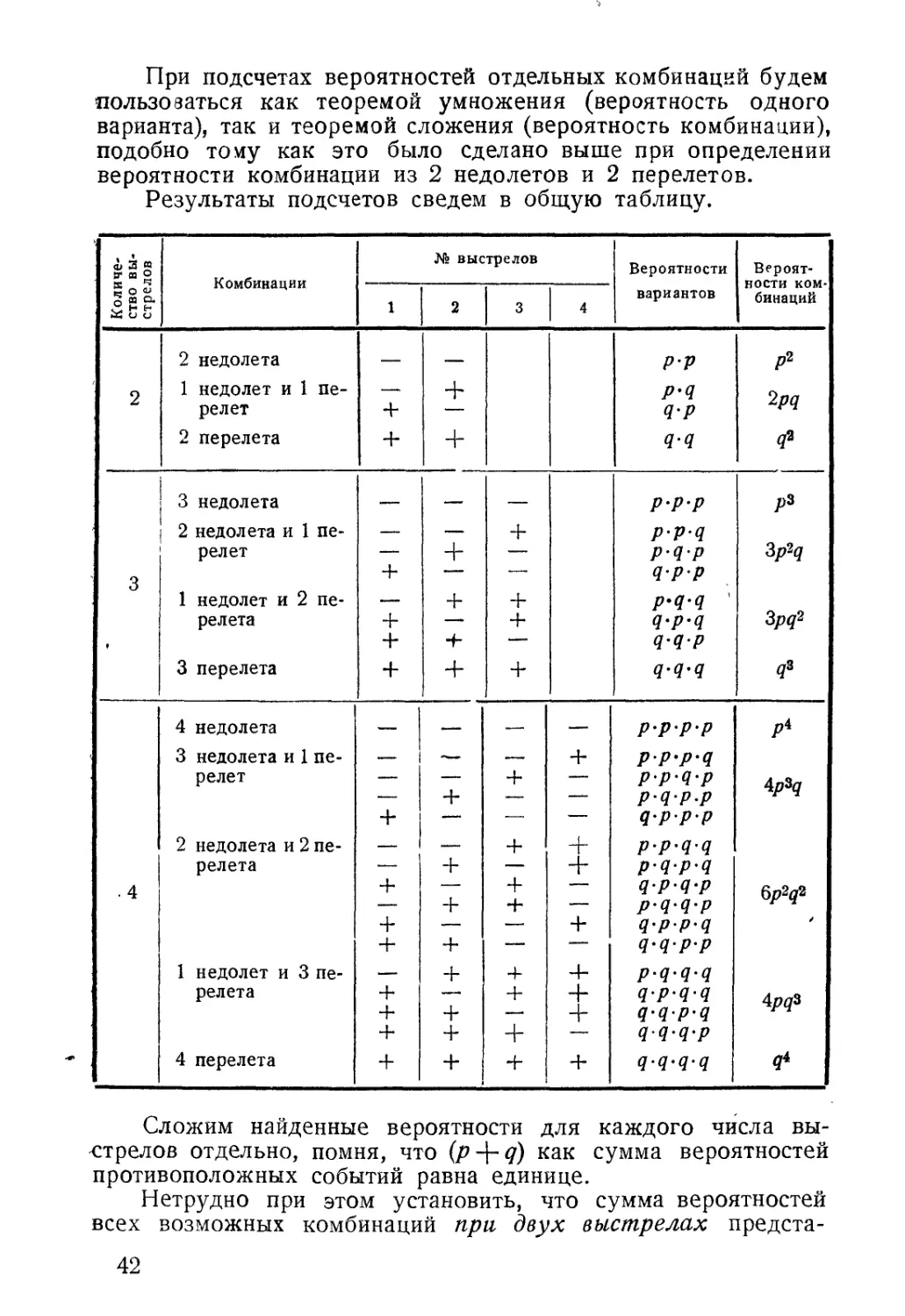
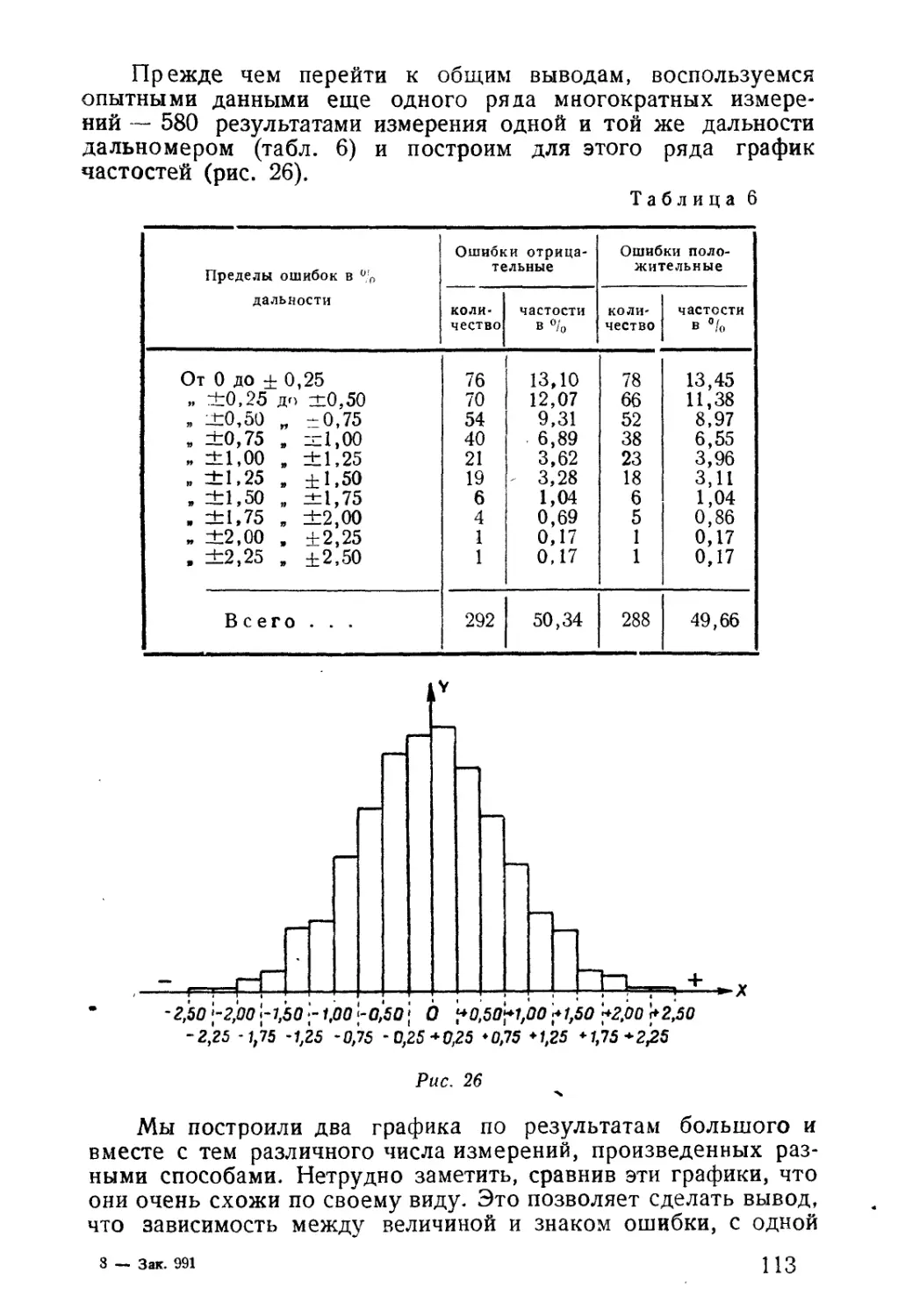
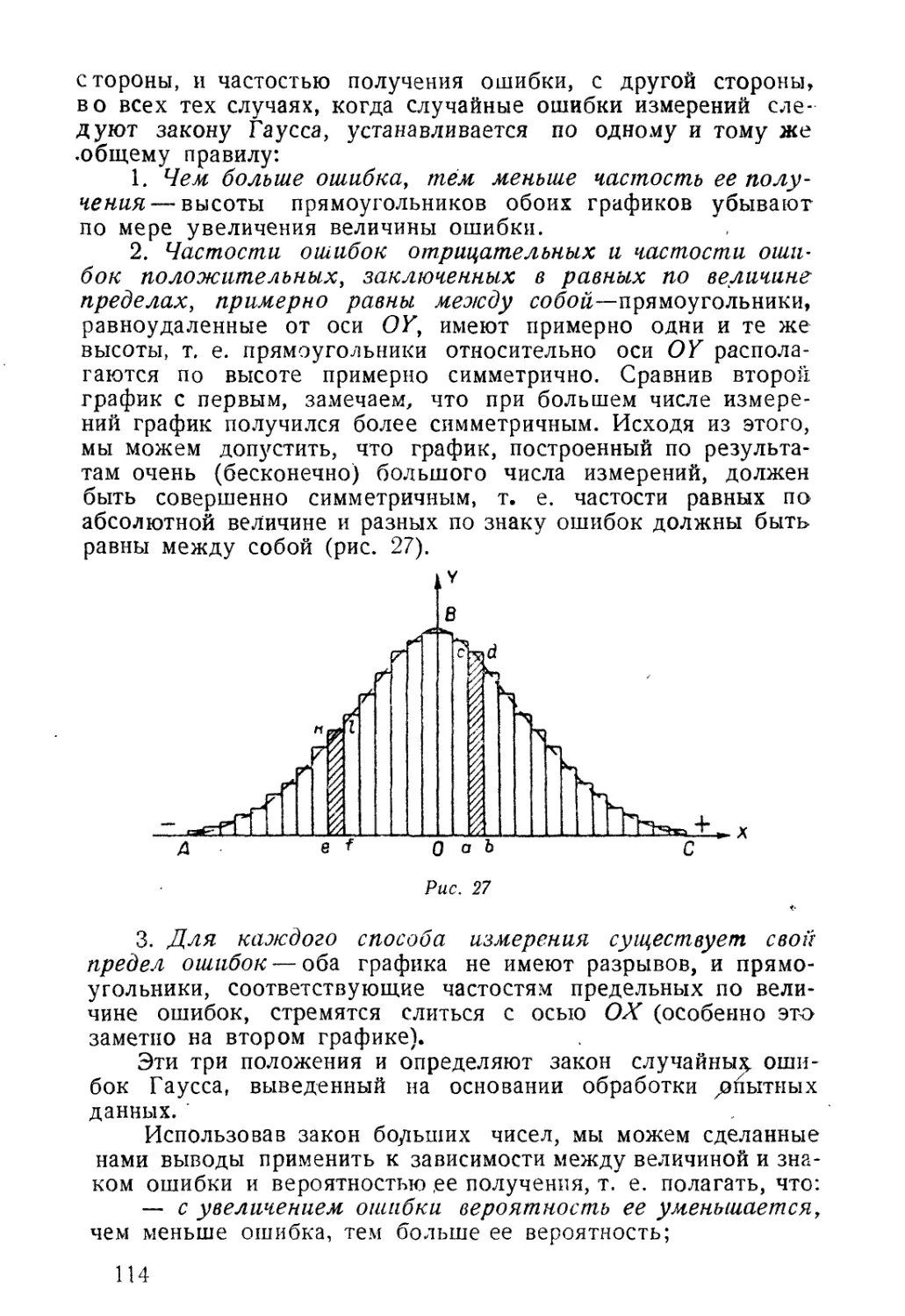
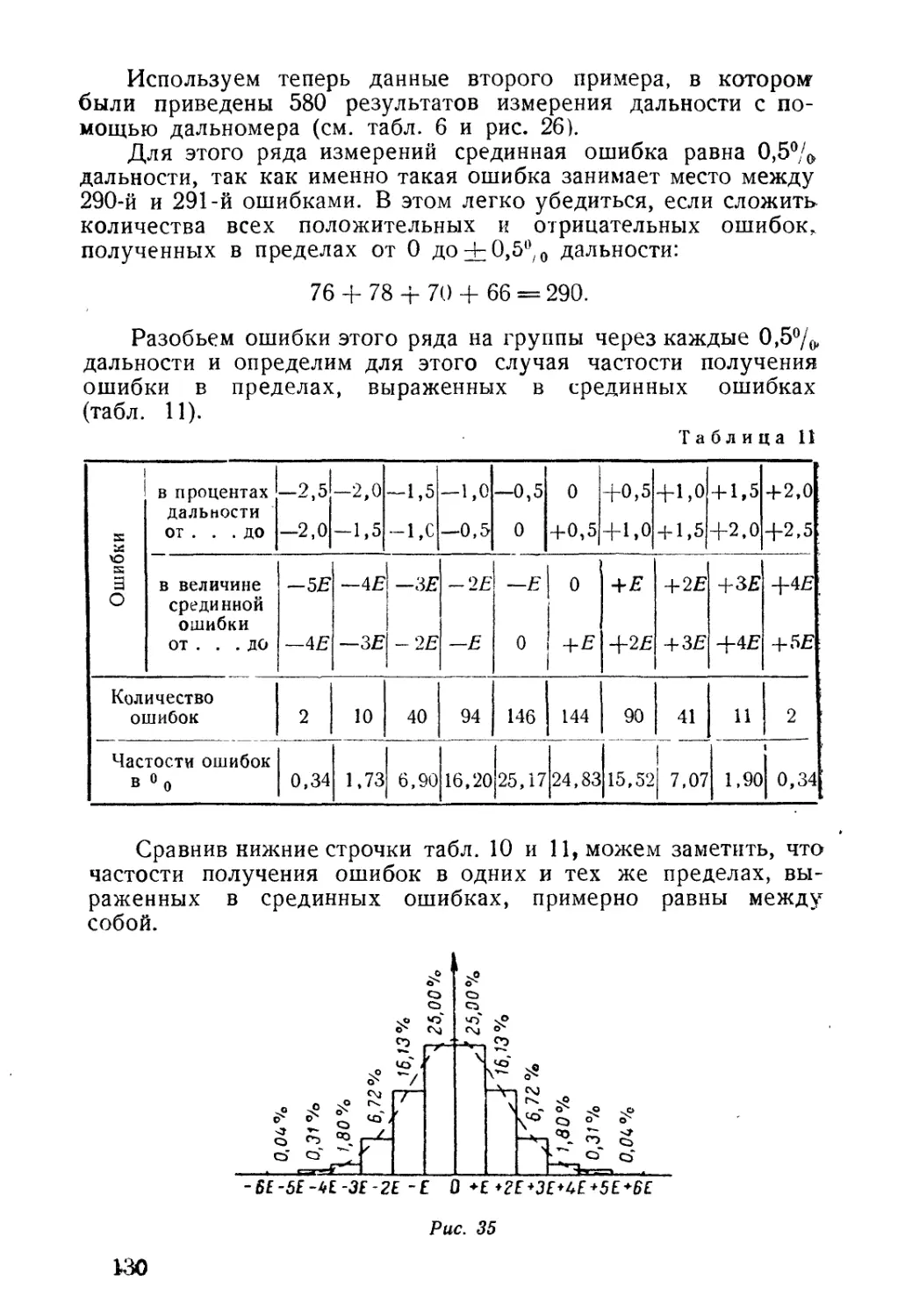
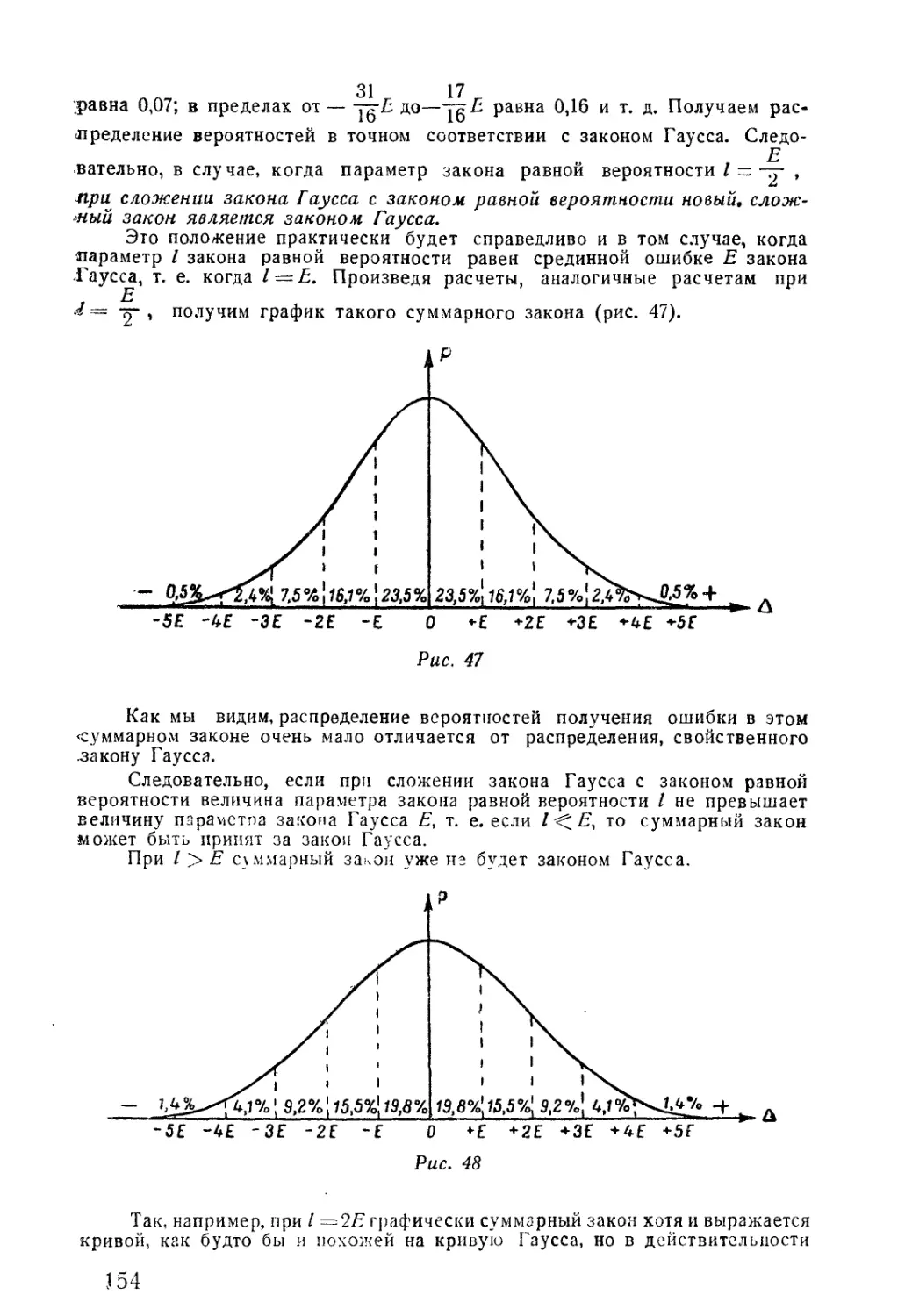
Автор: Блинов А.Д. Столбошинский А.П.
Теги: военное дело артиллерия артиллерийская подготовка
Год: 1949
Текст
КУРС
АРТИЛЛЕРИИ
КНИГА
8
полковник
А. П. СТОЛБОШИНСКИЙ
КУРС АРТИЛЛЕРИИ
КНИГА 8
ТЕОРИЯ ВЕРОЯТНОСТЕЙ.
РАССЕИВАНИЕ ПРИ СТРЕЛЬБЕ.
Под общей редакцией
генерал-майора инженерно-артиллерийской службы
БЛИНОВА А. Д.
ВОЕННОЕ ИЗДАТЕЛЬСТВО
МИНИСТЕРСТВА ВООРУЖЕННЫХ СИЛ СОЮЗА ССР
Москва—1949
Полковник А. П. Столбошинский. КУРС АРТИЛ-
ЛЕРИИ, книга 8. Теория вероятностей. Рассеивание
при стрельбе.
В книге освещены вопросы теории вероятностей^
теории ошибок и рассеивания при ударной и дистан-
ционной стрельбе.
Книга может быть рекомендована в качестве учеб-
ника для курсантов артиллерийских училищ. Кроме
того, она может служить пособием для офицеров,
Совеккой Армии при их самостоятельной работе.
РАЗДЕЛ 1
ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
ГЛАВА 1
ВЕРОЯТНОСТЬ СОБЫТИЯ
§ 1. ПРЕДМЕТ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Каждое явление, происходящее в природе или обществен-
ной жизни, неизбежно оканчивается некоторым результатом.
В зависимости от характера действия причин, вызывающих то
или иное явление, его конечный результат может быть неслу-
чайным или случайным.
Покажем на примере, при каких условиях конечный ре-
зультат явления носит случайный характер. Подбрасывается
вверх игральный кубик, на гранях которого нанесены очки:
от одного до шести. Кубик подбрасывается над столом. Кубик
неизбежно упадет на стол. Конечный результат падения — вы-
ход того или иного числа очков — результат случайный. Опре-
делить заранее нельзя, какое количество очков выйдет в ре-
зультате подбрасывания кубика. При повторении подбрасыва-
ния может выйти другое количество очков, хотя будет под-
брасываться тот же кубик над тем же столом и тем же лицом.
Все это объясняется тем, что выход того или иного числа
очков обусловливается очень многими причинами: положением
кубика в руке бросающего, высотой подбрасывания, положе-
нием кубика в момент его соприкосновения с поверхностью
стола, свойствами этой поверхности и т. д. Любую из этих
причин можно подразделить на ряд более мелких причин, из
которых каждая, может быть, и очень незначительно, но ока-
жет какое-то влияние на результат подбрасывания кубика.
Так, например, положение кубика в руке бросающего опреде-
ляется: какими гранями и насколько полно кубик соприка-
сается с ладонью, какие части ладони и как охватывают кубик,
насколько сильно при этом сжата рука и пр. Совершенно оче-
3
видно, что никакому учету все эти причины не поддаются,
а при каждом отдельном бросании действие их в своей сово-
купности носит, несомненно, случайный характер. Поэтому
при повторении бросаний и имеет, как правило, место выход
различного числа очков.
Этот пример достаточно наглядно показывает природу
случайных результатов явления. Как мы видим, явление, кото-
рому свойственны случайные результаты, может иметь их
несколько', какой из них будет иметь место при испытании,
заранее определить нельзя, так как любой из этих конеч-
ных результатов может быть, а может и не быть.
Это первая отличительная особенность случайных резуль-
татов явления, так как неслучайный результат может быть
только один и, что это за результат, можно определить зара-
нее; поэтому-то неслучайный результат явления так и называется.
Другая отличительная особенность случайных результатов
некоторого явления состоит в том, что при повторении этого
явления, иначе говоря, при повторении испытания в одинако-
вых по возможности условиях, можно установить вполне опре-
деленную закономерность, которой следуют эти случайные
результаты, притом тем яснее, тем полнее, чем больше был©
таких повторений.
В стрелково-артиллерийской практике постоянно прихо-
дится иметь дело со случайными результатами соответствую-
щего рода явлений.
Наиболее типичный пример — рассеивание снарядов. Явле-
ние полета снаряда неизбежно заканчивается падением этого
снаряда на землю. Результат падения снаряда — положение
точки падения на местности — результат случайный. Повторе-
ние выстрела в тех же условиях (орудие, снаряд, заряд, уста-
новки и пр.) даст, за очень редким исключением, другую
точку падения, не совпадающую с первой. Это объясняется
тем, что направление и дальность полета снаряда, а отсюда и
положение его точки падения определяются многими причинами:
формой и весом снаряда, весом и балистическими свойствами
пороха боевого заряда, положением ствола в момент выстрела,
скоростью и направлением ветра, температурой воздуха и т. д.
Для отдельных выстрелов снаряды будут несколько разли-
чаться между собой весом и формой, заряды — весом и свой-
ствами пороха, различны будут углы бросания и углы ЦО Тн,
меняться будут скорость и направление ветра и т. д. Учесть
все эти изменения при каждом отдельном выстреле нельзя,
а поэтому отклонения снарядов вследствие рассеивания носят
случайный характер. Если произвести достаточно большое
число выстрелов в одинаковых условиях, можно обнаружить
вполне определенную закономерность в распределении отдель-
4
ных точек падения относительно средней (центра рассеивания) —
известный нам закон рассеивания снарядов: неравномерность,
симметричность и небеспредельность этого распределения.
По результатам небольшого числа выстрелов такую законо-
мерность установить нельзя, и можно даже притти к неверным
выводам.
Когда мы говорим, что любой из нескольких случайных
результатов некоторого явления может быть, но может и не
быть, то это не означает, что степень возможности получения
(появления) таких результатов одна и та же. Наоборот, как
правило, эта степень возможности или, как мы будем гово-
рить, вероятность получения различных конечных результатов
тех явлений, с которыми нам обычно приходится иметь дело,
неодинакова. И действительно, мы знаем, например, что рас-
сеивание снарядов неравномерно — к центру эллипса рассеива-
ния они падают чаще (гуще), а к краям его реже. Очевидно,
что вероятность (степень возможности) получить точку паде-
ния снаряда вблизи центра рассеивания больше, чем вероят-
ность получить точку падения в удалении от этого центра.
Чтобы иметь возможность сравнивать вероятности отдель-
ных случайных результатов данного явления, а отсюда и иметь
возможность их предвидеть, необходимо знать численное (ко-
личественное) выражение закономерности, которой следуют
эти результаты.
Наука, занимающаяся изучением с количественной, сто-
роны закономерностей, которым следуют случайные резуль-
таты явлений, называется теорией вероятностей.
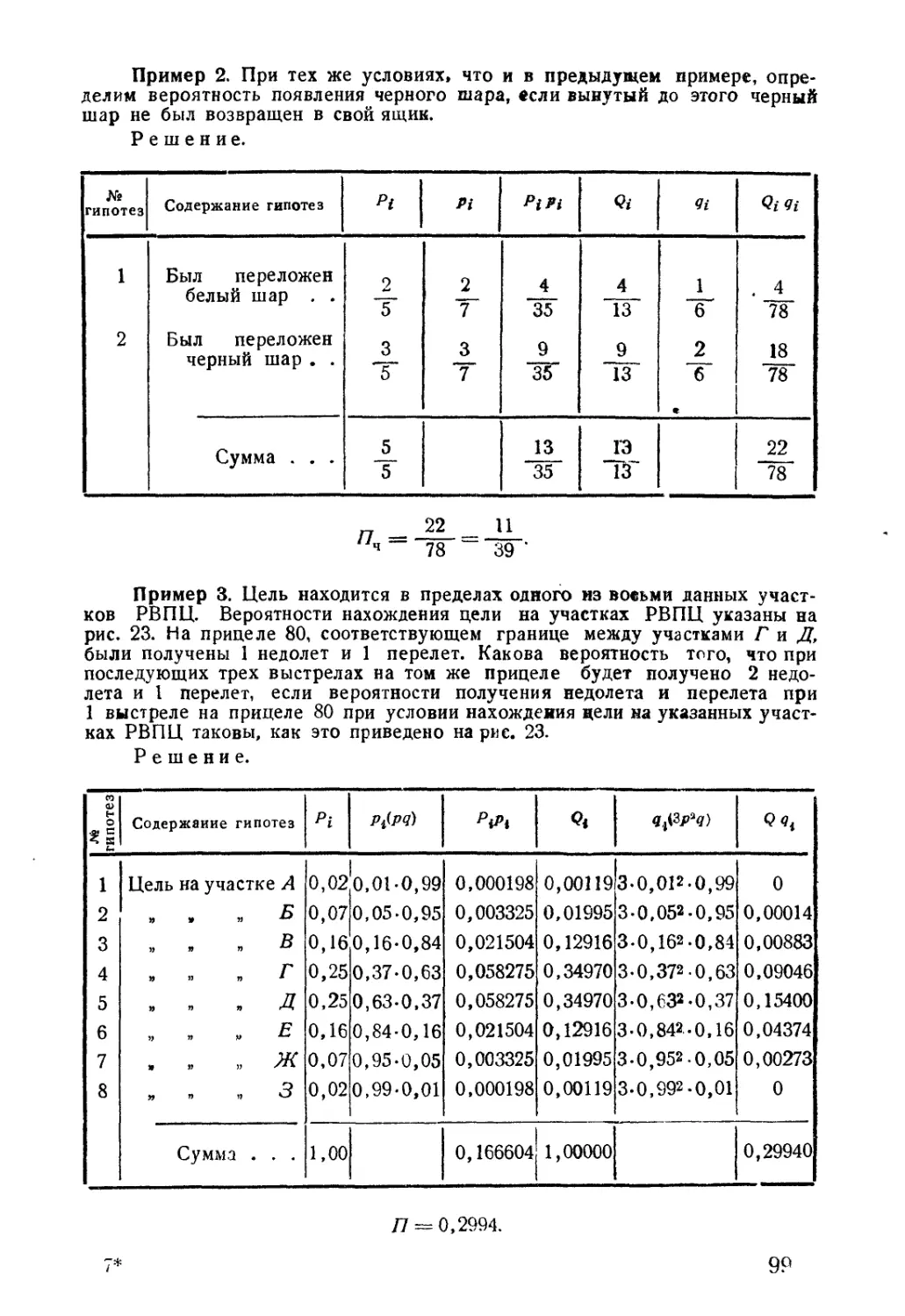
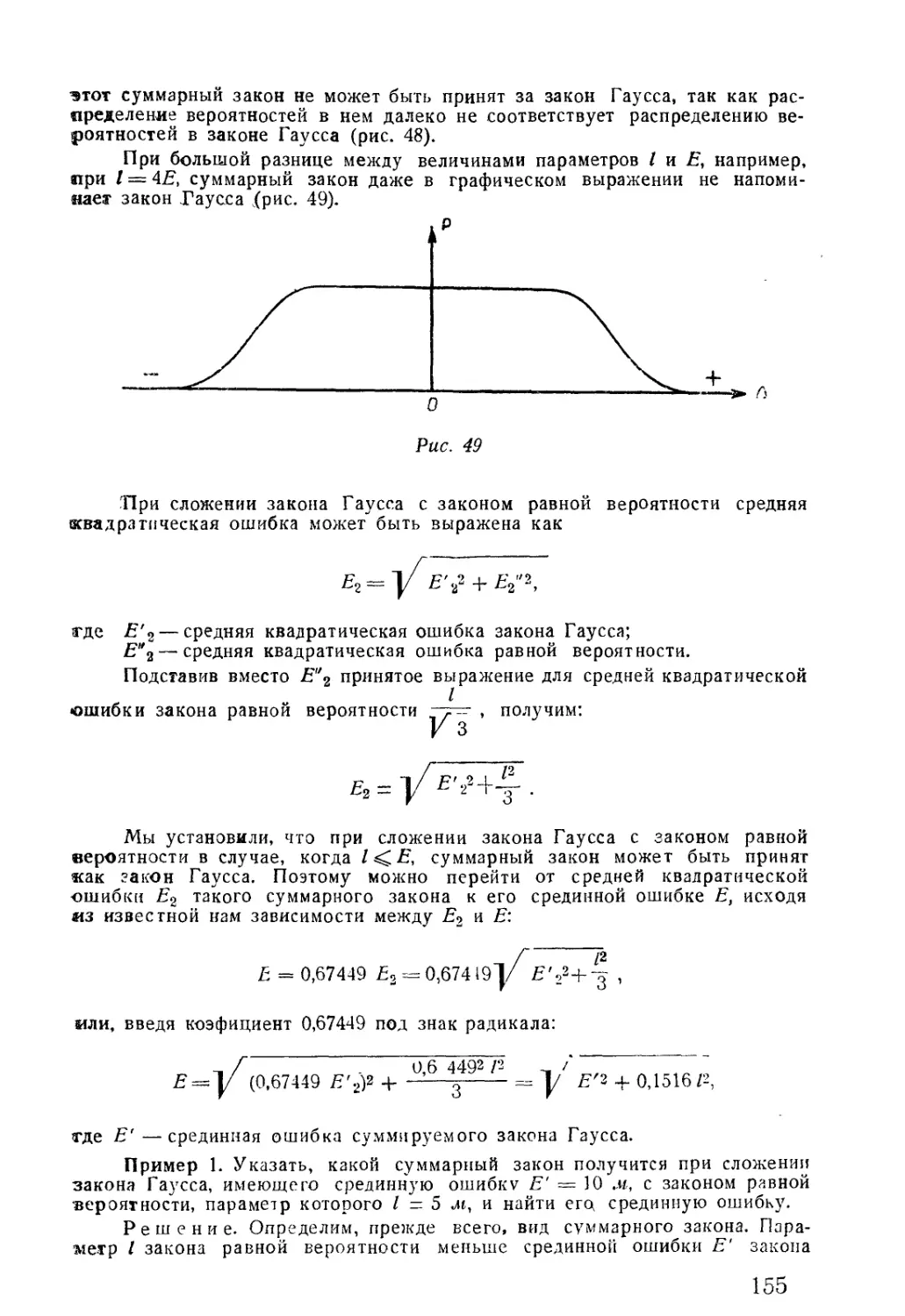
-4Вд-ЗВд -2Вд -Вд 0 +Вд +2Вд +ЭВд +483
Рис. 1
На примере того же рассеивания такая численная (коли-
чественная) закономерность выражается известной нам шкалой
рассеивания (рис. 1), которая в процентах дает численные зна-
чения вероятностей получения при одном выстреле точки па-
дения снаряда в определенных границах, выраженных вели-
чинами срединных отклонений (Вд, Вб и Be). Эта шкала, в ча-
стности, подтверждает, что вероятности получения различных
случайных результатов одного и того же явления неодинаковы.
Она позволяет рассчитывать такие. нужные артиллеристу ве-
роятности, как вероятности недолета, перелета, попадания,
промаха и т. д.
Теория вероятностей находит широкое применение в самых
разнообразных отраслях знания: социально-экономические науки,
5
астрономия, физика, метеорология и т. д. и, в частности,
артиллерийская стрельба. Везде, где она применяется, она
изучает с количественной стороны закономерность, которой
следуют случайные результаты исследуемого явления.
Нужно подчеркнуть, что качественную сторону этих
закономерностей теория вероятностей не исследует.
Применение теории вероятностей к артиллерийской стрельбе
позволяет научно предвидеть результаты стрельбы, устанавли-
вать правила стрельбы, обеспечивающие при систематическом
их применении получение наилучших результатов, позволяет
подыскивать методы стрельбы, дающие поражение цели с наи-
меньшим расходом снарядов и в наикратчайший срок, т. е.
позволяет так или иначе влиять на результат стрельбы.
Отсюда справедлива и такая формулировка: теория ве-
роятностей есть раздел математики, вырабатывающий
численные правила, от систематического применения кото-
рых следует ожидать наилучших результатов. Получение
наилучших результатов только при систематическом примене-
нии правил, основанных на теории вероятностей, обусловли-
вается тем, что количественные закономерности случайных
результатов явлений обнаруживаются только при большом
числе испытаний.
Теория вероятностей, как и всякая математическая наука,
пользуется рядом аксиом, положений и теорем, установление,
вывод и анализ которых, а также возможность их практиче-
ского применения (главным образом к артиллерийской стрельбе)
и составляют содержание настоящего Курса.
§ 2. СОБЫТИЕ
Событием в теории вероятностей называется случай-
ный конечный результат явления, независимо от степени
значимости этого результата1. Недолет, перелет, попадание,
промах при стрельбе, то или иное число очков при бросании
игральной кости, выигрыш или проигрыш в лотерее, — все это
события. События обычно обозначаются большими буквами
латинского алфавита: А, В, С, D и т. д.
Каждая математическая дисциплина исходит из некоторого
основного понятия: арифметика—из понятия числа, геомет-
рия — из понятий точки, линии, плоскости и т. д. Поскольку
теория вероятностей изучает закономерности случайных ко-
нечных результатов явлений, основным понятием в теории ве-
роятностей является событие.
События называются единственно возможными, если в дан-
ных условиях одно из них непременно произойдет. Например,
1 Необходимо отметить, что этот термин принят только в теории вероят-
ностей, так как вообще противопоставлять событие явлению нельзя.
6
при одном выстреле из винтовки попадание и промах — собы-
тия единственно возможные. При двух выстрелах из винтовки
•единственно возможными событиями будут, два попадания, по-
падание при первом выстреле и промах при втором выстреле,
промах при первом выстреле и попадание при втором выст-
реле и, наконец, два промаха.
Если имеется ряд единственно возможных событий неко-
торого явления, то отдельное испытание приводит лишь к од-
ному из этих событий, и появление одного такого события
исключает появление всех остальных событий того же ряда.
События, появление одного из которых исключает по-
явление всех остальных событий из ряда единственно воз-
можных, называются несовместными. Так, при двух вы-
стрелах из винтовки перечисленные выше четыре события не-
совместны, так как при получении, например, двух попаданий
невозможно получение при тех же выстрелах двух промахов
или одного попадания и одного промаха; два попадания исклю-
чили при этом испытании получение любого из трех осталь-
ных событий.
Если несовместных событий только два, они называются
противоположными (иначе — дополняющими). Получение недо-
учета и перелета, попадания и промаха при стрельбе, выигрыш и
проигрыш в лотерее — события противоположные.
Помимо событий несовместных, существуют события сов-
местные', это имеет место тогда, когда появление одного из
них не исключает возможности появления остальных. Напри-
мер, снаряд может попасть в цель и не разорваться; попа-
дание и неразрыв снаряда — события совместные.
При стрельбе на рикошетах может быть получен рико-
шет перед целью; в этом случае рикошет и недолет — собы-
тия совместные. Точно так же совместными событиями будут
рикошет и перелет (нерикошет и недолет, нерикошет и пере-
лет).
§ 3. ВЕРОЯТНОСТЬ СОБЫТИЯ
В § 1 было сказано, что вероятность события, как сте-
пень возможности его появления, может быть выражена
числом. Естественно возникает вопрос, какое это число и как
его определить.
Прежде чем перейти к численному выражению вероят-
ности события, необходимо предварительно установить, какие
события следует считать равновозможными.
События считаются равновозможными, если нет никаких
оснований полагать, что в данных условиях существуют ка-
кие-то причины, вследствие которых появление одного собы-
тия более возможно, чем появление другого.
Пример. В закрытом ящике имеется 10 совершенно оди-
наковых шаров, занумерованных по порядку: № 1, № 2, № 3
7
и т. д. до № 10. Если шары тщательно перемешать и затем,,
не глядя, вынуть из ящика один шар, то может появиться
любой из 10 шаров, так как при таком испытании нет ника-
ких оснований полагать, что появление шара одного какого-
либо номера более возможно, чем появление другого.
Наиболее наглядное представление о единственно воз-
можных, несовместных и равновозможных событиях дают
примеры с игральными костями, шарами и т. п. Поэтому
вывод и иллюстрация очень многих основных положений тео-
рии вероятностей производятся на подобных примерах.
Воспользуемся примером с шарами, чтобы установить
правило (общую формулу) математического выражения вероят-
ности события.
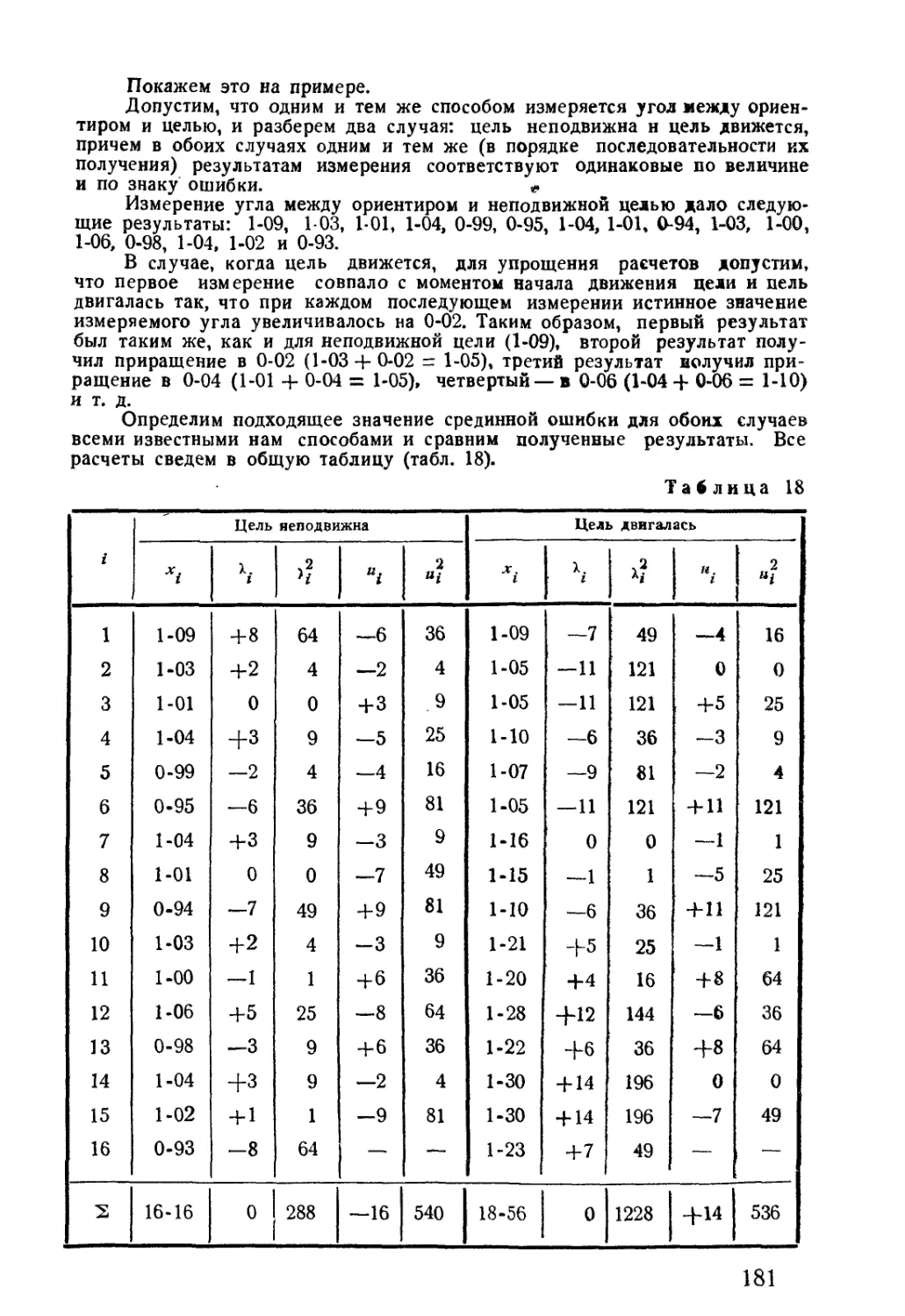
Положим, что в трех закрытых ящиках имеется по 4 шара
в каждом, причем в ящике №1—3 белых и 1 черный шар,
в ящике № 2 — 2 белых и 2 черных шара и, наконец, в ящике
№ 3 — 1 белый и 3 черных шара (рис. 2).
_ооо»1 1оо«<
№1 №2
Рис. 2
Шары различаются между собой только цветом и тща-
тельно в ящиках перемешаны. Испытание заключается в том,
что из ящика вслепую вынимается один шар.
Посмотрим, как можно численно выразить вероятность
появления белого шара из каждого ящика в отдельности.
Начнем с ящика № 1. В этом ящике имеется 4 шара. По-
условиям нашего испытания любой из этих 4 шаров может
появиться. Таким образом, случаев появления шара из ящика
№ 1 всего 4. Эти случаи (появления) единственно возможны
(других шаров в ящике нет), несовместны (вынимается один
шар) и равновозможны (шары различаются только цветом и
шар вынимается вслепую).
Нас интересует появление белого шара. Таких шаров
в ящике 3. Поэтому из 4 равновозможных случаев появления
шара (независимо от его цвета) 3 случая будут, как принято-
говорить в теории вероятностей, благоприятствовать по-
явлению белого шара.
Можно пояснить это иначе. Представим себе, что в наш
ящик одновременно опустили руку 4 человека и каждый из
них, не глядя, взял по одному шару. Положим, что человек,
вынувший белый шар, выигрывает, а вынувший черный шар —
проигрывает. Очевидно, что при одновременном вынимании
рук из ящика в трех руках окажется по белому шару — 3 че-
ловека будут иметь выигрыш. Также очевидно, что при повто-
рении такого розыгрыша всегда будут выигрывать 3 человека
из 4, ибо до тех пор, пока в ящике № 1 не изменится соотно-
шение между белыми и черными шарами, появлению белого
шара в руке каждого из участников всегда будут благоприят-
ствовать 3 случая из 4 возможных.
Перейдем теперь к ящику № 2. В этом ящике также
4 шара, но белых из них 2. Рассуждая аналогично, приходим
к заключению, что из 4 равновозможных случаев появления
шара 2 случая будут благоприятствовать появлению белого,
шара.
И, наконец, в ящике № 3 из 4 шаров только 1 белый.
Следовательно, из 4 возможных случаев появления шара
1 случай будет благоприятствовать появлению белого шара..
Итак, появлению белого шара:
— из ящика № 1 благоприятствуют 3 случая из 4;
— из ящика № 2 благоприятствуют 2 случая из 4;
— из ящика № 3 благоприятствует 1 случай из 4,
или, применительно к розыгрышу, если вынимать шары:
— из ящика № 1, всегда выигрывают 3 человека из 4;
— из ящика № 2, всегда выигрывают 2 человека из 4;
— из ящика № 3, всегда выигрывает 1 человек из 4.
Следовательно, до розыгрыша на каждого из его участни-
ков приходится, если взять:
— ящик № 1 - 3/4 выигрыша;
— ящик №2 — 2/4 выигрыша;
— ящик № 3—1 /4 выигрыша.
Поэтому вероятность (степень возможности) появления
белого шара или вероятность выигрыша из ящика № 1 можно*
выразить дробью 3/4, из ящика № 2 — дробью 2/4 и из ящика
№ 3 — дробью 1/4, т. е. отношением числа случаев, благо-
приятствующих появлению белого шара из данного ящика,
к числу всех равновозможных случаев появления шара неза-
висимо от его цвета.
Покажем, что выражение вероятности появления белого
шара таким отношением справедливо и тогда, когда мы имеем
дело с другим количеством белых и черных шаров в ящике.
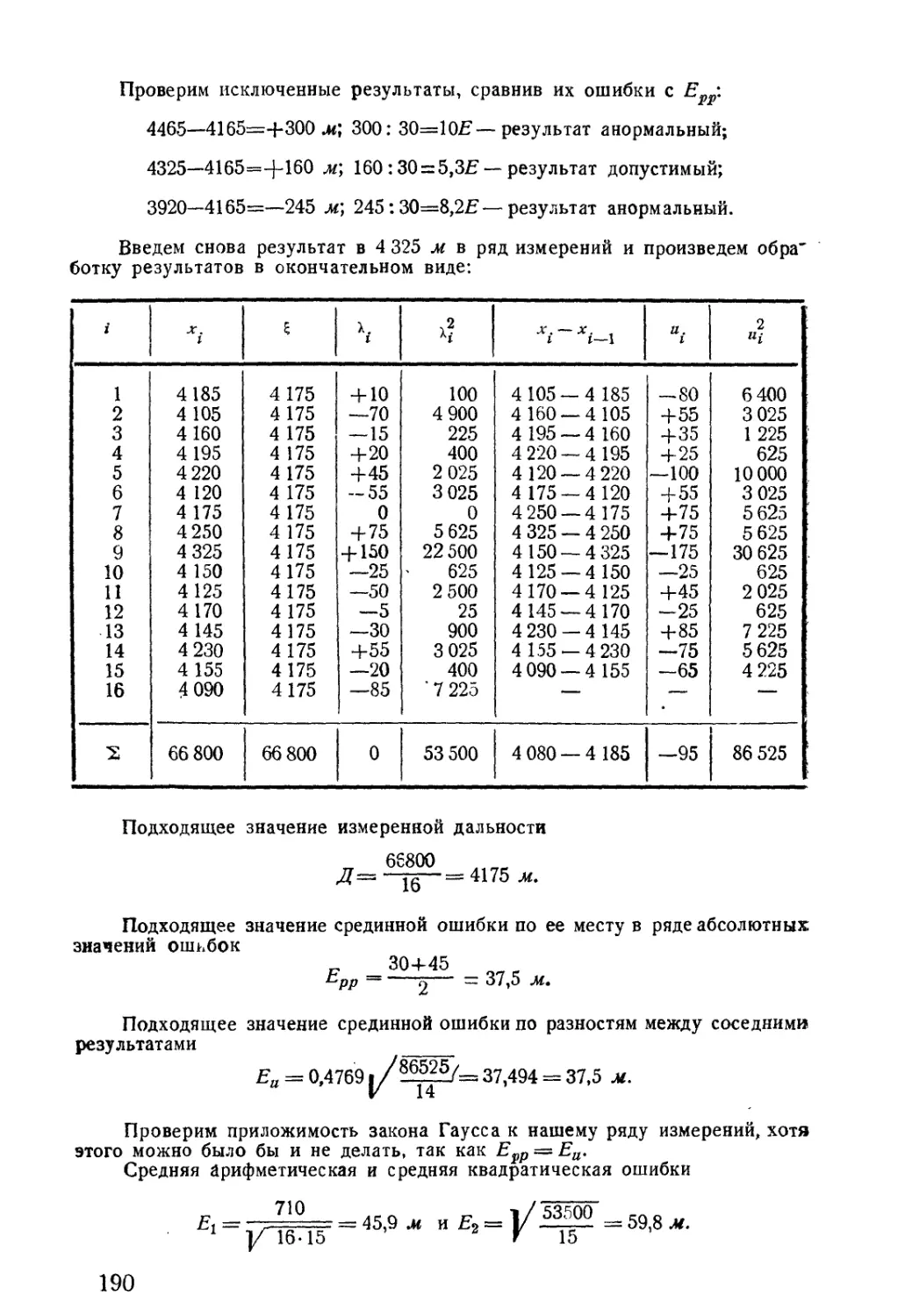
Положим, что имеется ящик № 4,
в котором 3 белых и 3 черных шара,
и сравним вероятность появления белого
шара из этого ящика с вероятностью
появления белого шара из ящика № 2
(рис. 3).
В обоих этих ящиках белые шары
составляют половину общего числа ша-
ров, т. е. соотношение между числом
случаев, благоприятствующих появлению
белого шара, и числом всех возможных случаев появления
шара здесь одно и то же. А если это так, то и вероятность
ЮО»»1
№2
ООО«»«
Рис. 3
9
появления белого шара из ящика № 4 равна вероятности
появления белого шара из ящика № 2. В самом деле:
3 __ 1 2 1
6 ~ 2 И 4 —' 2 •
Сопоставляя вероятности появления белого шара из ящи-
ков № 1, № 2 и № 3, мы видим, что эти вероятности 3/4, 2/4
и 1/4 прямо пропорциональны количеству случаев, благопри-
ятствующих появлению белого шара:
— — 3‘2*1
4 4 * 4 — ь
иначе говоря, во сколько раз число случаев, благоприят-
ствующих появлению белого шара из одного ящика, больше
(меньше) числа случаев, благоприятствующих появлению белого
шара из другого ящика, во столько же раз численное значе-
ние вероятности появления белого шара из одного ящика
больше (меньше) численного значения вероятности появления
белого шара из другого ящика. Поэтому в математическом
выражении вероятности появления белого шара из данного
ящика число случаев, благоприятствующих появлению такого
шара, и находится в числителе.
Сопоставляя вероятности появления белого шара из ящи-
ков № 1 и № 4, где число благоприятствующих случаев одно
и то же (3 и 3), а число всех возможных случаев различно
(4 и 6), видим, что вероятности появления белого шара из
этих ящиков обратно пропорциональны числам всех возмож-
ных случаев:
— • 3 = 6 • 4
4 • 6 ° ‘ '
иначе говоря, во сколько раз число всех возможных случаев
появления шара ‘ независимо от его цвета из одного ящика
больше (меньше) числа всех возможных случаев появления
шара из другого ящика, во столько же раз численное значе-
ние вероятности появления белого шара из одного ящика
меньше (больше) численного значения вероятности появления
белого шара из другого ящика. Поэтому в математическом выра-
жении вероятности появления белого шара число всех воз-
можных случаев мы поместили в знаменателе.
На основании приведенной пропорциональности можно
утверждать, что отношение числа случаев, благоприятствующих
появлению белого шара, к числу всех возможных случаев
действительно математически выражает вероятность появления
белого шара при любом соотношении между белыми и чер-
ными шарами.
Распространив этот вывод на любое случайное событие,
мы принимаем, что математическая вероятность события
10
равна отношению числа случаев, благоприятствующих по-
явлению этого события, к числу всех возможных случаев',
при этом случаи предполагаются единственно возможные,
несовместные и равновозможные, т. е.
р — —
п ’
где Р — (начальная буква латинского слова probabilitas, что
означает вероятность) — вероятность события;
т — число случаев, благоприятствующих появлению собы-
тия;
п — число всех возможных случаев.
Обычно слово „математическая* опускается, и говорят
просто: „вероятность события".
Пример. Чему равна вероятность появления 6 очков при однократном
бросании игральной кости?
Решение. Случаев, благоприятствующих появлению 6 очков, — один,
так как только на одной грани кости имеется такое число очков. Всех воз-
можных случаев 6, так как любая из 6 граней может оказаться сверху.
Отсюда вероятность появления 6 очков
Случаев, благоприятствующих появлению события, не мо-
жет быть больше числа всех возможных случаев, поэтому и
вероятность события не может быть больше единицы. Вероят-
ности, равной единице, отвечает достоверное событие, т. е.
такое событие, которое в данных условиях не может не
произойти — оно обязательно произойдет. Так, например,
появление белого шара из ящика, в котором находятся только
4 белых шара, есть событие достоверное. Вероятность появле-
ния белого шара из такого ящика:
Число случаев, благоприятствующих появлению события,
не может быть меньше нуля, отсюда и вероятность события
также не может быть меньше нуля. Вероятности, равной нулю,
отвечает невозможное событие, т. е. такое событие, которое
в данных условиях не может произойти. Например, появление
белого шара из ящика, в котором имеется только 4 черных
шара, есть событие невозможное. Вероятность появления
белого шара из такого ящика
А это означает, что вероятность события всегда выра-
жается правильной дробью, так как величина ее заключена
в пределах от единицы до нуля:
0<Р<1.
11
Вероятность события может быть выражена и в процен-
тах. Событие невозможно — вероятность его О°о, событие до-
стоверно— вероятность его 1ОО°/о.
При пользовании установленной выше формулой для выра-
жения вероятности события не исключены грубейшие ошибки,
если не учитывать со всей тщательностью несовместности и
равновозможности случаев.
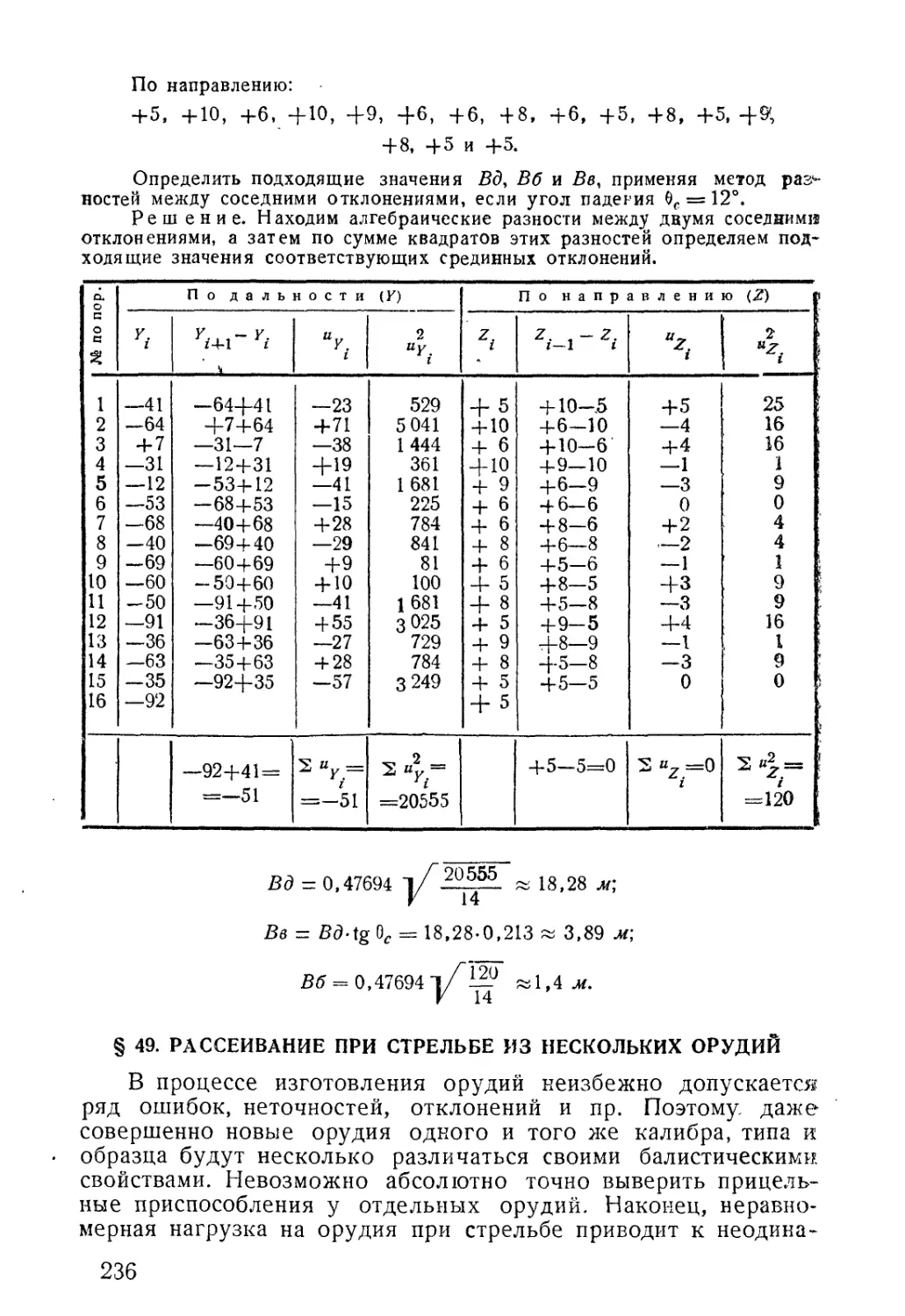
Пример 1. В ящике находятся 5 совершенно одинаковых шаров:
2 красных и 3 белых; шары занумерованы (рис. 4). Некто вынимает всле-
пую 1 шар и может при этом выиграть или проиграть — выигрывает, если
вытянет шар с № 1 или красный шар. Какова вероятность выигрыша?
Рис. 4
Решение. Всех возможных случаев появления шара — 5. Случаев,
благоприятствующих выигрышу, на первый взгляд 4: два шара с № 1 и два
красных шара. Отсюда вероятность выигрыша как будто
Но такое решение неверно, так как два случая, благоприятствующих
выигрышу — появление шара с № 1 и появление красного шара — случаи
совместные. Можно вынуть красный шар и вместе с тем шар с № 1.
Для правильного решения необходимо определить число несовместных
случаев, благоприятствующих выигрышу. Таких случаев 3: появление белого
шара с № 1 и появление 2 красных шаров. Тогда искомая вероятность
§ 4. ЧАСТОСТЬ СОБЫТИЯ
Чтобы обнаружить закономерность, которой подчинены
конечные случайные результаты явления, необходимо обра-
ботать результаты достаточно большого числа испытаний,
т. е. выяснить, как часто происходило то или иное событие
из всей совокупности событий, исчерпывающих рассматри-
ваемое явление.
Разделив число появлений интересующего нас события на
число всех произведенных испытаний (опытов), мы получим
ответ на этот вопрос. Например, если при 20 выстрелах полу-
чено 4 попадания, то, разделив 4 на 20, мы установим, как
часто происходило попадание при такой стрельбе.
Отношение числа появлений события к числу всех опы-
тов называется частостью события.
В приведенном выше примере частость попадания равна
4 __ •
20 ~~ 5 ’
эта частость показывает, что в среднем на каждые 5 выстре-
лов было получено 1 попадание.
12
В общем виде частость события выражается формулой
М
г~ W ’
где г — частость события;
М~ число его появлений;
2V—число произведенных опытов.
Пример. При 12 выстрелах было получено 3 недолета. Какова частость
недолета?
Решение. Число появлений события М — 3. число произведенных
опытов ^=12, тогда искомая частость
3 1
г ~ 12 — 4 •
Выясним, какими свойствами обладает частость. Положим,
что при 15 выстрелах было получено 5 попаданий. Отсюда
частость попадания
_ 5 1
Г~~ 15 “ 3 *
Произведем еще 3 выстрела. Если при этом будет полу-
чено 1 попадание и 2 промаха, то частость попадания не
изменится:
_ 5 + ! 6 1
Г~ 15 + 3 “ 18 ~ 3 •
Если при тех же 3 выстрелах получатся все попадания, то
частость попадания увеличится:
5 + 3 8 4
г15 + 3 “ 18“ 9 •
Если добавленные 3 выстрела дадут все промахи, то ча-
стость попадания уменьшится:
5 + 0 5
Г”~ 15 + 3 “ 18 •
Отсюда делаем вывод, что частость события изменяется
с изменением числа произведенных, опытов и с изменением
числа появлений события.
Событие при данном числе произведенных опытов может
появиться или при всех опытах, или только при части опытов,
или совсем не появиться, т. е. число появлений события может
быть равно или числу всех опытов, или числу части опытов,
или равно нулю. Поэтому частость события и выражается
числом, заключенным в пределах от нуля до единицы, т. е.
правильной дробью:
, 0<г<1,
или в процентах:
0°/0<г < 100%.
Остановимся на свойствах частостей противоположных
событий.
13
Положим, что при некотором испытании может появиться
или событие А или событие В, противоположное первому.
Положим также, что при М таких испытаниях событие А
появилось раз, а событие В — /И2 раз. Тогда частость
события А
Aft
д —
а частость события В
г _
гв— •
Так как события А и В противоположны, т. е.
то сумма частостей этих событий
r ( г ____ I М2 ________ ЛТл Л42 __ __ 1
г А * ' в ~~~ N * N ~~ N ' ~ N ~ *•
Пример. При 8 выстрелах было получено 3 недолета и 5 перелетов.
Тогда сумма частостей недолета и перелета
. _ 0.0 О -«
rn=-g- + -y— -8~— 1.
Сумма частостей противоположных событий равна
единице.
Исходя из этого вывода, зная частость одного события, мы
можем найти частость другого события, противоположного
первому.
Пример. Частость попадания равна -1-. Чему равна частость промаха?
Решение.
Л1р 1 гпоп 1 4 4 •
Очевидно, что и для любого числа несовместных событий^
которые произошли при данном числе опытов, сумма их часто-
стей также должна быть равна единице.
Пример. При 10-кратном бросании игральной кости:
6 очков вышли 3 раза;
4 очка— 1 раз;
3 очка — 4 раза;
1 очко — 2 раза.
Тогда частость получения:
6 очков: гс = -jq- ;
1
4 очков: r4 = -jQ-;
4
3 очков: r3 = -|q- ;
2
1 очка: /1 = -гтг.
Сумма этих частостей
3 1 4 2
/с Ъ -• а ’ Ч 10 + 10 + 10 г ю " 1 •
§ 5. СООТНОШЕНИЕ МЕЖДУ ВЕРОЯТНОСТЬЮ И ЧАСТОСТЬЮ
СОБЫТИЯ
Между вероятностью и частостью события имеется разница
по существу, которая заключается в следующем:
1. Вероятность события устанавливается до опыта и отве-
чает на вопрос: как часто (в среднем) можно ожидать появления
данного события. Для того чтобы определить вероятность
события, необходимо знать условия опыта, но производить
опыты нет никакой надобности.
Частость события определяется только после опыта и
отвечает на вопрос: как часто было появление данного события..
2. Вероятность события в неизменных условиях данного
опыта (для событий независимых)1 остается постоянной,
т. е. не зависит от числа опытов и их результатов. Так, если
из закрытого ящика, в котором находится 5 белых и 3 черных
шара, вынимают несколько раз по одному шару и каждый раз.
вынутый шар возвращают в ящик, то вероятность появления
белого шара перед каждым опытом будет равна независимо
от того, сколько раз перед этим был произведен такой опыт
и сколько раз появлялся шар того или иного цвета. Если же
мы изменим соотношение между белыми и черными шарами,
изменится и вероятность появления белого шара. Так, если
мы возьмем ящик с 4 белыми и 4 черными шарами, вероятность
появления белого шара будет уже равна —.
Таким образом, вероятность события остается неизменной,
для данного явления до тех пор, пока не изменятся условия,
при которых происходит явление.
Частость события непостоянна — она меняется с каждым
опытом и зависит от числа опытов и ог числа появлений
события.
Несмотря на указанные различия, между частостью и
вероятностью события можно установить одну зависимость,
которая выражается так называемым законом больших чисел.
Сущность этого закона заключается в том, что при увели-
чении числа испытаний, проведенных в одинаковых условиях,
частость события по своей величине приближается к вероят-
ности того же события, а при достаточно большом числе
таких испытаний частость события численно будет весьма
мало отличаться от вероятности этого события.
Значение закона больших чисел огромно, и он по справед-
ливости считается основой теории вероятностей2.
В тех примерах, которые мы разобрали, вычисление
вероятностей событий было так просто лишь потому, что
по условиям этих примеров число случаев, благоприятствующих
1 О зависимых и независимых событиях см. стр. 22.
2 Подробнее закон больших чисел рассматривается в §
15
по злению события, и число всех возможных случаев было
известно. В действительности же далеко не всегда условия
задачи заранее определяют число благоприятствующих и число
всех возможных случаев, и при отыскании численного значения
вероятности интересующего нас события приходится прибегать
к другому приему, основанному на законе больших чисел.
Определив частость события по результатам достаточно боль-
шого числа опытов, мы можем принять эту частость равной
неизвестной нам вероятности этого события.
У^сли вероятность события известна, то по этой вероятности
можно судить, не производя опытов, об ожидаемой частости
события.
В артиллерийской стрельбе закон больших чисел находит
самое широкое применение. Например, по частостям отклонений
снарядов определяются вероятности этих отклонений — средин-
ные (вероятные) отклонения; по частостям ошибок, получен-
ных в некоторых пределах, —- вероятности ошибок в тех же
пределах и т. д. По известной вероятности попадания рассчиты-
вают ожидаемое число попаданий, т. е. ожидаемые частости
попадания.
§ 6. ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ
При исследовании того или иного явления нас часто ин-
тересует появление не одного какого-то вполне определенного
результата (события), а появление одного, безразлично какого,
из нескольких результатов (событий), объединенных каким-то
общим для них признаком или свойством.
Так, при исследовании рассеивания при ударной стрельбе
нас интересует положение не какой-то одной определенной
точки падения, а положение совокупности (группы) точек
падения, дающих, например, недолеты, перелеты, попадания
в цель и т. п.
Отсюда и возникает необходимость определения вероят-
ности одного из нескольких событий без указания, какого именно,
так как появление любого из них в условиях данного испы-
тания достаточно для решения поставленной задачи. Эта
задача решается путем применения теоремы, сложения вероят-
ностей. Следует подчеркнуть, что теорема сложения веро-
ятностей применима только к несовместным событиям.
Покажем на примере, почему для определения вероятности
одного из нескольких несовместных событий без указания,
какого именно, необходимо вероятности этих событий склады-
вать.
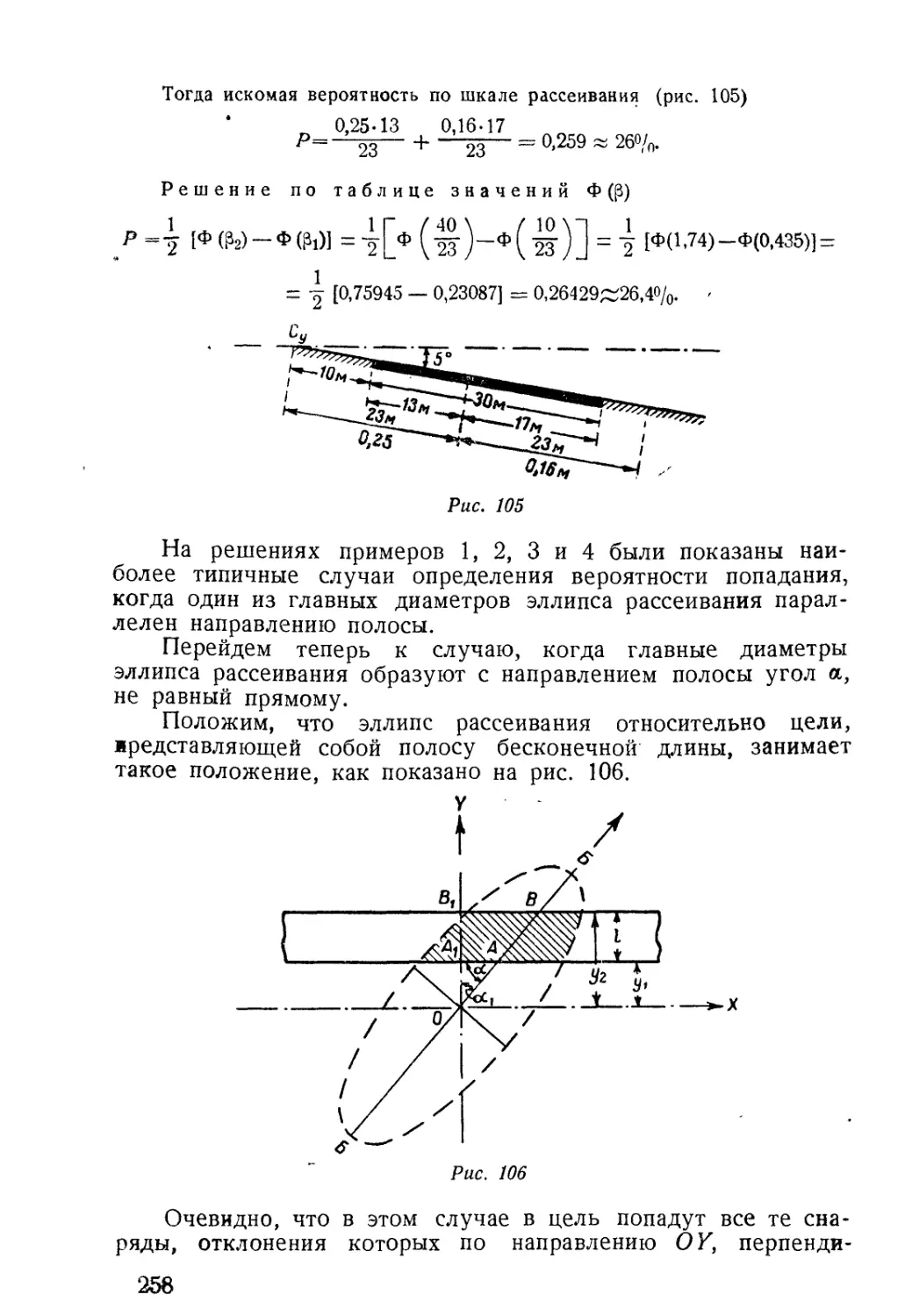
Положим, что стрельба ведется гранатой по полосе прово-
лочных заграждений, которая накрывается эллипсом рассеивания,
как это показано на рисунке (рис. 5).
Мы видим, что попадание в цель дают все те снаряды, ко-
торые приходятся как на полосу Д, так и на полосу Е.
16
Вероятность попадания в полосу Д равна 25%, а в полосу
Е—16%. Очевидно, что искомая вероятность будет равна
сумме
Р = Рд-]-РЕ= 25% + 16% = 41%.
Перейдем теперь к выводу теоремы сложения вероятностей,
т. е. докажем, что такой способ исчисления вероятностей справед-
лив для любой группы несовместных событий.
Рис. 5
Воспользуемся для этого следующим частным примером.
В закрытом ящике имеется 50 шаров, отличающихся друг от
друга только цветом: 8 белых, 10 зеленых, 5 синих, 12 черных
и 15 красных. Опыт заключается в том, что из ящика вслепую
вынимается один шар. Определим вероятность появления цвет-
ного, т. е. не белого и не черного шара.
Всех возможных случаев появления шара из ящика п = 50,
причем эти случаи единственно возможны, несовместны и
равновозможны.
Из этих 50 случаев по условию задачи нас интересует
появление либо зеленого, либо синего, либо красного шара.
Таких шаров в ящике 30: зеленых—10, синих —5 и красных —
15; отсюда, число случаев, благоприятствующих появлению
цветного шара, zn = 30.
Подставив найденные численные значения т и п в общую
формулу, мы и найдем вероятность появления цветного шара
р ___ т 30
/"ЦБ — — — - gg- .
Для вывода теоремы представим эту вероятность в ином
виде, помня, что т = 30 = 10 4-5 4- 15:
Р _ 30 _ 10 + 5 + 15 _ 10 , 5 , 15
^цв — 50 “ 50 ~' 50 + 50 4" 50 ’
и посмотрим, что представляют собой эти дроби.
В ящике на 50 шаров приходится 10 зеленых, т. е. 10
случаев из 50 всех возможных благоприятствуют появлению
2 — Зак. 991
17
зеленого шара. Следовательно, дробь —есть вероятность
появления зеленого шара из того ящика:
ю
Рассуждая подобным же образом, заключаем, что дробь
5 - 15
-эд- есть вероятность появления синего шара, а дробь ---------
вероятность появления красного шара. Отсюда
D 10 . 5 . 15 , ,
Г цв — "эд" “Г -эд- “г -эд- = рзел “г Рейн “Г Рк р ,
т. е. вероятность появления цветного шара оказалась равной
сумме вероятностей появления шаров — зеленого, синего и
красного.
Распространяя этот вывод на случайные результаты любых
явлений и на любое число несовместных событий, мы получим
выражение теоремы сложения вероятностей в общем виде:
/3 = Р14-Р2+РзН------+ря_14-рп .
Вероятность появления одного из нескольких несовмест-
ных событий без указания, какого именно, равна сумме
вероятностей этих событий.
Определяя вероятность появления цветного шара, мы
объединили в одну группу шары нескольких цветов, рассмат-
ривая появление цветного шара из этой группы как одно
событие, имеющее несколько разновидностей. Поэтому теорема
сложения вероятностей может быть сформулирована и так:
если событие распадается на несколько несовместных раз-
новидностей, то вероятность его равна сумме вероятностей
этих разновидностей.
Пример 1. Средняя траектория проходит к 1 Вд за целью. Чему равна
вероятность недолета при 1 выстреле?
Примечание. Во всех задачах, в которых глубина цели не
дается, предполагается, что цель не имеет глубины — линия, рубеж,
точка, т. е. предполагается получение только недолетов и перелетов.
Решение. Недолеты дадут все те снаряды, которые придутся на
полосы А, Б и В (рис. 6). Отсюда вероятность недолета при 1 выстреле
сложится из вероятностей попадания в полосу А, полосу Б и полосу В, т. е.
будет равна
Р ~ В а + Рб + В в — 0-02 4- 0,07 4- 0,16 — 0,25.
0,02 0,07 0J6 0,25 0,25 0,16 0,07 0,02
Рис. 6
18
Пример 2. В лотерее на 300 билетов приходится: 2 выигрыша по 50
рублей, 6 выигрышей по 20 рублей, 10 выигрышей по 10 рублей, 50 выигры-.
шей по 5 рублей и 100 выигрышей по 3 рубля. Чему равна вероятность,
имея 1 билет этой лотереи, выиграть не менее 10 рублей?
Решение. Условию удовлетворяют выигрыши в 50, 20 и 10 рублей.
Вероятности таких выигрышей равны:
2 . 6 10
Р50~~ 300 ’ P2Q~~ 300 и Ло ~ 300
Сложив эти вероятности, получим вероятность выигрыша не менее 10
рублей:
_ 2 б 10 18 __
Р = Рзо+Р2О +Р10- зоб- + "ЗОО" + ~3бб~--300“ °’06,
В тех случаях, когда вероятности несовместных событий
(разновидностей) равны между собой:
Р1=Р^=Рз •••
теорема сложения вероятностей принимает вид:
P kp,
где k — число несовместных событий; р — вероятность любого
из них.
Следствие теоремы сложения вероятностей: сумма вероят-
ностей всех возможных несовместных событий данного
явления равна единице:
р\ + рч + рз + _•' ’ + • • • + Ps—1 + Ps = 1 •
Проверим это следствие на разобранном выше примере
с шарами, сложив для этого вероятности появления шаров
всех цветов:
. , . . 8 . 12 . 10 , 15 , 5
Рбел+/?ЧерНН-Азел+Ркр+^сиН — 50 +-5б” + 5СГ + “бб" + 50 =~
_ 50 _ .
50 ““ Х-
Полученный результат указывает на достоверность собы-
тия. Это значит, что если вынимать один шар, то обязательно
должен появиться шар какого-либо цвета из всех шаров раз-
личного цвета, имеющихся в ящике.
Значение следствия заключается в том, что, пользуясь им,
мы можем проверить, все ли несовместные события данного
явления нами учтены полностью, т. е. всесторонне ли исследуется
это явление. Сложив вероятности всех возможных несовмест-
ных событий данного явления и получив в сумме результат
меньше единицы, мы имеем право утверждать, что была допуще-
на какая-то ошибка в определении вероятностей отдельных со-
бытий или совершенно не было учтено одно или несколько
из всех возможных событий. Руководствуясь следствием, мы
можем исправить эти ошибки.
ОФ
19
Пример 1. При стрельбе из пистолета стрелок попадает только в
черный круг мишени. Определить, какова вероятность выбить с одного
выстрела не менее 8 очков, если вероятность попадания в десятку равна 0,3,
в восьмерку — 0,2, в семерку — 0,1 и в шестерку — 0,05.
Решение. Нетрудно заметить, что в условиях примера не дана вероят-
ность попадания в девятку. Это подтверждается тем, что сумма заданных
вероятностей не равна единице:
Pv) + Ps + Рч+ Pg = 0>3 + 0,2 + 0,1-4- 0,05 — 0,65.
Чтобы учесть все возможные случаи попадания в мишень и получить
в сумме их вероятностей единицу, к полученному результату следует приба-
вить недостающую вероятность попадания в девятку:
0,65 + Pg = 1,
откуда
»9 = 1 — 0,65 = 0,35.
После этого мы можем приступить к определению искомой вероятности
выбить не менее 8 очков, т. е. вероятности попасть либо в десятку, либо
в девятку, либо в восьмерку
Р ==Рю “Ь Р9+ Ps ~ 0>3 + 0,35 4- 0,2 = 0,85.
Пример 2. В закрытом шпике имеется 10 одинаковых шаров с номерами
от № 1 до № 10. Требуется определить вероятность появления шара с номером,
кратным двум или трем.
Решение. Из 10 шаров имеется 5 шаров с номерами, кратными
двум*. № 2, № 4, № 6, № 8 и № 10. Вероятность появления такого шара
^2=4-
Шаров с номерами, кратными трем, имеется всего 3: № 3, № 6 и № 9.
Вероятность появления такого шара
3
Сложив эти вероятности, мы, невидимому, должны получить вероятность
появления шара с номером, кратным двум или трем:
_ 5 ( 3 _ 8
р2~грз ю + ю ю
Но такое решение неверно. В этом мы можем легко убедиться, исполь-
зовав следствие теоремы сложения вероятностей. Помимо шаров с номерами,
кратными двум или трем, в ящике имеются шары с номерами, не кратными
ни двум, ни трем: № 1, № 5 и № 7. Вероятность появления такого шара
Так как шар с каким-то номером должен появиться обязательно, то
сумма вероятностей появления всех различных по номеру шаров должна
быть равна единице, а она единице не равна:
5 3 3 11
7’z+/?3-+-/’h = io + ю + Ю = "10
Этот результат указывает, что была допущена какая-то ошибка. Эту
ошибку легко обнаружить. Она произошла от того, что мы не учли свойств
шара с № 6. Номер этого шара одновременно кратен двум и трем. Мы
нарушили требование, чтобы события были обязательно несовместными.
20
Чтобы исправить эту ошибку, необходимо взять сначала шары с номе-
рами, кратными только двум, — № 2, № 4, К® 8 и № 10, затем с номерами,
кратными только трем,--№ 3 и № 9 и, наконец, шар с № 6, кратный двум
и трем одновременно. Сложив вероятности появления таких шаров, мы и
получим искомую вероятность:
4 2 _1_____7_
Р =р<2 + Ръ +/>2.3= 10 + 10 + 10 - ю •
Прибавив к этому результату вероятность появления шара с номером,
не кратным ни двум, ни трем,-получим в сумме единицу:
что свидетельствует о правильности нашего решения.
Приведенный пример с достаточной наглядностью подтвер-
ждает, что теорема сложения вероятностей применима только
для несовместных событий.
Следствие теоремы сложения вероятностей важно еще и
тем, что при его помощи можно проверить правильность мате-
матических расчетов при условии, что в остальном ошибок
допущено не было.
Частный, случай следствия теоремы сложения вероят-
ностей: сумма вероятностей противоположных событий
равна единице:
p + q=\,
где р— вероятность одного события;
q — вероятность события, противоположного первому.
Доказательств здесь не требуется, так как то, что было
справедливо для нескольких несовместных событий, будет,
справедливо и для двух событий.
Зная вероятность одного из двух противоположных со-
бытий, , можно, вычтя эту вероятность из единицы, найти ве-
роятность другого:
Я', q = i-p.
Пример. Вероятность недолета при 1 выстреле равна 0,75. Чему равна
вероятность перелета?
Решение. Обозначив через р вероятность недолета и через q— ве-
роятность перелета и применив частный случай следствия, получим:
q = 1 — р == 1 — 0,75 = 0,25.
§ 7. ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
До сих пор нам приходилось иметь дело с так называе-
мыми простыми событиями^ т. е. с отдельными, единичными
событиями, которые являются конечным случайным результатом
того или иного явления: получением одного недолета, по-
явлением одного шара, выигрышем на один билет лотереи и т. п.
21
Помимо простых, очень часто происходят сложные собы-
тия, состоящие из нескольких простых событий, получаю-
щиеся в результате одновременного или последовательного
появления нескольких простых событий. Получение двух не-
долетов при двух выстрелах, одного попадания и трех про-
махов при четырех выстрелах, выход определенной суммы
очков при нескольких бросаниях игральной кости, получение
рикошета и в то же время перелета при одном выстреле гра-
натой— все это события сложные.
Определить вероятность сложного события можно при по-
мощи теоремы умножения вероятностей.
А. Случай независимых событий
Простые события, составляющие некоторое сложное собы-
тие, могут быть независимыми и зависимыми.
Независимыми называются события в том случае, когда
появление или непоявление одного из них не влияет на ве-
роятность появления других.
Зависимыми называются события в том случае, когда ве-
роятность появления одного события зависит от появления
других.
Например, выигрыш в одной лотерее и выигрыш в дру-
гой — события независимые, так как на вероятность выигрыша
в одной лотерее не окажет никакого влияния выигрыш или
проигрыш в другой. Выигрыш по двум билетам одной и той
же лотереи — события зависимые, так как выигрыш на первый
билет уменьшает вероятность выигрыша на второй, а проигрыш
на первый билет увеличивает эту вероятность.
Выведем теорему умножения вероятностей сначала для
независимых событий. Для этого воспользуемся следующим
частным примером.
Положим, что у нас имеется 2 закрытых ящика с шарами,
отличающимися только цветом. В первом ящике — 4 белых
и 5 красных шаров, во втором ящике — 3 белых и 2 красных
шара. Для удобства дальнейших рассуждений занумеруем шары
в обоих ящиках (рис. 7).
1-й ящик 2-й ящик
Рис. 7
Зададимся, исходя из этих условий, каким-либо сложным
событием и определим его вероятность. Найдем, например,
чему будет равна вероятность вынуть, не глядя, из обоих
ящиков по одному белому шару.
22
По общему правилу искомую вероятность находим по
формуле
Р = —
п
Определив т — число случаев, благоприятствующих по-
явлению сложного события, и п — число всех возможных слу-
чаев и взяв отношение первого ко второму, мы решим поста-
вленную задачу.
Интересующее нас сложное событие состоит из совпадения
двух простых независимых событий: появления белого шара
из первого ящика и появления белого шара из второго ящика.
Но, кроме таких совпадений, могут быть совпадения двух
красных шаров и совпадения белого шара с красным или крас-
ного с белым. Других совпадений быть не может, а поэтому
общее количество всех возможных совпадений двух шаров не-
зависимо от их цвета и будет равно числу всех возможных
«случаев появления интересующего нас сложного события.
Сколько же таких случаев?
Шар № 1 первого ящика может совпасть с любым из 5
шаров второго ящика, т. е. может быть 5 парных совпадений:
№ 1 с№ 10, № 1 с № 11, № 1 с № 12, № 1 с № 13 и № 1
е № 14. Такое же количество совпадений может быть для
каждого из остальных шаров первого ящика, а так как в этом
ящике всех шаров 9, то общее количество всех возможных
•совпадений будет
я— 9X5 = 45,
причем эти совпадения будут единственно возможны, несов-
местны и равновозможны.
Рассматривая совпадения шаров второго ящика с шарами
первого, придем к тому же результату, ибо для каждого из
5 шаров второго ящика может быть по 9 совпадений с шарами
700© -3@© 28®О 37®0
2О@0 2900 38 @©
/200 2700 3000 3900
7300 2200 3700 4000
7400 2300 3200 4100
1S®@ 25@® 34@0 4300
1700 2300 2500 4400
18©0 27©0 3300 45@0
Рис. 8
23
первого ящика. В этом случае общее количество всех возмож-
ных совпадений будет также
п = 5x9 = 45.
Для большей наглядности представим эти совпадения
в виде схемы (рис. 8).
Перейдем теперь к отысканию числа случаев, благоприят-
ствующих появлению рассматриваемого сложного события.
Любой белый шар первого ящика может совпасть с любым
белым шаром второго ящика, а так как в первом ящике
4 белых шара, а во втором 3, то число совпадений 2 белых
шаров, а отсюда и число случаев, благоприятствующих полу-
чению такого совпадения,
т = 4хЗ”12;
на схеме видны эти совпадения в комбинациях: № 1—4, 10 —
13 и 19 — 22.
Подставив найденные численные значения т и п в общую
формулу, определим искомую вероятность, т. е. вероятность
совпадения 2 белых шаров:
D т 12
И п 45 •
Для того чтобы вывести правило определения вероятности
сложного события, представим правую часть этого равенства
в несколько ином виде, помня, что т — 12 = 4 ХЗ и п = 45 =
= 9X5, и проанализируем его:
р__ т ___12__4-3__ 4 3
В первом ящике из 9 шаров 4 шара белого цвета, сле-
4
довательно, дробь есть вероятность появления белого шара
из этого ящика:
Во втором ящике на 5 шаров приходится 3 белых шара,—
дробь -г есть вероятность появления белого шара из второго
о
ящика:
Отсюда вероятность появления 2 белых шаров по одному
из каждого ящика равна произведению вероятности появления
белого шара из первого ящика на вероятность появления бе-
лого шара из второго ящика:
4 з
Рбб 9 ' 5 Р^'Рб.-
Таким образом, для определения вероятности сложного
события нам пришлось перемножить вероятности простых
событий, его составляющих.
24
Проверим этот вывод, задавшись при условиях нашего'
примера другим сложным событием — появлением 2 красных
шаров по одному из каждого ящика.
Вероятность появления красного шара из первого ящика.
5
Рк, — 9 •
Вероятность появления красного шара из второго ящика
2
— 5 *
Перемножив эти вероятности, мы должны получить вероят-
ность появления 2 красных шаров из обоих ящиков:
р ___п п ______ 5 2 __ Ю
^кк—РК1 -Рк2 — д • 5 — 45 •
На схеме (рис. 8) видно, что совпадений двух красных,
шаров—10 из 45 возможных (совпадения № 32—36 и 41—45)..
Следовательно, и для этого сложного события наш вывод,
справедлив.
Мы определили вероятность сложного события, состоящего
из двух простых событий. Посмотрим, чему будет равна ве-
роятность сложного события, если оно состоит из трех про-
стых событий.
Добавим к первому и второму ящикам третий ящик с 2
белыми и 4 красными шарами и определим вероятность по-
явления 3 белых шаров из 3 ящиков.
Мы имели 45 всех возможных парных совпадений шаров,
первого и второго ящиков. Каждая из этих пар может сов-
пасть с любым из 6 шаров третьего ящика, в результате чего
получится 210 совпадений (45 X 6), но уже из 3 шаров; это-
и есть число всех возможных случаев для появления нового
сложного события.
Парных совпадений белых шаров было 12. Каждая такая
пара может совпасть с любым из 2 белых шаров третьего
ящика, в результате чего получится 24 совпадения 3 белых
шаров (12x2) или 24 случая, благоприятствующих появлению
рассматриваемого сложного события. Отсюда его вероятность
р _ 24 __ 12*2 __ 4*3<2 _ 4 3 2
^ббб— 210- — 45,б — 9>5#6 — 9 • 5 • 6
= рб, • Рб, • рбл-
Следовательно, и в этом случае вероятность сложного со-
бытия равна произведению вероятностей простых событий, из-
которых состоит это сложное.
Нетрудно заметить, что определение численных значений
т и п следует некоторому общему для них правилу:
т — число случаев, благоприятствующих появлению слож-
ного события, всегда равно произведению чисел случаев, бла-
гоприятствующих появлению простых событий;
25
п — число всех возможных случаев появления сложного
события равно произведению всех возможных случаев появле-
ния простых событий:
т = т{-т2-т3 . . . ms',
П — Пу-П2’П3. . .ns.
Поэтому после подстановки значений т и п в общую
•формулу мы всегда будем иметь в итоге произведение вероят-
ностей простых событий, составляющих данное сложное:
р __ т ___ т1-т.2-ш3 . . . ms _ ms
п П1‘П2-П3 . . . ns пг п2 п3 ’ * ' ns '
или
• -Ps-
Вероятность сложного события, состоящего из совпа-
дения или последовательного появления нескольких простых
независимых событий, равна произведению вероятностей
.этих простых событий.
Следует отметить, что вероятность сложного события как
произведение правильных дробей будет всегда меньше любой
из вероятностей составляющих его простых событий. Если ве-
роятность каждого простого события равна единице, то вероят-
ность сложного события будет также равна единице.
Пример 1. При стрельбе из пистолета по круглой мишени вероятность
/попадания в десятку при 1 выстреле равна 0,2, в девятку — 0,25, в вось-
мерку— 0,3, в семерку — 0,15 и в шестерку—0,1. Чему равна вероятность
при 3 выстрелах выбить последовательно 8, 9 и 10 очков?
Решение. Последовательное попадание в восьмерку, девятку и де-
сятку — событие сложное, состоящее из 3 простых событий: попадания при
первом выстреле в восьмерку, при втором — в девятку и при третьем —
в десятку. Но теореме умножения искомая вероятность должна быть равна
произведению^верОятностей этих простых событий:
Р = p3-pQ-pio — 0,3-0,25-0,2 = 0,015.
Пример 2. В первой лотерее на 150 билетов^ приходится 20 выигры-
шей и во второй лотерее на 200 билетов 30 выигрышей. Чему равна вероят-
ность совпадения выигрыша на 1 билет первой лотереи с выигрышем
на 1 билет второй лотереи?
Решение. Вероятность выигрыша на 1 билет первой лотереи равна
20
^1= 150’
а на 1 билет второй лотереи
30
р2 ~ 200 ’
вероятность выигрыша на оба билета, т. е. вероятность совпадения выигры-
шей,
20 ‘30 1
Р=\-Р1 — 150 ' 200 ~ 50 — °’02-
26
Если вероятности простых независимых событий, соста-
вляющих некоторое сложное событие, равны между собой,
т. е. если
• • • =Р5,
то вероятность Р такого сложного события равна вероятности р
простого события в степени, равной числу простых событий:
P-ps.
Пример. Чему равна вероятность получить 4 недолета подряд при
стрельбе на одних и тех же установках, если вероятность недолета при
1 выстреле равна 0,75?
Решение. Так как установки при стрельбе не меняются, то веро-
ятность недолета для всех 4 выстрелов остается неизменной:
Pl = Р2=Рз = Р4 = М5-
Отсюда вероятность 4 недолетов как вероятность сложного события,
состоящего из 4 простых событий, вероятности которых равны между собой,
будет равна
р = = 0,754 = 0,3164.
Сложное событие, в свою очередь, может состоять из
сложных событий. Применение теоремы умножения вероят-
ностей в этих случаях никаких сомнений не вызывает, так как
любое сложное событие может быть представлено, как со-
стоящее только из простых событий.
Пример. Средние траектории, соответствующие прицелам 100 и 102,
занимают положение, показанное на рис. 9 (A2f=50 м, Вд = 25 м). Какова
вероятность захватить цель в вилку, на ближнем пределе которой должно
быть 2 недолета, а на дальнем — 2 перелета?
Рис. 9
Решение. Вилка, на ближнем пределе которой получено 2 недолета,
а на дальнем — 2 перелета, — событие сложное, состоящее из двух сложных
событий, каждое из которых состоит из двух простых событий.
Найдем сначала вероятность получения одного составляющего слож-
ного события, т. е. вероятность получения 2 недолетов на прицеле 100. Иг
рисунка видно, что вероятность одного недолета при стрельбе на этом при-
целе
о100 = 0,02 + 0,07 + 0,16 + 0,25 + 0.25 = 0,75;
отсюда вероятность получения 2 недолетов на том же прицеле
Лоо = .Р21Оо -0,752 = 0,5625.
27
Найдем вероятность другого составляющего сложного события, т. е.
вероятность получения 2 перелетов на прицеле 102. Вероятность получения
одного перелета при стрельбе на этом прицеле
9102 = 0,02 + 0,07 + 0,1р + 0,25 + 0,25 + 0,16 + 0,07 = 0,98;
вероятность получения 2 перелетов на том же прицеле
Лог = ?2Ю2 = 0.982 = 0,9604.
Зная вероятность обоих составляющих сложных событий, найдем ис-
комую вероятность, т. е. вероятность получения вилки, на каждом пределе
которой должно быть по 2 знака:
Рв = Лоо’Лоз = 0,5625-0,9604 = 0,5402.
К такому же результату мы придем, если сразу перемножим вероят-
ности простых событий, составляющих рассматриваемое сложное событие:
Л ~ Р100'Т’юо'*7102 • *7102 = 0,75-0,75-0,98-0,98 = 0,5402.
Во всех приведенных выше примерах мы имели дело со
сложными событиями, состоявшими из простых несовместных
событий, но теорема умножения вероятностей применима и
к совместным событиям.
Пример 1. Имеется закрытый ящик с 10 шарами, из которых 7 белых
и 3 красных. Все шары занумерованы: белые с № 1 по № 7 и красные
с № 8 по № 10. Какова вероятность вынуть, не глядя, белый шар с четным
номером?
Решение. Найдем сначала искомую вероятность как отношение числа
белых четных шаров к числу всех шаров, имеющихся в ящике. Из 10 шаров
3 белых шара имеют четный номер: № 2, NH и № 6. Следовательно, веро-
ятность выхода белого четного шара
Применим теперь теорему умножения вероятностей, рассматривая по-
явление белого четного шара как событие сложное, состоящее из совпадения
двух простых совместных событий: белого цвета с четным номером, или
четного номера с белым цветом.
Из 10 шаров 7 шаров белого цвета. Поэтому вероятность появления
белого шара независимо от его номера
7
Рв— ю •
Условию удовлетворяет только совпадение белого цвета с четным но-
мером. Из 7 белых шаров четных 3. Поэтому вероятность появления чет-
ного шара из числа белых
3
Рч-б = 7 •
Отсюда вероятность появления четного белого шара из числа всех
шаров
n__Z 3 __з
10 7 - 10 •
Оба решения привели к одному и тому же результату, так
как теорема умножения вероятностей справедлива и для тех случаев, когда
сложное событие состоит из совместных событий.
28
Необходимо иметь в виду, что при определении вероятности вынуть
белый шар с четным номером подсчитывается или вероятность совпадения
шара белого цвета (независимо от его номера) с четным номером шара
только из числа белых, или вероятность совпадения четного номера шара
(без учета его цвета) с белым шаром только из числа шаров с четным
номером.
Если эти условия нарушены, то возможно такое неправильное решение:
— вероятность появления шара с четным номером независимо от его
цвета
5
Рч - ю ’
— вероятность появления белого шара независимо от его номера
7
Рб - 10 *
Тогда вероятность появления белого четного шара из числа всех
шаров
_ А 7 _ 35 ,
Р - 10 * 10 - 100 ’
что противоречит отношению числа четных белых шаров к числу всех
шаров, имеющихся в ящике.
Разберем, почему произошла эта ошибка. Произведение дробей
5 7
10 ’ 10
7
•означает, что здесь берется либо-ууу от числа всех шаров с четным номером,
5
либо -ууу от числа всех белых шаров. По условию же мы имеем другие
. 7 3
соотношения: белых шаров среди четных не -гтг • а -г~ » и четных шаров
1 и 3
. з
среди белых не половина, а • 1
Пример 2. Вероятность нахождения целина том участке, куда напра-
влен огонь, рц — 0,3. Вероятность попадания при 1 выстреле и при условии,
что цель находится на обстреливаемом участке, р — 0,2. Определить вероят-
ности: а) получить попадание при 1 выстреле; б) получить 2 попадания при
2 выстретах.
Решение, а) Здесь мы имеем сложное событие, состоящее из совпа-
дения двух простых совместных событий — нахождения цели на данном
участке и попадания в эту цель. Отсюда искомая вероятность
Ра = рц • р - 0,3 • 0,2 = 0,06.
б) В этом случае сложное событие состоит из совпадения следующих
совместных событий: простого (нахождения цели на обстреливаемом участке)
и сложного (получения 2 попаданий подряд).
Если цель находится на данном участке, то вероятность 2 попаданий
подряд равна
рч = 0,22 = 0,04.
Вероятность двух попаданий с учетом вероятности нахождения цели
рб ~ • PZ ~ 0,3-0,04 = 0,012.
29
Было бы неправильно, использовав результат первого решения, возвести
его во 2-ю степень и считать, что
Рб = Ра2- 0,062 - 0,0036.
Ошибка станет очевидной, если мы этот результат представим в виде
произведения вероятностей простых событий:
0,0036 = 0,062 = (0,3-0,2)2 = 0,3-0,3-0,2-0,2 = Рц • рц • р-р.
В данном случае вероятность нахождения цели учтена дважды, т. е. она
поставлена в зависимость от числа произведенных выстрелов. В действитель-
ности вероятность нахождения цели от числа выстрелов не зависит, ибо она
показывает, какую часть от вероятности попадания следует брать при любом
числе выстрелов при условии, что цель обязательно находится на обстрели-
ваемом участке.
Пример 3. Вероятность попадания при 1 выстреле равна 0,4. Какова
вероятность получить 2 попадания подряд разорвавшихся снарядов, если
неразрывы составляют 6% от числа всех выпущенных снарядов?
Решение. При выстреле может быть попадание и промах, разрыв и
неразрыв снаряда. Поэтому наше сложное событие следует рассматривать
как состоящее из двух сложных событий, каждое из которых состоит из
двух простых совместных событий — попадания и разрыва снаряда.
Вероятность получения разрыва снаряда при 1 выстреле как вероятность
события, противоположного неразрыву,
рр = 1 — 0,06 = 0,94.
Вероятность получения попадания разорвавшимся снарядом при 1 вы»
стреле
рх = р . Рр = 0,4 • 0,94 = 0,376;
вероятность получения подряд 2 таких попаданий
P^Pf = 0,3762 = 0,1414.
Эти три примера показывают, насколько тщательным должен
быть анализ условий при определении вероятностей сложных
событий, в состав которых входят совместные события. Трафа-
ретный, поверхностный подход к решению таких задач является,
как правило, источником грубейших ошибок.
В теории вероятностей и, в частности, при артиллерийских
расчетах очень часто приходится применять одновременно и
теорему сложения и теорему умножения вероятностей.
Пример 1. Имеется 2 закрытых ящика с шарами: в первом 3 белых и
4 черных шара, во втором — 7 белых и 5 черных шаров. Чему равна вероят-
ность, вынимая из каждого ящика (не глядя) по одному шару, получить одно-
временно 2 шара одного и того же цвета?
Решени е. Решению этого примера удовлетворяет появление или
2 белых, или 2 черных шаров.
Вероятность появления 2 белых шаров по теореме умножения
_ 3 7 _ 21
рб -Рь,-Р(>. - 7 ’ 12 - 84 ’
Вероятность появления 2 черных шаров по той же теореме
4 5 20
/!ч - ^4,'Р'О - 7 ’ 12 ~ 84 *
30
По теореме сложения вероятность появления или 2 белых, или 2 черных,
шаров
20 _ 41
Р - рб + РЧ == 84 “Ь 84 ~ 84 ’
1
Пример 2. Вероятность недолета при 1 выстреле р — -у- Чему
равна вероятность получения накрывающей группы (наблюдений разных
знаков) при 3 выстрелах, произведенных на одних и тех же установках?
Решение. Если вероятность недолета при 1 выстреле равна 3- » то
вероятность перелета
« = 1 -р = 1 - -у = -у •
При 3 выстрелах можно получить накрывающую группу либо с пре-
обладанием недолетов (2 недолета и 1 перелет), либо с преобладанием
перелетов (1 недолет и 2 перелета).
Накрывающая группа, состоящая из 2 недолетов и 1 перелета, может
быть получена в виде одного из следующих трех вариантов: или-------
или----[--, или ------.
Вероятность любого из этих вариантов по теореме умножения равна
а так как порядок получения недолетов и перелетов нам безразличен, то по-
теореме сложения вероятность накрывающей группы с преобладанием не-
долетов
г. о 2 6
—-3р-д = 3- 27 — 27 *
Рассуждая аналогично, определим вероятность накрывающей группы
с преобладанием перелетов, исходя из того, что такая группа может быть'
получена в виде одного из следующих трех вариантов: или + н----, или
----И, или----h +:
1 /2V 12
— з- з • з J - 27 •
Отсюда по теореме сложения вероятность накрывающей группы неза-
висимо от соотношения знаков
Эту же задачу можно решить иначе: кроме накрывающих групп,,
оторые были рассмотрены, при 3 выстрелах могут быть получены все
едолеты или все перелеты.
Вероятность получения трех недолетоз
/IV 1
Р^-Р3={-3) =2Г
Вероятность получения трех перелетов
= V
__ _8_
“ 27
31
Если мы вычтем из единицы эти вероятности, то на основании след-
ствия теоремы сложения получим искомую вероятность накрывающей
группы:
( 1 8 \ 18 2
Р = 1 -(Р,+ Р4)= 1 - ( 27 + 27 ) = 27 = 3-
Сложив вероятности всех возможных
'перелетов при 3 выстрелах, получим:
6 12
Pi + Р-> 4- Р% + Р4 — 27 + 27
комбинаций из недолетов и
1 А
+ 27 + 27 = 11
что подтверждает правильность наших решений.
Б. Случай зависимых событий
Для зависимых событий выведем теорему умножения веро-
ятностей на следующем примере.
Положим, в закрытом ящике имеется 5 шаров: 3 красных
и 2 белых. Определим, какова вероятность вынуть, не глядя,
2 раза подряд красный шар, не возвращая в ящик шар,
вынутый первым.
'Здесь мы имеем дело с событием сложным, оно состоит
из последовательного появления двух простых событий. Эти
простые события зависимы — вероятность появления второго
красного шара зависит от того, какой шар был вынут
первый раз.
Если первым был вынут красный шар, то вероятность
г 2
вынуть вторым также красный шар будет равна , так как
число случаев, благоприятствующих появлению красного шара,
сократится с 3 до 2, а число всех возможных случаев — с 5 до 4.
Если первым был вынут белый шар, то вероятность поя-
- з
вления затем красного шара будет равна -у, так как число
случаев, благоприятствующих появлению
ярасного шара, не изменится, а сокра-
тится только число всех возможных
случаев.
Для удобства дальнейших рассуждений
занумеруем шары в ящике (рис. 10).
Рассуждая так же, как при выводе теоремы умножения
для независимых событий, опоеделим сначала число всех
возможных (единственно возможных, несовместных и равно-
возможных) совпадений двух шаров.
После шара № 1 может появиться либо шар № 2, либо
шар № 3, либо шар №4, либо шар№ 5, т. е. с шаром № 1 может
быть всего 4 парных совпадения. Столько же совпадений
может быть и с шарами № 2, 3, 4 и 5. Таким образом, всего
может быть 5X4 = 20 совпадений. Это и есть число всех
возможных случаев для появления рассматриваемого сложного
Рис. 10
32
•события. Представим эти совпадения (случаи) в виде схемы
(рис. И).
Число случаев, благоприятствующих появлению рассматри-
ваемого сложного события, должно быть равно числу совпа-
дений двух красных шаров. Таких совпадений по нашей
схеме—6: № 1 с № 2, № 1 с № 3, № 2 с № 1, № 2 с № 3,
№ 3 с № 1 и № 3 с № 2.
100
2®0
з®0)
4®©
5®®
В®® W00 w©0
70© ”00 «00
80© ’2©© '60© 2»©0
Рис. 11
Отсюда вероятность вынуть
возвращая в ящик шар, вынутый
равна:
подряд 2 красных шара, не
первым, по общей формуле
6
20
т
Вероятность появления красного шара первый раз —
3 2
рх = у, второй раз — р2 =2 , при условии, что вынутый красный
шар в ящик не возвращается. Представим найденную вероят-
ность в виде произведения двух дробей:
_ 6 __ з 2 —
Р~~ 20 ~ 5 ' 4 —Р1'р2>
т. е. вероятность вынуть 2 раза подряд красный шар при
условии, что вынутый в первый раз шар в ящик не возвра-
щается, равна вероятности выхода красного шара в первый
раз, умноженной на вероятность выхода красного шара во второй
раз, вычисленную при условии, что шар, вынутый первым, был
красного цвета.
В общем виде для любого числа простых зависимых
событий, составляющих сложное событие, вероятность слож-
ного события, состоящего из нескольких простых зависимых
событий, равна вероятности первого события, умноженной
на вероятность второго события, рассчитанную в предпо-
ложении, что первое событие произошло, умноженной на
вероятность третьего события, рассчитанную в предполо-
жении, что произошли первые два события, и т. д.
Пример 1. В лотерее на 10 билетов 3 выигрыша. Какова вероятность,
что взятые наудачу первые 3 билета будут выигрышными?
Р.е ш е н и е. Вероятность выигрыша на первый билет
3
- 10 •
3 ~ Зак. 991
33
Вероятность выигрыша на второй билет при условии, что первый
билет выиграл,
р2 = 4-
Вероятность выигрыша на третий билет при условии, что выиграли
первый и второй билеты,
Рз ~ ~8 *
Отсюда по теореме умножения вероятность выигрыша на 3 первых
билета
_ 3 2 . £ _ _б_____£
Р — РгРг’Рз - ю ’ g ’ 8 “ 720 ~ 120'
Пример 2. В урне 4 билета, один из них выигрышный. Билеты
распределены между 4 участниками розыгрыша. Участники розыгрыша
вынимают билеты из урны по очереди. Какой из участников имеет больше
шансов на выигрыш?
Решение. Вероятность выигрыша участника, вынимающего билет
первым,
Второй участник может выиграть только тогда, когда проиграет первый;
3
вероятность проигрыша первого равна -у» поэтому вероятность выигрыша
второго
______£ J._____1_
Р2— 4 ’ з — 4 *
Третий участник выигрывает при условии проигрыша первых двух,
и, наконец, четвертый участник выигрывает, если проигрывают все осталь-
ные участники. Вероятности выигрыша третьего и четвертого участников
’ 3 2 _1______£_ 3 2 1 _ 1
Т’з - 4 * з ' 2 ~ 4 и Р*~ 4 ’ 3 ’ 2 ’ 1 - 4 '
Таким образом, шансы на выигрыш у всех участников одинаковы.
§ 8. ГЕОМЕТРИЧЕСКАЯ ВЕРОЯТНОСТЬ
Нередко при определении вероятностей некоторых событий1
непосредственный подсчет числа случаев, благоприятствующих
их появлению, и числа всех возможных случаев бывает затруд-
нителен (случаев очень много) или вообще невозможен (слу-
чаев бесконечно много). Тогда отношение чисел благоприят-
ствующих случаев и всех возможных случаев заменяется отно-
шением величин, пропорциональных этим числам, если, ко-
нечно, такая пропорциональность существует.
Положим, что взяли 5 кг зерна, отделили 2 кг зерна и
окрасили его в красный цвет, а затем тщательно перемешали
с неокрашенным. Если все зерна одинаковы, то совершенно
очевидно, что и без подсчета окрашенных и неокрашенных
зерен можно утверждать, что вероятность появления окрашен-
-2 г
ного зернышка должна быть равна -у , так как на 5 кг зерна
приходится 2 кг окрашенного.
34
Здесь отношение числа случаев, благоприятствующих
появлению нашего события (числа окрашенных зерен), к числу
всех возможных случаев (числу всех зерен) мы заменили отно-
шением их весов, пропорциональных этим числам.
В приведенном примере число благоприятствующих слу-
чаев и число всех возможных случаев очень велико (доста-
точно сказать, что на. 1 кг зерна приходится около 150000
зерен), но эти числа конечны, и подсчет их хотя и затрудни-
телен, но возможен. Перейдем к примеру, по условию кото-
рого число случаев, благоприятствующих появлению какого-
либо события, и число всех возможных случаев бесконечно
велики.
Допустим, что имеется тонкий стержень АВ длиной
10 см, на котором сделано 10 зарубок — по одной на каждый
сантиметр. Допустим также, что при падении стержень пере-
ламывается на 2 части и этот перелом равновозможен на лю-
бой из этих зарубок. Определим вероятность перелома стер-
жня на участке CD длиной 3 см (рис. 12).
Л сив
I i ; :
I—I—.—I—г—1--1—|.!—^-.—>—I—I—!—Ч—г-Ь-г—t
0 1 23 't- 56789 ЮСМ
Рис. 12
Всех возможных (единственно возможных, несовместных
и равновозможных) случаев перелома стержня 10. Случаев,
благоприятствующих перелому на участке CD, -- 3. Отсюда
вероятность перелома на участке CD:
Увеличим число зарубок на стержне в 2, 5, 100, 1000 раз.
Очевидно, что во столько же раз увеличится число всех воз-
можных случаев перелома стержня и число случаев, благо-
приятствующих перелому на участке CD, поэтому искомая
вероятность не изменится:
3-2 3-5 3-100 3-1000 __ 3
Р~~ 10-2 “ 10-5 ~ 10" 100 10-1000 10 3
так как при любом увеличении числа зарубок количество
случаев, благоприятствующих перелому стержня на участке
CD, остается пропорциональным длине этого участка в сан-
тиметрах, а количество всех возможных случаев перелома-
пропорциональным длине всего стержня также в сантиметрах,
ибо на каждый сантиметр приходится равное число зарубок.
Теперь допустим, что число зарубок бесконечно велико
(зарубки как бы сливаются между собой) и стержень может
переломиться на 2 части в любой точке.
3=: 35
Несомненно, что установленная выше пропорциональность
сохранится и здесь—искомая вероятность будет равна отно-
шению тех же величин, т. е. отношению длины участка CD
к длине всего стержня, так как при бесконечно большом числе
точек перелома эти точки в своей совокупности (слитности) на
участке CD составят его длину, а на участке АВ — длину
стержня.
Следовательно, искомая вероятность может быть пред-
ставлена в виде отношения отрезка CD к отрезку АВ, т. е.
в виде отношения геометрических величин. Тогда, когда число
всех благоприятствующих случаев и число всех возможных
случаев могут быть заданы геометрическими величинами (отрез-
ками, площадями, объемами и т. п.), вероятность принято
называть геометрической.
Пример 1. Самолет бомбит НП, занимающий площадь, принятую за
круг, радиус которого г — 10 м. Бомбы при этом не выходят из предела
круга, радиус которого /? = 50л/, распределяясь внутри его равномерно.
Чему равна вероятность попадания в НП при сбрасывании одной бомбы?
Решение. Число-случаев, благоприятствующих попаданию в НП,
можно считать пропорциональным площади, занимаемой НП, а число всех
возможных случаев — пропорциональным площади, на которую может упасть
бомба. Поэтому искомую вероятность мы и найдем из отношения этих пло-
щадей:
№ ,-102 1
Р~~ — Я5О2 = 25 — °’04’
Пример 2. При стрельбе гранатой по блиндажу, занимающему площадь
прямоугольника размером 6 X 4 м, цель накрывается единичным эллипсом
рассеивания с главными полуосями 24 м и 3 м. Чему равна вероятность по-
падания в блиндаж при одном выстреле, если вероятность попадания в еди-
ничный эллипс равна 0,2 и если допустить, что снаряды на площади этого
эллипса ложатся равномерно?
Решение. Определим сначала вероятность попадания в блиндаж, не
учитывая вероятности попадания в единичный эллипс, как отношение пло-
щадей блиндажа и единичного эллипса:
6-4 1
р~ тг-24-3 “3-к-
Вероятность попадания в блиндаж, с учетом вероятности попадания
в единичный эллипс по теореме умножения
Р=~ - 0,2 0,022.
В практике артиллерийских расчетов нам постоянно при-
ходится пользоваться отношениями геометрических величин
при определении вероятностей. Достаточно сказать, что такие
вероятности, как вероятности попадания, получения перелета,
нахождения цели, — все это вероятности геометрического
порядка.
36
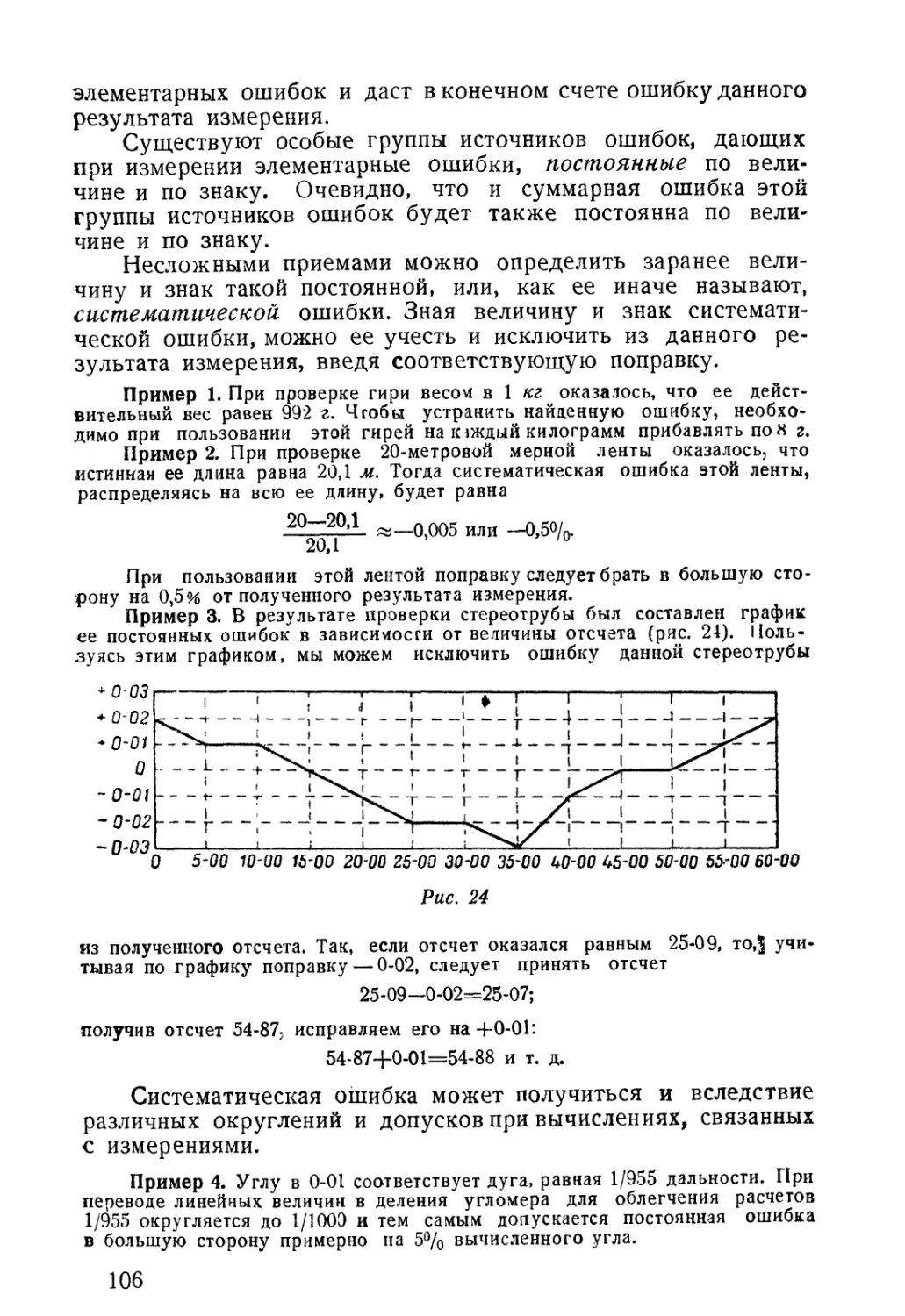
§ 9. ЗАДАЧИ НА ВЕРОЯТНОСТЬ И ЧАСТОСТЬ СОБЫТИЯ
Задача 1. В нише установлено 50 не рассортированных по весовым
признакам гранат, из которых 10 помечены двумя минусами, 25 одним плю-
сом и 15 тремя плюсами. Какова вероятность, что взятая наудачу граната
окажется с тремя плюсами?
Ответ. 0,3.
Задача 2. В закрытом ящике 30 совершенно одинаковых шаров, отли-
чающихся только цветом, — синие и красные. Сколько в ящике шаров крас-
ного цвета, если вероятность€,,взять, не глядя, один синий шар равна 0,4?
Ответ. 18.
Задача 3. В закрытом ящике находятся белые и черные шары, отли-
чающиеся только цветом. Каково общее число шаров в ящике, если веро-
ятность вынуть, не глядя, один белый шар равна -g- , а черных шаров 10?
Ответ. 15.
Задача 4. Из 28 тщательно перемешанных костей домино взята наудачу
одна кость. Чему равна вероятность, что на взятой кости окажется сумма
очков, равная 6?
Ответ, -у .
Задача 5. В урне 10 шаров, из них 7 белых. Берем одновременно
3 шара. Какова вероятность вынуть 3 белых шара?
Ответ. -Тэд- .
Задача 6. При 12 выстрелах было получено 2 попадания. Какова ча-
стость попадания?
1
Ответ, -g- .
Задача 7. Частость перелета равна 0,3. Каково количество перелетов,
если всего было произведено 20 выстрелов?
Ответ. 6.
Задача 8. При стрельбе гранатой частость рикошета равна 80 %. Чему
равна частость нерикошета?
Ответ. 20%.
Задача 9. Из ящика, содержащего 8 белых и 6 черных шаров, было
вынуто подряд 4 белых шара. Какова частость выхода белого шара?
Задача 10. В ящике имеются шары белого, красного и черного цве-
тов. Вероятность вынуть, не глядя, 1 белый шар равна , 1 красный — -g-
и 1 черный — -g-. Чему равна вероятность вынуть белый или черный шар?
2
Ответ, -g-.
Задача 11. Огонь ведется по цели, которая вся накрывается эллипсом
рассеивания. Какова вероятность получить при 1 выстреле перелет, если
средняя траектория проходит перед целью в 2 В д'?
Ответ. 0,09.
- Задача 12. В лотерее на 500 билетов приходится: 3 выигрыша по 100
рублей, 12 выигрышей по 50 рублей, 25 выигрышей по 20 рублей, 60 выиг-
рышей по 10 рублей и 100 выигрышей по 5 рублей. Чему равна вероят-
ность, имея 1 билет этой лотереи, выиграть не более 20 рублей?
Ответ. 0,37.
Задача 13. При стрельбе по участку траншей, состоящему из трех ли-
ний, вероятности попадания в I, II и III линии соответственно равны 0,08,
0,15 и 0,1. Чему равна вероятность попадания при 1 выстреле в одну из
линий траншей?
Ответ. 0,33.
37
Задача 14. Вероятность попадания при 1 выстреле равна 0,12. Чему
равна вероятность промаха?
Ответ. 0,88.
Задача 15. При стрельбе из винтовки по круглой мишени вероятность
попадания в десятку равна 0,15, в девятку — 0,25, в семерку — 0,2 и в ше-
стерку— 0,1. Какова вероятность выбить при 1 выстреле не менее 7 очков,
если стрелок кладет все пули в черный круг?
Ответ. 0,9.
Задача 16. Вероятность недолета при 1.’Выстреле равна 0,3. Какова ве-
роятность получения 2 перелетов подряд?
Ответ. 0,49.
Задача 17. Средние траектории, соответствующие прицелам 80 и 82,
занимают относительно цели такое положение, что вероятность перелета
при стрельбе на прицеле 80 равна 0,15, а вероятность недолета при стрельбе
на прицеле 82 равна 0,2. Чему равна вероятность, произведя по 2 выстрела
на каждом из этих прицелов, получить 2-деленную вилку, обеспеченную
2 знаками на каждом пределе?
Ответ. 0,4624.
Задача 18. Вероятность нахождения цели на том участке, куда напра-
влен огонь, равна 0,3. Вероятность попадания при 1 выстреле и при усло-
вии нахождения цели на данном участке равна 0,2. Определить вероятность
промаха при 3 выстрелах подряд.
Ответ. 0,8536.
Задача 19. Вероятность поражения цели осколками рикошетирующего
снаряда 0,25. Какова вероятность поражения цели при 1 выстреле, если ри-
кошеты дают в среднем 80% всех выпущенных снарядов?
Ответ. 0,2.
Задача 20. В закрытом ящике 5 белых и 3 черных шара. Какова ве-
роятность вынуть, не глядя, подряд 3 белых шара, если вынутые шары
в ящик не возвращаются и отличаются только цветом?
5
Ответ. -5J-.
Задача 21. Из 28 тщательно перемешанных костей домино берут на-
удачу 2 кости. Чему равна вероятность, что на первой кости сумма очкоз
будет равна 5. а на второй кости —10?
Ответ. 126*
Задача 22. Средняя траектория проходит в 1 Вд перед целью. Какова
вероятность получить при 2 выстрелах наблюдения одного и того же знака?
5
Ответ, -g- .
Задача 23. Имеется 3 ящика с шарами, отличающимися только цве-
том. В первом ящике 3 белых, 5 красных и 2 черных шара, во втором
ящике 6 белых, 4 красных и 5 черных шаров и в третьем ящике 1 белый,
2 красных и 3 черных шара. Определить, какова вероятность вынуть из этих
ящиков одновременно 3 шара одного и того же цвета. Шары вынимаются
вслепую и по одному из каждого ящика.
22
Ответ. 225.
Задача 24. Вероятность нахождения цели на обстреливаемом участке
0,4. Вероятность попадания при 1 выстреле и при условии нахождения цели
на участке, куда направлен огонь, равна 0,1. Какова вероятность поразить
цель при 2 выстрелах, если для поражения цели требуется 1 попадание?
Ответ. 0,076.
38
Задача 25. При стрельбе из винтовки в тире по круглой мишени все
пули ложатся в черный круг. Определить вероятность выбить с 2 выстрелов
не менее 18 очков, если вероятности попадания при 1 выстреле равны:
в десятку —0,15, в девятку —0,25, в восьмерку —0,3, в семерку —0,2 и
в шестерку —0,1.
Ответ. 0,25.
Задача 26. Какова вероятность при одновременном бросании 2 играль-
ных костей получить при первом бросании сумму очков не менее 10 и при
втором бросании сумму очков не менее 9?
Задача 27. В первом ящике 2 белых и 3 черных шара, а во втором —
4 белых и 5 черных шаров. Шары различаются между собой только цве-
том. Из первого ящика во второй, не глядя, переложен один шар. Опреде-
лить вероятность вынуть после этого белый шар из второго ящика.
Ответ. 0,44.
Задача 28. Найти вероятность подрыва танка, проходящего через одну
линию мин, если интервалы между минами равны 5 м, ширина гусениц
танка 1 м и танк движется перпендикулярно к линии мин.
Ответ. 0,2.
Задача 29. В окружность вписан правильный треугольник. Чему равна
вероятность, что поставленная наудачу внутри круга точка окажется вну-
три треугольника?
Ответ. 0,4135.
Задача 30. Самолет бомбит переправу, состоящую из 2 мостов: 6x30 м
а 8x30 м. Бомбы при этом накрывают переправу, ложась равномерно и не
выходя из пределов площади, имеющей вид прямоугольника 100x200 м. Ка-
кова вероятность хотя бы частично нарушить пользование этой переправой,
бросив 1 бомбу?
Ответ. 0,021.
ГЛАВА 2
ПОВТОРЕНИЕ ИСПЫТАНИЙ
§ 10. ВЕРОЯТНОСТЬ КОМБИНАЦИИ
Допустим, что при некотором испытании (например, вы-
стреле) непременно должно появиться одно из двух противо-
положных событий — событие А или событие В (например,
недолет или перелет), вероятности которых остаются неизмен-
ными при повторении такого испытания в совершенно оди-
наковых условиях (например, при повторении выстрела на од-
них и тех же установках, на том же заряде, тем же снаря-
дом и т. д.).
Если такое испытание мы повторим несколько раз, то по-
лучим какую-то совокупность или, как мы будем называть,
какую-то комбинацию из событий А и В (например, комбина-
цию из недолетов и перелетов).
При проведении артиллерийских стрельб очень часто при-
ходится иметь дело с комбинациями из недолетов и переле-
тов; попаданий и промахов, клевков и воздушных разрывов
и т. п. Поэтому знание вероятностей таких комбинаций,
имеет чрезвычайно важное практическое и теоретическое зна-
чение.
При определении вероятностей комбинаций как вероят-
ностей сложных событий можно было бы ограничиться уже
известными нам теоремами сложения и умножения вероятно-
- стей, если бы комбинации как сложные события не отличались
одной весьма существенной особенностью.
Эта особенность заключается в том, что комбинация с дан-
ным соотношением противоположных событий имеет ряд
вариантов, различающихся последовательностью (порядком)
появления этих событий. Эти варианты равновероятны —
любой из них может быть получен при повторении испыта-
ния, а поэтому, чтобы определить вероятность комбинации.^
необходимо знать число ее вариантов.
40
Покажем это на примере. Положим, нас интересует ве-
роятность комбинации из двух недолетов и двух перелетов, а
последовательность их появления нам безразлична.
Эта комбинация имеет 6 вариантов, различающихся по-
рядком (последовательностью) получения недолетов и переле-
тов.
Вариант № в ы с г р е л о в
1 2 3 4
1 Недолет Недолет Перелет Перелет
2 Недолет Перелет Недолет Перелет
3 Перелет Недолет Перелет Недолет
4 Недолет Перелет Перелет Недолет
5 Перелет Недолет Недолет Перелет
6 Перелет Перелет Недолет Недолет
Обозначим вероятность недолета при 1 выстреле через р,
а вероятность перелета — через q. Тогда вероятность одного
определенного (любого из 6) варианта по теореме умножения
вероятностей будет равна р2#2. А так как все 6 вариантов
равновероятны, то вероятность комбинации по теореме сложе-
ния вероятностей будет равна 6 p^q*.
Но особенность комбинации как сложного события этим
не исчерпывается — с увеличением числа испытаний резко уве-
личивается количество вариантов. Так, если комбинация в виде
равенства недолетов и перелетов при 4 выстрелах имела 6 ва-
риантов, то при 6 выстрелах такая же комбинация будет
иметь уже 20 вариантов, а при 8 выстрелах число их дойдет
до 70.
Совершенно очевидно, что определить количество воз-
можных вариантов данной комбинации методом их подбора,
как это мы сделали выше, допустимо лишь для очень неболь-
шого числа повторений испытания. При большем числе по-
вторений испытания такой метод очень сложен и, главное, не
дает гарантии, что все возможные варианты будут нами уч-
тены полностью.
Поэтому необходимо найти такую общую формулу, кото-
рая будет справедлива для вероятности любой комбинации
при любом числе испытаний.
Чтобы вывести такую формулу, рассчитаем вероят-
ности всех возможных комбинаций, получающихся при двух,
трех и четырех испытаниях, и обобщим результаты этих ра-
счетов. Для большей наглядности воспользуемся комбина-
циями из недолетов и перелетов при повторении выстрела,
обозначив при этом получение недолета знаком „минус" и
перелета — знаком „плюс".
41.
При подсчетах вероятностей отдельных комбинаций будем
пользоваться как теоремой умножения (вероятность одного
варианта), так и теоремой сложения (вероятность комбинации),
подобно тому как это было сделано выше при определении
вероятности комбинации из 2 недолетов и 2 перелетов.
Результаты подсчетов сведем в общую таблицу.
Количе- ство вы- стрелов Комбинации № выстрелов Вероятности вариантов Вероят- ности ком- бинаций
1 2 3 4
2 2 недолета 1 недолет и 1 пе- релет 2 перелета + + 1 4* 1 4- i Р-Р p-q q-p q-q P2 %pq
3 3 недолета 2 недолета и 1 пе- релет 1 недолет и 2 пе- релета 3 перелета + + 4 4- । 1 14-14 14 4 + + 4 4 Р-Р-Р p-p-q p-q-p q-p-p p-q-q ' q-p-q q-q-p q-q-q p3 ^q 3pq2 q3
. 4 4 недолета 3 недолета и 1 пе- релет 2 недолета и 2 пе- релета 1 недолет и 3 пе- релета 4 перелета J 1 1 1 + | | + | + 4 I + + + + 1 114 1 1 4 I 4 1 4 4 I ++ 4 1 1 + 1 1 4 1 4 4 ] 1 4 4 1 4- 4 1 4 1 1 1 Н—F 1 1 4 1 44—F 1 4 p-p-p-p pp-p-q p-p-q-p p-q-p-p q-p-p-p p-p-q-q p-q-p-q q-p-q-p p-q-q-p q-p-p-q q-q-p-p p-q-q-q q-p-q-q q-q-p-q q-q-q-p q-q-q-q p* 4psq 6p2q2 4pq$ 44
Сложим найденные вероятности для каждого числа вы-
стрелов отдельно, помня, что как сумма вероятностей
противоположных событий равна единице.
Нетрудно при этом установить, что сумма вероятностей
всех возможных комбинаций при двух выстрелах предста-
42
вляет собой квадрат суммы вероятностей недолета и перелета
при 1 выстреле:
р2 4- 2pq + q- = (р + qf = 1,
при трех выстрелах — куб этой суммы:
р3 4- Зр2<? 4- Зр<72 4- q3 == (р + Я? = 1,
и при четырех выстрелах — эту сумму в четвертой степени:
р* 4- 4р3? 4- 4- 4рЯ3 4- <74 = (Р + ЯУ = 1-
Прежде всего заметим, что для каждого числа выстрелов
сумма вероятностей комбинаций из недолетов и перелетов
равна единице. Это свидетельствует о том, что нами действи-
тельно учтены все возможные комбинации и их варианты при
данном числе выстрелов.
Теперь перейдем к обобщению полученных результатов.
Сопоставив эти результаты, мы можем допустить, что и при
дальнейшем увеличении числа повторений испытания вероят-
ности комбинаций будут следовать той же математической
закономерности, т. е. при любом числе(5) повторений испыта-
ния, в совершенно одинаковых условиях сумма вероятно-
стей всех возможных комбинаций из двух противополож-
ных событий может быть выражена суммой всех членов
разложения бинома Ньютона в степени, равной числу по-
вторений испытания, причем первая степень этого бинома
имеет вид: (р4-<7)=1, где р — вероятность события А и q —
вероятность события В, противоположного первому:
. С «Г 1 I 5(5—1) е 2 л , 5(5— 1)-(5—2) с о ч , ,
ps 4- Sps~l q 4- —Р Я 4------------—~ Р Я3 + •• +
4- 5(5—1)(5 —2). , .(5-Я+_1)_ ап , ,
1-2-3. . . (п—1)-я Р -t- • • • Т
+ Рг<?~ъ + -4~21) Л5-2 + Spqs~' + qs =
= + <7)s= 1,
или, сокращенно,
Ро 4- Р^ + + • • • ~^~Рп s—1 + Ps == 1 •
Здесь буквой п обозначен порядковый номер члена этого
ряда, если вести счет от нуля.
Член Р0=р5 выражает вероятность появления события
A S раз, член P1 — Sps~1 q выражает вероятность появления
события Д (5 — 1) раз и события В один раз; член
Р3 = _L pS-2 ц2 выражает вероятность появления собы-
тия A (S — 2) раз и события В — два раза и т. д.
43
Заметим, что индексы при Р соответствуют показателю
степени при q, т. е. числу появлений события В, чем и вы-
звано именно такое обозначение вероятностей комбинаций, на-
чиная с Ро и кончая Ps. Эти вероятности могут быть пред-
ставлены в виде:
Pq=PS(? и Ps~pQqs,
что соответствует появлению события В нуль раз в первом
случае и 5 раз во втором.
Очевидно, что член
_ S(S—• 1)(S —2). . .(S-n+1)
гп —
-----------------.-----nS—n . пп
1-2-3 . . . (п — 1)-л Р 4 ’
выражает искомую вероятность любой комбинации (5—^-крат-
ного появления события А и n-кратного появления события В.
„ , S(S— 1)(S — 2). . . (S-n+l)
При этом коэфициент — — (n-l)-n —количе-
ство вариантов данной комбинации, а произведение ps~n qn —
вероятность одного варианта.
Для удобства пользования этой формулой произведем
в ней некоторые преобразования: умножим числитель и зна-
менатель коэфициента на произведение всех натуральных, т. е.
целых и положительных чисел от (S — п) до единицы и заме-
ним (S—п) на т, исходя из равенства: m — S — п, откуда
т + п = S. Тогда
р — S(S-l)(S-2)...(S-n+l)(S-n)(5-n-l). . .3-2-1
и(и —1)(л —2). . . 3-2-1 (S — n)(S—и—1) . . .3-2-1 р 4 ’
Теперь числитель коэфициента представляет собой произ-
ведение всех натуральных чисел от 5 до 1. Такое произведе-
ние принято называть факториалом, (обозначается символом 5!).
В знаменателе же мы имеем произведение двух факториалов: п\
и (5— п}\, но так как S п = т, то и (5 — /г)!==т! и тогда
наша формула примет окончательный вид:
С’
Р —_______г>тпп
п т\п\ Р
Заметим, что 0! считается равным единице; это вытекает из следующего:
выразим S! равенством: S! = S(S—1)(S—2). . .3-2-1.
Заменив (S—1)(S — 2). . . 3-2-1 через (S — 1)!, имеем:
S!
S’ = S (S — 1)1, откуда (S — 1)'. = -у ;
приняв S=l, получим:
(1_1)!=0!=--у = 1.
Равенство 0! — 1 делает общую формулу справедливой и для вероят-
ностей Ро и Ps, которые можно представить в виде:
р _ nS _ S! _ _S qO u p _ ns _ о s*
po - P - 5Ю! p 4 и 4 — 0!S! P Q
* Следует помнить, что равенство 0! = 1 имеет чисто символическое
значение, а не выражает какое-то математическое действие, что было бы
явным абсурдом.
44
Если при 5 повторениях испытания событие А появилось т
раз, а событие В п раз, то это означает, что частость события А
равна -у-, а частость события В равна -у . Поэтому, определяя
вероятность комбинации с данным соотношением между обра-
зующими ее противоположными событиями, мы тем самым
определяем вероятность частости этих событий. Так, например,
определяя вероятность комбинации из 2 недолетов и 6 переле-
тов при 8 выстрелах, мы тем самым определяем вероятность
частости недолета, равной -у. Отсюда выражение „вероят-
ность комбинации" мы нередко будем в дальнейшем заменять
выражением „вероятность частости".
1
Пример 1. Вероятность недолета при 1 выстреле р — — . Чему рав-
на вероятность комбинации из 2 недолетов и 4 перелетов при 6 выстрелах?
Решение. По условию число повторений испытания (выстрелов)
<S = 6, число появлений одного события (недолета) т = 2, число появлений
события, противоположного первому (перелета), п = 4.
1
Если вероятность 1 недолета р = -у , то вероятность перелета
1 2
4 = 1— -у = -у. Подставив эти численные значения в общую формулу,
получим:
п Р 6! руру 6-5-4-3-2-1 J_ _16 =
л т\п\р 4 4 2!4! X 3 / X 3 / '2.1.4-3-2.1 ‘ 9 '81
16 80
1э‘ 729 = 243 •
Из анализа этого решения можно установить, что:
1. Вероятность одного варианта, т. е. одной определенной последова-
тельности появления недолетов и перелетов,
m п __
р q ~ 729 *
2. Всех возможных вариантов—15; эти варианты приведены в помещен-
ной ниже таблице.
№ вари- анта № выстрела № вари- анта № выстрела № вари- анта № выстрела
1 2 3 4 5 6 1 2 3 4 5 6 1 2 I 1 3 4 5 6
1 + + + — — 6 4" 4“ 4- — + — 11 + + 4~ + —
2 + + — — + 7 + + — + — + 12 + + — + + —
3 , + + — + + 8 + — + — + 4- 13 — + + — + +
4 + — — + + + 9 — _1_ — “Г _1_ 14 — + “Г —
5 _____ — + + + + 10 — + н- 4- + — 15 4- — + + — Д-
45
3. Вероятность этой комбинации в биноминальном ряде занимает пятое
место, так как индекс п при Р равен 4, а счет идет от нуля.
Примечание. Условие этого примера может быть сформули-
ровано иначе: чему равна вероятность получения частости недолета.
1 / „ 2 \
равной у или частости перелета, равной у j , при 6 выстрелах?
Пример 2. Вероятность разрыва бризантной гранаты в воздухе при 1
выстреле q = 0,8. Чему равна вероятность получения одной трети клевков
( вероятность частости клевка, равной -у) при 24 выстрелах?
Решение. Обозначим: S — - 24; т — 8; п = 16 и р = 1 — 0,8 — 0,2.
Тогда
24! о
₽1«=8ПбГ0’2 •°'811’-
В этом случае необходимо применять логарифмирование. По таблицам
логарифмов находим логарифмы факториалов, и тогда
lgP16 = + 1g 24! = 23,79271
— lg 8! = 5,39148
— lg 16! = 14,67938
+ 8 lg 0,2 = 6+0824
4- 16 lg0,8 = 2,44944
lgP16 = 2,72425,
откуда Pi6 = 0,053. Интересно отметить, что соответствующая этой
вероятности комбинация имеет 735471 вариант.
Если в этой же задаче обозначить: S = 24; т — 16 и п = 8, то тогда
р — 0,8 и q — 0,2.
Отсюда
24!
Очевидно, что ответ будет тот же, так как совершенно безразлично,
какое из двух противоположных событий будет занимать в общей формуле
первое, а какое — второе место. Необходимо только, чтобы показатели
ПРИ Рап У были равны числу появлений соответствующих событий.
§ И. НАИВЕРОЯТНЕЙШАЯ КОМБИНАЦИЯ
Чтобы ясно представить себе совокупность вероятностей
всех возможных комбинаций, получающихся при повторении
испытаний, рассчитаем такие вероятности, задавшись различ-
ными численными значениями S, р п q:
/ 1 и 2 \б
(-у-Г -у) = 0,0014 + 0,0164 4- 0,0823 + 0,2195 + 0,3292 +
+ 0,2634 + 0,0878= 1,0000;
(4+4- )12— 0,0000 + 0,0001 + 0,0005 + 0,0033 + 0,0149 +
'о о '
+ 0,0477 + 0,1113 + 0,1908 + 0,2384 +~ 0,2119 + 0,1272 +
-Н 0,0462 + 0,0077 = 1,0090;
46
(0,6 + 0,4)12 = 0,0022 4- 0,0174 + 0,0638 + 0,1419 + 0,2128+
+ 0,2270 + 0,1766 + 0,1010 + 0,0421 + 0,0025 + 0,0003 +
+-0,0000 = 1,0000.
Для большей наглядности выразим эти вероятности графи-
чески, отложив в произвольных масштабах по оси абсцисс
число равных отрезков по числу комбинаций, а по оси орди-
нат соответствующие им ве-
роятности. Таким образом, ве-
роятность каждой комбинации
будет выражена соответствую-
щим прямоугольником, а сумма
вероятностей всех возможных
комбинаций при данном зна-
чении 5 — площадью всего
графика (рис. 13, 14 и 15). Для
того чтобы в дальнейшем
иметь возможность сравнивать
эти графики, все они постро-
ены в одних и тех же мас-
штабах.
Рис. 13
После сопоставления результатов подсчетов и сравнения
построенных графиков, можно сделать следующие выводы.
1. Наименьшие численные значения вероятности комбина-
ций имеют в начале и конце каждого из этих трех биноминаль-
ных рядов, достигая по мере возрастания 5 пренебрежимо'
малых величин.
2. От края каждого ряда вероятности комбинаций увели-
чиваются, достигая в некотором месте этого ряда наибольшей
величины, которая соответствует так называемой наивероят-
нейшей комбинации {частости).
Следует отметить, что в некоторых частных случаях ве-
роятность наивероятнейшей комбинации может находиться
либо в начале, либо в конце биноминального ряда:
(0,8 + О,2)3 = О,512 + 0,384 + 0,096 + 0,008 = 1,0;
(0,1 4- 0,9)4 =0,0001 + 0,0036 + 0,0486 + 0,2916 + 0,6561 = 1,0.
Наивероятнейшая комбинация и ее вероятность предста-
вляют для нас большой интерес. Метод определения (выбора)
наивероятнейшей комбинации из ряда вероятностей всех воз-
можных комбинаций по своей громоздкости нас удовлетворить
не может.
Место вероятности наивероятнейшей комбинации в бино-
минальном ряде определяется численными значениями 5, р и q,
поэтому необходимо найти такую математическую зависимость
между этими величинами, которая позволит нам определить
место вероятности наивероятнейшей комбинации и ее величину
наиболее просто.
Обозначим вероятность наивероятнейшей комбинации
через
Р = pmqn
mini r v
Если Pn имеет наибольшее численное значение, то будут
справедливы следующие неравенства:
или
Рп > Рп—1 и Рп> Рп±1,
С| <?!
-—-Dman >----------—------ап~х -
mW. 4 (т + 1)! (п—1)! р 1 ’
-£! - птЛп "> ---—------от-1ап+1
mini " Ч (т—1)1{п + 1)1^ ’
48
Произведя возможные сокращения
ствах и заменив т на S — п, решим их
в этих двух неравен-
относительно и: •
n 1 1
I) — q > ё---------гт Р\
' п 4 5 — п -у 1
ox 1^1
») S~„ P> уг+i
q{S~п 4- 1) > рп\
qS — qn + q> pn-,
qS 4- q > pti 4- qtv,
qS + q> n(p 4- q)\
n < Sq + q.
p (nV) > q(S — n);
pn 4- p > qS — qn',
pn 4- qn> qS —p;
n(p + q)>qS—p;
n>Sq — p.
Заменив в полученных двух неравенствах п на S -т, мы
можем решить их относительно т:
I) 5 — пг <Sq + q;
S—Sq — q <nv,
S (1 — q) — q;
m> Sp — q;
II) S — m> qS — p;
S — qS 4- p m',
m < 5(1 — q) 4-A
m < Sp 4- P-
Таким образом, мы получили 2 пары неравенств, опреде-
ляющие пределы, в которых заключены численные значения
п и т:
п> Sq — р\ т > Sp-— q\
n<Sq 4- q.
тп < Sp 4- p>
Пользуясь этими неравенствами, можно по численным
значениям 5, р и q найти место наивероятнейшей комбинации,
а отсюда по общей формуле и ее вероятность. При этом
достаточно только одной пары неравенств, другая пара исполь-
зуется для проверки.
Пример 1. Найти наивероятнейшую комбинацию перелетов и недолетов
при 6 выстрелах и ее вероятность, если вероятность недолета при 1 выст-
1
реле р = -ту.
Решение. По условию S = 6. Обозначив вероятность перелета при
1 2
1 выстреле через q = 1 — -3 = -уи подставив численные значения и q
в пару неравенств, определяющих пределы п, в которых заключено число
перелетов, получим:
п ' 2 >б- з 1 ~~ 3 2 2 и п<6--3-4-3-
откуда
2 о
п >3 3 и п < 4 --у ,
или
„ 2 2
3 3 < :п<4-т.
4 — Зак. 991
49
Но так как п может быть только числом целым, то п = 4; тогда
т = 6 — 4 = 2, т. е. наивероятнейшая комбинация состоит из 2 недолеток
и 4 перелетов, а ее вероятность
о _ отап JLf _L Y (Л у __ 2_ Ш _
Гп~ т\п\ р 9 2!4'Л 3 / \3 / “2-1-4.3-2-1 ’ 9 * 81 “
80
243 =0’3292-
Проверим наше решение, определив т по неравенствам:
12 11
т > 6- Т - Т " т < 6- Т + 'з •
откуда
или
т — 2;
тогда
п = 6 — 2 = 4.
Пример 2. Найти наивероятнейшую комбинацию перелетов и недолетов
при 15 выстрелах, если вероятность перелета при 1 выстреле q = 0,75.
Решение. 6'= 15; р = 0,25; q = 0,75. Определим т\
ffi> 15-0,25— 0,75 и т < 15-0,25 + 0,25,
откуда
/п>3 и т<4.
Так как т есть число целое и не может быть одновременно больше 3
и меньше 4, то очевидно, что мы имеем две наивероятнейшие комбинации:
одна состоит из 3 недолетов и 12 перелетов, а другая—из 4 недолетов и 11
перелетов. В этом примере п и т имеют по два численных значения, отли-
чающихся друг ог друга на единицу:
тх = Sp — q == 3;
т2 = Sp + р -.= 4;
П1 = Sq 4- q — 12;
n2 = Sq — р — 11.
Вероятности таких двух комбинаций должны бьиь равны:
15!
- 0,233-0,75’2 ~ 0,2252;
15!
• 0,254-0,7511^0,2252.
Признаком наличия двух наивероятнейших комбинаций является полу-
чение ответов в целых числах при решении неравенств, определяющих
численные значения т и п.
Необходимо еще раз подчеркнуть, что вероятность наиве-
роятнейшей комбинации из двух противоположных событий
является в то же время и вероятностью наивероятнейших
частостей этих событий. Так, в примере 1 наивероятнейшая
комбинация из 2 .недолетов и 4 перелетов соответствует наиве-
2 4
роятнеишим частостям недолета -г- и перелета у, а в приме-
50
ре 2 наивероятнейшие комбинации из 3 недолетов и 12 пере-
летов и из 4 недолетов и 11 перелетов соответствуют наиве-
Л 3 4 12 и
роятнейшим частостям недолета уу и уу и перелета уу и .
Исходя из этого, неравенства, определяющие границы чис-
ленных значений т и п, позволяют нам сделать один весьма
существенный вывод.
Представим эти неравенства в виде:
Sq — р <п <Sq + q и Sp — q <ZSp + Р-
Разделив неравенства на 5 и произведя сокращения, по-
лучим:
р п . . а 0 т . р
q-f <~s<q + ^s И р--^< s-<p + ^-.
Так как р и q всегда меньше единицы, то по мере воз-
растания 5 дроби -у- и -у- становятся все меньше и меньше,
и наивероятнейшие частости -у- и — стр.емятся по своей ве-
личине приблизиться к соответствующим им вероятностям q и р:
п т
— -+дп-^р,
а при бесконечно большом числе 5 (при 5 -► оо):
п т
и -s-=p.
Это означает, что если некоторое событие А имеет вероят-
ность р, а противоположное первому событие В—вероятность q,
то при достаточно большом числе 5 повторений испытания
л л т п
наибольшую вероятность будут иметь те их частости у и у ,
которые по своей величине весьма близки к соответствующим
им вероятностям р и q.
Этот вывод подтверждает известный нам закон больших
чисел, принятый нами ранее на основе только опытных данных.
§ 12. КРИВАЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ КОМБИНАЦИЙ
Для дальнейших выводов нам необходимо знать, как изме-
няются вероятности комбинаций (частостей) по мере увеличе-
ния числа повторений испытания. Характер таких изменений
проследим на следующем примере.
Положим, имеется ящик с 4 шарами: 3 белыми и 1 красным.
Испытание заключается в том, что каждый раз вслепую выни-
мается 1 шар, который затем возвращается обратно в ящик.
Рассчитаем вероятности всех возможных комбинаций из
белых и красных шаров при 10, 20 и 100 повторениях испы-
тания. Вычисления будем доводить с округлениями до пятого
десятичного знака, пренебрегая вероятностями, меньшими
0,000005. Расчеты сведем в таблицы (табл. 1—3).
4* 51
•S—10 Таблица 1
Число лений появ- шаров Вероятность Число лений появ- шаров Вероятность Число леьий появ- шаров Вероятность
белого крас- ного Pi белого крас- ного Pi белого крас- ного Pi
0 10 0,00000 4 6 0,01621 8 2 0,28156
1 9 0,00006 5 5 0,05840 9 1 0,18771
2 8 0,00039 6 4 0,14600 10 0 0,05631
3 7 0,00309 7 3 0,25027
S Р{- 1,00000
*5—20 Таблица 2
Число появ- лений шаров Вероятность pi Число появ- лений шаров Вероятность Pi Число появ- лений шаров Вероятность Pi
белого крас- ного белого крас- ного белого крас- ного
5 15 0,00000 11 9 0,02700 16 4 0,18978
6 14 0,00002 12 8 0,06089 17 3 0,13389
7 13 0,00015 13 7 0,11240 18 2 0,06694
8 12 0,00075 14 6 0,16862 19 1 0,02114
9 11 0,00300 15 5 0,20233 20 0 0,00317
10 10 0,00992 —
3Pf= 1,00000
S—100 Таблица 3
Число лений появ- шаров Вероятность Pi Число появ- лений шаров Вероятность Pi Число появ- Вероятность Pi
лений шаров
белого крас- ного белого крас- ного белого крас- ного
54 46 0,00000 68 32 0,02475 81 19 0,03553
55 45 0,00001 69 31 0,03443 82 18 0,025<9
56 44 0,00002 70 30 0,04575 83 17 0,01652
57 43 0,00004 71 29 0,05800 84 16 0,01003
58 42 0,00008 72 28 0,07008 85 15 0,00566
59 41 0,00018 73 27 0,08064 86 14 0,0'>293
60 40 0,00036 74 26 0,08827 87 13 0,00142
61 39 0,00071 75 25 0,09180 88 . 12 0,00063
62 38 0,00135 76 24 0,09059 яа 11 0,00026
63 37 0,00244 77 23 0,08471 Ой 10 0,00009
64 65 36 35 0,00421 0,00702 78 79 22 21 0,07493 0,06262 91 Q9 9 8 0,00003 0,00001
66 34 0,01117 80 20 0,04931 7 0.00000
67 33 0,01700 УЗ
SP, = 1,00000
52
Для большей наглядности выразим рассчитанные вероят-
ности графически.
Начнем с графика при 5=10. В прямоугольной системе
координат (рис. 16) отложим по оси абсцисс число отрезков
по 1 см, равное числу всех возможных комбинаций, а по оси
ординат — соответствующие им вероятности в масштабе 0,1 в
1 см и подпишем под каждым отрезком частости того из двух
противоположных событий, вероятность которого равна q
(в нашем примере—частости появления белого шара, вероятность
которого равна -^- = 0,75).
Этот график даст нам весьма наглядное представление
о Соотношении или, как мы будем говорить, о распределении
вероятностей комбинаций (частостей) при 10-кратном повторе-
нии испытания.
Перейдем к графику распределения вероятностей при
5 = 20. Если бы мы сохранили те же масштабы построения,
то этот график по оси абсцисс занял бы 21 см, а по оси
ординат, вследствие уменьшения вероятностей отдельных ком-
бинаций, точность построения была бы меньше и распределе-
ние вероятностей было бы менее наглядным. Так как сумма
вероятностей всех возможных комбинаций при любом значе-
нии 5 равна единице, а площади обоих графиков должны
быть равновеликими, уменьшим величину отрезка по оси абс-
цисс в 2 раза соответственно увеличению 5, т. е. до 0,5 см,
и увеличим масштаб построения по оси ординат также в 2ьраза,
т. е. до 0,05 в 1 см (рис. 17).
При построении графика при 5=100 уменьшим величину
отрезка по оси абсцисс и увеличим масштаб построения по
оси ординат еще в 5 раз (рис. 18).
53
Таким образом, основание всех графиков осталось одно и
то же, величина отрезка по оси абсцисс во всех случаях равна
этого основания, а величина вероятности отдельной комби-
нации (частости) при этом выражается площадью прямоуголь-
ника с основанием и высотой, равной этой вероятности.
Сопоставив данные табл. 1, 2 и 3 и сравнив графики рас-
пределения вероятностей комбинаций (частостей), мы видим,
что с увеличением числа повторений испытания:
— выражаемые площадями прямоугольников вероятности
комбинаций уменьшаются неравномерно, — чем больше *5, тем
резче снижаются значения вероятностей относительно наиболь-
шей, тем меньше пределы, в которых вероятности имеют
существенное значение;
— прямоугольник вероятности наивероятнейшей комбина-
ции (частости), передвигаясь по оси абсцисс, стремится занять
з
положение, соответствующее вероятности ^ = 4 , т. е. под-
тверждается выведенное выше положение о том, что при уве-
личении числа 5 наивероятнейшая частость события стремится
приблизиться по своей величине к вероятности этого события;
— несимметричность графика постепенно сглаживается и
его ломаная линия по виду приближается к кривой, симмет-
ричной относительно ординаты, соответствующей вероятности
наивероятнейшей комбинации (частости).
Все это дает нам основание заключить, что при безгра-
ничном возрастании числа повторений испытания, т. е. при
•S-* со, ломаная линия графика распределения вероятностей
комбинаций (частостей) должна превратиться в кривую, симмет-
ричную относительно ординаты, абсцисса которой равна q
(рис. 19). Эта кривая носит название кривой нормального рас-
пределения вероятностей или кривой Гаусса. С ней нам часто
придется иметь дело в другом разделе теории вероятностей—
в теории ошибок.
55
§ 13. ЗАКОН БОЛЬШИХ ЧИСЕЛ
Сущность закона больших чисел сводится к тому, что при
достаточно большом числе повторений испытания частость
события очёнь мало отличается по своей величине от вероят-
ности этого же события.
Возникают два вопроса: что следует считать достаточно
большим числом повторений испытания и насколько частость
по своей величине может отличаться от соответствующей ей
вероятности?
Чтобы ответить на эти вопросы, зададимся каким-нибудь
вполне определенным отклонением (совокупностью отклоне-
ний в определенных пределах) частости от вероятности и по-
смотрим, как будет меняться вероятность такого отклонения
при увеличении числа повторений испытания.
Воспользуемся для этого распределениями вероятностей
частостей, уже рассчитанными нами для различных численных
значений 5 (§ 12).
Зададимся совокупностью отклонений частости появления
белого шара от его вероятности в пределах от —0,1 до +0,1
при 5 = 20.
Из всех частостей, которые могут быть получены при
таком числе повторений испытания, заданному отклонению
г л « 13 14 15 16 17
соответствует одна из следующих частостей: ™ , «х, бп и ни,
так как разности
13 15 _ п 1 17 I5 _ • п 1
20 20 0,1 И 20 20 4~ U, 1.
По теореме сложения вероятность получения одной из
этих частостей (см. табл. 2, § 12)
Р13_17 = 0,11240 + 0,16862 + 0,20233 + 0,18978 + 0,13389 =
= 0,80702.
Это значит, что, произведя большое число повторений
испытания, мы на каждые 20 таких повторений примерно в
81 случае из 100 в среднем будем иметь отклонение частости
появления белого шара от его вероятности, не выходящее из
пределов rt0,l. В остальных 19 случаях частость будет иметь
отклонения, большие ±0,1.
Теперь определим вероятность такого же отклонения при
5 = 100. Очевидно, что эта вероятность будет равна вероят-
„ „ 65
ности получения одной из частостей в пределах от до
85 / 65 75 , 85 75 . п , \ „
Too \Тоо ~~ Too = “ СМ и fog jog 4-0,1 j. Сложив эти вероят-
ности (см. табл. 3, § 12), получим:
Р65-85 ~-0,00702 + 0,01117 + . . .+ 0,01003 + 0,00566=0,9852,
56
т. е. в этом случае одна из частостей в указанных пределах
будет получена примерно в 99 случаях из 100 и только 1 слу-
чай даст отклонение, превышающее ±0,1.
Увеличим число повторений испытания до трехсот (5 =
= 300). Тогда вероятность отклонения частости в пределах
±0,1 или получение одной из частостей в пределах от до-
255 Л
300 бУдет:
7^195-255 = 0,99993,
т. е. практически при 5 = 300 частость из заданных пределов,
не выйдет.
Мы задались сравнительно большим отклонением частости
от вероятности. Возьмем другое, меньшее отклонение: ±0,02,
и рассчитаем вероятности этого отклонения при различных
значениях 5.
При 5 = 100 такому отклонению соответствуют частости
в пределах от 0,73 до 0,77; вероятность этого отклонения
Рть—п = 0,436.
При 5=300 вероятность того же отклонения
7^219—231 — 0,568.
При 5=1500 —
Т-’юэз—iiss — 0,92634.
И, наконец, при 5 = 6000 —
Р4380—4620 = 0,99965.
Таким образом, при уменьшении пределов отклонения
частости от вероятности и постепенном увеличении числа по-
вторений испытания можно добиться того, что вероятность
такого отклонения будет сколь угодно мало отличаться от
единицы. Очевидно, что можно задаваться и сколь угодно
малым отклонением.
Это положение формулируется в виде теоремы Якова
Бернулли.
При достаточно большом числе повторений испытания
с вероятностью, сколь угодно близкой к единице, можно
утверждать, что частость события будет отличаться от
вероятности события меньше, чем на сколь угодно малую
наперед заданную величину.
Несомненно, справедливым будет и такое утверждение,
обратное первому, что при достаточно большом числе повто-
рений испытания частость, полученная на опыте, может быть-
принята как вероятность этого события.
57
Теорема, обратная теореме Якова Бернулли, формули-
руется так:
При достаточно большом числе повторений испытания
с вероятностью, сколь угодно близкой к единице, можно
утверждать, что неизвестная вероятность события отли-
чается сколь угодно мало от полученной на опыте частости
этого события.
§ 14. ВЕРОЯТНОСТЬ ПОЯВЛЕНИЯ СОБЫТИЯ ХОТЯ БЫ ОДИН, ДВА,
ТРИ и т. д. РАЗ
При повторении испытаний в некоторых случаях задача
ставится так, что для ее решения достаточно появления одного
из двух противоположных событий хотя бы один, два, три
раза или, Что то же, не менее одного, двух, трех и т. д. раз.
Например, при артиллерийской стрельбе в зависимости от
числа попаданий, потребного для поражения данной цели,
задача решается при получении хотя бы одного или двух, или
трех и т. д. попаданий.
Отсюда возникает необходимость определения вероятностей
появления нужного нам события хотя бы один, два, три и
т. д. раз.
Покажем на примере, как вычисляются такие вероятности,
начиная с вероятности появления события хотя бы один раз.
Положим, что нам необходимо знать вероятность получе-
ния хотя бы одного попадания при 10 выстрелах, если вероят-
ность попадания при 1 выстреле /> = 0,1.
Обозначим вероятности комбинаций из попаданий и. про-
махов через Ро, Р1} Р2 и т. д. и составим таблицу.
58
имеется не менее одного попадания. Получение любой из этих
10 комбинаций дает решение поставленной огневой задачи.
Обозначив вероятность попадания хотя бы один раз через
Pi, по теореме сложения вероятностей получим:
Р\ ~ Pq 4- Pi 4- Р% 4- Р» 4- Р^ 4- Р$ + Р$ 4- Рч 4- Р^ 4- Р$-
Подставив численные значения вероятности попадания и
промаха при I выстреле, определим величины %, Ръ Р2 и т. д.
до Р9 и сложим эти вероятности.
Эту же задачу можно решить гораздо проще.
Известно, что сумма вероятностей всех возможных ком-
бинаций при повторении испытания равна единице. Следова-
тельно;
р. + Л 4- Л + % + Pi + % + Р л - Рп + Р. 4- % 4- Р1 о =
= Pi +Ло-1,
откуда
Р\ = 1 — Ло>
где Р10— вероятность всех промахов.
Обозначив вероятность промаха при I выстреле через q,
по теореме умножения вероятностей получим:
р ---Л10
— ч
Тогда вероятность попадания хотя бы один раз при 10
выстрелах в окончательном виде будет равна
— 1 — 210.
К этому же результату мы придем, если будем рассма-
тривать вероятность попадания хотя бы один раз и вероятность
всех промахов как вероятность двух противоположных собы-
тий:
Л 4- ?1е = 1,
откуда
A =l — qio.
Зная, что q = l—р=1—0,1 =0,9, мы можем довести
решение задачи до конца:
Р1 = 1 — 0,910 = 1 — 0,3487 = 0,6513 0,65 = 65%.
Это означает, что, произведя большое количество анало-
гичных стрельб, мы в 65 случаях из 100 в среднем будем
решать поставленную огневую задачу 10 снарядами. В осталь-
ных 35 случаях на выполнение этой задачи потребуется больше
снарядов.
£3 Распространяя сделанный вывод на любое событие и на
любое число повторений испытания, получим:
Pi 1 — qs—\ .
59
Вероятность появления одного противоположного собы-
тия хотя бы 1 раз при S повторениях испытания равна
единице без вероятности появления S раз другого противо-
положного события.
Пример 1. Вероятность недолета при 1 выстреле равна • Какова ве-
роятность получения хотя бы I недолета при 4 выстрелах?
Решение.
е /IV 1 15
Л = 1 - (1 -P)S I - (1 - 2 ) = 1 - 16 = 16 = 0)9375 ~ °’94-
Пример 2. Определить вероятность попадания хотя бы I раз при
24 выстрелах, если вероятность промаха при 1 выстреле равна 0,94.
Решение.
Рх = 1 — 0,9424;
24 lg0,94 =7,35512;
0,9424 = 0,2265;
/>!=!— 0,2265 = 0,7735 0,77.
Пример 3. Определить вероятность попадания хотя бы 1 разопри
16 выстрелах, если вероятность нахождения цели на обстреливаемом участке
Рц =0,25, а вероятность попадания при 1 выстреле и при условии, что цель
находится на участке, куда направлен огонь, р = 0,15.
Решение. Если бы цель находилась на обстреливаемом участке, то
Р} = 1 — (1 _ 0,15)16 - 1 _ (даб.
Логарифмируя, получаем:
16 1g 0,85 -2,87072;
0,8516 = 0,0743.
Тогда
Pj = 1 — 0,0743 = 0,9257;
учитывая вероятность нахождения цели, получим:
Р,ц == Р, • Рц = 0,9257-0,25—0,2313^23%.
Чтобы определить вероятность появления одного из двух
противоположных событий при S повторениях испытания хотя
бы два раза, от единицы следует отнять вероятности тех ком-
бинаций, в которых интересующее нас событие (попадание)
появляется менее 2 раз, т. е. вероятность появления 5 раз
события, противоположного первому (вероятность всех про-
махов), и вероятность появления первого события только 1 раз
(вероятность только 1 попадания).
Зная, что вероятность появления первого противополож-
ного события только один раз
Ps_x=Spqs~',
получим:
Р\\ — i — (Ps-i + Ps);
Ри - 1 - (W-1 + qs )•
60
Подставив в эту формулу значения: 5'= 10; р — 0,1 и
/у —0,9, получим вероятность попадания хотя бы 2 раза при
10 выстрелах:
Рп = 1 - (1 о • 0,1 • 0,99 + 0,910) =х 1 - (0,3874 4- 0,3487) =
= 1 —0,7361 — 0,2639^26%.
Рассуждая аналогично, заключаем, что вероятность появ-
ления одного из двух противоположных событий хотя бы
3 раза должна быть равна единице минус вероятности комби-
наций, в состав которых это событие входит менее 3 раз, т. е.
Р\\\ = 1 — (Ps—2 + Ps-\ + Ps),
или
рш=1 - р++/,2?5"2 + Spis~l + j •
Для любого заданного числа хотя бы К раз появления
события
Рк~ 1 — (Ps-k+i + Ps—к + Ps-k-i 4 • • • + Ps--i + Ps)-
Пример 1. Вероятность попадания при 1 выстреле />=0,05. Какова
вероятность попадания хотя бы 2 раза при 40 выстрелах?
Решение.
Рп = 1 — (40 • 0,05 • 0,9539 + 0,95*0);
40 1g 0,95 = Т,1088;
Pit) = 0,1285;
1g 40 + 1g 0,05 + 39 !g0,95 = 1,60206 + 2,69897 + f, 13108 = 1,43211;
P39 = 0,2705;
следовательно,
Pn = 1 — (0,2705 + 0,1285) = 1 — 0,399 = 0,601 60*>/о.
1
Пример 2. Вероятность нахождения цели на данном участке Ра=у-
При условии, что огонь ведется по этому участку, вероятность недолета
при 1 выстреле равна . Какова вероятность получения не менее 4 пере-
летов при 8 выстрелах?
Решение. При условии, что цель находится на данном участке,
вероятность получения не менее 4 перелетов
/1 1512 Ч- 252 4- 24 + 1 1789 _ 63747
+ X 4 / J ~ 1 “ 65536 “ 1 ~ 65536 " 65536 ~ 0,9/2
С учетом же вероятности нахождения цели
Р1Уц = 0,9727 | = О,4864 49<>/0.
61
§ 15. НАДЕЖНОСТЬ СТРЕЛЬБЫ
Каждая стрельба должна быть надежна, а так как конеч-
ной задачей стрельбы является поражение цели, то эта надеж-
ность оценивается вероятностью поражения цели.
В условиях современного боя, когда широко применяются
самые разнообразные оборонительные сооружения и брониро-
ванные машины, очень многие цели можно поразить только
прямыми попаданиями. Наилучшие результаты прямые попа-
дания дают при стрельбе и по таким целям, для поражения
(подавления) ^которых прямых попаданий не требуется (открыто
расположенные огневые точки, НП и пр.).
Поэтому принято надежность стрельбы оценивать вероят-
ностью хотя бы одного, двух, трех и т. д. попаданий, в зави-
симости от требуемого для поражения цели числа прямых
попаданий.
Чтобы иметь ясное представление о том, от чего зависит
надежность стрельбы, проанализируем формулу вероятности
попадания хотя бы один раз, как наиболее часто применяе-
мую в артиллерийских расчетах.
Эта формула:
показывает, что надежность стрельбы увеличивается с увеличе-
нием вероятности попадания при 1 выстреле и с увеличением
числа снарядов, расходуемых на поражение цели. Действи-
тельно:
— чем больше вероятность попадания при 1 выстреле
тем меньше (1 — р ;
—чем больше число расходуемых снарядов 5*, тем меньше
(1 - p)s , которое, как правильная дробь, уменьшается с
увеличением показателя степени.
Отсюда с уменьшением (1 — p)s естественно увеличивается
1 — (1 — ру _
Установив эту зависимость, посмотрим, как будут меняться
вероятности хотя бы одного попадания с увеличением числен-
ных значений р и 5. Расчеты сведем в таблицу.
S Вероятности попадания хотя бы 1 раз Увеличение вероятности попадания хотя бы 1 раз
при увеличении 5 при увеличении р
р~0.05 р=0,1 р=0;2 /7=0,5 р=0,1 р=0,2 0,05—0,1 0,1-0,2
10 0,4013 0,6513 0,8926 — — 620/0 - 37%
20 0,6415 0,8784 0,9885 58% 35% 11% 37% 13%
40 0,8715 0,9852 0,9999 36% 12% 1% 13% 1.50/0
80 0,9782 0,9998 — 12% '1.5% 0 2% —
62
Мы видим, что увеличение вероятности попадания при
1 выстреле в 2 раза дает большее увеличение надежности
стрельбы по сравнению с увеличением числа расхода снарядов
также в 2 раза. Так, при увеличении р с 0,05 до 0,1 при
<£=10 надежность стрельбы увеличилась на 62%, а при уве-
личении 5 < Ю до 20 надежность увеличилась на 58°/0 при
р — 0,05. При увеличении р с 0,05 до 0,1 при 5 = 20 надеж-
ность увеличилась на 37°/0, а при увеличении 5 с 20 до 40
при том же р = 0,05 надежность возросла на 36% и т. д.
Из этого можно сделать вывод, что увеличение надеж-
ности стрельбы примерно получается одно и то же как при
увеличении р, так и при увеличении 5 в одинаковое число
раз. Но это арифметический, а не артиллерийский вывод.
Известно, что вероятность попадания увеличивается по мере
приближения средней траектории к цели и достигает наиболь-
шей величины при совмещении средней траектории с центром
цели, что вытекает из неравномерности рассеивания снарядов.
Чтобы приблизить среднюю траекторию к цели, производится
пристрелка, а так как пристрелка по сравнению со стрельбой
на поражение требует значительно меньшего расхода снаря-
дов, то совершенно очевидно, что надежность стрельбы
должна увеличиваться, прежде всего, путем повышения точ-
ности проведения пристрелки, т. е. путем увеличения вероят-
ности попадания.
Вот почему Правила стрельбы наземной артиллерии 1945 г.
и указывают, что „действительность стрельбы на поражение
обеспечивается точностью пристрелки" (ст. 175) и что „необ-
ходимыми условиями для успешного выполнения задачи воз-
можно меньшим числом снарядов являются:
— пристрелка непосредственно по цели для определения
установок на поражение с возможно большей точностью;
— непрерывное наблюдение разрывов и своевременная
корректура с задачей приведения средней траектории к вы-
бранной точке цели и удержанию ее у этой точки" (ст. 195).
Артиллеристам важно знать не столько надежность стрельбы.,
сколько расход снарядов, обеспечивающий эту надежность.
При определении надежности стрельбы мы задавались,
численными значениями количества снарядов и вероятности
попадания при 1 выстреле и подставляли их в формулу ве-
роятности получения хотя бы 1, 2, 3 и т. д. попаданий. Чтобы
найти потребное для поражения количество снарядов, не-
обходимо в эту формулу подставить численные значения
вероятности попадания при 1 выстреле и надежности стрельбы.
Какова же должна быть эта надежность? Принято считать,
что стрельба достаточно надежна, если вероятность пораже-
ния цели близка к 90%, и вполне надежна, если вероятность
поражения порядка 96 — 98%. Задаваться вероятностями пора-
жения цели, весьма близкими к единице, нецелесообразно,.
63
гак как такое увеличение надежности стрельбы потребует
очень большого увеличения расхода снарядов.
Начнем с определения числа снарядов, потребного для
получения хотя бы одного попадания. Для этого представим
-формулу вероятности хотя бы 1 попадания в виде:
;и, прологарифмировав эту формулу, решим ее относительно S:
lg(l - A )==51g (1 -р);
Jg(l-P)
Покажем на примерах, как пользоваться этой формулой.
Пример 1. Каков должен быть расход снарядов, чтобы надежность
’была 0,95, если вероятность попадания при 1 выстреле равна 0,12 и для по-
ражения цели требуется одно прямое попадание?
Решение.
lg(l— 0,95) 1g 0,05 2,69897 - 1,30103 24
1g (1 — 0,12) 1g 0,68 1,94448 — 0,05552
Пример 2. Определить количество снарядов, необходимое для получе-
ния хотя бы 1 попадания, если вероятность попадания при 1 выстреле 0,07
.и надежность стрельбы должна быть равна 98%.
Решение.
Подставим численные значения р и Рх :
с 1g (1—0,98) 1g 0,02 2,30103 — 1,69897
5 =-----------=--------= -------------------- ^54 снаряда.
lg( 1 — 0,07) lg 0,93 1,96848 — 0,03152
Пример 3. Рассчитать при условиях примера 2 расход снарядов для
надежностей стрельбы 0,99 и 0,999.
Ре ш е н и е.
% = = I00000 = Z^OQOOL 64 снаряда;
1g 0,93 1,96848 —0,03152
s2 = ig0,001 = з.ооооо = -з,ооооо 9б с^рядов
1g 0,93 1,96848 —0,03152
Сравнив результаты расчетов в примерах 2 и 3, видим,.„гчто при
Рх = 0,98 средний расход снарядов на каждые 100 аналогичных стрельб
равен 5400, при этом, если снаряды не будут добавлены, в 2 случаях огне-
вая задача не будет выполнена. При Р^ = 0,99 средний расход снарядов
равен 6 400, т. е. увеличивается на 1000 снарядов, в то время как число
невыполненных стрельб уменьшится всего с двух до одной (при данном
отпуске снарядов на одну стрельбу). Еще резче скажется дальнейшее уве-
личение надежности стрельбы — при Рх = 0,999: расход снарядов увеличи-
вается еще на 3 200 снарядов. Все это еще раз с достаточной наглядностью
подтверждает, что задаваться очень большой надежностью стрельбы не
следует.
64
Значительно сложнее определение расхода снарядов, если
для поражения цели требуется 2 и более прямых попаданий,
так как привести формулы вероятностей хотя бы 1,2, 3 и
т. д. попаданий к виду, удобному для логарифмирования, не
представляется возможным. В этих случаях приходится при-
бегать к довольно сложному способу подбора.
§ 16. ЗАДАЧИ НА ВЕРОЯТНОСТИ ПРИ ПОВТОРЕНИИ ИСПЫТАНИЙ
Задача 31. Какова вероятность получения комбинации из 8 недолетов
и 4 перелетов при 12 выстрелах, если средняя траектория проходит в 1 Вд
за целью?
Ответ. 0,0024.
Задача 32. Вероятность попадания при 1 выстреле 0,05. Чему равна
вероятность получения 2 попаданий при 20 выстрелах?
Ответ. 0,1886.
Задача 33. Вероятность воздушного разрыва бризантной
3 1
1 выстреле равна-- . Определить вероятность получения —
4 3
гранаты при
клевков при
24 выстрелах.
Ответ. 0,1125.
Задача 34. Вероятность недолета при 1 выстреле равна 0,4. Какова
вероятность получить соотношение знаков 1:3 при 8 выстрелах?
Ответ. 0,25.
Задача 35. Вероятность нахождения цели на участке, куда направлен
огонь,- равна 0,6. Какова вероятность получения 5 попаданий при 24 выст-
релах, если вероятность попадания при 1 выстреле равна 0,15?
Ответ. 0,08831.
Задача 36. Вероятность недолета при 1 выстреле равна 0,3. Определить
наивероятнейшую комбинацию знаков при 16 выстрелах.
Ответ. 5 недолетов и 11 перелетов.
Задача 37. Вероятность попадания при 1 выстреле равна 0,07. Опре-
делить наивероятнейшую частость попадания при 8 выстрелах и ее вероят-
ность.
Ответ. Ноль попаданий; 0,5596.
Задача 38. Вероятность недолета при 1 выстреле равна
вероятность получения хотя бы 1 недолета при 8 выстрелах?
6560
Отве1- -656Г-
Задача 39. Определить вероятность получения хотя бы
при 12 выстрелах, если вероятность попадания при 1 выстреле
Ответ. 0,9313.
— . Какова
3
1 попадания
равна 0,2.
Задача 40. Вероятность воздушного разрыва бризантной гранаты при
I выстреле равна 0,75. Какова вероятность получения хотя бы 1 клевка при
32 выстрелах?
Отве т. 0,9999.
Задача 41. Вероятность попадания при первом выстреле при условии,
что цель находится на обстреливаемом участке, равна 0,12. Чему равна ве-
роятность получения хотя бы 1 попадания при 20 выстрелах, если вероят-
ность нахождения цели на участке, куда направлен огонь, равна 0,35?
Ответ. 0,3229.
Задача 42. Вероятность промаха при 1 выстреле равна 0,87. Чему
равна вероятность хотя бы 2 попаданий при 8 выстрелах?
Ответ. 0,28.
5 — Зак. 991
65
Задача 43. Чему равна вероятность получения хотя бы 2 попаданий
при 30 выстрелах, если вероятность попадания при 1 выстреле равна 0,06?
Ответ. 0,5445.
Задача 44. Вероятность попадания при 1 выстреле равна 0,1. Чему
равна вероятность получения хотя бы 3 попаданий при 20 выстрелах?
Ответ. 0,3232. I
Задача 45. Определить количество снарядов, необходимое для получе-
ния хотя бы 1 попадания, если надежность стрельбы должна быть равна 90%
и вероятность попадания при 1 выстреле равна 0,3.
Ответ. 6—7 снарядов.
Задача 46. Каков должен быть расход снарядов, чтобы надежность
стрельбы была 0,93, если для поражения цели требуется 1 прямое попадание
и вероятность попадания при 1 выстреле равна 0,15?
Ответ. 16—17 снарядов.
ГЛАВА 3
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
§ 17. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ.
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ СУММЫ И ПРОИЗВЕДЕНИЯ
В артиллерийской практике часто приходится иметь дело
с такими переменными, величинами, которые при повторении
аналогичного испытания принимают частные, случайные зна-
чения.
Так, например, при проведении стрельб (при повторении
стрельбы) в одинаковых условиях (система, установки, снаряд,
заряд и пр.) расход снарядов на поражение цели есть пере-
менная величина, так как в одних случаях поражение будет
получено при первых же выстрелах, а в других — поражение
будет достигнуто при значительном расходе снарядов. При
этом в каждом отдельном случае число снарядов, израсходо-
ванное на поражение цели, будет величиной случайной.
Так как расход снарядов на поражение цели в различных
случаях будет различным, то для приблизительного расчета
снарядов на проведение одной стрельбы в данных условиях
нужно брать какой-то средний расход снарядов.
На вопрос о среднем ожидаемом значении переменной
величины отвечает математическое ожидание этой величины.
Математическое ожидание расхода снарядов отвечает на
вопрос о среднем ожидаемом расходе снарядов на одну стрель-
бу при проведении большого количества стрельб в одних и
тех же условиях; математическое ожидание числа попаданий
отвечает на вопрос о среднем ожидаемом числе попаданий на
одну стрельбу при проведении большого числа аналогичных
стрельб; математическое ожидание расхода времени отвечает
на вопрос о среднем ожидаемом расходе времени на одну
стрельбу и т. д.
Математическим ожиданием величины называется сумма
парных произведений всех возможных частных значений дан-
ной величины на соответствующие им вероятности.
5* 67
Математическое ожидание обозначается буквой а или бук-
вами М.О. Тогда математическое ожидание величины х в общем
виде будет выражено равенством
М.О. (х) — а — 4- 4“ 4~ • • • 4-
s
4- ^гРг’4- • • • 4- xs Ds ~
где хг,х2, х3, . . . , х$ — частные значения величины х;
Ръ Ря, сРз> • • >Ps — вероятности, соответствующие этим
частным значениям.
Прежде чем приступить к доказательству справедливости
этого выражения, необходимо остановиться на среднем значе-
нии переменной величины, полученном из опыта, — на сред-
нем из опыта.
Вывод математического выражения средней величины из
опыта покажем на следующем примере.
Положим, при 22 стрельбах, произведенных в совершенно
одинаковых условиях, было получено при:
4 стрельбах по 5 попаданий;
7 стрельбах по 4 попадания;
5 стрельбах по 3 попадания;
3 стрельбах по 2 попадания;
1 стрельбе 1 попадание;
2 стрельбах все промахи (0 попаданий).
Применив простой арифметический способ решения, найдем
среднее число попаданий, приходящееся на одну стрельбу, для
чего общее количество попаданий разделим на число всех
стрельб:
5.4 + 4.7 + 3.5 + 2-3 + 1-1 + 0-2 70 о4 о 2
-------------22--------------------=22==^22==3ТГ попаДания-
Представим полученный результат в несколько ином виде,
проделав все расчеты в обратном порядке:
о 2 Q 4 70 5-4 + 4-7 + 3-5 + 2-3 + 1-1 ф-0-2 4 ,
6 11 ~~ d 22 ~ 22 ~' 22 ' 22 +
4- 4 - 22 4- 3 - 22 4- 2 - 22 4" 1 * 4~ У2 ‘
В этом выражении числа 5, 4, 3, 2, 1 и 0 показывают коли-
чество попаданий, полученных при отдельных стрельбах, т. е.
являются частными (отдельными) значениями рассматриваемой
тг . 4 7 5 3 1
нами переменной величины. Дроби же: ’ 22 ’ "22 ’ 22 и
2 „
22 являются частостями отдельных частных значении этой же
величины.
68
Произведение 5 • ~ показывает, что стрельб с 5 попада-
5
ниями в каждой было 4 из 22; произведение , что
стрельб с 3 попаданиями в каждой было 5 из 22; произведе-
ние же 0--22—, что все промахи были получены в 2 случаях
из 22, и т. д.
Обозначив через А'ср среднее из опыта, через xlf х2, х3, . . . ,
Xj, . . . ,xs —частные значения переменной величины и через
ri> гч, г %, • • • ,6, • • • , rs — соответствующие этим значениям
частости, получим:
Хср = хр\ + х2г2 + х8г3 + . . . + Xi rt 4- . . . 4-xs rs.
Среднее значение переменной величины (среднее из опыта}
равно сумме парных произведений из частных значений этой
величины на соответствующие этим значениям частости.
Пример. Найти среднее число очков, получившееся при 30-кратном
бросании игральной кости, если известно, что:
при 7 бросаниях вышло по 6 очков
я я
» 8 , „ „ 4 очка
» 4 „ , 3 ,
,6 „ „ 2 ,
. 2 „ „ , 1 очку.
Решение. Числа очков: 6, 5, 4, 3, 2 и 1—частные значения этой
переменной величины, — a — , JL , JL г , JL и ^-соответствующие им
30 30 30 30 30 30
частости. Тогда по общей формуле
у 7 . , 3 , , 8,ч 4 , Q 6 , , 2 _ 115 _
ср ‘ 30 + ' 30 + ' 30 + 30 + ‘ 30 + 30 30
= 3 — очка.
6
Арифметическое решение приводит к такому же результату:
у _ 6.7 +5.3 + 4.8 +3.4 + 2.6+1.2 115 Ч5П_Я
ср 30 30 6
На основании закона больших чисел по мере увеличения
числа повторений испытания частость события по своей вели-
чине стремится приблизиться к вероятности этого же события,
а при достаточно большом числе повторений испытания частости
очень мало отличаются от соответствующих им вероятностей.
Отсюда в выражении среднего из опыта можно частости
частных значений переменной величины заменить соответствую-
щими им вероятностями. Тогда, обозначив эти вероятности
соответственно через ръ р2, р3, . . . , pit . . . , ps, получим
выражение математического ожидания, данное выше:
М.О. (х) — a 4- ад, Ч-х3/?3 + . . . + ад + . . . +xsps.
69
Если при определении математического ожидания были
учтены все возможные частные значения переменной величины,
то согласно следствию теоремы сложения вероятностей,
Pi 4" Р2 4" Рз 4~ • • • 4- Pi 4- • • • 4~ ps — 1 •
Сравнивая выражения среднего из опыта и математического
ожидания, можем заключить, что между средним из опыта
некоторой переменной величины и ее математическим ожида-
нием существует такая же зависимость, как и между
частостью и вероятностью события, т. е. по мере увеличения
числа испытаний среднее значение величины будет прибли-
жаться к ее математическому ожиданию.
При достаточно большом числе повторений испытания
неизвестное математическое ожидание переменной величины
будет весьма мало отличаться от среднего значения этой же
величины, полученного из опыта. И наоборот, если математи-
ческое ожидание переменной величины известно, то при
большом числе повторений испытания полученное среднее зна-
чение этой величины будет весьма мало отличаться от ее
математического ожидания. В этом и заключается сущность
закона больших чисел применительно к среднему из опыта
и математическому ожиданию.
Пример 1. При стрельбе из пистолета по мишени, имеющей вид круга,
вероятность попадания в десятку равна 0,3, в девятку — 0,35, в восьмерку —
0,2, в семерку — 0,1 ив шестерку — 0,05. Определить математическое
ожидание числа очков при 1 выстреле.
Решение. В этом примере переменной величиной является число
очков, которое может быть получено при 1 выстреле. Частные значения этой
величины: 10, 9, 8, 7 и 6 очков. Вероятности этих частных значений соответ-
ственно: 0,3; 0,35; 0,2; 0,05 и 0,1.
Прежде чем перейти к определению математического ожидания числа
очков, проверим, полностью ли учтены в условиях примера все возможные
частные значения рассматриваемой переменной величины, для этого сложим
вероятности этих значений:
0,3 + 0,35 + 0,2 + 0,05 + 0,1 = 1.
Это показывает, что все частные значения в условиях примера учтены
и что при стрельбе исключается возможность попадания пули за пределами
черного круга мишени.
Убедившись в этом, подставим численные значения х, и pL в общую
формулу:
М.О. (х) = а =10-0,3 + 9-0,35 4- 8-0,2 + 7.0,05 + 6.0,1 — 8,7 очка.
’г* Это означает, что при проведении большого числа аналогичных стрельб
на каждый выстрел надо ожидать получение 8,7 очка в среднем.
Пример 2. Цель находится в пределах района, разбитого на участки
А, Б, В, Г и Д. При условии нахождения цели на участке А на пристрелку
расходуется 13 снарядов, на участке Б—11 снарядов, на участке В—8 сна-
рядов, на участке Г—10 снарядов и на участке Д—12 снарядов. Найти
математическое ожидание расхода снарядов на пристрелку, если вероятности
нахождения цели на участках Л, Б, В, Г и Д соответственно равны:
0,05, 0,15, 0,45, 0,25 и 0,1 (рис. 20).
70
Район возможных положений цели
5 А 1 6 . .. । $ v I / . . -J " i Д 1 । > —. »
0,05 0,15 0,45 0,25 0,10
13 он. Пен. Осн. Рис. 20 10 ОН. 12 сн.
Решение. Здесь переменная величина — количество снарядов, расхо-
дуемое на пристрелку. Частные значения этой величины 13, И, 8, 10 и 12.
По условию расход снарядов на пристрелку определяется нахождением цели
на том или ином участке района возможных положений цели. Отсюда вероят-
ности нахождения цели на различных участках этого района являются вместе
с тем и вероятностями соответствующих частных значений расхода снаря-
дов, и сумма этих вероятностей, если учтены все возможные положения цели,
должна быть равна единице. И действительно:
Рк + ръ + рв + рг + рд = °>05 + °»15 + °’45 + °>25 + О-1 = Е
Тогда
М.О.(х) = а = 13-0,05 + 11-0,154-8-0,45 + 10-0,25 + 12-0,1 =9,6 снаряда.
Пример 3. Найти математическое ожидание суммы очков, которая
может быть получена при одновременном и однократном бросании 2 играль-
ных костей.
Решение. Переменная величина — сумма очков. Частные значения
этой суммы Xi и соответствующие этим частным значениям вероятности Р,
даны в таблице.
X, 2 3 4 5 6 7 8 9 10 11 12
1 2 3 4 5 6 5 4 3 2 1
Pi 36 36 36 36 36 36 36 36 36 36 36
Сумма очков, равная 3, может быть получена как (24-1) или как (1 + 2),
а вероятность этой суммы независимо от того, на какой кости будет полу-
чено 2 очка и на какой 1 очко:
р _ 1 1 = 2
3 6 ' 6 6 ’ 6 36 ’
Сумма очков, равная 7, может быть получена как (6 + 1), или (5 4- 2),
или (4 + 3), или (3 4-4), или (2 + 5), или (1 + 6). Вероятность этой суммы
р _. 1 1+1 1д_1 1- L 1 + 1 1+1 1 = 2
1 б’б б’б^б’б^б'б^б'б^б'б 36 ‘
Сумма вероятностей всех возможных частных значений суммы очков
р.~ 1 Д-2^2+4Д.54-бД.54-44_3+24-1
1 ~ 36 + 36 + 36 + 36 + 36 + 36 + 36 + 36 + 36 + 36 + 36
^36 _
~~ 36 ~ 1 •
Тогда
М.О.(лг) = а = 2 .JL4-3. — + 4.2-р 5.-1+6.— 4-7..2 +
v ' 36 т 36 36 36 36 ~ 36
4-8.2. + 9.-1+10.2 4-И-2-4-12. 2 — 7 очков.
71
Разобранные примеры показывают, что математическое
ожидание переменной величины выражается любым дробным
или целым именованным числом.
В этих примерах математические вероятности были выра-
жены положительными числами, но они могут быть выражены
и отрицательными числами, если отрицательны частные значе-
ния переменной величины.
Мы разобрали случай, когда в условиях данного испыта-
ния были частные значения одной переменной величины.
Нередко конечный результат испытания определяется сово-
купностью частных значений нескольких таких величин. Напри-
мер, имея билеты нескольких лотерей, мы по окончании всех
тиражей получим какой-то суммарный выигрыш, слагающийся
из выигрышей на билеты различных лотерей, причем выигрыш
в одной лотерее не зависит от выигрыша в другой.
На вопрос о математическом ожидании такого суммарного
выигрыша отвечает математическое ожидание суммы несколь-
ких независимых переменных величин.
Выведем математическое ожидание суммы сначала только
для двух таких переменных величин.
Положим, что имеются две независимые переменные вели-
чины х и у, частным значениям которых: х2, -Х3, . . . >х$
соответствуют вероятности рг, р2, р& . . . ,ps, а _ух,_у2> • • • >
vs — вероятности qlt qz, qs, . . . ,qs.
Любое частное значение величины х может совпасть
с любым частным значением величины у. Такие совпадения
и дадут частные значения суммы:
^+У1 • • • • *1 + Ув
•*2 + У1 *2 + Ь • • . . + ys
Xs+Vi Xs+y^ .... xs + ^s
Сумма (a'x 4- j/J может быть получена только тогда, когда
величина х примет значение лх и величина у — значение у1У
а так как вероятность значения х{ по условию равна рг и
вероятность значения у1 равна qlf то по теореме умножения
вероятность такой суммы будет равна pxqx. Точно так же
вероятность суммы (а2 + у2) будет равна р2 q2, суммы (л3 +^4) —
p.iqi и т. д.
Подставив частные значения суммы и соответствующие им
вероятности в общую формулу математического ожидания,
яолучим:
М-ОДх-О)^*! + У^Р1Я1 + {Х1 +У2)Р1<Ь + • • • +
+ (a's + ys)psqs.
72
Раскроем скобки и произведем сравнительно несложные
преобразования, используя равенства
+ х2р2 + . . . +xsps = М.О. (х) = а,
. +ysqs^M>O.(y) = b
и помня, что
Р1+Р2+ • • • +ps= 1,
+ <?2 + • • *4- qs= 1,
после чего получим
М.О. (х 4-у) = а 4- Ъ = М.О. (х) 4- М.О. (у),
т. е. математическое ожидание суммы двух независимых пере-
менных величин равно сумме математических ожиданий этих
величин.
Этот вывод будет справедлив и для любого числа неза-
висимых переменных величин, так как легко представить
сумму нескольких величин сначала в виде суммы только двух
величин и затем решить задачу последовательно.
Например, если имеются три независимые переменные
величины х, у и z, математические ожидания которых соответ-
ственно равны а, b и с, то
М.О. (х 4-У + z) = М.О. (х + у) + М.О. (г) = М.О. (х) +
4- М.О. (у) + М.О. (г) — а 4- b 4- с.
Математическое ожидание суммы нескольких незави-
симых переменных величин равно сумме математических
ожиданий этих величин.
Пример. Стрельба ведется на трех установках прицела: 80, 81 и 82.
Определить математическое ожидание числа попаданий, если вероятности
попадания при одном выстреле соответственно прицелам 80, 81 и 82 равны:
0,05, 0,15 и 0,1 и на прицелах 80 и 82 намечено произвести по 8 выстрелов,,
а на прицеле 81—12 выстрелов.
Решение. Математические ожидания числа попаданий при стрельбе:
на прицеле 80 — аг = 8*0,05 = 0,4 попадания,
на прицеле 81 — а2 — 12*0,15 = 1,8 попадания,
на прицеле 82 — а3 = 8*0,1 =0,8 попадания.
Тогда сумма этих математических ожиданий
Gj 4- а2 + а3 — 0,4 4- 1,8 4- 0,8 = Зиопадания,
что и отвечает на вопрос о математическом ожидании числа попаданий
всей стрельбы.
Если частные значения нескольких независимых перемен-
ных величин не суммируются, а перемножаются, то можно
говорить о математическом ожидании произведения этих
величин.
Математическое ожидание произведения нескольких
независимых переменных величин равно произведению мате-
матических ожиданий этих величин
М.О. (x*y*z) = М.О.(х) X М.О. (у) х М.О. (2).
73
§ 18. ЧАСТНЫЙ СЛУЧАЙ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
В том случае, когда переменная величина при одном испы-
тании может принимать только два частных значения:
хг = 1 и х2 = О,
эти два значения соответствуют противоположным событиям
(например, недолет и перелет, попадание и промах). Выраже-
ние математического ожидания такой переменной величины
может быть значительно упрощено.
Выведем это упрощенное выражение применительно к наи-
более важному для артиллериста случаю — математическому
ожиданию числа попаданий. Заметим, что речь будет итти
только о прямых попаданиях и только при ударной стрельбе.
При одном выстреле может быть получено или попадание,
или промах, т. е. частные значения числа попаданий: ху~ 1
(попадание) и х2 = 0 (промах).
Обозначим вероятность попадания при 1 выстреле через
р и вероятность промаха через q, т. е. вероятности указанных
выше частных значений: рх=р и pt~q.
Тогда по общей формуле
М.О. (х) — ау —x-jj^ 4- х2/72= \ ‘р 4- 0 q = p попаданиям.
Следовательно, при 1 выстреле математическое ожидание
числа попаданий численно равно вероятности попадания при
1 выстреле. Это равенство только численное, потому что
вероятность попадания величина отвлеченная, а математиче-
ское ожидание — именованная.
Пример. Найти математическое ожидание числа попаданий при 1
выстреле, если вероятность попадания при 1 выстреле р — 0,15.
Р е ш е н и е: р = 0,15; а = 0,15 попадания.
Такое численное равенство справедливо только для 1
выстрела. Для 2 и более выстрелов этого равенства уже нет.
Действительно, вероятность получения всех попаданий, напри-
мер, при 3 выстрелах равна р-р-р~р\ т. е. меньше, чем при
одном выстреле (//3</?), а математическое ожидание числа
попаданий при 3 выстрелах, несомненно, будет больше, чем
при одном; чтобы определить, на сколько больше, рассчитаем
математические ожидания числа попаданий при 2 и 3 выстрелах.
При двух выстрелах будут следующие частные значения
числа попаданий (л^) и соответствующие им вероятности (/?,):
№ по пор. 1 Комбинации попаданий и промахов | xi Pi
1 2 попадания 2 Р2
2 1 попадание и 1 промах . . . 1 2pq
3 2 промаха 0 Q2
74
Подставив данные этой таблицы в общую формулу мате-
матического ожидания, получим:
М. О. (х) = а2 = хгрх 4- х2/ц + х3/ц = 2-р2 + 1 • 2pq 4- 0 • q2 =
= 2р2 4- 2pq — 2р(р 4- q) = 2p-l=2p попаданий,
т. е. при 2 выстрелах математическое ожидание числа попада-
ний численно равно удвоенной вероятности попадания при
1 выстреле.
При трех выстрелах частные значения числа попаданий
соответствующие этим значениям вероятности таковы:
и
по пор. Комбинации попаданий к промахов
1 3 попадания ........ 3 рз
2 2 попадания и 1 промах . . 2 3jp2g
3 1 попадание и 2 промаха . . 1 W
4 3 промаха 0 ?з
Тогда согласно общей формуле
М.О. (х) = а3 =ЛХ1 4- Р2*ъ + А*з 4- =
= 3>р3 4- 2-3p2q 4- 1 -3/2<72 4~ О-^3 — Зр3 4- 6p2q 4- 3pq2 =
— Зр (р2 4- %pq + q2) = 3р (р 4- Q)~ = 3р • 1 = Зр попаданий,
т. е. математическое ожидание числа попаданий при 3 вы-
стрелах численно равно утроенной вероятности попадания при
1 выстреле.
Сопоставив результаты наших расчетов:
ах = р попаданий;
а2 = 2р попаданий;
«3 = Зр попаданий,
можем считать, что и для любого 5 числа выстрелов мате-
матическое ожидание числа попаданий
М.О. (х) = as — Sp попаданий.
Пример 1. Найти математическое ожидание числа попаданий при 16 вы-
стрелах, если вероятность попадания при 1 выстреле равна 0,15.
Решение. М.О. (х) = а16 = S-p - 16-0,15 = 2,4 попадания.
Это означает, что при проведении большого количества ^стрельб в
условиях нашего примера среднее ожидаемое число попаданий на одну
стрельбу равно 2,4 попадания, хотя отдельные стрельбы дадут разное
число попаданий—от 0 до 16.
Пример 2. Вероятность нахождения цели на обстреливаемом участке
равна 0,3. Определить математическое ожидание числа попаданий при 12 вы-
стрелах, если вероятность попадания при 1 выстреле и при условии, что
цель находится на участке, куда направлен огонь, равна 0,08.
75
Решение. Вероятность попадания при 1 выстреле с учетом вероят-
ности нахождения цели
Р - Рц • р - 0,3-0,08 = 0,024.
Тогда
М.О. (х) = я12 — 12-0,024 — 0,288 попадания.
Задаваясь определенным математическим ожиданием числа
попаданий, можно рассчитать средний расход снарядов, не-
обходимый для решения поставленной огневой задачи.
a = S-p,
тогда
Р
Пример. Определить средний расход снарядов, если для поражения
цели требуется 3 прямых попадания и вероятность попадания при 1 вы-
стреле равна 0,05.
Решение.
а 3
•S = — = q-q5 = 60 снарядов.
Это означает, что при проведении большого числа стрельб при усло-
виях этого примера для получения 3 попаданий необходимо на 1 стрельбу
расходовать в среднем 60 снарядов.
§ 19. ЭКОНОМИЧНОСТЬ СТРЕЛЬБЫ
Каждая стрельба должна быть достаточно надежной, но
одной надежностью еще не исчерпываются все требования,
предъявляемые к стрельбе; стрельба должна быть экономич-
ной, т. е. огневая задача должна решаться с наименьшим рас-
ходом снарядов и времени.
Если при двух различных методах стрельбы математиче-
ское ожидание числа попаданий при первом методе больше,
чем при втором, то первый метод стрельбы более выгоден,
более экономичен, чем второй.
Положим, что при проведении стрельбы первым методом
математическое ожидание числа попаданий равно 2, а при про-
ведении стрельбы вторым методом—1, и для решения огневой
задачи требуется только 1 прямое попадание. Очевидно, что
при том же расходе снарядов, проводя стрельбу первым мето-
дом, можно решить 2 такие огневые задачи, так как на каж-
дую стрельбу расход снарядов будет в 2 раза меньше.
Следовательно, математическое ожидание числа попа-
даний характеризует экономичность артиллерийской
стрельбы.
Устанавливая те или иные положения (правила) артиллерий-
ской стрельбы, отыскивая наиболее выгодные во всех отноше-
ниях методы ее проведения, необходимо одновременно с на-
76
дежностью стрельбы учитывать и ее экономичность. Только
сопоставление надежности с экономичностью стрельбы позво-
ляет притти к правильным выводам.
Пример 1. Найти надежность и экономичность стрельбы при 40 вы-
стрелах, если вероятность попадания при 1 выстреле равна 0,1 и для раз-
рушения цели требуется 2 прямых попадания.
Решение. Надежность стрельбы определим как вероятность хотя
бы двух попаданий.
Ри = 1 — (Spqs~~l +qs)=\ — (40-0.1-0,939 + 0,9«») = 1 — 0,0805 а; 92%,
т. е. при данном расходе снарядов на 1 стрельбу огневая задача будет
решена в 92 случаях из 100, в остальных 8 случаях потребуется увеличить
расход снарядов.
Экономичность стрельбы найдем как математическое ожидание числа
попаданий:
а = S'p = 40-0,1 = 4 попадания,
т. е. на каждую стрельбу можно ожидать получения 4 попаданий в среднем.
Здесь мы натолкнулись, невидимому, на явное противоречие—требуется
2 попадания, а на 1 стрельбу можно ожидать получения 4 попаданий.
Если для уравнения математического ожидания числа попаданий с
требуемым по условию количеством попаданий уменьшить расход снарядов
вдвое, т. е. расходовать только 20 снарядов в среднем на стрельбу, то на-
дежность стрельбы понизится. Действительно,
Рп = (1 — 20-0,1.0,919 — 0,920) = 1 —0,3917 = 0,6093 » 610/0,
что явно недостаточно.
Пример 2. Определить надежность и экономичность стрельбы при
30 выстрелах, если вероятность попадания при 1 выстреле равна 0,2 и для
поражения цели требуется 1 прямое попадание.
Решение.
Надежность стрельбы Pi = 1 —0,83° = 0,9988.
Экономичность стрельбы а = 30-0,2 = 6 попаданий.
Очевидно, что надежность стрельбы слишком велика и может быть
снижена; снижение надежности, в свою очередь, повлечет уменьшение рас-
хода снарядов на стрельбу. Например, при надежности стрельбы, рав-
ной 96%,
1g (1—0,96) 1g 0,04 2,60206 — 1,39794
1g (1—0,2) lg0,8 1,90309 —0,09691 F
а экономичность стрельбы
a = 15-0,2 = 3 попаданиям.
Если условия стрельбы допускают меньшую надежность, например
90%, то
о 1g 0,1 — 1,00000
5 ~ lg0,8~ —0,09691 ~ 11 снаРяДам;
а ~ 11-0,2 = 2,2 попадания.
Таким образом, для выполнения указанной огневой задачи можно огра-
ничиться расходом 15 снарядов на 1 стрельбу в среднем. Дальнейшее сок-
ращение расхода снарядов на стрельбу нецелесообразно, так как получен-
ная экономия в снарядах очень незначительна (15—11 =4 снаряда), а на-
дежность стрельбы снизилась сразу на 6%.
77
§ 20. ЗАДАЧИ НА МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
Задача 47. По группе мишеней было дано 40 выстрелов, в результате
чего было поражено:
— при 6 выстрелах по 3 мишени;
— при 13 выстрелах по 4 мишени;
— при 12 выстрелах по 5 мишеней;
— при 9 выстрелах по 6 мишеней.
Определить среднее число пораженных мишеней на 1 выстрел.
Ответ. 4,6 мишени.
Задача 48. При стрельбе осколочной гранатой вероятность получения
воронки глубиной 30 см равна 0,2, глубиной 40 см — 0,4, глубиной 50 см—
0,3 и глубиной 60 см — 0,1. Чему равно математическое ожидание числа
пораженных мишеней на 1 выстрел, если известно, что при получении
воронки глубиной 30, 40, 50 и 60 см в среднем поражается соответственно
8, 7, 5 и 3 мишени.
Ответ. 6,2 мишени.
Задача 49. Определить математическое ожидание суммы очков для
одной, взятой наудачу кости домино?
Ответ. 6 очков.
Задача 50. Чему равно математическое ожидание числа прямых попа-
даний при 36 выстрелах, если вероятность попадания при 1 выстреле
равна 0,07?
Ответ. 2,52 попадания.
Задача 51. Вероятность нахождения цели на участке, куда направлен
огонь, равна 0,6. Определить математическое ожидание числа попаданий
при 16 выстрелах, если вероятность попадания при 1 выстреле при условии
нахождения цели на обстреливаемом участке равна 0,15.
Ответ. 1,5 попадания.
Задача 52. Определить средний расход снарядов на стрельбу, если
вероятность попадания при 1 выстреле равна 0,04 и для поражения цели
требуется 2 прямых попадания.
Ответ. 50 снарядов.
Задача 53. При стрельбе из пистолета по мишени, имеющей вид круга,
вероятность попадания в десятку равна 0,2, в девятку—0,3, в восьмерку—
0,25, в семерку — 0,15 и в шестерку — 0,1. Чему равно математическое
ожидание числа очков при 5 выстрелах?
Ответ. 41,75 очка.
Задача 54. Определить надежность и экономичность стрельбы при 16
выстрелах, если вероятность попадания при 1 выстреле равна 0,12 и для
поражения цели требуется 1 прямое попадание.
Ответ. 0,871; 1,92 попадания.
Задача 55. Определить средний расход снарядов на одну стрельбу и
надежность стрельбы при этом расходе снарядов, если вероятность попада-
ния при 1 выстреле равна 0,25 и для поражения цели требуется 2 прямых
попадания.
Ответ. 8 снарядов; 0,633.
ГЛАВА 4
ВЕРОЯТНОСТИ ГИПОТЕЗ
§ 21. О ВЕРОЯТНОСТЯХ ГИПОТЕЗ
При исследовании некоторых явлений нередко приходится
иметь дело с событиями, вероятности которых могут принимать
различные численные значения, в зависимости от того, в каких
условиях (какой обстановке) эти события происходят. Иначе
говоря, в зависимости от этих условий (этой обстановки) одному
и тому же событию могут соответствовать различные вероят-
ности.
В качестве очень наглядного и притом часто встречаю-
щегося -в артиллерийской практике примера можно указать на
вероятности недолета и перелета при ударной стрельбе. Эти
вероятности, как мы знаем, имеют различные численные зна-
чения в зависимости от того, где проходит средняя траектория
д б в \г д г ж з и
вероятность недолета 0 0,02 0,09 0,25 0,50 0,75 0,91 0,98 1,0
вероятность перелета 1,о 0,98 0,91 0,75 0,50 0,25 0,09 0,02 о
Рис. 21
относительно цели. Так, если цель находится в точке А
(рис. 21), вероятность недолета равна 0, а вероятность пере-
лета—1,0; при нахождении цели в точке Б вероятность недо-
лета равна 0,02 и вероятность перелета 0,98; при нахождении
цели в точки В вероятности недолета и перелета соответ-
ственно равны 0,09 и 0,91 и т. д.
Зная условия, в которых происходит интересующее нас
событие, мы можем найти частное значение вероятности этого
события, т. е. если положение цели относительно средней
79
траектории известно, то мы можем найти частное значение
вероятности недолета или перелета. Но вопрос может быть
поставлен и иначе: по частному значению вероятности собы-
тия мы можем определить конкретные условия, в которых
оно происходит; так, по частному значению вероятности недо-
лета или перелета мы можем судить о действительном поло-
жении цели относительно средней траектории. Такая поста-
новка вопроса имеет особо важное значение, так как знание
положения цели относительно средней траектории позволяет
нам рассчитать поправки для совмещения средней траектории
с целью и этим решить основную задачу артиллерийской
стрельбы.
Если бы представилось возможным произвести на одних
и тех же установках достаточно большое число выстрелов—
100, 200, 300, решение этой задачи было бы очень простым.
Рассчитав по результатам такой стрельбы частость недолета
или перелета и приравняв на основании закона больших чисел
(используя теорему, обратную теореме Якова Бернулли) най-
денное численное значение частости соответствующей ей
вероятности, мы по этой вероятности определяем интересую-
щее нас положение цели относительно средней траектории.
В действительности о таком числе выстрелов на одних и
тех же установках не может быть и речи. Как правило, стре-
ляющему приходится судить о положении цели относительно
средней траектории и принимать соответствующее решение о
корректуре установок по очень небольшому числу наблюде-
ний, зачастую даже по одному.
Вследствие неизбежности рассеивания при стрельбе дан-
ному положению (знаку) отдельного случайного разрыва или
группы разрывов могут отвечать различные положения цели
относительно средней траектории или различные положения
средней траектории относительно цели. Так, если на некото-
рой установке прицела были получены недолет и три пере-
лета, то средняя траектория может при этом проходить за
целью, перед целью и даже через цель (рис. 22).
Прежде чем принять решение убавить, прибавить или оста-
вить ту же установку прицела, у стреляющего, естественно,
возникает вопрос: какова же вероятность каждого из этих
80
положений, какое из этих положений является наиболее веро-
ятным? На этот вопрос отвечает теорема гипотез.
Сущность этой теоремы применительно к стрельбе по
наблюдению знаков разрывов заключается в следующем.
Зная, что цель относительно средней траектории может
занимать различные положения, мы еще до выстрела задаемся
рядом предположений (гипотез) об этих положениях цели.
Каждая такая гипотеза оценивается своей вероятностью.
Численные значения этих вероятностей вытекают из условий
подготовки исходных данных.
Произведя выстрел и получив то или иное наблюдение
(знак или знаки), мы по вероятностям гипотез о положении
цели до выстрела и по вероятностям получения наблюденного
знака (знаков) при различных положениях цели находим уже
новые вероятности гипотез о положении цели после вы-
стрела. Далее, основываясь на наивероятнейшей после вы-
стрела гипотезе, мы и принимаем соответствующее решение
о корректуре установок.
Чтобы показать, как результат испытания изменяет су-
ждение о вероятностях гипотез, воспользуемся следующим
примером.
В 2 закрытых ящиках находятся шары, различающиеся
только цветом: в первом ящике—3 белых и 2 черных шара
и во втором—только белые шары. Из первого ящика во вто-
рой, не глядя, перекладывают один шар.
О том, какой шар был переложен, мы можем сделать
два предположения, две гипотезы:
— переложен белый шар—вероятность этой гипотезы
3
равна -у;
— переложен черный шар—вероятность этой гипотезы
2
равна -у.
Предположим, что после этого из второго ящика выни-
мают, не глядя, один шар, и этот шар оказался черным.
Совершенно очевидно, что это могло произойти только в том
случае, если из первого ящика во второй был переложен
черный шар.
Вероятность второй гипотезы до испытания была рав-
2
на , а после испытания стала равной единице. Вероятность
з
первой гипотезы вместо у стала равной нулю. Результат испы-
тания в корне изменил суждение о вероятностях гипотез.
Вернемся к вероятности гипотез о положении цели. Рас-
считав вероятности всех сделанных нами гипотез о положении
цели относительно средней траектории, мы получим ряд (сово-
купность) возможных положений цели, каждому из которых
6 — Зак. 991
81
соответствует своя вероятность, т. е. получим, как это назы-
вается в теории стрельбы, —распределение цели.
Особенность теоремы гипотез по сравнению с другими
теоремами, которые применялись до сих пор, заключается
в том, что теорема гипотез не дает вполне определенного от-
вета на вопрос о вероятности события. Она дает ряд ответов,
ряд вероятностей или распределение вероятностей этого собы-
тия. Анализируя этот ряд, сравнивая вероятности гипотез, мы
приходим к наиболее целесообразному решению. При этом
необходимо особо подчеркнуть, что это решение будет спра-
ведливым только в условиях данной обстановки, только для
данного результата испытания, при стрельбе — только для
данного наблюдения (знака).
Получив первое наблюдение, изменив установки и про-
должая стрельбу, мы будем получать новые наблюдения. Каж-
дое такое новое наблюдение будет менять распределение цели.
С каждым новым наблюдением будет уменьшаться число ги-
потез (распределение цели будет сужаться) и вместе с тем
будут возрастать вероятности наивероятнейших гипотез. В ко-
нечном счете при сравнительно небольшом расходе снарядов
мы определим положение цели относительно средней траек-
тории с точностью, вполне обеспечивающей как надежность,,
•так и экономичность стрельбы на поражение.
В отличие от закона больших чисел теорема гипотез дает
основание для суждения о вероятности рассматриваемого собы-
тия по результатам небольшого числа испытаний. Этим обу-
словливается особенно широкое применение этой теоремы
в теории артиллерийской стрельбы.
§ 22. ТЕОРЕМА ГИПОТЕЗ
Для вывода численного выражения (общей формулы) ве-
роятности гипотезы воспользуемся следующим частным при-
мером.
Положим, что имеется 3 группы совершенно одинаковых
по виду, весу и форме закрытых ящиков. В ящиках нахо-
дятся шары, отличающиеся друг от друга только окраской.
Ящиков первой группы — 3, в каждом из них по 2 белых
и по 4 черных шара.
Ящиков второй группы — 2, в каждом из них по 4 белых
и по 3 черных шара.
Ящиков третьей группы — 4, в каждом из них по 3 белых
и по 5 черных шаров.
Ящики различных групп расположены вперемежку; из них
наудачу берут один ящик, из которого, не глядя, вынимают
шар, и оказывается, что этот шар белого цвета.
Определим, какова вероятность того, что этот шар был
вынут из первой группы ящиков?
82
До испытания белые шары имелись во всех ящиках. Сле-
довательно, белый шар мы могли вынуть из ящика первой,
или второй, или третьей группы. Следовательно, можно сде-
лать три предположения, сделать три гипотезы относительно
того, из ящика какой группы был вынут белый шар.
Появление белого шара из ящика первой группы в тех
условиях, при которых проходило наше испытаний, есть со-
бытие сложное, так как оно состоит из совпадения выбора ящика
первой группы с появлением белого шара из этого ящика. Ж1»
Всех ящиков 9, из них ящиков первой группы 3. Поэтому
вероятность выбора ящика первой группы, т. е. вероятность
первой гипотезы до испытания,
В каждом ящике первой группы по 2 белых и 4 черных
шара. Отсюда вероятность появления белого шара из ящика
первой группы, считая, что ящик именно этой группы уже
выбран, т. е. вероятность события по первой гипотезе
2
А=6-
По теореме умножения вероятность появления белого
шара из ящика первой группы, как вероятность совпадения
появления ящика первой группы с появлением белого шара
из этого ящика будет равна
п 32
^1 Рх — 9 ’ g •
Путем аналогичных рассуждений найдем, что вероятность
появления белого шара из ящика второй группы равна
р —2. ±
*2 Рч 9*7’
вероятность появления белого шара из ящика третьей группы
равна
о — ± 3
*зРз~~ 9 • у•
Откуда по теореме сложения вероятность появления белого
шара из ящика любой группы
т-г t-ч । о I г) ______ 3 2 2 4.4 3
П ^1Р1 ^2 Р ч. РзРз "д' ’ "б" д’ * У “Ь д' ’ g *
Приведём правую часть этого равенства к общему знаме-
нателю, умышленно не делая никаких сокращений, и закончим
вычисления:
п 3.2.7-8 2-4-6-8 4-3-6-7_336 + 384 + 504_1224
11 ~~ 9-6-7.8 + 9-6-7-8 + 9-6-7-8~ 3024 “3024 ’
Полученный результат позволяет сделать заключение,^ что
появлению белого шара из ящика любой группы до испытания
благоприятствовало 1224 случая из 3 024 всех равновоз-
можных случаев.
6* 83
Следует подчеркнуть, что .^4 не есть отношение числа
всех белых шаров к общему количеству шаров, а отношение
случаев, благоприятствующих появлению белого шара, к числу
всех равновозможных случаев.
Во всех 9 ящиках белых шаров по условию примера 26,
а всех шаров белого и черного цвета — 64. Определяя веро-
ятность появления белого шара из любой группы ящиков
26 1224
и взяв отношение , что не равно ^4» мы поступили бы
неправильно, потому что число шаров в ящиках неодинаковое.
Предположим теперь, что соотношение между белыми и чер-
ными шарами в ящиках осталось тем же, а число шаров
в каждом ящике одинаковое, а именно по 6-7-8, — всего по
336 шаров.
Тогда в каждом ящике первой группы должно быть по
2-7-8== 112 белых шаров, в каждом ящике второй группы по
4-6-8 = 192 белых шара и в каждом ящике третьей группы
по 3-6-7 = 126 белых шаров, что и даст нам те же численные
значения вероятностей появления белого шара:
__112__2. _ 192__ 4 . __ 126 _ з
^“336 6 ’ “336 7 ’ ^3“ 336 8 •
Учитывая общее число ящиков и число ящиков в каждой
группе, получим число всех равновозможных для появления
шара случаев:
п = 336- 9 = 3024,
а число случаев, благоприятствующих появлению белого
шара,
/п= 112-3+ 192-2 4- 126-4 —336 + 384 + 504 = 1224,
т. е. получим то численное значение вероятности появления
белого шара до испытания, которое мы вывели выше.
Вероятность появления белого шара до испытания из лю-
бой группы ящиков (без указания, какой именно) называется
полной или средней вероятностью появления белого шара.
В общем виде полная вероятность события выражается фор-
мулой
П= Ргрг + Р2Рч + ^зРз + • • • Л-PiPi + • • • Psps =
^=^PiPlf
1
где Pt — вероятности гипотез до испытания;
pi — вероятности событий по этим гипотезам.
Испытание было произведено—появился
белый шар.
Очевидно, имел место один из 1 224 случаев, благо-
приятствовавших до испытания появлению белого шара.
84
Выше мы установили, что из этих 1 224 случаев 336 слу-
чаев благоприятствовало появлению белого шара из ящика
первой группы, 384 случая — из ящика второй группы и 504
случая — из ящика третьей группы.
Определим вероятность появления белого шара из ящика
именно первой группы после того, как белый шар был уже вынут,
т. е. вероятность первой гипотезы после испытания.
Так как появлению белого шара из ящика первой группы
благоприятствовало 336 случаев из всех равновозможных для
появления белого шара 1 224 случаев, то вероятность появле-
ния белого шара из ящика именно первой группы или веро-
ятность того, что после появления белого шара имеет место
именно первая наша гипотеза,
п = 336
1224 ‘
Чтобы перейти от этого частного решения к общему вы-
воду, вспомним, как были получены числа 336, 384, 504
и 1 224:
336 = 3-2.7.8; 384 = 2-4-6-8; 504 = 4-3-6-7;
1224 = 336 + 384 + 504 = 3-2-7-8 + 2-4-6-8+ 4-3-6-7.
Тогда
о __ 3-2-7-8
"“3-2-7-8 + 2-4-6-8 + 4-3-6-7 *
В правой части этого равенства мы имеем только случаи,
благоприятствовавшие появлению белого шара. Для общего
вывода нам необходимо учесть и все равновозможные случаи.
Поэтому разделим числитель и знаменатель правой части
равенства на произведение 9-6-7-8 = 3024, т. е. на произве-
дение всех равновозможных случаев, после чего сделаем необ-
ходимые сокращения:
3-2-7-8 3 2
~ 9-6-7.8 9 ’ 6
Э-6-7-8 + 9-6-7-8 + 9-6-7-8 9 ’ б" + 9 ' 7 + 9 ' 8
Проанализируем полученный результат, разберем, что
представляют собой все эти дроби.
3 2 4
Дроби д', g и д-, по доказанному выше, являются веро-
ятностями выбора ящика той или иной группы, т. е. вероятно-
стями гипотез до испытания (до появления белого шара): Ри
Р> и Р3.
2 4 3
Дроби же -g , у и g являются вероятностями выхода белого
шара из ящика определенной группы, иначе говоря, вероятно-
стями события по вышеприведенным гипотезам: рг, р2 и ps.
85
Тогда, сохранив эти обозначения, получим:
л —
1 Р1Р1 + Р2Р2 + рзРз ’
Таким образом, вероятность того, что белый шар появился
из первой группы ящиков, т. е. вероятность того, что после
испытания имеет место первая гипотеза, равна произведению
вероятности выбора ящика первой группы до появления
белого шара (вероятности первой гипотезы до испытания) на
вероятность появления белого шара именно из такого ящика
(на вероятность события по данной гипотезе), деленному на сумму
таких произведений для всех групп (для всех гипотез).
Распространяя этот вывод на любое событие и любое чи-
сло гипотез, мы можем сформулировать теорему гипотез.
Вероятность гипотезы после испытания равна произ-
ведению вероятности этой гипотезы до испытания на ее-
роятностъ события по этой гипотезе, подобного происшед-
шему при испытании, деленному на сумму таких произве-
дений для всех возможных гипотез.
Или в общем виде для 5 гипотез
о __________________pi Pi_______________ pi Pi
1 Р1Р1+Р2Р2+РзРз~*Г • - -+Pi Pi + '”+PsPs 4pn
^iPi
При этом сумма
r • • + Pi 4“ • • • + Ps — 1,
т. е. при определении вероятности гипотезы после испытания
необходимо учесть все гипотезы, которые имеют место до ис-
пытания, что и подтверждается условиями нашего примера,
где
Л+₽г+/’з=4-+4+4 = 1-
Применительно к артиллерийской стрельбе теорему гипо-
тез можно сформулировать так.
Вероятность данного положения цели относительно
средней траектории после выстрела, давшего наблюдение
определенного знака, равна произведению вероятности этого
положения цели до выстрела на вероятность полученного
наблюдения при данном положении цели, деленному на
сумму таких произведений для всех возможных положений
цели.
Вывод теоремы гипотез мы могли бы сделать и не поль-
зуясь частным численным примером.
Положим, что относительно появления события А можно
сделать 4 гипотезы, вероятности которых до испытания
р _ §1 • р ______________р — $$. р _____"4
~ s ’ 2 ~ s ’ 3 ~ s ’ 4 s ’
86
Вероятности появления события А при условии, что имеют
место именно эти гипотезы, т'. е. вероятности событий по ги-
потезам
р — В- • р = ^2 • р — В и Р =
1 «i ’ 2 «2 ’ 8 я3 * п4 *
Тогда полная вероятность появления события А до испы-
тания (по всем гипотезам)
P^PiPi + Р2р2 + Р^ръ + P±pt =
__ Si ту . S2 , ^2 I $з , _£?з ^4
<S Hi S S * л3 "г S ’ ri4 ’
или, после приведения к общему знаменателю
р Sf • Л2 - Ид- • ^2 ‘ Я1 *я3* я44~^3 ‘ ^З'я1 ‘ я2' л44~<?4 • /W4 - • Л2 • яз
<9-ЯГИ2-Яз*я4
Испытание произведено—событие А появи-
лось.
Рассуждаем так же, как и ранее при решении частного
примера. Число всех равновозможных случаев до испытания
было
5*П1’П2,^3,Л4«
Число всех равновозможных случаев после испытания
стало
• т х • п2 • п, • п4 4- 52 • т 2 • п г и3 • и4 4- 53 • т 3 • пх- п2 • лг44-
4- <S*4 • mi • пх • м2 • zig,
причем из всех этих равновозможных случаев появлению события
А после испытания по первой гипотезе благоприятствует
S1'mi*n2-n3»ni случаев, по второй гипотезе 52• т2• пх• и8• п4 слу-
чаев, по третьей гипотезе—S^m^n^n^n^ случаев и, наконец,,
по четвертой гипотезе—S^m^ni-n^n^ случаев.
Тогда вероятность первой гипотезы после испытания
0 _______________________Sx-mi’ttyп±___________________
'*1 51-т1-Я2.Пз.Я44-52-7И2-яГ«3-«4+53*/яЗ-яГя2,я4+^4-/я4’я1 ‘№k '
Разделив числитель и знаменатель правой части этого ра-
венства на число всех равновозможных случаев до испытания,
т. е. на произведение З-п^п^п^п^ и произведя сокращения,
получим:
Si . т±
Q —__________________S Я1________________—-
т1 I ^2 . *И2 . $3 т3 ! S4 ^4
S Пу S я2 S S
___________Р\Р1______
Р\ Pl + Р2Р2+Р3 Рз + Р4 Pi
87
Таким образом, мы пришли к тому же выводу, что и на
численном примере.
Выше мы указали, что теорема гипотез дает нам возмож-
ность сравнивать вероятности гипотез после испытания.
Покажем это на нашем примере, определив по теореме
гипотез вероятности появления белого шара из ящика второй
группы и из ящика третьей группы, т. е. вероятности второй
и третьей гипотез после испытания.
Подставив в выведенную нами общую формулу соответ-
ствующие численные значения вероятностей, получим:
2 . 4
_ 9*7 384 384 .
1 . 1 4- 1.4 + 1 3 — 3364-384+ 503 — 1224 '
9 * 6 + 9 * 7 9*8
4 . 3
п _ 9*8 504 504
Чз— 3 2 2 4,4 3 ““ 3364-384+504 — 1224 ’
9 ' 6+9' 7 + 9'8
Нетрудно заметить, что достаточно рассчитать вероятность
только одной из всех сделанных гипотез. Вероятности осталь-
ных гипотез будут отличаться только числителем, который
представляет собой число благоприятствующих случаев для
появления данного события по каждой из всех остальных
гипотез.
Сравнивая Qn Q2 и Q3, мы видим, что вероятнее всего то,
что белый шар был вынут из ящика третьей группы, так как
после испытания третья гипотеза оказалась наивероятнейшей.
При этом
о 4.0 4.0 - 336 384 1 504 - 1 о
4/1+Q2+Q3— 1224 + 1224 + 1224
что и подтверждает правильность рассуждений и правиль-
ность всех сделанных расчетов.
Пример 1. Установлено, что в районе возможных положений цели
вероятности нахождения цели на отдельных участках этого района таковы:
Участки РВПЦ А Б В г Д Е ж 3. и
Вероятности нахождения цели . . . 0 0,02 0,10 0,23 0,30 0,23 0,10 0,02 0
88
Каждому участку района возможных положений цели (РВПЦ) соответ-
ствует некоторая установка прицела. Если на установке прицела, соответ-
ствующей участку Д, произвести 1 выстрел, то вероятности получения не-
долета (перелета) при условии нахождения цели на различных участках
РВПЦ будут следующие.
Участки РВПЦ А Б В г Д Е ж 3 и
Вероятность недолета . 0 0,02 0,09 0,25 0,50 0,75 0,91 0,98 1
Вероятность перелета . 1,0 0,98 0,91 0,75 0,50 0,25 0,09 0,02 0
Найдем вероятность нахождения цели на участке В после того, как
на прицеле, соответствующем участку Д, произвели 2 выстрела и получили
недолет и перелет.
Решение. Проверим, прежде всего, все ли возможные положения
цели учтены условием примера. Для этого сложим заданные вероятности
нахождения цели:
04-0,02+0,104-0,234-0,304-0,23 +0,104-0,024-0= 1,0.
Сумма вероятностей равна единице, что подтверждает полный учет
возможных положений цели.
Так как по условию примера цель может занимать в РВПЦ одно из
9 положений, то можно сделать 9 гипотез о положении цели. Вероятности
каждой из девяти гипотез до испытания приведены в первой таблице дан-
ного примера.
Каждому положению цели, т. е. каждой гипотезе при одном выстреле
на прицеле участка Д, соответствует определенная вероятность получения
недолета (перелета), отсюда и вероятность получения недолета и перелета
при 2 выстрелах, т. е. вероятность события по гипотезе, подобного проис-
шедшему при испытании.
Обозначив вероятность недолета через р и вероятность перелета через
q, представим вероятность события по гипотезе в общем виде:
Р.=р. q„.
Подставив численные значения р и q, определим вероятности получе-
ния недолета и перелета при различных положениях цели. Так, например,
при условии нахождения цели на участке В и при условии, что выстрелы были
произведены на прицеле, соответствующем участку Д, вероятность события
по данной гипотезе
рв =pq = 0,09-0,91 = 0,0519*.
* При расчете вероятностей событий по гипотезам (в примере—P^Q^)
не принят во внимание биноминальный коэфициент (в примере—2). Объяс-
няется это тем, что здесь рассчитываются вероятности события, подобного
происшедшему при испытании, а при испытании (при выстрелах) события
появляются в какой-то одной последовательности (в примере—сначала недо-
лет, потом перелет), и биноминальный коэфициент здесь неуместен.
89
Произведя аналогичные расчеты для всех возможных положений цели,
можем приступить к решению по общей формуле
(?в = __________________________РвРв____________________________
?аРа ~\-РбРб + ?вРв + PrPl + РдРд + РеРе + РжРж+ рз Рз +
+ риРи~ 0 +0,2.0,98-0,02 +0,10.0,91.0,09 +0,23-0,75.0,25+
0,10-0,91-0,09
+0,30-0,5-0,5+0,23-0,25-0,75+0,10-0,9-0,91+0,02-0,02-0,98+0 ~
0,008190
0+0,000392+0,008190+0,043125+0,075000+-0,043125+0,008190+0,000392
= °’008190 = 0,045903.
0,178414
Решение задач на применение теоремы гипотез удобнее производить
при помощи следующей таблицы.
Гипотезы Вероятность гипотез до испытания Pi Вероятность события по гипотезе Pi piPi Вероятность гипотезы после испытания Qi
Цель на участке А . 0 1-0 0 0
V V Б . 0,02 0,98-0,02 0,000392 0,002197
V V В . 0,10 0,91-0,09 0,008190 0,045903
V V Г . 0,23 0,75-0,25 0,043125 0,241713.
• • д . 0,30 0,50-0,50 0,075000 0,420374
V V Е . 0,23 0,25-0,75 0,043125 0,241713
п V • Ж . 0,10 0,09-0,91 0,008190 0,045903
V V п 3 . 0,02 0,02-0,98 0,000392 0,002197
V п И . 0 0,1 0 0
Суммы . . . 1,00 0,178414 1,000000
Сумма вероятностей гипотез после испытания получилась равной еди-
нице, что и должно быть, если рассуждения и расчеты были правильны.
Выше было указано, что каждое последующее испытание изменяет
вероятности нахождения цели, т. е. изменяет распределение цели.
Сравним распределения цели до выстрелов и после выстрелов, взяв
все вероятности с точностью до второго десятичного знака.
Действительно, количество гипотез сократилось; сократилась глубина
РВПЦ, так как вероятности нахождения цели на участках Б и 3 стали после
выстрелов настолько малыми, что ими можно пренебречь. Резко возросла
вероятность наивероятнейшей гипотезы—наивероятнейшего положения цели
(на участке Д): до испытания была 0,30, а после испытания стала 0,42.
90
Теорема гипотез применяется во всех тех случаях, когда
о появлении интересующего нас события можно допустить
ряд гипотез.
Пример 2. Имеются патроны трех партий:
Ns партии Количество пачек Вероятность осечки в °/0
8 20 0,2
11 25 0,3
16 15 0,5
Патрон из взятой наудачу пачки дал осечку. Из пачки какой партии
вероятнее всего был взят патрон?
Решение.
№ гипотез Гипотезы Pi Pi Pi Pi Qi
I Из 8-й партии 20 0,002 40 40
60 60000 190
II , 11-й 25 0,003 75 75
60 60 000 190
III . 16-й „ 15 0,005 75 75
60 60 000 190
Сумма . . . 1 190 1
60 000
После испытания получены две наивероятнейшие гипотезы: II и III.
Вероятности того, что патрон был взят из 11-й партии и из 16-й партии
одинаковы.
91
Частный случай теоремы гипотез
Нередко у нас не будет оснований считать, что до испы-
тания одна из гипотез более или менее вероятна, чем другая.
В этих случаях мы будем считать, что все гипотезы до испы-
тания равновероятны, т. е.
Л =Р2 = Р3 =... = . = Ps = P.
Возвращаясь к примеру, разобранному в начале пара-
графа, допустим, что число ящиков в каждой группе одина-
ково; тогда вероятности всех гипотез до испытания о том, из
ящика какой группы появится белый шар, будут равны между
собой.
Произведя соответствующие замены в общей формуле
вероятности гипотезы после испытания и сделав сокращения,
получим:
__________________________________________________ —
Ъ РР1 + РР2 + Ррз + • • • + Ppi + . .. + Рр$
________________Pi_____________.
Pl + P2 ~i~P3 + • • • + Pi + • • • + PS
Если до испытания все гипотезы равновероятны, то
вероятность гипотезы после испытания равна вероятности
события в этой гипотезе, деленной на сумму таких веро-
ятностей для всех возможных гипотез.
Нетрудно заметить, что вероятность гипотезы после испы-
тания пропорциональна вероятности события в данной гипотезе.
Пример 1. Цель может находиться на одном из следующих участков
РВПЦ: К, Л, М, Н и О. Вероятности нахождения цели на этих участках
равны между собой.
При выстреле на некоторой установке прицела вероятность попадания
в цель при условии нахождения ее на участке К равна 0,05, на участке Л—
0,07, на участке М—0,10, на участке //—0,08 и на участке О—0,06.
Определим, чему равны вероятности нахождения цели на указанных
участках, если на данной установке прицела с первого же выстрела было
получено попадание в цель?
Решение. Всего гипотез о положении цели по условию — пять.
Вероятности их до испытания одинаковы. Пользуясь формулой теоремы
гипотез для частного случая, получим:
0 __ 0,05 0,05 5
0,05+0,07+0,10+0,08+0,06 “ 0,36 ~ 36 *
Для остальных гипотез их вероятности после испытания будут найдены
путем замены числителя соответствующими вероятностями события, и тогда
7 . ~ 10. п 8 п 6
Чл- зё’Слг- и Qo= зб •
5 7 10 8 _6_
= 36 т зб + зб + 36 + 36 “ L
92
Пример 2. В закрытом ящике имеется 6 шаров, эти шары могут быть
только белого и черного цвета. Соотношение между белыми и черными
шарами неизвестно. Какова вероятность, что в ящике белых и черных шаров
поровну, если один за другим из ящика были вынуты 2 белых шара, причем
белый шар, вынутый первым, в ящик возвращен не был.
Решение. О составе шаров в ящике до испытания можно сделать
7 гипотез:
1. В ящике только белые шары.
2. В ящике 5 белых и 1 черный шар.
3. В ящике 4 белых и 2 черных шара.
4. В ящике 3 белых и 3 черных шара.
5. В ящике 2 белых и 4 черных шара.
6. В ящике 1 белый и 5 черных шаров.
7. В ящике только черные шары.
Все эти гипотезы до испытания равновероятны.
Вероятность появления двух белых шаров по этим гипотезам:
__ 6 _ 30 _ 3 _2 _ _6_
Л “ 6 ’ 5 “ 30 ; Л - 6 ’ 5 - 30 ’
_ 5 _4 _ 20 _ 2_ £_2_
р2 — 6 ‘ 5 — 30 ’ р5 = 6 * 5 “ 30 ’
4 £ _ 12 _ 1 2 _ п
б ' 5 — зо J Рб— б ’ 5 “ 0’
/>7 = 0.
Тогда искомая вероятность
6
30 6
^4 “ J30 20 12 6 2 “30 + 20 4-12+ 6 + 2“
30 + 30 + 30 + 30 + 30 + ° + °
6
= -уд- = 0,0857.
Пример 3. Условия те же, что и в примере 2, но белый шар, вынутый
первым, был^положен в ящик обратно.
Решение. Гипотезы о количестве белых и черных шаров до испыта-
ния те же, но вероятности события по этим гипотезам иные, так как измени-
лись условия испытания:
_2 2 _ 36 __ 2 3__9_
~ 6 ’ 6 = 36 ’ Pi~ 6 * 6 “ 36 ’
_ 2 2 _ 23 _ 2 2 А
^2 = 6 ’ 6 ~ 36 ' 6 = 36 :
_А 1_J2 _11_А_
рз — 6 • 6 “ 36 ’ р5 “ 6 ' 6 “ 36 ;
/>т = 0.
Отсюда
9 9
= ЗЬ + 25 + 16+9-|-4+1 = 91 ~ °-0989-
^Изменились условия испытания, изменилась и вероятность гипотезы
после испытания. Это еще раз подтверждает, что суждение о вероятности
события по результатам испытания справедливо только для условий данной
обстановки.
93
§ 23. ТЕОРЕМА БУДУЩИХ СОБЫТИЙ
Произведя испытание, мы по его результату можем, поль-
зуясь теоремой гипотез, определить вероятности всех сделан-
ных нами гипотез и принять соответствующее решение. Так,
при стрельбе мы определяем вероятности нахождения цели на
различных участках района возможных положений цели (РВПЦ),
чтобы выбрать установку прицела для очередной команды.
Продолжая испытания в тех же условиях, мы, естест-
венно, задаемся вопросом, что же мы можем получить в даль-
нейшем, т. е. возникает вопрос о вероятности так называемого
будущего события — события, ожидаемого после испытания,
давшего определенный результат. При стрельбе, например,
может возникнуть вопрос о вероятности получения недолета
или перелета при следующем очередном выстреле. На такой
вопрос отвечает теорема будущих событий.
Для вывода общей формулы теоремы будущих событий
воспользуемся тем же частным примером, что и при доказа-
тельстве теоремы гипотез.
Имеются 3 группы совершенно одинаковых ящиков: в пер-
вой группе 3 ящика, во второй — 2 и в третьей — 4. В каждом
ящике первой группы по 2 белых и 4 черных шара,
второй группы — по 4 белых и 3 черных шара и третьей груп-
пы •— по 3 белых и 5 черных шаров. Шары различаются
только цветом.
Из случайно взятого ящика был вынут вслепую один шар,
и он оказался белым. Какова вероятность, что в следующий
раз из того же ящика будет вынут черный шар, если белый
шар был возвращен в этот же ящик?
Обращаем особое внимание на постановку вопроса — оче-
редной шар вынимается из того же ящика, из которого перед
этим был вынут белый шар, ибо только при такой постановке
вопроса мы имеем право использовать результат предшество-
вавшего испытания для определения вероятности результата
последующего (будущего). К какой группе принадлежит этот
ящик, мы не знаем, так как мы его не вскрывали и состав
шаров в нем не известен.
Если бы это был ящик первой группы, то вероятность
появления из него черного шара
4
6 ‘
Вероятность того, что этот ящик принадлежит к первой
группе ящиков, как нам известно (§ 22), равна
л — 336 — 14
1224 ~ 51 •
94
Отсюда вероятность появления черного шара из данного
ящика, как ящика первой группы, т. е. вероятность совпаде-
ния принадлежности данного ящика к ящикам первой группы
с появлением черного шара из такого ящика, как вероятность
сложного события
Qi’?: =
Вероятность появления черного шара из данного ящика,
как ящика второй группы,
п __ 384 3 __ 16 3
42-^2 — 1224 ’ 7 ~ 51 ’ 7 •
И, наконец, вероятность появления черного шара из дан-
ного ящика, как ящика третьей группы,
П _______504 £_2£ 5
Чз*^з—1224 * 8 — 51 ’ 8 ’
Нам безразлично, к какой группе ящиков относится взятый
нами ящик. Поэтому вероятность появления черного шара не-
зависимо от принадлежности данного ящика к той или иной
группе ящиков, т. е. вероятность нашего будущего события,
по деореме сложения
77ч = • 4 ’ 7 +
I 21 5 _ 4925__
+ 51 8 ~ 8568 '
Для проверки наших расчетов найдем вероятность появле-
ния белого шара после испытания, вероятность вторичного
появления белого шара из того же ящика:
/7б = 14.2+26 4 21_ Л= 3643 _
776 51 6 51 7 51 8 8568
Сложив вероятности -обоих будущих событий, получим:
4925 3643 _ 8568 _
8568 + 8568 ~ 8568 b
что и должно быть, так как появления после испытания белого
и черного шаров — события противоположные.
Таким образом, вероятность появления черного шара после
того, как уже появился белый шар, равна сумме парных про-
изведений из вероятностей гипотез после испытания на веро-
ятности появления черного шара по всем гипотезам.
95
Распространяя этот вывод на любое будущее событие
при любом числе гипотез, можем дать следующую формули-
ровку теоремы будущих событий.
Вероятность будущего события после испытания, дав-
шего определенный результат, равна сумме парных произве-
дений из вероятностей гипотез после испытания на вероят-
ности интересующего нас будущего события, взятых для
всех гипотез.
Или в общем виде:
s
П == Qi^i 4- + • • • 4- Qi4i 4- • • • 4- Qsfls — 2 Q^.
i
Эту же формулу можно дать и в развернутом виде, исходя
из общей формулы теоремы гипотез:
0=__________________tjPi_____________.
4 PiPi 4- Р2Р2 4- • • • + Pipi 4- • •. 4- P$Ps
Тогда вероятность будущего события
j-j P\PiQi + P2PiQ2~\~ • • • + Р\Рfli + ••• 4- РsPs^s
Р1Р14- Р2Р2 + • • • 4- Ptрц + • • • 4- PsPs
Как мы видим, теорема будущих событий непосредственно
вытекает из теоремы гипотез, является логическим ее продол-
жением. Вместе с тем между этими двумя теоремами имеется
принципиальная разница. Теорема гипотез дает ряд вероятно-
стей — распределение вероятностей; теорема гипотез помогает
нам принять наиболее целесообразное решение в условиях
данной обстановки. Теорема будущих событий дает вполне
определенную вероятность — вероятность будущего события;
теорема будущих событий отвечает на вопрос, что можно
ожидать от решения, принятого по теореме гипотез.
'-Вернемся к нашему примеру и посмотрим, как меняется
вероятность ожидаемого события в зависимости от результата
испытания.
До испытания вероятность появления черного шара не-
зависимо от того, из ящика какой группы он может быть
вынут, равна
р __ 1800 — 25 ~ q где .
“ 3024 ~~ 42 ’
после испытания вероятность появления черного шара стала
равной
Пч * 0,575.
Как мы видим, выход при испытании белого шара умень-
шил вероятность появления черного шара. Логически так и
должно быть. Очевидно, после получения При первом выстреле
недолета вероятность получения перелета при втором выстреле
на .той же установке прицела должна быть меньше.
96
В то же время вероятность появления белого шара, кото-
рая до испытания была равна
Р.-2224 - Е«0 405
'о 3024 42 U,4U0’
после испытания стала равной
Пб ~ 0,425.
Вероятность ожидаемого события после испытания увели-
чивается для события, аналогичного тому, которое произошло
при этом испытании. Поэтому каждое новое испытание будет
давать новое численное значение вероятности будущего со-
бытия. > « .2$
Пример 1. Имеется 2 "закрытых ящика с шарами, различающимися
только цветом: в первом ящике — 2 белых и 3 черных шара и во втором
ящике — 4 белых и 2 черных шара. Из первого ящика во второй вслепую
был переложен один шар, после чего из второго ящика был вынут один
шар, который оказался черным. Какова вероятность того, что после этого
будет вынут из второго ящ 1ка белый шар, если вынутый перед этим черный
шар был положен в ящик обратно?
Решение. В этом примере будущим событием является появление
белого шара из второго ящика после того, как из этого ящика был вынут
черный шар. Перед появлением черного шара из второго ящика один шар,
неизвестного нам цвета, был переложен из первого ящика во второй.
О том, какой шар был переложен из первого ящика во второй, можно
сделать две гипотезы:
1. Был переложен белый шар; вероятность такого предположения, т. е.
вероятность первой гипотезы до испытания,
2. Был переложен чёрный шар; вероятность такого предположения,
т. е. вероятность второй гипотезы до испытания,
Если из первого ящика во второй был переложен белый шар, то во
втором ящике будет 5 белых и 2 черных шара, и вероятность появления
из второго ящика черного шара в этом случае, т. е. вероятность события
по первой гипотезе,
Р1 = 7 >
а вероятность появления из этого ящика белого шара, т. е. вероятность
будущего события,
5
41 = "у •
Если из первого яшика во второй был переложен черный шар, то во
втором ящике будет 4 белых и 3 черных шара, и тогда вероятность появле-
ния черного шара из второго ящика, т. е. вероятность события по второй
гипотезе,
3
Рч — 7 ’
а вероятность появления белого шара
4
42 = 7".
1 — Зак. 991
97
Испытание произведено — появился черный шар. Тогда вероятность
первой гипотезы после испытания по теореме гипотез
5 ’ 7 4
~ 2 2 3 J3 = 13 ’
5 ’ "7 + 5 ‘ 7
а вероятность второй гипотезы после испытания
3 3
_______5 ‘ 7___________9_
1 3 “ 13 •
5 ’ 7 + 5 ' 7
Отсюда вероятность будущего события, т. е. вероятность появления
белого шара из второго ящика после того, как из этого ящика был вынут
черный шар, и независимо от того, какой шар до этого был переложен, по
общей формуле теоремы будущих событий
п _ _ 4 . 5 9 4 20 36 56 8
— Qi<h + Q2Q2 — 13 *. 7 + 1з • 7 — 91 + 9J ~ 91 — 13 •
Для проверки рассчитаем вероятность противоположного будущего-
события — вероятность появления черного шара:
____£ _2 9 _3____£ 27 35 5
- 13 ‘ 7 + 13 • 7 = 91 + 91 = 9Г = 13 *
Сумма вероятностей этих противоположных событий дает нам единицу»
что и подтверждает прави ьность всех наших действий:
8 5
Пб + ПЧ — 13 + "13 = 1 •
Как и в задачах на применение теоремы гипотез, решение
задач на применение теоремы будущих событий удобнее про-
изводить по схеме, которая является дальнейшим развитием
принятой нами схемы для теоремы гипотез.
№ гипотез Содержание гипотез Вероятность гипотезы до испытания Pi £ о S с О а 5 со f-* S 1) а? н н 0 3 0 о-ю Е «8 5йГ ptpi Вероятность гипотезы по- сле испытания Qi Вероятность будущего со- бытия после испытания qi Q^i
1 Из 1-го ящика во
2-й был перело- жен белый шар _2 _2 4 4 5 20
5 7 35 13 7 91
2 Из 1-го ящика во
2-й был передо- 3 3 9 9 4 36
жен черный шар 5 Т 35 13 7~ 91
Сумма . . . 5 5 13 35 13 13 56 91
_5б_ 8_
—91 — 13-
98
Пример 2. При тех же условиях, что и в предыдущем примере, опре-
делим вероятность появления черного шара, если вынутый до этого черный
шар не был возвращен в свой ящик.
Решение.
№ гипотез Содержание гипотез Pi Pi Pi Pi Qi Qi Qi Qi
1 2 Был переложен белый шар . . Был переложен черный шар . . 2 5 3 5 2 7 3 7 4 35 9 35 4 13 9 13 1 6 2 6 . 4 78 18 78
Сумма . . . 5 5 13 35 ГЭ 13 22 78
_ 22 _ 11
7ч ” 78 39 ’
Пример 3. Цель находится в пределах одного из восьми данных участ-
ков РВПЦ. Вероятности нахождения цели на участках РВПЦ указаны на
рис. 23. На прицеле 80, соответствующем границе между участками Г и Д,
были получены 1 недолет и 1 перелет. Какова вероятность того, что при
последующих трех выстрелах на том же прицеле будет получено 2 недо-
лета и 1 перелет, если вероятности получения недолета и перелета при
1 выстреле на прицеле 80 при условии нахождения цели на указанных участ-
ках РВПЦ таковы, как это приведено на рис. 23.
Решение.
ЛЬ I гипотез! Содержание гипотез Pi P^PQ) piPi Qi <?«<
1 Цель на участке А 0,02 0,01-0,99 0,000198 0,00119 3-0,012-0,99 0
2 „ » » Б 0,07 0,05-0,95 0,003325 0,01995 3-0,052-0,95 0,00014
3 „„„ в 0,16 0,16-0,84 0,021504 0,12916 3-0,162-0,84 0,00883
4 » » „ Г 0,25 0,37-0,63 0,058275 0,34970 3-0,372-0,63 0,09046
5 » я » Д 0,25 0,63-0,37 0,058275 0,34970 3-0,632-0,37 0,15400
6 „ „ „ Е 0,16 0,84-0,16 0,021504 0,12916 3-0,842-0,16 0,04374
7 . „ ,, ж 0,07 0,95-0,05 0,003325 0,01995 3-0,952-0,05 0,00273
8 » я » *5 0,02 0,99-0,01 0,000198 0,00119 3-0,992-0,01 0
Сумма . . . 1,00 0,166604 1,00000 0,29940
77 = 0,2994.
7*
99
Пр. 80
Участки РВПЦ А Б В Г Д Е Ж 3
Вероятность нахож- дения цели 0,02 0,07 0,16 0,25 0,25 0,16 0,07 0,02
Вероятность полу- чения недолета 0,01 0.05 0,16 0,37 0,63 0,84 0,95 0,99
Вероятность полу- чения перелета. 0,99 0,95 0,84 0,63 0,37 0,16 0,05 0,01
Рис. 23
Если гипотезы до испытания были равновероятны, то вы-
ражение общей формулы теоремы будущих событий примет вид:
77— Р1<?1 + Р-Я2 + • • • + Pi<li + --+Psc!s
Пример 4. Имеется ящик с 5 одинаковыми шарами. Часть этих шаров
окрашена в белый цвет и часть — в черный. Сколько шаров того или иного
цвета — неизвестно. Из этого ящика был взят один шар, который оказался
белым. Какова вероятность того, что в следующий раз будет вынут черный
шар, если шар, вынутый первым, был возвращен в ящик?
Решение. О составе шаров в нашем ящике мы можем сделать 4 ги-
Пример 5. При тех же условиях, что и в примере 4, определим вероят-
ность появления двух черных шаров, если шар, вынутый первым, поло-
жен обратно в ящик.
100
Решение.
№ гипотез Содержание гипотез Pi Qi Qi<ii
1 4 белых и 1 черный шар . . 4 5 4 10 1 25 4 250
3 3 4 12
2 3 „ ,2 „ я . .
5 10 25 250
2 2 9 18
5 10 25 250
4 1 д 1 1 16 16
5 10 25 250
10 10 50
Сумма 5 10 250
Сравнив решения примеров 4 и 5, мы видим, что не равно П2. Это
объясняется тем, что вероятность появления второго черного шара зависит
от того, какой шар был вынут первым — черный или белый.
Пример 6. Вероятности нахождения цели на участках К, Л, М, Н и О
района возможных положений цели настолько мало различаются по вели-
чине, что их можно считать равными.
При условии нахождения цели на участке К вероятность недолета при
одном выстреле на прицеле 100 равна 0, на участке Л — 0,09, на участке
М—0,5, на участке Н— 0,91 и на участке О — 1. На прицеле 100» произ-
вели один выстрел и получили перелет. Какова вероятность того, что при
следующих двух выстрелах на том же прицеле будут получены один недолет
и один перелет?
Решение.
№ гипотез Содержание гипотез Pl Qi qflpq) QiOi
1 Цель находится на участке К 1,00 100 250 0 0
2 » » » л 0,91 91 250 0,1638 0,0596
3 » м 0,50 50 250 0,5000 0,1000
4 » » * н 0,09 9 250 0,1638 0,0059
5 » О 0 0 0 0
Сумма . . . 2,50 250 250 0,1655
/7 = 0,1655.
101
§ 24. ЗАДАЧИ НА ВЕРОЯТНОСТИ ГИПОТЕЗ
Задача 56. В одном ящике имеется 2 черных и 3 белых шара. Из дру-
гого ящика, в котором имеется 5 черных и 2 белых шара, в первый ящик
был переложен 1 шар, после чего шары в первом ящике были тщательно
перемешаны. Какова вероятность того, что был переложен черный шар, если
после перекладывания из первого ящика был вынут белый шар?
Ответ. ~.
Задача 57. На столе лежит 10 револьверов, из которых один не при-
стрелян. Вероятность попадания в цель из пристрелянного револьвера 0,73,
а из не пристрелянного — 0,23. При выстреле из взятого наудачу револьвера
получен промах. Какова вероятность того, что выстрел был произведен из
непристрелянного револьвера?
77
Ответ______
320
Задача 58. Имеется три группы совершенно одинаковых ящиков. В пер-
вой группе — 3 ящика, во второй — 5 и в третьей — 2. В каждом ящике
первой группы имеется по 2 белых и по 1 черному шару, в каждом ящике
второй группы — по 1 белому и 1 черному шару и в каждом ящике третьей
группы — по 1 белому и по 2 черных шара. Из взятого наудачу ящика
был вынут один шар, который оказался белым. Какова вероятность того,
что шар был вынут из ящика второй группы?
Ответ. .
Задача 59. Вероятности нахождения цели на участках А, Б, В, Г и Д
района возможных положений цели соответственно равны: 0,1, 0,2, 0-,4, 0,2 и
0,1. При условии нахождения цели на участке А вероятность недолета при
одном рыстреле на некоторой установке прицела равна -1-, на участке
112 3
Б — —, на участке В—— , на участке Г— — и на участке Д—
3 2 3 4
При двух выстрелах на данной установке прицела получили два недолета.
Найти наиболее вероятное положение цели после этих двух выстрелов.
Ответ. На участке В; QB = 0,366.
Задача 60. Допустим, что танк противника может двигаться при сле-
дующих курсовых углах: 0°, 45°, 90°, 135° и 180° относительно нашего ору-
дия ПТА. Вероятность того, что танк будет иметь курсовой угол в 0°. равна
0,1, угол в 45’—0,3, угол в 90’—0,3, угол в 135° — 0,2 и угол в 180°—0,1.
Вероятность попадания в неприятельский танк из нашего орудия при кур-
совом угле в 0° равна 0,35, при курсовом угле в 45° —0,27, при курсовом
угле в 90° — 0,24, при курсовом угле в 135° — 0,27 и при курсовом угле
в 180°—0,35.
С первого же выстрела нашего орудия танк противника получил пря-
мое попадание. Какова вероятность попадания в танк при первом выстреле
и под каким курсовым углом, вероятнее всего, шел танк?
Ответ. Р = 0,277; угол 45°.
Задача 61. В закрытом ящике имеется 6 одинаковых шаров, различаю-
щихся только цветом. Из этого ящика был вынут 1 шар, который ока-
зался черным. Какова вероятность того, что в числе 6 шаров, находившихся
в ящике, был только 1 черный шар?
Ответ. JL .
21
102
Задача 62. Имеется три коробки с патронами. В первой коробке 25
патронов, из них 2 неисправных. Во второй коробке 20 патронов, из них
1 неисправный. В третьей коробке 30 патронов, среди них неисправных нет.
Все коробки были вскрыты. Взятый наудачу из первой попавшейся под руку
коробки патрон оказался исправным. Какова вероятность того, что патрон был
взят из второй коробки?
„ 285
Ответ.------
861
Задача 63. В группе—10 человек, из них к зачету подготовили все
20 билетов программы 5 человек, 15 билетов — 3 человека и 10 билетов —
2 человека. На зачете каждому предлагается два билета. Первый вызван-
ный хорошо ответил на оба билета. Какова вероятность того, что вызван-
ный относится к группе знающих все билеты программы?
Ответ. 0,7.
Задача 64. У одного из четырех орудий батареи прицел 72, а у трех
остальных 73. При одном выстреле на прицеле 72 вероятность недолета равна
0,7 и вероятность перелета — 0,3. При одном выстреле на прицеле 73 вероят-
ность недолета равна 0,3 и вероятность перелета—0,7. Стрельба ведется
одним орудием. При первых двух выстрелах были получены недолет и пе-
релет. Какова вероятность того, что при следующем выстреле будет получен
недолет?
Ответ. 0,4.
Задача 65. Вероятности нахождения цели на участках I, II, III, IV и V
района возможных положений цели соответственно равны: 0,05, 0,25,0,40, 0,20
и 0,10. Вероятность перелета при одном выстреле на некоторой установке
прицела и при условии нахождения цели на I участке равна 0,75; при
условии нахождения цели на II участке —0,65; на III участке — 0,50; на
IV участке — 0,35 и на V участке — 0,25. При трех выстрелах на данной
установке прицела получили: недолет, перелет и недолет. Какова вероят-
ность при следующих двух выстрелах на той же установке прицела полу-
чить недолет и перелет?
Ответ. 0,4631.
Задача 66. Имеется 10 совершенно одинаковых закрытых ящиков с
шарами. Ящиков под № 1—три, в каждом из них находится по 2 белых и
по 2 черных шара. Ящик под№ 2—один и в нем находится 3 белых и 2 чер-
ных шара. Остальные ящики—под № 3, в каждом из них находится по 5 бе-
лых и 3 черных шара. Из взятого наудачу ящика 3 раза подряд вынимали
шар и клали его обратно. Были вынуты шары: белый, белый, черный. Ка-
кова вероятность после этого вынуть из того же ящика 2 белых и 1 чер-
ный шар?
Ответ. 0,42.
Задача 67. Имеется закрытый ящик с 3 шарами: белыми и черными.
Взятый из этого ящика шар оказался белым. Какова вероятность по-
явления белого шара еще 3 раза подряд, если вынутый шар каждый раз
кладется обратно в ящик?
Ответ. —.
81
РАЗДЕЛ II
ТЕОРИЯ ОШИБОК
ГЛАВА 5
ЛИНЕЙНЫЕ ОШИБКИ
§ 25. ОШИБКИ ИЗМЕРЕНИЙ
Чтобы определить численное значение интересующей нас
величины (расстояния, веса, объема, температуры и пр.), мы
производим измерение этой величины.
Повседневный опыт убеждает нас в том, что любое изме-
рение, независимо от способа, которым оно производится,
неизбежно сопровождается некоторой погрешностью, некото-
рой ошибкой.
В этом нетрудно убедиться, если одну и ту же величину
(например, расстояние между одними и теми же двумя точ-J
ками) мы измерим несколько раз одним и тем же способом,
одним и тем же прибором. Как бы тщательно ни производи-
лись измерения, получаемые при этом отдельные результаты
будут, хотя бы и незначительно, отличаться один от другого.
С каждым измерением мы будем получать новый результат,
отличающийся, как правило, от полученного ранее. Измеряе-
мая величина в процессе измерения оставалась одной и той
же, а мы получили несколько различных результатов измере-
ния. Очевидно, что ни один из этих результатов не дает
истинного (точного) значения измеряемой величины, каждый
из этих результатов дает только приближенное ее значение.
Отсюда мы делаем вывод, что ошибки при измерениях
неизбежны.
Разность между приближенным и истинным значениями
измеряемой величины называется ошибкой ' или погреш-
ностью измерения.
xi — Aj,
где х0 — истинное значение измеряемой величины;
х, — результат отдельного измерения;
\ — ошибка данного результата измерения.
104
Чем меньше абсолютная величина ошибки, т. е. чем ближе
отдельный результат измерения к истинному значению изме-
ряемой величины, тем точнее произведено данное измерение.
Например, если при измерении одного и того же расстояния
первый результат получен с ошибкой в 10 м, а второй — в
20 ж, то первое измерение было произведено более точно, чем
второе. Точность измерения в первом случае в два раза больше
точности измерения во втором случае.
Абсолютная величина ошибки характеризует точность
данного результата измерения1.
Ошибки отдельных результатов измерения различаются
между собой своими знаками. По знаку ошибки измерения
делятся-на: ошибки положительные, если приближенное зна-
чение измеряемой величины больше ее истинного значения,
т. е. если > х0, и ошибки отрицательные, если прибли-
женное значение измеряемой величины меньше ее истинного
значения, т. е. если хг < х0.
Например, если истинное значение измеряемого расстоя-
ния равно 3G00 м, а отдельные результаты измерения
л3 = ЗЮ0 м и я, = 2850 м,
то ошибки этих результатов:
Д3 = ЗЮ0—3000=+ЮО м (ошибка положительная)
и
Д7 = 2850—3000=—150 м (ошибка отрицательная).
Величина и знак ошибки — основные ее характеристики.
Неизбежность ошибок при измерениях обусловливается тем,
что любое измерение, несмотря на всю его тщательность,
точность применяемых приборов и учет влияния различных
факторов, всегда производится при наличии бесконечно боль-
шого числа источников ошибок. Назовем некоторые из этих
источников.
Несовершенство конструкции измерительных приборов —
неточность шкал (цена их делений), эксцентриситеты лимбов,
мертвые хода, неустойчивость треног и т. д.
Несовершенство наших органов чувств, например, зрения
при снятии отсчетов со шкал, совмещении указателей с деле-
ниями на шкалах, совмещении перекрестий с точками наведе-
ния, горизонтировании при помощи уровня и т. д., слуха при
звуковых засечках и пр.
Метеорологические условия — облачность, ветер, темпера-
тура воздуха, конвекционные токи и т. д.
Каждый источник ошибок дает при измерении свою так
называемую элементарную ошибку. Сумма же всех таких
1 Здесь речь идет о точности отдельного результата, а не о точности
способа измерения.
105
элементарных ошибок и даст в конечном счете ошибку данного
результата измерения.
Существуют особые группы источников ошибок, дающих
при измерении элементарные ошибки, постоянные по вели-
чине и по знаку. Очевидно, что и суммарная ошибка этой
группы источников ошибок будет также постоянна по вели-
чине и по знаку.
Несложными приемами можно определить заранее вели-
чину и знак такой постоянной, или, как ее иначе называют,
систематической ошибки. Зная величину и знак системати-
ческой ошибки, можно ее учесть и исключить из данного ре-
зультата измерения, введя соответствующую поправку.
Пример 1. При проверке гири весом в 1 «г оказалось, что ее дейст-
вительный вес равен 992 г. Чтобы устранить найденную ошибку, необхо-
димо при пользовании этой гирей на каждый килограмм прибавлять по К г.
Пример 2. При проверке 20-метровой мерной ленты оказалось, что
истинная ее длина равна 20,1 м. Тогда систематическая ошибка этой ленты,
распределяясь на всю ее длину, будет равна
20—20,1 ~_0 005 —0,50/0.
20,1 /(Ь
При пользовании этой лентой поправку следует брать в большую сто-
рону на 0,5% от полученного результата измерения.
Пример 3. В результате проверки стереотрубы был составлен график
ее постоянных ошибок в зависимости от величины отсчета (рис. 24). Поль-
зуясь этим графиком, мы можем исключить ошибку данной стереотрубы
из полученного отсчета. Так, если отсчет оказался равным 25-09, то,$ учи-
тывая по графику поправку — 0-02, следует принять отсчет
25-09—0-02=25-07;
получив отсчет 54-87, исправляем его на +0-01:
54-874-0-01=54-88 и т. д.
Систематическая ошибка может получиться и вследствие
различных округлений и допусков при вычислениях, связанных
с измерениями.
Пример 4. Углу в 0-01 соответствует дуга, равная 1/955 дальности. При
переводе линейных величин в деления угломера для облегчения расчетов
1/955 округляется до 1/1000 и тем самым допускается постоянная ошибка
в большую сторону примерно на 5% вычисленного угла.
106
В приведенных примерах даны типичные случаи проис-
хождения и учета систематических ошибок.
Таких источников, дающих постоянные по величине и знаку
элементарные ошибки, сравнительно немного.
Подавляющее большинство источников ошибок дает в усло-
виях данного измерения непостоянные по величине и по знаку
элементарные ошибки, которые имеют случайный, характер.
Случайный характер таких элементарных ошибок, естественно,
определяет и случайный характер ошибок отдельных резуль-
татов измерения, как ошибок суммарных.
Вполне понятно, что комбинация (совокупность) случайных
элементарных ошибок даст случайную суммарную ошибку,
которая и будет ошибкой нашего измерения. Повторив изме-
рение, мы получим другую комбинацию случайных элементар-
ных ошибок и другую суммарную ошибку.
Случайными, называются такие ошибки, которые, явля-
ясь результатом взаимодействия очень большого числа
источников ошибок, при каждом новом измерении получают
новые, случайные значения.
Величину и знак случайной ошибки заранее определить
нельзя, а поэтому и нельзя заблаговременно исключить ее из
данного результата измерения, введя соответствующую по-
правку.
К случайным относятся ошибки, возникающие при изме-
рениях дальностей различными способами, углов различными
приборами, барометрического давления, температур, весов и пр.
К случайным ошибкам относятся также такие величины
случайного характера, как отклонения, неточности, отступле-
ния. Так, если истинная дальность Д=5 200 м, а при изме-
рении получилась дальность Д = 5 050 м, то говорят, что
имеется отклонение, равное
Д — 4=5050-5200==—150 м.
Если снаряд должен иметь длину Zo= 1 010 мм, а в дей-
ствительности его длина /1=1012 мм, то говорят, что отсту-
пление или неточность в размерах равна
l1 — Zo == 1 012 — 1 010 = -+- 2 мм.
Из определения случайной ошибки видно, что ее можно
рассматривать как случайный результат некоторого явления.
Это означает, что к случайным ошибкам можно применить все
те выводы, которые были сделаны в разделе „Основы теории
вероятностей", и, в первую очередь, вывод о закономерностях
конечных случайных результатов явлений.
Раздел теории вероятностей, изучающий случайные ошибки
и закономерности, которым следуют эти ошибки, называется
теопией случайных ошибок или просто теорией ошибок.
107
Теория ошибок устанавливает закономерности, которым
следуют случайные ошибки, и, исходя из этих закономерностей,,
вырабатывает правила, при систематическом применении кото-
рых можно получать наилучшие результаты измерений.
Ошибки, которые характеризуются только величиной и
знаками, называются линейными или не зависящими от на-
правления, в отличие от ошибок, которые характеризуются не
только величиной и знаками, но и направлением (ошибки на
плоскости и в пространстве).
§ 26. ЗАКОНЫ СЛУЧАЙНЫХ ОШИБОК
Условия возникновения случайной ошибки не позволяют
определить заранее ее величину и знак, а отсюда и исправить
полученный результат измерения. Но это отнюдь не означает,,
что случайные ошибки вообще не подлежат учету. Наоборот,
учет этих ошибок необходим, иначе невозможно использовать-
результаты измерений. Надо лишь установить, в чем заклю-
чается и к чему сводится этот учет.
Представим, что требуется открыть огонь по цели, распо-
ложенной в непосредственной близости от своих передовых
частей. Измерили дальность до этой цели. Так как ошибка
при этом неизбежна и неустранима, то, открыв огонь на при-
целе, соответствующем измеренной дальности, мы можем пора-
зить свои войска. Но если нам будет известна величина той
предельной случайной ошибки, которая практически допустима
при данном способе измерения дальности, то, увеличив при-
цел на эту величину, мы гарантируем безопасность своих войск.
Другой пример. Цель не наблюдается. Пристрелка невоз-
можна. Координаты цели сняты с аэрофотоснимка. Произведя
необходимые измерения и расчеты, определили установки для
открытия огня. Неизбежность и неустранимость ошибок застав-
ляют нас вести огонь по цели на нескольких установках — огонь
по площади. Возникает вопрос о размерах этой площади.
Обстреливать площадь соответственно предельным ошибкам
невыгодно — слишком велик расход снарядов, слишком много
времени потребуется на выполнение огневой задачи. Следо-
вательно, необходимо ограничиться обстрелом только тех
участков района возможных положений цели (РВПЦ), где
вероятности нахождения цели значительны, а для этого мы
должны знать вероятности получения различных по величине
и знаку ошибок при определении установок для открытия
огня.
Приведенные примеры показывают, что учет случайных
ошибок не только возможен, но и необходим, ибо без него
невозможно правильно решать важнейшие практические задачи.
Для этого учета необходимо знать, какая при данном способе
измерения существует зависимость между величиной и знаком
108
случайной ошибки и вероятностью ее получения. Эта зависи-
мость выражается соответствующими законами случайных
ошибок.
Зависимость между абсолютной величиной и знаком
случайной ошибки и вероятностью ее получения называется
законом случайных ошибок.
Законов случайных ошибок много. Каждый из них выра-
жает определенную закономерность случайных ошибок, выте-
кающую из условий возникновения этих ошибок.
Например, закон равной вероятности выражает законо-
мерность случайных ошибок, возникающих при округлениях
при снятии отсчетов со шкал приборов. Закон арксинуса выра-
жает закономерность случайных ошибок, возникающих вслед-
ствие эксцентриситетов углоизмерительных приборов, и т. д.
Закономерности случайных ошибок можно найти двояко:
1. Опытным путем. Для этого производится большое
число измерений величины, истинное значение которой заранее
известно. Определяется для каждого отдельного результата его
ошибка. После распределения полученных ошибок по их вели-
чинам и знакам устанавливается зависимость между пределами
ошибок и частостями получения ошибок в этих пределах.
И, наконец, исходя из закона больших чисел, принимаются эти
частости равными соответствующим вероятностям.
2. Аналитическим путем — из анализа условий, в
которых возникают случайные ошибки рассматриваемого закона.
Установленные в результате таких исследований законо-
мерности могут быть выражены аналитически и графически.
Аналитически закон случайных ошибок в общем виде выра-
жается равенством
/7 = F(A),
где А—величина ошибки;
р — вероятность ее получения;
F (функция) — обозначение зависимости, связывающей А
с р, например р = А2.
Если вид функции ^(А) известен, закон ошибок может
быть выражен и графически. Закон ошибок выражается гра-
фически и тогда, когда он был выведен по результатам боль-
шого числа измерений1 2.
В практике артиллерийских измерений в подавляющем
большинстве случаев нам приходится иметь дело со следующими
двумя законами случайных ошибок: законом Гаусса и законом
равной вероятности.
Из этих двух законов наибольший интерес представляет
для нас закон Гаусса2. Достаточно сказать, что закону Гаусса
1 О графическом выражении закона ошибок подробно сказано в § 27.
2 Часто закон Гаусса называют нормальным законом случайных ошибок.
109
следуют рассеивание снарядов и ошибки таких измерений, как
измерения дальностей глазомерным способом, по карте и
дальномером, измерения азимутов, измерения температур,
весов и пр.
§ 27. ВЫВОД ЗАКОНА СЛУЧАЙНЫХ ОШИБОК ГАУССА
Уже было указано, что к выводу закона случайных оши-
бок можно подойти двумя путями — опытными аналитическим.
Найдем основные положения закона случайных ошибок
Гаусса сначала опытным путем, обработав результаты доста-
точно большого числа измерений, случайные ошибки которых
следуют именно этому закону.
Воспользуемся для этого таким примером. 170 одинаково
обученных разведчиков при производстве одной и той же марш-
рутной глазомерной съемки промерили шагами расстояние
между одними и теми же точками на местности и перевели
результаты своих промеров в метры. Таким образом было полу-
чено 170 приближенных значений величины этого расстояния.
Это же расстояние было промерено приборами с такой
точностью, что по сравнению со способом промера шагами
полученный результат без особых погрешностей может быть
принят за истинное значение величины данного расстояния.
Этот результат оказался равным 3 000 м.
Пользуясь этим точным результатом, определим ошибки
отдельных результатов промера шагами и сведем все наши
расчеты в следующую таблицу (табл. 4).
Таблица 4
i xi i xi i xi l xi 4 i xi
1 2 883 —117 1J 3021 +21 23 3 001 + 1 34 2 942 -58 45 3 047 +47
2 2 904 —96 13 2 955 -45 24 2 982 —18 35 3 025 +25 46 2 974 —26
3 3 119 4-119 14 3 093 +93 25 2 915 —85 36 2 996 47 2931 —69
4 2 859 —141 15 3 188 + 188 26 3 002 +2 37 2 884 —116 48 2 878 —122
5 ЗОЮ + 10 16 3 041 +41 27 3 140 + 140 38 28И —186 49 3 099 +99
6 3 062 +62 17 2 991 —9 28 3 014 + 14 39 3030 +30 50 3 147 + 147
7 3135 + 135 18 2 968 —32 29 2 960 —40 40 2982 -18 51 2 989 —11
8 2 986 —14 19 3 065 +65 .30 3 051 + 51 41 2 947 —53 52 2 923 -77
9 3 078 +78 20 2 998 —2 31 3 236 +236 42 2 930 —70 53 3 053 +53
10 3 107 + 107 21' 2 944 —56 32 3 124 + 124 43 3 022 +22 54 3 083 +83
11 2999 —1 22 2 925 —75 33 2 964 —36 44 3159 + 159 55 2 994 -6
110
1 xi i xi i xi i xi i xi
56 2 902 -98 79 2 990 —10 102 3 044 +44 125 2 921 1 1 —79 148 2 980 —20
57 3034 +34 80 3 019 + 19 103 2 873 —127 126 3 118 + 118*149 3 057 +57
58 2 940 —60 81 3 005 +5 104 2 832 —168 127 2 996 —4.150 3137 + 137
59 2 889 —111 82 2 900 —100 105 2 977 —23 128 2971 —29151 3 030 +30
60 3054 +54 83 3 032 ,+32 106 3 095 +95 129 3064 +64 152 2 993 —7
61 3128 + 128 84 3 121 + 121 107 2 967 -33 130 2 954 —46153 3 126 + 126
62 2 981 —19 85 2 959 —41 108 3 109 + 109 131 3 015 + 15i 154 3 039 +39
63 2 937 -63 86 3130 + 130 109 3196 + 196 132 2 941 -59 155 3018 + 18
64 2 851 —149 87 3 059 +59 ПО 3 033 +33 133 2 919 —81 156 2 965 —35
65 3 045 +45 88 2 896 —104 111 2 979 -21 134 2 807 — 193 157 2 903 —97
66 3 095 +95 89 2 776 —224 112 2 844 —156 135 3 004 +4 158 3 072 +72
67 3025 +25 90 2 951 —49 ИЗ 3 007 +7 136 3 085 +85 159 2908 -92
68 3 164 + 164 91 3115 + 115 114 3 021 +21 137 3178 + 178 160 3067 +67
69 2 984 —16 92 3 150 + 150 115 2 755 —245 138 3 103 + 103 161 2 948 -52
70 2 880 -120 93 2 929 —71 116 2 976 —24 139 2 910 -90 162 2 869 -131
71 3017 + 17 94 2 999 —1 117 3 133 + 133 140 2 962 —38 163 2 920 —80
72 2 909 —91 95 3 028 +28 118 3016 +16 141 3 003 +3 164 3 042 +42
73 2 952 —48 96 3 076 +76 119 2 898 —102 142 3 049 +49 165 3012 + 12
74 3037 +37 97 2 969 —31 120 2 927 —73 143 2 987 —13 166 3 088 +88
75 3 050 +50 98 3 055 +55 121 3 067 + 67 144 2 936 -64 167 2 871 —129
76 3 001 + 1 99 2 913 -87 122 3 144 + 144 145 3060 + 60 168 3045 +45
77 2 934 —66 100 2 866 —134 123 3 074 +74 146 3036 + 36 169 2 762 -238
78 2 947 —53 101 ЗОИ + 11 124 2 939 —61 147 3 089 +89 170 2 862 —138
Чтобы установить зависимость между величиной и знаком
случайной ошибки и частостью ее получения, разобьем
ошибки ряда измерений на группы через каждые 50 лг по их
величине и знаку. Так, в 1-ю группу сведем все отрицатель-
ные ошибки величиной от 201 м до 250 м, во 2-ю группу —
отрицательные ошибки величиной от 151 м до 200 м, и т. д.
Определим количество ошибок в каждой такой группе и най-
дем соответствующие частости их получения (табл. 5).
111
Таблица 5
По данным этой таблицы видно, как часто были получены
случайные ошибки в определенных по величине и знаку пре-
делах. Следует при этом отметить, что при разбивке ошибок
на группы именно через 50 м, мы исходим только из сообра-
жений удобства такой разбивки — предельная по величине
ошибка равна около 250 м, а 250 без остатка делится на 5.
Для большей наглядности представим зависимости, данные
в табл. 5, в виде графика. Для этого по оси ОХ в обе сто-
роны от точки О отложим пределы ошибок через 50 м в услов-
ном масштабе, а по оси OY — в другом условном масштабе
частости получения ошибок в этих пределах (рис. 25).
На этом графике площадь каждого прямоугольника в от-
дельности выражает частость получения случайной ошибки
в определенных по величине и знаку пределах, а площадь всего
графика — сумму частостей получения всех случайных ошибок.
112
Прежде чем перейти к общим выводам, воспользуемся
опытными данными еще одного ряда многократных измере-
ний — 580 результатами измерения одной и той же дальности
дальномером (табл. 6) и построим для этого ряда график
частостей (рис. 26).
Таблица 6
Пределы ошибок в % Ошибки отрица- тельные Ошибки поло- жительные
дальности коли- чество частости В °/о коли- чество частости В °/о
От 0 до ± 0,25 „ ±0,25 до ±0,50 „ ±0,50 „ = 0,75 „ ±0,75 „ ±1,00 .. ±1,00 , ±1,25 „ ±1,25 „ ±1,50 „ ±1,50 „ ±1,75 . ±1,75 „ ±2,00 „ ±2,00 , ±2,25 , ±2,25 „ ±2,50 76 70 54 40 21 19 6 4 1 1 13,10 12,07 9,31 6,89 3,62 - 3,28 1,04 0,69 0,17 0,17 78 66 52 38 23 18 6 5 1 1 13,45 11,38 8,97 6,55 3,96 3,11 1,04 0,86 0,17 0,17
Всего . . . 292 50,34 288 49,66
Рис. 26
•ч
Мы построили два графика по результатам большого и
вместе с тем различного числа измерений, произведенных раз-
ными способами. Нетрудно заметить, сравнив эти графики, что
они очень схожи по своему виду. Это позволяет сделать вывод,
что зависимость между величиной и знаком ошибки, с одной
8 — Зак. 991
113
стороны, и частостью получения ошибки, с другой стороны,
во всех тех случаях, когда случайные ошибки измерений сле-
дуют закону Гаусса, устанавливается по одному и тому же
.общему правилу:
1. Чем больше ошибка, пгём меньше частость ее полу-
чения— высоты прямоугольников обоих графиков убывают
по мере увеличения величины ошибки.
2. Частости ошибок отрицательных и частости оши-
бок положительных, заключенных в равных по величине
пределах, примерно равны между собой—прямоугольники,
равноудаленные от оси OY, имеют примерно одни и те же
высоты, т. е. прямоугольники относительно оси OY распола-
гаются по высоте примерно симметрично. Сравнив второй
график с первым, замечаем, что при большем числе измере-
ний график получился более симметричным. Исходя из этого,
мы можем допустить, что график, построенный по результа-
там очень (бесконечно) большого числа измерений, должен
быть совершенно симметричным, т. е. частости равных по
абсолютной величине и разных по знаку ошибок должны быть
равны между собой (рис. 27).
у
Рис. 27
3. Для каждого способа измерения существует свой
предел ошибок — оба графика не имеют разрывов, и прямо-
угольники, соответствующие частостям предельных по вели-
чине ошибок, стремятся слиться с осью ОХ (особенно это
заметно на втором графике).
Эти три положения и определяют закон случайны^ оши-
бок Гаусса, выведенный на основании обработки ^эйытных
данных. ‘
Использовав закон больших чисел, мы можем сделанные
нами выводы применить к зависимости между величиной и зна-
ком ошибки и вероятностью ее получения, т. е. полагать, что:
— с увеличением ошибки вероятность ее уменьшается,
чем меньше ошибка, тем больше ее вероятность;
114
— равные по абсолютной величине, но разные по знаку
ошибки равновероятны — вероятность получения ошибки по-
ложительной равна вероятности получения ошибки отрица-
тельной, равной первой по абсолютной величине;
— для каждого способа измерения существует свой
предел ошибок', ошибки, превышающие по своей величине
этот предел, имеют настолько малую вероятность получения,
что практически эту вероятность принимают весьма близкой к
нулю и такими ошибками пренебрегают.
Короче эти три положения можно сформулировать так:
ошибки распределяются неравномерно, симметрично и не-
беспредельно.
Это и есть выражение закона Гаусса в общем виде.
Если соединить середины верхних оснований прямоуголь-
ников общей кривой (см. рис. 27), то эта кривая, носящая
название палатки Эйлера, будет графически выражать те же
три основных положения закона Гаусса.
Вероятность получения ошибки в заданных пределах вы-
ражается отношением площади, ограниченной частью кривой,
заключенной между соответствующими ординатами, к пло-
щми, ограниченной всей кривой.
V Так, вероятность получения положительной ошибки в пре-
делах от а до b (см. рис. 27) выражается отношением пло-
щади abed к площади АВС; вероятность получения отрица-
тельной ошибки в пределах от / до ^-—отношением площади
efkl к площади АВС и т. д. Л
Обозначив площади, соответствующие пределам ошибок,
через sn s2, s3,..., и сложив эти площади, получим:
+ S2 + 53 + • • • +
где 5—площадь, ограниченная всей кривой.
Разделим левую и правую части этого равенства на 5,
и тогда
J4- J_ I _£з_ I I — 1
Это значит, что сумма вероятностей всех возможных в
условиях данного ряда измерений случайных ошибок равна
единице, что и должно быть согласно следствию теоремы
сложения вероятностей.
Так как площадь, ограниченная всей кривой, выражает
сумму вероятностей, равную единице, то можно принять эту
площадь также равной единице. Тогда элементарные пло-
щадки будут численно равны вероятностям, которые они
выражают.
Из выражения вероятности получения ошибки площадью,
•граниченной ординатами, соответствующими заданным преде-
Vе
115
дам, следует, что вероятность получения определенной по
величине и знаку ошибки равна нулю, так как в этом случае
ординаты, ограничивающие площадь, сольются и такая вероят-
ность будет выражена одной ординатой—линией. Поэтому
можно говорить о вероятности получения ошибки только в
некоторых пределах, как бы эти пределы ни были малы, на-
пример, о вероятности получения ошибки в пределах от
4,99999 и до 5,00001 м и т. п.
Рис. 28
Кривая закона Гаусса очень наглядно подтверждает все
уже известные нам основные положения этого закона. Поло-
жим, что разности пределов ошибок, вероятности получения
которых выражены площадями sn s2, Ss и s4> равны между
собой (рис. 28):
/2 —— /д '== /4 = /.
Тогда:
— чем меньше ошибка, тем больше вероятность ее полу-
чения: Si > s2 и s2 > s3;
— ошибки положительные и ошибки отрицательные, за-
ключенные в одинаковых по абсолютной величине пределах,
равновероятны:
$2 — S4;
— вероятность получения ошибки, превышающей по
своей величине некоторый предел (—ОА или + ОС), равна
нулю, так как кривая АВС на некотором удалении от
оси О Y — в точках А и С - - сливается с осью ОХ.
Для различных способов (рядов) измерения кривые закона
Гаусса будут также различны.
Но так как установленная в общем виде зависимость
между пределами ошибок и вероятностями их получения в
этих пределах выражается одними и теми же положениями,
то и кривые всегда сохраняют свой характер.
Для того чтобы иметь возможность сравнивать вероят-
ности получения ошибок в заданных пределах для различных
)16
рядов измерений, необходимо строить соответствующие этим
рядам кривые так, чтобы площади, ограниченные каждой из
этих кривых, были равновелики. Это требование, естественно,
вытекает из того, что такие площади во всех случаях прини-
маются равными единице. Для соблюдения этого требования
кривые должны быть построены в одном и том же масштабе
по оси ОХ, а по оси ОY в масштабе, измененном во столько
раз, во сколько раз основание одной кривой больше (меньше)
основания другой, т. е. необходимо соблюсти примерно тот
принцип построения, который ранее был применен при по-
строении графиков вероятностей комбинаций.
На рис. 29 показаны кривые закона Гаусса для двух раз-
личных способов (рядов) измерения.
Этот рисунок позволяет нам сделать следующие заклю-
чения:
1. Каждая из этих кривых полностью подтверждает поло-
жения закона Гаусса.
2. Вероятности получения ошибки в определенных по
величине и знаку пределах, например от а до Ь, для каждого
способа измерения свои, так как площади
abed ф abef.
3. Способ измерения, закон ошибок которого выражен
кривой более точен, чем способ, закон ошибок кото-
рого выражен кривой АВС, так как первому способу свой-
ственны меньшие предельные ошибки, чем второму:
ОА, <ОА и OQ < ОС.
4. По условиям построения обеих кривых ограниченные
ими площади равновелики. Отсюда чем меньше основание
кривой (чем меньше ошибки), тем больше ее наивысшая
ордината, т. е. тем точнее способ измерения. Следовательно,
117
по наивысшей ординате данного закона Гаусса можно судить
о точности способа измерений, сравнивать ее с точностью
другого способа, если, конечно, при построениях выдержаны
масштабы.
Очень наглядное представление о законе случайных оши-
бок Гаусса дает так называемый прибор Гальтона (рис. 30).
В воронку А бросают большое
количество дробинок (шариков).
Эти дробинки, падая по наклонной
плоскости дна ящика Б, встречают
на своем пути ряд тонких стерж-
ней (булавок или иголок, вбитых в
дно ящика). Ударясь об эти стержни,
играющие в приборе роль источ-
ников ошибок (отклонений), дро-
бинки, меняя при каждом таком
ударе направление своего движе-
ния, попадают в различные ячейки В.
Так как удары дробинок о стержни
и связанные с этими ударами изме-
нения движения каждой дробинки
носят, несомненно, случайный ха-
рактер, то в результате получается
распределение дробинок по ячей-
кам, весьма схожее с распределе-
нием случайных ошибок при изме-
рениях в том случае, если эти
ошибки следуют закону Гаусса. На рис. 30 показано такое
распределение пунктирной кривой.
Мы вывели основные положения закона случайных ошибок
Гаусса путем обработки и анализа опытных данных. К тем же
выводам мы придем, проанализировав условия возникновения
случайных ошибок этого закона.
Допустим, что в условиях данного ряда измерений имеется
восемь источников ошибок. Каждый из этих источников при
каждом отдельном измерении дает элементарные ошибки:
aj = + 1 или а2 = —1, т. е. элементарные ошибки, равные по
абсолютной величине и отличающиеся только знаками.
Допустим также, что вероятности получения положитель-
ной и отрицательной ошибок равны между собой:
Здесь было допущено две условности: взято небольшое
число источников дшибок и сделано предположение, что все
эти источники дают одну и ту же по абсолютной величине
элементарную ошибку. Поэтому величина элементарной ошибки
118
умышленно не выражена в принятых единицах измерения.
Далее будет видно, что эти условности не отразились на
правильности выводов.
Любой из восьми источников ошибок при каждом отдель-
ном измерении может дать как положительную ошибку, так
и ошибку отрицательную. В результате совместного действия
всех восьми источников ошибок может быть получена одна из
следующих суммарных ошибок:
Ai = +8; Д4 = +2; А7 = - 4;
Д2=+6; А5= 0; Д8 = - 6;
А3 = +4; А6 = - 2; Д9 ——8.
Суммарная ошибка Ai = +8 будет получена, если все
восемь источников ошибок дадут только положительные эле-
ментарные ошибки:
. Aj = + 1+1+1+1+1 Ч- 1 + 1 + 1 + 8.
Суммарная ошибка Д2 = +6 будет получена в том слу-
чае, когда семь источников ошибок дадут положительные
•элементарные ошибки и один источник — отрицательную:
Д2 — + 1 + 1-И + 1 + 1 + 1 + 1 — 1 = 4-6.
Суммарная ошибка А3 — +4 будет получена, если шесть
источников ошибок дадут положительные, а два источника
ошибок—отрицательные элементарные ошибки:
А3 = + 1 + 1 + 1 + 1 + 1 + 1 — 1—-1 = + 4 и т. д.
Так как элементарные ошибки всех наших источников
ошибок отличаются только знаками, то и любую из перечис-
ленных выше суммарных ошибок , можно рассматривать как
комбинацию из двух противоположных по знаку элементар-
ных ошибок при восьмикратном повторении действия одного
и того же источника ошибок.
Отсюда при определении вероятностей получения этих
-суммарных ошибок можно воспользоваться формулой вероят-
ности получения комбинации из двух противоположных со-
бытий при восьмикратном повторении испытания при условии,
что p — q — :
п <4 т п 8! / 1 \т[ 1 \п 8! / 1 у
’ /и!л! Р У т\п\ \ 2 ) \ 2 J т\п\ \ 2 ) ’
где т — количество источников, давших положительные эле-
ментарные ошибки;
и—количество источников, давших отрицательные эле-
ментарные ошибки.
119
Например, вероятность получения суммарной ошибки
А3 = 4-4 будет равна
р — ____[ J_\8— _2§ — о Ю94*
^3— б!2! \2 J— 256 ”
вероятность получения суммарной ошибки Де — --2(4-14-14-
4- 1 — 1 — 1-1-1 — 1)
п 8! / 1 56 aoiqq
— 3!5! \ 8 ) ~ 256 ~ 0,2188 И Т. Д.
Рассчитаем вероятности получения всех возможных в
условиях нашего примера суммарных ошибок и сведем эти
расчеты в таблицу (табл. 7).
Таблица 7
Pi A. i Pi A; Pi
4-8 0,0039 4-2 0,2188 —4 0,1094
4-6 0,0312 0 0,2734 —6 0,0312
+ 4 0,1094 2 0,2188 —8 0,0039
Сложив эти вероятности, получим:
9
2 ^=i.
1
что свидетельствует, во-первых, о полном учете всех воз-
можных по величине и знаку суммарных ошибок и, во-вторых,
о правильности расчетов.
Данные этой таблицы показывают, что:
— с увеличением ошибки вероятность ее получения
уменьшается;
— ошибки, равные по абсолютной величине и разные по
знаку, равновероятны;
— ошибки по своей величине не выходят за пределы zb8.
4Р. А это значит, что мы
“ 4 пришли к тем же трем по-
--I ложениям закона случайных
ошибок Гаусса, которые
~| ранее установили опытным
путем, — неравномерность,
симметричность и небеспре-
дельность.
Более наглядно эти же
. ~~ t— III —t -е г три положения выражает
-в-6-4-2 о +2 +4 *6 *8 график, построенный по дан-
Рис. 31 ным табл. 7 (рис. 31).
120
В приведенном выводе положений закона случайных оши-
бок Гаусса было сделано два допущения:
1. Число источников ошибок ограничено (8).
2. Все источники ошибок дают одни и те же по абсолют-
ной величине элементарные ошибки: «! = +! и а2 —— 1.
Выясним, не повлияют ли эти два допущения на правиль-
ность только что сделанных выводов.
Для этого прежде всего установим зависимость между
величиной и знаком ошибки и вероятностью ее получения
в том случае, если число источников ошибок станет увели-
чиваться.
Представим, что в условиях данного измерения действуют
не восемь, а шестнадцать источников ошибок, причем каждый
из них дает одинаковые по абсолютной величине элементар-
ные ошибки: «! = +! и а2 = —1.
Рассчитаем все возможные в данных условиях суммарные
ошибки и вероятности их получения. Расчеты эти представим,
в виде графика (рис. 32).
Этот график еще полнее выражает положения закона'
Гаусса. Так при восьми источниках ошибок вероятность полу-
чения предельной по величине ошибки (±8) нельзя еще счи-
тать пренебрежимо малой (0,0039), при шестнадцати же источни-
ках вероятности получения ошибок +16 (0,00002), +14 (0,00024)
и даже zt12 (0,00183) настолько малы, что такими ошибками
можно уже пренебречь.
Несомненно, что при дальнейшем увеличении числа источ-
ников ошибок выведенные нами положения закона Гаусса бу-
дут только подтверждаться, и в построении графиков для боль-
шего числа источников ошибок нет надобности.
Сравнивая графики рис. 31 и 32, построенные в одних и<
тех же масштабах, «мы можем заметить, что с увеличением
числа источников ошибок „ступенчатость" графика начинает
121
сглаживаться. Очевидно, что эта „ступенчатость" будет тем
меньше, чем больше источников ошибок, и при бесконечно
большом числе источников ошибок эта „ступенчатость" должна
исчезнуть — верхние основания прямоугольников графиков дол-
жны образовать плавную кривую, которая была получена при
обработке опытных данных (см. рис. 27). Такой же вид приняла
бы кривая распределения вероятностей комбинаций при беско-
нечно большом числе повторений испытания. Поэтому тогда
мы и назвали такую кривую кривой Гаусса1.
Итак, мы установили основные положения закона Гаусса,
допустив ограниченное число источников ошибок, и это допу-
щение не отразилось на правильности наших выводов. Теперь
посмотрим, как повлияет на эти выводы наличие в условиях
данного измерения нескольких групп источников ошибок, отли-
чающихся величинами своих элементарных ошибок.
Допустим, что в условиях данного измерения имеется три
группы источников ошибок:
— первая группа из восьми источников ошибок с элемен-
тарными ошибками: а\ = + 1 и а'2 = - 1;
— вторая группа из шести источников ошибок, элементар-
ные ошибки которых: а'4 = 4-2 и а% = —- 2;
— третья группа из пяти источников ошибок с элементар-
ными ошибками: а'4 = 4- 3 и а'4 = — 3.
Суммарные ошибки первой группы источников ошибок и
соответствующие этим ошибкам вероятности были нами уже
найдены (см. табл. 7).
При действии источников ошибок только второй группы
могут быть следующие суммарные ошибки: 1'4 = 4-12,
14 = 4-8, 1% = 4-4, 4"4==0, 4%=—4, 1% = — 8 и 1\ = —12.
Вероятности этих ошибок, как вероятности комбинаций из
.двух противоположных событий при шестикратном повто-
рении испытания, равны:
р7 ____ 1 pv ___ 6 . pv __ 15 р-, _ 20 р„ __ 15 pV ___ _6_
1 — 64 ’ 2 ~ 64 ’ 3 — 64 ’ 4 “ 64 ’ 5 64 ’ 6 64
И PV г- - ———
И У ‘ 64 •
При действии источников ошибок только третьей группы
суммарные ошибки таковы: 1'4 = 4-15, 1'4 =4-9, 1'4 = 4-3,
.1'4 = ~3, 4'4 — —9 и 4'4 = —15, а их вероятности:
рч'__1_1_ рч' _ 5 рт ___ 10 рщ ___ Ю pw ___ 5 pW ____1
32 ’ 2 32 ’ 3 — 32 » 4 “ 32 ’ 5 ~ 32 6 32 *
При совместном действии всех трех групп источников оши-
бок может быть любое совпадение суммарных ошибок этих
групп. Каждое такое случайное совпадение даст случайную же
результирующую ошибку, равную сумме суммарных ошибок.
1 См. § 12, рис. 19.
122
Например, если первая группа источников ошибок даст
ошибку Д'3 = +4, вторая группа —Д"6 = —8 и третья группа—
Д"'1 = +15, то результирующая для всех трех групп ошибка
Д = Д'3 + Д"6 + Д'\ = + 4 — 8 + 15 = + П;
другие совпадения дадут другие по величине и знаку резуль-
тирующие ошибки.
Предельная по величине результирующая ошибка будет
получена при совпадении предельных по величине суммарных
ошибок:
Д\ + Д\ + Д'\ = + 8 + 12 +15 = + 35 и
Д'9 + Д'\ + Д"6 = — 8— 12— 15 = — 35.
Остальные результирующие ошибки, которые могут быть
при совместном действии трех групп источников ошибок,
естественно, не выйдут из этих пределов: +35, +33, +31,
... +5, +3, +1, —1, —3, —5, . . . —31, —33, —35.
Что результирующие ошибки будут именно таковы, в этом
можно легко убедиться, если сложение отдельных суммарных
ошибок производить в определенной системе по следующей
схеме (табл. 8).
Результирующая ошибка, получающаяся при совместном
действии нескольких групп источников ошибок, есть событие
сложное. Поэтому и вероятность получения такой результи-
рующей ошибки, как вероятность сложного события, равна
произведению вероятностей суммарных ошибок ее составляю-
щих.
Так, вероятность результирующей ошибки +35 равна
произведению вероятностей составляющих суммарных ошибок:
Р^ = Р/ • Р,г • = - =0,000002.
Рассматривая табл. 8, можем заметить, что подавляющее
большинство результирующих ошибок имеет несколько
вариантов.
Так, например, результирующая ошибка +29 получилась
в двух вариантах:
+ 2 + 12 + 15 = + 29 и + 8 + 12 + 9 = + 29,
а результирующая ошибка +23 получилась в трех вариантах:
— 4+12+15 = -+23; +2-|-12 + 9 = +23 и
+ 8 + 12 + 3 = + 23 ит. д.
123
Т а б л и ц а 8
Д’ А" Д’” А Д’ А7 Д'7 А Д’ А7 Д'” д А’ А7 Д'" А Д’ д7 Д'" д
-4"8 + 12 + 15 + 35 +8 + 12 +9 +29 +8 + 12 +3 -4-23 +8 + 12 —3 + 17 +8 + 12 —9 + 11
4" 6 + 12 +15 +33 +6 + 12 +9 +27 +6 + 12 +3 +21 +6 + 12 —3 + 15 4-6 + 12 —9 + 9
+4 + 12 + 15 +31 + 4 +12 +9 +25 +4 4-12 +3 +19 +4 + 12 —3 + 13 +4 + 12- —9 + 7
+ 2 + 12 + 15 +29 +2 + 12 +9 + 23 +2 4-12 +3 + 17 +2 + 12 —3 + 11 +2 + 12 —9 + 5
0 + 12 + 15 4-27 0 + 12 +9 + 21 0 + 12 +з + 15 0 + 12 —3 + 9 0 + 12 —9 + з
—2 + 12 + 15 4-25 —2 + 12 +9 + 19 —2 + 12 + 3 + 13 —2 + 12 —3 + 7 —2 -1-12 —9 + 1
-4 + 12 + 15 4-23 — 4 + 12 +9 + 17 —4 + 12 4-3 + 11 —4 + 12 —3 + 5 -4 + 12 —9 — 1
-6 + 12 + 15 +21 -6 + 12 +9 +15 —6 + 12 +з -г 9 —6 + 12 —3 + з —6 + 12 —9 — 3
-8 + 12 + 1’5 + 19 —8 12 +9 + 13 —8 + 12 +з + 7 -8 + 12 —3 + 1 —8 + 12 -9 — 5
и т. д.
Отсюда следует, что при определении вероятности полу-
чения результирующей ошибки необходимо учитывать все ее
варианты, применяя теорему сложения вероятностей.
Табл. 8 не закончена, так как в ней только показан метод
определения величин результирующих ошибок. В полной та-
блице результирующая ошибка +29 имеет еще один вариант:
+ 6+ §+15 = +29. Таким образом, вероятность ее полу-
чения:
р —56 1 J_(_L 1 5 8 6 1 _
29 — 256 ’ 64 ‘ 32 “И 256 64 ‘ 32 + 256 64 ’ 32 —
= ~ 0,000208.
Результирующая ошибка -\-27 имеет уже четыре варианта:
1. + 8 + 4 + 15= +27. . - Л = 256' 64 ' 32 = 524288 ’
2. + 6+ 12 + 9= +27. . . Р2 = 256 ' 64 ' "32 ~ ’ 524288 ’
° Л _L ft 1 R 97 р — 28 6 1 — 168
9. + 4 + б , 10 > ... Н3 — 25б ' 64 ' 32 — 524288 ’
4. 0+12 + 15 = + 27. . . Р4 = 256 * 64 ' II ~ 524288 ’
откуда вероятность результирующей ошибки
р) 15 4- 40 + 168 + /0 _ 293 ___л лллггл
Р+27 524288 524288 0,000559 И Т. Д.
Для систематизации таких расчетов можно рекомендовать
в табл. 8 добавить вертикальные графы для вероятностей
Рис. 33
125
вариантов результирующих ошибок, после чего останется
только сложить вероятности одинаковых по величине и знаку
вариантов. Все такие расчеты для нашего примера, представ-
лены на рис. 33.
Рассматривая этот график, можно видеть, что и при дей-
ствии нескольких групп источников ошибок установленные
три основных положения закона случайных ошибок Гаусса
остаются в силе.
§ 28. ЧИСЛЕННОЕ ВЫРАЖЕНИЕ ЗАКОНА ГАУССА (ШКАЛА ОШИБОК}
Для практического использования выведенных трех поло-
жений закона случайных ошибок Гаусса необходимо устано-
вить численное выражение этих положений, т. е. необходимо
установить, какая существует численная зависимость между
заданными пределами ошибок и вероятностью получения оши-
бок в этих пределах.
Положения закона Гаусса едины для всех способов (рядов)
измерений, случайные ошибки которых следуют именно этому
закону. Очевидно, что численное выражение этих положений
должно быть также единым. Это значит, что пределы, отно-
сительно которых опр?Хёля1от вероятности получения ошибки,,
должны выражаться в каких-то единых мерах, общих для всех
рядов измерений, независимо от метрической величины оши-
бок (способа измерения и характера измеряемой величины).
Только при этом возможно оценить как точность отдельных
результатов независимо от способа измерения, так и точность
самих способов.
Точность данного способа измерений характеризуется
величинами возникающих при этом способе ошибок, — чем
точнее способ, тем меньше ошибки, тем больше вероятность
получения таких ошибок. Поэтому за общую, единую меру,
выражающую пределы ошибки для всех способов измерения,,
а отсюда и за меру точности любого способа измерения, сле-
дует принять величину какой-то ошибки.
Допустим, что два способа измерения одной и той же
величины дали следующие два ряда ошибок:
1-й способ: 4-5, — 7, — 2, 4-4, 4-8, — 3 и 4- 9;
2-й способ: -12, —6, 4-18, 4-1, —9, 4-12 и —10.
Очевидно, что первый способ по сравнению со 2-м явля-
ется более точным, так как он дал меньшие по величине
ошибки.
Если за меру точности брать отдельные случайные ошибки
из этих двух рядов, то выводы будут самые противоречивые.
Так, по ошибкам первых результатов измерения (4-5 и —12)
можно заключить, что 1-й способ точнее 2-го; ошибка же вторых
результатов (—7 и —6) приводит к противоположному выводу.
Нельзя также брать и наименьшие ошибки (—2 и 4-1), так
126
как в этом случае 2-й способ окажется точнее 1-го, что явись
не соответствует действительности. Отсюда следует вывод,
что за меру точности данного способа измерения отдельную
случайную ошибку брать нельзя.
При необходимости дать характеристику ряду (совокуп-
ности) различных величин (предметов) обычно берется какая-то
средняя величина.
Например, имея партию из 17 яблок различной величины
и желая одним яблоком, не показывая всех, дать хотя бы
приблизительное представление о величине яблок всей партии,
мы, естественно, выберем среднее по величине яблоко.
Аналогично этому при оценке точности данного ряда
измерений за меру точности, характеризующей этот ряд,
берется средняя ошибка.
Средних ошибок, как это будет видно дальше, несколько:
из всех средних ошибок в артиллерийской практике за меру
точности принято брать так называемую срединную ошибку.
Такое название этой ошибки объясняется тем, что она нахо-
дится в середине ряда ошибок, расположенных по своим абсо-
лютным величинам в возрастающем или убывающем порядке.
• Вернемся к двум рядам ошибок и расположим эти ошибки
по их абсолютным величинам в возрастающем порядке:
1-й способ: 2, 3, 4, 5, 7, 8, 9;
2-й способ: 1, 6, 9, 10, 12, 14, 18.
В первом ряду ошибка, занимающая срединное место,,
равна 5, во втором ряду—10. Из сравнения этих двух сре-
динных ошибок видно, что 1-й способ действительно точ-
нее 2-го.
Для оценки партии яблок было взято среднее по величине
яблоко. При расположении всех яблок в ряд в возрастающем по
их величине порядке (рис. 34) таким средним (срединным) оказа-
лось девятое яблоко.
1 2 3 4 5 6 7 в 9 10 11 12 13 14 15 16 17
Рис. 34
Занимая срединное место, это яблоко по своей величине
больше каждого из яблок одной (правой) половины и меньше
каждого из яблок другой (левой) половины всей партии
яблок. По аналогии, этим же свойством характеризуется и сре-
динная ошибка.
Срединной ошибкой называется такая ошибка, которая
по своей абсолютной величине больше каждой из ошибок
одной половины и меньше каждой из ошибок другой поло-
вины всех ошибок, расположенных в ряд в возрастающем
или убывающем порядке.
127
Таблица 9
№ д № д Ns д № д № д № д № д № д Ns д № д
1 —1 18 — 11 35 +21 52 + 32 69 —48 |86 +6О| 103 476 120 +95 137 -120 154 4144
2 — 1 19 + 11 36 +21 53 —35 70 -49 87 -61 104 —77 121 -96 138 + 121 155 + 147
3 + 1 20 +12 37 + 22 54 -36 71 + 49 88 +62 105 +78 122 -97 139 —122 156 —149
4 4-1 21 —13 38 -23 55 + 36 72 +50 89 —63 106 —79 123 -98 140 + 124 157 4150
5 —2 22 -14 39 —24 56 + 37 73 +51 90 -64 107 —80 124 +99 141 + 126 158 -156
6 + 2 23 + 14 40 +25 57 -38 74 —52 91 4 64 108 —81 125 —100 142 —127 159 + 159
7 4- 3 24 + 15 41 425 58 439 75 -53 92 +65 109 483 126 -102 143 + 128 160 + 164
8 —4 25 -16 42 -26 59 — 40 76 —53 93 -66 ПО -85 127 + юз 144 —129 161 — 168
9 —4 26 + 16 43 +28 60 —41 77 + 53 94 +67 111 485 128 — 104 145 + 130 162 + 178
10 +4 27 + 17 44 —29 61 +41 78 +54 95 467 112 -87 129 4107 146 — 131 163 —186
11 + 5 28 —18 45 +30 62 +42 79 + 55 96 -69 113 + 88 130 + 109 147 + 133 164 4188
12 -6 29 — 18 46 +30 63 + 44 80 —56 97 -70 114 +89 131 -111 148 -134 165 —193
13 —7 30 + 18 47 —31 64 —45 81 +57 98 —71 115 -90 132 +11э 149 4-135 166 + 196
14 + 7 31 -19 48 -32 65 +45 82 —58 99 + 72 116 -91 133 —116 150 + 137 167 —224
15 -9 32 +19 49 +32 66 +45 83 —59 100 —73 117 -92 134 —117 151 — 138 168 +236
16 —10 33 —20 50 -33 67 -46 84 +59 101 +74 118 +93 135 + 118 152 + 140 169 —238
17 +ю 34 -21 51 433 68 +47 |85_ -6°| 102 —75 119 +95 136 + 119 153 —141 170 —245
Исходя из этого определения, можно опытным путем най-
ти величину срединной ошибки, характеризующей точность
данного ряда (способа) измерений.
Из определения срединной ошибки следует, что вероят-
ность получения ошибки, которая по абсолютному значению
больше (или меньше) срединной ошибки, равна половине..
Так, если срединная ошибка способа измерений равна
25 м, то вероятность получения ошибки больше 25 м (или
меньше 25 м) равна половине.
Эти свойства срединной ошибки и обусловливают ее как.
меру точности, а отсюда и меру, посредством которой выра-
жается численная зависимость между пределами ошибки и
вероятностями ее получения в этих пределах.
Для отыскания такой численной зависимости применимы
те же методы, что и при выводе положений закона Гаусса.
Прежде всего, найдем такую зависимость путем обработки
опытных данных, использовав численные примеры, приведен-
ные в § 27.
В первом из этих примеров было 170 результатов проме-
ра расстояния шагами (см. табл. 4).
Расположим в возрастающем порядке абсолютные вели-
чины ошибок этих 170 промеров (табл. 9) и найдем срединную
ошибку этого ряда измерений, исходя из определения средин-
ной ошибки.
При 170 измерениях срединная ошибка в ряде ошибок
должна занимать место между 85-й и 86-й 'ошибками. Абсо-
лютная величина и 85-й и 86-й ошибок равна 60 м, следова-
тельно, срединная ошибка рассматриваемого ряда измерений
также равна 60 м.
Чтобы определить частости получения ошибки в пределах,
выраженных в срединных ошибках, разобьем все ошибки на
группы через каждые 60 м (табл. 10), обозначив при этом
величину срединной ошибки буквой Е.
Таблица 10
Ошибки в метрах от . . . до -300 —241 —240 -181 -180 -121 -120 -61 -60 0 0 +60 + 61 + 120 + 121 + 180 + 181 +240 + 240 +300
в величине срединной ошибки от . . .до —5Е —4Е —4Е —ЗЕ —ЗЕ —2Е —2Е —Е —Е 0 0 +f +£ + 25 +2Е + 35 Н-35 +45 +475 + 55
Количество ошибок 1 4 10 28 41 45 23 15 3 0
Частости ошибок В °/о 0,59 2,35 5,88 16,48 24,12 26,47 13,53 8,82 1,76 0
9 — Зак. 991
129
Используем теперь данные второго примера, в котором
были приведены 580 результатов измерения дальности с по-
мощью дальномера (см. табл. 6 и рис. 26).
Для этого ряда измерений срединная ошибка равна 0,5%
дальности, так как именно такая ошибка занимает место между
290-й и 291-й ошибками. В этом легко убедиться, если сложить
количества всех положительных и отрицательных ошибок^
полученных в пределах от 0 до+ 0,5% дальности:
76 + 78 + 70 + 66 = 290.
Разобьем ошибки этого ряда на группы через каждые 0,5%
дальности и определим для этого случая частости получения
ошибки в пределах, выраженных в срединных ошибках
(табл. И).
Таблица 11
S
в процентах дальности от . . .до —2,5 —2,0 —2,0 — 1,5 — 1,5 -1,С —1,0 —0,5 —0,5 0 0 +0,5 +0,5 +1,0 +1,0 + 1,5 + 1,5 +2,0 +2,0 +2,5
+ЗЕ
+Е
+4Е
—4Е
-ЗЕ
-ЧЕ
+ ЧЕ
-5Е
—Е 0
в величине
срединной
ошибки
от . . .до
—4Е
—ЗЕ
-2Е
0 I +Е
4-2Е
+ ЗЕ
+4Е
+ 5Е
Количество
ошибок
10
40
94
146
144
90
41
Частости ошибок
в 0 о
0,34 1,73 6,90 16,20 25,17 24,83 15,52 7,07
1,90 0,34
S
О
2
—Е
И 2
Сравнив нижние строчки табл. 10 и И, можем заметить, что
частости получения ошибок в одних и тех же пределах, вы-
раженных в срединных ошибках, примерно равны между
собой.
130
Взяв средние значения частостей, допустим, что при очень
большом числе измерений частости получения равных по аб-
солютной величине и разных по знаку ошибок равны между
собой. Тогда, применив закон больших чисел, можем числен-
ную зависимость между пределами ошибок, выраженными
в срединных ошибках, и вероятностями получения ошибок
в этих пределах представить графиком, изображенным на
рис. 35.
Источников ошибок, получаемых в условиях любого из-
мерения, бесконечно много. Не исключена возможность, что
источники ошибок дадут при отдельном измерении или только
положительные, или только отрицательные элементарные
ошибки. В этих случаях, несмотря на то, что элементарные
ошибки по своей величине бесконечно малы, суммарная ошиб-
ка может быть сколь угодно большой — теоретически от — оо
до 4- оо.
Вероятности получения таких ошибок ничтожно малы, и
ими можно пренебречь. Поэтому основание кривой Гаусса
ограничено пределами + 6 Е (см. рис. 35).
Но и вероятности получения ошибок в пределах от—-6Е
до — 4£ и от + 4£ до + 6Е также очень невелики:
0,0004 + 0,0031 + 0,0031 + 0,0004 = 0,007 == 0,7%.
Практически [такими ошибками можно также пренебречь,
и тогда численно закон Гаусса с некоторыми округлениями
может быть выражен шкалой, изображенной на рис. 36.
-»£ -ЗЕ -2Е -£ о ♦ £ +4£
0,02 0,07 0,16 0,25 0,25 0,16 0,07 0,02
Рис. 36
Эта шкала называется шкалой ошибок. Такой шкалой
ошибок, как правило, пользуются при расчетах, связанных
с теоретическими обоснованиями артиллерийской стрельбы.
По шкале ошибок можно видеть подтверждение основ-
ных положений закона Гаусса. Действительно:
1. С увеличением ошибки уменьшается вероятность ее
получения (0,25 — 0,16 — 0,07 — 0,02).
2. Вероятности получения ошибок отрицательных и оши-
бок положительных, заключенных в одних и тех же пределах,
равны между собой (0,25 и 0,25; 0,16 и 0,16 и т. д).
3. Практическим пределом ошибки для любого способа
(ряда) измерений является предел ±4£'.
К такой же шкале ошибок можно притти и другим пу-
тем— путем анализа возникновения случайных ошибок, следую-
щих закону Гаусса.
9: 131
На рис. 33 § 27 даны вероятности получения случайных
ошибок при совместном действии трех групп источников
ошибок.
Найдем для этого ряда ошибок такой предел, относи-
тельно которого вероятности получения большей и меньшей
по величине ошибки равны между собой, т. е. равны поло-
вине.
Сложив вероятности получения ошибок: — 5, -—3, —1,
4-1, 4-3 и 4- 5, получим:
2(0,088421 4- 0,084316 4- 0,076605) = 0,498684.
Результат сложения очень близок к 0,5, следовательно,
искомый нами предел лежит между 5 и 7, т. е. равен 6.
Приняв величину срединной ошибки равной 6, разобьем
все ошибки на группы через каждые 6 (единиц) и определим
вероятности получения ошибки для каждой такой группы
(табл. 12).
Таблица 12
Пределы ошибок - 6£ —5£ -5Е —ЛЕ ~АЕ —ЗЕ -ЗЕ —ЧЕ —2Е —Е —Е 0 0 +Е +ЧЕ 4-2Е +ЗЕ 4-3£ +4Я +4£ 4-5F +5£ +6£
Вероятность получения ошибок в °/0 0,0082 0,2068 1,6786 6,8203 16,3519 24,9342 24,9342 16,3519 о ОО 1,6786 0,2068 0,0082
Отбросив вероятности получения ошибки в пределах от
±42: до ±62: и произведя округления до целых процентов,
получим те же: 2%, 7°/., 16%, 25°/0, 25%, 16%, 7°/0 и 2%.
Пределы приведенной выше шкалы ошибок выражены
в целых Е. При расчетах, требующих большей точности, сле-
дует пользоваться шкалой, пределы ошибок которой выражены
в долях Е: 0,52: или 0,25Е (табл. 13).
Эта таблица показывает, что закон Гаусса графически
действительно может быть выражен кривой, так как по мере
уменьшения пределов ошибок вероятности их получения все
меньше и меньше отличаются друг от друга по своей вели-
чине и график, построенный в очень небольших долях Е, не-
сомненно, будет иметь вид кривой.
Шкала ошибок может быть построена и несколько иначе
(рис. 37).
Нетрудно заметить, что числа 0,50, 0,82, 0,96 и 1,00 по-
казывают вероятности получения ошибки в пределах от 0 до
± Е, от 0 до ± 2Е и т. д.
Вполне понятно, что такую шкалу можно составить с лю-
бой точностью — в любых долях Е. Шкала ошибок, состав-
ленная по этому принципу в сотых долях Е (с точностью до
132
Таблица
о 0,015 200*0
П)0*0
о 0,005 I 500*0
800*0
+ со о 110*0
о" Н0*0
о о о 610‘0
о Н,0‘0
+ о 180*0
о /80‘0
О со о Ж>*0
о 150*0
+ <м 950*0
1О о 190*0
см сГ со 990*0
О _ о /90*0
со /907)
ч ю о 990*0
о <м 190*0
Щ - о’ 950*0
1 со о 150*0
о Ж)‘0
о о /80*0
о- о 180*0
i о 1z60‘0
о 610*0
о со о ^10*0
о 110’0
со - ю 800*0
о о о 500 *э
о* ю Ш)‘0
<,00 *0 1
J
0,0IE), имеет вид таблицы [см. прило-
жение 1, таблица значений Ф(^)]. Этой
таблицей пользуются при расчетах, тре-
бующих особой точности. Кроме того,
эта таблица по сравнению с обычной
шкалой ошибок в некоторых случаях
упрощает технику расчетов.
-4£ -ЗЕ -2Е -Е о +2Е *3£
1-----L— 1 - 1 • —
0,02 । 0,07 1 0,16 ' 0,25 0,26 1 0,16 ' 0,07 0,02
I 1'1’ । I । ’
I > Ь*— 0.50 । •
I ' <1
। -------0,82-------।
U.-----------0,96 ----------
1,00
i
I
I
l
I
I
>
Puc. 37
Шкала ошибок, какой бы вид она
ни имела, дает возможность решить сле-
дующие две основные задачи:
1. Определить вероятность получе-
ния ошибки в заданных пределах.
2. Оценить точность данного резуль-
тата измерения, зная его срединную
ошибку.
Покажем это на примерах.
Начнем с определения вероятности
получения ошибки в заданных пределах.
Допустим, что дальность до цели стре-
ляющим определена в 4 000 м, а сре-
динная ошибка данного способа изме-
рения равна 80 м.
Найдем, прежде всего, какие ошибки
мог при этом допустить стреляющий
и каковы вероятности этих ошибок.
Построим для этого шкалу ошибок,
выраженную в величинах срединной
ошибки (рис. 38).
5 2 5 5 2 2 $
о о см со о 00 о оэ О О <3 см
♦ + ♦
-4/ -ЗЕ •2Е -Е 0 ♦и *2Е +4£
0,02 0.07 0,16 0,25 0,25 0,16 0,07 0,02
Рис. 38
При рассмотрении этой шкалы можно
сделать следующие выводы.
133
1. Наибольшая ошибка, которую практически мог допустить
стреляющий, не должна превышать 320 м как в большую,
так и в меньшую сторону (±4Е), т. е. истинное значение
величины измеренной дальности заключено в пределах: 4 000 м
zb 320 л/, от 3 680 до 4 320 м.
2. Вероятность того, что стреляющий ошибся в меньшую
сторону не более чем на 80 м, т. е. вероятность того, что
истинное значение величины измеренной дальности заключено
в пределах от 4000 м до 4 080 м, равна 0,25 = 25%. Вероят-
ность же того, что была допущена ошибка в большую сто-
рону от 160 м до 240 м, т. е. вероятность того, что истин-
ное значение величины измеренной дальности заключено
в пределах от 3 760 м до 3 840 м, равна 0,07 = 7°/0 и т. д.
^•3. Вероятность получения ошибки, не превышающей 80 м,
независимо от ее знака, т. е. вероятность того, что истинное
значение величины измеренной дальности заключено в преде-
лах 4 000 л + 80 м (от 3 920 м до 4 080 м), равна 0,25 +
+ 0,25 = 0,50 = 50%. Вероятность же ошибки, не превышаю-
щей 160 м в обе стороны (+2Д), т. е. вероятность того, что
истинное значение величины измеренной дальности заключено
в пределах от 3 840 м до 4160 м, равна 0,16 + 0,25 + 0,25 +
+ 0,16 = 0,82 = 82% и т. д.
По этой же шкале мы можем определить вероятность по-
лучения ошибки в любых заданных пределах, т. е. пределах,
не совпадающих с целыми Е.
Найдем, например, вероятность получения ошибки в пре-
делах от — 50 м до — 100 м.
Как мы видим, такая ошибка частично захватывает два
предела (рис. 39).
./60м -100м -80м *50м
-2Е '• -Е J
и.-------------------------------
20м ' 30м ।
* ’ U-- 50м
►ч--1--- Ю0м ------
Рис. 39
Допустив, что в пределах каждой Е ошибки распреде-
ляются равномерно, мы можем составить следующие про-
порции:
80 м — 0,25 и 80 м — 0,16
30 м — ру 20 м,—р2
Откуда
30-0,25 20-0,16 А п.
А = —8Q— = 0,09375 и р2 = —= 0,04.
Искомая же вероятность
Р=Pl 4- А = 0,09375 + 0,04 = 0,13375 13,4° в.
134
Несколько более точный ответ будет получен, если взять
шкалу ошибок, выраженную в долях Е, например в 0,5£
(рис. 40).
30-0,12 п пп 20-0,09
= —ад—= 0,09; А = —4Q— =0,045;
£> = 0,09 +0,045 = 0,135= 13,5%.
-»Б0м -120м -80м - 40м 0
: 0,07 i 0,09 0,12 , 0,13 !
*—. .1 *. .I < I. , ,, । . ।
--- 50м —
г»------- 100м ----------»Д
Рис. 40
И, наконец, наиболее точный ответ даст таблица значений
<>(£). В этой таблице приведены вероятности в пределах от
О до ± причем эти пределы выражены в сотых долях Е
(через 0,01/:). Ход решения при пользовании таблицей зна-
чений Фф) таков (рис. 41):
-1,25Е - 0,625 Е + 0,625 Е + 1,25Е
-100м -50м 0 +50м + 100м
к 0,13 709 к к 0,13 709 -н
I К---- 0,32665 ----»н [
-------------- 0,60003 -----------
Рис. 41
1. Выразим пределы нашей ошибки в долях Е, разделив
каждый из них на 80 м:
50:80- 0,625Е и 100:83- 1 ,25 Е.
2. Найдем по таблице значений Ф(3) вероятности получе-
ния ошибки в пределах от 0 до + 0,625 Е и от 0 до ±1,25/?:
рх = 0,32419 4- 0,00246 = 0,32665 и р.2 = 0,60083.
3. Вычтем из большей вероятности меньшую, т.е. найдем
вероятность получения ошибки в пределах от zt 50 м до + ЮОлс
(независимо от знака):
0,60083 — 0,32665 = 0,27418.
4. Определим искомую вероятность, разделив полученный
результат на 2, так как ошибки отрицательные и положитель-
ные, заключенные в одинаковых пределах, равновероятны:
р = = 0,13709 ~ 13,7° „.
135
Наибольшая точность решения по таблице значений Ф(^)
обусловливается тем, что допущение равномерности распреде-
ления ошибок в пределах, выраженных в сотых долях Е, ска-
зывается очень незначительно, так как малы сами пределы.
Зная величину срединной ошибки данного способа измере-
ния, а также величину ошибки отдельного- результата, поль-
зуясь шкалой ошибок, можно оценить точность этого резуль-
тата.
Допустим, что действительная дальность до цели равна
6000 м. Стреляющий, применив способ, срединная ошибка
которого равна 10% измеряемой дальности, определил даль-
ность до цели в5 500 лг, т. е. допустил ошибку, равную 500 м.
При рассмотрении шкалы ошибок, построенной по данной
срединной ошибке (рис. 42), можно сделать следующее заклю-
чение.
< । < <
-ЗЕ -ZE
‘ 0,02 ' 0,07 ' 0,16
5
О
С5
чэ
+
0 ♦£
0,25 0.25
0,16 0,0 7 0,02
Рис. 42
Ошибка стреляющего не выходит за пределы.+ 600 м, т. е..
за пределы rtf’. Вероятность получения ошибки в этих преде-
лах равна 0,50, т. е. ошибка, не выходящая за эти пределы,
может быть получена в среднем в 50 случаях из 100, а поэтому
можно считать, что определение дальности стреляющим было
произведено с достаточной точностью.
Если же дальность до цели стреляющим была определена
в 4 500 м, т. е. с ошибкой —1500 м, то такой результат для
данного способа измерения следует считать мало точным, так
как вероятность получения ошибки в пределах от zb 1 200 м.
до 4-1 800 равна всего 0,14, т. е. такая ошибка может быть
получена только в 14 случаях из 100 в среднем. Определение
дальности в 3500 м,, т. е. с ошибкой, превышающей 4Е, сви-
детельствует (за редким исключением) о том, что стреляющий
данным способом измерения не владеет.
Заметим, что такие рассуждения положены в основу оценки
точности подготовки исходных данных при выполнении артил-
лерийских стрельб.
§ 29. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ И СРЕДНЯЯ КВАДРАТИЧЕСКАЯ
ОШИБКИ И ЗАВИСИМОСТЬ МЕЖДУ НИМИ И СРЕДИННОЙ
ОШИБКОЙ
Определение величины срединной ошибки по ее месту
в ряде абсолютных значений ошибок (обозначается при
небольшом числе измерений не обеспечивает нужной точности.
136
При таких условиях не исключена возможность того, что даже
одно добавочное измерение может в значительной степени
изменить суждение о величине срединной ошибки, а отсюда и
о точности данного способа измерения.
Предположим, что в результате 11 измерений одной и
той же величины некоторым способом получили ряд ошибок
и расположили абсолютные значения этих ошибок в возрастаю-
щем порядке:
1, 2, 3, 3, 4, 6, 8, 10, 14, 17, 20;
срединная ошибка этого ряда
Ерр = б.
Допустим, что произведено еще одно измерение — 12-е.
Это измерение, очевидно, может дать ошибку, которая по-
своему абсолютному значению будет меньше или больше средин-
ной ошибки.
Если 12-е измерение даст ошибку, меньшую срединной
ошибки, например 2, то срединная ошибка нового ряда (1, 2,
2, 3, 3, 4, 6, 8, 10, 14, 17, 20)
Е — 4~^6 — 5
Если же 12-е измерение даст ошибку, большую средин-
ной ошибки, например 13, то срединная ошибка такого ряда
(1, 2, 3, 3, 4, 6, 8, 10, 13, 14, 17, 20)
р ___ 6 + 8 _„
Ерр — 2 —' ' *
Способ измерения оставался один и тот же, а срединная
ошибка в зависимости от результата только одного добавоч-
ного измерения приняла значения вместо 6: или 5, или 7.
Разница, как видим, весьма существенная.
Поэтому при определении величины срединной ошибки по-
небольшому числу результатов измерений, — а с таким числом,
как правило, и приходится иметь дело на практике,—необ-
ходимо учитывать численные значения всех ошибок данного
ряда измерений, т. е. применить, вместо расположения ошибок
в ряд, метод расчета. Тогда результаты отдельных измерений
не скажутся так значительно на величине срединной ошибки,
как это было в приведенном выше примере.
При определении величины срединной ошибки по резуль-
татам измерений методом расчета пользуются, как правило,
величинами средних ошибок: средней арифметической и
средней квадратической.
Как производятся эти расчеты, подробно будет разобрано-
дальше — в главе „Обработка результатов измерений". Здесь
только установим, какие численные зависимости существуют
137
в законе Гаусса (свойственны этому закону) между средней
арифметической и средней квадратической ошибками и средин-
ной ошибкой как общепринятой в артиллерийской стрельбе
мерой точности.
Средней ариф иетической ошибкой (Еу) называется мате-
.матическое ожидание абсолютного значения ошибки.
Или в общем виде:
Еу = М.О. {I ДI} = | | • рх 4- |Д21 'Ръ 4" I Дз । *^з + « • • 4-
4- =
где Еу — средняя арифметическая ошибка;
| А* | — абсолютные значения ошибок;
pi — соответствующие вероятности этих ошибок.
Исходя из этого определения, найдем зависимость между
средней арифметической ошибкой Ех и срединной ошибкой Е.
Для упрощения вывода сделаем допущение, что в преде-
лах, выраженных в целых Е, ошибки по своей величине рас-
пределяются равномерно, т. е. для этих пределов можно взять
•средние значения ошибки (рис. 43), выраженные в долях Е.
'4е ’21е -’iE 'V 4е ‘4е *-2 е
-4£ '-ЗЕ I-2E ! -Е ! О ! *Е 1*2£ '-зе
ь-... J - . 1 1-.I । - - j . —L L —I 1-1 < I •
0,02 0,07 0,16 0,25 0,25 0,16 О',07 0,02
Рис. 43
Так, для пределов от 0 до zcE такое среднее значение
ошибки может быть принято равным ± Е, для пределов от ± Е
:±:2Е— может быть принято равным ± 1 -^-Е и т. д.
Вероятности таких абсолютных средних значений ошибки
согласно шкале ошибок:
р . =0,25 4-0,25=0,50;
< *2*
р . =0,16 4-0,16 = 0,32 и т. д.
Тогда средняя арифметическая ошибка, как математическое
ожидание абсолютного значения ошибки:
Еу = ~ Е-0,50 4- 1-у £-0,32 4- 2~ F-0,14 4- 3~ 0,04 =
__ 50 4-96 + 70 4-28 F 244 р __ 122 р~ 6 р
~ 200 L ~~ 200 72 “100 ~ 5 С‘-
Откуда
Е------ Е
С.— Q Су.
13S
Если допустить равномерность распределения величин
ошибок в пределах, выраженных не в целых Е, а в долях Е,
результат получился бы более точным. Использовав таблицу
значений Фф), получим наиболее точный результат:
£ = 0,84535 Е. я Ev
Покажем справедливость установленной зависимости между
Е и ЕА на численном примере. На рис. 33 § 27 даны величины
ошибок и вероятности их получения при действии трех групп
источников ошибок.
Найдем математическое ожидание абсолютного значения
ошибки, учтя, что ошибки, равные по абсолютной величине и
разные по знаку, равновероятны, т. е. удвоим вероятности
получения ошибок:
= 1.0,088421 • 2 + 3 • 0,084316 • 2 + 5 • 0,076605 - 2 +
4-7-0,066296-2+9-0,054577-2+ 11-0,042646-2 + 13-0,031582-2 +
+ 15-0,022091-2+ 17-0,014530-2 + 19-0,008953-2+
+ 21-0,005129-2 + 23-0,002704-2 + 25-0,001301-2 +
+ 27-0,000559-2 + 29-0,000208-2 + 31 -0,000065-2 +
+ 33-0,000015-2 4- 35-0,000002-2 = 7,067888.
Откуда
£ = 0,84535 • 7,067888-5,975.
Ранее (см. стр. 132) было установлено, что срединная ошибка
этого ряда может быть принята равной 6.
Пример 1. Определить величину срединной ошибки способа измерений,
если средняя арифметическая ошибка равна 30 м.
5
Решение. Е — 0,84535• 30 = 25,3605 м, или Е — "g~ 30 — 25 м.
Пример 2. Определить величину средней арифметической ошибки, если
срединная ошибка способа измерения равна 20 делениям угломера.
Решение. Д — 20': 0,84535 = 23,651 деления угломера, или Ех ‘>=
5
= 20:-g- — 24 делениям угломера.
Перейдем теперь к средней квадратической ошибке,
которую принято обозначать через Е2.
За среднюю квадратическую ошибку принимают величину,
равную корню квадратному из математического ожидания
квадрата ошибки.
____________________________________ Г s
~ + ^Ч^Р2 + +2£з + • . • + &S2pS "у Pi •
откуда
= д12 Pi + VP2 Н- дз2Рз + - - - + ±s2Ps = 5 +/+
1
139
Исходя из этого последнего равенства, установим зависи-
мость между средней квадратической и срединной ошибками.
Возьмем для этого средние значения ошибок, выразив их
в долях £, аналогично тому, как это было сделано выше при
выводе зависимости между Ег и Е (см. рис. 43).
Произведя соответствующие подстановки в общей фор-
муле Е^, получим:
Е* = ^4" Е У ’ 0,50 + / 1 -i- Е У • 0,32 + ( 2-±- Е J - 0,14 +
+ ( 3± ^у-0,04 = 4- -0,50-£2 + •0,32-£2 +
-0,14-£2 + ~ - 0,04 • £2 = - + 2881Q-50----1— Е2 = 22*-£2.
Извлечем квадратный корень из обеих частей равенства:
£2= 1,48661 1,5£=4 Е>
откуда
2
£==4£,.
Более точные расчеты по таблице значений Ф(^) дадут:
£ = 0,67449 Е^ ^-Е2.
Покажем справедливость этой зависимости, воспользо-
вавшись тем же численным примером, что и для Ег:
£22 = I2 -0,176842 + З2.0,168632 + 52-0,153210 + 72-0,132592 +
+ 92-0,109154 + Н3-0,085292 + 132-0,063164 + 153-0,044182 +
+ 172-0,02906 + 192 - 0,017906 + 212-0,010258 + 232-0,005408 +
+ 252-0,002602 + 272-0,001118 + 292-0,000416 + 312-0,000130 +
4- ЗЗ2 • 0,000030 + 352 • 0,000004 = 76,999904.
Откуда
Е2 = К 76,999904 = 8,775.
Тогда
Е = 0,67449 Е2 = 0,67449 • 8,775 = 5,91864985 5,92.
Как видно, результат очень близок к тому, который был
цолучен при определении Е по Ег и разложением в ряд.
Пример 3. Определить величину срединной ошибки способа измерения,
если средняя квадратическая ошибка равна ЗаО м.
9
Решение £ = 0,67449-300 - ‘202,347 м, или Е = ~+ '300= 200 м.
140
Пример 4. Срединная ошибка равна 0-04. Найти величину средней
квадратической ошибки.
Решение. Е2 = 4 :0,67449 5,9301 деления угломера, или Л, —
2
= 4: -д- = 6 делениям угломера.
Между средней арифметической и средней квадратической
ошибками можно легко установить зависимость через средин-
ную ошибку:
р___ 2 р __ р
3 ^2 б"^1’
откуда
Ех = Е^, или Е,~ ^~ЕХ,
1 О 4 1
точнее
= 0,79787£2 и 52 = 1,25334£\.
Пример 5. Средняя арифметическая ошибка способа измерения равна
0-24. Найти величину средней квадратической ошибки.
5
Решение. Е2 ~ ~г -24 = 0-30.
£ 4
Следует заметить, что средняя арифметическая и средняя
квадратическая ошибки могут быть использованы и исполь-
зуются (в особенности последняя) как параметры, характери-
зующие точность способа измерения.
§ 30. ЗАКОН РАВНОЙ ВЕРОЯТНОСТИ
В практике артиллерийских измерений постоянно прихо-
дится сталкиваться с необходимостью округлять результаты
измерений, что, естественно, влечет за собой ошибки — ошибки
округления.
Такие ошибки возникают, прежде всего, в тех случаях,
когда мы, снимая отсчеты со шкал измерительных приборов,
вынуждены по тем или иным соображениям брать эти отсчеты
в целых делениях этих шкал, т. е. не можем или не хотим
брать на-глаз дробные части делений.
Например, измеряя дальность с помощью дальномера,
деления на шкале которого нанесены через 100 м, и округляя
результаты до сотен метров, мы будем допускать ошибки,
различные по величине и знаку в зависимости от того, какое
положение в момент снятия отсчета будет занимать указатель
относительно промежутка между двумя соседними делениями
шкалы.
Так, если указатель окажется в положении (рис. 44)
и будет принята дальность равной 2100 м, то будет допущена
ошибка в меньшую сторону примерно на 25 м. Если же
указатель в момент снятия отсчета займет положение
дальность будет определена в 2 200 м, то будет допущена
ошибка в большую сторону на те же 25 м. При положении
141
указателя дальность может быть округлена как до 2 100л«,
так и до 2 200 м— ошибки округления в этом случае будут
равны: либо — 50 м, либо + 50 м. И, наконец, если указатель
окажется в положении либо „а“, либо отсчеты будут
сняты без округлений, т. е. ошибки будут равны нулю.
Этот пример показывает, что ошибки округлений могут
быть как отрицательными, так и положительными, и что по
своей величине эти ошибки не могут превысить некоторого
вполне определенного предела — предела, равного половине
цены деления шкалы прибора ( + — 'j •
с
е - 2200
-2300
Рис. 44
Совершенно очевидно, что указатель при снятии отсчета
с одинаковой вероятностью может оказаться против любой
точки шкалы в пределах ее деления. Следовательно, ошибки
округления равновероятны. Поэтому и принимают, что ошибки
округления следуют закону равной вероятности.
Ошибки округления возникают и тогда, когда приходится
переводить результаты измерений в установки тех или иных
приборов.
Так, например, переводя исчисленную дальность до цели
в установки прицельных приспособлений, эту дальность выра-
жают в целых делениях прицела и уровня, оставляя зачастую
неучтенным остаток или излишек дальности. И в этом случае
ошибки округления не будут превышать половины цены
деления уровня ^от 0 до ± 4" ДУр) и будут равновероятны.
Таким образом, сущность закона равной вероятности
заключается в том, что вероятность получения ошибок*
следующих этому закону, не зависит от величины самих
ошибок и для некоторых пределов есть величина постоянная.
Для большей наглядности представим этот закон в виде
графика (рис. 45).
Обозначим цену одного деления прибора через 2Z и от-
ложим по оси ОХ в обе стороны от точки О в произволь-
ном масштабе отрезки, равные I. Это значит, что ошибки не
должны выходить за пределы от 0 дог+г/.
142
Ошибки равновероятны независимо от их величины..
Следовательно, вероятности их получения должны быть выра-
жены равными по высоте ординатами. Если мы построим такие
ординаты для всех возможных по величине и знаку ошибок
в пределах от 0 до±/ и соединим их вершины общей линией,,
то получим прямую CD, параллельную оси ОХ. Эта парал-
лельность и выражает равновероятность ошибок.
При графическом выражении вероятностей получения
ошибок в различных по величине и знаку пределах эти вероят-
ности принимают равными площадям, ограниченным ординатами,
соответствующими заданным пределам.
Например, вероятность получения ошибок в пределах от
Д-l до Д2 принимают равной площади abed-.
p = abcd = ab-h — {^ —
В этом выражении неизвестно h. Найдем зависимость
между h и I, так как именно I как половина цены деления
шкалы прибора характеризует точность этой шкалы.
Сумма вероятностей получения всех возможных по вели-
чине и знаку ошибок для закона равной вероятности может
быть выражена площадью ABCD, а эта площадь должна быть,
равна единице:
р-= ABCD— AB-h — Zl-h—X,
откуда
Тогда вероятность получения ошибки в указанных пре-
делах
р = (Д2-Д,)-Л = (Дг-Д,)- 47 = -?Г-
Пример 1. Деления на шкале дальномера нанесены через 100 м. Какова
вероятность того, что при считывании дальности будет допущена ошибка
в большую сторону не более 20 м!
Решение. По условию: 2/ = 100 м, А) = 0 и Д2 = + 20 м. Подставив
численные значения 2/, Д] и Д2 в общую формулу, получим:
д2 — Д1 +20 — 0 _
Р ~ 21 “' 100 “ °’2’
Пример 2. В условиях примера 1 определить вероятность допущения
ошибки в меньшую сторону не менее 10 м и не более 40 м.
Решение. Здесь Aj = — 40 м и Д2 = — Ю м. Тогда
— 10 —( — 40) +30_
Р~ 100 ~ 100 — и’й-
Пример 3. Какова вероятность того, что в установке прицела будет
допущена ошибка, не превышающая 10 м, если АХ = 50 м?
Решение. 21 = 50 м, Д5 = — 10 м и Д2 = + 10 м. Тогда
113
Перейдем теперь к мере точности для закона равной
вероятности. Найдем выражение для срединной ошибки этого
закона.
Срединная ошибка Е характеризуется тем, что вероятность
получения ошибки в пределах от нуля до ± Е равна 0,5.
Приняв \ — — Ер и Д2 — + Ер, где Ер — срединная ошибка
закона равной вероятности, и подставив эти значения Aj и Д2
в общую формулу, получим:
1 _ +Ер — ( — Ер} _ 2ЕР __ Ер
2 ~ 21 ~ 21 ~ I '
откуда
рр__ 1
~~ 2 ‘
Обычно для суждения о точности закона равной вероят-
ности пользуются другой его характеристикой — средней ква-
дратической ошибкой Ер.
Средняя квадратическая ошибка равна корню квадратному
из математического ожидания квадрата ошибки:
Ер— А*)/?! + Ajp2 4" - - • 4" &sps .
Так как для закона равной вероятности
P1=zp2=p3z=z . . . -psz=p~--~,
то
Ер =
^2 —
(Д? + Дг +
Aj 4- ^2 * • • +&$
+ 4) 4,
Выразим ошибки Др Д2, . . . ,Д$ в долях Z. Разобьем
для этого одно деление шкалы (2/) на 8 равных частей — пре-
Рис. 46
делов (рис. 46) и возьмем для каждого такого предела сред-
нее значение величины ошибки. Так, для предела от 0 доз±:^/
такое среднее значение
Д1=(о±| /) :2 = ± 1Z;
144
. 1 , , 2 r
для предела от 4: Z до ± Z
Д, = (±4 z + ±4z) :2 = ±11 и т- д-
Вероятности получения ошибки в каждом из этих преде-
лов равны между собой, а так как пределов по условию 8,
то и вероятность получения ошибки
_ 1 _
Р ~ 2/ “ 8 ’
Заменив в приведенной выше формуле Д2 • • • и т. д.
соответствующими средними значениями и подставив вместо
р — получим:
= vT-
В этом выражении коэфициент 2 показывает, что каждая
из ошибок может быть как положительной, так и отрицатель-
ной.
21 1
При округлении до была допущена ошибка:
1 21 _ 61 —63 _ 1
3 64 " 192 ““ 192 ’
Если бы отрезок 2Z был разделен не на 8, а на 16 равных
частей, то
РР__1 + 9 + 25 + 49 + 81 + 121 + 169 + 225) 2 Г _
И Z 256 ’ 16 “
V ’ 256 ~ V ' 3 “ v/з *
D ~ 85 1
В этом случае округление до у даст уже ошибку:
1 85 256 — 255 __ 1
3 256 ~ 768 — 768 ’
При делении отрезка 2Z на бесконечно большое число
равных частей мы получим точную зависимость:
£? = —U-.
уз
10 — Зак. 991
145
Пример. Определить срединную и среднюю квадратическую ошибки
при снятии отсчетов с угломерного кольца стереотрубы.
Решение. 21 — 0-01; I — 0-00,5 = 0,5 деления угломера. Тогда
I
2
Ер =
0,5
2
= 0,25
деления угломера;
_ 1 0,5
Е% = у~з'~ ~ ~ 0,29 ж 0,3 деления угломера.
§ 31. ЗАДАЧИ НА ЛИНЕЙНЫЕ ОШИБКИ
Задача 68. Найдены следующие величины ошибок отдельных результатов
измерения одного и того же угла: 4- 0-10, —0-05, 4- 0-07, —0-03, —0-01,
-f-0'04 , 4- 0-06, —0-02, 4-0-01, 0-00 и 4-0-02. Определить величину сре-
динной ошибки пп ее месту в ряде ошибок.
Ответ. 0-03.
Задача 69. При измерении одного и того же расстояния ошибки
отдельных результатов оказались равными: — 20 м, 4- 40 м, 4- 10 м, — 15 м,
4- 5 м, 4- 20 л/, — 5 м и -|- 25 м. Определить величину срединной ошибки
по ее месту в ряде ошибок.
Ответ. 17,5 л/.
Задача 70. Срединная ошибка способа измерения дальности равна 100 л/.
Чему равна вероятность того, что при определении дальности этим спосо-
бом будет допущена ошибка: а) не более 100 л/; б) не более 200 л/; в) не
более 50 м\ г) не меньше 100 м и не больше 200 .и; д) не меньше 25 м и
не больше 75 л/; е) не больше 50 л/ в меньшую сторон}' и не больше 100 м
в большую сторону?
Отв е ты. а) 0,5 (50%)*; б) 0,82226 (82%); в) 0,26407 (26%);
г) 0,32266 (32%); д) 0,25314 (25,4%); е) 0,38204 (38%).
Задача 71. Срединная ошибка способа определения установки угло-
мера равна 0-05. Какова вероятность, что, определяя угломер этим спосо-
бом, будет допущена ошибка: а) не более 0-02; б) не более 0-08; в) в пре-
делах от ± 0-03 до 4; 0-10; г) в пределах от —0-04 до—0-12; д) в пределах
от — 0-06 до 4- 0-03.
Ответы, а) 0,21268 (21°/0); б) 0,71949 (71°/0); в) 0,50836 (51%);
г) 0,24199 (24%); д) 0,44800 (44%).
Задача 72. Найти величину срединной ошибки, если средняя арифме-
тическая ошибка этого способа измерения равна 180 л/.
* Ответ. 152,163 л/.
Задача 73. Чему равна вероятность получения ошибки, не превосхо-
дящей 0-15, если средняя арифметическая способа измерения равна 0-12?
Ответ. Е = 10,1442 деления угломера; Р = 0,68141 (67,2%).
Задача. 74. Определить среднюю арифметическую ошибку данного
способа измерения, если его срединная ошибка равна 30 л/.
Ответ. 35,5 м.
Задача 75. Найти величину срединной ошибки, если средняя квадра-
тическая ошибка этого способа измерения равна 40 делениям угломера.
Ответ. Около 27 делений угломера.
1 В этой и последующих задачах ответы даны по таблице Ф (£);
в скобках — по шкале ошибок.
146
Задача 76. Какова вероятность получить ошибку в пределах от — 20 м
№—50 м, если средняя квадратическая ошибка способа измерения
равна 49 м?
Ответ. £ = 33,05 м~33 м; Р = 0,18794 (18,2о/с).
Задача 77. Срединная ошибка равна 150 м. Чему равна средняя ква-
дратическая ошибка того же способа измерения?
Ответ. £2 ~ 222,4 м.
Задача 78. Средняя арифметическая ошибка способа измерения равна
0-07. Чему равна средняя квадратическая ошибка того же способа?.
Ответ. £2~8,77 деления угломера.
Задача 79. Средняя квадратическая ошибка способа измерения
равна 53 м. Определить величину средней арифметической ошибки того же
способа.
О т в е т. £j ~ 42,3 м.
Задача 80. Какова вероятность того, что в установке уровня будет
допущена ошибка не более 5 м, если одно деление уровня равно 20 м7
О т в е т. 0,5. •
Задача 81. Деления на компасе нанесены через 1-00. Какова вероят»
ность, что при считывании азимута ошибка не будет превышать 0-30?
Ответ. 0,6.
Задача 82. При тех же условиях, что и в задаче 81, определить вероят;
ность получения ошибки в пределах от —0-20 до 4-0-50.
Ответ. 0,7.
Задача 83. Определить срединную и среднюю квадратическую ошибки
в установке прицела, если ДХ = 60 м.
О т вет. Ер = 15 м\ Ер = 17,3 м.
10?
ГЛАВА 6
СЛОЖЕНИЕ ЗАКОНОВ СЛУЧАЙНЫХ ОШИБОК
§ 32. СЛОЖЕНИЕ ЗАКОНОВ ГАУССА
Если при измерении возникают ошибки от нескольких
независимых друг от друга источников ошибок, то ошибки
измерения, как результат взаимодействия этих источников, бу-
дут ошибками суммарными.
Такие суммарные ошибки, очевидно, будут следовать
какому-то новому, суммарному (сложному) закону ошибок.
Также очевидно, что этот новый закон ошибок должен
отличаться от каждого из законов, которым следуют ошибки
отдельных источников (групп источников) ошибок.
Возникает вопрос, как найти этот новый закон, зная
взаимодействующие законы, т. е. возникает вопрос о сложе-
нии этих взаимодействующих законов.
Любой закон случайных ошибок характеризуется, во-пер-
вых, определенной зависимостью между величиной ошибки и
вероятностью ее получения, что выражается соответствующим
графиком, и, во-вторых, величиной срединной ошибки как
меры точности этого закона. Следовательно, и для нового,
суммарного закона необходимо найти эту зависимость и его
срединную ошибку.
Установим вид закона, получающегося при сложении
нескольких законов Гаусса.
Вспомним численный пример, в котором было установлено,
что при взаимодействии трех групп источников ошибок резуль-
тирующие ошибки следуют закону Гаусса, т. е. тому же
закону, которому следовали ошибки этих групп в отдельности
(§ 27, рис. 33). В дальнейшем (§ 29) этот вывод нашел
подтверждение в том, что для ряда таких результирующих
ошибок численные зависимости между Е, Ег и £2 оказались
такими, какие свойственны именно закону Гаусса. Можно
Считать законы, которым следуют ошибки различных групп
148
источников, независимыми друг от друга законами Гаусса, а
поэтому и сделать вывод, что при сложении нескольких зако-
нов Гаусса новый закон ошибок является также законом
Гаусса.
Остается для этого нового закона найти его срединную
ошибку.
Найдем для нового закона Гаусса сначала его среднюю
квадратическую ошибку Е^ а по ней — его срединную
ошибку Е, исходя из того, что в законе Гаусса между средин-
ной и средней квадратической ошибками существует зависи-
2 3
мость: Е = т К, или Ez — Е.
О Z
Допустим, что в условиях данного измерения имеют
место два закона Гаусса, средние квадратические ошибки
которых, выраженные через математические ожидания квадра-
тов, соответствующих этим законам ошибок Д' и Д", равны:
£7==М.0.(Д'«) и F2"2 = M.O.(Ab2),
Каждая результирующая ошибка Д нового закона равна
сумме ошибок взаимодействующих законов:
Д=ДЧД',
поэтому и средняя квадратическая ошибка Е может быть
выражена через математическое ожидание квадрата этой
суммы:
Е* = М.О. (А2) = М.О. [(Д' + Д")2] = М.О. [Д'2 + 2 Д'Д" + Д"2].
Применив теорему сложения математических ожиданий,
получим:
£22 = М.О. [Д'2 4- 2 Д'Д" + Д’2] = М.О. (Д'2) +
+ М.О. (2 Д'Д") + М.О. (Д"2).
В этом выражении М.О. (Д'2) и М.О. (Д"2) нам известны по
условию:
М.О.(Д'2) = £,'22 и М.О.(Д"2) = £2"2.
По теореме умножения математических ожиданий
М.О. (2 Д'Д") = 2 • М.О. (Д') • М.О. (Д").
Но закон Гаусса симметричен — одинаковые по величине
положительные и отрицательные ошибки равновероятны.
Поэтому и математическое ожидание первой степени ошибки
(с учетом ее знака) этого закона равно нулю, т. е.
2-М.О. (Д').М.О. (Д’) = 2-0-0 = 0.
149
Тогда
£22 —М.О. (Д'2) 4-М.О. (2Д'Д’) + М.О. (Д"2) = £'22 + 0 4- £2"2 =
= £'22 4-£2"2,
откуда
E2=VE'* + E'*.
* 3 3
Заменив в этом выражении Ег='^Е, Е\ — -^Е' и £1Г2==
з
= -^Е', получим:
f £=]/(|£' У + df У ;
после сокращения
Е = V£'2 4- £"2.
Для трех законов Гаусса, применив тот же метод расчета,
получим:
Сложив сначала два закона Гаусса и затем сложив полученный
результат с третьим законом Гаусса.
Очевидно, тот же вывод мы получим и для любого числа
взаимодействующих законов Гаусса:
При сложении нескольких независимых друг от друга
законов Гаусса срединная ошибка нового, сложного закона
Гаусса равна корню квадратному из суммы квадратов сре-
динных ошибок складываемых законов.
Проверим этот вывод, воспользовавшись тем же численным
примером получения случайных ошибок при взаимодействии
трех групп источников ошибок (см. § 27, рис. 33).
Там было три закона Гаусса, различающихся своими ошиб-
ками и вероятностями их получения. Определим для каждого
закона в отдельности его среднюю квадратическую ошибку.
Первая группа. Возможные ошибки: —8, —6, —4, —2,
О, 4-2, 4-4, 4-6, и 4-8; соответствующие этим ошибкам веро-
ятности их получения:
1 8 28 56 70 56 28 8 1
256 ’ 206 ’ 256 ’ 256 ’ 256 ’ 256 ’ 256 ' 256 И 256
Тогда средняя, квадратическая ошибка этого закона
£ 2 = 64- -Tjsg- • 2-J-36- • 24-16--2^ ’ 24-4- ^‘24-0«
150
Вторая группа. Возможные ошибки: —12, ——4,
О, +4, 4-8, +12; вероятности их получения соответственно:
1 6 15 20 15 6 1 ~
-s-r, -^7 , =7 , ?7 , ё7 , 77- и -77 . Средняя квадратическая
64 ’ 64 ’ 64 ’ 64 ’ 64 ’ 64 64 н г
ошибка этого закона
Е"г = . 2+М- А • 2+16 • + 2 + 0 • -g =
= V 7Г =/24.
Третья группа. Возможные ошибки: —15, —9, —3,
+3, +9 и +15; соответственные вероятности: — , ,
10 5 1 ГГ
32 ’ 32 И 32 • Т°гда______________________
E'”z = /225. 2+81-А-2 + 94-2 = /^ = V 45.
Подставив квадраты найденных средних квадратических
ошибок в общую формулу, получим:
£2 = У Е'\ + £^+ Е"'* = /"8+24 + 45 = ]/77 = 8,775.
При определении величины средней квадратической ошибки
по результирующим ошибкам (§ 29, стр. 140) был получен такой
же ответ: Е^ = 8,775, что подтверждает правильность выве-
денной нами формулы, ибо если справедливо равенство
Ez = V E'tf+ E‘l + Е"*,
з
то, на основании зависимости Е2 = ?Е, будет справедливо и ра-
венство
Е = У'Е'2 + Е"2 + Е”\
Пример 1. Имеем два закона Гаусса, срединные ошибки которых:
Е' =200 м и £"=60 м.. Чему равна срединная ошибка суммарного закона
Гаусса?
Решение. Здесь взаимодействуют два закона Гаусса, срединные
ошибки которых по условию: Е’ = 200 м и Е" = 60 м Подставив эти чис-
ленные значения в общую формулу, получим срединную ошибку нового,
сложного закона Гаусса:
Е = у Е^ + Е1^ = y+W+W^y+ЗбОЭ 209 м.
Пример 2. При определении исчисленной дальности срединные ошибки
законов Гаусса равны: при учете метеорологических, условий стрельбы —0,5%
дальности, при учете балистических условий стрельбы — О,3°/о и при опре-
делении топографической дальности — 0,8%. Определить величину суммар-
ной срединной ошибки.
Решение. Подставив численные значения срединных ошибок взаимо-
действующих законов Гаусса в общую формулу, получим:
Е = ]/F^++"2”+ £'"2 = j/0,52 40,32 + 0,8‘2 = У0,25 + 0,09 + 0,64 =
= j/0,98 1% дальности.
151
§ 33. СЛОЖЕНИЕ ЗАКОНА ГАУССА И ЗАКОНА РАВНОЙ ВЕРОЯТНОСТИ
Чаще всего при артиллерийских измерениях действуют одновременно^
и законы Гаусса, и законы равной вероятности.
Например, при изм^ рении углов стереотрубой, т. е. при наведении
трубы, мы допускаем ошибки, следующие закону Гаусса, а при снятии от-
счетов с шкал той же стереотрубы — ошибки, подчиненные закону равной
вероятности, и т. п.
Выясним, какой вид будет иметь сложный закон ошибок, получающийся
при взаимодействии этих законов.
Начнем со сложения закона Гаусса с законом равной вероятности,
когда I < Е.
Положим, что между параметрами Е и I законов Гаусса и равной ве-
Е
роятности имеется следующая зависимость: I = .
Найдем результирующие ошибки, получающиеся при взаимодействии
указанных выше законов. Для упрощения расчетов будем складывтть средние
значения ошибок для равных по величине пределов. Средние ошибки, сле-
дующие закону равной вероятности, выразим при этом в долях срединной
Е
ошибки закона Гаусса, исходя из того, что /=2' (тг)бл. 14).
Таблица 14
х. А б \ -4е -5-£ 4-1 ТЕ 4-2-Le 4-Зу Е
_J1Е 16 г 63 “16 £ -^Е 16 31 “ 16 Е _*Е 16: + — £ 16 £ 4- L7 Е 16 Е зз „ + 16£ 49 + 16 £
-~5е 16 с 61 45 “16 Е 16: 16ft + 3 Гб£ 4- 19 16 Е Uj 4- 51 + 16 £
16 59 “ 16 Е 16 27 “ 16 Е 4^ 4- -»£ 16 4- 16 е 37 + 16£ 53 + 16 £
_ЯЕ 16 16 25 “ 16 Е -Г6Е 4~ 7 16£ 4- 2-3£ 16 39 + 16f 55 „ + 16 £
+ 16£ _®Е 16 е -39д 16 с _™Е 16 --7в 16 4- rh 4- ?5 f 16 г 41 + 16 F 57 + 16 £
+ rh -5-3е 16 с 37 ~ 16 Е -24л 16 с -&-Е 16 с 4- + 27 £ К; 43 „ + 16 Е 59 + 16 £
+ Тб£ 16 е -3-5£ 16 16 __з£ 16 4- 13 £ 16 с 4* 29 16 Е 45 .. + 16 Е 61 + 16 £
7 „ + йЕ 49 “ 16 Е 33 “ 16 Е 17 ~ 16 £ -Г6£ 4- 15 16 Е 4- — Е 16 с 47 ,, + 16 £ 63 г. + 16 Е
В верхней горизонтальной графе А приведены средние ошибки, сле-
дующие закону Гаусса, в левой вер1икалгной графе Б - средние ошибки,
следующие закону равной вероятности, а на пересечении этих граф — ре-
зультируюп ие (суммарные) ошибки.
Рассчитаем теперь вероятности получения каждой из этих результи-
рующих ошибок.
152
ГЛ 63
Результирующая ошибка —-yg-E получается при сложении средней ошибки
1 7
закона Гаусса —З-^Е со средней ошибкой закона равной вероятности — yg Е<
Вероятность получения ошибки — Зу, Е равна 0,02. Вероятность получениям
7 1
ошибки — -yg-E равна ур = 0,125. Вероятность получения суммарной ошиб-
63 г.
ки—yg-E по теореме умножения равна 0,02X0,125 = 0,00250.
47
Вероятность получения результирующей ошибки — yg- Е как суммы.:
—22 Е f — yg Е равна 0,07 X 0,125 = 0,00875 и т. д.
Сведем все расчеты в общую таблицу (табл. 15).
Таблица 15’
Б А ~4Е 0,02 -4Е 0,07 -4 е 0,16 -ТЕ 0,25 + у Е 0,25 Е 0,16 +2тЕ 0,07 - +3Т Е 0,02 :
_1Е 16е 0,125 0,00250 L 00875 0,02000 0,03125 0,03125 0,02000 0,00875 0,00250
_^Е 16 е 0,125 0,00250 0,00875 0,02000 0,03125 0,03125 0,02000 0,00875 0,00250
_ 3 16 0,125 0,00250 0,00875 0,02000 0,03125 । 0,03125 0,02000 0,00875 0,00250 I
—16 Е 0,125 0,00250 0,00875 0,02000 0.03125 0,03125 0,02000 0,00875 0,00250
+ Г6£ 0,125 0,00250 0,00875 0,02000 0,03125 0,03125 0,02000 0,00875 0,00250
0,125 0,002500,00875 0,02000 0,03125 0,03125 0,02000’0,00875 0 00250 1 1
+11£ 0,125 0,00250 0,00875 0,02000 0,03125 0,03125 0,02000 0,00875 0,00250
+ Г6£ 0,125 0,00250 0,00875*0,02000 0,03125(0,03125 0,02000 0,00875 0,00250 I 1
2 0,02 0,07 0,16 0,25 0,25 0,16 0,07 0,02
Сложив в вертикальных графах вероятности получения ошибок, заме-
чаем, что вероятность получения ошибки в пределах от — —yg Е до—yg Е
47 33
равна 0,02; вероятность получения ошибки в пределах от — ygE до——pg Е.
153-
равна 0,07; в пределах от— -у^£ до—-jg£ равна 0,16 и т. д. Получаем рас-
пределение вероятностей в точном соответствии с законом Гаусса. Следо-
Е
вательно, в случае, когда параметр закона равной вероятности/ — — ,
при сложении закона Гаусса с законом равной вероятности новый, слож-
ений закон является законом Гаусса.
Это положение практически будет справедливо и в том случае, когда
параметр I закона равной вероятности равен срединной ошибке Е закона
.Гаусса, т. е. когда 1~Е. Произведя расчеты, аналогичные расчетам при
Е
Л= получим график такого суммарного закона (рис. 47).
Как мы видим, распределение вероятностей получения ошибки в этом
«суммарном законе очень мало отличается от распределения, свойственного
-закону Гаусса.
Следовательно, если при сложении закона Гаусса с законом равной
вероятности величина параметра закона равной вероятности I не превышает
величину параметра закона Гаусса Е, т. е. если 1^.Е, то суммарный закон
может быть принят за закон Гаусса.
При Z > Е суммарный закон уже не будет законом Гаусса.
Так, например, при 1-2Е графически суммарный закон хотя и выражается
кривой, как будто бы и похожей на кривую Гаусса, но в действительности
J54
этот суммарный закон не может быть принят за закон Гаусса, так как рас-
пределение вероятностей в нем далеко не соответствует распределению ве-
роятностей в законе Гаусса (рис. 48).
При большой разнице между величинами параметров I и Е, например,
при 1 = 4Е, суммарный закон даже в графическом выражении не напоми-
нает закон Гаусса /рис. 49).
Р
Рис. 49
'При сложении закона Гаусса с законом равной вероятности средняя
квадратическая ошибка может быть выражена как
£2=l/£'22 + j&2''2,
где Е'2— средняя квадратическая ошибка закона Гаусса;
£"2— средняя квадратическая ошибка равной вероятности.
Подставив вместо Е'2 принятое выражение для средней квадратической
I
ошибки закона равной вероятности у-- , получим:
£2 = /.
Мы установили, что при сложении закона Гаусса с законом равной
вероятности в случае, когда /СД суммарный закон может быть принят
как закон Гаусса. Поэтому можно перейти от средней квадратической
ошибки Е2 такого суммарного закона к его срединной ошибке Е, исходя
из известной нам зависимости между Е2 и £:
/ /2
£ = 0,67449 £2 -=0,674i9”|/ £'22+-з ,
или, введя коэфициент 0,67449 под знак радикала:
0 6 4 492 /2 /
(0,67449 £'2)2 + ——g------= ]/ Е'2 + 0,1516/2,
где Е'—срединная ошибка суммируемого закона Гаусса.
Пример 1. Указать, какой суммарный закон получится при сложении
закона Гаусса, имеющего срединную ошибку Е' = 10 м, с законом равной
вероятности, параметр которого I — 5 м, и найти его срединную ошибку.
Решение. Определим, прежде всего, вид суммарного закона. Пара-
метр / закона равной вероятности меньше срединной ошибки Е' закона
155
Гаусса. Следовательно, с достаточной для практики точностью суммарный
закон может быть принят как закон Гаусса.
По выведенной фЬрмуле срединная ошибка суммарного закона
Е - j/£'2 + 0,151672 = У 100 4-0,1516-25 — ]/ 103.79 « 10,2 м.
Пример 2. Срединная ошибка закона Гаусса Е' — 0-02. Параметр за-
кона равной вероятности I = 0-05. Определить вид суммарного закона, по-
лучающегося при сложении этих двух законов, и найти его характеристику.
Решение. Здесь дан случай, когда / > Е (1 = 2.5Е). Это означает,
что суммарный закон не является законом Гаусса, и формула
Е = У £'2+0,1516/2
для него не пригодна. Для этого закона можно определить только его сред-
нюю квадратическую ошибку
, / Р лГ ( Е’ \2 /2 / 4 ~“25
£2=)/ £'22 + 3 = |/ ^ ) + —- = у + “з ~ 4’14
деления угломера.
* *
*
Сопоставив приведенные случаи сложения законов Гаусса
и закона Гаусса с законом равной вероятности, мы можем:
сделать следующие выводы:
1. Закон Гаусса обладает устойчивостью, которая выра-
жается в том, что при сложении нескольких законов Гаусса
суммарный закон является также законом Гаусса.
2. Закон Гаусса обладает свойством поглощать другие за-
коны ошибок, в частности закон равной вероятности. Это
свойство закона Гаусса выражается в том, что, за сравнительно
редкими исключениями, при сложении закона Гаусса с законом
равной вероятности суммарный закон может быть принят за
закон Гаусса.
Эти свойства закона Гаусса обусловливают его чрезвычайно
широкое распространение; одно время даже полагали, что,
кроме закона Гаусса, никаких других законов случайных оши-
бок и не существует. Эти свойства закона Гаусса и позво-
ляют принимать ошибки, возникающие в процессе артилле-
рийских измерений, как ошибки, следующие закону Гаусса,
хотя при этих измерениях помимо закона Гаусса имеют место
и другие законы ошибок.
§ 34. ЗАДАЧИ НА СЛОЖЕНИЕ ЗАКОНОВ ОШИБОК
Задача 84. Определить характеристики закона ошибок, получившегося
в результате сложения трех законов Гаусса, срединные ошибки кото-
рых 4, би 12 м.
О т в е т. Е = 14 м: Ег = 16,6 м; Е2 — 20,8 м.
156
Задача 85. Определить характеристики Закона ошибок, получающегося
® результате сложения законов Гаусса, срединные ошибки которых
5, 11, 15 и 23 м
О т в е т. Е = 30 м; Et~ 35,5 м; Е2 — 44,5 м.
Задача 86. При измерении некоторого yr ia взаимодействуют два закона
Гаусса, срединные ошибки которых 0 06 и 0-08. Какова вероятность того,
>что угол будет измерен с ошибкой, не превосходящей 0-15?
Ответ. £ = 0-10; Р = 0,68833 (68°/0).
Задача 87. При определении исчисленной дальности сречинные ошибки
таковы: в учете метео юлогических условий стрельбы — 30 м, в учете ба-
листических условий стрельбы — 26 лив определении топографической
дальности—45 м. Чему равна вероятность того, что исчисленная дальность
•будет определена с ошибкой, не превышающей 50 лт?
Ответ. Е = 60 м\ Р — 0,42593 (42%).
Задача 88. При данном измерении взаимодействуют два закона Гаусса,
срединная ошибка одного из которых равна 32 м. Определить величину
•срединной ошибки другого закона Гаусса; если суммарная срединная ошибка
1равна 40 м.
О т в е т. 24 лс
Задача 89. Указать, какой суммарный закон излучится при сложении
закона Гаусса, срединная ошибка которого равна 12 м, с законом равной
вероятности, параметр которого I равен 4 м.
О твет. Закон близок к закону Гаусса: Е — 12,1 м.
ГЛАВА 7
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
§ 35. ПОДХОДЯЩЕЕ ЗНАЧЕНИЕ ИЗМЕРЯЕМОЙ ВЕЛИЧИНЫ
Артиллерийская стрельба, начиная с подготовки данных
для открытия огня и кончая последней командой, вся постро-
ена на использовании результатов различного рода измерений’
дальностей, углов, отклонений разрывов и т. д.
Ошибки при измерениях неизбежны, измерение никогда не
дает истинного (абсолютно точного) значения измеряемой ве-
личины. Поэтому при обработке результатов измерений прежде
всего возникает вопрос, какое значение в результате произ-
веденных измерений следует принять за истинное значение
измеряемой величины, какое значение будет более всего под-
ходить к этому истинному значению, т. е. будет иметь наи-
меньшую ошибку, если его принять за истинное. К отыска-
нию такого подходящего значения мы и приступим.
Допустим, что при измерении некоторой неизвестной нам
величины способом, ошибки которого следуют закону Гаусса,,
были получены следующие результаты:
Xj, Х2, Х3, ..., Xs—1, xs.
Обозначим истинное значение измеряемой величины че-
рез х0.
Тогда ошибки этих результатов
Aj — Xj Х0,
Д2 —- х2 Xq.
Ay — х3 х0.
‘S -- Xg Xq,
158
Сложим почленно эти равенства и определим истинное-
значение измеримой величины. 9
А1 + Д2 “F + • • • 4- — xi 4- хг 4- хз 4“ • • • 4~ xs — <Sx0,
откуда
+ х2 + х3 + • • • "Ь xs ^1+^2+ 4з 4- • • • 4" ^5
х0 = S •
Закон Гаусса симметричен — при достаточно большом числе
измерений S каждой положительной ошибке будет отвечать
примерно равная ей по абсолютной величине отрицательная
ошибка и при сложении всех таких ошибок алгебраическая
сумма их будет близка к нулю. Если же и получится неболь-
шой остаток, он при делении на S станет в S раз меньше. По-
этому последним членом правой части приведенного выше-
равенства можно пренебречь, и тогда
-*1 + х2 + хз + • • • -Г х$
Х„ =----------5—--------= г.
За неизвестное истинное значение измеряемой величины
принимают среднее арифметическое из всех отдельных ре-
зультатов измерений, т. е. средний результат.
Пример. Дальность до цели измерена одним и тем же способом 10 раз.
Результаты измерения в делениях прицела таковы: 125, 128, 116, 127, 121,
118, 123, 130, 120 и 122. Определить подходящее значение измеренной даль-
ности.
Решение. Подставим численные значения полученных результатов-
измерения в общую формулу:
я 125-4-128+116+127+121 + 118-М234-130+1204-122 _ 19Ч
ДсР 5 10
Следовательно, за истинное значение измеренной дальности можно при-
нять дальность, равную 123 делениям прицела.
Принимая средний результат % за истинное значение из-
меряемой величины х0, мы, естественно, и ошибки отдельных
результатов будем определять относительно среднего резуль-
тата. Обозначая такие ошибки через X, получим
— Хх £
)i2 — х2 £
^3 ~ Х3
Xs — xs Е
Ошибки, исчисленные относительно £, в отличие от оши-
бок истинных, исчисленных относительно х0, обычно назы-
ваются кажущимися ошибками.
159
Алгебраическая сумма кажущихся ошибок всегда равна
.'нулю..
Сложим почленно приведенные выше равенства:
У x1=S*i--S£;
шо условию
или 2х/ — S^
1
щ тогда действительно
s s
2л = 2^-^=°-
1 1
Проверим это положение. В приведенном выше примере было
10 отдельных результатов измерений, причем средний резуль-
тат оказался равным 123 делениям прицела. Рассчитав кажу-
щиеся ошибки отдельных результатов относительно среднего,
.получаем:
ю
2*г = + 2+5-7-Н—2—-5+04-7—3-1=0.
1
Если истинные ошибки Д2, Д,.., в условиях данного
измерения следуют закону Гаусса, то и кажущиеся ошибки
Xlt Х2, Х3... в тех же условиях должны следовать этому же
закону, как ошибки того же порядка.
В численном примере на 170 результатов измерения дальности
(§ 27, табл. 4) ошибки отдельных результатов были опреде-
лены относительно истинного значения величины измеренной
дальности, равной 3000 м.
Допустим, что это истинное значение было неизвестно и
ошибки отдельных результатов определены относительно сред-
него результата:
170
2 X;
е 1 510008 О АЛЛ Л Л 7
^Ттб" — ”Т7б~ = 30°0,047
Округлив полученный результат до 3000 м (отбросив
остаток в 47 м\ получим кажущиеся ошибки по величине
и по знаку, ничем не отличающиеся от соответствующих им
истинных ошибок, и исследование совокупности кажущихся
-ошибок приведет к тем же выводам.
160
При выводе формулы среднего результата как подходя-
щего значения измеренной величины мы допустили, что
Al + А2 + дз + • • • 4" п
- __и.
Это допущение полностью справедливо только при бес-
конечно большом числе измерений, так как только в этом
случае каждой положительной ошибке будет соответствовать
равная ей по абсолютной величине отрицательная ошибка
и алгебраическая сумма всех возможных ошибок будет равна
нулю.
При ограниченном числе измерений, с чем приходится иметь
дело на практике, принимая средний результат £ за истинное
значение измеряемой величины %0, мы делаем ошибку — ошибку
среднего результата
Aj + Д2 4- Ад + ... +
%о=----------ё----------.
Очевидно, что эта ошибка будет тем меньше, чем больше
число 5. Выше мы рассчитали среднюю величину дальности
по 170 отдельным результатам измерения; ошибка среднего
результата в этом случае
зооо-4_ 4_ 0,047 м.
Такая пренебрежимо малая величина ошибки среднего
результата еще раз подтверждает правильность сделанного
допущения.
С уменьшением числа 5 ошибка среднего результата при-
обретает все более и более существенное значение. Так, ошибка
среднего результата по первым 85 результатам измерения того
же примера
Ь —-------------------3 000—4-
447 . г-
4-5,259 м,
а по первым 35 результатам
d = _3000== 1дб29 м
35 35 ’
Помимо числа измерений, величина ошибки среднего ре-
зультата зависит и от точности самого способа измерения —
чем точнее способ, тем меньше отдельные ошибки, тем меньше
2 а.
их алгебраическая сумма и тем меньше В = —у2-•
Принимая средний результат за истинное значение изме-
ренной величины, необходимо учитывать ошибку среднего
результата.
11 — Зак. 991
161
§ 36. ПОДХОДЯЩЕЕ ЗНАЧЕНИЕ СРЕДИННОЙ ОШИБКИ
Выше была установлена (см. § 30) зависимость между ис-
тинными ошибками отдельных результатов измерения и сред-
ней арифметической и средней квадратической ошибками, а
через них и срединной ошибкой как основной характеристикой
закона Гаусса.
Приняв при обработке результатов измерений за истинное
значение измеренной величины средний результат, получают
не истинные, а кажущиеся ошибки. Отсюда, если значение
срединной ошибки данного способа измерения неизвестно, то
нужно установить правила определения подходящего значе-
ния срединной ошибки по этим кажущимся ошибкам.
Начнем с отыскания выражения для подходящего значе-
ния средней квадратической ошибки, а от него перейдем
уже к срединной ошибке.
Установим предварительно зависимость между истинной
и кажущейся ошибками.
Истинная и кажущаяся ошибки любого отдельного резуль-
тата измерения определяются формулами:
А{=^ —Хо И \=Хг — £,
или
^г + Х^Х, И +% = Xi,
откуда
At 4~ == \ 4"
или
А< — К 4" (£ — *о)= К 4"
т. е. истинная ошибка равна кажущейся ошибке плюс ошибка
среднего результата.
Перейдем теперь к решению поставленной задачи.
Положим, что имеется ряд отдельных результатов изме-
рения одной и той же величины:
ошибки которых следуют закону Гаусса.
Тогда, по только что установленной зависимости,
Al Aj ~Г 6
^2= А2 4" Ь
Аз = А3 4- Ь
А§ — As + 6
162
Ошибки и Ь могут быть как положительными, так
и отрицательными. Чтобы устранить влияние знаков при них,
возведем все эти равенства во вторую степень:
Д2 = Х32 + 2Х35 + б2
Д2 — X2+2Xsb + S2
Сложив почленно эти равенства, получим:
S S S
Sa<2=2V + 282X< + 552-
1 1 1
Алгебраическая сумма первых степеней кажущихся оши-
бок, как известно, всегда равна нулю. Отсюда и средний член
правой части нашего равенства
s
2&2><=0,
1
и тогда
S 5
Уд,2 = 2 v + ss2.
“1 1
В этом равенстве по условию нам неизвестны 2 А;2 и д2.
Чтобы избавиться от Ь2, воспользуемся выражением
4~ ^2 4~ Аз + • • • +
b— $
и возведем его в квадрат:
По общему правилу возвышения многочлена во вторую
степень будем иметь:
s s
(Д1 + Д2 + А3 + .. . + As)2 = А/ 4" ^2Д(Д/,
где 1 1
s
^1>2Д4Д< = 2(Д4Д2 4" AjAjj 4~ • • • 4~ A4As) 4" 2 (Д2А3 4- Д2Д4 -Ь
1
4- . .. + A2As) 4~ 2 (Д3Д4 4* А3А5 4-. • 4~ A3As) 4- 2 (As-2 As-i 4-
4- As- 2 As ') 4- 2As-1 As-
li* 163
Все эти произведения как произведения случайных ошибок,
следующих закону Гаусса, могут быть как со знаками „плюс",
так и со знаками „минус", и при достаточно большом числе
измерений их алгебраическая сумма будет очень близка к
нулю. Поэтому, пренебрегая в выражении
s 5
/д _|_д _|_д _р д \2 2Д(-2 22Д/Д/'
«•2 ( а1 + 2 + а3 п- • • • -Г \ 1 1
0 “ £2 -г 52
последним членом, получаем:
2Д/2 2Д?
б2 — -1— = 2--------L
u S’2 S S •
Сумма квадратов ошибок, деленная на число измерений,
может быть принята равной квадрату средней квадратической
ошибки. Отсюда
Вернемся к равенству
Sv
1 1
левая часть его может быть представлена, как
s
s -2Д/2
2 д| = 2^ 5=^5,
1
а после замены в правой ее части Ь2 = .£2--^-> получим:
s
SEl = 2 V + Ei,
1
откуда
s з
SEl— £? = 2V, или £1(5 — 1)= 2V,
1 1
или, решая относительно Еъ
р2__ 1
£2-5— >
тогда _______
__ 1 /~ Xi 4- Хг 4~ Хз • ~Ь
2 у
Подходящее значение средней квадратической ошибки
при обработке результатов измерения принимается равным
164
корню квадратному из суммы квадратов ошибок отдельных
результатов, деленной на число измерений без одного.
Для перехода от этой средней квадратической ошибки к
срединной ошибке будем пользоваться известной зависимо-
стью
Е = 0,67449 Е^^-Ег.
При выводе выражения для средней квадратической ошибки
по результатам обработки измерений было принято, что сумма
близка к нулю и математическое ожидание заменено
1
средним значением квадрата ошибки, что допустимо только
при очень большом (правильнее — бесконечно большом) числе
измерений. При ограниченном числе измерений эти допуще-
ния вызывают ошибку в определении средней квадратической
ошибки, а отсюда и срединной ошибки. Поэтому обработка
результатов измерений может дать только подходящее значе-
ние срединной ошибки, которое будет тем ближе к истинному,
чем больше было произведено измерений.
Пример 1. При измерении базы шагами были получены следующие
отдельные результаты измерения в метрах: 400, 360, 390 , 370 , 350, 360,380,
420, 390, 400, 380, 410, 370, 340, 370 и 390. Определить подходящее значе-
ние срединной ошибки по средней квадратической ошибке.
Решение. Ход решения подобных задач т<ков: сначала определяем
средний результат, приняв его за истинное значение измеренной величины,
затем рассчитываем кажущиеся ошибки отдельных результатов, возводим
эти ошибки во вторую степень, находим среднюю квадратическую ошибку
по выведенной нами формуле и, наконец, определяем величину срединной
ошибки. Удобнее всего решение производить, размещая все данные в
такой таблице. •
i Xl £ X2 7
1 400 380 + 20 ! 400
2 360 380 —20 ! 400
3 390 380 + 10 100
4 370 380 — 10 100
5 350 380 —30 900
6 360 380 —20 400
7 380 380 0 0
8 420 380 +40 1 600
9 390 380 + 10 100
10 400 380 +20 400
11 380 380 0 0
12 410 380 +30 900
13 370 380 — 10 100
14 340 380 —40 1 600
15 370 380 —10 100
16 390 380 + 10 100
2 6 0801 6 080 0 7 200
6080
£ = ie" = 380 м.
Е = 0,67449-21,91 14,78 м.
165
Пример 2. При подготовке исходных данных были по [учены следую-
щие исчисленные дальности до одной и той же цели в метрах: 4625, 4 590
4560, 4 620,4 600,4 655, 4635, 4610,4640, 4585, 4615, 4595, 4620,4675
и 4660. Определить число выполнивших подготовку на „отлично", „хорошо"
„посредственно" и „плохо*, если срединная ошибка определения дальности
выданных условиях неизвестна, а для получения отличной оценки ошибка
не должна превосходить одной срединной ошибки, для получения хорошей
оценки — двух срединных ошибок, для получения посредственной оценки —
трех срединных ошибок и для получения плохой оценки — более трех сре-
динных ошибок.
Решение.
i xi £ -2 'i Оценка
1 4 625 4 619 + 6 36 Отлично
2 4 590 4619 —29 841 Хорошо
3 4 560 4619 —59 3 481 Посред- ственно
4 4 620 4 619 + 1 1 Отлично
5 4 600 4 619 —19 361 Отлично
6 4 655 4619 +36 1 296 Хорошо
7 4 635 4 619 + 16 256 Отлично
8 4610 4 619 — 9 81 Отлично
9 4 640 4 619 +21 441 Хорошо
10 4 585 4 619 —34 1 156 Хорошо
11 4615 4619 — 4 16 Отлично
12 4 595 4 619 —24 576 Хорошо
13 4 620 4 619 + 1 1 Отлично
14 4 675 4 619 +56 3 136 Посред- ственно
15 4 660 4 619 +41 1 681 Хорошо
2 69 285 69 285 0 13 360 |
69285 ^4^9 м.
15
Е2 = 30,89 м;
Е = 0,67449-30,89 = 20,835 м.
£ = 20,835 м\ 1Е = ^1 м\ 3£ = 62,505 м.
Выполнение: „отлично"—7, „хорошо"—б, .посредственно" — 2.
Перейдем к отысканию подходящего значения средней
арифметической ошибки.
Для истинных значений ошибок средняя арифметическая
ошибка
s
166
и средняя квадратическая ошибка
A-V5-
При достаточно большом числе измерений кажущиеся
ошибки по величине и по знаку равны соответствующим им
истинным ошибкам. Исходя из этого, заменим в указанных
выражениях на /ч, и тогда
s l~s
/2Х?
а ^'= у V-
Подходящее значение средней квадратической ошибки
определяется формулой
а нужно найти подходящее значение средней арифметической
ошибки.
Полагая, что между подходящими значениями средней
арифметической и средней квадратической ошибок имеется та
же зависимость, что и между их истинными значениями, т. е.
Ег' = Ъ,7$787Е2' и Е1 = 0,79787Е2 (см. стр. 141),
составим пропорцию:
Е±: Е2 = Е/: Е2 ,
откуда подходящее значение средней арифметической ошибки
с2
или, произведя соответствующие подстановки,
а в окончательном виде
s
21^1
Е ______1
1
Пример 3. Определить при тех же условиях, что и в примере 2, под-
ходящее значение срединной ошибки по средней арифметической.
167
Решение. Слои.им абсолютные значения кажущихся ошибок отдель-
ных результатов: ,
15
2 Ity = 6Н-294-59+1 + 19+36Н-16+9+21+34-Н+24+1+56+41 =356.
1
Тогда подходящее значение средней арифметической ошибки
356 356 356
~ у 15 (15—1) ~ у210 ~ 14,4914 ~ 24’5663 м,
а подходящее значение срединной ошибки
Е = 0,84535-24,5663 » 20,867 м.
Часто, вместо выведенного нами выражения, пользуются
более простой для расчетов формулой
s
= -у
и тем самым получают несколько преуменьшенные подходящие
значения средней арифметической, а отсюда и срединной
ошибки.
§ 37. СРЕДИННАЯ ОШИБКА СРЕДНЕГО РЕЗУЛЬТАТА
Принимая средний результат за истинное значение изме-
ренной величины, мы допускаем ошибку среднего результата.
Очень легко убедиться в том, что эта ошибка при одном
и том же способе и одном и том же числе измерений для
каждого отдельного среднего результата будет различной по
величине и по знаку, если средний результат определять по раз-
личным отдельным результатам измерения.
Воспользуемся еще раз 170 результатами промера расстоя-
ния шагами (см. § 27, табл. 4).
Определив средний результат по первым 17 отдельным
результатам промера (с № 1 по № 17), получим:
= 3025,35 м,
Т1 17 ’
откуда ошибка этого среднего результата
— х0 = 3025,35 — 3000 = + 25,35 м;
вторая группа из следующих 17 результатов (с № 18 по
№ 34) даст нам:
Ь2 = £2 — х0 == - 3000 = 3013,59 — 3000 = + 13,59 м;
ошибка среднего результата третьей группы из 17 отдельных
результатов (с № 35 по № 51) будет равна
= = — 3000 = 2991,41 - 3000 = —8,59 м
и т. д.
168
Каждая из рассчитанных таким методом ошибок Ь2, 6;.;
и т. д. носит, несомненно, случайный характер, ибо случайна
последовательность получения отдельных результатов при мно-
гократном измерении одной и той же величины. Поэтому ни
одна из этих ошибок не может быть принята как мера, харак-
теризующая точность определения среднего результата при
данном способе измерения и данном числе измерений.
Очевидно, что точность среднего результата должна харак-
теризоваться какой-то своей срединной ошибкой—срединной
ошибкой среднего результата.
Срединная ошибка Е данного ряда измерений определяется
из совокупности ошибок отдельных результатов измерения,,
образующих этот ряд. Следовательно, по аналогии можно утвер-
ждать, что и срединная ошибка среднего результата также-
должна определяться из совокупности ошибок отдельных сред-
них результатов при том условии, конечно, что способ изме-
рения один и тот же и каждый отдельный средний результат
рассчитан для одного и того же числа измерений.
Найдем выражение для такой срединной ошибки.
Предположим, что одна и та же величина одним и тем
же способом была измерена W (например, 170) раз и все отдель-
ные результаты измерения в порядке последовательности их
получения были разбиты на К (например, 10) групп по S' (по
17) результатов в каждой.
Найдем для каждой из этих групп ее средний результат,,
а для каждого такого среднего результата его ошибку:
Ьр 52, Ь3, . . . .
В предыдущем параграфе (см. стр. 164) было установлено,,
что ошибка среднего результата связана со средней квадра-
тической ошибкой из квадратов ошибок отдельных результа-
тов следующей зависимостью:
Ошибки отдельных средних результатов, рассчитанных
для одного и того же числа, измерений, различны по своей
величине. Поэтому будут различны по величине и соответ-
ствующие им средние квадратические ошибки, т. е.
52 £’2.1
____ р’2 . 1
и2__z_2 5
$:2_ С"'2 1
о3 Е2 • $
Х2 _ PI& . 1
2 S
Сложим почленно эти равенства:
8* + 8| + &3 + . . . + 82.= I (Е? + < + £"2 + . . . + Ef).
169
В правой части этого равенства получена сумма частных
случайных значений квадрата средней квадратической ошибки.
Когда мы имеем ряд частных случайных значений изме-
ренной величины, за подходящее ее значение мы берем сред-
ний результат. Очевидно, что, имея ряд частных случайных
значений квадрата средней квадратической ошибки, мы можем
за подходящее его значение взять также средний результат,
т. е. взять среднее значение квадрата средней квадратической
юшибки:
Л »2 -м2 г2
р 2_ ^2 4* ^2 + ^2 + . . . + Е2
2 К ’
откуда
Е'2 + Е’2 + Е22+ . . . + Е«2= КЕ22.
Тогда сумма квадратов ошибок отдельных средних резуль-
татов
S] + 8? + 8=+. . .+8*.= 4z*
Разделив обе части этого равенства на К, получим:
+ +^ + • • • +*К __ А
К ~~ S •
Так же, как и для ошибок отдельных результатов измере-
ния, сумма квадратов ошибок отдельных средних результатов,
деленная на число таких результатов, есть не что иное, как
квадрат средней квадратической ошибки среднего результата.
Обозначив эту ошибку через /?2, получим:
р2
_
Срединная ошибка среднего результата, обозначаемая R,
•связана со средней квадратической ошибкой среднего резуль-
тата той же зависимостью, что и срединная и средняя квад-
ратическая ошибки Е и Е2:
Е = 0,67449 Е2 и R = 0,67449 R2.
Поэтому, заменив средние квадратические ошибки соот-
ветствующими им срединными ошибками, получим:
Р2
& = S’
или
Срединная ошибка среднего результата равна срединной
ошибке способа измерения, деленной на корень квадратный
из числа измерений.
Покажем справедливость этой формулы на численном
примере. Найдем для этого ошибки всех 10 средних резуль-
170
татов, о которых говорилось выше, и по этим ошибкам опре-
делим величину 7? всеми известными нам способами. Расчеты
сведем в общую таблицу (табл. 16).
Таблица 16
№ группы № измерений £ 8 82
1 1-17 51431 3025,35 +25,35 642,62
2 18—34 51 123 3013,59 + 13,59 184,69
3 35—51 50 854 2991,41 — 8,59 73,79
4 52—68 51 104 3006,12 + 6,12 37,45
5 69—85 50 737 2984,51 —15,49 239,94
6 86—102 50 967 2998,06 — 1,94 3,76
7 103—119 50 711 2983,00 —17,00 289,00
8 120-136 50 946 2996,82 — 3,18 10,11
9 137-153 51636 3037,41 +37,41 1399,51
10 154—170 50 391 2964,17 —35,83 1283,79
2|б| = 164,5 и .2 b2 = 4164,66.
Срединная ошибка среднего результата по данным этой
таблицы:
1. По средней арифметической ошибке:
п 0,84535-164,5 ллс.
RE1 =------=. - = 14,64 м.
У10-9
2. По средней квадратической ошибке
ЯЕ,= 0,67449]/ 4164J56 = 14 52
3. По месту в ряде абсолютных значений ошибок
+ 14,54 М.
Выше (см. § 28, табл. 9) было установлено, что срединная
ошибка способа измерения в условиях данного примера равна
60 м. Тогда по выведенной формуле
60
R — -р/-=— 14,55 м.
Как видно, по своей величине все эти численные значения
ошибки среднего результата очень близки между собой.
Пример 1. Определить срединную ошибку среднего результата, если
срединная ошибка способа измерения равна 40 м и средний результат был
найден„по четырем измерениям.
Решение. По условию £ = 40 и S = 4; подставив эти численные
значения в общую формулу, получим:
40
R = = 20 м.
171
Пример 2. Один и тот же угол был измерен одним и тем же способом
16 раз. Найдем срединную ошибку среднего результата, если срединная
ошибка способа измерения равна 0-02.
Решение. £ = 0-02 и 5=16, тогда
2
R = = 0,5 деления угломера.
Пример 3. При измерении одного и того же угла одним и тем же спо-
собом были получены следующие результаты: 8-69, 8-71, 8-70, 8-72, 8-66,
8-70, 8-73, 8-69, 8-68, 8-74, 8-69, 8-70, 8-72 и 8-67. Определим точность этого
измерения.
Решение. Найдем для этого срединную ошибку среднего значения
измеренного угла (среднего результата). Срединная ошибка способа измере-
ния не дана — определим ее по результатам (ошибкам) отдельных измерений,
а потрм по величине Е найдем и /?.
i 5 >-z л2 i
1 8-69 8-70 -0-01 1
2 8-71 8-70 +0-01 1
3 8-70 8-70 0-00 0
4 8-72 8-70 +0-02 4
5 8-66 8-70 —0-04 16
6 8-70 8-70 0-00 0
7 8-73 8-70 +0-03 9
8 8-69 8-70 —0-01 1
9 8-68 8-70 -0-02 4
10 8-74 8-70 +0-04 16
11 8-69 8-70 -0-01 1
12 8-70 8-70 0-00 0
13 8-72 8-70 +0-02 4
14 8-67 8-70 -0-03 9
EEi = 0,84535
= 121-80;
I
121-80
и
= 8-70;
2 |Xf| = 0-24;
--—= I о! деления
14 •
угломера.
ЗХ? = 0-66.
I
= 1,52 деления
угломера.
0-01+0-02
Ерр -----2-----= 1 »50 деления
угломера.
Получено три численных значения срединной ошибки способа (точнее —
ряда) измерения. Примем с округлением £=1,5 деления угломера, и тогда
1 5
R — —2—. = 0,4 деления угломера.
/14
Если срединная ошибка способа измерения Е служит для
характеристики того закона Гаусса, которому следуют ошибки
отдельных результатов измерения, то и срединная ошибка
среднего результата R будет характеризовать также закон
Гаусса, но применительно к ошибкам отдельных средних ре-
зультатов.
То, что ошибки отдельных средних результатов следуют
именно закону Гаусса, видно из самой формулы срединной
ошибки среднего результата. По этой формуле срединная
ошибка среднего результата R зависит только от величины
срединной ошибки способа измерения Е и числа измерений S.
Если же срединная ошибка способа измерения Е является
172
параметром закона Гаусса, то и срединная ошибка среднего
результата Z? будет параметром также закона Гаусса, но пара-
метром в VS раз меньшим.
Отсюда, зная величину срединной ошибки среднего ре-
зультата и пользуясь шкалой ошибок или таблицей значений
Ф($), можно рассчитать вероятности получения ошибки сред-
него результата в каких-то заданных пределах, или иначе го-
воря, вероятности того, что в этих пределах заключено истин-
ное значение измеренной величины.
Пример 4. Срединная ошибка среднего результата равна'10 м. Найдем
вероятности получения ошибки среднего результата в различных по вели-
чине и знаку пределах, выраженных в целых 7?, или, иначе говоря, найдем
вероятности того, что истинное значение измеренной величины заключено
в таких-то пределах.
Решение. Для большей наглядности построим шкалу ошибок, выра-
зив ее в Z?—10 м (рис. 50).
-40м -30м -20м -Юм +10м *20м +30м +Ь0м
• 4 Я -ЗЯ -Zff -R 0 +R * 2R +3R
0,02 0,07 0,16 0,25 0,25 0,16 0,07 0,02
Рис. 50
При рассмотрении этой шкалы можно сделать следующие выводы:
1. Практически предельной ошибкой среднего результата можно считать
ошибку, равную ±4/?= ±40 м. Это означает, что, приняв в условиях дан-
ного примера средний результат за истинное значение измеренной вели-
чины, мы ошибемся не более чем на ±40 м. В пределах от § — 4/? до
£±-4/? будет практически заключено это истинное значение.
2. Вероятность получения ошибки среднего результата в пределах от
О до ± R, т. е. от 0 до ± 10 м, равна по теореме сложения 0,25 -f- 0,25=0,5,
Иначе говоря, 0,5 есть вероятность того, что истинное значение измеренной
величины заключено в пределах от £—10 м до £±-10 м. Вероятность того,
что истинное значение измеренной величины заключено в пределах от £—20 м
до £±20 м (вероятность ошибки от 0 до ± 2/?) равна 0,16±0,25±0,25±0,16—0,82
(по таблице значений Ф(3)—0,82266) и т. д.
3. Вероятность получения ошибки среднего результата в пределах от
0 до ± R, т. е. от 0 до ± 10 м, равна 0,25; в пределах от ± R до ± 2R
(от ±10 до ±20 м) равна 0,16 и т. д.; те же значения вероятности будут
для пределов от 0 до — /?, от — R до — 2R и т. д.
Пример 5. При 16 измерениях дальности средний результат равен
3 200 м. Найти вероятность того, что истинное значение измеренной даль-
ности заключено в пределах:
а) от 3 180 м до 3 220 м\
б) от 3170 м до 3 230 м\
в) от 3155 м до 3 245 м;
г) от 3 140 м до 3 160 лг,
д) от 3 200 м до 3 250 м’,
е) от 3 150 м до 3 225 м\
если срединная ошибка способа измерения дальности равна 80 м.
Решение. Найдем сначала срединную ошибку нашего среднего
результата:
R ~_8L. = 20 .и.
:7з
Построим для этого значения R шкалу ошибок (рис. 51):
а) вероятность того, что истинное значение измеренной дальности за-
ключено в пределах от 3 180 до 3 220 м, равна вероятности получения
«шибки от 0 до ± 20 м (от 0 до ± 1,0/?), т. е.
ра -0,25 + 0,25 = 0,50;
- 00м +иом + 20м О 20м 0-Ом ~60м ~80М
—---------------1-------- 1-------------------1----------।
0,02 ' 0,07 ; o,is ; о,25 ! о,25 ! ops ! о,о? ; о,ог ;
3120н 31*0м 3160м 3180м 3200м 3220м 32U0M 3260м 3280м
Рис. 51
б) вероятность того, что истинное значение дальности находится
в пределах от 3 170 до 3 230 м или вероятность получения ошибки от 0 до
± 30 м (от 0 до ± 1,5 /?)
рб = 0,09 4- 0,25 + 0,25 + 0,09 = 0,68;
точнее, по таблице значений Ф(₽):
рб = Ф (1,5) = 0,68833;
в) вероятность ошибки в пределах от 0 до d:45 м, или — в долях R —
от 0 до ± 2,25/?, равна
рв = 0,0244-0,16 + 0,25+0,25+0,164-0,024 = 0,868 (по шкале);
рр — Ф (2,25) = 0,87088 (по таблице);
г) вероятность ошибки в пределах от ±40 м до +60 м, т. е. от +27?
до -j-З/?, равна
РГ =0,07,
или
Рг = ~ [ф (3,0) —Ф(2,0)] = 0’95698.~°>82266 = 0,06716;
д) вероятность ошибки в пределах от 0 до — 50 м, или от 0 до '—2.5/?;
равна
=0,254-0,16+0,04=0,45,
Рл “+ Ф (2,5) = 0,45413;
2
е) вероятность ошибки в пределах от —25 м до +50 м, т. е. от
—1,25/? до +2,5/?, равна
ре =0.05 + 0,254-0,25+0,16+0,04=0,75,
пли
Л = + [Ч> о .25) + Ф(2,5)) = адоозз+одаи, =
174
До сих пор по заданной величине срединной ошибки спо-
соба измерения Е и заданному числу измерений S опреде-
лялась величина срединной ошибки среднего результата R.
Понятно, что можно задаться определенными значениями Е и
R и по ним найти число S, удовлетворяющее заданному
соотношению между Е и 7?, т. е. можно найти такое необхо-
димое число измерений, при котором срединная ошибка сред-
него результата будет иметь желаемое численное значение.
£•
Решим равенство /? = —— относительно 5:
или
Пример 6. Сколько необходимо произвести измерений, чтобы средин-
ная ошибка среднего результата была равна 0-05, если срединная ошибка
способа измерения равна 0-20?
/ Е \2 /20\2
Решение. S = I / -g- } =42= 16 измерений.
Пример 7. Срединная ошибка способа измерения дальности равна 50 я.
Сколько следует произвести измерений, чтобы срединная ошибка в опреде--
лении дальности была равна 20 м!
Решение. <$ = -|2 у=2,52 « 6 измерений.
Можно задаваться и предельной по величине ошибкой
среднего результата, принимая такую ошибку, как правило,
равной zb 4/?.
Пример 8. Срединная ошибка способа измерения равна 0-05. Сколько
необходимо произвести измерений, чтобы средний результат был найден
с ошибкой, не превышающей 0-10?
Решение. Примем предельную ошибку среднего результата
ошах= ±4/?= ±0-10,
отсюда
R = 12. = 2,5 деления угломера.
а искомое число измерений
Если бы требовалось, чтобы предельная ошибка была равна не 0-10,.
а только 0-05, tq
5 / 5 V
R = -j- = 1,25 деления угломера и S= j-gg \ = 16.
Точность результата измерения можно повысить, повысив
точность самого способа измерения, т. е. уменьшив его сре-
динную ошибку или увеличив число измерений.
В конкретных условиях величину срединной ошибки спо-
соба измерения изменить невозможно, так как она опреде-
175
ляется свойствами приборов измерения, качествами самого из-
меряющего, обстановкой, в которой производится измерение,
и пр. Поэтому остается второй путь — повысить точность ре-
зультата измерения за счет увеличения числа измерений.
Увеличение числа измерений связано, прежде всего, с рас-
ходом времени, а при измерениях отклонений разрывов и
с расходом снарядов. Поэтому приходится ограничиваться,
как правило, сравнительно небольшим числом измерений.
Посмотрим, какое же увеличение числа измерений будет
наиболее эффективным с точки зрения повышения точности
результата измерения. Рассчитаем для этого срединные ошиб-
ки среднего результата R при различных численных значе-
ниях S и найдем изменения срединной ошибки среднего ре-
зультата &R в долях £ и в процентах для каждого последу-
ющего измерения (табл. 17).
Таблица 17
S R ДЯв £ ДЯ в S R Д Я в £ ДЯ в °/о
1 Е 6 same 0,039 8,2
2 0,707 £ 0,293 29,3 7 0,378 £ 0,030 7,4
3 0,577 £ 0,130 18,4 8 0,353 £ 0,025 6,6
4 0,500 £ 0,077 13,3 9 0,333 £ 0,020 5,7
5 0,447 £ 0,053 10,6 10 0,316 £ 0,017 5,1
Эта таблица показывает, что наиболее существенное при-
ращение точности может быть получено только при первых
измерениях. Так, при одном измерении R = E, при двух изме-
рениях R = 0,707Е, что по сравнению с первым результатом
уменьшило величину R на 0,293£\ или на 29,3°/0, при трех
измерениях R-~=0,b77E, что по сравнению с предыдущим ре-
зультатом дало уменьшение R на 0,130Я, или на 18,4°/0, и т. д.
Особенно резкое сокращение R дают второе, третье измере-
ния. Поэтому при всякой к тому возможности измерение ве-
личины следует производить не менее 2—3 раз.
После четырех измерений приращение точности резко
падает. Поэтому, определяя при стрельбе по отклонениям
разрывов положение средней траектории, ограничиваются
четырьмя измерениями, и только в случаях, требующих осо-
бой точности, доводят число измерений до девяти. Дальней-
шее увеличение числа измерений настолько незначительно
способствует повышению точности результата измерения, что
применяется, как правило, только при производстве измерений,
носящих научно-исследовательский характер.,
176
§ 38. ПОДХОДЯЩЕЕ ЗНАЧЕНИЕ СРЕДИННОЙ ОШИБКИ
ПО РАЗНОСТЯМ МЕЖДУ ОТДЕЛЬНЫМИ РЕЗУЛЬТАТАМИ
Подходящее значение срединной ошибки Е может быть найдено и не-
посредственно по результатам отдельных измерений, без предварительного
определения численных значений кажущихся ошибок. Этот способ заклю-
чается в том, что срединная ошибка определяется по разностям между со-
седними отдельными результатами измерения. Далее будут указаны случаи,
когда такой способ является не только более выгодным, но и единственно
возможным.
Допустим, что имеется ряд отдельных результатов измерения одной и
той же величины одним и тем же способом:
х1> х81 . . ., xs.
Условимся, что ошибки этих результатов следуют закону Гаусса.
Рассчитаем кажущиеся ошибки этих результатов:
Xi — X! — $
^2 == х2 — £
Х8 — х3 — £
— XS ~
откуда
Х1 = + £
х2 = ^2 + ?
*8 — ^8 ?
XS — + £
Возьмем разности между двумя соседними результатами, вычитая всег-
да предыдущий результат из последующего, и обозначим эти разности
через и:
х2 — х1 = (Х2 4- ?) — (Х4 4- ?) = Х2 — Xj =
хз — х2 — (Ха + ?) — (Хг + ?) = Хз — Х2 = и2
х^ — х3 = (Х4 + £) — (Х8 4- £) -- Х4 — Х8 = и2
xs — xs-i — + £) — 1 + ?) — Х$ X5—1 — i
Таким образом, разности между отдельными результатами мы заменили
разностями между соответствующими им кажущимися ошибками и получили
-S—1 значений таких разностей.
Возведем во вторую степень эти разности:
Xj —2 X2Xj Х| = ul
Х| —2 Х3Х2 4~ Х2 = п2
х| —2 Х4Х8 4~ х| = «з
4 — 2Х5 X<s_1 4-Xj_1 —
12 — Зак. 991
177
и сложим их почленно:
(^2+ Х|+ ^4 • • + ^s) — 2 (Х1Х2 + ^3 + ^4 + • • • 4* ^s—1Лs ) +
+ G1 + ^2 + ^3 + •" • + 4?—4 ~ и1 + и2 + «3 + • • • 4~ US~ 1 *
Исходя из симметричности закона Гаусса, мы можем пренебречь,
суммой парных произведений кажущихся ошибок
^1^2 4~ + ХдХ4 + • • • + 4 5 ,
так как она при достаточно большом числе измерений будет близка к нулю»
и тогда
5 5—1 S-1
2х2 + 2х2=2и2.
1
левая часть этого равенства. Нач-
2 1
Посмотрим, что представляет собой
нем со второго слагаемого
^х?.
1
Если бы мы имели S результатов измерения, а отсюда и S кажущихся
ошибок, то по известной формуле подходящее значение средней квадрати-
ческой ошибки
Но у нас в выражении
имеется сумма квадратов не <$ кажущихся ошибок, а £ без одной; при
таком числе кажущихся ошибок подходящее значение средней квадратиче-
ской ошибки должно быть выражено:
откуда
£22(S-2) = 2^-
1
Слагаемое
s
2х2
2 1
также представляет собой сумму (S—1) квадратов кажущихся ошибок.
Поэтому и это слагаемое мы можем заменить выражением
£| (S — 2),
и тогда равенство
5 2 5-^2 2
2 л; 4- 2 М = 2 Ui
2 1 1
178
примет вид
s-i
2 «2 = £22 (S - 2) + £22 (£ - 2) = 2£22 ($ __ 2).
Решая это равенство относительно £2, получим:
или
В законе Гаусса срединная ошибка Е связана со средней квадратиче-
ской ошибкой £2 следующей зависимостью:
Е = 0,67449 £2.
Допустив, что разности и как разности между случайными ошибками,
следующими закону Гаусса (см. стр. 177), следуют также этому закону,
заменим £2 на Е и получим:
£ =
0,67449
/2
или, после деления 0,67449 на /2,
/ ц.2 ц2„ _1_ ц2„ -и . . . -4- и? с ,
£«=•0,476941/ 1
S —2
Вернемся к равенствам:
U] = Х2— Х4
и2 — ^3 — ^2
ц3 = Х4 — Х3
11S—1 -
сложим их почленно:
М1 + и2 + из + . • • + us— 1= ^2 — Xi 4~ Х3 — Х2 4- Х4 — Х3 + . . . +Х5 — ^'5—1.
Тогда после приведения подобных членов получим:
S-1
S lit — Х5 Xj =
Алгебраическая сумма разностей равна разности между последним и
первым результатами измерения. Этим равенством будем пользоваться при
проверке правильности расчетов отдельных разностей.
12*
179
Пример 1. При засечке батареи противника с помощью БЗР были
получены следующие отдельные результаты 10 измерений в метрах: 5 750,
5 870, 5 940, 5 780, 5860, 5 840, 5 790, 5 900, 5800 и 5 820. Определить подхо-
дящее значение срединной ошибки этого ряда измерений.
Решение.
№ xi - Xi _ ! ui 4 Проверка:
1 5870-5750 + 120 14 400
2 5940—5870 + 70 4 900 5820—5750=+70 м.
3 5780-5940 —160 25 600
4 5860—5780 + 80 6 400 ' / 76700
5 5840—5860 — 20 400 E =0,476941/ —g—=46,31 м
6 5790-5840 — 50 2 500 и г о
7 5900—5790 + 110 12 100
8 5800—5900 —100 10 000
9 5820 -5800 + 20 400
S +70 76700
Пример 2. При определении начальной скорости стрельбой были полу-
чены следующие результаты 12 отдельных изме >ений в м/сек: 577,9;
582,1; 580,3; 581,6; 578,7; 579,6; 580,8; 578,2; 582,0; 581,1; 578,8 и 580,5.
Найти подходящее значение срединной ошибки.
Решение.
№ X. — х. , 1 i—1 ц.
1 582,1 —577,9 +4,2 17,64
2 580.3 — 582,1 —1,8 3,24
3 581,6 — 580,3 + 1,3 1,69
4 578,7 — 581,6 -2,9 8,41
5 579,6 — 578,7 +0,9 0,81
6 580,8 — 579,6 + 1,2 1,44
7 578,2 — 580,8 —2,6 6,76
8 582,0 — 578,2 +3,8 14,44
9 581,1 -582,0 —0,9 0,81
10 578,8 — 581,1 -2,3 5,29
11 580,5 — 578,8 +1.7 2,89
3 +2,6 63,42
Проверка:
580,5 — 577,9 = + 2,6 м/сек.
Еи = 0,47694 1/=1,2 м/сек.
Способом определения подходящего значения срединной ошибки по
разностям между отдельными результатами рекомендуется пользоваться
в тех случаях, когда условия, в которых производится измерение, непосю-
янны. Такие условия, в частности, могли быть в приведенных выше двух
примерах—непостоянство метеорологических условий при стрельбе с помощью
БЗР и разность температур боевых зарядов при определении начальной
скорости.
Этим способом необходимо пользоваться тогда, когда в процессе изме-
рения изменяется сама измеряемая величина, например при определении
дальности до движущейся цели. Определение в таких условиях подходя-
щего значения срединной ошибкл по кажущимся ошибкам приводит к не-
правильным выводам.
180
Покажем это на примере.
Допустим, что одним и тем же способом измеряется угол между ориен-
тиром и целью, и разберем два случая: цель неподвижна н цель движется,
причем в обоих случаях одним и тем же (в порядке последовательности их
получения) результатам измерения соответствуют одинаковые по величине
и по знаку ошибки. #
Измерение угла между ориентиром и неподвижной целью дало следую-
щие результаты: 1-09, 1-03, 1-01, 1-04, 0-99, 0-95, 1-04, 1-01, 0-94, 1-03, 1-00,
1-06, 0-98, 1-04, 1-02 и 0-93.
В случае, когда цель движется, для упрощения расчетов допустим,
что первое измерение совпало с моментом начала движения цели и пель
двигалась так, что при каждом последующем измерении истинное значение
измеряемого угла увеличивалось на 0-02. Таким образом, первый результат
был таким же, как и для неподвижной цели (1-09), второй результат полу-
чил приращение в 0-02 (1-03 4- 0-02 = 1-05), третий результат получил при-
ращение в 0-04 (1-01 4- 0-04 = 1-05), четвертый — в 0-06 (1-04 4- 0-06 = 1-10)
и т. д.
Определим подходящее значение срединной ошибки для обоих случаев
всеми известными нам способами и сравним полученные результаты. Все
расчеты сведем в общую таблицу (табл. 18).
Таблица 18
i Цель неподвижна Цель двигалась
Xi X. 1 >? 2 «1 Х i х. 1 /е. г 2 ai
1 1-09 4-8 64 —6 36 1-09 —7 49 —4 16
2 1-03 4-2 4 —2 4 1-05 —И 121 0 0
3 1-01 0 0 4-3 9 1-05 —11 121 4-5 25
4 1-04 4-3 9 —5 25 1-10 —6 36 -3 9
5 0-99 —2 4 —4 16 1-07 —9 81 —2 4
6 0-95 —6 36 4-9 81 1-05 —11 121 4-11 121
7 1-04 4-3 9 —3 9 1-16 0 0 —1 1
8 1-01 0 0 —7 49 1-15 —1 1 —5 25
9 0-94 —7 49 4-9 81 1-10 —6 36 4-11 121
10 1-03 +2 4 -3 9 1-21 +5 25 —1 1
11 1-00 —1 1 4-6 36 1-20 4-4 16 4-8 64
12 1-06 4-5 25 —8 64 1-28 +12 144 —6 36
13 0-98 —3 9 4-6 36 1-22 4-6 36 +8 64
14 1-04 4-3 9 —2 4 1-30 4-14 196 0 0
15 1-02 4-1 1 -9 81 1-30 4-14 196 —7 49
16 0-93 -8 64 — — 1-23 4-7 49 — —
2 16-16 0 288 —16 540 18-56 0 1228 4-14 536
181
Найдем сначала подходящее значение срединной ошибки для непо-
движной цели при ^=1616:16 = 1-01:
1. По средней арифметической ошибке
54
£pi = 0,84535----- — 2,95 деления угломера.
У 16-15
2. По средней квадратической ошибке
Ее^ - 0,67449 у/__— =2,96 деления угломера.
3. По месту в ряде абсолютных значений ошибок
Ерр = 3 делениям угломера.
4. По разностям между соседними результатами
Еи = 0,47694* / 549- = 2,96 деления угломера,
у 14
Все расчеты привели к одному и тому же численному значению сре-
динной ошибки, которое и примем за подходящее значение срединной
ошибки рассматриваемого способа измерения.
Теперь найдем подходящее значение срединной ошибки для движу-
щейся цели при £ = 1 856:16 = 1-16:
1. По средней арифметической ошибке
194
Ее = 0,84535-—===- = 6,76 деления угломера.
1 У 16-15
2. По средней квадратической ошибке
Ее* = 0,67449 у/ 1 ?28 = gj деления угломера.
3. По месту в ряде абсолютных значений ошибок
Ерр = 1 делениям угломера.
4. По разностям между соседними результатами
——— =2,95 деления угломера.
Сравнив эти расчеты, мы видим, что только способ разностей дал нам
подходящее значение, близкое к принятому значению срединной ошибки
способа измерения. Определение подходящего значения срединной ошибки
по кажущимся ошибкам дало нам неверные и различные значения Е.
Таким образом, в тех случаях, когда измеряемая величина изменяется
при измерении, для определения подходящего значения срединной ошибки
следует пользоваться только способом разностей.
Необходимо особо подчеркнуть, что при определении подходящего
значения срединной ошибки по разностям между соседними результатами
измерения необходимо эти результаты располагать в той последователь-
ности, в которой они были получены при измерении. В противном случае
нарушается закономерность изменений измеряемой величины, что приводит
к неверным выводам.
182
§ 39. ПРИЛОЖИМОСТЬ ЗАКОНА ГАУССА И ИСКЛЮЧЕНИЕ
АНОРМАЛЬНЫХ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯ
До сих пор во всех случаях обработки результатов изме-
рения было принято, что ошибки рассматриваемого ряда изме-
рений следуют закону Гаусса. Исходя из этого предположе-
ния и были сделаны все выводы.
Но помимо закона Гаусса при данных измерениях могут
иметь место и другие законы ошибок, и не всегда суммарный
закон ошибок будет законом Гаусса. Естественно, при обра-
ботке результатов измерения возникает вопрос: действительно
ли ошибки этих результатов являются ошибками, которые
следуют закону Гаусса, т. е. приложим ли закон Гаусса к дан-
ному ряду измерений? В противном случае применение фор-
мул, принятых для закона Гаусса, приведет к грубым ошибкам.
Выше было установлено, что только закону Гаусса свой-
ственны зависимости между средней арифметической, средней
квадратической и срединной ошибками, выражаемые равен-
ствами:
0,84535 Е = 0,67449 и Ег = 0,79787 £2,
или соотношениями, округленными до второго десятичного
знака:
=0,85, —= 0,67 и =0,8.
Еу ’ ’ Е2 ’ Е2 ’
Этими соотношениями пользуются для суждения о прило-
жимости закона Гаусса. Считается, что закон Гаусса практи-
чески применим к ошибкам данного ряда измерений, если
соотношения между Е, Еу и Е2, найденные путем обработки
результатов измерений, отличаются от соотношений, свой-
ственных закону Гаусса не более чем на 10%, т. е. если
-4-----0,85 <0,085;
Еу > ’
-----0,67 <0,067
Е2
и
-----0,8 <0,08.
Е2 ’
При этом подходящее значение Е определяется по месту
в ряде абсолютных значений ошибок или по разностям меж-
ду соседними результатами (Ерр и Еа).
Пример 1. Один и тот же угол одним и тем же способом был изме-
рен 15 раз, и при этом были получены следующие отдельные результаты:
1-30, 1-36, 1-33, 1-28, 1-36, 1-41, 1-45, 1-38, 1-27, 1-34, 1-29, 1-37, 1-31,
1-47 и 1-33. Проверить приложимость закона Гаусса к данному ряду изме-
рений и найти подходящие значения угла и срединной ошибки.
183
Решение. Произведем обработку результатов измерения.
X. 1 е *1 — J fi-l ai 2
1 1-30 1-35 —5 25 1-35 — 1-30 +6 36
2 1-36 1-35 +1 1 1-33 — 1-36 —3 9
3 1-33 1-35 —2 4 1-28- 1-33 -5 25
4 1-28 1-35 —7 49 1-36 — 1-28 + 8 64
5 1-36 1-35 +1 1 1-41 — 1-36 +5 25
6 1-41 1-35 +6 36 1-45 — 1-41 +4 16
7 1-45 1-35 + 10 100 1-38 — 1-45 —7 49 ,
8 1-38 1-35 +3 9 1-27 — 1-38 —И 121
9 1-27 1-35 —8 64 1-34 — 1-27 +7 49
10 1-34 1-35 —1 1 1-29 — 1-34 —5 25
11 1-29 1-35 -6 36 1-37 — 1-29 +8 64
12 1-37 1-35 +2 4 1-31 — 1-37 —6 36
13 1-31 1-35 -4 16 1-47 — 1-31 + 16 256
14 1-47 1-35 + 12 144 1-33 — 1-47 —14 196
15 1-33 1-35 -2 4 — — —
2 20-25 20-25 0 494 1-33 — 1-30 +3 971
2025
15
= 1-35;
70
Ei~ Я5П4
= 4,83
деления угломера;
494
14
= 5,94
деления угломера;
Ерр — 4
делениям угломера;
Еа — 0,47694
971
13
= 4,12 деления угломера.
Ерр-.ЕХ = 4,00:4,83 = 0,82;
Еа\ Е1 = 4,12:4,83 = 0,85;
0,82 — 0,85 = 0,03;
0,85 — 0,85 = 0.
0,03 < 0,085.
Е2 =
Ерр: Е2 =4,00 : 5,94 = 0,67;
0,67 — 0,67 = 0.
ЕВ:Е2 = 4,12:5,94 = 0,71;
0,71 —0,67 = 0,04;
0,04 < 0,067.
Ej: Е2 = 4,83: 5,94 = 0,81;
0,81 — 0,80 = 0,01
0,01 < 0,08.
Вывод. К данному ряду измерения закон Гаусса применим полностью*
Пример 2. Обработка результатов измерения расстояния дала следую-
щие численные значения параметров: Ерр = 20 м; Еи = 19,3 м\ Ех = 23,5 м
и Е2-=. 28,1 м. Установить приложимость закона Гаусса к этим результатам.
184
Решение. Найдем численные значения соотношений между парамет-
рами:
_£ _ 19'3 - 0 82-
— 94 А - u’oz’
Возьмем разности между этими соотношениями и соотношениями, тео-
ретически соответствующими закону Гаусса:
0,82—0,85=—0,03; 0,03<0,085;
0,69-0,67=4-0,02; 0,02< 0,067;
0,84—0,8 =4-0,04; 0,04<0,08.
Все разности меньше допустимых; следовательно, закон Гаусса приложим»
к этим результатам.
Для проверки сравним соотношения, рассчитанные относительно Ерр.
Ерр _ 20 о 85 и Ерр — 2° - о 71
' еТ~^~ °’/е
Тогда разности между соотношениями:
0,85—0,85=0;
0,71—0,67=0,04; 0,04<0,067,
т. е. эта проверка подтверждает приложимость закона Гаусса.
Пример 3. При обработке результатов измерения скорости самолета
были п олучены следующие численные значения параметров в м сек\ Еро = 4,5;
Еи = 3,9; Еу - 4,7 и Д2 = 7,5.
Установить приложимость закона Гаусса.
Решение.
е?£ El 4 5 - = 0,96; 0,96—0,85=0,11; 0,11>0,085;
Ерр Е* 4,5 = Уз = 0,60; 0,60-0,67=—0,07; 0,07^0,067;
Еи Ei z 3 9 = -уу = 0,83; 0,83—0,85=—0,02; 0,02<0,85;
Еи__ Еч 3 9 = у_ = 0,52; 0,52—0,67 = —0,15; 7,5 ’ ’ 0,15>0,067;
Е± Еч = 4,7 = тЧ- = 0,63; 0,63—0,80=—0,17; /,5 ’ 0,17>0,08.
Подавляющее большинство соотношений, рассчитанных по результатам измерения, превышает соотношения, свойственные закону Гаусса, более чем Е на 10%, а для соотношений и -р- это превышение достигает почти 20%,. Следовательно, в данном случае закон Гаусса не применим.
185
При обработке результатов измерений с вопросом о при-
ложимости закона Гаусса к данному ряду измерений связан
вопрос об исключении из этого ряда так называемых анор-
мальных результатов.
Производя измерение одной и той же величины одним и
тем же способом, мы нередко получаем отдельные результаты,
резко отличающиеся своей величиной от других результатов.
Очевидно, что такие результаты не могут не повлиять на
итоги обработки, и зачастую это влияние настолько велико,
что совершенно меняет суждение о законе ошибок данного
ряда измерений.
Положим, что в приведенном выше примере к 15 результатам измере-
ния угла был добавлен еще один, равный 1-67.
В этом случае средний результат будет уже не 1-35, а 1-37. Вследствие
этого изменятся значения кажущихся ошибок, и тогда
Ерр = 5 делениям угломера;
Ю6
£, = —7===. = 6,84 деления угломера
1 у 16-15
и
г / 1454 Л
£2 = t/ j-gr- = 9,85 деления угломера,
а соотношения:
Е 5
-^ = =0,73; 0,73—0,85=—0,12; 0,12>0,085;
0,о4 ’
Е 5
-^- = -==-=0,51; 0,51—0,67=—0,16; 0.16>0,067;
Z^2 У, оо
|1 = = 0,69; 0,69—0,80=—0,11; 0,11>0,08.
Обработав 15 результатов измерения угла, мы пришли к выводу, что
закон Гаусса к him применим, Включив в обработку 13-й результат, нам
пришлось отказаться от этого вывода, так как все разности соотношений
между Е, Ei и превысили допустимые для приложимости закона Гаусса
пределы.
Если имеются достаточно веские основания полагать, что
подобного рода результаты являются следствием причин, не
присущих данному способу измерения (грубые ошибки отсче-
тов и графических построений, математические просчеты, ошиб-
ки в наводке при стрельбе и т. п.), то исключение таких
анормальных результатов сомнений не вызывает. Например,
если при определении дальности до цели методом сокращен-
ной подготовки в одном случае точка цели была нанесена не
в тот квадрат карты, то очевидно, что при отыскании подхо-
дящих значений дальности и срединной ошибки способа этот
результат при обработке учитывать не следует.
Но далеко не всегда удается установить причину больших
отклонений отдельных результатов, и тогда к исключению их
из ряда измерений следует подходить с большой осторож-
186
ностью, так как известно, что в совершенно нормальных усло-
виях измерения ошибки отдельных результатов, а отсюда и
их отклонения могут быть очень велики.
В этих случаях следует исходить из численных значений
вероятностей получения ошибок, соответствующих отдельным
результатам, исключая те из них, вероятности ошибок которых
пренебрежимо малы.
До сих пор при всех расчетах мы принимали предельно
допустимой на практике ошибку, равную 4 срединным ошиб-
кам способа измерения, считая вероятности получения ошибки
свыше+42? пренебрежимо малыми.
Возможность такого допущения при обработке результа-
тов измерения, когда перед нами стоит задача определения
вида и основных характеристик закона ошибок, удовлетворить
нас не может.
Действительно, по таблице значений Ф(р) вероятность полу-
чения ошибки в пределах +42?
Ф (4,0) = 0,99302,
откуда вероятность получения ошибки свыше ± 42? равна
1—0,99302 = 0,00698.
Вероятность как будто не велика, но нас интересует не
вероятность получения одной ошибки свыше ±42?, а вероят-
ность получения хотя бы одной такой ошибки.
Положим, что произведено 20 измерений одной и той же
величины. Тогда вероятность получения хотя бы одной ошибки
свыше ± 42?
Pl = 1 _ (1—0,00698)*° = 1-0,993022° = 0,13072 13,1 %;
это означает, что в среднем на каждые 100 серий по 20 ана-
логичных измерений мы в 13 сериях будем получать резуль-
таты с ошибками, превышающими ± 42?. Очевидно, что отно-
сить такие результаты к категории анормальных оснований нет.
Примем практические пределы допустимой ошибки рав-
ными ±62?. Вероятность получения одной ошибки в преде-
лах ± 62?
ф (6,0) = 0,9999482,
откуда вероятность получения хотя бы одной ошибки свыше
±62? при 20 измерениях
Pl = 1—0,999948220 = 0,000961 «0,1%.
Это означает, что на каждую 1 000 серий по 20 измерений
в среднем получим только один результат с ошибкой, превы-
шающей+62?. Таким результатом можно пренебречь.
Известно, что с уменьшением числа повторений испытания
вероятность появления события хотя бы один раз также
уменьшается. Поэтому при небольшом числе измерений за
187
анормальные результаты можно принимать те результаты,
ошибки которых превышают ± 5Е.
Вероятность получения одной ошибки в пределах zt 5Е
ф (5,0) = 0,99926.
Допустим, что произведено 10 измерений, тогда вероят-
ность получения хотя бы одной ошибки свыше гЬ5£
,рг = 1 — 0,9992610 = 0,00734 «0,7%,
а для 5 измерений такая вероятность будет еще меньше:
А== 1-0.999265 = 0,00367 я 0,4%.
Получение отдельных результатов с ошибкой свыше ±:5Е
при таком числе измерений настолько маловероятно, что их
исключение из ряда измерений вполне допустимо.
Отсюда следует правило: анормальными, считаются ре-
зультаты, ошибки которых превышают ± 6£, а при неболь-
шом числе измерений, {меньше 10)—и те результаты,
ошибки которых превышают ±5Е.
В тех случаях, когда в ряде измерений были получены
отдельные анормальные результаты, порядок обработки всей
совокупности результатов измерения следующий.
Сначала исключают из обработки те результаты, которые
своей величиной резко отличаются от других результатов.
Затем по оставшимся результатам определяют подходящие
значения измеренной величины и срединной ошибки.
Относительно найденного среднего результата рассчиты-
вают ошибки исключенных результатов и, сравнив эти ошибки
со срединной ошибкой, устанавливают, какие из этих резуль-
татов следует совсем исключить, а какие снова ввести в ряд
измерений. После этого производится дальнейшая обработка
результатов измерения.
Пример 4. При определении дальности до одной и той же пели одним и
тем же способом были получены следующие результаты в делениях при-
цела: 131, 132, 133, 135, 130, 129, 148, 133, 137, 131, 122, 130, 133, 135, 131,
130, 132 и 130. Определить, какие результаты измерения следует отнести
к анормальным.
Решение. Резко выделяются два результата: 148 и 122; их мы и
исключим из первой обработки результатов измерения.
i xi k. 1 X? i Xi i Xi k. 1 X?
1 131 —1 1 7 Ц48| — — 13 133 + 1 1
2 132 0 0 8 133 +1 1 14 135 4-3 9
3 133 +1 1 9 137 -|-5 25 15 131 —1 1
4 135 +3 9 10 131 — 1 1 16 130 —2 4
5 130 —2 4 11 |T22| — 17 132 0 0
6 129 -3 9 12 130 —2 4 18 130 —2 4
188
Средний результат без исключенных
2И2
16 ~132-
Срединная ошибка по месту ее в ряде ошибок
1+2
ЕРР = ~2~ = !’5 ДХ-
Ошибки исключенных результатов:
Х7= 148—132 =+ 16ДХ и Хп = 122—132=—10 ДХ.
Эти ошибки, выраженные в Е:
16 10
1'7=='Т5' = Ю,7£Г и Хп = -y-g- =.&,1Е.
Следовательно, оба результата анормальны и включать их в обработку
измерений не следует.
Мы применили формулы, относящиеся только к закону Гаусса. Прове-
рим приложимость этого закона к данному ряду измерений (без исключен-
ных).
28
£>=рт§йз=1'814Хн^=
— = 2,22 ДАТ;
15
тогда соотношения между Е, Е± и Е^.
Е 15
= Р81=О,83; 0,83—0,85 = 0,02; 0,02<0,085;
Е 15
= Г?2 ==0»68; 0,68—0,67 = 0,01; 0,01<0,067;
Е, 1.81
-^А- ='2~2“? = 0,82; 0.82-0,80 = 0,02; 0,02<0,08.
Разности соотношений меньше допустимых — закон Гаусса приложим.
Пример 5. Засечка дальности до цели с помощью БЗР дала следую-
щие отдельные результаты измерения в метрах; 4 185, 4 105, 4 160, 4 190,
4 220, 4 465, 4 120, 4 175, 4 250, 4 325, 4 150, 4 125, 3 920, 4 170, 4 145,4 230,
4 155 и 4 090. Определить подходящие значения измеренной дальности и
срединной ошибки этого измерения.
Решение. Исключим из первой обработки результаты: 4465, 4 325 и
3 920 м, и определим подходящее значение измеренной дальности по остав-
шимся 15 результатам:
62475
£= —= 4165 м.
Найдем кажущиеся ошибки относительно этого среднего результата и
расположим их в возрастающем порядке по абсолютным значениям:
5, 5, 10, 10, 15, 20, 20, 30, 40, 45, 55, 60, 65, 75, 85.
Отсюда срединная ошибка по ее месту в этом ряде
Foo = 30 м.
189
Проверим исключенные результаты, сравнив их ошибки с Ерр:
4465—4165=4-300 м', 300:30=10F—результат анормальный;
4325—-4165=4-160 м\ 160:30 = 5,3F — результат допустимый;
3920—4165=—245 м\ 245:30=8,2F—результат анормальный.
Введем снова результат в 4 325 м в ряд измерений и произведем обра"
ботку результатов в окончательном виде:
1 Xi Е X. 1 X? Х1 *7—1 и. 1 2 “i
1 4185 4 175 + 10 100 4105- 4 185 -80 6 400
2 4 105 4 175 —70 4 900 4 160 — 4 105 +55 3 025
3 4 160 4 175 — 15 225 4 195 — 4 160 +35 1 225
4 4 195 4 175 +20 400 4 220 — 4 195 +25 625
5 4 220 4 175 +45 2 025 4 120 — 4 220 —100 10 000
6 4 120 4 175 -55 3 025 4 175 — 4 120 + 55 3 025
7 4 175 4 175 0 0 4 250 — 4175 +75 5 625
8 4 250 4 175 + 75 5 625 4 325 — 4 250 +75 5 625
9 4 325 4 175 + 150 22 500 4150 — 4 325 —175 30 625
10 4 150 4175 —25 625 4125 — 4 150 —25 625
11 4 125 4175 —50 2 500 4170 — 4 125 +45 2 025
12 4 170 4 175 —5 25 4145 — 4170 -25 625
13 4 145 4175 —30 900 4 230 — 4 145 +85 7 225
14 4 230 4 175 +55 3 025 4 155 — 4 230 —75 5 625
15 4 155 4175 —20 400 4 090 — 4 155 -65 4 225
16 4 090 4175 —85 ‘7 225 — — —
2 66 800 66 800 0 53 500 4 080 — 4 185 —95 86 525
Подходящее значение измеренной дальности
66800
4=-Ig-=4175 м.
Подходящее значение срединной ошибки по ее месту в ряде абсолютных
значений ошибок
„ 30+45
Ерр------2 — 37,5 м.
Подходящее значение срединной ошибки по разностям между соседними
результатами ____
Еа = 0,47691/37,494 = 37,5 м.
Проверим приложимость закона Гаусса к нашему ряду измерений, хотя
этого можно было бы и не делать, так как Ерр — Еа.
Средняя арифметическая и средняя квадратическая ошибки
с 710 лгп с 1/ 53500 ,ос „
Е, = •> - = 45,9 м и £о = I/ --------=— — <59,8 м.
1 У 16-15 ’ 2 V 15
190
Тогда соотношения:
Е _ 37,5
Ег ~ 45,9
= 0,82;
Е 37,5
Е2 — 59,8 = 0’б3;
Ег 45,9
Е2 — 59,8 — °’77-
Эти соотношения очень мало отличаются от соотношений, отвечающих:
закону Гаусса, что и подтверждает приложимость этого закона к исследо-
ванному ряду измерений.
§ 40. ЗАДАЧИ НА ОБРАБОТКУ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Задача 90. При измерении угла стереотрубой были получены следую-
щие результаты: 2-41, 2-37, 2-45, 2-40, 2-43, 2-38, 2-49, 2-44, 2-42 и 2-46.
Определить среднюю величину измеренного угла.
Ответ. 2-42,5.
Задача 91. При измерении дальности до репера были получены следую-
щие результаты измерения в метрах: 5 445, 5 384, 5 430, 5 515, 5 418, 5 406,
5392, 5525, 5468, 5 424, 5 452, 5 439, 5 398 и 5464. Определить подходящее
значение измеренной дальности.
Ответ. 5 440.
Задача 92. При измерении одного и того же угла биноклем были по-
лучены следующие результаты отдельных измерений: 1-59, 1-64, 1-61, 1-55,
1-62, 1-58, 1-52, 1-60, 1-72, 1-60, 1-65, 1-56, 1-60, 1-56, 1-67, 1-50, 1-63, 1-58,
1-49, 1-64 и 1-69. Чему равна величина измеренного угла?
Ответ. 1-60.
Задача 93. Найдены следующие величины кажущихся ошибок отдель-
ных результатов измерения в метрах: —13, —5, +16, —J-2, +24, —18, —20,
+8, —12, +10 и +8. Чему равна срединная ошибка способа измерения?'
Ответ. Е„„ 4- 12 м\ EF == 11,02 м', EF = 9,83 м.
Задача 94. При измерении базы мерной лентой были получены следую-
щие результаты отдельных измерений в метрах: 178,24; 178,31; 179,02; 178,64;
178,45; 178,36; 178,81; 178,54; 178,62 и 178,41. Определить величину средин-
ной ошибки способа измерения.
Ответ. Ерр = 0,155 м', Ее* = 0,166 м\ Ее^ = 0,162 м.
Задача 95. При измерении дальности до цели были получены следующие
результаты отдельных измерений в делениях прицела: 108, 112, 105, 106,
104, 105, 109, 105, 104, 106, 102, 107, 101, 109 и 107. Чему равна вероятность
того, что следующее измерение той же дальности и тем же способом будет
иметь ошибку:
а) не больше 2 ДХ;
б) не больше 5 ДХ?
О т в е т ЕЕ2 = 1,908 ДХ; Ра = 0,52035; Р6 = 0,92280.
Задача 96. При определении установки угломера были получены
следующие результаты отдельных измерений: 55-90, 55-45, 56-60, 55-80, 55-65,
56-00, 56-10, 56-15, 55-50, 56-05, 55-85, 55-95, 56-35, 56-20, 55-70, 55-95, 56-70,
56-20, 56-00 и 55-90. Чему равна вероятность того, что следующее определе-
ние угломера по той же цели и тем же способом будет иметь ошибку:
а) не более 0-10;
б) не более 0-35;
в; не меньше 0-50?
Ответ. £2 = 21,55 деления угломера; Ра — 0,24569; Рб = 0,72666;
Р, = 011763.
191
Задача 97. Чему равна срединная ошибка среднего результата, если
величина этого среднего результата была определена по данным 16 отдель-
яых результатов измерения и срединная ошибка способа измерения равна 80 м.7
Ответ. 20 м.
Задача 98. Срединная ошибка способа измерения равна 0-15. Чему
равна срединная ошибка среднего результата, величина которого определе-
на по данным 25 отдельных измерений?
Ответ. 0-03.
Задача 99. Определить срединную ошибку среднего результата, если
при измерении угла были получены следующие величины ошибок отдельных
измерений в делениях угломера: — 2, 4- 4, + 6, — 5, % 1, — 4, — 2, 4- 8 и — 6.
О т в е т. ЕЕз = 3,39 деления угломера; R = 1,13 деления угломера.
Задача 100. При измерении базы шагами были получены следующие
результаты отдельных измерений в метрах: 830, 750, 770, 820, 790, 870, 800,
780, 860 и 830. Определить срединную ошибку среднего результата.
Ответ. Ее% = 26,22 м\ R = 8,27 м.
Задача 101. При измерении дальности до цели дальномером были
получены следующие результаты отдельных измерений в метрах: 4 890,
4 850, 4 820, 4 860, 4 810 и 4 870. Определить наименьшие пределы, в которых
заключено истинное значение измеренной дальности, с вероятностью,
равной 50%, если срединная ошибка способа измерения равна 20 м.
Ответ. R « 8,2 м‘, от 4841,8 м до 4858,2 м.
Задача 102. При измерении угла были получены следующие результаты
«отдельных измерений в делениях угломера: 1-61, 1-69, 1-66, 1-60, 1-58, 1-65,
1-72, 1-64, 1-69, 1-65, 1-63, 1-54, 1-67, 1-63 и 1-64. Определить наименьшие
пределы, в которых заключено истинное значение измеренного угла, с веро-
ятностью, равной 0,82266.
Ответ. ЕЕг и 3,1 деления угломера; R ~ 0,8 деления угломера от
1-62,4 до 1-65,6.
Задача 103. При определении стрельбой начальной скорости были
получены следующие результаты отдельных измерений в м/сек: 420,3, 428,1,
-424,2, 426,7, 421,5, 420,8, 425,4, 422,1, 426,5, 421,8, 424,4, 427,1, 423,7, 425,9,
421,7 и 427,0. Найти подходящие значения начальной скорости и
•срединной ошибки способа ее определения.
Ответ, с'о = 424,2 м/сек\ Еи = 2,053 м/сек.
Задача 104. При определении дальности до цели с помощью БЗР были
получены следующие результаты отдельных измерений в метрах: 7 135, 6 915,
7 095, 7 350, 7 015, 7 210, 6 970, 7 320, 7 400, 7 040, 7 185, 6 960, 7 285, 7 150,
6 995, 7 250, 7 290, 7 035, 7 165 и 6 955. Найти подходящие значения дальности
и срединной ошибки.
Ответ. Д = 7 136 м; Еа = 113,8 м.
Задача 105. При измерении дальности до звучащей цели были получе-
ны следующие результаты отдельных измерений в метрах: 2 094, 2 071, 2 142,
2 104, 2 123, 2 082, 2 057, 2 095, 2 056, 2075, 2 085, 2 044, 2 099, 2 072, 2 100 и
2 043. Чему равна вероятность того, что, приняв средний результат за
истинное значение дальности, мы допустим ошибку, не превышающую
10 м.
Ответ. Еи — 18,28 м\ Р = 4,57 лт; Р = 0,86.
Задача 106. При определении дальности были получены следующие
результаты отдельных измерений в метрах: 4 255, 4205, 4 135, 4 235, 4 210-
4 315, 4 150, 4 2 20, 4 290, 4 195, 4170, 4 215, 4 305, 4 225, 4 275, 4 085, 4 220,
4 165, 4 185, 4 285, 4 260 и 4 130.
Проверить приложимость закона Гаусса для обработки результатов
измерений и найти подходящие значения дальности и величин характеристик
данного закона ошибок.
Ответ. Закон Гаусса применим; Д = 4 215 м\ Е± = 48,4 м\ Е% = 60,6 м;
£рр = 45 м; Еи — 45,24 м.
192
Задача 107. При определении расстояния были получены следующие
результаты отдельных измерений в метрах: 6188, 6195, 6130, 6068, 6 167,
6 111, 5 973, 6 156, 6 208, 6 257, 6 121, 6 035, 6 169, 6 274, 6 090, 6 198 и 6 074.
Проверить приложимость закона Гаусса для обработки результатов
измерений и найти подходящие значения дальности и характеристик данного
закона ошибок.
Ответ. Закон Гаусса приложим; Д = 6 142 м\ Ех — 65,9 м; Е% — 79,2 м;
Ерр = 53 м; Еи — 54,3 м.
Задача 108. При определении базы были найдены следующие резуль-
таты отдельных измерений в метрах: 85,9, 83,6, 84,8,78,8, 83,3, 85,4, 88,5,
94,0, 85,7, 84,0, 86,1, 92,8, 86,4, 84,9, 87,3 и 81,7. Найти подходящее значение
величины базы и указать, какие результаты измерений являются анормаль-
ными.
Ответ. Б = 85,2 м; 94,0 и 92,8.
Задача 109. Найти подходящее значение срединной ошибки и устано-
вить приложимость закона Гаусса для обработки 18 отдельных результатов
измерения скорости самолета: 31,5, 32,0, 31,5, 34,0, 36,5, 30,5, 33,5, 36,0, 35,5
31.5, 38,0, 34,0, 39,0, 35,5, 35,0, 37,0, 35,5 и 40,0 м/сек.
Ответ. Закон Гаусса применим; скорость 34,8 м/сек; Е— 1,6 м/сек.
13 — Зак. 991
ГЛАВА 8
ОШИБКИ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
§ 41. ОШИБКИ-ВЕКТОРЫ
Выше было указано, что все случайные ошибки могут быть
разбиты на следующие две категории:
1. Ошибки, не зависящие от направления, или ошибки ли-
нейные (иначе их называют скалярными ошибками).
2. Ошибки, зависящие от направления, или ошибки на
плоскости и в пространстве.
Ошибки первой категории определяются величиной (числен-
ным значением) и знаком. Например, измерив барометрическое
давление и установив, что ошибка этого измерения Д =— 2 л/л/,
мы получаем полное представление о точности произведенного
измерения. Кроме числа 2 и знака „минус", никаких других
характеристик ошибки не требуется.
К ошибкам, не зависящим от направления, т. е. не связан-
ным с каким-либо направлением, относятся ошибки при измере-
нии веса, давления, температуры, времени и т. п.
Для характеристики ошибок на плоскости и в пространстве,
кроме величины и знака, необходимо еще учитывать и их направ-
ление. В процессе измерений одной и той же величины одним
и тем же способом ошибки этой категории могут менять свое
направление, и каждое такое изменение будет сказываться на
результатах измерения. Поэтому такие ошибки и называются
зависящими от направления.
Покажем это на следующем примере.
Положим, что цель наносится на карту по углу между
направлениями на ориентир и цель и по дальности наблюдения.
Положим, что угол ро и дальность До соответствуют абсо-
лютно точному положению цели на карте. Допустим, что при
всех измерениях ошибки в нанесении цели на карту равны между
собой по абсолютной величине и различаются только направ-
лениями, т. е. допустим, что расстояния на карте между точкой
194
Ц» отвечающей действительному положению цели, и точками
Z/j, и Щ, полученными по отдельным результатам измерения,
одни и те же по величине, но направлены в разные стороны
(рис. 52).
По рисунку видно, что в зависимости от ошибок, допущен-
ных при измерении угла и дальности До, ошибки отдельных
результатов измерения Дп Д2 и Д3 имеют различные направле-
ния. Иначе говоря, при заданных направлениях ошибок Д15 Д2
и Д3, равных по абсолютной величине, результаты измерения
Следовательно, только зная величину, знак и направление
таких ошибок, можно определить ошибки отдельных резуль-
татов измерения.
Ошибки, которые помимо величины и знака характеризу-
ются еще и направлением, удобнее всего выражать графически,
т. е. в виде векторов.
Ошибка, значение которой определяется абсолютной
величиной и направлением, называется ошибкой-вектором.
Ошибки-векторы могут иметь любое направление на пло-
скости и в пространстве. Поэтому эти ошибки, в отличие от
ошибок линейных, носят название ошибок на плоскости и в
иространстве.
Ошибки-векторы, как и все векторы вообще, изображаются
в виде отрезка прямой, имеющего величину, точку приложе-
ния и направление. Под направлением следует понимать: во-
нервых, направление (положение на плоскости или в прост-
ранстве) прямой, на которой лежит ошибка-вектор, и во-вто-
рых, направление самой ошибки-вектора на этой прямой (рис. 53).
м
-------------------IV
Рис. 53
На рис. 53 АВ есть величина ошибки-вектора, А —- точка ее
ириложения и MN—направление прямой, на которой лежит
ошибка-вектор; стрелка показывает направление ошибки-век-
тора на прямой MN.
13*
195
Ошибка-вектор обозначается обычным символом, тольк®
с черточкой сверху — Д или двумя буквами с такой же чер-
точкой, причем первой ставится буква, соответствующая на-
чалу (точке приложения) ошибки-вектора {АВ).
Ошибка-вектор может быть задана и аналитически. В этом
случае ее величина выражается в каких-то линейных мерах,
точка приложения — координатами, прямая, на которой лежит
вектор,—уравнением, а стрелка заменяется знаками „плюс"
или „минус".
Отдельно взятая ошибка-вектор является следствием изме-
рения в каком-то одном направлении. Если при данном изме-
рении возникает несколько отдельных ошибок-векторов и
каждая из них имеет свое направление, то ошибка-вектор ре-
зультата измерения в целом носит суммарный характер. Такая
ошибка-вектор является результирующей отдельных состав-
ляющих ошибок-векторов. Наглядным примером может слу-
жить подготовка исходных установок для стрельбы, где
ошибка-вектор определения положения средней траектории от-
носительно цели, отвечающая исчисленным установкам,
является результатом взаимодействия ошибок-векторов опре-
деления направления на цель, дальности до цели и превыше-
ния цели.
Для отыскания результирующей ошибки-вектора необ-
ходимо сложить отдельные составляющие ошибки-векторы.
При сложении отдельных ошибок-векторов могут быть
следующие три случая:
1. Отдельные ошибки-векторы имеют общее направление,
т. е. направлены по одной прямой.
2. Отдельные ошибки-векторы имеют различные направле-
ния в одной и той же плоскости.
3. Отдельные ошибки-векторы имеют различные напра-
вления в пространстве, т. е. лежат в разных плоскостях.
1. Допустим, что при определении Дб глазомер-
ной подготовки ошибка измерения Дк (AJ равна + 100 м и
ошибка измерения отхода (Д2) равна + 30 м.
Эти две ошибки можно сложить как алгебраически, так и
геометрически.
При алгебраическом сложении результирующая ошибка
будет равна алгебраической сумме составляющих ошибок:
Д = Дг Д2 = ( + 100) + (+ 30) ~ + 130 м.
Для того чтобы произвести геометрическое сложение этих
же ошибок, изобразим их в одном и том же масштабе в ви-
де двух векторов и перенесем эти векторы на параллельную
им прямую ОА (рис. 54), при этом начало второго вектора
совместим с концом первого вектора.
196
Геометрически эта сумма может быть выражена отрезком О А.
Возьмем тот же пример, но допустим, что ошибка измере-
ния Дк = + 100 м, а ошибка измерения отхода Д2 — — 30 м.
При алгебраическом решении результирующая ошибка бу-
дет равна _
Д = (-Ь ЮО)+ ( — 30)== + 70лг.
Рис. 54
Рис. 55
Геометрически эта ошибка будет выражена отрезком ОА}
(рис. 55), равным _ _
Д = Д1 +
Порядок построения при этом будет тот же: начало вто-
рого вектора совмещается с концом первого.
При сложении отдельных составляющих ошибок-векторов,
лежащих на одной прямой, образуется результирующая
ошибка-вектор, как алгебраическая или геометрическая сумма
слагаемых ошибок-векторов. Направление результирующей
ошибки-вектора совпадает с направлением составляющих
ошибок-векторов.
Для геометрического сложения отдельных составляющих
ошибок-векторов необходимо начало второй ошибки-вектора
совместить с концом первой ошибки-вектора, начало третьей,
ошибки-вектора — с концом второй и т. д. Тогда начало
первой ошибки-вектора будет началом результирующей ошибки-
вектора, а конец последней ошибки-вектора — концом резуль-
тирующей ошибки-вектора.
Пример 1. При определении Дб методом сокращенной подготовки были
допущены следующие ошибки в дальности:
в определении координат ОП + 15 м",
в нанесении координат ОП на карту — 5 м\
в нанесении цели на карту—80 м',
в измерении расстояния на карте-1-10 м.1
Найти ошибку в определении дальности.
Решение. Имеем 4 отдельные составляющие ошибки-вектора,
направленные по одной прямой. Результирующую ошибку найдем как
алгебраическую сумму составляющих:
Д =(4-15)-U(-5)H-( — 80) + (+ 10) = -60 м.
Пример 2. Даны три ошибки-вектора дъ д2 и выраженные графи-
чески так, как это показано на рис. 56. Найти результирующую (суммарную)
ошибку-вектор.
Решение. Применим здесь геометрический метод решения. Совместим
для этого начало О% второй ошибки-вектора с концом Аг первой ошибки-
197
вектора и начало О3 третьей ошибки-вектора с концом Л2 второй ошибки-
вектора. Тогда точка будет начало.м результирующей ошибки вектора,
а точка А3 — ее концом (рис. 56) и результирующая ошибка-вектор будет
равна ____
Д1 + Д2 + Дз — А — ОМз-
0) <-----А;-------► Aj 0)1 ... Ai-------Aj
д2 —s------^2 - 1 ......102 А2г<-----------!----1 ^2
4?3 *------------- &S--------------*“^3 Оз*--------5--------- A3--------------
Ofi------------- А ------------JA,
Рис. 56
2. При сложении ошибок-векторов, имеющих разные направ-
ления, но лежащих в одной плоскости, применяется, как прави-
ло, геометрический метод сложения.
Сущность метода при этом основывается на том, что
векторы могут не’только переноситься вдоль какой-то линии,
но и перемещаться параллельно этой линии, т. е. параллельно
самим себе. В остальном построение результирующей ошибки-
вектора производится по тому же правилу, как и при сложении
ошибок-векторов, направленных по одной прямой: начало второй
ошибки-вектора совмещается с концом первой ошибки-вектора,
начало третьей — с концом второй и т. д. На рис. 57 даны
примеры сложения нескольких ошибок-векторов, имеющих
различные направления на одной плоскости1.
Частным случаем сложения ошибок-векторов, имеющих
различные направления в одной плоскости, является случай,
когда направления ошибок-векторов взаимно перпендикулярны.
К этому случаю сложения ошибок-векторов относится, напри-
мер, сложение ошибок в дальности и в направлении при под-
готовке исходных данных для стрельбы.
1 Перенесение вектора вдоль прямой является частным случаем его
параллельного перемещения.
198
Результирующая ошибка-вектор при этом может быть
определена аналитически как гипотенуза прямоугольного
треугольника, в котором катетами являются составляющие
ошибки-векторы, по формуле
^4- Д22,
а угол, составленный направлением результирующей ошибки-
вектора и направлением одной из составляющих ошибок-векторов,
— по формулам:
tg ai = -I2- или tga2 = _Al .
Д1 д3
Пример. При подготовке исходных данных были допущены ошибки
в дальности 4- 10J м и в направлении—60 м (влево). Найти результирую-
щую ошибку-вектор и угол, который образует эта ошибка с плоскостью
стрельбы.
Решение. По только что приведенным формулам 15еличина резуль-
тирующей ошибки-вектора
Д = j/-1002 + 602 = 117
а тангенс угла, составленного результирующей ошибкой-вектором и плос-
костью стрельбы
, 60 п с
tea=ioo =0’6’
откуда угол по таблице натуральных тригонометрических величин
а = 31° = 5-17.
Графическое решение этого примера показано на рис. 58.
Б
100м
Рис. 58
3. Сложение ошибок-векторов, имеющих различные направ-
ления в пространстве, в данном курсе не рассматривается, так
как со случаями сложения таких ошибок-векторов в наземной
артиллерии, как правило, иметь дело не приходится.
§ 42. ВЕКТОРИАЛЬНАЯ ОШИБКА
Предположим, что измерение некоторой величины сопро-
вождается ошибками-векторами, направленными по одной пря-
мой. Если каждый отдельный результат измерения дает свою
ошибку-вектор, то при многократном измерении одной и той
же величины получится совокупность ошибок-векторов или,
иначе говоря, система ошибок-векторов.
199
Система (совокупность) ошибок-векторов, направленных
в пространстве по одной определенной, прямой, называется
системой векториальных ошибок или, сокращенно, вектори-
альной системой.
Условно эту систему называют векториальной ошибкой,
понимая под этим не отдельную ошибку, а всю совокупность
ошибок.
Графически для системы векториальных ошибок, следую-
щих закону Гаусса, векториальная ошибка, изображается отрез-
ком, равным по величине срединной ошибке системы.
Так, например, если совокупность ошибок-векторов следует
закону Гаусса и имеет направление MN (рис. 59), то характе-
ризующая эту совокупность векториальная ошибка графически
может быть выражена отрезком ОВ (или ОС), приложенным
к точке О и направленным по линии MN. При этом точка
О — начало отсчета — отвечает истинному значению измеряе-
мой величины, т. е. результату, ошибка которого равна нулю.
Величина отрезка ОВ как величина срединной ошибки
совокупности ошибок-векторов, изображенных на рис. 59, может
быть легко найдена, если эти ошибки-векторы выразить чис-
ленно:
Д} = -Г ГО м; Д4 = ~Г 450 м; Д- = -Г 260 м; Д^о = -Г 200 м;
Д2 =— 350 м; Д5 =4-140 ж; Д8 =— 50 м; Ди = — 180 м;
Д3 —— 120 м; Д6 =— 400 м; Д9 = — 100 лг; 'Д12=-|- 80 м.
Тогда, расположив эти ошибки по их абсолютным величи-
нам в возрастающем порядке:
50, 70, 80, 100, 120, 140, 180, 200, 260, 350, 400, 450,
найдем, что
140 + 180
О В =.----2---= 160 М,
или, в масштабе рис. 59,-16 мм.
200
В приведенном примере отрезок ОВ выражает векториаль-
ную ошибку совокупности ошибок-векторов, направленных по-
линии MN; вместе с тем этот же отрезок ОВ по величине
(численно) равен срединной ошибке данной совокупности. По-
этому, когда говорят о векториальной ошибке, характеризую-
щей совокупность ошибок-векторов, направленных по одной
общей прямой, обычно под этим подразумевают срединную
ошибку данной совокупности, помня, что здесь речь идет
только о численном равенстве. В таком понимании векториаль-
ная ошибка обладает теми же свойствами, что и срединная
ошибка.
Если расположить (построить) все ошибки-векторы по их
абсолютным величинам в возрастающем или убывающем поряд-
ке, не обращая внимания на их направление, то векториальная
ошибка займет в этом ряде срединное место, т. е. будет больше
каждой из ошибок-векторов одной половины ряда и меньше
каждой из ошибок-векторов другой половины ряда.
Срединная ошибка не имеет знака, поэтому и векториаль-
ная ошибка не имеет направления на общей прямой, т. е.
изображается в виде отрезка прямой, а не вектором.
Векториальную ошибку обычно обозначают буквой R, хотя
может быть принято и обычное для срединной ошибки обозна-
чение Е. Если векториальная ошибка выражается отрезком
прямой, то над буквенным обозначением ставится черточка
с двумя стрелками, например: ОВ .
На рис. 60 показано положение векториальной ошибки R
в векториальной системе, как совокупности ошибок-векторов.
При измерении некото- ,,
рой величины могут иметь т
место несколько векториаль- -г
ных систем, направленных
по одной прямой; например,
векториальные системы, воз-
никающие при определении ----------------Т-?"-----------
различных поправок при т I t
полной подготовке исходных . ।
установок для стрельбы. __________________
Если эти векториальные д12д3 д3д5к
системы следуют закону
Гаусса,—а в дальнейшем с Рис- 60
такими векториальными си-
стемами мы только и будем иметь дело,—то сложение векто-
риальных ошибок, соответствующих этим системам, произво-
дится по известной нам формуле сложения законов Гаусса:
£ = Е'2 -j- F'2 + Р'2 + . . . + ES‘~ >
201
в которой вместо Е можно подставить суммарную (результи-
рующую) векториальную ошибку R, а вместо Е', Е”, Е", . . ,
Es — векториальные ошибки /?х, /?2, R3, . . . , Rs, характе-
ризующие отдельные векториальные системы. И тогда
R = + + + • • • +Rs-
Этот вывод можно сделать на основании той аналогии, кото-
рая была установлена между векториальной и срединной ошиб-
ками. Вместе с тем вывод показывает, что на векториальные
ошибки правило векторного сложения не распространяется.
Здесь складываются не отдельные ошибки-векторы, а системы
ошибок-векторов (срединные ошибки).
Пример. При определении исчисленной дальности векториальные
ошибки в определении метеорологических и балистических условий
стрельбы таковы:
В измерении температуры воздуха ................... 30 м
„ „ барометрического давления ...... 10 „
» , температуры заряда.......................20 „
„ „ скорости и направления ветра ........... 30 ,
, „ потери начальной скорости................40 „
Векториальная ошибка в определении дальности при топографической
подготовке равна 60 м.
Найти суммарную векториальную ошибку, т. е. векториальную ошибку
в определении дальности для всей подготовки в целом.
Решение. Подставив численные значения составляющих векториаль-
ных ошибок в общую формулу, получим численное значение суммарной
►(результирующей) ошибки:
R = у302 + 102 + 202 + ЗиЗ _|_ 402 _|. 602 = ]/ 7500 « 85,44 м.
Полученный результат означает, что в 50 случаях из 100 ошибки, про-
исходящие от неточного учета условий стрельбы, не превосходят 85,44 м.
При измерениях иногда ошибки-векторы, возникающие в
каком-либо одном направлении, сказываются на другом на-
правлении, с которым и связано решение основной задачи.
При целеуказании с одного наблюдательного пункта на
другой ошибки в определении положения цели дающим целе-
указание сказываются при отыскании цели принимающим целе-
указание.
Разберем этот случай в общем виде.
Положим, что дана векториальная- ошибка OR, напра-
вленная по линии KL (рис. 61). Это направление само по себе
нас не интересует, но для нас имеет существенное значение не-
которое другое направление MN, так как каждая ошибка-вектор,
возникающая в векториальной системе OR, вызывает откло-
нение от направления MN.
202
Так, если в системе О// получена ошибка-вектор О А, то
эта ошибка вызовет отклонение А "А от направления MN.
ошибка-вектор ОВ той же системы вызовет отклонение ВТ В
и Т. д. Все эти отклонения мы будем измерять по линии/MW',
перпендикулярной к направлению MN и составляющей с напра-
влением KL угол а, т. е. будем проектировать все эти от-
клонения на перпендикуляр к MN.
Рис. 61
Решая прямоугольные треугольники О А'А, ОВ'В и т. д.,
получаем: * ___ _____________
А" А = О А' = О А • cos а;
В"В = ОВ' =ОВ-созаи т. д.
Таким образом, каждая ошибка-вектор данной векториаль-
ной системы вызывает отклонение от некоторого направления,
равное проекции ошибки-вектора на перпендикуляр к этому
некоторому направлению. Зависимость же между ошибкой-век-
тором и вызванным ею отклонением выражается равенством
Д/= Д/’COsa,
где Д£— ошибка-вектор;
Д/— вызываемое этой ошибкой-вектором отклонение от
некоторого направления;
a — угол, составленный направлением векториальной
ошибки (системы) и перпендикуляром к некоторому
направлению.
Если ошибки-векторы следуют закону Гаусса, тому же
закону следуют и отклонения вызываемые этими ошибками-век-
торами, так как ошибки-векторы отличаются от соответствую-
щих им отклонений тем, что в выражении для отклонений
множителем входит cos а—величина постоянная при данных усло-
виях. Получается новая векториальная система, которая в дан-
203
ном примере с заданной векториальной ошибкой OR может
быть связана зависимостью:
OR' —OR «cosа.
Эта новая векториальная система существенно отличается
от обычных векториальных систем.
Во-первых, эта новая векториальная система не может
возникнуть самостоятельно — она вызывается какой-то другой
векториальной системой и зависит от нее.
Во-вторых, эта новая векториальная система представляет
собой систему отклонений., а не ошибок, причем эти отклонения
никогда не совпадают с линией, вдоль которой они направ-
лены, —они всегда параллельны этой линии и лежат от нее
тем дальше, чем больше соответствующие им ошибки-векторы
(отклонения А" А и В" В на рисунке).
Поэтому термин „векториальная ошибка" здесь не при-
меним; правильнее говорить: векториальное или срединное откло-
нение. Обычно же применяют термин „отклонение от некото-
рого направления", понимая под этим отклонение, вызванное
векториальной ошибкой и равное проекции этой векториаль-
ной ошибки на перпендикуляр к некоторому направлению.
Обозначив это отклонение через d (в отличие от вызы-
вающей его векториальной ошибки R), получим
d — /?-cosa.
Пример. Векториальная ошибка в дальности при определении положе-
ния цели с НП командира дивизиона равна 50 м, при этом ошибки при
определении положения цели в направлении (боковые) пренебрежимо
малы. Какова вероятность того, что командир батареи, направив стереотрубу
по данным целеуказания командира дивизиона, обнаружит цель в пределах
сетки стереотрубы, если угол, образованный линиями наблюдения команди-
ра дивизиона и командира батареи, равен 5-00, а дальность наблюдения
командира батареи равна 2500 м?
Решение. Ошибка в дальности, допущенная командиром дивизиона,
положения цели от линии наблюдения командира бата-
реи. Угол между линиями наблюдения по условию
равен 5-00, или 30°. Отсюда угол между линией наблю-
дения командира дивизиона (направлением векториаль-
ной ошибки) и перпендикуляром к линии наблюдения
командира батареи, как дополнительный до 90°, равен
(рис. 62)
a = 90° — 30° = 60°.
Спроектируем заданную векториальную ошибку
на перпендикуляр к линии наблюдения командира ба-
тареи (КБ), и тогда срединное отклонение от этой линии
d — 50-cos60° —50-0,5 = 25 м,
или в делениях угломера,
rf= 25:2,5 = 0-10.
вызовет отклонение
Рис. 62
204
Вероятность получения отклонения, не выходящего за пределы сетки
стереотрубы (±0-30):
а) по таблице значений Ф О
= Ф (3,0) = 0,95698;
б) по шкале ошибок
Р = 2 (0,07 + 0,16 4- 0,25) = 0,96.
Подобно тому, как проектировалась векториальная ошибка
на два направления, можно векториальную ошибку разложить
на два направления.
Рассмотрим случай разложения векториальной ошибки на
два взаимно перпендикулярных направления. Положим, что даны
векториальная ошибка ОВ и два взаимно перпендикулярных
направления ОХ и OY. При этом на-
правление OL этой векториальной
ошибки образует с направлением ОХ
угол а (рис. 63).
Спроектировав векториальную
ошибку на эти направления, получим
две проекции, как бы две векториаль-
ные ошибки:
В'
Рис. 63
В
О
X
ОВ'-- ОВХ= OB «cosа и ОВ" = OBV = ОВ - sinа.
Особенность этих двух векториальных ошибок, по сравне-
нию с любой другой парой векториальных ошибок, заклю-
чается в том, что они, во-первых, зависимы между собой, т. е.
возникают одновременно с векториальной ошибкой ОВ , и во-
вторых, при сложении вновь дают векториальную ошибку ОВ.
В этом можно легко убедиться, если спроектировать
ОВх и ОВУ на направление OL.
Проекция ОВХ на это направление равна
ОС = ОВ^.-cos а = ОВ cos2 а;
проекция ОВУ на то же направление равна
ОА — ОВу • sin а = ОВ sin2 а,
а сумма проекций
"ОС 4- ОА = ОВ cos2 а 4- ОВ sin2 а =
= ОВ (cos2 а 4- sin2 а) = ОВ .
Это означает, что проекции, получившиеся при разложе-
нии векториальной ошибки, складываются геометрически, т. е.
как векторы, а не как векториальные ошибки.
205
§ 43. ЭЛЛИПТИЧЕСКАЯ И ЭЛЛИПСОИДАЛЬНАЯ ОШИБКИ
Если ошибки-векторы, возникающие в процессе одного к
того же измерения, не совпадают по направлению, то и соот-
ветствующие таким ошибкам-векторам векториальные ошибки
также не будут совпадать по направлению.
Рассмотрим две векториальные ошибки, направленные по
взаимно перпендикулярным линиям.
Для большей наглядности возьмем частный пример, когда
для открытия огня по одной и той же цели одним и тем же
способом подготовляются исходные данные группой в несколько
человек, например группой курсантов.
Каждый из подготовляющих данные может допустить ошиб-
ку в направлении (ошибку в установке угломера) и ошибку
в дальности (ошибку в установке прицела)1. Получаются две
бистемы ошибок-векторов, направленные по двум взаимно
перпендикулярным линиям (рис. 64): одна — в определении по-
ложения цели по дальности (по линии ДД} и другая—в опре-
делении положения цели по направлению (по линии НН}. Допу-
стим, что первая система характеризуется векториальной ошиб-
кой /?д , а вторая система — векториальной ошибкой /?н . До-
пустим также, что точка До соответствует действительному
положению цели, т. е. абсолютно точным исходным данным.
Предположим, что первый курсант подготовил данные для
открытия огня с ошибками: Д^— в дальности и Д\ — в направ-
лении. Так как причины, вызвавшие эти ошибки, действовали
одновременно, то эти ошибки дадут результирующую ошибку-
вектор Д], и цель, нанесенная этим курсантом, окажется
в точке ДР Если второй курсант допустил ошибки: в даль-
ности Д'2 и в направлении Д"2, то результирующая ошибка-вектор
в этом случае будет Д2, и цель окажется нанесенной в точке Д2.
1 Ошибками в установке уровня пренебрегаем.
206
Ошибки в данных, подготовленных третьим курсантом, Д'3 и.
Д"3 дадут результирующую ошибку-вектор Д8, и цель ока-
жется в точке АД и т. д. Таким образом, при подготовке исход-
ных данных каждым курсантом возникают две ошибки-вектора;
каждая такая пара даст свою результирующую ошибку-вектор,
каждой результирующей ошибке-вектору будет соответствовать
свое положение пели.
Посмотрим, как складываются эти результирующие ошибки-
векторы, иначе говоря, установим, что представляет собой
совокупность всех нанесенных положений цели.
Ошибки подготовки исходных данных следуют закону
Гаусса, следовательно, как в дальности, так и в направлении
могут быть получены отдельные ошибки-векторы любой вели-
чины и любого знака, т. е. практически в пределах от £Z0 до
± 4/?д в дальности и от Цо до ± 4 RH в направлении. Поэтому
цель может быть нанесена в любой точке некоторой плоскости,,
на площади, ограниченной этими пределами (рис. 65).
Это означает, что ошибка подготовки исходных данных
в условиях данного примера будет выражена не одним каким-
то вектором, а совокупностью ошибок-векторов, расположен-
ных в одной плоскости, имеющих различные направления из
одной общей точки и ограниченных некоторой площадью.
Такая совокупность всех возможных ошибок-векторов на пло-
скости называется ошибкой на плоскости.
Распространяя это положение на любую пару взаимно
перпендикулярных векториальных систем, можно сделать сле-
дующий вывод.
Две взаимно перпендикулярные векториальные системы
пли две взаимно перпендикулярные векториальные ошибки
складываются в ошибку на плоскости.
207
Если складывать любое количество векториальных ошибок,
/направленных по двум взаимно перпендикулярным линиям, вывод
«будет тот же. -
Допустим, что по некоторому направлению действуют
векториальные ошибки /?/, /?2', R3' и т. д., а по другому
направлению, перпендикулярному к первому, — векториальные
ошибки /?/', /?2/', и т. д. Применив правило сложения век-
ториальных ошибок, направленных по одной прямой, получим
две результирующие векториальные ошибки:
R' = V R/* + + R3'* + • •. и R" =К/?1"! + й2"г + %"2+- • •,
сложение которых даст ошибку на плоскости.
Итак, при сложении векториальных ошибок (системы),
направленных по двум взаимно перпендикулярным линиям,
получается совокупность ошибок-векторов, концы которых не
выходят за пределы некоторой площади.
Для того чтобы определить вид (очертания) этой площади,
рассчитаем распределение вероятностей получения ошибки
в пределах интересующей нас площади, воспользовавшись тем
же примером подготовки исходных данных.
Построим две шкалы ошибок на взаимно перпендикулярных
линиях, по которым направлены векториальные ошибки, выра-
зив деления этих шкал в величинах векториальных ошибок
и /?н (рис. 65), и допустим, что векториальные ошибки
следуют закону Гаусса.
н
-ЭЯЭ -2Яд Нд 0 ’Rd *^5 *ЗЙЗ
Н
Рис. 66
Вероятность получения ошибки в пределах прямоугольника
Oabc, или вероятность того, что цель будет нанесена в пре-
делах этого прямоугольника, может быть найдена по теореме
умножения как вероятность совпадения ошибки в дальности
208
в пределах от 0 до + /?д с ошибкой в направлении в пределах
от 0 до + /?н •
Р = 0,25 • 0,25 = 0,0625 = 6,25%.
Вероятность получения ошибки в пределах прямоугольника
defg, или вероятность того, что цель будет нанесена в пределах
этого прямоугольника, может быть найдена как вероятность
совпадения ошибки в дальности в пределах от + 2 Рл до + 3 Ря
с ошибкой в направлении в пределах от — RK до — 2%
0,07-0,16 = 0,0112=1,12% и т. д.
Рассчитанные подобным образом вероятности дадут распре-
деление ошибок на плоскости при сложении двух взаимно пер-
пендикулярных векториальных ошибок.
Если пренебречь очень малыми вероятностями получения
ошибки (меньше 0,15%) и обвести оставшиеся прямоугольники
общей ломаной линией, то получится ступенчатая фигура,
пределом которой, по мере увеличения числа прямоугольников
(при построении шкал ошибок в долях /?д и /?н). является
эллипс.
Следовательно, при сложении векториальных ошибок,
направленных по двум взаимно перпендикулярным линиям
и следующих закону Гаусса, получается ошибка на плос-
кости в пределах эллипса. Такая ошибка называется эл-
липтической.
Эллиптическая ошибка будет g
иметь место и тогда, когда вектори-
альные ошибки не будут взаимно
перпендикулярны. Примером такой
ошибки может служить эллиптическая
ошибка, получающаяся в результате
засечки цели с двух наблюдательных
пунктов (рис. 67).
Положим, что ошибки наблюда-
телей при засечке цели следуют
закону Гаусса и что левый наблюда-
тель производит измерения абсолютно
точно, а правый с ошибками, причем
векториальная ошибка правого наблю-
дателя равна Ru. Очевидно, что цель
в этом случае окажется нанесенной
на линии наблюдения левого наблю-
дателя где-то между точками Цх и
Ц2, отстоящими от точки ZZo, соответ-
ствующей истинному положению цели,
на 4/?п.
Если же допустить, что правый
Рис. 67
наблюдатель производит измерения
14 —Зак. 991
209
без ошибок, а левый с ошибками, то цель будет нанесена на
линии наблюдения правого наблюдателя где-то между точ-
ками Ц3 и кЦ, отстоящими от точки Цо на 4/?л, т. е. на
величину предельных ошибок левого наблюдателя по линии
наблюдения правого наблюдателя.
Так как при засечке цели оба наблюдателя допускают
ошибки измерения, то цель окажется нанесенной в пределах
четырехугольника ABCD. Если теперь разбить этот четырех-
угольник на 64 четырехугольника, аналогично тому, как это
было сделано при сложении двух взаимно перпендикуляр-
ных векториальных ошибок (см. рис. 66), и отбросить те
четырехугольники, в которых нахождение цели мало вероятно,
то и в этом случае будет получена фигура близкая по очер-
танию к эллипсу. Следовательно, в конечном итоге при сло-
жении двух векториальных ошибок, направленных под любым
углом друг к другу, получается эллиптическая ошибка.
Таким образом, эллиптической ошибкой называется
ошибка на плоскости, получающаяся в результате сложе-
ния векториальных ошибок, имеющих различные направле-
ния в одной плоскости и следующих закону Гаусса.
Чтобы иметь возможность судить о точности измерения,
результатом которого является получение эллиптической
ошибки, необходимо знать характеристику этой эллиптической
ошибки. Как и для ошибок других категорий, которые были
рассмотрены до этого, так и для эллиптической ошибки такой
характеристикой должна быть какая-то срединная ошибка.
Очевидно,что такая срединная ошибка должна иметь вид
эллипса, связанного с теми векториальными ошибками, в резуль-
тате сложения которых получается данная эллиптическая
ошибка.
За характеристику эллиптической ошибки принимается
так называемый единичный эллипс, главными полуосями
которого являются складываемые векториальные ошибки
при условии, что эти ошибки взаимно перпендикулярны.
Единичный эллипс (рис. 68) обозначается буквой глав-
ные его полуоси —- буквами а (большая полуось) и b (малая
полуось).
210
Единичный эллипс определяет векториальные (срединные)
ошибки по любому направлению. Иначе говоря, любой полу-
диаметр единичного эллипса является в то же время векто-
риальной ошибкой по направлению этого полудиаметра. Так,
например, полудиаметр ОС является векториальной ошибкой
по направлению MN, а полудиаметр OD — векториальной
ошибкой по направлению KL и т. д.
Исходя из этого свойства единичного эллипса, легко можно
перейти к предельной по величине эллиптической ошибке —
к полному эллипсу (еШах). Для этого достаточно по несколь-
ким направлениям, проходящим через центр единичного эллипса,
отложить предельные по величине ошибки-векторы, приняв их
равными 4 или 5 векториальным ошибкам (полудиаметрам
единичного эллипса), соответствующим этим направлениям, и
затем построить полный эллипс (рис. 69). На любом диаметре
предельного эллипса можно построить шкалу ошибок, по
которой могут быть определены вероятности получения ошибок
в заданных пределах по направлению этого диаметра.
Вернемся к рис. 66, на котором было показано распреде-
ление ошибок в пределах эллиптической ошибки. Из этого
рисунка видно, что вероятность получения ошибки в пределах
прямоугольника, ограниченного в дальности + /?д и в направ-
лении ± /?п, равна
6,25% + 6,25% 4- 6,25% + 6,25% = 25%;
площадь же этого прямоугольника, называемого единичным
прямоугольником, равна 2/?д-2/?н или, приняв /?д = я и /?н—Л,
2а-2& = 4а6.
Единичный эллипс находится в пределах этого единичного
ирямоугольника. Взяв отношение площади единичного эллипса
к площади единичного прямоугольника, найдем приближенное
значение вероятности получения ошибки в пределах единич-
ного эллипса:
^ёг‘25 = 19>6<,/«« 20’ »-
14*
211
Если учесть, что ошибки в пределах единичного прямо-
угольника распределяются неравномерно, то эта вероятность
будет равна 20,3%.
Помимо единичного эллипса, в некоторых случаях при-
дется пользоваться так называемым половинным эллипсом,
главные полуоси которого равны половинам складываемых
векториальных ошибок. Вероятность получения ошибки в пре-
делах половинного эллипса равна 5,5%.
В частном случае сложения векториальных ошибок, когда
складываются векториальные ошибки, равные между собой по
величине и направленные по двум взаимно перпендикулярным
линиям в одной плоскости, получается так называемая круговая
ошибка. Круговая ошибка возникает, например, при нанесении
точек на карту или планшет по координатам или при снятии
координат таких точек.
Большое практическое значение имеет вопрос об откло-
нениях, вызываемых эллиптическими ошибками.
Допустим, что имеется единичный эллипс s, главные полу-
оси (составляющие векториальные ошибки) которого равны
а и Ь, причем главная полуось а направлена по линии KL.
Рис. 79
Допустим также, что имеется
некоторое направление MN,
перпендикуляр к которому
M’N' и направление KL обра-
зуют угол а (рис. 70).
Посмотрим, какое откло-
нение (срединное) вызовет еди-
ничный эллипс или эллипти-
ческая ошибка от заданного
направления MN.
Проекция большой полу-
оси а на перпендикуляр M'N',
т. е. отклонение, вызываемое
векториальной ошибкой а от
направления MN, по известной
нам формуле равна
а' = a-cos а;
проекция малой полуоси b на тот же перпендикуляр M'N'
(отклонение, вызываемое векториальной ошибкой b от напра-
вления MN)
b' -b- cos (90° — а) = b sin а.
Получили два независимых отклонения (срединных), напра-
вленных по одной прямой M'N'. По правилу сложения векто-
риальных ошибок, имеющих общее1 направление, суммарное
212
отклонение, т. е. отклонение, вызываемое эллиптической
ошибкой г,
D' — у а2 cos2a +- b2 sin2a.
Мы нашли отклонение, вызываемое эллиптической ошибкой
от направления MN по перпендикуляру к нему M'N'. Совер-
шенно очевидно, что можно найти отклонение, вызываемое
той же эллиптической ошибкой, и от направления M'N' по
перпендикуляру к нему, т. е. по направлению MN.
В этом случае отклонения а" и Ь", вызываемые соответ-
ственно теми же векториальными ошибками а и Ь, будут:
a"^«-Cos (90° — a) = a-sina и b", =^-cosa.
Тогда суммарное отклонение
Dv = у а2 • sin2a + b2 • cos2a.
Суммарное отклонение D", в отличие от суммарного откло-
нения D', часто называют отклонением по некоторому напра-
влению.
Этими двумя формулами будем пользоваться при опреде-
лении отклонений, вызываемых эллиптической ошибкой, от
некоторого направления и по некоторому направлению. При
этом под эллиптической ошибкой будем понимать единичный
эллипс1.
Пример 1. Имеется эллиптическая ошибка г, главные полуоси которой
равны 50 м и 20 м. Чему равны отклонения, вызываемые этой эллиптической
ошибкой от направления M.N и по направлению MN, если это направление
образует с направлением большой полуоси эллиптической ошибки угол 18°?
Решение. Обозначим главные полуоси эллиптической ошибки через
а — 50 м и b = 20 м.
Найдем сначала суммарное отклонение (срединное) от направле-
ния MN.
Отклонение, вызываемое векториальной ошибкой а,
a' =a-cosv. = 50-cos 18° = 50-0,951 = 47,55 м.
Отклонение, вызываемое векториальной ошибкой
b' — Z>-sina = 20-sin 18° = 20-0,309 = 6,18 м.
Тогда суммарное отклонение, вызываемое эллиптической ошибкой е,
D' = ]/'д'2 + 6'2 - у 47,552 + 6,182 ’^ 47,95 м.
Суммарное отклонение, вызываемое заданной эллиптической ошибкой
но направлению MN,
D" = ]/"502 sin2 18° + 202.cos2"18~ = J/ 15,452 + 19,022 ® 24,5 м.
1 Вывода правила сложения векториальных ошибок на плоскости не
дается ввиду его громоздкости. Частный случай сложения векториальных
•шибок на плоскости, наиболее часто используемый в артиллерийской прак-
тике, приведен в 10-й книге Курса артиллерии, § 3.
213
Пример 2. Эллиптическая ошибка, получающаяся при определении поло-
жения цели с НП командира батареи, имеет следующие характеристики:
векториальная ошибка в дальности /?д = 80 м и векториальная ошибка
в направлении А?н — 20 м.
Определить отклонения, вызываемые от линии наблюдения и по линии
наблюдения бокового НП, если уюл, образованный линиями наблюдения
обоих НП, равен 4-00.
Решение, а — Rr = 80 м; b = RK =20 м', а. = 4-00 = 24°.
а) Отклонение, вызываемое эллиптической ошибкой от линии наблю-
дения бокового НП:
£>" = J/"”802’. cos2 24° 4- 2G?-sin21r~ « 73,35 я.
б) Отклонение, вызываемое эллиптической ошибкой по линии наблю-
дения бокового НП:
D' = |/'8(j2-sin224° + 202Tos8 24°~ « 37*,31 м.
До сих пор мы складывали векториальные ошибки, лежа-
щие на одной и той же плоскости. В артиллерийской практике
нам приходится сталкиваться с одновременным действием не-
скольких векториальных ошибок (отклонений), не лежащих
в одной плоскости. В первую очередь это относится к откло-
нениям дистанционных разрывов.
Разберем наиболее простой и вместе с тем наиболее ти-
пичный случай — сложение трех векториальных ошибок, напра-
вленных по трем взаимно перпендикулярным линиям.
Положим, что имеются три векториальные ошибки Rr, R'
и R"', направления которых совпадают с направлениями осей
прямоугольной системы координат (рис. 71).
Сложим последовательно и попарно заданные вектори-
альные ошибки, зная, что при сложении двух векториальных
ошибок всегда получается эллиптическая ошибка.
Сложение векториальных ошибок R' и R", лежащих на пло-
скости ZXZ^Xy, даст нам эллиптическую ошибку s'. Сложение
векториальных ошибок R^' и/?'", лежащих на плоскости XYX^Yx,
даст эллиптическую ошибку г . Сложение векториальных оши-
214
бок R' и R", лежащих на плоскости ZYZxYy, даст эллиптиче-
скую ошибку s'". При этом плоскости всех трех эллиптических
ошибок будут взаимно перпендикулярны.
При одновременном действии заданных векториальных
ошибок (систем) каждый раз получаются три отдельные ошибки -
векторы, которые при сложении дадут какую-то суммарную
ошибку-вектор.
Если смотреть вдоль линии ХгХ, то отдельные ошибки-век-
торы относительно точки О могут быть направлены: в системе
R' — вверх и вниз, • в системе R" --- вперед и назад и. наконец,
в системе АГ — вправо и влево. Суммарная ошибка-вектор мо-
жет получиться в результате любого сочетания отдельных оши-
бок-векторов, а отсюда и может занять любое положение в
пространстве (в объеме), ограниченном некоторой поверхностью.
Мы установили, что сечения этого объема тремя взаимно
перпендикулярными плоскостями представляют собой эллипсы.
Очевидно, что и любые другие сечения этого же объема да-
дут также эллипсы, так как эти сечения можно рассматривать
как проекции эллипсов. А это значит, что такой объем пред-
ставляет собой эллипсоид.
При сложении трех векториальных ошибок, не лежа-
щих в одной плоскости, получается эллипсоидальная ошибка.
Эллипсоидальная ошибка обозначается буквой Э.
Эллипсоидальная ошибка, по аналогии с эллиптической,
характеризуется единичным эллипсоидом, главные полуоси
которого равны составляющим векториальным ошибкам (при
условии, что эти векториальные ошибки взаимно перпенди-
кулярны).
Если на направлениях соответствующих осей координат-
ной системы отложить по 4 векториальные ошибки и построить
эллипсоид, то получим эллипсоид ЭП1ах, поверхность которого
практически можно рассматривать как границу наибольших
из всех возможных ошибок-векторов данной системы.
Проекция Этах на любую плоскость дает эллипс, в кото-
ром проекции отдельных ошибок-векторов распределяются по
закону эллиптической ошибки, как это было показано на рис. 661.
§ 44. ЗАДАЧИ НА ОШИБКИ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
Задача 110. При полной подготовке исходных данных для стрельбы не
была учтена поправка на ветер, который уменьшал дальность полета снаряда
й отклонял его влево. Определить величину и направление допущенной
ошибки, если известно, что поправка на продольную слагающую ветра
равна 80 м, а на боковую слагающую 26 м.
Ответ. 84 угол с плоскостью стрельбы равен 18°.
Задача 111. Выполняя команду, наводчик ошибся и поставил угломер
7-35 вместо 7-55 и прицел 96 вместо 93. Определить величину и направле-
1 Более подробно об эллипсоидальной ошибке будет сказано в § 50 при
рассмотрении рассеивания дистанционных разрывов.
215
ние отклонения снаряда, которое будет вызвано ошибками наводчика
(±Х = 50 м).
Ответ. 178 угол с плоскостью стрельбы равен 32°41'.
Задача 112. При стрельбе производятся измерения отклонений разры-
вов от цели по дальности. Срединная ошибка прибора равна 30 м иВд=<2Ь м.
Найти срединную ошибку определения положения средней траектории отно-
сительно цели в дальности, если принять отклонение отдельного разрыва от
цели за отклонение средней траектории.
О т в е т. 39 м.
Задача 113. Производится пристрелка по измеренным отклонениям.
Срединная ошибка в определении отклонения по дальности равна 20 м', Bd=30 м.
Чему, равна срединная ошибка в корректуре дальности по группе из четы-
рех выстрелов?
Ответ. 18 м.
Задача 114. Срединные ошибки в дальности при учете метеорологиче-
ских условий стрельбы при полной подготовке таковы:
на продольную слагающую ветра.....................20 м
„ барометрическое давление ...................... 8 ,
„ температуру воздуха •..........................15 ,
Чему равна срединная ошибка поправки в дальности на отклонения ме-
теорологических условий стрельбы?
Ответ. 26,25 м.
Задача 115. При определении исчисленной дальности срединные ошибки
таковы:
— при учете метеорологических условий стрельбы — 0,6% дальности;
— при учете балисгических условий стрельбы — 0.4% дальности;
— при определении топографической дальности — 0,7% дальности.
Какова вероятность того, что исчисленная дальность будет найдена
с ошибкой, не превышающей 2% дальности?
Ответ. 7? « 1% дальности; Р = 0,82266.
Задача 116. Ведется пристрелка по измеренным отклонениям. Средин-
ная ошибка в определении отклонения в дальности равна 25 м; Ед — 36 м.
Сделано 6 выстрелов. Средняя точка нанесена на планшет со срединной
ошибкой 9 м. Чему равна вероятность того, что корректура дальности будет
произведена с ошибкой, не превышающей 25 .и?
О т в е т. R 20 м', Р — 0,60083.
Задача 117. Целеуказание передается с правого наблюдательного пункта
на левый. Векториальная ошибка в определении положения цели в дальности
дающего целеуказание равна 80 м. Какое отклонение вызовет эта ошибка от
линии наблюдения принимающего целеуказание, если угол засечки равен 2-00?
Ответ. 16,64 м.
Задача 118. Срединная ошибка в определении положения цели с пункта
командира дивизиона в направлении равна 20 м. Какое отклонение вызовет
эта ошибка от линии наблюдения командира батареи при приеме им целе-
указания, если угол, образованный линиями наблюдения командира дивизиона
и командира батареи, равен 4-00?
Ответ. 18,28 м.
Задача 119. Эллиптическая ошибка задана главными полуосями:
а = 30 м и Ь — 12 м. Чему равны отклонения, вызываемые этой эллиптиче-
ской ошибкой, от некоторого направления MN и по направлению MN, если
это направление с направлением полуоси а составляет угол 36° ?
Ответ. D' = 25,2 at; О" = 20,1 м.
Задача 120. Срединные ошибки в определении положения цели с НП
командира дивизиона равны: в дальности 150 м и в направлении 50 м. Опре-
делить отклонение, вызываемое этой эллиптической ошибкой, от линии на-
блюдения командира батареи при приеме им целеуказания, если угол между
линиями наблюдения командира дивизиона и командира батареи равен 1-50..
Ответ. 54,7 м.
РАЗДЕЛ III
РАССЕИВАНИЕ ПРИ СТРЕЛЬБЕ
ГЛАВА 9
РАССЕИВАНИЕ ТРАЕКТОРИЙ И ТОЧЕК
РАЗРЫВОВ
§ 45. ЯВЛЕНИЕ РАССЕИВАНИЯ ТРАЕКТОРИЙ И ЕГО ПРИЧИНЫ
Если бы снаряды данного калибра и типа обладали совер-
шенно одинаковыми весом и формой, если бы боевые заряды
к ним были совершенно одинаковы по весу и балистическим
свойствам пороха, если бы прицеливание орудия производи-
лось совершенно одинаково и стрельба производилась при
неизменных метеорологических условиях, то при ведении огня
на одних и тех же установках все снаряды описали бы одну
и ту же траекторию, и точка падения для всех снарядов была
бы одна и та же.
В действительности, вследствие наличия причин, о кото-
рых будет сказано ниже, добиться полного единообразия при
производстве отдельных выстрелов невозможно. Поэтому
каждый снаряд будет иметь свою траекторию и свою точку
падения, несмотря на то, что снаряд, заряд и установки
прицельных приспособлений при производстве выстрелов ме-
няться не будут. Такое явление называется рассеиванием сна-
рядов, точнее — рассеиванием траекторий.
Все причины, вызывающие рассеивание траекторий, могут
быть сведены в следующие три группы:
А. Причины, вызывающие разнообразие начальных скоро-
стей.
Б. Причины, вызывающие разнообразие в положении оси
канала ствола орудия в момент выстрела — разнообразие углов
бросания и положений плоскости стрельбы.
В. Причины, вызывающие разнообразие условий полета
снаряда после его вылета из орудия.
Рассмотрим отдельно каждую из этих групп, отметив наи-
более существенные причины.
217
А. Причины, вызывающие разнообразие начальных
скоростей:
1. Разнообразие весов боевых зарядов, являющееся след-
ствием ошибок (неточностей), допускаемых при развеске бое-
вых зарядов. Различие в весах боевых зарядов приводит
к различию начальных скоростей — больший по весу боевой
заряд сообщает снаряду большую начальную скорость.
2. Разнообразие балистических свойств пороха боевых
зарядов, вытекающее из природы самих бездымных порохов.
Несмотря на всю тщательность изготовления, сортировки
и хранения бездымных порохов, балистические свойства бое-
вых зарядов, изготовленных из пороха одного и того же сорта
и даже одной и той же партии, будут различны. Это разли-
чие сказывается на процессе горения боевого заряда в канале
ствола орудия и вызывает различие в начальных скоростях.
3. Разнообразие температур боевых зарядов-, различны
условия доставки боевых зарядов на огневую позицию (вид
транспорта, укупорка, состояние погоды и т. д.); различны
условия содержания боевых зарядов на огневой позиции
(в укупорке или без нее, в нишах, погребках или на открытом
воздухе, в тени или на открытом месте и пр.); различны, на-
конец, промежутки времени для отдельных выстрелов от мо-
мента заряжания до момента производства выстрела, следО’
вательно, различно влияние на боевые заряды нагрева ствола,
который при интенсивной стрельбе может нагреваться до тем-
пературы, измеряемой десятками и даже сотнями градусов. Все
это приводит к тому, что к моменту производства выстрелов
боевые заряды имеют различную температуру, а боевой заряд,
имеющий в момент воспламенения большую температуру, со-
общает снаряду и большую начальную скорость.
4. Разнообразие плотностей заряжания. Основные при-
чины: неодинаковый досыл снарядов при заряжании и разно-
образие размеров и положений ведущего пояска у различных
снарядов. Вследствие этих причин объем зарядной каморы,
а отсюда и плотность заряжания1 будут изменяться от вы-
стрела к выстрелу. Изменение плотности заряжания сказы-
вается на начальной скорости — при большей плотности заря-
жания горение боевого заряда происходит интенсивнее и на-
чальная скорость будет больше.
5. Разнообразие весов снарядов как результат ошибок
(неточностей, допусков) при изготовлении снарядов ,и взры-
вателей. Снаряд большего веса будет иметь меньшую началь-
ную скорость.
1 Плотностью заряжания называется отношение веса заряда к объему
зарядной каморы.
218
С изменением начальной скорости изменяется и дальность
полета снаряда — большей начальной скорости соответствует
большая дальность полета снаряда.
В Правилах стрельбы наземной артиллерии 1945 г. (прило-
жение 4) приведена таблица для приближенного учета усло-
вий стрельбы. Эта таблица показывает, что изменение началь-
ной скорости на 1°/0 вызывает изменение дальности от 1 до 2%.
Например, при стрельбе из 152-щж гаубицы-пушки обр.
1937 г. на третьем заряде и на дальности 7 000 ж изменение на-
чальной скорости на 1°/о изменяет дальность на 91 м, что со-
ответствует 1,3% дальности.
Таким образом, даже незначительные колебания начальной
скорости приводят к большим отклонениям снарядов, а так как
эти колебания достигают в отдельных случаях 1 — 1,5%, то
разнообразие начальных скоростей и является основной причи-
ной рассеивания траекторий по дальности.
Б. Причины, вызывающие разнообразие углов бросания
и положений плоскости стрельбы:
1. Разнообразие установок угломера, уровня и прицела
вследствие неодинакового для различных выстрелов совмеще-
ния указателей с делениями на соответствующих шкалах при-
цельных приспособлений.
2, Разнообразие в наведении орудия в горизонтальной и
вертикальной плоскостях в результате неточного и неодина-
кового совмещения перекрестия панорамы с точкой прицели-
вания (наводки), неодинакового подведения пузырьков уровней
на середину, а также вследствие мертвых ходов механизмов.
3. Разнообразие углов вылета и боковых смещений ору-
дия при выстреле, что в основном определяется конструктив-
ными особенностями самого орудия.
Эта группа причин приводит к увеличению рассеивания
по направлению и по дальности (по высоте).
Разнообразие углов бросания наиболее сильно сказывается
при малых углах бросания и в особенности при больших
начальных скоростях. При углах бросания, близких к 45°,
влияние разнообразия углов бросания сводится к нулю.
В. Причины, вызывающие разнообразие условий полета
снаряда:
1. Разнообразие атмосферных условий. Так как атмо-
сфера находится в постоянном движении, то атмосферные
условия полета различных снарядов неодинаковы. Это влечет
за собой увеличение рассеивания по направлению и по даль-
ности. Особенно сильно сказываются изменения направления
и скорости ветра, что может происходить в короткие про-
межутки времени.
219
2. Разнообразие балистических коэфициентов. Под разно-
образием балистических коэфициентов будем понимать коле-
бания в весе, форме, размерах различных снарядов и положении
их центра тяжести, а также неодинаковые размеры и распо-
ложение их ведущих поясков. Все эти колебания вызывают
изменения в ускорении силы сопротивления воздуха и, как
следствие, в дальности полета снаряда.
3. Разнообразие смазки наружной поверхности снаря-
дов, что также приводит к изменению силы сопротивления
воздуха.
Из всего сказанного следует, что рассеивание траекто-
рий неизбежно.
Однако, если рассеивание траекторий при стрельбе неиз"
бежно, то все же возможно и необходимо принимать меры
для уменьшения рассеивания, так как чем меньше рассеивание
траекторий, тем меньше требуется снарядов для решения
огневой задачи.
Уменьшить рассеивание можно, во-первых, путем повы-
шения качества производственно-технической работы (умень-
шение допусков, тщательность обработки, точность всех изме-
рений и пр.) и, во-вторых, путем соответствующих мероприя-
тий в процессе эксплоатации материальной части непосредственно
в артиллерийских частях и подразделениях.
Меры, принимаемые для уменьшения рассеи-
вания при эксплоатации материальной части:
1. Подбор боевых зарядов одной и той же партии изгото-
вления и хранение их в условиях, обеспечивающих одинаковую
температуру зарядов.
2. Подбор снарядов по партиям и весовым знакам, тща-
тельная очистка снарядов от лишней смазки, а главное — от
приставших частиц земли, песка и т. п.
3. Однообразный досыл снарядов при заряжании.
4. Однообразие и'тщательность установки угломера, уровня
и прицела; однообразие и тщательность наводки.
5. Уменьшение влияния мертвых ходов механизмов вра-
щением маховиков всегда в одну и ту же сторону1.
6. Установка орудия на орудийной площадке и устройство
орудийной площадки, устраняющие подпрыгивание орудия и,
в особенности, его боковые смещения в процессе стрельбы.
7. Выбор достаточно удаленной, хорошо видимой и-устой-
чивой точки наводки.
1 При совмещении перекрестия панорамы с точкой наводки, совмеще-
нии прицельной и орудийной стрелок, при подведении пузырьков уровней
иа середину и т. п.
220
§ 46. СНОП ТРАЕКТОРИИ
Совокупность всех траекторий, получаемых при стрельбе
из данного орудия в данных условиях при достаточно боль-
шом числе выстрелов, произведенных в течение небольшого
промежутка времени, называется снопом траекторий.
Все причины, вызывающие рассеивание траекторий, были
сведены в три группы. Посмотрим, как каждая из этих групп
причин влияет на положение отдельных траекторий в снопе
траекторий.
Начнем с группы причин, вызывающих разнообразие углов
бросания, допустив, что другие причины, вызывающие рассеи-
вание траекторий, отсутствуют (рис. 72).
Рис. 72
Если стрельбу ведут при малых углах бросания, то можно
считать, что при небольших изменениях угла бросания траек-
тории будут только отклоняться вверх или вниз, сохраняя
свою форму, т. е. получится пучок траекторий, имеющих
одинаковую кривизну и расходящихся в точке вылета О.
Условимся при этом, что траектория 1 соответствует случаю
полного отсутствия причин, вызывающих рассеивание траек-
торий.
f Если допустить, что действует только группа причин,
вызывающих разнообразие начальных скоростей, мы получили
бы пучок исходящих из точки вылета траекторий, но все эти
траектории шли бы от общей касательной^ точке вылета и
Рис. 73
имели бы различную кривизну (рис. 7.q). Условимся и здесь,
что траектория 1 соответствует случаю полного отсутствие;
причин, вызывающих рассеивание траекторий.
Объединим действия этих двух групп причин. Наложив
рис. 72 на рис. 73 так, чтобы траектории 1 обоих рисунков
221
совпали (рис. 74), получим пучок взаимно пересекающихся
траекторий, исходящих из точки вылета.
Еще больше точек пересечения траекторий'мы получили
бы, если бы учли влияние третьей группы причин — причин,
вызывающих разнообразие условий полета снаряда.
Рис. 74
В некоторых случаях даже одна и та же причина может
привести к пересечению траекторий. На рис. 75 показаны
траектории двух снарядов различного веса. Более легкий
снаряд вылетит с большей начальной скоростью, и поэтому
его траектория 1 на некотором расстоянии от точки вылета
пойдет выше траектории 2 более тяжелого снаряда. Но так
как более тяжелый снаряд имеет большую поперечную на-
грузку1, то, начиная с некоторого момента, он будет иметь
большую скорость полета, полетит дальше, и его траектория
пересечет траекторию более легкого снаряда (на рис. 75-
з точке К).
При одновременном действии нескольких причин могут
быть не только пересечения, но и переплетения траекторий.
Возьмем два снаряда, выпущенных при различных углах бро-
сания (рис. 76): более тяжелый снаряд при большем угле
1 Поперечной нагрузкой называется отношение веса снаряда к его
наибольшему поперечному сечению. Ускорение силы сопротивления воздуха
обратно пропорционально поперечной нагрузке снаряда. Снаряд, имеющий
большую поперечную нагрузку, лучше сохраняет свою скорость на полете.
222
бросания и более легкий — при меньшем. Вначале более лег-
кий снаряд полетит ниже более тяжелого, но так как более
легкий снаряд имеет большую начальную скорость, то он как бы
перегонит более тяжелый снаряд и пересечет его траекторию 2
в некоторой точке Кг. В дальнейшем скажется большая попе-
речная нагрузка более тяжелого снаряда, и получится вторая
точка пересечения траекторий Л”2.
Те же взаимные пересечения и переплетения траекторий
мы получим, если будем рассматривать влияние причин, вызы-
вающих боковые отклонения (боковое рассеивание) снарядов.
Так, разнообразие направлений полета снарядов даст пучок
траекторий, расходящихся от точки вылета, подобный тому,,
который показан на рис. 72, но только в горизонтальной пло-
скости, а разнообразие условий полета снарядов даст пучок
траекторий, идущий от общей касательной. Наложение этих
двух пучков один на другой приведет к взаимным пересече-
ниям и переплетениям траекторий.
Таким образом, сноп траекторий представляет собой пучок
пересекающихся и переплетающихся кривых, исходящих из
общей точки — точки вылета.
Явление рассеивания, изображенное на рис. 72—76, для
большей наглядности представлено в утрированном виде.
Чтобы показать взаимные пересечения и переплетения траек-
торий, отклонения концов траекторий построены в значительно
более крупном масштабе по сравнению с дальностями полета,
снарядов.
В действительности эти отклонения по сравнению с даль-
ностью настолько незначительны, что при построении снопа
траекторий в одном и том же масштабе, даже таком крупном,
как 1 :500, этих пересечений и переплетений невозможно
было бы показать. Поэтому, учитывая малую величину кри-
визны траекторий, принимают отрезки траекторий на неболь-
ших участках снопа траекторий как ряд параллельных прямых.
Воображаемая траектория, проходящая в середине снопа
траекторий, называется средней траекторией, (рис. 77).
Средняя траектория — это такая воображаемая траектория,
которая была бы получена при отсутствии причин, вызываю-
щих рассеивание траекторий (траектории 1 на приведенных
выше рисунках). Средняя траектория определяет положение
223
снопа траекторий в пространстве. Точка падения, отвечающая
средней траектории, называется центром рассеивания и обоз-
начается Су.
§ 47. ЗАКОН РАССЕИВАНИЯ ТРАЕКТОРИЙ
При полном отсутствии причин рассеивания всем снарядам,
выпущенным в одних и тех же условиях, будет соответство-
вать одна и та же траектория. Наличие же хотя бы одной из
этих причин приводит к отклонениям точек падения отдель-
ных снарядов от центра рассеивания, причем эти отклонения
носят случайный характер.
Допустим, что в данных условиях стрельбы имеется только
одна причина, вызывающая рассеивание траекторий, — разно-
образие весов боевых зарядов.
Вследствие ошибок, допущенных при развеске, боевые
заряды будут различаться своими весами. Центру рассеивания
отвечает боевой заряд абсолютно точного веса. Различные по
величине и знаку отклонения весов отдельных боевых заря-
дов вызовут различные по величине и знаку отклонения точек
падения отдельных снарядов от центра рассеивания. А так как
отклонения весов боевых зарядов, как следствие случайных
ошибок измерений, носят случайный 'характер, то такой же
характер будут иметь и отклонения отдельных точек па-
дения.
Рассматривая причины рассеивания, можно заметить, что
подавляющее большинство этих причин в той или иной сте-
пени связано со случайными ошибками различного рода изме-
рений. Имеются также причины рассеивания, возникновение
которых с ошибками измерений никакой связи не имеет. Но и
в этом случае можно считать, что такие причины связаны
с отклонениями случайного порядка (разнообразие температур
боевых зарядов, разнообразный досыл снарядов при заряжании,
различное состояние наружной поверхности снарядов и пр.).
Если случайные отклонения, вызываемые действием от-
дельных причин рассеивания, и не следуют закону Гаусса, то
отклонения точек падения, как результат взаимодействия всех
причин рассеивания, без особых погрешностей могут быть при-
няты как отклонения, следующие закону Гаусса или закону,
весьма близкому к закону Гаусса. Это со всей очевидностью
вытекает из свойств закона Гаусса (см. стр. 156).
Закон рассеивания траекторий (точек падения) — закон
Гаусса. Опытные данные подтверждают этот вывод.
Графически закон рассеивания может быть выражен кри-
вой Гаусса, показывающей зависимость между величинами
отклонений точек падения снарядов от центра рассеивания и
вероятностями их получения (рис. 78).
224
Так, например, вероятность получения отклонения в пре-
делах от а до b выражается площадью abed, вероятность по-
лучения отклонения в пределах от k до I — площадью klmn
и т. д.
Применительно к рассеиванию закон Гаусса может быть
сформулирован так:
1. Отклонения отдельных точек падения от центра •
рассеивания, малые по величине, имеют большую вероят-
ность, чем, большие — с увеличением отклонения вероятность
его получения уменьшается.
2. Отклонения отдельных точек падения от центра
рассеивания, заключающиеся в равных по абсолютной вели-
чине пределах, но разные по знаку, равновероятны.
3. Отклонения отдельных точек падения от центра
рассеивания, превосходящие некоторую вполне определенную
в данных условиях величину, имеют такую малую вероят-
ность, что практически ими можно пренебречь.
Короче, рассеивание неравномерно, симметрично и небес-
предельно.
- Эти положения закона рассеивания достаточно подробно
изложены в книге 1 Курса артиллерии.
Перейдем к оценке рассеивания траекторий.
Представим себе горизонтальную площадку и поставлен-
ный на ней вертикальный щит и допустим, что через центры
щита и площадки проходит средняя траектория, которой отве-
чает центр рассеивания Су (рис. 79).
4
Рис. 79
15—. Зак. 9‘. 1
225
Проведем через центр щита вертикальную (отвесную)
линию ББ и перпендикулярную к ней линию ВВ.
Если через этот же щит пройдут две случайные траекто-
рии 1 и 2, то на щите получатся две пробоины (две точки
попадания) Сг и С2. Положения этих пробоин относительно
центра рассеивания будут определяться соответствующими от-
клонениями: от линии ВВ — отклонениями по высоте, от линии
ББ — боковыми отклонениями. Поэтому в вертикальной плос-
кости линия ВВ принимается за ось рассеивания по высоте,
а линия ББ — за ось бокового рассеивания.
Проведем теперь через центр горизонтальной площадки
две взаимно перпендикулярные линии: Б'Б' и ДД, причем
линию Б1 Б' проведем так, чтобы она с линией ББ вертикаль-
ного щита лежала в одной и той же вертикальной плоскости.
Тогда положения случайных точек падения (воронок) и С2
относительно центра рассеивания могут быть определены: по
дальности — отклонениями от линии ДД и по направлению —
от линии Б'Б', т. е. в этом случае линия ДД принимается за
ось рассеивания по дальности в горизонтальной плоскости,
а линия Б'Б' — за ось бокового рассеивания в той же плос-
кости.
Таким образом, рассеивание точек попадания на вертикаль-
ной плоскости складывается из рассеивания этих точек по вы-
соте и их бокового рассеивания, а рассеивание точек падения
на горизонтальной плоскости — из рассеивания этих точек по
дальности и их бокового рассеивания. Допуская параллель-
ность концов траекторий, нетрудно установить (см. рис. 79), что
для одних и тех же траекторий боковые отклонения в вертикаль-
ной плоскости равны по величине и по знаку боковым отклоне-
ниям в горизонтальной плоскости. Это означает, что боковое
рассеивание в вертикальной плоскости равно боковому рассеива-
нию в горизонтальной плоскости.
Рассматривая рассеивание отдельных траекторий только в
одном направлении и учитывая, что рассеивание по дальности
(по высоте) не зависит от бокового рассеивания, можно счи-
тать, что это рассеивание следует закону Гаусса так же, как
л инейные ошибки. Отсюда по аналогии со срединной ошибкой,
за меру рассеивания по данному (одному) направлению при-
нимают срединное отклонение, т. е. такое отклонение, кото-
рое по абсолютной величине больше каждого из отклонений
одной половины всех отклонений и меньше каждого из откло-
нений другой половины. Следовательно, срединное отклонение
определяется тем, что вероятность получить отклоненйе, ко-
торое по абсолютному значению больше или меньше средин-
ного отклонения, равна половине (0,5). Отклонения, которые
по абсолютному значению меньше срединного отклонения, на-
зывают лучшей половиной отклонений, отклонения, которые
по абсолютному значению больше срединного отклонения,—
226
худшей половиной отклонений. Нередко вместо термина
срединное отклонение применяют термин вероятное откло-
нение.
Исходя из того, что рассеивание траекторий можно рас-
сматривать по трем направлениям, приняты следующие обоз-
начения срединных отклонений:
Вд — срединное отклонение по дальности,
Вв — срединное отклонение по высоте и
Вб—срединное боковое отклонение.
Численно закон рассеивания по одному направлению вы-
ражается шкалой, рассеивания, которая по своей сущности
ничем не отличается от шкалы ошибок. По шкале рассеива-
ния можно .решать те же задачи, что и по шкале ошибок,
только применительно к отклонениям траекторий. По внешнему
виду шкала рассеивания отличается от шкалы ошибок тем, что
на шкале рассеивания всегда прочерчивается средняя траекто-
рия. На рис. 80 показана шкала рассеивания по дальности при
Вд = 25 м.
-100м -75м -50м -25м 0 + 25м +50м +75м *100м
-ЬВд -ЗВд -2Вд -Вд\. 0 +Вд *2Вд +ЗВд *ЬВд
»— - I ! _____! ! _ ;______।
0,02 0,07 0.15 0,25 0,25 0.16 0,07 0,02 >
Рис. 80
По этой шкале можно, например, определить вероятность
получения отклонения в пределах от + 25 до + 50 м. Эта вероят
ность равна 0,16. Более подробно об использовании шкалы
рассеивания будет сказано в следующей главе.
Допустив, что конец траек-
тории на небольшом протяжении
может быть принят за прямую
линию, можно легко установить
зависимость между срединным
отклонением по дальности и сре-
динным отклонением по высоте
(рис. 81).
Рис. 81
Из прямоугольного треугольника АС В имеем:
Вв=- Вд • tg Gc,
или
Вд — Вв.- — Be - ctg Gc.
tg & °
15* 227
Эта зависимость позволяет по углу падения и величине
одного из этих срединных отклонений определить величину
другого срединного отклонения.
Пример. Опытными данными установлено, что fee = 8 м. Определить
величину Вд, если zf = 22°.
Решение. Находим значение tg 0с. По таблице натуральных лога-
рифмических величин tg22° = 0,404. Тогда
Be 8
Вд ~ “ 0,404 ~ 19,8 м’
На рис. 81 видно, что между перемещением траектории
по дальности (ДА') и перемещением траектории по высоте
(Д У) при изменении установки прицела на одно деление имеется
та же зависимость, что и между Вд и Be. Из прямоугольного
треугольника DCF имеем:
ДУ _+ а
дх —
откуда.
Be _ ДУ
Вд М '
Наклон местности в районе падения снарядов в сторону
стреляющего орудия и в обратную сторону влияет на величину
рассеивания.
Так как боковое рассеивание на вертикальной и на гори-
зонтальной плоскостях одно и то же, то боковое рассеивание
не зависит от наклона местности в сторону стреляющего ору-
дия и в обратную сторону. Очевидно, не зависит от наклона
местности и рассеивание по высоте, если плоскость цели зани-
мает строго вертикальное положение.
Что же касается рассеивания по дальности, то при стрельбе
по скатам, обращенным в сторону стреляющего орудия, рас-
сеивание по дальности уменьшается, а при стрельбе по обрат-
ным скатам увеличивается.
На рис. 82 показано влияние наклона местности на вели-
чину Вд. Так, если местность в районе падения снарядов
наклонена в сторону стреляющего орудия (ДА), то срединное
228
отклонение по дальности Вдх будет меньше табличного Вд,
т. е. данного в Таблицах стрельбы для горизонтальной мест-
ности. При наклоне местности в обратную сторону {ВВ) сре-
динное отклонение по дальности Вд2 будет больше табличного.
Найдем зависимость между величиной срединного откло-
нения по дальности и величиной угла наклона местности.
Положим, что местность имеет наклон в сторону стреляю-
щего орудия и угол этого наклона равен а (рис. 83).
Опустив из точки С перпендикуляр на продолжение линии
DB, получим два прямоугольных треугольника: САВ и CAD.
Из этих треугольников имеем:
С А — Вдг • sin (9е + а) и С А = Вд • sin 9С,
так как углы CDB и 0е равны между собой, как накрест
лежащие, а угол СВА равен сумме углов (6е -4- а), как внеш-
ний угол в треугольнике CDB. Следовательно,
Вдг • sin (0с 4- а) = Вд • sin Gc,
откуда
da __ Вд sin
0(7sin(9c + a) ’
Положим теперь, что местность имеет наклон в обратную
сторону — от орудия — и угол наклона равен а (рис. 84).
Опустив перпендикуляр из точки С на продолжение BD,
получим два прямоугольных треугольника САВ и CAD, из
которых имеем:
С А = Вд2 • sin АВС и С А ~ Вд • sin Gc.
Найдем, чему равен угол АВС:
4 АВС — 90° — [а +4 A CD] = 90° — [а + (90°— 0с)] =
— 90° — а — 90°4-Ое= 6е — а.
Тогда
Вд2 • sin (Ge — а) _ Вд • sin Ge ;
М _ Вд sin °с
sin(Oc —а) •
Пример 1. Цель расположена на переднем скате, угол наклона равен 3°.
Определить величину срединного отклонения по дальности Вд\, если
Вд = 24 м и = 31°.
Решение. Подставив численные значения Вд, а и в общую фор-
мулу, получим:
Вд • sin 24 • sin 31° 24-0,515
Вд1 = “Sin (0с + а) = sin (31° + 3°) = ~(Х559- к 22 м'
Пример 2. Стрельба ведется по цели, расположенной на обратном
скате, угол наклона которого равен 4°. Чему равна величина срединного
отклонения по дальности Вд2, если Вд = 30м и 0с = 32°?
Вд = Bdsin^c 30-sin 32°
2 sin (9С — a) sin (32° —4°)
30-0,530
До сих пор мы рассматривали рассеивание траекторий
только в одном направлении. В действительности рассеивание
происходит на некоторой площади.
230
Так как рассеивание траекторий в одном (данном) напра-
влении следует закону Гаусса, то, по .общему правилу сло-
жения векториальных ошибок на плоскости, рассеивание тра-
екторий на площади, как результат совместного действия рас-
сеивания по двум направлениям, должно иметь вид эллипти-
ческого рассеивания, т. е. дать эллипсы рассеивания точек
падения (попадания) на горизонтальной и на вертикальной пло-
скостях (рис. 85).
Распределение точек падения (попадания) в эллипсе рас-
сеивания следует закону эллиптической ошибки (см. рис. 66).
Распределение точек падения (попадания), рассчитанное через
0,5 срединного отклонения, дано в приложении 2 „Сетка кру-
гового рассеивания". Правила пользования этой сеткой даны
в следующей главе.
Рассеивание траекторий (точек падения) на плоскости, как
и любая эллиптическая ошибка, характеризуется единичным
эллипсом рассеивания е, расположенным внутри единичного
прямоугольника рассеивания, каждая сторона которого равна
двум срединным отклонениям. Вероятность попадания в единич-
ный эллипс рассеивания равна 0,203.
Помимо единичного эллипса рассеивания, приходится поль-
зоваться половинным эллипсом рассеивания, вероятность
попадания в который равна 0,055.
Причины, вызывающие рассеивание траекторий, а отсюда
и срединные отклонения как величины, характеризующие это
рассеивание, не остаются постоянными во всех случаях стрельбы
из данного орудия, снарядом определенного типа, на опреде-
ленном заряде и на определенную дальность. Наоборот, рас-
сеивание может изменяться от стрельбы к стрельбе вследствие
изменения условий проведения стрельб в различное время и в
различной обстановке, а также и в процессе самой стрельбы.
Например, партия боевых зарядов при одной стрельбе об-
ладает большим разнообразием балистических свойств пороха
по сравнению с партией боевых зарядов при другой*стрельбе.
Очевидно, что рассеивание по дальности при первой стрельбе
будет больше, чем при второй. Проведение стрельб в различ-
ное время суток обусловливает большее или меньшее разно-
образие температур боевых зарядов и т. д.
Рассеивание может меняться и в течение одной и той же
стрельбы, если эта стрельба продолжительна или производится
с небольшими перерывами. Изменения в величине рассеивания
происходят также при резких колебаниях метеорологических
и балистических ‘факторов.
Поэтому срединные отклонения данного момента будут
отличаться от своих табличных значений, т. е. значений, соот-
ветствующих некоторым средним условиям стрельбы. Рассеи-
вание данного момента характеризуется срединными отклоне-
ниями данного момента.
231
Срединным отклонением данного момента называется
такое срединное отклонение, которое будет характеризо-
вать рассеивание траекторий, если бы' в данный момент
можно было произвести большое число выстрелов.
Чтобы показать, насколько срединные отклонения данного
момента могут различаться своими величинами, приведем чис-
ленные значения срединных отклонений, полученные при стрельбе
из 7§-мм, пушки дальнобойной гранатой ОФ-350 (табл. 19).
Таблица 19
Углы бросания Углы бросания
10° . 20° 30° 40° 10° 20° 30° 40°
Вд В м Вб в м
26 49 36 60 12,6 7,9 17,7 13,4
20 26 45 27 6,9 22,0 9,5 8,1
21 38 47 45 13,1 14,1 34,5 34,0
8 22 29 43 7,6 16,7 13,0 8,6
30 37 42 34 4,8 6,5 6,4 15,6
25 25 25 56 3,1 6,0 6,7 9,4
Из табл. 19 видно, что при повторении стрельб для каж-
дого угла бросания были получены различные значения сре-
динных отклонений, причем колебания этих значений весьма
существенны.
Следовательно, необходимо учитывать возможность таких
колебаний значений срединных отклонений при выработке
правил стрельбы и норм расхода снарядов для поражения
различных целей.
§ 48. ОБРАБОТКА РЕЗУЛЬТАТОВ СТРЕЛЬБ
Если не считать стрельб, имеющих научно-исследователь-
ский или испытательный характер, обработка результатов
стрельб сводится к определению положения центра рассеива-
ния и к определению величин срединных отклонений данного
момента.
А. Определение положения центра рассеивания
Истинное положение центра рассеивания, по аналогии с
истинным значением любой измеряемой величины, может быть
найдено по результатам'только очень большого числа выстре-
лов. При ограниченном числе выстрелов можно определить
только приближенное положение центра рассеивания, т. е.
подходящие значения его координат.
При ограниченном числе выстрелов за центр рассеивания
принимается центр группирования точек падения (попадания)*
т. е. средняя из всех’ тех точек падения (попадания), которые:
232
были получены при данной стрельбе. Такой средней точке
будет отвечать приближенное положение средней траектории.
Положение центра группирования может быть определено*
двумя способами: графическим и расчетным. Сущность обоих
этих способов и приемы работ при их применении с исчерпы-
вающей полнотой изложены в книге 1-й Курса артиллерии.
Необходимо рассмотреть только вопрос о точности опре-
деления положения центра рассеивания, если вместо него при-
нять центр группирования.
Подходящие значения координат центра рассеивания нахо-
дятся как средние результаты из координат отдельных то-
чек падения (попадания). Следовательно, точность определе-
ния положения центра рассеивания по данному направлению*
определяется формулой срединной ошибки среднего резуль-
тата
в которой срединная ошибка способа измерения Е будет за-
менена соответствующими срединными отклонениями:
Вд .
*6 =
Пример 1. На одних и тех же установках было произведено 16 выст-
релов. По координатам воронок этих 16 выстрелов были найдены коорди-
наты центра группирования. Чему равна срединная ошибка в определении
центра рассеивания по дальности, если известно, что Вд = 20 м!
Решение. Срединная ошибка в определении положения центра рас-
сеивания как срединная ошибка среднего результата
Пример 2. Положение центра группирования определено по резуль»-
татам 12 выстрелов. Какова вероятность того, что, приняв центр группиро-
вания за центр рассеивания, мы допустим ошибку в дальности, не превы-
шающую 10 л/, и ошибку в направлении, не превышающую 2 л/, если*
Вд = 25 м и Вб = 4 м ?
Решение. Срединные ошибки в определении положения центра рас
сеивания:
в дальности
Rd
в направлении
R6
Тогда искомые вероятности по таблице значений Ф (^):
Рд = Ф (22^ = Ф (1,385) = 0,64978 « 0,65;
р, = ф<JLA = Ф( 1,739) =0,75918 « 0,76.
( 1,15/
- « 7,22 м\
/12
= J— « 1,15 м.
/12
233
Б. Определение подходящих значений срединных
отклонений
Подходящие значения срединных отклонений могут быть
«определены также двумя способами: графическим и расчет-
ным.
Графический способ достаточно полно изложен в 1-й книге
Курса артиллерии.
Расчетный способ определения подходящих значений сре-
.динных отклонений тот же, что и при определении подходя-
щих значений срединных ошибок, т. е. по месту в ряде абсо-
лютных значений отклонений, по среднему арифметическому от-
клонению, по среднему квадратическому отклонению и по
разностям между соседними отклонениями. При обработке ре-
зультатов стрельб используются последние два способа. Рас-
смотрим их на следующих примерах.
Пример 1. На одних и тех же установках произвели 20 выстрелов по
вертикальному щиту, все снаряды попали в щит. Путем обмера были най-
дены следующие отклонения отдельных пробоин относительно центра щита
л; метрах.
По высоте:
—1,6, 4-0,6, 4-2,4, 4-1,2, —0,6,—1,6, 4-1,0, 4-2,7, —0,3, —1,7, 4-1А
4-2,4, 4-0,6, —1,6, 4-1,9, —1,3, 4-2,3, 4-0,8, f 1,4 и 4-2,0.
«По направлению:
—1,0, —2,3, 4-0,8, —1,0, —2,1, — 1Д —0,4, —1,0, —1,9, —1,6, —0,4,
4-ОЛ, —2,0, —1,2, —1,3, —1,0, —2,5, —1,3, —2,7 и 4-0,3.
Определить подходящие значения Be, Вб и Вд, если известно, что угол
шадения Ос = 2°30'.
Решение. Определим сначала координаты центра группирования,
-взяв для этого алгебраические суммы отклонений по каждому направлению
в отдельности и разделив эти суммы на число отклонений. Затем найдем от-
к онения отдельных пробоин от центра группирования как алгебраические
разности между координатами отдельных пробоин и координатами центра
группирования. И, наконец, найдем значения Вв и Вб по соответствующим
«средним квадратическим отклонениям. Значение Вд определим через Вв и
tg 0С. Все решение сведем в таблицу.
П о высоте (У) По направлению (Z)
‘ Ns по Отклонение от Отклоне- ние от центра л Отклонение от Отклоне- ние от центра ,2
* пор. центра щита группиро- ХУ. центра щита группиро- XZ(.
У. i вания V. 1 1 А вания 1 >
1 —1,6 —2,2 4,84 — 1,0 +0,2 0,04
; 2 4-0,6 0,0 0,00 —2,3 -1,1 1,21
3 4-2,4 4-1,8 3,24 +0,8 +2,0 4,00
; 4 4-1,2 4-0,6 0,36 — 1,0 +0,2 0,04
. 5 —0,6 — 1,2 1,44 —2,1 -0,9 0,81
; 6 4 -1,6 —2,2 4,84 — 1,5 —0,3 0,09
234
№ по нор. По высоте (У) По направлению (Z)
Отклонение от центра щита Yi Отклоне- ние от центра группиро- вания V 1 2 ><У. 1 Отклонение от центра щита Отклоне- ние от центра группиро- вания xz. 1 ,2 KZ. i
7 + 1,0 +0,4 0,16 —0,4 + 0,8 0,64
8 +2,7 + 2,1 4,41 —1,0 +0,2 0,04
9 —0,3 —0,9 0,81 — 1,9 —0,7 0,49
10 —1,7 —2,3 5,29 — 1,6 . —0,4 0,16
11 + 1,4 +0,8 0,64 —0,4 4-0,8 0,64
12 +2,4 + 1,8 3,24 +0,1 + 1,3 1,69
13 +0,6 0,0 0,00 —2,0 —0,8 0,64
14 —1,6 —2,2 4,84 —1,2 0,0 0,00
15 + 1,9 + 1,3 1,69 — 1,3 —0,1 0,01
16 -1,3 —1,9 3,61 — 1,0 4-0,2 0,04
17 +2,3 + 1,7 2,89 —2,5 -1,3 1,69
18 +0,8 +0,2 0,04 —1,3 —0,1 0,01
19 + 1,4 +0,8 0,64 -2,7 —1,5 2,25
20 + 2,0 + 1.4 1,96 +0,3 4-1,5 2,25
2У.=+12,0 sxy =0 2Х* = 44,94 i ?Z~ — 24,0 s>,z=o I SX* =16,74 i
Координаты центра группирования:
по высоте
по направлению
Ь = 2^0= _ 1,2 м.
'б 20
Тогда искомые срединные отклонения:
Вв = 0,674491 /~-l4??4- 1,027 м',
I/ 19
Вб = 0,67449 1 [ -l^Z4 « 0,594 м\
I/ 19
Вд - -®21 . « 23,27 м.
tg 2 30'
Пример 2. При стрельбе по реперу было выпущено на одних и тех
же установках 16 снарядов. Местность в районе расположения репера ров-
ная, без наклона. Промером были найдены следующие отклонения отдель-
ных воронок относительно репера в метрах.
По дальности:
-^1, —64, +7, —31, —12, —53, —68, —40, —69, —60, —50, -91, —36,
—63, —35 и —92.
235
По направлению:
+5, +10, +6, -J-Ю, 4-9, 4-6, +6, 48, 46, 45, 48, +5, 4-9,
48, 45 и +5.
Определить подходящие значения Вд, Вб и Be, применяя метод раз*-
ностей между соседними отклонениями, если угол падения Gc = 12°.
Решение. Находим алгебраические разности между двумя соседними
отклонениями, а затем по сумме квадратов этих разностей определяем под-
ходящие значения соответствующих срединных отклонений.
Q. О По даль ПОСТИ (Г) По н а п p а в л e н и ro (2) I
С О У. У. , - У. и., 2 z. Z. - Z.
i 1 z+1 i * У. 1 Uy i i i—\ i zi «z. 1
1 —41 —64-1-41 —23 529 + 5 + 10-.5 45 25
2 —64 4-7+64 4-71 5 041 + 10 +6-10 —4 16
3 + 7 —31—7 —38 1 444 + 6 + 10—6 +4 16
4 —31 —12+31 4-19 361 4-Ю + 9—10 —1 1
5 —12 -53+12 —41 1 681 4 9 +6-9 —3 9
6 —53 —68+53 —15 225 4 6 + 6—6 0 0
7 -68 —40+68 +28 784 4 6 + 8-6 42 4
8 —40 —69+40 —29 841 + 8 +6—8 —2 4
9 -69 —60+69 49 81 4 6 +5-6 —1 1
Ю —60 -50+60 4Ю 100 4- 5 +8—5 4-3 9
И -50 —91+50 —41 1 681 4- 8 +5-8 —3 9
12 —91 —364-91 455 3 025 + 5 +9-5 4-4 16
13 —36 —63+36 —27 729 + 9 4-8—9 —I I
14 —63 —35+63 + 28 784 4 8 4-5—8 -3 9
15 -35 —924-35 —57 3 249 4 5 +5—5 0 0
16 —92 4- 5
—92+41 = з 4.= +5—5=0 S =0 s 4=
=—51 =—51 =20555 =120
Вд = 0,47694
п Г 20555
V 14
18,28 л;
Be = Вд-tg 0с = 18,28-0,213 » 3,89 л\
Вб = 0,47694 jZ ~1,4л/.
§ 49. РАССЕИВАНИЕ ПРИ СТРЕЛЬБЕ ИЗ НЕСКОЛЬКИХ ОРУДИЙ
В процессе изготовления орудий неизбежно допускается
ряд ошибок, неточностей, отклонений и пр. Поэтому, даже
совершенно новые орудия одного и того же калибра, типа и
образца будут несколько различаться своими балистическими
свойствами. Невозможно абсолютно точно выверить прицель-
ные приспособления у отдельных орудий. Наконец, неравно-
мерная нагрузка на орудия при стрельбе приводит к неодина-
236
новому износу каналов стволов. Поэтому к причинам рассеива-
ния, рассмотренным выше (см. § 45), при стрельбе батареей
добавляется еще одна—разнобойность орудий.
Разнобойность орудий батареи заключается в том, что
при стрельбе на одних и тех же установках центры группиро-
вания отдельных орудий не совпадают. При этом под разно-
бойностью орудий понимается только разнобойность в даль-
ности1.
Разнобой н остью (или разнобоем) орудий на-
зывается разность дальностей центров группи-
рования при стрельбе из различных орудий ба-
тареи при одном и т(ж же угле возвышения.*
При теоретических обоснованиях стрельбы исходят из
того, что разнобойность орудий отсутствует. Разнобойность
орудий при стрельбе батареей — явление неизбежное. Поэтому
необходимо установить: во-первых, насколько возможно прак-
тически устранить эту разнобойность и, во-вторых, какую
разнобойность следует считать допустимой.
Начнем с возможности устранения разнобойности.
Основной причиной разнобойности является неодинаковый
износ каналов стволов орудий, что приводит к разнообразию
начальных скоростей различных орудий батареи при стрельбе
на одних и тех же установках.
Определение разнобойности орудий производится двумя
способами: путем обмера длины зарядных камор орудий и
стрельбой по реперу. Оба эти способа подробно описаны
в Правилах стрельбы наземной артиллерии 1945 г. (приложения
2 и 3).
Рассмотрим способ сострела орудий с сопряженным наблю-
дением и определим величину ошибки, которая получается
в этом случае при определении разнобойности.
Большая полуось эллиптической ошибки засечки а опре-
деляется по формуле2
ад
а —----------.
1414-sin
Положим, что срединная ошибка прибора 5 = 1,5 деления
угломера, дальность наблюдения Д = 3000 м, угол засечки
7=3-00= 18° и Вд=25 м. Тогда по приведенной выше фор-
муле
1 При стрельбе батареей есть разнобойность орудий и по направлению.
Но эта разнобойность, являющаяся в основном следствием ошибок, неизбежно
допускаемых при построении параллельного веера, заранее (до стрельбы)
учтена быть не может и в процессе каждой стрельбы устраняется состре-
«ком веера требуемой ширины.
2 См. 10-ю книгу Курса артиллерии, § 3.
237
срединная ошибка в дальности засечки одного разрыва (с уче-
том рассеивания) по правилу сложения векториальных (средин-
ных) ошибок
= /а2 + Вд* = V202 + 252 32 я.
Согласно Правилам стрельбы, при состреле орудий данным
методом для определения положения центра группирования
одного орудия необходимо произвести из этого орудия 6—8
выстрелов. Это означает, что точность такого определения
(при 8 выстрелах) будет характеризоваться срединной ошибкой
о 32 __ 11 о
R = —7_=- — 11,3 я,
V* .
и тогда срединная ошибка, характеризующая точность опреде-
ления разнобойностй двух орудий,
Яр = У’1 1,32 + 11,32 == 16 я « 0,64 Вд.
Этот расчет показывает, что определение величины разно-
бойности орудий способом сострела неизбежно сопровож-
дается ошибкой и притом ошибкой сравнительно большой.
Поправка на разнобойность орудий учитывается уровнем.
При переводе поправки на разнобойность, выраженной в мет-
рах (разность корректур отдельных орудий батареи), в поправку^
выраженную в делениях уровня, также неизбежно допускается
ошибка — ошибка округления и, наконец, при введении такой
рассчитанной поправки в установку уровня добавляется еще?
одна ошибка — ошибка округления самой установки уровня.
Все это приводит к еще большему увеличению ошибки при
учете разнобойностй орудий батареи.
Отсюда можно сделать следующие выводы: во-первых,
при определении разнобойностй орудий способом сострела
полностью устранить разнобойность невозможно, во-вторых,
величина этой неустранимой (остаточной) разнобойностй до-
вольно значительна.
К таким же выводам мы придем при рассмотрении способа
определения разнобойностй путем измерения длины зарядных
камор орудий. Здесь будут ошибки при измерении длины за-
рядных камор, при определении по удлинению камор отклоне-
ний начальных скоростей отдельных орудий батареи, при
переводе этих отклонений в поправки уровня и, наконец, при
введении этих поправок в установки уровня.
Установлено, что при тщательном определении тем или
иным способом разнобойностй орудий и обязательном ее учете
при стрельбе неустраненная (остаточная) разнобойность не
превышает 1,5 — 2Вд. Такую остаточную разнобойность орудий
нужно иметь в виду при стрельбе батареей.
Перейдем теперь к вопросу о допустимой при стрельбе
батареей разнобойностй орудий, т. е. такой разнобойностй,
которая при ведении огня батареей не потребует применения
238
каких-то особых правил стрельбы по сравнению с правилами^,
выработанными для одного орудия. Получив ответ на этот
вопрос, установим, в какой степени остаточная разнобойность.
орудий скажется при стрельбе батареей.
Положим, что разнобойность двух орудий равна 2 Вд и
Вд = 20 м. Посмотрим, что будет представлять собой общая
шкала рассеивания этих орудий, т. е. шкала батарейного рас-
сеивания.
Если из каждого орудия произвести по 100 выстрелов на
одних и тех же установках и допустить, что точки падения
при этом распределяются в каждом орудийном эллипсе соглас-
но закону рассеивания (см. 1-ю и 2-ю строчки рис. 86), то
распределение точек падения в батарейном эллипсе может
быть легко найдено простым сложением (см. числитель 3-й
строчки). При пересчете на 100 выстрелов это распределение
будет вдвое меньше (см. знаменатель 3-й строчки).
Батарейный эллипс оказался равным 10 Вд, т. е. 200
Если рассчитать распределение точек падения в батарейном
эллипсе на 8 срединных отклонений, то это распределение
будет очень мало отличаться от распределения в орудийном
эллипсе (см. 4-ю строчку), и только величина срединного от-
клонения батареи увеличится до 25 м.
Графически батарейное рассеивание, получающееся при
такой разнобойности орудий, показано на рис. 87.
Рассчитав батарейное
рассеивание для случая,
когда в батарее 4 орудия,
и при условии их малой
разнобойности1, мы полу-
чим почти тот же ре-
зультат.
Отсюда делаем вывод,
что при разнобойности
орудий, не превышающей
2 Вд'.
1) закон рассеивания при стрельбе батареей практичес-
ки остается тот же, что и при стрельбе из одного орудия-
1 Т. е. разнобойности, не превышающей 2 Вд.
239
2) изменение величины Вд по сравнению с величиной
разнобойностй незначительно',
3) правила стрельбы, выработанные для одного орудия,
.применимы и для стрельбы батареей.
Поэтому, если в батарее разнобойность орудий определе-
на и при стрельбе учитывается, то неустраненная (остаточная)
разнобойность очень мало скажется на батарейном рассеивании.
Если же при стрельбе батареей разнобойность орудий не
учитывается, то батарейное рассеивание будет резко отличаться
-от орудийного и, что самое главное, уже не будет следовать
закону Гаусса.
Положим, что разнобойность двух орудий равна 4 Вд.
Найдем и для этого случая распределение точек падения при
-батарейном рассеивании, применив тот же метод, что и для
разнобойностй в 2 Вд (рис. 88 и 89).
Из рис. 88 и 89 видно, что при разнобойностй орудий
в 4 Вд распределение точек дадения батарейного рассеивания
закону Гаусса не следует, и правила стрельбы, установленные
для одного орудия, здесь не применимы.
В конечном счете это означает, что стрельба батареей по
общим правилам допустима только при учтенной.разнобой-
ности орудий. Если же разнобойность орудий батареи не
учтена и превышает 2 Вд, то, ведя огонь батареей, не-
обходимо корректировать стрельбу каждого орудия отдельно.
Этого и требуют Правила стрельбы наземной артиллерии.
240
§ 50. РАССЕИВАНИЕ ТОЧЕК РАЗРЫВОВ ПРИ ДИСТАНЦИОННОЙ
СТРЕЛЬБЕ
Дистанционной стрельбой называется стрельба снарядами,
способными разрываться в воздухе на желаемой дальности (ди-
станции) от орудия еще до встречи их с преградой, например
с поверхностью земли.
Такие снаряды снабжаются особыми дистанционными
взрывателями (трубками), конструкция которых позволяет
установить время действия снаряда, т. е. позволяет вызвать
разрыв снаряда в желаемый момент, в желаемой точке
траектории.
Этот разрыв может произойти на любой случайной траек-
тории снопа траектории. Это означает, что рассеивание точек
разрывов при дистанционной стрельбе определяется, прежде
всего, рассеиванием самих траекторий.
Помимо этого, вследствие разнообразия действия по вре-
мени дистанционных взрывателей разрыв может произойти
в различных точках данной траектории.
Таким образом, рассеивание точек разрывов при дистан-
ционной стрельбе слагается: из рассеивания траекторий и из
рассеивания действия дистанционных взрывателей.
К основным причинам, вызывающим рассеивание дистан-
ционных взрывателей, точнее — вызывающим рассеивание дей-
ствия по времени дистанционных взрывателей, можно отнести:
— разнообразие установок взрывателей, являющееся след-
ствием неодинакового совмещения указателя с делениями на
дистанционном кольце взрывателя;
— разнообразие горения дистанционного (порохового) сос-
тава как результат неодинаковых свойств этого состава у раз-
личных взрывателей;
— разнообразие балистических и метеорологических условий
стрельбы, влияющих на горение дистанционного состава по
времени.
Допустим, что причины, вызывающие рассеивание точек
разрывов при дистанционной стрельбе, полностью отсутствуют.
Тогда все снаряды, выпущенные при одних и тех же установ-
ках угломера, уровня, прицела и взрывателя, должны разор-
ваться в какой-то одной точке, лежащей на средней траекто-
рии — в центре рассеивания разрывов, обозначаемом Сд.
При наличии и совместном действии этих причин откло-
нения отдельных точек разрывов относительно средней точки
разрывов (центра рассеивания разрывов) могут иметь любое
направление в пространстве.
Рассеивание траекторий следует закону Гаусса. Без осо-
бых погрешностей можно считать, что и рассеивание дистан-
ционных взрывателей следует тому же закону. Поэтому можно
16—Зак. 991
241
принять, что рассеивание точек разрывов при дистанционной
стрельбе следует закону Гаусса. t
Это означает, что совокупность всех точек разрывов,,
которые могут быть получены при дистанционной стрельбе
на одних и тех же установках и при большом числе выстре-
лов, должна представлять собой эллипсоид — эллипсоид раз-
рывов. Следовательно, рассеивание точек разрывов при дистан-
ционной стрельбе будет эллипсоидальное.
Рассеивание точек разрывов в пространстве при дистанцион-
ной стрельбе, по аналогии с эллипсоидальной ошибкой, характе-
ризуется единичным эллипсоидом разрывов.
Рассеивание точек разрывов по дальности, направлению
и высоте характеризуется соответствующими срединными
отклонениями:
Врд—срединным отклонением разрывов по дальности;
Врб—срединным боковым отклонением разрывов;
Врв— срединным отклонением разрывов по высоте.
Так как боковое рассеивание разрывов при дистанционной
стрельбе зависит только от рассеивания траекторий, то Врб—Вб.
Если спроектировать эллипсоид разрывов на три взаимно
перпендикулярные плоскости: на плоскость стрельбы, на гори-
зонтальную плоскость и на вертикальную плоскость, то полу-
чится три проекции — три эллипса рассеивания разрывов
(рис. 90).
Рис. 90
Очевидно, что срединные отклонения, характеризующие
рассеивание разрывов по высоте и по дальности, не совпадают
с соответствующими главными полуосями эллипсоида разрывов.
В этом заключается особенность срединных отклонений при
дистанционной стрельбе. Отсюда и в единичном эллипсоиде
разрывов его главные полуоси не равны принятым на практике
срединным отклонениям — Врв и Врд.
Из показанных трех проекций эллипсоида разрывов
в теории стрельбы исследуются две проекции: на вертикаль-
ную плоскость, перпендикулярную к плоскости стрельбы, и на
плоскость стрельбы.
242
А. Эллипс разрывов в вертикальной плоскости,
перпендикулярной к плоскости стрельбы
6
Эллипс разрывов в вертикальной плоскости, перпендикуляр-
ной к плоскости стрельбы, дает картину рассеивания точек
разрывов, если смотреть вдоль направления стрельбы.
Построение такого эллипса разрывов несложно и произ-
водится в следующем порядке:
— прочерчиваются две взаимно перпендикулярные линии
ВВ и ББ, точка пересечения которых принимается за центр
рассеивания, а сами линии — за оси рассеивания;
— от этой точки по линии ВВ вправо и влево откладывают
по 4 Вб, а по линии ББ—вверх и вниз по 4 Врв\ численные
значения Вб и Врв берут из таблиц стрельбы;
— в полученный прямоугольник вписывается эллипс раз-
рывов.
На рис. 91 показан эллипс разрывов,
получающийся при стрельбе осколочно-
фуг; сной гранатой с взрывателем Д-1
из 122-л/л/ гаубицы обр 19^8 г. на заряде
втором. Дальность стрельбы 4 000 м\
Вб =2,4 м, и Врв = 7,4 м. Распределе-
ние точек разрывов, чтобы не загромо-
ждать чертежа, дано только по высоте.
При артиллерийских расчетах таким
эллипсом пользуются для определения
положения средней точки разрывов от-
носительно поверхности земли по соот-
ношениям между клевками и воздуш-
ными разрывами. Так как боковое рас-
сеивание при этом не учитывается, то
распределение разрывов строится только
по высоте.
Пример 1. В условиях построения эллипса разрывов на рис. 91 опре-
дели ib нанвероятнейшее положение средней точки разрывов относительно
поверхности земли, если щ и двух батарейных очередях на одних и тех же
установках было получено 2 клевка и 6 воздушных разрывов.
Pt шение Получено .5'/о клевков и 75% воздушных разрывов, что
соответствует пол< жению средней точки разрывов на высоте 1 Врв над
поверхностью земли, или, при переводе в метры, 7,4 м.
Вопрос может быть поставлен и иначе: по заданной высоте
средней точки разрывов требуется найти вероятность получе-
ния клевка или воздушного разрыва, или любой их комби-
нации.
Пример 2. Стреляет 122-л/л« гаубица обр. 1938 г. осколочно-фугасной
гранатой с взрывателем Д-1 на з ряде четвертом. Далтость стрельбы 2 500 м.
Какова вероятность получения в одной батарейной очереди 2 клевков и 2
воздушных । азрыв< в, если средняя точка разрывов относительно поверхности
земли находится на высоте 12 ж?
16* 243
Г 77о~1^ВрЗ
6
Рис. 91
, 146
Решение. По таблицам стрельбы № 146 и Д Для данных усло-
вий Врв ~ 6 м.
Строим распределение разрывов (рис. 92). Как мы видим, вероятность
клевка равна 0,09 и вероятность воздуш-
ного разрыва 0,91. Тогда искомая вероят-
ность
0.02
0.0 7
0.1 ь
0,25
1 0^5
12»-------------'-----------
1 0.1Ь
________0,07_
0,02
4-3-2-1
Р= 2^ТУТ0,092’0,912 ~ 0,°4-
>0,91
------0,09
Рис. 92
Определение положения центра
группирования точек разрывов в
вертикальной плоскости и подхо-
дящего значения величины средин-
ного отклонения по высоте по ре-
зультатам стрельбы производится
по тем же правилам, что и при
ударной стрельбе.
Б. Эллипс разрывов на плоскости стрельбы
Ограничимся рассмотрением единичного эллипса разрывов
на плоскости стрельбы.
Необходимо обратить внимание на то, что большая полуось
единичного эллипса разрывов не совпадает с направлением
средней траектории, образуя с ней некоторый угол (рис. 93).
Для того чтобы выяснить причины этого несовпадения,
рассмотрим рассеивание дистанционных разрывов в безвоздуш-
ном пространстве.
Причинами рассеивания при дистанционной стрельбе в без-
воздушном пространстве являются: разнообразие углов броса-
ния, разнообразие начальных скоростей и разнообразие времен
действия дистанционных взрывателей.
244
Отклонения (ошибки) отдельных точек разрывов относи-
тельно средней точки разрывов Сд, являющиеся следствием
совместного действия перечисленных выше причин, характери-
зуются следующими векториальными ошибками:
— векториальной ошибкой Врц, вызываемой ошибками (раз-
нообразием) в угле бросания; так как при ошибке только в угле
бросания разрыв может произойти выше или ниже линии
выстрела (правильнее — выше или. ниже линии, параллельной
линии выстрела и проходящей через точку Сд), то векториаль-
ная ошибка Вр9 будет направлена по перпендикуляру к линии
выстрела, т. е. под углом 90° + 90 к горизонту, где 6в — угол
бросания;
— векториальной ошибкой BpVf вызываемой ошибками
(разнообразием) в начальной скорости; эта векториальная ошибка
будет направлена по линии выстрела, т. е. под углом 0о к гори-
зонту; ошибка в начальной скорости вызовет отклонение
разрыва относительно точки Сд по линии, параллельной линии
выстрела;
— векториальной ошибкой Bpt, вызываемой ошибками
(разнообразием) во времени действия дистанционного взрыва-
теля; при изменении времени действия дистанционного взрыва-
теля разрыв переместится только по траектории, поэтому
векториальная ошибка будет направлена по касательной к трае-
ктории в точке Сд, т. е. под углом 180°—% к горизонту.
Рис. 94
Так как эти векториальные ошибки лежат в одной пло-
скости (плоскости цели) и имеют различные направления, то
при сложении они дадут эллиптическую ошибку с центром
в точке Сд (рис. 94). Направление большой полуоси этой
эллиптической ошибки (эллипса рассеивания) будет опреде-
ляться соотношением величин векториальных ошибок Bpv Bpv
и Bpt. В зависимости от этого соотношения большая полуось
эллипса рассеивания может совпасть со средней траекторией,
может пройти выше или ниже нее.
Для построения эллипса разрывов на плоскости стрельбы
необходимо по заданным табличным значениям срединных
245
отклонений Врд, Врв и Вв и угла падения 6С найти значения
главных полуосей единичного эллипса разрывов и угол, обра-
зуемый его большой полуосью и осью ОХ. Главные полуоси
единичного эллипса а и b и угол а, составляемый полуосью
а с осью ОХ, определяются по следующим формулам1:
Врд2 • cos2 а — Врв2 • sin2 а .
cos 2а ’
___"l/ Bps2 - cos2 а— Врд2 • sinEg .
Г COS 2a ’
Be2 — Врв2 — Bpd2-tg2 6
tg 2а (Врд2 — Врв2) tg
Принято считать угол а положительным, если положи-
тельное направление оси а единичного эллипса выше гори-
зонта, и отрицательным, если это направление ниже горизонта
(рис. 95). Угол ^падения Gc относительно горизонта всегда
положителен.
Пример. Стреляет 122-.и .и гаубица обр. 1938 г. осколочно-фугасной
гранатой с взрывателем Д-1 на заряде пятом. Дальность стрельбы 3 500 м.
Определить основные характеристики единичного эллипса разрывов на
плоскости стрельбы.
146
Решение. По таблицам стрельбы № 146 и'^Д для данных усло-
вий Врд — 30 м, Врв —10 м, Вв — 5,5 м и /^с = 17° 27'.
Определяем угол а, т. е. угол большой полуоси единичного эллипса
разрывов с горизонтом:
— Врв2 — Bpd*-tg2bc 30,25 -100 — 900-0,099
^2* ~ (Врд2 —Врв2) tgOf = (900 — 100) 0,314
тогда
2к«— 32’30' иа = — 16’15'.
1 Вывод формул не приводится ввиду его громоздкости.
246
Найдем главные полуоси единичного эллипса:
п f Bpd2-cos2 а—Врв2'Sin2a / 900-0,92— 100-0,08
= V cos 2а ” V 0,843
1^Bpe2-cos2a—Bpd2-sin2a 100-0,92 —900-0,08
° cos 2а ~ V 0,843
На рис. 96 показан единичный эллипс, построенный по этим данным.
§ 51. ЗАДАЧИ НА РАССЕИВАНИЕ ТРАЕКТОРИЙ И ТОЧЕК
РАЗРЫВОВ
Задача 121. Определить величину Вд, если Вв равно 1,4 м и угол
падения равен 5°.
Ответ. 16 м
Задача 122. Определить величину Вд, если Вв равно 53 м и угол
падения равен 40°.
Ответ. 63 м.
Задача 123. Определить величину угла падения, если Вд равно 15 м и
Вв равно 2 м.
Ответ. 7°36'.
Задача 124. Определить величину Вд, если Вв равно 6,3 м, ДУ равно
10 м и ДА равно 50 м.
Ответ. 31,5 м.
Задача 125. Стрельба ведется по цели, расположенной на переднем
скате. Определить величину Вд{, если Вд равно 25 м, угол падения равен
10°4' и угол наклона местности равен 2°.
Ответ. 20,9 м.
Задача 126. Стрельба ведется по цели, расположенной на обратном
скате. Определить величину Вд2, если равно 20 л/, угол падения равен
8°32' и угол наклона местности равен 0-50.
Ответ. 30,8 м.
Задача 127. Стрельба ведется по цели, находящейся на обратном
скате. Определить величину Вд2, если Вд равно 15 м- угол падения равен
9°03' и угол наклона местности равен 0-35.
Ответ. 19,5 м.
Задача 128. Стрельба ведется по цели, расположенной на обратном
скате. Определить величину Вд2, если Вд равно 35 зс ДА равно 50 м, ДУ
равно 23 м и угол наклона местности равен 0-45.
Ответ. 39 м.
247
Задача 129. При ударной стрельбе на одних и тех же установках были
получены следующие отклонения точек падения от репера по дальности
в метрах: 41, 62, 80, 60, 28, 96, 67, 53, 8 и 65. Определить положение центра
группирования относительно репера в дальности, если все разрывы были
недолетными.
Ответ. — 56 м.
Задача 130. При ударной стрельбе при одних и тех же установках
были получены следующие отклонения точек падения от репера по дальности
(у) и боковые (г) в метрах:
№ выст- рела у в м Z в м № выст- рела у в м Z в м
1 +72 —20 5 +40 —15
2 + 110 —16 6 + 130 —8
3 + 14 —5 7 +68 —28
4 +80 —24 8 +30 —12
Определить положение центра группирования относительно репера по
направлению и по дальности.
Ответ. = + 68; = — 16 м.
Задача 131. Найти величину Вд, если среднее арифметическое откло-
нение точек падения от центра группирования по дальности равно 24 м.
Ответ. 20,3 м.
Задача 132. Определить величину Вд, если среднее квадратическое
откл онение точек падения от центра группирования по дальности равно 33 м.
Ответ. 22,3 м.
Задача 133. Найти величину срединной ошибки определения положении
центра рассеивания по дальности, если Вд = 24 м и положение центра
группирования было определено по результатам 8 выстрелов.
Ответ. 8,48.
Задача 134. Положение центра группирования по направлению было
определено по результатам 16 выстрелов. Какова вероятность того, что,
приняв положение центра группирования за положение центра рассеивания,
получим ошибку, которая не будет превышать 1 м, если Вд = 3,2 м.
Ответ. 0,60083.
Задача 135. При ударной стрельбе на одних и тех же установках были
получены следующие отклонения отдельных точек падения от репера па
дальности (у) и боковые (z):
№ выст- рела у в м Z в м № выст- рела у в м 2 В М
1 —72 +2 6 + 38 +18
2 +142 —2 7 -26 +2
3 +48 —8 8 +22 0
4 +86 —4 9 +56 + 12
5 —8 — 14 10 —6 +14
Определить положение центра группирования относительно репера и
точность определения положения центра рассеивания.
О т в е т. + 28 м\ 2 м; Rd == 10,4 м\ R6 = 1,64 м.
248
Задача 136. При ударной стрельбе гранатой на одних и тех же уста-
новках были получены следующие отклонения отдельных точек падения
относительно репера в метрах:
по дальности (у):
4- 20, - 35, — 5,4- 15, 0, + 45, — 10, — 25, + 15, —60,-15 и — 5;
по направлению (г):
+ 6, 4-2, —4, + 8,-2, +3,+ 11, —6, —5, 4-2, 4-3 и+ 6.
Определить подходящие значения Вд и Вб по средним квадратическим
отклонениям, если известно, что ось OY прямоугольной системы координат
совпадает с направлением плоскости стрельбы.
Ответ. Вд — 18,6 м и Вб = 3,6 М.
Задача 137. На одних и тех же установках при стрельбе гранатой
с дистанционным взрывателем были получены следующие высоты отдельных
воздушных разрывов относительно поверхности земли: 0-10, 0-12, 0-11, 0-09,.
0-08, 0-12, 0-07, 0-05,0-08, 0-12, 0-07, 0-04,0-09, 0-15 и 0-06. Найти подходя-
щее значение Врв, если дальность стрельбы равна 3600 м.
Ответ. 7,3 м.
Задача 138. При испытании двух орудий одинакового калибра, но раз-
личных образцов, при стрельбе на одних и тех же установках и при прочих
равных условиях были получены следующие отклонения отдельных точек
падения относительно репера по дальности (у и _у3) и по направлению (znz$
в метрах:
№ Орудие образца А Орудие образца Л,
рела У Z Ух А
1 4-35 4-7 +12 4-2
2 —7 —13 +26 —3
3 4-18 4-2 0 + 1 4-7
4 4-26 0 4-17
5 0 4-10 —3 0
6 4-21 —3 +19 —8
7 4-14 —17 4-43 4-2
8 —25 4-3 4-7 —5
9 4-6 —8 -+-14 —1
10 4-62 —1 —15 4*5
Определить подходящие значения Вд и Вб для обоих орудий, если оси
OY и OY\ совпадают с направлением плоскости стрельбы.
О т в е т. О) удие образца А: Вд = 16,2 м\ Вб = 5,7 м. Орудие образца Zf.
Вд = 10,9 м‘, Вб = 3,03 м.
Задача 139. При ударной стрельбе на одних и тех же установках были
получены следующие боковые отклонения отдельных точек падения относи-
тельно цели в метрах:—12,4-2,4-9,4-2,— 6,4-5, — 3, — 10, + 7, +10 и
— 4. Определить подходящее значение Вб по разностям между соседними
отклонениями.
Ответ. 5,2 м.
Задача 140. При ударной стрельбе на одних и тех же установках были
получены следующие отклонения по дальности относительно репера в метрах:
4- 1‘5, 4- 35, 4- 75, 4- 55, 4- 15, — 45, — 15, 4- 5,— 35, 4- 40, — 10,— 75, — 45, 0,-5,
— 35, — 5, 4- 15, — 45 и — 55. Найти подходящее значение Вд по разностям
между соседними отклонениями.
Ответ. 20 м.
249
Задача 141. При ударной стрельбе на одних и тех же установках были
получены следующие отклонения отдельных точек падения относительно
ориентира (в метрах):
по дальности: 4- 46, 4-114, 4- 57, + 169, 4- 219, 4-284, 4- 145, 4- 86, + 240,
4- 160, 4- 16,+ 119, 4-238,4-120, 4- 150, + 184, 4-215, 4- 180, + 111, 4- 96;
по направлению: — 24, — 18, 4- 10, — 4, —10, 4- 15, — 20, — 34, — 46,— 47,
— 12, — 6, — 30, — 37, — 44, — 52, — 47, -48,-50 и — 52.
Определить по разностям между соседними отклонениями подходящие
значения Вд и В б", если плоскость стрельбы в районе падений снарядов была
провешена с достаточной точностью.
Ответ. Вд»43 м\ Вб = 7,75 м.
Задача 142. Определить вероятность получения воздушного разрыва
при стрельбе гранатой с дистанционным взрывателем, если средняя точка
разрывов находится в 8 м над поверхностью земли, а Врв = 5,5 м.
Ответ. 83,7% (83,2 70).
Задача 143. При стрельбе гранатой с дистанционным взрывателем
-средняя точка разрывов находится в 2 м под поверхностью земли. Какова
вероятность получения клевка, если Врв = 3,8 м7
Ответ.63,7% (63,2%).
Задача 144. Определить наивероятнейшее положение средней точки
разрывов относительно поверхности земли при дистанционной стрельбе,
-если при трех батарейных очередях на одних и тех же установках было
получено 5 клевков и 7 воздушных разрывов, а Врв = 7 м.
О т в е т. +2,2 м.
Задача 145. Определить наивероятнейшее положение средней точки
разрывов относительно поверхности земли при дистанционной стрельбе,
если при четырех батарейных очередях было получено 10 клевков и 6 воз-
душных разрывов, а Врв = 12 м.
Ответ. — 5,8 м.
ГЛАВА 10
ВЕРОЯТНОСТЬ ПОПАДАНИЯ
§ 52. ФАКТОРЫ, ОПРЕДЕЛЯЮЩИЕ ВЕЛИЧИНУ ВЕРОЯТНОСТИ
ПОПАДАНИЯ
Величина вероятности попадания является основой важ-
нейших артиллерийских расчетов.
Вероятность попадания определяет надежность и экономич-
ность стрельбы. Исходя из численного значения вероятности попа-
дания, находят наивыгоднейшие методы ведения огня, в частно-
сти — пристрелки. Зная вероятность попадания, можно рас-
считать средние нормы расхода снарядов для поражения раз-
личных целей.
Прежде чем приступить к рассмотрению способов опреде-
ления вероятности попадания, необходимо установить те
факторы, от которых зависит величина вероятности попадания.
Вероятность попадания зависит: от размеров цели, от вели-
чины рассеивания, от положения средней траектории относитель-
но цели и от направления стрельбы.
1. Размеры цела. При одной и той же величине рассеи-
вания, при одинаковом положении средней траектории отно-
сительно цели и при одном и том же направлении стрельбы,
но при различных размерах цели вероятность попадания будет
тем больше, чем больше размеры цели.
юо°/0
На рис. 97 показано, как уменьшается вероятность попада-
ния с уменьшением размеров цели при всех прочих равных
условиях, при этом размеры цели последовательно уменьшаются
251
в 2 раза, т. е. площадь цели уменьшается в 4 раза. Изменение
вероятности попадания не пропорционально изменениям раз-
меров цели, что, естественно, вытекает из неравномерности
рассеивания.
2. Величина рассеивания. При одних и тех же размерах
цели, при одинаковом положении средней траектории относи-
тельно цели и при одном и том же направлении стрельбы, но
при различном по величине рассеивании вероятность попадания
будет тем больше, чем меньше величина рассеивания (величи-
ны срединных отклонений). Например, если эллипс рассеивания
полностью укладывается в границах цели, вероятность попада-
ния будет равна 100%. Если же размеры эллипса рассеивания
таковы, что он накрывает цель только какой-то своей частью,
вероятность попадания будет меньше 100%, и тем меньше, чем
меньше накрывающая ее часть эллипса рассеивания (рис. 98).
3. Положение средней траек-
тории относительно цели. Из не-
равномерности рассеивания следует,
что вероятность попадания будет
наибольшей в том случае, когда
средняя траектория пройдет через
центр цели. С удалением средней
траектории от центра цели вероятность попадания будет умень-
шаться, и если это удаление будет превышать 4 срединных откло-
Рис. 98
Рис. 99
4. Направление стрельбы. Направление стрельбы опреде-
ляет положение эллипса рассеивания на цели. Боковое рас-
сеивание значительно меньше рассеивания по дальности. Поэтому
при одной и той же величине рассеивания, при одинаковом
положении средней траектории относительно центра цели и
при одних и тех же размерах цели вероятность попадания
будет наибольшей в том случае, когда ось бокового рассеивания
направлена вдоль наибольшего размера цели.
Так, например, если ось бокового рассеивания ББ напра-
влена вдоль цели, имеющей вид вытянутого прямоугольника
(рис. 100), и размеры эллипса рассеивания таковы, что он
полностью укладывается в границах цели, вероятность попадания
будет равна 100%. Если же ось бокового рассеивания будет
252
700%
Б
Рис. 100
Б
направлена перпендикулярно к той же цели, то вероятность
попадания будет меньше 1ОО°/о. Практически это означает, что при
всех прочих равных условиях при фланговом огне вероятность
попадания будет наибольшая, а при фронтальном — наименьшая.
Суммируя все то, что
было сказано о факторах, оп-
ределяющих величину вероят-
ности попадания, можно сде-
лать ряд практически важных
выводов.
1. Величина рассеивания
зависит от дальности стрель-
бы—чем меньше дальность, тем
меньше рассеивание. Поэтому,
чтобы иметь наименьшее рас-
сеивание, а отсюда и наиболь-
шую вероятность попадания, огневые позиции батарей следует
располагать возможно ближе к противнику. Опыт Великой
Отечественной войны показал всю целесообразность массового
применения орудий, стрелявших прямой наводкой из располо-
жения наших передовых частей. Здесь, помимо точности наводки,
исключительно большое значение имели и малые дальности
стрельбы, обеспечивающие большую вероятность попадания.
2. Пристрелку необходимо производить так, чтобы достичь
возможно более точного совмещения средней траектории
с целью, так как в этом случае огневые задачи решаются
с наименьшим расходом снарядов и времени.
3. Следует широко применять фланговый и косоприцельный
огонь, соответствующим образом располагая огневые позиции
батарей и распределяя огневые задачи между батареями.
§ 53. ВЕРОЯТНОСТЬ ПОПАДАНИЯ В ПОЛОСУ БЕСКОНЕЧНОЙ ДЛИНЫ
Известно, что численно закон рассеивания по одному направ-
лению выражается шкалой рассеивания, причем это направление
может совпадать или не совпадать с направлением одного из
главных диаметров эллипса рассеивания. Это следует из того
-свойства эллиптической ошибки, что на любом диаметре предель-
ной по величине эллиптической ошибки £тах можно построить
шкалу ошибок (см. стр. 211).
Поэтому, если цель представляет собой полосу бесконечной
длины (полоса проволочных заграждений, полоса траншей,
дорога, дефиле и пр.), то определение вероятности попадания
в такую цель сводится к определению вероятности получения
отклонения в заданных пределах по одному направлению.
Такая задача, по аналогии с определением вероятности полу-
чения ошибки в заданных пределах, может быть решена по
шкале рассеивания и по таблице значений Ф(^).
253
Шкалу накладывают на цель с учетом положения средней
траектории относительно цели, после чего определяют веро-
ятность попадания в ту часть эллипса рассеивания, которая
накрывает цель. Следует подчеркнуть, что шкала рассеивания
накладывается на цель, а не цель на шкалу рассеивания, так
как в противном случае при графическом решении задач на
чертеже строится совершенно ненужная часть шкалы рассеи-
вания — чертеж получается громоздким, мелкого масштаба
и не наглядным.
При пользовании таблицей значений Ф ф) удаление средней
траектории от границ цели переводится в доли соответствую-
щего срединного отклонения, а затем определяется вероятность
получения попадания в этих границах, т. е. при фронтальном
огне — между передним и задним краями цели, а при стрельбе
вдоль полосы — между левой и правой ее границами.
Рассмотрим два случая: направление одной из главных
полуосей единичного эллипса рассеивания параллельно направ-
лению (длине) цели и направление одной из главных полуосей
единичного эллипса рассеивания образует с направлением цели
некоторый угол а, не равный прямому.
Приемы определения вероятности попадания в обоих этих
случаях покажем на частных примерах, начав со случая, когда
направление одной из главных полуосей единичного эллипса
параллельно направлению цели (полосы).
Пример 1. Батарея стреляет по полосе проволочных заграждений
глубиной 30 м, Огонь фронтальный, т. е. плоскость стрельбы перпендику-
лярна полосе проволочных заграждений. Определим вероятность попадания
в эту полосу, если известно, что Вд = 22 м и средняя траектория проходит
через середину полосы. .
Решим эту задачу по шкале рассеивания и по таблице значений Ф
1. Решение по шкале рассеивания (рис. 101)
Рис. 101
Проведем две параллельные линии ПП и 33, расстояние между-
которыми в произвольно взятом масштабе равно ширине цели, т. е. 30 м.
Нанесем точку Су в полосе ППЗЗ так, чтобы средняя траектория
проходила через середину цели.
Проведем через точку Су линию ДД, параллельную линиям ПП и 33,.
т. е. параллельную направлению (длине) полосы, и линию ББ, перпендику-
254
лярно к линии ДД. Примем направления линий ДД и ББ за направления
главных диаметров эллипса рассеивания, иначе говоря, — за оси рассеивания
по дальности {ДД) и бокового рассеивания (ББ).
По линий ББ от точки Су в принятом нами масштабе отложим по
одному Вд в обе стороны (на чертеже — вверх и вниз, по условиям стрель-
бы— впе| ед и назад), т. е. наложим на цель ту часть шкалы рассеивания
по дальности, которая накроет полосу.
Составим пропорцию:
22 м — 0,25;
15 м — х;
откуда
х = 0,25 ' « 0,17.
t
Получена вероятность попадания в половину полосы.
Отсюда искомая вероятность
Р == 0,17 • 2 = 0,34 = 34%.
Эту же задачу можно решить, пользуясь шкалой рассеивания, постро-
енной с точностью до 0,5 Вд.
В этом случае цель будет накрываться полосами, содержащими по 13%,
попаданий и частями полос, содержащих по 12% попаданий.
Составляем пропорцию на ту часть глубины пели, которая накрывает-
ся полосой, содержащей 12% попаданий:
11 м — 0,12;
4 м— х;
откуда
х _ Oil2 :..±. ~ о,о44.
х~ н
Тогда искомая вероятность
Р = (0,13 + 0,044).2 = 0,348 к 35%.
2. Решение по таблице значенийФ(р)
По условию средняя траектория проходит через середину полосы
проволочных заграждений. Поэтому
может быть найдена как вероятность
получения отклонения в пределах от
0 до ± 15 м.
Переведем 15 му т. е. половину
ширины полосы, в доли срединного
отклонения по дальности:
В - 0,682.
Р - 22 L
Тогда по таблице значений Ф(р),
интерполируя, получим:
Р = Ф (0,682) = 0,35352 % 0,00097 = \
= 0,35449 « 0,355 = 35,5»/0.
Пример 2. Батарея ведет огонь
вдоль шоссе, ширина которого равна
6 м. Определить вероятность попа-
дания в шоссе, если средняя траек-
тория проходит через его левый край,
а Вб = 4,2 м.
255
1. Решение по шкале рассеивания (риб. 102)
Мы видим, что шоссе накрывается полосой, содержащей 25% попаданий,
и частью полосы, содержащей 16% попаданий. Составляем пропорцию
4,2 м — 0,16;
1,8 м — х",
откуда
0,16-1,8
х= —~ 0,069.
Тогда вероятность попадания в шоссе:
/>=0,254-0,069=0,319^32%.
Более точные расчеты по шкале рассеивания через 0,5 Вб дают:
/> = 0,134-0,12+ 0,029‘11 * * * *-8-^ 0,327.
2. Решение по таблице значений Ф(Р)
Определяем вероятность попадания в пределах от 0 до —6 м:
6
3 = ^2 = 1,429;
откуда, интерполируя, получаем:
Ф (р) = Ф (1,429) = 0,66521 — 0,00034 = 0,66487.
Тогда искомая вероятность
Р = у Ф(р) = 0,33243.
“Пример 3. Батарея ведет фронтальный огонь по полосе окопов,
общая глубина которой равна 40 м. Определить вероятность попадания
в эту полосу, если средняя траектория проходит в 15 м перед серединой пе-
реднего края полосы, а Вд = 38 м.
t
1. Решение по шкале рассеивания (рис. 103)
Здесь цель накрывается частью полосы, содержащей 25% попаданий, и
частью полосы, содержащей 16% попаданий. Составляем две пропорции
38 м— 0,25; 38 м — 0,16;
23 м — xf, 17 м — х2;
256
•ткуда
0,25-23 0,16-17
д-j = —2g— « 0,151 и х2 — - 88—' ~ 0,072.
Тогда вероятность попадания в полосу окопов
Р =0,151 4-0,072 = 0,223.
По шкале рассеивания, построенной через 0,5 Вд, та же вероятность
будет равна
„ 0,13-4 0,09-17
Р= - Jg 4- 0,12 -ь « 0,228.
2. Решение по таблице значений Ф (£)
Находим вероятность попадания в пределах от 0 до ± 55 м:
55
^з^ 1’447’
откуда
Ф (j32) = 0,66858 + 0,00235 = 0,67093.
Определяем вероятность попадания в пределах от 0 до ±15 м:
15
^= 28 =0,395,
откуда
Ф (р,) = 0,20749 ± 0,00260 = 0,21009.
Тогда искомая вероятность
Р = у [Ф(р3) — Ф (pi)] == (0,67093 — 0,21009) = 0,23042.
Пример 4. Батарея ведет фронтальный огонь по полосе окопов, рас-
положенной на обратном скате. Ширина полосы равна 30 м. Передний ее
край относительно гребня укрытия удален на 10 м. Определить вероятность
попадания в эту полосу, если средняя траектория проходит через гребень
укрытия, угол наклона ската а = 5°, угол падения 9^=22° иВ6=18л/
(рис. 104).
Решение. Прежде всего определим величину срединного отклоне-
ния Вд2 по направлению обратного ската по формуле (см. стр. 230)
Вд-sin 0 18-sin 22
--------С =------------- 23 м.
sin(6f — a) sin 17
17 - Зах. 991
257
Тогда искомая вероятность по шкале рассеивания (рис. 105)
~ 0,25-13
Р~ 23
0,16-17
+-----23— = 0)259 ~ 26%-
Решение по таблице значений Ф ф)
^=4 [Ф(^2)-ФФ1)] =4[ф(^г)-ф(4)] = 4 [ф(1’74)~_ф(°>435)] =
1
= 2 [0,75945 — 0,23087] = 0,26429~26,40/0. >
На решениях примеров 1, 2, 3 и 4 были показаны наи-
более типичные случаи определения вероятности попадания,
когда один из главных диаметров эллипса рассеивания парал-
лелен направлению полосы.
Перейдем теперь к случаю, когда главные диаметры
эллипса рассеивания образуют с направлением полосы угол а,
не равный прямому.
Положим, что эллипс рассеивания относительно цели,
иредставляющей собой полосу бесконечной длины, занимает
такое положение, как показано на рис. 106.
У
Рис. 106
Очевидно, что в этом случае в цель попадут все те сна-
ряды, отклонения которых по направлению OY, перпенди-
258
кулярному к направлению полосы, будут больше ух и меньше
у2. Поэтому найдем срединное отклонение, вызываемое еди-
ничным эллипсом рассеивания по направлению OY.
Отклонение, вызываемое эллиптической ошибкой по не-
которому направлению, равно (см. стр. 213)
D" — У a2 sin2 а -|- b2 cos2 а.
В нашем случае а — Вд, Ь = Вб и угол а — угол между
направлением главного большого диаметра эллипса рассеива-
ния (осью бокового рассеивания) ББ и направлением полосы.
Тогда приведенная выше формула примет вид:
В —УВд2 • sin2 а 4- Вб2 • cos2 а,
где В — отклонение (срединное), вызываемое единичным эллип-
сом рассеивания по перпендикуляру (нормали) к направлению
полосы.
Если в условии задачи будет дан не угол а, а угол а3,
образованный тем же главным диаметром и нормалью к на-
правлению цели, то
В = УВд2 cos2 ах 4- Вб2 • sin2 аР
Так как определяется вероятность получения отклонения
по линии OY, то необходимо удаление средней траектории от
переднего края цели, выраженное отрезком ОА, и удаление
от заднего края цели — отрезком ОВ, привести к направле-
нию OY, т. е. спроектировать на это направление.
Из чертежа видно, что эти проекции
ОАХ == ух = О А • sin а
и
ОВХ = у2 — ОАХ 4~ I — У1 4- I,
где I — ширина цели.
Если же удаление средней траектории относительно края
цели дается по нормали, то в таком приведении нет никакой
нужды.
В остальном приемы решения задач те же, что и в разо-
бранных нами примерах.
Пример 5. При направлении стрельбы, показанном на рис. 106, опре-
делить вероятность попадания, если Вд = 20 м, Вб = 3 м, а = 30°, ОА = 1? м,
/ = 20 м.
Решение. Независимо от способа решения прежде всего необхо*
димо найти значения В, ОАХ и ОВХ:
В =j/202 sin2 30°+ 32. cos2 30° - j/400-0,25 + 9-0,75 ж 10,3 м.
ОАХ ~ 12-sin 30°= 6 м и ОВХ — 6 м + 20 м — 26 м.
17* 259
Тогда искомая вероятность по шкале рассеивания (рис. 107)
+ 0,16 + ~ °’301 = ЗО’1О/о-
lv?O W,o
а по таблице значений Ф (^)
р = Т[ф ф ™ = Кф ( ТО-)-ф ( <з Д = I[ф (2'й4> -
— Ф [Ф (0,583)] — 2 (0,91382 — 0,30586) = 0,30398 « 30,40 0.
Рис. 107
Следует заметить, что формула
B — V Вд2 • sin2 а + Вб2 • cos2 а
выражает величину срединного отклонения в общем виде, т. е.
для любого направления стрельбы относительно цели.
Так, если огонь ведется фронтальный, т. е. а — 90°, то
В—]/Вд~ • sin2 90°+ Вб2 - cos2 906= Вд,
а при фланговом огне, т. е. при а —0°;
В = УВд2- sin2 0° + Вб2 cos2 0°= Вб.
§ 54. ВЕРОЯТНОСТЬ ПОПАДАНИЯ В ПРЯМОУГОЛЬНИК, СТОРОНЫ
КОТОРОГО ПАРАЛЛЕЛЬНЫ ГЛАВНЫМ ПОЛУОСЯМ ЭЛЛИПСА
РАССЕИВАНИЯ
Положим, что цель представляет собой прямоугольник,
стороны которого параллельны главным полуосям эллипса
рассеивания, и этот прямоугольник в эллипсе рассеивания
занимает такое положение, как показано на рис. 108.
Прямоугольник abed получился в результате пересечения
двух полос: полосы М, стороны которой параллельны боль-
шому главному диаметру ББ эллипса рассеивания, с полосой N,
стороны которой параллельны малому главному диаметру ДД
260
того же эллипса. Очевидно, что в этот прямоугольник попа-
дут все те снаряды, которые одновременно попадут в полосу М
и в полосу N.
В данном случае происходит слож-
ное событие—попадание в прямоуголь-
ник,—представляющее собой совпадение
простых независимых событий — попа-
дания в полосу М с попаданием в по-
лосу N. Обозначив вероятность попада-
ния в полосу М через рм, а в полосу
N — через pN, вероятность попадания
в цель найдем по теореме умножения
вероятностей:
Р=РМР„-
Следовательно, решение задачи на
определение вероятности попадания в
прямоугольник, стороны которого парал-
лельны главным полуосям эллипса рас-
сеивания, сводится к решению двух
задач на определение вероятности попа-
дания в полосы бесконечной длины, после
чего эти вероятности перемножаются.
Пример 1. Огонь ведется по блиндажу, имеющему вид прямоугольника
со сторонами в 6 и 10 м. Плоскость стрельбы перпендикулярна к меньшей
стороне блиндажа, а средняя траектория проходит через середину этой сто-
роны (рис. 109). Определить вероятность попадания в блиндаж, если
Вд = 28 м и Вб — 2,2 м.
рассеивания
Определяем вероятность попа-
дания по дальности
я °’09-
1. Решение по шкале
5
Рис. 109
А
Определяем вероятность попа-
дания по направлению
о /л ок । 0,16*0,08 \
Рб — 2 Г 0,25 + —*— \ 0,62.
Тогда искомая вероятность как
вероятность сложного события
Р=.рдрб=. 0,09*0,62 = 0,0558^5,6%.
2. Решение по таблице
значений Ф(Р)
Вероятность попадания по даль-
ности
Ро = -1ф(0,357)=0,09514.
261
Вероятность попадания по направлению
Тогда
Рб = ф (’тг)=ф (1,364)=0,64242‘
Р^рдрб =0,09514-0,64242 « 0,06112 ж 6,1°/0-
Пример 2. Орудие ведет фронтальный огонь по амбразуре ДОТ. Раз-
меры амбразуры 0,8 м X 0,2 м. Определить вероятность получения хотя бы
одного попадания в амбразуру при 6 выстрелах, если Вв = 0,2 м, Вб = 0,3 м
и средняя траектория проходит на 0,1 м ниже середины нижнего края
амбразуры (рис. 110).
0,1м 0,09
о,1м 0,1 г
—
о,1м 0,13 I
____L 1
— 0,2м- —
1 1*—,— 0,Ьм1------------г 0,4/и-,—।
0,75м ! О,75М ; 0,75м . /7,75м; 0,75м!
'*0,09 **0,72 ^0,13^ 0,13^0,12^0.09^
Рис. 110
Решение. Найдем сначала вероятность попадания в амбразуру при
одном выстреле.
1. По шкале рассеивания (с точностью до 0,5 Вв и 0,5 Вб):
рв =0,12 4- 0,09 = 0,21;
рб = 2 f 0,25 + « 0,62;
\ U,10 /
Р = рв Рб =0,21-0,62 ж 0,13.
2. По таблице значений Ф (р)
рв = 1Гф ('к^-Ф/'кк'] = 2ГФ (1,5) -Ф (0,5)1=
в 2L <0,2/ <0,2/_] 2L J
= 1 (0,6883—0,26407) = 0,21213;
= =1ф(1,333) = 0.6314;
р==Рврб- 0,21213-0,6314 жО ,134.
Теперь определим вероятность попадания в амбразуру хотя бы 1 раз
Рх - 1 _ (1 _ о,13)б = 1 — 0,876 = о,566,
или
рх = 1 — (I — 0,131)6= 1 —0,8666 = 0,576.
262
§ 55. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ ПОПАДАНИЯ В ЦЕЛЬ ЛЮБОГО
ОЧЕРТАНИЯ
В тех случаях, когда очертания цели таковы, что ее нельзя
представить в виде прямоугольника, стороны которого парал-
лельны главным полуосям единичного эллипса рассеивания,
определение вероятности попадания производится графическим
способом при помощи сетки кругового рассеивания.
Сетка кругового рассеивания строится и рассчитывается
в ^предположении, что рассеивание в эллипсе по его главным
диаметрам одинаково по величине. Вместо эллипса получается
круг, отсюда и название сетки. „
Для построения сетки кругового рассеивания на листе
клетчатой |или миллиметровой бумаги проводят две взаимно
перпендикулярные линии (рис. 111), принимая их за оси рас-
сеивания, а точку пересечения — за центр рассеивания Су. Сто-
рона каждого квадрата (клетки) сетки принимается равной
какой-то доле срединного отклонения: 0,5; 0,25 и т. д., в за-
висимости от требуемой точности.
После построения сетки рассчитывают вероятности попа-
дания в каждый квадрат, как в прямоугольник, стороны кото-
рого параллельны осям рассеивания. При этом используют
таблицу значений Фф), а точность расчетов доводят до 0,0001,
т. е. до 0,01%.
На рис. 111 показана часть сетки кругового рассеивания,
построенной в масштабе: в одной клетке — 0,5 срединного
отклонения. Прямоугольник abed получился в результате пе-
ресечения полосы М с полосой N.
Вероятность попадания в полосу М
= 4 Ф (0,5) = ^-7= 0,13204,
268
а вероятность попадания в полосу Л/
PN = ^[Ф(1,0) — Ф(0,5)] = 2^26407 = 0>i 1797.
Тогда по теореме умножения вероятность попадания
в прямоугольник abed
Рг РмРм^ 0,13204-0,11797 = 0,0155767588 0,0156.
Эту вероятность напишем в прямоугольнике abed.
Прямоугольник efgk получился при пересечении полосы К
с полосой L. Поэтому вероятность попадания в этот прямо-
угольник
Л = [Ф (1,0) - Ф (0,5)] • 1 [Ф (2,0) - Ф (1,5)]=:
0,5 — 0,26407 0,82266 — 0,68833 Л
—-----------------------------0,0079 и т. Д.
Полностью такая сетка дана в приложении 2.
Сетка кругового рассеивания построена в долях срединных
отклонений. Поэтому, чтобы по этой сетке определить вероят-
ность попадания в заданную цель, необходимо координаты
относительно осей рассеивания наиболее характерных точек
очертания цели выразить также в долях срединных отклонений,
после чего по этим координатам цель наносится на сетку и
суммируются вероятности попадания в те квадраты, которые
оказались накрытыми очертаниями цели. При этом вероятности
попадания в квадраты, накрытые целью только частично, опре-
деляются интерполированием на-глаз.
При перенесении очертаний цели на сетку кругового рас-
сеивания эти очертания по сравнению с действительными будут
искажены, что является следствием искажения масштабов сре-
динных отклонений при построении самой сетки, но на резуль-
татах расчетов это не скажется, так как сетка построена
в долях срединных отклонений, а не в метрических единицах.
В этом и заключается ценность сетки кругового рассеивания,
так как по ней можно определить вероятность попадания, во-
первых, в цель любого очертания и, во-вторых, в цель, лежа-
264
Пример. Цель представляет собой горизонтальный шестиугольник,
положение которого относительно центра рассеивания показано на рис. 112.
Координаты вершин шестиугольника в метрах таковы:
Вершины А в с D Е F
По оси ОХ .... —10 +20 +40 +20 —10 —20
По оси ОУ ... . 0 -2,5 +5 + 12,5 + 10 +5
Определить вероятность попадания в цель, если известно, чтоВд = 40 м
и Вб = 5 м.
Решение. Переводим координаты вершин цели: по оси ОХ — в доли
Вд и по оси OY—в доли Вб. Получаем:
Вершины А в с D Е F
По оси ОХ -0,25 + 0,5 + 1,0 +0,5 —0,25 -0,5
По оси OY 0 —0,5 + 1,0 +2,5 +2,0 + 1,0
По оси ОХ глубина цели от — 0,5 Вд до + 1 Вд и по оси ОУ ширина
цели от — 0,5 Вб до + 2,5 Вб. Поэтому на миллиметровой бумаге построим
ту часть сетки кругового рассеивания, которая накроет шестиугольник.
Воспользуемся при этом сеткой кругового рассеивания, данной в приложе-
нии 2.
Перенесем на сетку (рис. 113) вершины шестиугольника по координатам,
гыраженным в долях Вд и Вб, и соединим эти вершины прямыми линиями.
Следует обратить внимание на очертания цели, полученные на сетке, и ее дей-
ствительные очертания на рис. 112.
Теперь остается только сложить веро-
ятности попадания в квадраты, накрытые
целью. Если учесть, что один миллиметр
данного квадрата отвечает одной сотой
вероятности попадания в него, то, подсчитав
миллиметры в неполных квадратах, опре-
делим вероятность попадания в цель с
очень большой точностью, не прибегая к
интерполированию. «
Ниже показаны вероятности попадания
в отдельные квадраты, причем расположе-
ние слагаемых соответствует расположению
квадратов на рис. 113 (слева направо и
сверху вниз):
4+36+ 8 = 48
53 + 89 + 40 = 182
109 + 124 + 96 = 329
146 + 156 4- 128 = 430
ИЗ + 174 + 94 = 381
17 + 152 + 31 =200
что в сумме даст искомую вероятность
Р = 0,157 = 15,7%.
265
§ 56. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ ПОПАДАНИЯ
ПО ТЕНЕВОМУ ГРАФИКУ
До сих пор мы имели дело только с плоскостными це-
лями, т. е. с целями, расположенными либо только в гори-
зонтальной, либо только в вертикальной плоскости. В тех
случаях, когда требуется определить вероятность попадания
в объемную цель, применяют так называемый теневой гра-
фик.
Сущность этого способа заключается в следующем
(рис. 114).
Рис. 114
Параллельно траектории проводят касательные к цели до
их пересечения с горизонтом, в результате чего на горизон-
тальной плоскости получается теневая проекция (теневой гра-
фик) цели. На нашем рисунке этот теневой график получился
в виде прямоугольника EDCF.
Очевидно, что все снаряды, попавшие в прямоугольник
ABCD, дадут попадания в цель.
Из прямоугольного треугольника KED имеем:
ED =——
tg&c '
Обозначим длину теневого графика ED через d, высоту
цели ЕК—через h и глубину цели АЕ — через Z. Тогда длина
всего прямоугольника
AD = l + d~l+-±-.
Вероятность попадания в прямоугольник ABCD равна ве-
роятности попадания в цель, следовательно, решение задачи
сводится к определению вероятности попадания в прямоуголь-
ник, стороны которого параллельны главным полуосям еди-
ничного эллипса рассеивания. Если же теневая проекция цели
не имеет вида такого прямоугольника, применяется сетка кру-
гового рассеивания.
Пример 1. Положим, что цель (рис. 114) представляет собой неболь-
шое каменное здание с плоской крышей, причем высота h этого здания
равна 4 м, его длина (по фронту) б м и ширина /=3 м.
‘266
Определим вероятность попадания в эту цель, если Вд = 25 м, Вб =
= 2,4 л«, / $с = 21°48' и средняя траектория проходит в 10 м перед сере-
диной основания здания.
Решение. Находим длину прямоугольника на горизонтальной пло-
скости, отвечающего вероятности попадания в цель:
4
I + d — 3 + 0 — 13 м.
Тогда вероятность попадания в цель по таблице значений Ф (Р)
1 Г ( 23 \ ( 10 \1 ( 3 \
Р - Рд’Рб - 2 1ф \ 25 / ~ф\ 25 /ГФ \2?4/ =
= ~2~[Ф (°’92) ~ ф (°’40J ,ф (1’25) = 4“ (°>46509 — 0,21268) -0,60083 = 0,0758.
По шкале рассеивания с точностью до 0,5 Вд имеем:
( 0,13-2,5
Р ~\ 12,5
0,12-10,5 \
12,5 J
•2 0,25+
0,09-0,6
1,2
ж0,0749.
+
Пример 2. Определить вероятность попадания в остановившийся танк,
размеры которого: длина — 7 м, ширина — 3 м и высота — 2 если Вд —
— 15 м, Вб — 1,2 м и / = 5°. При этом средняя траектория совпадает
с серединой основания танка и до остановки танк двигался фронтально.
Т
Рис. 115
Решение. Принимая фигуру танка за прямоугольный параллелепипед
(рис. 115), определяем длину горизонтального прямоугольника, отвечающего
вероятности попадания в танк:
2
1 + d — 7 + го = 30 м.
ig °
Отсюда искомая вероятность:
а) по таблице значений Ф(£)
1 / 30 \ <1,5\ 1
Z3 = "2~Ф 5-J ''Ф^У = Т Ф (2.00)-Ф (1,25) =
= ^--0,82266-0,60083 ~ 0.24714 24,70/0;
б) по шкале рассеивания (рис. 115)
( 0,09-0,3 \
Р = (0,25 + 0,16) X 2 ^0,25 + оё = 0,41-0,59 0,2419 24,20/0.
267
§ 57. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ ПОПАДАНИЯ СПОСОБОМ
СОПОСТАВЛЕНИЯ ПЛОЩАДЕЙ
Для небольших участков эллипса рассеивания можно до-
пустить, что точки падения на этих участках распределяются
равномерно. При таком допущении можно определять вероят-
ность попадания в цели малых размеров способом сопоста-
вления площадей, т. е. принимать, что вероятность попада-
ния в цель так относится к вероятности попадания в участок
эллипса рассеивания, как площадь цели относится к площади
участка эллипса рассеивания.
Обозначим площадь цели через 5, вероятность попадания
в нее через Р, площадь участка эллипса рассеивания через х
и вероятность попадания в этот участок через р. Тогда, ис-
ходя из принятой нами пропорциональности, получим:
р=р^-
Следует подчеркнуть, что способ сопоставления площадей
дает лишь приближенное решение, причем ответ будет тем
точнее, чем ближе размеры цели будут к размерам сопоста-
вляемого участка эллипса рассеивания.
Наиболее широко в артиллерийской практике применяется
способ сопоставления площади цели с площадью единичного
прямоугольника рассеивания.
Нам известно, что площадь такого прямоугольника для
горизонтальной плоскости равна
2Вд-2Вб = 4Вд-Вб
и для вертикальной плоскости
2Вв-2Вб = 4Ве-Вб,
а вероятность попадания в него —0,25 (см. стр. 211).
Тогда приведенная выше формула примет вид:
4Вд-Вб ~ М)Вд>Вб ’
или
Р--- пле
4Вв,Вб — lQBe.B6 •
Пример 1. Блиндаж, имеющий вид прямоугольника размером 4x3 л,
накрывается единичным прямоугольником рассеивания. Определить вероят-
ность попадания в блиндаж, если Вд = 15 м и Вб = 1,5 м.
Ре ш е н и е. Подставив численные значения 5, Вд п Вб к общую фор-
мулу, получим:
4-3 1
Р ~ 16.15-1,5 ~ 30 ~ 3’3°/°-
Пример 2. Уязвимая часть напольной стенки ДОТ имеет ширину 2 м
и высоту 0,8 м. Определить вероятность попадания в эту часть напольной
стенки, если средняя траектория проходит через ее центр. Be = 1,1 м и
Вб = 1,2 м.
268
Решение.
2-0,8
Р = 16 1,1-Т,2 - °’076 = 7’6%‘
Средний расход снарядов на стрельбу определяется по
формуле
р ’
где а — требуемое число попаданий;
р — вероятность попадания при одном выстреле (см. стр. 76).
Заменим обозначение числа снарядов буквой N. Тогда
для одного попадания
W = ,
Р
а после подстановки вместо р выражения для вероятности по-
падания в единичный прямоугольник
кт 16ВдВб
или
16Вв-Вб
;v “ S
Эти формулы приведены в Правилах стрельбы наземной
артиллерии 1945 г., причем в ст. 318 указывается, что второй
формулой можно пользоваться только тогда, когда высота
уязвимой площади не превышает 2 Be, а ширина —2 Вб. Это
требование Правил стрельбы вытекает из сущности способа
сопоставления площадей.
Пример 3. При условиях примера 2 определить средний расход снарядов
для получения одного попадания.
Решение.
16-1,1-1,2
N : ----2-0 8-~ — I4 снаРядОВ-
Несколько более точный результат получим, если в фор-
муле вероятности попадания площадь единичного прямоуголь-
ника заменим площадью единичного эллипса рассеивания. При-
нимая во внимание, что площадь единичного эллипса рассеи-
вания равна т^Вд-Вб или т^Ве-Вб, а вероятность попадания
в него 0,203, получим:
р___л оно £ 0,065-S
или
р_ 0,065-5
Определим в условиях того же примера 2 вероятность
попадания в уязвимую часть напольной стенки, сопоставив ее
площадь с площадью единичного эллипса рассеивания.
269
Сделав соответствующие подстановки в только что выве-
денную формулу, получим
о — 0’0б5-2-0,8 q
‘ 1,1-1,2 v,v/y.
Для проверки произведем подсчет по таблице значений
Фф):
= 0,19394 • 0,42578 0,08258.
Совершенно очевидно, что сопоставление с площадью еди-
ничного эллипса рассеивания дало ответ, более близкий к точ-
ному.
Для целей очень малых размеров их площади можно со-
поставлять с площадью половинного эллипса рассеивания. Тогда
р — о 055 ___________________-_________0.07-S
Г- v’vuuK.o,5.Be-0,5^ ~ Вв-Вб •
Пример 4. Амбразура ДОТ имеет ширину 0,6 м и высоту 0,4 м. Опре-
делить вероятность попадания в амбразуру, если средняя траектория прохо-
дит через ее центр, Be = 0,6 м и Вб — 0.7 м.
Решение. Так как очертания амбразуры не выходят из пределов
половинного эллипса рассеивания, то искомая вероятность
Р =
0,07-0,6-0,4
0,6-0,7 “до-
вели размеры цели
плотно, — с небольшими,
таковы, что их можно достаточно
сравнительно, „зазорами", — вписать
в прямоугольник, стороны которого
параллельны главным полуосям еди-
ничного эллипса рассеивания, то способ
сопоставления площадей применим для
любого участка эллипса рассеивания,
независимо от его удаления от центра
рассеивания.
Пример 5. Цель — круглый блиндаж ра-
диусом 3 м. Центр блиндажа С относительно
центра рассеивания Су смещен, как это пока-
зано на рис. 116. Определить вероятность по-
падания в блиндаж, если 24.it и Вб=4м.
Решение. Вписываем круг в прямо-
угольник, стороны которого параллельны глав-
ным полуосям единичного эллипса рассеивания,
и определяем вероятность попадания в этот
прямоугольник:
вероятность попадания по дальности
рд ' ~ф “ 4 (Ф (0,75)-Ф (0,50)] =
= 4 (0,38705 — 0,26407) « 0,0615;
270
вероятность попадания по направлению
I г / 8 А / 2 \-| 1
Рб' =— ФкТЛ = -2 [Ф (2-00)-Ф (0-50)]-
= ~ (0,82266 — 0,26407) « 0,2793;
вероятность попадания в прямоугольник
Р' = pd'pgf =0,0615-0,2793 » 0,0172.
Подставляем эту вероятность в формулу сопоставления площадей; тогда
вероятность попадания в блиндаж
S л-9
Р - р —- - 0,0172 -gg- = 0,0107 w 10 0.
§ 58. ВЕРОЯТНОСТЬ ПОПАДАНИЯ ПРИ НАЛИЧИИ ОШИБКИ
В ОПРЕДЕЛЕНИИ ПОЛОЖЕНИЯ ЦЕЛИ
Перед переходом к стрельбе на поражение о положении
цели относительно средней траектории судят по результатам
пристрелки, причем результат пристрелки дает не одно
какое-то вполне определенное положение цели, а рас-
пределение цели (см. § 21). Это означает, что, перейдя на
поражение на установках, соответствующих наивероятнейшему
положению цели, можно допустить ошибку, так как действи-
тельное положение цели может и не соответствовать скоман-
дованным установкам.
Так как большая или меньшая ошибка в определении по-
ложения цели относительно средней траектории неизбежна,
то возникает вопрос: как же найти вероятность попадания
в цель при наличии ошибки в определении ее положения?
Ошибки в определении положения цели следуют закону
Гаусса. Этому же закону следуют ошибки, происходящие
вследствие рассеивания. Отсюда срединная ошибка В', харак-
теризующая взаимодействие (совокупность) этих двух систем
ошибок, по общему правилу сложения векториальных ошибок
будет равна
B' = VB2 + a\
где В — срединное отклонение по данному направлению;
а — срединная ошибка способа определения положения
цели.
В зависимости от направления эти срединные ошибки или
срединные отклонения выражаются следующими формулами:
по дальности
Вд' = Вд2 -f- а2;
по направлению
Вб' = УВбг + а2;
271
по высоте ________
Вв' = УВв- + а-.
Этими формулами будем пользоваться при определении
вероятности попадания. В остальном решение задачи произ-
водится одним из рассмотренных выше способов. Следует
подчеркнуть, что эти формулы справедливы только при под-
счетах вероятности попадания при одном выстреле и матема-
тического ожидания числа попаданий, но непригодны для
определения вероятности хотя бы одного, двух и т. д. попада-
ний.
Пример 1. Батарея ведет фронтальный огонь по железнодорожному
полотну шириной 6 м. Определить вероятность попадания в полотно, если
Вд = 20 ж. средняя траектория проходит в 10 м перед передним краем по-
лотна и положение средней траектории относительно полотна определено со
срединной ошибкой, равной 15 м.
Решение. Находим величину срединного отклонения с учетом сре-
динной ошибки определения положения цели:
Вд' = }/202 + 15-’ = 25 м.
Пользуясь найденным значением Вд', определяем вероятность попа-
дания в заданную цель:
1 г / 16 \ ( Ю 1
Pzz Ф^-25 Л = т [Ф (0.64)-Ф (0,40)] =
= (0,33402 — 0,21268) = 0,06067 6,10/0.
Пример 2. Батарея ведет фланговый огонь вдоль шоссе шириной 5 м.
Судя по результатам пристрелки, можно считать, что средняя траектория
проходит через край шоссе. Какова вероятность попадания в шоссе, если
Вб = 3,2 м и срединная ошибка в определении положения средней траек-
тории относительно цели равна 2,4
Решение.
Вб ’ = J/'3,22^H2j2 = 4 м.
1 / 5 \ 1
Р - — Ф J = -у Ф (1.25) - 0,30042 30%.
§ 59. ЗАДАЧИ НА ВЕРОЯТНОСТЬ ПОПАДАНИЯ
Задача 146. Определить вероятность попадания в каменную стенку вы-
сотой 4,5 м при фронтальном огне, если средняя траектория проходит че-
рез середину основания стенки и Вв~-3 м.
Ответ. 0,34417 (34®/0)1.
Задача 147. Определить вероятность попадания в полосу проволочных
заграждений глубиной 28 м при фронтальном огне, если средняя траекто-
рия проходит через середину переднего края полосы и Вд = 23 м.
Ответ. 0,29414 (29” 0).
1 В этой и последующих задачах в скобках даны значения вероятностей,
нодсчитанные по шкале ошибок.
272
Задача 148. Определить вероятность попадания в полосу проволочных
заграждений глубиной 35 м, если средняя траектория проходит через центр
полосы, огонь ведется перпендикулярно к фронту цели и Вд — 25 м.
Ответ. 0,3617 (35%).
Задача 149. Определить средний расход снарядов, необходимый для
получения четырех попаданий в полосу окопов общей глубиной 45 ж. если
средняя траектория проходит через центр полосы, Вд — 19 м и огонь ве-
дется фронтально.
Ответ, р = 0,5755 (56%); N = 7 — 8 снарядов.
Задача 150. Определить вероятность попадания в железнодорожное
полотно шириной 12 м при фронтальном огне, если средняя траектория
проходит в 20 м перед передним краем полотна и Вд = 26 м.
О т в е т. 0,09838 (9,7%).
Задача 151. Стрельба ведется вдоль железнодорожного полотна шири-
ной 9 м. Определить вероятность попадания в полотно, если средняя тра-
ектория проходит в 3 м левее его правого края и Вб — 3,4 м.
Ответ. 0,60723 (59,80/0).
Задача 152. Полоса проволочных заграждений расположена на перед-
нем скате. Глубина полосы 20 м. Угол наклона ската 1-00. Определить ве-
роятность попадания в полосу, если Вд = 20 м, — 18°, средняя траек-
тория проходит через середину переднего края полосы и плоскость стрельбы
перпендикулярна к направлению полосы.
О т в е т. Bdt = 15,2 м; Р = 0,31259 (30,9%).
Задача 153. Полоса траншей общей глубиной 25 м расположена на
обратном скате и ее передний край удален от гребня укрытия на 15 м.
Угол наклона ската 0-75. Чему равна вероятность попадания в эту полосу
траншей при фронтальном огне, если Вд — 24 м, = 36° и средняя тра-
ектория проходит через гребень укрытия?
О т в е т. Вд2 = 27 м\ Р = 0,19509 (19,4%)-
Задача 154. Батарея ведет огонь по железнодорожному полотну, ши-
рина которого равна 12 м. Плоскость стрельбы с направлением полотна
образует угол, равный 45°. Определить вероятность попадания в полотно,
если средняя траектория проходит через его передний край, Вд = 30 м и
Вб- 3 м.
О т в е т. В - 21,3 м\ Р = 0,14803 (14,5%).
Задача 155. Определить вероятность попадания в полосу бесконечной
длины шириной 5 м, образующую с плоскостью стрельбы угол, равный 60°.
если Вд = 15 м, Вб = 2 м и средняя траектория проходит в 3 м перед пе-
редним краем полотна, считая по направлению плоскости стрельбы.
Ответ. В=13ж;Р = 0,09977 (9,80/0).
Задача 156. Определить вероятность попадания в НП, имеющий вид
прямоугольника размером 10 х 5 м, при фронтальном огне, если Вд = 16 м
Вб = 1,4 м и средняя траектория проходит через центр НП.
Ответ. 0,121 (12,1%).
Задача 157. Блиндаж имеет вид прямоугольника размером 6x4 м.
Огонь ведется фронтально. Определить вероятность попадания в блиндаж,
если 5^ — 20 щ, Вб = 1,6 м и средняя траектория проходит через середину
меньшей его стороны.
Ответ. 0,04817 (4,6%).
Задача 158. Батарея ведет огонь по мосту длиной 22 м и шириной
6 м. Плоскость стрельбы направлена вдоль моста. Чему равна вероятность
попадания в мост, если Вд = 34 м, Вб = 4,8 м и средняя траектория про-
водит в 25 м перед центром моста?
Ответ. 0,05004 (4,9%).
Задача 159. Убежище размером 12 х 8 м имеет вид прямоугольника,
вытянутого вдоль плоскости стрельбы. Определить вероятность попадания
18 — Зак. 991
273
в убежище, если Вд — 18 м, Вб = 2,4 м и средняя траектория проходит
в 5 м перед левым краем убежища.
Ответ. 0,07998 (8,1%).
Задача 160. Координаты вершин четырехугольника относительно центра
рассеивания таковы:
Вершины | 1 А 1 в с D
По оси GX в м . . . | + 12 —12 0 д-36
По оси О У в м . . • | 0 + 8,4 + 14 * + 8,4
Определить вероятность попадания в четырехугольник, если Вд = 23 м,
Вб = 5,5 м и ось ОХ совпадает с направлением стрельбы.
Ответ. 11%.
Задача 161. Определить вероятность попадания в неподвижный танк
при'фронтальном огне (рис. 117), если средняя траектория проходит через
точку О- Вв = 1,5 м и Вб — 0,8 м. При
_ этом Г AM = 2 м, МН = 5. МОХ = 2-6 м,
2) ।------------------.с ВМ=1:8 м, ВС = 1 м-, CD = 1,5 м-
a DE = 4 м- FK = 2 м и ОХО = 0-9 м.
F----7^ Ответ. 49%.
/> у 0 / Задача 162. Батарея сосредоточенным
/ I । / веером ведет фронтальный огонь по камен-
д / ।______। % ной стене высотой 4 м и толщиной 2,5 м.
М Of Чему равна вероятность попадания в эту
стену, если Вд = 23 м. Z. 6С = 11 t20' и
Рис. 117 средняя траектория проходит в 5 м перед
стеной?
Ответ. 20,1%.
Задача 163. Определить вероятность попадания в остановившийся танк
размером 5 X 2 х 1-7 mz если средняя траектория проходит через основание
танка, Вд = 13 щ. Вб = 1,2 м и Z_ 0С = 4t24C Плоскость стрельбы напра-
влена вдоль танка.
Ответ. 17.3%.
Задача 164. Амбразура ДОТ размером 0-3 х 0,9 м накрывается еди-
ничным прямоугольником рассеивания. Чему равна вероятность попадания
в амбразуру, если Вв = 0,4 м и Вб = 0-5 ж?
Ответ. 8,4%
Задача 165. Цель — круглый блиндаж радиусом 2 м. Определить ве-
роятность попадания в цель, если Вд = 20 м- Вб — 3 м и блиндаж накры-
вается единичным эллипсом рассеивания.
Ответ. 1,35%.
Задача 166. Цель — окоп протяжением 5 м по фронту и 10 м в глу-
бину. Средняя траектория проходит в 15 м перед передним краем окопа.
Чему равна вероятность попадания в окоп, если срединная ошибка в опре-
делении положения средней траектории в дальности равна 18 м, Вд — 25 м.
и Вб = 2,5 м.
Ответ. 4,1%.
Задача 167. Цель — блиндаж размером 8 м по фронту и 12 м в глу-
бину. Огонь ведется фронтально. Средняя траектория проходит через се-
редину переднего края блиндажа. Известно- что срединные’ошибки в опре-
делении положения цели относительно средней траектории равны: в дально-
сти — 0.5 Вд и в направлении 0,8 Вб. Чему равны вероятность попадания
в блиндаж, если Вд — 30 м и Вб = 5 лЕ
Ответ. 2,9', 0
Приложение 1
ТАБЛИЦА ЗНАЧЕНИЙ Ф(р)
ВЕРОЯТНОСТЬ ПОЛУЧЕНИЯ ОШИБКИ В ПРЕДЕЛАХ ОТ О ДО ± р
§ Ф(Р) Diff. § Ф(Р) Diff. § Ф(Р) Diff.
0,00 0,00000 0,24 0,12860 0,48 0,25388 1
0,01 538 531 510
0,00538 0,25 0,13391 0,49- 0,25898
0,02 538 530 0,26407 509
0,01076 0,26 0,13921 0,50
0,03 538 530 508
0,01614 0,27 0,14451 0,51 0,26915
0,04 538 0,28 529 0,52 506
0,02152 0,14980 0,27421
0,05 538 528 506
0,02690 0,29 0,15508 0,53 0,27927
0,06 538 527 504
0,03228 538 0,30 0,16035 527 0,54 0,28431 503
0,07 0,03766 537 0,31 0,16562 526 0,55 0,28934 502
0,08 0,04303 0,32 0,17088 0,56 0,29436
0.09 537 526 0,57 500
0,04840 0,33 0,17614 0,29936
537 524 499
0,10 0,05377 537 0,34 0,18138 524 0,58 0,30435 498
0,11 0,05914 537 0,35 0,18662 523 0,59 0,30933 497
0Л2 0,06451 536 0,36 0,19185 522 0,60 0,31430 495
0,13 0,06987 536 0,37 0,19707 522 0,61 0,31925 494
0,14 0,07523 536 0,38 0,20229 520 0,62 0,32419 492
0,15 0,08059 535 0,39 0,20749 519 0,63 0,32911 491
0,16 0,08594 0,40 0,21268 0,64 0,33402
0,17 535 519 490
0,09129 0,41 0,21787 0,65 0,33892
0,18 534 0,42 517 0,34380 488
0,09663 0,22304 0,66
0,19 534 517 486
0,10197 534 0,43 0,22821 515 0,67 0,34866 486
0,20
0,10731 0,44 0,23336 0,68 0,35352
0,21 533 515 0,35835 483
0,11264 0,45 0,23851 0,69
0,22 532 513 482
0,11796 532 0,46 0,24364 512 0,70 0,36317 481
0,23 0,12328 532 0,47 0,24876 512 0,71 j 0,36798 479
0,24 0,12860 0,48 -0,25388 1 0,72 0,37277
18-
275
1 ₽ Ф (Р) Diff. Р Ф(Р) Diff. Р ф(3) Diff.
0,72 0,37277 478 0,98 0,49139 431 1,24 0,59705 378
0,73 0,37755 476 0,99 0,49570 430 1,25 0,60083 377
0,74 0,38231 474 1,00 0,50000 428 1,26 0,60460 373
0,75 0,38705 • 1,01 0,50428 1,27 0,60833
473 425 372
0,76 0,39178 471 1,02 0,50853 424 1,28 0,61205 370
0,77 0,39649 469 1,03 0,51277 422 1,29 0,61575 367
0,78 0,40118 468 1,04 0,51699 420 1,30 0,61942 366
0,79 0,40586 466 1,05 0,52119 418 1,31 0,62308 363
0,80 0,41052 465 1,06 0,52537 415 1,32 0,62671 361
0,81 0,41517 462 1,07 0,52952 414 1,33 0,63032 359
0,82 0,41979 461 1,08 0,53366 412 1,34 0,63391 356
0,83 0,42440 459 1,09 0,53778 410 1,35 0,63747 355
0,84 0,42899 1,10 0,54188 1,36 0,64102
458 407 352
0,85 0,43357 456 1,11 0,54595 406 1,37 0,64454 350
0,86 0,43813 1,12 0,55001 1,38 0,64804 348
454 403
0,87 0,44267 452 1,13 0,55404 402 1,39 • 0,65152 346
0,88 0,44719 450 1,14 0,55806 399 1,40 0,65498 343
0,89 0,45169 449 1,15 0,56205 397 1,41 0,65841 341
0,90 0,45618 446 1,16 0,56602 396 1,42 0,66182 339
0,91 0,46064 445 1,17 0,56998 393 1,43 0,66521 337
0,92 0,46509 443 1,18 0,57391 391 1,44 0,66858 335
0,93 0,46952 441 1,19 0,57782 389 1,45 0,67193 333
0,94 0,95 .0,47393 0,47832 439 1,20 1,21 0,58171 0,58558 387 1,46 1,47 0,67526 0,67856 330 328
438 384
0,96 0,48270 435 1,22 0,58942 383 1,48 0,68184 326
0,97 0,48705 434 1,23 0,59325 380 1,49 0,68510 323
0,98 0,49139 1,24 0,59705 1,50 0,68833
276
3 ф(₽; Diff. 3 Ф(Р) Diff. Р Фф) Diff.
1,50 0,68833 1,76 0,76481 2,02 0,82695
322 265 212
1,51 0,69155 1,77 0,76746 2,03 0,82907
319 1,78 263 2,04 0,83117 210
1,52 0,69474 0,77009
317 261 207
1,53 0,69791 315 1,79 0,77270 258 2,05 0,83324 206
1,54 0,70106 313 1,80 0,77528 257 2,06 0,83530 204
1,55 0,70419 310 1,81 0,77785 254 2,07 0,83734 202
1,56 0,70729 309 1,82 0,78039 252 2,08 0,83936 201
1,57 0,71038 306 1,83 0,78291 251 2,09 0,84137 198
1,58 0,71344 304 1,84 0,78542 248 2,10 0,84335 196
1,59 0,71648 301 1,85 0,78790 246 2,11 0,84531 195
1,60 0,71949 300 1,86 0,79036 244 2,12 0,84726 193
1,61 0,72249 297 1,87 0,79280 242 2,13 0,84919 190
1,62 0,72546 295 1,88 0,79522 239 2,14 0,85109 189
1,63 0,72841 293 1,89 0,79761 238 2,15 0,85298 188
1,64 0,73134 291 1,90 0,79999 236 2,16 0,85486 185
1,65 0,73425 289 1,91 0,80235 234 2,17 0,85671 183
1,66 0,73714 286 1,92 0,80469 231 2,18 0,85854 182
1,67 0,74000 285 1,93 0,80700 230 2,19 0,86036 180
1,68 0,74285 282 1,94 0,80930 228 2,20 0,86216 178
1,69 0,74567 280 1,95 0,81158 225 2,21 0,86394 176
1,70 0,74847 277 1,96 0,81383 224 2,22 0,86570 175
1,71 . 0,75124 276 1,97 0,81607 221 2,23 0,86745 172
1,72 0,75400 274 1,98 0,81828 220 2,24 0,86917 171 |
1,73 0,75674 271 1,99 0,82048 218 2,25 0,87088 170 |
1,74 0,75945 269 2,00 0,82266 215 2,26 0,87258 167
1,75 0,76214 267 2,01 0,82481 214 2,27 0,87425 166
1,76 0,76481 2,02 0,82695 2,28 0,87591
277
р Ф(Р) Diff. Р ф(?) Diff. Р Ф(Р) Diff,
2,28 0,87591 164 2,54 0,91332 124 2,80 0,94105 90
2,29 0,87755 163 2,55 0,91456 122 2,81 0,94195 89
2,30 0,87918 160 2,56 0,91578 120 2,82 0,94284 87
2,31 0,88078 159 2,57 0,91698 119 2,83 0,94371 87
2,32 0,88237 158 2,58 0,91817 118 2,84 0,94458 85
2,33 0,88395 155 2,59 0,91935 116 2,85 0,94543 84
2,34 0,88550 155 2,60 0,92051 115 2,86 0,94627 84
2,35 0,88705 152 2,61 0,92166 114 2,87 0,94711 82
2,36 0,88857 151 2,62 0,92280 112 2,88 0,94793 81
2,37 0,89008 149 2,63 0,92392 111 2,89 0,94874 80
2,38 0,89157 147 2,64 0,92503 ПО 2,90 0,94954 79
2,39 0,89304 146 2,65 0,92613 108 2,91 0,95033 78
2,40 0,89450 145 2,66 0,92721 107 2,92 0,95111 76
2,41 0,89595 143 2,67 0,92828 106 2,93 0,95187 76
2,42 0,89738 141 2,68 0,92934 104 2,94 0,95263 75
2,43 0,89879 140 2,69 0,93038 103 2,95 0,95338 74
2,44 0,90019 138 2,70 0,93141 102 2,96 0,95412 73
2,45 0,90157 2,71 0,93243 2,97 0,95485
136 101 72
2,46 0,90293 135 2,72 0,93344 99 2,98 0,95557 71
2,47 0,90428 134 2,73 0,93443 98 2,99 0,95628 70
2,48 0,90562 132 2,74 0,93541 97 3,00 0,95698 69
2,49 0,90694 131 2,75 0,93638 96 3,01 0,95767 68
2,50 0,90825 129 2,76 0,93734 94 3,02 0,95835 67
2,51 0,90954 128 2,77 0,93828 94 3,03 0,95902 66
2,52 2,53 0,91082 126 2,78 0,93922 92 3,04 0,95968 65
0,91208 124 2,79 0,94014 91 3,05 0,96033 65
2,54
0,91332 2,80 0,94105 3,06 0,96098
278
0 Фф) Diff. Р Ф(?) Diff. Р Ф([3) Diff.
3,06 0,96098 63 3,32 0,97486 44 3,58 0,98424 29
3,07 0,96161 3,33 0,97530 3,59 0,98453
63 43 29
3,08 0,96224 62 3,34 0,97573 42 3,60 0,98482 28
3,09 0,96286 60 3,35 0,97615 42 3.61 0,98510 28
3,10 0,96346 60 3,36 0,97657 41 3,62 0,98538 0’98565 27
3,11 0,96406 60 3,37 0,97698 40 3,63 27
3,12 0,96466 58 3,38 0,97738 40 3,64 0,98592 26
3,13 0,96524 58 3,39 0,97778 39 3,65 0,98618 26
3,14 0,96582 56 3,40 0,97817 38 3,66 0,98644 25
3,15 0,96638 3,41 0,97855 3,67 0,98669
56 38 25
3,16 0,96694 55 3,42 0,97893 37 3,68 0,98694 25
3,17 0,96749 55 3,43 0,97930 37 3,69 0,98719 24
3,18 0,96804 53 3,44 0,97967 36 3,70 0,98743
24
3,19 0,96857 53 3,45 0,98003 36 3,71 3,72 0,98767
23
3,20 0,96910 3,46 0,98039 0,98790
52 35 23
3,21 0,96962 51 3,47 0,98074 35 3,73 0,98813 23
3,22 0,97013 51 3,48 0,98109 34 3,74 0,98836 22
3,23 0,97064 50 3,49 0,98143 33 3,75 3,76 0,98858 22
3,24 0,97114 49 3,50 0,98176 33 0,98880 21
3,25 0,97163 3,51 0,98209 3,77 0,98901
48 32 3,78 21
3,26 0,97211 48 3,52 0,98241 32 0,98922 0,98942 20
3,79
3,27 0,97259 47 3,53 0,98273 31 20
3,80 0,98962
3,28 0,97306 46 3,54 0,98304 31 20
3,81 0,98982
3,29 0,97352 45 3,55 0,98335 30 20
3,82
3,30 0,97397 45 3,56 0,98365 30 0,99002 0,99021 19
3,83
3,31 0,97442 44 3,57 0,98395 29 19
3,84 0,99040
3,32 0,97486 3,58 0,98424
279
13 Ф(₽) Diff. 13 Ф(Р) Diff. (3 Ф(Р) Diff.
3,84 0,99040 19 3,95 0,99229 15 4,60 0,99808 40
3,85 0,99059 18 3,96 0,99244 15 4,70 0,99848 31
3,86 0,99077 18 3,97 0,99259 15 4,80 0,99879 26
3,87 0,99095 18 3,98 0,99274 14 4,90 0,99905 21
3,88 0,99113 17 3,99 0,99288 14 5,00 0,99926 16
3,89 0,99130 17 4,00 0,99302 129 5,10 0,99942 13
3,90 0,99147 17 4,10 0,99431 108 5,20 0,99955 10
3,91 0,99164 17 4,20 0,99539 88 5,30 0,99965 7
3,92 0,99181 16 4,30 0,99627 73 5,40 0,99972
3,93 0,99197 4,40 0,99700
3,94 0,99213 16 4,50 0,99760 60 6,00 0,9999482
16 48
3,95 0,99229 4,60 0,99808
СЕТКА КРУГОВОГО РАССЕИВАНИЯ Приложение 2
с масштабом в 0,5 срединного отклонения
0
5,0 4,5 4,0 3,5 3,0 2,5 2,0 1,5 1,0 0,5 [ 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
о,и 4,5 Л г> — — ч 3 1
1 1 2 1 3 | 1 3 1 3 1 1 0,1
1 1 1 2 1 1 0,2
3,5 3,0 2,5 2,0 1,5 1,0 0,5 0 —— 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0 1 1 2 4 5 7 8 8 7 5 4 2 1 1 0,6
1 1 3 5 8 12 15 16 16 15 12 8 5 3 1- 1 1,2
1 1 1 3 6 10. 16 23 29 32 32 29 23 16 10 6 3 1 1 2,4
2 5 10 18 29 40 50 56 56 50 40 29 18 10 5 2 1 4,3
1 1 2 4 8 16 29 45 63 79 89 89 79 63 45 29 16 8 4 1 1 6,7
1 5 12 23 40 63 89 111 124 124 .111 89 63 40 23 12 5 2 1 9,4
1 3 7 15 29 50 79 111 139 156 156 139 111 79 50 29 15 7 3 1 11,8
1 3 8 16 32 56 89 124 155 174 174 156 124 89 56 32 16 8 3 1 13,2
1 3 3 8 16 32 56 89 124 156 174 I 174 156 124 89 56 32 16 8 3 1 13,2
1 7 15 29 50 79 111 139 156 156 139 111 79 50 29 15 7 3 1 11,8
1 2 1 5 12 23 40 63 89 11Г 124 124 111 89 63 40 23 12 5 2 1 9,4
1 4 8 16 29 45 63 79 89 89 79 63 45 29 16 8 4 1 1 6,7
— 1 1 2 5 10 18 29 40 50 56 56 50 40 29 18 10 5 2 1 4,3
1 3 6 10 16 23 29 32 32 29 23 16 10 6 3 1 1 2,4
1 1 3 5 8 12 15 16 16 15 12 8 5 3 1 1 1,2
1 1 2 4 5 7 8 8 7 5 4 2 1 1 0,6
1 1 1 2 3 3 3 3 2 1 1 1 0,2
1 1 1 1 1 1 1 1 0,1
0,1 0,2 0,6 1,2 2,4 4,3 6,7 9,4 11,8 13,2 13,2 । 11,8 9,4 6,7 4,3 2,4 1.2 0;6 0,2 0,1
В квадратах, стороны которых равны 0.5 срединного отклонения, числа дают вероятность в сотых долях процента (О,О1°/0).
ПЕРЕЧЕНЬ ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Под редакцией В. Г. Дьяконова, Учебник-по стрельбе артилле-
рии, ч. I, II и III.
2. И. Ф. С а к р и е р, Теория вероятностей, изд. Артиллерийской акаде-
мии, 1932 г.
3. Г. Блинов, Теория стрельбы наземной артиллерии, ч. I, изд. 1940 г.
4. Задачник по теории вероятностей под ред. П. М. Прохорова.
5. В. А. У н к о в с к и й, Теория стрельбы и ее приложение к стрельбе
корабельной артиллерии, изд. 1939 г.
6. Его же, Стрельба морской артиллерии.
7. Л. Г. Гончаров, Теория вероятностей и теория ошибок в при-
ложении к вопросам морской тактики, изд. 1938 г.
8. С. И. Ермолаев, Рассеивание снарядов, изд. 1945 г.
9. В. Л. Гончаров, Теория вероятностей, изд. 1939 г.
• 10. А. Д. Б л и н о в и В. В. Дмитриев, Теория вероятностей (кон-
спект), изд. 3 ЛАУ, 1940 г.
11. Их же, Теория ошибок (конспект), изд. 3 ЛАУ, 1940 г.
ОГЛАВЛЕНИЕ
РАЗДЕЛ I
ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Глава 1
Вероятность события
Стр.
§ 1. Предмет теории вероятностей.................................. 3
§ 2. Событие ................................................... 6
§ 3. Вероятность события......................................... ,7
§ 4. Частость события ........................................... 12
§ 5. Соотношение между вероятностью и частостью события .... 15
§ 6. Теорема сложения вероятностей............................... 16
§ 7. Теорема умножения вероятностей.........,.................... 21
§ 8. Геометрическая вероятность.............’....•............... 34
§ 9. Задачи на вероятность и частость события.................... 37
Глава 2
Повторение испытаний
§ 10. Вероятность комбинации..................................... 40
§11. Наивероятнейшая комбинация................................. 46
§ 12. Кривая распределения вероятностей комбинаций............... 51
§ 13. Закон больших чисел...................................... 56
§ 14. Вероятность появления события хотя бы один, два, три и т. д.
раз............................................................ 58
§ 15. Надежность стрельбы........................................ 62
$ 16. Задачи на вероятности при повторении испытаний............. 65
Глава 3
Математическое ожидание
§ 17. Математическое ожидание переменной величины. Математическое
ожидание суммы и произведения.................................... 67
§ 18. Частный случай математического ожидания.................... 74
§ 19. Экономичность стрельбы..................................... 76
§ 20. Задачи на математическое ожидание.......................... 78
Глава 4
Вероятности гипотез
§ 21. О вероятностях гипотез..................................... 79
§ 22. Теорема гипотез...............................•............ 82
§ 23. Теорема будущих событий.................................... 94
§ 24. Задачи на вероятности гипотез............................. 102
2-S9