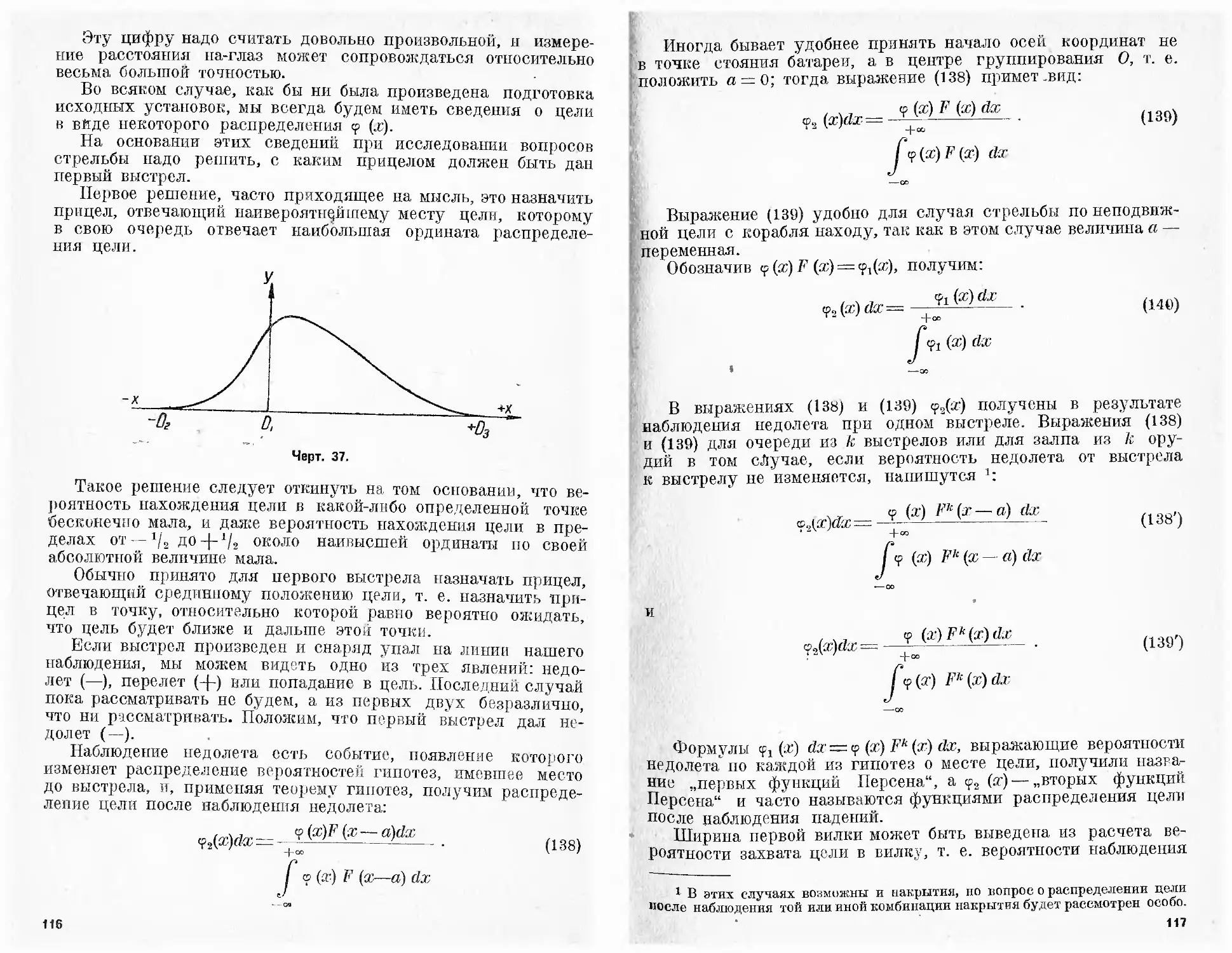
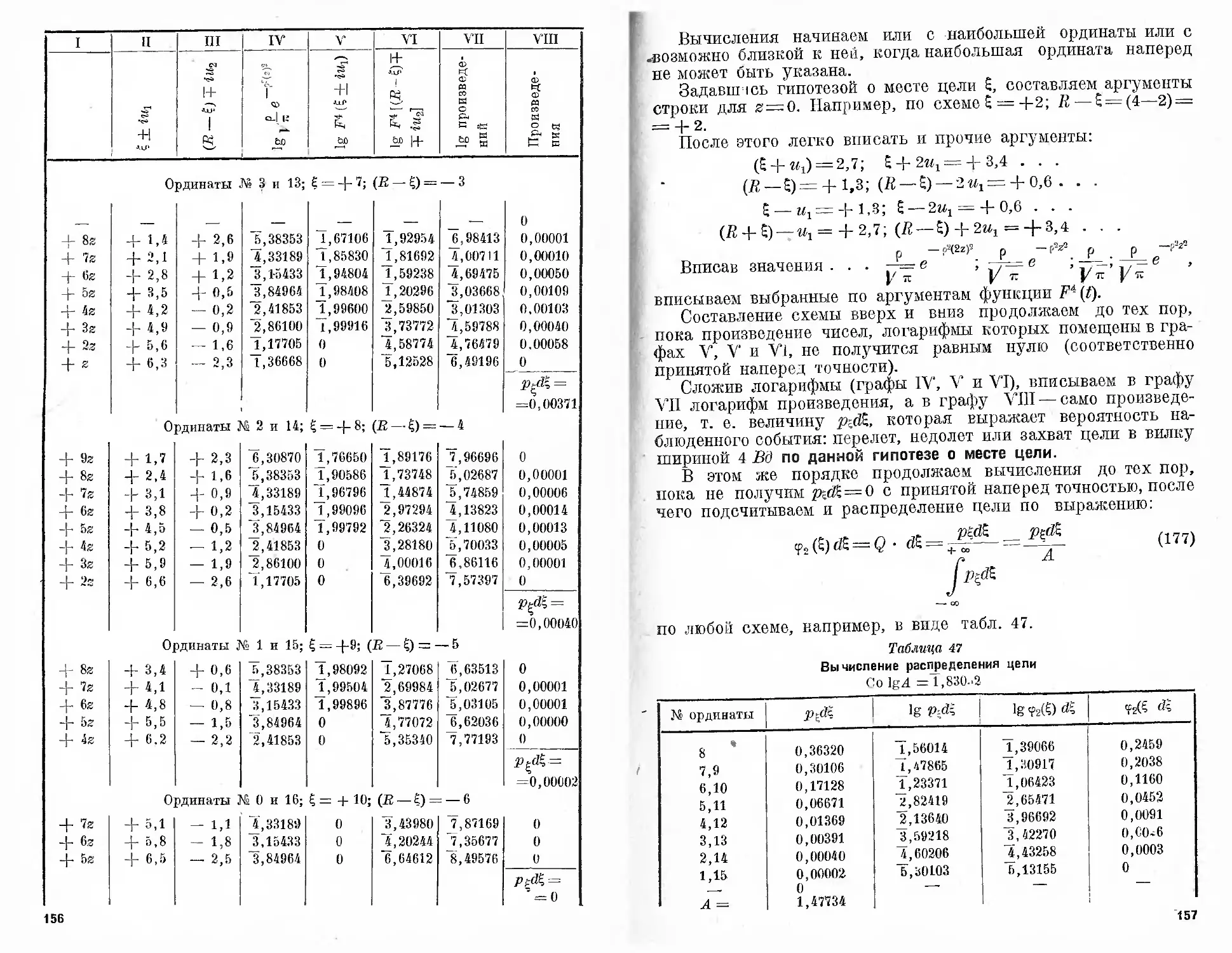
Текст
к к ймекиий
S1 ТЕОРИЯ .СТРЕЯЬБЫ
И ЕЕ ПРИЛОЖЕНИЕ К СТРЕЛЬБЕ
^BEEnbHOfSPTWWlEffi»
В06НИ9ДЛТ-1 93 J
Капитан 1-го ранга, доцент
В. А. УНКОВСКИЙ
ТЕОРИЯ СТРЕЛЬБЫ
И ЕЕ ПРИЛОЖЕНИЕ К СТРЕЛЬБЕ^
КОРАБЕЛЬНОЙ АРТИЛЛЕРИИ
ГОСУДАРСТВЕННОЕ ВОЕННОЕ ИЗДАТЕЛЬСТВО
НАРКОМАТА ОБОРОНЫ СОЮЗА ССР
МОСКВА—1939
Капитан 1-го ранга, доцент В. А. У н к о в с к и й. „Теория стрельбы и ее при-
ложение к стрельбе корабельной артиллерии".
Книга составлена в соответствии с современным состоянием теории
артиллерийской стрельбы и рассчитана на слушателей Военно-морской ака-
демии, которые, помимо теории, найдут в ней и ряд разработанных примеров,,
освещающих различные вопросы, возникающие на практике при исследо-
вании методов и правил стрельбы.
Редактор военинягенер 2-го ранга Мгисно. Техн, редактор Фрейман. Корректор Гиленко.
Сдано в производство 31.7.38 . Подписано к печати 4.5.39
Формат бумаги 60х92710. Объем 23 печ. л. и 1 вел. 7, и. п- 22,85 уч.-авт. я-
"Упоин. Главпита № Г—2910 Изд. № 417 Зак. .№ 5 96
Отпечатано в 1-й типографии Государственного военного изд-ва НКО СССР.
Москва, ул. Скворцова-Степанова, д. 3
ОТ АВТОРА
Настоящий труд имеет своей главной целью служить посо-
бием при исследовании методов стрельбы и при выработке
правил стрельбы корабельной артиллерии и артиллерии бере-
говой обороны в различных случаях боевой обстановки.
Руководствуясь этой задачей и учитывая объем труда, я на-
шел целесообразным не рассматривать ряд вопросов", которые
не являются актуальными именно для корабельной артиллерии
и имеются в других изданиях, и, напротив, в труде освещены
вопросы, связанные со стрельбой в морских условиях, которые
в существующих изданиях отсутствуют. Вследствие того, что
труд предназначается и в качестве учебника, в нем помещены
многочисленные примеры, большинство которых содержит пол-
ное решение. В части III „Стрельба снарядами дистанционного
действия" я употребляю, главным образом, графические методы
расчета, которые наглядны, обеспечивают, как и всякий графи-
ческий метод, от „неприятной" ошибки и дают точность,
которая практически более чем достаточна.
При составлении настоящей книги мною использованы все
капитальные труды в этой области и, прежде всего, труды
профессора П. А. Гельвиха.
Труд выходит первым изданием и, вероятно, не свободен от
целого ряда, недостатков. За указания на эти недостатки буду
признателен всем лицам, которые пожелают их сделать.
Ленинград, 1937 г.
В. Унковский
ЧАСТЬ ПЕРВАЯ
СТРЕЛЬБА УДАРНЫМИ СНАРЯДАМИ
Г Л А В А I
РАССЕИВАНИЕ ВЫСТРЕЛОВ
1. Сноп траекторий
Целый ряд причин, как-то: разнообразие начальных скоро-
стей, разнообразие углов бросания и разнообразие условий по-
лета, обусловливает известное явление, носящее название рас-
сеивания выстрелов (точек падения снарядов).
При малом числе выстрелов не удается наблюдать какой-
либо закономерности в рассеивании точек падения снарядов.
С увеличением же числа выстрелов в рассеивании точек паде-
ния снарядов начинает наблюдаться определенная закономер-
ность, и, насколько возможна вообще опытная проверка законов
рассеивания выстрелов, эта проверка приводит к выводу, что
рассеивание точек падения снарядов, как того и можно было
ожидать, следует закону Гаусса. Поэтому в дальнейшем, говоря
о рассеивании точек падения снарядов, мы будем считать, что
рассеивание выстрелов следует закону Гаусса.
Снопом траекторий называется совокупность всех траекторий,
которые могут иметь место в действительности при стрельбе из
одного орудия в данных условиях при достаточно большом числе
выстрелов, произведенных в течение небольшого промежутка
Бремени.
Из значительного числа причин, обусловливающих рассеива-
ние выстрелов, остановимся на случайных отклонениях в углах
бросания и в начальной скорости.
Эти причины обусловливают рассеивание в плоскости стрель-
бы и в плоскости, к ней перпендикулярной.
Рассматривая рассеивание в плоскости стрельбы, обуслов-
ливаемое только случайными отклонениями в углах бросания
(черт. 1), мы получим пучок траекторий, расходящихся уже
в самой точке вылета; эти траектории при небольших колеба-
ниях в угле бросания практически можно считать тождествен-
ными кривыми.
5
Рассматривая рассеивание в плоскости стрельбы, обуслов-
ливаемое только небольшими случайными отклонениями в на-
чальной скорости, мы получим пучок расходящихся кривых,
касательных к идеальной линии выстрела (черт. 2).
Черт. 1.
Эти кривые будут иметь различную ' кривизну, так как
с увеличением начальной скорости, вообще говоря, будем иметь
увеличение дальности полета и уменьшение искривления траек-
тории.
Черт. 2.
Так как в снопе должны быть все случайные траектории,
то, объединяя оба набора траекторий наложением одного (черт. 2)
на другой (черт. 1) так, чтобы точка О2 упала в точку Ог и
линия О2А2 совпала с линией 0^, получим новый набор
Черт. 3.
траекторий (черт. 3), строение которого уже не будет иметь
той правильности, которой обладают предыдущие наборы
(черт. 1 и 2); тут получаются уже пересечения отдельных
траекторий между собой.
Таким образом, строение снопа траекторий представляет
собой пучок пересекающихся и переплетающихся между собой
кривых, исходящих из одной точки. Обычно за эту точку при-
нимают точку вылета.
Средней траекторией называется такая идеальная траектория,
которая получилась бы при точном соблюдении всех условий,
считаемых нами условиями данного момента.
Картина рассеивания траекторий, изображенная на черт. 1,
2 и 3, вследствие несоблюдения масштаба не представляет
6
действительной картины рассеивания. Если бы мы поставили
себе задачей изобразить действительную картину рассеивания
какого-либо орудия, например, 130-ж.и пушки на дальность
60 каб., то для лучшей части снопа, вмещающей 82% всех
траекторий, при масштабе 1 :25 000 продольная ось снопа при
падении на землю выразится отрезком в 2,9 мм, а дальность
60 каб. — в 439 мм. Чтобы рассмотреть строение снопа в конце
нисходящей ветви траектории (что в данном случае нас только
и интересует), надо было бы взять масштаб по крайней мере
1 :1 000, а еще лучше 1:500.
Принимая во внимание очень большую величину радиуса
кривизны траекторий даже у конечной части снопа, практически
получаем ряд прямых параллельных линий, так как на чертеже
мы не заметим их расхождения. Поэтому вопрос о пересечении
траекторий на небольшом участке снопа рассеивания отпадает,
и обычно принимают случайные траектории в снопе рассеивания
параллельными между собой.
До настоящего времени мы рассматривали проекцию снопа
на вертикальную плоскость. То же полностью относится и к
проекции снопа на горизонтальную плоскость. Проекция снопа
рассеивания на горизонтальную плоскость также представляет
совокупность кривых, исходящих из одной точки, имеющих,
вообще говоря, разные касательные в точке вылета, пересекаю-
щихся и переплетающихся между собой, если мы будем рас-
сматривать весь сноп в целом. При рассмотрении же лишь не-
большого участка снопа, ввиду значительно меньшего размера
проекции рассеивания на горизонтальную плоскость, и подавно
мы можем принимать концы траекторий у точек падения парал-
лельными между собой.
Случайные траектории, встречаясь с преградой, пересекаю-
щей сноп траекторий под каким-либо углом, всегда дадут
распределение точек падений по закону Гаусса.
Для теоретических расчетов сноп траекторий обычно пере-
секают плоскостями: горизонтальной, вертикальной и по нор-
мали к средней траектории.
При пересечении снопа траекторий с плоскостью точки паде-
ния на ней распределяются по закону Гаусса, каково бы ни
было направление плсскости, и только величины срединных
отклонений будут различные.
Правильно изобразить характер строения снопа и распреде-
ление в нем траекторий по закону Гаусса—довольно затрудни-
тельно, так как для большинства орудий большая ось эллипса
рассеивания в 10—15 раз больше малой оси, а поэтому обычно
пользуются распределением по круговому закону Гаусса-
Сетки кругового распределения по закону Гаусса (черт. 4а
и 46) дают достаточно наглядную картину распределения точек
гадения по закону Гаусса при достаточно большом числе вы-
стрелов.
Для приближенных расчетов часто пользуются так называ-
емой „шкалой рассеивания** (табл. 1).
7
Таблица 1
Шкапа рассеивания (в процентах)
1 1 3 4 7 9 12 13 13 12 9 7 4 3 1 1
2 7 16 25 25 16 7 2
1 1 1 1 1 1 1 1 0,1
1 1 1 2 3 3 3 3 2 1 1 1 0,2
1 1 2 4 5 7 8 8 7 5 4 2 1 1 0,6
1 1 3 5 8 12 15 16 16 15 12 8 5 3 1 1 1,2
1 1 3. 6 10 16 23 29 32 32 29 23 16 10 6 3 1 1 2,4
г 2 5 ТО 18 29 40 50 56 56 50 40 29 18 10 5 2 1 4,3
/ 1 4 8 16 29 45 63 79 89 89 79 63 45 29 16 8 4 1 1 6,7
1 2 5 12 23 40 63 89 111 124 124 111 89 63' 40 23 12 5 2 1 9,4
1 3 7 15 29 50 79 111 139 156 156 139 111 79 50 29 15 7 3 1 11,8
1 3 8 16 32 56 89 124 156 174 174 156 124 89 56 32 16 8 3 1 13,2
1 3 8 16 32 56 89 124 156 174 174 156 124 89 56 32 16 8 3 1 13,2
1 3 7 15 29 50 79 111 139 156 156 139 111 79 50 29 15 7 3 1 11,8
1 2 5 12 23 40 63 89 111 124 124 111 89 63 40 23 12 5 2 1 9,4
1 1 4 8 16 29 45 63 79 89 89 79 63 45 29 16 8 4 1 1 6,7
1 2 5 10 18 29 40 50 56 56 50 40 29 18 10 5 2 Т 4,3
1 1 3 6 10 16 23 29 32 32 29 23 16 10 6 3 1 1 2,4
1 1 3 5 8 12 15 16 16 15 12 8 5 3 1 1 1,2
1 1 2 4 5 7 8 8 7 5 4 2 1 1 0,6
1 1 1 2 3 3 3 3 2 1 1 1 0,2
1 1 1 1 1 1 1 1 1 0,1
Черт. 4а. Сетка кругового распределения по закону Гаусса. Числа квадратов
дают вероятности в сотых долях процента (0,01%)
2. Величины, характеризующие сноп траекторий
Чтобы получить вполне определенное представление о вели-
чине рассеивания траекторий (растворения снопа), лучше всего
пересечь сноп плоскостью по нормали к средней траектории.
При этом площадь, на которой расположатся все пробоины, бу-
дет наименьшая и даст представление о характере и размерах
8
8
Черт. 5.
рассеивания для данного орудия на определенной дальности
стрельбы.
Ввиду того что путем опыта нельзя получить эту картину
на всех дальностях, а также и для целого ряда других надоб-
ностей, применяются величины отклонений не по нормали, а
по дальности Вд, по высоте Be (черт. 5) и боковые Вб.
Пусть средняя траектория
проходит через точку О (черт. 5);
она называется центром группи-
рования. Главные оси эллипти-
ческого закона рассеивания на-
зываются осями группирования.
Принимают, что большая ось
эллиптического закона рассеива-
ния совпадает с плоскостью
стрельбы (положение, невидимо-
му, весьма близкое к действи-
тельности).
Из черт. 5 видно соотношение
между срединными отклонения-
ми в плоскостях: горизонталь-
ной (ОА — Вд), вертикальной (ОС = Be) ненормальной (ОВ = Вп)
из треугольников ОАС, ОАВ и ОСВ:
Вд = Be ctg 0с ;
Be = Вд tg 0С ;
Вп = Вд sin0c ;
Вп
(1)
(2)
(3)
(4)
Вд „ >
S1H ъс
Вп — Be cos 6С ;
г, Вп
Ве= —д-.
cos 0С
(5)
(6)
Таким образом, зная одно какое-либо отклонение в пло-
скости стрельбы, всегда найдем и другие, так как угол падения
всегда известен из таблиц стрельбы.
3. Рассеивание данного момента
При исследовании вопросов стрельбы необходимо иметь в
виду, что строение снопа траекторий и величины, характеризу-
ющие рассеивание (срединные отклонения), не являются незыб-
лемыми и постоянными. Напротив, целый ряд факторов, напри-
мер, характер и сила ветра, различные партии снарядов и по-
рохов, изменяющиеся условия их хранения, величина и харак-
тер качки корабля, характер его маневрирования, искусство
маневрирования, состояние приборов, условия видимости и др.,—
все это действует на рассеивание * орудия, увеличивая или
уменьшая его.
s
3,2 3,4 3 0 2,6 2,2 ?, 8 1, 4 1,о о,б о,: 0,2 0, в 1, I 1, 4 IS 3,2 2,6 3,0 3,4 3,8 1
4,2 3,8 3, 4 3, 0 2, 6 2,2 1, 6 ’,4 1, ° 0,6 0,2 О,2 0,6 1, 0 1,4 /,8 2,2 2,6 М 3,4 3,8 4,2 2 5 7 9 12 15 20 26 32 39 47 55 64 73 81 89 96 101 105 90& 106 105 101 96 89 81 13 84 55 47 39 32 26 20 15 12 9 7 5 2
(L 0 0 0 0 0 1 0 0 0 0 1 0 0 7 1 0 0 1 0 0 0 0 1 0 0 0 0 0 0 2
1 0 0 0 0 0 0 1 0 0 1 0 1 0 7 1 0 1 0 1 0 0 1 0 0 0 0 0 0 1 5
0 0 0 0 1 0 0 1 0 7 0 1 0 1 7 1 1 0 1 0 1 0 1 0 0 1 0 0 0 0 7
0 0 1 0 0 1 0 1 0 1 1 1 1 1 2 2 1 1 1 1 1 0 1 0 1 0 0 1 0 0 9
0 0 0 0 1 1 0 1 1 1 1 1 1 2 2 2 2 1 1 1 1 1 1 0 1 1 0 0 0 0 12
0 1 0 0 0 1 0 0 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 0 0 1 0 0 0 1 0 15
0 0 0 0 0 0 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 0 0 0 0 0 0 20
0 0 0 1 0 0 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 2 2 2 2 2 2 1 1 1 1 1 1 0 0 1 0 0 0 25
0 0 0 0 0 1 1 1 1 1 2 2 2 2 3 3 3 3 3 4 4 3 3 3 3 3 2 2 2 т 1 1 1 1 1 0 0 0 0 0 32
0 0 1 б 1 1 1 1 1 2 2 2 2 3 3 3 4 4 4 5 5 4 4 4 3 3 3 2 2 2 2 1 1 1 1 1 0 1 0 0 39
0 0 0 1 1 1 1 1 2 2 2 2 3 4 4 4 5 5 5 5 5 5 5 5 4 4 4 3 2 2 2 2 1 1 1 1 1 0 0 0 47
1 0 0 0 0 1 1 1 2 2 2 3 4 4 5 5 5 6 6 6 6 6 6 5 5 5 4 4 3 2 2 2 1 1 1 0 0 0 0 1 55
0 1 1 1 1 1 1 2 2 2 3 4 4 5 5 6 6 6 7 7 7 7 6 6 6 5 5 4 4 3 2 2 2 1 1 1 1 1 1 0 64
.0 0 0 0 1 1 2 2 2 3 4 4 5 6 6 6 7 7 8 8 8 8 7 7 6 6 6 5 4 4 3 2 2 2 1 1 0 0 0 0 73
0 0 1 1 1 1 2 2 3 3 4 5 5 6 7 7 8 8 9 9 9 9 8 8 7 7 6 5 5 4 3 3 2 2 1 1 1 1 0 0 81
0 1 0 1 1 1 2 2 3 3 4 5 5 6 7 8 8 9 9 10 10 9 9 8 8 7 6 6 5 4 3 3 2 2 1 1 1 0 1 0 89
1 0 1 1 1 1 2 2 3 4 5 5 6 7 8 8 10 10 10 10 10 10 10 10 8 8 7 6 5 5 4 3 2 2 1 1 1 1 0 1 91
0 1 0 1 1 2 2 2 3 4 5 6 6 7 8 9 10 10 77 77 11 11 10 10 9 8 7 6 6 5 4 3 2 2 2 1 1 0 1 0 101
0 0 1 1 2 2 2 3 3 4 5 6 7 8 9 9 10 11 77 77 11 11 11 10 9 9 8 7 6 5 4 3 3 2 2 2 1 1 0 0 101
1 1 1 2 2 2 2 3 4 5 5 6 7 8 9 10 10 11 77 12 12 11\ 11 10 10 9 8 7 6 5 5 4 3 2 2 2 2 1 1 1 106
1 1 1 2 2 2 2 3 4 5 5 6 7 8 9 10 10 11 ‘77 12 12 11 11 10 10 9 8 7 6 5 5 4 3 2 2 2 2 1 1 1 106
0 0 1 1 2 2 2 3 3 4 5 6 7 8 9 9 10 11 77 11 11 11 11 10 9 9 8 7 6 5 4 3 3 2 2 2 1 1 0 0 ’05
0 1 0 1 1 2 2 2 3 4 5 6 6 7 8 9 10 10 77 11 11 11 10 10 9 8 7 6 6 5 4 3 2 2 2 1 1 0 1 0 101
1 0 1 1 1 1 2 2 3 4 5 5 6 7 8 8 10 10 10 10 10 10 10 10 8 8 7 6 5 5' 4 3 2 2 1 1 1 1 0 1 91
0 1 0 1 1 1 2 2 3 3 4 5 6 6 7 8 8 9 9 10 10 9 9 8 8 7 6 6 5 4 3 3 2 2 1 1 1 0 7 0 89
0 0 1 1 1 1 2 2 3 3 (4 5 5 6 7 7 8 8 9 9 9 9 8 8 7 7 6 5 5 4 3 3 2 2 1 1 1 1 0 0 81
0 0 0 0 1 1 2 2 2 3 4 4 5 6 6 6 7 7 8 8 8 8 7 7 6 6 6 5 4 4 3 2 2 2 1 1 0 0 0 0 73
0 1 1 1 1 1 1 2 2 2 3 4 4 5 5 6 6 6 7 7 7 7 6 6 6 5 5 4 4 3 2 2 2 1 1 1 1 1 1 0 64
1 0 0 0 0 1 1 1 2 2 2 3 3 4 5 5 5 6 6 6 6 6 6 5 5 5 4 4 3 2 2 2 1 1 1 0 0 0 0 1 55
0 0 0 1 1 1 1 1 2 2 2 2 3 4 4 4 5 5 5 5 5 5 5 5 4 4 4 3 2 2 2 2 1 1 1 1 1 0 0 0 47
0 0 1 0 1 1 1 1 1 2 2 2 2 3 3 3 4 4 4 5 5 4 4 4 3 3 3 2 2 2 2 1 1 1 1 1 0 1 0 0 39
0 0 0 0 0 1 1 1 1 1 2 2 2 2 3 3 3 3 3 4 4 3 3 3 3 3 2 2 2 2 1 1 1 1 1 0 0 0 0 0 32
0 0 0 1 0 0 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 2 2 2 2 2 2 1 1 1 1 1 1 0 0 1 0 0 0 25
0 0 0 0 0 0 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 0 0 0 0 0 0 20
0 1 0 0 0 1 0 0 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 0 0 1 0 0 0 1 0 15
0 0 0 0 1 1 0 1 1 1 1 1 1 2 2 2 2 1 1 1 1 1 1 0 1 1 0 0 0 0 12
0 0 1 0 0 Т 0 1 0 1 1 1 1 1 2 2 1 1 1 1 1 0 1 0 1 0 0 1 0 0 9
0 0 0 0 1 0 0 1 0 1 0 1 0 1 1 1 1 0 1 0 1 0 1 0 0 1 0 0 0 0 7
1 0 0 0 0 0 0 1 0 0 1 0 1 0 1 1 0 1 0 1 0 0 1 0 0 0 0 0 Т 1 5
0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 1 0 0 1 0 0 0 0 1 0 0 0 0 0 0 2
I
Рассеивание может меняться и в течение одной и той же
стрельбы, в особенности, если стрельба продолжительная или
происходит с небольшими перерывами. Имея это в виду, надо
наравне с несоответствием географической (или топографи-
ческой) дальности с табличной дальностью (прицел) данного
момента рассматривать и рассеивание данного момента, характе-
ризуемое срединными отклонениями данного момента.
Под срединным отклонением данного момента подразумевается
такое срединное отклонение, которое характеризовало бы распре-
деление точек падения, если бы мы могли в данный момент про-
извести большое число выстрелов.
При выработке правил стрельбы необходимо учитывать воз-
можность изменения величины срединного отклонения в тех
случаях, когда это изменение скажется на результате приме-
нения правил. Здесь могут быть два случая: случай резкого
перехода от условий более выгодных к условиям менее выгод-
ным, или наоборот, и случай . медленного изменения величины
срединных отклонений в течение стрельбы. Имея это в виду,
необходимо при выработке правил стрельбы исследовать, как
скажется на применении правил резкое изменение рассеивания.
Обычно правила вырабатывают для табличного рассеивания и
исследуют, какие необходимо ввести в них изменения для слу-
чаев рассеивания в два раза больше и в два раза меньше таб-
личного.
По окончании исследования необходимо объединить получен-
ный материал. Там же, где объединение без явного ущерба
для успешности стрельбы окажется невозможным или нежела-
тельным, должны быть указаны объективные признаки, на осно-
вании которых управляющий огнем может реагировать на ту
или иную обстановку стрельбы.
При резком изменении величины срединных отклонений
управляющий огнем всегда будет иметь возможность реагиро-
вать на обстановку момента, в случае же медленного измене-
ния рассеивания чаще всего не потребуется никаких мер, что-
бы парализовать его влияние, мало заметное.
4. Определение срединных отклонений путем опыта
на полигоне
Для определения срединных отклонений для пушек путем
опыта стрельбу следует производить на 3—4 дальности, выпус-
кая на каждой из них по 10—12 снарядов.
Для малых дальностей (до 10 кабельтовых) стрельба про-
изводится по вертикальному щиту, размеры которого должны
обеспечить улавливание щитом всех снарядов. Вследствие
трудности изготовления щитов очень больших размеров тре-
буется предварительная пристрелка, обеспечивающая положе-
ние центра группирования в непосредственной близости к цен-
тру щита.
ю
Щит должен быть установлен так, чтобы поверхность его
была строго перпендикулярна к вертикальной плоскости, про-
ходящей через направление: точка вылета —центр щита.
Пристрелка производится 3—4 выстрелами либо в тот же
щит, либо в щит, установленный рядом, и по полученным на
щите пробоинам определяется средняя точка попадания.
Пусть получены четыре пробоины (черт. 6) в правом верх-
нем углу щита и О,- — средняя точка попадания при наведе-
нии в центр щита и при строго одном и том же положении оси
пушки при каждом выстреле.
Не трогая установки пушки, направляют прицельную линию
в точку Ог, после чего снова обычными приемами наводят
орудие в центр щита и произ-
водят назначенное число выст-
релов.
Пусть Ci есть центр про-
боины г; координаты пробоин
удобнее мерить не от центра
щита, а от одного из его углов,
приняв начало координат, на-Q
пример, в точке О.
При данной установке щита
обработка ведется обычными
приемами или по среднему результату, или по разностям.
В первом случае определяем координаты центра группиро-
вания:
п
Затем находим величины кажущихся случайных ошибок:
— В;
Наконец, найдем срединные отклонения:
(9)
(Ю)
Вв = 0,67
В<7=0,67
(И)
(12)
11
где п — число выстрелов, произведенных после пристрелки
(пристрелочные выстрелы, конечно, во внимание не прини-
маются).
В том случае, когда мы не можем считать, что все выстрелы
произведены в строго одинаковых условиях, мы можем обра-
ботку произвести по разностям.
Пусть = —-Он (13)
и + ъ (14)
тогда 1/ VX Bd = 0,48 f 1 _ (15)
и 1/1* £6=0,48 f 2 . (16) т п — 2
При определении срединных отклонений на остальные даль-
ности измеряют отклонения по дальности и боковые и вычис-
ляют величины Вд и Вб, пользуясь теми же формулами (11) и
(12) или (15) и (16); координаты точек падения должны изме-
ряться: х{ в плоскости стрельбы, —в плоскости, к ней пер-
пендикулярной, от какого-либо произвольно выбранного начала
осей координат (начало осей удобно выбирать так, чтобы иметь
координаты точек падений одного и того же знака).
В том случае, когда мы не сможем иметь направление пло-
скости стрельбы, обработку придется . производить иначе.
В этом случае координаты точек падений измеряются относи-
тельно произвольно выбранных прямоугольных осей координат,
но направленных по возможности так, чтобы ось А'-ов была
ближе к плоскости стрельбы.
Пусть при этом измерены координаты точек падений хл,
•^2» *О(’ - • - , Хп И .<?2, г?;;, - • . , £п .
Пользуясь формулами (7), (8), (9) и (10), найдем „кажущиеся
ошибки" ж/ и у- относительно центра группирования. Опреде-
лим коэфициенты:
(17)
(18)
(19)
и
1
12
где ошибки по дальности обозначены через ?//, а ошибки в бо-
ковом направлении — через ж/.
Направление осей группирования найдем по формуле:
п
2
(20)
Формула (20) дает два значения ах и а2, различающиеся на
90°. Угол ах для направления большей оси надо выбрать так,
чтобы при cos2ax>0 и ах было в пределах от 0 до 45°
от оси У'-ов; при А < С cos 2ах < 0 и ах лежит вне этих пределов.
Найдя направление осей, получим и срединные отклонения
для пушки по формулам (21) и (22):
вя л 07 1/ 4 COS 2ах-j-Csin2ax JSsin 2ах (21)
Ий .= 0,67 / -----------------------------------
и /
Л, n- 1 / Д cos2a„ + Csin2a, 4- Б sin 2a, (22)
Вб = 0,6 i I/ —1--------—-------- ----------—
п — 1
Пример 1. На некоторую дальность произведено ю выстре-
лов и измерены координаты точек падения в плоскости стрель-
бы и в направлении, к ней перпендикулярном, в порядке их
появления; требуется определить срединные отклонения пушки
(табл. 2 и з).
Таблица 2
Определение срединных отклонений
(в саженях)
К точек падения X У
1 45 9
2 82 12
3 37 7
4 21 И
5 63 8
6 14 4
7 28 15
8 46 10
9 49 и
10 52 И
437 100
13
437
В = — =43,7 саж.1
100 ,
7] = — = 10 саж.
Таблица 3
Определение срединных отклонений
Vi Л? чу ж,-
45 + 1,3 1,69 9 —1 1
82 4-38,3 1 466,89 12 4-2 4
37 — 6,7 44,89 7 —3 9
21 —22,7 515,29 11 4-1 1
63 4-19,3 372,49 3 —2 4
14 —29,7 882,09 4 —6 36
28 —15,7 246,49 15 4-5 25
46 + 2,3 5,29 10 0 0
49 4- 5,3 28,09 13 +3 9
52 + 8,3 68,89 11 4-1 1
п V к? =3 632,1.
1
п
V>i = 90.
1
ВЗ = 0,67 1 / 3 632,1 _ 13 радк,
И 9
Ж.--0,6 7 1/ £2 = 2,1 саж.
|/ 9
Пример 2. Произведено 10 выстрелов и измерены в саженях
координаты точек падения относительно произвольно взятой
системы осей координат хоу при неизвестном направлении
плоскости стрельбы (черт. 7):
1 (5;105); 2 (8;97); 3(18;78); 4(8;75); 5(15;55); 6(22;55); 7(25;45);
8(18;43); 9(27;33); 10(25;10)2.
Требуется найти оси группирования и определить средин-
ные отклонения Вд и Во.
Обозначив через ж/ и у- координаты точек падения относи-
тельно центра группирования в прямоугольной системе осей
координат, параллельной системе хоу, для направления боль-
шей оси группирования имеем:
1 Пример решен арифметически точно. Обычно на практике ограничиваются
целыми числами, опуская дроби.
2 Начало координат выбрано так, что все координаты точек падения
положительны, поэтому знаки не показаны.
14
^Ъс-у{ 2 В
tg2a~ ^-YyF~A-c'
где у^В,^Г- = А в Ъу? = С.
При этом координаты центра группирования в системе прямо-
угольных координат хоу принимаем:
и
п
Обработка результатов опыта видна из табл. 4.
15
Таблица 4
Схема решения примера 2
№ па- дении Xi У% Xi У1 хА у г 2 (Г/ уС
1 6 105 —12,1 -|-45,4 —549,34 146,41 2 061,16
2 8 97 — 9,1 --37,4 —340,34 82,81 1 398,76
3 18 78 + 0,9 18,4 + 16,56 0,81 338,56
4 8 75 — 9,1 --15,4 —140,14 82,81 237,16
5 15 55 — 2,1 — 4,6 + 9,66 4,41 21,16
6 22 55 + 4,9 — 4,6 — 22,54 24,01 21,16
7 25 45 + 7,9 —14,6 —115,34 62,41 213,16
8 18 43 + 0,9 —16,6 — 14,94 0,81 275,56
9 27 33 + 9,9 —26,6 —263,34 98,01 707,56
10 25 10 + 7,9 —49,6 —391,84 62,41 2 460,16
—1 811,60= 564,90=4 7 734,40=
=13 =С
, о 2В —3 623,20 „ 3 623,20
& А—С 564,90—7 734,40 ^7 169,5 ’
откуда
2а = 26°48',6.
Так как А<^С, то для направления большей оси группи-
рования выберем а, при котором cos 2 < 0, тогда имеем:
аг = 103о24',3
И
а2=13°24',3;
Вд = 0,67 рЛ564,9COS2at+ 7 734sin2at—1811 sin2аг с&ж
j36 = 0,67 1 /564’9 cos2 a2 + 7 734 sin2 a2 —1 811 Sin 2 a2 _
г / - i . - Aj9\j vtwli.
На черт. 7 видим места точек падений и направление осей
группирования.
Следует иметь в виду, что полученное нами положение
центра группирования и направление осей группирования не
являются при десяти наблюдениях истинными положениями:
здесь мы имеем дело с распределениями центра группирования
и направления осей группирования, а потому всегда желатель-
но найти, хотя бы приближенно, эти распределения и, таким
образом, иметь суждение о точности работы. Полуоси единич-
ного эллипса распределения центра группирования получим из:
, Вд 21,2
a — —==—+=
]/п у ю
6,7 саж.
16
и
,, Вб 2,6
Ь =—7=——7==0,8саж.
У п у 10
Для получения распределения направления осей группиро-
вания имеем:
где
Применяя приближенный метод (п — 10), можно принять:
Ев = —7= И А
/4
п(1— г)2
2z
где
_В&
2~а*~Вд* ’
(2,6)2 _ 6,8
(21,2)2 ~ 449,4
и
10
1
6,8 V
449,4 )
2 • 6,8
449,4
-------= 322,4.
Срединная ошибка распределения направления осей выра-
зится так:
р _ 0,4769
УА У 322,4
0,0266=1°,5.
Построим распределение направлений осей через 1°, тогда
масштабная величина
Ея=^ = 1,5,
на стТ0₽01) ПОЛУЧИМ такое распределение (см. черт. 8 и табл. 5
2 Теория стрельбы
Из распределения имеем вероятность в 82%, что ошибка
в направлении осей не превосходит + 3°, и вероятность в 93%,
что эта ошибка не более + 4°,
Таблица 5 1
Распределение осей
(к черт. 8)
Да
О
±1°
±2°
±3°
±4°
±5°
±6°
+7°
+8°
0,174
0,167
0,120
0,072
0,035
0,013
0,005
0,001
о
Такие результаты мы получили благодаря большой разнице
в Вд и Вб, при которой А велико, и только благодаря этому,
так как число 10 (наблюдений) никак не может считаться доста-
точно большим.
5. Теоретический подсчет срединных отклонений
для пушек па основании данных валовой приемки
боевого запаса
Главнейшими причинами рассеивания точек падения снаря-
дов являются случайные отклонения в начальной скорости,
в углах бросания и в балистическом коэфициенте. Если на
основании опыта известны срединные отклонения, характери-
зующие законы случайных отклонений в указанных величинах,
то срединные отклонения для пушек могут быть подсчитаны
теоретически.
Обозначим срединные отклонения в дальности, проис-
ходящие от отклонений в начальной скорости, через Rv,
1 Это не единственный метод определения распределения направления
осей группирования: есть и другие методы, дающие приблизительно такую
же точность (см. Задачник по теории вероятностей, изд. Арт. академии
им. тов. Дзержинского).
18
от отклонений в углах бросания — через Ве и от отклонений
в балистическом коэфициенте — через Ес. Тогда срединное
отклонение по дальности может быть выражено:
Вд=(23)
Величины , Rv и Ес могут быть вычислены по любым
поправочным формулам внешней балистики.
Применяя поправочные формулы внешней балистики
(Б. Н. Окунев)1, будем иметь:
]/+ ( сОЫ 1+Н1-/Д) + А'(1 -т)-с] <24)
tg%
no = vocoseo;
i>o = tgO(l;
r'e = i',8 = 0,5 дел.;
(25)
(26)
(27)
r„ 1 1 / , 1 \
—=------------------ I чаще берут---------1;
V 250 300 \ Ш 300 )’
re _ 1 2.
C ~ 450 ’
X — дальность;
v0— начальная скорость.
Для получения боковых срединных отклонений пользуются
формулой:
Вб=л/ ( V+ (28)
I/ у cos О0 ) \ д J
где tg^ = Y’ (29)
Z —линейная величина деривации,
¥ — угол деривации.
г'е=1',8; ^- = 0,14",
д I
где I— длина снаряда в калибрах.
Изд. Военно-морской академии 1936 г. (на правах рукописи).
Иногда величину считают равной .
19
По вычисленным на несколько дальностей Вд вычисляют
Вп — Вд- sin 6С.
По Вп и Вб строят кривые, которые выравниваются в соглас-
ные кривые.
Снимая Вп с кривой через избранный интервал дальностей,
Вть
вновь вычисляют Вд — ——которыми и пользуются, а Вб
sinoc
прямо снимают с кривой.
Хорошие результаты получаются также при пользовании
формулой:
т
2 т—1
где
2 /е sin Г\
tg260 )
/у 2 т г„\2 / „ т—1 гЛ2
2т—1 vl ( 2т—1 С) ’
(30)
т —
v02 sin 2 6В
(31)
о
К—1 при выражении X в метрах и К = 182,9 при выражении
X в кабельтовых.
Примечания. 1. Вывод формул, входящих под знак радикала
в формуле (30), см. Уиковский „Стрельба морской артиллерии".
2. Всегда предпочитают пользоваться величинами срединных откло-
нений, полученными путем опыта, а формулами (24), (28) и (30) или
вообще какими-либо другими формулами для вычисления срединных
отклонений пушек пользуются только до определения этих отклонений
из опыта.
6. Стрельба из одного орудия
Выше (§ 5) мы приняли, что срединное отклонение орудия,
характеризующее закон рассеивания, является результатом
сложения срединных отклонений в дальности, характеризующих
законы случайных ошибок (разнообразия) в углах бросания,
в начальной скорости и в баллистическом коэфициенте. Это три
основных фактора; в действительности же этих ошибок значи-
тельно больше, например, вследствие разнообразия в весах
снарядов, в форме их, в расположении частей снаряда и т. п.
Отдельные ошибки, отражающиеся на положении точек
падения, вообще говоря, следуют закону Гаусса, что легко
может быть проверено, так как их величины доступны точным
измерениям. Следовательно, если отдельные ошибки подчи-
няются закону Гаусса, то и общая ошибка, получающаяся
в результате их сложения, будет также следовать тому же
закону.
Кроме этих ошибок, может быть еще ряд других причин,
вызывающих рассеивание, как-то: температура пороха отдель-
ных зарядов, колебания в силе и направлении ветра, изменение
20
температуры воздуха и др., которые могут следовать, но могут
и не следовать закону Гаусса; в последнем случае возможно
искажение картины рассеивания.
Так или иначе, для получения общего закона ошибки надо
сложить, что всегда возможно, если среди складываемых зако-
нов встречается не более одного несимметричного.
При исследовании вопросов стрельбы чаще всего случается,
что среди ошибок, следующих закону Гаусса, встречаются
ошибки, следующие закону равной вероятности. В большин-
стве случаев предел последних ошибок, по сравнению с сум-
марной ошибкой, подчиняющейся закону Гаусса, невелик.
В этом случае с точностью, совершенно достаточной для прак-
тических целей, можно принять, что при наличии нескольких
причин, вызывающих случайные ошибки по закону Гаусса и по
закону равной вероятности, мы можем их сложить в один закон,
который будет близок к закону Гаусса в том случае, если
предел ошибок по закону равной вероятности не более ошибок
по закону Гаусса, и этот сложный закон, близкий к закону
Гаусса, принять практически не отличающимся от закона
Гаусса.
Кроме закона равной вероятности, возможны и иные причины,
следующие неизвестным законам, но повседневная практика
стрельбы показывает, что параметры их столь малы, что при
рассеивании, насколько вообще возможна проверка зако-
нов рассеивания опытом, получается в результате закон Га-
усса.
Итак, при стрельбе из одного орудия в подавляющем боль-
шинстве случаев мы будем иметь распределение точек падения
снарядов по закону Гаусса или по закону, разница которого от
закона Гаусса практически не улавливается.
7. Стрельба из нескольких орудий. Явление разнобоя
й
В войсковой артиллерии стрельба из одного орудия —явле-
ние довольно частое; в береговой артиллерии такая стрельба
также может иметь место, если она будет вынуждена вести
огонь по суше при совместных действиях с войсками и при
обороне тыла; в морской артиллерии этот случай довольно ред-
кий даже при стрельбе по береговым целям, но тем не менее
исследование § 6 нам необходимо для перехода к случаю
обычных условий стрельбы, т. е. стрельбы из нескольких ору-
дий, так как придется считаться с законом рассеивания каж-
дого отдельного орудия.
При стрельбе из нескольких орудий, если их центры груп-
пирований точно совпадают друг с другом и срединные откло-
нения одинаковы, мы не получим никакой разницы по сравне-
нию со стрельбой из одного орудия.
Но совершенно другая картина получается при стрельбе из
РУшты орудий одного и того же калибра, если имеет место
21
несовпадение центров группирования (средних траекторий) из-за
разнобоя орудий, являющегося, главным образом, следствием
разнообразия в начальных скоростях, или различия в срединных
отклонениях.
Таблица 6
Вероятность хотя бы одного попадания из двух выстрелов при разнобое
орудий 2а
Положение
цели относи-
тельно точки
01
Вероятность хотя бы одного попадания
при 2 выстрелах
2а = 1Вд | 2а = 8Вд [ 2а = О
в процентах
Г"
О
1
2
3
4
46
46
37
22
9
27
25
16
7
4
47
44
29
14
4
Примечание. Глубина цели равна Вд при бесконечно большой ширине.
Разнообразие в начальных скоростях имеет место, главным
образом, вследствие неодинакового падения начальных скоро-
стей у разных орудий от изнашивания каналов стрельбой, от
разности температур помещений для хранения боевого запаса,
от разнообразия в весах снарядов и при стрельбе различными
партиями пороха.
Вред разнобоя осознан давно, и для парализования его вли-
яния принимается ряд мер, как-то: сострелка орудий, введение
поправок на температуру пороха, стрельба одинаковыми пар-
тиями зарядов и снарядов, полигонная разбраковка снарядов
и, наконец, разбор боевых припасов в портах и на корабле по
клеймам, чтобы одновременно к орудиям одного и того же
калибра подавать однообразные снаряды и заряды.
Учет разнобоя на основании результата сострелки и темпе-
ратуры пороха достигается введением индивидуальных попра-
вок на приборах управления огнем, а при отсутствии приборов
в сухопутной артиллерии — отдельной пристрелкой каждого
орудия.
При всех этих мерах все же не может быть и речи о пол-
ном уничтожении разнобоя, так как его определение базируется
на очень небольшом числе выстрелов и, конечно, заключает
в себе случайные ошибки измерения, а введение индивидуаль-
ных поправок всегда содержит в себе ошибку от округления.
Главная задача этого параграфа и заключается в том, чтобы
выяснить допустимую величину остающегося разнобоя, т. е.
такую величину, которая практически не отзовется на резуль-
татах стрельбы.
22
Этот вопрос рассмотрим сначала для двух орудий, которые
обладают разнобойностыо 2 а. За единицу длины примем сре-
динное отклонение по дальности Вд = 1.
Распределение точек падений определится по закону Гаусса
для каждого из орудий, например, для первого — кривой А1г
для второго — кривой А2 (черт. 9).
Если оба орудия стреляют либо одновременно, либо одина-
ково часто, то вероятность того, что выстрелит то или другое
орудие, будет равна половине С/2).
Вероятность падения снаряда около точки К будет: для
орудия № 1 — т/1 dx, а для орудия № 2 — y2dx.
Вероятность падения снаряда вообще около точки К для
двух независимых и несовместных (один и тот же снаряд не
может быть выстрелен из обоих орудий) событий будет:
Рх d^ = — У1 dx 4- — у2 dx,
Ci Cl
Pxd'x = ^~ (У1 + Мг) dx- (32)
Ci
—
Вычислив с помощью формулы у = —(табл. 5) орди-
у к
наты и пользуясь формулой (32), найдем закон рассеивания
Для стрельбы из двух орудий, изображенный кривой As
(черт. 9).
23
На черт. 9 мы видим, что кривая As, имея один максимум,
почти не отличается от кривых и А2.
Кроме того, на черт. 9 показана плотность для двух орудий
с разнобоем в 1 Вд и для двух орудий с разнобоем, равным нулю.
Сравнивая плотности, видим, что они также отличаются друг
от друга весьма мало. »
Подсчитав вероятность хотя бы одного попадания для двух
выстрелов по цели глубиной в Вд = 1 и бесконечной ширины,
лежащей серединой поражаемого пространства в точке О, полу-
чим, что эта вероятность при наличии разнобоя Вд— 1 = 2п
выражается в 44,8%; то же получим, если положение цели
будет такое же, а разнобоя не будет. Мы можем сделать эти
подсчеты для целого ряда положений цели для обоих случаев
и полученные результаты сравнить с таблицей, например, для
случая разнобоя 2а—8Вд (черт. 10).
Черт. 10.
Из сравнения приведенных выше данных видим, что разно-
бой 2« = 1=В0 почти неощутим, тогда как разнобой 2 а —
— 8Вд совершенно исказит картину (черт. 10) и в большинстве
случаев поведет к полному отсутствию поражения цели.
Сделаем вывод в общем виде для еще допустимой вели-
чины остающегося разнобоя, т. е. такого разнобоя, который на
стрельбе практически не скажется. Для этого возьмем начало
координат в середине между двумя центрами группирования
% и О2 (черт. 9 и 10) и, подставив в формуле (32) вместо уг и
у2 их значения для закона Гаусса, получим аналитическое
выражение для закона распределения точек падений кривой А&
для Е - Вд - 1:
1 Г Р — Р2(!В —«)2 р -р2(«? + а)21
pdx — — —г—е _|----'___е dx
2 L И * ]/л
или
— р2 (аг— я)2 —р2 (аг + я)2'
е
(33)
При небольших а будет один максимум, а при больших
а — два.
24
Распределение по закону Гаусса для неощутимости разно-
боя мы сохраним тогда, когда будет один максимум. Поэтому
найдем величину а, при которой будет один максимум.
Возьмем производную от выражения, стоящего в скобках, и
сделаем некоторые преобразования:
[е-₽3(«>-«)2 + е-р= + _2р2(ж — га)е~Р2 —
— 2p2(«4-«)e-Ps (® + «)2 — — 2р2(ж — а)е - р3«* + V - р3«3 —
— 2 р2 (х 4- а) е ~ р2®2 - 2р2«® ~ р2"2.
Чтобы получить одночлены в степенях при е, возьмем за.
скобку — 2 р2 е ~ р2®2 - р2“2 ; тогда получим:
[е-Р3(а>-а)3 е-р2 (® + “)2]' = — 2р2е -р“(®3 + «!) [(х—a)e + 2P2c®-j-
+ («4-«)e-2P2“®]. (34)
Из выражения (34) видим, что оно обратится в нуль при
ж —0.
Речь может итти только о небольшой величине разнобоя и
при достаточно малом х, так как при небольших а и боль-
ших величинах х вероятности у • dx в законе Гаусса уже
пренебрежимо малы, а потому, не прибегая ко второй произ-
водной, воспользуемся разложением выражения, стоящего'
в скобках в формуле (34), в ряд Маклорена и, ограничиваясь
двумя членами разложения, получим:
(х — а) (1 + 2р2 ax'] -f- (х + а) (1 — 2р2 ах) =»
=. х + 2р2«ж2 — а — 2р2о2ж 4- х — 2р2жс2 4~ а — 2 р2«2 х =
= 2х — 4р2«2Ж = 2Х (1 — 2р2 О2).
Заменяя полученным выражением выражение, стоящее
в скобках в формуле (34), получим:
[е - р2<® - «)3 4- e'-W + «)= ]' = — 4 е ~ р2 <®2 + (1 — 2р2»2). (35)
Выражение (35) будет иметь значение, меньшее нуля, и, сле-
довательно, один максимум при х^>0 до тех пор, пока
1 — 2р2о2<0. (36)
Решая неравенство (36) относительно а, получим:
и при Вд = 1 выражение ? у- представляет величину сред-
ней квадратической ошибки и численно равно 1,4826 Вд, т. е.
°Дин максимум будет до тех пор, пока величина а не превос-
ходит среднего квадратического отклонения пушки.
25
Таким образом, если примем, как правило, чтобы величина
разнобоя не превосходила среднего квадратического отклонения
орудия, то явление разнобоя на результатах стрельбы не будет
ощутимо.
При наличии нескольких орудий (более двух) мы получим
ту же картину, если, приняв какое-либо орудие за основное,
не будем допускать, чтобы разнобой каждого из остальных
орудий относительно основного был больше среднего квадра-
тического отклонения.
При решении этого вопроса дело осложняется тем, что вели-
чина среднего квадратического отклонения не есть величина
постоянная, но если принять даже табличное рассеивание, то
величина среднего квадратического отклонения все же будет
зависеть от дальности.
Черт. 11.
На черт. И построена кривая средних квадратических
•отклонений от 0 до 140 каб. для одного из орудий. Рассмот-
рение чертежа показывает, что для расчета допустимой вели-
чины разнобоя вполне достаточно взять наименьшую величину
среднего квадратического отклонения, т. е. для дальностей
порядка 25—ВО каб.
Разнобой пушек учитывается или индивидуальной при-
стрелкой орудий (войсковая артиллерия) или индивидуальными
поправками на корректорах, принимающих высоты прицела
(морская и береговая артиллерия).
В первом случае остающийся разнобой будет, главным обра-
зом, зависеть от точности пристрелки, от величины наимень-
шей поправки, обычно Р/2— 2Ёд; во втором случае это будет
сложный закон случайных ошибок эксцентрика, или множи-
тельного механизма (закон Гаусса), ошибки от округления
(закон равной вероятности,'в зависимости от точности уста-
новки корректоров, различной у различных систем), и наконец,
26
от ошибок сострелки, которые в свою очередь будут зависеть
от методов сострелки, точности приборов и числа выстрелов,
сделанных из каждого орудия на сострелке. Нетрудно показать
подсчетом, что при достаточной тщательности сострелки вели-
чина определенного опытом и учтенного на приборах разнобоя не
превысит одного среднего квадратического отклонения.
Закон (33) распределения точек падения при разнобое
может быть вычислен для разных х и а и сведен в таблицу,
но воспользоваться этим все равно не- удастся, потому что,
во-первых, разнобой может меняться, а во-вторых, нельзя иметь
правил для разных вариантов разнобоя; но тем не менее необ-
ходимо все же посмотреть, как велика будет наибольшая вели-
чина кажущегося рассеивания группы орудий после учтенного
сострелкой разнобоя.
Кажущаяся величина средней квадратической ошибки при
разнобое а найдется из формулы:
Е2 = /Е2'2 + «2
или
]/" Вд2 + (0,67449а)2,
где а — величина разнобоя, не больше среднего квадратиче-
ского отклонения пушки.
Окончательно примем:
)/В02+ 0,46 а2. (38)
Пример. Определить „кажущуюся" величину увеличения
рассеивания четырех орудий, если сострелка произведена изме-
рением начальных скоростей по четыре выстрела из орудия
при срединной ошибке в измерении скоростей 0,1%. Средин-
ная ошибка в измерении температуры пороха 0,2°. Наиболь-
шая ошибка в выточке эксцентрика, или множительного меха-
низма + Vs каб. Точность установки корректора + 0,05% от
начальной скорости.
дос
Табличные величины — = 60 саж., — = 70 саж., Вд = 28 саж.
dv dt
Срединная ошибка среднего результата при измерении ско-
рости будет:
о 1 °/
Дг= —^ = 0,05%.
V 4
Срединные ошибки по дальности:
ДХ- = — Дг = 60 • 0,05 = 3 саж.;
dv
= • 0,2 — 14 саж.;
27
Л v 12,5
ДАэкс. — —-— з саж.:
Д-Х~округ —‘ 3 ,
14* З2 +3 = 474
2 (0,6745)2 (0,6745)2 (0,6745)2
Таким образом, мы видим, что кажущееся увеличение рас-
сеивания при учтенном разнобое выражается ничтожно малой
величиной: 30,8 — 28 = 2,8 саж.
Несколько больше будет остающаяся величина разнобоя,
если вместо точной сострелки удовольствоваться пристрелкой
каждой пушки в отдельности.
Для сравнения примем, что пристрелка каждой пушки
оканчивалась обеспеченной нулевой вилкой из четырех выстре-
лов: 2 плюса и 2 минуса.
В этом случае срединная ошибка только от ошибки в учете
начальной скорости выразится:
. „ 0,90 -28 п
ДХ, —------=---= 17,9 саж.
К2
Все остальные величины останутся те же, а потому будем
иметь:
,2 17,92 142 З2
— (0,6745)2 + (0,6745)2 + (0,6745)2 + 3 —1 163;
Дз 489 .
|/ 4 ’
а — 1/ 0 • ——1163—+ 1 163—+ 1163-i- =
Вд'
Вд2 + 0,46
3 489
4 ”
282 + 0,46 = 34,4 саж.
Таким образом, в первом случае мы имеем кажущееся уве-
личение рассеивания па 10%, во втором случае — почти
на 24%.
Из этих цифр можно сделать вывод, что при уничтоженном
разнобое влияние остающегося разнобоя практически не будет
ощутимо, если выявление разнобоя пушек сделано достаточно
тщательно путем сострелки.
28
Закон рассеивания при стрельбе из группы орудий прак-
тически остается тот же, что и при стрельбе из одного ору-
дия. Правила стрельбы из одного орудия и из группы орудий
для случая стрельбы по неподвижной цели будут одни и те
же. Что касается различий в правилах стрельбы из одного и
из группы орудий для случая стрельбы по подвижной цели,
то причины этого различия совершенно иные и не имеют отно-
шения к вопросу о разнобое орудий, влияние которого в даль-
нейшем мы будем считать всегда уничтоженным.
Если сострелка производится отысканием прицелов на нулет
вых вилках, то это хотя и поможет делу, но величина остаю-
щегося разнобоя достигает 20—30%.
Наконец, укажем, что влияние разнобоя не может быть
учтено какими-либо правилами, основанными на определении
так называемого „батарейного" или „корабельного" рассеи-
вания.
Единственной мерой, парализующей вредное влияние разно-
боя пушек, является определение его величины путем сострелки
и введение индивидуальных поправок на корректорах, принимаю-
щих высоты прицела на пушках.
ГЛАВА II
ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТИ ПОПАДАНИЯ
8. Вероятность одного попадания при наличии
ошибок, не зависящих от орудия
К ошибкам, не зависящим от орудия, относятся ошибки
в определении расстояния до цели, ошибки в учете изменения
расстояния, ошибки в переходе от определенного расстояния
к табличной дальности (прицелу) и др.
Эти ошибки можно рассматривать или только в направлении
дальности, или на плоскости, или в пространстве, причем эти
ошибки, как и рассеивание орудия, будем принимать подчи-
няющимися закону Гауссф.
Независимо от того, будем ли мы рассматривать ошибки
или только в направлении дальности, или на плоскости, или
в пространстве, результат вывода сводится к одной и той же
весьма важной для нас теореме, которую можно формулиро-
вать так:
Если имеются ошибки в определении положения цели и поло-
жения средней траектории, то для определения вероятности
одного попадания все эти ошибки можно сложить в один закон, и
затем вычислить вероятность попадания в цель так, как будто мы
точно установили положение средней точки попадания относи-
тельно цели, но законы рассеивания характеризуются не средин-
ным отклонением, взятым для данного орудия, а срединным
отклонением, отвечающим суммарному закону всех ошибок.
Сначала докажем эту теорему для случая ошибок только
в положении цели в направлении дальности.
Пусть срединное отклонение пушки по дальности Вд = а.
Срединную ошибку, характеризующую закон ошибок в положе-
нии цели, обозначим Ъ.
Пусть средняя траектория направлена в точку О (черт. 12),
и мы предполагаем, что цель находится в точке Ц.
В действительности же цель находится не в точке Ц,
а может находиться где угодно, например, в
Зная срединную ошибку Ь, характеризующую закон случай-
ных ошибок в определении положения цели,' мы можем напи-
30
< Ть выражение вероятности для любого положения цели„
Вероятность положения цели в будет:
р
РаУ = 7^7=е dy.
by it
(39>
Если цель наверное находится в точке Ци то вероятность
попадания в нее при положении центра группирования в О
будет:
(40>
Вероятность попадания при положении цели в Ц1г а центра,
группирования в О с учетом вероятности попадания цели
в Цг будет:
„ W , (jg—уУП
Р2 f I “a , , ,
p dx dy — —=-7- e L J dxdy. (41)
к ab
Вероятность попадания при любом положении цели полу-
чится, если распространим эту вероятность на все возможные
положения цели; короче говоря, выражение (41) надо проин-
тегрировать по у, тогда получим:
, Р
р dx — -- -r
я ab
(42)
Для простоты письма при выкладках введем некоторые
обозначения постоянных величин:
Тогда выражение (42) примет вид:
Л Ул У 2 7
pdx=——-dx
— Fy* — *’х3 + 2 к^у — Лф/3
е ' dy.
(43)
31
Интегралы (42) и (43) рассматриваются и в теории случай-
ных ошибок, но ввиду важности вопроса повторим вывод.
Для этого сначала представим показатель степени при е
Ф виде
— (fc/ + fc22) у2 Д- 2 к22ху — к22х2. (44)
Умножим и разделим второй член (44) на и еще
вычтем из (44) и прибавим к нему выражение:
&24ж2 ___ к2х2
(/ kf~+k2)2 ~ V + V ’
тогда получим показатель при е в виде:
- (V + V) У2 + 2«/ V к2 4- к2
7л 4 /у»2
Jz __ 2 2 ___
’ 2 I I- 2 /1/2 11 ‘
«1 I ^2
=- (V+V)?/2
к22х
к2х2
fc24 х'
/с24ж2 . „ _
*____ . If а --
• 2 ! Ъ 2 Л2 ----
1 |~П2
-- I 1/ у 2 [ /. 2 , ^2 Х Т к2 к2
- [У \ +fc2 у w +
Введем новую переменную интегрирования, обозначив
( 7л 2/^»
w+v
х2.
(45)
~Z.
(46)
Имея в виду, что мы интегрируем по у, и потому считая х
постоянным и диференцируя (46), получим:
da = Vк-,2 -р fc22 • dy,
откуда
dy =
da
Fv+a2'
(47)
Подставляя (45), (46) и (47) в (43), получим:
pxdx= Ух
' fl?'4
ft? + fc?
da
?fci2 + V
—Q*
32
или
рх dx =
А 2
Kj/kJ+k?
+ х
--00
НО
+*:
/* — г
/ с 6/3 = 1/^,
%
а потому
7,- 7л 7-,2t.,2 ,
рх dx = —е - x- dx, (48)
1AW + V
но по обозначению
Д fc, ___________________ р2 _______________ р
WW ~ я6 ,/tt ~ т
у а2 bi
и
к*к22 р2
fc/2 + fc,2 а2 + Ъ2 ’
а потому, сделав соответствующую замену, получим:
__ > Х1
р р аа + г>2
рх dx — г---- е dx. (49)
/-(«2 + &2)
Сравнивая полученное выражение (49) с (40), видим, что
в числителе дроби показателя при е вместо (х— у)2 стоит х2,
а в знаменателе вместо квадрата срединного отклонения пушки
стоит сумма квадратов срединного отклонения пушки и сре-
динной ошибки в положении цели.
Но выражение (49) получено преобразованием выражения
(42), которое дает вероятность попадания при одном выстреле
с учетом закона ошибок в положении цели, а поэтому можем
считать доказанным, что вероятность попадания при одном
выстреле можно вычислять, не учитывая закона ошибок в поло-
жении цели отдельно, но считать положение цели достоверно
известным и рассеивание орудия характеризуемым не таблич-
ным отклонением а, а отклонением |/ч2 4- Ъ\ где Ъ — срединная .
ошибка, характеризующая закон ошибок в положении цели.
Для получения вероятности одного попадания в цель конеч-
/>• SY*
ных размеров (₽2 —₽J, где и Pi = 11(>
\/ а2 Д- Ь2 У а- -р- б2
обходимо (49) интегрировать по х в пределах . ₽2:
** Теория стрельбы 33
или
Распространяя этот вывод на случай наличия ошибок в опре
делении перемещения цели, кроме ошибок в определении е<
положения аналогичным выводом, получим:
(52
где с — срединная ошибка, характеризующая закон случайны?
ошибок в определении перемещения цели.
Если мы имеем дело с плоскостью или с пространством
т. е. с эллиптической или с эллипсоидальной ошибками, то
перемножая вероятности по сопряженным направлениям, мь
каждый раз будем приходить к тому же выводу, но только дс
тех пор, пока говорим о вероятности попадания в предполо
жении одного выстрела.
[9. Приемы вычисления вероятности одного
попадания при точно заданном положении цели
Для вычисления вероятности (одного) попадания при задан-
ном положении цели необходимо знать размеры цели, положе-
ние цели относительно центра группирования и величину сре-
динного отклонения орудия.
а) Пусть в О (черт. 13) центр группирования или место
прохождения средней траектории. Обозначим срединные откло-
нения орудия: по дальности — Вд и боковое—Вб.
Вероятность одного попадания в полосу MNRS, бесконеч-
ную по ширине, по глубине равную (ж2 — xj и расположенную
перпендикулярно к одной и параллельно другой оси группи-
рования, выразится в виде:
где
— р2^2 1
^=-[Ф(р2)-ФО
(53)
। __
Вд “ Вб'
34
В том 'случае, если центр группирования О будет лежать
в0утри полосы MNRS, то в силу нечетности функции, если мы
условимся считать направление орудие — цель положительным,
в формуле (53) в прямых скобках будем иметь не разность,
а сумму.
В частном случае, когда центр группирования лежит на
кромке цели и хг = 0, то = О и
ф(Рз)>
(54)
а при ..
М N
Х2 = О и х1 = — х, Ч
и тогда получим:
1 п.----
рж=^-ф(₽1)- (54') и~-----уг--------
В обоих случаях вероятно-
сти будут при той же глубине
цели равны, а аргументом будет
служить глубина цели, выра-
женная в срединных отклоне- с
ниях.
В том случае, когда центр Черт. 13.
группирования совпадает со сре-
диной глубины цели бесконечной ширины (см. черт. 13), выра-
жение (53) примет вид:
₽ = и х — половина ширины цели.
Если обозначить через 8 — глубину цели
мерно равным то это выражение примет вид:
ВО
и принять р при-
рх= ф
(55)
Для вычисления вероятности одного попадания в случае
ограниченной прял оугольной цели со сторонами, параллель-
ными главным осям группирования, и с центром группирования
® О надо найти ве} оятность попадания в полосу (черт. 14)
глубиной (х^ — Ху'), предполагая ее бесконечной по ширине,
потом в полосу шириной предполагая ее бесконеч-
ной по глубине (черт. 14).
35
Исходя из того, что оси группирования являются частны
случаем сопряженных диаметров эллипса, вероятность поп;
Дания в цель KLMN найдем как вероятность сложного собь
тия, состоящего из двух простых независимых событий, и эт
вероятность будет равна произведению вероятностей попадани
в каждую из полос.
Аналитически это выражение
0,68182
----= 0,34091;
Р=-ра.ри = 0,28955 • 0,34091 =0,09871 = 9,871%.
случаев будет достаточно ограничиться
процента и даже целыми процентами, и
В большинстве
десятыми долями
тогда
имеет вид:
Р=РхРу =
ri/y,
где
Л/
в
Черт. 14.
Вб’
Р‘2
Вб'
%
Вд
Интегралы (53) и (56)
слены и помещены в табл,
приложения).
Вд И
У,
La
центра цели Ц: — зо саж.
Вб~а саж.
и
(5f
Л
В
О
12
L
55
•U
В
Черт. 15.
вычи
з (см
Пример. Найти вероятность во
падания в прямоугольник ABGL
глубиной 50 саж. и ширино!
10 саж., если координаты центр;
группирования О относителык
— 7 саж. (черт. 15); ВЗ = 40 саж.
б) Вероятность попадания в полосу, когда ограничивающие
ее параллельные прямые не параллельны осям группирования.
Пример 1. Найти вероятность одного попадания в условиях
черт. 16; В0 = 4О саж.; Вб=Ь саж.
Предварительно надо найти отклонение, вызываемое эллип-
тической ошибкой, от направления полосы MN или Ве по направ-
лению оси ое:
Ве = У ВО2 cos2 ® Во2 sin2 да = ]/402 cos2110° 52 sin2 110°=
= 14,465 саж.
р
= Ф (1,73) —0,7567
5э
й)^1’375’
14,465
Пример ?. Найти вероятность одного попадания в условиях
черт. 17; Вд~ 40 саж.; Вб—а саж.
4U = 0’125’
12
— =2,4;
Ве= У402 COS2 70°+ 52 Sin2 70°= 14,465;
20 Y -
14,465 / ~
1 [Ф (4,84) - Ф (1,38)] = 0^9889-0^804 =
70
14,465
— ф
ол;
74 = ~ [ф (1,375) — Ф (0,125)] = °>64629 — 0,06719
ф35085- = 0,17543,
0,57910
=-----5----= 0,28955;
Ру — 1ф (23) — Ф (0,4)] = ^9450 — 0,21268
или, приближенно, 17,5%.
Если бы в условиях черт. 16 и 17 было предложено опре-
делить вероятность попадания в цель ограниченных размеров,
4'0 для точного решения этого вопроса необходимо условие,
чтобы цель представляла собой параллелограм, ограниченный
Прямыми, параллельными двум сопряженным диаметрам эллип-
37
36
са; но так как практически такого условия встретиться н
может, то обычно в таких случаях либо прибегают к графиче
Черт. 16.
скому методу, пользуясь сеткой кругового распределения по
закону Гаусса (см. приложения), при помощи которой можно
подсчитать вероятность по-
падания в цель любой фор-
мы, либо прибегают к при-
ближенному способу, обра-
щая цель любой формы в
равновеликий прямоуголь-
ник со сторонами, парал-
лельными осям группи-
рования, не изменяя при
этом относительного поло-
жения центра цели и сред-
ней траектории.
в) Для подсчета вероят-
ности попадания с помощью
круговой сетки цель и по-
ложение средней траекто-
рии относительно цели
трансформируют в масшта-
бе круговой сетки Гаусса.
Перенеся цель и точку по-
ложения средней траекто-
рии на прозрачную бумагу,
совмещают точку средней
траектории с центром сетки,
цель поворачивают вокруг
центра круговой сетки в положение, удобное для графиче-
ского подсчета, и подсчитывают вероятность попадания. Этот
38
способ при небольшой практике дает по точности очень хоро-
шие результаты.
Рассмотрим этот способ подсчета вероятности попадания на
частном примере.
Пример. Пусть на черт. 18 дана теневая проекция цели,
построенная для курсового угла 30° и угла падения 2б°33'.
Положение средней траектории задано (масштаб 1 саж.=
= 2 мм). Очертание цели дает возможность ограничиться
шестью точками. Начало координат произвольно берем в точке О
и ось УУ-ов направим в плоскости стрельбы.
Снимем координаты точек в саженях и, разделив на
величину ВЗ = 40 саж. и на величину Вб—5 саж., получим
координаты точек, выраженные в срединных отклонениях, но по
оси YY-ов в отклонениях по дальности, а по оси ХХ-ов — в откло-
нениях боковых (табл. 7).
Таблица 7
Координаты точек, выраженные в срединных отклонениях
Название Xi Vi Вб Вд Xi Вб Vi Вд
с а а е н и
Центр группиро-
вания —1 —15 —- — —0,2 —0,375
I +15 +26 — — +^ +0,65
II +14 4-ю — — +2,8 +0,25
ш —3,5 —20 5 40 —0,7 —0.5
IV —15 —26 — — —3 —0,65
V —15 —13 — — —3 —0,325
VI +2 +16,5 — — -1-0,4 +0,4125
В этой таблице выражены в боковых отклонениях и —
в отклонениях по дальности, а потому, если, пользуясь этими
координатами, построим положения точек, приняв за единицу
Вд = Вб в масштабе круговой сетки, мы трансформируем цель
для кругового рассеивания, т. е. для такого случая, при кото-
ром Вд = Вб~Е.
Черт. 19.
Приняв во внимание, что на черт. 19 Вд — Вб=20 мм, мы
олучим трансформированные координаты точек, которые све-
Дены в табл. 8.
39
Таблица 8
Координаты точек, показанные на черт. 19, в мм
Название точек Xi Hi Название точек Ш yi
м М ММ
Центр групппро-
вания —7,5 IV . . —60 —13
I 460 +13 V ... —60 —6,5
II + 56 + 5 VI ... + 8 +8,25
III —14 —10
Черт. 19 дает изображение цели, трансформированное для
круговой сетки Гаусса данного масштаба.
Пересняв трансформированное изображение цели и точку
прохождения средней траектории Ц на прозрачную бумагу и
наложив эту бумагу на круговую сетку Гаусса, совмещаем
среднюю траекторию с центром сетки. После этого изображе-
ние цели можно развернуть в положение, наиболее удобное
для подсчета. На черт. 20 цифры даны в тысячных долях
процента и показывают вероятность попадания в площадь
^ВдХ^-Вб.
146 288 504 792 111L
164 3^ 565 887 1243 1558
164 322 565 887 1243 1558 1743
146 288 504 792 1111 1392 1558
1558 НО 7УГ
JZ43 Ш W 164
1743 1558 1243 887 565 322 164
1558 1392 1111 792 504 288 146
Черт. 20.
Просуммировав эти числа и поделив их на тысячу, получим
вероятность попадания:
Р=13,9%
или
0 = 0,139.
Кроме разобранного способа, существуют и другие способы
трансформации цели для круговой сетки Ч
1 Капитан 1-го ранга У нк о некий, Расчет сеток распределения по
закону Гаусса, Военно-морская академия им. тов. Ворошилова, лптогр.
издание.
40
Из приближенных способов определения вероятности одного
попадания рассмотрим „способ прямоугольника". Сущность его
заключается в том, что принимают цель за геометрическую
фигуру, к которой по форме цель ближе всего подходит. Опре-
деляют площадь этой фигуры и один из размеров. Разделив
площадь на величину одного измерения, например, на „рабо-
тающую ширину у цели" или, что то же, на ее проекцию на
направление, перпендикулярное к плоскости стрельбы, полу-
чают другое измерение в плоскости стрельбы. Таким образом,
цель будет заменена равновеликим прямоугольником со сторо-
нами, параллельными осям группирования. Определить вероят-
ность попадания в такой прямоугольник затруднений не пред-
ставляет.
Разберем весьма частый случай замены теневой проекции
корабля прямоугольником. Для этого отдельно вычисляют
поражаемое пространство высоты борта или с помощью столб-
цов основной таблицы стрельбы, дающих цены делений по
высоте и по дальности, или по формуле
d = 7iCtg6c., (57)
где
h— высота цели,
6(. — угол падения.
Величина d зависит только от дальности, но от курсового
угла цели, конечно, не зависит.
Затем принимают палубу за эллипс, площадь которого выра-
зится через длину L и ширину I корабля:
P=^-Ll = 0,8Ll. (58)
х
При курсовом угле цели 0°, оставив ширину цели равной I,.
для глубины цели будем иметь 0,8 L.
При этом размеры прямоугольника определятся:
работающая ширина
К—1 (59)
и полное поражаемое пространство
D = 7ictgSe-|-o,8Z. (60)
Для курсового угла 90° глубина палубы принимается рав-
ной I. Размеры цели при этом определяются:
полное поражаемое пространство
D = h ctg 6С Д-1 (61)
и работающая ширина
/Г = 0,8П. (62)
Для любого курсового угла q работающая ширина цели при-
нимается равной проекции 0,8 L [см. формулу (58)] на плос-
кость, перпендикулярную к плоскости стрельбы:
К — 0,8 L sing. (63)
41
Глубина палубы полупится, если площадь палубы поделим
на К, и
Р 0,8 LZ
= ----— I- cosect/. (64)
К O.SLsmq J '
Тогда полное поражаемое пространство
D = Z cosec </-[-7ictg.6c. (65)
Ясно, что этот способ не только грешит численно, но и
•принципиально не верен, однако, ввиду его простоты, он
широко применяется в тех случаях, когда нужны приближен-
ные цифры.
Пример. Определить приближенно „по способу прямоуголь-
ника" вероятность одного попадания в корабль длиной 60 саж.,
шириной 8 саж. и высотой 3 саж. Угол падения 6С =
= 26°33' tg0e_; курсовой угол цели с/= 30°; Вд—10 саж.;
Вб~5 саж. Средняя траектория проходит через центр цели:
K=Q,8L sinq = 0,8 • 60 • 0,5 = 24 саж.;
a = l cosec 9 = 8 *2 = 16 саж.;
d = hctg0c = 3 -2 = 6 саж.;
D~ 16-|-6 = 22 саж.;
Рж==ф(“2Вй) и 1)г==ф(твб) ’
Рх=ф (Й)=ф (0,275) = °’15:
(24\
— ) = Ф(2,4) = 0,89;
I р=рвр, = 0,134 = 13,4%.
Из примера видно, что мы получили величину, очень близ-
1 кую к полученной в предыдущем примере.
। 10. Вероятность попадания при нескольких
выстрелах, когда положение цели относительно
центра группирования точно задано
Говорить о вероятности попадания при нескольких выстре-
। лах возможно только тогда, когда обусловлена та комбинация,
вероятность которой ищется.
В этих случаях можно говорить или о вероятности хотя бы
одного попадания, или о вероятности только одного попада-
। ния, или о вероятности не меиее одного и не более другого
42
числа попаданий, или, наконец, о вероятности отсутствия про-
махов. Понятия же просто „вероятности попадания" при несколь-
кИх выстрелах и без всякого оговоренного наперед усло-
вия не существует.
Иногда в этом случае говорят о „проценте попадания",
как >вым является не что иное, как математическое ожидание
числа п шаданий на выстрел. При этом необходимо подразуме-
вать, что вычисление делалось в предположении очень боль-
шого количества выстрелов.
Говоря о вероятности •той или иной комбинации попаданий
и промахов при нескольких выстрелах, заметим, что практиче-
ское значение им чот только три положения:
1) вероятность хотя бы одного попадания;.
2) вероятность иметь не менее заданного числа попаданий и
3) вероятность отсутствия промахов.
Для определения вероятности одной из указанных выше
комбинаций в том случае, когда положение цели точно задано,
необходимо найти вероятность попадания при одном выстреле
и подсчитать вероятность искомой комбинации.
Пример 1. Стречьба ведется одиночными выстрелами. Число
выстрелов р. Требуется найти: вероятность хотя бы одного
попадания, вероятность иметь не менее т попаданий и вероят-
ность не иметь промахов. Положение цели, ее размеры и рассеи-
вание орудия известны.
Если вероятность одного попадания будет р, то вероятность
промаха 4 = 1—р, а вероятность хотя бы одного попадания
будет:
Р = 1— (1 — p)v- =1 — р . (66)
Вероятность иметь не менее т попаданий будет:
р! (р — т)\
р!
(67)
или
пг = (т — 1)
р! (р — тУ.
т! р q
(68)
Пользоваться ли формулой (67) или (68) — безразлично, но
надо выбирать ту из них, которая решает задачу с меньшей
затратой труда и времени, что будет зависеть от величин ци®.
Вероятность не иметь промахов будет
11=^. (69)
Остальные комбинации практического значения не имеют.
Пример 2. Решим численно пример 1, если р = 80 и тре-
буется найти вероятность хотя бы одного попадания, вероят-
ность иметь не менее трех попаданий, вероятность иметь не
43
менее 15 попаданий и вероятность не иметь промахов. При этом
найдена вероятность одного попадания р = 0,2.
Вероятность хотя бы одного попадания:
Р=1 — д80=1 —10—8 . 17668 = 0,999999982332 1.
Вероятность иметь не менее трех попаданий:
П>3 —1 ~
80 - 79 „ „„ . Rn
——80р q,J <?80
= 0,9999961394 % 1.
Вероятность иметь не менее 15 попаданий получится по
интерполяционной формуле приближенно 64,4%.
Точный ответ на вопрос получим по выражению:
80!
11—1 > , —;—-————— rnm — т
1 _0 (80 — ту” ч
11. Применение теоремы гипотез к вопросам артил-
лерийской стрельбы для образования распределения
цели (распределение вероятностей гипотез о месте
цели после того или иного вида наблюдения)
Теорема гипотез отвечает на вопрос о вероятности той или
иной гипотезы после наблюдения и регистрации какого-либо
результата, полученного путем того или иного опыта; при этом
вероятность тех же гипотез до опыта может быть известна, но
может быть и неизвестна. В последнем случае решение вопроса
возможно, если гипотезы до опыта можно принимать равно-
вероятными.
Обычно основным вопросом при стрельбе является прицель-
ная дальность до цели, выражаемая или в табличных установ-
ках орудия, или в виде угла, соответствующего данной таблич-
ной дальности.
Обычно табличные установки орудия получаются введением
ряда поправок в непосредственно измеренную или снятую
с карты дальность.
Всякое измерение, а также учет факторов стрельбы, при
введении поправок сопровождается случайными ошибками изме-
рения и не может нам дать истинного значения прицельной
дальности.
Зная закон, которому подчиняются наши ошибки, а также
зная параметры, которыми характеризуются законы этих оши-
бок, и ноль уясь теоремой гипотез, мы можем по основному
признаку „прицельная дальность", регистрируя систематически
вспомогательные признаки (измерения, наблюдения знака паде-
ния и до.), значительно сузить пределы возможных ошибок и
не только сузить, но и указать их вероятное распределение.
Примем, что ошибки в измерении ргтсстояния до цели и
оши< ки при введении поправок подчиняются закону Гаусса.
До измерения расстояния до цели, в силу незнания коор-
динат цели, принципиально и теоретически мы можем считать
44
все наши предположения о месте цели равновероятными от
— со до 4-оо-
После измерения расстояния и по введении поправок при-
цельная дальность до цели, являясь определенной величиной,
будет содержать в себе некоторую случайную ошибку, и наши
предположения или гипотезы б величине этой ошибки хотя
принципиально и имеют пределы от —оо до-ф-оо, но уже на
основании частного случая теоремы гипотез не будут равно-
вероятны, т. е. мы придем к более узкому распределению
вероятностей гипотез о месте цели, или, как говорят, распре-
делению цели, которое появилось независимо от нас, но на
объективном основании регистрации некоторого признака, полу-
ченного путем опыта.
Поясним сказанное примером. Пусть по сложении законов
ошибок в измерении расстояния до цели и в учете всех фак-
торов, сопровождающих стрельбу, мы получим закон Гаусса
со срединной ошибкой Л’. Приняв за единицу измерения средин-
ное отклонение орудия Вд и обозначая Е масштабное черезЕм,
получим:
Положим, мы получим Ем —2.
Пользуясь выражением закона Гаусса через срединную
ошибку
Ж'2
?У==?(Х.)= Р---е
Ем
произведем вычисление ординат 7/ = ®(.t), которое и сведем
в табл. 9.
Таблица !)
Вычисление ординат у — ср (*)
К" ординат ГЕ» Xi Ем Ev. .’/«=? (О')
0 0 0 0,2691 0,1346
1,2 1 0,5 0,2537 0,1268
3,4 2 1 0,2143 0,1071
5,6 3 1,5 0,1613 0,0806
7,8 4 2 0,1083 0,0541
9,10 5 2,5 0,0652 0,0326
11,12 6 3 0,0347 0,0173
13,14 7 3,5 0,0168 0,0084
15,16 8 4 0,0071 0,0035
17,18 9 4,5 0,0028 0,0014
19,20 10 5 0,0009 0,0004
21,22 И 5,5 0,0000 0,0000
22
X г/i —1,0000
О
45
Построим по ординатам для наглядности кривую АВС
(черт. 21). Это будет кривая, характеризующая распределение
цели.
Рассмотрим подробнее эту кривую. Площадь, ограниченная
кривой (в пределах точности вычислений при применении пра-
вила трапеций), равна единице.
Каждая ордината кривой численно выражает площадь тра-
пеции, ограниченной осью абсцисс, двумя ординатами, нахо-
дящимися от данной на расстоянии-|-~Вди—— Вд.
2 2
Отношение этой площади или численно ординаты ко всей
площади, ограниченной кривой, дает вероятность гипотезы
о месте цели в этих пределах по отношению к прицельной
дальности.
Так как величины ординат численно равны элементарным
площадям, а вся площадь кривой равна единице, то сама вели-
чина каждой ординаты выражает вероятность гипотезы о месте
цели в пределах от-(--|- В0до—от этой ординаты.
Пользуясь кривой распределения, мы можем подсчитать
вероятность нахождения цели по отношению к прицельной
дальности в любых пределах. Пусть центр распределения О
является одновременно и прицельной дальностью. Вероятность
положения цели в пределах от А до С практически равна 100%.
Вероятность нахождения цели от К до L:
К---L- ' ' W +й,о4'^2 +
Ч-з/4 4- з/в -Ь з/8—;
46
р^,= 1 (0,0541 -J- 0,0806 4- 0,1071 + 0,1268 -}- 0,134 6 -}- 0,1268-}-
+ 0,1071 + 0,0806 + 0,0541 — 0,0541 ^ 0,Qo41 =
= 0,8177 = 81,77%.
Примечание. Собственно, для получения этой вероятности мье
должны бы были взять отношение площади KK^L к площади всей
кривой, но берем просто площадь KKpL^L в силу того, что вся площадь,
кривой равна единице.
Положим дальше, что по исчисленной нами прицельной даль-
ности до цели (ее основной признак), направив среднюю траек-
торию в центр распределения О, мы произвели один выстрел
и наблюдали попадание.
Наличие рассеивания пушки не позволяет нам утверждать,
что цель наверное находится в точке О, но, пользуясь теоремой
гипотез и на основании объективного признака — попадания,
мы можем снова подсчитать распределение цели.
По теореме гипотез имеем:
— вероятности гипотез до наблюдения попадания; мы их имеем
в виде ординат кривой распределения АВС, а вероятности
попадания, написанные в виде интеграла, мы подсчитаем для
каждой гипотезы о месте цели. Пусть цель имеет глубину, рав-
ную Вс1 = 1, при бесконечно большой ширине.
Тогда получим новое распределение (см. табл. 10 на стр. 48).
Построим для наглядности (черт. 21) кривую DEF. Одновре-
менно с прицельной дальностью, систематически регистрируя
результаты опыта (измерение расстояния, наблюдение попада-
ния), мы будем получать на основании теоремы гипотез новые,
более и более ограниченные распределения цели.
вн 1 Здесь z является линейной фувкпией от я1,- формула написанарв общем
зала вслеДствие того, что вопрос о вычислении вероятности попадания при
‘ А ином распределении рассматривается ниже.
4?
Таблица 10
Распределение цепи после наблюдения попадания (к черт. 21)
№ ординат о (ж) Pi = Ф(₽) Pi ?(«) Xpi <?(ac
0 0,1346 0,2651 0,0357 0,2981
1,2 0,1268 0,2121 0,0269 0,2246
3,4 0,1071 0,1100 0,0118 0,0984
5,6 0,0806 0,0368 0,0029 0,0247
7,8 0,0541 0,0079 0,0004 0,0035
9,10 0,0326 0,0010 0,000g1 0,0000
11,12 0,0178 0,0002 Щх) pi- 1,0005
13,14 0,0084 0,0000' =0,1197
15,16 0,0035 — —
17,18 0,0014 — —
19,20 0,0004 — —
21,22 0,0000
Произведя большое количество измерений или пользуясь
другими результатами наблюдений, например, измеряя откло-
нения или регистрируя наблюдения знаков падений, мы будем
приходить все к более и более ограниченным распределениям
цели, составляя эти распределения на основании правила, выте-
кающего из теоремы гипотез.
При таком статистическом методе подхода к вопросу совер-
шенно отпадают вопросы об „истинном положении цели", об
ошибках этого положения и др., и при решении проблем
стрельбы, вырабатывая наивыгоднейшие правила путем объек-
тивного метода решения этой задачи, мы должны будем счи-
таться и оперировать с распределением цели.
Основной задачей при выработке правил стрельбы для выяв-
ления наивыгоднейших методов, т. е. таких методов, которые
при их систематическом применении дадут в среднем наилуч-
ший результат, является получение распределения цели и его
наивозможное ограничение.
Полученное распределение даст нам возможность подсчитать
вероятности и математические ожидания попадания и решить
целый ряд других вопросов при тех или иных видах научных
исследований.
12. Подсчет вероятности попадания при заданном
распределении цели
В § 9 и 10 были даны методы подсчета вероятностен попада-
ния при заданном положении цели относительно центра груп-
пирования. При решении тех или иных вопросов стрельбы, как
1 При вычислении с точностью до четвертого знака.
48
мы видели в § 11, такое положение не может иметь места,
g этом параграфе мы познакомимся с аналитическим выраже-
нием вероятности попадания и с фактическими приемами раз-
личных подсчетов вероятности попадания при заданном рас-
пределении цели.
1. Вероятность одного попадания при распределении цели
только в направлении дальности.
Пусть имеем распределение цели (черт. 22), которое обо-
значим
у = <^(х).
Вид функции % (ж) будет зависеть от метода стрельбы и от
характера самих наблюдений: получено ли распределение на
основании наблюдения знаков падений снарядов, измерены ли
дальности с введением поправок для перехода к прицельной
дальности, измерены ли отклонения точек падений снарядов
от цели и т. п.
Так как в настоящем параграфе мы будем пользоваться
заданным распределением и не будем касаться способов его
получения, как зависящих от метода стрельбы, то распределе-
ние цели будем принимать в виде г/ = ср2(ж).
Пусть выстрел дан с прицельной дальностью в О1; в рас-
стоянии R от центра распределения О, которое примем за
начало координат.
При положении цели, например, в М и при срединном откло-
нении пушки Вд — 1 вероятность попадания при одном выстреле
в цель бесконечно малых размеров выразится так:
Для цели же конечных размеров 2d эта вероятность будет:
В 4- d
Н — d
Обозначив ( — В = Z, получим d£ = dz. Вводя новую перемен-
ную и подобрав пределы, получим (черт. 22):
G-R)+ d
Ф ^-/?) + d]-
(£ — R) — d
— Ф [(Е — R)-~ d] | . (70)
4 та '
°РВя стрельбы 49
Выражение (70) дает вероятность попадания при достоверном
положении цели в М. Учитывая вероятность этого положения,
получим:
a — R) + а
ds dx •
(71)
Принимая же во внимание распределение и распространяя
(71) на все распределение, получим окончательно:
или
Практически интегрирование, выражение (73), ведется по
правилу трапеций, причем ср2 (ж) задана либо в виде того или
иного закона, либо численно, а значение интеграла
(Е-Ц)+ а
(?. —В)- d
ds
дается численно в табл. 3 (см. приложения).
50
При этом формулы (72) и (73) морут быть приближенно пред-
ставлены в виде:
4- оо
Р =пред. V ср2 (Ж)
(74}
Интегрирование начинается от наибольшего значения ср2(я)
и ведется в обе стороны, пока мы не сможем принять ср2(я) = О
или Pi = ®-
В том случае, когда известна срединная ошибка распреде-
ления Е, для вычисления вероятности одного попадания нет
надобности производить вычисление сложной схемы (72), (73)
или (74), а вероятность одного попадания найдем, воспользо-
вавшись теоремой (11) по выражению:
1ГФ / \ ф / l-R-d \ j
2L \l/B92 + E2 / /]
(75)
В формуле (75) все выражено в табличных единицах, и при
Вд = 1 будем иметь:
1Г /£ — R-\-d\ —
— ф I — --j— I — Ф I —— ]
2 L / \/ i-b-E2 Л
(76)
Рассматривая формулы (72) и (74), видим, что они дают
не что иное, как правило для вычисления вероятности одного
попадания на основании теоремы будущих событий при бес-
конечно большом числе гипотез.
Пример. Найдем вероятность одного попадания при распре-
делении, изображенном на черт. 21 (§ 11) кривой АВС. Вероят-
ность одного попадания найдем, пользуясь формулой (76), а
для сравнения — формулами (72) или (74). После этого для
уяснения значения ограничения распределения вычислим вероят-
ность одного попадания для распределения DEF (черт. 21).
- Среднюю траекторию направим в центр распределения О.
Цель возьмем размерами по глубине 2d = Bd и бесконечной
ширины.
Тогда имеем:
р = Ф
____1
2/ 1 +.Е2
но Е = 2 и, следовательно,
= Ф (0,223) =11,96%.
+ о°
Вычисление формулы (74) p = nVeK X ъ(х)Р4 расположим в
ВиДе табл. п.
4*
51
Таблица 11
Схема вычисления формулы (74) для распределения АВС (черт. 21)
№ ординат ?2(ж) Vi 1g ?2 (ж) 1g Pi Ig?2(»)Pi ?2 (a=)Pi
0 0,1346 0,2651 1,12905 1,42341 1,55246 0,0357
1,2 0,1268 0,2121 1,10312 1,32654 1,42966 0,0269
3,4 0,1071 0,1100 1,02979 1,04139 1,07118 0,0118
5,6 0,0806 0,0668 1,90634 1,56585 1,47219 0,0030
7,8 0,0541 0,0079 1,73320 1,89763 4,63083 0,0004
9,10 0,0326 0,0010 1,51322 3,00000 5,51322 0,0000
11,12 0,0178 0,0002 1,25042 4.30103 1,55145 —
13,14 0,0084 0,0000 — — — —
+ °°
Р-пред. £ ср2 (ж)р,-= 0,0357 4-2(0,0269+ 0,0118+ 0,0030 +
— оо
+ 0,0004 + 0,0000)= 11,99%.
Разница по сравнению с предыдущим вычислением, равная
0,03%, происходит исключительно ввиду ограничений арифме-
тической точности работы по формуле (74), и ясно, что для
вычисления - вероятности одного попадания нет надобности про-
изводить только что проделанные вычисления, когда возможно
сложение законов ошибок, а также имея в виду, что формулы
(50) и (51) (§ 8) дают решения точнее.
Для распределения DEF (§ 11, черт. 21) имеем табл. 12.
Таблица 12
Схема вычисления формулы (74) для распределения DEF (черт. 21)
№ ординат Pi + т2(ж) Ig Pi Ig?2 {X\Pi <?2 +) Pi
0 0,2981 0,2651 1,47436 1,42341 1,89777 0,0790
1,2 0,2246 0,2121 1,35141 1,32654 1,67795 0,0476
3,4 0,0984 0,1100 1,99300 1,04139 1,03439 0,0108
5,6 0,0247 0,0368 1,39270 1,56585 4,95855 0,0009
7,8 0,0035 0,0079 1,54407 1,89763 1,44170 0,0000
9,10 0,0000 0,0010 — — — —
+ »
Р=пред. S ?2 (ж)Pi = 0,0790 4-2(0,0476 4-0,0108
4-0,0009) = 19,76% \
1 В последнем случае лучше применить эту схему, так как это проще,
чем определять „срединную" ошибку распределения DEF, которая к тому же
не является уже законом Гаусса.
52
2. Вероятность хотя бы одного попадания при р выстрелах
на одном прицеле, т. е. в ту же точку распределения.
Приняв те ясе обозначения, имеем для вероятности р про-
махов при данном распределении:
тогда для вычисления вероятности хотя бы одного попадания
будем иметь:
— Ф(£- R-d)]j dx. (78)
Интегралы вида (77), (78) вычисляются с помощью правила
трапеций и имеют довольно сложную схему вычисления.
Представив их в виде
+
—пред-Е (ж) (1—р/, (79)
можно предложить следующую схему вычислений (табл. 13).
Таблица 13
Схема вычислений вероятности хотя бы одного попадания при р. выстрелах на
одном прицеле
№ орди^ нат Pi (1—Pi) = =4i Igffi plgft Ig <f>2 (a;)
P-
53
3. Вероятность иметь не менее к попаданий при р. выстрелах
„на одном прицеле", т. е. в ту же точку распределения.
Для вычисления^ вероятности иметь не менее к попаданий
надо подсчитать сумму вероятностей комбинаций из попаданий
и промахов от р. попаданий до к попаданий, или чаще бывает
удобнее в смысле сокращения вычислительной работы подсчи-
тать сумму вероятностей комбинаций из попаданий и промахов
от О попаданий до (к—1) попаданий и вычесть эту сумму ком-
бинаций из единицы.
Выражение для вычисления вероятности не менее к попа-
даний в этом случае напишется так:
m = [л
п= £
т = к
т\ (р- — т)1
|Ф (S — к 4- d) —
— Ф(£ — к— d)]m ^[Ф(Е — k-\-d) —
I 2
— Ф(? — к — d)l} m % (ж) ‘ dx. (80)
Имея в виду интегрирование по формуле трапеций (80),
можно приближенно написать:
= H UJ +“
n=S дацДда)! прел- ?атт9г-т =
m = (R —1) . + 00
= 1- 2 п1,ед- £ (81)
или выражение (81) может быть представлено в виде:
/
i = у, i = к — 1
П=£Р(=1- у; Pit (82)
t = к i = О
где
! + 00
Р<= - и'—пред. У ?2(ж)рГ94 ~т
да!(р— да)!
Выражения (80), (82) показывают, что для нахождения
вероятности не менее к попаданий в цель потребуется вычис-
лить ряд значений Р4 по ряду аналогичных схем, после чего
полученные значения Р^ просуммировать.
Схема работы будет иметь вид табл. 14.
54
55
Число подлежащих вычислению аналогичных схем будет
равно числу комбинаций, вероятности которых придется опре-
делить, после чего вероятность не менее к попаданий в цель
следует найти, пользуясь формулой (82) при вычисленных уже
значениях 1\.
Пример 1. Найти вероятность хотя бы одного попадания из
30 выстрелов в центр распределения АВС (черт. 21, § 11) при
2d = 1 или одному срединному отклонению пушки при бес-
конечно большой ширине цели.
Схема вычислений дается в табл. 15 (стр. 57).
Пример 2. Найти вероятность не менее трех попаданий в цель
из восьми выстрелов при распределении цели DEL (черт. 21,
§ 11). Глубину цели возьмем равной 1 (глубина цели Вд=1
при бесконечно большой ширине цели).
Для вычисления воспользуемся формулой (82) и табл. 15.
В результате будем иметь три схемы вычислений (табл. 16.
17 и 18). Вычисления дают, что при данных условиях стрельбы
вероятность попасть в цель ,не менее трех раз из восьми вы-
стрелов выражается величиной всего в 22,2%.
4. Вероятность хотя бы одного попадания при обстреле пло-
щади только по направлению дальности.
При обстреле площади на нескольких прицелах, когда на
одном прицеле дается кА выстрелов, на втором — к2 выстрелов
и т. д., причем кА Д- к2 + ks . . . -}-Ли=р, вычисление про-
изводят по формуле:
+05
П>х = 1 — пред. U у2 (х) (1 —ft?' (1 — ft'?"... (1 -ft”) (83)
или по формуле:
4“ 00
= 1 - £ Ъ И Qik'
— ОС
(84)
Пример. Найти вероятность хотя бы одного попадания при
стрельбе на трех прицелах по 10 выстрелов на каждом при
распределении АВС черт. 21 (§ 11).
Прицелы — в точку К, h2 — в точку О и h.t — в точку L,
считая, что глубина бесконечно широкой цели 2<Z=Bd = l.
Для этого составим схему, в которую впишем номера орди-
нат, значения вероятности гипотез %(ж), определим для каж-
дой гипотезы и каждого прицела вероятности одного попада-
ния ft и промаха qit после чего произведем вычисление схемы
по формуле (84) (табл. 19).
При рассмотрении вопросов о вероятности попадания мы не
касались вопроса о цели конечных размеров по ширине, дабы
не усложнять выводы и расчеты схем, имея в виду, что в тех
случаях, когда при исследовании методов стрельбы и при под-
счетах вероятностей попадания приходится оперировать с целью
конечных размеров по ширине, почти всегда приходится
56
Вероятность хотя бы одного попадания на одном прицепе при у. = 30 выстрелам
(распределение цели АВС, черт. 21)
57
Таблица 18
Вероятность не менее трех попаданий в цепь из восьми выстрелов
, т = (к — 1) = (3 — 1) = 2
№ ординат Vi 1 ~Pi = Чх 1g Pi 1g 4i 21g 61g^ 1g ?2(®) 1g <?2(.Х)р№
0 0,2981 0,2651 0,7349 1,4234 7,8662 7,8468 7,1972 7,4744 3, 5184 0,0033
1,2 0,2246 0,2121 0,7879 7,3265 7,8965 7,6530 7,3790 7,3514 3,3834 0,0024
3,4 0,0984 0,1100 0,8900 7,0414 7,9494 7,0828 7,6964 7,9930 4, 7722 . 0,0006
5,6 0,0247 0,0368 0,9632 7,5658 T, 9837 7,1316 7,9022 7,3927 — —
7,8 0,0035 0,0079 0,9921 3,8976 7,9966 3,7952 7,9796 3,5141 — —
1 = 0,0093
O' V to 3,9685
Ко—1) (о— -2)... (р—т-г 1) 8 = 28 Iff e m! (p- -m) ! 1,4472
т! ((л— -т)! т ! 1
1g P p—2 1,4157
P u.—2 0,2604
t Таблица
Вероятность не менее трех попаданий в цепь из восьми
выстрелов
т = (к — 2) = (3 — 2) = 1
№ ординат IgPi HgQi 1g ?2(®) 1g ?2(O5)'PiQt7 ?2^)Pi4i7
0 7,4234 7,0634 7,4744 3,9612 0,0091
1)2 7,3265 7,2755 7,3514 3,9534 0,0090
3,4 7,0414 7,6458 7,9930 3,6802 0,0048
5,6 7,5658 7,8859 7,3927 7,8444 0,0007
7,8 3,8976 7,9762 3,5441 — 1 —
feCr/Mi7 = 0,0381
^-1 = 8- 0,0381 = = 0,3048
Таблица 18
Вероятность не менее трех попаданий в цель из восьми
выстрелов
т = (к— 3) = О
№ ординат 8igg» tg Ы®) йШ5
0 7,9296 7,4744 7,4040 0,0254
1,2 7,1720 7,3514 7,5234 0,0334
3,4 7,5952 7,9930 7,5882 0,0387
5,6. 7,8696 7,3927 7,2623 0,0183
7,8 7,9728 3,5441 3,5169 0,0083
Х?2(гг)9»8==0’2128
p ! 32 =1 p = 0,2128
m ! (p—m)! ! ~ 8 m ! (p—m)! p-
сп
ю
И ., = 1— s pi=:l —(0,2604 4-0,3048 4-0,2128)=!—0,7780 = 0,2220. ити 22,2о/0,
и.—2
Черт. 23.
пользоваться для подсчета вероятности одного попадания сет-
кой, а при этом конечные размеры цели учитываются автома-
тически. Однако, ниже остановимся и на этом вопросе.
5. Вероятность попада-
ния при распределении це-
ли на плоскости и в про-
странстве. В некоторых слу-
чаях стрельбы приходится
оперировать с распределе-
нием цели на плоскости
и в пространстве.
Не касаясь пока вопро-
сов построения самих рас-
пределений, укажем, что
распределение на плоско-
сти получается при стрель-
бе, когда нужно бывает вы-
брать дальность и направ-
ление; в этом случае по-
лучается распределение це-
ли в горизонтальной пло-
скости. При стрельбе шрап-
нелью при прямой наводке,
а также при стрельбе удар-
ными снарядами по зенит-
ным целям мы будем иметь
распределение цели в вер-
тикальной плоскости.
При стрельбе шрапнелью
по невидимой цели, когда
надо выяснить прицельную
дальность, целик (или угло-
мер) и трубку, распределе-
, ние будет в пространстве;
наконец, с распределением
в пространстве приходится
иметь дело при решении
вопросов стрельбы по зе-
нитным целям дистанцион-
ными снарядами.
Не касаясь здесь вопро-
Са Распределений на пло-
скости или в пространстве
одробно, покажем, что подсчет вероятностей попадания в этом
л5-чае принципиально не отличается от изложенного выше, и
Р зница только в объеме вычислительной работы.
по РимеР- Дано распределение на плоскости по закону Гаусса
Иц ДвУм независимым и взаимно перпендикулярным направле-
“ П0 Главным осям) со срединными ошибками по большой
25 саж. и по малой оси —10 саж. Плоскость стрельбы на-
60
61
правлена под углом 20' к большой оси. Цель имеет размеры
80 саж. по глубине (вдоль плоскости стрельбы) и 8 саж. в
перпендикулярном направлении, представляя прямоугольник.
ВО = 25 саж; В£=3 саж. Требуется найти вероятность хотя бы
одного попадания при четырех выстрелах, направленных в
центр распределения.
Построим распределение в масштабе через одно срединное
отклонение и впишем вероятности гипотез по закону Гаусса
(для простоты будем считать все распределение отЦ-4В до
— 4 В). При этом вследствие симметрии фигуры (черт. 23) впишем
цифры и будем делать подсчет только для половины распреде-
ления, а затем полученную сумму произведений для половины
фигуры удвоим.
Помещая центр цели в центр каждой клетки и вычисляя
для каждой гипотезы вероятность попадания, впишем эти ве-
роятности на чертеж.
Порядок дальнейшей работы ясен из черт. 23 и схемы вы-
числений (табл. 20), причем расстояние между центром цели и
центром группирования лучше всего снимать с чертежа графи-
чески.
Таблица 20
Вероятность хотя бы одного попадания при распределении цепи на
плоскости
№ ор- динат Pi 1g Qi 4 Ig Qi 1g ?2 (®) Ig?2(a5)««4 ?2 (®) 4?
1,2 0,0625 0,061 0,939 Г, 9727 1,8908 7959 2,6867 0,0486
3,4 0,0625 0,188 0,812 Г, 9096 Г, 6384 “ 7959 2,4343 0,0272
5,6 0,0403 0,037 0,963 Г, 9836 Г, 9344 2,6053 Т.5397 0,0346
7,8 0,0403 0,127 0,873 Г, 9410 Г, 7640 2,6053 2*, 3693 0,0234
9,10 0,0168 0,000 1 0 0 — — 0,0168
11,12 0,0168 0,000 1 0 0 — — 0,0168
13,14 0,0045 0,000 1 0 0 — — 0,0045
15,16 0,0045 0,000 1 0 0 — — 0,0045
17,18 0,0403 0,000 1 0 0 — — 0,0403
19,20 0,0403 0,035 0,965 Г, 9845 Ц9380 2,6053 2,5433 0,0349
21,22 0,0260 0,000 1 0 0 — — 0,0260
23,24 0,0260 0,107 0,893 Г, 9509 Г, 8036 Г, 4150 2,2186 0,0165
25,26 0,0109 0,000 1 0 0 — — 0,0109
27,28 0,0109 0,012 0,988 Г, 9948 Г, 9792 2,0374 2,0166 0,0104
29,30 0,0029 0,000 1 0 0 — — 0,0029
31,32 0,0029 0,000 1 0 0 — — 0,0029
33,34 0,0168 0,000 1 0 0 — — 0,0168
35,36 0,0168 0,000 1 0 0 — — 0,0168
62
Продолжение табл. 20
№ ор- динат Pi Qi 1g Qi 4 1g Qi 1g ?2 fa) 1g ?2(®)0i4
37,38 0,0109 0,000 1 0 0 — — 0,0109
39,40 0,0109 0,022 0,978 Г, 9903 Г, 9612 2", 0374 IT, 9986 0,0010
41,42 0,0045 0,000 1 0 0 3",6532 Г, 6532 0,0045
43,44 0,0045 0,020 0,980 Г,9912 Г, 9648 Г, 6532 Г, 6180 0,0042
45,46 0,0012 0,000 1 0 0 Г, 0792 Т,0792 0,0012
47,48 0,0012 0,009 0,991 Г, 9961 Г,9844 Г, 0792 Г, 0636 0,0012
49,50 0,0045 0,000 1 0 0 — — 0,0045
51,52 0,0045 0,000 1 0 0 — — 0,0045
53,54 0,0029 0,000 1 0 0 — — 0,0029
55,56 0,0029 0,000 1 0 0 — 0,0029
5'7,58 0,0012 0,000 1 0 0 — — 0,0012
59,60 0,0012 0,006 0,994 Г, 9974 Г, 9896 Г, 0792 8Д)688 0,0012
61,62 0,0003 0,000 1 0 0 — — 0,0003
63,64 0,0003 0,088 0,912 Г, 9600 Г, 8400 Г, 4771 4,3171 0,0002
0,3955
S = 0,7910
II >1=1 — 0,7910 = 0,2090 = 20,9%
ГЛАВА III
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ПОПАДАНИЯ
13. О математическом ожидании попадания
при одном выстреле
Согласно теореме Якова Бернулли, имеем, что при доста-
точно большом числе испытаний можно утверждать с вероят-
ностью, сколь угодно близкой в единице, что среднее значение
из полученных на опыте значений некоторой величины, на-
пример, числа попаданий при стрельбе, будет сколь угодно мало
отличаться от математического ожидания этой величины.
В том случае, если мы делаем по одному выстрелу ударным
снарядом в большом числе таких стрельб, мы можем иметь
каждый раз или одно попадание, или ноль попаданий.
При увеличении числа таких стрельб среднее значение числа
попаданий на выстрел мало отличается от математического
ожидания числа попаданий на выстрел.
С другой стороны, математическое ожидание определяется
выражением:
а=а?1р1-|-ж2р24-ж3р3-|- ...-\-хпрп.
Возвращаясь к случаю, когда мы только и можем говорить
об одном попадании, т. е. при одном выстреле, частное значе-
ние переменной величины может быть ^=1, вероятность чего
'будет р, где р— есть вероятность одного попадания, и я2 = 0,
вероятность чего будет (1—p) = q.
Подставив эти значения в определение математического ожи-
дания, получим:
а = 1 • р + 0 • (1— р)
или
а—р, (85)
т. е. при одном выстреле математическое ожидание попада-
ния численно равно вероятности попадания. Следует иметь в
виду, что равенство (85) имеет только численное значение.
Отсюда имеем правило: для определения математического
ожидания попадания при одном выстреле надо вычислить
64
вероятность одного попадания и полученную величину принять
равной математическому ожиданию попадания.
1. Математическое ожидание числа попаданий и числа попа-
даний на выстрел при у. выстрелах на одном прицеле. Исходя
из свойства математического ожидания, можем сказать, что
для определения математического ожидания числа попаданий
при р- выстрелах достаточно подсчитать его при одном выст-
реле и умножить на число выстрелов.
Математическое ожидание числа попаданий на выстрел при
р выстрелах на одном прйцеле, очевидно, будет равно мате-
матическому ожиданию попадания при одном выстреле.
Пример. Положим, что вероятность одного попадания р =
= 0,1196.
Определить математическое ожидание числа попаданий при
50 выстрелах, произведенных при аналогичных условиях.
Математическое ожидание « = 0,1196 попадания при одном
выстреле или числа попаданий на выстрел, а математическое
ожидание А числа попаданий при 50 выстрелах будет:
А = 0,1196 попадания X 50 = 5,98 попаданий.
Необходимо обратить внимание на то, что в то время как
вероятность попадания является числом отвлеченным, матема-
тическое ожидание попадания или числа попаданий, а также
числа попаданий на выстрел, числа именов-анные. Например,
5,98 попаданий, следует понимать так: при большом числе
стрельб в среднем на 50 выстрелов будем иметь число попа-
даний, близкое к 5,98. Это лишний раз подчеркивает, что пра-
вила, вырабатываемые на основании теории вероятностей,
оправдывают себя при их систематическом применении.
2. Математическое ожидание числа попаданий и числа попа-
даний на выстрел при стрельбе на нескольких прицелах. Для
вычисления математического ожидания числа попаданий на
нескольких прицелах надо найти таковое для каждого из при-
целов, помножить его на число выстрелов соответственно
каждому прицелу и полученные произведения сложить.
Если на прицелах hlf h2... hn дано ки к2... кп выстрелов и
математическое ожидание попадания на выстрел alt а2... ап, то
математическое ожидание числа попаданий
А = dj кг -р «2 к2 -р... -И «и кп , (86)
а Математическое ожидание числа попаданий на выстрел
«I к^ -р «2 к2 —р... —Р «и кп
k-i + kt -р ... -f- кП
(87)
j юрРимеР- В качестве примера подсчитаем для распределения
вы G 'чеРт- 21) математическое ожидание числа попаданий на
пн^ТреЛ С нрщелами hlf h2 и hs при 10 выстрелах на каждом
дин еле по цели глубиной 1 —Вд и' бесконечной ширины. Сре-
ь иная ошибка распределения Е—2.
отреаьби
Во-первых, найдем математическое ожидание попадания на
один выстрел для каждого прицела.
Согласно § 12 пишем:
R=y В02 4-Е2 ^j/l+25 = ]/5 = 2,23.
Приняв рассеивание пушки равным R, будем считать, что
распределения нет, а цель достоверно находится в О (черт. 21).
Глубина цели при этом будет:
Тогда
₽2=2,01 и ^ = 1,57;
«г = — Цф (2,01) —Ф (1,57)
= 0,0573;
«о=О,1198 (по § 12 среднее из двух вычислений);
«2=0,0573 (в силу симметрии);
10 • 0,0573-4-10 • 0,1198+ 10 • 0,0573 2,344
у —~ __________!______'_____'_______________ ___ __
30 30
= 0,0781 попадания, или среднее математическое ожидание
численно равно средней вероятности попадания.
Обращаем внимание на то обстоятельство, что математическое
ожидание подсчитывается значительно проще по сравнению с
вероятностью.
3. Математическое ожидание поражения цели при стрельбе
залпами. Математическое ожидание поражения цели при
стрельбе залпами мы рассмотрим для условий, когда огневая
задача поражения цели решается при одном попадании, т. е.
когда мы будем искать „математическое ожидание хотя бы
одного попадания". В этом, и именно в этом, случае задача
будет иметь иное решение по сравнению с изложенным выше.
При нахождении же вообще величины математического ожи-
дания попадания или числа попаданий на выстрел вычисления
производятся, как изложено было выше, и независимо от
того, ведется ли стрельба одиночными выстрелами или залпами.
Стрельба залпами может производиться как на одном, так
и на нескольких прицелах.
При стрельбе залпами математическое ожидание поражения
цели при одном попадании изменяется потому, что изменяется
самое явление, с которым связаны значения, определяющие
математическое ожидание.
Например, если будут даны т залпов из к орудий на одном
прицеле, то математическое ожидание числа попаданий на
выстрел определится так:
вероятность одного попадания.............р,
вероятность одного промаха...........9=1—Р,
вероятность не иметь попаданий в залпе будет . . . . qk,
66
вероятность не иметь попаданий в т залпах будет . . qkm,
вероятность хотя бы одного попадания .... 1 — qkm.
Применяя определение математического ожидания ах =
—:Pi 4- х2 Р2 и приняв = 1, Р1 = 1 — qKm, ж2 — 0 и Р2 = qkm,
получим:
аА = 1 • (1 — qkm) + О - qkm = 1 — qkm
или
flj = 1 — (1 —р)кт попаданий, (88)
а математическое ожидание числа попаданий на один выстрел
Пример. Найти математическое ожидание числа попаданий
на один выстрел при стрельбе на одном прицеле для четырех
залпов из трех орудий, если вероятность попадания р = 0,1196.
По формуле (89) имеем:
1—(1—77)12 1 _ (о 8804)12 0,7832
=---- - — =--------------— — 12 = 0,0653 попадания.
4. Математическое ожидание числа попаданий на выстрел
при стрельбе залпами на нескольких прицелах. На основании
изложенного аналогично получим математическое ожидание а
числа попаданий на выстрел:
(1—q1m‘ft>) + (l — + • • +(1 — qnnkn> <90)
а — - - ,
где qx, q2, . . . qn— вероятность одного промаха на каждом из
прицелов;
, к2, . • . ,кп — число орудий в залпе;
т1г т2, . • . ,тп — число залпов на каждом из прицелов;
р — общее число выстрелов.
Пример. Найти величину математического ожидания числа
попаданий на выстрел при условии, что будет дано по одному
четырехорудийному залпу на каждом из трех прицелов, причем
вероятность промаха на выстрел для каждого прицела опре-
делена: г/! = 0,0573; q2 = 0,1196; 73 = 0,0573.
Согласно равенству (90) будем иметь:
(1—0,94274) + (1—0,88044) + (1—0,94274)
-
0,2103-1-0,3992-4-0,2103 0,8198 л
= —------!——!------------— ——— = 0,0683 попадания.
X & А Zu
Для вычисления математического ожидания попадания или
числа попаданий при распределении на плоскости надо сло-
жить законы векториальных ошибок и определить величины и
направления главных осей суммарного единичного эллипса,
после чего, приняв его полуоси за срединные отклонения ору-
дия, трансформировать в этих отклонениях цель и обычным
приемом подсчета найти математическое ожидание пойадания
или числа попаданий.
Сравнивая вычисления вероятности попадания и математи-
ческого ожидания числа попаданий, видим, что последнее
вычисляется несравненно проще, а поэтому всегда, когда
возможно ограничиться вычислением только математического
ожидания числа попаданий, следует прибегать к вычислению
его по более простым формулам, приведенным в настоящем
параграфе.
Математическим ожиданием числа попаданий на выстрел
можно в большинстве случаев ограничиться для исследования
стрельбы на одном прицеле, для решения вопроса о среднем
расходе снарядов, когда надежность решения задачи не обу-
словливается вероятностью попадания, и во всех случаях
решения вопроса об экономичности стрельбы. Вероятность по-
падания требуется для определения степени надежности
стрельбы. Наконец, то и другое требуются одновременно, когда
приходится решать вопрос о методе стрельбы на поражение, т. е.
выгоднее ли стрелять на одном прицеле, или обстреливать
площадь и в каком порядке.
При исследовании вопроса о стрельбе на одном прицеле
обычно необходимо дать метод выбора наивыгоднейшего при-
цела и ширину последней вилки в зависимости от ряда объек-
тивных факторов, которыми располагает управляющий огнем,
а также дать и величину корректировки. На этот вопрос мы
можем получить ответ при сравнении математических ожиданий
попадания.
Для решения же вопроса о том, как выгоднее поражать цель:
на одном ли прицеле или на нескольких установках и на каких
именно, необходимо будет обратиться и к математическому
ожиданию числа попаданий на выстрел и к вероятности попа-
дания (обычно, хотя бы одного попадания).
Рассмотрим несколько из приведенных выше примеров. Для
этого сведем в табл. 21 вероятности хотя бы одного попадания и
математические ожидания при стрельбе на одном и на трех при-
целах, при 30 выстрелах и при распределении цели АЬбДчерт. 21).
Рассматривая табл. 21, мы прежде всего видим, что при
стрельбе на одном прицеле h в точку О распределения цели
АВС (черт. 21) математическое ожидание больше, чем при
обстреливании площади на трех прицелах hY, h2, h3 в точки
К, О и L того же распределения цели, при той же глубине и
при том же общем числе выстрелов 30, но, с другой стороны,
вероятность хотя бы одного попадания при обстреле площади
на трех прицелах значительно больше, чем при стрельбе на
одном прицеле.
Математическое ожидание дает нам, с одной стороны, сред-
нее число попаданий и среднее число попаданий на выстрел
при большом числе стрельб, а с другой стороны, оно отвечает
68
Таблица 21
Вероятности хотя бы одного попадания и математического ожидания при
30 выстрелах на одном и на трех прицепах
Прицел Число выстрелов Математи- ческое ожи- дание числа попаданий Математи- ческое ожи- дание числа попаданий на выстрел Вероят- ность хотя бы одного попадания
Центры группирования
К 0
h — 30 — 3,688 0,1196 73,0%
hi‘, Дз 10 10 10 2,342 0,0181 91,9%
и на вопрос о среднем расходе снарядов для решения той или
иной огневой задачи, но ни в одном случае математическое
ожидание не дает ответа на вопрос о надежности решения
огневой задачи.
Вероятность хотя бы одного попадания или вероятность не
менее заданного числа попаданий в цель дает нам возможность
судить о надежности решения той или иной огневой задачи.
Из приведенной выше таблицы трудно судить о надежности
решения огневой задачи при стрельбе на одном прицеле, так
как вероятность в 73% не говорит нам ничего ни в ту, ни в
другую сторону: она велика для того, чтобы сказать, что
стрельба безусловно ненадежна, и недостаточна для того, что-
бы сделать вывод о безусловной надежности стрельбы.
Вероятность же в 91,9% при обстреле площади вполне
может быть принята за критерий о надежности решения огне-
вой задачи, если таковая решается одним попаданием.
Если задача одним попаданием не решается, то все же
можно говорить, что при каждых 30 выстрелах хотя бы одно
попадание в цель весьма надежно.
Таким образом, математическое ожидание отвечает на во-
прос об экономичности стрельбы и о среднем числе попаданий
из большого числа стрельб, а вероятность попадания отвечает
на вопрос о надежности решения огневой задачи.
Параллельное же сравнение величин математических ожи-
даний и вероятностей попаданий является одним из лучших
вполне научных и численно обоснованных методов для выбора
наивыгоднейшего способа стрельбы.
Приведенный пример хотя еще и не дает полной картины
Для выбора метода стрельбы в данной обстановке (распределе-
аие цели), но уже позволяет сказать, что при данном распре-
делении цели обстрел площади выгоден.
Этот вывод можно сделать потому, что математические ожи-
дания числа попаданий на выстрел в обоих случаях близки
1е точностью до 0,1 попадания они равны), тогда как вероят-
юсть попадания возрастает очень резко при переходе к об-
стРелу площади.
69
Меняя шаг корректировки при обстреле площади, а также
и число выстрелов на каждом прицеле при том же общем числе
выстрелов и вычисляя параллельно математическое ожидание
числа попаданий и числа попаданий на выстрел с вероят-
ностью хотя бы одного попадания или с вероятностью не менее
заданного числа попаданий, легко из сопоставления получен-
ных цифр вывести и наивыгоднейший метод стрельбы.
При расчете обстрела площади одним из важных факторов
является равномерная плотность попаданий. Для выяснения
итого вопроса составим линейное распределение падений по
закону Гаусса при различных шагах корректировки для разных
прицелов и при одном выстреле на каждом прицеле. Распре-
деление составим через i Вд.
На черт. 24а, 245 и 24# показана „плотность11 при обстреле
Площади через 2 Вд.
Считая с точностью до 3%, видим, что при обстреле пло-
щади скачками через 2Вд с равномерной плотностью покрыты
районы: при стрельбе на 2 прицелах — в 2Вд, при обстреле на
3 прицелах — в 4 Вд и при обстреле на 4 прицелах — в 5 Вд.
Черт. 24г, 240 и 24е аналогичны черт. 24а — 24е, но обстрел
площади показан через ЗВд. Рассматривая черт. 24г — 24е,
видим, что и здесь получается равномерный обстрел площади
больших протяжений, а именно в 5, 7 и 10 Вд, но плотность
приблизительно в полтора раза меньше, чем при обстреле площа-
ди через 2 Вд, причем при обстреле на четырех прицелах в се-
редине обстрела заметно незначительное уменьшение плотности.
13 [4 7 9 йЙТй 12 3 f 11
-Ц-Ц-ПЛТ. Ф 13 13 13,9 7 ,4 3 1 1
|3|4 8 W|i7Wl№f7|f5Wl4 “
Черт. 24с.
1
1
1
1
3 1 и
е
9
3
1
9
3 4
314
10
3
12
15
4
13
17
7
13
1
21
9
12
22
13
7
4
13
4
7
241241124
12
3
1
24
9
1
12
22*
7
1
Й
21
13
17
3 1 1
12 9 7 4 3 1 1
15
10
1
7
8
4
8
4
3
1
Черт. 244.
На черт. 24 Ж, 24 3, и 24 И показан обстрел площади через
4 Вд на двух, трех и четырех прицелах. Полной равномерности
распределения плотности уже нет, хотя если пренебречь раз-
ностью в 3%, то до некоторой степени равномерная плотность
наблюдается на протяжении 6, 10 и 14 Вд при плотностях вдвое
меньших, чем при обстреле площади через 2 30.
Если на каждом прицеле производить не по одному, а по
несколько выстрелов, то, поделив плотность на lOO' и умножив
70
<
1
3
Черт. 240.
Черт. 24е.
_________________4В^_
5 5 3 4 7 77^53 12191
ТШуЫжпгизшНЗН2111.....
1311 НI
4б^
4
7
4^
4
7
5
53
5
12
52
5
52
5
53
5
53
5
1
53
5
52
,3
9
52
5
53
7 У12 13 <4^13 42'5? Л 52 53 54 54 53 52 55 55 52 5*311^2
12
53
53
52
53
52
4
7
9
3
9
7
4
9
3
9
3
7
4
3
9
9
3
4^
7
I 4
4
7
1
7
4
3
1
5
Черт. 24ы.
71
на число выстрелов на каждом прицеле, получим распределе-
ние математических ожиданий через каждую половину средин-
ного отклонения пушки на протяжении всего обстрела.
14. О распределении вероятностей падений. Кривая
распределения (вероятностей) падений
В некоторых случаях при исследовании методов стрельбы
картина распределения плотностей, или математических ожи-
даний может оказаться недостаточно наглядно характеризующей
распределение падений снарядов. В этом случае необходимо
обратиться к распределению вероятностей падения.
30
1.0
о,8:
о,8:
о,?;
о,б:
0,5.
о,<
оз:
02.
о,1.
Кривая распределение
падения снарядов <
0,2651
0,7349
186623
5,9869
0,00010
0,2121
0,7879
1,89647
лония
рос
0,8900
1,94939
цели
0,0368
0,9632
198372
0,0079
0,9921
199656
0,0010-
О,'9990
199957
0,0002
0,9998
1,99991
0,0000
1,0000
4,8941
2,4817
1,5116
1,8968
19871
1.9973
0,9999
Q00J78
0,9992
0,03032
0,9697
0,32479
0,6752
0,78850
0,2115
0,97072
0,0293
0,9938
0,0062
К
Вследствие симметрии кривых показаны только половины их
Черт. 25.
Под распределением вероятности падений снарядов мы будем
подразумевать закон, по которому распределяются вероятности
хотя бы одного падения или вероятности не менее заданного
числа падений относительно средней траектории (центра груп-
пирования) при стрельбе на одном прицеле или относительно
какой-либо точки (обычно центра распределения) при обстреле
площади на нескольких прицелах.
Обычно кривая, отвечающая этому закону, на каждом из
участков строится внутри распределения цели, но независимо
от него, так как эта кривая строится независимо от цели.
Расчет этой кривой очень прост, и мы его покажем на част-
ном примере. Пусть требуется внутри распределения цели АВС
72
(черт. 21) нанести кривую распределения падений через интер-
валы, равные глубине цели при 30 выстрелах, в центр распре-
деления и при тех же 30 выстрелах, произведенных в точки
К Ои L на трех прицелах Л2 и hs по 10 выстрелов на каж-
дом прицеле.
Пусть требуется построить кривую, отвечающую вероятности
хотя "бы одного падения в каждом из участков, равных глубине
цели, например, глубине цели, равной Вд = 1.
Так как в этом случае нам не придется производить сум-
мирования вероятностей, то расположим схему расчета парал-
лельно с черт. 25 и 26.
На схемах и черт. 25 и 26 представлены весь ход работы
и самые кривые.
^выстрелов
1Щ
Q9.
0,8.
0,7.
Об.
05.
Q4.
0,3.
02.
0,1.
0I
п
0,0079|0,0010
0,2651 02121
Q0079|QD368
0,992109990
0,734907879
0,9921 09632 108900
[99656(99957
КривЬя распределена
10 выстрелов
Кривая распределения
падений снарядов
? цели
\§вшрелов
4-
0,0002
0,1100
01100
09998
08900
0
00368
02121
1
09632
,07879 1Ц7349
0.0079
Д2651
0,0010
0,2121
0,0002 О
0,1100 [0,0368
Q0D7910,000
0,0002
9,9921
0,9990
0,7899
0,9998 1
08900 0,9632
09921 0,9990
0,9598
1.9965Щ99957 199991
[86623189647 194939
1.996560983721,94939
[9957 (9991 ТТЛ
29647 1/939 18372
1,8372 1,4939 р647
27976 £9869
00628 Q0970 0 0 634 0.0424
09372 10.9030
19656
О
198372
189647
[99656 ( 99957 1999911 0
1,86623 -------------------
1,89647194939)1.98372
<99656 1.99957193991
10006623
10 W 1.9656
О®
«а»
2,8019
2.6279
1,9991 L 0
1,49391(8372
1,49301 [8372
[9656 |1,9957 (9991
1,9656
09238
1,9957 19991
09901 0.9979
0,0099 0,0021
£9604 . ... .
0.0913 103112 ф.6873
09087 |О6888 |0,3127 |0,0762
£
Вследствие симметрии правых показаны только половины их.
0,9366
0,9576
0
0
Черт. 26.
Эти кривые также являются некоторой характеристикой в.
области исследования методов стрельбы, например, рассматри-
вая черт. 25, можно сказать, что кривая распределения паде-
ний снарядов не подходит к кривой Данного распределения
цели, так как первая кривая по отношению ко второй резко
падает.
Из чертежа же 26 видим, что кривая распределения падений
снарядов лучше подходит к кривой распределения цели, но
провалы в первой кривой указывают на неравномерность об-
стрела (неравномерная плотнос/ь), происходящую вследствие
излишне большого шага прицела в 4 Вд', поэтому лучше его
Уменьшить и ту же площадь/обстреливать на большем числе
прицелов. /
ЧАСТЬ ВТОРАЯ
ТЕОРЕТИЧЕСКИЕ ОСНОВАНИЯ
ВЫРАБОТКИ ПРАВИЛ СТРЕЛЬБЫ
УДАРНЫМИ СНАРЯДАМИ
ГЛАВА IV
О ПРАВИЛАХ СТРЕЛЬБЫ
15. Требования, предъявляемые к правилам стрельбы
При составлении правил стрельбы приходится в большинстве
’Случаев согласовывать два противоречащих друг другу усло-
вия: 1) правила стрельбы должны отвечать наилучшему пора-
жению цели с точки зрения математического ожидания попа-
дания и вероятности попадания при наибольшей действитель-
ности стрельбы (выбор снаряда и дальности) и 2) правила
стрельбы должны бр!ть просты, легко и удобно запоминаемы и
доступны нормальному уровню среднего командного состава
как по его интеллектуальному развитию, так и по подготовке
и выдержке. Кроме того, необходимо иметь в виду и ту обста-
новку, в которой стреляющему придется применять правила
стрельбы, т. е. обстановку боя. В этом отношении при состав-
лении правил следует быть осторожнее и всегда рассчитывать
на более тяжелые условия боя. В современном морском бою
обстановка может сложиться весьма разнообразно, например:
спокойное маневрирование и бой на больших дальностях; бой
на больших и даже средних дальностях при условии, что
управление огнем противника чем-то стеснено; внезапное появле-
ние цели на той или иной дальности, иногда весьма небольшой,
и на очень короткий промежуток времени; отражение атаки
быстроходных торпедных кораблей и катеров; различные случаи
ночного боя и т. п.
Ясно, что для всех случаев боевой обстановки иметь одни
универсальные правила невозможно и неизбежно придется иметь
ряд правил, отвечающих различным условиям боя, причем часть
этих правил может заключать в, себе совершенно конкретные
постатейные указания почти уставного характера, а часть пра-
вил, учитывая разнообразие боевой обстановки, может заключать
в себе ряд указаний, руководствуясь которыми управляющий
огнем должен сам уметь находить верные решения.
Что касается согласования указанных выше противоречивых
требований, то, чтобы дать правила, обеспечивающие наилучшее
поражение цели и одновременно простые и удобоприменимые,
рекомендуется сначала строгие требования теории, дающие
наивыгоднейший результат, оформить в виде определенных
правил, а затем эти правила привести к виду, удобному для
практического пользования, упростив их в тех частях, упро-
щения которых требуют условия боя.
Все упрощения правил необходимо особо тщательно прове-
рить расчетами, насколько они понижают математическое ожи-
дание попадания, или вероятность попадания, или, если это
требуется, то и другое вместе. Результат такой проверки по-
кажет, насколько приемлемо то или иное упрощение правил
стрельбы, после чего возможно приступить к окончательному
их оформлению.
16. Порядок выработки правил стрельбы
Дать общую схему на все случаи составления правил
стрельбы затруднительно, так как схема работы будет зависеть
от целого ряда причин, но все же некоторые руководящие ука-
зания дать возможно.
Во-первых, разделим процесс стрельбы на отличные по своим
характерным признакам периоды, а именно:
1) предварительная подготовка,
2) подготовка исходных установок,
3) пристрелка и
4) стрельба'На поражение.
Прежде всего необходимо исследовать и учесть ошибки
подготовок, вытекающие из точности имеющихся сведений о цели
до первых выстрелов и из методов стрельбы. Этот учет даст,
например, указание о величине первой вилки, необходимое при
пристрелке.
При исследовании периода подготовки стрельбы необходимо
найти и указать пути, ведущие к получению возможно полных
и точных сведений о цели.
Следующий период стрельбы — пристрелка — служит для
уточнения сведений о цели, т. е. для получения в конечном
итоге установок прицела и целика (угломера), наиболее отве-
чающих положению г цели в данный момент, а также для полу-
чения данных об элементах движения цели и своего корабля.
Каким бы способом эти установки ни осуществлялись,— с по-
мощью ли приборов управления огнем, или без них, — неиз-
бежно будут иметь место некоторые ошибки, которые должны
быть учтены при составлении правил стрельбы.
При исследовании периода пристрелки необходимо дать
указания о первоначальных действиях в этот период, исходя
из различной точности подготовки при всех ее градациях.
75
Вырабатывая правила стрельбы, учитывают уже возможность
поражения цели в процессе самой пристрелки. Но так как
главной задачей пристрелки является уточнение сведений о
цели в наикратчайший срок и с наименьшим расходом снарядов,
то такому положению должно быть подчинено все остальное,
а поэтому необходимо „нащупать" и обосновать те приемы,
которые наилучшим образом ведут к быстрому и экономичному
проведению пристрелки.
Момент окончания пристрелки определяется той степенью
уточнения или пополнения сведений о цели, дальше которой
итти нецелесообразно, так как ряд факторов, сопровождающих
стрельбу, и главным образом, рассеивание снарядов и время
не позволят улучшить сведения о цели, а иногда, например,
при стрельбе по подвижной цели, излишние старания в этом
направлении могут привести к упущению благоприятного мо-
мента для поражения цели.
Это обстоятельство стирает до некоторой степени искус-
ственный рубеж, разграничивающий периоды пристрелки и пора-
жения цели. Некоторые авторы в научном изложении вопросов
теории стрельбы предпочитают этого рубежа не проводить и не
делить стрельбу на периоды пристрелки и поражения, предпо-
читая вовсе не давать таких определений, которые нельзя
точно сформулировать.
Однако, не отрицается удобство разграничения периодов
стрельбы в правилах, а в некоторых частных случаях необхо-
димость разграничения признается и в научных трудах, напри-
мер, стрельба с пристрелкой по вспомогательной цели (реперу),
где рубеж между пристрелкой по реперу и обстрелом самой
цели обозначен резко. В нашем изложении курса будем про-
водить эту границу только там, где это окажется удобным, и
признаком конца периода пристрелки будем считать тот рубеж,
на котором кончается доминирующее значение уточнения све-
дений о цели и становится основным нанесение цели наиболь-
шего поражения. Конечно, и в период стрельбы на поражение
уточнение сведений о цели не прекращается, как и во время
пристрелки не отрицается возможность нанесения поражения
цели, с той разницей, что при пристрелке для скорейшего
уточнения сведений о цели жертвуют поражением ее, тогда
как при стрельбе на поражение стремление удержать и да-
же пополнить сведения о цели, используя для этого каждое
наблюдение, остается в полной мере, как и в период при-
стрелки.
Переходя к периоду поражения цели, необходимо найти и
указать:
1) наивыгоднейший способ перехода на поражение,
2) методы наивыгоднейшего поражения,
3) объективные признаки успешности поражения,
4) величины корректировок (там, где они имеют место),
5) объективные признаки необходимости возвращения к при-
стрелке и
76
6) руководящие указания о методах управления „прицелом",
„целиком" и ВИР (выбор метода поражения в данной обста-
новке).
Критерием целесообразности выбранного метода является
либо математическое ожидание попадания на выстрел, либо
вероятность хотя бы одного или не менее некоторого задан-
ного числа попаданий, либо и то и другое, либо, наконец,
вероятность наблюдения тех или иных комбинаций падений.
Необходимо отметить, что при выработке правил стрельбы
для корабельной артиллерии надо резко различать два случая:
1) обстановка стрельбы позволяет рассчитывать на более
или менее длительный огонь, когда можно базироваться на не-
котором равновесии между математическим ожиданием числа
попаданий на выстрел и вероятностью хотя бы одного или
не менее заданного числа попаданий, и
2) когда обстановка требует в исключительно короткий срок
хотя бы одного попадания в цель. В этом случае исключи-
тельно или главным образом базируются на том, чтобы дать
такой метод поражения цели, при котором хотя бы одно попа-
дание из выпущенных снарядов было обеспечено вероятностью,
близкой к единице, причем вопрос об экономичности стрельбы
отпадает и весь расчет следует вести, имея в виду исключи-
тельно надежность решения огневой задачи. Математическое
ожидание числа попаданий на выстрел, как критерий при
оценке метода стрельбы, нельзя упускать и в этом случае, но
только оно будет иметь значительно меньшее значение.
Правила стрельбы, выработанные на основании положений
теории вероятностей и с учетом опытных данных (рассеивание
падений и разрывов снарядов, распределение пуль или оскол-
ков, ошибки различных приборов и т. п.), будут верны, как и
всякий технический расчет, в обычных пределах 5—10%, и в
дальнейшем могут быть проверены в лаборатории стрельбы и
в порядке текущей боевой подготовки.
Особенно полезно выработанные правила предварительно
проверить в лаборатории стрельбы, допускающей весьма боль-
шое число испытаний и дающей возможность вводить различные
варианты рассеивания и создавать разнообразную обстановку.
В процессе выработки правила стрельбы могут проверяться
также при помощи исследовательского графика, но при этом
необходимо правильное введение рассеивания, и кроме того,
следует иметь в виду, что график может указать только на
пригодность или непригодность приема, но не дает возмож-
ности найти наивыгоднейшие приемы и численное обоснование.
Правила стрельбы могут содержать либо общие указания
и предоставлять управляющему огнем самому разбираться в
каждом частном случае и принимать соответствующее решение,
либо могут давать совершенно конкретные постатейные почти
уставного характера указания на различные комбинации усло-
вий стрельбы.
Первый вид правил легче вырабатывается, но от управляю-
77
щего огнем требует больше опыта и выдержки; правила вто-
рого типа легче для изучения и применения, но предъявляют
очень высокие требования к лицу, вырабатывающему эти пра-
вила, и требуют от него оолыпой предусмотрительности и учета
всех возможных обстановок стрельбы.
Правила стрельбы, заключающие в себе конкретные указа-
ния уставного характера, имеют преимущество перед прави-
лами, содержащими общие указания, и они не должны и не
могут допускать отступлений и упрощении; в тех же случаях
сложной боевой обстановки, когда конкретных указаний нельзя
дать из-за невозможности предусмотреть все ее комбинации, то,
пока не явится возможность их конкретизировать, правила долж-
ны содержать общие указания, в пределах которых управляющий
огнем сам должен уметь быстро найти верное решение; эта воз-
можность должна быть ему предоставлена правилами стрельбы.
17. Учет параметров, характеризующих рассеивание
орудий z
Меткость орудий характеризуется срединными отклонениями,
которые, как известно, не являются величинами постоянными .
и, кроме целого ряда факторов, зависят еще и от условий,
в которых протекает стрельба.
Посмотрим, как может отразиться на стрельбе изменение
меткости орудий, если это изменение не предусмотрено при
составлении правил стрельбы.
Правила стрельбы могут быть составлены так, что команды
даются либо в табличных единицах, например, в кабельтовых,
либо определяются числом срединных отклонений.
Если в первом случае при составлении правил ориентиро-
вались на какое-либо одно рассеивание, например, табличное,
то при значительно меньшем рассеивании для данного момента
правила окажутся не только грубыми, но применение их и
наблюдение результатов корректировок могут вызвать ряд
недоразумений и вынудить управляющего огнем к импровиза'
ции во время стрельбы, вследствие чего результаты такой
стрельбы легко могут свестись к нулю.
Если же рассеивание данного момента будет значительно
больше табличного, то правила окажутся излишне сложными
для такой меткости пушек и их применение может создать
такую путаницу, которая сведет к нулю и те скромные резуль-
таты, которые могли бы получиться при применении правил,
отвечающих рассеиванию момента.
При выражении команд в срединных отклонениях получится
та же картина, если в правилах стрельбы не предусмотрена
возможность изменения величины срединных отклонений, так
как команды все равно будут подаваться в табличных едини-
цах с ориентировкой обычно на табличную величину средин-
ных отклонений.
Во избежание подобных явлений правила должны преду-
сматривать изменение рассеивания и давать возможность менять
78
величины корректировок в зависимости от той меткости ору-
дий, которая имеет место в данный момент.
Отражение в правилах стрельбы всех условий момента,
могло бы сделать эти правила весьма громоздкими, а поэтому,
чтобы излишне не усложнять их, рекомендуется выработать
правила стрельбы до конца для трех случаев рассеивания:
табличного и в два раза меньше и больше табличного, а затем,
выписав их параллельно, сравнить и объединить те статьи,
которые для всех трех случаев рассеивания заключают равные
корректировки. Те же статьи, которые заключают разные кор-
ректировки, также следует попытаться объединить, предвари-
тельно исследовав путем подсчета математического ожидания
попадания и вероятностей наблюдения комбинаций падении,
а где требуется, то и вероятности попадания при одинаковых
корректировках для различных рассеиваний.
Подсчеты укажут на допустимость или недопустимость
объединения. Там, где это упрощение окажется недопустимым,
оно не должно иметь места, и для каждого случая рассеивания
должны быть даны свои правила, хотя бы они от этого и усложня-
лись. Возможно, что два случая рассеивания удастся объединить,
под одними правилами, а третий — потребует особых правил.
Во всех случаях, когда в правилах стрельбы приходится пре-
дусматривать различное рассеивание, должны быть найдены и
указаны объективные признаки, на основании которых управляю-
щий огнем может принять решение о применении того или
иного варианта правил.
18. Схема работы при составлении правил стрельбы
Исходя из изложенного в § 16—17, можно предложить сле-
дующую схему составления правил стрельбы, которая может
быть применена почти ко всем случаям, кроме стрельбы спе-
циальными снарядами (осветительными, ныряющими и т. п.).
1. Получение исходных установок.
2. Уточнение сведений о цели (пристрелка), которое дово-
дится до той степени, за которой при данном рассеивании
дальнейшее уточнение этих сведении затруднительно, беспо-
лезно и даже вредно.
3. Поражение цели: методы поражения с объективными ука-
заниями на необходимость применения того или иного метода и
с такими же объективными указаниями на момент возвращения
к пристрелке, если это потребуется.
't. Приспособление правил к практике или упрощение правил
с целью придать им простоту, гибкость и удобозапоминаемость
При наименьшем ущербе для их теоретической рациональности.
б. Окончательное оформление правил или в виде статей
готовых решений уставного характера, или в виде ряда руко-
водящих указаний, требующих умелого и искусного примене-
ния их в различной обстановке стрельбы.
ГЛАВA V
ОБ ОШИБКАХ ПОДГОТОВКИ
19. Ошибки предварительной подготовки
Предварительная подготовка состоит из сострелки орудий,
определения температуры зарядов, введения индивидуальных
поправок па корректорах принимающих приборов высоты при-
целов, обработки бюллетеня аэрометеорологического поста (АМП)
и составления таблиц балистических ветров, „поправок дня" и
поправок на плотность воздуха.
Ошибки предварительной подготовки и ошибки подготовки
исходных установок для первого залпа определят собой рас-
пределение цели к некоторому интересующему нас моменту.
Вследствие того что в ошибки подготовки исходных устано-
вок при стрельбе на море войдет ошибка ВИР, ошибки пред-
варительной подготовки, как не зависящие от ошибки в ВИР,
рассмотрим отдельно.
1. Ошибки балистической подготовки. Под ошибками бали-
стической подготовки будем подразумевать те изменения
в дальности, которые происходят от отступлений в начальной
скорости против табличной.
Причин, вызывающих изменения в начальной скорости,
много, и не все они поддаются учету. Перечислим главней-
шие из них:
а) износ канала орудия стрельбой;
б) изменение температуры заряда против нормальной;
в) отступление начальной скорости от табличной даже при
нормальной температуре пороха, различное для различных пар-
тий (ошибки при подборе зарядов на полигоне и при выделке
их в портах);
г) изменение балистических качеств пороха за время хра-
нения;
д) отступление веса снаряда от табличного.
а) Износ канала определяется перемещением конического
•ската зарядной каморы и выкрашиванием полей нарезов; оба
явления ведут к падению начальной скорости.
Как в основных таблицах стрельбы, так и таблицах стрельбы
на море, имеются специальные столбцы для помещения в них
80
поправок на так называемый „расстрел орудия", причем в ста-
рых таблицах аргументом служило число выстрелов, а в новых
основных таблицах дается в качестве аргумента расстрел ору-
дия на 25, 50 и 85%, при этом не указывается, какой смысл
заключается в этих процентах износа орудия.
Установить строгую зависимость между числом выстрелов
и падением начальной скорости нельзя, так как одно число
выстрелов, а тем более „приведенных" боевых выстрелов крите-
рием не является; важно, во-первых, с какой интенсивностью
произведено это число выстрелов, во-вторых, различные орудия
одного и того же калибра и при одном и том же числе выстре-
лов изнашиваются неодинаково, и в третьих, имеет значение и
различие в партиях порохов.
Единственно правильным критерием будет только опытное
определение падения начальной скорости либо по измерению
непосредственно начальных скоростей орудий, либо путем
сострелки при возможно точном измерении отклонений падений
снарядов; на основании результатов измерения отклонений
может быть рассчитано падение начальной скорости. Первый
способ, как более точный, менее дорогой и менее громоздкий,
должен быть предпочтен.
Срединная ошибка в определении начальной скорости при
ее измерении будет зависеть от ошибки прибора и может быть
установлена только путем опыта. Приближенно в среднем для
одного испытания ее принимают равной 0,5%, но нам думается,
что она может быть меньше.
Об ошибке в начальной скорости, полученной на основании
сострелки по измерению отклонений, скажем ниже в главе
о стрельбе по измеренным отклонениям.
б) Срединная ошибка измерения температуры пороха при-
нимается в среднем Д£=1°.
Срединная ошибка в скорости при этом будет:
Ди% = 0,11 Д/,
или, полагая Д/= 1°, получим:
Дг’%=0,11%.
в) и г) Что касается неточности изготовления и подбора
зарядов и изменения балистических качеств пороха при хра-
нении, то изменение начальной скорости по этим причинам
может быть установлено тиражными стрельбами на полигоне \
при этом ошибки в начальной скорости (при тарированных
зарядах) установлены Версальской пороховой комиссией в 5—
7 м/сек для 75-juju— 155-juju пушек, если тарирование было не
Раньше 15 дней перед стрельбой. С одной стороны, опытное
определение падения начальной скорости одновременно может
быть принято и за тиражную стрельбу, но, с другой стороны,
стрельбы для определения начальных скоростей вряд ли могут
1 ..Стрельба французской артиллерии", изд. 1926 г., стр. 225—230.
6 Теория стрельбы 81
производиться более одного-двух раз в кампанию, а поэтому
для учета срединной ошибки в начальной, скорости за счет
неточности изготовления заряда примем браковочную формулу
полигона: „Боевой запас принимается в том случае, если раз-
ность между средней скоростью из десяти выстрелов и наи-
большей и наименьшей не более 2% начальной табличной ско-
рости".
Полагая срединную ошибку равной одной пятой от наи-
большей, получим срединную ошибку в начальной скорости
за счет неточности и изменения качеств заряда:
Див = 0,4%.
Наконец, надо принять во внимание ошибку от округления
установки корректоров индивидуальных поправок. Такая ошиб-
ка дтя новых корректоров может быть принята в 0,2% и сле-
дующей закону равной вероятности. Следовательно, средняя
квадратическая ошибка будет:
Учитывая, что эта ошибка не больше других ошибок, сяе-
дующих закону Гаусса, можем принять приведенную средин-
ную ошибку:
• о 2
Дг?к = 0,67—.
Уз
Тогда будем иметь:
л /о/ -1 У/ °,5 V ~ ~ 1 0,2 \2 , ч
Дг.%=-|/ +0,ll2+0,42+^0,67y-j ’ (91)
где т—число выстрелов для определения средней начальной
скорости.
Вряд ли можно рассчитывать на ш>4, и для ш = 4 будем
иметь:
Дг/ = 0,49%.
Приняв согласно Версальской пороховой комиссии ошибку
за счет изменения свойств пороха при тарированных зарядах
в 5 м/сек, имеем:
0,01 v0 ’
Окончательно ошибка в начальной скорости будет:
Дг% = У(Дг7)2 + (Дг")2 . (92)
Ошибка балистической подготовки будет:
Я/У»
ДУ=^.Дг, (93)
dv v
82
где —----изменение в дальности от изменения начальной ско-
dv
рости на 1%.
Например, для 305-дьм пушки в 40 калибров длиной
(р0= 792,5 м/сек) получим:
Л» = |/ (0,49)’+ (~)' = 0.8%
Срединная ошибка подготовки, например, для Х=100 каб.,
будет по (93):
ДХ=103 • 0,8 = 82 саж.
Очень часто бывают попытки выяснить величину ошибки
балистической подготовки вне измерения начальных скоростей
или сострелки. Следует заметить, что без постановки очень
солидных опытов в этом направлении выяснить и хоть сколько-
нибудь научно обосновать эту ошибку нельзя.
2. Ошибки аэрологической подготовки. Под ошибками аэро-
логической подготовки подразумевают следующие ошибки:
а) ошибку в определении влияния балистической плотности
воздуха и
б) ошибку в определении влияния балистического ветра.
а) Ошибки в определении балистической плотности воздуха
зависят от ошибок в определении балистической температуры.
В настоящее время эту ошибку принимают:
Ет = 0,5% (срединная ошибка,
если обновление данных происходит через 2 часа, в случае
же обновления данных через 4 часа лучше считать
Е'Т=О,7% —1%.
б) В результате опытов Гаврской испытательной комиссии
(1921 г.) и опытов испытательной комиссии в Бурусе (1924 г.)
величина срединной ошибки в определении балистического
ветра дается от 1,5 до 2 м/сек.
Ошибка за счет обновления данных через 2 часа во фран-
цузской литературе 1 принимается равной 1 м/сек.
Эти цифры были пересмотрены в Главной геодезической
обсерватории и найдены чрезмерно большими, в особенности
Для высот больше 1 000 м и близких к ним.
Это положение было высказано на основании следующих
соображений:
1) кривая истинных значений вертикальной скорости ша-
рапилота с увеличением высоты постепенно приближается
1 I. Соurbis, Precision des tirs prepares. „Revue d’Artillerie“, январь
1925 г.
6*
83
к теоретической кривой, и на высотах свыше 1 000 м эти рас-
хождения незначительны;
2) характер вычисления балистических ветров таков, что
ошибки в скорости ветра с увеличением высоты уменьшаются и
3) опыты в Бурусе были слишком малочисленны для того,
чтобы на них можно было всецело основываться.
Исходя из опытов в Гавре-Бурусе, а также на основании
вышесказанных положений, у нас приняты следующие вели-
чины срединных ошибок в скорости балистического ветра:
срединная ошибка в балистическом ветре для высот не
менее 1 000 м — 1 м/сек',
срединная ошибка за счет времени обновления бюллетеня —
0,5 м/сек;
срединная ошибка в балистическом ветре за счет времени
обновления для высот менее 1000 м— 1 м/сек.
Таким образом, имеем для высот 1 000 м:
EWa, =ЕЮг = |Л24- 0,52 = 1,1 м/сек, (94)
а для высот менее 1 000 м
EWa,=EWz =У12-\-12 =1,5 м/сек. (94')
Срединные ошибки, происходящие от ошибок аэрологиче-
ской подготовки, будут ошибками в плотности воздуха:
д.т „ _ гЛ7°’0, (95)
d wx (96)
или л т- 9х Wx OWx • 1,5; (96')
LZW =-^-Е = “г dwe г дг = =—1,1, дгиг (96")
или = dz dw2 1,5, (96'")
где величины и найдутся по основной таблице
стрельбы.
20. Ошибки в подготовке исходных установок для
случая стрельбы по неподвижной цели
Переходя к ошибкам исходных установок для стрельбы по
неподвижной цели, заметим, что в этом случае к ошибкам бали-
стической и аэрологической подготовки прибавятся ошибки
84
в определении места цели, носящие в войсковой артиллерии
название „ошибки топографической подготовки". В море по
большей части это будет ошибка дальности.
Таким образом, мы будем иметь следующие ошибки подго-
товки:
1. Ошибки топографической подготовки —либо круговые,
либо эллиптические, либо ошибки в дальности по закону Гаусса.
2. Ошибки аэрологической подготовки—векториальные ошибки
по направлению плоскости стрельбы и ему перпендикулярному.
3. Ошибки балистической подготовки — векториальные ошиб-
ки по направлению плоскости стрельбы по закону Гаусса.
В тех случаях, когда нас интересуют только ошибки по
направлению дальности (довольно частый случай стрельбы на
море по видимой цели), мы можем учитывать только ошибки
по направлению стрельбы и тогда будем иметь срединную
ошибку подготовки в следующем виде:
где
Ду =0,8%;
= 0,5—1%;
ЕИа = 1,1—1,5 м)сек;
8 — срединная ошибка в дальности;
(12 5 \
0,67 - ’ ] — приведенная ошибка от округления в уста-
из/
новке прицела, выраженная в саженях шестифутовой меры.
В случаях распределения на плоскости будем иметь:
(97')
(97")
где г —радиус круговой ошибки топографической подготовки
или круговой ошибки в месте цели;
0,05 X
А —дальность в кабельтовых и величина ——=— • 0,67 —
Уз
приведенная ошибка от округления в установке целика, выра-
женная в саженях шестифутовой меры.
83
В том случае, когда ошибка в положении места цели выра-
жается эллиптической ошибкой с полуосями а и Ь, которые
могут и не лежать в направлении стрельбы и ему перпендику-
лярном, необходимо будет для получения распределения цели
произвести сложение векториальных ошибок.
Иногда в этом случае для упрощения прибегают к прибли-
женному расчету и заменяют эллиптическую ошибку круговой
на основании следующих соображений.
Пусть а и b — полуоси эллиптической ошибки и г— радиус
круговой ошибки, которой хотят заменить эллиптическую
ошибку.
Заменяя срединные векториальные ошибки векториальными
средними квадратическими ошибками и приравнивая их гео-
метрическую сумму радиусу круговой ошибки, получим:
а Т ' Ъ 12_ ' Д I2
р /л + LpWJ ~ L rW
откуда
(98)
Такую ошибку называют приведенной круговой ошибкой, но
такая замена допустима лишь в случае, когда разница между
а и b невелика.
Такая замена приближенна, но дает значительное упроще-
ние, так как позволяет воспользоваться формулами (97') и (97")
вместо сложных расчетов сложения векториальных ошибок, не
идущих под прямым углом, когда приходится делать расчеты
для ряда случаев разных направлений осей эллиптических
ошибок.
21. Ошибки в измерении расстояний на море
1. Ошибки в измерении расстояний горизонтально-базным даль-
номером по двум засечкам. Пусть О] и О2 (черт. 27) точки стоя-
ния визиров горизонталыю-базного дальномера; OjO2 — В —
база; / рх и / р2 — углы между базой и направлениями линий
визирования ООг и ОО2 на цель в один и тот же момент (что
возможно при непрерывном визировании) и в одну и ту же
точку цели.
Зная длину базы В и углы ₽х и ₽2 и решая треугольник
ОгОО2 графически или иным путем, мы будем знать в каждый
данный момент дальности O1O = d1 и O2O=d2.
Если точка стояния батареи (орудия) Б, то любая из даль-
ностей^ dr или d2 может быть трансформирована в дальность
Может быть трансформировано не только расстояние dx или
d2, но и угол от какого-либо ориентирного направления.
В настоящее время за ориентирное направление обычно берут
86
направление меридиана. Таким образом, визируя на какую-либо
точку цели с двух постов и О2, мы будем непрерывно иметь
расстояния и направления на цель О (углы между БО и мери-
дианом jVB).
Для исследования ошибок допустим сначала, что при визи-
ровании на цель появилась случайная ошибка визирования
только на посту О1г и пусть Дрг — срединная ошибка, характе-
ризующая закон случайных ошибок визирования.
Тогда, построив при точке О} угол Api и продолжив его
сторону ОХС до пересечения с верной линией визирования ОО2,
получим векториальную ошибку Дй2.
Полагаем, что ошибки визирования следуют закону Гаусса.
Поступив аналогично по отношению поста О2, получим
векториальную ошибку Д^.
Два направления Adj и Дй2 мы можем принять за сопря-
женные направления и построить на них эллиптическую
ошибку е.
Таким образом, видим, что горизонтально-базный дальномер
Бсегда дает эллиптическую ошибку.
Для определения срединной ошибки в дальности ОБ = d
Надо найти отклонение, равное ОК, вызываемое эллиптической
ошибкой от направления, перпендикулярного к ОБ (батарея-
Це ль).
87
Обозначив угол между Дй = ОК и Дс^ через ах и угол меж-
ду Дй2 и Дй—через а2, отклонение но направлению ОБ получим:
t^d — ^Дй/cos2 -|- Дй22С082а2. (99)
Для получения боковых отклонений следует найти откло-
нение, вызываемое эллиптической ошибкой, от направления
БОК, но при этом не надо забывать, что отклонение ОК и ему
перпендикулярное — зависимые отклонения.
Обозначив угол между и OL через -ц, а угол между Дй2
и OL через '(2, отклонение от направления ОБ получим:
Д£= У Дйх2 cos2 Дй22 cos2 у2. (ЮО)
Очень часто при исследовании бывает достаточно знать
наибольшие ошибки в дальности й, тогда достаточно найти
величины больших полуосей а эллиптических ошибок по ряду
направлений и для ряда значений углов засечки цели 6.
Для упрощения расчетов иногда прибегают к приведению
эллиптической ошибки к круговой по (98) § 20.
Самые дальности огоо^ й4 и й2 определятся из треугольника
- d± = В sin р2 sin 6 (Ю1)
и й2 = В sin р, sinO (Ю2)
Пределом возможности измерения расстояний горизонтально-
базным дальномером принимается угол засечки в 15° и угол
между направлением на цель и направлением базы в 15° как
одновременно, так и порознь.
Наибольшая срединная ошибка при угле засечки в 15°
обычно не превосходит 1/4%.
Условие, при котором угол засечки на предельную даль-
ность измерения расстояния будет не менее 15°, определяется
длиной базы, которая должна быть не менее */4 предельной
дальности.
Для определения ошибки в дальности от ошибки в измере-
нии базы из (101) и (102) имеем:
Дй ДВ
й ~ В ’
(103)
т: е. относительная ошибка в дальности равна относительной
ошибке измерения базы.
Из (103) можно заключить, что всегда и без особых трудно-
стей возможно достигнуть, что ошибка в дальности, происхо-
дящая от ошибки в измерении базы, будет пренебрежимо
малой.
88
Например, при дальности в 32 000 м и при базе в 8 000 м,
если допустить наибольшую ошибку в базе 0,01% (0,8 м), что
достигается без особых трудностей, то ошибка в дальности,
происходящая от этой причины, не превысит 3,2 м, т. е.
будет пренебрежимо малой.
2. Ошибки при измерении расстояний оптическими самсбаз-
ными дальномерами. В теории оптических дальномеров выво-
дится формула ошибки в измерении расстояний оптическими
самобазными дальномерами (монокулярными и стереодально-
мерами):
> (104)
где
Д — дальность;
7 — ошибка глаза дальномерщика (ошибка параллактиче-
ского угла);
В—база.
Если у—срединная ошибка глаза, то АД — срединная ошибка
измерения дальности (закон Гаусса).
Выражая у в секундах, Д— в кабельтовых и В — в метрах,
получим:
При наличии т равноточных дальномеров, одновременно
засекающих цель, срединную ошибку в дальности получим:
V т
(105)
В том случае, когда дальномером пользуются одновременно
и как угломером, эллиптическую ошибку и ее главные оси
получим сразу: одну ось, равную 8 (см. 105), которая пойдет
по направлению дальности, и другую ось, которая будет равна
0,001 ДДр и пойдет перпендикулярно дальности.
В последнем выражении Д—дальность; Др — срединная
ошибка в определении направления, выраженная в делениях,
соответствующих 0,001 дальности.
22. Ошибки в определении ВИР по графику
Непосредственное получение ВИР возможно различными
способами. Один из способов заключается в определении ВИР
по разности двух дальностей, измеренных непосредственно
одна за другой. ВИР (И7) в этом случае выразится так:
-^-1, (106)
т
83
* де
Дг— первая из измеренных дальностей,
Д2 — вторая из измеренных дальностей и
т — промежуток времени между измерениями дальностей,
выраженный в минутах.
Если ошибки измерения дальностей следуют закону Гаусса,
то и ошибки в ВИР будут следовать тому же закону. Средин-
ная ошибка ВИР, полученная по двум засечкам цели, произ-
веденным через некоторый промежуток времени между ними,
выразится:
(107)
т
где 8— срединная ошибкх средней дальности, определенной т
равноточными дальномерами:
8=4^;
V т
t — промежуток между двумя измерениями, выраженный
в минутах:
т— (в данной формуле 2) — число равноточных дальномеров,
одновременно засекающих цель.
Срединная ошибка ВИР при определении по двум засечкам
и промежутку между ними может принимать весьма большие
значения, в особенности, если т мало.
При т = 1 мин. величина п в 1,41 раза больше срединной
ошибки измерения расстояния. Увеличением промежутка t
можно получить большую точность в определении ВИР, но
необходимость быстрого выполнения подготовки и непрерывное
изменение ВИР не позволят значительно увеличить т. Для
увеличения точности определения ВИР прибегают к известному
графическому приему определения ВИР. В настоящем пара-
графе мы исследуем ошибки определения ВИР по графику.
Пусть через равные промежутки времени т в моменты Т1г
Тг, . . . , Тч измерены расстояния Ди Д2, . . . , Д, и из них
взято „среднее11.
Это „среднее" расстояние взято графически путем проведе-
ния прямой, ломаной или кривой, занимающей срединное поло-
жение между точками, нанесенными на график по измеренным
дальностям (по оси абсцисс) и времени (по оси ординат).
Таким образом, при измерении среднего расстояния ВИР
принимается во внимание, так сказать, автоматически. Пусть
истинное, неизвестное нам, значение ВИР за промежуток т
будет р. Истинное, неизвестное нам, расстояние в средний
момент Ti пусть будет X.
Тогда истинное расстояние в
момент Т\ будет Х-фзр,
» Т2 „ X -ф 2 р,
тй „ 14- з,
эо
Тогда истинное расстояние в момент
I
”
Т4 будет X,
Т- „ X — ₽,
Т6 „ X — 2р,
т, „ Х-Зр,
.я значение среднего расстояния будет:
(Z+3 Р) + (Х+2 Р)+ (Х+р) +Z+ (Х-р) + (А-2р) + (Х—3 Р)
7
Обозначим среднее арифметическое из измеренных нами
семи расстояний без учета ВИР через А, т. е.
Обозначим разность между средним арифметическим А и
каждым из измеренных расстояний в отдельности через ai;
т. е.
А — Дг — О.г-
Очевидно, что
7
—°-
1
Чтобы найти наивероятнейшее значение для ВИР, составим
выражение для вероятности получения дальностей Д1г Дг,—, Дц
или, что то же, для вероятности получения разностей аи
«2, -А-
Приняв проверенное опытом положение, что ошибки изме-
рения расстояний дальномерами следуют закону Гаусса при
какой угодно гипотезе об истинном расстоянии и гипотезе,
что ВИР будет
W=
вероятность иметь первую дальность в пределах между X 4- з р
и Д1 = А + aj будет равна
й, — ЛЫ«, —3₽г
—7=г-е
Для второй дальности
—е
и т. д.
91
Вероятность ошибки в среднем расстоянии будет
J/7
Вероятность иметь все эти ошибки совместно выразится про-
изведением их вероятностей:
7
g—Л2(а1—ЗР)“—^(аа—2Р)>—Л2(аа—Л2(а„+2₽)2—Л!(ат+3₽)2
ftV 7 —7 Л262
~7=е
рте
Чтобы исключить ошибку 8, найдем ту же вероятность при
всех гипотезах о 8, т. е.
h
Р —
_(108)
Преобразуя интеграл (108), заметим, что о входит не только
явно, но и в величины ап а2,. . ., а„ поэтому можно написать:
а. = а._р5.
Подставим выражение а4 = о4-pS в показатель степени выра-
жения (108), тогда в скобках первого члена получим:
(а,— 3₽)2 = (а1-р-з₽)2==а124-824-9₽2-|-
+ 2«j 8 — 2 ах 3 ₽ — 28 • 3 р;
скобки второго члена примут вид:
(а1 2 рр = ($2 -р о — 2 Р)“ = а22 -р ьа-р4р2-р
-j- 2 6t2 8 — 2 й2 2 р — 2 8 • 2 Р
И т. д.
Вынеся в показателе степени (108) Л2 за скобку и сделав
в скобках приведение подобных членов, получим:
- [(«1 - 3 Р)2 -Р (а2 — 2 р)2 -Р (а3 - р)а -р a42 + (а. 4- р)а +
+ («б+2Й2-Р(а, + Зр)2]=-/12[^^ + 7б2 + (9-Р4 + 1 + 1 + 4 +
1
7
+ 9)р2+ ^2 0,0 —2p(3«j + 2 О2-р«3 — «6 —2«6 — 3«,) —
-2 р-ргр + р-р-2 р-зр)].
Член
2 8 (3 Р-Р 2 Р-Р р — р — 2 р—3 Р) = 0.
92
Члены
^^24-7Й2 + ^2й<8=^(«4 +
1 1
где кг — постоянное в данном выражении число.
Поэтому интеграл (108) примет вид:
--ОО
[28^ — (За, + 2а, + а3 —- а., — 2а0 — За;)+Л,] д 1 / — 7 Л!а2
.е--.— • е di=
Г'
— 7№о2
dS.
— К2 [28₽2 — 2g (За, + 2а, + а3 — ав — 2ас—За,) ]
е
Примечание. В скобках второго члена показателя нет вели-
чины ait так как при а4 нет множителя р.
Обозначив постоянный множитель
e~7,*2 62 d8 через К,
.имеем:
р — h~ [28р2 — 2р (З^! + 2а2 + а3 —-• а5 — 2а6 — Зсг7)]
(109)
Чтобы найти наибольшую вероятность для всей комбинации,
надо найти максимум выражения (109). Это будет тогда, когда
показатель степени при некотором р = ро обратится в нуль,
т. е.
Ро [— 2 (3 Cl} -f- 2 . . • + 2 аб -|- 3 Clq) 28 р0] = О,
откуда
3 2 CI2 Ч* • • Ч- 2 CIq 3 drj
__________
или
3 ilj —2 CI2 ~|~
Ч 2 а6 -р- 3 ят == 14 р0
Это дает наивероятнейшее значение ВИР:
Ро 3 4“ 2 (12 Ч" • • • Ч 2 —f- 3 Cl-
т 14 т
93
Но ВИР неизвестен; пусть он будет:
Тогда выражение (109) примет вид:
Р — Хв — Л2 [28р2 — 2р (Зо, + 2а, + «, — «Е — 2ае — 2«-)] _
— Ke — h~ +«')!+ 28₽П - Wo + 28 «] _ — Л5 р028 a: g — 28 я? _
— Св-^ ^8)2«*,
(ИО)
где С — Ke-h-№Stt: — постоянная в данном выводе величина.
Значение С в (110) определится из того соображения, что
вероятность получить случайную ошибку в пределах от —ос
до + оо равна единице, или
dx = 1,
откуда
Итак, ошибки ВИР следуют закону!
J hl7 28
р dx = е dx,
V к
(111)
т. е. мера точности определения ВИР по семи засечкам цели
получилась в У 28 раз больше h — меры точности отдельного
измерения расстояния.
В сделанном выводе мы ограничились семью измерениями
расстояния, и величина <8' = 28 получилась как сумма удвоен-
ных квадратов простых чисел:
9 4-4-|-1 + 1 +4 + 9= З2-|-221212-|-22-|-32 = 28.
для
Сущность вывода позволяет
заключить по аналогии, что
К=8
К=5
К=7
K—Q
g=l2-|-l2 = 2
8 = 22 + I2-]- 12-|-22= 10
8 = 28
8 = 60 и т. д.,
где К — число засечек цели.
94
Таблица 22
Значения /ЦТ для разного числа К засечек цели
К 2 3 4 5 6 7 8 9 10 11 12
0,66 1,41 2,24 3,16 4,18 5,29 6,48 7,75 9,08 10,49 11,96
Таким образом, срединная ошибка при определении ВИР по
графику обратно пропорциональна и может быть выражена так:
п==±^., (112)
Vs*
где
и —срединная ошибка ВИР;
3 — срединная ошибка в измерении расстояния;
* —промежуток времени между первой и последней засеч-
ками цели, выраженный в минутах;
К — число засечек цели.
Из выражения (112) видно, что чем больше число засечек
и чем больше промежуток времени t, тем меньше срединная
ошибка ВИР и, следовательно, ВИР получится более
точно.
В действительности это не совсем так: метод графика дает
хорошие результаты только при достаточно постоянном значении
ВИР, что будет иметь место при маневрировании на постоян-
ных курсовых углах и только иногда на прямых курсах, как,
например, при маневрировании разноименными бортами, — и то
при медленном изменении курсовых углов.
Это обстоятельство, увеличивая ошибку ВИР, само по себе
заставляет сокращать промежуток времени для определения
ВИР и уменьшать число засечек.
Будущее принадлежит, бесспорно, инклинометру или иному
более точному прибору.
23. Ошибка в определении курсового угла цели по
видимой длине цели и измеренной до нее дальности
Из треугольника, в котором известны длина цели I, даль-
ность Д и угол р, под которым наблюдается длина цели,
имеем:
sin q — ~ sin р,
V
где q — курсовой угол.
95
Полагая, что ошибки в определении курсового угла про-
изойдут от ошибки в измерении дальности и угла, имеем:
Мд = ---sin р • АД
I cosq r
и
А —Ц- Д cos Р • Ар,
р Zcosp г
откуда срединную ошибку в курсовом угле М получим из
а<? = ТбЬг^(81п₽* ДДГ-НДсоэр. дрр (ИЗ)
Полагая по малости угла р, что sin р = р, a cos р— 1, и вынося
за скобку Д2 и р2, получим:
Из (113) и (114) видно, что с увеличением курсового угла
после 45° ошибки в курсовом угле быстро растут.
24. Ошибка в определении ВИР по курсовому углу
и скорости движения цели на основании измерения
курсового угла по видимой длине цели и дальности
до нее
ВИР в кабельтовых в минуту, в зависимости от курсового
угла и скорости движения цели, выражается:
W= -—vcosq,
о
где v — скорость в узлах.
Срединная ошибка в ВИР, в зависимости от ошибки в ско-
рости и курсовом угле, выразится так:
1 ,_______________________
п — -g-[/(cosq • Аг)2 + (гsin# • МУ’ (115)
Величины ошибок в скорости (Аг) и в курсовом угле (bq)
будут зависеть от способов измерения скорости и курсового
угла.
96
В частности, при определении курсового угла по видимой
длине цели и дальности получается по (115).
В табл. 23 приведены срединные ошибки ВИР, вычислен-
ные по формулам (113—115).
Таблица 23
Срединные ошибки при определении ВИР по скорости и курсовому угпу цепи
(стереотруба или бинокль—Др=1 делению (З',6); инклинометр—Af5=15"; ско-
рость движения цели 30 узлов; срединная ошибка ВИР — в кабельтовых)
\ Даль- \ ность Курсо-\ч вой угол\ Стереотруба или бинокль Инклинометр
60 80 кабель 120 Т'ОВЫ 160 60 80 кабель 120 то вы 160
30° 0,48 0,51 0,58 0,66 0,45 0,45 0,46 0,47
60° 0,63 0,78 1,10 1,50 0,30 0,33 0,41 0,50
80° 1,84 — — — 0,54 0,72 1,07 1,47
Рассмотрение ошибок ВИР при пользовании инклинометром
показывает некоторую парадоксальность,' но эта парадоксаль-
ность только кажущаяся и объясняется легко формулой (115).
При принятой для инклинометра ошибке Др = 15" до курсо-
вых углов 60—65° величина Д<? мала и второе слагаемое под
корнем мало влияет на величину ошибки ВИР по сравнению
с первым слагаемым (cos q&v). Величина Дг от курсового угла
цели не зависит, a cos<) тем меньше, чем больше q, почему
при точном измерении угла р ошибки ВЙР сначала умень-
шаются, а затем за пределами курсовых углов 60—65°,
несмотря на точность измерения угла р, начинает превалиро-
вать в формуле (115) второе слагаемое (г • sin q • Д<у), и ошибки
ВИР растут вместе с приближением курсового угла цели к 90°.
25. Ошибки в определении скорости и курсового
угла цели по ВИР и боковому перемещению
(БП) цели
Определение скорости и курсового угла цели основано на
построении вектора скорости, как замыкающего вектора ВИР
и вектора бокового перемещения (черт. 28 и 29). Пусть CF —
вектор ВИР и FO — вектор бокового перемещения. Замыкаю-
щий вектор 6’0 = г —скорости хода и угол OCF = q — курсо-
вой угол цели в начальный момент наблюдений; Д—дальность
в конечный момент наблюдения при определении ВИР, равного
Углу р. На черт. 30 треугольники COF и KOF построены
отдельно.
7 Теория стрельбы 97
98
С
К
Черт. 30.
(120)
Черт. 29<7.
Из треугольника KOF имеем:
БП — Д sin ₽,
откуда ошибки в боковом перемещении будут:
ДБ = У (snip • ДДУ-НДсойР • Др')2 (116)
(ошибки <5 и Др независимы).
Ошибка ВИР получится в зависимости от способа опреде-
ления, но при определении скорости и курсового угла цели
обычно применяется график, и ошибка най-
дется:; по (112) (§ 22). На черт. 28 и 29 по-
казано построение ошибок ДБ и п; срединная
ошибка ВИР пойдет в плоскости стрельбы, а
срединная ошибка ДБ пойдет по направлению,
ему перпендикулярному; таким образом, мы сра-
зу имеем главные оси эллиптической ошибки на
конце вектора скорости. Срединная ошибка в ско-
рости определится, как отклонение по направ-
лению скорости (черт. 28):
Л г = |/(ДБ cos <рц)2 + (n sin <p1)2 (117)
или (черт. 29)
Дг; == |/'(и cos cpj2 + (ДБ sin <fj)2, (118)
где cpj — q (всегда).
Для получения ошибки в курсовом угле
надо предварительно найти отклонение ОД по
направлению, перпендикулярному к Дг (черт. 28):
/ ОД = )/(ДБ cos?2)2 + (n sin?г)2 , (И9)
или
ОД = У (n cos <р2)2 + (ДБ sin ср,)2,
где
ср2 — 90° — q.
Для определения ошибки др в ВИП, принимая, что ошибки
визирования следуют закону Гаусса со срединной ошибкой,
равной 0,2 деления, будем иметь:'
др = У(о,2)2+ (о,2)2 = о,2 0,28 деления. (121)
Время для наблюдений по определению ВИР и ВИП (р)
(черт. 30) не следует брать менее ‘/3 мин. и более 1 мин.
На черт. 30 показан случай определения курса и скорости
с неподвижной точки К. Если это определение производилось
находу, то будет получено относительное боковое перемеще-
ние. Для построения треугольника COF (черт. 30) надо к по-
лученному БП придать алгебраически свое ВП для получения
абсолютного значения ВП цели.
На выводе ошибок пользование относительными величинами
ничем не скажется.
Ниже приводим табл. 24 срединных ошибок в определении
скорости и курсового угла цели по ВИР и боковому переме-
щению.' Таблица составлена для следующих условий: даль-
ность определяется как средняя из показаний трех 8-метро-
вых дальномеров; ВИР и величина изменения пеленга (ВИП)
определяются в течение 1 мин.; срединная ошибка параллакти-
ческого угла (а) принята равной 8"; число засечек при опре-
делении ВИР — 7; скорость хода цели — 30 узлов.
Таблица 24
Срединные ошибки в определении скорости и курсового угла цепи по ВИР и БП
Курсовой угол q = 0° д = зо° д = 90°
Дальность, каб. b.v де Дг> Дд Дг: Дд
60 0,9 уз. ' У2° 0,9 уз. 1J/4O 0,05 уз. 13/4°
120 2,2 „ 1° 1,9 ,, 2’/i°, 0,1 „ 4°
160 3,8 „ 1’/4° 3,3 ,, зу2° 0,1 „ 7’/4°
200 6,0 ,, 1У2О 5,1 „ 51/4° 0,1 „ lli/4°
26. Ошибки в ВИР и значение времени при стрельбе
по подвижной цели
На основании изложенного в § 21—25 мы можем принять,
что при измерениях достаточно точными способами ошибки
ВИР следуют закону Гаусса.
В этом параграфе мы рассмотрим только те ошибки ВИР,
которые изменяются либо при изменении условий маневриро-
вания, либо при получении новых-данных измерения, в осталь-
ное ясе время за весь период огневого маневрирования они
не меняют своего значения..
100
При условии, что ошибки ВИР следуют закону Гаусса,
вероятность ошибки в ВИР в бесконечно малых пределах z и
z + dz выразится:
, г’
• О ₽ п2
р dz = —е dz, (122)
п У л
где z— величина, выраженная в единицах скорости, а и — сре-
динная ошибка, характеризующая закон случайных ошибок
в ВИР.
Нам важны не ошибки в скорости, а ошибки в перемеще-
нии в плоскости стрельбы (ошибки ВИР) за некоторый интере-
сующий нас промежуток времени t, например, от момента
засечки цели дальномером до момента дачи или падения залпа,
а потому от ошибки z в скорости мы должны перейти к ошиб-
ке zt в перемещении (ВИР). Срединная ошибка при этом
будет nt. Вероятность получить случайную ошибку ВИР в пре-
делах z-l и выразится при этом в таком виде:
_ 2 ±1
pdz1 —----е dZp (123)
nt У к
Вероятность ошибки в перемещении zl = zt между преде-
лами z( и z" будет:
г”
Z*
и
_ 2
е nt (125>
nt у к
Формула (125) дает возможность при данных п и t построить
распределение ВИР. Очевидно, что при одном и том же п рас-
пределение для величины 2t будет вдвое хуже, чем для вре-
мени t. Рассмотрим распределение цели при простом измерении
дальности при ошибке в ВИР к моменту t и 2t после момента
измерения. Дальность к моменту t будет:
Д(=До+И7,
где До — дальность в момент измерения,
W—ВИР в 1 мин. и
t — время в минутах.
Дальность к моменту 2t будет:
Да< = До + 2 Wt.
Чтобы получить распределение цели к моменту t и 2t,
Учтем ошибки.
101
Пусть измерение До сопровождается случайной ошибкой Д
при срединной ошибке £.
Учет ВИР будет сопровождаться ошибками zt и 2zt со сре-
динной ошибкой nt.
Вследствие независимости ошибок 8 и nt имеем срединные
ошибки распределения цели:
f=V82+(«02
и
Е"=У 82 + (2и1)2.
Пусть 8—1; и—1; t=l мин., тогда
Е' = У2 =1,41
и
Е" = У5 =2,24.
Величины срединных ошибок распределения цели Е' и Е"
дают сами по себе ясную картину значения времени при
стрельбе по подвижной цели.
Еще нагляднее будет эта картина, если построить и самое
распределение цели:
«/ = ?(г) =
nt У п
Таблица 25
Распределение ВИР в зависимости от времени t и 2t
(к черт. 31)
№ ординат Е' = 1,41 Е"= 2,24
X te|8 1 У' II tel*®. X Е" у" v=y". 7 Е"
0 0 0 0,269 0,191 0 0,269 0,120
1,2 1 0,7 0,241 0,171 0,4 0,259 0,116
3,4 2 1,4 0,172 0,122 0,9 0,224 0,100
5,6 3 2,1 0,099 0,070 1,3 0,183 0,082
7,8 4 2,8 0,045 0,032 1,8 0,129 0,058
9,10 5 3,5 0,017 0,012 2,2 0,090 0,040
11,12 6 4,3 0,004 0,003 2,7 0,051 0,023
13,14 7 5,0 0,001 0 3,1 0,030 0,013
16,16 8 5,7 0 .— 3,6 0,014 0,006
17,18 9 .— — — 4,0 0,007 0,003
19,20 10 .— — — 4,5 0,003 0,001
21,22 11 — — — 4,9 0,001 0
23,24 12 5,4 0 —
102
На черт. 31 построены распределения цели при одних и
'тех же срединных ошибках измерения дальностей и ВИР, но
для разного времени: для / — кривая АВС и для 2/ — кривая
А^А-
27. Особенности счета времени при исследовании
стрельбы по подвижной цели
Получаемые сведения о цели должны давать нам возмож-
ность выводить правила рационального управления огнем и
должны быть использованы до следующего пополнения сведе-
ний о цели путем наблюдения падений. Поэтому сведения
е положении цели должны обрабатываться для того ближай-
шего залпа, который может или пополнить сведения о цели или
дать поражение.
В § 26 мы видели значение времени при стрельбе по по-
движным целям, когда с течением времени благодаря ошибке z
в ВИР увеличивается ошибка zt в перемещении, и сведения
о цели, полученные путем предварительной подготовки или
наблюдения, с течением времени будут тем более устарелыми,
чем больше протечет времени от момента их получения.
Сведения о цели, добытые путем подготовки, измерения или
наблюдения, нами используются для подачи команд, имеющих
в виду получение либо наибольшей вероятности попадания,
либо наибольшего математического ожидания попадания,
либо дальнейшее улучшение сведений о цели. Для возможно-
сти использовать и наблюдения падений, и предварительные
сведения, имевшиеся до падения, все это необходимо отнести
к одному и тому же моменту, именно — к моменту падения
ожидаемого залпа.
Это вытекает из того, что предварительные сведения о цели
можно использовать для расчетов к любому произвольно и
наперед выбранному нами моменту, тогда как фактическое
падение снарядов нельзя отнести ни к какому другому моменту,
как только к моменту их фактического падения; поэтому для
одновременного использования и предварительных сведений и
наблюдений падения надо отнести их к моменту падения, ибо
этот момент не произвольный.
Так как при стрельбе по подвижной цели удобнее вести
вее расчеты в относительном движении, то получается, что
тот момент, который в относительном движении должен быть
103
принят за начальный, есть момент падения ожидаемого (под-
готовляемого) залпа.
Для того чтобы при этом не иметь дела с отрицательным
счетом времени (падение залпа—момент последний), услови-
лись 1 считать время в обратном направлении, принимая момент
падения ожидаемого залпа за о мин. О сек.
Поясним изложенное примерами.
Пример 1. Положим, даны четыре залпа с промежутками
в 42 сек. и при времени полета 30 сек.
Условный счет времени ясен из табл. 26.
Таблица 26
Условный счет времени (к примеру 1)
№ залпов Фактическое время дачи залпов Фактическое время паде- ния залпов и знаки Время, отне- сенное к мо- менту падения по условному счету Время дачи первого заппа по счету
1 2 3 4 Ожидаемый 0 м. 00 с. 0 м. 42 с. 1 м. 24 с. 2 м. 06 с. 2 м. 48 с. 0 м. 30 с. (—) 1 м. 12 е. (+) 1 м. 64 е. (--) 2 м. 36 с. (4-) 3 м. 18 с. (?) 2 м. 48 с. 2 м. 06 с. 1 м. 24 с- 0 м. 42 с. 0 м. 00 с. /0=3 м. 30 с.
Пример 2. Цель засечена дальномером. Через 20 сек. дан
первый залп. Через 10 сек. после падения первого залпа дан
второй залп; через 10 сек. после падения второго залпа пред-
положено дать еще два залпа почти одновременно. Найти время
засечки цели дальномером в условном счете времени. Время
полета 32 сек. (см. табл. 27).
Таблица 27
Условный счет времени (к примеру 2)
№ залпов № засечек дальноме- ром Фактиче- ские момен- ты дачи залпов Фактиче- ские момен- ты падений залпов Моменты по условному счету времени
падений засечки цели даль- номером
0 1 0 м. 00 с. 2 м. 16 с.
1 — 0 м. 20 с. 0 м. 52 с. 1 м. 24 с.
2 — 1 м. 02 с. 1 м. 34 с. 0 м. 42 с.
Предпола- -— 1 м. 44 с. 2 м. 16 с. 0 м. 0 с.
гаемые 1 м. 44 с. 2 м. 16 с. 0 м. 0 с.
1 Такой порядок счета времени весьма удобен при исследовании вопро-
сов стрельбы по подвижной цели.
104
28. Ошибки подготовки при стрельбе по подвижным
целям
Ошибки предварительной подготовки при стрельбе по по-
движной и неподвижной целям ничем не будут отличаться
между собой.
Ошибки же подготовки исходных установок будут отли-
чаться тем, что для случая стрельбы по подвижной цели вой-
дут ошибки в определении ВИР, БП, ВИП, курса и скорости
движения цели. Влияние этих ошибок, вообще говоря, до-
вольно сложно, и исследование ошибок придется производить
в каждом конкретном случае особо.
Перед исследователем каждый раз будет стоять задача,
которую придется решать на основании положений теории
вероятностей и изложенного выше материала; дать какие-либо-
общие положения невозможно, вследствие чего мы предложим
частный пример.
Пример. Найти распределение цели к моменту падения вто-
рого или третьего пристрелочного залпа. Для расчета первой
вилки Д = 491/4 каб. Скорость цели 30 узлов. Курсовой угол
цели 9 = 30°. Произведена полная подготовка. Поправки на
изменение начальной скорости введены на корректорах, при-
нимающих высоты прицела. Дальности измеряются тремя
8-метровыми дальномерами: у = 0",9. ВИР и БП определяются
в течение 50 сек. при четырех засечках. Наводка прямая в при-
целы. Длина цели Z = 170 м. Пушка 305-лш в 40 кал. дли-
ной. Работающая ширина цели К—1 sin 7 = 170 sin 80° = 85 м.
Выпишем нужные нам табличные данные:
Т— 32 сек.; 0.Г
Вд = 43 саж.; т= = 16 саж.; о ср
Вб—2,3 саж.; дх
р, = 0°24' = 6,7 дел.; дх — =10 саж.; ot
==-=13,6 саж. (на 1 мсек); д Wx дх дх — =37 саж.; дП
-—— = 0,87 саж. (на 1 мсек); д W2 4 ' дх -==90 саж.
dv
Срединная ошибка в измерении
Срединная ошибка ВИР
п
ЪУк __Д4 • ]/4 • 6
“ у/ы ~ 2,24 • 5
дальности 6=14 саж.
= 15,4 саж.
Срединная ошибка в курсовом угле (§ 25)
Ату = 2°.
1 05
в
Срединная ошибка в скорости (§ 25)
Дг = 1,2 узла.
Теперь надо выяснить время, т. е. к моменту падения ка-
кого залпа нас будет интересовать распределение цели, полу-
ченное в результате инструментальной подготовки.
Так как цель видима и наводка производится помощью ви-
зирования цели, то ошибки будут направлены по двум взаимно
перпендикулярным направлениям: в плоскости стрельбы и
в перпендикулярном к ней направлении. Стрельба ведется по
наблюдению знаков падения, поэтому предварительно необхо-
димо выяснить, какая может быть ошибка по целику, так как
от этого будет зависеть время, которое протечет к моменту
Засечка цели
-f*
Залп N\ Мы.
Залп N2
40
Предполагаемые:
Залп N 4
0 (?)
Л=0л.00ся.
ЗалпЫЗ
О (?)
Черт. 32.
падения захватывающего залпа. Так, если вероятность не на-
блюсти знак падения первого залпа близка к нулю, то мы мо-
жем вести подсчет распределения цели к моменту падения
второго залпа, в противном случае будет осторожнее считать,
что первый залп потребуется повторить, и тогда распределение
цели по дальности надо рассчитать к моменту падения третьего
залпа. В случае пристрелки уступом промежутками времени
между залпами уступа можно пренебречь и оба падения зал-
пов уступа считать одновременными.
Произведем расчет времени. Для этого введем дополнитель-
ные условия. Положим, что первый залп после засечки цели
дальномером мы можем дать через 20 сек. Мертвый промежу-
ток времени между залпами —10 сек. Если залп № 1 (черт. 32)
не показал знака, его придется повторить, и тогда время
t=2 мин. 16 сек. — 2,27 мин. Если повторения первого залпа не
понадобится, времени потребуется меньше на 42 сек. (Т-{-10сек.)
и t= 1 мин. 34 сек. = 1,57 мин.
На основании § 26 можно заключить, что во втором случае
распределение цели будет лучше и ширина первой вилки мо-
жет быть меньше.
106
Поэтому подсчитаем раньше распределение цели в напра-
влении, перпендикулярном к плоскости стрельбы.
Здесь мы будем иметь следующие ошибки:
а) ошибки в боковом перемещении цели со срединной ошиб-
кой ДБ;
б) ошибки в учете отклонения средней траектории вслед-
ствие боковой слагающей балистического ветра;
в) ошибки от округления (ошибками в своей скорости
и своем курсовом угле и ошибками самих приборов прене-
брегаем).
Величина бокового перемещения цели выражается:
БП—vTsinq. (126)
Приводя скорость к сажени и минуте, получим:
llrr юо Т сек. .
ВЯ = • fi fin ^8-sm i27)
о • bO
Ошибка в боковом перемещении явилась следствием ошибок
в скорости и курсовом угле. Диференцируя (127) по v и q и
складывая независимые срединные ошибки, получим:
дй — _1£2—? С?К~ У (Дг sm с/)2 -4- (у cosq bq)2. (128)
6 60
Выражая &q = 2° в отвлеченной мере и подставляя в (128)
данные из условия (см. § 25), получим:
100 • 32 ,_________________________
ДБ = —6 gQ- ]/ (1,2- 0,5)2 —(30 • 0,87 • 0,0349)2= 9,16 саж.
Распределение цели в направлении, перпендикулярном
к плоскости стрельбы, получим:
// \2 / 0 0580 \2
9,1624- I 0,87 • 1,1 + 0,67 • —Ч—- ) =9,2 Саж.
\ ./ \ ИЗ /
За масштабную единицу примем величину Вб, тогда
м Вб 2,3
Подсчет по — е
в- сведен в табл. 28.
107
. Таблица 28
Распределение цели в направлении, перпендикулярном плоскости стрельбы
(черт. 33). Значения <р2 (х)
К» ординат ?2(ж) К» ординат ?2(«)
1 и 35 0 11 и 25 0,034
2 и 34 0,001 12 и 24 0,040
3 и 33 0,002 13 и 23 0,046
4 и 32 0,005 14 и 22 0,053
5 и 31 0,006 15 и 21 0,059
6 и 30 0,008 16 и 20 0,062
7 и 28 0,012 17 и 19 0,065
8 и 28 0,019 18 0,066
9 и 27 0,026 —
10 и 26 0,028 1,000
На черт. 33 показано распределение цели в направлении,
перпендикулярном к плоскости стрельбы, и показана рабо-
тающая ширина цели 76=46,5 саж. = 85 м, которая занимает
В
В=ДЬ,5с = В5метрое
Черт. 33.
только 0,57 всего распределения, т. е. вынос возможен, но
вероятность выноса, характеризуемая численно заштрихован-
ными площадями кривой АВС района, только 0,089, или 8,9°/0,
следовательно, мы можем заключить, что вынос первого залпа
при данной степени подготовки хотя и возможен, но мало ве-
роятен, а потому будем считать время / = 1,57 мин., так как
мы имеем достаточно оснований. принять, что первый же залп
покажет знак.
Тогда для распределения цели по дальности к моменту па-
дений „предполагаемых" залпов № з и 4, считая время
/=1,57 мин., имеем:
108
или, подставив данные условия, получим:
= /142 + (90 0,8)2 + (37 • 1)2Н-(13,6 1,1)2 +(15,4 • 1,57)2 +
1/ + (0,67 ^+Г = 87 саж.
к \ кз./
Примем за масштабную единицу величину Вб —43 саж.,
тогда
Е
Вд 43 саж.
Пользуясь формулой <р2 (X) = „ е Ем, построим
Вн у 7Г
распределение цели (табл. 29).
Таблица 29
Значения <f(x) при распределении цепи, показанном на черт. 34
№ ординат № ординат ?2 W
1 и 23 0 8 и 16 0,056
2 и 22 0,001 9 и 15 0,081
3 и 21 0,002 10 и 14 0,106
4 и 20 0,004 • 11 и 13 0,126
5 и 19 0,009 12 0,132
6 и 18 0,018
7 и 17 0,033 1,000
Это распределение показано на черт. 34. Изучая табл. 29 и
черт. 34, видим, что вероятность положения цели в пределах
от —2 каб. до + 2 каб. выражается цифрой 89,9°/0, и в пределах
от—з каб. до + 3 каб. вероятность нахождения цели будет 97,7%,
в чем легко убедиться/ подсчитав площади, ограниченные со-
ответствующими ординатами.
Мы не можем еще рассматривать вопроса о расчете ширины
«первой вилки'*, но приближенно уже можно сказать, что если
109
первый залп показал, например, (+) перелет, то уступ по 1 кйб.
©беспечивает захват с вероятностью, близкой к 90%, а уступ
по 2 каб. обеспечивает захват цели почти на 100%.
С другой стороны, сведения о цели, полученные только на
основании хотя бы и очень тщательной подготовки, очень еще
не полны и, например, вероятность накрытия цели четырех-
орудийным залпом в точку „12“ очень невелика и составляет
всего 37°/0, в чем также легко убедиться подсчетом.
Аналогичное исследование придется делать в каждом кон-
кретном случае, и задача исследования будет сводиться всегда
к выявлению ошибок подготовки в данной обстановке стрельбы
и в подсчете распределения цели на основании сложения вы-
явленных ошибок, причем в зависимости от условий и обста-
новки стрельбы иногда окажется возможным иметь дело с рас-
пределением цели только в одном направлении, а иногда этой
возможности может и не быть, и придется иметь дело с рас-
пределением цели на плоскости.
ГЛАВА VI
СТРЕЛЬБА ПО НЕПОДВИЖНОЙ ЦЕЛИ
ПО НАБЛЮДЕНИЮ ЗНАКОВ
29. Достоинства и недостатки метода стрельбы пи
наблюдению знаков
К достоинствам метода стрельбы по наблюдению знаков
относится, главным образом, простота оборудования и органи-
зации управления огнем. Этот метод может быть осуществлен
при отсутствии приборов управления огнем даже при стрельбе
по подвижной цели и требует только наличия хотя бы прими-
тивных средств для наблюдения падений, например, бинокля
в руках управляющего огнем. Кроме того, для стрельбы по
наблюдению знаков возможно ограничиться глазомерной подго-
товкой. Таким образом, достоинствами этого метода стрельбы
являются: простота оборудования, простота организации, про-
стота подготовки, а следовательно, и его надежность и живу-
честь, так как этим методом возможно вести стрельбу, когда
все приборы и дальномеры выведены из строя.
К недостаткам этого способа следует отнести требование
большого искусства управляющего огнем и сложность правил
стрельбы, а следовательно, и вытекающую отсюда сложность и
дороговизну боевой подготовки, большое время пристрелки и
большой расход боевого запаса на пристрелку, в особенности
при больших смещениях стреляющего корабля (батареи) от
плоскости наблюдения.
30. Вероятность недолета и перелета при заданном
положении средней траектории относительно цели
Вероятность недолета и перелета рассмотрим при условии
совпадения плоскости наблюдения с линией цели.
Пусть цель находится в точке С (черт. 35).
Центр группирования находится в точке О и за положи-
тельное направление примем направление от корабля (батареи)
к цели (корабль или батарею предполагаем на черт. 35 слева).
Все расстояния будем выражать в срединных отклонениях
пушки.
Если центр группирования в О, то вероятности недолета
будет отвечать вероятность попадания в полосу, пределами
которой будут с одной стороны—сю, а с другой стороны алге-
браическая величина р, равная расстоянию от центра группи-
рования до цели. При этих условиях вероятность недолета вы-
разится:
(129)
При пользовании таблицей Ф (р) выражение (129) может быть
представлено в виде:
Р^=гк [Ф(₽)4-ф(°°)]
или
р(_)=1/2[1+ф (?)].
(130)
Пользуясь таблицей Ф (Р), мы можем величину :/2 [14- Ф (р)]
вычислить наперед для р от — сю до + сю (обычно для практи-
ческих целей достаточно от — 5 до-}-5, при которых р(_} уже
мало отличаются от 0 и 1). Такая таблица носит название
.„Таблицы
--------------------- а
Черт. 35.
Из черт. 35 имеем, что р=ж—а, и вероятность недолета
может быть выражена
P<-}=F (х — а).
(131)
Для вероятности перелета на основании принятых условий
получим:
(132)
или
?(+)=4[ф ©1’
112
или
?(+)=g- [1 — ф(₽)]. (133)
Следовательно, вероятность перелета может быть предста-
влена в виде:
<7(+)=-F (-0, (134)
или
2(+)=-Р («-Я-) • (135)
Из (129) —(135) видим, что выражения для вычисления ве-
роятности недолета или перелета имеют один и тот же вид,
следовательно, для вычисления этих вероятностей достаточно
иметь одну таблицу F (f) (см. в приложениях табл. IV).
Так как таблица F (t) вычислена в пределах от — 5 до 5,
то для некоторых редких случаев научных работ, когда ве-
роятности недолета и перелета выходят из этих пределов,
пользуются обычно таблицей функции:
пределы которой значительно шире.
Для этого положим в (129) р е= t; продиференцировав по г и t,
получим:
ds =— dt •
Р
Подставив эти значения в (129) и подобрав пределы, по-
лучим:
Поступая подобным же образом по отношению выражения
вероятности перелета (132), получим:
1
1-©(р₽)
(137)
где р = О,4769364 11gр= 1,6784604].
'$ Теория стрельбы
113
Пример I. Определить вероятность недолета для дальности
до цели Х = 1С0 каб., если дальность до центра группирования
(прицел) « = 100 3/4 каб.; Вд—50 саж.
. 10 000—10 075 75
' = =--------50-----= -50 = -1’6;
р =F(0 = F(x — а)= f(— ) =F(— 1,5) = 0,156.
Пример 2. Определить для тех же условий вероятность пе-
релета.
q(+}=F (—t) = F(a — ж) = К (1,5) = 0,844 •
Примечание. Для одного выстрела q = 1 —р — 1—0,156 = 0,84 4.
Пример 3. Определить вероятность недолета для дальности
до цели х = 60 каб., если дальность до центра группирования
(прицел) а = 59 каб.; ВР = 40 саж.
м 6 000 — 5 900 100
t=------40----=ТГ=2-6;
р = F (/) = F (ж — а) = F (2,5) = 0,954.
Пример 4. Определить для тех же условий вероятность пе-
релета.
q — F (—t) = F (a—x) = F (—2,5) = 0,046.
Пример 5. Определить вероятность недолета для р = =б,25.
При этом аргументе мы выходим из таблицы F (t), а по (136)
имеем:
Р = Чг [1 + ® (Р ₽)] = J/2 [1 + © (-0,48 • 6,25)] =
= J/2 [1— 0 (3,00)1 =^2 [1 — 0,999978] = 0,000011.
Пример 6. Определить вероятность недолета для {?=-[-7,0
По (136) имеем:
Р=Ч, [1 + ©(РЮ] = [1+©(0,48.7,0)]=Ч2 [1 +
+ © (3,36)] = i/2 (1 + 0,999980) = 0,999990.
Пример 7. Определить вероятность перелета для р = 4-5,73
или (« — ж) = — 5,73.
<? = 1/2 [1-0(рР)] = 1/2 [1-© (0,48-5,73)] = */2 [1-
— ©(2,75)] =42 [1—0,9998994] = 0,0000503.
Пример 8. Определить вероятность перелета для р = — 6,67
или (а —ж) = 6,67.
? = 1/2 [1 —©(рР)]=1/2 [1— 0(—0,48 • б,67)] = 1/2 [1 +
4-0(3,20)] =!/2 (1 + 0,9999782) = 0,9999о91.
Кривая, изображающая F(t) (черт. 36), имеет асимптоты
т/ = 0 при ж= —оси ?/=1 при ж = 4-00.
114
Практически можно принять, 4Tof(7)=0 при / = — 5 и
F(t) = l при £ = -|-5. Часто для приближенных расчетов поль-
зуются сокращенной табл. 30 и принимают, что F (f) = о при
t— — 4 и F(t) = l при «= + 4.
Таблица 30
31. Распределение цели после первого выстрела
в случае, когда распределение цели до выстрела
известно. Расчет первой вилки
Распределение цели до выстрела будет известно на основа-
нии подготовки исходных установок, как бы таковая подготовка
ни производилась (§ 19 и 20).
Это распределение может быть выражено в виде симметрич-
ной кривой при полной или сокращенной подготовке, так как
в этом случае ошибки подготовки будут следовать закону
Гаусса с "некоторой срединной ошибкой Е в зависимости от
точности подготовки. В случае глазомерной подготовки кривая
распределения цели выражается, строго говоря, несимметрич-
ной кривой (черт. 37), так как ошибки в определении расстояния
на-глаз не следуют закону Гаусса, но обычно для удобства
анализа принято считать, что ошибки в определении расстоя-
ний на-глаз также следуют закону Гаусса с некоторой средин-
ной ошибкой, принимаемой в среднем для глазомера в 10% от
дальности.
8* ' 115
Эту цифру надо считать довольно произвольной, и измере-
ние расстояния на-глаз может сопровождаться относительно
весьма большой точностью.
Во всяком случае, как бы ни была произведена подготовка
исходных установок, мы всегда, будем иметь сведения о цели
в вйде некоторого распределения ср (х).
На основании этих сведений при исследовании вопросов
стрельбы надо решить, с каким прицелом должен быть дан
первый выстрел.
Первое решение, часто приходящее на мысль, это назначить
прицел, отвечающий наивероятн§йшему месту цели, которому
в свою очередь отвечает наибольшая ордината распределе-
ния цели.
Черт. 37.
Такое решение следует откинуть на том основании, что ве-
роятность нахождения цели в какой-либо определенной точке
бесконечно мала, и даже вероятность нахождения цели в пре-
делах от — 1/2 до Ч2 около наивысшей ординаты по своей
абсолютной величине мала.
Обычно принято для первого выстрела назначать прицел,
отвечающий срединному положению цели, т. е. назначить при-
цел в точку, относительно которой равно вероятно ожидать,
что цель будет ближе и дальше этой точки.
Если выстрел произведен и снаряд упал на линии нашего
наблюдения, мы можем видеть одно из трех явлений: недо-
лет (—), перелет (4-) или попадание в цель. Последний случай
пока рассматривать не будем, а из первых двух безразлично,
что ни рассматривать. Положим, что первый выстрел дал не-
долет (—).
Наблюдение недолета есть событие, появление которого
изменяет распределение вероятностей гипотез, имевшее место
до выстрела, и, применяя теорему гипотез, получим распреде-
ление цели после наблюдения недолета:
(138)
I ф («•) F (а?—a) dx
----ОН
116
Иногда бывает удобнее принять начало осей координат не
в точке стояния батареи, а в центре группирования О, т. е.
положить а = 0; тогда выражение (138) примет-вид:
. . , ср (ж) F (х) dx
a., (x)dx= —-------------- (139)
+“
J ср(ж)Г(ж) dx
--СО
Выражение (139) удобно для случая стрельбы по неподвиж-
ной цели с корабля находу, так как в этом случае величина а —
переменная.
Обозначив ср(ж)Г (ж) —ср5(ж), получим:
ср, (ж) dx =——. (140)
4-00
/ ср, (ж) dx
« -о»
В выражениях (138) и (139) ср3(ж) получены в результате
наблюдения недолета при одном выстреле. Выражения (138)
и (139) для очереди из к выстрелов или для залпа из к ору-
дий в том случае, если вероятность недолета от выстрела
к выстрелу не изменяется, напишутся
<р (ж) Fk(x — a) dx
ацжХж— '----------------—------ (138)
4-СО
ср (ж) Ек (ж — a) dx
•—00
и
(139')
Jср (ж) Ек (ж) dx.
Формулы cpj (ж) dx — ср (х) Fk (ж) dx, выражающие вероятности
недолета" по каждой из гипотез о месте цели, получили назва-
ние „первых функций Персена", а ср2 (ж) — „вторых функций
Персена" и часто называются функциями распределения цели
после наблюдения падений.
Ширина первой вилки может быть выведена из расчета ве-
роятности захвата цели в вилку, т. е. вероятности наблюдения
1 В этих случаях возможны и накрытия, но вопрос о распределении цели
после наблюдения той или иной комбинации накрытия будет рассмотрен особо.
117
перелета при следующем выстреле, близкой к единице, обычно
не менее 80—85°/0, или же из расчета дать следующий залп
(очередь, выстрел) в точку, отвечающую срединному положе-
нию цели. Выбор того или иного варианта зависит от характера
распределения цели после наблюдения недолета при первом
залпе.
В том случае, если точка, отвечающая срединному положе-
нию цели, занимает приблизительно среднее положение между
средней траекторией первого залпа и точкой, отвечающей ве-
роятности наблюдения перелета, не менее 8О°/о, то выгоднее рас-
считать ширину первой вилки для срединного положения цели,
так как в случае вторичного наблюдения недолета мы ничего
не теряем, повторив вилку, в случае же наблюдения перелета
в точке, отвечающей срединному положению цели, экономим
один залп, который пришлось бы израсходовать иа половиие-
нис первой вилки, выведенной для вероятности захвата, близ-
кой к единице.
Иногда бывает выгодно и третье решение: назначать команды
в точку, отвечающую наибольшему математическому ожиданию
попадания. *
Первые два решения в смысле исследования существенно
отличаются от третьего тем, что при расчетах вероятности
захвата цели в вилку мы не касаемся вопроса о размерах цели,
тогда как расчет математического ожидания попадания требует
задания конкретной цели и знания ее размеров.
В большинстве случаев третье решение при исследовании
периода, пристрелки бывает удобно при целях значительных
размеров, когда переход на поражение выгоден и возможен
при еще не совсем уточненном положении цели.
Пример. Стрельба трехорудийными залпами по видимой не-
подвижной береговой цели большой ширины. Подготовка, сокра-
щенная при определении расстояния по карте. Балистическая
и аэрологическая подготовки произведены полностью. Даль-
ность 40 каб. Произвести расчет первой вилки.
Табличные данные: угол прицеливания 5С49'; угол паде-
far, д'Т- с)'?- far,
ния 10°12'; = 50 саж.; ^ = 5,5 саж.; -3—= 17,4саж.; =
dv dt dll дев
QoC'
= 23саж.; Вд — 20 саж.; Вб —0,8 саж.; Т=258 м; —, —
dW№
=7,7 саж.
Срединная ошибка в определении места цели гч=30 саж.
круговая); срединная ошибка в определении места корабля
гк = 60 саж. (круговая).
При указанном выше виде подготовки мы будем иметь сле-
дующие ошибки: 1) ошибки в определении места цели со сре-
динной ошибкой гч = зо саж.; 2) ошибки в определении места
корабля со срединной ошибкой гк = 60 саж.; 3) ошибки бали-
стической и аэрологической подготовки и ошибку от округле-
на
ния прицела, характеризуемые соответствующими срединными
и средней квадратической ошибками (см. § 20).
По (97) § 20 имеем распределение цели по дальности;
302 + 60г 4-(50.0,8)2+ (5,5 • I)2 +
|/" +(17,4 • О,5)2-Ь(7,7 • l,5)2-f-fo,67
саж.
(По условию задачи можно считаться только с распределе-
нием цели по дальности.)
Возьмем за масштабную единицу величину срединного от-
клонения пушки Вд = 20 саж., тогда
_ 79,8
“ 20
Е
м
= 3,99^4
Функция © (ж), характеризующая распределение цели до
вы стрела, при ошибках, следующих закону Гаусса, будет:
_рг±
?(ж)=—16. (141)
i]/ к
Формула (139') примет вид:
— р2
—у=е 16 №(ж) dx
% (ж) dx = ----------------. (142)
рЗ
—^.е 1ЪР3(х)Ох
4^
Найдя по (141) величины <р (ж), вероятности трех недолетов
[Г3(ж)] по каждой из гипотез и произведения (ж) F3 (ж) = <?! (ж),
тем самым получим первые функции Персена. Найдя сумму
£cf>! (ж) и поделив на эту сумму каждую из функций фх(ж) =
= © (ж) Fs (ж), получим вторые функции Персена или ординаты
кривой распределения цели после наблюдения трех недолетов
(табл. 31).
По данным второго столбца построена кривая АВС распре-
деления цели до выстрела (черт. 38), по данным последнего
столбца на том же чертеже построена кривая DFK распределения
119
Таблица 31
Значения первых и вторых функций Персена после наблюдения трех недолетов
(черт. 33)
№ ординат <?(«) ВЦх) ? (ж) F3 (х) = ?1(ж)
— Л-И 00 / <f>] (ж) dx) .QO
1—20 1 0 0 0
21 0,0636 0,0007 0 0
22 0,0663 0,0156 0,0010 0,002
23 0,0673 0,1250 0,0084 0,020
24 0,0663 0,4219 0,0280 0,067
2Б 0,0636 0,7569 0,0481 0,116
26 0,0592 0,9368 0,0555 0,134
27 0,0511 0,9896 0,0506 0,122
28 0,0472 0,9989 0,0471 0,114
29 0,0403 1 0,0403 0,097
30 0,0336 1 0,0336 0,081
31 0,0271 1 0,0271 0,065
32 0,0213 1 0,0213 0,051
33 0,0162 1 0,0162 0,039
34 0,0121 1 0,0121 0,029
35 0,0087 1 0,0087 0,021
36 0,0061 1 0,0061 0,015
37 0,0042 1 0,0042 0,010
38 0,0028 1 0,0028 0,007
39 0,0018 1 0,0018 0,004
40 0,0011 1 0,0011 0,003
41 0,0007 1 0,0007 0,002
42 0,0004 1 0,0004 0,001
43 0,0002 1 0,0002 0
44 0,0001 1 0,0001 0
45 0 1 0 0
Сумма в пре- (ж) = 0,4154 (ж) - 1,000
делах точ- ности вы- числений близка к единице
цели после наблюдения трех недолетов со средней траекторией
в центр распределения АВС 2.
Для выявления наивыгоднейшей величины первой вилки
найдем срединное положение цели по распределению DFK.
Для этого найдем часть площади кривой DFK, равную по-
ловине. Сделав подсчеты, получим:
1 Значения о(ж) с № 1 по № 20 не вписаны, так как на этих участках
ГЗ(ж) = 0.
г Вследствие симметричности кривой АВС в данном случае срединное
положение цели совпадает с центром распределения.
120
I <p2 (ж) dx= 1 |o + 0,002 4- 0,020 + 0,067 + 0,116 +
— 2
+ 0,134 4- 0,122 — -| = 0,400;
Xu I
+ 5
I ^(x)dx—l jo + O,OO2+ . . . + 0,1141 = 0,518.
Простой интерполяцией находим, что площадь кривой DFK
делится пополам ординатой L между ординатами № 27 и № 28
или в 1 каб. от точки О (черт. 38).
F
О ОД 1 1,5 2 2Д ЗЫ
Черт. 38.
Аналогичными подсчетами найдем, что
+ ю
= 0,888.
Таким образом, при команде „2 больше44 вероятность захвата
цели в вилку шириной в 2 каб. (10 J90) выражается цифрой 88,8%,
т. е. близкой к единице. После захвата цели в вилку послед-
нюю надо будет сужать, и, для того чтобы найти наивыгодней-
шую команду, следует проделать такой же расчет при условии,
что залп в точку М показал перелеты.
Если же мы примем команду „1 больше44, то в случае за-
хвата цели в вилку залпом в точку L сразу получаем вилку
в два раза уже; в том же случае, если залп в точку L пока-
жет недолеты, то повторение вилки дает вероятность захвата
уже не 88,8%, а очень близкую к единице, так как наблюде-
ние трех недолетов в точке L еще сузит распределение цели.
В первом случае при команде „1 больше44 мы выигрываем
один залп, во втором случае ничего не теряем.
На основании этих рассуждений для условий данной задачи
первую вилку принимаем в 1 каб.
121
32. Распределение цели при отсутствии
предварительных сведений о положении цели
В § 31 при решении вопроса о первой вилке одновременно
было показано получение распределения цели после наблюде-
ния знаков падения при том условии, что до наблюдения зна-
ков падения или до выстрела распределение цели уже имелось
на основании каких-то других признаков, например, в резуль-
тате подготовки по карте.
Если пренебречь предварительными сведениями о цели, то
в результате наблюдения падений одного и того же знака
мы смогли бы ограничить положение цели только в одну сто-
рону, тогда как в другую сторону оно осталось бы не ограни-
ченным. Например, при наблюдении только недолетов мы полу-
чили бы фигуру, аналогичную черт. 36.
Для получения сведений о цели в виде некоторого распре-
деления ее в том случае, когда мы не хотим пользоваться све-
дениями о цели до выстрела (залпа или очереди), нам необхо-
димо наблюдать падения нескольких выстрелов, не менее двух,
по обе стороны цели или прямое попадание, причем эти
выстрелы (залпы) могут быть произведены либо с различными
установками прицелов (вилка), либо с одной установкой при-
цела (нулевая вилка или накрытие). Предварительные сведения
о цели заметно сказываются на распределении цели после
наблюдения вилки только в том случае, когда они достаточно
полны; в противном случае распределение цели после наблюде-
ния вилки получается почти таким же, каким оно получится и
в том случае, если сведениями о цели до наблюдения вилки
пренебречь вовсе.
Для подтверждения этого положения рассчитаем распреде-
ления цели для случаев, когда сведения о цели до наблюде-
ния вилки шириной в 4 Вд характеризовались срединной ошиб-
кой E — i и когда все гипотезы о положении цели до наблю-
дения вилки были равновероятны, что равносильно отсутствию
сведений о цели до выстрела.
При расчете будем полагать, что на каждом из пределов
вилки наблюдалось по одному знаку.
Полагая начало координат в точке О (черт. 39) для случая,
когда распределение цели до наблюдения вилки принято во
внимание, распределение цели после наблюдения вилки в 4 Вд
получим из выражения (143):
Р г2
—р и Е(ж)Е (4—ж) dx
ф'3(х)йх =------------------------------ (143)
С р р2 —
/ 4/тГ 6 16 F (ж) F (4—х) dx
•-GO
422
При отсутствии же сведений о цели до выстрела распреде-
ление цели после наблюдения вилки той же ширины будет най-
дено из выражения (144):
„, . , F (ж) F (4—ж) йж
<f>2 (x)dx= - v 7—1----------
J F(x)F (4—ж) tlx
—co
(144)
Вычисления (143) удобно расположить в виде табл. 32.
Таблица 32
Распределение цели после наблюдения вилки в 4 Вд, если сведения о цепи
учтены до выстрелов
№ орди- нат р —— е ‘ 16 = <р (ж) 4 И it Да?) Д(4—х) <Р1(а?) = = ? (a?) F(a?)F(4—ж)
15 0,0271 0 — 0 0
16 0,0336 0,0004 —. 0 0,0001
17 0,0403 0,0035 — 0,0001 0,0005
18 0,0472 0.02151 — 0,0010 0,0038
19 0,0511 0,0887 — 0,0045 0,0169
20 0,0592 0,2500 0,9996 0,0148 0,0553
21 0,0636 0,5000 0,99651 0,0317 0,1184
22 0,0663 0,7500 0,9785 0,0487 0,1818
23 0,0673 0,9113 0,9113 0,0559 0,2089
24 0,0663 0,9785 0,7500 0,0487 0,1818
25 0,0636 0,9965 0,5000 0,0317 0,1184
26 0,0592 0,9996 0,2500 0,0148 0,0553
27 0,0511 1 0,0887 0,0045 0,0169
28 0,0472 1 0,0215 0,0010 0,0038
29 0,0403 1 0,0034 0,0001 0,0005
30 0,0336 1 0,0004 0 0,0001
31 0,0271 1 0 0 0
S7l(a?) = 0,2575
Вычисления (144) расположены в табл. 33, где ввиду явной
симметрии дается только одна половина схемы.
0.24
Черт. 33.
123
Сравнивая последние столбцы табл. 32 и 33, видим, что <р2' (ж)
и <р2" (ж) практически дают одно и то же. Еще нагляднее это
видно по черт. 39, где кривая АВС дает распределение цели
р 0= —
до выстрела и построена по выражению —е ie .
4]/ л
Кривая DEF построена по (143) из последнего столбца
табл. 32, а кривая DKF — no выражению (144) из последнего
столбца табл. 33.
Таблица зз
Распределение цели после наблюдения випки в 4 Вд, если до выстрелов
сведения о распределении цепи отсутствуют
№ ордина т F(cc) f(4—as) ?1(Ж) = = F(x)F(i—х)
1 2 3 4 5
23 0,9113 0,9113 0,8307 0,2060
24 0,7500 0,9785 0,7340 0,1824
25 0,5000 0,9965 0,4983 0,1239
26 0,2500 0,9996 0,2499 0,0621
27 0,0887 1 0,0887 0,0220
28 0,0215 1 0,0215 0,0053
29 0,0035 1 0,0035 0,0009
30 0,0004 1 0,0004 0,0001
31 0 1 0 О
(ж) =4,023
Повторив аналогичные расчеты для других случаев, можно
убедиться, что чем хуже сведения о цели до выстрела, тем при
той же вилке ?2'(ж) и с?2"(ж) будут ближе друг к другу, а при
одинаковых сведениях о цели до выстрела ^./(ж) и с?2"(ж) будут
тем ближе, чем уже вилка.
33. Уточнение сведении о цели путем сужения вилки
(половинение вилки)
Вопрос об уточнении сведений о цели путем половинения
вилки рассмотрим при отсутствии предварительных сведений.
Рассмотрение вопроса начнем с вилки в 16 Вд и будем все
дальности выражать в величинах Вд.
Начало отсчета в этом случае будет удобно взять в средине
вилки в 16 Вд.
Пусть с каким-либо прицелом (h—8) в точке О (черт. 40)
наблюден недолет (—), а с прицелом (h + 8) наблюден пере-
лет (+), т. е. наблюдена вилка шириной 16 Вд.
До наблюдения недолета и перелета на пределах вилки,
вследствие отсутствия предварительных сведений о цели, все
гипотезы о месте цели равновероятны. После наблюдения вилки
вероятности различных гипотез будут пропорциональны вероят-
124
ности наблюдений недолета с прицелом (h—8) и перелета с при-
целом (Л + 8).
Принимая предыдущие обозначения и начало отсчетов в
точке О (черт. 40), подсчитаем первые функции Персена:
cpj (ж) = F (ж 8) F (8—ж). (145)
Подсчеты следует вести, начиная от средней ординаты 15
(табл. 34) в обе стороны, пока при выбранной точности, напри-
мер, четыре знака после запятой, не придем к нулевым отсчетам.
Кривая, построенная по этим значениям ^(ж), носит назва-
ние первой кривой Персена. Первую кривую Персена строить
не будем.
Л/
Черт. 40.
Имея первые функции Персена, по ним перейдем к кривой
распределения цели, пользуясь выражением (теорема гипотез)
, F(x + 8)F (8 — ж)йж
ср, (ж) dx — - (146)
С F (ж-ф 8)F(8—x)dx
Интеграл, стоящий в знаменателе (146), может быть найден
не посредственно.
Мы не будем останавливаться на этом вопросе и укажем, что
этот же интеграл может быть найден помощью квадратур (чаще
пользуются формулой трапеций).
Имея в виду, что интервал принят равным Вд=1 и конце-
вые координаты равны нулю, значение этого интеграла примем
равным:
2 К(ж + 8)F(8—ж) = 16, (147)
тогда получим:
<?3'(ж)=^Г(ж-4-8)Г(8—ж). (148)
На черт. 40 построена кривая АВС распределения цели п©
146) или.(148).
125
Таблица 34
Распределение цепи при получении вилки на прицепах (Л — 8) и (A-J-8) (черт. 40
кривая АВС)
1 II III IV V 1
№ ординат (8 + s' 1 СО 8* со со* д 1 S Ьч * II s' 1 со sf оо li II
1 0 1 0 0
2 0,0004 1 0,0004 0
3 0,0035 1 0,0035 0,0002
4 0,0215 1 0,0215 0,0013
5 0,0887 1 0,0887 0,0055
6 0,2500 1 0,2500 0,0156
7 0,5000 1 0,5000 0,0312
8 0,7500 1 0,7500 0,0469
9 0,9113 1 0,9113 0,0570
10 0,9785 1 0,9785 0,0612
11 0,9965 1 0,9965 0,0623
12 0,9996 1 0,9996 0,0625
13 1 1 1 0,0625
14 1 1 1 0,0625
15 1 1 1 0,0625
16 1 1 1 0,0625
17 1 1 1 0,0625
18 1 0,9996 0,9996 0,0625
19 1 0,9965 0,9965 0,0623
20 1 0,9785 0,9785 0,0612
21 1 0,9113 0,9113 0,0570
22 1 0,7500 0,7500 0,0469
23 1 0,5000 0,5000 0,0312
24 1 0,2500 0,2500 0,0156
25 1 0,0887 0,0887 0,0055
26 1 0,0215 0,0215 0,0013
27 1 0,0035 0,0035 0,0002
28 1 0,0004 0,0004 0
29 1 0 0 0
2¥1'(я0 = 16
126
Положим, что для. уточнения положения цели произведен
еще выстрел на средине вилки (h—8) и (Л-|-8). При этом мы
можем наблюдать: или перелет, или недолет, или попадание.
Попадание пока рассматривать не будем, а из прочих двух
случаев нам безразлично, какой ни рассматривать. Пусть при
выстреле с прицелом h наблюден недолет (—).
Теперь мы имеем случай, совершенно аналогичный случаю,
рассмотренному в § 32, с той только (не принципиальной) раз-
ницей, что в § 32 предварительные сведения о цели определя-
лись выражением
при срединной ошибке Ь' = 4, а теперь до третьего выстрела
мы имеем сведения о цели, определяемые распределением
<?2' (ж) = F (х +8) F (8—ж),
и, следовательно, распределение цели в результате наблюдения
на прицеле h недолета получится в результате вычисления
* П; (8—ж) F (х) ^х
Чг' (ж) dx =---+^—--------------------—- (149')
~J F(x-[-8)F(8—x)F(x)dx
—со
ИЛИ п"Мг1т - <?2<.X)F(X)dX
?2 №)dx— +оо . (149 )
--00
Эти вычисления показаны в табл. 35 к черт. 40, на котором
построена кривая распределения DEC, причем
4-00
(ЭН~8) 1'’ (8—ж) F (ж)(1х ~
У ^-F(х 4- 8) F(8 — ж) F(x) = ^~ ,
16 2
а потому
ф2" (Ж) = -1F (ж 4- 8) F (8 — ж) F (ж). (150)
• ‘ 8
127
Таблица 35
Распределение цепи при получении недопета на середине випки (h — 8) и
(Л 4-8) (черт. 40, кривая DEC]
II III IV V
1 1 "s'
1 ОО оо
оо + 4-
ос? -
ез 4- ICO
д и в
Д ьГ д т Л ?
о 8 8 5°
й 'э? II 5ч 9- • 9- -
9 0,0570 0 0 0
10 0,0612 0,0004 0,0000 0,0000
11 0,0623 0,0035 0,0002 0,0004
12 0,0625 0,0215 0,0013 0,0026
13 0,0625 0,0887 0,0055 0,0110
14 0,0625 0,2500 0,0156 0,0312
15 0,0625 0,5000 0,0312 0,0624
16 0,0625 0,7500 0,0469 0,0938
17 0,0625 0,9113 0,0570 0,1140
18 0,0625 0,9785 0,0611 0,1222
19 0,0623 0,9965 0,0621 0,1242
20 0,0612 0,9996 0,0611 О”1222
21 0,0570 1 0,0570 0,1140
22 0,0469 1 0,0469 0'0938
23 0,0312 1 0,0312 0,0624
24 0,0156 1 0,0156 0'0312
25 0,0055 1 0,0055 о'оно
26 0,0013 1 0,0013 0,0026
27 0,0002 1 0,0002 0,0004
28 0 1 0 0
Г'' (Ж) = 2- Vl ’ 2
— Р(ж4- 8)F(8 — ж) F(ж) F (ж — 4) F(6 — ж)йж
?2IV И йж=---------------------------------------------------
Д- 4*’(ж-|- 8)_F(8 — ж)F(x)F(x— 4)F(6 — x)dx
(153)
ИЛИ
<р21У(ж) = Д- F (х 4- 8) F (8 — ж) F (ж) F (ж—4) F (6 — ж). (154)
Весь ход вычислений показан в табл. 36 и 37.
Таблица 36
Распределение цепи при получении випки с прицепом (h — 2)M(h-j-2)
(черт. 40, кривая KLC)
Продолясая сужение вилки до 4 Вд и до
пределение при наблюдениях, например,
недолета, а на прицеле (h 4- 6) — перелета:
2 Вд, получим рав-
на прицеле (/г 4~4)
Д- F (х Ч- 8) F (8 — ж) F (ж) F (ж — 4) dx
О
(ж) dx-=----------------------------------------------
уIF (х 8) F (8 — ж) F (ж) F (ж — 4) dx
——о»
(151)
ИЛИ
<?/" (ж) = — F(х 4- 8) F (8 — ж) F (ж) F (ж—4), (152)
1 II III IV V
(ж) (84"аз) d (5—(«) •(8+®иД р Да „ив,
сЗ ^|СОЬ, и
К И II 1 д? Д *
И Рн О 1 а 8, 1 ** дД а ।
9- X - &- Ьч
13 0,0111 0 0 0
14 0,0312 0,0001 0,0005 0,0001
15 0,0625 0,0035 0,0002 0,0004
16 0,0988 0,0215 0,0020 0,0040
17 0,1139 0,0887 0,0101 0,0202
18 0,1223 0,2500 0,0306 0,0612
19 0,1241 0,5000 0,0620 0,1240
20 0,1223 0,7500 0,0917 0,1834
21 0,1139 0,9113 0,1038 0,2076
22 О', 0938 0,9785 0,0918 0,1836
23 0,0625 0,9965 0,0623 0,1246
24 0,0312 0,9936 0,0312 0,0624
25 0,0111 1 0,0111 0,0222
26 0,0027 1 0,0027 0,0054
27 0,0004 1 0,0004 0,0008
28 0 1 0 1?'1(ж) = 4 0
9 Теория стрельбы
129
128
Таблица 37
Распределение цепи при получении вилки с прицепом (h — 1) и (Л -j-1) (черт. 40.
кривая KMN)
I II III IV V
s' 1 s' 1
ci 1 CO
+ i + 1 + 7
А Д. 8 Рч l о г Д v- CM z—'
I4* s 1 s
се j и 1 Рч 1! -г- е? II II fcf
я t=t 8 1 ' 1
о ч—' оо ZD K>rH oo >CI OO
'Л Р4 Рч
13 0 1 0 0
14 0,0001 1 0,0001 0,0002
15 0,0004 1 0,0004 0,0008
16 0,0040 0,9996 0,0040 0,0080
17 0,0202 0,9965 0,0201 0,0402
18 0,0612 0,9785 0,0598 0,1196
19 0,1240 0,9113 0,1131 0,2262
20 0,1834 0,7500 0,1376 0,2752
21 - 0,2076 0,5000 0,1038 0,2076
22 0,1836 0,2500 0,0459 0,0918
23 0,1246 0,0887 0,0110 0,0220
24 0,0624 0,0215 0,0013 0,0026
25 0,0222 0,0035 0,0001 0,0002
26 0,0054 0,0004 0 0
27 0,0008 0 0 —
28 0 —. —• —
На черт. 40 кривые распределения цели при сужении вилки
до 4 и до 2 Вд — KLC и KMN.
При наблюдениях по одному падению обратим внимание на
то обстоятельство, что сужение вилки с 16 до 8 Вд резко
улучшает сведения о цели; при сужении вилки с 8 до iBd
уточнение сведений о цели хотя и значительное, но не столь
резкое, а при дальнейшем сужении вилки до 2 Вд (кривые KLC
и KMN) уточнение сведений о цели по сравнению с вилкой в
4 Вд уже совсем невелико.
34. Повторение пределов как мера, ведущая
к уточнению сведений о цели
Для рассмотрения этого вопроса положим, что после наблю-
дения на прицеле h недолета на прицеле (/г Д- 4) произведен
не один, а 4 выстрела и наблюдено 4 недолета, после чего на
прицеле (7> 8) произведено еще 4 выстрела и наблюдено
4 перелета.
130
До наблюдения 4 недолетов на прицеле (7z—f-4) и 4 переле-
тов на прицеле (/14-8) мы имеем уже сведения о цели в виде
распределения:
?2"(ж) = 4- F (ж + 8) F (8 — ж) F (ж)
О
(табл. 35 и черт. 40).
После наблюдения 4 недолетов на прицеле (/г 4- 4) и 4 пере-
летов на прицеле (h 4- 8) распределение цели выразится:
<?г"(ж)Р4(ж —4)F4(e —ж)йж
(X)-----—--------------------------------(i55)
'JЧз” (?) F* (ж — 4) F* (6 — ж) dx
Вычисления (155) сведены в табл. 38, и на черт. 41 построена
кривая распределения цели.
Таблица 38
Распределение цепи после повторения пределов випки
I II III IV V VI
"8 1
К, §
*“Н
4- 1
4- 8 Д о
т—1
[ f ь, Д тч |оо .8, О
се № К К т-< [оо 11 -? 1 8х II ь 1 8 II
рц — 1 8 1 й
о 8 » 8 СО ч—‘ оо
й fc, . э- К, & * 03 9-
16 0,0938 0 1 0 0
37 0,1140 0,0001 1 0 0
18 0,1222 0,0039 0,9986 0,0005 0,0037
19 0,1242 0,0625 0,9860 0,0077 0,0593
20 0,1222 0,3163 0,9166 0,0354 0,2748
21 0,1140 0,6898 0,6898 0,0542 0,4204
22 0,0938 0,9166 0,3163 0,0272 0,2109
23 0,0624 0,9860 0,0625 0,0039 0,0298
24 0,0312 0,9986 0,0039 0,0001 0,0009
25 0,0110 1 0,0001 0 0
S<?7 (Ж) =
= 0,1290
9*
131
Сравнивая кривые KLO (табл. 36, черт. 40) и (табл. 38,
черт. 41), мы видим, насколько лучше сведения о цели во вто-
ром случае.
Сравнивая кривую распределения цели KMN (табл. 37,
черт. 40), полученную в результате сужения вилки при одном
наблюдении на каждом пределе вилки шириной 2 Вд с кривой
распределения цели (табл. 38, черт. 41), полученной в
результате четырех наблюдений на каждом из пределов вилки
шириной в 4 Вд, мы видим,
втором
случае значительно
Черт. 41.
что уточнение сведении о цели во
лучше, и сведения о цели полу-
чаются значительно полней при
четырехкратном повторении преде-
лов вилки в 4Вд, чем при вилке
в 2 Вд, но при наблюдении по
одному падению на каждом ее
пределе.
Нетрудно аналогичным подсче-
том убедиться, что в результате
повторения пределов вилки шири-
ной в 16 Вд мы получили бы почти
такое же распределение цели, какое
имеем на черт. 40 при одном на-
блюдении на каждом из пределов
этой вилки, тогда как, споловинив
вилку в 16 Вд, мы сразу же полу-
чаем существенное уточнение све-
дений о цели при значительной
экономии снарядов. Повторением
пределов вилки шириной в 4 Вд
мы лучше уточняем сведения о
цели, нежели половинением этой
вилки, но производя по одному
выстрелу на пределе, расходуем 3
выстрела, тогда как повторяя пре-
делы вилки по 4 раза, мы расходуем 8 выстрелов, т. е. увели-
чиваем расход снарядов более чем вдвое.
Задачей расчетов при выработке правил стрельбы для периода
пристрелки и является сочетание достаточно надежного уточне-
ния сведений о цели с экономическим расходом снарядов и
времени.
В результате расчетов должны быть указаны: 1) ширина
„первой вилки11, 2) предел сужения вилки, з) когда следует
ограничиться одним выстрелом на пределе вилки и 4) когда
следует повторять пределы и по скольку выстрелов давать на
каждом пределе.
Повторение пределов называют обеспечением пределов вилки.
Основными указаниями при подобных расчетах являются
математическое ожидание числа попаданий на выстрел и вероят-
ность хотя бы одного или не менее заданного числа попада-
ний при том же расходе снарядов на поражение.
132
35. Распределение цели при наблюдении накрытия
цели
(нулевая вилка)
Рассмотрим распределение цели, которое получится в резуль-
тате накрытия при двух,- четырех- и трехорудийных залпах
(или очередях). При этом для четырехорудийного залпа пред-
положим, что были наблюдены 2 недолета и 2 перелета, а при
трехорудийном залпе — 2 недолета и 1 перелет.
Распределения цели в этих случаях мы подсчитаем по
выражениям:
1) для двухорудийного залпа
СР2^) =
F (ж) J1 (—ж) 2Дж) — Н2 (ж)
(156)
2) для четырехорудийного залпа
_ Н2(ж)Р2(—ж) _ F2 (ж) — Fi (ж)
V2 \F) , .
(157)
f F2(x)F2(—х) dx
3) для трехорудийного залпа
, . F2(x)F(— ж)
?2 (ж) = ——----------
F2(x) — F*(x)
(158)
В качестве примера получения распределения возьмем слу-
чай, когда наблюдено накрытие в двухорудийном залпе, т. е.
наблюдено по одному недолету и перелету.
Вычисления, сведенные в табл. 39, произведем через каждые
0,2 Вд, принимая попрежнему ВЭ = 1и пользуясь пятизнач-
ными логарифмами. (Эти расчеты в дальнейшем мы используем
и для примера вычисления средней квадратической и „приве-
денной срединной ошибки распределения цели.)
Для проверки имеем:
S2 = (2,65060 • 2 — 0,29894) • 0,2=1,000452,
что при данной точности вычисления можно принять равным
единице.
На черт. 42 построена кривая распределения цели в том же
масштабе, что и на черт. 40 и 41.
133
Таблица 39
Распределение цели при нулевой вилке + и —(2 выстрела)
Со 1g 81=0,07763
№ ор- динат F(.x) F2(«) F(x)- —F\x) lg[F(a5)— -F2(CC)] Ig ?2(*) ¥2 (*)
34 0,50000 0,25000 0,25000 T, 39794 T 47557 0,29894
33,35 0,55365 0,30653 0,24712 1,39291 1,47054 0,29549
32,36 0,60634 0,36765 0,23869 1,37783 1,45546 0,28541
31,37 0.65715 0,43186 0,22529 1,35274 1,43037 0,26938 co
30,38 0,70526 0,49738 0,20788 1,31781 1,39544 0,24857
29,38 0,75000 0,56250 0,18750 1,27300 1,35063 0,22420 o'
28,40 0,79085 0,62545 0,16540 1,21854 1,29617 0,19777 II
27,41 0,82749 0,68475 0,14274 T, 15442 1,23205 0,17063 J?
26,42 0,85974 0,73917 0,12057 1,08124 1,15887 0,14417 &-
25,43 0,88764 0,78792 0,09972 “2,99878 1,07641 0,11924
24,44 0,91133 0,83062 0,08071 2,90693 2,98456 0,09651 о Q
23,45 0,93108 0,86692 0,06416 2,80726 2,88489 0,07672
22,46 0,94725 0,89728 0,04997 2,69871 2,77634 0,05975
21,47 0,96025 0,92210 0,03815 2,58149 2,65912 0,04562 CO
20,48 0,97052 0,94194 0,02858 1,45606 2,53369 0,03417 О
19,49 0,97849 0,95744 0,02105 *2,32325 2,40088 0,02517 II
18,50 0,98455 0,96935 0,01520 2,18184 2,25947 0,01817 s
17,51 0,98908 0,97827 0,01081 2,03383 2,11146 0,01293 gP
16,52 0,99241 0,98487 0,00754 T, 87737 3,95500 0,09902 и
15,53 0,99481 0,98965 0,00516 3,71265 3,79028 0,00617 о"
14,54 0,99651 0,99305 0,00346 T, 53908 3,61671 0,00414 II
13,55 0,99769 0,99540 0,00229 3,35984 3,43747 0,00274 У
12,56 0,99850 0,99700 0,00150 3,17609 3,25372 0,00179
11,57 0,99904 0,99812 0,00092 4,96379 T, 04142 0,00110
10,58 0,99939 0,99880 0,00059 4,77085 T, 84848 0,00071 О
9,59 0,99963 0,99926 0,00037 4,56820 4,64583 0,00044 к
8,60 0,99977 0,99954 0,00023 4,36173 4,43936 0,00028 ёГ
7,61 0,99986 0,99972 0,00014 4,14613 4,22376 0,00017
6,62 0,99994 0,99988 0,00006 5,77815 5,85578 0,00007
5,63 0,99996 0,99991 0,00005 5,69897 5,77660 0,00006 II
4,64 0,99997 0,99994 0,00003 5,47712 5,55475 0,00004 75s
3,65 0,99998 0,99996 0,00002 5,30103 5,37866 0,00002
2,66 0,99999 0,99998 0,00001 5,00000 У, 07763 0,00001
1,67 0 0
Сравнивая кривую распределения цели черт. 42 с кривыми
черт. 40 и 41, можно заключить, что накрытие цели при наблю-
дении всего по одному падению по обе стороны от цели дает
распределение лучше, чем при захвате цели в вилку 4 Вд и
одном наблюдении на пределах вилки, немного лучше, чем
при вилке в 2 Вд и также с одним наблюдением на пределах
134
вилки (практически почти то же самое), но захват цели в вилку,
хотя бы шириной 4 Вд с четырехкратным обеспечением преде-
лов, дает распределение почти в два раза лучше, чем накры-
тие при одном наблюдении на каждом пределе вилки.
Из этого можно сделать вывод, что ценность накрытия реальна
только тогда, когда наблюдается по нескольку падений, а под-
счетами, аналогичными произведенным выше, можно убедиться,
что вилка в 4 Вд с четырехкратным повторением пределов почти
равноценна наблюдению накрытия по два падения с каждой
стороны цели (2 недолета и 2 перелета).
Это одна из причин, послуживших поводом к терминам
„надежное" или „ненадежное" накрытие и к стремлению в. мор-
ской артиллерии к четырехорудийным залпам.
36. Кривая распределения цели как кривая закона
ошибок
Пользуясь кривой распределения цели, мы можем найти
наивыгоднейший прицел, т. е. тот прицел, который будет отве-
чать или наилучшему поражению цели, или способствовать
дальнейшему уточнению сведений о цели.
В том случае, когда дальнейшее уточнение положения цели
уже не преследуется, прицел должен отвечать ее наилучшему
поражению и, выбирая тот или иной прицел, мы тем самым
как бы принимаем гипотезу об „истинном" положении цели.
Принимая то или иное положение цели за истинное, мы
неизбежно делаем ошибку, потому что цель может находиться
на различных участках распределения с различной вероят-
ностью, вероятность же положения цели в данной точке равна
нулю.
Положим, что, закончив пристрелку захватом цели в вилку
шириной 4 Вд при четырех наблюдениях на каждом пределе,
решено перейти на поражение цели с прицелом в точку М
(черт. 41).
135
В действительности цель может оказаться где угодно, в пре-
делах от Кг до Cv Если цель оказалась в точке N, то будет
иметь место случайная ошибка MN.
Вероятность нахождения цели в точке N равна:
ydx = срs 1 v (ж) dx. (159)
Этому же числу будет равна и вероятность ошибки MN.
Мы можем говорить о вероятности нахождения цели на
участке, например, NF. Вероятность этого предположения будет
равна:
+
п= Г <f^(x)dx. (160)
—
Этому же числу будет равна и вероятность случайной
ошибки в пределах от — хг до—или вероятность того, что
ошибка не выходит за пределы участка NF.
Таким образом, мы имеем здесь переход „закона распреде-
ления" в закон ошибок, причем моментом этого перехода
является утверждение, что некоторое значение, взятое в пре-
делах распределения, есть истинное значение величины.
Необходимо отметить, что и распределение цели и закон
ошибок, выраженные одной и той же кривой, заключают в себе
существенную разницу. Эта разница заключается в том, что
пока с кривыми, подобными черт. 40—42, мы имеем дело как
с кривыми распределений, нам совершенно безразлично, где
ни брать начало отсчета, но с того момента, как с этими же
кривыми мы начинаем иметь дело как с законами ошибок,
начало отсчетов должно брать обязательно в той точке, кото-
рую мы принимаем за истинное положение цели.
Рассматривая кривые черт. 40—42 и таблицы, по которым
они построены, мы видим, что при исследовании метода стрельбы
по наблюдению знаков мы можем встречаться с распределе-
ниями цели как симметричными, так и несимметричными.
С переходом от распределения цели к закону ошибок мы будем
иметь несимметричный закон всегда, если кривая закона ошибок
несимметрична.
В случае симметричной кривой мы будем иметь симметрич-
ный закон только в том случае, когда за «истинное» положение
цели примем основание наивысшей ординаты, во всех же осталь-
ных случаях закон ошибок будет несимметричен, хотя бы рас-
пределение цели и характеризовалось симметричной кривой.
Отсюда ясно, что вторые кривые Персена не являются зако-
ном Гаусса.
Закон, которому следуют случайные ошибки при стрельбе
по наблюдению знаков, мы будем иметь всегда, так как этот
закон всегда будет получен в виде таблицы, подобной табли-
цам, по которым построены кривые на черт. 40—42, и мы всегда,
имея эти таблицы и пользуясь формулой (160), вычисляемой
136
при помощи квадратур, можем найти вероятности ошибок
в любых наперед заданных пределах.
При исследовании методов стрельбы часто бывает необхо-
димо знать параметры, характеризующие распределение цели,
как закон ошибок.
При исследовании стрельбы по наблюдению знаков часто-
имеют место несимметричные распределения, переходящие в
несимметричный закон ошибок, но и при симметричных рас-
пределениях в зависимости от принятия того или иного поло-
жения цели за „истинное" могут иметь место несимметричные
законы и, наконец, даже и при симметричных законах, как
было уже указано, закон Гаусса не имеет здесь места.
Принимая все это во внимание, для определения парамет-
ров, характеризующих распределение цели, как закон ошибок,
следует обратиться к общему случаю, т. е. найти среднюю
квадратическую ошибку.
Квадрат средней квадратической ошибки в общем виде для
любого закона выражается:
+ оо
Е\ — Г ж2 ср (ж) dx
(161)-
(математическое ожидание квадрата случайной ошибки).
В качестве примера возьмем распределение после наблюде-
ния нулевой вилки при двух выстрелах:
. . , F(x)F(— x)dx
(ж) dx =----—— ---------—
* “ -1. ГЛ
(162).
и найдем для него величину средней квадратической ошибки
по выражению:
ж2 <f>2 (ж) dx.
(163)
Примем за истинное положение цели центр распределения
(34 на черт. 42).
Взяв из табл. 39 значения <р2(ж) и полагая ж = О; + о,2; +
+ о,4+ • • • + 6,6, подсчитаем величину Е2 по (163) и све-
дем вычисления в табл. 40.
Имея в виду, что табл. 40 обнимает только половину
симметричной кривой и интервал между ординатами равен
0,2, квадрат средней квадратической ошибки получим как-
137
Таблица 40
Схема вычисления кривой закона ошибок
№ орди- нат X 1g ¥2 (*) 2 1g х 1g 1'гг(я:)а52] X2 ?2 (ж)
34 0,29894 0 "1,47557 —. — 0
33,35 0,29549 0,2 1,47054 2,60206 2,07260 0,0118
32,36 0,28541 0,4 1,45546 1,20412 2,65958 0,0457
31,37 0,26938 0,6 1,43037 1,55630 2,98697 0,0971
30,38 0,24857 0,8 1,39544 1,80618 1,20162 0,1591
29,39 0,22420 1,0 1,35063 0,00000 1,35063 0,2242
28,40 0,19777 1,2 1,29617 0,15836 1,45453 0,2847
27,41 0,17063 1,4 1,23205 0,29226 1,52431 0,3344
26,42 . 0,14417 1,6 1,15887 0,40824 1,56711 0,3691
25,43 0,11924 1,8 ~1\07641 0,51056 1,58696 0,3864
24,44 0,09651 2,0 2,98456 0,60206 1,58662 0,3860
23,45 0,07672 2,2 2,88489 0,68485 1,56974 0,3713
22,46 0,05975 2,4 2,77734 0,76042 1,53776 0,3449
21,47 0,04562 2,6 2,65912 0,82995 1,48907 0,3084
20,48 0,03417 2,8 2,53369 0,89432 1,42801 0,2679
19,49 0,02517 3,0 2,40088 0,95424 1,35512 0,2266
18,50 0,01817 3,2 2,25947 1,01030 1,26977 0,1861
17,51 0,01293 3,4 2,11146 1,06296 1,17442 0,1494
16,52 0,00902 3,6 "3,95500 1,11261 "1,06761 0,1169
15,53 0,00617 3,8 3,79028 1,15957 2,94985 0,0891
14,54 0,00414 4,0 "3,61671 1,20412 2,82083 0,0662
13,55 0,00274 4,2 "3,43747 1,24650 2,68397 0,0483
12,56 0,00179 4,4 3,25372 1,28691 2,54063 0,0347
11,57 0,00110 4,6 3,04142 1,32552 2,36694 0,0233
10,58 0,00071 4,8 "4,84848 1,36248 2,21096 0,0163
9,59 0,00044 5,0 "4,64583 1,39794 2,04377 0,0111
8,60 0,00028 5,2 1,43936 1,43201 3,87137 0,0074
7,61 0,00017 5,4 1,22376 1,46479 3,68855 0,0049
6,62 0,00007 5,6 5,85578 1,49638 3,35216 0,0022
5,63 0,00006 5,8 "5,77660 1,52686 3,30346 0,0020
4,64 0,00004 6,0 5,55475 1,55630 3,11105 0,0013
3,65 0,00002 6,2 "5,37866 1,58478 4,96344 0,0009
2,66 0,00001 6,4 5,07763 1,61236 4,68999 0,0005
1,67 0 6,6 — —• — 0
удвоенную сумму чисел последнего столбца, умноженную на
0,2, или
ж2с?г(ж) 4,518 • 2 • 0,2=1,8072.
138
Отсюда
Е2 = )/ 1,8072 = 1,345.
Средняя квадратическая ошибка может служить характе-
ристикой закона ошибок.
По существу, здесь нет основания говорить о срединной
ошибке, так как мы имеем дело не с законом Гаусса, но вслед-
ствие ряда удобств, а также, принимая это распределение, весь-
ма близкое к закону Гаусса, за закон Гаусса, говорят о так
называемой „приведенной" срединной ошибке.
Срединную ошибку распределения цели после наблюдения
накрытия при двух выстрелах получим:
Е = р)/2 Е2 = р)/2 • 1,345 = 0,9012.
Имея в виду, что эти вычисления при пятизначных лога-
рифмах гарантируют только два знака, нам следует принять:
jE2 = 1,34
.И
Е = 0,90.
Подсчетом Персеи получил следующие срединные ошибки
для симметричных вилок шириной от о до 10 при одном на-
блюдении на каждом пределе (табл. 41).
37. Основания для выбора прицела по распределе-
нию цели
При выборе наивыгоднейшего прицела можно поступить
различно в зависимости от учета той обстановки, для которой
ведется исследование.
Мы можем иметь следующие случаи:
а) ошибка в ту или другую сторону безразлична;
б) ошибку в одну сторону иметь менее выгодно, чем в
Другую;
1 Величины В, начиная с вилки в 6 Вд и более, следует пересчитать по
Формуле р^2~Е2=Е.
139
в) часть распределения вовсе отпадает вследствие того, что на
этом участке распределения цели быть не может, например, отмель
в море, известное противнику заграждение, обрыв на суше ит. п.
В первом случае, когда нет оснований предпочитать ошибку
в одну сторону ошибке в другую сторону, можно рекомендо-
вать следующие три приема:
1. Найти срединное положение цели, т. е. ординату, деля-
щую площадь кривой пополам.
В этом случае ошибка в ту или другую сторону будет рав-
новероятна.
Определение положения ординаты, равноделящей площадь
кривой распределения, делается простым подсчетом площади,
пока не получится площадь, равная половине.
2. Найти такое положение, относительно которого математи-
ческое ожидание случайной ошибки равно нулю. В этом случае
мы будем иметь наименьшую величину средней квадратической
ошибки.
Для нахождения точки, относительно которой математиче-
ское ожидание первой степени случайной ошибки равно нулю,
заметим, что для этой точки и средняя квадратическая ошибка
принимает наименьшее значение.
Выражение (163) (§ 36) квадрата средней квадратической
ошибки тождественно с выражением момента инерции плоской
фигуры. Момент инерции плоской фигуры примет наименьшее
значение в том случае, если он взят относительно оси, прохо-
дящей через центр тяжести площади.
Таким образом, для нахождения точки, относительно кото-
рой математическое ожидание первой степени случайной ошибки
равно нулю, надо найти ординату, проходящую через центр
тяжести площади кривой распределения, для чего можно пли
применить общеизвестный прием, или воспользоваться „сет-
кой 2“ или, наконец, вырезав фигуру распределения, найти ось,
проходящую через центр тяжести путем уравновешивания
фигуры на острие ножа так, чтобы лезвие ножа было парал-
лельно ординатам кривой.
Последний прием наиболее прост при вполне достаточной
точности, так как команду все равно придется округлять не
менее как до J/4 кабельтова (45,72 м). При симметричном рас-
пределении одновременно удовлетворяются оба условия при
назначении прицела в центр распределения.
3. Наконец, можно указать и еще один прием, заключающийся
в том, что путем ряда попыток находят точку, отвечающую
наибольшему математическому ожиданию попадания.
В тех же случаях, когда ошибка в ту или другую сторону
при выборе наивыгоднейшего прицела "не безразлична, дать
конкретных указаний нельзя, так как это будет зависеть от
той предполагаемой обстановки, для которой вырабатываются
правила, и в большинстве случаев здесь приходится выбирать
более крайние положения, что часто будет иметь место, на-
пример, при стрельбе по подвижным целям при отражении атак.
140
38. Методы подсчета элементов кривых Персена
В предыдущем изложении курса мы уже имели случаи
подсчета элементов кривых Персена и здесь укажем только на
три способа подсчета:
а) Подсчет площадей по формуле трапеций:
с__к Уа++ Уч + • • • • (164)
О - II/ &
б) Подсчет площадей по формуле Симпсона:
У о + 4 Ух + 2 У 2 + 4 Уч + 2 Vi + •
. -ф4?/п_1 -\-уп
(165)
где в (164) и (165) h — интервал между двумя смежными орди-
натами, yi — величина ординаты, а число п в (165) — обязательно
четное. Последнее обстоятельство делает формулу Симпсона
мало применимой при подсчете элементов кривых Персена.
в) Подсчитать площадь графически, для чего кривую Пер-
сена вычерчивают на миллиметровой бумаге, подсчитывают
число клеток, занимаемое всей площадью кривой, и затем для
получения вероятности нахождения цели на том или ином
участке подсчитывают число клеток интересующей нас пло-
щади и берут отношение этой площади к площади всей кривой.
39. Один из приближенных способов получения
распределения цели и пределы его применения
Одним из приближенных способов получения распределения
цели является способ, при котором распределение цели после
наблюдения перелетов и недолетов при вилке той или иной
ширины приближенно принимают за закон Гаусса со срединной
ошибкой R.
Величина срединной ошибки R выбирается из табл. 41 сре-
динных ошибок распределения, данной Персеном (§ 36), в за-
висимости от ширины вилки.
Срединные ошибки распределения, взятые из таблицы Пер-
сена, отвечают случаю симметричной вилки и при наблюдении
по одному падению на каждом пределе вилки. В случаях, когда
имеет место повторение пределов, величины срединных ошибок,
выбранных из таблицы Персена, должны быть уменьшены в
корень квадратный раз из числа падений, наблюденных на каж-
дом пределе вилки. Например, при распределении цели после
захвата ее в вилку шириной 4 Вд и при четырех наблюдениях
на каждом пределе срединные ошибки надо уменьшить в )/4 =
==2 раза.
Распределение цели, если не прибегать к приближенному
методу, может быть вычислено по формуле:
141
<₽2 (ж) dx =
jF4 (х + 2) ,F4 (2 — a') dx
+<»
(166)
Fi (ж 4- 2) J’4 (2 — ж) dx
При применении приближенного метода имеем:
1 33
77 = 1,33 и Е = -^.= 0,665,
/4
откуда
_ 2
/л Р Р 0,665s
<р (х) = ------ _ е
0,665 У тс
(167)
Значения ®2(ж), вычисленные по (166) или по (167), приняты в
табл. 42.
Таблица 42
Значения tp2 (а;)
№ орди- нат по (166), Персеи <f2(x) по (167), Гаусс
5 0,401 0,404
4,6 0,244 0,243
3,7 0,052 0,052
2,8 0,003 0,004
1,9 0 0
К этой таблице нет смысла прилагать чертеж, так как
ясно, что при чертеже обычного масштаба обе кривые совпадут.
Аналогичными подсчетами можно убедиться, что с увели-
чением ширины вилки обе кривые будут отличаться одна от
другой все более и более.
Пределом применения приближенных методов является
вилка шириной в 8 Вд, когда вторые кривые Персена еще воз-
можно заменить, хотя и с большой натяжкой, законом Гаусса
с соответствующей срединной ошибкой.
Предел в 8 Вд объясняется тем обстоятельством, что при
этой ширине вилки вторая кривая Персена еще имеет один
максимум, а за этим пределом средняя часть кривой практи-
чески уже обращается в прямую, параллельную оси А-ов, и тем
на большей длине, чем шире вилка.
Другим условием, допускающим применение изложенного
приближенного метода, будет симметричность вилки, так как
142
при несимметричных вилках применение приближенного метода
будет сопровождаться уже более грубой ошибкой.
Приближенные методы подсчета распределений, вообще
говоря, следует применять только в тех случаях, когда при
исследовании' требуются подсчеты и построения большого числа
распределений.
В таком случае надо найти те крайние пределы, при кото-
рых замена кривых Персена палатками Эйлера практически при-
емлема, и тогда для всех промежуточных случаев расчет и
построение кривых Персена. заменяют расчетом и построением
палаток Эйлера при соответственно выбранных, срединных
ошибках.
Кроме рассмотренного приближенного способа, существует
еще способ Мангона, который можно считать равноценным рас-
смотренному. Этот способ в нашем курсе рассмотрен не будет.
40. Использование кривых Персена при выработке
методов стрельбы
Кривые Порсепа, как и вообще всякое распределение цели,
используются в самых различных направлениях. Укажем глав-
нейшие:
а) определение наивыгоднейшего прицела как при уточне-
нии положения цели, так и в период поражения;
б) решение вопроса о наивыгоднейшем способе обстрела цели,
т. е. стрельбы на одном прицеле или обстрел площади;
в) исследование выгоды того или иного метода стрельбы;
г) надежность решения огневой задачи;
д) расход боевого запаса, необходимого для достижения
заданной надежности решения огневой задачи;
е) выбор метода маневрирования (см. Стрельба по подвиж-
ной цели) для понижения успешности огня противника;
ж) исследование точности работы приборов и установление
предела точности, за которым прекращается улучшение резуль-
татов стрельбы.
Все указанные «задачи, а также и ряд других задач реша-
ются подсчетами математического ожидания попадания и веро-
ятности хотя бы одного или не менее заданного числа попада-
ний, о чем повторять не будем, так как приемы этих подсчетов
изложены в 1-й части курса.
Г Л Л В A VII
СТРЕЛЬБА ПО ПОДВИЖНОЙ ЦЕЛИ
ПО НАБЛЮДЕНИЮ ЗНАКОВ ИЛИ 111*11 НЕТОЧНОМ
ЗНАЧЕНИИ ВИР
41. Основные различия в условиях стрельбы по
подвижной цели по сравнению со стрельбой
по неподвижной цели
Стрельба по подвижным целям резко разнится от стрельбы
по неподвижным целям из неподвижных орудий. К стрельбе по
подвижной цели близко подходит стрельба с корабля находу по
неподвижной береговой цели, когда ВИР известен неточно, что
может иметь место при недостаточно уточненных координатах
невидимой береговой цели.
В этом случае ошибки в ВИР и БП своего корабля скажут-
ся на стрельбе, хотя и не так сильно, как при стрельбе по
подвижной цели.
Особенности стрельбы по подвижной цели будут следующие:
а) ошибка в учете ВИР и БП из-за неточного знания курса
и скорости цели, вследствие чего приобретает исключительно
большое значение время, в течение которого и будет накоп-
ляться ошибка в перемещениях по дальности и в боковом на-
правлении;
б) стрельба будет сопровождаться непрерывным изменением
аэрологических поправок вследствие непрерывного изменения
дальности и направления плоскости стрельбы (ВИП);
в) непрерывное изменение влияния несоответствия балистики
данного момента с табличной балистикой;
г) данные балистической подготовки будут также меняться
вследствие быстрого влияния числа выстрелов на изменение
начальной скорости у морских орудий калибром 180 мм и
крупнее.
Современные приборы управления огнем, решая в полной
мере задачу стрельбы, учитывают не только ВИР и поправки
на несоответствие условий данного момента с табличными усло-
виями, но учитывают и изменения поправок с изменением даль-
ности и направления плоскости стрельбы. Тем не менее, вслед-
ствие неизбежности ошибок при установке аргументов поправок
и изменения самих аргументов, сведения о цели непрерывно
144
устаревают, и требуется непрерывное пополнение этих сведений
' путем вепрерывной работы дальномеров, визиров и других при-
боров для наблюдения падений снарядов и введения корректур.
Эти факторы и составляют главный объект исследования при
выработке методов и правил стрельбы.
t локность явления не позволяет рассматривать вопрос сразу
во всем комплексе и требует его расчленения. Рассмотрим сна-
чала влияние ошибки в ВИР как главного фактора, сопровож-
дающего стрельбу по подвижной цели.
При изучении вопросов стрельбы по подвижным целям
вследствие непрерывного устаревания сведений о цели мы не
будем учитывать распределения цели до выстрела и, кроме
| случая расчета ширины первой вилки, будем считать все гипо-
I тезы о месте цели до выстрела равновероятными.
Что касается самой ошибки в ВИР, то здесь могут быть два
I случая:
а) ошибка в ВИР сохраняет свое значение на некоторый
промежуток времени и
б) ошибка в ВИР меняет свое значение от выстрела к вы-
стрелу (от залпа к залпу).
42. Вероятность наблюдения недолета или перелета
при захвате цели в вилку и при постоянной
ошибке в ВИР
За начало счета условного времени (§ 27) примем момент
падения будущего выстрела (залпа), который последует за па-
дением выстрела (залпа), захватившего цель в уступ или вилку.
Иначе говоря, за начало отсчета времени примем момент паде-
ния того выстрела (залпа), для которого используются сведе-
ния о цели, полученные в результате захвата цели в уступ
или вилку шириной R.
За начало отсчета дальностей примем табличную дальность
первого залпа. Начало координат при этих условиях располо-
жится, как показано на черт. 43. За положительное направле-
ние дальностей примем направление О'а, за положительное на-
правление счета времени — направление 0^.
Пусть с прицелом (табличная дальность) аг выстрел, направ-
ленный в точку Oj, показал недолет (—); вследствие рассеива-
ния пусть точка падения была в M’v
Через некоторый промежуток времени был произведен вто-
рой выстрел с прицелом (при табличной дальности) а2 — ал + R
с учетом ВИР. Вследствие рассеивания пусть точка падения
была в М2.
Назовем ошибку в определении ВИР через г, а ошибки в
Рассеивании—через и ж2.
Спроектировав точки М' и М2 на ось О'а и проведя линии
-М'Д и М'2А2 под наклоном соответственно ошибке ВИР, по-
лучим падения в точках Аг и А2, причем ошибки рассеивания
10 Теория стрельбы 145
суть О'М1 = х1 и 0”М2 — х2, а ошибки в перемещении вслед-
ствие ошибки в ВИР суть 214^.! = ^ и М2Ла = ^2.
При той же ошибке'в ВИР величины перемещений
так как
Обозначим абсциссу цели к моменту t = O через В.
Рассеивание следует закону (черт. 43)
)2Я?!2
О — Р2»,2 А — Р2®»2
рЖ1 dxt = -у— е dxt и Рх, dx2 = е dx2,
а ошибка ВИР подчиняется закону
где п — срединная ошибка, характеризующая закон случайных
ошибок BIIP.
Вероятность совместного появления этих ошибок будет:
pXl Рх, pz dxx dx2 dz=
о ~р2Й- p -p2^2 о
= , e dz • -~.e d:/\ r dx,. (168)
П V тс у тс у it
Взятые нами ошибки (черт. 43) таковы, что падения полу-
чены в Аг и А2, показав для первого выстрела недолет (—),
а для второго выстрела перелет (+). Наблюдения недолета и
перелета при тех же дальностях возможны и при других ком-
бинациях ошибок.
Для того чтобы получить вероятность недолета с прицелом
щ и перелета с прицелом а2 по гипотезе о месте цели около
Ц и при любых комбинациях ошибок, надо проинтегрировать
второй множитель выражения (168)в пределах, соответствующих
наблюдению недолета, а третий множитель в пределах, соот-
ветствующих наблюдению перелета.
146
Эти пределы получим из следующих условий: для наблюде-
ния недолета с прицелом ах необходимо, чтобы
^>«14-2^, (169)
а для наблюдения перелета с прицелом а2 необходимо, чтобы
— x2 + zt21. (170)
Для недолета имеем пределы: с одной стороны — оо, а с
другой—из неравенства (169)
—(169')
Для перелета имеем пределы: с одной стороны 4- со, а с
другой — из неравенства (170)
— — R — zt2. (170')
Тогда вероятность недолета и перелета для гипотезы о месте
цели около Ц можем написать:
Для того чтобы распространить выражение (171) на все воз-
можные ошибки в ВИР, его надо проинтегрировать в пределах
от — со до 4-со; кроме того, имея в виду, что
С, — zti
dxl — F(^—
и
R — i + zt?
dx2 — F(R—E 4- zt2),
1 Прп a?2 положительном неравенство (170) удовлетворится и подавно
если оно удовлетворяется прп х2 отрицательном.
10* W
окончательно получим вероятность захвата цели в вилку (пер-
вая функция Персена) в виде:
+ “ 2
Р;= I "2 F ^-ztJFfR-l 4- zt2) dz.
I n У тс
— oo
(172)
43. Приведение срединной ошибки ВИР к единице
Выражение (172) может служить для подсчета первых функ-
ций Персена, но для упрощения схемы расчетов его лучше
также упростить, исключив величину п, как явно входящую.
Для этого введем новую единицу времени 7',, которую будем
выбирать каждый раз так, чтобы срединная ошибка ВИР всегда
равнялась единице, тогда
nLT~l = l • LT,-'
или
п __ 1
откуда
Т.=-Т.
п
При таком переходе все времена должны быть заменены
другими числами, которые будут в п раз более принятых ра-
нее, где п будет численно равно срединной ошибке ВИР в еди-
ницах, которые были приняты для расчета.
Тогда выражение (172) приводится к более удобному виду:
Р^ = с£ / -Ue
— p-z-
F (В — z ntx) F (R — В 4- z nt2) dz. (173)
Какую величину мы примем за единицу — безразлично;
удобно брать за единицу или срединное отклонение пушки,
или какую-либо табличную величину, например х/4 каб., каб.,
1 каб. и т. д. Удобство расчета в табличных единицах заклю-
чается в том, что команды получаются сразу в кабельтовых,
-и очень наглядно видно влияние рассеивания, но пользование
таблицей F (I) так значительно усложняет расчеты, что обычно
при этих расчетах за единицу выбирают величину срединного
отклонения пушки.
Начало координат по дальности может быть отнесено куда
угодно, но удобно брать его йли на дальности прицела пер-
вого выстрела (залпа), или по середине первой вилки (уступа).
148
Если начало отсчета дальностей взять по середине первой
вилки, то выражение (173) примет вид:
+ со
— со
Если производится не один выстрел, а залпы в несколько
выстрелов, то функции F(t) войдут в выражениях (173) или
(173') в степенях, равных числу падений на каждом из преде-
лов вилок.
При захвате цели в уступ, когда падения на обоих преде-
лах принимаются одновременными, или при наблюдении накры-
тийв (173) и (173') tx=.t^=t.
В качестве примера со-
ставим выражение для под-
счета первых функций Пер-
сена при условиях, что
цель захвачена в вилку
шириной 8 Вд при наблю-
дении на дальности ах трех
перелетов (залпы трехору-
дийные) и на дальности
а2 = «1 — 8 трех недолетов;
на середине вилки наблю-
дено накрытие: 2 недолета
. (——) и 1 перелет (-ф-). Следующий залп будет дан через тот
же промежуток времени t, что и при первых залпах.
Возьмем' начало координат в О (черт. 44), тогда
+ <»
I di = di е ' F3 (8 — S + zntj) F3 (5 — znt2) F2 (? —
— со
— 4 znt3) F (4 — E 4- znt3) dz.
В этом случае влияние множителей F3(8 — i-\-znty) Fs (i—
— znt2) невелико, так как накрытие само по себе дает первые
функции Персена, и для приближенных быстрых расчетов
можно это произведение принять равным единице.
44. Распределение цели при стрельбе по подвижной
цели и постоянной ошибке в ВИР
Выражение (173') § 43 и другие, ему тождественные или
аналогичные, дают только вероятность наблюденного события
при любых гипотезах о месте цели. Чтобы найти распределе-
ние цели, надо найти площадь первой кривой Персена и, раз-
149
делив каждую ординату згой кривой на ее площадь, получить
ординаты кривой распределения цели.
Выражение (173') для распределения цели получим в таком
виде:
— p2z2 kJ \ K.J \
- е F \l — zntx) F \R — В snh)
(174)
Значение интеграла А, выражающего площадь первой кри-
вой Персена, может быть подсчитано по одной из формул
квадратур, причем по большей части применяется формула
трапеций.
45. Схема подсчета функций Персена
Схему подсчета рассмотрим для выражения (173) § 43.
Это выражение должно быть вычислено для ряда значений
Е до тех пределов, при которых ptcR обращается в нуль при
наперед принятой точности (характеризуем числом знаков).
Введем для упрощения письма обозначения zntx~ux и
znt2=u2.
Величина г произвольна, и ее следует выбирать так, чтобы
величины u-l и и2 выражались или целыми числами, или дро-
бями с одним десятичным знаком.
При этом следует иметь в виду, что чем меньше взято z,
тем длиннее и точнее вычисления, и, наоборот, чем больше взято
z, тем короче и грубее вычисления.
После этого надо наперед вычислить ряд значений
р ° О -Р2*8 р -Ps(2z)2 р -рДЗг)2
-7=е;~т=е ~т=е ; . и т. д„
у тс 1/ тс у тс ]/ тс
пока не получим нулевого результата при принятой наперед
точности.
^Затем подсчитывают все отдельные значения F \z-zntjv
F (в — $ 4- znt^ для разных z, причем ntx и nt2 остаются по-
стоянными, а Е берется то, для которого ведется подсчет p^dZ.
150
Таким образом сначала составляют схему аргументов
(табл. 43).
Первый ряд табл. 43 представляет собой соответственные,
значения ошибки ВИР, причем z—постоянное число, входящее
в (173') § 43 и ему аналогичные выражения.
Этот ряд тождественно повторяется для каждого почему
и функции этого ряда вычисляются наперед по таблице зна-
р —"
чений ср (г) — ~=е (закон Гаусса).
По аргументам (табл. 43) составляют функции (табл. 44).
После того как составлена табл. 44, следуя формуле (173)
§ 43 или ей аналогичной, надо перемножить стоящие друг под
другом в вертикальных столбцах числа и после этого сложить
полученные произведения. По сложении произведений получим
одно из значений p^dZ.
Таким же образом продолжаем вычисления каждого pydZ по
каждой из Ej до получения значений с принятой на-
перед точностью. Обычно берут пять, иногда и четыре, а иногда
и три знака после запятой.
В результате будут получены значения первых функций
Персена.
Для перехода ко вторым функциям Персена или распре-
делению цели надо найти
(175)
по одной из формул квадратур, для чего значения pt-cfc уже
имеются, и перейти к распределению цели
л p-,d^
<Р2(^)
(176)
Пример 1. Найти распределение цели после захвата ее в
уступ четырехорудийными залпами шириной 4 Вд, если на
дальности (прицел) щ = 80 каб. наблюдены недолеты (----),
а на дальности 81x/s— 813/4 каб. наблюдены перелеты (~|—Н~Н-
Время полета Т= 32 сек. Мертвый промежуток времени т=
= 10 сек. ВИР определяется по трем засечкам цели через
15 сек. двумя 6-метровыми дальномерами. Падения залпов
уступа, следующие друг за другом через несколько секунд,
примем одновременными. <5=20,5 саж., Вб—40 саж.
Найдем срединную ошибку ВИР:
20,5^3 50 , ос
п'— —/ - — =------—— % 50 саж.; п=ур: =1,25;
1/я. / 1
^=f2 = 0,7 мин. (32 4'16=42 сек.);
151
Схема аргументов
r(C?
+»?
гм 3 1
см CM <5
j +Y
_C1
1
fr2 +Э
•UJ»
<U-
о Л1Г 1
ВД
CM
tQ
—f- 1 -MJ* 1
CM
_GM
iQ GM A
+ -l‘Y
co $ + co
+ 1 w*
152
pzdZ = dt
д=е
— f?z’
F* (E — zntA) F* [(Я — E) 4- znt2\ dz
(черт. 45);
zntx=znt2=znt =z • 1,25 • 0,7.
Приняв (произвольно) г = 0,8, имеем:
«^=^2 = 0,8 • 1,25 • 0,7 = 0,7.
Предварительно выбираем из таблицы Дг) =
-~е
вели-
р — р (М2
чины ср (iz) — е (табл. 45).
Таблица 45
р — р2 (iz)2
Значения <р(1г)= р= е
1 iz Ig-JU г iz hr_P_ e
0 0 1,42088 5 4,0 1,84964
1 0,8 1,36668 6 4,8 3,15433
2 1,6 1,17705 7 5,6 4,33189
3 2,4 2,86100 8 6,4 5,38353
4 3,2 1,41853 9 7,2 "6,30870
Далее производим вычисления распределения цели или
вторых функций Персена, как показано в табл. 46 и 47.
153
Таблица 46
Вычисление векторных функций Персена или распределения цели
Ордината № в; £ = + 2; (В — £) = -р 2
I II 111 IV V VI VII VIII
+1 •'1с СО 5 1+ S Г дд +1 ЛАР До fini + ±(э—гт)1 1g произведе- ний Произведе- ния
+ 5г — 1,5 4- 5,5 *3,84964 0 4,77072 6,62036 0,00000
+ 4z — 0,8 4- 4,8 2,41853 1,99896 3,87776 4,29525 0,00020
+ 3z — 0,8 + 4,1 2,86100 1,99504 2,69984 3,55588 0,00350
4- 2г 4- 0.6 4- 3,4 1,17705 *1,98092 1,27068 2,42865 0,02683
+ 2 + 1,3 4- 2,7 1,36668 1,93936 1,63330 2,93934 0,08696
0 4~ 2 + 2 J1, 42988 1,83870 1,83870 1,10728 0,12802
— z + 2,7 4- 1,з 1,36668 1,93936 lj,63330 2,93934 0,08696
— 2г 4- 3,4 + 0,6 1,17705 1,98092 1,27068 2,42865 0,02683
— Зг + 4,1 — 0,1 2,86100 1,99504 2,69984 Ji, 55588 0,00350
— 4г 4- 4,8 — 0,8 2,41853 1,99896 /3,87776 4,29525 0,00020
— 5г 4-5-5 ( — 1,5 )рдинаты 3,84964 № 7 и 9; 0 5 = 4-3; 4,77072 (В-5) = 6,62036 + 1 0,00000 Pt (1^ = ^0,36300
-|- 6г — 1,2 4- 5-2 *3,15433 *3,28180 0 6,43613 0
4- 5г — 0,5 4- 4,5 3,84964 2,26324 1,99792 4,11080 0,00013
+ 4г 4- 0,2 4- 3,8 2,41853 2,97294 1,99096 1_3,38243 0,00241
+ Зг 4- 0,9 4- 3,1 2,86100 1,44874 1,96796 2,27770 0,01895
2г 4- 1,6 + 2,4 1,17705 1,73748 1,90586 2,82039 0,06613
+ г 4- 2-3 + 1,7 1,36668 1,89176 1,76650 1,02494 0,10591
0 + з + 1 1,42988 1,96222 1,50024 2,89234 0,07804
— Z 4- 3,7 4- о,з 1,36668 Т, 98904 1,05422 2,40994 0,02570
— 2г 4- 4,4 — 0,4 1,17705 1 99740 У, 38052 3,55497 0,00359
- - Зг 4* 5,1 — 1,1 2,86100 0 3,43980 /4,30080 0,00020
— 4г • — 1,8 Ординать 2,41853 I № 6 и 1 0 0; 5 = 4- 4,20244 4; (В-5) 6,62097 = 0 0 В/Й = =0,30106
+ 7г — 0,9 4- 5,2 1,33189 *3,73772 0 *6,06961 0
4- 6г — 0,2 4“ 4,5 3,15433 2,59850 1,99792 5,75075 0,00006
4- 5г + 0,5 4- 3,5 3,84964 1,20296 1,98408 3,03668 0,00109
4- 4г 4- 1,2 + 2,8 2,41853 1,59238 Т, 94804 3,95895 0,00910
454
I II III IV V VI VII vni
О1 1+ Ф
§ ДдР
”S> 1 ф ф
1+ Г +1 •UP РЗ W со S »=( ф
1—1 Д [ р 1 . о
0-1 к Рн
1 £ Ьн с « ° «
+1 LlP £ brj ьр 1+ _ьр g К и
Ординаты № 6 и Ю; 5= +4; (R— С) - -0
+ 3z + 1,9 + 2,1 2,86100 7,81692 1,85830 "2,53622 0,03437
+ 2г + 2,6 + 1,4 1,17705 1,92954 1,67106 2,77765 0,05993
+ 2 + 3,3 + 0,7 Т, 36668 1,97724 1,33408 2,67800 0,04764
0 + 4 0 1,42988 1,99394 2,79588 2,21970 0,01658
— z + 4.7 — 0,7 Т, 36668 1,99868 2,01200 3,37736 0,00238
— 2г + 5,4 — 1,4 1,17705 0 4,94724 4,12429 0,00013
— Зг + 6,1 — 2,1 Т, 86100 0 5,57572 6,43672 0
=
=0,17128
Ординаты № 5 и И; С = + 5; (В-© = — 1
+ 8.з — 0,4 + 4,6 5,38353 "2,38052 7,99836 7,74241 0
4- 7г + 0,1 + 3,9 4,33189 2,88688 1,99256 5,21133 0,00002
+ 6z + 0,8 + 3,2 3,15433 1,39338 1,97296 4,52067 0,00033
+ 5г + 1,5 + 2,5 3,84964 1,70566 1,91840 3,47370 0,00298
+ 4г + 2,2 + 1,8 2,41853 1,87596 1,79296 2,08745 0,01223
+ Зг + 2,9 + 1,1 2,86100 1,95562 1,54808 2,36470 0,02316
+ 2г + 3,6 + 0,4 Т, 17705 1,98676 1,13088 2,29469 0,01971
+ г + 4,3 — 0,3 1,36668 1,90674 _2,49228 3,85570 0,00717
0 + 5 — 1 1,42988 1,99936 3,59176 3,02100 0,00105
— Z + 5,7 — 1,7 1,36668 0 4,39832 5,76500 0,00006
— 2г + 6,4 — 2,4 "1,17705 0 6,88888 6,06593 0
Р^ =
=0,06671
Ординаты М 4 и 12; £ = +6; - 2
+ 8г + 0,4 + 3,6 5,38353 1,13088 1,98676 "6,50117 0
+ 7г + 1.1 + 2,9 4,33189 1,54808 1,95562 5,83559 0,00007
+ 6г + 1,8 + 2,2 "3,15433 1,79296 2,87596 4,82325 0,00066
+ 5г + 2,5 + 1,5 3,84964 1,91840 1,70566 2,47370 0,00298
+ 4г + 3,2 + 0,8 2,41853 1,97296 1,39338 3,78487 0,00609
+ Зг + 3,9 + 0,1 2,86100 1,99256 2,88688 3,74044 0,00550
+ 2г + 4,6 — 0,6 "1,17705 1,99836 2,14016 3,31557 0,00207
+ s + 5,3 — 1,3 7,56668 0 3,11768 4,48436 0,00030
0 + 6 — 2 Т, 42988 0 5,79112 5,22100 0,00002
— Z + 6,7 — 2,7 7,36668 0 6,14068 7,50736 0
Pg%> =
=0,01769
155
I II III IV V VI VII VIII
1+
£ S* з.М“' ф к . i
1+ Г +1 1 ф га со ф к ф
ЛД.Р S W
J.1J' > | о со
+1 вд 0.1 ц дл вд 5 ьр 1+ 1g пр НИЙ Про И НИЯ
0 рдинаты № 3 и 13; С = + 7; («-?) = — 3
— — — — — — 0
+ 82 4- 1.4 + 2,6 5,38353 1,67106 1,92954 6,98413 0,00001
+ 7г + 2.1 + 1,9 4,33189 1,85830 1,81692 4,00711 0,00010
-|- 62 + 2,8 + 1,2 3,1-5433 1,94804 1,59238 4,69475 0,00050
4- 5s + 3,5 + 0,5 3,84964 1,98408 1,20296 3,03668 0,00109
+ 4г + 4,2 — 0,2 2,41853 1,99600 2,59850 3,01303 0,00103
+ Зг + 4,9 — 0,9 2,86100 1,99916 3,73772 4,59788 0,00040
i -j- + 5,6 — 1,6 1,17705 0 4,58774 4,76479 0,00058
+ 2 + 5,3 — 2,3 4,36668 0 У, 12528 У, 49196 0
Pfdz, =
=0,00371
Ординаты № 2 и 14; С = + 8; (в-С) = — 4
+ 9г + 1,7 + 2,3 6,30870 4,76650 4,89176 4,96696 0
+ 8s + 2,4 + 1,6 5,38353 1,90586 1,73748 5,02687 0,00001
+ Ъ + 3,1 + 0,9 4,33189 1,96796 1,44874 5,74859 0,00006
+ 6г + 3,8 4- 0,2 3,15433 1,99096 2,97294 4,13823 0,00014
-|- 5г + 4,5 — 0,5 3,84964 1,99792 ~2,26324 4,11080 0,00013
+ 4г + 5,2 — 1,2 2,41853 0 3,28180 5,70033 0,00005
+ Зг + 5,9 — 1,9 2,86100 0 4,00016 6,86116 0,00001
+ 2г + 6,6 — 2,6 1,17705 0 У, 39692 7,57397 0
р^> =
=0,00040
Ординаты № 1 и 15; 5 = 4-9; (2?-5) = - -5
4- 8г + 3,4 + 0,6 5,38353 1,98092 1,27068 4,63513 0
+ 7г 4- 4,1 - 0,1 4,33189 1,99504 2,69984 5,02677 0,00001
4- 6г + 4,8 — 0,8 3,15433 1,99896 3,87776 5,03105 0,00001
+ az + 5,5 — 1,5 3,84964 0 Т, 77072 У, 62036 0,00000
+ 4s 4- 6.2 — 2,2 2,41853 0 5,35340 7,77193 0
pg№>=
=0,00002
Ординаты № 0 и 16; 5 = + Ю; (В-£) = — 6
4- 7г + 5,1 — 1,1 4,33189 0 4,43980 4,87169 0
+ 6 г + 5,8 — 1,8 3,15433 0 Т, 20244 7,35677 0
4- 5г + 6,5 — 2,5 3,84964 0 6,64612 8,49576 0
=
= 0
156
f Вычисления начинаем или с наибольшей ординаты или с
-возможно близкой к ней, когда наибольшая ордината наперед
не может быть указана.
Задавппсь гипотезой о месте цели Е, составляем аргументы
строки для 2=0. Например, по схеме Е =+2; R — Е=(4—2) =
= + 2.
После этого легко вписать и прочие аргументы:
(Е +«0 = 2,7; S + 2«^ = + 3,4 . . .
(R — Е)= + 1,3; (Я — Е) — 2«х —+ 0,6 . . .
Е — U1— +1,3; Е — 2^ = + 0,6 . . .
(/? + £) — «! =+ 2,7; (Л —E) + 2Uj, =4-3,4 - . .
р -P!(2z)’ р -fW р р -PV-
[Вписав значения. . . -+=е ; е ;-+_;+-=е
Г* V к J/тг У г.
вписываем выбранные по аргументам функции Я4 (t).
Составление схемы вверх и вниз продолжаем до тех пор,
пока произведение чисел, логарифмы которых помещены в гра-
фах V, V и VI, не получится равным нулю (соответственно
принятой наперед точности).
Сложив логарифмы (графы IV, V и VI), вписываем в графу
VII логарифм произведения, а в графу VIII — само произведе-
ние, т. е. величину pydZ, которая выражает вероятность на-
блюденного события: перелет, недолет или захват цели в вилку
шириной 4 Вд по данной гипотезе о месте цели.
В этом же порядке продолжаем вычисления до тех пор,
пока не получим pydH= 0 с принятой наперед точностью, после
чего подсчитываем и распределение цели по выражению:
?2(Е)dE = Q • dl = (177)
--- СО
по любой схеме, например, в виде табл. 47.
Таблица 47
Вычисление распределения цели
Со IgA =1,830-2
* № ординаты Р& 1g P-di 1g <Рг(?) di ТгС di
8 0,36320 1,56014 1,39066 0,2459
f 7,9 0,30106 Т, 47865 1,30917 0,2038
6,10 0,17128 1,23371 1,06423 0,1160
5,11 0,06671 2,82419 2,65471 0,0452
4,12 0,01369 2,13640 3,96692 0,0091
3,13 0,00391 3,59218 3,42270 0,00-6
2,14 0,00040 1,60206 4,43258 0,0003
1,15 0,00002 Т, 30103 5,13155 0
0 " 1 —
А = 1,47734
157
Во втором столбце табл. 47 вписаны из табл. 46 величины
рр]<. Дальнейший ход вычислений ясен из самой таблицы, по
последнему столбцу которой построена кривая распределения
цели (черт. 45).
Все вычисления сделаны для одной половины кривой рас-
пределения цели вследствие ее симметричности.
Симметричность вилок и кривой получена вследствие равен-
ства числа наблюдений на каждом пределе вилки и вследствие
принятия одновременности падения обоих залпов.
При отсутствии хотя бы одного из этих условий мы сим-
метричности кривой распределения цели не будем иметь, и в
этом случае необходимо вычислять обе ветви этой кривой.
Примечание. На черт. 45 и при вычислениях за масштабную
единицу принято Вд; за масштабную единицу можно брать любую
табличную величину, например, 4 каб., 1/-> каб. и т. п. Это будет иметь
свои преимущества, но пользование таблицей F(t) будет затруднено.
Пример 2. В качестве второго примера, даюшего образчик
несимметричного распределения, возьмем случай, когда вилка
в 8 Вд суживается до 4 Вд при промежутке между залпами
в 1 мин. Вд = 50 саж.
Как показано на черт. 46, залп № 1 (3 орудия) показал
3 недолета; залп №2 с прицелом на 8 Вд=В больше дал 3 пере-
лета; залп № 3 на середину вилки вынесен по целику и знаки
не наблюдены; залп № 4 с тем же прицелом (с учетом ВИР)
показал 3 перелета. Залпы № 1 и 4 дали последнюю вилку с
устаревшим пределом.
Для данного случая имеем значение pt,dZ:
-L ОТ
Г D “Р2^2 ZZ?
ptdk — dk I —Fsfi— snts)Fs(B — E-|-m£2)Fs I-------------
I v
— E + zntx j dz
(начало отсчета дальностей по залпу № 1).
При п =1 и г = О,8 имеем:
w1=m£1 = 0,8 • 1 1 = 0,8;
ад2 = ш4 = 0,8 • 1 • 3=2,4;
«3 = ж£3 = 0,8 • 1 • 4 = 3,2.
Подсчет первых и вторых функций Персена приводит к
кривой распределения цели (черт. 46).
Срединное положение цели — по ординате АВ, куда и сле-
дует перейти на поражение, т. е. за устаревший предел
залпа № 1.
Сравнивая распределение, полученное в результате уступа
(черт. 45), с распределением, полученным в результате за-
158
хвата цели в вилку с устаревшим пределом (черт. 46), видим,
насколько второе распределение хуже первого, хотя ширина
вилки и уступ равны. Срединная ошибка в ВИР от = 1, во вто-
ром случае (черт. 46) далее меньше, чем в первом, где п= 1,25
(черт. 45). Кроме того, распределение (черт. 46) в сильной
степени асимметрично, несмотря на равенство наблюдений на
пределах вилки.
Здесь сказалось влияние времени: при неподвижной цели
или при точном значении ВИР мы имели t= 0; во втором слу-
чае £ = 0,7 мин. и в третьем случае (черт. 46) /, = 1 мин,
(залп № 4); £2=3 мин. (залп № 2) и £3 = 4 мин. (залп № 1).
Черт. 46.
Несимметричность кривой является следствием устаревания
сведений 0 цели; более новые сведения, полученные в резуль-
тате наблюдения трех перелетов с падением залпа № 4, отбро-
сили срединное положение цели за устаревший предел
залпа № 1, несмотря на его три недолета. Значение же на-
блюдения трех недолетов с падением залпа № 1 сказалось тем,
что без этого наблюдения теоретически цель была бы отбро-
шена на — оо, при наличии же наблюдения трех недолетов
распределение цели вправо ограничено (практически) 81/2ВЭ,
а влево — 20112Вд от наивысшей ординаты, которая, в свою
очередь, лежит вне вилки между 21-й и 22-й ординатами.
Все зто есть результат значения времени при наличии ошибки
в ВИР.
Примечание. Подсчеты, приведенные выше, весьма сложны и
трудоемки, а поэтому при выполнении их обычно пользуются арифмо-
метром или логарифмической линейкой, ограничивая точностью окон-
чательных результатов распределения цели до третьего знака после
запятой.
46. Метод приближенного подсчета распределения
цели для некоторых частг ых случаев стрельбы по
подвижным целям при постоянной ошибке в ВИР
Для стрельбы по неподвижной цели, а также для случая,
когда ошибка ВИР равна нулю, Персеи подсчитал известную
таблицу срединных ошибок распределения цели для симметрич-
ных вилок при одном наблюдении на каждом пределе.
В теории стрельбы по наблюдению знаков при неподвижной
цели численно показано, что для симметричных вилок не шире
159
8 Вд закон ошибок, выраженный кривой распределения цели,
близок к закону Гаусса и для целого ряда приближенных
расчетов может быть заменен законом Гаусса со срединной
ошибкой E—R в зависимости от ширины вилки.
Можно численно показать, что нередко, если не требуется
особой точности, для частных случаев, когда и при стрельбе
по подвижной цели мы имеем симметричное распределение ее,
вторая кривая Персена может быть также заменена законом
Гаусса со срединной ошибкой
E==|/^~ + ^2 ’
(178)
где R— срединная ошибка распределения для неподвижной
цели, р —число наблюдений на пределе, п — срединная ошибка
ВИР и t — время, за которое происходит накопление ошибки в
ВИР. В случае стрельбы с ошибкой в ВИР симметричное рас-
пределение цели мы будем иметь только для уступа 'с одина-
ковым числом наблюдений на каждом из его пределов и для
чистого накрытия цели. Поэтому только для этих случаев и
возможна замена второй кривой Персена законом Гаусса.
Выведем выражение (178) для чистого накрытия в чыырех-
•орудийном залпе с двумя наблюдениями на каждом пределе.
Ординаты первой кривой Персена при этом выразятся:
+ со
С р -р2*8
pd£ = d£ I F2(^ — zt)F2(—^ + zt) ds, (179)
/ V я
где срединная ошибка в ВИР взята равной единице (п— 1).
Обозначим w-g-st; кроме того, Е~ -^=^2= о,64.
У 2 У 2
Заменяя законом Гаусса, имеем:
, ®2
F2\x) F2 (— х) = —L е~р2 (м4)’ ,
0,64 Утг
«следовательно,
9(;-г/)2
F2&-zt)F2(-t + st) =-----Le~pS_^F. (l80)
0,64 У «к
Заменив в (179) произведение F- (Н — zt) F2 (— В + st) из (180),
получим:
+
(Е — г/)-
(0-6,)г ds.
— оо
(181)
460
Выражение (181) представляет собой закон, получившийся
от сложения двух законов Гаусса, и, как известно, при этом
должен получиться опять же закон Гаусса. Наша задача — вы-
явить срединную ошибку, характеризующую этот закон.
Выражение (181) можно переписать так:
Ге [ (064) (182)
— со
Преобразуем формулу (182), обозначив
+ оо Г
; (183)
--------------------------- QO
тогда
(184)
Преобразуем показатель степени при е в (183):
0,642 0,642 0,642 ^0,642
11 Теория стрельбы
161
а потому
s!+4^=“!+w^+f- !1S1”
Подставив в (183) в показателе степени вместо двучлена,
в квадратных скобках равное ему значение (186), получим:
у
— Р 0,64- + с-
Величина е вынесена за знак интеграла как по-
стоянная при интегрировании по z, и, кроме того, в (187) мы
ввели из (185) новую переменную.
Диференцируя (185) по и и z, имеем:
откуда
Подставив в (187), получим:
Введя опять новую переменную $u—t,
по и и I, найдем du=^~dt и, подставив,
продиференцировав
получим:
и следовательно,
162
Е2
е~Р 0,64= + /2
А= -—
Р
Подставив (188) в
pdi — di—^-—
F 0,64тг
t2
0,642
(182) или в (184), получим:
~ Р 0,642 + f.
(188)
или
В2
0,6424-72
~Z2 У Г j/o,642 + Z2
0,642
— р
е
р tR —
Р ~p2 &
Д— е di,
где срединная ошибка, характеризующая этот закон,
E=J/o,642 + ^’
Величины 0,642 и t2 мы получили потомит, что взяли накры-
тие по два знака (+ + и ——) и п= Вд — 1.
Для уступов и любого п будем иметь:
Е =
(189)
Выражение (189) определяет срединную ошибку распределе-
ния цели для уступа шириной не свыше 8 Вд при любой сре-
динной ошибке ВИР (п).
Вычисление распределения цели по (189) значительно проще
и скорее, а потому и должно применяться везде, где это воз-
можно.
Для примера возьмем случай захвата цели в уступ шири-
ной 4 Вд при срединной ошибке w = o,75 и £=42 сек. = 0,7 мин.
При этих условиях у нас уже произведено вычисление функ-
ций <р2(?) распределения цели в § 45. Теперь для сравнения
сделаем то же, применяя приближенное решение для частного
случая симметричного распределения.
Для уступа в 4 Вдпо два наблюдения на пределе имеем:
R _ 1,33
1,33
^1 =0,943;
Е = \/ 0,9432 + (0,75 • 0,7)2 = 1,08.
Вычисления произведем по закону Гаусса:
е»
... Р ~р2 (1,68)2
Ю2 (а =-----1—7=. е
1,08 у-
и сведем в табл. 48.
11*
163
Таблица 48
Вычисление распределения цели
№ ординат 5 5 1,08 1,08 ?2(£) ?2© Вторая функ- ция Персена
8 0 0 0,2691 0,248 0,291
7,9 1 0,93 0,2210 0,205 0,245
6,10 2 1,85 0,1236 0,114 0,131
5,11 3 2,78 0,0464 0,043 0,046
4,12 4 3,70 0,0120 0,011 0,010
3,13 5 4,63 0,0021 0,002 0,001
2,14 6 5,56 0,0002 0,000 0
1,15 7 6,48 0,0001 0 0
Из сравнения двух последних столбцов видим близкое сход-
ство законов. Вычисления же математического ожидания попада-
ния или вероятностш! попадания как по одному, так и по дру-
гому распределению дадут почти одинаковые результаты.
17. Применение теоремы будущих событий к стрельбе
по подвижной цели
В части I курса разбирались методы подсчета математиче-
ского ожидания попадания и вероятностей различных комбина-
ций попаданий и падений.
Само по себе распределение цели служит только средством,
позволяющим найти эти вероятности с учетом обстановки и
решить вопрос о наивыгоднейшем прицеле будущего залпа
(выстрела) и способа обстрела цели, что, в свою очередь,
решается посредством подсчетов тех же вероятностей.
Вероятности различных комбинаций попаданий, вероятности
наблюдения различных комбинаций накрытий, а также матема-
тическое ожидание попадания в подвижную цель выражаются
так же, как и для неподвижной цели, так как эти вероятности
относятся к ожидаемому залпу и, следовательно, £=О.
Не касаясь порядка вычислений, изложенного в части I курса,
приведем для примера вероятности накрытий при распределе-
ниях, вычисленных по формулам § 45 для п—1, ^ = о,5 мин,
и t2 = l мин., для вилки J?=4 и ^==^ = 0,5 мин., для уступа
В = 4, при двух и четырех наблюдениях на пределах вилки
или уступа (табл. 49).
Эти цифры показывают преимущество уступа: уступ по 2
дает то же, что вилка по 4. Влияние времени еще нагляднее
будет видно, если подсчитать вероятности накрытий, например,
для уступа по 4, но не для ближайшего залпа, как подсчитана
табл. 49, а с опозданием через 0,5 мин. (когда ^ = ^ = 0,5 мин.)
или с опозданием на 1,5 мин. (табл. 50).
164
Таблица 49
Вероятность получить накрытие на середине уступа ипи вилки
(в процентах)
Характер накрытия Вероятность накрытия залпом по середине
уступа по 4 уступа по 2 вилки по 4
Чистое 22,4 19,5 19,4
Ненадежное 43,4 40,6 39,7
Всего 65,8 60,1 59,1
Таблица 50
Вероятность получить накрытие на середине уступа по 4
(в процентах)
Характер накрытия С опозданием на
0,5 мин. 1,5 мин.
Чистое 17,6 11,2
Ненадежное 36,0 25,4
Всего 53,6 36,6
48. Исследование стрельбы, когда ошибка в ВИР
меняет свою величину от залпа к залпу
При исследовании стрельбы по наблюдению знаков, когда
случайная ошибка в ВИР не сохраняет своей величины даже
на короткое время и меняет ее от залпа к залпу, могут быть
два случая; залпы падают либо одновременно (уступ), либо
разновременно (вилка).
' В первом случае для вероятности наблюдения недолета
и перелета (первые функции Персена) и для распределения
цели (вторые функции Персена) формулы, приведенные в § 45,
останутся в силе, так как ошибки ВИР скажутся одинаково.
Во* втором случае (вилка) эти формулы изменяют вид, при-
чем, принимая попрежнему для срединной ошибки в ВИР выра-
жение
-р=4
<19°)
165
при начале отсчета дальностей в О (черт. 43) для недолетг
имеем:
Для вероятности захвата в вилку шириной В в этом случае
надо написать:
а при новой единице времени Д =—Т
п
+°° 4-0=
pfc = d£ j ^~e~^Fk>^—ant1)dz рк‘ (R—t +
— 00 " „оо
-\-znt^dz, . (193)
где п — число, равное срединной ошибке в ВИР.
Называя
4-00
I pcR — A,
-—со
для распределения получим:
<p2(S)d^=£^. (194)
А
Особенность при вычислении (193) по сравнению с § 45
будет заключаться в том, что каждый интеграл, входящий в (193)
в виде множителя, надо вычислять отдельно, а затем брать их
произведение.
Для частного случая, когда предполагаются падения не
залпов в /Cj и fc2 выстрелов, а только по одному наблюдению
на каждом пределе вилки, выражения (193) и (194) значительно
упрощаются.
166
Возвращаясь к § 42 (черт. 43), для закона рассеивания при
одном выстреле мы. имеем:
р — к«2
pxdx—-j=e dx.
1/ ГС
Для ошибки в ВИР мы имели:
Вероятность совместного появления обеих ошибок получим:
р2 -р2(-^-+а?)
рхря dx dz ——е dx dz.
(195)
Заменим ошибку ВИР, выраженную в единицах скорости,
-ошибкой, выраженной в единицах перемещения; тогда, имея
в виду, что
_р2Д.
Р В , Р (ПО" з Z
—4= е dz = —= е d (zt),
пук nt У к
можем написать выражение (195) в виде:
рхр dxdz—-~-e ^(в,> dxdz. (196)
ntr-
Полагая x-\-zt=y, выражение (196) перепишем в виде:
, 7 Р2^
1 [ею2
+ (V - г»)2
dy dz.
(197)
Недолет будет наблюден при ? > х + zt.
Это даст границы для ж; с одной стороны, ж— zt, а с дру-
гой стороны, — со, но
х=у—zt,
следовательно,
у zt $ zt
или
Тогда при данной ошибке в ВИР
167
а при любых ошибках в ВИР от — со до + оо получим:
(198)
Преобразуем показатель в (198):
Г 1 2 Г (w02
Li + WJ у Li-f-W.
+ у2 =
1 /~i+W , у2
V (nty ' у i+W!l+iW
Заменяя в (198) показатель его преобразованным выраже-
нием, получим:
При одном выстреле на каждом пределе нам безразлично,
по какой переменной раньше интегрировать, а потому проин-
тегрируем (199) сначала по г:
168
Введем новую переменную:
|/ (И* ®И 1—
откуда, полагая при интегрировании по г вычитаемое
{/iOE
УУ 1+(«о2
постоянным, имеем:
dz —------. - - — du = _L J f(?z0 du.
f 14- (?i/)2 t у i -|- (nt)2
1 V (nt)2
(201 >
По подстановке (201) в (200) получим:
или
У ~ У1 4- (nt)2
ибо
(202:)
+ И
Введя новую переменную у— - ,—_ : -, имеем:
j/14-W
dy — У1 4* n2t2 • dv.
(203)
169.
откуда имеем:
По подстановке (203) в (202) получим:
P — F
_Е____
V i+«2z2
Произведя аналогичный вывод, мы придем для вероятности
<перелета к выражению:
Q+ — F
j В-1
где R — ширина вилки.
Для вероятности захвата цели в вилку (первая функция
Персена) имеем:
pd'=F
£
У1 -|-и2/2
(204)
Для распределения цели имеем:
(205)
Выражениями (204) и (205) можно пользоваться только для
•частного случая, при одном наблюдении на каждом пределе
вилки, когда ошибка в ВИР измечяется от выстрела к выстрелу.
Вычисление (198), кроме указанной уже особенности, ничем
больше не отличается от вычислений в § 44 и 45. Вычисления
же (204) и (205) никаких затруднений представить не могут,
я потому и примеров не приводим.
19. Исследование стрельбы при наличии большой
ошибки в ВИР, когда эта ошибка может быть
принята следующей закону равной вероятности
Ошибка в ВИР при ее большой величине может следовать
закону равной вероятности в том случае, когда ВИР против-
ника резко меняется через короткие промежутки времени и
невозможно учесть эти изменения. В этом случае ВИР цели
принимается постоянным, имеющим некоторое среднее значение
170
(чаше нуль), около которого ВИР цели меняется на одинако-
вую (приблизительно) величину в ту и другую сторону.
Стрельба при этих условиях потребует большой скорострель-
ности, позволяющей осуществить уступ, поэтому при исследо-
вании применим частный случай (§ 46), откуда имеем:
/ 7? \2
Е* = -/=) + (W
и среднюю квадратическую ошибку:
(206)
где В —срединная ошибка распределения неподвижной цели
характеризующая закон Гаусса при уступе шириной не более
8 Вд, когда F (5) 1 и F(—-5) % 0;
пъ=
п
Дб7
средняя квадратическая ошибка, характеризующая
закон ошибки ВИР.
Для случая равной вероятности
£
где I— предел ошибки в ВИР, следующей закону равной
вероятности.
Тогда квадрат средней квадратической ошибки распределе-
ния цели будет
(207)
Мы рассматриваем случай, когда величина I настолько
велика по сравнению с R что воспользоваться случаем
сложения срединной ошибки закона Гаусса с так называемой
приведенной f 0,67 —Е= Л срединной ошибкой нельзя.
\ V 3 /
В этом случае распределение цели мы получим по выра-
жению:
—
е
(208)
X — I
е ' — Ф(ж—Z)],
г — I
171
а потому, подставив в (208), получим:
? (•») = Д [ф(ж + Z) ~ ф (я — Z)] (209)
в: V
Выражение (209) дает нам распределение цели, для построе-
ния которого за единицу удобно взять величину срединной
ошибки в законе Гаусса и выразить в ней пределы ошибок
закона равной вероятности.
Ординаты кривой распределения могут быть найдены по
таблице, соответствующей значению выражения (208), а в слу-
чае выхода за пределы этой таблицы — вычисляют по вы-
ражению (209), что в некоторых случаях бывает даже удоб-
нее.
Пример. Противник маневрирует на курсовых углах около
траверза в пределах 70—110°, при скорости 33 узла. Время
полета Т= 35 сек.; мертвый промежуток времени -с = 10 сек.,
ВЭ = 20 саж. Требуется найти распределение цели к моменту
падения следующего залпа после захвата цели в уступ шири-
ной 8 Вд при четырех наблюдениях на каждом из пределов
уступа.
Время t = Т -}- т=45 сек. = 0,75 мин.
Колебания ВИР Z = + 200 • Z = + 200 • 0,75 = + 150 саж.
Е'
R 2,11 • 20
-==-------=— = 21 саж.
Приняв
Е'=1
имеем
150
V -- ~
21
Распределение цели получим по формуле (209):
Ts (®) = [Ф (« + О — Ф (ж - 01 =
= +Ай [ф(ж + 7>14) -ф & - 7’
Величинами ж будем задаваться через единицу, начиная от
а" = 0, до того момента, пока не получим «2(ж) = 0; точность
ограничим тремя знаками.
Вычисления приводят к следующему распределению цели
(черт. 47 и табл. 51).
172
Таблица 51
Вычисление кривой распределения цели
№ ор- динат X 'Е'х саж. <Рг(ж) № ор- динат X Е'х саж. <?2 (®)
12 <0 0 0,070 6,18 6 126 0,055
11,13 1 21 0,070 5,19 7 147 0,038
10,14 2 42 0,070 4,20 8 168 0,019
9,15 3 63 0,070 3,21 9 189 0,007
8,16 4 84 0,069 2,22 10 210 0,002
7,17 5 10Б 0,065 1,23 11 231 0,000
Яр2 (®)= 1,000
Изучение табл. 51 и черт. 47 даже без дальнейших под-
счетов дает указание, что потребуется обстрел площади или
через 8/4 каб. между ординатами 5 и 19, или через J/2 каб.
между ординатами 6 и 18, так как положение цели между орди-
натами 7 и 17 равновероятно и почти равновероятно между
ординатами 6 и 18.
э ib ii <г в <Г is й iiT is го as гГ
8] . ........... „ „ ... „ „„ ь,
2 Ш 1% 1 М УГУа 0 Уд 4 1 Ш V/г
Черт. 47.
В примере нарочно взято малое рассеивание, а при большем
рассеивании распределение цели будет приближаться к закону
Гаусса, и может даже представиться возможность воспользо-
ваться частным случаем сложения ошибок, из чего, конечно,
нельзя делать вывода, что большое рассеивание „полезно" В
50. Расчет ширины первой вилки при стрельбе по
подвижной цели и при ошибке в ВИР
Ширина первой вилки (Пр. В.) при наличии ошибки в ВИР
может быть найдена на основании распределения цели, полу-
ченного в результате подготовки исходных установок и пред-
положения о наблюдении знака залпа, направленного в центр
этого распределения.
Для расчета ширины первой вилки нам безразлично, какой
знак принять для первого залпа, и обычно принимают недолет.
Пусть случайная ошибка в ВИР будет ztv
Вероятность этой ошибки будет:
1 Некоторые высказывают мысль, что при обстреле площади небольшое
увеличение рассеивания даже полезно.
173
(210)
где п—срединная ошибка в ВИР.
Пусть случайная ошибка перехода от измеренной дальности
к прицелу (табличная дальность) ж; вероятность этой ошибки
будет:
Р Р Е2
——dx, (211)
Е У к
где Е — срединная ошибка перехода от дальномера к прицелу.
Величина
(ошибкой от округления в данном случае пренебрегаем).
Вероятность совместного появления ошибок х и st получим
из произведения (210) на (211):
Обозначив = и определив ж = $— sty, выразим в (212)
х через z — sty, тогда получим:
е» а-а,г
р р и3 Р 1 Е~ ,
-—!-=е dz—V^e dz. (213)
v У тг Е У тс
Выражение (213) дает распределение цели при определении
ошибки sty, сохраняющей свое значение в течение некоторого
времени.
Будем считать, что залп в к выстрелов, направленный в центр
этого распределения, показал недолет. В этом случае распре-
деление цели (213) дает первые функции Персена при том же
значении s к моменту падения будущего залпа, которым мы
хотим захватить цель в вилку.
Выражение для первых ф\ нкдий Персена получим:
„г2 (; —zf,)2
' п~ Р Е2 тчЬ
= С ds —е Fk(z — st,) dz.
тс eV ъ J
Упростим это выражение путем введения нов й единицы
времени Ту=~Т, и, переходя к любому значению s, получим:
174
+ »
Обозначив р^сК= А, переходим от (214) к распределению-
-—'СО
цели к моменту падения следующего захватывающего залпа:
+“
/_Р%= -г-
Рь0-^2)йг, (215>
— сю
где всегда t2 > 1Л (обычно tA212).
Ширину первой вилки R получим из того соображения, что
захват цели в вилку будет обеспечен в том случае, если при
ширине вилки В вероятность недолета будет равна нулю, что
приводит к выражению:
+»
р = J\(l)F*(l — R)cfc==O. (216)
— со
Вычисление (216) ведем попытками, задаваясь различными'
величинами R, пока не получим с удовлетворяющей нас точно-
стью, что {9 = 0.
Вместо вычисления (216) можно задаваться вероятностью,
перелета, равной единице, или
4“ оо
£ = f K®F*(R-t)dl = l. (216')
Схема вычисления (214) подобна схеме, приведенной в § 45..
Сперва составляем схему аргументов и функций (табл. 52).
Таблица 52
Схема аргументов и функций
2 г + z 0 — Z — 2z
£ — 2 и. £ — щ £ ? + 2«i
Е Е Е Е Е
2 С ? + «2 £ -|- 2 и2
? (2 г) о (г) <р(0) <р (г) ?(2 г)
1 fg-2^ Е Е ) Е ‘ \ Е ) 1 ($\ Е 4\Ej * М + “П Е ‘ \ Е J Е 1 k Е )
Fb (С — 2 и.) F*(0 Fk^+U2) Fk (С+ 2 и2)
175
Четвертая строка табл. 53 вычисляется один раз наперед
п повторяется для каждого значения p-dl.
В табл. 52 ux—zntx и = —простые обозначения, при-
чем желательно выбирать z так, чтобы ил и и2 были с простыми
.знаменателями (10).
Вертикальные ряды функций в табл. 52 надо перемножить
л произведения сложить, тогда получим значение p?dz для
«одного t
В качестве примера возьмем расчеты ширины первой вилки
при четырехорудипном залпе для случая полной подготовки
при п —1; 2? = 2,5; 4 = 0 (момент падения будущего захватив-
шего залпа); 4 = 0,8 мин.; 4 = 1,5 мин.; 3=1 (Вд=15 саж.).
Тогда
ил = zntx = 1 • 1- 1,5 = 1,5;
u2 = znt2 = l * 1 • 0,8 = 0,8.
Пользуясь табл. V (см. приложения), найдем и расположим
в табл. 53 значения ® (2) = —£=
Таблица 53
2 Z % OI о. 1 18
0 0 0,2691 1,4299
Z 1 0,2144 1,3312
2z 2 0,1084 1,0350
Зг 3 0,0348 _2,5416
4г 4 0,0071 3,8513
Бг Б 0,0009 4,9542
6г 6 0,0001 4,0000
7г 7 0 —
Эти значения —е или логарифмы их будут повторяться
для всех £; что же касается значений
1
1П
(Е — znt,)2
р Е2
поставляющих пятый ряд табл. 52, то для каждого рлК эти
значения приходится вычислять особо.
Далее приводится полная схема расчета ширины первой
вилкп для стрельбы по подвижной цели с ошибкой в ВИР
и для случая, когда ошибка в ВИР сохраняет свое значение
в течение некоторого времени.
476
Таблица 54
Вычисление распределения цели
I II III IV V VI VII
•5» +1 UP <м +1 •UP 1 , ч .Гр — р’2’ Igcp(z) = Ig —=-е L' л । j .S т I к; 9- L эр Е ’’ +1 ди» & tuO 1g подинтегртльных функций Подннтегральные функции
—0,5 4-1,0 4-2,5 4-4,0 4-5,5 —1,2 —0,4 +0,4 +1,2 4-2,0 Орд) 1,3312 1,0350 2,5416 3,8513 "4,9542 шата № 2; С 7,0280 7,0162 7,9332 2,7791 7.5540 = —2 7,2818 7,3805 2,1309 1,5924 1,8387 5,6410 2,4317 2,6057 2,2228 5,3469 0 0,0003 0,0004 О,0002 0
Р^ = =0,0009
—2,5 —1 4-0,5 4-2,0 4-3,5 4-5,0 4-6,5 —1,8 —1 —0,2 +0,6 +1,4 +2,2 +3,0 Орд 1,3312 7,4299 2,3312 2,0350 2,5416 3,8513 4,9542 ината № 3; ? 7,9332 2,0162 2,0280 2,9688 2,8384 7,6369 7,3643 = —1 "4,2024 7,5918 2,5985 2,2707 1,6711 2,8760 1,962 7,4668 4,0379 4,9577 3,2745 3,0511 4,3462 5,2807 0 0,0001 0,0009 0,0019 0,0011 0,0002 0
Pg£ = =0,0042
—3,0 —1,5 0 +1,5 +3,0 4-4,5 +6,0 4-7,5 —1,6 —0,8 0 +0,8 +1.6 +2,4 4-3,2 +4,0 Ор 7,0350 1,3312 1,4299 7,3312 7,0350 2,5416 7,8513 7,9542 дината № 4; 7,8384 2,9964 2,0320 2,9964 2,8384 2,6369 2,3120 2,2014 е=о "4,5877 3,8778 2,7959 2,3934 2,7375 1,9059 2,9730 1,9939 7,4611 2,2054 2,2578 2,7210 2,6109 2,0844 4,1363 0 0,0002 0,0018 0,0053 0,0041 0,0012 0,0001 0
Pg£ = =0,0127
12 Теория стрельбы 177
I II 1 Ш IV V VI VII
% 1 1 bp 7 £—1 1 II el 1 J 1 $ * ’«й 9- Г +1 UP X а к л св Он О? И 5S И S тегральные функции
: +1 UP +1 UP (2) i 3[ 1 ьс 11 Й, ,ьс ч ч ёё д к o’ td
—3,5 —1,4 Орди “2,5416 ната Я» 5; £ *2,8384 =+1 1,9472 “6,3272 0
—2 —0,6 1,0350 2,9688 2,1402 4,1440 0,0001
—0,5 +0,2 1,3312 1,0280 2,9729 3,3321 0.0021
4-1 +1 1,4299 ТД)162 +,5002 2,0463 0,0111
' +2,5 +1,8 1,33X2 "2; 9332 1,7930 2,0574’ 0,0114
+ 4,0 + 2,6 1,0350 2,7791 1,9295 7”, 7436 0,0055
+ 5,5 + 3,4 2,5416 2,5540 1,9809 3,0765 0,0012
+ 7,0 + 4,2 3,8513 2,2577 1,9960 4,1050- 0,0001
+8,5 + 5,0 4,9542 2,8903 1,9994 5,8439 0,0000 '
— •— 4,0000 *3",4517 0,0000 Т,4517 0
—4,0 —1,2 Орди "3,8513 чата № 6; £ = 2,7791 = + 2 7,2818 jsffZ£ = =0,0316 0
—2,5 —0,4 2,5416 2,9332 “2,3805 "5,8553 0,0001
—1 + 0,4 1,0350 1,0162 1,1309 3,1821 0,0015
+0,5 + 1,2 1,3312 1,0280 7", 5924 3,9516 0,0089
+ 2 +2 1,4299 2,9688 1,8387 2,2374 0,0173
+3,5 + 2,8 1,3312 2,8384 1,9480 2,1176 0,0131
+5,0 + 3,6 1,0350 2,6369 1,9868 3,6587 0,0046
+ 6,5 + 4,4 2,5416 2,3643 1,9974 4,9033 0,0008
+ 8,0 +5,2 3,8513 2,0206 0,0000 5,8719 0,0001
+9,5 + 6,0 4,9542 3,6058. 0 6,5600 0
—3,0 —0,2 Ордич "3,8513 гата № 7; £ = “2,8898 = + 3 1,5985 "5,3396 pg% = =0,0464 0,0000
—1,5 +0,6 2,5416 2,9964 1 1,2707 4,8087 0,0006
0 I + 1,4 1,0350 1,0320 | 1,6711 3,7381 0,0055
178 1
I II III • IV V VI VII
— КН
&
[ к
к
ii 2 И >>
3
Qi CD
1. S
„ Ik <s> 1 4 я
°- NT C5 д
, 1 , 1 PD
Jap I a. । S 1 «С* св Рм
II +1 К К £
[ —J и: i=r К
+1 UP -ей +Г. UP * “ ^bp Г ।“ bp 11 Jap 2 « Я о td
Ордината № 7; C = = +3
+1,5 +2,2 7,3312 2,9964 7,8760 “2,2036 0,0160
+3 7,4299 2,8898 1,9622 2,2819 0,0191
+4,5 + 3,8 1,3312 2,7120 1,9910 2,0342 0,0108
+6,0 +4,6 1,0350 *2,4631 1,8984 3,4965 0,0031
+7,5 +5,4 2,5416 2,1431 0 4,6847 0,0005
+9,0 +6,2 3,8513 3,7520 0 5,6033 0.0000
р^г =
=0,0556
Ордината № 8; ; = = 4-4
—3,5 0 4,9542 2,9331 “2,7959 "6,6832 0
—2,0 + 0,8 3,8513 2,9688 1,3934 4,2135 0,0002
—0,5 +1,6 2,5416 1,0280 1,7375 3,3071 0,0020
+1,0 +2,4 1,0350 1,0162 1,9059 3,9571 0,0091
+2,5 +3,2 T.3312 “2", 9332 1,9730 2,2374 0,0173
+ 4' +4 7,4299 2,7791 1,9939 2,2029 0,0160
+5,5 +4,8 7,3312 2,5530 1,9900 3,8742 0,0075
+7,0 +5,6 7,0350 2,2577 0 3,2927 0,0017
+8,5 +6,4 “2,5416 3,8903 0 4,4319 о.рооз
+io,o +7,2 3,8513 3,4517 0 5,3030 0
pgli =
=0,0541
Ордината № 9; С = + 5
—2,5 +1,0 4,9542 2,9332 7,5002 7,3876 0
—1 . +1,8 3,8513 1,0162 1,7930 4,6605 0,0005
+0,5 + 2,6 2,5416 7,0280 7", 9295 3,4991 0,0032
+2,0 + 3,4 7,0350 2,9688 1,9809 3,9847 0,0097
+3,5 +4,2 1,3312 2,8384 1,9960 2,1556 0,0143
+ 5 +5 1,4299 2,6369 1,9994 2,0662 0,0117
179
I II III IV V VI VII
$ £ T Qi bp П 'w' st 7 Г 1 0 _ ,.s ,ц0П с Ji 1 Г а-1 +1 4jlP динтегральиых ций нтегральные функции
ы ° И К
+1 ’J.P -H w 9- Г 1 ^ьр I ъь лс'-& о с
+ 6,5 +5,8 Орди 7,3312 ната № 9; ? = 2,3643 = +5 0 7,6955 0,0050
+8,0 +6,6 1,0350 2,0206 0 3,0556 0,0011
+9,5 + 7,4 2,5416 3,6058 0 4,1474 0,0001
+11,0 +8,2 3,8513 3,1199 0 6,9712 0
—3 +1,2 Орди 7,0000 ната К» 10; £ 7,8848 -4-6 7,5924 7,4822 р^> = =0,0456 0
—1.5 + 2,0 4,9542 2,9964 1,8387 5,7893 0,0001
0 +2,8 3,8513 1,0320 1,9480 4,8313 0,0007
+ 1,5 +3,6 2,5416 2,9964 1,9868 3,5248 0,0033
+3,0 + 4,4 1,0350 2,8898 1,9974 3,9222 0,0084
+ 4,5 +5,2 1,3312 2,7120 0 2,0432 0,0111
-J-6 + 6 1,4299 2,4631 0 3,8930 0,0078
+ 7,5 +6,8 1,3312 2,1431 0 3,4743 0,0030
+9,0 +7,6 1,0350 2,7520 0 3,7870 0,0061
+Ю.5 +8,4 2,5416 3,2898 0 5,8314 0,0001
+12,0 + 9,2 3,8513 3,7564 0 5,6077 0
—2,0 +2,2 Орди 4,0000 ната № 11; g 7,9688 = 4-7 7,8760 7,8448 Р^ = =0,0406 0
—0,5 +3,0 4,9542 1,0280 1,9622 5,9444 0,0001
+1,0 + 3,8 3,8513 1,0162 1,9910 4,8585 0,0007
+2,5 + 4,6 2,5416 2,9332 1,9984 3,4732 0,0030
+ 4,0 + 5,4 1,0350 2,7791 О 3,8141 0,0065
+5,5 + 6,2 1,3312 2,5540 О 3,8852 0,0077
180
I II III IV V VI VII
s CQ Г ЬХ) ’ll / ? — i uA~ \ E )]~ "1 p E . +1 Ay, динтегральных ций итегральные функции
’4 KJ be s К
+l Jjj' +1 ли* 1g? : I —' be II К ft +>e-- 4 о t:
-H +7 Орди1 1,4299 ;ата N» 11; C 1,2577 = + 7 0 "3,6876 0,0049
4-8,5 +7,8 1,3312 3,8903 0 3,2215 0,0017
4-10,0 4-8,6 1,0350 3,4517 0 4,4867 0,0003
4-11,5 ,+9,4 2,5416 4,9421 0 5,4837 0,0000
—1,0 +3,2 Орди 4,0000 ната N» 12; 1,0162 ; =+8 1,9730 "6,9892 р^ = =0,0249 0
+0,5 +4,0 4,9542 1,0280 1,9939 5,9761 0,0001
+2,0 4-4,8 3,8513 2,9688 1,9990 4,8191 0,0007
+3,5 +5,6 2,5416 2,8384 0 3,3800 0,0024
+5,0 4-6,4 1,0350 2,6369 0 3,6719 0,0047
+6,5 4-7,2 1,3312 2,3643 0 3,6955 0,0050
-|-8 +8 1,4299 2,0206 0 3,4505 0,0028
+9,5 +8,8 1,3312 3,6058 0 4,9370 0,0009
+n,o +9,6 1,0350 3,1199 0 4,1549 0,0001
4-12,5 +10,4 2,5416 4’, 5629 0 5,1045 0
+ o +4,2 Орди 1,0000 ната № 13; г 1,0320 = + 9 1,9960 "5,0280 Р^ = =0,0167 0
+1,5 +5,0 _4,9542 2,9964 1,9994 5,9400 0,0001
+3,o +5,8 3,8513 2,8898 0 4,7411 0,0006
4-4,5 +6,6 2,5416 2,7120 0 +,2536 0,0018
+6,0 +7,4 1,0350 2,4631 0 3,4981 0,0031
+7,5 -j-8,2 1,3312 2,1431 0 3,4743 0,0030
181
++++-.*-+ "i"t"t+++4'++ i "t i GO Q Qt W M W C GO СЛ >> M i w м о ел о ел о ел о о ел ел о ел о ел о ел о ел i + 1щ
±-1-++++ +++++++++ tt++ о ~ со ^.1 < Q )—iOO'-OGO<jQCiUT 1—i о о «О N 1й> с ОО О N ООО to £г» О ОО О ita- О ОО < ± *и2 Н-1
Орди] 1,4299 1,3312 7,0350 2,5416 Орди! ' 1,0000 4,9542 3,8513 2,5416 2,0350 J.3312 2,4299 1,3312 1,0350 Ордин 1,0000 2,9542 2,8513 2,5416 1,0350 7,3312 ig (z) = ig - р2^ >—<
ната К» 13; £ 1,7520 3,2898 4,7564 1ата № 14; t 2,9964 2,9332 2,7791 "2,5540 2,2577 “3,8903 “3,4517 4,9421 ата № 15; £ “2,9688 2,8384 2,6369 2,3643 2,0206 3,6058 и — 1 ! ffQ fej | t*f 1 Ц | -° J- съ . 1 1—^ II “5
1 II II "t + + О О О О О О ОООООООО® 5 о о о — 50 Ig Fi « + ш2)
3,1819 7,6210 “5,7914 "6,9964 "5,8874 4,6304 "3,0956 3,2927 “3,2215 4,8816 1,2733 1,9688 "5,7926 2,4882 4,9059 1,0556 4,9370 1g подынтегральных функций
= =0,0064 0 0,0001 0,0003 0,0008 0,0011 0,0009 =0,0106 0 0,0001 0,0004 0,0012 0,0020 0,0017 0,0008 0,0002 0 0,0015 0,0004 0,0001 0 Подинтегральные функции нч
5 ± iti'i
$ + iu2
Ig F4 (? ± iu.,)
Ig подинтегральных
функций
Подынтегральные функции
183
Выбрав из табл. 54 значения pd£, сведем их в табл. 55
и подсчитаем вторые функции Персена, дающие распределение
цели к моменту падения следующего залпа.
Таблица 55
Вторые функции Персена
№ ординат
А
1 0 0
2 0,001 0,003
3 0,004 0,011
4 0,013 0,036
5 0,032 0,090
6 0,046 0,129
7 0,056 0,157
8 0,054 0,145
9 0,046 0,129
10 0,041 0,115
И 0,025 0,070
12 0,017 0,047
13 0,011 0,031
14 0,006 0,017
15 0,004 0,011
16 0,002 0,006
17 0,001 0,003
18 0 0
+» +°°
Л = Сpgd%= У<<?г(О$=
—оо •—оО
=0,357 =1,000
На черт. 48 построено распределение цели к моменту паде-
ния следующего залпа. Для обеспечения захвата этим залпом
О~ 1 2 3 4 ~5 ЬКаб
Черт. 48.
цели в вилку необходимо, чтобы вероятность недолета для
этого залпа была равна нулю:
184
Fi (t—R)dt=O.
(217)
Вероятность, равную нулю, по (217) мы получим только в том
случае, если направим огонь в точку 18 (черт. 48), т. е. при
вилке шириной 14 Вд, которая при данном рассеивании выразится
в 6г/4 каб., и последнюю вилку придется взять в 3 каб. или
в Р/2 каб.
Исходить из первой вилки неудобно, а поэтому обычно исхо-
дят из последней вилки и выражают первую вилку в числе
последних вилок, что дает значительное упрощение правил
стрельбы.
Если принять последнюю вилку равной 4=Вд, то, исходя из
удобства расчета и команд, в данном случае величину первой
вилки придется взять в 16 Вд, как кратное четырем.
С другой стороны, учитывая то обстоятельство, что эконо-
мия времени при стрельбе по подвижной цели имеет исключи-
тельно большое значение, первую вилку желательно взять воз-
можно уже. Поэтому подсчитаем, насколько вероятность недо-
лета для вилок в 4 Вд и 8 Вд будет близка к нулю (табл. 56).
Таблица 56
Вероятность недолета для вилок в 4, 8 и 16 Вд
Ширина вилки 4 Вд 8 Вд 16 Вд
№ ор- динат ?2«) pi ?2 (0Pi* Fi (?—В) Р2 (О х X F^-R)
1 0 0 0
2 0,003 0 0 — — —
3 0,011 0 0 — — —
4 0,036 0 0 — — —
5 0,090 0 0 — — —
6 0,129 0 0 — — —
7 0,157 0 004 0,001 — — —
8 0,145 0,062 0,009 — — —
9 0,129 0,316 0,041 — — —
10 0,115 0,690 0,079 0 0 ——
11 0,070 0,917 0,06'< 0,004 0,001 —
12 0,047 0,986 0,046 0,062 0,003 —
13 0,031 0,999 0,031 0,316 0,010 —
14 0,017 1 0,017 0,690 0,012 —
15 0,011 1 0,011 0,917 0,010 —
16 0,006 1 0,006 0,986 0,006 —
17 0,003 1 0,003 0,999 0,003 —
18 0 1 0 1 0 —
+“= +“ 4-00
Pi=f?2 (О7™ (H-R)dL= 25<=/<Р2©-
=0,308=30,8% =0,045=4,5% Fi (ЬВ)=0
185
Рассматривая табл. 56, видим, что для вилки в 4Бд вероят-
ность недолета (30,8%) еще велика, чтобы ширину первой вилки
можно было принять равной 4Вд.
Вероятность недолета при вилке в 8 Вд уже весьма мала
(4,5%) и риск пойти на первую вилку в 8 Вд, имея в виду
экономию времени, будет вполне уместен, а поэтому и остано-
вимся на этой ширине первой вилки.
Наиболее рациональным видом пристрелки в этом случае
будет уступ по 4Вд. Двойной уступ по 4 Вд (всего 12 Вд) уже
дает весьма полное обеспечение захвата цели (вероятность недо-
лета для последнего залпа в уступе 0,1%).
Полная последовательность, исходя из расчета, была бы,
конечно, при уступе в 8 Вд.
Если сравнить расчет первой вилки при стрельбе с ошиб-
кой в ВИР с расчетом первой вилки для случая, когда ошибка
в ВИР равна нулю, или для неподвижной цели, то увидим
•существенную разницу.
При стрельбе по неподвижной цели для первой вилки при-
нималось во внимание срединное положение цели, при котором
перелет и недолет были равновероятны; для случая же
стрельбы с ошибкой в ВИР мы выбираем первую вилку, исходя
из вероятности недолета, равной нулю (или вероят-
ности перелета, равной единице).
В первом случае, т. е. при ошибке в ВИР, равной нулю,
если цель не будет захвачена вторым залпом в вилку, то при
захвате ее в вилку третьим залпом мы решительно ничего не
теряем; во втором же случае (при наличии ошибок в ВИР),
если цель не будет захвачена вторым залпом (или уступом), мы
упускаем время, и следующий шаг придется брать больше, что
в свою очередь вызовет потерю во времени при дальнейшем
сужении вилки, и к моменту перехода на поражение распре-
деление цели из-за потери времени будет хуже.
ГЛАВА UII
ВЛИЯНИЕ ФАЛЬШИВЫХ (НЕВЕРНЫХ)
НАБЛЮДЕНИЙ
51. Общие указания
Рассматривая вопросы теории стрельбы по наблюдению зна-
ков, мы предполагали, что все знаки падений или разрыва
ударных снарядов оцениваются верно. Между тем практика
стрельб показывает, что такое предположение не всегда имеет
место, так как в наблюдении знаков падений иногда также
бывают ошибки — принимают перелеты за недолеты и наоборот.
Такие ошибочные оценки носят название фальшивых или
неверных наблюдений.
При повторении пределов уступа или вилки, а также при
поражении цели залпами или очередями вероятность хотя бы
одного или не менее нескольких верных наблюдений увеличи-
вается, что может быть легко подсчитано, если известна вероят-
ность верного или вероятность фальшивого наблюдения. Это
обстоятельство послужило причиной названия процесса повто-
рения пределов обеспечением пределов.
Но как бы то ни было, а фальшивые наблюдения все же
имеют место, и иногда их влияние на успешность стрельбы
может оказаться немалым. В силу этого обстоятельства необхо-
димо рассмотреть, как ошибки в наблюдении знаков скажутся
на распределении цели.
Для решения различных задач при выработке правил
стрельбы и, главным образом, для получения распределения
цели с учетом возможности фальшивых наблюдений необходимо
знать закон, которому следуют ошибки наблюдений. Здесь воз-
можно предположить два случая: когда вероятность фальшивого
наблюдения зависит или не зависит от интервала падения
снаряда.
На втором случае, когда вероятность фальшивого наблюде-
ния не зависит от интервала падения снаряда и принимается
в виде постоянной конечной величины, мы останавливаться не
будем, так как этот случай, во-первых, опровергается стати-
187
стикой фальшивых наблюдений (правда, очень бедной), а, во-
вторых, теоретическое исследование этого вопроса приводит к
абсурду, давая распределение цели, уходящее в обе стороны
до бесконечности, причем получается
Доо
---00
несмотря на вилку с обеспеченными пределами.
В первом случае, т. е. при зависимости вероятности фаль-
шивого наблюдения от интервала падения, остановимся на двух
вариантах:
1) когда падения наблюдаются без помощи инструмента, из-
меряющего интервал падения, т. е. при помощи бинокля или
стереотрубы, и
2) когда наблюдение производится с помощью инструмента,
измеряющего интервал падения (стереодальномер, скартометр
и др.), но во внимание принимается только знак без учета ве-
личины интервала падения.
52. Влияние фальшивых наблюдений
при зависимости вероятности таких наблюдений
от интервала падения
Статистика фальшивых наблюдений показывает, что между
вероятностью фальшивого наблюдения и величиной интервала
падения существует зависимость, которую выразим в виде
рф=/(х),
где х—интервал разрыва.
гм
—2 —---------х '
О М ц
Черт. 49.
Положим (черт. 49), что через О проходит средняя траекто-
рия, М—точка падения снаряда и Ц—цель; возьмем направ-
ление осей так, что ®>0, тогда при интервале разрыва-}-®
верному наблюдению будет соответствовать недолет, и наблю-
дение перелета будет фальшивым.
При ж<0 (черт. 50), когда точка падения в М и цель в Ц,
наблюдение недолета явится фальшивым, так как в действи-
тельности имеется перелет.
Наша задача заключается в том, чтобы найти такой закон
ошибок, который давал бы для всех х ту же вероятность фаль-
шивого наблюдения, что и f (.г).
188
Пусть этот закон задан в виде
pxdx=<? (х) dx. (218)
Если недолет был принят за перелет (черт. 49), значит,
имела место ошибка, какая угодно, но обязательно больше х.
Вероятность такой ошибки по закону (218) будет:
X
dx — f (х).
(219)
Вероятность верного наблюдения, очевидно, будет:
X
откуда
+°°
у\р (ar) dx ~ 1,
—-00
что вполне отвечает закону случайных ошибок.
Если перелет был принят за недолет (черт. 50), то имела
место какая угодно ошибка от — со до х, и вероятность такой
ошибки выразится:
Рф = / <?(x)dx = f(_x\
(220)
Продиференцировав выражения (219) и (220) по х, получим:
при ж>0 (недолет принят за перелет)
<?(ж) = — f'(xy, (221)
при ж<0 (перелет принят за недолет)
?(ж) = /'(ж). (222)
Выражения (221) и (222) дают возможность правильно подоб-
рать закон <р (я?) dx в (218), (219) и (220), причем сама f(x) для
189
случая непосредственного наблюдения знаков может быть най-
дена только на основании обработки статистического материала
фальшивых наблюдений.
Однако, этот закон не должен давать отрицательных зна-
чений для вероятности фальшивого наблюдения й не должен
иметь никаких особенностей, которые сделали бы его неприем-
лемым в качестве закона случайных ошибок.
Если такой закон найден, то для нахождения функций Пер-
сена 'его надо сложить с законом рассеивания по правилу сло-
жения ошибок в один закон.
Поступая по правилу сложения законов ошибок и имея в
виду (черт. 49 и 50), что z = t — х, будем иметь:
+ «>
- С р
F(t)dt= I ~^=е ср (a?) dr,
J V*
--00
(223)
после чего, имея один закон „рассеивания наблюдений11, можно
составить функции:
(223')
(223")
t
—оо
Этими функциями (—Z) и I1\ (f) можно пользоваться прп
учете фальшивых наблюдений вместо J? (t), употребляемых в
предположении только верных наблюдений.
Получив из (219) и (220) закон (223), мы не рассмотрели слу-
чая фальшивого наблюдения при интервале X — Q.
К интервалу х = 0 надо подходить отдельно со стороны по-
ложительных х (недолет принят за перелет) и со стороны от-
рицательных х (перелет принят за недолет).
В первом случае из (219) имеем:
4-00
У ср (ж) dx. = f (0).
о
Во втором случае из (220) имеем:
о
dx=f(O).
190
При непрерывности f (0) можем написать:
-{-со 0
j\(x) dx= j<?(x)dx,
О — ОО'
+°°
что, исходя из условия, что J<р(ж) dx=l, даст:
— оо
f (°) = 2 (224)
И
П-0) = /(0). (225)
Если функция f (о) не непрерывна, то может быть
Н-о)=Г(о),
но при этом должно быть
П-0) + П+0)= 1. (226)
Выражения (224—226) указывают, что при х — Q без допол-
нительных указаний определить знак падения нельзя или, что
то же, будут иметь место только одни фальшивые наблюдения.
Это положение как обязательное, очевидно, не может быть
принято, так как часть знаков может быть наблюдена верно,
а поэтому
Г(-о)+Г(о)<1,
а это в свою очередь при положениях, которые легли в основу
наших рассуждений, приводит нас к выражению:
<?(ж) dx<Z 1-
•—со
Поэтому к системе ошибок с вероятностью <? (ж) dx надо при-
бавить ошибку, точно равную нулю, но с конечной вероятностью
при интервале ®=0:
► +“
1 — у1? (ж) dx.
—оо
Вероятность ошибки, равной нулю при интервале 0, мы по-
лучим, если вычтем из единицы сумму вероятностей фальши-
вых наблюдений при интервале 0, т. е.
1-[Л-0) + Г(0)], (227)
а в случае f (—0) = /'(+0)
1—2/(0). (228)
191
53. Применение выведенных законов к случаю
непосредственного наблюдения знаков без
измерения интервалов падения
На основании данных статистики фальшивых наблюдений
при непосредственном наблюден™ знаков инж. В. М. Трофи-
мовым предложен закон:
. 1 Л Ж
Г(Л)=Г р—Гр
что даст:
f (о) ==0,2000;
f (1)^=0,1667;
f (2) ==0,1333;
f (3) ==0,1000;
/ (4) == 0,0667;
f (5) ==0,0333;
f (6)-°-
Этот закон представляет простую линейную зависимость при
/ (х)=7(~ *)
По (221) имеем:
/1 Ixl V 1
(х) — — f (х) -- 30 j — 30 ’
а по (222)
/1 _ 1
? (*) — f (*) = ^5 зоу — зо ’
или вообще
? W ~ 30 • (229^
К этому, согласно § 52, надо прибавить вероятности ошибки,
равной нулю при интервале х==0-
Эта вероятность будет
Л°)=|(1-|)=|=0’2
и
1—2 /-(0) = 1 — 0,4 = 0,6
или
р - р*и2
0,6 е
у к
Подставляя (229) в (223), (2?3') и (223"), получим:
х В 6
192
р — р1 р
0,6 +зо )/Т
— р2г»2
е dx
dX. (230)
Применяя теорему сложения вероятностей, получим:
«? + б
F (ж) dx =
X— 6
Вычисление приводит к таблице F1(x).
Доказано, что практически получится тот же результат,
если вместо вычисления каждый раз, в зависимости от того или
иного закона F} (ж), определить „приведенную" срединную
ошибку Е и, применяя обычную таблицу значений F (f), делить
аргумент t на эту срединную ошибку рассеивания и закона
фальшивых наблюдений.
Последнее возможно, если получается закон, близкий к закону
Гаусса, подобно (230).
Ошибки рассеивания следуют закону Гауссу со средней
квадратической ошибкой
Р К 2
Для закона (230) средняя квадратическая ошибка может
быть определена как средняя ошибка по закону равной веро-
ятности в пределах + 6 и — 6 с вероятностью о,4 и ошибки, рав-
ной нулю, с вероятностью 0,6, так как вероятность ошибки,
равной нулю, будет 0,6 или
Е2=^0,4-1^ + 0,6 • 0“)/Н8-
Средняя квадратическая ошибка сложного закона будет:
Если закон (230) настолько близок к закону Гаусса, что
можно пользоваться таблицами, вычисленными для него, то
приведенная срединная ошибка будет:
Е = Е2'р}/2==]/9Гб”рЯ7^ (231)
или
Е= 1,785. ,
Поэтому для принятия во внимание фальшивых наблюдений
достаточно все значения аргументов поделить на 1,785 и
с этими аргументами рассчитывать кривые Персена при стрельбе
по цеям неподвижным или подвижным.
В случае принятия неодинаковой вероятности фальшивого
перелета и фальшивого недолета надо значения Е‘ при х >• О
и Е" при ж <С 0 найти указанным методом отдельно и аргументы
F (— t) делить на Е', а аргументы F (/) делить на Е".
13 Теория стрельбы 193
54. Применение выведенных законов к случаю
наблюдения знаков Па основании измерения
интервалов падений, когда ошибки измерения
следуют закону Гаусса
представляет закон
Если с? (ж)
о, ТО
при Л>0
Гаусса со средней ошибкой
яг2
г' dx
f(x) =
(О
Г «2
Р _₽ «Г ,
dx.
ё2
Эти выражения представляют уже известные нам функции
F(t) и F (— t) и потому можем прямо написать:
f(x) = F
Г—И
д
т
а срединная ошибка для сложного закона почудится по пре-
дыдущему
Е=У1+^, (232)
где <5 — срединная ошибка измерения интервала, но только для
принятия решения о знаке падения.
Таким образом, в этом случае мы имеем то же правило, но
значения аргументов надо делить не на 1,785, а на величину Е.
полученную от сложения срединной ошибки отклонения пушки
со срединной ошибкой измерения интервала.
Г Л А В A IX
СТРЕЛЬБА ПО ИЗМЕРЕННЫМ ДАЛЬНОСТЯМ
55. Общие основания метода стрельбы
по измеренным дальностям и табличные неувязки
Теорию метода стрельбы по измеренным дальностям мы
будем рассматривать только для случая стрельбы по морским
подвижным целям, так как для случая неподвижной береговой
цели метод стрельбы по измеренным отклонениям является
более рациональным и с успехом может быть применен при
обстреле невидимых береговых целей.
Что касается морских или береговых видимых неподвижных
целей, то по ним все методы могут быть применены с одина-
ковым успехом, и выбор того или иного из них будет зависеть,
главным образом, от обстановки стрельбы.
В основе метода стрельбы по измеренным дальностям лежит
работа дальномеров, а потому этот метод предусматривает
только видимые цели.
Самый метод стрельбы имеет ту особенность, что каждый
залп (выстрел, серия залпов или выстрелов) при поражении
цели либо предваряется измерением дальности до цели (засеч-
ка пели), либо залпы (выстрел, серии залпов или выстрелов)
даются на основании непрерывно измеряемой до цели дальности,
текущей в центральный дающий прибор.
Поправкой к измеренной дальности считают определяемое
несоответствие дальномерной (топографической) дальности с
табличной (пушечной) дальностью или прицелом. Эту поправку
называют балистической поправкой, учитывающей только недо-
выбранные вследствие различных ошибок балистические и
аэрологические поправки.
Кроме того, в измеренной дальности и в направлении должны
быть учтены и выделены упреждения на общий ВИР и общее
БП за время от момента засечки цели дальномерами до момента
залпа (выстрела) и упреждения на ВИР и БИ цели за время
полета снаряда.
Таким образом, в этом методе балистические (и аэрологиче-
ские) поправки и упреждения разделены.
Пусть, например, из неподвижной пушки в В (черт. 51)
произведен выстрел и снаряд упал в О. Выстрел произведен
13* 195
при тщательной подготовке с расчетом прохождения средней
траектории через цель.
Если прицел (табличная дальность) был he, а расстояние,
измеренное до точки падения, BO = De, то разность
а —- Jiq De
(233)
представит собой несоответствие между табличной дальностью
(прицелом) и дальномерной дальностью. Если эта разница не-
велика, то для поражения цели имеем
Нц — D„ -j- а Wt,
(234)
где 7г1( —прицел (табличная дальность) для поражения цели;
Черт. 51.
Du— дальность, измеренная до
цели;
а — поправка, полученная в ре-
зультате пристрелки по (233);
W—ВИР цели;
t—время от момента засечки
цели дальномером до момента па-
дения залпа.
Этот метод стрельбы в том виде,
как он изложен, является в сущности
методом стре 1ьбы, основанным на при-
стрелке по фиктивной вспомогатель-
ной неподвижной цели с последую-
щим переносом огня на действитель-
ную подвижную цель.
Фиктивной вспомогательной целью
(фиктивный репер) является непо-
движная точка моря, которая обо-
значается всплеском падения или
разрывом снаряда, до которого и из-
меряется дальномером расстояние.
Самый же перенос огня является „простейшим способом
переноса", основанным на гипотезе, что до некоторого определен-
ного предела (не более 10%) разности дальностей до всплеска
и до цели можно полагать, что
ТЪц Dn De,
откуда
Тьц— (7ie — De ) -|- D44- Wt — Оц -f- п -}- Wt. (235)
Можно наперед сказать, что сама эта гипотеза содержит
неточность и является приближенной.
Кроме того, вследствие изменения дальности и направления
определенная поправка на несоответствие дальномерной (топо-
графической) дальности и прицела (табличной дальности) будет
устаревать и потребует обновления.
196
(236)
(237)
Ввиду этого можно применить другой способ, так называ-
емый „способ коэфициента К“, который основан также на гипо-
тезе, что в некоторых пределах прицелы приблизительно про-
порциональны дальностям. Если положить, что для неподвиж-
ной цели
то
• 1гв=К11в,
и в
где коэфициент К — .
ив
При подвижной цели будем иметь:
Ьц — К he + Wt,
но при этом приборы, решающие эту задачу, получатся значи-
тельно сложнее.
Вопрос о переносе огня на цель и об обновлении поправки
на несоответствие в значительной мере облегчается тем, что при
стрельбе с приборами управления огнем изменение поправок
приборами учитывается, если аргументы поправок установлены
достаточно точно.
Достаточно точная установка поправок возможна либо при
наличии аэрометеорологического бюллетеня, либо без него при
полной подготовке для высот полета не более 200—300 м, что
при начальных скоростях 800—900 м/сек соответствует дально-
стям только до 60 каб.
Так как не всегда можно рассчитывать на наличие бюл-
летеня, произведем простой табличный подсчет для выяснения
вопроса как о точности переноса огня, так и об устаревании
поправки на несоответствие дальностей.
Для расчета возьмем умышленно пушку не с лучшей бали-
стикой, например, 305-.мл в 40 калибров длиной.
Этот подсчет, как касающийся только балистической поправ-
ки, произведен в предположении, что ошибки в измерении
дальности и в ВИР равны нулю.
Произведенные расчеты сведены в табл. 57—62.
Из рассмотрения табл. 57—62 видно значение тщательности
подготовки, что вытекает из сравнения табл. 57 с 58, 59 с
61 и 60 с 62.
Сравнение табл. 59 с 60 и 61 с 62 показывает преимущество
способа коэфициента К, но, имея в виду простоту приборов
управления огнем, возможно, что все же придется остановиться
на простейшем способе, уменьшив разность дальностей при
переносе до 5%, хотя, как показывают таблицы, перенос про-
стейшим способом до 10% возможен, тем более, что здесь
явятся, кроме табличных неувязок, и другие ошибки.
197
Таблица 57
1. Аргументы поправок, установленные на приборах.
2. Остающееся несоответствие прицела и дальности определено при-
стрелкой.
3. Срединные ошибки подготовки Аг =0,8%; At=l°; Д/7=0,5%; ДТ7 =
= 1 м/сек.
11. Изменение дальности 10%.
Дальности, каб. Табличные поправки саж. Срединные ошибки подготовки, саж. Средние! неувязки саж. Й СО С В с со еЗ
дх dv дх dt дх дП дх 0W 0® . —Дг dv dt ^Д/7 дП ДЖ dW
110 109 12 55 24 87 12 28 П 95
120 115 13 60 28 92 13 30 28 102 7
90 98 11 43 17 78 И 22 17 84
100 103 11 49 20 82 И 25 20 89 5
70 84 9 31 10 67 9 16 10 70
77 89 10 36 13 71 10 18 13 75 5
Таблица 58
Условия, аналогичные с табл. 57, но при больших ошибках подготовки.
Балистическая подготовка та же; Д®=0,8%; Д^=1°.
Аэрологическая подготовка: ДЯ=4%; ДТУ=5 м/сек.
Дальности, каб. Табличные поправки саж. Срединные ошибки под- готовки, саж. Средние неувязки, саж. Разность, саж.
дх dv дх dt дх ~оп дх dW дх дх ~dtht дх 0П^П дх dW^w
110 109 12 55 24 87 12 220 120 266
120 115 13 60 28 92 13 240 140 293 27
90 98 И 43 17 78 11 172 85 207
100 103 11 49 20 82 И 196 100 235 28
70 84 9 31 10 67 9 124 50 150 24
77 89 10 36 13 71 10 144 65 174
1 Определены, как корень квадратный из суммы квадратов срединных
ошибок.
198
Таблица 59
Перенос огня при больших случайных ошибках подготовки
(простейший способ) •
ДТГЛ.=10 лг/сек; Д+=4%; Д®=1%; Д#=1°.
Даль- ность до всплеска Прицел по всплеску Разность а Дальность до цели Прицел по цели Прицел Ли +<+ Ошибки пе- реноса
в к а б е л ь т О В Ы X
ПО 115,8 + 5,8 120 126,5 125,8 —0,7
ИО 115,8 +5,8 115 120,9 120,8 —0,1
90 94,6 + 4,5 99 104,1 103,5 —0,6
90 94,5 + 4,5 95 99,8 99,5 —0,3
70 73,2 +3,2 77 80,7 80,2 —0,5
70 73,2 + 3,2 74 77,5 77,2 —0,3
Таблица 60
Перенос огня при больших случайных ошибках подготовки
(способ коэфициента К)
ДЖх=10 .м/сек; Д/7=4%, Дц=Н%; М- =1°.
Даль- ность до всплеска Прицел по всплеску тс Дальность до цели Прицел по цели Прицел К v Ошибки переноса
в к а б е л ь т о в ы X
ПО 115,8 1,091 120 126,5 126,3 —0,2
по 115,8 1,045 115 120,9 121,0 —0,1
90 94,5 1,100 99 104,1 104,0 —0,1
90 94,5 1,056 95 99,8 99,9 +0,1
70 73,2 1,100 77 80,7 80,5 —0,2
70 73,2 1,057 74 77,5 77,4 —од
Таблица 61
Перенос огня при полной подготовке и при случайных ошибках подготовки
(простейший способ)
Д®=1%' Д1=1°; \ WX=2 м/сек; ДП=1%.
Даль- ность до всплеска Прицел по всплеску Разность а Дальность до цели Прицел по цели Прицел Дц Ошибка при переносе
в к 'а б е л ь т о в ы х
110 112,2 +2,2 120 122,4 122,2 —0,2
110 112,2 + 2,2 115 117,3 117,2 —0,1
199
Таблица 62
Перенос огня в условиях табл. 61
(способ коэфициента К)
Даль- ность до всплеска Прицел по всплеску К Дальность до цели Прицел по цели П рицел К Ошибка при переносе
в кабельтовых
110 110 112,2 112,2 1,091 1,046 120 116 122,4 117,3 122,4 117,2 0 “0,1
Эти же таблицы дают возможность
судить о степени уста-
ревания поправки на несоответствие дальностей,
Черт. 52.
но только
для данной балистики. Этот
вопрос для каждой балистики
при выработке правил стрель-
бы придется решать каждый
раз особо.
На черт. 51 показан слу-
чай стрельбы с неподвижно
стоящего корабля. При стрель-
бе же с корабля находу во-
прос осложняется тем, что за
время полета пристрелочного
выстрела (очереди, залпа) ко-
рабль меняет свое место.
Пусть выстрел произведен
при некотором прицеле 1гх в
тот момент, когда корабль был
в точке Ор причем установки
рассчитаны для попадания в
упрежденную точку цели А1
(черт. 52). Допустим, что сна-
ряд упал в точке Л2 к момен-
ту перемещения корабля в
точку О2 и OYO2=vT, где v —-
скорость хода корабля и Т —
получения величины несоответ-
знать Aj и Пр потому что а =
время полета снаряда. Для
ствия дальностей требуется
= /?! —Лр а дальность D фактически будет измерена. При
применении способа коэфициента К нам надо знать
Л)(,
А *
Величина может быть получена из” треугольника
по / qe, O1O2 = vT и Л, но удобнее будет воспользоваться
поправкой на несоответствие:
щ — й2 — Л,
200
потому что решение последней задачи в приборах осуще-
ствляется проще.
Необходимо подсчитать, как велика будет разница между
величинами щ и а2 при различных курсовых углах.
Подсчеты произведем для условий стрельбы: £9 = 100 и
150 каб.; v = 24 узла; 1%; барометр 760 .м.м; ^в = +10°Ц;:
Д/Ь--|-з%; 17=10 м/сек; курсовые углы: 90, 70, 50 и 20°;
угол ветра 45°.
Результаты подсчета приведены в табл. 63 (таблицы стрельбы
We указываются).
Таблица 63
Несоответствие дальностей вследствие хода корабля за время полета снаряда
Курсовой угол в градусах й| = 1 00 каб. hj = 150 каб.
а а—а. а «2 а—а2
В кабельтов Ы X
90 0,40 0,41 —0,01 1,0 0,94 +0,06
70 . . 0,40 0,45 —0,05 1,0 1,02 —0,02
50 0,40 0,39 +0,01 1,0 1,04 —0,04
20 0,40 0,38 +0,02 1,0 1,12 —0,12
Рассмотрение табл. 63 показывает, что ошибка пренебрежимо
мала.
56. Распределение цели при исследовании стрельбы
только в направлении дальности
Положим, что в Со (черт. 53) будет истинное положение цели
и р — расстояние, измеренное дальномером до цели, положение
которой при этом определилось в Сг с ошибкой Дх. Эта ошибка
будет характеризоваться срединной ошибкой дальномера о.
Черт. 53.
Пусть: СгС2=а — истинная величина суммы всех поправок
при переходе от дальномера к прицелу (несоответствие дально-
мерной и табличной дальностей);
6'3 — место цели при осуществлении этого перехода, причем
была сделана ошибка = Л,; эта ошибка будет характери-
зоваться срединной ошибкой при переходе от дальномера к
прицелу гпр;
201
Wt — истинное перемещение цели по дальности за время t.
Съ — окончательное место цели, если при учете ВИР сделана
ошибка zt', эта ошибка будет характеризоваться срединной
ошибкой ВИР, равной nt.
Условимся счет времени вести „назад" от момента падения
предполагаемого залпа до момента засечки цели дальномерами.
Исследование значительно упростится, если каждый залп
рассматривать в отдельности и независимо от других залпов,
считая, что постоянные ошибки Д2 и zt сопровождают каждый
залп.
Прицел (табличную дальность) при одном измерении мы
получим:
A — D + a+Wt, (238)
считая, что величина Дх вошла в Dlf Д2 —в а и zt—в Wt. Ошибки
Др Д2 и zt не зависят друг от друга, а потому можно напи-
сать:
Е=У&А-г„* + пЧ\ (239)
Если у нас работает не один, а несколько, например, т даль-
номеров, то (238) и (239) примут вид:
9Л
А =-----l-a+Wt (238')
т 1 а
и I
/- р2 ——— \
Е = л/ + (239')
у т
Имея величину Е из (239) или (239'), мы получим и закон
распределения цели по направлению дальности. В этом про-
•стейшем случае мы будем иметь линейное распределение цели.
Для вычисления Е необходимо знать величины о, гпр и nt.
Срединная ошибка дальномера 5 должна быть определена
из опыта или вычислением, и потому она известна.
Срединная ошибка гпр, которая будет сделана при переходе
от дальномера к прицелу, определится методом пристрелки.
Если пристрелка при стрельбе по измеренным дальностям
производится путем сравнения расстояния, измеренного до
падения снаряда, или среднего из измеренных расстояний до
нескольких падений с табличной дальностью (прицелом), опре-
деляемой углом возвышения, при котором произведены выст-
релы, то разность между табличной дальностью А и резуль-
татом измерения D должна для каждого залпа входить поправ-
кой в измеренные до цели расстояния.
Положим, что при прицеле А средняя траектория проходит
через точку О (черт. 54) и один снаряд вследствие рассеива-
ния пушки упал в М1г дав случайное отклонение от средней
траектории Дг Измеряя расстояние до М1г мы сделаем ошибку
202
Тогда получим результат несоответствия:
a —A — D, (240)
где ошибка Д2 вошла в D.
При этом величина а будет заключать в себе ошибку, кото-
рая будет характеризоваться срединной ошибкой, величину
которой найдем из
n>P=^ftd2+o2, (241)
где
Вд — срединное отклонение пушки и
В — срединная ошибка дальномера.
------Z7 —*-т—---Д| —-—-г----Лг ---
Черт. 54.
Если мы сделаем не один, а к выстрелов, и до каждого
падения будет измерено расстояние, то при среднем рас-
стоянии
и
т
Di (243)
acp=A-Dcp = A — -----
т
' Вводя поправку аср, мы сделаем ошибку, которая будет
характеризоваться срединной ошибкой и в этом случае опре-
делится из (244):
(244)
Величина срединной ошибки ВИР зависит от того, каким
способом измерена величина изменения расстояния.
57. Ошибки в определении упрежденной точки при
различных методах измерения
В § 55 и 56 рассмотрен случай стрельбы по измеренным
дальностям при визуальном наведении орудий и непосредст-
венной корректировке боковых отклонений средней траектории
(по целику). Вследствие этого при рассмотрении метода стрельбы
203
и системы ошибок интересовал нас только вопрос упреждений
по дальности, т. е. вектор перемещения що дальности Wt,
где Ж —ВИР, выраженный в единицах скорости; срединная
ошибка в векторе перемещения по дальности была nt, где п—
срединная ошибка ВИР, a t — „упредительное время", за кото-
рое рассчитывался вектор упреждения по дальности.
В силу этого мы рассматривали распределение цели только
в направлении дальности. Кроме того, в § 55 и 56 мы не каса-
лись вопроса о способах получения упрежденной точки цели.
Теперь мы рассмотрим ошибки в векторе упреждения, которые
в общем случае будут эллиптические, причем при распределе-
нии цели только по дальности мы должны найти отклонение,
вызываемое эллиптической ошибкой в направлении дальности,
а в случае рассмотрения системы ошибок, которая дает рас-
пределение цели на плоскости, необходимо получить эллиптш
ческую ошибку конца вектора упреждения.
Положение упрежденной точки цели может быть определено
различными способами. Мы остановимся на трех способах опре-
деления скорости и курсового угла цели, а именно: 1) отдельно
и независимо друг от друга, 2) путем измерения ВИР и БП
(бокового перемещения цели) и 3) последовательным измере-
нием координат цели (чаще всего в полярных координатах).
В первых двух случаях мы не имеем зависимости между
текущими координатами положения цели и произведением из
ошибок в скорости на упредительное время.
В первом случае в скорости, как в векторе, получается
эллиптическая ошибка прямо с полуосями Дг и г Дг/ (черт. 55),
причем в зависимости от способов измерения большая ось может
быть или Дг, или г Дгу.
Во втором случае в векторе скорости получается эллипти-
ческая ошибка с полуосями: срединная ошибка в ВИР (от) и в
БП (ДБ), причем ошибка в скорости получится как отклонение,
вызываемое эллиптической ошибкой в направлении скорости.
Оба случая разобраны при исследовании ошибок в опреде-
лении ВИР, БП, скорости и курсового угла цели.
В настоящем параграфе рассмотрим третий случай, когда
скорость и курс цели определяются последовательными изме-
рениями полярных координат цели. В этом случае всегда может
204
существовать зависимость между ошибками текущих координат
цели и эллипсом ошибки в векторе упреждения.
В дальнейшем мы будем предполагать гипотезу прямоли-
нейного и равномерного движения цели за все упредительное
время.
Рассмотрим два случая, когда положение цели определяется
либо в двух, либо в трех последовательных точках, но скорость
и курс цели при этом определяют все же по двум первым точ-
кам положения цели.
Последнее может иметь место, например, когда залп дается
с поджиданием подхода цели к наперед рассчитанной даль-
ности или к наперед рассчитанному направлению (азимуту),
или, наконец, когда третья точка положения цели может быть
определена так же, как и две первые, для уточнения упреж-
денного положения цели.
Пусть (черт. 56) определены полярные координаты цели
(OHi и Pj и ОЦ2 и р2) тем или иным способом (планшет, спе-
циальный прибор и пр.), определен курс Цх Ц2 Цап и скорость
где ^ — наблюдательное время.
Сама по себе скорость при таком способе определения теку-
щих координат цели не используется, а используется вектор
упреждения цели vtv, где tv — упредительное время, и в свою оче-
редь, в общем случае упредительное время сложится из работ-
ного времени /р и времени полета Т. Залп при этом будет дан
тогда, когда цель будет в точке Цзп , если система приборов
не позволяет дать залп в точке Ц2 при tp=o.
205
Ошибки в положениях точек ЦА и Д2 вызовут ошибки и в
векторе скорости и в векторе упреждения.
В общем случае все ошибки при наличии закона Гаусса
будут эллиптические, причем величины и направления полу-
осей будут зависеть от способов определения последователь-
ности положений точек цели. Например, при дальномерах,
имеющих одну точку стояния, одна полуось пойдет по направ-
лению дальности, другая — к ней перпендикулярно, и в этом
случае мы будем иметь сразу главные полуоси эллипса.
Этот случай будет наиболее общим, как пригодный и для
берега и для корабля. При горизонтально-базных дальномерах
мы получим сопряженные полуоси эллиптических ошибок.
В общем случае мы будем иметь эллиптические ошибки:
ej —в положении точки Ц1 и е2— в положении точки ______
Так как обе ошибки получены на концах вектора /Д Д2, то.
их можно сложить в одну (е), приписав ее концу вектора:
е = е1 + е2 (245)
[выражение (245) надо понимать, как сложение эллиптических
ошибок известным приемом].
Если можно принять ej % е2, то выражение (245) можно пре-
образовать так:
е = si У?Г, (246)
что означает, что полуоси эллипса е в у 2 больше полуосей
эллипса Ej.
Для нахождения эллиптической ошибки конца вектора упреж-
дения заметим, что ошибка в векторе скорости обратно пропор-
циональна наблюдательному времени Д, а ошибка в векторе
упреждения растет прямо пропорционально упредительному
времени ty.
Найдем предварительно численное выражение ошибки упреж-
денного положения цели, когда скорость и курс цели опреде-
ляются по измерению текущих координат в двух последова-
тельных точках.
Пусть Цх и Ц2 (черт. 57) две точки положения цели, опре-
деленные измерением координат цели.
При безошибочном определении положения обеих точек
упрежденную точку цели мы бы нашли, найдя величину
206
ц2ц—~*—- 1у=кц1ц2,
1'Н
где
Если положение точки Ц1 определено с ошибкой Цх Д/,
а положение точки Ц2 определено без ошибки, то упрежден-
ное положение цели определилось бы в точке Ц' из выражения
ТЦЦ'=кТ^ТЦ.
Из подобия треугольников Ц1Ц1’ Ц2 и Ц2 ЦЦ' имеем:
цц7 = == кг
Ц1Ц1 Ц\ Ц% Hz
откуда
~ЦЦ' = к • 7ЦЦ}'.
Но так как не только ошибке Ц1Ц1', но и всякой другой,
ошибке в положении Ц} будет соответствовать ошибка в поло-
жении Ц того же направления и численно в к раз большая, то
при наличии эллиптической ошибки ел только в положении
точки Hi в положении точки Ц будет эллиптическая ошибка ке,
т. е. эллипс с полуосями в к раз больше.
Теперь положим, что точка 1/л определена без ошибки, а в
положении точки Ц2 сделана ошибка Ц2Ц2.
Сделав подобное же построение, получим упрежденное поло-
жение цели в Ц", причем
U7U"=k
и
та"=та2'+• о?=+D-. • та/.
Из подобных треугольников Ц1Ц2Ц2 и Ц1ЦЦ" имеем:
w _та' та+р-та/ = к+1
Ц2Ц2 ЦгЦ2' ЩЦ,'
откуда
= Ц2Ц2’.
Рассуждая аналогично предыдущему, придем к заключению,
что при наличии эллиптической ошибки е2 только в положении
точки Ц2 положение упрежденной точки Ц будет сопровож-
даться эллиптической ошибкой (fc + l)e2.
При наличии эллиптических ошибок и в положении точки Цх
и в положении точки Ц2 получим на конце вектора упрежде-
ния эллиптическую ошибку:
еу — к ел + (к + 1) е2. (247)
207
В том случае, когда можно принять s1st;e2, выражение (247)
преобразуется в более простой вид.
Действительно, тогда
Sy = к2 г^~ -р (к2 + 2 к -р 1) гг2
или
sa = eiV2fc2 + 2fc+ 1.
(248)
Рассмотрим теперь, Kais велика получится ошибка упреж-
денного положения цели в том случае, если, найдя скорость
по измерению координат цели в точках Цх и Ц.г и рассчитав век-
тор упреждения, сделаем еще одно измерение координат цели
в точке Цо п от этого положения уже найдем упрежденное
положение цели.
Черт. 58.
*Эти действия могут быть выполнены двояко: либо, найдя
положение цели в Цо (черт. 58) по курсу найдем по
расчету (или механически, по работе прибора) точку Цап через
промежуток tp и в этой точке дадим залп по времени, либо,
рассчитав положение точки Ц6 (черт. 59), например, через про-
межуток времени (/р+Д), поджидаем подхода цели к точке Цо
и даем залп или по дальности, или по пеленгу, которые
всегда можем рассчитать или получить в результате работы
приборов управления стрельбой при систематическом измерении
координат цели.
Для определения эллиптической ошибки упрежденного поло-
жения цели в этом случае найдем ошибку в скорости, которая
в общем случае будет эллиптической.
Эллиптическая ошибка положения цели в Д2 будет
s' = Д' =2-
208
Ошибка в скорости будет
ев==±+^_. (249)
•Н
Если можно принять s1=e2> то ошибка в скорости будет
Формулами (249) и (249') можно пользоваться в том случае,
если нас интересует только ошибка в скорости.
Ошибку упрежденного места цели получим из (249^:
е/ = -^ (Sj + е2) — к (г1 г2).
f'H
"ti
Черт. 59.
Но нами делается третье измерение с ошибкой е0 для поло-
жения цели в точке Цо.
Так как скорость для расчета упреждения измерена между
точками Z/i и Ц2, то ошибка е0 в положении цели и в Цо при-
бавится просто как эллиптическая ошибка без множителя к,
и окончательно ошибку в упрежденном положении цели
получим:
ен~ ео~Ь^(Е1 "Ь еа)- (250)
Если можно принять е1 = е2, то (250) напишется так:
гу = е0 + ке1У2 . (250 )
Если же можно принять и £0 = s1, то (250) напишется так:
£y=ei]/2k2 + l. С250")
14 Теория стрельбы
209
Примечание. Если при третьей засечке цели мы стали бы вы
водить выражение для ошибки в упрежденном положении цели тем же
путем, как для двух засечек, то ошибки при трех засечках получились
бы больше, чем при двух, что, конечно, совершенно неверно, так как
каждое лишнее наблюдение увеличивает точность или, как говорят,
пополняет сведения о цели.
Вопрос может быть поставлен еще и так: не лучше ли изме-
рение скорости сделать по точкам 1Ц и Цо при третьей засечке
в Ц2. В этом случае выражение для ошибки в упрежденном
месте цели можно получить из (247) или (248), но при боль-
шем потому что наблюдение в Ц2 сказалось бы мало.
Кроме того, относительно наблюдательного и упредитель-
ного времени можно сказать, что эти времена от нас практи-
чески не зависят (при данной балистике), так как тактическая
обстановка и необходимость развить иногда полную скорострель-
ность всегда будут требовать уменьшения наблюдательного
времени, а упредительное время, главным образом, зависит от
времени полета снарядов (работное время при наличии прибо-
ров близко к нулю).
58. Ошибки в численном значении скорости
и в численном значении курсового угла
Численное значение ошибки в скорости (черт. 60) мы полу-
чим, как отклонение, вызываемое эллиптической ошибкой по
направлению скорости, а численную
ошибку в значении кур-
сового угла получим
Черт. 60.
л U2B
ЦуЦ.
При этом, если s =
= 01 + ег)> где ех И е2 суть
эллиптические ошибки
концов _ вектора, или
е = г1]/2, ТО ОШИбку В.
скорости получим из вы-
ражения:
Следует иметь в виду, что ошибки в скорости и курсовом
угле —ошибки зависимые и могут рассматриваться только от-
дельно.
Ошибка в скорости следует закону Гаусса со всей точностью,
а ошибка в курсовом угле может быть принята следующей
закону Гаусса постольку, поскольку В может быть принят
параллельным
210
59. Исследование стрельбы по измеренным
дальностям при распределении цели на плоскости
Распределение цели на плоскости будет иметь место в тех
случаях, когда, кроме измерения дальности, измеряется и на-
правление на цель, а орудия получают готовые установки по
дальности и по направлению.
В этом случае путем пристрелки приходится получать
поправки на несоответствие табличной дальности с измеренной
дальностью и на несоответствие табличного направления с изме-
ренным направлением.
Упреждения на движение цели производятся или по ВИР и
ВИП (или ВИН), или по курсу и скорости цели (§ 58), или же,
наконец, по скорости и курсовому углу цели.
В каждом случае получится эллиптическая ошибка в упреж-
денном месте цели с полуосями в зависимости от способа учета
движения цели.
Учет несоответствия табличных дальности и направления
с измеренными будет производиться на основании определения
точек падения снарядов в очереди или в залпе, причем опре-
деление точек падения будет сопровождаться эллиптической
ошибкой определения точек падения и эллиптической ошибкой
рассеивания с полуосями: Вд, направленной вдоль плоскости
стрельбы, и Вб— перпендикулярно к ней. При этом полуоси сум-
марной эллиптической ошибки будут зависеть от числа засекае-
мых всплесков, а при наличии оптических самобазных дально-
меров— и от числа дальномеров, засекающих всплеск (§ 56).
Окончательно в простейшем случае мы будем иметь:
1) эллиптическую ошибку в измерении дальности и направ-
ления или эллиптическую ошибку в положении цели;
2) эллиптическую ошибку рассеивания;
3) эллиптическую ошибку в учете несоответствий и
4) эллиптическую ошибку вектора упреждения. Все эти
ошибки сложатся в одну эллиптическую ошибку и дадут еди-
ничный эллипс распределения цели, причем координатами
центра распределения являются табличная дальность и таблич-
ное направление.
При выявлении системы ошибок и нахождении распределе-
ния цели главную роль будет играть система дальномера или
прибора, измеряющего текущие координаты цели.
В этом параграфе и в § 58 даны руководящие указания для
исследования стрельбы по измеренным дальностям на плоско-
сти; что же касается самого решения этой задачи, то в силу
исключительной многообразности вопроса эти решения можно
дать только на ряде частных примеров.
Пример. Береговая закрыто установленная батарея обслужи-
вается горизонтально-базным дальномером с базой 4 500 м
(24,61 каб.). Скорострельность — 1 выстрел в 1 мин. Пристрелка —
по определению несоответствия по трем выстрелам очередью
через 6—10 сек. выстрел. Время работы на приборе tnp = 3 сек.
14* 211
Прибор вырабатывает по скорости и курсу цели упрежденные
координаты цели. В точке Цг (черт. 61) первая засечка цели
при дальности 105 каб. Исследование произвести в условиях
черт. 61 для скорости цели г = 24 узла и при курсовом угле
цели 45° в точке Цг. Время полета Т = 39 сек., Вд = 30 саж.,
Вб—3 саж.
1. Определим эллиптическую ошибку в определении даль-
ности.
Черт. 61.
Ошибку в угле засечки примем ДВ = о,5 дел. = 0,0005. Ошибка
от округления будет ZCK/) = + o,5 дел., тогда
Д₽ = |/Г|(0,5)24-^°,67 =0,54 дел. = 0,00054.
Сопряженные полуоси эллиптической ошибки
др
1 sin 6
и
2 — sin е •
Тогда
е, 111-0,00054
ода-----=29’8 оаж-;
У , 100 • 0,00054
J, =-----—--------=26,4 саж.
Таким образом, имеем эллиптическую ошибку в положении
цели в точке Цг с сопряженными полуосями 29,8 и 26,4 саж.
при угле между ними 12°. В дальнейшем примем символиче-
ское обозначение ех (29,8; 26,4; 12°).
2. Определим величину изменения направления на цель при
ее движении на участке Цг Цу.
Исходя из цены деления, имеем, что при самом невыгодном
случае, когда цель идет при q = 90°, направление изменится на
**=60
10
дел.,
что составляет 3°,6.
3. Исходя из небольшой величины угла (3°,6), примем при-
ближенно, что в дальнейшем будем получать эллиптические
ошибки равными ед с осями, соответственно параллельными.
4. Исследуем, как скажутся наблюдательное время tn и метод
определения курса и скорости цели.
а) 4 — 15 сек., tnp=3 сек. Курс и скорость определяются
по двум первым засечкам; залп дается после третьей засечки
цели.
4 = 0,25 МИН.; 4 = 0,07 мин.
ь__.4 ___т tnp_____0,7 __
fC ~— = т----------------Z.o ,
tn tn 0,25
s,J~e1}/2k:! 4- l=ex V 2 • 7,84 1 = 4,08 ех И ey (122; 108; 12е).
б) 4 = 30 сек.; tnp — 3 сек. Курс и скорость определяются
по двум первым засечкам; залп дается после третьей засечки
цели; 4 = 0,5 мин.; 4=0,7 мин.
es, = S1|/ 2 . 1,96-4-1 =2,22 ех;
еу(64; 58; 12°).
в) 4 = 60 сек.; tnp — 3 сек. Курс и скорость определяются
по двум засечкам цели: залп следует после второй засечки
цели; 4 = 1 мин.; 4=0,7 мин.; fc = 6,7.
е„ = eJ/2 fc2 4- 2 jt-Fl =ех У 0,98 + 1,4 + 1 = 1,84 ех;
еу(57; 51; 12°).
г) Теперь посмотрим, какова будет эллиптическая ошибка
при определении курса и скорости цели как средних по пяти
засечкам, аналогично определению ВИР. Пусть засечки дела-
лись через 12 сек. в моменты: 0, 12, 24, 36 и 48 сек., причем
213
последняя засечка определяет и то положение цели, от кото-
рого берется упреждение.
Тогда
2 т
2 т + 1
У s~- т
где т — число засечек цели, S при пяти засечках равно. 22 +
+ I2 + I2 + 22 = 10 и т — промежуток времени в минутах между
двумя смежными засечками цели;
|/к)
еу(ЗО,6; 27,4; 12°).
д) При аналогично произведенных трех засечках через 15 сек.
будем иметь:
еу(53,2; 47,5; 12°).
Остановимся на случае г), тогда на конце вектора упрежде-
ния будем иметь:
1) эллиптическую ошибку вектора упреждения: %ДЗО,6;
27; 12°); "
2) эллиптическую ошибку в положении цели при последней
засечке: е, (28,7; 2d,9; 12°);
3) эллиптическую ошибку сострелки пушек с дальномером,
которая в свою очередь будет складываться из двух эллипти-
ческих ошибок:
а) из эллиптической ошибки засечки всплеска
б) из эллиптической ошибки рассеивания
Q \
-—=17,3; ^ = 1,7; 90° .
] ' 3 уз У
Для всех, кроме последней эллиптической ошибки, мы имеем
сопряженные полуоси, и для последней — главные полуоси
в плоскости стрельбы и в направлении, перпендикулярном к
этой плоскости.
Имея сопряженные полуоси всех эллиптических ошибок,
полз чим эллиптическое распределение цели к моменту паде-
914
пи.я залпа с центром в точке Цу. Начало координат возьмем
в точке Цу и ось Х-ов направим в плоскости стрельбы (черт. 62
и табл. 64).
Таблица 64
К примеру в условиях черт. 62
COS sin cpi 8i3 COS2 tpi sin2 BjS cos2 <fi 6<2 sin2 tfi 6j2 sin COS
17,3 0° 1 0 299,3 1 0 299 0 0
15 4° 0,998 0,070 225,0 0,996 0,0049 224 1,1 -- 15,7
25,9 4° 0,998 0,070 670,8 0,996 0,0049 668 3,3 — '45,8
27,4 4° 0,998 0,070 750,8 0,996 0,0049 748 3,6 — 52,4
1,7 90° 0 1 2,9 0 1 0 2,9 0
16,6 352° 0,990 —0,139 275,6 0,980 0,0193 270 5,3 — 37,8
28,7 352° 0,990 —0,139 823,7 0,980 0,0193 835 15,9 —114,3
30,6 352° 0,990 —0,139 936,4 0,980 0,0193 917 18,1 —128,8
3 961,9 50,2 —167,0
A C В
tg2 а =
2В
А —С
334
3911 • 7
0,0854;
А>С, следовательно, cos2a1>O, откуда
2 ccj = — 4° 53';
Ej = — 2° 26';
215
COS 04 = 0,999;
COS a2 = 0,042;
cos2 04 = 0,998;
cos2 a2 = 0,002;
2 a2 = 175° 07'
a, = + 87° 34';
sin 04 =— 0,042;
sin a2 = 0,999;
sin2 сц —0,002;
Sin2 a2 = 0,998;
sin 2 04 =— 0,085;
sill2a2= + 0,085;
a(b) = J/Л cos2 a1(2) + 1 sin2 a1(g) + В sin 2 a1(2) ;
a = ]/3 902 •“Щ998 + 50?2~^”0Д)02 + 167- 0,085 = 63 саж.;
Ь = У 3962 • 0,002 + 50,2 • 0,998— 167 0,085 =6,5 Саж.
Большая ось направлена под углом — 21/2° к плоскости
стрельбы (правее). Вследствие малой величины угла ях можно
принять, что большая ось совпадает с плоскостью стрельбы.
60. Поправка в ВИР при стрельбе по подвижной цели
а) Стрельба по наблюдению знаков падения
Наблюдение знака падения при различных методах стрельбы
по подвижным целям не только пополняет наши сведения
о цели, но в некоторых случаях позволяет судить о тех пре-
делах, в которых возможно предполагать величину случайной
ошибки в ВИР.
Расчет для выводов и необходимых при этом указаний может
быть сделан как для метода стрельбы по наблюдению знаков,
так и для метода стрельбы по измеренным дальностям, когда
обычная корректура не применяется, но расчет поправки ВИР
может быть полезен для некоторых частных случаев стрельбы
дальномерным способом. Поэтому остановимся сначала на
методе расчетов для выбора наивыгоднейшей величины по-
правки ВИР для случая стрельбы по наблюдению знаков.
Основным отличием стрельбы по подвижной цели является
изменение дальности, учет которой неизбежно сопровождается
случайной ошибкой, могущей в течение некоторого времени
сохранять свою величину или изменяться от одного залпа
к другому. Будем рассматривать только первый случай, счи-
тая, что ошибка ВИР подчиняется закону Гаусса. В этом слу-
чае вероятность ошибки ВИР в пределах и z и z-\-dz выра-
зится:
216
• Р Р” П2~
pdz*=- —~е dz, (251 >
11 У ТС
где z— случайная ошибка ВИР, выраженная в единицах ско-
рости, а п—срединная ошибка, характеризующая закон слу-
чайных ошибок ВИР, также в единицах скорости.
Переходя от ошибок в скорости к ошибкам перемещения,
будем иметь ошибку в перемещении zx — zt. Срединная ошибка
перемещения будет nt.
Имея в виду, что вероятность ошибки nt та же, что и
ошибки zt, можем написать:
pdz~-----(п1>2 dz, (251')
ntyn
или по сокращении будем иметь опять выражение (250):
о г2
р -р’~
pdz = е п" dz.
п у тс
За начало счета времени будем принимать момент падения
того последнего залпа, на основании которого сделаем вывод
о направлении и величи-
не ошибки в ВИР.
Счет времени по пре-
дыдущему будем вести
назад от падения послед-
него залпа.
Если, например, вре-
мя полета Т— 30 сек.,
мертвый промежуток т =
= 12 сек., то условное
время падения четырех
залпов (черт. 63) показа-
но в табл. 65.
Таблица 65
Условное время падения четырех залпов, показанных на черт. 63
№ залпа Время производ- ства залпа Время падения Время, отнесенное к моментам падения по условному счету времени
1 0 м. 00 с. 0 м. 30 с. 2 м. 06 с. = 2,1 мин. = Ц
2 Ом. 42 с 1 м. 12 с. 1 м. 24 с. — 1,4 мин. — Ь>
з 0 м. 24 с. 1 м. 54 с. 0 м. 42 с. — 0.7 мин. — /;(
4 2 м. 06 с. 2 м. 36 с. 0 м. 00 с. = 0,0 мин. = Ц
217
Наблюдение различных знаков на одном и том же пределе
указывает на направление ошибки ВИР и позволяет выявить
-закон случайных ошибок ВИР.
Вероятность захвата цели в эту растянутую по времени
„нулевую вилку“ будет для всех возможных г:
+“
—ОО
или, учитывая, что для принятого нами счета времени £4 = 0,
можем написать:
-J-O0
УРк(£ — ztj F*(—Е) (14.
Учитывая же вероятность ошибки z, получим:
-}-оо
Ф1(г)(Ь= р е ' "3 dz / Fk(4 — ztx) Fk(— l)dc, • (252)
ny iz I
—oo
Обозначив (s) dz = B, переходим от (252) к распределе-
нию ошибки в ВИР:
4-СО
cp,(S) fte=JL-P_ dz / F*(-E) d4. (253)
В J
I-00
Для производства расчетов будем иметь довольно сложную
схему. Во-первых, по (251) или по (251') вычисляем вероятность
гипотез z, пользуясь таблицей закона Гаусса: .
Схема этих вычислений показана в табл. 66.
Таблица, 66
№ ординат Z Z п ntf (г) <?(г)
0 0
1,2 1
3,4 2
218
Затем вычисляем
f*(E —
st,) Fk(-£) ds.
* Схему вычисления располагаем в табл. 67 (черт. 64).
Таблица 67
В одну сторону величина подинтегральной функции быстро
придет к нулю, в другую сторону число схем будет равно
числу строк табл. 66.
После этого подсчитываем распределение ошибки ВИР, рас-
полагая вычисления в табл. 68 [формула (253)], где величины
вероятностей © (г) берем из табл. 66.
Таблица 68
№ орди- нат Гипотеза об ошибке ВИР Величины из последней гра- фы табл. 67 Pi ср (3> = Pi * Pi'Pi ср2 (s) dz = Pipi
~*pipt
-PiPi
219
Полученное распределение ошибки ВИР позволяет выявить
наивыгоднейшую поправку ВИР при систематическом примене-
нии выработанного правила, но она не будет пригодна для
выявления наивыгоднейшего шага прицела в сторону цели, для
чего необходимо подсчитать распределения цели к моменту
падения следующего захватывающего залпа с новым началом
счета времени от момента падения этого предполагаемого залпа
(§ 43—45).
Например, если наблюдались знаки (—), (+), (+) и (~Н>
тогда рабочей формулой для вычисления распределения цели
будет:
(£) d z = —г- d С
Fk (— с 4- znti) dz
+ Znt^ Ffc (Я— 5 zn t3
(254)
или, приближенно, в более кратком виде:
®2 (?) d I = d ?
— &z-
у=е Fk(z — sntj) Fk (— ds. (255)
б) Стрельба по измеренным дальностям
При стрельбе по измеренным дальностям подобного рода
расчеты могут понадобиться лишь для некоторых частных
случаев стрельбы, но так как все же они могут понадобиться,
рассмотрим и этот случай.
Упрежденная табличная дальность при стрельбе по изме-
ренным дальностям выразится так:
h=D4~\-a~{- Wk6 Wtft, (256)
где D4 — измеренная дальность или средняя дальность, полу-
ченная в результате одновременного измерения дальности не-
сколькими равноточными дальномерами; а — поправка при .пе-
реходе от дальности, данной дальномерами, к табличной (к (при-
целу); t — время от момента засечки цели дальномерами до
момента падения залпа, равное (T-j-т), причем т —время от
момента засечки цели дальномерами до момента залпа и Т —
время полета снаряда; W„s— ВИР стреляющего корабля и
№ц — ВИР цели, оба выраженные в единицах скорости.
Причиной наблюдения недолета или перелета в этом случае
одновременно будут следующие ошибки: ошибки, сопровождаю-
щие измерение расстояния, ошибки перехода от дальности
к прицелу и ошибки в учете ВИР цели. Будем считать, что
99П
учет своего ВИР сопровождается пренебрежимо малой ошибкой.
Таким образом, для получения распределения ошибки ВИР
в этом случае нам надо учесть распределение цели к моменту
падения залпа, показавшего знак.
Рассмотрение этих ошибок позволяет считать, что ошибки,
сопровождающие измерения дальностей пристрелки или таблич-
ного перехода и учета ВИР, следуют закону Гаусса и, будучи
между собой независимыми, могут быть для получения сре-
динных ошибок распределения цели сложены:
(257)
где 8 — срединная ошибка, характеризующая закон ошибок
дальности, измеренной разноточными дальномерами; тпр — сре-
динная ошибка перехода от дальномера к прицелу; п— сре-
динная ошибка ВИР, ве-
личина которой зависит от
способа определения ВИР.
Полагая ошибку ВИР
равной z и ошибку пере-
мещения ^1 = ^, вероят-
ность этой шибки получим
по (251) или (251'), но счи-
тая время от момента за-
сечки цели дальномером до
момента падения залпа.
Тогда вероятность сложного события ошибки в ВИР при наблю-
дении недолета получится:
(t — zt) di. (258)
В данном случае мы имеем дело с зависимыми событиями,
и потому вероятность недолета должны вычислять в предполо-
жении, что первое событие — данная ошибка ВИР—имеет место.
Пусть черт. 65 дает распределение цели, вычисленное
по 257. Задаваясь ошибкой г, получим zy=zt, что дает поло-
жение средней траектории в О (начало координат полагаем
все время в О). Для этого положения вычисляем вероятность
недолета по (258).
В случае наблюдения перелета вероятность ошибки в ВИР
следует вычислять по (258'):
---00
Fk Zt) di. (258')
221
Полученную вероятность недолета или перелета Htajio умно-
жить на вероятность ошибки ВДОР z, вычисленную по (251).
Задаваясь всеми возможным#1 ошибками zr=^zt и повторяя
вычисления, получим вероятнос)ТЬ недолета (или пер611ета) ™
всем гипотезам об ошибке ВИР*- Распределение ошиРки Bill
получим из (259):
-г00
ср, (г) dz — ± е ' dz / е Е Fk (—Е + 2?) (25®)
t п V те / Г- V *
--00
+°°
где С= C^^dz, что и дае/Т распределение сшибки ВИР
в этом случае.
Схему расчетов в этом случае удобно располагать так. Во-
первых, вычислить
Е—1 f——F г’пр 4-
у т
и ординаты распределения цели к моменту падения тоГ° залпа,
на основании наблюдения знака которого хотим вывеет)1 наивы-
годпейшуго поправку ВИР (табл- 69)-
Таблы!'0- 69
№ ординат LJ— PiE Pi
После этого вычисляем веро.1ТНОСТ1, ошибки ВИР п(*
*
__ Р г («о2
nt ]/7
по схеме, аналогичной табл. 69.
Величины Ем и пм берем в зависимости от вьРРанных
единиц.
Затем вычисляем вероятност’ недолета (или перелет1), зада-
ваясь величинами z, начиная ots = O (табл. 70).
ООО
Таблица 70
z = z'
£,• — z't Р, (из табл. 69) Р;Рк&~-г't)
- Pi=rPiFk^ — S't)
И, наконец, вычисляем кривую распределения ВИР по схеме
данной в табл. 71. ’
Таблица 71
№ ор- динат Гипотезы ио ошибке ВИР Qi по фор- муле (251') Pi из табл. 70 0Р; OP- <?2 (г) dz - v & 1р _
^QiPi
Табл. 70 придется вычислять столько раз, сколько раз при-
дется задаваться ошибками ВИР.
ГЛАВА X
СТРЕЛЬБА ПО ИЗМЕРЕННЫМ ОТКЛОНЕНИЯМ
61. Различные случаи стрельбы по измеренный
отклонениям и способы измерения отклонений
Стрельбой по измеренным отклонениям мы будем называть
такой метод стрельбы, при котором поправки вводятся на осно-
вании измерения интервалов точек падения относительно' цели
или какой-либо другой точки, координаты которой относительно
цели известны. В частности, при стрельбе по морским подвиж-
ным целям интервалы точек падения измеряются всегда отно-
сительно цели.
Прп стрельбе по измеренным дальностям для каждого залпа
мы всегда имеем измеренные координаты цели, и измерение
координат цели предшествует каждому залпу или серии зал-
пов. При стрельбе же по измеренным отклонениям координаты
цели могут оставаться и неизмеренными, а измеряются коор-
динаты точек падения относительно цели или отклонения, на
основании измерений которых вводятся корректуры непосред-
ственно в установку прицела.
Это составляет одно из отличий метода стрельбы по изме-
ренным отклонениям от метода стрельбы по измеренным даль-
ностям, при котором корректур в этом смысле нет.
Существует несколько способов измерения отклонений:
а) сопряженные наблюдения при помощи светометрических
пли звукометрических засечек различной системы и точности;
б) наблюдения с самолета, также различной системы и точ-
ности ;
в) измерения отклонений в дальности, как разности даль-
ностей до цели и до точек падений снарядов, специальными
дальномерами (картограф) и, в крайнем случае, простым сте-
реодальномером.
Сопряженное наблюдение при стрельбе по подвижной цели
возможно при условии (черт. 66) одновременной засечки с обоих
концов Ог и О2 базы В цели и точек падения. Технически это
может быть осуществлено различными способами. В частности,
можно одновременно измерять углы сц и а2. С аргументами:
разность (а2 — aL), угол q и величина базы В — можно иметь до-
224
статочно подробную таблицу, в которой найдем величину и
знак интервала падения от цели по
может быть применен только при
непосредственной корректировке по
цели.
Измерения отклонений всегда бу-
дут сопровождаться большими или
меньшими ошибками этих измере-
ний.
В теории этого метода стрельбы
рассматриваются два случая измере-
ний вполне точных и не вполне
точных.
Вообще говоря, вполне точных
I измерений в жизни не бывает, а по-
тому надо уточнить понятие „вполне
I точных измерений".
Под измерениями вполне точными
I следует понимать измерения такой
точности, когда при дальнейшем
. уменьшении срединной ошибки из-
мерения отклонений увеличение ма-
i тематического ожидания попадания
практически прекращается (таким
I же критерием можно считать и рас-
дальности. Такой прием
пределение цели).
В дальнейшем мы рассмотрим случаи вполне точных и не
вполне точных измерений.
62. Средняя дальность до цели при вполне точном
измерении отклонений по дальности и при ошибке
ВНР, равной нулю
Пусть при выстреле с прицелом (табличная дальность) Хо
(черт. 67) ио цели Ц снаряд вследствие рассеивания упал
в точку if, причем отклонение ал~ ЦМ измерено.
, На основании этого изме-
рения мы будем иметь таб-
М Г 1 личную дальность до цели:
— ='Yo+ «v (26°)
причем знак поправки мо-
Черт‘ Б7, жет быть как положительный,
так и отрицательный.
Если бы орудие не имело рассеивания, а устройство при-
цела позволяло принять поправку ах, какой бы дробной вели-
чиной она ни выражалась, то при прицеле средняя траек-
тория должна пройти через цель, поскольку измерения ошибок
не содержат.
15 Теория стрельбы 225
В действительности орудие имеет рассеивание, а тогда ве-
личина X, явится табличной дальностью до цели с некоторой
ошибкой х. Таким образом, здесь мы можем смотреть на пушку,
как на дальномер, дающий табличные дальности до цели с си-
стемой ошибок, характеризуемой срединным отклонением Вд.
Это обстоятельство не позволяет ограничиваться одним
выстрелом и для получения среднего значения прицела X
требует производства нескольких выстрелов.
Кроме того, мы и не сможем ввести поправки а1г так как
ни прицелов, ни приборов управления огнем, позволяющих
вводить любые поправки, не существует. Измеренное отклоне-
ние, переходя к поправке, придется округлить до наимень-
шего деления прицела. Если ближайшая кратная делениям
прицела величина поправки будет а\, то второй выстрел будет
произведен с прицелом
Хо + а'1-
Если при этом будет измерено отклонение а2, то мы полу-
чим вторую табличную дальность до цели:
Х2 = Х0-[-<1 х(261)
Произведя третий выстрел с прицелом Х2 = Хо 4- а\ -j- а'2,
мы получим по измерении отклонения а3 третью табличную
дальность до цели:
Xs = Хо +’ «г а'2 а3. (262)
При производстве т выстрелов мы получим т измерений.
Принимая, что наиболее подходящим значением истинного при-
цела будет средний результат из т измерений, найдем сред-
нюю величину из всех результатов измерений табличной даль-
ности до цели.
’ Выпишем все полученные табличные дальности и найдем
эту среднюю величину:
X j = Хо - - О]
A2 = X04-«i —я2
Х3 = Xg -р Cl'^ “J" Cl 2 --fljj
— Xq + ci! + ci' 2 + a'3 ~~ai
Am-i = X0-J-«'14-a'24-«,3+• • +
__________Xm==X0 + -J-a'2-p a s + . . . -j- am
m , m
L X«= m Xo 4- (in — 1) a\ 4- (m — 2) a'2 4- (m — 3) a'3 4- ...4- a’m _ 4- £
i i
откуда
(in — 1) a\ 4- (m — 2) a'„ 4- (m — 3) a'3 4-... 4-
m
a 'm - 1 4- E Щ
226
Полученное выражение преобразуем, для чего по раскрытии
скобок прибавим и вычтем величину a'm_j. Тогда
после чего это выражение получим в виде:
X = Хо + d' 1 Т и 2,"Т з 4~ я m__ 1 -j- -—- | (di — a j) -j- (щ — 2а 2) *Т
'1)1/ I
4 (^з — 3 а д) [Щп—1 — (от — 1) ® »> — 1 ] Ч- | ‘ (263)
Выражение (263) дает среднее значение для табличной даль-
ности до цели с ошибкой, которая характеризуется величи-
нои —= , но, как мы увидим дальше, срединная ошибка сред-
у т
него значения табличной дальности до цели не может быть
сделана сколь угодно малой с увеличением числа наблюдений т.
Выражение (263) используется в дальнейшем для вывода основ-
ных правил стрельбы по измеренным отклонениям.^
63. Вывод Основных правил для стрельбы
по измеренным отклонениям
Для вывода правил воспользуемся выражением (263).
Можно представить себе три варианта:
1) поправка вводится после каждого отдельного выстрела;
2) поправка вводится после т выстрелов, как средняя из
измеренных отклонений, если все т выстрелов даны на одном
прицеле, и
3) для первых к выстрелов поправки вводятся по каждому
выстрелу, затем дается группа выстрелов на одном прицеле,
после чего вводится одна поправка, причем общее число вы-
стрелов т.
При всех трех вариантах возможны два случая:
1) когда
= (264)
г
откуда
а,- — ia'i = 0, (265)
что равносильно предположению о возможности ввести по-
правку любой величины;
2) когда
, аъ
а\ Ф —
’ ' г
15* 227
и, следовательно,
а,- — ia'i ф О.
Рассмотрим сначала случай, когда имеет место равенство (264).
1. Поправка вводится после каждого выстрела.
В этом случае в (263) а\ =f= 0.
Тогда при существовании равенств (264) и (265) имеем:
аА—й'1=0; й2— 2й'2 = 0... Om-i — (я?— 1)ат_!=о, и сле-
довательно, (263) обращается в
X = Xq ф й j й 2 ф й 3 ф ... Ц- й т — 1 “ - (266)
*
В выражении (266) сумма Хй ф а\ -] й'2 ф й'3 -j- ... -ф а'т _ t
является той дальностью, при 1соторой сделан последний вы-
стрел, а величина:
= (267)
представляет ту поправку, которую на основании теории ве-
роятностей надо принять для следующего прицела.
Отсюда вытекает правило: вводя поправки после каждого
выстрела при стрельбе по измеренным отклонениям, величину
каждой поправки берут равную последнему отклонению, поде-
ленному на номер соответствующего выстрела.
2. Поправка вводится после очереди в т выстрелов.
Если поправки после каждого выстрела не вводятся и все
выстрелы даны на одном прицеле, то
a'i =0
и выражение (263) дает:
т
Е й»
Х=Х0 + 1------ (268)
и т
Отсюда вытекает правило: для получения поправки после
первых т выстрелов следует алгебраическую сумму всех изме-
ренных отклонений поделить на число выстрелов.
3. При к первых выстрелах вводятся поправки после каж-
дого выстрела, после чего вводится поправка сразу по (т — к)
последним выстрелам.
При этом й\^0; й'2^0... й\/ 0, а
й /£ + j = 0; й +2 = 0... й m _ 1 = О,
и тогда (263) дает:
X = Хо ф- (й\ -фй'2 ф ... Ф й'Л ф + . (269)
Отсюда вытекает правило: если при первых к выстрелах
поправка делается после каждого измерения отклонения, а потом
99R
желатегьно ввести поправку по (т — к) выстрелам, то для по-
лучения этой поправки надо алгебраическую сумму (т—к) от-
клонений, полученных при одном прицеле, поделить на номер
последнего выстрела.
84. Ошибки от округления команд
В предыдущем параграфе мы рассмотрели случаи, когда
имели место равенства (264) и (265), что равносильно принятию
возможности вводить какие угодно поправки, чего в действи-
тельности не бывает, и команды приходится округлять. Округ-
ление возможно до наименьшего деления прицела. Следова-
тельно, если
г / ^‘i г !
a if — или —-a i f О,
ъ z
то, применяя систематически выработанные правила, мы каждый
раз будем вводить ошибку от округления.
Рассмотрим случай наибольшей ошибки от округления.
Если обозначим через ДХ наименьшую поправку при назначе-
нии команд, то наибольшее значение разности будет
откуда получим
ДХ .
— га\ = —— г i (2 /О)
Чтобы получить наибольшую величину ошибки от округле-
ния, найдем разность между поправкой по (263) и (266):
Для того чтобы получить величину наибольшей ошибки от
округления, подставим в полученное выражение значения
(а<—га! i) из (270), тогда получим:
S°KP~~m] 2 1+ 2
2 + ..
ДХ |
2 |
(т — 1) т
2
Окончательно
д
-1 ОКр
(271)
229
65. Замечания о стрельбе по измеренным
отклонениям. Распределение цели по дальности
В настоящем параграфе рассмотрим на частных примерах
несколько вопросов, относящихся к пристрелке по измерен-
ным отклонениям. При т выстрелах точность результата изме-
рения будет характеризоваться срединной ошибкой
Е
Вд
Ут
(272)
Эта же величина будет характеризовать и распределение цели.
Допустим, что мы можем округлять команды до J/4 каб.
(25 саж.). Подсчитаем срединные ошибки распределения цели
для случая, когда корректировка вводится после каждого вы-
стрела, при = саж.
Ошибка от округления будет следовать закону равной ве-
роятности. Мы воспользуемся для сравнения приведенной сре-
динной ошибкой:
4 уз
Для распределения цели будем иметь:
Е = 1 I Д'2 .
У т
Для одного выстрела
Е, = (ш-1) Д^- 0,67 =о
4 -J/3
И
Ид
Е^= ____=30 саж.
У т
Для двух выстрелов
,,, (2—1) 25 • 0,67 „
Е — --------~— = 2,4 саж.;
4 • Уз
Продолжив вычисления для разного числа выстрелов, све-
дем результаты вычисления в табл. 72.
Из табл. 72 видно, что при вполне точных измерениях де-
лать более двух-трех выстрелов при корректировке каждого
выстрела не стоит; третий и четвертый выстрелы уточняют
цель мало, пятый вовсе не уточняет, а с шестого начинается
ухудшение за счет растущей ошибки от округления. Седьмой
230
Таблица 72
Ошибки от округления, в саженях
))1 Е' Е Примечания
1 0 30 1
2 . 2,4 21,3 Вд
3 4,8 18,0 Е' <
4 7,3 16,7 Vm
5 9,7 16,6
6 12,1 17,1 . Ни V т
7 14,6 18,4 ) Вд
8 16,9 19,9
9 19,3 21,7 } V т
4
выстрел дает то же, что и третий; восьмой — хуже третьего,
а девятый хуже второго выстрела.
Поэтому при вполне точных измерениях после одного-двух
выстрелов, с корректировкой каждого из них, пристрелку, если
она еще нужна, следует заканчивать очередью в несколько
выстрелов на одном прицеле.
66. Распределение цели по дальности при стрельбе
по измеренным отклонениям при не вполне точных
измерениях и при ошибке ВИР, равной нулю
Наличие ошибок в измерениях отклонений не вы зывает прин-
ципиальной разницы со случаем стрельбы по точно измеренным
отклонениям. Эти ошибки скажутся лишь в том, что ухуд-
шается распределение цели и расходуется несколько больше
Черт. 68.
снарядов в периоде пристрелки, а иногда (при больших ошиб-
ках) и в процессе поражения.
Положим, что при средней траектории, проходящей через
точку О, падение снаряда вследствие рассеивания получено
в точке II (черт. 68). Обозначим через х случайное отклоне-
ние ОМ от средней траектории и через а — измеренное откло-
нение МЦ, которое сопровождалось случайной ошибкой изме-
рения Д.
Рассеивание характеризуется срединным отклонением Вд то-
чек падения. Пусть срединная ошибка, характеризующая закон
231
случайных ошибок измерений, будет Z (предполагаем закон
Гаусса, а в случае наличия другого закона мы всегда можем
найти среднюю квадратическую ошибку и воспользоваться „при-
веденной“ срединной ошибкой). Тогда при одном выстреле
распределение цели будет характеризоваться величиной.
Е — У'Вд2+гг, (274)
а при т выстрелах получим
(275)
При этом надо иметь в виду, что если поправка вводится
несколько раз, то еще войдет ошибка от округления команд
по закону равной вероятности.
Рассмотрим тот же пример, т. е. найдем распределение цели
для случая корректировки после каждого отдельного выстрела,
но при наличии ошибок в измерении отклонений. Пусть Вд —
— 30 саж.; г =60 саж.; Вд = 15 саж.; r = 60 саж.
Для распределения цели в этом случае будем иметь:
W + t2 .рп
т + ’
(276)
где величина Е' останется та же по (273).
В данном примере мы будем иметь г = 2 Вд и г = 4 Вд.
Срединные ошибки распределения цели показаны в табл. 73.
Таблица 73
т Е' (ошибки от округления) Средние ошибки измерения
Вд = 30 саж.; г = 60 саж. ВО = 15 саж.; г = 60 саж.
в сажен Я X
1 0 67,1 61,8
2 2,4 47,6 43,8
3 4,8 39,1 36,1
4 7,3 34,2 32,0
5 9,7 31,5 29,3
6 12,1 29,9 27,9
7 14,5 29,2 27,5
8 16,9 29,1 27,5
9 19,3 29,5 28,2
В обоих случаях, когда мы имеем значительные ошибки
в измерении отклонений по сравнению с рассеиванием пушек,
видим, что ошибка от округления с увеличением числа команд
не приносит такого вреда, какой она имела при точном изме-
рении отклонений.
232
Более или менее заметное улучшение распределения рели
кончается на 3—4-м выстреле, а после 6-го выстрела распре-
деление цели практически не изменяется, причем с 9-го вы-
стрела начинается ухудшение распределения.
Таким образом, и в этом случае вводить корректировку
после каждого выстрела стоит только для двух-трех первых
выстрелов, после чего следует произвести очередь в 3—(>
выстрелов.
Здесь, кроме того, необходимо заметить (как для случая
вполне точного, так и не вполне точного измерения), что при-
держиваться правила деления среднего отклонения в очереди
на номер последнего выстрела можно только в том случае,
если измерения отклонений могут считаться для всех выстре-
лов равноточными, в противном случае надо или вводить отно-
сительную точность или вес измерений, или аннулировать
вовсе измерения малой точности при наличии измерений боль-
шой точности. Это вполне допустимо, так как с принятием во»
внимание относительных весов наблюдений при наличии наблю-
дений большой точности измерения с малым относительным,
весом на окончательном результате почти не сказываются.
Например, при первом выстреле измерено отклонение
+ 300 саж. После введения поправки в 3 каб. произведен второй
выстрел, который дал отклонение —70 саж.; после этого при
том же прицеле, при котором был произведен второй выстрел,
дали еще три выстрела и измерили отклонения: —40 саж.;
— 50 саж.; —80 саж.
Совершенно ясно, что при том же способе измерений веса
этих наблюдений не могут считаться равноценными, так как-
условия измерения отклонений первого и остальных выстре-
лов совершенно неодинаковы.
Так, если веса последних четырех измерений порознь,
равны 1, а первого измерения 0,2, то при принятии во внимание
всех выстрелов с учетом относительных весов получим:
+ 70-f-40-f-50-}-80 _ 240
4 -J-1~0,2 ~ 4,2
4-57 саж. = 1/, каб.
Если вовсе откинуть первый выстрел, то получим:
240
—— =60 саж. = 1/2 каб. (разница на 3 саж.).
Вследствие неудобства учета относительных весов в про-
цессе стрельбы обычно выстрелы (первые 1—2 выстрела), про-
изведенные не в одинаковых условиях с остальными, просто*
аннулируются.
Кроме того, следует иметь в виду, что введение поправок
после каждого выстрела замедляет пристрелку и требует боль-
шого числа команд, в чем и состоит большое неудобство при-
стреливаться одиночными выстрелами.
233
Нормально как при точных, так и при неточных измерениях
пристрелка ведется так: дается очередь в 1—2 выстрела и
вводится поправка, равная алгебраической сумме измеренных
•отклонений, поделенной на номер последнего выстрела в оче-
реди. После этого дается вторая очередь в 3—4 выстрела
и вводится поправка, равная алгебраической сумме измеренных
при второй очереди отклонений, поделенная на номер послед-
него выстрела во второй очереди.
После этого дается третья очередь; если измерения откло-
нений и введение поправки еще возможны, то вводится по-
правка, равная алгебраической сумме отклонений в третьей
очереди, поделенная на число выстрелов второй и третьей
очередей.
Следует иметь в виду, что условия стрельбы могут меняться,
вследствие чего измерения отклонений предыдущих выстрелов
могут быть менее точны, чем последующих, именно из-за изме-
нения условий стрельбы; поэтому деление отклонений на номер
последнего выстрела должно применяться даже при одинако-
вой точности измерения только в том случае, когда все при-
нимаемые во внимание выстрелы произведены в такой короткий
промежуток времени, что условия стрельбы можно считать не
изменившимися. Последнее замечание относится как к точным,
так и к неточным измерениям отклонений.
67. Распределение цели на плоскости
Распределение цели на плоскости мы будем иметь в тех
случаях, когда приходится отдельно измерять отклонения по
дальности и в боковом направлении, или при сопряженных
наблюдениях, когда, оба или одно из направлений наблюдений
не совпадает с плоскостью стрельбы. В последнем случае мо-
гут иметь место две или несколько эллиптических ошибок. Во
всяком случае все эллиптические ошибки должны быть вы-
явлены, чтобы в результате их сложения получить распреде-
ление цели.
Пример 1. Отклонения в дальности определяются в плоскости
стрельбы с картометром при базе - 8 м; а— 5"; увеличение — 28;
дальность — 30 каб.; Вд = 20 саж.; Вб=3 саж. Боковые откло-
нения определяются с помощью стереотрубы при срединной
-ошибке 0,2 дел. При этих условиях 6] = 1,8 саж. и53 = 1,8 саж.
Срединная ошибка измерения по дальности 5 У 2 =1,8 • 1,4 =
= 2,5 саж. Срединная ошибка измерения в боковом направле-
нии 0,6 саж.
Так как полуоси обеих ошибок совпадают, то имеем:
а = р/2,52-|-202 = 20,2 саж.,
& = Уо,62-р 32 = 3,1 саж.
В результате имеем эллиптическую ошибку распределе-
ния цели:
е (20,2; 3,1; 0°).
234
Такая эллиптическая ошибка будет для одного пристрелоч-
ного выстрела. При группе в т выстрелов будем иметь эллип-
тическую ошибку
s ; -^L; 0°^) •
\Ут Ут /
В решенном примере предполагается точное знание коор-
динат цели, в противном случае прибавится еще эллиптиче-
ская ошибка в положении цели.
Пример 2. Пристрелка по графику (импровизированный план-
шет), Вд= 30 саж. и 5б = 3 саж. Угол между линиями наблюде-
ния— 35°; расстояние до цели: от левого наблюдателя — 6 240 м
и от правого наблюдателя 5 350 м. Плоскость стрельбы прохо-
дит под углом в 20° к линии наблюдения правого наблюдателя.
Наблюдения ведутся при помощи стереотруб. Срединная ошибка:
визирования цели — 0,5 дел. и визирования разрывов—1 дел.
Найдем распределение цели после очереди из четырех вы-
стрелов, данных по цели после пристрелки направления и мас-
штабов для графика.
При производстве только одного выстрела на концах век-
тора отклонения мы имели бы эллиптические ошибки с сопря-
женными полуосями:
а) на конце вектора у цели
(ч,_d2 Д ___5 350 • 0,0005
01 sin©
——-------= 4,65
0,576
,« = 2,54 саж.;
tZ, А Р 6 240 • 0,0005
sin© 0,576
— 5,42 ,« = 2,96 саж.,
где — расстояние между левым наблюдателем и целью и
d2 — расстояние между правым наблюдателем и целью;
б) на конце вектора у разрыва
с2
5 350 • 0,001
0,576
9,3 ж = 5,08 саж.;
6 240 • 0,001
0,576 ~
= 10,84
М = 5,93
саж.
Вследствие того, что разрыв после пристрелки направления
и масштаба получается в непосредственной близости от цели,
можно принять
а/ // в/' и а/ // ал
Тогда на конце вектора у цели будем иметь суммарную
эллиптическую ошибку с сопряженными полуосями:
8t = /2,52 + 5,082 = 5,7 саж. и о2 = V2,962 + 5,9s5 = 6,63 саж.
Ошибка будет направлена на 55° правее плоскости
стрельбы, ошибка будет направлена на 20° правее плоскости
стрельбы (черт. 69).
235
Кроме того, будем иметь эллиптическую ошибку рассеива-
ния орудия с полуосями Вд = 30 саж. в плоскости стрельбы и
Вб=3 саж. в перпендикулярной к ней плоскости.
Начало осей координат возьмем у цели и направим ось Хов
в плоскости стрельбы.
Произведя сложение векториальных ошибок, получим рас-
пределение цели на плоскости:
е4 (30,7 саж.; 3,8 саж.; большая ось на 6°55' правее пло-
скости стрельбы).
Учитывая же, что сделан не один выстрел, а четыре и что
поправки для перехода на поражение выведены как среднее
из четырех отклонений, показанных наблюдателями, будем
иметь распределение цели:
или
е4 (15,4 Саж.; 1,9 саж.).
Огонь следует открывать в центр распределения, но произ-
ведя еще контроль из четырех выстрелов, тогда получим:
s'e (5,5 саж.; 0,67 саж.).
При этом будем иметь наибольшую величину ошибки от
округления
Л т —1
^окр - ,
вызывающей отклонения: по дальности— •—= т/1£ каб. и
4 4
в боковом направлении 1/4 деления, что отвечает
236
при дальности 20 каб. отклонению т/2 саж.
» 77 40 „ 1 77
« 60 „ 1,5 77
М 77 80 П 2 77
Эти величины отвечают наибольшим отклонениям, вызывае-
мым ошибками от округления, и потому можно сказать, что
после второго контроля, по всей вероятности, будет возможно
вести стрельбу на одном прицеле и на одном направлении.
68. Стрельба по ненаблюдаемым неподвижным целям.
Общие положения
При стрельбе по неподвижным целям, когда в силу той или
мной обстановки корректировка огня непосредственно по цели
невыполнима, применяются, как известно, различные методы
стрельбы.
При наличии полной подготовки стрельбы мыслится воз-
можность открывать огонь просто по расчету, без всякого уточ-
нения положения цели пристрелкой, но при этом ошибки могут
оказаться настолько большими, что потребуются обстрел зна-
чительной площади и весьма значительный расход боевого
запаса, вследствие чего такой прием стрельбы без крайней
к тому надобности обычно избегают применять.
Второй прием заключается в пристрелке репера (вспомога-
тельной цели) с переносом огня на цель. При этом могут быть
такие случаи:
1) перенос огня ничем не ограничен, т. е. репер далеко от
цели и перенос следует не тотчас за пристрелкой репера,
а может быть отдален почти на все время обновления бюлле-
.теня АМП;
2) перенос, не ограниченный геометрически, происходит сейчас
же вслед за пристрелкой;
3) перенос ограничен геометрическим положением репера
относительно цели (репер недалеко от цели) и может быть
отдален по времени почти на все время обновления бюллетеня;
1) перенос ограничен геометрическим положением репера
относительно цели и происходит сейчас же после пристрелки.
Реперы, кагс известно, могут быть действительные, т. е.
какие-либо реальные предметы, и фиктивные, т. е. воздушные
или наземные точки, выбранные возможно ближе к цели.
Во всех случаях при этом виде стрельбы правила сводятся
к определению площади, подлежащей обстрелу, и к расчету
расхода снарядов, необходимых для решения поставленной
огневой задачи; для указания цели надо выявить ошибки и
найти распределение цели на плоскости, которое получится
в результате пристрелки репера и переноса огня на цель.
Из способов переноса огня от репера на цель остановимся
только на двух:
237
а) на простейшем способе, когда принимают, что разность
прицелов до репера и до цели равна разности дальностей или
11ц lip —— Рц ' Dp ,
откуда
11ц — hp ~Ь (D4 ~ Dp ), (277)
и б) на способе коэфициента К, когда принимают, что при-
целы изменяются пропорционально дальностям, или
"ч ___ | т
hp Dp — ’
откуда
Ьц = Кйр. (278)
Пределы применения этих способов определяются так:
а) простейший способ — репер в непосредственной близости
от цели и разность дальностей не более 5—10% меньшей из
них, а угол переноса—не более 300 делений;
б) способ коэфициента К — пределы применения опреде-
ляются неравенством
3 Рр 4
4 Рц 3 ’
что в большинстве случаев отвечает разнице между дально-
стями не более 30% меньшей из них; угол переноса —не более
300 делений.
Не касаясь в настоящем курсе техники производства
стрельбы, исследуем два рода ошибок, которые при этом будут
иметь место, а именно: геометрические или топографические
ошибки переноса и балистические и аэрологические ошибки,
в результате чего мы будем иметь эллиптическое распределение
цели и на основании исследования математического ожидания
и вероятности попадания сможем указать наиболее рациональ-
ный и выгодный путь решения данной огневой задачи.
69. Ошибки при стрельбе по ненаблюдаемой пели
без пристрелки
В этом случае будут иметь место топографические ошибки
в положении цели и ошибки в положении стреляющей бата-
реи (корабля) Пусть в Ц находится цель и в Б—батарея
(корабль, стоящий неподвижно) (черт. 70). В общем случае
ошибки будут эллиптические еч (а2; b2; aj и («2; Ь2; р2), где
ai и ₽i — углы относительно линии БЦ.
В этом случае геометрические ошибки определяются сле-
дующим образом. Мы будем иметь два отклонения, вызываемые
эллиптическими ошибками по дальности:
(?!=]/«j2 cos2 aj -|- Ьг2 sin2
238
и
d3 — |/ а22 cos2 pj + Ь22 sin2 р2,
и два отклонения, вызываемые эллиптическими ошибками
в направлении, перпендикулярном дальности:
d2 — У аг2 COS2 а2 4- V sin2 а2,
dt = y a2 cos2 р2 4- &22 sin2 р2.
Если при этом приходится пользоваться вспомогательной
точкой наводки Т (черт. 70), то скажется еще и ошибка в поло-
жении этой точки, причем эта ошиб-
ка будет иметь значение только в на-
правлении, перпендикулярном к даль-
ности.
Найдя величину rf'r и значение
Да из
по Да найдем величину йс, направле-
ние которой будет перпендикулярно
к дальности.
Тогда будем иметь геометрические
ошибки в дальности:
(1х = У^ + й-А
и в боковом направлении:
dz = yd.2 4-d^ + d-2 .
Имея в виду, что стрельба ведет-
ся без пристрелки, кроме этих оши-
бок, войдут еще ошибки балисти-
ческой и метеорологической подго-
товки. При принятых ранее обозна-
чениях имеем по дальности:
Черт. 70.
23 Ь-
н в боковом направлении:
ds \
дм)
где Е„, Et, Еп и Ew—срединные огДибки в v0, в t пороха, в плот-
ности воздуха, в скорости и направлении ветра.
Тогда окончательно будем иметР п0 направлению дальности.
а = У df + rf32 + ДХ„2 + Д А7 + А Ад2 + (270)
я по направлению, перпендикулярному к дальности.
Ъ = У d2 -[- dt + (к2 + J280)
Примечание. Если огонь открывается со
зданием после получения бюллетеня АМП, то необ» А У
ошибку за счет изменения ветра и ппотности воздуха-
70. Ошибки при стрельбе 0° ненаблюдаемой цели
с пристрелкой по действительному РеггеРУ>
значительно удаленному от цели
(1>олее 500 м ил!1 23/* 1;яб.)
При наличии пристрелки по реперу ошибкой в положении
«стреляющей батареи по дальности можно пренебречь, но есл
-эта ошибка велика, то она сыграет заметную роль в направлении-
При стрельбе корабельной артиллерии ошибка в положени
корабля будет значительно болыпЩ нем ошибка в определени
места сухопутной батареи, и не считаться с (ипиокои в поле
жении батареи в этом случае нельзя- „ ..
Пусть Б — место стреляющей батареи, Ц — щ'ль и к репе!
<черт. 71). После пристрелки при переносе ог?я на цель во.
никнут следующие геометрический ошибки переноса огня.
Если гв и е/?—эллиптические ошибки в положении батаре
и репера, то, найдя отклонения, вызываемые этими эллиптиче
скими ошибками в направлении, перпендикулярном к Kt,
получим на обоих концах вектора КБ боковые отклонения аБ
dn, которые и явятся ошибками концов вектора, как не связав
яые зависимостями в эллипсах. х .
В силу этих ошибок вектор* BR на местности будет занимат
зге то положение, которое он занимает на карте.
Сложив обе эти ошибки в одну
d= У&Г+ > (281)
мы всегда можем отнести ошибку к любому из концов веУ
тора БН.
Из черт. 71 имеем:
пристрелянную даль-
Черт. 71.
Величина угла Д£ при достаточной тщательности подготовки
не должна быть велика. При небольшой величине Др этот угол
приближенно, но с достаточной практически точностью может
быть принят за срединную ошибку в направлении вектора БЕ.
Для переноса огня на цель мы имеем:
ность до репера и снятые с карты даль-
ности до цели и угол переноса р.
Для удобства вывода ошибки при пе-
реносе огня примем пристрелянную даль-
ность до репера R и снятые с карты век-
тор переноса ЕЦ и угол ₽.
В действительности на местности мо-
жет оказаться угол больше или меньше
р, причем закон ошибок будет характери-
зоваться срединной ошибкой Др.
При этом огонь может быть направ-
лен не в Ц, а в какую-либо точку на ли-
нии Д1Д2. Закон этих ошибок будет ха-
рактеризоваться векториальной ошибкой
Е? , где
Е? = ВЦ • • -|- =
RH
’ (28“}
Направление этой ошибки, как видно
из чертежа, перпендикулярно к вектору
переноса ЕЦ. С направлением ЕЕ направ-
ление Е$ составит угол Р — 90°, а с на-
правлением дальности до цели БД--угол
[р 4-(Р — 90°)].
Кроме этих ошибок, мы будем иметь
ошибку пристрелки в зависимости от спо-
соба пристрелки и ее тщательности.
Окончательно будем иметь ошибку по-
сле переноса огня:
бс — £ц + + Ер , (283)
где гц — ошибки в положении цели на
конце вектора ЕЦ.
Суммирование ошибок в (283) надо понимать символически.
Исходя из того соображения, что пристрелка производится
по реперу, мы должны ожидать при переносе огня на цель
возникновения балистических и аэрологических ошибок, по-
скольку направление и расстояние до цели другие, но, конечно,
не в той мере, как это имело место при стрельбе вовсе без
пристрелки. Эти ошибки для случаев, когда имеет место при-
стрелка по реперу, рассмотрим отдельно.
16 Теория стрельбы
241
71. Ошибки при стрельбе по ненаблюдаемой цели
с пристрелкой по действительному реперу,
находящемуся в непосредственной близости отдели
При близком положении репера от цели (не более 500 м или
23/4 каб.) обе точки могут попасть на один фотоснимок или
могут быть засечены с одних и тех же пунктов. В этом слу-
чае'ошибки ец и будут зависимы между собой.
Если ошибка в векторе RR (черт. 71) мала, то мы будем
иметь равенство:
£ “ф £ пристр> (284)
где е — ошибка в векторе ЕЦ.
Если R и Ц получены с одного фотоснимка, то е можно
считать круговой ошибкой г = 10 м при масштабе карты не
мельче 1/25 000.
В тех случаях, когда репер и цель не попадают на один
фотоснимок, лучше пользоваться формулой (283) § 70.
72. Ошибки при стрельбе по ненаблюдаемой цели
с пристрелкой по фиктивному реперу
Фиктивный репер может быть воздушный и наземный.
Стрельба при фиктивном репере имеет ту особенность, что
ошибки в положении батареи (стреляющего корабля) значения
не имеют, так как будут полностью учтены пристрелкой, сам
по себе фиктивный репер ошибки также содержать не может,
но зато скажутся ошибки постов наблюдателей и ошибки при-
боров (ошибки в углах).
Воздушный или наземный фиктивный репер выбирается по
карте (по планшету). Иногда воздушный репер выбирается над
целью, но предпочтительнее выбирать его в стороне от цели
в какой-либо точке, нанесенной на карту; но так как в действи-
тельности цель может оказаться не в этой точке, то войдут
еще ошибки в положении цели, характеризуемые эллиптиче-
ской ошибкой еч.
Пусть в точках Нл и Нп места левого и правого наблюда-
телей (черт. 72), ел и г„ — эллиптические ошибки, характери-
зующие случайные ошибки в местах положения наблюдателей.
Если НпА — случайная ошибка в положении правого наблю-
дателя, то, найдя отклонение, вызываемое эллиптической
ошибкой е„ от направления НпЦ, по этому направлению
можем рассматривать отдельно ошибки Нп С и СА.
Ошибка НпС вызовет ошибку по дальности, которая будет
выбрана пристрелкой, ошибка же СА скажется в том, что при
верном угле а правый наблюдатель будет искать репер в направ-
лении Нп Ц совершенно так же, как будто вследствие ошибки
визирования была ошибка у цели////.
Срединная ошибка, характеризующая закон таких случай-
ных ошибок, будет равна dn —отклонению, вызываемому эллип-
242
тической ошибкой еп в направлении, перпендикулярном
Проведя касательную к еп параллельнр НпЦ, точкой пересе-
чения этой касательной с Нл Ц определим ошибку у цели 8„,
вызванную отклонением dn. Ошиб-
ка имеет направление по ЦНЛ .
Величина определится из:
Jn~ sin 6
(285')
Рассуждая аналогично в от-
ношении ошибки в положении
только левого наблюдателя, по-
лучим:
Черт. 72.
? __ (1Л
л~ sinT
(285")
Обе эти векториальные ошиб-
ки и 8Л сложатся с ошиб-
кой .
Неповторяющимися ошибка-
ми здесь явятся эллиптическая
ошибка приборов епр и эллип-
тическая ошибка рассеивания
ер с полуосями Вд и Въ, кото-
рые будут изменяться при за-
сечке каждого выстрела, а по-
тому при т выстрелах поде-
лятся на Ут.
Окончательно будем иметь:
(286)
--еЦ
Пример. Положение цели,
наблюдателей и направление
стрельбы показаны на черт. 73.
ец (17,17); Вд — 55 м; Вб=5 м;
еи (10,10); ел (10,10).
Срединная ошибка визиро-
вания др = о,ОО1. Пристрелка по
шести разрывам.
Для ошибки приборов имеем:
s, _ 4000 • Др _4000 • 0,001 _ . О7
О пр С\ г-Л»-» О К ° --- V, U 4 М у
sin 6 sin 35
ЗбОО^ЩОЩ
р sin 35
16*
243
; —; — а«
” ' sin О
10
sin 35°
= 17,4 м;
*пр У т 6,97 = —=- = 2,8 м; Уч
0 Пр У т 6,10 = - ---= = 2,5 м; Гб
2^ ф HI =~7==22,4 л; Гб
Вб_ У т = -^= = 2,0 м. Уч
Выбрав направление оси А-ов в направлении дальности
стрельбы, получим следующую систему ошибок:
22,4 М 0°
17,0 „ 0°
2,0 „ 90°
17,0 „ 90°
17,4 „ 105°
17,4 „ 140°
2,8 „ 320°
2,5 ,. 285°
(счет углов от положительного направ-
ления оси Аг-ов против часовой стрелки).
В результате сложения этой системы
ошибок получим эллиптическое распре-
деление цели с полуосями:
а = 33,5 м = 18,3 саж.
5 = 24,1 „ = 13,2 „
При этом большая ось направлена под углом — 29°16
к направлению дальности.
Фиктивный наземный репер следует выбирать в непосред-
ственной близости от цели, причем система ошибок остается
совершенно та же, что и при воздушном репере.
Если фиктивный репер по причине невозможности или труд-
ности наблюдать разрывы в непосредственной близости от цели
пришлось выбрать в удалении от цели, к разобранной системе
ошибок присоединяются ошибки учета изменения аэрологиче-
ских условий.
244
73. Балистические и аэрологические ошибки при
переносе огня от репера на цель
Балистические и аэрологические ошибки появятся при пере-
носе огня на цель и от пристрелянного репера, но в значи-
тельно меньшей мере, чем в случае стрельбы вовсе без при-
стрелки.
Перенос огня по способу „коэфициента всегда происхо-
дит при ограничении, при котором можно допустить, что при-
целы пропорциональны дальностям. Поэтому и рассмотрим
только случай ограниченного переноса.
Прицел по цели рассчитывается, исходя из допущения про-
порциональности поправок дальностям, обычно по формуле:
h и
Пц
Dr
Iir .
Для учета балистических ошибок (Дг0 и М) и ошибок в плот-
ности воздуха необходимо иметь или задаться наибольшими
значениями параметров отступлений (или избранными их зна-
чениями в зависимости от целей исследования).
Затем, задавшись условиями ограничения, т. е. максималь-
ным значением надо рассчитать для выбранных парамет-
Dr
ров численные значения поправок для дальности репера. Умне-
ем
жив эти поправки на отношение -угЦ получим поправки на
Ur
дальности до цели при допущзнии пропорциональности измене-
ния поправки.
Затем рассчитываем действительные величины поправок до
цели. Разности между рассчитанными поправками до цели и
поправками, полученными от умножения рассчитанных попра-
вок до репера на отношение •—-, дадут численные значения
Ur
ошибок от допущения, что поправки изменяются пропорцио-
нально дальностям.
Алгебраическую сумму этих поправок можно признать за
предел ошибок, следующих закону равной вероятности, и полу-
чить отсюда приведенную срединную ошибку.
Кроме этой ошибки, войдет ошибка от принятия постоян-
ства направления ветра для пристрелки по реперу и для
стрельбы по цели.
Пусть в точке Б—стреляющий корабль (батарея), в Б —
репер и в Ц — цель (черт. 74). Угол переноса у и дальности
Dr и иц подчинены тому пли иному ограничению; w—вектор
скорости ветра, который примем идущим под углом 90° к даль-
ности Dr , так как в этом случае ошибка от допущения
постоянства ветра будет наибольшая.
Из черт. 74 имеем:
(и.’ж ф = w • sin y, (287)
245
откуда получим значение lWx и затем приведенную срединную
ошибку:
^'. = 0,67-^.
(288)
Некоторые считают, что способ „коэфициента А'“ должен
быть переделан так, чтобы он применялся при полной подго-
товке стрельбы.
В этом случае способ „коэфициента А“ приобретет большую
громоздкость и потребует много времени на открытие огня по
цели по сравнению с настоящим приемом применения этого
способа. Но, имея в виду возможность такой переделки спо-
соба „коэфициента К'1, рассмотрим систему ошибок балистиче-
ской и метеорологической подготовок в при-
менении способа „коэфициента А“ при полной
подготовке.
Пусть прицел, рассчитанный на основа-
нии полной подготовки, по реперу — Нр и по
цели — Нц; прицел по реперу, полученный
пристрелкой,—hp, а неизвестный прицел по
цели — 11ц.
Допуская пропорциональность прицелов,
исчисленных при подготовке и полученных
пристрелкой, будем иметь:
Черт. 74.
откуда
— ф- • hp = Khp . (289')
-tip
В этом случае коэфициент К будет относиться только
к ошибкам подготовки и будет иметь своей целью возможный
учет этих ошибок.
Срединная ошибка балистической и метеорологической под-
готовки в этом случае может быть написана:
по дальности
Ех = + (ДХ,)\ + (Д1УП)\ +№)% <290)
и в боковом направлении:
+ (SZj\. (29 L)
Значения ДХ, входящие в правую часть равенства (290),
будут:
246
/дх \
\ /„
^ = 7дхГ^
и
(*хв\=
Примечание. Эллиптическая ошибка пристрелки учтена при
разборе геометрических ошибок переноса; эти же ошибки являются
ошибками только за счет переноса огня.
Имея в виду полную подготовку, мы при переносе огня от
репера на цель учтем не только угол переноса, но и измене-
ние балистического ветра, а следовательно,
/ \
/ дх VI ,
I I I
I ()lVz /J г
(292)
Очевидно, что в этом случае величины Ех и Ег будут зна-
чительно меньше, чем при применении этого способа без пол-
ной подготовки.
Срединная ошибка Ех будет лежать в направлении дально-
сти стрельбы, а срединная ошибка Ег —в направлении, перпен-
дикулярном к этой дальности.
74. Особенность учета ошибок и счета времени при
стрельбе с корабля на ходу по неподвижным берего-
вым целям (без вспомогательной точки наводки)1
Особенность учета ошибок, связанных с временем при
стрельбе на ходу, вытекает из того, что ошибка в положении
цели от времени не зависит, так как цель неподвижна, а ошиб-
ка в положении корабля будет накопляться во времени из-за
ошибок в скорости и курсе.
Вследствие неподвижности цели в относительном положе-
нии траектории и цели с момента производства залпа
(выстрела) ничего меняться не будет, а в положении стреляю-
1 В случае наводки по вспомогательной точке войдет эллиптическая
ошибка в положении этой точки.
247
щего корабля накопится ошибка к моменту производства
следующего залпа (выстрела).
Пусть к} (черт. 75) — место корабля в момент производства
залпа. Если цель наблюдаема, то для характеристики ошибок
в положении цели мы должны будем учесть срединную ошибку
пристрелки, а точку кл можем рассматривать, как не содержа-
щую ошибок, поскольку цель неподвижна.
Через некоторое время t к моменту производства следую-
щего залпа (выстрела) корабль придет в точку к2. Если
в точке A"i пристрелка закопчена, то в точке к2 и нескольких
последующих точках будет произведено по цели несколько зал-
пов на поражение без корректировки каждого из них, и эти
точки, подобно точке к2, будут содержать ошибки. Например,
при прямом курсе мы будем иметь эллиптическую ошибку &к
с полуосями kvt по направлению
/Ц вектора vt и vt Lq—AiG направлению,
перпендикулярному к кАк2, где
// bv и — срединные ошибки в
•< z^~7/ скорости и курсе. Эта ошибка
-S'"' // сложится с ошибкой пристрелки
/ / е„р, в результате чего будем иметь
/ / эллиптическое распределение цели:
/ / / e = enp4-efc (293)
/ KSit
/ъ S , (суммирование надо понимать сим-
/^>^4 волически).
Здесь необходимо оговорить,
что имеют место следующие до-
Черт< 75, пуски: во-первых, ошибки bvt и
vtbq нельзя считать независимы-
ми и, во-вторых, ошибка vt^q не следует закону Гаусса,
а мы ее приняли следующей закону Гаусса вследствие малой
величины vtAq по сравнению с вектором перемещения vt.
В тех случаях, когда стрельба на ходу производится по
ненаблюдаемым целям с пристрелкой по действительному репе-
ру и с переносом огня на цель, мы будем иметь ту же систему
ошибок, которая рассмотрена для случая стрельбы с непод-
вижного корабля (§ 70—73), но ошибки в положении стреляю-
щего корабля должны учитываться на основании изложенного
в настоящем параграфе при отнесении начала счета времени
к моментам производства залпов (выстрелов), а не к моментам
падений. В случае ненаблюдаемой цели ни одна из точек поло-
жения корабля не может считаться не содержащей ошибок, но
будет иметь место двоякая система ошибок: ошибки в опреде-
лении места корабЛя, которые будут зависеть от способов
определения места корабля, и ошибки счисления, накопляю-
щиеся во времени от момента определения места до момента
производства залпа (выстрела).
248
75. Стрельба по измеренным отклонениям
по подвижной цели (при наличии ошибки в ВИР)
Если стрельба по измеренным отклонениям производится по-
подвижной цели при наличии ошибок в ВИР, то по сравнению
со стрельбой по измеренным дальностям прибавится еще то об-
стоятельство, что измеренное отклонение падения от цели будет
заключать не только балистические и аэрологические ошибки,
из и накопившуюся ошибку в перемещении вследствие ошибки
в ВИР.
Следует различать два случая: 1) когда поправка вводится
после каждого выстрела (залпа) и 2) когда поправка вводится
после группы выстрелов, данных на одном прицеле с уче-
том ВИР.
Если поправка ввод itch по зле каждого выстрела, то ошибка
в ВИР будет накопляться за промежуток времени, протекаю-
щий от момента измерения отклонения до момента следующего
падения. В этом случае распределение цели к моменту паде-
ния будущего залпа (выстрела) вслед за измерением отклоне-
ния будет характеризоваться срединной ошибкой
E = + Е' + пЧ2 , (294)
где
п — срединная ошибка ВИР,
Z — время, равное времени полета Т плюс работное время т.
Срединная ошибка измерения отклонения для случая
стрельбы с корабля, когда отклонение может измеряться только-
как рапюсть дальностей до падения и до цели, выразится:
где о — срединная ошибка стереодальномера или картографа и
ш— число равноточных дальномеров.
Выражение (294) примет несколько иной вид, если, напри-
мер, после измерения отклонения и введения поправки дадим
очередь на одном прицеле с учетом ВИР и при этом будут
измерены отклонения каждого падения и введена поправка на
основании всех измерений.
Пусть при выстреле с прицелом h1 в точку (\ получено
падение в УД и измерен интервал ал до цели в точке Ц,
(черт. 76).
Затем с прицелом h1-[-al с учетом ВИР произведены три
выстрела, при этом первое в очереди падение произойдет через
промежуток времени t = Т + т.
При ошибке в ВИР, равной нулю, средние траектории от
линии ЦЛ\ прошли бы в одинаковом расстоянии.
При ошибке в ВИР, равной г и сохраняющей некоторое
время свое значение, через промежуток времени t расстояние
249’
между целью и средней траекторией будет О2Ц2, при этом
в измеренное отклонение М2Ц2 войдет ошибка в учете переме-
щения, равная zt. В момент второго измерения в величину М3Ц3
войдет ошибка в учете перемещения, равная z (Y + т2), где т2 —
промежуток между выстрелами (залпами). В момент третьего
измерения в измеренное отклонение войдет ошибка пере-
мещения, равная z (t + 2 т2).
При выводе средней поправки, если не будем учитывать
первого выстрела (залпа), как могущего быть данным при дру-
Черт. 76.
лих условиях, будем иметь ошибку в перемещении к моменту
падения будущего залпа, равную
Zt-^ z{t + ^ + z(t± 2т,)_
3 — П + ‘2)>
т. е. будет учтена ошибка в перемещении, имевшая место при
втором падении в очереди из трех выстрелов, что ясно видно
из черт. 76, где отклонение средней траектории О\ равно
+ Величина Д представляет ошибку от рассеивания,
а г(£-|-’т2) — накопившуюся ошибку ВИР.
Рассуждая аналогично, для очереди в четыре выстрела полу-
чим ошибку в перемещении к моменту падения будущего залпа,
равную той ошибке в перемещении, которая накопится к сред-
нему моменту в очереди, т. е.
^ + г(^ + т2) + г(^-|-2т2) + й!(^ + Зт2)__ , л „
— Z(i ~г 1,э
Вообще говоря, ошибка в перемещении, накопляющаяся к
моменту падения залпа после очереди, на основании которой
250
вводится поправка, будет равна той ошибке в перемещении, кото-
рая накопляется к среднему моменту в очереди выстрелов, дан-
ных на одном прицепе с учетом ВИР.
Величина накопившейся ошибки в ВИР при к выстрелах
будет равна: при к нечетном
z [t -J- (к — 2) t2]
и при к четном
г|7 + (к —2,5) т,].
Обозначая срединную ошибку ВИР через п, к моменту паде-
ния поражающего залпа будем иметь следующее распределе-
ние цели:
1/ ---Г---l-n’ft -Ь (Л — 2)т,р + £'2 (296)
* К
или
Лвэч-Т®
Е=Д/ --------+ п*[* + (*-2,5)(296')
" К
где все обозначения те же.
Если величинами (к— 2)~2 и (к — 2,5) т2 вследствие малой
величины т, можно будет пренебречь, то вместо выражений
(296) и (296') будем иметь выражение (294).
76. Стрельба но измеренным отклонениям
по подвижной цели прп сопряженных наблюдениях
Черт. 77.
Стрельба по измеренным отклонениям при сопряженных
наблюдениях возможна для береговых батарей, имеющих на
вооружении горизонтально-базные дально-
меры. При этом система дальномера долж-
на давать возможность производства од-
новременной засечки цели и падения с
трансформацией измеренного вектора от-
клонения на направление дальности
стрельбы и на направление, ему перпен-
дикулярное.
Положим, что падение снаряда про-
изошло в точке М в тот момент, когда
цель находилась в точке Ц (черт. 77),
причем обе точки одновременно засечены
дальномерами.
Вектор ЦМ можно автоматически раз-
ложить на ДХ по направлению ВЦ и на
ДУ—по направлению, перпендикулярно-
му к ВЦ.
Если при этом имеет место прямая
визуальная наводка и боковые отклонения
непосредственно, то система ошибок ничем
корректируются
не будет отли-
251
чаться от (296) и (296'), за исключением величины г, кото,мое
в данном случае следует получить как отклонение, вызывас
эллиптической ошибкой по направлению ВЦ.
В этом случае будут иметь место Две эллиптические ошис ди_
у точки Ц — £ц и у точки М—ем, причем ввиду малой в
чины вектора ЦП можно принять г,(.—£.«; тогда на конце ц
тора ЦМ можно считать эллиптическую ошибку
^пристр —- ец 4“ ’ гттгт
Найдя величину отклонения, вызываемого суммарной эл<,!вив
тической ошибкой по направлению дальности ВЦ, и подста^^
эту величину в (296) или (296') § 75, получим распределе
цели по дальности к моменту падения следующего залпа.
Черт. 78.
В том случае, если мы не имеем визуальной прямой наво/
и непосредственного наблюдения боковых отклонении, д у15' т
руководствоваться измеренными отклонениями и в наире в.Лу м
дальности и в боковом направлении. В этом случае мы У, _
иметь распределение цели на плоскости, совершенно анало
ное случаю стрельбы по измеренном дальностям, но с в
принципиальной разницей, что измерения производятс
моменты падений и поправки вводятся не посреди
вепно в прицел, т. е. имеемналиДО обычную корректир
с накоплением ошибки до нового измерения отклонения. ве_
Пример. Возьмем те же условия стрельбы, которые > ПРИ78)
дены в примере § 59 (стр. 211). Пусть в точке ^2
произведена первая засечка цели. Через 1Н— ои сек. ь iuik.
произведена вторая засечка цели. По определении курса и с д
роста цели через промежуток времени /Р = И сек. произве
первый пристрелочный выстрел, после которого через ь
второй и еще через 6 сек. — третий выстрел. 10_
Для всех трех падений измерены отклонения, причем с
следним падением произведена третья засечка цели в точке
За время /" = 62 сек. вновь взята* курс и скорость, а^
основании засечки в Цо — дальность, п°сле чего через tp Ис
О'
да)1 залп на поражение (BJ — 30 саж.; Вб = 3 саж.; Т=39 сек.).
Найти распределение цели в точке Цу к моменту падения
поражающего залпа.
Согласно формулам (250, 250' и 250") § 57 (стр. 209), но имея
в риду, что t'M ф t"H, можно написать:
% — го + fcisi + Л.’2г2 ,
где
7^ = А и fc2 = A.
н 1н
Имея в виду, что за время fH 4- /"-|-z?/ = 162 сек. = 2,7 мин.
дальность изменится не более 7 каб., а направление плоскости
стрельбы — всего на 3—4°, можем заключить, что условия
работы горизонтально-базных дальномеров не изменятся, и
М()жно принять
г0 ~ S2 — S1
и написать:
откуда
сг/ е1 1 4~ fcj + Zfj
Кроме эллиптической ошибки в^, на конце вектора упрежде-
ния будем иметь еще эллиптическую ошибку пристрелки
(enpwcmp + ер)> где Snpucmp— эллиптическая ошибка измерения
отклонений, а гр— эллиптическая ошибка рассеивания.
Тогда окончательно будем иметь:
с?/ == 4“ (Enpwcmp 4" Sp )
где все суммирования надо понимать символически.
Эллиптическую ошибку засечки цели et возьмем из примера
§ 59, так как условия работы горизонтально-базных дальноме-
ров те же, следовательно, имеем:
Ej (29,8 саж.; 26,4 саж.; 12°) (стр. 213),
причем ббльшая сопряженная полуось проходит правее плос-
кости стрельбы на 8°, а меньшая — левее па 4°.
При засечке цели и падении и при измерении отклонений
11Ы будем иметь одинаковые ошибки на обоих концах век-
тора—у цели и у точки падения. Относя по теореме об ошиб-
ках на двух концах вектора обе ошибки к одному концу его
V цели и учтя, что мы пользуемся средним результатом из
з’рех выстрелов, имеем:
е РА7_^. 25,9 . 2.
е„ристи^ , у- , 1-)^-
— e»lp«c>iP(33,8 саж.; 30,5 саж.; 12°).
253
Для ер будем иметь:
еР
гР(17,6 саж.; 1,7 саж.; 90°),
е. имеем главные полуоси с большей полуосью в плоскости
(Зтрельбы.
г.__^У __60 __
й
fr2 = A-=g=o,8o6,
откуда
/7+*; + ^= ^б’2-
Следовательно,
% (28,7 • 1,62; 25,9 • 1,62; 12°) =
= У (46,5 саж.; 42,0 саж.; 12°).
В результате получим следующую систему ошибок птир
ценную к прямоугольной системе осей координат, причем за
положительное направление оси плоскости стрельбы. А’-ов примем направление
О' (р-
33,8 саж. 352°
30,5 „ 4°
17,6 „ 0°
1,7 „ 90°
46,5 „ 352°
42,0 „ 4°
Произведя известным приемом сложение векториальных оши-
бок, получим единичный эллипс распределения цели:
« = 72 саж.; 6 = 7,5 саж.; а1 = — 2112°.
Большая ось проходит всего на 21/2° правее плоскости
стрельбы, что практически вполне допускает принять, что
большая ось совпадает с плоскостью стрельбы. Полученным
распределением цели удовлетвориться нельзя, и, изучая систему
ошибок, видим, что увеличение числа пристрелочных выстре-
лов особенно делу не поможет, так как главную роль играет
ошибка в векторе упреждения.
Следовательно, надо итти по пути изыскания мер в уточне-
нии вектора упреждения, а именно — по пути точности опре-
деления мест цели, т. е. увеличения угла засечки (увеличения
базы) и увеличения точности засечек.
Увеличение числа пристрелочных очередей, правда, помо-
жет в том отношении, что одновременно будет увеличиваться
2^4
и число засечек цели, но вряд ли правильно рассчитывать
на то, что цель будет долго итти одним и тем же курсом,
а если цель будет менять курс, то увеличение числа пристре-
лочных очередей только затянет время.
Выходом из данного положения может быть только обстрел
площади, причем при малой величине оси Ъ и при достаточно-
широкой цели обстрел площади понадобится лишь по даль-
ности без изменения направления.
Другой путь улучшения распределения цели лежит в-
направлении увеличения наблюдательного времени, но это суще-
ственно поможет лишь в том случае, если мало упредительное
время, т. е. сумма работного времени и времени полета. Отсюда
можно сделать вывод, что необходимо стремиться к усовер-
шенствованию приборов и балистики.
Само собой разумеется, что к одновременному удлинению
базы, уточнению засечек и уменьшению упредительного вре-
мени надо стремиться всегда и всемерно. Что касается увели-
чения наблюдательного времени, то это не всегда возможно,
так как уменьшается скорострельность и затягивается откры-
тие огня, что не всегда допускается тактической обстановкой..
77. Закон ошибок избирательного измерения
отклонений и дальностей до всплесков, когда
пристрелка по измеренным дальностям или по
измеренным отклонениям производится залпами1
При определении несоответствия между дальномером и таб-
личной дальностью (прицелом), а также при измерении откло-
нений точек падения снаряда относительно цели мы до настоя-
щего времени имели в виду или одиночный выстрел, или оче-
редь с такими промежутками между отдельными выстрелами,
которые обеспечивали бы измерение дальностей до каждого
из всплесков или измерение отклонений каждого всплеска
от цели.
Принимая за истинное значение дальности или отклонения
среднее значение из всех измерений, мы тем самым увеличи-
вали меру точности измерений и уменьшали влияние рассеи-
вания. Но одновременно с этим, в особенности при стрельбе
по измеренным отклонениям, вводили некоторую новую систему
ошибок в учете движения цели и своего корабля и увеличи-
вали время.
При использовании стереодальномера для измерения даль-
ностей до точек падений или отклонений точек падений от'
цели мыслится возможность избирательного измерения до того-
пли иного избранного падения из нескольких одновременных
падений залпа.
1 Разработка капитана 2-го ранга С. А. Венкстерна. Морской сборник, 1937 г...
255
Положим, что произведен залп в к выстрелов (черт. 79)
и точки падений получены в Ми М.2, при положении
цели в Цх.
Если дальность измерена до ближайшего • падения в Л/,
(стрельбу предполагаем слева) или будет измерено отклонение
то, обозначив МГО через £, имеем для вероятности паде-
ния у точки М,:
(297)
при Вд = 1.
Вероятность падения дальше точки Мх выразится:
Черт. 79.
(29S)
Вероятность же одного падения у точки и одновременно
(к — 1) падений дальше точки Мх будет:
_р2И (Л —1)
?1©d; = -£=e F (-$)d;.
I ~
(299)
сР1(?)й;==Л, для распределения средней траек-
тории будем иметь:
„ 1 р -р^=
<P2©d;=-jJ=e F (-g)d; . (300)
Совершенно такой же закон будет и в том случае, если
цель находится в Ц2, а измерены попрежнему или' дальность
до точки Мх или отклонение МХЦ2.
Если же при положении цели в Ц2 (или в Цх) будет изме-
рена дальность до точки падения (стрельба слева) или
отклонение (или то распределение средней траек-
тории выразится:
256
1 р -₽ч= (Л-1)
F (И-
л у к
(300')
Вычисление (зоо') приводим в табл. 74.
Таблица 74
Число орудий в залпе 4 3 2
£ ?2(0 ?2(?) ыо
- 4,0 0,00002
- 3,5 — 0 0,00015
- 3,0 0 0,00002 0,00076
- 2,5 0,00001 0,00020 0,00298
- 2,0 0,00015 0,00051 0,00960
- 1,5 0,00122 0,00587 0,02512
- 1,0 0,00669 0,02009 0,05354
- 0,5 0,03183 0,05160 0,09346
0 0,06713 0,10085 0,13442
Н 0,5 0,12811 0,15224 0,16053
- 1,0 0,18050 0,18007 0,16063
h 1,5 0,19369 0,17234 0,13607
- 2,0 0,16367 0,13490 0,09865
Ь 2,5 0,11298 0,08863 0,06191
9- 3,0 0,06847 0.05103 ОД-3476
- 3,5 0,03224 0.02444 0,01643
- 4,0 0,01395 0,01051 0,00703
- 4,5 0,00533 0,00401 0,00267
- 5,0 0,0**183 0,00138 0,00092
1- 5,5 0,00056 0,00042 0,00028
h 6,0 0,00038 0,00009 0,00006
- - 6,5 0,00004 0,0..003 0,00062
- 7,0 0 0 0
Из этих распределений видим, что измеренная дальность
(или отклонение до одного из крайних падений) должна быть
исправлена на величину, равную 1,5—2 срединным отклонениям
пушки в сторону остальных падений.
Можно произвести измерения до двух крайних падений
в залпе и принять за истинное положение средней траектории
среднее арифметическое из двух измерений, т. е. точку Ох.
Выведем закон для этого случая, для чего напишем вероят-
ность получить падения у точек МЛ и одновременно при гипо-
тезе о средней траектории в расстоянии $ (черт. 80) от точки Olt
например, в 02.
Эта вероятность напишется:
о — р2(» + Е)2 р — р2'•—£)=
a1(o;,^dxdz = —-~=е '/=е da; dt
17 Теория стрельбы
257
Преобразуем это выражение:
ср>! (х, В) dx dz
’ р \2 — р=(^ + 2я-.+ и + а®-2«';+»)
I е dx dz
У
или
Обозначив
®i (х, Е) dx tZE=
с₽х (х, Е) dx dz
dx dz.
(301)
получим распределение средней траектории:
1 р р2^2 о -р^2
<р2х (ж, Е) dx dz — ~т—У= е е dx dz.
A |/ к у к
(302)
Выражение (302) дает распределение средней траектории
в том случае, если был дан только двухорудийный залп; при
залпе в к выстрелов выражение (301) надо умножить на вероят-
ность наблюдения (А:— 2) падений между двумя крайними, до
которых измерены дальности.
Эта вероятность будет равна:
(* + Е)
Л —2
4-[Ф(*+ Е)-Ф(ж-Е)]1 .
(®—Е)
По перемножении будем иметь:
(х, Е) dx d% —
0 — р=2а= 0 -р22Р ( 1 ) fc-2
= ^=е. -^=е. [Ф^+О-Ф^-Е)]} . (303)
у ТГ у тс ( г J
Обозначив
J" ?i (х, В) dx (К = А2,
— со
для распределения средней траектории получим:
258
ср2 (х, В) dx di =
к — 2
j Р -p’2z’ р _p22^fl 1
=777=® -f=e |--[Ф (ж+?) —Ф (» — ?)][ da: d^. (304)
При нечетном числе выстрелов можно произвести измерение
до среднего падения в залпе.
Пусть при нечетном числе (2fc-f-l) выстрелов в залпе
(черт. 81) измерена дальность до среднего падения М8. В пред-
положении, что средняя траектория проходит через точку О,
вероятность падения около точки Ms выразится:
Но так как, кроме этого падения, наблюдено еще к паде-
ний ближе М3 и к падений дальше Мъ, то вероятность наблю-
дения к падений ближе М3 будет равна FR(?), а вероятность
Черт. 81.
наблюдения к падений дальше Ms будет равна Fk(—?), и рас-
пределение средней траектории получим из
E)dS
% (?) <К =------------------------------------. (305)
+ °°
/ Р e~^F1c(i)F1t (-£) di
I I' it
В дальнейшем мы не будем подробно останавливаться на
схеме расчетов формул (зоб), (300'), (302), (304) и (305), так как
все, что в этом случае необходимо,-—это иметь средние
квадратические и приведенные срединные ошибки, которые
уже вычислены.
Переходя от распределений к кривым закона ошибок, опре-
делим средние квадратические ошибки при условии, что за
истинное положение средней траектории принято положение,
отвечающее математическому ожиданию случайной ошибки,
равной нулю, что для случая (300) или (300') отвечает положе-
нию в 1,5—2 Вд от всплеска, до которого измерена дальность,
а в. остальных случаях, вследствие симметричности законов,
17* 259
это положение отвечает одновременно и срединному положе-
нию и наивысшей ординате.
Вычисления дают результаты, приведенные в табл. 75.
В табл. 75 величины Е2 и R даны в срединных отклонениях
пушки.
Таблица 75
До каких падений изме- рялись дальности Е2 и R Залпы
4-орудий- ный 3-орудий- ный 2-орудий- ный
До крайнего е2 1,059 1,107 1,228
R 0,71 0,74 0,82
До двух крайних е2 0,8001 0,856 —
R 0,54 0,57
До среднего е2 — 0,997 —
R • 0,67
Для получения срединной ошибки пристрелки в выведен-
ные ранее формулы как для стрельбы по измеренным дально-
стям, так и для стрельбы по измеренным отклонениям везде
вместо величины Вд необходимо взять значения R из приве-
денной выше таблицы.
Изложенное в настоящем параграфе является только иссле-
дованием, которое теоретически можно считать доведенным де
конца. Что же касается применения этого вида пристрелки на
практике, то необходимо предварительно произвести экспери-
ментальное исследование вопроса о возможности избирательной
засечки всплесков при одновременном падении нескольких
снарядов.
При исследовании предполагалось, что засечка имени®
избранных всплесков достоверна, и не учитывалась вероятность
ошибки, дабы не усложнять исследования, так как усложнение
исследования в данном случае было бы весьма значительным.
Этот допуск не является существенным, так как при большом
и среднем рассеиваниях вероятность ошибки близка к нулю,
а при малом рассеивании ошибка на результатах стрельбы почти
не скажется.
ЧАСТЬ ТРЕТЬЯ
ТЕОРЕТИЧЕСКИЕ ОСНОВАНИЯ
ВЫРАБОТКИ ПРАВИЛ СТРЕЛЬБЫ
СНАРЯДАМИ ДИСТАНЦИОННОГО
ДЕЙСТВИЯ
ГЛАВА XI
СТРЕЛЬБА ШРАПНЕЛЬЮ
78. Задачи и общий порядок выработки правил
стрельбы дистанционными снарядами
Основной задачей при выработке правил стрельбы дистан-
ционными снарядами является выявление тех условий, при
которых получается наилучшее поражение цели и указаны
ебъективные признаки, по которым можно судить о степени
поражения цели.
Критерием, характеризующим успешность поражения цели,
примем математическое ожидание либо числа пораженных целей,
либо попадания в зависимости от характера цели и поставлен-
ной задачи. Так, например, если поставлена задача поражения
большого числа живых целей, за критерий принимают матема-
тическое ожидание числа пораженных целей, а при необходи-
мости поражения одной цели за определенный промежуток
времени — математическое ожидание попадания.
Поражение цели снарядами дистанционного действия немыс-
лимо вне убойного интервала разрыва; поэтому первая задача
заключается в том, чтобы найти величину убойного интервала
разрыва.
Дистанционные снаряды, разрывы которых происходят в пре-
делах убойного интервала, не все могут поражать цель своими
элементами, а только те из них, разрывы которых произойдут
внутри области опасных разрывов; поэтому следующей задачей
будет найти эту область опасных разрывов.
Ясно, что для поражения цели интервал разрыва не должен
быть более убойного, но может быть сколько угодно менее
261
убойного, и тот интервал, при котором математическое ожида-
ние числа пораженных целей или попадания наибольшее, будет
наивыгоднейшим.
Таким образом, следующей задачей является найти наивы-
годнейший интервал разрыва.
Математическое ожидание числа пораженных целей при
данном интервале разрывов будет зависеть от положения сред-
ней траектории относительно цели, причем, как увидим далез,
в этом случае существуют допуски, в пределах которых мате-
матическое ожидание меняется весьма мало; поэтому следующей
задачей явится найти наивыгоднейшее положение средней траек-
тории и установить границы допусков.
Положение средней траектории относительно цели опреде-
ляется углом прицеливания или углом возвышения („прицел"),
причем в известных пределах можно считать, что интервал
разрыва не зависит от прицела. При одном и том же положе-
нии средней траектории на величину интервала разрыва будет
влиять установка дистанционной трубки. Пусть, например, при
положении цели в Ц (черт. 82) средняя траектория будет О/ц
и средняя точка разрывов Ох — на высоте Но.
Черт. 82.
Изменив установку прицела, например, на величину ДХ,
мы одновременно перенесем среднюю траекторию в O2h2 и под-
нимем среднюю точку разрывов до высоты Н в точку 02, не
изменив интервала разрыва 1г.
Если мы теперь удлиним трубку на величину, отвечающую
положению средней высоты разрывов Но, то средняя точка
разрывов переместится по траектории O2h2 в точку О3, причем
интервал разрыва неизбежно уменьшится до величины 12.
Таким образом, через подсчет наивыгоднейшего интервала
разрывов и наивыгоднейшего положения средней траектории
мы придем к наивыгоднейшим для данных условий стрельбы
установкам прицела и трубки.
Но найти наивыгоднейшие установки еще недостаточно, —
надо указать и объективные признаки, по которым стреляющий
может с достаточной вероятностью утверждать, что указанные
262
в правилах стрельбы и в таблицах стрельбы установки им най-
дены и он может рассчитывать на надежное поражекиэ цепи.
Пусть средняя точка разрывов находится в О, и эллипсоид
разрывов е, проекция которого на плоскость стрельбы изобра-
жена на черт. 83, вмещает практически все разрывы; АВ— гори-
зонт цели (вода, земля); все разрывы ниже АВ будут клев-
ками К; CD—-верхняя граница низких разрывов Н; EF — верх-
няя граница нормальных разрывов N; KL — верхняя граница
высоких разрывов В и нижняя граница очень высоких разры-
вов ОВ.
Тогда положению цели в точке Ц и средней траектории Oh
будет отвечать определенное распределение клевков, низких,
нормальных и высоких разрывов, что служит объективным
указанием на высоту средней точки разрывов.
Черт. 83.
Данное на черт. 83 положение отвечает определенному рас-
пределению захватывающих разрывов (низких и клевков).
Распределение средней точки разрывов по высоте может
быть получено на основании непосредственного измерения
высоты разрывов как в случае, когда все разрывы воздушные,
так и в том случае, когда измерены высоты воздушных раз-
рывов, но имеются и клевки.
Распределение цели по дальности может быть также полу-
чено па основании измерения отклонений по дальности как воз-
душных разрывов, так и клевков.
Так или иначе, но для стрельбы по наблюдению знаков или
по измеренным отклонениям указанные выше признаки дают
соответствующие распределения средней точки разрывов и цели
и позволяют составить правила стрельбы, причем в основе
работы лежит изучение действия отдельного снаряда и дей-
ствия группы дистанционных снарядов, вытекающего в свою
очередь из- действия отдельного снаряда и закона рассеивания
точек разрывов.
Изучение закона рассеивания точек разрывов дает возмож-
ность установить направления и размеры осей эллипсоида раз-
рывов, получить распределения захватывающих разрывов, под-
считать наивыгоднейший интервал разрывов, установить гра-
ницы разрывов различных категорий и дать совершенно объек-
тивные признаки для стреляющего по выбору установок прицела
263
и трубки, отвечающих наилучшему поражению цели, и указать
возможные допуски во избежание' излишней траты снарядов
и времени на ненужные уточнения.
При выработке правил стрельбы снарядами дистанционного
действия, как и ударными снарядами, необходимо учитывать
рассеивание данного момента, для чего правила должны быть
выработаны для нескольких рассеиваний. Обычно вырабатывают
правила для рассеивания табличного и для рассеивания, в два
раза более и менее табличного, после чего делаются возмож-
ные обобщения и упрощения и указываются объективные при-
знаки, по которым надо следовать тем или другим правилам,
если обобщение невозможно.
Может быть предложен следующий порядок работы при
исследовании стрельбы и выработке правил стрельбы снаря-
дами дистанционного действия:
1. Изучение действия отдельной шрапнели.
2. Изучение рассеивания.
3. Подсчет напвыгоднейшего интервала разрыва и нормаль-
ной высоты разрывов.
4. Разделение разрывов по высоте на категории и выявле-
ние признаков категорий.
5. Выявление допусков:
а) влияние интервала разрыва на поражение при условии
прохождения средней траектории через цель (ошибки в уста-
новке трубки);
0) влияние удаления средней траектории от цели при неиз-
менном среднем интервале до цели (ошибки в установке
прицела);
в) влияние удаления средней траектории от цели при неиз-
менной нормальной высоте средней точки разрывов (ошибки
прицела).
6. Выбор средней высоты разрывов, необходимой для при-
стрелки.
7. Пристрелка высоты разрывов.
8. Оценка пригодности установки трубки.
9. Пристрелка возвышения (прицела) и стрельба на пора-
жение.
10. Исследование накрытий.
На изложенный порядок выработки правил стрельбы снаря-
дами дистанционного действия следует смотреть только, как
на указания, облегчающие путь исследования, но само собой
разумеется, что порядок работы при том или ином исследова-
нии будет зависеть от цели и характера исследования и в каж-
дом отдельном случае лицо, ведущее исследование, этот поря-
док должно установить само.
Указанный порядок ближе всего подходит при исследовании
стрельбы пулевой шрапнелью.
При исследовании применяют частью аналитические, а частью
графические методы подсчетов. Так как графические методы
подсчетов при этом характере исследования дают точность,
264
значительно превосходящую точность самой стрельбы, то гра-
фический метод подсчетов в дальнейшем будет широко исполь-
зован.
Стрельба снарядами дистанционного действия может вестись
как при неизменной, так и при непрерывно меняющейся даль-
ности.
Особого метода выработки правил стрельбы снарядами ди-
станционного действия по наземным и надводным целям давать
не будем и исследование будем вести для стрельбы при не-
изменной дальности. Переходя же к движению стреляющего
корабля или цели, примем метод стрельбы завесами при пере-
менном интервале на постоянной трубке для каждой завесы,
причем установим пределы обстреливаемой площади с учетом
выявленных допусков и обстановки стрельбы.
Исключением будет стрельба по быстро движущимся целям
в тех случаях, когда стрельба по наземным и надводным целям
ведется методами стрельбы зенитной артиллерии.
При стрельбе снарядами дистанционного действия по назем-
ным и надводным целям можно иметь дело не с эллипсоидом
рассеивания точек разрывов, а с его проекциями на плоскость
стрельбы, на вертикальную плоскость, перпендикулярною к
плоскости стрельбы, и на горизонт цели. Это в значительной
степени упрощает весь метод исследования, поэтому в даль-
нейшем мы будем говорить об эллипсах рассеивания точек раз-
рывов, понимая под этим всегда соответствующие проекции.
79. Свойства пулевой шрапнели
Свойства пулевой шрапнели характеризуются:
1) пробивной способностью пуль в зависимости от дальности
стрельбы и интервала разрыва,
2) углом разлета пуль и
3) законом распределения пуль в круге сечения конуса
разлета.
Указанные выше характеристики действия шрапнели лучше
всего получаются путем правильно поставленного опыта, но
пробивная способность пуль и величина угла разлета пуль
могут быть приближенно подсчитаны и наперед.
80. Скорость, сообщаемая пулям разрывным
зарядом
Скорость, сообщаемая пулям разрывным зарядом, опреде-
лена из опыта инж. Трофимовым для шрапнели 76-мм пушки
обр. 1902 г. Шрапнель при этом находилась в покое и, следо-
вательно, было принято положение, что скорость, которую при-
обретают пули от действия разрывного (вышибного) заряда, не
зависит от того, находится ли шрапнель в движении или в
покое. Таким образом, было принято, что начальная скорость
пуль слагается из скорости шрапнели в момент действия раз-
265
рывного заряда и той дополнительной скорости пуль, которую
они приобретают под действием только разрывного заряда, при
условии, что стакан остается целым.
Инж. Трофимов получил скорость пуль г„ = 77 м/сек, а ско-
рость летящего назад стакана гст=115 м/сек.
Вес частей, летящих вперед, был % з,8 кг, а летящих
назад —рст 2,6 кг.
Из этого была выведена формула, дающая возможность хотя
бы приближенно подсчитать скорость пуль по весу пуль, ста-
кана и разрывного заряда дымного пороха.
Эта формула получена на основании следующих сообра-
жений.
Отношение веса частей, летящих вперед, к весу частей,
-летящих назад:
14=1’46-
Рст 2,6
Отношение скорости частей, летящих назад, к скорости частей,
летящих вперед, будет:
Гст. ___ 11Э
Принимая во внимание, что действие пороховых газов на
стакан вследствие его формы выгоднее, чем на части, летящие
вперед, приближенно принято, что
Рст Vcm — Рп (306)
Полагая, что сумма живых сил частей, летящих вперед, и
частей, летящих назад, пропорциональна весу заряда, будем
иметь:
_рст г2с,ц = А (307)
20 ~2£ ’
где И —постоянный коэфициент пропорциональности, а <о —
вес разрывного заряда, выраженный в килограммах.
Из (306) имеем:
Рст
и, подставив значение vcm в (307), получим:
Рет Рп2У„2
2 У Р“ст
Рп?п
?У
Аш,
или
. 2 / Рет Рп
” I 2 др2Ст
Рп
2 у
,= Аш,
266
или
9 77 ( Рст +^« = Аю>
£ У \ ] Рст
откуда
гД = 29 А —= 7?2----------------“-----= В2 ~ ,
Рст + Рп рп Рст -1-79. Рп 1 Рп
где
В=]/ 2дА
и
Р——Рст + рп‘,
тогда окончательно имеем:
кп = Вл /~HL . P^L.. . (308)
V Р Рп
Для 76-лки шрапнели имеем:
ш = о,О85 кг-, pcm—2S> кг; р„~3,8 кг; В—6,4 кг и из опыта
г’„ —77 м)сек.
Значение скорости vn обозначают обычно символом а.
81. Пробивная способность пуль
Шрапнельная пуля, вообще говоря, должна обладать доста-
точной живой силой для вывода бойца из строя. Но в морской
артиллерии шрапнельные пули должны обладать большей живой
силой, чтобы при стрельбе по торпедным катерам пробивать
и легкие преграды (прикрытия) с расчетом повредить скрытые
за ними механизмы.
= С кг!м, (309)
где С— численное значение живой силы, достаточное для вы-
вода человека из строя. Из (309) имеем:
(ЗЮ)
V Рп
Для действия по живым целям считают необходимым, чтобы
пуля обладала живой силой (7> 10 кг/м.
Для определения убойного интервала разрыв^ внешняя
балистика дает:
_ _____«о
’ (311)
Е
где v0 = ve + a; ц, — окончательная скорость в момент разрыва
шрапнелью и a=v„; Е — постоянный коэфициент. Для пули в
шрапнелях калибром до 152 мм £'==39100.
267
Решая уравнение (311) относительно 1уб, получим:
г E(v0 — vve)
vS vv6
пли
Л/'7 (гс + a)vyS
Из (312) видим, что убойный интервал разрыва зависит от
дальности стрельбы.
Формула (312) может служить лишь для ориентировочных
подсчетов, так как из опыта известно, что не все пули обла-
дают одинаковой скоростью.
Обычно убойный интервал определяется путем опыта.
Иринято считать убойным интервалом тот интервал разрыва,
при котором отношение числа пуль, пробивших сосновую доску
толщиной 2,5 см, и половины застрявших в ней к числу всех
пуль в шрапнели равно половине.
82. Угол разлета пуль в пулевой шрапнели
Угол разлета пуль обычно определяется путем опыта, при-
чем этот угол получается попутно с определением распреде-
ления пуль в конусе разлета.
Для производства этого опыта на полигоне устанавливают
3 щита В, A-l и Д (черт. 84). Щит В служит как „взводящий11
только для того, чтобы вызвать ударное действие трубки
(трубка двойного действия); щит Аг—из легкого картона и слу-
жит только для определения угла разлета пуль; щит А2 —
для определения распределения пуль в сечении конуса раз-
лета, о чем будет сказано ниже.
Обозначив половину угла разлета пуль через В, имеем
(черт. 84), что
tgp=-^2L. (313)
Величина угла разлета пуль (шаровых) может быть полу-
чена путем вычисления без опыта, причем получается резуль-
тат, весьма близкий к опытному.
Угол разлета пуль определится на основании следующих
соображений.
В момент разрыва шрапнели пули ее имеют следующие
скорости:
1) поступательную (гс-|-а), где vc — окончательная скорость
шрапнели в моменты разрыва и а — добавочная скорость, полу-
ченная в результате действия разрывного (вышибного) заряда;
2) скорость Ъ, сообщаемую разрывным зарядом по нормали
к боковой поверхности шрапнели;
3) скорость с от вращения снаряда, направленную по каса-
268
тельной к окружности, проходящей через центры наружного
ряда пуль.
Скорости бис, будучи взаимно перпендикулярны, сложатся
в одну скорость: _ ______
и — -|- с2,
Черт. 84.
которая будет перпендикулярна к оси шрапнели и, следова-
тельно, к скорости vc + а.
Крайние пули шрапнели (черт. 85), обладая скоростью vc + а
и^ скоростью и, к ней перпендикулярной, отклоняются от оси
шрапнели на угол р. При этом
(314)
Черт. 85.
Определим величину скорости с.
Обозначив внутренний радиус шрапнели через 1{, расстоя-
ние от оси шрапнели до центра крайней пули — через г и длину
хода нарезов у дула —через т;, для выражения числа оборо-
тов в 1 сек. будем иметь:
»]
269
где v0 — начальная скорость шрапнели, откуда линейная ско-
рость вращения будет:
c = ^2w.
Подставив значение с в (314), получим:
tg? =
£>2 + | — 2w
\ »!
vc + а
(315)
Опыт показывает, что если в (315) положить Ь=О, то углы р
получаются весьма близкими к полученным из опыта. Полагая
в (315) Ъ — 0, для вычисления половины угла разлета шрап-
нельных пуль будем иметь:
tgp =
2 л г v0
ri (vc' h й)
(316)
Этой формулой и будем пользоваться для определения угла
разлета шрапнельных пуль.
S3. О случайной группировке попаданий
Когда действие шрапнели оценивается не числом попавших
в цель элементов (пуль, осколков и пр.), а числом поражен-
ных единиц цели или числом пораженных целей, нас будет
интересовать только „полезное11 поражение цели, т. е. только
то число попаданий, которое достаточно для вывода цели из
строя, так как все остальные попадания в уже пораженную
единицу цели могут считаться бесполезно пропавшими.
Если для поражения цели достаточно одного попадания, то
одно попадание будет „полезным", и при большем числе попа-
даний все остальные будут потерянными.
Выведем выражение для вероятности попадания и для мате-
матического ожидания поражения цели (числа пораженных
целей) при заданной средней плотности поражения:
где т— число снарядов, осколков, пуль и других элементов,
падающих на некоторую поверхность, содержащую 8 равных
по площади единиц цели.
При этом примем условие, что каждый из т снарядов,
осколков, пуль и т. п. может попасть в каждую единицу с рав-
ной вероятностью.
При этом условии вероятность попадания в одну определен-
ную единицу цели будет
1
8 ’
270
а вероятность, что осколок не попадет, будет
Вероятность же того, что ни один осколок не попадет в опре-
деленно выбранную нами единицу цели при числе снарядов или
элементов, равном т, будет
/ 1 V"
= I 1 — у 1 • (317)
Выражение (317) представляет собой вероятность, что при сред-
да .
ней плотности попадания « == некоторая цель не будет пора-
• о
жена вовсе.
Вероятность одного попадания хотя бы одним снарядом или
элементом получим, вычтя выражение (317) из единицы:
/ 1 V" 4
р = 1 —2?0 = 1—( 1 —у I • (318)
Упростим выражение (318) и приведем его к более общему
виду. Для этого из выражения а = =-определим т = а8, где
о
о—средняя плотность попадания.
Подставив значение т в (318), получим:
Р=1 — Ро = 1 —
(319)
[1 Is -1
1 — —-I =е ,и при 8 = 100 это выражение уже мало
<8==оо
отличается от своего среднего предела, а именно:
(1-s)=2’73 •
Поэтому, полагая в (319) для достаточно большого &
л 1 v -1
р gj—е ,
получим- -а
р = 1—р0 = 1 — е . (320)
Для математического ожидания числа пораженных целей
при 8 единицах цели из (320) получим:
М=8(1‘— р0) = 8(1 — е-“). (321)
Это выражение мы используем при исследовании стрельбы
дистанционными снарядами очень широко.
В современных условиях стрельбы как дистанционными сна-
рядами, так и снарядами ударного действия, могут быть случаи,.
271
когда для надежного поражения цели необходимо иметь не
менее двух, трех и более попаданий в единицу цели.
Распространим выражение (321) для вероятности иметь не
менее двух попаданий в том случае, когда можно исходить tb
средней плотности попадания.
Вероятность, что не попадет в цель ни один снаряд или ни
один элемент его, по (317) будет:
Вероятность, что попадет один определенный снаряд, пуля,
осколок или другой элемент, а остальные не попадут, будет:
Вероятность, что попадет какой-нибудь один из элементов
в единицу цели, будет:
ш / 1 V1-1
А==8’(1“8’) ’ (322)
Выражение (322) можно преобразовать так:
1
При достаточно большом S молено принять:
Тогда на основании (320) = ае ~а.
Вероятность, что попадет какой-либо один элемент или ни
одного, будет:
е~а —“ = е~° (1 -р «).
Вероятность получить попадания хотя бы двумя какими-
либо элементами получим в таком виде:
P>g = 1 — е ~»(1 + «). (323)
Для вероятности попадания хотя бы двумя, тремя, четырьмя
и т. д. какими-либо элементами в единицу цели будем анало-
гично иметь:
тСт— 1) / 1 \т —2
lh~' 218* ( 1 “8*) ’
__ т(т— 1) (т — 2) / 1 \m —3
Ps ~ 318s 1 ~ ~S j ;
_ т (т — 1) (га — 2) (га — 3) / 1 \ст-4
~4Г& ( 1-8/ ’
272
т(т—-1) . . . [т— 1 \№ —п
™ 2! о2
_т / 1 \,B-i
~ 1 ~ S)
" / т
Для определения вероятности, что попадут хотя бы три эле-
мента в какую-либо единицу цели, преобразуем выражение:
(£ \ т — 2
1 “ s' /
т — 1 / 1 1
1 \ _ а2
2S 2S / 2 е '
При этом при достаточно большом S принято, что
1
2 S'
0.
Вероятность неблагоприятного для нас события будет:
9 / .9
d" —• а — a I (£.“
е~аае~ а—е =е 11+« + -у
Искомая вероятность напишется так:
/ \
1 + « + —. (324)
Аналогичным путем получим вероятность попадания хотя
бы четырех элементов в какую-либо из единиц цели:
^>4 = 1 — е“°(1+« + -5у + тг)’ (325)
<5*^* I Zj i О . J
и вообще вероятность не менее п попаданий в какую-либо из
единиц цели
...+F=T)"i) ,826)
Следует иметь в виду, что формулы (320), (321), (323)—(326)
дают приближенные решения, что видно из самого вывода.
Рассматривая допуски при выводах, можно сказать, что чем
больше S, тем результат точнее, и при S^>100 можно при-
нять, что для практических целей мы будем иметь достаточно
точные решения.
Примечание. Очень часто для всех случаев можно пользоваться
а3 а”-1
формулой (323), так как сумма слагаемых— ц--др ’
вообще говоря, мала.
18 Теория стрельбы
ГЛАВ А XII
РАССЕИВАНИЕ РАЗРЫВОВ СНАРЯДОВ
ДИСТАНЦИОННОГО ДЕЙСТВИЯ
84. Рассеивание разрывов в безвоздушном
пространстве при временной трубке
Изучая рассеивание точек падения снарядов ударного дей-
ствия, мы обошлись без рассмотрения этого явления в безвоз-
душном пространстве. Рассеивание разрывов снарядов дистан-
ционного действия сложнее, и поэтому для лучшего уяснения
этого явления рассмотрим его сначала в пустоте.
Черт. 86.
Причин рассеивания разрывов в безвоздушном пространстве
три: разнообразие углов бросания, разнообразие начальных
скоростей и разнообразие во времени действия трубки. Никаких
других причин в безвоздушном пространстве быть не может.
Рассмотрим сначала картину рассеивания точек разрывов
при идеальной трубке, положив, что Д£=0 и t— const.
Если время полета от Л до О (черт. 86) равно t, то при
отсутствии каких бы то ни было ошибок все разрывы получи-
лись бы в точке О.
Предположим, что в начальной скорости ошибок нет, а имеют
место только ошибки в углах бросания, которые характеризу-
ются срединной ошибкой Д6.
Векториальная ошибка, порожденная ошибками в углах бро-
сания, будет:
274
0D = 0Dl = Връ = v01 ДОо.
Направление этой ошибки будет перпендикулярно оси канала.
Величина и направление этой ошибки получаются из сле-
дующих рассуждений.
При v0 — const и t— const все осевые дальности будут равны
между собой и равны vot.
При случайной ошибке в угле бросания, равной нулю,
точку разрыва получим, отложив по направлению АОг величину
, „ „ qt2
vot и отложив затем по вертикали вниз величину Ofi — —--
Проведем из А, как из центра, окружность радиусом АО =
= v01. Из каждой точки окружности проведем вниз вертикальные
qt2
линии, на которых отложим величины, равные^-; тогда окруж-
ность, проходящая через эти точки, представит геометрическое
место точек разрывов при наличии ошибок в угле 0о.
Имея в виду, что величина рассеивания незначительна по
сравнению с v01, мы можем в пределах рассеивания дугу окруж-
ности заменить прямой половина которой и будет равна
указанной выше векториальной ошибке.
Предположим теперь, что имеют место только ошибки
в начальной скорости, характеризуемые срединной ошибкой Д«о.
Эти ошибки вызовут рассеивание точек разрывов по направ-
лению СОС1г и при этом получится векториальная ошибка
OC=OC1~t^vo=^Bpv.
Направление этой векториальной ошибки будет параллельно
оси канала орудия.
Величину и направление векториальной ошибки Bpv — t Дг0
мы получим из следующих соображений.
При отсутствии ошибок в углах бросания, но при появле-
нии ошибок в начальной скорости, все осевые дальности раз-
рывов будут откладываться по направлению АОг.
Отложив по направлению АО, величины t Дг0, проведя верти-
gt2
кальные линии и отложив вниз СС3 и С^, порознь равные —,
получим векториальную ошибку
00=001 = Bpv = tAv0.
Эта векториальная ошибка будет направлена параллельно
оси канала орудия.
При идеальной трубке нет никаких других причин для обра-
зования ошибок, кроме двух, рассмотренных выше ошибок:
Bpv!Д^’о
и
Эти две векториальные ошибки вызовут эллиптическую
ошибку, причем Врс и Вт, являясь ее со пряженными полудиа-
18* 275
метрами, одновременно будут и ее главными полуосями, из
которых одна полуось идет параллельно оси канала орудия.
Обращаем внимание, что направление большой оси единич-
ного эллипса рассеивания точек разрывов при идеальной трубке
не совпадает с направлением средней траектории. Это несовпа-
дение является характерным для рассеивания разрывов снаря-
дов дистанционного действия.
При неидеальной трубке прибавится третья векториальная
ошибка • vc — M • г>0, которая будет характеризовать ошибки
во времени, благодаря которым при отсутствии других ошибок
снаряды будут рваться на траектории и дальше и ближе
точки О (черт. 86). Очевидно, что векториальная ошибка Bpt =
= Д£ • v0 будет направлена под углом 6с = Оо. Три векториаль-
ные ошибки BPv, BPfj и Bpt создадут эллиптическую ошибку
с полуосями ОС/— ОСХ' и ОТ)'~О1){' (черт. 87 и 88), причем
большая ось этой эллиптической ошибки может иметь самое
различное направление, проходя выше и ниже средней траекто-
рии и в частном случае совпадая с ней.
Если мы проведем касательные к единичному эллипсу раз-
рывов, параллельные горизонту и перпендикулярные к нему,
то образовавшиеся длины ОГ и ОВ носят названия срединного
отклонения разрыва по дальности и срединного отклонения
разрыва по высоте, соответственно и обозначаются ВРэ и Врв
(черт. 86).
Эти два взаимно перпендикулярные направления не являются
сопряженными, а потому и не являются независимыми.
Величинами Вре и Врэ характеризуют рассеивание точек раз-
рывов снарядов дистанционного действия.
При исследовании рассеивания в безвоздушном простран-
стве выявлены два обстоятельства: 1) большая ось эллипса раз-
рывов, вообще говоря, может не совпадать и по большей части
не совпадает со средней траекторией и 2) величины ВРд и Врв,
как два взаимно перпендикулярных направления, не совпадаю-
щих с главными полуосями, суть направления не сопряжен-
ные, и ошибки по этим направлениям, как события зависимые,
совместному рассмотрению не подлежат. Эти два положения
остаются справедливыми и для рассеивания в воздухе.
На этом мы закончим рассмотрение вопроса о рассеивании
276
разрывов снарядов дистанционного действия в безвоздушном
пространстве *.
85. Определение величин Врв и Врд из опыта
Самое точное определение величин Вр0 и Вре из опыта дости-
гается путем фототеодолитной съемки разрывов с последую-
щей проработкой результатов съемки на специальном компара-
торе, после чего вычисляют величины Bpg, Врв и Вр6.
В некоторых случаях, при отсутствии соответствующей аппа-
ратуры для фототеодолитной съемки, опытное определение вели-
чин ВРд и Врв производится непосредственным измерением углов,
под которыми видны интервалы и высоты разрывов, и обычной
обработкой результатов наблюдений. Этот способ основан на том
свойстве эллипсоида разрывов, что боковые отклонения малы.
Пусть в точке Т (черт. 89) установлен теодолит или иной
точный угломерный инструмент. R—пристрелянная средняя
точка разрывов по дальности. Направление ВТ перпендику-
лярно к плоскости стрельбы. Р,-—точка г-го разрыва (после
пристрелки), а р/—проекция /-го разрыва на горизонт.
Тогда по отношению к фиктивной цели В интервал h будет
интервалом /-го разрыва, a Hi — высота того же разрыва, при-
чем /. = dtgp4- и Hi =dtgai .
1 Лиц, желающих подробно ознакомиться с рассеиванием в пустоте, отсы-
лаем к курсам теории стрельбы, изд. Арт. академии РККА.
277
По получении ряда значений Л и Я» обработка результатов
наблюдений для определения Вр0 и Вре производится обычными
способами с последующим обязательным определением центра
и осей группирования и их распределений для суждения о
качестве опыта и для решения о принятии его или о повторении.
Лучше при производстве опыта иметь два рядом поставлен-
ных угломерных инструмента: один — для измерения углов
а другой — для измерения углов |Э,- . Наблюдатели должны быть
очень опытны и хорошо натренированы, так как разрывы отно-
сятся ветром, а потому засечки разрывов должны произво-
диться почти мгновенно в самый момент разрыва.
При этом опыте, кроме нахождения распределений, обяза-
тельна и проверка применимости закона Гаусса и очень осторож-
ное и внимательное отношение к исключению анормальных
наблюдений, которые могут появиться вследствие несвоевремен-
ной засечки разрыва, отнесенного ветром.
По определении величин ВРэ и Врв обязательно должны быть
подсчитаны полуоси эллипса разрывов и их направления.
86. Одни из способов теоретического вычисления
величии Врд и Врв
К теоретическому вычислению величин Вр0 и Вре следует
прибегать только в том крайнем случае, когда почему-либо их
нельзя получить путем опыта, а иметь необходимо хотя бы
приближенно.
Вычисления величин Вр0 и Вре ведутся по следующим фор-
мулам:
Bp0 = VRnz + R2 + Rc2' (327)
где Rn— срединная ошибка в интервале разрыва вследствие
рассеивания трубки;
Bn = vc cos ecr„, (328)
где vc — окончательная скорость, 6е — угол падения и гп — сре-
динная ошибка рассеивания трубки.
г„ = 0,06+ 0,003 Т сек. (329)
Величина Rn— одного наименования с гс .
Rv — срединное отклонение в интервале разрыва вследствие
ошибок в начальной скорости.
(ззо)
Гв=(о,1 + ^%. (331)
Rc — срединное отклонение в интервале разрыва вследствие
разнообразия балистических коэфициентов.
Rc^lQQ~rc,
Oil
278
где принимают
1
.
100
BP°=V(Rn2 + Rv2) tg20c + AV ’ (332)
где
7?» = 0,001 X r.f ; (333)
здесь: X— дальность, R,. =0,3 — 0,7 — срединная ошибка в угле
бросания.
Остальные обозначения те же, что и в формулах (328) и (330).
Вычисления производятся через определенные интервалы;
полученные значения ВРо и Врв выравниваются по кривым и
вписываются в таблицы стрельбы через интервалы, допускаю-
щие линейное интерполирование.
87. Рассеивание разрывов снарядов дистанционного
действия по табличным данным
Без исследования вопроса о рассеивании разрывов невоз-
можны ни исследование, ни выработка правил стрельбы снаря-
дами дистанционного действия. Впервые этот вопрос был иссле-
дован проф. П. А. Гельвихом и с исчерпывающей полнотой
изложен в его труде „Стрельба", т. I обоих изданий. В изда-
нии 1934 г. этот вопрос трактуется на стр. 61—97, причем сюда
же входят исследования вопросов о распределении низких раз-
рывов и клевков. Поэтому в настоящее время уже нет необхо-
димости повторять ряд выкладок, и мы ограничимся только
выводами и методами их применения для ряда подсчетов, кото-
рыми придется заниматься при исследовании и выработке мето-
дов стрельбы снарядами дистанционного действия.
Исследование рассеивания разрывов должно нам дать поло-
жение единичного эллипса разрывов 1 и его размеры, что опре-
деляется соответствующими уравнениями эллипса.
Для этого служат данные проф. Гельвихом уравнения эллипса,
вписанного в четырехугольник NKPS (черт. 90) и в шестиуголь-
ник К1гЛ28ЯД8, образовавшийся из того же четырехугольника
NKPS и двух прямых ДИ2 и 43Л4, проведенных на расстоя-
нии fi — Btt от центра группирования О параллельно средней
траектории.
Начало координат принимаем в центре эллипса О.
Уравнение
напишется:
эллипса, вписанного в четырехугольник KPSN,
х2 2кху ,У2.
аГ'~аЬ~ 1-/1
(334)
1 В сущнссти, в воздухе мы имеем не эллипс, а эллипсоид разрывов, но
вследствие того, что цель находится на плоскости прицеливания и большая
ось эллипсоида разрывов лежит в плоскости стрельбы, можно иметь делонс
с эллипсоидом, а с его проекциями на вертикальную плоскость стрельбы и
на вертикальную плоскость, перпендикулярную плоскости стрельбы. В этом
смысле и употребляют выражение „эллипс разрывов".
279
для четырехугольника
= Ц-—г
2 a ab
(335)
Если положить: « — Вр8-, Ь — Врв; Р = Вв и a = tg0c, то урав-
нение единичного эллипса разрывов, вписанного в четырехуголь-
ник NKPS, будет:
х2
2 к ху
ВрдВрв
рв
(334')
к = В2в+В20 1ё20с-Дй2
2 Врд Bpe^g 0С
(335')
Уравнение эллипса, вписанного в шестиугольник A3KLA2SR,
будет:
х2
р2 — а2 а2 — Ь2
а2
а а2 Ь2
yL
ъ2
—ft2CT2_b2K2
2а ab Г
У
и
Приняв те же обозначения для а, Ъ, р и а, получим уравне-
ния проекции единичного эллипсоида разрывов на плоскость
стрельбы, касательную к прямым: двум вертикальным в рас-
стоянии Врд от центра, двум горизонтальным в расстоянии Вре от
центра и двум параллельным средней траектории, пересекаю-
щим ось У-ов в расстоянии Вв от центра.
Врд tgJ 6С Врв .
В2рд Bid В1в tg 0с J 4
Bl В2рд tg2 0С —В|й
У
В2рв
\ 2
= 1 —
(336')
2 Врв Врв tg 0С
280
Уравнения (334), (334'), (336) и (336') дают возможность полу-
чить нужные нам сопряженные направления и длины нужных
' нам сопряженных полудиаметров единичного эллипса.
На черт. 90 эти полудиаметры будут:
1. OMi —вертикальный полудиаметр.
Ему сопряженный полудиаметр будет ОМЛ, который полу-
чится, если соединить центр О с точкой касания вертикальной
прямой Д& в расстоянии Врд от центра (не проведен, чтобы
не затемнять чертежа).
2. 0М2— горизонтальный полудиаметр.
Ему сопряженный полудиаметр будет 0М2, который полу-
чится, если соединить центр О с точкой касания М2 горизон-
тальной прямой, проходящей в расстоянии Вре от центра.
3. 0М\— полу диаметр, идущий по средней траектории. Ему
сопряженный полудиаметр будет OMS, который получится, если
соединить центр О с точкой касания Ж3 линии, параллельной
средней траектории.
Уравнения (336) или (336') дают координаты концов этих
сопряженных полудиаметров.
(Врв; — к Врв) — сопряженный вертикальному 0Мг';
М2 (— к Вр0; Вре) — сопряженный горизонтальному 0М2;
М.
Врд(Врд tg ---к Вре) . Врв(Врв fe Врд tg 6C )
Вв ’ Ве
— сопряженный идущему по средней траектории OM'S.
Уравнения этих полудиаметров будут:
Орд
— со пряж енны й вертикальному;
К 1эрд
— сопряженный горизонтальному;
..__Вре (к Врд tg 6С Вре)
J~ BpdUiBpe-BpdtgGo)
— сопряженный средней траектории.
Длины полудиаметров OJf/ = d/; OA^ — d^ 0M2' — d2; ОМ.
= d2; OMS' = d'3 и 0Ms = d3 выражаются:
вертикального:
cli=BpeV\— /r2;
сопряженного вертикальному:
(338).
(339)
(310)
(341)
(342)
горизонтального:
(343)
281
•сопряженного горизонтальному:
d2=y/^Bi,d +ВР7 ; (344)
по средней траектории:
йв'=^^|/| (l-fc2)(14-tg26c) (345)
•сопряженного средней траектории:
= Bfo+Bre--^^ (l-fc2)(l+tg26c). (346)
Для того чтобы полоясение проекции эллипсоида разрывов
на плоскость стрельбы было вполне определенно, надо иметь
выражения для направления (угол от оси Х-ов) большой оси
группирования и длины осей группирования единичного эллипса.
Угол т (черт. 90) определяете! преобразованием известной
формулы
tg 2 -г = —
g ‘ А —С
м в окончательном виде выражается:
tg2T =
Bl -BPpe- В*о tg20c
(В"р0 — Вре) tg бс
(347)
При этом, придерживаясь правила Декарта, в зависимости
от знака получим направление оси ниже или выше горизонта
в четвертой или в первэй четверти.
Обозначив главные полудиаметры эллипса разрывов через
-а0 и Ъо и имея в виду обозначения а=Вр0 и Ь—Вре, являю-
щиеся отклонениями, вызываемыми эллиптической ошибкой,
можем написать из выражений:
а2 = а02 cos2 7 + b2 sin2 7,
Ъ2 — a2 sin2 7 b02 cos2 7
я уравнения, связывающих величины a=BpS; Ь = Врв; а0 и Ьо:
Bpa = а02 cos2 у + Ь2 sin27,
Врв = a2 sin2 7 + b02 cos2 7.
Решая эту систему уравнений относительно а0 и Ьо, получим:
«0=1/ Вр& cos- у Врз sin- . (318) cos2 7 — sin2 7
fc0 = |/ Bpd sin2 Bpe cos- у (319) sin2 7 —- cos2 7
282
В качестве рабочих формул для построения сеток распре-
деления разрывов (рассеивание точек разрывов следует закону
Гаусса) (335), (335'), (337), (338), (340), (341), (346), (347), (349)
используются либо формулы (335), (337), (341), (343) и (345),
либо (335') и (338—319).
88. Построение сетки распределения разрывов
дистанционных снарядов по направлению горизонта
и ему сопряженному
В настоящем параграфе будет изложен способ графического
определения распределения низких разрывов дистанционных
снарядов. Для получения этого распределения построим сетку
по двум сопряженным направлениям: по направлению гори-
зонта и ему сопряженному. Покажем на частном примере
построение этой сетки при использовании уравнений и фор-
мул § 87.
Пример. Построить сетки распределения разрывов по направ-
лению горизонта и ему сопряженному для следующих таблич-
ных условий:
бс = зз°; #„0=18 саж.; Врв^=^ саж. Вд— 16 саж.;
Вв = 10 саж.; Вб = 2,8 саж.; Я0=15 саж.
tgOc = 0,619; tg2Oc = 0,421; 1 + tg2 6С = 1,421.
Найдем величину коэфициента к по (335'):
ДД+#+tg+c-/?2 =
2 Врд Вре tg 6е
_ 81 + 324 • 0,421 — 100
~ 2 • 18 • 9 • 0, 649 “~°’о74:
Л;2 = 0,3295;
1 — к2 = 0,6705.
Для диаметра, сопряженного горизонту, воспользуемся урав-
нением (339):
Задаваясь произвольно ж=100, получим:
У = — 87,1.
Координаты точки (100;—87,1) по соединению ее с центром О
дадут нам направление диаметра, сопряженного горизонту.
Дальше вычислим длину диаметра, сопряженного горизонту,
по (344):
^2 = VV0,3295 • 324 + 81 = 13,7 саж.
Вычислим длину диаметра, идущего параллельно горизонту,
по (343):
d2 — Врд р 1 — /г2 — 18 р 0,6705 —14,7 саж.
283
Теперь мы имеем все данные для построения сетки.
Приняв для построения сетки точку О (черт. 91) за среднюю
точку разрывов и одновременно за начало координат, проведем
координатные оси XX и У У, расположив ось абсцисс гори-
зонтально.
Теперь мы имеем одно направление по горизонту. Для того
чтобы провести направление, сопряженное ^горизонту, из (339)
имеем: если ж = Д-1ОО, то «/ = — 87,1. Построив по этим коор-
динатам точку и соединив ее с точкой О (центр группирования
и начало координат), продолжим ее в обе стороны и получим
направления двух сопряженных полудиаметров: по гори-
зонту ХОХ и ему сопряженное АОВ. Отложив О6\ = ОС2=</./ =
= 14,7 саж. и O/1 = O/'3 = d2 = 13,7 саж., получим сопряженные
полудиаметры единичного эллипса разрывов; увеличив ОС\, ОС2,
Of. и Of., в четыре раза и проведя через точки отложения
параллельные линии, получим сетку распределения разрывов,
построенную по двум сопряженным направлениям: по гори-
зонту и по направлению, сопряженному горизонту.
Так как ошибки по этим направлениям, как по сопряжен-
ным, независимые, мы можем перемножить вероятности слу-
чайных ошибок по ОБ (черт. 91) и по ОХ и вписать произве-
дения в клетки. На черт. 91 это сделано для низких разрывов,
а на черт. 92 показано все распределение точек разрывов по
закону Гаусса.
Пользуясь черт. 91, найдем распределение низких для
До =15 саж. на горизонте. Для этого, во-первых, подсчитаем
процент разрывов в полосе от горизонта до границы низких.
Подсчет дает цифры, показанные на черт. 92.
Просуммировав эти цифры, получим:
2 (1,334 4- 0,867 + 0,364 + 0,097) = 5,324.
284
Поделив каждую из этих цифр на 5,324, получим:
0,0182—0,0678—0,1602—0,2501—0,2501—0,1602—0,0678—0,0182.
Отсюда видим, что получили закон, настолько близкий к
закону Гаусса, что можем заключить, что это отклонение от
закона Гаусса есть не что иное, как результат графического
метода работы, находящийся в пределах точности графического
подсчета.
0,02 0,07
——।------
0J6 ; 0,16 ! 0,07 ; 0,02
I П ! Единичный эллипс распределения
I—17,2 с—< \ низких на горизонте
\-2^с—;
Черт. 92.
Из последнего вытекает, что низкие разрывы распреде-
ляются по закону Гаусса и для данного примера полуоси еди-
ничного эллипса распределения равны 14,7 саж. и 2,8 саж.,
центр распределения может быть принят в точке пересечения
диаметра, сопряженного горизонту, с самим горизонтом; коор-
динаты его (17,2 саж.;—15,0 саж.), и находится он в расстоя-
нии 5,8 саж. от средней траектории (черт. 92).
Задаваясь различными гипотезами о месте цели, мы можем
подсчитать и вероятности различных комбинаций наблюдения
недолетов и перелетов из числа низких разрывов по каждой
из гипотез. Если при этом мы имеем распределение цели, то
можем и вообще подсчитать вероятности различных комбина-
ции недолетов и перелетов из числа низких разрывов.
При этом вместо срединного отклонения точек разрывов по
дальности мы должны брать величину полу диаметра, сопря-
женного горизонту (в данном примере 14,7 саж.), а для центра
распределения разрывов должны брать точку С (черт. 92) пере-
сечения с горизонтом оси эллипса разрывов, сопряженной гори-
зонту, а не точку О пересечения средней траектории с гори-
зонтом.
По черт. 92 можно сказать, что при прохождении средней
траектории через цель вероятность недолета из числа низких
больше, чем вероятность перелета.
Имея распределение низких и центр этого распределения
285
на горизонте по наблюдению знаков разрывов из числа низких
или измеряя отклонения, мы можем получить и распределение
цели на горизонте.
89. Аналитический способ подсчета распределения
низких разрывов
В § 87 были приведены уравнения и формулы для расчета
сеток распределения по закону Гаусса разрывов дистанцион-
ных снарядов по сопряженным направлениям и в § 88 пока-
зано построение сетки по направлениям горизонта и ему сопря-
женному, а на черт. 91 было получено распределение низких
на горизонте и центр этого распределения. Но система графика
несколько громоздка, и распределение низких разрывов, что
очень важно в процессе выработки правил стрельбы шрап-
нелью, легко может быть найдено и аналитическим путем.
Для этого проекцию единичного эллипсоида разрывов е
(черт. 93) мы можем рассматривать, как эллиптическую ошибку,
образовавшуюся от сложения двух векториальных ошибок cl2 и
d,', из которых d2' имеет горизонтальное направление, а ошибка d,,
ей сопряженная, может иметь различное направление в зави-
симости от положения эллипса е, но координаты конца диа-
метра будут всегда М2(— кВрв; Врв).
Ошибки d2 и d2', как сопряженные, независимы, а следова-
тельно, векториальная ошибка d2' определяет рассеивание около
диаметра М2Ь, оставаясь постоянной, независимо от того, выше
или ниже это рассеивание происходит.
Таким образом, диаметр М2Ь, сопряженный горизонту,
является геометрическим местом центров распределения низ-
ких разрывов и, будучи продолжен до горизонта цели (вода,
286
земля), даст в точке С центр распределения разрывов, полу-
ченных непосредственно у земли (воды).
Центром распределения низких разрывов на границе низких
будет точка Сг Если слой низких разрывов является неболь-
шим слоем всех разрывов, то можно принять среднюю точку
за центр всего рассеивания низких, в противном случае надо
каждый слой рассматривать в отдельности, причем метод под-
счета будет оставаться для каждого слоя один и тот же.
Проведем на черт. 93 среднюю траекторию и найдем поло-
жение центра рассеивания низких разрывов С на горизонте
относительно точки пересечения средней траектории с горизон-
том О1; а также и полуоси эллипса рассеивания низких в плос-
кости горизонта.
Для этого но табличным данным имеем: Вр0; Вря; Be; Вб;
tg 0с и, кроме того, должна быть известна высота средней точки
разрывов Но.
Для направления, сопряженного горизонту, имеем уравнение:
(339) § 87:
Вря
У=~тв;^
где
,,__Вре -|- Брр tg2 0е — Be
2 вРд вРе tgec
Положив у——Нй , получим:
____ BLo к Врд
Х0__т> - •
и ре
Кроме того, дэ -Цл-'о = Я0 ctg0c, откуда
х'о =н0 ctgec —ж0
и
d'2=BPd
(35О>
(351)
(343, § 87).
Пример. Требуется определить распределение низких раз-
рывов у горизонта цели при средней высоте разрывов Но =
= 15 саж. и при тех ясе табличных условиях, как в примере
§ 88, т. е.:
6 = 33°; etg 0 = 1,540; Врд —18 саж.; Вре = 9 саж.; Be = 10 саж.;
Вб=2,8 саж.
Из примера § 88 берем к= 0,574, положив в уравнении
По (350) получим:
15 • 0,574 • 18
х0 =---------а--------
= 17,2 саж.;
287
но (351) получим расстояние от Ог до С (черт. 94):
ж'0=15« 1,540— 17,2 = 6,9 саж.
и, наконец, главную полуось единичного эллипса распределения
низких разрывов:
d'2 = Врв |/ 1— fc* — 18 р^о,б7О = 14,7 са.ж.
Из этих цифр видно, что центр распределения низких раз-
рывов отстоит от средней траектории ближе на 6,6 саж.
Для наглядности построен черт. 94. Точка О — средняя
почка разрывов. Начало координат взято именно в средней
точке разрывов, а ниже на 15 саж. («/ — — 15) проведен гори-
зонт. Средняя траектория, идущая под углом 6е = 33°, пересе-
кает горизонт в точке Оо-
O'О1=Не^Ьс—23,саж.
Отложив ж0=17,2 саж. от точки О', получим центр распре-
деления низких разрывов в 5,9 саж. от (средняя траектория).
Ниже показан единичный эллипс распределения низких
разрывов с полуосями d'2 = 14,7 саж. и Вб=2,8 саж.
90. Распределение клевков на горизонте
В § 88—89 мы видели, как легко может быть подсчитано
распределение низких разрывов; отсюда естественно вытекает
вопрос — возможно ли распределение низких разрывов распро-
странить и на распределение клевков или, что то же, считать,
что клевки распределяются так же, как и низкие разрывы.
На этот вопрос можно ответить элементарно просто: возьмем
весь эллипс разрывов (черт. 95, 96 и 97). На этих чертежах:
288
Черт. 95.
pR — средние траектории, MN — диаметры, сопряженные гори-
зонту, являющиеся геометрическими местами центров распре-
делений низких разры-
вов; заштрихованные слои
ABBAAt — области низких
разрывов, КВ2 — случайные
траектории, касательные к
нижней части эллипсов раз-
рывов jLBj—случайные тра-
ектории, проходящие через
дальнюю границу клевков,
и В2ВХ — области клевков.
На черт. 95 видим, что
при данном положении
средней траектории и боль-
шой оси эллипса с некото-
рым допуском возможно
считать, что клевки распре-
деляются одинаково с низ-
кими разрывами.
Из черт. 96 и 97 ясно
больших осей эллипсов
клевки распределяются так же, как и низкие разрывы, никак
нельзя и такой допуск будет неприемлем.
Итак, вообще говоря, клевки распределяются неодинаково
с низкими разрывами, и, как дальше увидим, распределение
клевков не следует закону Гаусса и представляет несиммет-
ричный закон.
Из черт. 96 и 97 также можно заключить, что наиболее
удобной сеткой для подсчета распределения клевков будет
сетка, составленная по направлению средней траектории; тогда
другим направлением, чтобы ошибки были независимы, должно
быть направление сопряженной средней траектории.
видно, что при таких положениях
и средних траекторий считать, что
Черт. 96.
Таким образом, прежде всего надо построить сетку по
направлению средней траектории и по направлению, ему
сопряженному. Это построение покажем на частном при-
мере § 88.
19 Теория стрельбы 289
Ос —33°; —18 саж.; Врв = 9 саж.; Вд —16 саж.; В<?=ю саж.;
Вб — 2,8 саж.; Яо = 15 саж. tgОс = 0,649; tg20c = 0,4316; 1 +
+ tg2 0с = 1,4316; fc = 0,574; к2 — 0,3298; 1—fc2 = 0,6702.
Направление, сопряженное средней траектории, по ’(340):
„. _ Врв (к Вро tg 6С Врв) __
J Врд(кВрв—Врд^^ —
9(0,574 - 18 - 0,649—9) . —,'20,7 ,
~1« (0,574 • 9—18 • 0,649) — 117 Д—°>177ж-
Приняв произвольно х = 100 саж., найдем П/’=17,7 ]саж.
По этим координатам, приняв среднюю точку разрывов и нача-
ло координат в О, проведем направление, сопряженное средней
траектории (черт. 98).
Черт. 98.
Среднюю траекторию проведем непосредственно по углу
Падения 6С = 33°.
Длина полудиаметра, идущего по средней траектории, по (345):
290
(l_fc2)(1 + tg2ec) =
18 9
10
|//Л0,6702 • 1,4316 =15,9 саж.
Длина полудиаметра, сопряженного средней траектории,
по (346):
d3 = -1 / Врд + В2рв -. (i- к2) (1+ tg2 ьс ) = 12,6 саж.
V Ве
Имея оба сопряженные направления и длины полудиаметров
по сопряженным направлениям, производим построение сетки,
на которой (черт. 98) вписано полностью распределение по за-
кону Гаусса.
Произведя по сетке подсчет, получим, процентное распре-
деление клевков из всех разрывов вообще (черт. 99, верхняя
строка).
-^0
^0,53 1,48 ^3,11 ^7^2,94 ^23 Ъ,27 0,09
0,040 0,112 0,236 0,263 0,223 0,094 0,025 0,007
Черт. 99.
Общая сумма клевков выразится:
0,53 -L-1,48 Д- 3,11 Д- 3,47 Д- 2,94 + 1,23 + 0,27 + 0,09 = 13,12%.
Поделив каждое из этих чисел на 13,12, получим распреде-
ление клевков (черт. 99, нижняя строка).
По этим числам на черт. 100 построена кривая распределения.
Из изучения этой кривой мы видим, что клевки распреде-
ляются не по закону Гаусса и распределение несимметрично.
19* 291
91. Построение сетки ио главным полуосям эллипса
разрывов
Главные полуоси эллипса разрывов являются частным слу-
чаем сопряженных полудиаметров, а потому в тех случаях,
когда окажется удобнее' пользоваться сеткой, построенной по
главным полуосям, может быть построена и эта сетка.
Построим'сетку по главным полуосям для того же примера
(§ 90).
6С = 33°; Врб = 18 саж.; Врв = Ч) саж.; Вв = 10 саж.;
tg6c = 0,649; tg20c = 0,421; Я0 = 15 саж.
fc = 0,574; /г2 = 0,3298 И 1 — к2 = 0,6702.
По (347) § 87
tg2T =
откуда
и
По (348) § 87
= _ 0 747
(В^— B|B)tgOe
Т1 = —18°22'
= + 71°38'.
д _ AB'id cos2 7 — B-pe sin27__ / 324 • 0,901 — 81 - 0,099__
|/ cos2 f — Sill2 у у 0,901—0,099
= 18,9 саж.
и по (349)
Bpd sin2 у — B2pe cos2 у _ /~324 • 0,099 — 81 • 0,901
sin2 7—cos2 Y У 0,099 — 0,901
= 7,1 саж.
Черт. 101.
Для построения сетки (черт. 101) возьмем начало координат
в средней точке разрывов О, проведем горизонт АгА2 и по-
строим направление большой полуоси под углом к горизонту
Y = —18°22' и направление малой полуоси — перпендикулярно
к большой. Имея размеры полуосей, строим сетку.
292
92. Применение для подсчета распределения клевков
круговых сеток распределений но закону Гаусса
В § 88 и 90 был показан подсчет распределений низких
разрывов н клевков по сеткам, построенным по сопряженным
направлениям.
Значительно удобнее и точнее эти же подсчеты могут быть
произведены по круговым сеткам Гаусса.
Для подсчетов распределения низких разрывов или клев-
ков по круговой сетке необходимо правильно трансформиро-
вать на круговую сетку линию горизонта цели, после чего
подсчет ведется так же, как и по основной сетке (черт. 92,
98, 101).
Покажем это трансформирование для подсчета распределе-
ния клевков при трансформировании горизонта с основной
сетки, построенной по направлению средней траектории и по на-
правлению, ему сопряженному (черт. 98), на круговую сетку
(черт. 102).
Для переноса линии горизонта возьмем на основной сетке
(черт. 98) какие-либо две точки пересечения горизонта с лини-
ями, параллельными средней траектории, например, и К2, и
снимем их координаты, причем за ось абсцисс примем диаметр,
сопряженный средней траектории, а за ось ординат—диаметр,
идущий по средней траектории. Начало координат —в центре
рассеивания О.
Координаты точек Кг и К., самое удобное снимать в произ-
вольных единицах, например, в миллиметрах. Тогда имеем:
/Д (о; —27,5) и К2 (50,4; —43,3).
О
2
^~2^мм^те доли^
50)791111 Ыйб 156139
15
29,
4 Iff
2 5
10
6
18
Ю
29
40
16 23
12
50
29,
15
56
32
561
Г50
32
29
16
16
15
3 |3
45
16
63
29
29
23
50
40
79
63
111
89
16
23
10
5
12
5
2
2
1
8
4
5 12
1 3
3
5
2
1
8
4
1
1
5
2
7
8
8
1
£
2
з
1
~Рв %.
0,ОзЬр7 [й151033 [055'|0Я< (30'161 ЦЖз|О,0б№2Ц(и1о £#=13,01
Черт. 102.
Эти координаты и будем трансформировать на круговую
сетку. Для этого заметим, что на круговой сетке по обеим осям
единица одна и та же; в нашем примере (черт. 102)
Е-„ — Еу = Е — 20 мм.
293
На основной же сетке единицы неодинаковы: по оси абсцисс
единицей является d3 = 12,6, а по оси ординат d's= 15,9. Тогда
для трансформации будем иметь:
к' (° ' 20 —
1 12,6 ’ 15,9 j
и
, / 50,4 • 20 . 43,3 20 \
2 15,6 ’ ~’ 15,9 у '
Окончательно получим:
К\ (0; —34,6)
и
К'2 (80; —54,5),
где координаты К\ и К\ выражены в миллиметрах.
Нанеся по этим координатам точки К\ и К'2 на круговую
сетку (черт. 102), проводим линию горизонта А К\ К'2 Вг.
На сетке цифры даны в сотых долях процента. Подсчитав
суммы сотых процента, стоящих под линией горизонта, и поде-
лив эти суммы на 100, получим вероятности клевков (см. черт. 102).
Поделив каждую из этих цифр на их сумму (£р» —13,01%), по-
лучим распределение клевков.
Это распределение построено на черт. 103.
Обращаем внимание, что грубый подсчет по основной сетке
дал Spz=13,l% (т. е. разница на 0,09%).
Распределение на черт. 103 теоретически должно быть со-
вершенно одинаково с черт. 100, и некоторая разница как в
цифрах, так и в чертежах объясняется только степенью точ-
ности графического подсчета (на черт. 102 и 103 подсчет сделан
через Вд, а на черт. 98 и 99 — через 1 Вд) и большей точно-
стыо сетки.
Для подсчета распределения клевков сетка по направлению,
294
сопряженному средней траектории, является наиболее удоб-
ной еще и потому, что на этой сетке горизонт делится ли-
ниями, параллельными средней траектории, на величины, равные
Вд, тогда как на сетке, построенной по направлению, сопря-
женному горизонту, эти деления равны величине сГ2, т. е. длине
полудиаметра, сопряженного горизонту в единичном эллипсе.
Для тех случаев, когда можно принять, что клевки распре-
деляются так же, как и низкие разрывы, можно вообще обой-
тись без построения сеток, а расчет произвести аналитически
(§ 89), приняв полученное распределение одинаково и для
клевков и для низких разрывов; что же касается общего про-
цента низких разрывов и клевков, то его можно подсчитать
просто по проекции эллипсоида разрывов на плоскость, пер-
пендикулярную к плоскости стрельбы.
Имея законы распределения низких разрывов и клевков, мы
можем подсчитать и вероятности недолета и перелета или любой
комбинации захватывающих разрывов для различных положений
цели, что и дает возможность получать распределение цели.
При выработке правил стрельбы шрапнелью часто доволь-
ствуются определением вероятности недолета и вероятности
перелета при некотором заданном, обычно наивыгоднейшем
положении средней траектории; это положение средней траек-
тории относительно цели определяется наибольшим математи-
ческим ожиданием числа пораженных целей, причем объектив-
ным указанием на такое положение средней траектории служит
относительное количество наблюдений недолетов и перелетов
из числа захватывающих разрывов (низких и клевков).
Вероятность недолета низкого разрыва подсчитывается по
сетке, построенной по направлению горизонта и по направлению,
ему сопряженному, а вероятность недолета клевка подсчиты-
вается по сетке, построенной по направлению средней траекто-
рии и по направлению, ему сопряженному.
При употреблении круговой сетки вероятность недолета как
низкого разрыва, так и клевка может быть подсчитана при
трансформации сетки, построенной по направлению горизонта и
по направлению, ему сопряженному.
Для подсчета вероятности недолета из числа захватывающих
разрывов на сетке должна быть проведена средняя траектория
и нанесено положение цели, для которого ведется подсчет.
Пример. Подсчитаем вероятность недолета из числа захва-
тывающих разрывов по сеткам (черт. 91 и 98) и по сетке кру-
гового закона (черт. 104) при трансформации сетки (черт. 91)
для случая прохождения средней траектории через цель.
Сетка черт. 91 дает;
вероятность низкого разрыва................. 0,05224
вероятность низкого недолета..........0,03180
Сетка черт. 98 дает:
вероятность клевка...........................0,1301
вероятность клевка недолета.......... 0,0847
285
Число случаев благоприятных наблюдений недолета из числа
захватывающих будет пропорционально сумме вероятности недо-
летов низкого разрыва и клевка:
Число всех равновозможных случаев для захватывающих
будет пропорционально сумме вероятности всех низких разрывов
и всех клевков:
п—к (0,05224-J-0,1301) — к • 0,18234.
Вероятность наблюдения недолета из числа захватывающих
выразится:
^=™1г=о^зз=бз’з%-
То же можно сделать по сетке кругового закона при транс-
формации линии горизонта, средней траектории и цели с сетки,
построенной по направлению горизонта и по направлению, ему
сопряженному.
Координаты точки Сг (черт. 91) трансформируются в коор-
। динаты точки С" (черт. 104):
(23 1 \
0; -7А-20) или С'(0; 28,5).
16,2 /
Координаты точки Ц (черт. 91) трансформируются в коорди-
I наты точки Ц' (черт. 104):
(йу ‘ 20; Ж 20 )’ или Ц'(8,0; 28’5)
296
и, наконец, координаты какой-либо точки на границе низких
разрывов, например (О; 18) трансформируются:
I 0; —• 20 |, или (0; 22,2).
\ й16’2 /
Нанеся (черт. 104) точки С, Ц' и точку (0; 22,2), лежат} к>
на границе низких разрывов, проводим линии F' К', PR и
ОЦ'.
Вероятность недолета из числа захватывающих будет равна
отношению суммы всех цифр, заключенных в фигуре PRST до
границы низких разрывов, к сумме всех цифр, заключенных
во всей фигуре черт. 104.
Непосредственно подсчет дает:
t-l
Очевидно, эта цифра более точна, чем предыдущая (63,3),
но во всяком случае разница невелика.
Если мы примем, что в данном случае клевки распределя-
ются так, как и низкие разрывы, то вероятность недолета за-
хватывающего разрыва можно получить непосредственно из
черт. 94:
(Р, Q \
_g_j=F(0,4) = 61%,
что дает уже более значительную разницу, -которая получилась
вследствие допуска об одинаковости распределений низких
разрывов и клевков.
Разница между цифрами 63, 67 и 61% во всяком случае
такова, что такой допуск вполне возможен.
Примечая ие. Подсчет вероятности недолета из числа низких
разрывов с черт. 91 дает также 61%.
Обращаем внимание на то обстоятельство, что при прохож-
дении средней траектории через цель вероятность недолета из
числа захватывающих больше вероятности перелета. Вероят-
ность недолета для всего эллипсоида рассеивания будет еще-
больше, что наглядно видно из черт. 98 и 101. Это явление
вообще характерно для шрапнели, когда средняя точка разры-
вов лежит выше горизонта.
ГЛАВА XIII
ПОРАЖЕНИЕ ПУЛЯМИ ОТДЕЛЬНОЙ ШРАПНЕЛИ
93. Распределение пуль в конусе разлета
Для решения целого ряда вопросов при выработке правил
'Стрельбы шрапнелью и, главным образом, для выявления наи-
выгоднейшего интервала разрыва при стрельбе группой шрап-
нелей необходимо изучить предварительно действие отдельной
шрапнели, начиная с распределения пуль или других пора-
жающих элементов в конусе разлета.
Это распределение может быть получено только из опыта.
В качестве примера сошлемся на опыт со 120-.мл шрапнелью,
произведенный в 1931 г. Для этого на щите с уловленными
пулями проводилась окружность, концентрично охватывающая
пробоины почти всех пуль. Радиус этой окружности делили на
10 равных частей (черт. 105) и через точки деления описывали
концентрические окружности, после чего подсчитывали число
пуль, попавших в каждую из кольцевых полос.
Результат опыта сведен в табл. 76.
Таблица 76
Распределение пуль в конусе разлета на основании опыта 1931 г.
со 120-.ЛМ1 шрапнелью
№ колец Опыты Среднее число по- павших пуль Распреде- ление пуль по кольцам в процентах
1 2 3
1 22 14 15 17,0 2
2 61 27 40 42,7 6
3 53 62 90 68,3 10
4 72 93 137 100,7 14
5 110 106 123 113,0 16
6 133 125 116 124,6 17
7 130 112 88 110,0 15
8 80 93 57 80,0 И
9 44 54 23 40,3 6
10 21 21 18 20,0 2
Вне окруяг- ности . . 20 6 5 10,3 1
Итого пуль 756 713 712 727,0 !
298
Изучая табл. 76, видим, что в центре круга и в крайнем
кольце наблюдается наименьшее число пуль, а где-то ^между
5-м и 6-м кольцами (черт. 106) — наибольшее. Иную картину
дает относительная плотность попадания пуль, которая полу-
чится при делении числа пуль на площадь’ кольца, выраже'н-
Черт. 106.
ную в площади 1-го кольца. Площади колец, если принять
площадь маленького круга в центре за единицу, относятся, как
1:3:5:7:9:11:13 :15 :17 :19;
следовательно, если поделить число пуль в каждом кольце на
его относительную площадь, получим относительную плотность
(табл. 77 и черт. 107).
299
Таблица 77
Плотность попадания шрапнельных пуль в концентрические кольца
на вертикальном щите
А» колец 1 2 3 4 5 6 7 8 ° 10
Число пуль . Относительная 17,и 42,7 68,3 100,7 113,0 124,6 110,0 80,0 40,3 20,0
площадь .... Относительная 1 3 5 7 9 11 13 15 17 19
плотность . . . 17,0 14,2 13,7 14,4 12,5 11,3 8,5 5,3 2,4 1,1
Черт. 107.
Интересно отметить, что опыт со 120-м шрапнелью дал
результаты, совершенно противоположные результатам опытов
инж. В. М. Трофимова с 76-и.и шрапнелью.
Инж. Трофимов брал средние цифры из семи опытов. При
опыте со 120-м шрапнелью было произведено только три вы-
стрела. Тщательность производства опытов как в том, так и в
другом случае сомнений не оставляет, но причину диаметрально
противоположных результатов надо’ искать не в числе опытов,
так как средние цифры из трех любых опытов, взятые из семи
опытов Трофимова, с качественной стороны дают совершенно
то же и почти то же с количественной стороны, что и средние
цифры из семи опытов.
Причину такого несоответствия следует искать в устрой-
стве снаряда и именно в том, что в 120-л л шрапнели три ряда
пуль, а в 76-м —два ряда, а также и в разнице окончательных
скоростей.
94. Математическое ожидание числа пораженных
единиц цели для отдельной шрапнели
при различных интервалах разрыва
В § 83 было указано, что для случаев стрельбы дистанцион-
ными снарядами часто успешность стрельбы оценивают числом
пораженных единиц целей; при этом были выведены формулы,
дающие вероятности полезных поражений для 1,2...п попаданий
в единицу цели.
Рассмотрим случай, когда для вывода цели из строя доста-
точно одного попадания.
Для этого случая мы имеем формулу:
Pi = 1 — Ро = 1 — е- “. (320, § 83)
300
При S единицах цели математическое ожидание числа по-
раженных целей будет
M = S(1 — p„) — S (1—-е~с), (321, § 83)
где « — плотность попадания.
Формула (321) дает математическое ожидание числа пора-
женных целей.
Покажем на частном примере для 120-ллг шрапнели прак-
тический прием подсчета математического ожидания числа по-
раженных целей.
Предварительно подсчитаем угол разлета пуль шрапнели.
В § 82 была выведена формула (316) для угла разлета
шрапнельных пуль:
W В(г/с + а)
Для 120-хи шрапнели: R=0,06 м: г = 0,048 .и; 0, = 6° (угол
наклона нарезов); т0 = 823 м'сек; а = 92 м,сек (из опыта).
Вычисления по этой формуле для разных дальностей пока-
заны в табл. 78.
Таблица 78
Угоп разпета пупь 120-.M.W шрапнели
Дальность в каб. 10 20 40 60
Окончательная скорость . . 570 388 261 247
Угол разлета (2(3) . . 13°06' 16°00' 24°16' 2а°16'
Половина угла разлета (3) . . . 6°33' 8'00' 12°08' 12°38'
Для использования формулы (321) § 83 надо найти значения
(1 — е~а) для различных значений а. Самос удобное значение
(1— е~а) вычислить наперед, задаваясь произвольно величинами
а, и с такими интервалами аргумента, при которых возможна
линейная интерполяция.
Таблица численных значений (1 —е~а) помещена в прило-
жениях к настоящему курсу (табл. IX).
Рассматривая эту таблицу, видим, что для практических
целей в тех случаях, когда не требуется большой точности,
можно принимать, что для плотностей «< 0,1 численные значе-
ния выражения рх = 1— е~а равны плотностям а, а при плот-
ностях п>5,2 они равны единице.
Кроме того, для использования формулы (321) надо знать
число единиц цели S. Для подсчета единиц цели вообразим
себе круг сечения конуса разлета пуль. Так как при опыте по
определению распределения пуль в конусе разлета круг сечения
301
конуса делился на десять колец, то разделим радиус взя-
того нами круга (масштаб произволен) на десять равных ча-
стей и, проводя через точки деления окружности, получим
десять колец, которые и перенумеруем арабскими цифрами
(черт. 105).
Проведем касательные к кольцам и положим, что круг сече-
ния конуса разлета пуль взят при таком интервале I, при
котором цель по высоте равна ширине кольца; тогда мы будем
иметь бесконечные горизонтальные полосы целей, причем в
круге сечения конуса разлета их уместилось 20 рядов.
Математическое ожидание числа пораженных целей мы будем
подсчитывать для каждой полосы в отдельности.
Положим, что для поражения цели достаточно одного попа-
дания, тогда при этом условии мы используем формулу (321)
§ 83.
Совершенно ясно, что для тех случаев, когда для пораже-
ния цели требуется не одно, а например, п попаданий, мы
должны бы были воспользоваться и соответствующей форму-
лой § 83.
Определим масштаб чертежа, исходя из размеров цели.
Пусть наша цель имеет размеры по высоте 8/4 м и по
ширине х/3 м (стрелок с колена). Тогда ширина кольца будет
8/4 м, а ширину цели, вследствие того, что масштаб взят про-
извольный, определим в долях ширины кольпа; для этого надо
ширину цели С/3 л) разделить на ширину кольца (3/4 л), что
дает:
1'3/ 1-4 4
/з- /4=5—у = о ширины кольца
/ 1 \
I что составит немного менее — ширины кольца .
\ £1 I
В радиусе поместится целей:
4 90
10 : — = — — 22,5 23 цели.
9 4
Разделим радиус круга сечения конуса разлета на 23 равные
части и проведем через точки деления линии, перпендикуляр-
ные к полосам (полосы на черт. 105 перенумерованы римскими
цифрами). На концентрических окружностях мы получили
бесконечные полосы рядом стоящих целей.
Очевидно, что если бы цель была других размеров, то
черт. 105 представил бы несколько другую картину. Например,
при цели высотой 2 м и шириной 5 м, положив на черт. 105
ширину кольца и полосы по 2 м, ширину цели в долях полосы
или кольца, получим:
5
- — 2,5 ширины кольца.
302
Разделив 10 на 2,5, получим, что по ширине уместят-
ся 4 цели, и, разделив радиус на 4 части, мы также
проведем через точки деления линии, перпендикулярные
полосам.
При больших размерах цели по высоте и, следовательно,
при 20 рядах таких больших целей мы могли бы получить
несуразно большой интервал разрыва. В таком случае можно
уменьшить число колец, но для этого надо пересчитать рас-
пределение пуль по меньшему числу колец.
Этот метод подсчета, как видим, представляет собой абст-
ракцию, которой в данном случае мы пользуемся исключительно
с целью выявления наивыгоднейшего интервала разрыва, наи-
выгоднейшей высоты разрыва и других условий наивыгодней-
Черт. 108.
шего поражения цели данных размеров.
Подсчитаем теперь число целей в полосах и в кольцах и
результаты подсчета сведем в табл. 79 с двумя входами: но-
мера полос (левый верти-
кальный столбец) и но-
мера колец (верхняя го-
ризонтальная строка).
Ввиду симметрии распо-
ложения целей подсчеты
сделаем для четверти
круга (черт. 105).
Для определения чи-
сла целей в части коль-
ца данной полосы до-
статочно подсчитать пло-
щадь соответствующей
фигуры и разделить эту
площадь на площадь
цели, выраженную в отвлеченных единицах.
При подсчете площадей все время придется вычислять
площади полусегментов, подобных BCD (черт. 105), и площади,,
подобные фигуре DCEF.
Для подсчета площади полусегмента вычисляем раньше
площадь сегмента ABCD (черт. 108).
Эта площадь будет равна:
чт гп
(352) (чеРт- 108>
Разделив половину площади Sj на площадь цели, выражен-
ную в отвлеченных единицах (в нашем примере 4/9 кв. ед.),
получим число целей в площади BCD.
Для определения числа целей в площади DCFE (черт. 105)
имеем:
пл. DCEF —
пл. KBFM—
пл. ABCD-YLDEM
(353)
ЗОУ
причем площадь S2 сегмента KBFM выразится:
^ = ^~(r-2)2ctg13- (354)
Для получения величины р для формулы (352) имеем:
sin Р = 1 —-j, , (355)
а для формулы (351):
sin 3=1— (356)
Г
<р==180° —2р
(357)
Вычисления для некоторого неизвестного интервала I прп
пользовании формулами (352) — (357) и для площади цели
7s кв. ед. дают табл. 79 для круга.
Таблица 79
Число целей по полосам и кольцам в конусе разлета для цепи
площадью */о кв. ед.
Кольца По.тосьт^'-^ 1 2 3 'к 5 6 7 8 9 10
I 1,75 2,45 2,29 2,22 2,22 2,21 2,21 2,21 2,21 2,21
II — 2,68 2,98 2,43 2,30 2,29 2,27 2,24 2,24 2,23
III — — 3,40 3,43 2,61 2,58 2,41 2,33 2,36 2,27
IV — — — 3,97 3,83 2,95 2,66 2,49 2,47 2,37
V — — — — 4,41 4,32 3,06 2,77 2,64 2,53
VI — — — — — 5,01 4,51 3,28 2,94 2,75
VII — — — — — — 5,42 4,82 3,53 3,05
VIII — — — — — — 5,72 5,22 3,66
IX — — — — — — — 6,12 5,46
X 6,46
Для того чтобы определить этот интервал I, надо знать
угол разлета пуль или элементов. Угол разлета будет зависеть
от снаряда и дальности. Покажем определение этого интервала
для 120-м пулевой шрапнели для дальностей 10 и 40 каб.
На черт. 109 показано продольное сечение конуса разлета
с числом полос 20.
Ширина полосы в нашем примере 3/4 м, следовательно,
2 г = 3/4 • 20—15 М
и
г = 7,5 .И.
Кроме того,
I=rctgp = 7,5 ctgp.
Из табл. 78 находим рн т. е. половину угла разлета пуль:
304
для Х=10 каб.; pi0 = 6°33'; ctgp10 = 8,7!;
„ Л’=40 каб.; Р40 = 12°О8'; ctgp40 = 4,65.
Тогда для 10 каб. 7 = 7,5 • 8,71=65.4 л = 35,8 саж.
„ 40 ,, 7 = 7,5 - 4,65 = 34,9 .«=19,1 саж.
Таким образом, должны быть найдены интервалы для всех
чех дальностей, для которых производятся расчеты правил
стрельбы.
Само собой разумеется, что для того же снаряда и тех же
дальностей, но для другой высоты цели при том же числе
полос значения интервалов I получатся другие.
Определим для интер-
вала I среднюю плотность
попадания по кольцам
черт. 105.
Если обозначим число
пуль в г-ом кольце nt, а
число единиц цели пли
число целей в том же коль-
це Si, то средняя плот-
ность попадания для 7-го
кольца будет:
77. •
(358)
В табл. 79 указано число
целей в четверти кольца, а
ПОТОМУ ДЛЯ получения ВС- Черт. 109.
личины достаточно сло-
жить вертикальные столбцы этой таблицы и суммы умно-
жить на 4.
Значения числа пуль по кольцам определены опытом и их
возьмем из табл. 76 распределения пуль в конусе разлета
(§ 93); полученные значения SL и сведены в табл. 80.
Таблица SO
Значения величин числа цепей по кольцам и среднего числа пуль и»
Кольца 1 2 3 4 Б 6 7 8 9 10
Число це- лей Si 7,00 20,62 34,68 48,20 61,48 77,44 90,16 103,44 118,68 131,96
Среднее значение числа ПУЛЬ Щ 17,0 42,7 68,3 100,7 113,0 124,6 110,6 80,00 40,3 20,0
20 Теория стрельбы
305
Подставив значения п,- и 8,- в (358), получим среднее значе-
ние плотностей для интервалов I (табл. 81).
Таблица 81
Средние значения плотностей попадания по кольцам
Кольца 1 2 3 4 5 6 7 8 9 10
2,43 2,08 1,97 2,07 1,82 1,61 1,22 0,77 0,34 0,15
Пользуясь табл. 81, мы можем составить таблицу значений
вероятности полезных поражений, т. е. в данном случае веро-
ятностей хотя бы одного попадания в единицу цели:
^ = (1 — р0)=(1 -е~а).
Эти значения могут быть взяты по аргументу at непосред-
ственно из табл. 82.
Таблица 82
Значения 1 —е
Кольца 1 2 3 4 5 6 7 8 9 10
1 — е~а 0,914 0,865 0,861 0,865 0,838 0,800 0,700 0,546 0,288 0,140
Математическое ожидание числа пораженных целей (сред-
него числа пораженных целей), равное Si (1 —е~а), для каждой
полосы найдем, если, взяв по кольцам значения (1—е~а), по-
множим их на значения 8(- и произведения просуммируем. Кроме
того, имея в виду, что полос каждого номера — две, эту сумму
надо удвоить.
Например, для I полосы будем иметь математическое ожида-
ние (м. о.) : М. О. = 2(1,75 • 0,914+2,45 • 0,865 + 2,29 • 0,861Д-
2,22(0,865 + 0,838) 2,21 (0,800 + 0,700 + 0,546 + 0,288 + 0,140)] =
= 29,14.
Для VIII полосы будем иметь:
м. 0. = 2 • (5,72 0,546-[-5,22 • 0,288 + 3,66 • 0,140)= 10,28.
Для X полосы будем иметь:
М. о. = 2 • (6,46 • 0,140)= 1,81
• (все для Интервала I).
В табл. 83 показано математическое ожидание числа пора-
' женных целей при интервале I по всем полосам.
Табл. 83 дает математическое ожидание числа пораженных
целей при определенном интервале I для отдельной шрапнели.
306
Таблица 83
Математическое ожидание числа пораженных цепей при интервале Г
дпя отдельной шрапнели
X» полос I II III IV V VI VII VIII IX X
Математи- ческое ожидание 29,14 29,10 28,10 26,52 23,82 20,38 15,74 10,28 5,04 1,81
Для расчета наивыгоднейшего интервала разрыва нам не-
обходимо найти математическое ожидание числа пораженных
целей для отдельной шрапнели для ряда интервалов, чтобы,
введя рассеивание, путем подсчета найти математическое ожи-
дание числа пораженных целей группой шрапнелей с учетом
рассеивания для ряда интервалов; затем, построив кривые, да-
ющие зависимость математического ожидания поражения от
интервала разрыва, вывести наивыгоднейшие интервалы разрыва
для разных дальностей
Обычно для удобства вычисления выбирают следующие
интервалы разрывов:
ЧД; ЧЛ Щ; i’AJ; 21; зд з1/^ 4Д 4V; &г,
54-2 Г, 67 . . . и т. д.,
немного перейдя за наибольший убойный интервал разрыва
(грубо).
Посмотрим сначала, как получить математическое ожидание
числа пораженных целей для интервалов, больших I, поль-
зуясь тем же кругом разлета пуль (черт. 105).
Для этого заметим, что если интервал увеличится в к раз,
то число целей в полосе также увеличится в к раз, а плот-
ность попадания уменьшится в к2 раз.
Поэтому для каждой из полос I, II, Ш . . . IX, X подсчет
математического ожидайия числа пораженных целей необхо-
димо произвести по следующей формуле.
Для I полосы:
Для VI полосы:
1 В большинстве случаев „нормальный" интервал разрыва сохраняет или
почти сохраняет свое значение для всех дальностей.
20* 307
и вообще для да-й полосы:
V (<>
м. о. = 2 к Zj Snt
(359)
Пример. Подсчитать математическое ожидание числа пора-
женных целей при интервале, равном 2 /.
Предварительно подсчитаем плотности попадания:
так как к = 2 и значения pi = l—е
Ui __CL; _
к’~~ 4 ’
4 (табл. 84).
Таблица 84
а
„ И ~ “4
Значения "ЧТ и pi~i — в
Кольца 1 2 3 4 5 6 7 8 9 10
4 0,61 0,52 0,49 0,52 0,46 0,40 0,31 и,19 0,09 0,04
1-е 4 0,46 0,41 0,39 0,41 0,37 0,33 0,26 0,17 0,09 0,04
Примечание. При вычислении значений 1—е & следует иметь
_______________________________________________a_i
в виду, что при плотностях, меньших 0,1, значения 1—е к- можно прак-
тически принимать равными плотностям попадания.
Тогда для I полосы при интервале, равном 21, по (359)
получим:
м. О. = 4 [1,75- 0,46 + 2,45 -0,41 +2,29 - 0,39 +
+ 2,22 • (0,41 0,37) + 2,21 (0,33 + 0,26 + 0,17 -(-
+ 0,09 + 0,04)] —25,64 ед. цели.
Для УШ полосы получим по (359):
М. О. = 4(5,72 -0,17 + 5,22 • 0,09 4-3,66 • 0,04) = 6,36 ед. цели.
Для X полосы получим по (359):
м. о. = 4(6,46 • 0,04)= 1,03 ед. цели.
Результаты вычислений показаны в табл. 85.
Таблица 85
Математическое ожидание числа пораженных цепей дпя отдельной шрапнели
________________________дпя интервала, равного 21__________
Полосы I И III IV V VI VII VIII IX X
Математи- ческое ожидание 25,64 24,52 22,76 21,84 18,64 15,04 10,68 6,36 3,08 1,03
308
Совершенно так же вычисляется математическое ожидание
числа пораженных целей и для остальных интервалов, боль-
ших I.
Рассмотрим случай, как надо вычислять математиче-
ское ожидание числа пораженных целей при интервалах,
меньших I, используя тот же круг сечения конуса разлета пуль
(черт. 105).
При уменьшении интервала площадь круга сечения конуса
разлета пуль уменьшается пропорционально квадрату числа
раз уменьшения интервала, например, при интервале, в 2
раза меньшем I, площадь круга уменьшится в 4 раза,
при интервале, равном г141, площадь круга уменьшится в 16
раз и т. д.
Пусть S^; — числа целей по полосам и коль-
цам, взятые из г-й горизонтальной строки табл. 79, и а — пло-
щадь цели, тогда после уменьшения интервала в к раз площадь
/-Й полосы в круге разлета будет:
2а
Разделив что выражение на а, получим число целей в поло-
сах после уменьшения интервала в к раз.
Для того чтобы избежать при уменьшенном интервале нового
круга разлета, условимся площадь круга разлета считать для
всех интервалов постоянной, а увеличивать соответственно
площадь самих целей.
Рассмотрим этот случай для уменьшения интервала раз-
рыва в два раза ^2-7^.
Положим, что с уменьшением интервала в 2 раза площадь
круга не уменьшается в 4 раза, а остается та же, а площадь
отдельной " цели увеличивается в 4 раза, так что из двух
рядом стоящих полос образуется новая полоса с числом
единиц цели:
&+& + i
4
Пусть в I полосе число ед. цели=8Г
во II ,, ,, „ „ 8о
в -Л. „ ,, ,, ,,
Обозначим через а площадь цели.
Нормальная площадь круга равна
°- (814_$2~Ь • • • +^ю)-
I
Оставляя для интервала — ту же площадь круга, площадь
i-J
309
единицы цели примем равной 4а, и тогда новое число еди-
ниц цели по полосам получим из выражения:
I полоса II полоса V полоса
a (Sj + S2 + ••• + &1о) Si + S2 S3 + S4 <S9 + Slo
----------_----------+ +. . .+__---------------------------,
но уже вместо прежних 10 полос имеем только 5.
Плотность попадания при уменьшении интервала в 2 раза,
очевидно, увеличится в 4 раза.
Для математического ожидания числа пораженных целей
будем иметь:
для I новой полосы:
для V новой полосы:
5,46 4- 6,46
4
Аналогично при уменьшении интервала в 4 раза для
математического ожидания числа пораженных целей будем
иметь:
для I новой полосы (I + II + II1-|-1V старые полосы):
м. о. = 2
1,75 —j- 0 + 0 4“ О
~16 “
2,45 2,68 + 0-|-0
16
+ -- -16 ' I1-* )+
, 2,22 4-2,30 4- 2,66 + 3,83 / ~16аА
4-------------------!-----II — в I 4- .
16 \ /
. 2,21 4-2,23 4-2,27 4- 2,37 / -М«Ю\П
• • • 4-------------—----------- 1 — е ;
16 \ /J
для II новой полосы (V+VI4- VJI 4- VIII старые):
п Г 4,41 4-04-04-0/ - 16аА ,
=2[---"16~—(1-е ;+• •
, 2,53 + 2,75 4- 3,05 4- 3,66 / ~16М'|
+ ~Чб------------~е } ]•
310
Для III новой полосы (IX Ч-X старые):
При дальнейшем уменьшении интервала разрыва схема
расчета остается совершенно такой же.
Пример. Подсчитать математическое ожидание числа пора-
женных целей для интервала разрыва 1/4/.
Предварительно составим табл. 86 плотностей, увеличенных
в 42 = 16 раз, и соответствующих им вероятностей хотя бы
одного попадания в единицу цели.
Таблица 86
Плотности попадания и вероятности хотя бы одного попадания в единицах
цепи для интервала, равного 1/4 I
Кольца 1 2 3 4 5 6 7 8 9 10
16 щ 38,89 33,28 31,52 33,12 29,12 25,76 19,52 12,32 5,44 2,40
„ — 16 «г 1 — е г 1 1 1 1 1 .1 1 1 0,996 0,909
Полосы I, II, Ш и IV:
М. О. = 2
1,75 , . 2,45 + 2,68 1 .
ле- ‘1 + —16-------------1+
2,29 + 2,98 4-3,40 , 2,224-2,43 + 3,43 + 3,97
16 1 16
- , 2,22 + 2,30 + 2,61 4-3,83
16
+ 2,21+2,23+2,27+ 2.37 0>9091 = 10>вв единиц цели.
16
Все эти подсчеты по окончании следует свести в общую
табл. 87, которая, будучи вычисленной для произвольного
интервала 7, годна для всех дальностей для данной таблицы
стрельбы (в нашем примере 12О-лм< шрапнель времен мировой
войны 1914—1917 гг.).
Табл. 87 годна для всех дальностей, но для каждой даль-
ности величина интервала 1 будет своя, и, как было указано
выше, для дальности
10 каб. 7=65,4 м = 35,8 саж.
20 „ 7=47,4 „ =25,9 „
40 .. 7=34,9 „=19,1 „
60 „ 7=33,5 „=18,3 „
311
Таблица 87
Математическое ожидание числа пораженных цепей, размерами 3/4 м X1 з м,
для 120--и>и отдельной шрапнели и для различных интервалов разрыва
X. Полосы Интер- X. валы I II III IV V VI VII vni IX X
1/8 I 1,4 1 1/2 1 19 10 55 ,66 19 4, ,09 89 16 8, ,83 55 12 ,59 1 0,56 2,12 5,10
I 29,14 29,10 28,10 26,52 23,82 20,38 15,74 10,28 5,04 1,81
1,5 / 2 1 28,98 27,90 27,03 25,08 21,84 17,97 13,14 8,10 3,72 1,36
25,64 24,52 22,76 21,84 18,64 15,04 10,68 6,36 3,08 1,03
2,5 I 21,75 20,75 19,92 18,38 15,65 12,68 8,83 4,89 2,20 0,78
3 1 18,90 18,18 17,40 15,96 13,32 10,68 7,80 4,44 2,10 0,62
3,5 ] 16,94 16,20 15,47 14,28 12,11 9,83 6,86 3,88 1,76 0,55
4 I 15,08 14,00 13,45 12,43 10,54 8,71 5,97 3,35 1,44 0,49
4,5 I 13,65 13,18 12,63 11,54 10,01 7,85 5,40 3,10 1,30 0,43
5 7 12,93 12,19 11,47 10,64 8,80 7,06 4,82 2,70 1,16 0,39
5,5 7 6 1 11,48 10,90 10,04 9,58 7,84 6,39 4,36 2,45 1,06 0,36
10,48 9,94 9,46 8,77 7,37 5,77 4,00 2,23 0,97 0,32
Примечание. Математические ожидания, полученные в решенных
ранее примерах, в таблице подчеркнуты.
В настоящем параграфе математическое ожидание числа
пораженных целей для отдельной шрапнели нами рассмотрено
на частном примере для цели размерами 3/4 м X Дз м- В случае
цели иных размеров горизонтальных полос (I, 11 . . .) будет
попрежнему десять, так как при расчете плотностей попадания
мы исходим из опыта, при обработке которого сечение круга
разлета пуль (элементов) было разделено на 10 колец. Что же
касается вертикальных полос, то число их при других разме-
рах цели будет, конечно, иное, так как ширина цели при этом
методе расчета всегда выражается в долях высоты цели.
В зависимости от высоты цели и углов разлета определятся
и величины интервалов I для любой дальности.
Для подсчета математического ожидания мы пользовались
для частного примера формулой (320) § 83, исходя из того, что
для поражения цели необходимо и достаточно одного попадания.
Для тех же случаев, когда для поражения цели требуется иметь
не менее п попаданий, следует пользоваться одной из формул
(323)—(326) § 83.
Полученная нами (на частном примере) табл. 87 содержит
математическое ожидание числа пораженных целей отдельными
шрапнелями при определенных интервалах и является только
вспомогательной таблицей, которая нужна для тарирования
„области опасных разрывов" для дальнейших расчетов.
Г ЛАВА XIV
ДЕЙСТВИЕ ГРУППЫ ШРАПНЕЛЕЙ
95. Область всех возможных разрывов и область
опасных разрывов
Для выяснения наивыгоднейшпх условий поражения цели
снарядами дистанционного действия необходимо принять во
внимание: во-первых, действие отдельной шрапнели, характе-
ризующееся математическим ожиданием числа пораженных
единиц цели или целей на том или ином интервале разрыва, и,
во-вторых, рассеивание точек разрывов, характеризующееся
законом рассеивания.
Таким образом, говоря о поражении цели группой шрапнелей,
приходится говорить не о том или ином определенном интер-
вале разрыва, а об интервале средней точки разрывов или о сред-
нем интервале.
В этом случае полный эллипсоид разрывов представит
„область всех возможных разрывов". Размеры и положение
осей эллипсоида разрывов для любого положения средней
точки разрывов могут быть всегда получены, если известны
параметры, характеризующие закон рассеивания точек разры-
вов (ВРд', Врв; Вв и угол падения).
Не каждый из разрывов в области всех возможных разры-
вов будет наносить поражение цели, хотя бы он и был заклю-
чен внутри убойного интервала. Поражающими разрывами будут
только те разрывы, которые произойдут внутри некоторого
пространства, представляющего вид либо конуса, либо клина,
что зависит от боковых размеров цели. Это пространство, кото-
рое включает в себя разрывы, могущие нанести поражение
цели, называется областью опасных разрывов.
Пусть (черт. 110) средняя траектория МЦ проходит через
цель Ц', в точке О —средняя точка разрывов; е— эллипс всех
возможных разрывов (проекция эллипсоида разрывов на пло-
скость стрельбы); точка М ограничивает предельный убойный
интервал разрывов (ЦсУ, угол разлета пуль KML = 2[i.
Построим треугольник ЕГ)Ц, стороны которого ЕЦ // КМ,
ВЦ // ML и DE _L МЦ.
Треугольник ЕВЦ представляет сечение области опасных
разрывов, которые при незначительной ширине цели имеют
313
вид конуса, а при широкой цели —вид клина. Этот конус или
клин и называется областью опасных разрывов, так
как только те разрывы, которые произойдут в этом простран-
стве, могут нанести поражение цели. Например, разрыв Ах
является поражающим разрывом, так как цель всегда будет
находиться в конусе разлета его пуль (элементов).
Разрывы, происшедшие на линиях ВЦ и ЕЦ, поражающие
па пределе; все же разрывы, подобные й3, как видно из чер-
, :тежа, дают конусы разлета пуль, не задевающие цели.
Черт. 110.
Из черт. 110 ясно и построение области опасных разрывов,
для чего надо при цели Ц так построить угол, равный углу
разлета пуль (элементов), чтобы средняя траектория являлась
его биссектрисой, а затем ограничить эту область убойным
интервалом.
96. Математическое ожидание числа пораженных
целей для группы шрапнелей
Для выяснения математического ожидания поражения цели
(числа пораженных целей) при определенном среднем интер-
вале и при некоторой высоте средней точки разрывов подсчет
ведется, во-первых, только для тех разрывов, которые проис-
ходят внутри области опасных разрывов, а во-вторых, учиты-
вается и рассеивание точек разрывов или вероятность разрыва
в той или иной точке.
Вообразим (черт. 111) область опасных разрывов ВЦЕ, на
которой проведены сечения кругов разлета пуль (черт. 105),
•314
11 1
на интервалах-j-Z: -j-Z, Z, 1 —У . • . и т. д. Какой-либо круг,
например, ED, разделим на 20 (или иное число) равных частей,
представляющих горизонтальные полосы (черт. 105) I, II . . .
и т. д. Через точки делений из вершины опасных разрывов про-
ведены радиальные линии. На полосах вписывают математиче-
ское ожидание числа пораженных целей для отдельной шрап-
нели. Биссектриса МЦ представляет среднюю траекторию. Для
того чтобы получить математическое ожидание, например, для
среднего интервала 31, наложим на область опасных разрывов
эллипс всех возможных разрывов, который для удобства заме-
няется параллелограмом с сеткой, построенной по двум сопря-
женным направлениям. На черт. 111 взята сетка для паралле-
лограма по направлению средней траектории и по направлению,
ему сопряженному. Положим, что параллелограм начерчен на
прозрачной бумаге и на нем вписаны вероятности разрывов по
закону Гаусса.
Наложение области всех возможных разрывов параллело-
грама ABCD на область опасных разрывов для случая, когда
средняя траектория проходит через цель, произведем так,
чтобы средняя точка разрывов упала на средней траектории МЦ
на интервале 31 и линия МК совпала с биссектрисой МЦ.
В каждой точке этой области, например, в точке а, будут два
числа: одно, дающее математическое ожидание поражения цели,
если снаряд разорвется наверное в а, а другое — вероятность
разрыва в а. Взяв произведение таких чисел для всех точек
области ABCD и сложив их, получим математическое ожидание
поражения с учетом закона рассеивания.
315
Произведя эти подсчеты для ряда средних интервалов раз-
рыва п для различных положений средней траектории относи-
тельно цели, мы сможем построить кривые зависимости мате-
матического ожидания поражения от интервала разрыва и от
положения средней траектории относительно цели, из которых
и определим наилучшие условия поражения. После этого надо
дать объективные признаки, по которым управляющий огнем
сможет судить о среднем интервале разрыва, о положении
средней траектории относительно цели и о высоте средней
точки разрывов.
Из сопоставления условий наилучшего поражения и его
объективных признаков оформляются правила стрельбы.
В § 96 и на черт. 111 показана, так сказать, принципиаль-
ная сторона решения задачи; практически же делать так под-
счет неудобно по двум причинам: во-первых, угол ЕЦГ), равный
углу разлета пуль (элементов), может быть очень мал, и, для
того чтобы произвести подсчеты, потребуется неудобно боль-
шой масштаб чертежа, а во-вторых, при таком построении при-
дется для каждой дальности производить новое построение и
тарирование области опасных разрывов. В дальнейшем покажем
удобный практический прием построения и тарирования одной
области опасных разрывов. Что касается построения параллело-
грамов области всех возможных разрывов, то таковые надо для
каждой дальности строить особо, но это большого труда не
составит.
Для построения области всех возможных разрывов может
быть взята любая сетка, построенная по двум сопряженным
направлениям, но наиболее удобными являются две: или сетка,
построенная по главным полуосям эллипса разрывов, или сетка,
построенная по направлению средней траектории и по направ-
лению, ему сопряженному, причем первая сетка удобна только
в том случае, когда большая полуось эллипса разрывов совпа-
дает со средней траекторией или когда угол между большой
осью п средней траекторией пренебрежимо мал и допустимо
принять совпадение большой оси со средней траекторией,
1)7. Практический прием построения и тарирования
области опасных разрывов
Для построения области опасных разрывов примем, что она
представляет прямой угол (черт. 112). Это, кроме удобства
графических подсчетов, дает еще п то преимущество, что для
подсчета математического ожидания на любую дальность мы
сможем пользоваться во всех случаях одной и той же областью
опасных разрывов, но вводя в области всех возможных разры-
вов соответствующее искажение масштаба в направлении, пер-
пендикулярном к средней траектории.
Будем считать, что фигура ЕЦБ (черт. 112) представляет
область опасных разрывов и что сечения этого конуса (клина)
на любом интервале Ц представляют собой известный нам круг
316
(черт. 105), разбитый на 10 колец (20 полос) и покрытый пора-
жающими пулями (элементами), распределенными по выведен-
ному из опыта закону.
Эти сечения мы можем провести на произвольных расстоя-
ниях от вершины конуса Ц по биссектрисе ОЦ (она же сред-
няя траектория). На черт. 112 принято 7=20 мм (обычно
практически для работы этот масштаб берут много больше,
например, /=100 мм или даже 7 = 200 мм).
Наиболее удаленное сечение ED при Л = 6 / разделим на
20 (по числу горизонтальных полос черт. 105) равных частей и
через точки деления проведем радиальные линии, которыми
круги разлета пуль (элементов) на всех интервалах Е будут
разделены на 20 равных частей.
Примечание. Если при обработке опыта по распределению пуль
(элементов) в конусе разлета число колец было бы не 10, а меньше,
то и прп тарировании области число делений будет соответственно
меньше.
Дальнейшее тарирование покажем на частном примере для
120-лл шрапнели.
В каждом делении впишем найденное нами математическое
ожидание поражения для отдельной шрапнели из табл. 87 (§ 94).
Затем для каждой из дальностей, для которых производятся
подсчеты, надо нанести те интервалы разрыва, для которых
мы будем подсчитывать математическое ожидание поражения.
Производить подсчеты для интервалов */47, 1j2l, I, I,
21. . .67 неудобно, потому что эти интервалы хотя и вполне
определенные, но произвольные и ничему реальному не отве-
чают.
Для целей стрельбы наиболее удобно интервалы разрыва
выражать в табличных дальностях, отвечающих делениям при-
цела. В частности, для прицелов морской артиллерии наимень-
ший интервал разрыва удобно принять равным ДХ = 1/4 каб. =
= 25 саж. (6-футовые меры) и протарировать область опасных
разрывов через интервалы ДХ, 2 ДХ, 3 ДХ . . . и т. д. до пре-
дела убойности.
Определим прежде всего масштаб области опасных разры-
вов для дальности, например, 10, 20, 40 и 60 каб.
Для 10 каб. мы имеем 7=35,8 саж., но так как на области
опасных разрывов 7=20 мм, то, следовательно, для 10 каб.
имеем, что 1 саж. = 0,55 мм.
Подобным образом получим цену 1 саж. для всех дально-
стей (табл. 88).
Дальше определим цену ДХ = 1/4 каб. для тех же дально-
стей в масштабе области опасных разрывов (табл. 89).
По этим данным на области опасных разрывов проводим
однотипные линии перпендикулярно к биссектрисе (средней
траектории) через деления, равные ДХ, 2 ДХ . . . и т. д. при-
близительно до предела убойности.
Для удобства работы пунктиры делают цветными и для
каждой дальности берут свой цвет.
317
Таблица 88
Цена 1 саж. для дальностей в 10, 20, 40 и 60 наб.
X каб. 10 20 40 60
20-лмг области опасных ра'зрывов соответствуют 1 саж. области опасных разрывов соответствует Цена \Х = каб 1=35,8 саж. 0,55 мм Таблиц дпя дальнее 1=25,9 саж. 0,77 Jt.w а 89 тей в 10, 20 1=19,1 саж. 1,077 мм 40 и 60 наб 1=18,3 саж. 1,093 мм j
X каб. 10 20 40 60
ДХ = каб. = 25 саж. 13,8 мм 19,2 мм 26,2 мм 27,3 мм
На черт. 112 тарирование по ДХ показано для дальностей
10 и 40 каб.
Затем определим величину предельных убойных интервалов
и выразим их для удобства в величинах ДХ в масштабе обла-
сти опасных разрывов.
Величину убойного интервала найдем по формулам § 81:
= ,W±g) М г (312) (v„ + a) Vy5 v 7
где 0«.=1/-9~ (31«) у Рп
Для 120-.W34 <7^10 кг/м. Подсчеты по шрапнели Е= 39100 и для живых целей (310) и (312) сведены в табл. 90.
Таблица 90
Убойный интервал Туб для дальностей в 10, 20, 40 и 60 каб.
X каб. 10 20 40 60
Дб в м 229,5 207,0 174,4 173,0
1уб-в мм 69 87,2 99 103
1уб ® • 5 4 4 4
318
п
Значения предельных убойных интервалов принимаются во
внимание в том смысле, что за их пределами математические
ожидания поражения не подсчитываются и наносить их на
«область опасных разрывов нет никакой надобности, так как это
Черт. 113.
случаях, когда средняя
только будет пестрить чертеж и мешать подсчетам. Затем надо
протарировать область опасных разрывов по А//, т. е. нанести
линии средних траекторий параллельно биссектрисе угла в тех
траектория проходит дальше и ближе
цели на ДХ, 2 ДХ, 3 ДХ и т. д.
(черт. 113). Это требуется для под-
счета математического ожидания
поражения в тех случаях, когда
средняя траектория проходит не
через цель, а дальше или ближе
цели.
Для этого предварительно надо
найти величины Д?/, 2 А?/ и т. д„
соответствующие изменению при-
цела на ДХ, 2 ДХ и т. д. Эти вели-
чины мы найдем в основной таб-
лице стрельбы.
— /----------4 Найденные величины Д?/, 2 Аг/
Черт. 114. и т. д. непосредственно наносить
на область опасных разрывов нель-
зя, потому что масштаб области в направлении, перпендику-
лярном к средней траектории, искажен вследствие того, что
угол разлета пуль (элементов) 2 р заменен для всех дальностей
прямым углом, а потому надо найти искажение масштаба в
направлении, перпендикулярном к средней траектории, что
производится на основании следующих соображений.
Пусть 1)Ц (черт. 114) —- средняя траектория. Вместо поло-
вины угла разлета р взят угол в 45° и, следовательно, вместо
радиуса круга разлета Ъ на каком-либо интервале I взят
радиус а.
Из черт. 114 имеем:
а = 1 tg 45° = I,
b—I^
320
или
b= (itgp,
откуда
a = bctgp. (360)
Таким образом, все величины в направлении, перпендику-
лярном средней траектории, должны быть увеличены в котан-
генс половины угла разлета раз.
Выпишем величины Дг/ для ДХ = 1/4 каб. из основной таб-
лицы стрельбы, где они даны в тысячных дальности, и пере-
ведем их в сажени (табл. 91).
Таблица 91
Перевод в сажени значений Ду, выраженных в тысячных дальности
X в каб. 10 20 40 60
Д/у в тысячных даль- ности . 0,6 1,0 2,1 4,0
Ху в саж 0,6 2,0 8,4 24,0
Ьти значения Дг/ мы имеем в направлении, перпендикуляр-
ном горизонту или вообще линии цели. Вам же они нужны
в направлении, перпендикулярном к средней траектории. Чтобы
получить Дг/ в направлении, перпендикулярном к средней
траектории, умножим их на cosOe (табл. 92).
Таблица 92
Перевод Ду I пинии цели в Ду I средней траектории
X в каб. 10 20 40 60
Дг/ I линии цели, в саж. У., 0,6 1°18' 2,0 4С22' 8,4 18°27' 24,0 45°30'
cos 0С 1,00 0,99 0,95 0,71
Д?у I средней траектории, в саж 0,6 1,98 7,98 17,03
Масштаб в направлении, перпендикулярном к средней траек-
тории, как выведено выше (360), должен быть увеличен в ctg р
раз, и для 120-лглг шрапнели он показан в табл. 93.
Таблица 93
Масштаб в направлении, перпендикулярном средней траектории
X в каб. 10 20 40 60
₽ 6°33' 8°00' 12°08' 12°38'
Увеличение масштаба в направлении, перпенди- кулярном к средней траектории 8,7 раза 7,1 раза 4,7 раза 4,5 раза
21 Теория стрельбы
321
Выведем величину Д?/ в масштабе области опасных разры-
вов для дальности в 10 каб.
По табл. 93 мы имеем, что для 1=20 мм в направлении
средней траектории он будет 20Х8>7=174 мм, но для Х =
= 10 каб. 1 = 35,8 саж., следовательно, для Д// = о,6 (табл. 91)
соответственно XX = 1li каб. получим:
для X = 10 каб.
20 • 8,7 • 0,6
35,8
для А’= 20 каб.
&Уы
2,92 мм;
20 • 7,1 • 1,98
------28Щ-------= 1°’9 ММ’
для Х = 40 каб.
А?/40
20 • 4,7 • 7,98
19,1
39,2 мм;
для Х = 60 каб.
20 • 4,5 • 17,03
-------—— ------ =83,7 ММ.
Горизонтальные линии, проведенные на области опасных
разрывов параллельно биссектрисе и в расстоянии от нее
2,9 мм; 10,9 мм; 39,2 мм и 83,7 мм, будут отвечать положе-
ниям средней траектории, проходящей в расстоянии ДХ =
= Х каб. от цели, причем линии, проведенные выше биссек-
трисы, отвечают положению средней траектории дальше цели
на 71 каб., а линии, проведенные ниже биссектрисы, отвечают
положению средней траектории на г/4 каб. ближе цели.
Этим тарирование области опасных разрывов может быть
закончено, но, кроме этого, необходимо иметь таблицу значе-
ний коэфициентов убойности, выражающих отношение числа
пуль (элементов), пробивших сосновую доску толщиной 2,5 см,
и половины засевших в ней к числу всех попавших в нее
пуль (элементов).
Примечание. Для элементов, которые сами содержат разрывной
заряд, этих коэфициентов не требуется.
На черт. 112 показана протарированная область опасных
разрывов, но не для всех дальностей, дабы не пестрить излишне
чертежа. Величины 2 Ху и 3 Ху по той же причине не тари-
рованы.
98. Построение параллелограма (сетки) области всех
возможных разрывов
В § 96 было указано, что в качестве области всех возмож-
ных разрывов удобнее взять сетку параллелограмов, построен-
ных по главным полуосям эллипса разрывов или по направ-
лению средней траектории и направлению, ему сопряженному.
Обычно строится единичный параллелограм в масштабе обла-
322
сти опасных разрывов для соответствующей дальности; потом
параллелограм искажается в направлении, перпендикулярном
к средней траектории, в ctg₽ раз (₽—половина угла разлета
пуль или элементов); затем из единичного, уже искаженного,
параллелограма. строится сетка области всех возможных разры-
вов; наконец, в малых параллелограмах сетки вписывается
распределение точек разрывов по закону Гаусса (обычно для
полного параллелограма области всех возможных разрывов
довольствуются четырьмя срединными отклонениями по обеим
полуосям).
Пример. Построить параллелограм (сетку) области возмож-
ных разрывов для 120-льл шрапнели для дальности 40 каб. по
направлению средней траектории и по направлению, ему сопря-
женному.
Данные для Х = 40каб.:
Д,й=49 саж.; Врв=15 саж.; Вв = 6,9 саж.; бс —18с27'.
По (335', § 87) имеем:
В2е + В2д tg2 Ос - В2е
2 Врд Вре tg 6е
= 0,9067;
к- = 0,8222;
1— к- =0,1778;
tgOc = 0,3336;
tg2 ес = о,шз;
1 4-tg26c = 1,1113.
Длина срединного отклонения по средней траектории
по (345):
Врд Вре -----------------
—-----Be----Р С1-А:2И1+^“6е) =47,4 СаЖ.
Длина срединного отклонения по направлению, сопряжен-
ному средней траектории, по (34з):
^=|/ + ^2^-(1-л2)(1+^ос) =
= VВ2рд + В2ре —d's2 =16,73 саж.
Для направления, сопряженного средней траектории, имеем
уравнение прямой, проходящей через начало координат,
__ Врв ВРд °C — Вре) „ „ „ _
V/ уч . уч X Л \ " V • U 1. О гЛ/у
Врд (к Вре —Врд tg )
а полагая произвольно, что ж = 100 саж., получим:
у~ 18,9 саж.
Для Х = 40 каб. мы имели масштаб: 1 саж. = 1,047 мм.
Возьмем (черт. 115) произвольно систему прямоугольных
осей координат XOY, направив ось Х-ов горизонтально (или по
линии цели, если угол места не равен нулю). Среднюю точку
разрывов примем в начале координат.
21* 323
Под углом падения 0С = 18°27' проведем направление сред-
ней траектории, по которой отложим отрезки OB1 = OB2 = d'g =
= 47,4 саж. В масштабе области
OBL = ОВ2 = d'3 = 49,7 мм.
По координатам Мв (+ 100; + 18,9 саж.) проведем направле-
ние сопряженное средней траектории, и отложим отрезки
0Ег = 0Dt = d3 — 16,73 саж.
В масштабе области опасных разрывов
0Е1 = 0DL = d3 = 17,5 мм.
По этим двум сопряженным направлениям построим паралле-
лограм
Параллелограм А^Р^ мог бы быть использован в том
случае, если бы область опасных разрывов не была искажена
в прямой угол.
Вследствие искажения области опасных разрывов мы должны
исказить параллелограм в направлении, перпенди-
кулярном средней траектории.
Все длины в направлении, перпендикулярном средней траек-
тории, увеличиваются в ctg р раз, а для дальности 40 каб, в
4,7 раза (§ 97, табл. 93).
Проведем перпендикуляры к средней траектории: Лр42, С\С2,
E\F, и КгКг и, продолжив их, отложим:
ЛД = 4,7 А^.,;
С02 =4,7 С,С2;
FF2 =4,7 FjF2
и КК2 =4,7 КХК2.
324
Соединив последовательно точки А, С, F и К, получим парал-
лелограм ACFK.
После этого проведем линию ED // АС или ED // KF. При
проверке точности построения должно быть:
АС // KF и CF // АК
и, кроме того, линии /1(7 и FK должны пройти через точки
Л', и В.,.
Черт. 116.
Фигура ACFK и есть единичный параллелограм в нужном
нам искажении в масштабе области опасных разрывов для
дальности 40 каб.
После этого развертываем единичный параллелограм в сетку,
но осей координат не наносим (они больше не нужны), а сред-
нюю траекторию проводим горизонтально (черт. 116). Построе-
ние сетки делают на прозрачной бумаге.
99. Практический прием подсчета математического
ожидания числа пораженных целей, пользуясь
областями опасных и всех возможных разрывов.
Влияние интервала разрыва на поражение цели
(ошибки в установках трубки)
Прием подсчета математического ожидания числа поражен-
ных целей покажем на частном примере для Х = 40 каб., для
7= 4 АХ и для случая, когда средняя траектория проходит
через цель, так как о принципиальной стороне вопроса сказано
в § 96.
325
Для подсчета накладываем область всех возможных разры-
вов средней точкой рассеивания О на точку, отвечающую выб-
ранному нами интервалу 4ДХ (на черт. 112 точка О). При этом
среднюю траекторию направляем по биссектрисе ОЦ.
Под каждым малым параллелограмом сетки мы видим
математическое ожидание поражения тарированной области.
Для четкости подсчета будем придерживаться правила, что
для всей площади малого параллелограма вероятность раз-
рыва одна и та же, и из всех цифр математического ожидания
поражения, которые пришлись в данном малом параллело-
граме, будем брать среднее арифметическое.
Подсчеты будем вести по вертикальным рядам и только
в тех малых параллелограмах, которые не выходят за пределы,
убойных интервалов.
Для каждого вертикального ряда будем брать сумму про-
изведений из средних значений м iтематического ожидания
поражения отдельной шрапнелью для данной точки разрыва
на вероятность разрыва в этой точке.
Подсчетами находим:
IV ряд. +4 = (0,553 • 0,01684-1,98 • 0,0403 + 10,55 • 0,0625) =
= 0,749 ед. цели;
V ряд. +в = (3,38 • 0,0403-|-12,72 • 0,0625 + 12,21 • 0,0625 +
-|-4,38 - 0,0403 + 0,50 • 0,0168)= 1,878 ед. цели;
VI ряд. Л6 = (16,13 • 0,0403 + 15,19 • 0,0403 + 2,38 • 0,0260) =
= 1,325 ед. цели;
VII ряд. 47 = (2,72 • 0,0168 -(-2,73 • 0,0168 + 7,11 • 0,0168) =
= 0,211 ед. цели.
Просуммировав эти результаты для дальности 40 каб. при
интервале 4ДХ = 1 каб. и при прохождении средней траекто-
рии через цель, получим, что математическое ожидание
М. 0. = 0,749-]-1,878 + 1,325 + 0,211=4,163 ед. цели.
В сущности слагаемые 0,749; 1,878; 1,325 и 0,211 следовало
бы умножить на коэфициенты, равные отношению числа всех
пробивших и половины всех засевших пуль к числу всех
попавших пуль, но так как эти отношения можно получить
только из опыта, а опыта для 120-jo шрапнели не было, то
мы должны принять, что внутри убойного интервала все пули
убойные, и эти коэфициенты считать равными единицам.
Таким же образом подсчитывают математическое ожидание
и для остальных интервалов от интервала, равного нулю, до
предельного убойного интервала (для Х = 40 каб. 1уо 4 ДХ).
Эти подсчеты делаются для всех тех дальностей, для кото-
рых разрабатываются правила стрельбы.
Подсчеты сводятся в таблицы, по которым строятся кривые.
Из черт. 117 видим, что наивыгоднейший интервал при про-
хождении средней траектории через цель для всех дальностей
326
примерно один и тот же, а именно —около 23/4 ДХ — 683/4 саж. %
чг 70 саж., грубо s/4 каб. Одновременно черт. 117 дает измене-
ние математического ожидания поражения при изменении интер-
М.О.
Черт. 117.
вала разрыва и при прохождении средней траектории через
цель (ошибка в установке трубки).
100. Влияние удаления средней траектории от цели
при неизменном среднем интервале разрыва (ошибка
в установке прицела) и влияние высоты разрыва
Для того чтобы выявить влияние удаления средней траек-
тории от цели при неизменном интервале, необходимо подсчи-
тать математическое ожидание поражения на тех же интервалах,
что и при прохождении средней траектории через цель, но
при этом наложение области всех возможных разрывов на
Область опасных разрывов делается несколько иначе.
Во-первых, необходимо найти понижение или повышение
средней точки разрывов. При прохождении средней траектории
ближе (или дальше) цели на величину ХДХ (черт. 118) средняя
точка разрывов понизится (или повысится) на величину КДу.
Величина КДу может быть найдена или решением треугольни-
327
ков ОАЦ, О1АА1 и О2АА2, или расчетом с помощью основ-
ных таблиц стрельбы. Обычно применяется последний спо-
соб.
Из таблиц стрельбы мы имеем величину Дг/ при изменении
прицела на величину ДХ. Прп отклонении средней траектории
От цели на величину КЬХ
Принимают изменение сред-
«Л1/' ~ Ней высоты разрывов по от-
4-0 Ношению к нормальной вы-
л''-- Соте разрывов Яо = НО рав-
цЫм
Например, для Х = 4О
л /7\ К’аЙ- ^У —8’4 саж- Если
----------I ^С1--Средняя траектория прой-
Act Дальше цели на 1 каб.=
~~---------------Jq ----i ‘ == 4 ДХ, средняя точка
Разрывов поднимется на
Черт. 118. величину 4Д«/ = 8,4 • 4 =
===33,6 саж.
Для подсчета математического ожидания поражения, напри-
мер, для интервала Zo = 3 ДХ (черт. Хю) проведем в области
опасных разрывов прямую, параллельную биссектрисе угла на
расстоянии 4 Ду cos Не от
биссектрисы. Центр об-
ласти всех возможных
разрывов наложим на
точку Oj и среднюю тра-
екторию этой области
совместим с О1А1, после
чего подсчет производим
приемом, изложенным в
§ 99. ,
Подсчеты производят-
ся обычно для наивыгод-
нейшего интервала и для
ряда удалений средней
траектории от цели, чем
и выясняется влияние
высоты разрыва при не-
изменном интервале.
В частности для
120-льл« шрапнели под-
счеты дали, что наилуч-
шее поражение дости-
гается при прохождении
средней траектории через
цель и при высоте разрыва
= Io tg 0С = 23/4 ДХ tg 0>с _. 2з/4 д?/
328
101. Влияние удаления средней траектории от цели
при неизменной нормальной высоте средней точки
разрывов и влияние интервала разрыва
(Ошибки в установке прицела)
Осуществить сохранение неизменной средней высоты раз-
рыва при изменениях положения средней траектории относи-
тельно цели, т. е. при изменении прицела, возможно только-
при параллельном изменении прицела и трубки одновременно;
при этом неизбежно будет меняться интервал разрыва.
Для подсчета математического ожидания поражения в этом
случае необходимо предварительно рассчитать интервал разрыва..
Пусть при средней
высоте разрыва Но сред-
няя траектория проходит
через цель Доприсредней
точке разрыва в О (черт
120).
При уменьшении при-
цела на величину КАХ,
где ДХ — наименьшее де-
ление прицела, напри-
мер, для морских при-
целов ДХ —’/4 каб., па-
раллельным изменением трубок среднюю точку разрывов удер-
жим на той же высоте И,,; средняя точка разрывов при этом по-
лучается в Ov Новый интервал разрыва будет: t
^ = /0-}- ХДХ = но ctg 0С + хдх. 1 * (361)
Поделив Д на величину ДХ, получим интервал разрыва,
выраженный в величинах ДХ, которые для ряда дальностей
нанесены на область опасных разрывов.
При увеличении прицела на величину ХДХ и при сохране-
нии средней высоты разрыва в 02 (черт. 120) новый интервал
разрыва получим:
Д = Но ctg бс — ХДХ. (362)
Зная среднюю высоту разрывов и рассчитав средний интервал
разрывов, мы будем иметь координаты точки наложения центра
области всех возможных разрывов на тарированную область,
опасных разрывов для подсчета математического ожидания
поражения.
Сделав такие подсчеты для каждой из дальностей и для
ряда интервалов при одной и той же наивыгоднейшей средней
высоте разрывов, мы можем построить кривые, выражающие
зависимость математического ожидания поражения от удале-
ния средней траектории от цели.
В качестве примера рассмотрим случай прохождения сред-
ней траектории в ДХ = ]/4 каб. = 25 саж. перед целью и в 4 ДХ =
329
—100 саж. за целью при наивыгоднейшей средней высоте раз-
рывов Я0 = 23/4Д?/ для дальности Х = 20 каб. (бс=4°22').
Для случая, когда средняя траектория проходит в ДХ перед
целью, для дальности 20 каб. имеем:
23/4 Дг/ = 5,3 саж.; 10 = 7Д ctgОс 70 саж.;
j. 70 саж. + 25 саж. _ 95 саж. 3 g д у
' * 25 саж. 25 саж. ’
Таким образом, координаты точки наложения области всех
'возможных разрывов на область опасных разрывов Ох на черт. 121
будут Oj (3,8 ДХ; Ai/cos6c).
Область всех возможных разрывов для подсчета математи-
ческого ожидания поражения должна, быть наложена на область
опасных разрывов (черт. 121) так, чтобы центр рассеивания
-совпал с точкой % и средняя траектория совпала с линией
О.А. || ОЦ0.
Для случая прохождения средней траектории в 4 ДХ дальше
цели для дальности 20 каб. имеем:
т 70 саж. —100 саж. 30 саж. „ . v
25 саж. 25 саж.
Таким образом, координаты точки 02 на области опасных
разрывов (черт. 121), на которую надо наложить область всех
возможных разрывов для подсчета математического ожидания
поражения, будут 02(—1,2 ДХ; 4 Дг/4 cos bc).
Эти подсчеты для 120-лкн шрапнели показаны в виде кри-
вых на черт. 122 и 123. На черт. 122 показана зависимость
математического ожидания поражения от средней высоты раз-
рывов при одном и том же интервале, а на черт. 123 — зависи-
мость математического ожидания поражения от положения
средней траектории относительно цели при одной и той же
средней высоте разрывов.
Из черт. 122 видно, что отклонение средней точки разрыва
до 1 Дг/вызывает небольшое падение математического ожидания,
а отклонение на 2 Дг/ уменьшает его приблизительно в два раза.
Из черт. 123 видно, что отклонение средней траектории от
цели на величину ДХ немного (приблизительно на 25%) умень-
шает математическое ожидание поражения, а отклонение сред-
ней траектории на 2ДХ уменьшает это ожидание приблизи-
тельно в 2 раза.
102. Классификация разрывов по высоте
В § 100 и 101 показана зависимость математического ожи-
дания поражения от высоты разрывов. Для удобства в прави-
лах стрельбы разрывы разделяются на категории, и для каждой
из них обычно указывают верхнюю границу, выраженную
в делениях угломера (в тысячных дальности).
330
331
Для разделения разрывов по высоте предварительно удобно
их разделить на четыре категории.
К I категории причисляют все разрывы, заключающиеся
в пределах (черт. 117, см. кривую для ЛГ = 4О каб. и черт. 124)
от подошвы цели до такой высоты, при которой математиче-
ское ожидание поражения, увеличиваясь, достигает
наибольшего возможного.
Ко II категории причисляют все те разрывы, при которых
математическое ожидание поражения не менее Б/6 наибольшего
возможного.
К III категории относят такие разрывы по высоте, при кото-
рых математическое ожидание поражения, убывая, доходит
до х/з наибольшего возможного.
К IV категории относят все остальные разрывы.
Верхи грншлень
высонихдО-В} \К> К
Л Кривая мо число поразк целей
В
В.гр-цалт-
ламнык\В]
М.
1J.Пети.
'/? )1 ' IП
]капг\\[кот ;
Уфшбкзм яо)
. Н ’> ’ •’
й "
Г'/г ••
ЛЛ.........
ГЛ.........
Гр-цаллевкь
Гл
О
?5\
а
4
Черт. 124.
Разделение разрывов на категории обычно делают только
для наивыгоднейшего положения средней траектории относи-
тельно цели.
На черт. 124 кривая АВС дает зависимость математического
ожидания поражения от интервала разрыва, при наивыгодней-
шем положении средней траектории относительно цели, т. е.
при прохождении ее через цель. Проведя границы, разделяю-
щие разрывы на категории, получим, что к 1 категории отно-
сятся разрывы от нуля до высоты Оъ ко II категории — разрывы
между высотами Ot и О2, к Ш категории — между высотами О2
и Os, к IV категории — выше 03 и клевки.
Возьмем проекцию эллипсоида разрывов в KJJX на плоскость,
перпендикулярную к плоскости стрельбы. Линия MN прохо-
дит на границе высоты Но; РК является верхней границей
разрывов I категории, ST—верхней границей разрывов II кате-
гории, QZ—верхней границей разрывов Ш категории. Разрывы
выше QZ и ниже горизонта (клевки) относятся к IV категории.
После этого разделения для удобства и простоты правил
придают разрывам следующую классификацию: клевки (К) ниже
горизонта: низкие (Н)—-до 3 саж. (около 6 лг) выше горизонта,
причем клевки и низкие разрывы, как дающие знак по даль-
ности, называются захватывающими. Остальные разрывы I кате-
гории и все разрывы II категории носят название нормальных (7V),
332
причем ST является их верхней границей. Все разрывы Ш кате-
гории называют высокими (В), причем QZ — их верхняя гра-
ница, а разрывы выше этой границы — очень высокими (ОБ).
В зависимости от рассеивания возможны случаи, что все
три категории могут быть отнесены к низким и нормальным
или даже к одним низким разрывам.
В качестве примера распределим разрывы для дальности
Х--40 каб. при табличном рассеивании.
По черт. 117 можно снять непосредственно верхние границы
категорий разрывов, а именно:
I категория 8,75 саж., что дает 2,2 деления
П „ 28,8 „ „ „ 7,2
Ш „ 41,2 „ „ „ 10,0
При нежелании проводить средние траектории, это же можно
рассчитать по снятым с чертежа интервалам разрывов и тан-
генсу угла падения:
Ос = 18°27' tgl8°27' = 0,334.
Для I категории разрывов имеем:
h = 25 саж.
Верхняя граница h tg6c = 25 • 0,334 = 8,4 саж., или 2,1 дел.
Для II категории разрывов
1/2 = 86,2 саж.
Верхняя граница In tg 6С = 86,2 • 0,334 = 28,7 саж., или
7,2 дел.
Для III категории разрывов
1/2/= 127,5 саж.;
1щ tg6c = 127,5 • 0,334 = 42,5 саж., или 10,1 дел.
Таким образом, для X = 40 каб. имеем:
верхняя граница „низких" — 0,75 дел. 1 дел.,
„ „ „нормальных" — 7 дел.,
„ „ „высоких"—10 дел.
Проделав подобные расчеты для ряда дальностей, обычно
яти цифры по возможности оггругляют, придавая правилу удобо-
запоминаемую форму, например: „считать за верхнюю границу
нормальных разрывов 5, 7, 10 и 15 дел. соответственно даль-
ностям 30, 40, 50 и 60 каб., а за верхнюю границу высоких —
удвоенное число делений соответственно тем же дальностям".
103. Процентное распределение разрывов
по категориям их по высоте
Процентное распределение разрывов по высоте зависит от
высоты средней точки разрывов и рассеивания, а поэтому
может служить для выбора высоты средней точки разрывов
333
для пристрелки по наблюдению знаков при рассеивании дан-
ного момента, так как для пристрелки по наблюдению знаков
необходимо иметь достаточное количество захватывающих раз-
рывов. С другой стороны, процентное распределение разрывов
по высоте может служить объективным признаком наивыгод-
нейшей высоты разрывов. Подсчет процентного распределения
разрывов по высоте покажем на частном примере для 120-л/„и
шрапнели при дальности Х = 40 каб. и при наивыгоднейшей
Вре^ЭОс
1
Врр-ЛЪс.
7
16
Врсг]_с-
__2
16
16
65,7%
'2%
77~25------р7
ад
>__с
25
25
7,5% __7
2
Верхи граница В.
Верхи граница N
>21,7%
Горизонт
1б;
____>307?.%
£
Черт. 125.
средней высоте разрыва /70 = 23.,4 Д?/. Для этой дальности
5pe = 15 саж.; Ду = 8,4 саж.;
Яр = 23/4 Д7/ = 23,2 саж. 23 саж.
Расчет может быть сделан и аналитически, и графически.
Обычно для практических целей вполне достаточно произ-
вести грубый графический подсчет. Проведя линию горизонта
(черт. 125), отложим вверх от нее 23 саж. в каком-либо мас-
штабе по трем вертикальным линиям и нанесем средние точки
разрывов О. От точек О в обе стороны отложим по 4Вре при
рассеивании, в два раза меньшем табличного, при табличном
п при рассеивании, в два раза большем табличного, после чего
1 впишем числа Гаусса.
334
Затем, отложив вверх от горизонта 3 саж., проведем верх-
нюю границу низких разрывов; отложив вверх от горизонта
29 саж., проведем верхнюю границу нормальных разрывов и,
отложив вверх от горизонта 40 саж., проведем верхнюю гра-
ницу высоких разрывов.
Теперь простым подсчетом получим, что при нормальной
средней высоте разрывов Н0 = 23 саж. при рассеивании, в два
раза меньшем табличного, нормальных разрывов около 66%
и захватывающих разрывов около 4%, причем клевки, как ред-
кое исключение. При табличном рассеивании —нормальных раз-
рывов около 40%, причем клевки также редки (около 7%). При
рассеивании, в два раза большем табличного, нормальных раз-
рывов около 22%, а захватывающих около 32%, причем клев-
ков около 2/з всех захватывающих разрывов.
Из этого же подсчета видим, что когда рассеивание дан-
ного момента велико, например, раза в два более табличного,
пристрелку следует вести на нормальной высоте разрывов, так-
как захватывающих разрывов вполне достаточно. При рассеи-
ваниях табличном и меньшем табличного на период пристрелки
требуется понизить среднюю точку разрывов на столько, чтобы
число захватывающих разрывов довести по крайней мере
ДО 30%.
Положение средней точки разрывов относительно горизонта
легко найдется из того же черт. 125.
104. Необходимое и достаточное число наблюдений
для пристрелки высоты разрывов
Введение поправки в высоте разрывов можно делать после
различного числа наблюдений. Если суждение о средней точке
разрывов сделать на основании наблюдения одного разрыва, то
срединная ошибка в оценке средней высоты разрывов будет
равна
+ (363)
где Врв — срединное отклонение, характеризующее рассеивание
по высоте, а Ъ— срединная ошибка, характеризующая закон
ошибок измерения высоты разрывов.
Величину Ъ в (363) следует выражать в величинах Врв.
В угловых величинах срединную ошибку измерения обычно
принимают на основании опыта наблюдений равной 2 дел.
в тысячных дальности.
Для любой дальности X каб. при срединной ошибке в угле,
равной 2 дел., величина b в Врв получится так:
где X — дальность в кабельтовых, Врв — в саженях.
335»
При т
выразится
наблюдениях срединная ошибка в оценке высоты
так:
= (365)
У in
принимают ^максимально необходимое число наблю-
Обычно
.ценил т, при котором
R <0,8 Врв,
и вполне достаточным, когда
R<0,5 Вре
(366)
(367)
гак как за этим пределом уменьшение величины R с увеличе-
нием числа наблюдений т идет очень медленно.
105. Пристрелка высоты разрывов
Пристрелка средней высоты разрывов может быть произве-
дена на основании наблюдений разрывов, или только по раз-
делению разрывов на воздушные и клевки, пли на основании
•счета клевков с одновременным измерением средней высоты
•воздушных разрывов, когда и клевки и воздушные разрывы
получаются при одних и тех же установках. Второй способ
дает более полные сведения о высоте средней точки разрывов,
но первый проще, вследствие чего чаще применяется.
Рассмотрим оба способа. В обоих случаях для вывода пра-
вил и указаний необходимо получить или распределение сред-
ней точки разрывов, или распределение горизонта. При выра-
ботке правил стрельбы дистанционными снарядами обычно
предпочитают первое, т. е. находят распределение средней
точки разрывов, хотя в расчетах нет никакой разницы. В пер-
вом случае мы берем начало отсчета на горизонте и делаем
различные гипотезы о средней точке разрывов; во втором слу-
чае, принимая начало отсчета в средней точке разрыва, делаем
различные гипотезы о горизонте.
Рассмотрим сначала случай обработки результатов наблю-
дения клевков и воздушных разрывов без измерения высоты
последних, тогда мы будем иметь полную аналогию с обработ-
кой наблюдения знаков падений, причем проведем аналогию
между клевками и недолетами и между воздушными разрывами
и перелетами.
Для распределения средней точки разрывов при той или
иной гипотезе о высоте точки разрывов Но и при начале отсчета
на горизонте вероятность получения tn клевков будет:
WK^Fm(-H0), t (368)
при этом вероятность получения п воздушных разрывов будет:
We = Fn(H0). (369)
,336
Распределение средней точки разрывов:
?2(H0)dH0 =
Fm(—Но) Fn(H0)dH0
+ °°
J‘ F™ (—Не) F* (HJ dHQ
— oo
(370)
Некоторые предпочитают иметь дело с распределением гори-
зонта, тогда при начале отсчета в средней точке разрывов
вероятность т клевков при той или иной гипотезе о горизонте
будет
Ж*=Г(Я0), (371)
причем вероятность п воздушных разрывов будет
W„ = F(—Ho), (372)
и распределение горизонта при этом
?2(Нв)йЯ0=
Ит(Я0)Я(-Я0)^Я0
+ "
/ Fm(H0)F\-H0)dH0
(373)
Вычисление выражений (370) или (373) известно, поэтому
приводить здесь этих расчетов не будем, а приведем в виде
частного примера распределения
по выражениям (370) и (373) для
случая наблюдения 3 клевков и
1 воздушного разрыва, полученных
при одних и тех же установках.
На черт. 126 показана кривая
А^С^, представляющая распреде-
ление средней точки разрывов,
построенное по (370), и кривая
А2В2С2 — распределение горизонта,
построенное по (373) после наблю-
дения 3 клевков и 1 воздушного
разрыва; и по тому, и по другому
распределению наивероятнейшей
гипотезой является положение
средней точки разрывов ниже го-
ризонта на 0,9 Врв — 1Врв.
Если принять не вероятнейшую гипотезу, а срединное поло-
жение средней точки разрывов или горизонта, то положение
средней точки разрывов определится на 1,1 Врв ниже горизонта,
т. е. почти то же. Итак, при наблюдении 3 клевков и 1 воз-
душного разрыва можно принять за наиболее подходящее
положение средней точки разрывов точку, лежащую ниже гори-
зонта на 1 Врв.
22 Теория стрельбы 337
Дальнейшее будет зависеть от того, куда мы хотим пере-
местить среднюю точку разрывов. Например, при табличном
рассеивании для пристрелки на дальности 40 каб., чтобы обес-
печить не менее 30% захватывающих разрывов, среднюю точку
разрывов следует поднять на величину 1 Врв4-Дт/= 15 саж. -|-
-|-8 саж. = 23 саж., или на 6 дел., для чего потребуется
соответственное укорочение трубки.
Подобным же образом может быть произведен расчет по
(370) или по (373) для любой комбинации из клевков и воздуш-
ных разрывов.
Несколько особо стоят две комбинации: наблюдение только
клевков или только воздушных разрывов.
Наблюдение только клевков распределения дать не может,
но может дать кривую Персена по
^(H0)dH0 = Fm(-H0)dH0 (374)
или
(375)
причем по (374) мы будем иметь кривую вероятностей
наблюдать т клевков при различных гипотезах о средней точке
разрывов (черт. 127), а по (375) —
кривую вероятностей наблюдать
т клевков при различных гипо-
тезах о горизонте (на черт. 127
не показана).
В этом случае можно заклю-
чить, что вероятнее всего сред-
няя точка разрывов ниже гори-
зонта не менее, как на 4 Врв,
и следовательно, для поднятия
средней точки разрывов поправ-
ку надо брать на величину, не
менее 4Вро-|-Н, где И—желае-
мая высота средней точки раз-
рывов над горизонтом.
Эту поправку надо повто-
рять до наблюдения части или
всех разрывов над горизонтом.
При наблюдении только воздушных разрывов, если не будем
делать измерений, мы также получим незамкнутую кривую
Персена, но эта кривая будет весьма нерациональна, так как
среднее арифметическое из измеренных высот или (при навыке
измерения) высота воображаемой средней точки разрывов дает
нам распределение средней точки разрывов и позволит сразу же
принять решение о средней точке разрывов, причем срединная
ошибка средней высоты разрывов будет:
338
где b — срединная ошибка измерения, а п — число воздушных
разрывов.
При измерении высот п воздушных разрывов и выводе сред-
ней высоты разрывов Нср над горизонтом, как
Нср
п
распределение средней точки разрывов получим из
* (1Н0 (376)
R У л
[вычисление (376) уже известно].
Заметим, что наблюдение в первой очереди (залпе) только
воздушных разрывов очень выгодно, так как в этом случае мы
имеем измерения и хорошие сведения о средней точке разры-
вов, а кроме того, сразу получаем представление о рассеива-
нии момента и можем проверить ширину веера.
В том случае, когда измеряют высоты воздушных разрывов
при одновременном наблюдении клевков, сведения о средней
точке разрывов получаются полнее, нежели при разделении
разрывов только на воздушные и клевки без измерений высот
воздушных разрывов.
В этом случае распределение средней точки разрывов при
измерении средней высоты Нср из п воздушных разрывов и при
одновременном наблюдении т клевков, очевидно, получится
из выражения:
(gp-gg,)5
Р F™(-H0)dH0
^(H0)dH0=------------------------------------------ (377)
Л (gp-gpp)5
/ Р 7^(-Н0)^Я0
/ й|/к
или для распределения горизонта:
р? (g^-gp)2
-Le рт(+Нй)&Н0
?2(H0)dH0 =-----------------------------------. (378)
Г „(»еР-н«)2
/ Р ^~Fm(+H0)dH0
/ Ry-^
22* 339
Формулы (377) или (378) дают распределение лучше, нежели
(370) или (373), только в том случае, когда измерения точны
и R мало отличается от единицы или лучше меньше единицы;
в противном случае измерение высот разрывов особой пользы
не принесет, а только усложнит организацию наблюдений
и правила стрельбы.
106. Пристрелка дальности (высоты прицела) на
основании наблюдения знаков захватывающих
разрывов. Поражение цели
Теория пристрелки дальности при стрельбе дистанционными
снарядами имеет целью не только найти прицел для лучшего
поражения цели, но определить и пределы рационального суже-
ния вилки и вывести правила для наивыгоднейшего пораже-
ния цели, т. е. дать указания, на скольких прицелах следует
поражать цель, с каким шагом и, наконец, дать объективные
признаки наивыгоднейших условий поражения цели.
Выводы делаются на основании подсчета математического
ожидания поражения, исходя из распределения цели, получен-
ного в результате захвата цели в вилку той или иной ширины.
Распределение цели получается совершенно так же, как
и при исследовании стрельбы снарядами ударного действия,
но для вероятности недолета и перелета надо пользоваться не
обычной таблицей F (t), а таблицей, составленной для данного
случая по распределению захватывающих разрывов, как то
было изложено в § 87—92.
Величины математических ожиданий для различных гипотез
о месте цели относительно средней траектории получим с чер-
тежей, подобных черт. 117, 122, 123.
Распределение цели после наблюдения кг недолетов с при-
целом h и к2 перелетов с прицелом h Ц- 2а получим, как обычно,
по выражению:
—**’<*+») т"1 (я-*)<^ , (379)
+ °°
/ рк* (х Ц- а) р*» (а — х) dx
а в случае накрытия на одном прицеле h
i Fk‘(x)Fki(—x)dx ,.}Qn4
С?2 (х) dx =-----—--------<------. (380)
+ »
У Fk' (x)Fk*(— x)dx
— oo
Имея распределение цели, математическое ожидание пора-
жения для любого положения средней траектории получим для
стрельбы на одном приц.-ле из выражения:
А = Х AfW2(x)dx. (381)
340
При стрельбе на нескольких прицелах надо произвести под-
счет по (379) для каждого прицела, полученные величины мате-
матического ожидания сложить и разделить на число прицелов
при обстреле площади.
Пример. Дальность Х%40 каб. На прицеле 39 каб. наблю-
дали: воздушный разрыв и минус клевок, а на прицеле
41 каб. наблюдали два воздушных разрыва со знаком плюс.
Подсчитать математическое ожидание поражения на середине
вилки при нормальной высоте разрывов и табличном рассеива-
нии (120- мм шрапнели).
Во-первых, надо подсчитать вероятность недолета (—) и пере-
лета (+) захватывающего разрыва (§ 87—92) и подсчеты свести
в таблицу, которую даем в готовом виде для дальности 40 каб.
при табличном рассеивании (табл. 94).
Затем подсчитываем математическое ожидание поражения
при различном удалении средней траектории от цели и при
нормальной высоте разрывов (£0 = 23/4 Д?/) (черт. 123 и табл. 95),
после чего переходим к подсчету по формуле (379) распреде-
ления цели (табл. 96).
Этот подсчет показал, что при вилке в 1 каб. и при переходе
на поражение на ее середине математическое ожидание числа
пораженных целей при одном выстреле будет 0,365 ед. цели.
Подсчет приведен как пример подобных подсчетов. Подоб-
ные подсчеты следует сделать для разных вилок и для стрельбы
на разном числе прицелов (обычно не более трех).
Сравнение математических ожиданий поражения дает воз-
можность вывести правило. При этом следует иметь в виду,'
что сужение вилки выгодно только до тех пор, пока оно суще-
ственно увеличивает математическое ожидание поражения;
в противном же случае дальнейшее сужение вилки следует
прекратить.
Если при обстреле площади по дальности математическое
ожидание поражения не очень отличается от того же ожи-
дания при стрельбе на одном прицеле, то обстрел площади
выгоден.
Наконец, необходимо указать, что для случая поражения
цели на одном прицеле при стрельбе -дистанционными снаря-
дами поражение не всегда выгодно вести на середине вилки,
а поэтому необходимо подсчитать математическое ожидание
поражения для ряда прицелов и выбрать наивыгоднейшие
условия поражения.
107. Стрельба при измерении высоты и интервала
разрывов
Если имеется возможность производить измерение высот //,
и интервалов разрывов до цели Ц (черт. 128), то получение
наивыгоднейших установок, отвечающих напвыгоднейшсму
интервалу и высоте разрывов, достигается скорее, проще и точ-
нее, нежели при стрельбе по наблюдению знаков разрывов.
341
Таблица 94
Вероятность наблюдения (—) и (+) захватывающих разрывов при X = 40 каб.
Рассеивание табличное (Но = \у)
+ о
>Х
о
X
с CQ
го со
Z ।
О. |
о
X
X
О.
С (ч.
X + т—1
X
с
о
»- СО
о
X +
X
О-
О
ь-
X
трае 123) о СО
>х ь
X ф
ЕС X
о> Q. со
1 •«J
х <
к
га Хи~
0 04
S- с и 1О
S? га
» ЕС ' ‘
<3 X ч—'
Еч 3
X
3* CQ
X о S “ со" ’—Ч
ГО Р О
Q.B-
со
X 2
о. °-
= о
5 ° т—<
X О
ф -°
Й °
CD
О.
С
си X К в се Рн • о
X Ри
со о
ЕС
X « ф
й ф ГО . и . X
РнЮ га -
ш Н сЗ И"
о ьм W *
X о о> О И к ож
X s
X ф ф •
f- Рн Ф о
га О Д’ М -
ЗЕ о
п> Р ф •
к- К о в
го р х •
2 ф
X Й s
о « д
W й §
о £
342
Одновременно мы можем иметь и отклонение средней траекто-
рии х, так как
х = Ц~То и = .
При введении поправок следует придерживаться общей
теории стрельбы по измеренным отклонениям, но здесь необхо-
димо иметь в виду, что измерения производятся не по сопря-
женным наблюдениям, и построение распределения цели по
дальности и по высоте было бы неверно. Распределение цели
и в этом случае получается путем других соображений.
Здесь могут быть те же случаи, какие мы имели при иссле-
довании стрельбы снарядами ударного действия по измерен-
ным отклонениям: 1) поправки вносятся на основании измере-
ния нескольких высот и интервалов разрыва по средним ариф-
метическим из измеренных высот и интервалов; 2) поправки
вводятся после каждого отдельного выстрела и 3) поправка
вводится сначала по каждому отдельному выстрелу, а затем
для введения поправки дается группа выстрелов.
Мы рассмотрим только два первых случая, так как этим
охватываетря и третий случай. Кроме того, следует различать
случаи, когда имеют место только одни воздушные разрывы
и когда вместе с воздушными разрывами наблюдаются и клевки.
В случае наблюдения в группе выстрелов только клевков
может быть получено распределение цели по дальности и при-
стреляна табличная дальность (прицел), -после чего, вводя
поправки в установку трубок, пристреливаются высота и интер-
вал разрыва. Этот случай отдельного рассмотрения также не
потребует, потому что исчерпывается рассмотрением двух пер-
вых случаев.
Рассмотрим сначала случай наблюдения одних воздушных
разрывов в группе выстрелов при одинаковых установках,
когда поправка вводится на основании получения средней
высоты и среднего интервала разрыва.
При стрельбе снарядами дистанционного действия, вслед-
ствие того, что приходится рассматривать вопрос в двух изме-
рениях, удобнее считать цель находящейся в определенной
точке и исследовать распределение средних точек разрывов,
343
отвечающих или одной, или различным табличным дально-
стям.
Пусть при отдельном выстреле точка разрыва получена
в О4 (черт. 129) и при этом измерены высота Н1 и интервал Zv
Для получения распределения средней точки разрывов на
основании только одного наблюдения нам надо построить эллипс
разрывов, что может быть выполнено по вертикальному направ-
лению и по направлению, ему сопряженному, из которых одно
(вертикальное) известно, а другое легко может быть найдено.
Пусть единичный эллипс распределения будет ег Если произвести
Черт. 129.
не один, а 4 выстрела и принять за среднюю точку разрывов
точку О, по координатам
тт ___ Н1 + Н2 + Из + Н4 Zj + Z2 + Д + Л
11ср —----------—--------- и 1ер =— ---------------
и на основании этих измерений принять поправку для даль-
нейшей стрельбы, то единичный эллипс распределения е2
с центром в точке О2 найдется по разделении полуосей эллипса Sj
на у т. е. мы получим сведения о цели в 2 раза лучше.
Рассмотрим теперь случай распределения, когда произве-
дена группа выстрелов и поправка вводится после каждого
из них.
В этом случае единичный эллипс распределения средней
точки разрывов получится в результате объединения распреде-
344
лений. Для удобства объединения распределений обычно на
чертеж не наносят для каждой новой установки новых эллип-
сов, а пользуются „приведенным" положением разрыва, т. е.
действительные точки разрывов заменяют другими точками,
которые отличаются по высоте и интервалу от действительных
точек разрывов на столько, на сколько по данным основной
таблицы стрельбы должны отличаться соответственные средние
точки от средней точки при первой установке.
Пример. При прицеле 7^=40 каб. и при трубке ?ц = 5,4сек.
измерены Zj = 10 саж. и Ну — 10 саж. (черт. 129), а при при-
целе 7t2 = 393/4 каб. и при трубке п2 = 4,8 сек. измерены Z2 =
= 70 саж. и Н2 = 20 саж.
Табличные данные следующие: Z0 = 7O саж. Изменение при-
цела на ДХ = 1/4 каб. меняет высоту разрыва на Д^ = 8,4 саж.
Изменение трубки на сек. меняет интервал разрыва на
ДХ = 105 саж. и высоту разрыва на Ду, = 26 саж.
Распределение средней точки, отвечающее разрыву, полу-
ченному с прицелом 40 каб. и трубкой 5,4 сек., характеризуется
единичным эллипсом с центром в точке Оу.
Точку разрыва, полученну ю при прицеле 393/4 каб. и трубке
4,8 сек., приведем к прицелу 40 каб. и трубке 5,4 сек., т. е.
найдем при помощи табличных данных, какой интервал 12Пр
и какая высота Н2Пр были бы при прицеле 40 каб. и трубке
5,4 сек., если с прицелом 393/4 каб. и трубкой 4,8 сек. были
получены Z» = 70 саж. и ZZ2 = 20 саж.
По табличным данным имеем: с увеличением прицела на
каб. высота разрыва должна увеличиться на 8,4 саж.,
а с удлинением трубки на 0,6 сек. эта высота должна умень-
шиться на 26 • 0,6 — 15,6 саж.
В результате получим
Н2Пр — 20 + 8,4 —15,6 — 12,8 саж.
Интервал разрыва при удлинении трубки на 0,6 сек. должен
уменьшиться на 105 • 0,6 = 63 саж.
Z2„p = 70 — 63 = 7 саж.
По интервалу Z2np = 7 саж. и высоте 772кр = 12,8 саж. нане-
сем точку О2, которая и явится приведенной точкой разрыва
при втором выстреле и дает распределение средней точки раз-
рывов для прицела 40 каб. и трубки 5,4 сек. Это распределе-
ние будет характеризоваться эллипсом е2, равным и параллель-
ным эллипсу Sj.
Вследствие параллельности двух распределений и е2 они
объединяются в одно е0 по принципу нахождения центра тяже-
сти. Таким образом, распределение средней точки разрывов,
полученной в результате двух измерений, будет характеризо-
ваться единичным эллипсом s0 с полуосями, меньшими в 2 раз
полуосей эллипсов ej и е2 и им параллельными. Если к точ-
кам Оу и О2 прибавится третья точка О3 в результате измере-
345
ния высоты и интервала разрыва третьего выстрела с новым
прицелом, то объединять распределения надо так: раньше
соединить точки О{ и О2 и линию OtO2 разделить пополам
и найти эллипс е'о с центром О', потом соединить точки О' и О3
и найти центр нового распределения О" по принципу нахож-
дения центра тяжести. Полуоси эллипса е"0 будут параллельны
полуосям эллипсов еъ е2 и е, и в / з раз меньше полуосей
этих эллипсов. Поступая таким образом, мы можем найти рас-
пределение средней точки разрывов для любого числа выстрелов.
Исследование значительно сложнее, если вместе с воздуш-
ными разрывами наблюдаются и клевки. Пристрелка на осно-
вании измерения интервала и высоты разрывов при наличии
только одних воздушных разрывов значительно выгоднее, чем
пристрелка при одновременном наблюдении воздушных разры-
вов и клевков, а поэтому в случае получения в очереди части
клевков лучше поднять среднюю точку разрывов настолько,
чтобы обеспечить получение одних воздушных разрывов, и дать
новую очередь выстрелов.
Указание о том, насколько надо поднять среднюю точку
разрывов, когда одновременно с воздушными разрывами наблю-
даются и клевки, должно быть дано на основании подсчетов
по (377) и (378) § 106.
108. Замечания об исследовании стрельбы снарядами
дистанционного действия на ходу по неподвижной
цели
Исследование стрельбы дистанционными снарядами на ходу
по неподвижной цели, когда дальности и направления непре-
рывно изменяются, но достаточно точно учитываются, ничем не
отличается от исследования стрельбы при отсутствии измене-
ния дальности, так как вследствие неподвижности цели мы
будем иметь тот же абсолютный интервал разрыва.
Вопрос встает о самом методе стрельбы, при этом надо
учесть, во-первых, сложность организации управления непре-
рывным изменением трубки, а во-вторых, крайнюю трудность
непрерывно удерживать наивыгоднейшее положение средней
траектории. Наконец, угол возвышения орудий в случае пря-
мой визуальной наводки (непосредственно от пушек или при
помощи центрального визира) будет непрерывно меняться вслед-
ствие непрерывного изменения угла места.
Лучшим методом в этом случае, обеспечивающим „прохож-
дение цели11 под наивыгоднейшим интервалом и при нормаль-
ной высоте разрывов, будет метод „неподвижных завес**.
Задачами исследования, кроме тех задач, какие стоят и
при стрельбе из неподвижной батареи, будут:
1) установить пределы сужения вилки,
2) определить глубину обстреливаемой площади и
3) указать объективные признаки того, что прохождение
.346
цели под наивыгоднейшим интервалом обеспечено, и объектив-
ные признаки моментов оттягивания или закидывания прицела
с параллельным изменением установки трубки.
109. Замечания об исследовании стрельбы снарядами
дистанционного действия по подвижной цели
Исследование стрельбы снарядами дистанционного действия
по подвижной цели будет отличаться, во-первых, тем, что при-
дется иметь дело не с абсолютным, а с относительным интер-
валом разрывов, а во-вторых, необходимо учитывать не только
упреждение на движение цели по отношению к снаряду за
время его полета до момента разрыва, но брать упреждение
и за время полета пуль. Все расчеты и построения паралле-
лограмов надо вести по относительному интервалу и по отно-
сительной траектории.
Черт. 130.
Относительный интервал и относительная траектория полу-
чатся на основании следующих соображений. Пусть О — точка
разрыва (черт. 130). Построим от точки разрыва вектор окон-
чательной скорости vc под углом падения 6С; от конца век-
тора vc построим вектор vx продольной слагающей скорости
цели в направлении, обратном ее движению. Замыкающий век-
тор v'c и будет вектором относительной скорости, угол 6'с —
относительным углом падения. При этом угол разлета пуль,
их распределение и плотности следует брать так же, как и при
стрельбе по неподвижной цели из неподвижного орудия.
При отсутствии специальных приборов управления огнем
стрельба ведется методом неподвижных завес с постоянной
трубкой для каждой завесы. При наличии специальных прибо-
ров наилучшими методами явятся, повидимому, методы стрельбы
зенитной артиллерии.
ПРИЛОЖЕНИЯ
Табл ица I
2 —ас2
Значения Ф (ж) = -у= е
X Ф(ж) X Ф(ж) ж Ф(ж)
0 1,128 1,00 0,415 2,00 0,021
0,05 1,126 1,05 0,375 2,05 0,017
0,10 1,117 1,10 0,336 2,10 0,014
0,15 1,103 1,15 0,301 2,15 0,011
0,20 1,084 1,20 0,267 2,20 0,009
0,25 1,060 1,25 0,236 2,25 0,007
0,30 1,031 1,30 0,208 2,30 0,006
0,35 0,998 1,35 0,182 2,35 0,004
0,40 0,961 1,40 0,159 2,40 0,004
0,45 0,921 1,45 0,138 2,45 0,003
0,50 0,879 1,50 0,119 2,50 0,002
0,55 0,834 1,55 0,102 2>55 0,002
0,60 0,787 1,60 0,087 2,60 0,001
0,65 0,739 1,65 0,074 2,65 0,001
0,70 0,691 1,70 0,063
0,75 0,643 1,75 0,053
0,80 0,595 1,80 0,044
0,85 0,548 1,85 0,037
0,00 0,502 1,90 0,030
0,95 0,458 1,95 0,025
1,00 0,415 2,00 0,021
348
Таблица IT
а
2 f — i2
Значения 0 (а) = е dt
V « J
о
a 0(a) a 0(«) a 0(a)
0 0 1,00 0,84270 2,00 0,99532
0,05 0,05637 1,05 0,86244 2,05 0,99626
0,10 0,11246 1,10 0,88020 2,10 0,99702
0,15 0,16800 1,15 0,89612 2,15 0,99764
0,20 0,22270 1,20 0,91031 2,20 0,99814
0,25 0,27633 1,25 0,92290 2,25 0,99854
0,30 0,32863 1,30 0,93401 2,30 0,99886
0,35 0,37938 1,35 0,94376 2,35 0,99911
0,40 0,42839 1,40 0,95229 2,40 0,99931
0,45 0,47548 1,45 0,95969 2,45 0,99947
0,50 0,52050 1,50 0,96611 2,50 0,99959
0,55 0,56332 1,55 0,97162 2,55 0,99969
0,60 0,60386 1,60 0,97635 2,60 0,99976
0,65 0,64203 1,65 0,98038 2,65 0,99982
0,70 0,67780 1,70 0,98379 2,70 0,99987
0,75 0,71116 1,75 0,98667 2,7505 0,99990
0,80 0,74210 1,80 0,98909 3,123 0,999990
0,85 0,77067 1,85 0,99111 3,460 0,9999990
0,90 0,79691 1,90 0,99279 3,77 0,99999990
0,95 0,82089 1,95 0,99418 4,06 0,999999990
Формула интерполирования для табл. II:
0 (a, +h) = 0 (Cj) +
О (a.,) —0(01)
a2 —aj
1 — hat
1 ~ (a2 — «1) «1
349
Тай/пща III
₽
2p f
Значения величин Ф (p) = 7- e
r* J
0
dz-, ₽ = _£_
Ф(₽) W Ф(3) Diff Ф(₽) w
0,00 0,00000 538 0,39 0,20749 519 0,78 0,40118 468
0,01 0,00538 538 0,40 0,21268 519 0,79 0,40586 466
0,02 0,01076 538 0,41 0,21787 517 0,80 0,41052 465
0,03 0,01614 538 0,42 0,22304 517 0,81 0,41517 462
0,04 0,02152 538 0,43 0,22821 515 0,82 0,41979 461
0,05 0,02690 538 0,44 0,23336 515 0,83 0,42440 459
0,06 0,03228 538 0,45 0,23851 513 0,84 0,42899 458
0,07 0,03766 537 0,46 0,24364 512 0,85 0,43357
0,08 0,04303 537 0,47 0,24876 512 510 0,86 0,43813 454 452
0,09 0,04840 538 0,48 0,25388 0,87 0,44267
0,10 0,05378 536 0,49 0,25898 509 0,88 0,44719 450
0,11 0,05914 537 0,50 0,26507 508 0,89 0,45169 449
0,12 0,06451 536 0,51 0,26915 0,90 0,45618
0,13 0,06987 586 0,52 0,27421 506 0,91 0,46064 44b 445 443 441 439 438 435 434 431 430
0,14 0,07523 536 0,53 0,27927 50b 504 503 502 500 499 498 497 495 0,92 0,46509
0,15 0,16 0,08059 0,08594 535 535 0,54 0,55 0,28431 0,28934 0,93 0,94 0,46952 0,47393
0,17 0,18 0,19 0,09129 0,09663 0,10197 534 534 534 0,56 0,57 0,58 0,29436 0,29936 0,30435 0,95 0,96 0,97 0,47832 0,48270 0,48705
0,20 0,21 0,22 0,10731 0,11264 0,11796 533 532 0,59 0,60 0,61 0,30933 0,31430 0,31925 0,98 0,99 1,00 0,49139 0,49570 0,50000
0,23 0,12328 532 532 0,62 0,32419 494 1,01 0,50428 428
0,24 0,12860 0,63 0,32911 492 1,02 0,50853 425
0,25 0,13391 531 0,64 0,33402 491 1,03 0,51277 424
0,26 0,13921 530 0,65 0,33892 490 1,04 0,51699 422
0,27 0,14451 530 0,66 0,34380 488 1,05 0,52119 420
0,28 0,14980 529 0,67 0,34866 486 1,06 0,52537 418
0,29 0,15508 528 0,68 0,35352 486 1,07 0,52952 415
0,30 0,16035 527 0,69 0,35835 483 1,08 0,53366 414
0,31 0,16562 527 0,70 0,36317 482 1,09 0,53778 412
0,32 0,17088 526 0,71 0,36798 481 1,10 0,54188 410
0,33 0,17614 5^6 0,72 0,37277 479 1,11 0,54595 407
0,34 0,18138 524 0,73 0,37755 478 1,12 0,55001 406
0,35 0,18662 524 0,74 0,38231 476 1,13 0,55404 403
0,36 0,37 0,19185 0,19707 э23 522 522 520 0,75 0,76 0,38705 0,39178 474 473 1,14 1,15 0,55806 0,56205 402 399
0,38 0,39 0,20229 0,20749 0,77 0,78 0,39649 0,40118 471 469 1,16 1,17 0,56602 0,56998 397 396
350
Ф(?) Di/Г ₽ Ф(₽) w ₽ Ф(3) Diff
1,17 0,56998 393 1,60 0,71949 300 2,05 0,83324 206
1,18 0,57391 391 1,61 0,72249 297 2,06 0,83530 204
1,19 0,57782 389 1,62 0,72546 295 2,07 0,83734 202
1,20 0,58171 387 1,63 0,72841 293 2,08 0,83936 201
1,21 0,58558 384 1,64 0,73134 291 2,09 0,84137 198
1,22 0,58942 383 1,65 0,73425 289 2,10 0,84335 196
1,23 0,59325 380 1,66 0,73714 286 2,11 0,84531 195
1,24 0,59705 378 1,67 0,74000 285 2,12 0,84726 193
1,25 0,60083 377 1,68 0,74285 282 2,13 0,84919 190
1,26 0,60460 373 1,69 0,74567 280 2,14 0,85109 189
1,27 0,60833 372 1,70 0,74847 277 2,15 0,85298 188
1,28 0,61205 370 1,71 0,75124 276 2,16 0,85486 185
1,29 0,61575 367 1,72 0,75400 274 2,17 0,85671 183
1,30 0,61942 366- 1,73 0,75674 271 2,18 0,85854 182
1,31 0,62308 363 1,74 0,75945 269 2,19 0,86036 180
1,32 0,62671 361 1,75 0,76214 267 2,20 0,86216 178
1,33 0,63032 359 1,76 0,76481 265 2,21 0,86394 176
1,34 0,63391 356 1,77 0,76746 263 2,22 0,86570 175
1,35 1,36 1,37 0,63747 0,64102 0,64454 355 352 350 1,78 1,79 1,80 0,<7009 0,77270 0,77785 261 258 257 2,23 2,24 2,25 0,86745 0,86917 0,87088 172 171 170
1,38 0,64804 348 1,81 0,77785 254 2,26 0,87250 167
1,39 1,40 0,65152 0,65498 346 343 1,82 1,83 0,78039 0,78291 252 251 2,27 2,28 0,87425 0,87591 166 164
1,41 0,65841 341 1,84 и,7оо4л 248 2,29 0,87755 163
1,42 0,66182 339 1,85 0,78790 246 2,30 0,87918 160
1,43 1,44 1,45 1,46 1,47 1,48 1,49 1,50 1,51 1,52 1,53 1,54 1,55 1,56 1,57 1,58 0,66521 0,66858 0,67193 0,67526 0,67856 0,68144 0,68510 0,68833 0,69155 0,69474 0,69791 0,70106 0,70419 0,70729 0,71038 0,71344 337 335 333 330 328 326 323 322 319 317 315 313 310 309 306 304 1,86 1,87 1,88 1,89 1,90 1,91 1,92 1,93 1,94 1,95 1,96 1,97 1,98 1,99 2,00 2,01 0,1 УОЗи 0,79280 0,79522 0,79761 0,79999 0,80235 0,80469 0,80700 0,80930 0,81158 0,81383 0,81607 0,81828 0,82048 0,82266 0,82481 0,82695 0,82907 0,83117 244 242 239 238 236 234 231 230 228 225 224 221 220 218 215 214 2,31 2,32 2,33 2,34 2,35 2,36 2,37 2,38 2,39 2,40 2,41 2,42 2,43 2,44 2,45 2,46 0,88078 0,88237 0,88395 0,88550 0,88705 0,88857 0,89008 0,89157 0,89304 0,89450 0,89595 0,89738 0,89879 0,90019 0,90157 0,90293 159 158 155 155 152 151 149 147 146 145 143 141 140 138 136 135
1,59 1,60 0,71648 0,71949 301 2,02 2,03 2,04 212 210 2,47 2,48 2,49 0,90428 0,90562 0,90694 134 132
2,05 0,83324 207
351’
Ф(?) Diff P Ф(₽) Diff Ф(₽) w
2,49 0,90694 131 2,87 0,94711 82 3,24 0,97114 49
2,50 0,90825 129 2,88 0,94793 81 3,25 0,97163 48
2,51 0,90954 128 2,89 0,94874 80 3,26 0,97211 48
2,52 0,91082 126 2,90 0,94954 79 3,27 0,97259 47
2,53 0,91208 124 2,91 0,95033 78 3,28 0,97306 46
2,54 0,91332 124 2,92 0,95111 76 3,29 0,97352 45
2,55 0,91456 122 2,93 0,95187 76 3,30 0,97397 45
2,56 0,91578 120 2,94 0,95263 75 3,31 0,97442 44
2,57 0,91698 119 2,95 0,95338 74 3,32 0,97486 44
2,58 0,91817 118 2,96 0,95412 73 3,33 0,97530 43
2,59 0,91935 116 2,97 0,95485 72 3,34 0,97573 42
2,60 0,92051 115 2,98 0,95557 71 3,35 0,97615 42
2,61 0,92166 114 2,99 0,95628 70 3,36 0,97657 41
2,62 0,92280 112 3,00 0,95698 69 3,37 0,97698 40
2,63 0,92392 111 3,01 0,95767 68 3,38 0,97738 40
2,64 0,92503 110 3,02 0,95835 67 3,39 0,97778 39
2,65 0,92613 108 3,03 0,95902 66 3,40 0,97817 359
2,66 0,92721 107 3,04 0,95968 65 3,50 0,98176 306
2,67 0,92828 106 3,05 0,96033 65 3,60 0,98482 261
2,68 0,92934 104 3,06 0,96098 63 3,70 0,98743 219
2,69 0,93038 103 3,07 0,96161 63 3,80 0,98962 185
2,70 0,93141 102 3,08 0,96224 62 3,90 0,99147 155
2,71 0,93243 101 3,09 0,96286 60 4,00 0,99302 129
2,72 0,93344 99 3,10 0,96346 60 4,10 0,99431 108
2,73 0,93443 98 3,11 0,96406 60 4,20 0,99539 88
2,74 0,93541 97 3,12 0,96466 58 4,30 0,99627 73
2,75 0,93638 96 3,13 0,96524 58 4,40 0,99700 60
2,76 0,93734 94 3,14 0,96582 56 4,50 0,99760 48
2,77 0,93828 94 3,15 0,96638 56 4,60 0,99808 40
2,78 0,93922 92 3,16 0,96694 55 4,70 0,99848 31
2,79 0,94014 91 3,17 0,96749 55 4,80 0,99879 26
2,80 0,94105 90 3,18 0,96804 53 4,90 0,99905 21
2,81 0,94195 89 3,19 0,96857 53 5,00 0,99926 16
2,82 0,94284 87 3,20 0,96910 52 5,10 0,99942 13
2,83 0,94371 87 3,21 0,96962 51 5,20 0,99955 10
2,84 0,94458 85 3,22 0,97013 51 5,30 0,99965 7
2,85 0,94543 84 3,23 0,97064 50 5,40 0,99972
2,86 0,94627 84 3,24 0,97114
2,87 0,94711
352
Таблица IV
Значения функций: F(£)=% Р+? (0L гДе ? (О определена табл. Ill
F (—7,5) = 0,0000002; F (—7,0) = 0,0000012;
F (—6,5) = 0,0000058; F (—6,0) = 0,0000209;
F (—5,5) = 0,0001038; F (—5,0) = 0,0003729.
1 И III IV V VI VII VIII IX
/ F (t) 1g F(t) рт (/) 21gF(0 рт (0 3 1g F (7) F* (t) 4 IgF(i)
—- 0, 0. 0, 0,
5,0 00037 "4,56820 "7,13640 '10,20460 14,27280
4,9 00047 "4,67210
4,8 00060 4 77815
4,7 00076 4,88081
4,6 00096 Т, 98227
4,5 О0120 "3,07918 "6,15836 9,23754 12,31672
4,4 00150 "3,17609
4,3 4,2 00186 00230 J3.26951 3,36173
4,1 00284 3,45332
4,0 00349 "3,54283 00001 5,08566 "8,62849 “9,17132
3,9 3,8 (.0427 00519 "3,63043 3,71517 00002 00003 1,26088 5,43034
3,7 3,6 00622 00759 3,79379 3,88024 00004 00С06 5,58758 5,76048
3,5 00912 "3,95999 00.08 "5,91998 “7,87997 “9,83996
3,4 01(91 "2,03782 00012 4,(17564
3,3 3,2 3,1 01301 01545 01827 1,11428 2,18893 2,26174 00017 00024 00033 4,22856 _4,37786 4,52348
3,0 02151 "2,33264 00046 “4,66528 00001 6,99792 "7,33056
2,9 2,8 02523 02947 "2,40192 “2,46938 00064 00087 "4,80384 4,93876 00002 00003 “5,20576 5,40814
2,7 2,6 03429 03974 2,53517 2.59923 00118 00158 J), 07034 3,1984( 00004 00006 "5,60551 "5,79769
2,5 04587 2,66153 0021(1 "3,3231)6 00010 "5,98459 “6,64612
2,4 05275 2,72222 00278 "3,44444 00015 7,16666 00001 ”6,88888
2,3 06044 2,78132 00385 3,56264 00022 7,34396 00001 5,12528
2,2 06892 12,83835 00475 3,67670 00033 4,51505 00002 5,35340
2,1 07833 2,8931'3 00614 3,78786 00048 4,68179 00004 5,57572
2,0 08867 "2,94778 00768 "3,89556 00070 4,84334 00006 "5,79112
1,9 10001 "1,(0004 01000 7,10(108 00100 "3,00012 00010 1,00016
1,8 1,7 11236 12577 1,05061 1,09958 01262 01582 J2,10122 2,19916 00142 00199 JI, 15183 3,29874 00016 00025 4,20244 4,39832
23 Teos ия стрел ьбы 3S3
I II III IV V VI 1 j VII VIII IX 1
t F (I) lgF(f) 21gF(O F3 (f) 31gF(0 f14 (0 4 IgF(f)
1,6 0, 14026 1, 14694 0, 01967 "2,29387 0, 00276 "3,44081 o, 00039 1,58774
1.5 15584 1,19268 < 2429 "2,38536 I 00379 3,57813 00059 1,77072
1,4 17251 "1,23681 02976 "2,47362 00513 1,71043 00088 4,94724
1,3 19029 1,27942 03621 2,55884 00689 3,83826 00131 3,11764
1,2 20915 1,32045 04374 2,64090 00915 >,96135 00191 3,28180
1,1 22906 1,35995 05247 2,71990 01202 1,07985 00275 1,43980
1,0 25000 1,39794 06250 "2,79588 01562 2.19382 00391 1,59176
0,9 27191 1,43443 07394 "2,86886 02010 1,30329 00547 3,73772
0,8 29474 1,46944 08687 2,93888 02560 2 40832 00755 3,87776
0,7 31842 1,50300 10139 1,006. 0 03228 2,50900 01038 1,01200
0,6 34285 1,53504 11751 1,07008 04028 2,60512 01381 2,14016
0,5 36797 1,56581 13540 1,13162 04982 1,69743 01833 1.26324
0,4 39366 1,59513 15497 1,19026 06101 1,78539 02402 2,38052
0,3 41983 1,62307 17625 1,24614 07400 2,86921 03106 1,49228
0,2 44635 1,64967 19918 1,29925 08892 2,94902 03967 2,59850
0,1 47311 1,67496 22383 1,34992 10590 T, 02488 05010 2,69984
0 50000 1,69897 25000 1,39794 12500 1,09691 06250 1,79588
+ 0,1 52689 1,72172 27761 1,44344 14627 1,16516 07707 1,88688
0,2 55365 1,74323 30653 1,48647 16971 1,22970 09396 2,97294
0,3 58017 1,76356 33660 1,52711 19529 1,29067 11329 1,05422
0,4 60634 1,78272 36765 T, 56544 22293 1,34816 14821 1,17088
0,5 63203 1,800'4 39946 1,60148 25248 1.40222 15957 1,20296
0,6 65715 1,81767 43186 1,63534 28380 1,45301 18650 1,27068
0,7 68158 1,83352 48455 T, 66704 31664 1,50056 21581 1,33408
0,8 70526 1,84835 49738 T, 69669 35079 1,54505 24739 1,39338
0,9 72809 1,86218 53011 T, 72437 38594 1,58654 28102 T, 44874
1.0 750«0 1,87506 56250 1,75012 42187 1,62518 31640 1,50024
1,1 77094 1,88702 59434 T,77404 45820 1,66106 35325 1,54808
1,2 79 85 1,89809 62545 1,79619 49463 T, 69425 39118 1,59238
1,3 80971 1,90832 65561 1,8H 65 53085 T, 72497 42983 1,63330
1,4 82719 1,91777 68475 1,83553 56520 T, 75220 46888 1,67106
1,5 84416 1,92642 71257 1,85283 6i 151 1,77925 50780 1,70568
1,6 85974 1,93437 73917 1,86874 63549 1,80311 54636 1,73748
1,7 87423 1,94162 76428 1,88325 66823 T82486 58411 1,76650
1,8 88764 1,94824 78792 1,89648 69939 1,84472 6:081 T, 79296
1,9 89999 1,95423 80995 1, 90846 72893 1,86269 65603 1,81692
2,0 91133 1,9.9157 83062 1,91935 75687 1,87902 68973 1,83868
2,1 92167 1,96457 84948 1,92915 78292 1,89372 72160 1,85830
I 11 HI IV V VI VII VIII IX
t F (0 1g F (0 F2 (f) 21gF(f) F3 (f) 31gF(O F* (I) 41gF(f)
0, 0, 0, 0,
2,2 93108 1,96899 86692 1,93798 80718 1,90897 75154 1,87596
2,3 93969 T, 97294 88284 1,94588 82950 1,91882 77940 1,89176
2,4 94725 T, 97646 89728 1,95293 84994 1,92939 80511 1,90586
2,5 95412 1,97960 91034 1,95920 86856 1,93880 82870 1,91840
2,6 96025 1,98238 92210 1,96477 88540 1,94714 85023 1,92954
2,7 96570 1,98484 93256 1,96968 90058 1,95452 86967 1,93936
2,8 97032 1,98701 94194 1,97402 91418 1,96103 88723 1,94804
2,9 97477 1,98890 94888 1,97721 92622 1,96671 90035 1,95442
3,0 97849 1,99055 95744 1,98111 93682 1,97166 91664 1,96220
3,1 98173 1,99199 96378 1,98398 94617 1,97597 92887 1,96796
3,2 98455 T, 99324 96935 1,98648 95438 1,97972 93964 1,97296
3,3 98698 1,99431 97414 1,98862 96146 1,98293 94893 1,97724
3,4 98908 T, 99523 97827 1,99046 96758 1,98569 95701 1,98092
3,5 99088 1,99602 98184 1,99204 97288 1,98806 96400 1,98408
3,6 99241 1,99669 98487 1,99338 97740 1,99007 96997 1,98676
3,7 99371 1,99726 98746 1,99452 98125 . 1,99178 97508 1,98904
3,8 99481 1,99774 98965 1,99548 98450 1,99322 97940 1,99096
3,9 99573 1,99814 99146 1,99628 98722 1,99442 98301 T, 99256
4,0 9.1651 1,99848 99305 1,99697 98957 1,99545 98610 1,99392
4,1 99715 1,99876 99430 1,99752 99147 1,99628 98864 1,99504
4,2 99769 1,99900 99540 1,99800 99312 1,99700 99082 199600
4,3 99813 1,99918 99624 1,99837 99435 1,99754 99252 T, 99674
4,4 99850 1,99935 99700 1,99870 99552 1,99805 99402 T99740
4,5 99880 1,99948 99760 1,9989 99642 1,99844 99522 1,99792
4,6 99904 1,99950 99812 1,99918 99717 1,99877 99622 1,99836
4,7 99924 1,99967 99838 T, 99934 99772 i ,99901 99696 1,99868
4,8 99939 1,99974 99880 T, 99948 99820 1,99922 99760 1,99896
4,9 99952 1,99979 99902 T, 99958 99855 1,99937 99808 1,99916
5,0 99963 1,99984 99926 1,19968 99892 1,99958 99853 1,99936
5,1 99971 1,99987 99940 1,99974 99910 1,99961 99880 1,99948
5,2 99978 1,99990 99954 1,99980 99931 1,99970 99908 T, 99960
5,3 99982 1,99992 99963 T, 99984 99944 1,99976 99926 T99968
5,4 99986 1,99994 99972 1,99.88 99958 1,99982 99944 T, 99976
5,5 99988 1,99995 99977 1,99990 99965 1,99985 99954 1,99980
5,6 99990 1,99996 99981 1,99992 99972 1,99988 99963 1,99984
5,7 99992 1,99997 99986 T, 99994 99979 1,99991 99972 1,99988
5,8 99994 1,99997 99988 T, 99995 99981 1,99992 99977 T, 99990
5,9 99996 1,99998 99991 1,99996 99986 1,99994 99981 T, 99992
6,0 99998 1,99999 99995 1,9999s 99991 "9,99996 99991 1,99996
23*
355
354
Таблица V
Значения функции <р(ж) =
X ¥ (») Diff X о (ж) w X о (Ж) w
0, 0, 0,
0 26908 61 2,4 07261 766 4,8 00143
0,1 26847 2,5 06495 29
183 711 4,9 00114 23
0,2 26664 301 2,6 05784 657 5,0 00091
0,3 26363 2,7 05127 17
416 603 5,1 00074
0,4 25947 526 2,8 04524 550 5,2 00057 17
0,5 25421 2,9 03974 12
628 03475 499 5,3 00045 10
0,6 24793 3,0
722 03025 450 5,4 00035 00028 7
0,7 24071 3,1
807 02621 404 5,5 7
0,8 23264 3,2 00021
883 02261 360 5,6 6
0,9 22381 3,3 00017
946 01942 319 5,7 4
1,0 21435 3,4 00013
1 ООО 01660 282 5,8 3
1,1 20435 3,5 00010
1 041 248 5,9
1,2 19394 3,6 01412 00008 2
1 072 3,7 01196 216 6,0 2
1,3 18322 00006
1 091 187 6,1
1,4 17231 1 100 3,8 01009 162 6,2 00004
1,5 16131 1 098 3,9 00847 140 6,3 00003 1
1,6 15033 1 087 4,0 00707 119 6,4 00002 1 1
1.7 13946 1 067 4,1 00588 101 6,5 00001
1,8 12871 4,2 00487 00001 0
1 039 00402 85 6,6 0
1,9 11840 4,3 00001
1 005 00329 73 6,7 0
2,0 10835 4,4 00001
965 60 6,8
2,1 09870 4,5 00269 50 6,9 00001 0
919
7 9 08951 4,6 00219 00000 0
871 42 7,0
2,3 08080 819 4,7 03177 34
2,4 07261 4,8 00143
Таблица VT1
Значения функций F(t), f(t), — f'(16
t F(0 ftt) -Л«) t F(f) -Г (0
— 5,0 0,000 5,37 0,92 0,0 0,500 1,18 0,64
— 4,9 0,000 5,28 0,92 0,1 0,527 1,12 0,62
— 4,8 0,001 5,19 0,92 0,2 0,554 1,06 0,61
~ 4,7 0,001 5,10 0,92 0,3 0,580 1,00 0,59
— 4,6 0,001 5,00 0,92 0,4 0,606 0,94 0,57
— 4,5 0,001 4,91 0,92 0,5 0,632 0,88 0,55
— 4,4 0,002 4,82 0,92 0,6 0,657 0,83 0,54
— 4,3 0,002 4,73 0,92 0,7 0,682 0,78 0,52
— 4,2 0,002 4,64 0,91 0,8 0,705 0,73 0,51
— 4,1 0,003 4,55 0,91 0,9 0,728 0,68 0,49
— 4,0 0,003 4,45 0,91 1,0 0,750 0,63 0,47
— 3,9 0,004 4,36 0,91 1,1 0,771 0,58 0,45
— 3,8 0,005 4,27 0,91 1,2 0,791 0,54 0,43
— 3,7 0,006 4,18 0,91 1,3 0,810 0,50 0,41
— 3,6 0,008 4,09 0,90 1,4 0,827 0,46 0,39
— 3,5 0,009 4,00 0,90 1,5 0,844 0,42 0,37
- 3,4 0,011 3,91 0,90 1,6 0,860 0,38 0,35
— 3,3 0,013 3,82 0,89 1,7 0,874 0,35 0,33
— 3,2 0,015 3,73 0,89 1,8 0,888 0,32 0,31
— 3,1 0,018 3,64 0,89 1,9 0,900 0,29 0,29
— 3,0 0,022 3,55 0,89 2,0 0,911 0,26 0,27
— 2,9 0,025 3,46 0,88 2,1 0,922 0,24 0,25
— 2,8 0,029 3,37. 0,88 2,2 0,931 0,21 0 23
— 2,7 0,034 3,28 0,88 2,3 0,940 0,19 0,21
— 2,6 0,040 3,19 0,87 2,4 0,947 0,17 0,20
— 2,5 0,046 3,11 0,87 2,5 0,954 0,15 0,18
— 2,4 0,053 3,02 0,86 2,6 0,960 0,13 0,16
— 2,3 0,060 2,94 0,86 2,7 0,966 0,12 0,15
— 2,2 0,069 2,85 0,85 2,8 0,971 0,10 0,13
— 2,1 0,078 2,77 0,84 2,9 0,975 0,09 0,12
— 2,0 0,089 2,69 0,84 3,0 0,978 0,08 0,11
— 1,9 0,100 2',60 0,83 3,1 0,982 0,07 0,10
— 1,8 0,112 2,52 0,82 3,2 0,985 0,06 0,09
— 1,7 0,126 2,44 0'81 3,3 0,987 0,05 0,08
— 1,6 0,140 2,36 0,81 3,4 0,989 0,04 0,07
1Й» «»5 CQ Т-1 1 1 1 1 1 0,156 0,173 0,190 0,209 0,229 2,28 2,20 2,12 2,04 1,96 0,80 0,79 0,79 0,78 0,77 3,5 3,6 3,7 3,8 3,9 0,991 0,992 0,994 0.995 0,996 0,04 0,03 0,03 0,02 0,02 0,06 0,05 0,04 0,04 0,03
4,0 0,997 0,02 0,03
— 1,0 0,250 1,88 0,76 4,1 0,997 0,02 0,03
— 0,9 0,272 1,81 0,75 4,2 0,998 0,01 0,02
— 0,8 0,295 1,73 0,74 4,3 0,998 0,01 0,02
— 0,7 0,318 1,66 0,73 4,4 0,998 0,01 0,02
- 0,6 0,343 1,59 0,72 4,5 2,999 0,01 0,01
- 0,5 0,368 1,52 0,70 4,6 0,999 0,01 0,01
— 0,4 0,394 1,45 0,69 4,7 0,999 0,004 0,01
— 0,3 0,420 1,38 0,68 4,8 0,999 0,003 0,01
— 0,2 0,446 1,31 0,67 4,9 1,000 0,003 0,01
— 0,1 0,473 1,25 0,65 5,0 1,000 0,002 0,005
1 К способу Мангона.
357
356
Таблица VII1
Таблица IX
_ 1 Р / — о2 (я? — а)2 , — р2 {х + о)2'
Значения ?/= — -7=1 е ’ -f- р • '
г 1 - \
\ х а \ 0 0,5 1,0 1,5 2,0 2,5 3 3,5 4,0 4,5 5,0
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0 269 254 214 161 108 064 035 006 007 003 001
0,2 267 252 213 161 109 066 036 017 007 003 001
0,4 259 246 210 161 111 069 039 019 009 004 001
0,6 248 236 205 161 115 074 043 023 011 005 002
0,8 233 223 • 198 161 120 081 050 028 014 006 002
1,0 214 208 189 160 124 089 058 034 018 008 004
1,2 194 190 178 157 129 098 067 041 023 011 005
1,4 172 171 166 154 134 106 077 050 029 015 007
1,6 150 152 153 149 137 115 087 060 036 020 010
1,8 124 132 139 143 138 122 098 070 045 026 013
2,0 108 ИЗ 124 135 138 128 108 081 054 032 017
2,2 090 095 110 126 136 133 117 092 064 040 023
2,4 073 079 096 116 131 134 124 102 075 049 029
2,6 058 064 082 105 125 135 130 112 086 059 036
2,8 045 052 069 094 117 132 133 120 097 070 045
3,0 035 041 058 082 108 127 135 127 107 081 054
3,2 026 032 047 071 097 120 133 132 116 092 064
3,4 019 024 038 060 086 112 130 134 124 102 075
3,6 014 018 030 050 075 102 124 134 130 112 086
3,8 010 013 023 041 064 092 116 132 133 120 097
4,0 007 010 018 033 054 081 107 127 134 127 107
4,2 004 007 013 026 045 070 097 120 133 132 116
4,4 003 005 010 020 036 059 086 112 130 134 124
4,6 002 003 007 015 029 049 075 102 124 134 130
4,8 001 002 005 011 023 040 064 092 116 132 133
5,0 001 002 004 008 | 1 017 032 054 081 107 127 134
1 Влияние разнобоя.
Таблица VIII
Вероятности попадания в эллипсы, подобные единичному, и в кольца,
ограниченные такими эллипсами
Границы эллипсов или колец Срединные отклонения
4 1 4 2 2-t 3 з4 4 4— 2 5
Вероятность попадания
В эллипс Вероятность попадания в эллиптиче- 5,5 20,3 40,0 59,7 75,8 87,0 93,7 97,3 98,9 99,6 %
ское кольцо 5,5 14,8 19,7 19,7 16,1 11,2 6,8 3,5 1,6 0,7
358
Значения р! = 1 — е ир« = 1 — е (1 4- а)
а ?1 dm Р2 dm а diff Pi diff
0,00 0,0000 198 0,0000 2 0,70 0,5034 99 0,1558 70
0,02 0,0198 194 0,0002 о 0,72 0,5132 97 0,1628 70
0,04 0,0392 190 0,0008 9 0,74 0,5229 95 0,1698 71
0,06 0,0582 187 0,0017 13 0,76 0,5323 93 0,1769 71
0.08 0,0769 183 0,0030 17 0,78 0,5416 91 0,1840 72
0.10 0,0952 179 0,0047 21 0,80 0,5507 89 0,1912 72
0,12 0,1131 175 0,0067 22 0,82 0,5596 87 0,1984 72
0/14 0,1306 172 0,0089 26 0,84 0,5683 85 0,20э6 73
о’16 0,1478 169 0,0115 29 0,86 0,5768 84 0,2129 73
0,18 0,1647 166 0,0144 31 0,88 0,5852 82 0,2202 73
0,20 0,1813 162 0,0175 34 0,90 0,5934 81 0,2275 74
0,22 0.1975 159 0,0209 37 0,92 0,6015 79 0,2349 73
0*24 (1,2134 156 0,0246 39 0,94 0,6094 77 0,2422 73
0,26 О', 2290 152 0,0285 41 0,96 0,6171 76 0,2495 74
0,28 0,2442 149 0,0326 44 0,98 0,6247 74 0,2569 73
0,30 0,2592 147 0,0370 45 1,00 0,6321 73 U,2642 74
0,32 0,2738 144 0,0415 47 1,02 0,6394 71 0,2716 74
0.34 0,2882 141 0,0462 49 1,01 0,6465 70 0,2790 73
0,36 0,3023 138 0,0511 51 1,06 0,6535 69 0,2863 73
0> 0,3161 136 0,0562 53 1,08 0,6604 67 0,2936 74
0,40 0,3297 133 0,0615 55 1,10 0,6671 66 0,3010 73
0,42 0,3430 130 0,0670 56 1,12 0,6737 65 0,3083 73
0,44 0,3560 127 0,0726 57 1,14 0,6802 63 0,3156 73
0,46 0,3687 125 0,0783 59 1,16 0,6865 62 0.3229 72
0,48 0,3812 123 0,0842 60 1,18 0,6927 61 0,3301 73
0,50 0,3935 120 0,0902 61 1,20 0,6988 60 . 0,3374 72
0.52 0,4055 118 0,0963 63 1,22 0,7048 08 0,3446 72
0,54 0,4173 115 0,1026 63 1,24 0,7106 58 0,3518 71
0,56 0,4288 ИЗ 0,1089 65 1,26 0,7164 56 0,3589 71
0,58 0,4401 111 0,1154 65 1,28 0,7220 5b 0,3660 71
0,60 0,4512 109 0,1219 66 1,30 0,7275 54 0,3731 71
0,62 0,4621 106 0,1285 67 1,32 0,7329 53 0,3802 71
0,64 0,4727 104 0,1352 67 1,34 0,7382 51 0,3873 70
0,66 0,4831 102 0,1420 70 1,36 0,7433 51 0,3943 69
(<68 0,4934 100 0,1490 68 1,38 0,7484 50 0,4012 70
0,70 0,5034 99 0,1558 70 1,40 0,7534 49 0,4082 69
359
i a Pi tZiff P-i a Pi Pi <Ziff
1,40 0,7534 49 0,4082 69 2,10 0,8776 24 0,6204 51
1,42 0,7583 48 0,4151 68 2,12 0,8800 24 0,6255 51
1,44 0,7631 47 0,4219 68 2,14 0,8824 23 0,6306 50
1,46 0,7678 46 0,4287 68 2,16 0,8847 23 0,6356 49
1,48 0,7724 45 0,4355 67 2,18 Q.,8870 22 0,6405 49
1,50 0,7769 44 0,4422 67 2,20 0,8892 22 0,6454 49
1,52 0,7813 43 0,4489 66 2,22 0,8914 22 0,6503 48
1,54 0,7856 42 0,4555 66 2,24 0,8936 21 0,6551 47
1,56 0,7898 42 0,4621 65 2,26 0,8957 20 0,6598 47
1,58 0,7940 41 0,4686 65 2,28 0,8977 20 0,6645 46
1,60 0,7981 40 0,4751 64 2,30 0,8997 20 0,6691 46
1,62 0,8021 39 0,4815 64 2,32 0,9017 20 0,6737 45
1,64 0,8060 38 0,4879 63 2,34 0,9037 19 0,6782 45
1,66 0,8098 38 0,4942 (13 2,36 0,9056 19 0,6827 45
1,68 0,8136 37 0,5005 63 2,38 0,9075 18 0,6872 44
1,70 0,8173 36 0,5068 62 2,40 0,9093 18 0,6916 4.3
1,72 0,8209 36 0,5130 61 2,42 0,9111 18 0,6959 43
1,74 0,8245 35 0,5191 61 2,44 0,9129 17 0,7002 42
1,76 0,8280 34 0,5252 60 2,46 0,9146 17 0,7044 42
1,78 0,8314 33 0,5312 60 2,48 0,9163 16 0,7086 41
1,80 0,8347 33 0,5372 59 2,50 0,9179 16 0,7127 41
1,82 0,8380 32 0,5431 59 2,52 0,9195 16 0,7168 40
1,84 0,8412 31 0,5490 58 2,54 0,9211 16 0,7208 40 .
1,86 0,8443 31 0,5548 57 2,56 0,9227 15 0,7248 39
1,88 0,8474 30 0,5605 57 2,58 0,9242 15 0,7287 39
1,00 0,8504 30 0,5662 57 2,60 0,9257 15 0,7236 39
1,92 0,8534 29 0,5719 56 2,62 0,9272 14 0,7365 38
1,94 0,8563 28 0,5775 55 2,64 0,9286 14 0,7403 37
1,96 0,8591 28 0,5830 54 2,66 0,9300 14 0,7440 37
1,98 0,8619 28 0,5885 55 2,68 0,9314 14 0,7477 37
2,00 0,8647 27 0,5940 54 2,70 0,9328 13 0,7514 36
2,02 0,8674 27 0,5994 53 2,72 0,9341 13 0,7550 35
2,04 0,8700 26 0,6047 53 2,74 0,9354 13 0,7585 35
2,06 0,8726 25 0,6100 52 2,76 0,9367 13 0,7620 35
2,08 0,8751 25 0,6152 52 2,78 0,9380 12 0,7655 34
2,10 0,8776 24 0,6204 51 2,80 0,9392 12 0,7689 34
a Pi diff 1>2 Mff a Pl 1 1'2 1 diff
2,80 0,9392 12 0,7689 34 3,50 0,9698 6 0,8641 21
2 82 0 9404 12 0,7723 33 3,52 0,9704 6 0,8662 21
2 84 0,9416 11 0,7756 33 3,54 0,9710 6 0,8683 20
2,86 O', 9427 12 0,7789 33 3,56 0,9716 6 0,8703 20
2^88 0^9439 11 0,7822 32 3,58 0,9722 5 0,8723 20
2,90 0,9450 11 0,7854 32 3,60 0,9727 5 0,8743 20
2 92 0,9461 10 0,7886 31 3,62 0,9732 6 0,8763 19
294 O', 9471 11 0,7917 31 3,64 0,9738 5 0,8782 19
2’96 0,9482 10 0,7948 31 3,66 0,9743 5 0,8801 19
2^98 0^9492 10 0,7979 30 3,68 0,9748 5 0,8820 18
3,00 0,9502 10 11,8009 29 3,70 0,9753 5 0,8838 18
3 02 0,9512 10 0,8038 29 3,72 0,9758 5 0,8856 18
304 0',9522 9 0,8067 29 3,74 0,9763 4 0,8874 18
3 06 0,9531 9 0,8096 29 3,76 0,9767 5 0,8892 17
3,08 0,9540 9 0,8125 28 3,78 0,9772 4 0,8909 17
3,10 0,9549 9 0,8153 28 3,80 0,9776 5 0,8926 17
3 12 0,9558 9 0,8181 27 3,82 0,9781 4 0,8943 17
314 0 9567 9 0,8208 27 3,84 0,9785 4 0,8960 16
3 16 O’9576 8 0,8235 27 .3,86 0,9789 >> 0,8976 16
3'18 O’9584 8 0,8262 26 3,88 0,9794 4 0,8992 16
3,20 0,9592 8 0,8288 26 3,90 0,9798 4 0,9008 16
3 22 0 9600 8 0,8314 25 3,92 0.9802 4 0,9024 15
3’24 0,9608 8 0,8339 26 3,94 0,9806 3 0,9039 15
3'26 0 9616 8 0,8365 25 3,96 0,9809 4 0,9054 15
3’28 0,9624 7 0,8390 26 3,98 0,9813 4 0,9069 15
3,30 0,9631 8 0,8414 24 4,00 0,9817 4 0,9084 15
3 32 0,9639 7 0,8438 24 4,02 0,9821 3 0,9099 14
3’34 0,9646 7 0,8462 24 4,04 0,9824 4 0,9113 14
3'36 0'9653 7 0,8486 23 4,06 0,9828 3 0,9127 14
3^38 0^9660 6 0,8509 23 4,08 0,9831 3 0,9141 14
3,40 0,9666 7 0,8532 22 4,10 0,9834 3 0,9155 13
3 42 0,9673 6 0,8554 22 4,12 0,9837 4 0,9168 14
344 O', 9679 7 0^8576 22 4,14 0,9841 3 0,9182 13
346 0,9686 6 0,8598 22 4,16 0,9844 3 0,9195 13
3*48 0,9692 6 0,8620 21 4,18 0,9847 3 0,9208 12
3,50 0,9698 6 0,8641 21 4,20 0,9850 3 0,9220 1 13 1
361
360
a Pi diff P2 diff a Pi diff P2 diff
4,20 0,9850 3 0,9220 13 4,90 0,9926 1 6,9561 7
4,22 0,9853 3 0,9233 12 4,92 0,9927 1 0,9568 7
4,24 0,9856 3 0,9245 12 4,94 0,9928 2 0,9575 7
4,26 0,9859 3 0,9257 12 4,96 0,9930 1 0,9582 7
4,28 0,8862 2 0,9269 12 4,98 0,9931 0,9589
4,30 0,9864 3 0,9281 11 5,00 0,9933 6 0.9596 32
4,32 0,9867 3 0,9292 12 5,10 0,9939 6 0,9628 30
4,34 0.9870 2 0,9304 11 5,20 0,9445 5 0,9658 27
4,36 0,9872 3 0,9315 11 5,30 0,9950 5 0,9685 25
4,38 0,9875 2 0,9326 11 5,40 0,9955 4 0,9711 23
4,40 0,9877 3 0,9337 11 5,50 0,9959 4 0.9734 22
4,42 0,9880 2 0,9348 10 5,60 0,9963 4 0,9756 20
4,44 0,9882 2 0,9358 11 5,70 0,9967 3 0.9776 18
4,46 0,9884 3 0,9369 10 5,80 0,9970 3 0,9794 17
4,48 0,9887 2 0,9379 10 5,90 0,9973 2 0,9811 16
4,50 0,9889 * 2 0,9389 10 6,00 0,9975 3 0,9827 14
4,52 0,9891 2 0,9399 10 6,10 0,9978 2 0,9841 13
4,54 0.9893 2 0,9409 9 6,20 0,9980 2 0,9854 12
4,56 0,9895 2 0,9418 10 6,30 0.9982 1 0,9866 11
4,58 0,9897 2 0,9428 9 6,40 0,9983 2 0,9877 10
4,60 0,9899 2 0,9437 9 6,50 0,9985 1 0,9887 9
4,62 0,9901 2 0,9446 9 6,60 0,9986 2 0,9896 9
4,64 0,9903 2 0,9455 9 6,70 0,9988 i 0,9905 8
4,66 0,9905 2 0,9464 9 6,80 0,9989 i 0,9913 7
4,68 0,9907 2 0,9473 9 6,90 0,9991) i 0,9920 7
4,70 0,9909 2 0,9482 8 7,00 0,9991 i 0,9927 6
4,72 0,9911 2 0,9490 8 7,10 0,9992 i 0,9933 6
4,74 0,9913 1 0,9498 9 7,20 0,9993 i 0,91'39 3
4,76 0,9914 2 0,9507 8 7,30 0,9994 0 0,9944 5
4.78 0,9916 2 0,9515 8 7,40 0,9994 i 0,9949 4
4,80 0,9918 1 0,9523 8 7,50 0,9995 0,9953
4,82 0,9919 2 0,9531 7 8,00 0,9997 1 0,9970 11
4,84 0,9921 2 0,9538 8 8,50 0,9998 1 0,9981 7
4,86 0,9923 1 0,9546 7 9,00 0,9999 0 0,9988 4
4,88 0,9924 2 0,9553 8 9,50 0,9999 1 0,9992 3
4,90 0,9926 1 0,9561 7 10,00 1,0000 0,9995
362
Таблица X
Распределение по круговому закону Гаусса в процентах (три варианта)
I вариант (всего 98,6% = ф(4) ф(4)
4 3 2 1 0 1 2 3 4
0,03 0,12 0,29 0,45 0,45 0,29 0,12 о,бз 4 3 2 1 0 1 2 3 4
0,12 0,45 1,09 1,68 1,68 1,09 0,45 0,12
0,29 1,09 2,60 4,03 4,03 2,60 1,09 0,29
0,45 1,68 4,03 6,25 6,25 4,03 1,68 0,45
i 4 4 4 6 4 2 1
1 4 1 2Л 4 4 4 3 1
1 4 _1_ 1 1=/4 2 1
0 1 4 1 т 1
II вариант
III вариант
ОГЛАВЛЕН HE
Стр.
От автор а................................................... 3
ЧАСТЬ ПЕРВАЯ
СТРЕЛЬБА УДАРНЫМИ СНАРЯДАМИ
Глава I. Рассеивание выстрелов
1. Сноп траекторий........................................... б
2. Величины, характеризующие сноп траекторий................. 8
3. Рассеивание данного момента......................... ... Я
4. Определение срединных отклонений путем опыта на полигоне . . 10
5. Теоретический подсчет срединных отклонений для пушок на осно-
вании данных валовой приемки боевого запаса................. 18
6. Стрельба из одного орудия........................... ... 20
7. Стрельба из нескольких орудий. Явление разнобоя.......... 21
Глава II. Вычисление вероятности попадания
8. Вероятность одного попадания при наличии ошибок, не завися-
щих от орудия.............................................. 3(1
9. Приемы вычисления вероятности одного попадания при точно за-
данном положении цели....................................... 34
10. Вероятность попадания при нескольких выстрелах, когда положе-
ние цели относительно центра группирования точно задано ... 42
И. Применение теоремы гипотез к вопросам артиллерийской стрельбы
для образования распределения цели (распределение вероятно-
стей гипотез о месте цели после того или иного вида наблюдения) . 44
12. Подсчет вероятности попадания при заданном распределении цели 48
Глава III. Математическое ожидание попадания
13. О математическом ожидании попадания при одном выстреле ... 64
14. О распределении вероятностей падений. Кривая распределения
(вероятностей) падений.....................•.................. 72
ЧАСТЬ ВТОРАЯ
ТЕОРЕТИЧЕСКИЕ ОСНОВАНИЯ ВЫРАБОТКИ ПРАВИЛ СТРЕЛЬБЫ
УДАРНЫМИ СНАРЯДАМИ
Глава IV. О правилах стрельбы
15. Требования, предъявляемые к правилам стрельбы............. 74
16. Порядок выработки правил стрельбы......................... 75
17. Учет параметров, характеризующих рассеивание орудий..... 78
18. Схема работы при составлении правил стрельбы.............. 79
364
Стр.
Глава V. Об ошибках подготовки
19. Ошибки предварительной подготовки.......................... 80
20. Ошибки в подготовке исходных установок для случая стрельбы
по неподвижной цели . ......................................... 84
21. Ошибки в измерении расстояний на море........................ 86
22. Ошибки в определении ВНР по графику.......................... 89
23. Ошибка в определении курсового угла цели по видимой длине
цели и измеренной до нее дальности.............................. 95
24. Ошибка в определении ВИР по курсовому углу и скорости дви-
жения цели на основании измерения курсового угла по видимой
длине цели и дальности до нее................................... 96
25. Ошибки в определении скорости и курсового угла цели по ВИР
и боковому перемещению (БП) цели................................ 97
26. Ошибки в ВНР и значение времени при стрельбе по подвижной
цели........................................................... 100
27. Особенности счета времени при исследовании стрельбы по подвиж-
ной цели....................................................... 103
28. Ошибки подготовки при стрельбе по подвижным целая......... 105
Глава VI. Стрельба по неподвижной цели по наблюдению знаков
29. Достоинства и недостатки метода стрельбы по наблюдению знаков . 111
30. Вероятность недолета и перелета при заданном положении сред-
ней траектории относительно цели............................... 111
31. Распределение цели после первого выстрела в случае, когда рас-
пределение цели до выстрета известно. Расчет первой вилки . . 115
32. Распределение цели при отсутствии предварительных сведений
о положении цели................................................ 122
33. Уточнение сведений о цели путем сужения вилки (половннение
вилки).......................................................... 124
34. Повторение пределов как мера, ведущая к уточнению сведений
о цели.......................................................... 130
35. Распределение цели прп наблюдении накрытия цели (нулевая
вилка).......................................................... 133
36. Кривая распределения цели как кривая закона ошибок........ 135
37. Основании для выбора прицела по распределению цели.......... 139
38. Методы подсчета элементов кривых Персена................... 141
39. Один из приближенных способов получения распределения цели
и пределы его применения...................................... 141
40. Использование кривых Персена при выработке методов стрельбы . 143
Глава VII. Стрельба па подвижной целп по наблюдению знаков
или при неточном значении ВИР
41. Основные различия в условиях стрельбы по подвижной цели по
сравнению со стрельбой по неподвижной цели...................... 144
42. Вероятность наблюдения недолета или перелета при захвате цели
в вилку и при постоянной ошибке в ВИР........................ 145
43. Приведение срединной ошибки ВИР к единице .................. 148
44. Распределение цели при стрельбе ио подвижной цели и постоян-
ной ошибке в BIIP............................................... 149
45. Схема подсчета функций Персена.............................. 150
46. Метод приближенного подсчета распределения цели для некото-
рых частных случаев стрельбы по подвижным целям при постоян-
ной оши ке в ВИР................................................ 100
47. Применение теоремы будущих событий к стрельбе по подвижной
цели........................................................... Ю4
48. Исследование стрельбы, когда ошибка в ВИР меняет свою вели-
чину от залпа к залпу............................................ Юа
365
Стр.
49. Исследование стрельбы при наличии большой ошибки в ВИР, .
когда эта ошибка может быть принята следующей закону равной
вероятности.................................................. 170
БО. Расчет ширины первой вилки при стрельбе по подвижной цели
и при ошибке ф ВИР.......................................... 173
Глава VIII. Влияние фальшивых (неверных) наблюдений
61. Общие указания.............................................. 187
52. Влияние фальшивых наблюдений при зависимости вероятности
таких наблюдений от интервала падения.......................... 188
53. Применение выведенных законов к случаю непосредственного на-
блюдения знаков без измерения интервалов падения............... 192
54. Применение выведенных законов к случаю наблюдения знаков на
основании измерения интервалов падений, когда ошибки измере-
ния следуют закону Гаусса...................................... 194
Глава IX. Стрельба по измеренным дальностям
55. Общие основания метода стрельбы по измеренным дальностям
и табличные неувязки........................................... 195
56. Распределение цели при исследовании стрельбы только в напра-
влении дальности............................................... 201
57. Ошибки в определении упрежденной точки при различных ме-
тодах измерения.............................................. 203
58. Ошибки в численном значении скорости и в численном значении
курсового угла................................................. 210
59. Исследование стрельбы по измеренным дальностям при распреде-
лении цели на плоскости...................•.................... 211
60? Поправка в ВИР при стрельбе по подвижной цели............... 216
Глава X. Стрельба по измеренным отклонениям
61. Различные случаи стрельбы по измеренным отклонениям и спо-
собы измерения отклонений ..................................... 224
62. Средняя дальность до цели при вполне точном измерении откло-
нений по дальности и при ошибке ВИР, равной нулю................ 225
63. Вывод основных правил для стрельбы по измеренным отклоне-
ниям ......................................................... • 227
64. Ошибки от округления команд................................. 229
65. Замечания о стрельбе по измеренным отклонениям. Распределе-
ние цели по дальности ......................................... 230
66. Распределение цели по дальности при стрельбе по измеренным
отклонениям при не вполне точных измерениях и при ошибке ВИР,
равной нулю.................................................... 231
67. Распределение цели на плоскости............................. 234
68. Стрельба по ненаблюдаемым неподвижным целям. Общие поло-
жения ......................................................... 237
69. Ошибки при стрельбе по ненаблюдаемой цели без пристрелки . . 238
70. Ошибки при стрельбе по ненаблюдаемой цели с пристрелкой по
действительному реперу, значительно удаленному от цели (более
500 м или 2% каб.).......................................... 240
71. Ошибки при стрельбе по ненаблюдаемой цели с пристрелкой по
действительному реперу, находящемуся в непосредственной бли-
зости от цели.................................................. 242
72. Ошибки при стрельбе по ненаблюдаемой цели с пристрелкой по
фиктивному реперу.............................................. 242
73. Балистические и аэрологические ошибки при переносе огня от
репера на цель............................................. . 245
74. Особенность учета ошибок и счета времени при стрельбе е ко-
рабля находу по неподвижным береговым целям..................... 247
75. Стрельба по измеренным отклонениям по подвижной цели (при
наличии ошибки в ВИР)........................................... 2!9
66
Стр,
76. Стрельба по измеренным отклонениям по подвижной цели при
сопряженных наблюдениях........................................... 251
77. Закон ошибок избирательного измерения отклонений и дально-
стей до всплесков, когда пристрелка по измеренным дальностям
или по измеренным отклонениям производится залпами............... 255>
ЧАСТЬ ТРЕТЬЯ
ТЕОРЕТИЧЕСКИЕ ОСНОВАНИЯ ВЫРАБОТКИ ПРАВИЛ СТРЕЛЬБЫ
СНАРЯДАМИ ДИСТАНЦИОННОГО ДЕЙСТВИЯ
Глава XI. Стрельба шрапнелью
78. Задачи и общин порядок выработки правил стрельбы дистанцион-
ными снарядами........................................... 261
79. Свойства нулевой шрапнели............................. 265
80. Скорость, сообщаемая пулям разрывным зарядом.......... 265
81. Пробивная способность пуль............................ 267
82. Угол разлета пуш в нулевой шрапнели................... 268
83. О случайной группировке попадании..................... 270
Глава XII. Рассеивание разр явив снарядов дистанционного действия
84. Рассеивание разрывов в безвоздушном пространстве при времен-
ной трубке..................................................... 274
86. Определение величин Врв и Врв из опыта..................... 277
86. Один из способов теоретического вычисления величин Вр0 и Врв . 278
87. Расс иванпе разрывов снарядов дистанционного действия по та-
бличным данным................................................. 279
88. Построение сетки распределения разрывов дистанционных сна-
рядов по направлению горизонта и ему сопряженному.............. 283
89. Аналитический способ подсчета распределения низких разрывов . 286
90. Распределение клевков на горизонте......................... 288
91. Построение eeiKii по главным полуосям эллипса разрывов .... 292
92. Применение для подсчета распределения клевков круговых сеток
распределении по закону Гаусса................................. 293-
Глава XIII. Поражение пулями отдельной шрапнели
93. Распределение пуль в конусе разлета........................ 298
94. Математическое ожидание числа пораженных единиц цели для
отдельной шрапнели при различных интервалах разрыва .... 300
Глава XIV. Действие группы шрапнелей
95. Область всех возможных разрывов и область опасных разрывов . 313
96. Математическое ожидание числа пораженных целей для группы
шрапнелей.................................................... 314
97. Практический прием построения и тарирования области опасных .
разрывов ................................................... 316-“
98. Построение параллелограма (сетки) области всех возможных раз-
рывов ....................................................... 322
99. Практический прием подсчета математического ожидания числа
пораженных целей, по ьзуясь областями опасных и всех возмож-
ных разрывов. Влияние интервала разрыва на поражение цели
(ошибки в установках трубки)................................. 325-
100. Влияние удаления средней траектории от цели при неизменном
\ среднем иитерва е разрыва (ошибка в установке прицела) и влия-
ние высоты разрыва............................................. 327
101. Влияние удаления средней траектории от цели при неизменной
нормальной высоте средней точки разрывов и влияние интервала
разрыва (ошибки в установке прицела; .......................... 329
367
Стр.
102. Классификация разрывов по высоте........................... 330
103. Процентное распределение разрывов по категориям их по высоте . 333
104. Необходимое и достаточное число наблюдений для пристрелки
высоты разрывов.................................................. 335
105. Пристрелка высоты разрывов................................ 336
106. Пристрелка дальности (высоты прицела) па основании наблюде-
ния знаков захватывающих разрывов. Поражение цели........... 340
107. Стрельба при измерении высоты и интервала разрывов...... 341
108. Замечания об исследовании стрельбы снарядами дистанционного
действия находу по неподвижной цели.............................. 346
109. Замечания об исследовании стрельбы снарядами дистанционного
действия по подвижной цели....................................... 347
Приложения
2 • - •а?
Таблица!. Значения Ф(х) = ~-=е ..................... 348
) "
а
2 Г —12
Таблица II. Значения 0 (а) = —= I a dt........................... 349
К« J
о
2 р f — р’г5 Я
Таблица III. Значения величин Ф (Р) = I е dz; р — — 350
У 7Г J Е
о
Таблица IV Значения функций F (7) I 1Ц-?(7) I, где с(7) опре-
делена табл. III........................................... 353
Таблица V. Значения функции (ж) = —е ' х .................... 356
Таблица VI. Значения функций F (t), f(f),— f'(t)............. 357
1 D / —p2(*—«Я —р2 + с)'2 \
Таблица VII. Значения / е + е ) • •
2 j/к \ )
Таблица VIII. Вероятности попадания в эллипсы, подобные еди-
ничному, и в кольца, ограниченные такими эллипсами.......... 358
Таблица IX. Значения = 1 — е а и р2=1 — в а (1 + а) . . . . 359
Таблица X. Распределение по круговому закону Гаусса в процен-
тах (три варианта)........................................... 363
Опечатки к книге В. А. Унковского „Теория стрельбы и ее приложение
к стрельбе корабельной артиллерии"
Стра- ница Строка Напечатано Следует читать
45 Таблица 9 ' У1 Ем У1
114 18 сверху . . . для Р = = 6,25. . . . для р = — 6,25.
160 1 снизу p — dE, — dE, pd С = d£,
168 1 „ р2 t п = -4— nt-г. P?t Р ~ —— r nt г.
4-со 4~СО
189 6 сверху A = J <p(x)dx=/(x). (219) Pi=j* 4{x)dx=f(—x). (219)
+оо 4-00
190 3 снизу J <p(x)dx =/(0). 1” o(x)dx = /(—0).
191 7 сверху /(-0)=/(0), /(-0) #^/(0),
222 Таблица 69 В графе второй должно быть 4
223 Таблица 71 в Pi Qi Pi
239 1 снизу — №-\ F ^Wg \dw J ’ _ (дх \ ( дщ, ) P"wx',