ВОЕННАЯ КРАСНОЗНАМЕННАЯ АКАДЕМИЯ
КОМ АНДНОГО И III ГУРМАНСКОГО СОСТАВА ВВС
ВООРУЖЕННЫХ С Н Л СОЮЗА ССР
РАТЦ В. Г.
КУРС
САМОЛЕТОВОЖДЕНИЯ
ЧАСТЬ I
КАРТОГРАФИЯ

Военное Издательство
Министерства Вооруженных Сил Союза ГСР
Москва — 194в
О П В Ч А Т К И
Стра- ница	Стрэка	Напечатано	Должно быть
6	1 сверху	Глава	Глава 1
62	19 сверху	_	Р-**5 /?-sin dX	_	P'd8 П /?-sin zd\
98	18 сверху	3 ,	9	2 /?ср	(1— qsin2tp0) М У 1 - <?2 (1 — ₽3 sin2 ер) 1 __1_ = (1 — ё2 sin2 %) 2 (1 — ё2)	=	3 m -	=	(1 — easin2y) 2	_ M Vl — ef-(l — e2 sin2 ep) 1	1 2	2 = (I — e2 sin2 <p) (1 — e2)	=
99	2 сверху	Л=Л±1т	Т\ = 7\ ± 180°, где 7j — обратный азимут.
* 101	12 сверху	ctg/7 = tg tps-cos ep-cosec X— sinep-tgX.	ctg П = tg «pj-costp-cosec X — sin tp-ctg X.
102	2 сверху	a, i — угол	az — угол
102	12 снизу	. . mn -^a=Ml =	.	mn — tg a = —T = 6	ml
102	9 снизу	tg s'n Ф + cos Фcos X ctg /7-cos X — sin X’Cos cp ’ -			L	tg cp5- sin q> + cos ep- cos X ctg//-cos X — sinX-siny *
118	14 сверху	если подставим	если представим
124	1 снизу	j	 cos2 £ cos2 a	_ j	cos2 e ~	COS2 a
Зак. 1683.
ВОЕННАЯ КРАСНОЗНАМЕННАЯ АКАДЕМИЯ
КОМАНДНОГО И ШТУРМАНСКОГО СОСТАВА ВВС
ВООРУЖЕННЫХ СИЛ СОЮЗА ССР
РАТЦ Б. Г.
КУРС
САМОЛЕТОВОЖДЕНИЯ
Ч АСТЬ I
КАРТОГРАФИЯ
УЧЕБНИК
для высших военных учебных заведений
— ВВС Вооруженных Сил Союза ССР
Военное Издательство
Министерства Вооруженных Сил Союза ССР
Москва — 1946
«Курс самолетовождения0 предназначен в качестве учебника
для высших учебных заведений ВВС Вооруженных сил СССР.
Учебник может быть использован и в других высших учебных
заведениях, где читается аналогичный курс, а также штурманским
составом строевых частей ВВС Вооруженных сил СССР.
Курс состоит из четырех частей:
Часть 1 — Картография.
Часть 2 — Компасная навигация.
Часть 3 — Радионавигация.
Часть 4 — Авиационная астрономия.
Каждая часть выпускается отдельным изданием.
ВВЕДЕНИЕ
Современное самолетовождение пользуется следующим?
основными способами навигации: компасной навигацией, радио-
навигацией и авиационной астрономией.	:
Компасная навигация, несмотря на все более широкое рас-
пространение радионавигационных и астрономических методов,
остается пока еще основным методом самолетовождения; Даже
в тех случаях, когда навигационная обстановка, т. е. условия
видимости земли и небесной сферы, характер местности, время
года и суток, высота полета, его скорость и дальность, состав
экипажа, оборудование самолета, наконец, боевая задача ijo-
лета, — даже в тех случаях, когда эти условия полета требую-
и позволяют применение радио и астрономии, все же методы
компасной навигации находят себе применение в той или иной
форме и размерах.
Основным методом компасной навигации является прокладка
(счисление) пути. Этот метод требует от экипажа знания,
во-первых, направления движения, во-вторых, скорости полета
относительно земли и, в-третьих, времени полета.
Если бы не было ветра, то задача прокладки пути была бь
во много раз проще, чем это есть в действительности: курс
самолета, воздушная скорость и время, найденные по приборам,
давали бы возможность довольно быстро определять место
самолета с точностью, зависящей от точности показания компаса,
указателя воздушной скорости и часов. Однако наличие ветра
сильно осложняет прокладку пути. Причины этого заключаются,
во-первых, в том, что в полете ветер можно определить, за ред
ким исключением, только при условии видимости земли, и, во-
вторых, в том, что величина и направление ветра сильно7
изменяются во времени и в пространстве. Эти два обстоя-
тельства делают прокладку пути настолько неточной, что обычно
через 30—40 минут полета после определения места по земным
ориентирам приходится его опять повторять. Чем дольше длится
полет вне видимости земли без использования других методов
аэронавигации, тем менее точно известно местоположение само-
лета. Таким образом, т о ч н о сть п р о к л а д к и пути зави-
сит от расстояния, пройденного с начала ее (прокладки)
ведения. Этим отличается способ прокладки пути от всех дру-
гих способов самолетовождения. Практически точность про-
кладки составляет 5—8% от пройденного расстояния. Напри
меР, для расстояния 300 км это составляет 15—25 нм
а
Другим методом компасной навигации является визуальная
пеленгация, позволяющая определить расчетное место самолета
с точностью, зависящей от дистанции до пеленгуемого ориен-
тира. Считают, что точность визуальной пеленгации составляет
3—5% от дистанции. При дистанции 50 км это составляет 2—3>км.
Метод этот, по ряду причин, получил весьма ограниченное
применение.
Весьма мощным и все развивающимся средством самолето-
вождения является радионавигация. Если до последнего времени
все методы радионавигации были основаны на измерении углов
(азимутов, или пеленгов), то в последнее время получили рас-
пространение дистанционно-метрические методы определения
позиционной линии самолета или его расчетного места, извест-
ные под названием радиолокационных методов.
Методы, основанные на измерении углов, или азимутальные
методы, дают возможность определить расчетное место самолета
с точностью, зависящей от дистанции до пеленгуемой радио-
станции. Точность радиопеленгации составляет 3—10% от этой
дистанции в зависимости от способа пеленгации и некоторых
других причин. При дистанции 300 км это составляет 10—30 км.
Несмотря на сравнительно небольшую точность, какую дают
эвимутальные методы радионавигации на больших дистанциях,
методы эти получили весьма широкое распространение, особенно
в слепом самолетовождении, так как с помощью их самолет
имеет возможность выйти к местоположению радиостанции
с достаточной для практики точностью.
Радиолокационные, или дистанционно-метрические, способы
радионавигации, основанные, как показывает название, на изме-
рении дистанций от самолета до радиостанции, дают возмож-
ность определить позиционную линию самолета или его рас-
четное место с весьма большой степенью точности, что делает
этот метод исключительно ценным, особенно для такой задачи
военно-воздушных сил, как отыскание цели над территорией
противника и выход на нее.
Точность, даваемая радиолокационными системами, опреде-
ляется несколькими десятками метров и даже выше на дистан-
циях нескольких десятков и сотен километров. Такая высокая
точность ставит новые проблемы перед другими областями
навигационной науки, в частности перед картографией, должен-
ствующей своей точностью составления карт не отставать от
радиолокации.
Авиационная астрономия позволяет определять расчетное
место самолета с точностью, не зависящей ни от взаимного
расположения самолета и различных ориентиров на земле
.'например радиостанций), ни от времени полета, как это имеет
место в методе прокладки пути. При помощи последних образ-
цов секстантов можно получить расчетное место самолета
с точностью 5—10 км.
Из сравнения всех описанных способов самолетовождения
видно, что они далеко не равноценны и могут найти примене-
4
ние в полете только при определенной навигационной обста-
новке.
Искусство штурмана заключается в правильной оценке этой
обстановки и, на основе этой оценки, в правильном и умелом-
использовании того или иного способа, дублировании различ
ных способов.
Только умелое сочетание разных способов навигапии в различ-
ной обстановке может служить залогом успешного выполнения
полета в навигационном отношении,
ГЛАВА
ПОЗИЦИОННЫЕ ЛИНИИ НА ЗЕМЛЕ
§ 1. ОСНОВНЫЕ СВЕДЕНИЯ О ЗЕМЛЕ
Земля по своей форме подходит к эллипсоиду, форма и
величина которого определяются размерами его полуосей и
сжатием. Величина сжатия с — —- - , где а и b — боль-
шая и малая полуоси эллипсоида.
Размеры полуосей, полученные различными исследователями,
следующие:
	а	b	С
ЦНИИ ГА и К (совет- ский эллипсоид) . По Бесселю	 По Хейфорду (между- народное) 		6378,2 км 6 377,4 км 6 378,4 км	6356,9 км 6356,1 км 6 356,9 км	1:298 1:299 1:297
Для целей самолетовождения Землю принимают за шар,
радиус которого определяют из условия равенства объемов
земного сфероида и шара, т. е.
о	О
откуда
Подставляя сюда значения а и Ь, получим приближенно
/? = 6371 км.
Положение любой точки на земной поверхности опреде-
ляется географическими координатами: широтой ср и дол-
готой X (рис. 1).
Широта отсчитывается от 0 до 60° в обе стороны от эква-
тора и получает наименование северной (N, Nord) или южной
(S, Sud).
Для определения долготы один из меридианов принимают
за начальный.
Большинством стран за начальный принят Гринвичский
оидиан, проходящий через астрономическую обсерваторию
гор. Гринвиче (вблизи Лондона). На некоторых старых кар-
тах У нас ведут счет Д°лгот от меридиана Пулково или о. Ферро
Долгота Пулково от Гринвича составляет:
А = 30°19'38",55 Е, или прибли-
женно 30°20'Е;
долгота Ферро от Гринвича со-
ставляет;
X = 17°39'46",05 W, или прибли-
женно 17°40'W.
Для перехода от одного счета
долгот к другому могут служить
простые зависимости:
ХгР
*Гр
= 30-20' + кпулк;
= >-фер-17°40'
Долготу считают к востоку и к западу от начального мери-
диана от 0 до 180°; восточной долготе присваивается знак
плюс (+) или Е (East), а западной — знак минус (—) или W (West).
Длина дуги 1° меридиана (или экватора) приближенно может
быть получена из соотношения:
2л.6371	.
Пэкв — 360	360	~ 111,18 КМ.
Более точно: эта длина меняется в пределах от 110,56 км
у экватора до 111,68 км у полюса.
Для получения длины дуги 1° параллели на какой-либо
широте <р можно воспользоваться соотношением = 111,18 cos <р,
что следует из треугольника О МО' (см. рис. 1), так как
r = /?cos% где г—радиус параллели.
Длины дуг в 1° меридиана и параллели на различных широ-
тах даны в приложении 1.
Длина дуги земного меридиана приблизительно составляет
40000 «.«, или километр равен Дуги меридиана.
Морская миля равна 1'дуги меридиана; следовательно,
2л/?	2К.6371	, осо
1 морская миля = ~збо-~бй~ ~” 36О-6О ' ~ 1»°52 км.
Так как длины дуг меридиана меняются от экватора к по-
люсу, то длина дуги 1' меридиана не всюду равна 1852 м —
ближе к экватору она несколько меньше, а к полюсу больше
этой величины.
Перевод морских миль в километры и обратно см. в при-
ложении 2.
Кабельтов равен морской мили, или 185 м.
7-
Английская (статутная) миля равна 1,6 км.
В этих мерах длины оцифрованы все приборы на английских
и американских самолетах (но не в морских милях!).
Перевод английских миль в километры и обратно см. в при-
ложении 3.
§ 2. ОСНОВНЫЕ ЛИНИИ ПОЛОЖЕНИЯ
Дуга большого круга иначе называется в навигации орто-
дромией.
По ортодромии измеряется кратчайшее расстояние между
двумя точкам ia земной поверхности.
Ортодромия составляет с меридианами различные, неравные
между собой углы я,, я2, а8... (рис. 2). Разница в этих углах
при одной и той же длине
ортодромии будет тем
больше, чем ближе к по-
люсу расположена ортодро-
мия.
На ортодромии (или на
ее продолжении) всегда
можно найти точку, где
ортодромия составляет с ме-
' ридианом угол 90°. Такая
точка называется вертек-
сом (V). Из всех точек
ортодромии вертекс имеет
максимальную широту.
Линия, пересекающая ме-
ридианы под одинаковыми
углами я, называется л о-
ксодром ней (см. рис. 2). Локсодромия, как правило, длин-
нее ортодромии, но в некоторых частных случаях совпадает
с ней, например, меридиан является одновременно ортодромиче
ской и локсодромической крш ой.
То же самое относится и к эква-
тору. Более подробный анализ
сравнения этих двух кривых дан
в конце настоящего раздела.
Линией равных азиму-
тов (ЛРА) называется кривая,
из всех точек которой направле-
ние на одну какую-либо посто-
янную точку, считаемое по ор-
тодромии, составляет с меридиа-
нами один и тот же угол П (рис.З).
Эта кривая является линией воз-
Рис. 3
можных положений, т. е. позиционной линией самолета,
пеленгующего какую-либо радиостанцию с помощью радиопо-
лукомпаса (радиокомпаса).
6
Малый круг1 наземном шаре, являясь геометрическим
местом точек, равноудаленных от одной точки — центра круга,
используется в самолетовождении как позиционная линия само-
лета при астрономической и радиоориентировке.
Наконец, позиционной линией самолета при радионавигации
могут быть гипербола и эллипс.
Разберем подробнее каждую из указанных нами позицион-
ных линий.
§ 3. ОРТОДРОМИЯ
Уравнение ортодромии
уже сказано, ортодромия
На рис. 4 Р—полюс :
между точкой А,
Как было
шого круга,
ортодромия
лежащей на экваторе, и точкой В
с координатами <р и X. Тогда из
сферического треугольника РАВ
можно получить уравнение орто-
является дугой боль-
АВ —
земли, EQ — экватор,
дромии.
По формуле четырех элемен-
тов2 имеем, принимая за четыре
элемента угол а, сторону РА,
угол ДХ и сторону (90 — ср):
cos РА- cos ДХ — з1пРД-
• ctg РВ — sin ДХ • ctg а.
Так как РА = 90°, то получим:
Рис. 4.
tg ср = ctg a-sin ДХ. w	(1)
Здесь а—угол, который составляет ортодромия с меридиа-
ном в точке пересечения с экватором.
Уравнение (1) является уравнением ортодромии. Задаваясь
разностью долгот ДХ точки А и текущей точки, можно полу-
чать широту этой точки.
Ниже, при расчете промежуточных точек ортодромии
(формула 7), дан другой вид уравнения ортодромии, в которое
в качестве постоянных входят координаты вертекса.
Из уравнения (1) имеем:
при а = 0°, sin ДХ — 0, т. е. ДХ = О или 180°.
Это значит, что при любой широте разность долгот точек
ортодромии равна (г или 180°, т. е. ортодромия обращается,
в меридиан.
При а = 90°, tg <р — 0°, т. е. ортодромия обращается в экватор
1 Правильнее следует сказать малая окружность, но мы будем поль-
зоваться принятым в навигации термином малый круг (так же, как и тер-
мином большой круг).
а Формулы сферической тригонометрии даны в приложении 18.
9
При дальних перелетах основное направление полета прокла-
дывается по ортодромии, которая разбивается на ряд участков.
Внутри каждого из участков путь прокладывается по локсодро-
мии (рис. 5), по которой уже совершается полет. Для разбивки
ортодромии на участки
необходимо как-то выбрать
промежуточные точки.
Параллельно с этим опре-
деляют ортодромические
путевые углы и расстояния.
Вычисление всех этих эле-
ментов составляет предмет
того, что обычно называют
расчетом ортодромии,
способов которого существует довольно много. Здесь мы раз-
берем два аналитических способа расчета. В дальнейшем, при
анализе некоторых проекций, мы укажем и на графические
методы расчета ортодромии с помощью тех или иных проекций
Ортодромический путевой угол
На рис. 6 Я и В — точки с координатами <рь кг н <р2, к2,
дуга АВ — ортодромия, а — ортодромический путевой угол
в точке А. Применим к сфе-
рическому треугольнику РАВ
формулу
тов:
четырех элемен-
sin PA  ctg PB — sin (k2 —kJ •
• ctg a=cos PA • cos(k2—kJ,
или
sin (90 — ср J • ctg (90 — <р2) —
—sin(k2 — kj-ctga =
= cos (90 — <р J  cos(k2 — kJ,
р
90
Рис. 6.
s v«t0^ В('Ъ
откуда

ctg а= cos • tg <?2 • cosec (k2—k J — sin <f>i • ctg (k2 — kJ.	(2)
По этой формуле может быть вычислен ортодромический
путевой угол.
откуда
Ортодромическое расстояние
Из рис. 6 имеем по теореме синусов:
sin АВ sin РВ
sin (Х3 — )-i)	sin а '
; с___ cos %-sin (Х2 — ki) ,
О 111 О   ---а;------— ,
sm а
(3)
10
Чтобы получить расстояние в километрах, необходимо после
вычисления 5 по формуле (3) умножить его значение в мину-
тах дуги на 1,852.
Вычисление ортодромического путевого угла по формуле (2)
и расстояния по формуле (3) удобно производить по схеме
(см. приложение 4).
Можно вычислить ортодромическое расстояние, не прибегая
к формуле (2). По теореме для косинуса косоугольного тре-
угольника имеем:
cos АВ — cos РА• cos РВ + sin РА • sin РВ • cos (Х2 — к,),
откуда
cos 5 == sin • sin <p2 + cos <fi • cos <j>8 • cos (X2—Xx).	(4)
После получения 5 по формуле (4) необходимо умножить
его значение в минутах дуги на 1,852 для перевода в кило-
метры. Вычисление удобно производить по схеме (см. прило-
жение 5) в случаях, когда необходимо вычислить только орто-
дромическое расстояние. При необходимости же вычисления,
параллельно с расстоянием, и ортодромического угла, удобнее
воспользоваться схемой, данной в приложении 4.
Координаты промежуточных точек
1-й способ.
При этом способе можно получить промежуточные точки,
задаваясь их долготами. Искомые широты определяются по
соответствующей формуле.
Способ использует вспомогательную точку вертекса. По
рис. 6 найдем координаты	вертекса из прямоугольного
сферического треугольника PVA:
sin Р V — sin РА • sin а,
откуда
cos<?0 = cosft-slna.	(6)
Из того же треугольника имеем:
cos РА = ctg (k0 — kJ • ctg a,
откуда
Ctg(ko —X1) = sin<prtga.	(6)
По формулам (5) и (6), после предварительного определе-
ния а по формуле (2), определяются координаты вертекса.
Из прямоугольного треугольника PBV имеем:
tg РV = tg РВ • cos VPB,
откуда
tg <р = tg ?о ’ cos (Хо — X).	(7)
11
Давая различные значения долготам X, по этой формуле
можно получать соответствующие широты <?. Вычисление ко-
ординат промежуточных точек по формулам (6) и (7) удобно
производить по схеме, данной в приложении 6, после того как
вычислен путевой угол по схеме приложения 4. Таким образом,
полный расчет ортодромии может быть произведен по схемам,
данным в приложениях 4 и 6.
2-й способ.
Способ позволяет вычислять координаты промежуточных
точек, выбранных, как это нам угодно, например, через опре-
деленные расстояния по ортодромии или через расстояния по
ортодромии, соответствующие изменению путевого угла на 1°.
1) Объединяя формулы (2) и (6), получим:
tg(\> — >ч) = tg <р2-ctg	cosec (Х2 — X,) — ctg(X2 — X,).	(8)
2) Из треугольника PAV имеем:
tg Р V = tg РА • cos APV,
откуда
tg?o = tg<prsec(Xe —Xj).	(9)
Формулы (8) и (9) служат для определения координат вертекса.
3) Из треугольника PBV имеем:
tgBV
sin РУ »
откуда
tgS = tg(Xo —X)-cos<p0.	(10)
По этой формуле можно вычислить расстояние по ортодро-
мии от точки с долготой X до вертекса. Если весь маршрут
полета лежит по одну сторону от вертекса
Р (рис. 7), то после вычисления по формуле (10)
\	= и S2 — IW, находят искомое рас-
\ стояние S как разность и S2, т. е.
Т' / \	5= —<S2.
/ I \ Если же маршрут проходит через вер-
/ I | текс, то
/	1	5 = ^ + 5,.
4)	После вычисления расстояния 6" по
формуле (10), эту же формулу можно исполь-
Рис. 7. зовать в другом виде:
ctg(X0 —X) = ctgS-cos<p0.	(11)
Задаваясь определенными, обычно равными, промежутками
по ортодромии 5, начиная от места вылета, вычисляют долготы
соответствующих точек.
12
Для получения широт этих точек можно использовать фор-
мулу (7):
tg<p = tg<p0-cos(X0 — >.).	(12)
5)	На основании той же теоремы, по которой написана
формула (10), можно написать из треугольника PAV:
откуда
tgax = ctg cosec 6^ ,
где а.А —путевой угол у точки А;
—расстояние по ортодромии от точки А до вертекса.
Соответственно для любой точки ортодромии будет спра-
ведливо:
tga = ctg ср0- cosecS,	(13)
где 5—расстояние по ортодромии от точки до вертекса.
Подставляя в формулу (13) вместо 5 те же расстояния, что
и в формулу (11), получим путевые углы при промежуточных
точках.
6)	Наконец, формулу (13) можно написать так:
sin .5 = ctgcpo-ctga.	(14)
Задаваясь здесь путевыми углами (например, через каждый
градус), будем получать расстояния по ортодромии (до вер-
текса) и, следовательно, все промежуточные точки.
Все вычисления по 2-му спо-
собу по формулам (8) — (14) удобно
производить по схемам, данным
в приложениях 7, 8 и 9.
Пользование этими схемами ис-
ключает необходимость вычисле-
ния расстояния по схеме прило-
жения 5, так как это расстояние вы-
числяется по схеме приложения 7.
увеличится пропорпио-
Зависимость длины ортодромии
от высоты полета
При увеличении радиуса орто-
дромии на величину высоты по-
лета /V (рис. 8) длина ортодромии
нально ему, т. е.
или
Sq
sn_____R ±_Н_
R
Обозначив
выоажение 11 4-
через о, получим:
— °«50.
В табл. 1 даны значения а для некоторых значений Н.
Таблица 1
Н км	1	2	3	4	5	8	10	15
б	1,000157	1,000314	1,000471	1,000628	1,000786	1,001256	1,001571	1,002356
Из таблицы видно, что увеличение ортодромии невелико,
но в некоторых случаях практики радиосамолетовождения его
следует учитывать.
§ 4.	ЛОКСОДРОМИЯ
Как было упомянуто выше, локсодромия пересекает все
меридианы под одинаковыми углами. Как правило, она длиннее
ортодромии, однако на
сравнительно неболь-
ших расстояниях эта
разница не слишком
велика. На практике
при расстояниях до
500—600 км путь про-
кладывают по локсо-
дромии. На полетных
картах путь по локсо-
дромии прокладывают
следующим образом.
Соединяют точки вы-
лета и назначения пря-
мой линией и измеря-
ют путевой угол у
среднего меридиана
участка пути. После
этого полученный пу-
тевой угол строят последовательно у всех меридианов на карте,
начиная от пункта вылета. При таком способе построения по-
лучают ломаную линию (рис. 9), практически близко подходя-
щую к локсодромии.
Можно построение локсодромии произвести графическим
путем на сетке меркаторской проекции, о чем речь будет
ниже.
При отсутствии карты меркаторской проекции, а также при
необходимости получить большую точность, расчет локсодро-
мии может быть произведен аналитически.
14	*
Уравнение локсодромии
Построим на земной сфере весьма малый треугольник АВС
- ---------------- а АВ является локсодромией.
. ис Ю), У которого сторона
'Р уГОЛ ’а —локсодромическим
путевым углом. Сторона АС
является разностью широт то-
чек А и В и обозначена Д<р. Сто-
рона ВС является разностью
долгот. Она равна ДХ-cos?. При-
нимая треугольник АВС за пло-
ский, найдем:
ВС —AC-tg а,
или
Д). • cos ? = Д? • tg а.
Переходя к бесконечно малым величинам, получим:
(В - = tg а
</ф
cos ф
(15)
Интегрируя это выражение, найдем:
X = tga-lntg(45 + -£)+ С.
Постоянную интегрирования С можно получить, положив
? = 0. Тогда Х0 = С и уравнение принимает вид:
X = tg a- In tg (45 + -тг) + хо.
(16)
Величина л0 представляет собой
долготу точки пересечения локсодро-
мии и экватора (так как ?=0).
Выражение (16) может быть пред-
ставлено в виде:
, 6г । ф\	a—Xo)Ctga
tg^45 + yj=e	(17)
Выражение (17) или (16) предста-
вляет собой спиралеобразную кри-
вую, оборачивающую Землю бесчи-
сленное число раз и асимптотически
Р|1С- и-	приближающуюся к полюсу (рис. 11).
Действительно, если задавать дол-
готе X значения Xt 4- 2к, kj 4-4я и т. д., то выражение (17),
а следовательно, и широта <р будет беспрерывно расти, между
тем как долгота будет оставаться неизменной (прибавление 2п,
т- е. 360°, долготу не меняет). Следовательно, локсодромия будет
Пересекать один и тот же меридиан бесконечное число раз, а точки
пересечения будут беспредельно увеличивать свою широту ?.
15
Из формулы (16) следует, что при а = 0 или а = 180° X = к0,
т. е. долгота локсодромии остается постоянной (и равной дол-
готе точки ее пересечения с экватором). Это значит, что в этом
случае локсодромия совпадает с меридианом.
Если проинтегрировать выражение (15) в пределах от
до <ра, то получим:
Х2 —Xt = tga [in tg (45 +	— In tg (45 +	],
или
tg а = ---------1---------------—.	(18)
In tg I 45 +	- In tg (45 4-	1
При а = 90е или 270°, т. е. при tg а = то, знаменатель этого
выражения должен быть равен нулю, так как числитель Х2— X,
не может быть равен бесконечности. Равенство же нулю знаме-
нателя приводит к равенству широт, т. е. <р2 = <р1.
Отсюда следует, что при курсовых углах 90° или 270°
широта остается неизменной, т. е. локсодромия обращается
в параллель.
Расчет локсодромии
Путевой угол локсодромии выражается формулой (18).
Величина In tg 45 + входящая в эту формулу, назы-
вается меридиональной частью и обозначается обычно
буквой D.
Следовательно,
£>= In tg(45 + f).
Здесь D выражено в радианах. Умножая D на 57,3-60, т. е.
принимая радиус Земли R = 3437,75 морской мили, а также
переходя от натуральных логарифмов к десятичным через
mod = 0,43429..., получим:
п 3437,75 .	(. _	<р \
~ 0,43429 g tg (,45 + 2 )’
ИЛИ
Э = 7915,705 lg tg(45 + |-).	(19)
Значения величины D в морских милях, в зависимости от
широты ср, даются в таблицах меридиональных частей (см. при-
ложение 10).
Формула (18) принимает вид:
tga =
Хд “— Х|
(20)
Здесь D2 и — меридиональные части, а весь знаменатель
называется меридиональной разностью широт. Формула (20)
16
является
ческого
формулу
рабочей формулой для расчета путевого локсодроми-
тла. Для расчета промежуточных точек можно эту же
представить в следующем виде:
D = D^ -f-ctga-(X — XJ.	(21)
Задаваясь долготой X, находят D и затем — по таблице
меридиональных частей —широту.
Можно итти и обратным путем, задаваясь широтой и находя
соответствующую долготу по формуле:
k = (D —DjJtga+Xj.	(22)
Длина пути по локсодромии может быть найдена следую-
щим образом. Из весьма малого треугольника АВС (см. рис. 10),
который мы примем за плоский, имеем:
Д<р = AS-cos а.
Переходя к бесконечно малым величинам, получим:
d<? = dS-cos a.
Интегрируя в пределах широт <рх и <р2, найдем:
5=	.	(23)
cos а	'
Для получения длины локсодромии в километрах необхо-
димо умножить выражение (23) на 111,18, т. е.
Skm = 111,18-^^l_.	(24).
’	cos а	4 1
Здесь и <р2 следует брать в градусах.
Формула (24) не дает желаемых результатов, когда угол a
близок к 90 или 270°, а разность (<р2— <Pi) близка к нулю.
В таком случае следует пользоваться другой формулой. Из
рис. 10 имеем:
АХ• cos <р = AS-sin a.
Переходя к бесконечно малым величинам, получим:
dS = dk^~.	(25)
sma	4 '
Принимая во внимание небольшую разность широт (<р2 — Ti)»
можно положить
__	<р, 4- <рд
?ср	2
и проинтегрировать выражение (25)
величиной постоянной и проинтегрировать выражение (25)
в пределах от Хх до Х2. Тогда 5
5 = (Хг —k1)-°S?cp- .
v £	sin a
Ни. зеки И и- титут ГВО:17,
2-1ВД.1
Е- IT ПЫ
I
I
I
I
I
I
I
I
I
I
I
I
I
I •
Умножив это выражение на 111,18, найдем:
Skm = 111,18(1, -	 -°^р-.	(26)
Если разделить выражение (24) на выражение (26), получим
приближенную формулу для локсодромического путевого угла:
tg а = cos <?„ .	(27)
6	 <?2 — 91 ,СР	' 7'
Для расчета локсодромии (вычисления путевого угла, длины
локсодромии и координат промежуточных точек) по приведен-
ным формулам можно воспользоваться схемой, данной в прило-
жении И. В схеме приведен пример расчета локсодромии для
маршрута Москва — Ныо-Йорк.
Графический расчет локсодромии, который применяется
обычно на практике, приведен нами ниже, при рассмотрении
равноугольной цилиндрической (меркаторской) проекции.
§ 5.	РАЗНОСТЬ МЕЖДУ ДЛИНАМИ ЛОКСОДРОМИИ И ОРТОДРОМИИ
Как известно, путь по локсодромии, как правило, длиннее
пути по ортодромии и только в некоторых частных случаях
совпадает с ним.
Р	Интересно проследить, ка-
/Тк	кова разница в длинах между
/C.VX	ними, поскольку эта разница
/Ah	может оказать влияние при
/212 \	дальних полетах на выбор
/	1	\	маршрута.
/	I \	Максимальной величины
/	I	\	разность ДУ между локсодро-
/	I	-\	мией и ортодромией достигает
/	икад”	\	при полете вдоль параллели.
I	У\ \90	\	Для определенной разности
°mодромия	долгот эта разность ДУ по
Atyity Локсодромия"	абсолютной своей величине
имеет максимум на некоторой
1>ис- 12-	параллели. Проф. Витковский
приводит формулу для опре-
деления такой параллели. На рис. 12 AVB—ортодромия, про-
веденная между точками А и В, находящимися на одной
параллели. Проведя PV перпендикулярно к ортодромии, полу-
чим сферический прямоугольный треугольник APV с прямым
углом при точке вертекса ортодромии V7.
, Из треугольника имеем:
sin А V— sin АР-sin APV.	728)
18
s c
Ho AV —	> где длина, ортодромии, a R— радиус Земли,
/Р=90е —?> а угол *4Plz= _; Где ДХ —разность долгот то-
чек А и В. Подставляя это в выражение (28), получим:
откуда	/ д>
Sc,pT= агс sin (s’n ~2~cos ®J.	(29)
Длина локсодромии между точками А и В определится как
длина параллели, т. е.
S,okc = Д’-АХ-cos®.
Следовательно,
= 5»кс — 5орт	[ДХ - cos ? — 2 arc sin (sin ~ cos <р )"|. (30)
При © = 0° выражение (30) обращается в нуль, при ? = 90°
локсодромия й ортодромия, а следовательно, и AS также обра-
щаются в нуль.
Следовательно, где-то в промежутке значение AS должно
иметь максимум. Найдем его. Для этого возьмем первую про-
изводную AS и приравняем ее нулю.
4 »	О a f ЬкК
А/. • cos а — 2 arc sin sin -к-  cos ©
Принимая ДХ за постоянную величину, найдем [а>.-cos v — 2 arc sin fsin -cos ®	= — Дл мп	ср +	4i~ =—=0. / . ДХ	у у 1 — (sin-—-cos ф 1 Отсюда . - •• Д>- 4 sir)- — AX2 =	—	 .1—sin2 2 cos2<p ИЛИ ДХ2 — 4 sin2 COS2 ©  	p—, T	*19	• Л ДЛ AA2-sm4 откуда	AX-sin -f
19
Подставляя это в уравнение (30), получим:
д^„=2/?
Ах\2 .„ДХ
2-;-sinT
---ДХ---- — аГС Sin
sin-3-
По этой формуле подсчитана наибольшая разность ДУмакс для
различных значений ДХ. Значения ДУ приведены в табл. 2.
Как видно из таблицы, наиболь-
шей величины ДУ достигает на средних
широтах.
Достигая максимума на некоторой
широте, разность ДУ принимает по
абсолютной величине меньшие значе-
ния как при уменьшении, так и при
увеличении широты. Уменьшение ДУ
с уменьшением широты при некото-
рой разности долгот объясняется тем,
что, хотя по абсолютной величине
длины локсодромии и ортодромии
растут, но локсодромия при прибли-
ближе подходит к ортодромии, сливаясь
Таблица 2
Д).		й5макс B KM
30°	54°30'	15
60°	53°35'	120
90°	52°O1'	419
120°	49 31'	1047
150°	45°40'	2 200
180°	39°32'	4 185
к экватору все
жении
с ней на экваторе. Уменьшение же ДУ с увеличением широты
связано с тем, что хотя при приближении к полюсу локсодро-
мия все дальше отходит от ортодромии, но по абсолютной
своей величине длины локсодромии и ортодромии быстро умень-
шаются.
Полученные нами значения по абсолютной
являются столь интересными, как относительные
AS
локсодромии, т. е. величины -т.— .
-орт
На рис. 13 приведены графики величины —
^орт
ных разностей долгот при постоянной широте. Из графиков
видно, что с приближением к полюсу величина непрерывно
^орт
растет, достигая вблизи полюса своего максимума. Для каждой
AS
разности долгот величина т— имеет свои максимум, из
"^OP'i
рых самый большой приходится на разность долгот 180°.
AS	п
чину — для этого случая нетрудно определить. Для
*\рт
разделим выражение (30) на (29), тогда получим:
величине не
увеличения
для различ-
KOTO-
Вели-
этого
AS
7?
cos <р — 2 arc sin (sm — cos
ДХ
cosq>

дХ
27? arc sin (sin — cos
2	а'.	\	1
arc sin ^sin cos ф \
20
<р подставить у. Однако это выражение приобретает при этом
неопределенность. Применяя правило Лопиталя, берем производ-
ные числителя и знаменателя, тогда получим:
. 7е
ДХ	— sin о	_ ДХ	Sln 2	ДХ
2	.да	2	.Да . г.	ДХ* *
— sinysm<f>	sin —sin—	2sin —
При максимальной разности долгот, равной к, получим:
s	— 1 = 0,57, т. е. 57%.
*^орг шах
Таким образом, теоретически максимальное уве-
личение длины маршрута, взятого по локсодро-
мии, по сравнению с длиной, взятой по ортодро-
мии, может быть 57% (вблизи полюса), что и видно на
графике рис. 13. В этом случае ортодромия представится диа-
метром, а локсодромия — полуокружностью, которая больше
своего диаметра на 57%.
„	Д5
Величина — зависит от взаимного расположения начальной
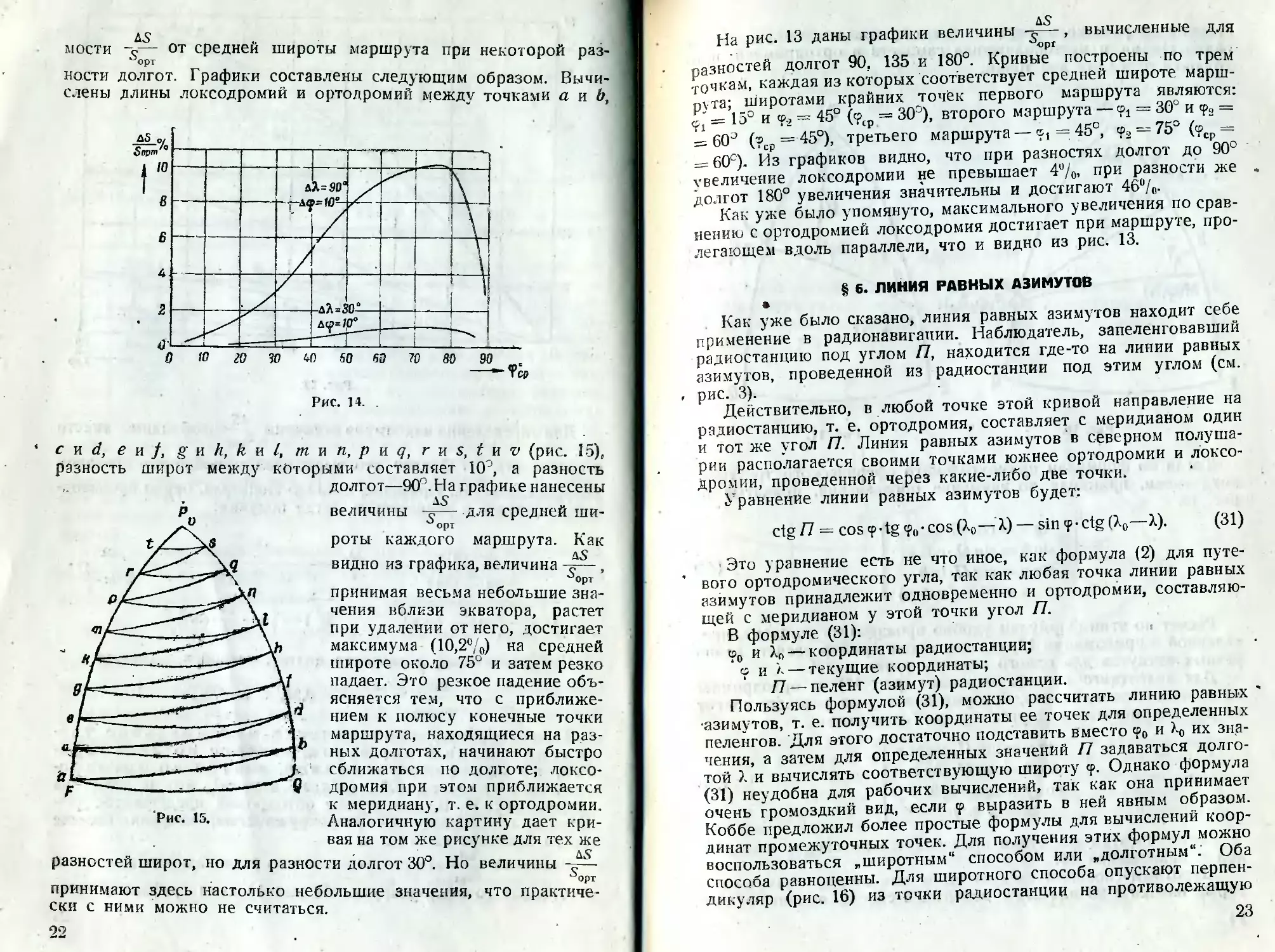
к конечной точек маршрута. На рис. 14 даны графики зависи-
21
мости -о— от средней широты маршрута при некоторой раз-
°орт
нести долгот. Графики составлены следующим образом. Вычи-
слены длины локсодромий и ортодромий между точками а и Ь,
end, ей}, g и h, k и /, т и п, р и q, г и s, t и v (рис. 15),
разность широт между которыми составляет К)1, а разность
долгот—90°. На графике нанесены
aS
величины -Q— для средней ши-
^орт
роты каждого маршрута. Как
видно из графика, величина ,
•^орт
принимая весьма небольшие зна-
чения вблизи экватора, растет
при удалении от него, достигает
максимума (10,2%) на средней
широте около 75° и затем резко
падает. Это резкое падение объ-
ясняется тем, что с приближе-
нием к полюсу конечные точки
маршрута, находящиеся на раз-
ных долготах, начинают быстро
сближаться по долготе; локсо-
дромия при этом приближается
к меридиану, т. е. к ортодромии.
Аналогичную картину дает кри-
вая на том же рисунке для тех же
aS
"<’орт
что практиче-
Рис. 15.
разностей широт, но для разности долгот 30°. Но величины
принимают здесь настолько небольшие значения,
ски с ними можно не считаться.
На рис. 13 даны графики величины -к—, вычисленные для
*\>рт
разностей долгот 90, 135 и 180°. Кривые построены по трем
точкам, каждая из которых соответствует средней широте марш-
рута; широтами крайних точёк первого маршрута являются:
= 15° и ср., — 45° (<? = 30°), второго маршрута —— 30° и ср2 =
= 60э (?СР = 45°), третьего маршрута — = 45°, <р2 —75°(® =
= 60е)- Из графиков видно, что при разностях долгот до 90°
увеличение локсодромии не превышает 4%, при разности же
долгот 180° увеличения значительны и достигают 46%.
Как уже было упомянуто, максимального увеличения по срав-
нению с ортодромией локсодромия достигает при маршруте, про-
легающем вдоль параллели, что и видно из рис. 13.
§ 6.	ЛИНИЯ РАВНЫХ АЗИМУТОВ
•
Как уже было сказано, линия равных азимутов находит себе
применение в радионавигации. Наблюдатель, запеленговавший
радиостанцию под углом П, находится где-то на линии равных
азимутов, проведенной из радиостанции под этим углом (см.
, рис. 3).
Действительно, в любой точке этой кривой направление на
радиостанцию, т. е. ортодромия, составляет с меридианом один
и тот же угол П. Линия равных азимутов в северном полуша-
рии располагается своими точками южнее ортодромии и локсо-
дромии, проведенной через какие-либо две точки.
Уравнение линии равных азимутов будет:
ctg П = cos<p-tg<?0-cos(X0—X) — sin<p-ctg(X0—А).	(31)
Это уравнение есть не что иное, как формула (2) для путе-
вого ортодромического угла, так как любая точка линии равных
азимутов принадлежит одновременно и ортодромии, составляю-
щей с меридианом у этой точки угол П.
В формуле (31):
®0 и Хп— координаты радиостанции;
а и X— текущие координаты;
П — пеленг (азимут) радиостанции.
Пользуясь формулой (31), можно рассчитать линию равных '
•азимутов, т. е. получить координаты ее точек для определенных
пеленгов. Для этого достаточно подставить вместо ®0 и их зна-
чения, а затем для определенных значений П задаваться долго-
той X и вычислять соответствующую широту ср. Однако формула
(31) неудобна для рабочих вычислений, так как она принимает
очень громоздкий вид, если ср выразить в ней явным образом.
Коббе предложил более простые формулы для вычислений коор-
динат промежуточных точек. Для получения этих формул можно
воспользоваться „широтным*1 способом или „долготным".' Оба
способа равноценны. Для широтного способа опускают перпен-
дикуляр (рис. 16) из точки радиостанции на противолежащую
23
сторону сферического треугольника, образованного меридианами
радиостанции и местоположения самолета и ортодромией, про-
ходящей через эти две точки.
Е
Рис. 16.
Рис. 17.
Тогда по формулам прямоугольного сферического треуголь-
ника имеем, принимая во внимание обозначения, принятые на
рис. 16:
tg х = cos ДХ  ctg ср0
sin & = sin ДХ - cos <Ро
sin у = ctg П-tg ft	'
<P = 90— (x+_y)
Расчет по этим формулам удобно производить по схеме, при-
• веденной в приложении 12, где дан также пример расчета линии
равных азимутов для одного пеленга, равного 80°.
Для долготного способа опускают (рис. 17) на ортодромию
из полюса перпендикуляр, который делит угол разности долгот
на два вспомогательных угла х и у. Тогда имеем:
tg х = ctg П • cosec ср
sin & = sin П-cos
cos j/ =tg То-tg8
ДХ = x + у
(33)
Расчет по этим формулам производится по схеме, приведен-
ной в приложении 13.
Широтным способом следует вычислять линии, азимуты ко-
торых близки к 90 или 270°; долготный способ применяют для
24
вычисления линий, расположенных в меридиональном направле-
нии. Для линий, азимуты которых близки к 45, 135, 225 и 315е,.
можно воспользоваться любым из способов.
Вычислив координаты точек линии равных азимутов, наносят
их затем на рабочую карту и соединяют плавными кривыми.
Кроме этих способов, существуют еще некоторые приемы
расчета точек линий равных азимутов.
На практике большей частью линии равных азимутов нано-
сят на карту графическими способами, связанными с характером
картографической проекции. Об этих способах будет итти речь
при рассмотрении этих проекций.
§ 7. МАЛЫЙ КРУГ
Как было упомянуто, малый круг используется как позицион-
ная линия при радио- и астрономической ориентировке.
При радионавигации бывают известны радиус малого круга?
и положение его центра.
Из рис. 18 и 19 можно получить уравнение малого круга..
Возьмем малый круг радиуса г (г выражено в дуговой мере)?
с центром в точке О и на окружности точку М. Отметим, что
радиус г круга является ортодромией. Обозначив координаты
центра круга через <р0 и Хо и координаты точки М — через f и X,
напишем выражение для косинуса стороны ОМ сферического>
треугольника РОМ:
cos ОМ = cos OP- cos PM -f- sin OP-sin PM cos P,
или
cos r = sin • sin <f 4- cos <рс • cos <p• cos (Ac—I).
(34>
25.
Полученное выражение является уравнением малого круга,
в котором ср и >. являются текущими координатами.
Определим из уравнения (34) cos(k0—л). Тогда получим:
cos (Хо->) =	. «I
Полученное выражение представляет собой формулу для ра-
счета точек тех участков круга, которые расположены в мери-
диональном направлении и для расчета которых удобно зада-
ваться широтой и находить соответствующую ей долготу.
Для получения удобной расчетной формулы для участков
круга, расположенных в направлении Е—И/ опустим перпенди-
куляр из точки О на сторону РМ и обозначим его через У, а от-
резки дуг стороны РМ — через х и у. Тогда, пользуясь форму-
-лами для сферического прямоугольного треугольника, найдем:
tg х = ctg ®0 • cos (а0—X)
'sin 8 = cos ?0 • sin (k0—).)
cos y~ cos r-sec &	'
® — 90' — (x + j)
Задаваясь значениями а, можно определять соответственные им
.значения <?, когда известны координаты центра круга и его радиус.
Расчет и нанесение малого круга на карту по приведенным
-формулам не всегда может нас удовлетворить по точности, так
как формулы не учитывают сжатия Земли и составлены для
шара, а не для сфероида.
Например, при пользовании дистанционно-метрическими мето-
.дами радионавигации (радиолокации) для целей бомбометания
по Невидимым целям точность знания точек малого круга должна
быть в пределах нескольких десятков метров. В таких случаях,
кроме нанесения на полетную карту сетки малых кругов, рас-
считанных по формулам (35) и (36), необходимо точно рассчи-
тать участок района пели для одного круга, проходящего через
цель. Этот расчет ведется по формулам высшей геодезии.
В частности, расстояние между7 двумя точками может быть
вычислено по строгой формуле Кларка:
24/?, +	•	(37)
Здесь k — длина хорды между конечными точками; _____________
R— среднегеометрический радиус кривизны, т. е. R=VRi’R2,
где и R2— радиусы конечных точек.
Для расчета величины k служит формула:
k = а ’ (cos «J — cos u.,)2 + (sin ил — sin м2)3 + .
+ 4 cos  cos a., • sin2 —1 y—J 2 .	(	(38)
26
Здесь а и b—большая и малая полуоси эллипсоида;
и и2—приведенные широты, т. е.
ь	ь ,
tg«l = ^tg?i И tgK2 = -tgO2.
Формула Кларка (37) применяется для расстояний, превышаю-
щих 800 км. Для меньших расстояний может быть применена
формула, дающая ошибку не больше 3—4 м в диапазоне широт
44-57°N:
S = k+ 1023-10-18&3 + 28-10~31-^5.	(39)
Здесь все величины выражаются в метрах.
§ 8. ЛИНИЯ РАВНЫХ РАЗНОСТЕЙ (СУММ) РАССТОЯНИЙ
При использовании дистанционно-метрических методов радио-
навигации (радиолокации) позиционной линией самолета может
быть линия равных разностей (или сумм) расстояний о.т двух
точек — фокусов, в которых расположены радиолокаторные стан-
ции. По аналогии с плоскостной гиперболой (или эллипсом),
такая линия на сфере называется сферической гиперболой (или
эллипсом).
Выведем уравнение сферического эллипса в сферических ко-
ординатах.
За сферические координаты точки Л/ (рис. 20) принимают
тангенсы дуг £ и отсчитываемых от начала координат 0 до
оснований перпендикуляров, опущенных из полюсов (х и у) на
начальные круги у—у и х—х через данную точку М. Таким
образом,	*
х = tg$ и у = tgф
27
Из треугольников уАМ и хМВ имеем:
tgV == tgiq-COsE И tg 5' = tg Е  COS 7].
(40>
Пусть на рис. 21 оси х—х и у—у совпадают с большой и ма-
лой осью эллипса, f и f—его фокусы, точка М лежит на эллипсе,
точка S также лежит на эллипсе, причем OS — малая полуось
эллипса. Тогда fOS и fOS являются прямоугольными треуголь-
никами, у которых гипотенузы fS = fS = а, если 2а—большая
ось эллипса, а катет OS— р, если 2р—малая ось эллипса. Кроме
того, р + р' = 2а.
Из треугольника f'OS имеем:
cosa = cos £• cose.	(41)
Отсюда
или
l + tg2e = (l+tg2a)TT^-,
откуда
g i + tg^₽ •
(42)
Из прямоугольных треугольников fMA и fMA имеем:
cosp' — cos-*]'-cos (е — ?);	(43)
cosp •= cos тр cos (е-R).	(44)
Обозначим р^-р' = 28 и, помня, что р + р' = 2а, получим:
р = а ф- 8; р' = а — 8,
отсюда
cosp = cos (а + 8) = cos a-cos 8 — sin a-sin 8;	(45)
cosp' = cos (a — 8) = cos a-cos 8 4- sin a-sin 8.	(46)
Сложив эти равенства, получим:
у (cos р + cos р') = cos a • cos 8.	(47)
Сложив равенства (43) и (44), получим:
4 (cosр' 4- cosр) = cos V• cosе•cos 6 = _£Bst‘cotL.	(48)
z	V1 + <
Сопоставляя выражения (47) и (48), получим:
cos a-cos 8
cos e-cos g
^l/l + tg24'
28
Подставляя сюда значение tg ц' из уравнения (40) и cos а из
уравнения (41), найдем:
о 5	cos Е
V 1 + cos^-tg2-»]
sec2p• sec28 =	= 1 4~ tg2 E 4- tg2tj,
(1 + tg2₽)(l 4- tg28) = 1 + tg2E + tg2T).	(49)
Отсюда
или
Выразим 8 через а и Е.
Вычтем и сложим уравнения (45) и (46). Тогда найдем:
cosp — cosp' = — 2 sin a-sin 8;	(50)
cos р + cos р'= 2 cos а-cos 8.	(51)
Вычтя и сложив уравнения (43) и (44), найдем:
cosp — cos р' = — 2 cos т]' • sin е • sin Е;
cos р 4-cos р'= 2 cos т]'• cos е • cos Е.
Сопоставляя эти равенства с выражениями (50) и (51), получим:
sin а • sin 8 == cos tj’ - sin e • sin E;
cosa-cos8 == cos tj'-cose-cos E.
Разделив первое на второе, получим:
tg8==2g^gA
s tg а
Отсюда, принимая во внимание уравнение (42),
tg2a-tg2P
lb°-tg2a l+tg20 ’
отсюда
1 4- tn28 - 1 4-
1 4-tg 0—14- tg2a l + tg2₽ •
Умножив обе части на (1 4-tg2₽), найдем:
(1 4- tg2 ₽)(1 4- tg28) = 1 4- tg2₽ 4- tg2E-tg2-°=gtg-2^ .	(52)
Сопоставляя (49) и (52), получим:
tg2 4- tg2$ = tg2 ₽ 4- tg2E--^f- .
Отсюда
tg2 t] 4- tg2 E = tg2 ₽ 4- tg2 E - tg2 E .
29
(53)
Отсюда, разделив на tg2 р, найдем:
tg8?  t^7)
tg8» tg8₽
Это есть уравнение сферического эллипса. Аналогично этому,
обозначив разность р' — р = 2а, а мнимую ось гиперболы через
2£, найдем:
Рис. 22.
_ 1	(541
tg2» tg2₽“L
Связь сферических коорди-
нат с географическими выра-
жается следующими зависи-
.мостями, которые легко полу-
чаются из сферических тре-
угольников МРу и ОРу
(рис. 22). На этом рисунке
Р — полюс Земли, EQ — эква-
тор, у—у и х—х — новые на-
чальные круги (оси координат
гиперболы или эллипса). Все
обозначения ясны из рисунка.
sin ®у cos (><„—/-) = tg «p-coscy, —ctg(8—£)-sin(X0—К),
sin V = sin © • sin vy + cos ?-costiy cos (Xv—X)
sinaycosPy—xo) = costytgtpc —sinPy—X0)ctg8.
(55)
рис. 23.
$г2а

Расчет точек гипербол неудобно производить по приведенным
формулам и может быть произведен по следующей схеме (рис. 23).
1. Определяют координаты
промежуточных точек орто-
дромии АВ — оси х — х семей-
. ства сферических гипербол,
через которые должны пройти
гиперболы.
Так как гиперболы обычно
должны проходить через оди-
наковые расстояния, то расчет
промежуточных точек следует
производить по способу, изло-
женному на стр. 12 и 13. Зада-
ваясь равными промежутками
расстояний S, по формулам (8),
(9), (10) и (12) вычисляют иско-
мые координаты.
2. Точки гипербол, не лежащие на оси х—х, вычисляют так:
а) Изменяют путевой угол а на величину Да и проводят орто-
дромию АС, пересекающую гиперболу в точке С(о').').


x—x, вычисляют так
30
б) Решают сферический треугольник АВС, у которого сто-
лаАС = •S'p ВС — (Sj — 2а) и АВ=2с, где 2а — разность расстоя-
ний для рассчитываемой ветви гиперболы, а 2с— ортодромиче-
ское расстояние между точками А и В. Зная также угол Да, по
формуле косинуса стороны определяют длину Sl—2a и затем
и Sv
Величину 2а можно вычислить как разность ортодромических.
расстояний DB и AD после определения координат точки D.
г в) По формулам (5) и (6) определяют вертекс ортодромии,
а затем, задаваясь промежутками расстояний по формулам.
(11) й (12) определяют координаты X' точки С.
При необходимости весьма точных расчетов, что может быть
при дистанционно-метрических методах радионавигации (радио-
локации), следует пользоваться более точными способами и
формулами высшей геодезии, в частности формулами (37) и (39),
ГЛ А В А 2
ОБЩИЕ СВЕДЕНИЯ О КАРТОГРАФИЧЕСКИХ ПРОЕКЦИЯХ
§ 9. СВЕДЕНИЯ ИЗ ТЕОРИИ ИСКАЖЕНИЙ
О масштабе
Масштабом называется отношение бесконечно малого от-
резка некоторой линии на карте к отрезку соответствующей ли-
нии на местности. Если это отношение' выражают отвлеченным
числом, например 1:100 000, то такой масштаб называют числен-
ным масштабом. Если указанный масштаб выразить числом единиц
Длин, которыми измеряют расстояние на местности и на карте,
например 1 км в 1 см, то такой масштаб называют линейным.
При построении картографических проекций земной шар умень-
шают в некоторое заданное число раз до размеров глобуса,
соответствующего заданному масштабу, а затем уже поверх-
ность глобуса переносят на карту различными способами.
Масштаб глобуса, выражающий степень общего уменьшения >
земного шара, называется общим или главным масшта-
бом. Этот масштаб подписывается под картой.
Однако он лишь приблизительно характеризует отношение
длин на карте к соответствующим действительным длинам.
Причина этого заключается в невозможности изображения ша-
ровой поверхности на плоскости без искажений. На различных
картах эти искажение имеют различную величину и характер,
в зависимости от назначения карты. Масштаб в данной точке
карты по данному направлению, в отличие от главного масштаба;
называется ча с т н ы м масштабом. Если главный масштаб
принять равным единице, то частные масштабы будут больше
или меньше единицы.
Одна из основных задач картографии состоит в том, что-'
бы выбрать и рассчитать такую проекцию карты, в кото-
.	31
рой частные масштабы возможно меньше отличались бы от
единицы.
Увеличением масштаба или просто увеличением назы-
вают отношение частного масштаба в данной точке по данному
направлению к главному масштабу карты. Если через р обозна-
чить частный масштаб, то разность v = р. — 1 называется отно-
сительным искажением длины в данной точке по данному
направлению.
На аэронавигационных картах, предназначенных для про-
кладки пути, искажения длин невелики даже на краях проек-
ции. Например, карта в равноугольной конической проекции
масштаба 1:1 500 000 имеет максимальный частный масштаб 1,04,
т. е. искажение длины достигает на ней величины v = 0,04,
или 4°/в. Однако аэронавигационные карты специального назна-
чения могут иметь частные масштабы, сильно отличающиеся
от единицы; так, например, на карте центральной (гномониче-
ской) проекции частный масштаб по меридиану на широте 30°
равен 4,0, а по параллели—2,0, или на карте равноугольной
цилиндрической проекции частный масштаб на широте 60° как
по меридиану, так и по параллели равен 2,0. Давая такие боль-
шие искажения длин, эти карты обладают некоторыми свой-
ствами, с успехом используемыми для решения специальных
задач аэронавигации. На этих особенностях мы будем оста-
навливаться при рассмотрении проекций.
Эллипс искажений
Возьмем на сфере (рис. 24) круг бесконечно малого радиуса,
отнесенный к прямоугольным координатам, совпадающим с
Рис. 24.
.диаметрами круга, и на окружности круга—точку А с коорди-
натами х и у. Диаметры Ох и Оу изобразятся на плоскости
в виде линий О'х' и О'у', которые, вообще говоря, будут пере-
секаться под некоторым углом, не равным 90°. Координаты
точки А'—-изображения точки А на плоскости—обозначим через
32
i у'. Обозначая частные масштабы по направлениям О'х' и О'у‘
через р и V, получим:
X1 = fix И у' = ХУ, или х= — и у =
Если в уравнения круга радиуса г
х2 + у2 = Г2
подставить значения х и у, то найдем:
Мы получили уравнение эллипса с сопряженными полудиа-
метрами уг и vr.
Так как при перенесении круга на плоскость мы не ограни-
чивали себя никакими условиями, то справедливо будет поло-
жение: всякий бесконечно малый круг на земном шаре изобра-
жается в общем случае бесконечно малым эллипсом, причем
два взаимно перпендикулярных диаметра круга изображаются
сопряженными диаметрами эллипса.
Из аналитической геометрии известно, что эллипс имеет
одну и только одну пару сопряженных взаимно перпендикуляр-
ных диаметров — оси эллипса. Следовательно, на земном шаре
в каждой точке существуют два взаимно перпендикулярных
направления, которые дают на проекции также взаимно пер-
пендикулярные направления — оси эллипса. По одному из этих
направлений—большой оси — масштаб будет максимальным, по
другому — малой оси — минимальным. Эти направления называ-
ются главными направлениями п р о е кци и. Уравнение
бесконечно малого эллипса, отнесенного к главным осям, будет:
где а = р.г и b — vr (рис. 25).
Рис. 25.
3-1883
33
Если принять r= 1, то а = ций = у, т. е. полуоси беско-
нечно малого эллипса равны частным масштабам по главным
направлениям проекции. Такой эллипс называют эллипсом
искажений или индикатрисой (указательницей). Таким
образом, а и b являются максимальным и минимальным мас-
штабом в данной точке.
Искажение длин
Из рис. 25 имеем, обозначая (УА'=г*-.
/ = j/х'2 +у2.
Так как х' = ах и у1 = by, то
И = 1/(ах)2 + (&у)2.
Обозначая частный масштаб по направлению (УА1, опреде-
ляемому углом а на сфере, через , получим:
Из рис. 25 имеем:
X	у
— = COS а и У = sin а.
Следовательно,
у. = j/а2 cos2 а + Ь2 sin2 а.	(56)
По этой формуле можно подсчитать частный масштаб по
любому направлению, если известны максимальный и минималь-
ный масштабы в данной точке.
Искажение углов
Из рис. 25 имеем:
= tg₽ = 5’= В’
отсюда
tg° _ а
tg₽ b •
Составляя производные пропорции, получим:
tga — tg₽ = -^-tga
и
tg«+tg₽= -^-Jltga.
Разделив первое на второе, получим:
sin (a — ₽) __________________ а — Ь
sin (a + ₽) а + b
(57)
34
Здесь (<* — ₽) есть величина искажения угла а; желая полу-
чить максимальное значение этого угла, мы должны положить
sin (а + ₽) = 1, ИЛИ а + р = 90°.
Тогда
sin (а — Р)	= а~~г .	(58)
\	max д 0	v '
Возьмем на окружности (рис. 25) точку В, выбранную так,
что ОБ расположено симметрично ОА относительно оси у.
На плоскости мы получим соответственно точку В' и линию
О'В, расположенную симметрично О'Л' относительно оси О'у'.
Тогда углу АОВ = S на сфере будет соответствовать угод
ДО’В' = 5' на плоскости. Искажение этого угла будет
&' — &=( 180 — 2₽) — (180 — 2а) = 2 (а — р).
Обозначая 2 (а — р) „„ = <о, или (а — р) = 4» заметим, что
искажение угла при данной точке равно о>, т. е. удвоенному
искажению направления. Подставляя это в выражение (58), полу-
чим формулу для наибольшего искажения угла между двумя
направлениями:
s,n7 = T+T-	(59)
Искажение площадей
Площадь бесконечно малого круга на глобусе равна р0 = -кг*.
Площадь эллипса искажений, соответствующего указанному
кругу, равна р^ = nab.
Найдем отношение -%— = р, называемое масштабом пло-
Ро
щадей в данной точке и характеризующее, во сколько раз
увеличилась или уменьшилась площадь некоторой фигуры при
перенесении ее с глобуса на карту:
а-Ь
Р = -^.
'а
Положив r0 = 1, найдем:
р = а-Ь,
(60)
т. е. масштаб площадей в данной точке равен произведению
максимального и минимального масштабов в этой точке.
Обозначим масштабы по меридиану и по параллели проек-
ции через тип.
Почти во всех проекциях, нашедших себе применение в аэро-
навигации, главные направления совпадают с меридианами
и параллелями. Поэтому для этих проекций будут справедливы
равенства
а = т и b = п.
5»
35
В таком случае формулы искажений (56), (59) и (60)
вид;
примут
Р-а — Vm2 cos2 а	n2 sin- а;
ш т — п
Р = т-п.
Для некоторых проекций бывает а = п и Ь — т.
(61)
(62)
(63)
способ
сетки
§ 10. О КАРТОГРАФИЧЕСКИХ ПРОЕКЦИЯХ
Картографической проекцией называют
условного изображения на плоскости географической
меридианов и параллелей.
В геометрии проекцией (рис. 26)
точки М на некоторую поверхность И
называют точку т, в которой поверх-
ность Н пересекается с лучом ОМ, иду-
щим из точки зрения О через проекти-
руемую точку.
В картографии поверхность Земли
может проектироваться на плоскость
или на различные поверхности, кото-
рые затем разворачиваются на пло-
скость. Однако такое геометрическое
представление проекции не может пол-
ностью характеризовать картографи-
ческие проекции, так как построение
этих последних большей частью производится не по правилам
геометрических перспектив, а по законам, которые не всегда могут
получить простое геометрическое толкование. Поэтому в карто-
графии термин „проекция11 понимается в более широком смысле,
а именно: картографической проекцией называется такое изо-
бражение земной поверхности, при котором каждой точке этой
поверхности соответствует одна точка на плоскости (изображе-
нии), и, наоборот, каждой точке на изображении соответствует
одна точка на сфере. Другими словами, изображение на плоско-
сти любой точки на сфере должно быть взаимно-однозначно.
При этом непрерывному перемещению точки М на сфере
соответствует непрерывное перемещение точки т на плоскости.
Как бы ни была задана картографическая проекция, всегда
можно указать связь между координатами точки М (X, <р) на
сфере и соответствующими ей прямоугольными декартовыми
координатами на плоскости (х, у). Аналитически это может
быть выражено так:
x = f (К <?);
у= Ф 0-, ?)•
(64)
Таким образом, уравнения (64) вполне определяют карто-
графическую проекцию.
36
Задача картографии состоит, с одной стороны, в том, чтобы
дать возможно более простые уравнения типа уравнений (64)
для построения картографической проекции, а с другой сто-
роны, — и это главное, — в том, чтобы удовлетворить требова-
ния потребителя, сводящиеся обычно к тому, чтобы проекция
давала возможно меньше искажений или же чтобы характер
этих искажений следовал определенному закону, с помощью
которого искажения могли быть легко определены и учтены.
Классификация проекций по характеру искажений
Выше уже было сказано, что изображение сферы на плоскости
сопряжено с искажением длин, углов или площадей. В зависи-
мости от этого, проекции могут быть классифицированы по
характеру искажений на четыре группы:
1)	равноугольные;
2)	равновеликие;
3)	равнопромежуточные;
4)	произвольные.
В равноугольных проекциях сохраняется равенство
углов между направлениями при перенесении их с глобуса
на карту. Обратившись к формуле (62), характеризующей
искажение углов, мы, соблюдая условие равноугольности, т. е.
отсутствия искажения углов, должны положить в ней ш = О,
что приводит к равенству т = п. Это значит, что масштабы
по главным направлениям равны. В таком случае формула (61)
примет вид:	____________
= т cos2 а -р sin2 а = т — п.
Отсюда следует, что частный масштаб по
нию остается величиной постоянной, т. е.
обратится в круг (рис. 27).
Это значит, что беско-
нечно малые фигуры в
равноугольных про-
екциях изображаются
подобными бесконеч-
но малыми фигурами.
Поэтому равноугольные :
проекции называют еще
конформными, т. е. „подоб-
ными". Масштаб равно-
угольной проекции, сохра-
няясь в точке по всем направлениям постоянным, изменяется
при переходе от точки к точке, так как в противном случае нам
пришлось бы притти к выводу, что сферу можно изобразить
на плоскости без искажений масштабов и углов, что, очевидно,
невозможно.
Равноугольные проекции наиболее распространены в аэро-
навигации.
любому направле-
эллипс искажений

Рис. 27.

37
Равнопромежуточными называют такие проекции,
в которых масштаб сохраняется по одному из главных напра-
влений. Следовательно, в этих проекциях или а — 1, или Ь=\.
На рис. 28 представлен бесконечно малый круг на сфере
и его изображение на равнопромежуточной проекции в виде
вллипса, в котором b — 1, а следовательно, п = 1.
Условие равнопромежуточности исключает, конечно, условие
равноугольности и, следовательно, подобия фигур.
Равновеликими называются такие проекции, в которых
изображения сохраняют величину площадей.
Формула (63) для равновеликой проекции будет иметь вид:
а-Ь = 1, или а= -г ,
т. е. произведение экстремальных масштабов равно 1.
Эллипс искажений для равновеликих проекций будет иметь
вид, изображенный на рис. 29, т. е. каждая из его полуосей
не равна радиусу круга оригинала, но сохраняется равенство
яЬ = 1.
88
Равновеликие проекции не получили распространения
0 практике аэронавигации.
Наконец, произвольными называются те проекции,
в которых не соблюдается ни одно из условий, положенных
в основу указанных трех групп проекций.
Классификация проекций по способу построения
Из большого числа видов проекций мы рассмотрим только
те из них, которые получили применение в авиации, а именно:
1)	цилиндрические проекции;
2)	перспективные проекции;
3)	конические проекции;
4)	поликонические проекции;
5)	многогранные проекции;
6)	произвольные проекции.
Всякая картографическая проекция определяется видом
сетки координатных линий. Система сферических координат,
у которой координатные линии проще всего изображаются
в данной проекции, называется нормальной системой, а соответ-
ствующая ей сетка — нормальной сеткой данной проекции.
Цилиндрическими
называются такие проек-	i	Г"
ции, у которых меридиа-	_____________-__-
ны нормальной сетки	________________
суть прямые параллель- 'll- Ц-У1
ные линии, отстоящие ~	~
одна от другой на рас-
стояния, пропорциональ-	----------------
ные долготам; параллели 
суть прямые линии, пер- <_______
пендикулярные к мери-
пианам. Расстояния меж-	Рис. 30.
ду параллелями могут
быть различные; они определяют характер искажений проекции.
Сетку меридианов и параллелей такого вида можно получить,
если представить сферу спроектированной на цилиндр, разверну-
тый затем на плоскость (рис. 30). Отсюда и произошло назва-
ние— цилиндрические проекции. Следует только помнить, что
построение цилиндрических проекций происходит не по правилам
геометрической перспективы, а по законам, описываемым ниже.
Перспективными называются такие проекции, которые
получены в результате проектирования земной поверхности из
какой-нибудь точки на плоскость (рис. 31). Это единственный
вид картографических проекций, в которых слово „проекция*
всегда соответствует его геометрическому смыслу.
Коническими называются такие проекции, в которых
меридианы нормальной сетки изображаются пучком прямых
линий, углы между которыми пропорциональны долготам,
а параллели — концентрические окружности.
39
Сетку меридианов и параллелей такого вида можно полу-
чить, если проектировать сферу на конус, касательный (или
секущий) по некоторой параллели и развернутый затем на
плоскость (рис. 32). Как и цилиндрические проекции, конические
проекции строятся не по правилам геометрических перспектив,
а по законам, описываемым ниже.
S
Рис. 31.
Рис. 32.
Нетрудно заметить, что цилиндрические и перспективные
проекции являются частными случаями конических проекций.
Действительно, если параллель касания конуса приближать
к экватору, то угол при вершине конуса будет уменьшаться
и в пределе, когда параллелью касания
будет экватор, вершина конуса уйдет в бес-
конечность и конус превратится в ци-
линдр. Наоборот, если параллель касания
конуса приближать к полюсу, угол при
вершине конуса будет увеличиваться,
вершина будет приближаться к сфере и
в пределе конус обратится в плоскость,
касательную в полюсе. Таким образом,
коническая проекция является общим слу-
чаем указанных трех видов проекций.
П ол и кон иче ск и м и называются про-
екции, для нормальной сетки которых
Рис. зз.	средний меридиан — прямая линия, осталь-
ные меридианы — симметрично располо-
женные кривые; параллели — разноцентренные окружности,
центры которых расположены на среднем меридиане (рис. 33).
Многогранными называются проекции, при построении
которых земная поверхность переносится на ряд плоскостей,
касающихся шара в центральных точках сфероидических
трапеций, ограниченных меридианами и параллелями, взятыми
через определенные промежутки.
Произвольными называются проекции, которые нельзя
отнести ни к одной из перечисленных групп.
40
ГЛАВА 3
ЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ
В зависимости от изображения сети координатных линий
цилиндрические проекции могут быть нормальные, попе-
речные или косые.
Нормальная проекция получается при проектировании
глобуса на цилиндр, ось которого совпадает g осью вращения,
глобуса (рис. 34, а).
Рис. 3».
Поперечная проекция получается при проектировании
глобуса на цилиндр, ось которого перпендикулярна к оси
вращения глобуса (рис. 34, б).
Косая проекция соответствует промежуточному положению
глобуса (рис. 34, в).
§ 11. ПРОСТАЯ ЦИЛИНДРИЧЕСКАЯ ПРОЕКЦИЯ
Простая цилиндрическая (квадратная) проекция была предло-
жена в 1438 г. Генрихом Мореплавателем и является
наиболее простой из всех суще-
ствующих проекций. Она полу-
чается следующим образом (рис. 35).
Плоскости меридианов глобуса, во-
круг которого описан касательный
по экватору цилиндр, продолжают
до пересечения с цилиндром и вы-
прямляют каждый меридиан в его
плоскости до совпадения его с по-
верхностью цилиндра. Таким обра-
зом, на меридианах проекции будут
отложены выпрямленные дуги ме»
ридианов глобуса. Очевидно, ме-
ридианы на цилиндре суть его обра-
зующие, а параллели — окружности
одинаковых радиусов, равных ра-
диусу экватора. Если теперь разрезать цилиндр по одной
из образующих и развернуть затем цилиндр на плоскость, то
получим сетку простой квадратной цилиндрической проекции,
41
^принимая во внимание, что промежутки между меридианами
и параллелями взяты нами одинаковые. Обозначив эти проме-
жутки через Д<р и ДХ и радиус глобуса — через /?, можем написать:
Дф = /?-ДХ.
Простая цилиндрическая проекция является равнопромежу-
точной по меридианам, т. е. для нее т = 1, что следует из
'условия ее построения. Параллели сетки растянуты тем больше,
чем ближе они расположены к полюсу. Очевидно, бесконечно
малому кругу на глобусе соответствует бесконечно малый
эллипс на карте, расположенный своей большой осью вдоль
параллели (рис. 35). Из рис. 1 мы имели:
г — /?-cos <р,
или	(65)
R— г-sec <р.
Здесь г—радиус параллели.
Отсюда видно, что длины параллелей проекции увеличива-
ются в sec <р раз, следовательно, если т = 1, то п = sec <р.
В табл. 3 даны изменения масштаба и искажения углов,
подсчитанные по формулам (65) и (62).
Таблица 3
<₽	Масштаб		Наибольшее искажение углов <ш)
	по меридиану (т)	по параллели («)	
0°	1,о	1,000	0° 00'
10°	1,0	1,015	0° 52'
20°	1,0	1,064	3° 28'
30°	1,0	1,155	7° 40'
40°	1,0	1,305	13° 46'
50°	1,0	1,556	25° 08'
60°	1,0	2,000	38° 58'
О
На рис. 35 представлены схематично эллипсы искажений
проекции на различных широтах; эллипсы, сохраняя неизменной
свою малую ось, увеличивают большую ось по мере удаления
от экватора.
Обладая существенными недостатками, проекция не получила
применения в авиации. Изложена она нами в целях методических,
так как через нее облегчается переход к весьма распространенной
равноугольной цилиндрической проекции Меркатора.
§ 12. РАВНОУГОЛЬНАЯ ЦИЛИНДРИЧЕСКАЯ ПРОЕКЦИЯ
В квадратной цилиндрической проекции п — sec <р, т. е. парал-
лели в каждой точке проекции растянуты в sec<p раз, что
лишает проекцию весьма важного для навигации свойства
равноугольности. Для сохранения этого свойства необходимо,
'чтобы в каждой точке проекции т = п.
42
Напрашивается вывод: необходимо в квадратной цилиндри-
ческой проекции меридианы в каждой точке растянуть также
в sec<p раз.
Тогда для каждой точки проекции будет справедливо равен-
ство т = п = sec <р, и проекция будет равноугольной. Если рас-
стояния между меридианами останутся неизменными, то рас-
стояния между параллелями будут увеличиваться по мере уве-
личения широты. Полюсы в этой проекции, очевидно, вообще
не могут быть изображены, так как они уйдут в бесконечность.
Найдем выражение для расстояния D каждой точки проекции
от экватора.
Масштаб по меридиану найдется, как отношение бесконечно
малого участка длины меридиана на карте к соответствующей
длине на Земле, т. е.
Масштаб по параллели
dy _______ R'd\ __________ 1
y?-cos	R • cos <j> • d'K cos <p ’
Для равноугольной
тельно,
проекции должно быть т = я, следова-
dx ___	1
R • d<? cos <p ’
ИЛИ
dx = R-^.
cos ф
Но расстояние х на проекции и есть искомое расстояние D от
экватора до точки проекции, следовательно,
dD = R-^-.
coscp
Интегрируя это выражение в пределах от 0 до <р, получим:
<66>
о
_	Г d<0
Неопределенный интеграл дает:
+ ^ + с.
Тогда по выражению (66) получим:
D = R In tg (45° + J).	(67)
43
Переходя от натуральных логарифмов к десятичным и выра-
жая D в морских милях, получим:
D = 7915,7051g tg(45 +	.	(68)
Эта формула нам уже знакома под номером (19) на стр. 16,
Величина D называется меридиональной частью и дается в спе-
циальных таблицах в приложении 10.
Так как на проекции минуты дуги (морские мили) растянуты
по меридианам, то меридиональная часть какой-либо параллели,
выраженная в минутах дуги
экватора, будет всегда больше,
чем число минут в дуге мери-
диана от экватора до данной
параллели.
Поэтом)' величина D, вообще
говоря, всегда больше соответ-
ствующей широты места. Раз-
ница между ними, небольшая
вблизи экватора, растет по мере
удаления от него. При ср — 90°
D ~ со, т. е. полюс уходит в бес-
конечность.
Искажения масштабов в
равноугольной цилиндрической
проекции, как уже было упо-
мянуто, будут:
т = п — sec <р.
Искажения углов проекция
не дает, так как при т = п, ш = 0.
Искажения площадей, со-
гласно формуле (63), следуют
закону:
т2 = sec2 <?.
Отсюда следует, что площади фигур сильно увеличиваются
по мере приближения к полюсам.
Действительно, карты в меркаторской проекции, составлен-
ные для больших районов, вытянутых по широте, дают неесте-
ственно увеличенные изображения в полярных широтах по срав-
нению с экваториальными.
Весьма малые круги на глобусе изображаются в любом
месте карты также кругами тем больших радиусов, чем они
ближе к полюсам (рис. 36). Однако круг конечного радиуса
имеет вид на проекции не круга, а сложной фигуры MN, имею-
щей приблизительно вид, изображенный на рис. 36. Ниже дается
таблица искажений меркаторской проекции (табл. 4).
44
Таблица 4
V	т = п	СО	Меридиональные части в градусах
0°	1,000	0°0'	0,0
15°	1,035	0°0'	15°, 18
30°	1,155	0°0'	31 °,47
45°	1,414	0°0'	50°,50
55°	1.743	0° 0'	66°, 13
60°	2,000	0°0'	750,46
75°	3,864	0°0'	116°,17
Пользуясь формулой (68) или таблицей меридиональных
частей, а также выражением для разности долгот, можно
построить сетку меркаторской проекции. Выражения для коор-
динат будут:
Сетка меркаторской проекции дана на рис. 37.
Необходимо отметить, что вычисление координат точек при
построении точных сеток проекций (как меркаторской, так и
других проекций) на практике производят не по формулам (69),
а по несколько видоизмененным формулам, учитывающим
сжатие Земли.
§ 13. ЛОКСОДРОМИЯ И ОРТОДРОМИЯ НА МЕРКАТОРСКОЙ ПРОЕКЦИИ
Локсодромия является линией, составляющей с меридианами
постоянный угол. Так как меридианы на меркаторской проек-
ции прямые линии, параллельные одна другой, то, очевидно,
локсодромия на меркаторской проекции также прямая. Это
следует также из уравнения (16). Заменив в этом уравнении
In tg f45 4- на D, получим:
X = £Mga + X0.
Но для меркаторской проекции D = х, а Х = ^, что следует
из (69). Следовательно,
у = /?(% tga + >о)-
Это выражение является уравнением прямой, наклон которой
к оси х составляет угол о..
Простая форма локсодромии на меркаторской проекции
позволила этой последней получить широкое распространение
в морской и в воздушной навигации. Имея сетку мерка-
торской проекции, можно произвести довольно быстро гра-
фический расчет локсодромии. Для этого необходимо соеди-
нить прямой конечные точки А и В маршрута (см. рис. 37).
45
Долгота (Л)
угол между проведенной прямой и любым из меридианов будет
путевым углом. Расстояние же измеряют по рамке сетки, памя-
туя, что одной минуте дуги соответствует одна морская миля.
Так как масштаб сетки увеличивается с увеличением широты,.
то и линейная величина отрезков, равных одной минуте дуги
меридиана, т. е. одной миле, различна. Поэтому при измере-
нии расстояний необходимо всегда пользоваться делениями
боковой рамки, соответствующими тем широтам, в которых,
лежит измеряемый отрезок пути. Для этого переносят изме-
ряемое расстояние на боковую рамку так, чтобы середина его
приходилась против широты средней точки измеряемой линии.
Число минут дуги, отсчитанное при этом на рамке сетки, будет
соответствовать числу морских миль. На рис. 37 длина локсо-
дромии АВ составляет 32 , или 1 920 миль.
Ортодромия на меркаторской проекции имеет вид кривой,,
обращенной своей выпуклостью в сторону большего масштаба,,
т. е. к полюсам (см. рис. 36). В пересечении с экватором орто-
дромия имеет точку перегиба. Будучи на шаре (в действитель-
ности) короче локсодромии, на меркаторской проекции она
оказывается длиннее локсодромии. Это объясняется тем, что
масштабы на этой проекции растут в направлении к по-
люсам.
При необходимости нанести на карту меркаторской проек-
ции ортодромию, рассчитывают ее промежуточные точки, кото-
рые затем наносят на карту. Точки соединяют между собой
прямыми, т. е. локсодромиями.
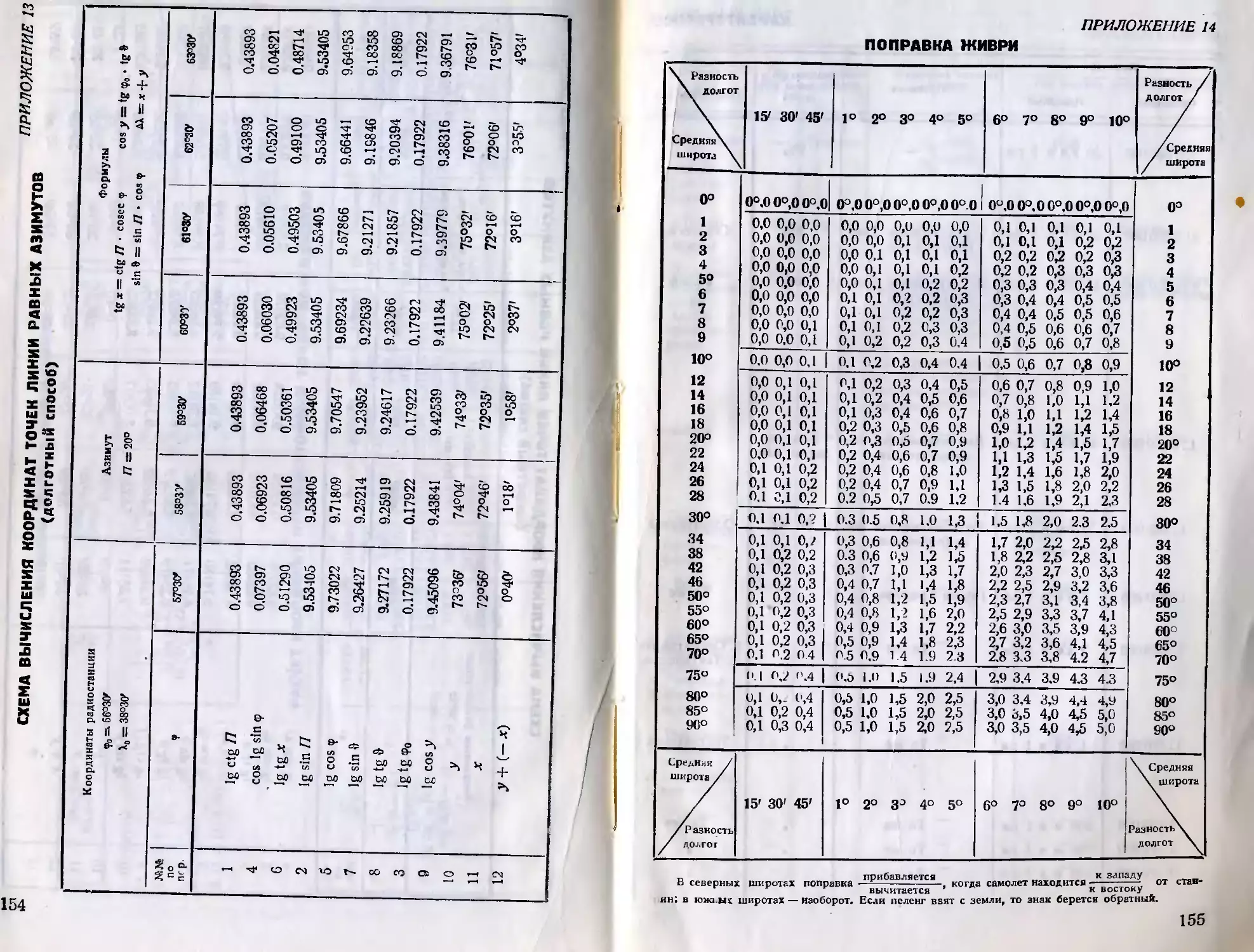
Поправка Живри
При прокладке линий радиопеленгов на карте меркаторской
проекции приходится производить операцию,
название: перевод ортодромиче-
ского пеленга в локсодромический.
Рассмотрим сначала существо во-
проса на сфере (рис. 38).
На рис. 38 EQ — экватор, N—
полюс, Р — место радиостанции,
С—место самолета, пеленгующего
радиостанцию. Линия радиопелен-
га — ортодромия Л’—пересекает ме-
ридиан радиостанции под углом
Пр> а меридиан самолета — под
углом /7с, не равным углу /7р.
При пеленгации экипаж са-
молета определяет с помощью
радиополукомпаса угол 77с. Для
которая носит
прокладки ортодромии (т. е. ли-
нии пеленга) от точки Р экипаж должен исправить угол Пе
на величину, равную Пр — Пс. Найдем эту величину. Из
47
•сферического треугольника NCP, согласно неперовой анало-
гии, имеем:
tg^
<Рр — ?с
cos —--------£
2
. <?с + <Рр
sin---------Е.
2
, АХ
cte-y
Но
* Пс+П»	х ^c+lW-П-
tg - С 2 Р- = tg ----Е
t ПР~П<
= Ctg 2-
При небольших значениях углов можно положить:
tg
cos
. АХ АХ
tg 2 — 2 
Тогда
нп ?с + ?р . АХ	Пр-Пс
ЫП 2	2	2	,
откуда
8 = Пр — Пс = дХ sin .	(70)
Таким образом, поправка в обратный радиопеленг равна
разности долгот, умноженной на синус средней широты само-
лета и радиостанции. Очевидно,
эту поправку можно получить, зная
хотя бы приближенно место са-
молета.
Определим теперь, чему будет
равна искомая поправка на мер-
каторской проекции. На рис. 39
дуга PC — линия ортодромического
пеленга, прямая PC — линия локсо-
дромического пеленга. Из рисунка
видно, что если самолет принял
ортодромический пеленг радиостан-
ции под углохМ Пс, то он должен
дромический обратный (т.
углом П.
Из рисунка имеем:
отложить от радиостанции локсо-
е. исправленный на 180°) пеленг под
& = /7 —/7 .
р с
48
Для сравнительно небольших расстояний можно положить
8. = 8О. Тогда
282 = 8,
или
2-8=4-(д-ч)-
Подставляя сюда из уравнения (70) значение /7р — Пс
лучим:
дх
8g = у sin
Фс + Фр
2
ПО-
СТ!)
Это выражение, служащее для перевода ортодромического
пеленга в локсодромический, получило название поправки
Живри, по имени французского гидрографа, предложившего ее.
Правило знаков поправки Живри для северных широт сле-
дующее: при пеленгации с самолета поправка прибавляется
к измеренному пеленгу, когда самолет находится к западу от
радиостанции, и наоборот. При наземной пеленгации правило
знаков обратное.
Если в выражении (71) заменить ДХ на Хр—X., где Хр — долгота
радиостанции, Хс — долгота самолета, то знак поправки будет
получаться сам собой, если долготы Хр и Хс восточные, а широты
северные:
X — 1р~ Хс . Фс + Фр
*2 - -^2— sin —2“5
(72)
Вычисленные по формуле (71) поправки Живри для опре-
деленных разностей долгот и широт даны в приложении 14.
Необходимо добавить, что прокладку локсодромического
пеленга следует производить при расстояниях до радиостанции
до 300 — 400 км. При больших расстояниях необходимо про-
кладывать линии равных азимутов.
§ 14. КАРТЫ В МЕРКАТОРСКОЙ ПРОЕКЦИИ
В меркаторской проекции составлены все морские навига-
ционные карты, а также полетные карты в некоторых иностран-
ных государствах.
Морские навигационные карты, в зависимости от их назна-
чения, подразделяются на генеральные, путевые и частные.
Генеральные карты предназначаются для выбора кур-
сов плавания, нанесения общего пути и изучения условий плава-
ния. На этих картах обычно изображаются целиком моря, океаны
или большие заливы. Они составлены в мелком масштабе.
Путевые карты предназначаются для работы на них
в плавании, т. е. для прокладки пути и определения места ко-
рабля. Масштаб путевых карт бывает в пределах 200000—350000.
Частные карты предназначаются для плавания вблизи
берегов, фарватеров и т. п. Они составляются в крупных мас-
штабах (50000—200000), и на них наносятся подробно берего-
вые районы.
4 1683
49
Каждая морская карта имеет свой номенклатурный номер
(в нижнем углу за рамкой карты). На карте указан численный
масштаб по главной параллели, пользоваться которым можно
только вблизи этой параллели. При измерении расстояний
в других широтах следует поступать, как указано выше, т. е.
пользоваться боковыми рамками карты.
Полетные карты морской авиации, составленные в мерка-
торской проекции, предназначены для ориентировки и самоле-
товождения над морем и над прибрежной полосой. Они соста-
влены в масштабе для главной параллели 300000. Для измере-
ния расстояний не только в милях, но и в километрах на рам-
ках этих карт даны километровые деления, которые, так же
как и минуты дуги, изменяются по длине в зависимости от
широты. Однако ввиду того, что каждый лист карты охваты-
вает всего 2° по широте, масштаб по всей карте для практики
можно считать постоянным и пользоваться, следовательно,
средним масштабом для всей карты.
§ 15. ПОПЕРЕЧНО-ЦИЛИНДРИЧЕСКАЯ ПРОЕКЦИЯ
Поперечно-цилиндрические проекции получаются в резуль-
тате проектирования глобуса на цилиндр, касающийся какого-
либо меридиана (см. рис. 34, <5). Поперечно-цилиндрическую рав-
ноугольную проекцию, построенную аналогично меркаторской
проекции, предложил
Гаусс (рис. 40). Сред-
ний осевой меридиан
изображается в попе-
речно-цилиндрической
проекции прямой ли-
нией, вдоль которой
сохраняется масштаб,
равный единице. Эква-
тор изображается пря-
мой, перпендикуляр-
ной к осевому мери-
диану, причем точки
экватора, отстоящие
на 90° к востоку и за-
паду от осевого мери-
диана, на проекции
изображены быть не
могут, так как они
уходят в бесконеч-
ность, аналогично по-
люсам в нормальной
меркаторской проек-
ции. Также в виде
бесконечных прямых,
перпендикулярных к
50
осевому меридиану, изображается меридиан, отстоящий на 90°
от осевого меридиана. Остальные меридианы и параллели изо-
бражаются трансцендентными кривыми. По аналогии с мерка-
торской нормальной проекцией, искажения масштабов попе-
речно-цилиндрической проекции пропорциональны секансу рас-
стояния (выраженному, конечно, в угловой мере) от осевого
меридиана.
Если это угловое расстояние принять за новую координату
<р', а угловое расстояние от экватора обозначить через X', •to
прямоугольные координаты точки в поперечно-цилиндрической
проекции будут:
х = /?1п tg(45 + £)
k }•	(73)
у = №
Здесь новые координаты <?' и X' могут быть получены из старых
координат <р и X из сферического треугольника РАМ (рис. 41).
Рис. 41.
По формуле косинуса стороны имеем:
cos (90 — <р') = cos (90 — <р) • cos 90° +
+ sin (90 — <p)-sin 90°-cos(90 — X).
По формуле четырех элементов имеем:
cos (90 — X) • cos 90° =
= sin 90 • ctg (90 — <p) — sin (90 —X) • ctg (90 — X’).
Отсюда находим:
sin<p' = cos <p-sin X;
tg X' = tg <p • sec X.
В проекции Гаусса новые меридианы и параллели имеют вид
двух групп параллельных прямых, пересекающихся под прямым
4*
51
углом. Как уже было упомянуто, искажения в проекции Гаусса
пропорциональны секансу новой широты, т. е.
т = п = sec <р'.
Ниже приведена табл. 5 искажений масштабов проекции
Гаусса.
Таблица 5
Л ф	0°	15°	30°	45°	60°	75°	90°
0°	1,000	1,035	1,155	1,414	2,000	3,863	СЮ
30°	1,000	1,026	1,109	1,265	1,512	1,825	3,863
60°	1,000	1,008	1,033	1,069	1,109	1,142	1,155
90°	1,000	1,000	1,000	1,000	1,000	1,000	1,000
Как видно из таблицы, проекция дает небольшие искажения
вблизи осевого меридиана, почему она и применяется для
изображения стран, вытянутых по меридиану.
Рис. 42.
Так как проекция равноугольна, то всякий бесконечно малый
круг на шаре изображается на проекции также бесконечно
малым кругом, увеличивающимся по мере удаления от осевого
меридиана (рис. 42).
Немецкий геодезист Крюгер разработал теорию равноуголь-
ной поперечно-цилиндрической проекции, учтя сжатие Земли.
Новая проекция, известная под названием проекции Гаусса-
Крюгера, принята в СССР для обработки геодезических на-
бугюдений в прямоугольных координатах.
52
Карты в проекции Гаусса-Крюгера строятся в полосе, соответ-
ствующей столбцу листов международной миллионной карты
(см. ниже, стр. 90), ограниченной двумя соседними меридиа-
нами с долготами от Гринвича, кратными 6°. На среднем мери-
диане проекции масштаб равен единице, а во всей меридиан-
ной полосе от полюса до полюса искажения весьма невелики
и практического значения для аэронавигации не имеют.
В проекции Гаусса-Крюгера построены у нас наиболее рас-
пространенные во фронтовой авиации карты масштаба 500 0001,
200 000 и другие карты более крупных масштабов (см. прило-
жение 15).
Проекция Гаусса-Крюгера широко применяется для крупно-
масштабных карт в артиллерии для целеуказаний.
Косая равноугольная цилиндрическая проекция
При больших перелетах важно иметь карту, которая обла-
дала бы двумя свойствами: равноугольностью и ортодромич-
ностью. Последнее свойство выражается в том, что ортодромия
на проекции изображается прямой линией. Теоретически ни одна
проекция не обладает этими двумя свойствами одновременно.
Однако равноугольная цилиндрическая проекция для полосы
шириной 30° (считая по 15° в стороны от оси полосы) практи-
чески является ортодромичной. Действительно, из рис. 40
видно, что в равноугольной цилиндрической проекции большие
круги (на данном рисунке меридианы) имеют точки перегиба
на осевом меридиане и потому весьма близки к прямым вблизи
него. Эти же свойства сохраняет и косая цилиндрическая про-
екция в полосе вдоль какой-либо оси, совпадающей с большим
кругом. Отношение наибольшего масштаба к наименьшему
в пределах такой полосы будет равно sec 15°, т. е. 1,035. Косая
цилиндрическая проекция была применена Каном для трансат-
лантического перелета Коста и Белонте в 1928 г. по маршруту
Париж—Нью-Йорк, причем осью проекции являлась ортодромия
между этими двумя пунктами.
ГЛАВА 4
ПЕРСПЕКТИВНЫЕ ПРОЕКЦИИ
Выше было уже упомянуто, что перспективные проекции —
это единственные картографические проекции, где слово „проек-
ция" отвечает его геометрическому смыслу, так как они строятся
по законам геометрической перспективы.
В зависимости от положения картинной плоскости относи-
тельно поверхности глобуса проекции могут быть (рис. 43):
а) полярные (или нормальные), когда картинная плоскость
касается поверхности глобуса в полюсе;	-г
1 До 1940 г. эта карта строилась у нас в видоизмененной поликонической
проекции.
63
б) экваториальные (или поперечные), когда картинная
плоскость касается экватора;
в) горизонтальные (или косые), когда картинная плоскость
касается глобуса в любой точке.
проекции могут быть (рис. 44, а, б,
Рис. 44.
В зависимости от положения точки зрения перспективные
в и г):
а) центральные, когда
точка зрения располо-
жена в центре глобуса
(D = R)-
б) стереографические,
когда точка зрения рас-
положена на поверхности
глобуса (D — 2/?);
в) ортографические,
когда точка зрения уда-
лена в бесконечность
(D = ~);
г) внешние, когда точ-
ка зрения находится вне
глобуса на некотором
конечном расстоянии D
от точки касания.
В аэронавигации на-
ходят себе применение
центральные и стерео-
графические проекции,
которые мы и рассмо-
трим.
§ 16. ЦЕНТРАЛЬНАЯ ПОЛЯРНАЯ (ГНОМОНИЧЕСКАЯ) ПРОЕКЦИЯ
Центральная полярная проекция, иначе называемая гномони-
ческой, получается проектированием поверхности глобуса на
плоскость, касательную глобуса в полюсе; точка зрения поме-
щается в центре (рис. 44, а и 45). В результате простой геомет-
рической перспективы получается сетка меридианов и парал-
лелей, причем нетрудно видеть, что меридианы представляют
54
собой пучок прямых, исходящих из одного центра изображе-
ния полюса, а параллели — концентрические окружности. Мери-
дианы пересекаются между собой под углом, равным разности
долгот, т. е. 8 = ДХ, где 8 — угол схождения меридианов на
проекции. Из рис. 46
X	можно написать:
Рис. 45.
p = /?-Ctg<p,
где
Р — радиус какой-либо
точки на проекции,
<? — ее широта.
Очевидно экватор на
этой проекции изображен
быть не может, так как
р = /?-ctg 0°=
Рис. 46.
Из рис. 45 видно, что координаты некоторой точки Л1 (х,у)
равны:
х = p-cosX = 7?-ctg<p cosX;
у = p-sinX = 7?-ctg <?• sin X.
Разделив второе уравнение на первое, получим:
т. е. меридианы суть прямые, проходящие через начало коор-
динат под углом одна к другой X.
Возведя наши уравнения в квадрат и сложив их, получим:
х2 + у2 = (R • ctg <р)2.	(7 4)
Это есть уравнение параллелей — окружностей радиусов:
p = /?ctg<p.
Найдем искажения на гномонической проекции. Длина беско-
нечно малой дуги меридиана на шаре равна R-dq, а длина
бесконечно малого отрезка меридиана на проекции равна dp.
Их отношение есть масштаб по меридиану. Поэтому
/re=^r = ^M = _^_==_cosec2	(75)
R-dq> R-dy	sir? ср	47
55
Знак минус означает, чта масштаб растет с уменьшением
широты.
Длина бесконечно малого участка дуги параллели на шаре
равна r-tZX, где г—радиус параллели, равный /?-cos<p. Следо-
вательно, искомая длина будет равна 7?-cos <р-с?Х. Длина беско-
нечно малого участка дуги параллели на проекции равна р-<Й.
Помня, что о==Х, получим:
e-d8 1
п = т—£---— -т- = cosec с₽.	''
/?-cos<p-dX	sin 9	‘	' >
Искажение углов определится по формуле:
<77>
sin3 ф "I" sin ср
Из формул (75), (76) и (77) следует, что гномоническая про-
екция не равноугольна и не равнопромежуточна, причем мас-
штабы растут у нее по мере удаления от полюса. Рост этот
идет быстрее по меридианам, чем по параллелям. Поэтому бес-
конечно малые кружки на глобусе изобразятся на проекции
бесконечно малыми эллипсами, все увеличивающимися по мере
удаления от полюса (рис. 45). Большая полуось эллипса на-
правлена по меридиану. Ниже приводится табл. 6 искажений
гномонической проекции.
Таблица 6
ф	т	п	
90°	1,000	1,000	0°00'
75°	1,072	1,035	1°59'
60°	1,333	1,155	8° 14'
45°	2,000	1,414	19°45'
30°	4,000	2,000	38=07'
15°	14,928	3,864	72°20'
Сетка гномонической проекции дана в приложении 17.
§ 17. ОРТОДРОМИЯ НА ГНОМОНИЧЕСКОЙ ПРОЕКЦИИ
Как было показано (стр. 9), уравнение ортодромии имеет
вид:
tg <р = ctg а • sin ДХ.	(78)
С другой стороны, для центральной полярной проекции мы
имели (стрг 55):
P = /?-ctg <р.
56
Подставляя отсюда значение ctg<p в (78), найдем:
p==A?-tga-cosec ДХ.	(79)
Это выражение представляет собой уравнение прямой в по-
лярных координатах (рис. 47) вида:
р — у • cosec ДХ,	______р=г/cosec дХ
где у = -tg а = const для
данной ортодромии.
Отсюда следует, что
ортодромия на гно-
монической проек-
ции изображается
прямой линией.
Это же самое можно	Рис. 47.
показать на рис. 48.
Плоскости больших кругов шара проходят через его центр.
Поэтому все лучи, проектирующие большой круг из центра
шара, лежат в плоскости этого круга. Но плоскость круга
пересекается с картинной плоскостью по прямой. Следовательно,
проекцией любого большого круга на картинную плоскость
будет прямая. Это свойство гномонической проекции — изобра-
жать ортодромию в виде прямой линии — определило примене-
ние проекции в морской и воздушной навигации; пользуясь
57
сеткой гномонической проекции, можно произвести графический
расчет ортодромии. Соединив заданные две точки — вылета
и прилета — прямой линией, мы получим ортодромию. В изме-
ренный на проекции путевой угол ортодромии необходимо
ввести поправку.
Так как гномоническая проекция не равноугольна, то углы
на проекции не равны углам на местности. Зависимость между
путевым углом (азимутом) на местности и на проекции можно
получить из формулы (57) на стр. 34:
tg«=”tg₽,	(80)
где а — путевой угол на местности;
Р — путевой угол на проекции.
Подставляя сюда значения т и п из (75) и (76), получим:
tga= cosec <p-tgp,
или
tg р = sin<p-tga.	(81)
Отсюда видно, что a = р при значениях a = 0°, 90°, 180°, 270°, т. е.
при маршруте вдоль параллели и вдоль меридиана. Во всех
остальных случаях угол на проекции меньше угла на местности.
Из формулы видно также, что на полюсе, где sin <р — I,
искажения угла а нет; по мере удаления от полюса это иска-
жение растет.
Для быстрого определения угла р по а и наоборот на рис. 49
дана номограмма, пользование которой не представляет
затруднений.
Следует только помнить, что измеренный на проекции путе-
вой угол необходимо привести к первой четверти перед тем,
как входить в номограмму. Например, дано: угол на проекции
315°, <р — 60°. Определить путевой угол.
Решение.
1.	Приводим угол к первой четверти: 360°—315° = 45°.
2.	По номограмме находим a = 49°.
3.	Путевой угол равен 360°—49° = 311°.
Измерить на гномонической проекции длину ортодромии
непосредственно невозможно, так как масштаб проекции сильно
меняется от точки к точке. Для целей измерения расстояний
на сетке нанесены кривые (пунктиром), все точки которых
соответствуют точкам на шаре, одинаково удаленным от мери-
диана, являющегося средним для данной сетки. Это удаление
указано возле каждой кривой в километрах. Пунктирные кри-
вые построены по формуле (10) на стр. 12.
Для того чтобы измерить длину ортодромии, ее необходимо
расположить так, чтобы она оказалась перпендикулярной к сред-
нему меридиану (рис. 50). Для этого на ортодромии находят
точку вертекса V и затем перемещают линию АВ так, чтобы
точка вертекса V легла на среднем меридиане на том же
расстоянии от полюса, что и точка V. При этом ортодромия
58
<|Г
10'
65'
IS*
70*
2° 1
20° .
75°
25° .
- 3“
зов.
- 4!
ЗБ’
80°
81*
82*
83'
40°
5°
84*
6‘
7'
8°
9°
10'
46'
50'
55°
85°
86"
60е-
87'
65'
15*~.
70'
88
-20
-25'
I
75'
-*80°
П Ш
89'

2'
6
10'
20'
30'
40°
50°
БО*
Рис. 49.
89'
88*
87° -
86°
85‘
84*
83'
82°
81°
80°
75'
70'
65‘
%
80'
75'
'25'
'20
70°--К'
65°
60
55'
10'
8°
: т
50
45
40
35°
‘ 30
’ 25°
20
6'
4‘
3'
12'
 15°
10 L-
Ш’ П'
’ V
Рис. 50.
окажется перпендикулярной к среднему меридиану. Длина
ортодромии 5орг будет равна сумме длин отрезков AV и V'B'.
Длина каждого из этих отрезков определяется по соответ-
ствующей пунктирной кривой линии.
На рис. 50 приведен пример определения длины ортодромии
между Москвой и Хабаровском.
5орт = 51 + 52 = 3700 4- 2500 = 6200 км.
Иногда вертекс располагается не между начальной и конеч-
ной точками ортодромии, а вне их. В таком случае прямую АВ
необходимо продолжить и на ее продолжении определить точку
вертекса V. Перемещение ортодромии производится, как и в
предыдущем случае. Длина ортодромии определится как раз-
ность длин 5Х и S2, т. е.
5, =5,— 5,.
На рис. 50 приведен также пример определения длины орто-
дромии между Ленинградом (<р = 60°, X = 30°19') и островом
Рудольфа (ср = 81°47', Х = 57°57').
5орт = 3300 — 780 = 2520 км.
Промежуточные точки ортодромии легко определяются по
сетке и переносятся на полетную карту по географическим
координатам.
По сетке, данной в приложении 17, можно производить гра-
фический расчет ортодромии описанным способом.
Центральная полярная проекция может применяться в аэро-
навигации не только для графического расчета ортодромии,
но также для отыскания созвездия или звезд на небе. Гномо-
ническая проекция, искажая конфигурацию созвездий, позво-
ляет переходить от знакомых созвездий
к незнакомым по створам, т. е. по дугам
больших кругов, проводимым через опре-
деленные пары звезд на небе в виде прямой.
§ 18. СТЕРЕОГРАФИЧЕСКАЯ ПОЛЯРНАЯ
ПРОЕКЦИЯ
Стереографическая полярная проекция
получается в результате проектирования
глобуса на плоскость, аналогично цент-
ральной проекции, но здесь точка зрения
помещается не в центре глобуса, а на его
поверхности (рис. 44, б и 51).
Сетка меридианов имеет вид пучка прямых линий, пересе-
кающихся, как и в центральной проекции, под углом & = ДХ,
а параллелей — ряда концентрических окружностей, радиусы
которых нетрудно определить из рис. 51:
P = 2/?-tg-J,	(82)
Рис. 51.
где z = 90 — ч}.
61 ’
Координаты некоторой точки ix, у) равны (рис. 52):
х = p-cosX = 2/?-tg -j-cos А;
у = р • sin X — 2R • tg у • sin X,
откуда
7
т. е. меридианы будут прямые, проходящие через начало
координат под _у гл ом одна к другой X.
Уравнение параллелей
''	будет:
Рис. 52Г
х2+У = 4/?2-tg2y =
-=4/e2-tg2(45-y), (83)
что является уравнением
окружности радиуса
2^-tg(45 —|).
Найдем масштабы по
меридиану и параллели:
1,
R-dz	R-dz
с—2-------- —---------•
~ о „„.я г	1 + cos г *
Р.<Го	2/?^7	2
ft-sindA	R-smz	1 + cosz"
Следовательно, т — п, т. е. стереографическая проекция
является равноугольной, и искажение углов для нее“> = 0.
Круги искажений для этой проекции показаны на рис. 52.
Величины искажений приведены в табл. 7.
Таблица 7
ф	90°	75°	60°	45°	30°	15°	0°
т = п	1,000	1,017	1,072	1,172	1,333	1,589	2,000
Карты, составленные в стереографической полярной проекции,
иногда применяются в аэронавигации для полетов в северных
широтах, так как они, во-первых, равноугольны, а во-вторых
62
практически ортодромичны, т. е. дуги больших кругов на них
близки к прямым.
Стереографическая проекция обладает одним, весьма важ-
ным свойством: всякая окружность, лежащая на поверхности
шара, изображается в стереографической проекции также
окружностью.
Докажем это.
На рис. 53 АМВ— окружность на шаре, amb — его проекция,
конус SAMB касается шара по данной малой окружности, s—
Рис. 53.
проекция вершины 5 конуса, МТ—касательная к окружности
в точке М, перпендикулярная к образующей конуса SM. В силу
равноугольности проекции, угол между проекциями sm и mt
прямых SM и МТ также равен 90°. Следовательно, касательная
mt в любой точке кривой amb перпендикулярна к прямой sm,
проведенной в точке т из постоянной точки s; иначе говоря,
кривая amb пересекает под прямым углом все лучи пучка пря-
мых, проведенных из точки $. А это значит, что кривая amb
есть окружность, центром которой является проекция вершины
конуса, касающегося данной окружности на шаре.
Как видно из рисунка, центр окружности amb не совпадает
с проекцией центра окружности АМВ.
Найдем широту точки Е, проекция которой является цент-
ром искомой окружности amb
63
Обозначим длину радиуса окружности АМВ, считаемого по
ортодромии, через d, т. е. AD — d. Тогда DCA = -~ — u.. Из
прямоугольного треугольника ACS имеем:
CS=^~ .
cos а
Из треугольника OCS по теореме синусов имеем:
CS _ ___R____
sin х cos (<Ро 4- х) ’
Подставляя вместо CS его значение и сокращая на R, полу-
чаем:
cos(?0 + х) == cos a - sin х,
откуда
etc X —sin * cos а
ё	cos фи •
Обозначим искомую широту точки Е через <рж.
Тогда из рисунка можно написать
- £Q = 90° — '-'РКЕ,
или
<рж = 90° —2х,
откуда
л = 45 —
Подставляя значение х в выражение для etgx, найдем:
ctg (45-	= sin<₽° + cos“.	(84)
ь	I )	COS <Pu	'	'
Для частного случая, например, когда d = 1 000 км, <р0 = 60°,
<РЛ = 59°44'.ч
Долгота центра окружности остается неизменной.
Нанесение малых окружностей на стереографическую сетку
может быть необходимым при использовании дистанционно-
метрических методов радионавигации (радиолокации).
Свойство стереографической проек-
ции изображать всякий круг на шаре
в виде круга на проекции используется
в астрономической ориентировке, где
применяется экваториальная стереогра-
фическая проекция, в которой картинная
плоскость касается не полюса, а экватора,
точка зрения помещается также на эква-
торе с противоположной стороны. Сетка
меридианоз и параллелей выглядит в
этом случае, как показано на рис. 54,
причем все меридианы и параллели
остаются окружностями на проекции
(но разноцентренными).
64
ГЛАВА б
КОНИЧЕСКИЕ ПРОЕКЦИИ
Из большого числа разновидностей конических проекций мы
остановимся только на некоторых, получивших применение
в авиации.
Конические проекции получаются в результате проектиро-
вания глобуса на конус, так или иначе расположенный относи-
тельно оси вращения глобуса.
Рис. 55
Конические проекции называются нормальными, когда ось
конуса совпадает с осью вращения глобуса (рис. 55, а, б и в),
поперечными — когда ось конуса перпенди-
кулярна к оси вращения глобуса, и косыми —
когда ось конуса расположена под любым
углом к оси вращения глобуса. Мы остановимся
только на нормальных проекциях, в которых
построены почти все встречающиеся в практике
авиации карты. Нормальные конические про-
екции могут быть построены на касатель-
ном (см. рис. 55) или секущем (рис. 56) ко-
нусе.
§ 19. УГОЛ СХОЖДЕНИЯ МЕРИДИАНОВ
На рис. 57 в точках А и В проведены две образующие ко-
нуса, являющиеся касательными в этих точках к меридианам
АР и ВР. Угол 8 между касательными называется углом
схождения меридианов. Величина этого угла может быть полу-
чена из рисунка. Вспомнив, что длина дуги равна радиусу, умно-
женному на величину угла (выраженному в радианах), можно
написать, пользуясь обозначениями рисунка:
'-'АВ — г- ДА;
'~'АВ = р-?>,
откуда
г-ДА = р-8.
Из треугольника ASC имеем:
r=p-sin <р.
5—К 33
65
Следовательно,
о — AX-sin %
т. е. угол схождения меридианов на широте касания равен
меридианов, умноженной на синус
широты касания.
Нетрудно сообразить, что угол
схождения меридианов меняется в
пределах от 0° на экваторе, где ка-
сательные к меридианам параллельны
одна другой, до величины, равной
разности долгот меридианов на по-
люсе. Действительно, на экваторе
при <р = 0° sin <р — 0 и о =0. На полюсе
при ср = 90° sin ср == 1 и 8 _ дХ.
разности долгот этих
Рис. 57.
на карте конической проекции.
So
Рис 58
§ 20. ПРОСТАЯ КОНИЧЕСКАЯ
ПРОЕКЦИЯ
Для построения простой кониче
ской проекции представим себе ко-
нус, касательный к глобусу по парал-
лели на широте <р0, выбранной нами
как широте касания. Разрежем конус
по одной из образующих и развер-
нем его на плоскость (рис. 58); полученный пучок образующих
принимают за сетку меридианов
Очевидно, угол между двумя
образующими, т. е. меридианами,
является углом схождения мери-
дианов для широты, соответ-
ствующей ^принятой широте ка-
сания данного конуса.
Таким образом, на карте ко-
нической проекции угол схожде-
ния меридианов для любой ши-
роты выражается формулой:
8 = ДХ  sin ср0,
где % — широта касания конуса.
Для каждой проекции (карты)
широта касания конуса-характе-
ризует вид ее сетки меридианов. Поэтому величину sin<ра на-
зывают постоянной проекции; ее обозначают буквой а.
Таким образом,
8 — а ДХ.
Для того чтобы задать вид сетки меридианов конической
проекции, необязательно, следовательно, представить себе конус,
на который проектируется поверхность глобуса, а достаточно
66
гГ. ать величину а, характеризующую величину угла схождения
Меридианов.
‘ Для построения сетки параллелей необходимо определить
иХ радиусы. Из рис. 57 получаем радиус параллели касания:
= ctg %.	(85)
За параллель касания принимают, следовательно, дугу окруж-
из центра пучка меридианов.
пости радиуса р0, проведенную
Остальные параллели
представляют собой дуги
концентрических окружно-
стей, радиусы которых
лучаются по формуле:
Р = Ро +£(% — ?)•
по-
(86)
что
Из формулы видно,
эти радиусы отличаются от
радиуса параллели касания
на величину/?(<р0 — <f), пред-
ставляющую собой длину
дуги меридиана, заключен-
ную между широтами <р0 и
(см. рис. 58). Таким образом,
длина отрезка меридиана
на проекции равна выпрям-
ленной дуге соответствую-
щего участка меридиана
глобуса, т. е. вдоль мери-
дианов масштаб проекции
не претерпевает искажений
и т = 1. Следовательно,
проекция является равнопромежуточной по меридианам. Масштаб
по параллели
p-tZo	p-a-rfX.	p-a
/?-COS<p-<ft	R-COio-dK	7?-C0S? ’
(87)
Так как все параллели при перенесении их с глобуса на ко-
нус растягиваются (рис. 59), то п>1. Только на параллели каса-
ния П—1. Действительно, из формулы (87) для параллели каса-
ния имеем:
и — р,а = fl-CtgCp-a _ J
A>cos<j) R-costp0
Искажение углов равно
=	=	(88)
z т -j- п I. + п
Вид эллипсов искажений для простой конической проекции по-
казан на рис. 58.
Б*
67
Нетрудно сообразить, что цилиндрическая и центральная про. 
екции являются частными случаями конической проекции. Дей. 
ствительно, если принять экватор за параллель касания, то ко- ]
нус обращается в цилиндр, вершина которого уходит в беско-
нечность; при этом, так как <р0 = 0, получим:
S = AX-sin?0 == 0.
Ро = R • Ctg % = CV>.
Это значит, что угол схождения меридианов на карте цилиндри-
ческой проекции равен нулю, т. е. меридианы параллельны друг j
другу. Так как все радиусы р равны бесконечности, то парал- 1
лели обращаются в прямые, им перпендикулярные, — кониче- I
ская проекция обращается в цилиндрическую.
Для центральной проекции необходимо положить <р0 = 90°.
Тогда & = Дк и Ро = О.
Это значит, что угол схождения меридианов на карте цен- I
тральной проекции равен разности долгот, а радиус параллели I
касания равен нулю, т. е. касание имеет место в точке полюса,—
конус обращается в плоскость.
В таблице 8 приведены искажения простой конической про- I
екции с параллелью касания 55° и с крайними параллелями
<₽N = 70° и <ps — 40°. Из таблицы видно, что искажения на край- |
них параллелях неодинаковы: на крайней северной параллели I
оно составляет 5%, а южной — 2,9%. Можно построить проек- I
цию, у которой искажения на крайних параллелях равны; в таком
случае параллель касания не придется на среднюю широту. I
В табл. 9 приведены искажения масштабов для тех же крайних
параллелей, что и в табл. 8, но параллель касания здесь равна
Фо — 57°1'. Как видно из табл. 9, искажения масштабов здесь
были сглаженьТ и уменьшены по сравнению с искажениями, при-
веденными в табл. 8.
Таблица 8
ф	т	п	ш
70°	1	1,050	2°48'
65°	1	1,019	1°04'
60°	1	1,004	0°14’
55°	1	1,000	0°00'
50°	1	1,004	0°12'
45°	1	1,013	0°46'
40°	1	1,029	1°37'
Таблица 9
Ф	т	п	СО
70°	1	1,036	2°01'
65°	1	1,012	0°40>
60°	1	1,001	Э°05'
55°	1	1,001	0°02'
50°	1	1,007	0°23'
45°	1	1,019	1°04'
40°	1	1,036	2°0И
В конической равчопромежуточной проекции (проф. Каврай-
ского) составлена карта СССР масштаба 1:2 500 000.
Ввиду наличия угловых искажений карта эта, однако, рас-
пространения в авиации не получила.
68
£ 21. ПРОЕКЦИЯ НА СЕКУЩЕМ КОНУСЕ
Проекция на секущем конусе применяется для того, чтобы
уменьшить искажения длин и углов. Чтобы получить секущий
конус, можно провести параллельно касательной SA секущую
S'BC (рис. 60), пересекающую
окружность в точках В к С.
Найдем зависимость между ши-
ротами параллелей сечения и
углом схождения меридианов.
Так как ' АВ АС,
то
Z BOA — / АОС, т. е.
<Fo —Ф1 = % —?о,
или
_ __ Ф1 + ф»
<Ро-----2	.
Но, как видно из рисунка, <f0
является широтой параллели ка-
сания; подставляя ее значение
в формулу угла схождения ме-
ридианов, получим:
8= Aksin’li’i.	(89)
Л
Таким образом, для секущего конуса
постоянная проекция
а = sin’l+jPi.
Из треугольников StBO и StCO можно получить выражения
для радиусов параллелей сечения. По теореме синусов имеем:
SiC = _R_. StB = R
sin (90 — Ift)	sin % ’ sin (90 — <pa) sin o0 *
Отсюда, принимая во внимание, что 5tC — pj и
получим:
Радиусы р параллелей на карте вне параллелей сечения по-
лучаются так же, как и в простой конической проекции, т. е.
P = Pi +	—?);
р = р2 + Ж<р2 —?)•
69
Радиус средней параллели на карте р0 = найдется из
рис. 60;
p0 = O/10ctg <?0,
но
ОЛ0 = OB-cos = Я-cos
где Д? = <р2 —Ф1-
Следовательно,
Ро = Я-cos-^ -ctg%.
Для получения радиусов параллелей внутри параллелей се-
чения хорду АВ (но не дугу!) делят на равные части. Так
как хорда меньше стягивающей дуги, то масштаб по мери-
дианам внутри параллелей сечения будет меньше единицы:
ВС = 2/?sin—j-	мп-у
ВС R <~а — о,) др
~2~
Для получения масштаба по параллелям следует пользоваться
общей формулой (87), а для искажения углов — формулой (62).
В труде Траура при-
ведена табл. 10 искаже-
ний, вычисленная по ука-
занным формулам.
Таблица 10
9	т	п	(1)
70°	1.С00	1,036	2°!'
65°	1,000	1,008	0°27'
62°30'	1,000	1,900	0°0'
60°	0,995	0,992	0°18'
55°	0,991	0,988	0°30'
50°	0,995	0,992	0°18'
47°30'	1,000	1,000	0°0'
45°	1,000	1,006	0°20'
40°	1,000	1,022	1°16'
В этой таблице парал-
Рис- 61.	лели сечения взяты для
ср, = 47°30' и ср2 = 62°30’.
На этих параллелях проекция не дает искажений. Масштаб по
меридианам вне параллелей сечения равен единице, внутри их —
меньше единицы. Масштаб по параллелям вне параллелей се-
чения больше единицы, внутри их — меньше единицы, это
наглядно видно из рис. 61. Проекция не равноугольна. Как
70
Рис. 62.
видно из табл. 10, проекция дает меньшие искажения, чем дает
их проекция на касательном конусе. Эллипсы искажений
для секущего конуса показаны на
рис. 62.
§ 22. РАВНОУГОЛЬНАЯ КОНИЧЕСКАЯ
ПРОЕКЦИЯ
Простая коническая проекция
является более общим случаем по
отношению к квадратной цилин-
дрической проекции. Последняя,
так же как и простая коническая,
равнопромежуточная по меридиа-
нам, не равноугольна, вследствие
того, что параллели у нее растя-
нуты тем более, чем дальше они
отстоят от параллели касания. Для.
того чтобы сделать проекцию рав-'
ноугольной, известный математик
Ламберт предложил растянуть ме-
ридианы сетки в такой же степени,
в какой растянуты ее параллели, по аналогии с тем, как по-
лучена меркаторская проекция из квадратной цилиндрической.
Таким образом, в каждой точке проекции масштаб по мери-
диану оказался равным масштабу по параллели, т. е. т — п.
Масштаб по параллели, согласно формуле (87), равен;
Р-Д
/?-cos<p 
Масштаб по меридиану т = —	. Знак минус означает
уменьшение радиуса р с увеличением широты <р.
Таким образом,
р • 1	da
11! cos ср	к-d? ’
отсюда
. 7
р cos <р
Интегрируя, получим:
In о = — a In tg ^45 + у) + In k,
или
_ k
tg’(45+’
где k — постоянная интегрирования.
(90)
(91)
(92)
71
Обозначив tg (45 +	= U, получим:
ъ
Р = -^-	(93)
Для отыскания значения k положим <р = 0. Тогда
tg(45 +	1 и k = p,
т. е. k — радиус экватора на проекции. Масштаб в любой точке
равноугольной проекции:
где г—радиус параллели.
Можно доказать, что постоянная проекции а представляет
собой синус широты той параллели, для которой масштаб наи-
меньший. Для этого найдем min функции:
/(•cos ф ’
предварительно прологарифмировав ее:
In п — In а + In р — In R— In cos <р;
диференцируя, получим:
d (In n)_______1
d<?	~ f
dp , Sin ф
cos? '
Согласно формуле (90),
1 dp ______ a
p dtp ~ cos ф *
Следовательно,
d (In ri)   a
dtp	cos <p
sin ф
COS ф *
Приравняв нулю это выражение, найдем экстремальное зна
чение <р, которое обозначим через <р0- Тогда получим:
-----+ = 0
cos ф0 COS ф0 1
откуда
a = sin <р0.
Вторая производная In п дает:
<Р (In Я> _ d / sin ф — «
dtp3 dtp \ cos ф
72
откуда
(In n) _ cos’ ф 4- sin2 9 — a-sln<p _ 1—a-sinq?
dtf2 ~	cos2 ф	cos2 о
Так как a = sin ?0> то произведение a-sin<?o<L и вся дробь
чт0 соответствУет т*п Функции п =	 при
a = sin <р0.
Таким образом, доказано, что <?0 есть широта той параллели,
для которой масштаб п наименьший.
В зависимости от способа выбора произвольных постоянных
а и k можно получить различные равноугольные конические
проекции. Рассмотрим некоторые из этих способов.
1. Масштаб на средней параллели наименьший и равен еди-
нице.
В соответствии с только что доказанным положением по-
стоянная а определится из условия:
a = sin<p0>	(94)
где <р0— заданная широта средней параллели проекции.
Кроме того, необходимо, чтобы п0 = 1, т. е.
а-ро _ .
П°- —	1.
Но
_ Л
Ро rjl ’
ио
следовательно,
У;-	(95)
a
Таблица 11
<р	т = п	ш
70°	1,042	0°0'
65°	1,017	0°0/
60°	1,004	0°0'
55°	1,000	0°0'
50°	1,004	0°0'
45°	1,014	(W
40°	1,032	0°0'
Пользуясь формулами (89), (92), (94) и (95), можно вычислить
картографическую сетку.
Ниже приведена табл. 11 искажений равноугольной конической
проекции, вычисленной по указанному способу (по Трауру).
Рассмотренный случай равно-
угольной конической проекции
применен при составлении „Кар-
ты Азиатской России" в мас-
штабе 100 верст в 1" (на 8 ли-
стах) и при составлении „Карты
пограничной полосы Азиатской
России" в масштабе 40 верст в 1"
(на 32 листах).
2. Масштаб равен единице
на двух заданных параллелях
?! И <р2.
73
Геометрически это условие соответствует проекции на секу-
щем конусе с параллелями сечения и <?t.
Из условия следует:
а-р.
Но
k _ k
rt-u; ~ гГ1Д'
следовательно,
Логарифмируя, получим:
Ig f'2 + a!g U2 = 1g + a 1g Ux,
откуда
a = П ~ lg °
lg£A —igiA ’
(96)
Принимая во внимание, что -^- = “‘Рг = 1 получим:
Г1	Г2
(97)
В равноугольной конической проекции на секущем конусе
построено много карт, напрг?мер:
— карта Европы в масштабе 25 км в 1 см изд. Генераль-
ного штаба Красной Армии — параллели сечения = 45е,
<?_> = 60°, осевой меридиан 31°Е;
— карта масштаба 1:1500000 для некоторых районов Азиат-
ской части СССР—параллели касания — средняя параллель
каждого листа карты. Карта дает небольшие искажения в пре-
Таблица 12
<р	/п = п	W
70°	1,037	0°0'
65°	1,013	0°0>
60°	1.000	0°0'
55°	0,996	0°0'
50°	1 000	0°0'
45°	1,011	0°0'
40°	1,028	0°0'
Существуют ещ		? некоторые
постоянных а и k,		однако они
получили.
делах каждого листа, но при
склеивании листов между ними
образуются разрывы.
А. В. Траур приводит табл. 12
искажений для равноугольной
конической проекции, где ши-
рота параллелей сечения взята
ft — 50° и ср3 = 60°.
Из таблицы видно, что иска-
жения длин здесь меньше, чем
в аналогичной проекции на ка-
сательном конусе (см. табл. 8).
способы задания произвольных
распространения в авиации не
этими точками.
§ 23. ОРТОДРОМИЯ НА КОНИЧЕСКОЙ ПРОЕКЦИИ
Ортодромия на конической проекции представляет собой
трансцендентную кривую, весьма близко подходящую к окруж-
ности большого радиуса.
При расстояниях до 1 000 км прямую, соединяющую две
точки, принимают за ортодромию между
При больших расстояниях орто-
дромию наносят на карту по точкам,
вычисленным заранее одним из из-
вестных способов.
Проф. Иммлер предложил фор-
мулу для угла между ортодромией
и конической прямой (т. е. прямой на
конической проекции). На рис. 63,
который представляет собой кони-
ческую проекцию с нанесенной на
ней ортодромией АВ, можно при-
нять углы между ортодромией и пря-
мой в конечных точках маршрута
равными один другому.
Из рис. 63 имеем:
а + ?4-р + 54’8 = 180’,
откуда
5 = 90о_л+2~1.
(98)
Обозначим
90 —
Рис. 64.
2
4
Из рис 61, па котором изображен треугольник РАВ на сфере
и линия АВ — ортодромия, имеем по аналогии Непера:
tg с' = tg ~ sec sin ----^ .	(99)
По формулам (98) и (99) подсчитана
таблица углов между ортодромией и
конической прямой для карты равно-
угольной проекции, имеющей постоян-
ную а = 0,793 (<рср = 52°30') (см. прило-
жение 16).
Таблицы подсчитаны для точек, имею-
щих различные разности широт и долгот.
На
углов
одной
что угол ? может принимать
расположенных на известном
карты, и при значительной разности долгот.
рис. 65 изображены графики
Е для точек, расположенных на
параллели. Из графиков видно,
большие значения для прямых,
удалении от средней параллели
75
Рис. 65.
76
На рис. 66 показан вид ортодромии на конической проекции.
Как видно из рисунка, ортодромия обращена своей выпукло-
стью в сторону большего масштаба и в пересечении с парал-
лелью наименьшего масштаба имеет точку перегиба, подобно
тому как это имеет место на меркаторской проекции при пере-
сечении ортодромией экватора.
На этом же рисунке дан вид локсодромии на конической
проекции.
§ 24. ЛИНИЯ РАВНЫХ АЗИМУТОВ НА ИОНИЧЕСКОЙ ПРОЕКЦИИ
Линия равных азимутов на конической проекции предста
вляет собой трансцендентную кривую, довольно близко под
ходящую к окружности боль-
шого радиуса. Действительно,
если на рис. 67, изображающем
сетку меридианов конической
проекции, считать все ортодро-
мические направления на точку А
(радиостанцию) прямолинейными
(что близко к истине для рас-
стояний до 1 000 км), то линия
равных азимутов будет пред-
ставлять собой геометрическое
место точек, обладающих тем
свойством, что все вписанные
углы П, опирающиеся на хорду
-4S (расстояние между полюсом
и радиостанцией), равны между
собой. Таким свойством обладает
только окружность. Насколько
близко эта окружность подхо-
дит к точно вычисленной линии
Рис. 67.
равных азимутов, видно из следующей таблицы.
Точное вычисление
ф	X
59°02'	2°
58°01'	4°
57°08г	6°
56° 14'	8°
55°22/	10°
54°32'	12°
Приближенное вычисление
ф	»
59°02'	2°
58°03'	4°
57°07'	6°
56°14'	8°
55°22'	10°
54°31'	12°
Из таблицы видно, что приближенное вычисление почти
не отличается от точного.
77
Вид линий равных азимутов (ЛРА) на конической проекции
дан на рис. 68.
Линию равных азимутов на картах конической проекции
прокладывают обычно графическим способом. Для этого можно
воспользоваться прокладчиком НИИ ВВС, представляющим собой
соединение линейки с транспортиром (рис. 69). В линейке сде-
лана прорезь, вдоль которой ходит движок с иглой. Линейка
вместе с транспортиром передвигается относительно движка.
Транспортир вращается на оси вокруг своего центра. Для
прокладки линий равных азимутов транспортир устанавливается
таким образом, чтобы против линейки пришлось деление, соот-
ветствующее истинному пеленгу П. Острие движка линейки
78
накалывают на место радиостанции на карте. Передвигая линейку
относительно движка и устанавливая каждый раз транспортир
делениями 0°—180° на меридианы, карандашом отмечают сквозь
отверстие в центре транспортира течку на меридиане. Соеди-
няя затем последовательно полученные точки, получают линию
равных азимутов. Вид подготовленной таким образом карты
конической проекции показан на рис. 68.
Н. Ф. Кудрявцев предложил другой, весьма простой про-
кладчик (рис. 70), представляющий собой Шаблон из целлулоида,
позволяющий откладывать углы в 1°,6 и 3°,2. На карте, на
которой меридианы проведены через 2°, линию равных азиму-
виде ломаной (рис. 71), причем первый
тов прокладывают в
отрезок ломаной от-
кладывают (с помощью
шаблона) под углом
1°,6 к линии пеленга,
все последующие от-
резки откладывают (с
помощью другой сто-
роны шаблона) под
углом к предыдущему
отрезку 3°,2. Таким
образом, линия равных
азимутов изобразится
вписанным многоуголь-
ником, стороны кото-
рого равны между со-
бой, так как все они
являются хордами дуг,
на которые опираются
равные вписанные углы
(углы схождения ме-
ридианоз). Шаблон с
указанными углами
(1°,6 и 3°,2) предна-
значен для карт конической
и разность долгот между соседними
В таком случае для этих карт угол схождения соседних мери-
дианов S = 1°,6. К этим картам относятся карты масштабов
2 500 000, стоверстка, сорокаверстка.
проекции, для которых а = 0,8
меридианами АХ =2°.
79
§ 25. ПОЛИКОНИЧЕСКАЯ ПРОЕКЦИЯ
Поликоническая проекция возникла в связи с необходи-
мостью уменьшить те искажения, которые дают конические
проекции, в особенности для стран, вытянутых по широте.
Сетка простой поликонической проекции строится следую-
щим образом.
Вспомнив, что радиус параллели касания конической проекции
равен р0 = /? ctg <Ро, условимся, что радиусы всехпараллелей
на поликонической проек-
ции будут paBHbip = /?-ctg<p>
где — любая параллель,
а р — радиус ее на проек-
ции. Если на конической
проекции все параллели
представляют собой концен-
трические окружности,то на
поликонической проекции
все параллели проведены
из разных центров, рас-
положенных на среднем
меридиане. Центры этих
окружностей можно найти
следующим образом.
На среднем меридиане
проекции, проведенном в
виде прямой, намечают
центр и проводят радиусом
Р1=/?-ctg <р! параллель для не-
которой широты <pt (рис. 72).
После этого от точки А
пересечения найденной па-
раллели со средним мери-
дианом откладывают по
среднему меридиану его
длину АВ до следующей
параллели. Длина АВ опре-
деляется как длина выпрямленной дуги меридиана, т. е.
AB — R (?1 —<р3).
Подобным образом откладывают расстояния между парал-
лелями вдоль среднего меридиана; отложив от найденных точек
радиусы (вдоль среднего меридиана), соответствующие своим
параллелям, найдем положения центров окружностей, пользуясь
которыми можно провести параллели.
Для проведения меридианов поступают следующим образом.
Вдоль каждой параллели в обе стороны от среднего мери-
диана откладывают длины параллелей в главном масштабе
проекции. Эти длины определяются по известной формуле:
S = R • ДХ • cos <р.
80
Точные значения этих дуг, вычисленные с учетом сжатия
Земли, даются в специальных таблицах. Точки на параллелях,
с одноименной долготой соединяют плавной кривой, предста-
вляющей собой меридиан.
Построенная таким образом сетка является сеткой про-
стой поликонической проекции.
Таким образом, простая, или американская, полико-
ническая проекция обладает следующими особенностями;
1)	масштабы по
среднему меридиану и
по параллелям равны
единице;
2)	масштаб по ос-
тальным меридианам
тем больше единицы,
чем дальше он отстоит
от среднего меридиана;
3)	проекция не яв-
ляется равноугольной:
кружки, перенесенные
с глобуса на проекцию,
будут иметь вид, изо-
браженный на рис. 72.
На международной
географической кон-
ференции в Лондоне
в 1909 г. была принята
предложенная профес-
сором Пенк карта масштаба 1:1 000 000, в основу которой была
положена простая поликоническая проекция. Эта видоизме-
ненная поликоническая проекция, названная проекцией
международной карты мира 1:1000000 (с поправками
геодезиста Щеткина), обладает следующими особенностями.
Каждый лист карты ограничен по широте четырьмя, а по
долготе — шестью градусами (рис. 73).
Меридианы представляют собой прямые линии, причем на
двух меридианах, отстоящих вправо и влево на 2° от среднего
меридиана, масштаб равен единице. Вследствие некоторого
укорочения этих меридианов, средний меридиан также укоро-
тился на некоторую величину К (К меняется в пределах от
0,08 мм до 0,27 мм; в средних широтах К равно около 0,1 мм),.
значение которой дается в специальных таблицах (например,
у В. В. Каврайского).
Таким образом, масштаб по среднему меридиану несколько
меньше единицы, а по крайним меридианам — несколько больше,
единицы.
Сетка строится по прямоугольным координатам х и у, дава-
емым в специальных таблицах. При этом построении, по пред-
ложению геодезиста Щеткина, учитывается необходимость
уменьшения разрывов, неизбежных при склеивании листов карты.
S—1683	81
Следует отметить, что этот способ построения сетки в смысле
жолучения искажений практически почти не отличается от спо-
соба, предложенного в первоначальном варианте международ-
ной карты мира, а именно: проводить крайние параллели листа
в виде дуг разноцентренных окружностей радиуса p = /?’Ctg<p,
как это делается в простой поликонической проекции.
Промежуточные параллели при этом проводят следующим
образом: все меридианы делят на равные отрезки, причем точки
деления отстоят одна от другой на 1°. Точки на всех меридианах
листа с одинаковой широтой соединяют плавными кривыми.
Меридианы проводят, деля крайние параллели, как в про-
стой поликонической проекции, и' соединяя соответственные
точки прямыми, которые принимают за меридианы. Поэтому
масштаб по крайним параллелям равен единице.
Здесь также следует отметить, что в иных случаях парал-
лели проводят иначе (например, в виде дуг окружностей), однако
все методы их построения дают точность, близкую к пределу
графической точности рисунка карты, т. е. 0,1 мм. Вид сетки
листа международной карты дан на рис. 73. Эллипсы искажений
показаны на рисунке утрированно; считают, что в пределах
одного листа карта не дает практически ощутимых искажений.
В описанной нами проекции международной карты мира
построена общевойсковая стратегическая карта масштаба
1:1000000. В такой же видоизмененной поликонической проек-
ции строилась до 1940 г. карта масштаба 1:500000, которая
сейчас, однако, издается у нас в проекции Гаусса-Крюгера.
Склейка листов этих карт не вызывает затруднений при
небольшом числе их. В противном случае мы неизбежно
столкнемся с разрывами и морщением листов. Объясняется это
тем, что, заменив внутри каждого листа кривую, изображающую
меридиан, прямой, мы тем самым представили меридианы в виде
ломаных линий. При склейке четырех листов карты мы получим
между двумя листами разрыв, угловая величина которого для
миллионки не превышает 20—25'. Соответственно этому линей-
ная величина разрыва будет около 2 мм.
§ 26. МНОГОГРАННАЯ ПРОЕКЦИЯ
Многогранные проекции применяются для крупномасштабных
карт, т. е. тогда, когда необходимо пользоваться одновременно
ограниченным участком земли. Давая небольшие искажения,
в пределах одного листа карты, проекция, конечно, не допу-
скает склейки карт без разрывов.
Международную карту мира, а также карту 1:500000 по-
иеречно-цилиндрической проекции Гаусса-Крюгера относят
к многогранным проекциям (такие надписи на листах этих карт
можно встретить). Если бы мы склеили листы этих карт для
всего земного шара, то получили бы многогранник.
Карты масштабов 1:200000, 1:100000, 1:50000, 1:25000 и
1:10 000 строились у нас в многогранной проекции Мюфлинга^
82
для построения сетки этой проекции глобус делят на сферои-
^ические трапеции, ограниченные меридианами и параллелями,
реличина площади трапеции зависит от масштаба карты. Каждая
трапеция проектируется на плоскость,
касательную глобуса в центральной"
точке сфероидической трапеции. Фи-
гуру» полученную при проектировании
на плоскость, можно считать плоскост-
ной трапецией, у которой стороны
являются хордами дуг соответствующей
сфероидической трапеции. Ошибка от
такого допущения, как видно из при-
водимой ниже табл. 13, невелика и со-
ставляет для карт 1:200 000 и 1:100000
величину порядка 0,5 мм (рис. 74).
Рис. 74.
Таблица 13
I
Масштаб кг рты	Разность долгот	Величина стрелки h на земле в м	Величина стрелки А на карте в мм
I ( 1: 50 000	15’	7,5	0,15
1:100 000	S0'	30	0,3
1:200000	60'	120	0,6
В этой таблице разность долгот взята между крайними
меридианами листа карты. (
ГЛАВА 6
ПРОИЗВОЛЬНЫЕ ПРОЕКЦИИ
4
§ 27. ОБРАТНАЯ РАВНОАЗИМУТАЛЬНАЯ ПРОЕКЦИЯ
(сетка Вейерса)
Проекция обладает той особенностью, что на ней линия
равных азимутов изображается прямой линией. Выше было
приведено уравнение линии равных азимутов:
•	I	*
ctgП = costg«Ро*cosec ДА — sin?-ctg ДА. (100)
Разделив обе части этого уравнения на произведение
ctg 77-cos <р-cosec ДА, получим:
sec? • sin ДА = >— tg/7-tg?-cos ДА + tg/7-tg?0.	(101)
83
с»
Введем обозначения:
sec f-sinAX — И
tg <р • cosAX = xf ‘
Тогда уравнение (101) перепишется:
у = — tg Пх 4- tg /7- tg %.
(102)
(ЮЗ)
В прямоугольных координатах это выражение представляет
собой уравнение прямой линии, образующей с осью к угол П
(рис. 75). Если теперь построить координатную сетку, опре-
деляемую уравнениями (102), т. е.
сетку, имеющую переменные мас-
штабы по осям, то на такой сетке
уравнение линии равных азимутов
(101) изобразит прямую линию.
Рассмотрим, что представляет со-
бой сетка, определяемая уравне-
ниями (102).
Возведем эти уравнения в квад-
рат:
у2 = sec2 <р-sin2 ДХ;
х2 = tg2<p-cos2 ДХ.
Разделив первое уравнение на
сложив оба уравнения, получим:
see2?, а второе — на tg2<р и
х2 д у'3
tg2 <р ~ St-C* ф
(W4)
Разделив первое уравнение на
Sin’AX, а второе на cos2AX и ввгчтя
из первого второе, найдем:
Выражение (104) представляет со-
бой уравнение эллипса. Так как оно
не содержит долготы, то эллипсы
изображают параллели картографиче-
ской сетки. Аналогично этому выра-
жение (105), являющееся уравнением
гиперболы, изображает меридианы,
так как не содержит широты. Сетка
Рис. 76.
проекции представлена на рис. 76.
В соответствии с уравнениями (102) значения абсцисс на про-
екции пропорциональны sec<p, а ординат — tg <р.
На такой сетке, как показано было выше, линия равных
азимутов изображается прямой линией, причем, как показывает
84
уравнение (103), эта прямая образует угол П (т. е. пеленг радио-
станции) с осью х, т. е. с центральным меридианом, являющимся
прямой линией, в отличие от всех остальных меридианов-гипер-
бол.
Масштабы по меридиану н параллели найдем, продиферен-
цировав выражения (102):
_	— cos AX-d Ф _ cos АХ
т~ U-dtf ~ /?-dcp-cos’ <р 7?-cos3<p ’
dy _ cos ДХ-d ДХ _ cosAX
П ~ R • cos ф • d Д к Н. • cos2 ср • d ДХ	соб2ф *
Поскольку т = п, проекция равноугольна.
Проекция Вейерса находит себе применение в радионавига-
ции, так как линия равных азимутов является позиционной
линией самолета, запеленговавшего радиостанцию под некото-
рым пеленгом П. Использование проекции указано в части III
„ Радионавигация".
§ 28. СПЕЦИАЛЬНАЯ ПРОЕКЦИЯ
В авиации находит себе применение для некоторых специаль-
ных целей нижеописанная проекция.
Представим себе, что на-
блюдатель, находящийся на
самолете на некоторой высоте
Н, замеряет каким-либо спо-
собом расстояние по прямой
от самолета до предмета и
затем это расстояние 5 откла-
дывает от центра проекции О
на сетке под таким же ази-
мутом, каков он есть в дей-
ствительности. На рис. 77 а —
угол визирования предмета
A, da — элементарное измене*
ние угла я, АС—дуга радиуса
<$; тогда угол САВ = а. Из
элементарного треугольника
АВС, принимая его за прямо-
угольный, имеем:
ВС = ЛВ-sin а,
или
dS
Ав “ dD
= sin а.
Но dS есть изменение расстояния 5 на сетке, a dD — измене-
dS ,
ние расстояния на земле, следовательно, отношение = sin а = т
есть масштаб по „меридиану", называя „меридианами" здесь
лучи, расходящиеся из центра („полюса") проекции (рис. 78).
85
„Параллели" проекции будут представлять собой концентри-
ческие окружности радиусов •$ = //• sec а. Масштаб по параллели
также нетрудно получить.
Дуга окружности радиуса
S равна 5)., где X — у гол между
„меридианами". Следователь-
но, на проекции длина эле-
ментарной дуги равна S-d\.
На Земле длина элемен-
тарной дуги равна ОАсГк =
= S-sin a-dk.
Отсюда масштаб по „па-
раллели" равен
S-rfk
п —	= cosec a.
6-Sina-dX
Следует оговориться, что
описанная проекция приме-
няется для ограниченных рай-
онов, определяемых теоретической дальностью видимости гори-
зонта С самолета.
Сравнительно небольшие значения дальностей позволяют
принять за плоскость ту часть сферы, которую мы проекти-
руем на сетку.
Искажения масштабов проекции, пропорциональные sin а и
cosec а, в произведении дают единицу, следовательно, проек-
ция является равновеликой. Эллипсы искажений проекции пока-
заны на рис. 78.
Проекция дает наименьшие искажения контуров объектов
на своих краях и увеличивает эти искажения по мере прибли-
жения к центру проекции. Самый центр проекции вместо точки
изображается окружностью радиуса, равного высоте полета //,
что согласуется с тем, что при а = 0 масштаб по параллели
я = cosec a = се, т. е. точка растягивается в бесконечно боль-
шое число раз, получая конечные размеры.
Поэтому на описанной проекции весьма искаженно (вытянуты
по „параллелям" и сжаты по „меридианам") выходят объекты,
расположенные вблизи полюса проекции. Эти искажения умень-
шаются с уменьшением высоты и теоретически исчезают
при Н — 0.
Проекция не равноугольна, но не искажает углов к между
^меридианами".
§ 29. НОМЕНКЛАТУРА КАРТ
Систему деления картографического изображения террито-
рии на отдельные листы называют разграфкой карты, а си-
стему обозначения отдельных листов называют номенкла-
турой карт.
86
Существует два типа разграфки:
1) международная;
2) прямоугольная.
Каждому из этих типов разграфки соответствует своя номен-
клатура.
Рис. 79.
Основанием для международной разграфки служит лист
карты масштаба 1:1000 000. Краями изображения этого листа
являются меридианы и параллели. Размеры листа —4° ио ши-
роте и 6° по долготе.
Для получения такого листа весь земной шар разбит на
пояса, имеющие буквенное название, и на колонны, имеющие
числовое обозначение (рис. 79). Пояса обозначаются буквами
латинского алфавита от А на экваторе до V вблизи полюса. Ко-
лонны нумеруются от 1 до 60; начало счета колонн—меридиан 180°.
87
Рис. 85.
N 36
Рис. 82.
W-36-J24
Лист карты имеет номенклатуру, например для Москвы
N—37. Кроме номера, на листе ставится название наибольшего
города, расположенного на данном листе.
Дл^ получения листов карт масштабов 1:500000, 1:20'0000,
1:100 000 лист карты масштаба ItlOOOOOO делится соответст-
венно на 4, 18 и 144 части (рис. 80, 81 и 82). Номенклатура
этих листбв указана в табл. 14.
I	Таблица 14
Международная разграфка и номенклатура
Масштаб		Размеры оамки			Количество	Пример номен- клатуры листа
численный	линейный	по мери- диану	по парал- лели	Основной лист для разграфки	листов, уме- щающихся f основном листе	
1:1000 000	10 км в 1 см	4°	6°		1	N-36
1 :500 000	5 км в 1 см	2°	3°	1:1000 000	4	N-36-A
1 -.200000	2 км в 1 см	0°40'	2°	1: 1 000 00С	18	N—36-XIV
1;200 000	2 км в 1 см	0°40f	1°	1: 1 000 000	36	Ч -36-XJV3. п.
1 -.100 000	1 км в 1 см	0°20'	0°30'	1 • 1 000 000	144	N—36-124
1:50 000	>00 м в 1 см	0°10'	0°15'	1: 100 000	4	N—36-124-В
1:25000	?50 ж в 1 см	0°05'	0°7'30"	1:	50 000	4	N —36-124-В-а
1:1и000	i00 м в 1 см	0°02'30"	0°9'45"	1:	25000	4	Ч —ЗС-124-В-а-2
Иногда листы карты 1:200 000 издают разделенными на две
половины: западную и восточную. В таком случае номенклатура
Рис. 85.
карты остается прежней, но
к ней добавляются две бук-
вы— 3. П. или В.П. (западная
или восточная половина). Для
получения карт масштаба
1:50000, 1:25000 и 1:10000
делят каждый предыдущий
лист на четыре части и обо-
значают листы буквами или
цифрами, как показано на
рис. 83,84 и 85. Пример между-
народной номенклатуры дан
в табл. 14.
Основой для разграфки
и номенклатуры карты мас-
штаба 1:1 500 000 служит лист
карты размерами в 6° по ши-
роте и 9° по долготе; рамками
листа являются параллели и
меридианы.
Для получения такого листа земную поверхность разбивают
;на пояса и колонны и обозначают их буквами русского алфавита
и номерами, как это показано на сборном листе (рис. 86). При-
мер номенклатуры листа карты: Е—6.
S0
Рис. #6.
При прямоугольной разграфке картографическое изобра-
жение делится на листы, имеющие форму прямоугольников,
причем крайние линии листа карты не совпадают с параллелями
и меридианами.
Номенклатуру листа карты составляют номер ряда и номер
колонны для крупномасштабных карт, или же просто поряд-
ковый номер листа карты для средне-и мелкомасштабных карт.
Пример прямоугольной разграфки карты 1:2500000 дан на
рис. 87.
Рис. 87.
§ 30. ТРЕБОВАНИЯ К АВИАЦИОННЫМ НАРТАМ
Карта необходима при выполнении всякого полета, какого бы
назначения он ни был: боевой или просто перелет из одного пункта
в другой.
С качеством и особенностями карты связано обычно и каче-
ство выполнения полетного задания.
В первое время своего существования авиация пользовалась
картами, созданными для наземных потребителей. Практика,
однако, показала, что наземные карты не удовлетворяют требо-
ваниям авиации. Разнохарактерность и даже известная проти-
воречивость этих требований делают вопрос о картах для ВВС
довольно сложным.
S2
Требования, предъявляемые к авиационным картам, вытекают
д13 тех задач, которые приходится решать с помощью карт;
задачи эти в основном сводятся к следующим проблемам:
1)	визуальная детальная ориентировка;
2)	визуальная общая ориентировка;
3)	прокладка пути;
4)	пеленгация радиостанций;
5)	дистанционно-метрия радиолокаторных станций;
6)	прокладка астрономических позиционных линий;
7)	расчет полета.
Кроме этих чисто навигационных проблем, на авиационных
картах приходится решать задачи, связанные с бомбометанием,
фотосъемкой, разведкой и т. п.
Если к этому добавить, что все перечисленные задачи
требуют обычно письменной работы на карте, т. е. нанесения
надписей, линий, условных знаков и т. п,, то станет понятным
наличие большого количества различных карт, применяемых
в настоящее время в ВВС.
Требования, предъявляемые к авиационным картам, касаются
следующих элементов:
1)	масштаб;
2)	проекция;
3)	содержание.
1.	Основным масштабом для полетной карты почти
во всех странах принят масштаб 1:1000000.
Этот масштаб позволяет вести общую визуальную ориенти-
ровку, прокладку пути, а также производить некоторые другие
навигационные расчеты и построения. В последнее время в дальне-
бомбардировочной авиации начали применяться карты масштабов
1:1500000 и 1:2000000. Эти масштабы оказываются более
удобными в случае, когда экипаж самолета не привязан к земле
на маршруте, например, в дальних ночных или заоблачных
полетах, так как более мелкий масштаб требует меньшей
по величине площади карты, что для авиации имеет важное
значение.
В ближних полетах, какие приходится обычно выполнять
фронтовой авиации, более удобным является масштаб 1:500 000.
Удовлетворяя навигационным целям, этот масштаб, однако, не
позволяет отыскивать мелкие цели, какие бывают, например,
в пределах оборонительной полосы противника. Для этого могут
служить карты масштаба 1:200000.
Таким образом, во фронтовой авиации возникает необходи-
мость пользования в полете картами двух разных масштабов,
что весьма затруднительно. Принимая во внимание эту трудность,
в некоторых странах создали карту масштаба 1:300000 с целью
соединить в ней необходимые качества масштабов 1:500000
и 1:290000, В ВВС была создана карта 1:300000 для некоторых
районов. Однако распространения эта карта не получила.
93
Для целей азимутальной радионавигации удобными масшта-
бами являются 1:2500000 и 1:5000000. Удобство применения
мелких масштабов здесь объясняется возможностью одновре-
менного нанесения и пользования на ограниченном участке
карты положениями нескольких радиостанций и самолета. Так как
точность радиопеленгации на далекие расстояния невелика,
то ошибки от неточности графического построения на карте
мелкого масштаба не имеют существенного значения.
Дистанционно-метрическая радионавигация (радиолокация) не
требует для чисто навигационных работ Специальной карты
и может выполняться на карте масштаба 1:1000000. Однако
радиолокация для целей бомбометания и фотографирования
требует таких точностей, каких не может дать ни одна карта.
Эта работа выполняется по таблицам, которые должны быть
рассчитаны с геодезической точностью.
Боевые действия ВВС могут потребовать карты крупного
масштаба порядка 1:25000 или даже 1:10 000, являющейся
по существу уже планом. Такие карты бывают необходимы
при подготовке и проведении бомбардировочных ударов по
крупным целям оперативного и стратегического значения: же-
лезнодорожным узлам, промышленным объектам и т. п.
Таким образом, ВВС, в зависимости от характера действий,
могут пользоваться картами и весьма мелких (до 1:5000000)
и очень крупных (1:10 000) масштабов.
С какой точностью следует изготовлять карты для ВВС?
Предельная точность, которую может рассмотреть человече-
ский глаз, равна 0,1 мм. Та длина на местности, которая соответ-
ствует 0,1 мм на карте, называется предельной точностью
масштаба. Для карты 1:1000000 предельная точность
масштаба составляет 100 м. Меньше этого расстояния простым
глазом на карте 1:1000000 рассмотреть нельзя.
Ниже приводятся предельные точности масштаба для неко-
торых карт, применяющихся в авиации.
Масштабы карт	Предельная точность масштаба в м	Точность определения и отклады- вания расстояний в м
1 :2500 000	250	1250
1 : 1000 000	100	500
1:500 000	50	250
1:200 000	20	100
Предельная точность масштаба определяет те подробности,
которые могут быть нанесены на карту.
В авиации измерение и откладывание расстояний в обычной
рабочей обстановке производятся с помощью линейки, имеющей
самые мелкие деления в 1 мм. Принимая во внимание, что
толщина карандаша бывает около 0,5 мм, следует считать, что
точность, с какой обычно измеряют или прокладывают рассто-
яние на карте, не превышает 0,5 мм, что в пять раз ниже пре-
дельной точности масштаба.
94
Отсюда нельзя, конечно, сделать вывод, что карты для ВВС
можно изготовлять с точностью до 0,5 мм, так как и в ВВС
могут быть случаи, когда измерение расстояний требуется
произвести с предельной точностью масштаба кдрты.
2.	Проекции авиационных карт должны, по возможности,,
удовлетворять условиям, во-первых, равноугольности и, во-вто-
рых, равномасштабности. Требование равновеликости (равенство
площадей) для ВВС несущественно. Проекций, которые одно-
временно удовлетворяют равноугольности и равномасштабности,
нет, да и быть не может. Поэтому при создании какой-нибудь
карты необходимо поступиться каким-либо из требований.
В морской навигации, например, пользуются равноугольной
проекцией с переменным масштабом. В ВВС пользоваться пере-
менным масштабом затруднительно, поэтому при проектировании
авиационных карт стараются, сохраняя равноугольность, одно-
временно сохранить практически (с известной степенью точности)’
и равномасштабность на некотором ограниченном участке карты-
Это удается хорошо для маршрутных карт (полос) какой
угодно длины и ограниченной ширины (200—300 км). Для обыч-
ных же карт в авиации применяют равноугольные проекции,,
дающие искажения масштабов около 1% в своем рабочем рай-
оне и до 2—3%—на краях проекции (но не на краях листов
карты!).
Для некоторых специальных целей в ВВС применяют карты,
не обладающие свойствами ни равноугольности, ни равнопроме-
жуточности, но на этих картах одна из позиционных линий'
изображается прямой. Например, на гномонической проекции
ортодромия прямая, на меркаторской — локсодромия прямая,
а на обратной равноазимутальной — линия равных азимутов— 
прямая. В зависимости от этого свойства проекцию называют
ортодромичиой, локсодромичпой или равноазимутальной.
3.	Содержание или нагрузка карты определяется ее
назначением. Карта для детальной ориентировки должна содер-
жать все подробности земной поверхности, которые необходимы
для отыскания самых мелких ориентиров, однако эта нагрузка
лимитируется масштабом. Так, на карте 1:500000, служащей’
для детальной ориентировки, не удалось нанести все населен-
ные пункты, что является существенным недостатком карты.
На старой десятиверстке нанесены все, даже очень мелкие
деревни, но обилие надписей на этой карте в заселенных мест-
ностях делает карту совершенно неудобочитаемой.
Сравнительно сложным является вопрос обозначения рельефа
на авиационных картах.
На картах 1:500 000 и крупнее рельеф дается горизонталями
через 50 или 40 м и чаще. На картах 1:200000 и мельче рельеф
может даваться в виде гипсометрического изображения, а
именно: каждой ступени высоты присваивается свой оттенок
светлокоричневого цвета. Весьма важно распределить оттенки
так, чтобы самый темный из них все же не затемнял карты.
95-
В равнинных местностях овраги и балки отмечают отмывкой
-что облегчает пользование этими объектами для детальной
ориентировки.
Условные знаки для полетных карт должны по возможности
облегчать чтение карты. Наиболее резко должны быть выделены
железные и шоссейные дороги, реки, озера. Населенные пункты
следует давать не в виде кружков различной величины, а со.
блюдать их конфигурацию.
Ниже дается таблица характеристики некоторых, наиболее
распространенных в ВВС карт (приложение 15).
ДОПОЛНЕНИЯ
§ 31. ЗЕМНОЙ СФЕРОИД
Земля имеет неправильную математическую форму, весьма
близко подходящую к сфероиду — эллипсоиду вращения вокруг
малой оси. Два сечения в любой точке сфероида — меридианное
и ему перпендикулярное — из бесчисленного множества верти-
кальных (нормальных) сечений являются главными сече
ниями, причем сечение, перпендикулярное меридиану, назы-
вается первым вертикалом. Меридианное сечение является
плоскостью симметрии сфероида. Радиусы кривизны меридиана
и первого вертикала обозначаются соответственно М и N. Они
равны:
М =	— <*)	. л/ =	Д(1 — г2)
Д’	Р 1 — е2 sin- <р
(1 —e2sin2<?) 2
Среднее арифметическое из всех радиусов кривизны верти-
кальных сечений в данной точке равно:
^cp = 1//WN =
а V 1—е2
1 — е2 sinz <р
В формулы радиусов входит географическая широта <р,
т. е. угол, который составляет отвесная линия в данной точке
с плоскостью экватора (рис. 88.) Угол ср', составленный радиу-
сом-вектором ОА с плоскостью эква-
тора, называется геоцентрической
широтой. Если описать около центра
сфероида О окружность радиусом, рав-
ным большой полуоси сфероида а, и
продолжить перпендикуляр С А, опу-
щенный из данной точки А на экватор,
До пересечения с окружностью в точке А'-
то угол и, составленный радиусом ОА1
с экватором, называется приведен-
ной широтой.
Формулы для геоцентрической и
приведенной широт следующие:
*S?' = (1—e2)-tg<p; tgu = ]/l—£2 tg=p.
Т-1683
97
Разность между географической и геоцентрической широтой
достигает максимума 12' на широте 45°, для приведенной
широты эта разность равна 6'.
§ 3?. ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ
Кратчайшее расстояние между двумя точками на сфероиде
считают по геодезической линии. Основное свойство ее
состоит в том, что в каждой ее точке произведение синуса ее
азимута а на расстояние точки от малой оси сфероида г есть
величина постоянная, т. е. г-sin а — const.
Геодезическая линия совпадает с меридианами и с экватором,
т*. е., когда а = 90° или 270°. В остальных случаях геодезиче-
ская линия не совпадает с ортодромией.
Посмотрим, насколько могут расходиться расстояния, вычи-
сленные по ортодромии и по геодезической линии. Найдем
соотношение радиусов /? и М для широты 45°, которое будет
характеризовать искажение длин по меридиану, при принятии
нами сфероида за шар радиуса /?,р:
з
/?__	fl — ei sin2	2	-i- .	_ —i-
-------------------= (1 _sin2?о) * (1 _е
7И	|/ 1 — (Л (1 — sin2 ср)
. . ё1 ,,	.1
= l+-ycos% = l w,
т. е. искажение длин составит 0,16%. Для расстояния
это составит 160 м, что значительно превышает ошибки
100 км
радио-
локационных систем. Однако для широт, более удаленных от
широты 45°, принятой нами в данном примере для определения
радиуса шара, — ошибки будут еще больше.
Расчет геодезической линии может вестись различными спо-
собами и по различным формулам, в зависимости от степени
требуемой точности. Кроме формул Кларка, приведенных на
стр. 26, могут быть рекомендованы формулы Шрейбера и Гаусса,
по которым составлены Таблицы для вычисления геодезических
координат, Геодезиздат, 1944 г.
Сравнительно простое решение получается в конформных
сфероидических плоских координатах Гаусса-Крюгера. Если
пренебречь искажениями длин порядка 0,05%—0,07% и напра-
влений порядка сотых долей секунды, то задачи решаются
следующим образом: принимают расстояния (хорды) Az, АВ,
Bz (рис. 89) за геодезические линии; имея плоские азимуты
(дирекционные углы) XAz, ХАВ, XBz и координаты точек А,
В, z, — нетрудно рассчитать расстояния Az, АВ, Bz (обратная
геодезическая задача). Точно так же, задаваясь величинами 1\
и расстоянием Аа — Az, Ab = Az, Ac = z, легко рассчитать
координаты точек а, Ъ, с, а по ним расстояния аВ, ЪВ, сВ
и т. д.
98
Для прямой задачи служат формулы:
xz ~ xi + cos Ту; у2 =	+ d sin Ту; Ту = Ту ± 180°.
Для обратной задачи служат формулы:
tg Т2 = —
ь х2 — л.
х 2 Л1 __ У'2  У1
cos 7'2 sin 7 2

и а
Кроме аналитического,
можно воспользоваться и
графическим решением за-
дачи, когда это позволяет
требуемая точность. При
графическом решении мо-
жет определяться выраже-
ние для геометрического
места точек, равноудален-
ных от заданной точки —
положения радиостанции.
Эту кривую называют
и зо орт ой. Можно вычи-
слить и построить по точ-
кам сеть изоорт по следу-
ющим формулам в прямо-
угольных координатах:
(л — xf + О —х)2 = d?;
d — k-s
Рис. S9.
006,
Здесь х и у — координаты текущей точки;
xs и Уз — координаты радиостанции;
s — длина геодезической линии;
— основание неперовых логарифмов;
d—длина хорды, стягивающей геодезическую
линию;
/? —средний радиус кривизны на средней широте
относительно линии.
Пользуясь формулами (106), можно вычислить и нанести
изоорты на любую проекцию.
Для графического расчета изоорт можно воспользоваться
стереографической сеткой, помня, что на этой сетке все окруж-
ности на шаре изображаются окружностями. При этом проек-
цию сфероида можно рассматривать при допустимых для нас
искажениях для расстояний до 500—600 км как проекцию шара,
на которой сфероид отображен конформно.
99
Принимая за полюс проекции радиостанцию, мы получим си-
стему изоортв виде ряда концентрических окружностей радиусов:
P = ktg^.
Здесь К — постоянная проекции;
R—радиус шара;
s — заданное расстояние, равное на проекции полярному
расстоянию.
Разницу Д/7 межд> ортодромическим и геодезическим ази-
мутами можно получить по следующей формуле:
tg Д/7 = —c2cos<pf-sin /7^sin<fftg у — cos /7-cos<$Q.	(107)
Ошибка Д/7 может достигать максимального значения 11', 2.
Она больше в экваториальных широтах и уменьшается к полю-
сам. На рис. 90 приведены линии равных поправок геодезиче-
ских азимутов к ортодромическим для радиостанции, располо-
женной на широте = 48°.
100
§ 33. ЛИНИЯ РАВНЫХ АЗИМУТОВ (ПЕЛЕНГОВ)
Позиционной линией самолета, пеленгующего какую-либо
радиостанцию при помощи радиополукомпаса, является, как
было указано, линия равных азимутов пеленгов (ЛРА). ЛРА,
следовательно, есть такая кривая, из всех точек которой орто-
дромическое направление на радиостанцию составляет с мери-
дианами один и тот же угол П (рис. 91).
Принимая обозначения по рисунку, можно написать по фор-
муле четырех элементов:
ctg П sin А = tg • cos — sin <р - cos л,	(108/
или
ctg П—tg <?s- cos <р • cosec X — sin • tg A.	(109)
Последнее уравнение есть одновременно формула для путе-
вого ортодромического угла, так как любая точка линии рав-
ных азимутов принадлежит одновременно и ортодромии, соста-
вляющей с меридианом у этой точки угол П.
В формулах (108) и (109)	— широта радиостанции, Л — раз-
ность долгот радиостанции и текущей точки, <р— текущая ши-
рота. Если определение линий равных азимутов применить
к плоскостному изображению, заменив все большие круги пря-
мыми, то линия равных азимутов изобразится дугой PM2S
окружности, проходящей через полюс и место радиостанции
(рис. 92), причем углы П будут равны между собой, как впи-
санные, опирающиеся на хорду PS, длина которой равна рас-
стоянию между полюсом и радиостанцией, при этом углы на
дуге PM^S, являющейся дополнением дуги PM.,S до 360°, равны
180°—П, т. е. дополнениям углов П до 180°.
Следует не путать ЛРА с локсодромией, которая сама соста-
вляет с меридианами постоянный угол (рис. 93), между тем как
ЛРА составляет с меридианами разные углы. На рис. 94 ЛРА
в точке М составляет с меридианом РМ угол PMk = а, где Mk —
касательная к ЛРА в точке Л1. Таким образом, из рисунка
101
г
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
видно, что a = n + i, где П— азимут (пеленг) радиостанции S,
a, i — угол между ортодромией и касательной МК.
Найдем углы а и г.
Переместим точку М на бесконечно малое расстояние Мт
в точку т. Тогда, принимая обозначения по рисунку, можем
написать:
Mn = ml = d<z\
Ml = mn — d). • cos <p.
Из элементарного треугольника Mmn имеем:
, mn	d\
— tg = c°S т	(ПО)
Считая П и % постоянными, продиференцируем уравнение
(108), взяв производную от X по <р.
А   tg ip,,-sin <p + cos <p-cosX
d<?	ctg /7 • cos X — sin X • cos 9 ’
или
A   (sin <рЛ-sin 9 + cos <p?-cos 9-cos X)-sin П
d<? (cos/7-cosX — sin ZAsinX.sintppcos®,'
Выражение, стоящее в числителе в скобках последней дроби,
есть косинус дуги MS, т. е. coss, а в скобках знаменателя —
косинус угла р, следовательно,
А.   coss-sin П
dtp cosp-cos<?5 ‘
По теореме синусов из треугольника PSM имеем:
sin П   sin Р
cos 9^	cos 9
102
Следовательно,
dl____________________ coss sin p _ , p _ cos
d<? ~~ cosp-cosq> ° ‘ cos9
Подставляя это в выражение (ПО), найдем:
tga = — coss-tgp.	(Ill)
Найдем теперь выражение для угла i — a.— /7.
Имеем:
tg/ = tg(a-/7) = i^J5g^-r
Подставляя сюда значение tga из формулы (111) получим:
. • _ tg 77 4- coss-tgP
cos s-tg fl-tg/7 — 1 ’
Умножив числитель и знаменатель этой дроби на cosfPcos/7,
найдем;
, -__jsir./7-cos 8 + cos 77-sin В-cos s
b coss-sin p-sin П — cosp-cos/7 '
Числитель полученной дроби есть, по формуле пяти элемен-
тов, sinX-sin®, а знаменатель есть косинус угла X. Поэтому
tg г — sin ср • tg X.	(112)
Из формул (111) и (112) следует, что угол а между ЛРА
и направлением меридиана меняет свое значение при переме-
щении точки М по кривой равных азимутов. Из формулы (111)
видно также, что угол а связан определенным образом с углом 8,
который образует ортодромическое направление с меридианом
в месте радиостанции.
Из формулы (112) видно, что угол i между ортодромией
и ЛРА не зависит от параметров ЛРА—П, %, а зависит только
от широты <р точки на кривой и от разности долгот X между
этой точкой и радиостанцией.
Для меридиана радиостанции X — О; следовательно, из Лор-
мулы (112) имеем:
tg i - - 0; i — 0 и а = П + г,
т. е. в точке радиостанции ЛРА пересекает мери-
диан под углом, равным азимуту (пеленгу) П.
Для полюса р = 0, так как ортодромия о. впадает с мери-
дианом радиостанции; следовательно, из формулы (111) имеем:
tg а = 0; а — 0; i -- а — П = — П.
Известно, что сближение (схождение) меридианов В двух
точек определяется следующей формулой:
tgS = sino-tgX.	(ИЗ)
Здесь ® — широта точки, для которой определяется сбли-
жение, а X — разность долгот двух точек.
103
Формулу сближения меридианов точек М и L можно полу«
чцть следующим образом (рис. 95).
Опустим из точки М на меридиан точки L сферический
перпендикуляр МК. Если теперь через точку М провести дуГу
MN параллельно меридиану РК, то угол а, образуемый этой
дугой с дугой большого круга, соединяющей точки М и L,
называется дирекционным углом. Разность между дирек-
ционным углом а и азимутом точки L— сц называется сближе-
нием меридианов. На рис. 95 она обозначена 8. Следовательно,
8 = а — <Xj.
Принимая во внимание, что угол Р/И/С=9О — 8, из прямо-
угольного треугольника РМК имеем:
cos (90 — <р) = ctg (90 — 8) • ctg X,
откуда и получаем формулу (113).
Очевидно, что сближение меридианов точки М имеет одно
и то же значение для всех точек, лежащих на меридиане PLK.
Название „сближение меридианов* произошло от сравнения
дуги ML с прямой ML, если изобразить ее на плоскости
с путевыми углами (азимутами) а и а, (рис. 96). При этом
предполагается, что расстояние ML невелико. Тогда разность
углов (а — аД равная углу 8, представит как раз сближение
меридианов РМ и PL точек М и L.
Сравнивая уравнения (112) и (113), мы видим, что угол i
между ортодромией и ЛРА равен сближению мери-
дианов.
§ 34. ИССЛЕДОВАНИЕ УРАВНЕНИЯ ЛРА
Кривые равных азимутов имеют на сфере более сложный
вид, чем ортодромия и локсодромия. Общий вид этих кривых
на сфере дан на рис. 97 и 98 для радиостанции, расположен-
ии
«ой в точке 5 на широте ?л = 40°. На рис. 97 меридиан PS
здиостанции совпадает с плоскостью чертежа, на рис. 98 этот
Меридиан перпендикулярен плоскости чертежа.
Пользуясь уравнением (108) ЛРА, исследуем вид кривых не
сфере.
а)	Из геометрических соображений следует, что азимуту
/7=0° соответствует часть меридиана PS, а азимуту П = 180° —
часть меридиана PS.
б)	Если в уравнении (108) положить X = 0, то
О — tg?f-cos?— sin ?,
или
tg? = tg?, И ? = ?,.
Это значит, что все линии равных азимутов проходят через,
радиостанцию.
в)	При Х= 180е имеем:
О — tg ?s- cos ? + sin ?,
или
tg ? = — tg ?, И ? = — v
iC5
Рис. 98.
Отсюда следует, что все кривые равных азимутов проходят
"через точку S' с широтой — являющуюся антиподом точки
-5 — места радиостанции.
г)	Если в уравнении (108) переменить знаки одновременно
У X и П, то уравнение не изменится. Но перемена этих знаков
означает, что вместо азимута П взят азимут 360—П. Сле-
довательно, линии равных азимутов симметричны отно-
сительно меридиана радиостанции PSP', что и видно на ри-
сунке.
Таким образом, например, кривой равных азимутов 80°, рас-
положенной в западной (относительно радиостанции S) полу-
сфере, соответствует симметричная ей кривая равных азимутов
360°—80° = 280°, расположенная в восточной полусфере. Ввиду
полной симметрии мы в дальнейшем будем рассматривать
только одну, например западную, полусферу.
д)	Если в уравнение (108) подставить 180 4-/7 вместо /7, то
уравнение не изменится. Это значит, что кривая, соответствую-
щая азимуту П на одной половине сферы, переходит в кривую
для азимута 180 + П на другой половине сферы, например, кри-
вые азимутов 80° и 260° являются продолжением одна другой.
306
е)	Положим, <? —О, т. е. найдем точки пересечения линии
равных азимутов с экватором. Тогда из уравнения (108) полу-
чим:
ctg П- sin X = tg
или
sinX = tg77-tg<ps.	(114)
Так как синус не может быть больше единицы, то должно
иметь место неравенство
tg/7-tg<ps<l,
или
tg/7-ctg (90—?f)<l.
Но эго возможно только при условии, если
77<90 — ъ.
Следовательно, экватор пересекают только те Л РА,
азимут которых меньше либо равен 90 — <р5.
Кр и в ы е ти п а /7<<9С-— <ps, пересекая экватор, соединяют
две точки: радиостанцию S и противоположный полюс Р или
антипод радиостанции 5' и противоположный полюс Р, образуя,
таким образом, две ветви для одного и того же азимута.
На рис. 97 и 98 эти кривые соответствуют азимутам от 0°
до 50° в западной полусфере и от 310° до 0° в восточной
полусфере.
Долготы Хо пересечения этих кривых с экватором опреде-
ляются уравнением (114). В случае, когда Хо = 90°,
tg 77-ctg (90—<ps) = 1.
Отсюда 77=90— <р5. Значит, кривая равных азимутов, соот-
ветствующая значению азимута 77 = 90— tp5, пересекает экватор
в точке Ро, отстоящей от меридиана радиостанции на 90° (или
на 270°).
Кривая типа 77 = 90 — ?s имеет две ветви: одна проходит
через радиостанцию 5 и ее антипод S', другая — через полюса
Р и Р. Обе ветви пересекают экватор в точке PQ (на рис. 98 —
в точках Е и Q).
Справедливость этого следует из уравнения (108), если поло-
жить в нем 77 = 90 — <ps. Тогда получим:
tg^-sin X = tg<p.?-cos<p — sin tp-cos X.
Это x равнение имеет следующие решения:
при X = 0°, 'p=4-|Pj—кривая проходит через точку 5;
при Х = 180°, ® = — —кривая проходит через точку S'-
при Х = 90°, <р = 0— кривая проходит через точку 7%;
при X — 90° + <р = + 90°— кривая проходит через точку Р-
при X = 90c— <?„ <р =—90°—кривая проходит через точку Р.
107
Для нашего случая, когда = 40°, эта кривая соответствует
азимуту /7 = 50° для западной полусферы и азимуту 310° — для
восточной полусферы.
В случае, когда /7>90 — <ps, кривые равных азиму-
тов не пересекают экватора.
ЛРА этого типа имеют две ветви: одна проходит через
радиостанцию S и полюс Р одноименной широты, другая про-
ходит через антипод 5' радиостанции и соответствующий ему
полюс Р'. Для нашего случая эти кривые соответствуют
азимутам от 50° (исключительно) до 180° для западной полу-
сферы и азимутам от 180° до 310° (исключительно) для восточ-
ной полусферы.
§ 35. УРАВНЕНИЕ ЛРА Р ВИДЕ П1 ОСТРАНСТВЕННЫХ
ОВАЛОВ КАССИНИ
Уравнение (108) ЛРА не дает возможности непосредственно
по его внешнему виду определить характер кривой. Это можно,
однако, сделать, если вывести
уравнение кривой в ноеой
системе координат.
Примем меридиан радио-
станции PS за экьатор, к се-
редине которого в точке О
восставим перпендикуляр
(рис. 99). В точке Ро пересе-
чения этого перпендикуляра
со старым экватором полу-
чим новый полюс системы.
Возьмем на ЛРА точку М и
проведем дугу Р0МС, кото-
рая разделит угол П на два
угла а и р и образует два
сферических прямоугольных
треугольника Л4РС и MSC.
Рис. 99.
Приняв за новый начальный
меридиан дугу 0Ро, получим долготу точки М, равнуюОС — X.
Обозначим широту точки М в новой системе через <?, причем
из рисунка имеем ч — '^МС, а дополнение широты до 90°
(дугу РйМ) — через &.
Кроме того, дополнение до старой широты радиостанции
обозначим через т], таким образом ИО = ~ и РО==^.
Из прямоугольных треугольников РМС и MCS имеем:
tg
tga= —
cos 0
и tg В = -----------------77-
ь r	COS
Подставим эти выражения в формулу тангенса суммы:
108
tg/7=tg(« + ₽) = T^^P=’
tg(i + x) +tg(j—x)
eos»&-tgQ--x).tg (y—xj
cos&.
Умножив числитель и знаменатель последней дроби на
cos
(у +	’ COS Q — • COS2 &>
Но
COS fy + COS ^у — *) = у (cos 73 + cos 2\
и	,	\	.	\	1 ,
sin у + Xj Sin (у — X — — у (cosiq—cos2X
Следовательно,
„___________________2 sin у cos 8________________
» (cos tj + cos 2X) cos2 a + cos nj — cos 2z.'
Подставляя сюда
tg/7 =
sin П
cos 77
i-tg8!
И cos ’> =----7Г-,
l + t^
получим;
( a 2	/
cos n f 1 — tg’ 2 1 +cos 2X
sin П
cos/7
2 sin 7] ('l — tg4y)
»\a 7 a ?	7 a \»
— tEa у J + cos t) 1+tg2 у j — cos 2X +tga у}
sin П
cos П
sinij^l — tg4y)
~ —
cos i] + cos tg4 —----2 cos 2X tg2 у
Q,
tg4 у (cos tj  sin П + sin >j-cos/7) — 2 cos 2X • sin П- tg2 у +
+ cos ц sin /7 — sin ri cos /7=0;
'tg 2cos 21 + -еГм/уЛ = °-	0 15>
l Л
Это есть уравнение пространственных овалов
Кассини.
Действительно, овалом Кассини является геометрическое
место точек, произведение расстояний которых до двух точек —
фокусов овалов — есть величина постоянная. Уравнение (115)
можно представить в виде
r‘r2 = W^^ = const-	(И6)
Здесь
	.	I
l.o^i sin г/	г sin П "12.	1 И 1 тт
| tg-2 +5TnT/;+v-2cosXLm77+^)-J	(117>
1x9^1 sin Г/ . n - Г sin П
| tg- 2 + sin (11 + 7j) + 2 C0S 7 |_sin (11 + V)) J 2 
Действительно, из уравнений (116), (117) и (118) имеем:
1
i \ч	! sin/7 I2	8 Г sin П 2	,
(гГгг)—[tg' 2 + sin (77+ч) J Гtg 2 L sin (/7 + rj _ cos)J =
sin2 7]
~ sin2(/7 + >j) ’
. . 8 , „ , о 8 sin П ,
tg^ + 2tg--F--.n-;+- +
। slnS/7 _ 4 tp2 JL . - sinZ7 рпч2 X — - sir,2 f‘ 711 Q\
+ sina(/7 + 4)	2 sin (//+ t;) COS Л sin2(/7 + rj) ' 'Пу)
Принимая во внимание, что
sin2 П	sin2 у]_sin (П— ц)
sin2 (П + т;) sin2 (11 4- ij) sin (11 + ij)
И ЧТО
2 cos2 X — 1 — cos 2z,
из уравнения (119) легко получим указанное выше уравнение (115).
Расстояние P0Q равно:
— Р 0^2
sin П
sin (/7 + тр
не Cj и С2 — фокусы овалов (рис. 100).
Рисунок можно легко разобрать, сравнив его с рис. 97 и 98,
на которых соответственные точки обозначены одними и теми
же буквами. Из рисунков видно, что дуга СГС2 (она же ОО'),
соединяющая фокусы овала, является кругом симметрии всех
ЛРА. Большой круг NN, перпендикулярный кругу ОС, также
является кругом симметрии ЛРА.
Как было уже исследовано, для случая П <90—<рл овал
Кассини состоит из двух замкнутых ветвей (на рис. 100—PmS
ПО
л PnS); для случая, когда П>90 — <р5, овал Кассини имеет
jBe разорванные ветви SBP1 и PAS'; наконец, для случая /7 =
90 — <pt овал Кассини имеет форму двух пересекающихся кри-
вых SP0S' и РРОР\ которые носят название пространственной
Бернуллиевой лемнискаты, по аналогии с плоскостной лемни-
скатой.
Уравнение (115) имеет при этом следующий вид, принимая
во внимание, что для наших обозначений надо положить П =--
= 90 —= •»]:
to4 4_tg2 — —°—= 0
ь 2 ь 2 cos т; ’
г}
tg2— = sec vj • cos 2X.
откуда
Для точки Po мы должны положить в этом уравнении 8 =J
— 90° (см. рис. 99 и 100). Тогда получим:
1 = sec Vj • cos 2Х,
или
1 . ,
2 '1 —Х-
Это соответствует положению точки Ро, в которой пересе-
каются обе ветви лемнискаты.
111
$ 36. УРАВНЕНИЕ ОРТОДРОМИИ НА МЕРКАТОРСКОЙ
ПРОЕКЦИИ
Ортодромия на меркаторской проекции имеет вид трансцен-
дентной кривой, обращенной своей выпуклостью к полюсам
«(см, рис. 36). В пересечении с экватором ортодромия имеет
точку перегиба. Уравнение ее можно получить следующим
образом. Координаты точки на меркаторской проекции:
х = D = In tg ^45 + -f*) и у = >..
От сюда имеем:
эли
р е* — 1
Подставляя это значение в уравнение ортодромии (1), по-
лучим:
ctg я - sin X = — (е* — е~ х),
или
ctg а • sin X — sh х.
При необходимости нанести на меркаторскую сетку орто-
дромию, рассчитывают ее промежуточные точки, которые затем
наносят на карту и соединяют плавными кривыми.
J 37, УРАВНЕНИЕ ЛИНИИ РАВНЫХ АЗИМУТОВ НА МЕРКАТОРСКОЙ
ПРСЕ^ ДИИ
Напишем уравнение линии равных азимутов в таком виде:
ctgП• sec ? sin X = tg — tg<» • cosX.	(120)
Координаты точки на меркаторской проекции:
х = D = In tgf45 + -£•); у = X .
Отсюда имеем:
ф
= tg(45 + 4-) - ---
v '	1-tg-|-
или
112
180° 170“ 160° 150° 140” 130° 120° 110° 100° 90° &0° .70° 60°
Г80°
20°,
-50т
-40е
70°-
-J-60?
10°~Т)'
60° 40е 30° 20° 10° 0° 10° 20° 30° 40° 50° 60° 70° 80° 90° 100° 110° 120° 130°
140“ 150° 160° 170° 180?
....* 80°Т
iH70?
130°
110° 1
|O
100°
SQ°
Й
о
10
20
О
30
50-
50“
100°
80° “ 90°
Г 740
20°
1 30е
80°
'60°
40° 30° 20е 10"
0° 10°
130“
О
iton II ..,.,,11111111111111 п Н ,И НИ НИИ НИИ НИИ ИИ и
180° 170° 160° 1Б0°140° 130° 120° 110° 100° 90° 80° 70° 60° 50°
20° 30°
20° 30° 40° 50° 60° 70° 80° 90° 100° 110° 120° 130° 140° 150° 160° 17.0° 180'
Nia°iQ
Рис. 101.
да
о? Те
30?-
7
P1I 1150°
16Q?
60?,
Зак. Ns 1681
804
шв
50?
10°
Но
2
tg <р = ----------
ctg-g-—tg-g-
следовательно,
tg^=^(ex — e~x) = shx,	(121)
sec <p = ]/ 1 + tg2 <p = l/i + -Le2x+±e~2x-~ =
= )/-^(ex + ^2.
или
sec <p = -g- (e* + e~x) — ch x.	(122)
Подставляя уравнения (121) и (122) в (120), получим:
ctg/7  chx • sinX = tg<j>s — shx-cosX.	(123)
Уравнение (123) дает трансцендентные кривые, изображен-
ные на рис. 101 для радиостанции, расположенной на широте
= 20°. Уравнение ЛРА на поперечной меркаторской проекции
дает также трансцендентные кривые, которые можно построить
только по точкам.
§ 38. КОСАЯ ПОЛЯРНАЯ И ДВУАЗИМУТАЛЬНАЯ ПРОЕКЦИИ
Центральная полярная проекция находит применение в ра-
дионавигации. При пеленгации с земли место самолета опреде-
ляется на пересечении двух позиционных линий, проведенных
на карте в виде ортодромий от двух пеленгаторных станций.
Для удобства пользования радиопеленгаторные станции приме-
няют карты центральной проекции, на которой заранее от стан-
ции проведены лучи ортодромий в виде прямых линий. Полюс
проекции (сетки) выбирается так, чтобы он оказался в середине
района, предназначенного для обслуживания данными двумя
станциями. На такой сетке — косой центральной проекции — ’
ортодромии, проведенные от радиопеленгатора для пеленгов
через равные углы, например через 2°, не будут, конечно,
отстоять одна от другой на эти же углы на карте, ввиду иска-
жений, которые дает проекция. Поэтому густота лучей в раз-
личных направлениях будет неодинакова.
Каждая пеленгаторная станция может избегнуть для себя
этого неудобства, построив сетку таким образом, чтобы место
станции оказалось полюсом проекции, т. е. точкой касания про-
ективной плоскости. Тогда все ортодромии отойдут от радио-
станции в виде прямых, углы между которыми будут соответ-
ствовать углам на местности, т. е. измеренным пеленгам.
8—1633
113
Формулами для построения сетки косой центральной проек-
ции могут быть:
х — R • ctg <р' • cos X' >
у = R • ctg <?' • sin X'. j	(124)
Здесь <?' и X' — новые координаты, зависимость которых от
координат ср и X легко получить из рис. 102 по формулам четы-
рех элементов:
ctg X' = cos То ’ tg <р • cosec X — sin <?0 • ctg X |
tg ср' = cos X' - tg To + sin X' • ctg X - sec To- )
(125)
Здесь X и X' считаются от

меридиана точки касания.
Таким образом, сетка ко-
сой центральной проекции
для радиопеленгаторной стан-
ции с полюсом проекции в
месте ее расположения может
быть построена по формулам
(124) и (125), где т и X геогра-
фические координаты станции,
причем долготы считаются
от меридиана радиостанции.
При построении лучей —
ортодромий от радиопелен-
гатора— эти лучи будут иметь
одинаковую густоту во всех
направлениях только для этого
пеленгатора, другие станции
на этой же сетке будут обла-
дать указанным недостатком:
неравномерностью густоты
лучей.
Однако и этого недостатка можно избегнуть, построив такую
сетку, у которой две заданные точки будут обладать таким
свойством, что все построенные вокруг них неискаженные кар-
тушки будут иметь деления, соответствующие круглым значе-
ниям пеленгов. Такая проекция носит название двуазимуталь-
ной. Идея ее построения заключается в следующем: соединим
(рис. 103) две точки 5, и S2, для которых должна быть пост-
роена двуазимутальная проекция, ортодромией, и середину ее
отметим точкой А. Эту точку примем за полюс нашей проек-
ции. Тогда, очевидно, искажения в точках 5, и S2 будут оди-
наковы, так как они расположены симметрично относительно
полюса (с разницей новых долгот X' на 180° и на одинаковой
новой широте </)• Согласно формулам (75) и (76), искажения
масштабов в точках и 52 пропорциональны:
т — qosec2 п — cosec .
114
Уменьшим масштаб т в точках 3, и 32 в cosec ср' раз, умно
жив его на sin </, а масштаб п оставим неизменным. Геометрв
чески это будет соответствовать ортогональному проектировл
нию картинной плоскости на плоскость, повернутую на уго.
(90 — <р') относительно картинной плоскости вокруг прямо!
Рис. 103.
перпендикулярной к дуге 5j 32 или ее изображению на картин
ной плоскости. После такого проектирования в точках З) и 3.
т = п — cosec <р', т. е. проекция будет равноугольной. Во все)
остальных точках проекция не будет равноугольной, но свой-
ство ортодромичности сохранится.
Таким образом, в точках 3j и 32 можно будет построил
неискаженные картушки, проведя из них ортодромии в вид»
прямых линий.
S 39. УРАВНЕНИЕ ЛИНИИ РАВНЫХ АЗИМУТОВ
НА ГНОМОНИЧЕСКОЙ ПРОЕКЦИИ
На рис. 104 картинная плоскость Н касается шара в точке
Меридиан РЕР' принят за начальный, он составляет угол 9С
с меридианом PQP’, принимаемым за нулевой на плоскости пре
екции. Сферические координаты точки М будут тд и 5. Из чер
тежа видно, что на гномонической проекции, т. е. на плоскост
Н, этим координатам соответствуют координаты х, у, приче>
связь между сферическими и плоскостными координатами
такова:
x = tgE и у = tg>j.
Связь между сферическими и географическими координа-
тами такова:
<р = т)' и В = 90° — X,
следовательно,
ctgA = tg£ = x .
8!

Найдем выражения для sin\ cosX, sin <р и cos<p через коор-
динаты х и у для подстановки их в уравнение (108) линии рав-
Рис. 104.
аых азимутов. Из прямоугольного сферического треугольника
EML имеем:
tg П' = tg ? = tg 7] • cos? = р==.
Отсюда
tg ф	у_____
s'n ~ V 1 + tg2 <р ~ V 1 + аг + у2 >
cos <? = _7~, ,	= 1/-----——---------
у 1 + tg2 ? у 1 + х2 + у2
Так как
tg£ —ctgX = x,
то
V 1 + ctg2 л У 1 + х2 ’
V 1 + ctg2 К У 1 + х2 ‘
Подставляя заготовленные выражения в уравнение (108)
гинии равных азимутов, получим:
Fl+x* 6Т1Г1 + хЧУ У1+х2 У1 + х2 + у2
откуда
ctg П-)/ 1 + л2 +У = tg (1 + Л2) — ху. (126)
116
Это уравнение дает трансцендентную кривую, кроме одного
случая, когда /7—90° и левая часть уравнения (126) обращается
в ноль. Правую часть уравнения преобразуем, повернув ос»
координат на угол 45 4--^-.
Это необходимо потому, что ось симметрии ЛРА составляет
с экватором угол 45 + -у- (см., например, рис. 97).
По правилам поворота осей
х = Xi cos а—yl sin а;
у — Xj sin а + .Vi cos а,
где а — угол поворота, хи ух — новые координаты.
Положив 45 + -V- = а, подставим значения х и у в уравне-
ние (108) и будем новые координаты обозначать х, у. Тогда
получим:
tg?j[l +(*cosa—J/sina)2] —(xcosa—у sin a) (x sin a	cos a) = Q->
tg + *2 COS2 a tg <ps — xy sin 2a • tg + J2 sin2 a • tg —
— (x2—j2) — sin 2a — xy cos 2a = 0,
или
tg 4* (1 + COS 2a) tg % — xy sin 2a • tg 4-	(1 — COS 2a) tg
— C*2 —У) j sin 2a—xy cos 2a — 0.
Умножим все уравнение на cosfj и заметим, что при
a = 45 4-	, cos 2a — — sin % и sin 2a = cos
тогда получим:
sin Фх + у sin % • (x2 + J2) — 4 (x2 —у2) = 0,
откуда
ха ,	уа	п
sin <?,-------+-----2----- 0,
1	— sin	1 + sin
X2 ___ У2 _ |
2	sin <p5	2 sin tpv
1 — sin <ps 1 + sin <ps
Отсюда видно, что кривая представляет собой сферическую
гиперболу.
Во всех других случаях уравнение (126) не дает алгебраи-
ческого решения.
ПТ
§ 40. УРАВНЕНИЯ ЛОКСОДРОМИИ И ОРТОДРОМИИ
НА ПОЛЯРНОЙ СТЕРЕОГРАФИЧЕСКОЙ ПРОЕКЦИИ
Для полярной стереографической проекции при /? = 1
р = 2 tg-J = 2 tg (45 — yj = 2 ctg(45 + у),
«ли
l-2tg(45 + i).
Подставляя это значение в уравнение локсодромии (17)
см. стр. 15), найдем:
р = 2e“4kctga.
(127)
Как следует из уравнения, локсодромия на проекции
ямеетвид логарифмической спирали, составляющей
с меридианами (т. е. с радиусами-векторами) постоянный угол ДХ,
«то объясняется, очевидно, равноугольностью проекции.
Уравнение ортодромии на проекции получим, если подста-
вим уравнение ортодромии в следующем виде:
ctg 8 = ctg а • sin X.
2tg|
Лодставляя сюда значение tg8=---и Х = Х', найдем:
1
2tgy • ctgа - sinX' = 1 —tg2y.
Подставляя сюда р = 2 tg у, получим:
у р2 + p-ctga-sinX'= 1.	(128)
Это есть уравнение окружности, что согласуется с изве-
стным нам свойством стереографической проекции изображать
конечные окружности окружностями же.
§ 41. УРАВНЕНИЕ ЛИНИИ РАВНЫХ АЗИМУТОВ
НА СТЕРЕОГРАФИЧЕСКОЙ ПРОЕКЦИИ
Лодставляя в уравнение (115) координаты X'= X и
/ . _ т \	0
- = tgf45 — _i = tgy по уравнениям стереографической проек-
;ин для случая, когда картинная плоскость не касается полюса,
совпадает с экватором, получим:
Р4----т p2cos2X' + -	= 0.
r sin (Z7 + V]) г	sin (/7 + ij)
Как видим, уравнение (115) не изменило своего характера.
Поэтому все, что говорилось о характере кривой ЛРА на сфере.,
U8
относится и к стереографической проекции, а именно: кривые
являются овалами Кассини (уже на плоскости), одна из кото-
рых при /7=90 — обращается в Бернуллиеву лемнискату
с уравнением
р2 = sec т; • cos 2>Л	(130)
Вид кривых ЛРА на стереографической проекции показан
на рис. 105 для станции, расположенной на широте = 20°.
рис. 105.
Ввиду совпадения вида уравнений и кривых ЛРА на сфере
и на стереографической проекции, анализ этих кривых зачастую
производят на указанной проекции.
§ 42. УРАВНЕНИЕ ОРТОДРОМИИ НА КОНИЧЕСКОЙ ПРОЕКЦИИ
Ортодромия на конической проекции представляет собой
трансцендентную кривую, довольно близко подходящую к окруж-
ности больщого радиуса, т. е. к прямой. Уравнение ее можно
119
получить, представив уравнение ортодромии (1) в следующем
виде:
Ctg a-sin X-tg& + 1.
Подставляя сюда значение tg&
2tg|
1- tg2y
получим:
Так как
В	S
2tgy • ctga-sinX = 1 — tg2у.
то
i	1
2p“ • ctga-sin-^-+ p“ =1.
При a — 0,5 имеем:
p4 + 2p2 • ctg a - sin 2k’ = 1.
(131)
(132)
Это есть уравнение овала Кассини.
£ 43. УРАВНЕНИЕ ЛИНИИ РАВНЫХ АЗИМУТОВ НА РАВНОУГОЛЬНОЙ
КОНИЧЕСКОЙ ПРОЕКЦИИ
Уравнения равноугольной конической проекции:
X' = a-k и р = tg“j,
(133)
где 9 = 90 — <р, причем k — 1, что не повлияет на последующий
анализ.
Чтобы получить уравнение ЛРА на конической проекции,
подставим координаты (133) в уравнение овала Кассини на
сфере (115). Из уравнения (133) имеем:
v х » V
Л = - Htgy=p ,
следовательно,
a ____п Sitl П
Р sin (У/4 tj
2
•р cos 2— 4-
stn(/7—7}) _ с
sin(/7 + i])
Это уравнение изображает трансцендентную кривую, которая,
однако, обращается в окружность при a = 2, как это показал
Каврайский. Действительно, при a = 2 имеем:
Р2
2 sin П
sin (П + ij)
pcosk'+
sin (П — к;) _ «
sin (/7 4- ч) —
(134)
120
и
Если положить
siti п
а ~~ sin (П +1))
/ sin’ П sin (П —_ s*"7!	,
г = у Sin' (/7 + ч) sin (П + 1)) sin (Л + ч)
то уравнение (134) перепишется так:
sin’ П Г sin3/7 — /Гп(У-~-^-П - О,
р»—2a-p-cosX' + ^(Й+V-1«ш3(“ + 1|1)	«п(/7 + ч> -1
Рис. 106.
121
Это есть уравнение окружности, центр которой О лежит
на начальном меридиане в расстоянии РО = а от полюса
проекции, а радиус окружности равен г.
Таким образом, сетка равноугольной конической проекции,
удваивающая долготы (а = 2), может служить для быстрого
графического нанесения на ней линий равных азимутов в виде
окружностей.
На рис. 106 изображена такая сетка с нанесенными на ней
линиями равных азимутов для радиостанции, расположенной
на широте <р5 = ЗО°Л/.
Сетка дает изображение одной четверти шара, расположен-
ной к западу от радиостанции для северного и южного полу-
шарий, Однако ввиду симметрии сетка соответствует анало-
гичному району и к востоку от радиостанции. Таким образом,
диапазон долгот сетки составляет ±90°, диапазон широт от
северного до южного полюса.
Как было указано, на конических проекциях, имеющих
а~0,7 — 0,8, т. е. принятых для наших карт (например, 1:1 500000,
у
Рис. 107.	Рис. 108.
1:2500000 и др.), линия равных азимутов близко подходит
к окружности. Действительно, если на рис. 107, изображающем
сетку меридианов конической проекции, считать все ортодро-
мические направления на радиостанцию 5 прямолинейными, что
может быть принято в авиации для расстояний до 1 С00 км, —
то линия равных азимутов будет представлять геометрическое
место точек вершин вписанных углов — азимутов 77, опираю-
щихся на хорду PS.
Таким геометрическим местом является, как известно, ок-
ружность.
Широта <р0 центра О окружности получается из треуголь-
ника ОРК, где ОК делит пополам хорду PS (базу): ОР =
= РК-cosec П (угол РОК=Г1, как центральный, опирающийся
на половину дуги PS, на которую опираются все вписанные
углы /7).
122
Обозначая OP = р0, PK — ^ps, получим:
1	ГТ
Po = 2-Prcosecn,
где	, t х
P, = A-tg -f.
Долгота центра О относительно места радиостанций Хо =
==90 — /7, что следует из треугольника ОРК.
§ 44. УРАВНЕНИЕ ЛИНИИ РАВНЫХ РАЗНОСТЕЙ РАССТОЯНИЙ
Выведем уравнение линии равных разностей расстояний (ги-
пербол) в сферических координатах. Воспользуемся зависи-
мостями, которые можно получить по рис. 104 из треугольни-
ков РКМ и EML-.
tg ч1 — tgipcosE и tg£' = tgE-cos4-	(136)
Пусть на рис. 108 ось х — х совпадает с осью гиперболы,
у—у — с ее осью симметрии, f nf — ее фокусы, точка М лежит
на гиперболе. Принимая обозначения по рисунку, напишем
условие для сферической гиперболы по аналогии с плоскостной
гиперболой:
р — р' = 2а.
Кроме того, положим:
cose = cos а-cosр.	(137)
Отсюда
1 + tg2e = (1 + tg2a) (1 + tg2₽),
или
tg2 е = tg2 а + tg2 ₽ + tg2a • tg2₽.	(133)
Из прямоугольных треугольников MfA и MfA имеем:
cosp = cos1»]'-cos (e + $) = cos ч' (cose-cos E — sin e-sin$), (139)
cosp' = cos ч'-cos (e — E) = cos ч' (cos e-cosE + sin e. sin 6). (140)
Сложив и вычтя эти равенства, получим:
cosp + cosp’ = 2 cos ч’• cose-cos $,	(141,
cos p — cos p' = — 2 cos ч • sin e - sin 5.	(142)
Обозначим p + p'= 28 и, помня, что p — p'= 2a, получим:
p = a 8 и p' = 8 — a.
Отсюда
cos p = COS (a + 8) = cos a-cos 8 — sin a-sin 8,
cos p' = cos (8 — a) = cos a • cos 8 + sin a • sin 8.
Сложив и вычтя эти равенства, получим:
cosp + cosp' — 2 cos a -cos 8,	(143)
cosp — cosp'= — 2 sin a-sin 8.	(144)
123
Сопоставляя (141) и (143;, найдем:
cosa-cosB = cos 7]'-cose-cos 5= _C0Se‘C0SL
V 1 + tg’ V)'
Подставляя сюда значение tgr/ из (136) и cose из (137)
найдем:
Отсюда,
получим:
или
Выразим '
(144), найдем:
5 cosB-tgE
COS 8 = ,	- * — .
Vl + cosa£-tg24
возводя в квадрат и заменяя секансы тангенсами
1+tg2s=L+-cXVg217 о+
1 4-tg28 = (1 + tg2$ 4-tg2Tj) (1 +tg2₽).	(145)
8 через а и E. Сопоставляя (141) и (142) с (143) и
cos a-cos 8 = cos V'cose-cosE;
sin a sin8 — cos?)'-sine-sinE.
Разделив второе уравнение на первое, получим:
tg8 = t8±Igi.
Б tga
Отсюда, принимая во внимание (138), получим:
tg2 8 = a + te2 ₽ + tg2«• tg2 ₽)•
Сравнив это выражение с (145), получим:
(1 + tg2 Е 4- tg2 Ч) (1 4- tg2 ₽) - 1 4- (tg2 a 4- tg2 ₽ 4- tg2 a • tg2 ₽).
Отсюда
tg2a-tg2₽ 4-tg2ч’tg2 a 4-tg2ч  tg2₽-tg2 a = tg2₽-tg2E.
Разделив на tg2a-tg20, получим:
tg2E tg’4(l +tg’P) = .
tg’a	tg’₽
или
tg’m == .
tg2 a sin’ p
Положим здесь sin2p = tg2y, получим уравнение сферической
гиперболы:
Здесь a—действительная ось гиперболы, а у — мнимая ось
гиперболы, определяемая соотношением
tg2r = sin2₽ = l-cos2₽ = l-^.	(147)
ПРИЛОЖЕНИЕ 1
ДЛИНЫ ДУГ МЕРИДИАНА И ПАРАЛЛЕЛИ В 1° в м
	Длина дуг в j j и			Длина дуг в 1° в м	
Широта			Широта		
9	меридиана	параллели		меридиана	параллели
				111 109	
Юн* ® о	110 564 110 564 110 566 110 568	111307 111290 111239 111 155 111 037	45° 46 47 48 49	111 129 111 149 111 168 111 188	78 837 77 134 76 047 74616 73163
5° 6 7 8 9	110 570 110574 110 578 110583 110588	110 886 110 701 110482 110230 109945	50» 51 52 53 54	111 207 111226 111245 111264 111288 111 301	71687 70189 68 670 * 67129 65568
10° 11 12 13 14	110 594 110 600 ПО 608 110615 110 624	109 627 109275 108 890 108 472 108 021	55° 56 57 58 59	111 320 111338 111 355 111374 111390	63 986 62385 60765 59126 57468
15° 16 17 18 19	110 633		60°		55793
	110 643 110 653 110 664 110675	107538 107022 106 473 105893 105280	61 62 63 64	111 408 111424 111440 111456 111475	54101 52392 50667 48 926
20° 21 22 23	110 688 110 699 110713 110 726	104 635 103958 103250 102 511	65° 66 67 68 69	111486 111502 111515 111529	47170 45 399 43614 41816 40005
24	110 740	101 740	70° 71 72 73 74	111542	
25» 26 27 28	110 754 110 769 110 785 110 800	100 938 100 106 99 243 98 350		111554 111 567 111 578 111589	38 182 36346 34500 32 643 30775
29 30» 31 32 33	110 816 110833 110849 110 867 110 884	97 427 96 475 95 493 94 482 93 442	75° 76 77 78 79	111 600 111 609 111 619 111627 111636	28 898 27 012 25118 23 216 21307
34	110 901	92 374	80»	111 642	19 391
35» 36 37 38 39	ПО 920 110 938 110 957 110 975 110 994	91277 90153 89001 87 822 86 616	81 82 83 84 85°	111 630 111 655 111661 111 665 111670	17469 15 542 13 610 11673 9 733
40® 41 42 43 44	111013 Ш 032 111051 111071 111091	85384 84125 82841 81531 80 197	86 87 88 89 SO»	111 672 111676 111678 111 679 111680	7 79(3 5845 3 898 1949 0 000
125
ПРИЛОЖЕНИЕ 2
ПЕРЕВОД МОРСКИХ МИЛЬ В КИЛОМЕТРЫ
Азор- ские | МИЛИ 1	.0	.1	.2	.3	.4	.5	.6	.7	! 8	.9	Мор- ские 1 мили
1				К и	ЛОМ	е т р	ы				
0	0.000	0.185	0.370	0.556	0.741	0.926	1.111	1.296	1.482	1.667	0
1	1.852	2.037	2.222	2.408	2.593	2.778	2.963	3.148	3.334	3.519	1
2	3.704	3.889	4.074	4.260	4.445	4.630	4.815	5.000	5.186	5.371	2
3	5.556	5.741	5.926	6.112	6.297	6.482	6.667	6.852	7.038	7.223	3
4	7.408	7.593	7.778	7.964	8.149	8.334	8.519	8.704	8.890	9.075	4
5	9.260	9.445	9.630	9.816	10.001	10.186	10.371	10.556	10.742	10.927	5
6	11.112	11.297	11.482	11.668	11.853	12.038	12.223	12.408	12.594	12.779	6
7	12.964	13.149	13.334	13.520	13.705	13.890	14.075	14.260	14.446	14.631	7
8	14.816	15.001	15.186	i 5.372	15.557	15.742	15.927	16.112	16.298	16.483	8
9	16.668	16.853	17.038	17.224	17.409	17.594	17.779	17.964	18.150	18.335	9
Мор- ские мили	.0	.1	.2	Л	.4	.5	.6	.7	.8	.9	Мор- ские мили
ПЕРЕВОД КИЛОМЕТРОВ В МОРСКИЕ МИЛИ
Кило- метры	.0	.1	.2	.3	.4	Л	.6	.7	.8	.9	Кило- метры
				Мор	С К И	е м и л и					
0	0.000	0.054	0.108	0.162	0.216	0.270	0.324	0.378	0.432	0.486	0
1	0.540	0.594	0.648	0.702	0.756	0.810	0.864	0.918	0.972	1.026	1
2	1.080	1.134	1.188	1.242	1.296	1.350	1.404	1.458	1.512	1.566	2
3	1.620	1.674	1.728	1.782	1.836	1.890	1.944	1.998	2.052	2.106	3
4	2.160	2.214	2.268	2.322	2.376	2.430	2.484	2.538	2.592	2.646	4
5	2.700	2.754	2.808	2.862	2.916	2.970	3.024	3.078	3.132	3.186	5
6	3.240	3.294	3.348	3.402	3.456	3.510	3.564	3.618	3.672	3.726	6
7	3.780	3.834	3.888	3.942	3.996	4.050	4.104	4.158	4.212	4.266	7
8	4.320	4.374	4.428	4.482	4.536	4.590	4.644	4.698	4.752	4.806	8
9	4.860	4.914	4.968	5.022	5.076	5.130	5.184	5.238	5.292	5.346	9
Кило- метры	.0	.1	.2	.3	.4	.5	.6	.7	.8	.9	Кило- метры
126
ПРИЛОЖЕНИЕ 3
ПЕРЕВОД АНГЛИЙСКИХ МИЛЬ В КИЛОМЕТРЫ
.Лили	.0	Л	.2	.3	.4	.5	.6	.7	.8	.9	Милн
				к	И л о	метр	ы				
0	0,00	1,61	3,22	4,83	6,44	8,05	9,66	11,27	12,88	14,48	0
10	16,09	17,70	19,31	20,92	22,53	24,14	25,75	27,36	28,97	30,58	10
20	32,19	33,80	35,41	37,02	38,63	40,24	41,84	43,45	45,06	46,67	20
30	48,28	49,89	51,50	53,11	54,72	56,33	57,94	59,55	61,16	62,77	30
40	64,38	65,99	67,59	69,20	70,81	72,42	74,03	75,64	77,26	78,86	40
50	80,47	82,08	83,69	85,30	86,91	88,52	90,13	91,74	93,34	94,95	50
60	96,56	98,17	99,78	101,39	103,00	104,61	106,22	107,83	109,44	111,05	60
70	112,66	114,27	115,88	117,49	119,10	120,70	122,31	123,92	125,53	127,14	70
80	128,75	130,36	131,97	133,58	135,19	136,80	138,41	140,02	141,63	143,24	80
90	144,85	146,46	148,06	149,67	151,28	152,89	154,50	156,11	157,72	159,33	90
Мили	.0	Л	.2	.3	.4	.5	.6	.7	.8	.9	Мили 	
ПЕРЕВОД КИЛОМЕТРОВ В АНГЛИЙСКИЕ МИЛИ
Кило- метра	.0	.1	.2	.3	.4	.5	.6	.7	.8	.9	Кило- метры
					М и	Л и					
0	0,00	0,62	1,24	1,86	2,49	3,11	3,73	4,35	4,97	5,59	0
10	6,21	6,83	7,46	8,08	8,70	9,32	9,94	10,56	11,18	11,80	10
20	12,43	13,05	13,67	14,29	14,91	15^3	16,15	16,78	17,40	18,02	20
30	18,64	19,26	19,88	20,50	21,12	21,75	22,37	22,99	23,61	24,23	30
40	24,85	25,47	26,09	26,72	27,34	27,96	28,58	29,20	29,82	30,44	40
50	31,07	31,69	32,31	32,93	33,55	34,17	34,79	35,41	36,04	36,66	50
60	37,28	37,90	38,52	39,14	39,76	40,38	41,01	41,63	42,25	42,87	60
70	43,49	44,11	44,73	45,35	45,98	46,60	47,22	47,84	48,46	49,08	70
80	49,70	50,33	50,95	51,57	52,19	52,81	53,43	54,05	54,67	55,30	80
90	55,92	56,54	57,16	57,78	58,40	59,02	59,64	60,27	60,89	61,51	90
Кило- метры	°		.2	.3	.4	.5	.6	.7	.8	.9	Кило- метры
127
ПРИЛОЖЕНИЕ 4
СХЕМА ВЫЧИСЛЕНИЯ
ОРТОДРОМИЧЕСКОГО ПУТЕВОГО УГЛА И РАССТОЯНИЯ
Схема маршрута:
Москва
Нью-Йорк
Формулы:
ctg а = cos <Pt tg ф2 cosec (Х2 — XJ —
— sin tpi ctg (Х2 — Xt)
sin S = cos q>a cosec a sin (Х2 — X])
А — Нью-Йорк				?1 = 40°43'	Xj = —74°
В — Москва				Фа = 55°47'	X2 =37°34'
1	Х2 — Xj	111°34'	5	lg COS Ф,	9.74999
2	1g cos ф1	9.87964	15	colg sin a	0.24706
4	lg tg <?i	0.16748	6	lg sin (X2—Xj)	9.96848
7	colg sin (X2 — X,)	0.03152	16	lg sin S°	9.96553
9	lg (cos ф, tg ф2 cosec (X2 — Xj)]	0.07864	17	S°	67°28'
10	cos o, tg ф2 cosec (X2 — X^	1.1985	IS	S'	4048
3	lg sin ср.	9.81446	:9	IgS'	3.60724
8	lg ctg (X2 —xt)	9.59688n	20	lg 1,852	0.2676
11	lg [sin ctg (X2 — X,)]	9.41134n	21	IgS	3.87484
12	sin Ф! ctg(X2 — X,)	-0.25784	22	S km	7496
13	ctg a	1.4563			
14	a	34°29'			
15	a				
128
ПРИЛОЖЕНИЕ 5
СХЕМА ВЫЧИСЛЕНИЯ ОРТОДРОМИЧЕСКОГО РАССТОЯНИЯ
Фопмула: cos S = sin 9, sin ®2 + cos 9i cos ЧЪ cos P-a — ^1)
— A — Москва	<?! = 55°47'	Xi = 37°34'
В— Нью-Йорк	®a = 40°43'	X2=—74°C0'
1	X2 	 Xj	—Hl°i4'
2.i	lg sin Ф!	9.91746
4	ig sin ®2	9.8.446
6	lg sin sp, sin <p2	9.73192
7	sin (Pi sin ?2	0.53941
3	lg cos <p.	9.<4ft99
5	lg COS <p2	9.87964
6	lg COS (X2 — Xj)	9.56536n
9	lg [cos ?, cos <p2 cos (X2 — Xj']	9.1949)n
10	cos ®j cos q>a cos<X3 — Xj)	-0.15667
11	cos S	0.38274
12	S°	67 30'
13	S'	4050'
14	IgS'	3.60746
15	if 1,R52	0.2676
10	IgS	3.87506
17	S km	7500
»-1683
129
ПРИЛОЖЕНИЕ 6,
to
СХЕМА ВЫЧИСЛЕНИЯ КООРДИНАТ ПРОМЕЖУТОЧНЫХ ТОЧЕН ОРТОДРОМИИ
а =34°29'
Ф1 = 40°43'
Ф3 = 55°47'
X, = -74°
Х2 = 37°34'
Формулы:
cos Фо = cos Ф181П а
ctg (Хо — Х:) = sin Т1 tg а
tgq> = tg фа cos ()0 — X)
Вертекс			Промежуточные точки						
1	1g sin a	9.75294	Xo	X	Xo-X	lgcos(X0-X)	1g tg <Po	Igtgt?	<P
3	1g cos ep,(a)	9.87964	—08°08'	37°34'	—45°42'	9.84411	0.32313	0.16724	55°46'
5	1g cos tpo	9.63258 64°35'	—08°08'	30°	—38°08'	9.89574	0.32313	0.21887	58°52'
6	<Po		—08°08'	20°	—28°08'	9.94540	0.32313	0.26853	61°41'
6	1g tg Фо	0.32313	—C8°08'	10°	—18°C8'	9.97788	0.323'3	0.30101	63°26'
7	Igtga	9.83686	—08c08'	0°	—08°08'	9.99561	0.32313	0.31874	64°21'
	1g sin ф1(3)	9.81446	—08°08'	—10°	1°52'	9.99977	0.32313	0.32290	64°34'
4	Igctg (Xo — X,) (Xa)	9.65132	—08°08'	—20°	11°52'	9.99062	0.32313	0.31375	64°06'
8	).0-Xt	65°52'	—08°08'	-30'	21°52'	9.96757	0.32313	0.290/0	62°53'
10 11	Хо к E		—08°08'	-40°	31°52'	9.92905	0.32313	0.25218	60°46'
	Xo к W	—08°08'	—08°08'	—50°	45°52'	9.87198	0.32313	0.19511	57°27'
			—08°08'	-60°	|	5l°52'		9.79063	0.32313	| 0.11376	52°25'
			—08°08’	-70°	|	61°o2'		9.67350	|	0.32313	| 0.99b63	44°47'
ПРИЛОЖЕНИЕ 8
СХЕМА ВЫЧИСЛЕНИЯ ПРОМЕЖУТОЧНЫХ ТОЧЕК
(путевой угол по расстоянию и расстояние по путевому углу)
Формулы:	tg а = ctg (р0 cosec S
sin S = ctg tp0 ctg a
<s„ = 64°35' lg ctg ?1) = 9.67687
43°46'	colg sin S	lg tga	a	a	a	lg Ctg a	lg sin S	S	5n-l ~ 5п	
									Град, мин	К
	0.16007	9.83694	34°29'	—	34°29'	0.16314	9.84001	43°47	ю-оп	1113.22
33°46'	0.25507	9.93194	40°32'	—	40°32'	0.06799	9.74486	23°46'		
									10°00'	1111.00
23°46'	0.39-t68	0.07155	49°42'	—	49042/	9.92843	9.6053)	239461		
									10°00'	1111.00
13°46'	0.62348	0.30035	63°24’	—	63°24'	9.69963	9.37650	13°46'		
									ic°oo'	1111.00
3°46'	1.18248	0.85935	82°08'		82°0<>'	9.14041	8.81728	3°46'		
									—	
0°00'	—	—		—	—		—	—		
									10°00'	1111.00
6°14'	0.96426	0.64113	i°08'	102°52'	77°08'	9.35.873	9.( 3560	6-14'		
									10-00'	1111.00
16°14'	0.55354	0.23041	59°32'	120°28'	59°32'	9.76957	1.44644	16°14'		
									7-30'	833.25
23°44'	0.39526	0.07213	49044г	130°16'	49044г	9.92792	9.60479	23°44'		
										
ПРИЛОЖЕНИЕ 9
СХЕМА ВЫЧИСЛЕНИЯ ПРОМЕЖУТОЧНЫХ ТОЧЕК
(широта и долгота по расстоянию)
Формулы: ctg (Хо — X) = ctg S cos tp0
tg ер = cos (Xo — >) tg <p0
q>0 = 64°35'; Xo = — 8°08'; lg cos ep0 = 9.63258; lg tg ep0 = 0.32313
№ по пор.	От места вылета мили	От вертекса град. мин.	lg Ctg S	lg ctg (X0-l)	lo-X	lg cos (X, — 1)	ig tg <p	f	X
•—— 1	Нью-Йорк	43°46'	|	0.01870	9.65128	65-52'	9.61158	9.93471	40°43'	74°00’W
2 1	600'	33°46'	0.17483	9.80741	57°18'	9.73259	0.05572	48°40'	63°26'
з	1200'	23°46'	0.35619	9.98877	45°42'	9.84385	0.16698	55045'	53’52'
4	1800'	13э46'	0.61082	0.24340	29’43'	9.93876	0.26189	61019'	37051'
5	2400'	3°46'	1.18154	0.81412	8°43'	9.99495	0.31808	64°19'	16°51'
6	2626'	0°00'	—	—	—	—	—	64°35'	8°08'W
7	3000'	—6° 14'	0.96168 п	0.59426	—17°17'	9.98636	0.30949	63053'	ОООУЕ
8	3500'	—16-11'	0.53587П	0.16845	—34009'	9.91781	0.24094	60°C8'	26°01'
9	Москва	|	— 23°44'	0.35688п	9.98946	—19°42'	9.84411	0.16724	55°46'	37O34'E
ПРИЛОЖЕНИЕ 19
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В МОРСКИХ МИЛЯХ
	ill				И	P О	T	A				
X.	° i V.	0°	1°	2°	3°	4°	5°	6°	7°	8°	9°	10°	
0	0.0	6J,0	120.0	100,1	240,2	330,4	360,7	421,1	481,6	542,2	803,1	0
1	1,0	61,0	121.0	181,1	241.2	301,4	361,7	422.1	482,6	543,2	604,1	1
2	2,0	62,0	122,0	182.1	242,2	302,4	362,7	423,1	483,6	544,3	605,1	1
3	3,0	63,0	123,0	183,1	243,2	303,4	363.7	424,1	484,6	545,3	636,1	3
4	4,0	64,0	124,0	184,1	244,2	304.4	364,7	425.1	485,6	546,3	697,1	«
1	5,0	65,0	125.0	185,1	245.2	305,4	365,7	426,1	486,6	547,3	698,1	S
6	6,0	66,0	126.0	186,1	246,2	306,4	366,7	427,1	487,6	548,3	609,2	6
7	7,0	67,0	127,0	187,1	247,2	307,4	367,7	428,1	488,6	549,3	610,2	7
е	8.0	68,0	128,0	188.1	248,2	308,4	368,7	429,1	489,6	550,3	611,2	в
9	9,0	69,0	129,0	189,1	249,2	309,4	369,7	430,1	490,7	551,3	612,2	0
10	10,0	70,0	130,0	190,1	25-3,2	310,4	370,7	431,1	491,7	552,4	613,2	10
11	11,0	71,0	131,0	191,1	251,2	311,4	371,7	432,1	492,7	553,4	614,2	11
12	12,0	72,0	132,0	192,1	252,2	312,4	372,7	433,1	493,7	554,4	615,3	12
13	13,0	73,0	133,0	193,1	253,2	313,4	373,7	434,1	491,7	555,4	616,3	13
14	14,0	74,0	134,0	194,1	254,2	314.4	374,7	435,2	495,7	556,4	617,3	14
It	15,0	75,0	135,0	195,1	255,2	315,4	375,7	436,2	•96,7	557,4	618,3	It
10	16,0	76,0	136,0	196,1	256,2	316,4	376,8	437,2	497,7	558,4	619,3	IB
17	17,0	77,0	137,0	197.1	257,2	317,5	377,8	438,2	498,7	559,5	620,3	17
18	18,0	78,0	138,0	198,1	258,2	318,5	378,8	439,2	499,8	560,5	621,4	16
10	19,0	79,0	139.0	199,1	259,2	319,5	379,8	440,2	500,8	561,5	622,4	19
20	20,0	80,0	140.0	200,1	200,2	320,5	380,8	441,2	101,8	862,5	623,4	20
21	21,0	81,0	141.0	201,1	261,3	321,5	381,8	442,2	502,8	563,5	624.4	21
22	22,0	82,0	142,0	202,1	262,3	322,5	382,8	443,2	503,8	564,5	625,4	22
23	23,0	83,0	143,0	203,1	263,3	323,5	383,8	444,2	504,8	56э, 5	626,4	23
24	24.0	84.0	144,0	204,1	264,3	324,5	384,8	445,2	505,8	566,5	627,5	24
я	25,0	85,0	145,0	205,1	265,3	325,5	385,8	446,2	506,8	567,6	628,5	26
20	26.0	86,0	146,0	206.1	266,3	326,5	386,8	447,3	507,8	568,6	629,5	20
27	27,0	87,0	147,0	207,1	267,3	327,5	387,8	448,3	51-8,8	569,6	630,5	27
20	28,0	88,0	148,0	208,1	268,3	328,5	388,8	449,3	509,9	570,6	631,5	20
2S	29,0	89,0	149,0	209.1	269,3	329,5	389,8	450,3	510,9	571.6	632,5	29
30	30,0	00,c	150,0	210,1	270,3	330,5	390,8	461,3	811,9	572,6	633,6	30
31	31,0	91,0	151,0	211,1	271,3	331,5	391,8	452,3	512,9	573,6	634,6	31
32	32,0	92,0	152,0	212,1	272,3	332,5	392,9	453,3	513,9	574,7	635,6	32
зз	33,0	93,0	153,1	213,1	273,3	333,5	393,9	454,3	514,9	575,7	36,6	33
34	34,0	94,0	164.1	214,1	274.3	334,5	394,9	455,3	515,9	576,7	637,6	34
SS	35,0	95,0	155,1	215,1	275.3	335,5	395,9	456,3	516,9	577,7	638,6	35
36	36,0	96,0	156,1	216,1	276,3	336,5	396.9	457.3	517,9	578,7	639,7	36
37	37,0	97.0	157,1	217,1	277.3	337,5	397,9	458,4	519,0	579,7	649,7	37
38	38,0	98,0	158.1	218,1	278,3	338,5	398,9	459,4	520,0	580,7	641,7	30
39	39,0	99,0	159,1	219,1	279,3	339,5	399,9	460,4	521,0	581,8	642,7	39
40	40,0	too.c	160,1	220,2	280,3	340,6	490,9	461,4	£22,0	E82,8	8<3,7	40
41	41,0	101.0	161,1	221,2	281.3	341,6	401,9	462,4	523,0	583,8	644,7	41
42	42,0	102,0	162,1	222.2	282,3	342,6	402,9	463,4	524,0	584,8	645,8	42
43	43,0	103,0	163,1	223,2	283.3	343,6	403,9	464,4	525,0	585,8	646,8	43
44	44,0	104.0	164,1	224,2	284,3	344,6	404,9	465,4	526,0	586.8	647,8	44
4S	45,0	105,0	165,1	225.2	285,3	345,6	405,9	466,4	527,1	587,8	648,8	46
40	46.0	106,0	166,1	226,2	286,3	346,6	40G.9	467,4	528,1	588,9	649,8	<6
47	47,0	107,0	167,1	227,2	287,3	347,6	408,0	4(8,4	529,1	589,9	650,9	47
46	48,0	108,0	168.1	228.2	288,3	348,6	409,0	469,5	530,1	590,9	651,9	46
49	49,0	109,0	169,1	229.2	289,3	349,6	410,0	470,5	531,1	591,9	652,8	49
SO	60,0	110,c	170,1	230,2	290,3	350,6	411,0	471,5	>32,1	692,9	683,9	to
tl	51.0	111,0	171,1	231,2	291,3	351,7	412,0	472,5	533,1	593,9	654,9	11
S2	52,0	112,0	172,1	232,2	292,4	352,6	413,0	473,5	534,1	594,9	655,9	Б2
S3	53.0	113.0	173,1	233.2	293,4	353,6	414,0	474,5	535,1	596,0	657,0	S3
64	54,0	114.0	174,1	234,2	294,4	354.6	415,0	475,5	536,2	597,0	6'.8,0	54
65	55,0	115,0	175,1	235.2	295,1	355,6	416,0	476,5	537,2	598,0	659,0	66
66	56.0	116,0	176,1	236,2	296,4	356,6	417,0	477,5	538,2	599,0	669,0	60
67	57,0	117,0	177,1	237.2	297,4	357,6	418,0	478,5	539,2	600,0	661,0	17
50	56,0	118,0	178,1	238.2	298,4	358,6	419,0	479,5	540,2	601,0	662,1	68
89	69,0	119,0	179,1	239,2	290,4	359,7	420,0	460,5	841,2	902,1	643,1	60
	0°	1°	2°	3°	4©	5°	6-	7°	8°	9°	10°	
134
(Продолжение"}
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В МОРСКИХ МИЛЯХ
				111	И Р	О	Г А				
	11°	12°	13°	14°	16°	16°	17®	18°	18°	20°	
U 1 2 3 4 6 6 7 В 0 10 11 12 13 14 « 10 17 W 19 20 21 22 23 24 № 20 27 28 20 30 31 32 33 34 36 36 37 ЗВ 36 40 41 42 43 44 46 46 «7 46 40 69 51 S2 БЗ S4 66 К 67 66 69	664,1 665,1 66'3,1 667,1 668,2 669,2 670,2 671,2 672,2 673,3 674,3 675,3 676,3 677,3 678,4 679.4 681,1 681,4 682,4 683,5 684,6 685,5. 686,5 687,5 688.6 689,6 <9),6 691,6 692,6 693,7 634,7 695,7 696,7 697,7 698,8 699,8 700,8 701,8 702,8 703,9 704,9 705,9 706,9 708,0 709,0 710,0 711,0 712,0 713,1 714,1 715,1 716,1 717,1 718,2 719,2 720,2 721,2 722,3 723,3 724,3	721,3 726,3 727,4 728,4 729,4 730,4 731,5 732,5 733,5 73-1,5 730,6 736,6 737,6 738,6: 739,6, 740,7 741,7 742,7 743,7 744,8 746,0 716,8 747,8 748,9 749,9 750,9 751,9 752.9 754,0 755,0 769,0 757,0 758,1 759,1 760,1 761.1 762,2 763,2 764,2 765.2 769,3 767,3 768.3 769.3 770,4 771,4 772,4 773,4 774,5 775,5 776,6 777,5 778,6 779,6 78>,6 781,6 782.7 783,7 784.7 786,0	7ЕВ,В 787,8 788,8 789,9 790,9 791,9 792,9 794,0 795,0 796,0 707,0 798,1 799,1 800,1 801.2 802,2 803,2 804,2 805,3 806,3 807,3 808,3 809,4 810,4 811.4 812,5 813,5 814,5 815,5 816,6 617,6 818,6 819,7 820,7 821,7 822,7 823,8 824,8 825,8 826,9 127,9 828,9 829,9 831,0 832,0 833,0 834,1 835,1 836,1 837,2 838,2 839,2 810,2 841,3 842.3 843,3 844,4 845,4 846,4 847,6	848,5 849,5 850,6 851,6 852,6 8 >3,6 854,7 855,7 856,7 857,8 868,8 859,8 860,9 861.9 862,9 861,0 865,0 866,0 867,0 868,1 669,1 870,1 871,2 872,2 873,2 874,3 875,3 876,3 877,4 878,4 679,4 880,5 881,5 882,5 833,6 881,6 885,6 866,7 887,7 888,7 889,8 890,8 891,8 892,9 893,9 894,9 89>,0 897,0 898,0 899,1 806,1 901,1 902,2 933,2 994,3 905,3 906,3 907.4 908,4 809,4	916,5 911.5 912.5 913.6 914,6 915,6 916,7 917,7 918,' 919,8 92.,8 921,9 922,9 923,0 925,0 926,<> 927,0 9’8,1 929,1 930,1 641,2 932,2 933.3 931,3 935,3 936,4 937,4 938,4 939,5 940,5 941,6 942,6 943,6 944,7 945,7 946,7 947,8 948,8 949,9 950,9 851,6 953,0 954,0 955,0 9'6,1 957,1 958,3 959.2 960,2 961,3 082,3 963,4 964,4 965,4 966.5 967,5 9.8,6 969,6 970,6 971,7	972,7 973,8 974,8 975,8 976,9 977,9 979,11 980,0 981,1 982.1 £83,1 98-1,2 985,2 986,3 987,3 988,3 9Ч9,4 990,4 991,5 992,5 693,6 994,6 995,6 996,7 997,7 9’8,8 999,8 1000,8 1001,9 1002,9 1004.0 1005,0 1006,1 1007,1 1008,1 1009,2 1010,2 1011,3 1012,3 1013,4 1714,4 1015,4 1016,5 1017,5 1018,6 1019.6 1020,7 1021,7 1022,8 1023,8 1'24,9 1025,9 1026,9 1'128,0 1029,0 1030,1 1031,1 1032.2 1933,2 1334,1	1033.3 1036,3 1037,4 1038,4 1039,5 1040,5 1041,6 1042,6 1043,7 1044,7 104S,t> 1046,8 1047,9 1048,9 1050,0 1051.0 1052,0 1053,1 1054,1 1055.2 1086,2 1057,3 1058,1 1059,4 1060,4 1061,5 1062,5 1063,6 161,6 1065,7 1066,7 1067,8 1068.8 1069,9 1070,9 1072,0 1073,0 1074,1 1075,1 1076,2 1077,2 1078,3 1679,3 108'1,4 1081,4 1082,5 1083,5 1084,6 1085,6 1086,7 1007,7 1088,8 1089,8 1'190,9 1'191,9 1093,0 1094,0 1095,1 1096,1 1097,2	1093,2 1099,3 1100,3 11 1,4 1102,4 1103,5 1104,5 1105,6 1106,6 1107,7 1108,7 1109,8 1110,8 1111.9 1112,9 1114,0 1115,1 1116,1 1117.3 1118.2 111 1,3 1120,3 1121,4 1122,4 1123,5 1124,5 1125,6 1126,6 1127,7 1128,7 1129.В 1130,9 1131,9 1133.0 1134,0 1135,1 1136.1 1137,1 1138,2 1139,3 1143,4 1141,4 1142,5 1143,5 1144,6 1145,6 1146,7 1147,7 1148,8 1149,9 1160,9 1152,0 1153,0 1154,1 1155,1 1156,2 1157,3 1158,3 1159,4 1160,4	1161,5 1162,5 1163,6 1164,7 1165,7 1166.8 1167,8 1168,9 1170,0 1171,0 1172,1 1173,1 1174,2 1175,2 1176,3 1177,4 1178,4 1179,5 1180,5 1181,6 1182,7 1183,7 1184,8 1185,8 1186,9 1188,0 1189,0 1191,1 1191,1 1192.2 1103,3 1194,3 1195,4 1196,4 1197,5 1198,6 1199,6 1200,7 1201,8 12'12,8 1203,9 1204,9 1206,0 1207,1 1208,1 1209.2 1210,3 1211,3 1212,4 1’13,4 1214,6 1215,6 1216.6 1217,7 1218,8 1219,8 1220,9 1221.9 1223,” 1224,1	1226,1 1226,2 1227,3 1228,3 1229,4 1230,5 1231,5 1232,6 1233,7 1234,7 1235.8 1236,9 1237,9 1239,0 1240,0 1241,1 1242,2 1243,2 1244,3 124.5,4 1246,4 1247,5 1248,6 1249,6 1250,7 1251,8 1252.8 1253,9 1255,0 1256,0 1267,1 1258,2 1259.2 1260,3 1261,4 1262,5 1263,5 1264,6 1265,7 1266,7 1267,8 1268,9 1269,9 1271,0 1272,1 1273,1 1274,2 1275,3 1276,4 1277,4 1273,6 1279,6 1280,6 1281.7 1282,8 1283,8 1284.9 1286,0 1287,1 1288,1	0 1 2 3 4 6 6 7 8 8 10 11 12 13 14 IS 18 17 10 19 20 21 22 23 24 26 20 27 20 29 30 31 32 33 34 36 36 37 30 39 40 41 42 43 44 46 40 47 48 49 50 61 52 63 64 68 56 67 68 89
о	11°	12°	13°	14°	18°	16°	17°	18°	19°	20°	
135
(Продолжение}
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В МОРСКИХ МИЛЯХ
	ш				И Р	О	Т А				
t 'к	21°	£2°	23°	24°	25°	26°	27°	2В°	29»	36°	
в	1269,2	13(3,7	141В,6	1484,1	1(10,0	1016,5	1633,9	1781,2	1819,4	1869,4	в
1	1290,3	1354,8	1419,7	1485,2	1551,1	1617,6	1684,6	1752,3	1820,6	1889,5	1
2	1291,3	1355,8	1420,8	1486,2	1552,2	1618,7	1685,8	1753,4	1821.7	1890.7	2
3	1292,4	1356,9	1421,9	1487,3	1553,3	1619,8	1686,9	1754,9	1822,9	1891,8	3
4	1293,5	1358,0	1423,0	1488,4	1554,4	1620,9	1688.0	1755,7	1824.0	1893,0	4
S	1294,6	1359.1	1424,1	1489,5	1555,5	1622,0	1689,1	1756,8	1825,2	1894,2	К
6	1295.6	1360,2	1425.1	1490,6	1556,6	1623,2	1690,3	1758.0	1826,3	1895,3	0
7	1296.7	1361,2	1426,2	1491,7	1557,7	1624,3	1691,4	1759,1	1827,4	1896,5	7
6	1297,8	1362,3	1427,3	1492,8	1558,8	1625,4	1692,5	1760,2	1828.6	1897,6	в
8	1298,8	1363,4	1428,4	1493,9	1559,9	1626,5	1693,6	1761,4	1829,7	1898.8	9
10	1290,0	1364,В	1420.5	1405,0	is6i,o	1827,В	1694,7	1762, S	1(30,9	1699,9	113
11	1301.0	1365,6	1430,6	1496,1	1562,1	1628,7	1695,9	1763.5	1832,0	1901,1	11
12	1302,1	1366,6	1431,7	1497,2	1563,2	1629,8	1697.0	1764,6	1833,2	1932,2	12
13	1303,1	1367,7	1432,8	1498,3	1564,3	1630,9	1698,1	1765.9	1834,3	1933.4	13
1<	1304,2	1368,8	1433,9	1499,4	1565,5	1632,1	1699,2	1767,0	1835,5	1904,6	14
1»	1305,3	1369;9	1434,9	1500,5	1566,6	1633,2	1700,4	1768.2	1836.6	1935,9	15
10	1306,3	1371,0	1436,0	1501,6	1567,6	1634,3	1701.5	1769,3	1837,7	19 6,2	16
17	1307,4	1372,0	1437,1	1502,7	1568,8	1635,4	1702,6	1770,4	1838,8	1938,5	17
10	1308,5	1373,1	1438.2	1503,8	1569,9	1636,5	1703,7	1771,6	1840,0	1909,2	1В
10	1309.6	1374,2	1439,3	1504,9	1571,0	1637,6	1704,9	1772,7	1841,1	1910,3	19
20	1310.В	1376,3	1440,4	1500,0	1(72,1	1638,0	1706,0	1773,0	1842,3	1911,9	29
21	1311,7	1376,4	1441,5	1507,1	1573,2	1639,9	1707,1	1775,0	1843,5	1912,7	21
22	1312,8	1377,5	1442,6	1508,2	1574,3	1641,0	1708,2	1776,1	1844,5	1913,8	12
23	1313,9	1378,5	1443,7	1569,3	1575,4	1642,1	1709,4	1777,3	1845,8	1915.0	23
24	1314,9	1379,6 1380,7	1444,7	1510,4	1576,5	1643,2	1710,5	1778,4	1846,9	1916,1	24
2S	1316,0		1445,8	1511,5	1577,6	1644,3	1711,6	1779,5	1848,1	1917,3	2S
20	1317,1	1381,8	1446,9	1512,6	1578,7	1645,5	1712.8	1780,7	1849.1	1918,5	2В
27	1318.2	1382,9	1448.0	1513,7	1579,8	1646,5	1713,9	1781,8	1850,4	1919,6	27
<8	1319,2	1383,9	1449,1	1514,8	158),9	1647,7	1715,0	1782,9	1851,5	1926,8	28
23	1320,3	1385,0	1459,2	1515,9	1582,1	1648,8	1716,1	1784.1	1852,7	1921,9	26
30	1321,4	1360,1	1451,3	1(17,0	1(63,2	1049,9	1717,3	1765,2	18(3,0	1323,1	30
31	1322,5	1387,2	1452,4	1518.1	1584,3	1651,0	1718,4	1786,4	1855,0	1924,3	31
32	1323,5	1388,3	1453,5	1519,2	1585,4	1652,2	1719,5	1787,5	1856,1	1925,4	32
S3	1324,6	1389,3	1454,6	1520,3	1586,5	1653,3	1720,6	1788.6	1857.3	1926.6	33
34	1325,7	1390.4	1455,6	1521,4	1587,6	1654,4	1721,8	1789.8	1858,4	1927,7	34
85	1326,8	1391,5	1456.7	1522,5	1588,7	1655.5	1722,9	1799,9	1859 6	1928,9	3S
30	1327.8	1392.6	1457,8	1523,6	1589,8	1656,6	1724,0	1792,0	1860,7	1930.1	30
37	1328.9	1393,7	1458.9	1524,7	1599,9	1657,7	1725,2	1793,2	1861,9	1931,2	37
зв	1330,0 1331,1	1394,8	1160.0	1525,8	1592,0	>658,9	1726,3	1794.3	1863,0	1932,4	30
39		1395,8	1461,1	1526,9	1593,1	1660,0	1727,4	1795,5	1864,2	1933,6	36
4?	1332,1	1396.9	1462,2	1528,0	1(94,3	1661,1	1728, В	1796,0	1065.3	1934,7	40
41	1333,2	1398.0	1463,3	1529,1	1595,4	1662,2	1729,7	1797,7	1866,5	1935.9	41
42	1334,3	1399.1	1464,3	1530,2	1596,5	1663,3	1730,8	1798,9	1867 6	1937.0	42
43	1335,4	1400,4	1465,5	1531,3	1597.6	1564,5	1731,9	1800,0	1868,8	1938,2	43
44	1336,4	1401.3	1466.6	1532.4	1598,7	1665,6	1733,1	1891,1	1869 8	1939,4	44
4S	1337,5	1402,3	1467,6	1533,5	1599.8	1666,7	1734,2	1802,3	1871,1	1910,5	45
40	1338,6	1403.4	1468,7	1534,6	160ъ’,9	1667,8	1735,3	1803,4	1872,2	1911,7	40
47	1339,7	1404.5	1469,8	1535,7	1602,0	1668,9	1736,4	18-04,6	1873,4	1942,9	47
40	1340,7	1405,6	1-170,9	1536.8	1633.1	1670,1	1737,6	I8C5.7	1874.5	1944.0	40
49	1341,8	1406.7	1472,0	1B37.S	1004,2	1871,2	1738,7	1800,9	1875.7	1045,2	49
во	1342,9	1407,0	1473,1	1539,0	1608,4	1672,3	173В,В	1ЕОВ,0	1870,8	1846,4	89
61	1344,0	1408.9	1474,2	1540,1	1606,5	1673,4	1741,0	1809,1	1878.0	1947,5	(1
82	1345,1	1469,9	1475,3	1541,2	1607,6	1674,5	1742,1	149,3	1879.1	1918,7	62
S3	1346,1	1411,0	1476,4	1542,3	1608,7	1675,7	1743,2	1811,4	1880,3	19-19,9	£3
Б4	1347,2	1412.1	1477.5	1543,4	1609,8	1676,8	1744,4	1812,6	1881,4	1951,0	£4
М	1348.3	1413,2	1478,6	1544,5	1611),9	1677,9	1745,5	1813,7	1882,6	1952,2	65
во	1349,4	1414,3	1479,7	1545,6	1612,0	1679,0	1746,6	1814,9	1883,8	1933,3	БО
S7	1350,4	1415,4	1481,8	1546,7	1613,1	1680.1	1747.8	1816,0	1884,9	1954,5	£7
ВО	1351,5	1416,5	1481,9	1547,8	1614,2	1681,3	1748,9	1817,1	1886,1	1935,7	50
К9	1352,6	1417,5	1403.0	1548,0	1615,6	1682,4	17В3.0	1818,3	1887,2	1656,9	50
	21°	22°	23°	24° |	25°	25°	27°	28°	£9°	36° |	\
136
(Продолжение}
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В МОРСКИХ МИЛЯХ
ш					И Р	О	А				
X	| 31°	32°	33°	34°	35°	36°	37°	08°	38°	40°	
О	1968,0	2020,4	2069,G	2171,5	2244,3	2310,0	2392.6	2489,3	2644,0	2622,7	ч 10
1	1959,2	2029,6	2100,7	2172,7	2245,5	2319,2	2393,9	2469,5	2546,2	2624,0	1
2	196'1,3	2030,7	2101.9	2173,9	2246,7	2320,5	2395,1	2470,8	2547,5	2625,3	2
3	194.5	2031,9	2103.1	2175,1	2248,0	2321,7	2396,4	2472.1	2548,8	2626,6	3
4	1962.7	2933,1	2104,3	2176,3	2249,2	2322,9	2387.6	2473,3	2550,1	2627,9	4
В	1963,8	2034,3	2105,5	2177,5	2250,4	2324,2	2398,9	2474,6	2551,4	2629,2	Б
6	1965,(1	2035,5	2106,7	2178,7	2251,6	2325,4	2400,1	2475,9	2552,7	2630,5	6
7	1966,2	2036,6	2107,9	2179,9	2252,8	2326,6	2401.4	2477,2	2553,9	2631,8	7
в	1967.3	2037,8	2109,1	2181,1	2254,1	2327.9	2402.7	2478,4	2555,2	2633,1	0
9	1968,5	2039.0	2110,3	2182,3	2255,2	2329,1	2403.9	2479,7	2556,5	2634,5	9
10	1969.7	2С4й,2	2111,3	2103,5	22ВВ,Б	2330,4	2405,2	2401,0	2857,0	2631,8	10
11	1970,9	2041,4	2112,7	2184,8	2257,7	2331,6	2406.4	2482,2	2559,1	2637,1	11
12	1972,0	2042,5	2113,8	2186,0	2259,0	2332,8 2334,1	2407,7	2483.5	2560,4	2638,4	12
13	1973.2	2043,7	2115,0	2187.2	2260,2		2408,9	2484,8	2561,7	2639,7	13
14	1974,4	2044,6	2116,2	2188,4	2261,4	2335,3 2336,6	2410,2	2486,1	2563,0	2641,0	14
1В	1975,5	2'146,1	2117.4	2189,6	2262,6		2411,4	2487,3	2.364,3	2642,3	1S
16	1976,7	2047,3	2118,6	2190.8	2263.9	2337,8	2412,7	2488,6	2565,6	2643,6	16
17	1977.9	2048,5	2119,8	2192,0	2265,1	2339.0	2414,0	2489.9	2566,8	2644,9	17
10	1979.1	2049.6	2121.0	2193,2	2266,3	2340,3	2415,2	2491,1	2568,1	2646,2	10
19	198'1.2	2050.8	2122,2	2191,4	2267,5	2341,5	2416.5	2492,4	2569,4	2647,6	19
20	1S61.4	2082,0	2123,4	2195, Б	2268,6	2342,0	2417,7	2433,7	2070,7	2648,9	20
21	1982,6	2053.2	2124,6	2196,9	2270,0	2344,0	2419,0	2495,0	2572,0	2650,2	21
22	1983,7	2054,4	2125,8	2198,1	2271,2	2345,2	2420,2	2496,2	2573,3	2651,5	22
23	1981,9	2055,6	2127,0	2199,3	2272,4	2346,6	2421,5	2497.5	2374,6	2652,8	23
24	1986,1	2056,7	2128,2	2200,5	2273,7	2347,7	2422,8	2498.8	2575,9	2654,1	24
26	1987 2	2057,9	2129,4	2201,7	2274,9	2349,0	2424,0	2500.1	2577,2	2655,4	2S
20	1988,4	2959,1	2130,6	2202,9	2276,1	2350,2	2425,3	2501,4	2578,5	2656,7	26
27	1989.6	2060,3	2131.8	2204,1	2277,3	2351,5	2426,5	2502,6	2579,8	2658,1	27
28	1991.8	2061,5	2133.0	2205,3	2278.6	2352,7	2427,8	2503,9	2581,1	2659,4	28
20	1991.9	2062,7	2134.2	2206,6	2279,8	2353.9	2429,1	2505.2	2592,4	2660,7	29
30	1383,1	2063,9	2133,4	25.07,8	2201,0	23Б5.2	2430,3	2506,5	2883,7	2662,0	30
31	1991,3	2065,0	2136 6	2209,0	2282,2	2356,4	2431,6	2507,7	2585,0	2663,3	31
32	1995.4	2066,3	2137.8	2210,2	2283,5	2357.7	2432,8	2509,0	2586,3	2664,6	32
33	1996,6	2067.4	2139.0	2211.4	2284,7	2358,9	2434.1	2510,3	2587,6	2665,9	33
34	1997.8	2068,6	2140.2	2212,6	2285,9	2360,2	2435,4	2511.6	2588,9	2667,3	34
36	1999,0	2069,8	2141,4	2213,8	2287,2	2361,4	2436,6	2512,9	2593,2	2668,6	ЗБ
30	2000,1	2071,0	2142,6	2215,1	2288,4	2362.7	2437,9	2514,1	2591,5	2669,9	30
37	2001,3	2072,2	2143.8	2216,3	2289,6	2363,9	2439,1	2515,4	2592,7	2671,2	37
36	2002,5	2073,3	2145.0	2217,5	2290,9	2365,1	2440,4	2516.7	2594,0	2672.5	30
39	2003.7	2074,5	2146,2	2218,7	2292.1	2366.4	2441,7	2518,0	2595,3	2673,8	39
40	2004,8	2076,7	2147,4	2219,9	2293.3	2367,6	2442,0	2519,3	2096,Б	2878,2	«
41	2006,0	2076.9	2148,6	2221,1	2294,5	2368.9	2444,2	2520,5	2597,9	2676,5	41
42	2007,2	2078,1	2149,8	2222,3	2295,8	2370,1	2445,5	2521.8	2599,2	2677,8	42
43	2008,4	2079,3	2151,0	2223,6	2297,0	2371.4	2446,7	2523,1	2690.5	2679,1	43
44	2009.5	21'89,5	2152.2	2224,8	2298,2	2372,6	2448,0	2524,4	2601,8	2680,4	44
46	2010,7	2081.7	2153,4	2226,0	2299,5	2373,9	2449,3	2525,7	2602,1	2681,8	4Б
40	2011.9	2082,9	2154,6	2227,2	2390,7	2375,1	2450,5	2526,9	2604,4	2683,1	40
47	2013.1	2084,0	2155.8	2228,4	2301,9	2376,4	2451,8	2528,2	2605,7	2681,4	47
40	2014,2	2085,2	2157,0	2229,7	2303,2	2377,4	2453,1	2529,5	2637,0	26^5.7	48
49	2015,4 2016,6	2086,4	2158,2	2230,9	2394,4	2378,9	2454,3	2530,8	2608,3	2687,0	49
60		2087,7	2159,4	2232,1	2305,0	2380.1	2455.7	2032,1	2609,7	2688,4	50
61	2017,8	2088,8	2160,6	2233,3	2.306.9	2381,4	2456.9	2533,4	2611,0	2689,7	61
52	2019,0	2699,0	2161,8	2234,5	2308,1	2382,6	21.8.1	2534,6	26123	2691,0	S2
53	2020,1	2091,2	2163,0	2235,7	2399,3	2383,9	2459,4	2535.9	2613,6	2692,3	53
64	2021,3	2692,4	2164,2	2237,0	2310,6	2385,1	246'),7	2537,2	2614,9	2693,7	S4
5S	2022,5	2093.6	2165,4	2238,2	2311,8	2386,4	2161,9	2538,5	2616,2	2695.0	Sfi
53	2023,7	2Р,94,8	2166,7	2239,4	2313,0	2387,6	2463,2	2539,8	2617,5	2696,3	S6
57	2'124,8	2096,0	2167,9	2240,6	2314,3	2388,9	2464.5	2541,1	2618.8	2697,6	67
58	2026,0	2097.1	2169,1	2241,8	2315,5	239 ),1	2465,7	2542,4	2620,1	269s,9 27С0,3	50
69	2С27.2	2098,3	2170,3	2243,1	2316,8	2391,4	2467.0	2643,6	2621,4		59
Z	31°	32°	33°	34°	35°	зс°	37°	38°	39°	4С°	
137
(Продолжение)
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В МОРСКИХ МИЛЯХ
	Ш				И Р	О	Г А				
X. о г \	41°	42°	43°	44°	49°	46°	47°	48°	40°	и°	
в	2751.6	2701,7	2863,1	2945,8	3029,9	3115,6	3202,7	3291,6	3382,1	3474,6	8
i 1	2702,9	2783,1	2864,5	2947,2	3031,3	3117,0	3204,2	3293,0	3383,6	3476,0	1
2	2704,2	2784,4	2865,8	2918,6	3032,8	3118,4	3205,6	3294,5	338э, 1	3477,6	2
а	2705,6	2785,8	2867,2	2950,0	3934,2	3119,9	3207,1	3296,0	3386,7	3479,1	8
4	2706,9	2787,1	2868,6	2931.4	3035,6	3121,3	3208,6	3297.5	3388,2	346 ),7	4
К	2708,2	2788,4	2869.9	2952,8	3037,0	3122,7 3124,2	3210,0	3299,0	33ь9.7	3 *82,3	Б
6	2709,6	2789,8	2871,3	2954,2	3038,4		3211,5	3300,5	3391,2	348л .	8
7	2710,9	2791,1	2872,7	2955,6	3039,8	3125,6	3213,0	3302,0	3392,8	3486,4	7
6	2712,2	2792',5	2874,0	2956,9	3041,3	3127,1	3214,5	3303,5	3 94,3	3486,9	8
9	2713,5	2793,8	2875,4	2958,3	3042,7	3128.5	3215,9	3305,0	3395,8	3488,5	8
10	2714,9	2795,2	2876 Л	2955,7	3044,1	3136,0	3217,4	3306,6	3397,4	3490,1	10
11	2716,2	2796,9	2878,2	2961,1	3045,5	3131,4	3218,9	3308,0	3398,9	3491,6	11
12	2717,5	2797,5	2879^5	2962,5	3046,9	3132,9	3220,3	3309,5	3490,4	3493,2	12
13	2718,9	2799,2	2880,9	2963,9	3048,4	3134,3	3221,8	3311,0	3401,9	3494.7	13
14	2720,2	2800,6	2882,3	2965,3	3049,8	3135,7	3223,3	3312,5	3403,5	3496,3	14
Я6	2721,5	2801,9	2883,6	2966,7	3051,2	3137,2	3224,8	3314,0	3405,0	3497,9	1Б
16	2722,8	2893,3	2885,0	2968,1	3052,6	3138,6	3226.2	3315,5	3406,5	3499,4	16
17	2724,2	2804,5	2886,4	2969,5	3054,0	3140,1	3227,7	3317,0	3408,1	3501,0	17
16	•2725,5	2896,0	2887.8	2970,9	3055,5	3141,5	3229,2	3318,5	3499,6	3502,6	18
19	2726,8	2897,3	2889,1	2972,3	3056,9	3143,0	3230,7	3320,0	3411,1	3504,1	19
20	2720,2	2808,7	2890,Б	2973,7	30SB.3	3144,4	3232,1	3321,6	3412,7	3606,7	20
21	2729,5	2810,0	2891,9	2975,1	3059,7	3145,9	3233.6	3323,0	3414.2	3507,3	21
22	2730,8	2811,4	2893,3	2976 5	ЗС61.1	3147,3	3235,1	3324,5	3415,7	ЗоО8,8	22
23	2732,2	2812,8	2894,6	2977,9	3062,6	3148,8	3236,6	3326,0	3417,3	3510,4	23
24	2733,5	2814', 1	2896,0	2979,3	3064,0	3150,2	3238,0	3327,5	3418,8	3512,0	24
2Б	2734,8	2815,5	2897,4	2950,7	3065,4	3151,7	3239,5	3329,0	3420,3	3513,5	25
26	2736.2	2816,8	2898,8	2982,1	3066,8	3153,1	3241,0	3330,6	3421,9	3515,1	26
27	2737,5	2818,2	2900,1	2983,5	3068,3	3154,6	3242,5	3332.1	3423,4	3516,7	27
26	2738,8	2819,5	2901,5	2934,9	3069,7	3156,0	3244,0	3333,6	3425,0	3518,2	26
29	2740',2	2820,9	2902,9	2986,3	3071,1	3157,5	3245,4	3315,1	3426,5	3519,8	29
1 30	2741,5	2822,2	29С4.3	2967,7	3072,Б	3158,0	3246,0	3336,6	3420,0	3621,4	30
|	31	2742,8	2823,6	2905,7	2989,1	3074,0	3169,4	3248,4	3338,1	3429,6	3523,0	31
и 82	2744,2	2824,9	2907,0	2990,5	3975,4	3161,8	3249,9	3339,6	3431,1	3524,5	32
! зз	2745,5	2826,3	2908,4	2991,9	3076,8	3163,3	3251,3	3341,1	3432,7	3526,1	33
[	34	2746,8	2827,7	2909,8	2993,3	3078,3	3164,7	3252,8	3342,6	3434,2	352/ ,7	34
30	2748,2	2829,0	2911,2	2994,7	3079,7	3166,2	3254,3	3344,1	3135,7	3529,3	3S
1 36	2749,5	2839,4	2912,6	2996,1	3081,1	3167,7	3255,8	3345,6	3437,3	3530,8	36
37	2750,9	2831,7	2913,9	2997,5	3082,5	3169,1	3257,3	3347,2	3438,8	3532,4	37
36	2752,2	2833,1	2915,3	2998,9	3084,0	3170,6	3258,8	3348,7	3440,4	3534,0	36
39	2753,5		9916,7	3000,3	3985,4	3172,0	3260,2	3350,2	3441.9	353о,6	39
40	2754,8	2836^9	2618,1	3001,7	3066,6	3173,6	3261,7	3361,7	3443,5	3637.1	40
41	2756,2	2837,2	2919,5	3003,1	3088,3	3174,9	3263,2	3353,2	3445,0	3538,7	41
j 42	2757,5	2838,5	2920,9	3004,5	3089,7	3176,4	3264,7	3354,7	3446,5	3540,3	42
1	43	2758,9	2839,9	2922,2	3006,0	3991,1	3177,9	3266,2	3356,2	3448,1	3541,9	43
I 44	2761\2	2841,3	2923,6	3007,4	3092,6	3179,3	3267,7	3357,8	3449,6	3543,4	44
| 4S	2761,6	2812,6	2925,0	3008,8	3094,0	3189,7	3269,2	3359.3	3451,2	3545,0	4S
1 40	2762,9	2844,0	2926,4	3010,2	31'95,4	3182,2	3270,6	3360,8	345 !./’	3546.6	46
М	47	2764,2	2845,3	2927,8	3011,6	3096,9	3183,7	3272,1	3362,3	3454,3	4548,2	47
|	48	2765,6	2846,7	2929,2	3013,0	3098,3	3185,2	3273,6	3363,8	3455,8	ЗУ.9.8	49
1 49	2766,9	2848,1	2930,5	3014.4	3099,7	3186,6	3275,1	3365,3	3457,4	3551,4	49
10	2769,3	2849,4	2931,9	ЗВ1S,8	3161,2	3180,1	3276,6	3366,9	3458,9	3562,9	Б0
61	2769.6	2850,8	2933,3	3017,2	3102,6	3189,5	3278,1	3368,4	3460,5	3554,5	Б1
1 и	2771,0	2852,2	2934,7	3018,6	3104,0	3191,0	32/9,6	3369,9	3462,0	Зо<э6,1	Б2
БЗ	2772,3	2853,5	9936,1	3020,0	3105,5	3192,5	3281,1	3371,4	3461,6	зЬз/,7	БЗ
Б4	2773,6	2854,9	2937,5	3021,5	3106,9	3193,9	3282 6	3372,9	3465,1	3559,3	54
ББ	2775,0	2856,3	2938,9	3022,9	3108,4	3195.4	3284,1	3374,5	3466,7	3569.9	56
Б6	2776,3	2'57,6	2940,3	3024,8	3109,8	3196,9	3285,6	3376,0	3468.3	3562,4	66
Б7	2777,7	2859,0	2911,6	3025,7	3111.2	3198,3	3287,0	3377,5	3469,8	*564,0	Б7
Б6	2779,0	2869,4	2943,9	3027,1	3112,7	3199,8	3288,5	3379,0	3471,4	3565,6	Б8
Б9	2780,4	5861,7	2944,4	3028,5	3114,1	3201,2	3290.0	3380,6	3472,9	3567.2	Б9
	— 										
	41°	42°	43°	44°	46°	46°	47°	48°	49°	60°	-
188
(Продолжения)
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В МОРСКИХ МИЛЯХ
ШИРОТА
X	51°	82°	83°	64°	65°	66°	870	1В°	89°	во°	
0	3568,8	3668,2	3763.8	3884,6	2968,0	4073,9	4182,В	4294,3	4409,1	4027.4	8
1	3570,4	3666,8	3765,4	3866,3	3969,7	4075,7	4184,5	4296,1	4411,1	4529,4	1
2	3572,0	3668,4	3767,1	3868,0	3971,5	4077,5	4186,3	4298,1	4413.0	4531,4	1
3	3573,6	3670,1	3768,7	3869,7	3973,2	4079,3	4188,1	4300.0	4415,0	4533,4	1
4	3575,2	3671,7	3770,4	3871,4	3974,9	4081,1	4190,1	4301,9	4416,9	4535,4	4
*	3576,8	3673,3	3772,1	3873,1	3976,4	4082,9	4191,8	4303,7	4418,9	4537,4	
6	3578,3	3675,0	3773,7	3874,9	3978,7	4084,6	4193,6	4305.6	4420,8	4539,4	В
7	3579,9	3676,6	3775,4	3876,6	3980,5	4086,4	4195.5	4307.5	4422,8	4541,4	7
6	3581,5	3678,2	3777,1	3878,3	3981,4	4087.2	<197,3	4309,4	4424,7	543,4	fl
9	3583,1	3679,8	3778.7	3880,0	3983.5	4099,0	4199,2	4311.3	4426,7	4545,4	
10	3684,7	3681,8	3780,4	3681,7	3965,4	4061,8	4201,0	4313,2	4420,6	4047,4	10
11	3586,3	3683,1	3782,1	3883,4	3937,2	4093,6	4202,0	4315,1	4439.6	4549,4	11
12	3587,9	3684,7	3783,7	3885.1	3988.9	4095.4	4291,7	4317,0	4432 5	4551,4	12
1’	3589,5	3686,8	3785,3	3886,8	3990,7	4097,8	4236,6	4318,9	4434,5	4553,5	13
14	3591,1	3688,0	3787,1	3888.5	3992,4	4-399,0	•1208,4	4320,8	4436,4	4555,5	14
15	3592,7	3689,6	3788.8	385'9,2	3994,2	4130,8	4210,3	4322,7	4438,4	4.57,5	1В
te		3691,3	3790.4	3891,9	3996,0	4102,6	4212,1	4324.6	4440,3	4559,5	16
17	3595,9	3692,9	3792,1	3893,7	3997,7	4104,4	4214.0	4326,5	4442,3	4561.5	17
1В	3597,5	3694,5	3793,8	3895,4	3999,5	4106,2	4215,8	4328,4	4444.2	4563,5	IB
19	3599,1	3696,2	3795,4	3897,1	-•001,2	4108,0	4217,7	4139,3	4446,2	4565,6	19
20	3600,7	3837 Ji	3797,1	3698,8	4003,0	41С8,8	4219,5	4332,2	4448,2	4667,6	20
21	3692,3	3699,4	3798,8	3990,5	4004,7	4111 6	4221,4	4334.1	4450,1	4569,6	21
22	3693,9	3701,1	3890,5	3902,2	4006,5	4113,4	4223,2	4336.0	4452,1	4571,6	22
23	3695,5	3702,7	38)2,1	3903,9	4008.3	4115.7	4225.1	4337,9	4454,0	4573,6	23
24	3607,1	3704.4	3803,8	3905,7	4010,0	4117,0	4226,9	4339.8	4456,0	4575,7	24
25	36-'8,7	3706,0	3805.5	3907,1	4011,8	4118.8	4228,8	4341.8	4458,0	4577,7	28
26	3619,3	3707,6	3897,2	39 9.1	4013,5	4120,7	4230,6	4343,7	4459,9	4579,7	26
27	3611,9	3709,3	3898,9	3910,8	4015,3	4122,5	4232,5	4345,6	4461,9	4581.7	27
26	6613,5	3710,9	3810,5	3912,5	4017.1	412-1.3	4231.4	4347,5	4463.9	4583.8	26
29	3615,1	3712,6	3812,2	3914,3	4018 8	4126,1	4236,2	4349,4	4465,8	4585,8	29
ЗЭ	3610.7	3714,2	3813,0	3616,0	4020,6	4127,0	4238.1	43S1,3	4467,8	4587,0	36
31	3618,3	3715,8	3815,6	3917,7	4022,4	41297	4239 9	4353,2	4469,8	4589,9	31
32	3619,9	3717,5	3817.3.	3919,4	4924,1	4131,5	4211.8	4355,1	4471,8	4591,9	32
33	3621,7	3719.1	3818,9	3921,3	4025 9	4133,3	4213.7	4357,1	4473,7	4’93,9	33
34	3623,2	3720,8	3829,6	3922,9	4027,7	4135,2	4245,5	4359,0	4175,7	4’>96,0	34
35	<162-1,8	3/22,4	3822,3	3924,6	4029,4	4137,0	42-17,4	4360,9	4477,7	4598,0	30
36	3626,4	3724,1	3824,0	3926,3	4031,2	4133,8	4249,3	4162,8	4179,7	4690,0	38
37	3628,0	3725,7	3825,7	3928,1	4033,0	4140,6	4251.1	4361,7	4481.6	4602,1	37
38	.3629,6	3727.4	3827.4	3929.8	4034,7	41-12,4	4253.0	4366,9	4483,6	4604,1	38
39	3631,2	3729,0	3829,1	3931,5	4036,8	4144.2	4254,9	4368,6	4485,6	4606,1	39
43	4632,8	3730,7	3030,7	ЗЭЗЗ.2	4638,3	4146,1	4256,7	4370,5	4487,6	4608.2	40
41	363»,4	3732,3	3832,4	3935,0	4040.1	4147,9	4258.6	4372,4	4189,5	4610,2	41
42	3636,5	3734.0	3834,1	3936,7	4041.8	4149,7	4260,5	4374,3	4491,5	4612,3	42
43	3637,7	373,.6	3835,8	3938,4	4043.6	4151,5	4262,3	4376,3	4493,5	4614.2	43
44	3639,3	3737,3	3837,5	3940,2	4045,4	4153,3	4264,2	4378,2	4195,5	4616,4	44
4S	3640,9	3738,9	3839,2	3941,9	4047.2	4153,2	4266,1	>380,1	4-197,5	4618,4	48
46	3642,3	3740,6	3840,9	3943,6	4048.9	4157,0	4268.0	4382,0	4199.5	4620,4	46
47	3644,1	3742,2	3842,6	3945,4	4050,7	4158,8	4269,8	1384,0	4501,5	4622,5	47
48	3645,7	3743,9	3844,3	3947,1	4052,5	4160,9	4271,7	4335,9	4503,4	4624,6	4В
49	3647,4	3745.5	3846,0	3948,8	4054,3	4162,5	4273,6	4387,8	4505,4	4626,6	4В
50	3649,0	3747,2	3847,7	3960,6	4856,1	4164,3	4275,5	4389,8	4007,4	4628,0	60
S1	3650,6	3748,8	3849,4	3952,3	4057,8	4166.1	4277.3	4'91,7	4509,4	4630,7	81
82	3652,2	3750,5	3851.0	3954,0	4059,6	4168,0	4279,2	4393,6	4'11,4	4632,8	62
S3	3653,8	3752.1	3852,7	3955,8	4061,4	4169,8	4281,1	4395,6	4513,4	4634,8	63
Б4	3656,5	3753,8	3854,4	3957.5	4063,2	4171,6	4283,0	4397,5	4515,4 4517,4	4636.9	04
S5	3657,1	37а5.5	3856,1	3959.3	4065,0	4173,4	4284,9	4399,4		-i638,9	во
66	3658,7	3757,1	3857.8	3961,0	4066,8	4175,3	4286,8	4401,4	4519,4	4641.0	80
и	3669.3	3758,8	3859,5	3962,7	4968 5	4177,1	4288.6	4403,3	4521,4	4613,0	87
68	3661,9	3760,4	3861,2	3961,5	4070,3	4178,9	4290,5	4401,3	4523,4	4645.1	68
S9	3663,8	3702,1	3062,9	3966,2	4972,1	4180,8	4282,4	4407,2	4НМ	4647.2	69
	81°	62°	63°	54°	88°	86°	67°	68°	89°	63°	X,
139
(Продолжение}
(Продолжение}
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В МОРСКИХ МИЛЯХ
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В МОРСКИХ МИЛЯХ
ШИРОТА
	61°	82°	63°	| 64°	6S°	86°	67°	66°	69°	70°	
0	4649,2	4775,0	4904,9	1039,4	1178,8	0323,S	1174,0	6630,8	6794,6	59B5.S	в
1	4651,3	4776,1	4907,1	5041,7	8181,2	5326,0	5476,6	5633,5	5797,3	5968.8	1
2	4653,3	4779,2	4909,3	5044,0	5183,5	5328,4	5479,1	5636.2	58)0,1	5971 8	2
а	4655,4	4781,4	4911,5	5046,3	5185,9	5330,9	5481,7	5638,8	5892,9	5974,7	3
4	4657,5	4783,5	4913,8	5048,6	5188,3	5333,4	5484,3	5641,5	5805,7	5977,7	4
К	4659,6	4785,6	4916,0	5050,8	5199,7	5335,8	5486,8	5644.2	58)8,5	598 ),6	1
в	4661,6	4787.8	4918,2	5053,1	5193,0	5338,3	5J89,4	5646,9	5811,3	5981,5	в
7	4663,7	4789,9	4920,4	5055,4	5195,4	5340,8	5492,4	5649,6	5814,1	5986,4	7
В	4665,8	4792,1	4922,6	5057,7	5197,8	5343,2	5494,5	5652,2	5816,9	5989,4	в
9	4668,8	4794,2	4924,8	5060,0	5200,2	5345.7	5497,1	5654.9	5819,3	o992,3	9
10	4069,9	4795,3	4927,0	S062,3	S202.S	5348,2	5489,7	S6S7.li	S82z,6	6995,3	10
11	4672,0	4798,5	4929,2	5064,6	5204,9	5350,7	5502,3	5660,3	5825,4	5998,2	11
12	4674,1	4800,6	4931,5	5066,9	5207,3	5353.1	5504,8	5663,0	5828,2	6001,2	12
13	4676,1	4802,8	4933,7	5069,2	5209,7	5355,6	5537.1	5665,7	5831,0	6904,1	13
14	4678,2	«804,9	4935,9	5071,5	5212,1	5358.1	5519.0	5668,4	58’33,8	6007,1	14
15	4680,3	4807,1	4938,1	5073,8	5214.5	5369.6	5512,6	5671,1	58 36.7	6310,')	IS
16	4682,4	4809,2	4940,3	5076,1	5216.9	5363.1	5515,2	5673,8	5839,5	6013,0	16
17	4681,4	4811,4	4942,6	5078,1	5219.2	5365,5	5517,8	5676,5	5842,3	6016,0	17
10	4686,5	4813,5	4944.8	5080,7	5221,6	5168,0	5520,4	5679,2	5845,1	6018,9	18
19	46°8 6	4815,7	4947,0	5083,0	5221,0	5370 5	5523.0	5681.9	5848,0	6021,9	19
20	4€80,5	4917,8	4949,2	S06S,3	5226,4	6373,0	ES26J	5Б84.Б	1653,6	6024,3	20
1 21	4-92,8	4820,0	4951,5	5087.6	5228.8	5375,5	5528,1	5687,3	5853,6	6027.8	21
22	4694,9	4822,1	4953,7	5089,9	5231,2	5378.0	5530,7	569),0	5856,5	6030,8	22
23	4697,0	482 i,3	4955,9	5092.3	5233,6	5380.5	5533,3	5692.7	5859,3	6033,8	23
24	4699,0	4826,4	4958,3	5094,6	5236,0	5383,0	5535.9	5695,4	5862,1	6036,8	24
25	4701,1	4828,6	4960,4	5096.9	5238.4	5385.5	5538,5	5698,2	5865.9	6039,8	25
26	4703,2	4830,8	4962,6	5099,2	5240,8	5388.0	551 .1	5700,9	5867,8	6042,7	26
27	4701,3	4834,9	4964,9	5101,5	5243.2	5390,5	5543,8	5703.6	5870.7	6045,7	27
28	4707,4	4835,1	4967,1	5103,8	5245.6	5393,0	5546.4	5706,3	5873,5	6048,7	28
29	4709,5	4837,2	4969,4	5106.2	5248.1	539 ,6	5549,0	5709,1	5876,4	6051,7	29
30	4711,6	4239,4	4971,6	5108,6	6250,5	5330, o	'.SI ,6	6711,8	5879,2	6064,7	30
31	4713,7	4841,6	4973,8	5110,8	5252,9	5400.5	5554,2	5714,5	5882,1	6057,7	31
32	4715,8	4813,7	4976,1	5113.1	5255,3	5493,0	5556,8	5717,2	5886,0	6060.7	32
33	‘717,9	4845,9	4978,3	511-5,5	5257,7	5405,5	5559,4	6720,0	5887,8	6063,7	33
34	4*720,0	4848,1	4980,5	5117,8	5260,1	5408.0	5562 1	5722,7	589*),7	6066,7	3*
3S	4722,1	4850,3	4982,8	5120,1	5262,5	5410,6	5564,7	5725,4	5893,5	6669,7	35
36	-1724,2	4852,4	4985,1	5122,4	5265,0	5413,1	5567,3	5728.2	5896,4	6072,7	30
37	4726,3	4854,6	4987,3	5124.8	5267,4	5415,6	5569,9	5730,9	5899,3	6075,7	37
38	4728,4	4856,8	4989,6	5127,1	5269,8	5418.1	5572,6	5733.7	5902,2	6078,7	ЗВ
39	4730,	4859,0	4991,8	5129,4	5272,2	542-\6	5575,2	5736,4	5905,0	6081,8	39
40	4732,6	4861,1	4994,1	Б1Ы.8	6274,7	5423,2	6877,в	6739,2	6947,0	6084,6	40
41	4734,7	4863,3	4996,3	5134,1	5277,1	5425,7	5589,4	5741.9	5910,8	6087,8	41
42	<736,8	4865,5	4998,6	5136,5	5279,5	5428,2	5583,1	5744,7	5913,7	6090,8	42
43	4738,9	4867,7	5000,8	5138,8	5281,9	543'?,7	5 >85,7	5747,4	5916,5	6093,9	43
44	4741,0	4869,0	5003,1	5141,1	5281,4	5433.3	5588,4	5750,2	5919,4	6996.9	44
45	4743,2	4872,0	5005,4	5143,5	5286.8	5435.8	5591,0	5752,9	5922,3	6099.9	45
4	4745,3	4874,2	5007,6	5145,8	5289,2	5438,3	5593,6	5755,7	5925,2	6103,0	46
47	4747,4	4876,4	5009,9	5148,2	5291,7	5140,9	5596,3	5758,5	5928,1	6106,0	47
48	4749.5	4878,6	5012,1	5159,5	5291,1	5443,4	5598.9	5761,2	59-1,0	6Ю9.О	48
49	4751,5	4880,8	5014,4	5152.9	5296,6	5446,0	5601.6	5764,0	5933.9	6112.1	49
SO	4753,7	4893,0	SOIc,’’	£155,2	b'99,u	5443,6	6604,2	5766,6	5936,8	6115,1	50
61	4755,9	4885,2	5018,9	5157,6	5391,5	5451,0	5696,9	5769.5	5939,7	6118,2	61
62	4758,0	4887.4	5021,2	5159,9	5303,9	54-ю .6	5609,5	5772,3	5912,6	6121,2	62
53	4760,1	4889,5	5023,5	5162,0	5306,3	5-156.1	5611,2	5775,1	5915,5	6124,3	S3
54	4762,2	4891,7	5025,8	5161,6	5308,8	5458.7	5614,8	5777,9	5948.4	6127,3	54
SB	4764,3	4893,9	5028,0	5167,0	5311,2	5461.2	5617,5	5780,6	5951,3	6130,4	65
156	4766,5	4896,1	5039,3	5169,4	5313,7	о464,8	5620,2	3783,4	5954.2	6133,4	56
•	67	4768,6	4898,3	5032.6	5171,7	5316,1	5-166.3	5622.8	5786,2	59-57.2	6136,5	57
68	47/0,7	490 ),5	5034,9	5174,1	5318,6	5468,9	5625.5	5789,0	5960,1	6139,6	58
63	4772,9	4902,7	£037,1	£176,4	5321,1	5471,4	6628,1	S7S1,8	5363,0	6142,6	59
											9
	61°	62°	63°	64°	65°	EE°	67°	6У3	69°	70°	О
Ll.					i Р	О	А				
	71°	72°	73°	74°	75°	76°	77°	73°	79°	80°	° / / 9
0	6146,7	6334,8	6634,4	6745,7	6970,3	7210,1	7437,2	77446	6045,7	8375,2	0
1	6148,8	6338 1	6537,8	6749,4	6974,2	7214,2	7471,7	7749,4	8050,9	8381,0	1
2	6151,8	6341,3 6344.6	6541,3	6753,9	6978,1	7218,3	7476,1	7754,2	8)56,2	8386,7	2
з	6158,9		6544.7	6736.6	6981,9	7222,5	7480,6	7759,0	8061,5	8392,5	3
4	6159,:»	6347,8	6548,1	6760.3	6985,8	7226,6	748о 0	7763,9	8)66,7	8398,3	4
к	6161,1	6351,1	6551,6	6763.9	6989,7	7230,8	7489,5	7768,7	8972,0	8404,1	S
6	6164,2	6354,3	6555*0	67^7,6	6993.6	7235,0	7494,0	7773,5	8077,3	8409,9	6
7	6167,3	6357,6		6771,2	6997,5	7239.1	7498,5	7778,4	8482,6	8415,7	7
6	6170,4	6360,8 6364 1	6561,9	6774,9	7901,4	7243,3	7502,9	7783,3	8087,9	8421,6	8
9	6173,5			6778.5	7005,3	7247,5	7507,1	7788,1	8093,2	8427,4	9
10	BIIBJ	6367,2	6566 Л	6782,2	7009,2	7261,6	7611,9	7733,1)	6028,5	8433,3	10
11	6179,6	*•370,9	6572,2	6785,9	7013,1	7255,8	7516,4	7797,9	8103,8	8439,1	11
12	6182,7	6373,9	6575.7	6789,5	7017,0	7263,0	7521,0	7802,8	8109,2	8445,0	12
13	618 \9	6377,2	6579,2	6793,2	7020,9	726- 2	7525,5	7807,7	8114,5	843° 9	13
14	6189,•	6380,4	6582.6	6796.9	7024,8	7268,4	7530.0	7812,6	849,9	Ь456,8	14
15	6192 Л	6383,7	6586,1	6800,6	7028,8	7272.8	7534,5	7817,5	8125,2	8462,7	15
1Б	6106,2	6387,0	6589,6	6844,3	7032,7	7276,8	7539,1	7822,4	8130,6	8468,6	1Б
17	0198,3	6390,3	6593.0	6808.0	7036,6	7281,0	7543,6	7827,3	8136,0	8474,6	17
18	62Л-1 /1	6393,6		6811,7	7040,6	7285,3	7548,1	7832,2	8141,3	8480,4	18
19	620-1,5	6396,9	6690,0	6815.3	7044,5	7289,5	7552,7	7837,2	8146,7	8486,4	19
20	6207,7	6400,1	6003,6	6810,0	7048,6	7293,7	7567,2	7842,1	8162,1	0402,3	20
21	6210,8	6403,4	6607,0	682*2,8	7052,4	7298,0	7561.8	7847,0	8157,5	8498.3	21
22	6213.9	6406,7	6610,5	6826,5	7056,4	7302,2	7566,4	7852.0	8162,9	8584,2	22
23	6217,0	6410,0	6614,0	6830,2	7060,3	7306,4	6571,0	7857.0	8168,4	8510,2	23
24	6220.2	6413,4	6617,5	6833.9	7064.3	7310,7	7575,5	7861,9	8173,8	8516,2	24
26	6223,3	6416,7	6621,0	6837,6	7068.8	7314,9	7683,1	786: 9	8179,2	8о22,2	25
26	6226,5	6420.0	6624,5	6841,3	7072,2	7319,2	7584.7	7871,9	8184,7	8528,2	26
27	6229.6	6423,3	6628,0	6845.1	7076,2	7323,5	7589.3	7876,9	819°,1	8534.3	27
28	6232,7	6426.6	6631.5	6848 8	7080.2	7327,7	7593,9	7881,9	8195,6	8540,3	29
j 29	6235,9	6429.9	6635.0	6852,5	7084.2	7332,0	7598.5	7886,9	8201,1	8546,3	29
ЗЭ	038,»	6433,3	6638,7	08SS.3	7088,2	7336.3	7603,2	7891,3	8206,6	8562,4	30
31	6242,2	6436,6	6642.0	6860,0	7092,2	7340,6	7607.8	7896 9	8212,1	8558,4	31
32	6245^3	6439,9	6645,6	6863,8	7096.2	7344,9	7612,4	7902,0	8217,6	8564,5	32
33	6248*5	6443.2	6649.1	6867,5	7100,2	7349.2	7617,0	79)7,0	8223Л	8570,6	33
34	6251,7	6446.6	6652,6	687 ,3	7104,2	7353,5	7621,7	7912,0	8228,6	8576,7	34
35	6254,8	6449,9	6656.2	6875,0	7108.2	7357,8	7626,3	7917,1	8234,1	8о82,7	35
36	6258,0	6453,3	6659,7	6878,8	7112,2	7362,1	7631,0	7922Л	8239,7	8588,9	30
37	6261,2	6456,6	6663,3	6882,6	7116.2	7366,4	7635,6	7927,2	8245,2	8а95,1	37
38	6264,3	6460.0	6666.8	6886.3	7120.3	7370,7	7640,3	7932,3	8250, 7	8601,2	38
30	6267,5	6463,3	6670,4	6891,1	7124,8	7375,1	7645,0	7937,3	8256,3	8607,3	39
40	6270,7	6406,7	6673,0	6393,0	7128,3	7373,4	7649,7	7942 4	8261 ,В	86111	40
41	6273,9	6470,0	6677,5	6897.7	7132,4	7383,7	7654,3	7917.5	8267,5	8619,7	41
42	6277,1	6473,4	6681.0	6991,5	7136.4	7388,1	7659,0	7952,5	8273,0	8625,9	42
43	6283,2	6476,7		6905,3	7140,5	7392,4	7663.7	7957,7	8278,6	8632Д	43
44	6283.4	6480,1	6688.2	6919,1	7144,5	7396,8	7-£68,7	7962.8	8284,2	8638,3	44
46	6286,6	6483,5	6691,7	6912,9	7148,6	7401,1	7673,1	796!	8289,9	8644,5	45
48	6289,8	6486,9	6695.3	6916,6	7152.7	7405.5	7677,9	7973,1	8295.0	8650,7	
47	6293,0	6490,2	6698,9	6920,5	7156,7	7409.91 7682,6		7978,2	8301Л	8656,9	47
48	6296.2	6193,6	67С 1. 5	6924.3	7160.8	7414,3	7687,3	7983,4	8306,8	8663,2	48
49	6299,4	6497,0	6706,1	69.8,1	7164,9	7418,5	7692,1	7988,5	8312,4	8669.4	49
60	63& 2, Б	0500,4	6709,6	6031,0	7169,0	7423,0	7В96,8	7993.7	6318,1	8676,7	КО
51	6305,8	6503,8	6713,2	6935,7	7173.1	7427,4	7701,Б	7998,8	8323,7	8682,0	51
62	*•309.0	6507,2	6716.8	6939,6	7177,2	7431,8	7706,?	v004,4	8329,4	8688,3	S2
63	6312,3	6510,6	6720,4	6943,4	7181,3	7436,2	7711,1	8009,2	8335,1	8694,6	53
54		6514,0	6724,0	6947,2	7185,4	7440,6	7715.8	8014,4	8340.8	8700,9	54
55	*318,7	6517,4	6727,6	6951,1	7189.5	7445,0	7720,6	8019.6	8346,5	8707,2	5Б
5S	6321,9	6'20.8	6731,3	6954,9	7193,6	7449,5	7725,4	8024,8	8352,2	8713,6	ЕО
67	6125,1	6524.2	6734,9	6958,8	7197,7	7453.9	7730,0	8030.0	8358,0	8719,9	67
68	6328,4	6527,6	6738,5	6962,6	7201,8	7458,3	7735.0	8035,2	8368,7	8726,3	КО
so	0331,6	6931,0	6742,1	6900,6	7206,9	7462,8	7739,8	6040,S	8369,4	8732,7	58
	71°	72°	73°	74°	76°	76°	77°	78°	78°	1 ю°	
140
141
(Продолжение)
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В МОРСКИХ МИЛЯХ
	111 И				Р	э т	А			
X о / X.	61°	Б2Э	83°	04°	8Б°	86°	87°	88°	89°	
0	6739,1	9143,5	9605,0	10130,9	10764,6	11632,8	12622,1	13916,4	16299,6	0
1	8745,5	9152,7	9614,0	10146,5	10776,1	11546,9	12541,3	13945,2	16357,3	! 1
2	8751,9	9159,9	9622,3	10156,1	10787,6	11561,3	125693	13974,2	16166,1	2
3	8758,3	9167,1	9630,5	10165,7	10799,2	11575,8	12579,9	14003,5	16475,9	3
4	8764,7	9174,3	9638,8	10175,4	10810,8	11590,3	1259911	14033,0	16-536,8	4
Б	8771,2	9181,6	9647,1	10185,0	10822,5	11695,0	12619,0	14062,8	16598,7	5
в	8777,6	9188,8	9655,4	10194,8	10834,2	11619,6	12638,7	14092,8	16661,8	6
7	8784,1	9196,1	9663,7	10204,5	10845,9	11634,4	12658,5	14123,1	167'26,0	7
6	8799,6	9203,4	9672,9	10214,3	10857,7	11649,2	12678,5	14153,7	16791,5	8
9	8797.1	9210,7	9680,5	10224,1	10869,5	11664,0	12698,5	14184,5	16858,3	9
10	8803,6	3216,1	0688,9	10233,9	10801,4	11678,9	12718,7	14216,6	16926,4	10
11	8810,1	9225,4	9697,3	10243,7	10893,2	11693,9	12739,0	14247,0	16995,8	11
12	8816,6	9232,8	9705,7	10253,6	10995,1	11709,0	12759,4	14278,7	17066,7	12
13	8823,2	9240,1	9714,2	10263,5	10917,1	11724,1	12779,9	14310,7	17139,1	13
14	8829,7	9247,5	9722,6	10273,5	19929,1	11739,3	12890,6	14343,0	17213,0	14
11	8836,3	9254,8	9731,1	10283,4	10941,2	11754.6	12821,4	14375,6	17288,6	16
16	8842,9	9262,4	9739,7	10293,4	10953,3	11769,9	12842,3	14408,5	17365,8	16
17	8849,5	9269,8	9748,2	10303,5	10965,4	11785,3	128э3,3	14441,7	17444,9	17
16	8856,1	9277,3	9756,3	10313,5	10977,6	11890,7	12884,5	14475,2	17525,8	18
16	8862,7	9284.7	9765,3	10323,6	10989,8	11816,3	12905,8	14599,1	176-18,6	19
20	6669,3	6292,2	0773,9	10333,7	11002,1	11831,9	12827,2	14543,3	17693,6	28
61	,876,0	9299,7	9782,6	10343,9	11014,4	11847,5	129-18,7	14577,9	17789,5	21
22	8882,6	9307,2	9791.2	10354,0	11026,8	11863,3	12970,4	14612,8	17860,8	22
23	8889.3	9314,8	9799,9	10364,2	11039,2	11879,1	12992,3	14648,0	17961,5	23
24	8896,0	9322,3	98п8,6	10374,5	11051,6	11895,0	13911,2	14683,7	18055,7	24
26	89'12,7	9329,9	9817,3	10384,7	11064,1	11910,9	13036,4	14719,7	18152,5	25
26	8939,4	9337,5	9826,0	10395,0	11076,6	11927,0	13058,6	14756,1	18252,2	26
27	8916,1	9345,1	9834,8	10405,3	11089,2	11943.1	13081.0	14792,8	18354.8	27
26	8922,8	9352,7	9843,5	10415,7	11101,8	11959,3	13103,6	14830,0	18460,6	26
29	8929,6	9360,3	9852,3	10426,1	11114,5	11975,6	13126.3	14867,6	18569,8	28
30	6936,3	9368,0	6861,2	10436,5	11127,2	11 Вв1,9	13149,1	14905,6	18692,6	30
31	8943,1	9375,7	9870,0	10447,0	11140,0	12008,3	13172,1	14944,0	18799,0	31
32	8949,9	9383,4	9878,9	10457,4	11152,8	12024,8	13195,3	14982,8	18919,7	32
33	8956,7	9391,1	9887,8	10467,9	11165,7	12041,4	13218.6	15022,1	19044,7	33
34	8963,5	9398,8	9896,7	10478,5	11178.6	12058,0	13242,1	15061,9	19174,4	34
ЗБ	8970,3	9406,5	9995,6	10489,1	11191,6	12074,8	13262,7	15102,1	19309.3	35
36	8977,2	9414,3	9914,6	10499,7	11204,6	12991,6	13289,5	15142,8	19449,6	36
37	8984,0	9422,1	9923.6	10510,3	11217,6	12108,5	13313,5	15183,9	19595,9	37
S3	8993,9	9429,8	9932,6	10521,0	11230,7	1212-5,5	13337.6	15225,6	19748,7	39
ЗБ	8997,8	9437.6	9941,6	10531,7	11243,9	12142,6	13361,9	15267,8	199)8.7	39
40	9004.6	9446,6	9950,7	10542,6	11237,1	12159,7	13386,4	16310,6	20076.4	40
41	9311,6	9453,3	9959,7	10553,2	11270,4	12177,0	13411,0	15353,8	20252,7	41
42	9018,5	9461,2	9968,8	10564,0	11283,7	12194,3	13435,9	15397,6	20438,6	42
43	9025,5	9469,1	9978,0	10571,9	11297,0	12217,7	13460,9	15441,9	20635,1	43
44	9932,4	9477,0	9987,1	10585,8	11310,5	12229,2	13486,0	15486,9	20843,5	44
45	9339,3	9484,9	9996,3	10596,7	11323,9	12246,8	13511,4	15532,4	21065,4	46
46	9946,4	9492,8	1:1005,5	10697,6	11337,4	12264,5	13537.0	15578,5	21302,5	46
47	9053,3	9500,8	10014,7	10618,6	11331,0	12282,3	13562,7	15625,3	21557,3	47
48	9069,3	9508,7	10923,9	10629,6	11364,6	12300,1	13588 7	15672,7	21832,5	49
49	9167,3	9.516,7	10033,2	10640,7	11378,3	12318,1	13611,8	15720,8	22131,6	49
Б0	9074,3	9524,7	10042,5	10631,7	11392,1	12336,1	13641,2	16769,9	22469,3	50
61	9081,4	9532,7	10051,8	10662,9	11405,9	12354,3	13667,7	15819,1	22821,5	61
Б2	9088,4	9540,8	10061,2	10674,0	11419,7	12372.5	13694,5	15869,3	23226,4	62
БЗ	9095,5	9548,9	10070,6	10685,2	11433,6	12399,9	13721,5	15920,2	23685,4	БЗ
64	9102,6	9556,9	10080,0	10696,5	11417.6	12109,3	13748,7	15971,9	2421-5,3	Б4
ББ	9109,7	9-565,0	10989,4	10707,7	11461.6	12427,9	13776,1	16)24.4	24842,1	Б5
	9116,8	9573,2	10098,8	10719,0	11475.6	12446,5	13803,7	16077,7	256)9,2	Б6
87	9124,0	9581,3	10108,3	10730,4	11489.8	12165,3	13831,5	16131,8 I	26698,2	Б7
66	9131,1	9589,4	10117,8	10741,7	11594,0	12481.1	13859,6	16186,8 I	27992,1	68
Б9	9139,3	6697,6	10127,3	10763,2	11618,2	12693,1	13887,9	16242,7 ।	30376,0	19
	81°	82°	33°	84°	81°	88°	•7°	66’	В9°	о\
142
(Продолжение?
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В ГРАДУСАХ
				ш	И	Р о	т	А				i
	0°	1°	1°	8°	4°	6°	О’	7°	6°	6°	10°	X
0	0,00	1,00	2,00	3,00	4,00	5,01	6,01	7,02	8,03	9.04	10,0В	• 1
1	0,02	1,02	2,02	3,02	4.02	5,02	6,03	7,04	8,04	9,06	10,07	1 J
2	0,03	1,03	2,03	3,04	4,04	5,04	6,01	7,05	8,06	9.07	10,08	2 г
3	0,05	1,05	2,06	3,05	4,05	5.06	6,06	7,07	8.08	9,09	10,10	?	1
4	0,07	1,07	2,07	3,07	4,07	5,07	6,08	7,08	8,09	9,10	10,12	4 h
8	0,08	1,08	2,08	3,08	4,09	5,09	6,10	7,10	8,11	9,12	10,14	* 1
8	0,10	1.10	2,10	3,10	4,10	5,11	6,11	7,11	8.13	9.14	10,15	6	1.
7	0,12	1,12	2,12	3,12	4,12	5,12	6,13	7,11	8,14	9.16	10,17	’ 1
в	0,13	1,13	2,13	3.14	4,14	5,14	6,14	7,15	8,16	9,17	10,19	8
9	0,15	1,15	2,15	3,15	4,15	5,16	6,16	7,17	8,18	9,19	10,20	9	|
10	0,17	1,17	2,17	3,17	4,17	5,17	6,18	7,18	8,20	9,21	10,22	10 к
11	0,18	1,18	2,18	3,18	4,19	5,19	6,23	7,20	8,21	9,22	10,24	11 г
12	0,23	1,23	2,20	3,20	4,29	5,21	6,21	7,22	8,23	9,24	10.26	12 г
13	0,22	1,22	2,22	3,22	4,22	5,22	6,23	7,24	8,24	9,26	10,27	13	»
14	0,23	1,23	2,23	3,24	4,24	5,21	6,21	7,25	8,26	9,27	10,29	14
18	0,2 >	1,25	2,25	3,25	4,25	5,26	6,26	7,27	8.28	9,29	10.30	19
16	0,27	1,27	2,27	3,27	4,27	5,27	6,28	7.29	8,3')	9,31	10.32	18 L
17	0,28	1,28	2,28	3,28	4,29	5,29	6,30	7,30	8,31	9.32	10.34	17
18	0,39	1,39	2,30	3,30	4,30	5,31	6,31	7,32	8,33	9,31	10,36	18
19	0.32	1,32	2,32	3,32	4,32	5,32	6,33	7,34	8,35	9,36	10,37	19
20	0,33	1,33	2,33	3,34	4,34	5,34	6,38	7,35	8.3В	9,38	10,39	20
21	0,35	1,35	2,35	3,35	4,36	5,36	6,36	7,37	8,38	9,39	10,41	21
22	0,37	1,37	2,37	3,37	4,37	5,38	6,38	7,39	8,40	9,41	10,42	22
23	0,38	1,38	2,38	3,38	4,39	5,39	6,49	7,40	8,41	9,42	10,44	23
V	0,40	1,40	2,40	3,40	4,40	5,41	6.41	7,42	8,43	9,44	10,46	24
28	0,42	1,42	2,42	3,42	4,42	5,42	6,43	7,41	8,45	9,46	10,48	2Б
28	0,43	1,43	2,43	3,44	4,44	5,44	6,45	7,46	8,16	9,48	10,49	26
27	0,45	1,45	2,45	3,45	4,46	5,46	6,46	7,47	8,48	9,49	10,51	27	,
21	0,47	1.47	2,47	3,47	4,47	5,48	6,48	7,49	8,53	9,51	10.52	20	['
29	0,48	1,48	2,48	3,48	4,49	5,49	6,50	7,50	8,52	9,52	10,54	29	I'1
30	0.S0	1,60	2,60	3,so	4,60	В,В1	6,51	7,52	8,53	9.S4	10,S6	30	(
31	0,52	1,52	2,52	3,52	4,52	5,52	6,53	7,54	8.55	9,56	10.58	31 f
32	0.53	1.53	2,53	3,54	4.54	5,54	6,55	7,56	8,56	9,58	10,59	32
33	0,55	1,55	2,55	3,55	4,56	5,56	6,56	7,57	8,58	9,6)	10.61	33 J;
34	0,57	1,57	2,57	3,57	4,57	5,57	6,58	7,59	8,60	9,61	10,63	34 h
3S	0,58	1,58	2,58	3,58	4,59	5,59	6,60	7.63	8,62	9,63	10,64	35
36	0,69	1,69	2,60	3,60	4.6')	5,61	6,62	7,62	8.63	9,64	1066	36	(
37	0,62	1,62	2,62	3,62	4,62	5,62	6,63	7,64	8,65	9,66	10,68	37	।
36	0,63	1 64	2,64	3,64	4,64	5,64	6.65	7.66	8,67	9,68	10,70	
39	0,65	1,65	2,65	3,65	4,66	5,66	6,66	7,67	8,68	9,70	10.71	39
4G	0,67	1,67	2,67	3,67	4,67	6,68	6,68	7,68	8,70	9,71	10,73	40
41	0,68	1,68	2.68	3,69	4,69	5,69	6,70	7.71	8,72	9.73	10,74	il
42	0,70	1,70	2,70	3,70	4,70	5,71	6,72	7.72	8,73	9,75	10,76	
43	0,72	1,72	2,72	3,72	4,72	5,73	6,73	7.74	8.75	9,76	10,78	43
44	0,73	1 73	2.74	3,74	4,74	5,74	6,75	7.76	8,77	9,78	10,80	45
4S	0,75	1,75	2,76	3,75	4,76	Т>,76	6,76	7,77	8.78	9,80	10,81	
48	0,77	1.77	2,77	3,77	4.77	5,78	6,78	7,79	8,81	9.82	10,83	
47	0,78	1,78	2,78	3,79	4.79	5,79	6,80	7,81	8,82	9,83	10,85	
4В	0,83	1,83	2,8)	3.80	4.80	5,81	6,82	7,82	8,81	9,85	10,86	
49	0.82	1.82	2,82	3,82	4,82	5,83	6,83	7.81	8,85	9,86	10.88	4S	i
80)	0,83	1,63	2,84	3,84	4.84	6,84	6,85	7,86	6,87	9,60	10,90	
и	0,85	1.85	2,85	3,85	4,86	5,86	6,87	7,88	8,88	9.91	10,92	SI
02	0,87	1,87	2,87	3,87	4.87	5,88	6,88	7,89	8,9.)	9.92	10,93	
ВЗ	038	1.88	2,88	3,89	4,89	5,89	6.90	7.91	8,92	9,93	10,95	
84	0,93	1,90	2,90	3,90	4.91	5,91	6,92	7,92	8,91	9,95	10,97	
1 И	0.92	1,92	2,92	3,92	4.92	5.93	6,93	7.94	8.95	9,97	10,98	
66	093	1,93	2,94	3,94	4,91	5,94	6,95	7,96	8,97	9,98	11,00	
Б7	0,95	1,95	2,95	3,95	4,96	5,96	6.97	7.98	8.99	10,00	11.02	
89	0,97	1,97	2 97	3,97	4,97	5,98	6,98	7,99	9,00	10,02	11,04	89
89	0,98	1,98	2,98	3,90	4,99	6,00	7,09	8,01	9,02	10,04	11,0В	
												__l
	60	1°	2°	8°	4°	5°	во	7°	6°	ээ	10°	°	1?  p
14^
(Продолжение)
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В ГРАДУСАХ
	Ш				И Р	О	Г А				
	11°	12°	13°	14°	16°	16°	17°	10°	18э	20°	
0	11,07	12,09	13,11	14,14	16,18	16,21	17,2В	18,30	19.36	23,42	8
1	11,08	12,10	13,13	14,16	15,19	16,23	17,27	18.32	19.38	23,44	1
2	11,10	12,12	13.15	14.18	15,21	16,25	17 29	18.31	19,39	20.46	2
3	11,12	12,14	13.16	14,19	15,23	16.26	17.31	18,36	19,11	21,47	3
4	11,14	12,16	13,18	14,21	15.24	16.28	17,32	18.37	19.43	2Э.49	4
Б	11,15	12.17	13,zO	14,23	15.26	16,30	17,31	18,39	19,45	20.51	Б
в	11.17	12,19	13.22	14,24	15.28	16,32	17,36	18,11	19 46	20.52	6
7	11,19	12.21	13,23	14.26	15 39	16.33	17.38	18 13	19.48	20,54	7
в	11,20	12,22	13.25	14,28	15.31	16,35	17,1 >	18.41	19. X)	2') .56	6
9	11,22	12.24	13.27	14,30	15.33	16.37	17,11	18.46	19.52	20,58	9
10	11.24	12.26	13.28	14,31	16.35	16,38	17,43	18,46	19,54	2Р,6*	10
11	11.26	12,28	13,30	14,33	15,36	16,49	17.45	18,50	19,-55	2Ъ62	11
12	11,27	12,29	13,32	14,35	15.38	16,42	17.46	18,51	19.57	21.61	12
13	11,29	12.31	13.34	14.36	15 40	16.44	17.48	18,53	19.59	11 6.5	13
14	11,31	12,33	13,35	14,38	15.42	16.16	17,5'1	18.55	ПД»	29.67	14
1Б	11,32	12.34	13.37	14,40	15.13	16 47	17,52	18.57	19.62	21.68	1fi
16	11,34	12,36	13,39	14,42	15.15	16,49	17,53	18,58	19,64	20.70	16
17	11,36	12,38	13.10	14,43	15.17	16.51	17,55	I8 60	19.66	20.73	17
1В	11,37	12,40	13,12	11.45	15.18	16,52	17.57	18.62	19.68	2'74	18
19	11,39	12.-11	13,11	14,47	15.50	18,54	17,59	18,64	19.69	20.76	19
20	11,41	12,43	13,46	14.4В	16,62	16.56	17,60	18,66	19,71	20, Т.	20
21	11,42	12,45	13,17	14,50	15,54	16.58	17 62	18 67	19./3	20.79	21
22	11.44	12,46	13,49	11.52	15,56	16,59	17.61	18.69	19,75	20.81	22
23	11,4b	12,48	13.51	14,54	15,57	16,61	17,66	18,71	19,/6	2\8>.	23
24	11,48	12,50	13 52	14,55	15.59	16,63	17,67	18,72	19.78	2'31	24
25	11,49	12,52	13.54	14.57	15.61	19.65	17 69	18.71	19.8	2X86	2Б
26	11,51	12,53	13,56	14,58	15,62	16.66	17,71	18.76	19.82	2 >Xs	28
27	11,53	12,55	13,58	14.60	15.64	16 68	17 73	18.78	19.8-1	20,9'	27
28	11,54	12.57	13.59	14,62	15.66	16.70	17,74	18.8)	19 85	2-1.92	28
29	11,56	12.58	13.61	14,64	15,68	16,72	17,76	18.81	19,8/	21,9 i	29
30	11.SS	12,6’3	13.63	14.66	15,69	16,73	17,78	16,83	19,89	20,85	30
31	11,60	12.62	13.64	14.68	15,71	16 75	17.83	18,85	19,9)	20,97	31
32	11,61	12.64	13.66	14,69	15,73	16.7/	17.81	18.86	19,92	2.1.99	32
33	11,63	12.65	13,68	14,71	15.74	16,78	17.83	18.88	19 94	21,’Ю	33
34	11,65	12 67	13,70	14,73	15,76	16,80	17,85	18.9-	19,96	21,-12	34
ЗБ	11,66	12,68	13.71	14.71	15.78	16.82	17,87	18.92	19.98	21.04	ЗБ
36	11,68	12,70	13,73	14,76	15.8л	16,84	17,88	18,94	19,99	21,96	36
37	11,70	12.72	13,75	14.78	15,81	16.86	17,91	18,95	20,01	21J8	37
36	11.71	12,74	13.76	14,81	15,83	16.87	17,92	18.97	23,03	21.1)	38
39	11,73	12,75	13.78	14,81	15,85	16,89	17,94	18,99	29,05	21,11	39
43	11,75	12,77	13.80	14,83	16,8В	16,91	17,95	19,61	20.06	21.13	49
41	11,76	12,79	13,82	14,85	13.88	16,92	17,97	19,02	20.08	21,15	41
42	11,78	12.80	13,83	14,86	15.90	16,94	17,99	19.04	23.10	21.16	42
43	11,80	12,82	13,85	14.88	15,92	16.96	18,01	19,06	2).12	21,18	43
44	11,82	12.84	13 87	14.93	15,94	16.98	18.02	19,98	2J.14	21,2 -	44
4Б	11.83	12.86	13.88	14,92	15,95	16.99	18,04	19.09	20,15	21.22	4Б
46	11.85	12.87	13.93	14.93	15,97	17,01	18.06	19,11	23.17	21.21	46
47	11,87	12,89	13,92	14,95	15,99	17,03	18,08	19.13	20,19	21,26	47
48	11.88	12,91	13.94	14,97	16.00	17.05	18.09	19,15	20,21	21.27	40
49	11,99	12,92	13.95	11,98	16.02	17.07	18,11	19,16	20,22	21.29	49
tfl	11.92	12,94	13,97	1S.00	10.04	17,0В	10,13	19,18	20,24	21,31	БЗ
51	11,94	12,96	13,99	15.02	16,06	17.10	18.15	19,20	20,26	21,33	il
Б2	11,95	12,98	14,00	15,04	16,08	17,12	18,16	19.22	20,28	21.31	Б2
53	11,97	12,99	14,02	15,05	16,09	17,13	18.18	19,24	20,30	21,36	БЗ
54	11,99	13,01	14,04	15,07	16,11	17,15	18,2-0	19,25	20,31	21..38	14
ББ	12,00	13,03	14,06	15,09	16,12	17,17	18,22	19,2'	20,33	21,40	БЕ
50	12,02	13,04	14,07	15,10	16,14	1 ,18	18,23	19.29	20,35	21,42	66
57	12,04	13,06	14.09	15,12	16,16	17,20	18,25	19.30	23.36	21,43	67
Б8	12,06	13,08	14.11	15,14	16.18	17.22	18,27	19,32	20,38	21,45	Б9
59	12,07	13,10	14,12	16,16	16.20	17,24	18,24	19,34	20.49	21,47	89
	11°	12°	130	14°	11°	16°	17°	18°	18°	20°	
144
J jput ил.п t n-
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В ГРАДУСАХ
				ш	И Р	ОТА				37	° X
°	21°	22°	23°	24°	25°	26°	27'	26	2S		
	21 49	52,56	23,64	24,74	25,83	26,94	26,05	28,13	36,32	31,47	е
	91 «50	22,58	23,66	24.75	25.85	26,96	28,08	29.20	30,34	31,49	1
п 2	21,52	22Л>6	23,68	24,77	25,87	26,98	28,10	29,22	30,36	31,51	2
й S	21,54	22,62	23,70	24,79	25,89	27,00	28,12	29,24	30.38	31,53	3
"	4	21,56	22^63	23,72 23,74	24,81	25,91	27.02	28,13	29.26	30,40	31,55	4
В £	21,58	22.65		24,82	25,92	27,03	28,15	29,28	30.42	31,57	
S	21,59	22,67	23,75	24,84	25,94	27.05	28,17	29,30	30.44	31,59	6
7	21,61	22,69	23,77	24,86	25.96	27,07	28,19	29,32	30.46	31,61	
В	21'63	22,70	23,79	24,88	25,98	27.09	28,21	29,34	30.48	31 6 i	Б I
S	21,65	22,72	23,81	24,90	26,00	27,11	28,23	29,36	30,5?	31,65	S
1 10	21,67	22,74	23,82	24,92	26,02	27,13	26,24	29,38	35 52	31,68	1С
11	21,68	22,76	23,84	24,94	26,04	27,14	28,26	29,39	30,53	31,68	11
12	21,70	22,78	23,86	24,95	26,05	27,16	28,28	29,41	30,55	31,70	12
13	21,72	22,80	23,88	24,97	26,07	27,18	2830	29,43	30,57	31,72	13
14	21,74	22,81	23.99	24,99	26,09	27,20	28,32	29.45	30,59	31,74	14
1Е	21,76	22,83	23,92	25,01	26,11	27,22	28,34	29,47	30,61	31,76	15
16	21,77	22,85	23,93	25,03	26,13	22,24	28,36	29,49	30,63	31,78	16
17	2L79	22,87	23,95	25,04	26,15	27,26	28,38	29.51	30,65	31,69	17
18	21,81	22',88	23,97	25,06	26,16	27,28	28,40	29,53	30,67	31.82	1В
19	21.83	22,90	23,99	25,08	26,18	27,29	28,42	29,51	30,69 30,70	31,81	1S
29	21,64	22,92	24,01	26,10	26,20	27.31	28,43	29,55		31,86	20
21	21,86	22,94	24,02	25.12	26,22	27,33	28,45	29.58	30,72	31,88	21
22	21,88	22196	24,04	25,14	26,24	27,35	28,47	29,60	30,74	31.90	22
23	21,90	22,98	24,06	25,16	26,26	27,37	28,49	29,62	30,76	31,92	23
24	21,92	22,99	24,08	25,17	29,28	27,39	28,51	29,64	30.78	31,94	24
2Б 2В	21',93 21,95	23,01 23.03	24,10 24,12	25,19 25,21	26,29 26,31	27,40 27,42	28,53 28.55	29,66 29.68	30.81 30,82	31,96 31,98	25 2G
27	21/17	23,05	24,13	25,23	26,33	27,44	28 .<56	29,70	30,84	31, с9	27
26	21,99	23,06	24,15	25,25	26,351	27.46	28,58	29.72	39,86	32,01	28
29	22,00	23,08	24,17	25,26	26,37	27.48	28,60	29,74	30,88	32.03	29
80	22,02	23,10	24,10	25,20	26,39	27 ДО	28,62	29,75	30,90	32,05	30
31	22,04	23,12	24,21	25,30	24,40	27.52	28.64	29,77	30.92	32,07	31
32	22,06	23,14	24,22	25,32	26,42	27,54	28,66	29.79	30,94	32.09	32
S3	22.08	23',16	21,24	25.31	26,44	27,56	28,68	29.81	30,96	32,11	S3
S4	22,10	23117	24,26	25,36	26,46	27,57	28,70	29.81	30,97	32,13	34
ЗЕ	22,11	23,19	24,28	25,38	26,48	27,59	28,72	29,85	30,99	3 .*,1а	35
36	22,13 22,15	23,21	24,30	25,39	26,50	27,61	28,73	29,87	31,01	32,17	38
37		23,23	24,32	25,41	26,52	27.63	28.75	29.89	31,03	32.19	37
38	22,17	23,25	24,33	25,43	26,5.3	27,65	28,77	29.95	31,05	3 ',21	3S
39	22,18	23,26	24,35	25,45	26,53	27,67	28,79	29,92	31,07	32.23	3^
«	22,20	23.28	24,37	26,47	26,57	27,68	28,61	29,94	31,OS	32,24	40
41	22,22	23,30	24,39	25,48	26.59	27,70	28,83	29,96	31,11	.32,26	41
42	22’24	23,32	24,40	25,50	26.61	27,72	28,85	29,68	31,13	32,“8	42
43	22,26	23,34	24,42	25.52	26,63	27.74	28,86	30,00	31,15	32,30	41
44	22,27	23’,36	24,44	25,54	26,64	27,76	28,88	30,02	31.16	37,32	44
45	22,29	23,37	24,46	25,56	26,66	27.78	28,90	30,04	31,18	32,34	4Е
46	22,31	23,39	24,48	25,58	26,68	27,80	28,92	30,06	31,20	32,36	45
47	22,33	23,41	24,50	25,60	26,70	27.82	28,94	30,08	31,22	32,38	47
48	22,34	23.43	24,52	25,61	26,72	27,84	28,96	30,10	31,24	32,49	48
49	22,36	23.44	24,53	25.63	26,74	27,85	28,98	30.12	31.26	32,42	49
to	22,30	23,46	24,55	26,66	26,76	27,87	28,00	30,13	31 28	32,44	S9
£1	22,40	23,48	24,57	25.67	26,78	27,89	29,02	30,15	31,30	32,46	61
52	22.42	23,50	24,59	25,69	26,79	27,91	29,04	30,17	31.32	32,48	Б2
63	22,44	23,52	24,61	35,70	26,81	27.93	29.05	30,19	31,34	32,50	53
54	22,45	23,54	24,62	25,72	26,83	27,95	29,07	30,21	31,36	32,52	54
56	22,47	23,55	24,64	25,74	26,85	27,96	29,09	30,23 4	31,38	32,54	55
56	22,49	23,57	24,66	25,76	26.87	27,98	29,11	30,25	31,40	32.56	5S
Б7	22,51	23,59	24,68	25,78	26,88	28,00	29,13	30,27	31,42	32,58	57
58	22,52	23,61	24,70	25.80	35,90	28,02	29,15	30,28	31,44	32,60	58
59	22,54	23,62	24,72	25,62	26.92	78,04	29,17	38,30	31 45	32,61	^'3
у/*	21°	22°	23°	24°	25°	а°	270	2Е	29е	30°	
JO-1683
145
(Продолжение'
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В ГРАДУСАХ
				u	И P	о T					
											0 /
	IP	31°	33°	34°	35°	36°	37°	38°	33°	46°	/ t
0	32,63	33,81	34,93	36,19	37,45	39,63	39/8	41,14	42,42	43,71	8
А	32,65 32,67 32,69 32,71	33 83	35,01	36,21	37,42	38,65	39,90	41,16	42,44	43,73	1
2		33,85 33,86 33,88 33,90 33,92 33,94 33,96 33.98	35,03	36,23	37,44	38,68	39,92	41,18	42,46	43,76	2
2			35,05	36,25	37,47	38,70	39,94	41,20	42,48	43.78	3
			35,07	36,27	37,49	38,72	39,96	41,22	42,50	43,80	4
5			35/9	36,29	37/1	38,74	39,98	41/4	42/2	43,82	S
g	32,75 32,77 32,79 32,81 3 ,11		35,11	36,31	37,53	38,76	40,00	41,26	42,54	43,84	8
*]			35,13	36,33	37,55	38,78	40,02	41,28	42,56	43,86	7
g			35,15	36,35	37,57	38,80	40,04	41,31	42,59	43,88	6
д			35.17	36,37	37,59	38,82	40,06	41,33	42,61	43,91	9
18		34,00	36,19	36,39	37,01	38,54	40/9	41,35	42/3	43,93	10
If	32,85 32,87 32,89 32,91 32,92	34,02 34,04 34,06	35/1	36,41	37,63	38,86	40.11	41,37	42/5	43,95	11
flfll			35/3	36,43	37,65	38,88	40,13	41,39	42,67	43,97	12
1g			35,25	36,45	37,67	38,90	40,15	41,41	42,70	44,00	13
14		34,08	35^27	36,47	37,69	38,94	40,17	41,44	42,72	44/2	14
IS		34,10	35/9	36,49	37,71	38,94	40,19	44,46	42,74	44,04	18
16	32,94 32,96 32,98 33,00 33,02	34/2	35,31	36,51	37,73	38,96	40,21	41,48	42,76	44,06	11
17		34,14 34,16 34,18	35,33	36,53	37,75	38,98	40,23	41,50	42,78	44.08	17
IS			35,35	36,55	37,77	39,00	40,25	41,52	42,80	44,10	16
19			35,37	36,57	37,79	39,02	40,28	41,54	42,82	44,13	19
20		34,30	35,39	35,59	37,01	30,05	45,39	41,66	42,84	44,16	20
21	33,04 33,06 33,08 33,10	34,22	35,41	36/2	37,83	39,07	40,32	41,58	42,87	44,17	21
72		34/4	35,43	36,64	37,85	39,09	40,34	41,60	42,89	44,19	22
2J		34/6	35’45	36,66	37.87	39,11	40,36	41,62	42,91	44,21	23
24		34/8	35,47	36,68	37,90	39,13	40,38	41,65	42,93	44,24	24
26	33,12	34,'30	35,49	36,70	37,92	39,15	40,40	41,67	42,95	44/6	25
jfi	33,14	34/2	35/1	36,72	37,94	30,17	40,42	41,69	42,98	44,28	26
23	33,16	34,34	35/3	36.74	37,96	39,19	40,44	41,71	43,00	44,30	27
2S	33,18	34,36	35,55	36,76	37,98	39,21	40,46	41,73	43,02	44,32	29
29	33,20	34,38	35/7	36,78	38,00	39,23	40,48	41,75	43,04	44,34	29
30	33,22	34,40	35/9	36,&o	36,02	39,25	40,'O	41,78	43/6	44,37	30
31	33,24	34,42	35/1	36,82	38,04	39,27	40,53	41,80	43,08	44,39	31
32	33> 33,28 33,30	34 ,44	35,63	36,84	38,06	39,30	40,55	41,82	43,10	44,41	32
33		34,46	35/5	36 86	38,08	39,32	40,57	41,84	43,13	44,43	33
34		34,48	35,67	36,88	38,10	39,34	40,59	41,86	43,15	44,46	34
35	33,32	34/0	35,69	36,90	38,12	39,36	40,61	41,88	43,17	44,48	35
Ж	3334 33,36	34/2	35,71	36,92	38,14	39,38	40,63	41,90	43,19	44,50	36
37		34/4	35,73	36,94	38,16	39,40	40,65	41,92	43,21	44,52	37
31	33’38	34/6	35/5	36,96	38,18	39.42	40,67	41,94	43,23	44,54	31
31	33,40 11,41	34,58	35,77	36,98	38,20	39,44	40,70	41,97	43,26	44,56	39
48		34,00	35,П	37,00	30,2»	39,46	40,72	41,N	41,21	44,68	40
41	33,43	34,62	35,81	37,02	38,24	39,48	40,74	42,01	43,30	44,61	41
42	33,45	34/4	35,83	37,04	38,26	39,50	40,76	42,03	43,32	44/3	42
4Q	33/7 33,49	34,56	35,85	37,06	38,28	39,52	40,78	42,05	43,34	44,65	43
44		34,68	35,87	37,08	38,30	39,54	40,80	42,07	43,36	44,67	44
45	33’,51	34,70	35,89	37,10	38,32	39,56	40,82	42,10	43/(8	44,70	48
4C	33/3	34,72	35,91	37,12	38,34	39,58	40,84	42,12	43,41	44,72	46
47	33/5	34,73	35,93	37,14	38,36	39,61	40,86	42,14	43,43	44,74	47
44	33/7	34,75	35,95	37,16	38,39	39,63	40,88	42,16	43,45	44,76	40
43	33/9	34,77	35.97	37,18	38,41	39/5	40,93	42,18	43,47	44,78	49
50	33,61	34,79	35,19	37/0	38,43	39/7	40/3	42,20	44,30	44,81	SO
51 62	33,63 33,65	34,81 34,83	36,01 36,03	37,22 37,24	38,45 38,47	39/9 39,71	40,95 40,97	42,22 42,24	42,52 42,54	44,83 44,85	51 52
!3	33/7	34,85	36,05	37,26	38,49	39,73	40,99	42,26	42,56	44,87	53
54	33/9	34,87	36,07	37/7	38,51	39,75	41,01	42,29	42,58	44,89	54
55	33/1	34,89	36/9	37.30	38,53	39,77	41,03	42,31	4’,60	44,92	56
SB	33,73	34,91	36,11	37,32	38,55	39,79	41,05	42,33	42,62	44,91	56
57	33/5	34,93	36,13	37,34	38,57	39.83	41,07	42,35	42/5	44,96	57
58	33/7	34/5	36,15	37,36	38/9	39,81	41,10	42,37	42/7	44,98	58
59	33/3	34,97	36,17	37,38	38,61	30,96	41,12 1	42 39	42,69	45/0	59
//®	31°	32'	33°	34°	36°	36°	ЯР j	38“	39°	40°	
											0
146
( Продолжение)
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В ГРАДУСАХ
ШИРОТА
х	О											0 /
X	41°	42°	43°	44°	46°	46°	47°	48°	49°	50°	
0	45,03	46,36	47,72	49,10	58,60	51,92	63,38	54,86	60,37	*7,91	0
1	45.05	46,38	47,74	49,12	50,52	51,95	53,40	54,88	56,39	57,93	1
2	45,07	46,41	47,76	49,14	50,55	51,97	53.43	54.91	56,42	57,96	2
3	45,09	46,43	47,79	49,17	50,57	52,00	53,45	54,93	56,44	57,98	3
4	45',12	•16,45	47,81	49,19	50,59	52,02	53,48	54,96	56,47	58,01	4
5	45,14	46,47	47,83	49,21	50,62	52,04	53,50	54,98	56,50	58,04	6
6	45,16	46.50	47,86	49,24	50,64	52,07	53.52	55,01	56.52	58,06	в
7	15,18	46,52	47,88	49,26	50,66	52.09	53,55	55,03	56,55	58,09	7
9	45*20	46,54	47,90	49,28	50,69	52,12	53,58	55,06	56,57	58,12	8
9	45,22	46,56	47,92	49,30	50,71	52,14	53,60	55,08	56,60	58,14	9
10	45.25	46,69	47,86	49,33	60,74	52,17	63,62	56,11	56,62	68,17	10
11	45,27	46,61	47,97	19,35	50,76	52,19	53,65	55,13	56,65	58,19	11
12	45'29	46,63	47,99	49,38	50,78	52,22	53,67	55,16	56,67	58,22	12
13	45J2	46,65	48,02	49,40	50,81	52,24	53,70	55.18	56,70	58,24	13
14	45,34	46,68	18,04	49.42	50,83	52,26	53,72	55,21	56,72	58,27	14
15	15,36	46,70	48.06	49/4	50,85	52,29	53,75	55.23	56,75	58,30	1Б
16	45,38	46,72	48,08	19,47	50,88	52,31	53,77	55,26	56,78	58,32	16
17	45,40	46,74	18,11	49,49	50,90	52,34	53,80	55,28	□6,80	58,35	17
18	45,42	46,77	18,13	19,52	50,92	52,36	53.82	55.31	,56,83	58,38	16
19	45,45	46,79	18,15	49,54	50,95	52,38	53,84	55,33	•56,85	58,40	19
20	46,47	46,61	4В.13	49,56	60,97	52,41	53,87	55,36	36,80	68,43	26
21	45,49	46,83	48,20	48,58	51,00	52,43	53,89	55,38	56,90	58,46	21
22	45,51	46.86	48,22	49,61	51,02	52,46	53,92	55,41	56,93	58.48	22
23	45,54	46 83	48,24	49,63	51,04	52,48	53.94	55,43	56,96	58,51	23
24	45,56	46,91	48,27	49,66	51,07	52,50	53,97	55.46	56,98	58,53	24
25	45,58	46,92	48,29	49,68	51,09	52,53	53,99	55.48	57,00	58,56	25
26	45 6")	46,95	48,31	49,70	31,11	52,55	54,02	55,51	57,03	58,58	26
27	4о,62	46,97	48,34	49,72	51,14	52,58	54,04	55.54	57,06	58,61	27
08	45,65	46,99	48,36	49,75	51,16	52,60	54,07	55,56	57,08	58,64	28
29	45,67	47,02	48,38	49,77	51,18	52,62	54,09	55,58	57,11	58.66	29
30	45,69	47,04	4 В,40	49,80	51,21	52,65	54,12	16,61	57,13	50,69	39
31	45,71	47,06	48,43	49,82	51,23	52,67	54,14	55,64	57,16	58,72	31
32	45,74	17,08	18,45	49,84	51,26	52,70	54,16	55,66	57,18	58,74	32
33	4.5,76	47,10	48,47	49 86	51,28	52,72	54,19	15,68	57,21	58,77	33
34	45,78	47,13	48,50	49.89	51,30	52,74	54,21	55,71	57,24	58,80	34
35	45,80	47,15	48Л2	19,91	51,33	52,77	54,24	55,74	57,26	58,82	ла
36	45,82	47,17	18,54	49,94	51,35	52,80	54,26	55,76	57,29	58,85	
37	45,'5	47,20	48,56	49,96	51,38	52,82	54,29	55,79	57.31	58,87	at
ЗВ	45,87	47.22	48,59	49.98	51,40	52,84	54,31	55,81	57,34	58,90	л о
39	45,89	47,24	48,61	50.00	51,42	52,87	54,34	55,84	57,36	58,93	•SU
40	46,92	47,26	48,64	SC.03	51,46	S2.89	64,36	66,86	57,39	68,96	
*1	45,94	47,29	48,66	50,05	51,47	52,92	54,39	55,89	57.42	58,98	41 АО
42	4 ,96	47,31	48,68	50,08	51,50	52,94	54,41	55,91	57,44	59,00	
43	45,98	47,33	48,70	50,10	51,52	52,96	54.41	55,94	57,47	59,03	чл
44	46,00	47,36	48,73	50,12	51,54	52,99	54,46	55,96	57.49	59,06	AC
45	46,03	47,38	48,75	50,15	51,57	53,01	54,49	55,99	57,52	59.08	АП
4S	46,05	47,40	18,77	50,17	51,59	53,04	54,51	56,01	57,54	59,11	АО
47	46,07	47,42	18,80	50,19	51Д>2	53,06	54,54	56,04	57,57	59,15	48
4В	46,09	47,44	18,82	50,22	51,64	53,09	54,56	.56,06	57,60	59,16	49
49	46,12	47,47	18.84	50,24	51,66	>3,11	54,58	56,09	57,62	59,19	*n
50	46,1ч	47,49	48,86	50,26	51,00	53,14	64,61	16,12	67,65	59,22	
51	46,16	47,51	48,89	50,29	51,71	53,16	54,64	56,14	57,67	59,24	61
S2	46,18	47,54	48,91	50,31	51,73	53,18	54,66	56.16	57,70	59,27	52
53	46,20	47,56	48,94	50,33	51,76	53,21	54,68	56,19	57.73	59,30	S3
54	46,23	47,58	48,96	50,36	51,78	53,23	54,71	56,22	57.75	59,32	14
И	46,25	47,69	48,98	50,38	51,81	53,26	54,74	56,24	57,78	59,35	Б|
56	*6,27	47,63	49,00	50,40	51,83	53,28	54,76	56,27	57,80	59,37	во
17	46,30	47,65	49,03	50,43	51,85	53,30	54.78	56,29	57,83	59,40	*7
58	46,32	47,67	49,05	50,45	51,88	53,33	54,81	56.32	57,86	59,43	18
59	45,34	47,69	49,07	50,48	51,90	53,3В	24,83	66,34	57,88	80,46	59
	41°	| 42°	43°	44°	45°	46°	470	48°	49°	50°	
											о
10»
147
(Продолжение/
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В ГРАДУСАХ
		ш			И Р	О	Г А				
\ °									1		° /
\	51°	52°	53° |	54°	н°	56°	57°	53°	53° |	60° |	/
0	59,48	61,09	62.73	64,41	66,13	67.90	69,71	71,67	73,40	75,46	0
1	59,51	61,11	62,76	64,44	66.16	67,93	69,74	71,60	73,52	75,49	1
2	59,53	61,14	62.78	64,47	66,19	67.96	69.77	71,64	73,55	75,52	2
3	59,56	61.17	62,81	64,50	66,22	67,99	69,80	71,67	73,58	75,56	3
4	59,59	61,20	62,84	64,52	66,25	68.02	69,83	71,70	73,62	75,59	4
б	59,61	61,22	62.87	64,55	66,28	68,05	69,86	71,73	73,65	75 62	5
6	59,64	61,25	62,99	64,58	66,31	68,08	69,89	71,76	73,68	75,66	6
7	59,66	61,28	62.92	64,61	66,34	68,11	69,92	71.79	73,71	75,69	7
8	59,69	61,30	62,95	64,64	66,36	68,15	69.96	71,82	73,74	75,72	8
9	59,72	61,33	62,98	64,67	66,10	63,17	69,99	71,86	73,78	75,76	9
10	59,74	61,36	63,01	64,70	66,42	68,20	70,02	71,09	73,01	75,79	10
11	59,77	61,38	63,04	64,72	66,45	68,23	70,05	71,92	73,84	75,82	11
12	59,80	61,41	63,06	64,75	66,48	68,26	70,08	71,95	73,88	75,86	12
13	59,82	61,44	63,09	64,78	66,51	68,29	70,11	71.98	73,91	75,89	13
14	59.85	61,47	63,12	64,81	66,54	68.32	70,14	72,01	73.94	75,92	14
15	59,88	61,49	63,15	64,84	66,57	68,35	70,17	72,04	73,97	75,96	15
16	59,93	61,52	63.17	64,86	66,60	68,38	70,20	72,08	74,00	75,99	16
17	59,93	61,55	63.2С	64,90	66,63	68,41	70,23	72,11	74,04	76,02	17
1S	59,96	61,58	63,23	64,92	66,66	68,41	70,26	72,14	74,07	76,06	10
19	59,98	61,60	63,26	64,95	66,69	68,47	70,30	72,17	74,10	76,09	19
20	00,61	61,63	63.29	64,98	68,72	68,60	70,92	72,20	74,14	70,13	20
21	60,04	61,66	63,31	65,01	66,74	68,53	70,36	72,24	74,17	76,16	21
22	60,06	61.68	63,34	65,04	66,78	68,56	70,39	72,27	74,20	76.19	22
23	60,09	61.71	63,37	65.06	66,80	68,59	70,42	72,30	74,23	76.23	23
24	60,12	61,74	63,40	65,10	66.83	6«,62	70,4>	72,33	74,27	76,26	24
26	60,14	61,77	63,42	65,12	66.86	68,65	70,48	72,36	74,30	76,30	2£
26	60,17	61,79	63,45	65.15	66,89	68,68	70,51	72,40	74,33	76,33	26
27	60,20	61,82	63,48	65,18	66,92	68,71	70,54	72,43	74,36	76,36	27
28	60.22	61,85	63,51	65,21	66,95	68,74	70,57	72,46	74,40	76,40	29
29	60,25	61,88	63.54	65,24	66,98	68,77	70,60	72,49	74,43	76,43	29
30	60,28	61,90	63,56	65,27	67,01	68,80	70,64	72,62	74,46	76,40	39
31	60,30	61,93	63,59	65.30	67,04	68,83	70,66	72,55	74.50	76,50	31
32	60,33	61,96	63,62	65,32	67,07	68,86	70,70	72,58	74,53	76,53	32
33	60.36	61,98	63,65	65,35	67,10	68,89	70,73	72,62	74,56	76,56	33
34	60,39	62,01	63,68	65,38	67,13	68,92	70,76	72.65	74,60	76,60	34
35	60,41	62.04	63,70	65,41	67,16	68,95	70,79	72,68	74,63	76,63	35
3G	60,44	62,07	63,73	65,44	67,19	68,98	70,82	72,71	74,66	76,67	36
37	60,47	62,10	63,76	65,47	67,22	69,01	70,85	72,74	74,69	76.70	37
38	60,49	62,12	63,79	65,50	67,24	69,04	70,88	72,78	74.73	76,74	36
39	60.52	62,15	63,82	65,52	67,28	69,07	70,92	72,81	74,76	76,77	39
40	60,66	62,18	63.84	&s,s:	67,30	69,10	70,94	72,84	74,79	76,80	40
41	60,57	62,20	63.87	65,58	67,34	69.13	70,98	72,87	74,82	76,81	41
42	60,60	62,23	63,93	65,61	67,36	69,16	71,01	72,93	74.86	76,87	42
43	60,63	62.26	63,93	65,64	67,39	69,19	71,04	72,94	74,89	76,90	43
44	60,66	62,29	63.96	65,67	67,42	69,22	71,07	72.97	74,92	76,94	44
45	69,68	62.32	63,99	65,70	67,45	69,25	71,10	73,00	74,96	76,97	46
46	60,71	62,31	64,02	65,73	67,48	69.28	71,13	73,03	74,99	77,01	46
47	60,74	62,37	64,04	65,76	67,51	69.31	71,16	73,07	75,02	77,04	47
48	60,76	62.40	64,07	65,78	67,54	19,34	71,20	73,10	75,06	77,08	48
49	60,79	62.42	64,10	65,81	67,57	69,38	71.23	73,13	75,09	77,11	49
60	60,82	62,46	64.13	65,84	67,60	60,40	71,26	73,16	75,12	77,14	50
51	60,84	62,48	64.16	65,87	67,63	69.44	71,29	73,20	75.16	77,18	51
52	60,87	62.51	64,18	65,90	67,66	69,47	71,32	73,23	75.19	77,21	S2
S3	60.90	62,54	64,21	65,93	67,69	69.50	71,35	73,26	75,22	77,25	53
54	60,92	62,56	64,24	65,96	67,72	69,53	71,38	73.29	75,26	77,28	54
66	60,95	62,59	64,27	65,99	67,75	69,56	71.42	73,32	75,29	77,32	56
56	60.98	62,62	64,30	66,02	67,78	69.59	71,45	73,36	75,32	77,35	S6
17	61,00	62,65	64,32	66,04	67,81	69,62	71,48	73,39	75,36	77,38	57
Б8	61,03	62,67	64,35	66,08	67,81	69,65	71,51	73.42	75,39	77,42	88
59	61,66	62,70	64,38	66,10	67,87	В9,62	71,64	73,45	75.42	77.45	69
	S1°	52°	53°	54°	ss°	ИР	67°	58°	59°	60е	
148
I
(Продолжение)
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В ГРАДУСАХ
	ш				И Р	О	Г А				
\ °											° /
X	61°	62°	63°	64°	65°	66°	67°	68°	69°	70°	S
0	77,40	79,58	81,75	83,99	80,31	68.72	61,23	93,85	96,18	99,43	0
1	77,52	79.62	81,78	81.03	86,35	88.77	91,28	93,89	96,62	99,48	1
2	77*56	79,65	81,82	84.07	86,39	88,81	91,32	93,94	96,67	99,53	2
з	77*59	79,69	81,86	84,10	86,43	88.86	91,36	93,98	96,72	99,58	3
(	4	77,62	79,72	81,90	84,14	86,47	88,89	91,40	94,02	96,76	99,63	4
с	77^66	79,76	81,93	84,18	86,51	88,93	91,45	94,07	96,81	99,68	5
6	77*69	79,80	81.97	84,22	86,55	88,97	91,49	94,12	96,86	99,72	6
7	77,73	79,83	82.01	84,26	86,59	89.01	91,53	94,16	96,90	99,77	7
8	77,76	79,87	82,04	84.30	86,63	89,05	91,58	94,20	96,95	99,82	8
8	77»80	79,90	82,08	84,33	86,67	89,10	91,62	94,25	97,00	99,87	9
10	77,03	73.94	82,12	84,37	86,71	69,14	61,66	94,29	97,04	99,92	10
11	77,87	79,97	82,15	84,41	86,75	89,18	91,70	94,34	97,08	99,97	11
12	77,90	80,01	82,19	84,45	86,79	89.22	91,75	94,38	97,14	100,02 130,07	12
13	77,94	80,05	82,23	84,49	86,83	89,26	91,79	94,43	97,18		13
14	77,97	80,08	82,26	81,52	86,87	89,30	91,83	94,47	97,23	100,12	14
15	78,00	80,12	82,30	84,56	86,91	89,34	91,88	91,52	97,28	100,17	15
18	78*04	80.15	82,34	84,60	86.95	89,38	91,92	94,56	97,32	100,22	18
17	78.07	80,19	82,38	84,64	86,99	89,42	91.96	94,61	97,37	100,27	17
16	78,11	80,22	82,41	84,68	87,03	89,47	92,01	94,65	97.42	100,32	18
19	78,14	80,26	82,45	84,72	87,07	89,51	92.05	94,70	97,47	100,36	19
20	78,18	60,30	82,49	84,76	87,11	69.56	92,00	94,74	97,61	106,42	20
21	78,21	80,33	82,52	84,79	87,15	89,59	92,14	94,79	97,58	100,46	21
22	78,25	80,37	82,56	84,83	87,19	89,63	92,18	94,83	97,61	100,51	22
23	78,28	80.40	82.60	84,87	87,23	89,68	92,22	94,88	97,66	100,56	23
24	78,32	80,44	f<2,64	84,91	87,27	89,72	92,26	94.92	97,70	100,61	24
25	78,35	80,48	82,67	84,95	87,31	89,76	92,31	94,97	97,75	100,66	25
28	78,39	80,51	82,71	84,99	87,35	89,80	92,35	95,02	97,80	100,71	26
27	78',42	80,55	82,75	85,02	87,39	89,84	92,40	95,06	97,84	100,76	27
28	78,46	80,58	82,78	85,06	87,43	89,88	92,44	95,10	97.89	100,81	28
29	78,49	80,62	82,82	85,10	87,47	89,92	92.48	95,15	97,94	100,86	29
»0	78’53	00,66	82,86	65,14	87,51	89,97	92,53	98,20	97,90	100,91	33
31	78,56	80,69	82,90	85,18	87,55	90,01	92,57	95,24	98,04	100,92	31
32	78',60	80,73	82,94	85,22	87,59	90,05	92,61	95,29	98,08	1 >1,01	32
33	78*63	80.76	82,97	85,26	87,63	90,09	92,66	95,33	98,13	101,06	33
34	78,67	80,80	83,01	85,30	87.67	90,13	92,70	95,38	98,18	101,11	34
35	78.70	80,84	83,05	85.34	87,71	90.17	92,74	95,42	98,22	101,16	35
36	78,74	80,87	83,08	85,37	87,75	90,22	92,79	95,47	98,27	101,21	36
37	78,77	80,91	83,12	85,41	87,79	90.26	92,83	95,52	98,32	101,26	37
38	78,81	80,95	83,16	85,45	87,83	90,30	9238	95,56	98,37	101,31	38
36	78*84	80,98	83.20	85,49	87,87	90,34	92,92	95,61	98.42	101,36	39
40	78,88	81,02	33,24	85,53	87,91	90,39	82,66	16,65	98,46	101,41	40
41	78,91	81,06	83,27	85,57	87,95	90.43	93,01	95,70	98,51	101,46	41
42	78,95	81,09	83,31	85,61	87,99	90,47	93,05	95,74	98,56	101,51	42
43	78’,98	81,13	83,35	85,65	88,03	90,51	93,10	95,79	98,61	101,56	43
44	79,02	81,16	83,38	85.68	88,07	90,56	93,14	95,84	98,66	101,62	44
45	79,05	81,20	83,42	85,72	88,11	90,60	93,18	95,88	98,70	101,66	45
46	79,09	81,24	83,46	85,76	88,15	90.64	93,23	95,93	98,75	101,72	46
47	79,12	81,27	83,50	85,80	88,19	90,68	93,27	95,98	98,80	101,77	47
48	79,16	81,31	83,54	85,84	88,24	90,72	93,32	96,02	98,85	101,82	48
49	79.19	81,36	83,57	85,88	88,28	90,77	93,36	96,07	98,90	101,87	49
so	70.23	81.38	83,61	65,92	98,32	90,01	93,40	66,11	98,95	101,92	50
51	79,26	81,42	83,65	85,96	88,36	90,85	93,45	96,16	99,00	101,97	и
52	79£0	81,46	83,69	86,00	88,40	90,89	93,49	96,20	99,04	102.02	52
КЗ	79,34	81,49	83,72	86,04	88,44	90,94	93,54	96,25	99,09	102,07	ВЗ
54	79,37	81 £3	83J6	86,08	88,48	90.98	93,58	96,30	99,14	102,12	54
55	79,40 79,44	81,56	83,80	86,12	88.52	91,02	93,62	96,34	99,19	102,17	55
56		81,60	83,81	86,16	88,56	91.06	93,67	96,39	99,24	102,22	56
57	79,48	81,64	83,88	86,20	88,60	91,10	93,71	96,44	99,29	102,28	57
во м	79,51 79,85	81,68 81.71	83,92 83,45	86,24 86,27	88.64 88.68	91.15 91.19	93,76 63,80	96,48 96,53	99,34 89,38	102,33 102.38	58 1"
	61°	62°	63°	64°	65°	66°	67°	68°	69°	70°	° 'ч
149
{Продолжение)
( Продолжение)
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В ГРАДУСАХ
МЕРИДИОНАЛЬНЫЕ ЧАСТИ В ГРАДУСАХ
				ш	И Р	О	1’ А					—
\	| 71°	72°	73°	74°	78°	76°	770	78°		79°	80°	
0 1 2 3 4 .	5 •	6 7 6 8 10 ; и 12 13 14 18 16 17 1	10 1 19 20 21 22 23 24 2S 26 27 |	28 29 30 31 32 33 34 36 36 37 38 39 40 41 42 43 44 4Е 46 47 48 49 50 S1 52 S3 54 5S 56 57 68 59	102,43 102,48 102,53 102,58 102,63 102,68 102.74 102,79 102,84 102,04 102,84 102,99 103,04 103,10 103.15 103.20 103,25 103,30 103,36 103,41 103,46 103,51 103.56 103.62 103.67 103,72 103.78 103.83 103.88 103,93 103,88 104,04 104,09 104,14 104,20 104,25 104,30 104,35 104,40 104,46 104.61 104,56 104,62 104,67 104.72 104,78 104,83 104,88 104,94 104,99 186,04 105,10 105,15 105,20 105,26 105,31 105,36 105.42 105,47 108,83	106.88 105,64 105,69 105,74 105.80 105,85 105,90 105,96 106,01 106,07 106,12 106,18 106,23 106.29 106,34 106.40 106,45 106,50 106,56 106,62 106,67 106.72 106,78 106,83 106.89 106.94 107.00 107.06 107.11 107,16 107.22 107,28 107,33 107,39 107,44 107,50 107,56 107,61 107.67 107.72 107,78 107,83 107.89 107,94 108,00 108.06 108.12 108.17 108,23 108.28 108.34 108.40 108.45 108,51 108.57 108,62 108.68 108.74 108,79 108,05	108,01 108.96 109,02 109.08 109.14 109.19 109.25 109,32 109,36 109,42 109,48 109,54 109.60 109,65 109.71 109.77 109.83 109,88 109.91 110,00 110,06 110,12 110,18 110.23 110,29 110,35 110,41 110,47 110.52 110,58 110.64 110,70 110,76 110.82 110,88 110,91 111.00 111.06 111.11 111,17 111,23 111,2'1 111,35 111,41 111,47 111,53 111,59 111.65 111,71 111,77 111.83 111.89 111,95 112.01 112,07 112,13 112.19 112.25 112.31 112.37	112,43 112,49 112,55 112.61 112.67 112,73 112.79 112,85 112.92 112.98 113,04 113.10 113,16 113.22 113,28 113,34 113.40 113.47 113.53 113.59 113,66 113.71 13.78 H3.8I 113,9' 113,96 111.02 114.08 114.15 114.21 114,27 114.33 111.40 114,46 111.52 114,58 114.65 114.71 114,77 114.84 114,00 114,96 115,02 115,09 115.15 115.21 115,28 115,34 115.40 115.47 116.53 115.60 115.66 115.72 115,79 115,85 115,92 115,98 116,04 116,11	116.17 116.21 116,36 116,36 116,4.5 116.50 116.56 116.62 116.69 116,76 116.82 116.88 116,95 117,02 117.08 117.15 117,21 117,28 117,34 117,41 117.48 117.54 117.61 117.67 117,71 117 80 117.87 117,94 118 00 118.07 118.14 118.20 118.27 118.34 118.10 118,17 118,54 118.60 118,67 118,71 118,82 118,87 118.91 119.01 119,08 119.14 119.21 119.28 119,35 119.42 119,48 119,55 119.62 119.69 119.76 119,82 119.89 119.96 120.03 120,10	120,1- 120,24 123.3 ' 120,38 120,4-1 120,51 123,58 120.65 120.72 120.79 120.86 12.3,93 121,00 121.07 121.11 121.21 121.28 121.35 121.42 121.19 121.56 121 63 121,70 121.77 121 84 121 92 121.96 122.06 122,13 122.23 122.27 122.31 122.12 122.49 122.56 122.63 122,70 122,77 122.84 122.9"' 122.99 123.06 123.14 123.21 123.28 123.35 123.42 123.50 123.57 123.61 123,72 123,79 123.86 123,91 124.01 124.08 124.16 124.23 124.33 124,38	124.45 124.53 124.63 124.68 121.75 124.82 124.9 124,98 125,05 125.12 125.20 125.27 125,35 125.42 125.50 125,5- 125.65 125,63 125.81 125.88 125.96 126.03 126.11 126.18 126.26 126.33 126.11 126.49 126.56 126.64 126.72 126.80 126.87 126.95 127.03 127.10 127,18 127,26 127.34 127.42 127,50 127.57 127.65 127,73 127,81 127.88 127.96 128.04 128.12 128,23 128.28 128.36 128,14 128,52 128.60 128.68 128.76 128.83 128.92 129,00	129.08 129.16 120,21 12932 129.43 129,18 1’9/6 129,61 129 72 129 80 129.38 129,96 130,95 130,13 133.21 133.29 133.37 130.46 130.51 133,62 13»,70 133.78 130.87 130.95 131.13 131.12 131.20 111.28 131.36 1-31.45 131,53 131.62 131.70 131.78 131.87 131.93 132.04 132.12 132.20 132.29 132,37 132.46 132.54 132.63 132.71 132.80 132.88 132.97 133.06 133.14 133,23 133,31 133.10 133,49 133.57 133.66 133.75 133.83 133,92 134,01		134.10 131,18 131.27 111,36 131,11 111.53 1.34 62 1 41.71 131.83 134.89 134.98 135.06 135.15 135,24 135.33 135.42 135,51 135.61 135.69 135.78 133.37 135.96 136,0.5 136.11 136.23 136.32 136.41 136.5"' 136.59 136.68 136,78 136,87 136,96 137.05 137,14 137,24 137.33 137,42 137,51 137.60 137,70 137.79 137.88 137.98 138.07 138,16 138,26 138.35 138.45 138.54 138.64 138.73 138.82 138.92 139.01 139.1) 139.20 139.30 139.40 139.49	139,59 139 68 1 '-9.78 119.84 139.9/ 111,07 110,16 14--.26 140.16 UO.it 140,66 140.65 140,7 140.8’ 110.91 111.01 1I1.H 141.24 141.3' 141,41 141,64 1 П .61 111.71 111.91 1 >1.9< 142,01 142.1' 112.2 112.3 X. 142.11 142,54 142,64 14 '.74 142.84 142.94 113.9" 143,1 143.25 143.3' 143.41 143.56 143.66 143.76 113.8, 113.9; 144,ПЯ 114.18 141.28 141.39 144,49 144.6J 144.70 144.8 144.91 145.02 145.1.’ 145.2.1 145.33 145.41 145,54	0 1 2 3 - 7 8 9 10 11 12 13 14 1S 16 17 10 19 20 21 0 22 J 23 24	| 25 26 27 ? 28 29 30 31 4 32 I 33 | 34 g 36 й 3S 37 39 39 43 41 42 43 44 45 46 47 49 49 50 SI Е2 S3 64 | 55 56 57 EO 59 I
	71°	72°	73°	740	7Б°	7G	77о	78°		73°	80°	°
ш и					P о	T	1.			
	01°	82°	83°	84°	85°	86°	87°	88°	89°	
0	140,05	152,42	180.10	160.98	170.41	1 132,21	1 208,70	231.94	271,66	0
*1	145,76	152,54	160,23	169,11	179.60	192,45	209,02	232,42	272,62	1
2	145’86	152,66	169,37	169,27	179,79	192,69	209,34	232,90	273,60	2
3	145,97	152,78	160,51	169,43	179.99	192,93	209,66	233.39	274,60	3
4	146,08	152,95	160,65	169,59	181,18	193.17	209,99	233.88	275,61	4
s	146.19	153.03	160,78	1, 9.7.>	18 ),38	193,42	210,32	234.38	276,64	E
в	146,29	153.15	160,92	169.91	18),5/	193.66	210,64	234.88	277,70	6
7	146,40	153.27	161,66	170,08	18 1,76	193,91 194,15	210,68	2 3o,33	278,77	7
8	146,51	153.39	161.20	170,24	180,96		211,31	235,90	279,86	8
9	146,62	153,51	161.34	170,40	181.1«	194,4)	211,64	236,41	280,97	9
10	146,73	113,64	161.48	170,56	101.36	194,65	211.98	238.93	262,11	10
11	146,84	153,76	161.62	170,73	181,55	194,93	212,32	237,45	283,26	11
12	146,94	153,88	161,76	170,89	181,75	195.15	212,66	237.98	284.44	12
13	147,05	154,00	161,9J	171.16	181,9 j	195,40	213,00	238,51	285,65	13
14	147,16	154.12	162.04	171,22	182,15	195.65	213,34	239.05	286,88	14
15	117.27	154,25	162,18	171.39	182,3o	195,91	213/9	239.59	288,14	15
16	147,38	154,37	162,33	171.56	182,56	196,16	214,04	240,14	289.43	IB
17	147,49	154,50	162,47	171,72	182,76	196,42	214,39	240.70	290,75	17
18	147.60	154,62	162,61	171,89	182,96	196,68	214,74	241,25	292,10	10
19	147,71	154,74	162,76	172,06	183,16	196.94	215,10	241,82	293,48	18
20	147,82	184,87	162,00	172,23	163,37	197,20	218,48	242,39	294,89	20
21	147,93	155,00	163,04	172,40	183,57	197,46	215.81	242,96	296,34	21
22	148,04	155.12	163,19	172,57	183,78	197,72	216,17	243,55	297,83	22
23	148,16	155,25	163,33	172,74	183.90	197,98	216,54	244,13	299.36	23
24	148,2/	155,37	163,48	172,91	184,18	198,25	216,90	244,73	300,93	24
25	148.38	155,50	163,62	173,08	184,41	198,52	217,27	245,33	302,54	2E
26	148,49	155,62	163,77	173,25	184,61	198.78	217,64	245.94	304,20	26
27	148,60	155,75	163,91	173,42	184,82	199,04	218,02	246,55	305,91	27
28	148,71	155,88	164,06	173,6'1	185,03	199.32	218,39	247,17	307,68	28
29	148.83	156,00	164.20	173,77	185 24	199.59	218,77	247.79	309.50	28
30	148.04	186,13	164.38	173,94	(85,45	199,96	219,15	248,43	311.36	30
31	149,05	156,26	164.50	174.12	185.67	200,14	219,54	249,07	313.32	31
32	149'16	156,39	164,65	174,29	185,88	200.41	219,92	249,71	315,33	32
33	149.28	156.52	164,80	174,46	186.10	200,69	220,31	250,37	317,41	S3
34	149,39	156.65	164,94	174,64	186.31	200,97	220.70	251,03	319,57	34
35	149.50	156,78	1 5,09	174,82	186.53	291,25	221,10	251,70	321,82	3E
36	149,62	156,90	165,24	175,00	186,74	201,53	221.49	252,38	324.16	38
37	149,73	157,04	165.39	175.17	186,96	201,81	221.89	253,06	326,60	37
38	149,85	157.16	165,54	175,35	187.18	202,09	222,28	253,76	329,14	38
39	149,96	157,29	165.69	175,53	187,40	202,38	222.70	254,46	331,81	39
4J	100,08	157,42	165,84	176,71	187,62	202,66	223,11	255,18	334,61	40
41	150,19	157,56	166.00	175,89	187,84	202,95	223,52	255,90	337,54	41
42	150.31	157.69	166,15	176,07	188,06	203,3-1	223,93	256.63 25736	340,64	42
43	150,42	157,82	166,3 >	176.25	188.28	203,53	224,3a		343,92	43
44	150,54	157,95	166.45	176.43	188,51	203,82	224,77	258,12	347,39	44
45		158,08	166,60	176.61	188,73	204,11	225.19	258,87	351,09	45
46	150.77	158,21	166,76	176.79	188.96	204,41	2 5.62	259,64	355.04	46
47	150,89	158,35	166.91	176.98	189.18	204,70	226,04	260.42	359,29	47
48	151,00	158.48	167.06	177.16	189,41	205,00	226,48	261,21	d63,88	|	48
49	151,12	158,61	167,22	177,34	189,61	205.30	226.91	262,01	368,86	
SO	151,24	158.74	187.38	177.83	189,87	2i6,63	227,36	262,83	374,32	
51	151,36	158.88	167,53	177.72	190,10	205,93	"227,80	263,65	380,36	51
Б2	151,47	159.01	167.69	177.9 ।	199.33	206,21	228,24	264.49	387,11	62
S3	1 il ,59	159.15	lb7.84	178/9	191,56	206.52	228.69	265,34	394,76	S3
64	151,71	159,28	168/6	178.28	190.79	206.82	229,14	266,20	403,59	55
55	151,83	159,42	168,16	178.16	191,03	207.13	229,60	267.07	414,04	
56	151.95	159.55	168,11	178,65	191,26	207.41	230,06	267,96		
57	152,07	159,69	168.47	178,84	191,50	207,76	230,51	268,86	443,30	S3
58	152,18	159,82	168.63	179.03	191,73	208,07	230,99	269,78	466,-54	
59	152,30	109,08	168,79	173,22	191,87	206,36	231.48	270,71		
	81°	82°	83°	84°	05°	86°	87J	88°	89°	
151
150
М		 	 	 	 	 		 Сл г»₽мл олги». -	ПРИЛОЖЕНИЕ 11 ,			 СХЕМА РАСЧЕТА ЛОКСОДРОМИИ а	—.	- — , ..					
1	Москва I	Нью-Йорк	х3 х,	37°34' —74°00'	ф2 «Pi	55°47' 40°43'	£>3 =	4050', 7 £>,=	2679', 1
Формулы 1. tga =	~ Х’]' Г^2-А]' 2.S= 1852’sec а [<р3 — 3.0 = ZX1 + ctge0[X-X1]	п2~ [Х? — X,]' Jg Р;2 — X,] 1g [£>2~£),] Igtg® а	111°34' 6694 3.82569 3.13723 0.68846 78°25'	[Фз— Ф1] [%—?,]' 1g >2-9,]' 1g sec а0 Ig 1.852 IgS o KM	15°04' 904' 2.95617 0.69725 0.26764 3.92106 8.338	£>3 — £>, =	1371',6
					Схема маршрута
					Москва 5=8342 КЛ1		-0
•					О'		 Н ЬЮ-Йорк	!
РАСЧЕТ КООРДИНАТ ПРОМЕЖУТОЧНЫХ ТОЧЕН ЛОКСОДРОМИИ
х° . [Х-Х,]' Ig [х-М , 1g Ctg а0 1g Ctga0[X —X,] Ctg a0 [X — X] £>i D	—74°00' —74W 40°43'	-60°00' —74°00' 840' 2.92428 9.31168 2.23956 172.2 2679.1 2851.3 42°51'	—50°00 —74°00 1440' 3.15836 9.31168 2.47004 295.1 2679.1 2974.2 44° 20'	—40°00 —74°00 2040' 3.30963 9.31168 2.62131 418.1 2679.1 3097.2 45°46'	—30°00 —74°00 2640' 3.42160 9.31168 2.73328 541.1 2679.1 3220.2 47012'	—20°00 — 74°00' 3240' 3.51055 9.31168 2.82223 664.1 2679.1 3343.2 48°34'	—10°00' —74°00' 3840' 3 58433 9.31168 2.89601 787.1 2679.1 3466.2 49°55'	0° —74°00' 4440' 3.64738 9.31168 2.95906 910.0 2679.1 3589.1 51°13'	10°00' —74°00' 5040' 3.70243 9.31108 3.01411 1033.0 2679 j 3712.1 52O29<	20°00 —74°00 5640' 3.75128 3.31168 3.06296 1156.0 2679.1 3835.1 53°43'	30°00 —74°00 6240' 3.79518 9.31168 3.10686 1279.0 2679.1 3958.1 54°54'	37°34' —74°00' 6694' 3.82569 9.31168 3.13737 1372.1 2679.1 4051.2 55°47'
ПРИЛОЖЕНИЕ 12
СХЕМА ВЫЧИСЛЕНИЯ КООРДИНАТ ТОЧЕК ЛИНИИ РАВНЫХ АЗИМУТОВ
(широтный способ)
Координаты радиостанции To = 56030* Xo = 38°30*			Азимут П = 80о		Формулы			
					tg X = COS A) - ctg Фо sill 0 = sin • cos		sin у = ctg П  ig » <p = 90- (*+»	
		40030*	42°30*	44°3C*	46°30*	48°30*	50°30'	52030*
№№								14°
no nop.	AX	2°	4°	6°	8°	10°	12°	
4	1g cos AX	9.99974	9.99894	9.99761	9.99575	9.99335	9.99040	9.98690
2	1g ctg tp0	9.82078	9.82078	9.82078	9.82078	9.82078	9.82078	9.82078
6	Igtgx	9.82052	9.81972	9.81839	9.81653	9.81413	9.81118	9.80768
5	Ig sin AX	8.54282	8.84358	9.01923	9.14356	9.23967	9.31788	9.38368
3	1g cos <p0	9.74189	9.74189	9.74189	9.74189	9 74189	9.74189	9.74189
7	Ig sin 0	8.28471	8.58547	8.76112	8.88545	8.98156	9.05977	9.12557
8	Ig tg »	8.28479	8.58579	8.76185	8.88673	8.98358	9.06265	9.12950
1	Ig ctg П	9.24632	9.24632	9.24632	9.24632	9.24632	9 24632	9.24632
9	Igsiny	7.53111	7.83211	8.00817	8.13305	8.22990	8.30897	8.37582
10	У	0°12'	0°23'	0°35'	0°47'	0°58'	l°10'	1°22'
11	X	33°29'	33°26'	33°21'	33°15’	33°06'	32°55'	32°43'
12	x+y	33°41'	33°49'	33°56'	34°02'	34°04'	34°05'	34°05'
13		56° 19'	56°11'	56°04'	55°58'	55°56'	55°55'	55°55'
СП
СХЕМА ВЫЧИСЛЕНИЯ КООРДИНАТ ТОЧЕК ЛИНИИ РАВНЫХ АЗИМУТОВ
(долготный способ)
Координаты радиостанции <ро=ь56°ЗО» 10 = 38°30»			Азимут П = 20°		Фо tg x = ctg П  cosec <p sin 8 = sin П • cos		рмулы cos у = tg фо • tg » Ф	ДХ 5= X -f- у	
№№ по пер.		57030»	58°33*	59°30'	60°3T	61°3(У	62’30*	63030*
1	lg ctg п	0.43893	0.43893	0.43893	0.43893	0.43893	0.43893	0.43893
4	cos lg sin <p	0.07397	0.06923	0.06468	0.06030	0.05610	0.05207	0.04821
6	lg tgx	0.51290	0.50816	0.50361	0.49923	0.49503	0.49100	0.48714
2	lg sin П	9.53-105	9.53405	9.53405	9.53405	9.53405	9.53405	9.53405
5	lg cos cp	9.73022	9.71809	9.70547	9.69234	9.67866	9.66441	9.64253
7	lg sin 8	9.26427	9.25214	9.23952	9.22639	9.21271	9.19846	9.18358
8	IgtgO	9.27172	9.25919	9.24617	9.23266	9.21857	9.20394	9.18869
3	lg tg <Po	0.17922	0.17922	0.17922	0.17922	0.17922	0.17922	0.17922
9	lg cos у	9.45096	9.43841	9.42539	9.41184	9.39779	9.38316	9.36791
10	У	73°36'	74°04'	74°33'	75° 02’	75°32'	76°01'	76°31'
11	X	72°56'	72°46'	72°35'	72°25'	72° 16'	72°06'	71°57'
12	У + (- X}	0°40'	1°18'	1<>58'	2°37'	3°16'	3=55'	4°34'   —
lOJYOV / ЧАЭоневс]/ oOl об 08 ci o9 oS of c8 оЪ ol /St /08 /SI	/ / вгоДипт	80°	ОД	0,.	0,4	0,5	1,0	1,5	2,0	2,5	3,0	3,4	3,9	4,4	4,9 85°	0,1	0,2	0,4	0,5	1.0	1.5	2,0	2,5	3,0	3,5	4,0	4,5	5,0 90°	0,1	0,3	0,4	0,5	1,0	1,5	2,0	2,5	3,0	3,5	4,0	4,5	5,0	75°	| О.| 0,2 о,4 | <45 1.<> 1,5 1.9 2,4 | 2,9 3,4 3.9 4.3 4.3	34	0,1	0,1	0,2	0,3	0,6	0,8	1,1	1,4	1,7	2,0	2,2	2,5	2,8 38	0,1	0,2	0,2	0.3	0,6	0,9	1,2	1,5	1,8	2,2	2,5	2,8	3,1 42	0,1	0,2	0,3	0,3	0,7	1,0	1,3	1,7	2,0	2,3	2,7	3,0	3,3 46	0,1	0,2	0,3	0,4	0,7	1,1	1,4	1,8	2,2	2,5	2,9	3,2	3,6 50°	0,1	0,2	0,3	0,4	0,8	1,2	1,5	1,9	2,3	2,7	3,1	3,4	3,8 55°	0,1	0,2	0,3	0,4	0,8	1,2	1,6	2,0	2,5	2,9	3,3	3,7	4,1 60°	0,1	0,2	0,3	0,4	0,9	1,3	1,7	2,2	2,6	3,0	3,5	3,9	4,3 65°	0,1	0,2	0,3	0,5	0,9	1,4	1,8	2,3	2,7	3,2	3,6	4,1	4,5 70°	0.1	0.2	0 4 I 0.5	0,9	1.4	1.9	2.3	2.8	3.3	3,8	4.2	4,7	1	30°	| О.1 0,1 0,2 | 0.3 0.5 0,8 1,0 1,3 | 1,5 1,8 2,0 2.3 2.5	12	0,0	0,1	0,1	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0 14	0,0	0,1	0,1	0,1	0,2	0,4	0,5	0,6	0,7	0,8	1,0	1,1	1,2 16	0,0	0,1	0,1	0,1	0,3	0,4	0,6	0,7	0,8	1,0	1,1	1,2	1,4 18	0,0	0,1	0,1	0,2	0,3	0,5	0,6	0,8	0,9	1,1	1,2	1,4	1,5 20°	0,0	0,1	0,1	0,2	0,3	0,5	0,7	0,9	1,0	1,2	1,4	1,5	1,7 22	0.0	0,1	0,1	0,2	0,4	0,6	0,7	0,9	1,1	1,3	1,5	1,7	1,9 24	0,1	0,1	0,2	0,2	0,4	0,6	0,8	1,0	1,2	1,4	1,6	1,8	2,0 26	0,1	0,1	0,2	0,2	0,4	0,7	0,9	1,1	1,3	1,5	1,8	2,0	2,2 28	0.1	0,1	0,2	0.2	0,5	0,7	0.9	1,2	1.4	1,6	1,9	2,1	2,3	10°	1 0,0 0,0 0,1 | 0,1 0,2 0,3 0,4 0.4 | 0,5 0,6 0,7 0,8 0,9 |	1	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,1	0,1	0,1	0,1	0,1 2	0,0	0,0	0,0	0,0	0,0	0,1	0,1	0,1	0,1	0,1	0,1	0,2	0,2 3	0,0	0,0	0,0	0,0	0,1	0,1	0,1	0,1	0,2	0,2	0,2	0,2	0,3 4	0,0	0,0	0,0	0,0	0,1	0,1	0,1	0,2	0,2	0,2	0,3	0,3	0,3 5°	0,0	0,0	0,0	0,0	0,1	0,1	0,2	0,2	0,3	0,3	0,3	0,4	0,4 6	0,0	0,0	0,0	0,1	0,1	0,2	0,2	0,3	0,3	0,4	0,4	0,5	0,5 7	0,0	0,0	0,0	0,1	0,1	0,2	0,2	0,3	0,4	0,4	0,5	0,5	0,6 8	0,0	0,0	0,1	0,1	0,1	0,2	0,3	0,3	0,4	0,5	0,6	0,6	0,7 9	0,0	0,0	0,1	0,1	0,2	0,2	0,3	0.4	0,5	0,5	0,6	0,7	0,8	© о ъ о £ о о о	 о о © © о О О о © © о © о О © © с © о © © о © е о © © о *©	\ Разность \ долгот \	15' 30' 45' 1° 2° 3° 4° 5° 6° 7° 8° 9° 10° СредняяХ широта \
\ Средняя \ широта РазностьХ долгот \	«scoop	«4	О/ЯОПСЛСЛЛф.СйЫ	W	—	..... _ о о. ©	ел	© сл © сл © 55 ьа ос и*	о	оо а ф. гЗ о ое	© 4» ю о со <х> м а ел 4» u to ►-	© ооооооооо	о	о	о	о								Разность / долгот / / Средняя / широта
сл
СП
о
К
I
i
характеристика
Масштаб- - =- * Численный	Линейный		Проекция	Максимальное искажение мас- штаба	ь а. з и а Общевойсковое	
1:5 000 000 1:2 500 000 1:1 500 000 1:1 000 000 1:500 000 1 :500 000 1:200 000 1:100000 1:50 000 1:25 000 1 :ЮООО	50 км в 1 см 25 кл Е 1 см 15 км в 1 см 10 км в 1 см 5 км в 1 см 5 км в 1 см 2 км в 1 см 1 км в 1 см 500 м в 1 см 250 м в 1 см 100 л в 1 гл	Равноугольная Лам- берта-Гаусса Равноугольная Лам- берта-Гаусса Видоизмененная по- ликоническая Видоизмененная по- ликоническая Гаусса-Крюгера То же То же То же То же То же	6% 6% 6% Практи- чески нет То же • » в » 9 В В	Стратеги- ческая То же л Оперативная То же 1. Оперативная 2. Тактическая Тактическая То же в в	<<
156
ПРИЛОЖЕНИЕ 15
НЕКОТОРЫХ КАРТ
ч е н и е		Род авиа- ции	Начальный меридиан	Параллель касания (сечения)	Год издания	Район обеспечения
	в ВВС					
	1. Радионави- гация 2. Астро- ориенти- ровка То же 1.	Полетная 2.	Радионави- гация 3.	Астро- ориенти- ровка Полетная 1. Полетная 2. Детальная ориенти- ровка То же 1.	Детальная ориенти- ровка 2.	Разведка 3.	Фотораз- ведка 1.	Разведка 2.	Фотораз- ведка 3.	Бомбомета- ние То же Я V	ДБ ДБ ДЬ ББ ДБ. ББ, ША, ИА То же я я я я я	Гринвич То же • • я я V я я 	<PN =60° ' <Ps =50° <₽М = 60° ?s = 45° 1. Для листов се- вернее параллели 48° за параллель касания принята средняя па- раллель каждого ли- ста 2. Южнее паралле- ли 48° — единая па- раллель касания на широте 51°	1938 1940 1940 1943 1939 (нзда нием пре- кращена) 1943 1943 1925	Европа СССР и сопре- дельные страны То же я я 9 9 * Я •
1Б7
ПРИЛОЖЕНИЕ 16
УГЛЫ МЕЖДУ КОНИЧЕСКОЙ ПРЯМОЙ И ОРТОДРОМИЕЙ
= 0	“ = °>793 (’ср = 52°’5)
АХ 9	10°	20°	30°	40°	50°	60°	70°	80°	90°	100°	110°	120°
30°	—1°28'	—2°55’	—4°17'	—5°34'	—6°43'	—7042'	—8°29'	— 8°57'	—9°06'	—8°51'	—8°05'	— 6°41'
40°	—0е 45'	—1°29’	—2°08'	—2°42'	—3°34'	- 3°57'	-3°33	—3°22'	—2°56'	—2°11'	-1004'	0°30'
50°	—0008'	—0015'	—0°19'	—0°28'	—0°11'	0°03'	0°16'	1°02'	1°47'	2°55'	3°58’	5°25'
60°	0°22'	0°45'	1009'	1°37'	2°09'	2°45'	3°28'	3°41'	5°13'	6016'	7°27'	8°44'
70°	0°44'	1°28'	2014,	3001'	3°52'	4°41'	5°34'	6°28'	7°33'	8°36'	9°42'	10°46'
Д? = 10°
Ак ’Ср\^	30°	60°	90°
25°	—5°52'	—10°57	-14°04'
35°	—3°35'	—6°19'	—7°08'
45°	— 1035'	—2°26'	-1°45'
55°	0°04'	0°41'	2°22'
65°	1°21’	3°00'	5°14'
Д<Р = 20°
	30°	60°	90°
30°	—4°15'	- 7°38'	—9°02'
40°	—1°58'	-4004'	-2°11'
50°	—0°02'	0°30'	2OQ7'
60°	1°35'	3°19'	5°37'
До = 30°
ДХ Фер	30°	60°	90°
35°	-2°17'	—3°47'	—3°37'
45°	-0°01'	0°32'	2°11'
55°	1°52'	3°56'	6°21
65°	3°19'	6°26'	9°15'
ПРИЛОЖЕНИЕ 18
ФОРМУЛЫ СФЕРИЧЕСКОЙ ТРИГОНОМЕТРИИ
При выводе различных формул мы пользуемся следующими
основными формулами сферической тригонометрии:
1.	Косинус стороны сферического треугольника равен про-
изведению косинусов двух других его сторон плюс произведе-
ние синусов тех же сторон на косинус у.гла между ними.
cos a — cos6-cosc4- sin 6-sinc-cos А.
2.	Синусы сторон сферического треугольника пропорциональны
синусам противолежащих им углов.
sin а   sin Ь _ sin с
sin A	sin в ~ sin С ’
3.	Произведение косинусов средних элементов сферического
треугольника равно разности между произведениями синуса
средней стороны на котангенс крайней стороны и синуса сред-
него угла на котангенс крайнего угла.
cos с  cos В =sin с ctg а — sin В ctg А.
4.	Для прямоугольного сферического треугольника:
а)	если три элемента треугольника лежат рядом, то косинус
среднего элемента равен произведению котангенсов крайних
элементов:
cos С = ctg а  ctg (90° — 6);
б)	если элементы не лежат рядом, то косинус отдельно
стоящего элемента равен произведению синусов рядом лежащих
элементов:
cos (90° — с) = sin а • sin С.
При этом катеты заменяются их дополнениями до 90° и счи-
таются лежащими рядом, а прямой угол, как известный, не счи-
тается.
5.	Произведение синуса стороны сферического треугольника
на косинус прилежащего угла равно разности произведений
синуса другой стороны, ограничивающей указанный угол, на
косинус третьей стороны и косинуса стороны, ограничивающего
тот же угол, на синус третьей стороны и на косинус угла,
противолежащего первой стороне:
sin a-cos В = sin с-cos b — cos с-sin b-cos А.
Произведение синуса угла на косинус прилежащей стороны
равно сумме произведений синуса другого угла, прилежащего
к той же стороне, на косинус третьего угла и косинуса при-
лежащего угла на косинус третьего угла и на косинус стороны,
противолежащей первому углу:
sin А  cos b — sin С-cos В + cos С- sin В  cos а.
159
6. Формулы Непера:
а— Ь
, А + В C0S 2 С
C°s^-
, а — Ь
А —В
tg —
. а 4- b
а — b

sln— L С
—ГйС‘§Т
sin —-—
A-В
C0S ~2~ с ,
А + В* 2 1
c°s-2-
. А-В
sia-2~, с
A + BtS 2 ’
sin-J-
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
1-	Траур, Математическая картография, 1938.
2.	Каврайский, Математическая картография, 1934.
3.	Макаров, Основы картографии, 1940.
4.	Поляк, Материалы диссертации, 1945.
5.	Ратц, Кривоносов, Сороковик, Васильков, Кар-
тография, 1941.
6.	Соловьев, Математическая картография, 1937.
7.	Матусевич, Определение места корабля по радиопелен-
гам, 1940.
8.	Витман, Вычисление кратчайших расстояний на земной
поверхности.
9.	В и т к о в с к и й, Практическая геодезия.
10.	Immler, Grundlagen der Flugzeugnavigation.
IL -1&S3
ОГЛАВЛЕНИЕ
Стр.
Введение.................................................... ...	3
Глава 1. Позиционные линии на Земле................................ 6
< §	1.	Основные сведения о Земле............................... —
§	2.	Основные линии положения ............................... 8
* §	3.	Ортодромия.............................................. 9
v §	4.	Локсодромия............................................ 14
§	5.	Разность между длинами локсодромии	и	ортодромии ....	18
§	6.	Линия равных азимутов.............................. 23
§	7.	Малый круг........................................... 25
§	8.	Линия равных разностей (сумм)	расстояний............. 27
Глава 2. Общие сведения о картографических проекциях............	31
§ 9.	Сведения из теории искажений.............................. —
§ 10.	О картографических проекциях . .	.	.	36
Глава 3. Цилиндрические проекции.................................. 41
§ 11.	Простая цилиндрическая проекция.......................
§12.	Равноугольная цилиндрическая проекция................... 42
§ 13.	Локсодромия и ортодромия на меркаторской проекции ...	45
§ 14.	Карты в меркаторской проекции........................... 49
§ 15.	Поперечно-цилиндрическая проекция....................... 50
Глава 4. Перспективные проекции .................................. 53
§ 16.	Центральная полярная (гномоническая) проекция........... 54
§ 17.	Ортодромия на гномонической проекции.................... 56
§ 18.	Стереографическая полярная проекция..................... 61
Глава 5. Конические проекции...................................... 65
§ 19.	Угол схождения меридианов.............................
§ 20.	Простая коническая проекция............................. 66
§ 21.	Проекция на секущем конусе.............................. 69
§ 22.	Равноугольная коническая проекция....................... 71
§ 23.	Ортодромия на конической проекции ...................... 75
§ 24.	Линия равных азимутов на конической проекции............ 77
§ 25.	Поликоническая проекция................................. 60
§ 26.	Многогранная проекция................................... 82
Глава 6. Произвольные проекции.................................... 83
§ 27.	Обратная равноазимутальная проекция...................... —
§ 28.	Специальная проекция.................................... 85
§ 29.	Номенклатура карт....................................... 86
§ 30.	Требования к авиационным картам......................... 92
Дополнения........................................................ 97
§ 31.	Земной сфероид.......................•................... —
§ 32.	Геодезическая линия..................................... 98
§ 33.	Линия равных азимутов (пеленгов).......................  W1
§ 34.	Исследование уравнения ЛРА.............................. Ю4
§ 35.	Уравнение ЛРА в виде пространственных овалов Кассини . .	108
§ 36.	Уравнение ортодромии на меркаторской проекции.......... 112
162
§ 37.	Уравнение линии равных азимутов на меркаторской проекции 112
§ 38.	Косая полярная н двуазимутальная проекции................ ИЗ
§ 39.	Уравнение линии равных азимутов на гномонической проекции 115
§ 40.	У равнения локсодромии и ортодромии на полярной стерео-
графической проекции.......................................... 118
§ 41.	Уравнение линии равных азимутов на стереографической
проекции ....................................................... —
§ 42.	Уравнение ортодромии	на конической	проекции............. 119
§ 43.	Уравнение линии равных азимутов на равноугольной кониче-
ской проекции................................................. 120
§ 44	Уравнение линии равных	разностей	расстояний........... 123
Приложения'.
1.	Длины дуг меридиана и параллели в 1° в м............... 125
2.	Перевод морских миль в километры и обратно............. 126
3.	Перевод английских миль в километры и обратно......... 127
4.	Схема вычисления ортодромического путевого угла и рас-
стояния .................................................. 128
5.	Схема вычисления	ортодромического расстояния........... 129
6.	Схема вычисления координат промежуточных точек орто-
дромии ................................................... 130
7.	Схема вычисления широты н долготы вертекса и ортодроми-
ческого расстояния........................................ 131
8.	Схема вычисления промежуточных точек (путевой угол по
расстоянию и расстояние по	путевому	утлу)................ 132
9.	Схема вычисления промежуточных точек (широта и долгота
по расстоянию)............................................ 133
10.	Меридиональные части в морских	милях................... 134
11.	Схема расчета локсодромии.............................. 152
12.	Схема вычисления координат точек линии равных азимутов
(широтный способ).......................................... 153
13.	Схема вычисления координат точек линии равных азимутов
(долготный способ)........................................  154
14.	Поправка Жнври......................................... 155
15.	Характеристика некоторых карт.......................... 156
16.	Углы между конической прямой	и	ортодромией............ 158
17.	Гномоническая сетка.................................вклейка
18.	Формулы сферической тригонометрии...................... 159
Использованная литература.................................. 161