Текст
ВК. ЕВСТВ4ЮВ
ТЕОРИЯ ОБРАБОТКИ МЕТ4<ИОВ ДИВИЕНИЕМ
Допущено Министерством высшего и среднего специального образования УССР в качестве учебника для студентов вузов, обучающихся по специальности «Машины и технология обработки металлов давлением»
ХАРЬКОВ
ИЗДАТЕЛЬСТВО ПРИ ХАРЬКОВСКОМ ГОСУДАРСТВЕННОМ УНИВЕРСИТЕТЕ ИЗДАТЕЛЬСКОГО ОБЪЕДИНЕНИЯ
• 8ИЩА ШКОЛА»
1981
34.62я73 Е26
УДК 621.77.001
Теория обработки металлов давлением. Евстратов В. А. — Харьков: Вища школа. Изд-во при Харьк. ун-те, 1981.—248 с.
В учебнике отражено современное состояние теории обработки металлов давлением. Рассмотрены основы механики сплошных сред и пластической деформации металлов и сплавов. Изложены основные законы и методы решения задач теории обработки металлов давлением. Сформулированы основные задачи теоретического анализа процессов обработки и показаны пути их оптимизации численными методами с использованием цифровых ЭВМ. Теоретические положения тесно связаны с их практическим использованием.
Для студентов, обучающихся по специальности <Машины и технология обработки металлов давлением!. Может быть полезен инженерно-техническим и научным работникам кузнечно-штамповочного производства.
Табл. 4. Ил. ПО. Список лит.: 191 назв.
Рецензенты: кафедра обработки металлов давлением Киевского политехнического института, кафедра машин и технологии обработки металлов давлением Запорожского машиностроительного института
Редакция научно-технической литературы Зав. редакцией Л. А. Гаврилова
31205—092_ _ 2704030000
С М226(04) —81 «vwww
(^Издательское объединение «Вища школа», 1981
ПРЕДИСЛОВИЕ
Повышение эффективности производства, качества, надежности и долговечности изделий — одна из главных задач современной промышленности. Решить ее можно только путем широкого использования прогрессивных технологических процессов, в частности обработки металлов давлением (ОМД). Базой всех процессов ОМД является теория обработки металлов давлением (ТОМД). Основам этой науки посвящены учебники [28, 31, 53, 132, 138, 1701. Что же побудило автора по-новому изложить курс?
Известно, что студенты усваивают теорию обработки металлов давлением с большим трудом из-за насыщенности фактическим материалом, сложности математического аппарата, абстрактности феноменологического подхода. В то же время усвоение ТОМД в значительной мере определяет уровень подготовки специалиста по обработке металлов давлением. Поэтому при подготовке книги автором проведен тщательный отбор необходимого материала, исключены второстепенные вопросы и детали. Автор руководствовался принципом: от известного к неизвестному, от простого к сложному. Он стремился представить теорию обработки металлов давлением как стройную науку, имеющую свою логику, противоречия и трудности, непрерывно развивающуюся, как арену борьбы ученых за знания, где каждый новый шаг дается с большим трудом, где с каждым годом число неясных вопросов увеличивается; показать преемственность знаний и раскрыть способы их получения; подчеркнуть тесную связь теории с практикой и указать пути использования теоретических знаний для совершенствования технологии ОМД.
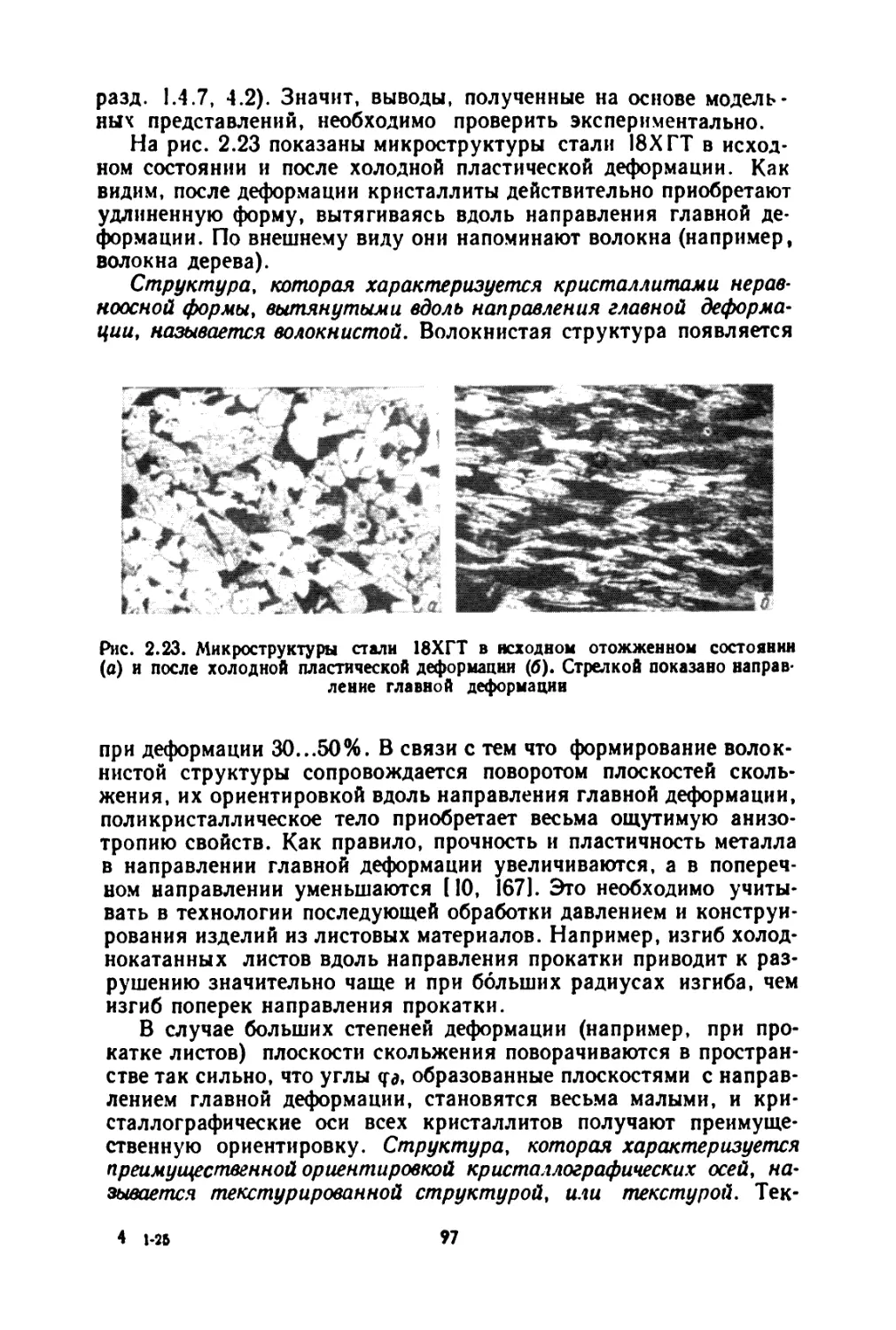
Теория обработки металлов давлением — молодая наука. Чтобы читатель увидел, как она развивалась, автор дает маленькие исторические справки, ссылается на многочисленные работы советских и зарубежных ученых и подчеркивает, что именно благодаря их трудам мы можем успешно решать те или иные важные задачи совершенствования технологии ОМД. Читатель должен иметь представление о диалектическом развитии науки. С этой целью в курсе отмечены трудности, противоречия, нерешенные вопросы, показаны подходы к решениям разнообразных задач, пути преодоления тупиков, источники открытия.
С расширением области познанного появляется все больше точек соприкосновения с непознанным. Познание нового представляется в виде ступенчатого процесса. «От живого созерцания к абстрактному мышлению и от него к практике — таков диалектический путь познания истины, познания объективной реальности» [В. И. Ленин, Поли. соб. соч., т. 29, с. 152—1531. Вторая ступень познания— это абстрактное описание изучаемого объекта, обобщение его основных черт. Такое упрощенное описание реаль
ного объекта принято называть моделью. Анализ модели позво-ляет получить новые знания об изучаемом объекте. Изучение последовательно усложняющихся моделей — наиболее эффективный путь познания. Создание моделей, достаточно точно описывающих реальные объекты, их анализ численными методами с использованием быстродействующих цифровых ЭВМ служит основой для решения исключительно важных для практики задач оптимизации. Современная технология ОМД ждет от теории не только разработки методов анализа процессов, а комплексного решения проблемы получения изделий наиболее высокого качества при наименьших издержках производства. Вот почему во всех случаях, где это было возможно, использовались модельные представления и обсуждались пути оптимизации процессов.
Важная роль в книге отведена справочному и методическому аппарату.
Чтобы облегчить читателю запоминание материала, акцентировать внимание на главном, термины, определения и ключевые слова в тексте выделены курсивом. Большинство их заимствовано из наиболее авторитетных источников, перечисленных в списке литературы. Краткие вступления к важнейшим разделам имеют целью показать читателю основную идею, а выводы резюмируют содержание. Материал, который частично известен из других курсов, набран петитом.
Автор выражает искреннюю благодарность тт. О. А. Ганаго, А. Г. Овчинникову, Е. А. Попову, а также своему учителю проф. Л. И. Живову, труды и советы которых с благодарностью были использованы при подготовке учебного пособия.
ВВЕДЕНИЕ
Обработка металлов давлением — это видовое наименование группы методов изготовления деталей, заготовок или полуфабрикатов, основанных на пластической деформации металлов. Таких основных методов шесть: прокатка, волочение, прессование, ковка, объемная и листовая штамповка.
Значение обработки металлов давлением в народном хозяйстве исключительно велико: методами ОМД изготовляют самые ответственные и тяжело нагруженные детали турбин, станков, автомобилей, тракторов, самолетов, ракет, атомных и химических реакторов и других изделий, получают дешевые и высококачественные изделия массового производства (болты и гайки, детали электрических машин и аппаратов, корпуса транзисторов и реле, металлическую посуду и холодильники). Практически любое промышленное предприятие, выпускающее металлические изделия, имеет в своем составе цех для ОМД.
Рассматриваемая наука является прикладной дисциплиной, которая объясняет процессы, происходящие при пластической деформации, описывает изменения структуры и механических свойств металлов в результате деформации, дает возможность определить усилия деформации, нагрузки на инструмент, конечную форму заготовки и ее предельное формоизменение, позволяет создавать оптимальные технологические процессы обработки давлением, обеспечивающие получение изделий наиболее высокого качества при минимальной затрате труда и материальных ресурсов. Это — молодая дисциплина. В 1935 г. С. И. Губкин писал: «Самые разнообразные отрасли техники требуют знания тех законов, которые управляют деформацией... пластической. В недалеком будущем должна сформироваться новая дисциплина — теория необратимых (пластических) деформаций, и эта дисциплина получит большое прикладное значение» [29, с. 3]. В 20—30-х гг. появились работы Т. Кармана, Э. Зибеля, Г. Закса, А. Ф. Головина, С. И. Губкина, И. М. Павлова, посвященные частным вопросам теории обработки металлов давлением. Они подготовили появление первого учебника, который вышел в свет в 1947 г. [31].
Теория обработки металлов давлением возникла как наука, призванная решать технические задачи технологии ОМД. Обработка давлением известна человечеству со времен бронзового и железного веков. Ковка орудий труда и оружия, изготовление украшений из волоченой проволоки, чеканка монет используются человечеством с незапамятных времен. Более поздними достижениями являются прокатка (1495 г.), объемная штамповка (1819 г.), прессование (1894 г.) [28, 99, 1561. Однако до начала 30-х гг. технология была искусством: ее уровень определялся только умением мастера. Индустриализация производства привела к бурному
s
развитию технологии ОМД. Это поставило ряд важных проблем, решить которые можно было лишь на основе теоретического подхода. Задачи теории стали гораздо сложнее в военное время и в послевоенный период восстановления народного хозяйства. Нового, еще более высокого уровня развития теории обработки металлов давлением потребовало решение задач, выдвинутых XXVI съездом КПСС и постановлениями ЦК КПСС и Совета Министров об экономии металла и внедрении малоотходной технологии.
В]теории обработки металлов давлением можно выделить два главных направления: механико-математическое и физико-химическое. Первое основано на феноменологическом подходе, второе — на физическом. Первое использует для исследования процессов ОМД методы механики сплошных сред и теории пластичности, второе — методы физики металлов, металловедения, физико-химической механики материалов. Каждое из указанных направлений ставит и решает разнообразные задачи.
Задачи первого направления: определить усилия и работу деформации различных технологических процессов; установить характер распределения напряжений по контактным поверхностям рабочих частей штампов и вычислить нагрузки, действующие на них; вычислить показатели конечного формоизменения, т. е. определить форму и размеры детали после выполнения заданной операции; вычислить показатели предельного формоизменения, т. е. определить наибольшую деформацию, при которой заготовка не разрушится. Решение указанных задач позволяет правильно выбрать технологическое оборудование, рассчитать на прочность рабочие, крепежные и базовые детали штампов, найти предельные значения основных технологических параметров процесса деформации, при которых можно не опасаться разрушения инструмента или заготовки. Такие задачи решены для многих процессов ОМД: усилия деформации определены практически для всех известных операций, задачи конечного формоизменения решены для основных процессов, в том числе и с двумя степенями свободы течения. Но до сих пор в числе нерешенных остаются многие задачи распределения напряжений, первые шаги сделаны в решении задач предельного формоизменения.
Задачи второго направления: установить механизмы пластической деформации металлов; определить зависимость структуры, механических и физических свойств металлов от степени предшествовавшей деформации; определить зависимость сопротивления деформации и пластичности металлов от их химического состава, температуры, скорости и механической схемы деформации; исследовать закономерности контактного трения, определить его влияние на силовой режим и характер формоизменения, разработать способы уменьшения его вредного влияния и полезного использования. Решение перечисленных задач позволяет установить научно обоснованные технологические режимы деформации, обеспечиваю*
щие получение изделий наиболее высокого качества. Эти задачи решены в первом приближении для большинства металлов, исполь-зуемых в производстве для обработки давлением.
В развитии теории обработки металлов давлением можно выделить (конечно, с известной условностью) четыре характерных периода. Первый период (1915—1945 гг.)—становление ТОМД как самостоятельной дисциплины. В работах этого периода даны решения простейших задач: на основании общих уравнений теории пластичности определены усилия деформации наиболее распространенных операций ОМД (С. И. Губкин, Г. Закс, Э. Зибель, Н. С. Петров, Л. Прандтль, Е. П. Унксов, А. И. Целиков). Второй период (1945—1960 гг.)— развитие общих приближенных методов решения более сложных задач, связанных с определением усилий деформации, нагрузок на инструмент и конечного формоизменения. Совместными усилиями советских и зарубежных ученых в этот период были разработаны инженерный метод анализа процессов ОМД (С. И. Губкин, Г. Закс, Э. Зибель, И. М. Павлов, Е. А. Попов, В. С. Смирнов, М. В. Сторожев, Е. П. Унксов), метод линий скольжения (Г. Генки, X. Гейрингер, В. Прагер, И. П. Ренне, В. В. Соколовский, А. Д. Томленое, Р. Хилл, Л. А. Шзфман), энергетический (О. А. Ганаго, В. Джонсон, В. Л. Колмогоров, А. А. Поздеев, И. Я- Тарковский, Э. Томсен), метод сопротивления металлов пластическим деформациям (Г. А. Смирнов-Аляев), визиопластический (Ю. Н. Алексеев, Э. Томсен). Третий период (1960—1975 гг.) — развитие методов теоретического анализа процессов ОМД численными методами с применением цифровых ЭВМ. Он имеет две особенности. Во-первых, благодаря достижениям вычислительной техники, а также физики металлов, металловедения, физико-химической механики материалов произошло значительное сближение феноменологического и физического подходов, создались предпосылки для построения и анализа моделей процессов ОМД, более полно учитывающих реальные условия деформации, и решения новых задач (предельное формоизменение). Во-вторых, усилиями ведущих ученых-теоретиков в нашей стране были созданы научные школы, в частности московская (А. А. Ильюшин, Н. Н. Малинин, Е. А. Попов, М. В. Сторожев, А. Д. Томленое, Е. П. Унксов, Л. А. Шофман), ленинградская (В. С. Смирнов, Г. А. Смирнов-Аляев), уральская (О. А. Ганаго, В. Л. Колмогоров, А. А. Поздеев, И. Я. Тарновский), минская (Е. М. Макушок, В. П. Север-денко, В. М. Сегал), тульская (И. П, Ренне), харьковская (Ю. Н. Алексеев, Е. Ф. Шарапин). Четвертый период (с 1975 г.) — разработка экспериментально-аналитических методов и окончательное объединение феноменологического и физического подходов. Важными вехами этого периода следует считать работы Г. Д. Деля 133), Е. И. Исаченкова 1481, В. Л. Колмогорова [ 109], А. Н. Леванова, В. Л. Колмогорова [61], П. И. Полухина,
7
Г. Я. Гуна, А. М. Галкина (1101, Г. А. Смирнова-Аляева (1331, В. И. Уральского (34), Н. А. Чиченова, А. Б. Кудрина, П. И. Полухина (1701. В них теоретический подход базируется на данных эксперимента, их статистическом анализе, использовании новых представлений о контактном трении и разрушении материалов, роли температуры, скорости и механической схемы деформации.
Значительный вклад в развитие теории обработки металлов давлением внесли зарубежные ученые: Дж. Александер, Дж. Бишоп, П. Бриджмен, В. Бэкофен, О. Гофман, В. Джонсон, Г. Закс, Ш. Кобаяши, X. Кудо, А. Надаи, X. Пью, Э. Томсен, Р. Хилл, Ч. Янг. Многие их работы переведены на русский язык и используются советскими специалистами [ 16, 26, 36, 80, 86, 150, 1651.
Таким образом, теория обработки металлов давлением стала наукой, которая не только объясняет экспериментальные факты, но и предсказывает течение конкретных процессов деформации, дает возможность управлять ими и решать важные технологические задачи, показывает пути и направления дальнейшего развития технологии обработки металлов давлением.
ГЛАВА 1
ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД
1.1. ОБЩИЕ ПРЕДСТАВЛЕНИЯ О ДЕФОРМАЦИИ
Рис. 1.1. Схема ссадки заготовки на гидравлическом ковочном прессе
Обработку металлов давлением осуществляют воздействием рабочего инструмента на деформируемую заготовку. Например, операцию осадки на гидравлическом ковочном прессе выполняют следующим образом. Заготовку 3 устанавливают на нижний боек 2, прикрепленный к столу пресса (рис. 1.1). Верхний боек 4 н подвижная поперечина пресса 5 в процессе осадки перемещаются при помощи плунжера рабочего цилиндра 6 по некоторому закону Н = H(t), задаваемому типом привода пресса. Пусть в момент времени /0 верхний боек коснется деформируемой заготовки. Дальнейшее движение бойка сопровождается перемещением ее верхнего торца. За время At верхний торец заготовки переместится на расстояние АН = Но— H(tQ + At). Схематически это показано на рис. 1.2. В момент времени tk заготовка получит заданную деформацию и будет иметь высоту Hk. Произвольно выбранный элемент деформируемой заготовки М можно представить в виде системы частиц, закономерно рас
положенных в пространстве и удерживаемых на расстояниях г силовыми полями (на рис. 1.2 они показаны схематически в виде пружинок). Выделим для простоты изложения только две частицы
9
(например Ль Лж). Силу их взаимодействия Л/? можно выразить уравнением [461
Г/г /г V*l
ДК = ВП£) I. (1.1)
Здесь В — константа; г0 — равновесное расстояние между частицами, параметр решетки; г— фактическое расстояние между ними.
Рис. 1.2. Схема формоизменения заготовки при осадке:--------исходное, —-------промежуточное,
-------конечное состояние
Геометрическая интерпретация этого уравнения (рис. 1.3) позволяет более наглядно представить зависимость Д/? от г. Из рисунка
Рис. 1.3. График силового взаимодействия двух частиц (атомов) >41( Ла по уравнению (1.1)
следует, что в естественном равновесном состоянии, когда г = г0, Д/? =* 0. При уменьшении расстояния между частицами Лх, Л, от г = г0 до г — г' возникают силы отталкивания Д/?'. Поэтому для получения равновесного состояния, точнее квазиравновесного, при котором частицы /41, Л, остаются на расстоянии г' друг от друга, к ним необходимо приложить внешние силы 4- Д/?',—Д/?'. С увеличением расстояния между частицами Л1( А, до г = г" возникают силы притяжения Д/?’. Поэтому для сохранения между частицами расстояния г* к ним необходимо приложить внешние силы —Д/?’, +Д/?’. Квазиравновес-ное состояние, которое имеет место расположения частиц под действием
при изменении взаимного
внешних сил, принято называть напряженно-деформированням.
Теперь возвратимся к рассмотрению процесса деформации заготовки на прессе (рис. 1.2). При осадке высота заготовки Но из-
Ю
меняется в связи с изменением расстояний г между соседними парами частиц, а также в связи с другими более сложными явлениями, обусловленными пластической деформацией (о них пойдет речь в гл. 2). Изменение г вызывает реакции А/?. Равнодействующая этих реакций /?, приложенная со стороны деформируемой заготовки к инструменту, препятствует движению инструмента (бойка) и поперечины пресса. Следовательно, для дальнейшего движения бойка и деформации заготовки рабочий цилиндр пресса должен развивать силу Рд, которая уравновешивает равнодействующую R.
Осадка—наиболее простая операция обработки давлением. Поэтому схема взаимодействия частиц деформируемой заготовки друг с другом и деформирующим инструментом получилась такой простой и наглядной. Но и в других, более сложных процессах обработки металлов давлением необходимые деформирующие усилия и воздействие деформируемой заготовки на инструмент определяются силовым взаимодействием ее частиц, зависящим от степени нарушения равновесного состояния между частицами.
Таким образом, на примере осадки можно установить следующие важные факты: воздействие инструмента на деформируемую заготовку приводит к нарушению естественного равновесного состояния частиц; изменение расстояний между частицами вызывает появление внутренних сил А/?, которые определяют реакцию взаимодействия деформируемой заготовки с инструментом /?; в каждый момент времени реакция R деформируемого тела на инструмент уравновешивается действием деформирующей силы Рд, которую развивает главный исполнительный механизм кузнечноштамповочной машины. Отсюда следует, что для вычисления усилия Рд необходимо задаться деформацией заготовки АЯ, установить, каким образом деформация распределяется внутри тела между отдельными частицами, как изменяются естественные расстояния между частицами, какие реакции А/? возникают между ними, как эти реакции воздействуют на инструмент. Иными словами, необходимо детально проанализировать цепочку взаимосвязанных факторов: перемещение — деформация — напряжение — сила.
1.2. ФЕНОМЕНОЛОГИЧЕСКИЙ ПОДХОД К ИССЛЕДОВАНИЮ ПРОЦЕССОВ ДЕФОРМАЦИИ
Уравнение (1.1) позволяет определить силовое взаимодействие двух частиц при любых значениях г. Казалось бы, это дает возможность проанализировать силовое взаимодействие всей системы частиц, образующих рассматриваемое деформируемое тело. Но это не так. В 1 см3 твердого металлического тела содержится 10м... ... Ю34 частиц (атомов). Для описания взаимодействия только каждой пары понадобилось бы около 10’° уравнений. Совершенно очевидно, что справиться с такой огромной системой немыслимо
11
даже при использовании самой быстродействующей цифровой ЭВМ. Значит, возможность анализа напряженно-деформированного состояния на атомарном уровне пока исключается.
Выход из создавшегося тупика в использовании так называемого феноменологического подхода к анализу напряженно-деформированного состояния. Суть подхода состоит в том, что свойства реального деформируемого тела схематизируют настолько, насколько это необходимо и допустимо, чтобы, с одной стороны, получить возможность достаточно простыми средствами решить задачу, а с другой — отразить в этой схеме все наиболее важные черты рассматриваемого тела. При анализе процессов деформации важно поведение не отдельных атомов, а всего тела как целого. Поэтому вполне допустимо отказаться от учета атомарного строения деформируемого тела. Такой подход позволяет рассматривать деформируемое тело как некую субстанцию, непрерывно заполняющую объем тела и называемую сплошной средой.
Сплошная среда (материальный континуум)* — это модель реального деформируемого тела, которая сохраняет основные его свойства, кроме атомарного строения, микро- и макроструктуры. Идеализация очень важна потому, что она дает возможность использовать для анализа деформации математический аппарат непрерывных функций, дифференциальное и интегральное исчисления.
С помощью феноменологического подхода к анализу напряженно-деформированного состояния современная математическая теория пластичности выражает основные уравнения связи между напряжениями и деформациями в виде физических законов (уравнений состояния), полученных на основе обобщения опытных данных или принятых как некоторая система аксиом. Поясним это на примере. Пусть дан цилиндрический стержень диаметром d и длиной /. Необходимо установить зависимость между его удлинением Д/г в направлении оси г и напряжением ог, соответствующим удлинению. Воспользуемся опытом. Нагружая стержень различными силами Р, измерим удлинения Д/г, соответствующие приложенным силам, вычислим напряжения ог и составим уравнение ог = /(Д/г), график о2 —Д/2 или таблицу о2—Д/2, которые будут выражать физический закон (уравнение состояния). Из курса сопротивления материалов известно, что это закон Гука, описываемый уравнением о2 = ЕД/2//. Конечно, его можно распространить только на узкий класс деформируемых тел (стержни постоянного сечения, нагруженные только осевой силой), но получить такой закон достаточно просто.
Простота установления уравнений состояния (в рассмотренном выше примере определение модуля упругости Е) в известной мере компенсирует многие недостатки феноменологического подхода.
* В дальнейшем будем употреблять преимущественно сокращенный термин «среда».
12
Во многих случаях уравнения состояния выводят на основании различных допущений о связи между напряжениями и деформациями. Несмотря на аксиоматический характер уравнений состояния, полученных на этой основе, они широко используются для решения прикладных задач. Термодинамический анализ показывает допустимость такого подхода, а многочисленные решения важных практических задач подтверждают правильность принятых допущений. Феноменологический подход дает возможность широко использовать модели сплошных сред.
1.3. МОДЕЛИ СПЛОШНЫХ СРЕД
Модель — это объект любой природы, который способен замещать исследуемый объект так, что его изучение дает новые знания об изучаемом объекте (105]. Модель создают путем абстракции и идеализации, стремясь чтобы между нею и изучаемым объектом было сходство в главных чертах, имеющих значение в данном исследовании. Материалы, которые рассматриваются в ТОМД, ТУ и ТП, обладают различными свойствами: упругостью, пластичностью, вязкостью. Для описания их свойств с наибольшей полнотой при наименьшей сложности используют модели сред (6, 30, 116, 128, 146|.
Жесткой называется среда, деформация которой остается равной нулю при любых напряжениях. Если объектом исследования служит деформируемая заготовка, то почти всегда можно без ощутимой погрешности считать, что деформации инструмента равны нулю. Так приходим к модели жесткой среды.
Упругой называется среда, для которой зависимость между напряжением о и деформацией е выражается однозначной для нагрузки и разгрузки функцией
а = Де)е, (1.2)
где /(е) > 0. Это означает, что упругая деформация — процесс обратимый Если зависимость между напряжением и деформацией подчиняется закону Гука, т. е. уравнение (1.2) имеет вид линейной функции
а = Ее, (1.3)
то среда носит название линейно-упругой, или среды Гука. С такими средами мы встречаемся при анализе напряженно-деформированного состояния различных деталей машин и строительных конструкций, нагруженных умеренными напряжениями (не более 0,5... 1,0 ГПа).
Анализ модели взаимодействия двух атомов (уравнение (1.1) и рис. 1.3) позволяет сделать предположение о том, что в общем случае металлы можно отнести к нелинейно-упругим средам. Однако при умеренных напряжениях для некоторых из них, например сталей, нелинейность настолько мала, что в технических расчетах ею можно пренебречь.
Пластической называется среда, для которой зависимость между напряжением и деформацией выражается функцией
о = о, + Е(е)8, (1.4)
где Е(е) >0; cs — предел текучести. Если Е(е) = 0, то уравнение (1.4) определяет пластическую неупрочняющуюся среду. Такую среду часто называют жесткопластической неупрочняющейся (46, 116, 128]. Если F(e) + 0, то среда упрочняющаяся: при Е(е) = const—линейно-упрочняющаяся, при Е(е) 7b const — нелинейно-упрочняющаяся.
Модели пластических сред хорошо описывают свойства металлов при их обработке давлением. В дальнейшем будем широко использовать эти модели для анализа технологических задач обработки металлов давлением.
13
Вязкой называется среда, для которой зависимость между напряжением о и скоростью деформации £ выражается функцией
а = Фа)£. (1.5)
где Ф($) > 0. Если Ф(£) = const, то среда носит название линейно-вязкой, или среды Ньютона. Материалы, используемые при обработке давлением, редко проявляют линейно-вязкие свойства. Поэтому чаще используется модель нелинейно вязкой среды, для которой Ф(£) const. Чтобы полнее учесть свойства реальных деформируемых тел, следует комбинировать свойства простых сред. Например, соединяя упругость и пластичность, можно получить модель упругопластической среды, поведение которой при нагрузке определяется уравнениями
о «= f (в) в при е < е$;
о — / (е) е$+ F(e) (в — ъ) при в > в,, а при разгрузке — уравнением
а = / (в) в, 4- F (в) (ер — е,) — f (в) (ер — в).
<16) (1.7)
(1-8)
Здесь 8а — деформация, соответствующая началу пластического течения; вр — деформация, соответствующая окончанию нагрузки н началу разгрузки. Если упруго-пластическая среда
Cl
К'
К 6
6t—
a
€
Рис. 1.4. Телесная модель упругой среды (а), график зависимости о-в для этой среды (б)
не упрочняется, т. е. F (в) — 0, она носит название среды Сен-Венана.
Для наглядного представления о свойствах сред часто применяют механические модели [6 46, 116, 146). В основу моделей кладут различные механические образы. Условимся использовать так называемые телесные модели. Деформируемое тело представим в виде двух полых цилиндрических стаканов Ср Са, перемещающихся один в другом без трения (рис. 1.4). Если длину модели /и и площадь поперечного сечения FM принять равными соответствующим единицам, то перемещение стакана Са численно равно относительной деформации 8, а сила Р численно равна напряжению о. Свойства тела, которые определяют зависимость о — в или о — В, будем характеризовать механическими аналогами, например упругость показывать упругим элементом У (пружина), расположенным внутри стаканов Q, Cj.
Совершенно очевидно, что при растяжении тела, т. е. при перемещении цилиндра Са из положения К в положение К', возникнет реакция и состояние тела определится точкой К{ на диаграмме а — е. Сжатие тела (перемещение К в положение /С) вызовет реакцию Ра, а состояние тела определится точкой Ка на диаграмме о — в. Наделив тело С>— Са соответствующими свойствами, можно получить телесные модели простых сред (рис. 1.5). Свойство упругости среды принято изображать упругим элементом (пружина с линейной У или нелинейной характеристикой УН, как это показано па рис. 1.5, а, б). Пластические свойства среды представляют элементом трения (рнс. 1.5, а). В нем поверхности Пр Па прижаты друг к другу постоянной силой. Поэтому, если о < о,, поверхности ПР Па неподвижны и тело не деформируется. Деформация начинается н протекает только при а > о,. Если яараллельно элементу трения установить упругий элемент, получим модель упрочняющейся среды (рис. 1.5, г). Элемент, характеризующий вязкие свойства среды, показывают чаще всего в виде поршня н цилиндра,
цилиндра Ca из положения
14
заполненного жидкостью [6, 116, 146]. Но это громоздко н не дает воз* можности продемонстрировать линейность или нелинейность вязких свойств среды. Поэтому для вязкого элемента с линейной характеристикой В и нелинейной характеристикой ВН примем обозначения, представленные на рис. 1.5, д, е. Чтобы получить телесные модели со сложными свойствами, применим различные элементы У, П, В в определенных сочетаниях. При последовательном соединении элементов в них действуют одинаковые силы, численно равные напряжениям, а деформация тела находится как сумма
Рис. 1.5. Модели простых сред и соответствующие нм графики зависимости а—е, о —
а — линейно-упругая среда, б — нелинейно-упругая, в — жесткопластическая неупроч-яющаяся, в — жесткопластнческая упрочняющаяся, д — линейно-вязкая, « — нелинейно* вязкая
деформации составляющих элементов. При параллельном соединении элементов деформация каждого равна деформации тела, а сила, действующая на модель, получается суммированием сил, действующих на каждый из влементов.
Классификация сред, приведенная выше, не исчерпывает всех их свойств. Упругость, пластичность, вязкость могут изменяться в объеме тела. В зависимости от характера изменения свойств по координатам различают однородную и неоднородную среды. Однородной называется среда, свойства которой не зависят от координат. Неоднородной называется среда, свойства которой изменяются вдоль координатных осей по определенным законам. В большинстве случаев металлы обладают однородными свойствами. Исключение составляют слоистые материалы, слитки, а также все ваготовки, нагретые неравномерно по сечению или длине, В некоторых случаях свойства одинаковы в разных точках деформируемого тела, но различны в одной н той же точке в зависимости от выбранного направления, Это характерно для тонколистового проката. Прочность и пластичность таких материалов сильно зависят от выбранного направления: вдоль прокатки они выше, поперек — ниже. Среда, свойства которой зависят от
15
выбранного направления, называется анизотропной. Большинство металлов, обрабатываемых давлением, не обладает анизотропией. Среда, свойства которой не зависят от выбранного направления, называется изотропной.
Таким образом, используя модельные представления, можно доста* точно детально описать свойства реальных металлов, применяемых в про* изводстве.
1.4. ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ
Состояние тела, при котором его частицы выведены из первоначального равчовзсного положения, называется деформированным состоянием. Частицы деформируемого тела могут находиться в движении. Такое состояние характерно для процесса обработки давлением, когда инструмент непрерывно изменяет форму и размеры обрабатываемой заготовки. Частицы деформированного тела могут быть и неподвижными, если тело уже подверглось воздействию инструмента. В первом случае говорят о текущем деформированном состоянии, во втором — об итоговом деформированном состоянии [ 133].
Ранее (см. подразд. 1.1) установлено, что при нарушении естественного равновесного состояния атомов деформируемого тела возникают внутренние силы — напряжения. Поэтому деформации и напряжения тесно связаны друг с другом. Любая текущая деформация вызывает напряжения*, итоговая деформация — не всегда**. Особенность напряжений, действующих в деформированном теле, состоит в том, что они самоуравновешены. Это означает, что и текущее, и итоговое деформированное состояния являются одновременно и напряженными. Такое состояние можно охарактеризовать определенной деформационно-силовой схемой. Но в методических целях пока забудем об этой связи и рассмотрим вначале деформированное состояние, а затем— напряженное.
1.4.1. Способы описания движения сплошной среды. Переменные Лагранжа и Эйлера. Движение материальных частиц деформируемого тела можно описать с различных точек зрения: в переменных Лагранжа и переменных Эйлера (46, 78, 114, 1281. Для описания закона движения по Лагранжу достаточно определить функции х = Fx(t), у = Fy(t), г = Ft(/), связывающие координаты частицы х, у, zco временем t. Рассматривая состояние частицы в моменты времени /0> t2, .... tn, можно определить ком-
поненты ее перемещения и скорости:
«х = (f) — Fx (t0) = Фх (x, у, z, vx = duxtdt\ uv = Fu (/) —
— Fv (А>) s % (x, y, z, t)\ vy = duy/dt-, иг = Ft(f) — Ft (/0) => вфх(^. У, 2, ty vz = duzldt. (1.9)
Чтобы описать движение сплошной среды материального тела» необходимо установить закон движения каждой ее частицы. Для
* Одно исключение из этого правила: при равномерном нагреве тела в нем возникают только деформации.
м Детальный анализ этого вопроса дан в подразд. 4.2.4, 4 2.6.
16
этого нужны правила индивидуализации отдельных (совершенно одинаковых с геометрической точки зрения) частиц сплошной среды. Данное требование означает, что необходимо задать закон движения в виде
x = fx(x°, у9, z?, t); y = fv(x?, у9, z°, /); z = f2(x°, у9, z9, t), (1.10, где x°, y°, z° — координаты произвольно выбранной в деформируемом теле частицы в начальный момент времени t9.
Если в уравнениях (1.10) х°, У’, z° фиксированы, a t— переменная величина, то уравнения определяют движение одной частицы деформируемого тела (той, которая в начальный момент деформации имела координаты х°, у0, z°). Если зафиксировать /, а х°, у9, г9 сделать переменными, функции (1.10) дадут распределение частиц деформируемого тела в пространстве в рассматриваемый момент времени. Если же переменными будут х°, у0, г° и время t, то уравнения (1.10) можно рассматривать как закон движения деформируемого тела в целом, поскольку они определяют движение каждой материальной частицы этого тела. Переменные х°, у9, и t принято называть переменными Лагранжа, хотя исторически это и не совсем оправдано 190, 1141.
Рассмотрим описание движения в переменных Эйлера. Пусть через точку пространства А (х, у, г) в моменты времени tlt tit t3 и т. д. проходят материальные частицы деформируемого тела М2, М3 и т. д., имеющие скорости vt, vs и т. д. В соответствии с представлением Эйлера, движение сплошной среды считается заданным, если компоненты vx, vv, vz вектора скорости v определены функциями
их = их(х, у, г, /); vy=vu(x, у, z, /); vt = v2(x, у, г, t) (1.11) при фиксированных значениях координат. Координаты пространства х, у, z и время t называют переменными Эйлера [46, 1281. Переменные Эйлера широко используются при теоретическом анализе многих процессов обработки металлов давлением. Они особенно удобны для описания стационарного движения сплошной среды, т. е. движения, при котором уравнения (1.11) не зависят от времени.
Значит, переменные Лагранжа определяют законы изменения координат, перемещений, скоростей, ускорений для каждой индивидуальной частицы сплошной среды, а переменные Эйлера— законы изменения тех же исследуемых величин, но в каждой фиксированной точке пространства, через которые последовательно проходят материальные частицы сплошной среды. Описания движения в переменных Лагранжа и Эйлера в механическом отношении эквивалентны.
1.4.2. Движение сплошной среды и деформации. В общем случае при пластической деформации тела все три компоненты скорости vx, vy, vz каждой материальной частицы (или частиц, про
17
ходящих через фиксированную точку пространства при описании движения в переменных Эйлера) отличны от нуля. Такое движение называется трехмерным. Анализ процессов обработки давлением с трехмерным движением —задача исключительно сложная. Она упрощается, когда движение материальных частиц деформируемого тела описывается в цилиндрической системе координат и и» = = 0. Такое движение называется осесимметричным. Задача упрощается еще больше, когда движение частиц двумерное (плоское), т. е. одна из компонент скорости, например vy, равна нулю. Эти виды движения характерны для большинства операций обработки металлов давлением. Так, плоское движение имеет место при изгибе широкой полосы, осадке полосы неограниченной длины, осадке с ограничением уширения, объемной штамповке поковок удлиненной формы, волочении полосы, прокатке тонкого листа и т. д. Осесимметричное движение типично для большинства процессов листовой и объемной штамповки деталей круглой фэрмы, волочения и прессования осесимметричных изделий.
Одномерное движение (vx = оу = 0, vt Ф 0 или vr = и» =« 0, vt 0) в процессах пластической деформации осуществимо только для пористых материалов или порошков. В этом случае изменяется удельный объем тела.
При определенных условиях движение частиц тела вызывает его деформацию. Деформация — смещение частей или материальных частиц тела, при котором изменяются взаимные расстояния между ними, но не нарушается непрерывность самого тела. Обратимая деформация называется упругой, необратимая— пластической.
Для количественной оценки деформации можно использовать различные показатели. Два из них уже известны читателю из курса сопротивления материалов:
абсолютная деформация тела ДЛ = L& — Lo, (1.12)
относительная деформация тела* е = &LIL9. (113)
Здесь L9, Lt — любой начальный и конечный размер тела (высота, длина, ширина).
Связь показателя деформации е с характеристиками движения установить несложно. Обратимся к примеру осадки заготовки (рис. 1.1). Если движение бойка определено законом Н =» H(t) и при t = to боек касается верхнего торца заготовки, то абсолютная деформация ДЯ = H(t0) — Я(/). Размер заготовки Яо задан. Поэтому легко вычислить и относительную деформацию по высоте заготовки: ен(Л в 1Я(/0) — H(t)]/H(t9).
Опыт показывает, что при выполнении операций обработки металлов давлением деформация не бывает одинаковой во всех точках тела. Поэтому в ТОМД нас интересуют не только деформации
* Относительную деформацию часто выражают в процентах: в =□ « (AL/L<»)IOO%.
18
тела в целом, определяемые показателем е, но и локальные деформации, т. е. относительные смещения частиц внутри тела. Представление о картине локальной деформации можно получить различными способами [ 127, 134, 164, 170], например методом координатной сетки. Для количественной оценки локальной деформации используют формулу (1.13), но вместо размера всего тела Lo подставляют в нее шаг координатной сетки а0, а вместо AL — абсолютную деформацию каждой ячейки Да.
При вычислении показателя локальной деформации еА под а0 можно понимать расстояние между двумя любыми точками, лежащими на одной прямой, параллельной оси k, а не только шаг координатной сетки.
Показатель е в форме (1.13) предложен Коши и в специальной литературе нередко носит его имя [78, 1281. Его значение просто вычислить, он достаточно универсален. Но этот показатель имеет два существенных недостатка: неточно отражает физический смысл больших деформаций и не обладает свойством аддитивности*. Поэтому кроме показателя Коши в теории пластичности используют и другие: показатель Свейнгера, Грина, Альманси, Генки [114, 120]. Первые три имеют те же недостатки, что и показатель Коши. Показатель Генки е вычисляют по формуле
е = ln(Ld/L0). (1.14)
Показатель Генки свойством аддитивности обладает.
1.4.3. Деформированное состояние сплошной среды. Неоднородная деформация приводит не только к изменению расстояния между точками, но и к искажению первоначально прямых линий и углов между ними. Поэтому задача описания и количественной оценки деформации тела в целом представляется весьма сложной. Определим деформацию тела V, движение которого задано в переменных Лагранжа (1.10). Геометрическое изображение движения представим в четырехмерном пространстве х, у, г, t (рис. 1.6). Такая геометрическая интерпретация показывает, как стечением времени при движении координатной системы хуг вдоль оси t изменяется форма тела. Для упрощения рассуждений возьмем точки М, N и проследим за их движением в процессе деформации тела. Пусть конечное состояние тела соответствует времени /к. Вследствие деформации расстояние между точками М, N изменится. Совместим координатные оси хуг при t = tK с координатными осями начального положения при t = /0 (рис. 1.6,6). На рисунке MqN0—начальное, a MKNK— конечное положение отрезка, соединяющего точки М, N. Выберем какую-либо координатную плоскость, например хОу (рис. 1.6,в), спроектируем на нее точки. Мо, #0, Мк, и обозначим их проекции через ш0, л0, /пк, п*
• Аддитивность — свойство физических, геометрических и других величин. состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям при любом разделении объекта на части.
19
Спроектируем точки т0, п0, тк, пк на координатную ось х. Очевидно, что т^тк— проекция на хОу вектора полного смещения им точки Л4, а отрезок АС — проекция им на ось х; ПоПк— проекция на хОу вектора полного смещения «л/ точки У; отрезок BD — проекция un на ось х. Примем топо за начальную, а ткпк за конечную длину отрезка тп. и вычислим для него показатель деформации в направлении оси х.
Рис. 1.6. Схема движения частиц сплошной среды К, М, N в четырехмерном пространстве xyzt (а), изменение положения проекций частиц на плоскости
*У (б)
Возьмем АВ — dx. Условимся, что прямая /попо параллельна координатной оси х, причем
_CD — AB_ (<b+uxN-uxM)—dx АВ dx • '
Функции смещения любой точки тела (1.9) предполагаются заданными и непрерывными. Поэтому значения uxn можно вычислить, использовав разложение функции их в ряд Тейлора
। dux . . dux . , дих , UxN = ихм + dx + dy + dz (Б)
и ограничившись линейными членами. По принятому условию расстояние АВ бесконечно малое, равное dx, ЛВЦОх, откуда dy = dz = 0. Из этих условий и уравнений (А), (Б) следует, что ех = дих/дх. Рассмотрев движение проекций точек М, N в координатных плоскостях xOz, r/Oz, пэлучим гу =диу1ду, гг — диг!дг.
Перейдем к рассмотрению угловых деформаций. Возвратимся к рис. 1.6. Выберем в деформируемом теле произвольную плос
20
кость, параллельную какой-либо координатной плоскости, например хОу. Возьмем в ней точки М, N, К, образующие прямой угол, стороны которого параллельны координатным осям. Как и в предыдущем случае, обозначим проекции точек М, N, К на плоскость хОу через т, п, k. Индекс 0 приписываем начальному состоянию тела, а индекс к — конечному. Углы обозначим так, как показано на рис. 1.6. Вычислим искажение yxv первоначально прямого угла <р0 при переходе точки М из положения Мо в Л4К. На основании рис. 1.6
Уху = Фо фк = Фху 4“ Фух- (В)
Здесь <ржр — отклонение луча ткпк от оси х в сторону оси у qyx— отклонение луча ткпк от оси у в сторону оси х. Сумму Фж₽ 4- фух = уху назовем углом сдвига. Из рис. 1.6 следуют соот-алк . bkK
ношения tg Фху = — ; tg фрх = • Отрезки апк, атк и bkK, Ьтк
легко вычислить, разложив функции (1.9) в ряд Тейлора. Подставив в выражения найденные значения отрезков и предположив, что деформация тела бесконечно мала, по уравнению (В) находим yx₽=~-f--^. Рассматривая изменения относительного положения двух троек точек в плоскостях yOz, zOx, получаем формулы для определения углов сдвига по другим к орди-дии , ди2 ди2 . дих
натам: ууг = 4- ; у в —? 4- . Следовательно, показа-тел и деформации е, у выражаются через градиенты функций перемещения (1.9):
дих ех = -д- ; * дх *
дих дии ' диу. ___ди у , дих .
в ду + dx ’ = dy ’ “ dz + dy ’
_ du, , dux dx ’ dz
(1.15)
Эти уравнения впервые вывел Коши, поэтому в специальной литературе по теории упругости они носят его имя. Для осесимметричного движения среды уравнения Коши выводят аналогично:
„ . Ur диг ди. . диг ..
е-=а7; е'=~; = + <||6>
Таким образом, если движение тела определено функцией перемещения и, то показатели деформации е, у в направлении координатных осей легко вычислить по уравнениям (1.15) или (1.16).
Приведем решение задачи в общем виде. Сформулируем ее следующим образом. Задано тело V. В нем выделена частица М с координатами х, у, г. Движение частицы М определено уравнениями (1.9). Необходимо определить локальную деформацию тела в окрестности заданной частицы М в заданном направлении. Выделим в окрестности частицы М частицу W, удаленную от М по координатным осям х, у, г на бесконечно малые расстояния
21
dx, dy, dz так, чтобы отрезок MN был параллелен заданному направлению. Направление отрезка MN охарактеризуем углами ах, а₽, ах, которые он образует с координатными осями х, у, г. Обозначим длину отрезка MN до деформации через Lo. а после деформации через La. Для характеристики локальной деформации примем показатель Коши е = (La—Lo)/Lo. Опустив достаточно громоздкие преобразования, приведенные в работе [26], дадим окончательную формулу:
С = ₽ХОХ 4- 4” Ух!РхРу 4- Ууг^у^г 4~ Угх^гРх- (1-17)
Здесь ах = cos ах, ау = cos ау, аг = cos аг. Из уравнения (1.17) следует, что в рассматриваемой точке М деформируемого тела по любому произвольно выбранному направлению, которое характеризуется направляющими косинусами ах, а₽, а2, можно определить показатель Коши через показатели деформации ех, е. и т. д. Это значит, что задача решена и можно перейти к сообщениям.
1.4.4. Тензорные характеристики деформации. Для полной характеристики деформации в общем случае необходимо иметь функции компонент перемещения (1.9) и вычислить девять их производных, определяющих коэффициенты уравнения 1.17. Производные duxldx, duyldy и т. д. образуют тензор второго ранга*, так называемый тензор единичного относительного перемещения [261:
дх
ди,
диг 51
дих дих ду дг диу диу ду дг дих диг ду дг ]
(1.18)
В общем случае этот тензор несимметричен относительно главной диагонали. Представим его в виде суммы симметричного и кососимметричного тензоров [1, 26, 1281:
дих 1 1дих . диу\ I (дих диг\ дх 2 \ду ' дх J 2 {дг дх J
1 /диу . дих\ диу 1 (диу . диж\
~2 ‘ ду ) ду~ 2" дг ду ) | •
1 /диг । дих \ I /диж । диg
Т дг / "2 + дГ/ Л j
(1.19)
(1.20)
* Тензор второго ранга — это физическая величина, определяемая в любой системе координат девятью числами или функциями Ai/, кото-рые при изменении системы координат преобразуются в A’i/ по закону А’I/ = аг/ aip А//, где аг/,аи'—направляющие косинусы новой системы в данной системе координат (1).
22
дих fojA 1 /&/* ди? ду дх I 2 I дг дх
1 1дии______5ux\ ~ 1 !дии_____диг\
~2 дх ду j 2 у дг ду J
1 /диг_______ЯмЛ 1 (диг диу\ о
2 \<?х дг / 2 дг /
(1.21)
J
Тензор Г. называется тензором деформации, или тензором чистой деформации; тензор Т.— тензором поворота, или тензором вращения.
Компоненты тензора деформации Т. читателю уже известны (см. соотношения (1.15)). Компоненты тензора Г. обозначим dujdy — du9fdx = <Dxp и т. д. При этом тензоры 7\, можно представить в более компактном виде:
еж 2 2 "^хг
_ 1 1
О 2 2
1 л 1
2 ®ух 0 2
• 1 А
2 2 О
(1.22)
В курсах теории упругости и пластичности 16, 78, 1281 показано, что при изменении положения координатных осей одно и то же деформированное состояние выражается различными тензорами Т«, компоненты которых при повороте координатных осей монотонно изменяются, достигая максимума или минимума. При определенном положении координатных осей тензор Т, может иметь форму
(ех О О О е, О О 0 е8
(1.23)
Тензор, у которого Уху = Ууг = у« “ Ух* = Угу = Уи*= О называется тензором главных деформаций. Координатные оси, по которым компоненты тензора деформации ухи, уУг, Угх обращаются в нуль, называются главными осями тензора деформации. Особенность главных осей состоит в том, что линейные элементы, ориентированные вдоль этих осей до начала деформации, остаются взаимно перпендикулярными и в процессе малой деформации, и после завершения его. Если деформация однородная, главные оси имеют одинаковые направления во всех точках деформируемого тела. Но чаще всего направления главных осей различны в разных точках деформируемого тела. Компоненты тензора деформации ех, е2, е3 в направлении главных осей называются главными деформациями. Особенность главных деформаций состоит в том, что одна из них наибольшая, другая — наименьшая из всех возможных, взятых в окрестности данной точки по любому произ
23
вольному направлению. Чтобы определить главные деформации необходимо решить кубическое уравнение 16, 901:
е8 - /х (Т.) е2 + 7» (Г.) е - 7Э (Т.) = 0. (1.24)
Здесь 7Х (7\), 7, (7\), 7, (7\) — коэффициенты, инвариантные к преобразованию координат, составленные из компонентов тензора деформации 7\:
7« (Л) =
2
I 2 ^иг
*2
2 У*г
~2 е»
= const;
7, (Л)
сж 2 2 ^хх
~2 У и* ~2
1 I 2 Уг* 2 “^гЧ
= const.
(1-25)
Эти коэффициенты носят название инвариантов тензора деформации Г,. Корни уравнения (1.25) — это главные деформации. В курсах теории упругости и пластичности 190, 1611 доказано, что все корни уравнения (1.25) действительные. Значит, в любой точке деформированного тела есть главные оси, вдоль которых деформация определяется компонентами еь е,, е3, а сдвиги по этим осям отсутствуют (уху = ууг = =0). Первый инва-
риант тензора деформаций 7|(7'.) имеет определенный физический смысл: с точностью до бесконечно малых второго порядка он выражает относительное изменение объема деформируемого тела или его элемента:
Л (Л) = ч + е, 4- еа = (V, - Уо)/Уо. (1.26)
Из курса сопротивления материалов известно, что при одноосном растяжении или сжатии = е8 = —vev Поэтому /JT.)^ = 8i(l — 2v). Здесь v — коэффициент поперечной деформации (коэффициент Пуассона). Для упругой деформации различных металлов v = 0,25...0,33. Значит, при растяжении в упругой области объем тела увеличивается (ei > 0), а при сжатии — уменьшается (е, < 0). Тщательные эксперименты по определению изменения объема при пластической деформации показали, что v = = 0,5, а следовательно, при пластической деформации объема тела или его элемента не изменяется:
7i (Г.) = ех 4- с* 4- г, = et + е, + е8 = 0. (1.27)
Эго равенство принято называть законом или условием постоянства объема. Условие (1.27) можно представить и в дифферен
24
циальной форме, если вместо компонент тензора деформаций взять их значения по уравнениям Коши (1.15), (1.16):
+ ^ +1 “ 0 < L28>; £* + 7 + £ = °- 0-29)
Из уравнений (1.28), (1.29) вытекают важные следствия: для описания двумерного или осесимметричного движения достаточно задать одну функцию, а другая однозначно определяется интегрированием уравнения (1.28) или (1.29). Для описания трехмерного движения необходимо задать две функции (например иг, uv), а третью найти интегрированием. Это позволяет значительно упростить подход к описанию движения деформируемых тел при анализе технологи-гических процессов ОМД. Тензор Т, характеризует полную деформацию тела: он определяет изменение формы тела (компоненты е, у) и объема (компоненты е). Чтобы разделить эти виды деформации и дать наглядное представление о них, тензор 7, раскладывают на две тензора Т. = Т? 4- D,, где
еж вер 2 Тхр 2 ^хг
2 Vpx Ер Еср 2 Трг ’ • (1.30) ~2 Yzx *2* ₽с₽ 1
Тензор называют шаровым тензором деформации. Его особенность заключается в том, что компоненты у равны нулю, а диагональные компоненты еСр равны средней деформации. Из выражения (1.27) следует, что «ср = у /1(Т«). Значит, тензор определяет только изменение объема. Для упругой деформации е^ =/= */= 0. Поэтому 7Т =#= 0 и объем деформируемого тела изменяется в зависимости от значения и знака величины еср. Для пластической деформации еср = 0. Следовательно, 71й = 0 и объем деформируемого тела не изменяется. Тензор £>« называется девиатором деформации. Его важная особенность состоит в том, что /i(D.) = 0- Это означает, что девиатор деформации характеризует только изменение формы тела. Для пластической деформации еСр = 0, поэтому D. = Tt. Исключительно важную роль играет в ТОМД второй инвариант девиатора деформации D«. Функция е<=^=ГмёГ)=1рх
х V('«—(«,—«.)' + («»—«.)’ + 4 ?£,+ v?x)
называется интенсивностью деформации и устанавливает условия пеоехода тела в предельные состояния.
25
1.4.5. Условия совместности деформаций. Деформированное состояние тела однозначно определено, если заданы компоненты функции перемещения ых, uyt иг или компоненты тензора деформации ех, гу, ег, уХ1Р ууг, угх. В первом случае требуется всего три функции, а во втором — шесть. В связи с этим возникает вопрос: а можно ли все компоненты тензора Т, задавать совершенно произвольно или имеются какие-либо ограничения, наподобие условия постоянства объема при выборе функций ых, иу, иг.
Продифференцируем дважды первое уравнение Коши (1.15) по у, второе — по х и результаты сложим. Четвертое уравнение продифференцируем по х и у. В итоге получим два уравнения с одинаковыми правыми частями. Приравнивая и левые, установим, что деформация уху однозначно определяется через деформации ех ev. Два других уравнения выводят аналогично:
д*еж , дЧи _ d*yxy. д* у , дЧг _ д*уух . а»ех , д*гх _ д*угХ
ду* ' дх* дх ду * дг* ду* ду дг * дх* ' дг* дг дх' ' ’ ' Эти соотношения называют уравнениями Ссн-Венана. Они выражают условия совместности деформаций. Из уравнений Сен-Ве-нана следует, что, если заданы три функции ех, еу, г2, то этого вполне достаточно для однозначного и полного описания деформированного состояния, так как три оставшиеся (уху, ууг, угх) определяют по уравнениям (1.32). Можно установить и обратную связь между у, е. Для этого продифференцируем четвертое уравнение (1.15) по z, пятое — по х, шестое — по у. Последнее уравнение умножим на —1. Результаты сложим. Полученное уравнение продифференцируем по у. В итоге выведем уравнение, связывающее деформации е с перемещением и. Приняв во внимание, что дуу/ду = еу, найдем уравнение, связывающее у и е. Два других уравнения выводят аналогично:
£ №1! _ 4_ ^У«\ = 9 дЧк — (tly* _ =
дх дг dx * dy j dydx’dyy dx dy ‘ dx j
n дЧУ . /&Угх &Уху I &Ууг\ n д*гг /1 oo\
a^-dxdx' dx\dy дг dx ) £dydx' I1-’3’3/
Эти уравнения также называются уравнениями Сен-Венана и выражают условия совместимости деформации, но в другой форме. Из них следует: если заданы три функции уху, ууг, угх, то этого вполне достаточно для однозначного и полного описания деформированного состояния, так как три оставшиеся (ех, еу, ег) определяются по уравнениям (1.33). Аналогично из уравнений (1.16) можно получить условия совместности деформаций и для осесимметричного течения сплошной среды.
1.4.6. Скорости деформации. При выводе уравнений (1.15), (1.16) отмечалось, что деформация тела бесконечно мала, расстояние между точками бесконечно мало и т. д. В реальных производственных процессах обработки металлов давлением деформации тела исключительно велики, и показатели деформации е, у, обра
26
зующие тензор Т«, оказываются лишенными свойства аддитивно* сти. Поэтому для анализа производственные процессы приходится разбивать на этапы так, чтобы в пределах каждого из них деформации можно было бы считать малыми [133, 146, 1761. Задача упрощается, если движение сплошной среды описать в переменных Эйлера, задав поле скоростей. Поле скоростей — это совокупность значений компонент вектора скорости и, заданных в каждой точке рассматриваемой области. Поле скоростей можно получить аналитически. Пусть,например, движение инструмента определено законом
= — /?<1)(sin а 4- 4- Xsin 2а + Xacosa). (1.34)
\ ш /
Эго уравнение характеризует движение инструмента, закрепленного на ползуне кривошипного пресса или горизонтально-ковочной машины. Очевидно, что по такому же закону движутся частицы деформируемой заготовки, непосредственно примыкающие к рабочим поверхностям инструмента, т. е. vx = при z = = zB (здесь Zu —координаты рабочей поверхности инструмента. Значит, можно установить связь уравнений (1.34) с характеристиками движения исполнительного механизма оборудования: определить ог = иДх, у, г, t) и найти функции vx, vy на основании условия постоянства объема и дополнительных уравнений, которые связывают их, vy, vx и вытекают из кинематических особенностей процесса деформации или принятых упрощающих допущений. Есть и другой путь для определения поля скоростей: экспериментальное исследование деформируемой заготовки или ее модели (127, 133, 134, 145, 164, 170, 1781. Имея уравнения (1.11), можно найти скорости деформации сплошной среды. Обозначим
дх 1*’
до до ди ди до
ду “ дх *xlh ду дг ду
(1.35)
Структура этих уравнений аналогична структуре уравнений Коши (1.15). Величины £х, — линейные относительные
скорости деформации. Они имеют размерность 1/с. Их физический смысл вытекает из следующего преобразования. Предста-а ~ д рил д /дид де
вим Vg как oug dt. Тогда L = = т- Нт = ~ hr- = si •
* я дх dx\dt / dt\dx J dt
Таким образом приходим к определению. Скорости деформации Ъ — это показатели изменения степени деформации 8 в направлении соответствующих координатных осей в единицу времени. Аналогично устанавливаем смысл и определение скоростей деформации сдвига. Скорости деформации сдвига %ху, 1уг, 1гх — это показатели изменения первоначально прямых углов в единицу времени. Скорости деформации сдвига также имеют раз*
мерность 1/с. Скорости деформации £ образуют тензор скоростей деформаций
л =
2 2 ^хг
~2 ^ух ^у ~2 ^ух ’ *
Л t JLt t 2 vzx 2 «1/ *z
(1.36)
Свойства тензоров T\, Т, во многом схожи. В частности, для пластической деформации
Л (Л) = k-Н,-Нг = 0.
(1.37)
Это уравнение выражает условие постоянства объема в скоростях. По аналогии с условиями (1.28), (1.29)
Для скоростей деформаций £ можно определить положение в пространстве главных осей и найти тензор главных скоростей деформации
0 О' 0 0
10 0 J
(1.39)
Здесь, как и в тензоре главных деформаций, — наибольшая, а $з — наименьшая скорость деформации в данной точке из всех возможных по любому направлению. Для компонент тензора Т% можно составить уравнения совместности, имеющие полную аналогию с уравнениями (1.32), (1.33), и определить интенсивность скоростей деформации &, заменив в формуле (1.31) компоненты деформации е, у компонентами скоростей деформаций £.
Скорость деформации в любой точке деформируемого тела в направлении любой главной оси определяется однозначно скоростью деформирования v# и видом функций (1.33). Например, для плоского движения сплошной среды, когда vx = — Cz, vu « vd
= 0, vx = Cx, имеем , L = ^ • Здесь H — размер тела
в направлении оси z. Отсюда следует вывод: при однородной деформации тела скорость его деформации £ прямо пропорциональна скорости деформирования и обратно пропорциональна линейному размеру Н в направлении вектора о#.
Таким образом, описание движения сплошной среды в скоростях деформации позволяет дать такую же детальную характеристику деформации, как и описание в перемещениях, не прибегая, однако, к допущению о ее малости.
28
1.4.7. Схемы и виды деформации. Чтобы язык формул перевести на язык графики, введем понятие «схема деформации» [28, 30, 138]. Схема деформации—это условное графическое изображение
компонент. тензора главных деформаций Т[.
Допустимые схемы деформаций ограничиваются условием постоянства объема /1(7\) = 0, из которого устанавливаем, что
главные деформации et, еа, е3 не могут иметь одинаковых знаков.
Значит, для трехмерного движения сплошной среды возможны
только две схемы деформации: одна деформация сжатия и две рас-
стяжения (рис. 1.7, ДО1) или две деформации сжатия и одна рас-стяжения (рис. 1.7, ДО2). Для плоской деформации е3 = 0 и et +
+ е3 = 0, что определяет единственно возможную схему, при которой еа = —е3 (рис. 1.7, ДП). Для осесимметричного движения сплошной среды характерны схемы ДО1, ДО2. При радиальной раздаче длинных труб иг= = 0, «е = 0, а и, =#: 0. Тогда ег = е3 = диг 1дг =£ 0, ее = Ej = ur/r 0 и схема де-
Рис. 1.7. Схемы деформаций: ДО — объемные, ДП — плоские
формации приобретает вид ДП. Такое движение сплош-
ной среды — единственно
возможный вариант одномерного движения, вызывающего пластическую деформацию. Понятие «схема деформации» можно распространить и на случай, когда движение задано в переменных Эйлера и деформированное состояние тела определено тензором главных
скоростей деформаций 71. Так мы приходим к общему определению понятия «схема деформаций».
Схема деформации —это условное графическое изображение компонент тензора главных напряжений Т\ или тензора главных скоростей деформаций 71. Отметим важную особенность компонент тензора деформаций еж, еу, ez и скоростей деформации £ж, Ъу, Одна из этих компонент — компонента вынужденной деформации,которая однозначно задается движением инструмента, а две других — компоненты свободной деформации. Они определяются законом наименьшего сопротивления (см. подразд. 4.1) и условием постоянства объема. В некоторых случаях, например при прессовании, вынужденными являются две компоненты ег, Ее, а третья — компонента свободной деформации. Деформация может быть однородной и неоднородной. Однородная деформация — это деформация, при которой тензор Т[ или Т\ и положение главных осей не зависят от координат. При однородной деформации прямые и параллельные линии остаются таковыми и после деформации, хотя их направление может изменяться. По
29
добные и подобно расположенные фигуры во всех точках тела деформируются подобно [ 17, 301. В процессах обработки металлов давлением однородная деформация возможна при растяжении гладкого образца, цилиндрического или листового, и осадке без трения. Во всех остальных случаях деформация неоднородна.
Неоднородная деформация — это деформация, при которой тензор Т\ или Т[ и положение главных осей является функциями координат деформированного тела. Неоднородность деформации сильно усложняет анализ процессов обработки металлов давлением. Поэтому часто деформируемое тело разделяют, конечно, условно на ряд элементов, в пределах которых деформацию можно считать однородной.
1.5. НАПРЯЖЕННОЕ СОСТОЯНИЕ
При обработке давлением положения материальных частиц де-фэрмируемого тела изменяются под действием инструмента. В ответ на эти изменения между частицами возникают внутренние силы и тело переходит в напряженное состояние. Напряженное состояние — это состояние тела, находящегося под действием уравновешенных внешних сил при упругом равновесии или движении его частиц.
1.5.1. Поверхностные и объемные нагрузки. Силовое взаимодействие двух тел можно.представить двумя моделями: как действие одного тела на другое в виде сосредоточенной силы или в виде распределенной поверхностной нагрузки. Первая модель широко применяется в теоретической механике и сопротивлении материалов, нередко используется и в обработке металлов давлением. Однако из-за сравнительно грубой схематизации взаимодействия двух тел она пригодна лишь для решения таких задач, как определение усилия и работы деформации. При обработке давлением силовое взаимодействие двух тел можно с достаточной точностью охарактеризовать только второй моделью — моделью распределенной поверхностной нагрузки. Под поверхностной нагрузкой S(x, у, г) условимся понимать интенсивность действия внешней силы, приложенной к поверхности деформируемого тела. Для вычисления S(x, у, г) в точке поверхности деформируемого тела необходимо в окрестности этой точки взять площадку Д£, найти силу ДР, действующую на площадку, вычислить lim (&P/&F) и при-
AF-»0
нять S(x, у, г) = lim (&P/&F). Размерность поверхностной нагрузки Па. iF-0
В общем случае при взаимодействии двух тел вектор силы не совпадает с нормалью к площадке ДР. Силу ДР можно разложить на нормальную ДРЯ и тангенциальную ДР/ составляющие. Поэтому и распределенную нагрузку на поверхности деформируемого тела можно представить как нормальную Sn и тангенциальную S/. Составляющая St по своей природе является силой трения. Напряжение S можно разложить на компоненты по координатным осям Sx, Sy, Sx. Знаки этих величин будут установлены в подразд. 1.5.2. На деформируемую заготовку, кроме поверхностных, действуют также объемные (массовые) нагрузки: силы тяжести, инерции и магнитного взаимодействия. При анализе процессов ОМД силы тяжести никогда не учитывают. Силы инерции, а также магнитные силы учитывают только при выполнении специальных процессов ОМД — высокоскоростной, взрывной, электрогидравлической или магнитно-импульсной штамповки. Для вычисления интенсивности действия объемной нагрузки q(x, у, z) в ив*
>0
которой точке необходимо в ее окрестности выделить элементарный объем AV, определить силу AQ. действующую в этом объеме, вычислить lim(AQ/A V) ди-о
и принять q(x, у, z) = lim (AQ/ДИ). Размерность этой величины Н/м’. Ин* дУ-»о
тененвность объемной силы q можно разложить на компоненты по координатным осям qx. q*, q*. Знаки этих величин устанавливаются по соглашению, на* пример qx > 0, если направление qg совпадает с положительным направлением оси х.
1.5.2. Тензор и девиатор напряжений. Силовое воздействие ин-
струмента на заготовку вызывает в ней напряженное состояние. Из курса сопротивления материалов известно, что в большинстве
случаев напряжения, как и деформации, распределяются в теле крайне неравномерно. Поэтому для описания напряженного состояния необходимо решить сложную задачу: для любой точки деформируемого тела определить напряжения на любой произвольной площадке. Рассмотрим стержень, нагруженный силами + Р и —Р (рис. 1.8). Условимся, что стержень имеет постоянное сечение и достаточно большую длину. В соответствии с принципом Сен-Венана можно считать, что напряжения распределены равномерно, за исключением областей, непосредственно примыкающих к точкам приложения сил. Если площадь сечения стержня F, то напряжение в любой точке на площадке Уь нормаль к которой nj совпадает по на
Рис. 1.8. Схема действия внутренних сил при растяжении стержня постоянного сечения
правлению с осью стержня, можно опреде-
лить как о = Р/F. Возьмем в теле произвольную точку М, проведем через нее плоскость Nt, нормаль которой nt расположена под углом <р к оси стержня. Пользуясь методом сечений, известным читателю из курса сопротивления материалов, определим напряжение S, действующее в точке М по плоскости У,. Воспользовавшись условиями равновесия, находим $/7со5ф — Р, откуда
S = Pcos ф/F = ст cos ф. (1.40)
Полное напряжение S разложим на составляющие — нормальную оя и касательную т. Из треугольника МАВ (рис. 1.8) находим
on = Seos ф = стсоб’ф; т = S sin ф =ст sin 2ф. (1.41)
Следовательно, напряжения стл, т на любой площадке У, произвольно наклонной к оси стержня, можно найти однозначно, если известны напряжение ст и угол ф, определяющий положение площадки. Это дает основание поставить задачу в общем виде. Сформулируем ее следующим образом. Пусть в теле, нагруженном заданной системой нагрузок, в координатных площадках, проведенных через точку Mt действуют известные напря
31
сия тетраэдра МА ВС. Из услс — Рвмс^ху — Fcma^xi 4- Fabc
Рис. 1.9. Схема к «определению напряженного состояния в точке
жения ?/’ °у' a” т^’ Т</г’ T«* T«’T?v» тух (рис. 1.9). В окрестности точки М проведем плоскость А ВС, нормаль к которой п образует с координатными осями х, у, z углы, косинусы которых аж, ау, аг соответственно. Определим напряжение S, действующее в площадке АВС.
В направлении оси х действуют напряжения их, хху, тжг, а также компонента напряжения Sx. Составим условие равнове-зия S Рх = 0 находим — FambQx — »х » 0. Из условий Ру = 0, S Рг = 0 пат учим два аналогичных уравнения для Sy, St. Разделив почленно каждое из уравнений на Fabc и приняв во внимание, что FambIFabc = Ох, F вне! F авс = ау, Fcma/Fabc = аг, найдем уравнения, определяющие компоненты напряжения и полное напряжение в площадке АВС:
Sx = Ох^Х 4~ ^xjfly 4“ ТхА‘» Sy = "tyxQx -f- ОуЯу 4* S2 = ltxax 4* 4“
S2 = 5« + sj + s;. (1.42)
Нормальное напряжение an в площадке АВС можно определить, проектируя 5Ж, Sy, S2 на нормаль п:
on = S^x-f- Syfly+ (1.43)
Наконец, касательное напряжение т в площадке АВС можно найти по правилу параллелограмма:
т2 = S2 — о*. (1-44)
Итак, если заданы напряжения в координатных площадках, проведенных через рассматриваемую точку М, то по уравнениям (1.42) можно однозначно определить напряжение S, действующее в любой площадке, положение которой задано направляющими косинусами аж, ау, at. Это означает, что для характеристики напряженного состояния в точке М необходимо и достаточно задать девять величин: ож, тЖу, тЖ2, хух, хуг, ог, тжж, тжу. Таким образом, приходим к следующему выводу.
Напряженное состояние в точке— это физическая величина, для количественной характеристики которой необходимо и достаточно задать девять чисел (напряжения в координатных площадках), которые в совокупности образуют тензор напряжений
G
®х *ху ^хг Т’ух &V *
Дхх ^ty °, .
(1.45)
32
Числа ах, тхи, тХ2 и другие называются компонентами тензора напряжений. Знаки нормальных напряжений ох, ау, а, устанавливаются так: напряжение, растягивающее элемент, считается положительным (например их> иу, и2 на рис. 1.12), сжимающее — отрицательным, знаки касательных напряжений тху, тХ2 и т. д. устанавливаются по соглашению*. Заметим, что Та — симметричный тензор второго ранга. Поэтому нельзя принимать условие парности касательных напряжений в виде тхр =—т₽х, = — —®= —тхх» как это обычно делают в работах по сопротивлению материалов [8, 147]. По-видимому, впервые эта неточность отмечена Ю. И. Ягном [180].
Компоненты тензора напряжений Та могут быть числами или функциями. В первом случае тензор Та характеризует напряженное состояние тела в точке, во втором — напряженное состояние тела в целом. В курсах тензорного анализа [ 1, 1281 доказано, что лю5ой тензор второго ранга можно разложить на два тензора: Г, = Т “4- где
аср 0 0 Ох Оср ТХ2
Т“ = 0 оср 0 ; Da = °СР . (1.46)
0 0 стСр ^гх "*гу & г ®сР
Тензор называется шаровым. Его компоненты оср—среднее напряжение: оср = j (ах 4- оу 4- о2) = у /, (Т9). Тензор De называется девиатором напряжений. Важная собенность девиатора напряжений состоит в том, что его первый инвариант тождественно равен нулю. Величина oz, пропорциональная второму инварианту девиатора напряжения,
о(= 1Z3|/,(D.)| =
= 4? lz(°» — °»)’ + (°,—oJ1 -Но.—о,)' + 6 hi, + + 4J
(1.47)
называется интенсивностью напряжений и определяет переход тела в первое предельное состояние.
1.5.3. Главные напряжения. Возвратимся к рассмотрению рис. 1.8 и формул (1.41). Если <р — 0, то в площадке действует только напряжение о„ = о, а касательное напряжение т обращается в нуль. Из курса сопротивления материалов известно, что и в общем случае площадку АВС (рис. 1.9) можно расположить в пространстве так, что касательные напряжения в ней обратятся
* Особое правило знаков для касательных напряжений вводят только при построении круга Мора: т > 0, если для совмещения с его направлением внешнюю нормаль к площадке действия т необходимо повернуть на 90’ по ходу часовой стрелки; т < 0 — если против хода часовой стрелки [160]. При этом tjcy = — и т. д.
2 1-25
33
в нуль, а будут действовать только нормальные. Площадки, по которым действуют только нормальные напряжения, называются главными площадками', напряжения в главных площадках — главными напряжениями; координаты оси, перпендикулярные к главным площадкам,— главными осями тензора напряжений. Чтобы определить главные напряжения в площадке АВС, необходимо решить кубическое уравнение [90, 128, 1381
о3- К (Тв) а2 + /, (Л) а — 73 (Т.) = 0. (1.48)
Здесь 7j (Т„) = ох + оу 4- о2,
/з (Л) =
О» ^ху ^хг ух Uy lyg .
Tzp О2
Уравнение (1.48) имеет три корня oni, а„2, ол3. Доказано, что все корни действительные [128, 138]. Эти корни — главные напряжения. Обозначим их ох, о2, о3 так, чтобы о3^о2^ох. Определив численные значения главных напряжений, можно найти положение соответствующих им главных осей и главных площадок [6, 160]. В главных осях тензор напряжений приводится к виду
0
0
0 0 ст2 0
0 о3
(1.49)
Его называют тензором главных напряжений.
По физическому смыслу задачи главные напряжения <тх, о2, о3 должны быть одинаковы независимо от того, в какой координатной системе рассматривается напряженное состояние тела. Поэтому и коэффициенты уравнения (1.48) должны быть одинаковыми. Следовательно,
Il (Тд ~ ох + Оу 4- о2 = ох + и2 + а3 = const;
72 (Т в) = а^у — х2ху + о^г — т?г + огох — =
— ^i^2 I а2а3 4’ a3<h const, 73 (7*а) — охох 4- ^хХуХу2х2Х~~ — охх*2—о„т2х — а2т*и = охо2о3 = const. (1.50)
Эти коэффициенты называются инвариантами тензора напряжений Т„. Из уравнения (1.48) выходит, что два тензора Т‘9,Т" определяют одно и тоже напряженное состояние, т. е. дают одинаковые главные напряжения тогда и только тогда, когда Л (То) я Л (Т1*); Ц (П = /3 (Т'в) = 73 (77). Таким образом,
напряженное состояние можно задать в любой координатной системе хуг тензором Та. По уравнению (1.48) можно определить
34
главные напряжения olt а2, о8 в координатной системе 123. Следовательно, напряженное состояние можно передать тензором главных напряжений Т«.
1.5.4. Главные касательные напряжения. Анализ уравнения (1.41) показывает, что в простейших случаях напряженного состояния, например при одноосном растяжении и сжатии, касательное напряжение т достигает максимума на площадках, расположенных под углом 45° к главным осям. Наибольшие коса-тельные напряжения называют главными касательными напряжениями.
Попытаемся решить задачу в общем виде для трехосного напряженного состояния. Пусть напряженное состояние в точке М задано тензором главных напряжений TJ. Определим положение площадок, в которых действуют главные касательные напряжения. Из уравнений (1.42)— (1.44) получаем
т2 = oJa* + 4- (ф2 — (Oja? 4- (Jta* + o^2)2. (1.51)
Здесь аъ аг, а3 — направляющие косинусы, определяющие положение наклонной площадки, где действует напряжение т, относительно главных осей /, 2, 3. Касательное напряжение т является функцией трех переменных а2, а3. Одну из переменных, например а3, можно исключить, воспользовавшись условием
а} 4-o’4-aJ = а2 4-а? + «1 = 1. (1.52)
Тогда уравнение (1.51) примет вид
т2 « о2п2 4- 4- а2 (1 — а? 4- о?) —
— [о1а?4-а2а24-а3(1 — а2 —а|)]2. (1.53)
Читателю известны способы исследования функций на экстремум, поэтому промежуточные выкладки опустим. Уравнения дт2/5а1= О, дт2/уа2 = 0 представим в виде системы
Ci
(<*! — о8) а? 4- (а2 — а8) а* — у (ах — о3)
«J (<*i — Оз)4- (oa — а8) а\ — у (о2 — а3)
= 0;
= 0.
(1.54)
Тривиальные решения системы очевидны: а2 = 0, а3 = 0. Из условия (1.52) находим а3= ±1. Они определяют положение координатной плоскости, перпендикулярной к главной оси 1. Как известно, в этой площадке касательные напряжения равны нулю. Нетривиальное решение первого уравнения системы (1.54) получим, предположив av Ф 0, аа = 0. Тогда (о, — о3) а} —у (<jj — а8) = 0. л»
Отсюда fl] = ± , а2 = 0, а3 = + |/ ~. Аналогично, приняв
<*1=0, а8=5«ь0, из второго уравнения (1.54) найдем ах = 0, а3 =
2*
35
= a3 = i у т>-• Исключая из уравнения (1.54) последовательно a,, и выполняя аналогичные исследования на экстремум функции т2, получим следующие значения направляющих косинусов, определяющих площадки, в которых действуют максимальные касательные напряжения г:
Gj = 0, Ga = Qf = 4; ♦ Яа = О, = Оз = + j/" ’
а8 =0, Gi = аа= ± У у. (1.55)
Первые три направляющих косинуса определяют две взаимно перпендикулярные площадки, проходящие через заданную точку М и ось /, равно наклоненные к осям 2, 5; вторые три — две взаимно перпендикулярные площадки, проходящие через заданную точку М и ось 2, равно наклоненные к осям 1, 3, последние три — две взаимно перпендикулярные площадки, проходящие через заданную точку М и ось 3, равно наклоненные к осям /, 2 (рис. 1.10).
Главные касательные напряжения обозначают т1а, таа, та1. Здесь индексы показывают оси, к которым равно наклонена площадка, где действует данное касательное напряжение. Направление вектора главного касательного напряжения устанавливают по следующему правилу: вектор т перпендикулярен к той оси, наименование которой не входит в индекс т. Например, вектор т1а перпендикулярен к оси 3 и т. д.
Определим численные значения главных касательных напряжений. Для этого воспользуемся формулой (1.51) и значениями направляющих косинусов (1.55):
*13 = ± 4 <ai ~ Ьз = ± у — аа)« T»i = ± 4 <аз—^i)- О-56)
Таким образом, любое главное касательное напряжение равно полуразности соответствующих главных нормальных напряжений, взятой со знаком 4- или —. Воспользовавшись уравнением (1.43), найдем нормальные напряжения, действующие в площадках, определяемых направляющими косинусами (1.55):
<Чз = ± 4 = ± 4(°* + G3i = ± 4 (аз+°г1)- О-57)
1.5.5. Эллипсоид напряжений. Виды и схемы напряженного состояния. Пусть в некоторой точке напряженное состояние задано тензором 71. Проанализируем возможные изменения напряжения S, действующего в любой площадке, наклоненной к главным осям под углами, косинусы которых alt оа, gs. Уравнения (1.42) преобразуем
36
возведем в квадрат и почленно сложим. Учитывая соотношение (1.52), получаем
°i °i °»
(1.58)
Это уравнение описывает трехосный эллипсоид с полуосями ot, °з— эллипсоид напряжений (рис. 1.11). Поверхность эл* липсоида — геометрическое место точек, которое описывает конец вектора полного напряжения S при любых положениях наклонной площадки, если начало вектора находится в начале координат.
Рис. 1.10. Площадки действия главных касательных напряжений Рис. 1.11. Эллипсоид напряжений
Из уравнения (1.58) следует важный вывод: абсолютное значение вектора полного напряжения S на любой площадке, наклоненной к главным осям, не может быть меньше минимального главного напряжения о9 и больше максимального Пр Анализ уравнения (1.58) и его графического отображения (рис. 1.11) позволяет осуществить классификацию видов напряженного состояния.
Напряженное состояние называется объемным, или трехосным, если все три главных напряжения а>, а2, а3 отличны от нуля. Анализ задач с объемным напряженным состоянием наиболее сложен: для их решения необходимо определить в общем случае шесть компонент напряжений ох, ог, хху, xyt, хгх. Поэтому при решении технологических задач ОМД пытаются свести рассматриваемую задачу с объемным напряженным состоянием к более простой. Во многих случаях деформируемую заготовку можно разделить (конечно, условно) на части, в пределах которых напряженное состояние определяется меньшим количеством неизвестных.
Важное место в теории обработки металлов давлением занимает напряженное состояние, которое характеризуется равенством всех трех главных напряжений. В этом случае эллипсоид обращается
в шар и по любой площадке, наклоненной ко всем трем главным осям, действует только нормальное напряжение <тср = уЛ(Т.). Значит, любая площадка, проведенная через рассматриваемую точку,— главная площадка, любая тройка ортогональных осей — главные оси. Такое напряженное состояние бывает при всестороннем равномерном сжатии или растяжении. Оно определяется шаровым тензором 7Т. Напряжение аСр называется гидростатическим давлением.
Рис. 1.12. Схемы напряжений: НО —объемные, НП — плоские, НЛ —линейные
Достаточно простым напряженным состоянием является плоское. Напряженное состояние называется плоским, или двухосным, если одно из главных напряжений равно нулю. В этом случае эллипсоид превращается в эллипс и напряженное состояние можно задать тензорами
П = (®‘ 01 или Т. = 1°' «1.
10 ов1 I гх ог )
Самое простое напряженное состояние линейное. Напряженное состояние называется линейным, или одноосным,' если только одно из главных напряжений отлично от нуля. Линейное напряженное состояние определяется тензорами
Г __ fal 0|
’ “ 10 о/
или Т,=
0 (М
0 а,)
, или Т.=
a, J
При линейном напряженном состоянии всегда бывает известно положение главных осей. Поэтому анализ задач сводится к нахождению единственного главного напряжения или а3 и вычислению по формулам (1.41) компонент тензора Т в площадках, заданных углом <р. Чтобы наглядно представить множество возможных раз-
38
новилностей напряженного состояния, введем понятие «схема напряжений» [30, 1381. Схема напряжений — это условное графическое изображение тензора главных напряжений 7*. Возможные схемы деформаций определяются условием постоянства объема Л(?\) = 0- Для компонент тензора напряжений такого жесткого ограничения нет, так как в общем случае ЩТ,) ф 0. Следовательно, возможно девять схем напряженного состояния (рис. 1.12). Схемы НО (схемы напряжений объемные) характеризуют наиболее общий вид напряженного состояния. Такие схемы типичны для процессов холодной и горячей объемной штамповки, прессования, выдавливания, волочения, прокатки фасонных профилей и сортового металла. Анализ процессов ОМД, для которых характерны такие схемы, наиболее сложен. Схемы НП (схемы напряжений плоские) характеризуют более простой вид напряженного состояния — плоское напряженное состояние. Они типичны для процессов листовой штамповки. Самый простой вид напряженного состояния характеризуют схемы НЛ (схемы напряжений линейные). В обработке металлов давлением эти схемы встречаются исключительно редко: при испытании на растяжение гладких образцов, правке растяжением, а также вне очага деформации при волочении, редуцировании и вытяжке.
1.5.6. Уравнения связи между напряжениями и деформациями в упругой области. Из формулы (1.1) следует, что напряжения и деформации связаны однозначно. На феноменологическом уровне эта связь устанавливается на основании экспериментальных исследований или модельных представлений. Для упругой деформации при линейном напряженном состоянии вид функции а = f(e)e определен известным из курса сопротивления материалов законом Гука (1.3). В общем случае, когда рассматривается объемное напряженно-деформированное состояние, связь между напряжениями и деформациями выражается следующим соотношением между девиаторами напряжений и деформаций:
O.-55O.. (1-69)
где G — модуль сдвига. Раскрывая это тензорное соотношение, получаем уравнения связи между напряжениями и деформациями в упругой области:
«Ж = [ох — v (Оу + ог)); Уху = Хху, ty — j(Oy — v (о, + ох)];
У ух = q~ Туг! Ъг~~Ё — V V» “ ~О *60)
Из уравнений (1.60) можно сделать три важных вывода. 1. Если равны две компоненты о* тензора напряжений Тв то равны и соответствующие компоненты деформации, и наоборот. 2. Если в направлении координатной оси k деформация ед равна нулю, то напряжение в направлении этой оси отлично от нуля и пропорционально среднему напряжению аср. 3. Если в направлении координатной оси k напряжение а* равно нулю, то деформация е* в направлении этой осн отлична от нуля и пропорциональна средней деформации еср.
39
*1.5.7. Механическая схема деформации. В большинстве технологических процессов ОМД состояние деформируемого тела задается частично напряжениями и деформациями. Это соответствует наиболее общему случаю смешанных граничных условий в напряжениях и перемещениях или скоростях перемещения. Поэтому для описания состояния деформируемого тела только схемы напряжений или деформаций недостаточно. Значит, необходимо новое понятие — «механическая схема деформации»*.
Механическая схема деформации — это совокупность схемы напряжений и схемы деформаций. Сочетание девяти схем напряжений с каждой из трех схем деформаций позволяет получить 27 механических схем деформации. Одни из них часто встречаются при обработке давлением. Другие принципиально осуществимы, но пока не реализованы ни в одном из известных процессов ОМД. Третьи принципиально невозможны, как, например, схемы НП1— ДП, НП2—ДП, НПЗ—ДП (рис. 1.7, 1.12), что следует из выводов 2, 3 в подразделе 1.5.6.
1.5.8. Плоские задачи. Kpvr Мора. В теории обработки металлов дав* лен нем различают две плоские задачи: плоское напряженное и плоское деформированное состояние.
Для первого
е*
О
1 у Yw
О
JO
I уТ«
О
«I
(1.61)
Для второго
Т9
о
Оу О
О ог
8х
1 у Y«
!
у Y«
еа
(1.62)
где ву ж» -% (ох 4- а,).
При решении плоских задач приходится определять напряжения в различ -ных площадках, наклоненных к координатным. Формулы преобразования можно получить нз общих уравнений (1.42) — (1.44). Главные напряжения определяем, пользуясь формулой (1.48) и принимая Оу » 0, хХу Хуг =* О, Л (^e) m °х + ог, охог — т*г, /, (Тв) = 0;
ст1. з = у (°* + °*) ± у <CTjt" °***+ 4т« • (1-63)
Формулы преобразования значительно упрощаются, если напряженное состояние задать в главных напряжениях, а координатными выбрать главные оси 1, 3. В этом случае по формулам (1.43), (1.44) после подстановки ах =» cosa, аг » i«na и замены cos*a, sin*a функциями двойного
• Введено в ТОМД С. И. Губкиным [29, 30).
40
угла находим нормальные н касательные напряжения, действующие во взаимно перпендикулярных площадках, проходящих через некоторую точку М:
ах ) 1 . 1 1
а J 2" + °з) ± Т (°1 ““ °») cos 2а; т« “ ± у <ст1 “ аз) s,n 2а* 0 в4)
Эти формулы имеют простую геометрическую интерпретацию: в координатной системе о— т они определяют в параметрической форме окружность радиусом —(Oj — оа), смещенную от начала коор-*
динат по оси о на у (аа + а,). Построив в координатах о — т по формулам (1.64) окружность, можно просто и наглядно перезадавать напряженное состояние в любой фиксированной точке деформируемого тела, т. е. от тензора Т\ переходить к тензору Тв в любой произвольной координатной системе и наоборот. На рис. 1.13 показано, как определить компоненты тензора Тв через компоненты тензора Т°. Впервые такое построение предложил О. кругом Мора.
Рис. 1.13. Круг Мора —геометрическая интерпретация уравнений (1.64)
Мор. Поэтому оно называется
1.5.9. Уравнения движения и равновесия. Движение сплошной среды обусловлено действием внешних сил. Определим уравнения, которые описывают движение элемента, выделенного в окрестности точки М (х, у, г), напряженное состояние которой определено тензором напряжений Та (рис. 1.14). Пусть компоненты напряжений тензора Т9 заданы функциями ах = ах (х, у, г), тху = xxiz(x, у, г) и т. д. Возьмем точку /V, расположенную на бесконечно малом удалении от точки М. Координаты точки N примем xN = xM + dx, yN = yM + dy, zN = zM + d!. Чтобы определить напряженное состояние в точке воспользуемся разложением функций а, т в ряд Тейлора. При бесконечно малых значениях dx, dy, dz можно ограничиться первыми членами разложения. Поэтому напряженное состояние в точке N получим в виде тензора
(1.65)
Проведем через точки М, Л/ площадки, параллельные координатным. Полученный прямоугольный элемент объемом dV = dxdydz находится под действием поверхностных сил (они определяются компонентами тензоров Т'М, Твн), сил тяжести и сил инерции. Оце-
41
ним порядок силы тяжести. Возьмем кубик с ребром 1 см. В зависимости от рода металла (от магния до вольфрама) на кубик действует сила тяжести 0,02...0,2 Н. При пластической деформации напряжения в очаге деформации составляют Ю...1000 МПа. Это означает, что на грани кубика действуют силы 103... 10ь Н.
Рис. 1.14. Схема равновесия элементарного объема деформируемого тела. Напряжения ах, cjj^, Oj, ху* tyx’ Хгх компоненты тевеора TaN (см. формулу (1.65))
Таким образом, силы тяжести на несколько порядков меньше поверхности сил, определяемых тензором Т9. Поэтому в процессах обработки металлов давлением силами тяжести всегда пренебрегают. В высокоскоростных процессах обработки металлов давлением (взрывная, магнитноимпульсная, электрогидравлическая штамповка) силы инерции соизмеримы с поверхностными силами, определяемыми тензором Та. Пренебречь этими силами без большой погрешности уже невозможно (см. подразд. 6.4.7).
Предположим, что деформируемое тело имеет плотность р и движется так, что в точке М компоненты ускорения равны wyt wt. В соответствии с принципом Даламбера движение элемента dV в направлении оси х можно определить уравнением (рис. 1.14) —ох dy dz 4- [ох 4- dxj dy dz
ду
wxp dx dy dz « 0.
Аналогичные уравнения можно составить для осей у, z. преобразований выводим уравнения движения: дох . дКху I дххг _ . дХух I дау дТуг _а .
дх ' ду ' дг ' *’ дх ду ' дг ? у' дх„ . дххи , диг
= ₽®-
Таким же образом получаем уравнения движения для метричных задач ОМД:
дпг дг
<jr — <*е
После
(1.66)
осесим-
(167)
дхгг । Хгт , до» -5^ + 4- -Г2 = (’»*•
дг г 1 дг ' 1
Анализируя процессы ОМД, протекающие с малыми скоростями (ковка, объемная и листовая штамповка на прессах и штамповочных молотах), можно пренебрегать членами рк*. При этом уравнения движения (1.66), (1.67) превращаются в уравнения равновесия.
42
1.5.10. Граничные условия. Силовое взаимодействие деформируемой заготовки с рабочим инструментом определяется нагрузкой S(x, у, г), распределенной по поверхности заготовки. Чтобы установить связь между приложенной нагрузкой S(x, у, z) и напряженным состоянием заготовки Тв(х, у, г), возьмем произвольную точку М, лежащую на бесконечно малом удалении от поверхности, где приложена нагрузка S, и выделим в ее окрестности тетраэдр (рис. 1.9). Для равновесия тетраэдра нагрузки на его грани должны удовлетворять условиям (1.42). Поэтому уравнения (1.42) называют также статическими граничными условиями в напряжениях, или условиями на контуре тела.
Во многих задачах ОМД бывают известны кинематические или динамические граничные условия, т. е. условия, которые определяют перемещения или скорости перемещений отдельных объемов, поверхностей или частиц деформируемого тела. Например, для осадки цилиндрической заготовки (рис. 1.2) динамические граничные условия для торцовых поверхностей имеют вид vx = 0 при г = 0, иг = при z = Н, где рн — скорость перемещения инструмента. Имея кинематические или динамические граничные условия, можно найти деформированное состояние заготовки, распределение напряжений, усилие, работу деформации.
1.6. ПРЕДЕЛЬНЫЕ СОСТОЯНИЯ
1.6.1. Общие представления о предельных состояниях. Представление о предельных состояниях можно получить на основании анализа процесса растяжения гладкого цилиндрического образца (рис. 1.15). Пусть головка А неподвижно закреплена в захвате испытательной машины, а головка В перемещается с помощью подвижного захвата. При увеличении длины образца нарушается равновесное состояние его частиц и возникают как реакция на это внутренние силы. Их результирующая Р является силой сопротивления деформаци... Растяжение образца приводит к его удлинению, уменьшению площади поперечного сечения, образованию шейки и разрушению в ней. В процессе растяжения сила Р изменяется. Графическое изображение зависимости Р от М в процессе растяжения называется диаграммой растяжения. Диаграмма растяжения позволяет наглядно отобразить механическое состояние образца в процессе его нагружения. На ней можно выделить несколько характерных точек: L, Е, S, В и /?* **, которые делят кривую OLESBR на пять характерных участков, определяющих специфические состояния деформируемого образца (рис. 1.15, в).
Участок OL — это линейный участок диаграммы растяжения, в пределах которого справедлив закон Гука, а сила Р увеличи
* Форма и размеры образцов для механических испытаний регламентированы Государственными стандартами [22—25].
** По первым буквам английских слов linear, elastic, slip flow, break upture.
43
вается пропорционально Л/. Участок LE криволинейный, в его пределах деформация остается упругой. Таким образом, если деформация не превосходит Д/я, а сила — Ре, то после разгрузки образца его исходная форма и размеры восстанавливаются, риска N возвращается в первоначальное положение. В пределах участков 0L — LE деформация обратима: зависимость Р — Ы описывается кривой OLE при нагрузке и разгрузке.
Участок ES — это участок малых упругопластических деформаций. На нем происходит качественное изменение состояния образца, которое приводит к необратимому изменению размеров. При
Рис. 1.15. Схема растяжения стандартного пятикратного образца (а), диаграмма его растяжения (в) и типовые диаграммы растяжения с увеличенным масштабом по оси А/ (б). Пунктиром показан контур образца в момент разрыва шейки С
нагрузке сопротивление деформации изменяется по кривой OLES, а при разгрузке — по прямой SQ, параллельной OL. Риска W после разгрузки занимает положение Ns. Следовательно, образец получает остаточную деформацию Д/ = 0Q, а точка S определяет переход деформируемого образца в первое предельное состояние.
Первое предельное состояние — это такое напряженно-деформированное состояние тела, при котором наступает переход от его упругой деформации к пластическому течению.
Усовершенствование методов измерения и повышение чувствительности испытательных машин и регистрирующих приборов позволили установить, что положения точек L, Е, S на диаграмме растяжения весьма условны и тем ближе к началу координат О, чем выше точность измерений. Поэтому в физике металлов и теории обработки металлов давлением точки L, Е на диаграмме растяжения не выделяют [76, 179]. Точка S определяет переход
44
в первое предельное состояние. Значит, выделить ее необходимо, причем однозначно. Условились точку S брать на кривой так, чтобы при разгрузке образец получал остаточную деформацию Als, равную 0,2% первоначальной длины рабочей части образца /0. Участок SB — это участок квазиравномерной деформации образца (см. подразд. 2.5.5). На этом участке происходит интенсивная пластическая деформация образца в пределах всей длины рабочей части 19 4- Д/. В соответствии с законом постоянства объема площадь поперечного сечения рабочей части образца уменьшается обратно пропорционально увеличению ее длины. Участок BR — это участок локальной, сосредоточенной деформации образца. В точке В на рабочей его части формируется шейка (рис. 1.15, участок С). Поэтому дальнейшая деформация осуществляется при уменьшении сопротивления деформации от Рв до Pr. Наступает потеря несущей способности образца, в нем накапливаются повреждения, по сечению шейки развивается магистральная трещина. При деформации Д/я в точке R образец разрушается. Таким образом, R —точка перехода во второе предельное состояние.
Предельное напряженно-деформированное состояние тела, при котором наступает разрушение, называется вторым предельным состоянием.
Для построения диаграммы растяжения масштаб по оси Д / берут обычно большим 1. При этом кривые OSBR вытягиваются в направлении оси Д/ и приобретают вид, показанный на рис. 1.15, б. При механических испытаниях разнообразных металюв и сплавов встречаются диаграммы растяжения трехосновных типов. Диаграмма первого типа (рис. 1.15, в; 1.15, б, кривая /) характерна для большинства металлических материалов, применяемых в практике ОМД Для растяжения отожженных малоуглеродистых сталей, вольфрама, молибдена, кадмия, цинка, некоторых алюминиевых и медных сплавов характерны диаграммы второго типа (рис. 1.15, б, кривая 2) 11111. Особенность этих диаграмм — наличие площадки текучести (участок SS0. Заметим, что если от точки начала площадки текучести S осуществить разгрузку, то остаточная деформация Д/s окажется равной О,002/о. Участок SSX — это участок развитой пластической деформации (как и участок SiB), в пределах которого сопротивление деформации Р остается неизменным. Диаграммы растяжения третьего типа (рис. 1.15, б, кривая 3) характерны для некоторых высокопрочных малопластичных сталей и сплавов цветных металлов, чаще всего термически упрочненных. В практике ОМД диаграммы этого типа встречаются редко*.
* В учебниках по сопротивлению материалов диаграммы с площадкой текучести дают, к сожалению, как основной тип диаграмм. В историческом плане диаграммы второго типа были первыми диаграммами, с которыми познакомились ученые и инженеры в XIX веке, когда начались систематические исследования механических свойств сталей. Однако с появлением новых материалов диаграммы этого типа отошли на второй план»
45
Переход в первое предельное состояние образцов различных размеров, изготовленных из одного и того же материала, происходит при различных усилиях Ps- Однако условное напряжение
= Ps/Fo практически не зависит от размеров образцов (в пределах, регламентированных ГОСТами) и служит объективной характеристикой перехода данного металла в первое предельное состояние. Это напряжение называют пределом текучести. Различают условный и физический пределы текучести [22].
Условный предел текучести o0»i — условное напряжение, при котором остаточное удлинение достигает 0,2% начальной длины рабочего участка.
Физический предел текучести ат — условное напряжение, при котором образец деформируется без заметного увеличения растягивающей нагрузки.
Растяжение цилиндрического образца осуществляется в условиях одноосного нагружения, т. е. характеризуется наиболее простой схемой напряженного состояния. Однако и в более сложных случаях первое предельное состояние означает начало пластической деформации тела, а второе — ее предельное значение, за которым наступает разрушение. Поэтому при обработке металлов давлением необходимо так строить процесс, чтобы состояние деформируемого тела всегда находилось между первым и вторым предельными состояниями. Для этого следует найти математические зависимости, определяющие условия перехода в предельные состояния.
1.6.2. Первое предельное состояние. При одноосном растяжении гладкого образца переход в первое предельное состояние определяется условием ах = от,. При одноосном растяжении реализуется простейшая схема напряженного состояния, для которой {о, 0)
q1 Qi и тензор не зависит от координат (разумеется, в пределах длины рабочей части /0). В практике ОМД чаще всего встречаются схемы, для которых напряженное состояние определяется тензором
|ст* Хху ^ух °у ^уг ^гх ^ty ^2
, где
од ss Оц (х, у, г), xkl = tw (х, у, г). Поэтому понятие «предел текучести», определяющее переход в первое предельное состояние при одноосном растяжении, необходимо обобщить на случай объемного напряженного состояния, т. е. найти функцию компонент тензора напряжений F (Та) = 0, аналогичную по содержанию УСЛОВИЮ Oj =о,.
Уравнение F (Т9) = 0, связывающее компоненты а, т тензора напряжений Та при объемном или плоском напряженном состоянии с пределом текучести деформируемого материала при ли
44
нейном напряженном состоянии и определяющее переход тела в первое предельное состояние, называется условием пластичности.
1.6.2.1. Условие пластичности Треска—Сен-Венана. Совершенно очевидно, что вид функции F(Ta) — 0 можно установить только на феноменологической основе. Опыт показывает, что переход в первое предельное состояние зависит от свойства материала, температуры и скорости деформации, предшествующей обработки материала и т. д. В связи с этим установление универсального условия пластичности, учитывающего все факторы, влияющие на переход в первое предельное состояние,— задача чрезвычайно сложная. Поэтому упростим ее, разделив на две части. Вначале установим вид функции F(T9) = 0 для определенной исходной структуры, заданной температуры и скорости деформации. Затем учтем влияние остальных факторов: температуры, скорости и степени предшествовавшей деформации, которая сильно влияет на структуру деформируемого тела. Этот подход считается общепринятым и обеспечивает достаточную для практики точность 130, 138, 146, 150, 1651.
Именно такой подход использовал французский инженер Г. Треска. В 1864 г. он провел большую серию экспериментов по выдавливанию различных металлов через матрицы круглой и прямоугольной формы. Он показал, что переход в первое предельное состояние происходит в том случае, когда максимальное касательное напряжение достигает заданного значения, однозначно связанного с пределом текучести при одноосном растяжении.
Существует мнение о том, что Г. Треска, основываясь на собственных весьма грубых опытах и общем законе разрушения грунтов, установленном Кулоном в 1773 г., угадал форму условия пластичности (1651. Но даже в этом случае заслуга Треска очень велика. Математическую формулировку условия пластичности, установленного Г. Треска, в 1871 г. дал Б. Сен-Венан:
<h —<*з=а,- (1.68)
Это выражение вошло в литературу как условие постоянства разности главных напряжений, или условие Треска—Сен-Венана 186, 138, 150, 1651. Оно показывает, что тело переходит в первое предельное состояние тогда, когда разность максимального и минимального главных напряжений станет равной пределу текучести деформируемого материала при одноосном растяжении. Значит, если деформируемое тело находится в таком объемном напряженном состоянии, при котором ах — cr3 < os, оно деформируется упруго; если ох — а3 = а,, тело переходит в первое предельное состояние и деформируется пластически. Условие ах—o3>os неосуществимо.
В общем случае напряженное состояние деформируемого тела неоднородно и компоненты аь о2, а3 являются функциями координат. Поэтому условие пластичности (1.68) приходится применять
47
для каждой частицы деформируемого тела или небольшого объема, в пределах которого напряженное состояние может считаться однородным. Соотношение между напряжениями аь о8, оа и их знаки бывают известны лишь в простейших схемах нагружения. Из-за этого условие (1.68) записывают в таком виде:
1(71 — 0,1=0,; |о3 — а,|= а,; |о, —^1=0,. (1.69)
Условие пластичности Треска—Сен-Венана в форме (1.69) имеет достаточно наглядную геометрическую интерпретацию: в ко
Рис. 1.16. Поверхность пластичности Треска — Сен-Венана S в пространстве напряжений OiG3(t3
ординатных осях а^Оп.Оз уравнения (1.69) отображаются в виде трех пар пересекающихся плоскостей (рис. 1.16), образующих правильную шестигранную призму, ось которой 001 проходит через начало координат и одинаково наклонена к координатным осям Qi, о,, а,. Поверхность призмы называется поверхностью пластичности и обозначается буквой S.
Напряженное состояние тела (или его малого элемента), заданное тензором главных напряжений 71, определяется в пространстве напряжений OjOoGs точкой М (ах, аа, о3). Если М лежит внутри призмы S, то тело находится в упругом состоянии. Если М лежит на поверхности S, то тело деформируется пластически. Напряженные состояния, при которых точка М выходит за пределы поверхности S, неосуществимы.
Пусть напряженное состояние задано тензором главных напряжений 71. В пространстве напряжений отобразим его вектором ОМ, имеющим компоненты оь а2, а3. Разложим вектор ОМ на составляющие так, чтобы одна из них ОК лежала на оси поверхности пластичности 00ъ а другая ON — в плоскости, перпендикулярной к 00,. Можно показать, что компоненты вектора ON численно равны компонентам вектора КМ, т. е. Oi — оср, о,— ®ср> (73 ~~ ^ср. Таким образом, компоненты вектора ON численно равны компонентам девиатора напряжений, отвечающего заданному тензору Тга. Вектор ОК определяется шаровым тензо-Гш
»•
48
Сечение поверхности пластичности плоскостью ст, = 0 показано на рис. 1.17. Линию пересечения поверхности S с координатной плоскостью (например, Ох0ст3) условимся называть контуром.
пластичности S. Форму контура пластичности легко получить из уравнений (1.69) при ст, = 0 (или ст, = 0, или Ст1 = 0). Отметим на контуре пластичности характерные точки: Es(Clt С,) — переход в предельное состояние при одноосном растяжении (сжатии) в направлении осей /, 3 соответственно; Ei,(C13) — переход в предельное состояние при двухосном растяжении (сжатии).
Приведенный анализ условия пластичности Треска—Сен-Венана позволяет сделать следующие выводы.
1. Шаровой тензор напряжений 7Т не может вызвать пластической деформации ни при каких значениях компонент оСр. так как вектор ОК лежит внутри поверхности пластичности S при любых значениях оср. Шаровой тензор вызывает только упругую деформацию тела. Этот вывод находится в хорошем согласии с
Рис. 1.17. Контуры пластичности Треска — Сен-Венана S и Губера — Мизеса в плоскости напряжений ОхО,
данными практики и результатами
специально поставленных экспериментов [86, 116, 1601.
2. Девиатор напряжений D, вызывает пластическую деформацию, если
компоненты Oi,ct„ct3 удовлетворяют
условию пластичности (1.69), т. е. конец вектора ОМ лежит на поверхности пластичности S.
3. Любое напряженное состояние 71 можно представить как сочетание двух наложенных друг на друга напряженных состояний, определяемых шаровым тензором ТГ и девиатором D9. Это соответствует разложению вектора ОМ на две составляющие ОК, ОМ.
Экспериментальная проверка условия пластичности Треска— Сен-Венана, выполненная многими зарубежными и советскими учеными, показала, что оно правильно и с достаточной точностью описывает переход в первое предельное состояние.
1.6.2.2. Условие пластичности Губера—Мизеса. Получим условие пластичности, исходя из того, что переход в первое предельное состояние обусловлен только девиатором напряжений D„. Пусть напряженное состояние однородного изотропного тела при заданной температуре и скорости деформации в некоторый момент, соответствующий переходу в первое предельное состояние, определяется тензором 71, а деформированное — тензором 71. Если к первому предельному состоянию подходить из упругой области, то связь между компонентами тензоров 71, Т\ можно установить
49
по уравнениям (1.59) или (1.60). Разложим тензоры Т9, Тг, на шаровые тензоры Т“, w девиаторы D9, De Г, =» 7Т + Trt = + Dt. Перемножим эти уравнения почленно и каждый
член умножим на . Учитывая, что при перемножении Т™ на
D, и 7“ на D9 получаем нули, приходим к уравнению
4 Т'.тг. = | + I D.D.. (А)
Это уравнение имеет ясный физический смысл. Произведение =y(<h£i + о2е3 + ®зез) выражает удельную потенциальную энергию деформации (т. е. работу сил рх = Од • 1 • 1, pt = = о, • 1 • 1, р3 = а3 • 1 • I на соответствующих перемещениях Д/д = ех • 1, Д/2 = е3 • 1, Д/3 = е3 • 1), отнесенную к единице объема деформируемого тела. Аналогичный смысл имеют и члены, расположенные в правой части уравнения (А): — удельная
работа изменения объема; ^-D9Dt— удельная работа изменения формы. Воспользовавшись уравнениями связи между напряжениями и деформациями (1.60), после несложных преобразований находим у Т9ТГ, = + а* + аз — 2v (ст1аз + + <Vi)J;
1 т'шу’ш _ ’ (J _ 2v) (Од + ст2 4- а3)2. Полученные значения под-ставим в уравнение (А), обозначим D,Dt = Аф и разрешим его относительно Аф: Аф = «н (а? + o’ + oj — 2v (адо2+а2о3 +а3ад)1— ALi
— (1 — v) (Од + а2 + о3)3. После преобразований имеем
А» = [(а, - а,)2 + (о, - а,)2 + (а, -а,)2]. (1.70)
В процессе формообразования тела, определяемого девиатором D., возникают внутренние силы сопротивления деформации,определяемые девиатором D,. Для их преодоления необходимо затратить работу Аф, однозначно вычисляемую по уравнению (1.70) компонентами тензора напряжений Т9 и упругими постоянными материала Е, v. Предположим, что величина Аф не зависит от схемы напряженного состояния и к моменту перехода в первое предельное состояние получает некоторое предельное значение АфП, характерное для данного материала. Очевидно, что при этом допущении значение величины Афп легко определить по результатам испытаний на одноосное растяжение гладких образцов. Действительно, при одноосном растяжении имеет место линейное напряженное состояние, для которого а2 = а3 = 0, а в момент перехода
50
в первое предельное состояние Oj = cg. При этом АфП= ~б£~2о’. Подставив значение Афп в уравнение (1.70), получим условие пластичности в таком виде:
(<Ч — а,)2 + (а, — 4- (а, — а,)2 = 2aJ. (1.71)
Конечно, первоначально условие пластичности (1.71) было полу* чено не так просто. В 1904 г. появилась статья польского ученого М. Губера, где предлагалось новое условие пластичности. Однако языковый барьер (работа написана на польском языке) помешал широкой известности этой работы. Спустя почти десятилетие, в 1913 г., немецкий ученый Р. Мизес предложил призму пластичности Треска—Сен-Венана заменить цилиндром, описанным около призмы. Анализ показывает, что уравнение цилиндра как раз совпадает с (1.71). Интересно отметить, что Мизес считал условие (1.68) точным, а условие (1.71) приближенным. Значительно позже (в 1924 г.) немецкий ученый Г. Генки показал, что условие (1.71) означает следующее: переход в первое предельное состояние начинается тогда, когда работа изменения формы достигает некото-Гюй критической величины, характерной для данного материала 51, 75, 1651. Как видим, для формулировки условия пластичности и уяснения его физического смысла ученым потребовалось около 20 лет.
Условие пластичности в форме (1.71) можно получить и для общего случая напряженного состояния, заданного тензором Тв. Читатель самостоятельно может решить эту задачу (теперь уже нетрудную). Условие пластичности в общем виде приводится к следующему уравнению:
(а, — о „у 4- (<уу — а,)2 + (а, — аж)2 + 4-6(<4-т;,4-т;ж)=2< (1.72)
В формулах (1.71), (1.72) условие пластичности вошло в литературу как условие Губера— Мизеса. Учитывая физический смысл, его нередко называют энергетическим. Условие Губера—Мизеса как и условие Треска—Сен-Венана, имеет наглядную геометрическую интерпретацию: поверхность пластичности отображается ци-1 Г 2^ линдрической поверхностью S, радиусом Rt = у 3-о,, ось которой 001 проходит через начало координат и одинаково наклонена к координатным осям а2, о,. Сопоставляя уравнения (1.71) и (1.69), нетрудно убедиться в том, что поверхность пластичности 3, описана вокруг призмы пластичности 3. Поэтому при некоторых напряженных состояниях (вточках соприкосновения поверхностей S9, 3) условия пластичностиТреска—Сен-Венана и Губера-Мизеса тождественны. Сечение поверхности пластичности Зэ плоскостыоа2 » 0 (илиах = 0, илиа3 =0) называется контуром пластичности, имеет вид эллипса (рис. 1.17) и обозначается 2>.
S1
Экспериментальное определение условий перехода в первое предельное состояние было предметом многих исследований. Наиболее часто для этой цели использовали тонкостенные трубы из различных материалов. Трубы нагружали растягивающей или сжимающей силой, закручивали, подвергали гидростатическому давлению. Используя различные комбинации нагрузок, получали различные схемы напряжений и различные точки в пространстве (или в плоскости) напряжений. Необходимо отметить работы В. Лоде 1861, М. Роша и А. Эйхингера [75], Дж. Тейлора и X. Куини (751, А. М. Жукова [40], Г. Б. Талыпова [ 139], И. И. Гольденблата и В. А. Копнова [18]. Результаты некоторых работ представлены на рис. 1.17, где рядом с контурами пластичности 2, S, нанесены экспериментальные точки. Как видно из рис. 17, эксперименты свидетельствуют о большей точности энергетического условия пластичности (1.71). В точках Ех, Е3, Ехз, Ci, С3, С13 оба условия дают одинаковые результаты, весьма точно соответствующие экспериментальным данным.
Уравнениям (1.71), (1.72) можно придать и другую форму. Различные напряженные состояния могут приводить к одинаковым значениям левых частей уравнений (1.71), (1.72) и быть эквивалентными с точки зрения перехода в предельное состояние. Поэтому левые части уравнений (1.71), (1.72) называют эквивалентными напряжениями, эффективными напряжениями, обобщенными напряжениями или интенсивностью напряжений [26, 138, 150, 1601. Обозначим
/(а, — а,)’ 4- — о2)’ + (о,—аж)3 + 6 (tJ, + tJ, + т^) =
= у= / (ах — а,)1 + (а» — aj* + (°з — <h)8 = (1.73)
и условимся называть а{ интенсивностью напряжений. Тогда условия пластичности в форме (1.71), (1.72) можно представить как
a/=af (1.74)
и трактовать следующим образом: тело (или его частица) переходит в первое предельное состояние тогда, когда интенсивность напряжений о1 достигнет значения, равного пределу текучести деформируемого тела а, при одноосном растяжении.
1.6.2.3. Условия пластичности для различных схем напряженно-деформированного состояния. Условия пластичности Треска—Сен-Венана и Губера—Мизеса имеют принципиальные отличия. В первом из них фигурируют только наибольшее ох и наименьшее о3 напряжения, а во втором — все три: ох, о„ оя. Тем не менее оба критерия достаточно хорошо описывают условия перехода в первое предельное состояние. Это может быть лишь в том случае, когда среднее главное напряжение о, или совсем не оказывает влияния, или это влияние крайне незначительно. Чтобы оценить влияние напряжения оа, выразим его через at, as и полученное соотношение подставим в условие пластичности (1.71). Сконструируем для о, такую
52
функцию /(Qf, аа), чтобы она могла принимать значения, не большие ot и не меньшие аа:
<*« в у (°1 + °з) + у va (°i ~ <*>)•
В этом уравнении ve— переменная величина (—I < v9 < 1). Подставив выра-
Г/1 — Ve\> /l+ve\« жен не (Б) в условие (1.71), находим (<4 — <?а)* 11—я—I +1—;r— j + 1
«= 2aJ. Отсюда после преобразований получаем
2 <
ИЗ + vJ
(Б)
(В)
При v9sb ±1 условие (В) приводится к виду уравнения (1.68). Наибольшее отличие первого от второго имеет место при плоском деформированном со-2 стоянии, когда v0 =0. В этом случае ах— аа » 1,155аа. Обозначим —= at=*
= 1,155а» через a*, а a, = 0,577a, через k. Последнюю величину (А
-0,577а») условимся называть постоянной пластичности. 2
Коэффициент зависит от схемы напряженно-деформированного
K3 + v«
состояния и изменяется в очень узких пределах; от 1 до 1,155. В литературе по теории пластичности его обозначают через 0 и называют коэффициентом Л оде. Значит, в общем случае условие пластичности можно записать в форме
а» — а, «= ро»,
(1-75)
где Р = - z . Так как —1 < ve < 1, то 1 < Р < 1,155 и последнее не-
H+v«
равенство показывает, что влияние среднего главного нормального напряжения аа весьма несущественно. Влияние аа следует учитывать при анализе таких процессов, для которых деформированное состояние близко к плоскому. Важной характеристикой напряженного состояния является среднее напряжение аср = у /j (Тв). Существует мнение о том, что оно значительно влияет на переход в первое предельное состояние [31, 62, 115, 116, 150, 190]. Чтобы отразить это влияние аср, условие пластичности представляют в форме Ми-аеса—Шлейхера [116]:
a<-/(acp). (1.76)
В зависимости от предпосылок, положенных в основу теоретического подхода, н экспериментальной базы условие пластичности (1.76) получает f азличное содержание. В общем виде оно сформулировано Ю. И. Ягном 180]. В зависимости от свойств материала это условие в пространстве главных напряжений определяет либо параболоид, либо гиперболоид, либо цилиндр. В последнем случае оно приводится к энергетическому условию (1.72). К сожалению, критерий Ягна не подвергался в достаточной мере экспериментальной проверке и границы его применимости не исследованы. Аналогичные недостатки присущи и другим условиям предельного состояния [115].
На основании экспериментальных исследований авторами работ [62, 190] установлено, что среднее напряжение аср оказывает влияние не на
53
форму записи условия пластичности, а на истинное сопротивление деформации а,. По данным этих работ, условие пластичности можно записать в такой обобщенной форме:
<Ji — о« = р/(аср). (1-77)
Здесь а1( а»—наибольшее и наименьшее главные напряжения; р—коэффициент Лоде; / (аср) — переменное истинное сопротивление деформации, зависящее от <гср. По данным А. А. Коставы [62],
f (<*Cp) = ст«о (1 + «к аср>« 0 -78)
а по данным Г. Стюве [190], /(<*ср) » + асаср- Здесь aso — истинное
сопротивление деформации при атмосферном давлении; ак, ае — коэффициенты чувствительности к среднему напряжению по Коставе и Стюве. А. А. Костава связывает коэффициент чувствительности с пределом прочности деформируемого материала ав (в МПа) [115]. а* =» 0,015е °-003’в, Г. Стюве предлагает принимать коэффициент чувствительности в зависимости от вида материала. Так, для сталей он рекомендует ас аз 0,1 [190]. Из формулы (1.77) следует, что в процессах обработки металлов давлением, для которых характерны схемы напряженного состояния со всесторонним неравномерным сжатием, например при выдавливании, прессовании, гидропрессовании, истинное сопротивление деформации ож = ^(°ср) может превышать в 1,5...2 раза. Однако ни в одной экспериментальной ра. боте по выдавливанию, прессованию, гидро прессованию эффекта такого значительного повышения истинного сопротивления деформации пока не отмечено. Поэтому нам представляется, что пока (до получения более широких экспериментальных данных, подтверждающих влияние среднего напряжения <тср на истинное сопротивление деформации) следует пользоваться условиями пластичности (1.69), (1.72) без каких-либо ограничений.
Итак, в общем случае трехмерного напряженно-деформированного состояния переход в первое предельное состояние определяется условием (1.72). Если напряженное состояние задано тензором главных напряжений Тга, условие пластичности упрощается (1.75).
Для трехосного напряженного состояния в цилиндрической системе координат и осесимметричного нагружения условие пластичности можно получить из выражения (1.72), заменив ах на аг, аи на о9 и приняв тху ™ туг = 0, = тг1,
(<т, - Ов)» + (ств - о,)« 4- (а3 - Or)’ + 6т^ = 2о». (1.79)
Таким образом, условия перехода в первое предельное состояние определяются уравнениями (1.69), (1.72), (1.75), (1.79), в которых компоненты тензора напряжений Г, (7^) связаны с пределом текучести о, деформируемого металла при данной температуре, скорости и степени деформации в условиях одноосного растяжения или сжатия.
1.6.2.4. Условие пластичности и упрочнение. Выше показано, что переход в первое предельное состояние определяется условием пластичности (1.74), которое включает предел текучести а, как константу. Однако анализ диаграмм растяжения (рис. 1.15, в) показывает, что в процессе деформации о, изменяется. На участке SB образец равномерно удлиняется, а площадь его поперечного сечения F уменьшается. Напряжение а = Р/F, которое действует в сечении образца, непрерывно увеличивается по мере деформации.
54
Это напряжение, в отличие от о0>2, от, является истинным сопротивлением деформации (оно рассчитывается по истинной, а не начальной площади поперечного сечения образца). Условимся истинное сопротивление деформации при любом виде испытания обозначать символом as и называть истинным напряжением. Рассмотрим особенности деформации образца при ступенчатом нагружении. Растянем образец до точки М (рис. 1.18). Так как в точке М Рм > Ро.^ образец получит некоторую необратимую деформацию Д1ОСТ > 002/о. Разгрузка из точки М пойдет по линии МО',
которая близка к прямой и параллельна упругой части кривой OL. Это соответствует теореме А. А. Ильюшина о разгрузке [461 и поведению упругопластического тела (см. подразд. 1.3, уравнение 1.8). Повторное растяжение этого же образца будет идти по линии О' М', которая также близка к прямой и параллельна упругой части кривой 0L. До точки М' образен деформируется упруго. В точке М' начинается пластическая деформа ция. Как показывают эксперименты 175, 861, точка М' ложится на продолжение кривой 08гМ и почти совпадает с точкой М (если нагрузка и разгрузка не разделены большим промежутком време-
Рнс. 1.18. Диаграмма растяжения при ступенчатом нагружении и разгрузке образца
ни и не успевают происходить
процессы старения). Если забыть на время о предыстории деформирования образца, его состояние при повторном нагружении можно рассматривать в координатных осях Р'О'Ы как независимое и можно определить точку S2, соответствующую условному пределу текучести. Если в точке jV снова прервать деформацию и разгрузить образец, а последующее нагружение рассматривать в координатных осях Р”О'Ы, то и для него можно определить точку S3, соответствующую условному пределу текучести. Таким образом, для каждого цикла нагружения можно определить значения условного предела текучести a0t2, a0,2 соответственно точкам Sb St, S3 и т. д. Сравнение показывает, что после каждого этапа пластической деформации образца его сопротивление деформации увеличивается. Это явление называют упрочнением* (см. подразд. 2.4.6, 2.5.4).
Упрочнение значительно усложняет анализ перехода деформируемого тела в первое предельное состояние, так как в каждый
* В научных и технических работах по металловедению это явление называется наклепом.
55
текущий момент в условие пластичности необходимо подставлять значение истинного сопротивления деформации о,, которое за* висит от предыстории нагружения. Упрочнение означает, что в процессе деформации поверхность и контур пластичности (рис. 1.16, 1.17) непрерывно расширяются. Поэтому для поддержания процесса пластического течения необходима непрерывная догрузка тела, т. е. увеличение интенсивности напряжений с(. Упрочнение означает, что условие пластичности (1.74) должно непрерывно изменяться. Это изменение в общем случае можно представить в таком виде: ct =* о,(е). Отсюда следует, что для анализа процесса пластической деформации необходимо научиться определять истинное напряжение в зависимости от предыстории нагружения деформируемого тела, т. е. научиться определять вид функции
о, =Ф(е). (1.80)
Здесь под е можно понимать любой из показателей деформации (см. подразд. 1.4.2.). Ранее показано (см. подразд. 1.1), что на современном этапе развития ТОМД установить связь между о, и е можно только на феноменологической основе. Наиболее часто эту связь представляют в графической форме и называют диаграммой истинных напряжений*.
1.6.3. Диаграммы истинных напряжений. Диаграмма истинных напряжений — это графическое изображение зависимости истинного напряжения о, от степени предшествовавшей деформации е.
Диаграммы истинных напряжений можно строить по результатам испытания на растяжение, сжатие, кручение. В качестве показателя деформации можно принимать S, ф, е, е и т. д. Однако наибольшее применение для практических целей получили диаграммы построенные в координатах а, —ф, а, — е по результатам испытания на растяжение и сжатие соответственно. Многочисленными экспериментальными исследованиями доказано, что показатели деформации ф = (Fo — Fd)/F0» е = (ft0 — Ла)/Л0 эквивалентны по упрочняющему эффекту. Это означает, что в пределах точности эксперимента графики зависимостей а, = Ф(ф), а, = Ф(е), полученные для одного и того же материала, совпадают [30, 165, 1781.
Диаграмму истинных напряжений а,—ф можно построить по диаграмме растяжения Р — Ы. Однако такая диаграмма будет
* Диаграммы <Jt Ф(е) в литературе часто называют кривыми упрочнения [28, 56, 138, 146 и др.]. С этим нельзя согласиться, так как упрочнение определяется производное dos/de, а значит, строить кривую упрочнения необходимо в координатах dojdt — в. Зависимость os =» Ф(е) называют по-разному: кривая течения [29], кривая напряжения — деформация [86], кривая предела текучести [36], кривая истинных напряжений [30, 31]. кривая зависимости между истинным напряжением и истинной деформацией [1501, зависимость между напряжением и деформацией [173], диаграмма растяжения [1461, диаграмма деформирования [111], диаграмма деформации (163, т. 1], истинная диаграмма деформации [163, т. 2], диаграмма истинных напряжений [132]. Последнее название определяет кривую о, = Ф(е) наиболее точно и кратко.
56
отражать зависимость истинного сопротивления деформации от степени деформации только на начальном этапе растяжения образца (до момента образования шейки). Поэтому для построения диаграмм истинных напряжений используют преимущественно испытание на сжатие. Условия испытания в наибольшей степени приближаются к условиям, характерным для большинства процессов объемной штамповки, высадки, выдавливания, прессования. Широкому распространению испытания на сжатие препятствовали технические трудности, связанные с исключением влияния внешнего трения. Различные искусственные способы (осадка коническими бойками цилиндрических сплошных (301 и трубчатых образцов [661, способ осадки трех образцов [66, 1761 и т. д.) оказались трудоемкими и недостаточно точными. Наиболее универсален, прост и точен способ осадки цилиндрических образцов с торцовыми выточками (рис. 1.19). Выточки В заполняют эффективной смазкой (см. подразд. 3.5), которая практически полностью устраняет трение между торцами образца и рабочими поверхностями инструмента в процессе осадки [661. Детальные исследования показали, что деформация происходит в условиях одноосного сжатия. При
испытании углеродистых и легированных ста- риС. иэ. образец лей оптимальные размеры образцов определи- с торцовыми вы-ются такими соотношениями [661: d0 = точками = 16.-.30 мм; Лб = (0,015...0,020)do*» = d0\
/б = (0,030... 0,035)</0- Для медных и алюминиевых образцов диаметром до 30 мм можно принимать Лб = 0,60...0,65 мм, /б = = 1.7...2.3 мм [661.
При осадке образцов с торцовыми выточками истинное сопротивление деформации а, совпадает с ох и ах. Поэтому для построения диаграммы истинных напряжений достаточно зафиксировать несколько значений усилия Р/, соответствующих значений диаметра dj и высоты образца h/. По этим данным определяют значения ст,/, е/ в каждой точке /:
4PZ h9 - h/
’•'=,7-= e'—4"
(1.81)
Для построения диаграммы а, — е достаточно испытать один образец и взять 6... 15 точек. Учитывая статистическую природу зависимости о, — е, для повышения точности диаграммы истинных напряжений обычно испытывают 3—5 образцов и строят диаграмму по средним значениям г/. Диаграммы истинных напряжений построены для большинства металлов и сплавов, имеющих технические применение [66, 151, 152]. Как пример, приведен рис. 1.20.
При теоретическом анализе процессов ОМД оперировать диаграммами истинных напряжений очень неудобно. Истинное напря-
57
жение Как сомножитель входит в подынтегральные выражения, определяющие усилие, работу и мощность деформации, изгибающий момент и т. д. (см. подразд. 6.3), поэтому зависимость (1.80) стремятся выразить какой-либо аналитической функцией. Требования к этой функции весьма противоречивы: с одной стороны, она должна с наименьшей погрешностью аппроксимировать диаграмму истинных напряжений, а с другой — быть короткой, простой и легко интегрируемой. Для аналитического описания диаграмм истинных напряжений предложено большое количество раз-
Рис. 1.20. Диаграммы истинных напряжений [152]:
/ — сталь ЗОХГСА. 2 — сталь 45, 3 — сталь 08кп, 4 — латунь Л68, S — алюминиевый сплав Д1
Рис. 1.21. Диаграмма истинных напряжений для стали 08пс (показана пунктиром) и графики аппроксимирующих функций:
/ — а, — 448 + 882»; 2 — о, — 972»0-276; 3 — а, —308 +2276» — 3882»» + 2579»•; 4 —о,— — 308+ 14»0,6
нообразных по структуре формул. В процессе теоретического анализа часто применяют функции вида
а, = А 4- Вфл; о, = А + Вел. (1.82)
Для определения коэффициентов уравнения (1.82) С. И. Губкин предложил формулы [31]
и = 1, 4 = (1б(1 — 2фш)/(1 — Фш)*» В = (Ть/(1 — фш)*»
А = 0, В = Ош/Фш, л ==> Фш (1 — Фш)»
которые позволяют получить линеаризованную диаграмму истинных напряжений (п = 1, А =/=0) или аппроксимировать ее степенной функцией (Я = 0, п 1) по результатам однократного испытания на растяжение и вычисления оь, аш, фш-
Во многих работах коэффициенты А, В, п определены экспериментально как среднестатические для групп материалов. Напри
58
мер, для углеродистых сталей с содержанием углерода 0,1...0,4% предложена функция ot = <j0,2 4- 14e°*e [152]. Эта функция проста и достаточно универсальна, так как для ее определения требуется лишь одна постоянная о0,#, значения которой приведены в любом справочнике. Однако для многих сталей она дает очень грубое приближение. Наиболее точную аппроксимацию диаграммы истинных напряжений, заданной таблично или графически, можно з
Рис. 1.22. Характер разрушения образцов при механических испытаниях (а), вытяжке (б) и выдавливании (в)
нома Ап вычисляются на цифровых ЭВМ методом наименьших квадратов по экспериментально построенным диаграммам. Анализ показал, что уже при трех-четырех членах полинома погрешность аппроксимации составляет 2—5%. Как видно из рис. 1.21, наибольшая точность достигается при аппроксимации полиномом.
1.6.4. Второе предельное состояние. 1.6.4.1. Второе предельное состояние в технологии ОМД. Все процессы обработки металлов давлением построены на использовании свойства пластичности . Пластичностью называется способность твердых тел необратимо изменять форму и размеры без макроскопических нарушений сплошности. Чем более пластичен металл, т. е. чем большее формоизменение можно сообщить заготовке за один переход, тем выше производительность и экономическая эффективность процессов ОМД. Мерой пластичности может служить степень деформации, накопленная телом к моменту разрушения. При механических испытаниях материалов мерой пластичности считают предельные значения относительных величин удлинения б, поперечного сужения ф или осадки е, которые получает образец в момент перехода во второе предельное состояние. Критерием перехода во второе предельное состояние служит разрыв образца при испытании на растяжение и появление первой визуально обнаруживаемой трещины на боковой поверхности образца при испытании на сжатие (рис. 1.22). Показатели 6, ф, 8 наряду с о„ аь и твердостью определяют механические свойства материалов.
59
Пластичность сильно зависит от химического состава и структуры материала, температуры и скорости деформации, схемы напряженного состояния и характера приложения нагрузки (рис. 1.23). Такая зависимость пластичности от температурноскоростных условий деформации и схемы напряженного состояния дает основание считать, что пластичность — это не столько свойство, сколько состояние деформированного тела (см. подразд. 2.8).
При механических испытаниях материалов реализуется наиболее простая схема напряженного состояния —линейное растяжение или сжатие. Это дает возможность достаточно просто оценить пластичность показателями б, ф или е. Однако в реальных процессах ОМД деформация распределяется по объему заготовки, как правило, крайне неравномерно: в одних ее элементах преобладает деформация сжатия, в других — растяжения, в третьих —сдвига; в одних элементах деформация невелика, в других — приближается к предельно допустимой или даже превышает ее. В последнем случае деталь разрушается (рис. 1.22, б, в). Разрушение деталей в условиях действующего производства — явление крайне нежелательное. Поэтому при разработке технологического процесса изготовления какой-либо детали технолог исходит из двух противоречивых требований: с одной стороны, он стремится предотвратить образование брака и назначить небольшие степени деформации, а с другой — получить за один переход максимальное формоизменение, так как при этом удается резко увеличить производительность труда, снизить капитальные расходы на оборудование и текущие расходы на изготовление штампов, повысить рентабельность производства. В технологических процессах,которые принято называть разделительными, наоборот, нужно преднамеренно создавать такие условия, когда деформируемая заготовка разрушается в заданном месте. Чтобы помочь технологу решать эти сложные проблемы, необходимо разработать методы определения предельно допустимого формоизменения заготовки, при котором ни один из ее элементов не переходит во второе предельное состояние, либо, наоборот, происходит преднамеренное разрушение. Задача эта исключительно сложная, и лишь в последнее десятилетие, когда ученые разработали теорию деформируемости и научились строить диаграммы пластичности, ее решение стало вполне реальным.
1.6.4.2. Деформируемость и диаграммы пластичности. Условимся называть пластичность, которую обнаруживают материалы при механических испытаниях, природной пластичностью [1341. Пластичность зависит от схемы напряженного состояния и других факторов, поэтому при выполнении заданной технологической операции пластичность заготовки может измениться. Пластичность, обусловленную механической схемой деформации, характерной для данного технологического процесса, условимся называть технологической пластичностью, или деформируемостью [28, 30, 971.
60
Деформируемость определяется способностью заготовки не разрушаться в процессе выполнения заданной технологической операции. Представление о разрушении материалов прошли достаточно сложную эволюцию. В начале XVII в. Г. Галилей считал, что разрушение наступает тогда, когда наибольшее нормальное напряжение Oj достигает критического значения (59). Совершенно очевидно, что для пластичных материалов это утверждение не соответствует действительности. Поэтому в XIX в. Б. Сен-Венан предложил другой критерий, который лучше описывал поведение
Рис. 1.23. Графики зависимости относительного удлинения б (/—3) и относительной осадки 8 (4—6) от температуры испытания [35, 77].*
1, 4 — сталь 45; 3, 6 — сталь У8А; 3, 6 — бронза БрБ2
Рис. 1.24. Диаграммы пластичности различных материалов [34, 59, 109]:
I — бериллий, 3 — титановый сплав BT9. 3 — цинк литой. 4 — сталь XI8HI0T, 5 — медь, 6 — алюминиевый сплав Д18
пластичных металлов. Он установил, что разрушение не наступает до тех пор, пока относительное удлинение 6 (укорочение е) не достигнет критического значения характерного для данного материала и определяемого из опытов на растяжение (сжатие). Конечно, такое представление о переходе во второе предельное состояние можно использовать только при простейших схемах напряженного состояния, которые мало отличаются от схем одноосного растяжения и сжатия. Для более сложных схем предлагалось много различных подходов [30, 59, 109]. Наиболее обоснованную оценку условий перехода во второе предельное состояние дали в последнее десятилетие Г. А. Смирнов-Аляев [ 133], В. Л. Колмогоров [59, 109], В. А. Огородников [96, 971. В их исследованиях разрушение ставится в зависимость от степени деформации сдвига.
Под степенью деформации сдвига понимают всю накопленную частицей материала пластическую деформацию в течение определенного отрезка времени, которую подсчитывают вдоль траектории ее движения по формуле [ 1091 t
A = (1.63)
61
Здесь 5/ — интенсивность деформации (см. подразд. 3.4.6). Деформацию сдвига, соответствующую переходу во второе предельное состояние, принято обозначать Лр [34, 109J. Показатель Ар наиболее полно характеризует пластичность при любой схеме напряженно-деформированного состояния. В частном случае при испытании на растяжение однозначно связан с показателем относительного поперечного сужения [34[:
Ар = 1.73 In (1.84)
Величину ф можно выразить через диаметры исходного образца di — d9
d0 и шейки dm ф = 0 - ш 100%. После подстановки значения ф d0
в выражение (1.84) получаем формулу для вычисления деформации сдвига Лр при испытании на растяжение:
Лр = 3,46 In (do/dn,). (1.85)
Многочисленными исследованиями [97, 109, 1331 установлено, что величина Лр однозначно зависит от показателя жесткости схемы напряженного состояния
Пв = (а, 4- а, +
Графическое изображение зависимости Лр от Пв называется диаграммой пластичности [34, 1091.
Показатель жесткости схемы напряженного состояния Пв в различных технологических процессах может изменяться в широких пределах. Например, для двухосного растяжения листовой заготовки Пв = +2,0, для одноосного сжатия П, = —1,0, а для выдавливания и гидропрессования Пв = —3...—10. Численное значение Пв изменяется в процессе выполнения технологической операции. Например, при осадке цилиндрического образца П, увеличивается от — 1 в начале процесса до —0,17 при деформации на 82,5% [591.
В настоящее время диаграммы пластичности (рис. 1.24) построены для большого числа материалов [34, 59, 97, 1091. На основании анализа диаграмм можно установить, что деформация бериллия, титанового сплава ВТ9, литого цинка (кривые 1...3) путем растяжения (П, = +1) неосуществима вообще или крайне неэффективна, так как разрушение наступает при очень малых деформациях. Изменение схемы напряженного состояния (уменьшение По путем использования процессов всестороннего неравномерного сжатия) позволяет резко повысить пластичность большинства сплавов, однако далеко не всех. Например, пластичность стали Х18Н ЮТ (кривая 4) очень слабо зависит от показателя П9. Диаграммы пластичности показывают, что по результатам испытаний на растяжение нельзя судить о пластичности металлов и сплавов в процессе осуществления технологических операций. Пластич
62
ность стали 45 при растяжении (П, = +1) примерно вдвое меньше чем стали X18Н ЮТ, а при выдавливании (П, = —3) примерно вдвое больше. Очевидно, что чем больше dAp/dno, тем более эффективно применение процессов ОМД со схемами всестороннего неравномерного сжатия, для которых П9 0.
Таким образом, при помощи диаграмм пластичности можно установить предельное значение деформации сдвига Лр, накопленной к моменту разрушения. Однако этого все еще недостаточно для количественного решения задачи о возможности осуществления заданной операции без разрушения или, наоборот, с разрушением заготовки в заранее заданной области. Чтобы решить и эту задачу, рассмотрим условие деформируемости без разрушения.
1.6.4.3. Степень использования ресурса пластичности. Пусть некоторая частица деформируемого тела dV с координатами х, у, г находится в напряженно-деформированном состоянии, которое определяется тензорами Тв = Та(х, у, z, t), Tt=7\(x, у, z, f). За промежуток времени t частица получит деформацию
t
Л (х, у, г, о = /3 f h (х, у. г, f) dt. (1.86)
о
Такая деформация не вызовет разрушения, если выполняется условие
Л (х, у, г, *)<Лр(х, у, z, t), (1.87)
Показатель жесткости схемы напряженного состояния /7а для частицы dV легко определить, имея
/1 (Л) /з/| lt(Dg)]
0.88)
Поэтому на основании экспериментальной зависимости Ар — — П, (диаграммы пластичности) можно найти предельное значение Ар(х, yt z, t) для данной частицы. Условие (1.87) удобнее представить в виде
о-89)
Функция координат и времени ф называется степенью использования ресурса пластичности 159, 109). Очевидно, что при ф < 1 разрушения не произойдет, а при ф > 1 — разрушение неизбежно.
В работах 159, 97, 1091 подчеркнуто, что условие (1.89) должно учитывать историю деформирования. Для этой цели в условие (1.89) вводят функцию B(t) и получают окончательное условие деформируемости без разрушения в таком виде:
/
* = /3 j В (Г) -x'l’n’»)/-< '• U-90)
v 4Жп I1 *0 \*/J
63
Использовать формулу (1.90) для практических расчетов трудно, так как неизвестен вид функции B(t). Автором работ 196, 97] на основании нелинейной теории накопления повреждений установлена функция B(t), а выражение (1.90) приведено к виду, более удобному для практического использования:
ЛаФДЛ
Л1+аФ р
(1.91)
Здесь Ф = dTIa Л/Л — функция изменения показателя схемы напряженного состояния; а — константа, слабо зависящая от свойств материала. Эта формула позволяет вычислить степень использования ресурса пластичности ф и для наиболее опасной точки установить возможность сохранения целостности или разрушения (см. подразд. 6.7).
ГЛАВА 2
ФИЗИЧЕСКИЕ ОСНОВЫ ОБРАБОТКИ МЕТАЛЛОВ ДАВЛЕНИЕМ
2.1. СТРОЕНИЕ МЕТАЛЛОВ И СПЛАВОВ
Из предыдущей главы известно, что различные модели сплошных сред с достаточно хорошим приближением описывают поведение металлов. Это позволяет изучать процессы пластической деформации на феноменологической основе. Пластическая деформация приводит к необратимому изменению формы и размеров, а также к значительному изменению механических и физических свойств металлов. Чтобы изменять эти свойства в нужном направлении необходимо установить оптимальную последовательность операций, правильно выбрать граничные условия и рассчитать технолс-
64
гические параметры процесса. Для этого нужны знания физических основ обработки металлов давлением.
2.1.1. Строение металлов. Для описания характерных особенностей строения металлов* введем понятия фазы и структуры. Фаза — однородная составная часть системы, имеющая одинаковый состав, одно и то же агрегатное состояние и отделенная от остальных частей поверхностями раздела. Большинство металлов, применяемых в технике, имеет многофазное строение. Например, стали 08кп, 45, Ст. 3 содержат ферритную и перлитную фазы, закаленные стали У12, X 12М, Р6М5 — мартенситную, карбидную
Рис. 2.1. Микроструктуры армко-железа (а) и стали 20 (б): I — зерна феррита; 2 — зерна перлита
и аустенитную фазы. Структура — характеристика фазового состава металла, которая определяется формой, размерами и особенностями взаимного расположения соответствующих фаз. Различают макроструктуру (без увеличения или с увеличением до 40) и микроструктуру (увеличение 50 и более).
Чтобы изучать структуры металлов, необходимо соответствующим образом подготовить их поверхности: сделать макро- или микрошлиф**. Изучение'макроструктуры помогает установить направление главной деформации, некоторые виды брака, нарушения технологии, неправильную конструкцию штампа, а микроструктуры— наличие мелких дефектов, нарушения температурно-скоростного режима деформации, неравномерность дефэрмации и др.*** Микрофотографии дают основание считать, что металлы имеют зернистое строение. Более тонкие методы исследования (рентгенографические, электронографические) позволили установить, что каждое зерно — кристаллическое образование, в котором атомы
* Под металлом условимся понимать вещество с металлическими свойствами, независимо от того, является ли оно химическим элементом или сплавом.
•* Методике изготовления шлифов и их исследованию посвящены работы |67, 68].
*** Здесь указана лишь область использования структур для изучения прикладных вопросов, связанных с обработкой давлением.
3 t -2в
45
f>acn<wiaraiOTCH в определенной закономерной последовательности 68, 71, 135, 157, 1791.
Кристалл — это твердое тело, в котором пространственное расположение атомов повторяется периодически и которое ограничено плоскостями, образующими друг с другом вполне определенные углы. Кристаллы неправильной огранки, из которых состоят технические металлы (рис. 2.1), называют кристаллитами. Размеры кристаллитов обычно невелики (от миллиметров до микрометров). Поэтому детали машин и другие металлические изделия состоят из большого количества кристаллитов [53, 68, 741. Тело,
Рис. 2.2. Модели расположения атомов, соответствующие неупорядоченному (аморфному) состоянию (а) и упорядоченному (кристаллическому) (б)
состоящее из большого количества сросшихся друг с другом кристаллитов, называют поликристаллическим. В технике нередко используют тела, представляющие собой один большой кристалл. Такое тело называют монокристаллическим или просто монокристаллом.
Почему кристаллы имеют правильное строение? Чтобы ответить на этот вопрос, рассмотрим рис. 1.3. В естественном состоянии атомы располагаются на расстоянии г0другот друга. Поэтому можно представить атомы Л,, Л, в виде двух соприкасающихся шариков диаметром d = 2г0. Как расположить множество шариков в пространстве? Как угодно. Расположение, показанное на рис. 2.2. а, неустойчиво. Если шарики встряхнуть, они расположатся в некотором закономерном порядке (рис. 2.2, б). В реальном кристалле роль такой встряски выполняет тепловое движение атомов и связанная с ним диффузия. Следовательно, закономерное расположение атомов — это естественное состояние, обусловленное силами их взаимодействия и свободой перемещения друг относительно друга.
Для характеристики закономерности расположения атомов в пространстве введем понятие о кристаллической решетке [ 135, 1791. Кристаллическая решетка — это простейшая модель кристалла, представляющая собой совокупность точек — центров колебания атомов, расположенных в пространстве так, что каждая точка имеет соседей, положение которых по отношению к ней
Рис. 2.3. Схема простой кубической решетки, KLM NOPQR — элементарная ячейка
совершенно одинаково. На рис. 2.3 показана схема простой кубической решетки. Любая точка в ней, например Д’, имеет шесть ближайших соседей. Каждая из соседних точек в свою очередь имеет шесть ближайших соседей, расположенных точно так же, как соседи располагаются вокруг точки К- Для наглядного изображения кристаллических решеток удобно их точки соединить прямыми (рис. 2.3). Тогда сразу становится очевидным, что свойства симметрии решетки можно определить при помощи небольшого количества точек, образующих элементарную ячейку. Элементарная ячейка — это наи-меньший комплекс точек, обладающих всеми свойствами симметрии решетки, который при многократном повторении в пространстве вдоль координатных осей позволяют воспроизвести кристаллическую решетку. Размеры элементарной ячейки (рис. 2.3, а—с) определяются расстоянием меж
ду ближайшими соседями, окружающими данную точку. Длина ребра элементарной ячейки которая соответствует линейному сдвигу, необходимому для нового совмещения ячейки с решеткой, называется параметром решетки.
Для однозначного описания элементарной ячейки в общем случае нужно задать три параметра а, Ь, с вдоль осей х, у, г, а также три угла а, ₽, у, которые образуют оси х, у, г. Очевидно, что для кубической решетки а = Р = == у = 90°, а а = b = с.
Математически доказано, что имеется четырнадцать (и только четырнадцать!) различных типов кристаллических решеток (135]. Однако для описания строения металлов, имеющих широкое промыв) ленное применение, достаточно трех, представленных на рис. 2.4.
Кубическая объемно-центрированная (ОЦК) (рис. 2.4, а). Для нее а = b = с, а=»Р = у = 90°. в центре которого расположен атом. Эта решётка характерна для а железа, ванадия, вольфрама, калия, лития, молибдена, натрия, хрома, а также их сплавов 1179]. Параметр решетки а равен (2,5... ...3,5) • 10’7 мм. Например, для Fea а = 2,87 • 10“7 мм, для Моа = 3,15 • 10-* мм 1179].
Рис. тки,
2.4. Кристаллические реше-типичные для большинства металлов:
ОЦК (а), гцк (б) и ГПУ (•)
я ячейка —
3*
67
Кубическая гранецентрированная (ГЦК) (рис. 2.4, б). Для нее также а = 6 = с, а = р = у = 90°. Элементарная ячейка— куб, в центре каждой грани которого расположено по атому. Эта решетка характерна для у-железа, цветных и благородных металлов: алюминия, золота, меди, никеля, платины, серебра, свинца, а также их сплавов [179]. Параметр решетки а равен (3,5...5,0) • 10_? мм. Например, для Fe7a = 3,65-Ю"2 мм, для А1 а = 4,05 • 10"? мм, для РЬ а = 4,95 • 10“7 мм [ 179].
Гексагональная плотноупакованная (ГПУ) (рис. 2.4, в). Для нее а = b с, а = 120°, Р = у = 90°. Элементарная ячейка — прямоугольная шестигранная призма, внутри которой расположено три атома. Эта решетка характерна для бериллия, кадмия, кобальта, магния, осьмия, рения, титана, цинка, циркония 11791. Параметры решетки: а = (2,5...3,5) • Ю"2 мм, с= (3,5...5,5) х X Ю”2 мм. Например, для Ti а = 2,95 • 10"2 мм, с = 4,68 X X 10“2 мм, для Mg а = 3,21 • Ю"2 мм, с = 5,21 • 10“2 мм 11791.
Как видно из рис. 2.4, расстояния между соседними атомами существенно зависят от выбранного направления. Для ОЦК-ре-шетки расстояние между атомами А, К равно а, между атомами А, N— аИ2, между А,М — 0.5J/За. Поэтому силы взаимодействия между атомом А и К, N, М ощутимо различны. Вследствие этого физические и механические свойства зависят от выбранного направления. Например, для железа модуль упругости Е в направлении AM составляет 2,90 • Ю2 ГПа, а в направлении АК — 1,35 • 102 ГПа, т. е. в 2,15 раза меньше 11601. Таким образом, все кристаллические тела, следовательно, все металлы необходимо отнести к анизотропным (см. подразд. 1.3). Из курса сопротивления материалов известно, что все технические металлы изотропны. Для стали, например, независимо от направления, можно брать модуль упругости £ = 2,1 • Ю2 ГПа [8, 1601. Эти факты не противоречат друг другу. Действительно, все кристаллические тела анизотропны. Все технические металлы представляют собой поли-кристаллические тела, в которых кристаллографические оси кристаллитов ориентированы случайным образом. Если воспользоваться методами математической статистики и теории вероятности, то для поликристаллического железа можно найти теоретическое значение модуля £ = 2,07 • 102 ГПа. Это значение практически совпадает с полученными экспериментально и приведенными в справочниках и курсах сопротивления материалов (8, 116]. В технических металлах изотропность кажущаяся. Она обусловлена осреднением свойств, в том числе и модуля упругости £, кристаллитов в объеме тела в целом. Такая изотропность в отличие от идеальной называется квазитропностью материала. При специальной обработке тюли кристаллические тела могут приобретать значительную анизотропию физических и механических свойств (см. подразд. 2.5.6, 2.7.4).
Точки кристаллической решетки — это центры, вокруг которых атомы, образующие реальный кристалл, совершают колеба
68
тельные движения. При комнатной температуре амплитуда коле* баний атомов составляет около 2 • 10"• мм, т. е. примерно 1% параметра решетки, а частота колебаний — около 1013 1/с [ 160, 179). Учитывая сказанное, модель кристалла можно представить в виде шариков, соединенных друг с другом пружинками (рис. 1.2) 1111, 1571. Пружинки позволяют атомам—шарикам не только колебаться вокруг положений равновесия, определяемых уравнением (1.01), но и смещаться от положений равновесия под нагрузкой в ту или иную сторону в зависимости от знака нагрузки (рис. 1.3).
2.1.2. Индексы плоскостей и направлений. Пластическая деформация металлических кристаллов осуществляется только по определенным плос-костям и направлениям. В кристаллографии положение плоскостей в пространстве характеризуется индексами плоскостей 174, 135, 157]. Чтобы найти индексы для любой плоскости S (рис. 2.5), необходимо выбрать в пространственной решетке координатную систему; определить отрезки /, т, п, отсекаемые плоскостью на координатных осях — кратные параметру или в долях параметра; взять обратные величины 1//, 1/т, 1/п и привести полученные числа к виду наименьших возможных дробей, имеющих общий знаменатель; числа, полученные в числителе, заключить в круглые скобки.
Если плоскость S расположена так, что отсекает на оси отрицательный отрезок, то минус соответствующего индекса располагают над ним, как, например, для плоскости (110) на рис. (2.5, б). Плоскости, параллельные друг другу и находящиеся по одну сторону от начала координат, одинаковы по своим свойствам и имеют одни и те же индексы. Они образуют систему плоскостей. В кубических решетках плоскости (100), (010), (001), образующие грани куба, совершенно эквивалентны. Поэтому их часто объедг ’яют в семейство плоскостей {100}.* -
В одной и той же плоскости пространственной решетки можно указать различные направления. Для этого используют индексы направления. Чтобы найти индексы направления, необходимо взять две любые точки пространственной решетки, например А, В, через которые проходит вектор выбранного направления; одну из точек, например Л, принять за начало координат и провести через нее оси х, у, г, определить координаты X, г, Z второй точки, кратные параметру решетки; вычислить наибольший общий делитель D координат X, Y, Z, найти целые числа и = Х/D, о = Y/D, w = Z/D и заключить их в квадратные скобки. Индексы направлений могут быть положительными и отрицательными, например [101] и [101]. В пространственных решетках различных типов имеются семейства эквивалентных направлений. Например, при повороте кубической ячейки на 90° вокруг
Рис. 2.5. Основные плоскости (а—в) и направления (а) в кристаллических решетках
69
оси г направление [1001 переходит в направление [010] и наоборот. Эквивалентные направления [100], [010], [100] принято описывать как семейство направлений <100>. Направления типа [ПО], [101], ]011] включаются в семейство (ПО), а направления типа [111], (Г11) —в семейство (111).
2.1.3. Особенности строения металлических сплавов. В природе встречаются разнообразные сплавы естественного и искусственного происхождения. Для обработки давлением используются металлические сплавы. Под сплавом условимся понимать вещество с металлическими свойствами, полученное при кристаллизации расплава из нескольких компонентов*. Сплавы — это основа современного машиностроения, металлообработки, всей техники в целом. Наиболее широкое распространение получили сплавы черных металлов — углеродистая и легированная сталь, медные — латунь, бронза, алюминиевые, магниевые, титановые сплавы.
Различные сплавы состоят из одной или нескольких фаз, которыми могут быть твердые растворы металлов (например никеля в железе, цинка в меди, меди в алюминии), химические соединения металлов с неметаллами (например карбиды, сульфиды, фосфиды, нитриды, окислы), а также интерметаллические соединения металлов. Объем фаз, которые представляют собой химические или интерметаллические соединения, в деформируемых сплавах невелик. Однако их влияние, особенно карбидов, на процесс деформации весьма значительно. Основа сплавов — это твердые растворы [68, 135, 179].
Твердый раствор —это фаза сплава, состоящая из двух или нескольких компонентов, в которой атомы компонентов примесей занимают места в узлах или междоузлиях кристаллической решетки компонента растворителя. Металлы с небольшим различием атомных радиусов образуют твердые растворы замещения. Им свойственно незначительное искажение кристаллической решетки. Любой ее узел может быть занят атомом компонента примеси. Атомы примесей распределяются в решетке статистически равномерно, но случайным образом (неупорядоченные твердые растворы) или в закономерном порядке (упорядоченные твердые растворы). Параметр решетки твердых растворов замещения изменяется почти линейно с изменением концентрации примеси. Микроструктура твердого раствора — это обычно однородные кристаллические зерна. Как правило, сплавы такого типа обладают высокой пластичностью и небольшим сопротивлением деформации. Твердые растворы внедрения характерны для сплавов, один из компонентов которых имеет большой атомный радиус, а другой (или другие) — намного меньше (например железо и углерод). У растворов этого типа решетка искажается сильно, что связано с расположением атомов примеси в междоузлиях решетки основного компонента. Высокие локальные напряжения, возникающие в решетке раствора внедрения, приводят к тому, что внедренные атомы располагаются, как правило, в областях искажения решетки вокруг дислокаций, образуя атмосферы Коттрела [68, 88, 167]. Важнейшие твердые растворы, которые часто встречаются в металлах, используемых для ОМД — феррит (раствор углерода в а-железе) и аустенит (раствор углерода в у-железе). Предельная растворимость углерода в а-железе — 0,02%, в у-железе — 2,14% [£Я]. Феррит и аустенит обладают высокой пластичностью и относительно небольшим сопротивлением деформации.
Таким образом, металлы и их сплавы имеют кристаллическое строение. Однако динамическая модель кристалла и представление о металлах как о пол и кристаллических телах — лишь грубая схематизация строения металлов. Чтобы уточнить наши представления, необходимо рассмотреть процесс кристаллизации.
* Сплавы получают также методами порошковой металлургии.
70
2.2. КРИСТАЛЛИЗАЦИЯ МЕТАЛЛОВ
До середины XX столетня единственным промышленным способом по* лучения металлических тел была кристаллизация из расплава. Этот спо* соб и в наше время является основным. Кинетика кристаллизации изложена в курсе «Технология конструкционных материалов и материаловедение». Здесь важно обратить внимание на следующие особенности процесса
кристаллизации.
1. Образование кристаллов в расплаве идет одновременно из многих центров. Скорость образования центров кристаллизации н скорость роста
кристаллов зависят от степени переохлаждения расплава, т. е. от разности между температурой плавления и фактической температурой кристаллизации.
2. Кристаллографические оси в различных центрах кристаллизации ориентированы случайным образом.
3. При кристаллизации расплава, содержащего такие примеси, как углерод, сера, фосфор, марганец, кремний и легирующие добавки хрома, никеля, титана, вольфрама, ванадия, их распределение происходит неравномерно: на границах кристаллитов примесей и легирующих добавок, как правило, значительно больше, чем в объеме. После затвердевания расплава образуется поликристалл ическое тело. В процессе кристаллизации температура переохлаждения расплава изменяется, и структура литого металла (слитка) получается неоднородной. Например, при кристаллизации стального слитка вначале появляются мелкие кристаллиты глобулярной формы (рис. 2.6). Когда изложница нагреется, скорость образования зародышей уменьшится, а отвод тепла станет направленным, начнут формироваться кристаллиты удлиненной формы. При кристаллизации средней части слитка число центров кристаллизации резко уменьшается и кристаллиты могут вырастать до огромных размеров. В связи с особенностями теплоотвода кристаллизация идет интенсивно по всем направлениям. Как следствие образуются так называемые дендриты. В процессе кристаллизации атомы примесей и легирующих •лементов оттесняются в расплав. Содержание
Рис. 2.6. Строение стального слитка [153]:
1 — зона мелких кристаллитов глобулярной формы; 3 — эона столбчатых кристаллов; 3 — дендритная зона; 4 — пустоты усадочного происхождения; 5 — усадочная раковина; 6 — график распределения содержания серы по сечению слитка
инородных атомов в расплаве непрерывно увеличивается, что приводит к ликвация. На •-'’лее сильно ликвируют углерод, сера, фосфор, вольфрам, ванадий (рис. 2.6). При кристаллизации удельный объем металла уменьшается. Это связано с тем, что в твердом теле упаковка атомов наиболее плотная. Например, при кристаллизации стали удельный объем уменьшается на 3...4% [179]. Кристаллизация начинается с поверхности. Из-за этого уменьшение удельного объема неизбежно приводит к образованию усадочной раковины и пустот усадочного происхождения.
Снижение температуры приводит к уменьшению растворимости примесей и легирующих элементов. Поэтому при кристаллизации и последующем охлаждении сплава до комнатной температуры на границах зерен выделяется еще одна фаза, например углерод в виде цементита (если содержание углерода в стали превышает 0,8%), Из-за этого многие стали и сплавы цветных металлов состоят из двух и более фаз. В большинстве случаев
71
свойства фаз сильно различаются. Например, высокоуглеродистая сталь состоит из перлитной основы и включений цементита. Твердость перлита HV« 250, твердость цементита HV« 1000. Перлит обладает высокой пластичностью, цементит очень хрупкий и разрушается практически без остаточной деформации. Эти различия существенно влияют на характер пластической деформации литой стали. Кристаллизация металлов сопровождается образованием большого количества разнообразных дефектов не только в пределах слитка, но и в пределах монокристальных зерен, образующих слиток. Несовершенства кристаллической решетки зерен оказывают исключительно большое влияние на свойства литых металлов и механизм их пластической деформации. Вот почему, прежде чем перейти к изучению деформации металлов, необходимо рассмотреть основные дефекты их кристаллического строения.
2.3. ДЕФЕКТЫ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ МЕТАЛЛОВ
Кристаллическая решетка даже очень чистых металлов по различным причинам содержит большое количество разнообразных дефектов. Например, искажения, размеры которых не превышают нескольких параметров решетки, обусловлены флуктуацией энергии; искажения, простирающиеся на миллионы межатомных расстояний, обусловлены поликристаллическим строением металлов. Известно четыре типа дефектов кристаллической решетки металлов (табл. 2.1).
2.3.1. Точечные дефекты. Динамическая модель кристалла (см. подразд. 2.1.1) показывает, что атомы, образующие кристалл, движутся вокруг положений равновесия — узлов решетки. Энергия колебаний каждого атома может существенно отличаться от среднестатической, характерной для данного металла и заданной температуры. Эго явление называется флуктуацией энергии.
Флуктуация энергии приводит к образованию различных дефектов кристаллической структуры металлов. При кристаллизации некоторые атомы, расположенные на поверхности твердой фазы, могут покинуть предписанные им положения, и в решетке получаются отдельные незаполненные узлы — вакансии. Обмениваясь энергией с атомами жидкой фазы, атом, получив импульс, направленный в сторону твердой фазы, может проникнуть в уже сформировавшийся кристалл и застрять в нерегулярном положении. Это второй вид точечных дефектов — межузельный атом. Вакансии и межузельные атомы могут возникать из кристаллах и после их затвердевания, так как в кристаллической решетке атомы имеют достаточную подвижность и могут обмениваться энергией. Если из-за флуктуации атом получит энергию, достаточную для преодоления сил взаимодействия с соседями, и выйдет из узла решетки, то образуется дефект, представляющий собой сочетание вакансии и межузельного атома (параФренкеля).
Вокруг вакансии и межузельного атома происходит возмущение, и атомы смещаются от положений равновесия, характерных для бездефектной решетки. Однако вакансия вносит меньшие искажения, чем межузельный атом, поэтому количество межузель-
72
Таблица 2.1. Классификация и характеристика дефектов кристаллической решетки (10, 63, 74, 157, 159, 160, 167]
Тмп дефекта Наименование дефекта Сущность дефекта
Точечный Вакансия Отсутствие атома в одном из узлов кристаллической решетки
Межузельный атом Находящийся в нерегулярном положении атом, лишний с точки зрения правильного строения кристаллической решетки
Пара Френкеля Сочетание близко расположенных вакансий и межузельного атома, образовавшихся вследствие выхода одного атома из регулярного положения
Примесный атом Инородный атом, расположенный в узле решетки или междоузлии
Линейный Краевая дислокация (рис, 2.7, а) Нарушение регулярного строения кристалла, обусловленное наличием избыточной атомной плоскости
Винтовая дислокация (рис. 2.7, б) Нарушение регулярного строения кристалла, обусловленное изгибом части решетки
Двумерный Дефект упаковки Отклонение от нормальной для данного кристалла последовательности расположения атомных слоев, например скопление вакансий или дислоцированных атомов, расположенных в одной плоскости
Граница между зернами »д Нарушение регулярного расположения атомов вблизи границы между двумя смежными кристаллами поликристалл нческ ого тела
Мозаичная структура кристалла Нарушение регулярного расположения атомов вблизи границы между блоками, образующими кристаллит
Трехмерный Пустота Дефект усадочного или дислокационного происхождения в виде мн к роили макроскопической полости
73
них атомов неизмеримо меньше количества вакансий. Вакансии образуются главным образом по механизму Шоттки, в соответствии с которым кристалл как бы растворяет пустоту, начиная с поверхности (88, 166]. Вакансии очень подвижны: они почти непрерывно перемещаются из одного узла решетки в другой, выходят на поверхность кристалла и исчезают. Однако взамен исчезнувших образуются новые, и общее количество вакансий в кристалле остается практически неизменным. Для каждой температуры устанавливается равновесная концентрация вакансий
np/W = ехр(—Q,/7?T), (2.1)
где Q. — энергия образования вакансии;./? — постоянная Больцмана.
Из формулы (2.1) следует, что равновесная концентрация вакансий исключительно сильно увеличивается с повышением температуры. Вакансии легко взаимодействуют с другими дефектами и поэтому играют важную роль в процессе пластической деформации.
Рис. 2.7. Модели линейных дефектов.
в — краевая дислокация (£ — экстра плоскость. L — линия дислокации. D — ядро дислокации. а — параметр решетки; S — плоскость скольжения); б — винтовая дислокация (Ь — вектор Бюргерса)
2.3.2. Линейные дефекты-дислокации. Первые упоминания о дислокациях относятся к 1934 г. 163, 179]. Представления о дислокациях возникли в связи с противоречиями между теоретическими расчетами и экспериментальными данными, относящимися к скольжению в кристаллах. Дислокации послужили основой для создания такой модели кристаллического тела, которая позволила устранить отмеченные противоречия, объяснить механизм пластической деформации и упрочнения кристаллических тел, предсказать некоторые эффекты, связанные с ростом кристаллов, их пластической деформацией, повышением прочности кристаллических тел. " ’ '
74
Установить существование дислокаций экспериментально, изучить их свойства и обнаружить источники оказалось возможным лишь в 50-х годах после создания достаточно совершенных электронных микроскопов. Поэтому теория дислокации завоевывала признание с большим трудом. Лишь когда при помощи ионного микроскопа удалось прямо наблюдать дислокации и отдельные точечные дефекты, когда открылась возможность выполнить ряд количественных исследований, теория дислокаций стала теорией механических свойств кристаллов [ 10].
Различают краевую (рис. 2.7, а) и винтовую (рис. 2.7, б) дислокации. Краевая дислокация — это дефект, связанный со смещением
нескольких рядов атомов из регулярного положения, соответствую-
щего представлению об идеальном кристалле. Чтобы получить краевую дислокацию, необходимо взять идеальный кристалл, расщепить его по кристаллической плоскости на некоторую глубину и в образовавшийся зазор вставить дополнительную плоскость — экстраплоскость. Введем следующие понятия и дадим их определения [11, 63, 68, 88]. Линия дислокации — линия L, соединяю-
б
щая атомы, лежащие на краю экстраплоскости. Ядро дисло-
кации — множество атомов, окружающих линию дислокации и отстоящих от нее примерно на один параметр решетки. Вектор Бюргерса — вектор b идеальной решетки, соответствующий разрыву контура A BCD А в дефектном кристалле (рис. 2.8). Чтобы получить вектор Бюргерса, образуем замкнутый контур Бюргерса A BCD А в идеальной решетке и аналогичный контур, который включает такое же количество узлов, охватывающий дислокацию. Последний окажется незамкнутым. Чтобы его замкнуть, необходимо добавить вектор Бюргерса b (рис. 2.8). Вектор Ъ наглядно показывает, в каком направлении смещается материал при перемещении дислокации. Как видно из рис. 2.8, модуль и направление вектора Бюогерса не зависят от того, какой первоначальный контур выбран и в каком направлении осуществляется обход контура. Вектор b — койетаНта для всех участков дислокационной линии и остается константой при движении дислокации.
- Дислокации обладают подвижностью. Достаточно приложить к кристаллу сравнительно небольшое напряжение, чтобы вызвать перемещение дислокации. Наиболее легко дислокация движется в направлении оси х (рис. 2.7, а), так как при перемещении дислокации на один параметр а вправо по оси х энергия, которую необходимо сообщить правому соседу дислокации, практически равна освобождаемой при перемещении левого. Такое движение (перпендикулярно экстраплоскости) называется консервативным движением дислокации, или скольжением. Плоскость S, перпендикуляр
75
ную экстра плоскости Е, проходящую между линией дислокации L и ближайшей атомной плоскостью, называют плоскостью скольжения.
Экстраплоскость может располагаться выше плоскости скольжения или ниже ее. Условимся в первом случае приписывать дислокации знак плюс, а во втором — минус и обозначать их соответственно _1_ или Т.
Сила, необходимая для консервативного движения дислокации, называется силой Пайерлса. Эта сила относительно невелика. Например, для металлов с ГЦК-решеткой она составляет около 0,05 МПа. При низких напряжениях дислокации скользят очень медленно, со скоростями порядка 10“• мм/с. Однако с увеличением напряжения скорость движения дислокации резко увеличивается. Теоретическая оценка зависимости скорости дислокации Цдисл от приложенного касательного напряжения т приводит к следующей формуле [88]:
Одисл = ехР (—Л/тТ), (2.2)
где Т — температура; и0. Л — константы материала.
Консервативное движение дислокаций не сопровождается переносом массы и не обусловлено диффузионными перемещениями атомов. Поэтому оно может происходить при каких угодно низких температурах, вплоть до абсолютного нуля. В процессах пластической деформации консервативное движение дислокаций играет исключительно важную роль.
Второе возможное направление движения дислокации — по оси г(рис. 2.7, а). Однако простое движение экстраплоскости в направлении оси z, как и в направлении оси у, неосуществимо, требует исключительно больших затрат энергии. Движение краевой дислокации в направлении осн z может осуществляться только путем диффузионного перемещения линии дислокации и называется неконсервативным движением дислокации, или переползанием. Если линия дислокации поглотит цепочку межузельных атомов, то экстра плоскость удлинится на один параметр. Если линия дислокации поглотит цепочку вакансий, то экстраплоскость укоротится на один параметр и дислокация как бы сместится вверх на один параметр решетки. Переползание дислокации вызывает деформацию кристалла—его изгиб. Подвижного точечных дефектов сильно зависит от температуры. Поэтому переползание дислокации может происходить достаточно интенсивно только при температурах, значительно превышающих комнатную. Переползание дислокаций играет очень важную роль в высокотемпературных процессах деформации.
Винтовая дислокация (рис. 2.7, б) — это дефект, обусловленный искривлением части кристаллографических плоскостей, когда контур Бюргерса образует виток винтовой линии. При таком искажении кристалла экстра плоскость отсутствует. Представление о винтовой дислокации впервые введено Дж. Бюргерсом в 1939 г.
76
[1791. Линия, параллельная вектору Бюргерса b (на рис. 2.7, б, параллельная оси у) и соединяющая узлы решетки, в которых начинается искривление плоскостей, называется линией дислокации. В зависимости от направлений искривления кристаллографических плоскостей различают правую и левую винтовые дислокации (на рис. 2.7, б показана правая дислокация).
Винтовые дислокации также обладают подвижностью. Движение винтовой дислокации не сопровождается переносом массы и не обусловлено диффузионными перемещениями атомов. Поэтому, как и консервативное движение краевой дислокации, оно может происходить при каких угодно низких температурах, вплоть до абсолютного нуля. Направление движения винтовой дислокации,
Рис. 2.9. Схемы нагружения кристалла (а), образования и движения смешанной дислокации (б) и сдвига а в результате выхода дислокации на поверхность кристалла (в)
перпендикулярное линии дислокации и вектору Бюргерса b (на рис. 2.7, б дислокация движется в направлении оси х), называется поперечным скольжением. Других направлений движения винтовая дислокация не имеет.
Деление дислокаций на краевые и винтовые в известной мере условно: оно используется главным образом в методических целях, чтобы упростить подход к изучению линейных дефектов кристаллической решетки. В действительности дислокации являются смешанными. Для примера возьмем совершенный кристалл и приложим к eri грани (010) нагрузку (рис. 2.9, а). Грань — основание (в плоскости ху) — закрепим неподвижно. Под действием нагрузки на грайл (100) образуется краевая дислокация, на грани (010) — винтовая дислокация (рис. 2.9, б). В точках А, С — чисто краевая и чисто винтовая дислокация, а в любой другой точке линии АВС дислокация будет смешанной (частично краевой и частично винтовой). Это значит, что при движении вдоль АВС краевая дислокация постепенно переходит в винтовую. При увеличении нагрузки дислокации начнут перемещаться в направлениях М и N, линия дислокации станет расширяться, и когда она пересечет весь кристалл по плоскости АВС, произойдет смещение верхней части кристалла относительно нижней на один параметр решетки (рис. 2.9, в).
п
Линии дислокации не обязательно должны быть плоскими: они могут образовывать ступеньки и разветвляться. Например, в кристалле с отрицательной дислокацией, у которой экстра плоскость Е имеет форму, показанную на рис. 2.10, линия дислокации ABCDFG имеет две ступеньки: СВ и DF. Движение такой дислокации в направлении вектора Бюргерса (напомним, что для всей дислокационной линии его значение и направление постоянны) является консервативным. В результате скольжения дислокации Е и выхода ее на поверхность кристалла образуется ступенчатая поверхность Р. Такое скольжение называется карандашным. Движение винтовой дислокации со ступенчатой линией порождает точечные дефекты.
Рис. 2.10. Модель дислокации со ступенькой (а) и схема карандашного скольжения (б)
Краевая и винтовая дислокации — это простейшие модели линейных дефектов. Сейчас известны и другие, более сложные: геликоидальная, двойникующая, призматическая, расщепленная, сверхструктурная, сидячая, частичная дислокации. Несмотря на некоторые их отличия друг от друга, в процессах пластической деформации все они играют одинаковую роль. Дислокационные линии могут разветвляться. При этом образуются дислокационные сетки. Например, в кристаллах с ГЦК-решеткой часто образуются гексагональные сетки дислокаций в плоскости (111) [631. Встречаются частичные дислокации. Образование вакансионного диска и его захлопывание приводят к формированию замкнутой дислокационной петли, которая представляет собой частичную дислокацию, известную в литературе как сидячая дислокация Франка [ 1661. Особенность этих дислокаций — их низкая «идвижность.
Важной характеристикой состояния кристалла служит плотность дислокаций. Плотность дислокаций р -г- это суммарная длина линий дислокаций /а, приходящихся на единицу объема кристалла V:
Р « S h/V. (2.3)
Плотность дислокаций в кристалле меди, приготовленном обычным способом, составляет 10е см-’. После специального длительного отжига ее удается снизить до 106... 10* см'*. В особых условиях кристаллизации можно вырастить кристаллы с плотностью дисло
78
каций 10s... 15 • 10s см"3. Изменение плотности дислокаций приводит к существенному изменению свойств кристаллов.
2.3.3. Двумерные и трехмерные дефекты. В табл. 2.1 приведены лишь основные виды двумерных и трехмерных дефектов. Специалистов по обработке металлов давлением они интересуют лишь постольку, поскольку способствуют образованию и движению точечных и линейных дефектов или являются барьерами на их пути. Дзумерные и трехмерные дефекты служат источниками точечных дефектов. Именно на поверхностях двумерных или трехмерных дефектов зарождаются по механизму Шоттки и двигаются в глубину кристалла вакансии, если их концентрация меньше равновесной (например, при нагреве). Поверхности двумерных или трехмерных дефектов могут служить и стоками точечных дефектов, т. е. местами, куда устремляются вакансии и межузельные атомы, если их концентрация оказывается выше равновесной (например, при медленном охлаждении кристалла). Двумерные дефекты — эффективные барьеры на пути движения дислокации. Поэтому при пластической деформации в области малоугловых границ, особенно границ зерен, наблюдается скопление дислокаций. Трехмерные дефекты — это превосходные стоки дислокаций (как и свободные поверхности кристаллов). При выходе дислокации на свободную поверхность трехмерного дефекта на последней образуется ступенька, равная вектору Бюргерса дислокации.
Таким образом, двумерные и трехмерные дефекты оказывают значительное влияние на характер движения дислокаций, а значит, и на пластическую деформацию кристаллических тел.
2.4. ХОЛОДНАЯ ПЛАСТИЧЕСКАЯ ДЕФОРМАЦИЯ МОНОКРИСТАЛЛОВ
Пластическая деформация реальных металлических тел — процесс исключительно сложный. Начнем рассмотрение с простейшей модели холодной пластической деформации монокристалла. Монокристалл — это такое кристаллическое образование, в котором нигде, кроме поверхности, не нарушено закономерное расположение атомов.
2.4.1. Модели деформации совершенных кристаллов. Рассмотрим модель механизма пластической деформации тела в виде кристалла с простой хубической решеткой. Нагрузим его так, чтобы напряженное ссиЛояние определялось шаровым тензором Т“, причем аср < 0. Теперь поставим вопрос, как тело будет деформироваться.
Выделим в теле элементарную ячейку кристаллической решетки. Если при деформации атомы из положений А переместятся в положения А' (рис. 2.11) и параметр решетки уменьшится от а0 до аэ, то в соответствии с формулой (1.1) между атомами возникнут силы отталкивания /?х, /?,. При уменьшении параметра а силы /?х, Rt
79
будут непрерывно и неограниченно увеличиваться. После снятия нагрузки атомы А согласно формуле (1.1) возвратятся в исходные
*Z1
*4
К Ар| IX А
R
2
^x2
ЯхЗ
t„ g.i
____Ва-
Аз
*з
рне. 2.11. Модель деформации элементарной ячейки при равномерном сжатии
положения, а кристалл примет первоначальную форму и размеры. Значит, всесторонне равномерное сжатие не может привести к пластической деформации. Если оср>0, то на начальных этапах деформации изменение расстояний между атомами будет обратимым и после разгрузки кристалл примет первоначальную форму и размеры. Однако если при деформации перейти границу гкр» то внутренние силы взаимодействия между атомами не смогут уравновесить внешние нагрузки и кристалл разрушится. Следовательно, всестороннее равномерное растяжение также не приводит к пластической деформации, но при определенных условиях такая нагрузка
может вызвать разрушение тела.
Теперь рассмотрим схему нагружения кристалла, при которой Л = |т О**} и оси х’ гсовпаДают с кристаллографическими
осями. Выделим в теле небольшой элемент кристаллической решетки (рис. 2.12). Пока
тело не нагружено, атомы занимают положения устойчивого равновесия, определяемые узлами кристаллической решетки (рис. 2.12, а). Под нагрузкой тхх тело деформируется, решетка искажается и атомы занимают новые положения (рис. 2.12, б). Расстояния между атомами Ль As уменьшаются, а между Л2, Л4 увеличиваются. В связи с этим между ними возникают силы взаимодействия R4 и /?з, Rt и R4, горизонтальные составляющие которых 7\ и Тг, Т3 и Т4 уравновешивают внешние силы, вызывающие напря-
Рис. 2.12. Модель деформации элемента кристалла при сдвиге:
жение т„. С увеличением тжг решетка все более
искажается, увеличивается угол возрастают
a — исходное состояние; б — упругая деформация; в — упруго-пластическая деформация; а — остаточная деформация
80
силы взаимодействия Rlt Rt, R3, R4. Будут ли они возрастать неограниченно? Ответ на этот вопрос дают следующие расчеты*. Пусть атомы Л4, А3 неподвижны, а атом At перемещается из положения 4? в положения А\, 4J и т. д. (рис. 2.13). Если пренебречь влиянием других атомов и предположить, что все атомы, лежащие в слое 4t—А, перемещаются синхронно с атомом 4Ь то
касательное напряжение тх„ которое ренние силы Rt и R4, с достаточной точностью можно выразить функцией
тХ2 = ткр sin (2л VJ). (2.4)
При малых значениях х/а «и (2лх/п)^ ~ 2лх/а. Поэтому т;££ь гкр2лх/а. Отношение х/а характеризует степень искажения решетки. Изрис. 2.13 видно, что х/а «= tg yxz. При малых значениях х/а tgY„ = yxx. Тогда уравнение (2.4) примет вид тхг = = 2лткруХ2. Обозначив 2лткр через G, преобразуем его в уравнение, выражающее закон Гука тХ2 = Gyxx. Связь между ткр и модулем сдвига G определит соотношение
ткр = 0/2л. (2.5)
может уравновесить внут-
Рис. 2.13. Схема к расчету критического касательного напряжения
Значения модуля сдвига G приведены в) справочниках практически для всех используемых в технике ме таллов. Поэтому функцию (2.4) можно записать так:
G . х
T~efctS,n а
(2.6)
Отсюда следует, что т„^6/2л и возрастать неограниченно не может. Кроме того, при х/а = 1 тХ2 = 0. Значит, после того как атом А4 перешел из положения 4J в положение 4}, решетка вновь возвращается в естественное ненапряженное равновесное состояние. Возвратившись к рис. 2.12, обнаруживаем, что при перемещении атома Аг в новое положение все атомы, лежащие выше плоскости скольжения S, должны сместиться относительно атомов, лежащих ниже плоскости скольжения S, на расстояние а (рис. 2.12, в). Такая деформация называется сколь-жением и уже не является обратимой.
После разгрузки кристалл получает остаточную деформацию (рис. 2.12, г). Очевидно, что сдвиг верхней части кристалла в плос
* Впервые такие расчеты выполнил Я< И. Френкель в 1926 г, [184, 1621.
81
кости скольжения S относительно нижней на ka, где k — целое число, также приведет к равновесному состоянию кристалла. Естественен вопрос: является ли плоскость S (или другая, параллельная ей) единственно возможной плоскостью скольжения? Может ли деформация осуществляться по другим плоскостям, например Д1Л4 или AtA4 (рис. 2.12)? Экспериментальные данные свидетельствуют о том, что модуль сдвига G зависит от выбранного направления: для плоскостей, где атомы упакованы наиболее плотно, значение величины G наименьшее. Поэтому для плоскостей с наиболее плотной упаковкой атомов и напряжение ткр наименьшее. Следовательно, такие пл<Лкости— это плоскости наиболее легкого скольжения Из рис. ,2.12 следует, что плоскости ЛхЛа и Л1Л4 имеют наибольшую Ф*yiocrb упаковки атомов, а плоскости А4А3 и ЛаЛ4 — наименьшую^ Поэтому под действием касательных напряжений скольжение возможно по плоскостям ^p4t, А4А4 и мало вероятно по плоскостям Д^з, А3А4.
На основании детального анализа принятой модели пластической деформации можно сделать следующие выводы. Нормальные напряжения не приводят к пластической деформации, а вызывают упругое обратимое изменение размеров и объема тела. Касательные напряжения, не превышающие критического значения ткр, также не вызывают пластической деформации. Тело деформируется упруго, подчиняясь закону Гука. Пластическая деформация осуществляется только в том случае, когда касательные напряжения достигают критического значения ткр. Происходит она путем скольжения, т. е. сдвига одной части кристалла относительно другой, причем сдвиг должен быть кратным параметру решетки. Скольжение происходит в плоскости, наиболее плотно упакованной атомами.
2.4.2. Экспериментальные данные. В лабораторных условиях удается выращивать монокристаллы больших размеров. Благодаря этому возможна экспериментальная проверка выводов, полученных на основе модельных представлений о деформации металлов.
Рентгенографические исследования [10, 11, 71, 74 , 85, 1671 подтверждают вывод о том, что сдвиг при пластической деформации действительно происходит в плоскости с наиболее плотной упаковкой атомов. Для кристаллов с ГЦК-решеткой такими плоскостями являются (111), для кристаллов с ГПУ-решеткой — плоскости базиса (0001). В кристаллах с ОЦК-решеткой, плотность расположения атомов по различно ориентированным плоскостям отличается незначительно. Поэтому скольжение в этих кристаллах может осуществляться по плоскостям, (НО), (112), (123) и др. Кроме того, установлено, что скольжение происходит только в определенных направлениях. Для кристаллов с ГЦК-решеткой оно осуществляется в направлении < 110), с ГПУ-решеткой — в направлении < 1120), с ОЦК-решеткой —в направлении <111). Совокупность плоскости и направления скольжения называется системой скольжения.
82
Хорошо подтверждается данными экспериментов и вывод о том, что пластическая деформация происходит путем сдвига одной части кристалла относительно другой. Например, если стержень из монокристалла цинка подвергнуть значительной пластической деформации, то на его поверхности легко обнаружить полосы скольжения (плоскости скольжения) и уступы, образованные при смещении одной части кристалла относительно другой. Экспериментально установлено, что полосы скольжения удалены друг от друга на расстояния порядка 1 мкм (11, 741. Это означает, что сдвиг происходит только в небольшом количестве плоскостей. Расстояния между соседними атомными плоскостями для разных кристаллов составляют ^Среднем 5 • 10“* мкм (см. подразд. 2.1.1). Стедовательно, только оДна из двух тысяч смежных плоскостей является плоскостью скольжения. Чтобы при этих условиях получить ощутимую деформацию, необходимы значительные смещения в каждой из действующих плоскостей скольжения. Экспериментальные исследования показывают, что смещение в действующих плоскостях скольжения достигают (50...100)а, где а — параметр решетки.
Обратимся к изучению силовых условий деформации. В соответствии с принятой моделью к кристаллу необходимо приложить касательное напряжение ткр = 6/2л, чтобы вызвать в нем пластическую деформацию. Расчеты 1166] позволили уточнить значение ткр и считать, что
тКр = 6/30. (2.7)
Воспользовавшись данными 'работ [ 160, 167], найдем значение Ссч для цинка, меди и железа: по формуле (2.5) — 6500; 7350; 11000 МПа и по формуле (2.7) — 1360; 1540; 2300 МПа соответственно.
Теперь обратимся к экспериментальным данным по растяжению монокристаллов (74, 167, 174]. Уже в ранних исследованиях Е. Шмида и В. Боаса [ 174] установлено, что при растяжении монокристаллов напряжение течения of сильно изменяется в зависимости от ориентировки плоскости скольжения и направления скольжения. Однако, если действительное напряжение растяжения о = Р/F преобразовать в приведенное критическое
ткр = a sin % cos X, (2.8)
то это последнее оказывается константой для каждого металла. В выражении (2.8) % — угол между плоскостью скольжения и осью образца; X — угол между направлением скольжения и осью образца. Иными словами, напряжение ткр в системе скольжения, характерной для данного металла, константа. Уравнение (2.8) выражает закон Шмида для критического касательного напряжения. Для цинка, меди, железа получаем соответственно следующие значения ТкрСП : 0,30...0,94; 0,40... 1,0; 15,0...29,0 МПа. Сравнение значений т{£с’ и т’рСП не вызывает оптимизма: расхождение на
83
3...4 порядка дает основание считать, что принятая модель неточно отражает действительный механизм деформации. Попытаемся уточнить модель. Для этого проанализируем влияние различных дефектов кристаллической решетки на характер деформации кристалла. При комнатной температуре концентрация вакансий ничтожно мала. Искажения, которые вносит вакансия, распространяются только на два-три ближайших слоя. Поэтому мало вероятно, чтобы вакансии (а тем более межузельные атомы, которых еще меньше, чем вакансий) могли так сильно повлиять на критическое напряжение ткр.
В монокристаллах, выращенных при малой скорости кристаллизации, двумерные и трехмерные дефекты практически отсутствуют. Поэтому можно с уверенностью сказать, что различие т£рсч и Ткр" вызвано не этими дефектами. Остается предположить, что снижение ткр определяется влиянием дислокаций. Такое предположение впервые высказали Я. И. Френкель [162], Дж. Тейлор, Е. Орован и М. Полани [63, 179]. Чтобы подтвердить его или отвергнуть, необходимо из одного и того же металла получить два кристалла: один с дислокациями, другой^ без них. Современная техника позволяет сделать это. В особых условиях можно вырастить практически бездислокационные монокристаллы —усы, или нитевидные кристаллы [9]. Результаты испытания нитевидных и обычных кристаллов дают однозначный ответ: действительно, дислокации очень сильно влияют на значение ткр и предел текучести. Это влияние показано ниже [9, 167, 179]:
Металл Fe Си Zn
Предел текучести монокристаллов, МПа: нитевидных 10000 3 000 380
обычных 15...29 0,4 ... 1,0 030 ... 0,94
Как видно, уменьшение плотности дислокаций приводит к увеличению сопротивления деформации на 2...4 порядка. Аналогичные данные получены и для других металлов. Они позволяют утверждать, что для объяснения механизма деформации металлов необходимо рассмотреть дислокационную модель.
2.4.3. Дислокационная модель деформации. Рассмотрим кристалл с некоторым количеством положительных и отрицательных дислокаций, расположенных в плоскостях скольжения SIt Sa, S8 и т. д. (рис. 2.14, а). Выделим в нем область М, окружающую положительную дислокацию, лежащую в плоскости Sa. Если кристалл деформируется и решетка получает угловую деформацию ухг (рис. 2.14, б), то в ядре дислокации происходит изменение взаимного положения атомов и перераспределение напряжений. При деформации, соответствующей напряжению тХ2 = тКр. начинается консервативное движение дислокации (рис. 2.14, в). Обычно начало движения соответствует напряжению ткр = (10-s... 10-4)G 1159].
84
Такую легкость движения дислокации можно объяснить следующим. Искажение решетки под действием напряжения ххг приводит к тому, что линия дислокации Lo приближается к цепочке атомов расположенной под плоскостью скольжения, а цепочка атомов Lj удаляется от цепочки Ах (рис. 2.14. б). Экстра плоскость K0Lq разрывает атомную плоскость KjLiAiBi и образует вместе с частью плоскости Д1В1 полную атомную плоскость Ko^o^i^i. а часть плоскости KXLX становится экстра плоскостью (рис. 2.14, в). Под действием напряжения ткр этот процесс может многократно повторяться до тех пор, пока экстраплоскость выйдет на поверхность кристалла и на последней образуется ступенька (рис. 2.14, г.)
Рис. 2.14. Дислокационная модель деформации элемента кристалла: а — кристалл с дислокациями в плоскостях скольжения S, — 3»; б — упругая деформация решетки; в — начало движения дислокации к поверхности кристалла; в — разгрузка кристалла после выхода дислокации на поверхность
Следовательно, происходит как бы перемещение экстраплоскости, хотя в действительности все атомные плоскости перемещаются на расстояние, меньшее параметра-решетки а. В плоскости скольжения может находиться т дислокаций одного знака, как например, в плоскости S, (рис. 2.14, а). Под действием напряжения ткр все они могут пройти через кристалл и выйти на его поверхность. Тогда ступенька станет равной та.
Наконец, рассмотрим движение дислокаций в самом общем случае, когда в плоскости скольжения расположено несколько дислокаций разных знаков (рис. 2.14, а плоскость S3). Нетрудно установить, что при встречном движении дислокаций разных знаков произойдет взаимное уничтожение, или аннигиляция дислокаций. Последовательная аннигиляция дислокаций разных знаков и выход дислокаций на поверхности кристаллов приводят к уменьшению плотности дислокаций.
С помощью понятия о дислокациях легко объяснить, почему реальные кристаллы деформируются при напряжениях, которые на несколько порядков ниже предсказанных по формулам (2.5), (2.7). На первый взгляд все ясно и логично. Но сделаем простой расчет. Возьмем кристалл в виде кубика с ребром 1 см и плотностью дислокаций 10е см-2. Предположим, что линии всех дислокаций в нем непрерывны и идут от одной грани к другой, а плоскости скольжения расположены равномерно, через
85
каждый микрометр. Эти допущения вполне соответствуют экспериментальным данным (см. подразд. 2.3.2, 2.4.2). Рассчитаем среднее количество дислокаций, лежащих в каждой плоскости скольжения. В кубике с ребром 1 см имеется 10* плоскостей скольжения. Пусть в каждой из них л дислокаций. Тогда их общее количество и суммарная протяженность Zld = п • 1 • Ю4 см. Сбъсм кристалла V = 1 см3. При плотности дислокаций р = 10е см-3 согласно формуле (2.3) п = 10’. Предположим, что одна половина дислокаций положительна, другая отрицательна и при деформа-
ции они не аннигилируют, а все выходят на поверхность кристалла (рис. 2.15). При этих условиях образуется 104 ступенек, каждая
Рис. 2.15. Схема к расчету деформации кристалла:
а— исходное яедгфсрмврованпос состояние; 6 — деформированное состояние после выхода всех двелокаций на боковые грави кубика
из которых имеет протяженность па = 10’ • а. Общее смещение верхней грани кристалла по отношению к нижней составит ДЛ =« I04 х X 10’ • а. Примем а = = 5 • 10мм. Тогда ДЛ = Ю’х 5 • Ю-7 = = 0,5 мм. Это соответствует относительной деформации кристалла ел = (0,5/10) • 100% = = 5%. Иными словами, если взять даже не очень тщательно выращенный
кристалл и предположить, что ни одна пара дислокаций не аннигилировала, а все они вышли на поверхность деформируемого кристалла, то и в этом невероятном случае остаточная деформация окажется ничтожно малой, примерно на порядок меньше наблюдаемой в экспериментах с реальными монокристаллами. Кристалл же превратится в бездислока-ционный, и его сопротивление деформации станет исключительно высоким. Соответствует ли это действительности? Нет. Реальные монокристаллы деформируются на 50% и более. При этом сопротивление деформации (критическое напряжение сдвига) увеличивается крайне незначительно (для металлов с ГПУ-решеткой) или довольно значительно (для металлов с ГЦК и ОЦК-решеткой, но до уровня, который на несколько порядков ниже теоретического, характерного для бездислокационных кристаллов. Именно это и было причиной длительного отрицания теории дислокаций.
В 50-х годах было установлено, что после деформации обычных монокристаллов плотность дислокаций в них возрастает до 10*° ... ... 10” см~’ и что при деформации совершенных бездислокационных монокристаллов (усов) в них появляется большое количество дислокаций, а критическое напряжение сдвига резко снижается и ста-
86
новится соизмеримым с критическим напряжением сдвига обычных монокристаллов, содержащих дислокации [9, 10, 68, I67J.
Таким образом, для доказательства истинности теории дислокаций необходимо было обнаружить механизмы образования дислокаций в процессе деформации.
2.4.4. Источники дислокаций. Механизм образования дислокаций в процессе пластической деформации предсказал в 1940 г. академик Я. И. Френкель 168, 162), а экспериментально подтвердили в 1950 г. Ф. Франк и В. Рид [ 1831. Рассмотрим кристалл со ступенчатой линией дислокации ABCDFG (рис. 2.10, а). Если при карандашном движении дислокации участки ВС и DF (рис. 2.16)
Рис. 2.16. Схема образования дислокаций по механизму Франка — Рида (вид сверху на кристалл с дислокацией, показанной на рис. 2.10.):
а — исходное состояние; б—в — этапы движения дислокации L* и образования иоео* дислокации L,
встречают какое-либо препятствие (точечные дефекты, дислокации, движущиеся в перпендикулярной плоскости), то эти участки закрепляются. Линия дислокации CD, продолжая двигаться, выгибается, краевая дислокация превращается в смешанную, начинается поперечное скольжение (движение винтовой дислокации в направлении оси у), затем петля дислокации смыкается в точке К, образуя внешнюю линию дислокации Lo и новую линию дислокации При дальнейшей деформации кристалла картина повторяется: линия дислокации выгибается, образует петлю, которая смыкается в точке Ki, порождает новую дислокацию L2 и т. д. Закрепленная по концам линия дислокации, которая может выгибаться, образовывать петли и новые дислокации, называется источником Франка~Рида. Каждая петля, возникшая в плоскости скольжения, при выходе на грани кристалла образует ступеньку — единичный сдвиг. Если источник Франка—Рида порождает большое количество дислокаций, то в плоскости скольжения получается сдвиг на сотни и тысячи параметров решетки. Это и объясняет возможность значительной пластической деформации реальных металлических кристаллов. Линия дислокации ведет себя как упругая струна. В ней возникает сила сопротивления растяжению, направленная к центру кривизны. Эта сила уравновешн-
вт
вает приложенные к кристаллу нагрузки. Критическое касательное напряжение, при котором начинается движение дислокации» обратно пропорционально длине линии дислокации I (рис. 2.16,6):
ткр = Gb/l, (2.9)
где G — модуль сдвига; b — вектор Бюргерса дислокации. Из формулы (2.9) следует, что сопротивление сдвигу при деформации кристалла существенно зависит от его дислокационной структуры.
Ф. Франк предположил, что в кристаллах, полученных кристаллизацией из расплава, дислокации образуют трехмерные сетки, обладающие устойчивой конфигурацией. В дальнейшем его предположение было подтверждено экспериментально [111. Такие сетки обусловливают образование в кристаллах своеобразной
Рис. 2.17. Модель механизма гомогенного зарождения дислокации (£.£) и ее движения через кристалл:
□ — упругая деформация кристалла; б — зарождение; а —движение дислокации; а — выход дислокации на поверхность кристалла; д — разгрузка и необратимая деформация кристалла
ячеистой структуры. Сетки дислокаций делят монокристалл на ячейки (бездислокационные области), развернутые друг относительно друга на небольшие углы. Средняя длина ячейки для различных металлов составляет 10“1...10_* мм. Размеры и форма ячеек оказывают очень сильное влияние на свойства кристаллов и их пластическую деформацию. Эти особенности строения монокристаллов определяют как субструктуру*.
При деформации кристаллов с ячеистой структурой движение дислокаций происходит в трех взаимно перпендикулярных плоскостях. Это приводит к многократному поперечному скольжению и образованию новых дислокаций. Такой механизм действует подобно механизму Франка—Рида. Однако в отличие от последнего он определяет не только размножение дислокаций в данной плоскости скольжения, но и распространение скольжения на соседние.
До сих пор мы рассматривали размножение дислокаций. А как образуются дислокации в первоначально бездислокационных кристаллах?
* Под структурой металла понимают форму, размеры и характер взаимного расположения соответствующих фаз в металлах или сплавах ; под субструктурой — форму, размеры и разориентировку ячеек, образованных дислокационными сетками в монокристаллах или зернах поликристалли-ческих металлов. Для характеристики субструктуры широко используются термины ячеистая структура, мозаичная структура, блочная структура.
88
Их образование происходит по механизму гомогенного зарождения (рис. 2.17). Для этого, как правило, требуются очень высокие напряжения, приближающиеся к теоретическим, рассчитанным по формуле (2.7). Наконец, в поликристаллических телах возможно образование дислокаций по механизму гетерогенного зарождения (см. подразд. 2.5).
2.4.5. Модель деформации двойникованием. Скольжение дисло
каций — не единственный механизм пластической деформации монокристалла. Деформация при повышенных скоростях и низких температурах может осуществляться двойникованием. При двойниковании кристаллит скачкообразно делится на две части, в кото-
рых решетка становится зеркально-симметричной относительно плоскости двойникования (рис.
2.18) . Двойникование при растяжении монокристалла сопровождается характерным потрескиванием, а деформация протекает скачкообразно.
В ГПУ-кристаллах двойники
образуются по плоскостям {1012], в ОЦК-крнсталлах — по плоскостям {112], а в ГЦК-кристаллах — по плоскостям (111] 174, 159, 167]. В ГЦК-кристаллах двойникование осуществляется с большим трудом и только в специально созданных условиях. Эти трудности давали основание считать двойнико
Рис. 2.18. Модель двойникования монокристалла с ОЦК-решеткой [74] (стрелками показаны направления перемещения атомов)
вание в таких кристаллах невозможным. Хотя сейчас этот механизм и обнаружен, тем не менее при деформации ГЦК-кристаллов двойникование не имеет практического значения 11591. Экспери-
ментальные исследования, выполненные на монокристаллах цинка, показали, что двойникование чрезвычайно чувствительно к концентрации напряжений. Для начала его необходимы напряжения до 30 МПа, а затем процесс идет при значительно меньших напряжениях (около 5 МПа) [ 111.
Двойникование — это механизм деформации преимущественно ГПУ- и ОЦК-кристаллов, роль которого сильно возрастает с увеличением скорости и (или) понижением температуры, так как при
понижении температуры критическое напряжение сдвига увеличивается быстрее, чем критическое напряжение двойникования. Двойникование считается специфическим механизмом деформации по-ликристаллнческих металлов 150, 1661. В самом деле, для деформации монокристалла достаточно существования одной системы скольжения. Поэтому монокристаллы металлов с ГПУ-решеткой (при благоприятной ориентации плоскости скольжения относительно системы приложенных сил) могут деформироваться значительно. Для деформации поликристаллических металлов необходимо оу-
89
ществование пяти независимых систем скольжения 1166]. В поликристаллах с ГПУ-решеткой это требование не выполняется, и их деформация была бы невозможной без двойникования. Двойникование приводит к изменению ориентации части кристалла и увеличению количества систем скольжения В поликристаллических металлах выход дислокаций на поверхности зерен вызывает значительные локальные напряжения (рис. 2.19). При благоприятной ориентации плоскостей скольжения в смежных зернах может происходить не сдвиг, а двойникование. Примеси и легирующие добавки существенно влияют на механизм деформации. Например, фосфор и кремний сильно облегчают двойникование в железе даже при обычных температурах и скоростях деформации (111). Я. И. Френкель и Т. А. Конторова теоретически установили, что двойникование имеет дислокационное происхождение. В работах последних лет это убедительно доказано экспериментально [1661.
2.4.6. Механизм упрочнения. Деформация монокристаллов приводит к увеличению плотности дислокаций. Казалось бы, что по мере деформации скольжение должно облегчаться. Однако опыт показывает, что истинное сопротивление деформации увеличивается. Попытаемся разрешить это противоречие.
Дислокации легко перемещаются в кристалле, если не встречают препятствий. В реальных кристаллах имеется большое количество различных дефектов, в том числе дислокационных сеток, полос двойников или линий двойникования. Поэтому свободное движение дислокаций может происходить только на небольших участках пути через кристалл. Кроме того, барьерами для дислокации могут служить поверхности кристалла, если они окислены или и кажены. Пластическая деформация кристалла может осуществляться как направленное смещение дислокаций, или как двойникование. Двойникование в обычных условиях требует большего напряжения, поэтому основным механизмом деформации является скольжение. Предположим, что в плоскости Ss (рис. 2.14, а) действует источник дислокаций R. Пусть в этой плоскости имеется дефект D. Даже атом примесей или легирующих добавок— трудно проходимое препятствие. Такие же дефекты, как окисленная граница зерен,— непроходимый барьер. Подойдя к дефекту D, головная дислокация останавливается, движение последующих дислокаций в плоскости S3 очень затрудняется.
Скольжение в плоскости Ss большого количества дислокаций одного знака сильно искажает кристалл и увеличивает его внутреннюю энергию. По мере увеличения плотности дислокаций вблизи препятствия D движение новых дислокаций от источника R требует все больших напряжений. Поэтому открываются новые источники дислокаций Rlt Rt и т. д. (с меньшей длиной дислокационной линии I и большим значением ткр). а дислокации получают возможность двигаться и в других плоскостях. Источник R может продолжать действовать совместно
90
c Z?i, Ri и другими, а может и блокироваться плотностью. Таким образом, по мере деформирования кристалла и повышения плотности сопротивление их движению все более увеличивается. Это явление называется упрочнением. Экспериментальные исследования показывают, что критическое касательное напряжение увеличивается пропорционально корню квадратному из плотности дислокаций: ткр = СИр НО, 85).
Таким образом, пластическая деформация монокристаллов может осуществляться скольжением, двойникованием и сбросообра-зованием. Скольжение происходит как направленное смещение дислокаций в плоскости скольжения. Этот механизм деформации является основным. Двойникование и сбросообразование имеют место только при определенных условиях, неблагоприятных для скольжения (низкие температуры и высокие скорости деЗюрмации). В процессе деформации в кристалле действуют источники дислокаций. При деформации плотность дислокаций в кристалле увеличивается, их движение затрудняется, в результате сопротивление деформации возрастает, т. е. при деформации кристалла происходит его упрочнение.
2.5. ХОЛОДНАЯ ПЛАСТИЧЕСКАЯ ДЕФОРМАЦИЯ ПОЛИКРИСТАЛЛИЧЕСКИХ МЕТАЛЛОВ
В технологии обработки металлов давлением холодная пластическая деформация находит широкое применение. Она используется при выполнении большинства технологических операций листовой и объемной штамповки, при выдавливании, прессовании. Поэтому рассмотрение механизма холодной пластической деформации поликристаллических металлов имеет большое практическое значение. Вместе с тем оно подготавливает читателя к изучению деформации при повышенных температурах.
2.5.1. Особенности пластической деформации. Ранее установлено, что технические металлы и сплавы, используемые для обработки металлов давлением,— это поликристалличе-ские тела. Поликристаллическое тело можно представить как совокупность большого количества монокристаллов. При таком подходе пластическую деформацию тела можно рассматривать как среднестатистический результат пластической деформации каждого монокристального зерна. Каждое отдельное зерно может деформироваться скольжением и (или) двойникованием*. Эти механизмы принято называть внутрикристаллитной деформацией.
Однако поликристаллическое тело может деформироваться еще одним специфическим способом, который называется межкристаллитной деформацией. Для наглядности создадим модель тела, в ко
* Сбросообразование как самостоятельный механизм характерен только для деформации монокристаллов [74, 167].
91
тором кристаллиты не могут деформироваться. Таким телом может быть, например, смесь глины с песком (и водой). Частички кварца — недеформируемые кристаллиты; глина, обволакивающая частички кварца,— межзеренные прослойки. Свойства такого тела хорошо известны: ему можно придавать самые разнообразные формы, хотя ни один кристаллик кварца свою форму и размеры не меняет. Но каждый кристаллик изменяет свое положение относительно других. Это оказывается возможным благодаря подвижности межзеренных прослоек и межкристаллитной деформации.
При деформации пол и кристалл и чес кого тела внутрикристаллит-ная и межкристаллитная деформация не могут протекать обособленно: внутрикристаллитная обязательно вызывает деформацию
Рис. 2.19. Схема движения дислокаций через смежные зерна полякристаллн-ческого металла:
а — начало скольжения в зерне А: б — распространение скольжения на зерно В; в— форма границы KL зерна В при условии свободной деформации; в — форма границы KL при совместной деформации аерен В, С
межкристаллитную; межкристаллитная — внутрикристаллитную, но не во всех случаях. Рассмотрим связь между внутрикристал-литной и межкристаллитной деформациями. Возьмем однофазный поликристаллический металл, например чистое железо. Выше уже установлено, что формоизменение образца происходит в связи с направленным смещением дислокаций в каждом монокристаль-ном зерне (рис. 2.19). Выход дислокаций на поверхность зерна А приводит к образованию на ней ступеньки и концентрации напряжений на грани смежного зерна В (рис. 2.19, а). Если ступенька достаточно велика, то в последнем начинает действовать гетерогенный источник дислокаций (рис. 2.19, б). Выходя на поверхность, эти дислокации в свою очередь создают концентрацию напряжений на грани соседнего зерна С и вызывают в нем пластическую деформацию. Так, пластическая деформация идет от одного зерна к другому. Деформируются и зерна, плоскости скольжения которых ориентированы неблагоприятно относительно системы внешних сил. Значительная деформация поликристалла проявляется как результат смещения большого количества дислокаций в большом количестве плоскостей скольжения в каждом зерне. Если бы зерна С, В деформировались обособленно, то их форму и положение можно было бы представить, как показано на рис. 2.19, в. В реальных условиях такая схема невозможна, ибо при деформации без раз
92
рушения выполняется условие сплошности. Поэтому кристаллиты С, В получают форму, показанную на рис. 2.19, г. Сопоставляя исходное и деформированное состояния, можно убедиться в том, что изменились форма и взаимное расположение кристаллитов С, В. Их поверхности стали ступенчатыми из-за выхода дислокаций на грани. Длина границы между ними G увеличивалась по сравнению с первоначальной. Совокупность этих изменений представляет одну из особенностей межкристаллитной деформации. Следовательно, внутрикристаллитная деформация обязательно сопровождается межкристаллитной.
Теперь установим связь межкристаллитной и внутрикристал-литной деформации. При относительном перемещении и повороте зерен ребра одних надавливают на грани других. В области надавливания в зерне по гетерогенному механизму могут зарождаться дислокации (рис. 2.19, а). Следовательно, в зерне может происходить скольжение или двойникование. Это значит, что при межкристаллитной деформации возможна и внутрикристаллитная, если напряжения в области надавливания зерен превысят ткр для скольжения или двойникования данных монокристальных зерен.
Есть еще один механизм деформации, присущий поликристаллам — механизм межзеренного проскальзывания. Он характерен для горячей деформации металлов. С повышением температуры межзеренные границы разупрочняются и при Т = 0,5ТПл их сопротивление деформации снижается до уровня сопротивления деформации зерен. Поэтому межзеренное проскальзывание, которое происходит как сдвиг одного зерна относительно другого, с энергетической точки зрения становится равноправным с процессами перемещения дислокаций внутри кристалла 1151. Межзеренное проскальзывание обычно идет одновременно с движением дислокаций внутри зерен. Благодаря этому сплошность поликристалла сохраняется и в процессе деформаций. При определенных температурно-скоростных условиях можно получить идеальное сочетание механизмов деформации и перевести металл в состояние сверхпластичности 150, 1231 (см. подразд. 2.8.2.1).
2.5.2. Критическое напряжение сдвига. Поликристаллический металл можно рассматривать как совокупность монокристальных зерен. Механические свойства монокристаллов известны достаточно хорошо. Казалось бы, предсказать свойства поликристаллов можно на основе статистических представлений, как это сделано, например, для модуля упругости. Однако теории поликристалли-ческого металла, при помощи которой это можно было бы сделать, пока еще не существует. Такое положение обусловлено тем, что процесс деформации монокристальных зерен протекает не обособленно, а кристаллиты деформируются как система.
Рассмотрим деформацию поликристаллического металла. Возьмем стандартный разрывной образец (рис. 2.20) и нагрузим его силой Р, изменяющейся во времени по некоторому закону P(t), например линейному Р = Ct. Предположим, что в начальный
93
момент (при t =а О, Р = 0) все кристаллиты находятся в естественном ненапряженном состоянии. Такое предположение будет достаточно близким к истине, если перед деформацией образец отжечь. Выделим в образце плоскость ЛГХ, наклоненную к оси г под углом 45°. Как известно (см. подразд. L5.4), в ней действует максимальное касательное напряжение т>иХ = 0,5о, где а = P/F. Пусть в кристаллите Кп плоскость скольжения S„ совпадает с где действует напряжение ттах, равное тхр для данного металла. В соответствии с законом Шмида (см. подразд. 2.4.2) кристаллит должен бы начать деформироваться. Но деформироваться как отдельный монокристалл он не может в силу того, что у него
&
Рис. 2.20. Схема деформации кристаллитов (б) при растяжении образца (а)
есть соседи Кл_х, Kn+i. Плоскости скольжения в них 5Л+Х образуют с осью углы (p„_x, <р„+х, отличные от 45°, а касательные напряжения тл_х, тл+х в плоскостях S„_x, Sn+i меньше тл = ткр. Поэтому кристаллиты Кп_и Kn+i могут деформироваться только упруго. Кристаллит Кп зажат соседями. Даже малая внутри-кристаллитная деформация обязательно вызывает межкристаллитную. При нагрузке образца напряжения в кристаллитах K„_i, Knt Kn+i будут перераспределяться: малые пластические деформации кристаллита вызовут его разгрузку, а упруго деформированные кристаллиты Хя_х, Kn+i станут догружаться. Перераспределение будет продолжаться до тех пор, пока касательные напряжения тл_х, тл, тл+1 не выравняются и не достигнут значения ткр в каждом кристаллите. В результате все кристаллиты Kn_i, Кп, K„+i одновременно перейдут в состояние интенсивного пластического течения. Подобным образом деформируются группы кристаллитов, которые пересекаются любой другой плоскостью АГ, наклоненной к оси образца под углом 45°.
Еще раз обратимся к рис. 2.20, чтобы выяснить, будет ли локальная деформация еж в каждом из кристаллитов одинаковой и равной средней деформации образца в целом еср (точнее, его
94
рабочей части). В кристаллите Kn+i плоскости скольжения Sn+i расположены так, что после сдвига по ним значительно увеличится размер вдоль оси г. А в кристаллите Kn-i размер в направлении оси z может уменьшиться.Следовательно, деформация поли-кристаллического тела весьма неравномерна. Экспериментальные данные хорошо подтверждают такое модельное представление. Как видно из рис. 2.21, при средней деформации образца е.» = 7,3% локальная деформация ех колеблется от —8% до -f-24%, т. е. некоторые зерна даже укорачиваются в направлении растяжения образца. Это результат перераспределения напряжений, обусловленного совместной деформацией в?ех кристаллитов как системы.
на поверхность кристаллита, 221 распределение частот образуется силовое поле, на- удлинений при растяжении плоско-правленное против ее движения. го образца [163]
В связи с этим на границе кристаллита плотность дислокаций повышается, их движение затрудняется. Поэтому критические напряжения сдвига для поликри-сталлических металлов выше, чем для монокристаллов, и тем в большей степени, чем более деформирован поликристалл (табл .2.2) [77, 110, 151, 152, 160, 167, 174]. Критические напряжения сдвига Ткр и пределы текучести о, для основных металлов приведены ниже:
Металл ткр МПа о* МПа МПа
Алюминий 0,6 ... 1,0 15 .. .300 100 .. . 500
Цинк 0,3 ... 0,9 10 ... 100 100 .. . 300
Медь 0,4 .. . 1,0 75 ... 300 150 .. . 1000
Железо 15 ... 29 150 ... 500 350 .. . 1200
* Предел текучести отожженного полнкристаллнческого металла. Между о4 и т существует зависимость сг,»2ткр.
•• Предел текучести для полнкристаллнческого металла после деформации.
Как видно из таблицы, поликристаллнческие металлы при деформации упрочняются. На феноменологическом уровне упрочнение уже рассмотрено (подразд. 1.6.3). Чтобы понять природу этого процесса и научиться управлять им, необходимо изучить
95
механизм упрочнения. Упрочнение определяется изменением структуры металла при деформации.
2.5.3. Изменение структуры металлов. В общем случае дефор* мация описывается тензором деформации Г, (1.20) и тензором вращения 7. (1.21). При деформации изменяется не только форма отдельных кристаллитов, но и их положение в пространстве. Вначале попытаемся описать изменение структуры поликристалличе-ского тела на основе модельных представлений. Возьмем полукристаллическое тело Ао в виде куба и выделим в нем элемент Мо, геометрически подобный рассматриваемому телу (рис. 2.22). Осуществим равномерную деформацию тела так, чтобы получить заданное относительное удлинение еср вдоль оси г. Элемент Мо также
а б
Рис. 2.22. Исходное (а) и деформированное (б) состояние кристаллита К в поли-кристаллическом теле А
получит удлинение е, = еСр и останется геометрически подобным деформированному телу Ад (см. подразд. 1.4.7). Макроскопическая деформация тела в целом — это результат микроскопической деформации кристаллитов, образующих его. Если в исходном состоянии кристаллиты имеют форму, близкую к равноосной, то элемент Мо можно выделить так, чтобы он был описан вокруг неко-
торого кристаллита Ко (рис. 2.22, а). Пусть плоскости скольжения в этом кристаллите образуют с осью гугол <р«. При деформации кристаллита К сдвигом он приобретает форму Кд (рис. 2.22, б). Но в процессе деформации элемент Мо преобразуется в элемент Мд, а кристаллит Кд не выходит за пределы элемента Мд. Это значит, что при деформации кристаллит поворачивается, а угол между плоскостями скольжения и осью z уменьшается до фа. Легко убедиться, что первоначальная ориентировка плоскостей скольжения, определяемая углом ф0, не изменяет общей картины: угол фа всегда оказывается меньшим, чем ф0. Следовательно, при пластической деформации кристаллиты приобретают удлиненную форму, вытягиваясь вдоль направления главной деформации, а плоскости скольжения, поворачиваясь в пространстве, получают преимущественную ориентировку в направлении главной деформации. К такому выводу мы пришли на основании модельных представлений. Действительная картина деформации гораздо сложнее полученной для простой модели. Пластическая деформация осуществляется скольжением и (или) двойникованием (см. подразд. 2.4.3, 2.4.5). Она может происходить по нескольким плоскостям, например для металлов с ОЦК-решеткой по семействам плоскостей {110), {112}, {123) (см. подразд. 2.1.2, 2.4.2, 2.4.5). Деформация в большинстве случаев бывает неравномерной (см. под-
96
разд. 1.4.7, 4.2). Значит, выводы, полученные на основе модельных представлений, необходимо проверить экспериментально.
На рис. 2.23 показаны микроструктуры стали 18ХГТ в исходном состоянии и после холодной пластической деформации. Как видим, после деформации кристаллиты действительно приобретают удлиненную форму, вытягиваясь вдоль направления главной деформации. По внешнему виду они напоминают волокна (например, волокна дерева).
Структура, которая характеризуется кристаллитами неравноосной формы, вытянутыми вдоль направления главной деформации, называется волокнистой. Волокнистая структура появляется
Рис. 2.23. Микроструктуры стали 18ХГТ в исходном отожженном состоянии (а) и после холодной пластической деформации (б). Стрелкой показано направление главной деформации
при деформации 30...50%. В связи с тем что формирование волокнистой структуры сопровождается поворотом плоскостей скольжения, их ориентировкой вдоль направления главной деформации, поликристаллическое тело приобретает весьма ощутимую анизотропию свойств. Как правило, прочность и пластичность металла в направлении главной деформации увеличиваются, а в поперечном направлении уменьшаются [ 10, 1671. Это необходимо учитывать в технологии последующей обработки давлением и конструирования изделий из листовых материалов. Например, изгиб холод-нокатанных листов вдоль направления прокатки приводит к разрушению значительно чаще и при больших радиусах изгиба, чем изгиб поперек направления прокатки.
В случае больших степеней деформации (например, при прокатке листов) плоскости скольжения поворачиваются в пространстве так сильно, что углы <р, образованные плоскостями с направлением главной деформации, становятся весьма малыми, и кристаллографические оси всех кристаллитов получают преимущественную ориентировку. Структура, которая характеризуется преимущественной ориентировкой кристаллографических осей, называется текстурированной структурой, или текстурой. Тек
4 1-25
97
стура появляется при деформации 70...90% и обусловливает сильную анизотропию свойств деформированных металлов. Во многих случаях это приводит к нежелательным последствиям. Например, при вытяжке цилиндрических стаканов образуются фестоны, и значительная часть детали удаляется при обрезке кромки.
Итак, холодная пластическая деформация приводит к существенному изменению структуры: при умеренных степенях деформации исходная структура с равноосными кристаллитами преобразуется в волокнистую, а при весьма больших степенях деформации — в текстурированную структуру. Соответствующей термической обработкой волокнистую структуру можно устранить и возвратить металлу квазиизотропные свойства. В зависимости от природы металла текстура, полученная при деформации, после термической обработки может исчезнуть, остаться неизменной или превратиться в текстуру рекристаллизации [10, 28,167].
2.5.4. Механизм упрочнения. В процессе деформации металлов их структура претерпевает глубокие изменения: кристаллиты дробятся на блоки, образуется волокнистая структура и текстура. Это сильно затрудняет движение дислокаций через монокристаль-ные зерна, образующие рассматриваемое деформируемое тело.
Пусть в каком-либо зерне Кт пол и кристаллического тела в плоскости скольжения Sj действует источник Франка—Рида (рис. 2.20, б). Он генерирует дислокации, которые направляются к границам кристаллита. Однако границы — это эффективные барьеры, и дислокации останавливаются у границ, образуя силовые поля т, направленные против движения дислокаций. В процессе деформации образца плотность дислокаций в зерне Кт увеличивается, на его границах образуются ступеньки, которые порождают дислокации в соседних зернах по гетерогенному механизму. Поворот кристаллита Кт вызывает появление новых плоскостей, например Ss, в которых действующее напряжение т при-ближаетсяи к критическому. Это создает благоприятные условия для возникновения новых источников дислокаций, например Движение дислокаций по системам взаимно пересекающихся плоскостей, параллельных $>, Sa, вызывает образование ячеистой дислокационной структуры. Эта структура проявляется уже на начальных этапах деформации. Образование ячеистой структуры начинается от границ зерен, где плотность дислокаций наиболее высока. Уже при деформации 5% дислокации образуют объемные сетки, в которых участки, свободные от дислокаций, имеют средний размер около 3 мкм. С увеличением деформации до 30% средний размер ячеек уменьшается до 2 мкм, а плотность дислокаци й в скоплениях значительно увеличивается [111.
Образование ячеистой структуры приводит к значительному сокращению длины свободного пробега дислокации и увеличению интенсивности силовых полей, направленных против движения дислокаций, что обусловливает возрастание сопротивления деформации. Многочисленные исследования позволили установить,
98
что предел текучести о, связан с плотностью дислокацийр соотношением 110, 68, 851
о, = о»о + a-Gb ]/р. (2.10)
Здесь aJO — предел текучести металла после отжига; а — коэффициент упрочнения, зависящий от природы металла. Плотность дислокаций р тесно связана с длиной их свободного пробега, а эта последняя зависит от размера зерна или субзерна (ячейки) d. Поэтому формула (2.10) может быть представлена в виде так называемой формулы Хола—Петча:
о, = (ho + (2.11)
где <тяо, С — постоянные для данного металла. Постоянная С явно не зависит от температуры. Поэтому упрочнение одинаковым образом зависит от размера зерна в широком диапазоне температур 11111. Формула (2.11) точно выполняется для железа и других металлов с ОЦК-решеткоЙ. Для металлов с ГПУ- и ГЦК-решеткой она дает достоверные результаты, если под d подразумевать размер субзерна, а не зерна. Хотя формула (2.11) пока теоретически не доказана, тем не менее Н. Петч дал весьма правдоподобное ее обоснование [ 1591.
Формулы (2.10), (2.11) можно дополнить данными, приведенными'в табл. 2.2. В исходном отожженном состоянии металлы имеют малую плотность дислокаций и большой размер зерна. В результате деформации плотность дислокаций увеличивается, зерна дробятся на блоки и в соответствии с формулами (2.10), (2.11) предел текучести возрастает. В этом смысл так называемой нагартовки, т. е. упрочнения металлов путем холодной пластической деформации.
2.5.5. Влияние упрочнения на характер деформации. Упрочнение оказывает существенное влияние не только на силовой режим, но и на характер деформации. Чтобы показать это, рассмотрим растяжение гладкого образца (рис. 2.24). Примем во внимание, что площадь поперечного сечения образца F(z) изменяется по длине случайным образом в пределах Fo — AF из-за неточности изготовления, а также из-за наличия трехмерных дефектов, ослабляющих образец; сопротивление деформации a,(z) изменяется по длине образца в пределах а, Да, в связи с различной структурой и более или менее благоприятной ориентацией групп кристаллитов. Поэтому в образце всегда найдется «слабое сечение», т. е. сечение, для которого несущая способность F(z)a,(z) наименьшая.
При растяжении образца деформация начинается именно в этом слабом сечении. В его окрестности наметится шейка, площадь поперечного сечения F (г) уменьшится на ДГШ и станет равной ^ш = ^(гш) — ДГШ. Если предположить, что деформация не сопровождается упрочнением, то несущая способность образца Лц<Мгш) си*е более уменьшится, и после некоторого удлинения
4*
99
Д/ш образец разрушится (рис. 2.24, б). Совсем иной характер деформации при растяжении образца из упрочняющегося металла. Уменьшение площади поперечного сечения F(z) в слабом сечении di (рис. 2.24, в) сопровождается интенсивной пластической деформацией области, примыкающей к сечению. Это приводит к деформационному упрочнению и возрастанию о, (zj, а несущая способность слабого сечения F(zl)os(z1) увеличивается. Затем находится второе слабое сечение, деформация локализуется в области этого слабого сечения d2, последнее в свою очередь упрочняется, несущая способность его возрастает, деформация в нем
а о б е д
Рис. 2.24. Схема растяжения стандартного разрывного образца: а — в сходное состояние; б — разрушение в первом слабом месте (при отсутствии упрочнения); е. е — квазиравномерная деформация путем последовательного образования многочисленных шеек at, dt. а, и т. д.; д— образование последней шейки и разрушение
прекращается. Далее находится третье слабое сечение ds и т. д. Таким образом очаг деформации периодически перебрасывается из одного места в другое по всему объему рабочей части образца (рис. 2.24, в).
Локальное удлинение в области слабого сечения приводит к образованию шейки на его поверхности. Но в связи с тем что деформация охватывает последовательно всю длину рабочей части образца, происходит кажущаяся равномерная или квазиравномерная деформация (рис. 2.24, г). На стадии квазиравномерной деформации процесс растяжения образца можно описать математической моделью.
Рр =/%<ho(l —W + Л^о(1 —ф)фл, (2.12)
где Рр — усилие растяжения (несущая способность образца); а,о. Д, п — константы металла; ф — относительное поперечное сужение.
Первый член уравнения показывает, как уменьшается несущая способность образца при уменьшении площади его поперечного сечения; второй — как увеличивается несущая способность образца при упрочнении. Поведение функции (2.12) зависит от постоянных а<0, А, п, которые определяются природой деформируемого металла. Например, для стали 20 ож0 = 375 МПа, А =
100
® 568 МПа, п = 0,57. При ф < 0,20 функция (2.12) возрастает, достигает максимума при ф = 0,20, а затем происходит ее заметное убывание. Если усилие растяжения Рр возрастает, то слабое сечение интенсивно упрочняется, его несущая способность увеличивается, и растяжение устойчиво идет в условиях квазиравномерной деформации. Если усилие Рр уменьшается, это свидетельствует о неустойчивости процесса: упрочнение не может компенсировать снижение несущей способности, обусловленное образованием шейки. Деформация локализуется в шейке и продолжается в ней до разрушения образца (рис. 2.24, д).
Таким образом, упрочнение изменяет характер деформации: делает ее более равномерной. Это обстоятельство оказывается чрезвычайно важным при разработке технологических процессов. Например, при вытяжке цилиндрических станков и коробок прямоугольной формы утонение стенок и количество брака тем меньше, чем интенсивнее упрочнение. Поэтому сложные детали, требующие глубокой вытяжки, штампуют только из сильно упрочняющихся сталей и сплавов цветных металлов.
2.<5.6. Влияние деформации на физические и механические свойства. В процессе холодной пластической деформации поликристаллических металлов значительно изменяется структура, повышается плотность дислокаций, увеличиваются концентрации вакансий и количество трехмерных дефектов. Это приводит к изменению физических свойств деформированных металлов. Плотность металлов уменьшается и тем больше, чем выше среднее напряжение. Поэтому при двухосном растяжении плотность снижается сильнее, чем при трехосном сжатии. Однако и в том и в другом случае изменение плотности очень незначительно, не более 0,1...0,2% [53, 1031. Это дает основание считать, что условия постоянства объема (1.27), (1.28), (1.29), (1.37) выполняются с достаточной для инженерных расчетов точностью.
Упругие постоянные Е, G, v в результате холодной пластической деформации практически не изменяются, но лишь до тех пор, пока не образуется текстура. В этом случае в связи с преимущественной ориентировкой кристаллографических осей проявляется анизотропия свойств, и упругие постоянные увеличиваются в одних направлениях и одновременно уменьшаются в других.
Совсем иначе обстоит дело с электрическими и магнитными свойствами. При взаимодействии дислокаций образуется большое количество точечных дефектов, что приводит к изменению электрического сопротивления. Экспериментально установлено, что изменение удельного электросопротивления Дрэ тесно связано со степенью деформации е и может быть выражено эмпирическим уравнением 11591:
Др9 = Се°, (2.13)
где С, а — постоянные, зависящие от природы металлов. Для многих металлов а= 1,0... 1,4. Значение величины С изменяется
101
в очень широких пределах. После деформации электрическое сопротивление, как правило, увеличивается всего на 2...5%. Однако некоторые металлы весьма чувствительны к деформации: например, электрическое сопротивление никеля увеличивается на 8%, молибдена — на 18%, а вольфрама — на 40...50%. При ОМД могут происходить межкристаллитная деформация, разрушение меж
зеренных прослоек и снижение электрического сопротивления. Это характерно для сложных сплавов, например хромеля, алюмеля и других, деформация которых приводит к уменьшению электри-
Рис. 2.25. Графики зависимости твердости НВ от степени деформации е [151]: / — стяль ЗОХГСА. г — У10А.
3 — 08пс. 4 — 45. S — латунь Л68. 6 — медь техническая. 7—• алюминиевый сплав АМг
ческого сопротивления.
При холодной деформации, особенно с большими степенями, которые приводят к образованию текстуры, сильно изменяются магнитные свойства железа, никеля, кобальта и их сплавов. Холодная пластическая деформация переводит металлы в термодинамически неравновесное состояние. Резко снижается их коррозионная стойкость, что широко используется в металлографии для приготовления шлифов. В остальных случаях это приводит к весьма вредным последствиям. Например, латуни и некоторые сплавы алюминия после холодной пластической деформа-
ции подвержены коррозионному растрескиванию, которое происходит в
присутствии кислот, щелочей и просто во влажной атмосфере, содержащей следы сернистых газов или аммиака. Чтобы устранить коррозионное растрескивание, необходимо отжечь деформированные изделия (301.
Влияние холодной пластической деформации на механические свойства уже частично рассмотрена. Установлено влияние деформации на изменение сопротивления деформации (см. подразд. 1.6.3; 2.4.6; 2.5.4) и ресурс пластичности (см. подразд. 1.6.4.3). Здесь покажем влияние деформации на твердость. Твердость находится в тесной корреляционной зависимости от сопротивления деформации а, [1511 и увеличивается тем интенсивнее, чем круче кривая истинных напряжений (рис. 2.25). Эго следует учитывать при конструировании деталей, изготовляемых методами холодной пласт» -
ческой деформации, и выборе исходных материалов: во многих случаях возможно использование менее прочных, более дешевых и более технологичных материалов.
2.5.7. Тепловой эффект деформации. Ранее установлено, что
упругая деформация — процесс обратимый, а пластическая — необратимый. В соответствии с законом сохранения энергии работа пластической деформации Л пл = D,Dt изменяет внутреннюю энергию кристалла. Деформация приводит к увеличению плотности дис
102
локаций и образованию различных дефектов кристаллической решетки. Поэтому внутренняя энергия кристалла возрастает. Экспериментальные исследования показывают, что только незначительная часть работы Апереходит в энергию искажения решетки. В основном затраченная на пластическую деформацию работа переходит в тепловую энергию.
Обозначим работу деформации, переходящую в тепло, Лт и выразим ее через полную работу пластической деформации Лпл и коэффициент выхода тепла т)т:
Л^ПтЛпл. (2.14)
На основании экспериментальных данных установлено 130, 36, 178), что т]т = 0,85...0,90 для чистых металлов и Т)т — 0,75...0,85 для сплавов. Это означает, что свыше трех четвертей работы деформации переходит в тепловую энергию и температура тела в очаге деформации повышается.
2.6. НАГРЕВ И РАЗУПРОЧНЕНИЕ ДЕФОРМИРОВАННЫХ МЕТАЛЛОВ
Нагрев и последующее охлаждение деформированных металлов приводят к существенным изменениям, связанным с упорядочением решетки, уменьшением количества дефектов и обусловливают разупрочнение металлов. Причинами этих изменений являются возврат и рекристаллизация.
2.6.1. Возврат. Упрочнение металла при деформации определяется совместным влиянием дефектов. Однако подвижность точечных, линейных и двумерных дефектов различна. Поэтому при нагреве и последующем охлаждении деформированных металлов наблюдаются изменения, обусловленные прежде всего точечными и линейными дефектами, которые обладают наибольшей подвижностью. В литературе эти изменения связывают с возвратом [68, 135, 159). Возврат — »то процесс упорядочения кристаллине' с кой решетки деформированных металлов при их нагреве и охлаждении, приводящий к изменению субструктуры металлов. При возврате упорядочение кристаллической решетки происходит в пределах субзерен и не вызывает структурных изменений. Поэтому механические свойства деформированных металлов изменяются, как правило, не очень значительно (рис. 2.28).
В процессе возврата принято различать две стадии [68, 159]: отдых и полигонизацию. Нагрев деформированного металла до температуры Т » « 0,2Тпд, выдержка и последующее охлаждение приводят к отдыху. В результате отдыха значительно уменьшается количество точечных дефектов (см. подразд. 2.3.1); избыточные вакансии устремляются к стокам, и их концентрация приходит к равновесной. Межузельные атомы занимают места вакансий. Дислокации противоположных знаков, лежащих в одних и тех же плоскостях скольжения в пределах субзерен, частично аннигилируют (см. подразд. 2.3.2; 2.4.3). В процессе отдыха происходят несущественные изменения, связанные с упорядочением решетки. Поэтому ощутимо изменяются только физические свойства, например электропроводность, которые сильно зависят от концентрации точечных дефектов. После нагрева до температуры 0,2Тпл < Т < О,ЗТПЛ, выдержки и охлаждения происходит полигонизация. Под влиянием нагрева дислокации приобретают более высокую подвижность и образуют устойчивые конфигурации, которые приводят к уменьшению внутренней энергии решетки. Такими конфигурациями являются стенки дислокаций. Следовательно, после нагрева до тем
103
пературы Т<0,ЗГпл, выдержки и охлаждения строение деформированного металла (его субструктура) существенным образом изменяется: снижаются концентрация вакансий и плотность дислокаций, дислокации выстраиваются в стенки и образуют субграницы, формируются области, почти свободные от дислокаций. Это вызывает ощутимые изменения физических и механических свойств: снижаются твердость и предел текучести, повышаются пластичность, уменьшается (в большинстве случаев) электрическое сопротивление.
2.6.2. Рекристаллизация. Дальнейшее повышение температуры обусловливает подвижность двумерных дефектов. По этой причине изменения в строении деформированных металлов захватывают уже структуру (зерна поликристаллических металлов). Такие глубокие изменения в структуре металлов обусловлены рекристаллизацией [10, 20, 68, 89, 135, 159|.Рекрм-сталлизация — это процесс образования новых равноосных зерен вместо ориентированной волокнистой структуры деформированного металла. Новые зерна, в основном свободные от напряжений, имеют гораздо меньшую твердость и сопротивление деформации. Они образуются и растут за счет искаженных и поэтому неравновесных зерен деформированного металла. Процесс продолжается до тех пор, пока в структуре не исчезнут искаженные неравновесные зерна. А. А. Бочвар установил, что рекристаллизация различных металлов начинается при температурах около 0,4Тпл [89]. Эта температура весьма условна и характерна для металлов технической чистоты. Для химически чистых металлов она снижается до (0,1...0,2)7'пл [89], для различных сплавов увеличивается до (0,5...0,6)Тпл, для гетерофазных сплавов при надлежащем размере и расположении частиц второй фазы до 0,8Тпл [10].
При рассмотрении кинетики рекристаллизации принято различать следующие три стадии: первичную, собирательную и вторичную рекристаллизации [20, 68, 159].
Первичная рекристаллизация — это процесс образования устойчивых зародышей, из которых растут новые неискаженные зерна. Металлографическими методами получены прямые доказательства того, что зародыши при рекристаллизации появляются на участках с наибольшими искажениями, т. е. на границах зерен и субзерен [20, 159]. Критический размер зародыша, который способен к устойчивому росту, должен быть не менее значения d0, которое зависит от природы металла и условий деформации. Такие зародыши образуются в результате термической активации, т. е. увеличения подвижности атомов, вызванного диффузией. Кроме того, согласно современным воззрениям они могут также образоваться в процессе дорекристал-лизацнонного нагрева при полигонизации и даже в процессе деформации [10, 159]. Чтобы ясно представить кинетику собирательной рекристаллизации, необходимо учесть, что повышение температуры металлов вызывает диффузию [71, 179].
Диффузия — это перемещение атомов в кристаллическом теле на расстояния, превышающие параметр решетки. Одна из важнейших характеристик диффузии — ее скорость, т. е. количество вещества т, перемещающегося через единицу площади поверхности за единицу времени. В соответствии с первым законом Фика [68, 179]
^dC
m = ~Ddt' <215)
где D — коэффициент диффузии; — градиент концентрации. Коэффи-ц иент диффузии D сильно зависит от температуры, природы металла и сте-п ени его неравновесности:
D = Doexp(-Q/RT), (2.16)
104
где Do. Q — константы для данного металла: R — постоянная Больцмана. Например, для у-железа D, = 0,58 • 104 м’/с; Q= 284,3 кДж/моль (179). R = 8,31 Дж/моль * К- При этих данных увеличение температуры от 20 до 100u С и от 20 до 500° С приводит к увеличению значения D в 103 и Ю1’ раз соответственно.
Резкое повышение подвижности атомов прн нагреве вызывает перестройку кристаллической структуры деформированных металлов: из состояний неустойчивого равновесия в сильно искаженных областях кристаллитов атомы переходят в положения устойчивого равновесия, подстраиваясь к неискаженным решеткам зародышей новых зерен. Этот процесс начинает интенсивно протекать при температуре, превышающей 0,47^, и называется собирательной рекристаллизацией. В процессе собирательной рекристаллизации размеры зерен увеличиваются (рис. 2.26). Однако зерна растут не беспредельно: процесс роста останавливается по достижении зерном равновесного размера dp, который определяется температурой нагрева при рекристаллизации. Равновесное состояние наступает в тот момент, когда
Рис. 2.26. Кинетические кривые роста зерна
Рис. 2.27. Пространственная диаграмма рекристаллизации стали 50 [121]
новые рекристаллизованные зерна полностью поглощают те, которые были в структуре металла до рекристаллизации. Новые зерна близки к равноосным и относительно однородны по размерам. В большинстве случаев процесс рекристаллизации на этом завершается. Однако при повышении температуры нагрева некоторые зерна могут преимущественно расти за счет других, что приводит к аномальному росту этих отдельных зерен. Эта третья стадия называется вторичной рекристаллизацией. Таким образом, при нагреве выше температуры рекристаллизации структура деформированного металла преобразуется в структуру рекристаллизации, которая характеризуется равноосными зернами, относительно однородными по размеру. Ниже представлены температуры плавления /м, возврата (в, порога рекристаллизации ta) и полного раскристаллизационного отжига технических металлов в °C [68, 89, 135). Температуры /пл и установлены экспериментально, температуры /в и /пр определены по формулам <. = (0,2...0,3)ТПЛ - 273- С, = 0.4Тпл - 273° С.
Металл ^ПЛ *пр *ро
Свинец 327 —153... 4-93 —33
Алюминий 660 -86... 4- 7 100 300 ...500
Медь 1083 —2... 4-134 269 500... 700
Железо 1539 89...271 452 650 ...710
Вольфрам 3380 458... 823 1188 1800... 2300
I0S
Конечный размер зерен зависит от температуры нагрева, а также в значительной мерс от степени предшествовавшей холодной пластической деформации. Чтобы наглядно представить эту связь, С. П. Чохральский предложил строить трехмерные диаграммы рекристаллизации [179]. Анализ диаграмм показывает, что рекристаллизация начинается только по достижении критической степени деформации ек (рис. 2.27). При в « еКр происходит резкое увеличение размера зерна [56, 121]. Для чистых металлов вкр лежит в интервале 1...5% [20, 135], для сплавов — в пределах 5... 15% [20]. В большинстве случаев с повышением температуры значение екр уменьшается. При увеличении степени деформации размер зерна, как правило, уменьшается. Однако для некоторых сплавов (например, алюминиевых) обнаружен значительный рост размера зерна и в области больших степеней деформаций при высоких температурах [56, 121]. Эти важные свойства диаграмм рекристаллизации следует иметь в виду при назначении режимов деформации холодной штамповки. Если в процессе ОМД деформация попадет в интервал критических, соответствующих данной марке материала, то после нагрева и рекристаллизации получим деталь с крупнозернистой структурой и пониженными механическими свойствами.
Итак, в зависимости от природы металла, степени предоест-продолжительности нагрева разу-
прочняющне процессы (возврат н рекристаллизация) могут приводить к глубоким изменениям структуры, механических и физических свойств. Указанные изменения происходят в процессе нагрева и выдержки при заданной температуре, а фиксируются уже после охлаждения разупроч-ненного металла до комнатной температуры (рнс. 2.28).
Рнс. 2.28. Изменение структуры, механических ов, а0 2, б и физических свойств (электросопротивления р») при разупрочнении деформированных металлов после нагрева [89]:
В — возврат; ПР. СР в ВР — первичная, собирательная н вторичная рекристаллизация вовавшей деформации, температуры н
2.7. ПЛАСТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРИ РАЗЛИЧНЫХ ТЕМПЕРАТУРНО-СКОРОСТНЫХ УСЛОВИЯХ
Технологические процессы обработки металлов давлением выполняют в широком диапазоне температур и скоростей деформации: в холодном, полугорячем и горячем состоянии; на тихоходном, быстроходном и высокоскоростном оборудовании. Температура, скорость и степень деформации оказывают очень большое влияние на сопротивление деформации и пластичность обрабатываемых металлов. Расчеты технологических усилий выполняют по теоретическим или эмпирическим формулам, в которые величина сопротивления деформации а, входит как сомножитель. Это означает, что точность расчетов усилия зависит не только от адекватности теоретической модели, положенной в основу вывода формулы, или статистической достоверности эмпирической формулы, но в значительной мере и от точности определения а,.
106
В результате пластической деформации структура и механи-ческие свойства металлов коренным образом изменяются. Эти изменения сильно зависят от температуры и скорости деформации. Поэтому изучение пластической деформации при различных температурно-скоростных условиях имеет большое значение для теории и практики обработки металлов давлением.
2.7.1. Особенности динамического возврата и рекристаллизации. Если технологические процессы ОМД осуществляются при высоких температурах, то в деформируемом металле процессы упрочнения и разупрочнения протекают одновременно. С изменением температуры механизм упрочнения практически не изменяется. Разупрочняющие процессы, которые происходят одновременно с деформацией, развиваются и протекают иначе, чем при нагреве после деформации. Эго обусловлено особенностями процесса возврата и рекристаллизации. В отличие от статистического возврата и рекристаллизации, которые рассмотрены в подразд. 2.6, процессы возврата и рекристаллизации, происходящие во время деформации, принято называть динамическими 110, 68). Они обладают рядом особенностей. Во-первых, при высоких температурах резко увеличивается количество точечных дефектов, что приводит к облегчению переползания дислокаций. Благодаря этому значительно возрастает подвижность дислокаций, динамический возврат протекает с высокой скоростью и приводит к более существенным изменениям структуры, чем возврат при последеформационном нагреве (статический). Во-вторых, с увеличением степени деформации из-за сильного искажения решетки снижается энергия активации Q, что обусловливает значительное уменьшение температуры рекристаллизации. В связи с этим при деформации нагретого металла процесс рекристаллизации идет значительно интенсивнее и с большей скоростью, чем при обычном последеформационном нагреве. Скорость рекристаллизации увеличивается и потому, что под действием напряжений облегчается миграция границ зерен. В-третьих, рекристаллизация может начаться только по достижении критической степени деформации екр. Это приводит к тому, что рекристаллизация непрерывно деформируемого металла происходит периодически.
Чтобы выяснить характер динамической рекристаллизации, возьмем какой-либо однофазный сплав и проследим за происходящими изменениями в нем. В начале деформации зерна находятся в равновесном состоянии. В процессе деформации упрочнение идет известным образом: резко возрастают концентрация точечных дефектов и плотность дислокаций, сетки дислокаций делят кристаллиты на субзерна, структура металла становится неравновесной, сопротивление деформации увеличивается от а10 до некоторого значения а, по кривой АВ (рис. 2.29). Накопление искажений в зернах приводит к значительному уменьшению энергии активации Q, и после достижения критической степени деформации Схр (в точке В) начинается процесс рекристаллизации. По
107
мере увеличения доли рекристаллизации Хр по кривой Ьс интенсивность упрочнения снижается и в некоторый момент (в точке В') влияние разупрочнения начинает преобладать, а сопротивление деформации падает (по кривой ВС). Когда значение Хр достигнет I, рекристаллизация снимет все предшествующее упрочнение, структура вновь станет равновесной, а сопротивление деформации снизится до первоначального значения ст,0 (в точке С). Дальнейшая деформация до критической степени екр вновь вызовет упрочнение (кривая CD). Затем опять начнется рекристаллизация (точка
d), которая приведет к восстановлению равновесной структуры (точка е) и сопротивления деформации а, (точка Е). Очевидно, что по такой схеме деформация может продолжаться неограниченно, а структура и свойства будут периодически изменяться. Описанная модель динамической рекристаллизации грубо отражает реальный процесс деформации поликристаллического тела. Разупрочнение не может идти одновременно во всех зернах по двум причинам: из-за колебаний екр, обусловленных различиями химического состава, а также из-за неравномерной деформации зерен. Поэтому точки Ь, в которых начинается разупрочнение в каждом отдельном зерне, смещаются по координатной оси е, а кривые of — е для каждого зерна
тинного сопротивления деформации от степени деформации в и доли рекристаллизации деформированной структуры Хр
смещаются друг относительно друга. Разупрочнение в каком-либо одном зерне идет одновременно с интенсивным упрочнением в других. В результате изменяется форма кривой а, — е: она приобретает вид, показанный линией АЛ1. Последняя описывает такую деформацию, при которой упрочнение непрерывно и почти полностью снимается рекристаллизацией. В структуре металла, деформированного в указанных условиях, наблюдаются в основном рекристаллизованные зерна равновесных размеров. Но часть зерен, деформация которых меньше критической для данного металла, остается нерекристаллизованной.
Деформация, в процессе которой динамическая рекристаллизация снимает упрочнение и приводит к образованию равновесной для данной температуры структуры, называется горячей деформацией. Горячая деформация возможна только при температурно-скоростных условиях, обеспечивающих полное завершение рекристаллизации. Если температуры близки к порогу рекристаллизации, горячая деформация осуществима только при очень малых скоростях деформации. С увеличением температуры до Т > 0,7Гпл скорость диффузии согласно формуле (2.16) резко повышается, а поэтому
108
рекристаллизация идет с очень высокой скоростью и успевает завершаться даже при относительно высоких скоростях деформации. Если соотношение между скоростями упрочнения и разупрочнения меняется так, что последнее не завершается полностью (точка С на рис. 2.29 не успевает опуститься до уровня о|0). то в процессе деформации упрочнение накапливается и сопротивление де* формации о( непрерывно увеличивается (см. кривую AN на рис. 2.29).
Деформация, при которой динамическая рекристаллизация не приводит к полному разупрочнению и в результате которой образуется структура с большим количеством упрочненных перекристаллизованных зерен, называется неполной горячей деформацией.
Неполная горячая деформация происходит при относительно низких температурах, когда рекристаллизация идет с малой скоростью, или высоких скоростях, когда для завершения рекристаллизации не хватает времени. После горячей деформации, даже с полным разупрочнением, металл имеет повышенную против равновесной концентрацию точечных дефектов и дислокаций и некоторое время находится в нагретом состоянии. Благодаря этому происходит повторная рекристаллизация 110].
Повторная рекристаллизация — это разновидность статической рекристаллизации, отличающаяся от последней тем, что новые зерна не образуются, а кристаллизация приводит к росту зерен только в результате миграции большеугловых границ. Наряду с повторной рекристаллизацией происходят полигонизация и отдых. Эти процессы приводят к уменьшению количества дефектов кристаллической решетки и изменениям механических и физических свойств металлов, деформированных при повышенных температурах (см. подразд. 2.6).
Таким образом, выбирая соответствующие температуры, скорости и степени деформации, можно в широких пределах управлять механическими и физическими свойствами металлов в процессе их деформации и после нее.
2.7.2. Классификация процессов деформации по температурноскоростному признаку. Знание особенностей процесса деформации при нормальных и повышенных температурах, низких и высоких скоростях позволяет все процессы обработки металлов давлением разделить на четыре вида: холодную, неполную холодную, неполную горячую и горячую деформацию [30, 31]. Холодная деформация — это деформация, которая не сопровождается разупрочнением. Холодная деформация осуществляется, как правило, при низких и умеренных скоростях, когда влияние теплового эффекта не приводит к существенному изменению температуры заготовки. Температура холодной деформации для различных металлов очень различна, например: для свинца — (100... 150)° С, для вольфрама + (450...800)° С. Холодная деформация приводит к значительным изменениям структуры, физических и механических свойств металлов (см. подразд. 2.5.3; 2.5.6; 1.6.3). При холодной деформации
109
сопротивление деформации о, (высокое уже вначале) непрерывно увеличивается в процессе формообразования изделия, а пластичность уменьшается. Это требует больших усилий для ОМД и ограничивает возможность получения изделия заданной формы за один переход.
Неполная холодная деформация — это деформация, которая сопровождается значительным разупрочнением в форме возврата. Неполная холодная деформация обычно осуществляется в температурном интервале (0,3...0,5) Г™, когда интенсивно протекают процессы возврата, а рекристаллизация не идет совсем или идет с очень малой скоростью. Скорость деформации может быть любой, однако не слишком высокой, чтобы влияние теплового эффекта не приводило к значительному повышению температуры и активизации диффузионных процессов. Неполная холодная деформация приводит почти к таким же изменениям структуры и механических свойств металлов, как и холодная. Физические свойства в результате неполной холодной деформации изменяются менее заметно в связи с протеканием процессов возврата (см. подразд. 2.6.1).
Неполная горячая деформация — это деформация, которая сопровождается значительным разупрочнением в форме возврата и частичной рекристаллизации. Неполная горячая деформация обычно осуществляется в температурном интервале (0,5...0,7)Тпл, когда интенсивно протекает динамическая рекристаллизация, ио ее скорость недостаточно высока и не происходит полного разупрочнения металла. Изменение скорости деформации может привести к существенному изменению полноты разупрочняющих процессов. Поэтому структура и механические свойства металлов после неполной горячей деформации очень чувствительны к скорости деформации.
При неполной холодной и неполной горячей деформациях сопротивление деформации а, значительно ниже, чем при холодней. Это дает возможность осуществлять обработку давлением даже крупногабаритных деталей на оборудовании сравнительно небольшого тоннажа. Пластичность при этих видах деформации, как правило, выше, чем при холодной, т. к. повышение температуры, во-первых, обусловливает появление новых систем скольжения и облегчает переползание дислокаций, а во-вторых, приводит к активизации разупрочняющих процессов, способствующих восстановлению высокой пластичности. В последние годы эти два вида деформации применяются все шире. В практике ОМД неполную холодную и неполную горячую обычно не разделяют и рассматривают как один вид деформации, называя его полугорячей (или теплой) деформацией. Термин «полугорячая деформация» чаще используется в кузнечно-штамповочном производстве, термин «теплая деформация» — в прокатном.
Горячая деформация — это деформация, которая протекает с полным разупрочнением. Горячая деформация осущ ствляется при
110
Рис. 2.30. Диаграммы истинного сопротивления деформации для различных видов деформации:
I — холодной; 2 — неполной холодной; 3 — неполной горячей; 4 — горячей
температурах 0,7TM и выше. В процессе горячей деформации литого металла, особенности строения которого описаны в подразд. 2.2, происходит существенное изменение его структуры: залечивание дефектов, дробление дендритов и межкристаллитных прослоек, получение равноосных зерен равновесного размера. Благодаря этому механические свойства литых металлов после горячей деформации значительно повышаются. Однако после того, как литой металл получит деформацию, достаточную для преобразования структуры в деформированную, его свойства и структура остаются неизменными на протяжении всего процесса обработки давлением (разумеется, если температура в процессе обработки не меняется).
При горячей деформации истинное сопротивление деформации не изменяется (рис. 2.30, кривая 4), а при холодной — кривая а, — е идет наиболее круто (рис. 2.30, кривая /). Неполную горячую и неполную холодную деформации, для которых кривые о, — е определяются неоднозначно, объединяют в область полугорячей деформации (между кривыми 2, 3). Кривые а, — е позволяют отнести деформацию к тому или иному виду. Например, деформация свинца при комнатной температуре идет с полным разупрочнением (кривая 4) и, следовательно, является горячей, а деформация вольфрама при 400’С холодная, так как идет по кривой 1 без разупрочнения.
2.7.3. Влияние температуры, скорости и степени деформации на сопротивление деформации. В самом общем виде истинное сопротивление деформации а, обусловлено совместным влиянием физико-химических свойств материала ФХ, температуры деформации Т, скоростью g и степенью деформации 8, а также характером изменения деформации во времени Tt(t) (ПО]:
о, = <р(ФХ, Т, е, 7\(0). (2.17)
Влияние каждого из факторов настолько многообразно, что установить вид этой функции не представляется возможным даже на феноменологическом уровне. Поэтому ученые и практические работники — специалисты по ОМД — предпринимали многочисленные попытки установить на экспериментальной основе хотя бы частные зависимости о, от основных фактов. Влияние температуры на сопротивление деформации сплава заданного состава может быть установлено на основании температурного закона Курнакова [30, НО]:
о, =Оплехр[^ (Тпл —Г)], (2.18)
111
где аПл — сопротивление деформации, экстраполированное до температуры плавления Тпя\ m — константа, зависящая от физико-химических свойств материала. На основе термодинамических представлений М. А. Зайков подтвердил справедливость формулы (2.18) [411. Многочисленные экспериментальные исследования по
казали, что она хорошо описывает зависимость а$ от температуры. Однако на значения входящих в нее констант Опл, m сильно влияют химический состав сплава, степени и скорость его деформации [811. Сопротивление деформации при данной температуре
Рис. 2.31. Графики зависимости предела текучести от температуры, скорости и степени деформации [81]: / —Е —0.05 1/с; 2 —
6 - 7.5 1/с; 3 - Е =
-150 1/с ----в — 10%:
------- - 30%
очень чувствительно к скорости и степени деформации (рис. 2.31). Частные зависимости а, от скорости деформации установлены на основании многочисленных экспериментальных исследований в такой форме:
a, = 4 + Cln(J/b): (2-19)
<т,= 8(№)п- (2.20)
Здесь А, В, С, £0, п —параметры, обусловленные физико-механическими свойствами металла и температуры.
Первая формула описывает зависимость между о, и при холодной и неполной холодной деформации, вторая — при неполной горячей и горячей [30, 411. Несмотря на простоту, формулы (2.19), (2.20) не нашли широкого применения, так как для каждого металла необходимо определять значения А, В, С, £0, л, а они существенно зависят от химического состава. Поэтому использование формул (2.18)...(2.20) для условий, отклоняющихся от тех, при которых найдены
входящие в них параметры, может давать ощутимые ошибки, но
создавать опасную иллюзию «научности» расчета.
Выражения (2.18) и (2.20) можно объединить и получить обобщенную формулу для вычисления сопротивления деформации 11761:
os =обехр[/л (Тпд — Т)]^., (2.21)
где Об — константа, характеризующая сопротивление деформации при Т = Тпл. £ = 1 1/с, k, = 1; kt — коэффициент, учитывающий влияние степени деформации. Л. А. Шофман экспериментально установил, что формула (2.21) удовлетворительно описывает зависимость са от температурно-скоростных условий при Т 0,65Г™ и 0,1 < е < 0,7 [ 1761. Здесь также необходимо предостеречь читателя от опасной иллюзии «научности» расчетов по формуле (2.21). Закономерное изменение значения характерно для ограниченного интервала температур, скоростей и степеней деформации. Во многих случаях переход к другим температурно-ско*
112
ростным условиям может сопровождаться фазовыми превращениями или структурными изменениями. Поэтому необходимо расчеты по формуле (2.21) сверять с экспериментальными данными.
В последние годы достаточно успешно развивается направление, предложенное В. И. Зюзиным [ 1511. Сопротивление деформации можно представить как функцию некоторого базисного значения сопротивления деформации аб и коэффициентов kt, k^, учитывающих влияние температуры, скорости и степени деформации в таком виде;
о, = ОбМ&- (2.22)
Эта формула по существу представляет собой модификацию формулы (2.21), но отличается от предыдущей чисто эмпирическим происхождением коэффициентов и базисного значения об. Значения Об, kt, kt для различных сталей, медных и алюминиевых сплавов приведены в работе 11511. Определение значения о, по формуле (2.22) и графикам позволяет сделать расчет наглядным и создает предпосылки для оптимизации температурно-скоростных режимов обработки различных металлов. Кроме того, расчет по формуле (2.22) никогда не приведет к большой ошибке, так как графики, по которым находят коэффициенты, одновременно показывают и область достоверности формулы.
2.7.4. Влияние различных видов деформации на структуру и механические свойства металлов. Структура и механические свойства металлов после обработки давлением зависят от вида деформации, т. е. от того, какие разупрочняющие процессы протекают во время деформации и насколько полно они завершаются. Влияние холодной деформации рассмотрено ранее (см. подразд. 2.5.6).
Горячая деформация осуществляется при температурах Т > > 0,7Тлл, когда интенсивно протекают диффузионные процессы, она сопровождается полным разупрочнением в форме динамической рекристаллизации (см. подразд. 2.6.2, 2.7.1) и приводит к значительному изменению структуры металлов.
Структура литого металла преобразуется в полосчатую структуру деформированного (рис. 2.32). Название этой структуры связано с ее особенностями, обусловленными характером расположения вредных примесей, неметаллических включений и вторых фаз. При горячей деформации, как и при холодной, зерна изменяют форму, вытягиваясь в направлении главной деформации. Это приводит к образованию волокнистой структуры. Однако в связи с высокой подвижностью дефектов кристаллической решетки при горячей деформации интенсивно происходят динамическая рекристаллизация и очень быстрое преобразование уже непосредственно в процессе деформации волокнистой структуры в рекристаллизованную. Поэтому основная масса зерен в структуре горячедефор-мированного металла — это рекристаллизованные зерна глобулярной формы равновесного размера. Неметаллические включения, вредные примеси и вторые фазы (например, карбиды) в литой
113
структуре располагаются по границам зерен, образуя межзеренные прослойки. При деформации межзеренные прослойки частично разрываются, вытягиваются в направлении главной деформации (как и сами зерна до рекристаллизации) и образуют строчки или полоски (они хорошо видны на рис. 2.32). Образование полосчатой структуры связано со строчечным расположением межзеренных прослоек. Поэтому при обработке давлением однофазных сплавов, не содержащих вредных примесей и неметаллических включений, полосчатая структура не образуется. Горячая деформация двухфазных сплавов, например заэвтектоидных сталей, приводит к образованию ярко выраженной полосчатости.
Рис. 2.32. Полосчатая структура горячедеформированной стали 20 (а) и инструментальной стали Х12 (б). Стрелками указано направление главной деформации
Преобразование литой структуры в деформированную сопровождается залечиваяием дефектов усадочного происхождения. При деформации какого-либо элемента заготовки в условиях двух-или трехосного сжатия полость усадочного происхождения смыкается и происходит сваривание металла по поверхности соприкосновения. В связи с залечиванием дефектов литой структуры плотность металлов после горячей деформации увеличивается. Например, для стали 40 плотность повышается в зависимости от коэффициента укова (отношения площадей поперечного сечения исходной заготовки Го и деформированной Fg) следующим образом [55]:
Коэффициент укова У I 1,5 2,5 3,5 5
Плотность р, кг/м* 7819 7824 7825 7826 7824
Здесь наибольшее увеличение плотности (на 0,1%) имеет место при коэффициенте укова У = 3,5. Дальнейшая горячая деформация (вплоть до У = 10 и выше) не приводит к изменению плотности металла. При горячей деформации слитков кипящей стали плотность увеличивается значительно больше (до 5%) в связи с тем что при раскислении металла в изложнице в слитке образуется большое количество газовых пузырей, которые при последующей деформации тоже залечиваются. В процессе горячей деформации
114
Рис. 2.33. Зависимость относительной деформации ел, при которой происходит залечивание дефекта, от относительной ьеличнны дефекта А»
- 100% 155]
происходит залечивание дефектов даже очень больших размеров (рис. 2.33). При деформации 60...70% залечиваются дефекты, относительный размер которых 10% и более от размера заготовки.
Преобразование литой структуры в деформированную приводит к значительному изменению механических свойств (рис. 2.34). Уже при сравнительно небольшом коэффициенте укова (у = » 2...3) происходит интенсивный рост всех механических характеристик. Это связано с залечиванием дефектов усадочного происхождения, разрывом межзеренных прослоек (обычно хрупких и менее прочных, чем сам металл) и образованием прочных связей между кристаллитами непосредственно. Однако с увеличением степени деформации полосчатость приводит к появлению анизотропии механических свойств: вдоль направления строчек прочность и пластичность несколько увеличиваются, поперек строчек —значительно уменьшаются значения показателей пластичности б, ф, а также ударная вязкость. Это необходимо учитывать при
разработке технологических процессов ОМД деталей ответственного назначения. Например, в тонкостенных сосудах высокого давления напряжение <те в два раза больше напряжения ох.
Рис. 2.34. Влияние коэффициента укова У на изменение механических свойств продольных (—) и поперечных (—) образцов хромоникелевой стали [55]: а — предел прочности ав(/) и текучести es (2>; б — относительное поперечное сужение ф (/) в удлинение в (Л
Поэтому технологию ОМД следует строить так, чтобы полосчатость горячекатанного листа соответствовала варианту А, а не Б (рис. 2.35).
Горячая деформация литых металов в к у знечно-прессовых и кузнечно-штамповочных цехах используется для изготовления только крупных поковок. Поковки мелких и средних размеров изготав-
115
ливают из проката, прессованных или кованых заготовок, т. е. из металла, который предварительно был подвергнут горячей обра-ботке давлением. Нагрев, деформация и охлаждение таких металлов сопровождается изменением фазового состава и структуры (рис. 2.36). Например, нагрев доэвтектоидной стали, которая в исходном состоянии имеет размер зерна d0. До температуры никаких фазовых и структурных превращений не вызывает (линия d0B). При t = ti начинается а — у-превращение, которое приводит к изменению фазового состава и структуры стали: ферритноперлитная смесь превращается в аустенит и переходит в однофазное состояние, размеры аустенитных зерен оказываются намного
Рис. 2.35. Возможные направления полосчатости (Л и В) в тонкостенном сосуде высокого давления, изготовленном из горячекатанного листа
Рис. 2.36. Зависимость размера зерна d от фазовых и структурных превращений, происходящих при нагреве, деформации и охлаждении стали [99]:
<пр — температура порога рекристаллизации; /я. /в — нижний ки верхний пределы температурного интервала ОМД; — температура начала а -» ^-превращения; G — температура начала т — а-превращепия; d« — исходный размер зерна; d,. dt — размеры верна после различных режимов деформации
меньше, чем d0 (точка С) [68, 89]. Для стали = 727° С. При этой температуре, а особенно при более высокой, вплоть до /в, зерна интенсивно растут (по кривой CD). В точке D заготовка нагрета до необходимой для ОМД температуры. Ее извлекают из печи и передают на штамповочную машину, например ковочный пресс или молот. За это время заготовка остывает, но размер зерна остается неизменным (линия DE). В точке Е начинается деформация. В связи с пластической деформацией зерна дробятся, а тепловой эффект деформации может приводить к повышению температуры заготовки. Это изображается на схеме кривой EF. При высокой температуре с большой скоростью идут процессы и динамической, и последеформационной рекристаллизации. Поэтому зерно увеличивается. В точке G происходит второй нажим пресса или удар молота: снова зерна дробятся, температура повышается. Если процесс закончить в точке Н (после второго нажима или удара), то в результате последеформационной рекристаллизации по линии НКК' после охлаждения поковки зерно будет иметь раз
116
мер di, превышающий исходный d0. Если процесс ОМД закончить в т'очке L, то после охлаждения поковки (линия LMM') зерно приобретает размер dt, соответствующий исходному. При значи-тельной деформации и подстывании заготовки (точка М) после охлаждения поковки зерно может получить размер d8, меньший чем d0. Здесь важно подчеркнуть, что а—у-превращение приводит к значительному измельчению зерна (линия ВС). Обратное а—у-превращение не приводит к изменению размеров зерна [68, 891. Поэтому крупное зерно, полученное в результате последефор-мщионной рекристаллизации (например, по линии НКК'), при температуре t < t3 (точка К') не будет претерпевать никаких изменений, а структура останется крупнозернистой.
При однократной деформации (например, когда ОМД осуществляется на кривошипном прессе, горизонтально-ковочной машине, фрикционном молоте) нагрев заготовки до верхней температуры /в всегда приводит к получению изделий с крупным зерном d > d0. Дальнейшей термической обработкой такую структуру не всегда можно исправить. Для получения мелкозернистой структуры необходимо греть исходную заготовку до температуры tM < /в.
Итак, после холодной деформации структура металлов получается волокнистой, а их свойства становятся анизотропными. Это обусловлено вытягиванием зерен в направлении главной деформации, их поворотом и появлением преимущественной ориентировки кристаллографических осей. После горячей деформации структура металлов приобретает полосчатость, а свойства металлов становятся анизотропными из-за влияния вредных примесей, неметаллических включений, вторых фаз, например карибидов. Термическая обработка позволяет полностью устранить волокнистость структуры и анизотропию механических свойств, вызванную холодной деформацией. Полосчатую структуру и анизотропию свойств, полученную в результате горячей деформации, устранить термической обработкой почти невозможно. Поэтому процессы горячей обработки давлением необходимо строить так, чтобы полосчатость проявлялась в наименьшей степени (для этого следует назначить оптимальные коэффициенты укова) и чтобы направление строчек наилучшим образом соответствовало условиям работы данной детали.
2.8. ПЛАСТИЧЕСКАЯ ДЕФОРМАЦИЯ В ОСОБЫХ УСЛОВИЯХ
Конструирование и технология всегда находятся в противоречивых отношениях: чем выше требования к прочности конструкций, тем труднее обрабатывать элементы этой конструкции; чем больше габаритные размеры и сложнее конфигурация деталей, составляющих конструкцию, тем больше усилий требуется для их обработки, сложнее штампы и оборудование, дороже их эксплуатация. Уже сейчас многие высокопрочные и малопластичные материалы и многие сложные н крупногабаритные детали практически не поддаются обработке традиционными способами ОМД. Вот почему в последние десятилетня интенсивно ведутся исследовательские и опытно
117
конструкторские работы по расширению технологических возможностей обработки металлов давлением. Наметилось три важные направления обра-бот к и давлением высокопрочных и малопластичных сплавов, а также изготовления крупногабаритных деталей, деформация в условиях высокого давления, свеохпластичност и и циклического нагружения.
2.8.1. Высокое давление. 2.8.1.1. Общие сведения. При некоторых условиях деформации даже очень хрупкие материалы обнаруживают значительную пластичность. Так, при измерении твердости пластическая деформация в области лунки составляет 10... 12%, но следов видимого разрушения не обнаруживается даже у сталей, закаленных на очень высокую твердость и разрушающихся без видимой остаточной деформации при обычных испытаниях на растяжение и сжатие (27J. Исследования Т. Кармана [30], П. Бриджмена [14], Л. Ф. Верещагина [87] показали, что пластичность является не свойством вещества, а его состоянием. Классический эксперимент, показывающий зависимость пластичности от схемы напряженного состояния, выполнен Т. Карманом [30]. Исследователь осаживал цилиндрические образцы из мрамора в условиях одноосного сжатия на плоских бойках и трехосного неравномерного сжатия в специальном устройстве, где путем нагнетания в рабочую камеру глицерина можно было создавать регулируемое радиальное давление на боковую поверхность образца. В первом случае образец разрушался практически без остаточной деформации, во втором — в зависимости от радиального давления пластическая деформация е2 достигала 8...9%. М. В. Растегаеву удалось довести степень деформации ег мраморных цилиндров до 78% [30].
Деформация с наложением давления жидкости на свободную поверхность заготовки оказалась очень аффективным способом повышения пластичности не только мрамора, но и всех металлов и их сплавов. Экспериментальные исследования П. Бриджмена позволили установить, что при растяжении цилиндрических образцов из различных металлов сужение шейки тем больше, чем выше давление жидкости в рабочей камере, где осуществляется деформация. Предельную пластичность епр при давлении жидкости р можно выразить уравнением [14]
% « А» + kp, (2.23)
где е9 — пластичность при р = 0 (см. подразд. 1.6.4); k — коэффициент пропорциональности, зависящий от свойств материала. Для углеродистых сталей = 0,5...0,9, Л « 2 • 10“’ (если р — выражено в мегапаскалях). Следовательно, при увеличении давления жидкости р от нуля до 1000 МПа предельная пластичность возрастает в 3...6 раз. Такое сильное влияние давления на пластичность объясняется изменением схемы напряженного состояния и механизмов деформации. Рассмотрим малый элемент деформируемого тела (рис. 2.37, а) и выделим в нем произвольный кристаллит А. Проведем через точку М, лежащую в пределах кристаллита, главные оси напряжений 1, 3. Пусть S — плоскость скольжения. Для простоты предположим, что деформированное состояние в точке М плоское, например, при осадке плоской заготовки и задано тензором Тд. Отобразим его на плоскости напряжений с помощью круга Мора. Очевидно, что в площадке S действуют напряжения ом, тм (рис. 2.37, б). Наложим на деформируемое тело давление р. Напряженное состояние в точке М изменится, и в площадке S станут действовать напряжения о^, тм, соответствующие точке М' на круге Мора. Из построения точек М, М' следует, что тм = тм, °м = °м — Р' стср = °ср — Р' Значит, наложение гидростатического давления р не изменяет условий перехода в состояние пластического течения, но должно влиять на механизм деформации.
При деформации под давлением плотности дислокаций уменьшаются, линии дислокаций спрямляются, клубки дислокаций отсутствуют или слабо выражены и немногочисленны. Основная масса дислокаций выстраивается в стенки, образуя субструктуру, сходную со структурой полигонизации.
118
Это объясняется значительной активизацией неконсервативного движения дислокаций. Облегчение переползания под действием высокого давления — явление барополигонизации — предотвращает скопление дислокаций и образование микротрещин [108].
а б
Рис. 2.37. Схема деформации кристаллита (а) и изменение напряженного состояния в нем при наложении гидростатического давления р (б)
С ростом давления р повышается равномерность деформации и уменьшаются дополнительные напряжения. При высоких давлениях дополнительные растягивающие напряжения не возникают вовсе. Поэтому подавляются силы, которые стремятся раскрыть имеющиеся в теле трещины. Берега трещины сближаются и в процессе относительного перемещения на их поверхностях образуются мостики схватывания. Это приводит к залечиванию дефектов и значительному повышению пластичности при деформации в условиях действия высокого гидростатического давления (14, 87).
Рост пластичности с увеличением давления характерен для всех материалов. Однако исследования советских ученых позволили установить, что зависимость предельной пластичности епр от приложенного гидростатического давления р сложнее, чем предполагал П. Бриджмен, и в общем случае описывается кривой, которая делится на три участка характерными давлениями (рнс. 2.38) [87, 108). Давление рп, при котором начинается интенсивное увеличение предельной пластичности, называется пороговым.
Давление рж, при котором рост пластичности сильно замедляется, называется давлением насыщения. Для многих пластичных металлов пороговое давление очень мало, и поэтому не обнаруживается при испытании алюминия, латуни, железа, стали и других пластичных металлов [87, 108]. Для малопластичных металлов пороговое давление определения передельной пластичности в формулу (2.23) необходимо внести уточнение:
Это приводит к зале-епр
Рп Рп Р
Рис. 2.38. Обобщенная зависимость предельной ностыо е^ н
ем р (/) и возможные частные зависимости (2, 3) [108]
между пластич-давлени-
очень велико, и для
тпр = 'о + k(p - рп). (2.24)
Давления насыщения у металлов настолько высоки, что в экспериментах обнаружены лишь для некоторых металлов, например, для вольфрама рн = а 2800 МПа [108]. Поэтому в пределах практически используемых давлений расчет можно вести по формуле (2.24).
2.8.1.2. Технологические возможности. Один из наиболее эффективных способов повышения пластичности — деформация жидкостью высокого
119
7
давления. В производственной практике его называют гидропрессованием. Осу» ществляется гидропрессование так. Деформируемая заготовка помещается в контейнер с матрицей (рис. 2.39). Полость матрицы заполняют рабочей жидкостью и запирают плунжером. Чтобы предотвратить утечки жидкости на плунжере и матрице, делают уплотнения, а заготовку подгоняют по матрице проточкой. При рабочем ходе ползуна пресса плунжер постепенно сжимает жидкость и вытесняет заготовку через отверстие в матрице. В зависимости от формы отверстия заготовка после гидропрессования приобретает форму стержня с круглым, многогранным или любым заданным профилем сечения. Давление на боковую поверхность заготовки создает в ее объеме схему всестороннего неравномерного сжатия,поэтому значительно Еозрастает пластичность металла.
Поверхности контейнера, матрицы и заготовки в процессе деформации разделены слоем смазки (рабочая жидкость одновременно служит и смазкой). Благодаря высокому давлению в полости контейнера смазка принудительно подается в зону трения, что обеспечивает поддержание достаточной толщины смазочной пленки и гидродинамический режим трения. Потерн на трение сводятся к минимуму, и на 20...40% снижается усилие деформации (по сравнению с обычным прессованием). Уменьшаются неравномерность деформации, дополнительные и остаточные напряжения. Вот почему процесс гидропрессования находит все более широкое применение в производстве фасонных профилей высокой точности из пластичных металлов или простых профилей из труднодеформируемых металлов, которые другими способами ОМД получать невозможно или экономически’ нецелесообразно.
Для повышения пластичности металлов совсем не обязательно при деформации воздействовать на свободную поверхность заготовки гидростатическим давлением жидкости. Достаточно изменить схему напряженного состояние оср. Например, при осадке цилиндриче
ских образцов из закаленной стали 45 разрушение происходит уже при е2 вв 2%. Однако, если перед осадкой образец из той же стали поместить в цилиндрическую обойму из пластичного металла, например стали 20, то разрушение может не наступить даже при е2 =» 60% [27]. Аналогичные результаты можно получить и при других способах изменения схемы напряженного состояния. Например, диаметр прутка можно уменьшить с d9 до dK равномерным растяжением, волочением, прессованием. Для перечисленных операций характерны различные схемы напряженного состояния и существенно отличающиеся средние напряжения. Поэтому резко отличаются и технологические возможности каждой операции: равномерным растяжением можно уменьшить диаметр прутка до dK = (6,83...0,87)do, волочением — до dK = (0,75...0,80)do, а прессованием—до dK = (0,1... ...0,5)4,.
Для повышения давления оср используют различные приемы, каждый из которых может служить основой для разработки более совершенных технологических процессов ОМД. Так, в последние годы широко применяют прессование в оболочках [80, 99], штамповку и прессование с противодавлением [80, 108], чистовую вырубку |80], резку прутков с осевым подпором [80] и другие.
Рис. 2.39. Схема гидро-прессования:
/ — стол пресса, 1 — контейнер. 3 — матрица; 4 — заготовка; 5 —> рабочая жидкость, 6 — пуансон. 7 — ползун пресса, 8 — уплотнения
ния и повысить дав
120
2.8.2. Сверхпластичность. 2.8.2.1. Общие сведения. Повышение пластичности металлов путем увеличения среднего напряжения— задача достаточно сложная. Поэтому в последние годы все чаще применяется деформация в условиях сверхпластнчности 113, 501. Сверхпластичностью называют способность металлов и сплавов равномерно удлиняться без разрушения на сотни и тысячи процентов.
Работы последних лет [50, 123] позволили обобщить огромный фактический материал и установить, что сверхпластичность— это не уникальное явление, как считали первые его исследователи, а состояние материала. В работе [ 1231 приведен перечень металлов и сплавов, которые при определенных условиях можно перевести в состояние сверхпластнчности. Он включает 66 различных сплавов на основе алюминия, цинка, магния, меди, хрома, титана, никеля, железа. Многие из них имеют широкое промышленное применение. Деформация этих сплавов в условиях сверхпластичности открывает новые технологические возможности их обработки давлением и позволяет получать практически неограниченные степени деформации при напряжениях, которые на порядок меньше обычных. Механизм деформации в условиях сверхпластичности интенсивно изучается. Однако сейчас уже твердо установлено, что существует два принципиально отличных друг от друга типа сверхпластичности [50, 123]. Первый характерен для полиморфных металлов и сплавов, испытывающих при определенных температурах фазовые превращения. Например, чистое железо испытывает а— у-превращение при температуре 910° С, а при температуре 850... ...910° С — находится в состоянии сверхпластичности. Пластическое течение в этих условиях можно представить как результат направленного смещения отдельных атомов под действием напряжений, возникающих в образце при его деформации. Такой вид деформации обычно называют диффузионной ползучестью. Этот процесс протекает с малой скоростью, что значительно ограничивает возможные скорости деформации заготовки в условиях сверхпластичности. Однако, если обработку давлением осуществлять с малой скоростью (например, £ = ЮА..10"4 1/с), то для железа можно получить деформацию до 500%, а сопротивление деЛорма-ции (предел текучести nf) не будет превышать 2 МПа [501. Для сравнения отметим, что при растяжении в обычных условиях и близкой температуре относительное удлинение составляет для железа всего 45...50%, а предел текучести а, = 30...50 МПа 1152]. Как видим, деформация в условиях сверхпластичности сулит значительные выгоды. К сожалению, металлов, испытывающих фазовые превращения, совсем немного (железо, титан, олово, кобальт, уран, цирконий и некоторые другие).
Значительно больший практический интерес представляет второй тип сверхпластичности. Он характерен для металлов и сплавов, которые имеют специфическую микроструктуру (ультрамел-кое зерно со средним диаметром 1...5 мкм), стабильную в процессе
121
деформации при постоянной температуре. Поэтому второй тип сверхпластичности носит название структурной сверхпластичности.
Структурная сверхпластичность имеет место в условиях горячей деформации при температуре свыше 0,4Тпл и скоростях деформации lOA.JO-1 1/с (50, 123]. В таких условиях свойства сплавов значительно отличаются от свойств обычных металлов
и сплавов и приближаются по реологическим характеристикам к вязким веществам и полимерам. Реологические характеристики
металлов и сплавов достаточно хорошо описывают уравнение о, = = Сел£'я 1501, где п — показатель упрочнения; т—показатель
скоростной чувствительности
Рис. 2.40. Схема пнсвмотермиче-ской формовки [106]:
напряжения течения. При обычных условиях деформации п = 0,2...0,5, т = 0,01... 0,20 и образование шейки определяется преимущественно влиянием упрочнения. В условиях сверхпластнчности т = « 0,3...0,8. Поэтому локализация деформации в шейке и увеличение скорости £ приводит к резкому повышению сопротивления деформации. Это означает, что в шейке деформация немедленно прекращается, и очаг деформации
1 — матрица. 1 — нагревательные вле- ПОСЛеДОВЭТеЛЬНО Н раВНОМерНО ОХ-ватывает весь объем растягивае-быточного - устройство мого образца (см. подразд. 2.5.5).
По этой причине при деформации в условиях сверхпластичности получаем удлинение 500... 1000% и более.
Механизм деформации при структурной сверх пластичности уже достаточно глубоко изучен. Установлено, что в процессе деформации в условиях структурной сверхпластичности проявляются диффузионная ползучесть, дислокационное скольжение, зернограничное проскальзывание, миграция границ зерен и т. д. С каждым годом все более расширяется номенклатура сплавов, которые могут деформироваться в условиях сверхпластичности. Следовательно, уже сейчас можно ставить вопрос об использовании явления сверхпластичности для производства различных изделий.
2.8.2.2. Технологические возможности. Широкие возможности открываются перед технологами при использовании эффекта сверхпластичности для изготовления куполообразных и коробчатых деталей (рис. 2.40) 11061. Преимущества такого способа весьма разнообразны. Во-первых, можно получить за один переход колпак (цилиндр, коробку) с очень большой степенью деформации. Во-вторых: для деформации тонких листов (до 1...2 мм) можно использовать сжатый воздух давлением не более 0,6...0,8 МПа. Это позволяет обойтись без дорогостоящего и дефицитного специального оборудования и осуществлять деформацию в простых штам
122
пах, снабженных пневматической системой избыточного давления (рис. 2.40, позиция 5). Наконец, в результате деформации можно получить детали с заданным утонением и определенными механическими свойствами. В простейшем случае деформация сопровождается неуправляемым утонением стенок. Однако уже найдено несколько способов управления утонением 1106). Один из них состоит в том, что в начале деформации устройство поддержки 6 (рис. 2.40) затрудняет деформацию центральной части заготовки 4. Когда заготовка получит заданную расчетную деформацию АЛ, устройство поддержки опускается в крайнее нижнее положение и происходит окончательная деформация заготовки. Таким способом удается формовать детали из сплавов АМГ6, МА8, ЦА22, ВТ6, ОТ4-) и др. Технологические режимы обработки этих сплавов приведены в работах [123, 1061.
В современном машиностроении велика потребность в крупногабаритных деталях, например панелях с вафельным оребрением. Изготовление этих деталей методами ОМД тем сложнее, чем меньше толщина изделия. Нередко для этого требуются уникальные прессы усилием 30...75 тыс. тонн. Поэтому естественно, что при изготовлении таких деталей используют любую возможность, чтобы снизить усилие деформации. Наиболее эффективно эта задача решается при деформации в условиях сверхпластичности.
Одна из важнейших задач ОМД — применение пластической деформации для формообразования различных видов инструмента. Такие изделия, как элементы пресс-форм, матрицы и пуансоны для объемной штамповки и высадки, фрезы, зенкеры, развертки, пока изготовляют резанием. Это сопряжено с большими потерями дефицитных и дорогостоящих инструментальных сталей (свыше 50% материала заготовки идет в стружку), высокой загрузкой инструментальных цехов и, что самое главное, приводит к снижению стойкости инструмента. Выдавливание полостей матриц и пресс-форм, фрез, зенкеров и разверток в холодном или горячем состоянии позволяет повысить коэффициент использования металла до 0,85...0,95. Однако для деформации инструментальных сталей требуются инструменты с еще более высокой прочностью. Выдавливание инструментальных сталей в условиях сверхпластичности дает возможность успешно преодолеть это техническое противоречие. Быстрорежущие инструментальные стали (Р18, Р6М5) имеют мелкокристаллическую структуру в состоянии поставки. Поэтому для перевода их в состояние структурной сверхпластичности достаточно выбрать оптимальную температуру и скорость деформации. Углеродистые инструментальные стали (У8А, У10А) такой структурой не обладают. Поэтому они требуют предварительной термической или термомеханической обработки, которая обеспечивает измельчение зерен и насыщение их границ дефектами кристаллической решетки.
Исследования показали, что развертки, фрезы, зенкеры из стали Р6М5 можно выдавливать в условиях сверхпластичности при
123
температуре 810...820° С и скорости деформации 10~1 1/с. Удельное усилие деформации составляло 180...250 МПа, что на порядок меньше, чем при обычных условиях [5]. Матрицы штампов и пресс-форм выдавливали из стали У8А при температуре 720... ...730° С и скорости деформации 10-I 1/с (скорость деформирования 0,2...0,5 мм/с). Удельные усилия не превышали 400 МПа, что в 6,5 раз ниже, чем при холодном выдавливании этой же стали, и в 3...3.5 раза ниже, чем при полугорячем выдавливании. Важно, что при выдавливании в условиях сверхпластнчности возможно получить в матрице полость с относительной глубиной до 2,8, в то время как при полугорячем выдавливании предельной оказывается относительная глубина полости 1, а при холодном — 0,5. Наконец, при выдавливании в условиях сверх пластичности возможно получение высокого уровня механических свойств по всему сечению изделия, а это обусловливает значительное повышение стойкости инструмента (в 1,8 раза и более).
Таким образом, есть все основания считать, что деформация в условиях сверхпластнчности в ближайшие годы найдет широкое промышленное применение в обработке металлов давлением, особенно при штамповке крупногабаритных деталей, требующих для изготовления высоких степеней деформации, а также различных видов режущего инструмента, матриц и пресс-форм.
2.8.3. Циклическое нагружение. Анализ процессов обработки металлов давлением позволил установить, что формоизменение заготовки в обычных условиях сопровождается большими потерями энергии деформации на трение. Например, при волочении прутков и проволоки эти потери составляют 30...42% от общей энергии, затраченной на осуществление процесса 154]. При осадке без смазки низких заготовок потери на трение могут достигать 50% и более 11381. Поэтому ученые и практические работники непрерывно ведут поиски, направленные на уменьшение вредного влияния трения. Одним из перспективных направлений оказалось деформирование в условиях циклического нагружения, т. е. так называемое циклическое деформирование.
Все процессы циклического деформирования металлов в зависимости от частоты приложения нагрузки можно разделить на простое пульсирующее деформирование, вибрационное деформирование, деформирование в ультразвуковом поле 154].
Простое пульсирующее деформирование осуществляется с малой частотой нагружения (до 10 1/с). Этот процесс широко используется при выполнении многих операций ковки на молоте, например осадки. В некоторых случаях его применяют для получения равномерной деформации образцов при испытании на сжатие.
Вибрационное деформирование в общем случае осуществляется с частотой от 10 до 16000 1/с. Однако наиболее распространен в промышленности низкочастотный процесс (от 10 до 300 1/с и лишь в отдельных случаях до 1000 1/с). Вибрационное деформирование уже нашло применение для волочения, вырубки — пробивки, за
124
чистки, вытяжки; ведутся успешные работы по его использованию для объемной штамповки, прессования.
Деформирование в ультразвуковом поле осуществляется с частотой 16000 1/с и выше. При такой высокой частоте нагружения деформация сопровождается повышением температуры заготовки. Это приводит к значительным изменениям характера деформации. Высокая эффективность деформирования в ультразвуковом поле доказана экспериментально. Однако из-за технических трудностей, связанных с подводом к заготовке ультразвуковых колебаний большой мощности, этот процесс пока широко не используется.
Для всех видов деформации в условиях циклического нагружения характерно существенное изменение контактного трения на рабочих поверхностях инструмента. Прямыми экспериментами установлено, что при прессовании с наложением ультразвукового поля коэффициент трения в 2...8 раз ниже, чем при обычном прессовании (126]. Вибронагружение также приводит к значительному снижению сил трения на контактной поверхности. Улучшение условий трения приводит к тому, что шероховатость поверхности изделий, полученных в условиях циклического нагружения, как правило, снижается на 1...2 класса.
Второй важный фактор, влияющий на характер и силовой режим деформации,— это механизм разупрочнения при циклическом нагружении. Циклическое нагружение способствует неконсервативному движению дислокаций и релаксаций напряжений [45, 54]. Следовательно, действие циклического нагружения аналогично нагреву деформируемой заготовки. Исследование деформированного состояния заготовок, подвергнутых обработке давлением с наложением вибрации и ультразвука, показали, что сдвиговые деформации при этом значительно уменьшаются, заметно снижаются остаточные напряжения второго рода. Структура металлов, деформированных в условиях циклического нагружения, как правило, получается более однородной и мелкозернистой.
В промышленном производстве наиболее часто используют вибрационную штамповку. Она наиболее эффективна для глубокой вытяжки, зачистки вырубленных заготовок, осадки, объемной штамповки. Эти процессы весьма перспективны для деформации малопластичных и труднодеформнруемых сплавов (54, 126].
125
ГЛАВА 3
КОНТАКТНОЕ ТРЕНИЕ
3.1. ФИЗИЧЕСКИЕ ОСНОВЫ
При взаимодействии деформируемой заготовки с инструментом на контактных поверхностях возникают силы трения, которые оказывают исключительно большое влияние на силовой режим деформации, характер формоизменения, износ инструмента, качество деталей.
Используя различные способы снижения сил контактного трения, можно уменьшить усилие деформации в 5... 10 раз, а износ — в 100... 1000 раз. Условия контактного трения могут коренным образом изменять характер формоизменения при деформации с двумя степенями свободы течения металлов. Например, осадка кольцевой заготовки на шероховатых бойках приводит к уменьшению диаметра отверстия, а осадка на гладких смазанных бойках — к его увеличению. Таким образом, важность изучения контактного трения и его влияния на процессы ОМД очевидна.
Контактное трение—это механическое взаимодействие между твердыми телами, которое возникает в местах их соприкосновения и препятствует (или только стремится препятствовать) относительному перемещению тел в плоскости их соприкосновения. Сила взаимодействия двух элементов заготовки и инструмента на площадках ДГз, ДГи в общем случае направлена под углом а к нормали п (рис. 3.1). Касательная составляющая Т силы R называется силой трения. В соответствии с третьим законом Ньютона силе /?з, действующей на заготовку, отвечает такая же сила /?и» приложенная к инструменту. Таким образом, на контактной поверхности заготовки Д^з возникает сила трения сопротивляющегося действия Тз, которая затрудняет перемещение заготовки относительно инструмента и сильно влияет на качество деталей, а на контактной поверхности инструмента ДГи возникает сила трения активного действия 7и, которая стремится увлечь инструмент
126
в направлении движения заготовки и обусловливает износ. Это положение известно как положение о парности сил контактного трения сопротивляющегося и активного действия (1021.
Для удобства сравнения силы трения Т относят к единице площади и величину тж = limT AF называют контактным касатель-ним напряжением. При анализе силового режима и формоизменения заготовки учитывают напряжение ткз. действующее со стороны инструмента на заготовку. Анализируя нагрузки на инструмент, оперируют с напряжением тки-
z
X
Рис. 3.1. Силы, действующие на контактных площадках заготовки AF, н инструмента AFg при осадке
Рис. 3.2. Схема взаимодействия элементов поверхностей деформируемой заготовки 3 и инструмента И
Трение в процессах обработки металлов давлением качественно отличается от трения в машинных парах. Во-первых, при пластической деформации поверхность соприкосновения заготовки с инструментом непрерывно обновляется, так как увеличивается площадь контактной поверхности. Например, при осадке цилиндрической заготовки диаметром d и высотой h до высоты Лк площадь контактной поверхности увеличивается в h/hK раз, при волочении прутков и проволоки увеличение контактной поверхности пропорционально d/dK. Во-вторых, относительные перемещения де^юрми-руемого тела и инструмента в большинстве процессов ОМД незначительны и различны для различных точек контактной поверхности. В-третьих, для обработки давлением характерны высокие давления или температуры на поверхности трения. В подшипниках и направляющих машин общего назначения давления не превышают 20...40 МПа, в тяжело нагруженных парах трения кузнечного оборудования они возрастают до 50... 100 МПа, а при холодной пластической деформации —до 2000...2500 МПа. В случае деформации с нагревом давление уменьшается, однако на поверхности трения развивается высокая температура — 800... I0004 С и более. Влияние высокого давления и температуры, в большинстве случаев совместное, вносит существенное изменение
127
в процесс взаимодействия инструмента с обрабатываемой заготовкой по сравнению с трением в машинах.
Перечисленные особенности приводят к тому, что в процессах ОМД бывает только три вида трения. Сухое трение возникает между заготовкой и инструментом в том случае, когда их контактные поверхности не разделены каким-либо третьим телом: смазкой, окислами, воздухом. В момент соприкосновения инструмента с заготовкой контакт осуществляется по небольшой поверхности ГКф в = 2ДГ/, образуемой вершинами выступов микронеровностей заготовки (рис. 3.2). Поверхность фактического контакта Гкф значительно меньше номинальной Гкн. Поэтому пластическая деформация заготовки начинается на поверхностях фактического контакта ДГ/. В процессе деформации происходит согласование поверхности заготовки с поверхностью инструмента по достижении предела текучести испытываемого образца 157]. В области выступов металл получает значительные пластические деформации и упрочняется. Большие давления на контактных площадках ДГ/ в сочетании с относительным перемещением и значительной местной пластической деформацией обусловливают образование узлов схватывания, т. е. поверхностей, по которым вследствие адгезии образуется металлическое соединение трущихся тел (61, 65, 129]. При сухом трении прочность металлического соединения в узле схватывания в большинстве случаев выше, чем прочность заготовки. Поэтому дальнейшее относительное перемещение заготовки по поверхности деформируемого инструмента возможно лишь при разрушении металла заготовки. Где будет происходить разрушение? Проследим за образованием узла схватывания, например, на площадке ДГ/ (рис. 3.2). В начальный момент сближения поверхностей инструмента и заготовки деформация локализуется у вершины выступа, так как в этом месте площадь сечения наименьшая, а следовательно, напряжение оп наибольшее (рис. 3.3). По мере увеличения площадки контакта от ДГи до ДГа очаг деформации распространяется в глубину выступа по нормали п. Вследствие упрочнения предел текучести металла на сдвиг т$ в объеме выступа оказывается переменным, так что в направлении от поверхности контакта материал деформируемой заготовки получает отрицательный градиент механических свойств dxjdn. = arctgtp. В этих условиях трение внешнее переходит в трение внутреннее [64]. Дальнейшее перемещение заготовки относительно инструмента в направлении их оказывается возможным лишь в том случае, если узел разрушится по поверхности среза ab, для которой произведение &FabXt будет наименьшим. Опыт показывает, что поверхность среза располагается преимущественно у основания узла схватывания.
Очевидно, что при сухом трении контактное касательное напряжение должно определяться сопротивлением деформации материала заготовки т, и площадью фактической поверхности контакта ГКф. При развитой пластической деформации ГКф -> Гки.
128
Поэтому контактное касательное напряжение соизмеримо с пределом текучести на сдвиг т,. Силовой режим деформации в этих условиях исключительно тяжелый. Кроме того, схватывание при сухом трении приводит к резкому ухудшению поверхности деформируемой заготовки, износу инструмента, иногда совершенно катастрофическому. Металлические соединения трущихся поверхностей в узлах схватывания образуются при повышенных температурах и комнатных, при достаточно больших скоростях относительного движения и статическом’ контакте [12]. Прочность контакта в узле схватывания определяется сродством деформируемого инструмента и заготовки. Если сродство велико, то металлический контакт очень прочен и при трении металл заготовки налипает на инструмент, т. е. реализуется схема, показанная на рис. 3.3. Если же сродство небольшое, то металлический контакт при низких температурах очень непрочен и с увеличением температуры его прочность изменяется незначительно. Поэтому в случае деформации инструментом, свойства которого сильно отличаются от свойств заготовки, сопротивление срезу по поверхности ab больше, чем сопротивление сдвигу по поверхности cd, служащей границей между заготовкой и инструментом. В этих условиях схватывание имеет место, но налипание металла заготовки на поверхность инструмента не происходит. Конечно, такие условия трения благоприятнее по всем критериям: силовому режиму, качеству изделий, износу инструмента.
В чистом виде сухое трение возникает лишь при обработке металлов давлением в глубоком вакууме. В обычных условиях деформации без смазки поверхности заготовки и инструмента покрыты окислами, пленками влаги, газов, различными загрязнениями. Поэтому условия, близкие к сухому трению, существуют лишь на отдельных участках поверхности деформируемой заготовки (главным образом на тех, которые образовались в результате увеличения общей площади контакта и выхода на поверхность глубинных слоев), да и то при отсутствии эффективной смазки.
Гидродинамическое трение* возникает при холодной пластической деформации с обильной смазкой: волочении прутков и проволоки (60, 1681, вытяжке листового металла (48, 49, 611, холодной осадке заготовок на плоских плитах (491, гидропрессовании (341, прессовании, в том числе горячем (61, 141, 150). Особенность этого вида трения состоит в том, что во всех точках контактной поверхности заготовка и инструмент разделены толстой, более 10мм, пленкой смазки. Для этого вида трения контактное касательное напряжение определяется по формуле Ньютона:
т»=Н£й-с. (3.1)
* Этот вид трения нередко называют жидкостным.
5 1-15
129
где цс — динамическая вязкость смазки; —градиент скорости в слое смазки в направлении нормали к контактной поверхности.
При использовании эффективных смазок толщина пленки оказывается достаточно большой, трущиеся поверхности надежно разделяются, а контактное касательное напряжение оказывается минимальным: примерно на два порядка ниже, чем при сухом трении. Это приводит к резкому снижению деформирующих усилий, повышению качества изделий и увеличению стойкости инструмента. Например, известны случаи, когда применение напор-
Рис. 3.3. Схема деформации отдельного выступа
Рис. 3.4. Вытяжка в условиях гидродинамического трения [34 , 49]: 1 — пуансон, 2 — прижим, 3 — заготовка, 4 — вытяжная матрица, 5 — смазка
ных трубок, создающих гидродинамический режим трения, позволяло в десятки раз повысить стойкость инструмента для волочения прутков и проволоки, резко снизить брак [60].
В процессе обработки металлов давлением смазка выжимается с контактной поверхности под действием высоких нормальных давлений. Для поддержания гидродинамического режима трения необходимо создавать условия, способствующие образованию смазочного клина. Проще это сделать при волочении, гидропрессовании, прессовании, осадке, вытяжке (рис. 3.4). Относительное перемещение деформируемой заготовки по инструменту и вязкость смазки обусловливают вовлечение частиц смазки в зону деформации. Поэтому при движении вязкой жидкости в сходящемся канале давление повышается. При высоких давлениях вязкость смазок резко увеличивается. Например, легкие минеральные масла при давлении 210 МПа переходят в твердое состояние, коэффициент вязкости возрастает примерно на один порядок. Другие смазки переходят в твердое состояние при давлениях 1500...3000 МПа [120]. Большие давления и сравнительно высокие скорости относительного скольжения в плоскости контакта вызывают высокие локальные температуры, что приводит к падению вязкости смазки и резкому уменьшению толщины смазочного слоя. По этой причине
130
условия гидродинамического трения нарушаются и трение переходит в граничное.
Граничное трение при обработке металлов давлением встречается чаще других видов. Оно характеризуется тем, что поверхности инструмента и заготовки разделены тончайшим слоем смазки, обычно не более 10“®... 10"4 мм. Контактное касательное напряжение тк при граничном трении на порядок больше, чем при гидродинамическом. Здесь особо важное значение приобретают свойства смазки и состояние контактирующих поверхностей. Причины столь значительного повышения контактного касательного напряжения состоят в следующем. Во-первых, смазочные пленки толщиной менее 10-4 мм (граничный слой) качественно отличаются от нормальной жидкости, из которой они образованы. Во-вторых, неровности контактирующих поверхностей местами прорывают смазочную пленку, образуя узлы схватывания. Если пленка обладает малой механической прочностью, то количество узлов схватывания может быть весьма большим и граничное трение приближается к сухому.
Таким образом,применением эффективных смазок, образующих прочные смазочные пленки, или созданием гидродинамического режима трения можно в десятки раз снизить контактные силы трения, предотвратить схватывание, в сотни и тысячи раз повысить стойкость инструмента и улучшить качество изготовляемых изделий.
3.2. ГРАНИЧНЫЕ УСЛОВИЯ
Для теоретического анализа процессов ОМД необходимо задать граничные условия, т. е. указать закон, по которому должны изменяться касательные напряжения на контактных поверхностях деформируемой заготовки. В зависимости от вида операции и состояния контактных поверхностей заготовки и инструмента граничные условия могут задаваться по-разному.
В соответствии с законом Амонтона—Кулона контактное касательное напряжение тк пропорционально нормальному давлению в плоскости контакта [48, 61, 103, 1071:
тк = ро„. (3.2)
Теоретический расчет усилия осадки тонкой цилиндрической заготовки при задании граничных условий в форме Амонтона—Кулона приводит к нереально завышенным результатам: расчетное усилие в 22,6 раза больше полученного экспериментально [311. Этот факт обязывает определить возможность применения формулы (3.2). Рассмотрим некоторую область ДГз контакта заготовки с инструментом в окрестности точки А с координатами хл Уа< гл (Рис- 3.1). Пусть апА = —5о„ р = 0,4 (такие значения ц вполне реальны при горячей деформации). В соответствии с этими исходными данными согласно формуле (3.2) ткд =«—2о,.
5* 131
вуют оольшие нормальные > 0,50а,. Если рая<О,50а„
Возьмем произвольную точку В деформируемой заготовки с координатами xfl, ув, гв. Очевидно, что Т,в =[ (х, у, г), однако Тшах = o,5(amax —amir). При пластической деформации ат.х — — атщ =00,. Поэтому в любой точке деформируемой заготовки, в том числе и точке А, ттах = 0,50а,. Очевидно то, что | тк | С ^ттах. Таким образом, приходим к противоречию: по формуле (3.2) в точке А |тл|=2о„ а по уравнениям механики сплошных сред | т*| 0,577а, ® k. Это означает, что условие Амонтона —
Кулона нельзя применять, если на поверхности контакта дейст-напряжения ал, при которых роя> то частицы деформируемой заготовки могут перемещаться относительно инструмента со скоростью vx = = их(х. У» 2) (рис. 3.2), зависящей от скорости деформирования и размеров очага деформации. При рая > 0,50а, характер течения металла существенно меняется: частицы, лежащие на поверхности инструмента, как бы прилипают к нему, скорость vx = = vx (х, у, z), в точках с координатами г = zK обращается в нуль, а течение переходит в приконтактные слои, толщина которых больше высоты микронеровностей поверхности инструмента.
Для деформации в условиях граничного трения сопротивление сил трения на площадке AF должно определяться в зависимости от сопротивления на сдвиг деформируемого металла т, и граничной смазки тсы:
Рис. 3.5. Схема взаимодействия заготовки 3 с инструментом И при граничном трении со смазкой С 112]
ДТ == т,ДГс 4-тсмДГсм,
(3.3)
где ДГС— часть площадки ДГ, по которой происходит сухое трение; ДГСМ— часть площадки ДГ, по которой деформируемая заготовка взаимодействует с инструментом через слой смазки (рис. 3.5). Очевидно, что ДГС = £ Д/о ДГСМ = £ ДГО ДГС 4-4- ДГСМ = ДГ. Следуя Боудену и Тейбору [12], обозначим ДГр' /ДГСМ = а, примем т, = 0,50а,. Разделив почленно выражение (3.3) на ДГ, после преобразований получим т* = 0,50а, [а 4-+ (1—а) Тем/bl-Обозначив 0,50 [а 4-(1 — а)тс„/т,1 через р, придем к формуле
тк = ра„ (3.4)
известной в литературе как формула Зибеля. Здесь коэффициент р можно считать коэффициентом трения.
Физическая сущность коэффициентов трения р, входящих в формулы Амонтона—Кулона (3.2) и Зибеля (3.4), различна.
132
В соответствии с рекомендациями И. Л. Перлина [ 107], формулы (3.2), (3.4) можно привести к виду
тк = (3.5); тк = пл (3.6).
В общем случае так как из уравнений (3.5), (3.6)
следует рл в р/т,/] ап |. Для процессов со схемой всестороннего неравномерного сжатия | ол |> о,, поэтому рл < ps. К сожалению, в справочной литературе коэффициенты трения во многих случаях приводятся без указания формулы, по которой выполнялся расчет, или условий испытания, из которых определялись значения р„ или |л, (64, 168 и др.]. Формулу (3.5) следует применять для теоретического анализа процессов ОМД, в которых преобладают растягивающие напряжения и выполняется условие | ол | о„ т. е. для волочения, вытяжки листового металла, прокатки с небольшими обжатиями толстых листов, начальной стадии осадки высоких заготовок и др. Для теоретического анализа процессов, характеризуемых схемой всестороннего сжатия с большим отрицательным средним напряжением — прокатки тонких листов с большими обжатиями, прокатки в калибрах, осадки тонких заготовок, объемной штамповки, прессования и других—следует применять формулу (3.6.). В сомнительных случаях целесообразно выполнить предварительные расчеты по формуле (3.5), построить эпюры <зп, тк и сравнить тк с а,: если тк 0,5ра„ то расчет можно считать правильным [107].
Экспериментальные исследования показывают, что площадь ДГС, по которой происходит металлический контакт заготовки с инструментом, зависит от нормального давления в пределах площадки ДГ, шероховатости инструмента R^ и заготовки Rz3, степени деформации е, температуры приконтактного слоя заготовки /к, свойств и распределения смазки и др. Поэтому р является сложной функцией вида
Р = Ф (*, У, z = zK, Тсм> Ra*, R„. 8, /, ...). (3.7)
Вид функции (3.7) установить теоретически пока не представляется возможным. Поэтому в первом приближении принимают, что силы трения равномерно распределены по контактной поверхности. Чтобы учесть влияние формы очага деформации, в работах И. Я. Тарновского и его учеников предложено контактное касательное напряжения тк определять через т, и функцию фк, которая зависит от коэффициента трения р для пары инструмент— заготовка [141, 1461. Например, для осадки цилиндрической заготовки диаметром d и высотой h, предложены формулы
= фкт,; фк = р + (1 — р) / р. (3.8)
К сожалению, функции вида (3.8) установлены только для простейших схем деформации. Поэтому в дальнейшем используются граничные условия в форме Амонтона—Кулона (3.2), Зи-
133
беля (3.4) или условия гидродинамического трения (3.1). При обращении к работам И. Я. Тарновского граничные условия даются в форме (3.8).
3.3. ОСНОВНЫЕ ФАКТОРЫ, ВЛИЯЮЩИЕ НА КОНТАКТНОЕ ТРЕНИЕ
Сила трения Т зависит от многих факторов. Рассмотрим влияние некоторых из них.
Сродство материала инструмента и деформируемой заготовки — один из важнейших показателей, определяющих не только силы контактного трения, но и износ инструмента, качество изготовляемых деталей, требования к технологии подготовки исходных заготовок. Обычно сродство материалов тем меньше, чем больше различаются параметры их решеток 1129]. При малом сродстве материала инструмента и заготовки мостики схватывания разрушаются по границе инструмент—заготовка и налипание материала заготовки на инструмент не происходит даже при отсутствии смазки. Приведем иллюстрацию к сказанному. В одном из кузнечных цехов при обжиме стальной толстостенной трубы в жесткой матрице условия на контактной поверхности приближались к сухому трению, так как острая кромка, полученная при отрезке трубы, сдирала смазку с поверхности матрицы. Стойкость стальных матриц составляла в среднем 100...200 деталей. Уже после изготовления 50... 100 деталей на поверхности матриц образовывались наросты налипшего металла, на поверхности обжимаемых труб появлялись глубокие задиры. Применение матриц из твердого сплава BKI5 позволило в 1500 раз повысить их стойкость, а качество деталей резко улучшить 1144]. Причина повышения стойкости — малое сродство твердого сплава и стали. Этот пример подчеркивает важность правильного выбора марки инструментального материала при конструировании штампов. В некоторых случаях хороших результатов можно достигнуть применением соответствующих покрытий, например хромированием матриц для вытяжки листовых заготовок.
Второй важнейший фактор — смазка. Надлежащим подбором смазки можно снизить усилие тем значительнее, чем больше отношение контактной поверхности ко всей поверхности деформируемого тела. Рекомендации по применению различных смазок даны в подразд. 3.4. Подчеркнем, что с помощью смазок оптимальной вязкости можно создать режим трения, приближающийся к гидродинамическому 148, 49].
Шероховатость поверхности инструмента играет важную роль лишь постольку, поскольку способствует удержанию смазки и созданию режима, приближающегося к гидродинамическому. Поэтому наименьшие силы контактного трения возникают на поверхности инструмента с регулярным рельефом, созданным специаль-
134
ними методами обработки [175]. Стремиться к чрезмерно высокой чистоте поверхности инструмента нецелесообразно из-за интенсификации процесса образования узлов схватывания [ 129] и ухудшения условий смазки [21]. Шероховатость поверхности, обработанной обычными методами, характеризуется рельефом с преимущественной ориентировкой: после строгания, фрезерования, шлифования образуются риски, ориентированные вдоль направления обработки. Поэтому трение на контактных поверхностях инструмента, как правило, бывает анизотропным, т. е. зависящим от выбранного направления [ 103, 173]. Так, даже после двойного чистового шлифования (в двух взаимно перпендикулярных направлениях) сопротивление течению вдоль рисок на 20% меньше сопротивления поперек рисок 1103]. Во многих случаях это явление можно обратить на пользу (см. подразд. 4.1). В тех случаях, когда на контактных поверхностях инструмента необходимо получить изотропное трение, применяют специальную обработку: торцовое шлифование, обработку ручным наждачным инструментом в разных направлениях и т. п.
Роль поверхности деформируемой заготовки существенна только в начальный момент деформации. В процессе деформации поверхность заготовки полностью согласуется с поверхностью инструмента. Шероховатость с регулярным рельефом на поверхности заготовки может способствовать захвату смазки и созданию режима трения, близкого к гидродинамическому. При увеличении скорости деформации силы трения, как правило, уменьшаются. Однако этот параметр процесса деформации всегда строго определен типом машины, на которой выполняется заданная операция. Поэтому технолог не может варьировать скоростью в пределах, позволяющих ощутимо снизить силы трения. Температура деформации оказывает очень сложное влияние на силы контактного трения. При повышении температуры резко меняются физико-химические свойства смазки, на поверхности деформируемой заготовки образуются окисные пленки. Вследствие этого силы трения могут возрастать. Но, с другой стороны, при нагреве снижается сопротивление деформации металла а„ и силы контактного трения возрастают или убывают в зависимости от того, какой из упомянутых выше процессов преобладает.
Характер приложения сил и дробность деформации также существенно влияют на контактное трение. При пульсирующей нагрузке, когда инструмент в результате упругого восстановления отходит от поверхности деформируемой заготовки, сплошность смазочной пленки восстанавливается, а силы трения Т снижаются (см. подразд. 2.8.3). С увеличением степени деформации смазочная пленка, как правило, выдавливается, утоняется и разрывается, на поверхность контакта выходят глубинные слои металла, и силы трения значительно увеличиваются. Поэтому во многих процессах, например при холодном выдавливании деталей типа стаканов, предельное формоизменение ограничивают не в связи с исчерпа
135
нием ресурса пластичности, а из-за утонения и разрушения слоя смазки, увеличения сил трения, развития процесса схватывания, ухудшения качества деталей и поломок инструмента [38].
3.4. СМАЗКИ ДЛЯ ОБРАБОТКИ МЕТАЛЛОВ ДАВЛЕНИЕМ
В процессах обработки металлов давлением условия трения на контактных поверхностях (давление, температура, скорость и т.д.) изменяются в очень широком диапазоне. Чтобы обеспечить оптимальные режимы деформации, необходимо использовать смазки с разнообразными свойствами. В одних случаях смазка должна снижать трение и усилие деформации, в других — охлаждать инструмент и предотвращать его разупрочнение, в третьих — улучшать качество поверхности изделий. По этой причине для обработки металлов давлением используют большое количество смазок, свойства которых и условия применения указаны в работах [21, 48, 60, 61, 82, 120, 141, 1681. Основное требование к смазкам — хорошая экранирующая способность (способность надежно разделять поверхности деформируемой заготовки и инструмента). Установлено, что именно это свойство смазки определяет силовой режим деформации, износ инструмента, качество изделий. При ухудшении экранирующей способности смазки контактное трение возрастает не так значительно, как износ инструмента. Например, если в связи с ухудшением условий контактное трение т* возрастает в 3...4 раза, то износ может возрасти в 100... 1000 раз [ 12).
3.5. ОСНОВНЫЕ НАПРАВЛЕНИЯ ПОЛЕЗНОГО ИСПОЛЬЗОВАНИЯ СИЛ ТРЕНИЯ
В большинстве технологических процессов ОМД контактное трение приводит к нежелательным последствиям: повышению технологического усилия, неравномерности деформации, износу инструмента, снижению качества изготовляемых деталей. Однако во многих случаях силы контактного трения можно обратить на пользу. Например, при холодном выдавливании деталей типа стаканов трение на поверхности матрицы приводит к тому, что в очаге деформации получается схема всестороннего неравномерного сжатия (рис. 3.6,а). Такая схема,повышая пластичность, обусловливает увеличение усилия сопротивления деформации. Чтобы силы контактного трения при выдавливании обратить на пользу, достаточно сообщить матрице перемещение в направлении оси г со скоростью им, превышающей скорость истечения металла сс. Тогда в очаге деформации схема напряженного состояния изменится и станет сжаторастянутой (рис. 3.6, б). В этом случае потребуется значительно меньшее усилие деформации. Хотя такая схема приводит к снижению пластичности, при выдавливании малоуглеродистых сталей и сплавов цветных металлов с большими степенями деформации бывает очень важно снизить нагрузки на инструмент. Экспериментальные исследования показывают, что выдавливание и прессова
136
ние с использованием активных сил трения позволяет на 20...30% уменьшить усилие деформации 195, 100]. Благодаря этому удается значительно повысить стойкость инструмента.
Активные силы трения можно использовать при осадке цилиндрических заготовок. Если между бойками и осаживаемой заготовкой поместить мягкие прокладки (из материала с меньшим пределом текучести), то деформация начнется с прокладок. Вытекая из-под осаживаемой заготовки, прокладки увлекут за собой ее торцовые поверхности и предотвратят образование бочки. Если прокладки излишне мягкие, боковая поверхность осаживаемой заготовки становится корсетной. Применение мягких прокладок
Рис. 3.6. Схемы течения и напряженного состояния при выдавливании в обычных условиях (а) и с использованием активного трения (б)
Рис. 3.7. Напряжения в течке М при ссадке заготовки с кручением [61]
усложняет технологию. Образование бочки можно предупредить путем компенсации трения на контактных поверхностях. Бочко-образность получается вследствие вредного влияния контактного касательного напряжения тк (рис. 3.7). Сообщим верхнему бойку вращательное движение вокруг оси г. В каждой точке, например М, будет действовать два взаимно перпендикулярных вектора касательных напряжений тКг, ткв. Напряжения тКЛ, тк»— это компоненты вектора полного касательного напряжения тк, действующего в точке Af, т. е. т£ = tJ, -f- tJb. Напряжение ткв можно изменять, изменяя скорость вращения инструмента. Напряжение тк зависит от граничных условий на контактной поверхности, но не может превышать Tmax = 0,5ро$. Поэтому при возрастании ткв значение ткг должно снижаться. Благодаря этому существенно изменяется схема напряженного состояния, уменьшается неравномерность деформации и в 3...5 раз снижается усилие деформации. Детальный теоретический анализ процесса осадки с вращением инструмента дан в работах [52, 61].
Совершенно очевидно, что такой метод уменьшения усилия деформации можно использовать и для других процессов, которые характеризуются осесимметричной схемой напряженно-деформированного состояния. Например, при объемной штамповке в от
137
крытых пггампах вращение инструмента может приводить к снижению усилия деформации в 2...5,5 раз. Поэтому для штамповки требуется оборудование меньшего тоннажа, а главное — резко возрастает стойкость инструмента. Анализ влияния вращения инструмента на усилие деформации объемной штамповки дан в работах 161, 104]. Аналогичные эффекты отмечены при волочении и других процессах ОМД.
Следовательно, во многих процессах обработки металлов давлением силы трения можно частично или полностью компенсировать. Если выбрать такую схему деформации, при которой инструмент можно принудительно перемещать в направлении течения металла, то силы трения на контактных поверхностях инструмента можно обратить на пользу. Этот принцип широко применяется в промышленности [48, 61, 95, 100].
Подчеркнем, что стремиться к снижению контактного трения не всегда целесообразно. Например, при осадке заготовок перед штамповкой на прессе или молоте можно совершенно не заботиться об условиях контактного трения, так как усилие машины определяется не этой операцией и износ поверхностей для осадки не влияет на стойкость штампа в целом. Уменьшение сил контактного трения, а значит и деформирующих усилий, имеет практическое значение лишь в том случае, если позволяет выполнить операцию на оборудовании меньшего тоннажа или резко повысить стойкость инструмента и качество изделий, снизить брак.
ГЛАВА 4
ОСНОВНЫЕ ЗАКОНЫ ПЛАСТИЧЕСКОЙ
ДЕФОРМАЦИИ
Между явлениями существуют объективно необходимые связи, которые принято называть законами. Познанные на эмпирическом уровне, они устанавливают внутренние связи между причиной
138
и следствием. Например, движение электрического тока определяют законы Ома и Кирхгофа, состояние газа — закон Бойля— Мариотта, преобразование электрической энергии в тепловую — закон Джоуля—Ленца. По определенным законам происходят и процессы пластической деформации. Закон постоянства объема и закон Шмида читателю уже известны (подразд. 1.4.4, 2.5.2). Ниже рассмотрим еще три, играющие исключительно важную роль в процессах пластической деформации (законы наименьшего сопротивления, неравномерности деформации, подобия), а также основные следствия, вытекающие из них.
4.1. ЗАКОН НАИМЕНЬШЕГО СОПРОТИВЛЕНИЯ
Эго один из важнейших законов, определяющих характер формоизменения и силовой режим пластической деформации. Любая материальная частица деформируемого тела, имеющая несколько кинематически возможных направлений перемещения, движется в направлении наименьшего сопротивления. Практическое значение закона наименьшего сопротивления в указанной формулировке относительно невелико, так как решение задач конечного формоизменения невозможно, если не установлены направления наименьшего сопротивления в деформируемом теле и неизвестны количественные соотношения между сопротивлениями и объемами металла, которые смещаются в различных направлениях. Закон наименьшего сопротивления в такой формулировке позволяет решать задачи формоизменения лишь на качественном уровне. Однако ряд важных следствий, вытекающих из него, особенно принцип минимума полной энергии деформации (см. подразд. 5.2.3.), дают возможность подойти к изучению формоизменения при пластической деформации на количественном уровне.
Приближенная связь между перемещениями частиц деформируемого тела и сопротивлениями перемещению этих частиц установлена в работах [17. 30, 43, 103, 140, 173, 1781. При осадке на плоских бойках в условиях изотропного трения перемещение частиц в плоскости, параллельной плоскости бойков, происходит по кратчайшей нормали к контуру, внешнему или внутреннему. С достаточной точностью можно считать, что перемещения частиц в различных направлениях обратно пропорциональны сопротивлениям перемещению, а последние пропорциональны квадрату расстояния частицы от контура.
Поэтому при осадке призматической заготовки ее контур преобразуется по схеме, представленной на рис. 4.1. Кинематически возможные перемещения частицы К — это перемещения их, йд. В связи с тем, что К. лежит ближе к контурной линии ВС. чем к А В, согласно закону наименьшего сопротивления действительным оказывается перемещение их. Все частицы, лежащие правее биссектрисы ВМ угла АВС, должны перемещаться по направле
139
нию нормали к ВС, а частицы, лежащие левее ВМ — по направлению нормали к АВ. Это означает, что ВМ — линия раздела течения. Таким образом, основание прямоугольной призмы (или любое сечение, параллельное основанию) можно разбить на четыре зоны, в пределах которых перемещения одинаковы по направлению и знаку. Как видно из рис. 4.1, при достаточно большой деформации (третий и последующие этапы) прямоугольный контур исходной заготовки преобразуется в контур, близкий к окружности. Это проявление принципа наименьшего периметра, вытекающего из закона наименьшего сопротивления [17, 30, 43, 103]. При осадке на плоских бойках в условиях изотропного трения заго-
Рис. 4.1. Этапы преобразования контура призматической заготовки при осадке на плоских бойках [43]
(а — первый, б — второй втап): — исходный контур; — — контур после этапа деформа, дни; —»— линия раздела течения; направление наименьшего сопротивления
товки постоянной высоты любой формы в плане внешний контур ее принимает форму, имеющую при данной площади наименьший периметр, т. е. в пределе стремится к кругу.
Такая схема деформации (рис. 4.1) справедлива только при большом влиянии внешнего трения [1401. Если трение отсутствует или влияет очень мало, справедлива радиальная схема и поэтому контур исходной заготовки преобразуется в геометрически подобный. Указанные схемы течения являются предельными, т. е. имеют место при тк =» k, тк =• 0. Для производственных условий характерны промежуточные схемы. Как видим, даже в простейшем случае осадки призматической заготовки формоизменение определяется сложными закономерностями. Добавим к этому, что изотропное трение на контактных поверхностях инструмента встречается в производственных условиях сравнительно редко (см.подразд. 3.3). При анизотропном трении поперечное сечение заготовки любой формы в результате осадки преобразуется в эллиптическое.
Несмотря на то что закон наименьшего сопротивления сформулирован в самом общем виде, он широко используется для анализа формоизменения и имеет ряд важных практических приложений. Из закона наименьшего сопротивления вытекает принцип минимума полной энергии деформации. Следуя Л. М. Качанову [511, его можно сформулировать следующим образом. Действительная форма равновесия тела отличается от всех возможных форм тем, что сообщает полной энергии минимальное значение. Поясним
140
сказанное на примере (рис. 4.2). Дадим заготовке бесконечно малую осадку АЛ. Кинематически возможные направления перемещения частиц А, В, С (их радиальные компоненты) суть перемещения -\~иг или — иг. Опыт показывает, что игд > 0, a Urc < 0. Это означает, что часть металла деформируемой заготовки перемещается от центра к периферии, а часть в противоположном направлении. Материальные частицы деформируемого тела (рис. 4.2, В), для которых иг = 0, образуют поверхность, называемую поверхностью раздела течения. При осадке на плитах с отверстиями поверхность раздела течения цилиндрическая диаметром Dp (140). Предположим, что в некоторый момент деформации на свободной поверхности заготовки изменятся граничные условия (рис. 4.2,
Рис. 4.2. Схема осадки цилиндрической заготовки на плитах с отверстиями: а — естесненная деформация с двумя степеням! свободы течения; б и в — стесненная деформация с одно* степенью свободы течения
б, в). В обоих случаях деформация характеризуется одной степенью свободы течения металла. Следовательно, кинематически возможными и одновременно действительными станут перемещения от центра к периферии (рис. 4.2, б) или от периферии к центру (рис. 4.2, в). При деформации с двумя степенями свободы течения металла частица А перемещается от центра к периферии. Это направление наименьшего сопротивления. Наличие связи, запрещающей подобное перемещение, заставляет частицу А двигаться в другом направлении наименьшего сопротивления, например, игд < < 0 (рис. 4.2, в). Но направлением абсолютно наименьшего сопротивления оно уже не будет. Для деформации по схемам б, в на перемещении A/i потребуется большая работа, а следовательно, и большее усилие, чем при деформации по схеме а. Факт значительного увеличения усилия деформации при переходе от схемы с двумя степенями свободы течения металла к схеме с одной степенью свободы подтверждается экспериментально.
Приведенный пример показывает, что между силовым режимом и характером формоизменения существует тесная связь 1143, 1461. В рассмотренном случае она может быть выражена функцией вида Ад = f(DP), где Ад — работа внешней деформирующей силы на перемещении A/i[ 143]. Исследуя эту функцию на экстремум, можно отыскать значение Dp, соответствующее минимуму Ад, затем решить все вопросы, связанные с формоизменением и силовым режимом.
141
Рис. 4.3. Особенности течения металла при штамповке звездочки в штампе с облойной канавкой III типа(56] (стрелками указаны направления течения металла)
или к повышенному
Действие вакона наименьшего сопротивления необходимо учитывать при теоретическом анализе, проектировании инструмента, разработке тех* нологическнх вопросов. Во многих случаях для этого достаточно общей формулировки закона. Так. для получения круглых в плане поковок ковкой и штамповкой с применением операции осадки, в качестве исходной заго* товки можно принимать прокат не только круглого, но и квадратного профиля. При протяжке для повышения эффективности вытяжки необходимо ограничить подачу (укоротить очаг деформации).
В процессе штамповки деталей типа звездочек возможен брак — неза-полнение в местах А (рис. 4.3) даже при сравнительно большом отходе металла в облой. Для его предупреждения достаточно изменить на участках L сопротивление течению металла из ручья: применить облойную канавку типа III [56], как это показано на рис. 4.3, или изменить параметры принятой для штамповки канавки на участках L (уменьшить толщину облоя h или увеличить ширину облойного мостика в).
Детали типа шестерен (рис. 4.4) можно штамповать из заготовок одинакового объема, но различных размеров. Наилучший вариант можно определить на основании закона наименьшего сопротивления. Если штампуется заготовка /, металл имеет одну степень свободы течения, а значит, работа деформации, усилие, износ ручья наибольшие. Штамповка заготовки 3, осаженной до диаметра поковки, нецелесообразна по другой причине. Для заполнения ступицы необходимо на начальном этапе деформации ограничить течение металла в облой чую канавку, но именно на начальном этапе штамповки высота облойной щели наибольшая, а сопротивление течению металла в облойную канавку наименьшее. Поэтому при деформации заготовки 3 в соответствии с законом наименьшего сопротивления течение металла в облойную канавку очень интенсивное. Это приведет к незаполнению ручья расходу металла. Наилучшей является заготовка 2,
при штамповке которой металл течет одновременно в ступицу и обод.) С достаточной для практики точностью можно принять Dp = 0,5(4< + dt). Тогда для выполнения поставленного условия необходимо равенство объемов частей заготовки и поковки, заключенных внутри поверхности раздела течения nRfyt « Vf. Объем У< можно рассчитать по размерам поковки: V, « 3ir*hi + я(^р — r*)As. Следовательно, оптимальной оказывается заготовка высотой А = VilnR^. Указанный расчет дает возможность значительно снизить усилие штамповки и повысить качество изделий. При штамповке поковок с развилинами применяют заготовительно-предварительный и чистовой ручей (56]. Конструируя чистовой ручей, необходимо предусматривать специальные компенсационные полости для размещения избыточного металла. В этом случае согласно закону наименьшего сопротивления деформация осуществляется по схеме с двумя степенями свободы течения металла, для чего требуется наименьшее усилие. Штамповка в ручье без компенсационной полости потребует большего усилия (или числа ударов), вызовет чрезмерный износ ручья и появление брака по прострелам (см. подразд. 4.2.6).
Идея штамповки поковок по схеме с двумя степенями свободы течения металла весьма плодотворна, особенно применительно к таким поковкам, как турбинные диски, тонкие фланцы и другие подобные детали диаметром свыше 300 мм. Обычно на их доштампо'вку затрачивается 50% и более общей энергии деформации. И все же поковки получаются недоштампован-аыми. Расчленение процесса на два перехода н применение штампа с ком
142
пенсационными полостями непосредственно в ручье позволяет осуществить штамповку по на неугоднейшему силовому режиму (рнс. 4.5). Изменение схемы деформации при штамповке турбинных дисков диаметром свыше 500 мм из стали ЭИ961Ш позволяет в среднем в два раза уменьшить число ударов молота и на 10—14% снизить массу поковки [130].
На характер течения металла существенно влияет анизотропия внеш* него трения. Во многих случаях это можно использовать для повышения эффективности деформации. Например, обработка абразивным инструмен* том пережнмных, подкатных и протяжных ручьев вдоль их оси приводит к повышению коэффициента вытяжки, а в поперечном направлении — к увеличению уширения. Поэтому для интенсификации перераспределения металла и снижения износа инструмента необходимо, чтобы риски от обработки были ориентированы вдоль желаемого направления перемещения частиц деформируемой заготовки. Рассмотренные примеры далеко не исчер-
Рис. 4.4. Варианты штамповки поковки типа шестерни из заготовок различных размеров
Рис. 4.5. Схемы течения металла (а, б) и эпюры нормальных напряжений (в, г) при штамповке тонких дисков:
а — по обычно! технологии: б — по технологии [130], К — компенсационная полость
пывают возможностей использования закона наименьшего сопротивления при проектировании технологических процессов и конструировании оснастки. Этот закон в форме принципа минимума полной энергии деформации широко используется для количественной оценки формоизменения (см. подразд. 5.2.3, 6.6).
4.2. НЕРАВНОМЕРНОСТЬ ДЕФОРМАЦИИ, ДОПОЛНИТЕЛЬНЫЕ И ОСТАТОЧНЫЕ НАПРЯЖЕНИЯ
С физической точки зрения даже деформация монокристалла неравномерна. В поликристаллических телах неравномерность ее усугубляется тем, что в каждом зерне плоскости и направления скольжения ориентированы по-разному (см. подразд. 2.5.1). И все же при определенных условиях такую квазиравномерную пластическую деформацию можно считать равномерной, если оценивать ее с геометрической точки зрения и рассматривать формоизменение в объемах, значительно превышающих объем отдельного кристаллита. Равномерной называется пластическая деформация, показатели которой не зависят от координат. Из этого определения следует, что интенсивность деформации тоже не зависит от коорди
143
нат, остается постоянной по всему объему деформируемого тела. Пример равномерной деформации — осадка цилиндрической заготовки на плоских бойках при отсутствии трения. Однако большинство процессов обработки металлов давлением характеризуется крайней неравномерностью деформации. Ее причины определяются действием геометрических и физических факторов.
4.2.1. Влияние геометрических факторов. Рассмотрим поперечную осадку цилиндрической заготовки диаметром D (рис. 4.6, а). Из-за несоответствия формы заготовки форме инструмента абсолютная деформация в различных вертикальных сечениях цилиндра неодинакова, поэтому неодинаковой оказывается и относительная деформация: в сечении — Аг она наибольшая, а в окрестности
Р,;с. 4.6. Влияние геометрических факторов на характер деформации (слева — до деформации, справа — после деформации):
а — при поперечной осадке цилиндра; б — при осадке на кояусяых бойках; • — при без. облойной штамповке
точки Вх тело вообще не деформировано. На рис. 4.6, б форма заготовки в точности соответствует форме инструмента. Однако из-за особенностей формы бойков деформация оказывается неравномерной. Хотя заготовка в целом получает одинаковое обжатие ДА, относительная деформация е" = ДА/Ао получается переменной по радиусу. В практике ОМД чаще встречается третий случай (рис. 4.6, в), когда различны и абсолютная и относительная деформации.
Неравномерность деформации, обусловленная действием геометрических факторов, проявляется и при операциях листовой штамповки. Например, при пластическом изгибе листовой заготовки волокна получают разную деформацию не только по абсолютному значению, но и по знаку. Наиболее резко выражена неравномерность деформации при разделительных операциях листовой штамповки. В процессе вырезки — пробивки очаг деформации охватывает очень узкую область, примыкающую к режущим кромкам матрицы и пуансона, а интенсивность деформации настолько высока, что вызывает местное разрушение заготовки.
4.2.2. Влияние физических факторов. Рассмотрим осадку цилиндрической заготовки на плоских бойках (рис. 1.2). Форма заготовки соответствует форме инструмента, все сечения заготовки получают одинаковые абсолютные и относительные деформации
144
ен = ДЛ/Л0. Но опыт показывает, что деформация распределяется далеко неравномерно: вблизи торцов локальная относительная деформация ег = диг1дг намного меньше средней по объему ®ср = ₽н, а в средней части заготовки, наоборот, она значительно превосходит еср (рис. 4.7). Это объясняется следующим. При деформации без нагрева трение на контактных поверхностях изме
няет схему напряженного состояния заготовки и затрудняет переход в первое предельное состояние приконтактных слоев. При де-
Iz
формации с нагревом сказывается подстуживание торцов.
4.2.3. Количественная сценка неравномерности деформации. Сложность механизма деформации при выполнении операций обработки металлов давлением затрудняет количественную оценку неравномерности деформации. Количественная оценка основана обычно на одном из экспериментальных методов [118, 133, 134, 140, 164, 170, 1781.
Наиболее распространенным показателем является коэффициент неравномерности деформации [99, 1011 Кп = ел/еср, где ел « = Да/а — относительная локальная деформация; еср = ДЛ/Д — относительная средняя деформация; А — габаритный размер за-
Рис. 4.7. Изменение показателя относительной лекальной деформация ед после осадки образца 0 25 X X 37,5 мм из стали Ст. 3 при /= = 1000° С на фрикционном прессе [991
готовки (высота, длина, ширина, диаметр); а — база координатной сетки (шаг винта, толщина слоя и др.); ДД, Да — приращения соответствующих размеров после
деформации.
На рис. 4.7 приведена кривая изменения показателя относительной локальной деформации ел, построенная по данным, полученным при осадке стальных образцов с дезаксиально ввернутыми винтами с шагом t =0,8 мм [ 1011. Дезаксиальность выбирается так, чтобы образующая винта совпала с осью образца. При этих условиях кривая выражает неравномерность высотной деформации по продольной оси осаживаемого образца. Коэффициент неравномерности деформации Кв изменяется по высоте заготовки: для области затрудненной деформации (сечения, прилежащие к торцам) 0 < < Кп < 1, а для области интенсивной деформации (средняя часть заготовки, заключенная между сечениями В—В и С—С) 1 < Кн <
< 2.
Оценивая количественно неравномерность деформации, можно использовать и другой показатель — градиент неравномерной деформации Гн=д₽л/дЛ [Ю11. Здесь k—координата вдоль которой исследуется деформация (k = х, у, г, г, 0). Практически Ги выражается через тангенс угла наклона кривой ел = /(£) к оси k. Например, на рис. 4.7 k = г и градиент неравномерной дефор
145
мации в точке Л —это rHx=tga>i. Однако неравномерность деформации одинаково трудно определять и с помощью Хи и с помощью Гн, так как необходимо иметь функции ел = / (k) по всем координатам (или графики этих функций). Закономерности неравномерной деформации при обработке металлов давлением весьма сложны. Поэтому в литературе приводятся подробные сведения о неравномерности деформации только для простейших операций ОМД, главным образом ковки и прокатки (99, 101, 103]. Результаты исследования неравномерности деформации при объемной штамповке, выдавливании, прессовании и других процессах ОМД, представлены в работах [32 , 34 , 43, 73, 134, 145, 164, 170].
Рис. 4.8. Механизм возникновения дополнительных напряжений при неравномерной деформации элементов А, В:
а — исходное состояние элементов; б — деформированное состояние при наличии физического раздела между элементами А и В по поверхности тп; в — силовое воздействие элементов друг на друга; » — деформированное состояние элементов А и В, условно выделенных в сплошном теле
4.2.4. Закон неравномерности деформации и дополнительных напряжений. Неравномерность деформации при обработке металлов давлением обусловливает неодинаковое необратимое изменение размеров отдельных элементов тела. Пусть в деформируемом теле два элемента А, В (рис. 4.8, а), разграниченные условной поверхностью тп, под действием приложенных внешних сил получают различное изменение размеров. Если бы элементы А, В могли изменять форму обособленно, то в результате деформации приняли бы вид, показанный на рис. 4.8, б. Но так как в процессе деформации соблюдается условие сплошности и частицы элемента А (например, частица К') взаимодействуют с частицами элемента В (например, /("), то элемент В передает на элемент А силы Та (рис. 4.8, в), стремящиеся увеличить размеры последнего. В то же время элемент А передает на элемент В силы 7д, стремящиеся сдержать его деформацию. Частицы Л', /(* при совместной деформации получают перемещение большее, чем К', но меньшее, чем /(’.
Таким образом, в теле на границе элементов, деформирующихся с разной интенсивностью, имеет место градиецт неравномерной деформации Гн, возникают взаимно уравновешивающиеся внутренние напряжения адЛ, адв. которые обусловливают формоизменение тела по схеме, приведенной на рис. 4.8, г. Напряжения Одл, ояв называются дополнительными, так как они не зависят от схемы на
146
пряженного состояния, определяемой действием внешних сил и тензором Тв. Это положение известно как закон неравномерности деформации и дополнительных напряжений. Следуя С. И. Губкину [30, 311, сформулируем его следующим образом.
В процессах обработки металлов давлением в связи с неравномерным распределением напряжений и деформаций отдельные слои и элементы тела, стремящиеся к большему изменению размеров против среднего, передают слоям и элементам, стремящимся к меньшему изменению размеров, силы такого знака, которые увеличивают изменение размеров, а слои и элементы, стремящиеся к меньшему изменению размеров, передают слоям и элементам, стремящимся к большему изменению размеров, силы такого знака, которые уменьшают изменение размеров.
Дополнительные напряжения, возникающие при неравномерной деформации, принято классифицировать следующим образом [30, 76, 125].
Напряжения первого рода — это микроскопические зональные напряжения, охватывающие целые области деформируемого тела и имеющие ориентацию, связанную с его формой. Иными словами, напряжениями первого рода называются дополнительные напряжения, которые возникают при взаимодействии макроскопических элементов А, В, составляющих значительную часть деформируемого тела. Если же размеры элементов А, В микроскопические (кристаллиты или группы кристаллитов деформируемого тела), то дополнительные напряжения называются напряжениями второго рода. Как правило, напряжения второго рода не имеют преимущественной ориентировки. Напряжения третьего рода возникают при взаимодействии субмикроскопических элементов деформируемого тела: блоков мозаики, полигонов, дислокаций. Их ориентация связана с направлениями кристаллографических осей зерен.
Учитывая неоднородность пластической деформации в физическом отношении, можно утверждать, что появление дополнительных напряжений второго и третьего рода сопутствует любому виду пластического формоизменения любого поликристаллического тела. Напряжения первого рода возникают только в том случае, когда деформация тела неравномерна в геометрическом отношении.
4.2.5. Остаточные напряжения. Остаточными называются напряжения, которые возникают из-за неравномерности пластической деформации и остаются в теле после снятия внешних сил или устранения других причин, обусловивших неравномерную пластическую деформацию. При горячей обработке давлением с малой скоростью остаточные напряжения практически полностью снимаются вследствие рекристаллизации. Холодная деформация вызывает остаточные напряжения, мало отличающиеся от дополнительных.
Остаточные напряжения классифицируются так же, как и дополнительные. В большинстве случаев они нежелательны, так как
147
ухудшают служебные свойства изделий; резко снижают коррозионную стойкость, пластичность, ударную вязкость и предел выносливости, вызывают коробление изделий. Складываясь с напря-
когда к остаточным добавляются напряжения, возни-действия неравномерного температурного поля. Иногда напряжения улучшают служебные свойства изделий, создание в поверхностном слое деталей сжимающих
жениями от внешних сил, остаточные напряжения могут привести к разрушению тела под нагрузкой, значительно меньшей, чем расчетная. Нередко разрушение тела под действием остаточных напряжений происходит даже в ненагруженном состоянии. Это бывает в случаях, каю цие от остаточные Например,
остаточных напряжений приводит к повышению их усталостной прочности [45].
Для определения величины остаточных напряжений, направления их действия и знака применяют химические, механические и рентгеновские методы [30, 76, 125]. Химические и
Рис. 4.9. Образование прострела в процессе доштамповки поковки в открытом штампе
механические методы позволяют выявить напряжения первого рода в изделиях простейшей
формы (проволока, прутки, трубы). Остаточные напряжения первого, второго и третьего рода в деталях сложной формы находят с помощью рентгеновских методов. Остаточные напряжения зависят от неравномерности деформации. Поэтому, пользуясь рентгеновскими методами, можно с достаточной точностью судить о характере деформации в
процессе изготовления детали.
4.2.6. Влияние неравномерности на характер деформации и качество деталей. Неравномерность деформации затрудняет процесс деформирования, снижает пластичность и отрицательно влияет на качество изделий. Накопление больших локальных деформаций приводит к превышению ресурса пластичности, что обусловливает образование внутренних трещин и расслоения [76, 125]. Так, при штамповке поковок типа шатунов, вилок и других деталей, имеющих ребра, кольцевые выступы, часто встречается дефект, называемый прострелом [30, 73].
Прострел образуется в том случае, если конфигурация ручья штампа способствует образованию так называемых застойных зон (рис. 4.9). На стадии доштамповкн, когда в облойную канавку вытесняется избыточный металл, в кольцевом выступе А формируется застойная зона, где скорости смещения ох, vv равны нулю. На поверхности тп, отделяющий очаг деформации ОД от застойной зоны, возникают большие градиенты деформации, ресурс пластичности исчерпывается н происходит разрушение (см. подразд. 1.6.4.3). Аналогичные результаты неравномерности деформации отмечены при осадке низких заготовок (кузнечные расслоения), а также при протяжке (ковочный крест) (73, 1011. Предупредить образование прострела можно двумя способами: уменьшением избыточного объема металла, вытесняемого в облойную канавку на стадии доштамповки, или повышением пластичности деформируемого металла. Иными словами, необходимо умень
148
шить объем исходной заготовки или взять для штамповки другой металл, с более высокими показателями б, ф.
Неравномерность деформации приводит к разрушению сравнительно редко, но на качестве поковок сказывается отрицательно. В результате не* равномерности деформации изделия получаются с неоднородной структурой} и пониженными механическими свойствами. Чтобы не попасть в область критических степеней деформации и не получить в отдельных объемах поковки крупнозернистой структуры и пониженных механических свойств, приходится назначать более высокие коэффициенты укова, что также связано с увеличением трудоемкости. Неравномерность деформации при ковке вызывает бочкообразность и другие искажения формы поверхностей поковок. Из-за этого приходится увеличивать припуски на механическую обработку, вводить дополнительные отделочные операции (обкатку, выглаживание), увеличивающие трудоемкость. При изготовлении деталей из листовых затотовок неравномерность деформации вынуждает вводить дополнительные операции, иногда очень трудоемкие. Например, из-за неравномерности деформации при гибке имеет место значительное пружинение. Для получения точного угла изгиба применяют дополнительную операцию калибровки, выполняемую в штампе или вручную с помощью шаблона.
Лишь в некоторых случаях неравномерность деформации можно использовать для повышения качества поковок. Изготовляя поковки из слитков, обычно назначают высокие коэффициенты укова (3 и более), чтобы в процессе деформации заварить внутренние пузыри, рыхлости и несплош-ности. Использование повышенной неравномерности деформации, например ковка узкими бойками нагретого слитка с подстуженной поверхностью, дает возможность ликвидировать внутренние дефекты в слитке при обжатиях порядка 10% [99].
4.2.7. Способы снижения неравномерности деформации. Источниками неравномерности деформации являются геометрические и физические факторы (см. подразд. 4.2.1, 4.2.2). Поэтому для снижения ее необходимо стремиться, чтобы заготовка соответствовала форме инструмента. При объемной штамповке стадия доштамповки должна быть минимальной. Эти меры позволяют снизить влияние геометрических факторов. Важнейшие физические факторы — равномерное температурное поле и силы контактного трения. Благодаря использованию современных нагревательных устройств и средств механизации для вспомогательных приемов ковки и штамповки, заготовка нагревается равномерно, ее подстуживание в процессе обработки предотвращается. Силы контактного трения можно уменьшить применением смазок, мягких прокладок (при ковке) или оболочек (при прессовании). Соприкасаясь с поверхностью инструмента, прокладки с более низким пределом текучести, чем у металла заготовки, деформируются интенсивнее и компенсируют силы трения, частично или полностью. Благодаря этому заготовка деформируется равномернее.
Неравномерность деформации при осадке можно значительно снизить с помощью рельефных бойков [ 101) или спаренной осадки [55].
В процессах объемной штамповки неравномерность деформации всегда выражена достаточно ярко, так как стенки ручьев штампов стесняют деформацию и способствуют образованию застойных зон. Чтобы снизить локализацию деформации на стадии доштамповки
149
и предупредить образование брака (прострелы, неравномерность структуры и механических свойств), необходимо следующее: рассчитывать объем заготовки так, чтобы стадия доштамповки была предельно короткой; приближать форму заготовки к форме поковки, пользуясь заготовительными ручьями; при проектировании штампов избегать резких переходов, способствующих образованию застойных зон; применять эффективные смазки.
Неравномерность деформации зависит также от плавности контуров ручья: с увеличением радиусов перехода от вертикальных и наклонных стенок ручья к горизонтальным (рис. 4.4, радиусы Z?i, Rt, Rs) она значительно снижается. Однако применять этот путь рекомендуется лишь в случаях крайней необходимости, так как он чреват увеличением расхода металла, ухудшением условий обрезки облоя и прошивки отверстий, повышением трудоемкости механической обработки.
4.3. ЗАКОН ПОДОБИЯ И МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ОМД
При создании новых технологических процессов, совершенствовании существующих часто бывает необходимо определить основные параметры: удельное усилие, усилие и работу деформации, распределение напряжений по контактной поверхности инструмента и т. д. Детальный теоретический анализ исследуемого процесса можно выполнить далеко не всегда. Кроме того, при теоретическом анализе принимаются упрощающие допущения физического, геометрического и математического характера, влияние которых на точность результатов оценивается только экспериментальной проверкой. Из-за этого приходится обращаться к экспериментальному исследованию. Постановка эксперимента на натурных изделиях сопряжена с большими затратами и нередко требует применения уникального оборудования. Поэтому исследования часто проводят на моделях,размеры которых значительно меньше размеров изделий, и результаты исследования переносят на процесс, подлежащий освоению. Чтобы данные, полученные в лабораторных условиях на модели, можно было распространить на натурный объект, необходимо выполнить ряд условий, вытекающих из закона подобия.
4.3.1. Закон подобия. Этот закон устанавливает соответствие силовых условий деформации двух тел разных размеров (модели и натуры), если тела геометрически и физически подобны, а их формоизменение осуществляется в определенных условиях. При деформации двух тел (модели и натуры) удельные усилия деформации одинаковы, деформирующие силы относятся как квадраты, а работы деформации — как кубы сходственных размеров, если выполняется подобие условий пластической деформации. Подобие условий пластической деформации включает геометрическое и фи-зическое подобие.
150
Тела считаются геометрически подобными, если имеют одинаковую форму и постоянное отношение сходственных размеров ZH/ZM = = Ьи1Ьц = Лц/Лм = ... = fi. Здесь lu, bu, hu — размеры натуры, a ZM, Ьм, Лм —соответствующие размеры модели. Величина п называется константой подобия. При этих условиях отношение поверхностей натуры и модели равно квадрату, а объемов — кубу константы подобия. Геометрическое подобие деформируемых тел должно выполняться от начала до конца процесса деформации. Требование геометрического подобия приводит к необходимости подобия рабочих элементов деформирующих инструментов.
Физическое подобие включает следующие требования.
1. Физические (химический состав, фазовое состояние, микро-н макроструктура) и механические свойства модели и натуры должны быть одинаковы в исходном состоянии и в любой момент деформации (см. подразд. 2.5, 2.7.3).
2. Температурные режимы деформации модели и натуры должны быть тождественными на протяжении всего процесса деформации (см. подразд. 2.7.3).
3. Скорости и степени деформации модели и натуры должны быть одинаковыми (см. подразд. 1.6.3, 2.5.6, 2.7.3).
4. Трение на контактных поверхностях модели и натуры должно быть идентичным. Это требование выполняется, если материал и шероховатость рабочих поверхностей штампов, качество применяемой смазки, скорость скольжения металла по инструменту одинаковы для модели и натуры. Отсюда вытекает необходимость равенства скоростей деформирования модели и натуры (см. подразд. 3.3).
Анализ требований физического подобия приводит к выводу о том, что они противоречивы в своей основе. Для тождественного распределения температуры в модели и натуре (требование 2) необходимо, чтобы время их деформации удовлетворяло условию /м = /н/п’ (44]. Отсюда следует равенство = £нл1, которое противоречит требованиям 3 и 4, так как из третьего вытекает равенство £м = £н, а из четвертого — = £нл.
Как известно, равенство £м = £н (требование 3) обусловливает одинаковое время деформации модели и натуры /м = /н. При пластической деформации с нагревом полнота разупрочняющих процессов определяется длительностью их протекания (см. подразд. 2.7). Если то модель и натура могут деформиро-
ваться по разным схемам: например, разупрочнение в натуре успеет завершиться полностью и деформация окажется горячей, а деформация модели из-за недостатка времени для полного разупрочнения может быть неполной горячей. Поэтому при деформации с нагревом соблюдение условия (или эквива-
лентного ему = £н) совершенно необходимо. Но, с другой стороны, при tu — tn нельзя выполнить требование 2, если деформация не протекает в изотермическом режиме. В самом деле, у образца для моделирования меньше объем и больше отношение
151
поверхности к объему, чем у натуры. Поэтому образец, соприкасаясь с холодным инструментом, остывает быстрее натуры, а его сопротивление деформации может значительно изменяться. Опыт показывает, что при обработке давлением геометрически подобным инструментом геометрически подобных заготовок, нагретых до одной и той же начальной температуры, конечная температура увеличивается, а сопротивление деформации уменьшается с увеличением объема заготовки [29, 44, 79, 169].
Таким образом, точное моделирование процессов пластической деформации неосуществимо. При холодной пластической деформации вследствие незначительного влияния скорости деформации условия физического подобия в основном выполняются, что позволяет моделировать производственные процессы с достаточной для практики точностью. При горячей пластической деформации, а также при деформации с высокими скоростями возможно только приближенное моделирование. Но в одних случаях основным требованием физического подобия является температура, в других — внешнее трение, в третьих — скорость деформации.
Погрешность, вносимая при невыполнении каких-либо требований физического подобия, может быть учтена коэффициентами несоответствия, т. е. поправочными коэффициентами, которые определяются опытным путем [84, 169]. Различия в скоростях деформации модели и натуры можно учесть с помощью скоростного коэффициента т]5, а различия в условиях теплоотдачи и температурах конца деформации — с помощью масштабного коэффициента <рм:
Ра = Л&А*» Р» = Ч'мРм* (4.1)
Значения скоростного и масштабного коэффициентов для различных условий деформации приведены в работах [30, 44, 84. 138, 169].
4.3.2. Основные направления моделирования. Моделирование — одна из важных практических задач теории обработки металлов давлением. Следуя С. И. Губкину [301, можно выделить пять основных направлений моделирования.
1. Изучение влияния пластической деформации на изменение структуры и свойств металлов. Обработка давлением — один из наиболее эффективных способов изменения свойств металлов (см. подразд. 2.5, 2.7, 2.8). Поэтому важно исследовать влияние пластической деформации на изменение структуры и свойств изделий. Для этой цели моделирование осуществляют при точном выполнении требований 1,2,4.
2. Изучение влияния различных способов деформации, режимов обработки давлением и контактного трения на пластичность и сопротивление деформации в процессе выполнения операций ОМД. Пластичность ограничивает предельное формоизменение заготовки за один переход, а сопротивление деформации оказывает исключительно большое влияние на стойкость инструмента и потребное усилие деформации. Поэтому применение эффективных
152
способов и режимов деформации, обеспечивающих высокую пластичность и низкое сопротивление деформации, позволяет значительно увеличить производительность и использовать менее мощное (следовательно и более дешевое) оборудование. Решение этих задач обеспечивается точным выполнением требований 1, 4 и приближенным выполнением требований 2 или 3 в зависимости от того, какое из них оказывает более существенное влияние.
3. Исследование формоизменения. Закономерности формоизменения в значительной мере определяют качество изготовляемых деталей: неравномерность и локализация деформации приводят к ухудшению структуры, образованию различных дефектов, например прострелов. Закономерности формоизменения зависят от геометрических особенностей деформации (формы инструмента и заготовки) и реологических характеристик деформируемого материала (упрочнения, неравномерности свойств по объему заготовки). Если свойства деформируемых заготовок достаточно однородны, то формоизменение различных материалов практически не отличается (при сохранении геометрического подобия). Поэтому для исследования формоизменения моделирование можно осуществлять, выполняя лишь требование 4. Это открывает широкие возможности моделировать формоизменение на образцах из пластилина, свинца и других мягких и пластичных материалов.
4. Моделирование существующих технологических процессов с целью определения их основных параметров (удельного усилия, усилия, работы деформации) и распределения деформаций и напряжений в очаге деформации. Эго одна из наиболее сложных задач моделирования. Хотя ее решению посвящено немало специальных работ [28, 30, 31, 44, 47, 79, 84, 122, 125, 138, 155, 169, 170, 188 и др.], общая теория моделирования находится еще в процессе становления. В том случае, когда требования физического подобия не выполняются или выполняются с грубым приближением, закон подобия дает основание записать
Рн я ПРм» р» = Ли = пл’Лм, (4.2)
где п — константа подобия (коэффициент, определяющий геометрическое подобие модели и натуры): т] — коэффициент несоответствия, который характеризует влияние отступления от точного выполнения требований физического подобия. При реальном моделировании т) определяется несоответствием химического состава материала модели и натуры, различиями условий трения, скоростного и температурного режима деформации. Поэтому общий коэффициент несоответствия можно представить как произведение частных коэффициентов, каждый из которых отражает несоответствие условий подобия для отдельных параметров процесса 1169]:
Л = (4-3)
где Лло !10> Лг — частные коэффициенты несоответствия, учитывающие соответственно влияние химического состава и
153
структуры материала, условия контактного трения, скорость деформации, скорость деформирования, температуру.
Указанные коэффициенты с достаточной точностью можно определить экспериментально (например, скоростные коэффициенты С. И. Губкина т]; приведены в работе (30), коэффициенты Т]т, зависящие от массы поковки,— в работе (44)). Поэтому в пределах технически необходимой точности по формуле (4.3) можно найти значение ц, по формулам (4.2) — значения рв, Ря и Аа.
5. Моделирование новых технологических процессов, намеченных для внедрения в производство. Решение этой задачи преследует цель — оптимизировать технологический процесс и оснастку, применяемую для его реализации. Как правило, отмеченная задача — одна из самых сложных. Приходится определять влияние разработанного процесса на структуру и механические свойства, пластичность и сопротивление деформации, изучать особенности характера формоизменения, находить значения р, Р, А, анализировать качество получаемых изделий, выяснять возможность и условия получения брака.
Таким образом, моделирование процессов ОМД дает возможность решать сложные задачи совершенствования существующих и оптимизации вновь создаваемых технологических процессов и штампов при наименьших затратах материалов, времени и использовании дешевого и универсального оборудования. В связи с трудностями выполнения требований температурного подобия до последнего времени многие специалисты отрицали возможность достаточно точного моделирования процессов горячей деформации. Сейчас можно с удовлетворением отметить, что теория подобия и моделирование все более широко используются в практике ОМД.
4.3.3. Критерии подобия и планирование экспериментальных исследований процессов ОМД. Теория подобия — это учение о подобных явлениях. Геометрическое подобие определяется константой п. При физическом подобии все величины, характеризующие состояние деформируемых тел (например, плотность р, температура Г, скорость v и др.), должны быть также подобными:
Рм/Рн = Лр, Ты/Ти = Л^, Vm/Vh = Лр,
где лр, пт, по — константы подобия физических величин р, Т, о.
Сложные физические процессы, а именно к ним относятся процессы пластической деформации, определяются многими физическими величинами, которые связаны между собой определенными законами. Поэтому константы подобия для этих величин нельзя выбирать произвольно. Например, для любой равномерно движущейся частицы скорость v — это отношение пути / ко времени t. Для модели и натуры = /М7М. = VfH-
Разделив второе равенство на первое, получим
— = 7-7- или
„ п‘ л» = ~.
nt
(4.4)
1S4
Отсюда следует, что для рассматриваемого процесса (при моделировании равномерного движения) можно произвольно задавать две константы, а третья определяется из уравнения связи между ними (4.4). Сгруппируем в левой и правой частях величины с индексами мин соответственно:
. (4.5)
*м * *и
Размерность этих частей [(м/с) • с/м] = [/°, /°], т. е. обе части — безмерные комплексы физических величин, характеризующих изучаемое явление. Поэтому их называют критериями подобия. Для подобных процессов критерии подобия сохраняют одно и то же числовое значение:
vt/l = К = idem. (4.6)
На основании второй теоремы теории подобия любая зависимость между переменными, характеризующими явление, может быть представлена в виде зависимости между критериями подобия Ki. К2. Кз и др. [79, 169]:
(КР ...» Кп) = 0. (4.7)
Это открывает широкие возможности для планирования экспериментальных исследований. Пусть, например, задана математическая модель процесса в форме
Рд = Ф (о,, р, a, b, I, h). (4.8)
Для проверки ее точности и установления допустимой области применения можно взять несколько материалов, изготовить из них образцы и осуществить деформацию в штампах, имеющих различные размеры a, b, I, h при разных условиях контактного трения. Если для a, b, I, h взять по пять значений, а для as, р — по три, то потребуется 5х5х5х5хЗхЗ = 5625 опытов.
Уравнение (4.8) можно представить в критериальном виде, например*
Fa, “ЦП. » у » yj- (4-9)
В этом случае правая часть уравнения определяется всего четырьмя комплексами р, a/h, b/h, Uh, а иногда и тремя р, аЫ№, Uh. Для проверки потребуется в 5 или даже в 25 раз меньше экспериментов, если взять (как и в первом случае) по три значения
р
* Критерий подобия —— принято называть относительным удельным Fa,
усилием деформации и обозначать р. Этот критерий широко используется при теоретическом анализе процессов ОМД (см. гл. 6).
155
at и p, по пять значений a!h, b/h, Uh (или ab!h\ Uh). Количество информации окажется большим, так как каждый из критериев, например a!h = const, можно рассматривать как отношение множества значений а = ih к множеству значений Л (i — действительное число).
Таким образом, приведение уравнения к критериальному виду позволяет сократить объем экспериментального исследования и, что не менее важно, представить в графической форме и проанализировать полученные данные гораздо быстрее и с большей точностью.
ГЛАВА 5
МЕТОДЫ ТЕОРЕТИЧЕСКОГО АНАЛИЗА ПРОЦЕССОВ ОБРАБОТКИ МЕТАЛЛОВ ДАВЛЕНИЕМ
5.1. ОБЩИЕ ПРЕДСТАВЛЕНИЯ О МЕТОДАХ
С развитием технологии обработки металлов давлением возникают сложные вопросы, связанные с определением усилий, затрат энергии, выбором оптимальных технологических параметров деформации и др. Ответы на них можно дать лишь на научной основе, используя различные методы исследования процессов обработки металлов давлением. Все методы исследования процессов ОМД можно разделить на три класса: аналитические, экспериментальные и экспериментально-аналитические.
Аналитические методы основаны на замене исследования реального физического объекта математической моделью, поведение которой с достаточной точностью отражает поведение физического объекта. Для аналитического исследования необходимо реальный материал и реальный процесс заменить их моделями. О моделях материалов речь шла в гл. 1. Модель процесса — это упрощенное представление о действительном процессе. Упрощения позволяют
154
описать процесс математически. Второй этап аналитического ио следования — детальный анализ математической модели процесса, т. е. получение зависимости усилия, работы деформации и других величин от параметров процесса деформации. Пластическая деформация сопровождается сложными физическими явлениями. Это приводит к тому, что зависимость между напряжением и деформацией в реальном деформируемом теле оказывается намного сложнее, чем в модели. Некоторые исходные величины (сопротивление деформации о,, контактное трение тж и др.) определяются на основании экспериментальных исследований с ограниченной точностью. Поэтому и результаты теоретического анализа необходимо оценивать критически. «Математика подобно жернову перемалывает то, что под него засыпают, и, как засыпав лебеду, вы не получите пшеничной муки, так, исписав целые страницы формулами, вы не получите истины из ложных предпосылок» [133, с. 231. Нужно обращать пристальное внимание на «засыпку», т. е. на исходные данные, которые используются для теоретического анализа, и соразмерять точность метода с точностью исходных данных.
В литературе по теории пластичности часто встречается термин «точные методы», означающий получение теоретического решения путем интегрирования дифференциальных уравнений равновесия совместно с условием пластичности. Действительно, с точки зрения механики сплошных сред это решение точное, но лишь до тех пор, пока считаем точными значения а,, тк и других исходных величин. Второй источник погрешностей при теоретическом анализе — это замена реального процесса деформации его моделью. Модель процесса тоже не может быть точной. Таким образом, ошибки, связанные с неточностью описания свойств тела, накладываются на ошибки, связанные с неточностью описания процесса. Если ошибки велики, то точность решения оказывается низкой. Чтобы оценить полученное аналитическое решение, необходима экспериментальная проверка.
Экспериментальные методы основаны на исследовании реальных материалов в реальных процессах. Иногда с целью уменьшения затрат на материалы и штампы исследования проводят на геометрически подобных заготовках уменьшенных размеров (см. подразд. 4.3). Однако и в том, и в другом случае удается обходиться без упрощающих допущений. Экспериментальные методы исследования детально описаны в работах [30, 36, 118, 127, 134, 145, 150, 170, 1781. Широкое распространение получили экспериментально-аналитические методы. Объединение эксперимента и теоретического анализа позволило создать мощный метод исследования даже самых сложных процессов ОМД.
Для исследования процессов ОМД используются разнообразные методы, изложенные ниже. Выбрать наиболее подходящий из них для анализа конкретного технологического процесса — нелегкая задача. Чтобы облегчить инженеру ее решение, отмечены до
157
стоинства и недостатки каждого из них, а в гл. 6 приведена табл. 6.1, где указаны классы решаемых задач и ограничения.
5.2. АНАЛИТИЧЕСКИЕ МЕТОДЫ
5.2.1. Инженерный метод. Теоретические основы инженерного метода заложили Э. Зибель [431, Г. Закс, С. И. Губкин [291, И. М. Павлов 11031 и другие ученые. Окончательная его разработка принадлежит Е. П. Унксову [1541, а уточнения и дополнения — М. В. Сторожеву, Е. А. Попову [1381. Идея метода про-
Рис. 5.1. Напряженное состояние в точке М при осадке полосы неограниченной длины:
а — в физическое полости; б — плоскости напряжений
ста. Поясним ее на примере осадки полосы неограниченной длины (рис. 5.1, а). В соответствии с законом наименьшего сопротивления
8^ = 0, =у (ох + aj. Пусть в некоторой точке М, лежащей вблизи контактной поверхности, напряженное состояние определено тензором
т я f <*х тжх 1
Для точки М условия равновесия
до ~ 0Т-- da,
—L J----H s Л- —— -I____- =
дх дг ' дх дг
Условие пластичности (о, - а,)’ + 4?Х1 = 4Л2.
(5.1)
(5.2)
Эта система содержит неизвестные величины ах, ах, тхх=тгх. Теоретически ее можно решить. Однако нелинейность уравнения (5.2) делает задачу практически неразрешимой. В нашем распоряжении имеется и другое условие пластичности — линей
158
ное (1.75). В нем фигурируют главные напряжения, которые нам не заданы. Конечно, пользуясь уравнением (1.48), тензор То можно перезадать тензором но и это не спасает положения, так как полученные компоненты alt os можно выразить через ох, ог, тХ2 только с помощью нелинейных функций. Пойдем по другому пути. Отобразим напряженное состояние в точке М на плоскость напряжений (рис. 5.1,6). Приняв тХ2>0, а т^сО (см. правило знаков в подразд. 1.5.2), построим для точки М круг Мора. Напряженное состояние в площадке F, проходящей через М и перпендикулярной к оси х, отображается точкой F на круге Мора, а напряженное состояние в площадке G — точкой G. Проведем FP^KL и GP'^KL, тогда точка Р — плюс. Проведем через нее линии* РК и PL. Они дадут направления главных осей /, 3 (и главных напряжений alt о,). Если тХ2<^Л, то a3 практически совпадают с ах, о, по направлению и по значению. Это даёт основание без большой погрешности заменить условие пластичности (1.75) условием
ох — ог = + о*. (5.3)
Если же тХ2->-Л, то
ох —о2 = 0. (5.4)
Присоединив выражение (5.3) или (5.4) к условию (5.1), можно легко разрешить полученную систему. Правда, для этого необходимо принять два упрощающих допущения: а) касательное напряжение линейно зависит от координаты z, т. е. тхг = ±Az; б) контактное касательное напряжение тк = тхг|г=л не зависит от координаты х и определяется условием Амонтона — Кулона или условием Зибеля (см. подразд. 3.2). Примем тк = цо2. Тогда
------г.
Продифференцировав условия (5.3), (5,4) по да
-г— »-г- . Воспользовавшись этим соотношением, <ur ох
(5.5), получаем из условия равновесия (5.1) да, 2ц а,
•Н — -~- = о. дх h
Решение этого уравнения имеет вид
о, = С ехр (—2цх/Л).
С помощью уравнений (5.3) или (5.4) находим ах, а (5.5) получаем тХ2.
Таким образом, для решения задачи инженерным обходимо заменить точное условие пластичности (5.2) ным (5.3) или (5.4) и принять допущения а), б). Е
(5.5)
х, находим уравнением
(5.6)
(5.7) из формулы
методом не-приближен-. П. Унксов
159
выполнил детальный теоретический анализ влияния этих допущений на точность решения и показал, что погрешность не превосходит 5% при тк < 0,ЗЛ, достигает 10% при тх « 0,4Л. По мнению Е. П. Унксова, условие пластичности в форме (5.3) можно с достаточной для инженерных расчетов точностью принимать, если 0 тк 0,7Л, и в форме (5.4), если 0,7Л < тк < k (154]. Аналогично решаются осесимметричные задачи. Инженерный метод дает возможность получать приближенные решения при определении усилия деформации и анализе простейших задач конечного формоизменения. Поэтому он постепенно уступает место более точным и универсальным методам.
5.2.2. Метод линий скольжения. Теоретические основы метода линий скольжения разработали Г. Генки [ 185], Л. Прандтль, X. Гейрингер, Р. Хилл (1651, В. Прагер и Ф. Ходж [114], В. В. Соколовский (136], С. А. Христианович. Большой вклад в его развитие применительно к решению задач ОМД внесли А. Д. Томленое [ 148], Л. А. Шофман (1781, И. П. Ренне 1117], Е. М. Макушок 1145], В. Джонсон и X. Кудо [361. Идея метода линий скольжения, к сожалению, не так проста, как идея инженерного метода. Поясним ее на следующем примере. При растяжении листовой заготовки на ее поверхности появлется специфический рисунок в виде линий Чернова—Людерса. Эти линии — следы сдвиговой деформации. Они совпадают с траекториями действия максимальных касательных напряжений. Если описать линии скольжения аналитическими функциями, то появится возможность определить компоненты тензора Т9 в любой точке.
5.2.2.1. Теоретические основы. Пусть напряженное состояние точки М задано тензором
Т = f 1
I ТХХ J
в произвольной координатной системе (рис. 5.1, а). Перезададим
напряженное состояние тензором Тга. Для этого воспользуемся
кругом Мора (рис. 5.1,6). Определим угол <р между осями х, z и главными осями /, 3. Выразим напряжения ох, ог, тХ2 через полусумму главных напряжений аср « 0,5 (а, 4- стз) и угол <р. Из треугольника AOF имеем ах = аСр+ОА, ОА — OF cos 2^. OF = = Tmax. Отсюда ox = <тср + тгоах cos 2q>. Аналогично из треугольника OBG находим ог = оср — ттах cos 2<р. Кроме того, из треугольников OAF и OBG определяем*
1тХ21 = | Т„ I = ± т = Tmax sin 2ф.
* Только при построении круга Мора знаки касательных напряжений определяют по правилу, принятому в курсе сопротивления материалов (см. подразд. 1.5.2).
160
Рнс. 5.2. Схема изменения положения главных осей 1 и 3 и направлений действия тпих = k в физической плоскости хг (MN, АВ — траектории главных касательных напряжений)
При пластической деформации ттах=^ (см. подразд. 1.6.2). Сле-дозательно,
°* = <*ср 4- k cos 2<р; а, = сгСр — k cos 2<р; т„ = + k sin 2<p. (5.8)
Эта система тождественно удовлетворяет условию пластичности (1.72). Положение главных осей /, 3 изменяется в пространстве координат хг и зависит от угла <р. Изменяется также положение главных площадок, по которым действуют главные касательные напряжения т13. Обозначим угол, образованный направлением действия т13 и осью х, через со. Величины со, ф связаны соотношением со = ф 4- л/4 (рис. 5.2). Воспользовавшись этим соотношением, можно выразить компоненты тензора напряжений через угол наклона площадок действия максимальных напряжений
ох = оср 4- k sin 2ш;
о2 = оСр — k sin 2(о;
т = + k cos 2<о. (5.9)
< Эта система должна удовлетворять условиям равновесия (1.66). После дифференцирования каждо
го из уравнений (5.9) по х и г соответственно, подстановки их в выражение (1.66) и упрощений получаем
4- 2Л (cos 2<о Т sin 2(0 = 0;
дх 1 \ дх дг ]
— 2Л (cos 2(0 + sin 2(0» 0. (5.10)
Система (5.10) определяет изменение первого инварианта тензора напряжений Т„ вдоль линии скольжения — траектории главных касательных напряжений. Возьмем произвольную точку L на линии скольжения MN. В точке L имеются две взаимно перпендикулярные площадки, в которых действуют напряжения Tmax = k Одна из них касается линии скольжения MN, другая линии скольжения А В. Выбор координатных осей х, г произволен, поэтому можно от системы хОг перейти к системе x'Lz, проходящей через точку L. При этих условиях со = 0 или (о = л/2. Сле-дэвательно, cos2(o = 1, sin2(o = 0, и систему (5.10) приводим к виду
^+2*^=0; ^-2*^=0. (5.11)
В каждой точке пространства, а значит, и в точке L, линии скольжения образуют естественную криволинейную систему ко
6 1-25
161
ординат т)£. В окрестности точки L производные по х и т>, по г и £ от переменных оср, <о одинаковы. Поэтому систему (5.11) можно преобразовать так:
£ (оср + 2*<о) = 0; - 2*ш) = 0. (5.12)
Интегрирование уравнений при k = const дает
оср 4- 2Л<о = F (С); оср — 2Л(о = Ф (л). (5.13)
Здесь F (С), Ф(т])— произвольные функции, постоянные вдоль координатных осей т], С соответственно. Уравнения (5.13) называются интегралами Генки (185). С их помощью можно иссле-
Рис. 5.3. Сетка линий скольжения и круги Мора для точек D и С при осадке заготовки трапецеидальной формы
довать напряженное состояние в плоских задачах. Для этого возьмем две точки (например, Л, В) на линии скольжения Л В, для которой С—const. Пусть напряжения в этих точках осрл, асрв, а углы сод, (од соответственно. Кроме того, пусть на линии скольжения АВ имеем С = Со- Тогда для точек Л, В из первого уравнения системы (5.13) осрл 4- 2Л(од = F (Q; асрв 4- 2Л(ов = = В(£о). Отсюда Осрл — асрв = —2Л((ол ~<ов).
Аналогично для точек М, N аСрм — = 2Л (ом — сод,).
Объединив оба выражения, получим основное уравнение метода линий скольжения:
^срм — = ±2Лсол<лг, (5.14)
где (&MN = (ом — (Од, — угол поворота линии скольжения при переходе вдоль нее от точки Af к точке N.
Таким образом, при движении точки вдоль линии скольжения т) или С среднее напряжение оср (и, следовательно, ст1 4~оя = = ох 4- изменяется прямо пропорционально углу поворота линии скольжения (о. Покажем, как с помощью уравнения (5.14) определить компоненты тензора напряжений 7\ в любой точке деформируемого тела. Пусть дана заготовка, имеющая в сечении форму трапеции (рис. 5.3), а также сетка линий скольжения т),
162
£ (метод построения сетки описан ниже). Определим компоненты тензора Тв в точке С. Воспользоваться уравнением (5.14) можно в том случае, если известно напряженное состояние хотя бы в одной точке. В рассматриваемом случае на гранях АК, BL напряжения известны. Возьмем например, точку D, лежащую на линии скольжения ц, проходящей через точку С, напряженное состояние которой нас интересует. В точке D имеем Oj =<тл=0; tbl =0; а/ = а* или ттах = k. Напряжение о3, действующее параллельно BL, неизвестно. Для его определения воспользуемся кругом Мора (рис. 5.3, OD). Из построения ясно, что осро =—к. Теперь можно воспользоваться уравнением (5.14) и определить осрс =acpD ± 2кшСо. Значение величины (aCD = у определяем через углы а, ₽ с помощью соотношения (лей = а 4- Р — л/4. Знак coCD можно установить, рассуждая таким образом. На свободной поверхности деформация нестесненная. В глубине деформируемого тела и на контактных поверхностях инструмента она всегда стесненная, поэтому абсолютное значение ]сгср возрастает. В точке С деформация стесненная. Значит, |асрс| > |осро|. Отсюда асрс = —k — 2k (а 4- Р — л/4). Чтобы определить компоненты Т„с, воспользуемся кругом Мора (рис. 5.3, Ос). В точке С для него задано oc₽c и ттах = к. Построение выполняем так: из точки С перпендикулярно CF проводим СМ, из произвольной точки Ot — ось т. Откладываем Ofic =оСрс. Из точки Ос, как из центра радиусом k, проводим окружность. В точке С в площадках CF и СМ действуют напряжения ттах=£, 0пс=0срс. Напряженное состояние в этих площадках отображается на круге Мора точками Clt С2. Чтобы найти напряжения ах, иг и Oj, а3 в точке С, находим полюс круга Мора Р. Для этого из Ct проводим С,Р параллельно CF и С2Р — перпендикулярно CF-, так как Р = л/4, полюс Р совпадает с точкой С3. Поэтому направление главной оси / определяется линией МС2, а главной оси 3 — линией NC2. Направление МС2 совпадает с Охх. Значит, = ах. По той же причине и3 = о2. Из круга находим Охе — = 0с₽е 4- k = —2Дга;
0х? = 0Я = 0cpc — k = —2k (1 4- а). Аналогично можно найти напряжения в любой другой точке деформируемой заготовки (в пределах очага деформации). Совершенно очевидно, что при а?=0, т. е. когда осаживаем прямоугольную заготовку, ах = 0, а напряженное состояние описывается известным соотношением ох = — 2k.
Иногда не удается найти линию скольжения, проходящую через нужную нам точку, где есть другая точка с известным напря-Ж'нным состоянием. Тогда находим любую точку, где напряженное состояние известно (например, D), и соединяем ее любой ломаной линией (желательно кратчайшей и с наименьшим количеством переломов), проходящей по линиям семейства q. £, с той точкой (например, Е), напряженное состояние которой необходимо вычислить. Если сетка линий скольжения описана аналитически или
6*
163
построена графически, то совсем нетрудно определить (oDe. а затем по формуле (5.14) вычислить осрв и с помощью круга Мора найти компоненты тензоров 7\, Тга. Применение круга Мора не обязательно. Для определения компонент тензоров Та, Т, можно воспользоваться формулами преобразования, но это, как правило, приводит к более громоздким вычислениям и, что более важно, скрывает физический смысл рассматриваемой задачи.
Таким образом, задача исследования напряженного состояния (при плоском напряженном или плоском деформированном состоянии) решается с помощью уравнения (5.14) достаточно просто, если известна сетка линий скольжения. Поэтому один из главных вопросов в методе линий скольжения — это способ построения сетки линий скольжения.
5.2.2.2. Способы построения сетки линий скольжения. Построить сетку линий скольжения, пользуясь аналитическим ее описанием, удается только для небольшого класса задач ОМД. Например, при вытяжке детали с фланцем в нем возникает на-пряженное состояние, характеризуемое тензором Т9 = |о aJ- Так как тге = Т9Г = 0, то аг, сте — главные напряжения. Значит, линия скольжения в каждой точке фланца пересекает радиус под углом л/4. Как известно, таким же свойством обладает логарифмическая спираль. Ее уравнение
г—ае*. (5.15)
Уравнение (5.15) дает возможность построить два семейства линий скольжения ц, С. На наружной поверхности аг = 0 и в точке А асрл = —Л- Это следует из круга Мора (как на рис. 5.3, Od) или из условия пластичности иг — ое = 2Л, откуда при аг = = 0 имеем ст® = — 2k, осрл = 0,5 (ог +<*•) = —k. На внутренней поверхности (на начале изгиба фланца по вытяжному ребру) в точке В напряжение осрВ можно определить по формуле (5.14). Обозначим ОА = ₽н, OB = Rt. Согласно формуле (5.15) при переходе из точки А в точку В линия скольжения поворачивается на угол солв = InПоэтому осрв— осрл = ±2k In /?н/₽в-Отсюда осрв = —k ± 2k In /?я/₽в- Вопрос о знаке при втором числе пока оставим открытым: выясним его позже на основании физического смысла задачи. По определению, асрв = 0,5 (агв + + аев). Следовательно, агв + = — 2k ± 4k In /?и/₽в. Кроме
того, из условия пластичности агв— оьв = +2к. Объединим эти два уравнения в систему, решим ее: игв = + 2k In RH/R», 09в = = —2k(l + In Rh/Rb). Теперь знак можно установить без труда: фланец деформируется за счет втягивания металла в матрицу, поэтому Огв — напряжение растяжения, т. е/ о,в>0. Значит, нужно взять знак 4-. Тогда получим окончательно
о,В = 2Л In «,//?,; OIB = —2* (1 — In /?„/?.). (б. 16)
164
Аналогично решаются задачи о растяжении внутренним давлением длинной трубы, сжатии трубы наружным давлением, деформации кольцевой части заготовки при открытой прошивке. Однако класс задач, для которых сетку линий скольжения можно описать аналитическими функциями, очень ограничен. Поэтому приходится прибегать к другим, более сложным методам построения линий скольжения.
В работах Р. Хилла (165), В. В. Соколовского (136), Е. М. Макушка (145) даны точные методы построения сеток линий скольжения с использованием функций Бесселя. Пользуясь этими методами, можно вычислять координаты узловых точек сетки (например, рис. 5.4, табл. 5.1) и решать некоторые прикладные задачи ОМД. Покажем это на примере прессования плоской заготовки в шероховатом контейнере. Построим на листе ватмана двухцентровую веерную сетку (рис. 5.5) по табл. 5.1.
Таблица 5.1. Координаты узловых точек двухцентровой веерной сетки линий скольжения с шагом 15° [165|
Индекс Координата Индекс Координата Индекс Координата
X 2 X х | X г
1,1 0,428 0,000 2,3 1,333 0,413 3,6 2,804 2,414
1,2 0,647 0,286 2,4 1,552 0,944 4,4 3,134 0,000
1,3 0,792 0,639 2,5 1,634 1.571 4,5 3,830 0,937
1.4 0,845 1,040 2,6 1,545 2,256 4.6 4,370 2,205
1.5 0,789 1,464 3,3 1,867 0,000 5,5 5,060 0,000
1.6 0.617 1,880 3,4 2,338 0,615 5,6 6,170 1,453
2,2 1,018 0,000 3,5 2,673 1.429 6,6 8,040 0,000
Нанесем на полученный чертеж контур штампа для прессования в масштабе М так, чтобы точки А, В веерной сетки совпали с началом калибрующего пояска матрицы. Пусть стенки матрицы КС, LD касаются линий скольжения AA4Q, BNQ соответственно*. Тогда контур ABNRMA ограничит очаг деформации, а контуры RNDCMR, АКМ, BLN — жесткие зоны. Имея сетку линий скольжения в очаге деформации, можно выполнить детальный анализ напряженного состояния.
К сожалению, такой стандартный прием подходит для решения ограниченного класса задач (внедрение пуансона в пластину, волочение листа через клиновидную матрицу, выдавливание в клиновую полость, прессование), только при условии [тк| = k. Большинство задач объемной штамповки приходится решать иными способами, ибо построить для них сетки линий скольжения таким стандартным приемом невозможно. В этих случаях приходится использовать графические методы построения сетки линий сколь
• Если КС, LD не пройдут через узловые точки М, N, то нужно взять сетку с меньшим шагом (например, 5° 1150]).
165
жения. Рассмотрим некоторые из них. Однако прежде остановимся на свойствах линий скольжения, облегчающих построение.
Линия скольжения— это траектория максимального касательного напряжения. Отсюда вытекает четыре простейших свойства
Рис. 5.4. Двухцентровая веерная сетка линий скольжения с шагом 15° [165]
Рис. 5.5. Сетка линий скольжения для прессования плоской заготовки через шероховатый контейнер
линий скольжения: линии скольжения непрерывны; образуют два семейства ц, как угодно густо п жрывающие очаг деформации; линии скольжения семейства т] ортогональны линиям скольжения . семейства £; линии скольжения пересека-
ют траектории главных напряжений под уС углам. п/А.
/ \ Еще одно свойство доказывается с по-
/ V. мощью теоремы Генки (136, 148, 1851.
Угол между касательными, проведенными к ДВУМ линиям скольжения одного семей-ства в точках пересечения их линиями другого семейства, остается постоянным * вдоль линий скольжения.
л Для доказательства рассмотрим криво-‘ * линейный четырехугольник ABCD, обра-Рис. 5.6. Схема к дока- зованный точками пересечения линий зательству теоремы Генки скольжения q. $ (рис. 5.6). Через точки А, В, С, D проведем касательные к линиям семейства т] до пересечения их в точках Р, Q. Обозначим <4РВ = <р, <CQD = ф. Очевидно, что ф = ыв — шд, ф = = со© — о>с. Установим связь между ф, ф. Для этого каждое из уравнений системы (5.12) продифференцируем по т), £ и вычтем
166
одно из другого. Получим дифференциальное уравнение второго порядка = 0. После его интегрирования имеем
со = Ф(Л) + F(£). (5.17)
Здесь Ф(п). F(C) — произвольные функции от т), С, постоянные вдоль координатных осей т), £.
Пользуясь уравнением (5.17), определим углы «о, образуемые касательными АР и BP, CQ и DQ с осью х:
“л = ф (Пл) + F (Сл); “с = ф (*1с) + Г (W:
% = ф (nfl) + f (Св); “о = ф (По) + F (Со). (5.18)
z
Рис. 5.7. Сетка линий скольжения для осадки ступенчатой полосы неограни* ценной длины (для упрощения рисунка взят большой шаг Д<р)
В координатной системе т]£ при движении вдоль линии t значение величины т) остается постоянным. Поэтому Ф (т]л) = Ф(т]а) и Ф(Лс) = Ф (%)• Углы <р, ф найдем путем почленного вычитания уравнений (5.18):
Ф = F (Q - F (Q; ф = F (Q - F (£с). (5.19)
При движении вдоль линии т] значение величины $ остается постоянной, поэтому F(£B)=F(l^D) и F (£л) = F (£с), а из выражения (5.19) вытекает очень важное для практического использования соотношение ф = ф. Оно и выражает содержание теоремы Генки. Теорема Генки позволяет использовать графические методы для построения сетки линий скольжения. Наиболее широкое распространение получили графические методы построения кусочно линейных сеток (98, 176].
Рассмотрим осадку ступенчатой полосы неограниченной длины. В силу симметрии задачи возьмем только четверть заготовки, расположенной в первом квадранте (рис. 5.7). Под углом л/4 к оси х проведем линию АВ. Она выделит область деформируемой заготовки АОХВ, примыкающую к свободной поверхности ЛОР Это
167
область равномерного напряженного состояния. В ней линии скольжения семейства т|(аЬ) располагаются параллельно АВ, а линии семейства t(ac) — перпендикулярно АВ. Обычно сетку ab~ас в области AOJ3 не показывают. К области AOiB примыкает область АВС. Здесь имеем веерную сетку линии скольжения: линии семейства т] — радиусы, а линии семейства С — дуги окружности. В пределах области ЛВС дуги (например, de) не показываем. Проведем из особой точки А пучок прямых с шагом Дгр. Для получения приемлемой точности необходимо принимать в пределах л/24...л/36. Перенумеруем полученные линии (0, 1, 2 и т. д.). Линии семейства £ тоже перенумеруем, начиная с ВС (О, 1, 2 и т. д.). Условимся называть узлы, образованные пересечением линий семейств г) С. двумя цифрами — номерами пересекающихся линий. Заменим дугу ВС ломаной 0,0—1,0—2,0 и т. д. Эта линия — исходная для построения кусочно-линейной сетки. Построение начинается на отрезке 0,0—1,0. В любой точке, в том числе и в точке 1,0, линии семейств т), С ортогональны. Проводим линии 1,0—1,1 перпендикулярно линиям 0,0—1,0. Из точек 2,0 и 1,1 проводим линии 2,0—2,1 и 1,1—2,1 перпендикулярно линиям 1,0—2,0 и 0,1—1,1 до пересечения в точке 2,1. Полученный четырехугольник—типичный элемент сетки линий скольжения. Он имеет два прямых угла (в вершинах 2,0 и 1,1) и два угла, отличающихся от прямого (в этом единственная неточность метода построения): в вершине 1,0 угол равен ~ + 4Дф, а в вершине
2,1 — ~ Д<р. Эти углы характерны для всех элементов сетки линий скольжения (см. четырехугольник 6,5—7,5—7,6—6,6). Отсюда выводим простой алгоритм построения: любой последующий узел /, т получаем как точку пересечения прямых 1(т — 1)—1т и (/—1)/п—тп, проведенных перпендикулярно прямым 1(т — 1) — —(/ — 1)(/п — 1) и (/ — 1)/п — (/ — 1)(/п — 1) соответственно.
При построении сетки может встретиться несколько особых точек. В рассматриваемом случае — это точки A, D. Здесь сетка образует веер. Последняя линия скольжения семейства т), выходящая из D, должна обязательно проходить через точку О (проекция на хОг линии пересечения плоскостей симметрии Ох и Ог). Чтобы добиться этого, необходимо подобрать такой угол 6,2—D—7,2, при котором линия 7 пройдет через О. Обычно это удается достигнуть обратным построением линии 7 от точки О. Как видно из рис. 5.7, сетка линий скольжения делит поковку на две области: очаг деформации (40j0D/1) и жесткую зону (DOFE). Очаг деформации включает область равномерно-напряженного состояния (ЛО1В), веерную область (АВС), где напряжение изменяется только вдоль С, и область неоднородного напряженного состояния (BCDOB), где напряжение изменяется и вдоль т], и вдоль £.
Имея сетку линий скольжения, можно определить напряженное состояние в любой точке по формулам, которые легко получить
168
на основании интеграла Генки и формул преобразования (176,
°х) = оСр(0,0) — 2Л (/ 4- т) Дф ± k cos 2(1 — т) Дф;
тя = k sin 2 (I — т) Дф. (5.20)
Здесь /, т — индексы узловой точки.
Точность построения кусочно-линейной сетки линий скольже-ния по методу Л. А. Шофмана высока. При шаге Дф = ... по-
грешность не превышает 1,5% (1761. Это позволяет использовать кусочно-линейные сетки для решения любых технических задач. Но сетку линий скольжения для данной задачи можно построить не единственным способом. Например, есть различные сетки для осадки заготовки трапецеидальной формы, внедрения плоскою штампа в пластическую среду и др. Поэтому вопрос о корректности построения решается путем анализа кинематических граничных условий (36, 114, 136, 149, 150, 165, 178, 189, 191].
5.2.3. Энергетический метод. Теоретические основы энергетического метода разработали Н. С. Петров 11381, Э. Зибель [43], И. Я. Тарновский, А. А. Поздеев, О. А. Ганаго [143, 146]. Большой вклад в его развитие внесли А. Г. Овчинников [95], Л. Г. Степанский [ 137]. Идея этого метода достаточно проста и очень наглядна. Поясним ее на примере, хорошо знакомом читателю из курса теоретической механики. Пусть дано тело, равномерно движущееся вверх по наклонной плоскости с углом подъема ф. Пренебрегая трением, определим силу /?, приводящую тело в движение. Решение этой задачи можно вести с позиций статики, рассматривая условия равновесия тела под действием силы тяжести G и движущей силы R. Можно вести его и с позиций энергетических, рассматривая уравнение баланса работ сил R, G: при бесконечно малом перемещении тела 6R в направлении силы R затрачивается работа, которая равна работе силы тяжести G на перемещении 60 вдоль направления действия силы G, т. е.
/?6Л=С6О. (5.21)
Перемещения 6G, связаны очевидной зависимостью 6G = «= 6^ sin ф. Поэтому силу R легко определить из условия (5.21). С таким же успехом вместо перемещения 6R можно задать скорость движения тела по наклонной плоскости vR, определить из геометрических соотношений скорость подъёма тела vQ и найти силу R на основании условия сохранения мощности. По этой причине в литературе встречается несколько названий: метод работ, метод баланса работ, метод баланса мощностей и т. д. Однако во всех случаях используется закон сохранения энергии. Следовательно, точнее называть его энергетическим. Такое название является более
169
обобщенным и охватывает как частные разновидности метод баланса работ, метод баланса мощностей.
5.2.3.1. Теоретические основы. Пусть тело, находящееся в состоянии пластического течения, имеет форму, описываемую уравнением Ф(х, у, z, t) = 0. Возьмем бесконечно малый промежуток времени dt, за который тело получит дополнительную деформацию, а внешние силы совершат дополнительную работу dA9. Эта работа затрачивается на преодоление внутренних сил сопротивления де-формаци dAd и сил трения на контактных поверхностях dAT. На основании закона сохранения энергии можно записать
dAB = dAd + dAr. (5.22)
В процессах ОМД всегда известно направление перемещения деформирующего инструмента, а направление активной силы Рд, вызывающей деформацию тела, совпадает с направлением перемещения. Поэтому
dAB = Pddu, (5.23)
где Рд — переменная в процессе деформации активная сила, численно равная силе сопротивления деформации (см. подразд. 1.1); du — бесконечно малое перемещение деформирующего инструмента за время dt. В силу принятого условия dt -+ 0, можно считать, что на малом этапе деформации Рд = const. Подставив выражение (5.23) в уравнение (5.22), найдем
Р«-Ё(Л4э + Л4т). (5.24)
Эта формула дает возможность рассчитать деформирующее усилие Рд в момент деформации t, если известны значения dAd, dAT.
Работу внутренних сил сопротивления деформации dAd за время dt можно вычислить следующим образом. В объеме деформируемого тела выделим элемент с ребрами dx. dy, dz. В общем случае на гранях элемента действуют напряжения Sx, Syt S,, а каждая грань получает перемещения dux, duy, du,. На это затрачивается работа
dАд = f J (Sxdux + Svduy + S,du,)dF. (5.25)
F
Напряжения Sx, Sy, S, выразим через компоненты тензора напряжений по уравнениям (1.42). Тогда уравнение (5.25) примет вид
dAa = Й U°x du* + х*у fay + т« dui)а* +(Ь« fa*+ F
+ о у du у + ху, du,) ау + (ти dux + х,у duy + о, du,) a,] dF. (5.26)
Это уравнение имеет ясный физический смысл: выражает работу всех компонент напряжений тензора Т„ на соответствующих перемещениях в элементарном объеме деформируемого тела. На осно
170
вании формулы Гаусса—Остроградского уравнение (5.26) можно преобразовать в следующее:
+ a*didu* + avdyduv + a*d2 du* +
Х*и [ду du* + дх dUyj Ti* dUy + ду du^ + Ьх du, ч- du,)] dV.
Приняв во внимание условия равновесия (1.66) и уравнения Коши (1.15), получаем для dA# уравнение более простого вида:
dAd = И J (а* + Оу dev + °*de> + х*и d4*y + 1уг dyVz +
+ T„dV2x)^. (5.27)
При пластической деформации девиаторы деформаций и напряжений связаны соотношением D. = Wa, где X = Зе{/2а(. Отсюда легко опр$д£лить компоненты деформации и их дифференциалы:
Зв/ 3dez
6* = 2а^ (<Т* “ ас₽); Yw в 2^ <а* ОсР); dykt =
3det-= 2^7 т«-
Здесь k, I — обобщенные координаты, последовательно принимающие значения х, у, г. Подставив значения deA, dyA/ в формулу (5.27), после преобразований получим
dAd ” № & К’»-’»)2 + -°«)2 +
I
+ 6 (< + т’, + rL)J dV. (5.28)
Выражение в квадратных скобках — это удвоенный квадрат интенсивности напряжений а/. При пластической деформации oi = а,. Поэтому уравнение (5.28) можно представить в более компактном виде:
d'4‘, = JH<’.<ie<dV- (5.29)
Определим работу сил трения dAr. Пусть F — площадка контактной поверхности, ориентированная в пространстве произвольным образом. Работа — величина инвариантная к преобразованию координат. Поэтому изменением положения координатных осей можно сориентировать площадку перпендикулярно какой-либо
171
оси, например, z. Тогда полное напряжение S, действующее в площадке, можно разложить по осям на составляющие ох, тХ2, тух. Если осьз совпадаете направлением перемещения инструмента, то работа силы OgdF учтена как работа силы сопротивления деформации, а работа сил xxxdF и TygdF — искомая работа сил трения dA-t. На контактной поверхности деформируемой заготовки тхх + тух = тк. Вектор тк направлен в сторону, потивоположную направлению вектора перемещения du. Величина du определяется как геометрическая сумма компонент перемещения duxt duy. Поэтому работу сил трения на поверхности F выразим как
dAT = ( J тк V du2x + dufaF. (5.30)
f
Если ось z не совпадает с направлением перемещения инструмента, то работа силы axdF обратится в нуль, так как перемещение деформируемой заготовки в этом направлении запрещено инструментом. Сила atdF вызывает упругую деформацию инструмента и обусловливает его износ.
Таким образом, вычислив для данного момента деформации приращения работы деформации dAe, dAr на бесконечно малом перемещении du за бесконечно малый промежуток времени dt, можно по формуле (5.24) определить усилие деформации Р^. Решение этой задачи достаточно четко алгоритмизируется. Основные шаги алгоритма можно охарактеризовать следующим образом.
1. Задаемся бесконечно малым перемещением деформирующего инструмента du на любом интересующем нас этапе деформации и определяем во всем объеме деформируемой заготовки приращения перемещений по координатам х, у, z как функции du:
dux = fx (du); duy = fy (du); du2 = fz (du). (5.31)
2. На основании полученных функций dux, duy, du2 находим компоненты девиатора приращений деформации и вычисляем приращение интенсивности деформации de(.
3. По формуле (5.29) находим dAd как функцию du: dAd s
= Фд (du) = asde£ dV.
V
4. По формуле (5.30) вичисляем dAT как функцию du: dAr = = Ф (du) = j J тк Vdul + du2dF.
F
5. По формуле (5.24) определяем усилие деформации
± a, de, dV + f j т, Vdui + du?df]. (5.32)
Наиболее сложный шаг этого алгоритма — получение функций приращения перемещений (5.31). Чтобы его облегчить, используют простейшие модели течения: очаг деформации разделяют на ряд
172
областей, в пределах которых деформацию с достаточной для технических расчетов точностью можно считать однородной. Тогда функции (5.31) оказываются линейными, их легко получить из граничных условий на контактной поверхности заготовки и условия постоянства объема. Значительно облегчаются и последующие этапы, например, интегрирование для вычисления работы Ад. Но при использовании такой модели течение металла в очаге деформации схематизируется сравнительно грубо. Чтобы не получить большой погрешности, затраты энергии на неравномерность деформации необходимо учесть как дополнительную работу. Проще это сделать путем введения работы сдвига. Предположим, что в очаге деформируемого тела выделены две области, в которых
Рис. 5.8. Схема к определению работы сдвига
Рис. 5.9. Схема осадки кольца, — радиус поверхности раздела течения
приращение перемещения dux изменяется по координате (рис. 5.8). Описать аналитически такое поле перемещений сложно. Поэтому допускаем, что переходная область dxx, в которой duz изменяется достаточно сильно, сужается до dx= 0. Тогда на границе областей А, В появляется разрыв перемещений &(dux). В областях А, В принимаем соответственно duXA = const, diitB = const.
Работа, которая в реальных условиях деформации затрачивается на деформацию в области dx, частично учитывается как работа внутренних сил в областях А, В. Чтобы учесть ее полнее, введем работу сдвига dA0 на поверхности разрыва G:
dA<*=
xJdUtB — duxA IdG.
(5.33)
Совершенно очевидно, что для определения усилия деформации необходимо в формулу (5.24) добавить работу сдвига и учесть, что очаг деформации разбивается на ряд областей. Таким образом, приходим к первому основному уравнению энергетического методам н м
[2 dV+S Ит* ^du*+du‘dF+
N
— du/|dG], (5.34)
л—1 G
173
где k, I — обобщенные координаты (х, у, г. г, 6); Н — количество облает чй, на которые разбит очаг деформации; М — количество поверхностей трения, где рассчитывается работа dAT; N — количество поверхностей разрыва перемещений.
В уравнении (5.34) усилие определено через перемещения. Поэтому оно позволяет не только определять усилие дефэрмации, но и решать задачи, связанные с анализом конечного формоизменения. Например, при осадке на плитах с отверстиями (рис. 4.3) или осадке кольца (рис. 5.9) усилие Ра зависит от того, какие значения Rn будут взяты в качестве исходных для определения функций (5.31). Конечная формула для определения усилия осадки кольца (см. подразд. 6.6)
Р& — F (of, И» Рн» Н, ^р)- (5.35)
Подставляя в нее различные значения /?р при постоянных of, р, /?я, /?в, Я, получим кривую Рд = Р(/?Р). Вид этой кривой можно прогнозировать на основании закона наименьшего сопротивления. Эксперименты показывают, что при осадке с трением диаметр кольца увеличивается, а диаметр отверстия уменьшается. Это значит, что течение металла происходит в двух направлениях наименьшего сопротивления от поверхности раздела течения. Изменим граничные условия так, чтобы = 0. Это можно сделать, вставив кольцо в матрицу. Очевидно, что прежнее направление наименьшего сопротивления частиц А, для которых /?р^г< /?н, изменится на новое, противоположного знака, которое не будет направлением абсолютно наименьшего сопротивления. Следовательно, при /?р = RH усилие больше, чем при /?в < Rp < R„ (см. подразд. 4.1, рис. 4.3, 4.4). Аналогичная картина получится и в том случае, если запретить движение частиц В (для которых Rb<r^Rp) в направлении к центру. Таким образом, кривая Pd = F(Rp) — это унимодальная функция, выпуклая вниз, имеющая минимум при R*< Rp< R„. Если функция Pd = F(/?p) известна, легко определить положение поверхности раздела течения Rp из уравнения
дРл
3^ = 0. (5.36)
р
Это второе основное уравнение энергетического метода*. Оно дает возможность исследовать конечное формоизменение (см. подразд. 6.6).
Наконец, аналогичные уравнения можно получить, рассматривая процесс деформации в переменных Эйлера. Перемещения du, dux, duy, dut происходят за время dt. Разделив каждое из них на dt, получим du/dt = о0 — скорость перемещения деформирую*
* В знаменателе уравнения (5.36) может стоять любая координата, определяющая положение раздела течения (см. подразд. 6.6.3).
174
щего инструмента (скорость деформирования);dux/dt = их, duyldt » = vy, dujdt = vz — компоненты скоростей перемещения частиц деформируемого тела (составляющие поля скоростей). Имея их, vz, определяем компоненты тензора скоростей деформации 7\ (см. уравнения (1.35)), находим интенсивность скоростей деформации
и приводим уравнение (5.35) к виду н м
W т« +
ft=i J V m-1 F
N
+ 2 (5-37)
n«l G
где — интенсивность скоростей деформации (см. подразд. 1.4); V*, Vi — компоненты скоростей перемещения частиц деформируемого тела (составляющие поля скоростей). Остальные об<> значения такие же, как и в уравнении (5.34).
Второе основное уравнение энергетического метода (5.36) не зависит от того, в каких переменных (Лагранжа или Эйлера) рассматривается процесс деформации.
Итак, задача определения усилия деформации Рд и исследования формоизменения решается при помощи уравнений (5.34), (5.37) достаточно просто, если известны функции перемещения (5.31) или функции скоростей перемещения vx = fx(y0), vy~ = fy(v0), vtv=tz{vaY Поэтому один из основных вопросов в энергетическом методе — это способ определения функций перемещения их, Uy, иг или скоростей их, vy, иг.
5.2.3.2. Способы определения функций перемещения или поля скоростей. Способы описания движения сплошной среды в переменных Лагранжа и Эйлера равноправны. Но последний дает некоторые преимущества. В дальнейшем нам чаще придется пользоваться переменными Эйлера. В этой связи рассмотрим способ определения функций скоростей перемещения. Пусть необходимо решить задачу выдавливания цилиндрического стакана (рис. 5.10). Эксперименты показывают, что деформация в этом процессе весьма неравномерна, но значительные сдвиги имеют место в области, примыкающей к цилиндрической поверхности АВ. Применяя схему разрывных решений, разделим очаг деформации на области 1, 2, отделенные друг от друга поверхностью г = гП. Считаем, что деформация в областях /, 2 однородная, а сдвиги сосредоточены на поверхности г — гп. Функции vr, t>e, vz определяются просто. В силу осевой симметрии задачи ив = 0. Рассмотрим деформацию области / (рис. 5.10, б). На ее границах г = 0, z = h известны скорости и2 = 0, v2——v0. Принятое допущение об однородности деформации дает основание считать, что иг1 =—Аг. Из граничного условия Vziz^h = — Vq находим А — v0/h. Тогда
= —VnZ/h, 0 г h. (5.38)
175
Для определения v, воспользуемся условием постоянства объема в дифференциальной форме (1.38). Преобразовав его, полу* чим
(5.39)
Рис. 5.10. Расчетная схема выдавливания детали типа стакана (а), динамнче* ские граничные условия и поля скоростей для областей 1 (б) и 2 (в)
Это общее уравнение позволяет находить компоненту скорости vr при любой осесимметричной деформации. Для рассматриваемой области vr = 0 при г = 0, поэтому С = 0. Подставив выражение (5.38) в (5.40), находим
Vri^o^r/ih. (5.41)
По уравнениям Коши (1.35) получим компоненты тензора скоростей деформации
= v9/2h’t e = = 0. (5.42)
Как видно, компоненты Ьь bi являются также компонентами скоростей главных деформаций, а оси г, г — главными осями /, 3. Легко убедиться, что £,i, gei, £zi удовлетворяют условию постоянства объема (1.38). Это должно следовать из условия (5.40). Тем не менее, такая проверка позволяет обнаружить возможные ошибки в выкладках, особенно, если приходится иметь дело со сложными выражениями. Воспользовавшись уравнением (1.31), определим интенсивность скоростей деформации
Ь » v0/h. (5.43)
176
Таким образом, функции (5.38), (5.41) дают возможность де* тально описать состояние деформируемого тела в области 1. Как видно из выражений (5.38), (5.4 I), функции vn, vzl не зависят от г, г соответственно, а поля скоростей во всем объеме области / имеют вид, показанный на рис. 5.10, б.
Перейдем к анализу деформации кольцевой области 2. Для нее имеем следующие граничные условия (рис. 5.10, в): ufjx»os = 0; в 0; Ur|r-rn= vrp. Компоненту определяем из уравнения (5.41) при гвгп. Допущение об однородности деформации в области 2 дает основание считать иг? = Вг. Постоянную В легко определить из условия постоянства объема: nr2}v9 == л (Rl—
ОоГ2 г2
— r£) »z2iz-h- Отсюда dz2|z=a = -2 п 2; Я = v zr" -2 • Следова-^м~гп *ы~гп
тельно,
= (5-44>
Скорость 0г2 найдем, воспользовавшись уравнением (5.40): [2
Ро ГП Г* .
л • ^77» • 2 + с •
Произвольную постоянную интегрирования С получаем из граничных условий. На поверхности раздела г = га не может быть разрывов компонент скорости, нормальных поверхности. Поэтому 1>г2|л-гп = Oriir-zn* Значение при г = гв легко установить из уравнения (5.41). Значит,
=_____1 Гр« г" г2 I г!
2* " г„ [2* +
Отсюда р °* г2- п р* г"
С 2Л р2 2 г"« Vr2 ~ 2Л /?2 2 г • (5.45)
Определяем компоненты тензора скоростей деформации:
Г2 fD2 \ г2 ю2
t = - °0 " I и • =°* г"___
6/1 2Л/?2_2^^
п t °о гп 5x2 = Л -г2 ’ гп
(5.46)
Подставив эти значения в формулу (1.31), найдем интенсивность скоростей деформации для второй области:
(5.47)
177.
Таким образом, функции (5.44), (5.45) дают возможность детально описать состояние деформируемого тела в области 2. Как видно из выражений (5.44), (5.45), функции vri, vxt не зависят от г, г соответственно, а поля скоростей во всем объеме области 2 имеют вид, показанный на рис. 5.10, в.
Совершенно очевидно, что система уравнений (5.38), (5.41), (5.43), (5.44). (5.45), (5.47) позволяет достаточно легко решить задачу об определении усилия выдавливания детали типа стакана при использовании основного уравнения энергетического метода (5.37). Если бы пришлось решать задачу выдавливания в условиях плоской деформации, то вместо уравнения (5.40) можно получить аналогичное
v, = -j^dx + C. (5.48)
Для решения трехмерных задач нужны дополнительные уравнения (их получают на основе экспериментов или упрощающих допущений), связывающие скорости перемещения vx, vy и v2. Тогда, приняв vz= Az и определив связь их, иу в виде vy = = f(vx), можно найти необходимые функции и решить поставленную задачу.
Итак, приняв простейшую модель деформации, мы смогли определить поле скоростей и построить функции (5.38), (5.41), (5.44), (5.45) для обеих областей однородной деформации. Однако поле скоростей для всей деформируемой заготовки в целом получилось разрывным. Действительно, при г — г„ 4- Дг иг > 0, а при г = г„ — — Ar < 0. Разрыв Дц = |цХ2 — | увеличивается с увеличе-
нием координаты z и при z = h достигает (Ди)т„
“Гп
Чтобы учесть работу внутренних сил на поверхностях разрыва скоростей и получить приемлемую точность расчёта, нужно в формуле (5.37) учесть все поверхности, где есть разрыв скоростей. Аналогичным образом можно строить функции приращения перемещения.
5.2.4. Вариационные методы. Теоретические основы вариационных методов разработали А. А. Ильюшин 1461, Л. М. Качанов {511, Л. С. Лейбензон 1691, С. Г. Михлин (831, И. Я. Тарковский, А. А. Поздеев, О. А. Ганаго 11431, В. Джонсон 11871, X. Кудо [189]. Вариационные методы основаны на использовании закона сохранения энергии, т. е. по сути являются энергетическими. Однако они отличаются большей гибкостью. С одной стороны, они позволяют очень простыми средствами получить приближенную верхнюю оценку усилия деформации даже для сложных задач, а с другой стороны, обеспечивают точное решение (на основании модели течения, в максимальной степени приближающейся к реальному процессу). Широкому распространению этих методов способствовало расширение возможностей ЭВМ и создание надежно
178
работающих стандартных программ. Важно, что во многих случаях вариационные методы дают возможность найти решение, оптимальное по какому-либо параметру.
5.2.4.1. Прямой вариационный метод. Идея этого метода основана на принципе минимума полной энергии деформации. Предположим, что для описания поля скоростей вместо линейных функций (5.31) использованы произвольные нелинейные vx — fx(x, у, г}, vy = fy(x, у, z), vx = fz(x, у, г) и по этим функциям рассчитано усилие деформации какого-либо процесса. Если функции описывают такое течение металла, как и происходящее в дейепи-тельном процессе (последнее определяется законом наименьшего сопротивления), то, очевидно, усилие деформации, рассчитаннсе по формуле (5.37), должно быть абсолютно наименьшим или очень мало от него отличаться. Конечно, угадать вид функций невозможно. Но их можно задать в виде многочлена с варьируемыми параметрами. Тогда задача сведется к анализу процесса деформации со многими степенями свободы (каждый варьируемый параметр дает одну степень свободы), а решать ее можно по схеме решения задач с одной степенью свободы энергетическим методом (см. уравнение (5.36)).
При использовании прямого вариационного метода, который известен в литературе как метод Ритца, функции для компонент скоростей vx, Vy, vz (или компонент приращения перемещений dux, diiy, duz) принимают в виде ряда, обычно содержащего от 2...3 до 5 членов:
Vk = Я1Ф1 № + OjTj (*) Н---Ь (k), (5.49)
где k — обобщенная координата (k = x, у, г, г, 0); at — численные коэффициенты — неизвестные варьируемые параметры; <рДЛ) — координатные функции.
Координатные функции нужно выбирать так, чтобы ряд (5.49) удовлетворял заданным граничным условиям задачи. Кроме того, модель течения, полученная на основе этих функций, должна иметь принципиально такой же характер, как реальный процесс ОМД, анализ которого выполняется. Например, при осадке цилиндрической заготовки или полосы vr = f(r, г) или vx = f(x, z) являются функциями параболического типа. Значит, координатные функции <pt(&) надо выбирать тоже из класса функций параболического типа. Отсюда следует важность экспериментального исследования. Даже качественные результаты эксперимента оказываются весьма полезными при установлении вида координатных функций. Эксперимент позволяет определить наиболее подходящие для рассматриваемой задачи координатные функции. По этой причине функции ср, (k) и называют подходящими 1146].
Сложность решения и объем вычислений зависят от выбора подходящих функций <рДЛ) и количества членов ряда (5.49), т. е. от количества варьируемых параметров л. Имея подходящие функции, составляем функции vx, vy, vz, куда входят неизвестные
179
варьируемые параметры а{. Предполагаем, что а{ известны. Решаем задачу энергетическим методом. Определяем по формуле (5.37) усилие деформации Ра и получаем решение Ра = Ф(Д1, о2. ...» ап), где at — варьируемые параметры. Чтобы их определить, используем принцип минимума полной энергии деформации, в соответствии с которым из всех кинематически возможных перемещений частиц деформируемого тела действительно сообщающее деформации минимальное значение [51, 69, 1431. Из этого принципа следует, что каждый из параметров а{ необходимо выбирать так, чтобы он минимизировал усилие деформации Р«. Это означает, что варьируемые параметры at можно определить из системы уравнений
£/>» = 0(1 = 1,2,3........л). <5.50)
Если воспользоваться уравнением (5.37) для усилия деформации, то каждое уравнение системы (5.50) можно преобразовать-в следующее:
н м
S Ш a^idV + S И + v'dF + Л—l ' V m-Г F
N
+ V — О/JdGpO. (5.51)
л-l G
Прямой вариационный метод приводит к системе уравнений (5.51). Решение этой системы дает возможность определить значение варьируемых параметров а/. Зная варьируемые параметры, можно найти функции vXt vu, vx и составить модель течения для исследуемого процесса. Имея модель течения, вычисляем компоненты тензора 7\, интенсивность скоростей деформации а затем по уравнению (5.37) усилие деформации Р$. Кроме того, зная компоненты тензора Л или функции vx, vu, v2, можно решать задачи конечного формоизменения.
Таким образом, решение задачи прямым вариационным методом достаточно четко алгоритмируется. Алгоритм включает следующие шаги.
1. Выбор подходящих функций. Это один из наиболее ответственных шагов. От того, насколько удачно выбраны подходящие функции, зависят точность решения и трудоемкость вычисления (или программирования, если задача решается на ЭВМ). К сожалению, здесь трудно дать какие-либо конкретные рекомендации, так как для одной и той же задачи можно почти с равным успехом использовать разные подходящие функции. В отличие от энергетического метода, где функции vxt vy, vz определяются однозначно, в прямом вариационном методе выбор функций — это скорее искусство и интуиция, чем наука. Однако при выборе подходящих функций обязательно следует опираться на результаты экспери
180
ментов. Кроме того, первый член ряда (5.49) нужно брать таким, каким он получался бы по уравнениям (5.38), (5.41) в условиях однородной деформации. Например, при осадке полосы неограниченной длины боковая поверхность принимает форму, близкую к параболической. Поэтому для vx нужно взять такую функцию, которая содержала бы za. Исходя из этого соображения и граничных условий, принимаем [ 146]
। (1 х1 \(, Зг*\
+ 36’Д1 Л« / *
(5.52)
Здесь первый член найден из условия равномерной деформации. Второй член содержит варьируемый параметр а. Очевидно, если а = 0, то их = С при любых значениях г. С увеличением значения г значение их убывает по параболической зависимости, которая определяется множителем (1—Зг’/Л2). Чтобы вычислить функцию vIt используем уравнение (5.48). В нем оси х, г равноправны. Значит, = —l^dz-f-C. Подставив функцию получим
= —а*(1 — p)(l — £). (5.53)
Эта функция удовлетворяет граничным условиям ог = 0 при z = 0 и vx = —и0 при z = h.
2. Определение компонент тензора скоростей деформации 7\, интенсивности скоростей деформации Этот шаг алгоритма — один из наиболее простых. По уравнениям (1.31), (1.35) находим для приведенного выше примера осадки полосы
3. Составление и решение системы (5.50) для определения варьируемых параметров а(. Это один из сложных и наиболее трудоемких шагов алгоритма. Вначале покажем, как решается
181
задача при анализе процесса осадки полосы. Функции (5.52), (5.53) содержат один варьируемый параметр. Поэтому система (5.51) приводится к одному уравнению. В нем Н — I, М = I, N = О (мы рассматриваем четверть заготовки, а в связи с простой формой заготовки очаг деформации не делится на области, и, следовательно, разрывы скоростей отсутствуют). Значит, получаем
Д ШУ a^{dv + Тк dF
« 0. Подставив сюда vx, имеем
1 f ? С ст> да U J /31 о о
4-36а Л< 4-4а ^1 Л>) 24а
_L ь
— + / С тк х 4-1 ——j') (1 — I = 0. Как ви-
Л’/J ,) I п \ эо / \ Л / 1
дим, это уравнение громоздко. Дальнейшие преобразования, связанные с дифференцированием выражения, стоящего в фигурных скобках, приводят к еще большему усложнению. Получить решение в замкнутом виде не представляется возможным даже в том случае, когда приходится отыскивать только один варьируемый параметр.
Для решения задачи предложено несколько обходных путей. Введением упрощающих допущений приводят уравнение к такому виду, при котором математические трудности преодолеваются. Но это наименее удачный путь, так как упрощения математического характера вносят неконтролируемые погрешности. Задачу решают численным методом. Привлечение ЭВМ дает возможность вычислять интегралы с заданной погрешностью, не превышающей заранее заданной величины. Это наиболее эффективный способ решения задачи. Однако программирование и отладка программы требует больших затрат времени. Наконец, можно использовать приемы приближенного вычисления интегралов вида °9^dV.
v
Для любой функции £ (о,) имеем (5 (а/)]2 = 2$ (а() Д £ (а/). Отсюда — ft д ' В° многих процессах ОМД значение g/ в каждой точке деформируемого тела не очень сильно отличается от среднего £ср, рассчитанного по уравнению (1.31) в предположении равномерной деформации 1143, 1461. Отсюда следует, что
(5.55)
182
Используя это приближенное равенство, преобразуем систему (5.51) таким образом:
н м
Л—1 V m=l F
N
4-V {j T«^| vA —V/|dG = 0. (5.56)
n=»l 6
Для осадки полосы система (5.56) сводится к одному уравнению вида
Ш Й' dV + Л Т“ & dF = °’ V F
2v
Здесь ^ср = -7^- рассчитываем по уравнению (5.54) при а = 0; у 3 h
значение £* берем из выражения (5.54); vx—из уравнения (5.52).
Вычисляя почленно, находим j J J [а* дБ х
ср V 000
X dx dy dz = о, £ abh (0,213 + 0,64 £ + 0,026 ; JJtk Д vx х
р
ъ I
X dF = j фкт, dxdy = —0,833фк йа. Суммируем и полу-
0 *0
ченное уравнение решаем относительно а:
0,416% V а = Ч>______________" *
h b* W
0,213 + 0,648 £5 + 0,026
(5.57)
Для каждого момента деформации t считаем заданными и0, ^к; текущую высоту заготовки h определяем по изменению начальной высоты h = h0 — J* vodt, а ширину b находим из условия по-о
стоянства объема. Таким образом, имея значения и0, h, b, вычисляем а, затем по формулам (5.52), (5.53) определяем функции компонент скоростей vx, vx. Пользуясь (5.37), ищем усилие деформации Рд. Кроме того, имея функции (5.52), (5.53), можно решать задачи конечного формоизменения, т. е. определять форму заготовки после осадки на некоторую заданную величину Дй. Решение прикладных задач ОМД прямым вариационным методом рассмотрено в гл. 6.
5.2.4.2. Метод верхней оценки. Из-за сложностей, связанных с вычислением работы (мощности) внутренних сил, исследователям
183
пришлось искать новые подходы к решению задач пластического течения. Возникла идея, нельзя ли обойтись без вычисления работы (мощности) внутренних сил? В энергетическом методе такая идея уже частично реализована: работу, связанную с неравномерностью деформации, мы определили как дополнительную работу сдвига. Пойдем дальше. Представим, что очаг деформации разбит на треугольные блоки (жесткие области), в которых дефсрмация отсутствует, а формоизменение тела осуществляется путем относительного сдвига этих блоков. Такое представление соответствует механизму межзеренной деформации (см. подразд. 2.5.1). В этом и заключается суть идеи метода верхней оценки.
Однако путь от идеи до создания метода был довольно долгим. Необходимо было доказать, что такой подход не вносит значительной погрешности. Д. Друккер, X. Гринберг и В. Прагер (182], а затем В. Джонсон 136] и X. Кудо (189] разработали теоретические основы метода верхней оценки. Очаг деформации разбивают на некоторое (желательно небольшое) количество жестких треугольных блоков (это равносильно замене действительного непрерывного поля скоростей разрывным кусочно-линейным) и на основании энергетического подхода определяют усилие деформации по формуле:
м N
=г (S +X «) • <5 58)
° Л1—I п-1
Здесь у0 — скорость перемещения инструмента; ис — скорость относительного сдвига смежных треугольных элементов; ск — скорость скольжения элемента по контактной поверхности инструмента; т, — предел текучести деформируемого металла на сдвиг; тк — контактное касательное напряжение; Гс и — площади поверхности относительного сдвига элементов и контактной поверхности; N — количество поверхностей сдвига; М — количество контактных поверхностей.
Эта формула вытекает из первого основного уравнения энергетического метода (5.37), если принять = 0, т. е. элемент считать недеформируемым; vK(x, у, z) = const, vi(x, у, z) = const, т. e. скорости в пределах каждого элемента считать постоянными. При этом интегрирование по поверхностям трения F и сдвига G в уравнении (5.37) заменяется суммированием мощностей трення и сдвига для каждого треугольного элемента, на которые раебн-вается очаг деформации, в уравнении (5.58). Однако доказано, что в задачах, где внешними силами являются нагрузки деформирования и не зависящие от них силы контактного трения, а также заданы скорости деформирования, равенство мощностей внешних сил на кинематически возможных скоростях устанавливает верхнюю оценку нагрузок (36, 51, 136, 1371. Это и послужило основанием для названия метода. Доказательство теоремы о верхней оценке выходит за пределы программы. Читатель сможет найти
184
его в работах [36, 51]. Поэтому основу метода рассмотрим на конкретном примере прессования полосы через клиновую матрицу (рис. 5.11).
В силу симметрии задачи рассмотрим половину полосы ABCDOE. Выделим очаг деформации в виде треугольной области BCQ. Точки В, С однозначно определены геометрией матрицы. Точку Q возьмем на оси 2 произвольным образом. Ее положение можно однозначно задать, например, углом у, а угол Р выразить через у и размеры матрицы Р = arctgU>e/(Z,cosa — bactgy)).
Piic. 5.11. Расчётная схема прессования полосы через клиновую матрицу (а), кинематически возможные перемещения отдельных областей заготовки (б) и годограф скоростей (а)
Мысленно разделим деформируемую заготовку на отдельные области BCQ и CDQE (рис. 5.11, б), определим кинематически возможные перемещения каждой из них (на рисунке перемещения показаны пунктиром) и построим годограф скоростей (рис. 5.11, в).
Годограф скоростей — это векторная диаграмма, построенная из одной точки (полюса) и показывающая скорости определенных точек или областей деформируемого тела.
Из полюса Р проведем вектор PR, численно равный скорости движения области /. Очевидно, что PR = = t>n. где t>n — ско-
рость пуансона. Область 2 движется совместно с областью 1 со скоростью I»! = ип и относительно этой области со скоростью plwl. Вектор скорости должен быть параллелен стенке матрицы ВС Отсюда следует способ определения направления и модуля век-Dpa и2 на годографе: через точку Р проводим PS параллельно ВС и PS параллельно BQ. Тогда PR = — скорость движения
области 2 совместно с областью Г, RS =« ua_j — скорость движения области 2 относительно области Г, PS = и2-о — скорость
185
Рис. 5.12. Зависимость относительного удел ьного усилия прессования полосы р от угла у: /-ц-0,1; 2 — и =0.5
движения области 2 (скорость скольжения области 2 по матрице 0). Теперь можно перейти к анализу движения области 3. Она движется совместно с областью 2 со скоростью vt и относительно этой области со скоростью и^_г. Вектор скорости I», должен быть параллелен оси матрицы Ог. Отсюда следует способ определения направления и модуля вектора с8 на годографе: через конец вектора и2 проводим ST параллельно QC до пересечения с продолжением вектора Тогда PS = v2 — скорость движения области 3 совместно с областью 2, ST = — скорость движения области
3 относительно области 2, а РТ = р3 — скорость движения области 3 (скорость выдавливания металла из матрицы).
Из построения годографа следует, что углы <RPS, <SRT, <STR равны углам а, р, у соответственно. Поэтому векторы и2, и2_д, t’3_2. t'3 однозначно определяем через вектор ©д и углы а, Р, у.
Примем ширину полосы ABCDOE (размер в направлении оси у) равной 1. По формуле (5.58) определим верхнюю оценку усилия
= + CQ-TS +
4- ра, • 1 • АВ • PR 4- pa, • 1 • СВ • PS 4-4-poi-l-CD Рг). (5.59)
Очевидно, что величина Р^ зависит от положения точки Q (углов Р и у). Поэтому необходимо выполнить анализ уравнения (5.59) на экстремум и взять наименьшее из всех возможных значений Рд- Таким образом, углы р, у выступают в роли варьируемых параметров. В рассматриваемой задаче только один из углов (Р или у) независим. Но во многих других задачах варьируемых параметров может быть два и более. Вот почему метод верхней оценки относят к вариационным.
На рис. 5.12 приведена зависимость относительного удельного усилия р = Pd!Fat от угла у, определяющего положение точки Q, для прессования полосы при Ьо = 50 мм, Ь$ = 25 мм, /д = = 60 мм, /2 = 50 мм, /8 = 10 мм, a = 30°, р = 0,1 и р = 0,5, вычисленного по формуле (5.59).
Аналогично можно решать и другие задачи ОМД. Метод верхней оценки широко применяется для решения задач, которые пока не решены более точными методами. Если для расчета принять достаточное количество жестких треугольников, то, используя минимизацию усилия деформации по углу наклона элементов (как на рис. 5.11, 5.12) или по их размерам, можно получить вполне удовлетворительную для технических целей точность решения задачи. Верхние оценки, полученные выбором наилучших возмож
186
ных полей скоростей, дают значения усилий, которые всего на 10...20% превышают усилия, вычисленные методом линий скольжения.
Если для рассматриваемой задачи известен вид сетки линий скольжения, то построение расчетной схемы (как на рис. 5.11, а) значительно облегчается: нужно сетку линий скольжения покрыть небольшим числом треугольных блоков. Метод верхней оценки используется и для анализа осесимметричных задач 136, 150, 1771.
5.2.4.3. Метод конечных элементов. Простота метода верхней оценки достигнута дорогой ценой: разрывное поле скоростей позволяет анализировать только силовой режим и простейшие задачи конечного формоизменения. Однако современная практика выдвигает значительно более сложные задачи. Поэтому ученые всех стран активно разрабатывали методы расчета, обладающие более широкими возможностями и универсальностью.
Созданию такого универсального метода способствовали значительные успехи вычислительной техники. Назвали его методом конечных элементов (МКЭ). Хотя первые упоминания о конечных элементах появились в 1956 г„ интенсивное использование МКЭ началось лишь с семидесятых годов, когда вышли в свет работы 142. 1131 и некоторые другие.
МКЭ нашел широкое применение в первую очередь для решения задач строительной механики. Затем появились работы,( в которых метод использовался для анализа упругих деформаций штампов (1811, пластической деформации 170, 1241 и даже расчета деформаций и температурных полей в задачах обработки металлов давлением (921. Считают, что МКЭ открывает новую эру в расчетах напряженно-деформированного и температурного состояния сложных неоднородных сред. Важно, что в нем объединены механика сплошных сред и современные методы численного анализа. При использовании .метода конечных элементов ЭВМ помогает не только решать задачи, но и частично строить решения этих задач. Особенно успешно метод стал применяться после создания надежно работающих универсальных программ, например (19, 421.
Метод конечных элементов широко применяется для решения плоских и осесимметричных задач. С математической точки зрения МКЭ — это обобщение вариационного метода. Его отличие от прямого вариационного метода состоит в одной детали: координатные функции (5.49) выбирают в виде кусочно-линейных функций. Однако эта деталь резко расширяет возможности метода и значительно упрощает решение задачи. Процедура построения таких функций легко алгоритмируется и может быть поручена машине. Линейность координатных функций позволяет свести решение системы сложных интегродифференциальных уравнений вида (5.51) к системе линейных уравнений. Хотя порядок системы оказывается весьма высоким (более 10s), ЭВМ успешно справляется с решением. К сожалению, жесткие рамки программы курса не позволяют рассмотреть этот очень перспективный метод.
187
5.3. ЭКСПЕРИМЕНТАЛЬНО-АНАЛИТИЧЕСКИЕ МЕТОДЫ
Аналитические методы не позволяют учесть многообразие факторов, определяющих протекание реальных процессов ОМД, так как рассматривают сильно упрощенные модели процессов и модели деформируемых сред. В то же время производство выдвигает перед теорией все более сложные задачи для решения которых необходим детальный учет многочисленных факторов, влияющих на деформацию. Успехи в области измерений и статистической обработки экспериментальных данных позволили резко повысить точность экспериментального определения перемещений и деформаций. Благодаря этому появились предпосылки для использования экспериментальных данных в теоретических решениях. Так возник качественно новый подход к решению задач ОМД, основанный на объединении экспериментального исследования и теоретического анализа.
Экспериментально-аналитические методы объединяют одна идея: на основании экспериментальных исследований получить функции, описывающие перемещение частиц деформируемого тела. Затем, используя уравнения Коши, вычислить деформации и с помощью уравнений связи между напряжениями и деформациями определить напряженное состояние, силы, нагрузки на инструмент и т. д.
5.3.1. Метод сопротивления материалов пластическому деформированию. Теоретические основы метода сопротивления материалов пластическому деформированию (МСМПД) разработали Г. А. Смирнов-Аляев и В. М. Розенберг 11331. Идея этого метода основана на предположении о том, что главные оси деформаций и главные оси напряжений совпадают, т. е. тензоры 7», Тв коа-ксиальны. Экспериментально установлено, что для малых деформаций это предположение выполняется всегда, а для больших — только в случае монотонной деформации. Под монотонной подразумевается такая деформация, при которой две любые материальные частицы деформируемого тела постоянно сближаются или удаляются друг от друга. Для монотонной деформации справедливы соотношения
= ga~~gl (5.60); v9 = v, (5.61).
<4 — с, с,— as Cj — a/ ' 9 * ' '
2a« a, —— c« 2ft *—
Здесь v0 — —=--; v, — —------------’; e — показатель де-
Ci — c8 — e3
формации Генки (см. формулу (1.14)).
Значение величины \в можно получить на основе анализа изменения формы заготовки. В операциях листовой штамповки деформации материальных частиц q, et, е3 в большинстве случаев однозначно установлены законом движения инструмента. В операциях объемной штамповки е1( et, е3 определяют с помощью коорди
188
натных сеток. Приняв во внимание выражение (5.61), находим
2а, — ах — а3 = * (<т> — а,). (5.62)
*1 ^3
Присоединяем условие пластичности в форме —ов = Р°,. Получаем однажды статически неопределимую] систему. Для ее разрешения нужны дополнительные условия, например, условия равновесия, условия равенства нулю какой-либо компоненты напряжений (в процессах листовой штамповки это выполняется с Высокой точностью) и др.
СМПД был первым методом, в котором экспериментальному исследованию уделялось очень большое внимание. Эксперименты используются, во-первых, для точного определения истинного сопротивления деформации о,, во-вторых, для исследования конечных пластических деформаций. Г. А. Смирнов-Аляев разработал микроструктурный метод исследования, а также метод анализа искажения координатной сетки.
Методом СМПД успешно решены многие важные прикладные задачи обработки металлов давлением. Детальное изложение этих решений приведено в работе 1133).
5.3.2. Визиопластический метод. Теоретические основы визио-пластического (ВПМ) разработали Ю. Н. Алексеев [2, 3] и Э. Томсен с сотрудниками [ 1501. ВПМ — единственный метод, позволяющий получить теоретические решения для высокоскоростных процессов ОМД. Обобщение опытов по сложному нагружению позволило установить, что при пластической деформации справедливо следующее тензорное соотношение:
D, = 2рА, (5.63)
где ji/ = af/3£z.
В случае деформации несжимаемых материалов, т. е. практически всех металлов, применяемых в ОМД, за исключением кипящей стали и порошковых материалов, Di «= 7\. Поэтому уравнение (5.63) можно представить в виде
о* = Оср 4* 2ц^х; тХу в Оу в Оср 4~
Туж = р&уг, Ог « аСр 4- 2р/Ь; в Р/Ь*. (5.64)
Из этих соотношений следует, что для определения напряженного состояния деформируемого тела достаточно определить компоненты скорости деформации и т. д. Действительно, — однозначная функция и т. д.:
Ь - £ /(Еж- Е,)’+ (Е, - Ь)’+ (5. - Ь)’+ 4 (Е« + EL + Е.*ж).
(5.65)
189
Интенсивность напряжений ot при пластической деформации численно рав'на истинному сопротивлению деформации а,. Она однозначно связана с интенсивностью деформации (см. 1.6.3):
N
а, = А 4- Be" или и, = £ Лле". (5.66)
л—1
Интенсивность деформации можно вычислить, имея интенсивность скоростей деформации
t
г, = f hdt. (5.67)
О
Таким образом, задача анализа напряженного состояния деформируемого тела сводится к определению его деформированного состояния и анализу уравнений (5.64). Функции
(5.68)
выражаются через скорости частиц деформируемого тела в переменных Эйлера. Поэтому задача сводится к построению поля скоростей.
Поле скоростей получают экспериментальными методами. Для эгой цели деформируемое тело разрезают так, чтобы в плоскости разреза не действовало растягивающих напряжений и чтобы плоскость разреза совпадала с направлением главной деформации. В плоскости разреза наносят какую-либо координатную сетку (рис. 5.13). Осуществляют поэтапную деформацию. После каждого очередного приращения деформации сетку фотографируют и измеряют координаты узловых точек. Если этапная деформация небольшая, а положение координат узлов сетки измеряется с высокой точностью, то можно с достаточной точностью вычислить две компоненты скоростей деформации (например, £г), а третью найти из условия неразрывности скоростей деформации (1.37) или (1.38).
Полученное экспериментальное поле скоростей (5.68) и уравнения (5.64) позволяют определить напряженное состояние деформируемого тела, если известно среднее напряжение оср. Чтобы найти аср, рассмотрим деформацию элемента тела dV, имеющего плотность р и поверхность dF, на которую действуют поверхностные нагрузки Sx. Sy, Sz. Пусть элемент dV движется с ускорением w. Как и в других случаях анализа процессов ОМД, влиянием силы тяжести тела пренебрегаем. В соответствии с основным уравнением механики получаем ( f f pwdV — J f S^dF = 0. Boc-’ V F
пользовавшись преобразованием Гаусса — Остроградского поверхностного интеграла в объемный, представим уравнение в виде
ш - ш (%+%+=°- <а’
V
190
где первый интеграл выражает силу инерции, а второй — поверхностную силу, которая действует на деформируемое тело. Каждый вектор поверхностной нагрузки 5Х, Sy, Sz можно представить как векторную сумму составляющих (см. подразд. 1.5.2): Sx = = iox +Jrxy + Лгхж; Sy = ixyx 4- kxyx\ Sz = Zt2x 4-/тад + k<jx, где /, J, k — орты. Подстановка значений Sx, Sy, Sx и преобразование подынтегрального выражения позволяют свести векторное интегральное уравнение (А) к трем дифференциальным [2]:
Л 4. 4 п д°х г. 1 .
Р\дГ х дх у ду ' ’ дг / дх ' ду ' дг *
р \ дг * дх ' 11 ду ' * дг / дх ду ' дг *
п1^г 4. » 4-п *°г 4- г, 4- 4- ва‘
р\-57 + р'17 +о>-^ + е‘-д^)--^+-^+-дГ- <Б>
Подставив в первое уравнение (Б) значения напряжений из выражения (5.64), получим первое уравнение движения, содержащее неизвестное среднее напряжение:
П 4- n дх>х 4- я дх>х 4- я 4- .1 (d*Vx 4- d*Vx 4-
i । n tex , dpt (dvx *>y\ dp/ (dvx dox\ fiq.
дг* / ' дх дх ‘ ду \ dy ' dx / ' дг \дг ' dx) ‘ '
Два других уравнения имеют аналогичную структуру. Их можно получить циклической перестановкой индексов. Обозначим левую часть уравнения (5.69) как ФХ|, а все члены правой части, не содержащие <тср, как Ф^. Тогда выражение (5.69) примет вид
dcr da„_
Фж1 = -^-₽ + Фх2 ИЛИ = ФХ1 — Фх2 = Фх. (В)
Здесь ФХ|, ФХ2 — функции, содержащие производные компонент скоростей перемещения частиц деформируемого тела их, vy, vz и производные р/ = р/(х, yt z). Это означает, что Фхь Фх2 однозначно определены, если задано поле скоростей vx, vy, vx и закон упрочнения as = Ф (ef). К виду (В) можно привести все три уравнения (Б):
^£Р = фж; 5^Р = Ф : !^р = Ф2. (Г)
дхх,дуыдг ' '
Уравнения (Г) дают возможность вычислить среднее напряжение
<УсР = \ Ф*^х 4- J ФуАу 4- j Ф^г. (5.70)
Таким образом, решение задачи визиопластическим методом не встречает никаких принципиальных затруднений. Однако для решения необходимо построить поле скоростей. Проще его построить
191
для стационарного процесса, т. е. такого, в котором функции (5.68) не зависят от времени (прессование, волочение, прокатка).
Рассмотрим процедуру построения поля скоростей на примере прессования цилиндрической заготовки через коническую матрицу
(рис. 5.13). Пусть в момент времени t координатная сетка имеет вид, показанный на рисунке. За промежуток времени Д/ сетка изменится. Выделим узел сетки, например Мо, имевший до де-
формации координаты r0, г0
Z
Рис. 5.13. Схема процесса прессования составного образца с координатной сеткой, нанесен-
. За время Д/ он сместится в положение Mi, а его координаты станут гР Смещение узла М можно определить с помощью компонент иг = г0— — = Дг, иг = г0 — Zi = Дг, а сред-
нюю скорость на участке МйМг — компонентами
vr = Дг/Д/, V,s bzlkt. (Д)
Очевидно, чем меньше Дг, Дг, Д/, тем лучше приближение средних скоростей (Е) к мгновенным скоростям в точке Мо. Однако не следует забывать, что Дг, Дг, а также Д/ определяются экспериментально. Поэтому их нельзя брать слишком малыми. Наилучшими результаты
оказываются в том случае, когда значения этих величин берут такими, при которых относительная по-
ной на поверхность разъема грешность измерения не превышает 5%. Само собой разумеется, что для измерения Дг, Дг (и Д/) необходимо пользоваться средства-
ми, которые дают наименьшую абсолютную погрешность, например, инструментальным микроскопом. Аналогично по формуле (Д) рассчитывают компоненты скоростей всех узловых точек координатной сетки (см. рис. 5.13):
Индекс узла 0,0 1.0 2,0 0.1
Радиус узла г 0 Г(1.0) Г(2.0) 0
Ордината узла 2 0 0 0 Г<0.1)
Компонента vr 0 °г(!.0) °г(2.0) 0
Компонента vg Ро V«(0.1)
По этим данным можно построить поверхности vn vz, а затем аппроксимировать их функциями vr = v,(r, z) uz—vz(r, z). Например,
V, = S (m, n — 0, 1, 2, ...» л). (E)
Однако это сопряжено с двумя трудностями. Первая состоит в том, что значения иг, полученные экспериментально, опре-
192
делены с неизбежными ошибками, из-за чего поверхности vr(r, z), u2(r, z) не получаются гладкими. Вторая трудность связана со свойствами аппроксимирующего полинома (Е): чем выше порядок полинома, т. е. чем более высокие степени г, z он содержит, тем лучше можно приблизить его к точному описанию значений v в узлах координатной сетки (с меньшей суммой квадратов невязок). Но качество производных dvr/dr, dvjdz значительно ухудшается, что приводит к большим погрешностям при решении уравнения (5.70).
Чтобы улучшить качество функций vr= vr(r, z), vt= vz(r, z), поступают следующим образом. Во-первых, поверхности находят не во всей области определения переменных г, г, а в некоторых сечениях, образующих ортогональную сетку, т. е. vr = v, (г, z == = Ci); vt = v2 (r, z = C2); v, = vr(r = C3, z); v2 =>v2(r = Cit z).
Во-вторых, для аппроксимации берут полиномы не выше четвертой-пятой степени. В-третьих, осуществляют сглаживание экспериментальных функций (170, 171). Сглаженная функция должна удовлетворять условию постоянства объема и граничным условиям. Например, для сечения г = С (рис. 5.13) должно выполняться условие
R
v2 (г, z = С) 2nrdr = n₽Ju0. (5.71)
Визиопласгическим методом выполнен анализ напряженно деформированного состояния многих стационарных задач ОМД [2 3, 91, 127, 150, 170, 1711. Анализ задач нестационарного течения значительно усложняется тем, что необходимо строить поля для нескольких этапов деформации, несколько раз осуществлять сглаживание функций vr, vt (или в общем случае vx, vy, v2) и несколько раз решать сложную задачу интегрирования среднего напряж ния по уравнению (5.70). Еще сложнее анализировать высокоскоростные процессы. Это связано со значительными техническими трудностями фотографирования координатной сетки в процессе деформации. Однако визиопластический метод — это пока единственный метод анализа высокоскоростных процессов ОМД. Именно с его помощью выполнен анализ большого количества высокоскоростных процессов ОМД, особенно в листовой штамповке [2, 71. Е. П. Унксов отмечает, что необходимость прерывания процесса деформации для поэтапного фотографирования координатной сетки может приводить к значительной погрешности 11561. Это действительно так, но для многих процессов совсем не обязательно прерывать деформацию. Например, при обжиме, раздаче, вытяжке, гибке и других операциях листовой штамповки, осуществляемых даже взрывом или импульсным магнитным полем, поле скоростей можно получить при непрерывной деформации с помощью сверхскоростного фоторегистратора. Кроме того, успешно применяют метод непре
*/, 7 1-25
193
рывного фотографирования координатной сетки в процессах объемной штамповки, прессования и выдавливания 172, 91].
При малых скоростях деформации, когда действием инерционных сил можно пренебречь (имеются в виду процессы листовой и объемной штамповки, осуществляемые на прессах и обычных молотах двойного действия),уравнения визиопластического метода значительно упрощаются.
Для плоского деформированного состояния в работах [150, 170] приведены следующие уравнения:
п (* (д /dvx I 9 Г /дох , диг\ ]] , . . .
~ 2 .’ ("57 д?/] 2 дх + ЛГ/JJ Л
0
=2 .( U [н< (% - £)] - Н Ь (£+£)]} <572>
о
Здесь (ох)0, (ог)0 — напряжения в начальной точке интегрирования. Они определяются по граничным условиям, или по усилию деформации, или экспериментальным путем. Решение этих уравнений находят численным с помощью ЭВМ или графическим методом 1150. 170].
5.3.3. Метод муаровых полос. Этот метод представляет собой модификацию визиопластического метода. Метод муаровых полос (ММП) отличается от ВПМ только способом определения функций компонент скоростей (5.68). Суть метода состоит в том, что при наложении двух координатных сеток образуются картины квази-интерференционных полос, которые характеризуют несовпадения в шаге и направлении этих линий. Однако в отличие от метода координатной сетки ММП, дает качественно новую форму информации: вместо дискретных значений величин имеем их непрерывные поля [ 127, 170].
В методе муаровых полос на поверхность заготовки наносят фотослой, экспонируют на него эталонную решетку, проявляют и получают рабочую решетку. Затем образец поэтапно деформируют. После каждого этапа рабочую решетку фотографируют через эталонную. На фотографии фиксируют картину муаровых полос. Расшифровка ее позволяет определить поля скоростей с достаточно высокой точностью 1127]. К сожалению, технические трудности получения картин муаровых полос пока препятствуют широкому распространению этого метода. Тем не менее, методом муаровых полос решены многие сложные задачи обработки металлов давлением 1124. 145. 1701.
5.3.4. Метод определения напряжений по распределению твердости. Рассмотренные выше экспериментально-аналитические методы (МСМПД, ВПМ, ММП) дают возможность определить напряженно-деформированное состояние в процессах ОМД тем точнее, чем точнее найдено значение истинного сопротивления дефор
194
мации о, = Ф(е). в каждой точке деформируемого тела и в каждый момент деформации. Аппроксимация зависимости а, = ф(е) функциями (5.66) может давать ощутимую погрешность. Чтобы повысить точность значений величин, входящих в уравнения (5.64), (5.70), (5.72), необходимо точнее найти значения о, в каждой точке деформируемого тела. Это можно сделать, воспользовавшись методом определения напряжений по распределению твердости(МРТ). В основу этого метода положен экспериментально установленный факт однозначной связи твердости НУ (или НВ) с интенсивностью напряжений а( = о,.
Первая попытка осуществить анализ напряженного состояния по распределению твердости принадлежит Г. А. Смирнову-Аляеву [133].
Сейчас МРТ усовершенствован настолько, что стал одним из эффективных методов анализа технологических задач ОМД. Большой вклад в развитие этого метода внесли Г. Д. Дель [32, 33] и В. А. Огородников [97].
МРТ — это модификация визиопластического метода. Он отличается от последнего только тем, что дополнительно к компонентам vr, vg или их, vz, (если решается задача в прямоугольной системе координат) определяют еще и твердость. Например, для анализа задачи прессования (рис. 5.13) экспериментально получают следующую информацию:
Индекс узла 0,0 1.0 2,0 0,1
Радиус узла г 0 Г(1.0) Г(2.0) 0
Ордината узла t 0 0 0 *(0.1)
Компонента vr 0 °Г(1.О) ar(2,0) 0
Компонента иг Vo Рг(0.1)
Тгердость HV WV(o.o) ^(1.0) ^(2.0)
Одновременно с проведением эксперимента выполняют построение градуировочной (тарировочной) кривой твердости. Для этого делают образцы с торцовыми выточками из того же материала, что и испытываемая заготовка, осаживают их до различных степеней деформации. В процессе осадки фиксируют усилие деформации и по фактической площади поперечного сечения образца рассчитывают интенсивность напряжений оР После испытания измеряют твердость НУ всех осаженных образцов. Затем методом наименьших квадратов строят тарировочную кривую о( — НУ. Дальнейшая процедура расчета напряжений выполняется так же, как и при вязкопластическом методе.
Анализ технологических задач ОМД при помощи МРТ (как и других экспериментально-аналитических методов) требует обработки больших массивов информации. Чтобы решить задачу в приемлемые сроки и с нужной точностью, используют ЭВМ. Этим методом решены многие важные задачи ОМД: прессование, осадка, радиальное сжатие цилиндров, гибка и др. [321.
‘/,7*
195
ГЛАВА 6
ЗАДАЧИ ТЕОРЕТИЧЕСКОГО АНАЛИЗА ПРОЦЕССОВ ОБРАБОТКИ МЕТАЛЛОВ ДАВЛЕНИЕМ
6.1. КЛАССЫ ЗАДАЧ ТЕОРЕТИЧЕСКОГО АНАЛИЗА И МЕТОДЫ ИХ РЕШЕНИЯ
Технологические процессы ОМД можно совершенствовать, используя два разных подхода: экспериментальный и теоретический. Проведение экспериментальных исследований связано со значительными материальными и трудовыми затратами. Поэтому эксперименты проводят, как правило, в ограниченных объемах, преимущественно для проверки теоретического анализа. Именно теоретический анализ того или иного процесса ОМД позволяет детально изучить его особенности, определить силовой режим деформации и характер формоизменения. Роль теоретического анализа в последние десятилетия сильно возросла, так как во-первых, получили развитие новые методы теоретического анализа и появилась возможность создавать достаточно точные математические модели технологических процессов ОМД, а во-вторых, практика поставила перед наукой задачи оптимизации процессов ОМД, решить которые можно только моделированием на ЭВМ.
Рассмотренные в предыдущем разделе аналитические и экспериментально-аналитические методы анализа процессов пластической деформации можно применять для решения различных технологических задач и оптимизации параметров процессов ОМД и штампов.
Первый класс задач теоретического анализа —анализ силового режима, т. е. определение усилия и работы деформации. Решение этих задач позволяет правильно выбрать технологическое оборудование и в первом прхближении рассчитать на прочность детали штампа. В последние годы решение этих задач используют для оптимизации параметров технологических процессов и штампов.
196
В общем случае усилие деформации — это функция комплекса параметров технологического процесса Kt (температура, скорость деформирования, степень деформации, форма исходной заготовки, род применяемой смазки и т. д.) и комплекса параметров /<к. определяющих конструкцию формоизменяющих деталей штампа (штамповочные уклоны, толщина облоя при штамповке в открытых штампах; конусность матрицы, радиусы скругления калибрующего пояска матрицы при прессовании; радиус вытяжного ребра матрицы при вытяжке и т. д.):
= Г (Кт, Л\). (6.1)
При изменении параметров /<т, К* усилие Рд может значительно изменяться. Задача исследователя —проанализировать зависимость (6.1), выбрать такие комплексы параметров технологических процессов и форму инструмента, которые дают минимум усилия (конечно, с учетом ряда ограничений, накладываемых на выбор параметров реальными производственными условиями).
С развитием техники задачи, стоящие перед технологией ОМД, усложняются: нужно обрабатывать все более прочные материалы, получать все более точные изделия, применять все более напряженные режимы деформации. В этих условиях нагрузки на инструмент приближаются к предельно допустимым даже для самых прочных инструментальных сталей. Для расчета тяжело нагруженных штампов, оптимизации технологических параметров процесса и параметров, определяющих конструкцию формоизменяющих деталей штампа, необходимо знать уже не только усилия деформации, но и распределение нагрузок, действующих на рабочих поверхностях инструмента:
о„ =-- Ф„ (Кт, Кк); тк = Фк (Кт, Кк). (6.2)
Уравнения(6.2) дают возможность рассчитать на прочность формоизменяющие детали штампа и выбрать такие комплексы параметров Кт и Кк, которые позволяют получить необходимые запасы прочности. Это второй класс задач теоретического анализа.
Процессы ОМД осуществляются чаще всего в несколько переходов. Форма исходной заготовки и промежуточных переходов, как правило, не заданы. Поэтому выбор заготовки в известной мере произволен. Так, при штамповке поковок типа шестерен (рис. 4.4) можно брать любые различные по высоте Н3 и радиусу R3 исходные заготовки, лишь бы они удовлетворяли условию постоянства объема и сохраняли устойчивость при осадке. Установить, какая из заготовок окажется наилучшей, можно лишь после анализа формоизменения. При многопереходной штамповке нужно выбрать и наилучшие промежуточные формы заготовки. Анализ формоизменения, выбор рациональных размеров исходной заготовки и ее промежуточных форм — третий класс задач теоретического анализа.
7 1-25
197
Основная задача прикладной науки состоит в том, чтобы изыскивать пути повышения эффективности производства. Совершенно очевидно, что наиболее высокая производительность и эффективность процессов ОМД достигается тогда, когда заготовка приобретает требуемую форму за минимальное число переходов. Но при некоторых условиях такой процесс может оказаться совершенно неэффективным из-за большого количества брака по трещинам (см. подразд. 1.6.4, 4.2.6). Поэтому инженер должен строить технологический процесс так. чтобы не исчерпать ресурс пластичности ф и получить детали без каких бы то ни было дефектов по трещинам. Это четвертый класс задач теоретического анализа.
Задачи третьего и четвертого классов касаются анализа формоизменения. По содержанию и методам анализа они разные. Условимся называть их соответственно задачами конечного формоизменения и задачами предельного формоизменения.
Таблица 6.1. Возможности и ограничения использования аналитических и эксперимеиталько-аналитическнх методов для решения задач анализа процессов ОМД
Методы Класс решаемых »«Д«ч Ограничение
1 2 3 4 А Б в
Аналитические
1. Инженерный (5.2.1) + 4“ 4* —• ПО —— УО
2. Линий скольжения (5.2.2) 4> 4- — + П,1СТ тгп БУ
3. Энергетический (5.2.3) + — 4- — ТП, БОП
4. Прямой вариационный (5.2.4.1) + 4- 4- + — ТП. БОП —
5. Верхней оценки (5.2.4.2) 4- — + — по ТГП. ТП УО
6. Конечных элементов (5.2.4.3) 4- 4" 4- 4" ТП. БОП —
Экспериментально-аналитические 1. Сопротивления материалов плас-
тической деформации (5. 3. 1) 4- 4“ — 4" по ТЭ —
2. Вязкопластический (5.3.2) -j- *4“ 4” 4~ по тэ, сэт, ТП —
3. Муаровых полос (5.3.3) + 4- — 4е по тэ, сэт, ТП —
4. Распределения твердости (5.3.4) + 4" — 4* по тэ, сэт, ТП —
Решение перечисленных задач основано на феноменологическом подходе и общих методах механики сплошных сред (см. гл. 1,5). Теоретический анализ процессов ОМД осуществляется различными методами. Каждый из них характеризуется возможностями и ограничениями (табл. 6.1). Крестиком указана возможность решения задач четырех перечисленных классов. Здесь же отмечены ограничения:
А — на область применения метода (П — преимущественно для плоских и осесимметричных задач; ПО — преимущественно
1»1
для плоских и осесимметричных задач; 1СТ — в основном для задач с одной степенью свободы течения металла);
Б — на методику решения задач (ТГП — для решения задачи необходимо выполнить большой объем графических построений и расчетов; ТП — необходимо составлять сложную программу для ЭВМ и долго ее отлаживать; БОП — требуется цифровая ЭВМ с очень большим объемом памяти; ТЭ — нужно провести трудоемкий эксперимент и его обработку; СЭТ —для проведения экспе римента используется специальная сложная техника и аппаратура);
В — на результаты решения (БУ — без учета упрочнения; УО — учет упрочнения осредненной оценкой (по методике, изложенной в подразд. 6.3).
Таким образом, в зависимости от класса решаемой задачи анализа процесса ОМД по табл. 6.1 можно выбрать соответствующий метод. Привлечение физических представлений (гл. 2, 3) позволяет обоснованно выбрать исходные параметры и таким образом получить более точные окончательные результаты. Особенно важен правильный выбор истинного сопротивления деформации и граничных условий на контактных поверхностях инструмента.Это именно та «засыпка», которую перемалывают математические жернова и от которой зависит истинность или ложность результатов расчета (см. подразд. 5.1, 3.2, 2.7.3, 1.6.3).
6.2. ИСПОЛЬЗОВАНИЕ ЭВМ ПРИ ТЕОРЕТИЧЕСКОМ АНАЛИЗЕ
Историю развития теории обработки металлов давлением с известной условностью можно разделить на два периода. Первый — разработка методов теоретического анализа,экспериментального исследования, а также определения главным образом усилий деформации и конечного формоизменения. Второй период начался сравнительно недавно —использование различных методов для оптимизации технологических процессов и конструкций штампов. Это принципиально новый подход к решению прикладных задач ОМД, который требует огромной вычислительной работы.
Оптимизацию можно осуществить на основе сравнения по какому-либо критерию результатов расчета при различных исходных параметрах процесса. Например, если необходимо оптимизировать конструкцию штампа для выдавливания детали типа стакана с двухсвязным контуром (рис. 6.16, б), то в качестве варьируемых можно взять следующие конструктивные параметры: толщину Наружной 5Я и внутренней стенки стакана SB, высоту калибрующих поясков на пуансоне /кн и /Кв» уклоны матрицы ан, ав, уклоны пуансона рн, рв. Пусть известна математическая модель процесса, т. е. уравнение Рд » Ф($я, SB, /ки, /кв, ая, ав, рн, рв), связывающее усилие деформации с перечисленными параметрами,
7*
199
а в качестве критерия оптимизации принят минимум Рд. Если каждый из параметров варьировать всего на трех уровнях, то потребуется 3е = 6561 раз вычислять усилие Рд. Конечно, такой колоссальный объем работы можно выполнить только о помощью цифровых ЭВМ. Многие технологические задачи ОМД можно решать численными методами на машинах «Наири» МИР-2. Для решения сложных задач прямым вариационным и визиопластическим методами нужны машины с большим объемом памяти, например М-222, БЭСМ-6, ЕС 1020 и другие аналогичного класса. К сожалению, объем книги и ее направленность не позволяют представить программы даже для типовых задач ОМД.
6.3. УЧЕТ УПРОЧНЕНИЯ В ТЕОРЕТИЧЕСКИХ РЕШЕНИЯХ
Формулы для анализа напряженно-деформированного состояния и силового режима содержат в качестве независимой переменной величину истинного сопротивления деформации af, значение которой в процессе деформации непрерывно возрастает в связи с упрочнением. Значение aj может оставаться неизменным только при горячей изотермической штамповке, когда разупрочнение идет с высокой скоростью. Такие условия в производстве встречаются крайне редко. Поэтому при теоретическом анализе практически всех технологических операций ОМД необходимо учитывать упрочнение металла и изменение истинного сопротивления деформации.
Интегрирование уравнений равновесия совместно с условием пластичности (5.1), (5.2) легко удается лишь в том случае, когда а, = const. Такое же положение характерно для методов линий скольжения и верхней оценки. Достаточно принять at =* Ф(е), как задача станет практически неразрешимой [361. Вот почему в большинстве решений технологических задач, полученных инженерным методом, а также методами линий скольжения и верхней оценки принято а, = const. Это один из существенных недостатков указанных методов.
Во многих работах предлагается уточнять решения путем осред-нэния истинного сопротивления деформации о, [4, 36, 137, 1501. Пусть для заданной операции каким-либо из аналитических методов определено усилие деформации Рд при условии а, =• const. Уточним значение Рд, воспользовавшись осредненной оценкой упрочнения металла 11371. Из уравнения баланса мощностей имеем
где — скорость деформирования; (а,)Э| к •
(£,)э — эквивалентные значения интенсивности напряжений и интенсивности скоростей деформаций, которые учитывают упрочнение металла в среднем; V—полный объем очага деформации. На основании теоремы о среднем значении интеграла находим
= («а» (6-3)
200
где (<тД, (БД — среднеинтегральные значения о(, в расчетной модели. С достаточной для практики точностью можно считать, что уравнение (6.3) справедливо для упрочняющихся и неупрочняю-щихся металлов. Запишем его дважды: для деформации с упрочнением и без (в первом случае величины, входящие в уравнение, пометим индексом у) и разделим первое на второе: р*--- =
(°<)су (b)cyVy Л _
= —(Б<) V ’ Опыт показывает, что средняя величина интенсивности скоростей деформации (БД практически не зависит от свойств материала, т. е. (БЗсу = (£Д. Форма и размеры очага деформации при обработке давлением упрочняющегося и неупроч-няющегося материалов отличаются незначительно. Скорости voy, v0 для одной и той же операции ОМД одинаковы. Следовательно,
<6Л>
При деформации не упрочняющегося материала a, = const = Поэтому уточнение усилия деформации путем осредненной оценки упрочнения сводится к определению среднеинтегрального значения истинного сопротивления деформации с учетом упрочнения (аДу и вычисления Рду по формуле (6.4). Чтобы найти значение (оДу. нужно построить диаграмму истинных напряжений о,— для данного деформируемого металла (см. подразд. 1.6.3). Из уравнения (6.3) найти (БЛс и для исследуемого этапа деформации рассчитать (еД по формуле г t п
Г (* Р№
(е<)с = = \ -^Г dt. (6.5)
‘о о
Отметив на оси е, диаграммы истинных напряжений координату (еД, вычисленную по формуле (6.5), легко найти соответствующее значение (оДу на оси о, и затем по формуле (6.4) рассчитать уточненное усилие с учетом упрочнения.
Экспериментальная проверка теоретических решений, уточненных по изложенной методике, показала, что для прессования ошибка осреднения не превышает 10% [41.
Значительно проще учесть упрочнение в теоретических решениях, полученных энергетическим, прямым вариационным, визио-пластическим методами. Диаграмму истинных напряжений аппроксимируем какой-либо функцией, например в виде полинома ae = = уМив", который дает погрешность, не превышающую 3% на л=0 всем интервале допустимых значений интенсивности деформации 0 ef 1. Подстановка значения а,, выраженного полиномом*, в формулы для вычисления усилия или работы деформации, например в формулу (5.34), не вызывает никаких принципиальных за
201
труднений, так как интеграл, определяющий работу внутренних сил, приводится к сумме четырех интегралов, достаточно просто вычисляемых на ЭВМ:
(6.6) V п=о у
где е( = е((х, у, z, t) — известная функция (1.31). Конечно, трудоемкость вычисления по формуле (6.6) значительно возрастает. Ошако при использовании ЭВМ это мало отражается на продолжительности расчета.
Упрочнение учитывается в теоретических решениях наиболее просто в том случае, когда используется метод определения напряжений по распределению твердости (см. подразд. 5.3.4). Решение задачи этим методом достаточно легко алгоритмизировать и запрограммировать для ЭВМ [32, 331. Однако при большом количестве узловых точек резко возрастает трудоемкость получения экспериментальной информации, а при малом числе узлов — сильно снижается точность решения [1561.
6.4. АНАЛИЗ СИЛОВОГО РЕЖИМА
6.4.1. Постановка задачи. Определение деформирующего усилия имеет большое прикладное значение как один из этапов разработки технологического процесса, конструирования штампов и выбора оборудования. Рассмотрим какой-либо процесс ОМД, например штамповку на кривошипном горячештамповочном прессе (рис. 6.1). Считаем, что эпюры распределения контактных нормальных ап и касательных напряжений тж заданы в виде функций
= Фя(х, у, z,/);
Рис. 6.1. Схема к определению деформи- Тк Фк(*» У* г» Л» (6.7) рующего усилия известных на контактной по-
верхности f(x, у, z} = 0.
Выделим на контактной поверхности инструмента площадку dF. Пусть нормаль к площадке п образует с координатной осью z* угол <р. Тогда
j (on cos ф 4- тк sin ф) dF — Р&; j (о„ sin ф + тк cos ф) dF Т. (6.8) f р
Равнодействующую Ра вертикальных составляющих распределенных сил, действующих на контактной поверхности деформирую
* Ось z выбираем так, чтобы она совпадала с направлением перемешен ня ползуна пресса.
202
щего инструмента, условимся называть усилием сопротивления дв-формации.
Силу Рд. которая передается деформируемой заготовке контактной поверхностью инструмента и развивается главным исполнительным механизмом кузнечной машины, условимся называть деформирующим усилием, или усилием деформации. Будем считать, что —Рд — усилие активного действия кузнечной машины, а 4- Рд — усилие сопротивления деформации обрабатываемой заготовки. Сила Т представляет собой горизонтальную составляющую полного усилия сопротивления деформации. Она уравновешивается реакцией направляющих ползуна пресса или специальными элементами штампов, которые называют замками.
Таким образом, задача определения деформирующего усилия легко решается, если известны функции (6.8). Найти их можно разнообразными методами, рассмотренными в гл. 5.
Однако это не единственный путь решения задачи: для вычисления деформирующего усилия часто используют энергетический подход. Работу деформирующей силы — Рд на перемещении — du (или мощность Рди0) приравнивают к работе (или мощности) всех внешних и внутренних сил сопротивления деформации. С решением таких задач читатель уже знаком (см. подразд. 5.2.3). При выборе метода решения задачи об определении деформирующего усилия необходимо учитывать следующее. Во-первых, нужно использовать такой метод, который ведет к цели кратчайшим путем. Например, при определении усилия горячей осадки цилиндрической заготовки достаточную точность решения обеспечивают инженерный метод, метод верхней оценки или энергетический. Во-вторых, не следует упускать возможности оптимизации исследуемого процесса. Инструмент для обработки давлением работает в исключительно тяжелых условиях. Поэтому любое изменение параметров технологического процесса или параметров, определяющих конструкцию штампа, которое приводит к снижению усилия деформации, как правило, обеспечивает значительное повышение стойкости штампа, стабильности технологического процесса и эффективности производства.
Деформирующее усилие— важная характеристика технологического процесса ОМД. Наряду с ней для выбора технологического оборудования во многих случаях необходима еще одна характеристика — работа деформации. Работа деформации—основной параметр, по которому выбирают оборудование для магнитно-импульсной, электрогидравлической, взрывной и высокоскоростной штамповки.
Работу деформации Ад легко определить, имея зависимость усилия деформации от перемещения инструмента Рд = Ф(ДЛ):
h
Aa - J Pt dll. (6.9)
0
203
Отсюда следует важная задача теоретического анализа: вычислить не только наибольшее усилие деформации Рюах, которое для
многих процессов соответствует ее окончанию, но также его изменение в процессе деформации.
При штамповке магнитным полем или жидкостью подвижный инструмент отсутствует. Для этих процессов работу деформации можно найти как сумму работ внутренних сил и сил трения в объеме деформируемой заготовки (см. уравнения’(5.22), (5.29), (5.30)).
6.4.2. Плоские задачи объемной штамповки. Пусть необходимо определить усилие осадки полосы, длина которой значительно превышает ширину. В соответствии с законом наименьшего сопротивления можно считать, что еи “ 0, т. е. деформированное со-
отояние плоское. В очаге деформации имеем 7. »
1 р* у Ухг . 4 е«
, где (jy = 0,5 (ож+<тг). Для решения такой
задачи чаще всего используются методы верхней оценки, энергетический и инженерный.
В зависимости от условий трения на контактной поверхности можно принять два вида разрывных полей для метода верхней оценки (рис. 6.2). Обозначим ширину и высоту полосы как b, h. Построим годографы скоростей (рис. 6.2, б, е) и по формуле (5.58) определим усилия деформации (на единицу длины осаживаемой полосы).
Для варианта а имеем тк = k = о,/КЗ; Рд = — 4т,исГс; т, =» “аХЗ; о. = Г Л’ + 6’; F. = 4 У Л’ + Л
После подстановки этих значений и преобразований находим
о, w b' + h* /3 ’ Л ’
Определим относительное удельное усилие деформации'. ~р
- 1 + м
р Уз bh •
(6.10)
Задавшись значениями b/h = 2, 3, 4, 5, вычислим р и нанесем полученные значения на график (рис. 6.3). Для варианта b имеем тк = 0,1а* = 0,1 • 2о,//3. Следовательно, Рд = Д [т, АВ u2-i -f-“f- Te ВС j “f” Tk AC Vg—e “1“ BZ) ^3-ol«
204
Из рис. 6.3 следуют соотношения между искомыми и заданными величинами (для удобства расчетов принимаем v0 = 1, h = « 1): У2-в = vt = tga; = °3-° = из e
= tga4-tgP; tgp=^ — tga; AC = ~ ; BD =
= _ tg a; BC — /1 + — tg a) . После подстановки и
преобразований получаем
п 2<*s /11 Ь* . 1 I +rr2 а\ •
P', = V5(l+,‘~+^ + tg Т
Рис. 6.2. Кинематически допустимые разрывные поля скоростей (а, в) н соот» ветствующие им годографы (б, г) для осадки полосы:
а, б — для тк — А, в и в •— для тк < А
В уравнении (6.11) угол a — варьируемый параметр. Чтобы получить верхнюю оценку, необходимо функцию (6.11) минимизировать.
Задавшись значениями b/h = 2, 3, 4, 5, вычислим минимизированные значения р и нанесем их на график (рис. 6.3). Решим эту же задачу энергетическим методом. Примем линейное распределение скорости v, по высоте заготовки z: vz = —Сг. При г = h vx — — v0. Отсюда С = v0/h, иг = —v^z/h. По уравнению (5.48) определяем vx = — Ц—dx = ух, Имея папе скоро
205
стей, находим компоненты и интенсивность скоростей деформации:
= “7Г ’» £« = ~= — -j-; е« = 0; & = . Подставляем
найденные значения в формулу (5.37). Приняв тк = ро*, получаем
2 1 Л
ООО
Отсюда находим относительное удельное усилие деформации р = -^1+|Л£). (6.12)
Примем ЫН. = 2, 3, 4, 5 и рассчитаем р для двух значений коэффициента трения р=0,1, р = 0,5. Результаты расчета нанесем на график (рис. 6.3). Решим эту же задачу, воспользовавшись инженерным методом. Возьмем уравнения (5.1) и приближенное условие пластичности в форме (5.3) или (5.4). Дифференцируя последние два уравнения по х, получаем
= (6.13)
дх дх ' '
Заменяем в первом уравнении системы (5.1) первый член дих1дх равным ему членом dajdx. Имеем
^£-+^Д? = 0. (6.14)
0Х 02
Примем закон изменения тХ2 по г в виде линейной функции На плоскости симметрии при z = 0 сдвиги отсутствуют, поэтому тхх = 0, Ао = 0. При г = + 0,5й т„ = тк. Отсюда тХ2 = 2тк2/й. Примем тк = —ро*. При этих условиях
2р о?
<615>
Дифференцируя уравнение (6.15) по г и подставляя получен-qo 2ра*
«ое значение в выражение (6.14), найдем ----j—= 0. Реше-
ние этого дифференциального уравнения легко найти в виде 2ра? _ ,
+ Постоянную интегрирования С определим из
204
следующего условия: если бы трение по контактной поверхности отсутствовало, то в любой точке деформируемого тела мы имели бы а2»—0*е Трение затрудняет деформацию заготовки только в областях, удаленных от свободных поверхностей. Поэтому можно принять а, — —а* при z = 5/2. Откуда
о,—
h \2
(6.16)
Воспользовавшись общим уравнением (6.8) и учитывая, что для рассматриваемой задачи costp — 1, sin<p » 0, вычислим деформирующее усилие
ь
Т 1
Ш2ца, (Ь \ •] . . 26а, , 6\
-7nU_x)-0‘ 1+l*2*)-
Определим относительное удельное усилие деформации
+ (6J7)
Как видно из уравнений (6.17), (6.12), энергетический и инженерный методы дают совпадающие значения р. Ранее для а, мы нашли инженерным методом другое решение (5.7): af =» Сехр (—. Оно получено в предположении, что контактное касательное напряжение тк зависит от нормального an в форме Амонтона—Кулона: тк = Постоянную найдем из граничных
условий, принятых ранее: при х = Ы2 аг = —о*. Тогда
* у-, ( 2ц б\ л ♦ /2цб\
— о, =жСехр(— f • -yj; С = — a, exp|^-§-J;
в—а»ехр[1г(т—*)]• (6.18)
После интегрирования а, по контактной поверхности заготовки имеем
ь 2 I
Pd=2 ,f У о*ехр[2т(4“"х)]ах^='й'4*[ехр(»х4)’"1]-0 0 L 1J У L\/J
Разделив Рд на 1 • b • о„ получим относительное удельное усилие
₽“-^т[ехр(иЯ-1]’ <619)
207
Рис. 6.3. Графики зависимости относительного удельного усилия осадки полосы, построенные по различным формулам:
1—(6.12) и (6.17): 2 - (6.19); 3 - (6.11) при ц " 0,1; 4 —
(6.12) и (6.17); 5 — (6.10); 6 — (6.19) при ц — 0.5
Примем b/h = 2, 3, 4, 5 и рассчитаем относительное удельное усилие р для двух значений коэффициента трения р = 0,1, р «= = 0,5. Результаты расчета нанесем на график (рис. 6.3).
Итак, одну и ту же задачу мы решили методами верхней оценки, энергетическим и инженерным. Получили различные формулы для определения относительных удельных усилий. Результаты расчетов представлены на графиках (рис. 6.3). Как видно нз рис. 6.3, при р = 0,1, b/h > 3 все три метода и все четыре формулы дают практически совпадающие результаты. Для осадки узких полос (b/h < 3) метод верхней оценки дает завышенные значения. Это связано с тем, что принятое для расчета поле оказывается слишком грубым для таких условий.
Менее отрадной оказывается картина при осадке с большим трением на контактных поверхностях (р = 0,5, кривые 4, 5, 6). Формула (6.19) дает нереально завышенные результаты. Детальный анализ причин этого явления сделан в подразд. 6.5.2. Задаваясь условиями трения на контактных поверхностях, необходимо учитывать рекомендации, изложенные в подразд. 3.1, 3.2. Используя условие тм = ра, для
осадки, мы не обращали внимания на то, что при р = 0,5 контактное касательное напряжение тк сразу же достигает предельного значения и дальше увеличиваться с увеличением о, не может. Поэтому формула (6.19) некорректна для р = 0,5.
Разрывное поле, принятое для осадки полосы при р = 0,5 (рис. 6.2, е), также слишком грубо схематизирует процесс, а поэтому ..качения р сильно отличаются от действительных.
Для этих условий наиболее точные результаты можно получить по формулам (6.12), (6.17). Осадка полосы — самая простая операция ОМД. Однако ее анализ принципиально не отличается от анализа других, более сложных процессов. Прав
да, лишь в том случае, если анализируются задачи с одной степенью свободы течения металла. Действительно, при осадке полосы уширение заготовки (компонента vx) однозначно определяется по известной скорости движения инструмента vt = vo, независимо от условий трения на контактных поверхностях и влияния
других факторов.
Большая группа процессов ОМД характеризуется двумя степенями свободы течения.К их числу относится процесс выдавливания деталей типа коробок. Если длина коробки значительно больше ее ширины, то деформированное состояние заготовки можно считать плоским. При выдавливании коробок ось пуансона всегда смещена относительно матрицы на величину 6. В одних случаях не-
206
соосность преднамеренная, т. е. вызванная стремлением получить деталь с различной толщиной стенок, в других — непреднамеренная, т. е. обусловленная неточностью изготовления или наладки штампа. И в том, и в другом случае осевая симметрия течения металла в очаге деформации нарушается: течение в толстую стенку встречает меньшее сопротивление, чем в тонкую. Поэтому толстая стенка оказывается более высокой. Анализ таких задач сопряжен с известными трудностями.
Для исследования процессов ОМД с двумя степенями свободы течения металла наиболее часто используют вариационные методы.
Рис. 6.4. Кинематически допустимое разрывное поле (а) и годограф скоростей (б) для нестационарной стадии выдавливания [361
Приведем, как пример, решение задачи о выдавливании разностенной коробки методом верхней оценки (рис. 6.4). Несоосность пуансона и матрицы б определяется конструкцией или наладкой штампа, а положение точки М (или размер А) — законом наименьшего сопротивления. По формуле (5.58) найдем усилие деформации,
а затем и относительное удельное усилие Р =-^-4-
n
4-т,АСс3_а 4- + xiBDvl)_i +чкСМи2+хкОМи4 + хкСЕиа +
4- xkAL (v0 4- u3) 4- tkBN (y0 4- wB) 4- tkDFv6]. Вычислим значения входящих в формулу величин. Положение точек А, В, а следовательно, и углов <р, ф однозначно определяется смещением пуансона б и размерами выдавливаемой заготовки; tg ф = (7?м — — гп — б)/h\ tg = ()?м — гп 4- б)/Л. Величину б условимся считать независимой переменной. Положение точки М и углов а, р определяется смещением Д точки М от оси пуансона: tga=(rn— — Д)/Л; tg р = (гп 4- ty/h. Величину Д условимся считать варьируемым параметром. Из рис. 6.4 находим
AM = Л/cos a; AC = Л/cos ф;
CM = Л(sin ф 4-sin a);
СЕ = Л4-/к; AL«=/K;
BM = Л/cos p; BD = Л/cosф;
DM = Л (sin ф 4- sin p);
BN = /KT; DF ~ h + (6.20)
209
Может возникнуть вопрос, почему в выражении (6.20) принято СЕ = h 4- /к. а не СЕ = h 4- /, как это следует из рис. 6.4. Объяснение заключается в следующем: в связи а неравномерностью деформации выдавленная стенка детали ощутимо изгибается внутрь и ее контакт с поверхностью матрицы имеет место только на участке CL = Л 4-1*- Этому способствует также изготовление матриц с уклонами стенок порядка 0,5°. По этой же причине DF — « h 4- /кт, а не DF =• h 4- 4- Из годографа находим
vt-i = t/o/cos a; v9_t = v0 tg «/sin Ф; = Ц»/соз 0;
= »o tg P/sin ф; v3 = v0 tg a; t>4 •= u0 tg 0;
v9 *= ?o tg a/tg 0; v9 = v0 tg 0/tg ф. (6.21)
После подстановки найденных значений и упрощения получаем
- = 1_______Л Г 1 1 1 , 2tga . 2tg0 ,
" У'З * 2r п |cos*a * cos* 0 "t” sin 2<p ' sin 2ф
। o„ F tg a (i I . tg 0 /. . i 2 (/M 4" ;кт) 1 । PL tg«p \ Л / tgt\ “* Л / "" h Jf
4- 2щ [(sin a 4- sin <p) tg a 4- (sin 0 4- sin ф) tg 3]}. (6.22)
Уравнение (6.22) в неявном виде выражает зависимость р • «= Минимизация р по варьируемому параметру Д позволяет установить положение раздела течения МК, построить годограф, отвечающий минимуму полной энергии деформации и вычислить скорости течения металла в [тонкую f, и толстую стенку. Для производственных задач необходимо оптимизировать размеры конструктивных элементов штампа так, чтобы получились детали с наименьшей разновысотностью. Этого можно достигнуть, увеличив высоту калибрующего пояска пуансона /к, а также ухудшением условий трения на участках MD, DF. С этой целью мощности трения на участках матрицы MD, DF введены в уравнение (6.22) с коэффициентом трения щ, который можно преднамеренно увеличить по сравнению с ц.
Уже минимизация р требует многих повторений достаточно громоздких вычислений. Оптимизация размеров конструктивных элементов штампа, в частности выбор высоты калибрующего пояска /к, число повторений расчета р увеличивает во много раз. Поэтому такие задачи решают, используя ЭВМ.
Усилия деформации различных технологических задач ОМД, рассчитанные методом верхней оценки, как правило, превышают действительные, если даже подобрано корректное поле. Поэтому для решения сложных задач с двумя степенями свободы течений Широко используют прямой вариационный метод [28, 143, 146, 1501. Преимущество его не только в более высокой точности, но и в общности решения. Рассмотрим, например, модель течения, Предложенную в работе [391. Очаг деформации принят в первом Приближении (рис. 6.5) ступенчатым: линия EGMN отделяет очаг деформации (области /, 1т, 2 и 2т) от жесткой зоны (область 4).
210
КМ —линия раздела течения, т. е. линия, на которой vx = О для любого г. Если ось пуансона смещена относительно оси мат* рицы на заданное расстояние б, то, как показывает опыт, линия раздела течения получает смещение относительно оси пуансона в сторону тонкой стенки на расстояние Д, однозначно связанное с величиной б. Поэтому, как и выше, считаем б независимой переменной, а Д варьируемым параметром. Учитывая принятые допущения и граничные условия задачи, поле скоростей представим в таком виде: для области /, где —(гп 4- б) х —(б 4- Д);
О, = о, = -^-(х+Д + «);
для области /т, где — (б 4- Д) х (гп — б),
— -г2- [г — (h— Аат]; »,я-г-(х4- Д + б); лд т пдт
для области 2, где — /?м<х^ — (гп 4- б),
Оо (гп-Д)(₽м + х)
Rtt гп &
дли области 2т, где (гп—б)^х^/?м,
__ С'о (гп + М (Ям х) х “ ?<?т *м-'п + а
Здесь и0— скорость перемещения пуансона. По уравнениям (1.35) нахочим скорости деформации, по выражению (5.65)— интенсивность скоростей деформации.
Далее можно воспользоваться классической схемой решения вариационных задач (см. подразд. 5.2.4.1). Составив систему (5.51) или (5.56), находим варьируемые параметры, а затем строим действительное поле скоростей и по уравнению (5.37) решаем поставленную задачу. Однако такой путь оказывается более громоздким, чем предложенный в работе [391. Его суть состоит в том, что функции vx = vx (х, у, z), vx =« vx (х, у, z), содержащие варьируемые параметры (в рассматриваемом случае Д, Aj, А^). вводят в уравнение (5.37). Выполнив все необходимые подстановки и преобразования и разделив левую и правую части на площадь пуансона 2гп1 и истинное сопротивление деформации о,, найдем относительное удельное усилие деформации
Р в о9 4- аг 4~ а9 . (6.23)
Здесь а9 = 4- рх/г ; а «--------*------(р. (1 4-
ИЗ (I — г) (1 — 60) 1 4(1 _г)(|4-в0) (
+ д, + |2 + 2М, _7) _; _ дя} + Д f П) <_-#; а> _
211
= Г Л 4-+Д)’-L И М» 1 1 [ <> + бр) (1 + А) .
771(1 + иУ 3)1~тг“ + ( 1-Д) ~77ТИ » +
+ (1 — 6О) (1 — А)],
Уравнение (6.23) объединяет силовые и кинематические характеристики процесса выдавливания в условиях несоосного расположения инструмента и содержит три варьируемых параметра: А — показатель смещения линии раздела течения КМ от оси пуан-
Рис. 6.5. Модель течения, принятая для анализа процесса выдавливания ко* робок [39]
Рис. 6.6. Зависимость относительного удельного усилия выдавливания р от несоосностн инструмента б0 и относительного размера пуансона г [39]:
1 — 7—0.8; 7 —7—0,7; 3 — 7—0,8; 4 — г — 0.9
сона; п — показатель формы очага деформации; Ла— глубина распространения очага пластической деформации. В соответствии с принципом минимума полной энергии деформации действительные значения Ла, л, А должны минимизировать функцию р = = /(Ла, л, А). Отсюда следует, что dp/dhd = 0; др/дп = 0\ др/д&=0. Эти уравнения эквивалентны системе (5.50). Из первого уравнения находим dp/dh^ ajR*—aa/?M//ia = 0;
Ла =: Rm 7” (6.24)
Подстановка hd из выражения (6.24) в уравнение (6.23) приводит к функции
Per = л0 + 2 7" OjOj. (6.25)
Эту функцию можно записать как рст =« /(л, 3). Значит, на стационарной стадии Рат зависит от двух варьируемых параметров.
212
Минимизируя per по п и Д численным методом, можно получить
зависимость относительного удельного усилия выдавливания от относительного смещения пуансона 60 при различных степенях деформации, характеризуемых относительным размером пуансона г (рис. 6.6). Пользуясь формулами (6.23)—(6.25), можно построить график изменения деформирующего усилия по ходу инструмента. Перемещение ho — h# происходит в условиях стационарной стадии. Для этого участка усилие определяем по формуле (6.25). Дальнейшее движение пуансона приводит к изменению схемы деформации, так как очаг пластической деформации охватывает всю
толщину донышка выдавливаемой детали. Задавая различные текущие значения его толщины h в пределах О < h < hdt по формуле (6.23) рассчитываем соответствующие относительные удельные усилия р и находим усилие деформации Pa«2rn/pa,. График Рд — — &h позволяет вычислить работу де формации Да и таким образом решить все вопросы, связанные с выбором оборудования.
6.4.3. Плоские задачи листовой штамповки. Особенность большинства задач листовой штамповки состоит в том, что контактные напряжения являются сравнительно небольшими и не могут оказывать существенного влияния на переход заготовки в пластическое состояние. Поэтому с достаточной
Рис. 6.7. Графики распределения напряжений стг, во фланце заготовки, подвергаемой (ытяжке
для практики точностью можно счи-
тать, что при деформации листовой заготовки напряженное состояние плоское. Такая схема напряженного состояния характерна для вытяжки, отбортовки, обжима, раздачи, формовки 11121. Благодаря этому уменьшается число неизвестных, упрощаются уравнения равновесия и их интегрирование. Например, для осесимметричного деформирования фланца заготовки при вытяжке (рис. 6.7) уравнения равновесия (1.67)
дст ст. — ств приводятся к одному уравнению 4---------— = 0.
Присоединив к нему условие пластичности ог — as = о,, легко найти напряжение аг в функции радиуса
аг = о, In RH/r.
(6.26)
Из условия пластичности и формулы (6.26) находим вторую компоненту напряжения
а® = —о, (1 — In Rjr). (6.27)
213
Таким образом, напряженное состояние фланца при вытяжке заготовки определяется двумя главными напряжениями о,, (рис. 6.7) по формулам (6.26), (6.27). Если вытяжка заготовки осуществляется с прижимом Q, то силы трения, приложенные к фланцу, создадут дополнительное растягивающее напряжение [112].
Дох = . при переходе от фланца к скруглению вытяжной
кромки матрицы гм в точке В металл претерпевает изгиб. В результате появляется дополнительное напряжение До, =« 0,5о, х с
X л—т-ё . В точке С металл распрямляется. Это также приводит к увеличению напряжения на Дет, = Дста. В точке С напряжение, действующее вдоль сбразующей, которая до вытяжки имела радиальное направление, можно определить, суммируя все напряжения о„ Дох, Даа, Даа:
°с в °«(,п 7; + nR^Sa, + 2rM + i) *
Наконец, при движении контактной поверхности деформируемой заготовки по поверхности вытяжного ребра ВС трение приводит к увеличению напряжения. Это можно учесть множителем ехр(рл/2) [ 112]. При малых значениях р можно ехр(рл/2) заменить первыми двумя членами разложения в ряд:
ехр(рл/2) =* 1 + 1,6р. (Б)
Объединив выражения (А), (Б), получим окончательное выражение для определения напряжений в точке С:
+ + + (6.28)
Теперь несложно перейти к усилию деформации. В точке С площадь поперечного сечения деформируемой заготовки найдем из рис. 6.7: F = 2лгв5. Огсюда усилие деформации при вытяжке стакана
Ра - 2пг,Sa,(in £ + (1 + 1.6Ю- (6.29)
По формуле (6.29) можно построить график изменения усилия деформации по ходу пуансона. В процессе деформации S изменяется мало; rB, р, Q допустимо считать постоянными. Поэтому усилие изменяется в связи с упрочнением и уменьшением радиуса R„. Упрочнение оценивается путем осреднения о, для каждого этапа деформации. Задав для каждого этапа деформации /?и, вычисляем Рд и строим график Рд — Связь между ходом пуансона ДА и размером фланца /?и легко установить на основании условия постоянства объема.
214
Интегрирование усилия по ходу пуансона позволяет получить работу деформации [931
Ад = 2nR,Sa, (1 + 1,6ji) (й; - зл; + 1) +
+ nSaf + +2$ J ’
где R9 — радиус исходной заготовки; = RJR*.
Уравнения (6.26), (6.27) можно использовать для анализа целого класса задач листовой штамповки — задач раздачи и обжима кольцевых и трубчатых заготовок. При этом следует учитывать знаки напряжений: для раздачи а, <0, а® > 0; для обжима а, <0, < 0. Большое практическое значение имеет анализ
задачи изгиба широкой полосы. Изгиб — сопутствующий элемент таких процессов, как вытяжка, формовка и др.
При изгибе моментом широкой полосы (ее ширина значительно больше толщины S) деформированное состояние можно считать плоским, а напряженное — объемным (рис. 6.8). Напряжения af, ae — главные нормальные напряжения. Интегрирование дифференциальных уравнений равновесия совместно с условием пластичности позволяет определить функции распределения напряжений ar, at по толщине полосы:
для зоны растяжения для зоны сжатия
<Jr в — о* In /?н/г; а, = —at In r/RB;
ae = at (1 — In /?B/r); ae = —at (1 + In r/Rj. (6.31)
Здесь /?н» Rt—радиусы наружной и внутренней поверхности полосы. Они выражаются через радиус срединной поверхности изгиба полосы Ro и толщину полосы S соотношениями R*= =* + 0,55, /?в= Ro — 0,55.
Исследования показывают, что при RofS < 25 толщиной упруго-деформированного слоя полосы можно пренебречь и считать, что пластическая деформация распространяется по всей толщине полосы [1121. Из уравнений (6.31) следует, что по мере удаления от поверхностей напряжения о, возрастают по абсолютному значению, а напряжения о# меняют знак.
Назовем поверхность, на которой напряжения ar, рассчитанные по уравнениям (6.31), становятся одинаковыми, а напряжения а« меняют знак, нейтральной поверхностью. Обозначим ее радиус через гв. Радиус г№ найдем из выражения (6.31); at In ₽в/гив ** at In rB/RB. Откуда
Гв = V (6.32)
Эта формула показывает, что в общем случае при изгибе полосы нейтральная поверхность не совпадает со срединной и располагается между последней и внутренней поверхностями, так как
215
< /&hR* <R0=s 0,5 (Ян + RJ. По уравнениям (6.31), (6.32) можно построить графики распр?деления напряжений ае (рис. 6.8) и найти изгибающий момент:
Рис. 6.8. Эпюры напряжений для изгиба полосы без упрочнения (--------) и с
упрочнением (------):
а — с большим радиусом изгиба (R^S — 5); б — с малым радиусом изгиба (RB/S »1)
После подстановки значения га из (6.32) в уравнение (6.33) находим
Мя = 4 bS*o* 4 •
(6.34)
Формула (6.34) получена для oj = const и может быть исполь-вована только для определения момента изгиба толстых листов в горячем состоянии. Изгиб тонких листов в холодном состоянии происходит с упрочнением металла. В этом случае кривая истинных напряжений достаточно точно аппроксимируется степенной функцией (см. подразд. 1.6.3). Совместное решение дифференциального уравнения равновесия и условия пластичности с переменной правой частью в фэрме at = А (In — | позволяет получить уравнения для определения аг, ав в таком виде [112]:
для зоны растяжения при г>гя
216
для зоны сжатия при г<гн л Г. г \л+1 / f V>+>1
а,=-----тп 1Пй-Н - 1П^) ;
' п 4-1 [\ /?,/ \ г / J ’
(г \л л Г/ г V*+l / г \л+11
lnz) ~гпК,пй;) ~(|пт) ]• (6.35)
Подставляя значения а,, <?• в подынтегральные выражения (6.33), находим момент изгиба полосы с упрочнением.
Многие задачи листовой штамповки можно анализировать также методами линий скольжения, верхней оценки, энергетическим, по распределению твердости и др. В качестве примера приведем опре-деление усилия вытяжки стакана с утонением стенки (рис. 6.9)
Рис. 6.9. Схема вытяжки с утонением детали типа стакана (а, б), сетка ли* ний скольжения при тк = 0 (а), разрывное кинематически допустимое поле (б) и годограф скоростей (а) [178]
[178]. Эту задачу отнесем к плоским (плоская деформация), так как тангенциальная деформация е» незначительна по сравнению с радиальной е . Условие et<ef вытекает из уравнений Коши е9 = ur/r, er = oujdr. Очевидно, что при большом радиусе г и малой толщине стенки S На рис. 6.9 сетка линий сколь* жения построена в предположении, что Sj/S0 s 1/(1 4- 2sina). Имея сетку, легко рассчитать относительное удельное усилие деформации [178] р = и определить деформирую-
щее усилие
р . f1 +°)sina n ((fn 4- sd)2 _ r«j, (6.36) УЗ 14-2 мп a n । »/ n>. \ /
В формуле (6.36) не отражено влияние трения на контактных поверхностях инструмента и упрочнение металла. Согласно рекомендации Р. Хилла [ 1651 трение на поверхности матрицы можно учесть множителем 1 4- pctga. Эго дает основание формулу (6.36) представить в таком виде:
Ра = (1 + Н ctg а) " (2г„$а + S’]. (6.37)
6 1*25
217
Рис. 6.10. Характер локализации деформации при штамповке осесимметричных поковок в открытом штампе
При вытяжке с утонением площадь поперечного сечения исходной заготовки Fo= л Цгп + «$0)2 — уменьшается до Fd = = л[0’п+<$д)2 — г2]. Это позволяет рассчитать показатель Я? « Г»— = —р—, по диаграмме истинных напряжении определить сопро-• о тивление деформации а, н подставить его в выражение (6.37).
При больших коэффициентах вытяжки ft, = S0/Sd напряжения в стенке вытянутой части стакана могут превзойти предел прочности ав и вызвать обрыв стенки. Поэтому одна из важных задач анализа состоит в том, чтобы найти не толоко усилие деформации /V но также оптимальный угол а, при котором Рд получает минимальное значение. Наиболее просто это можно сделать методом верхней оценки. На рис. 6.9 приведены кинематически допустимое разрывное поле б и годограф скоростей в. По формуле (5.58) определяем усилие Рд и минимизируем его по углу а. Результаты минимизации, представленные в работе [178), показывают, что аО1гг = 15...25°.
6.4.4. Осесимметричные задачи объемной штамповки. Для анализа этого класса задач можно использовать практически любой аналитический метод.
Анализируя силовой режим штамповки в открытом штампе (рис. 6.10), можно воспользоваться вариационным методом. В работах М. В. Сторожева, Е. И. Семенова, Ш. Гелей установлено,
что при окончательном формообразовании поковки (доштамповке) очаг деформации охватывает не весь объем металла, находящегося в ручье, а сравнительно небольшую область, примыкающую к об-лойной канавке [138, 146). Это позволяет сложную задачу анализа штамповки детали с контуром A BCDEFGHKL свести к более простой, задаче анализа штамповки детали с контуром MEFN. В работе [ 146) очаг деформации MEFN отделен от жестких зон поверхностью ft = zt: [Ло + oft0(l — r2//?J)l, где ft, г — текущие координаты поверхностей ME, NF\ 2ft0 — толщина облоя; R„ — радиус поковки, а — варьируемый параметр, определяющий глубину, распространения очага деформации (рис. 6.10).
Радиальные перемещения частиц металла в очаге деформации описаны функцией ur=* br (1 — z2/ft2)2.Параметр b находим из условия h
постоянства объема nr*&h = J 2nru,dr. Отсюда b = 15АЛ/16А; о
иг = 15ДЛг (1 — z2/ft2)2/ 16ft. Вторую компоненту можно определить л пл, ЗОДЛг/. 2z’ . z4 \ .»
по уравнению (1.29): II — 4- 1. Имея и„ и„ вы-
218
числим йг, сг ег, с,. Используя уравнение (5.37), определим усилие деформации и найдем
₽= 1,15 j j YС\ + С,С, + CJ + CJr dr di. О о
(6.38)
Здесь г = г//?п» z = z/h — безразмерные координаты; Clt Са, С8 — ~ 15 (1+а) (1-г’)4-а?(1—г’) (1—9?)
переменные коэффициенты; Сг = j • 1-----—----। + а a~'i--------*
. _ 15/1-2X2. г а [2а7»? - (1 - 7») (I + а)1 - т« i— 8v г;, g3— 2- т(1 + а— ат)
В уравнении (6.38) не учтено усилие, необходимое для дефор мации облоя. Приняв в объеме облоя схему равномерной дефор
мации, получим относительное удельное усилие
- _ | , |Л ^0
р‘~ +зм/?;-я«)
(6.39)
Полное усилие доштамповки можно определить на основании выражений (6.38), (6.39):
Рд = nRnpc, 4- л (₽J — Rl) pfPs. (6.40)
Уравнение (6.40) — вариационное уравнение с одним варьируемым параметром а, определяющим глубину распространения очага пластической деформации. Минимизация Рд по а_ при помощи ЭВМ позволила определить параметр а, вычислить рш для различных соотношений Rn/h0 [ 1461. При штамповке поковок в открытых штампах значение величины Rn/h0 обычно находится в_ пределах 60... 100, что дает возможность считать приблизительно рш — 5...6. Для решения уравнения (6.38) приходится выполнять громоздкие вычисления. Поэтому предложена его аппроксимация, позволяющая определить усилие деформации при штамповке по следующей приближенной формуле:
[р Id \i»5 //? \з.51
1+0,17^-0,013(g) ]. (6.41)
Приближенная формула (6.41) во-первых, справедлива только До ₽п/Ло С 80- Во-вторых, она как и уравнения (6.40), (6.38), применима лишь в том случае, когда глубина полости штампа в любой точке поверхности разъема больше глубины распространения очага пластической деформации [ 1461. Аналогичные результаты можно получить и при использовании других методов [131, 142, 138, 150].
6.4.5. Осесимметричные задачи листовой штамповки. Осесимметричное напряженное состояние в задачах листовой штамповки 8* 219
Рис. 6.11. Разбивка призматической заготовки на области, в которых деформацию можно считать плоской
встречается сравнительно редко. Это связано с характером при-ложен и я нагрузки в технологических задачах листовой штамповки (см. подразд. 6.4.3). К числу осесимметричных можно отнести разделительные операции, выполняемые цилиндрическим инструментом, а также вытяжку с утонением цилиндрических деталей. К сожалению, теория разделительных операций пока не создана. Вытяжку с утонением можно свести к плоской деформации. Р. Хилл показал, что пластическое течение при вытяжке с утонением можно считать плоским, если диаметр и толщина стенки заготовки свя-30S [ 165]. Решение плоских задач листовой штамповки, в том числе и вытяжки с утонением, рассмотрено ранее (см. подразд. 6.4.3).
6.4.6. Объемные задачи. Объемные задачи — наиболее сложный класс задач ОМД. Решаются они двумя путями. Наиболее простой — расчленение заготовки на области, в которых напряженно-деформированное состояние можно считать плоским или осесимметричным.
Использование этого пути можно проиллюстрировать на примере осадки призматической заготовки (рис. 6.11) 1138]. В соответствии с законом наименьшего сопротивления при осадке призматической заготовки течение металла происходит по кратчайшей нормали к периметру (см. подразд. 4.1). Поэтому заготовку можно
условно разбить на две треугольных области ABE, CDF и две трапециевидных ADFE, BCFE, в которых деформацию можно считать плоской. Предполагая, что напряжения о2(х, у) известны для каждой области, деформирующее усилие можно определить интегрированием ог(х, у) по всей контактной поверхности:
Рд = 2 j o2i dFt 4- 2 J ст22 dF,. Fl Ft
(6.42)
Здесь F,— площади трапеции AEFDn треугольника ABE. Из рис. 6.11 имеем
dF, = [(/ - b) + 2x] dx; dF, = [2y — (I — b)] dy.
Остается найти функцию o2t, огг. Используя уравнение равновесия, приближенное условие пластичности, условие на контактной поверхности в форме Зибеля и допущение о линейной зави-dUr . dtxi л _ _*
симости между т„ и z, получаем ~ 4- = 0; их — о, = о;;
тд = —poj; тЖ2 = 2tbz//i. Из этих уравнений находим —
220
2РП» л 2 ц а*
----j- =0, откуда после интегрирования ог = -~JX4-C. По-
стоянную С определяем из условия о, = —о* при х = 0,56: С =>
в —о? — • 4 • Отсюда
a,i = -о* - (А - х). (6.43»
Л , л /
Аналогичным образом для оси у получаем --------------------------(6.44)
нЧ1 _ Ь
2h\ 31
Подставив значения of|, dFx, а22, dFt в уравнение (6.42), определим усилие деформации Рд- Разделив усилие Рд на площадь контактной поверхности заготовки Ы и предел текучести о,, найдем относительное удельное усилие деформации р = р[1 +
. Если принять р = 1, р = 0,5, то получим извест
ную формулу Губкина [31) Формула получена в предположении чисто плоской деформации в областях Fu F2. В действительности это предположение справедливо только при /^>6. Поэтому для 6</<56 вместо о* необходимо принимать Рст, и коэффициент Р определять линейной интерполяцией по формуле
₽= 1 +®45(4 — 1). (6.45)
4 \ и /
G учетом этого уточнения
р = [ 1 + 0,0375 (А - 1)1 1 + (1 - £)1 • (6.46)
L \ v / j \ о»/ j
Такой путь возможен только для решения простейших задач ОМД. Наиболее часто для анализа объемных задач применяются вариационный или визиопластический методы [2, 92, 146, 150, 170].
6.4.7. Особенности анализа высокоскоростных процессов. Высокоскоростные процессы ОМД с каждым годом получают все более широкое распространение. Уже четко определились области применения различных видов высокоскоростной штамповки — взрывной, электрогидравлической и магнитно-импульсной. Особенность этих процессов —исключительно высокие скорости деформирования и, как следствие, очень высокие ускорения и инерционные силы, действующие на элементы деформируемой заготовки. Под влиянием внешних нагрузок частицы деформируемого тела разгоняются, накапливают огромный запас энергии, соизмеримый с энергией деформации. Эту стадию процесса высокоскоростной деформации принято называть стадией разгона. Дальнейшая деформация происходит за счет инерции частиц заготовки. Запасенная
221
кинетическая энергия расходуется на дополнительную деформацию. Эту стадию, которая протекает, как правило, без воздействия рабочей нагрузки, называют стадией торможения. Инерционные силы сильно изменяют поле напряжений.
Определить влияние инерционных сил и вычислить обусловленные ими напряжения можно только визиопластнческим методом, который разработан Ю. Н. Алексеевым именно для анализа высокоскоростных процессов ОМД [2, 3).
Рассмотрим растяжение цилиндрического образца с высокой постоянной скоростью v0 (3J. Основные уравнения движения (5.69) для рассматриваемой задачи (в цилиндрической системе) имеют вид
„„ 52-5^! 4-., Р*' I
Wr dr ~ дг +^‘\дг* + г дг г / + 2 дг дг •
„„ — 4- и 4-9^5!’
Р г дг дг дг* дг дг *
(6.47)
Скорости vft иг являются функциями скорости растяжения образца и0 и координат г, z:
и,
2/
г;
Подставляя их значения в уравнения (6.47) и выполняя необходимые преобразования, находим
^вр_1гвф- = Ф
дг р 4/« Г дг 1 I* z *'
После интегрирования этих функций по формуле (5.70) определяем среднее напряжение
аср = з + 2 \7* + 47* / ’
а затем по формуле (5.64) — осевое напряжение
(6.48)
Уравнение (6.48) показывает, что напряжения в образце зависят от координат. Это связано с действием инерционных сил, которые учитываются конвективными членами уравнений движения (левые части уравнений (5.69)). Оценим порядок второго слагаемого (6.48). Обозначим его через ДаКОм- Примем обычное для высокоскоростных процессов значение и0 = 100 м/с. При этом для стали, имеющей в среднем р = 7850 кг/м3, находим, приняв z = /, г == 0, что соответствует точке на оси образца в конце его рабочей части, Даконв, = 0,5 • 7850 • Ю0а (кг/м8) • (ма/са) «
40 • 10е кг/мма = 40 МПа. Для стали 15of « 200 МПа, следо
222
вательно ДвконвА. 0,2. Для меди и алюминия at « 100 МПа и 50 МПа, а р = 9000 кг/м3 и 2700 кг/м3соответственно. Поэтому для меди ДоконвУ”, « 0,45, а для алюминия Доковв./”, « 0,30. Совершенно очевидно, что пренебрегать такими добавками можно только в очень грубых расчетах.
При деформации с высокой скоростью инерционные силы возникают в образце также и в связи с изменением во времени скорости перемещения частиц металла. Вследствие этого изменения появляются добавочные члены (локальные члены уравнений движения (5.69)), которые дают дополнительное увеличение напряжений (6.48) на Долок-
В работе [3] добавочные напряжения определены следующим образом: Дал<ж = Для высокоскоростных процессов
ОМД dvQ/dt имеет порядок 10е м/с’. Поэтому при r = 0, z = = / = 30 мм = 0,03 м (это стандартный пятикратный образец диаметром 6 мм) для стали 15, например, имеем Додок/о, « 0,6. Примеры показывают, что при высокоскоростных процессах ОМД в деформируемой заготовке возникают дополнительные напряжения, обусловленные действием инерционных сил, которые соизмеримы с основными напряжениями.
- Рассмотрим анализ процесса раздачи тонкостенной трубчатой заготовки импульсным магнитным полем [7). Пусть на заготовку действует давление магнитного поля q(t), которое изменяется во времени по закону
q (/) = <7тахв“28/ sin’cot (6.49)
Здесь </tnax — наибольшее давление; 6 —коэффициент затухания; (о — круговая частота разрядного контура.
Экспериментально установлено, что при оптимальном соотношении длины индуктора и заготовки компонента скорости vr не зависит от г и описывается функцией (рис. 6.12) vr = Аг 4- В/г, где г — текущий радиус. Из условия постоянства объема (1.38) находим осевую компоненту vg = —2Аг + С.
Примем во внимание следующие граничные условия (рис. 6.12): vr « о0 при г п= r0; v2 = t>i при z = h; vz = 0 при г = 0. Введем обозначение Vj/и0 «= а. При этих условиях легко определить постоянные А, В, С и в окончательном виде получить поле скоростей:
v, s § (^ + Л//г); vt = г, (6.50)
где V » 2Лг0 — Далее выполняется известная процедура (см. подразд. 5.3.2) определения компонент скоростей и интенсивности скоростей деформации, вычисления коэффициента рр интегрирования уравнений движения и определения среднего напряжения. Опуская эти промежуточные преобразования, приведенные в ра
223
боте [7] со всеми подробностями, дадим окончательные выражения для компонент напряжений:
=о? 1п£ +р^(г —Я);
♦ I Г I <4 / 1
•i ' I о\ о*(Заг*—Н)
а,=а, 1пу+р-^(г-Я)--^- . (6.51)
Здесь А = av0/2h; R—радиус внешней поверхности заготовки.
Скорость v0 пока остается неизвестной. Чтобы ее определить, вое-
Рис. 6.12. Схема раздачи трубчатой заготовки импульсным магнитным полем
Рис.6.13. Графики изменения давления магнитного поля q(l), скорости перемещения внутренней поверхности заготовки о9 (2) и работы деформации A# (3) при раздаче [7]
пользуемся условием равенства радиальной составляющей поля напряжений и давления магнитного поля на внутренней поверх* ности заготовки:
<7тахв-2М sinW = О* In + Р (Гв — R). (6.52)
/у
Численным интегрированием этого уравнения можно получить значение скорости и0 для любого момента t.
Имея поле напряжений и скорость v0, можно определить работу деформации А^. При высокоскоростной деформации полная работа определяется суммированием работы, затраченной на формоизменение Е, и работы, затраченной на изменение кинетической энергии частиц заготовки L [2,31:
Ад = (Е + L) dVdt; Е =
, (до. Зр \ (до. до.\
L = р"' (м +Vr аг)+₽0« (* + )• <6-53)
_ до. до. др. до
Для тонкостенной заготовки -нт + Or -5- « -zr , так как ->0. or or or or
224
Расчеты давления магнитного поля q, скорости va и работы деформации Аз, выполненные по формулам (6.49), (6.52), (6.53) для процесса раздачи заготовки 054 X 2 длиной 2Л = 40 мм из сплава АМгбМ, приведены на рис. 6.13. Как видим, графики q, v0 сдвинуты примерно на 30 мкс. Поэтому деформация заготовки продолжается и после прекращения действия магнитного поля в течение 30 мкс. Эта деформация происходит на стадии торможения за счет накопленной кинетической энергии.
6.5. АНАЛИЗ НАГРУЗОК НА ИНСТРУМЕНТ
6.5.1. Постановка задачи. Инструмент для ОМД работает в чрезвычайно тяжелых условиях. Чтобы рассчитать его на прочность и оптимизировать конструкцию, нужно определить действующую на него систему сил и установить законы их распределения по контактной поверхности. Ранее мы установили, что усилие Рд характеризует условия работы инструмента далеко не полностью (см. подразд. 6.4.1 и рис. 6.1). Поэтому сформулируем задачу следующим образом.
Задана технологическая операция ОМД, указаны комплексы параметров технологического процесса Кт и комплексы конструктивных параметров инструмента Кк. Найти на контактной поверхности инструмента /(х, //, z)=0 напряжения ип=ап(х, у, z), Тк =тк(х, у, г), а также систему сил Рх, Ру, Рг и моментов Мх, Му, Мг, к которым приводится воздействие деформируемого металла на инструмент. В общем виде такая задача неразрешима. Поэтому пути ее решения покажем на некоторых частных примерах.
6.5.2. Плоские задачи. Рассмотрим нагрузки, действующие на плоские плиты при осадке полосы в условиях плоской деформации и предельного трения тк = к (рис. 6.14). Наиболее точно решение этой задачи можно получить методом линий скольжения.
В области ADC металл находится в однородном напряженном состоянии, следовательно аСр = —k (см. подразд. 5.2.2 и рис. 5.3, 5.7). Поэтому, двигаясь из области ADC в направлении любой линии скольжения, можно найти компоненты напряжений ах, аг, тхг в любой точке, в том числе и лежащей на поверхности контакта деформируемой заготовки с инструментом, например, пользуясь формулами (5.20). Это легко сделать для участка контактной поверхности АЕ. Однако при построении сетки линий скольжения получаем жесткую зону OEOlt на границе которой OtE заканчиваются все линии скольжения. Поэтому выйти на границу контактной поверхности ОЕ не представляется возможным. Чтобы получить и на участке ОЕ можно поступить следующим образом.
Во-первых, принимать = const, как это сделано Р. Хиллом 1165), и определять значение из условия равновесия области OEOt. Это легко сделать, так как напряжения на границе ЕОХ
225
известны. На рис. 6.14 показана эпюра, построенная по Р. Хиллу (кривая /). Как видно, она имеет разрывы в точке е. Поэтому предпочтительнее эпюра аг, полученная А. Д. Томленовым 11491 (кривая 2). Такой эпюра оказывается, если на участке ЕО принять
= flo + аре2 + atx*. Коэффициенты а0, аг определены из условий равновесия элемента ОЕОХ и гладкого сопряжения в точке с кривой be. Решение позволяет определить напряжения в точках А, В, Е, О и координаты этих точек [149]:
а л = ив = — 1,285(7,; хА = 0,56; хв — 0,56 — 0,7076;
а£-----1,154а, + 1,28б); хЕ = 1,285Л;
оо =—1,154(7, 2,14о); х0 = 0. (6.54)
Рис. 6.14. Эпюры распределения нормальных напряжений при осадке полосы в условиях плоской деформации:
/ — по Р. Хиллу [165]; 2 — по А. Д. Томленой у [149]; 3 — по А. Г. Овчинникову [94] и В. М. Сегалу [127]
Рис. 6.15. Эпюры распределения нормальных и касательных напряжений при осадке полосы в условиях плоской деформации
Имея ох = 0г(х), легко найти деформирующее усилие
Рд = 1,154Ь/а,(| +^ + 0,57). (6.55)
Здесь п = b/h — относительная ширина заготовки; b— ширина; / — длина; h — высота заготовки.
Решения Хилла и Томленова не учитывают бочкообразность заготовки в процессе осадки. В работах [94, 1271 даны уточнения, показывающие, что искажение формы заготовки приводит к существенному изменению эпюры ог (рис. 6.14, кривая 3).
226
Жесткие зоны во многих случаях значительно затрудняют получение эпюры напряжений оп на контактной поверхности инструмента, а поэтому для решения задачи используются другие методы, например инженерный. Покажем возможности этого метода на примере осадки полосы в условиях плоской деформации (рис. 6.15). Пусть О А = 0,56 — половина ширины заготовки. В точке А имеем о-л = —aj. Найдем закон распределения ot на поверхности АвСО. В подразд. 5.2.1 такая задача решена. В предположении, что тЛ = раж, получено уравнение (5.7):
аг = С ехр (—2рх/6). (А)
Постоянную С найдем из условия аг = —а* при х = 0,56. Подставив значение С в выражение (А), получим
ох = — и* exp[ j (у — *)] • (6.56)
Зависимости о, от х по уравнению (6.56) и тк от х по уравнению тк = рах показаны на рис. 6.15 (кривые abd и a'b'd' соответственно). При анализе граничных условий установлено, что формулу Амонтона—Кулона тк = раж можно использовать только в том случае, если |art|<a,. Из уравнения (6.56) следует, что |ax|>af. Поэтому необходимо проверить условие I тк | < 0,5Pas (см. подразд. 3.2). Если это условие не выполняется и тк возрастая, достигает ттах =—0,5a*, то внешнее трение переходит во внутреннее и дальнейшее возрастание |тк| прекращается. Пусть в точке В тк=ттах =—0,5a*. Тогда
-0.5a,*
-0.5a,* =
— pa* exp
. Отсюда
= paxB;
a*
a'fl = “2p; xb = °»56 — mh
(6.57)
где tn = In 2p/2p. При x > хв, t. e. на участке контактной поверхности АВ, аж изменяется по кривой ab, а тк — по кривой а'Ь'. При х<хд условие тк = pat не выполняется, его необходимо заменить условием тк = —0,5a*. При этом уравнения (5.5), 2 0 5a*
(5.6) преобразуем: тХ1 =—~—-z; -f- ~ =0. Интегрируя вто-
а*
рое уравнение, находим az = х 4- С. Определив постоянную С из граничного условия аж = ахв при х = Хв, найдем закон изменения напряжения ах по координате х:
ах = а,в — (хв — х). (6.58)
227
При х< Хв напряжение <зг изменяется на контактной поверхности ВСО по линейному закону (Ьсе), а тк — остается постоянным (Ь'с'е').
Исследования, выполненные методом фотоупругости, показывают, что в точке С, где хс « Л, касательное напряжение начинает убывать по линейному закону. Поэтому на участке СО имеем тк=тсх/хс, или тк=—0,5о,*х/хс. При этом условии уравнения (5.5), (5.6) преобразуются:
— h* 2’ дх + Л1 °’
Интегрируя второе уравнение, находим
°ж = 2h«х2 +
Постоянную С найдем из условия: ог=игс при х = хс. В итоге получим
(6.59)
Следовательно, при х < хс напряжение ог изменяется на контактной поверхности СО по параболе со, а касательное напряжение тк убывает линейно по с'О.
Таким образом, в общем случае контактная поверхность АО разбивается на области скольжения АВ, торможения ВС, прилипания СО. В каждой из них нормальные и касательные напряжения изменяются по разным законам согласно выражениям (6.56), (6.58), (6.59). При горячей деформации р « 0,5, т = 0. Поэтому хв = 0,5Ь, т. е. зона скольжения отсутствует. Если полоса узкая, может отсутствовать область торможения.
6.5.3. Осесимметричные задачи. Анализ осесимметричных задач можно выполнять практически теми же методами, что и анализ плоских. Достаточно точные решения осесимметричных задач получены и методом линий скольжения [1771. Однако это справедливо до тех пор, пока речь идет об анализе задач с одной степенью свободы течения. Для задач с двумя степенями свободы применение метода линий скольжения наталкивается на большие трудности, связанные с построением корректных сеток линий скольжения (98, 150]. Экспериментально-аналитические методы позволяют получать достаточно точные решения, но они весьма трудоемки. Энергетические методы для анализа распределения напряжений неприменимы. В тех случаях, когда не требуется высокой точности, решение можно получить инженерным методом.
Пусть необходимо найти распределение напряжений и усилие при осадке кольца (рис. 5.9). Используя инженерный метод, Л. А. Шофман (1781 получил следующие уравнения:
228
для внутренней зоны, где гв<г</?р, „ ^3ri + <Ф , 2Н®« <' ~ '.)
СТ, — ~~г~ 1П , _ "т" l »
У3 '2 (*J + V3H + /?J) Л
для внешней зоны, где Rp^.r Ra, а - °’ + +
/3 nr,(Rp + /3«J + «J) *
для всей контактной поверхности
3+^/г1
аг = 0, + a, _ ----;.
Уз (3+ /?*/,«)
(6.60)
(6.61)
Чтобы воспользоваться этими уравнениями, необходимо знать положение поверхности раздела течения, т. е. иметь значение Rp. Значение величины Rp для данных размеров кольца R№, rB, h и условий трения р можно определить из условия неразрывности напряжений а,. Приравнивая правые части выражения (6.60) для внутренней и внешней зон и принимая г «= /?р, приходим к уравнению вида Fi(Rp, rB) = Ft(/?P, Ru), откуда находим Rp.
В работах 1143, 178] эта задача решена инженерным и энергетическим методами. Более точные значения Rp, получены энергетическим методом. Инженерный метод дает значения Rpt вполне пригодные как первое приближение. Определив Rp, по уравнению (6.61) можно найти распределение напряжений а2 на контактных поверхностях инструмента.
К сожалению, приходится констатировать, что задачи распределения напряжений решены пока в небольшом количестве [ 136, 149, 1781. Особенно сложными оказываются задачи с двумя степенями свободы течения.
6.6. АНАЛИЗ КОНЕЧНОГО ФОРМОИЗМЕНЕНИЯ
6.6.1. Постановка задачи. Обработка металлов давлением приводит к значительному необратимому формоизменению изделий. Конечная форма и размеры изделия всегда заданы, но получить их можно, используя заготовки различной формы и размеров (рис. 4.4), даже различные способы. Конечная форма заготовки и ее размеры зависят от формы инструмента и его размеров, а также от ряда технологических параметров: температуры, степени и скорости деформации, условий трения на контактной поверхности инструмента и т. д. Инженер должен выбрать наилучший вариант технологии. Для этого необходимо научиться решать задачу конечного формоизменения. Сформулируем ее следующим образом.
229
Заданы заготовка, имеющая форму Ф(х, у, г) = 0, инструмент, имеющий форму f(x, у, г) = 0 и движущийся по закону v(f), температурно-скоростные условия деформации и граничные условия. Определить форму заготовки Ф8(х, у, z, t) = 0 в любой момент времени t. В общем виде такая задача не решается. Покажем ее решение на частных примерах.
6.6.2, Процессы ОМД с одной степенью свободы течения металла. К процессам с одной степенью свободы течения условимся относить такие, в которых конечная форма заготовки «почти однозначно» определяется законом движения инструмента. Эго осадка цилиндрической заготовки (рис. 1.2, 4.7), осадка полосы (рис.6.14), штамповка в открытом штампе (рис. 6.10) и др. Для этих процессов средний диаметр заготовки, средняя ширина полосы, форма поковки однозначно определены условием постоянства объема. Однако форму боковой поверхности даже и в этих задачах приходится определять, исходя из закона наименьшего сопротивления. Одну из таких задач мы уже рассмотрели (см. подразд. 5.2.4.1).
Движение боковой поверхности осаживаемой полосы в направлении оси х можно описать функцией (5.52), а варьируемый параметр а найти по формуле (5.57). Пусть заготовка имеет начальные размеры Ьо, Ло, а верхний боек движется по закону и0 = = u0(f). Можно считать, что за малый промежуток времени Д^ варьируемый параметр а сохраняет постоянное значение Вычислим hjbo и по формуле (5.57) рассчитаем ах. По формулам (5.52), (5.53) вычислим иХ|, v,i и для фиксированных точек боковой поверхности (например, z = 0, z = 0,25/;о, z = O,5/io, z = = O,75ho, z = Zz0) рассчитаем перемещения ых1= vxl Д/j u2l = vzi
По перемещениям uxlt un найдем форму боковой поверхности заготовки после первого этапа. Очевидно, что для получения точной формы необходимо взять достаточное число точек и небольшой промежуток Д/р Величина игХ = vxi = ДЛХ при z = h0 определяет перемещение верхнего бойка. Следовательно, после первого этапа деформации высота заготовки = Ао — ДЛХ. Аналогичным образом анализируется второй, третий и последующие этапы деформации (до тех пор, пока не будет получен заданный конечный размер высоты заготовки Лк = Ло — ДЛ, — ДЛ, —-----ДМ-
Детальный анализ осадки полосы и цилиндрической заготовки дан в работах [143, 1461.
6.6.3. Процессы ОМД с двумя степенями свободы течения металла. К процессам со многими степенями свободы течения условимся относить такие, в которых конечная форма заготовки определяется не только законом движения инструмента и его формой, но и технологическими параметрам'!, в том числе трением. Сюда отнесем осадку на плитах с отверстиями (рис. 4.2), осадку кольца (рис. 5.9), штамповку в открытых штампах с компенсационной полостью (рис. 4.5, б), комбинированное выдавливание (рис. 6.16), выдавливание в условиях несоосного расположения инструмента (рис. 6.4, 6.5), прессование через многоочковые матрицы и т. д.
230
Рассмотрим осадку кольца на плоских бойках. В подразд. 6.5.3 приведены уравнения (6.60), по которым можно определить положение поверхности раздела течения Rp. Чтобы вычислить конечные размеры кольца, которое до осадки имело размеры rM, ho, необходимо процесс деформации разбить на ряд этапов и для каждого из них найти положение поверхности раздела течения Rp. Считая в пределах каждого этапа Rp = const, можно вычислить приращения радиусов Дг, А/? и определить размеры кольца на любом п-м этапе деформации:
= ^л—1 &hn‘, гп = Агя, Rn — Rn—i 4~ ^Rn,
р2 __-2 р2 ____ г>2
= ДЛ„ \ ; Д/?„ = дл„ • (6.62)
*ХЛ-1«Л-1
Таким образом, задача анализа конечного формоизменения сводится к определению положения поверхности раздела течения. Для решения таких задач в наибольшей степени приспособлены вариационные методы. При осадке кольца течения металла можно описать простыми функциями vr, v2. Использовав уравнение (5.36), можно найти положение поверхности раздела течения [146]: = OJ4g_l) + ^(^ + O (6 63)
р 0,6 (Я -1) 4- 2fKrR
где фк = Н 4-0,125(1 — р) /p(R — 1); ~r = rjh\ R = RJr^ Rp = •= RP/rв.
Эго уравнение достаточно точно описывает процесс осадки кольца. Имея Rp, по формулам (6.62) легко найти размеры кольца на любом этапе деформации.
Аналогичным образом решают более сложные задачи конечного формоизменения. Например, при выдавливании в условиях несоосного расположения инструмента (см. подразд. 6.4.2 и рис. 6.4) определены скорости течения металла в тонкую и толстую стенки v3, и8. Разобьем процесс деформации на У этапов, каждый продолжительностью Д/. Если время Д/ мало, то скорости ц3л, на л-м этапе можно считать постоянными и приращения высоты тонкой и толстой стенок определять по формулам Дй3л = и3лД/, Дй5л = и5л Д/. Полную высоту стенок можно получить суммиро-W N
ванием этапных приращений /?, = V Д/13л; Л5 = Чтобы
Л=1 п=1
определить »3л, v^n, нужно для n-го этапа определить Д и построить годограф скоростей. С увеличением количества этапов N трудоемкость расчета возрастает, быстрее чем точность определения размеров й3, Л8. Поэтому для технических расчетов можно приниматьN — 5... 8 в зависимости от того, как сильно изменяется положение плоскости раздела течения.
В работе [58] дано решение очень сложной задачи: комбинированного выдавливания цилиндрической заготовки с двухсвязным
231
контуром. Результаты решения (рис. 6.16, а) достаточно близки к действительным. В задачах этого класса геометрия инструмента играет исключительно важную роль. Например, изменяя размеры калибрующих поясков /к по внутреннему и наружному контуру пуансона, выполняя уклоны на матрице ан, а, или уклоны на пуансоне 0Ж, 0В, можно очень сильно изменять соотношения ско* ростей течения металла в стенки SB, SB и тем самым управлять их высотой (рис. 6.16, б).
Рис. 6.16. Модель течения металла при выдавливании контуром (а) и вариант конструктивного оформления
стакана с двухсвязным матрицы и пуансона (б)
6.7. АНАЛИЗ ПРЕДЕЛЬНОГО ФОРМОИЗМЕНЕНИЯ
6.7.1. Постановка задачи. Задачи анализа предельного формо* изменения относятся к числу самых сложных. Именно поэтому в теории обработки металлов давлением сделаны только первые шаги в данном направлении. В исследованиях В. Л. Колмогорова [59, 1081, В. А. Огородникова [96, 971 разработана теория деформируемости и пэлучены диаграммы пластичности для различных металлов и сплавов, а также выведены формулы для определения степени использования ресурса пластичности (см. подразд. 1.6.4.3). Значительный вклад в развитие теории предельного формоизменения внес И. П. Ренне [117, 1181. Предложенная теория позволяет перейти к решению задач анализа предельного формоизменения. Сформулируем эту задачу следующим образом.
Дано деформируемое тело, для которого определены тензоры Т„, Г,. Вычислить степень деформации сдвига А, сравнить ее с предельно допустимой Ар и установить степень использования ресурса пластичности Т для любой (или наиболее опасной) точки деформируемого тела.
В общем виде такая задача не решается. Покажем ее решение на частном примере.
232
6.7.2. Пример анализа задачи выдавливания. Современное производство ставит перед наукой сложные вопросы, касающиеся оптимизации технологических процессов. Оптимизацию можно осуществлять по различным критериям: минимуму усилия деформации. максимуму равномерности деформации или минимуму степени использования ресурса пластичности [ 108, 119, 1781. В процессе обработки давлением заготовок с высоким пределом текучести и при высоких степенях деформации нагрузки на инструмент достигают предельно допустимых значений. Поэтому оптимизацию
таких процессов ведут по условию минимума усилия деформации Рд-Однако во многих случаях (например, при холодной штамповке) ограничения степени деформации вызваны необходимостью предотвратить брак. Тогда оптимизацию процесса ведут по условию минимума степени использования ресурса пластичности.
Покажем решение этой задачи на примере выдавливания [371. На рис. 6.17 показана сетка линий скольжения и линии тока для стационарной стадии выдавливания клиновым пуансоном в условиях плоской дефор
Рис. 6.17. Разрывное поле скоростей и линии тока для выдавливания плоско-клиновым
пуансоном стали 20 при у = 0,1, графики интенсивности деформации (Г) н степени использования ресурса пластичности (Ф) 137J
интегрирование необходимо
мации и непредельного трения (у. = = 0,1 по всем контактным поверхностям). Степень использования ресурса пластичности при движении материальной частицы вдоль соответствующей линии тока можно определить по формуле (1.89). Однако, учитывая, что поле скоростей, принятое для анализа, имеет разрывы,
заменить суммированием приращений интенсивности деформации сдвига ДА;/ при пересечении линий разрыва скоростей:
ф = У
V ZjApCn,)*
(6.64)
Значение величины Лр(Па) можно вычислить по аппроксимирующей функции [37, 109]:
Лр (Пв) = A -f- В<7ср.
(6.65)
Для стали 20, например, А = 1,9, В = — 1,1. Вычисляя ДА// вдоль линии тока, получаем значения Т. Это дает возможность определить степень использования ресурса пластичности для каждой линии тока (рис. 6.17). Как видно из рис. 6.17, значение на
233
копленной интенсивности деформации сдвига ЕЛ// ® Л сильно изменяется по толщине стенки: на внутренней поверхности значение Л в два с лишним раза выше, чем на внешней. Поэтому и степень использования ресурса пластичности на внутренней поверхности стенки значительно больше, чем на внешней.
В рассмотренном примере значение Т не превышает допустимого, т. е. Т < 1. Поэтому процесс можно осуществлять без опасения получить брак по трещинам. Однако при выдавливании другого, менее пластичного металла (например, стали 35) есть вероятность получить Т > 1. Предупредить появление брака можно путем оптимизации профиля пуансона, изготовления детали за два перехода с отжигом между ними, наложения противодавления на верхний торец выдавливаемой детали. Резервы первого пути весьма незначительны. Третий путь приводит к резкому увеличению нагрузок на инструмент и усложнению конструкции штампа. Поэтому в производстве чаще используют второй путь. Выдавливание в два перехода дает возможность уменьшить в формуле (6.64) числитель, а отжиг — увеличить знаменатель. Поэтому степень использования ресурса пластичности уменьшается.
Таким образом, решение задачи предельного формоизменения позволяет прогнозировать возможность появления брака и своевременно предотвращать его. Это одна из важнейших задач совершенствования производства.
СПИСОК ЛИТЕРАТУРЫ
1. Акивис М. А., Гольдберг В. В. Тензорное исчисление.— М.: Наука, 1969.— 351 с. 2. Алексеев Ю. Н. Введение в теорию обработки металлов давлением, прокаткой и резанием.— Харьков: Изд-во Харьк. ун-та, 1969.— 108 с. 3. Алексеев Ю. Н. Вопросы пластического течения металлов.— Харьков: Изд-во Харьк. ун-та, 1958.— 188 с. 4. Алюшин Ю. А., Еленев С. А. Применение энергетического метода для расчета и анализа процессов пластического формоизменения металлов.— В кн.. Исследование процессов пластической деформации мета л лор. М.: Наука, 1965, с. 106—133. 5. Ба-зык А. С., Пустовгар А. С., Казаков М. В. Выдавливание заготовок инструмента с использованием эффекта сверхпласти«ности.— Кузнеч.-штам-повоч. пр-во, 1978, № 6, с. 5—8. 6. Безухов Н. И. Основы теории упругости, пластичности и ползучести.— 2-е изд.— М.: Высш, школа, 1968.— 512с. 7. Белоглазов И. М. Определение основных технологических параметров процесса раздачи тонкостенного цилиндра импульсным магнитным полем.— Обработка металлов давлением в машиностроении, 1969, вып. 5, с. 110—115. 8. Беляев Н. М. Сопротивление материалов.— 12-е изд.— М.: Физматгиз, 1959.— 629 с. 9. Бережкова Г. В. Нитевидные кристаллы.— М.: Наука, 1969.— >58 с. 10. Бернштейн М. Л. Структура деформированных металлов.— М.: Металлургия, 1977.— 431 с. 11. Бернштейн М. Л., Займовский В. А. Структура и механические свойства металлов.— М.: Металлургия, 1970.— 472 с. 12. Боуден Ф. П., Тейбор Д. Трение и смазка.— М: Машгиз, 1960.— 151 с. 13. Бочвар А. А. О зависимости механических свойств сплавов от их состава и строения.— Иэв. АН СССР. ОТН, 1946, № 5, с. 743—752. 14. Бриджмен П. В. Исследование больших пластических деформаций и разрыва.— М.’ Изд-во иностр, лит., 1955.— 444 с. 15. Булат С. И., Тихонов А. С., Дубровин А. К- Деформируемость структурно неоднородных сталей и сплавов.— М.: Металлургия, 1975.— 352 с. 16. Бзкофен В Процессы деформации/Пер. с англ.: Под ред С. Е. Роко-тяна.—М.: Металлургия, 1977.- 288 с. 17. Головин А. Ф. Прокатка,— М.. Металлургиздат, 1933 — Ч. I.— 237 с. 18. Гольденблат И. И., Коппов В. А. Критерии прочности и пластичности конструкционных материалов.— М.: Машиностроение, 1968.— 192 с. 19. Гордон Л. А., Заливай-ко С. Б., Храпков А. А. Программа решения осесимметричной задачи теории упругости методом конечных элементов для ЭВМ типа М-220.— Л.: Б. и., 1974.— 63 с. 20. Горелик С. С. Рекристаллизация металлов и сплавов.— М.: Металлургия, 1967.— 402 с. 21. Горенштейн М. М. Трение и технологические смазки при прокатке.— Киев: Техшка, 1972.— 190 с. 22. ГОСТ 1497—73. Мегаллы. Методы испытания на растяжение.— Введ. 1.01.1975. 23. ГОСТ 8817—73. Металлы. Метод испытания ня осадку.— Введ. 1.07.1973. 24. ГОСТ 11150—75. Металлы. Методы испытаний на растяжение при повышенных температурах.— Введ. 1.01.1978. 25. ГОСТ 11701—66. Металлы. Методы испытания на растяжение тонких листов и лент.— Введ. 1.07.1966. 26. Гоффман О., Закс Г. Введение в теорию пластичности для инженеров/Пер. с англ.: Под ред. Э. И. Григолюка.— М.: Машгиз. 1957.— 351 с. 27. Грозин Б. Д. Механические свойства закаленной стали.— М.: Машгиз, 1961.— 281 с. 28. Громов Н. П. Теория обработки металлов давлением. 2-е изд.— М.: Металлургия, 1978.— 360 с. ?9. Губкин С. И. Пластическая деформация металлов.— М.—Л.: Б. и., 1935.— 448 с. 30. Губкин С. И. Пластическая деформация металлов: В 3-х т.— М.: Металлургиздат, I960.— Т. 1. 376 с.; Т. 2. 416 с.; Т. 3. 306 с. 31. Губкин С. И. Теория обработки металлов давлением.— М.: Металлургиздат, 1947.— 532 с. 32. дель Г. Д. Определение напряжений в пластической области по распределению твердости.— М.: Машиностроение, 1971.— 200 с. 33. Дель Г. Д. Технологическая механика.— М.: Машиностроение, 1978.— 174 с. 34. Деформация металлов жидкостью высокого давления.— М.: Металлургия, 1976.— 423 с. 35. Деформируемость ме
235
та л лов/Под ред. С. И. Губкина.— М.: Металлург из дат, 1963.—200 с. 36. Джонсон В., Кудо X. Механика процесса выдавливания металла/Пер. с англ.: Под ред. М. 3. Ерманка.— М.: Металлургия. 1965.— 174 с.
37. Евдокимов А. К. Влияние формы пуансона на неравномерность деформации и использование ресурса пластичности при плоской закрытой прошивке (стационарная стадия).— Обработка металлов давлением. (Тула), 1972, вып. 17, с. 78—85. 38. Евстратов В. А., Даниленко В. Я. Методика оценки качества фосфатного покрытия и оптимальное конструирование стальных деталей, изготовляемых холодным выдавливанием.— В кн.: Объемная штамповка: Материалы семинара.— М.: Б. и., 1973, с. 155—161. 39. Евстратов В. А., Куликов И. В., Иванов О. М. Влияние несоосности инструмента на характер деформации, силовой режим и нагрузки, действующие на пуансон при выдавливании.— Вести. Харьк. политехи, ин-та, 1977, № 131. Прогрессивная технология обработки металлов, вып. 4, с. 38—44. 40. Жуков А. М. О пластических деформациях изотропных металлов при сложном напряженном состоянии.— Из в. АН СССР. ОТН, 1956, № 12, с. 231—252. 41. Зайков М. А. Режимы деформации и усилия при горячей прокатке.— Свердловск: Металлургиздат, 1960.— 302 с. 42. Зенкевич О. Метод конечных элементов в тех нике/Пер. с англ.: Под ред. Б. Е. По-бедрн.— М.: Мир, 1975.— 541 с. 43. Зибель 3. Обработка металлов в пластическом состоянии.— М.: Б. и., 1934.— 287 с. 14. Золотухин И. М. О подобии процессов горячего деформирования металла.— Кузнеч.-штампо-воч. пр-во, I960, № 3, с. 1—3. 45. Иванова В. С., Терентьев В. Ф. Природа усталости металлов.— М.: Металлургия, 1975.— 456 с. 46. Ильюшин А. А- Механика сплошной среды.— М.: Изд-во Моск, ун-та, 1971.— 247 с. 47. Ильюшин А. А. Моделирование горячих и скоростных процессов обработки металлов давлением.— Изв. АН СССР. Прнкл. математика и механика, 1952, 16, вып. 4. с. 386—398. 48. Исаченков с. И. Контактное трение и смазки при обработке металлов давлением.— М.: Машиностроение, 1978.— 208 с. 49. Казаченек В. И. Штамповка с жидкостным трением.— М.: Машиностроение, 1978.— 77 с. 50. Кайбышев О. А. Пластичность и сверхпластичность металлов.— М.: Металлургия, 1975.— 280 с.
51. Качанов Л. М. Основы теории пластичности.— 2-е изд.— М.: Наука, 1969.— 420 с. 52. Качество и эффективность при листовой и объемной штамповке: Материалы семинара.— М.: Б. и., 1977.— 209 с. 53. Кириллов П. Г. Теория обработки металлов давлением.— М.: Высш, школа, 1965.— 296 с. 54. Клименко В. М„ Шаповал В. И. Вибрационная обработка металлов давлением.— Киев: Техшка, 1977.— 128 с. 55. Ковка крупных поковок/ Под ред. В. Н. Трубина, И. Я. Тарновского.— М.: Машгиз, 1962.— 224 с. 56. Ковка и объемная штамповка стали: Справочник: В 2 -х т. /Под ред. М. В. Сторожева.— М.: Машиностроение. 1967.— Т. I. 435 с. 57. Кокрофт М. Смазка в процессах обработки металлов давлением/ Пер. с англ.: Под ред. М. 3. Ерманка.— М.: Металлургия, 1970.— 111 с. 58. Колесников В. М., Евстифеев В. В. Разработка алгоритма и программы расчета на ЭЦВМ силовых и кинематических параметров операции холодного обратного совмещенного выдавливания.— В кн.: Машины и технология обработки металлов давлением. Омск: Б. и., 1975, с. 68—77. 59. Колмогоров В. Л. Напряжения. Деформации. Разрушение.— М.: Металлургия, 1970.— 230 с. 60. Колмогоров В. Л., Орлов С. И., Колмогоров Г. Л. Гидродинамическая подача смазки.— М.: Металлургия, 1975.— 256 с. 61. Контактное трение в процессах обработки металлов давлением.— М.: Металлургия, 1976.— 416 с. 62. Костава А. А. Об условии пластичности при высоких гидростатических давлениях.— Науч. тр./ЦНИИТМАШ, 1969. вып. 89. Вопросы пластичности н технологии обработки металлов давлением, с. 15—20. 63. Коттрел А. Теория дислокации/Пер. с англ.: Поз ред. А. Л. Ройтбурда.— М.: Мир, 1969.— 96 с. 64. Крагельский И. В., Виноградова И. Э. Коэффициенты трения. Справочное пособие.— М.: Маш-гнз, 1955.— 188 с. 65. Крагельский И. В., Любарский И. М., Гусля-ков А. А. Трение и износ в вакууме.— М.: Машиностроение, 1973.— 216 с. 66. Кроха В. А. Кривые упрочнения металлов при холодной деформации.—
236
М : Машиностроение, 1968.— 131 с. 67. Лаборатория металлографии/ Под ред. Б. Г. Лифшица.— 2-е изд.— М.: Металлургия, 1965.— 439 с. 68. Лахтин Ю. М. Металловедение и термическая обработка металлов. 2-е изд.— М.: Металлургия, 1977.— 407 с. 69. Лейбензон Л. С. Вариационные методы Кешения задач теории упругости.— М.: ГИТТЛ, 1943.— 128 с. 70. Ли К., ’вас аки X., Кобаяши Ш. Вычисление остаточных напряжений в процессах пластической деформации.— Тр. Америк, о-ва инж.-мех., 1973, № 1, Конструирование и технология машиностроения, с. 199—208. 71. Лифшиц Б. Г. Металлография. 2-е изд.— М.: Металлургия, 1971.— 406 с. 72. Лобанов В. К., Пилипенко В. М. О выборе оптимального профиля и материала матриц для обжима поковок.— Кузнеч.-штамповоч. пр-во, 1976, № 8, с. 36—38. 73. Лошкарев В. Ф. Производство стальных поковок.— М.: Ме-таллургиздат, 1953.— 299 с. 74. Макклинток Ф., Аргон А. Деформация и разрушение материалов/Пер. с англ.— М.: Мир, 1970.— 443 с. 75. Малинин Н. Н. Прикладная теория пластичности и ползучести.— М.: Машиностроение, 1968.— 400 с. 76. Манасевич А. Д. Физические основы напряженного состояния и прочности металлов.— М.—К-: Машгиз, 1962 — 199 с. 77. Материалы в машиностроении.— М.: Машиностроение, 1967.— Т. I. 304 с. 78. Мейз Дж. Теория и задачи механики сплошных сред/Пер. с англ.: Под ред. М. Э. Эглит.— М.: Мир, 1974.— 318 с. 79. Метод подобия в теории прокатки.— Л.: Наука, 1971.— 178 с. 80. Механические свойства материалов под высоким давлением/Под ред. X. Л. Пыо.— М.: Мир, 1973.— 296 с. 81. Механические свойства стали при горячей обработке давлением.— Свердловск: Металл у ргиздат, 1960.— 264 с. 82. Миронов Л. И. Применение смазочно-охлаждающих жидкостей в процессах механической обработки и штамповки.— М.: Б. и., 1974.— 30 с. 83. Михлин С. Г. Вариационные методы в математической физике.— М.: Б. и., 1957.— 83 с. 84. Мошнин Е. Н., Золотухин Н. М. Определение усилия осадки поковок.—Кузнеч.-штамповоч. пр-во, 1960, № 6, с. 1—5. 85. Набор-ро Ф. Р. Н., Базинский 3. С., Холт Д. Б. Пластичность чистых монокри-сталлов/Пер. с англ.: Под ред. Л. М. Утевского, А. Л. Ройтбурда.— М.: Металлургия, 1967.— 214 с. 86. Надаи А. Пластичность и разрушение твердых тел/Пер. с англ.: Под ред. Г. С. Шапиро.— М.: Изд-во иностр, лит., 1954.— 647 с. 87. Некоторые вопросы больших пластических деформаций металлов при высоких давлениях.— М.: Изд-во АН СССР, I960.— 162 с. 88. Новиков И. И. Дефекты кристаллической решетки металлов.— М.: Металлургия, 1968.— 188 с. 89. Новиков И. И. Теория термической обработки металлов.— М.: Металлургия, 1974.— 400 с. 90. Новожилов В. В. Теория упругости.— Л.: Судпромгиз, 1958.— 287 с. 91. Норицын И. А., А кара И. Л., Перфилов В. И. Влияние профиля матричной воронки на параметры прямого прессования.— Кузнеч.-штамповоч. пр-во. 1971, № 12, с. 1—8. 92. Няшин Ю. И., Скороходов А. Н., Ананьев И. Н. Вариационный метод расчета температурных полей в процессах обработки металлов давлением.— Изв. вузов СССР. Черная металлургия, 1973, № 9, с. 91 — 94. 93. Овчинников А. Г. О выборе кривошипного пресса для вытяжки. Кузнеч.-штамповоч. производство, 1961, № 1, с. 30—33. 94. Овчинников А. Г. Осадка бесконечно длинной полосы.— В кн.: Машины и технология обработки металлов давлением. М.: Машиностроение, 1973, с. 178— 180. 95. Овчинников А. Г. Исследование процессов выдавливания. Дисс... докт. техн. наук. М., 1975.—275 с. 96. Огородников В. А. Деформируемость металла при обработке давлением.— Изв. вузов СССР. Черная металлургия, 1976, № 3, с. 74—78. 97. Огородников В. А. Оценка деформируемости металлов при обработке давлением.— Кузнеч.-штамповоч. пр-во, 1977, № 3, с. 15—18. 98. Основы теории обработки металлов давлением/Под ред. М. В. Сторожева.— М.: Машгиз, 1959.— 359 с. 99. Охрименко Я- М» Технология кузнечно-штамповочного производства. 2-е изд.— М.: Машиностроение, 1976.— 560 с. 100. Охрименко Я. М., Ливанов В. А., Бережной В. Л., Щерба В. Н. Анализ и разработка новых схем прессования.— Кузнеч.-штамповоч. пр-во, 1973, № 8, с. 8—12. 101. Охрименко Я. М., Тюрин В. А. Неравномерность деформации при ковке.— М.: Машинострое-
237
ние, 1969.— 184 с. 102. Павлов И. М. Контактное трение сопротивляюще-гося и активного действия.— В кн.: Обработка металлов и сплавов давле* нием. М.: Б. и., 1965, с. 7—14. 103. Павлов И. М. Теория прокатки.— М.: Металлургиздат, 1950.— 428 с. 104. Паршин В. А. Исследование напряженного, деформированного состояния металла и совершенствование технологии при производстве железнодорожных колес: Автореф. дне. ... канд техн. наук.— Свердловск, 1970.— 18 с. 105. Патрунов Ф. Г. Электронные модели.— М.: Моск, рабочий, 1973.— 112 с. 106. Пашкевич А. Г., Орехов А. В., Тюпич Ю. П. Управление распределением толщины при пнев-мотермической формовке листовых деталей в режиме сверхпластнчности.— Кузнеч.-штамповоч. пр-во, 1978, № 8, с. 36—39. 107. Перлин И. Л. Виды расчетных коэффициентов трения при обработке металлов давлением и области их применения.— Цветн. металлы, 1956, № 2, с. 75—82. 108. Пластичность и прочность твердых тел при высоких давлениях.— М.: Наука, 1970.— 162 с. 109. Пластичность и разрушение/Под ред. В. Л. Колмогорова— М.: Металлургия, 1977.— 336 с. ПО. Полухин П. И., Гун Г. Я., Галкин А.'М. Сопротивление пластической деформации металлов и сплавов: Справочник.—М.: Металлургия, 1976 — 488 с. 111. Поль Б. Макроскопические критерии пластического течения и хрупкого разрушения.— В кн.: Разрушение. М.: Мир, 1975, с. 336—520. 112. Попов Е. А. Основы теории листовой штамповки.— М.: Машиностроение, 1968.— 283 с. 113. Постнов В. А., Х.архурим И. Я- Метод конечных элементов в расчете судовых конструкций.— Л.: Судостроение, 1974 — 344 с. 114. Прагер В. Введение в механику сплошных сред.— М.. Изд-во иностр, лит., 1963.— 312 с. 115. Прозоров Л. В., Костава А. А., Ревтов В. Д. Прессование металлов жидкостью высокого давления.— М.: Машиностроение, 1972.— 152 с. 116. Прочность. Устойчивость. Колебания: Справочник.— М.: Машиностроение, 1968.— Т. 1. 831 с. 117. Ренне И. П. Приближенные методы определения значений интенсивности деформаций при установившемся плоском течении.— Изв. вузов, 1965. № 7, с. 160—167. 118. Ренне И. П., Иванова Э. А., Бойко Э. А.. Филигаров Ю. М. Неравномерность деформации при плоском пластическом течении.— Тула. Б. и., 1971.— 159 с. 119. Рен-не И. П., Ренне Т. И. К вопросу об оптимальном угле клиновых пуансонов при плоской закрытой прошивке.— В кн.: Обработка металлов давлением. (Тула), 1971, вып. 8, с. 27—31. 120 Реология. Теория и приложения/ Под ред. Ф. Эйриха: Пер. с англ.— М.: Изд-во иностр, лит., 1962.— 824 с. 121. Рогельберг И. Л., Шпичинецкий Е. С. Диаграммы рекристаллизации металлов и сплавов: Справочник.— М.: Металлургиздат. 1950.— 280 с. 122. Сафаров Ю. С. О моделировании пластических деформаций____
Кузнеч.-штамповоч. пр-во, 1974, № 8, с. 1—6. 123. Сверхпластичность металлических материалов.— М.: Наука. 1973.— 219 с. 124. Свирид Г. П. Численное исследование осесимметричных вязкопластических течений методом конечных элементов.— Докл. АН БССР, XVII, № 9, 1973, с. 819— 821. 125. Северденко В. П. Теория обработки металлов давлением.— Минск: Вышайш. школа, 1966.— 223 с. 126. Северденко В. П., Клубович В. В. Степаненко А. В. Ультразвук и пластичность.— Минск: Наука и техника. 1976.— 448 с. 127. Сегал В. М. Технологические задачи теории пластич-ности/Под ред. В. П. Северденко — Минск: Наука и техника, 1977.— 256 с. 128. Седое Л. И. Механика сплошной среды.— М.: Наука, 1970.— Т. I. 492 с. 129. Семенов А. П. Схватывание металлов.— 2-е изд.— М.: Машгиз, 1958.— 280 с. 130. Сконечный А. И. Новая технология штамповки дисков.— Кузнеч.-штамповоч. пр-во, 1969, № 8, с. 1—5. 131. Смирнов В. С. Развитие обработки металлов давлением в СССР за 50 лет.— Кузнеч.-штамповоч. пр-во, 1968, № 9. с. 3—6. 132. Смирнов В. С. Теория обработки металлов давлением.— М.: Металлургия, 1973.— 496 с. 133. Смирнов-Аляев Г. А. Сопротивление материалов пластическому деформированию.— 3-е изд.— Л.: Машиностроение. 1978.— 368 с. 134. Смирнов-Аляев Г. А., Чикидовский В. П. Экспериментальные исследования в обработке металлов давлением.— Л.: Машиностроение, 1972.— 360 с. 135. Смит М. К. Основы физики металлов/Пер. с англ.: Под ред. Б. Я. Любова.— М.: Металлур
238
гия, 1962.— 456 с. 136.' Соколовский В.' В. Теория пластичности.— 3-е изд.— М.: Высш, школа, 1969.— 608 с. 137. Степанский Л. Г. Расчеты процессов обработки металлов давлением.— М.: Машиностроение, 1979.— 215 с. 138. Сторожев М. В , Попов Е. А. Теория обработки металлов давлением.— 3-е изд.— М.: Машиностроение, 1971.— 424 с. 139. Талыпов Г. Б. Пластичность и прочность стали при сложном нагружении.— Л.: Изд-во Ленингр. ун-та, 1968.— 134 с. 140. Тарковский И. Я. Формоизменение при пластической обработке металлов.— М.: Металлургиздат. 1954*— 534 с. 141. Тарковский И. Я., Леваков А. Н., Поксеваткин М. И. Контактные напряжения при пластической деформации.— М.: Металлургия, 1966.— 279 с. 142. Тарковский И. Я-, Поздеев А. А. По поводу энергетических принципов расчета в теории обработки металлов давлением.— Кузнеч.-штамповоч. пр-во, 1970, № 6, с. 47—48. 143. Тарковский И. Я., Поэ-деев А. А., Такого О. А. Деформации и усилия при обработке металлов давлением.— М.: Машгиз, 1959.— 304 с. 144. Твердосплавные штампы/Под ред. С. М. Хмары.— Харьков: Прапор, 1971.—78 с. 145. Теоретические основы ковки и горячей объемной штамповки.— Минск: Наука и техника, 1968.— 408 с. 146. Теория обработки металлов давлением'Под ред. И. Я. Тарковского.— М.: Металлургиздат, 1963.— 672 с. 147. Тимошек-ко С. П. Сопротивление материалов/Пер. с англ.— М : Физматгиз, I960.— Т. I. 379 с. 148* Томлеков А. Д. Механика процессов обработки металлов давлением.— М.: Машгиз, 1963.— 235 с. 149. Томлеков А. Д. Теория пластического деформирования металлов.— М.: Металлургия, 1972.— 408 с.
150. Томсен Э., Янг Ч., Кобояши 111. Механика пластических деформаций при обработке металлов.— М.: Машиностроение, 19S9 — 503 с. 151. Третьяков А. В., Зюзин В. И. Механические свойства металлов и сплавов при обработке давлением: Справочник.— 2-е изд.— М.: Металлургия, 1973.— 224 с. 152. Третьяков А. В., Трофимов Г. К., Зюзин В. И. Механические свойства металлов и сплавов при обработке давлением.— М.: Металлургия, 1964.— 223 с. 153. Трубик К. Г., Ойкс Г. Н. Металлургия стали.— 4-е изд.— М.: Металлургия, 1970.— 616 с. 154. Укксов Е. П. Инженерные методы расчета усилий при обработке металлов давлением.— М.: Машгиз, 1955.— 280 с. 155. Укксов Е. П. Методы моделирования процессов обработки металлов давлением.— Кузнеч.-штамповоч. пр-во, 1975, № 4, с. 1—5. 156. Укксов Е. П. О развитии теории обработки металлов давлением.— Кузнеч.-штамповоч. пр-во, 1978, № 6, с. !—5. 157. Уэрт Ч., Том-сок Р. Физика твердого тела/Пер. с англ.: Под ред. С. В. Тябли-кова. 2-е изд.— М.: Мир, 1969.— 558 с. 158. Феодосьев В. И. Сопротивление материалов.— 3-е изд.— М.: Физматгиз, 1963.— 539 с. 159. Физическое металловедение/Под ред. Р. М. Кана: Пер. с англ.:— М.: Мир, 1968.— Вып. 3. 484 с. 160. Филин А. П. Прикладная механика твердого деформируемого тела.— М.: Наука, 1975.— Т. 1. 832 с. 161. Филонекко-Бородич М. М, Теория упругости.— 4-е изд.— М.: Физматгиз, 1959.— 364 с. 162. Френкель Я- И Введение в теорию металлов.— М.: ГИТТЛ, 1950.— 383 с. 163. Фридман Я. Б. Механические свойства металлов.— М.: Машиностроение. 1974.— 472 с. 164. Фридман Я. Б., Зилова Т. К., Демина Н. И. Изучение пластической деформации и разрушение методом накатанных сеток.— М.: Оборонгиз, 1962.— 188 с. 165. Хилл Р. Математическая теория пластичности/Пер. с англ. Э. И. Григолюка.— М.: ГИТТЛ, 1956.— 40/ с. 166. Хирт Дж., Лоте И. Теория дислокаций/Пер. с англ.: Под ред. Э. М. Надгорного, Ю. А. Осипьяна.— М.: Атомиздат, 1972.— 600 с. 167. Хоникомб Р. Пластическая деформация металлов/Пер. с англ.: Под ред. Б. Я. Любова.— М.: Мир, 1972.— 408 с. 168. Чертовских А. К.. Белосевич В. К. Трение и технологическая смазка при обработке металлов давлением.— М.: Металлургия, 1968.— 362 с. 169. Чижиков Ю. М. Теория подобия и моделирование процессов обработки металлов давлением.— М.: Металлургия, 1970.— 295 с. 170. Чичеков Н. А., Кудрин А. Б., Полухин П. И. Методы исследования процессов обработки металлов давлением.— М.: Металлургия, 1977.— 311 с. 171. Шабейк А., Кобаяши 111, Применение вычислительных машин к методу визиопластично-
239
сти.— Тр. Америк, о-ва инж.-мех., 1967, № 2. Конструирование и технология машиностроения, с. 165—174. 172. Шапошников И. А. Механические испытания металлов-— М.: Машгиз, 1954.— 443 с. 173. Шарапин Е. Ф. Элементы теории обработки металлов давлением.—Металлургнздат, 1961. — 208 с. 174. Шмид Е„ Боас В. Пластичность кристаллов, в особенности металлических.— М.—Л.: Б. и., 1938.— 316 с. 175. Шнейдер Ю. Г. Образование регулярных микрорельефов на деталях и их эксплуатационные свойства.— Л.: Машиностроение, 1972.— 240 с. 176. Шофман Л. А. Основы ?асчета процессов штамповки и прессования.— М.: Машгиз, 1961.— 340 с.
77. Шофман Л. А. Приближенные решения некоторых трехмерных задач обработки металлов давлением.— Кузнеч.-штамповоч. пр-во, 1966, № 4, с. 1—7. 178. Шофман Л. А. Теория и расчеты процессов холодной штамповки.— 2-е изд.— М.: Машиностроение, 1964.— 375 с. 179. Шульце Г, Металлофизика/Пер. с англ.: Под ред. Я. С. Уманского.— М.: Мир, 1971.— 503 с. 180. Ягн Ю. И. Конспект лекций по курсу механики твердого и деформируемого тел а.— 2-е изд.— Л.: Б. и., 1970.— 216 с. 181. Dalheimcr R.t Diet er le К. Die Berehcnung Elastischer Formanderungen von belasteten Strang-preBmatrizen.—Ind.— Anz., 1970, № 57, p. 92. 182. Drucker D. C.. Grinberg H. J., Prager IF. The Safety Factor of an Elastic — Plastic Body in Plane Strain.—Trans. ASME, J. Appl. Meeh., 1951, 18.—371 p. 183. Frank F.C., ReadW.T. Multiplication Processes for Slow Moving Dislokations.— Phys. Rev., 1950, 79, p. 722. 184. Frenkel J. ZurTeorie der Elastizitiitsgrenze und der Fes-tigkeit kristallischer Kdrper.—Z. Phys., 1926, 37. p. 572—609. \9b. HenckyH. Uber einige statisch bestimmte F3Ile des Gleichgewichts in plastischen Kor-pern.— Z. Angew. Math. Meeh., 1923, 3, p. 241—251. 186. Jain S. C., Brantley A. N. Speed and frictional effects In Hot Forging.—Proc. Inst. Meeh. Engrs, 1968, № 39, p. 192. 187. Johnson W. Estimation of Upper—Bound Loads for Extrusion and Coining Operations.— Proc. Inst. Meeh, Engrs., 1959, 173, 61—72. 188. Kast D. Modellgesetze in der Umformtechnlc.— Ind. Anz. 1969, № 22, p. 91. 189. Kudo H. An Upper—Bound Approach to Plane—Strain Forging and Extrusion.— Int. J. Meeh. Sci., 1960, I. p. 57—83. 190. Stu-we H. P- Die FlieBspannung bei der Kaltumformung.— Z. Meta I Ik., 1970, N3, p. 61. 191. Thomsen E. G. A New Method for the Construction of Hcncky-Prandtl Nets.— Trans. ASME, J Appl. Meeh., 1957, 24, p. 81—84.
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Ад — работа деформации b — вектор Бюргерса Dt, D^, D3— девиаторы деформации, скоростей деформации и напряжений Е — модуль упругости е—показатель деформации Генки F — площадь сечения или поверх* ности G — модуль сдвига k — постоянная пластичности k, I — обобщенные координаты Nd — мощность деформации Рд — усилие деформации р — относительное удельное усилие деформации
Sx, Sy, Sx — полное напряжение в наклонной площадке и его компо* ненты
7*,, 7'ш, Т\, Тя — тензоры деформаций, поворота, скоростей деформаций и напряжений
Г“, — шаровые тензоры деформа-
ций и напряжений 7’, / — температуры t — время u, их, uv, иг — полное перемещение частицы и его компоненты V — объем о» о*» vy, vg — скорость частицы и ее компоненты «р, v>y, Wg — ускорение частицы и его компоненты
в — показатель деформации Коши 81, еа, е>—главные деформации е( — интенсивность деформации еср—средняя деформация
е*, 8у, е„ Уху, Уух, Угх — компоненты тензора деформаций
Л — степень деформации сдвига ц — коэффициент трения v — коэффициент Пуассона £ — скорость деформации
£1* £«• Ь —главные скорости деформации
^ — интенсивность скорое left деформации
U tv Ь. k*-компоненты
тензора скоростей деформаций р — плотность дислокаций °i> ст»> а» — главные напряжения а{ — интенсивность напряжений ап — нормальное напряжение оср —среднее напряжение ох, Оу, Og, хХу, Xyg, ххх — компоненты тензора напряжений а» — предел текучести о02, от-условный и физический пределы текучести
тм, Т»1— главные касательные напряжения тк — контактное касательное напряжение ткр — критическое напряжение сдвига ф — степень использования ресурса пластичности
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Анизотропия 68, 115, 117 Аннигиляция дислокаций 85 Атмосфера Коттрела 70
Барополигонизация 119
Вакансия 72, 73
Вектор Бюргерса 75
Возврат 103 — динамический 107 — статический 107
Гидропрессование 120 Главные оси тензора деформации 23 -----— напряжений 34 —площадки 34 Годограф скоростей 185
Градиент неравномерной деформации 145
Градуировочная кривая твердости 195
Граничные условия 43, 131 -----динамические 43 ----- кинематические 43 ----- статические 43 Граница между зернами 73
Давление гидростатическое 38 — насыщения 119 — пороговое 119
Движение дислокации 75
----- консервативное 75 ----- неконсервативное 76 Движение сплошной среды 16, 17 ----- двумерное 18 — — — нестационарное 17 ----- одномерное 18 -----осесимметричное 18 -----плоское 18 ----- стационарное 17 ----- трехмерное 18
Двойникование 89
Девиатор деформации 25 — напряжений 33 Дефект упаковки 73
Дефекты кристаллической решетки 72
-------- двумерные 73, 79
-----линейные 73, 74 -----точечные 72, 73 -----— трехмерные 73, 79
Деформация 18 — абсолютная 18 — внутрикристаллитная 91 — главная 23 — горячая 108, НО — квазиравномерная 100
— локальная 19
— межкристаллитная 91
— монотонная 118
— неоднородная 30
— неполная горячая 109, НО — неполная холодная ПО — неравномерная 113, 145 — однородная 29 — остаточная 80, 81 — относительная 18 — полугорячая НО — равномерная 143 — теплая ПО — холодная 109
Деформирование вибрационное 124 — в ультразвуковом поле 125 — простое пульсирующее 124 — циклическое 124 Деформированное состояние 16 — — итоговое 16 ----- объемное 29 ----- плоское 40 -----текущее 16 Деформируемость 60 Деформирующее усилие 203 Диаграмма истинных напряжений 56 — пластичности 62 — растяжения 43 — рекристаллизации 106 Дислокация 74 — винтовая 73, 77 ----- левая 77 -----правая 77 — краевая 73, 75 — сидячая Франка 78 — смешанная 77
Дислокационная сетка 88, 98
Диффузионная ползучесть 121 Диффузия 104
Закон 138 — Гука 12 — наименьшего сопротивления 139 — неравномерности деформа* ции 146, 147 — подобия 150 — постоянства объема 24 — Шмида 83 Залечивание дефектов 114
Инварианты тензора деформации 24 -----напряжений 34 Индексы направления 69 — плоскостей 69 Интегралы Генки 112
242
Интенсивность деформации 25
— напряжений 33, 52
— скоростей деформации 28, 189
Источник дислокаций 87
-----Франка — Рида 87
-----гетерогенный 92
-----гомогенный 88
Квазиравновесное состояние 10
Квазиизотропность 68
Компоненты тензора деформации 23
-----напряжений 33
Константа подобия 121
-----геометрического 151, 153
-----физической величины 154 Контактное касательное напряжение 127
Контур пластичности 49, 51
Коррозионное растрескивание 102
Коэффициент выхода тепла 103
— Лоде 53
— неравномерности деформации 145
— несоответствия 153
-----частный 153
— укова 153
Кривая упрочнения 56
Кристалл 66
— нитевидный 84
Кристаллит 66
Критерий подобия 155
Критическая степень деформации 106
Критическое напряжение сдвига 81, 93
Круг Мора 41
Линия дислокации 75, 77
— раздела течения 140 — скольжения 166
Макроструктура 65
Макрошлиф 65
Межзеренное проскальзывание 93
Межузельный атом 72, 73
Метод Ритца 179
Механизм зарождения дислокаций 87
— гетерогенный 89. 93
— гомогенный 88, 89
— межзеренного проскальзывания 93
— упрочнения 90, 98
— образования вакансий 72, 75
— — — Френкеля 72
-----— Шоттки 74
Механическая схема деформации 40
Микроструктура 65
Микрошлиф 65
Модель 13
— деформации 79
— — двойникованием 89
— — дислокационная 84
-----монокристалла 79
-----поликристалла 91
* — скольжением 81
-----совершенного кристалла 79 — сплошной среды 13 -----— телесная 14 Монокристалл 66, 79
Нагрузка массовая 30 — объемная 30 — поверхностная 30 Наклеп 55 Напряжение 31 — истинное 55, 56 — контактное касательное 127 — критическое касательное 81 — приведенное критическое 83 — среднее 33 — условное 46 Напряжения главные 33 -----касательные 35 — дополнительные 146 -----второго рода 147 — — первого рода 147 ----- третьего рода 147 — остаточные 147
Напряженное состояние 30 ----- в точке 32 — — двухосное 38 — — линейное 38 ----- объемное 37 — — одноосное 38 -----плоское 38, 40
Напряженно-деформированное состояние 11
Нейтральная поверхность 215
Неравномерность деформации 143
Область прилипания 228 — скольжения 228 — торможения 228 Оптимизация 199 Отдых 103 Относительное удельное усилие деформации 155, 204
Пара Френкеля 72, 73
Параметр решетки 67
— варьируемый 179
Переползание дислокации 76
Переменные Лагранжа 17
— Эйлера 17
Пластичность 60
— • природная 60 — технологическая 60 Плоскость скольжения 76, 81 Плотность дислокаций 78 Поверхность пластичности 48 — раздела течения 141 Подобие геометрическое 150 — физическое 150 Показатель деформация Коши 19 Генки 19
243
—* жесткости схемы напряженного состояния 62
Поле скоростей 27
Ползучесть диффузионная 121
Полигонизация 103
Поликристалл 66
Постоянная пластичности 53
Предел текучести 46 -----условный 46 -----физический 46 Предельное состояние 43 ----- первое 44 -----второе 45, 59 Примесный атом 73 Принцип минимума полной энергии деформации 140 — наименьшего периметра 140 ----- сопротивления 139 Прострел 148 Пустота 73
Работа деформации 203
Растрескивание коррозионное 102
Рекристаллизация 104
— вторичная 105
— динамическая 107
— первичная 104 — повторная 109 — собирательная 105 — статическая 107 Решетка кристаллическая 66 ----- гексагональная плотноупа-кованная 68
----- кубическая гранецентриро-ванная 68
------- объемноцентрированная 67
Сбросообразование 91 Сверхпластичность 121 — структурная 122 Сетка линий скольжения 164 -----веерная двухцентровая 165, 166 ----- кусочно-линейная 167 Сила Пайерлса 76 — трения 126 -----активного действия 126 -----сопротивляющегося действия 126
Система скольжения 82
Скольжение 81
— карандашное 78
— поперечное 77
Скорость деформации 27 ----- сдвига 27 — деформирования 28 Сплав 70
Среда анизотропная 16
— - вязкая 14 — жесткая 13 <— жестко-пластическая 13
---линейно упрочняющаяся 13
---нелинейно упрочняющаяся 13
---неупрочняющаяся 13
— изотропная 16
— линейно вязкая 14
— нелинейно вязкая 14
— неоднородная 15
— однородная 15
— пластическая 13
---неупрочняющаяся 13
— простая 15
— сложная 15
— сплошная 12
— упругая 13
— упруго-пластическая 14
Стенки дислокаций 103
Степень деформации сдвига 61
---критическая 106
— использования ресурса пластичности 63
Структура 65
— блочная 88
— волокнистая 97
— мозаичная 88
— полосчатая 113
— текстурированная 97
— ячеистая 88
Схватывание 128
Схема деформации 29
— напряжений 39
--- линейная 39
--- плоская 34
--- объемная 39
— разрывных решений 175
Твердый раствор 70
--- внедрения 70
---замещения 70
Текстура 97
— рекристаллизации 98
Тензор 22
— второго ранга 22
— главных деформаций 23
---напряжений 33, 34
---скоростей деформаций 28
— деформаций 23
---шаровой 25
— единичного относительного перемещения 22
— напряжений 32
---шаровой 33
— поворота 22
— скоростей деформаций 28
Теорема Генки 166
Тепловой эффект деформаций 102
Трение 126
— анизотропное 135
— гидродинамическое 129
— граничное 131
— жидкостное 129
244
— изотропное 135
— контактное 126
— сухое 128
Угол сдвига 21
Узел схватывания 128
Упрочнение 55, 90, 91. 98
Уравнение состояния 12
Уравнения движения 42
— Коши 21
— равновесия 42
— Сен-Венана 26
— энергетического метода, основные
173, 174
Усилие деформации 203
Условие деформируемости без разрушения 63
— парности касательных напряжений 33
— пластичности 48
-----Губера — Мизеса 49
-----Треска — Сен-Венаиа 47
----- энергетическое 51
— постоянства объема 24, 28
— совместности деформаций 26
Фаза 65
Феноменологический подход 11
Физический закон 12
Флуктуация энергии 72
Функция координатная 179 — подходящая 179
Экранирующая способность смазкн 136
Экстр а плоскость 75
Элементарная ячейка 67
Эллипсоид напряжений 37
Ядро дислокации 75
ИМЕННОЙ УКАЗАТЕЛЬ
Александер Дж. 8
Алексеев Ю. Н. 7, 189
Альмансн Э. 19
Амонтон М. 131. 133. 159, 207. 227
Бессель Ф. 165
Бншоп Дж. 8
Боас В. 83
Больцман Л. 74
Боуден Ф. П. 132
Бриджмен П. В. 8. 118, 119
Бэкофен В. 8
Бюргерс Дж. 75, 88
Верещагин Л. Ф. 118
Галилей Г. 61
Галкин А> М. 7
Ганаго О* А. 7, 169, 178
Гаусс К. Ф. 171, 190
Гейрингер X. 7, 160
Гелен Ш. 218
Генкн Г. 7, 19.51, 160, 166, 167. 169, 188
Головин А. Ф- 5
Голъденблат И. И. 52
Гофман О. 8
Грин А. I9
Гринберг X. 184
Губер М. 49. 51
Губкин С. И. 5. 7, 147, 152.
154, 158
Гук Р. 12. 13
Гун Г. Я. 7
Даламбер Ж. Л. 42
Дель Г. Д. 7. 195
Джонсон В. 7, 8, 160, 178. 184
Друккер Д. 184
Жуков А. М. 52
Зайков М. А. 112
Закс Г. 5. 7, 8. 158
Зибель Э. 132. 133. 158, 159.
169. 220
Зюзин В. И. 113
Ильюшин А. А. 7, 55, 178
Исаченков Е. И. 7
Карман Т. 5
Качанов Л. М. 51, 178
Кобаяши Ш. 8
Колмогоров В. Л. 7, 61. 232
Кон торов а Т. А- 90
Койнов В. А. 52
Костава А. А. 54
Коттрел А. X. 70
Коши О. Л. 19. 21. 22, 25. 217
Кудо X. 8, 160. 178. 184
Кудрин А. Б. 8
Куини X. 52 Кулон Ш. О. 47, 131, 133. 159, 207, 227 Курнаков Н. С. 111
Лагранж Ж. Л. 16, 17
Леванов А. Н. 7 Лсйбензон Л. G 178 Лоде В. 54
Макушок Е. М. 7. 160. 165
Мизес Р. 49, 51. 53
Михлин С. Г. 176 Мор О. 159, 160
Надаи А. 8
Ньютон И. 129
Овчинников А. Г. 169 Огородников В. А. 61, 195* 232
Ороваи Е. 84
Остроградскнй М. В. 171, 190
Павлов И. М. 5, 153
ПаЙерле Р. 76
Перлин И. Л. 133
Петров Н. С. 7, 169
Петч Н. 99
Поздеев А. А. 7, 169, 178
Полани М. 84
Полухин П. И. 7, 8
Попов Е. А. 7, 158 Прагер В. 7, 160, 184 Поаядтль Л. 7, 160
Пью X. 8
Растегаев М. В. 118 Ренне И. П. 7, 160, 262 Рид В. Т. 87 Ритц В. 179 Рощ М. 52
Свейигер К. 19
Северденко В. П. 7 Сегал В. М. 7. 226 Семенов Е. И. 218 Сен-Венан Б. 26, 47, 48. 51
Смирнов В. G 7
Смирнов-Аляев Г. А. 7, 61. 188, 189
Соколовский В. В. 7, 160, 165
Сторожев М. В. 7, 158, 218
Слове Г. 54
Степанский Л. Г. 169
Талыпов Г. Б. 52 Тарковский И. Я- 7, 133, 134, 169. 178
Тейбор Д. 132
Тейлор Б. 20
Тейлор Дж. 84
Томленой А. Д. 7. 160, 226
Томсен Э. 7, 8, 189
Треска Г. 47, 48, 51
Унксов Е. П. 7, 158, 159. 160, 193
Уральский В. И. 8
Франк Ф. К. 87, 88 Френкель Я- И- 72, 81* 84, 87, 90
Хилл Р. 7. 8, 160, 165, 217* 220, 225
Ходж Ф. Г. 160
Хол Е. 99
Христианович С. А. 160
Целиков А. И. 7
Чернов Д. К. 160
Чнчеяев Н. А. 8
Чэхральский G П. 106
(Царапин Е. Ф. 7
Шлейхер К. 53
Шмид Е. 83. 139
Шофман Л. А. 7, 112,160, 169
Эйлер Л. 16, 17
Эйхингер А. 52
Ягн Ю. И. 33,53
Янг Ч. 5
ОГЛАВЛЕНИЕ
Предисловие .................................................... 3
Введение ....................................................... 5
Глава 1
Основы механики сплошных сред.............................9
1.1. Общие представления о деформации ........................ 9
1.2. Феноменологический подход к исследованию процессов деформации 11
1.3. Модели сплошных сред.......................................13
1.4. Деформированное состояние .................................16
1.5. Напряженное состояние .....................................30
1.6. Предельные состояния.......................................43
Глава 2
Физические основы обработки металлов давлением ... 64
2.1. Строение металлов и сплавов................................64
2.2. Кристаллизация металлов....................................71
2.3. Дефекты кристаллической решетки металлов ..................72
2.4. Холодная пластическая деформация монокристаллов............79
2.5. Холодная пластическая деформация псликрнсталлических металлов 91
2.6. Нагрев и разупрочнение деформир< ванных металлов..........103
2.7. Пластическая деформация при различных температурно-скорсст-ных условиях..................................................106
2.8. Пластическая деформация в особых условиях.................117
Глава 3
Контактное трение................................•.............126
3.1. Физические основы.........................................126
3.2. Граничные условия.........................................131
3.3. Основные факторы, влияющие на контактное трение..........134
3.4. Смазки для обработки металлов давлением...................136
3.5. Основные направления полезного использования сил трения ... 136
Глава 4
Основные законы пластической деформации...................139
4.1. Закон наименьшего сопротивления...........................139
4.2. Неравномерность деформации, дополнительные и остаточные напряжения .........................................................143
4.3. Закон подобия и моделирование процессов ОМД ..............150
Глава 5___________________________________________________________
Методы теоретического анализа процессов обработки метал* лов давлением..................................................156
5.1. Общие представления о методах.............................156
5.2. Аналитические методы!.....................................158
5.3. Экспериментально-аналитические методы.....................188
Глава 6___________________________________________________________
Задачи теоретического анализа процессов обработки металлов давлением..................................................196
6.1. Классы задач теоретического анализа и методы их решения ... 196
6.2. Использование ЭВМ при теоретическом анализе...............199
247
6.3. Учет упрочнения в теоретических решениях
6.4. Анализ силового режима ...............
6.5. Анализ нагрузок на инструмент ........
6.6. Анализ конечного формоизменения ....
6.7. Анализ предельного формоизменения . . .
Список литературы . Основные обозначения Предметный указатель Именной указатель .
200
202 225 229
232
235
241
242
246
ВИТАЛИЙ АЛЕКСЕЕВИЧ ЕВСТРАТОВ
ТЕОРИЯ ОБРАБОТКИ МЕТ44ИОВ ИИВ/1ЕНИЕМ
Редактор А. М. Видмиш
Переплет художника Ю. Г. Неровни Художественный редактор В. Б. Мартыняк Технический редактор Г. Л. Александрова Корректоры В. В. Николаева, Л. А. Федоренко
Информ, бланк № 4450
Сдано в набор 20.01.31. Подл, в печать 10,12.81. БЦ 09343.
Формат в0х90'/1«. Бумага тнпогр. № 1. Лит. гари. Выс. печать.
15,5 усл. печ. л. 15,5 усл. кр.-огт. 18,3 уч.-иад. л.
Тираж 5000 эка. Изд. № 822. Зак. 1*25. Цена 85 к.
Издательство при Харьковском государственном университете издательского объединения «Вища школа». 310003, Харьков-3, ул. Университетская, 18
Книжная фабрика ям. М. В. Фрунзе, 310057, Харькоа-57. уд, ДонеЦ'Захаржеаская, 6/8