Н.И.ЛОБАЧЕВСКИЙ
ПОЛНОЕ
СОБРАНИЕ СОЧИНЕНИЙ
под общей редакцией
В.Ф. КАГАНА, А Н.КОЛМОГОРОВА
А П.НОРДЕНА, ИГ ПЕТРОВСКОГО
В.В.СТЕПАНОВА
ГЛАВНЫЙ РЕДАКТОР
В.Ф. КАГАН
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МО СКВ А — ЛЕНИНГРАД
1951

НИ ЛОБАЧЕВСКИЙ
том пятый
СОЧИНЕНИЯ
ПО МАТЕМАТИЧЕСКОМУ
АНАЛИЗУ,
ТЕОРИИ ВЕРОЯТНОСТЕЙ,
МЕХАНИКЕ
И АСТРОНОМИИ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МО СКВ Д—ЛЕНИНГРАД
1 951

СОДЕРЖАНИЕ !)
От редакции &
I. Сочинения по теории рядов. Об исчезании
тригонометрических строк (1834). Способ уверяться в пс-
чѳзании бесконечных строк и приближаться к значению
функций от весьма больших чисел (1835). О сходимости
бесконечных; рядов (1841). (Перевод В. В. Степанова).
Вводная статья и комментарии Г. Л. Лунца 11
II. Значение некоторых определенных интегралов (1852>.
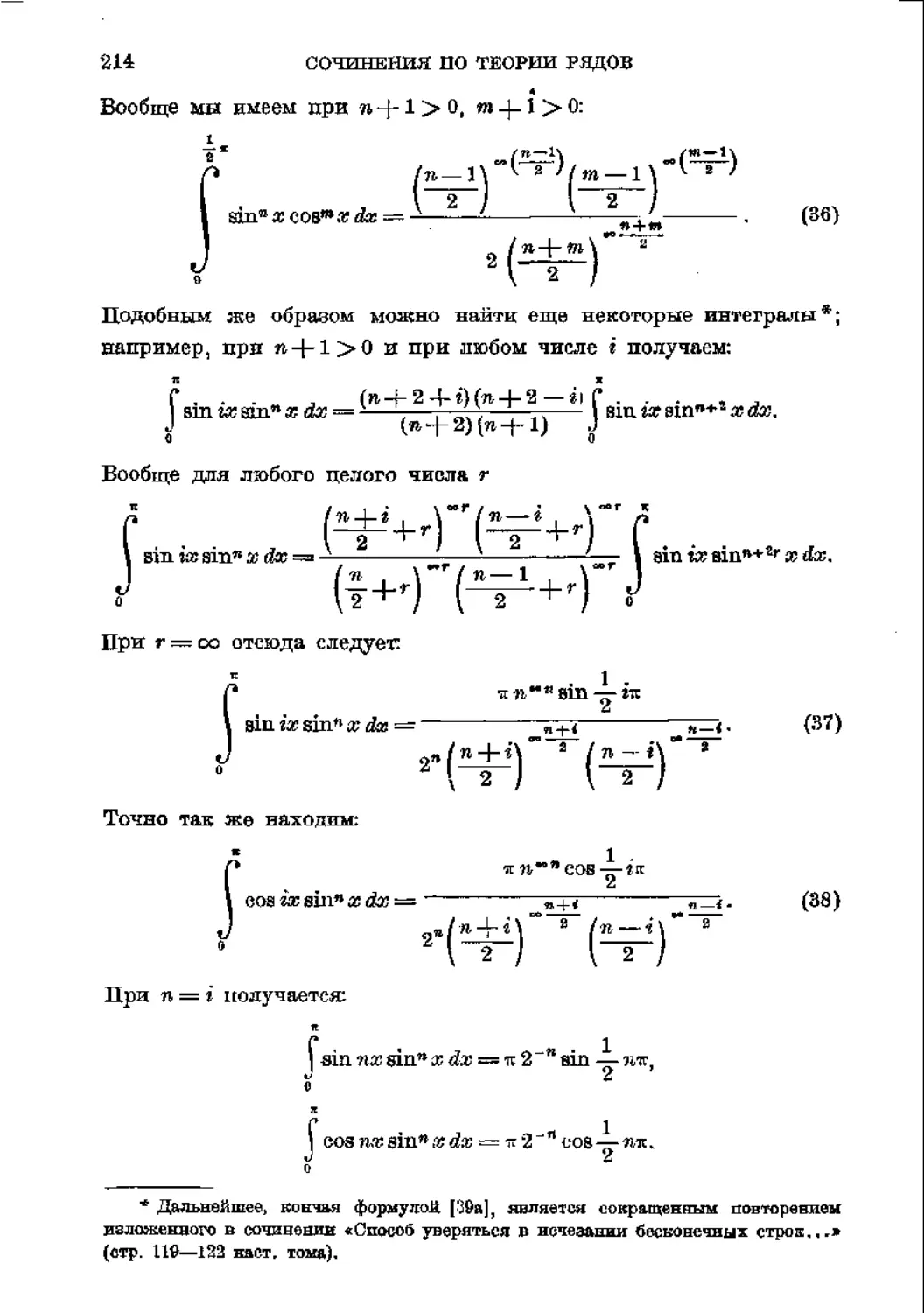
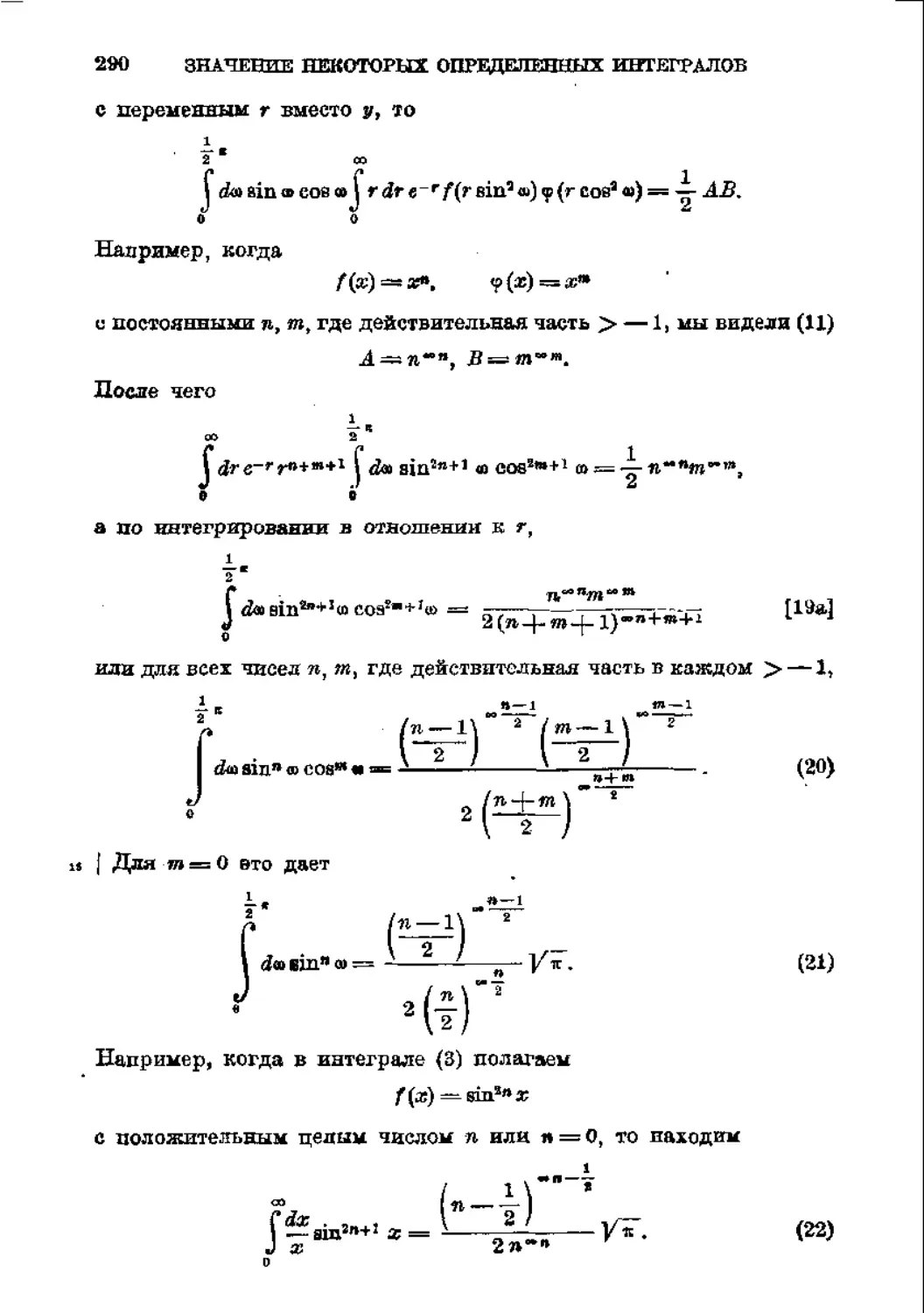
Вводная статья и комментарии Г. Л. Лунца 267
Ш. Вероятность средних результатов, полученных из
повторных наблюдений (1842). Вводная статья А. 3.
Колмогорова. Перевод A. S. Хованского. Комментарии
А. И. Колмогорова и А. В.. Хованского 327
IV. Условные уравнения для движения и положение
главных осей в твердой системе (1835). Вводная статья и
комментарии Я. К. ИЪельсопа 349
V. Подробный разбор рассуждения, представленного
магистром Поповым под названием «Об интегрировании
дифференциальных уравнений гидродинамики,
приведенных к линейному виду» (1845). Комментарии Г. Г. Ту-
машева 379
VI. Полное затмение солнца в Пензе 26 нюня 1842 года
(1842). Вводная статья ч комментарии А. Д. Дубяю . 41S
г) Здесь указана первая страница соответствующего отдела тона. Подробное
содержание каждого отдела помещено на обороте указываемой здесь страницы

H. IE, Л! о 5&ч. е к и киіг.
С л-^тр^іі *удя;£ннг::і Л. Д, К^еоий,
Г^ стр. ,-і.

от і'щищин
Настоящим пятым томом полного собрания сочинений
Н. И. Лобачевского исчерпываются его работы по математическим
наукам. Этот том содержит работы по анализу, к которым
примыкают статьи по теории вероятностей, механике и астрономии. Все
яти работы после опубликования при жизни Лобачевского в
повременных изданиях прошлого века появляются в печати в первый раз.
Первые их издания етали мало доступны, и только теперь
советские математики получают полную возможность ознакомиться с
трудами нашего великого геометра, лежащими за пределами
геометрии.
Бесемѳртную свою славу Лобачевский заслужил, конечно,
созданием неевклидовой геометрии. Но его труды по другим
математическим дисциплинам также представляют большой интерес как сами
по себе, так и по тому яркому освещению, которое они проливают
на личность Лобачевского, на разнообразие его научных
интересов, на глубину ого замыслов ').
Время, когда Лобачевский писал эти труды, ушло далеко от
эпохи Эйлера, которого вполне справедливо относят к числу
основоположников математического анализа. Многочисленные и глубокие
труды Эйлера составили славу нашей Академии в первую четверть
века ее существования; они дали первое систематическое
изложение анализа бесконечно малых. Но это построение было еще
далеко от логического совершенства, вызывало сомнения и
справедливые возражения. Первая половина прошлого века, время, когда
писал Лобачевский, было проникнуто стремлением довести
построение анализа до совершенства, устранить вей не только неправильное,
') В «Иеторико-матеаатических исследованиях* (выпуск П, И. — Л., 1919)
помещены работы Г. Л. Лунцв, А. П. Юптевичв. и И. Г. Бвшмавовой, В. В. Гнѳ-
деняо, Н. И. Идальсона, посвященные трудам ЛоОачевсвого ао математическом
дисциплинам, не входящим непосредственно в состав геометрии.

в ОТ РЕДАКЦИИ
но и неточное, неясное. Большие заслуги в этом отношении
принадлежали Гауссу, Кожи, Фурье, Пуассону, Дирихле, работы
которых уже были хорошо известны Лобачевскому. Живя далеко
от центров математической мысли, Лобачевский все же ясно
ощущал важнейшие . вопросы и задачи дня, сосредоточил свои
мысли на обосновании анализа, на исходных его понятиях, на
начальных положениях его построения. И то, что было
сделано названными выше корифеями науки, Лобачевского всё же
не удовлетворяло. Эта тенденция к строгому обоснованию
математики составляет наиболее характерную черту всего творчества
Лобачевского, красной нитью проходит через все его работы.
Лобачевский ищет правильной постановки исходных положений,
начиная с самого понятия о функции. Взгляд на функцию, как на
величину, выражаемую рядом действий над значением независимой
переменной, — эта точка зрения Эйлера, которую многие
математики еще принимали в эпоху Лобачевского, для него неприемлема;
он дает определение функции, которое по существу сохранилось
и до настоящего времени. Он отчетливо понимает значение
непрерывности функции при ее исследовании, очень близко подходит
к понятию равномерной непрерывности; он правильно пользуется
предельным переходом и на нем основывает учение о сходимости
ряда вообще, тригонометрического ряда в частности. Он
устанавливает теорему о законности почленного интегрирования ряда
Фурье, в то время как сама необходимость теоретического
применения подобных операций стала понятной большинству
математиков лишь много позднее. Он ясно видит, что учение о рядах,
об их сходимости, о точном и асимптотическом их суммировании
составляет центральное место анализа; этому он посвящает главные
свои работы по анализу. Не желая повторять здесь соображения,
изложенные во вводных статьях и в комментариях, нужно все же
отметить данный Лобачевеким своеобразный признак сходимости
бесконечного ряда. Нельзя, конечно, сказать, что этот признак
сохранил свое значение и в настоящее время. Но Лобачевскому он
сослужил большую службу: при его стремлении исходить в
развития своих идей из возможно более общих положений, Лобачевский
систематически пользуется этим признаком в большинстве выводов,
относящихся к теории рядов.

ОТ РЕДАКЦИИ 7
Из упреков, которые Лобачевскому делал М. В. Остроградский '),
справедлив только один: все работы Лобачевского читаются с
большим трудом, требуют исключительного внимания. Именно поэтому
редакция настоящего издания считала совершенно необходимым
очень обстоятельно их комментировать. Такое комментирование
статей по анализу было поручено В. В. Степанову и Г. Л. Лунцу.
К несчастью, болезнь и кончина В. В. Степанова не дали ему
возможности выполнить эту задачу до конца. Он оставил только
перевод основного мемуара Лобачевского «О сходимости бесконечных
рядов» с немецкого оригинала. Но он имел еще возможность
обсудить совместно с Г. Л. Лунцем все творчество Лобачевского в области
математического анализа.
С выходом в свет настоящего тома три основные работы
Лобачевского по математическому анализу, относящиеся к теории рядов,
становятся доступными широкому кругу математиков.
К этим работам Лобачевского примыкает его сочинение
«Значение некоторых определенных интегралов», напечатанное в атом
томе также с комментариями Г. Л. Лунца. Своеобразные методы
вычисления определенных интегралов составляли одну из тем,
к которым Лобачевский систематически возвращался. Они играют
очень важную роль почти во всех геометрических работах
Лобачевского: в первом же его мемуаре «О началах геометрии* 5) и
затем в сочинениях «Воображаемая геометрия» и «Применение
воображаемой геометрии к некоторым интегралам» а). Но в этих
работах Лобачевский приходит к вычислению значений
определенных интегралов от геометрии, в поисках доказательства логической
правильности созданной им «воображаемой геометрии». К значению
некоторых определенных интегралов он приходит также в своих
рассуждениях, относящихся к теории вероятностей *). В названной
же специальной работе, написанной Лобачевским уже к концу его
жизни, оп вычисляет значения ряда определенных интегралов
аналитическими средствами. Найденные Лобачевским значения многих
интегралов некоторое время пользовались большей известностью,
і) Ом. его отзыв на етр. 265 наст. тома.
3) Папечатано в I томе нает. издания.
3) Напечатаны в Ш томе наст, издания.
*) Сочиаевке «О вероятности средник результатов, полученных на повторных
наблюдений», напечатанное в наст. тоне.

S ОТ РЕДАКЦИИ
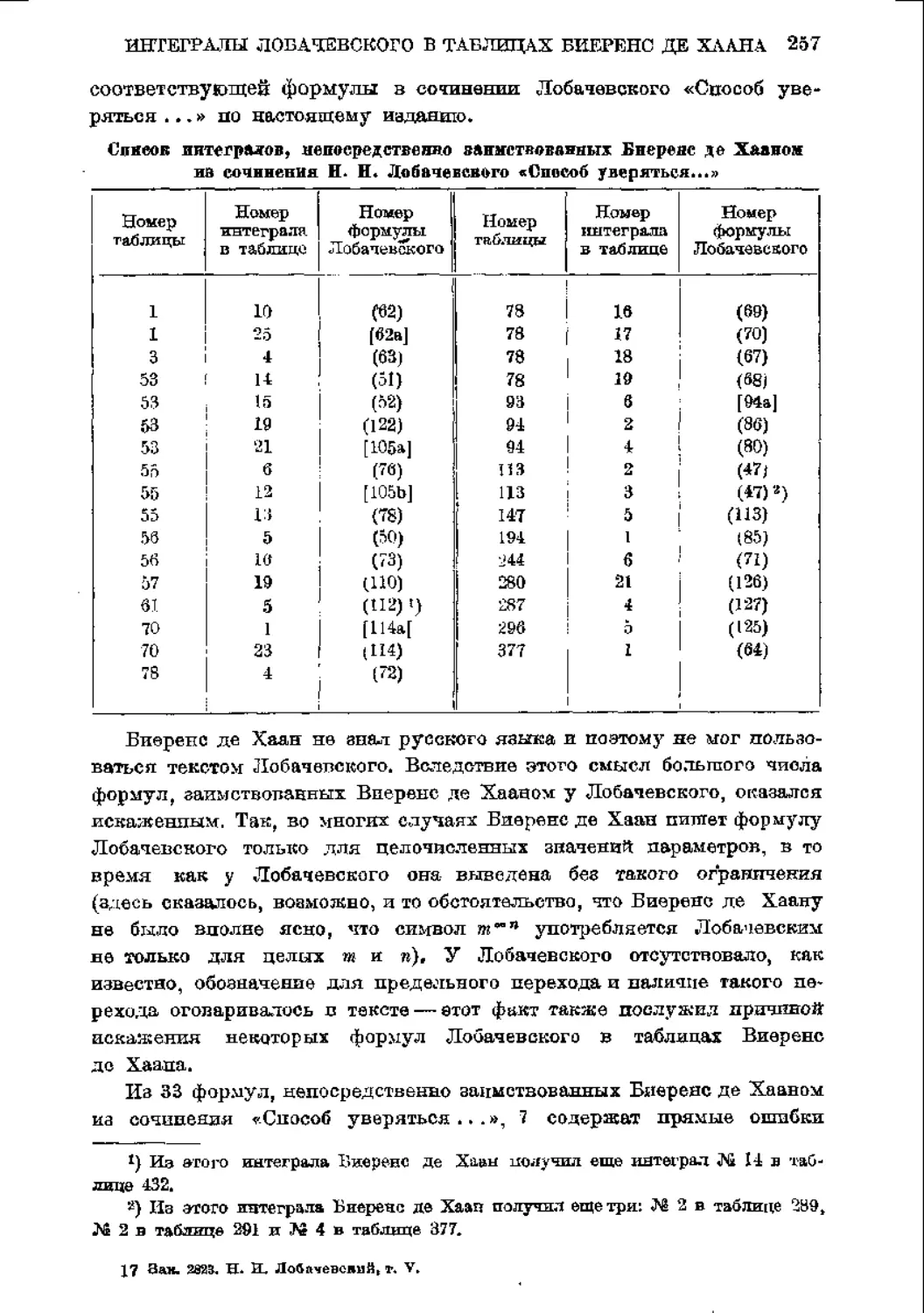
чем другие его работы. Об этом можно нудить по обилию этих
значений, приведенных в известных таблицах интегралов Виеренс
до Хаана.').
Особняком стоит статья Лобачевского, содержание которой
относится к области механики—«Условные уравнения для движения и
положение главных осей в твердой системе». Она состоит из двух
частей: первая часть посвящена основной теореме Эйлера, а
вторая относится к так называемой геометрии масс. Это —
единственная работа Лобачевского, опубликованная не в изданиях Казанского
университета, а в «Ученых записках Московского университета».
Вряд ли можно сомневаться, что в этом отношении сыграл роль
Н. Д. Брашман, состоявший уже в »ту пору профессором
Московского униперситета. Специальный характер этой работы
потребовал особого выяснения, которое нашло себе место во вводной статье
и комментарии Н. И. Идельсона; этот комментарий не носит
характера текстуальных примечаний, какие сопровождают другие
сочинения Лобачевского в настоящем издании; вместе с вводной статьей
он посвящен обстоятельному выяснению содержания и значения
работы Лобачевского.
К области механики относится также отаыв о докторской
диссертации А. Ф. Попова. Приложенная к нему статья Д. Д. Дубяго 2)
содержит не только данные о возникновении этой работы, но и
интересные сведения, характеризующие моральный облик
Лобачевского. Чтобы читатели могли уяснить себе отзыв Лобачевского,
здесь помещено краткое изложение содержания диссертации Попова,
составленное, как и комментарии к этой работе, Г. Г. Тумашевым.
Выбор темы и самый разбор диссертации свидетельствуют о
глубине математического образования, о разнообразии научных
интересов Лобачевского.
Он не был чужд и теории вероятностей, к области которой
относится небольшая статья «Вероятность средних результатов, полученных
из повторных наблюдений», печатаемая в настоящем томе в
переводе с французского, сделанном А. Н. Хованским под редакцией
:) См. статьи Б. Л. ЛіМеви Г. Л.Лунца «Интегралы Лобачевского
в таблицах Виеренс дѳ Хаана* (стр. ИЗ Ш тома и стр. 256 нает. тома).
s) «Историво-библиографические сведения о диссертации Лопов» и
раэборе ее Лобачевский», стр. 412 наст. точа.

ОТ РЕДАКЦИИ 9
А. Н. Колмогорова1). Эта статья представляет собой развитие
рассуждений, нашедших место в XII главе сочинения «Новые начала
геометрии е полной теорией параллельных» а). Занимаясь численным
решением прямолинейных и сферических треугольников, Лобачевский
имел и специальную задачу: на основе астрономических наблюдений
он вычислял сумму углов треугольника, вершины которого лежат в
центре Земли, вцентрѳСолнцаивзвезде;ѳтнвычисления
производились на основе многочисленных наблюдений. Требовалось не только
установить наиболее вероятное значение этой суммы; нужно было
судить о том, насколько получаемый результат дает основание считать,
что сумма углов треугольника равна тс. Это заставило Лобачевского
заняться выяснением закона распределения среднего
арифметического из результатов отдельных наблюдений. Лобачевский
ограничивается специальным случаем задачи, но для избранного им
случая он дает ее исчерпывающее решение, позволяющее при любом
числе наблюдений точно вычислить пределы погрешности,
соответствующие любому заданному уровню вероятности. Попутно
Лобачевский получает интересные формулы теории соединений и
вычисляет значения некоторых определенных интегралов.
Эта задача Лобачевского была, таким образом, тесно связана
с астрономическими наблюдениями. К астрономии, к ее
теоретическим и практическим задачам Лобачевский стоял очень близко').
Он своеобразно построил астрономическую обсерваторию Казанского
университета, он два года читал курс астрономии в отсутствие
Н. М. Симонова, он еше в раннем возрасте наблюдал комету 1811 г.,
а в 1832 г. —комету Энке. Неудивительно, что в 1842 г. для
наблюдения в Пензе полного солнечного затмения во главе экспедиции
Казанского университета был поставлен Н. И. Лобачевский
(профессор астрономии Н. М. Симонов находился в заграничной
командировке). Отчет об этой экспедиции под заглавием «Полное
затмение солнца в Пензе 26 июня 1826 г.» заключает настоящий том.
Это — единственная работа Лобачевского, предназначенная не для
узких специалистов; отчет написан очень ярко и читается с живым
і) 0G этой работе см. тавасе статьи Б. В. Гнѳденко «О работах Н. И.
Лобачевского по теории вероятностей» и Н. И. Идельоона яЛобачевский-астронои-
(«Исторпко-мвтематическиѳ исследованжя», выіь П).
s) Напечатано во Д томе наст, издания.
») См. статью Н. И. Ияельсоаа, указанную в сноске1).

10 ОТ РЕДАКЦИИ
интересом. Редакция сочла целесообразным дать к нему несколько
более подробную вступительную статью и более доступные комментарии,
составленные А. Д. Дубяго. Отчет Лобачевского о солнечном
затмении будет прочитан широким кругом читателей; он даѳт яркое
представление о взглядах Лобачевского на физику Солнца, тогда
еще только зарождавшуюся, о его отношении к теориям света,
стоявшим тогда в разгаре дискуссии.
Редакция настоящего издания имеет полное основание считать,
что с выходом настоящего тома собрания сочинений Н. И.
Лобачевского научный облик нашего великого геометра будет освещен
гораздо ярче, чем это было еделано до сих нор.
После выхода в свет IV тома редакция полного собрания
сочинений Лобачевского вновь понесла большую потерю — скончался
Б. В. Степанов. Его обязанности взяли на себя А. Н. Колмогоров
и И. Г. Петровский.

СОЧИНЕНИЯ
ПО ТЕОРИИ РЯДОВ
ОБ ИСЧЕЗАНИИ
ТРИГОНОМЕТРИЧЕСКИХ СТРОК
-<=••«»
СПОСОБ УВЕРЯТЬСЯ
В ИСЧЕЗАНИИ БЕСКОНЕЧНЫХ СТРОК
И ПРИБЛИЖАТЬСЯ К ЗНАЧЕНИЮ ФУНКЦИЙ
ОТ ВЕСЬМА БОЛЬШИХ ЧИСЕЛ
О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ
ПЕРЕВОД В.В.СТЕПАНОВА
а т & а
ВВОДНАЯ СТАТЬЯ И КОММЕНТАРИИ
ГЛ. ЛУНДА

СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Вводная статья;
Обаор сочинений Н. И. Лобачевского по теории рядов 13
Н. И. Лобачевский — «Об иечезании тригонометрических
строк» 31
Н. И. Лобачевский — «Способ уверяться в исчезании
бесконечных строк и приближаться к значению функций
от весьма больших чисел» 81
Н. И.Лобачевский — «О сходимости бесконечных рядов»
Перевод с немецкого В. Б. Степанова 163
Примечания 219
Приложения:
1. Признав сходимосіи Лобачевского 252
2. Интегралы Лобачевского в таблицах Б нервно де Хаян» 256
3. Иеторнко-библиографические сведения о сочинениях Н. И.
Лобачевского по теории рядов 261
4. Отзыв М. В, Остроградского о сочинения Лобачевского *0
сходимости бесконечных рядов» 265

ОБЗОР СОЧИНЕНИЙ Н. И. ЛОБАЧЕвСКОГО
ПО ТЕОРИИ РЯДОВ
Н. И, Лобачевским опубликованы следующие сочинения по теории
рядов: в 1834 году—«Об исчезании тригонометрических строк» (дальше
обозначается через |1]), в 1835 г. — «Способ уверяться в исчезании
бесконечных строк и приближаться к значению функций от весьма
больших чисел» (дальше обозначается через {2)) и в 1841 г. — «Ueber
die Converges der unendlichen Reihen» («О сходимости бесконечных
рядов», дальше обозначается через {3}); последнее сочинение
печатается в переводе В. В. Степанова. Эти работы тесно связаны между
-собой по содержанию. Сочинение J3) представляет собой, в основном,
резюме двух предыдущих работ. Мы сочли поэтому целесообразным
дать общий обзор всех работ Лобачевского по теории рядов.
По своему идейному замыслу сочинения Лобачевского по теории
рядов примыкают к его «Алгебре» J). Не подлежит сомнению, что
отправной точкой в исследованиях Лобачевского по теории рядов
явилась его работа над перестройкой «Алгебры» (которая в
первоначальном варианте предназначалась в качестве учебника для гимназий) и
в особенности широкое использование в «Алгебре» бесконечных рядов,
в частности, для определения основных трансцендентных функций.
Интерес Лобачевского к теории рядов не имеет самодовлеющего
аначения. Цель Лобачевского во всех его сочинениях по теории рядов
одна и та же—подвести прочный фундамент под здание
математического анализа, под основные понятия, которыми он оперирует, и
теория рядов должня, по мнению Лобачевского, сыграть здесь решающую
роль.
Некоторое влияние на содержание работ Лобачевского по теории
рядов оказали также его геометрические работы. Так, например,
Лобачевский в сочинении «Об исчѳзании тригонометрических строк» 2),
■ ссылается яа своп работы по геометрии, проводя доводы в пользу
расширения понятия функциональной зависимости. Кажется также
!) «Алгебра пли вычисление конечаыі» — напечатано в IV тоые наст, издании.
2) Ом. стр. 44 наст. тома.

11
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
весьма вероятным, что большое внимание, уделяемое Лобачевским
в своих аналитических работах теории гамма-функции, объясняется,
в некоторой степени, ролью, которую играет вта функция при
вычислении определенных интегралов, в частности интегралов,
вычисленных Лобачевским в сочинениях по геометрии.
Однако в целом сочинения Лобачевского, посвященные теории
бесконечных рядов, носят вполне независимый от его геометрических
исследований характер; содержание их связано с самыми актуальными
проблемами математического аналива того времени, и полученные
Лобачевским в этих работах результаты дают полное основание утверждать,
что Лобачевский был не только гениальным геометром, но и
выдающимся авалистом.
Переходя к обзору сочипояий Лобачевского по теории рядов, мы
приводим, ввиду того, что наш обзор не исчерпывает, конечно, всего
содержания сочинений, а также в связи с тем, что в оригинальном
тексте оочинений Лобачевского отсутствует какое-либо деление на главы,
план каждого из сочинений.
{1} — «Обисчеаанни тригонометрических строк»
I — Ряд Фурьѳ (стр. 31 ваот. тома)
П — Признак сходимости (стр. 35)
ЛТ — Ряд Фурье (продолжение) (стр. 40)
IV — Определение функции, определение днфференпи-
руѳмостя, доказательство теоремы
существования определенного интеграла,
несобственные интегралы (стр. 42)
V — Ряд Фурье (окончание) (стр. 54)
{2} — «Способ уверяться в исчезании бесконечных строк
и приближаться к значению функций
от вееьма больших чисел»
I — Признак сходимости (с приложениями) (стр. 81)
II — функция гамма (с приложениями) (стр. 97)
Ш —Ряд Фурье (стр. 125)
IV" — Приложение рядов Фурье и функции гамма к
вычислению определенных интегралов и к
суммированию рядов (стр. 138)
V—Функция гамыа (окончание) . . (стр.15*)
{3} — «О сходимости бесконечных рядовв
I — Признан сходимости , . (стр. 163)
II — Определение с помощью рядов показательной
фунвцнн, степенной функции и логарифма . (стр. 166)
Ш — Разложение функции sia.K в бесконечное
произведение и другие аналогичные разложения . (стр. 178)
IV —Примеры на применение приавака сходимости . . (стр. 184)
V — Ряд Фурье (стр. 187)
ЛТ—Функция гамма и ее приложении (стр. 109)

16
СОЧИНЕНИЯ ПО ТЕОГИИ РЯДОВ
только что приведенной выдержки. Дело в том, что термин
Лобачевского «постепенность» равносилен современному «непрерывность».
Следует, однако, отметить, что строгое определение этого термина вводится
Лобачевским только в сочинении «Способ уверяться...> 1, хотя, вводя
.етот термин, Лобачевский ошибочно сам указывает на то, что
соответствующее опрѳделѳвлё было им сформулировано еще в статье
«Об исчезании тригонометрических строк». Правда, не формулируя
определения, Лобачевский в (1) кое-где пользуется, тем не менее,
оловом «по степенность», как термином. Однако, когда Лобачевский
говорит, что функция есть число, которое «вместе с ж постепенно
изменяется», то его обозначает только, что функция иамѳняетоя по мере
того, как изменяется ж. Примерно в таком же смысле употребляет
Лобачевский слово «постепенно» также в конце страницы 44 и на
странице 45. Тот факт, что Лобачевская не связывал понятие функции
о еѳ непрерывностью, бесспорен хотя бы потому, что он во многих
местах специально оговаривает «постепенна» ли в данной точке
функция или нет, исследует сходимость ряда Фурье в точках, где
нарушается «постепенность» функции и т. д. Следует, таким образом,
считать бесспорно установленным, что Лобачевскому принадлежит
приоритет в современном определении понятия функции (аналогичное
определение Дирихле относится к 1837 году).
Лобачевский первый разграничил понятия дифферѳнцируёмос'ж и
непрерывности. Сначала он определяет понятие диффѳренцаруеыосгя2)
(«непрерывности» в терминологии Лобачевского), л потом *)
специально подчеркивает различие между диффереипяруемостью и
непрерывностью («непрерывностью» и «постепенностью»). Определение
дифферѳнцируемости функции, сформулированное Лобачевским, —
«внутреннее»; для того, чтобы не выходить за пределы числовых
множеств, определяющих данную функциональную зависимость, он
вводит в само определение дифференцируемооти критерии сходимости
Коши. Таким образом, функция F(ai) называется дифференцируемой
(«непрерывной»), если разность
F(et + k) — F(x) F(x + k')—F(&_
А Ъ?
где I A' j «С | A j, можно сделать по абсолютной величине сколь угодно
.малой, когда величина \h\ достаточно мала.
Следует все же отметать, что, во всяком случае в сочинении [1],
Лобачевский фактически исходит аз предположения, что непрерывная
') Стр. 131 наст. тома.
•) <1}. «Р. 45.
в) <3}, стр. 130—131.

ОВЗОР СОЧИНЕНИЙ
17
функции мовет иметь только . изолированные точки
недифференцируемости.
Весьма вероятно, что именно потому, что Лобачевский не мог
ни доказать, на опровергнуть такое предположение, он, желая явно
сформулировать налагаемые на функцию при докавательствѳ теоремы
о разложении в ряд Фурье условия, вводит понятие в аналитической»
функции 1).
«Аналитической» Лобачевский навываег функцию f(&),
дифференцируемую всюду, кроме отдельных точек, где величина f (ж)
бесконечна. На дальнейших замечаний и рассуждений Лобачевского следует,
что «аналитическая» функция может также иметь изолированные точки
разрыва первого рода.
Как мы видели из приведенной выше выдержки, в которой
Лобачевский определяет понятие функциональной зависимости,
Лобачевский первоначально, как »то вообще было принято в то время,
называл функцию аналитической, если она задана формулой («прямо или
условно»). Для того чтобы подчеркнуть, что такое ограничение
понятия функции не оправдано, он, при доказательстве теоремы о том,
что функция, имеющая производную, равную тождественно нулю,
постоянна, специально предполагает, что функпия ведана не
аналитически, а ев числах», и доказывает упомянутую теорему (это
доказательство не является вполне строгим) дважды: один раз в общем
виде, а другой раз, исходя из возможности аироксимации етой
функции аналитической функцией—многочленом г). Тот факт, что, как
отмечено выше, Лобачевский придал впоследствии понятию
«аналитической» функции совсем другой, но уже точно определенный смысл,
свидетельствует о том, что он осознал беспредметность этого понятия
в прежнем смысле.
Интересно отметить, что Лобачевский близко подошел к понятию
равномерной непрерывности. Доказывая теорему о существовании
определенного интеграла 8), он исходит из утверждения, что величина
|9(я-|-о)—9 (я)! может быть, для непрерывной на некотором огревав
функции <р (at), сделана меньше любого положительного числа, каковы бы
ни были х ш а, если только величина |«І достаточно мала.
Закончив доказательство, он продолжает*):
«До сих пор однако ж значение ^ (ж) не предполагалось
бесконечно великим, иначе могло бы случиться, что
9 (at Ч-«)—?(*)
Ч <3>. игр. 130.
3) {!}, стр. 47—49.
Ч {1}, стр. 40.
*) Сѵр.61.
2 Зав. 3813. Н. И. ЛоОтпямн*. т. V.

ОБЗОР СОЧИНЕНИЙ
15
В тексте сочинений Лобачевского нами, для удобства, произведено
разделение каждого сочинения на главы. Номера глав обозначены
в тексте римскими цифрами в соответствии с приведенным выше
планом.
Обзор дается нами не в том порядке, в котором строит наложение
Лобачевский, а по отдельным вопросам, служащим предметом его
исследований.
Начнем с основных понятий анализа и, в первую очередь, с
определения понятия функциональной зависимости.
Бот каким образом Лобачевский вводит это определение1);
«Общее понятие требует, чтобы функцией от х пазывать число,
которое дается для каждого я? и вместе с х постепенно изменяется.
Значение функции может быть дано или аналитическим
выражением, или (условием, которое подает средство испытывать все
числа п выбирать одно из них [,..]. Наконец, условия, которым
функция подчинена, могут быть^еще неизвестны, тогда как
зависимость чосел уже существует несомнительно. В таком случае
предположение, будто функция вілражаетея аналитически, должно
назваться произвольным. Правда, что еще не встречено таких
примеров, где бы зависимость чисел не могла быть представлена
прямо пли ус.іовно аналитическим выражением; однако ж нельзя
быть уверѳну совершенно и в том, чтобы другое предположение
не привело также и к новому решению [...]. Кажется нельзя
сомневаться ни в истине того, что всё в мире может быть
представлено числами, ни в справедливости того, что всякая в нем
пере лена и отношение выражается аналитической функцией.
Между тем, обширный взгляд теории допускает существование
зависимости только в том смысле, чтобы, числа, одни с другими в связи,
принимать как бы данными вместеs). Лагранж и своем вычислении
функций (Calcul das functions), которым хотел заменить
дифференциальное, столько же, следовательно, повредил обширности
понятия, сколько думал выиграть в строгости суждения».
Сопоставление приведенной нами выдержки со всем содержанием
работ Лобачевского по математическому анализу не оставляет
сомнения в том, что роль определения понятия функции пграет
выделенная нами курсивом фраза. Можно иногда слышать мнение о том, что
Лобачевский связывал определение понятия функции с ее
непрерывностью. В качестве аргумента выдвигается при ѳтом первая' фраза
!) {1}, стр. 43—44 наст. тома. В дальнейшем все страницы, указанные в этой
статье, приведены по настоящему тому.
!) Курсив наш. — /'. Л.

18 СОЧИНЕНИЯ ПО ТЕОРИИ РВДОВ
не будет уменьшаться беспредельно вместе с «. Например,
у я;
дает
1 — ѴИ
?(8«) —Т(д) = ' ,
У 2а
которая разность увеличивается с уменьшением а».
Говоря о том, как Лобачевский определял основные понятие
анализа, нельзя, наконец, не отметить, что Лобачевский безусловно
понимал необходимость обоснования предельного перехода под знаком
интеграла и фактически пользовался понятием равномерной сходимости.
Так 1), доказав сходимость последовательности о общим членом
п
»-!- + '
он получает оценку вида
. |A»-S(3)|<s(*).
где 3(a)—предел последовательности, a Jim е(в) = 0, и специально
я-*а
подчеркивает, что в (и) не зависит от а (0 ^ а ^ 1). На основании
указанной оценки Лобачевский получает неравенство вида
| J An (a) da — j S (я ) da | < а - s (n),
о о
из которого следует, в частности, существование предела
и а
Um f Лл(а)гіа= fs(a)d<x.
Замечательным образцом строгости изложения может служить
вывод разложения функции віп а) в бесконечное произведение, где также
фактически используется равномерная сходимость s).
Сначала Лобачевский доказывает сходимость, при любом
конечном х, ряда
Далее Лобачевский пишет тождество:
Iog8in3 = 2nlogcos~ + log(2»tg^4-f J] h_tg«^ctg*~)
і) {3}, «р. 200.
3) <3}г отр. 178—182.

ОБЗОР СОЧИНЕНИЙ 19
справедливое при любом целом м, и доканывает, что при достаточно
большом г величина
а также
l|4-*s°*'-£)|.
|£-(.-^.*£)|
может быть сделана сяоль угодно малой и останется таковой, к&к бы
мы ни увеличивали п (то-ѳсть равномерно относительно я). Так как,
кроме того, 2вlog008-^-+О и ^°s(—^e-^)-* 0 Щ>и и->со, то
абсолютная величина разности между
8ШЖ
log-
is
bm X log
л-»-™ / і , я*
*=n
1В1Г*
может быть сделана околь угодно малой, если г достаточно велико.
Но, каково бы ни было і,
Ьш = 1
и, следовательно, при любом постоянном г
Ьт N log -J =0.
П->-со /I •&
Г
11m "^1
1-»-™ ./, I
_ „ . НІПЯ
Таким образом, log .. . отличается от нуля на величину сколь угодно
'> j , вісат
малую при достаточно большом г, но log—зу-г от г нѳ вависит и, сле-
доватѳльно,
. sin я
2*

20
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Значительное место в рассматриваемых сочинениях Лобачевского
занимает найденный им признак сходимости знакоположительных
рядов, основанный на разложении каждого члена ряда в двоичную дробь.
Прием, на котором основан этот признак, впервые был Лобачевским
применен при исследовании сходимости одного ряда ещев «Алгебре» 1).
В {1} s) Лобачевский подробнее останавливается на своем способе
исследования сходимости, иллюстрируя его на двух примерах и производя
оценку остатков соответствующих рядов, но все же нѳ приводя
точной формулировки ѳтого признака. Формулировка и доказательство
признака, сопровождаемые далее многочисленными примерами, имеются
в {2] и {3} '), причем сходимость всех без исключения встречающихся
в этих сочинениях рядов, последовательностей и бесконечных
произведений исследуется только о помощью ѳтого признака в каждый раз
производится оценка соответствующего остатка, Лобачевский
формулирует свой признак, как достаточный; между тем, если общий член
ряда положителен и монотонно убывает (вернее, не возрастает), то
признак Лобачевского не только достаточен, но и необходим.
Доказательство как достаточности, так и необходимости признака
Лобачевского дано в приложении 1 на стр. 252 настоящего тома, и здесь мы
ограничимся только его формулировкой (и притом в простейшем
случае):
Если функция целочисленного аргумента f(n) положительна,
монотонна и не возрастает, то ряд
•—1
сходится или расходится одновременно с рядом
где рт определяется из неравенств
В центре исследований Лобачевского по теории рядов находится
теория рядов Фурьѳ. Ею он занимается во всех рассматриваемых
сочинениях*); кроме того, он применяет разложение в ряд Фурье
к суммированию числовых рядов н вычислению определенных
интегралов в),
•) Том IV наст, иаданнн, стр. 233 я 234.
*) Стр. 35—30 наст. тока.
*) <3>, стр. 82—90, {3>, стр. 1вЗ—185.
*) {!}. «яр. 31—35, 40—41, 54-80 {2}, «р. 83-83, 83-87; <3}, етр. 108-1©
в) <2>. «Р. 138-150.

ОБЗОР СОЧИНЕНИЙ
81
Лобачевскому было иввеотно докѵвахвяьотво Дирихле теорема
о разложении функции в ряц Фурье1); однако оа, йѳ бее основания,
не был удовлетворен тем обстоятельством, что Дирихле пользуется
значением интеграла
I
ипат , к
ах-
х 2
в
без всякого обоснования. Дирихле, по всей видимости, впоследствии
и сам осознал отот дефект в своем доказательстве к в 1887 году
изменил его так, чтобы не пользоваться значением указанного интеграл».
Известны были Лобачевскому также докааатѳльотва Копта и Дирк-
сена; ѳти доказательства тем более не могли его удовлетворить.
Лобачевский указывает только на один недостаток втих
докаватѳльств—-отсутствие обоснования оходимости ряда
^ einfec
отмечая при этом, что втот недостаток менее существенен, чем
остальные.
Действительно, Коши налагает на разлагаемую в ряд функцию очень
сильные ограничения (аналитичность в некоторой полосе плоскости
комплексного аргумента), а доказательство Дирксѳна порочно во
многих отношениях.
Схема доказательства сходимости ряда Фурье, данного
Лобачевским0), такова:
Выполняя интегрирование по частям, Лобачевский получает
і
J «■<*«—і.) f(x) <fe« _ ^ i(-iyf (1)_/-(Q)) +
о
і
+ -^-К-1)'Г(1)-Г(0)}—^-JowCfta-iaijrCaJ.to
о
и доказывает сходимость рядов, общими членами которых являются
члены правой часта: ѳтого равенства. При этом предполагается {не все
условия явно оговорены Лобачевским), что функция f (х) в
соответствующем интервале равномерно ограничена, имеет не более чем
конечное число точек раврыва 1-го рода, функция f {х) непрерывна [в
дальнейшем8) Лобачевский показывает, что можно допустить наличие
конечного числа точек, где она обращается в бесконечность]. Функция
f{x) может обращаться в бесконечность конечное число раз.
!) Journal flir die reine und angewandte MathematJb, 1829.
a) {1}. стр. 32—35, 40-41, 54—56.
1) Стр. в5—66.

22
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Хотя вти условия весьма ограничительны, однако они, в некотором
смысле, шире условий Дирихле, так как допускают наличие
бесчисленного множества точек экстремума (ограниченность вариации
функции f(x) этими условиями обеспечивается).
Далее, длн отыскания суммы ряда Фурьѳ Лобачевский повторяет
расоуядения Пуассона.
Исходя из разложения
—— ^£ т—j s =1 + 2 V |l*O0fl(*1GC Йо),
1 — 2j*cos(xa;—to) -\-у? ' ** ' '
справедливого при j j* [ < 1, он получает
1 — 2[хеоа(іга:—ш) -|-[ів
= j /'(яОЙЕ+г 2 (і* Гсоз(«па; — ш)/Ч«).*в jlj, (10a), (10b)1)
о (=і о
и, после ряда выкладок, приходит к равенству
1 к> 1
Г(і —о) + ?(^ + о) —J/to'fc + aE Jooe(*»~*«)f(a!)<te.{l},(ie)
11 о t=i о
Хотя в действительности выкладки Лобачевского обосновывают
лщщ, равенство
следует заметать, что в отличие от Пуассона2), метод которого он
излагает, Лобачевский доказал, как мы видели, предварительно
сходимость ряда
і
2 ( соа(іісге— ta)f(ss) их,
а так как нетрудно убедитьсяв), что ряд в правой части (10Ъ)
сходится относительно ц равномерно при 0 0^1, то предельный
переход под знаком суммы в правой части (10Ь), приводящий к (13),
оправдан, и, таким образом, теорема о разложении функции в ряд
Фурье доказала Лобачевским, по сути дела, строго,
В связи с рассмотренным выше доказательством Лобачевскоі-о
сходимости ряда Фурье интересно отметить, что Пуассон впервые попы-
*) Нумерации формул в этой вводной статье совпадает с нумерацией в теевте
Лобачевского.
s) Journal de Ѵбаоів polyt, сяМег IS, 1823.
Е) См. примечание [*] на сгр. 221 нает. тома-

ОБЗОР СОЧИНЕНИЙ
28
■тадоя доказать (при ввоъма ограничительных условиях) сходимость
рада только в 1883 году1), тая асе как и Лобачевский выполняя
интегрирование по частям (но однократное) в формуле общего члена, но
доказал лишь отрвидение общего члена к нулю. Лишь в 1885 году8)
он, дважды применив интегрирование по частям к общему члену ряда
Фурье функции f(ts), доказал сходимость этого ряда в интервале (О, іи)
при условии, что f (тс) = f (0) = О и имея в виду непрерывность
функций f(x), f(x), f (я) во воем интервале (0, те).
Преобразовав, далее, частную сумму ряда Фурье о помощью
интеграла Дирихле, Лобачевский допускает, что в отдельных точках
функция / (ж) становится бесконечной, оставаясь при «том интегрируемой
(что влечет за собой и абоолютвую интегрируемость, так как
фактически предположено, что с каждой стороны от рассматриваемой точки
функция стремится в бесконечности определенного знака), и
доказывает, что при етом теорема о разложении функции в ряд Фурье остается
справедливой всюду, аа исключением точек, в которых функция
бесконечна. Тем самым Лобачевский, по существу, пришел к «принципу
локализации», много позже сформулированному Риманом8); в
соответствии с агам принципом сходимость и значение суммы ряда Фурье
в данной точке связаны с поведением функция только в окрестности
ѳтой точки.
Наконец, пользуясь равенством
—(«—м)^2 *-fehlim' UU25)
справедливом в интервале (0, 2к), положив
і «
—t —а
где на функцию f(x) иѳ налоксено никаких ограничений, кроме
требования ее интегрируемости (а по существу абсолютной
интегрируемости), проинтегрировав обе стороны последнего равенства в пределах
от Ъ до с (—а^&< С^.а) и перейдя к пределу при І-*оо,
Лобачевский, пользуясь (25), доказывает, что
е е
lim [Ft(*)dm*=x{fte)(kt. {1J, (27)
') Poisaon—Trait6 de m&anique, t. I, 1933.
*) Poisson — Tbeorie math, de la chaleur, 1835, стр. 180.
B) E. Biemajm—TJeber die D.irstellbarkeit einer FQnkdon durch eine tngono-
metrisetie ЕѳШо, 1353. Русский перевод в «Сочинениях В. Римана>, Гостехжота?,
М,—Л., 1948, стр. 225—281.

24
СОЧИНЕНИЯ ПО ТВОРИИ РЯДОВ
В равенстве (27) содержится теорема, утверждающая, что
почленное интегрирование ряда Фурьѳ функции f(x) (даже расходящегося)
приводит к оходищемуая ряду, сумма которого равна ннтагралу от / (ж).
Ѳта теорема была впоследствии: вновь доказана Лебегом, во только
в 1906 году1). Следует, однако, указать, что предельный переход
при і -*■ со, приводящий в (37), Лобачевский адесь не обосновывается й),
а отоутвміие каких бы то ни было обозначений для предельного
перехода и неаккуратность записи [выражающаяся в том, что левая часть (2в)
обозначен» не черев Ft (а), а черев F(o>), жотя Лобачевский и дояоняѳт,
что era функция зависит от г], приводят к следующему: подменив фаити-
с с
чески lira Г Ji(ai)(foi через Г Ню і^(ш)Йію, Лобачевский делает из (27)
о о
совершенно необоснованный вывод о том, что
Ііш Ff (о>) = іѵ f (a),
И считает, что таким образом доказана теорема о разложении функции
в ряд Фурье.
В )2{ Лобачевский опять возвращается к доказательству теоремы
о разложении функции в ряд Фурье.
Для етого он доказывает сходимость ряда
со
2 -j-ей» (*» + «),
снова получает равенство {1}, (27), преобразует частную сумму ряда
Фурье с помощью интеграла Дирихле к виду
V" *ш(і+—)х
&Ff(»)=> \ і -L f(x + o>)dx
—- em-
я, выполняя в правой части последнего равенства интегрирование по
частям, приходит, переходя к пределу при і->сс, к теореме о
разложении функции в ряд Фурье. Функідая f (ж) при втом
предполагается «аналитическое» (определение «аналитической» функции ом.
выше), то-еоть условия, налагаемые на f (х), адесь значительно тире,
чем в {1}, так как функция f (х) вообще не участвует в
рассуждениях. Эти условия, как уже отмечалось, в определенном смысле шире
и условий Дирихле.
Сами рассуждения Лобачевского при доказательстве теоремы
являются, по существу, строгими.
*) Lebesgue—Ьертад аяг lee series trigonomefcriouee, Parfe, 1B06.
") См, примечание р] на стр. 225.

ОБЗОР СОЧИНЕНИЙ
25
В {3} Лобачевский снова докалывает теорему (1), (27) ж делает и»
нее тайне ив необоснованные выводы, как и в {1}. Само
доказательство этой теоремы в принципе таноѳ see, вав и в {1), по ему
предшествует вывод оценки вида
я — а; ѵі sin tx
S;
<
*(-+тѴ)
ѵ sin— '
О
или, что то асе,
я вшіг-!- — I
-Йш— тс
<-И'+^Ѵ).
где а, Ъ, а', Ь'—некоторые положительные постоянные (0<я<[іг).
Вромв того, прежде чем интегрировать равенство jl}, (26), он
преобразует его правую часть с помощью интеграла Дирихле и говорит,
что будет следовать методу Дирихле, который заслуживает
предпочтении перед всеми прочими. Между тем, метод Дирихле делает оценку
вида
t em
J
-К)
■ da
<с
<•*)
(О < t <те, О—постоянная, і—любое целое число) тривиальной, а, как
показано в примечании р8], строгое обоснование предельного перехода,
ведущего в {lj, (27), основано именно на неравенствах вида (*) и (**).
Последним из основных вопросов, которым посвящены сочинения
Лобачевского ло теории рядов, является определение, исследование
свойств и многочисленные приложения функции гамма1). Хотя из
заглавия сочинения {2} («Способ ... пржближатьея к значению
функций от весьма больших чисел)) можно заключить, что в разделе,
посвященном функции гамма, будет итти речь только об асимптотически!
формулах, в действительности Лобачевский отроит весьма
оригинальную и достаточно полную теорию этой функции.
В )2}, пользуясь обозначением
(я + а)-» = (* + в)(*+о —1)... (ч+1),
где х—целое и положительное число, Лобачевский вводит функцию
/(&, а) (мы несколько наменяем обозначения) при помощи равенства
!) (2>, стр. 97—225, 154—162; {3}, стр. 198—218.

26 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
откуда для [з?~|-а1>1 получает
f(x —1,а.)
fjx — 1, а.) у п
g />, *) e.fl1(»+4(*+2)(*H-«)*+1'
Иа сходимости ряда
у /(» + *—1,«)
следует существование при любом <х функции
ф(а)=1іт Дх, а).
Фунвдщя Xfx-\-a) о помощью равенства
со со со
определена нѳ только для целых положительных значений ж, а для
всех вначениі* а: —J— ol, для которых (ж + "*-^Л|>1, где к—любое целое
положительное число; следовательно, равенство
/(*, а) «■}(<*)-^ (.»+*)
определяет в указанной области функцию f(x, <х), а следовательно, и
функцию
(a+«)"a = 4(a)(a-f а)*+,+ *е-*Х(:к+оО.
и, в частности,
Так как
lim X(x-j-a) = 1,
то при а:—*-со имеет место асимптотическое равенство
(*+«)-вРаф (а) (*+ а)*+"+"» «-•.
Добачевовнй находит, что
и, следовательно, по определению,
ж"в=«у^ж*+»«-*Х(а;) = Г(ж + 1). {2}, (32)
Эту последнюю формулу приписывают обычно Бишэ; однако
Лобачевский пришел к ней на четыре года раньше, чем Вине1).
После втого Лобачевский переходит к уточнению асимптотической
формулы для функции х"х.
*) Journ. de l'&jole polyt, eabier 27,1839, мр. 226.

ОБЗОР СОЧИНЕНИЙ
27
Так как первый член разложения по отрицательным степеням х
функции
-^
совпадает о первым членом аналогичного разложения для
„, <а(х— 1)
Т (*)
]
где (р (а;) = ess*, то Лобачѳвовяй полагает
X(x)^e^fs(X),
то-есть
х™<* = "|/'^ГяЯ'"і"і'е~я+55/і (ж).
Продолжая так дальше, Лобачевский получает, член за членом,
разложение функции \ogX(x) в ряд по отрицательным степеням х
(ряд Стерлинга) и показывает, как такое же разложение можно
получить из формулы Эйлера—Маклорена. При атом Лобачевский
приводит (бѳв доказательства) найденные им рекуррентные формулы для
вычисления чноел Бернулли
где Tt—коѳффициенты в разложении
^*=2Г*
х**-1
(=і (Si —1)1'
связанные о числами Бѳриулли формулами
Далее Лобачевский показывает, что для того, чтобы введенное нм
определение функции гамма не противоречило определению с помощью
эйлерова интеграла, необходимо положить
ГС + 0-- Щ^-
Этим равенством определение функции а™1 распространяется на всю
комплексную плоскость3} (целые отрицательные значения а являются
1) В обозначениях Лобачевского (к — целое положительное число)
„™fc_ J*
Я) Это обстоятельство Лобачевский отмечает в коепѳ рассматриваемого
сочинения, стр. 154—155.

28 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
полюсами втой функции). Непротиворечивость втого определения о
определением )2}, (32) пояавана в примечании!10]. Лобачевский выводит
ооноввоѳ соотношение:
(я+в)--*"«(ш + в) —в—, {2}, (42)
из которого, в частности, далее получает многочисленные свойства
функции гамма и которое фактически служит Лобачевскому также
для аналитического продолжения функции {ат-}-а)'"!Е, так как
функция а"" уже определена во всей плоскости. Не останавливаясь
на выводе свойств функции гамма, отметим лишь, что, в частности,
Лобачевский пришел к формуле
также имеющей место во всей плоскости (кроме целых отрицательных
значений и). Эта формула была получена Эйлером еще в 1729 г.
(письмо к Гольдбаху), однако впоследствии была забыта, и вновь
докававший ее Гаусс считал, что она найдена им впервые.
Лобачевский также считал, что именно он открыл эту формулу.
Нѳ касаясь многочисленных приложений функции гамма в
вычислению определенных интегралов и суммированию рядов, отметим,
что ии было доказано равенство, которое в современных обозначениях
имеет вид
р + ісо
J ^ = РЙ <Р>°> ВеЯ>0). {2}, (118)
Этот интеграл был в некоторых частных случаях ранее вычислен
Лапласом1) и Лѳяс&ндром *). В общем виде в том же году, что и
Лобачевский, его вычислил Лиувилль8), однако вывод Лиувнлля
весьма далек от строгости. Представляет интерес также иайдениое
Лобачевским выражение модуля функции гамма в виде ряда о
действительными членами [формула {3], (129)*)].
В сочинении {3} Лобачевский в качестве определения функции
гамма принимает формулу {2}, (54) н совершенно строго доказывает
существование предела в правой части этой формулы, исходя из
тождества
в t
t*r\
> + 2)...(« + г)
(схема этого доказательства была приведена выше, на стр. 18).
') La Place, Osuvres, том ѴП, стр. 134—135.
*) Legeadre — Exercises de ealeu! futSgcal, том I, 18П, стр. 354.
*) Jottrn. f. ralno mid angew. Math., 13, 1835.
«) Стр. 182.

0В80Р СОЧИНЕНИЙ
26
Ов приходит также снова я. равенств у {2}, (82) тем же способом,
чаю и в {2}, однако же пользуется им для продолжения функции я"*,
во6 время очитая х целый положительный числом; непротиворечивость
определения {2}, (54) в опутав, воли я — цвлое положительное число,
о равенством {2} (82) Лобачѳвезай доказывает. В качестве
определения функции »"■* при любых я и а он принимает равенство {2}, (42)
в форме
я-"
(Ж — в)-»—
Записав равенотво J2J, (82) в виде
Добачевокии показывает, что коэффициента .4^ при а:-1 разложения
функции (р (ж) по отрицательным степеням х определяются, ив. равенства
В {8} Лобачевский выводит также различные свойства функции гамм*
(однако, менее подробно, чем в (Е)), применяет ету функцию к вычисдв*
ннк> различны! определенных интегралов и, в частности, снова
находит интеграл )2), (113).
Итак, в своих сочинениях по теории рядов Лобачевский получил
ряд оригинальных результатов первостепенной важности. К сожалению,
ѳти работы Лобачевского оставались по существу неизвестными до
самого последнего времени.
Не подлѳгвит сомнению, что это обстоятельство в немалой степени
связано с рапортом М. В. Остр оград евого, адресованным Академии
Наук, в котором он высказал свое отрицательное отношение в
присланному ему на отвыв сочинению Js] *).
Остроградский обвиняет в этом рапорте Лобачевского в нарочито
применяемых странностях при изложении, в пренебрежении *первей-
шиыи принципами точного рассуждения», в том, что в работе
Лобачевского нет ничего нового. Сам тон рапорта свидетельствует о его
предваятоеги, связанной с отношением Остроградекого в
геометрическим работам Лобачевского; Оотроградсвий, впрочем, и не скрывает
ѳтого в своем рапорте. Об этом же свидетельствует ни на чем не
основанное обвинение Лобачевского в том, будто он приписывав*
себе открытие возможности определить тригонометрические функции,
не прибегая в кругу (при помощи рядов).
*) См. приложение 4 на стр. 285 нас*, тома.

30
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Конечно, стиль изложения в рассматриваемых сочинениях Лобачев-
екоіч) оставляет желать лучшего, имеется вакже нарядное количество
опечаток и допущенных по невнимательности ошибок, мяогве
рассуждения чересчур лаконичны, имеются и нарушения систематичности
наложения. Лобачевский также несколько «злоупотребляет» и своим
признаком сходимости, пользуясь всюду только им (ѳто делается им,
повидимому, умышленно, для того, чтобы продемонстрировать силу
ѳтого признака), хотя в большинстве случаев можно проще решить
соответствующую задачу другими общеизвестными средствами.
Наконец, как ѳто уже отмечалось, сама запись ведется Лобачевским, порой,
небрежно; в частности, не всегда ясно, совершен ли уже предельный
переход. Однако не подлежит сомнению, что если бы такой
выдающийся математик, как Остр оград ский, подошел к рассмотрению работы
Лобачевского объективно или даже вообще потрудился с ней
внимательно познакомиться (он утверждает в рапорте, что работа
Лобачевского им тщательно изучена), то он нѳ мог бы проглядеть имеющихся
в ней интереснейших результатов (часть из которых, впервые
полученных Лобачевским в Jl} и {2}, была, правда, к моменту выхода
в свет сочинения )3(, вновь получена другими математиками).
Совершенно очевидно, что Острогр&дский внимательно сочинение {3J (нѳ
говоря уже о предыдущих работах Лобачевского в этой области) нѳ
читал, а ограничился ѳго беглым просмотром.

'ШПЕРАТ^КЖЛГО КАЗАНСКАЯ) УНИ-
ВЕРСИТЕТА.
■'■'rSr' 1834. '
I. НАУКИ.
1. Овъ иэзвзднін ті яг ономВТ#аі«-
сквх» стгокг.
( В, Лобаъевсхаго. J
Везконечныя строки, расположенный въ сввусахБ
или косавусэхъ крашдой дуги, названы тршокометри-
Хесками. Их% нрітаѣнеаіе весьма важно въ ивтаегриро-
ваиів лянеішшсь ураащшй еъ частншт диФФереаціала-
КЯ, а следовательно въ рѣшевіи самыхъ дюботшш-
гыхъ задачь шъ Фвза&н « Механики. Между тѣагь
80йАйд безвднечнаа строка мояепгь назваться
только аналишягескяпъ вырашѵіехъ в оставят ел безъ
упатреблешя, ноьуда ей не принадлежит*, извѣстщмі
аначшііе, К* коше-рощу она приближается, ш«к»«
&б пвслѣдаихъ члешхъ. Вошь позему гарщчщомегарц-
тескіл сшрсаш были предзіетомъ подобных* таслѣдо-
ванів, как» нолно читать въ записках1» Гг. Еош»
(Mfaolres de Г Acad, d. sciences, an 1823), ДярШ-
ле Д Дирасевь (Journal £ &. хѵха u* aage-w- ИаШда. .
Первая странвиа оригинального изданан сочинения
аОб иечезавии трнгонометричоския строк»
{107-я стр. П книжки «Ученых записок Казанского университета» я а 1834 г.).
К стр. эі.

OB ИСЧЕЗАЕМ
ТРИГОНОМЕТРИЧЕСКИХ СТРОК
га*
В Бесконечные строки *, расположенные в синусах или косинусах
кратной дуги, названы тригонометрическими. Их применение весьма
важно в интегрировании линейных уравнений с частными
дифференциалами, а следовательно в решении самых любопытных
задач, из Физики и Механики. Между тем всякая бесконечная строка
может назваться только аналитическим выражением и оставаться
без употребления, покуда ей не принадлежит известное значение,
к которому она приближается, исчезая в последних членах. Вот
почему тригонометрические строки быди предметом подобных
исследований, как можно читать в записках Гг. Коши (Мепюігеа
de Г Acad, d. sciences, an 1823), Диряпше и Диркеен (Journal f. d.
reine u. angew. Mathem. 11829. S. 157, Sur la convergence dee series
trigonome'triques. Par M. Lejeune-Dirichlet; S. 170, Ueber d. Gon-
vergenz nach den Sinussen u. Cosinussen der Vielfachea eines Win-
kels fortgchr. Eeihe. Von. H. Dirksen). О сочинении Г. Коши дал
уже свое мнение Г. Диришле, который н сам, кажется, без
должной осторожности допускает исчезашге строки®
я Их Зе
о т * т at *
потому только, что внак меняется в членах, которых сумма должна
представлять
со
С sin <р , 1
о г
* Тѳкет Лобачевского на главы не расчленен. Номер» подразделений
сочинений по теории рядов введены редакцией; уаловные ах наэвваня пврмиоаены
во вводной статье (стр. 14 наст, том»),
* В современной терминологии—бесконечные ряды,
* В современной терминологии— еяхнНиюеть ряда.

32 СОЧИНЕНИЯ НО ТЕОРИИ РЯДОВ
значение определенного интеграла, давно принятое Математиками
и может быть также без дальней строгости р]. Если мне и
показалось, что в названных сочинениях находятся какие нибудь
недостатки, то я хочу однако ж ограничиться одним тольео
замечанием, менее даже важным, нежели другие, а именно тем, что
здесь лѳрвым основанием служит предположение, будто строка
sin и 4- -=■ еіп 2м -f- — sin Зш -f- ... (1)
исчезает для всякого ю, на что однако ж хотелось мне сыскать
наперед совершенно удовлетворительное доказательство. Чтобы судить
об исчезании тригонометрической строки, стоит только взглянуть
на уравнение
і
J
cos («м-») f{x) <fcs = — ^HL. {(_ iy f(i)—f(p)\ +
I
cos«o
^-K-l),r(l)-/'(0)}-^rJeoB(«B-»)r(*)<te, (2)
a
которое легко вывести помощию интегрирования но частям и где і
целое положительное, х и со произвольные числа, jc содержание*
окружности в поперечнику,
Здесь можно видеть с первого раза, в чем должно заключаться
доказательство на исчезание строки
для всякой функции Д«), как скоро исчезание строки (1) уже
допущено.
Итак я начну сперва говорить о еумме
Пусть она прерывается на і = 2°. Соединяя по два члена
е ряду, получим
21 . . ѵі вш(2»—1)и , 1 ѵ 1 - /„• 1\
* То-есть отношение. Лобачввекжй всегда применяет евово соЭержюмік в атом
смысле.

Н. И. ЛОБД.ЭЕВСКИЙ--.ОЕ ИСЧЕЗАШІИ ТРИГОНОМЕТР. СТРОК. 88
ire [Подобным образом
a""2, , а -д»~Е sin (бі— — \ <в а"'3
Si-(«-|)--S-i}5!=nL+«-toST*'(ul'-T)'-
Вообще для всякого делого положительного числа г
Из всех уравнений выводим
S1 . - ѵ< аіп(2« — 1)ш .
2ti-s ein|4i -~| а,
, 1 V \ " / і
„и-а
s"-*sin tlfi* ~ la
+ CO32'tac0S(0CQs2'u2i 2i(M-l) +
-J~ и проч.
2rj — )ш
1-™-j-««uu»...w»i* -; ^ ai(M —1)
+ cos-^<ucos<o...cos(2''-a<o) 2"ТВІП(2Г* 2—l"
3 Зак. S88B. H. И. ЛобнчевокаН, т. Ѵ.

<0
- +
84 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
А если делаем г = п, то
S1 . . ѵ еіп(2І —1)(о
«"-'■шп/ач--'2'' „1"1)
г—а і 1 '
~Ь еов "5" а соа ш eos 2m ... cos (2п~г«о) sin —^— (о. (5)
Последний член, яакая бы дута <в<тс ни была*, с возрастанием п
или должен делаться нулем, или по крайней мере не
чувствительным. Он делается нулем и один раз навсегда уничтожается,
когда в
число членов ограничено*. Если ж оно бесконечно, и следова
теиьно между целыми отрицательными показателями —р будет
недоставать также бесконечно много целых чисел0, то с каждым
пропущенным членом 9 я 2 будет по величине I
оов(2*-'«)<]/'-і
* Лобачевский проводит доказательство в случае, когда 0 < щ < я. При ш = О
и » = я равенство нулю рассматриваемого вырвдюния очевидно, так как
обращается в нуль либо первый, либо последний множитель.
* Бели в выражении
• - « S VJ,>
где о» принимает только значения 0 и 1, число членов, для которых а„ = 1,
конечно, то
__ я*
где п к q — целые положительные числа я и — нечетное. Но тогда множитель
сов^"ю, гдеяі = 2е_1, обращается в нуль,
° Если число членов суммы
СО
s *>-*
для которых Ир = О, конечно, то так же, кис и в предыдущем случае, ш = ——,
где я и д — целые положительные числа я и—нечетное число.
8 То-есть таким, что aq = 0.
% «По веянчине» всегда обозначает у Лобачевского «по абсолютной
величине*.

Н. И. ЛОБАЧЕВСКИЙ —«OB ИОЧЕ8АНИИ ТРИГОНОИЕПТ. СТРОК» 86
а произведение
сое — л cos се еов 2м...
до крайней мере уменьшаться в содержании к т/Л. и наконец
делаться нечувствительным.
Теперь во второй части уравнения (5) принимаем все
остальные члены за положительные и увеличиваем, поставивши единицы
вместо синусов. После втого можно всегда взять п довольно
большое число, чтобы по величине
1 1 ^ ' г=2
[Щ
Рассматриваем наперед производитель *
Доказать исчезааие этой строки моием по способу, который
наложен в моей Алгебре (Алгебра или Вычисление конечных 1884 г.
стр. 387*) и который применяется ко всем подобным случаям®.
Полагаем, что для какого нибудь г дробь
1
2Ц2І— 1)'
«а | будучи разложена по степеням -^, дает самую низшую
степень 2-г и которая следовательно встречается не далее, как до
члена
4І(4* — 1) '
* То-ееть множитель.
* Страница укааава Лобачевским по оригинальяому изданию сочинения
«Алгебра ели вычисление конечных*. Она соответствует егранвде 233 ГѴ тона
яапт. издания (статья 182).
а Способ, о которой говорит здесь Лобачевский, представляет собоВ, по
сути дела, необходимый и достаточный признак сходимости ряда о
положительным и монотонно невозрастающин общим членом. Этик лрнзнашц Лобачввовиа
пользуется почти во всех своих сочинениях по анализу (см. анодную статью,
стр. 20 наст. тона). Подробное обоснование этого признака дано в приложении 1
(отр. 252 вест. тома).
3*

86 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
потому что для всякого t > 1
4і(4г — 1) — £і(2і— 1) > О*.
Итак
L<r^'i21~r*.
Между тем неравенство ■ . -^-> 2~г дает
*<2 а .
Лосле чего
£<2Г^ ил, £<^IS.
і 2
17* | Если бы в таком еуммованми, остановившись на известном
члене, захотели судить о величине остатка в строке, то не трудно
видеть, что вообще
СО СП г —1
S *(*-!)< 2 2~~- Е5а]
начиная с г, которое удовлетворяет условию
2і(2і-~ 1)<2ГТ
* Иа этого неравенства следует, что
Если, ш предположено, разложение -arm-.—-.-=- в двоичную дробь аачн-
г ! w Я<2і —1)
ниѳтея с члена 2 , то -^-д; -г- -^ 2 , и, следовательно, ■
Таким образом, число „ ... . уже не содержит в своемразложении ілѳна 2 .
* Здесь і — число членов ряда, содержащих в своем двоичной разложении
на нервом месте член 2 и, следовательно, меньших чем 2 . •
"> Эта оценка слишком грубая. Ив предыдущего неравенства следует, что
to"5™1.
$ В оригинале L < 2 + Ѵ"2-
Т В этом неравенстве і и г—наименьпгав значения индексов суммирования
в левов к правой частях [5в].
Наименьше© значение индекса г должно быть таким, чтобы хоть какой-нибудь
(а следовательно, первый) член ряда в левой части [5в] содержал в своем двонч-
воіі .разложении Ъ~г, а значит, был больше чем 2-'.

Н. И. ЛОБАЧЕВСКИЙ— -ОБ ИСЧЕЗАНИИ ТРИГОНОМЕТР. СТРОК» 87<
и откуда находим
следовательно
^ 2г(2г — 1) УЯ(2і —1)
значение, которое исчезает с возрастанием к Например, взявши
і=3, получим
L < 1,47 ®.
Чтобы пояснить более применение нашего способа, берем еще
другую бесконечную строку, которая в последствии будет нужна
as |и которая необходимо исчезает вмеоте с L, потому что Ж<4£.
Полагаем
г* = 2
или непосредственно 5
ів<2Г
с пѳлым показателем г. После чего
і г т
Для і = 4 находим
і=4
Jtf<3,07T.
* Здесь і и г обозначают то ate, что а в предыдущем неравенстве;
следовательно, левая часть этого неравенства является первых членом ряда в правой
частя [5а].
* В оригинале в правой части неравенства [5с] отсутствует множитель 2.
Так как
<и , г-' ''-1 m _.*. *•—і
то е учетом [5Ь] получаем [5е].
и В оригинале £<^1,03, Эта ошибка связана с отмеченной выше ошибкой
в [5с].
S То-есть г — наибольшее целое число, для которого выполнено следующее
далее неравенство.
{ввІСО
I В оригинале V ~<Ц№, *Г<2,43-

88 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Другой способ предложим еще следующий. Пусть для какого
нибудь г
2І(2І — 1) = аг,
Для всякого другого *' > і,
1 2і'(2і'~ 1) ^«*'
где А < а9 и где знак суммы относится к целым положительным
числам те*. Пусть далее N то целое, которое дает
2N(2N — l) = a*"
или непосредственно
2N(2N— 1)<<*Е«*.
Отсюда
* J. вавиент вдась только от і'.
Так иав
S1 = 1 дв
то ко всякому члену ряда at. можно подобрать такое к, что
I 1
я такое Лц, удовлетворяющее уелоаню —-g—<4s<0*—і, 4IO имеет место
разложение
* То-есть W — наибольший номер члена ряда, превосходящего ~gr ^
следовательно, содержащего ■—=м" в своем разлоясенив: (а). Тогда количество членов ряд&
содержащих в своих разложениях —g^, нѳ превосходит У— і, а сумма всех чже-
^ вЯ і
нов разложений вида -gr- яе превосходит ——=j^— (W—і).
а В оригинале

Н. И. ЛОБАЧЕВСКИЙ — *ОБ ИОЧЕЗАШИ TPИГOHOME,K■. ОТРОК» 39
После чего
V 1 1 a'-l/l + VT+fai \
ЛЙ(Й-1)^ ая ^ а* \ 4 / +
, «' — 1 /І + Vl+to* Л і в1 —1 /1 + Ѵі+4<*в Л ,
"^ ^*~V * V"*—^~1 і Ч+
+ и т. д. * [6еІ
Отбрасываем везде единицу под квадратный корней:
у 1 5—4І е + 1*
Л2І(2г—1)^ 4аа "г" 2а к 1°Ч
ігт [Полагаем * = 2:
"у і < 1 і 1+2¥*
(^2І(2г —1) 1в"*~ 4КЗ '
L 1_ 1 + 2Д
16 41/3
* В оригинале иод аеавоы ваявдога радикала в правой частя этого
неравенства коэффициент при второй члене не 4, а 8. Это связано с отмеченной выше
сшибкой в неравенстве [5d].
* В оригинале в свази с отпеченной выше ошибаой неравенство [Щ имеет
вид
^2і(2і—1) 4оВ ауа '
Однако даже исправленное намн неравенство [5f] во обосновано, так как
отбрасывание первых слагаемых под аниками радикалов уменьшает правую
часть [5ѳ]. Для получения обоснованной оценки можно иод знаком каждого рада-
капа заменить первое слагаемое черев <$ иди даже через -^-, так как в
рассматриваемом случае о* ^ 2 ирн всякой і.
° В оригинале последние неравенства в связи с ошибной, идущей от неверного
неравенства [5d], имеют вид
*\Г і ^ L 1 1 + 3Ѵ¥
і<Х + 1±і^<1,ад.
16 зут
Однако исправленные в тексте неравенства также не обоснованы, так зав они
получены вв неравенства [Щ. Правильные оценки мокво получить способом,
укявааным в предьцдгщой еиоеве.

40 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
{Ш]
Переходим к другой строке
V-^sinwi<£|l-j- Vcos — шео8іаеоа2ю ... cos(2r~3 is) [.
Заметим, что
1 sin 2ш і sin 4o>
cos ■— «и сов to = ————, cos — oj cos cd cos 2co
Вообще
2s sin -^ in 2s sin — ш
1 .. y0»— a , sin2r_4ai
coa -—-» cos in ... cos (2 я>) =
и следовательно
2 v „,-i . 1
2Г sin —ui
Г = Л—1
т&іпш<і 1+ >, - * ■
i l r=i 2 sin —<u '
Принимая на правой стороне вое синусы в числителях за
единицы, находим
2
а полагая м = со, переходим к строке (4)
2
1 BlIl-x-Ul
* В лавой части этого неравенства стоит абсолютная величина предполагаемо!!
суммы ряда, а не сумма ряда, составленного иа абсолютных величин
соответствующих членов; одаяво сходимость ряда (I) теа ае менее следует из рассуждений
Лобачевского, так как предгдеетвутогаие выкладки показывают, что ряды,
получаемые в правой части равенства (5) (на стр. 34) при а =* со, сходятся (я притом
т
даже абсолютно), а ішзиюеть между частной суммой V ——;— н суммой, стоящей
в правой части (5) при соответствующем выборе п, Еак нетрудно показать,
стремится к нулю при т -> со (см., например, найденное Лобачевским
неравенство І18а! на стр. 191).

Н. И. ЛОБАЧЕВСКИЙ- «ОБ ИСЧЕЗАЕИИ ТРИГОНОМЕ'ГР. СТРОК» 41
Обратимся теперь к уравнению (2), откуда выводим
бесконечную строку
2j \ сов(мса:—m)f(x)dx =
— Zj \-^-i^os{ivx—m)f"{u:)<lx. (6)
1 0
Здесь по величине
™
ism
^[(-1)V(1W(0)J<AZ(1:+.—^—)\
dnT"
І^К-і)'Г(і)-Г(0)3<£^
icosim
i
где J. по величине самое большое из двух
f(l) + r(0) f(X)~ f (О)
1С IT
i^ [.В таким же образом самое большое из двух
Л(і)+/Ч0) Г(і)—Г(о)
1Г ' 1С
Остается в уравнении (6) рассмотреть бесконечную строку
yW cos (іъх—іа>) f"(%)dx
і о
дня /"(ж) произвольной функции. Прежде однако ж нахожу нужным
сказать несколько слов вообще о дифференцировании и
интегрировании.
* Эта оценка {в левой часта подразумевается знак абсолютной величины) —
необоснованная. Для получения правильной оценки нужно применить отдельно
я каждому чз радов
^-^гувіп(й"+і)<° и St""2'1
рассуждения, примененные выше в ряду (4).

но
42 СОЧИНЕНИЯ ПО ТЕОРИИ РДДОВ
ІЩ
Пишем для краткости tp (а;) вместо
df(x)
dx '
Под у (at) должно разуметь функцию от ж, которая происходят
а уравнении
когда с уменьшением А исчезает Н. Обратно
такая функция от х, которой дифференциал дает <?(ге) или, все
равно, которая* представляет границу приближения, когда в
содержании
1 h
h уменьшается. Как скоро это условие выполнено, то f(x)
определено достаточно, кроме того, что f(x) допускает еще прибавле?
ние произвольного постоянного. Действительно, цуеть
Надобно, чтобы
где 3' исчезает вместе с Ъ, и И, а следовательно
F(x + k) — F(x)
h
тоже должно исчезать вместе с ft, не представляя никакого
постепенного и непрерывного изменения еж*. Между тем, если это
содержание зависит от а и А вместе, то с уничтожением k должно
бы еще оставаться функцией от х, а потому оно и для всякого h
не может быть функцией от х. Это значит, что F(x) постоянное.
* Вместо еяова «которая» доладао быть «по отношению в которой у (х)*.
,. F[x + h)~-F'(a:)
* То-есть величина lim ■—-——~і і-і- равна нули) тождественва (незавн-
«mm от х).

б: и. лобачевский—«об исчезании тригоношггр. строк» 48
Впрочем, заключение, будто функция от двух переменных чн-
сед х, h для & = 0 остается еще функцией от х*, во всей
обширности понятия: было бы несправедливо, а потому и нужно обратить
внимание на то, каким образом
іа1 ! h
принадлежит именно к тем функциям от двух чисел х, k, которые
всякий pas делаются функциями от х, если А = О и если F(x)
действительно изменяется вместе с х.
Общее понятие требует, чтобы функцией от х называть число,
которое дается для каждого х и вмеете с ж постепенно * изменяется.
Значение функции может быть дано или аналитическим
выражением, или условием, которое подает средство испытывать все числа
ж выбирать одно из них; или наконец зависимость может
существовать и оставаться неизвестной. Например хг функция от х,
которая выражается аналитически; но корень в уравнении пятой
степени будет функция последнего члена®, для которой
аналитического выражения еще не найдено и которая определяется самым
уравнением, как условием. Б строгом смысле должно екааать, что
ни тех и ни других; функции значения не даются прямо, но всегда
ограничиваются условными уравнениями, а потому и вычисляются
большею частию только приблизительно. Например квадратный
корень целого числа, если не будет также целое, выражается уже
бесконечной дробью, где десятичные одна за другой отыскиваются
помощиго испытания. Наконец условия, которым функция подчи-
ііі нена, могут быть еще неизвестны, | тогда как зависимость чисел
уже существует несомнительно. В таком случае предположение,
будто функция выражается аналитически, должно назваться
произвольным. Правда, что еще но встречено таких примеров, где бы
зависимость чисел не могла быть представлена прямо или условно
аналитическим выражением; однако ж нельзя быть уверену совер-
* То-ееть не может обратиться в аостояяяую величину.
* Здесь (как и во миогих других местах), олово «постепенно»
применяется не пак математлнеский термин, равносыьный современному термину
емелрзръкио*. Смысл фразы, очевидно, состоит в том, что значения
функции даются для каждого х и изменяются по мере того, как изменяется я. См.
ой втом во вводной статье, стр. 15—13 нам. тона.
а При заданных значениях: коэффициентов.

44
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
втенао и в том, чтобы другое предположение пе привело также и
к новому решению. Б рассуждении моем о началах Геометрии
(Каа. Вест. 1830 г.) принимал я зависимость утла от расстояния
вершины до точки на боку, где перпѳндияул делается с другим
боком параллелен, разумея под линией параллельной такую, которая
начинает пересевать с малейшей переменой направления к одной
стороне*. Ясно, что здесь понятие о зависимости заключается
в самом определении; но допускать какое нибудь аналитическое
выражение, значило бы ограничивать уже обширность
предположения. Бот почему, означая х расстояние вершины от нерпеидикула,
назвал я І1 (at) самый угол, нисколько однако ж не разумея под этим
знаком какую нибудь аналитическую функцию от х, а желая только
сказать, что угол ¥(х) всякий раз дан вместе с расстоянием х.
В последствии уже доказывается, что F(a;) действительно
аналитическая функция и определяется уравнением
cot i-F (*)-*■,
из Iгде е основание Непнеровых логарифмов*. Жажется нельзя
сомневаться ни в истине того, что всё в мире может быть представлено
числами; ни в справедливости того, что всякая в нем перемена
и отношение выражается аналитической функцией. Между тем
обширный взгляд теории допускает существование зависимости
только в том смысле, чтобы числа, одни с другими в связи,
принимать как бы данными вместе®. Лагранж в своем вычислении
функций (Calcul deg reactions), которым хотел заменить
дифференциальное, столько же, следовательно, повредил обширности
понятия, сколько думал выиграть в строгости суждения.
Итак под названием функции должно вообще разуметь число,
которого постепенные э изменения даны и зависят от изменений
другого, хотя бы совершенно неизвестным образом. Означаем F(x)
s Си. той I наст, недавня, стр. 185. Речь идет о функции Лобачевского И (х),
которая в сочинении еО началах геометрии» обовначалась чарѳз Г (ат).
* Он. том I наст, аздааия, стр. 205, формула (13).
° Б этой фраае содержится строгое определение понятии функциональной
зависимости. Дирихле сформулировав определение функции, равносильное
определению Лобачевского, тремя годами позднее (в І837 г.). См. вводную статью,
стр. ]Ь я 18 нает. тома,
9 Слово «постепенные» здесь имеет смысл «последовательные».

Н. И. ЛОБАЧЕВСКИЙ— «ОБ ИСЧЕЯАНИИ ТРИГОЯОМЕТР. СТРОК» 4S
функцию от х, которая, меняясь с х, непрестанно возрастает* от
определенного х до ж™ а. Разделяем а — х на г равных частей и
полагаем
г
Пусть числа в ряду
1\х), F{x + h), F(p-\-2k), ..., F(a)
*ы I всегда известны, как бы ни было мало А, которое уменьшается
беспредельно с возрастанием і. Содержание
k
.должно изменяться вместе с А. Пусть для *'>*' —р— = h'. Если
.к тому
F(x->rh) — F(x) F{x + h')—F(x)
h ft'
или, все то же, если
WF& + А) — hF{x 4- А') 4- (h—h') F(x)
-Ж
= £
АЛ'
для всякого х постепенно уменьшается вместе с А до того, что
может сделаться как угодно малым, то функция F(x) получает
название непрерывной* и предполагает для содержания
F(x-\~h) — F(x)
h
границу, к которой ведет постепенное уменьшение А и которая
будет
dF(x)
1 " Лв "
Напротив, если Е с уменьшением А приближается к какому ня-
будь числу более нуля ж перейти за такое число не может, то
функция F(x) разделяется на две, которых соединение
представляет точку грубого излома в кривизне линии 0, где оканчиваются
* Это ограничение нужно Лобачевскому толыю для того, чтобы разностные
отношения ^ ~—— были положительны н тгобы избежать, таким обра-
h
зом, необходимости говорить об их. абсолютных величина*.
* Слово •непрерывная» Лобзтавсвий всегда употребляет вместо хдифференци-
руемая*, в еѵвето современного «непрерывная» говорит «постепенная» (си. стр. 49
■ наст. тока). См. такясе вводную статью, стр. 15—16.
аРечь едесьядвт о нарушении гладкости линии, а не об «шламе в врнвяада>
в современном смысле, который евнэан с поведением второй производной.

46 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
вершины ордонат F(x), перпендикулярных к оси х. Если этот
перелом кривизны происходит именно в точке, которой коордонаты
<e,F(x), то полагая А' = — А, получим выражение
F(x-\-h) + F(x — h)—2F(x)
А
которое для непрерывной функции F(x) уменьшается беспредельно
с А, а для: ломаных функций F(x) и для некоторых х не
переступает ва известную границу уменьшения*.
Когда число г так велико, что разность
F(x-\-h)—F(x)
для всякого х нечувствительна, тогда все данные значения F(x),
от х = а до х = а, могут быть заменены аналитическим
выражением
F(x) = J1(a)-j-^AJP(a)-t-E0-!!A»^Ca)+ ... -J-er*A*F(e)*, (7)
us (где
a — a x — a f
i ' to '
A*F(a) => F(a + 2m) — 2F(a + <fl) + F(«),
I
Д*Р(я) = .?» —iP(e — в) + С".Р(в — 2a)—..
Если к атому полагаем
AF(x) = Щв) + ЕД?^(в)-f ... -f «,'~1A*J*(e), '
ДѴ(х) = №F(a) + ... + ET'^'AWfe)
и т. д.,
то содержание
F(x + \e>) — F{x)
с уменьшением \ приближается к границе
(8)
* Вторая часть утверждения наварна. Указанное выражение может
стремиться к нулю, корца F(x) не дифференцируема (и даже когда эта функция
разрывна) в точке х.
* Лобачевский здесь (я всюду вообще) применяет обозначение
„„ ѣ(п— !>...(»— т+1)
® Выражеаяе, стоящее в оравой чаетж внутри фигурной скобки, представлявг
собой коэффициент при первой степени X в разложении F(x-^-}.io) — #{*),
которое нетрудно получить не предыдущих формул.

Н. И. ЛОБАЧЕВСКИЙ —«OB ИСЧЕЗАНИИ ТРИГОНОМВТР. СТРОК» 47
которая может почитаться только в том случае га
dF(x) ^ F(x-\-v) — F(x)
dx <n
для си = 0, когда функция F{x) непрерывная ж когда, следовательно,
с уменьшением в> исчезает вместе
| — Д«Р(а), — &F(a)...
Пусть теперь
dF{x)
■О
dx
для всякого х от э!=а до аз = я,ж для которых значений
рассматриваем также все числа F(x) данными. Увеличивая число і,
должны находить
F(x~\-a>) —Fix) dF(as) ,
где число & с возрастанием г уменьшается и делается наконец
нечувствительным. Если F(x) постоянно растет от а;=а до х = а,
то числа Те должны быть положительные вместе о равностию
F{x~\~m)—F(x)*. Называя Ж самое большое из них, получим
F{a-\-m)—F(d)
ш
F(a~h2<s>)-F(a + a>)
Jfa + to)—Д> +2«) <к
и так далее до
Fja + Ы)— F(a-\-\a> — e>) R
ш
| для всякого целого числа X > 1. Складывая все уравнения,
находим
т
или, полагая 'т = Ь,
F{*-!rb) — F{o.)<bK
* Зная величины к связан со знаком W {х), н поэтому в такоя общей
формулировке утверждение Лобачевского несправедливо; однако в рассматриваемом
елутае, когда F' (х) = 0, величина к действительно положительна.

48 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОК
для произвольного Ь от й = 0 до 5 = а — а. Число К можно
уменьшать также произвольно и брать как угодно близким к нулю*,
а следовательно для всякого числа Ъ
или вообще
F{ss)<=F{a)
число постоянное.
Если даже F{x) будет заменено аналитическим выражением (7), то
da.'
даст уравнение
&F(x) ~A"F{x)-\-^^F(x)—...-\-(-^^'^F(x) = Q>
куда вставляя значевия AF(x), ua_F(a?)... из уравнений (8), получим
- &F(a)
^-^^й-'+.-.-с-ч'т"
и которое уравнение должно быть справедливо для
£=.0,-6 = 1, (-2,..., І^і.
После чего находим
iF(a) —~A«F(e)+ ... —(—1)' Д-Д*ВД = 0
А»*»—4 A3_F(a)+ ... +(-l/ -Д-дѴо^О,
д«р(«) _ 1 Д4jj.(B) _!_.„_(_!)* _J_ д Ѵ(а) и 0
і г — ^
ДО (
Д !?(«) = О.
Откуда легко заключить, что
АР(д) = 0, Д9^(а) = 0, ..., дѴ(а) — 0.
* Это утверждение Лойачевеяим, но существу, ие доказано. Понятие равно-
черной непрерывности в то врема,. когда писалась ѳта статья, отсутствовало.

Н. И. ЛОБАЧЕВСКИЙ —«ОБ ИОЧЕЗАНИИ ТРИГОНОЫБТР. СТРОК» 49
Таким образом, для всякого х находим из уравнений (7)
F[x) = F{a)
— постоянное число *.
«о Итак, будет ли предположено, что F{x) дает|ся в числах для
всякого ж, или F(x) разумеем как аналитическое выражение,
которое без чувствительной погрешности заключает в себе все данные
значения F(x), всегда
dF(x) e0
dx
требует, чтобы F{x) было постоянным, а потому все возможные
значения
должны разниться только в прибавочном постоянном, которое
определяется вместе с началом интеграла, именно
\<?(x)dx = f{x)-f(a)*.
а
Обратно, помощию <?(я) накодим f(x), положивши для целого числа І
х—а
і
и принимая
^(а;) = «{<р(а: —а)+ <? (ж —2a)-j-...+<?(.г —й)}, (9)
тем вернее находим F(x) = f(x), чем а менее. Здесь надобно
следовательно показать, что с возрастанием і функция F(x)
приближается к известной границе, которая должна быть f(x).
(9і I Пусть г' > і и пусть еще
х—а „ х—а
■ = ?>
г- ■ ' гѵ
Если я> (#) от крайнего зпачеиия х = а До другого х = Ь постепенно 0
увеличивается и уменьшается, то можно взять і всегда так велико,
чтобы разность двух смежных чисел в ряду
<Р (а), <? О + а)> 9 (« +2*), ...
* Для того чтобы доказательство было строгим, нужно сначала доказать
возможность равномерной апрокиииации функции F(x) многочленом.
* Обозначение I ѵ (х) их употребляется Лобачевским в том же смысле, что и
j<t (х) dx.
а
а Здѳеь слово «постепенно» уже термин, равносильный современному
«непрерывно».
4 Зак. І8Щ. H. И. Ло&ачевскиЙ, т. V.

50 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
была по величине менее Е. После чего такая же разность в ряду
?(*). ?(я + Р), ?(о + 2р),...
должна быть Й' еще менее по величине, нежели і£*. Итак
?(* — т) + Т(я~8т)+... + »(« —і'т) —*'?(* —а)<*'Д
4- <р (» — 2/f)—*'« (ж — 2а) < *'Д
? (* — w't + і'7 — і) + г (я — я'т + t'-f — 2у) + ...
-f- в (ж — й'т) — і'в (ж — го) < i'JE*.
Складывая все уравнения, получим
г
, (я, — Т) + <р(ж — 2-х) + ... -f-<?(а) — -F(x)<ii'K
а
ш [Подобным образом нашли бы
*(* — Т) + ?(« — 2т) +■••+ 9 («) —§- ^1 <«•)< «'-Е'-
Отсюда
*Ч*) — F, (я)< {ж—а) СЯ+ЛО-
Молшо следовательно г всегда взять довольно большим числом,
чтобы для всякого V > г почитать без приметной погрешности
В таком случае уравнение (9), когда вместо я: ставим сюда ж-}- я,
а і-j-l вместо *, дает
.F(a;-f а)~ а {?(*) + ? (я— *)Н- • ■ ■ + ?(«—**)}•
После чего
это значит,
тем вернее, чем в менее. К тому уравнение (9) требует, чтобы
* Эхо и дальнейшее следует не из непрерывности, а из равномерной
непрерывности функции ? (*У-
* Левые іастж вгих неравенств иодрвэумеваюмя находящимися под внюш
абсолютной величины.

Н. И. ЛОБАЧЕВСКИЙ — «ОБ ИОЧЕЗАНИИ ТРИГОНОМЕТР. ОТРОК» 51
і»! [следовательно,
F(x) = f{x)-f{a)
тем вернее, чем г в уравнении (9) более.
До сих пор однако ж значение ір (да) не предполагалось бесконечно
великим, иначе могло бы случиться, что <р(х-{-а) — у(х) не будет
уменьшаться беспредельно вместе с а. Например,
Ух
дает
1 — 1/2
ф(2«) —tp{a) = -
Y%~a
которая разность увеличивается с уменьшением а а.
Пусть <в(х) делается бесконечно великим для крайнего только
значения х, которым интеграл начинается или оканчивается. На
такого рода интегралы разделяется всякий интеграл
хотя бы <р (х) несколько раз делалось бесконечно великим. Также
іа* довольно, если мы будем говорить | только о том случае, когда
этот интеграл начинается с х=а и когда у (а) = со. Собственно под
Г в (х) dx
а
должно теперь разуметь границу, к которой приближается
I в (х) dx,
с уменьшением ю и когда я + ю взято между а и другнм
значением х. Выражение (9.) всегда может заменять этот последний
интеграл, покуда а> не нуль и когда г достаточно велико. Затем
остается решить, какое значение принадлежит интегралу
а+ч>
\ в (ж) dx
а
или, все равно, интегралу
і
ад 1ір((і-|-ніа:)<&е,
* Этот пример оокяяыввет, что Лобачевский бливко подошел к понятию
равномерной непрерывности.
4*

62 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
который надобно присоединить к прежнему, положив »= 0 после
интегрирования. Принимая следовательно и весьма малым и
пользуясь таким обстоятельством, очень часто можно будет видеть
границу приближения с уменьшением <я. Здесь должны встречаться
два только случая: или интегралу
■ ев | \<p(x)dx
а
принадлежит действительное значение с тем вместе, как
і
О)
о
для ш = 0; или
і \ <a(a-\~tax)clx=0,
і
і <р (х) их = со,
когда
не делается нулем для со = 0 *. Например
уж
j
в)
Берем еще
находим
is* следовательно
Если
) \ со (а 4- шж) dx = j/ій I ——
і
01
jV^M^-jf;
тле
l — = со.
J ж
* Это не совсем верно, так как на того, ч-іа предел Ііщ і f(x) dx
■во cjnjecTBjeT, не следует, что этот предел бесконечен. " "* а + а

Н. И. ЛОБАЧЕВСКИЙ— «OB ИСЧЕЗАШЯИ ТТЖГОНОЫЕТР. ОТТОК» 58
ТО
і і
о о
С (for
сл ед оват ельно
Когда
то
;со.
эша
а (ж) = -у=======,
У sins а — sin4 ж
і _ і
Г,. , , Утяни f (fe n *
о j <в (a -f- ax) dx = — I —■— = v .
% V — sin 2a v1 у ж
Вообще если <?(х) or х*=а до гв=6 не делается бесконечно
великим кроме ш(5) = ±(хз, и если к тому
j <р (ж) &s=*f(x)
аг |так, что для неопределенного х
df(x)
то
= <р(аО,
j" ¥ (я:) 4в = /(*) — /(a).
Если ж между границами х=а, % = с функция ф(ж)делается
бесконечно великой, то нельзя еще утверждать, чтобы
е
С <о (х) t& = Г(с) — f (a),
хотя бы для неопределенного х и находили
а надобно прежде увериться, что ни который из двух интегралов
ь с
f ? (ж) йж, V ? (ж) Ак
* Имеется в виду предел при ш -> 0. Первое равенство щшбиижѳнное, в
правой части отброшены члены, содержащие более высокие степени в; второе
равенство получено при щ = 0.
В оригинале перед знаком интеграла пропущен инояигаель аіса.

54 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
не деяается бесконечно великое число, потому что
с Ь а
f <р (х) dx = j <р (ж) <fce -f- f <p (ж) dar.
а й Ь
Например,
1 J Ж* Я! '
но отсюда аще не следует, чтобы
+ і
С dx
—j.
потому что
О +1
С dx Cdx
— 1 О
Bes такие случаи можно соединить в уравнениях:
df{x)
^{х)йх = Пх), ^ = ?(а.),
9 (6) — сю, ^ (&') = оо...
§<t(x)dz^f(c)—f(a) -f J <p(i+ «)&■-{- J «p^' + ojffa.-!-...*,
где b, b' ... падают между ж = a, re = с, и где после
интегрирования должно полагать ш = О.
[VI
Все сказанное до сих пор о дифференцировании и
интегрировании применяем к интегралу
і
j cos (йке — !<в) f" (х) dx
о
б уравнении (2). ІЕсли здесь f(x) не деяается бесконечно великим
числом ни для какого значения х от ат = 0 до ж—1, то
основываясь на уравнении (9), легко заключить, что
і
j |оов(іет—*»)Г(э;)Ле = МЛ(1)—Л<0)), (10)
* Смысл етой. формулы непонятен. Ояа верна, если функция f(x) непрерывна
в интервале (а, с), но в этой случае все интегралы в правой части стремятся
к нулю; вопи же не существует такой непрерывной функции, производная
которой во веек точках интервала (о, с), кроме точек Ь, І/, ... , равна f (x), то неясно,
что следует поииыать под f(cs).

ft И. ЛОБАЧЕВСКИЙ —«OB ИОЧЕЗАНИИ ТРИГОНОМЕТР. ОТРОК» 55
где X < 1*, а следовательно
2iJeog(«w — »)Г(*)Лв = {Л(1) — Г (О)} У—
<-і * ° СІ *'
представляет исчезающую строку, которой значение, сколько бы
членов взято ни было, всегда менее
3,07{Г(1) —Л(0)}*.
Хотя бы /"(*) н делалось бесконечно великим числом -для
некоторых х между границами ж = 0, ж = 1, но и тогда уравнение (10)
справедливо, покуда f (х) не делается бесконечно великим от а; = 0
до ж = 1, потому что г таком случае на правой стороне уравнения
(10) должно бы прибавить интегралы
Г cos (ivx — іія-\- mr) f (х -}- г) dr e
дли всех х, которые делают f (х) бесконечно великим, после
интегрирования положив г = 0. Пусть вообще
N^^(x)f(x)dx, N = ),{f'(x)~f'(a)].
a
I Дифференцируя, находим
dN^dk tf(x)—К
N л * ф{ж) '
Отсюда видно, что покуда &(х), Г(&) сохраняют свои знаки, а
следовательно № растет ?, необходимо по величине
* Точнее, р.] < 1. Равенство (10) справедливо, если функция f (.с)
знакопостоянна на интервале (0,1). Впрочем, дла дальнейшего, до существу, достаточно,
чтобы f (х) била равномерно ограничена, что и предположено Лобачевским, так
і
і С09 (ЙІЛ »в) f (x) UX
как в атом случае
< (7 при любом і (С — постоянная).
Это неравенство остается в силе ж тогда, когда f" (х) неограниченна, как это
дальше предполагает Лобачевский, но абсолютно интегрігруемя в жатервале (0,1).
* В оригинале вместо 3,07 стоит 2.45 (см. сноску I к стр. 37),
а См. сноску на стр. 54.
9 По абсолютной величшіе.
I Это ■ заключение, вообще говоря, несправед;іиво, во ври знавопостояыстве
4>(х) и f(x) можно, конечно, утверждать, что \Ц меньше максимального
значения |«1> (х)\ и интервале интегрирования.

56 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Так в интеграле
+ г
J сов («таг — !о> -f- (да) Г (яг + г) dr = X {/' (э; + *•) — С (ж — *•) 1
—г
всегда г можно ваять довольно мало, чтобы во всем пространстве
интегрирования
С08{мкв — і<а-\-іъг), f{x~\-r)
сохраняли сеой знак *, а следовательно но величине Х<1, и для г = О
Г соз(ідаг — іш-}-и»")/"(ж-|-«")<&■=! О.
— Г
После всего этого мы в праве заключать, іто строки на обеих
сторонах уравнения (6) исчезают, по крайней мере покуда /"(ж), f (ж}
от х = 0 до аг = 1 не делаются бесконечно великими.
Чтобы найти самое значение строки
аоі |мы воспользуемся тем же способом, которому следовал Г.Пуассон
(Sur le ealeul immerique des integralos defimes. Memoires de l'Acad.
d. sciences, 1'an nee 1823, p. 571) и наперед рассматриваем строку
і і ._
X=^f[x)dx -\-2 |*2°^ cos (mar — ie,)f(x)dxt [10a]
о о '"=l
которая для p^l также исчезает, как и строка У*.
Известное разложение
со
1 — р*
1 _—2[ь сов (іга — (и) 4- }і'
- y = 1 + 2 V [і* cos (гітж — й) '
* Как бы мало щг было полояситольвде число г, величина cos (fac — іш + inrj
но будет знакопостоянной в интервале (— г, г) для всех г, но, несмотря на ато,
первую теорему о среднем применять, конечно, можно, если функция f" (я}
знакопостоянна в интервале (х — г, х -J- г), что Лобачевский, но-сущэству, предпо*
лаштг. Для дальнейшего достаточно іг знакодостоянства f" (х) при достаточно
малом г в каждом ив интервалов іх — г,х), (х, я;-["г)-
со
* При |ц|<1 ряд ^ Iх*сов (*"*"~*ш) сходится равномерно, откуда
і і
со - - со
2 »*" 1 соа (Іг^е — іиі)/"(іс)(ім!= I Г V S*( cos (іга; — leu)] f{x)dx. (a)
Однако ври [і = 1 равенство (а) теряет смысл, так как ряд 2 еоёііхх — («У
расходится. * ™і
® Это рааложение лмеет место при |[і|<4.

Н. И. ЛОБАЧЕВСКИЙ— *ОБ ИОЧЕЗАНИИ ТРИГОНОІІЕТР. СТРОК» 57
даат
Чт-
(1—ll»)f(«)<fe>
- 2[і СОѲ (іМ! — <ц) -j- jab '
[10bJ
а с переменой [і на 1 —[»
*=/
р(2 —rt/(*)«to
о [i.3-f-4sins — (па;—и) • (1 —|і)
Чем менее ji, тем вернее следовательно можно принимать
і і
f /»<fe-f 2У~2 Г ^Ф
(И)
о І*а -j- 4 sin3 — (кх—о»)
Здесь границы интеграла могут быть сближаемы до тех значений
из х, для которых уже нельзя без [ чувствительной погрешности
пренебрегать |і в знаменателе и для которых можем следовательно почитать
I «*>**+* WirfSSSgr*-
* То-ѳси.
2yf(x)dx
|1Э -[" * 8'п3
2 и г ■ —~ 2
Подробное доказательство дано в примечании р].
* Действительно, как бы мало ни было положительное число 5,
ш— &
ііш Г ^'»>Д" =iim f ^Wto
= 0
^у.
оі + г
LU-J-B
J
ц /'(ж) іх
у. f{x} их
ш-Н
(те — сп)я — 4 sicB ■
j^ ^ + 4ііві^-^)[Р« + («-.Л
/Чз)*в
<
м-f t
О
J
_£g-«)*l/<»Ug_<Op>_>0
sma ^— (we — w)a
прн [i-*-0 и постоянном 5 (С— некоторая положительная постоянной).

58 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Если (о > о, < л, то, полагая
получим
где крайние значения г подчинены только тому условию, чтобы
за малостиш ри* можно было пренебрегать разность
|W:—sm([ir),
а потому чем меньше fiS, тем вернее уравнение
г
\ f(x)dx-l-2V=~lf(^^rb\-{-fl^r — b Uaretangr
с уменьшением [t можно, следовательно, увеличивать г до
бесконечности и переходить к границе приближения со всей строгоетяго *
2ЧТ/ j" ffadx + Z^ \ <x>3(i%x — iat)f(x)ex, (12)
О 10
w (покуда fix) в переходе от Д—— 81 к /{—-f-8j сохраняет
постепенность. В противном случае
1 - « J
/■/л_а)-)-/■(— +а] = [ f(x)dx + 2 ^ {cosукх—ш)г(х)Лх, (із>
где под Д— В1, Д—+ 8]0 должно разуметь те два
значения f{x), которые отвечают я;в— е нарушением постепенности!1].
к При помощи преобразования В = \іг, кх—ш = |а< получаем:
Ч IE
J P*+(ms —»)* ~~ J p.*+(*« — «>)* ~
іи— 5 as — ju
' * J 1 + £ ^ л J ! + *»
(И
а о
прячем г -»- со при [і -+ 0 к постоянном В.
* Обоснование этого еы. в примечания [*].
а В современных обозначавши: /*( — — 0), ц — -j-Ol.

Я. И. ЛОБАЧЕВСКИЙ —«ОБ ИСЧЕЗАШШ ТРИГОНОМЕТР. СТРОК» 69
Если m = 0,. то полагая
и принимая у.г столько малым, чтобы дозволено было перебрать
[пренебрегать] раѳность
(М*— 6ІП(1І.Г),
уравнение (11) надобно будет переменить на такое:
О U
Наконец если ш = я, то ставя
пх = it — (іс
я принимая [іг столько же малым, как и прежде, из уравнения (И)
находим
і
о с
После чего уменьшая jw и увеличивая г, приходим к границам
/(0)=j /■(«) (fe + 2 2 j C09 (дат) f (#)<&;, (14)
о * о
f(l) = j f(e)(fe + 2 2 j (—1)«<юв(«и>)/(*)А»\ (15)
о ' о
Если «<0, > — я, то в уравнении (11) нельзя сделать
вш — (itx — да)
2t
бесконечно малым, а следовательно в таком случае
J" У (да) dar -J- 2 2 j cos (іяж — да) f(x) dx^Q*. (16)
* Е более общем случае нужно в левой часта равенства (14) писать f (+0),
а в левой части равенства (15) писать f(\ — 0)нли,в обозначениях Лобачевского,
соответственно /{Ь} и /(1—8).
* Этим доказано, что равенства (12) и (13) дают вря — я < » < я разложение
в рвя Фурье функции, совпадающей с 2f (я) в нвтвраапе (0, 1) и равной нулю
в интервале (—I, 0).

60 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Если сюда ставим —х вмеето ж, потом f(x) вместо f(—х), —»
вместо <я, то для о>> 0, <к получим
о со °
j* f(x)dx-\-2^ J соѳ(іта; — ад)/"(ж) сйв = О*,
а в соединении с уравнением (12)
f{—)=-|-[ Г(я)<&е + V f соа(мга—Wl^cfe. (17)
Eos 1 Если в уравнении (12) ставимж-j-l вмеетож, потом f(x) вместо
f(x-{-l), то для щ<0, > — к находим
2f(-^\*= [C(s;)<te-h2 V f cob(w# —ги>)Л»<Ь*.
—i l —i
а в соединении с уравнением (16) снова получим уравнение (17),
которое таким образом поверяетея для значений да>0, <я шли
<°<0, >—ft.
Если в уравнении (15) ставим —х вместо х, потом f(x) вместо
f{ — х), то сделается
« ™ о
f(—\) = § f(x)dx +%~2> J( — l)*coe(wa?)f(ar)(uc,
-i * -і
а в соединении с уравнением (15)
■§-{/(-1) + Г(+1)} = у J /C«0*fc+ J j (-1)*«я(*«>)««)<&. (18)
—і i—i
Б уравнении (14) поставя -—ж вмеето іс, потом /(#) вместо f{—x),
получим
f (0) = Т I /(Ж) + 2 S I соэ (ііта) Я я> *">
* f(—ж), а следовательно, и /"(в) в этом равенстве — произвольная функция
(удов.-іѳтворяницая, коаечно, условиям, ври которых доказан» сходимость ряда
Фурье), и левая часть этого равенства дает, следовательно, разложение в ряд
Фурье любой, фупкцни, равной нулю при 0 <^ ц> <^ я, в частаоага функцвн,
совпадающей с f {%) в интервале (—1, 0).
* Ѳто равенство нопучаетен из (12) подстановкой х = t + 1 при помогай
обозначений и = оі — зи, f{x -J-1) = f(,x).

Н. И. ЛОБАЧЕВСКИЙ —«ОБ ИСЧЕЗАНИИ ТРИГОНОІШТР. ОТРОК» 61
а в соединении с уравнением (14)
Г(0)=2-J f(x){lx + 2£\ сов («»)/(*) Лв.
—і і —і
зое | Итак если в уравнение (17) ставим та» вместо to, то для всех
значений <о между границами —1, -|-1 и покуда функции /*(»)
принадлежит единственное значение *, находим
Я» = у] Я^ЙЯ+^І <Я>ВІ1С{Х— m)f(x)dx. (19)
—1 1 —1
Если ж функция f(x) прерывается, а потому f(m) принадлежат
два значения, то, как требует уравнение (13),
~ {/(»—J) + /(e + 8)} = ± j f(z)dx+ £ j cos »(* — ■)«*)*!. (20)
—l i —l
Наконец, если о) = і=1, то уравнение (19) заменяется уже
уравнением (18).
К уравнениям (18), (19), (20) можно идти прямо, доказывая
наперед исчезаиие написанных здесь строк и основываясь в этом
доказательстве на уравнении
+ (- 1/ SS^L {Г (+1) - Г (- D) - ~ j cos і* (»—)Г<*) *t, (21)
которым должно теперь заменить уравнение (2), будет лн функ-
w ция f(tc) постепенная илн нет; но [ где однако ж, как мы уже
заметили, /(ж) и f (х) нельзя еще предполагать бесконечно
великими. Так например, в уравнениях (18), (19), (20) можем
принимать f(x) = 1 от а; = — 1 до as = +1; после чего из уравнения (19),
* То-есть, пока f(x) в здчде х = ш непрерывна. В точке разрыва первого рода
функция имеет, по терминологии Лобачевского, два аначения.

62 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
положивши здесь для сокращения ш = 0, находим
Отсюда
sin I г -+- — ] тее
2= I ; і— ' йс
ИЛИ
, (Ні+?)
1
лат
—-dm,
где поело интегрирования должно ставить г = со.
Если же в уравнении (19) пошагаем ш = 0, f(a) = l от # =— яг
до »=-•}-а, разумея а<1; для прочих значений х принимаем:
/(ж) = 0 от ж = — 1 до х=—я, от -f-a до jb = -|-1, то находим
подобным образом
t M'+t)
1
8ш —-тог
ЮТ
— <fe (22)
о
ив тем вернее, чем г более, хотя-бы число я бы|ло столько малюг,.
что беа чувствительной погрешности могли бы написать
р зіп (г-{-—ітіжяа;
■-J . *■
* Здесь запись у Лобачевского неаккуратная. Нужно писать:
г S е г г і,
2= I dx + 2, У. \ совйксйя = \ ic + 2 1im \ (V соа«іа;)Лв,
как это следует из (19).
Впрочем несколькими строчками ниже Лобачевский сам указывает, что пере*
ход к пределу совершается после интегрирования,
* Действительно,
а . (. . 1\ £ . /. . 1\
1«аз
Jn(*+T)«, Ляш^-+_)
Йа;— I - dx
КС \ ИХ

Н. И. ЛОБАЧЕВСКИЙ —«ОБ ИСЧЕЗАНИИ .ТРИГОНОМЕ?ГР. ОТРОК» 6»
Пусть теперь
то для * = со получим
I ісж =і и.
1 Г (й* . ѣ
— тг = 1 — sin и *.
2 J и
(28)
Этот интеграл, таким образом, выведен из уравнения (11), где
положив о) = о, а границы интегрирования назначив х = -\-а,
х = -\~ о *, получим
а
I
y>dss
[*в + 4 sin1 — «ж
о ^
DO
2-Я + 2^8ІПІ,сй
[24]
&
— уравнение, где после интегрирования должно полагать 5*- = 0,
и в справедливости которого нѳ иначе можно быть уверену, как
доказавши наперед исчезайте здесь бесконечной строки. Далее,
интегрируя, находим
2
*Ѵ 44Ѵ
-Arc tang (tang
■(Н/"
СО
1 , 1 V ! ■ ,- ^
ikc die | = lim
i-»co
(tkc)b
3126
-»K)
itcds
<яз)а
. /. , 1\ 1 ЗІ2Я T"'"
s= lim ami 14- — in I — -—
*»
О
a 2
(0<а<;а), как мало бы ни было полоаяивльноѳ число в, если а достаточно шло.
* С учетов доказанного рапеѳ
0 . /.. і\ 0+1)™
-=- = lira Ііщ
о о-»-0 f->eo
-<£с = 1іт. lim Г 5^1 д» =
f 8ІПИ Г 8ІП.И ,
= І13П I вИ = I du.
o-»oj « J *
о о
* То-есть положив f(x) = 0 в интервале (о, 1) я f (да) = 1 в ияіѳрвал*
(О, а) (а<1).
в Номер формулы (24) в оригинале пропущен.

64 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
а полагая [і = О,
СО
— тс (1 — а) = ^ f 8ІП («<*)-
і
Уравнение (24)* можно еще представить так:
а
!' ji tun
или
[Is + 4 sin8 — тес
[АЙЙ
— І (1 -]- 2 V cos ш) йя
о
8111 (*+т)яа
1 - 2 1 .1 da
(J.2 -{- 4 sin2 — tea } sin — пд
^ о ^
с тем условием однако ж, чтобы после интегрирования на одной
стороне полагать ц = 0, на другой і = оо, как бы а впрочем ей было
мало. Полагая а столько малым, чтобы вместо віп-^-тсй можно было
ставить самую дугу, потом принимая |і — О, г = оо, получим
определенный интеграл (23).
Если которая-нибудь из функций f(%), f fa) делается бесконечно
великим числом для х=а мѳищу границами х=-{-1, х = — 1,
то взявши 3 произвольным числом, интегралы в уравнении (19)
должно распространять от ж = — 1 до х = а — 8, от % = а-\-Ъ до
о = -\-1, потом во второй части уравнения присоединять интеграл
J»—-|-J{l-f.22]eoa«t(o —г—«)}/(в —8)Д +
0 со
* Б теките здаоь ссылка на фориуду (23).
* Б правильной записи
Р=іі Да —B)dB+V і costs (a — В — «>)f(a — B)dB +
+41/,'°+B)dB+2 Iші,і(',+!і-и')/'("+«)л
/=1 О

Н. И. ЛОБАЧЕВСКИЙ--.ОБ ИСЧЕЗАШШ ТРИГОНОМЕТР. ОТРОК» 65
2іо |шда, все равно,
s
*~Т —^^ U(«-»)*+
J 8іп~я(а—В—«.)
в
f 81Д
+ 2" ~-^~1 і-/-(а + в)Л* [24а]
J вш—*(а + в —■)
о ^
Когда а—ш не нуль, то можно 8 взять так малым, что
s
р = an|(t+i.)(o —«—в)*1/(о —8)Л +
2 віп ■£-«(*—•) J lV ' '
S
-j-——~ -—(ml(* + -U(a._-* + 8)*}r(e + »)<B*. (24b]
.2 u
Если теперь f (e) =s oo, ho
ff(a-f-»)rf8
is
с уменьшением 8 исчезает, то мы видели уже выше, что в таком
случае Р—О®.
Если f{a) число конечное, но f (а) = со, то всегда можно 8 взять
так малым, "чтобы почитать
p=_j^__ * и і)(в_ш_Е) іл +
/(a+ 8)
9
2 sin—іс (а—ш)
fem{(t + i)(a—Ш+»)*ІЛ*.
* Здесь в левой части лучше писать Р (t, 8), причем Р = lim. Р (», S).
* Точнее: абсолютная величина разности между правой: частью Р' (г, Ь) этого
равенства и правой частью Р ((, 3) предыдущего равенства можег быть при: дю-
бом » сделана меньше любого положмтемьного числа, есян. 5 достаточно мало.
Подробное доканатдаьство еы. в примечании р].
0 Обоснование втого утверяедения см, в примечании р),
9 Точнее: если Р {». В) — выражение, стоящее в правой части этого равенства,
іоР(і, В) —Р(І, В)-+0 при£-кО.
5 3eit. 28S3. Н. И. ЛобачевснвВ, т. V.

66 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
После чего
it (2г -{-1) 8Іп -5- it (a—m)
/■(a+ 5)
it(2i+l)sin— it (a—a)
^— fC0B|(i + l)(a-«-H»)«|-
■cos
{(*+£)<e—4
следовательно J" уничтожается с возрастанием **.
Если a = «, то
,1 sin -— icS
2
r:S
sin
~!—Г{а + Ъ)(Я.
2
о Л о
Если л тому /(a) —оо, то само по себе разумеется, что
уравнение (19), давая на одной стороне значение f(ct), не может
представлять на другой исчезающую строку.
Если ж Дм) конечное число, по /"(«) = со, то всегда 8 может
быть так мало, чтобы почитать
зіп (* + -2"1 я*
( 8Ш
P=f(f(»-8) + №+8)! 1 <®-
J вш—іг8
о ^
Вставляя сюда значение интеграла (22)*, получим
■Р—5" ('<«-*> + /'(«+8>Ь Н
где 8 бесЕонечно малое, а потому f(a—8), /(a-J-6) будут два
значения f(x), когда постепенность функции нарушается для х=а.
«> Если ж в переходе от | f(a—:8) к /(a-J-8) сохраняется постепѳн-
еость, то F^f(a).
Между тем уравнения (19), (20), когда на другой стороне
в бесконечной строке отделяем часть Р, должны представлять
* Здесь доказано только, что Ііш Р (і, 6) = О, доказательство того, что
І-уса
Ііш Р{і, 8) = 0, приведенное в приметаняи [&J, годится я для этого случая.
* И перехода я пределу при і -+ си.

Н. И. ЛОБАЧЕВСКИЙ —.ОБ ИОЧЕЗДНИИ ТРИГОНОМЕРР. СТРОК. 87
значение /(а) в случае /(ж) = 0 от х = а— S до х = а-\-Ъ;
следовательно, оба уравнения и теперь верны для f (а) =00.
Иечезание и значение строки (19) кажется мне теперь вполне
доказано; однако ж предложу я здесь еще другое решение, которое
с такою же строгости*) может быть соединяет боаее простоты я
краткости.
Доказательство, которое дано было выше на исчезание строки.
™ 1
V -г- аіп м>
і
остается без существенной перемены и двд всякой строки. _ ,.
^ -|- sin (w -fa),
когда знак суммы относится к. числу І, какие бві впрочем дуги <о, я
ни были. Например строку
со
, -г- соѳ ііа
5.
ни ] надобно почитать тоже исчезающей, а следовательно и допускать
уравнения
со
log (1 + в»ѵ=і) — — 2 (-1)' -І- (cos *и + Ѵ^Тяп м),
і
log (I -f e-"v-1) <- — 2 (—!)• т {сое ш — У— 1 sin »}
1
которых разность дает
Присоединяя сюда
получим
0-|- + 2(-І)'4
1 . .
Bin «о.
5"

68 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОИ
Отсюда для положительного о» < -к
со
y (- —)=2 4віп іш * (2б) *
і
как ѳто было уже найдено выше по другому способу.
Теперь рассмотрим зависимость двух функций F(ss), f{%),
предположив для произвольного числа а>0®
F(<a)*=-~ Г ^cosHx—^f^dx?, (26)
-а —™
,іі | где знак суммы относится к і, и где впрочем нет необходимости
разуметь число членов в строке бесконечно великим, оставляя
назначать г в последствии, как точность вьтчиолѳния того потребует т.
Умножаем уравнение (26) на da и интегрируем от т = 5 до
<я = е.
я +а +
(^(mJUj^ — I Ѵ<-т-С08Іж(зІпгй — 8ІПІ6)4-
6 —о —со
-(- — sin гх (cos іб—cos іс)і f (а;) йс,
где для і = 0 надобно принимать
1 . ., . 1 . . L . .
-i-smw = S, — атге = с, --вша=і.
t t ■ г
а следовательно и уравнение писать иначе;
(ѴН&^І J[« — 6 + 22{-7-dn^t!~ж) —4-smi(6—fe)|jf(a)dB.
* Это равенство справедливо при. О <«) <[ 2к,
*■ В оригинале здесь опшбо"шо стонт шмер (23)j уже встречавшийся выше,
° В дальнейшем, как это видно ив текста, предполагается, что 0<a<it.
В В правильной записи:
I То-есть. в дальнейшей под J*1 (о)) Лобачевский понимает частную сумку
ряда (28), и, таким образом, в следующих далее выкладках крайние значения
индекса суммирования следовало бы обозначать не через — со a -j- со, как ею
делает Лобачевский, а, соответственно, через — іиі.

Н. И. ЛОБАЧЕВСКИЙ ~«0В ИОЧЕЗАНИИ тВГОНОМЕГР. СТРОК» 68
Здесь
—о ( 1 '
Вели разумеем е>0, <а, то, основываясь на уравнении (26),
находим:
I Ив + й24-шіІ((і-а!)}/С«)йв =
О ' 1 '
Д ™ а го
= ]|с-{-22~ЁІП^С — ^[/'(«Jde + Jie-—2 2Jj8in*'(*—C)jf (»)<&! =
о ' і J и I і '
с а
— Г(* + в>)/(аО&—J(«—«)Г(«)*в*.
О о
° со я
Я с + 2 2-f sin г (е + ж)1/■(—!»)<&: ==J(«—x)f{—x)dx
..Л ' ft
После чего
+ а
= (е+яОДя!)^— (я — »)/'{а:)Й8+і (T — x)f(—x)dse.
* Ссылка ва равенство (35) показывает, что Лобачевский переходит к
пределу при t-* со. В правильной записи равенство, к которому приходит
Лобачевский, таково:
Of С в
lira ||e+2yi-sm*(c —«)W(w)*e= [ (it + х) f (x) fa— \ (с —as)/* (*)*«-
Ззтіись всех дальнейших предшествующих равенству "(27) преобразований
также неудачна: предельный переход при і->со должен следовать за
вычислением соответствующих интегралов. Обоснование предельного перехода под
знаком ттатеграла см. в примечании f]. Аналогичным образом обосновывается
предельный переход и в следующих далее равенствах.

70 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Таким же образом для Ь^О, < с
+ а со
Г !& + 2J]isini(6— x)lf{x)dx =
baa
= {(^-\-x)f(x)dcs— )(*— x)f(x)dx-^-\(Tc—x)f{—x)dx.
о ь о
Наконец
e n
j F(n) dm = it J /■(«) ate *. (27)
«« I Так как границы Ь, с интегралов совершенно произвольны и:
могут быть сближаемы до равенства иди по крайней мере до
элементов [F(x) — f[x)]dx с одинаковым знаком, то необходимо для
F(x) = Kf(x)*. (28)
Таким же образом могли бы доказывать справедливость
последнего уравнения для х < О.
* В правильной записи
о л
Ііго Г Ft(<о) Ля = Tt f Дл:) ііж,
f-l-CO ■
0
где
P((<i,) = -g- U Veosi(.E —ffl)|f(x)d;c.
-a —i
В этом равенстве содержится теорема, утверждающая, что если функция fix)
абсолютно интегрируема, то почленное интегрирование ее ряда Фурье (даме
в том случае, когда этот ряд расходится) приводит к сходящемуся ряду, сумма
которого равна интегралу от функяяи f(x). Эта теорема быяа вновь доказана
лишь в 1903 г. Лебегом (Lebesgue — Leeons sur les aeries trigonometriques,
Paris, 1906).
* Здесь p Лобачевского ошибка, сэяаанная с отмеченной выше
неаккуратностью обозначений, не позволяющей судить о том, совершен ля уже предельный
переход или нет. Равенство (28) справедливо лишь в том случае, когда заранее
н.эвеетЕО, что ряд Фурье функции f (х) сходится, т. Ѳ. существует предел
Р{и0=1іт Fa(<a)
н-*ся
и что
ее о
lira Г F„ (ш) dai = Г ІІш Fn (ш) <Іш = Г F (ш) dw.
b о о
Таким образом, выводы, которые в дальнейшем Лобачевский делает па (23),
обоснованы только при этих предположения! и поэтому не представляют ивтврвса.

Н.,И. ЛОБАЧЕВСКИЙ —«ОБ ИСЧЕЗАЛИ!! ТРИГОНОМЕТР. СТРОК. 71
Если напротив предположим О а, то
о ' і '
а
о
О ' I ' и
следовательно
И с -f- 2 Ѵ-=- sin г (с — ж) >/(я)<£с —
—о і
а а
= j (к + ж) /(л) <£е 4- j (я — ж) /(- и) <Ь.
о о
Если к тому снова 6^0, то
е а
ь ь
| Если ж &<—а, то не трудно таким же образом найти, что
а -1-я
В —о
Из последняя: двух уравнений и с помощью (27) следует, что
для b > а, с > £
с —6
Г,Р(іи)<&а = 0, f F(a>)<f«o = 0.
6 —с
Это значит, что для х>а, х<—а всегда
F(x) = 0.
Другое заключение можно отсюда вывести еще то, что
уравнение (28) справедливо и для f(x) = 0 между известных границ;
а следовательно и тогда, когда между тех же границ поставится

72 СОЧИНЕНИЯ ПО ТЕОМШ РЯДОВ
новая функция от х, так что в уравнении (26) функция f(x) может
быть постепенна или нет, всегда
F(x) = *f{x)
для х <-{-«, > — а. Так же
для х вне границ -J- о, — а.
" 1 Уравнение (28) не должно быть еще принято для всех
значений JP(x), потому что оно выведено из сравнения интегралов (27),
которых елемѳнты могут разниться, как скоро число таких
ограничено. Итак, остается исследовать, не принадлежит ли
функции F{x) особенных значений, которые нарушают постепенность.
Выражение для F(x) в уравнении (26) можем представить еще
в другом виде, как это делали и прежде:
4-о
М(г+{>-.)}
J sin—(я — а)
■**<•) =-§■ I- ' , ' !~f(x)dx*. (29)
Если f{x)=l, то
*>(.) = A J Іі + г^соегСж —оі)|йсс«*
—а 1
<х* со
■= а -{- V -г- віп і (а — о») -j- V -г- віп г (а -f- «)
і і
после чего находим, основываясь на уравнении (25)
+о
С* sm
и» |(*+-2-J (* — «)}
2к= \ — - '-'-- — ■■ ■— - ■■■- dx
J sin ~ (as — «)
—о *
илн, ставя а; -}- а вместо х,
віп \і + ~-\ х
гіп(і + 4")
2* = \ і ~-і dan,
sin — а:
* В правой частя имеется в виду предел при г -* со. Это замечание относится
также ко всей дальнейшим выкладкам.
* В правильной записи
і
^(Ш} = і lim j |l + 3 ѴРОЧг-(х_ш)\

Н. И. ЛОБАЧЕВСКИЙ —«OB И0ЧЕ8АНИИ ТРИГОНОМЕТР. СТРОК» 7S
sis ІЦОТОМ ДЛЯ «0 = 0
6111
Ы)-
J sm — х
Откуда, для S бесконечно малого положительного:
S
Г sin
для й, ft произвольных с одинаковым знаком:
С am Н + ■— | ат
™ (*+і)
(30)
0= \ х ' fa. (81)
а £
Если в уравнении (30) ставим
и принимаем і = оо, то получим
1 Tdu .
■— л: = I — ВШ « *,
2 J и
о
Уравнение (29) делается, когда вместо « пишем т-|-В*
*Чш+8) = І I * ^' ffr+tt-H)^,
тогда как для 3=0
J sin —ж
• Строгое обоснование этого равенства см. в лоненѳииях и выводу
формулы (23) (сгонит * на мр. 02 ж * на стр. 63).
* Сначала додается подстановка x = t+<e, а ватем и заменяется через m-f В.

74 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Далее
4-0—ш
sin И + ~1я
Ы)
1_
2 1 .1
J 6ПП — Ж
—о—ш ^
■ {ДЖ + а> + В) — f (» + *°)! ^ "
■ sin(# + —)(»+вН-«)
+ _і. I \_±/____д_в,-*4-»>*»-
J sin — (ж+ «-{-*)
о -=
J ЁІП— (Ж — Д + ш)
Последние два интеграла для 5 бесконечно малого могут быть
-заменены такими:
J sin -^- ж J sin — х
и еоглаено с уравнениями (30), (3L) делаютея нулями, кроме еиучаев
<o==t:a, дня которых обращаются в -~rnf{— а), либо в --п^-|-я)*.
Итак полагаем
і Г зіп(^1)
J sin — ;С
Означая k какое нибудь положительное число < я— ш, интеграл
принятый для ^*(ш-[-ё) — F(e>) можем разложить па три:
sin
Ы)
д^А. \ _ 1"' {/(« + « + 8) —/(g4-«))<te.
sm — at
-О—<е -
* Это утверждение но обосновано. Для его строгого обоснования можно, яонечао,
предположить кусочную монотонность функция f(x) н повторить доказательство
Дирихле.

И. И. ЛОБАЧЕВСКИЙ— «ОБ ИСЧЕЗАНИИ ТРИГОНОМЕТР. СТРОК» 75
4-я—и
ЙІП ( І -\- -І- } X
{f(X -f о, -f Щ — f(x -f- О))} (for,
+ 8) —/(«+•)}**.
sin — ж
-ft 2
Покуда /О) от ж = — а до :с =—h-j-ai-j-b и от ж=А + ш до
■ж=а-(-8 сохраняет постепенность и непрерывность*, разность
/■(ж-|_,я-[-8)—/"(яЦ-ю) с уменьшением 5 может быть сделана как
угодно малой и представляет 8 '/"(ar-j-tB) *, а следовательно
ВШ 4 -j- — Ж
Ѵ ^ ! f'{x + m)ta,
sin —a;
ВШ I * -г — I Я!
. 1
sin — х
-/'{а! + «)А-вв;
таким же образом нашли бы
f sin (і -Ь 4) (* + 8)
= .B+s+-±. -_L_^ {/(я! + «-М)-/'(*+<»)!<**5.
J вш4(* + «)
—ъ —
Предполагая однако ж нарушение постепенности значений F(x)
в переходе от х — ш-\~Ь к # = <п, как бы 8 мало ни было, мы должна
допускать уже, что постепенность сохраняется в значениях F(x)
от « = e>—В до ж —<о, я потому разность /'(«О — F(<с — В) почитать
* То-есть вяпрерьданоеть и дифференцируе порть.
* Точаее, а/"(*+<о+в8>, где 0<в<1.
° В правые частях этих двух равенств вместо /' (л -J- о>) нужно писать
/"{я: + в + вВ).
Если фуввцин /"' (а:) такова, что пределы интегралов в правых частях этих
равенств при і -*■ со существуют, то lim И ^= Ііш S — 0-
3-»о 8->-о
S Здесь чѳрея Лив обозвачены не те величнаы, что раньше; одааяо н адееь,
при соответствующих преддоложевинх, Ііш Н = lim Л = 0.
і-і.0 I +0

76 СОЧИНЕНИЯ; Ш ТЕОРИИ РЯДОВ
за нуль*. После этого
Г sin U + T )*
I Ѵ х ' -{fix + ш + Ъ) — /■(« + ■")}<*» —
еіп. ™зт
Jh яіп і («+ 8)
Произвольное число h можем принимать столько малым, что под
знаком / в праве дочитать х постоянным и затем уже писать
ь
. ёіп {г -|- — j х
am — ж
1
(* sin (* + _) х
J віпі-(яН-8)
J sin—(ic-f-S)
Здесь, согласно с уравнениями (30) и (31), для k положительного
* То-есть Лобачевский, по онредедеаню, полагает F(a) = F(a — 0), во не
объясняет, почему это не противоречит прентему определению F{x). Вообще,
начиная с этого места и до конца стр. 223 оригинала (стр. 77 настоящего
издания), не только обозначения, ко и сами раесувденид Лобачевского в значительной
мере аѳ ясны. Наряду с ошибками и необоснованными «шеявдиаия, цель которых
состоит в обосновании утверждения, содержащегося в первых строках стр. 2Э4
оригинала (стр. 78 нвет. издания), на тексте этих двух страниц сказалось и то-
обстоятельство, что Лобачевский, оовидимому, перерабатывал свою рукопись во
время ее печатания, и до недосмотру текст последних страниц либо был
неаккуратно сверен, диво попал в набор же чернового наброска рукописи. Ошибки,
отмеченные в сносках на стр. 79 к 80, объясняются, вероятвя, етой же причиной.
Этот факт, а тааже и то обстоятельство, что Лобачевский сам не был
удовлетворен заключительной частью сочинения «Об исчезашн трнгонометрнче-

Н. И. ЛОБАЧЕВСКИЙ —*0Б ВСЧЕЗАНИИ ТРИГОНОЫЕТР. СТРОК. 77
и отрицательного
I sin
і L___/—йж=,Ж) I Л—і Лв«иО.
J sin-ж J rin — (e-f-e)
,u IК тому если разность f(v>)— /"(л — 8) также исчезает в постепенном
ходе f(x) от ж = <п—8 до »=*», то
Не трудно видеть также и то, что в разности .F(<n-j-B)—F(a)
часть Д 4-^ = 0-
Наконец, если постепенность функции f(x) нарушается для
;е = т-|-*, то интеграл Q* можно разложить на три:
ЗІП — X
л
ЭШ — #
r=Y \ —; і w»+«-i-»W(«4-«),*».
sin —ж
из которых первые два снова уничтожаются для Е = 0, А = 0, а
последний делается
!'-{{/'(»+« + *)-№ + •-*)) I ч г "' **
іп(* + 1)я
ь—ft
8ШІЖ
и следовательно У = 0 согласно с уравнением (31).
ім Итак, особенные значения, кроме яДя), функция | ІГ(ж) может
только приобретать с ж = ±а ж с теми ж, для которых нарушается
постепенность функции f (я?). Все такие случаи мы теперь рассмотрим.
еісих строк», подтверждаются следующим замечанием Лобачевского в его сочинении
^Способ уверяться ...» (стр. І2І—125 наст, тома): «Ксчатя здесь в повторяю с
новынк пононениямк тют способ, который изложен был в конце моего иочикевин
аод названием .Об исчезавжя тригодаметрячѳекжх строк"; тем более, что сюда
вярались ошибки во время печатание е переменой означения».
* Швидимому, Q= F{(o -j- Ь) — Л*Н-

78 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Пусть x = -±za. Значения функции f{x) должно почитать
данными только от х=.— а до х = -\-а, вне которых границ можно
полагать f(x) произвольной, и потому, сохраняя далее
постепенность, принимать для всякого положительного 8
«* + *) = /(«-«), \
f(--a — i) = f(— и+ 8). | Vй*
Затем для известного В пусть
*(*)=/(* + *), *<*)=/(* — »),
где ?(&), ^(аг)— две функции от яг для всех чисел от ar=s — а до
я;= +и. Разумея в бесконечно малым и следовательно <р (-f- я — 3),
і(—a—f-S) постепенно изменяющимися вместе ев, можем допускать,.
основываясь на уравнениях (28) и (29)
1 ЛвяпЛ- + -|-)(«—а + 8)
*:<f>Ofa — 3) = — I —^—- - ? (аО dm,
вт -- (ж — а -)- 8)
*5
Г sb [» + _ (я + о-
■«-+Ч-Н ■ ,; ,
J am—(a:-fa —8
-3)
— <Ь (аг) йв
«ss ]или, все равно,
(яг —8)<&Т,
J em —(ж —a)
-fa-5 , 1 .
Г вЫ(»+-й- (*+а)
J 8ІІ1Ѵ(ЯГ + Д)
— о— 5 й
Потом
р віп (•+-S-)(*—«)
tt/(+el = f(+e) + — 1 —Ѵ t ' «<а — 8)&г—
J sin—(ж —а)
а л
( К1П Г J -I I IV. Л1

Н. И. ЛОБАЧЕВСКИЙ—«ОБ ИСЧЕЗАНИИ ТРИГОНОМЕТР. СТРОК. 79-
*/(—а) —*Ч— а)+ 4- \ і —-1 ф(«-(-В)(Ь» —
J ein —(я+о)
—о—* £
а)
или наконец:
а—ъ
віп~-(а; + а)
■ф(* + »)Лг„
1 f *п(*+т)*
smTB
f ^(*+т)»
Bui»
f(— о + *)Д*,.
я/-(_о) = **(_л) + -|-
1 Г »(♦ + ■!■)*
еіп¥8
/'(—а — В),
' 8ІП('+І)
«ш-і-8
-/(<* — *)**-
* Здесь у Лобачевского ошибка. В действительности
' и» f
2 (-»■» J
sto-g-(S-ai)
f (-* + *> *-
* Здесь также отябка. На самой деле
г та.(і-\--^)і
*/-(_«),= *(_ «) + .£■ И» ^-г^—Г(-а-»)
2 і-±а> J
sin— (в~ 2а)
dB-
Г(-в + г>л

80 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
«е j' [ Отсюда, принимая в помощь уравнения (32) и (30), находим:
F(-a) = ±«{f{+a) + f(-a))*.
Если же постепенность функции Дсе) нарушается для ж = ш, так
что f(m) принадлежат два значения, которые оаначим f(a> -(-8),
/(в> — 8} с помощию бесконечно, малых 8, то постепенность
функции f(x) будет соблюдена, когда, начиная с х = ш до х = а, вместо
f(x) будем разуметь
/(*)—/(• + ») + /(—»),
а следовательно
-рвш (*+-=-)(» — «»)
sin -^ (ж — w)
Здесь
Ѵ ,2/ -&>- Ѵ 12; -л»,
8ІЛ -5"(Я! —*) J 8ІП —Ж
следовательно
* Это воряо (при условиях, в которых имеет место теорем» разложения)
только, волн я = я, как это видно на двух предыдущих оаосок. Если же а<^п,
то на основании равенства (30) получим;

-ИМОКРАТОРСКАГО КАЗАНСКАГО
УНИВЕРСИТЕТА.
1835.
I. ПАУКИ
^ I, Cjl О СОВ* УВѣГЯТЬСЯ В ■» ЯЭЧЕЗЛНІЙ В В 3-
конечныхг стюкъ я приближаться к.%
ЗВЖ ЧВ НІЮ ФУНКЦГЯ ОТІ ВЕСЬМА БО ДЫНЯХЪ
',- ' ' ЧИСвД Ъ.
( ff. Лобаиасксиа.)
Нзвѣслшо, что безкоиечняя строка всякой разъ
азчезаешть, иогда %ъ еей содевжлнів <тва н.ъ пред-ь-
идуіцему постоянно іненыяе единицы, съ которой
рмзиосгаь одаакозкъ не должна переходить за какое
добудь опредѣлеаноа число. Въ шакоаъ сдучаѣ
прикладывая адеЕгь за чденомъ, приближаемся къ тому
зваченію , на которое влідше проэихъ ожчасу сгааво-
Первая страница ориі'изадшого издания сочпнешш
«Способ уверяться п исчезапии боскоиечиыі строк
и яриблиэдатыііі к аішчеігят функциіі от весьма бодыннх чисел»
(211-я стр. II книжки «Ученых зашшак Казанского университета» за 1S35 г.).
Ы отр. S1.

СНОСОВ УВЕРЯТЬСЯ
В ИСЧЕЗАИИИ БЕСКОНЕЧНЫХ СТРОК
Я ПРИБЛИЖАТЬСЯ К ЗНАЧЕНИЮ ФУНКЦИЙ
ОТ ВЕСЬМА БОЛЬШИХ ЧИСЕЛ
м
■д51 Известно, что бесконечная строка всякий раз исчезает*, когда
в ней содержание * члена к иродъидущему постоянно меньше
единицы, с которой разность однако ж не должна переходить за какое
нибудь определенное число. В таком случае прикладывая член за
членом, приближаемся к тому значению, на которое влияние про-
sia- чих отчасу становится менее, покуда с достижением назначенной
точности сделается совершенно нечувствительным. Напротив, когда
сказанное содержание постоянно больше единицы, то строка
растет и не может служить для вычисления. Остается решить, из
двух случаев к котором;' принадлежит та строка, где содержание
члена к предъидущему хотя везде меньше единицы, но разность,
уменьшаясь, наконец уничтожается а.
О таких строках Г. Диркеен напечатал недавно рассуждение,
читанное в заседании Берлинской Академии наук 16 Февраля
1832 года (ТТеЬег die Bedingungen der Convergenz und der Diver-
genz der uneudliehen Koiheii. v. Dirksen). Сочинитель обнимает свой
предмет во всей обширности, разделяя строки на классы, роды,
виды с отменами, которых число восходит до 23; потом дает
9 предварительных положений, основывая ыа них пять
предложений для различных случаев. Способ Г. Дирксена нельзя назвать
* Напоминаем (ем. стр. 31), что Лобачевский всегда нааынает ред строкой,
я, еаодимость ряда — исчезангіе.к строки,
* Лобаіеюевнй: всегда применяет вместо дотнотенно» слово «содержание»,
ч> Ре-5Ь идет о том случав, когда известный нрнвнав Далимбера сходимости
вя-f-I
бесконечных рядов отказитяется служить, т. е. когда отношение *^ постоянно
меньше единицы, но lim —^-"г— = ).
Я-* но ап
6 Эая. 2B8S. H. И. Либаченскаіг, т.

82 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
общим; к тому ж в его главных положениях есть одно (Htttfeata 1),
которое не должно быть принято бев ограничения. Это положение,
е употреблением тех же знаков, какие придумал Г. Дирксен,
заключается в том, что когда г можно ваять довольно большое число,
чтобы неравенство
Ѵ.І1. («,.,.„ — ОгХе*
in | оставалось справедливо для произвольного т и как бы в ни было
мало; то
Gr «„ = &,*.
Между тем полагая
ат = log m,
Н&ХОДИМ
Т- п- (*пт — <Ѵ> = bg (1+Т") "
Здесь можем взять г так велико, чтобы log (1 + ~) для
всякого т был уже меньше какого нибудь данного числа а0, тогда
как logm = co для т = оо.
Кажется надобно дать преимущество тому способу, который я
придумал и применил к двум случаям (Алгебра или вычисление
конечных 1881 года; стр. 337 в. О тригонометрических строках,
в Ученых Записках Казанского Университета за 1884 год *), и
который не только подает средство судить об исчѳзанин бесконечной
строки, но вместе назначает самые границы приближения. Здесь
намерен я говорить об втом способе гораздо' пространнее **.
и» I Пуеть /(і), положительное число, представляет какую нибудь
функцию целого і, а вместе всякий член в бесконечной строке
СО
* Здесь т. п. — символ абсолютной величины (пстцднмому, таіеиг sram&ique).
* Обоаначвние Gr о„ равносильно современному tha о„.
ю-уса
в Это, конечно, неверно. Некоторые пояснения даны в примечании ['].
Э Страница указана по оригинальному нвданию «Алгебры». В настоящем
надыши она соответствует охр. 233—234 IV тома (статья 182).
Т Си. стр. 35—39 наст. тона.
•* Речь ждет о найденном Лобачевским признаке сходимости. Подробнее об
атом нрвяніяѳ см. приложение 1 (стр. 362 наст. тома). Там же дано
доказательство не только достаточности, но в необходимости приаяава сходнкоотк Лоба-
чтаиао.

Ц. И. ЛОБАЧЕВСКИЙ—.СПОСОБ УВЕРЯТЬОЯ» 88
которая происходит, когда складываем: значения /(*), ставя на
место і по порядку числа 1, 2, з... ж т. д. до бесконечности.
Функцию f(i) можем снова предполагать значением бесконечной
строки
которая происходит с разложением но степеням от 2, так что
здесь а постоянное для всех членов, X или нуль gjra целое
положительное число, 2=1 для А = 0, потом или ( = 0, иди 1=1 для
всякого другого К. Ставя такое значение (2) функции f(i) в
уравнение (1), должны подучить
us ]с целыми положительными числами L. Пусть теперь р—такое
целое, для которого
Г(ЮЗй2-\ Пѵ.+1)^2*-*: (8)
После чего L^p, а следовательно
*<2^ {IZl. W
Условия (S) служат в определению границы:, за которую ц на
переходит, и которая, будучи поставлена в уравнение (4), назначает
вместе границу для значения самой строки, по крайней мере
всякий раз, когда в этом виде суммование возможно. Такого рода
способ яснее будет виден на примерах.
Пусть
с постоянным числом те для всех членов в строке. Надобно теперь
полагать
I—a
не |и следовательно
1*<2_5~.
* Еелн №Ш неравенстве определяю! немеолько вяачвянй р, м> жужяо взять
наибольшее ня нкч доетому лучше писать:
в«

8+ СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Основываясь далее на' неравенстве (4), получим
g<S2(.-)»-» {-
Откуда для п > 1
і
о — — о
г<-?-4-,
1 — 2» 1
так что в этом случае бесконечная строка
со
і
исчезает всегда, как бы разность п — 1 ни была мала.
Пусть еще
яіг Іс постоянными положительными числами п, р. Надобно полагать
где 5^0. Находим
1-я
(„_4,),_(,4—н4,),-,і
и следовательно
Если к число так большое, что
Ь1-о,_й
то для »^1
■тем; сильное
Носло чего
*2*-Ч<1,
Ц-,2>-Ча1+^2^-Ч.
1 +i,2Tfe-4 < { 1 +^ а***-4}».
К^+а^-*",
а ставя такую границу вначений у. в неравенство (4), получим

а Ж. ЛОВА.ЧЕВОКВЙ—«СПОСОБ УВЕРЯТЬСЯ»
Итак для nfel
Если ж п < 1, однако ж > -^, то предполагая снова
пишем
<Jpi+^-12i'1-'"+i,2^'^'«+2^R-i4.
Лотом, смотря на неравенство (4),
J л = оо.
51S
[Наконец отеюда
Вв—1 / J \
J- Jl-і Л0 ._ «2"*»"* ' йѴ1_*г)'
1 — 2 *»»" 1 —22(* *
Итак, бесконечная строка
s=y I
исчезает для всякого и > -s-, как бы разность 2w — 1 мала ни была.
Если нужно доказывать это последнее предложение, не заботясь
о степени приближения, то довольно заметить, что дня
* Нужно было, конечно, предположить, что рфтР, где т — дедое
положительное число. В остальной сходимость ряда при П>1 доказана Лобачевским
строго, однако оденва суммы проведена не вполне аккуратно, так как Лобачевский
пользуется тем, что X достаточно велико жр2 <1> а суммирование
распространяет на все индексы от X = 0.
Такое же замечание можно сделать я к следующей далее одеавѳ суммы в елу-
■чве, когда -^ ■< « <, 1.

se
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
необходимо
Откуда
|потом
Р<2 » ,
и следовательно для ^>-g-
8<~—хгг-
Обратимся к самым основаниям нашего способа. Здесь из двух
условий (8) довольно которого нибудь одного для назначения
границы числам р,, тогда как другое заменяется неравенством (4) *.
К тому данная строка (1) необходимо предполагает уменьшение f(i)
с возрастанием »*; следовательно, граница для р может только
выходить из первого условия (3), именно
Пгі>2А~\ (5)
которое дозволяется впрочем соединять и со вторым
Г(р4-1)<Й"\
{лишь бы в этом соединении не уничтожался показатель X®,
в зависимости с которым должна быть назначаема граница числам р.
Вели /(|t) .алгебрагичѳская функция, то граница может быть
отыскана для р, так жѳ как его делается для положительных
корней в уравнении, по способу всем известному.
Чао касается до числа а, так его можем определять или
неравенством
* Лобачевский имеет в виду, что первого не неравенств (3) достаточно для
оценки суммы ряда сверху; если жѳ пользоваться тоаьво вторым не неравенств (3),
то ив определяемых при помощи вето значений, ц нужно брать то, при котором
справедливо и (4), т. е. наибольшее.
* Для оценхя суммы ряда сверху при; ломолщ (4) и, следовательно, при аоль-
вованнк способом Лобачевского ш достаточным признаком сходимости
требование монотонности функции fff) нелишне.
ф Неясно, чтб Лобачевский: называет «уничтоженном» покавателя і.

Н. И. ЛОВАЧЕВОКНЙ—гіЛІОаОВ УВКРЯТЬОЯ» 87
или лучжѳ строгим уравнением
Ш-зГ1, (в)
равумея под г число, воторое иринадлаашт первое не тех членов,
откуда схрова начинает исчезать *. В ѳтом последней ояучаѳ
Пусть например
.и |где те, ж произвольные числа, и где
ті_ я(м—1)0 —2)... (п—»'-М)
И° - 1 - 2 • 8- ... І
по принятому мной означению для членов в строке, которая пред-
етавляет етепень от суммы (l+as) с показателем п (Алгебра паи
вычисление конечных). Вообще буква в внизу, по примеру Г. Вар-
тельса (Vorlesimgen liber Math. Дпаіув.)0, будет означать деление
на произведение делых, от единицы по порядку до того числа,
какой вверху шжаватель.
Теперь надобно полагать
пГѴ>2—*
и первую часть этого неравенства принимать всегда
положительной. Если к тому х положительное, n-j-l^O, ц так велико, что
находим »■<}», для которого
г + 1 sl'
то
*м [следовательно,
а переходя к Непперовым логарифмам, получим
(X-a)log2+log{7Cr)^plog(-|)
* То-есть, начиняя с которого, члены ряда монотонно убнввюі.
. * Обычное обозначение у Лобачевского. См. т. IV, стр. 184 и наст, torn, стр. 4в.
" J.M. С. Bartels—Vorlemmgen fiber тяіЬвпийіясЬе Analysis. Dorpa*> івЗЗ.
H. И. Лобачевский олушво лввции М. ф. Бартепьс» в Кмянскон университете.
9 В левой части подразумевается ваше абсолютной величины.

88 . . СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
— неравенство, которое впрочем определяет границу чисел у. только
для х < 1. В этом предположении бесконечная строка
со
■ ч
всегда исчеаает, потому что неравенство (7) дает
{(1 - e) log 2 + log («?*)}-г2а*1,
logic
куда вставляя значение я из уравнении
я.-ѵ=2в+і;
,и (получим
Для n-f-l — О можно принимать »- = 0, и тогда
1—#^
Ці)'
Откуда находим, ставя — вместо #,
я?
_loga:<-^_ + _log^Ta)
для всякого а: > 1, а < а:. Увеличивая сперва произвольное
положительное число а, потом также х до бесконечности, заключаем,
что для х = со
—log3T = 0.
Это последнее предложение можно доказать еще простее, когда
заметим, что для ж > 1
* Здесь, давидаиоыу, ошиаса, не аиеющая, впрочем еущеотввваого анячвнкя.
Из вравддущвго равенства сведет, что
г -г г
S-2»rf^<-~-Jf21og2-l-(l_log2)logn-'-j.

Н, И, ЛОБАЧЕВСКИЙ— «СПОСОБ УВЕРЯТЬСЯ» 89
Цосле чего
11.
l~->-logx,
ass [Ставя сюда — вместо ж, получим
1.1,1, . 1,
Всегда, следовательно, х с а можем увеличивать до того, чю
ilog*
будет менее всякого данного числа.
Для ті-]-1<0, <в<1 можем взять р. так велико, что найдем
целое *"<ц, дал которого, как выше заметили,
где в < 1. В таком случае
Условие (5) будет, следовательно, выполнено, как скоро
. _„г( r-t-1 W., „о-*
*» I «• \T=irj B >2 ■
Теперь если хотим судить об остатке S' в бесконечной строке
о
за членом f(r), то должны полагать
и тогда
*ГУ=>2"+1
21+1>
(тГ-
Откуда
11 Г< log8
Потом из неравенства (7) выводим
a+alog2
S <~2 logB
эіт I иди, наконец,

90 -СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Итак, строке для степени (1 + я) с показателем п, расположенная
по восходящим степеням: ж, исчезает для всякого числа п, как
скоро а<1 по величине.
Пусть еще требуется решить, приближается ли выражение
Е определенному числу, с возрастанием целого положительного т,
в для всякого а, кроме целых отрицательных.
Для я»=со можно рассматривать Лш как значение бесконечной
строки
где общий член
Следуя нашему способу, полагаем
или, по разложении в бесконечную строку,
(«+і)-| («+1У--І- С+іУ-^
<(fl+«i—I)" (,»4-та~1)"'^ (i*-j-m —1)*
Пусть
1
а~Х
«>
Ѵ8"
— случай, к которому приводится всякий другой. Берем еще ц
так велико, чтобы
(■«4-IV —Л > t Ё__і_
или, все равно.
(.+„ »>j!±aL
3 -p-j-*»-|-« 4((i + m —1) ' 5(ii + m—l)a *""
*» IА как ни (ѵ, ни т не должны быть < 1, то последнему требованию
будет удовлетворено предположением
t«-j-i> 3 ^ p-fm + a *

Н. И. ЛОБАЧЕВСКИЙ ~ «СПОСОБ УВЕРЯТЬСЯ» 91
откуда
Число )і может быть, следовательно, всякое целое, как скоро
Далее,
■2(р+т-1)"'
потом отсюда
і
-{І-а-ц
itn [Между тем, основываясь на неравенстве (7), должна почитать
теи сильнее
и наконец
Число а дается здесь уравнением
следовательно,
После чего
Л —А — а"*1-
2 =log 1 -4 р —- -
& \ ' т) ' m-J-a-j-1
Итак А^ не только приближается к известной границе с
возрастанием числа т, но даже разность Ащ о этой границей всегда менее
(1+ Ѵ2) /Я. + 1 /ь*(і + £) -5+Ірі~

92
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
какие бы числа ѵа, а. ни были, как скоро при том
3(а + 1)2 —1 '
Довольствуясь первым членом в разложении по степеням
отрицательным от т, заключаем, что
L | 8>Аа; 3<АШ+^±±(1 + Ѵг).
Взятый теперь пример из сочинения Г. Дирксена принадлежит
в тем случаям, где требуется сыскать значение функций от
чрезвычайно больших чиеел. Б решении такого рода задач обыкновенно
следуют Лапласу (TMorie analytique dee probabilitCs). Я бы мог
предложить в замен, даже е выгодой, употребление строки Макло-
реня для разности суммы с интегралом; но замечательно, что
значение функций представляется бесконечным рядом, который не
исчезает. Итак, строгость и возможность назначать границы
приближения составляют уже преимущество нашего способа. Прежде,
нежели буду говорить здесь об этом новом применении, надобно
сказать еще несколько слов о произведениях с бесконечным числом
производителей.
Разложение функций на бесконечное число производителей
требует осторожности, как и самое разложение в бесконечные
строки. Г. Бартельс (Vorlesungen tiber math. Апаіув.) может быть
первый еще доказал со всей строгости© такое разложение для
синусов и косинусов*. Между тем, если частные случаи доставляют
особенные к тому средства, то по крайней мере в общем способе
и» должно предпочесть простую теорию Ейиера, как | скоро пополняем
ее доказательством на то, что произведение с возрастанием числа
множителей приближается к определенной границе.
Пусть F(x), функция х, делается нулем только для ж = /(») и
так, что функция f(n), оставаясь всегда положительной или всегда
отрицательной, приобретает различные значения, когда вместо п
* Лобачевский ошибается. Разложение с.іауса в бесконечное произведѳняе
было строго обосновано еще Эйлерам.

Н. И. ЛОБАЧЕВСКИЙ —«СПОСОБ З^ЕРЯТЬСМЬ 98
ставим по порядку целые числа до бесконечности. С атии
предположением
если к тому постоянное А поверяет уравнение для какого нибудь xt
а произведение бесконечного числа множителей приближается к иа-
вестному значению вместе е тем, как производитель за
производителем прибавляется*. Это последнее требование будет всякий рае
выполнено, когда полагая
Ѵ"Чі-тЫ
находим, что бесконечная строка
iogj»=iogA+2bg^( [l^lc
an I исчезает с возрастанием целого і. Итак, условие будет заключаться
в том, чтобы начиная с.известного г = г в
для всех других чисел' j* > г, выходило
с числом ш <1, > 0. В таком случае до величине
logF{x) -log {А ■ А, ■ А, ... А^) < 22*—>(—»
и следовательно
log*4a>) —bg(^Mi -~ iN1)<~3.
То же самое должпо бнть выведено как для множителей, где f(n)
положительные, так и для множителей особо, где f(n)
отрицали тельные; или в [ противном случае по крайней мере для
соединения тех и других вместе.
Например,
аштас
1 = 0
тех
Это утверждение в общем случае, как известно, несправедливо.

9* СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
делается единицей для ж = 0 и нулей для всех х = ±а целых.
После чего надобно полагать
ашяа; = та;(1~ я*)(і — ~(А [і-|А.. (8)
Остается доказывать, что здесь произведению с бесконечный числом:
множителей принадлежит определенное значение. О этой целию
пусть
Ці-£)>2=-:
отсюда
Тем сильнее
ін |или
Наконец,
р.* ~ 2у* ^ 3|*в
-,а-\ , х>
2а_"<—:
р<*{1 + 8"* *"}.
Х = 0
со
Теперь [енот, неравенство (7)1
<2(Р-Г)2а-І<а;22^а-Ч(*-Г)2 20-1= {[
Число а находим из уравнения
і«_-Ці_£).
Возьмем еще1 функцию
2кя '
пг | которая делается единицей для х = 0 и нулем для ж = zt rt У^І
е целыми числами п. Надобно следовательно принимать
Далее пусть
bg(i + ^)>2-

В. И. ЛОБАЧЕВСКИЙ— «СПОСОБ УВЕРЯТЬСЯ» 96
иди, после разложения в строку,
2"-*<.£ £-J__£L_ .
следовательно, у. всегда можно взять так велико, чтобы
Отсюда
Потом
<log{(l + ^(l+4«")...(l + ^)}+^(l + V2)2^°+"-r2"+'.
Число а должно быть взято в уравнении
Этих примеров уже довольно, чтоб отсюда заимствовать
правила для всякого другого случая в разложении функций на
производители. Переходам теперь к значению функций F(x), когда х
весьма большое число *. Здесь все дело состоит в том, чтоб
удовлетворить уравнению
отыскавши постоянные Л, а, Ь, с и новую функцию <р(х), которая
делается единицей для х = со *. Показатели могут также содержать
не степени j выше первой от х, если б это было нужно в некоторых
случаях.
О этой целига Лаплас (ТЬёогіе analytique dee ргоЬаЬШійа, 1814,
р. 175) составляет наперед уравнение для F{x) с приращениями а.
Потом выражает F(x) определенным интегралом, где переменное
число ш заключается в элементе под видом
* То-ееть в асимптотическим формулам щга х -* со.
* Такого вида асимптотическая формул» нѳ всегда, конечно, существует,
в То-вотъ уравнение в конечных равносташ

96 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
с постоянными А, а, Ъ и с функцией у от х, <о, которую надобно
всякий раз определять, а также границы интегрирования, чтоб
уравнение е приращениями поверялось. Столь искусственный способ
справедливо может казаться весьма далеким от сущности в
решении. К тому ж здесь интегралы разлагаются^ предельные строки
(series limites), как, их назвал Лаплас, которые в начале только
исчезают, а потом растут до бесконечности. Замечание, сделанное
самим Лапласом (Theorie analyt. des prob., 1814, p. 174), будто
можно довольствоваться приближением с первыми членами, трудно
было бы распространить на все случаи; ,тем. менее доказывать это,
когда надобно прибегать к обращению строк,
і | Напротив, следуя тому способу, который здесь изложен, думаю,
что вычисление вероятностей можем обратить в алгебр агичѳское
учение, кроме тех случаев, где по роду самых задач
интегрирование необходимо.
Пусть требуется найти значение функции
F(x)
-М"
с постоянным <о для чрезвычайно большого числа х. Взявши
логарифм и разлагая в строку, получим
і3 ft|3 л,4
logJ,(£0) = <o-
2х ' Зжа 4й3
Так как эта строка всегда исчезает для dl > w'z, то, предполагая х
чрезвычайно большим числом, можем довольствоваться
приближением
которого границы легко назначить. Они будут дня ш
положительного
. X Зчі1 ш'
hi)
<e~a'e *=-*"> >е~
* То-есть

Н. И. ЛОБАЧЕВСКИЙ — «СПОСОБ УВЕРЯТЬСЯ» 97
Потом
J^___^_, —^_і, 2ш _■. 2і° )^
шг ( ^ ш , в2 «в , о)
>
После чего
2ж ( * я "*" 2жа я* ' &в*
Ша 1 1 «Ж I
<о3 j Ж8 ІОШ! 1 «
2ж \ жа— в»*'-' 15;еа — 9»*/ *-
Ы)
ѵі*аг ь«г3
ал1—юа+ аа*—l-o,» *
[П]
| Предлагаем еще найти приближенное значение к выражению
(*+«)—= («4-1)(а + 2)...<«4-*) (Ю)
с произвольным числом а и с весьма большим целым
положительным х. Переходя к логарифмам, получим
bgOe+a)-"—logts + e — l)"—1 = bg(ai+«).
Чтоб уничтожить в этом уравнении log (г-J-<*)и, должно ставить
(аг-i-a) —-(аг+я)"^^^ 01)
и потом определять новую функцию f(x) в уравнении
log «я-fa) — log/(а;+ «_!)=. (л—1) log (l — "T^i")'
Разложение в строку по степеням отрицательным от х-\~а дает
, і™. /<* + ") = 1( 1±2а 1 + За 1 + 4а
1 ■ *Ѵ(аН-в—1) ^ 2(даН-я) ■" 2-3(a?-j-n)s ~ 8 ■ 1 (ж-(-*)в "
* То-есть
За! I «•* з* — uiH Г ^~2зГ Зз" + ••■<- 2х \ з^ —мв 15з£--Вівв J"
^_"*__ , а»' в
* То-ееть е •« М + "жУ "^ '
&Ю1— Зер-
и Смысл этого предлоисеввн становится очевидный из дальнейшего.
9 Обозначение неудачно. Вместо f (ж4-«) нужно бы писать Дх, о) и дальше,
соответственно, f(x — 1, я) вместо /(.£ + =— 1).
7 Зяк. 3623. Н. И. Лобаіавскиа, т. V.

98 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Чтоб уничтожить в этой строке первый я второй чпее, надобно
принимать
Д (* + «)« (*-Ь*)'+Ѵ,(іВ'4-а),1 (13)
где Л (я), ^(ж)— функции х. Теперь находим:
(14)
г-ЗСіС+а)* ' 3.4(ж-)-*}в ' 4-5(ж + а)4 "" '
Можно бы продолжать таким образом уничтожение первого члена
в строках, вводя каждый раз новую функцию. Довольствуясь
однако ж этой степенью приближения, полагаем
s« |где ф(а)—такая функция от а, в которую /^(да+а) переходит с
а; = со. Когда ат чрезвычайно большое число, то уравнения (14), (15)
показывают э, что можно принимать без чувствительной разности
f,(*+«) = «(«).
Досле чего уравнения (11), (12), (13) дают
* См. предыдущую сноску. Вместо ft (ж + о) и /а (я + о) следовало бы писать
соотвѳтствевно /і (я, а) и ft (д о).
* В правильных обозначениях в левой части следует юкать:
а В правильных обозначениях под знаком суммы б правой чаяш нужно
писать:
9 Из (14) следует, ио при достаточно большом і
Ul0=fiW+<-i,»)l<. і
н, следовательно, ряд в правой части (15) сходится при всех значениях а^ кроме
тез, ври которых я-\-а есть целое отрицательное число, и существование
предела ф (°) = 1іш /і (*■ °) Іеш самым обосновано.
Т Это равенство— асимптотическое (при х-+ оо).

В. ИГ. ЛОБАЧЕВСКИЙ— «СПОСОБ УВЕРЯТЬСЯ. . 99
Чтоб судить о степени приближения в этом уравнении, надобно,
следуя нашему способу, начинать с неравенства
ftQg+q + E —1) х
ІОё №+* + ?) >2
или, принимая е помощь уравнение (14), полагать
2 <12(я;-]-а-!-^ + 24(ж+а + ^'+'-- <І7)
или, наконец, еще сильнее;
Отсюда
2 <12(!S+a+llf • [т
Между тем, к уравнению (15) применяя неравенство (7), должны
почитать
І0^ ф(а) <10?^(Ж + а + 1)^^^ ^ U = oor
а в соединении с неравенством (18) и сделавши суммование,
находим:
iflg/r-(g+B)<iog-r'Cw+') .+A±Jg.84-_(g+a+1)g-+4
Здесь
и следовательно
Уравнение (14) дает
2Я+1 < '
12(fis-j-«)<a + a —1)'
* Это неравенство не следует из (17). Для справедливости дальнейшего нужно,
чтобы в [17а] правая часть быка не меньше чем в (L7). Например, если jas + ej >3,
достаточно вдвое увеличить правую часть [17а], ч»о приведет к соответотвующему
увеличению правых частей (18) и (10).
7*

100 СОЧИНЕНИЯ ПО ТЕОРИЙ РЯДОВ
После чего
log/,(*+«)<log*W + ^( ,—І+2^ І—1. (19)
Итак мы справедливо сказали, нто для весьма большого х можно
без чувствительной погрешности функцию ft (<с -f- а) принимать
за ф(«). Эту последнюю функцию постараемся теперь определить
из уравнения (16), которое строго справедливо для г=со. В этом
предположении *
, —at—а—-
ф(«)~<а> + «Г>+«) "Л (20)
і
$(0)=-а:—х~'"~'4', (21)
ф(—•«) — (« — «)""(« —а)~"+*-^ 8я. (22)
я« |В уравнение (20) поставивши 1 — а вместо а, потом х — 1 вместо х,
получим
ф(1_а) = (« —«Г—^ів —оГ*+"~"Ь"-\
а в соединении с уравнением (22)
(1 — аЖ1 —в) = 4-Ф<—*>- f23)
Далее, произведение уравнений (20), (22) дает
а пользуясь уравнениями (21), (23), находим
сц ; Ф(0)*
или основываясь на уравнениях (8), (9),
ф(в)М1_.)в + (0,.._^_. (24)
«в | Откуда для а = -к-
Ф(0) = ~ф(у)ѵ^. (25)
* Эп> значит, что в правых чаіітяі следующих далее равенств
подразумеваете» переход к лрѳдолу пря ж-*со.
* В оригинале в левой части этого равенства пропущены первые два «гаоаси-
тела е{1— о).

Н.И. ЛОБАЧЕВСКИЙ—.СПОСОБ УВЕРЯТЬСЯ» 101
Ъ уравнение (21) ставим теперь 2ж вместо &:
К0) = (23;ГВЯ2~'И"^"ЗЯ~Ѵ*. ■
Сличая значения ty(0) в этом последнем уравнении с значением
в уравнении (21), заключаем:
1 / 1 \~"с
1 = —■== ж х-* е"
Ѵ2\ 2/
или
(•+тГ
ѵ~2-' 2*4-1 «—'■
Между тем уравнение (20) для а = -^ делается
- *(і)-('+т)">+^Г'--
Из соединения двух последних уравнений находим:
ж | потом из уравнения (25):
у (0) = У2І.
Итак, уравнение (16) для з=0 и для х чрезвычайно большого
числа будет
a5"*™ySat"+»e-", (26)
как и Лаплас назодит (Theorie analytique des probabilites). Для
всякого ж вообще ж должно полагать
х~ш=.ха+»ё-вЬ(х), (27>
и, следовательно, неравенство (19) дает опшбяу в уравнении (26):
f , ■, >-+у* L_
Лаплае находит:
=*° I }/~2я 12а; 288ж'
Уравнение (14) для * = 0 делается
g /j(a:) 2-За;4 ^3-4я* ~ 4 - 5ж*

102 СОЧИНЕНИЯ НО ТЕОРИИ РЯДОВ
Если хотам продолжать приближение к значению функции /а(ат),
то должны в последней строке уничтожить первый член, полагая
Ш = е^Гй{х). (28)
После чего находим
ft (х) ѵ І(і + І)
а соединяя (27) и (28), получим
Для ж чрезвычайно большого можем довольствоваться
приближенней:
Ml |
или, разлагая в строку,
Чтоб судить о степени такого приближения, заметим, что
со
los/;(aO-los*(0)+2log ^tZi?1
fa(x-\-i)
Надобно, следовательно, полагать
иля, еще сильнее, основываясь на уравнении (29),
^<^ 1 -
120 (х+р.)4 "
Отсюда находим
J/120
5=і | а применяя неравенство (7), заключаем:
і а*" _.. {х_
~т- л
/120 x_24-
■ х2а+1. 1Лі=і °°
* Здесь та же неточность, что а в неравенстве [17aJ (ом, сноску* на етр. 88).

Н. И. ЛОБАЧЕВСКИЙ —«СПОСОБ УВЕРЯТЬСЯ» 108
Число а определяется уравнением
/в (ж) -%а+1.
следовательно,
2«+і > -J— <- L „*
120sb*^ 120а;8(я —2) '
После чего
bg/e(ar)>logV'&r~—^—і-г^—-4-======г--—I.
ё 120ж2 | (./g-^ ^ж(з._2)в «J*
sss |В уравнении (29) уничтожаем первый член, полагая
Так находим.
720 log
Л И -? (» + &)(* 4~ 6) a;(+s ' (31)
,і і і
В уравнении (31) уничтожится первый член, когда ставим
После чего находим
, ^і і і , і
«-»= (/2л х *е~*е Ѵ2Х •w*"' 1Яйкв*/6 (ж).
-JS4 | Так продолжая, всегда приходим к строкам, подобным этой
последней и каковы были в уравнениях (29), (31), которые все при
том исчезают. После чего не трудно видеть, что вообще
х"ж = уІ2* х *е~*Х, (32)
где функция X вычисляется помощию строки для logX, которая
сколько бы ни продолжалась, нѳ перестает исчезать, будучи
расположена по нисходящим степеням ж. В ней останавливаясь на
каком нибудь члене, можем назначать даже границы приближения,
как и даны были выше примеры.
* То-есть
. ча + і. - 1
,. о" + ' <"
120.Е* <~" ^ 130*'(* — 2) '

104 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Впрочем, значение log X заключается прямо в отроке Маклореня
для всякой функция и от х и для всякого приращения их от х.
Еоли ставим сюда
u = \ogx, Дж = 1,
ці |то находим
2к*«-^+(—^)і»,.-.+§-г!Ьг-І-^г+...-,
где А — постоянное перед интегралом. Между тем, логарифмы на
обеих сторонах уравнения (32) дают
loga;+ ^}ogx^logV2K-l-{x + -\log% — x-j-logX.
После чего нетрудно видеть, что
А = log УйГ.
Числа
Jfn Jfi.Jf* ...
определяются, как известно, помощию множителей в строке для
tang ж при степенях дуги х. Тая, если
іаПеіС = -2(-і)'ѴоМ~!0 |!~^ (35)
* Здесь ЛобачевокиН пользуется следующими обозначениями:
Д;е{І = -р-; ЛГ»в=(—l)ft + JJBlb (Вй — числа Бернуліш).
Сама запись формулы Эйлера-Яаклорена недостаточно аккуратна; оютзатвн,
имеющиеся в оригинале в этой формуле и в ряде другях предшествующих равенству
(36) формул, r настоящем ивдании исправлены.
j—і
* В левой части подравумевается "V '°£ х-\ вт* же сумма понимается под
2 log х и в следующем равенстве.
СО
э Эта формула неверна. Должно быть или th х = — 2 (— & 7Ѵ***—1 , нлн

Н. И. ЛОБАЧЕВСКИЙ ~ «СПОСОБ УВЕРЯТЬСЯ» ІОЬ
|то
Jtf, — J
2S(2B— 1) '
a_2*(2*—1) *
^"av*1—і)
и т. д.
Множители в строке (36) при степенях х вычисляются различным
образом. К этому может служить найденное мной уравнение
і,д = — ^(—1)2 —^—(яі—1), і„_і ,
которое делает вычисление гораздо короче, нежели все подобные
уравнения до сах пор употребительные. Начиная с Г, = 1 и ставя
вместо т по порядку числа, получим:
Тъ «2Г„
2,-24-,,
Т4 =2-
заг8~
Ть ~*2&Tt—2*
1 Те =2
Г7 =23
Гв-2
5-Г,-
•з2т6-
7"Г,-
Гв = 27Г8-2*
Г,о = 2
Отсюда
* Суммиров
чисть от ~ \.
8*Т,-
анке ря
*г.,
•8Г8,
■2е-52;+24,,
-2'.5'ГВ4 28Г„
-28 . з ■ 5 - 7Гв + 2« ■ 5 ■ 7IS—ОД,
■ 73T1-j-2B. 7Гв —5 ■ 2eTf„
-27-3 ■ 7Г8 + 2*.3. 72!Г7 — 2S . 3flTe + ^Tj.
Уа=2,
Г, =2*,
Г4 =2*-17,
Г5 =28-31,
У6 = 2е-691,
Г7 = 21г - 5461,
Ts =2U- 929 569,
Te = 21в ■ 320 229 1,
Гц, = 2"-221 930 581.
■пространшо па значения і от 1 до 1 — {! "г 1

106 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Строка {34) для logX будет, следовательно,
0g 12ж 360^3 "г 1260а£ 1680а:7 ~!~
j _J 6Э1 I 1 * (т
^ 1188Ж» 360 360а» ^ 156#13 "" ' Ѵ ■*■
•-■is | Кстати скажем здесь, что строка (35) для tang ж исчезает, когда
*а< 1, потому что в ней каждый множитель
Ті<(2і — 1)'а*-і.
Еще скорее должна исчезать известная строка
когда г<1 по величине. Но сомнительно, чтоб можно было
подобным образом доказывать исчезание строки (33) и при том для
всякого а<1. Способ, которому следовал я здесь, приводит,
собственно, только к тому заключению, что всегда можно взять х так
большое число, чтоб остановись на каком нибудь члене,
пренебрегать остатком отроил за маяоетшо, О строке (33) в праве,
следовательно, утверждать, что всякий раз, когда с уменьшением Да;
уменьшается в геометрической прогрессии
шли, все равно, когда но величине
- I О»—а)—1 ®К=Г
не переходит за какую нибудь определенную границу; можем
ваять Дж столько малым, чтоб остановись в строке на известном
члене, пренебрегать остатком за малоетию, хотя бы самые члены
поодиночке не уменьшались*. Это составляет особый род иечеза-
ния в таких строках, которые, собственно, растут0. Для них можем
оставить название предельных (aeries limitea), данное Лапласом
* В орнгашле ошьбочао
1 1 1 17
log А— 12и ЗѲ0^ -\- 12в0& 29 8Шві +
31 бѲІ . 5481
т 14281а* 15345а;Ч "^ 38 ОІОаЯ
* Это утверждение Лоба'тевскшс вѳ обосновано.
в То-есть раеюдятек.

Н. И. ЛОБАЧЕВСКИЙ —«СПОСОБ УВЕРЯТЬСЯ.
107
(Тдёогіе anaiytique dee probabilites), распространяя такое название
даже на те строки, где знак перед членами не меняется, под
условием: однако ж, чтоб остаток в строке можно было рассматривать
разложением функции, которой значение уменьшается до
бесконечности. О этим ограничением только должно допускать употребление
возрастающих строк (series divergeates). Подобное замечание делает
Лвжандр о строке (В4), не дав никакого впрочем доказательства
и предлагая название полуисчезающих строк (demiconvergentes) *
Посмотрим теперь, к каким заключениям может привести
сличи чѳние двух решений. По способу [ Лапласа (Theorie aualytique dea
probabilites, ed. de 1814, p. 126) надобно полагать
(Я+ «)—^ ?. (87)
Q
Между тем найдено выше, что
(Ж +*)-* = ,!,(*) (я + зГ+*+т е-*-X', (37')
где под X' разумеется функция, которая происходит, когда в Z
ставим as-j-a вместо х*. Итак
со і оо
raa>+«e-o,2a = <H3)(a;-f-<0" * 2 е~*Х' j a«e-*da (36)
о о
— уравнение справедливое для произвольного переменного se®.
Пусть теперь
я = з!-{~а-{-й.
Отсюда t определяем функцией 0:
». I — /т-^'^Кгт-.) '•
* Ехегсіеев do calcul totegral, par Legendre. T.I,p.394 [ТГр^неткибЛооачеесиом,]
* В прежних обозначениях logX'(x-\-a) = log/3 (л>-|-а)— logi(o). Иа (14) и
(15) следует, что яга величина дѳйстааіѳльво зависит только от х -f- a,
ф В равенстве (37) предположено, что а>— 1 и я:>0.
S Лобачевский: пишет это равенство внесто
дай того, чтобы установить взаимно однозаачноѳ еоотиетеівие меаыо"" значениями
а ж t (значениям о от 0 до х-\-а еоответстврот отрицательные эвачеяия t, аначв-
НЯЯМ ОТ 35+11 ДО СО— ЩМЮЖИТѲЛЬЯЫв).

о
4- со
10Й СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Это значение t показывает, что границам а = 0, а = оо отвѳчалэт
t=—oo, t=-\-co. После чего
о
Уравнение же (38) переменится в такое:
со
= ф(в).ЗГ' [ a*e-»dfl.
D
Для а; = со оно сделается
>" какое бы число а ни было; так что полагая а=0 | и ставя
найденное выше значение У~2к для ^(О), получим
+™
— ™
— известный интеграл. Для всякого Другого числа а будет
СО
$ (a) J а" е-» йя = Уйя «-*. (S9)
о
Уравнения (23), (24) могут следовательно быть представлены
теперь:
га со
о о
w со
J J Sin out
* В оригинале отсутствуем мвожтель е—« в правой части. В следующей,
формуле и формуле [38а] этот же множитель отсутствует в левой части, а в (30)—
снова в правой части.
* Равенство [38а} иояучево Лобачевеииы да предыдущего формальный нере-
ходом к пределу под знаком интеграла при --~ -*со. Обоснование предель-.
аого перехода отсутствует.
в В орвтаяаде в этой формуле имеется лишня» множитель е в левов: чаегк
равенства, в в следующей форыуле — в правой части равенств*.

а И. ЛОБАЧЕВСКИЙ —«СПОСОБ УВЕРЯТЬСЯ» 109
Их произведение дает
оа од
t х3 е-" dx ■ \ х-" е~ш dx = —^-— UQ\
J J атак ѵ '
о о
-™ 1 —известное свойство таких интегралов н которое теперь доказано
новым способом.
Надобно заметить однако ж, что здесь о может быть только
число по величине менее единицы, так же как и: в уравнении (37),
если « отрицательное; потому что
\ a*+Ie~e<to =— й^+«е—"-j~ (з;-j-а) Го»+°—1 е~"da,
где свободный член от знака интеграла делается нулем для
границ й = 0, я = са, покуда .«-}-«> О, и следовательно уравнение
ОО СО
ГаЖ4-«й-о^й — (а;4-а)*я,Г cPe-ada
о в
предполагает 1-(-а>0. Лаплае хотя не сказан, но вероятно
подразумевал такое ограничение (Theorie aaalyt. dea probab., ed. de
1814, p. 130). Его способ переходить отсюда к воображаемым не
может однако Ж назваться строгим (там же, стр. 132),
-J5J Функция, для которой употребляли до сих і пор знак ф, весьма
примечательна по своим свойствам и заслуживает особенного
внимания, встречаясь очень часто в аналитике. Здесь намерен я
говорить об этих свойствах, по крайней мере главных, следуя своему
способу, может быть более других единообразному; а также,
занимаясь применениями, вывести значение некоторых известных и
даже новых определенных интегралов.
По примеру Лежандра должно бы писать
Ш-Г(в+1,л
Однако ж. я хочу предпочесть означение
+ <*)
уже не без пользы раз принятое для целых а::", и которое теперь
* Это не совсем точно. С помощь» равенств {II) — (15) функция (х + а)"я
определена ав только дзя целых положительных значений х, а для любых, а а х,
.для коюрьи при всяком делом пешоиителыгом к имеет кесто неравеиство
[a:-f a-f-'I>*■ Функдвя х"" в частности, определен» в области |я + А|>1.

110 СОЧИНЕНИЯ ПО ТЕОРИИ РЯД013
распространяется на все прочие числа*. Уравнение ^ч7') будет*
иначе выражено
(*+«Г'--^(ИѴ+'+Ѵ^7(*+«Г, (43)
!«■> где logf(a?) представляет бесконечную строку | (34), делаясь ну л ем
с ге = оо[10]. Найденное наше значение $(0) = У2т: дает теперь
о-° = і.
Разумея под ж всякое число, можем в уравнении (41) п ілагать
а = О, потом ставить ж -j- а вместо се. Так получим
(Я+*)"Я,+Я = Ѵ"^(«+«)ІС+11+ѴЯ-7(Ж+*)^
а следовательно
(я+»)-•+" = («+«)-*а" (42>
— свойство рассматриваемой здесь функции, которое принадлежит
ей с произвольными числами а, х, и Еоторое выражалось
обыкновенно, хотя не в такой обширности, уравнением
Г(1+п) = пГ(я).
Умножив уравнение (41) на такое же с —а вместо з, получим
ася I (»+■«)"% —а)"*а"*( —д)"~" —
Присоединяя сюда уравнение
ж-и,= уг2ісжв,+те~*/(з!),
в которое переходит уравнение (41) с а = 0, находим
(aj-J-a)"" (ж— о)"л
ж"*
-а-*(—а)—* =
* Функция ф (а) определена для всякого а.
* В оригинале в правой чисти этого равенства вместо множителя е * "
стоит множитель в—и.
в В оригинале отсутствует множитель у~3тс в правой: части втого равенства.
S Б оригинале в этой формуле в правой части равенства отсутствует
множитель 2тг, а в елѳдуяапвй формуле — ъгаожитеяь У 2а.

Н. И. ЛОБАЧЕВСКИЙ —«СПОСОБ УВЕРЯТЬСЯ. 111
и, наконец, для ж = со, как выше [ур. (24), (40)]
*-■<_«,)-- = ^И_, {43)
но здесь * произвольное, тогда как в уравнении (40) необходимо
предполагалось л<1 по величине. Уравнение (43)~-то же, что
с означением Лежандра будет
| Г<1 + *)Г(1 —а);
Пользуясь уравнением (42), можем ставить
и дать уравнению (43) другой вид
(а —1)— ^-а)—'™_Д_, (44)
а но Лезкандру
ГС«)Г<1 —а).
it
вшаіи
Полагая здесь а = -^, получим
(-|) '-Ѵ^. . (45)
Делая то же в уравнении (43), находим
Рассматриваем теперь интеграл
і
у"
} Г ѳіп*в«соегтФЙі
о
с произвольными положительными и, »j, или "отрицательными по
величине < -тг • Интегрирование по частям дает
4- I-
sin3» <в cos2" ч> dv = 2 —3—=—1— вт2»+гФсов2"а^Ф.
J ' ' 2я + 1 j ...

112 СОЧИНЕНИЯ ПО ТЕОРИИ РДЦОВ
Продолжая такое превращение, притом означая г целое
положительное, находим
і і
С (ti-l— т -4- т\'яг с
Здесь выражение
под интегралом приобретает самое большое значение, когда
tang2 <о = -
Л " + г
т
aw [а потону можно всегда взять г довольно большим числом, чтобы
на правой стороне начальную границу в интегрировании сближать
как угодно с последней ^-тс и довольствоваться без чувствительной
разности положениями
? = —іѵ —а>, sm« = e а ( ео8|р = <о.
Так приходим к уравнению
і
а" ш
которое тем вернее, чем г боле?*; а следовательно для г —со
полутам со всей строгостшо
і
-го | Между тем, уравнение (39) е нашим означением и для всякого з®
дает
(,е-*явЙЕ = а*"". (47)
3 Хотя форма р&сеужденяй, приводящих a [48aj, необычна длл совреиепного
читателя, они тем не менее е помощью соответствующих: оценок могут быть
обоснованы без особого труд».
* Это равенство получено формально из [48а] оодствноваой ш! (» -(- г) = х.
* »> —1.

Н. И. ЛОБАЧЕВСКИЙ — .СПОСОБ УВЕРЯТЬСЯ» 118
После чего
А как здесь интеграл должен оставаться тот же с переменою
чисел п, т одно на другое, то не трудно заключить, что для всех
положительных щ т и отрицательных < 1 по величине
m (и -|- г;
где г = оо. Это последнее уравнение, как сейчас увидим, справед- _
либо для всех вообще чисел п, т. Оно никем; еще не было
замечено [п] и служит основанием а исследования» всех свойств
функции *"\
sn ] С переменой 2п, 2т на 2n + l, 2m-J-l уравнение (48) делается
і.
Между тем, уравнение (49), когда ставим сюда п-\~т-[-1 вместо т,
дает
(* + ')"' <п + »+1)-,,+-н
После чего
л
7"
Г ■ »»„»«
2 \ siuto+I-peo82m+la!d!B= — т—п. (50)
Полагая едееь a: = tan.g*<p, потом ставя и — 1, да—1 вместо », т,
получим с означением Лежандра
со
x»-3dx Г(и)Г(м)
Jtl + aO"**-]^»-!-»)
— то гее самое, что другим образом доказывают Лежандр (Ехѳгс.
,7, de ealoul integ. Т. I, p. 279) и [ Г. Пуаесон (Jour, de Гёсоіе polyt.
1823, Т. ХП, р. 278).
8 Зал. азав. В. И. Ло6»чевокт1, I- V.

114, СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Для п=т уравнение (50) делается
f вша»+1?йт = 2й' * " „.,. (51)
J <8п-И)-"+1
Если ж полагаем снова 2m-f-l = 0> то
Г """ВР
как найдено было по другому способу в изданной мною
Воображаемой Геометрии (стр, 88*). Вставляя значение (45)
ГиЬ"И4т^-.І.у; * j-, (52)
V £ ооИ-1
получим
в
Ы)
а сравнивая с другим значением этого ас интеграла, заключаем, что
-+|
Полагая т=0в уравнении (49), находим
для всякого числа ть. Чтоб это доказать, то разумея под р >эт два
положительных числа, пишем, основываясь на уравнении (42),
(-„r^-fr-»)""".
(р—«)-"
Здесь для р—»>0 уравнение (54) дает
(р_п)-*—-=■—^1—г»—.
(і> — п+г)
* Страниц» укапана по орирннальиоыу иаданззо сочинения «Воображаемая
геоиетрия». В настоящем аадакаи ей соответствует стр. 38 Ш тома.

Н. И. ЛОБАЧЕВСКИЙ—«ОПОООВ УВЕРЯТЬСЯ. 116
После чего
<-»)'
"(р_»ц_ ,)-*+<■'
^р~».
И» г"'
(*—«+*■)"*'(-n + r)"r (# — я+ *■)-* ' (_я+г)"г
"* | Откуда дня г = оо
(—n-j-r)
— то же самое уравнение (54), аогда здесь вместо п ставим —п;
а следовательно в уравнении (49) числа п, т произвольные.
Например, полагая 2»+1 = 0 в уравнении (54), получим
^ = (2г-1) (г-Ѵ-'-Чг-іГ-1
НгГЫГ
Это значит,
2 К~ 1-3 ' 3-5 * 5-7'"'
— известное выражение Баллиса.
Вели в уравнении (49) ставим —-, п вместо п, т и разумеем
теперь под п, т целые положительные числа, то находим
—2- Л.
>'» [Это значив
\т/ \n-\-m}
2т ѣт ....
х і ІГі'~ л "-^і— (55>
(n + m)m(n + 2m) ™ (я + 2я*)*{»-}-Зя|) "
Например, и = 1, т = 4 дают
[? ~.\л /4\* 8* 12* 16*
о
Если в уравнении (49) вместо «, то ставим ар, в и разумеем под а, Р
произвольные числа, то подучим
8*
(«»**-«--;-, '.г-

116 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Это значит
Например, «^у, Р = у Дают
^.^ ^._.___ jTjp-...» (57)
о
-Выражению (54) можно дать еще такой вид:
(__ l)rrn
(-Л-1)
«г '
;(58)
где, как и прежде, г=*оо.
Если ставки сюда вместо п но порядку
1 , 2 . 71 — 1 ,
\-х, \-я, .... \-х,
разумея теперь п целое, под х произвольное число; потом-
умножаем уравнения, то получим
(_1)Ж.-,г(»-і)(.+»)
І_-1 а, |_ і_ я ._ .1 — 1 х\
^ (_ і)пг-г/"-ц (*+т) (_а -ж)--(г ~г)''~1пяг __
= (— й — 1 — ТКС)"1*'
8=3 («г+mas-(-та)"""'
* В оригинале правая часть формулы (57) имеет вид
3» ffl-ffl 5Д-7Д

Н. И. ЛОБАЧЕВСКИЙ—.СПОСОБ УВЕРЯТЬСЯ» 117
ігг (Пользуясь ураввенвем (41), ставим езода для г = со
V- -г *■)
г
^~г + і
"'«/hr •г',
Так находим
(і+-)4+"(І+«)*"і+"-^+«)-'+-=
Или, ставя а;—|1 вместо к и г = оо,
*~(^rVf)""-(*-^)
п
"-1 -*ш- 1
= (я*)"яаі(2іг) » та 2 9. ^59)
Для # = 0
Дринимая в помощь уравнение (44), выводим отсюда для веяного
целого числа и
. к , 2я . (я, — 1)іс -„ .,-г
еш — am — ... am - ~ = м.2"п+І *
?і п п
'* В оригинале вместо ігамкителя е~ѵ+в,+ Ч в правой -частя этого равенств»
стоит мвожи*ель е ".
* В оригинале вместо множителя е~~<яг+»*+») а правой части втого равен-
*іт
ства стоит мномите.-іь е .
0 В орагнпале отсутствует мнояситсль «fn~*4(*+4 в щаво8 часта втого
равенства.
2 Первый множитель правой частя этого равенства имеет в оригинале
вид (iw)™*; кроме того, в связи с отмеченными выше ошибками в предыдущих
равенствах в правой части (59) в оригинале имеется лишний чножигель «~п*+*.
1 В оригинале последний множитель в правой части Hums вид 2»—'.

118 СОЧИНЕНИЯ ПО TSOFEH РЯДОВ
—-известное всем уравнение, на котором Лежандр основался, чтобы
притти к уравнению (60), потом уже к уравнению (59) [іа].
Если в уравнении (59) вместо х ставим —, потом ——и
перемножим два уравнения, принимая в помощь уравнения (48), (44),
то получим
»-і . . lie \ . /2к , \ . [(та—1W. 1 .„„,
8Шиівз=2 вша;em I—|-a;jsml \-х\ ,.. вті~ -—\-я\. (61)
Берем снова интеграл (50), который с положением ж = віпв7
переменяется в такой:
і
I
п~»т~т
яр(1 — *)-& = ...,,. (62)
'і» | После чего
і
а с переменой п, шна и-[-8, —1 — 8*
х
J
а^Н-1 (-8)—'-1 ач._,(» + 8)-+'-Д-Ч [в2Ы
Откуда для 8 = 0, н>1
о
• Здесь от ■<[ — 1 при S > 0; одтатс жнтѳграл сходится в оипу условия,
наложенного нва№ до 1».
* В оржгяналв правая часть равенства [S3bJ имеет следующий вод:
(_t)--»_l («-f-5)""4-8 —»""
В первом члене вдѳсь явная огаетатва, а пропуск мвожзтѳяя (— В™-*) во второй
члене не скавывается на форнулѳ (ИЗ), тав вав іітп (—в) ""~! = 1.
а->-о
Приводам промежуточные вывладви к равенству [flSbj:
-s l ' to-"

Я. И. ЛОБАЧЕВСКИЙ — -СПОСОБ УВЕРЯТЬСЯ» 119
где постоянное
G=> 0,577 215 664 901 582 5.
Между тем, поставивши п в уравнении (47) вместо а и
дифференцируя в отношении к и, находим
со
\er-*x*lcgxdx=^^~; (64)
следовательно
СО СО 1
\e-'x»logxdx= \^&fa{\'~^r &»— О)* (65)
0 0 0
Веяв логарифм от уравнения (62) и дифференцируя потом в
отношении к п, получим с помощню уравнения (63)
і іі
J^(l—^)»l0g!C^=e j^(l—я!)*ЙжГ^^~ dx. (66)
« 0 0
Способ Дежандра, чтоб доказать эту зависимость трех интегралов,
мне кажется весьма затруднительным (Exerc. de oaloul. iateg.
Т. I. p. 259). Сравнение интегралов (62), (58) он делает только
в предположении показателей т целых; а распространение потом
на произвольные числа не может уже назваться совершенно
строгим (Ехег. de eatc. rnteg. Т. П. р. 7 at 99).
Рассматриваем теперь интеграл
ж
lsmra;smna;<b;
о
щ1 [для те-|-1>0 и числа г произвольного. Интегрирование по
частям дает
«Э аЯ
»
-1 sin ias em"
xdX'
=—sin «в sin"-1 ж cos as-)— соэ «я? sin» х-\-(ѣ — 1) і ein іх sin»-8 x dx;
* В оригинале правая часть равенства (85) имеет вид
щ і

120 СОЧИНЕНИЯ ДО ТЕОРИИ РЯДОВ
следовательно
и вообще для положительного целого г
f . . №+')"(5fi+')"Y
I sin w; ein" xdx= ■>— ■■■ — -г-,-— . " ' . — l sin ia; віпп+*' ж <is,
J (- +,p(^+,)- J ■
а для r =oo, основываясь на уравнении (49), можем сюда ставить
/я.—г , \"г ( п\'
п
'■г
а. [После чего в том асе предположении
•Ч1
о
sin іж вга"+Яг a? tfe.
Здесь элемент второго интеграла приобретает самое большое
значение для
tang х = — ■■ ■ *■:■ ■■■ tang г#,
а следовательно е возражением г разность-=-тс—хаи
уменьшается так, что наконец можно прижимать по примеру выше *
к 4-™
|шпй;ашя+-йгаГ(?я;=8Іп — ік \ е~ГШІсІіа=8ш-^ші/ — ,
* См. вывод формулы (43) и сноску * в стр. 112, Здесь Лобачевский, кроме
того, полагает

Н, И. ЛОБАЧЕВСКИЙ —«СПОСОБ УВЕРЯТЬСЯ. 121
ПОТОМ
с
еткввііі»а!Йа! = —^—^—-ф7 ■■-■ /■ ^j уЧвт'-—І**
3*1 Iили, поиьвуяеь уравнением (53), всегда для n-f"l>0
к
Г - - . , я . 1. . п-п
1 вш гхвт" z ах=—віп—«г п ?*■ ГѲ7>
I 2 ; \ 2 ;
Подобным образом находим
*
Для і = п
IE
| sin тсс sin" ж {£с = и 2 sin — яле, (69)
о
я
1савмжвтп;в<&; = гс2 сов-^-п-к. (70)
D
Для і = 0 ®
. "*П
ia!8m'»a;(fo! = x3 2 ""' ^ 5, (71)
т) *(т)
I віа*1 я4с = 1г2
—я П
(72)
(т) "(т
* В оригинале отсутствует множитель нш—tit в правой частя втого
равенства.
* В оригинале вместо множителя 'віп-д-ія наяетатаво sin -х- it.
® Лобачевский получает (71) ив (87) с помощью предельного пѳреіода при
*-*0.

132 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
ш j Для n -f-1 > * уравнение (50) дает
и переменяет уравнения (87), (68) в такие:
і
IsmwJein^icda: I Bm"+J+<aseoan+1-(;e<ic = -ттйш —«г, (74)
1 савіхвтпхске \ 8т"+1+(жeosn+1—{xdx*=— -гг.cos-5-й. (75)
cJ eJ (« + 1)2 2
От двух интегралов (67), (68) легко перейти к одному такому,
в котором оба заключаются:
і
Т'
I соаіяеоѳ"^^--^ Л±Г~ *Н.' <76)
2 (. і л" ! /. 1\ °" а
№) W) '
*« ІЭто значит
1 cos»a;cos',aj(bc j sinn+1+*a;eosn+1_'#<ie = J_ 2~~" (77)
под условием и + 1>«, *>0, хотя затем п, і могут быть уже
произвольные числа*.
Для і = п интеграл (76) делается
і
Г"
I cos па; соая xdx = -^rj. (78)
о 2
как и Г. Пуассон находит по другому еноеобу *.
* пкі совершенно произвольными быть яе могут. Для оходакости
интегралов в левой части (77) щужво, чтобы »>. — 1, »+l-f-i> — 1, »-f-l —*">— 1.
* Journal de Гёооіе polyt. Т. ХП, p. 490. Здесь, однако as, дошввж бить
опечатка в авяганяя интеграла. [Примечание Лобачевского.\

Н. Ж. ЛОВАЧЕВШИЙ—«ОДОСОВ УВЕРЯТЬСЯ» 128
Дифференцируя уравнение (77) в отношении к г, получше
с пособием уравнений (68), (78):
| I х вшіх сов" xdx I em1**'-** х сов**1"1 х dx я=
1 Я+( Я—*
-ж
Пользуясь уравнением (76), находим для всякого т-|-1>0 для і
целого, «в произвольного
Г ■ / ■, - j я я-«{1 + (—1)"+М cos ѵо
I совг(ж—ю)со8яж<£с=— • ' „^і =у.
Сюда можем ставить, основываясь на уравнении (42),
п
(80)
»—1 , . Я—1
-и ,.. . -. —I-
(п— 1 . Л в /п —1 , Д-*/* —1\
(»4Ч
(!_,р •
/*—і л 3
* В оригинале левая часть этого равенств» имеет вид I —к 1J
То же относится и ао вторым множителям левых частей равенств [SOfa] и
следующего еа ани.

124 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
«яг [и следовательно
Последнее уравнение можем еще переменить [уран. (53}] в такое:
я-1 я + 1 ^—-|-*\ "
После чего уравнение (80) дает для целых чисел *
сов2і(х—«) сое» #<&! = ——— —^—— *, (81)
{(тП(т+'Г
f еов(2і — 1)(ж~ «) сое" я <£с =
{(т)"гГ(=^Г'
-gf|l-(-iri " ' , ,.< с«(2.--1).. (82)
.-(і + і)
*н . Два последние уравнения служат дня лредставле|ния степеней
косинуса, какой бы показатель ни бил, в тригонометрически!:
строках с косинусами кратиой дуги. Этот род разложения, понимаемый
под общим видом, требует большой осторожности в суждении, чтобы
соблюсти должную строгость. К стати здесь я повторю с новыми
* В орягвналв отсутствует множитель л"*" в числителе правой Ч*етн.

Н. И. ЛОБА1ШВеКИЙ-~ «СПОСОБ УВЕРЯТЬСЯ. 125
пояснениями тот способ, который изложен был в конце моего
сочинения яод названием об исчезант* тригонометрических строк; тем
более что сюда вкрались ошибки во время печатания е переменой
означения.
[ГЩ
Рассматриваем значение суммы
S= УІвш(» + «) { І==1
^ г ѵ ' 1 І = 2П
с произвольными дугами а>, а и с делымн положительными
числами г, п. Соединяя по два члена, первый со вторым, третий
■с четвертым и т. д., получим
+««~.«2тІгіп(йв-|-*-т") {Иг-*-1.
ч«в | Итак, е условием заменять только положительные числа, меньшее
большим, находим постепенно:
^<ье2+соал^1,51=2;тйЬ1(2^+я-¥т) {jii«,
я, < log 2+см «я* >?a = 2Tain(2afai+a-Tw) I \Zl*+,
ff^ioga+coato^ 58 = 2т8Іп(28і'в+а"~ТС0) I I~2"-»
-S'.r-I<log2 + ooe2e-<«S,1„ [#я<1.
Соединяя все такие неравенства, к тому замечая, ято для всякого
целого положительного п
1 п „« віп2л+"І(о _, 1
СОЭ -ГГ-« С08 И COS 2ш . .. COS 2 <В = — <
2 smTffl 2 sm — л
находим
2nsiH-s-o> ^ 2 sm — o/ \ i = n,
<l0g2 + ^±^ (83)
sin —я

l2ff СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
.ао | а следовательно, бесконечная строка
™ 1
t
і
исчезает * для произвольной дуга а и для всякой ю > 0, < 2*_
Полагая здесь я «О, потом я = -^т:, получим две строки, из
которых первую помножав на У—1 и приложив к другой, получим:
где £ знав функции. Чтоб определить теперь
і J ___' 1— = У-г-вш*»,
2 У—1 і *
заметим, что строка
£[l + e] = _]g(_iyi*< [83а]
і
принадлежит такое свойство (Алгебра Лобачевского, стр. 322 *)
Х[1+* + У + а*] = £[1-М + .Е[1 + у], [83Ь]
яаі {какие числа а;, у ни будут [ieJ. После чего
а следовательно дин а>>0, <тс
£[1_е—ѵ=і] —£[1 —e^^l^
= і Гі + У^Л oot-i- «1 — £ Гі — Ѵ^Т eot-і.«1 ц»
СО
1
Итак
= 2
і
2Твіпг'« (84)
* Ив самого равенства (83),к дающего оценку для абсолютной величины
частной суммы рада, еіодниооть рассматриваетич» ряде не следует; однако не
существа предшествующих преобразований от* сюдиыость следует (ом, свяову на
стр. 40 нает. тома в сочинения) «Об ясчвввнни тригонометрических строи»).
* Страниц» указана по оригинальному надавив) сочинение «Алгебра или шлиі
еленне конечных*. В настоящем издания ей соответствует стр. 223 ГѴ тома.

Н. И. ЛОБАЧЕВСКИЙ — «СПОСОБ УВЕРЯТЬСЯ» 127
для всех углов в» > О, < іс ж как бы впрочем т ни был мшгаЯ угол *.
Ставя сюда га = х, «= &х, получим для всякого приращения Дж
со
і
потом заменяя знаки приращения и суммы знаками
дифференциалов и интеграла,
о
Подобный переход от суммы к интегралу предлагал Г. ЗКопш
принять аа основание в интегральном вычислении. (Journal de
Гёсоіе polyt. Tome jXH, p. 690). В сочинении моем OS нечеткий
тфтономеггѵрических ат$ок (стр. 29 ©) я старался доказывать строгость
таких начал. Настоящий случай требует увериться только, что
L = I — sin x
J X
а
уменьшается беспредельно с возрастанием я, как бы х при том
ни было велико. Действительно
Выше доказано было, что значение бесконечной строки, которая
входит здесь под знаком интеграла, с возрастанием х приближается
к нулю; при том 8шж<1, следовательно X может сделаться как
угодно малым числом Т, Впрочем интеграл
„ Cdx .
* Равенство (34) имеет, как известно, место, есгаО<<о<2п. Вывод
Лобачевского связан со сходимостью разложения функции aretgic в степенной рад н
пригоден, если -н- < w < ~іг ■ Следует также заметить, что в втом вывода под Ъ [1 + !с]
нужно понимать рад [85а], так ют равенство [85Ь] опрѳдеияет функцию £[1+ж)
неоднозначно (при помощи этого равенства определяются вое ветви:
логарифмической функции).
* Обоснование етого заключения ск. в примечание [Щ.
0 Страница указана Лобачевским по отдельному оттиску оригинального
нэдания, нто соответствует стр. 49—50 наст. тома.
9 В оригинале отсутствует множитель к перед знаком, интеграла,
1 Рассуждения Лобачевского правильные, однако вались несколько небрежна.
Си. подробнее в примечании р].

128
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
какое бы число положительное а ни бшго, может быть найден еще
другим образом. Заметим, что
D о •
или, полагая х = -ка>,
J - (~=і+,р
где после вычисления должнр почитать г = оо. Основываясь на
уравнении (49), заключаем, что
N=* I einrcwdlog
о
Или [ур. (43)]
С-^)
ю—1
—5-
(1Н'
2а
я*—
die . , .
m
co+I
I (i)"
asi |A как здесь м>0, то [ур. (6Э)]
2. 11
„ {'dx , , Г С^+^ІПігш , ,
N= \ —am х 4- 1 1 -——г—:—ахаш.
J х ' J J ж + 1
Интегрируя аперва в отношении в ю, получим
2s
,, f(fe . , Г е-*"» As
ДГ= I — em» + I . . . .
■і х ' J 14- »s
Пусть теперь
Чт
•—'"'dx
4-з*
* Это ваияючввие не обосновано, Си, примечание [М].

Н. И. ЛОБАЧЕВСКЩЙ—«СПОСОБ УВЕРЯТЬСЯ» 129
с произвольным положительным числом а. Дифференцируя в
отношении я а, находим
Ѵ+Г~Т ■ *■■]
— уравнение, которого интеграл должен делаться -д-п для а = 0;
ел е д оват ельно
F=eintf — сова — cos» — sin а-4—s-тс сов а, . [85b]
в о
!as |s для я = 2я
о
что вставляя в последнее уравнение для N, получим, как выше,
Дт=-=-«. Уравнение (85), таким образом, служит дополнением
к уравнению (84), которое, следовательно, должно почитать
верным в непрерывном уменьшении дуги « до ш = 0.
От этого предложения переходим к другому, не менее
примечательному. Начнем с того, что для всякого целого
положительного числа г
1 -f 2 У cos кс =5 .
1 sm—ж
Умножая на <&е, потом интегрируя от ж = 0, получим
, р sin (*-Нг) ж
ie+2Srsin^= — і а
J sin —я
Разумея теперь і= со, под и или нуль, или целое
положительное, под я угол > О, < я, легко находим с пособием уравнения (84)
* -^- Де=(2п-|-1)іс для ге=2гаіг-}-«,(2т-(-1)*+«>
. 1
81П -^Г-Ж
= яя а; = в»,
= 0 ж = 0,
= — (2ті-}-1) іе а; — —2тмс—а,—(2п-{-1)я—а,
— —те х = —jwe.
(86)
w Формула [85cj верна, so получена путем недостаточно аккуратных проме-
ясуточных вычислений. См. нрамечанжѳ рі].
9 Sue. 2823. Н. И. ЛобачевоанВ, т. V.

180 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Теперь для всех значений х, от х = — іг до х = -\- іг, означаем f (#)
какую нибудь аналитическую функцию*, давая такому названию
тот обширный смысл, который предполагает только возможность
для всякого х, между сказанных границ, отыскивать
хотя бы f (%) для некоторых х делалось бесконечным *. Пусть еще
Дат) в промежутке х= — it, a; = -j-n не переходит за какое нибудь
определенное число. При таких условиях ищем другую функцию
F{m) от переменного да, начиная с т = — я до ю = -f-it, из уравнения
2F(<o) = ^{l + 2^eoei(x — <»))f(x)dx® I i = co (87)
от | Останавливаясь в.бесконечной строке на члене с известным числом»,
которое можем потом увеличивать произвольно, полагаем сперва
+*вш(і + — \(х— «)
2*» = і—j—і f(x)&V
*f ein — (а: — ю)
или, все равно,
+ ж—е
-±1
віп (*+-§-)ж
2^(ві)= I і— :—/(да+ »)<&. (88)
Во всякой аналитической функции, какова здесь /(ж), обращать
должно внимание на постепенность и непрерывность. В сочинении
моем 05 исчезании трѵяаномещпічесѵтх строк ^ я доказывал
необходимость этого различия, называя функцию f(x) постепенной, когда
приращения в ней уменьшаются до нуля вместе с приращениями
* Си. вводную статью, стр. 17 наст1, тома.
* Как видео аз дальнейшего, Лобачевский фактически предполагает, что во
всякой такой точке левый и правый предали f(z) равны бесковезносжЕ опре-
делевного знака.
° Запись неудачна, так как ряд под энакок интеграла расходится. Щш вра-
вильноЁ записи формула (S7) имеет вид
■ і
<-*™ J tZi
9 Tuuni оброаом, в левов частя нужно бы писать 2F((oi),
I См, вгр. 45 надо, таив, а таяпе вводную етвтьго (стр. 1в—17).

И. И. ЛОБАЧЕВСКИЙ —«ОПОСОБ УВЕРЯТЬСЯ»
131
переменного х;—непрерывной, когда содержание двух втих
приращений с их уменьшением переходит нечувствительно в новую
функцию, которая будет, следовательно, дифференциальным мно-
яттелем. Интегралы должны быть всегда разделяемы так на
промежутки, чтоб елементы под знаком каждого интеграла
сохранили постепенность и непрерывность. Применяя теперь общее наше
>» рассуждение к интегрированию в уравнении (88), рассмотрим сперва
случай, когда f(x) — постепенная функция. Интегрирование по
частям дает
ВШ^ + І):
8Ш | «-+■ -s- I X
- f(x -f- to) dx =
. 1
ain-j-a;
sm
= /(» + •) '
іп(«-1-і)и р peinji-j-i-l*
—і— д/ Да,_ 1 f(x+n)an I —і— ' dx,
sin-^-a: J J ѳіп— х
будет ли /(ж) непрерывной или ломаной функцией, с тою разницей,
что в последнем случае каждый интеграл должен быть сумкою,
нескольких интегралов с елемептами, в состав которых войдут
одни непрерывные функции. Распространяя между назначенных
границ, получим
Г_<0 / J \ —1-е / j\
2F(a)c=f(«) ( 1 2 / (to: — /(—к) I і LL.dx —
sin — ж J sin -^- я:
J sin-^- я
Г (* + «)*! \ S—J <**■
о о *
Пусть і так уже велико, что во всяком интеграле
J ѳш-2-я
е*

132 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
можем почитать І = со без приметной разности, которая будет
собственно
со
Y] -?- 8ІП ІХ *
і
и, следовательно, либо нулем, либо приближаться к нулю с
возрастанием г, как видели выше. О таким предположением и
с пособием уравнений (86) находим для аі=50, <я
»іп(і + І-)
8Ш \t-\- — \Х
. 1
SID — ГЯ
О Л
— к —щ
[* вш 1 і-\—=-1 х
3іп(і+А).
. і
еш~- х
ІІП(^ + Т)
smu-ь- іх
J sin ~ ж J
и і о
J J sin —a;
О 0 й
dn (i+4)
С fain І + -- a:
= 1 f(m — x)dx \ \ i*' <fe —w{f(») —Г(—»)}•
J J sin —ж
» и i
После чего
І*» = *:Л» (89)
кроме (о = я, для которого случая должны писать
Л»(і+-§-)* ?" ряп/і + і)*
«)=_/(_«) I 1 _fJ_^4- Л(* + «)Ле \ Ѵ ^ ' <fo.
J sin—a; J J sin —a:
2F(-
* Это не соасем точно, Рааноеть, о которой идет речь, равна
ао
1 .
t
* Это равенство, равно как н следующее за азы, справедливо. Подробное
обосяованне предельного перекола см. в примечании {Щ.
2 Ѵ-г 8ІП. КС.

Н.И. ЛОБАЧЕВСКИЙ—«ШОСОБ УВЕРЯТЬСЯ» 188
Здесь в последнем интеграле пренебрегая тем единственный
«цементом, который отвечает х =— 2тг, и таким образом, основываясь
на уравнениях (86), к тому принимая
—з—рі-лг—ас, | —і—?-L
о
2
I. . 11
X
— dx'
. 1
sm— x
получим
*Ч*)~!-«{/'( + *) + Л-«)}. (90)
Чтоб не оставить сомнения в отношении к строгости, можем также
прибегнуть к вспомогательному числу S > 0, < те и писать
ЯШ--Х
J J втТж
■dx-
2
Sic
* I 1\
Г Г.™ И+2"Г
— a*+ — eb+s
шг
* Здесь второй член правой части должен иметь вил
— ас
нов в обовнвчѳвияі Лобачввеаого
—зк
X
я»(*+ -g-)*
1 Л (» + «)*: 1 —^ ~-te.
J J япТ
—a*+s о
Ѳта и дальнейшие вытщпкн, имеющие целью обоснование равенства,* (90)
вепошргны. Строгое обоснование равенства (90) строится аналогично обоснованию,
равенства (89), приведенному в примечании [Щ.

134 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Здесь
1п(*+т)ж
dx =
»» [После чего
(*■•*(»+4-1*
J sin-a
= _re f ^ (& + *)&•_ « |Y(b + «)** =
о —t* -i-в
о
В сочинении моем 06" гккезании тригонометрических строк
употребил я другой способ, чтобы притти к уравнению (90)*. Так как
значения f(x) собственно даны от х =—тс до х = -{-%, и
следовательно произвольны для х > ж, то принимая
для всякого ж>0; потом разумея под f(x) новую постепенную
функцию х, которая происходит, когда в f(x) ставим % -\- Ь вместо х
с известным числом 8>0, можем писать, смотря на уравнения
(88), (89),
f'niL [(*+-£-) (*-« + »)]
| 2тгф(тс —8)= 1 ^—j-=-i +-<?(x)(lx. [90a]
J Bih-g-(S —K + ft)
Си. стр. 78—80 вата. том».

Н. И. ЛОВІЛЕВОІШЙ— «СПОСОВ УВЕРЯТЬСЯ. 166
Это значит
7^ta[Y<+i.)(*—«+8)1
2к/(тс) = I u а ' і/(я! + 8)йг™
sin—(ж—іг + 8)
"•"^•шп^і+і-)^-.)]
- LL_AL_ 1д»)л=
J ЭІП—(Ж—7Г)
—11 + 1 й
p'sin Г(* + 4) (*-«>1 "р'шпГ(*+ і) (*-«)]
J ѲШ — (« —*) J 8Ш—(ж —я)
ЙВ +
■+»
sm r t
'1" " ' Г(ж)Лс =
sin—(ж—тс)
psinji+ib p«hi(» + i)a>
— aP(*)-l —v ' f{x—«)<to+\ —* 1 ' Г(«+«)Дв. [90b]
J 8ІП-Ж J 8ІП-*
2
Для В столько малого, чтоб f{x-\-b), f(x—8) можно было
принимать за f(x), получим
х
I 2я/(*) = агч*)+{/(+«)—Г(—«)} * г &»»■ рюе]
J ^т*
Последний интеграл представляет я, кав бы дуга 8 мала ни была
[урав. (86)]; после чего получим опять уравнение (90).
* В правых частях [90а], [90Ь] и [90в] подразумевается яервюд к пределу
при і-*-оо после вычисления соответствующих интегралов. Равенство [90с]
Лобачевский получает из [00Ь| фактически применением первой теоремы о среднем
(под внавом предела) и переходом к пределу при В-*-0, ео применять эту *ѳо-
рему нельзя, так как, каа вы мало ни было В, функция — при доста-
атт
точно большом г не является знакопостоянной в интервале (0, S). Обосновать
равенство [90с] можно при помощи рассуждении, аналогичны! тем, которые яри-
ведеиы в примечании [ІВ]-

136 СОЧИНЕНИЯ ПО ТЕОРИИ Р.ЙДОВ
Так как f(x) в уравнения (87)—произвольная функция, то
поставя /(—х) вместо f(x), потом —х вместо х, наконец f{—<о)
вместо /(<»), как сейчас доказано было для непрерывных функций
кроме случая <вг=те, находим
+■
2ягД— о>) = J \l-\-4^40^i{X'\-o>)\f{x)dx*.
Это значит, что предложение (89) справедливо для всех
отрицательных значений «о по величине <гс; а в уравнении (90) вместо
F(-k) можем писать F{—тс). Итак, дня всех углов в» внутри
границ —т, -\-чс и для всякой непрерывной функции f(x),
будет
+к +* , -
it/H^j J /(»)<**+21f «»»(*—e)rc»j«fc 'j)^,^ (9i)
1С К
Если ж а> = тс в бесконечной строке, то
+," +«
= ¥ J rt*)*4-2 J (— D* cosixf(x)dx (J = ^>
(92)
Особенного внимания не нужно было до сих пор обращать на тот
случай, когда f (х) для какого нибудь х делается бесконечно
великим, потому что в интегральном исчислении принимают всегда
ь
lfix)fa = f{b) — f<a),
а
каковы значения Р(х) ни будут, лишь бы f(x) не делалось
бесконечно великим между границ а, Ъ интеграла *.
Если ж f{x) не постепенная функция, так что х = а отвечают
два значения/(:e) = j1, f(x) — B, из которых одно переходит грубо
в другое с возрастанием х, то стоит только под /(я) разуметь А,
* В правильное з&вяси
2яД— «>)= Iim f (14-2 V вов»{ж+ш)} Дж)^Ж.
* Если функция f(x) непрерывна на отрезке интегрирования.

н. и. лоблчевокийѵ- «даосов уверяться» 187
за х — а* вместо f(%). писать f(x)-\-A. — Bt чтобы поотепевность
уже везде сохранялась. Уравнения (88) и (8В) должны,
следовательно, теперь давать для tn<a
J Sin —(а:—о.)
2*/(.)- L' 1 ' Jy(aO(d») +
sin — (as—•)
Здесь
J sin — (х—о>) J sin—ж
о о —ш
Для <о > я те же уравнения (88), (89) дают
2ж {f(m) + А-3} -
Bin ji-f—)(ж—«) 7» em(i + -i)a:
ніп— (ж—«) J sin — х
Здесь
ТЧ'+т)' д„Т'^(;+^)^+'Г°(;+^)^=.2,.
J sin-^-ж J 8ІП-І-Ж J sin—ж
зог | Таким образом, уравнение (91) в этих двух случаях остается
верный; но для х = а находим
Ъ*А-=
^sin (t + i}(*— а) р віп(і+—L
1 LV 2/ -ІДх)Лг+(^-Л) I Ѵ 1 ' dx,
sin—(ж—а) 1 sin ^-х
где последний интеграл представляет ж. Отсюда
sin у (я—а)
* То-есть spa x>a.

IS8 СОЧИНЕНИЯ ПО ТЕОРИИ РВДОВ
Это значит:
+■ +■ .
SM
веяний раз, когда с # = а постепенность функции/"(а;) нарушается
грубым переходом от f(a) =jl в f(a) = B.
Применяя предложение (91) к уравнениям (80), (81), получим
для всякого 'числа п>0 и для всякой дуги <о>—іс, <-f-w
№"'
(84)
Если здесь я = 2от чотное 'число, то
2*» сое"» «■= (2Т"}"2" (1 + 8 У ""' « соз 2т )
или можем написать иначе
2**»соч*"« = -—- z, >,m~%"-(Cos2ia>* I .
Поетавя сюда
і = X. — иг,
(2w)"aB, = (2m)~42m—A)"»"1»-",
«—=«-"-Ѵ\
получим
2s™ совад и = 2 (2т)ГУ cos (2m — 2Х) ш I
2я»
* Из основного равенства (х + *)**"+" = (ж + >)"*«"*,івію!Шв ar-f-a = »>
ж™ —і, идеек т"т = т™~*(т-\-і)■*•*+', откуда
Щ = - —-,

Н. И. ЛОБАЧЕВСКИЙ —.СПОСОБ УВЕРЯТЬСЯ» 189
•»» | — известное разложение четной степени косинуса в косинусы
кратной дуги,
О нечотным числом п = 2m -J-1 уравнение (94) делается
а ставя сюда
г = і — т,
получим известное выражение
2йв+1со8йв+1о) = 2(2т+1)Гхоо8(2ст+1— 2Х)« |.Х = ° , ,
Если в уравнении (91) полагаем f(x) — GQBnos от а?=^——к до
і
a;=-[--j11' а внѳ тавия; границ дочитаем Дат) = 0, то с пособием
уравнения (76) для всякого целого і находим
+*'
Г ■, ч - j> кп-псовіа г„, ,
I сое* (я;—n>)eosna;ate = ^ jj^j- ». [94а]
Отсюда, поставя 2і вместо вдтного, 2г~|-1 вместо нечотного *
[урав. (42)]*,
Г '" Ы Ы
М!, | і соѳ2е(ж—о>)соввжі&г; = -—~——■ г соа2ио,
о- ■=•»
*1Й* (Я
+Т-
cos [(2г -[-1) (ж—«)] сов" xda=
_( Я-r-J. 1
«и*
-^^003(21+1)01.
»+і
«•(•44 W)
* Это равенство непосредственно следует из (79).
* Следующие далее равенства вытекают из равенств [80а], [80Ь], если учесть
окованное в сноске в егр. 13S.

140 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
После чего для «feO, -=;-утс
2ncos"o)=
И и
^s(^)"(^)""'-^-
(95)
з;,(|+2(-ч,(2-»)"'(|')"",™2Ч-
n°
1
d»)* (H
n+I
PiX
X |(-1)« (^"(^"^(Й+І)-. [96.]
Последнее уравнение справедливо также для положительных углов
«1 ш > -J я, < я, как можно видеть j из сличения двух уравнений
(94), (95) в предположении oofeO, ^-s-it*. А когда сюда ставим
-5" чс—|— т вместо в), то получим для всех углов от ш с
2
іидо«=ги
і і
* Равенство (95) дает разложение в ряд Фурье непрерывной функции, равной
2" сое "ш в интервале ( — — _j и равной нулю в интервалах (—я, —^ і, (-sTj51);
поэтому при замене ю -теред т-)—— сумма ряда будет равна нули, если
тс ^
0O<-g-; эта замена и приводит к [95af.
Но таи дав сумма ряда (95) является нѳрнодичеокой функцией в периодом 2іс,
то ока равна нулю и в интервале (я, —1; следовательно, равенство [95aJ имеет
также место в интервале {
і-Ш-

Н. И, ЛОБАЧЕВСКИЙ — .СПОСОБ УВЕРЯТЬСЯ. 141
После чего уравнение (96) может быть представлено двояннм
образок для всех углов от м = 0 до в = -к-іг *.
r-w— ^ ^х
x|(iFi)"'(^)""-(«+««. <m
2"-1 cos"* = * г X
><{1+|(1*Г(Н"^е<*2Ч- (98)
Для и ■=■ 2т чотного числа последнее дает то же, что было выше;
между тем, в первом
и следовательно
.й'-'еов"—, чітт\ ^_Х
Ц2т)"2т{т^±)
OS
* Равенства (97) и (98) справедливы не только в интервале (О, -=-), но и во
( « и\ \ <*/
веем интервале I — -=-, -д-11 так к*18 в этом интервале имеют место равенства
(95) и (88). Иа непрерывности разлагаемой в ряд функции следует также снра-
ведливоеть атих равенств и на концах интервала ( ——, —).
* В оригинале отсутствует множитель т -\- — в числителе дроби, стоящей
й
в правой части этого равенств.

142 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Это значит:
,. . ,. 1 , 2m(2m—-2)...2 1 .
<2m+1>TKCOB'"n> = (2m-l)(2W-3)...l(C08t0 +
. 2т~ 1 0 . (2т—1)(2т—3) л . \
+ 2^+3-СОЭ +(2^ + ^)^ + 5)СОд5<И + ---Ь-
Для 7i = 2m-f-l нечотного уравнение (97) дает обыкновенное
разложение на косинусы нечотно кратной дуги. Напротив,
уравнение (98) делается
Ы) Ы)
х|І"+Ё(т+т) (и + ^) *»*«}• (10°)
и, | Это значит
1 , , 2т(2т — 2) ...2 (1 , 2т4-1 „ ,
— я сое *т+ 'да = ■ ■-- ■ ■ ■■ ■— < 1 " соа 2о) -4-
4 (2n-|-l)(2n—1)...1 1 2 ^ 2т-ЬЗ ""'"Т
(2т 4-1) {2т — 1)
(2т 4- 3) (2т 4- 5) №
+ ...}*.
Уравнение (96) умножая на dm и интегрируя от <и = О, получим
для всех углов от ю = О до а = -д- тс
і і
■•-=—=—• - - ■ • - п-і х
2 „!і±і
х?вфт(ті)"'(^і)"",-(*+ч-
- ІІ(т)"(*Г""—■ сад
* В оригинале это равенство имеет вид
1 ■ * 8 2ш 1-2то—3...1 \2т — Л '
2» —1-2ні —3 _ , 2т,-— 1.2м — 8-2ш — 5 t , 1
+ 2H.+3.3OT45cos3'"+a» + s-2M+5.am+'?cog5a+"-}-
* В оригинале вместо множителя — з левой части равенства напечатано-^,
а Равенство (101) имеет место, «аи асе вал а (96), в интервале {— -=- —1. Оно
я \ 2 2/
справедливо хщсже и. при и = і: -д-.

Н. В: ЛОБАЧЕВСКИЙ —«СПОСОБ УВЕРЯТЬСЯ. 148
Чтоб уверѳну быть б справедливости такого выражения, надобно
только доказать исчезание бесконечной строки". Это можно видеть,
принимая тотчас і так большим числом, чтобы беа чувствительной
равноети полагать уже
!„_!
[101в]
И -———^
(т») = W—т*-
Откуда
Таким же образом
1+1
(-1)4-4 s
**-> "(_-±»-^' ll0Ml
* Это иаяипшв, іаа как Лобачевским доказана (см., например, сочинение
«Об исчвввкии тригониметричесаих строк», стр. 66—70 наст, издания) воамоав>
восяь почленного интегрирования ряда Фурье.
* Наши неправлены почти все правые части формулы [101b] — [101b].
В оригинале:
1) в формуле [101b] вместо множителя (-^і напечатано (—1)',
3) в формуле [101с] отсутствуют множители (—1)< и f-н-) г •
3) в формуле [101 ѳ] вместо множителя (—if—) напечатано (— 1)*,
4) в формуле [lOlfj отсутствуют множители (—1)* и (—-—1 ,
R
5) в формуле [10Ig] отсутствуют множители <~1)* "(дО - я+1
Гп + 1\"~Т~
в) в формуле [101h] в знамдаатепе имеется липший множитель I—-—I

144 -. , СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
[101е]
я + 1
• —
2
•Ч*
«4-1 / П + 1\
\ 2 / ■ ■ «-*
М-'РРГ-— Ч4т-. ^
а следовательно множитель при эіп2гю в строке (101) будет
аі5 j множитель при sin (2»-f"i)«:
-(-!)« 2^Г , х _, І [Ю1Й
-—j-e—i
(4*) ' (Н
После того, что было доказано выше, строка (101) должна,
следовательно, под конец делаться исчезающей:.
В уравнении (101) полагая <ю=—тс, подучим
і і
4_к ~~~ ' ' я+і* ' я-і^
х£|^ВГНИ~~ч с»»
Если же поставим сюда,
* В оригинале вместо ыноядателя -у- напечатано —.

X
Н.И. ЛОБАЧЕВСКИЙ-.СПОСОВ УВЕРЯТЬСЯ» 146
то находим
чо (где *», ji —произвольные числа. Для т = оо с пособием:
уравнения (41) последняя строка обращается в
1 , 1,1 1 .
Для всякого другого т уравнение (103) с обыкновенным
означением представляет
№
•*&
(і>)
^_l/\ І 2«+.р —1 | 1 (2»+f-^I)(2« + g —8)
' 8 2m-f-j)-f 3 ^ Ь (2»і+і) + 3)(2т+у4-5)
Уравнение (102) помножив на такое ate с переменой » на м+1
получим весьма примечательное выражение
£-=&?Щ-Н""(т*+'Гх
которое значит
і 1. г "- + 1 U 1 д | * "(» —2)
1 16 л+2\ 3»+4т5(»+4)(»-|-6)
1 »(» —2)(п^- 4) 1
ѵІі 1 *—1 I 1 (»-!)(»—3) 1 иг — 1)(п — 3)(»-5) 1
Х1ІГ~8 п + 8~*"'6(ji+'8)(n-f-5) 7 («4-8)<* + &)(*+Ч"*""*! ■
Ю 8«в. 5S2S. Н. И. Лобачевский, т. V

146 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Для и = 0 это будет
ДЛЯ 71 = 1, П = 2
Л. j = JL 1 1 1
32 " 3 " 1 ■ З5 - 5 3 ■ 6s • 7 5 - 7s • 9
Для n = 3, ft = 4
na = 2 . 1 . 1
16-32 3-5-7 + 1 -3- 52. 7-9 ~T" 3 • 5 • 72 • 9- 11
1
-{-...
1 5 - 7 • Я3 • 11 -13
ян I Подобных уравнению (104) можем найти много, продолжая брать
интегралы в обеих частях уравнения (101). Так, следующий
интеграл дает
(і-Г*'(і-Г*' ;;
х|Ш,(^Г'(-Ці)-'р-«*+^-
Полагая здесь <в = -g-ir, потом умножая на такое ж уравнение с
переменой » на n-j-1, получим
І^+|Ш'(І»Г+'(1*Г>
х{1-4(^)'(^)"а+,(-^)""^>
* В оригинале в этой и в следующей формулах в начале каждой скобки в
левой часта вместо <— напечатано -,«в начале правой частя вместо 4 напечатано 2.
8 &

Н.И. ЛОБАЧЕВСКИЙ—«ШОСОБ УВВРЯТЬОЯ» 147
si» j Это значит
| 8 ^ и + 2 З1 (я-{~2)(« + 4Ѵ ' /Л
Л1 8 ^п-і-3^3* (n±&)(n-f-5) -Г ■•■js=
и + 2 [ 81 n-f4. 5* (* + 4)(n + ej ^"-* |л
1 п —1 , 1 (ті — 1){л~8) . ]
Для п = 0 будет
А і|_1 и_І- 1 , } 1 , 1
-.(і-£+£-4+...)'.
Дли и=1
8 \ 8 ~ 2/1 8
8 '3 3* - 5 ' 5* ■ 7 7'. 9
1,1 1 .
3 ' 3* • 5 3 ■ 5* . 7 ~ 5 - 7* • 9
іи [Уравнение (105) разделяя на такое же с переменой п на »+!„
находим
8
1 і , V/ * V/1 V"*"1"1/1 \—и~1
у/ 1 \»/п-1\-'/я + 1\--'
* В оригинале вто равенство имеет вид
1
а левая одеть следующего равенства —вид
* В оркгинавѳ в числителе ж в энаиенателе левой частя вместо -ё-&в*алш~
10*

i&St СОЧИНЕНИЯ ПО- ТЕОРИИ -РЯДОВ
Например для п = О
1 1 4-' 1 Х -|_
3 ^ 3s • 5 3 ■ 53 ■ 7 ^ 5 ■ 7s • 9
Когда в уравнение (98) ставим у it — <а вместо <о, потом, умножив
на cos™ to do>, интегрируем, от ш = О до <о = — іс, то подуши
вт" ѵ> сое" ш dm ==
и"»
і
і вііі»
—г— 1 -д- I C03m e>d»-\-
-}- V { 1)* ( "=- « } ( ~5~ т ) 1 cos 2^° С08И1 м *° [ -
in | Здесь, как видели выше [ур. (76)],
I еоат ю <&в = —— ———j j—, [105а]
*~(Н (И
\ соа 2 т со9т<о Лв = — ■-
м""(іт) (тт)
.1.-*
После чего
*"+'(4»Г(Н
і
[105b)
і
2п+ш ein"»coe"«(fa = - *» " j X
*/ ва — ft ао — tit a
Кі-Пі-ГГ
х{*+£<-*(Н"'И"'(Н''(т-П-
* В оригинале левая часть втого равенетва имеет вид

Н. И. ЛОБАЧЕВСКИЙ—«СНОСОВ УВЕРЯТЬСЯ. lifl
в.е переменой п, т на 2п, 2т и принимая в раосуждйнне
интеграл (&0), находим
2*і+»п-
- ЫРѴ4)
1
(n-j-m)
—n+t
s« /n_\ "•Ml
тг(2к)"г"(2т)
/1
eh (Наконец, отсюда
^Г = 1 + 2^(-1)£п-'п"~(ш"%—(*. (106)
Например, для m = — n это дает*
итс 1 иа и8 ns
2 sin ми 2 n*— 1 ' n9 — 2J na
Для m = 1 — 5i
* 1 1
2n (1 — и) ѳіп т*я 2и2 (» — 1)* я (мв — 1) (м — 2)
1 1
^(п+1)(па — 2а)(п — 8) {п + Ъ)(п* — 3s) (и — 4)
Для да» = 2 — и
те 1
ь4и (и — 1) (»—2) sin яіг 2ft2 (n — l)s (и — 2)2
1
(и — 1) (п? — Is) (те — 2) (п — 3)
1
+
(107)
(108)
1 й(й-(-1)(п!-2!)(№-3)(№-4)
Уравнение (107) умножив на dn и интегрируя, получим
і j_
. f^ —sin та: . . | 1-{-х (2—х\*(3-і-а;\ѣ )0
(І09)
* Это равенство поиучаетея не предыдущего, если воепольвовдться теореаюк
умножения ганма- функции (5В), на основании которой
і
•я—т 1 _ 1
»-"(»—5") =(2я)в2 в(2»)
-ЕЯ
+ На основания (*3).
® В оригинале в знаменателе под знаком интеграла пропущен множитель А
Если |я |< 1, го ввиду равномерной сходимости рода (107) в интервале (0, #)
почленное интегрирование этого ряда допустимо.

160 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Еедга at уравнение (107), разделив сперва на п, умножаем потом
на йті и интегрируем, то приходим к известному выражению
а^і- (»-g)(i-$)-,
log—— — =log-i— <■■■>■■ 5--^ *.
(1_n.)^__j...
В уравнении (106) полагая п = m = —, получим
1109а]
Откуда
или
1
64Х-
1
"64*
9-16
1
8Я =
1
16
1
r Sa-
1
5
1 1
2 3е
1
3-5а
(
.7' 1
1 1
1 3s-5г
1
о3 - 7 ■ 9й
1 .
7а•9 • 11* '
_ 1 _і
5= ■ 72 ^
1
9а- 11
1
11я - 13
* і *
13"
15а
0
[109Ъ]
Делая же « = ■»» = —,
4
Заметим еще интеграл
2
sin й; cqb" х аіп а; Йж =
1
о
B + t-И Я+1—і 1
(ПО)
2-»(^±і) ' (=*£=!)
* В оригинале левая часть этого равенет вя. ямѳѳт анл
logf «Sctang-s-»!!],
* В оригяаа.те вместо последнего члена — ■ а напечатано-.-^—- ■ ■„. Это
равенство подучено из [І09а] попарный соединением членов правой чавти,
начинав со второго, Анаиогичаов соединение члеаоа правой части |10йа|, начиная
с первого, приводит я [lQ9b].
в В оригинале первый член правой части этого равенства равѳп -~-^.
4 /~І—
9 В оригинале амеето первого множителя правой части л/х ввпечатаао 1/ -к-я.
• 1/8

Я. И. ЛОБАЧЕВСКИЙ — .СПОСОБ УВЕРЯТЬСЯ» 161
который легко вывести с пособием интеграла (78) и уравнения
J сое (і -j-1) х cos" х dx = Г cos іх сов»+' ts dx — Г ain ix cos» x ein x dx.
Перейдем теперь к интегралу
і
Х= 1 сов (иж — jj tang ж) сов""* xdse, [110a]
о
где р произвольное, и всякое положительное. Бѳа назначения границ
интегрирование по частям дает на правой стороне
1 п Г -
| совяжвш(«ж—# tang #)-)- — I сое" ж cos («ж—ptangx)dx—
Р Р ■>
— —J cos"-1 хsin (пх—ptang#)8m#(&c; [110b]
следовательно, для п > 0 [*°]
і
Х = — j cos (пх-{-х ■—-pt&ngx) cos"-1 ж«йв, (111)
d(pX)
р „
dp
потом интегрируя:
(р-*)Х-0*;
Х=рп 1е "N. [111а]
Чтоб определить функцию N, которая не содержит более р,
называем X' выражение X, ноставя сюда р-\~г вместо р и разумея
под г целое положительное чиело. Основываясь на уравнении (111),
* Пра помощи [110b] получаем:
£ -
рХ = п f cos" х cos (nx —p tgx) dx — n \ cos»-* x sin (пж —p tg я) sin x dx.
0
Отсюда легко найти, что
в
£(Р-Х) _і_рх = я | c09n-s^cos(ni— р tg x) da: = «X

152 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
получим
(Л_1)—"СЯ + г/Ж- .
= | сов(пх-^-гх—jptanga; — rta,ngx)aoan+r~1xd№*. [11 lb]
о
s« [Если г — чрезвычайно большое число, то под интегралом можно
довольствоваться весьма малой дугой х, а потому для г = оо
почитать со всей етрогостию*
1
-2*
Х' = -— \ сов»4-"-* х dx [lllct
и поетавя значения интеграла [ур. (76)],
х,= rc(w + r-2)-*+r-2
или [ур. С54)]
Х1^
ж(» + г —2Г*,+Г-Ѵ-Ѵ-1
п+г г'
я^-Ч—D—^^f^-1)" а "(иг"1)'
Между тем для г=>со [ур. (26)]
=-r+*
f-r = yW'Vr.
* Иѳ сопоставления [110а] и (111) еяѳдует:
Х(р. »)=^Х(р, »-f-l),
откуда
X(ft »)»B<'' + 1>"f + ,-1Ix(|.. * + r).
P
Подставив сюда p + r вместо р, получим:
у_(»+Г-1)"
(l» -ь г)
то-веть, веян учесть, что {«-J-»"— 1)"""= ■-■ - _ , равенство [111b].
(п— 1)°*
* Подробное обоснование ем. в примечании [Щ.

Н. И. ЛОБАЧЕВСКИЙ — .СПОСОБ УВЕРЯТЬСЯ» 15ft
ist (После чего
и следовательно
N
(«
Здесь для г = со [ур. (9)]
('
Так находим
N-
(п-іГ'-^+гу
*
„gP^+r-l
-і)-',-І(р+»-)п+^1
,-И-Г-!
. гш
и наконец для всякого и > О
[llldj
—р «~1
1 чов(пх—рЪа,п%х)со8п-^х(1х = *--.-. . (112)
о ^ '
О переменой tang я; на х этот интеграл принимает вид
который дал ему Г. Пуассон с доказательством собственно для
целых чисел и (Journal de Гёсоіѳ Polyt. Tom. XII, p. 480),
Случай jp = w рассматривая Лаплас еще прежде, переходя а
воображаемым от действительных. Впрочем, этот способ, как эамечает
сам Лаплас, может елужигь только руководством в исследованиях
я первым средством к открытиям, не представляя должной
строгости (ТЫогіе analyt. des probability's, ed. 1814, p. 134, introd.
p. 82).
Уравнение (112) помножив вафи интегрируя от jj = о, получим
примечательное выражение
і
"в"*
I . J s—- сов"-1 xdx = i!, (114>
J dILL OS

154
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
где после интегрирования должно полагать г = со и где п не только
положительное число, но может быть нулем, потому что
sin fr tang ж) (* dx .
же = I — am гх = іс'
(* sin
J ~~эі
яш г соз я
[114а]
о 5
39 | До сих пор прижимали в рассуждение только х°°п с
показателей п действительным числом, хотя затем уже произвольным.
Теперь будем говорить более в обширном предположении,
допуская в п даже воображаемый множитель У—і.
[VJ
Уравнения (И), (12), (18), (14), (15) соединяются в такие три*:
(х-\-а)"а = е-а'(х-\-<гУ
Ѵ(аЧ-«).
log f(x 4- «) = log + (■) + £ log '~^±^>,
2 log
/Ч«-
■1)
/(*+«)
:Y ..-*_ .--
+ l>
(115)
где ж целое число, а произвольное, знак суммы относится к целым
положительным і; наконец
может быть принимаема за функцию я 'всякий раз, когда
бесконечные строки (115) исчезают, хотя бы х представляло не только
целое, но произвольное действительное или воображаемое число.
Этот последний случай остается - теперь доказывать и при том
разумея под а; вею действительную, под а всю воображаемую часть.
Здесь у Лобачевского отибяа. В деиствительнппти
віигх
I-
и, таким образом, формула (114) ае ворна, ьыш и. = 0.
* В равенствах (115) нужно вжсагь f(x, а) вместо /(ж-f-a) и соответственно
/(л—1, я) вместо f(3t + « — l), f(x + i,a) вместо Да;+ « + »), f(x + i~ I, a)
вместо /'(l-f-a-fi —1).

Н. И. ЛОБАЧЕВСКИЙ -*- .СПОСОБ УВЕРЯТЬСЯ» 156
Итак, ставе <ху — 1 вместо а, полагаем
*-2
* cos [{*+ 1)4]
Получим
і±1 '
1 («+2)(«+1)(а*+<і») ■
М= L tang в 2j —і+Г*
і (i_j_2)(t + l)(*» + e>)~
а следовательно, по величине лак L, так и Ж всегда будут менее
Этого замечания довольно, чтобы принимать ^і(а) за функцию
только «, всегда с определенным значением!3*]. Таким образом,
недостаток в сличении двух выражений
ал | исчезает вместе с возрастанием ж, будут ли ж, а действительные
числа или заключать в себе множителя Y—1- Весьма
примечательную здесь функцию а™" Дежандр предлагал назвать гамма,
которое название можно распространить даже на все выражения ж™",
с каким бы то показателем п ни было.
* Б оригинале
со
L = cob6 У ' -f+i, M=Lt«ng6.
i (і +2)0 + 1) (а*+ «•)""*"
* В оригав&ле в знаменателе вместо (3s + a') a напечатано (я — в)

166 СОЧИНЕНИЯ ПО «ТЕОРИИ РЯДОВ
Уравнение (116), как видели прежде, дает 0"° = 1; а потому
для произвольных х, п я целых чисел г можем допускать
x~" = x"r(a: — r)""-r [116aJ
и таким образом определение гаммы пополнять тем самым
положением, которое приводит к уравнения» (116)*. Сюда поставя се-}-£!,,
а — (3 вместо х, з, е произвольными з, р, должны, следовательно,
получить
Ѵ ~ ' (а—Р)""-р
После чего
w» j и для другого произвольного f
«-■ = *-!(«_.,)-»-* (в_Р)—3^
а потому
какие бы числа а, 3, Т ни были, действительные или воображаемые..
Пусть в а заключается р действительная часть не—р
воображаемая е У—1. Интегрирование по частям дает
J в + 1 « + 1J
Для всякого, следовательно, дедого положительного г, как скоро
P + 1>0,
со со
J е-* я" йж = в " -т J e~<»£>+rdx [Н7&1
* Неясно, о каком дотолнеяик определения идет речь. Равенство [116а] ш
следующее далее равенство (І17) следуют яѳ свойства (43).
Действительно,
,Ч_ " -.«!• _ « fj rl**"~)'— * J
{*-»)-•-*' (и-г)-*-*"* l ' <*_«)—*_'
откуда л™'1 =аг'"г (х — г)""-г, причем г совсем не обязательно целое.
* В оравой части этого равенства, а также в правой часта (116) следует
приписать мшикитолъ X (х -f- о); иначе эти равенства — только асимптотические.

Я. Ж. ЛОБАЧЕВСКИЙ — «СПОСОБ УВЕРЯТЬСЯ» 167
ИЛИ [урВДі (Ив))
(* И-0 —г—« — (*
| \е-<й2?'сіх*=~у=(г-\-а) * ег+|" 1 е-"&+*dor,
о j
е возрастанием г границы второго интеграла сближаются s самому
большому значению, которое приобретает ѳлеменх вместе с тем,
как будет удовлетворено требованию
Откуда в нраве заключить, что воображаемая часть интеграла
уничтожается для г = оо, тогда как в действительной можно
довольствоваться значением
ж = г+р+.**
е числом t действительным и весьма малым; а следовательно
О . ' —t '
Мы видели выше, что для весьма большого г
кг-*-*-
После чего с переменой t на х ^г получим [№]
та
j. е-* & dx = &— (118)
О
для всякого я, лишь бы в нем действительная часть была > — 1.
Рассматриваем интеграл
J'
аіцЭп+i х cos3"14-1 xdx =
-і— sin2»+23;cos»™ж + —^-т Г sin2»-*-8*соа^-1*»<£с«;
і + 2 п + 1.1
'2/1 + 2" ' п + 1.)
.* Если а = р + іт, где *"= Y — 1. то ]е-яз^+я J = е-» я'+Р. Левая тасть
равенства является производной этого выразвѳнвя. В оригинале равенство имеет аид:
е-ххг+<цг^.а — г) = 0. •
* В оригинале: т = а-f-р +.t,'
а Правая часть этого равенства в оригинале иыѳет вид
2я -4- 1 ' » + І J

158 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
как скоро здесь вп-|-1 действительная часть > 0, то для всякого
целого положительного г находим, продолжив интегрирование по.
частям,
і і
т* -г"
f віпап+ія:со8я*+1жо!іс==п"~г»в~'' f sm^+^+^cos3*-^*1»^
о о
"6 (покуда действительная часть в m — r-j-1 более нуля. Ставя сюда-.
m-\-r вместо га, получим
\ Bm^+^cos^+^+'ajffo™ V аша"+в'+1 х сов8"*1 х dx Щ8аѴ
о о
всякий раз, когда действительная часть в я-+1, m-f-1 превышает-
нуль. Поставя г = оо, можем довольствоваться в первом интеграле
весьма близкими значениями к ж = 0, вовтором—кд;=-д- я,а
следовательно
Ге-і-**а;а»+і da: = ^^. fe-™*;E*»+l йе. [И8Ъ]
в о
Откуда для всякого числа н, когда ви-f-I действительная часть > О,.
со
{е~*х*&е = А г-г и- -г г*. [118с]
о
Здесь А = 1 для п = 0, а следовательно, вообще [ур. (118)]
, | »-» = »•-гй--»>» (119^.
— то же уравнение, какое было выше (54), но теперь уже
доказанное без всякого ограничения для всех как действительных, так и
воображаемых чисел п [*].
С условием, чтобы в п~\~1, т-\-1 действительная часть была,
положительной, интегрирование по частям дает
і і
Т" ?■
1 вш*"-1 жсов*"-*-' xdx=t -■ ~^!~ ■ Г ат*п+,а!Соя*"+вж*Ь:
J я-И J

Н. Ж. ЛОБАЧЕВСКИЙ —«СПОСОБ УВЕРЯТЬСЯ» 16»
и следовательно для всякого целого положительного г
\ ain^+^coB^+'artfa; =■ -■■■-?* _ f аш^+'жсов^+^+^вй»*!
о о
По примеру выше для г — оэ, вставляя
о а
и принимая в помощь уравнение (119), получим
і
j 2(и-+-»»Н-1) п+ш+1
о
— то же уравнение, какое было выше (60), но здесь уже я, т могут-
быть воображаемые числа.
Например для 2ji-f-l~«-f Ъ У~1, 2m-J-l=«0,. с а, 6
действительными числами- находим после всех приведений
I sin° х {cos (6 log sin a;) + Y— 1 віп (6 log sin x}} dx ■■
или в другом виде
m
VI—е-»
9 В оригинале в множителе перед интегралов в правой чкстн переставлены
чиояитедь и ннамеватель.
* В оригинале формул» (121) имеет следующей вид:
и . ^__ _
і(в_і+цт;)
!
Равенство (121) получается из предыдущего водмвя^аиой Jogвіпі = —5 и
ааменой а аа a— 1-

160 СОЧИНЕНИЯ НО ТЕОРИИ РЯДОВ
Для 6 = 0
і
т" ѵ--
\ smazdxt=——?—^—— (122)
Уравнение (119) будучи помножено на такое же с переменой п на
—п, дает
ѣ"»(_—п) "-«-■= r"r»--*-n"-'"(—п°°у.
Это значит
Итак для п действительного
(^=4)-^(-ЛЯ[)—• V=7D___^E_ (123)
in [Если же в уравнении (119) вместо п ставим a-\-bY~-1 и
переменяя внаки перед а и 6, после перемножим, то находим:
— log{(a + 6y^l)4«+»v:::T(a — &і/^Т)-«-*ѴГЛх
Это значит
со со со to
е-.-»—»(^)в(нгк 'й^йлв
Берем наконец интеграл
J (n+2)(n + l)J
о . u
а« ]е произвольными числами г, и, лишь бы действительная часть
вк-)-1 была >0. Продолжая интегрировать по частям, находим
для целого положительного г

Н. Ж. ЛОБАЧЕВСКИЙ —«СПОСОВ УВЕРЯТЬСЯ» 191
Для г — оо получим
■ ів і ■
о о '
Что вставляя, находим
Jn + iV-lY-'fn — iV^Y'*'
Ѵп
а принимая в помощь уравнѳмие (119),
еіх еіи« а; ^ -
' П + іѴ — І я—1^—1 '
2"(і±І]^і)" * (±Zzi£=l\~ B (126)
Отсюда нетрудно заключить, что
1
е*" sin" xdx =
i
'Н.(126)
Интегралы (125), (126) относятся к произвольным числам (', « под
условием, чтобы в п+1 действительная часть была положитель-
* Это равенство получается из предыдущего, если вырааять я"-**-,
I ? "Г J . I и ( ■ j- -—— ) яо Формуле (118) и вошольэоватьоя
асимптотическими формулами
* В оригинале множитель {[—( — І)"^"} стоит авв знаменателе, а в
числителе.
11 Зли. веяв. Я. И. Лобаченокий, т. V.

162 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
ной. Первому можно дать еще другой вид;
(е"* -і- е.- **») cos9" х dx =
«(2л)-*
22"(и + гѴ/=1)-,,+і1/-І('*-^:::1)"п~'Ѵ~і
s« [Вставляя сюда значение (08) для cos'™», находим
(127)
-*+»2(-=&іг-- «l28>
і
где знак суммы относится к целым числам X. О переменой г на
іѴ—1 подучим
* (127) легио получить аз (125), еояе учесть, что
I я
Я И 2
f «M^airim а: !&;=:«*■ f е-Ж* eo&Z* x dx = ё* Г ((£»* +е-*"} сов"» а: *в.
о __«_ о
в
В оригинале в знаменателе правой части (127) отсутствует множитель 2Е".

г
METEOROLOGISCHE ВШВАСНТЩСЕЯ
V;'' " AtJS DEM иШМЗШ DEB ІЛВВШШ ВІЗ&ИЖН
UMVEBSITAET КА8АЛ.
AUF ROSlliN BER ШІѴЕШТАЕТ HEKAl'SCEGEBEN
ERNEST UNORH,
, flr.'Ar №«. ff. Л. йЛфта ~ flu*, J"rt£ ord. dn- РЛ^аЗ end fiyii, tkupafkk fry ifrr >
HEFT I.
iSS5 - 1836-
KASA».
<H Pfcl LmVBS*lTaBTJ~EljeBD»VEKB«fit p
184t-
Титульниіі лист «Метеорологических наОліоденпіі учебного округа
Казанского университета»; тетрадь I,
ы клтороН йгіло напечатано сочинение чО сходимости бесконечных радов».
К стр. ісз.

UEBKR DIE COIfVERGENZ PER ШЕІЧШЛСНЕЕЧ
. 8БШБІЧ,
ияі sicol- LOBATsaiEwsar.
PlOf. 01». Din Mil"? Ѵ1Г1Е \x И к К І'вІЧІЧТЧІ К ЛЯ».
S*At uneiidlicbp Reihe Іывп dargtstelll wrr^i-n ilaicli Ааь 'Lwiivn
CO
wu.'sirb die angnlHttele Sanunattm Wf a]It gnnrrn пччіпсв Wetlbe rou i ЬсііеЫ, \on
i=l an, viaread fit) irgani dot Ьнііштіе Fimtiion ™ > ЬекЫякі- Nfbmen die WciUw
der FiurlioQ /T*J "^ iraehwAm v dargesfalt ab« dast ilire Бѵшпи aich от ю аліи «nrr
bniiBMlta Crane S Bibert. je grflfur die ЛпіаЫ йегкІЬса is*, к wirJ die Reihe couw-
girrpd gBBMHl. den Wtrtb 5 der Reibe kam nun al*lani mil beiirbiger Gcrouiglirii Ьвіім-
mii» i iiub-ш пазя ah lelflvn Werlh van i an Zabl r ninmil, die eo grau irt, d.iu щ.ш ■&*
Siuiime alter Gfcfcr jcnsdU f[i) trrnacblanigai Ьаіш. ЛІЬ.- IteiheB daieti ilfiw Eigsasrliall
iir.ii [ шкот ml. Ьлмеи airbl iu BertcliBung™ dientn. and ddl™ laae Ixsiui.nile ZM -Uii.
П.ія charafteri*lM''he Uvrluu.il еілгг contorgQalfD uDradliebeii Reihe betfeht demiuvJi iJj-
linn , djss die Bumnie alter Gbeder inn t=r-f-l bis izzp du4 чгасііншіеві г fnrtwabrctid ;ib-.
піні<. »іе grot* мсЬ i> gnln'bl wRTik; Kill oian |е=мя, so loll Леи Swanie der «hi rftr
llriht jrnttili dci Gliedet f(r) gciuDnt werden. Kin solrlwir Hat капа urieder afs fine unniil-
li. lis Keihe falracblet, and rfartfa
. dargpslelll asiten.
Ки nj I. B. f\i)=jf u bal nan
Первая страница оригинального издания сочинения
«О сходимости бесконечных рядов»
(1-и стр. приложения к «Метеорологическим наблюдениям учебного округа
Казанского университета я, тетрадь I, 1841 г,).

О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ
Перевод е немецкого В. В. Степанова
m
Каждый бесконечный ряд может быть представлен при помощи
обозначения
где показанное суммирование относится ко всем целым
положительным значениям і, начиная с і = 1, тогда как /(*) обозначает
какую-нибудь определенную функцию от і. Если значения
функции f(i) убывают при возрастании г таким образом, что их сумма
тем более приближается к некоторому определенному пределу St
чем больше их число, то ряд называется сходящимся; тогда можно
определить значение ряда 3 с любой точностью, если брать в
качестве последнего значения і число г столь большое, что можно
пренебречь суммой всех членов после f(i). Все ряды, не
обладающие этим свойством, не могут служить для вычислений и не
представляют определенного числа.
Таким образом, характеристический признак сходящегося ряда
состоит в том, что сумма всех членов от і = г-\-1 до г=р все
больше убывает при возрастании г, как бы велико ни было jj; если
положить р = со, то эта сумма называется остатком ряда после
члена f(r). Такой остаток опять может быть рассматриваем как
бесконечный ряд и представлен выражением
Пусть, например, f{%) = x*; тогда
1 . ѵ* ■ і ^+1 1
11*

164 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Далее, мы имеем для каждого действительного значения а;<1*:
СО
г^= 2*-
Остаток этого ряда после члена г = г есть
он убывает при возрастании г и имеет пределом нуль.
Вообще, если f(i) принимает положительные значения для всех
І>г и, кроме того, убывает с возрастанием *, то для таких членов
ряда имеем:
где I хотя и зависит от к, мыслится таким образом, что для
каждого к оно равно О или 1.
Уравнение (1) дает в этом случае для остатка ряда после
члена f(r)
где целое- положительное число L зависит от л.
Если теперь определить величину р. так, что она не меньше
значения, получающегося из уравнения *
ffr) = fir)2-\ (2)
то отсюда следует, что при разложении f(i) по убывающим
степеням числа 2 член 2~* в остатке R может войти только со
множителем L, который не больше чем р. —г. Поэтому равенство (1) дает
всегда
ПО
где величина ji должна быть определена из уравнения (2) или но
* — 1<х<1.
* Функция f(i) определена, по сути: дела, юлько для целочисленных значений
аргумента, и поэтому с помощью равенства (Э), вообще говоря, нельзя определить р
как функцию от X. Вместо равенства {2} следует писать неравенства:
■сяк это Лобачевский и делал в предыдущих гочннѳнннх (си. стр. 37 в 8В наст-
ТОНА).

Н. И. ЛОБАЧЕВСКИЙ — «О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ» 165
крайней мере должна быть не меньше, чем получаемое яз этого
уравнения значение ji, и где р. должно быть выражено как
функция Я.
В качестве примера рассмотрим опять ряд
Уравнение (2) дает:
откуда следует:
tf=xrT\
* ; Аі<*2
следовательно, в силу (3)
Суммирование дает:.
2 log 2
В < f-Y a?.
-ш'
Сравнивая с точным выражением для й, мы получаем для
положительных значений ж<1:
•rlog(-M<(l —a:)21og2.
Если сюда подставить ах < 1 на место х, го получится:
a:log ( —I < I ж) 21og2-f-#Ioga*.
Принимая здесь а произвольным, можно всегда мыслить х настолько
уменьшившимся, что в конце концов получим:
, /1\ 21og2
Отсюда следует для х = 0 в качестве границы приближения:
/1 \ 1 — .г
* В оригинале вместо множителя I х I стоит —-—.

166 , СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
[И]
Для краткости в дальнейшем мы будем под символом
П
понимать произведение
п(п— 1)(п — 2) ... (к — і + 1), [За]
содержащее і множителей, которые начинаются спи следуют друг
за другон, уменьшаясь на единицу. Если такое произведение
разделено на подобное же, в котором п = і, то это будет записываться
так:
и, кроме того,
п = 1, пв = 1, я„= 1,
и для всякого положительного значения г полагаем:
(_i)--'=eoo*. [8Ъ]
* Яри-кйч. Чтобы облегчать рассмотрение некоторых последующих
приведений мы добавим адесь некоторые предложения, относящиеся к применению
знака ж"". Если р и m — целые долоасительныѳ^иела и р~>т, то легко получается:
(я + и^)"ІJ,"^-и') = (r^-(-m)",в■^^"',., ,Д
Если полагать уравнение I справедливым и в случае отрицательного т и если
подставить —m на место т, то получается:
„-(-я) =.— -. щ
(« + «>"*"
Древ,
(—п)",м = (— іСіл + т-І)"" TV
откуда
Далее
в если г = со или по крайней мере означает весьма, большое число,
»-" =
[Дрм.кечачие Лобачевского.]

Н. И. ЛОБАЧЕВСКИЙ —«О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ. 167
Наконец, обозначение
для всякого целого положительного значения і равнозначно
выражению
Предпослав это, переходим к рассмотрению ряда, который
получается из разложения показательной функции. Он таков:
S=^i (4)
Для положительных значений х в салу (2) значение р
получается из уравнения
а£ = я£ 2~ ,
откуда следует:
(р—r)loga: = log(!i-i—'-) — Uog2;
следовательно,
(р — г) log х > fa —г) log (г-\-1) — к log 2
и, наконец,
^ a log 2
Отсюда получается для остатка' ряда (4) после члена і = г:
**№
Теперь, если г так велико, что г-і-1>а;, то при дальнейшем
увеличении г остаток Л убывает до нуля; следовательно, ряд (4)
сходится для всякого положительного х, тем более для
отрицательных значений х. Если бы мы пожелали рассмотреть этот
последний случай отдельно, то мы должны были бы положить
-£*.•* Ьттт)
и определить [д. по (2) из уравнения
* Здесь 0О<Зг + і.

168 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
но из него следует:
2г-НІ
(2р _- 2r) log х = log [(2^) " *-2r] — >. log 2 + log x ■
l~ 2\і.-\-Л
Отсюда мы имеем:
(2^ —2r)log?i^<Alog2-log(l—^ф^);
следовательно,
log(l
a log 2 ь \ 2»' +1
2l0R-X 21og——
и, наконец (до *Ns 3),
й<(1~27+і) ■
і /2/- + 1Х
Если мы будем продолжать увеличивать г после того, как уже
2г -}-1 >■ ж, го мы можем сделать й сколь угодно малым.
Следовательно, ряду (4) при всех действительных х, а также,
как легко видеть, и при всех мнимых принадлежит определенное
значение, которое мы обозначим через f(x).
Следовательно, если х и у обозначают две любые величины,
можно положить
г
где В и It' обозначают две величины, которые можно сделать «соль
угодно малыми, увеличивая г. Произведение этих рядов дает:
t{*)№=iL £«-*+/'*-,
р -0 і ™ ty
"* Нетрудно найти это выражение, если рассматривать произведение обоих
рядон, но его тагсже легко получить, если заменить ряды суммами, ибо, например,
іх і »;= і і: *:*;-"і" і ^~я,
f~>0 k_Q >. —0 I—11 рві 1 — 0
где о для всякого І произвольно; следовательно, можно также положить а = І, от-

II. И. ЛОБАЧЕВСКИЙ —«О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ. ' 169
где
*
если здесь сначала отброшены все члены, относящиеся к
пополнению двойной суммы, б которой мы можем положить
следовательно, мы имеем также
Но так как Р состоит из произведений, л которые входят
целиком или частично множителя Л и В', то, увеличивая г, можно
сделать также и Р произвольно малым; следовательно,
Предшествующее служит для определения степеней с
действительными показателями, тогда как ряд (4) распространяется на
действительные и мнимые показатели. С основанием неперовых
логарифмов е этот ряд дает:
«■ж Ѵ~і
= cos as-f- У — 1 sin x.
куда получаем:
- і 2*;*гі-'2 2 <^r' =
St- 2r r—1 3r 2*" -r
= 2 2 *o*r'-2 2 *i»r(-2 2 4.<-' =
Отсюда сразу яидяо, какие члены яз MR' нужно вяять для пополнения.
[Примечание Лобачевского. В оригинале некоторые из стоящих рядом знаков ^
переставлены местами. В преобразованиях Лобачевский нсімѵіьзуот равенство
(— я)™-" = 0 (если «>0л целое), из которого следует, что ;/^ —" = 0].

170 ' СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Таким образом, тригонометрические функции могут быть введены
в анализ независимо от геометрических рассмотрений, как я это
показал в алгебре, изданной много в 1832 г. *.
Теперь мы перейдем к рассмотрению ряда ,
S=% «Г* **. (5)
(—0
Чтобы здесь найти границу, которую не превосходит остаток
ряда, надо сначала рассматривать все члены ряда как
положительные числа. Тогда уравнение (2) дает:
откуда следует:
21
(,*_»_ I)-!*-' - ' і ^-г
-(іР
При «-[-1^0 коэффициент при 2х состоит из множителей вида
і п+х
і '
где г надо полагать равным всем целым числам от г-f-l до ji;
поэтому мы имеем ®:
л1ое2
ц —г --=: — .
откуда
Здесь наибольший множитель в п™г есть
Д< 81о«Д »г^-
* Ом. сочинение «Алгебра или вычисление конечных», т. ГѴ наст, издания,
«тр. 230. Это сочинение вышло в свеі в 1834 г.; указывая 1832 г., Лобачевский
имеет в виду год утверждения девзурой (см. т. IV, стр. 9).
* В обеих частях этого и предыдущего равенств подравуыевается знав
абсолютной величины.
ф При достаточно большом г.
_я—г-j-l я—г-у-
s »Г= г
^■■^^г^^-ту^-ч1)-

Н. И. ЛОБАЧЕВСКИЙ— «О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ. 171
следовательно, «~г убывает при возрастании г, если г > и -f-1,
тогда как абсолютное значение величины
хг
при ж < 1 может быть сделано произвольно малым.
Если в случае п-}-1 < 0 положим
1 « + 1
Ш = 1
г '
то необходимо только взять г достаточно большим, чтобы по
абсолютной величине было аи;< 1; тогда мы имеем:
Uog2
ц_г <
*Ш'
Е< 21°«г, „-У.
Ці)
Хотя здесь п"г возрастает одновременно с г, все же оказывается,
если подставить r-\~t на место г, если только <иж<1:
В < -. 2 yg,2 t и-'a?" (еж)» *,
iog(-L
а эта последняя величина при возрастании t убывает до нуля.
Следовательно, ряд (5) сходится для веек действительных
значений 7і, а также для всякого х или для х Y— 1 вместо х, если только
по величине х < 1.
Для целых положительных значений п легко показать, что
и что, следовательно, произведение двух таких сумм для двух
положительных чисел пит должно дать:
а, га і
d-fffl), х = 2іх Zin>= тв •■
• Чтобы d этои убедиться, достаточно учесть, что
,-,4.« „~г (»-r)<«-r-l)...f—Г-М-1)
"о -"« (г + 1)(г + Ч...(г + 0
и применять преобразование, подобное указанному в предыдущей сноске.

172 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
откуда следует:
Для того чтобы это уравнение, в котором г-—наивысший
показатель чисел и и т, было справедливо для любых целых
положительных чисел, оно должно быть верным вообще для всех значений:
п и т s.
Если поэтому обозначить значение ряда (5) через f(n), то мы
будем иметь вообще для всех значении п и т:
f{n)f(m)=--f(n + m). (7>
Ряд (5) служит для обобщения при определении степеней, если
подставить х Y—1 на место х; но этот случаи в соответствии
с уравнением (7) должно всегда предварительно свести к случаю,
где входит степень l-\-xY~-1, и по абсолютной величине ж<1.
Например,
(-1)7-/=1,
[7а]
следовательно, по уравнению (7) для всех действительных
значений к
и, наконец, полагая —1 -J- 1^2 = ш,
l"-{—'p-f %№»ѵьѵ=У-
№
Если подставить сюда— на место «, ввести величину і из
условия мі = 16 и понимать под ѵ > 2 целое простое число *, то
* Если два многочлена равны при любых целых значениях аргументов, то
они тождественны.
* Для дальнейшего вуисно только, чтобы 16 не делилось на ».

К И. ЛОБАЧЕВСКИЙ —«О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ» 178
найдем мнимый корень
t
[7с]
где L н Ж могут быть вычислены с помощью рндоп
со
і- 2(— і)Ч"Ѵ,
*= 2(--1)'ти+,-"+1.
Остается только показать, что М не обращается в нуль, если
только t — не целое число и не больше 3 -^ *. В ряде для М двѴ
последовательных члена объединяются в следующее выражение:
(—1)Ч-"+1«*+Ч(2І + 2)<2*+8Н8 + 2У'2) +
+ (4г + 3) *— С — (2і + 1)(2/-І- 2) ] ® [7d]
Это выражение не меняет своего алгебраического знака с
возрастанием «, как только 2» > t. Если в этом выражении положить
і = 0, то в качестве суммы двух первых членов М получим:
i-fe>i{(t+4)(7 — *) —10+12/21 >
> -^to3{ (* + *)(7- 0 — 18+12 J/2 } *. [7е]
/ о -і- Y" V
* В оригинале отсутствует множитель I — -г— I
* Из того, что п ~£> 3, следует, чтп (<!5-, -
* В оригинале [7d] имеет нид
(-I)<(-* + 1.f + >{(2i + 2)(2i + 3H2 + -J>'"f)-r-(4i + 3)(-t») =
= (-l)*(-M + 1^ + 3{(t+4)t7-!-«_0 +
4- В? (1+ l^"} + li (L + 5 /2~) - IS + 12 /2 }.
Аналогичная ошибки, оставшаяся, к сом;алепию, не испраіі-тенпоіі н в настоящей
издании, имеется и в «Алгебре» Лобачевского (ГѴ том наст, издания, стр. 203).
Так пак
(йЧ-2)(2» + 3)(3 + ЗѴа") + (4( + 3)' —Р —(2(4-1)(2» + 2)>
>(2і + 1)(2і' + 3)(Э + 2>г2") + <4і-М)*-/3 — (:>*+-2><2І-|-3) =
= (Йі + 2} (2< + 3) (3 + о /2 ) + <** + 3) < - Р.
то следующие далее из (7d] заключения все же еправѳдлішы.
9 В оригинале формула [Те] в связи с отмоченной выше ошибкой в (Tdj
имеет вид
JLfoy*{(f + 4)(7-f) — ie-j-12 l'"3 }>-i-fe.»(f + 4)(7-0-

174 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
что является положительным числом для всех t < 6.
Следовательно, при (<2 в ряде Ж суммы всяких двух последовательных
членов положительны.
Для (>2<3* 3-й и 4-й члены дают:
сѴ{і-<'-^~6>},
что является положительным числом; начиная отсюда, остальные
члены объединяются но два в положительные суммы.
Для *> 8 < 4 три первых члена Ш дают:
f01_(o-V + CV>to3J-i.(( + 4)(7-f)~~u)aj>3g(a>e* [7ff
— положительное число; начиная отсюда каждые два члена,
соединенные по порядку, дают только положительные числа.
Для t > 4 < 5 первый член М со вторым и далее по два члена
дают только положительные числа0.
Для t > 5 < 6 первые три члена М дают:
Ы __ ;-V + С V >*Ш3{-|-((+ 4) (7 - І) -5°^ I * >
■ > *шЗ { ю у^2 —13,5 | >0,64fcu8.
Начиная отсюда, соединение следующих членов по два дает
только положительные числа.
Этим способом я показал в своей Алгебре ^, кйк всегда можно
найти по крайней мере один мнимый корень из единицы, если
показатель есть простое число. При помощи одного корня легко
* То-ѳеть 2<(<3. Аналогичные смысл имеют и последующие неравенства
такого жѳ вида.
о
* В оригинале в последней части неравенств [7f] напечатано В Іф\
Ом. примечание [И].
в Положительность суммы первых двух членов следует из [7ѳ]; с помощью-
[7d] легко убедиться, что сумма третьего и четвертого членов тоже
положительна, а дальше 2і >1н, следовательно, суммы всех других пар также
положительны.
Я Это неравенство справедливо; однако, по всей вероятности, адѳеь у
Лобачевского ошибка в вычислениях, так как из [7і] немедленно следует более-
сильное неравенство
to _ іо"3ш +1 - V > -і to* ((+ 4) (7 - О
ввида того, что (0°*J>'0 при (>4.
I Си. т. IV наст, издания, стр. 203—305.

Н.И. ЛОБАЧЕВСКИЙ —аО СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ» 17»
найти также остальные мнимые корни также и в случае, когда
показатель — составное число.
Если подставить на место действительного числа п мнимый
показатель ѵ,у—1, то ряд (5) служит также для определения
степеней, если только абсолютная величина ж< 1, так как только-
в этом случае ряду соответствует некоторое значение. Чтобы
. доказать это, достаточно заметить, что если для некоторого
действительного числа п предположить сходимость обоих рядов
со
2к"-(-»)ГѴ,
в которых множитель при х1, расположенный по степеням пг
состоит из членов с одинаковыми знаками, то ряды тем более
будут сходящимися, если подставить »]/'—1 на место п, так как
вследствие этого входят члены с переменными знаками.
Все остальные случаи возведения в степень могут быть сведены
к этим, если пользоваться уравнением (7).
Возведение в степень с мнимым показателем п Y—1 может быть
произведено также при помощи ряда (4), который всегда сходится,,
как это только что было доказано; но для этого мы должны
сначала определить две действительные величины « и р из
уравнений
pes
ре 8
Откуда получается:
У =
- = і-к-
"-l-t-
* ;«-
■1 + /2) Ѵ—\ ,
-1 + ^2) 1^=1,
ѵ~^-\{ъ']-
2 + У2
Рассмотрим еще ряд
-«!-*)-£ 4-^ (8>
Для него ц определяется из уравнения
(±Г-7*

176 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
следовательно,
(^->\)log^= Uog 2+ log (-£-)< Uog2".
Следовательно, остаток ряда после члена і = г есть
В < 4 log 2 ■ з* ■ —^—.
log --
Таким образом, ряд (8) сходится для любого положительного
х < 1 и тем более он сходится, если на место х поставить —х или
х V—1> если только по абсолютной величине ж<1.
Если в ряд (8) на место х подставить выражение —(х -\-y-\- ХУ)<
то получится*:
~f[ (1+х) (1 + !/) j = ^^—rL(x + s-\-x!)Y -~
.t = i
^(-і/О'-іГ1-1 <* + * + *</>; =
со
= _^ С— !> С* — !) a^c (ан/)с
где целым числам « и «і должно быть придано любое значение,
при котором ?'-—п — т не отрицательно. Пусть теперь
і — т=р, і—п = 9;
тогда множитель при х"уі в ряде для —/j (1 -\~x)(l-J-y) |
выразится через
2,
(-і)Ч'-і)'
где знак суммы распространяется на нее значения /, для которых
і—J), г — q, p-\-q — і пе отрицательны. Для jj.= 0 или q = Q этот
коэффициент соответственно равен
(-1)" (- If
-—— или - — .
Ч JP
* В оригинале в яевоіі части этого равенства н в правой части следующего
далее неравенства отсутствует множитель log — .
* Предполагается, что | х + >/ + j-y \ < 1.

Н. И. ЛОБАЧЕВСКИЙ — «О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ» 177
Если {>0и если, кроме того, положить p = g-f-f, i = gr-j_(4-A, то
этот множитель можно представить следующим образом:
і
=<-1',+Ііт-<«+'+і-1''"'"1
, -'■■-'"
к—о *
Отеюда следует, что этот множитель равен нулю Іур. (6)] я что
ряд (8) обладает свойством
П(і+*ні+у)}-/'а+*)+/<і+у). w
откуда мы далее заключаем, что /,(ж) = 1о£ж*1 пока я; обозначает
действительное число. Ряд (8) служит также для вычисления logic
для мнимых значений я, пока этот ряд не перестанет сходиться,
или пока он при помощи (9) может быть сделан сходящимся. На-
жример, ряд (8} дает для ю = — У — 1
СО UO
= І.Ѵ * і * г/~Т У * в
* Суммирование распространено на значения ^ от 0 до q, потопу что ори
*-<0 и при q — X <0 знаменатель делается беиксшечаым, так как (—г)" = со,
если г>0 и целое.
* Это нѳ совсем ясно. Казалось бы, что равенство (8) служит определением
лод-ардфма.
3 В оригинале второй член последней частя этих равенств имеет вяа
*' 2d/.. зѵ->*
12 За». WS3. Н. И. Лобачевввнй, т. V.

178 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Входящее сюда ряды, которые всегда сходятся, как мы покажем
ниже, дают:
іов(і+у=і) = -ііЧС2+-і-*Ѵг:гТ*,
где іг обозначает отношение окружности к диаметру. На. том же
основании [ур. (9)] находим:
log (— 1) = 2 log (V=l) = it ]/~.
То, что здесь сказано о рядах для степеней, логарифмов и
показательных функций, я привел в такой же форме в изданной мною
Алгебре*, чтобы не лишить этот отдел математики существенной
пользы, которую можно извлечь из тригонометрических функций
и из разложения в бесконечные ряды, а также чтобы дать
прочное обоснование вычислениям с мнимыми величинами.
[Ш]
Разложение тригонометрических и показательных функций не
может в современных доказательствах рассматриваться как вполне
обоснованное. Если рассмотреть ряд
Я-Щі—£), [100]
то из уравнения
Сумму ряда
2
? (-1)'
і = и
Лобачевский, повидимому, получает из разложения в степенно» ряд арктангенса,
как и в своей ■Алгебре», где определение чясл» л основано на атом ряде
(см. т. IV наст, издания, стр. 232),
* См. т. IV наст, издания, гл. XI—XIV.
э В оригинале номер формулы пропущен.

Ы. И. ЛОБАЧЕВСКИЙ —«О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ» 179*
следует, что
І»Ѵ—.*' >
гхъ*(і-&):
а отсюда
Наконец,
х^/1 *('-£)■
і
*
Таким образом, остаток ряда (10) после члена і = г
<
следовательно, он убывает до нуля при возрастании г. Поэтому
произведение бесконечного числа множителей
П*) =
* Есліт 0<f<l, то
-iog(l-() = * + -J + f + ...<M-P+P+...=j3T
а?
Положив ( = —j-j , получим:
-М1—ж? <
* Если (>0. то Vl + t<l+ Vt •
э Здесь используется неравенство logf<f—1, а также неравенство ісг —#<
< Уп^гЗ — дрі справедливое, если з;>0 и г достаточно велико (члены
исследуемого ряда содержат только четные степени х, я можно считать, что г>0).
12*

180 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
представляет функцию f(x) переменного ж, какое бы конечное
значение мы ни придали х. Чтобы определить эту функцию,
рассмотрим известное выражение
]ogaina; = 2»tlogeos;r—\-log(2np) + "У, bg(l—j^coti»1)*, [10a]
2n #—і
в котором m есть любое целое число, »=-з—, р = tang —-. Если п
достаточно велико, так что можно принять г < п, да* > а;, и если
положить
log(l —j)s cota іыо) = 2~4og (1 —ps cot2 гш),
ТО получим:
/_bg(l— jt'cotffv)
Следовательно, остаток суммы*
к
2 log (1 —р* cot* wo)
і—1
после члена, для которого і = г:
< — (■£ — »")(1 — 2 "llogCl— ^cotsH4-
где для і. надо взять значение из уравнения для у., в котором на
место |і подставлено п®. Далее имеем:
tang2 ru» —-j?8 ~ ui (tang r® —#} '
[10b]
* Доназательетво атого тождества см. в примечании j85].
* Вернее, абсолютная величина этого остатка.
& На основания признана еходииости Лобачевского
х -і.
1
где верхний индекс суммирования представляет собой то значение X, которое
соответствует [д. = я.
Я Здесь Лобачевский пользуется неравенствами
-logU-tX—i-. (0<(<1) и Ѵ'^г№>а — Ь (а>6>0).

Н. И. ЛОБАЧЕВСКИЙ— «О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ» 181
и если г настолько велико, что гт>р, то имеем также:
-4*
<
д<і.М(і + /2)(і-2 * ) 1-2-М
ш I гда —j> гш -|- j) J
*'{ 1/2 I 2j> „-.Г (і + уТ)2т* 1_]| [10с]
<а(Гіи — %> Гаи)2—J9a j_ ПО+.Р. '"«O+J'J/
Если здесь отбросить те члены, которые заведомо отрицательны,
то получим:
о) \rat — р ггш' — р')
Следовательно, можно всегда взять г < п настолько большим, чтобы
остаток S ряда стал сколько угодно малым и далее при
возрастании п таким и оставался.
В то же время
2ftl°scos£ и kg (vtang£:)
при возрастании п приближаются к нулю; следовательно,
равенство
sin ж ѵі, 1 — »aeot2w>
'*/<*) Jf1 !_■
при возрастании и может быть сделано справедливым с любой
точностью *.
Если здесь положить
1 — рг cot2 ш ч ,
1-f
1*я
то а представляет величину, которая при возрастании п убывает
до нуля; но так как г, число логарифмов в сумме, является огра-
• По поводу неравенств (10с] и [I0dJ см. примечание рт|.
* При достаточно большом г. Иныыи словами, каково бы ни было «>■ 0, если
г достаточна велико, то
г
^ах и V1 і 1 — i»Bctg**e» I
lfan 2j IoS —J— | < E-
xfi?) «*-« — г_

182 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
ниченжым, то мы необходимо имеем:
а следовательно,
/(») =
8Ш.С
X
ІІодобным же образом можно показать, что
log cos х =
ь»(^^)-|^{(і+Й)|.
(П)
(12)
(13)
если применить здесь известные равенства,, справедливые для
любого целого числа и*:
logcos.i; = 2«Iogco8-—h ^ log
taQs5<fe
»/2І — 1 \ '
л ля а; 2
Ьв(-|-)-21овЦ^Г-) +( -2—) (ео*-ЕГ-) }'
4 То-есть, как велико бы ей было г,
и» s
Я -* со .«■.
t.io.i'легально.
( = і
sin j-
так как эта величіша оі г не зависит.
■ Первое пэ следующих далее равенств можно получить подобно тоыу, как
вто было показано дня равенства [10а]. Второе и третье равенства получаются
соответственно из первого и [Ша) с помощью формул, выражающих тряшномет-
ряческие фувкцнн через гиперболические.

Н. И. ЛОБАЧЕВСКИЙ —«О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ. 188
Чтобы найти для ряда (11) остаток Я после члена і = г, полагаем
bgjl- / *!„ } = 2'?logfl-
= log І2«-
ЫГ
тез
:';■
Кі)"
Отсюда следует *:
_1
"2
?+ <
/
1- -,
2
('+ 2") *"
: , 1 Ж
1 + 2*" log
-+т)'-
- -.С
и, наконец,
1Г
(2+Ѵ2)х + ^('-!-4)Ѵ"2,
—(гг^і—-
Для ряда (12) <а определяется и-ч ураг.кеаия
log(l^^)=^log(n-^).
Отсюда следует, если г и [і весьма бо.іыіше чш via:
,. Л. і
І1< — 2-
* В оригинале в левой части предыдущего равенства стоит log(pr + f *),
а зтого равенства: log {f — е~х); имеются и другие опечатки, которые адесь
исиравлены,
* Следующие далее вшыадки повторяют соответствующие вычислении при
яыволе оценки для остатка ряда (10J,
J В оригпаале отсугстнует множитесь 1 + У% прн х в числителе нравой
части итого неравенства.

184 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
и, наконец,
ж
если только
~rlog(l + ^)+(l+V-2)f]/log(l-h^)<^2, [13а]
а это условие выполняется, ©ели я с >■ х *.
Для ряда (13) имеем:
Если »■ настолько велико, что |»' + -^-1 ^ >ж, то
1 , х „-4-х 1
* + Т<Т2
■ /Н'+'і^трЬ
Отсюда для остатка ряда (13) после члена і = г получаем:
й<-(,+І)іоё{1+-^-{+
V^j/logj
-f (1 + ^2)^1/ log 14 _ Vn— <
2э;5Ѵ^2
|1Ѵ|
Разложение функции в сумму бесконечного числа дробей
требует такого же уточнения, как и разложение на множители; между
тем с помощью изложенного здесь метода легко доказать
сходимость таких рядов. Пусть, например,
8=ш 2і~": (14>
тогда имеем:
Л.
[і. = г ■ 2 " ,
* Подробное обоснование неравенств» [13а] см, в примечании psj.
* Ом. примечание (За],

Н.И. ЛОБАЧЕВСКИЙ —«О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ» 185-
н следовательно, остаток ряда поеле члена і = г:
on і
ДО-1- ^ *.
1 — 2 »
Поэтому ряд (14) всегда сходится при и > 1 и представляет
некоторое определенное значение S, как бы мала, впрочем, ни была,
разность п— 1.
Для ряда
га
5в,?<н-«н«+в5' (і5>
где разность а — Ь^-0, надо положить
отсюда следует:
Р= —\ {а + 6) + |/(г + я) (г + 6) 2l-f1 (« ~ й)\
откуда
j><—* + 2s У>-|-в) (»■ + &)*.
Остаток ряда (15) после члена і = г оказывается, таким образом,
В<_ 1 + _Jd^_ (16)
Если а и b — положительные числа и если положить г = 0, то
получается:
в ^ ѴаЬ
Пусть теперь
Я= V І (17)
" В соответствии с признаком Лобачевского
Л<г- >:Сг2»-г)2^<Г1-В У,2 -"^Н---^-^-.
t<f-.2(r2«_r)2V-2!i"l=rl"
Ь=і 1~і 1_3 в
* Так как Уа^ -(- pa ^ | а | +1 j) |. Предполагается, что г достаточно яелико-

186 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
где р обозначает положительное число. Уравнение
(!«(у,п —pf — 2Ѵ (г»—р)
дает:
1»" - у*+\/ -\-*»+ *- (г - р) 2";
следовательно,
Рп<2-\-2* У»-»(г» — р).
Если к тому же заметить, что когда т, а, Ь положительны и сверх
того т < 1, а > Ь, то
•+(4Г>'+4>
loga+log|l+l—I |>mloga + «»logH+ —1
поэтому
и, наконец, учитывая
а™ + 6"' >(а + 6)», [l7al
получаем для л > 1;
_ Л. -і. -L
Следовательно, остаток ряда (17) после члена * = г будет:
В<
г" (г" — р) ' t - і—-
(2 '»—1)(1— JW-") -"
Ряд (17) сходится также при п >-д-. В этом случае имеем:
,4м-і
[i2"<j)-4-p23 j/^« (,-»—_^у_j- 21 г" (»■*• — у),
* В оригинале ыэдздяаіе-іь степени множителя (1—Р*"~І() имеет вид —— — !■■
* В оригинале показатель степени множителя (2р) тшеѳт вид — ,
п

Н. И. ЛОБАЧЕВСКИЙ —«О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ» 1Ѳ7
Отсюда получаем для остатка ряда (17) после члена г —г:
■і - -і-і -L-i
j._ г (2р)ая(1— gr-»)^ , (1—gr-»)» ^
г г(2 4" —1) /а»-і(2 "» —1)
Таким образом, этот ряд сходится при возрастании г, как бы мала
ни была разность Чп—ь
[V]
Перейдем теперь к рассмотрению тригонометрического ряда
со
Пусть сначала для целых и положительных значений п
Р_ VИД(«« + «)
r Z* і+р '
где р означает любое положительное число. Если в этой сумме
объединить каждые два следующих друг за другом члена и
поступить так же со вновь образованными суммами, то получим:
Р,=соаа; Р3+ (?.,,
P^cos^Pa + ft.
Вообще мы имеем для целых значений т і^ »:
где
»»-• da {2тіх -\- <* — і (2т — 1) я'
р __ у Н_
г"— sm |2тІх + я — і- (3 ■ 2*—1— 1)а:
е--2
(£- (2«-И>2~**)(2і+і>2~ -1)
В орикшале это неравенство иыэет вид
_L A -L-i 1--
г -(2 4п-1) г*»~Ч2 '" —1)

188 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Таким образом, получаем:
P-ft-l-У ИДЕ*"1») Q | гіп(2"~1а>) р,
«'
и для »»= и:
Здесь s
він (2*_1ж) 0Ш < У, з—— т -" <
<ІѴ.
и, наконец [ур. (16)],
eiii(2i-1a;)Q4+1<
1 , if I
^(24ч>2-')<1+*2-<Г * i&(l+J,2-«-» +4)(x+*a—Чі>
<
(2-+-jt2-)(l+j2-*) 2d.2-'+2)' 2^(p2^+2)(p2~' + l)
< .- . «-»w, , „п-*\ -.-.,. -.+ ., V ■ ; <
0-р2-г) + (1+У2){У2+2 » Vsp+J2-*}* =
2(2 + і,2-<){14-р2-')
==8+K2+j2~<+~i+(l+Vr2>2~T* /«У ■ '
2(2-Ь^2^)(1+^2-0
* По абсолютной величине.
* Здесь испольеуется неравенство [17а].

Н. И. ЛОБАЧЕВСКИЙ — .0 СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ. 189
следовательно,
,-ц.1
P<Q + L.Vf8 2 +д+Ѵ2)ѴЗр.2 **+3 + У2
j» am — я
Здесь *
1 ^ 1 , 1 + Ѵ2
■^ ('9І _1_ и» /9*' . 1._ « 1 \
Остальные бесконечные ряды в выражении для границы Р оуть:
1
1. S
'^CH-^oH-a'+y
s.fl'-S
1 .
2-т*
ЛІСр + г^ич-а*) '
1:0 — і
,±і(р-И*>(р+2'+У
Для ряда £ мы имеем:
(P + 2|,)(p + 2'l+1) = 2l(p + 2)(p4-l)e.
откуда следует:
2^<2 2 /№ + 2)(р + І) ;
далее
* Подразумевается, что каждый члея как левой, так и правей частей этого
неравенства наіодатея под анавом абео.іютной величины.
Само неравенство в оригинале содержит две ошибки: под званом У в числителе
вместо 2 а напечатано КЗ- , а в знаменателе пропущен множитель 2.
* По абсолютно И велнчине.
э Здесь Лобачевский пользуется своди признаком для оценки остатка ряда,
положив г = О-
Э В оригинале отсутствует двойка пѳрол логарифмом в знаменателе; нет
множителя 2 также в обом знаменателях следующего неравенства.

190 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
еле до вате ль но,
ѵ^ 1 , 1<Ц[(Р + 2)(Р-И)]
Для ряда 8' в свою очередь
<р+ 2^+1)(р + 2^2 * Р =21{р + 2) (р+ 1);
отсюда
далее
ах—а _а_
2І'<2 а (р2 + 3р + 2)5
я, наконец,
1*<та~1)+ 5ІОІ2- —'
у ^ 2 ,2і?&КргЫН£±2Л*
° ^50+1)(р + 2Г 51og2.(p+l)(>+2) '
Для бесконечного ряда S" имеем уравнение
(p+a')(p+2,l+1)^=2lu. + l)tP + 2J,
а отсюда
х—і ^_
2^2 8 [<р + 1)<р+2)]<;
наконец,
„ ^ .1 а-і)4- log[Q> + i)Q» + a)]
Р < -j- (А—1)1 ^^2
1 , bg[(g + l)<g + 2)] »
° ^ 3{p + l)(Pl-2)"I"3log2.(i' + l)(i' + 2) "
После подстановки найденных границ для Q]t S, 6", S" получаем:
1 , 1+^2 ,
і><
рУ2 Ъ$Ур — 1
х ,у(3 + Ѵ2)+|-{1 + і/2)Ѵ^+^Ѵ^
2Sin' J (*+l)(P1-2>
* В оригинале чис.іитель первого члена правой части равен 4.
* В оригинале числитель первого члена ярвво* части равен 2.

Н. И. ЛОБАЧЕВСКИЙ —«О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ» 191
■ log(p+l) + Iog(p + 2)
"•" 30(j> + l)(p + 2)log2 л
х[*в+15Ѵ2 + (12+12^2)Ѵ^ + 10рѴ^|| + *• [18а]
Так как при возрастании р оба отношения
log (j +1) iogCp + 2)
J> + 1 ' P + 2
становятся исчезаюгце малыми, то Р тем более приближается
к нулю, чем больше взято число р, если только віп-к-я>0*.
Найденная граница для Р, которая не зависит от дуги о®, служит
также границей для остатка после члена і=р в ряде (18) е,
который тем самым предстазляет определенную функцию дуги а;<2тг.
Отсюда, далее, следует уравнение
со
9 (#) sin я -J- ф (ж) cos а = V -г- віп («в -+- а) Т7
<=1
где в(і)я|(ж) обозначают две функции, не зависящие от а. Если
* В связи с отмеченными выше ошибками в предшествующих вычислениях
неравенство ]19а] в оригинале имеет вид
р< 1 л-.А+У2 +-—і—і 5 — — j-
"рѴТ 2ру7=і aein^.^1 (p + i)(j» + 2j
+ togfy + D + tog(P+a (4а + ]5 у-2" +{12 + 12 |^2) УТ* + 20р У^І.
* Вернее, если sin-s-^tO.
т
ffl А также и от и.
Э Действительно, для ряда (18) имеем:
в» ~ 2 TO"sio Ш +р) х + "' = S TTFsin l" +а'''
І"1
где а' = j«;-}-a.
там со
I V ^ Sin (S3-f-я) — ЗІП Я У — Яш((а:+-|Л + СОва Ѵ-тг 8ШІГ =
і—1 1 = 1
= sin а V -г cos іх + сов а >^ -г віпіх.
Токе к образом,
в со
<рИ = ^ тсозіг- *(*) = ^ т8ІПІГ"

192 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
■к
здесь положить сначала а = 0, затем я = -^, то получим:
т(ж) + ^П.ф(ж)==^І^-
г
Вместо этого последнего ряда, в сходимости которого мы теперь
уже убедились, мы вправе положить —log (1 —е~аѴ~~^), что легко
обнаружить, если при помощи равенства (9) так изменить ряд, чтобы
получить другой сходящийся ряд, значение которого уже известно.
Для ж^-т-я, <« можно написать:
— log(l—e3,y:::T) = — log (2віп*-і-я!І — log(1 — l^Tcot— x\ =
Еслж х ■< — я, > 0t то мы имеем:
— log(l — e*^-1)^ — log(sina;) — log I tang Л я • V—1) =
= log Y— 1 — l°g sin х — log j 1 -}- tang — x ■ Y— 1J =
Отсюда для любой дуги #>0Т <я
-log (2sin±х) = %1
■ cos гж,
* a,
V (-1)'
i — 1

Н. И. ЛОБАЧЕВСКИЙ — .О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ. 198
СО
-!(*-«)-. 2 Т "*»«>*■ (19)
г
Если в последнем ряде подставнть ти — х на место х, то получается
і ѵ(-і)<_1 ■ ■
-"-.■);= ». ■——; shims
2 ^ г
і = 1
для всех значений от ж= 0 до х < п.
Ряд (19) можеі' быть также представлен в виде
—+«Si
1 . .
sin «a;
рвІп(*-|--5-) X
:= \ L ^1 dx*, (20)
8Ш — X
* Си. сноску £ на стр. 1Й1.
* Мы имеем;
3inf;-t-~"W — sin f i — -^\х = 2 сое іх eta. — х,
sinf i — ~w)x — яіп (*~ ~2ІХ "=Зсов(І — 1) ^вів-д-з;,
.3 .1 „ . . 1
sin — х — вш — х = I сов л; siu -5- #,
•ln((+fl
откуда ——Ь___—і— = і -j_ 2 > cosix.
2 і —j
Если здось умяоясить на dx н проинтегрировать, то получим:
іе
sin ( »'+тг)*
dB('+y)J
21
— sm іх.
1
Следовательно,
х
( sinfi + ^-j х
— -dx + K(i),
I SlH — я;
и
где К,() при возрастающем г приближается к нулю. [Дрклмчвнм ЛЪйчмекою.]
13 Зав. S8SJ. В. И. ДойачевичіВ, т. V.

15*4 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
если последнему выражению придать тот смысл, что пока ж<я,.
значение интеграла тем менее отличается от тс, чем больше взято і
так что разность может быть сделана произвольно малой.
Значение вышенаписанного интеграла для других значений х, которые
не заключаются в указанных границах, легко определяется. Если ю-
означает острый угол и п — любое целое положительное число, тс-
получаем *;
('аіа\і + -\х
\ ___!—-__і— dx== (2и-}-1}к для ж=2»ж -fa», и х = (2»-|-l)ic-f-<o
J ЗІП — X =7ИГ ... Х=Пъ
и і.
= — (2п-\-1)к ... х=— 2итс—ш...ж——(ги-І-І)"—ш
= —тан ... ж™—nit.
Все эти случаи содержатся, таким образом, в следующем правиле:
«Значение интеграла не изменяется, иока х не достигает
границ 2jc, 4it, и т. д.; при достижении одной из этих границ
значение интеграла увеличивается всегда на -к, и такое же увеличение
еще происходит, когда одна из этих границ становится
превзойденной. При достижении границ —2я,— 4іг и т. д. в значению
интеграла должно прибавить — т и еще раз — к, когда эта граница
превзойдена».
С помощью интеграла (20) можно показать известное
разложение любой функции в тригонометрический ряд. Этот метод
впервые изложен г-ном Дирихле и заслуживает предпочтения перед
всеми другими;мыповторим здесь его в несколько измененном виде.
Пусть
*•(•)- \ і Х f(x)dx, (21)
J sin—(a: — <e)
а £
где пределы интеграла а и Ь произвольны, ((х) обозначает
произвольную непрерывную или разрывную функцию от х1 которая,
однако, здесь сначала должна рассматриваться как непрерывная, и
где<п представляет некоторую определенную величину, в то время
как F(v>) — искомую функцию от ш.
* В следующих далее равенствах нужно, как это, иярочем, указано выше
Лобачевским, перейти к пределу при і -* со.

Н. И. ЛОБАЧЕВСКИЙ — «О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ. 195
Если умножить равенство (21) на і&п, затем проинтегрировать
по ш от w = а до ш = {3, предполагая а > a, fi < Ь, то получим:
J J sin—(я:—а)
а а £
J J sin —(»—и)
-f
f [^[(h-tw--)]
I <&/<*) —LV t2/ J л-
J J sin —(jc —ш)
= \ dxf{x) \ V -..- /.-rfa,
sin — «
Г sin
in (і + -к-)щ
nnT"
^sin (* + -5-)(э: —ш)
-f I dsf{x) \ V 1 7 A».
sin T (a;—a)
Так как *—%, Э—x положительные числа, если х заключено
в границах а, а и отрицательные для X в границах р и Ь, то для
таких значений х, если предположить р — »£2n, а—й^ — 2х, мы
будем иметь в силу равенства (20)
іі+і)"
. 1
am — яі
2
" 81П і
* В левой части подразумевается переход к пределу при t-*co
IS*

196
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
с л ѳ доват ѳ л ьно,
sm(i + -s-) (* —•)
?(ш)йш= \ Aef{x) 1 і—~' dm =
sin — (ж — <о)
sin -г- ш J ./ sin — ш
9
= 2к§<іх /(ж)*, [21а]
как бы пи были близки между собою, пределы а и р. Если f(a*)
есть непрерывная функция и кроме того ш > а, < S *, то
сближение пределов » if приводит в конце кондов к заключению, что
или
Ёіп(і + -і)Ж
2*;» = I Г (я-г") * 1—*—<&,
J sin --- х
а—ш &
если 6 — a^z2r.; но так как ш должно быть заключено между
границами а и Ь, то отсюда следует, что значение ж = 0 лежит между
границами Ь — ш и а — ш.
Еслиш <тг, > —тг э не заключено между границами й и а и,
следовательно, значение ж = 0 не лежит между & — ю на— ш , то можно
* Здесь Лобачевский производит предельный переход при і -j- со, я в левой
тасти этого равенства следу еі1 писать:
е
Шп I F(in)du>.
Законностыгрѳдолі.ыогоперехода в правой части равенства может быть обоснована
бѳа особого труда (см. примечании [№\)-
* В оригинале о> > — т;, < + іс.
* Здесь в левой части вместо Р(ш) нужно писать lira Р(м). Это равенство
не обосновано. Оно справедливо, если предел limF(ui) существует (т. е. соответ-
стиующий ряд Фурье сходится) и стремление к пределу равномерно в некоторой
окрестности точки о>.
Э В оригинале <а<^2г.,^>—2я.
3 Точнее: ѳелк—-я<»<я и i»-[-2ftit (fr = 0, ± 1, — 2, ...) пе заключено
ы^зеду а и Ь, т. ѳ. если значение #=2fcn не находится между 6 — ш и а—»
ІФуакциа F(w), определенная « помощью (21), имеет период 2т].

В. И. ЛОБАЧЕВСКИЙ — «О СХОДИМОСТИ ВЕОКОНЕЧНЫХ РЯДОВ» 197
так удалить друг от друга границы а и Ь, чтобы <в * лежало между
ними, и в то же время положить f(<a) равным нулю, так как
значение f(x) вне границ «, Ь произвольно. Отсюда следует F(<a) = О,
за-исключением значений, соответствующих самым границам яиі,
для которых не могла бы иметь места непрерывность функции.
Если юі= тс или чі = — г к кроме того
sin—(ж —«}
smH-b-g-ja;
F(*) = \ dxffr—x) — V *'
I
din ~X
sin \t+ — \x
dxf(x — v)- ^~
Если 8 означает произвольное сколь угодно малое число, то
г -in/i+f)* У ■* (*+■£-)*
sin (* + -=-)*
sin — лг
»n(f4--s-)!C
* Точнее: ш + 2Aic.
* Здесь ааять производится ее отраженный в обозначениях предельный
переход при t-юо. Окончательный результат справедлив, если яа функцию Да;)
наложить условия, позволяющие совершить предельный пѳрвюд под вняном
интеграла.

198 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Подобным же образом получается:
F(— я) "=*/(*) + */(— it).
Если непрерывность функции f(x) нарушается при ж = о» между
границами а и Ь, когда Ъ — a^2it, так тіто f(x) начинается ео
значений А с той стороны, где х уменьшается и со значения В с
противоположной стороны, то непрерывность сохранится, если при
х><и вместо f(x) взять [(.«)-{- А—В; тогда мы получим:
sb(i + — )(* — я)
ЛвДя) — і-г—' +
аіп--(да — <о)
sin(« + ^-)(* — «)
rf»[/(s)+A —Д] Ѵ г ' +
8ІП—(я: — ш)
эі» {* + -«"](«—»)
+(Л—J) » <'- ѵ 2/
9Н1 ~г-(Х — ш)
Здесь два первых интеграла объединяются в один между
пределами а и Ь и дают, как было выше показано для непрерывной
функции f(x), значение 2,кА, тогда как последний интеграл
представляет значение іг; следовательно, теперь
Р{») = т.А-ігтіВ*.
В дополнение к предшествующему заметим еще,что непрерывность
функции F(v>) нарушается только вместе с непрерывностью f(x)
при я = «, за исключением случаев, где <и= pit или <в = — к, в чем
легко убедиться яа рассмотрения выражения (21).
[VI]
Теперь займемся еще решением задачи:
Определить, может ли положительное число А(„), которое
находится в некоторой определенной зависимости от числа п и
возрастает вместе с п, превзойти некоторую определенную границу?
* Здесь тоже осуществлен предельный переход при і -* _о.

Н. И. ЛОБАЯЕВСКИ Й — «О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ» 199
Пусть
со
Применяем изложенный вначале метод. Полагаем
отсюда следует, что
СО СО
1 = 1 ^~1
значит,
со
Пусть, например,
і—і '
тогда мы имеем:
^+'—4«*«-'el(«(1+S+T=i)-^
+»'
далее,
Разлагая в ряд, расположенный по отрицательным степеням
■}* + '« — 1, получаем:
Если, кроме того,
то можно взять п настолько большим [*>], что
■+|
(n + !*-lf
■откуда следует:
>«-'Кет-^Ы.
' *«— 1 п-\-а

200 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
и, наконец,
іЛі(п—1)
Это последнее выражение определяет точность вычисления во всех
случаях, когда а> — 1 —f—^= *; если же а меньше этой границы,
то можно положить
1 1 , t «^ 1
■Гн; + -ГнГ+Т + 1овя- Ss+TR- (22>
Это означает не что иное, как то, что в Ап на место а доставлено
а-j-l, и, продолжая таким образом, можно довести а до желаемой
величины.
Если умножить Ап на da и проинтегрировать от « = 0, то
получим:
^^^logj^^p^,)^] [22а].
для а>0 и <1, с точностью
,(1 + ^2) УЗ ^(1+V2)VS°
уп(п— 1) и—I
* В оригинале последняя часть неравенств [21с] имеет вял
Y2 и —1
Ум(в-1) »(»-Ь1) *
* В нераленствах [21с) последняя строчка дает оценку в случае, когда О^я^ I,
а дае предыдущие — когда а > -— 1 -| =.
® В оригинале
1+7^ »-і ) ! а і і
в евяэн с отмеченной выше ошибкой к [21с].

Н. И. ЛОБАЧЕВСКИЙ —«О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ» 201
Отсюда находится значение функции
тем точнее, чем больше взято целое положительное число г *,
а именно с приближением, которое характеризуется множителей
е г_1 *.
Если а > 1, например а^р-^-а,, где ш> 0, < 1, а р — целое
положительное число, то мы получаем из (23):
Наконец, если а < о и если положить в—— р-\~ш, где ji означает
целое положительное число, далее ш>о, <1, то с помощью (28)
получаем s:
((0 «)"»W^= .
ѵ -с' ш— р
Если функция от п неограниченно возрастает вместе с п, то можно-
получить приближенное значение, если отделить такую ее часть,
что остающаяся не превзойдет некоторой определенной границы.
Лусть, например, дана функция (ж + а)***, где х означает
некоторое целое_ положительное число; пусть, далее, F(х) — новая
функция, такая, что
(.!; + ■)-*:= (я-|-а)-1»;-
* То-есть Лобачевский, do определению, полагает (ем. примечание [*])
С С М|.»Г
logn — D= 1 8 (a) da = lim I A, da = lim log
J r-*oo J r-+™ (e+ •")■*r
о с
где i? (a) = lim A„.
* В оригинале б связи и ошибками в [21с] и [22а] это выражение имеет вил.
13 Действительно,
9 Авалогично тому, как ато показано в предыдущей сноске.

202 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОП
тогда мы имеем:
log
^«(*-l)loe.(l-^-).
F{x-
Чтобы здесь уничтожить тот член, который в разложении по
отрицательным степеням x-j-a не зависит от х, принимаем еще:
J?(x) = e~* в (ж),
а чтобы уничтожить ѳщѳ один член ряда, пусть
?(x)^(r, + *f+~b(x).
Таким образом, можно было бы продолжать, чтобы уничтожать
один член за другим. Если мы ограничимся уже сделанным, то
получим:
<» + «)-« = (х + *?+'+т (-.$&), (24)
где
Если, кроме того, обозначить значение ^(#) при # = °° через /(<*),
то в согласии с излагаемым методом для определения f(a) нужно
прибегнуть к ряду
log<,(*) = log/(«)+gbg ^|~lj-, (26)
который тем точнее даст значение f(a), чем большим взять х.
Предполагая /"(а) определенным, имеем:
(я + «)"я = />)(;с + а)3'+в+Зе-*Х, [26aJ
где
+ (* + * — ■!)
іоеХ=Уіоё^±і~!
■К*) = ' —т;
следовательно,
^^а—'+(-+-І)^('+^=т)
или
00
w *<?=±> _ 1V '(-1Г1 (27)

Н.Ж. ЛОБАЧЕВСКИЙ —*0 СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ» 203
Из этого последнего ряда и из (25) следует, что х всегда можно
взять достаточно большим, чтобы было
ФИ ^ 12(ж + а)''
1
<
12(я; + в — I)2"
Вместо первой из этих двух границ можно также положить
ф((в) "I2(a;-f-e)(a; + a-l-l) ~12[x-j-a a;-f*+i"
я, следовательно,
logX = glog -' \ £^ > Т8(Я + ,-Ц)-
Вторая граница дает:
"*'-£-«і?йг1<^і
Применением нашего метода и при помощи значения
5» = (,і- + а —1)(2*"''— 1)
получаем:
Ѵ2
Следовательно, всегда можно взять х достаточно большим, чтобы
без заметной разницы иметь:
(х + *Г" = №&+в)'*"~*е-я, (29)
причем это равенство тем вернее, чем больше ж.
Значение функции f(a) должно быть вычислено здесь при
помощи равенства (26), т. е. с помощью выражения
. *
* /'(а) является пределом выражения, стоящего в правой части этого рівен-
ства, при іс-»оо.

204 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Если здесь положить в=0, а = -^, а—■ — -^ , то получим *:
Если в последнем равенстве подставить ж-^-1 на место я;, то
получим: ,
Подобным же образом в выражении для /(0) можно подставить
2я? на место ж, откуда получим:
/ 1 \*°а
/■(о)= L_/A___*
а;
ЧЧ-7.ГТ
а
/2
Отсюда следует;
=^-Ѵгі(і-іТ- [28аі
* В правых частях атих в всех последующих равенств, служащих для
определения /"(О), Л-s-j. М —"5")* подразумевается предельный переход при ж-ют.
* Здесь вужао воспользоваться тождеством:
<2х)-9я = я
, 1 -, w X

Н.И. ЛОБАЧЕВСКИЙ—«О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ. 205
а при х = оо это равенство дает;
Следовательно,
Между тем мы имеем также:
12,1 2) (-Ч)Ѵі)
е2л
-^і ^»+] =
и, следовательно, при # = со
,(i).,(-i)-fw.
* Это равенство немедленно следует иэ [28а], так как
Wx-Jjf *
* Пользуясь исходными выра-жеянями: для м-у) и /'( ~-5"Ь получаем
«едленно
'©
і \«
3 Последняя часть этих равенств в оришвале имеет вид
г^ Здесь оледѵет воспользоваться равенством )іт — ,—; г^- = 1 и
разложением функции sin хс в бесконечное произведение, из которого следует,
что

206 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
и, наконец,
Выражение (28) переходит, таким образом, при я = 0 в
с тем большей точностью, чем больше взято х. Подобным образом
мы имеем для всякого значения а:
/(«) = —-^— ■ --— ■—-— ■
Ы)
Здесь fai-j-a-f- 2")logf 14--—J тем ближе к я, чем больше х;
следовательно, имеем:
„.)_«!±£_Ѵ.!?*.
х е
Это выражение-—то же, что и следующее из (23) для
а"'
Таким образом, снова показано, что выражение (28) представляет-
значение некоторой функции от о тем точнее, чем большим взято
число г. Таким образом, при принятом обозначении мы можем
теперь написать:
Из найдѳняых значений для f\^A t fi —---)' ^W получаем:
* В правой части цодрааумеваетіія иереход к пределу при х-*-ас Это равенство,
следует иа (28) » [3Sb].
* В правой части следует перейти в пределу при й-»іл.
ф Это равенство — аиныптотическоо (при х-*-оо).

П. И. ЛОБАЧЕВСКИЙ —.О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ» 20Г
и вообще
с тем большей точностью, чей большим взято х.
Это выражение в своем значении совпадает с тем, которое
принято для случая, когда а—целое положительное число и,
следовательно, п.""" представляет произведение целых чисел от 1 доа.
В дополнение к предыдущему мы примем, что для любого
значения и и а выполняется равенство
я""
которое само собою выполняется для целых чисел [**].
Идя по избранному ранее пути, можно продолжить
приближение к значению функции от большого числа. В качестве примера
рассмотрим равенство
*—-УК»*4"*"*—+,(">* (31)
где, как мы видели, функция <о(х) разлагается в ряд но
отрицательным степеням х. Если бы в этом разложении мы дошли
до х~п и при этом показали, как это имело место при и = 0, что
сумма остальных членов заключена между определенными
границами, которые сами при возрастании х уменьшаются до нуля, тс*
можно показать то же для следующего члена ж-"-1.
Итак, пусть
Равенство (31) дает:
(*—§-) log (l ~ "У - " 1 +*<»)-*<*-1).
откуда следует:
в (ж—1) — <в(х) =

■208 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Далее
Бели здесь подставить г — >- —|— 1 на место г, то получится:
со . Я со .ф\_і
да в со .«х-1 » .
j(—і)-та=s8(t+i)(;+2)^" s^s^r+si?-*
i—i ѵ ' ' ѵ ' ' \ = \ і—1 J,—a
2(« + 2)-Ѵ+1 ^.^«*n ■
Подобным же образом мы найдем:
F(as — l)—F(x) =
;-2S(-ir*A(i+2)0-1+1(A+ir2 —» ,
Для определения и неизвестных коэффициентов, которые по
порядку получаются из Ах, служат п уравнений
2 ы
* Здесь используется тождество пв™ ™ = ио"°я—".
* Если «<^то (п ч Щ-—лелые положительные числа), то п"*л = 0.
п » —1
° В оригинале а втях равенствах пропущены слагаемые \^—г я: Л,—ттт-
1—2 (=1
9 В оригинале это равенство, частично п связи с ошибкой в предидуіди
равенствах, имеет вид
I В оригинале в атом равенстве верхний индекс суммирования не І, а » — *»о
связано с отмѳчевпыми в предыдущих сносках ошибками.

Н. И. ЛОБАЧЕВСКИЙ —«О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ. 209
где на место * надо последовательно подставить все числа от г = 1
до » = «[«]. Тогда разность F(x— 1) — F(x) оказывается
выраженной двояким образом, а именно:
- '-2І(^+1)-а(г + 2ГХ+%
'"-"-'"-кг 2^+2)-ѵ+-— ■ ™
Здесь п есть наибольшее значение А; следовательно, и—1 есть
высший показатель при і- если теперь рассматривать все Лх как
положительные, то получим, что каждый член ряда (34) по
абсолютной величине меньше чем
А
о-І—1
^'КІ,<-
1)°
(а-_ і)і+'
следовательно, надо только взять х настолько большим, чтобы
log(,-1)>log(,+ 1» + ^bgj|- + 4-|i^A^-|
и тогда каждый член ряда по величине станет меньше единицы
и при дальнейшем увеличении х будет убывать в любом
отношении. Если увеличить х таким образом, то можно наконец,
достичь того, что по величине
Р
Р(я-1)_-F(x)<-
>
(я —1)в+4'
Р
аЯ+2'
где Р зависит от п [**]. Так как доказано, что F(x) становится
нулем при я! = оо, то имеем:
^x^Sfa+iliy.^-
* В оригинале под еваком внутренней суммы в числителе дроби пропущен
множитель (—1) ~1.
£4 Зэк. S82G. И. И, ЛойачевсвиА, т.Ѵ.

210
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Если применить к этому случаю иаш метод суждения о
сходимости рядов, то получим:
С другой стороны, мы имеем [ур. (38)]:
=^+і 1(«-і-пГ'=+і ~ (я+п-иГя+і)
[34а]
откуда следует:
Обе границы, между которыми заключено F{x), определяют вместе
с тем точность вычисления в предположении, что в равенстве (31)
х взято достаточно большим.
Числа Аі, которые мы сейчас рассмотрим ближе, должны быть
определены из выражения (32), в которое на место і подставляются
по порядку все целые числа от 1 до п. Таким образом, для
определения любого А„ служит уравнение
2
или в другом виде
5-»=2(*+і)"в(» + 2)ГІ+1^
2(»+2)(И + 1)-ІіП° А*
(35)
* Б оригинале вто неравенство имеет вид
і_
2р 1 "+2
FW<
(X— !,«+!
я + 1
* В этом неравенстве вместо F(x) следует писать jF(s)|. Знал абсолютной
величины подразумевается и в предшествующих неравенствах.
Ия (33) следует, что при достаточно большом я: анак величины F{x— 1) — F(x)
совпадает со знаком коэффициента при г-"-3 и остается, следовательно,
неизменным; это дает основание для получения неравенства [34Ь] при помощи
суммирования неравенств вида [34а].

Н.И. ЛОБАЧЕВСКИЙ —«О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ» 211
Отсюда видно, что множители А^ принадлежат ряду
L = A1 + A&^As4 + Aia:t-\-.., =% Аь£-\
і-=і
произведение которого с другим
* = &*
дает:
со со со со
л.«2 2<*+*-і)Г^,л4+1-1=2 2 «г*-1.^*-
1=1 і=0 1=1 П=1—1
п=0 X— 1
Применяя равенство (35), мы заключаем отсюда, что
<*> „ »
= -4(е»-1)-^(е»-1-а>-г-£,
откуда следует:
і=і і=і
Мы теперь закончим наше исследование некоторыми замечаниями
о функции, значение и способ вычисления которое определены
равенством (29).
* В оригинале в втой части равенств переставлена знаки У Кроые того,
а оригинале вслед за этой частью равенств следует исключенная ваий следующая
част і.:
™ п + і
= 2 <1»?^*А =
В = 1-1 1 = 1
* Так как п"т = 0, если ів>л Ш н п — целые положительные числа), та
2 2 »і-'л<=2 2-о"1"Ч^=
ІП СО 11 fl-f-1
= ^^2«Г-Ч= 2<2»Г1-Ч-
П=0 1 = 1 П=0 >=1
14?

212 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Для любых положительных чисел п, т и далее для
отрицательных, меньших ^ по абсолютной "величине, интегрирование по частям
дает*:
л ft —Г *и I 1 />
1 aiainxco&imxdx=———~— I ѳшая+8;ссо9атжй!а:;
вообще мы имеем, если г означает целое положительное число:
{* (ft __[-_ ■№ _|_ f\ p
Здесь выражение
достигает своего наибольшего значения при
■• /~п-\-г
tangs =j/ -3_;
следовательно, можно всегда взять г настолько большим, чтобы
сколь угодно приблизить х к пределу интеграла -=■, и
одновременно принять, что
1
а7=,_.,с_(0?
sin ж = е а ,
С08 X = (О.
Таким образом, мы получим равенство
(» + *— т) °
* Следующие далее выкладки, кончая равенством [35а], являются, в основной,
повторением аналогичных выкладок в сочинения 'Способ уверяться в исчѳзаяии
бесконечных строк...» (стр. 111—113 наст. тона).

Н.И. ЛОБАЧЕВСКИЙ —«О СХОДИМОСТИ БЕСКОНЕЧНЫХ РОДОВ» 218
которое тем вернее, чем большим взято г. Следовательно, при г=оо
мы имеем е полной строгостью [ур. (29)]:
о 2
і
dx =
^rjVV z*fe. [35a]
2(« + «)"
Отсюда мы заключаем, что для любых чисел n-j-l>0, »»-|-1>0
ао со
С »*•*• Г
1 e-3>3Pdx = —— I e-xxmdx*.
J я»"1».]
о о
При »і = 0 это дает:
СО
о
„11
При п = —-, п = — -=- получаем:
га
Г — 1
о
* Эта равенство легко получить иа (35aJ, если заменить соответственно » и «
через re + -s- иів + ти учесть тождество
Г япв»+1 a;cos8"**1 *dx « Г ain*»+l a:соя <™+1 aids.

214 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Вообще мы имеем при n -f-1 > О, m-j-l>0:
і
а ж In —1\ /И—1\
am"» сов™» dx = ———' . (36)
Подобным же образом можно найти еще некоторые интегралы*;
например, при п+1>0 и при любом числе г получаем:
f • ■ -«л (ft-f-2-H}(n + 2— «if . . .
\ am га; sin" xdx = ;—т——-,—— I em гх вт"*1 х ах.
Вообще для любого целого числа г
г.. (^+'Г(^-Ч°"Г
\ sin іж аіп" й! (йв = — \ ѳіпксвіпп+г,а;(Ь;.
) (т+') (^+'1 •>
При г = со отсюда следует:
тгпия8Ш —іте
8Іп гж sin" ж (to = ■——і-+'( 7Г=і ■ (37)
Точно так же находим:
" 1
Р тип"" СОВ— Іх
\ еоэіз;sin"хdx = —я+* " —й11*- (38)
j 2.(»4і)"т(^і)"т
Прл п = і получается:
п
| sinnxma.nxdx = %2~nsiii-s- пъ,
• 2
IE
I oosnxem.nxdx = ъ2~п <!OS-£--t>m.
J 2
* Дальнейшее, кончая формулой [39а], является совращенным повторением
изложенного в сочинении «Способ уверяться в иечезании бесконечных строк...»
(стр. 119—122 наст. тома).

Н.И. ЛОБАЧЕВСКИЙ — «О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ» 215
Оба случая (87) и (38) объединяются в одном интеграле
з
а"
і
О
coBixcosaxdx = —. г (39)
*»№ '№)
и при г = 7і
1_
а
ТС
J
cosnarcosntftfo: = -~~* [39а]
Этот интеграл впервые найден Пуассоном (Journ. de 1'ёсоіе polyt.
т. ХП, р. 490).
Нет никаких препятствий рассматривать а в уравнении (29) как
мнимое, откуда следует, что интегралы (36) и (39) остаются еще
верными, если в n-J-1 и т-[-1 действительная часть больше нуля.
К этим интегралам можно присоединить следующий *:
і
я"
J
(е3'* -f « ~Ux) соэ3» х dm =
it (2л)-2"
(,1_|_іУ^1}-("+'>'-^(п_і1ЛІЛ)
—г.-(*_іП) '
где п > ^ і или п0 крайней мере его действительная часть
удовлетворяет этому условию. Этот последний интеграл можно
или непосредственно получить из (39), или получить тем же
методом.
Наконец, рассмотрим еще интеграл
/(»)=■ j
e»v-1d«
где # означает любое положительное число, а п также любое
положительное число или мнимое, у которого действительная часть
положительна.
* См. формулу (127) в сочинении «Способ уверяться...» (стр. 162наст. тома).

216 СОЧИНЕНИЯ ПО ТЕОРИЙ РЯДОВ
Если продифференцировать по р и проинтегрировать по частям,
то получим:
Следовательно,
где ->(«.) не зависит от р. Выражению для і/{п) можно еще придать
такой вид:
Ф(«) = 2 -^ГТ f сов («ж—J) tang ж) cos»-г х Же * [*]. (39b)
Интегрирование по частям показывает также, что*
^ (л) = п ^ (п -f-1).
Вообще для любого целого числа г получается:
+ («) —(п + г —1)-'ф(п + г),
т. е.
і
ф(»)= „~_і——Г cos(jwe—ptanga: + rai)cos',+''-,ar(fo:®1
или, если подставить р~(-г на место р,
і
1""
■}>(»)= ' ' .„^-j \ cos(иж—ptangx-\-rx—rtalngx)cosn*r~3xdx.
Если j- — весьма большое число, то элемент под знаком интеграла
принимает свое наибольшее значение, когда а; очень близко к нулю;
* В оригинале отсутствует множитель 2 в правой части [39Ь].
* См. формулу (111) сочинения «Способ уверяться. .. » (стр. 151 наст. тома).
э В оригинале отсутствует множитель 2 в правой части этого и следующих:
двух равенств.

Н. И. ЛОБАЧЕВСКИЙ — «О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ» 217
следовательно, в этом случае
і
*ы=2{п£17)»!'Т $ «*—-*• [39с]
(р + г)
или [ГР- (29), (39)]
*(«)-
2a.r"rr»-ieP+>-(n + r—2)~'l+t~*
()^1)-»-1(р+г)"+'-12»+'-1/'—-Л"* я Ѵ^+Г-Л" 2 '
Здесь [ур. (31)]
.У&г'+К-*,
,.+^
\ 2
Отсюда имеем:
и так как
то
(и-|-г—2)w"l+»'-a = y/2ir(n4-»-—2) ае-»-"-а,
ф(я) =
(»—i)-»-»(jp+r)»+»—* '
exV=Idx , 2ке-Р
J„ <J>+xV~l)n (и—I)"*-1
для всех положительных значений р и я, а также и для тех
мнимых значений, у которых действительная часть положительна.
Из уравнения (29) непосредственно следует:
а-"(— «)--« =-т
sin (air) '
* Подробное обоснование этого равенства см. в примечания [И].
* В оригинале отсутствует множитель 2 а числителе и множитель (« —1)~*~1
в знаменателе.
я Здесь, как и выше, предположено, что г-»-со.
9 Вывод этого равенства дав Лобачевским в сочквении «Способ уверяться »
[формулы (24), (40), (43)).

218 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
что справедливо также для мнимых значений а; например, для
действительных значений х имеем:
(ѵѴ~іГхУ^(-хѴ^і)
а для действительных значений вир
sin аіс (е1* + е-1^) + J/ — 1 cos ait (е*Р — е-"Р)

ПРИМЕЧАНИЯ
Ш
Oft исчезанин трнгоьожетрическш строк
і1] Доказательство сходимости ряда, данное Дирихле в
цитированной статье, вполне строгое. Однако равенство
со
О
действительно не было в этой статье обосновано. См. об ѳтом
подробнее во вводной статье1).
|а1 При [L < І- и Ъ > а
v.(2—f.)f(pe)dx
2\if(x)dx
тех — и>
1*4-4 (1 — ^}8іп» 2
[J.2 -f- * Sm!
ц»(*.іп»~!-ц»)«*)
ate
<
4 sin*-
!]
<
<2^
|/4*)|4»
J (^+3*1"^) (^ + 4***^) > + 4Sin*
ТГХ —«
С другой стороны, если функция f(x) равномерно ограничена в
интервале (0,1), то, как бы малы ни были положительные числа е и S,
'} Стр. 21 ваоі, тома.

220 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
можно выбрать столь малое положительное числа р0, что при ft <С Т*о
ш—В
\f(x)\dx . С \f(<e)\dx
2[і3
,8-f 4ems
ткс — а,
<Е.
В то жѳ время при любом ц. (О < ]і ■< 1)
\fix)\dx
*'J
м—* iA2-j~4ains
тсс—а»
<<Л
где С > О — постоянная.
Таким образом,
і
І/Ч*)!**
о [»а+4вша
из; — m
<* + съ
и, ввиду произвольности величин з и 8, утверждение Лобачевского
доказано.
[3]Еслифун«ция/(#)непрерыввапря ж = —, то, каково бы ни было
е > О, можно взять S = [іг столь малым, чтобы
5
if
1
■'(^)-'(ѵ)
1+H
<-(іт^<
■па
-j-rs ^Т
йг
<
и, следовательно.
Аналогично
Ііш
■t-i-0
№
(4е)
А-
+ г*
■(т)
^ 2

ПРИМЕЧАНИЯ
221
Но, по доказанному ранее
_t lim
1С ц->0
J 1+г» +J 1-t-r»
= lim Г
p(2-i0f<ar)At
- 4 (1 — [») sin;
и, следовательно, era величина от 8 не зависит.
[41 Повторенные Лобачевским рассуждения Пуассона, строго
говоря, доказывают только, что
I ос. 1
f (Л — о) +/■(— -Ь°|= f f(x)dx-\-2 Hm У |**Ѵоов(ііиг—«»)/(*) <te.
*
Однако, в отличие от доказательства Пуассона, доказательство
Лобачевского теоремы о разложении функции в ряд Фурье является, по
существу, строгим. Действительно, рассуждениям Пуассона у
Лобачевского предшествует доказательство (справедливое при
определенных условиях) сходимости ряда
і
со »
V I сов(«ят — iu>)f (x)dx.
*ri,J
Следовательно, каково бы ни было s ~> 0, при заданном w можно найти
такое К", что при п > N и р > и имеет место неравенство
і
г Г I
2 J cos (tier — !іо) f(x) dx J < !
и, на основании известной леммы Абеля, если 0<![і<!!1,
і
2 І1*] сов(ітгх — i<a)f(x) dx
Таким образом, ряд
і
2(*( COS fee— iia)f(x)dx
< р"а < в.
сходится равномерно относительно ц, если О-^ji-^l и, следовательно,
Urn S I*1 і cos (іты; — w*1) /"(*) *е — 2 I сов ("^ ~~~1*) f (x) dx'
Ѵ. + 1 і-1 ? і = 1 oJ

222
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
[ь] Разность, например, между первыми членами правых частей
[24а] и [24Ъ] легко преобразуется к виду
X
^[(г+2)<а 8 ^^^^^..^^^.^д, (а)
sin—{а — 8— ю)
it
Лобачевский фактически допускает лишь изолированные точки
неограничен: ности для f{x) и f (х) и притом только такие, что при
приближении к ним как слева, так и справа, эти фѵнкции стремятся
к бесконечности определенного знака. В силу этих условий,
интегрируемость функции f{x) в окрестности точки а равносильна ее ебеолютной
интегрируемости и в интервале (л, а — 80) при достаточно малом S0
функция f{x) монотонна; следовательно, произведение f(a — В) аіп —
ограничено, и если 3 < | а, — ш |, то под интегральная функция в (а)
равномерно ограничена и величина (а) стремится к нулю при й-* О
равномерно относительно г.
\е] Если Р(і, 8)—выражение [24а], то для того, чтобы доказать,
что ,Р = 1іт.Р(г, 8) —*-0 при 8—>-0, нужно сначала доказать, что1іт.Р(г, 5)
существует.
Докажем прежде всего существование предела lim Р' (г, 8), где
Р'іі, 8) — выражение [24b].
Как уже отмечалось в предыдущем примечании, Лобачевский
фактически предполагает, что при достаточно малом 3 функция f(x)
монотонна п знакопостоянна в интервалах (а —8, а) и (и, a-f-8).
Если Ж;, х„, ..., хп~ нули функции sin /г-|~--](а — ш — 8)іг
в интервале (О, 8), то
х
J віп[(*'+т)<й~« —В)«1л = ±—t^~y\-
"* ЧС(І+Т)
j 8щГ/і+і-|(а — « — 8)Tt]r(a + 8)(f8
«(''+т)і

ПРИМЕЧАНИЯ 223
С другой стороны, члены последовательности.7,, /„ Ія, ... , где
"к
по абсолютной величине монотонно убывают и знаки всяких двух
соседних членов ѳтоіЧ последовательности взаимно противоположны;
следовательно
|вш[(г+-|)(а-ш-8)л]^(а + 3)й8 < 2 j'|/-(a+8)|^^0
при г —у со.
Применяя такие же рассуждения к другому члену
выражения JP'fi, S), убеждаемся, что 1шіР'(і, 8) = 0 при любом достаточно
малом 8.
Переходя к выражению Р (г, 8), имеем, сохраняя прежние
обозначения:
3\
sin
івГ(і+т)<а+в-10>1І1
ein —(a-f-8—ш)
sin —-(« + 8о—ш)
іп[(і+т)(а+8~0,),г1'Г(а f8,dS-
I ..АЛ И і{(а х8)db =
sin — (a -j- Б — w)
8)d8,
= I 8m|(i-|-~)(a tS— «")*W + ;
.шіС + Ц—, J U 2> J
гдеО<гоОІР хк<Ьк<лк+1.
Можно ваять S столь малым, чтобы функция sin ■=■ (a -j- 8 — ш)
была знакопостоянной и монотонной в интервале (О, S); тогда
множитель перед интегралом в правой части последнего равенства
определит монотонную последовательность и, на основании известной
леммы Абеля и раесуждениі, примененных выше к выражению

224 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Р'(і, 8), получим
•шп[(і+4) <*+*—•>*]
sin -— (д -f- 8 — ш)
Па + Ь)Л
<
<а
■(<+i)J
|«а + *)|Л,
где а — наибольшая ив величин
1
(Ь=0,1,2,...,н).
Проведя подобные выкладки для другого члена, входящего
в Р(і, В), легко убедиться, что lira Р (і, 8) = О при всякой достаточно
малом В. '"*■"
Таким образом, утверждение Лобачевского справедливо, хоти
переход к пределу при 8 —*■ 0 излишен.
П То-есть HmP(t, t)=l\f(a — 0) + f(a + Q)].
Здесь опять-таки доказано не существование limP(i, 3), а суте-
ствование предела выражения, отличающегося от Р(і, 8) на величину
бесконечно малую вместе с 8.
Для того, чтобы доказать существование lim Р(і, 8), достаточно
*->СО
воспользоваться равенством
ism
Ы)
тсВ
sin —
■in (< + -§")
w8
-/'(в + 8)Л +
эш-
sin
+
*+І
Г(а+»)Д+...
■-- +
Р-(' + !)
*5
аш
*8
/-(а+ 8) Л,

ПРИМЕЧАНИЯ
225
монотонностью ffa-f-S) при достаточно малом S и применить
рассуждения, которыми пользовался Дирихле при доказательстве теоремы
о разложении функции в ряд Фурье и которые были хорошо иавѳ-
стны Лобачевскому, как это видно, в частности, из ссылки на статью
Дирихле в начале настоящего сочинении.
п
Р] Пусть Л„(і) = і-і-2\|іт,к Тогда
II L fc=l -1
IT " 1 1 Г Г " 1 1
^JU^Y^sinM f(c~t)dt+\\c-\-2 2 j-віпЫ /(<:-*)<« =
e L i=l -1 ft L ft=1 J
= (Ѵ + тт — f)f(c —()Л— U„(fjf<c — ')<« +
T (
0 frail ^
где s произвольно (0 < e < с).
Функция f(x) предположена, конечно, интегрируемой, а, как уже
отмечалось выше, Лобачевский, повидл мом у, не делал различия
между интегрируемой и абсолютно интегрируемой функциями, так
как под неограниченностью функции в точке он всегда понимает
стремление ее к бесконечности определенного знака с каждой
стороны от этой точки.
Тождество 2 V -"-'- = _±—-d! — / показывает, что вели-
W л J I
і J зш -.;-'
чина \ ■• am kt\ ранаоыерно ограничена в интервале {О, s) и, сле-
доватѳльно, каково бы ни было В > 0, при достаточно малом s
■+22 4«-«
j f [ с 4- 2 Л' ~ sin ht
f(e— t)dt <S.
В сочинении «О сходимости бесконечных рядов»1) Лобачевский
покалывает, что
|яиИК—^Ц->
!) Стр. 190—161 наст. тон».
15 Век, 2823, H. И. ЛобачевіЧіИгі. т. V.

226
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
где Л — постоянная. Следовательно, каково бы ни было а, ложно
выбрать п столь большим, чтобы
JRn(t)f(c~ ()dt\<b
и, таким образом,
lim \
в
=1
-\-2 V -т-8Ів.і(с—х)
с
*=1
f(x)dx--^
о
(с 4-к — t)fic — t)At= (r.-]-x)f(x)dx.
Точно так же доказывается, что
lim 1 с—2 V — віпй (.с —г) ffx)dx = - - | (тг — x)f(x)dx.
Способ уверяться в нечеаанин бесконечных строк
и приближаться к значению функций от весьма больших чисел.
I9] Трудно объяснить вту ошибку Лобачевского, так как он сам в
других местах *) пользуется критерием Кошя. Нам кажется, что эта ошибка
может быть объяснена лишь следующим образом: Лобачевский сам нѳ-
употребляет никаких специальных символов для обозначения
предельного перехода и только о помощью словесных пояснений (не всегда
четких) даѳт знать читателю о том, что такой переход совершен.
Повидимому, слова «можем взять г так в ѳ лак о...» или «когда г можно
взять довольно большое число» обозначают у Лобачевского, что
предельный переход при г —у оо произведен. Иными словами, Лобачевский
воспринял критерий Коши в изложении Дирксена как утверждение о тол,
что lim am существует, если неравенство lim | ar+m — aT ] < е имеет место
ш -> оа г -*>-0
при любом положительном а, каково бы ни было м, т. е. если
lira. (ttr + „ — ar) = 0 при всяком т, а потому и привел пример, проти-
г-*со
воречащий такому неправильному утверждению,
I1"] Лучше сказать, что f{x -\-a) представляет собой ряд в правой
части (15), причем каждый член этого ряда определяется с помощью (14),
то-ѳсть исходить из основанного на (11), (12), (13), (14) и (15) равенства
(х [-а)-" = ф(*)(» + аГ+"і""* Г'Гух-^-л), (а)
') Си., например, стр. 127 этого сочинения (страница укааана по наст. тому).

ПРИМЕЧАНИЯ
227
где
со «
Следует, однако, показать непротиворечивость определения
функции х"", получаемого из (а) при а •= 0, и определения этой же функ-
пяв с помощью равенства
ѵъ ..... (Ь)
(Лобачевским доказана, по сути дела, непротиворечивость этих
определений только для целых положительных значений а.) Пользуясь
исправленными в сносках к формулам (18) и (14) обозначениями '),
имеем, если 11 -\~ я \ > 1,
и
A (0. a) _ (l-j-«)° + T
Положив в равенстве
(* + *)"* = (*-|-af+0 + *•-«/-, (x, «}
x = 1, получим
/oil, Я) = .
] I
следовательно,
Л(0,я) = —
Положив в 8том же равенстве д; = 0, будем иметь я"° = 1. Из
равенства (а), таким образом, получаем (при х = О)
С другой стороны, это jse равенство при я = 0 дает
ж"* = У^к x"+'Je-''f(x).
Если в атом равенстве заменить х через а и соиоотавить его с
предыдущим, то получим равенство (Ъ).
') См. стр. Ш наст. тома.
15*

228
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
[и] Лобачевскому не было известно, что Эйлер еще в 1729 году
(письмо к Гольдбаху) нашел формулу
I' (s -f 1) = Um —- -
то-еоть формулу (54) этого сочинения Лобачевского х). Формула (49)
следует отсюда немедленно. Олѳлует отметить, что вообще формула
Эйлера была аабыта, так что, например, Гаусс, который также пришел
к этой формуле, тоже счнта,ч, что она найдена им впервые.
[]SJ Формула (59), известная иод названием теоремы умножения гамлчв-
функции была сначала доказала Лѳжанлром для и =2 (Exercises tie
calcul integral, Paris, 1811), а в общем случае сперва Гауссом
(Comment, soc. tegiae acient, Gotting. tec, том П, 1813), а потом Лежан-
дром (Traite des fonctioiis elliptiques, том II, 1826).
[") Если под L(l-\-iV) понимать ряд (83а], то свойство [83Ъ] имеет
место только при \х' < 1, \у1 < 1, |х~\-у -(-ху ] ■< 1 [кап Лобачевский
и указывает в своей «Алгебре» 3)], а также в случае, когда одна или
несколько на величин ;?, у, х-|-у/-j-.су имеют модуль, равный 1 (а
модуль каждой из остальных меньше 1) и все ряда в равенстве [83Ъ] —
сходящиеся. Однако по существу Лобачевский понимает под L (1 -j- х)
функцию, совпадающую с рядом [83а]. когда этот ряд сходится, и
продолѵкенную с помощью fS3b).
Именно в ѳтом и состоят смысл утверждения Лобачевского, что
(83bj справедливо для всех & и у. В сочинении «О сходимости
бесконечных рядов» в) определение функции loff(l -j- ж) = і(1 -J- х)
сформулировано более четко.
Iй] При любом а > 0, если -т целое число,
а _а_
" ІХ . их
sin к й.? . ,. ѵі smA-Дз;
\ dx = hm У — Д.е = Um \ -
J X А.т-*(1 -^ К AX ,™ -л ^J
Способом, при помощи которого получена оценка (83), легко придти
к неравенству вида
\ 2і г, |^ . х '
■ п = !■■! 1 ! и діп --
]) Стр. 11+ наст. тома.
а) См. т. IV, стр. 222 наст, издании,
-ч) Стр. 177 наст тома.

ПРИМЕЧАНИЯ
229
где .1 —постоянная, полученному Лобачевским в статье «О
сходимости бесконечных рядов» J). Следовательно,
іі sin к Да;
k
Дат '
<
.1
а , &в
— sin
Да; 2
<•
равномерно относительно Дг, как мало бы ни было положительное
число г, если а достаточно велико.
Таким образом, при достаточно большом а
_!* Ле—lim V ******
J Т. ІІЕ-» 1) ^J
['"] Если ;< — четное и яте ^.х < (и-\- 2)п, то
<*
^S I °"-+l^-.
*; = О п 4- Iti
а тате как
ч—і"±"
2 J ^*~2 І<^>'^ =
k=0 O-L-JiK
tl ' IE
±J (« + 2fcr)[a:-f-(2A-J- І)я]
<£e
і™ H 7Г-
ft -— П
^0,
то нетрудно убедиться в справедливости доказываемого утверждения.
["] Непосредственные вычисления показывают, что
Ііиі -т— log
1)"
і + Ь '
а следовательно, также
lim -r- log
. г,0-1"
= 2(-і)'
і
(я + А- "
!) Стр. 190—1Ѳ1 наст. томи.

230 СОЧИНЕНИЯ НО ТЕОРИИ РЯДОВ
Равенство (49) позволяет утверждать, что
lira log
Г->00
(f-H'
(—+*■)
— log-
^'
_._!
Ч-'"
Но отсюда еще не следует соответствующее равенство для
производных.
[17J Запись промежуточных выкладок, приводящих к ѳтому
равенству, неправильная; в частности первый из интегралов в прав о it
части [85Ъ] — расходящийся. Общий интеграл [85а] при а > О
имеет вид (а > 0)
а а
~,r, \ - і і ■ Г аояп j Г s^aa j
¥ (а) = вj sin а -(- с3 соэ a -(-sin а I аа — соа а 1 аа.
т я
Так как F-+-—при а-* 0 и
в
а
ѵ Г ■ Г COS а 1 .
lira, ми а I аа = 0.
п_»о L J а I
a
то
і>
п , 1* sin a
С = — -+- I tfn
2 ' J й
а
и, полагая а = 2іг, имеем
о а к аі
^/« . * . Г sin a , С sin a , С sin a
(le) При любом е
da -I
г -^
( 8Ш
f' (х-\~ш) dx I ——■-■■ ' ■ dx =
J sin -^
d- '
I f (я-J-ltt) (fe
Г sin (г -j--i J
to —
./ sin —
V 2
+ n*-
В>^ " i"2-
dx. (a)

ПРИМЕЧАНИЯ
281
Яо
Г 8іп(і+у)а;
Их
<с.
где О — постоянная; следовательно, вви-jy абсолютной интегрируемости
С sin (» + у I а;
f(x + m)dx \ -1——I fa

Sinai
< С*.
где С —постоянная,
В то яге время
■ ~ ■ -~і ах = г— 2 у — suit
.■к
sin —
2
і+і
Сумма ряда в правой части этого равенства сгрѳмитси при І—* оо
к нулю равномерна относительно ж, если 0 <| s<,c<2it (см., например,
примечание [14]) и, следовательно, каково бы ни было в ]> 0, второй
член в правой части (а) может быть стелан сколь угодно малым по
модулю при достаточно большом У. Учитывав, наконец, произвольность
числа s, имеем:
У->со
= « \ /*(* + »)<& = іг[Д*) — f{m)\.
[19] равенство [101 а] — асимптотическое (при % -> оо). Получить
его можно следующим образом. Если I — целое и полокитѳльное число,
то, исходя непосредственно из определения (10), имеем

232 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Из (42) легко получить
,( _. 1
(а)
а так как при *—>■ со имеют место а сим итог очес кие равенства
■і—=-> ч'і4 , ,-4-» -«■"+»
М-) ' «^(<-Н "Оч
!
то при г—* оо асимптотически
/. » \ £ » , і
(-Т-) ~^П(,-М
Но
е-
т-Ѵ-т -"- .. ('-т-0"
/ 2 \ г -"-і
Urn 11 : 1 = е - и 1
і -*со \ г I і
Іііи =1;
- і-
ел ѳ лов ате льно
(«-Н"'"*-'-г''"*-'. (Ь)
Равенство [lOlaJ немедленно следует из (а) и (Ъ).
Для получения равенства [101b] представим его левую часть в
следующем виде:
т
1 (—IV
in, \"г / и \ " <
т+') (~г—
Если воспользоваться для і — — — 1 асимптотическим
равенством [101а), заменив -^ череа — -.,— 1, то получим [JOlbj.

ПРИМЕЧАНИЯ 23»
[3(|| Выражение [110Ъ] показывает, что интеграл [iiOaJ сходится
ирв jiijfcO и н >■ 0. Прн р = 0 интеграл (110а] расходится, если п < 1.
Интегралы, входящие в [ІІОЬ] в пределах от 0 до *-, при л > О
сходятся абсолютно и равномерно относительно р в интерпале (—со.оо);
следовательно, интеграл (110а] сходится равномерно и интервалам.
(—оо, —е) и (а, со), как мало бы ни было положительное число е.
Равенство, получаемое иа (Щ) дифференцированием по р,
справедливо, если п > 0 и і> ф 0.
[21] Непосредственное исследование функции
на экстремум показывает, что если г достаточно велико, то при jxT»
мта функция положительна и монотонно возрастает в интервале (0,.с0),
г,-us .в0 = aretg 1/ '■' . , а в интервале (л0, -^-1 монотонно убынает,
причем
5
■?(^) = 0(. + ,-)arctgl/ -!L=£- _ |/(я —,0 (р -L- г j < ^Г^: ;
если :ке р >■ п, то j о (зг) | монотонно возрастает во всем интервале (0, -^-1.
Так как легко доказать, что lim у (»■-*) = 0Т если Л- > -^ , то, каковы
бы ни были р и ji, неравенство 1и (#) | < е(г), где lim г ()*) = 0, имеет
место ■ для всех значений .г из интервала (0, г-*'), если - <fc< .,-
(х„ < г-*, если к < тг и г достаточно велико |.
Кроме того,
1 cos [(и -4- г)х — (р -J- г) tgж] со8ч+'"-') хdx < I cos" + '-гж rfa; <
<(T^i'"i)cos"fr"5,r'*)<Y(1 2^)П+Г 2<Се ' ' (а>
где G > 0 — постоянная.
Но из (49) я (50) следует, что при г --► со асимптотически
^7
!■
Crts» + '—-'.r<tess- Л-^ / -г- I (Ь)

234 СОЧИНЕНИЯ НО ТЕОРИИ РЯДОВ
Сопоставляя (а) и (Ь), легко придти к выводу, что
Ига —
Г cos [(я -\-г) х —(р-(-»■) tg#J еод"+г_ *х
-*xdx
г -*oj —
Гсояп+г-Еа-'Ас
о
Г eoa[{n-\-r)x—~(p-\-r)t^x]cos"*'—^xdx
= Цш :г* (с)
г-!-со г
I со8п+7'_! ят rfa:
о
■если к < —.
С другой стороны, при - - < к < -,-
і еоз І(я + г) ж —(p-j~''l tg.»icos"Tj'_! j-rfr =
о
г"* t-ft
Г „ Г . , («4-'*);*-—(Р -f >'і ta ->■
= 1 cos»+'—-fedx—2\ sm2!—і—-- -^-J—— - -cos»->-r--.<:dx =
0 II
r-« ,.-k
= oos"+^aartig~2amaV ^ ' —^£-J -+■ °- 1 cos»+r-5 ж Ac,
it и
где 0<в<у-*.
По доказанному ранее
І(и+г)в —(р + г)ія(і;<«(г),
прпчѳм lim е|>) = 0, и из (с) следует, что
| eos [|м -j-r) .-с— (р -f-r) tg■ х\ con"~r--xdr
lim u—— = l.
(aos"*r-^xdx
а
Равенство [111с] (в котором предполагается переход к пределу при
г.-> са), такин образом, обосновано.

ПРИМЕЧАНИЯ
235
[2а] Как это следует иа сказанного в примечании [so], равенство
вила [111а] справедливо для (значений р а каждом из интервалов
(—со, 0) и (0, со); однако вычисление константы JF (вависящѳй от и)
следует производить для каждого ив этик интервалов отдельно. Между
тем значение [llldj было получено при помощи замены р через j>-\-r
и перехода в пределу при г->со; таким образом, равенство [11 Id.)
найдено для р~> 0.
[2S] Иа равенств
л
"■Г
cos(nx—р tg се] cosn"i х dx =
(п — і)~«-і
f siii{wx—р tgx) сов"-!жйх = о
получаем (і = ]/ — 1):
(' . ., 2ке-"р"-1
= I (созж-[_*8т;,;)" е~р' **соз"--х dx ■-
{« — 1)"»
Замена —ptgx=*t (как уже было отмечено в предыдущем
примечании, р>0) приводит к равенству (113), справедлив о л у при р > О,
п > 0| которое можно также записать в виде
1 г е' dz _ 1
[**] Таким образом, строго говоря, построенное Лобачевским
определение функции я."*- таково.
Бели X — целое и положительное число, то
(в + о)-* —(» + »)(*+« —1)...(*+1).

230
СОЧИНЕНИЯ ПО ТКОРИИ РЯДОВ
При помощи первого на равенств (По) определяется для целых,
положительных значений х функция fix, а)
/ (х, а) = г .
т+г + —
(* + *)
причем для однозначности следует пол (х -\- а) г понимать.
(.т + «-[--1-)]о^(лг + *) .
^ s/ , где имеется в лиду главное значение логарифма,
то-есть — я < Іпіlog(х-\-а) <Съ\ при таком условии непрерывность
ао отношению к ъ функции f{x, а) нарушается только при
отрицательных значениях х-\-а и при 3j-{-a = 0.
Далее, ко всякому (комплексному) я можно подобрать целое и
положительное число хп так, чтобы при а; ^ #ц величина я -f- я не могла
принимать отрицательные значения и обращаться в нуль и чтобы ряд
СО .35
при х^>хл сходился равномерно.
Поэтому второе и третье иа равенств (11.5) определяют
функцию <Ъ (а):
1о?,'Ь(*)=!1іпі log f(x, я) = log /"(ж, і) — log X(#-4-tx),
причем функция ^ (а) —аналитическая во всей плоскости, а с
помощью первого равенства (115) определяется функция (*4-а)ЯЗ!
і
J'i »-і— г... , ., (Ъ)
в области, где ряд (а) схолится абсолютно и равномерно, то-есть при
всех значениях х и а, для которых (ж-|-я-[-ft | >■ 1, где 4 —любое
целое положительное число.
В частности,
x~^ss=Y^xlt'vi с-хх(ж), (°)
так как ф (0) = V 2гс.
Равенство (с) служит, таким образом, определением функции х"х
в области, определяемой неравенствами ) х -j- к | >■ 1, где к — любое
целое положительное число. Бинѳ, которому приписывался приоритет
в получении равенства (с), пришел к нему лишь в 1S39 году, то-есть
на четыре года позже, чем Лобачевский *).
) См. вводную статью, стр. 26 наст. типа.

ПРИМЕЧАНИЯ
287
Распространение определения функции і~' на любые комплексные
значения а производится Лобачевским е помощью равенства
"~*—щ-> (*>
пе противоречившей, которого с равенством (с) была покааана в
примечании [І0].
ІТэ определений (Ь) и (d), как показал Лобачевский '), следует, что
(,г -{-«)"« + » = (дг+й)"* я~«. (ѳ)
Это равенство обосновано, волн | х~^-а-\-к\ > 1 ((.* — любое целое поло-
вштельное число).
Из равенства (с) следует, что, при Re а ^> 0, функция в"* не имеет
особых точек, целые отрицательные' значения а являются полюсами
этой функции, как ато видно из (d); гак, если я—целое и
отрицательное, то (ж-{~в)~л = 0 при любом целом и положительном #.
Следовательно, при а целой отрицательном fix, а) =э 0, а потому и ^ (я) = О.
Основываясь на равенстве (ѳ), легко заключить, что никаких других
особых точек функция о"" иметь (в конечной частя плоскости) яе
может, так как, если х—целое и положительное, го при любом
значении а, кроме целого отрицательного, («4~ о.)™^■ф. О, и если бы точна
а (а не равно целому отрицательному числу) была особой, то точка
x-j-a, при достаточно большом целом положительном .с также была
бы особой, что противоречит тому, что н особогі точке функции я™"
действительная часть аргумента не может быть положительной.
Так как функция я*** определена во всей плоскости, то
равенство (ѳ) может служить определением функции (я-j-я}™". Исходя из
этого определения, нетрудно заключить, что (jr-L3)"^ = go, если ж-|-з
— целое отрицательное, а а не равно целому отрицательному числу;
если а —целое отрицательное, а .ж-j-* не равно целому
отрицательному числу, то функция (ж-)""1*)"* имеет устранимую особую точку
и для сохранения непрерывности следует положить (.г 4- а)--г =*■ 0.
Устранимыми особыми точками являются также точки, в которых
как я, так и я-j-a являются целыми отрицательными числами; при
атом, если х > О, то следует положить
(,; + а) -' = {.с + «) (* -)- і — 1) . . . О -г D-
если жѳ х < ") І0
и если х = 0, то
(*4*)"е=1.
і) Стр. 110 наст. тома.
*) Ом. сноску ,+ к стр. 1.1S.

238 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
[56] Очевидно, ход рассуждений Лобачевского таков.
Если а = р -j- я (г = У— 1), то модуль под интегрально го выражения
в правой части [117а] (под х1' следует понимать главное значение
и |з;(т|=1) равен е~* х**г и достигает максимального значения при
Подстановка х = г -f- p -f-1 дает
f «—af+'de= j e-C-+f+')(r + p + t)r+a
dt
—r —p
Наибольшее значение модуля подинтегрального выражения в правой
части соответствует значению t = 0, и чем больше *-, с тем меньшей
ошибкой можно в качестве пределов этого интеграла брать — I та. і,
где ( мало сравнительно с г. Поэтому можно под внаком интеграла,
считать, что
-(і+-| "_ряа(і+_І_р/1 *-р«
■г + «)
Таким образом, при большом г
1
о"" I е *ѵт"' ,
1/2* J іЛ'+*
а после подстановки ( = г у 2 \г-^-п и перехода к пределу при г—» со
со со
■> I 2т: >І
Замечание Лобачевского о том, что «... воображаемая часть
интеграла уничтожается для г = со» обозначает, повидішому, что, хотя
после подстановки ( = гУ 2у г -f-a интеграл вычисляется не и о
действительной оси. а по определенной втой подстановкой прямой в
плоскости комплексного переменного, тем не менее эта прямая при г—* ее
приближается к действительной оси.
Хотя рассуждения Лобачевского и нѳ являются вполне строгими,
однако при помощи соответствующих опепок их нетрудно обооновать.

ПРИМЕЧАНИЯ
239
[м] Лобачевский считает, что в левой частя [118а] при достаточно
большом г можно заменить верхние предел интегрирования через
сколь угодно малое положительное число а в положить
/ Х- l-",+S''-1 J.!
,,f+1iss 1 :- I «jI— (2w + 2f — 1)—Pal — r^sae-'»".
я»и + 1
a в правой части [118а| произвести подобные замены после
преобразования
Г sin2n*^T+1 хсо^*1 х dx= Г sin2™-*1 xcost't+1ir+ixdx.
О 6
Таким образом, он прахоцит к асимптотическому равенству (118Ь].
Далее, с помощью подстановки гхг = г, легко получить
1 га-
J 2»*+'J
0 D
и, положив >« = 0[тогда = r"*n придти к (118), минуя [118с],
причем в правой части (119) подразумевается предел при г-+со.
Все эти рассуждения можно строго обосновать, сопровождая их
соответствующими опенками.
["] sin0-*-11 ѵ~^х = s\naxeb r=> '"f»1" *.
Отсюда, с учетом (42),
Г sin«3;[cos(61ogsmx)-f- V—lsin(blogsini)[rfj? =
/e+ft^-l-
/ п
вЧ-ЬѴ'_і —I I
-) ' И) '
а+ЬѴ'—і
Ы/ і \ " г
^
/а + Ь^-ІХ"»

240
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
[S81 Это равенство нетрудно получить из предыдущего, если
учесть, что
Й([ЮѴ$][('-т)'-^
ft*
-) СО
п
1 —
~~ я2 (a2 -+- 6S>
[м] Здесь, как и во многих ранее отмеченных случаях, раосужде-
ния Лобачевского таковы:
тс
* " ■( — — \
|301 Если Л'—-целое и положительное число, то
Г еіз>sin"a?da; = (— 1)" *(2*- '> ** [ с*1 sin" x<Lr,
f eix ein" «ds= е**'к Г <?'* яІп" a: dr
е'*віп."ж<Іж--=(і4-{— 1)" с'*-j-е-'с 4-(~ 1Г eMe + ---М е*л эіп"жЛс =
1 + (-1Уе<-
1—<■*
е>« sin» х dx =■=
_a2_^i_?_[i±(-j) <■ ] _
." — л —i
«+<1 —1
(a)
я 4-1)/—l\ ■ (v—iV—X
(1 — ри.)

ПРИМЕЧАНИЯ
241
«ели, конечно, І<0 или, в более общем случае, Rei<0. В протин-
OQ
ном случае 1 е** sin* а; е?ж расходитея.
о
Если к—-целое положительное или нуль, то
1 + (- 1)%*' 1
и в этом случае формула (126) справедлива.
{И
U сходимости бесконечных рядов
[Э|] ж log—< (■ х\ 2 log 2-\-х log а < - 1- х log a.
Ко всякому положительному числу в можно подобрать такое а, что
—2^- <; — , а к определенному таким образом значению а подбирается
такое положительное г, что о.г < 1 и х log а < -s- при х < е. Таким
образом, при я < а
х Jog — < 8
и, следовательно,
lim [жlog— 1 =0.
[е5] Равенства I и II следуют из [За]; равенство III является
определением символа «"""в случае, если т — целое отрицательное число
и получается формально из I или П, если учесть, что. по
определению, п-п=1; V следует из ІГС и II (или I); [ЗЬ] следует из V; VI
следует из I (или П); VII следует ив определения символа и" ; ѴШ можно
получить из [За], так как
»"">-f-r)"r |-г1 г-\-і г + п
*• II • г ч, » Г
[ай] На основании [7е]
> |.>[1(| + 4)(7-()т ^ »!(»-1)('-2)('->)('-<)] ■
(а)
1{і Зое. авЗЭ. Ы. 31. Лобичовсвий, т. V.

242 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
В интервале 3 < ( < 4 выражение ((—1)(( —2)((-—3} (£— 4)
отрицательно, и, как показывают вычисления, достигает экстремального
значения
, равного —1 I при t = _-_.- I; поэтому
tta — tc а» -- ta а> > *<в
|((Н_4)(7_0—^-»
Нижняя граница величины -^-(' + 4)(7— () при 3<і<4 равна 4
(достигается при ( = 4), а так как ш2= 3 —2 ]/1Г< 1, то
1 1 1Q
б" т м ' 20 "^20
Неравенства {Tf), таким образом, справедливы, а в коэффициенте при
fro5 в последней части неравенств имеется, иоаиджмону, опечатка или
описка.
[Я4] Повидимому, Лобачевский имеет в виду следующее. Для того,
чтобы при извлечении корня ряды (4) и [ТЬ] давали одпо и то же
_і_
значение корня, нужно, чтобы значение (—1) й выражалось по
формуле 17 а].
Пусть
Из свойств ряда (4) следует, что число е~ ~~ отличается от числа
в ~~г только знаком коэффициента при У—1; следовательно,
л-.ѵ=і = (і±^І)Т(1_(_1+/т)/^Т,.
Обоэначжв
І2
Ь
2 + VYJ ' '■ 8'
Лобачевский приходит к равенствам [7hJ.
Следует, однако, заметить, что ни равенство [7g], ни, тем более,
второе из равенств [71і| не определяют однозначно числа it. Так,
например, равенства [7g] не нарушатся нри замене ~ на я — lGirfc
(fc=0, ztzl, z£2, ...I.
[зъ] Для дальнейшего достаточно предположить, что и = 2 , где
м— целое положительное число.

ПРИМЕЧАНИЯ 243
Тогда
„ . х х . х . х— іѵ
віпа; = 2 8ш---ео8—- = — 2 sin —-sin
2 2 2 2
„, . х х , х— к х— тс
— — 2а sin — cos — вт-—;— cos-
4 4 4 4
„, . ж . эт— ir х—2іг . х—St.
= —■2'* sin — em—-—sin am
, TT ■ x — fcjr
4 4 4 4
I
й- а
Более общее равенство
sin 2 = (— іу-Ѵ1-1 TTsin - — (b)
можно доказать для любого целого положительного в, исходя на
иеаеотного тождества
гдѳ г — "(Л— * ■
Далее, ив (а) или (Ь)
«—I тт / х . кг. . х кт\
вша; = -—2 II (cos — sin— — sin — cos — 1 =
,-M » » и я /
n-l
п
fr=l V
э; тт . for ТТ / х кп\
— 1 I sm II 1 — tg — ctg 1 .
п—' . X ТТ / se . Атт j: fcru ,
= 2 sm— I I cos—эт—- — sm—-008—1 =
n J-f; \ « и n
П—1 Я—1
n—1 X
= 2 tg — cos" ■
Следовательно, при любом х
П—1 H—1
in x n-i x TT - k" TT / a: ftit \
— = 2 сов«_Ддт—-ЦДі-tg^ctg-j
sin
tg
n
и, переходя к пределу яри х-* 0, получаем
к —1 .
2" Двіп—= «•).
* = і
') См. также сочинение Лобачевского «Способ уверяться в нкчеэании
бесконечных строк...», стр. 117 васт, тома.
16*

244 СОЧИНЕНИЯ ПО ТЕОРИЙ РЯДОВ
Таким образом,
Но
X я ТТ / ж кк\
msc = »tg — cos"— II [ 1 — tg—ctg — =
» при к = п
x fcrc as , кк
l_tg_ctg_-l+tg —otg—=1.
Следовательно,
[3G] Так как ж ■< тиг и р->г, то
J,etg|« = t(rls.«g_<_—<і.
В то же время, если U < t < 1, то
Сд едовате л ьно,
р2 ctg3 рш ^ _0-і
1 — рв ctg2 [>w
Отсюда
>—2 log(I— р* ctg* no).
— 2 'log(l— p" otgs ro)
/)2ctg- fio> > --j — .
1 — 2 log(l—j>actgam)
l/ 2^
t*<ig?*<Py '--log(L_p.ctgVtu)<
* 1
/— log(l— j>>otg*r») J'
хак какУі-|-' < l + l^'. если '> °-
J*1] Первое на неравенств [10с] получено из [10b] заменой tg г*
черѳа гоі, что оправдано для второго члена неравенства [10Ь], но
неверно для первого члена, так как он отрицателен. Таким образом,

ПРИМЕЧАНИЯ
245
это и последующие неравенства, служащие для оценки В, не
обоснованы; однако нетрудно убедиться, отбросив все отрицательные члены
в правой части, что следующее далее заключение о том, что
величина \В\ при достаточно большом г становится сколь угодно малой,
и притом равномерно относительно п, справедливо.
Действительно, учитывая сказанное выше, следовало бы вместо [10d]
писать
ІЯ|<ІІІ±Ѵ1.
№ р
Но величина — равномерно ограничена flint Л—Л ] И] следова-
тельно, каково бы ни было г > 0, можно к нему подобрать такое г0,
чтобы при т > г0 и всех » имело место неравенство | R | < *■
[*SJ Если тиг>'^|, то
и условие [13Ь| сводитоя к неравенству
(а;1 \ ж3
которое, конечно, выполнено.
Далее, если положить
/
1 2гѴ- + ~ЗіѴ " '" 1_ "'
Ч1+^)+(1+КГ)?/Ч1 + ^) =
— (^-^+-)+<1+^)^/і-і^+5І-..
=ж-#+г(2-^~^г+...)-а+^,^,=
д^уТ яг* Г., . .,-. / х- ** , 'И^£ІКА
так как
ЗА* ' ЗА4
^ ...=1 — 2« + *а

246
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
и, следовательно, 2д ~> „jj-ъ—а-< "і ~Ь ■ • ■' поѳтому тем более
Таким о бравом, неравенство [13а] обосновано.
{'*] Из (18aJ следует, что
ип [г
Й» — it
■ш-
<т "
em
2'
где 0 < ж < 2іи, а и Ь — некоторые положительные достоянные и, таким
образом, как малы бы ни были положительные числа е н 6, можно
ваять і столь большим, чтобы
t
sin
-■— Л) — и
sin(i+"2")lU
<«,
если 8<;;<;27г — 3; следовательно, при достаточно большом і
sin. | і —|—^-1 аі
ІШ2
-rf<e ;< 2г,
если S <^ (j <^ (2 <^ 2и — S.
Кроме того, каковы бы ни были ( (О ,^ £ <; Л, где Л —любая
положительна» постоянная) и г,
\ - -—^ '-— dm
ш
sia-—
2
<С,
где С — некоторая положительная постоянная, так как при О ^ і ^ іс
8іп[*+т)m
< I * Г1^— *и<

ПРИМЕЧАНИЯ
247
С другой стороны,
f(l«)rfU) =
в — Т
Р-ІГ
sin—-
. tJ зга т
I j sm(i+— jot Г Г sm
+ \ f(x)dz \ —^ ^-rfa + \ ^)4в I —
('+т)
sin
О)
2
81П -
■Л» +
Я—J -і р И— Lt
Г* sin (І + —-} в> Г Л sin (і-(---)■»
fC»)to\ —' =-t—d«—\ f(^)d« I —* '
if a ■
0 l
г—аЛ-г
Ш
,y sm —
Pain[i + — L Г Г" sin It-)-—) »
/■(ж) da: I 1 ^—rfoj—l f(x)dx \ i li_ rfa
Если функция f{-t') абсолютно интегрируема, то при достаточно
большом і получаем
Р Р sinli + TJ ш Г*
\ f(x)dx \ ^ ^ от
< 2s I f(x)\d.c.
1—X
В-ж
sm —-
f{x)dx
*Ы)
?+*
1—.г
3-.1-
Г(х)<іл
1 віп(':+|)
|«-3
а—іГ
3-j-
f(x)dx
sm —
-('+!)
rfu)
(/ш
S1T1
(0
Э,П--
l&O
<2« |/Ѵ)І<**,
■
<C I \f(x)\dx,

248
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
<е I \f(x)\dx + C
<г \ \f(x)\dx±C
\НЩ<&,
а+8
а так вше с и о произвольны, то
lim [ F(m)do> = 2x [f{x)dx.
\№\**>
f(x)\dx.
f{x)\dx,
Равенство (21a], полученное Лобачевским еще в 1834 году (см.
стр. 70), содержит теорему о том, что почленное интегрирование
ряда Фурье абсолютно интегрируемой функции f(x) приводит к
сходящемуся ряду, сумма которого равна интегралу от f(x). Эта теорема
была вновь доказана лишь в 1906 году Лебегом.
[*'] Правая пасть [21Ъ] имеет вид
(1+ =)—!• 0-Мг-у (1 + а)« —і-
(Р+М_1)» (р + я — і)! (^ + „ — і)* ' ■■■
Если л > —і4-—, то (1 -\-af-—->0 п ft -{-«) — у>°. a ПРИ
достаточно большом и абсолютная величина суммы всех членов ряда,
начиная с третьего, меньше абсолютной величины второго члена;
следовательно, абсолютная величина суммы ряда в правой части [21Ъ]
меньше первого члена ѳтого ряда.
Далее (для обоснования |21с]) следует учесть, что:
log
и—і я —1 2(и — l)s
...<
и—1'

ПРИМЕЧАНИЯ
249
откуда
log . — —-—- <" — в !__
"я —1 п + « » —1 и-(-а (п~1)(н~^-а)
Кроме того, так как
(„_i)/bg-!! ]~)
lim ^ в „ + ^ > я,
п -*■ <
то при достаточно большой п
, , к , к — 1 и — 1
_l,i_1)log_ + -—(<_,___s.
[41J В [?2aJ подразумевается предельный переход при я ->■ со.
Лобачевский совершенно строго доказал существоаание предела
lim f Л„<іі = fs («)<*«. (a>
"*'°о о
где S (я) = Ііш 1п.
Именно для этого он в последней строке {21с] пришел к
неравенству вила
13(a)-А. !<■(»),
гце 1іте{и) = 0 и е(п) не зависит от з, если О^а^І (тот факт,
что г (п) от в не зависит, специально отмечен Лобачевскпм).
Отсюда он получает
ъ a
0 0 0
то-ѳсть опенку [22Ъ], из которой и следует существование предела (а).
Лобачевский, таким образом, близко подошел к понятию
равномерной сходимости.
[43] В атом сочинении Лобачевский принимает в качестве
определения функции a"n при любом а равенство (23) и не пользуется тем,
что равенство [2ба] также может служить определением функции
(а:-{-в)™*, й, следовательно и х":г, не только для целых
положительных значений .к [как это было показано в сочинения «Способ
уверяться в иечезанпп бесконечных строк...»1)]. Поѳтому адееь нет
необходимости доказывать непротиворечивость равенств (23) и [26а],
і) См. стр. ПО васт. тома.

250
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
и Лобачевский ограничивается указанием на непротиворечивость
равенства (23) и определения функции а.°" для целик положительных
значений в, а равенство (30), справедливое также для целых
положительных значений я, принимает за определение функции и~° для
любых п и а.
[481 Для того, чтобы разложение F{x — 1) — F{х) не содержало
членов с покавателями при т, меньшими, чем п -[- 2, следует поло-
ZC ■—г Д.
зкнть
ч
-^'=2<Л+І>"а^+2)"І+1^~^2>и3^-М (* = 1.2 «-1) (а)
ft
4-"-2 (>. + і)"*-(п + 2)а-у+1Л;:, (Ъ)
но, так как (і~\- 2)" +1 = 0 при к > t-f- 1 и (і-\- 2)"(_г~ = 1, то
равенства (а) и (Ъ) сводятся к равенствам (32).
[**) Это не совсем точно. Иа равенств (34) следует, что. как мало
бы ни бьіло положительное число г, можно найти такое Х(в, и), что
при х > X. (s, и) имеют место неравенства
где Р(я)— коэффициент при (х—1)~"—s s ряде (34).
\<ъ] Действительно
tb (я) —: «*/"(я) = в* -г—■ -- - = яр —- где г= I/—-1.
' ' J (р -4- за;)" J (я — tx)n ' '
—со —оя '
Подстановка х=р tg ( дает
со 2
f e*arf.c (' еЪЬг pdt __
J (р + м)"~ J pB(l-f-(tef}"* coPT™
^ "J
Г gifts t „ 1 Г
J p" ' (co8f~f-»sin()» p"-1 J

ПРИМЕЧАНИЯ 251
Аналогично
J (р — ixY
—м
и, следовательно.
e~tmdx
tdt
I e'W-jn,(| cos"-=i
p"-1 J
ф(п) = — I [eUnt—ptgtj _j_e-i(n<-/itef)]Cos«-s tdf-
r I cos (nt —pig I) oos"~"-idt = rl GO&Int —ptg?)cosn_sf dl.
p"-1 J p" 1 J

Ири-дожемыи I
ПРИЗНАК СХОДИМОСТИ ЛОБАЧЕВСКОГО.
Одним ив наиболее интересных оригинальных результатов
Лобачевского, опубликовантіх в сочинениях по теории рядов, является
найденный им признак сходимости знакоположительных рядов.
Лобачевский пользуется этим признаком для доказательства сходимости многих
рядов и бесконечных проивведенпН з для оценки сверху их остатков.
Поэтому Лобачевский формулирует »тот признак, как достаточный
признак сходимости, и доканывает только его достаточность. Между
тем, признак Лобачевского для знакоположительных рядов с монотонно
неввзрастающим общим членом является также необходимым. Ниасѳ
мы приводам формулировку и доказательство как достаточности, так
и необходимости признака сходимости Лобачевского.
Пусть дае знакоположительный ряд
2 и»),
м=1
причем f(k-\-l)>f(k) и f{n-\- 1)>/"(«) при и > к.
Определим величину рт (рт > к) из неравѳнотв
f(k) ^- ' f(Jc) ^
Тогда
as ей со
~rm 2ср«—*)2—< £ ^в>< S fr»-*)2-"1)
■t=l !1 = A +1 Bl=[
и, в частности, данный ряд сходится или расходится одновременно
с рядом
]) Для одопкп суммы ряда или егч> остатка сверху, а следовательно, и для
доказательства достаточности признака Лобачевского требование монотонности
функщш /"(«) излишне, если под рт понимать наибольшее из чисел,
определяемых неравенствами, служащими для вычисления^ (в этом случае указанные
неравенства не определяют j>m однозначно). Аналогично, если под рт понимать
наименьшее из чисел, определяемых этими неравенствами, то сохранится оценка
остатка ряда снизу.

ПРИЗНАК СХОДИМОСТИ ЛОБАЧЕВСКОГО 258
Лобачевский доказывает, как уже отмечалось, только достаточность
ианака. Для э1
двоичной дроби
признака. Для этого Лобачевский представляет величину ^Лгг в виде
ft*) — V rf)2"m
~ 2 %
П*)
(мы несколько наменяем применяемые Лобачевским обозначения),
где 1„ равно или 0, или 1; изменив порядок суммирования, он
получает
2 /■(«)=/■(*) ЬВ'Л
п^к + г т=1
где
А„ = 2 С,
я утверждает, что Lm < pm — fc, что и дает оценку остатка ряда сверху.
Строгое доказательство можно построить следующим образом. Так
как Ц^- < 1,TO^7jr- = 0n2~Mn, где №„ и 0Я одноакачно определяются
условием -н--^9п < 1 (тп—целое положительное число или нуль);
группируя члены ряда, для которых шп одинаково, получим
п—44-1 1 ' т = й *—і ^
Далее, так как рт — номер последнего члена ряда, отношение
которого к f(le) еще больше, чем '1~'" (или равно 2-'"), то
Р,„ — ^ = »о "Г »і + ■•■ -Ь»я-і (т=1, 2, ...),
рс —* = 0.
С одной стороны, ім — количество членов ряда, отношение кото-
— т
рыя к f(k) содержит в своем двоичноя разложении член 2 , а
следовательно, таких, для которых это отношение и подавно больше чем 2-'"
(или равно 2 ); следовательно.
fin) , — (»—'>
С другой стороны, если отношение —ф имеет вид Ьп2 , то
двоичное разложение этого отношения заведомо содержит член 2 ~
я, следовательно,
Учтя, что >іт_,=Рт— Рт-і, имеем

254
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Следовательно,
= /■(*) 2 £.г--<Л*) 2 (ft.-*)»""
Но
со оо ■■*> ее
так как рв = к и
со
Таким образом
со со
л окончательно
СО СО СО
jfW 2 (р»-*)2-*"< 2 f(»)<№ 2 (р»-*)2""-
w ■= 1 л ™ fr -4-1 m = і
Лобачевский ') предлагает еще другой способ исследования
сходимости ряда, который представляет собой, по существу, некоторое
обобщение только что рассмотренного признака сходимости. Он не
формулирует содержание этого способа, а только применяет ѳго к
доказательству сходимости и опенке остатка одаого ряда. Эта болѳѳ общая
форма признака, сходимости Лобачевского может быть обоснована и
сформулирована следующим обрааом.
При тех же условиях относительно общего члена ряда, что и прежде,
положим f(k) = a~^ <Г 1.
Так как
ПО
Ч 1 1
V _2_ = _
п.— к ѵ '
! ^ , 1
то всякое число і, для которого —^ .< і < —г-—, может оыть единствен-
ным образом представлено в виде
* = -4.2 а'т'
где ^-Л^Аш<а — і.
I) <1}, стр. 38—39 иаст. тома.

ПРИЗНАК СХОДИМОСТИ ЛОБАЧЕВСКОГО 266
При н > к по условию f(n)<f(k) и, следовательно,
f(n) = An 2 в"»,
где А-„>-2.
Разложив таким образом каждый член ряда, начиная с /(fe-|-l),
и объединив члены с одинаковыми степенями а, получим
СО СО
2 /Ч«)= 2 £„«--■
п^Л + 1 в=а
О другой стороны, каждый член ряда, номер которого больше, чем А-,
имеет вид І»я-т, где — -^ Ѳ < 1 и ш~>-\. Следовательно
се оэ чт
2 г(«)- 2 <*- 2 el"*.
n = fc + l ш—1 ft—1
где 1<(4"1<1.
Нетрудно видѳгь, ч'іо цри таких обозначениях
С«і + "* + -••+ ч»-і) -~- < А» < (»і + »*+•■• + *«<-і) (о—І).
■ Определив теперь целое положительное число рш пз неравенств
Получим
Рл~~ *=.»1 + »а+ .. .-(-"„_,
и, таким образом,
со со со
»І = * «el!+l 111—2
откуда, в частности, следует, что данный ряд сходится или расходится
одновременно о рядом
со
2 А, в"".
И—2

Приложение Я
ИНТЕГРАЛЫ ЛОБАЧЕВСКОГО
В ТАБЛИЦАХ БИЕРЕНС ДЕ ХААНА
Как было уже указало в статье Б. Л. Лаптева «Интегралы
Лобачевского в таблицах Биерѳес де Хаана», помещенной в Ш томе
настоящего изданиях), автор ѳтих первых весьма обширных «Таблиц
определенных интегралов»2) ссылается, как на один иа источников,
которыми он пользовался при составлении таблиц, на сочинение
Лобачевского «Способ уверяться в исчезавши бесконечных строк и
приближаться к значению функций от весьма больших чисел»3).
В таблицах Биеренс де Хаана имеются формулы, сопровождающиеся
указанием, что они прямо заимствованы из работы Лобачевского
«Способ уверяться в исчеааниа бесконечных строк » (иногда, при
ѳтои, наряду о работой Лобачевского, перечисляются и работы других
математиков, нрншедших к той же формуле); в других случаях имеется
ссылка на заимствованную из сочинения Лобачевского формулу, иа
которой рассматриваемая формула легко выводится 4).
Ниже приводится список интегралов, непосредственно ааимство -
ванных Биеренс де Хааном из сочинения «Способ уверяться ...»ь).
В первом столбце обозначен номер таблицы Биеренс де Хаана, во
втором — номер интеграла в таблице, в третьем столбце указан номер
і) Стр- 413 III тома.
3}Bierens de Haan— Tables d'iutegrales defines. Verhandeliugen ilei-
Koninklijke Akademie van Wetenschappen, Amsterdam, 1858.
3) Кроме этого сочинения, Биереые до Хаан указывает еще следующие
сочинения Лобачевского: * Воображаемая геометрия», «Применение воображаемой
геометрии к некоторым интегралам» и «Вероятность средних результатов,
полученных иа повторных наблюдений». Об интегралах иа первых двух сочцненніі
ом. указанную статью Б. Л. Лаптева; ой интегралах на сочиненна «Вероятность
средних результатов .. .» см. на стр. 348 наст. тома.
4) В сносках аа следующей странице перечислены 4 ингегра.ш, выведенное
Биеренс лѳ Хааном из формул Лобачевского.
») Список не содержит тех заимствованных Биеренс де Хааном у
Лобачевского и встречающихся в сочинении «Способ уверяться ...» формул, относительно
которых Бяѳренс да Хаан указывает, что они заимствованы и;і другого сочинении
Лобачевского.

ИНТЕГРАЛЫ ЛОБАЧЕВСКОГО В ТАБЛИЦАХ БИЕРЕНС ДЕ ХААНА 257
соответствующей формулы в сочинении Лобачевского «Способ
уверяться ...» по настоящему изданию.
Спнеов интегралов, непосредстве ни о ванистнованньп Бнереас де Хаанож
иа сочинения Н. И. Лобачевского «Способ уверяться...»
Номер
таблицы
1
1
3
53
53
53
53
55
55
55
58
56
57
61
70
70
78
Номер
интеграла
в таблице
10
25
4
14
15
19
аі
б
12
Ѵі
5
W
19
5
1
23
4
Номер
Формулы
Лобачевского
(Ѳ2)
[в2а]
(68)
(51)
(52)
(122)
[105*]
(76)
[105Ь]
ста)
(*>)
(73)
(ПО)
(112) t)
[1На[
II И)
(72)
Номер
таблицы
78
78
78
78
93
94
94
113
ИЗ
147
194
Ш
280
£87
Ш
377
Номер
интеграла
в таблице
16
17
18
19
в
2
і
3
3
5
1
6
21
*
5
I
Номер
формулы
Лобачевсаого
(Ю)
(70)
(67)
(68)
[94а]
(86)
(80)
(47|
(47)*)
(ИЗ)
(85)
(71)
(126)
(12?)
(125)
(М)
Биѳрепс де Хаан нѳ звал русского языка и поэтому не мог
пользоваться текстом Лобачевского. Вследствие этого смысл большого числа
формул, заимствованных Впервые де Хаавом у Лобачевского, оказался
искаженным. Так, во многих случаях Биѳренс де Хаан питает формулу
Лобачевского только для целочисленных значений параметров, в то
время как у Лобачевского она выведена без такого ограничения
(здесь сказалось, возможно, и то обстоятельство, что Биѳренс ле Хаану
нѳ было вполне ясно, что символ т —" употребляется Лобачевским
не только для целых ш и п). У Лобачевского отсутствовало, как
известно, обозначение для предельного перехода и наличие такого
перехода оговаривалось в тексте — ѳтот факт также послужил причиной
искажения некоторых формул Лобачевского в таблицах Биѳренс
до Хаапа.
Из 33 формул, непосредственно заимствованных Биереяс де Хаавом
из сочинения «Способ уверяться .. .в, 7 содержат прямые ошибки
') Из этого интеграла Вихрено дѳ Хавы получил еще интеграл J4J 14 в
таблице 432.
й) Из этого иатегра.та Биеренс дѳ Хаап получил еще три: Л 2 в таблице 289,
Лі 2 в таблице 291 и Л 4 в таблице 377.
17 Ван. 2823. Н. И. ЛовпчевояиН, г. V.

258
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
(юга опечатки) либо в таблицах Биѳрѳнс лѳ Хаана, либо в сочинении
Лобачевского, либо, наконец, и там и здесь. Ниже приводится
перечень этих формул о указанием ошибок (при этом учтен список опечаток
и исправлений, помещенный Биеренс де Хааном в конце своих таблиц).
Формула 1 таблицы 70 соответствует формуле [114а] Лобачевского.
У Лобачевского имелась ошибка, исправленная Биеренс де Хаянои.
Формула 23 таблицы 70 соответствует формуле (114) Лобачевского.
У Лобачевского формула верна. Биеренс де Хаав перепечатал
формулу Лобачевского, не указав, что следует произвести предельный
переход и, кроме того, дал неправильный ответ, считая, что
исправляет ошибку Лобачевского. Ошибка Биеренс де Хаана вызвана, по-
видимому, том, что формула Лобачевского [114а] формально является
частным случаем формулы (114), и Биерепс де Хаан «исправила
формулу (114) (которую трудно непосредственно проверить) так, чтобы
формальная подстановка частного значения параметра завала
правильный результат для формулы [114а]. Но отмеченная выше ошибка
Лобачевского в формуле [114а] явилась как раз следствием
необоснованного использования формулы (114) для значения параметра, не
принадлежащего той области, в которой формула справедлива.
Формула 18 таблицы 78 соответствует формуле (67) Лобачевского.
Биеренс де Хаан исправил имевшуюся у Лобачевского опечатку.
Формула 4 таблицы 94 соответствует формуле (80) Лобачевского.
У Лобачевского формула верна. Биеренс де Хаан перепечатал ее
в том же виде, в каком она помещена у Лобачевского, но в списке
исправлений укавал, что формула не верна, не приведя в то же время
правильного, по его мнению, значения интеграла. Невидимому, дело
объясняется тем, что ета формула верна только при целочисленных
значениях одного из параметров (что специально и оговорено
Лобачевским), а Биеренс де Хаан обратил лишь внимание на сразу
бросающийся "в глава абсурд, к которому приводит применение формулы
к дробным значениям ятого параметра.
Формула 21 таблицы 280 соответствует формуле (126) Лобачевского.
У Лобачевского имеется ошибка. Эта ошибка осталась
неисправленной у Биеренс де Хаана, но кроме нее появились еще новые опечатки
(или ошибки).
Формула 4 таблицы 287 соответствует формуле (127) Лобачевского.
У Лобачевского имеется ошибка, которая «исправлена» Биеренс де
Хааном неправильно.
Формула 5 таблицы 296 соответствует формуле (125) Лобачевского.
У Лобачевского формула верпа. Биеренс де Хаап перепечатал ее
неправильно.
Таким образом, в трех случаях правильные формулы Лобачевского
были заменены Биеренс де Хаааом неверными, в двух случаях ошибки

ИНТЕГРАЛЫ ЛОБАЧЕВСКОГО В ТАБЛИЦАХ БЖЕРЕНС ДЕ ХААНА. 269
имеются и у Лобачевского и у Биерѳнс дѳ Хаана и только в двух
случаях Виерѳно дѳ Хаан действительно исправил результат
Лобачевского (в одном случае опечатку и в одном случае ошибку).
В 1867 году вышло новое издание таблиц Виѳрѳнс дѳ Хаана1).
При атом многие формулы были исключены из таблиц: это либо те
формулы, которые являлись чаете гам случаем других, имевшихся
в таблицах, либо те формулы, которые в новом издании были заменены
более общими, либо те, где были обнаружены ошибки, исправить
которые автор не сумел, либо, наконеп, те, которые могут быть
просто получены с помощью соответствующих неопределенных
интегралов. Ниже приводится таблица устанавливающая соответствие между
поморами таблиц и формул по обоим изданиям таблиц Биѳренс де
Хаана для интегралов, непосредственно заимствованных из сочинения
«Способ уверяться ...»
Переход от старого издания таблиц Екеренс де Хаіша в иовох/
1-ое издание
номер
таблицы
1
1
3
53
53
53
53
65
55
55
56
56
57
61
70
70
78
номер
интеграла
10
25
4
14
15
19
2L
6
12
13
5
16
VJ
5
1
23*
4
2-ое издание
номер
таблицы
номер
интеграла
1 ' 3
— —
2 і 2
і
і
— —
41 ' 3
41 21
— ' „
4і ! а
42 ! 5
— 1 —
42 18
43 j 2
51 j l
— —
1-ое издіяже
номер
таблицы
78
78
78
78
93
94
94
113
ИЗ
147
! 164
244
280
! 287
. 296
377
номер
иптеграла
16
17
1Я
19
6
2
4*
2
3
5
1
8
31*
4*
.5*
1
2-оѳ издание
номер
таблицы
62
—
62
62
69
—
—
—
—
100
—
218
—
270
277
_
номер
ИЕтеграла
7
—
9
10
6
_
—
— *)
_в)
4")
-')
7
—
8*
1*
-в)
і) Віогенз do Haan — Nouvellea іаЫез d'intfigrales definite. Leydeii, 1367.
a) Заменен во втором издании более общим (таблица 81, интеграл 1).
') Эта формула во втором издании но форме отличается от указанной
формулы первого издания, но полностью совпадает С формулой 3 таблицы 142
первого издания.
*) Заменен во втором издании более общим (таблица 151, интеграл 1).
9) Запенен во втором издании более общим (таблица 353, интеграл I).
17*

260
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
По второму изданию таблиц проставлены номера лишь тех формул,
которые полностью совпадают е соответствующими формулами первого
издания (без учета, конечно, изменения обозначений и формы
записи). Звездочками отмечены те формулы, которые содержат ошибки.
Пи одна из пяти формул, заимствованных Биѳренс до Хааном из
сочинения «Способ уверятьоя ...», в которых в первом издании
имелись ошибки (только две из этих формул были неверны и у
Лобачевского), не была при переиздании исправлена: три из пяти формул
были исключены из второго издания, а две перепечатаны без
исправлений.

Приложение З1)
ИСТОРИКО-БИБЛИОГРАФИЧЕСКИЕ СВЕДЕНИЯ
О СОЧИНЕНИЯХ И. И. ЛОБАЧЕВСКОГО ПО ТЕОРИИ РЯДОВ
Первые два сочинения {1} — «Об иечезании тритоном етричеоких
строка- и {2] — «Способ уверяться в иечезании бѳскопѳчных строк и
приближаться к значению функции от весьма больших чисел» были
напечатаны в «Ученых запасках Казанского университета»: {1}—во
второй книжке за 1834 г. (стр. 1G7—226), {2} — во второй книжке за
1835 т. (стр. 211—342). 05а сочинения вышли также отдельными
оттисками с новой нумерацией страниц и с указанием на обороте
титульного листа: «Перепечатано иа Ученых Записок на основании
дозволения высшего учебного начальства».
Третье сочинение {3} — «Ueber die Convergenz der nnendliclien
Reihen» было напечатано в 1841 г. в издававшемся в Казани на
немецком языке сборнике «Meteorologisohe BeobacMnngen aus dem Leur-
bezirk der Kaiserlicli Russischen Univeisitai, Kasan» 2), тетрадь 1, 1835—
1836. Этот сбооник, издававшийся, как сказано на титульном листе,
«Эрнстом Кнорром на средства университета» $), содержит
метеорологические наблюления за 1835 и 1836 гг. в городах Казанского
учебного округа (Нижнем Новгороде, Симбирске, Саратове, Астрахани,
Вятке, Екатеринбурге и Оренбурге); после результатов наблюдений
следует два приложения с отдельной нумерацией страниц): 1)
сочинение Лобачевского «Ueber die Convergent der unendlicben Reihen»
и 2) работа Э. Кнорра «Allgemeine Beraerknnjren iiber den Yortrag
der Physik anf G-ymnasiens).
Включение в сборник метеорологических наблюдений приложений,
не иметощих к метеорологии никакого отношения, производит, конечно,
странное впечатление; причина этого включения еще не выяснена.
') Составлено И. Н, БронттѳЕіном.
-) =МиТйоро логические наблюдения а учебном округе имп, российского
Казанского университетам. Титульные лист этого сборника воспроизведен после стр. 1Й2
наст. тома.
8) Э. Кнорр — ирофѳсеор Казанского университета. Подробнее о ней см.
стр. 457 нает. тома (примечание [°] к сочинению «Полное аатмение Солнца в Пензе
20 нюня 18*2 года»).

262
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
Не ясно также, когда было написано сочинение Лобачевского (3} —
в период 1835—1836 годов, в которым относятся наблюдения, или
ближе к 1841 г., когда был напечатан сборник. Во всяком случае
сочинение J3( написано Лобачевским не позднее 1840 г. — это видно
ив следующих обстоятельств.
В отчете о состоянии Казанского университета за 1840—1841
академический год, составленном по поручению совета университета
профессором Н. Ивановым'), между прочим сказано:
«Ректор Университета, ординарный профессор Лобачевский
напечатал в Берлине, на немецком языке, сочинение под заглавием: Веі-
trage zu der Theorie tier parallellen Linien3) и послал туда же, для
помещения в Крѳллѳвом журнале, рассуждение: Ueber die Convergena
der xmendlichen Eeiheii».
Аналогичная запись имеется в отчете Казанского университета и
учебного округа за 17 лет (1827—1844)3), причем в этом отчете точно
укааано, что статья «Ueber die Convergenz der unendlichen Reihen»
была послава в журнал Крелпя в 1840 году.
Эти указания говорят о том, что в 1840 году Лобачевские направил
в журнал Крелля «Journal fur die reiae und angewandte Mathematit»
свое сочинение «О сходимости бесконечных рядов» на немецком языке.
Но оно в этом журнале напечатано не было, хотя другпѳ его
сочинения «Geometrie Imaginaire» и «Probability dee resultats нюуепв...»,
направленные Лобачевским в тот же журнал, были в нем
напечатаны— первое спустя два гола, а второе спустя 3—4 года после
получения4). Возможно, что Лобачевский одновременно с отправкой
своего сочинения в журнал Крелля передал другой экземпляр для
напечатания в сборнике Кнорра.
Отзывов на сочинения {1} и |2( при жиани Лобачевского не было
(если не очитать краткого указания на сочинение {1} в заметке,
помешенной в журнале «Библиотека для чтения»5) и одной общей
фрааы в отзыве Остроградского на сочинение {3}). Сочинение {3)
') Обозрение преподаваний в имп. Казанском университете на 1841—1842
учебный гад». Казань, 1841, стр. 11. Ноечроизвѳдено Л. Б. Модзалввским
в сборнике «Материалы дли биографии Н. И. Лобачевского», изд. АН СССР,
Ы.—Л., 1948, документ № 453, стр. 422.
2) Речь идет о сочинении Лобачевского «Геометрические исследования по
теории параллельных линий», помещенном в I томе настоящего издания.
а) К. К. Фойгт— Отчет имп. Казанского университета и учебного округа за
17 лет с 1Э27 по 1-е геннаря 1844 года по управлению Тайного советника -Мусина-
Пушкина, Казань, 1844, стр. ЗОі. Воспроизведено Л. Б. Мод залевским
ъ том же сборнике, документ № 515, стр. 498.
*) Си. т. Ш наст, издания, стр. 171 и наст, том, стр. 347.
Б) Т. X аа апрель 1335 г. Эта заметка воспроизведена в IV тоне наст, издания
на стр. 436—437.

ИСТОРИКО-БИБЛИОГРАФИЧЕСКИЕ СВЕДЕНИЯ
263
было в 1842 г. направлено министром народного просвещения и
президентом академии иаув в Физико-математическое отделение Академии
с просьбой дать на него отзыв. Отрицательный отзыв академика
Оотроградского был совершенно необоснован1).
Сочинения Лобачевского по теории рядов никогда не
перепадав ались ни в России, ни аа границей, и в настоящем
издании воспроизводятся впервые; сочинение {8} переведено на
русский язык В. В. Степановым незадолго до его смерти.
Имеющиеся в иностранной литературе немногочисленные ссылки
на вти сочинения2) носят случайный характер и к тому же нередко
искажают содержание соответствующих работ Лобачевского. Биереас
дѳ Хаан в своих известных таблицах интегралов указывает, что 37
интегралов он заимствовал из сочинения (2)а). В нашей литературе
до самого последнего времени имелись лишь отрывочпые сведения
об этой стороне деятельности Лобачевского*); достаточно широко
известны были только сформулированные Лобачевским
определения основных понятий анализа. Лить недавно появились
статьи, специально посвященные работам Лобачевского по
анализу6).
В настоящем издании сохранены обозначения оригинального издания,
за исключением обозначения степеней тригонометрических функций
(в оригинале sin ж" вместо sinnar и т. д), обозначения радикалов
(в оригинале иногда у вместо у" ) и некоторых других, явно
противоречащих обозначениям, общепринятым в настоящее время.
В переводе сочилення {3} применяется современная терминология.
Редакцией добавлены (в квадратных скобках) номера глав (см,
вводную статью, стр. 15), а такжо номера формул с литерами a, b
и т. д., еа которые имеются ссылки в комментариях.
Все явные опечатки и описки в формулах оригинального иэдшгая
исправлены без специальных оговорок ц разъяснений. Что касается
тех случаев, когда Лобачевский допускает ошибки в формулах или
вычислениях, или когда трудно решить вопрос о том, является
і) Отзыв Острчградского помещав: на стр. 266 наст. тона. Подробнее об этом
см. во вводной статье (стр. 20—30).
з) Burkhardt — Enz. der Math. Wiea., Bd. Пь Н. 7, 8; N. Nielsen — Hand-
buch der Theorie dor Gamma-Funktion, Leipzig, 1Э0Ѳ.
в) См. статьи «Интегралы Лобачевского в таблицах Биеренс де Хаяяа»,
стр. 413 II тома л стр. 256 наст. тома.
«) В. Ф. К а г а н — Лобачевский. Изд. АН СССР, М, —Л, 1Ш н І9ІЗ гг.
А. В. Васильев — Математика. Петроград, 1921.
в) Г. Л. Луац — О работах Лобачевского по математическому анализу.
Историко-математичѳекиѳ исследования, вып. П. Гостехяздат, М. — Л,, 1946;
Аналитические работы Н, И. Лобачевского, «Успехи математических наук», т. V,
вып. I, I950.

264 СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
данная ошибка опечаткой или нет, то, как правило, ошибки поправлена,
а в сносках приведен: оригинальный текст. В немногих случаях, когда
исправление ошибки в формуле невозможно без изменения текста,
формула напечатана в том виде, как она помещена в оригинале,
а в сносках приводится, с соответствующими пояснениями,
исправленная формула.
Согласно общей установке, принятой в настоящем падании, начало
каждой страницы оригинального издания отмечено в тексте знаком [,
а номер соответствующей страницы указан на полях. (Это не относится
к сочинениям, которые даются в русском переводе с иностранных
языков.)

При.юшенчк &
ОТЗЫВ К. В. ОСТРПГРАДСКОГО О СОЧИНЕНИИ
ЛОБАЧЕВСКОГО «О СХОДИМОСТИ БЕСКОНЕЧНЫХ РЯДОВ»
Ниже приводится перевод о французского языка двух документов:
I—извлечения из протокола Физико-математического отделения
Академии наук о отзывом Остроградского о «мемуаре о сходимости рядов»
я II—письменного рапорта Острогр адского на эту лее тему,
адресованного отделению и приложенного к этому протоколу. Точное
название сочинения Лобачевского ни в одном иа документов не приведено, но
иа первых строк протокола («доклад о сборнике Казанских
метеорологических наблюдений») ясно, что речь идет о сочинении «О сходимости
бесконечных рядов», напечатанном в 1841 году в качестве приложения
к «Meteorologiache Beobachtungen aus dem Lehrbezirk der Kaiserlicli
RHSsiechen (Jniversitat Каяап». Оба документа хранятся л Архиве
Академии наук СССРі) и были воспроизведены вместе с их
переводом Л. Б. Модэалевским а).
I. Из протокола Фиянко-иатематического отдаления Акадешш Наук
Класс физико-математический
No XI
От среды 10 июня 1842
§ 1Ѳ8
Г. академик Остроградокпй сделал доклад о сборнике Казанских
метеорологических наблюдение и сообщил, что, отвечая на желание
г-на министра и президента, он прочел ыемуар о сходимости рядов,
который в нем содержится. Г. Остроградский нашел, что эта новая
работа г. Лобачевского похожа на его предыдущие работы; автор
пренебрегает в ней первейшими принципами точного рассуждения, точно
с предвзятым намерением осложняет понимание хода своей мысли,
и эти недостатки пе искупаются ни новизной результатов, ни удроще~
ниѳм в изложении того, что уже известно. Г. Остроградокпй не считает,
поэтому, атот .мемуар заслуживающим одобрения Академии [... ]
і) I — Архив АН СССР, Ф. 3, он. 1. Js£ Э4, Протоколы за 1842 г.; черновик —
Ф. 1, он. 1-а, М 66. II — Архив АН СССР, Ф. 1, он. 2-1812, ФМ, § 188.
2) Материалы для биографии Н. И. Лобачевского. Собрал и редактировал
Л. В. Нодэалевский. Изд. АЕ СССР, 1948, документы Ж^ 470—4S0,
стр. 444—447. Перевод второго документа сделан неточно н нами исправлен.

266
СОЧИНЕНИЯ ПО ТЕОРИИ РЯДОВ
П. Рапорт И. В. Остроградского
Рапорт
Первому Отделению императорской Академии Наук
Академия поручила мне рассмотреть мѳмуар о сходимости рядов
и дать о нем отчет. Автор ©того мѳмуара, г-н Лобачевский, ректор
Казанского университета, ужа известен, ао правде говоря, с довольно
невыгодной стороны, новой геометрией, которую он называет
воображаемой, достаточно объемистым трактатом об алгебре и несколькими
диссертациями по различным вопросам математического анализа.
Мѳмуар, представленный моему рассмотрению, не содействует
изменению репутации автора. Г-н Лобачевский пренебрегает в нем
первейшими принципами точного рассуждения, словно с предвзятым
намерением осложняет понимание хода своей мысли, и эти недостатки не
искупаются ни новизной результатов, ни упрощением в изложении
того, что уже известно.
Можно превзойти самого себя и прочесть плохо ере тактированный
мемуар, если затрата времени искупится поанапием новых истин, но
более чем тяжело- расшифровывать рукопись, которая их но содержит
и которая трудна нѳ возвышенностью идей, а причудливым оборотом
предложений, недостатками в хода рассуждений и нарочито
применяемыми странностями.
Эта последняя черта присуща рукописи г-на Лобачевского; всё
же мы прочли ее и не нашли в ней ничего, кроме известных
разложений в ряды наиболее простых иа трансцендентных функций. Эти
разложения доказаны тяжеловесно в пред став лены обозначениями,
которые, кроме автора, никто не употребляет, и не сопровождаются
никакими действительно новыми замечаниями.
Автор поистине считает, что он сделал открытие; так, например,
он говорит, что он первый обратил внимание на то, что теория
тригонометрических функций может быть объяснена беа помощи круга;
однако, мы полагаем, что уже Лейбниц анал это.
Нам кажется, что мѳмуар г-яа Лобачевского о сходимости рядов
не заслуживает одобрения Академии.
Сего июня 1842.
М. Остроградекий
На рапорте имеются пометы академика О. Н. Фуеа «Lu Іѳ 10 Зот 194:!» я
«] (Л., М 1S8-.

ЗНАЧЕНИЕ
НЕКОТОРЫХ
ОПРЕДЕЛЕННЫХ
ИНТЕГРАЛОВ
ВВОДНАЯ СТАТЬЯИКОММЕНХАРИИ
Г.Л.ЛУНЦА

ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Вводная статья:
Обзор сочинении «Значение некоторых определенны!: интегралов» 269
Н. И. Лобачевский — «Значение некоторых
определенных интегралов»: ,
Статіл I 275
Статья П 303
Примечании 313
Приложение:
Историко-библиографические сведения о сочиненші «Значение
некоторых определенных интегралов* ..,,,., 325

ОБЗОР СОЧИНЕНИЯ
«ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ»
Сочинение Н. И. Лобачевского «Значение некоторых определенных
интегралов», состоящее из двух статей, является его последней
работой, посвященной вопросам математического аналиаа, и хотя оно
(его в особенности относится ко второй статье), несомненно, тесно
примыкает к его работам по теории рядов, тем не менее существенно
отличается от ѳтих работ как по содержанию, так и по характеру
изложения.
Ъ работая по теории рядов Лобачевским был получен ряд выдающихся
результатов; однако, эа исключением, раввѳ, найденного им признака
сходимости, остальные открытия были сделаны им как бы мимоходом:
основная цель этих работ состояла не столько в получении новых
результатов, сколько в обосновании всего фундамента анализа,
основным элементом которого, по мнению Лобачевского, должна
стать теория рядов, И то большое внимание, которое Лобачевский
уделяет в сочинениях по теории рядов своему признаку сходимости,
объясняется, главным образом, тем, что его не удовлетворяло «легкое»
отношение к вопросу о сходимости со стороны своих современников,
иногда даже таких, как Копш. В сочинениях по теории рядов
Лобачевский старается соблюдать исчерпывающую строгость в
рассуждениях (что ему, с современной точки зрения, конечно, ое всегда
удается) л оговаривать при доказательствах все нужные условия.
В противоположность этому, основная цель сочинения
«Значение некоторых определенных интегралов» вполне конкретна я отражена
в названии сочинения.
Известно, что вычисление определенных интегралов занимало
значительное место в сочинениях Лобачевского как по геометрии,
так и по анализу, хотя и в геометрических и в аналитических работах
оно играло, в основном, лишь роль средства, иллюстрирующего силу,
полезность или правильность полученных Лобачевским результатов.
Вполне естественно, что Лобачевский любил ето, сослужившее ему
добрую службу, средство и, как всегда, стремясь к обобщениям,
поставил своей задачей наложение некоторых способов, позволяющих

270 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
«соединить» значения некоторых определенных интегралов, т. е.
способов, каждый ив которых может служить для вычисления
различных интегралов.
Главное место среди этих способов занимают различные
интегральные преобразования, которым посвящена, в основном, статья I.
Соотношения (3), (4), [46 а] принадлежат к числу оригинальных
результатов Лобачевского.
Статья И содержит приложения к вычислению определенных
интегралов свойств функции <гамма».
Что касается формы изложения, то следует отметить, что
большинство выводов дается Лобачевским чисто формально, без
обоснования по существу; в ряде важнейших мест не оговариваются даже
условия, при которых ѳти выводы справедливы. Если учесть, что
его сочинение было надиоано Лобачевским в после ~шяѳ годы его
жизни, то кажется весьма правдоподобным, что, не обладая уже
полной трудоспособностью, Лобачевские решил опубликовать
накопившиеся у него за десять с лишним лет со времени написания
последней работы по теории рядов результаты, хотя бы и в не
совсем отделанном виде, так как он с по.'іным основанием имел право
считать ѳти результаты и в такой форме достойными самого
глубокого внимания.
Переходим к обзору содержания сочинения «Значение некоторых
определенных интегралов».
Сначала, пользуясь интегралом
I
е >™ain bxdx-.
a* -f- b3 '
Лобачевский, дифференцируя по параметру а интеграл
fe-X Ctga
— sin a; dx.
приходит к справедливому при 0<а^— равенству
со
о
на которого, в частности, получает
J
smz .it
—-—<&= — . (1)
') Нумерация формул в настоящей статье совпадает с нумерацией в тексте
Лобачевского.

ОБЗОР СОЧИНЕНИЯ 271
Далее Лобачевский рассматривает интеграл
со
о
где функция f(x) удовлетворяет условиям
f(K + x) = fi«—*)~Mf(x)
и, пользуясь разложением
-і ±-_діу-(-і)'
sin а; х ^4 і'я1—х1 '
приходит к общей формуле
и и
которую применяет к вычислению некоторых интегралов.
Если же функция f{x) такова, «то
f(*-\-x) = f(K — x) = —f(x),
те аналогичные выкладки приводят к равенству
со г
| f(x)dx = \ f(x)coaxdx. (4)
о »
Следует заметить, что функция, удовлетворяющая условиям, при
которых выведено это равенство, может быть непрерывной в точках
fcir -[-—--(& = 0, 1, 2,...) только если она. в этих точках обращается
в нуль.
Положив f (х) = , Лобачевский получает из (4)
cos а;
со
О
Этот интеграл расходится; однако вывод Лобачевского справедлив,
если под главным значением интеграла в левой части (5) понимать
сумму ряда
СО
п —о
где Іп — главное значение интеграла
R
х j
ах.

272 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Затем Лобачевский переходит к теории гамм а-функция.
Положив для целого положительного г
п"'<=к(и — 1) ... (и—r-J-1),
Лобачевский определяет функцию < гамма от и с показателем »*»
с помощью равенства
»-»■=. hm \ JJ (б)
и ссылается на то, что существование предела, стоящего в правой
части этого равенства, было им доказано для любых комплексных
к и ж в сочинении «Способ уверяться в исчезании бесконечных строк. .. »
Показав непротиворечивость этого определения с определением
для случая, когда m целое и положительное, Лобачевский выводит
основное соотношение
л-"* —»-*(* —р)--^», (7)
с помощью которого выражает функцию «гамма с показателем» через
«гамма полную»
я-»
п"Р =а .
После этого Лобачевский выводит некоторые свойства функции гамма
(«полной») а вычисляет некоторые ее частные значения. Положив
далее, как и в своих сочинениях по теории рядов, для целого
положительного г
і
(Я-)-.г)-г=(М + г)Я+Г+^е-^(г), (10)
Лобачевский получает
log w=D=т 2 !нЛГе+2)(»+^іГ'' і10а1
и показывает, что Km ф (г) == f(n) существует прщ любом комплекс-
г -Ь со
ЫОМ П И
1овГ(«)-1ов*М + ІУ У (~*'* [ЮЪ]
2 «ГІS (*+ 1)<*-М)(* + г+ Х)1+1
Равенства (10) и (10b) могут служить определением функции
(я-|-»")™г при любых комплексных те и г. Они по существу отличаются
от соответствующих равенств, встречающихся в сочинениях Лобачевского
по теории рядов1), лишь тем, что в правой части [10Ь] изменен порядок
суммирования. Но произведенное Лобачевским изменение порядка
суммирования делает двойной ряд в правой части [10Ъ] сходящимся
при любых комплексных п и г (кроме »-[-г = 0и целых отрицательных
I) См. статью «Обзор сочинений Н. И. Лобачевского ио теории рядов»
стр. 25—26 вост. тома.

ОБЗОР СОЧИНЕНИЯ 273
значений »-j-r) и служит, следовательно., средством аналитического
продолжения функции (»4-»")"г- Лобачевский, правда, не
останавливается на этом вопросе, тан как равенство [10b] ему нужно только для
оценки асимптотического поведения функции (я-|-»-)"г, однако вряд ли
можно считать такую перестановку порядка суммирования случайной.
Доказав далее, что интеграл
со
\ e-xx"dx
а
сходится, если Ееи>-—1, и воспользовавшись асимптотическим
равенством, основанным на (10), Лобачевский показывает, что
о
e-xx"dx = n"n. (11)
Показав, что равенство
1
И'
,--*»,**=,_ (12>
а
'Справедливо и для комплексных значений a(Beft>-Q), Лобачевский
применяет это равенство к вычислению интегралов
«1 СО
\xne~a<Booabxdx, I xne~B'ain ЬхЗх (13), (14)
о о
и ряда других.
Далее Лобачевский показывает, как можно применять замену
переменных под знаком двойного интеграла для вычисления аначеняв
определенного интеграла, и применяет этот способ к вычислению
интеграла
«
Jsin^-HoDCOS^+Woi (Re»> —1, Rem > — 1) [19*1
в
в других.
Пользуясь специальным приемом, обоснование которого дано
в примечании [aJ, Лобачевский, исходя из равенства (12), доказывает,
как и в сочинениях по теории рядов, что
If
еіх *° = І1£і і) (Be й > О, Be И > - 1), (28,
і + іх)
—со
а также получает, что при тех же условиях
"" e-*xdx
I,
= 0. (2в)
— ш
1) Здесь г — у"— I. Лобачевский никогда не пользуется этим обозаачеаком.
19 Воя. S82S. Ы. И. Лобачевский, т. V.

274 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Обобщив этот прием (ом. примечание I14]), Лобачевский приходит
к примечательному интегральному преобразованию1)
со ft со
J&Jf(«)?M*-*)]<fc-[m-o)+m+o)i р-М^ЛІ-^^ (аз>
—со 0 в
где <!/' (х) = ^ (х) и О < А < А. При й = со его равенотво превращается
в [33а] и имеет место при любом А > 0.
Это весьма общее преобразование содержит, в частности,
интегральную формулу Фурье
оо со
ДА—0) -|-f(*. + 0) = — fete (7(a:)eoslz(A —а;)]*Е.
— со в
Иг (33) и полученного аналогичным путем равенства
со Ь
J ds jV(a:)<B[^(A-(-a:)] Ae=.0 (35)
Лобачевский получает, положив і (ж) = зіп аг, оинус-трансформацию
в косину с-трансформацию Фурье.
Формулы (28) п (29) также легко получаются на (33) и (35).
Наконец, в первой статье рассматриваемого сочинения Лобачевский
находит еще равенство
а+і со , л со X
о — і а> о 0
валяющееся обобщением преобразований Лаплас а-Мѳллина, и поль-
вуетоя им также для вычисления определенных интегралов.
Вторая статья посвящена целиком приложению гамма-функции
Ж вычислению определенных интегралов вида
feinbasinx , (* /sin&x\™ р ( тй.Ъх\п .,
1) Как выяснил Б. М. Гагаев (доклад на научной конференции Казанского
университета, посвященной 135-летию создания Н. И. Лобачевский неевклидовой
геометрии, февраль 1951 г.), формула «ила (33) была получена в 1838 г. Лиувиллеи
(Note sur іше шапіёге de generaliser la formula d« Fourier, Jour», de math, pure»
et appliquees, т. 10, стр. 102—105).

УЧЕНЫЯ
ЗАПИСКИ,
ПЗДШЕМЫН
к л :t л и«: кинь ушшерснтктонъ.
1852.
ШАЖКА ІГ.
1
MsaaiftBWw —
КАЗАНЬ,
■ к гнНВВГСВТВТСКвЯ ТНПОГИ»]И.
1853.
Титудьныіі лист IV книжки «Ученых аяидсок Казанском университета»
па, 18">2 г., в которой было напечатана сочинение
«Значение некоторых определенных иятегралов».
К стр. 27 j.

ЗНАЧЕНіЕ
НЪБОТОРЫХЪ ОНРЕДЪЛЕНВЫХЪ ИНІК11'.І.ЮН Ь.
статья і
3. Доваѵшкяго Ла£лі)і|<с>Шіо ІГрофиюра'.
ОпрсдЬдопиыв интегралы слу;кап- часто боллшмт. нмогчемт, ѵь агилггическии, рѣ-
теігіяѵя , H.itijiiiutpi вь ішііч |іи|!ізиаиіи ди.рФерпнііа.іі.ныѵь урзміенІй. Однлижъ учвніе
оВь опредѣ.іеіШЫХ'Ь Вигегргимъ дксни поръ еиш ііс могло Оыіь iijiase.wiiu иь сдетмл,
Ш » оііюшміІц къ яіачстячъ ннитрэлои, пи въ отношеши ьь раздичвывъ оимибаиъ
достигать этмі-ь аоачеиііі. Надобно іксыіь , чіибы шс-гіишащ» (кмік расирисграняла,
мшму доічавигі напередь бо-іѣе нашиты ;чсиіш.
Здісь енрдиншь а амдчеігіи; иікиіорыіь «іі|«ді.іеішыхі> интеграле» с* уіаэашеш
в рл-івшыіъ (посововъ выводить эти іш-теыіи.
Шчиенъ къ интеграла
ев
I —iiill =s-.T fl)
г*і гг окружность кр)іл въ чагтш-ь поигреюяка. Этег* нптегралъ заключается п друге**
К = і — г . sib J
глі й проплольпыИ пмтияшіый угол < 1 ?г. Дв*дереіщіір}я »' »і отвопгенш *ъ а,
полупит*
00
-/
#**«. /»*, 185* і і
.«<іп'= <І». «иг. і
da
Первад страница оригинального издания сочинения
•Значение некоторых определенных интегралов»
(1-я стр. IV книжки «Ученых зашіоок Казанского университета); :ta 1852 і'.)-

ЗНАЧЕНИЕ НЕКОТОРЫХ
ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
СТАТЬЯ I
іѵ Ц Определенные интегралы елужат часто больший пособием
в аналитических решениях, например в интегрировании
дифференциальных уравнений. Однако ж учение об определенных
интегралах до сих нор еще не могло быть приведено в систему ни
в отношении к значениям интегралов, ни в отношении к
различным способам достигать этих значений. Надобно желать, чтобы
исследования, более распространяясь, могли доставить наперед
более полноты учению.
Здесь соединил я значения некоторых определенных интегралов
с указанием и различных способов выводить эти значения.
Начнем с интеграла
«
о
где тс — окружность круга в частях поперечника. Этот интеграл
заключается в другом
-J*
**«—«»■ .вш».
где а произвольные: постоянный угол <^к*. Дифференцируя У
в отношении к а, получим
dY . . ..
-5— 8ш*о= I diesiax'f,
со
'=1
' Вернее 0<а<^-.
1В*

27в ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
1 [Но вообще для постоянных at b*
I
со
1
, —<га . , Ь
ах е вш ох —
а5-+-і
следовательно
dare costa^^-p-
-j- = 1.
da.
А как F должно делаться нулем для а = о *, то
Так для всех углов а< —тс
со
С (&В . —root»
| —-sinік* е =а. (2)
о
Впрочем, угол а может быть как угодно близкий к -s-it, а
следовательно з праве допускать a = --j-*®. В таком случае интеграл
(2) переходит в интеграл (1).
Интеграл (1) заключается опять в интеграле более общего вида
\ — sm а; - f (х),
J х
о
где f(x)— такая функция от х, которой значение не меняется
с прибавлением х к углу ж и с переменой х на — хя. В таком
случае [']
со со *
Г dx . ,, , ѵі (*(—IV da; sin а;,. .
где знак суммы требует складывать члены, которые происходят,
когда вместо і ставим по порядку все целые положительные числа
от і = О. Такое означение будем везде употреблять и в последствии.
* »>0.
• Urn Т = 0.
я-»»
"Интеграл (2) сходится равномерно при 0<;а^ —.
S Так как функция fix) должна быть определена только для х^О, то
второе условие, по сути дела, обозначает, что ((я—1) = f{x).

Н.И. ЛОБАЧЕВСКИЙ —СТАТЬЯ I 277
Далее
со 2
і * ** •'«- .2 I Ч£?*-ѵ»+ S №£=«*
і~0 О
+ж «f.lJ «+<
э | Когда в последнем интеграле ставим ті— х вместо а;, то
сделается
Cdx . ... ѵ^ Г (—1)* da? sin ж „. . . ѵ Г (—1)* da: sin я ,, .
в S — 00 ' ( = 00 Ѵ ' '
1 1 I
f *** ■ „ , , V f (-—1)*<Ас8шзт « f (—lYdx einx
=j T „in «■«») +J, j _7_F_-r(»)+Sj |І+1),_Т/М-
о j_iо ' (<iо х
i І. 1
f dat . .. . . ri f (— IV die sin ж., . v Г (— l)'d«sma: .
* f™JO (ИІО
1
«Г А>ппш./(ш)| —~2ж V *ZlA>M.
J. ' wi ж M tV— ж* I
о l (—1 '
Известно, что
1 * n„V.H)' *
811» XX
После чего
i
J'
о о
Так, полагая f(x) — l, находим
dx . 1
— sin ж = —it,
к 2
о
1
как и выше (1). Полагая /(#) = еіп'ж,
СО
і —вшяж=—я.
J ж 4
* См., например, Уитгевер и Ватсон — Вурс современного ажигава,
ч. I, стр. 181, ГТТИ, М.-Л, ШЗЗ.

276 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Вообще положив
f(x) = em2™ x,
• I получим для п целого положительного
і
ТЕ
I — sin8"*1 x = I dx eina" x.
0 0
Бели же функция f(x) такова, что
f (_*) = +/(*); Гіъ + Я):=-Гіх)*,
ТО П
о о і—О
1
5"
= 2 J Kq^-«w««)-i J -srrr'W-
i~IO ' I—1 0
1 1
X 1
г 3"
* То-еоть /(*-)-я) = f(jt — x) = — f[x). Так кік отсюда, в частности, следует,
что f!~j= — гіѵіі то Фуякяая. обладающая атими свойствами, моасат быть
непрерывной а точках fcn-).— только, когда f(fcicf--K-) =и0 {кш=0, 1, 2, ...)-
* Так как
etg
ж = ~ - 2х 2j fc*^ — я> •

Н. И. ЛОБАЧЕВСКИЙ —СТАТЬЯ I
279
Таким образом,
і
J —sinх-f(aO«= J dxeosx-f(x). (i)
л о
Например положив
f(x)t
cos it
находим
J
— tang* =-«[»]. .(5)
6
Лежандр приходит к этому интегралу другою дорогой (Ехегсісев
de calcul integral, Tome I. p. 181).
| Значение многих определенных интегралов может быть дано
помощию функции, которую Лежандр назвал гамма и для которой
я предложил название уступа в моем ^Способе уверяться в исчеза-
нии бесконечных строк и проч.» *, желая тем выразить, что
функция происходит подобно степени, но что здесь множители, ие
будучи равны, следуют один за другим, отступая назад единицей.
Название не составляет еще сущности, но я удержу по крайней
мере означение более удобное и более выгодное для вычисления*.
Для всякого числа п и для целого положительного г, под
я разумею произведение из г производителей, от первого и- и
потом уменьшая единицей по порядку, до последнего « —?--|-1.
Так, что
п~г = п(п — 1)(я — 2) ... О—r-L-l).
Затем для всяких двух чисел и, т,
(»_j_r)-r
* Лобачевский цитирует по памяти и не гочао. Термином «устуц» в
сочинении «Способ уверяться в исчезании бесконечных строк...» он не пользовался.
Этот термин встречается в сочинении Лобачевского «Новые начала геометрии
с полной теорией параллельны» (см. том II наст, издания, стр. 398).
* Обозначения Лобачевского совпадают, по сути дела, с общепринятыми
в настоящее время обозначениями для фякториальноН функции. Поскольку
Лобачевский рассматривает фунвдию гамма как частный случай обозначаемой им
с помощью символа л**** функции, зависящей от двух аргументов, то естественно,
что ему неудобно пользоваться обозначениями Лежандр*.

280 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
где целое положительное число г = оо *. В упомянутом моем
сочинении * я доказал, что значение выражения (6) всегда
приближается к известной границе с возрастанием числа г, каковы бы
числа п, т ни были °, действительные или воображаемые под
видом а-\~р Ѵ~—І, е действительными числами «, р. Значение
выражения (6) для г = со будет то, что я называю гамма от и с
показателем т. Если же т = 7і, то гамма от п делается той функцией,
которую Лежандр означает
Г 0 + 1).
Различные свойства гаммы могут быть непосредственно
выведены из данного выражения (6), которое служит определением,
этой функции.
Бели т—целое положительное число, то
(я — т-\-г)"Т
М~т=з Г™-
(« + *■)-
(м— m~\-r)°
(n + r)"™-(n + r — m)""-m
п (п — 1)... (п — m -+-1)
(» + »•)
Здесь с возрастанием г дробь
(» + ,)—
j обращается в единицу, следовательно гамма от я с показателем m
целым положительным делается произведением
п(п-—1) ... (п—m-j-l)
из я» производителей.
* Лобачевский обычно оговаривает продельный переход в тексте, не
пользуясь никакими специальными обозначениями. Формула (б) со сделанной
оговоркой может быть записана в более привычной для современного читателя форме
. !■->» (В _|_Г)*"Г
* То-ѳсть в сочинении «Способ уверяться ...в (см. формулы (42) па етр. ПО,
(54) иа отр, 114 и (118) на стр. 15Ѳ нвет. том»].
э За исключением случаи, когда » — целое отрицательное число, а и — m ие
является целым отрицательным (см. примечание (м] к сочинению «Способ
уверяться...» на стр. 235—237 наст. тома).

Н. И. ЛОБАЧЕВСКИЙ —СТАТЬЯ I 28І
Для т = 1 и для всякого п
и"1 =и.
Для от = 0 ж для всякого и
т"° = 1.
Уравнение (6) для произвольных чисел п, т, р дает
п~*_7* (п—р + гУ
(» + г)-' '
(я—_р + г)
Отсюда следует, что
Для я = я» это дает
п р = ———— ■.
(п-рГп-р
Итак, гамма с показателем определяется помощию гаммы полной,
для которой Лежандр дал таблицы и которой значения известны
для всех чисел, как скоро даны для чисел от нуля до единицы.
Для и = п уравнение (6) делается
<» + »•)-'
а когда ставим сюда ~и вместо п,
*-™ г
(—n)--» = r-w
С*- — »)
Произведение двух последних уравнений дает
1 2! Зг
• —(—п) "=■
1-Я2 2В —«а З1 —71s ' '
Это значит, для действительных чисел п,
I »-«(_„)—» = _!2_.) (8)
(пУ — 1) (—«у —1) д,^,._,-я. ■ <9>
где е основание Непперовых логарифмов.

"282 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Для п = "т в уравнении (8)
ШЧНР=4-
Между тем, согласно с уравнением (7),
После чего
(1) --Н-і) '■
Полагаем для г целых положительных чисел
(» +г)"г = («-і-г)п+г+^е-г .<-(»■), (10)
тде ф (г) "число в зависимости от г и ?і, как это требует самое
уравнение. Подобным образом
■ (n-t-r —1)"г_1 =(ft_t-r —1}"+г"^е'-7' й(Ѵ— 1).
Иа этих двух уравнений следует
ф(г) /и + г —?\"т" 2
+ (г_1) 2 «Ті<* + !)(• + 2)(п + ^)(+і-
Или, когда располагаем по степеням от п-\-г — 1,
log *(*•> =ІѴ (-Wi Г10.і
Два выражения для разности Iogij>(*-) — logfy(r — 1) показывают,
что с возрастанием числа г эта разность двух логарифмов
обращается в нуль и что, следовательно, ty(r) перестает зависеть от г
и начинает быть функцией от одного числа п, которую означим f{n)
и которой значение может приблизительно быть вычислено помощи»

Н.И. ЛОБАЧЕВСКИЙ —СТАТЬЯ I 283
уравнения
Здесь всегда можно взять г довольно большим числом, чтобы ^ (г)
принимать за f(n) как для действительных чисел п, так и для
чисел под видом а-\-$Ѵ—1 с действительными числами а, [J.
В этом последнем случае полагая
получим
3 *
р = а + *" + К tang ш=— ,
WrIM-i-Y V (-!)'' =
Таким образом, разность log/(?!•) — log ^ (г) состоит из двух частей,
действительной и воображаемой, которые обе делаются
нечувствительными для весьма большого числа г.
Переходим теперь к интегралу
со
\dx Xя е~ш = А''.
а
Во первых заметим, что этому интегралу принадлежит
определенное значение, как функция от п *. "Чтоб в этом увериться, ставим ах
вместо х, разумея под а положительное число; получим
о
Далее интеграл N можем рассматривать как сумму из бесконечного
числа интегралов; таким образом
со » ° .
* Вместо j» и и следовало бы писать соответственно j»^ и
* Еояя п> — 1.

284 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Если в бесконечной строке останавливаемся перед тем членом,.
где і = г, то остаток в строке будет
со *
B = a"e-™Ve-fo Иг-|-г + —J е-» ей»;
1=0 0 ' '
і следовательно
<; а» е-™ V е~іа \(г-\-і +.1)" е~" dx,
-8
fa
В этой последней строке содержание* каждого члена к предъ-
пдущему
-(^Г-Ті)"
следовательно, это содержание сделается везде менее единицы,
как скоро г довольно велико, чтоб
1
r>-j—,
е"— 1
которому условию всегда можно удовлетворить для всех
действительных чисел а, п. Содержание, о котором здесь говорится, для я
положительного числа, менее
-w>
следовательно для такого числа п
1 —«-" /, , 1 \в
7 П5ГТ + Т
может быть сделано как угодно малым с возрастанием г.
Для п отрицательного содержание двух членов в строке S
постоянно менее
остаток строки R < an е~аг (г 4- 1)п, следовательно, увеличением г
может быть сделан как угодно малым.
* Словом содержание Лобачевский всегда называет отношение двух величин-

Н. И. ЛОБАЧЕВСКИЙ- СТАТЬЯ I 285
Итак для всех чисел действительных п, положительных и
отрицательных, строка для N исчезает, а следовательно
интегралу N принадлежит определенное значение. Отсюда не следует
однако ж, чтобы значение N не могло бить бесконечно великим,
потому что таковы могут быть значения первых членов в строке
для N. | Впрочем, этот случай только предполагается для п
отрицательных, когда самые елементы интеграла увеличиваются до
бес конечности.
Интегрирование по частям и когда действительная часть в
»> — 1 дает
со со
I daneae~<a= ■= уёяи-ях***,
І (» + *)";!
где г — целое положительное число. Отсюда видно, что интеграл
с отрицательным числом п приводится к тому случаю, когда
показатель этот положительный и если к тому
m +1 > О.
■Следуя принятому означению (6), можем написать
СП СО
о г о
и наконец, основываясь на уравнения (10), поставить сюда, когда г
чрезвычайно большое число,
где ?(0)* — число независимое от г. После чего
со СО
\ dxxne-a^n~°\ (0) T~T\dx (—Y+re>--*.
о о * '
Поставя *■-(-£ вместо ж, получим
со со
Г*ваг-яе-*'.= т"я»(0)г~'і" (<гЕе-ф + —]"+Г =
о -г ^ '
і * ™
= »->(0)r-i-{J«rf(l-A)',"," + J<«e-*fl + f)"+r}
а ^ ' о \ / ■
* В правой части подразумевается переход к пределу яри г-кя.
* В обозначении формулы [10Ь]
і_
2„-г

386 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Для г чрезвычайно большого числа, как здесь предполагается,
можем довольствоваться первой степенью от г а знаменателе,.
а потому принимать
^-ІГЧ-тИ-
]t | После чего и для »- = оо
— 2п""т(0)г * 1 Дв *
о
а поетавя
1 d»s»»e-*s= ^?(°)к""1 йжж"те^^ pj-
дѳлая « =к——, находим
?(0) =
с лед оват епьно,
со си
(■ п"» (* L
1 dxxn£-* = --;= dxx * е-*.
Лоставя сюда п = 1, получим
™ і
\ dm х - е~" = У к
и наконец
а
для всех чисел п действительных я воображаемых, еели только-
действительная часть в п > — 1.

Н. И. ЛОБАЧЕВСКИЙ—СТАТЬЯ I 287
В уравнение (11) ставя ах вместо х, для действительного
положительного числа а находим
со
J ^<^e'om=-—. (12),
js [Впрочем, приложив ЬУ — 1 к а с действительным числом 6<а
по величине* находим
™ со , ™
о і—о о
_ пя" у (» + *)"** /—дѴ^іу _
_ая+1А г' I в і ~
<—о ' ' '
_ »— / ■ *Ѵ^Тг"_І = -ft""
_а«+Ч + а У (а+&^—1)"+1'
Продолжая ставить а-\-ЬУ— 1 вместо а, таким образом уверяемся,,
что значение интеграла (12) верно для всех положительных чисел а,
для всех вообще действительных чисел b и покуда действительная
часть в п> — 1.
Другим образом приходим к тому же заключению, рассматривая
в интеграле (12), значение которого пусть будет У, число а
переменным. Интегрируя по частям и дифференцируя V в отношении
к а, находим
da ' а
отсюда
7=-С
йя+1-
Постоянное
С = п**я,
как мы нашли для действительного числа а [*].
* То-ееіь по абсолютной величине.
* Так век
ь-»у^. ѵ(-аѴ-і)< ,
2(-»у -чу

288 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
В уравнении (12) поетавя а-\-ЬѴ~* вместо а и разделяя
действительные части от воображаемых, при которых
множитель V—1, получим
со
а
I tfeж»sin bx • е_ои =
*
=£^!=^(в+бK=rтг"~1--(я-бJ^гв-,)■ (14)
із | Полагая здесь 6*=atanga и разумея а< —тс положительный
It
угол*,
to
Г Я"™
j <&ra*« е-оа;соа(ож tang a) t=s-^ соЖ1*1** сов (п-{-1) a, (15)
о
Или, поетавя acota вместо а*,
со
J йезГе—^оол (ах) = -J^. sinn+1acos(n+I)a, (17)
f Ас я" «-«««*" аіи („д.) = jQ_ віп»+ > а gin (и + 1) а. (18)
» а
Например для m —■ — -$-
™ т ——— —
f ^«-""^"eoeCaarj^ і/^віпа соя-і-«,
(for
J ^"^'^М^)^ j/^-ain. выі-в.
* Это условие ізлипше. Можно считать, что —^<^а<^-тгі так как Фор-
пулы (13), (14) справедливы при любой конечном Ь, если я^>0.
* Здесь уже 0 < а < — .

Н. И. ЛОБАЧЕВСКИЙ— СТАТЬЯ I 28В
Соединение двух интегралов (12), (17) дает
f «fee-0*001" в?-1{1 - cos ах) = ^—— tang" а [I - cos я> соа'а} .[18а]
е по
Для числа и весьма малого можно принимать
1 — соа пз. еоа" я = — n3ns — в log сов я
и следовательно
I dajaj»—!(1 — созаж)е^'"'со1,'' = —— tang" а! — паг — log соа в [,
а полагая здесь п = 0, получим
со
С dx
_(1 — wsax)e.-ax'"*f== — log COS а П. (19)
t) X
а
Для каких нибудь двух функций f(x), y(x) от переменного х
пусть известны два интеграла
со оэ
Аж= [ dxe-"f(x), B={dxe-*<o(x).
о о
и | Произведение двух этих интегралов выражается двойным
интегралом
f dx f dy e—* -» f (ar) <? (y) = A£
о и
или, когда поставим сюда х-, у1 вместо ж, j/,
со ев
о о
Полагая здесь
[dx\dyxye-x'-ff(x^'?(yt) = ~AB.
х = у tang ш
и рассматривая <и неременным вместо х, получим
!
— с
f-^Й-™ f */ У3 e'^fW tang'«) 9 (у3) = І АЯ-
J COS oi J *
и О
Наконец, пусть _
у = сов со . у г

290 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
с переменным г вместо у, to
і
Т"
1 doi аіп а> сов <о 1 г &r e~r f(r віѵ? ш)у{г со& я») = —- АВ.
о о
Например, когда
с постоянными в, от, где действительная часть > — 1, мы видела (11)
А = п~я, В = т-™.
После чего
і
I dre-'r»*"1*1 1 de> smSn+1 «о cos8»*1 ш = —n"*nm-™,
о в
а по интегрировании в отношении к г,
і
7"
Jn," "»і **m
с&овіп^+'шеоа*—і-'ш = ——, , „ „.-„tin 11а»3
или для всех чисел те, т, где действительная часть в каждом > — 1,
і Е П—1 И — 1
йш sin" . cos« ■ — i-J_J і—^-jX . (20)
u I Для m = Q вто дает
В
I.
Bin"o»= ' п V*. (21)
Например, когда в интеграле (3) полагаем
f{x) ~ вш*пх
с положительным целым числом п или и = 0, то находим
і
п — —
Г^riaiwi г = ѴП 2^ ѴТ. (22)

Н. И. ЛОБАЧЕВСКИЙ — СТАТЬЯ I 291
Для п = О это снова даст интеграл (1), потому что в таком случае
Ы)"~*-п
п-" = 1.
Для ябів уравнении (22) будет
Ы) '-Ш'-^
п-"=1;
следовательно,
со
J
dx . . 1
— яш»а; = — іг,
как было найдено выше (4).
Другим образом приходим к интегралу (20) от двойного
интеграла
со со
f dxtf* \ dyy^e-'-v = п-пт"т.
о it
Вместо у ж х поетавя сюда
у уи
1 + м' 1 + м
и рассматривая потом м переменным вместо х, получим
со оэ
fundu С
u (l-f«)"+w+\-
а произведя интегрирование в отношении к у,
n-nm-m
С undu _
п^\-т-^-і)°°п+т+1'
который интеграл и переходит в интеграл
dm ИП**1*1 W COS*"*+1 О) = -г т ; : ; ; , (23)
когда делаем
и = tang5 <и
10*

292 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕІТАЛОВ
с условием, чтобы действительная часть в и, т была в каждом
> — 1. Так для 2ws4-l=0 получим
(24)
Если в
і
Т"
1 Йш8Іп5я+!»в =
0
интеграле (23)
полагаем
п —
т =
tango) =
(-
Р-
ч —
1
п"п ]Лс
+
.—I
1
Р~
ч
1\-"+*
*}
-1,
то условия для чисел и, *в теперь для р, q сделаются такими:
р>0, Q>p.
Самый интеграл (23) примет вид
1
і£е Р"Ѵ(Ч —Р — I) - *- » -'
(25)
і, ' {? — I)"»-1
Для 8=1 и для р<1 последний интеграл делается
со
J Л am иг:
" 1 + ятР
Вообще для р>0, <1>р можно интегралу (25) дать такой вид:
J
1, ((/_і)»ч-і sin pic'
ir Весьма примечательный определенный интеграл
+ ■»>
(25
<£ве*ѵ'-' 2тсе-« ,д.
JL (а+яК-!)"*1
может быть доказан различным образом. Здесь и—число, в
котором действительная часть > — 1 *,
* Следует также предположить, что о>0(а«ід, в более общем случае, Re в>0).
Интеграл (28) был вычислен Лобачевский в сочинениях -Способ уверяться...»
и «О сходимости бесконечных рядов» другими способами (см. стр. 151—153 и
215—217_ наст, тома)

Н. И, ЛОБАЧЕВСКИЙ — СТАТЬЯ I 298
В интеграле (12) ставя a-j-iV—1 вместо а, получим
о?
fds *-*•+» ^^-as» — ?—L- .
J (a + 5J/-l)n+1
Умножая на $>еьГ~1 и интегрируя от —Ь до -\-Ь, находим
ао , 4-t»
\dxxne~ax ;—- = n-n I __
UJ (1-ж)У— 1 _-i («-J-6J/—I)»*'
Или, разложив первый интеграл на два с границами от ж = 0 до
ж = 1, потом от х=1 до ж=со,
»-» \ —І—_ГГ -=, Д»з»е—■ 7Ѵ^=т—~~ +
J (а + іК—-1)™+1 ^ '—ж> С —'
С g» <і—«) Ѵ^і ,—ь а—«) Ѵ^Т
^J (1_И)ѴСГІ
Если ate во второй части этого уравнения поставим в последний
интеграл 1-{-х вместо х\ в первый интеграл 1—х вместо х, то
получим
1* epV^db С еЬяУ^і—g-ЬхУ^І
С -fcc J' —Д в—&вѴ — 1
+ *>-<•] (^(І + я-)"*-"* = [28а]
По ставя сюда у вместо х,
х \" - £ » е* ѴГІ — е- *ѵ=і
+'-/*(1+т)"-' я/=і
DO
+ 2«-°J^«iiitf-(l+f-)VI*. [28Ъ]

294 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Для й = оо это последнее уравнение делается
+™
„-« f g»y *g =4е--» Г— sins ГО [28c]
_І(« + »К-1)Я+1 J*
или наконец, внеся сюда значение (1) последнего интеграла:
как и предполагалось (28), покуда действительная часть в а
положительная, в к> — 1.
Если, поставя a-j-i^—1 вместо а, умножаем уравнение (12) на
и потом снова интегрируем в отношении к & от —Ъ до ~\-Ь, то
получим
+6 _ +6 ее
-J
<£пвпе-™-
(1 + яОѴ-І
ОО СО
= 2 \dxx^t^^^^- = 2t*" f—(я — I)»e—8in6x. [28dl
0 ' 1
А когда поставим сюда
к I вместо а-, то
Вторая часть этого уравнения уничтожается для 6»оо и джя
it > — 1 и следовательно
е-ьѴ-хйЬ
если в о и в п-(-1 действительная часть положительная.
1й££5--п-

Н. И. ЛОБАЧЕВСКИЙ— СТАТЬЯ I 295
Из двух интегралов (28), (29) следует
Г ^8'пж те-0
Интеграл (30) для п = 0 дает
со
Г tfe-cosa; яс~а* л^}
J а»-і-а;5 — 2я '
о '
Способ, который употребили мы, чтоб от интеграла (12) перейти
ж интегралу (28), может быть представлен в общем виде *. Пусть
№, +(*)
две функции от х, и пусть
Рассматриваем двойной интеграл
+ь h
7= j" <fej"<&/(a:)<p(iz-atf),
—ь о
где А>Х, 5 — все три числа действительные и положительные.
Интегрируя в отношении к з между назначенных границ, получим
я
7», ф^ФСЦ-а*)-^.^
Л — X
о
Разделяем этот интеграл на две части Р, Q, так что
а
. — far) — $(&г — 6і)
а
X
В интеграле Р поставя к—х вместо я, получим
4 Чтобы получить (32), нужно интеграл (30) сложить с интегралом,
получаемым ев него заменой а: на — я.
* Обоснование следующих далее рассуждений си. в приме-щннж [Щ.

296 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
В интеграле Q поставя \-\-x вместо х:
і/ ft*
Поставя
Дня і =
А
J
оо
вместо
Р--
Q--
х:
f
dxf
*Н(*)—т
(1+.)Ш=
-*)
-Ф(—
1
»)
о
D
Если /(ж) — функция постепенная*, то в интегралах Р, Q
значение f(k) одинаково. Если же постепенность нарушается для х=\,
то в интеграле Р надобно поставить то значение f[k), к которому
приближается f(k — х) е переходом х в нуль, а в интеграле Q
надобно поставить то значение f(l), к которому приближается f(k-\-x)
с переходом х в нуль.
Так составляются образцовые уравнения и условия к отысканию
определенного интеграла
<р(аг) =
db{x)
dx '
о
™ ft
(33)'
# То-ееть непрерывная.
* В тексте Лобачевского номером (33) обозначены только формулы Для <J

Н. И. ЛОБАЧЕВСКИЙ —СТАТЬЯ I
297
Здесь f(x), ф(ж) — произвольные функции от х\ k, Х^-постоянные
числа действительные и положительные; при том
В интегралах Р, Q множители f(\ — В), fQ--\-b)* представляют те
значения, которые эти функции принимают с переходом S в нуль.
Если/(ж) функция непрерывная*, то /■().— 5) = f(k), f(k-\-S) = f(i.),
P=Q.
Граница h, перейдя за величину л, может произвольно быть
увеличена. Так условие h > А будет выполнено, если к = со. В таком
случае уравнения (88) сделаются
у(х) = -
<ІХ
■' X
с
Р+«= J dQ§ axf(x)?Q.H—яС).
[ВЗа]
Например для
, находим
fix).
ts (х) = ё
хУ—1
P = 2f(k) \ — smx = vf(к)®,
J X
о
«-"*/(*),
+ »
2jt/(1)= J (K §dxf(x)coeM~zC),
(34)
— известная формула Фурье.
* В современных обозначениях /(X — 0), fQ. -f- 0).
і * ^го — первый случай, яогда Лобачевский употребляет тернии «иепрсрыв-
аості.в в современном смысле.
и Перед этим равенством, по всей видимости, имеется пропуске тексте.
Выписанные выше выражения дли функций fix), і (#) и f (х) при подстановке в [33а]
приводят к выведенным ранее формулам (28) и (29). а для того, чтобы получить
интегральную формулу Фурье (84), вужно положить ty(x) ■= sinх, <?{х) = еоаж
оставляя функцию f(x) произвольной.

298 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Рассматриваем еще двойной интеграл
—Ь О
где А, Ъ, Л, как и прежде, положительные числа. Интегрирование
в отношении к г дает [10]
а когда поставим х— і. вместо х,
Мшщ J %п*-щиь')-и-Ь')}-
= Г *r(*-4{ + (**)-t(-M-J^«*-^){t(te)-*(-te)b
о о
потом а; вместо Ьх,
Ь*+ (A И.
ж= J ^',(т-4)(*и-ф(-*)і-1т^(т-,1)І*(а!>-+(-аі)|-
о * ' о ^ '
Если Х>0 н 6 = со, то М=0. Если же і = 0 и & = со, то
со
м=но)^щх)—и-«)ь [348]
о
Итак для X > О, А > О
+ я> h
0=> f <fej(te/(a:)e(l?-|-a!^). (35)
—со О
| Если же \ = 0t то
■4-со & с»
J (faJ(fa/'(*)9(») = /'(0)J^{*(a.)-t(-*)}, (36)
—во о о
где /(а:) непрерывная функция от а; и где

Н. И. ЛОБАЧЕВСКИЙ—СТАТЬЯ Т 299
Между теи для к > 0 было тоже найдено уравнение (33), которое
соединяя о уравнением (35), получим для л > О
» +и> It
'WjflH'HMH J <frJ«faA*)(*(A*—a*) — «(іг-j-aw)}. (38)
0 —CD 0
Например, когда ф(ж)=8Іп:£, <в (ж) = соаа;, то
-*™ о
яДХ) = J Ж j"da/fa;)віпУ;sinа£ (40)
-m 0
и которые" уравнения заменяются еще такими;
со h
— ■к f (# = §<%.§ dxf(x)cosK<;oBzZ., (41)
о в
со h
і. я f(k) = j Ж j" dx f(x) sin AC em asC (42)
о о
Если полагаем
/,(ж) = е-в"а;'»
так, чтобы действительная часть в я была положительная н в п > — 1,
то уравнение (39) дает, после интегрирования в отношении к х,
(4S)
е-* С dz cos Хг
- j, (а + гі/^Т)^' '
а уравнение (40) подобным образом
j -^ПЬ~1^= ( Д«^С (44)
' *—/-1 i(a + ^l/-l)-+''
как было найдено выше (30), (31).
Бели в уравнениях (33) полагаем
ф (х) = tang ж,
то

300 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Далее, если f(i) произвольная, но постепенная функция от Л, то (б)
+™ А
-—» о ѵ '
Произведя здесь интегрирование от —з до -{-г, получим
D
где предполагается X > О, А > А и где после интегрирования в
отношении к а: надобно 2 почитать бесконечно великим числом f11].
Для произвольной функции f(x) от х находим двойной интеграл *
£ = f dz ^L^-\ dxfix)*-**-***=*-
f" +f" A^'-f)*"1
tf jL(«a + *V-i)"+I
= Г dxe-*»f(x) С
1-T -Wri +
/31
г
'-т
,n+i
S ^ *' jL(«* —0* + *^ —1)"+»
А как та часть интеграла, где &>і, делается нулем по
примеру интеграла (29), то
L=[ dxe~<«/<*)( 1 — — Г f -
о ' о
1
* Дальше предполагается, что о>0 (или Ееа>0).

Н. И. ЛОБАЧЕВСКИЙ— СТАТЬЯ I 301
Так значение двойного интеграла делается
us -—■ - I dxe x f(x) =
i
= 1^" J ^Ѵ(Х-.т)Н- [4ea]
i
Например для f(x) = 1 сделав интегрирование в отношении к х,
получим
+ « 1Л_ і
•L(ox+*v— i)n+a xe+i»-" J " (*-
^(яА+жУ— 1)-+= X- + 1»-" J (* + l) —+ >'
,в | как было найдено выше (28). Положив
f(a)_*»,
находим
і
1 dx я" (X — х)т = -, ѵ—^ і—і-г .
Поетавя сюда
получим
| (йоаіп-
» ™ " -т ■" т
>-МаіС08=»+1аі =
2(п + т-|-1)""+"+1 '
как доказано было прежде (23).
Интеграл (2), когда поставим «ода а вместо cot а, можем напи-
еать в таком виде:
?dx . 1 , fa + V=l\*
\ — sin.-g ■ е-"3'— — >- — log I —!—-, -.1 ,
"\ * В тѳнете Ловачевевого а этой формуле пропущена двойка в знаменателе.
* Так как
1 , а + У-Л
arctg о = -^^ log ——Т=.
ЧУ—\ а- Ѵ—1

302 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
где а может быть всякое положительное число. Означая Ъ какое
нибудь другое положительное число, заключаем, что
J к У ЧѴ—I *\а — у—1 Ь+У—1/
Ставя сюда а + 1, 6 + 1 вместо а, 6; потом а + 2. *+- 2 вместо
я, 6 и так продолжая, если складываем все такие интегралы,
получим для целого числа г
СО
Же . e-*r_e-ta
— яп ж • (1 — е — **) =
ж 1-е-»
., (а+г-1 + К-1)-'(й + г-1-Ѵ-1)^
2]/ЗГТ *(в + г_ і_ Y~l)~*{b-\-r — I-)-/— i)-f
Для г = со это дает
е — ож_ е — Ьх
віп а;*
X ех—1
2/-1 (a+V^Ti>- + ''-i(6„j/„1)

СТАТЬЯ П
іѵ | После того, как значение определенного интеграла
CD
п vtn
1
dxsf* e~ax =
о *
доказано для всех чисел п, а, действительных и воображаемых *,
стоит только сюда поставить один раз а-\-ЬУ— 1, в другой раз
а — Ьу — 1 вместо а, потом взять рааноеть двух интегралов, чтобы
получить интеграл
со
I dzm"e—аг8Іпйа;= *
о
\(а + ЬУ=1)-»-~ '-(а — бу^Гі)—'-і). (48)*
— п'
ч.\Г^\
Полагая здесь 7ь = 8—1 и В тасло весьма малое, чтобы при
разложении довольствоваться первой степенью, получим
[&*« — ^~
Основываясь на том свойстве гаммы, что для всяких чисел іъ, а, т
п-"ю = п-"(п — в)-"--,
можем писать
(•-О-'-'-т.
* Кѳо>0, Ввя> —1.
* В тексте Лоб»чвееяого номер формулы (43) отсутствует неоониенно по
ошибке; на ѳтот шшер в дальнейшем имеется ссылка.

304 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
| а для 3 чрезвычайно малого числа
(в —1)-»-івІ-«.
Далее
(а — ЬѴ^І) ~3 = 1 — Й log ft — ЬУ=1) *.
После-чего и для 3 = 0
\ Охе-0* = —т={ log r,=),
J * 2/-1 й — f'V— lJ
[48a]
и
согласно с тем, как было найдено прпжде.
Вместо а ставя сюда по порядку о-j-l, а-\-2, ..., потом
складывая все интегралы, получим для целого числа і
С, einbx 1-е-** 1 ѵі. (а4-і — l + W— 1 \
J х 1~е-<» 21/—1^, \а-{-і—1—Ь\/—1/
или с принятым означением
die-——е-<и__- _ = ___.iog.L_-J- ~ ■ , —'—Q.
я? 1 — е-я 2 У— 1 (я + г— 1 — Ъу— 1)"*
Для весьма большого числа г, основываясь на том уравнении,
которое служит определением гаммы, и для всех чисел р, q
подобным образом
* То-ееть
,______._____._
5-ю 1
а
* То-есть
1ІШ _-t° + »»_gL_.-_ ц- 1-Іа-ЬѴ-^=1_
а В тексте Лобачевского в этой формуле в знаменателе под знаком
интеграла ошибочно поставлен лишний множитель х.

Н. И. ЛОБАЧЕВСКИЙ — СТАТЬЯ П 305
а когда поставим а вместо а:
После чего для і = со получим
ос
tfcg sin &g [e-<& — e ~°д) 1 (о — 1 — ЪУ— 1) — 2bV~l
1-е— 2J/^T' °S~(s —1"_~&7^l)--»»^3~*
Если сюда ставим
то находим
а = 1— у— 1,
а=1 + У=~І,
ее
«fe sin to sin ж ^ 1— (1 + ^)К— lj—^' -J
Далее, основываясь на общем уравнении для гаммы
п "п = п ~х ■ (к — а) - я ~«,
можем написать
,. .— І-/І4.») і/— і! - -11 + ь>ѵ zri
}_(1_]_й)У_1) — *м -і= < Uf^f М ^_
> * "Г " » t_(i_u)/_i} — d-чѵ-.і
J
«Ьв еіп г, sin foe
гс е* —1
в і_1о {—(! + *)/— М—» + "у'-'Ч(1 + ^)/— ц-p + w-»
4 °g { —(1 —6)[/^Т} (<-0)J'^i{(i_6)l/:Zrtj-(i-»]l'r:i
Между тем, для всякого числа п, действительного и
воображаемого (ур. 8}
;і-я(-
После чего
ао
f da; sin .г sin йж
J * е1—1
D
' Sill niz
1 ] \t>~\-l ee«-«—es—ta
4 E|t —1 e»" + "—«-"-»■
30 Яяк. 58S3. И. В. Лобачевсии», т. Ѵ.

306 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Если предполагаем Ь — 1 столь малым числом, что можем
довольствоваться первой степенью от 6 — 1 в разложении, потом Ь
почитаем за единицу, то приходим к такому интегралу:
Т их 8Іп2э; 1, /е2* — е-*«\*
о 1 '
Если в уравнении (48) снова ставим а-\-ЬУ — 1 вместо а, потом
а — bY—1 в том же уравнении вместо а, наконец берем разность
двух интегралов, то получим
со
1 Дг х" е — ах віпа Ьх =
о
= —І-я-*1{(а + 2ЬѴ=гІ)-я-1—2а~п-і-\-(а — 2ЬУ^І)гп-1), <49)
и | а когда поставим сюда п = 8 — 2,
S *•>•--(^)'
= ^-(8 — 2)-'-*{(а + 2*у^1)*-* — 2а»-Ч-(а — 25^— I)1-').
Для § чрезвычайно малого числа
j"*""-(^r-
+ (я —26Ѵ^І)[1 —81og(a —26lA^a)|[ *.
Принимая 8 = 0, находим
* В тевете Лобачевского под внаком хогарнфга вместо 4л ошибочно стоит 2.
* См. сноску * к стр. 304.

Н. Ж. ЛОБАЧЕВСКИЙ —СТАТЬЯ II 807
Если к тому а = 0, то должно принимать
«i4f(i + 5)-o.
Так приходим к интегралу
о ^ '
для 6 = 1:
который интеграл можно также найти, начиная с неопределенного
Г dx . . 1 . . . Г <fc . п
I -TsmBa: = — — sina;e4- 1 —8іп2зт:
J x2 x ' J x .
с уменьшением х
1 . „
-—sin*»
X
переходит в нуль, а следовательно
CO CD CO
f Ле . - f <** • « f <fc; . 1
I —sim"i'= 1 —вш2ж= 1 —eina: = —it.
J x2 J cc J ж 2
ч I В уравнении (49) ставя a-\-b]/—l, а — ЪУ—1 вместо а, потом
вычитая один интеграл иа другого, получим
со
I Зххпе~-аз:віпяЬх*=
в
п*
__.|(а4-зб)/—Т)-'»-І-з(а+іѴ~і)-п~,+
+ 3(а— 6/^Т)——' — (а — Зб/^Т)-»-1}.
Полагая вдесь 8—>8 = я и 8 столько малым, чтобы довольство-
го*

308 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
ваться первой степенью от S в разложении
j *,«.,-«. (f^1
. -S—з
■■1\у— І(*+аьѴ-іПі-ііое(о+8бѴ-і)}-
— S(a-hbV~l)*[l~~blog(a-{-bV=ri)]-\-
_|_ з(а — Ь Ѵ^ІУ [1 —Slog (а — Ь Ѵ^Т)]—
— (а — 36 Ѵ^І? [1 — * bg (а — Зй У^1)Ц
Здесь
(3_3)"5-а=.
что вставляя и удерживая только первую степень S, находим
8-«
?, . „„/einto\»
.{_(a_|_3&l/^T)4og(a+3bt^I) +
8(8—1J(5 —2)|/^І
+ 3 (а + Ь /=l)Uog (а + 6 У=1) — 3 {«-& Ѵ^У log (а — 6 VZZl) +
4- (а — 36 V^lf log (а — 3* У^І)},
а когда делаем S = 0, то
7 л /вшбаЛ8
. {- (а + S6 К-1)« log (а + 36 Ѵ~ 1) +
ібѴ—і
4- 3 (а + 6 yZTi)4og (а + 6 К13!) — 3 (а — 6 l^=l)a log (а — 4 Ѵ^Л ■
+ (о — 36 Ѵ^і? log (а — 36 У~*)} *=
-аЯ -iog.'+;;^-i-a^(fl'+«y)+
16^—1 а —36 (/"—1
8
За*
l°g
а+6"
, 3 ,,,..,,. , 362 , а — Ь Ѵ~
4 а£ log (аа -f б1) -[ т=- log ~г=-

Н. И. ЛОБАЧЕВСКИЙ — СТАТЬЯ П 309
Итак если полагаем
зй „ ь
— = tangp; — = tangf,
то
{"«..--(-£■)■_
= і р (эй* „ а-) + J-1 (в» - 6') - -| об log (а* + 9S*) +-| oft log (а* + Ъ*).
Для а = 0 делается
и следовательно
И^)'-т--
Так продолжая, находнм для всякого целого положительного
числа т и для S чрезвычайно малого
о
В»*
[^«-«(і^)"^
7=^гХ
«(в — і)""-1.(—21^—1)"
та , »
xS(~f„f"-'[a+(>«-206VA=I]"-4(l-Blog["+('«-2»)^]/I=l])*-
1 = 0
Рассматриваем теперь сумму
т
* Дальше Лобачевский пользуется методом полной индукции. Поэтому саму
вту формулу следовало бы тоже проверить методом индукции.
* Здесь Ь заменяет о У"— і в прежних обозначения!.

810 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
находим
яі-И
(-1?Ѵ ■,<-1[«+& + ("t-2i)&]"-'-
ТП+1 - ѵ у
— 2ft У(— 1)^т\,]'" [а4-Д + (« —ЭО6]"-' =
—(а+6+. «914(0+й)_(а+*+ИІй)я.1(а-в)—
1+1
—<—і
= (а —& + m&)ZM(a+S) — (а + Ь+тЬ)Хт(а — Ь) +
т ,
-(<* — * + «*)№.(« + *) — A.(o-ft)} [15]- [49а]
п | Итак, если Д„ (a) = 0 для всякого а, как это можно поверить
для т = 1, т*=2, то
и, следовательно, для всякого целого положительного числа ад
После чего
Г . / 8ІП&в\™
X
(m —іГ'—'рі/— 1)и
х|;Ь^^{в-1-(»_2і)йУ=іГ-11ов{в + («-Й)4Ѵ^1}.
Если делаем
(т — 2г) — = tang щ f,
то
/ sin 5ж \m
о
С / sin Ъх \"
X
(m_l)-™-!(2V—1)"
*_о * cosuii

Н, И. ЛОБАЧЕВСКИЙ—СТАТЬЯ II 311
а когда поставам значение eoswj,
!-r-fflm-
;Х
(»-1)—1(2/=І/
Если о = 0, то для всех і
После чего
«, = т«г.
І*(^Г-
&"-1е в у
(т-1)""-'(2Ѵ"-1)'
xjSc-O'^fm-ao-^jiogKM-a^ftH-i-*»^!}}.
Здесь множитель при -^-^"^—1, как было доказано выше,
т
г'
(=0
л | следовательно, значение интеграла представляется короче
HW
(»-J1vr-i
_ Vя-1е - у
^(т-1)-я,-1(2/^ІГ
X 2<-iy^(»-20--4og[(m-«)4.
Здесь число & разумеется положительным; а когда число под
знаком логарифма сделается отрицательным, то множитель —1
надобно заменять множителем

312 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Так находим для т чотного
т-і (»-і)^ та и
Для т нечогного
~(»-Ч
• х ' (» — l)"m-12"(— 1) a f=»
Например,
со
Г da; . , 1
I -—■ SID ОЖ = — It,
а
о
р\ /sin fa \* 1 „
f , /sin&e\s 115 ,,
* 8 оригинале поеяеддае два интеграла даны с опечатками:
со со
$ „Jwabx-y 235 Р. /біпЬа:\* 33 ,,

ПРИМЕЧАНИЯ
['] Если иятѳграл
С,. . віпа;,
f(x) dx
J х
о
несобственный, то для справедливости дальнейшего нужно
предположить, что он сходится, что влечет за собой также сходимость
интегралов
\m^f^ (*-ip8l...>
о
[:] Следующие далее выкладки справедливы, если интеграл
¥
С ,, . sin х ,
J f№ ~1Г~ '
о
а следовательно и интегралы
■
С f{x)sinxdx _
о '
сходятся.
[3] дтот интеграл рааходится. Однако произведенное Лобачевским
вычисление вполне обосновано, как в втом нетрудно убедиться,
проследив выкладки, приводящие к (4), если под значением интеграла
в левой части (5) понимать
с»
II =-0
где І„— главное значение интеграла

314 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
[4] Из одного того, что lim [logt|i (г) —log>Ji{r— 1)] = 0, нѳ следует,
конечно, что lim^r) существует. Однако существование этого предела
г-» и»
немедленно следует из [10а]. В самом деле, если п-|-г;> 1, то
log
*(r+H
♦ (г)
<
12 (в+ »■)*'
а так как ряд
СП
+kf
сходится, то Нтф(г) оущеотвует и
г->со
lim log ф (г) — log ф (г) =
= Vlo;;^f+Hl)=l V у (-!)'■ (а)
ft—a
J_0 №1
Перестановка порядка суммирования в правой часта (а) приводит
к равенству [10Ъ]. Двойной ряд в правой части JlOb] сходится при
любых комплексных значениях г-(-я, кроме целых отрицательных и
r-j-» = o, а так как функция f(n) определена для любых значений»
[если и—целое отрицательное число, то ^ {г) ^ 0, при достаточно
большом г и, следовательно, /"(«)= 0], то равенства (10) и [10bJ
могут служить определением функции (п-{-г)"г для любых комплексных
значений И и г, кроме »-[-г = 0 и тех, при которых г4-и целое
отрицательное число. Значения п -J- »■ = О и некоторые из значений г и я,
для которых w-j-r целое отрицательное число, соответствуют
устранимым особым точкам функции (w-j-r)~r. См. об этом подробнее в
примечании [аі] к сочинению сСпособ уверяться ...» на стр, 235—237
наст. тома.
|6) Хотя рассуждения Лобачевского при выводе втого равенства
весьма нестрогие, однако с помощью соответствующих оценок их
можно обосновать беа большого труда.
[6] Если Г(«, и) = I е~"язУЧкс, то интегрирование по чалтям
U
(Кеа>0, Ее«>0) дает
со
Via, и) = —~ £~«';сп+1Ас = —£—Г(а, п + 1).
я -f-1 J n —j— 1

ПРИМЕЧАНИЯ 815
С другой стороны,
дГ(а, и)
да
ел ѳдоватѳ льно,
откуда
, „ e-<^x"+1dx = —V(a, n + 1);
дѴ(а, п) , к 4-1
да
п«, і-т.
Но С(я) не зависит от а, а так как О (и) = и~" при действительном а,
го равенство (12) справедливо при комплексном а.
Лобачевский, невидимому, считал необоснованной, в случае, если
а — комплексное число, подстановку ж = а( в интеграле (11),
приводящую к (12), так как путем интегрирования в (12) при этом стано«
вится нѳ положительная вещественная полуось, а некоторый луч
в правой полуплоскости.
[*] Несмотря на внешнюю нѳ строгость, рассуждения Лобачевского
при выводе равенств (19) правильные. Действительно,
1 — еоэ па соз™ а = 1 — I 1 — -{-... I cos" % =
= 1 — соа" а -| — cos" а I 1 — -—- —j— ■ - - I =
, (1 -—cos" а)5
= —-nlog cos a-~-
2
так как
log cos" a = — (1 — cos"a)-
Ввиду того, что
(1 — C08"5)3
,. (1 — cos" a)2
bm -—■——■ '■ = 0,
отсюда следует, что
1 — соа яа сое" a
Іпн ■■ ■ ■— ■ = —logcoaa.
Это последнее равенство проще, впрочем, получать, пользуясь обычным
правилом раскрытия неопределенностей.
Что касается предельного перехода под знаком интеграла,
приводящего от [18а] к (19), то очевидно, что, благодаря наличию в [18а]
под знаком интеграла множителя 1 — cos ах, этот интеграл сходится
равномерно не только в окрестности точки »= 0, но даже при
и > — 2 4-е, где s — любое положительное число.

316 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
[э] Предельный переход от [28Ъ] к [28о] Лобачевским не обосновав.
Приводим здесь обоснование равенства [28о).
Нижа (ом. примечание (10]) доказывается следующее предложение.
Если функция f(x) имеет ограниченную вариацию в интервале (О, ft),
где h >■ О, и интеграл
и
сходится, то
lim ff(,)^mto = r( + o)fiH(b.
Функция f{x) = (1 -^-х)'Іе~аа' имеет ограниченную вариацию в
интервале (0, ее) и, положив Р(х) = 9ти, имеем для второго интеграла
в правой части [28а]
ГО
г еьх К—і е-fc" V—1
lim 1 (1 -i-x^e-*31 ■ <b: =
»-*„J ^ x\f~l
о <□
„ ,. С , , , einfor , f.sini ,
= 2 lim (1 -4- а;)» е-"* -Ac =2 dx.
ъ-*а,<} x J x
о о
Что касается первого интеграла в правой части {28а], то
і і
С рЪя V—1 fi — Ьх V—1 (• -:„ ь_
J хѴ-l У
= 2 j (l-^-^^dx+S Jo-^e-^de, (a)
0 1—t
где s — произвольное положительное число.
Так как я > — 1, то модуль последнего интеграла в право- части (а)
может быть сделан сколь угодно малым для всех значений Ъ при
соответствующем выборе числа е, а
Hi со
.■ Г /, ,„ „. 8ІП&С fsillX .
lim I (1 — х)певх ita=l dx
Ь •& оэ *J X J X
О О
ж равенство [28с], таким образоѵ, обосновано.
[э] Обоснование предельного перекода можно построить аналогично
тому, как это показано в предыдущем примечании. Предварительно
нужно только следующим образом преобразовать интеграл в послед-

ПРИМЕЧАНИЯ
317
ней части [28d]:
і
, , sin Ьх .
(а; — і)пе-аа———4х--
X
С, ч, sin bx , f*, . ч sin Ьх ,
= I (ж — l)"e-™.—-—dx— {х— і)»е-«» dj =
о о
f sin 6а: , Г sin Ьж ,
О 1—■
J * X
I)
где* — произвольное положительное число, а ®(х)— функция, равная
нулю в интервале (1 — а, 1-|~е) и совпадающая с (х—iytg-ая внѳ
этого интервала.
J10] Проводим обоснование следующих далее выкладок, кончая
равенством (36). Начнем с доказательства основное леммы:
Лемма. Если ft > 0, функция f(x) имеет ограниченную вариацию
в интервале (О, &) и интеграл
J
*&-** (а)
сходится, то
Um|/(0imaef{.i.o)JiM4fa. о,)
Т-*"Е
Заметам, что из справедливости (Ъ) для функций f1 (х) и /2 (х)
следует его справедливость для функции fc,/\ (х) -f- fcaf» (*)> г^е fei я *j —
постоянные; так как, кроме того, очевидно, что равенство (Ь) имеет
место, если /(x)sl, то будем считать, что в интервале (О, Д)
функция f{x) действительная, неубывающая и / (-(- 0) = 0.
Взяв произвольное положительное г, выберем а так, чтобы
О < а < А и f(x) < s при 0 < з; < а.
Применяя вторую теорему о среднем, получим
о ъ
Слѳ д овате л ьно,
I" WlTI\
<Ом,
J
«о-^і*

318 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
где С — некоторая достоянная, так как
F{Tt)
t
dt
dx
<C
в силу предположенной оходимоетн интеграла (а).
С помощью второй теоремы о средней имеем также
■3* -[Г
(о)
где а ^ у -^ А. Ввиду сходимооти интеграла (а), модуль интеграла
в левой части (с) можно сделать сколь угодно малым, если Т
достаточно велико, а так как число а произвольно, то равенство (Ъ) доказано.
При тех же условиях относительно функция f(x), если сходится
интеграл
—"л
J
F(x)
dx,
(»')
аналогичным образом можно доказать, что
Если функция F{x) равномерно ограничена в интервале (О, со) или,
соответственно (О, —со), то равенства (Ъ) и (V) остаются
справедливыми и в случае, когда в окрестности конечного числа точек
интервала (0, ft) функция f(x) имеет неограниченную вариацию (в
частности, становится неограниченной), лишь бы она была абсолютно
интегрируемой в окрестности ѳтих точек.
Действительно, если «о—такая точка, a S—произвольное
положительное число (0 < <п — S, і» + в < ft), то
$т*Шл^т^«+^1(р_ь (d)
о О (о —5
где Д() = 0 в интервале (ш — S, m-j-B) и f(t) = f(t) вне этого
интервала. В силу (а)

ПРИМЕЧАНИЯ
319
я так как модуль второго слагаемого в правой части (d) при
достаточно малом 8 и любом Т произвольно мал, го равенство (Ь) остается
в силе. Так же обстоит дело и с равенством (Ь').
Пусть теперь функция f(x) имеет ограниченную вариацию в любом
конечном интервале и абсолютно интегрируема в интервале (—со, со),
функция F(x) равномерно ограничена в интервале (—то, оо) и
интеграл
— ОО
сходятся, .
Докажем, что
со
1ІЮ f,(.)^C—Я*,
*— со
m О
а —со
В самом деле, при этих условиях можно выбрать так В и Б, яв
вавиоящие от Т, чтобы Л > tt R > — £ и чтобы
со
11
-S
<
со
|««)|*<.,
I—GO ~~' —CO
как мало бы ни было а > О, н следовательно, интеграл
со
« ев
сходится при любом * равномерно относительно Т.
Но
—К
о

320 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
и в соответствии с (Ь) а (Ь'), если — £ < (< В, то
-я
Отсюда и из равномерной сходимости интеграла (/) немедленно
следует (е).
Нетрудно видеть, что равенство (е) остается справедливым при
наличии конечного числа точек, а окрестности которых функция f(x)
имеет неограниченную вариацию (н частности, становится
неограниченной), если только она имеет ограниченную вариацию в окрестности
точки (.
Из равенства (ѳ), в частности, следует, что
ш [пш) *ІТ«—Я * = о. (,)
в
если ( < я или £>■[}, так как в этом случае функцию Да;) можно
положить равной нулю в интервалах (— со, а) или (|3, со).
Предположим теперь, что функция а(х) интегрируема в любом
конечном интервале, обозначим
.г
F(x)=[v(x)dx
о
и допустим, что функции f(x) и F{x) удовлетворяют условиям,
оговоренным при выводе (е).
Тогда
- ft О И
так как условия, наложенные на функции f(x) и f{x), делают
возможный изменение порядка интегрирования.
Если считать, что f(x)sszO в интервале (—оо, 0) и (А, со), то при
0 ■< ( < h на основании (е) получим
ft й <и
Urn f dz (7<*Ж*(* —x)]dx=lf{t — о)+ f(t +0)1 f-^H<te=
т. ■* о ■ *г, J j х
(Я
^^-OJ + rtf + OMJi^^I^*,,
а
т. е. формулу (33) Лобачевского.

ПРИМЕЧАНИЯ
321
Вслш і = 0, то, полагая f(x) = 0 прп I < 0, приводим к формуле
Лобачевокого (36).
Если же ( < О (ила t > k), то, пользуясь (g), найдем, что
СО h
\ Az \ f(x)w[z(t — x)]dx = 0,
со n
1 dz\ f(x)<i[!:(t-irx)\dx = Q
apir t > О (или t < — h). Этим обоснована формула Лобачевского (35).
Если интеграл
to
\ f(x)a[z(t — x)\dx
u
сходится равномерно относительно z во всяком конечной интервале,
то наряду с формулой (33) справедлива и формула [ЗЗаІ, а также
формулы (35) п (36) при fi = co.
Из приведенных рассуждений нетрудно видеть, что все
выведенные выше формулы остаются в силе, когда интеграл
ее
*ѵ> *.
х
расходится, но существует главное значение
т*»±т х .) х
Запись формул Лобачевским этот случаи предусматривает.
Формулы (28) и (29) получаются, если положить |в обозначениях
Лобачѳвекого) f (ж) == ж» e~<™, «(ж) =еІ*г-1, а= 1, прячем прп п > — 1
легко убедиться в выполнении всех оговоренных выше условий.
Заметим, наконец, следующее.
Если функция Ф (,г) становится неограниченной в точках
?*(-.-<P-j<P-i<0<P«<Pi<P!< •■■)• Іпі (Pfc —Р»-і)>0 " воли
главным значением» интеграла
Ф (х) dx
*'
О
называть величину
І 4,
* си

322 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
где 1^—главное значение интеграла
2
\ Ф (a;) dx,
а
то при некоторых дополнительных условиях, которые мы здесь
приводить не будем, можно доказать, что формула (е) останется
справедливой, если под значениями интегралов понимать главные значения
в указанной смысле.
(uj Формула (45) лишена смысла, так как внутренний интеграл
в ее правой часта расходится и не имеет даже главного значения;
тем не менее формула (46) справедлива (см. примечание [,0]), если
в правой ее части подразумевать главное значение соответствующего
интеграла, как это следует из формулы (ѳ) примечания [і0] и из
равенства (5) (см. также примечание [3J).
I11] Далее в оригинале в результате недосмотра ') следует текст,
почти дословно повторяющийся после равенства [46а]. Приводим втот
текст полностью:
«Например, для f(x) = lr сделав в L наперед интегрирование в
отношении к х, получим
— і
(* dze*v~* 2яе-<* С 3
\ =- = I dxxn =
-n+l >
как было найдено выше (28).
Поставя f (х) ■= ж™, получим
і
dx ж" (к — х)т =
Xffl+n+V
(» + ш+1)
«-n+m + 1
который интеграл переходит в интеграл (23), когда адесь делаем
х = 'К sin2 u>» .
I1*] В современных обозначениях и если положить « + ?- = (,
равенство [46а] примет вид:
а-і-ісо со X
<) Это сочинение ЛобачевсккЯ диктовал, будучи crntaam.

ПРИМЕЧАНИЯ
828
В отом равенстве содержится преобразование, полученное формально
из пари трансформаций Лапласа
а^-іао
2™eito
("+ і)-вратным интегриройаниѳм второй формулы, что даст
а—ісо
Подставив сюда ф(?) из первой формулы (а], получим
а —/со О (I
и, положив a("'+1,(a:) = 1f(a;)I приходим в формуле (46а|.
Однако формула [46aJ является более общей, чем (Ь), так как
в равенстве (Ь) и — целое положительное число или нуль.
Iй] При вычислении предела, приводящего к правой части (47),
удобно воспользоваться тождеством
/_ і .л ••*+»■
и асимптотической формулой
х - е~
Равенство (47) получается из предыдущего при помощи предельного
перехода при г —> со и замены а — 1, Ь — 1 соответственно через
а и Ъ.
[IS] Так как
[,, .4- ь-\- (т—2і) Ь]т =
= (e^_6_(-»tu)[u-f-64-0»—21)*]""1 — 2Ы\а-\-Ь-\-{т — 2і)*Г""'
и
21*

324 ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
ТО
і-0 1
={0 + 6+м6)2(_і/^ІІ±^±^_[а+й + (т_2і)бГ-і_
t—о
і-о 1
„(«+6+»Ь> £»(« + *)+
1 ь*Ь 1
+ (a+bJrmb)%(~l)'-J!!-—i:r-[a±b + (m~2i)br-,~
і = 1 ^ '
если учесть также, что (—1)"*~'=00 и m"m+1 =0.
Лобачевский, невидимому, пропустил под знаком суммы в третьей
строчке равенств [49а] множитель і в числителе.
Далее замена і на і-\-\ дает
* -і
= — У(-1)'^[а__Ь + (™ — 2і)&Г_І = — ■&■,'(* — Ь)
,а+1 . ,*-*
D _ (« -f1) 2] (— 1)* -^- [а — 6 + (щ _ Zt) ИГ" 1=— (я) + 1) £„ (а—6)
і = о г
и, следовательно,
А»+і (а) = (« + * + ™ь) І\і (<* + 6) —Ьт (а — &)J -[- 2Ь(т-\- 1) Ьт (д — ft).
Таким образом, действительно из тождества Lm(a) = 0 следует тожле-
«*■<» А»+1 («) —О.

Приложение
ИСТОРИКО-БИБЛНОГРАФИЧЕСКИЕ СВЕДЕНИЯ О СОЧИНЕНИИ
«ЗНАЧЕНИЕ НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ»
Последнее сочинение Н. И. Лобачевского до математическому
анализу «Значение некоторых определенных интегралов» было напечатано
в (Ученых записках Кааанского университета* за 1852 гол, в книжке IV
на страницах 1—34. Две ее части, озаглавленные сСтатья I» и
«Статья ТІ», следуют подряд (статья I—на стр. 1—26, статья Д — на стр.
27—Зі) и имеют общую нумерацию формул; в то же время каждая
из них снабжена заглавием сочинения и фамилией автора1). Это
производит странное впечатление. Возможно, что сначала
предполагалось поместить эти статьи в разных книжках «Ученых записок»
и что Лобачевский сдал в редакцию свое сочинение в два приема,
но их оказалось возможным напечатать вместе.
Журнал с сочинением Лобачевского вышел в 1853 году. В том же
году это сочинение вышло отдельным списком с надписью на обложке:
чЗначение некоторых определенных интегралов. Сочинение Николая
Лобачевского, заслуженного профессора императорского Казанского
университета»; в конце 34-й страницы оттиска указано: «Перепечатано
из 4-Й книжки Ученых валисок за 1852 год».
Сочинение на русском языке ни разу не переиздавалось.
В 1855 году в «Архиве Эрмана» (Arohiv fiir wissenschaftliche Kunde
von Ruseland, Берлин, том 14, стр. 232—272] был опубликован
перевод этого сочинении на немецкий язык под заглавием: «Ueber den
Wertb. einiger bestimmten Integrale. Naeh dem Russischen von Herrn
Lobateohewakij, Prof, emerh. zu Kazan».
Текст настоящего издания воспроизводит текст оригинала;
исключено только нескодько строк, по ошибке напечатанных дважды (см.
примечание [1-] на стр. 322); порядок дополнительной нумерации формул,
направления ошибок п опечаток, а также изменения обозначений тот
же, что и в сочинениях Лобачевского по теории рядов3).
') Фотография стр. 1 помещена перед стр. 27о наст, тома; заглавие второй
статьи (стр. 27 оригинального издания) имеет точно такой же вид.
-} Си. стр. 263 л 364 наст. типа.

ВЕРОЯТНОСТЬ
СРЕДНИХ РЕЗУЛЬТАТОВ,
ПОЛУЧЕННЫХ
ИЗ ПОВТОРНЫХ
НАБЛЮДЕНИЙ
a s-ui.
ВВОДНАЯ СТАТЬЯ А.Н.КОЛМОГОРОВА,
ПЕРЕВОД АН. ХОВАНСКОГО,
КОММЕНТАРИИ А.НКОЛМОГОРОВА
И АН. ХОВАНСКОГО

ВЕРОЯТНОСТЬ СРЕДНИХ РЕЗУЛЬТАТОВ,
ПОЛУЧЕННЫХ ИЗ ПОВТОРНЫХ НАБЛЮДЕНИЙ
Вводная статья:
Обзор сочинения «Вероятность средних результатов, полученных
нэ повторных наблюдений»
К. И. Л о б а ч е в о к и и — «Вероятность средних результатов,
полученных из повторных наблюдений» Перевод с
французского А. Л. Хованекого
Примечания
Приложение;
Иеторико-библиографические сведения о сочинении кНероятвость
средин* результатов полученные иа повторных наблюдений» .

ОВЗОР СОЧЯЯЕЯИЯ
«ВЕРОЯТНОСТЬ СРЕДНИХ РЕЗУЛЬТАТОВ.
ПОЛУЧЕННЫХ ИЗ ПОВТОРНЫХ НАБЛЮДЕНИЙ»
Статья Лобачевского (Вероятность средних результатов, полученных
its повторных наблюдений:», напечатанная а 1842 году на французском
языке в журнале Крелля, является переработкой статей (параграфов)
104—165 его «Новых начал геометрии с полной теорией
параллельных» *). В некоторых частях французский текст статьи является
простым переводом русского текста «Новых начал». Некоторые чисто
технические выкладки текста «Новых начал» в журнальной статье
сокращены или опущены, но зато в ней добавлены сопоставление
нолученных результатов с результатами Лапласа и применения к
вычислению определенных интегралов.
В современной терминологии исследование Лобачевского посвящено
нахождению закона распределения суммы, или среднего
арифметического )' взаимно независимых и одинаково распределенных случайных
величин. Лобачевский ограничивается двумя специальными задачами
этого рода. Первая из решаемых им аадач заключается в нахождении
распределения суммы
!*г = J4-На І- ■•• + *г>
і'дѳ д( взаимно независимы и каждое из них принимает только целые
значения I, заключенные в пределах
— а ^ I ^ -\- а,
с одинаковой вероятностью -—г—-. Очевидно, что сумма а, способна
принимать только пелілѳ значения т, заключенные в пределах
— га г£ т ^ -j- га,
н задача состоит в нахождении соответствующих вероятностей
СГЫ)
Рг («) =
(*»+ 1Г
!) Т. И наст, издания, стр. 397—403.

330 ВЕРОЯТНОСТЬ СРЕДНИХ РЕЗУЛЬТАТОВ
где Gr(m) обозначает «число шансов> получить iir = m. Вместо
обычной в современных исследованиях формулы «компоаиции»
распределений
p,+1W = 2-Рг (»)рі (»—»)
•и
Лобачевский пользуется формулой
Сг+1(») = 2 0,(11)0,(1— я),
п
которая позволяет последовательно вычислять Сг(»*) при г = 2, 3, 4
отправляясь от
І1 при \т\^а,
ОприМ>«.
Вторая задача, рассмотренная Лобачевским, заключается в
нахождении распределения среднего арифметического
£r=l(B1 + 8,+ ...+8r),
где каждая из взаимно независимых величин 8( распределена
равномерно на отрезке [—1; -\-1]. В настоящее время такая задача
решалась бы на основе формулы композиции для плотностей вероятности,
Лобачевский получает ее решение предельным переходом при
а —* со,
ш
га
из решения первой задачи.
Наиболее замечательным является то, что Лобачевский совершенно
элементарными методами находит для чисел Сг (т) в первой задаче
и вероятностей
Pr(x)--P{\lr\^x\
во второй задаче явные формулы, которые в современных обозначе-
яиях имеют вид1);
0г(т)= 2 (—1>10ІС^л)Втт+г_,_,, (1)
Pr{r) = l Л-; 2 (_i)'c;0--v.r^2/.f. (2)
') Где С" — биномиальные коэффициенты
С? =
я ml (» — *»)! '

ОБЗОР СОЧИНЕНИЯ 331
В заключительной части статьи Лобачевский пользуется формулой
Лапласа
Binla-f-if ) °Л
1 ВШ|
Сг(т) = — 1 cos ши ■-—— ——| dm, (3)
'J . [ -у
и получает для Р,(х) интегральное выражение
ао
Сопоставление (4) и (2) приводит в выражению в виде конечной суммы
интеграла, стоящего в правой части равенства (4). Попутно
Лобачевский получает еще формулу
JoM(W)(^)'^--—^— ^ <г-1?$(г-Ы±г*)*-\ (Ь)
где знак перед гх можно выбрать по произволу.
Наконец, полагая в (5) г = 1, я = 0, Лобачевский получает новое
доказательство известной формулы
ее
J
tfnz it .„.
— dz^—-. (ft)
о
Относительно формулы (5) Лобачевский указывает, что она была
получена Лапласом, хотя и «несколько обходным путем». Кроме ука-
ваний на сложность рассуждений Лапласа, Лобачевский отмечает, что
Лаплао интересовался «собственно говоря лишь случаем очень
большого числа наблюдений». Лобачевский, наоборот, подчеркивает
существенность получения точных количественных результатов,
применимых уже при ограниченном числе слагаемых г. В частности, для г = 10
он дает таблицу функции Ріа(х) с интервалом в 0,1 но ж и пятью
знаками после запятой в значениях функции.
Обращение к вопросам теории вероятностей в параграфах 164—165
(Новых начал» и в статье (Вероятность средних результатов» осталось
незначительным эпизодом в научном творчестве Лобачевского! В этой
побочной для него области математики Лобачевский оказался вполне
на уровне лучших специалистов того времени; поставив перед собой
конкретные и вполне естественные с точки зрения теории ошибок
аадачи, он решил их с исключительной простотой. Найденные им

332
ВЕРОЯТНОСТЬ СРЕДНИХ РЕЗУЛЬТАТОВ
формулы (1) н (2) сохраняют интерес и до настоящего времени, хотя
для второй иг них мы предпочли бы теперь другой способ ѳе вывода.
С методологической стороны интерес представляет стремление
Лобачевского получить точные количественные результаты,
применимые уже при ограниченном числе слагаемых г, т. е. о практической
точки зрения — при обработке небольшого числа наблюдений. Это
связано, поаидимому, с тем, что результаты, относящиеся к обработке
наблюдений:, Лобачевский предполагал применить к оценке
надежности выводов в высшей степени важных1).
Отметим, наконец, что основная часть статьи Лобачевского
находится на очень высоком уровне в смысле логической строгости
выводов. Большей ясности, чем это имеется у Лобачевского при предельном
переходе от первой аадачи о распределении сумм [ѵг ко второй задаче
о распределении средних арифметических ^ в его время требовать
было невозможно. Слабее в этом отношении заключительная часть
статьи, где Лобачевский допускает смешение предельных и
допредельных соотношений в стшіе чисто эвристических приемов, свойственных
Лапласу (см. примечания (lB], [I9J, [ЗІ1).
Трудно сказать, как относился Лобачевский к проблематике,
связанной с предельным переходом при г —> оо, которую он оставляет
в стороне. Как известно, ее полпое исследование вполне строгими
методами является заслугой русской чебыіпевской школы. Сравнение
таблицы функции PlQ(x), составленной Лобачевским, с таблицей
нормального интеграла
показало бы, что на самом деле в случае, разобранном Лобачевским
уже при г = 10, нормальное приближение удовлетворяет всем
практическим потребностям. Но во времена Лапласа и Лобачевского вряд ли
имелась возможность доказать ѳто, не производя расчетов по
формулам Лобачевского.
') См. по этому поводу обзор сочинения «Новые начади геометрии» во втором
томе настоящего издания, стр. 115.

1М 13. l.obaticlieieity, рпЬвЫШ* dciravll-emg. fail іГвІФпШ. гфиМм.
13.
ProbahilUe des resultate raoyens tiv&s d'obscrvalions
repetics.
(Ptt Mi. (te6n(scAitniiyj исіни do ruuiversUc de Сим.)
Je me sets dc fespressioii r*" pour reprueenter ie produil des * Гзс(сиг>
Г(Г-1}<Г-3).«.<•—■+!),
ie noisbrc я (Haul entier el pwitif, quel que soil an resle Tantre nombre r.
Ронопя lie plus que r"" = l poor Bs=0 « г"=з<> (ouiee lee ГоІ* que
fexposant n uuvient negaliy. On a de eeUe raaniere
i 111 ~ <tz:lTl j. trJZT1
»-" ,i- T"(n-.i)-«-i-
Je consider* a present 1» function algebrique
uti ie eigne 2 s'eiend a loutes les -vatenn du nombre eutiei poaitif Tv de-
риів Л. ss О, tant qne
іея uitres погаЬгея r, a elsot eutiers posUife, m est ааяві ов eatiei- ртмІіГ
ou rtegatif. Par ехеяріе ео mettaut r = 0, 1, 2, etc. et en regard»» »
«опте posilif. os Ігавте
' C„{«.) = 0,
iC,<«.) «l,
3. ^(-«0=1,
|C,(«) ™ За —m + i,
,€,(—«.)=» 2e-M+l,
Л Г aide des equations (1), (3) on txoo»e
Пернаи страница орнгггналг.иого іе.'ідішші сочинении
"Нероптност], средних результатов, яо.іученаых іи повторных наилюденкіі»
(1154-я tip, 24-іі книжки журна.іа Крсі.гн аа 184"- г.).
Еі <т|>. Г1ЯЭ.

ВЕРОЯТНОСТЬ СРЕДНИХ РЕЗУЛЬТАТОВ,
ПОЛУЧЕННЫХ ИЗ ПОВТОРНЫХ НАБЛЮДЕНИЙ
Перевод с французского Л. И. Хованского
Я пользуюсь выражением г™" ['] для обозначения
произведения и множителей
где число «— целое и положительное, каково бы ни было другое
число г. Положим, кроме того, г~я — 1 для п = 0 и г™™ —о
каждый раз, когда показатель -п становится отрицательным. Тогда
имеем
1.
С»- — !)'
(г — І)*
Ц=іП.
пп л"" 0 — 1)
Я рассмотрю теперь алгебраическую функцию
2. <?,(«)= % (f^Г^-Т^ЛС—а)"+'» + '—1-Ч"""1'
где знав 2 распространяется на все целые положительные числа і
от А = О до
2а+ 1
1.
и где числа г, а целые положительные, а т целое положительное
или отрицательное. Например, полагая ?=0, 1, 2 и т. д. и считая
т положительным, находим
с, и = о,
<?!((»)- I,
3. <?,(—м)=і,
С2(ві)=2а—'»+!,
С8(—»») = 2а —т+1.

334 ВЕРОЯТНОСТЬ СРЕДНИХ РЕЗУЛЬТАТОВ
С помощью уравнений (1), (2) находим [*]
Ст (т+1) = Сг (*») + J Г ^'Т^Г.-іН'--^) я + m + '-1-Ч
ѵ* 2) А.
= СгИ+У(~1)Х(^'^-Л^-2Х)а + т+/— 1-Ц—' +
— г—2
-С,(ж)+ 0,^(0 ^-яl^-l) —
ч
-Г—2
X]"'-2,
или, наконец,
4. Or(»+l)=Of.(M)+0I._1(a + « + l)—C-^Cm-o).
Функция Gr(m) обладает еще свойством не менять свое значение-
при замене -}~т на —т, так что
5. ' <7,(m) = CU—»).
Уравнения (3) уже подтверждают это свойство для г = 0, 1, 2.
Предположим, что это свойство верно для всех чисел г от г = 0
до данного г. Подставляя »--|-1 вместо г и т-\-1 или —«і вместо т
в уравнение (4), имеем
Сг+1(« +1) = Gr+1{m) + Ог(« + « + 1)— Or(« - a),
СѴ+)(-«0 = Сг+і(—*»-!) +Cr(a-m) _CT(—m_a_i) =
= cP+1(—»-])+c„(»—e) _ar(»4-e+i);
следовательно,
Сг+і(*+1)=С,+д(-м~1)+(7,.+1(і») -С,+1(-м).
Полагая здесь по порядку т = 0, 1, 2 и т. д., заключаем, что
данное утверждение верно для индекса г-]-1 и для всех делых
чисел т.
При г =2, т = 2а имеем
6. Сг(га)=1,
что также верно для всех чисел г; последнее утверждение
доказывается с помощью выражения (2), где А в этом случае не может
быть больше нуля [Б].

Н. И. ЛОБАЧЕВСКИЙ —«ВЕРОЯТНОСТЬ СРЕДНИХ РЕЗУЛЬТАТОВ» 335
При г = 2, т~2а-\-а и а >0 функция Ог(т) становится
7. СР(гл+в)_0,
что также верно для всех целых положительных ■чисел г, и что
можно доказать, рассмотрев сперва уравнение (7) для всех
индексов, меньших г.
В самом деле, уравнение (4) нам дает
8. С,(/а-|-а) =
= Сг(га-\-я — 1) + Сг_і(га-\-а—а) — Сг_і(гя — я+а —1).
Но уже было доказано по уравнению (в), что
С,(»-и) = і, Ct__j(ra — я)=.1,
а так как мы только что предположили, что
Сг-і (•*« + *)=■ О,
то уравнение (8) нам дает сначала для а = 1
Ог(гя + 1) = 0.
Если предположить затем, что
CT_s(ra-\-a + a)^Q, Cr.t (га~а + с — 1) = 0,
то из того жѳ уравнения (8) получим:
Cr(ra+*)=Cr(ra + a-l).
Подставляя сюда а = 1, затем а = 2, 3 и т. д., мы докажем
правильность уравнения (7) для всех чисел а.
Определим теперь вероятность ошибок в средних результатах.
Предположим, что в каком-нибудь наблюдении все ошибки равно
возможны и являются целыми числами, заключенными между -\- а
и —а. Сочетая между собой наблюдения, число которых есть г,
мы будем иметь в сумме ошибку т, которая не может выйти за
пределы -f- га, — га. Это число сочетаний есть та же функция
отгия, которую мы обозначили выше через Сг(т). В самом деле,
это выражение уже удовлетворяет условню обращаться в нуль
всякий раз, когда т превышает га\ затем оно равно единице при
от = га и, наконец, оно обладает свойством не менять свое
значение при замене -\-т на —т (см. уравнения (5), (6), (7)). Остается
лить рассмотреть случай т положительных и меньших га.
При г 8= 1 число сочетаний равно единице, что также является
значением СТ{т), как видно из одного из уравнений (3). Для всех

336 ВЕРОЯТНОСТЬ СРЕДНИХ РЕЗУЛЬТАТОВ
других чисел г необходимо и достаточно, чтобы функция <7Г+1(»»)
была суммой всех значений произведения
Сг(р)-Огіт—р)
от р=т — а до j) = m-f-a. Но так как С1{т — р) = 1, то
необходимо, чтобы
внутри тех же пределов для р, что также проверяется и
доказывается путем подстановки сюда выражения (2) для Сг(р). Таким
образом, мы получим
где двойное суммирование распространяется на все значения риі,
отр = я» — а до p = m-j-a и от А = о до
Произведя суммирование по р, мы имеем
где следует положить р —ж^-я и определить постоянную J так,
чтобы Gr^l(m) обращалось в нуль для р = т — а—1. Следовательно,
-*=-£(7-1£-"Ѵ-а>а+д-в-і+'-ц"'''
где А меняется в пределах от А = О до
, ^га\- т — й
Л£: 2а -fl '
или, заменив А на А — 1, получим
где А меняется в пределах от А = 0 до
f r-J-1) a-j-1»-f-1

Н. И. ЛОБАЧЕВСКИЙ— «ВЕРОЯТНОСТЬ СРЕДНИХ РЕЗУЛЬТАТОВ* 3S7
Таким образом, значение Су+1(т) равно
+£ гЦ^ір [(*-4-i-2^)«+>:+*-->]"f,
причем пределы суммирования по а одинаковы в обеих суммах,
т. е. і. = 0 и
'' — 2в -)- 1
Соединив эти две суммы в одну, получим
что действительно является выражением С>+І(»і)і как мы его дали
выше (уравнение (2)), и в котором, как было доказано, можно
поставить — т вместо f«H обозначить тем самым величину числа
сочетаний, могущих произвести ошибку то,
причем суммирование ведется от а = 0 до
га—т-[-1
А- 2а+1 "■
Соединив все значения Ог{т) от т=1 до данного числа т,
находим
V С, (т) = А - V (~5^ГЛ (О" ~ &) а- m + г - a] "f.
Постоянная А определяется тем условием, чтобы певал часть
этого равенства обращалась в нуль при т —0. Следовательно.
9- ^Х(-^Й0--2А)а + г-ХГ'
от л — 0 до
Умножив на 2 уравнение (9) и прибавив к этому произведению
Сг(0), мы получим полное число сочетаний, приводящих к тому,
22 Ямс. ЗйіЯ. Н. П. Лобачевский, т. V.

838 ВЕРОЯТНОСТЬ СРВДНИХ РЕЗУЛЬТАТОВ
чтобы ошибка т оставалась внутри границ —f—я», —т. Это число
будет
ю. 2<?г(«)=
■2%~^£г№-Ы)<* + г~\Г'-1(г-2к)а-т + г-КГг}
І1"Х
т"ТК
(-if r
ѵ — Ll А
где X под знаком 2 возрастает от л = О до тех пор, пока в
произведениях не будет больше положительных множителей.
Ясно, что число сочетаний, которые производят все возможные
ошибки, должно равняться (2a-f-l)r. Необходимо, следовательно,
чтобы [5]
11. (2«+1)г =
Обозначив через Рт(т) [8] вероятность того, что ошибка ж
среднего результата г наблюдений должна быть заключена в границах
+ »*, —то, имеем, очевидно,
Сочетав это уравнение с уравнениями (10), (11), разделив
предварительно два последние на (2я-|-1)г и полагая затем
m
— = х, а = со
га '
имеем
ига) і _ .а*
где Рг(ж) представляет вероятность того, что ошибка среднего
результата, полученного из г наблюдений, не выходит из границ
-\-х, —х, когда наибольшая ошибка каждого наблюдения не вы-

Н. И. ЛОБАЧЕВСКИЙ —«ВЕРОЯТНОСТЬ СРЕДНИХ РЕЗУЛЬТАТОВ» 339
ходит за пределы -J-1 и —1. Соединение двух последних
уравнений дает для этой вероятности
где сумма распространяется на все целые J., начиная с А = 0, для
которых г — гх—2\ положительно [•].
Взяв, например, г =10, имеем [10]
для 0,8s£#s£l
„ . . , 390 625.
72 576
для 0,6 й£ х й£0,8
Р /rf^i 390 625 (4-5*)"
для 0,4s£:cs£0,6
Рід(*) = 1
для 0,2^а:^0,4
Р1В(*) = 1
390 625 (* —te)" (8 —toy
72 576 ѵ ' "т" 18X440 40 320 '
390 625,
(1 - -ли. 4- (Ы*1° _ (S-to)" (2-to)"
72 576 *• ' ~ 181440 40 320 "т" 15 120 '
для 0^ят«0,2
= 1-
390 625
Р„(«)-
м -у. і (*—б«)10 (a-to)" , (2-to)" (i-бя)"
72576 ѵ" ' ' 181440 40320 ' 15120 8640
Вычисляя с точностью до пятого десятячного знака, имеем [п]:
Ошибка
1,0
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0.0
Вероятность
1,00000
1,00000
1,00000
0.9В997 *
0,99944
0,Э950в
0,97310 *
0.89807*
0,72220
0,41087 *
0,00000
Можно, следовательно, держать 18 против 7, что при наблюдении,
повторенном десять раз, ошибка среднего числа не превзойдет
22*

340 ВЕРОЯТНОСТЬ СРЕДНИХ РЕЗУЛЬТАТОВ
одной пятой наибольшей ошибки, которая может быть допущена
в отдельном наблюдении [п].
Лаплас в своей «Аналитической теории вероятностей»
занимается, собственно говоря, лишь случаем очень большого числа
наблюдений. Путем чрезвычайно сложных рассуждений и
постоянно пользуясь определенными интегралами, он пришел к
выражениям, которые вполне совпадают с только что приведенными
здесь. Число сочетаний, в которых сумма ошибок есть т, а число
повторений есть г, можно выразить следующим определенным
интегралом
г,. 'L MitM
СТ (т) = - Л cos mm —. '—. | .
\) \ йі. J
Разделив этот интеграл на (2а-\-І)Т, т. е. на полное число
сочетаний, имеем [,я]
о \ Z I
для вероятности того, что сумма ошибок равна т. Теперь
вероятность того, чтобы эта сумма была внутри пределов -j- т и —т,
должна быть J1*]
р. . 2 f^sin^f 6ІП(а + 1)^
Ат) ~~ и j <u (2а+1)'\ sin « У ■
Положив m = г«ж, затем я = со и обозначив о<о = г, имеем |16]
со
™ а?
13. Рг(я) = ^| |йг^С08(ггэ;)/,^Лу.
НО l '
Но мы нашли для Сг(т) выражение (2), которое в случае я = со
позволяет нам установить, что интеграл б уравнении (12) равен[1и]
со
, , -г—I
zhra:)

Н. И. ЛОБАЧЕВСКИЙ —«ВЕРОЯТНОСТЬ СРЕДНИХ РЕЗУЛЬТАТОВ» 341
Сумма здесь распространяется на все значения Х^-0, для
которых величина, стоящая под показателем г—1, положительна ["J,
причем знак перед х можно выбрать произвольно. Лаплас также
приписывает это значение определенному интегралу, но приходит
к этому несколько обходным путем [18j.
Выражение, которое мы нашли для Рг(ж>, служит также для
вычисления двойного интеграла (13), откуда мы заключаем,
произведя интегрирование по х, что[19]
2 С Ог . , .(тпг\г
15. т „аИ—^
причем сумма распространяется на все значения /.от л = 0, для
которых г — 2сс — 2\ положительно [*°], число х положительно,
меньше или равно единице, а г есть целое положительное
число. Уравнения (Н), (15) должны быть верны п при г = 1,
причем оба они согласным образом приводят к известному
интегралу ["]
СО
Cdx . 1
1 —йтж = — іг
J ж 2
и
и доставляют, таким образом, новое доказательство этого
равенства.

ПРИМЕЧАНИЯ
['] В (Новых началах» Лобачевский называет такое выражение
уступом, а число п — показателем уступа1),
[*1 Здесь и далее Лобачевский отказывается от употреблявшегося
„-а
им в «Новых началах» обозначения *>"а= ——— .
[a] В журнале Крелля опечатка, отсутствующая в «Новых
началах» т
га — т -J- 1
^ 2а +1 '
Легко заметить, что член с л =—^ . ,— равен нулю и мог бы быть
поэтому отброшен.
I*] В первой строке этой формулы в журнале Крелля вместо г"
Ошибочно поставлено (г — 1) . Этой опечатки нет в «Новых нача-
л ах», где Лобачевский вместо ■ _^ употреблял обоаначѳние г^**- .
А
Кроме того, в журнале Крелля вместо Cr_t(a-\- т-\-1) ошибочно
напечатано Cr_,(a-j-w»). Эта опечатка имелась ив «Новых началах».
[b) Подробный вывод этого равенства находится в «Новых
началах» а).
[е] У Лобачевского здесь, как и в «Новых началах», пропущено
слагаемое —А в квадратных скобках. Эта ошибка повторяется и
дальше в формуле для Сгі1 (»і) и в соединении обеих сумм в одну.
(ТІ В журнале Крелля при второй квадратной скобке формулы(И)
имеется лишний множитель г, отсутствующий в «Новых началах».
(s) В «Новых началах» Лобачевский обозначает вероятность
буквой В.
і) См. і. II наст, издании, стр. 398.
э) Там же, стр. ЗАВ—*00.

ПРИМЕЧАНИЯ
343
[9] Буквальный перевод этого шеста гласит: «на все значения X,
вплоть до степеней отрицательных чисел».
[,0] В подлиннике во всех нижеследующих неравенствах для х
указан лишь нижний предел, а в последнем неравенстве указан лишь
верхний предел: х<<0,2. Как н в «Новых началах», мы везде
уточнили эти неравенства. Индекс г в выражениях для Рг(х) при с=10
мы заменили индексом 10, как это сделал сам Лобачевский в «Новых
началах*.
["] В четырех местах, отмеченных нами звездочкой, числовые
значения Р10(ж) указаны у Лобачевского не вполне точно. Мы везде
приводим правильные значения Р^(х).
1 ' 18 + 7 25 '
В «Новых началах» Лобачевский дает более грубое приближение:
7
7-f-a
= 0,7.
[le] Лаплас приходит к этому интегралу путем следующих
соображений (мы пользуемся обозначениями Лобачевского).
Пусть ошибки для каждого из г наблюдений могут быть с
одинаковой вероятностью некоторыми из чисел —а,■— а+1, ..., 0, 1 а.
Всего, таким образом, имеется 2а -J- 1 возможных значений для каждой
ошибки, и вероятность того, что она примет данное значение, равна
. Тогда число сочетаний, в которых сумма ошибок еоть т,
2а + 1
а число наблюдений г есть коэффициент при етші в разложении
выражения
|е-<ші + e-fa-цв* 4-... + е-щ| + і -f- <?"'+... -+■ еаші\г
в ряд по целым степеням еш*.
Но
e-avt_L.e-te-i)«>i 4- ... + е-,аі -J- 1 +ещ'4- ... +«"*•<=.
e(sa+)imi і (е(а-*-і)щ( e_0lu*) (е_ш( — 1)
V — 1 (е"» — 1) ((-«•* — 1)
2 — 2 cosiu
. 2а+1
віп ■— т
совоа» — coa<a-|-l)w 2
1 — сое ш . ю
am —

sa вероятность средних результатов
Поэтому наше разложение имеет вил
. 2а+1 У
ВІП -г-— 10 х
= 2 Сг(к)ооаІ№.
Но коэффициенты этого тригонометрического ряда определяются
соотношением
*іп («+■!) Л
1 т\
Сг(ш) = — 1 008 »іш ■ -— | del,
что и является интегралом, применяющимся Лапласом.
[и] Формула верна, конечно, только в качестве асимптотической
при a ~-> со.
[161 Лобачевский здесь слишком рано полагает к = со. В формуле
(12) при а = со обе стороны обращаются в пуль.
Положив m = rax, имеем:
* п і \ * L oos(raxz)
'вІП(й+і)<В| .
Обозначив аіат=я, получим:
і „, , і Г соВ(гаг) ( *іа(в+т)т\л
OS
11,, \ ' a I 1
= — I cos (гаг)—~ - . —— dz.
2Гатвшг —
2a
При помощи втого соотношения моясно повязать, ,что в случае
Сг(ш) 1 С , % IsmsY,
llm "«, "і"Т^ = — \ сое (ггя) ) -—- <fer
равномерно относительно m, находящегося, как было с самого начала
предположено, в пределах
— ra -^ w ^ -J- га.

ПРИМЕЧАНИЯ 345
Таков точный смысл, который надо приписать формуле (12) для
того, чтобы из нее ложно было вывести, что при г > 1
X со
Ііш Рг (т) = — | dx 1 cos (rzx) I J dz.
°->™ oo '
Отсюда естественно заключить, что во второй эадаче о непрерывно
и равномерно на отрезке [— 1, -{-1) распределенными слагаемыми Вг
имеет место формула
Рг (л;) = -— 1 (Jj? 1 соэ {rzx) I 1 dz,
о о ' '
которая после замены порядка интегрирования, не вызывающей
сомнений при г > 1, превращается в формулу Лобачевского (13).
11в] Формула (2) вместе с уточненной, в соответствии с предыдущий
примечанием, формулой (12) дает:
, ч /sins\r ,
cos (rzx) I —— I dz =
о ' '
,. і ■■ ». , »r ■ i ,. , . r—1 —л
откуда уже легко получается формула (14).
В журнале Крѳлля в (14) опечатка: вместо 2Г поставлено 2Г ■
Знак =t перед х поставлен Лобачевским потому, что в левую часть х
входит под знаком косинуса, и поэтому обе части равенства являются
четными функциями х.
I11] В подлиннике здесь пропущено несколько слов. Напечатано
только: «Ьѳ eigne qui exprime ici la somme, аѳ rapportant a toutee
les valeure de k, juaqu'aux quantises sous l'exposant r—1», что не имеет
ясного смысла.
\1S] См. La Place-—«Theorie analytique des probabilites», aeconde
edition, Paris, 1814, стр. 157—169.
[ie] См. формулу для Pr (x) на стр. 339 наст. тома.
[50] В подлиннике: «от 1 = 0 до степеней отрицательных чисел».

316
ВЕРОЯТНОСТЬ СРЕДНИХ РЕЗУЛЬТАТОВ
["] Полошив в (14) г=1, получим [так как правая часть при г =
равна Ct (те) = 1] при любом х
(X
J
cos за;-
:* = т-
В самом деле, ков известно,
си
J
em г ,
cos zx —— az =
упри |а:|<1,
— при (а;| = 1,
О ПрЕТ | X | > 1.
Согласно определению у Лобачевского |ж|^1, так как |т[^|га|.
Но, как было уже указано в примечаниях [1б] и [16], вывод формулы
(14) для случая г = 1 встречает некоторые затруднения. На самом
деле оказывается, что она верна в случае г—1 лишь при |ж|<1.
Остается неясным, каким образом ЛобачевевиН получает интеграл
□о
I
——~dx — ~
х 2
из формулы (15).

ЯСТОРЛКО-БИБЛИОГРАФИЧЕСКИЕ СВЕДЕНИЯ О СОЧИНЕНИИ
«ВЕРОЯТНОСТЬ СРЕДНИХ РЕЗУЛЬТАТОВ, ПОЛУЧЕННЫХ
ИЗ ПОВТОРНЫХ НАБЛЮДЕНИИ»
Сочинение было напечатано в 1842 году на французском языке в
журнале Крелля «Journal fiir die тѳіпе unil angewandte Mathematik»
в 24 томе под номером 13 ва отр, 164—170. Название работы
Лобачевского: «Probabilite dee resultats moyens tires d'obaervatioos repetees».
После ааглавия стоит (в скобках) фамилия автора: «Par Mr. Loba-
tschewsky, recteur de i'univereite de Саиап».
Эта работа в дальнейшем пе переиздавалась и на русском языке
появляется впервые (в переводе А. Н. Хованского).
Сочинение «Вероятность средних результатов» является
переработанным переводом ст. 164—165 его сочинения сНовые начала геометрии».
Статьи 164—165 «Новых начал» были напечатаны в I книжке
«Ученых эаписок Казанского университета» за 1838 гол, а сочинение
«Вероятность средних результатов» вышло в свет только в 1842 году.
Такой разрыв объясняется тем, что сочинение пролежало в редакции
журнала Крелля более трех лет: Лобачевский отправил его для
помещения в журнале почта одновременно с соответствующим текстом
«Новых начал». В издании «Обозрение преподаваний в императорском
Казанском университете» ') помещена «Краткая историческая записка
о состоянии Казанского университета за 1837/58 и'1838/39
академический год», в которой между прочим говорится:
«Ординарный профессор Лобачевский напечатал в ученых записках
Казанского университета новые начала геометрии, решение
прямолинейных треугольников *} и решение прямоугольных сферических
треугольников, отправил для помещения в журнале, издаваемом г. Крел-
лем, статью: Sur la probability des resultats moyena, tire's des
observations repe"tees».
Шесть опечаток, имевшихся в соответствующем тексте «Новых
начал», исправлены в тексте французской статьи, но зато добавлены
1) Казань, 1830, приложение. Цитируемый текст воспроизведен в сборннаѳ
Л. Б. Модвалевского «Материалы дли биографии Н. И. Лобачевского*, изд.
АН СССР. М. — Л., 1948, на стр. 402—403 (документ ІМ 431).
*) Глава «Решения прямолинейных треугодьяяков» сочинения «Новые начала
геометрии» и содержит ст. 164—165. составяащие содержаний сочинения аВеронт-
ность средних результатов наблюдений».

348
ВЕРОЯТНОСТЬ СРЕДНИХ РЕЗУЛЬТАТОВ
пять новых. Если учесть при втом, что французокий текст совращен
по сравнению с текстом «Новых начал», то следует признать, что Крѳл-
левскии журнал, считавшийоя тогда одним из лучших математических
журналов, не уступал по числу допускавшихся опечаток казанским
«Ученым запискам». Ѳта замена одних опечаток другими лишний раз
доказывает, что их пѳ следует ставить в вину самому Лобачевскому:
очевидно, что в рукописи перевода большинство опечаток «Ученых
записок» было поправлено.
Насколько нам известно, печатных отзывов на статью «Вероятность
средних результатов> не было. Только Биѳрѳнс де Хаан в своих
известных таблипах определенных интегралов •) указывает, что два из них
a — btr
Яда)'— 4-і-і^2(-1,-?('-^Ч
и
а±Ъд
|со,м(^ = ^2(-1>-^-1(Ь±,-2..>»
О
(помещенные в таблице 202 под номерами в и 7) извлечены из работы
Лобачевского «Probabilite.. .> (это—формулы 15 и 14
Лобачевского)3). Недавно появилась статья В. В. Гнедѳнво «О работах
Н. И. Лобачевского по теории вероятностей» s), посвященная атому
сочинению.
Рукописи Лобачевского, как и почти всех его сочинений, не
сохранилось. В геометрическом кабинете Казанского университета
сохранилось несколько отдельных листов с черновыми записями Лобачевского.
На одном из них, написанном, очевидно, на части бланка
университетского диплома, имеются запаси карандашом — вычисления
вероятностей Вп{х), вошедшие в ст. 1С5 «Новых начал геометрии» и в работу
«Вероятность средних результатов». Снимок этого листка помещен
в настоящем томе.
В настоящем издании сочинение Лобачевского сопровождается
примечаниями, составленными А. Н. Колмогоровым (примечания [l*J, [lsl,
І16Іі Р1] ІГ частично [*], [п]) и А. Н. Хованским (остальные).
Ч Bierens de Наин — Tables d'integrales definies. Vflrhandelingec der Konin-
fclijka Afcarfemie таи Wetenaeiiappea (Amsterdam, Deal IV, 1858, стр. XXXI-j-572.
s) Во втором интеграле можно взять любой яз двух енаков.
■) «Историке-математические исследования», вып. II, Гостехиздат, М. —Л.,
1А49, стр. 128—Ш.

■;*■£
-1- ».*. > '- -■
—'; : . --г,<>. ,^.
У**Л*
■ •' _
»к
- - П'
. *
■^
*■#.'*!■'•
- >;
Ѵ*&ъ
L ■ '■'Л
#**Г-
f-'4
.**■ -*."-?■■*
Лг-Ч
»*3
jfa
&л
'-І-
Чъ*
'-Ч.
■..*
... . V. . ■ Л' .. . '
' ( - -■■ - - - - Л -" - -■*-
:.' ^'••-••1
Чь
> -.^
1*&
"А?
-****■
#і
^-
* х^Ч
:^--^ч
**#*■
^-^7&г^-?
і( 4-
г ■.: -\ «-■
■«Л
»: *£.,?■
■£■' '
:^-к-
■іі ''•■
іік
'±f L Ѵ ' • " '
"■г
f-^+f
#*у* £*%"*
>#■
ж
-'■•■'■.LV. ^Ч-f^i*
t
^/4^М^
5Ш?* ■;;,;■
hf-^i-f- у
'і
^> ^і
(й - * ■
*^%4^^W
ІІ^*4 W
д >^#
f^i
*%У
^У
*-*
у.
*-*<**. *.г^*
-t
U:^
- :£Ь
^,"г.-5-
^
*™*,
(Ч4*$
г'
^
Л4"ѴЖ
...?Ч
.'■С..Ч Гф..-.,,
^- ,'"'^.^
;^'
^
.>^.
7*
>^!*ь
•-ІУ<-
♦
*-А"
V
.«г
. If ■
»*-' «^
>vw^*-**--«v
-,м.*іі—і^іИьЧЧііь.^ **"- -^-!Wi'"'l*""."*<'*"^
^
X
г***
**?
■"Пій-
і%
о^Л г^гЛ-*гЛ>а
*'» *
-' * * ■' -^
І і»,- .
.%**
--*$■?
*<:*,
" „^"Si
" »■
■ ™
^ Г'Ч
* 4.
^^ч*иѴЬ^*-«жЛь^*-*--;^.*ѵА-' *>»ми.^
.іЛ; іЗьі
\ ^
/•\
'ИІИ>'
...- ,<*у^ »и ;>ѵ^
ѵ ѵ
+ г
*+ **.
ѵ**^. *
**' *,
4 <.
&*■. №
.-* ^t» уЧ, ]4
.^■•?ѵ.
•^■^');-Ч ЧІ^ЛѴ'%1^'
■• ^ - '^- ^ -„Хч
. -■■• ■... /
-' :
»
, .-ч*»'--.■"--'
■Л'
iff
■**т——ч> Щщ .
££В"
t
\
-ч
*ЧІ"-***№
.%*■
г -* л \
* *Г ■*
"^л^іЩі^Щи.
**** ч
ft-!%4XW-
^-:^^лфл -
V^if
~ і - {ь:
3*
4
=ч ^-о"1"-'-
■«.
>
4* -
F
■ t
TL t
т<
%
_^
•«. 4
"* -44*
w[i^ i,^./- i i.-^Z L,
V^
11
■>4^f- Sly.* ,■■*■■
:.'..--;J№t
■т"^Ч#ч^і*+^^_.
^-?A)
;-;b:
•:х^з&£&>к
Ьм^тті ■'^■■■-^
.^HlSifcLi.S'
">Д-*
I; If-
k^^A*^^sSeiSi*sa^>
i»t*
ь>
.fei
**5 -
#*
-j*»_
n
■" -Г
О
M
^ * ^
»U
il/
. (f-^
-#
r
'•'Ч?
:і 4^ f
^flwjfc...
Записи H. И. Лобачевского, относящиеся к вычислениям вероятностей, помещенным в сочинениях «Новые начала геометрии»
и «Вероятность средних результатов, полученных яз повторных наблюдений*. (Написано карандашом, очевидно, на части бланка
университетского диплома. Хранится в геометрическом кабинете Казанского университета.)
К стр. Й49.

УСЛОВНЫЕ УРАВНЕНИЯ
ДЛЯ ДВИЖЕНИЯ
И ПОЛОЖЕНИЕ
ГЛАВНЫХ ОСЕЙ
В ТВЕРДОЙ СИСТЕМЕ
а а з s
ВВОДНАЯ СТАТЬЯ И КОММЕНТАРИИ
Н.ИИДЕЛЬСОНА

УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ
И ПОЛОЖЕНИЕ ГЛАВНЫХ ОСЕЙ
В ТВЕРДОЙ СИСТЕМЕ')
Вводная статья:
Основные работы по вопросам кинематики и динамики твердого
теля, предшествовавшие сочинению Лобачевского 351
Н. И. Лобачевский — «Условные уравнения для движения
я положение главных осей в твердой системе» 357
Комментарий 366
1) Опубликовано в «Ученых записках Московского уянверситотй», ч. ѴШ,
февраль ІѲЗэ р., стр. ISO—190. В перечне сочичепнй Лобачевского, помещенной
в I томе настоящего издания (стр. 21), в названии сочинения допушева ошибка:
после слова «осей» стоит ненужное слово «обращенная, отсутствующее в
подлиннике. Эта же ошибка имеется во маогих биянографнческих указателях, например,
в списке издании сочиыеанй Н. И. Лобачевского, приводимом Л. Б. Модз&лсн-
ским в сборнике «Материалы для биографии Н. И. Лобачевского», изд. АН СССР.
М,—Л., 1948.

ОСНОВНЫЕ РАБОТЫ НО ВОПРОСА» КИНЕМАТИКИ
И ДИНАМИКИ ТВЕРДОГО ТЕЛА, ПРЕДШЕСТВОВАВШИЕ
СОЧИНЕНИЮ ЛОБАЧЕВСКОГО
Сочинение Лобачевского «Условные уравнения для движения и
положение главных осей в твердой системе» содержит
оригинальные я глубоко задуманные доказательства двух осяовныі положений
теоретической механики. Первая часть сочинения относится к
кинематике системы точек, расстояния между которыми остаются
неизменными при ее движении; здесь выводится основная теорема Эйлера,
утверждающая, что произвольное бесконечно малое перемещение такой
системы приводится к бесконечно малому поступательному
перемещению и к бесконечно малому вращению вокруг мгновенной оси
вращения. Вторая часть сочинения, совершенно независимая от первой,
принадлежит к тому разделу механики, который носят теперь нааванпе
«геометрии масс»; здесь Лобачевский доказывает существование для
любой системы материальных точек трех взаимно перпендикулярных
осей — главных осей тензора инерции данной системы.
Оба эти положения, лежащие в основе кинематики и динамики
твердого тела, была установлены в ХѴШ в. в работах Даламбера,
Эйлера и Л&гранжа. Лобачевский ссылается на некоторые из этих
рабит. Поэтому целесообразно представить о них краткую
историческую справку.
Даламбер
Общие принципы составления уравнений движения любой
материальной системы под действием каких угодно сил были установлены
Даламбѳром в его знаменитом «Трактате по динамике» (1743) '); через
несколько лет, отправляясь от весьма актуальной тогда
астрономической проблематики, именно от теории прецессии и нутации земной
оси в системе ньютоновского тяготения, Даламбер дал чрезвычайно
важную работу: сО предварении равноденствий» 5). Для истории меха-
') D'Alembert — Traite de Dynamique, 1-е изд., 1743; 2-еивд., 1758. Русский
перевод: Даламбер — Динамика, Гостохиздат, М, — Л., 1950.
Э) D'Alembert — Recherehea яиг la precession des equinoxes et sur la
nutation de l'axe de la Terre dans le Systems Newtoaien, 1749.

352
УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ
вики она существенна тем, что в ней были впервые выведены все
шесть дифференциальных уравнений движения твердого тела; в три
уравнения второй группы — уравнения вращения системы вокруг ее
центра инерции — естественно вошли и величины, эквивалентные
моментам и произведениям инерции, в современной терминологии, —- но с тем
существенным отличием, что Даламбер относил уравнении движения
к неподвижным осям, в силу чего все эти величины входили как
переменные в уравнения вращения. Вопроса о свободном вращении
твердого тела при отсутствии внешних сил Даламбѳр в этой работе
не рассматривал, поскольку в ней была поставлена и решена задача
о вращении Земли в заданном поле сил притяжения тела Земли Солнцем
и Луной; однако впоследствии, в одной работе 1768 г. '), когда вопрос
о свободном вращении и об осях, вокруг которых такое вращение
возможно, приобрел существенную важность в динамике твердого тела,
Даламбер напоминал и подчеркивал, что его работа о предварении
равноденствий от 1749 г. «содержит все принципы, необходимые
для того, чтобы определить в общем случае законы движения тела
произвольной формы». Но только в этой работе 1768 г. Даламбѳр
развил полную теорию главных осей инерции и получил
характеристическое уравнение третьей степени, корнями которого
определяются направления этих осей.
Эйлер
Цикл работ Эйлера по механике твердого тела начинается с мему-
ара 1750 г. «Открытие нового принципа механики»5). Здесь впервые
дан чисто кинематический анализ задачи о вращении твердого тела
вокруг неподвижной точки и доказана фулдамептальная теорема о
распределении скоростей точек системы: оно оказывается таким, как если
бы система вращалась в данный момент вокруг некоторой оси,
проходящей через неподвижную точку, — т. е. именно та теорема, которой
посвящена первая часть мемуара Лобачевского. К проблемам динамики
твердого тела Эйлер подошел несколько поаже, в мемуаре 1760 г.
«О движении произвольного твердого тела, вращающегося вокруг
подвижной оси» а). Методическое значение згой работы чрезвычайно велико,
прежде всего, потому, что здесь Эйлер впервые перешел к осям, неиа-
J) D'A Іега 1) er t—Heeherches sur les axes rte icrtation d'nn corps do figure
quekonque, qui n'est аштй риг aueirae force acceleratrieo (Opusc. Mathem., t. IV,
178B, стр. 1—31).
s) L. Euler— DArauverte d'un nouveau principe de МёсішІіще. Hist. Acad, <le
Berlin, 1750, стр. 1Ѳ5—217; особенно стр. 198—205.
°) L. Euler —Du mouveraeat d'un corps solide quelconque, lorsqu'il tourne
autour d'un axe mobile. Hist. Acaei de Berlin, 1760, стр. 176—227; особенно
стр. 212-213.

РАБОТЫ, ПРЕДШЕСТВОВАВШИЕ СОЧИНЕНИЮ ЛОБАЧЕВСКОГО 353
менно связанным с твердым телом, в силу чего те величины, которые
в уравнениях Даламбера являлись переменными, теперь превратились
в постоянные. Здесь же в полном объеме рассмотрен и вопрос о
свободных осях вращения1) и доказана теорема: «Какова, бы ни была
форма тела, можно всегда указать в ней такую ось, проходящую через
центр тяікеоти, вокруг которой тело может вращаться свободно и
непрерывным движением»; вслед ва этим Эйлер выводит то кубическое
уравнение, от которого зависит определение осей свободного вращѳ>
ния s). Наконец, еще через пить лет Эйлер опубликовал знаменитый
трактат; «Теория движения твердых или жестких теле 3), в котором
кинематика и динамика тнѳрлосо чела представлены, л основном, в том
самом виде, в котором они налагаются и по настоящее время.
Лагранж
Аналитическая механика ЛагранжаJ) в каждом из ее разіелов
представляет собой гармоническое сочетание всех результатом,
полученных в предыдущем развитии науки, с новыми, порою граядиоапыми
концепциями ее автора. Это относится и к обеим интересующим нас
здесь задачам кинематики неизменяемой системы п геометрии .масс.
Первая иэ них трактуется в дпух разделах «Аполитической механики»:
«Свойства равповесия по отношению к вращательному движению» s)
и «О равновесии твердого тела конечной величины и любой формы,
все точки которого находятся под действием любых сил»6). Таким
образом, оба эти вывода соподчинены задачам статики: Даі'р&шк ищет
здесь те выражения виртуальных перемещений жесткой системы,
которые, в сочетании с основным началом статики, могут обеспечить
равновесие системы при тех или иных распределениях действующих сил.
Тем не менее оба эти вывода представляют независимый и выдаю-
Ч Вирочеи, самое открытие этих otwti принадлежит не ДаламЗсру, но Эйлеру
а II. Сегнеру (1704—1777), изобретателю «Сегнерова колеса», обрати пшюту внимание
на их значение в 17оэ г. (Job. Segjier — Specimen Theoriae TurLiiium).
ИІ Вопрос о приоритете Даламбера или Эйлера здесь все и?о остается довотіыіи
спорным, так как Даламбер п работе, опубликованной уже в 1761 г., дал еонер-
піізнно корректную формулировку условий, необходимых и достаточных длн тоі*о,
чтоііы данная ось ыоіла быть осыо свободного вращения (D'A liimb ег t-—Du
шопvciuont d'lm corps de figure lueleonque auimu par des forces quelconijues. l.)piii,c.
ilatii., t. I, 1761, стр. ii—Loll). (Лишни по.тньШ анализ веян, цроилймы нышхшеи
Даланйеріім только в раооте 1769 г., от.чеченноіі выше.
s, L. Euler— Tiienria Mot us Corpormn solidorum sed rigidoruio. Rofetotk, 1765.
*l J. Lagrange — Mecaniqiin Analytique, пар, 1787 и 1813. Русский перевод
JK, Л а гранок — Лнаднтичесііаіі механика» нор. под ред. Л. Г, Лоііцянскоіо и
А. И. Лурье, 2-е изд., т. I—П, Гостехиздат, М. — Л., 1950.
5) См. русский перевод, т. 1, стр. 72—93.
■£) 'Гам же, стр. 337—^33.
23 Зак, 28ЙЗ. Н. И. ЛоОачевсккіі. - V

354
УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ
щийея интерес. Лобачевский в своей работе исходит от второго лагран-
жѳва доказательства, но придает ему существе/то ббльтуго общность
и полноту. Действительно, Лаграаж рассматривал «большое количество
расположенных друг за другом точек» неизменяемой системы и обо-
вначал их координаты через
х, у, г;
x-\-dx, y~\-dy, z-f-гіг;
Таким образом, символу d придается здесь значение бесконечно
малого приращения координаты; по в то яге время Лаграяж
применяет в нему и схемы исчисления конечных разностей, именно
формулу Ньютона
**=<1+ <*/*.
Расстояния между всеми точками рассматриваемой совокупности
должны бглть неизменными при движении; обозначая соответствующие
приращения координат через S.c, Ьу, Зг и учитывая очевидную здесь
коммутативность операторов d и 3, Лагранж приходит в «условным
уравнениям» для прирагценнп Ьх, by, bz:
dx d Ъх-j- dy d Ьу -j- dz d 5г = 0,
d?x, <P &x -|- d*y d- by -\- d^z d~ hz = 0,
d3xd3 3a; -j- d3y ds ay -j йягй>о;г = 0.
Все эти уравнения заключены в одной общей формуле й)
dnxdabx + dTy dnly-\-dnz (TSz = 0 (l')
или
8 [(d"x)* + {dPyf + (pgft = 0. (2)
Для того чтобы вывести те значения йж, 6|/, 8г в фуыгсции от
х, у, z, которые могли бы удовлетворять условным уравнениям (2) при
любом п, Лаграпж применяет следующее раееуждепие. Символ d,
говорит он, можно понимать теперь в смысле дифференциала
координаты; примем одну из координат, например х, за независимую
переменную -); т.-гда все дифференциалы от х порядка выше пирвого обратятся
в жуль; уравнения (1) и (2) '-удут заключать только по два члена;
второе и третье уравнения группы (1) иосле определения <РЪу на второго,
его дифференцирования (т. е. применения оператора d) и подегапоскн
!) См. сцоску ■>) на предыдущей странице, стр. 217 и 229 I тома русского
перевода.
3) По старинной, терминологии это выражаетсн словами «приыем dx
постоянный», .

РАБОТЫ, ПРЕДШЕСТВОВАВШИЕ СОЧИНЕНИЮ ЛОБАЧЕВСКОГО 355
в третье уравнение, приводят к основной формуле 2)
После двух интегрирований эта формула дает:
где а и ^<£с—две произвольные постоянные.
Подставляя выражение d* Ьг во второе уравнение группы (1) и снова
дважды интегрируя, найдем
&Ъу = — «ііг -|- Т dx,
где ~idx ость третья произвольная постоянная.
Подстановкой обоих полученных выражений в первое уравнение
этой же группы получим
d Вя = р dz — ч dy.
Интегрируя еще раз и обозначая через а, 6, с три новые
произвольные постоянные, найдем окончательно:
&Ѵ = Ь-{-->х—аг, \ (4)
Ьг = с -|- ау — рж. I
В этих формулах и содержится теорема о перемещениях жесткой
системы, данная в 1750 г. Эйлером. От вывода их, предложенного
Лагранжеы, остается впечатление некоторой искусственности, именно
потопу, что, трактуя символы (( как дифференциалы, Лаграеж, как
уже отмечено, применяет к ним п правила исчисления конечных
разностей. Несомненно, это обстоятельство имеет в виду Лобачевский,
начиная свой исследование следующими словами:
«Лагранж в Аналитической Механике выводит условные
уравнения ^), которые первый дал Эйлер, для движения сплошного твердого
тела, полагая бесконечно малые расстояния вещественных точек
постоянными и принимая, для простоты решения, тоже постоянным
дифференциал одной из трех перпендикулярных друг к другу координат,
которыми определяется положение точки в теле» 3).
В разделе «Аналитической механики), озаглавленном «Свойства
неподвижных осей вращения свободного тела любой формыз *)
і) Ж. Лагранж — Аналитическая механика, нал, 2-е, Гостехиздат, Ы. —Л.,
1950, г. I, стр. 228.
2) То-есть уравнения (4).
3j Стр. 357 наст, тома,
*) См. сноску і), стр. 357—3flG кешги Лагранжа,
23*

35G
УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ
Лаѵран-іК дает теорию осей свободного вращения. Для современного
читателя, привыкшего к наложению динамики твердого тела в эйлеровых
осях, неиамеыно связанных с телом, и к конструкции эллипсоида инер-
пии по Нуансо ') вывод Лагранжа представляется необычайно
сложным. В общем, Лагранж довольно близко следует за рассуждениями
Даламбера в упомянутом выше мѳмуаре 1768 г. Здесь, прежде всего,
составляются выражения проекций вектора момента количеств
движения твердого тала на неподвижные <даламбѳровы» осп; в случае
равенства ну л го моментов действующих сил, укааавнне проекции
постоянны. Но входящие в них выражения моментов в произведений
инерции тела по отаошению к неподвижным осям (или плоскостям)—
переменные. Задача состоит н определении положения осп, вокруг
которой тело могло бы вращаться с постоянной угловой скоростью;
Лаіранж принимает за неизвестные отношения двух направляющих
косинусов этой оси )с третьему, и, исключай олпо нэ этих отношений
из тех трех уравнений, к которым в данном случае привотятся три
уравнения моментов, получает для другого отношения косинусов
кубическое урапненне; исследование этого уравнения и дает полное
решение задачи о свободных осях.
Лобачевский был, невидимому, первым лзтематпком, обратив шил
внимание на то, что такой метод определения осей свободного праще-
шія, подчиняет задачу, связанную только с распределением масс
данного тела, сложному динам пч ее кому анализу. «Между тем, — говорит
он, — геометрическое свойство этих осей может быть доказано без
помощи Механики и даже Дифференциального Исчисления» 2).
Такпм образом, предвосхищая метод Пуапсо, Лобачевский
открывает здесь новую главу теоретической механики, ту именно, которая
получила название «геометрии масев. В этом — историческое значение
второіі чаеги сочинения Лобачевского.
Детальный анализ этого сочинения дан в комментарии ").
!) Роічзог. — Тііеогін oouvelle do la rotation (les согря, 1Я52.
2i Стр. 360 ааит. тома.
3) Стр. 369 -378 наст. тома.

УЧЕНЫЯ
і ЗАЖЖ@ЖЖ
ІІМПЕРАТОРСКАГО
МОСКОВСКАГО УНИВЕРСИТЕТА.
ГОДЪ ВТОРОЙ. .
ЧАСТЬ ВОСЬМАЯ.
МОСКВА.
Еъ Университетской 1'ипографіи.
18 3 5.
Тнтулыіиіі гшст 8-іі часттт «Утиных :шті'ик ^Госкоіз^кого уншзкрг^ттетая,
в котором йыяо ншючатапо еочннвнчо «Уелопнью уравнении ;піі л.пп;і.'ении
и наложение глліііімх осоіі в тверди it енвтеме^.
К стр. а;?.

ИЙВДАТОРСКАЗ^І МОСКОВСКАГО
УНИВЕРСИТЕТА.
1835* Февраль, Nft ѴШ.
I. НА У К И.
А. МЕХАНИКА.
1. Условны* ттлвідоп* для. дмикгны, и поль ,
ЖЕНИ МіЛЯЫХъ ОСЕЙ ВЬ ТВЕРДОЙ СИСТЕМ».
Профессора, ЛобаЪб*ска,со.
* Лагранхъ вь Аналитической Механике
выводить условныя урзіненія, который первый
#хк*Э&ерц для движенія спдошнаго гавердаго
яйшц (іолагая беэконечно малыя разстоянія ве^
щеслпенныхь точекъ постоянными и
принимая, для простоты рѣшенія, гаоже постояв-
аымъ диФФеренціадъ одной изъ трехь
перпендикулярный, другъ кь другу коордияагаъ, ко-
Уч. Зап. Часть VII. 1
Первая страница оригші;ілі,ні>Гіі несший сочинения
■ Условные ураннеямн д.ш дииження и положение глпшімх осп
(169-я стр. 8-ІІ ча"-тіІ «Ученых записав ІГискі.викоічі уялиерсптста»),

УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ
И ПОЛОЖЕНИЕ ГЛАВНЫХ ОСЕЙ
В ТВЕРДОЙ СИСТЕМЕ
№ *,
"ш II ,'Іаг^анж в Аналитической Механике выводит условные
уравнения, которые первый дал Эйлер, для движения сплошного твердого
тела, полагая бесконечно малые расстояния вещественных точек
постоянными и принимая, для простоты решения, тоже постоянным
дифференциал одной из трех перпендикулярных друг к другу
1Г„ координат, которыми определяется положение точки в теле (Моса-
nique analytique, par Lagrange. 1811. Т. I. p. 108). Можно к таким
уравнениям притти, хотя бы число вещественных точек в твердой
системе было ограничено, а расстояния между ними конечные.
Назначаем, по выбору произвольному, в каком порядке
вещественные точки твердой системы должны быть рассматриваемы
одна за другой. В этом порядке называем х, у, 2
перпендикулярные друг к другу координаты одной точки; х, у', г' — следующей
за него; х", у", г" — третьей; %'", у'", г'"—-четвертой. Пусть по
известному принятому озпаченпю в вычислении приращений
х' — х = Дж, У —х' = Д г 4- &х, х'" — -с" = \х + 2 Д4ж + Д=х,
так и для других координат у, z. Расстоянии между
вещественными точками в твердой системе не должны изменяться от
движения, а следовательно значение их квадратов
(x' — xT + iif — yf +(г'-г)\
(ar — afy + tf—yy +(*"-2')3,
(я*—«V + G/'-ff)' +(г"-г)\
'" і {х"'—хУ + (1,"1-у"Г + (г'"-г'У,
(а/" _ ху _|_ (/" — iff + (S"—z'Y,
(«" - rf + (у'" - yf + (2'" - z?
* Разделение сочинения Лобачевикого аа частя I и II сделано пани.

358 УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ
ее зависит от времени. Вставляя сюда
а/ = х -\- Да1,
У — х-^-2&х-{-&х,
х'" = х А- 3 At 4 3 Ь?х -j- Д8ж,
подобным образом и для других координат у, г, выражая к тому
знаком В впереди то изменение бесконечно малое, которое
происходит в движении, должны почитать
Й [(Да; -j- tfxf + (Ay + Д2г/)5 + (Дг 4 Д2*)а] = О.
8 [(2 Да; 4 Дах)2 + (2 Ду + Л1У)г "Г (2 іг + д2г)г] = ° *.
8 [(Дж + 2 №х -j- Д3ж)2 + (Д</ -|- 2 Дау + Д'у)3 + (Дг -[- 2 Д*г + Д3*)2] = О,
a[(2ii;4-3A*a:4-A3*f4-(2i?/+3iV + iV)s + (2i2+3A=2f Д'г)»] = О,
S[(,4Ax + 3A!aT + AV + (3i!/ + 3AV + As?/r-b(3A2+3A22-LAVI = 0.
Второе и третье с помощию первого из этих уравнений дают два
таких:
S (Да; 6?х -\- Ду Д!у + Дг Д=г) = О,
S (ДЪ:2 + Д V 4 Д3гг) = О.
іі» | которыми пользуясь, находим из трех остальных
S (Ах Д8х + Ду Д3# + Дг ДМ = О,
3 (Да# Дв.е 4" Д!У Д V + ДІ? Д'^) = °.
а (д3х3 4- ДУ + Д3-*2) = °;
идя той же дорогой, можно бы доказать вообще для целых чисел
п, т, что
з (Дя# ь?»х 4 Д™г/ Д™г/ 4 Д™^ Д"Ч) = °- С1)
Лшранж замечает, что условие для движения твердого тела
выражается дифференциальным уравнением
d"x dn Ьх 4 <%пУ rf" Ъ</ 4 ^2 <Z" 5z = 0,
или иначе
5 (*'.*■* 4 <?".'/" 4 d"?-) = О,
іі где, следовательно, как это показывает уравнение (1), квадраты
дифференциалов от координат могут быть заменены произведением
двух приращений какого угодно порядка.
* В оригинале начало этой формѵлы ошибочно шшѳч&таао так:
8 [(ія + да»)! + ...

Н. И. ЛОБАЧЕВСКИЙ — «УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ» 359
Берем еще тожественные уравнения
8 (As1)
Ах*
8 (Д V)
8(А'л1)
8(ДѴ)
ДѴ
S (АѴ)
ДѴ
S (Джа)
Дажг
Да:2
8(Да:А%)
Ах ДѴ
8 (А?а: Дэж)
Д2ж Д3;с
6(А'з;Ад:)
Д'.ж Дж
= 0,
= 0,
= 0.
[la]*
in | Основываясь на уравнениях (1), заключаем отсюда, что
8{Д2/5-Ь^2) , В(ДѴ-ЬДѴ)_2§(Д1ДѴЬДгДІі) = 0
Да:2
Д2ж3
Ах А'1,г
»(ДѴ + А'^) , В (Дя^ + ДУ) В fД°і/Д5у + Asz АЬ) _
Ах3 т ДѴ ДУД'ж '
й(ду-|-ДѴ) 8(А?/=4-Аг*) 08(ДуД3у + ДгД'г) _
АЧ* + 'дл;* ДжД'а: '
которым уравнениям можем дать еще такой вид:
\А2х
у\ /А'8у АЬу\ /А'г Дг\/АЧ
.с j I ДѴ Да; j "г" I, ДѴ Да: Д Д2а
'АѴ
Ау
"д! ,
д^\/д%
ДѴ./ ^ Д8а;
Aff\ /A'Stf
Д*8г Д8г
АЧу\ IАЪ АЪ\ I
!~т~\Айх Ах}\
ДѴ
АЧ?
Ах
Д*8г
Д3ж
A»5j
Д'я
АЙ2
= 0,
= 0,
н-
(2)
Д'я; Да: / \ ДѴ Да; / ' \ ДѴ Да; ) \ Агх Ах
іі4 I Умыожая первое из этих уравнений на ДѴ и разделяя на Да; -f- Д'я;.
получим
Д.у Ах '
As
д"1=о.
Ах
(3)
Подобным образом, умножая второе из уравнений (2) на ДѴ и
разделяя на ДѴ -j- ДѴ, находим
л *У
ДѴ
ДѴ ' ДѴ ДѴ
(4)
Иа последнего в уравнениях (2) берем первый член
іі?у Ау\(АЧу А8у'
I ДѴ Д.с У ^ Д3^ А
А (Ах Ahj — Д V Ду)—(Д V ДЧ/ — Д V Дау)
Я-
Да; ДѴ
X
X
А(Аа-Д% —AyA'SaQ —(АѴА'8,у—А^А'&с)
Да: Д V
* Номера формул о литерами сделаны нами для удобства ссылок в комментарии.

360 УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ
Положив здесь для краткости
X = Ах2 -f tee А*х, X' = ifsfl -J- А"-х Ух,
продолжаем вычисление так:
\ Аах Ах I \ А*х Ах )
[4а]
+і"а£-4£-
Даа;
Потом
(^)-(ХД^)-
= (Х + АХУА^.^4
"У
Ах
+(х+дг)дх|д^
=,Х{Х + АХ)А*^.А*±Р-
'Ах Ах
АІу
Ах
Дж Д.г'
-АХ-
Ду
Дй
да?/
д#
^Д^.Д^-.Д^І,
1 Дж Ах
+ ІХ
д Лгг/ ^ ДЕу ^ Ду А Дг 5?/
ДѴ
Дх
Д2а-
В орішшнле в этоіі формуле вместо ■■;„■■ я -ts-^ напечатано соо гветствеЕіыо
Дя Дж '
tf# дах.

Н. И. ЛОБАЧЕВСКИЙ —.УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ» 361
Заметим, что
_Д3
дг
н1+£)4£-
ду
Ах'
'M'+^^)*s+ft'^
I После чего
Ду
Д!ж ^^ДМП Д*л/ Аі+[ + 4»я) Аі
Д5і/
[4Ь]
[4в]
Д#
Д«М&
Дж
Ах
Да-
' Ах
)-
-(^•т+»и)^-4,^+('+4и)4(^-^)-м
A!*. aA*w,. д» дд!^~
Д3а: ' Да; 1" Дж ' Д!я
\ ~Дая- ' &?х) [ V д'г Дж / Дж ДіС .
+
+»(і+*£)*£-Ц?-і*]
Соединив всё вместе, попучим
д,.д.д.(^-^)(^-А?»
\А*% Ах I \ А6 л Ах
)"
Да;
+*(4")!<*+дх)("-ы'дШ-
-^Ч+Й + ^Н-
+ *£-а4?{«-"-ах(і+а
Да^
Д'жі
1 Л ~і-
Д=ж
ДЧу
Да.я '

362
УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ
Поставивши сюда г вместо у и складывая, находим, основываясь
на уравнениях (2), (3), (4)
\ Да; Да: ' Да: Дж }
Х{^Х+Д^-Х'ДХ.^-Хх(і + 2^ + Д^)}. [40
Здесь
^+Д^=л^ +
Ха , XX'
"Дж2 ' ДжЛ5*'
' — х
'й?х ' ~ Дгя1— Ах№х "т" Дж.X'
, Ь ,Ь= X , ХД'ж
"Г Д2„ ~Г AS™ Л.л Л3„- '
следовательно,
Х(Х+ДХ)-Х'ДХ^--ХХ'(і + 2^ + Д^) =
т ( Ха Х'а Т Ах XX' X Двж | __
— J Джа Д*ж! ' Д5ж Дж Д2ж Да; j
= Дж (Да; + Д%) [(Да: + Даа:)а — (Д2Я + Д8ж)а — Д2ж (Дж + 2 Д2а? + Даж)] =
= Да: • (Дж -j- Д2ж) (Да; + 2 Даа; -j- №х) (Дж — Д*г — Д3ж).
Так как
Дж Дж
іч | содержат в знаменателях произведение
Да; (Да; -f Д!ж)5 (Дг + 2 ДѴ + Двж),
то необходимо
4 \ Дж Да; Дк Д.е / ѵ '
Пусть для краткости
Дж Д.е Да' Дя;
Находим
, /ду* д/ ДуИДУ „дг/ , Д8у\
U** Да^ Дж/ \ Д*" Д»-' Дж /
/Д/'_ ДУ ^WAS," 9W Д8£\
■" \ Дж" Дт/ ^ Д.е/ \ Д.г-" " Дж' ' Да- j '
* Номер формулы (4) у Лобачевского здесь повторивши.

Н. И. ЛОБАЧЕВСКИЙ— «УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ» 368
или, основываясь на уравнении (3),
р- (**", л?/1 (дз-ѵ" j.**y\j-(Аг" j_ Лг\ fд 6г" _і_ даг\
г [^+^}\~^^ + -^ } + [-&?+j-z){-&sr+-K£ )-
Ду'/ДЗу" Д6у\ „Дг'/ДЕУ А5г\
Дат' \ Дж" ^taj d Дж' \ Да;'" "•" Д., )
2-д^ід^+ді)-2^(д^+д^- [4gJ
ITS
| Здесь
Ду' дгу , да./ іе,_а£' A^l-lA^ ^£
Дж' ' Да; Дж' ' Дж ' Дж' " Ду "*~ Дж' ' Да;
= 2 ( *2 - А^ + — ■ — ) + Д (^ • ^4- — ■ — 1 -
\ Дж Дж Дж Дж / ' \ Дж Дж "^ Дж Дж /
_/д^.4^ + Д—-А—\-
\ Дж Да; Дж Дж /
„ Д8ж , ДВж
Дж Дж
После чѳго
Р-/Ѵ,Д»\ №" , ASjA , /А?" і ДЛ/ДоУ' , А3г\
~ \ Д** "^ Дя/ I Дж" "•" Аж/"Г"\Дж""1" Дж/ ^ Дж" Г Дж/
Д вж „ Д Зж' . А Еж . Д 8ж' г,. , „
Да; Да/ Да: Дж L Jl
Отсюда следует, что значение Р не переменяется, когда вместо
координат ж, у, г ставим ж', j/', /, делая то же наоборот. Б таком
случае уравнение (4) должно давать
(Дж—Д*ж —Д8ж)Р = (ж'" —2ж"-|-ж)Р=(.г'" — 2ж" + ж')Р;
следовательно, хР = ж'Р. Если ж = ж', то не может быть вместе у' — у,
„и г' = г, а так как означение координат произвольно, | то, принимая
ж, ж' неравными, должны почитать Р=0; это значит:
ді^.4.4^ + Д»^.Д^в0. (5)
Дж Дж Дж Лж
О помощию этого уравнения и дифференцируя уравнение (3),
находим
д.^.д^ + Д.^.дАН + д^.а>А** + д^.Д^-о.
Дж Дж ~ Дж Да; ~ Дж Дж > Дж Дж
* Эта формула не обосиовава (си. комментарий, стр. 375 наст, тома).

364
УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ
Вставляя сюда из уравнении (3), (5) значения Д-т—, Д -т—, получим
Да:
Дж
Д*
Да; Да; Да; &хі
ДЕУ
Да;
да
Д8у
Да;
Да;
Д3
*1
Ах
= 0.
\В этом произведении можем тот или другой производитель
полагать нулем. Если принимаем
Л*
или, все то же,
Да; Ах Ах Ах
= 0,
д^
Да;
Ах
то интегрирование даст
ѵ = Ся + Сх + СГ,
которое уравнение с постоянными С, С, С" должно быть
справедливо по крайней мере для четырех точек по порядку; а как
ничто не мешает четвертую точку всякий раз выбирать вне
плоскости трех предшествовавших и даже, в случае невозможности
из остальных, возвращаться к прежним точкам, то остается
необходимое условие, чтобы
Д%
Да;
Д!
Да;
= 0,
1 или иначе
АЬу
' Да;
. Дг Дг As
А —— Дг -— Д -
■ 0.
[5а]
Да; Да; Да;
Это последнее уравнение интегрируя, находим
Дйу = Лг-5з — Дж.З'г, В?/= £&-]-г Ва — а;Вт,
где оЬ, uat S-f произвольные постоянные. Вставляя значение АЬу
в уравнение (3), получим Д-т—= — из Д-г2-, интегрирование чего
дает
52 = 8с + а;53 —т8а,
где Ее, 8р новые произвольные постоянные. Наконец уравнение (1)
для п = 1, »і = 1 делается
АхАЬх-]~Ау Д5у-|-ДгЛ6.г = 0,

Н.И. ЛОБ;ПЕВСКИЙ — «УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ. 365
куда поставя значения 8і/, ог, паходші
Интегрируя, получим
1S, |где Ьа новое произвольное постоянное. Таким образом, условия
для движения твердой системы будут;
Ьх = За -f- у of — z 39,
Ъу = ЪЬ + гЪа~ гЛу,
Ьг = Ье-і-хЬ?—уЬя,
Для одного обращателъного движения они сделаются
bx = ybf — гЗр,
Зі/ = гВз — хЬу,
Зг = а;5[5— г/Вя.
Если оси координат вместе главные оси обращения, го
2 туг = О, 2 тгх = 0, 2 тдаУ = ^
где яг — масса вещественной точки, а сумма берется в отношении
ко всем таким точкам системы. Эйлер открыл первый
существование трех главных или свободных осей обращения и взаимную
перпендикулярность нх, определяя самое большое и самое моньшое
значение момента косности. Лаграною в Аналитической Механике
приходит к тому зке заключению, рассматривая свободное
движение около оси, которой положение само гобой сохраняется. Между
іаі тем геометрическое свойство этих осей может быть доіказано без
полощи Механики и даже Днффсрепппялыюго исчисления.
[П]
Воображаем чрез начало координат плоскость, к которой
перпендикулярная дает і, т], С косинусы ее углов с осями координат
х, у, г. Расстояние р всякой точки (х, у, г) от этой плоскости будет
і> — д + г/*і+-г*
Для двух новых плоскостей, также проведенных чрез начало
координат, различая буквы ударениями, должны писать
* В оригинальном тексте вместо р', р" ошибочно напечатано g', q".

366 УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ
После чего
р'р" = х* ■ ЕГ + у* - т,'Ѵ -f г* ■ W + у>г (г,Ѵ + W) + я; (С'Г + С"£') +
J^P = ** • Ь"Е -г t/2 • Vl +Ѵ1 • СС -1- уз (ч"С + чС") + «« (С 5 + «") +
ЯР' = я3 ■ «' + ys ■ щ' + *а • «' + г/^ « + ті'С) + ^ (СЕ' + СЕ) +
Умножая все три уравнения на т, ставя перед каждым членом
знак суммы и полагая
2 tnp'p" = О, 2 мУ'Р = 0, 2 ЩРР' = О,
2«^5 =А 2™уа =Д 2 «и" =с,
2ту2 =я, J)™-337 = ^> S*?1^ =еі
і» | получим
0 = ,1Е'Г + 5ѵіѴ+СС/С"1-а(ѴС'Ч-Ѵ'С') + г,(-''" + ^"'')Ч-
о«дй'+5ччч-ок'+о(іісч-ѵс)+ь(«'+се)4-
+ сОп'-Н'ч).
Если к тому плоскости, от которых расстояния точки назвали
р, р', р"7 все три перпендикулярны друг к другу, то
ET-i-TjY + C':" = 0, ГЕ-|-Ч"1 + ^'С = «, КЧ чѴ + К' = 0. (7)
Присоединяя сюда еще уравнения
Е9-И9-К* = і, Е,а+ѵа-К'- = і, Г'+Ѵ»+;*»=і, (8)
получим всего 9 уравнений (6), (7), (8) для определения девяти
пеизиестпых £, t|, £'. ;' и проч. Чтобы избегнуть затруднений
не в обыкновенном способе исключения, заменим три уравнения (6)
новыми
\Y—Bi\ + a', + t&, (9)

Н. И. ЛОБАЧЕВСКИЙ — -УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ» 367
(10)
ѴХ'=>АѴ -Ьсп'-И*',
X'Z1 = СС' -\- Ы' 4- аѴ,
А"Г"=5ч" + вС" + еЗ",
где А, X', ^" произвольные числа и где
Х = чГ —П"С, Г=С'Е* —СГ, Z = Vif — V%
y = Vt-<. F-CS — СГ, ^ =Г-п — En',
X* —4C —tfC, F"=CE' — C'£, 2" — 6ч' —*Ч
is7 (Отсюда
ХХ'+ГУ + ^г'^О; J
Z"+Prt + £'* —1,
Xй3-f Г"3 + г""
L
(11)
(12)
(13)
(14)
(16)
(16)
Произведение первых из уравнений (9), (10) даѳг
)ХХХ' =
= J'Ef -f с*трі* + ИХ' 4 йс« + t/C) + 45(tf + СЕ) + Ас(ЕѴ + !\).
Таким же образом находим лА'УІ", \t!ZZ'\ а складывая все три
уравнения вместе и принимая для краткости
А' = А9-
В' = £* — 6=
С = С* —с»,
(17)
a' = 6e-)-a(JJH-0), &' = м + 6(с+А с' = а& + с(А + В),
с помощию уравнений (15) и с переменой ударений над буквами,
получим
] 0 = А'ІІ" + 5 Ѵм" + W + а' (І'Г + ѴѴ) + &'(6Ѵ4- ^Ѵ) +
О = Д'£"£ + ВV ч + С >" + а' (— + «") + Ѵ С^Ч + W) +
+ С (ч^ + тГ).
0-=.1'ЕЕ'4-В'»,Ѵ + С'«/4-«'(«'4-С'Е) + 4/(Ьі' + е/ч) +
Уравнения, подобные уравнениям (6) и которые приводят к
заключению, что если в одном теле
2 «я?— 4, 2му2 = -В, 2™"—С,
2»і(/2 = а, 2ni■гa;=, 6> 2та:У —с>

368
УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ
В другом
2 тз? = А? — аа, 2 "»/э =■ -В5 — 6я, 2 отгя = С* — с\
тяг/ = a6+fi(A+i?),
то положение трек главных осей в обоих телах одинаково.
Два последние из уравнений (17) можем снова заменить
уравнениями
pX = A'l+<f-4 + ffc, v.Y=B'-q + aX-\-c% v.Z=C'Q~\-l/Z + a% (18)
и* I где p произвольное число. Сличая уравнения (18) с уравнениями (9)
и полагая ^=рѵ, получим:
(A' — Av)l-j- (с'~ сѵ)ц-\- (b' — bv)', = 0, ]
(с'_cu) £+(#'—Щі\+ (а' — аѵу, = 0, (19)
(У — Ь»)І-\-(^ — аѵ)іі + (С~Сѵ)Л = 0. І
Отсюда исключая которые нибудь два числа из і, ч;, С, потом отбра-
сывая третье, находим
(А' — Аѵ) {В' — Аѵ)(С—Си) — (A'—Av) (a'-avf — (B'-Bv) (b'—bvf-
— (С — Сѵ) (с' ~ cvf + 2 (а — а'ѵ) (Ь — Ь'ѵ) (с — с'ѵ) = 0 (20)
— уравнение третьей степени и которого по крайней мерс один
корень необходимо действительный. Отыскавши ого, потом
содержание друг к другу чисел і, tj, ', помошню двух из уравнений (19),
получим самые числа Е, ч\, \, всегда действительные, из первого
уравнения (8):
H+tf + t^l.
Зная Е, % С, определяем содержание друг к другу чисел £', т/, г-'•
соединяя последнее из уравнений (6) с последним из уравнений (7);
hi а наконец получим а самые числа | і', tj, (,', тоже действительные,
из уравнений (8). Подобным образом находим и числа Е", г", С".
Надобно заметить, что если множитель в уравнении (20) при
ѵя будет нуль, то можно принимать г» = со, поело чего уравнения (1!))
сделаются
А% + <я\-\-К = 0, с',-|-Д*і-і-а; = 0, Ь- + а-ц + С,*-і> (21)
и предполагают
ABC— aU — №В - c'JC+ 2aic = 0.
Б таком случае уравнения (21) в соединении с первым из
уравнений (8) дают всегда действительные значения чисел £, tj, С

КОММЕНТАРИЙ
В первой части своего сочинения Лобачевский ставит задач у
вывести эйлеровы уравнения'), применяя общий ход рассуждений
Лагранжа, но допуская, что «число вещественных точек в твердой
системе... ограничено, а расстояния между ними конечные»8).
При такой постановке вопроса дагранжев оператор d должен
уступать место оператору конечной разности Д; обозначая координаты
последовательных точек через х, у, г\ а/, у', г'; х", у", г", ..., имеем:
яГ = х+ Да:, х" = х1 + Да:',
Да;' = Да: + ДЧ х" = х -\- 2 Да; + Даа-,
Этими и аналогичными равенствами определяются разности первого
я высших порядков от координат. Наряду с конечными разностями
вводятся символы Ьх, Ьу, Ьг; их нужно понимать как дифференциалы
координат при ігк дифференцировании по времени.
Так как
8 Дат = S (а/ — х) = 8л-' — Ьг = Д За:,
то операторы Д и 3 коммутируют; то же самое имеет место ;іля й и
для равноетей высших порядков.
Оба символа Д и 8 входят во все формулы Лобачевского; сопоставляя
их с основными формулами Лагранжа, приведенными во вводной статье'),
мы должны проследить, как отражается па fhx оамена символа d на Д.
Мы наметим сначала только оояовные этапы вывода Лобачевского.
Здесь фундаментальными являются четыре формулы, которые мы
обозначим (А), (В), (С) и (D).
Первая из них гласит:
8(Д»*.Д'»а; + Д"да. Д»'^-}-Д»г-Д|»*) = 0, (А)
нри любых целых и положительных и и *и *).
J) Уравнения (і) на стр. З&З (во вводной статье). Н дальнейшем вое ссылки
на страницы относятся к настоящему тому.
*) Стр. 357.
8) Формулы (1), (2) и (3) на стр. 3&4-355.
') ЛиЗачввекого — формула (1) на стр. 358.
2* Эш. 88». Н. И. ЛобачевеянЙ, т. V,

370
УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ
Уравнение (А) имеет фундаментальное значение в работе
Лобачевского; оно выражает в наиболее общей форме условие
неизменяемости ори движений расстояний между точками твердой системы,
ввятьшн в ограниченном числе.
Очевидно, что основная формула Лаграяжа
S [(#•*)* + (#»!»)* + (**Л = °
является только частным случаем уравнения (А), при замене Д на d
и при условии тп = и.
На следующем этапе анализа Лобачевский получает уравнение:
Это соотношение переходит во вторую формулу лагравжевой группы
формулг), если только считать Дя; постоянным и заменить символ Д
лаграажѳвым d.
Далее, после весьма утомительных выкладок Лобачевский
приходит к уравнению
д.* д.^ + д^.д»*^ О»). (0)
Ах Ьх ' Ас Да; '
Очевидно, при Ас = const мы пришли бы к третьему уравнению
системы лагранясевов группы при Ar = conBt,
Путем весьма замечательного анализа уравнений (В) и (С)
Лобачевский приходит*) к последнему основному уравнению:
Д__4^- = 0. (D)
Ас
Это уравнение, по его структуре, аналогично уравнению
Д^.Д^ + Д^.дІ^О
ах Ас Ас Ас
в методе Лаграяжа: оно является разрешающим для метода
Лобачевского; интегрируя его, как уравнение в конечных разностях, затем
привлекая снова уравнения (В) и (А), Лобачевский получает (в
несколько иной записи) те эйлеровы выражения для Ьх, &у, йг, которые
были приведены нами во вводной статье ь); на этом и завершается
первая, кинематическая, часть исследования Лобачевского.
J) У Лобачевского — формула (3) я» стр. 35Р.
") Формулы (1) во вводноК статье (стр. Зоі).
3) У Лобачевского — формула (5) на стр. 363.
*) У Лобачевского — формула [5а| на стр. 364.
5) Уравнения (4) на етр. Н.іэ.

КОММЕНТАРИЙ 371
Проследим теперь более детально за главными этапами выкладок
Лобачевского и для этого приведем, прежде всего, основные формулы
того алгоритма, которым он пользуется.
По самому определению конечных разностей, имеем для
произведения и для частного переменных и, ѵ:
Д (нѵ) = и Дѵ -(- ѵ Ли + Дм ■ Лг,
и о Дм — и Д ѵ
ѵ ѵ {ѵ -\- Дг)
при v^zO, v-j-Ьѵ фО.
Отсюда, для « = Да;, г = 4#,
Ду __ іс ■ Д4у—Ag/ ■ Д*х
Д^Г Дж.(Дж+Д*ж) <а)
и точно так же, при м*=Л5.г, « = Д*р,
Аау Даа=-Д»у—ДУ-Д3ж
ДЪ™ Д2а;(Д% + Д%У"' <Ь>
Знаменателе дробей в (а) и (Ь) обозначаются у Лобачевского')
через X и X', так что
X ■ Д ^ = Дх ■ ДѴ — Ду - Д=.г, (с)
Взяв разность от обеих частей (с) и вычитая почленно (іі), получим:
А (х'А ІІ) - х' ■д Ё - **'Айу - *,J ■ДЗз;- w
Для некоторых выводов Лобачевского важно заметить, что в
выражение второй разности
Дл;
войдет произведение
Да; (Да: + Д1*)8 {±х + 2 Д!.с -j- ДЧс).
Отметим еще применяемые Лобачевским соотношения:
Д (к Дг) = Ди Де + (а -г іи) -*!»
п. наконец,
Д (мо) ■ Д («'с) = »(«-)- Д") ■ Д» ■ Д'« -г -^" (" Н~ ^'0 " •* (vw) ~Т -^"а ' "'*■
') Формулы |4а] на стр. 36*}.
24*

372
УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ
Эгимн формулами исчерпывается тот аппарат, которым пользуется
Лобачевский в первой части своей работы.
Вывод основной формулы, обозначенной ваше через (А),
проводится Лобачевским') шаг ва шагом, всходя ив неизменяемости при
движении квадратов расстояний между первой и второй, первой н
третьей, второй и третьей точками и т. д.; етот вывод особых
пояснений не требует; подчеркнем только, что обозначения:
Да;2, Дг£2, Д8»:1 и т. п.
применяются всегда для квадратов соответствующих разностей,
ко никогда как разности от ж2; эти последние у Лобачевского вовсе и
не встречаются.
Весь дальнейший анализ Лобачевского основан на трех
«тождественных уравнениях! '), которые все заключены в тождестве:
8«s 8иг_ 28 (иѵ)
в. первом из них и = Лх, ѵ = Агх, во втором и = А?х, ѵ = Аъх, в третьем
я = Дяд:, ѵ = Ах.
Но в силу условия неизменяемости расстояния между точками
(х, у, г), {т.', у', z') и из уравнения (А) при m = n = 2 имеем:
Ъ(Ах*-\-Ау°--\-Аг*) = 0,
8 (ДѴ + ДѴ -f АѴ) = 0.
Поэтому, например, из первого тождественного уравнения по
выполнении дифференцирований под анаком 8 найдем, обозначая
многоточием члены соответственной структуры с Дг и 8г:
Ау Afy_ | ДV AsZg , Ду Аг3у ДѴ Аѣу (_
Да: Ах Д2а; Агх Ах Д.г ДЕа; Да;
или
Лг# Ду \ / Дг Sy Д 3^ \ . [ аналогичное про-
Л2л Да; / \ Д5я Д.г | ' | наведение с Дг и Вг
Но й силу формулы (с),
А^_Д^:=ДД£ £___
А"х Ах Ах Да: ■ Д5.с
") На стр. 353.
*) Формулы [iaj яя стр. 359.
Э) Формулы (2) на стр. 359.
*) Формула [4Ь] на стр. 361.
= 0.») (t)

КОММЕНТАРИЙ
373
Последний множитель едрава появится и в тех членах (f), где у в г
заменены на 5у и на 8г; сокращая этот множитель, получим одно на
основных соотношений, уже отмеченных выше, именно формулу (В).
Столь же просто производится обработка второго «тождественного
уравнения». Учитывая теперь, что в силу формулы (d)
А3х Д2,е Ах1 Д5я ■ і8ж'
Лобачевский пргіходит к уравнению (4) т), именно:
, Дау .АЧу . дД2Вг Д«8*
4^-д-д^ + д-д?--дді^0-
Существенно сложнее выполняется замечательная обработка третьего
* тождественного уравнения»:
адваа йДж3 ___ 2о(Д% - Дх)
"ДЭ^ "■" "Д-ё5" ~~ ~~"Два: ■ Дл; '
Эта обработка эанимаѳт у Лобачевского страницы 350—362 наст,
тома; здесь мы отметим ее основные моменты. -Иа третьего уравнения
системы (2) в), учитывая значения X и X' и применяя формулу (ѳ),
Лобачевский приходит к уравнению в):
[А(Х Аѵ) — X' Aw] ■ [А(Х Аѵ') — X' Aw')+ ... = 0, (g)
где нами для краткости положено
Ау , Д% А-у , АЧу
Ах Ас Джа Дя
н где многоточием обозначены аналогичные члены с г и Ъг.
Выполняя перемножение, получим:
а) члены, пе содержащие X', именно:
Д(ХД«)' Д(ХДі'') =
= Х(Х\ АХ) АН ■ АѴ-\-АХ{Х-^АХ)А(Аѵ ■ Ал,') -f АХ' Аѵ - Ді/,
б) члены с множителем X', именно:
Aw - Д (ХАѵ')^-Аю' • Д(ХДи) =
= (Х+ АХ) {Aw ■ ДѴ J- Дч/ Д2«) 4-ДХ(Ди ■ До' -j- Av ■ Aw') *)
и, наконец,
в) член
Л"'" Дці ■ Ati/.
J (Г')
1) См. етр. 35Ѳ.
2) Стр. 359.
3) Стр. 360.
') Ьішнкитель X' оиущен.

374 УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ
откудаг)
Аналогичные соотношения имеют место между Д«/ и At/, ДѴ. Они
приводят в равенствам8):
І№. ДѴ-|~Дм>' ■ 4=41 =
= 2(і + ^ + А-^)д^.ДѴ+(і + ^).Д(Д,-Д,'). (і)
Дм; ■ ДѴ -[- Д« • Дм/ =
-(l-|_^-L4-^-)l4(A..iO -ДЧ--4ѴЛ-г(ц-Д^)д,.Д;.(Ь)
Подставляя (h), (і) и (к) в указанные члены а), б) и в), мы получим:
1) члены с Д!и ■ ДЧ''; коэффициент при них обозначим через К,
2) члены с Дг-Дг~'; их коэффициент обозначим через Кѵ
8) члены о Д(Д« ■ Дѵ'); их коэффициент обозначим через К2.
Но, очевидно, те же самые коэффициенты К, К, и К2 получатся
при разложениях тез членов уравнения (g), в которые входят г и 8-
вместо у и %у. Поэтому, восстанавливая значения ѵ, ѵ', w и и-' uq ig')<
придем к уравнению
+Ч4£-*£+4#-4£
= о. (1)
Здесь сумма при коэффициенте JE, равна нулю в силу основного
уравнения (В); следовательно, равен нулю и коэффициент при Кй,
как разность этой суммы. Поэтому уравнение (1) приводится к виду
■[»£
Дз; ' Ах Ах
= 0 »). (ш)
Вычисление коэффициента К проведено у Лобачевского на стр, 362.
В конечном итоге уравнение (т) принимает форму:
(Дж ■— Д2.г — &?х)
Д.г Да: ' Да: Дж ' '
■) Формула [4с] на стр, 361.
*) Формулы [Id] и [іе) на стр. 361.
■) Формула [4f| на стр. 382.
■*) У Лобачевского — формула (4') на итр. 36:2

КОММЕНТАРИЙ 375
После этого Лобачевский проводят довольно сложные выкладки,
чтобы показать, что из (и) вытекает уравнение (С), которое и есть
третье фундаментальное уравнение его исследования, как уже было
отмечено выше. К сожалению, именно эти страницы в работе
Лобачевского содержат либо пропуск текста, либо искажение в печати, так
как, вычисляй Р1), он приравнивает нулю сумму
Лх' Да:' ' Ах1 Ах' '
Между тем, иа уравнения (В) а), на которое ссылается здесь
Лобачевский, равенство нулю этого выражения никак не следует; к тому
же, применяя условие неизменяемости квадрата расстояния между
точками (а/, у', /) и <х", у", г"), имеем
8 (Да:'2 + V3 + Д*'8) = °>
откуда, дифференцируя и деля на Дж' :
_Ѵ_ AS/ А/_ Д8т^ Ш_
Аз/ ' Ах' + Дд/ да,.' — Ах' '
В салу этого, выражение для величины Р, которое Лобачевский
получает3), места не имеет, и утверждение, что выражение
Ах Да: Дж Ах
симметрично относительно координат точек (х, у. z) и (ж', #', г'), не
доканывается проведенным Лобачевским рассуждением. Но по счастью,
в этом и нет необходимости; действительно, коэффициент прп Р
в уравнении (п), как было указано выше, есть Дж—-Д*;с— ДАв; но
Д.т — Д3ж — Л8ж = ж'" ~- 2х" + ж,
и поетому при произвольном расположения трех точек (я, у, г),
(хѵ, у", г") и (я/'', 7'", ?'") этот коэффициент в нуль ее обращается.
В силу этого иа уравнения (п)
(.с'" —2ат"4-'-)? = 0.
которое имеет места при любых значениях координат назваеныі точек,
необходимо слѳдѵет, что
Р = 0,
чем и устанавливается третье фундаментальное уравнение метода
Лобачевского.
В заключение весьма топкам анализом уравнений (В) и (G)
Лобачевский приходит к тому уравнению (D), которое мы назвали
1) Формула [4g] на стр. 363.
*) У Лобачевского —уравнение (3) на стр. 3W.
') Формула [4hj на стр. 364,

376
УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ
выше разрешающим в его исследовании; после этого он без труда
получает эйлеровы выражения ох, 8у, 8? для бесконечно малых
перемещений точек твердой системы.
На -сказанного нельзя не усмотреть, с каким замечательным
искусством Лобачевский провел всё ѳто доказательство, несмотря на
существенные осложнения, которые возникли перед ним в силу отказа от
лаграыжева допущения о том, что Да; является бесконечно малой
величиной, которую можно понимать в смысле дифференциала
независимой переменной, уничтожая тем самым ее разности второго и
высших порядков.
Вторая часть исследования Лобачевского имеет своим предметом,
как уже упомянуто, задачу об определении главных осей тензора
инерции любой системы материальных точек. Для пояснения приемов,
которыми пользуется Лобачевский в этом классическом вопросе,
пѳлесообразно применить векторные обозначения. Пусть р, р', р"—
три взаимно перпендикулярных орта; их проекции на заданные оси
х, у, з, иными словами — направляющие косинусы этих ортов, назовем,
как у Лобачевского, через
I і) L- с' т/ V- V і," r"-
проведем чѳрѳз начало координат три плоскости, перпендикулярные
к этим ортам; возьмем точку системы с массой т{ и с координатами
жо Уі, г(; ее радиус-вектор относительно начала координат назовем rt;
обозначим через pif р'( и р". расстояния этой точки до плоскостей,
образуемых соответственно ортами р' и р"\ р" и р, р и р'; эти
расстояния выразятся, очевидно, скалярными произведениями:
Положение трех «главных плоскостей» Лобачевский определяет
условиями:
из них, в связи с ортогональностью трех ортов, и надлежит
определить их проекции; но каждая из сумм типа V т(р',р' приводится
к билігаѳйноіі форме проекций тех двух ортов, через которые
получаются соответствующие расстояния. Коэффициентами в ѳтих формах
являются те величины, которые обозначены у Лобачевского через
А, В, С, а, Ъ, с. Обозначим эти билинейные формы соответственно через
1, Т' и Т". Развернутые их выражения даны Лобачевским в правых
частях формул (<5) >).
і I Ніі гтр. Угі'і.

КОММЕНТАРИЙ
877
Рассмотрим одну из втих форм, например Т". Поскольку она
билинейна в проекциях (£, *], С) и (£', т\', £'), имеем по теореме Эйлера:
дТ" ЬТ" ЬТ"
Но по условию о главных плоскостях Т" *= 0; следовательно,
вектор а проекциями
дГ 9Т' дТ"
W ' дц' ' ас (р)
ортогонален к орту р'\ далее, непосредственным вычислением
убеждаемся, что
RT" дТ" дТ"
дІ' е "■" ЙѴ ^ "'"' К'"" ~~ '
и поскольку 2" = 0, то введенный выше вектор (р) ортогонален в
к орту р"\ следовательно, его направление совпадает, с точностью
до знака, с направлением векторного произведения р' X Р"■
Проекции вектора (р) обозначены у Лобачевского через кХ, kY, kZ,
где к—неопределенное вещественное число. Вместо того, чтобы
писать три скалярных равенства для проекций этого вектора, обозначим
его через кВ и напишем в очевидной символике:
дТ"
~=кВ = Х(р'Хр"). (q)
Три соответствующие скалярные равенства совпадают а
формулами (9) и (12) текста Лобачевского1); аналогично найдем:
ІІТ
^L = \'b? = i'(p"xp) ir)
и
?±- = к''М"^к"(рХр'). (s)
В скалярной записи мы получили здесь группы формул (10) и
(13), (11) и (14) исследования Лобачевского2).
Но векторы _В, Л', -В", очевидно, попарно ортогональны; образуя
их скалярные произведения, мы получим снова три билинейные формы,
которые обозначим через S, S' и S"; по структуре они вполне
аналогичны рассмотренным выше формам Т, Т' и Т', с замеяой
коэффициентов А, В, О, а, Ь, с па Л', В', G', а'. !/, с', причем
А' = А" + Ь- -j- с", а' = ас + Ъ (А -\- С),
В'= №-\-<:* Л- а-, Ъ' = аЬ-^с(А-\- В),
С' = О5 + а"- + !>-, с' = Ьс-\-а(В + С) а).
і) На стр. аве, 367.
3) Ом. стр. 367.
3) Этими выражениями следует заиеиить формулы Лобачевского ;і:ія .1' С
ел стр. 3S7.

.378
УСЛОВНЫЕ УРАВНЕНИЯ ДЛЯ ДВИЖЕНИЯ
Условие перпендикулярности векторов К, R' Л" приводит к
уравнениям (17)1):
S = 8' = S" = О.
Но теперь очевидно, что формы S можно подвергнуть такой же
обработке, как и формы 5"; в частности, мы получим
где |t — неопределенный множитель. В скалярной записи это дает
три уравнения (18) s); Лобачевский полагает р —А.ѵ, и получает,
сопоставляя уравнения (q) и (q'):
дѵ , as*
w=*vH=*w (t)
Три соответствующих скалярных уравнения — это уравнения (19) ');
они линейны и однородны в проекциях Е, ij, £ вектора р\
приравнивая нулю их определитель, Лобачевский получает уравнение (20),
т. е. то характеристическое уравнение третьей степени относительно
параметра ѵ, которое приводит к решению задачи о главных
плоскостях системы.
В современных трактатах теоретической механики сохранились,
в основном, лишь два метода определения главных осей: метод Эйлера
определения экстремальных-значений моментов инерции и
геометрическое построение Пуансо. Но за методом Лобачевского навсегда
сохранится значение исследования, в котором эта задача была
представлена именно как проблема из «геометрии масо, и ее
замечательное решение проведено-с точек зрения, едва намечавшихся в эпоху
тридцатых годов прошлого столетия.
і) На стр. 367.
*) На стр. 388.
*) На стр. 368.

ПОДРОБНЫЙ РАЗБОР
РАССУЖДЕНИЯ,
ПРЕДСТАВЛЕННОГО
МАГИСТРОМ ПОПОВЫМ
ПОД НАЗВАНИЕМ
«ОБ ИНТЕГРИРОВАНИИ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ГИДРОДИНАМИКИ,
ПРИВЕДЕННЫХ
К ЛИНЕЙНОМУ ВИДУ »
І34І
КОММЕНТАРИИ ГГТУМАШЕВА

ПОДРОБНЫЙ РАЗБОР РАССУЖДЕНИЯ
Н. И. Лобачевский — Подробный разбор рассуждения,
представленного магистром Поповым под названием
«Об интегрировании [дифференциальных] уравнений
гидродинамики, приведенных к линейному виду» . . 381
Примечания 395
Приложения:
1. А. Ф. Попов. Введение к диссертации ЗВ&
2. Г. Г. Тумашев. Краткое изложение содержания диссертации
А. Ф. Попова 400
3. А. Д,. Дубяхо. Иморяно-библиографические сведения о
диссертации Полова и разборе ее Лобачевпшш 412

л- *
ОБЪ ИНТЕГРИРОВАНИИ
лмегвдынмъ лшш пиптюи.
ПРВВГДЕНЯЫХЪ КЪ ЛИНЕЙНОМУ ВИДУ-
РАЗСУ9КДЕНІЕ
НА
НАТЕИДТЯКК S AEtBtffftXH.
КАЗАНЬ, 1845 ГОДА.
1Ъ УНИВЕРСИТЕТСКОМ ТИПОГРЛФЩ
Титульный лист докторской диссертации Л. Ф. Попова,
к которой был приложен печатный отзыв Н. II. Лобачевского.
I
і
К. стр. S91.

РАЗСУЖДЫПЯ, ЯРЕДСТАВЛЕННАГО МАГИСТРОМЪ ПОПОВЫМЪ.
ПОД* КЛ]»Н|СНЪ '
•ОСТ интатиншши УШНШй гидродинамики . приведглкых'ъ къ
ЛИНЕЙНОМУ ВИДУ» ' •, "
НА СТЕПЕНЬ ДОКТОРА МАТЕМАТИКИ В АСТРОПОМІВ..
«HIMWi
До tan пор* еще вигеогіе язь члююпмюп яшшинеі инесрирошйап. тіѵь jfa§-
наш! Дишю, eotojwu врадсгаымоя ада nuenii mi п ѵп[иг«ъ «ивит, или
квярв т пшсраюсга виамщиыи жидкостей. Bet іюловвьи уриивй стзрэнш пра-
■щн к» лшягОаан] ші; , чювь авлегчга. якягряржик. Оригір*, tunn ибригап
■■■ Иііыи дтмреяіиаивыа лтаеш отораго порядка, им^ть hwjh& fem аптегрирашы,
шэдмп j wpmro фур, ** его соигасиІа TMorie ииІ]іЦое de la cbattur. Напграрив-
ае лагіЬаго дмвернпіыывп) ;рамкві, которое іфедпаымгь расоросіражм япп гь
юдукк, дать иврвой П]іШвп ■* обпиог* іоді (Juan») de litelt рЫіІкЬпЦое, Т. VII) и
ю оэслідсін, кпртпшя ;вяв прииошкеіветп, чѵАы (триста дипиии «о ■»■
пуіиіИ' шриадпрарш» оссЛ, был чатыжя лч^ерявіыим одаЫІ «пш (иг !•
ркдеиюя to noamunt dan let шНігаі rlutirMi ■ M«o- ta ■ I'Aradew, It 11 Otlabn
1ІЭ0; Штоіп» 4« 1'ІмІіЫ, Т. X.). Някгриросшіа ли+атртишдатг \(овпн, numpua
qutaumn кипам ai ммроосш икжиывя* жмкосіа. jbjo. -пчн* пгртчі HjxMtt,
п tan» иіПНі Ѵівоіге «ar fa іЬсогіо do oodci, 1я k 3 ectvbv « IS dntman- HI I
(Hianiret d« ftadilnl, T. t). HoRifapnavie» rt«. a» fpuamt nmnu жт» Ім,
iiuuauu аяае», "Шел* da h ргира^имв <ki «ida i b яѵЬкя d'm Daife final fan
■гоіоавмг nictaa*, jrtmsa ttuo Ац.тияі uin n rjsfawt » шплли ■» Мгаиім*
■гмиЦ» ртг una йіш , Т. I, I'ao ІШ.
1йр№!1 страшит от tuna 11, II, Лойл-іоис-uoLO на диссертацию А. Ф. Ноіііпи.

ПОДРОБНЫЙ РАЗБОР РАССУЖДЕНИЯ,
ПРЕДСТАВЛЕННОГО МАГИСТРОМ ПОПОВЫМ
ПОД НАЗВАНИЕМ «ОБ ИНТЕГРИРОВАНИИ
УРАВНЕНИЙ ГИДРОДИНАМИКИ.
ПРИВЕДЕННЫХ К ЛИНЕЙНОМУ ВИДУ-,
НА СТЕПЕНЬ ДОКТОРА
МАТЕМАТИКИ Я АСТРОНОМИИ
] До сих пор еще немногие из математиков занимались
интегрированием тех уравнений Динамики, которые представляют или
явления звука в упругих жидкостях, или волнение на
поверхности несжимаемых жидкостей. Все подобные уравнения стараются
приводить в линейному виду, чтоб облегчить интегрирование.
Пример, каким образом линейныя дифференциальный уравнения
второго [порядка могут вполне быть интегрированы, находим
у первого Фурье, в его сочинении Theorie analytique de la cha-
leur. Интегрирование линейного дифференциального уравнения,
которое представляет распространение звука в воздухе, дал
первый Пуассон в оощем виде (Journal de Гёсоіе porytechnique, Т. ѴІТ)
и впоследствии, не ограничиваясь даже предположением, чтобы
■скорости движения по направлению перпендикулярных осей были
частными дифференциалами одной функции (Sur la propagation
du mouvement dans les milieux eiastiques, Me"m. lu a 1'Academie,
le 11 Octobre 1830; Memoires de l'lnstitut, T. X.)- Интегрирование
дифференциальных уравнений, которые представляют волнение на
поверхности несжимаемой жпдкости, дал тоже первый Пуассон
в своем сочинении ЭДёяшіге эш' la theorie des ondes, lu le 2 Oetobi'p
et 18 D6cembre 1815 (Memoires de l'lnstitut, T. I).
Интегрированием тех же уравнений занимался потом Коти, которого
сочинение, Theorie de la propagation des ondes a. la surface d'un fluide
pesftnt d'une profondeur indeiinie, увенчано было Академией наук

-ІВ2 ПОДРОБНЫЙ РАЗБОР РАССУЖДЕНИЯ А. Ф. ПОПОВА
в Париже и напечатано в Memoir ее presentee рал- divers savans,
Т. I, l'an 1827 *.
I Во всех этих теориях уравнения для распространения звука
в упругой средине и для волнения несжимаемой жидкости на.
поверхности или внутри ничего между собой общего не
представляли. Это не могло быть иначе, потому что в одном случае
предполагали жидкость упругой, а в другом совершенно
несжимаемой. Между тем упругость принадлежит всем жидкостям без
исключения, так что самое движение, собственно говоря, без
упругости в них происходить не может.
Теория волнений и звука представляла еще то несовершенство,
что в ней сообщение движения предполагалось по тому же закону,
как и распространение давления во время покоя. Навье старался
поправить этот недостаток предположением хотя вероятным, но
за всем тем произвольным. Взгляд Пуассона в теории движения
жидкостей может назваться совершенно основательным, когда он
представляет себе жидкость рядом упругих тел (Journal de l'ecole
poly technique, Т. XIII)*. Так он приходит к общим уравнениям
Гидродинамики, где явления звука и волнений заключаются как
частный случай при различных ограничениях и предположениях.
Интегрирования уравнений в этом виде оставалось еще желать.
Г. Попов выбрал это предметом для своего рассуждения.
Он ограничивается во-первых тем случаем, когда члены с
двойным размером в отношении к скорости движенияе делаются
* Приводим библиоірафггчеевив данные сочняѳшій, упоминаемых ЛоОа-
чевеким:
Fourier — ТЬёогіе analytique de la chaleur. Paris, 1822.
Poisson — Sur la tbeorie du son. Journal de 1'EeoIe poly technique, т. VII.
1808, стр. Зіе—ЗѲ2.
Роіээоп — Sur la propagation du raouvement dans lea milieux Slastiques.
Ifiimoires de I'institut, т. X, 1931, стр. 549—605.
Poieson— Memoire sur la tbeorie des ondea. Meraoires de Г Academic royale
<1« I'institut do France, Алокѳ І81Ѳ, т. I, 1818, стр. 71—S86.
С a u с h у — Memoirs sur la propagation des oudes a la surface d'nne fluide
pesant d'une profondeur іпгШіпіе. Memoires presentee par divers savans a
['Academic royale des sciences de i'institut de France. Sciences mathematiques et physiques
t. I, 1827, стр. 3—312.
* Po i ss on— Memoire sur ies equations generales d'equilibre et du Mouve-
meufc dea Corps solides, elastiques et dea fluides. Journal de l'Ecole polytechnique,.
20 eahier. т. ХШ, 1831, стр. 1—174.
® То-есть члены, содержащие квадраты а произведения проекций скоростей,,
я такте их производных.

Н. И. ЛОБАЧЕВСКИЙ — «ПОДРОБНЫЙ РАЗБОР. 388-
нечувствительны — предположение, которое обыкновенно
допускают в теории звука и волнении. Потом сочинитель приводит
дифференциальные уравнения к линейному виду, предполагая
во время движения изменение плотности весьма малым (ур. 10)*.
Однако ж это предположение надобно разуметь ток, что в урав. (10)
ішотнооть р' принадлежит в равновесии месту, куда частичка
принесена движением. Далее уравнение (11) заключает в себе
новое предположение, что давление р', которое надобно разуметь
подобно р', разнится с р в движении для того же места
пропорционально изменению в плотности р'я, какое на месте произошло.
Эта пропорциональность выражается множителем —, где числу t
принадлежит определенное значение, как видно из уравнения (7)!1]-
Уравнение (11) может быть заменено таким:
p = ep-j-(A — 1)р'* — еЯ,
которое и приведено тут же выше, или еще уравнением
р 1 — ля
или. Баковеп, за малоетию s можно принимать
Р — Я=-|-[1 — (a — l)s].
> Откуда видно, что предположение сочинителя заключается в том,
что изменения в давлении должны быть пропорциональны
изменениям в плотности, покуда те и другия очень малы; далее, что
эта пропорциональность может быть различна в зависимости новой
плотности от прежней и новой упругости от прежней плотности.
Предположение дозволенное и столько же общее, как и принятое
Пуассоном в содержании * давления к степени от плотности. (Traite
de Мёс. Т. Ц, р. 647) ®. Если колебания в жидкости чрезвычайно'
* Ом, «Краткое изложение содержанки диссертации А. Ф- Попова» (стр. 400—
411 наст, тома). Все формулы, на которые имеются ссылки в отзыве
Лобачевского, приведены * «краткой изложении»,
• Хо-есть в отношении.
° Poise on —Traite de Metanique. Second» 6dltion, т. II, 1833. Здесь имеете»
P
в веду выведенное Пуассоном уравнение адиабатического процесса ~г = е- где
Р
і — показатель вдиабаты.

384 ПОДРОБНЫЙ РАЗБОР РАССУЖДЕНИЯ А. Ф. ПОПОВА
малы, то известно, что предположение р«е(^) — Н), которое
собственно принадлежит равновесию, удовлетворяет и явлениям
движения, а следовательно во всяком другом случае, которая здесь
рассматриваются, число к должно весьма мало разниться от
единицы. На это замечание сам сочинитель намекает в след за
уравнением (22), Далее, сравнение того предположения, которое сделал
здесь сочинитель, с тем, которое принадлежит Пуассону, ведет
к заключению, что число к можно принимать за постоянное, как
опыты показали в подтверждение теории Пуассона.
С такими предположениями общие уравнения для движения
(а), (Ь), (с), (d), (е)І!І принимают линейный вид дифференциальных
с постоянными множителями, каковы (12) и (13). Четыре
уравнения (12) и (13), которыя должны определять движение вполне,
заменяет сочинитель одним (14), где уже предполагается
существование трех уравнений (б). Таким образом, все решение
зависит от интегрирования одного уравнения (14). Из этого
последнего в статье 4, довольствуясь предположением Даламберта и
пренебрегал действием тяжести, сочинитель выводит уравнения,
обыкновенно принимаемые в теории звука. Далее в статье о,
предполагая жидкость несжимаемой, сочинитель находит отсюда
также известные уравнения в теории волн. Итак достоинство
теории, предположенной сочинителем, уже заключается в том,
что она обнимает собою до того две раздельные теории.
Впрочем, для такого перехода от одного случая к другому,
надобно собственно довольствоваться уравнениями (11), (12) и (14),
в которых заключается уравнение (13) само собою. Этот переход
должен быть сделан в предположении весьма малой сжимаемости,
которой значение, выраженное числом, может быть только прене-
брежено в конце счета. Действительное понятие о природе
жидкостей делает невозможным и самое движение без способности
сжиматься. Для k = 0 или следуя теории Даламберта *, получим
вместо сказанных уравнений такие:
| р^р' \р',, (П)
' D'Alembert— Traite de l'equilibre et du mouvement dee fluides.
Paris, 17M.

Н. И. ЛОБАЧЕВСКИЙ — «ПОДРОБНЫЙ РАЗБОР» 385
du ____ \ ds dv к ds dw л ^ _i_,- ,ч
~dt~~^'~dx' rf( —T"^' Ж^Т'йг"1-^- ■'?**
По свойству текучих жидкостей * должно почитать как $, так и
X — 1 весьма малыми, а следовательно, движение таких жидкостей
достаточно представят уравнения
p=p' — -t-s,
ii« 1 is _ de 1 ds dw 1 ds
dt s. d% ' dt & dy , dt e dz'
Итак, во-первых надобно определить а такую функцию от х, у, г
и t, чтобы
d2® d^v , (Рф , tPc . <2« ,_ .
После чего полагать *
и следовательно
dy
dl
d? tf» dv
d-r ' ~~~dy ' dz
Предположение несжимаемой жидкости превращает уравнение (24)
в такое:
dor di/- ds" '
которое действительно выражает собою неизменяемость объема.
Итак, предполагал это уравнение во всей строгости справедливым
* То-ссть капгльных жіідкостеіі.
* Если рассматривать случэіі потенциал і.ного течения, то пррдпоследние
уравнения mopj"t быть переписаны следующим образом:
~<ix\di)~~~s dx' dy\dt)~ e dy ' dz\ttt)^' s its'
Отсюда., полагая 1= 1, t s — величиной постоянной, находим:
dtp
25 Зак. 9«2U. H. II, „Іо^ачѳеркий, т. і\

386 ПОДРОБНЫЙ РАЗБОР РАССУЖДЕНИЯ А. Ф. ПОПОВА
и относя это условие собственно к роду движения, из уравнения
(24), оставаясь верными общей теории, получим
[В дополнение к уравнениям (25) и (33) надобно принять
уравнение
—-«'
или, что вое равно, на основании уравнения (11) прибавить
Куда поставя I) вместо р', плотность несжимаемой жидкости,
а вместо р' поставя &дг, приходим к уравнению
£-»-§■' <28>
Три уравнения (26), (83) и (28) представляют собою теорию
волнения несжимаемых жидкостей, как она до сих пор
рассматривалась в строгом предположении несжимаемости, и как она следует
в виде частного случая из общей теории в предположении
собственно нечувствительного сжатия.
Вместо того, чтоб итти прямым путем, которым я здесь
прихожу к уравнениям (25), (33) и (28), сочинитель заменяет
уравнение (25) таким
^-и&Рл-^Р — п
da? ■ dy2 "г rfz2 *
присоединяя сюда уравнение (28), которое должно служить потом
для определения «. Далее обращает он внимание на то, что выбор
функции р ограничен как последним уравнением, так и в
уравнениях (3), где предполагается р данной функцией для всех ж, у
при начале движения, если я хорошо отгадываю его мысль,
которая впрочем тут не совсем ясно выражена s. Наконец, решение
будет окончено, когда придем к уравнению
* При решении уравнения Ляалаоа, которому удовлетворяет давление Р,
нужно считать эту величину заданной на координатной плоскости для любого
момента времени.

Н. И. ЛОБАЧЕВСКИЙ —«ПОДРОБНЫЙ РАЗБОР* 387
начиная с г данной функции от .г-, у для і=0 н для свободной
поверхности, для которой р дано в продолжении всего движения.
Итак, ограничиваясь одною свободной поверхностью и
дифференцируя уравнение (29), получим
где пренебрегая двумя последними членами за малостию, можем
почитать
которое уравнение в соединении с уравнением (28) дает для р'
постоянного
Для переменного р' должно бы написать, как делает сочинитель,
dp' (ftp tPtp
Ddt~ 9Ж~~Ш'
где переменная часть в jj' может быть впрочем пополнена в
интегрировании прежних уравнений (25), (23) и (28). Итак, вывод,
сделанный сочинителем, предполагает в уравнении (29) свободную
поверхность с сохранением своих материальных частичек в про- "
должении всего движения. Между тем, такое ограничение для
движения можно рассматривать, наоборот, следствием из
уравнений (25), (28) и (28).
Впрочем Г. сочинитель в интегрировании общих
дифференциальных уравнений собственно следует указанному мной способу
для перехода от теории звука к теории волн на поверхности
жидкостей *.
Способ интегрирования, которым пользуется сочинитель,
составлен по образцам, какие мы находим в творениях Фурье и
Пуассона.
Уравнение (14), которого интегрирование, с удовлетворением
особенных условий, должно заключать в себе полную теорию звука
* Здесь Н. И. Лобачевский, очевидво, имеет и виду сделанное иы уехнос:
указание А. Ф. Попову.
35*

8Ѳ8
ПОДРОБНЫЙ РАЗБОР РАССУЖДЕНИЯ А. ф. ПОПОВА
и волн, когда сюда ставим
принимает вид
д£» л*9 d^
^+'л е і**~,~<^і~т"&»}+ТГл",~~л~~І S~| ^'*
и может быть удовлетворено предположением
1=*'2T-ft'-rt*=icoaa(3!_ a).eos&tjf — Р)> (38)
г |где я, &, а, р, y, s*— произвольные постоянные, к различному
значению которых относится знав суммы. Множитель Т должен служить
интегралом уравнению
g!+l(d. + e. + ^(A^ + T)-(.„y—LT-Q
и следовательно
Іш-А^ + В*'1
с А, В—произвольными постоянными, с £', V —■ корнями уравнения
ея+~ («а+*■+ѵ-*) «+4 <аВ+6Э+'tS)+^^-1=°- <89)
Корням этого уравнения можно всегда дать такой вид:
$'= _ р-L » —qV^l, 5" = — р — »+«V—L
С этим представлением интеграла в общем виде надобно достигнуть
еще той цели, чтобы в интеграле заключались данные функции при
начале движения.
Для волн па поверхности текучей жидкости, при том в
беспредельной массе, достаточно принимать
9 = 2e~|lte+i')cosa(a: — a)cos6(j/ — $){Auos(t\/'gYu?~+b'i -\-
-j-В sin (t Уду& + '&')}, (44)
где а, 6, і, %, А, В, si, г' — произвольные постоянные. Последнее
постоянное г' должно сохранять сумме г-{-/ положительное
значение; иначе, как доказывает последствие, функция о получает
неопределенное значение для весьма малого г*.
* Последнег предложение следует понимать в том смысле, что ряд (44)
расходится, когда сумма г + г' имеет отрицательное значение. В атом случае при
произвольном положительном ц члены ряда могут стать сеоль угодно большими.
Интересно отметить, что во времена Лобачевского сумму расходящегося ряда
называли неопределенной.

Н. И. ЛОБАЧЕВСКИЙ —«ПОДРОБНЫЙ РАЗБОР. 389
Вообще в теории волн как воздухообразных, так и текучих
жидкостей, можно довольствоваться выражением интеграла в таком
виде:
■i = ^cosa(x — я)стЬ(у — $)e~pt{(Aent -[-Be-^cosqtcoap(z — f) +
\-(Ае** —Ве-»>) am qt sin? (г — t))[3J, (42)
где а, Ъ, А, Д а, р, у, і1 — произвольные постоянные, р, q, п — числа,
которых значения даны выше; а знак суммы относится только
к положительным а, Ь, р.
б | Если интеграл (42) для (=0 должен обращаться в данную
функцию от х, у, г, то
А + .В=^*'(«,р.-Г)-І
где .F—знак функции, а знак суммы в уравнении (42) представляет
уже кратный интеграл для з, р, у и кратную сумму для а, Ь, (*
с постоянным множителем. Крайние значения а, р, ? при
интегрировании те самые, между какими крайними значениями х, у, г
заключается масса.
Далее сочинитель предполагает І = В с тою целшо, чтобы для
(=0 член в <р с синусом от [х(г—-f) уничтожался. Таким образом,
в интеграле остается одна произвольная функция. Б этом
ограничении не нахожу никакой надобности, потому что в интеграле
для полноты можно ввести две произвольные функции, означив
вторую f{x, у, г) от х, у, s и полагая
А — В = — ±-еТщ \[f(a., ^ y) + pF(*,$, -[)]«" в""1 da d$ dt Ьа \Ь ЬѴ~.
Здесь начало интеграла в отношении к і произвольно; но чтоб
выражение (42) удовлетворяло уравнению (37), надобно располагать
этой границей и самой функцией f(x, у, z) так, чтобы А — В
сохраняло свое значение для крайних границ f, где уже как
частный случай заключается условие f(x, у, z)-\~j3F(x, у, г) = 0,
которое принимает сочинитель [ур. (52)].
В случае беспредельной массы надобно ставить dadbdp вместо
ДаДбД;і, знак суммы заменять тройным ннтегрэлом с границами
нуль и -j-oo,
* В оригинале эта формула яо недосмотру имеет вид:
А + В = dad^t ДоdbipF(а, р, і).
В саыои тексте дисоерташда она напечатана правильно (ем. стр. 404 наст, тома).

890 ПОДРОБНЫЙ РАЗБОР РАОСУЖДЕНИЯ А. Ф. ПОПОВА
В теории для волнения всех жидкостей сочинитель справедливо
довольствуется нервный степенями от s и —, принимая
9Ѵ-
и = -
Ѵі
| При изменениях в самой причине волнения сочинитель пользуется
законом наложения малых движений.
В движении жидкости прикосновенной к стенам сосуда
предположение сделано то, без которого обойтись нельзя, что частички
не оставляют прикосновения1.
Теперь следует переход к волнению текучих жидкостей,
которые рассматриваются собственно сжимаемыми, как и должно
понимать в них сообщенное движение. В этой теории сочинитель из
общего уравнения (37) откидывает член с А и принимает Х = 1.
Уравнение делается
(Ра
^t(s+^s)+^' <74)
где сжатие
■-■№)•
скорости по направлению коордонат
df (Up
dx' dy' " dz'
К тому уравнение (28) для свободной поверхности, где р = О и
'-да (7б>
Уравнению (74) удовлетворяет
>?=:'%{АйовіѴХ! + ВвіаііПГ}е-**сова(х— а)<ювЪ(у—р), (77)
где я, &, а, Э, р — произвольные постоянные, -і, В — произвольные
функции от а, J3, и где
* То-«ть частицы жидкости прилегают к стенкам.

Н. Ж. ЛОБАЧЕВСКИЙ— «ПОДРОБНЫЙ РАЗБОР- 391
Из значения для w находим коордонату z, разумея^од г0 ее
начальное значение для t — 0,
* = Ч — У {A sin * ]/"¥—,#cos t/Ж] —=6"^соа а(#—a)cos Ь (у—3)—
-л ІДля частички, приведенное на свободную поверхность, в этом
уравнении дод знаком суммы, почитая приближенно г' = О, получим
г,=>гц—~'^{Ае&а tVW — В cos t Vw\ -~ cose (as— а)совй(^—р>—
— E 7^ eos a (x ~~ я) coa b & ~ &
Между тем уравнение (76) дает з' для точек на свободной
поверхности
з' = — 2 {В сов t VW — A sin t ѴЖ\ VTcos«(# — a) cos & (у — р). (80)
Разность двух значений У должна быть нечувствительной, а потому
г«= Sfe cos tt О — а)cos * (У — Ю-
Если оба значения г' принимаем для одной материальной точкн,
то последнее уравнение сделается уравнением для начальной
поверхности, которое пусть будет
z = f(x, у)
н вместе
fix, У) = ^Аыъа(х-*)ыяЬ{у — $. (81)
■Сличение прочих членов в двух значениях для г' дает
После чего
e = 2iJ.cos(y"]V:-l-Sain/VTje-lvS:+Fcoea(a; — a)cos6(y — % (t)
Выражение (81) требует принимать
и разуметь знак суммы двойным знаком интеграла в отношении
к а, р и двойным знаком суммы в отношении к а, Ь.

S92 ПОДРОБНЫЙ РАЗБОР РАССУЖДЕНИЯ А. Ф. ПОПОВА
Сочинитель замечает, что интеграл (I) удовлетворяет
уравнениям (25) и (33), как выражение, куда е не входит, тогда как
жидкость предполагалась вначале сжимаемой. | Я с своей стороны
могу прибавить, что этот интеграл должен таким образом
принадлежать предположению жидкости, как доказал я «ьіпте для самых
уравнений (25) и (33).
Выражение (I) с двойным интегралом вместо двойной суммы
в отношении к а и b для беспредельной жидкости будет
V—;-Г75 со со + +
Хе 40sa(x — a)cQsb(y — ?)dadbda^, (84)
о о — —
Если в начале движения поверхность изменяется без удара на нее,
то А = 0 и выражение (84) будет то же, какое дал Пуассон в Мб-
moire de l'Institut, Г. I*.
Если к тому начальная скорость дана
w0 = -!f(x у),
то уравнение
для і = 0 требует принимать
df=SW
А -^—.
В этом виде, с данными скоростями, определение начального
состояния представляет совершенно ясное понятие, тогда как Копш
в его записке sur la propagation des ondes* говорит об ударе0
(percussion), не соединяя при этом никакой определенной мысли»
От новых ударов на жидкость волнение может быть
присоединяемо к прежнему, и таким образом в их непрерывном
исследовании представлять движение с неременным давлением. Сочинитель
достигпул той же дели, рассматривая переменное давление как
побудительную силу к движению, именно присоединяя -уАт к д -г
ъ уравнении (33). Таким образом, уравнение (97) дает значение
* См. сноску * на стр. 382 (третий меыуар Пуассона).
* См. ту же сноску.
J Тѳриин «удар» нужно пониыать в смысле пыпульса сил давлвняЁ.

В. И. ЛОБАЧЕВСКИЙ —^ПОДРОБНЫЙ РАЗБОР» 39S
Функции ір из трех членов, аз которых первый происходят от
изменения в поверхности, второй — от удара на поверхность, третий —
от непрерывно переменного давления. Сочинитель рассматривает
еще случай, когда волнение происходит от плывучего тела с
равномерным движением.
В движении воздухообразной жидкости сочинитель, отбрасывая
в уравнении (ЗГ) член о множителем </, пишет
] ** >•(*•* л.** j_**\_i.A М* л. *Р , &*\ „от
разумея
h'h
не принимая, следовательно, в рассуждение тяжести, но обращая
внимание на сопротивление в сообщенном движении.
Интеграл уравнения (100), когда пренебрегаем £3, берет такой
вид
<р = 2е s (A'cosTtcf-j-fi'sinwef) Q,
где
Q = cos a (x — а) сов b(y — $) cos ji (г—7).
Для беспредельной массы
1 С С С Г С С — кеч 1 с? оз си -і- -г +
«р = -Л 1 ||/(«, P,t)* * (coenet-!r—lce*siiitiet)Qdadbdpd!td$di+
в где
функции f{x, у, г), й(ж, у, г) представляют начальные сжатие и
скорость.
Другой вид (111) тому же интегралу дают полярные коордо-
наты -и, Ѳ, (в вместо а, 6, ц. Интегрирование в отношении к У, оі
может быть произведено непосредственно. Таким образом выходит
выражение (117) для о с четверным интегралом. Значение
функции о для первых мгновений движения дается тройным
интегралом (126) и по прошествии значительного времени двойным
интегралом (125), где с і = 0 приходим к формуле Пуассона.

394 ПОДРОБНЫЙ РАЗБОР РАССУЖДЕНИЯ А. Ф. ПОПОВА
Сочинитель в конце своего рассуждения дает решения
некоторых вопросов, которыми до него еще никто не занимался.
Рассматривает, в закрытом параллелепипеде, происхождение звука
мгновенно произведенного или продолженного, с отражением от стен,
л Принимая в j рассуждение действие тяжести, говорит вообще
о волнении в жидкости, текучей и воздухообразной, которая
опирается на горизонтальную плоскость. В решении всех этих
любопытных и трудных в анализе вопросов он умел пользоваться
образцовыми способами знаменитых математиков, применять их в
настоящему случаю и распространять в новом или более обширном
виде. К чести сочинителя могу сказать вообще, что в этом
соединении двух теорий, о волнении текучих и воздухообразных
жидкостей, вижу большую услугу для науки.
Заслуженный Профессор Лобачевский.
11 Апреля 1845.

ПРНМЕЧАНЯЯ
[3] г — величина, обратная квадрату скорости авука [см,
формулу (7) диссертации Попова1)]. Величина А при любой зависимости
Р
вида —= с, где с—постояннал, равна единице.
В самом деле, по формулам (10) и (11) а), имеем
w(-4£).
■откуда следует
р р' : /
b"~p'T'~~(\^f
или, при достаточно малом х,
г р'
Принимая во внимание выражение квадрата скорости звука
легко находим '/. = 1.
['] Уравнения (а) имеют в диссертации вид
где X, У, % — проекции массовой силы на оси х, у, г; (S—коеффя-
. ,/dp , dp i rfp i dp\
диент вязкости, ш =J)J-ft^ ^_M__j_t^4- «, j£j .
') Стр. 402 ниот, тона,
a) Стр. 400.

396 ПОДРОБНЫЙ РАЗБОР РАССУЖДЕНИЯ А. Ф. ПОПОВА
Эти уравнения получены Навьѳ и Пуассоном на основании
различных соображений о веаиыодеиствин между молекулами.
В современных руководствах по гидромеханике дается вывод,
свободный от подобного рода предположений *).
Выражение h легко может быть найдено, если принять во
внимание равенство
ѵ —
Пользуясь уравнением неразрывности, последнее можно представить
в виде
или
. и. Эр / др , др , др , dp \
отсюда
3prfp
Очевидно, величину ft можно считать постоянной только при малых
скоростях движения жидкости.
Величина к обращается в нуль в двух случаях:
1) при [t = 0, т. е. для жидкости, не обладающей вяакостыо,
2) при-р = 0, т. е. для несжимаемой жидкости.
Is] В данном случае правая часть формулы (42) представляет
собой интеграл Фурье. Как показывается в теории интегралов
Фурье, любая функция переменного х, имеющая период 2-аі. и
удовлетворяющая условиям Дирихле, может быть, представлена следующим
о бравом;
Вводя обозначения -s- = а, у = Да, это равенство можно переписать
в следующей форме:
Пт: ЯК
° СО "
f(x) = -^. \ f(t)badt + — VJ Да f /(*) совв(ж—0^-
И* и = 1 —ПК
!) См., например, Н. Е. Кочив, И. А. Кабель и Ж. В. Розе —
Теоретическая гидромеханика, т. П, Гостехивдат, 1S48, стр. 285.

ПРИМЕЧАНИЯ
397
Отсюда, переходя формально к пределу при Да -► О, получим:
со со
f(x)=— da f(_t)ooea(x—t)dt.
О — со
Последняя формула легко обобщается на случав функций трех
переменных следующим образом:
f{x, У. г) =
= -^jffjf fft». Р. "Г)оова(я — a)cosb{y — ?)совс(г — ■[) X
X (*« dfi di da db dc.
Приведенное рассуждение, принадлежащее в основном Фурье, с
современное точки зрения не представляет доказательства1). В
последнем интеграле а, Ь, С меняются от нуля до со. Пределы
интегрирования по о, [5, і совпадают о пределами изменения переменных х, у, z
в области, в которой f(a, $, ^)^fcO.
В диссертации Попова и отзыве Лобачевского пределы
интегрирования поставлены снизу и сверху дифференциалов.
Приведем в качестве примера формулу (84):
* = &JJj№ М + А C0S1 Ѵ^ * ^l^ Г ' ГаГ^ Х
СИ СО + ~\-
X сое а (а; — а) сов Ь (у — (3) da db do. d$.
л о — —
Эдѳсь знаки минус и плюс указывают на то, что интегрирование
по а и р производится между крайними значениями х, у,
принадлежащими области, в которой подинтегральное выражение отлично от
нуля.
') Ом. Е. Тнг чыар га —Введение а тоорию интегралов Фурьа. Гмтехиздат,
М, —Л., 1948.

Приложение 1
ВВЕДЕНИЕ К ДИССЕРТАЦИИ1)
А. Ф. Попов
Способы настоящего Анализа позволяют предпринять
интегрирование дифференциальных уравнений Гидродинамики только в двух
общих предположениях: 1) если движение жидкости представляет
поток постоянного вида, и 2) если скорости частичек в жидкой маосе
вообще незначительны. В первом предположении уничтожаются члены,
которые представляют частные дифференциалы для функций
движения в отношении ко времени, потому что две частички постоянного
потока, проходя чрез одну точку в пространстве, описывают ту же
кривую линию. Напротив, в последнем предположении частные
дифференциалы в отношении времени остаются, тогда как члены, для
главной части движения в потоке, уничтожаются.
Такое уничтожение, в последнем случае, позволяет привести
дифференциальные уравнения Гидродинамики к линейному виду. С втой
простотой в уравнениях, доказывают равномерное распространение
звука в воздухе, также законы распространении волн на поверхности
воды. Однако же, решение обеих задач может подлежать еще
сомнению, или, по крайней мере, почитаться неполным; потому что
начинают обыкновенно с уравнений, составленных Д'Аламбѳртом, где члены,.
с чувствительным влиянием на образование и распространение волн,
опущены.
В предлежащем рассуждении мы начинаем с уравнений
Гидродинамики в том общем виде, в каком их предложили Навьѳ и
Пуассон, приводим их к линейному виду, сохраняя возможную общность.
при выборе вспомогательных условий; указываем члены, опущенные
другими авторами; наконеп, интегрируем составленные линейные
уравнения в тех случаях, которые непосредственно применяются к Теории
волн. Наложение, по сущности самого предмета, нельзя было сделать
чисто аналитическим и независимым от фивнческих положений;
а потому, пользуясь ученым языком, я почел необходимым объяснить
1) Этот текст предшествует диссертации А. Ф. Попова без всякого названии
(см. статью «Йсторико-библиографкіесвие сведения», стр. 414 наст, томя.)

ВВЕДЕНИЕ К ДИССЕРТАЦИИ А. Ф. ПОПОВА
39»
о некоторою подробноотию не только положения, но д принятые
названия в Теории волн,
С того времени, как это сочинение поступило на раосмотрение
Физико-Математичвского отделения, Г. Заслуженный Профессор
Лобачевский, мой наставник в высшем Анализе, указал мае, в своих
ученых замечаниях и советах, некоторые новые точки взгляда на мою
задачу. Постараюсь оправдать и заслужить внимание, которым Его
Превосходительство почтил мое сочинение.

Приложение 3
КРАТКОЕ ИЗЛОЖЕНИЕ СОДЕРЖАНИЯ ДИССЕРТАЦИИ
А. Ф. ПОПОВА
Г. Г. Тумашее
Диссертация состоит из небольшой вводной части и двух глав, первая
из которых содержит в «статей» (параграфов), а вторая — 16. В первой
главе изложен метод приведения уравнения волнового движения
жидкости к линейному виду, а во второй — интегрирование этих
уравнение.
В настоящей статье все формулы и обозначения даны в том виде,
в каком они приведены в работе А. Ф.Попова и п отзыве Н. И.
Лобачевского. Сохранена также нумерация формул.
Во вводной части диссертапии-приввдвпи полные уравнения
гидродинамики в виде
( d-x\ dot fd*u d?u d*w
x-!e)=di^?[d^ + df+d?-
?\ dt*) d»^* \dx* ^ dy"- ^ dx* )
(„ d*z\ dm „ ld?w d3w ,
dhe
dY-
Г»)
где
d-x
dP '
d-y
dl- =
#2
АГ- *
dx
dtT
ffw , du , du da
dl ' dx ' dy ' dx '
dt; dv dv , d'-
dt • dx ' dy ' dz >
dw dw , dw . dw
= -——-!(-- U V —~-f- W—-
dl ' dx ' dy ' rfj>
= K' di=r' 5Г = Ю:
\dt ' dv dy dz}'
dp dpu dpi- dpw
dl
dx
dy
ds
= 0.
(b)
(o)
(d)
(•)

КРАТКОЕ ИЗЛОЖЕНИЕ СОДЕРЖАНИЯ ДИССЕРТАЦИИ
401
«, ѵ, а; — проекции скорости на оси координат х, у, г,
j), р — соответственно давление и плотность,
ft, р — постоянные1).
В статье 1 дается общая характеристика волновых движонип.
Указывается, что .движение частиц жидкости, приведенной и «волпение»,
заключается в малых колебаниях около положения равновесия;
волновое движение газообразных тел состоит ив последовательного
расширения и сжатия слоев.
В статье 2 производится упрощение уравнений (а) и (Ь).
Пренебрегая членами, содержащими квадраты и произведения проекции
скоростей, а также их производные, к полагая |3 = 0, автор приводит
эти уравнения к виду
(3)
<*>
"■; (3)
= 0. (6)
Уравнении (3) совпадают с уравнениями Эйлера при h = О. что п
предполагается в дальнейшем.
В статье 3 вводится предположение о том, что плотность во время
двизкснил изменяется незначительно и определяется по формуле
Р = Г'' С1—*), (10)
где s — функция от х, у, г, t остается малою, каково бы ни было
значение переменных; р'— плотность в состоянии равновесия.
Далее выводится формула (11), выражающая зависимость давления
от функции я:
d.i:
dl
dp
Ж
Р
Р
Р
= і
+
(-'
('"
(«
du\
' ~dt) "
dr\
-dij'
dn\
~dt) '"
0) =JJ -(-
j
dy
dl^"'
d pit . d pr
dx dy
da,
"dx-
da,
dai
~~d7>
A*.
df
ds
dl~~
1 di
p = V — -- p .■>',
где /. — некоторая постоянная.
(И)
i) См. примечание [-] на і:тр. ;Ш.
-6 ЗаК* -2&J3. Н. П. Лпйачриский. г. V-

402
ПОДРОБНЫЙ РАЭБОР РАССУЖДЕНИЯ А. Ф. ПОПОВА
Величина в (сжатие) определяется как производная от плотности
по давлению для состояния равновесия;
<ір' = в dp'.
(7)
Таким образом, s —величина, обратная квадрату скорости звука.
Рассматривая состояние покоя, уравнения (31 можно заменить
другими;
dp' ,
V dp'
ах аѵ
Эти уравнения и соединении с уравнением (7) дают
•V
-V = W da,
Р
откуда, после ігятвгриронания получается
(9)
гдй В—-плотность жидкости при г — 0.
Вставляя в уравнения (3), (4) значения р, р из соотношение (10),
(II) и пренебрегая вторыми степенями и произведениями малых
величин, получаем следующую систему уравнений;
dT=-'--A
dv
d7
a (ds
e \d\j
^le_ =L , A
die '. . „.
4
~dT
d<
d*
^)+('--i).^-!-^^
ds du . di: , die
Дифференцирование этих уравнений по х, ц, г, і дает
(12)
(13)
d —
d-s л id-s , d-я і й\ . hk I dx-
d/* = T \rfje= ' dy-' d?) ~T"T \~d7~'
rf7-
d(
(ft
)
+Чг+'т)+«*(•+4) -=—"■ <">

КРАТКОЕ ИЗЛОЖЕНИЕ СОДЕРЖАНИЯ ДИССЕРТАЦИИ
40?
Б статье 4, приравнивая величину h нулю, иа уравнения (14)
выведено уравнение
if* а / d2s , d"s , d?s \ , , , , ds , „,, , ,
Вопи при том же предположении пренебречь силой тяжести, то
уравнения (12) и (14) заменятся уравнениями
du к ds I
dt ~ s dx'
dv a ds
<ft $ dy>
dw л <is
(16)
S life2
Полагая
E dtp
T'di'
(17)
(21)
где о — потенциал скорости, уравнение (17) можно записать в виде
<И'
Для капельной жидкости, вместо уравнений (12) п (13), получается
d''ta 1 /d!tp , d5<? , d-'t\ (ftp
tf^~ = T (Ar*"^ rfj^ **IF) i q dz■
(24)
В статье 5 показано, что для несжимаемой; жидкости уравнение (22)
переходит в уравнение Лапласа
с!х- ' <fy3 dz1
которое совместно с интегралом Лнграніка
-0.
(25)
р dv
(28)
определяет функцию ?.
Из уравнений: (2о) п (28) вытекает, что р — функции гармоническая.
Далее, если принять во внимание постоянство давления на
слово дно It поверхности, получается условие
d-v
d<a
W = aH7-
(331
В статье 0, завершающей первую главу диссертации, дан
небольшой обзор развития теорип волновых движений.
2d'

404 ПОДРОБНЫЙ РАЗБОР РАССУЖДЕНИЯ А. Ф. ПОПОВА
В статье 7 с помощью подстановки
(3?)
d-f d'-v rfs(p
d -~ d-—r d-r-J-K
уравнение (14) приводится к виду
Решение ищется в виде
<р = 2 7>р<*~1) Ѵ ~J cos я (ж —a) cos Ь {у — Щ, (38)
где а, Ь, |і, з, р, -J— произвольные постоянные.
В статье 8 получено значение <в:
<Р = 2 2 е_р(( J.e'"'+ Be "') oos g/ соя а (х- — a) cos 6 (у — р) ооз ji (г — 1) -)-
"Ь 22 e~p\Arnt — Ве~пі) sing; созл (ж—a) cos Ь {у—?) sin и- (г—?), (42)
где j), «, g определяются иа соотношений
В статье Й показано, что если значение о при £ = 0 дано формулой
?о = 2*Ча> Р. Т) соза(.е —a)cosb(j —Э)сов(і(г-~і)( (48)
то
Л+Л-ІГ<*,?, -г). (49)
В формуле (48) каждый член, стоящий под знаком суммы,
предполагается умноженным на дифференциалы da, d$, df и на конечные
разности Да, ДЬ, Ду. Интегрирование по й, |3, -у производится между
пределами изменения ж. j/, г, а суммирование по к, Ь, |а от ^со до -)-оо.
Далее показано, что общий интеграл уравнения (37) будет
9 = 2 2 -^ "' (е"' 4- f ""') cos q! cos «(.в—a) cos b ()/ —j3) cos ji (г — -;} —
4-2 2 -l''~*' (*"' — e~"*) sin gi cos а (х—я) cos & (г/ ?) sin ]*(z — T). (53)
Величины /', ij, л определяются до формулам (40) и выбирается
то решение уравнения (37), которое обращается в нуль при г = со.
В статье 10 даны пргсблияеенные выражения р, q, n, которые автор
получает^ пренебрегая в равенствах (40) членами степени выше nepBOft
относительно а и —. Эти выражения приведены в отзыве Н. И. Лоба-
чевокого.

КРАТКОЕ ИЗЛОЖЕНИЕ СОДЕРЖАНИЯ ДИССЕРТАЦИИ 405
В следующих статьях 11 п 12 получена формула для потенциала
скорости в предположении, что причина, вызывающая волновое
движение, непрерывно изменяется:
с
9 = 2%ѵ{лащ + j4(( —в)^<м), (58)
ГДв
Q = соэ а(х — «) eos Ь (у — р)
і(І) = (-"(е"' + «-"')виді.
В статье 13 рассматривается вопрос о граничных условиях.
Ставится требование, чтобы на поверхности твердого тела z = г (х, у)
выполнялось условие
dz &z
&х ! dy ѵ '
Подобным жѳ образом условие на свободной поверхности <!* (ж, ?/, г, t) =0
записываѳтоя в виде
В статье 14 разложение правой часта формулы (9) в ряд дает:
с другоі* стороны, согласно формуле (11)
Принимая во внимание постоянство давления на свободной
поверхности, из двух последних формул находим:
Отсюда, считая заданным уравнение свободной поверхности в
начальный момент
«; = /(». *)> (72)
легко получаем
/V, .'/)=А С™)
При рассмотрении случая волн значительной длины, уравнение для
определения потенциала скорости принимается в визе

406 ПОДРОБНЫЙ РАЗБОР РАССУЖДЕНИЯ А. Ф. ПОПОВА
и показывается, что решение имеет вид
9 = 2 (Л coat УИ~ + В sin (ѴЮ^**™* "('■'--«) сов 6 (у — 3), (77)
где W, а, Ь, \і, з, |3 — постоянные, связанные соотношением
Ws = a2 -f- 6a — |J.5 -f- ?a|i; (78)
jlj В — произвольные функции постоянных а, [Э.
Воавытаение частиц над нѳвоам у щепным уровнем определяется по
формуле
U
подставив сюда вместо <о выражение (77), находим:
z' = ?0—V (,ізіп( V № —В cost ]/W) -р= cos я (я — ?)соз Ь (у —3)—
— > ._ ооз а [х-— *) соз Ь ('/ — 8); (79)
с другоі стороны, соглаоно уравнению (7Н)
г' = — У (if cos f У~Ѵ — A sin ( J/ІѴ) l^JTcos ,і (г — і) ооз Ь (?у — 3). 180)
Сравнение уравнение (79) и (80) дает
e'a = f{x, ;/) = У-£=-cos «(.с — ■x)cosb(y-~ 3). (31)
*■ ѵ ^
Принимая во внимание (78), находим
'•p = S(-4eosiV^+Rsinf УУ)е л1а'+6"'сова(а; — «)coSf>ljr — "?)■
Если [{х, у) представить по формуле Фурье:
f[x, !/) = 2f(a- s)cosa(a?— a)cos&(^ — p) Да ДЬЛя dS,
то предыдущую формулу можно переписать в виде
\ у у /
Хе~гІ'а,"І"','соэо(^ — a) cos Ь {у — 3) Да Ді> dec <ф. (34)
Полученная функция удовлетворяет уравнениям (25) и (33). Таким
образом, как справедливо указывает Н. И. Лобачевский, полученное
решение соответствует случаю движения несжимаемой жидкости.
Отбрасывая в формуле (84) величину .1, автор получает формулу,
найденную ранее Пуассоном (Memoirs de Г Acad., т. I, 1816). Этим
предполагается отсутствие импульса давления в начальный момент.

КРАТКОЕ ИЗЛОЖЕНИЕ СОДЕРЖАНИЯ ДИССЕРТАЦИИ
407
В статье 15 рассматривается случай, когда на поверхность
действует последовательность импульсов давлений и выводится
■формула
*~*ші2^=^
■х
X е~*У п*4'*'сов а (х — л) cos b(y — $)dadb ск $; \ ИЗ)
о о — —
обозначения над и под дифференциалами показывают, что
интегрирование производится по a, ji между пределами изменения х, у, а по а, Ь
от — са до -\- со. At — импульс давления для момента
времени ti.
В статье 16 выведена формула, на которую ссылается II. I?,
Лобачевский:
9^_4 f f f f F(., ^-'-QdadbJadU-
Ж J J v' J С о » — —
— T7T- <M I \ Ш*' ?. Ooose((— t')Qdadbdad$, (97)
и
где для сокращения введено обозначение
Q = е~г Ѵ ф +№ cog а (.с — а) соэ й (у — §).
Формула (97) дает выражение потенциала скорости в виде суммы
трех членов. Первый член определяет влияние формы свободной
поверхности в начальный момент; второй и третий члены выражают
потенциал скорости в зависимости от импульса и переменного
давления на эту поверхность.
При выводе формулы исходными являются уравнении (25) и (34),
которые теперь обозначаются автором через (а) и (Ь):
d-'a d-ro , d-o
dr- ' d\r dz~
1 dp' __ <to >l"v
~D~di~~'J'dz^'W' i-
Возвышение частицы свободной поверхности над не возмущенным
уровнем определяется по формуле

408 ПОДРОБНЫЙ РАЗБОР РАССУЖДЕНИЯ Л. Ф. ПОПОВА
Отсюда, полагая p' = ty(x, у, t), -j- = Q, при ( = 0, находим:
*>; = *(*, И, О)-^дПг'0. (в)
Уравнению (а) удовлетворяет функция
fix, у, z, f),= JLjj f j"?(«, р, (|Х
Х ,,-*' ^^ cos „ (х— ,) соа h (у — 3) ,i/i db ,Іі 4- (illi)
О II — —
Для определения произвольно ft функции ?(п, р, (| предыдущее
выражение вставляется в уравнение |Ь), причем предполагается
приближенно г' = 0. Величина р' заменяется выражением
1 С С С (' со о) + +
Т ) I ) I Ф (а> ?' 0 С08 а (х — а)оов Ъ (У — Р) de ^ ^я ^?*
Уравнение для определения '? (а, р, () имеет вид:
Решением этого уравнения будет
<р(а, р, 0-=еоасЛ Л + - frinci ^^'f' " Д< Ц-
1 * i-' U tit j
где
Подставляя это иыраікевіге в уравнение (Ь) и сравнивая
полученное уравнение п уравнением (f), находим:
,**!^^?<а,М) = о.
С л ед оватѳл ьно,
Т(.,М>- -,-^Д, (ь>

КРАТКОЕ ИЗЛОЖЕНИЕ СОДЕРЖАНИЯ ДИССЕРТАЦИИ 409
где F(a, Э) — вертикальная составляющая скорости. Теперь, если
вставим выражение ?{а, £, () в уравнение (Ѳб) и значение <р (з, |3, 0)
нз уравнения (1і), то получим после простых преобразований
формулу (97).
В статье 17 рассматривается частный случай, когда давление
перемещается поотупательно в направлении оси х с постоянной
скоростью к.
Выражение потенциала скорости для ѳтого случая имеет вид:
+ /)fl J)J ^ '^ a^ — c1 - cos b(i/ — j3) da Й6 da 4Э.
№)
В статье IS получено решение уравнения (37) для случаи
безграничной среды; отбрасывая в формуле (37) член д-£. зависящий от
тяжести, и полагая
). „ т..
т = „-, т = *,
гІ'в <JS« ,^ф
ПРИВОДИМ (37) К ВЕЕДу
#-"-(*?+5F+rf?)+*(-ar ■*--*-+—)■ <im>
Его решение:
f = -j \ U I П /'(3lP. 1)* - (соч IFCl J- ^ Sin »tA Q rf« (ІЫ'[1 fb 4 dT+
1 i1 Г С С С I* ~'~ ' ain яс) со л д, + + +
— -•■! U U m». P. l)' " ^=^-Qdadbd».dad^d-!, (112)
" . ... . , "c on»-
где
Q = cos a (x — a ] cos b (>/ — fl) cos ji (; — -[),
/'(a;, v, 3) —значение плотности в начальный момент движения.

410 ПОДРОБНЫЙ РАЗБОР РАССУЖДЕНИЯ А. Ф. ПОПОВА
В статье 19 вводятся вместо х, у, z сферические координаты
«, Ь, ш и формула (113) записывается в виде
?==в^ J f f f J ff(e>M)«~^'(°"«»' + ^f *"> пирсов *ДХ
« I'll 5 + + -|_
X **s sin 'I du dtn dst dv d$ d^ -f-
0 ft 1} - - -
•л 2i т. + + +
0 0 1! - - -
где для краткости обозначено:
R = (х — a) sin ft cos w-\-(y — Э) э^п 9 зіп щ + (г — f) eos ,J*
Вводя далее обозначение
(* —«O' + fe-^ + C-'-Tj'-P2 (45)
и пользуясь известным интегралов
\\ cos uR sin Ѳ d<) dm = — ?Ы!_^£. (liej
правую часть формулы (114) можно представить следующим образом:
<? = —~г I j М f (а, 3, т)е a I cos*uf-|—— sin ни* I—— uditd* d$ df -j-
f ! Г Г l" Г i / о ■ - -^-' 8Іи к»( зіп ир , . .„ , ,,, ,,
+ ^Л ) 11 1 'И0' ?• Ч)е —-=-d» из (*Э <^1« (u't
Sit'
Г SUl К «( SI
p
Для больших значений I правая часть формулы может быть
заменена двойным интегралом
к Іъ тс 2~
?' = 4^І \ Li,'mPd>>dt "Г gZ^rff I ji'hj-Ь'Ч/'Ф''?. И351
где
L = i(j:-;-- н( C04J), // -[- нійінр cosi/, ;-}" »'sin/i sing);
ji, 7— сферические координаты.
Для малмх значений I выражение потенциала скорости будет
о' = -І- -L-.AJ \^{а' 3' т)<Г^0Г^'— «Г^Щя.Й.Ег. (126)
4ит(Ѵ 2-М J J J p
В последней частя диссертации (статьи 20—23) получено решение
ряда частных задач. В статье 21 рассматривается волновое движение

КРАТКОЕ ИЗЛОЖЕНИЯ СОДЕРЖАНИЯ ДИССЕРТАЦИИ 411
а слое, ограниченном двумя горизонтальными плоскостями; как
предельный случай, отсюда получается волновое движение в бесконечном
полупространстве, ограниченном горизонтальной плоскостью. В статье 22
рассматривается волновое движение жидкости, имеющей свободную
поверхность и ограниченной горизонтальной плоекостьт.
Как видно иа приведенного краткого изложения, Л. Ф. Попов
в своей дисеертадии значительно обобщил имевшиеся результаты
в теории волновых движений. Оо вывел более общие, чем у Копт и
Пуассона, уравнения волнового движения, в которых частично
учитывается и вязкость жидкости. Отсюда, как чаотные случаи,
получаются уравнения волновых движений на поверхности капѳдьноі)
жидкости и уравнения распространения звука, рассматривавшиеся до
А. Ф. Попова раздельно.
Идеи совместного рассматривания етих двух явлений, как это
видно из замечании в отзыве, подсказана Попову Лобачевским.
При интегрировании уравнений волнового движения А. Ф. Ионон
в основном следует методу Пуассона.
В последних разделах диссертации рассмотрены частные случаи
волновых движений, которые ранее не изучались.

Приложение 3
ИСТОІ'ИКО-БНБЛЛОГРАФИЧЯСКИЕ СВЕДЕНИЯ
О ДИССЕРТАЦИИ ПОПОВА И РАЗБОРЕ ЕЕ ЛОВАЧЕВСКИИ
-1. Д. Дуояго
6 нюня 1845 г. в Казанском университете пропеходил публичный
диспут па соискание степени доктора математики и астрономии.
Диссертантом был Александр Федорович Попов (1815—1870),
окончивший в 1835 г. Казанский университет со степенью кандидата
математических паук, учитель математики Казанской первой гимназия,
к тому времени уже имѳппшй и следующую степень магистра.
Оппонентами ему выступали ординарные профессора Н. И. Лобачевский
и Л. И. Котельников. Докторская диссертация А. Ф. Попова [как и
кандидатская, защищенная в 1842 г., причем оппонентами были те же
Н. И. Лобачевский п П, И. Котельников, а также п Н. Н. Звнип1))
досшпцена была гидродинамике и имела ваглавае; «Об интегрировании
дифференциальных уравнений гидродинамики, приведенных к
линейному виду».
Казанская газета сообщает -), что это событие рассматривалось,
как торжество, давно уже не повтор я вшѳеся в университете.
Специальный характер темы диссертации был причиной «незначительного
стечения посторонних посетителей, тем не менее развитие выбранных
докторантом положений, доведенных в этом ученом споре до ясного
понятия всех присутствующих, делало его чрезвычайно занимательным».
В «Деле об утверждении магистра Александра Попова доктором
математики и астрономии» и в протоколах Совета Казанского универ-
1) Знаменитый утгмиг: Н. Н. Зннин (18ГІ—1880) получил в Казанском
университете блестящее образование в области математики, астрономии в механики'
При окончании университета и 1333 г. он был удостоен степени кандидата и
золотой медали .зя. ночігнеине ^Теория ігертѵрбапий», отзыв на которое лил
Н. И. Лобачевский (это сочинение и отзыв в настоящее вредя, пони дин ому,
утрачены). В 1831—183І іт. Зігаип преподавал аналитическую механику,
гидростатику и гидродинамику, после чего посвятил себя химии.
=) Казанские губернские ведомости, часть неофициальная [11 июня 1845],
Л° 24, столб. 239—210, -Заметка воспроизведена Л. Б. Модзалевскии в сборнике
«Материалы дли биографик Н. И. Лобалевского», изд. АН СССР, М. — Л., І84&.
документ Лі 518, стр. 504—У1,і.

ИОТОРИКО-БИБДИОГРАФИЧЕСКИЕ СВЕДЕНИЯ
413
ситета за 1845 г., хранящихся в Центральном государственном архиве
Татарской АССР, имеются весьма интересные и, в большей части, до
■сиз: пор неопубликованные документ», из которых выясняется роль
Н. И. Лобачевского при защите этой дисгертации.
Из подробного «Журнала испытания магистра Александра Попова
на степень доктора математики», состоящего из отдельных «статей»,
каждая из которых подписана всеми присутствовавшими членами
философского факультета, мы узнаем, что в заседании второго отделения
философского факультета 12 октября 1844 г. слушано было прошение
магистра Александра Попова о допущении его к испытанию на
степень доктора математики, причем он представил свою диссертацию.
После ее просмотра, 16, 17 и 28 февраля, 1 и 26 марта 1845 г. были
последовательно проведены устные и письменные испытания по чистой
математике, устные и письменные испытания по прикладной
математике (т. е. по механике) и устные испытания по астрономии и
геодезии. Ответы Попова (письменные ответы частично хранятся в деле)
іс изложением истории и литературы предмета» по каждому вопросу
были «совершенно (или вполне) удовлетворительный, кроме ответов
по астрономии и геодезии;, которые были найдены только
«удовлетворительными». По окончании последнего экзамена второе отделение
философского факультета. 2G марта 1845 г. определило; допустить
Попова к публичному защищанию диссертации.
12 июня 1S45 г. дѳван П. И. Котельников писал Совету о
состоявшейся защите и от имени второго отделения философского факультета
просил Совет ходатайствовать об утверждении Попова в степени
доктора математики и аотрономии !). 26 июня проректор К. К. Фойгт
сообщил Совету, что управляющий Казанским учебным округом
(Н. И. Лобачевский) разрешил отправить в цензурный комитет 6
экземпляров дисоертацик Попова, отпечатанной в типографии Казанского
университета, и по одному экземпляру в русские университеты и
научные учреждения; еще несколько экземпляров было передано
Казанскому университету, а остальные выданы Попову. Этим
устанавливается дата выхода в свет диссертации А. Ф. Попова; как мы увидим,
отзыв К. II. Лобачевского был напечатан одновременно, или почти
одновременно.
Диссертация А. Ф. Попова напечатана отдельной книжкой в
формате 4°; на титульном листе напечатано2); «Об интегрировании
дифференциальных уравнений гидродинамики, приведенных к линейному
виду. Рассуждение магистра Александра Попова аа степень доктора
1) Центральный гос. архив Татаріжой АССР, ф. 977, Совет, ,\і Н91В, я. !6.
Ц Фотографии титульного листа диссертации воспроизведена в наст, томе
леред стр. 381.

414
ПОДРОБНЫЙ РАЗБОР РАССУЖДЕНИЯ А. Ф. ПОПОВА
математики и астрономии. Казань, 1845 года. В Университетской
типографии». На обороте титульного листа имеется указание: «Печатано-
с доаволенип университетского начальства». В книжке после
титульного листа идут две ненумерованные страницы, составляющие нечто
вроде введения к диссертации1), и 59 страниц текста, за которыми
следуют две (опять не нумерованные) страницы: Положения [Тезисы].
В том же формате 4° напечатан и составляет как бы продолжение
диссертации Попова отзыв Лобачевского под названием: «Подробный
разбор рассуждения, представленного магистром Поповым под
названием „Об интегрировании8) уравнений гидродинамики, приведенных
в линейному виду" на степень доктора математики и астрономии».
Отзыв Лобачевского содержит 13 отдельно нумерованных страниц и
подписан: Заслуженный Профессор Лооачееский. 11 апреля 1845.
Вот что писал далее Лобачевский 25 августа 1845 г. за № 3824
Совету университета:
По представлению Совета Казанского Университета 3
минувшего Июля, и согласно разрешению Господина Управляющего-
Министерством Народного Просвещения, Товарища Министра
3 текущего Августа № 7546, я утверждаю Старшего Учителя
первой Казаиекой Гимназии Магистра Александра Попова в звании
Доктора Математики и Астрономии.
Уведомляю о том Совет Университета, в ответ яа означенное
представление, для надлежащих по сему распоряжений.
В моем представлении Г. Министру Народного Просвещения
объяснил я свое мнение, что нахожу приличным по примеру,
как зто сделано с диссертацией) Г. Попова, присоединять всякий
раз печатный подробный разбор.
Г. Управляющий Министерством в отношении к атому
последнему обстоятельству предоставил поступить по моему
усмотрению. Между тем я желаю знать предварительно мнение Совета,
чтобы принять за постоянное правило: к Докторским
диссертациям прилагать печатный подробный разбор.
Управляющий Казанским Учебным Округом
Ректор Университета — Лобачевский.
Правитель канцелярии И. Цепелев 8).
22 сентября 1845 г. Совет Казанского университета заслушал это
предложение Н. П. Лобачевского, который, хотя и оставался ректором,
і) Это внсденце помещено в качестве дриложе&иа 1 на стр. 398 наст. тома.
2) Слово «дифференциальных» в заглавии отзыва, вероятно да недосмотру,
отсутствует.
3) См. саоеву :) на стр. 413, л. 2Ъ. Фотоснимок итого документа помещен после
стр. 41Ѳ наст. тома.

ИіУГОРИКО-ІЗЕВЛИОГРАФИЧЕСКИЕ СВЕДЕНИЯ
415
но уже редко участвовал в заседаниях Совета. Черновая запись
постановления Совета университета, аа исключением ее начала, написана
рукой председательствовавшего проректора К. К. Фоигта. По вопросу
о печатании рецензий на диссертации Фойгт сначала записал одно
мнение, затем его зачеркнул и тут же заменил другим. Вычеркнутый
текст, в котором, в свою очередь, есть небольшие помарки и поправки,
с трудом можно прочесть; он глаовт:
2. Г-ну Управляющему Каз. Учебным Округом донести, что
Совет У-та [начиная отсюда зачеркнуто] вполне разделяет
мнение Его Превосходительства') насчет приложения к
диссертациям на высшие ученые степени и притом [неразб. — наиболыпѳ?)
Доктора или Магистра, подробных разборов, представленных
г. профессорами по принадлежности. Такие раэборы, с одной
стороны, должны служить открытым засвидетельствованием [и]
доказательством всей [той — зачеркнуто] строгости приговоров,
. которые Университет произносит над подобными трудами, а с
другой стороны, охранными, так сказать, грамотами, под защитою
которых молодой ученый вступает па литературное поприще а).
Как сказано, сразу вслед аа этим Фойгтом написано совершенно
другое мнение и в таком виде запись была перенесена в книгу
протоколов Совета:
§ 3. от 25 августа 1845 г, за № 3624 об утверждении старшего
учителя первой Казанской гимназии магистра Александра Попова
в звании Доктора математики и Астрономии. — Определено:
1. Предписать начальнику типографии напечатать г. Попову
диплом на степень Доктора Математики и Астрономии и представить
с отпуском в Совет; по напечатании диплом, утвѳрдя подписом
и приложением печати, выдать г. Попову, взыскав с него
следующие деньги, а 2-е отделение философского факультета о сен
уведомить для сведения. 2. Г. Управляющему Казанским
учебным округом донести, что Совет университета на счет печатания
подробных разборов к диссертациям Докторов полагает, что такое
печатание, подвергая профессора суду публики против его воли
и тем требуя от него большей 3) строгости, иногда
обременительной для Докторантов, не должно быть поставляемо в настоящую
обязанность, но представлено собственному усмотрению и
желанию профессоров, представавших вти разборы *).
') То-елтг. Лобачевского.
*) Центр, гос. архив Татарской АС* Р, Ці, 977, Совит, Лі 6916, л. 20.
*■) Так в черновике Фоііі'та. В протоколе — «большой».
*) Центр, гос. архив Татарское АССР, Фонд 077, Совет, ."V 8082, л. 96.

416
ПОДРОБНЫЙ РАЗБОР РАССУЖДЕНИЯ А. Ф. ПОПОВА
Кем были высказаны эти противоречащие друг другу мнения по
пункту 2, что побудило Совет отступать от первого из них и
остановиться на втором, мы вряд ли узнаем, и все-таки крайне странно
постановление, с которым, в конце конпов, ооглаоилясь
многочисленные присутствовавшие члены Совета и все без оговорок подписали
протокол. Среди них были ученые, широко известные своими научными
трудами и открытиями, но ни один из них не пожелал прибавить
к протоколу особого мнения по столь принципиальному вопросу. Итак,
Совет решил и записал, что если отзывы профессоров будут
печататься, то им будет труднее проявлять снисходительность к
докторантам I
Не такого мнения ожидал Лобачевский от Казанского университета,
и он с горьким разочарованием и сурово отвечает Совет;- (27 октября
1S45 г. ."Ns 4583):
На представление Совета Казанского университета, 17
текущего октября, с мнением яа счет печатания подробных разборов
к диссертациям Локторов, даю знать, что суду публики
подвергается сочинитель против своей воли за всякое вообще изданное
им сочинение. Итак, если бы приводимая Советом причина была
достаточной в этом случае, то она служила бы заявлением от
профессоров их намерения вообще не печатать своих сочинений.
Впрочем, не вводя теперь еще никакого постоянного, на такой
случай, правила вперед, предлагаю Совету Университета,
представляя диссертации на звание Доктора, всякий раз излагать
подробно причины, которые побуждают удерживаться пѳчатапием
полного разбора диссертаций.
Управляющий Казанским Учебным Округом
Ректор Университета—'Лобачевский.
Правитель канцелярии И. Деие.ив 1).
Со страниц архивного дела встает перед нами благородный облик
Лобачевского в его неустанной заботе о развитии русской пауки. Он
справедливо считает необходимым условием ее процветания высокий
уровень подготовки молодых ученых и требует о те глухие годы всей
возможной гласности в самом трудном и ответственном деле —
присуждении степени доктора, наук. Не только диссертации, но и разборы
их профессорами должны печататься и широко обсуждаться — так
полагает Лобачевский, и сам подает первый пример. Испытав в своей
жизни вместо справ ѳ д лив ого суда критика бессмысленные
издевательства людей, не цоннмавших его великих открытий, Лобачевский не
і) Центр, гос. аріиа TAGCP, фонд У77, Сонет, J* 89ів, л. 28. Фотоояимок
этого документа помещен вдесь вслед за первой дикументом, о котором
говорилось на стр. 4U.

е/У~ $ff- jey&ttzac eSSei^G*1^. '£0г-£аг**еД&&іШие*
Л'^ХХш ^SU**"*"*** ^А«№ЛЬ-/
с;
Мерная .іаппока П. И, Л</»;ічі?іи:Кі>го ^'иііетѵ І^яг^ии-ін'игп ѵіті!і']нчпѵт;і—
ufx'.vjM^euiK' Еіріінѵпч* ;ія но ііг.ігіііиі' гфдіі;игіч-
<*& ДІЖІѴр^КІІМ -Ш^^ИЧИНИШ ILj>J]. kU'UI L іі^'ІЛШЫ^ ІІ<]..фийі1],І.І ра.илфл
IV UT(>. II?.

^*л**й^*^ ^ье# -^«7 аввдая..
У У
7 с^__— '^Ідг^^
ѵ^
/'Аглщълл*.- ..-J.' Stnt,.y-^.., 'i% /ft si^<^^.-u_
Окинчішік- и.'іікіііі .і.ціцсі;и .'[и<'ачі-иі'і.нііі Гі.мту jimis'-pci юп.

{-*>-&*brrw /Ьлъ&гъсмюео ,Уш4~*
I *&&*"&ЬЬГЖ&**-*ъ4Я*г-
УЧШЛБНЫН ОКРУГІЬ. ^*" stf S
•Ли*-«ф наг- се**—в *ь«*л»*і-«*"»****-'
^ft_.
Л* л»лсгги-аи*/ сА^_, / £ui^-u.
•3™ 5
1і'ііі(і:(і( :щгш<-і.чі If. II. Лобіі'ГРШ'КііГіі Сшн-гу 1і!іі.іангі(ііГіі унііт-рсііпчи -
іііі:!]імч:і>нііо NlI [ичіи'ітіці (JoBivra но нцс i.ln'.wiiino Лчпичригюч'и

,&&***/Ъъ**+*Аър Ле-яп^г^сл*--- А^ЛОй^лит^ -tf>$&LJ**i*s
'^&&rrb£-f»$ J£?t*>-
PCJtt-ь*',
? /fu^j «-^ 0. г^^и^
U*u*',™ua I""i авчмщі -■І.і.іічо^-к,,,-., ,;,,№ry yU,шерсти та.

ИСТОГИКО-БИБЛИОГРАФИЧЕСКИК СВЕДЕНИЯ
4І<
смутился и твердо продолжал итгя по своему пути. Вот почему он
осудил малодушие Совета университета, не сумевшего удержаться на
«толь высокое точке зрения.
Рассылка Советом диссертации А. Ф. Попова по университетам и
иаучным учреждениям России, невидимому, затянулась до окончания
приведенной нами переписки и была осуществлена только в конце 1845 г.
Некоторые зкзѳмпляры диссертации не содержат при себе отзыва
Н. И. Лобачевского. Чем это было вызвано, выяснить трудно.
7 июля 1846 г. кончалось пятилетие, на которое был избран
Н. И. Лобачевский на должность профессора чистой математики, сверх
уже истекшего в 1841 г. 25-летнѳго срока службы. Л. Б. Модзалев-
ский впервые установил, что Лобачевский, в связи с этим, добровольно
уступил кафедру своему ученику А. Ф. Попову. Являясь в то время
управляющим Казанским учебным округом, Лобачевский написал
3 июля 1846 г. представление министру народного просвещения
С. С. Уварову об оставлении проф. И. М. Симонова (в отношении
которого возникал подобный же вопрос) «еще пять лет на службе
в аванип заслуженного профессора».
«Что же касается до меня,—пишет Лобачевский,—то со воѳй
приэнатвльностию к заключению университетского Совета об
оставлении меня на службе в должности преподавателя, честь имею
представить на благоусмотрение В-го В-ва, что кафедру чистой
математики более с пользою, вероятно, может аанять учитель
1 -ой Казанской гимназии Попов, получивший степень доктора
в прошедшем году и для которого такое повышение не только
будет совершенно ааслуженное, но даже должное, с той целию,
чтобы поощрить далее к занятиям при несомненных его хороших
способностях. В силах еще первое молодости, неотвлеваѳмый,
подобно мне, другого рода занятиями по службе и обязанностями
семейственными, он не замедлит показать себя достойным
профессором и встать в кругу самых известных европейских ученых.
При таких обстоятельствах желание с моей стороны оставаться
в должности профессора не могло бы почитаться справедливым;
а потом;- прошу покорнейше В. В., уволив меня от ученой службы,
наградить производством пенсии...»').
Вступив н 1846 г. экстраординарным профессором на кафедру
чистой математики, А. Ф. Попов был избран 7 сентября 1849 г.
ординарным профессором по той же кафедре я занимал ее до 8 августа
1866 г., когда был вынужден оставить службу по болезни.
!) Воспроизведено Л. D. Ыодзалѳвскіш в ши сборнике (см. стр. 411І наст,
тома), документ ?£ 532, стр. 513—514. См. также предисловие Модэалевсвого (там
же, стр. 17).
27 8ая. аам. н. н. Лдвачявонив. т. ѵ.

418
ПОДРОБНЫЙ РАЗБОР РАССУЖДЕНИЯ А. Ф. ПОПОВА
Ученая деятельность Попова была обширна и разнообразна. Мноі'ие-
его работы были посвящены, как и обе его диссертации,
гидродинамике, в особенности теории волн и связанным с ней вопросам теории
упругости и теории звука.
Однако преемник Лобачевского, А. Ф. Попов, не оценил значения
того переворота в геометрии, который совершил его учитель. В
интересных и важных для историка воспоминаниях о Лобачевском,
изданных в 1S57 г., Попов кратко и сдержанно упоминает об атом: «...
чтения для избранной аудитории, в которых Лобачевский развивал свои.
Новью начала геометрии, должно назвать по справедливости
глубокомысленными». В другой месте Попов указывает: «В числе восемна--
дцати или двадцати рассуждений, книг и брошюр Лобачевского одни
относятся к теории числ, другие к теории интегралов и важнейшие
к строгой теории параллельных линии .. .я1).
1) А. Ф. П о и о в — Воспоминания о службе н трудах профессора Назанского-
университета Лобачевского. Ученые записки, издаваемые императорским
Казанский университетом эа 1857 г., кн. IV, стр. 153—159; воспроизведено Л. Б. Иодва-
левскнм в его сборнике, стр. 58в—580.

ПОЛНОЕ
ЗАТМЕНИЕ СОЛНЦА
В ПЕНЗЕ
26 ИЮНЯ 1842 ГОДА
—•-Тіі—
ВВОДНАЯ СТАТЬЯ И КОММЕНТАРИИ
А.Д.ДУБЯГО

ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА В ПЕНЗЕ 26 ИЮНЯ 1842 ГОДА
Вводи ая статья:
Отчет Н. И. Лобачевского о наблюдениях солнечного затмения
в 1842 году 421
Н. И. Лобачевский — «Полное затмение солнца в Пензе
26 июня 1842 года* 433
Примечания 458
Приложения;
1. Заыетк& в Пензенской газете 1342 г. о аатмении, вероятно,
принадлежащая Н. Е. Лобачевскому 485
2. Первые астрономические наблюдении Н. И- Лобачевского .... 433
3. Историко-бибпнографичѳские сведения о сочинении «Полное
затмение солнца в Пѳнаѳ 26 июня 1842 года*. 494

ОТЧЕТ Н. И. ЛОВАЧЕВОКПГО О НАБЛЮДЕНИЯХ СОЛНЕЧНОГО
ЗАТМЕНИЯ В 1842 ГОДУ
Из все: известных нам оочинѳний Н. И". Лобачевского к области
астрономии относится только отчет о наблюдении полного солнечного
затмении 26 июня (строго стиля) 1842 г. в Пензе, если не считать
его юношеских наблюдений кометы 1811 I1). Между тем, на
продолжении своей многолетней научной н учебной деятельности
Лобачевский немало занимался астрономией, как в ѳтом можно убедиться
до очень интересной статье Н. И. Идельсона «Лобачевский —
астроном» 2). К сожалению, утрачено сочинение магистра Лобачевского
«Об эллиптическом движении небесных тел», я' сохранился лишь
лестный отзыв о нем профессора математики Бартельса. По
собственному свидетельству Лобачевского, он много занимался наблюдениями
в 1819 году, когда профессор астрономии Казанского университета
И. М. Симонов уехал о екепедидией Беллинсгаузена и Лазарева
в Антарктику, а Лобачевский его замещал. Одним из следов
преподавания им астрономии осталось предвычислениѳ студентами Юфѳ-
ровым, Токаревым и Пякторовым кольцеобразного затмения 26 августа
(старого стиля) 1S20 г, в Казани, где оно было частным с фазой
немного более -j-3). Б своем отчете о затмении 1842 г. Лобачевский
пишет, что os наблюдал кимету Ѳякѳ в 1832 г. и комету Галлея
в 1835 г. В 1838 г. Лобачевский написал отзыв на сочинение «Теория
пертурбаций» кончавшего курс студента, в будущем знаменитого
химика Н. Н. Зинина; последний sa это сочинение получил золотую
медаль.
Повидимому, до сих пор никто не пытался осветить все содержание
отчета Лобачевского о затмении 1S42 г., хотя оно очень интересно.
Это сочинение отличается от прочих трудов Лобачевского
разнообразием затронутых в нем тем: опиоывавтся поездка в Пензу и наблю-
і) См. стр. 489 наег. -іома (приложение 3).
3)111. И. Идельсоя. Лобачевевий — астроном. «Исторшсо-математические
исследования», вып. И, Гостехиадат, 1949, стр. 137—167. Также: «Вопросы истории
отечественной науіш», кал, АН СССР, ІѲ49, стр. 142—164.
3) «Казанские Известия», Х- 62, 4 августа 1820 і\, стр. 268.

422
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
даыия ватмения, неоднократно упоминаются спутники и коллеги
Лобачевского, перечисляется масса фактов по истории науки и разбираются
мнения ученых по многим проблемам физики и астрономии. Отчет
Лобачевского о затмении относится к далекому от нас этапу развития
науки, и для его полного понимания необходим подробный
комментарий, который приводится здесь и в примечаниях к отчету.
Укажем, прежде всего, какие материалы были использованы для
Этой цели.
После изысканий Л. Б. Модаалевокого стали доступными широ-
комукругу читателей многочисленные и важные документы о жиани
и деятельности Н. И. Лобачевского; здесь мы отметим тѳ из них,
которые непосредственно свяэаны с его поездкой в Пензу для
наблюдения солнечного затмения 1842 г.: они в некоторых случаях
добавляют существенные детали к повествованию самого Лобачевского,
но новых сведений научного характера мы почти не находим1).
Мы не знаем никаких подробностей О наблюдательной
деятельности Лобачевского, кроме того, что он сам нам сообщает в немногих
фразах; сохранившиеся его листы с черновыми теоретическими
выкладками лишь в небольшой части относятся к астрономии; наконец,
нет самых важных документов, относящихся к его отчету о затмении.
"Чтобы стало ясно, почему до нас дошло так мало сведений, надо
вспомнить, что страшный пожар 24 августа 1842 г., уничтоживший
бблыпую часть Казани, захватил и астрономическую обсерваторию
университета. От огня частично пострадали инструменты и, невидимому,
сгорел архив обсерватории, так как в нем не осталось никаких
научных материалов ранее 1842 г. Эта судьба, очевидно, постигла и записи
астрономических наблюдений Лобачевского. Сгорели многие книги
и бумаги, которыми пользовался Лобачевский при составлении отчета
о затмении, происшедшем за два месяца до казанской катастрофы.
Даже первый вариант отчета Лобачевского о затмении 1842 г. стал
жертвой пламени. Поэтому теперь остается очень мало надежды на
отыскание таких интересных документов, как, например, письмо
В. Я. Струве к И. М. Симонову с предложением наблюдать затмение
в Пензе и с программой наблюдений; также нет никаких следов
инструкции для наблюдений, которую нанисал Симонов, уезжая
ненадолго до затмения за границу, своему заместителю, астроыому-наблю
дагелю М. В. Ляпунову. Поиска в других Казанских архивах,
предпринятые в надежде, что удастся найти новые сведения об
экспедиции Лобачевского и его коллег в Пензу, дали до сих пор немного
') Материалы для биографии Н. И. Лобачевского. Собрал и редакгировал
Л. Б. Модзавевский, Иад. АН СССР, 1948 (далее цитируется: Модзалѳв-
ский). Документы J*?6 473, 47в, 478, 481, 483, 493, 494, 498.

ОТЧЕТ Ы. И. ЛОБАЧЕВСКОГО О НАБЛЮДЕНИЯХ ЗАТМЕНИЯ 423
результатов. Среди сохранившихся в Казани архивных материалов
интересны записи книг, выдававшихся библиотекой университета его
профессорам и преподавателям, расположенные по учебным годам 1).
Эти записи, в частности, могли бы быть" пенны потому, что
Лобачевский, как правило, не указывает в отчете использованную им
обширную литературу. В записях нехватает 1843/44 года, но это не имеет
значения, ибо к лету 1843 г. рукопись Лобачевского заведомо была
окончена. Надо сказать, однако, что Лобачевский в связи с
составлением отчета, повидимому, вовсе не брал книг из библиотеки.
Немногочисленные книги, взятые им после поездки в Пензу, относятся к
другим темам. Конечно, оп мог читать журналы в самоа библиотеке,
а часть нужных ему книг находилась на руках у других лиц, или,
может быть, в астронома чес кон обсерватории. Кое в чем помог при
комментировании отчета Лобачевского просмотр записей книг и,
частично, самих книг, взятых 9. А. Кеорром и М. В. Ляпуновым
(спутниками Лобачевского по поездке в Пензу на затмение), а также
И. М. Симоновым,
Чтобы отчет Лобачевского предстал в правильной перспективе, мы
предпошлем некоторые исторические замечания о солнечных
затмениях и, в частности, о полном затмѳнни 1842 г.
Причины солнечных и лунных затмений были понятны еще
древним грекам. Однако только в 1(>04 г. Кеплер показал, что солнечные
затмения могут- быть и полными и кольцеобразными, то-ѳсть, что
видимый поперечзик Луны во время затмения может быть и больше,
и меньше, чем видимый поперечник Солнца, вследствие того, что
расстояния іэгнх небесных тел от Зем.чн изменяются в некоторых
пределах. Как раз по вопросу о расстояниях светил от Земли в системе
мира Птоломея господствовала путаница. Тогда же Кеплер описал
корону, появляющуюся вокруг Солнца, во время полных ватмекий,
о чем имелось свидетельство еще у Плутарха. Кеплер приписывал
корону либо сиянию эфира вокруг Солнца, либо атмосфере Луны
{которая во время затмения располагается для нас перед Солнцем).
Полные солнечные затмения, из-за сравнительной узости полосы
полной фазы на аемноп поверхности, видимы в данной местности
через большие промежутки времени, измеряемые столетиями. Точное
их предсказание для определенного географического места было в те
далекие времена затруднено несовершенным знанием видимых
движений Солнца и Луны. Еще в ХѴТЛ веке солнечные затмения подчас
наблюдались случайными и неподготовленными наблюдателями, кото-
!) На существование таких записей нам указал Г. А. Скопин.

424
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
рые за короткое время полной фазы, пораженные картиной
торжественного и грозного явления природы, не успевали сделать
объективных и сколько-нибудь ценных наблюдение. Почти полный список
исторических наблюдений над солнечной вороной приведен
Лобачевским в его отчете, но Лобачевский только глухо памекает на
наиболее поразительные примеры тех иллюзий, жертвами которых стали
наблюдатели. Так, во время затмения 1778 г., наблюдавшегося с корабля
в открытом море, Уллоа видел, что корона вращалась наподобие
фейерверочного колеса, и отметил дыру в Луне, близ ее края,,
сквозь которую просвечивало Солнце. Аналогичные «наблюдения»
повторялись и позже, во время других затмений (л том числе и
в 1842 г.); некоторые астрономы даже решались их серьезно
обсуждать.
Долное затмение 20 июня (S июля) 1S42 года должно было быть-
видимо в Европе после многолетнего перерыва, за время которого-
астрономия и физика сделали большие успехи; не удивительно, чго-
ученые готовились к наблюдениям заранее и впервые снаряжали
особые экспедиции в полосу полной фазы. Условия для наблюдений
ожидались хорошие: лунная тень пробегала через всю Европу от
Испании до Урала и продолжала путь по Сибири; длительность
полной фазы была значительной.
Директор Пулковской обсерватории академик Б. Я. Струве возглавил
организацию наблюдений в России. По его плану было проведено-
четыре акспедиции для наблюдения полного затмения — в Дубно,
Чернигов, Липецк и Пензу. В этих первых широко организованных
наблюдениях солнечных затмений и России приняли участие ае
только астрономы-профессиональЕ, но и ученые других
специальностей (как Лобачевский и Кнорр) и простые любители астрономии.
Наблюдениям в Дубно, как об этом сообщает Славянский'), и в Пензе,,
как видно из отчета Лобачевского, помешала пасмурная погода. Ясное
небо благоприятствовало наблюдениям в Липецке, куда выехали
О. В. Струве и Шидловокий. Статья О. В. Струве о наблюдении
затмения очень интересна3). Е Чернигове наблюдал затмение
киевский профессор астрономии В. Ф. Федоров; там небо было покрыто-
тонко!* пеленой облаков 3).
і) Astronomicі'ііо Kachricliten, В. 20, 1343, стр. іЗ—76.
2) О. StriiYe — BeobachtUDg der totalen Soimenfiusttrnb am 7. Juli 1842 in
Lipezk, таи же, стр. 227 -234. (По астрономическому счету времени сутки до
1025 г. начинались в полдень, а затмение нш'шю да лось в Европе в утренние
часы, поэтому оно отнесено к 7 июля нового етиля.)
3) В. Федоров — О солнечном затмешш, бышвем 28 июня 1842 года в
Чернигове, Журнал Министерстна народного просвещения, часть 35, отд. 2, 1S42,
гтр, 154—164. Такте Astronomische ІчасдпеІіЬеп, В. 20, 1843, стр. 235—240.

ОТЧЕТ Н. И. ЛОБАЧЕВСКОГО О НАБЛЮДЕНИЯХ ЗАТМЕНИЯ 425
Кроме этих четырех экспедиций, организованных Пулковской
обсерваторией, в России наблюдали затмение и не
астрономы-профессионалы ').
Результаты важнейших сделанных за границей наблюдений над
короной и протуберанцами приводятся в отчете Н. И. Лобачевского-
и в прекрасно написанно» статье профессора астрономии
Петербургского университета (позже академика) A. EL Савича2).
Затмение 1842 г. не внесло новости в вопрос о природе солнечной
короны. Для простого глаза и в трубу (в отличие от фотографий)
корона имеет довольно размытый вид и не представляет каких-либо-
вполне резких и четких деталей. Поэтому, наблюдая визуально, нельзя
воспользоваться движением Луны относительно Солнца во время
затмения, чтобы уверенно заметить, по отношению к какому из ѳтих
светил корона остается неподвижной и, таким образом, решить, свя-
аана ли она с Солнцем или с Луной. Некоторые ученые считали даже,
что корона происходит вследствие диффракции солнечных лучей
у краев Луны. Во время затмения 1851 г. была получена первая
фотография (дагерротип) солнечной короны, по только после
затмения 1860 г. и после изобретения спектрального анализа окончательно
рухнул старый взгляд на Солнце, как на тело, в основном
твердое—как и планеты, —но лишь окруженное оболочкой сияющих
облаков, и вместе с тем было неопровержимо доказано, что корона
п протуберанцы принадлежат Солнцу.
Мы переходим теперь к обзору содержания отчета Н. И.
Лобачевского о затмении 1842 г. Отчет начинается с указания на задачи,
стоящие перед астрономами и физиками при наблюдении полного-
затмения Солнца. Далее Лобачевский излагает обстоятельства,
сопровождавшие организацию экеиѳдшши Казанского университета в Пензу,
и перечисляет лиц, участвовавших в ней.
Спутниками Лобачевского по экспедиции были
астроном-наблюдатель Казанской обсерватории Михаил Васильевич Ляпунов и
профессор физики Казанского университета Эрнест Августович Кнорр..
і) Д-р Штубспдорф в сѳае Корякове (аыне Павлодарской области
Казахской ССР, долгота 77°15'. широта 52324'-, см. AstronomiscUe Naahrichten, В. 20,
ІЬ'43, стр. 17Э—184), врач К у рови цви іі в Семипалатинске (см. там же,
Стр.Зээ—358). военный врач С то ао в в Вани Ауле (ШежідарсноНоо.таіли,
долгота 75°45', шпрота 50°39'; ем. там яів, стр. 357—330). Во веек этих местах jaa-
таение наблюдалось около полудни.
*) А. Савич — Известия о любопытных явлениях, запеченных it разных
местах Европы во время полного солнечного затмения 1842 года. Журнал
министерства народного просвещения, часть 40, отд. 2, 1843, стр. 1—1В.

426
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
Оба они были незаурядные люди, и у обоих научная
деятельность кончилась не особенно удачно (как это часто бывало в ту
эпоху).
М. В. Ляпунов (отец знаменитого математика и механика А. М.
Ляпунова и его братьев — академика Б. М. Ляпунова и композитора
С. М. Ляпунова) был учеником И, М. Симонова и Н. И.
Лобачевского. Истинным призванием М. В. Ляпунова были астрономические
наблюдения. Но не успела вполне развернуться его научная
деятельность, как в 1855 г., в возрасте 34 лет, Ляпунов оказался перед
необходимостью оставить ее навсегда и уйти из Казанского
университета из-за недоразумений, связанных с преподаванием астрономии.
Ляпунов умер, когда ему было всего 48 лет. Во время поездки
в Пензу он только недавно покинул студенческую скамью; том не
менее он проявил себя хорошим организатором.
Э. А. Кнорр по возрасту занимал среднее место между
Лобачевским и Ляпуновым и уже девять лет был профессором физики,
поступив в Казанский университет по рекомендации столь крупного
ученого, как А. Гумбольт. Интересы Кнорра были разнообразны: он
положил много забот для правильной постановки метеорологических
наблюдений в Казани и в Поволжьи, производил магнитные
наблюдения, а в области собственно физики занимался изучением явлений
■света. После путешествия для наблюдения затмения в 1842 году он
недолго проработал в Казани и в 1846 г. (в том же году, когда
Лобачевский ушел с поста ректора) переехал в Киев и занял такую
же кафедру — физики и физической географии (метеорологии), — что
и в Казани. Отелужив 25 лети получив право на пенсию, Кнорр покинул
в 1858 г. Киевский университет и Россию, а вместе с тем и оставил
научную деятельность. Кнорр не создал себе крупного имени как
ученый и теперь почти забыт.
Добавим, что Кнорр много путешествовал. Он изучал восток России,
уезжая далеко от Казани, ездил за границу (и это было одним из
самых успешных путешествии казанских профессоров в SIX веке):
переехав в Киев, он вторично отправился наблюдать полное
солнечное затмение 18/28 июля 1851 г., потерпев, впрочем, полнейшую
неудачу. Лобачевский в своем отчете неоднократно и не случайно
упоминает о себе совместно с Кнорром и наряду со своими приводит
и его мнения — вряд ли можно сомневаться, что между ними были
хорошие отношения. Более того, пересмотров опубликованные, по,
очевидно, забытые статьи того времени, приходится убедиться, что
именно Киорр переслал Гауссу в конце 1840 г., или в самом начале
1841 г., одно яз сочинений Лобачевского по неевклидовой геометрии'
тот же Кнорр, вероятно, передал издательству Финке в Берлине
* Геометрические исследования по теории параллельных линий» Лоба-

ОТЧЕТ Н. И. ЛОБАЧЕВСКОГО О НАБЛЮДЕНИЯХ ЗАТМЕНИЯ
427
•чѳвского. Впрочем, сам Кнорр так и не понял значения неевклидовой
геометрии Лобачевского.
Мы приводим ниже1) еще некоторые подробности об Э. А. Кнорре,
чтобы оживить забытый облик спутника Лобачевского по доездке
в Пензу на солнечное затмение 1842 года.
Описав кратко приезд в Цензу и перечислив взятые в экспедицию
инструменты, Лобачевский останавливается на предполагавшихся
фотометрических измерениях постепенного потемнения во время затмения,
а также сообщает о наблюдениях Ляпунова, сделанных для
определения географической широты и долготы временной обсерватории
в Пензе. ТІо этим результатам приходится заключить, что долгота
Пензы была получена ненадежно.
Инструментальное оборудование Казанской обсерватории в 1842 г.
уже нельзя было назвать бедным (как во время Литтроиа), но в нем
было слабое место — имелось только два хронометра карманного типа.
В поездку был взят один из них, и он останавливался как по дороге
в Пензу, так и обратно. Поэтому нельзя было определить долготу
Пѳнаы перевозкой хронометра из Казани, как это обычно делали в то
время.
В следующем разделе отчета, после краткого сообщения о
пребывании в Пензе до затмения и приготовлений к наблюдениям,
приводятся результаты наблюдений Ляпунова вал моментами начала и
конца полной фазы затмения.
Далее идет выразительное и художественное описание картины
самого затмения и сопровождавших его обстоятельств. Затем
Лобачевский подробнее останавливается на виденной им и Кноррон
солнечной корове (в отчете нет никаких упоминаний, видел ли корову
Ляпунов) на заре у горизонта и делает некоторые замечания о темноте
во время полного затмения и о видимости звезд. После этого сообщается
о наблюдениях Кнорра над поляризацией короны и неба и ставится
основной вопрос всего отчета: «Но как истолковать происхождение
светлого кольца вокруг Солнца? Составляется ли венеи этот собственно
вокруг Солнпа, или вокруг Луны, или гораздо ближе к нам, в нашей
атмосфере?»*). Лобачевский отмечает, что первый опыт еі-о отчета
сгорел 24 августа 1842 г., но что он может зато воспользоваться
дошедшими до него сведениями о наблюдениях затмения, и заключает:
«Я намерен здесь рассмотреть вое предположения, какие можно бы
сделать о происхождении венца вокруг Луны во времн
затмения» в).
*) В примечания (5) на стр. 457 наст, тома.
*) Стр. 439 наст, той»,
3) Там же.

428
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
Сперва Лобачевский подробно обсуждает предположение, что вен ей
(корона) принадлежит самому Солнцу (как это и есть в
действительности). Правильное мнение о существовании атмосферы у Солнпа
сочетается в тексте с теорией Солнца Гѳршеля, по которой Солнце —
твердое и темное тело, наподобие планет, окруженное светящейся
оболочкой облаков. Здесь Лобачевский только разделяет общепринятое
в то время представление о Солнце.
Араго, имевший большое влияние на оовременную ему наукут
незадолго до смерти (1853 г.) писал в «Популярной астрономии»:
«... если спросят: могут ли на Солнце существовать обитателя,
организованные подобно жителям Земли, то я немедля дам
утвердительный ответ. Существование на Солнце темного центрального ядра,
окруженного непрозрачною атмосферою, за которого находится
светоносная атмосфера, отнюдь не противоречит подобному
предположению» 1),
Этот отрывок наглядно показывает, в каком состоянии находились
знания о Солнце до изобретения спектрального анализа и до
установления в финике неба важнейших следствий закона сохранения
энергии.
По расчету Пулье, на мемуар которого Лобачевский ссылается
немного далее, температура поверхности Солнца составляет 1761°С,
что гораздо ниже ее действительного значения; если бы последнее
было известно, теория Гершеля должна была бы сразу рухнуть.
Температура Солнца может быть выведена многими способами, в том числе
и на основании измерения значения солнечной постоянной (г. е.
количества тепла, получаемого аа минуту времени на один квадратный
сантиметр поверхности, поставленной за пределами атмосферы
перпендикулярно к солнечным лучам). Именно так поступил Пулье, причем
его измерения дали уже довольно близкое к истине значение
солнечной постоянной, но он пользовался неверным законом излучения.
Выведенная по закону излучения Стефана температура Солнца
равна приблизит ель цо 5750° от абсолютного пуля, или около
5500°С. По другим способам температура Солнца выходит немного
выше.
Изложив общие соображений об атмосферах небесных тел,
Лобачевский переходит к опенке высоты земной атмосферы и температуры
мирового пространства, делая различные предположения об убывании
температуры с высотой над земной поверхностью и ссылаясь на
измерения температуры во время полета Гей-Лгассака и на работы Фурье
и Пулье. После этого Лобачевский заключает, что наблюдавшиеся во-
]) Араго — Общепонятная астрономия, перев. Хотинского, т. 2, 1861, стр. 139.

ОТЧЕТ Н. И. ЛОБАЧЕВСКОГО О НАБЛЮДЕНИЯХ ЗАТМЕНИЯ
129
время затмѳння 1842 года протуберанцы не могут быть солнечными
тора мв.
Лобачевский полагает, что корону нельзя считать за «вторую
солнечную атмосферу, кроме той, которая нас освещает» ') (г. ѳ. фотосфера
Солнца). С одной стороны, атмосфера Солнца должна быть, при
наблюденном протяжении короны, весьма сплюснута к полюсам Солнца (этот
вывод нѳ подтверждазтся расчетом, см. примечание [85] на стр. 467—4G8).
С другой стороны, наблюдения затмения в разных места* дали много
отличий в форме короны и в расположении ее лучей. В таком случае
пришлось бы считать, что «тонкое вещество, раз отделившись от Солнпа,
движется с чрезвычайной скоростию, повинуясь отталкивающей силе.
Это бы значило пронимать Солнце за большую комету, окруженную
весьма пространной атмосферой»г). Но и это предположение
Лобачевский отвергает, сопоставляя наблюдения короны во время многих
полных затмений Солнпа.
Заметив, что «вокруг Луны атмосфера, если существует, должна
быть ничтожная, которая не может быть причиною приметных
явлений»8), Лобачевский исследует, возможно ли объяснить корону диф-
■фракцией света («погибанием лучей») близ лунной поверхности. Он
приводит результаты опытов над диф фракцией солнечного света
в условиях искусственного солнечного затмения. При этом Лобачев-
«кий сперва исходит из «теории вытекания» (эмиссионной теории)
■свет» Ньютона и заключает, при помощи остроумных доводов
(привлекая и наблюдения покрытий звезд Лукой), что таким способом нельзя
объяснить солнечную корону. Но к такому же заключению приводит
его и рассуждение с точки зрения волновой теории Декарта, Гюйгенса
и Эйлера, развитой Юнгом и Френелем.
Велед за этим Лобачевский ставит высокие требования к волновоЧ
-теории света и считает, что она им не удовлетворяет. Наряду с
замечаниями о теории света Коши, здесь особенно следует выделить мысль
об универсальности в взаимной овяаіі сил притяжения и отталкивания;
всестороннее развитие ѳтой мысли находим в «Диалектике природы»
Энгельса (см. примечание [6S] на стр. 480). Лобачевский характеризует
формальный характер волновой теория того времени н следующих
оловах: «Говорить о волнах, значит основывать все суждение на том,
что в строгом смысле не существует, подобно тому как мы говорим
о линиях и поверхностях, тогда как в природе находятся только тела.
Теория волнений представляет верно некоторые законы в явлениях
света, но на дает еще понятия, в чем существенность заключается»*).
1) Стр. 442 васт. тома.
2) Стр. 44а наст. тома.
3) Стр. 44а паст. томя.
*) Ctji- 449 каст. токв.

430
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
Это отношение Лобачевского к волновой теория интересно для нас
тем, что оно было высказано в такую эпоху, когда волновая теория
света праздновала наибольшие успехи, а эмиссионная теория была
оставлена всеми виднейшими физиками.
Лобачевский сообщает замечание Кнорра, «что нет еще достаточной
причины вооружаться против теории Ньютона, так же как
неблагоразумно было бы не пользоваться преимуществом другой системы» 1)
(волновой теории), и показывает, к&к можно было бы построить
объединение обеих теорий для объяснения всех явлений света. Акад. С. И.
Вавилов подчеркивал, что такое понимание света — как истечения
световых частиц, сопровождающегося волновыми процессами,—было иногда
свойственно Ньютону.
С. И, Вавилов пишет: «К Ньютоновой попытке соединения теории
истечения и во л ново» теории физика все же время от времени
возвращается, забывая при этом о первоисточнике. В 1Ѳ42 г. Е. И.
Лобачевский попытался, например, так соединить эмиссионную и волновую
теории...» (далее следует цитата из отчета Лобачевского, и никого
другого С. И. Вавилов здесь не упоминает)а).
Лобачевский затем приводит свое мнение, что ни изгибание света
около Лупы, ни диффракция не в состоянии произвести корону (это
тем более верно, что вследствие больших размеров Луны никаких
заметных диффракционных явлений при солнечных затмениях вообще
не будет). Сообщив о наблюдениях над температурой воздуха во время
затмения, он пишет, что на образование кольца вокруг Луны можно
подозревать большое влияние воздуха. В пользу этого предположения
приводятся разные доводы, в том числе из области фотометрии, но
ни на одном из них Лобачевский не настанваѳт.
Выше уже было упомянуто, что истинная природа солнечной
короны выяснилась много позже 1842 г.; это было достигнуто новыми
методами фотографии и спектроскопии8).
J) Стр. 440 наст. тома.
S) Акад. С. И. Вавилов- Исаак Ньютон, 2-е над., изд. АН СССР, 1845,
етр. 78—79.
я) В соответствии с современными взглядами, нороной можно назвать самые
внешние слои атмосферы Солнца. Условно ее можно разделить на две части —
внутреннюю и внешнюю корону. Внутренняя корона, более яркан, окружает во
время затмения Луну кольцом шпрнвоіі в несколько мннут дуги; в настоящее
время возможны наблюдения внутренней коровы и вне затмений Солнца.
Внешняя корона значительно шире н слабее внутренней и на своей границе незаметно
переходит в фон неба. Дли вее характерно лучистое строение, и значительную
долю света она получает за счет отражения свата от пылевьтс частиц,
движущихся в соседстве с Солнцем; именно поэтому спектр внешней короны является
обычным спектром Соявца. После классических исследований А. П. Ганского
стало несомненным, что корона не обладает шаровой формой; изменения формы

ОТЧЕТ Н. И. ЛОБАЧЕВСКОГО О НАБЛЮДЕНИЯХ ЗАТМЕНИЯ 431
В заключение отчета о затмении Лобачевский приводит результаты,
магнитных наблюдений в Пенае по сравнению с Казанью, делает не-
сколько замечаний о климате в связи с садоводством и, наковегі,
приводит мысль Кнорра об образовании рек, — мысль для того времени
замечательную и предвосхищающую один иа возможных способов
образования речных долин по В. В. Докучаеву,
Этот обзор содержании сочинения Н. И, Лобачевского о затмении
1842 г. в некоторой мере показывает, какое богатство и разнообразие
идей сумел развернуть Лобачевский по поводу виденного им
величественного явления природы. Тщетно стали бы мы искать этому
параллель в отчетах других наблюдателей, которые, за немногими
исключениями, ограничивались отметкой моментов фаз затмения и голым
описанием того, что они видели, или думали, что видели, подвергаясь
подчас самым странным обманам зрения.
По некоторым намекам текста можно предполагать, что
Лобачевский думал позже вернуться к затронутым им общим вопросам физики
и астрономии и разработать их подробнее, ибо ѳти вопросы, повиди-
лгому, глубоко интересовали его в зрелом возрасте, когда он писал
отчет о затмении. Многое выражено им весьма кратко. Чтобы дать-
возможность оценить с исторической точки зрения взгляды и
суждения Лобачевского, высказанные только в атом сочинении, а иногда
и просто понять их, в примечаниях к отчету даны довольно
обстоятельные пояснения (относящиеся, преимущественно, к истории науки),
приведены питаты из многих авторов, упоминаемых Лобачевским,
собраны подробные литературные указания. В виде приложения дан
(с некоторыми примечаниями) текст заметки о затмении, появившейся
10 июля 1842 г. в М 2S «Прибавлений к Пензенским губернским
ведомостям» и почти несомненно написанной самим Лобачевским1).
короны связаны с однввядцатилетяии циклом изменения солнечной
деятельности.
Многие проблемы, связанные с солнечной к-ороаой, и до сих пор представляют
значительные трудности. Так, ваприыер, общая масса вещества короны в тысячи
рва меньше массы земной атмосферы; тем не менее, корова простирается на
несколько радиусов Сеянца, После того как в 1839—1941 гг. был расшифрован
спектр коровы, оказалось, что яркие линии коровального спектра соответствуют
запрещенным переходам с одного энергетического уровня на другой у высоко
ионизированных атомов железа, никеля и т. д, Температура короны дол;ква быть
весьма высока, порядка миллиона градусов. По мнению И. С. Шкловского, в
короне нет так называемого лучистого равновесия и в ней существуют большие
отклонения от термодинамического равновесия. И. С. Шкловский полагает, что
высокая температура короны может быть объяснена джоулевьш теалом,
выделяющимся благодаря наличию слабых электрических нолей.
і( См. стр. *85 наст, тома, приложение 1.

432
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
Предпринятое Н. И. Лобачевским, Э. А. Кморром и М. В.
Ляпуновым первое путешествие ученых Казанского университета для
наблюдения полного затмения Солнца положило начало традиция,
которая далее не прерывалась до нашего времени. Экспедиции казанских
астрономов — при участии иногда и фиеиков (проф. Д. А. Гольдгам-
мер), и математиков (проф. А. Ф. Попов) — на полные солнечные
затмения 1851, 1887, 18Ѳ6, 1914, 1936, 1941 и 1945 гг. дали много
интересного и ценного для науки. Неразрывная нить ввязывает
Н. И. Лобачевского с настоящим и будущим советской астрономии.

ПОЛНОЕ ЗАТШіНІЕ СОЛНЦА
ВЫГЕИЗЪ 28 ІЮНЯ 1842 ГОДА.
(Ошчвтя Орд. Проф. Аобачевышо.)
Полное солнечное затиівіс по справедливости назваться
мнжсі-f. явлеиіега примечательным» я р-йдкнит,. Ееів коку
лопаюсь разъ аадѣіъ его въ своей жвтв, то конечно в*
лруіѵй уже не случится, развѣ захотѣд-* бы переіхать для
того весьма большое разстояш'е. Это мжіше ее должно
казаться преувелкченвыігь, если прнбавяігь къ тону пеобхо-
лнчость услонл і чтобы небо для нЁста вабдюдеша было
бсэобдачнмнъ. Вогъ почему полное солнечное затагішіа
почитается ве во всѣхъ подробностохъ еще до сяхтѵ яоръ
ііклѣдоваігнмігь. Въ особенности фшвкъ желает* слышать
удоплетіюрнтельвые ответы на мвогів вопросы: охлажденіе
въ воздугЬ, теплота солнечвых/ь лучей, постепенность онра-
ченія, свѣтъ прямой, отраженной, погвбь лучей вокруг»
лункой поверхности. Астровоѵъ дорожить своиия наблюдении»
\ яъ ахонъ случаѣ, какъ ветртлею двугь главных.!, для насъ
I свѣгиль аа небѣ, которых* пути до тЬхъ пор* иаслѣдовалъ
Книжка Ш. 1843 >. t
Первая страшит оригинального ллдашія сочинения
вПо.тное ялтирнпе ооляця ч Прияе Jt> июня Н42 годіі-ч
51-я іір. Ш книжки -.Ученых ашшиок Кагсанскпги уыииеуентета" an 184.'.! г.).
і; стр. 433.

ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
В ПЕНЗЕ 26 НЮНЯ 1842 ГОДА
щ || * Полное солнечное затмение по справедливости назваться может
явлением примечательным и редким. Если кому довелось раз
видеть его в своей жизни, то конечно в другой уже не случится,
разве захотел бы переехать для того весьма большое расстояние.
Это мнение не должно казаться преувеличенным, если прибавим
к тому необходимость условия, чтобы небо для места наблюдения
было безоблачным. Вот почему полное солнечное затмение
почитается не во всех подробностях еще до сих пор исследованным.
В особенности физик желает слышать удовлетворительные ответы
на многие вопросы: охлаждение в воздухе, теплота солнечных
лучей, постепенность омрачения, свет прямой, отраженный, погибь *
лучей вокруг лунной поверхности. Астроном дорожит своими
наблюдениями в этом случае, как встречею двух главных для нас
si светил на небе, которых пути до тех пор исследовал | он отдельно ['].
Наконец любопытно для каждого видеть, как отсутствием света
внезапно среди дня бывает поражено в чувствах своих все то, что
живет одушевленное в природе. Г. Штруве [!]° представлял
Академии наук отправить для наблюдений в Дубно, Чернигов,
Курск и Пензу 2. В последний из этих городов, тоже на
центральной черте затмения, предлагал он ехать Г. Симонову, с
инструментами Казанской обсерватории [8]. Готовясь тогда к отъезду за
границу, Г. Симонов принужден был передать поручение Г. Астро-
* После названия сочиненна в оригинале напечатано: {Отчет, Орд. Проф.
Лобачевского.). Сы. фотоснимок, помещенный перед этой страницей.
* Изгибание.
э Лобачевский в отчета о затмении писал фамилию директора Пулковской
обсерватории В. Я. Струве в согласии с ее произношением по- ненецки — Штруве',
однако в предписании Ляпунову 21 мая 1843 г. он пишет «Струве» (см, М о д з а-
п е в с и. и Н, стр. 439).
9 Фраза остается незаконченной.
28 Зап. ііяаа. II. И. ЛобачевсииН. т. V,

434:
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
ному наблюдателю Ляпунову [*], к которому присоединились
Г. Профессор физики Кнорр [в] и я, желая воспользоваться таким
случаем для наблюдений физических и чтоб удовлетворить
собственное любопытство [*]. Г. Ляпунов отправился ранее нас в Пензу 10,
я с Проф. Кнорром 20 Июня. Инструменты положены были для
безопасности в отдельном устроенном нарочно возке: труба
прохождений, ахроматическая большая труба, две малых
ахроматических труб, секстант с искусственным горизонтом, хронометр Брѳге,
магнитный инклинаторий и деклинаторий Гамбе, качательный
магнитный снаряд, нагревательный снаряд Пулье, психрометр
Аугуста, барометр, небесный глобус и хронометр Бреге с меткой
(a pointage) ["].
Нам желательно было с Г. Кнорром наблюдать постепенность
темноты и соединенного с ней охлаждения, как в атмосфере, так
и в самых солнечных лучах *. Определять эту постепенность чрезвы-
>і чайно затруднительно. | Все до сих пор известные способы
фотометрических измерений весьма недостаточны, в особенности тем,
что не могут служить для наблюдений над явлениями мгновенными.
Г. Штруве предлагал замечать, как будут показываться звезды
различной величины. Соображаясь с его желанием, взяли мы с собой
небесный глобус, чтобы заранее познакомиться с местами на небе,
где во время затмения должно было ждвть появления планет и
звезд. Отказаться совсем от этого рода наблюдении мы не хотели,
хотя не надеялись, чтобы невольным образом развлеченное
внимание могло дозволить нам улавливать с верности» те мгновения,
когда звезды там и сям на небе покажутся. Появление звезд не
только зависит от их величины, но дадее от их возвышения над
горизонтом, и наконец от света постороннего, который во время
затмения бывает разлит весьма неровно в атмосфере. Мы с Г. Кнорром
придумывали новые фотометрические способы, но, к сожалению,
не могли достигнуть вполне желаемой дели. Сначала надеялись,
что можно будет хорошо судить об освещении по ясности в кругах,
начерченных на белой бумаге и разделенных черными вырезками
различной меры [8]. Опыт показал, что ясность в разделении кругов
далеко не отвечает той постепенности, в какой свет уменьшается.
То-есть повижеяие температуры в тени и на солнце.

Н. И. ЛОБАЧЕВСКИЙ —«ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА» 435
Я предложил еще составить снаряд из полупрозрачных пластинок,
которых бы число, как скоро произведет уже совершенную темноту,
могло служить мерой освещения. В этом способе также заключался
свой недостаток: свет, поляризуясь в первых пластинках, приобре-
я тал способность проходить легче сквозь остальные. К тому же
трудно сделать такой снаряд вместе ручным, складным и
непроницаемым для постороннего света. Наконец в том и другом
способе, ко всем сказанным уже недостаткам еще присоединяется
главный тот, что глаз нащ, сначала ничего не примечая в темноте,
скоро потом в состоянии бывает уже видеть и самый слабый свет [в].
Г. Ляпунов, прибыв 15 Июня в Пензу, выбрал удобное место
для временной обсерватории, где и занимался предварительными
наблюдениями для верной установки своих инструментов, а потом
определением географического положения. Пасмурная погода
дозволила ему не прежде 21 испытать ход хронометра и поставить
приблизительно трубу прохождений. С 21 по 28 продолжал он
наблюдения соответственных высот и над прохождением звезд чрез
полудѳнник. После чего с верностию можно было полагаться на
хронометр, который однако ж к сожалению показывал истинное
время только для Пензы, потому что раз остановился на пути туда,
В другой на возвратном до Казани [|0]. Широта места вычислена
53°10'30",5 из наблюдений с 27 Июня до 4 Июля, по способу
Г. Бесселя, над звездами первого вертикального круга [и]. Из
прохождений луны чрез полуденник найдена долгота Пензы от
Берлина 2Ч6 50 .' из затмений спутников Юпитера, первого — 2Ч6 20 ,
второго — 2*6 30 ; последнее наблюдение сомнительно.
Довольствуясь первым и прибавляя поправку 14",5, находим .долготу
ti самого города Пензы от | Берлина 2*6 34",7; от Казани к западу
16'18*,6 во времени; 4°5' в градусах экватора J1*].
По приезде вечером 23 Июня, на другой день утром поспешили
мы с Г. Кнорром отправиться в Императорский сад,
расположенный под самым городом. Здесь взгляд на временную
астрономическую обсерваторию приятно нас поразил и выбором открытого
возвышенного места и постройкой удобной, достаточной, под
защитой от солнечных лучей и непогоды. Обязаны свидетельствовать
нашу благодарность за ревностное содействие Г. Директору сада
Магзигу, так же как и за внимание Г. Гражданского Губернатора
28*

436 ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
Панчулидзева, по приказанию которого градская полиция охраняла
целость инструментов и ненарушимое спокойствие наблюдателей
в их занятиях. Обсерватория была даже местом жительства для
Г. Ляпунова; а нас пригласил Г. Магзиг в свой дом, которым
предложением по доброте хозяина мы возпользовалиеь [18].
В приготовлениях и совещаниях скоро протекли два дня, хотя
с нетерпением ожидали мы видеть солнечное затмение. Наконец
утром 26 Июня проснулись мы весьма рано, но с грустию при
виде покрытого неба, пасмурной и дождливой погоды. Несмотря
на то собрались в обсерваторию, поставили зрительные трубы и
сидели ничего не делая. Уже прошло несколько минут после
назначенного времени для начала, как сквозь туман облаков нако-
ІБ нец ] ущерб солнца показался. Г. Ляпунов измерял секстантом
расстояния между остреями серпа до начала и после затмения
полного; замечал также прохождение на микрометре двух краев.
Не льзя много полагаться на те и другие наблюдения как но
трудности наблюдений этого рода, так и потому, что туман мешал
ясности. Микрометрические измерения дают начало затмения
в среднем Пензинеком времени 9*9 24 ,3; измерения секстантом —
94lo'47w,7. Начало а конец частного затмения не были совсем видны;
начало полного затмения по хронометру 942 15 ,4; конец полного
затмения — 9 15 14 *,- а с присоединением поправки среднее время
для Пензы будет при начале 9Ч9 22 ,4; при конце 9'112 21 ;
следовательно, полное затмение продолжалось 2'58",6; средина
затмения в 9"l0'5l",7 ["].
Астрономические наблюдения делал Г. Ляпунов, которому
помощником был студент Магзиг. Мы с Г. Кнорром оставили для
себя другого рода занятие: наше внимание обращено было на самое
явление, по истине великолепное, хотя многое скрыто было для
наших глаз под завесой облаков. На месте дневното светила, когда
последний его луч исчез, явился темный круг; как бы само
солнце, но теперь уже черное стояло на небе. В трепетном ожидании
чего-то неизвестного, с торопливым желанием все видеть, с
опасением чего-нибудь не заметить, стояли мы, зрители, среди
призраков во мраке, с обращенным взором к потухшему солнцу, как
* Очевидная ошибка в одном из двух последних-мочентов. См. об этом в ори-
лѳчаним [Ч].

Н. И. ЛОВАЧКВСКИЙ —«ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА» 437
!7 обворо|жеиные, постигнутые страхом и беспокойством,
вдохновенные чувством возвышенным и торжественным. С этим душевным
волнением так трудно было внимательно наблюдать и замеченное
сохранить в памяти, что, возвратившись домой, мы находили нужным
в разговоре нашем друг друга поверять, так-ли и то-ли мы все*
видели. Полное затмение поражает сильно всех животных. Птиц
оно тревожит в особенности: из лесу поднялись с криком стаи
галок и грачей, взвились на воздух и потом опять спустились на
деревья. Перед нами невдалеке паслось стадо, пригнатое сюда
к этому времени по приказанию Г. Магзига. За криком птиц вскоре
послышалось мычанье коров и блеяние овец, которые все пустились
бежать по дороге домой. На Пензинской торговой площади, где
продолжалась ярмарка, собралось много народа. Там случилось
в это время быть одному из моих знакомых, Г. Каховскому [1В].
Он рассказывал, что солнечное затмение в начале заставило народ
толковать и беспокоиться; но когда солнце совсем закрылось, то
послышались голоса, вероятно городских жителей: ах, что-то
делается дома; ах, пойти-было домой! С мыслей о преставлении
света люди пали на колена, с воплем и молитвой ожидали над
собой страшного суда. Но [первый проскользнувший луч солнца
прогнал и мрак в природе и страх в сердце людей. Г. Каховский
любовался, как черная тень прибежала по равнине, по горам, и
скрылась потом за лесом. Переход от темноты к свету казался
>8 разительнее, чем от света к темноте. В помрачешш [ сохранялась
какая-то постепенность до последнего мгновения, тогда как первый
вырвавшийся луч из за лупы вдруг переменил ночь на день;
черная завеса вдруг упала. Когда затмение оканчивалось, Г.
Губернатор, который был все время с нами близь обсерватории, подозвал
к себе крестьян. На вопрос, что думали, они отвечали: ничего не
думали, но мы перепугались.
В продолжении полного затмения темный круг пуны был
окружен светлым широким венцом. По словам Г. Ішорра, со
вступлением полного затмения светлый венец: несколько медлил
показываться. Сначала был оп растянут в две стороны горизонтально.
* В оригинале стоит ес§. По лпеншо Л. Б. Модэалсвекого здесь нужно
читать-— erf, а не все (Иодзалевский, стр. 465).

438 ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
может быть случайным сгущением облаков, хотя случайность эта
теряет что-нибудь из своей вероятности, как скоро направление
было не другое, но именно горизонтальное [16]. Потом светлое
пятно делалось почти треугольным, уменьшалось, округлилось,
опять увеличилось и было под конец по крайней мере вдвое шире
против солнца. С моим товарищем согласны мы в том, что свет
на кольце казался менее близь лунного края, потом сгущался и
затем постепенно слабел и терялся на небе. Ничего не могли мы
заметить особенного местами j17]. Свет на венце был сплошным и
с пепельным оттенком во всех направлениях, как бы свет дневной,
проникнутый сквозь отверстии на своде, в пространство
наполненное дымом. Между тем заря, занявшись от горизонта, разливала
is по всему небу хотя чистый, но желтоватый свет, который |
отражался слабо вокруг нас на всех предметах. Трудно судить, как
велика была темнота; но мы друг друга видели хорошо. Студент
Магзиг не мог читать книгу. Саженях в 50 от нас, в стаде заметил
я ' светлую шерсть, но не в состоянии был различить, на какой
скотине. Г. Кнорр признал пастуха только по движению и по
очертанию. Тень от предметов нигде на земле не падала. Свет
следовательно со всех сторон приходил равно сильный, от кольца
вокруг луны, от зари по горизонту, от всех частей неба. Г. учитель
Пензенской гимназии Трофимов заметил звезду в самом зените.
Б это время должна была действительно тут проходить Вега. На
возвратном пути в Казань сказывали нам многие, что звезды
видели, даже в городе Буинеке, где затмение не было полное, но
серп оставался едва заметным [1Н].
Г. Кнорр, испытывая в поляр изоекоп, нашел, что свет кольца
вокруг луны не был поляризованный [і0], тогда как поляризование
во всей остальной части неба казалось весьма сильное. Этот
желтоватый поляризованный свет * был отраженный свет на верхние
слои воздуха земной поверхности, освещенной вне лунной тепи.
Б справедливости такого толкования ие льзя сомневаться, когда
свет от обитаемой нами планеты, пройдя все расстояние до своего
спутника, падая на темную его половину, потом отражаясь отсюда,
приходит снова к нам и дает луне пепельный цвет, видимый близь
Свет кольца аари.

. Н. И. ЛОБАЧЕВСКИЙ— «ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА. 439
тонкого серпа в первой четверти. Надобно заметить, что свет от
«о земли много теіряетея, потухает в атмосфере, прежде нежели
проникает в пустое пространство; за всем тем ыы светим на нашу
спутницу, может быть, еще более, нежели она светит на нас в ясные
лунные ночи. И так понятно, что во время затмения полным
отражением лучей па верхних слоях воздуха приходит к нам
довольно свету, чтобы составить эту зарю, которую мы видели
разлитой по всему небу. Но как истолковать происхождение
светлого кольца вокруг солнца? Составляется ли вѳнец этот собственно
■вокруг солнца, или вокруг луны, или гораздо ближе к нам, в нашей
атмосфере? Бот вопросы, решение которых представляет уже
большие затруднения. В Заседании Парижской академии наук, где
присутствовал тогда ваш Профессор астрономии Г. Симонов,
Г. Драго рассказ свой о затмении нынешнего года, которое
наблюдал он сам в Нерпиньяне, заключил откровенным сознанием, что
светлый венец в все видимые в нем явления для него совершенно
непонятны Р°].
* Теперь я принимаюсь уже в другой раз за свой отчет
о поездке в Пензу. Первый мой опыт сделался добычею
пламени в несчастный день для Казани 24 Августа [и]. По крайней
мере вторичный труд мой вознаграждается тем, что могу
пользоваться сведениями, которые между тем до меня дошли в описании
всех наблюдений над полным солнечным затмением нынешнего
года. Я намерен здесь рассмотреть все предположения, какие
можно бы сделать о происхождении веица вокруг луны во время
затмения.
сі | Еще Буге заметил, что солнце в середине светлее, чем на краях,
тогда как напротив здесь должен бы свет быть сильнее, на круглой
поверхности, сжатой для нашего глаза. По своим измерениям нашел
он от края на расстоянии в одну четверть солнечного
полупоперечника свет слабее, нежели к середине, в содержании чисел 35
к 48 [23]. Лаплас заключил отсюда, что солнце должно быть
окружено атмосферой, которая свет поглощает, и так много, что без
этой атмосферы солнце на нас светило бы сильнее в 12 раз [**].
Мы с Г. Кнорром, наблюдая ход солнечного затмения, не могли
удержаться, чтобы друг другу не заметить, сколько резким казался
* Здесь абэагс сделан редакцией-, в тексте Лобачевского его нет.

440
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА.
край луны, тогда как солнечный ограничивается чертой весьма
нежной, хотя при всем том явственной и правильно закругленной.
Это различие в двух пограничных чертах особенно противупола-
галось в остреях серпа. И так надобно думать, что свет выходит
не из одной поверхности, но рождается вместе sa какой-то глубине.
Впрочем, нет еще необходимости, чтоб этот свет брал свое начало
от солнечного ядра, потом большею частию потухал, проникая
сквозь атмосферу. Довольно, что атмосфера вокруг солнца
существует, что свет происходит в ней к ее пределам, как явление
теплотвора в грубом его переходе из средины, где внутренним
равновесием он удерживался, к пустому пространству, которое не
противупоставляет уже никакого сопротивления. Эта мысль
подтверждает и то мнение Г. Гершеля, что солнце само должно быть
а темным, что светит только вокруг него тонкая | оболочка, что по
временам и местами эта оболочка, разрежаясь, бывает усеяна
черными пятнами. Это значит отверстиями, сквозь которые мы видим
темное солнечное ядро [**].
Атмосферы надобно почитать собственным произведением
мировых тел. Если б они сгущались из той средины, в которой наша
солнечная система двигается, тогда бы плотность их была в
содержании* к массе тел, чего не находим однако ж но сравнению земли
с луною [м]. Надобно полагать также, 'іто атмосферы составляются
из жидкостей воздухообразных*. Мы знаем, что жидкости текучие
не могут существовать без наружного давления, следовательно
должны быть покрываемы по крайней мере тем паром, который
от них самих отделяется. Правда, что вокруг луны заметной
атмосферы нет, но может быть на ней разлиты такие жидкости, которые
дают только чрезвычайно тонкие лары. Вокруг солнца, при той
сильной теплоте, которая в нем сохраняется, без сомнения
атмосфера должна быть воздухообразная, подобно как и вокруг
обитаемой нами земли. Г. Араго даже доказал, что свет от солнца
именно с теми свойствами, какие могут принадлежать свету
воздухообразных жидких тел [!Ь]. Трудно судить о пределах солнечной
атмосферы, когда ничего верного не можем даже сказать, как
далеко простирается воздух над поверхности») земли. Если при-
* Т. е. в отношении
* Жидкости воздухообразные — газы.

Н. И. ЛОБАЧЕВСКИЙ —«ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА» *41
пимаем в основание, что граница там устанавливается, где тяжесть
•> уравновешивается с упругостию*, то находим, ] что высота нашей
атмосферы должна бы в пять раз быть более земного
полупоперечника, следовательно восходит до 32 060 верст [*7]. Это
чрезвычайно большая высота не подтверждается появлением зари, которая
состоит в освещении верхних слоев нашей атмосферы. Легко понять,
что упругость воздуха должна вместе уменьшаться с температурой,
а следовательно гораздо ближе над поверхностию земли
уравновешиваться с тяжестию. Гѳй-Лгаесак в своем аеростатическом
путешествии нашел, что температура в воздухе уменьшается одним
градусом сотенного термометра на 175 метров или 82 сажени. Если
так охлаждение продолжается в воздухе до самых его пределов,
то высота атмосферы будет выходить не более сотой части земного
полупоперечника, около 57 верст, а температура должна бы
понижаться до 350 сотенных градусов [2В]. Таким образом уже высота
делается слишком малой, а температура слишком низкой. Другое
предположение, что температура в атмосфере так же уменьшается,
как при нагревании твердых тел, в геометрической прогрессии,
ведет к заключению, что воздух простирается на 30 часть земного
полу поперечника, или на 190 верст, а температура доходит до
200 градусов ниже нуля, — выводы более других вероятные [w].
Г. Пульс недавно предложил теорию, которая во
многих'отношениях оправдывается различными наблюдениями и согласно с которой
температура на пределах нашего воздушного неба должна быть
не выше—144°С [*"]. Фуррье*, неизвестно впрочем в следствие
<і какого рода вычислений, утверждал, что тем|пература пустого
пространства, где двигается наша солнечная система, должна быть
не выше —50° J*1]. Если теперь эти понятия применяем к
солнечной атмосфере, то со всей вероятностиго должны думать, что
вокруг солнда воздухообразная жидкость простирается далеко выше
всех неровностей твердого ядра; что пограничные слои к пустому
пространству, в переходе к весьма низкой температуре,
производят явление света, который начинается па значительной глубине
* Несоыпеяяая ошибка: дзлжно быть «с цоитробеашои силой*. См. прішв-
чютге Р1.
* Так в оригинальном издания. Правильно — Фурье (J. В. Fourier).

442
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
в солнечной атмосфере. Если бы теперь какие нибудь твердые
части выдавались вон ив атой атмосферы, то по свойству таких
тел, остынув в чрезвычайно холодной средине, они казались бы
нам постоянными черными пятнами, которых однако ж на солнце,
кроме подвижных, совсем не примечаем [м]. Если Гг. Тулуаекие
астрономы и Г. Шумахер видели во время последнего полного
затмения светлые, розового цвета возвышения на лунном крае, то
после всего сказанного здесь, трудно согласиться, чтоб эти
возвышения могли быть солнечные горы [*э].
Светлый венец вокруг солнца не льзя почитать за вторую
солнечную атмосферу, кроме той, которая нас освещает; по крайней
мере, если под атмосферой хотим разуметь всегда жидкую средину
вокруг ядра в одинаковом с ним обращатѳльном движении [34].
Б таком случае атмосфера должна представляться сжатой ог
полюсов обращения к своему экватору. Хотя солнечное кольцо, как
ю нам казалось, занимало на небе до 2 градусов в шири) не своей, и
хотя атмосфера при такой обширности может еще держаться
в равновесии, но сжатие должно бы происходить весьма сильное [№].
Между тем оно никем не было замечено, ни в последнем, ни
в прежних солнечных затмениях. Расширение, которое мы видели
в начале, именно потому, что направление было горизонтальное,
скорее щадобно приписать нашей земной атмосфере или
случайному расположению в облаках [•*]. Наконец объяснить надобно те
особые принадлежности*, которые никак не льзя допускать в
составе воздушной атмосферы, потому что производить их обраща-
тельное только движение не может. Рассказ о наблюдениях в этом
отношении весьма разнообразен. В Нарбонѳ * видели на юговосточ-
ной части лунного круга, в пространстве 45 градусов, сноп лучей
неправильно раскинутых. От крайних лучей свет был слабее внутри
снопа, от снопа в обе стороны ровный, но на конце северозападном
выходил конусом, сгущаясь в острее. Г. Профессор Симонов в
заседании Парижской академии наук слышал, как Г. Араго описывал
явление совсем иначе по своему наблюдению. В Перпипьяпе видел
он вокруг солнца светлый венец из лучей прямых и потом загну-
* Смысл таков: наблюденные особенности.
* Так в оригинале. Правильно: лИарбонне».

Н. И. ЛОБАЧЕВСКИЙ —.ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА» 443
тых подобно плицам в колесе Пенселе * [3J]; лучи выходили под
различными углами к еолацу, даже в линиях касательных, и
вообще давали венцу вид многоконечной звезды. В Монпелье также
заметили, что край югозападный и северовосточный светил * сильнее;
что на первом в начале показалась багряная черта, потом на
т север о западном такого же двета возвышение в 45"; | наконец еще
два на востоке е раздвоенной вершиной. Аетроном здесь находил
большое сходство лучистого венца с распущенными по ветру
волосами®. Мы видели в Пензе, как я*сказал уже выше, свет около
солнца в начале растянутый, потом треугольный, наконец ровный
сплошной, или с некоторым разнообразием, от неодинаковой
густоты вероятно в облаках, но без особенных принадлежностей
самому вепцу9. Г. Ляпунов заметил в начале полного затмения
на югозаиадном краю луны небольшое, может быть до I1/: минуты,
возвышение красного цвета, потом недалеко к северу показалось
еще раздвоенное возвышение [**]. Вот это разнообразие,
замеченное с различных мест наблюдения, мудрено толковать, допуская,
что венец производит каким нибудь образом само солпце вокруг
себя. Если бы требовалось объяснить только лучистый неровный
состав вевтца, тогда бы можно было прибегнуть к предположению,
что топкое вещество, раз отделявшись от солнца, двигается
с чрезвычайною скоростию, повинуясь отталкивающей силе. Это
бы значило принимать солнце за большую комету, окруженную
весьма пространной атмосферой. Далеко растянутый хвост комет
на стороне, противоположной от солнца, заставляет думать, что
здесь отделяется вещество, которое солнцем отталкивается. Это
действие солнечных лучей или самого ядра в солнце весьма хорошо
можно видеть, как мне случилось и самому наблюдать в 1832 году,
на комете Энкѳ, которой атмосфера представляет еллипсоид, вытя-
(, нутый прочь от солнца. Подобным образом и в самом | солнце
могут заключаться частички, которые, сделавшись свободными на
поверхности ядра, разлетаются в разные стороны, по различным
* Так в ортігсшаде. Правильно: ІТолоеле.
* Правильнее было бы: «что кран юго-западный и северо-восточный еве/гшш*.
Q См. примечание [Щ.
Э Смысл конца этоіі: фразы таков: « но без особенностей, принадлежащих
самому венцу.. Лобачевскаіі хочет этим отметить, что у солнечного венда не
наблюдалось каких-либо определенных очертаний в целом иди в отдельных частям.

444
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
направлениям, различно сгущенные, е быстротой, где круговое
движение солпца пе может уже быть чувствительным. Это
предположение не льзя допустить однако ж со всей вероятностию, по
причинам, о которых упомянул я выше [30]- Действительно, в таком
случае должно бы, кажется, ожидать гораздо более согласия в
наблюдениях. Мы знаем, что светлые атмосферы вокруг комет от времени
все более и более уменьшаются. Знаменитая комета Галлея, которая
в прежних своих появлениях поражала всех ужасом, расстилая свой
хвост до трети неба, пришЛа к нам в 1835* году, окруженная
светом очень скудным [*°]. Напротив, светлый венѳц вокруг солнца
бывает различной величины, не представляя приметного
постоянного уменьшения. В 1567 году полное солнечное затмение приняли
за кольцообразное: следовательно, кольцо вокруг луны показалось
остатком в солнечном круге. В начале 1605 года видели полное
затмение в продолжение нескольких мгновений, и темный круг
луны казался окруженный светом, который распространялся на
большую часть неба. Плантад и Кляпье рассказывают, что они
видели, в 1706 году, полное солнечное затмение: вокруг луны было
белого цвета кольцо шириной около трех минут, следовательно не
более двенадцатой части лунного поперечника. Галлей описывает
полное затмение 1715 года: за несколько секунд до наступления
• полного затмения луна показалась окруженной ] бледным светом,
может быть шириною в десятую * или двенадцатую часть своего
поперечника. Это же затмение наблюдал Французский академик
Лувиль в Лондоне. Кольцо вокруг луны казалось ему серебристого
■ цвету, гуще к внутреннему краю, слабее к окружности, которая
за всем тем однако ж ограничпвалась чертой определенной. В этом
кольце свет промежутками® был различной густоты. Лувиль
утверждал, что кольцо было одноцентрным с луною; напротив, Маральди
пашсл при затмении 1724 года, что кольцо в начале было шире
к -западу, в конце к востоку. В 1778 году Испанский адмирал
Уллоа наблюдал полное затмение* о котором пишет; кольцо во&руг
луны показалось чрез 5 или ti секунд после начала полного затме-
* В оригинале ошибочно напечатано: 1838.
* В оригинале опжйочпо напечатано: девятую. "У Галлон — десятую; в «Журнале
Министерства Народного Щюевѳщенияв (см. стр. 494 наст, тома) напечатано верно.
ф Очевидно, — промежутками по направлению лучей.

Н. И. ЛОБАЧЕВСКИЙ—«ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА» 445
ния, пропало в такое же время до конца, составляло около шестой
части лунного поперечника, внутри было красноватого, далее
желтоватого, наконец к окружности совершенно белого цвете. По
местам из кольца выходили лучи, длиною в лунный поперечник.
Бовдшчь и Ферре * 1806 года видели полное солнечное затмение
в Америке. Бенец был одноцентрным с луною, 3 минуты в ширину,
перловой белизны; из краев выходили лучи, простираясь градуса
на два [41]. — Те же явления повторялись, следовательно, всякий
раз, но в различном только размере. Если мы видели в Пензе
венец гораздо шире, то нет сомнения, что причиной тому было
пасмурное небо.
Кеплер, рассуждая о затмении 1598 года, светлое кольцо думал
ко объяснить или воспламенением эфира вокруг солнца, | или
преломлением лучей в лунной атмосфере [43]. Первое объяснение не
заключает в себе ничего, кроме понятий неопределенных и
предположений без основания. Второе допускать не льзя потому, что
вокруг луны атмосфера, если существует, должна быть ничтожная,
которая не может быть причиною приметных явлений. В
последствии опыты Фложерга, Делиля и Майера, кажется, наклонили
астрономов более к тому мнению, что кольцо происходит от поги-
бания лучей близ лунной поверхности [43]. Фложерг, подражая
ватмеішю, подвешивал темный шар против солнца, и брошенную
тень принимал на полотно. Когда видимый поперечник шара
составлял 1964",6, то в средине тени появлялась светлая точка,
которая, с приближением полотна, расширялась, и наконец, когда
видимый поперечник гаара доходил уже до 4°4б'54",
распространялась на всю тень слабым полусветом. Поперечник солнца был
вымерен при опытах в 1927",76, почти равный с поперечником
шара в то время, когда свет внутри тени соединяется в одну
точку. Подобное бывает и в солнечном затмении; откуда Фложерг
заключил, что кольцо происходит от лучей, которые, погнувшись
у лунной поверхности, проникают в средину тени. Опыты Делиля
были в том же роде, но явление думал он приписать разнос}'
лучей (irradiation), тогда как оно собственно заключается в поги-
бании света (inflexion). Повторяя опыты фложерга, хотя не делая
Так и оригинале. Прави.тыю: Феррер (Ferrer).

*46
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
самых измерений, мы с Г. Профессором Кнорром нашли то же.
Впрочем, погибание лучей в середину тени физикам известно
то хорошо; но те[перь остается сделать из этого применение к кольцу
в затмении. По теории вытекания (emission) надобно предполагать
действие темных тел на свет только в неприметном расстоянии,
а следовательно луч, погибаясь у поверхности темного тепа, должен
за тем уже продолжать свой путь но прямой линии. Теперь
прямая, от наблюдателя до внешнего края на светлом кольце,
проходит мимо луны на расстоянии но меньшей мере в одну
двенадцатую долю лунного поперечника—расстояние слишком большое,
чтобы здесь могло происходить какое нибудь действие на свет.
Эта теория вытекания, придуманная Невтоном*, предполагает еще
в светлых частичках попеременную наклонность отражаться или
проникать ["]. По такому свойству своему луч может сначала
принимать кривизну темного тела, потом, изгибаясь в противную
сторону, приходить уже к нашему глазу; но в таком случае
последнее направление будет по прямой, которая падает на тсмоое
тело. От этого край, из за которого свет приходит, будет нам
казаться прозрачным или выщербленным в том месте, где светлое
тело начинает скрываться за темным, как это действительно всегда
так и бывает. Бот почему покрытие звезды луною замедляется
до 8-^- секунд времени, в продолжении которого звезда как бы
продолжает уже свое движение ао лунному кругу, или другими
словами, луна в этом месте бывает как бы вырезанной. Это
замедление должно бы составлять около 50" в дуге по наблюдениям
Сежура, Мешеня и Лекселя (Histoire de llAstrxmomie, parDelambre)*,
п тогда как Леменье0 | назначает не более 13" [■<*]. Сжатие в видимой
величине планеты Венеры, когда проходит ова по солнцу,
оказывается еще менее, около 6 секунд {*'], вероятно потому, что
крайние погнутые лучи к средине тени по слабости своей делаются
нечувствительны для глаза при солнечном сиянии. Этой же
причине надобно приписать и все разнообразие в замедлении звезд,
" Фамилия Ныотояа в других местах тевста «Ученых записок» пишется:
Нюток; здесь — исключение.
* Delambre — Histoire de FAstronomie au dixhuitieme віёсіе, 1827 (стр. 718,
731—722).
э Обычно© написание: Лемоны (La Monnier).

Н. И. ЛОБАЧЕВСКИЙ—«ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА» 4*7
емотря по тому, какой величины самая звезда и какая часть луны
бывает освещена. И так от погибания лучей пуна во время
затмения должна быть окружена светом, который, собственно,
представляет не расширение солнечного круга, но сжатие лунного, и
который ни в каком случае не может составлять более -^ лунного
11
поперечника, тогда как его находят от Тч д0 То > а мы в ^ензе
видели сквозь облака приметный свет по крайней мере на 2
градуса по небу [*']. Скажем и то, что погибаниѳ лучей должно бы
давать свет сильнее к наружному краю. Хотя некоторое
послабление* заметил я близ самой луны, но вообще явление происходило
совсем в другом роде.
Переходим теперь к другой теории, Декарта, сильно
поддерживаемой Гугенеом и потом Эйлером, известной под названием
системы волнений (ondnlations), которой физики принуждены были
во всех отношениях дать преимущество, особенно когда Г. Юнг
прибавил к тому перекрестывание лучей (interference) [*!].
Пользуясь этой теорией и с помощию своих новых предположений,
Френель вычислял гиперболическую линию в уклонении света,
п подтвердил эту кривизну действительным измерением, наконец
хотел уже здесь видеть несомнительиое опровержение системы
Нютона ['"]. Не прямое движение света, после того как он прошел
мимо темного края, приличнее называть разЗрасывением (diffraction),
следуя системе волнении, нежели потбапием (inflexion), которое
должно быть постоянным при всяком размере непрозрачного тела,
завися, по теории Нютооа, от действия только в неприметном
расстоянии. Система волнений, с предположением к тому Френеля,
достаточно нам объясняет, каким образом возле пограничной черты
на тени, в обе стороны, ложится кайма Гримальди, где красный
цвет уклоняется всегда менее, следовательно менее покрывается
другими, отчего бывает господствующим, когда тень происходит
от сложного солнечного света [S0J. Нет сомнения, что багряная
черта, которую видели к Монпелье по краю луны, была явлением
в этом роде. Г. Ляпунов в Пензе заметил эту черту даже сквозь
облаков. Покуда не наступало полное затмение, мы с Г. Кнорроы
* В «Ученых записках» стоит вѳ послабление, а поги&тия. В «Журнале
министерства народного просвощепиж (ем. стр. 492 иаст. тома) напечатано — и,
несомненно, правильно—посла&генгк.

448 ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА.
долго любовались яркой красной чертой на солнце воале лунного
края; слабый отблеск виделя также на темной половине к верху [Б1],
Мне кажется более основательным приписывать тому же
разбрасыванию лучей от лунных гор и происхождение тез:
возвышенностей, которые были замечены как бы выдвинутыми из-за луны.
Об них упоминает и Г. Ляпунов, назначая величину до 1-^- минуты,
слишком уже большую для гор на самом солнце, чтоб это
последнее мнение могло казаться сколько нибудь вероятным, тогда как
г1 окрашенная кайма красным | цветом вне теня, брошенной
незначительным возвышением луны, легко может достигать до такого
расширения на расстоянии до нашей земли [6!]. Что же касается
до светлого кольца, то хотя кривизна лучей ж подает с первого
раза повод предполагать здесь именно такое направление, которое
бы свет расширяло для наших глаз вокруг луны, но вникнув,
каким образом это направление должно быть определено, находим,
что кольцо так же мало может быть произведено разбрасыванием,
как и погибанием лучей. Юнг доказал наблюдениями, что кайма
пропадает внутри тени, как скоро другой край темного тела
закрывается; следовательно, для каймы необходимо взаимное действие
двух краев, которые Френель и принимает за место, где начинают
образоваться новые волны. Эти последние волны почитает он
единственной причиной, почему свет распространяется внутри тени,
так что здесь в согласном перекрѳетывании свет усиливается,
в противоположном — уничтожается. Если таким образом цветные
полосы могут образоваться на всяком месте, внутри или вне тени,
то направление света но теории должно быть всегда
перпендикулярно к поверхности составной волны. Возьмем теперь в пример
освещенное место в самой средине тени. Сюда волны приходят
от всех краев одинаково; нормальная линия составной волны
должна, следовательно, быть направлена к центру луны, но не
выходить вон за темный круг. Из других мест внутри тени
нормальные принимают различные направления, которые тем не менее
іі все бея исключения выходить вон из | тени не могут, чтобы
составить потом светлое кольцо вокруг луны [*'].
Систему волнений не льзя справедливо называть теорией, а только
выражением тех явлений, которые желают объяснить. Истинная
теория должна заключаться в одном простом, единственном начало,

Н. И. ЛОБАЧЕВСКИЙ — «ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА» 449
откуда движение берется, как необходимое следствие, со всем
своим разнообразием. Еще Пуассон в письме к Френелю (Annales
de СЬ. et de Ph., 1823, p. 270*) заметил несообразности, как скоро
хотим итти далее тех случаев к которым теория волнений
приспособлена {**]. Говорить о волнах, значит основывать все
суждение на том, что в строгом смысле не существует, подобно тому
как мы говорим о линиях и поверхностях, тогда как в природе
находятся только тела. Теория волнений представляет верно
некоторые законы в явлениях света, но не дает еще понятия, в чем
существенность заключается. То не сомнительно, что пространство
повсюду наполнено центрами, откуда вытекает или сила
притягательная или сила отталкивающая; что центры таким образом
между двух противоположных сил держатся в равновесии; что
нарушение равновесия бывает или причиной изменения
совершенного, или только колебаний внутри тел [й5]. Г. Коти первый
вздумал этим путем идти в изложении теории для света. Однако ж,
предполагая качания для частичек эфира, не принимает в
рассуждение того, как это движение' должно начинаться; почему свет
is пробегая всегда прямую линию, не примечается | более на
пройденном пути, тогда как еще качания должны бы продолжаться?
Г. Копта доказывает эллипсоидное движение частичек в их
качании; затем в трех осях эллипсиса произвольно хочет
допускать две оси для поляр из алии и третью ось для явлений
теплоты [ы].
Г. Профессор Кнорр однажды в разговоре со мной остроумно
заметил, что нет еще достаточной причины вооружаться против
теории Нютона, так же как неблагоразумно было бы не
пользоваться преимуществом другой системы. Можно верным остаться
теории Нютона, прибавя только, что поток эфира, встречая
препятствие на пути, приходит в волнение, подобно тому как вода
в реке встретив плотину, поднимается волной, разделяется на две
струи, между которыми происходит пустота, наконец вода
соединяется снова в общий поток; или подобно воздуху, который
встречая препятствие, также волнуется, разделяется на два потока,
с пустотой между ними; волнение здесь производит иногда звук
* Библиографические данные ом. в примечании [н| на стр. 4Г8.
29 Зав. £823. Н. И. Побачеиоиві, т. V.

460 ПОЛНОЕ ЗА'ГМЕНИЕ СОЛНЦА.
в прежнее течение за пустотой восстановляется. Падение воды
за плотиной и пустота, воздухом оставляемая за стеной, отвечают,
следовательно, брошенной тени позади непрозрачных|тел;
стремление воды или воздуха с двух сторон сливаться вместе
представляет нам уклонение снета к ередине тени. Таким образом две
теории соединяются в одну для толкования всех явлений света ["].
Оставалось бы решить, какою силой в эфире надобно заменить
тяжесть воды или упругость воздуха; при том выбрать эту силу
те так, чтобы са|мая большая часть светлых частичек сохраняла
прямолинейное движение — отличительная принадлежность света.
Этот взгляд приобретает тем более вероятности на своей
стороне, что представляет теорию света с теорией теплоты в
той же тесной связи, в какой находятся самые явления; тогда
как система волнений оставалась без всякого применения ко
всему тому, что мы до сих пор из опытов уже хорошо знаем
о нагревании тел.
Рассуждая во всей обширности, не стесняя себя никакими
предположениями покуда без необходимости, надобно думать, что
частички света в своем источнике получают как погонное, так
и качательное движение. Первое можно почитать причиною как
освещения, так и нагревания, разумея здесь динамическое действие
соединенным с накоплением теплотвора от проникнутых частичек
внутрь тела. Наконец в карательном движении можем отыскивать
происхождение цветов и всех явлений поляризованного света [ts].
Я не берусь еще на таких новых началах построить всю теорию,
но последнее солнечное затмение, которого был я свидетелем,,
подало мне повод к этим замечаниям, тем более что почел своей
обязанности!» сказать что-нибудь о светлом кольце вокруг луны.
Мое мнение таково, что ни погибание (inflexion), ян разбрасывание
лучей (diffraction) не в состоянии производить подобное явление.
Погибание лучей уменьшает во время затмения видимый
поперечник луны, следовательно еолнце должно выставляться кольцом,
гі но кольцом тонким, не шире | нескольких секунд, как должно
заключать по замедлению в покрытии звезд, где величину поги-
бания наблюдают вполне. Разбрасывание лучей, напротив, нисколько
не участвует в образовании кольца, и даже не бывает
чувствительно в средине тени, где бы должно обнаруживаться красным

Н. И. ЛОБАЧЕВСКИЙ — «ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА»
451
цветом, как таким, который в кайме Гримальди другими не
покрывается. Повторив опыт Фпожѳрга*, могу сказать только, что хотя
видел я свет вокруг темного края, но свет в том же роде, как
видим его близ непрозрачных тел, куда бы к освещенной части
неба ни обращались. На расстоянии, где темный шар одинаковой
величины с солнцем, красный свет появляется в середине, потом
с уменьшением расстояния хотя расширяется по всему темному
кругу, но вон не выходит и кольца не составляет.
На образование кольца вокруг луны можно подозревать
большое влияние воздуха. Чтобы судить об этом влиянии, позволил
я себе в начале, с некоторой подробностию даже, говорить о
границах и составе нашей атмосферы. Первое, что надобно заметить
в этом отношении — понижение температуры во время затмения.
Наблюдения делал Г. учитель математики в Пензинской гимназии.
Хватунов.
26 Июня .1842, утром, в4 о'
8 15
8 30
8 45
7. | 9 0
9 11
9 30
15",2
14,4
14, 7
14,5
14, О
13, 4 начало полн. затмен.
13,9
Показания термометра в градусах Реомюра. Ветер был юго-
западный, весьма тихий; барометр стоял на 727,9 миллиметрах
и приметно не менялся, И так, самое большое падение термометра
составляло 1°,8, несмотря на то, что за продолжительным дождем
с утра небо начинало проясниваться, отчего воздух должен бы
нагреваться скоро [**]. Если теперь от лунной тени произошла
в температуре столь значительная разность у земной поверхности,
то без сомнения на границах самой атмосферы должна быть эта
разность чрезвычайно резкая, особенно е том месте, где тень
разграничивалась со светом. После чего делается вероятным, что
солнечные лучи, менее других погнутые близ луны, следовательно
самые обильные светом, должны преломляться в отенѳнном воз-
. * Относительно каймы Гримальди ей. [WJ; об опытах Фложерга ем. [&\.
29*

452 ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
духе так, что большая часть из них могла приходить к нашему
глазу в том самой направлении, какое требуется для произведения
кольца вне темного лунного круга. От охлаждения должно
происходить движение в воздухе: стремление со всех сторон в тень,
и течение к низу внутри тени. Это движение, соединенное с
движением самой тени, вероятно причиной и неравного преломления,
которое в светлом венце производит искривленные полосы. Может
быть присоединяется к тому различное состояние воздуха на
границах атмосферы, представляя переход к жидкому капельному,
п {даже к твердому телу, при чрезвычайном холоде в
прикосновенном пустом пространстве. Итак, не мудрено, что здесь бывают
внезапные превращения, которые по временам и местами дают
солнечным лучам особенное направление, отчего происходит
явление, какое находим в описании Уллоа [*°].
Может быть светлое кольцо вокруг луны составляет явление
более сложное, нежели как я здесь его представил, и как вообще
все явления света физики до сих пор разумеют [еі]. Возьмем в
пример освещенные тела, которых отраженный свет обыкновенно
принимают, с одной стороны, слабее в содержании к квадрату
расстояния, с другой усиленным в том же содержании сжатием видимой
величины. Между тем, если напряжение света должно быть
независимым от расстояния, то трудно понять, каким образом наша
мрачная земля на весьма большом расстоянии делается светлым
пятном, подобно прочим планетам и луне. М" видим, что облако
вдали гораздо более светится, нежели тот туман, которого вид оно
должно принять, когда мы к нему прнближимся. Представим
себе светлые тела, размещенные с промежутками на такой глубине,
что свет от них кажется непрерывным. Теперь в конусе видимой
величины за каждым телом должны скрываться другие, которых
евет уже до нашего глаза не доходит, и число которых будет
тем более, чем ближе находимся к куче тел. Отсюда необходимо
ів происходит уменьшение в свете, ко|торое совсем не предполагают,
доказывая равную силу в освещении на различных расстояниях.
По примеру таким образом скученных тел можем заключать о всяком
теле, которое должно разуметь собранием атомов, размещенных
иа расстояниях. Без сомнения, не в этом одном состоит усиление
«вета на большом удалении. Трудно согласиться, чтоб от этой одной

Н. И. ЛОБАЧЕВСКИЙ — «ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА» 453
причины наша темная земля могла принадлежать на небе е числу
светлых планет. Мысль, что на планетах плоскости в различных
направлениях отражают свет, эта мысль не может быть допущена
даже для металлических * зеркал, в противность основного
понятия, как мы внутренний состав тел должны себе представлять.
За тем какие зеркальные грани свет может встречать на тумане
в облаках или на тонких парах кометного хвоста, чтоб отразившись
приходит[ь] еще приметным для нашего зрения? Предположение,
что свет, коснувшись твердого тела, заставляет каждую точку
делаться новым центром волнения, это предположение Френеля
хотя произвольное, подтверждается тем не менее на самом деле [и].
Не льзя сомневаться, чтобы свет в прикосновении не возрождался
снова, чтоб это возрождение не было тем сильнее, чем более
сопротивления для света, чем разительнее, следовательно, переход из
одной средины в другую. Когда теперь идем от этих положений,
то делается вероятным, что в прикосновении света поверхность
нашей атмосферы сама начинает светить, и что в кольце вокруг
луны мы видим также собственный свет от верхних воздуш-
(і ных | слоев, подобно тому как эта тонкая оболочка нашей земли
должна гореть ярким светом для жителей на прочих планетах
и на луне ["].
Вот все, что мог я сказать за моих товарищей и за себя, как
очевидцев полного солнечного затмения в Пензе. Г. Ляпунов свои
наблюдения изложил особо [и]. Пользуясь нашим пребыванием
в ѳтоы городе, мы сделали также несколько магнитных наблюдений.
Для магнитного наклонения был употреблен снаряд и стрелка
работы Гамбея в Париже. Два ряда наблюдений сделаны, как
обыкновенно, ■ с перекладыванием и перемагничиванием стрелки.
Первый ряд дает 65°33',25; второй 65°34',19. Однако ж мы
заметили, что стрелка Гамбея в одном конце принимала более
магнетизма. Наблюдения с другой стрелкой, приготовленной в
механическом заведении нашего университета, дали магнитное наклонение
66°19',9. Прежде того 21 Октября 1836 года Г. Профессор Кнорр
определил в Пензе наклонение 66°19',1.
* В «Журнале министерства народного просвещения» (и у Модзалевского)
вместо металлических напечатано математических. Это — безусловное искаженна
текста Лобачевского.

154
ПОЛНОЕ 8АТМШИЕ СОЛНЦА.
Магнитное отклонение в Пензе Г. Ляпунов находит как
среднее из своих наблюдений для северного конца V^b'i'J
н. востоку.
Горизонтальное напряжение магнетизма можно заключить из
сравнения наблюдений, сделанных тем же снарядом в Казани
и в Пензе, при равных дугах качания [6В].
аі | 1836 июня 29. В Казани, время 10 качаний при 0° Е 50", 35
1836 октября 22. В Пензе 48",187
1842 июля 18. В Казани 50",391
1842 июня 25. В Пензе ■ 48",156*
В отношении к физической географии город Пенза заслуживает
внимание своим гористым положением и потому климатом более
суровым, нежели как бы должно было ожидать, судя по
географической широте. Эта возвышенность, открытая на пространную
степь к востоку, бывает причиною грубых перемен в температуре
и составляет отличительную принадлежность стран в соседстве
с северной Азией. Особенно весной, после теплой погоды в апреле,
когда плодовые деревья начинают уже двести, северозападный
порывистый ветер приносит холодный дождь и даже снег. В Казани
1842 мая 31 снег покрыл совершенно землю; в это же время
термометр в Пензе спускался до нуля, снежинки летали по воздуху,
хотя таяли, падая на землю ['*]. Далее к Саратову, на равнинах
по берегам Волги, с уничтожением гор, климат делается столько
теплым, что растет уже виноград. Пенза хорошо выбрана местом
для садоводства, которому принуждены здесь учиться как
искусству, тогда как в южной России на согретой почве, под
благоприятным небом, не нуждаются и пренебрегают пособием для
природы, без того богатой растительною силой. Напротив,
подобное небрежение к северу бывает причиною неудач, в
которых по незнанию дела часто хотят обвинять несправедливо самое
садоводство [6~].
* В .Журнале министерства народного просвещения» эти числа заменены
еле дующими: 50",ЗѲ; 4#",087; 50*,39l; 4S",1S5. Причины такого расхождения не
удалось установить. В статье Н. Й. Иванова «Ученые собрания профессоров
Казанского университета» (см. стр. ЮТ наст, тома) приводятся некоторые числовые
результаты из сообщения Лобачевского о затмения, в частности, вместо двух
последних чисел дается 68"391 в Пензе (явная ошибка) и 48", 156 в Кавави.

Н. И. ЛОБАЧЕВСКИЙ-—«ПО ЛНОЕ ЗАТМЕНИЕ СОЛНЦА» 455
43 | Гористое положение Пензенской губернии не представляет
никакой правильности в своем образовании, тогда как от Симбирска
до Казани господствует одна только возвышенность правого берега
Волги, от которой в Симбирской губернии начинается уже степной
вид полей. Г. Кнорр полагает, что вода на земной поверхности
сначала долго пребывала запертая в случайных углублениях; потом,
проложив себе дорогу, произвела реки, где течением углубилось
дно и придало возвышенность берегам, которые может быть совсем
и не должно почитать за ветви горных хребтов. Такое мнение
совершенно подтверждается при первом взгляде на холмиетую
поверхность Пензенской губернии. Падение реки Свияги произвело
в высоком Волжском береге разрыв, где в промежутках еще видны
■остатки. На одном из таких возвышений уделенного берега построен
город Свияжск [*в].

ПРИМЕЧАНИЯ
I1! Перед наблюдателями полного солнечного еатмения 26 июня
(8 июля нов. ст.) 1842 г., которое ожидалось в Европе после
длительного перерыва, впервые встала важная цель — разрешить при помощи
физических наблюдений вопросы, связанные с природой Солнца и с
явлениями, происходящими при затмениях на поверхности Земли и
в ее атмосфере. Лобачевский особо обращает внимание на эту, самую
актуальную в ту эпоху, сторону наблюдения затмения, вместе с тем,
выделяя феномены, предположительно вытекающие из теории света,
как погибь (нагибание, диффракдия) лучей Солнца.
Астроном в старом смысле слова, в отличие от физика, должен
был решать только задачи, относящиеся к положениям светил на небе;
он использовал затмение для определения относительных координат
Солнца и Луны при особо благоприятных условиях.
При наблюдении солнечного затмения различают четыре так
называемых контакта. Первый контакт соответствует началу частного
затмения (внешнее касание круглых дисков Солнца и Луны); второй и третий
контакты—началу и концу полной фазы (внутренние касания Солнца
с Луной); четвертый, или последний контакт—концу затмения
(внешнее касание дисков). В случае полного затмения диск Луны, конечно,
должен иметь больший диаметр, чем солнечный диск. Если же Солнце
во время затмения имеет больший видимый диаметр, чем Луна, то
второй и третий контакты будут внутренними касаниями Луны с
Солнцем, соответствующими началу и кончу кольцеобразного затмения
(так как в промежутке между этими контактами темный диск Луны
будет окружен светлой каемкой Солнца).
Из наблюдений моментов контактов можно получить относительное
положение центров Солнца и Луны на небесной сфере, что важно
для проверки таблиц их движения. При этом должно быть известно-
положелие наблюдателя в пространстве, для чего, в свою очередь,
требуется точное звание его географических координат на земной
ловерхвости.
[*] В. Я. Струве (1793—1864) —крупнейший русский астроном,.
академик, основатель и первый директор Главной обсерватории в
Пулкове.

ПРИМЕЧАНИЯ 457
[3] И. М. Симонов (1794—1855) — профессор астрономии и директор
астрономической обсерватории Казанского университета, участник,
знаменитой экспедиции Беллинсгаузена и Лазарева в Антарктику
в 1819—1821 гг.
У первого профессора астрономии в Казани И. А. Литтрова вместо
обсерватории имелось только небольшое и неудобное для наблюдений
помещение и очень мало инструментов. Современное здание
университетской обсерватории было выстроено в 1834—1836 гг. при самом
непосредственном участии И. М. Симонова и Н. И. Лобачевского,
бывшего председателем строительного комитета. Обсерватория была
открыта в 1S38 г., причем для нее был приобретен ряд первоклассных
по тому времени инструментов (9-дюймовый рефрактор, большой
пассажный инструмент, несколько позже — меридианный круг, многие
другие инструменты)1). Вскоре после поездки Лобачевского и
Ляпунова па затмение здание обсерватории сгорело при страшном пожаре
Казани 24 августа 1842 г. (Симонов в это время был аа границей)..
[*] М. В. Ляпунов (1820—1863) — с 1840 г. астроном-наблюдатель,
о 1850 г.—директор Казанской университетской обсерватории, в 1855 г.
ушел из Казанского университета. См. о нем во вводной статьеs).
[&] 3. А, Кнорр (1805—1879)—профессор физики и физической
географии (метеорологии) Казанского университета с 1832 по 1846 г.
С 1846 по 1858 г. занимал ту же должность в Киевском
университете, после чего ушел в отставку. См. о нам во вводной статьеs).
Мнение Эыгеля, что Лобачевский, был с Кнорр ом в хороших
отношениях, находит себе подтверждение в общем тоне высказываний
Лобачевского о Кнорре в отчете о затмении, а предположение того же
Энгеля, что Кнорр передал Гауссу в 1840г. «Геометрические
исследования» Лобачевского*) может быть подкреплено очень вескими доводами.
') См. И. М. Симонов —Описание астрономической обсерватории ими.
Казанского университета, Журнал Министерства народного просвещения, часть VII,
1838, отд. П, стр. 1—22.
') Стр.426 наст. тома. См. также Н. П. Загоскин —Биографический
словарь профессоров и преподавателей mm. Казанского университета (1804—1904),.
ч. 1. Казань, 1904, стр. 419—122.
*) Стр. 4ЭѲ наст. тома. См, также: Н, П. Загоскин, дит. соч., стр. 355—357,
В. С. Иконников — Биографический словарь профессоров и преподавателей
ими. университета св. Владимира (1834—1884), Киев, 1384, стр. 202—264; Nikolaj
Jwanowifsch Lotetacbefskij. Zwci geometriache Abhandlungen aus Дега Ruesischen
Qbersetzt roit Anmerimngen und einer Biographie des Verfassers, von F. Engel, 1890,
стр. 438—44&
4) Cm. t. I eacl. издания, стр. 172. При всем том остается весьма вероятным
предположение, что в издательство Финке Лобачевский направил «Геометрические
исследования* при посредстве профессора И. А. Финке (им. там же, стр. 174).
[Примечание главного редактора,]

468
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
1В большой отчетной статье «Об ученых путешествиях профессоров,
преподавателей и воспитанников Казанского университета с 1827
ао 1843 год *) имеется подробный и очень любопытный отчет о
поездке Кнорра за границу в 1840 г. Вскоре после начала своего
путешествия Кнорр посетил Берлин. «Тут возобновлены ил прежние
связи с многими учеными, особенно с знаменитым бароном
Александром Гумбольтом, Леопольдом Буком, Поггеидорфом, Дирксѳном, Энке,
Лихтенштейном и Мич ер лихом » э). После Германии Кнорр посетил
Австрию, Францию и Англию. Вот что сказано о последнем этапе
его поездки: «Посему, проведя 14 дней в столице Великобритании,
лроф. Кнорр поехал, через Роттердам, в Геттингѳн, гдѳ возобновил
прежнее знакомство с профессорами Гауссом и Вѳбером и вотупил
в новые связи о Гг. Листингом и Штерном. Заказав у механика'
Мейерштейна некоторые магнитные аппараты, изобретенные Гауссом
и Вѳбѳром, проф. Кнорр отправился, через Берлин, С.-Петербург
и Москву, в Казань, куда и прибыл в начале февраля 1841 г. Все
действия проф. Кнорра в чужих краях для пользы науки,
Университета и учебного округа, приобретают ему в высшей степени
признательность его сочленов и ставят это путешествие наряду с теми,
которые принесли Казанскому университету наиболее известности
за границей»*).
Совершенно очевидно, что известное письмо Гаусса к Энке от
20 января/1 февраля 1841 г.*) написано под свежим впечатлением
только что происшедшей встречи с Кнорром, который, как видно из
приведенных цитат, был с ними обоими давно знаком. Естественно,
'іто Гаусс при овидании с Кяорром должен был повести разговор
о том, что его всего более интересовало в Казаки-—именно, о
Лобачевском. Интерес, возбужденный у Гаусса этнм разговором, отражён
и в письме к Энке, Очевидно, Кнорр, взяв рукопись «Геометрических
исследований» для издания (и передав ее в первом этапе своей поездки
издательству Финке в Берлине), имел при себе и оттиски какой-то
другой геометрической работы Лобачевского. Эту работу (написанную
по-русски) он и прислал Гауссу после еаидания с ним. Столь же
понятно, что и Гаусс, после долгого перерыва в знакомстве, не
вспомнил точно фамилию Кнорра в письме к Энке. Наконец, весьма вероятно
и то, что общее суждение о поездке Кнорра, высказанное в конце
') «Журнал Министерства народного просвещения», часть 40, 1843, отд. 3.
стр. 53—104; перепечатано в «Прибавлениях к Казанским губернским ведомостям»,
J6 8, 21 февраля 1344 г., стр. 114—121 (ж в других номерах); отчет о поездке
Кнорра — на стр. 75—80 «Журнал министерства.» я стр. UT—121 «Прибавлений*.
з) Там же, стр, 77, соотв. 11Ѳ.
а) Там же, стр. 80, соотв. 121.
*) Т. I наст, издания, стр. 173.

ПРИМЕЧАНИЯ
459
■отчете (си. выше), принадлежит не кому иному, как ректору
университета Лобачевскому; оно вполне подтверждает все сделанные здесь
-заключения.
Рі Л. Б. Модвалевский опубликовал ряд документов, касающихся
Казанской экспедиции на затмение 1842 г.1). Мы отметим только, что
в документе № 473 от 21 мая 1842 г.2). Лобачевский сообщает М. В,
Ляпунову о письме директора Главной обсерватории Струве к Симонову,
«которым он изъявляет желание, чтобы 26-го июня сего года было
наблюдаемо в Пенаѳ солнечное затмение». Лобачѳвокий просит
Ляпунова «составить примерное счисление, какие издержки потребуются
для проезда в город Пензу>.
К этому можно добавить, что на путевые расходы Лобачевского,
Кнорра и Ляпунова было израсходовано 256 р. 46 в- серебром8).
В своем предписании 5 нюня 1842 г,*) Лобачевский дает указания
Ляпунову о сдаче им обсерватории (которой Ляпунов заведывал в виду
■отъезда Симонова за границу) профессору П. И. Котельникову, а также
о наблюдении за перевозкой инструментов и об откомандировании с
Ляпуновым одного на служителей обсерватории. К сожалению, как уже
«тмечѳно во вводной статье °), письмо В. Я. Струве и инструкция
Симонова о наблюдения затмения не сохранились: тис не удалось найти
ни в Центральном гос. архиве 'ГАССР, ни в переписке Симонова,
хранящейся в отделе рукописей и редких книг научной библиотеки
Казанского университета. Нужно думать, что все эти документы
сгорели при пожаре 24 августа 1842 года.
I7] Некоторые из перечисленных инструментов уже не существуют
в их прежнем виде, но их описание имеется в каталоге инструментов
Казанской университетской астрономической обсерватории; другие
инструменты существуют и теперь6).
Труба прохождения (или, иначе, переносный пассажный
инструмент Эртѳля) была приобретена в 1840 г. Она имеет объектив в 43 мм,
ломаную трубу и горизонтальный круг в 30 см диаметром, ори
котором четыре нониуса с точностью отсчетов до 10". С этими
инструментами М. В. Ляпунов производил наблюдения для определения гео-
I) Материалы для биографии Е. И. Лобачевского. Собрал и редактировал
.X В. М о д з а л е в с в и й. Изд. АН СССР, М. — Л., 1948. (В дальнейшей цитируется:
Модаалавскнй). Документы ЖЧа 473, 476, 478, 481, 482, стр. 439—443
3) Модзалевский, стр. 439—440.
3) Протокол Совета Университета от 14 августа Ш'З г., пункт 2од. Центр
гос. архив Татарской АССР, фонд 977, і& 8703.
*) Модзалевеккй, документ Л£ 478, стр. 444.
s) Стр. 4.22 наст. тона.
') См, фотографию на следующей странице.

460
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
графических координат пункта наблюдения в Пензе. Ахроматическая
большая труба Фраунгофера, заказанная И. М. Симоновым в Венском
политехническом институте в 1823 г. и полученная в 1828 г., имеет
объектив в 97 мм; две малых трубы —Рамодѳна и Тавгета—еще
до основания университета принадлежали казанской гимназии. Все
эти трубы обладают хорошими оптическими качествам и. Секстант,
работы Траутона, ХѴШ века; хронометр Бреге № 3874, карманного-
типа, был куплен Симоновым в Париже в 1825 г. Инструменты для
Пассажный инструмент («труба прохождений») Эртеля н хронометр Броге,
взятые экспедицией Казанского университета в Пензу в 1842 г.
магнитных наблюдений были приобретены у Гамбея в 1835 г. и,
насколько можно судить по их описанию, должны были давать точные
результаты; в каждом ив них имелось по два микроскопа для
отсчетов. Прибор Пулье, психрометр и барометр, вероятно, были ааяты
ив физического кабинета. Наконец, довольно громоздкий небесный
глобус имел 50 см в диаметре и покоился на треноге. Хронометр
Бреге с меткой — это, в сущности, счетчик секунд, действующий
в течение 10 минут, который может быть в любой момент пущен в ход
и остановлен. Его секундная стрелка снабжена подачей чернил и, при
нажиме пруясины, ставит в качестве отметки момента чернильную
точку на эмалевом циферблате. Этот любопытный и недорогой прибор
был приобретен незадолго перед поездкой на затмение.

ПРИМЕЧАНИЯ
461
I9] Из описаяяя б тексте неясно, как были разделены круги.
Is] Лобачевский отчетливо обрисовывает те трудности, с которыми
■сопряжены фотометрические измерения во время полного затмения.
Непосредственно перед полной фазой затмения (и сразу же но ее окон-,
чании) освещенность земной поверхности меняется очень быстро в
громадных пределах, так что Лобачевский совершенно правильно говорит
■о мгновенных явлениях. Впрочем, неблагоприятная погода помешала
поставить намеченные фиаичеекие наблюдения.
[1а] Следовательно, нельзя было определять долготу Пензы отно.
-ситѳльно Казани способом перевозки хронометров. Однако, имея один
хронометр (к тому же, карманного типа), трудно было рассчитывать
•на точность относительной долготы бблыпую, чем 2—3 секунды
времени, при сравнительно длительных переездах иа Казани в Пензу
и обратно на лошадях. Заметим, что в то время в Казанской
обсерватории имелось только два не особенно хороших хронометра; моает
■быть, второй хронометр Гаута был не в исправности и Ляпунов не мог
веять его о собой.
Iй] Наблюдения прохождений звезд через первый вертикал
позволяют определить широту места; соответствующие способы наблюдений
разработаны Бессѳлѳм1).
I1*] Определение долготы, до применения для этой цели телеграфа
и радио, обычно опиралось на перевозку хронометров. Так как в
данном случав хронометр в дорого останавливался, М. В. Ляпунов не мог
применить зтот метод. Он использовал наблюдения Луны, координаты
которой быстро меняются; поэтому по Луне можно в любой момент
найти время гпо основному меридиану, а следовательно, и долготу.
Однако наблюдения Луны около эпохи затмения (новолуния) должны
производиться днем, что невыгодно отзывается на их точности.
Затмения спутников Юпитера тоже не могут дать большой точности, так
как при погружения спутника в тень Юпитера блеск спутника
убывает постепенно и наблюденный момент затмения зависит от
оптической силы трубы. Введенная поправка в 14 ,5, может быть,
учитывает его обстоятельство. В итоге, полученная долгота 2 6 34 ,в
(из приведенных чисел следует 2 6m34s,5) опирается только на
затмения первого спутника Юпитера. Сколько наблюдалось этих затмений,
из отчета Лобачевского не видно; возможно, что лишь одно.
і) Beasel — liber den allgemeiuen Gebranchdes Passagen-lnstrumentea. Astrona-
шіясЬе Machrichten, В. fl, 1328, стр. 221—248. Beobacbtiragen mit ѳівст tragbarea
Paaaagen-Inatntmente in Miinchen und Marienbad. Там ясѳ, В. 9, I83i, стр. 413—136.
Эти труды Беоеѳля читал Ляпунов перед поездкой в Пензу, как видно из atumcefi
взятых юс книг.

462
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
Поэтому долгота Пензы может быть ошибочна на 10s в более, что
создает значительную неуверенность в положении наблюдателя на
земной поверхности и мешает использованию наблюденных моментов
второго и третьего контактов затмения для их прямой цели — определения
взаимного расположения дисков Солнца и Луны. Из приведенных
в тексте результатов следует, что Ж. В. Ляпунов принимал восточную
долготу Казани от Берлина равной 2 22m53s,3, что на О3,8 меньше
ныне принятого значения.
В настоящее время методика определения широт и долгот
существенно изменилась; способы, упомянутые выше, можно найти в более
старых руководствах по практической астрономия.
[1В] Упоминаемый Н. И. Лобачевским сад принадлежал к училищу
садоводства, директором которого был Э. И. Магзиг, А. А. Панчулид-
зев (1789—1867) был длительное время пензенским гражданским
губернатор ом.
|14} Наблюдения с секстантом к кольцевым микрометром (у трубы
Фраунгофера был такой микрометр), как справедливо отмечает
Лобачевский, не могли дать большой точности. По существу дела,
постепенное убывание расстояния между остриями солнечного серпа может
дать момент его исчезновения, т. ѳ. момент начала полного затмения.
Такие наблюдения М. В. Ляпунова дают для начала полной фазы
результаты, которые плохо сходятся между собой. Вероятно,
убедившись в ненадежности наблюдений, Ляпунов не повторял их во
всем объеме после конца полной фазы.
В виду плохого состояния неба нельзя было быть заранее
уверенным, что удастся вообще увидеть полную фазу затмения и
непосредственно отметить момент ее начала, почему Ляпунов и
производил намерения серпа только до полной фазы.
Как правило, начало и конец полного затмения могут быть
замечены по хронометру до немногих десятых долей секунды. В одном
из неисправленных моментов по хронометру ') ошибка на 10
(продолжительность полной фазы — 12m58s,fi). В каком моменте имеется ошибка,
сказать нельзя, но его и но столь важно, так как исправленные моменты,
очевидно, даны верно. Это подтверждается заметкой о затмении в
«Прибавлениях к Пензенским губернским ведомостям», весьма вероятно
принадлежащей Н. Н. Лобачевскому s). Там моменты пачала и конца
полной фазы затмения, с приблизительно вычисленной поправкой
хронометра, даны как 9Ь9Ш22Я и 9І112Ш22Э среднего пензенского
времени, что сходится с текстом отчета Лобачевского.
>) В обоих текстах (см. стр. 494), а следовательно, и в подлинной рукописи.
>) Си. приложение 1 на стр. 486 наст, тома.

ПРИМЕЧАНИЯ . 463
[1В] Ф. А. Каховский (1808 —1875) — помещик. См. о нем: Модаа-
левокий, стр. 738—740.
І1в] Смысл конца этой, не вполне ясной фразы тот, что слои
облаков часто кажутся нам параллельными горизонту из-за перспективы,
то-есть, уже не случайно.
['''] В (Журнале министерства» в этой фразе выпущено последнее
слово смеотами», а между тем, только с ниц она имеет смысл: в
светлом кольце не было особенных мест, то-есть, определенных отдельных
деталей. 9то не удивительно при наблюдении сквозь облака. Труднее
понять, почему Лобачевскому и Кнорру корона казалась слабее у
лунного края. Другие наблюдатели затмения 1S42 г. подобного явления
не замечала.
[1SJ Относительно Беги—ошибка; недалеко от зенита была Капелла.
Звезды видели и в Воронеже, где затмение не было полным.
[1Э] Наблюдения поляризации короны, произведенные во Франции
во время затмения 1842 г., оказались не очень удачными; поѳтому
результат Кнорра представлял в то время определенный интерес 1).
І20І Араго делал отчет о наблюдениях затмения во Франция на
заседании Академии Наук 22 и 29 августа 1842 г. -). Он указал,
что из-за противоречий в наблюдениях не может пока дать статью о
затмении. Полный обзор наблюдений аатмения в июля 1842 г. Араго
дал гораздо позже отчета Лобачевского3). Следовательно, Лобачевский
в отношении наблюдений затмения во Франции в значительной мере
пользовался сообщениями Симонова (см. также примечание I37]).
[гг] В етот день в 1842 г. грандиозный пожар уничтожил
значительную часть Казани; в университете сгорела обсерватория.
["SI Для измерений яркости на Солнце Буге *) использовал изобре-
тенньій им гелиометр (у Буге гелиометр имел два объектива, каждый
!) Ср. Ф. Араго— Общепонятная астрономия, 18Ѳ1, т. 3, стр. 424—42Ѳ.
а) Comptas rendus bebdomadairee da ГАеаййтіе dea Sciences, т. 15, Paris,
1842, стр. 396 и 465. 12 сентября 1842 г. Краткой изложение доклада Арагс-
имеется в журнале L' Institnt, Journal пшѵегвеі des sciences, 10 агшёе, 1342, J4s 452.
(Этот номер отсутствует в библиотеке Казанского университета. Имеющиеся
документальные данные недостаточны, чтобы установить, был ли он получен
и читал ли его Лобачевский, вообще регулярно просматривавший этот журнал.)
') Arago — Sor Гйсііряе totale du Soleil du 8 juillefc 1842. Annuaire pour Гап
18*6, public par le Bureau des Longitudes, Paris, 1345, стр. 271—477.
*) P. Bouguer — Traite d'optiipie but la gradation de la lumiexe. Ed. poathume.
Paris, 1760, стр. 30—96. Русский перевод: Бугвр Пьер —Оптический трактат
о традашш света. Иэд. АН СССР, 1В50, стр. 76 — 80.

464
полное затмение солнца.
из которых давал свое изображение Солнда). Byre сначала приводит
причини, по которым яркость солнечного диска должна возрастать
к его краю до бесконечности, то-ѳсть Буге принимает, что поверхность
Солнца равномерно покрыта светящимися точками, ни при каких
обстоятельствах не закрывающими друг друга. Однако на следующих
страницах он заключает, что это рассуждение не отвечает
действительности. В том же 1760 г. Ламберт, рассматривая излучение не точек,
а элементов поверхности светила, вывел- свой закон освещения, но
которому диск светящегося тела должен иметь равномерную яркость.
Однако и втот закон верен только Для абсолютно черного тела.
Измерения Буте были качественно верны и его результаты намного
опередили свою впоху. Еще в первой половине XIX века Араго и
другие астрономы считали, что Буге ошибся, а Солнце имеет одинаковую
яркость по всей поверхности.
Рэ] Лаплас ') исходил из своей теории поглощения света в
атмосферах небесных тел и из первого ошибочного допущения Буге (см.
предыдущее примечание). С современной точки зрения результат
Лапласа но имеет смысла.
[**J Лобачевский и Кнорр тонко подметили различие в очертаниях
краев Солнца и Луны. Объяснение дано совершенно правильное:
основная причина, почему солнечный край во время затмения кажется
более нежным — быстрое падение яркости Солнца у самого края диска,
отчего уменьшается контраст с фоном неба. Кроме того, известную
роль в подчеркивании края Луны могут играть его неровности (горы).
Б ту эпоху, когда Лобачевский писал свой отчет, среди
большинства ученых еще были распространены, восходящие к первой половине
ХѴШ столетия, представления о «твплотворе» (теплороде) Хр. Вольфа,
хотя уже Ломоносов считал теплород вымыслом. Нужно напомнить,
что на концепции теплорода были построены в начале XIX века
фундаментальные сочинения о теплоте Фурье и Кар но. С другой стороны,
почти все астрономы тогда безоговорочно разделяли упомянутую
Лобачевским теорию Солнца, разработанную Уильямом Гершелем
в 1S01 г., во восходящую еще к 1769 г., к наблюдениям Уильсона
нал положением тени в солнечных пятнах, когда они подходят к краям
диска Солнца2).
[іа] Трудно сказать, на чем основано утверждение о
пропорциональности плотности атмосфер тел солнечной системы их массам при
•) La Place — Mecanique celeste, 2 partie, livre 10, cnap. 3. Oeuvraa, t. i, 18*4,
стр. 318—323.
*) W. Herachel—Observations tending to investigate the nature of the Sun.
Philosophical transactions of the Royal Society of London, 1801, стр. 265—353.

ПРИМЕЧАНИЯ
465
допущении, что атмосферы сгущаются из мировой среды. Повидимому,
Лобачевский рассматривал это просто как вероятную гипотезу.
Iй6] Сообщение Араго было сделано на заседании Академии Наук
14 июня 1В24 г. Сает, исходящий от самосветящихся тел, если эти
тела твердые или жидкие, частично поляризовал, когда лучи образуют
малый угол с поверхностью выхода. Раскаленные газы дают свет,
который ни при каких углах наклона не показывает чувствительных
следов поляризации; отсюда Араго заключает, что заметная часть света
от газов идет изнутри, с некоторой неопределенной глубины.
Результаты, полученные по етому методу, подтверждают предположений
Боде. Шретѳра и Гершѳля (т. е. что Солнце окружено светящейся
газовой атмосферой).
[2~] Здесь в тексте описка: вместо упруі ости должна быть
центробежная сила. На экваторе Земли отношение эхо я силы к силе
притяжения составляет только 1/2S9, но первая из ѳтих сил возрастает
пропорционально расстоянию от центра Земли, а вторая — убывает
обратно пропорционально квадрату этого расстоянии. Следовательно,
на расстоянии к 289 = 6,61 радиусов от центра Земли обе силы
сравняются и, так как их направления противоположны, там будет предел
атмосферы; следовательно, ее высота на экваторе составит 5,01 радиусон
Земли, или 35800 «.« = 33500 ворст. Лобачевский проделал
приближенный расчет.
Фигура атмосфер небесных тел, в частности, длн этого предельного
случая, была рассмотрена Лапласом в его «Небесной механике» (см.
примечание [3S]).
[w\ Полет Гсй-Люссака был соиершен 16 сентября 1804 г. На
наибольшей: высоте 0977 .« над Парижем (пли 7016 м над уровнем моря)
температура была —9,5°, в это же время н Париже было -| 30,75е.
Отсюда Гей-Люссак виводит падение температуры атмосферы на 1э0
в среднем на 173,3 .« высоты п).
Результаты наблюдений Гой-Люссака приводятся во многих книгах
(например, у Лапласа), а Лобачевский взял их, очевидно, не из
первоисточника (отсутствовавшего в университетской библиотеке). Принимая
градиент постоянные, он нашел приведенную в тексте высот;-
атмосферы и общее пониженно температуры (82X^50 = 28 700 силкоп г=
— 57,4 верст). Однако обычно наблюдаемый градиент температуры
больше того, который был получен Гѳп-Люссаком, и составляет
') Relation d'un "voyage ayrofitatique fait par M, Gay Lussac le 29 frnctldor
an 12. Journal de physique, de chiraie, d'hiitoire naturelle «t dea arts, t. 59, 1804,
стр. 454—462,
30 Заж. 2№3. H. И. Л о Паче воин В, т. V.

466
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
—0,009s1 С на 1 м. Равномерное падение температуры атмосферы с
высотой соответствует адиабатическому состоянию (которое в
действительности никогда на осуществляется во всей атмосфере). Высота
адиабатической атмосферы равна только 27,9 км (273:0,0098 = 27900 м),
если считать, что на поверхности земли температура равна 0°, а на
границе атмосферы она падает до абсолютного нуля (—273°С).
[м] В предположении, что температура убывает с высотой в
геометрической прогрессии и с градиентом температуры по Гѳй-Люссаку,
получается, что на высоте 190 км температура гораздо ближе к
абсолютному нулю, чем это дает Лобачевский. Как он пришел в своему
результату, выяснить не удалось.
[зс] В своей важной работе 1) Дулье домерил солнечное излучение
при помощи изобретенного им пиргелиометра и нашел, что Солнце
посылает на землю (за пределами земной атмосферы) 1,71333 малых
калории на 1 ем"1 в минуту, т. е. он произвел определение солнечной
постоянной. Но все теоретические выводы Пульѳ опираются на
неверный аакон излучения Дюлонга и Пти. Вследствие этого Пульѳ
вычислил, что температура Солнца составляет только 1761°С. Пулье
измерял актинометром ночное излучение Земли, а ватем рассчитал, что
вероятиейнгѳѳ значение температуры мирового пространства равно
—142° С. Здесь нет возможности останавливаться на ряде других
интересных заключений Пулье.
I"1) Фурье 2) устанавливает три источника тепла на земной
поверхности: излучение Солнпа, излучение остальных бесчисленных светил
и внутреннее тепло Земли. Он впервые заметил, что последний
источник дает ничтожно мало тепла. Главный аргумент, что температура
мирового пространства должна быть около -—40°R (—50ЭС, то-есть,
довольно высока), состоит в том, что если бы земной шар находился
в окружающем пространстве, лишенном всякого тепла, то полярные
области испытывали бы чрезвычайный холод. Самые низкие
температуры в полярных областях (насколько их знал Фурье) должны уже
быть близки к температуре мирового пространства.
Фурье пишет, что он не ставит овоѳГг целью математическую
трактовку предмета, но желает лишь привлечь к нему внимание, как
я вопросу натурфилософии. Желание Фурье исполнилось: после него
') Pouillet — Щтоіге sur la chaieur воіаіге, sur lea pouvoirs rayoonaats et
abeorbantea da I'air atmoepherique et sur la temperature de l'&pace. Comptes rendus
de I'Academie dee Sciences, t. 7, Paris, 183S, eip. 24^05.
a) J. B. Fourle r —Memoire sut lea temperatures du globe terrestre et des
ёзрасеэ ріалбШгеа. Мётоігез de I'Acad&mie des Sciences de l'lnetitut de France>
t. 7, 1837, crp. 589—801.

ПРИМЕЧАНИЯ
46Т
Сванбѳрг, Пуассон, Пульѳ, Лив и другие занялись тем же вопросом
о температуре мирового пространства.
t88) Здесь Лобачевский воввращается к теории Солнца Гершеля
(см. примечание I5*]). Подвижные пятна-—вто обычные солнечные
пятна, возникающие и уничтожающиеся, меняющие свою форму я
могущие, перемещаться по поверхности Солнца.
}за1 «Возвышения», то-ееть, протуберанцы (в действительности
являющиеся выброшенными на значительную высоту газами
хромосферы), наблюдались в Нарбоннѳ тулузскими астрономами Пино а
Буажиро, о чем есть сообщение в отчете Араго (см. примечание [*°])
и у И. М. Симонова1). Аналогичные наблюдения Шумахера
упоминаются там же; Шумахер*) пишет, что три возвышенности имели
большое сходство с вершинами глетчеров в розовом свете.
Любопытно, ■что о солнечных горах говорят, в связи с
протуберанцами, и другие астрономы, наблюдавшие это затмение.
I34] Лобачевский рассматривает атмосферу Солнца, как гавоэуе»
среду о постоянной угловой екороатьвд вращения, равной угловой
скорости твердого ядра Солнца.
[9Bj фигуры атмосфер небесных тел и, в частности, Солнца, были
рассмотрены Лапласом в); чтобы сравнить с заключением Лобачевского
о сжатии солнечной атмосферы, выведем здесь один из результатов
Лапласа, не следуя строго его изложению.
Солнце можно принять за почти точный шар о маосой М и
угловой скоростью вращения ш. Допустим, что Солнце окружено
атмосферой ничтожной уаосы, вращающейся с той жѳ угловой, скоростью о»,
и определим форму внешней поверхности атмосферы. Это будет
поверхность уровня потенциала Солнца W на границе атмосферы, на
переменном расстоянии р от центра Солнца:
_ m . «у ««* <?
W= і- — = с = const.:
Р ' 2
■
причем здесь f -^постоянная тяготения, е-—широта точки поверхности
атмосферы относительно солнечного авиатора (другая координата —-
долгота — не входит в уравнение). Первый член представляет
потенциал ныотонианского притяжения, второй-—потенциал центробежной
силы (ибо pcoatp есть расстояние переменной точки от оси вращения),
1) И. М. Симонов — Ззпяскп и воспоминания о путешествии по Англии:,
Фратщии, Бельгии и Германии. Казань, 1844, стр. 145.
3) Schumacher — Eeobachhjn™ der total™ Sonnenfinsternis auf der Wiener
Sternwartc. Astronomiacbe Naehrichfcen, B. 20, 18*9, стр. 1—4.
3) La Place — Mecaaique celeste, livre III, chap. 7. Oeuvrea, t. H, 1343,
стр. 194—197.
HO*

468
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
Обозначим через ре и рр значения р для точек, лежащих на
экваторе, соответственно, на полюсе поверхности атмосферы Солнца. Для
полюса у нас будет c=fM/pp, ибо ф=-90°. Подставляя ѳто, получим
для экватора (<р = 0°)
іА* /1 I
~J* = fM{—-
2 \РР Рс
откуда
Рв—Р. "*Й
р, 2/аг
Воспользуемся обычной в физике системой единиц CffS и лодета-
вим числа: /■=(!,7 ■ ІО"3, Ж=2,0 ■ 1039, ш = -=-,гдеУ—оборот Солнца
вокруг оеи (который Лаплас принимал равным 251/,; суток и который
надо выразить в секундах), или №= -^-г—24". во"ёб == а'9 ' 10_6-
Примем далее ре=8 радиусам Солнца, что соответствует радиусу короны
в 2° (зотя в тексте речь идет, скорее, о диаметре), и мы найдем
ре= 5,6 • 1011. В результате будет
Ре—Рр 1
рр ^190-
Следовательно, сжатие атмосферы даже на столь значительном
расстоянии будет мало. Это — следствие медленного вращения Солнца.
Іж] Затмение наблюдалось в Пензе утром и видимое направление оси
вращения Солнца образовывало с горизонтом угол, сильно
отличающийся от 90°.
I3'] Литературные указания, относящиеся к отчету Араго о
затмении 1842 г., даны в примечании [і0]. В записках Симонова (см.
примечание Е83!) есть описание упомянутого в тексте заседания Париж-
ской Академии Наук; приведем из них две цитаты. Араго начал овой
доклад о наблюдениях затмения следующими словами;
«Эти явления не представляют ничего любопытного для
астрономов и мы положили не делать астрономических наблюдений, но
так как трудно астроному не заметить времени начала и конца
затмения, то мы это и сделали».
Здесь мы снова встречаем отмеченное в примечании [']
характерное разделение наблюдений на астрономические {в нынешнем смысле
слова — аетрометрическиѳ, т. е. относящиеся к положениям небесных
тел) и физические. До поводу своих наблюдений короны Араго сказал:
*Венец оканчивался остроконечиями, загибаясь в них так,
я скажу с позволения г. Президента, comme le roue a aubes cour-
Ыв de Mr. Poncelet, и вот явление, которого мы не понимаем».

ПРИМЕЧАНИЯ
4вй
Понеѳлѳ председательствовал на заседании Академии 22 августа
1842 г.; следовательно, тогда Симонов ж слышал сообщение Араго.
Понселе, в то время академик, прежде был военным инженером и
изобрел свое водяное колесо в 182G г. Колесо Понселе принадлежит
к числу подливных (колесо находится над потоком воды); лопасти его,
отходя радяально, затем изгибаются навстречу потоку воды. Вода,
покидая колесо, обладает отань малой скоростью, так что наибольшая
часть живой силы воды обращается в полезную работу.
J88] В описаниях протуберанцев, наблюдавшихся М. В. Ляпуновым
* и другими астрономами во время полного солнечного затмения 1842 г.,
нет большого сходства. Это объясняется, вероятно, тем, что в равных
местах затмение происходило в различные физические моменты и форма
протуберанцев могла меняться. Кроме того, наблюдатели явно не были
подготовлены видеть их.
[аа] Мьтслъ о влиянии отталкивания Солнца на образование комет-
пых хвостов была высказана еще Кеплером, но построение на ее основе
класоичѳекой теории кометных форм было осуществлено Ф. Д.
Бредихиным уже поело Лобачевского. Лобачевский признает, в принципе,
возможность выброса Солнцем частиц, освобождающихся на его
поверхности (и только отрицает пригодность такоя гипотезы для
объяснения солнечной короны). Как теперь известно, Солнце действительно
посылает в окружающее пространство поток корпускул.
О наблюдениях Лобачевского над кометой Энкѳ ничего, кроме
сказанного в тексте, мы не знаем. Комета Ѳнке прошла перигелий своей
орбиты в начале мая 1882 г.
[и] Факт убывания блеска комет верен, но, что касается кометы
Галлея, то она в появлении 1910 г. слова достигла значительного
блеска.
[*1] Наблюдения этих затмений содержатся в редких старинных
изданиях, большинства которых нет в библиотеке Казанского
университета. При составлении отчета Лобачевский, повпдимому, использовал
статью Араго, появившуюся перед самым затмением І).
В статье Араго (длинное название которой должно было подробно
охарактеризовать еѳ новую и непривычную тему) имеются все приве-
!) А г a g о — Snr №lipse totale du Soleii; eur Іѳэ phSnomenes, qui devront plus
particniieremeiib filter I'atteutioa des astronomes; sur lea questions de physique celeste
dont la solution semble devoir etre Dee aux observations qui ponrront etee faites
pendant lea eclipses totelea du Soleii. Comptes renrfus de l'Acadetnie des Sciences, Paris,
T. 14, В тоня 1842 г., стр. 843—361; существенная часть втоЙ стаіыі появилась
также s журнале L'Institat, 10 ашібе 1842, етр. 221—236. ■

470
ПОЛНОЕ ЗАТИЕНИЕ СОЛНЦА
денныѳ Лобачевским и многие другие подробности, по большей частя
переданные словами самих наблюдателей затмения ѵ).
У Лобачевского есть только одна небольшая неточность: Феррер
наблюдал вѳнѳц 6' шириной, а лучи доходили до 3°.
■
["] Кеплер !) первый связал ворону, видимую во время полных
■солнечных затмений, с самим Солнцем. Оа пишет:
«Таким образом, очевидно, что, хотя скрывается все Солнце,
но вовдух (атмосфера — аёг), окружающий Солнце, чем ближе
к Солнцу, тем более сияет. .,>').
«Или воздух, или даже эфирная субстанция, которая, конечно,
еѳ есть ничто, но имеет ту или иную отепень плотности,
освещенная Солнцем, воспринимает блеск (eplendorem. concipiat),
который должен имитировать (воспроизводить — repraesentat.)
солнечный свет при закрытом Солнце» *).
Еще немного далее Кеплер выдвигает я другое объяснение короны,
связанное с лунной атмосферой.
[*81 Дѳлиль, бывший впоследствии первым
академиком-астрономом Российской Академии ІІаук, произвел свои опыты, чтобы
объяснять светлое кольцо, видимое вокруг Луны при полных
солнечных затмениях (солнечную корону) 6). Упомянем один из опытов Делили,
в котором солнечный диск покрывался каким-либо
шаром—деревянным, металлическим, каменным, или даже просто куском черного
картона, вырезанным в форме круга — вокруг екрана совершенно
ясно было видно светящееся кольцо. *
Исследования Фложѳрга над диффракциѳй света (аа которые он
получил премию от Академии Гардокого департамента Франции) были
основаны на ряде опытов, большей частью новых. Опыт, о котором
!) Ор. такие: Араго— Общепонятная астрояомігя. Перев.- Хотинсісого, т. 3,
1831, стр. 412—414.
в) Ad Vitellionem psralipomon», quibus Asfcrononiiae pars optica tcaiiilur, 1604.
J. Kepleri Opera omnia, ed. Frisch, t. 2, 1859.
^ Там же, стр. 318.
*) Таи же, стр. 319. В этом отрывке отдельно ваятоѳ вддешшое выражение
eplendorem concipiat допускает нѳ только наш перевод — «воспринимает блеск»,
во и «воспламеняется», кик в тексте, которым швьзовался Лобачевский. Однако,
еепн в»о илоао наставать в фраѳу Кдалера, она потеряет смысл.
°) Юеіівіе Іе Cadet — Reflexions aur Гсхрепепсе que j'ai rapportee i, ГАсв-
damie d'xm Anneau lununeux serablable a celui que l*on aper?oit aiitouc de la Ілте
dans les Eclipeee toUIes du Soleil, ffietoire de l'Aead&nie royaledes sciences, азшёе І715,
Paris, 1718, Мёшоігея de Ія Mathematique et de Physique, стр. 160—169.

ПРИМЕЧАНИЯ
471
пашет Лобачевский, является самым первым. Вот он в несколько
сокращенном изложении.
Посредине открытого окна подвешен черный шар; тень его падает
на белый картон. Когда картон находится рядом с шаром—тень шара
представляется как черный круг, диаметр которого немного меньше,
чем диаметр шара; воя тень равномерно интенсивна. Круг тени
окружен очень узкой полутенью, а полутень, в овою очередь, одрушев»
светящимся кольцом—-короной. При удалении экрана тень
уменьшается, полутень увеличивается, светящееся кольцо становится шире
и бледнеет. Когда экран удален на расстояние, равное 5—6 диаметрам
шара — середина тени заметно светлеет, край остается черным; когда
расстояние между экраном и шаром достигает 12 диаметров — тень еще
больше светлеет, становится похожей на полутень, но продолжает быть
окружена таким же черным кольцом. Когда экран удален на 104—105
диаметров, посредине тени получается почти белая точка и она
находится в пѳнтре маленького черного кольца. При дальнейшем
увеличении расстояния остаемся одна черная точка; когда аяран удаляется
на 107 диаметров, черная точка исчезает и остается полутень,
окруженная широким светящимся кольцом; при ѳтом шар своими краями
как раз покрывает Солнце.
На основании ѳтого и трех других опыгов, Фложѳрг пришел к
заключению, что если свет проходит около края какого-либо тела, то
часть его лучей (погибаѳтсяі (s'inuechie), входит в тень и освещает ее;
явление это не зависит от формы и материала тела, от состояния его
поверхности, температуры и т. д., не зависит также йот среды,
окружающей тело ' |.
Майер проделал такой же опыт, но не получил каких-либо новых
результатов. Мы здесь не говорим о его других опытах я не
останавливаемся подробнее на взглядах Майера па природу света (он был
сторонником теории истечения Ньютона, но с некоторыми изменениями);
интересующиеся могут найти это в его статье в).
Яи одного ие этих мемуаров не было в библиотеке Казанского
университета, и Лобачевский, несомненно, писал это место отчета не
по первоисточникам. С некоторой подробностью опыты Делиля,
Фложѳрга и Майера переданы в обширной енциклопедии финики
і) Мекуар Фложерга был опубликован в виде четырех сообщений; все
изложенное содержится а первом из них: Flaugergues — Мйюоігѳ аог la diffraction
<1ѳ 1а ІішіІёгѳ, premier extrait. Journal de physique, de cbimie, dliistofre naturelle
et des arte, t 75, 1812, стр. 16—29.
э) J. T. Mayer—Pbaenomenorum abinflexions ІЩвіпк pendetitim»expropriisob-
aervationibaa et cxpartmentle rocensio et compatatlo. Commentatianies societatis regiae
seiectiarum Gotfcingengis recentioree, v. 4, ad a. 181S—1818, Gottmgse, 1820, Сіаааів
matttematicae, <-лр. 4S—80.

472
ПОЛНОЕ ВАТМЕНИЕ СОЛНЦА
Гѳлера1). Оттуда их и мог взять Лобачевский:; но любопытно, что,
вероятно, оя сам обратил расстояния: шара от вкрана, выраженные
Фложергом в .диаметрах шара, в видимые угловые диаметры
последнего. Действительно, нетрудно, нользуясыаблицами тангенсов,
получить такие результаты:
Расстояния
в диаметрах шара
107
105
12
Угловые
диаметры шара
ШГ',7
1964*4
4Ч6'19"
они в достаточной мере согласуются о числами Лобачевского.
Многочисленные опыты по диффракции света были произведены
н другими авторами в ХѴШ вене и в начале XIX века; их завершили
в свое время блестящие исследования Френеля, вытеснившие ив
памяти даже современников Лобачевского работы Фложѳрга и Майера,
о которых нет никакого упоминания во многих исторических и
монографических сочинениях по физике и специально по учению о свете,
изданных начиная с 30-х годов ХТХ века.
По существу, результаты опытов Фложѳрга ни в коѳа мере не
могут быть перенесены на маоштабы солнечных затмений, несмотря
на внешнее сходство условий. Ира столь большом непрозрачном теле,
каиим является Луна, теоретически мыслимые диф фракционные
явления внутри границ лунной тени па Эѳмле, практически будут
совершенно отсутствовать. Тень останется темной. Повидимому, это
было впервые выяснено варшавским физиком Биекѳ не так давно8).
Не лишено интереса, что еще в 1748 г. астроном Тобиао Майѳр
(отец физика Майера, упомянутого Лобачевским), когда он доказывал
отсутствие атмосферы на Лупе, сослался на опыты, сделанные для
объяснения солнечной короны. Он говорил (довольно иронически),
что круглый кусок олова, диск дерева или бумаги, даже железный
гвоздь и волос могут вызвать подобные явления. Но, как эти тела не
обладают атмосферой, так нет нужды предполагать атмосферу на
Луне, чтобы понять корону Солнца.
Далее он выоказываѳт то же предположение о короне, что и
Лобачевский3), который, впрочѳмі вряд ли читал ѳто: «Возможно, что
это наш земной воздух единственно виноват. .. в отношении светлых
1) J.S.T. Gehler-Physikaliscbejj Worterbuch, В. 2,1830 (стр.837— о Деднлѳ,
стр. 860—691 — о Фложоргѳ и стр. 707 —о Майѳрѳ).
а) F. Вівке — Are diffraction phenomena possible at solar eclipses? The Aetro-
phyaical Joaraal. v. 38, 1913, стр. 1S2—198.
*} Ом. стр. 451 паст. тома.

ПРИМЕЧАНИЯ 473
полос около тѳл, когда последние помещаются перед Солнцем; по
крайней мере, обратное не показано»1).
Хотя в впоху Лобачевского объяснение солнечной короны диф-
■фракциѳй света далеко не было отвергнуто астрономами и фиаимамя,
■сам он в конце отчета о еатмѳнии от него откааался.
[4,3 Взгляды Ньютона на природу света вовсе не были
односторонними и его нельзя считать только создателем эмиссионной теории
(теории вытѳваиия), как ею было принято в XIX веке1). Оп отчетливо
представлял себе вовможность соединяя теории, которая объединяла бы.
преимущества волновой и корпускулярной гипотезы о свете, хотя.
в действительности ©то было осуществлено только в паше время.
Академик Г. С. Ландейерг пишет 8):
«Нельзя не отметить, что современная квантован теория света
(теория фотонов) характеризуется чертами, которые напоминают
ньютоново представление о свете даже в большей степени, чем
ото может показаться с первого взгляда. Корпускулярные
свойства света получили ѳвспѳримѳнтальпоѳ обоснование гораздо
более серьезное и разнообразное, чем его было во времена
Ныотоыа, а теория „приступов11 легкого отражения и легкого
прохождения, придуманная Ньютоном для объяснения
интерференционных явлений, содержит черты, напоминающие
современную концепцию волнового поля, определяющую вероятность
нахождения фотона в том или ином месте пространства».
Эмиссионная (корпускулярная теория света) .подразумевается
Ньютоном уже в определении I «Оптики» *) и особенно ясно выражена
в вопросе 29Б) «Но являются ли лучи света очень малыми телами,
испускаемыми светящимися веществами?»
I45] Замедление в 8 -д- секунды в моменте покрытая звезды Луной
■соответствует перемещению Луны на небе менее 2". Как раз Дюсѳжур
!) См. редкое сочинение, имеющееся в библиотеке Казанского университета;
Т. Mayer — Beweia daaa der blond кеіпѳд LuftkreiB habe. Kosmogtapliische Nach-
rickten uad Sammlungen auf das Jatir 1748, Шеи, Nurnberg, 1755, стр. 37S—419;
в частности, стр. 418 — 417.
3) Историю работ Ньютона но опд'иие можно найти в книге акад. С. И. В а-
пааова— «Исаак Ньютон*, 2-е изд., 1945,главы 5, 6, J и 8, Классический,
обобщающий труд Ньютона, на который в данном вопросе обычно делаются ссылки:
Isaac Newton — Opticks, London, 1704, 3-е зад. 1721; русский перевод-. И оаак
Ньютон — Оптика, перѳв. С. И, Вавилова, изд. АН СССР, М,—Л., 1627.
я) Г. С. Ланд с бѳрг — Оптика. 2-е изд^ Гоетехиздат, М. —Л., 1947, стр. 578,
*) Стр. 14 русского перевода.
6) Стр. 288 русского шринода.

474
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
дает для изгибания лучей 3" и не согласен а Лемояье, который
доводит изгибание до 13". Лекселя Деламбр вовсе не упоминает; в итоге
просмотра ряда работ Лекселя, а также специальных трудов по
вопросу о замедлении моментов покрытий звезд Луной, аѳ удалось
найти упоминания о подобных его наблюдениях.
Лобачевский, составляя вторично отчет о затмении, вероятно,
написал его место на память, не обращаясь сыова к Деламбру (бывшему
на руках у И. В. Ляпунова); поэтому отсутствует указание страниц
ffistoire; вместе с тем, при обращении и дугу 3 ^ секунд времени
опоздания в покрытии звезды, было использовано правило для
суточного движения звезд (3— X 15 = 32"і5). после чего получились
приведенные в тексте 50", вместо 2я.
Явление кажущегося перехода звезды через край диска Луны
объясняется, с одной стороны, несовершенством толоскопон, дающих
вследствие сферической и хроматической аберрации расширение
лунного диска, с другой стороны —- неточностью фокусировки, ибо яркие
звезды и темный край Лупы (при пепельном свете) не поѳволяюг
уверенно наводить ка фокус. Возможно, что здесь имеют место и
зрительные иллюзии.
Телескопы XVІЛ вена были не слишком хороши, а в самих
наблюдениях много противоречий; одни наблюдатели видели звезды
внутри края Луны, другие, находившиеся на той же обсерватории и
в то же время, — нет.
[*Ц Дѳламбр1), приводя эту величину, говорит об иррадиации.
Явления иррадиации при прохождениях Вѳиеры по диску Солнпа
проявились очень резко в заметно уменьшили точность наблюдении.
f+1J Указанная здесь максимальная величина сжатия — -ш лунного-
диамѳтра — соответствует ошибочному расчету 50" для замедления
при наблюдении покрытий звезд Луной (см. примечание [*5]). Однако
»та ошибка в расчете значения не имеет, так пая верный результат
только усилил бы заключение Лобачевского,
lts} Декарт считал, что свет распространяется в пространстве путем
передачи давления в эфирной среде; при этом .давление может
сообщаться отдельными импульсами. В этих взглядах только с большой
натяжкой можно видеть намек на волновой принцип. С точки зрения
Декарта пѳльвя объяснить одновременную передачу света в двух
') Сочинение, цитированное на стр. *4в пает. тома, стр. 585.

ПРИМЕЧАНИЯ 476
противоположных направлениях — два человека но могут видеть друг
Друга1).
Теория овѳта Гюйгенса8) много совершеннее, чем у его предше-
ствѳнников. Именем Гюйгенса назван принцип, согласно которому
«вокруг каждой частицы» (до которой распространяется световая
волна) «должна образоваться волна, центром которой она является»;
однако удары в центрах волн совершаются без определенной
последовательности и волны следуют не на равных раоотояниях.
Невидимому, Гюйгенс считал световые волны продольными колебаниями.
В ряде сочинений Эйлер отвергает теорию истечения Ньютона
и высказывается в пользу волновой теории. Он связывает различные
цвета с продолжительностью световых колебаний, но ни Гюйгенс, ни
он еще не сумели использовать важнейший аргумент в пользу
волновой теории — явления интерференции, открытые в XVIIвеке3).
Принцип интерференции световых волн был установлен Юнгом
в 1801 г., несколько позже он уточнил его и дал самое название
«интерференция». «Когда два колебательных движения различного
прохождения совпадают либо точно, либо весьма близко по
направлению, то нх совместное действие является комбинацией движений,
принвдаѳжащих каждому в отдельности»4).
Френель упоминает не раз имена основателей волновой теории
света. В начале его популярной статьи о светеа) мы моасем прочесть,
следующий отрывок, сходный с текстом Лобачевского.
«Волновой принцип, обязанный своим происхождением
Декарту и в выводах, из него вытекающих, с большим искусством
развитый Гюйгенсом, был принят также Эйлером, а в самое
последнее время доктором Томасом Юнгом, которому оптика
обязана многими важными открытиями».
!) Впервые Декарт высказал свои взгляды па природу евета в написанном
до конца 1632 г., но опубликованном значительно повмсе сочинении: Desoarte в—
Le Monda он traite de la lumicre, 1864, 1S67. Русский перевод; Ренэ Декарт—
Трактат о свете. Избранные произведения, перѳв. В. В. Соколова, 1В50, стр-
240-2*5.
^Huygene — Traite de la lumi&re, 1690. Русский перевод: Xp.Гюйгенс —
Трактат о свете, перев. Фредерике, 1935, стр. 31.
3) Си. прекрасный очерк: Акад. О.И. Вавилов—Физическая оптика Лаовардя
Эйлера (Леонард Эйлер, 1707—1783, сборник статей и материалов я 150-летшо
со дня смерти. Академия паук СССР, 1Q35, етр, 29—38),
*) Young — On the theory of light and eolonrs. Philosophical transactions of tee
Royal Society of London, 1802, стр. 34.
6) A. F r e s и ѳ 1 — De la lumlere. Supplement a la traduction fran$aise de la
cinqnieme edition du Systeme de chimie, par Th. Thomson,... par J. RiHsult, Paris,
1822, стр. 1. Русский перевод: О. Ж. Френель — О свете, перев. Фредерике,
1U28, стр. 7.

476
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
(*9] Б опыте ФренеляL), сыгравшем важную роль в обосновании
волновой теории, свет от источника, пропущенный через красный
■светофильтр (чтобы получить свет определенной длины волны),
отражался от двух зеркал, составлявших между собой угол, очень близкий
к 180°. В зеркалах получаются два изображения источника света,
расположенные близко друг к другу. В каждой точке пространства,
куда попадает свет источника от обоих зеркал, могут наблюдаться
явления интерференции, так как лучи, идущие от обоих изображений
источника, когерентны, т. е. имеют постоянную разность фаз в течение
времени, достаточного для наблюдения. В точке, где разность длин
путей, пройденных светом от обоих изображений источника,
составляет четное число полуволн света, будет максимум оевѳщѳннооти;
минимум освещенности будет соответствовать разности путей в
нечетное число полуволн, В случае точечного источника света какая-нибудь
поверхность равной освещенности (например, соответствующая ее
максимуму! представит в пространстве часть двуполоотного
гиперболоида вращения. Фокусами его будут оба изображения источника
света: разность расстояний от них до любой точки гиперболоида будет
ооотоявжа и равна данному четному числу полуволн света, эта же
разность расстояний будет действительной полуосью гиперболоида.
Если пересечь гиперболоид любой плоскостью, проходящей через оба
иаображѳния источника света, следом на плоскости будет гипербола
■с теми же фокусами.
Опыт, аналогичный по выводам, был произведен Френелем с
непрозрачным телом, помещенным в пучке света; роль фокусов
гиперболы (рассматривая построение на плоскости) играли края тела.
Хотя и в этом мѳмуарѳ Френель неоднократно подчеркивает
значение своих исследований для опровержения теории истечения, но
•еще яснее он выражается в популярной статье о свете 5).
«Но только что приведенного опыта достаточно, чтобы
поставить вне сомнения заметную кривизну траекторий, по которым
распространяются внешние полосы.
Этот замечательный результат представляется весьма трудно
совместимым с принципом испускания; в самом деле, самое
естественное объяснение внешних полос с точки зрения этого
принципа состояло бы в предположении, что световой поток,
коснувшись экрана, испытывает в его близости попеременно
расширения и сжатия, которые и порождают темные и светлые
1) Fresnel — Мйтоіго sur la diffraction <Іѳ 1а Іитіёгѳ. Аішаіез de скішіе et
■da physique, t. 11, 1819, стр. §37—338, 351. Б полном виде в Мбшоігее do Г
Academic des Sciences de 1'Institufc de France, t 5. 1336, стр. 416—418, 432.
a) Соч., пат. в саояаев) и» предыдущей странице.

ПРИМЕЧАНИЯ
477
попоен. Но тогда ѳти различные пучка—сжатые или
расширенные— долйвны были бы, перейдя за экран, идти по прямой
линии, ибо, воли в теории Ньютона допускается, что тела могут
производить на световые молекулы сильные притяжения и
отталкивания, то воѳ исѳ никогда не предполагается, что действия
этих сил могут распространяться на расстояния столь
значительные, как размеры тех траекторий, которые обладают заметной
кривизной на протяжении нескольких метров... » г).
[м] Хотя указания на явления диффракдии света можно найти
у Леонардо да Винчи, но более определенные наблюдения были
сделаны Гримальди в середине XVII века3). В одном из его опытов
евет Солнца, проходил черев малое отверстие в темную комнату, где
на пути пучка солнечных лучей ставилось узкое непрозрачное тело,
а диффракционныо явления наблюдались на экране сзади. Диффрак-
ционпые полосы, располагавшиеся вне геометрической теня, белые
посредине, имели с внутренней оторояьг синюю кайму, а с внешней—-
красную. Тая как из всех лучей видимого спектра красные обладают
наибольшей длиной волны, для пях разность длин путей света от
краев непрозрачного тела до диффракционной полосы на вкране,
пропорциональная длине волнн, будет наибольшей, а поэтому они
всего сильнее уклонятся наружу от геометрического вчая тени.
[S1J Речь идет о верхнем слое солнечной атмосферы-~так
называемой хромосфере, которая кажется розово-красной из-за обилия в неП
водорода (в видимом спектре водорода преобладает яркая красная
линия). Хромосферу можно без труда наблюдать во время полных
солнечных затмений и ее видели многие наблюдатели затмения 1842 г.
Iм] Протуберанцы (выступы газов хромосферы), описаипыѳ
М. В. Ляпуновым, наблюдались многими астрономами; см.
примечание Р3].
[ъз] Опыт Юнгаа) был похож на опыт Гримальди (ом.
примечание [5(IJ), но Юнг, кроме того, закрывал часть потока овега,
проходившего мимо одного из краев непрозрачного тела, причем тогда
немедленно исчезали полосы интерференции внутри тени.
Этот вазкный. для волновой теории опыт и другой, ему
аналогичный по результатам, упоминает Френель в своем сочинение «О свете» *).
і) Там sse, стр. 26; русский перевод — стр. 35 (здесь немного исправлено).
2) Эти исследования Граыаиьди: были опубликованы после его емертш:
Grimaldi — PhyBLeo-mathesis de lumiae, coloribua et iride, 1665.
3) J о ц n g — Experiments and caleulatione relating to physical optics. Pbiloso-
phical transactions of the Royal Society o£ London, 1804, стр. 1.
t) Cm. сноску fJ на стр. 475.

478
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
Рассуждения Френеля, кратко приведенные Лобачевским,
основываются на видоизмененном принципе Гюйгенса (см. примечание ['*]).
Далѳе Лобачевский остроумно и просто опровергает объяснение короны
диффракпиеВ солнечного света. Уже тогда укоренявшийся термин
«интерференция» (взятый с английского выражения Юнга) он
переводит русским словом «перекрестываниѳ».
[B*J Возражения Пуассона !), направленные против волновой теории
света, основаны на решении уравнений распространения упругих
волн от точечного источника в двух различных средах, каждая на кото-
рык однородна, Обе среды разделены плоскостью; колебания в етих
средах продольные. Следствия, выведенные Пуассоном для
интенсивности отраженного света, не сходятся с опытом; еще более важное
возражение заключается в необъяснимости рассеяния света при
преломлении: так как скорость волн не зависит о* их длины, показатели
преломления для разных цветов должны быть одинаковы. Пуассон не
отрицает принцип Френеля (дополненный принцип Гюйгенса сложения
»лементарных яолѳбаний, приходящих в данную точку от всех чаотей
световой волны, см. в примечании [сг]), но оспаривает его
преимущество. Пуаеоон пишет, что из етого принципа вытекает необходимость
существонания, наряду с волной, распространяющейся вперед, также
и волны, идущей обратно (чего, конечно, не наблюдается). Исходя из
развитой им теории, он считает, что Френель незаконно оперирует
с интерференцией всевозможных элементарных волн, ибо колебания
на некотором расстоянии от источника света будут распространяться
только ортогонально к поверхности основной волны, а не по всем
направлениям, как полагал Френель. На некоторых других возражениях
мы нѳ останавливаемся, но приведем следующую характерную фразу:
«В своих исследованиях физики часто руководствуются
индукциями, которые мы не можем принять за достаточные
доказательства, но яоторые, тем не менее, очень ценны, потому что они
замещают теории, пока те не полностью построены; к тому же
науки им [индукциям] обязаны большим числом прекрасных
открытий>.
Вот заключение письма Пуассона:
«Я закончу ети заметки, повторяя, что они яѳ направлены ни
в коей мере к тому, чтобы посеять сомнения в результатах Ваших
# опытов, к которым никто не относится справедливее меня; они
і) Extrait d'une lettre de M. Poiseon. i M. Freaael, Annates de caimie et de
physique, t. 22, 1823, стр. 270—280. См. тякям статью Пуассон*, непосредственно
предшествующую его письму ж ивяваиную с нам: Роіввод — Exfraifc d'un М&шяге
йпг la propagation du mouvesment done lee fluides elsstiquee. Тан жѳ, стр. 242—269.

ПРИМЕЧАНИЯ 479
также не направлены против теории волнений, верность или
ошибочность которой, по-моему, могут быть доказаны только строгим
анализом, сравнением его во всех следствиях с
наблюдениями; но они [ваметки] имеют целью доказать, что если ета теория
есть истина, можно в настоящий момент уверять, что это
наверняка нѳ вследствие тех доводов, которые давались до сих
нор в се поддержку и чтобы объяснить явления, представляемые
светом».
Ответ Френеля появился в следующем томе журнала1); он
направлен, главным обравом, в защиту принципа Гюл^енеа и его
плодотворности; кроме того, в ответе подчеркиваются поперечные колебания
световых волн.
Чтобы, объяснить явления поляризации, допуская продольные
колебания ефира, нужно иметь две различные жидкости, наполняющие
одну и ту же часть пространства. Нѳ воспроизводя всей обстоятельной
аргументации Френеля, приведем немногие выдержки. Френель питает,
■например:
*С помощью одного принципа сложения малых движений,
ив которого следует принцип интерференции, я нашел общие
ааконы диффракции, которые не смогли бы быть открыты одними
наблюдениями».
В другом месте:
«Гипотеза поперечных колебании в световых волнах не только
необходима, чтобы объяснить особенное явление
пе-интерференции лучей, поляризованных под прямым углом, но еще и для
того, чтобы понять самую поляризацию, потому что, если
допустить, вместе с Вами, колебания только перпендикулярные в
волнам, то-еоть направленные по лучам, всё становится подобным
вокруг этих лучей, и они долины иметь одинаковые свойства
со всех сторон. Я удивлен, что размышление, столь простое, не
отняло у Вас надежду представить явления оптики с теми
определениями световых волн, которые Вы приняли».
Как общий итог, Френель не без яда замечает, что когда Пуассон
достаточно разовьет свои теории, он своими строгими методами придет
ко всем выводам, полученным Френелем из его основного принципа.
Теория света Френеля, являясь громадным шагом вперед, все-таки
в существенных пунктах требовала дополнений и уточнений, которые
и были постепенно сделаны на протяжении всего XIX века. Ее
прочной опорой были многочисленные и остроумные опыты, резко противо-
і) Т. 23, стр. 32—50 и ИЗ—122.

480
ПОЛНОЕ ЗАТМЕНИЕ СОЛНДА.
рѳчившие эмиссионной теории Ньютона. В 1816 голу, за семь лет дсѵ
описанной полемики, академики Пуассон и Араго рассматривали
первую работу Френеля о диффракпии. Проверяя его выводы, Пуассон
нашол, что в центре тени от круглого тела должно быть, на основе
волновой теории, светлое пятнышко, как если бы лучи света падали
сюда беспрепятственно. В этом Пуассон усмотрел опровержение
волновой теории, но Араго сделал опыт, который полностью подтвердил
теорию и произвел громадное впечатление. Несколько странно, что
академикам тогда не пришли на память опыты Делиля, Маральди и
Фложѳрга (ср. примечание [48]), в которых уже вѳ раз был получен
этот результат.
Поперечные колебания в эфире плохо укладывались в умы
тогдашних физиков. Но здесь позиция Фрѳполя несомненно была исторически
оправдана: об эфире известно было только, что он носитель света, и
требовать, чтобы он во всех отношениях подходил под категорию обычных
жидкостей—было метафизикой. Позже Стоке показал, что и в жидком,
эфире возможны поперечные колебания.
[Ь6] К 1842 г. взгляды Френеля временно восторжествовали, и
в учении о природе света это было в то время тагом вперед. Но
затруднения в теории света етим не исчерпывались, и Лобачевский
предусмотрел, что эта победа—нѳ окончательная, что волновая теория
не завершена, а природа света далеко не уяснена. Вслед за тем оп
высказывает глубокую мысль об универсальности сил притяжения и
отталкивания. Напомним, что пишет Энгельс по поводу притяжения
и: отталкивания 3):
«Обыкновенно принимается, что тяжесть есть наиболее всеобщее
ощеѲедеше маіщпюлтости, т. е- что притяжение, а не
отталкивание есть необходимое свойство материи. Но притяжение а
отталкивание столь же неотделимы друг от друга, как положительное
и отрицательное, и поэтому уже на основания самой диалектики
можно предсказать, что истинная теория материи должна отвести
отталкиванию такое же важное место, как и притяжению, и что
теория материи, основывающаяся только на притяжении, ложна,
недостаточна, половинчата».
«Там, где имеется притяжение, оно должно дополняться оттал--
киванием».
[D*J Теория света Коши, постепенно дополнявшаяся, а*в некоторых,
пунктах и изменявшаяся ее автором, содержится в целом ряде
мемуаров и заметок, и было бы затруднительно дать ее краткий очерк..
1) Ф. Энгельс — Диалектика природы. Госполитвадат, 1948, стр. 185, 196.

ПРИМЕЧАНИЯ 481
Она явилась существенным шагом вперед в развитии теории Френеля;
учитывая влияние молекул вещества на частички светоносного вфира,
Коши показал, что волновая теория может объяснить дисперсию
света—явление, которое оставалось непонятным после работ Френеля.
В 1830 г. Коши писал1):
«Гипотеза, которую принял Френель, стала реальностью,
несмотря на аргументы; и вычисления его знаменитого
противника» (т. е. Пуаоеона, ср. примечание [м]).
В начале этого момуара Коши сообщает:
«Я первый дал общие уравнения равновесия и движения
молекул, подверженных силам вваимиого притяжения и
взаимного отталкивания, допуская, что эти силы являются функциями
расстояний между молекулами».
Там же встречается упоминание о трех системах плоская волн,,
сопровождающих распространение света.
В 1839 г. Коши ссылается на этот мечуар 1830 года и, между
прочим, пишет s):
«Если теплота есть колебательное движение, как воб
заставляет ѳтому верить, и если она может распространяться в пустоте,
то-есть в ѳфире, рассматриваемом отдельно, — нужно, чтобы она.
была одним ив колебательных даиясейий, в которым эфир оно--
еобен. Но, так как колебания, распространяющиеся в ефирѳ,
доходят до больших расстояний от центра возбуждения, так что-
повѳрхности волн, взятые в ограниченном простирании, могут-
бѳз чувствительной ошибки рассматриваться как плоскости, йти
колебания необходимо еводягоя к таким, которые допускаются
движениями плоских волн, то-ѳоть к поперечным, или
продольным колебаниям. Итак, ввиду того, что поперечные колебания,
происходящие бѳв изменения плотности, представляют свет, для
представления теплоты остаются только продольные колебания,
или, что то же самое, колебания, сопровождаемые изменениями
плотности».
Впервые это предположение было высказано Коши в 1836 г.
в письме к Амперу 8).
Лобачевский был прав в своей критике: ѳта часть теории света
Коши оказалась мертворожденной. Пусть в некоторой среде оуще-
і) A. Сатіеьу— Мётоіге апг la iheorie de la Inmiere. Paris, 18S0.
2) A. Cauehy—Mfimoire ou Гол monire comJuent іддѳ seule et memethecrle
peut fournir Іѳв lois de la propagation de la lumiere et de la chaleur. Comptcs геи-
due de l'Aesdfinrie dee Sciencee, t. 9, Paris, 1839, frp. 285.
=) Comptes тѳіиіиэ, t. 2, 1838, етр. 2О7—20С.
31 Зал. 2823. H. И. Лоббчеиовнй, т. У-

482 ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
опяуют только поперечные волны света; при каждом преломление,
или отражении на границе с другой средой, должны возникнуть и
продольные волны, которые потребуют себе часть энергии пришедшиж
поперечных волн. Опыт втому противоречит: при прохождении светом
границы двух оред энергия световых колебаний не терпит заметной
потери.
[и] Это место цитирует акал- О. И. Вавилов, отмечая попытку
И. И. Лобачевского соединить емисоионную и волновую теории света *).
Перед ѳтим *) он говорит о гипотезе Ньютона, по которой световые
частицы возбуждают колебания в ѳфире, находящемся в веществе и
около него. Но в XIX веке, после триумфа волновой теории, идея
Лобачевского являлась неожиданной н смелой. Иа текста видно, что
исходная мысль была подана Кнорром, но где-то Лобачевский
незаметно переходит к положению собственных воззрений (см. следующее
примечание) — может быть, сразу же после первой фравк абзац», но,
может быть, и далее, например, со слов: «Оставалось бы решить,
какою силой в эфире...».
р8] Следующая еа этим фраза ясно показывает, что высказанный
в тексте взгляд на связь теории света и теории теплоты принадлежит
самому Лобачевскому (а не Кнорру). «Погонное» и «качатѳльноѳ»
движения— поступательное движение и поперечные колебания. Эфир
Лобачевского — его не просто носитель колебаний, как у физиков его
века, его-—поток частиц, которым свойственны волновые колебания.
С проницательностью, поистине поразительной, Лобачевокий в
значительной степени предусмотрел то направление, по которому пошло
учение о свете через ряд десятилетий после него,
[іэ] По наблюдениям О. В. Струве во время затмения в Липецке
падение температуры было более значительным.
[ео) Приведем это достопримечательное описание Уллоа 8):
«Черва пять или шесть секунд после погружения [в тень]
мы начали наблюдать вокруг Луны весьма яркий круг света,
который, казалось, имел быстрое круговое движение, до
некоторой степени подобно ракете, вращающейся вокруг своего
центра».
») С. И. Вавилов-Исаак Ньютон. 2-е изд., 1945 г„ стр. 78.
з) Таи асе, стр. 70—78.
е) XI] 1 о а — Observations о£ the total and annular eclipse of the Sun, t&fcen on
the 21th of Jane_17?8... Philosophical transactions □£ the Royal Society of London,
1779, стр. 10&—119.

ПРИМЕЧАНИЯ
433
Подобная иддювия повторялась у некоторых зрителей других
затмений и, вероятно, объясняется утомлением и плохой адаптацией глав,
до того направленных на яркий солнечный серп (это подтверждается
тем, что корона была замечена на сразу после начала полной фазы
затмения).
Iм] Отвергнув объяснение солнечной короны при помощи диффрав-
ции света у краев Луны, Лобачѳвокий считает недостаточной
рефракцию (преломление) солнечных лучей в аѳмной атмосфере,
[es] Принцип Гюйгенса получил у Френеля новую формулировку ').
«Колебания световой волны в каждой ее точке могут
рассматриваться как сумма влемѳнтарных движений, которые досылают
сюда в этот момент времени, действуя отдельно, вое части етой
волны, взятой в каком-нибудь из ее предшествующих положений».
Добавим, что формулировка принципа Френеля не вполне строга;
более строгая формулировка была дана Кирхгофом в 1882 г., но и та
не свободна от теоретических недочетов. Тем нѳ менее, для решения
многих задач оптики на практике вполне достаяючен принцип
Гюйгенса в том виде, в каком его применял Френель.
[т] Причина, по которой Луна и планеты нам кажутся светлыми,
заключается в том, что мы их наблюдаем на темном фоне ночного неба,
между тем как они освещены Солнцем. Лобачевский, в сущности, не
пользуется своим рассуждением, что яркость (по терминологии
Лобачевского «напряжение света», «сила в освещении») собрания
светящихся тел зависит от расстояния до наблюдателя, как бы чувствуя
ненадежность вывода.
По поводу его объяснения солнечаой короны следует еще раз
напомнить, что астрономы не скоро после затмения 1842 г. решили
окончательно, что она принадлежит Солнцу. Тем не менее, вполне
справедливо мнение Лобачевского, что свет Солнца, рассеиваемый
аѳмной атмосферой, еначительно повышает отражательную способность
Земли, если ее рассматривать иа мирового пространства. Альбедо Земли
(отношение светового потока, отражаемого Землей во всех
направлениях, к потоку солнечного света, падающему на Землю) равно 0,23,
тогда как для Луны, лишенной атмосферы в воды, альбедо равно
только 0,07.
Характерно упоминание Лобачевским жителей небесных тел, — может
быть ѳто не более, чем оборот речи, но и то свидетельствует, что
Лобачевский не отрицал обитаемости Вселенной.
і) См. напр: сочинение Френеля, приведенаов в сноске на стр. 475 наот
тона,— стр. 65 нодлинвика и 56 русского перевода.
31*

484
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
[w] О наблюдениях М, В. Ляпунова и его отчете ■см., кроме текста
отчета Н. И. Лобачевового, примечания [*], R, [І0І, [п], р], [14], [и],
вводную статью -1) и приложение 8 s).
[66] Отношение вначения горизонтальной составляющей земного
магнетизма в Пензе к ее значению в Казани может быть найдено по
обычному правилу: оно обратно пропорционально квадратам периодов
колебаний стрелки. Ив наблюдений 1336 г. это отношение получается
1,0918; из наблюдении 1842 г. —1,0950.
[56] Подобные похолодания и поздние снегопады олучалиоь и в
последующие годы. Небывалый снегопад имел место в 1916 г.: снег выпал
в Казани 1 июня и лѳясал до 3—4 июня (нового стиля), толщина
снегового покрова достигла 20 см, а в других местах—до 27 см Е).
1^] В втих высказываниях виден глубокий интерес Лобачевского-
к природе и сельскому хозяйству своей родины. Непосредственным
поводом к его замечаниям могло послужит* пребывание на
территории Пензенского училища садоводства, где была расположена
временная обсерватория Казанской експѳдицаи.
j6Bj •уттітмнттнтгид о гористом положении Пензенской губернии нѳ
следует понимать буквально. В первой половине XIX века холмы нередко
назывались горами. Следы ѳтого словоупотребления со хранились и до
сих пор, и, например, возвышенности правого берега Волги иногда
в разговоре называются горами. Эти возвышенности, как правильно
отмечает Лобачевский, отнюдь не связаны с горными хребтами,
например с Уралом (как думали выдающиеся геологи того времени), на
имеют эрозионный, размывной характер. Действительно, Свияасск
расположен на «останце», вырезанном иа правоеолжской
возвышенности размывом впадающих в Волгу рѳчев.
') Стр. 421 наст, тома.
г) Стр. 494 наст. тома.
s) См. П. Т. Смоляков — Кшшат Татарии, Казань, 1947, стр. 31.

Приложение 1
ЗАМЕТКА В ПЕНЗЕНСКОЙ ГАЗЕТЕ 1842 г. О ЗАТМЕНИИ,
ВЕРОЯТНО, ПРИНАДЛЕЖАЩАЯ Н. И. ЛОБАЧЕВСКОМУ
В «Прибавлениях в Пензенским губернским ведомостям» М 28 от
10 июля 1842 г., вскоре после наблюдений казанских ученых над
полным еолнечним затмением, появилась заметка (без подписи),
относительно которой X. Чаливов в 192В г. 1) высказал предположение,
что она может принадлежать перу Лобачевского. X. Таликов
приводит текст заметки и аргументирует свое мнение, ссылаясь на
употребление некоторых чиото технических терминов, на самый стиль вамѳтки
и: на глубокое понимание происходящего явления. Предположение
X. Чаликова кажется очень правдоподобным, и -в его пользу можно
привести дополнительные соображения.
Ниже следует текст заметкиа).
«1842 года 26 июня, происходило в Пензе полное затмение
солнца. К сожалению, для наблюдений столь редкого и
любопытного явления погода была не совсем-благоприятная. За густыми
облаками на возможно было видеть ни начала, ни конца
общего затмения. Солнце появилось, когда уже часть его была
покрыта луною, но в неясном и не рѳеко ограниченном виде.
Наблюдения ' производились в присутствии Ректора Казанского
Университета Г. Действительного Статского Советника
Лобачевского н Профессора Физики Коллежского Советника Кнорра,
Астрономом наблюдателем Кандидатом Ляпуновым, с помощию
большой Венской Ахроматической трубы и Брѳгетова хронометра,
принадлежащих Астрономической Обсерватории Казанокого
Университета. Начало затмения по приблизительно вычисленному
') X. Чаликов— ft И. Лобачевский в Пензе. «Трудовая правда» (Пенза),
J4 51, 4 марта 1026 г., стр. 3. См. также С. А. Каеьянюк —Поездка Н.И.
Лобачевского в Пензу для набшодееяя шлного солнечного затиекия 1842 г.,
«Природа», 1050, М 10, стр. 69—71.
Я) По точной ее копии, сделанной о подлинного редкого издания Г. О. Кар-
ыедош, зав. Пензенской обл. библиотекой им. Ж. Ю. Лермонтова.

486-
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
состоянию хронометра г) определено вН. 9'22" среднего
Пензенского времени, а конец полного затмения в9ч. 12J22"cp. П. вр.
Таким образом, полное ватмениѳ продолжалось 2'Ь§" *). Сильное
уменьшение света сделалось заметным за несколько минут до
начала полного затмения. Впрочем об втом предмете ничего нельзя
сказать удовлетворительным образом. Пасмурное время
принудило отказаться от всех физических наблюдений, какие
предположено было сделать над степенью уменьшения солнечного света
и солнечной теплоты. Утвердительно сказать можно только то,
что темнот» во время полного затмбняя была совершенно
полуночная, и, вероятно, при ясном небе открылась бы многие ввеады
и для простого глаза. Всего более поразителен был удивительно
быстрый переход от этой темноты к свету, когда появился
первый луч солнца. С втим появлением все исчеапо: дымчатый
отлив, каким одеты были все окружающие предметы, особенный
вид облаков, мрак, покрывающий восточную часть горизонта,
и заря, освещающая противоположную часть неба, одним словам,
вой, что явление полного аатмѳния далаіо столько 3)
величественным и удивительным для всякого внимательного наблюдателя
чудес природы».
Описание ерѳяища полного затмения при облаках на небе,
изображение полной фазы замечательны но краткости, точности и
картинности*). Нельзя допустить, чтобы все ото мог написать Кяорр, в ту
пору явно не владевший столь свободно художественными средствами
русского языка. В той же книжке Ученых записок Казанского
университета, где впоследствии появился отчет Лобачевского, есть статья
*) Ляпунов, вероятно, еще нѳ вакончил обработку своих наблюдений; поэтому
поправка хронометра была вычислена только приблизительно.
3) Расхождение в ! секунду с предыдущими моментами начала и: конца
полной фазы, повидиыомѵ, вызвано округлением дееятак долей секунд.
*) Особоваость стиля Лобачевского, ер. стр 439 част, тома («сколько резким»),
стр. 454 (■стодьяо теплый»; исправлено в «Журнале Министерства» на «столь
теплым*).
*) Во время пошгой фазы солнечного аатмеаия небо опоясано со всех сторон
кольцом эари, так как воздух освещен за праце.таш* конуса лунной тени, кото-
ран движется по эвмиой поверхности с запада на восток со скоростью порядка
1 мв секунду. Пока длится полное аатмепне, ширина кольца вари в разных
направлениях горизонта меняется; только в середине полной фазы и к тому ше
на нейтральной линии аатмеаия горнаонт оенещев зарей равномерно со всех
сторон. Чем шире конус лунной тони у земной поверхности и, следовательно,
длительнее полное ватменаа, тем уже полоса зари у горизонта н тем
ощутительнее теинота. Перед самым кондом полной фазы заря поднимается на западе
со все аараегаящей быстротой, а тень спускается на востоке. Когда край вари
доычнтея по небу до Ооянца я пронольвнет перед ним, мгновенно блеснет еол-
нвчтай ауч, ж полное затмение кончается.

ЗАМЕТКА. В ПЕНЗЕНСКОЙ ГАЗЕТЕ О ЗАТМЕНИЕ
487
Кнорра «О темных лучах света». Чувствуется, что текст етой статьи
был не то написан по-немецки и почти дословно переведен на
русский яаыя, не то ее автор сразу пользовался русскими словами, строя
шри ѳтом фразы по немецкому образцу. Ляпунов, с другой стороны,
был 'все время [занят наблюдениями в телескоп. Он просто не мог
одновременно отмечать по хронометру точный момент конца полной
фазы и рассматривать окружающий ландшафт.
Если к етому добавить, что Лобачевскому, как ректору и главе
ѳкспѳдиции, было всего естественнее сообщить о наблюдениях ватмѳ-
вия, то мы придем к выводу, что он и был автором заметки в
«Пензенских губернских ведомостях». Конечно, характерное сокращение «Г,в
только перед фамилией Лобачевского и, вероятно, чины участников
экспедиции приписала редакция газеты.

Приложение It
ПЕРВЫЕ АСТРОНОМИЧЕСКИЕ НАБЛЮДЕНИЯ
П. И. ЛОБАЧЕВСКОГО
Казанские известия № 21 (вреда 6 сентября 1811 г., с.тр. 1—2)
содержат сообщение о наблюдениях кометы 1811 г., проиѳвѳдѳняых
Н. И. Лобачевским и И. М. Симоновым. Сообщение это сделал И. А. Лит-
тров (1781—1840), первый профессор астрономии в Казанском
университете, приехавший в Казань в 1810 г., но уме в 1816 г. покинувший ѳѳ.
История возникновения школы астрономов а Казани ж усилия,
которые положил Литгров, чтобы основать хоть самую скромную
обсерваторию, подробно описаны Н. П. Загоскиным 1). Одним из первых
учеников Литтрова явился 18-летний Н. И. Лобачевский,
зарекомендовавший себя еще на студенческой скамье как талантливый астровюм,
в особенности блестяще овладевший теорией.
На следующий год после прибытия Литтрова в Казань появилась
комета, которая впоследствии получила обозначение 1811 I (т. ѳ.
первая комета, прошедшая через перигелий овоей орбиты в 1811 г.). Это
была одна из самых блестящих комет за последние столетия,
обладавшая очень ярким, хотя и не слишком длинным:, хвостом. Открытая
25 марта 1811 г. Фложѳргом й Вивьѳ, она прошла через перигелий
12 сентября (нового стиля), как раз тогда, когда она наблюдалась
в Казани. В это время она обращала на себя всеобщее внимание.
Еще нѳ совсем угасшие астрологические суеверия связали
появление кометы с бурными политическими событиями той эпохи, и комета
1811 I прочно вошла в историю. Считали, в частности, что ѳе действие
проявилось в необычайно высоком качестве вина урожая 1811 г.
Именно ее имеет в виду стих Пушкина:
«Вина кометы брызнул ток» s)
и описанием этой кометы заканчивается второй том «Войны и мира>
Л, Н. Толстого.
1) Н. П. Загоаянн — История императорского Казанского университета за
первые сто лет его сущестаовашш 1804—1904, т. Ш, Казань, 1004, глава 5.
*) •Евгений Онегин», ги. I, XVI.

ПЕРВЫЕ АСТРОНОМИЧЕСКИЕ НАБЛЮДЕНИЯ Н.И. ЛОБАЧЕВСКОГО 489
Но для наблюдения над этим необычайным светилом казанские
аотрономы располагали ничтожными средствами: у них был только
секстант, о которым они измеряли расстояния кометы до звезд и днем
наблюдали Солнце для определения поправки обычных стѳвжых часов,
которыми они были выну ведены пользоваться при наблюдения*.
Загоскин пишет:
«Наблюдения вти, произведенные Литтровым 1) при содействия
его учеников И. М. Симонова и Н. И. Лобачевского, были
обставлены самым примитивным образом и могли представить значение
разве только исключительно пропедевтическое; производившиеся
с 80 августа через окно комнаты советской канцелярии, при
неблагоприятных атмосферных условиях, плохими инструментами,
даже без помощи астрономических часов, которые заменялись
обыкновенными степными часами, находившимися в зале советских
заседаний 2) — эти наблюдения не представляли никакого научного
значения [„шіШш pretii" ')], как отозвался об них и сам Литгров
в письме к попечителю! *).
Это и справедливо и не справедливо. Конечно, в настоящее время
значение ѳтих наблюдений только историческое- Но не следует
забывать, что в ту эпоху наблюдения комет, вообще, часто страдали
большими погрешностями, и е этой точки зрения наблюдения Лобачевского
и Симонова, хотя их и немного, вероятно, не хуже наблюдений
многих других астрономов. По крайней мере, отсчеты секстанта для
расстояний кометы от звезд сходятся между собой неплохо. По ѳтам
расстояниям вполне могли быть вычислены координаты кометы на
небе (как это и было сделано Литтровым), Что же касается часов,
то их роль при наблюдениях комет не так велика—только для отметан
момента наблюдений; при умеренной скорости движения кометы
ошибка в поправке часов на несколько секунд не могла играть ровно
никакой роли.
С наблюдениями кометы І81І I впервые появилось имя Н. И.
Лобачевского в печати. Прямо установить, какие Ha6jnofleHHH принадлежат
ему, а какие — Симонову, нельзя: это не указано в тексте. Но легко
видеть по моментам чаеов, что наблюдения идут попарно, с
некоторыми перерывами. Очевидно, что наблюдения, сделанные первым
наблюдателем, повторялись вторым и, надо полагать, как правило,
!) Наблюдения дрояазодались ЛоОяіавоким и Симоновым — и только в
присутствии Литтрова.
*) То-всть заседаний Совета.
' э) Никакое цены.
*) Загоскин, т. ПГ, стр. 70. Попечителем Казанского университета был
ясивший в Петербурге престарелый астроном академик С. Я. Румовеккй.

490 ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
первым наблюдателе и был старший — магистр Е. И. Лобачевский,
вторым — студент И. М. Симонов.
Текст заметки написал, несомненно, Литтров; с его немецкого
подлинника был сделан (слишком буквальный!) перевод.
В практика астрономов давно принято, что сообщения в печать
о наблюдениях, сделанных на тон или иной обсерватории, дает ее
директор (точно так н поступил Литтров), однако сами наблюдения
рассматриваются как научный труд астронома, непосредственно их
выполнившего, следовательно, в данном случае мы имеем первую
научную работу Н. И. Лобачевского и И. Ж. Симонова.
Приводим полностью текст заметки *).
Казань
Комета, ныне видимая, находится между звездани (омега и пси грвч.
оукв.) Большой медведицы. Она удаляется уже от солнца. При ее
приближении к оному, первый ее наблюдал Г. Фложѳрк5) в Вивие (*)
25 марта (нового гати.) сего года; но тогда она была гораздо менее.
Можно надеяться, что она будет видима и в Ноябре; свет ее и величина
станут в продолжении месяца умножаться; она теперь в Казани уже
не заходит, а бывает и днем над горизонтом.
Наблюдения, деланные над сею кометою Гг. Магистром
Лобачевским І-м и студ. Симоновым под руководством и в присутствии
Г. проф. Литрова здесь сообщаются:
30 Авг. „
ггт> "асы набяюд.
11 Септ.
10Ч21'4Ѳ"
10 2410
10 2519
10 28 20
11 540
Двоив, высоты
верхв. солн. края
71°20'О"
71 400
71 МО
72 0 0
76 250
откуда ускорение часов против среднего Казанского времени в 10*42'
найдено 5'12",3.
1) Заметка воспроизведена {без данных наблюдения) в книге «Материалы для
биографии Н. И. ЛоЗачеанвого». Собрал и редактировал Л. Б. Модзаяевсиий.
Изд. АН СССР, M. — JL, 1948. Документ № 29, стр. 49.
2) Фложерг.
(*> Город во Франции под 44°28'57" северной широты и 22°20'55'7 долготы от
Парижского3) меридиана [Прам. подлинника].
в) Не от Парижского меридиана, а от меридиана Фѳрро, лежащего на 20°0'0Я
к западу от Парижа,

казанскія извъстія.
<#
21
Сред» СвйячіСй*-'$г*о ,№Я ]Sil год».
: ,,fiaujwfa^- 1.
Кааяпь .
Комета. вйШЖидвнМ в«
< я уже віпь ' ЩИЬ,& Щм Ш ШШ
Слпіыѵіч и* сяіояуіпирьпрй'ея-иаф^^
,п,л.п Г. і[і.чі*срк*'и> Втііѣ (Г *') ябиар-
им {iiaeaiQ «№% } (fere кДОіііф nittv
,Ѵ> она Рыла іораздо* Ьмі&ѵ'ЗДэЬяе
на,і%ншѵ;я, что она . будет* ' яИі
Дима и вт. ШнбгЛ; свЬвів *■>-?*
{"} ХЪрИДЪ В* Ф|1ШГ[ІГ
Cbwjthfiff Ю' pMtijj i;l\
f ^.і,искаі и Мь J'H V u; f.
nfii-
.-гІ.;дІ1
«*■
ДО
''"'ушяаялтнещ ом шеяарь
адшші ma* горизонтов».
jHrCjhom *> ***•■№* вад» е«о
ЙОЙспГОю Гг. Мм«е>пр<іиі Лобачея-
пішіпі ГОТА- Смкяквви* ппл»
руипнодсшкмі* к я» при сушения* Г.
Проф. Ангаром адіс* сообіцяк>ВЕі:я:
.1" Двг. часы н«6*юд. д»о*». шсомя
11 (>нш. Btjam. о<ия. при
to'. Si'. 4f'---" Т»** ао", о"
Первая страница сообщения о наблюдении кочеты 1811 г.—
периов упоминание в печати имени Н. И, Лобачевского
(«Казанские известия», Л? 2! да 1811 г.).

ПЕРВЫЕ АСТРОНОМИЧЕСКИЕ НАБЛЮДЕНИЯ Н. И. ЛОБАЧЕВСКОГО 498
Часш набл.
8Ч18'28"
8 23 2
8 32 в
8 36 33
10 6 38
10 14 8
Часы набл.
e^sas"
8 40 9
8 45 44
10 8 37
10 15 54
31 авг.
12СВНТ. ^«ваблюд
10* 8'1б"
10 15 46
10 16 49
10 17 59
Расст. от (Гр. вита)
Больш. медведицы
15°7'40я
15 8 0
15 8 10
15 7 50
15 4 40
15 5 0
Расст. от (Гр. альфа)
Больш. медведицы
20D2e' О*
20 26 О
20 26 О
20 21 50
20 21 30
Двойн. высоты
верх. солв. края
68°40'0"
69 50 0
70 0 0
70 10 0
откуда следует, что ускорение часов против среднего времени для
Казани в 10ЧВ' будет 4'43",5.
Расст. от (Гр. вита)
Часы набл.
7Ч57' 8"
8 2 45
9 56 8
10 0 48
Часы наб.і.
7,59'47"
8 И 23
9 43 9
9 49 10
9 14 51)
Большой медведицы
14°47'20"
14 47 20
14 44 30
14 45 0
Расст. от {Гр. альфа)
Больш. ыедвед.
20° 2'20"
20 1 40
19 5S 10
19 58 20
19 58 30
Непостоянная погода не позволила снять ни одних соответственны!
высот солнца.
{Сообщено от г. профессора Лгтрова).
') Вероятно, должно Оить: VfWb".

Приложение 3
ИСТОРИКО-БИБЛИОГРАФИЧЕСКИЕ СВЕДЕНИЯ
О СОЧИНЕНИИ «ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА В ПЕНЗЕ
26 ИЮНЯ Ш2 ГОДА»
Отчет Н. И. Лобачевского о полном ватмении Солнца в Пензе
2G июня/8 июля 1842 г. появился в печати дважды — в «Ученых
записках, издаваемых императорским Казанским университетом», 1842,
книжка Ш, Казань, 1843, стр. 51 — 83 (имеется также в виде
отдельного оттиска с самостоятельной нумерацией страниц) и в «Журнале
министерства народного просвещения», часть XXXIX, 1843, отд. II,
стр. 65—S6.
Лобачевский сам сообщает, что его спѳрвый опыт> отчета
«сделался добычей пламени в несчастный день для Казани 24 августа».
Повидимому, первый текст был написан незадолго до 24 августа 1842 г.
К вторичному писанию отчета о затмении Лобачевский, вероятно,
приступил не сразу, будучи занят ликвидацией последствий пожара в
университете. Может быть даже он стал писать его только после
возвращения И. М. Симонова из заграничной командировки —14 ноября
1842 г.2), а связи с рассказами последнего о наблюдениях затмения
за границей. Сославшись на сообщения Симонова5), Лобачевский
пишет через несколько строк о затмении «ныпеишего года». Итак,
можно утверждать, что отчет был окончен Лобачевским во второй
половине ноября или в декабре 1842 г., а скорее всего, и написан
целиком в это время. К концу года отчет был представлен, ибо сам
Лобачевский пишет:
«Ординарные профессора Лобачевский и Кнорр с астрономом-
наблдадателен Ляпуновым ездили в город Пензу для наблюдения
полного солнечного затмения 28 июня 1842 г. Хотя погода не
благоприятствовала в день затмения, однако ж астрономические
наблюдения заслуживают доверия, а физические могут идти в сравнѳ-
J) Н. Л. Загоскин—Биографический словарь профессоров и
преподавателей императорского Казанского университета (1801—1904), часть I, Казань,
19U4, стр. 490,
3) См. стр. 438 наст. тома.

ИСТОРИКО-БИБЛИОГРАФИЧЕСКИЕ СВЕДЕНИЯ 495
виѳ о подобными на других местах, где астрономы видели то же
затмение. В Панзѳ сделаны тоже наблюдения над силой и
направлением земного магнетизма. Подробный отчет об ѳтой поездке
и свод всех наблюдений прѳдотанлены Лобачевским и
Ляпуновым» ').
Обращаясь к интересному документу, опубликованному Л. Б. Мод-
валевским2) («Отношение Канцелярии министра народного
просвещения непременному секретарю Академии Наук Я. Н. Фусу с
представлением отчета М. В. Ляпунова3) о наблюдении солнечного затмения
в Пензе, 10 мая 1843 г.»), мы читаем:
«Командированные в Пензу для наблюдения над бывшим
в протекшем году полным солнечным затмением, ординарные
профѳссоры Казанского университета Лобачевский, Кнорр и
астроном-наблюдатель Ляпунов, возвратись в Казань, занялись
составлением отчетов; но пожар 24 августа лишил профессора
Лобачевского и наблюдателя Ляпунова весьма многих книг, записок
и бумаг. По приведении всего оставшегося в известность и
порядок, составлены ими два отчета: один профессорами Лобачевским
и Кнорром, а другой астрономом-наблюдателем Ляпуновым.
Г. министр народного просвещения, получив ныне от г.
попечителя Казанского учебного округа сии отчеты, приказал передать
первый, заключающий в себе общее описание затмения, в
редакцию Журнала министерства для напечатания, а второй,
состоящий из астрономических выкладок, в императорскую Академию
Паук.
Вследствие сего, препровождал при сел к Вашему
превосходительству отчет г. Ляпунова, имею честь...»
Академия Наук постановила 19 мая 1843 г. послать отчет М. В.
Ляпунова директору Главной обсерватории 4). Но в это время Ляпунов сам
уже был в Пулкове с инструментами Казанской обсерватории,
пострадавшими от пожара (24 августа 1842 г, сгорело алание обсерватории).
Весьма вероятно, с согласия Ляпунова В. Я. Струве, получив отчет
о затмении, не стал публиковать его. Причиной тому могла быть
ненадежность определенное Ляпуновым географическое долготы мест
') Отчет императорского Казанского университета аа 1842 г., составленные
ырофессором Лобачевским (чорноник отчета целиком написан рукой Лобачевского).
В. Часть ученая, 2. Ученые экспедиции. Центральный гос. Архив Татарской АССР,
фонд 977, J& 8705а. л. 40.
а) ЫодзалевскиЙ, докумеиг № 4Я2, стр. 457—458.
в) У Модзалевского ошибочно: Н. И. Лобачѳвккого.
*) Модаалавский, стр. 458.

496
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
наблюдения затмения в Пѳнзе'). Дальнейших сведений об отчете
Ж. В. Ляпунова о затмении мы не имеем.
Любопытно отметить, что в приведенном выше документе говорится
о совместном отчете Лобачевского и Кнорра. Между тем, это или
ошибка (ибо иначе имя Кнорра как соавтора, конечно, фигурировало
бы и в печати в <Журнале министерства народного просвещения»)
или неточность выражения, возникшая из-за того, что Лобачевский
часто говорит в отчете о себе и Кнорре совместно. Сам Кнорр,
невидимому, ничего о затмении 1842 года не писал.
То, в сущности, редкое и особенное обстоятельство, что мы
располагаем двумя печатными отчетами Лобачевского о затмении 1842 г.,
позволяет проверить весь текст и, в частности, сверить все числовые
данные. Основной текст, каким следует считать опубликованный
в «Ученых записках», содержит очень немного искажающих смысл
опечаток и, без сомнения, в нем не внесено никаких изменений
в рукопись Лобачевского, который, может быть, сам правил
корректуры.
Опубликованный в «Журнале министерства народного
просвещения» отчет Ы. И. Лобачевского подвергся редакционным поправкам
стилистического характера. Во многих местах были переставлены слова,
заменены выражения. Характерный стиль Лобачевского был
редактором почти всюду «причесан»; в результате этого текст получился
глаже, по в значительной степени потерял свойственную языку
Лобачевского образность. Приведем следующие примеры разночтений
в обоих изданиях:
1) В «Ученых записках» Лобачевский пишет: «солнечное затмение
в начале заставило народ толковать и беспокоиться». В «Журнале
министерства» редактор исправляет: «затмение в начале произвело
в народе толки и беспокойство».
2) Лобачевский пишет: «ые можем даже сказать, как далеко
простирается воздух». Редактор для гладкости вставляет два
паразитических слова: «не можем даже сказать относительно того, как далеко
простирается воздух».
3) Лобачевский пишет; «иа комете... атмосфера представляет
эллипсоид, вытянутый прочь оі' солнца». Редактор вычеркивает не
необходимое, но очень образное слово «прочь».
4) Лобачевский пишет: «чем ближе находимся к куче тел... По
примеру скученных тел... Причиною грубых перемен в температуре...».
Редактор заменяет «грубые», по его мнению, слова; в «Журнале
') Ср. примечание [i*j на стр. 481—462 наст. тома.

ИСТОРИКО-БИБЛИОГРАФИЧЕСКИЕ СВЕДЕНИЯ 497
министерства» напечатано: «чем ближе находимся к группе теп,... по
примеру сгруппированных тел,. .. Причиною быстрых перемен в
температуре. ..».
б) Текст Лобачевского: «Пенза хорошо выбрана местом для
садоводства» редактором заменен на следующий: «Местоположение Пензы
весьма благоприятно для садоводства».
Существенных изменений в наложение Лобачевского в «Журнале
министерства», за очень редкими исключениями, нѳ внесено, но
при печатании появились кое-где серьезные опечатки, в одном месте
выпало несколько слов, в другом — пелая строка.
Приведем некоторые выдержки из документа, опубликованного
Модзалевским ') («Из статьи Н. И. Иванова „Ученые собрания
профессоров Казанского университета" о докладе Н. Й. Лобачевским
результатов наблюдений солнечного затмения в Пензе»). Числовые
результаты, которые пе дают ничего нового, здесь опущены.
«Собрания происходят в зале Физического кабинета. Поныне
их было десять. Члены с удовольствием видели, что и
посторонние лица, даже некоторые путешественники, принимали участие
в их беседах. Бросим беглый взгляд на результаты собраний.
Ректор Университета, заслуженный профессор чистой
математики Лобачевский сообщил весьма любопытные известия
о поездке, предпринятой им в прошедшем году с профессором
физики Кнорром и астрономом-наблюдателем Ляпуновым в Пензу
и о произведенных им там астрономических и физических
наблюдениях, особенно над полным солнечным затмением, бывшим
20-го июня 1842 года. [...]
Во время затмения небо покрылось облаками, однако ж
астрономические наблюдения над началом в концом полного
затмения могли быть сделаны с достаточною верностью.
Температура воздуха в продолжение аатмеыия понизилась на 1",2Р2).
Вокруг солнца виднелся светлый венед, которого вид менялся
в своем очертании, может статься, от расположения в облаках.
Одушевленный, превосходный свой рассказ г. Лобачевский
пополнил описаниями многих известных наблюдений над
солнечными затмениями, сделанными как прежде, так и в последнее
время; присоединил собственные исследования, как надлежит
объяснять явления, замечаемые при полном солнечном аатменип;
1) Модаалевский, стр. 458—160. Статья оцубликоваиа в ^Северной
Пчеле» 3 нюня 1843 г., J* 121, на стр. 483—484.
я) Неверно, должно быть 1°,8.
32 Зав. азаз. Н. И. Лобачевский, т. V.

498
ПОЛНОЕ ЗАТМЕНИЕ СОЛНЦА
представил доводы, почему возвышения на лунном крае,~пока-
вавшиѳся во время полного затмения и окрашенные розовым
дветом, нѳ надобно почитать солнечными горами. Почти всеми
астрономами принятое мнение, что светлое кольцо вокруг солнца
должно происходить от погибания лучей близ луны, кажется
г. Лобачевскому не вполне основательным, потому что подобное
действие тел на свет еще не известно физикам и не может быть
соглашено ни с какоЧ теорией. Г. Лобачевский находит более
вероятным, что явление совершается собственно в нашей
воздушной атмосфере. Таким образом, возможно понять и все
особенные явления, разнствующие по месту наблюдения, в последнее
и прежние затмения, как например, снопы лучей в светлом
венпе, различное направление и кривизну, примеченную в лучах
кольца вокруг лупы.—В высокой степени занимательное и
превосходно изложенное повествование г. Лобачевского доставило
собранию самый приятный вечер».
И. М. Симонов в 1844 г. упоминает об отчете Лобачевского в
следующих словах:
«В Пензе наблюдала полное солнечное затмение 1842 года
два профессора им п. Казанского университета Лобачевский и
Кнорр и астроном Казанской обсерватории Ляпунов. Из
подробного и любопытного описания ѳтих прекрасных наблюдений,
изданного г-м профессором Лобачевским, видно, что в Пензе
полное солнечное затмекие сопровождалось почти теми же
явлениями, какие замечены были Киевскими наблюдателями1) в Чѳр-
Отчет II. И. Лобачевского о затмении 1842 г. иногда отмечался
в позднейшей литературе, вплоть до последних лет
В 18ііЗ г.. на праздновании столетия со дня рождения
Лобачевского, профессор Л. В. Васильев произнес большую блестящую речь,
нааеч.танаѵю в юбилейном издании Казанского университета и вскоре
переведенную в разных странах на иностранные языки.
Останавливаясь на различных этапах научной деятельности Лобачевского,
А. В. Васильев говорил о его поездке в Пензу для наблюдения
солнечного затмения и цитировал взгляды Лобачевского на солнечную
корону и на теорию свита3).
') Пр Ф. В. Ф. Федоровым и его спутниками, см. стр. 421 наст, тома,
г) И. м. Симончк — Записки и воспоминания о путешествия по Аягляя,
Франции, Бельгии и Германии, Казань, 1844, стр. 1J0.
В) 1793—1993. Празднование императорским Каеаискны университетом
столетней годовщины дня рпжлеяия Н. И. Лобачевского. Казань, 1894, Речь проф.
А. В. Васильева, етр 125—126.

ИСТОРИКО-БИБЛИОГРА.ФИЧЕСКИЕ СВЕДЕНИЯ 499
В 1943 г. акад. С. И. Вавилов цитирует из отчета Лобачевсяого
то место (стр. 449 наст, тома), где Лобачевский пишет об
объединении эмиссионной и волновой теории света1). Н. И, Иде ль сон в своем
очерке «Лобачевский — астроном» посвящает отчету Лобачевского
о затмении V раздел, в котором особо отмечает глубокие мысли
Лобачевского о сущности физических теорий и о трудностях, с которыми
сталкивается теория света').
Отчет Н. И. Лобачевского о полном затмении Солнпа в Пензе
26 июня 1842 г. перепечатан Л. В. Модзалевским по тексту сУчѳных
записок» 3). Им введена новая орфография. В тексте опечаток мало
(в том числе в заглавии), но имеются стилистические отклонения от,
подлинника, хотя и не очень важные и обычно взятые из «Журнала
министерства народного просвещения» (между прочим, Модзачевский
везде писал Пептон, тогда как в «Журнале министерства» — Ньютон,
а сам Лобачевский в своем отчете в «Ученых записках» писал, в
согласии о английским произношением, — Дютон и лишь один раз там
фигурирует Невтои, причем ѳто наверное описка или опечатка). Кроме
втого, у Л. Б, Модэадевекого есть только одна серьезная погрешность.
Именно (см, стр. 453 наст, тома), Лобачевский говорит об отражении
света на планетах в различных направлениях, и указывает что эта
мысль не может быть допущена даже для металлических зеркал.
В «Журнале министерства* слово «металлических» совершенно
напрасно заменено на «математическим» и так же у Модзалевского4).
Наконец, специально путешествию Н. И. Лобачевского в Пензу
для наблюдения полного солнечного затмения посвящены сіатья
~К. Чачикова, появившаяся в 192G г., и статья G. А. Касьянгака,
опубликованная в 1950 г.; см. о них в приложении 1 6).
') С. И. Б авилов — Ислав Ньютон, 2-е изд., 1945, стр. 78.
2| См. сноску 2) на стр. 42L наст. тома.
3) МодвалевскпП, стр. 4ѲЗ—І78.
♦) Модзалевский, стр. 477.
') Стр. 485 наст. тома.

.Редактор Я. Я. HfWKtuoteflif.
Тещ. редактор О. S. А.хяажн.
Отв. корректор Г- я; лё-tuSosa
Подписано в печать 24/Х 1951 г,
В)тиаг&?0Х1«уи.
Тираж 5 000 вкз. 10,375 бун. я,
42,813 нач. Л.+12 вклеек.
■ 30,84 уч.-иэд, лиата. т-олиі. Заказ J* «S23.
Цева 18 pjfl. 15 яоа. Нераліет 3 ру&
4^я тИЕОГрафвя им. Ear. Соколовой
ГлаытолиграфпадатіЬ
при Совете Министров СССР,
Лепяеград, Измэйдовсява пр., 39.