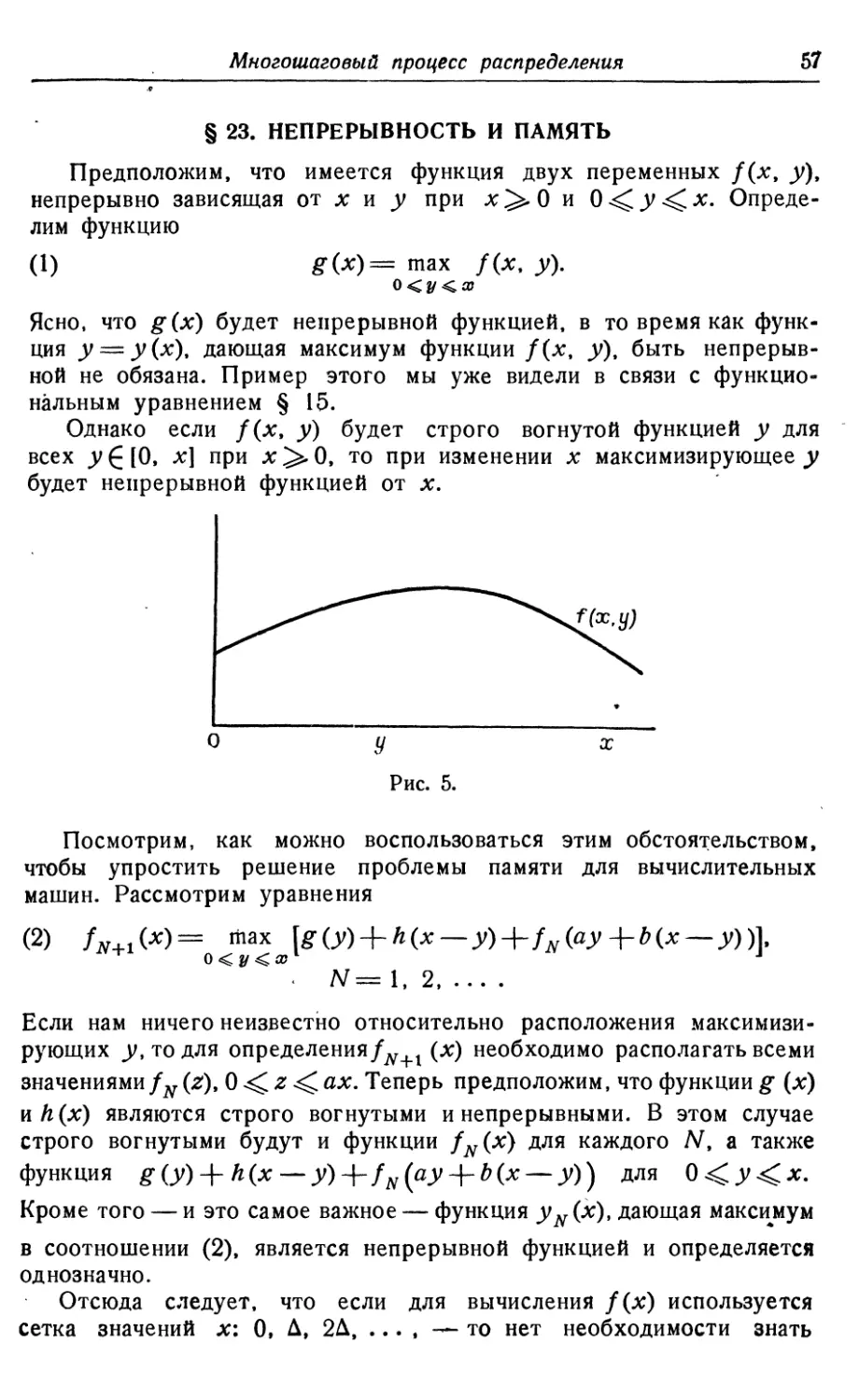
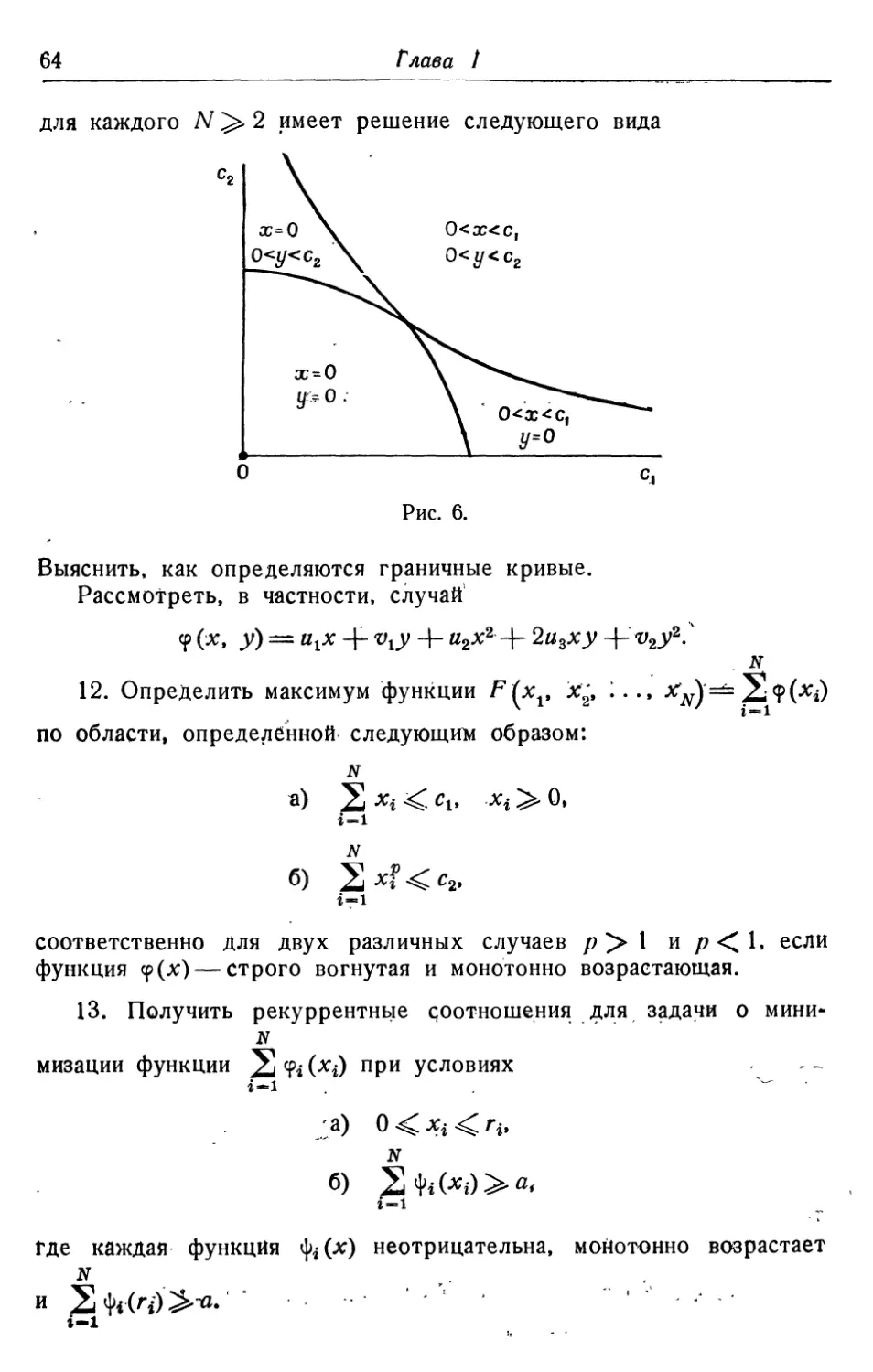
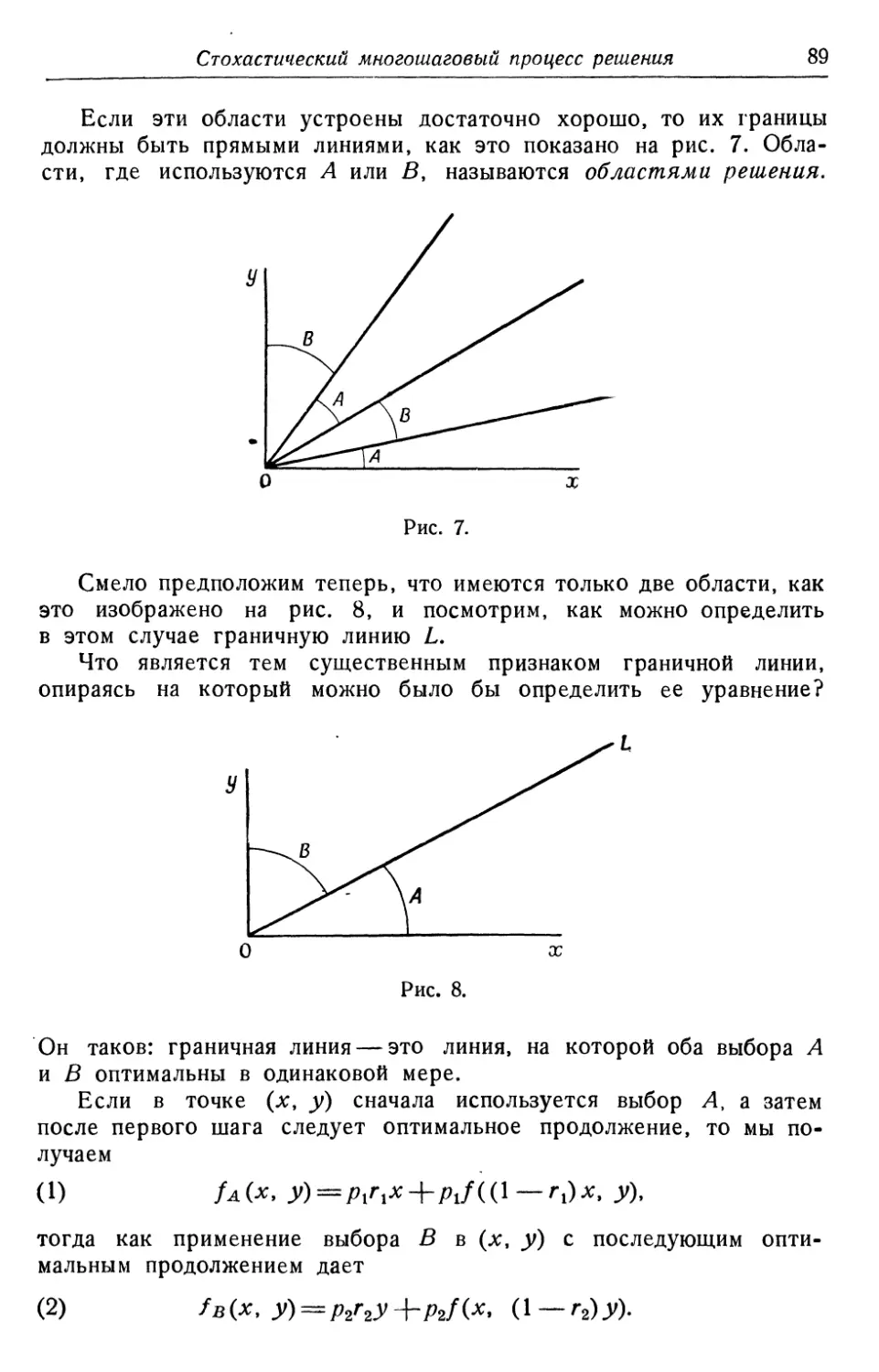
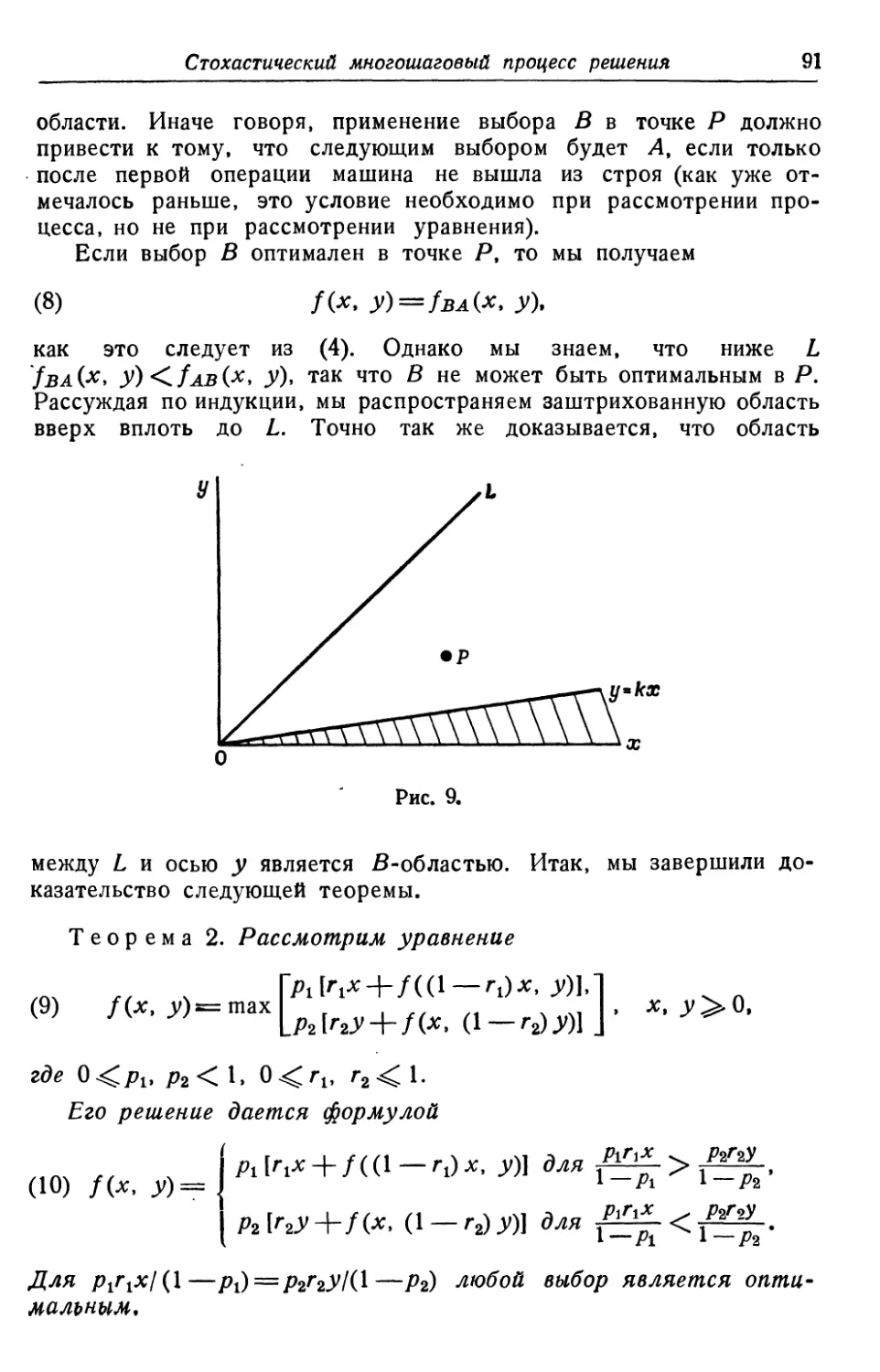
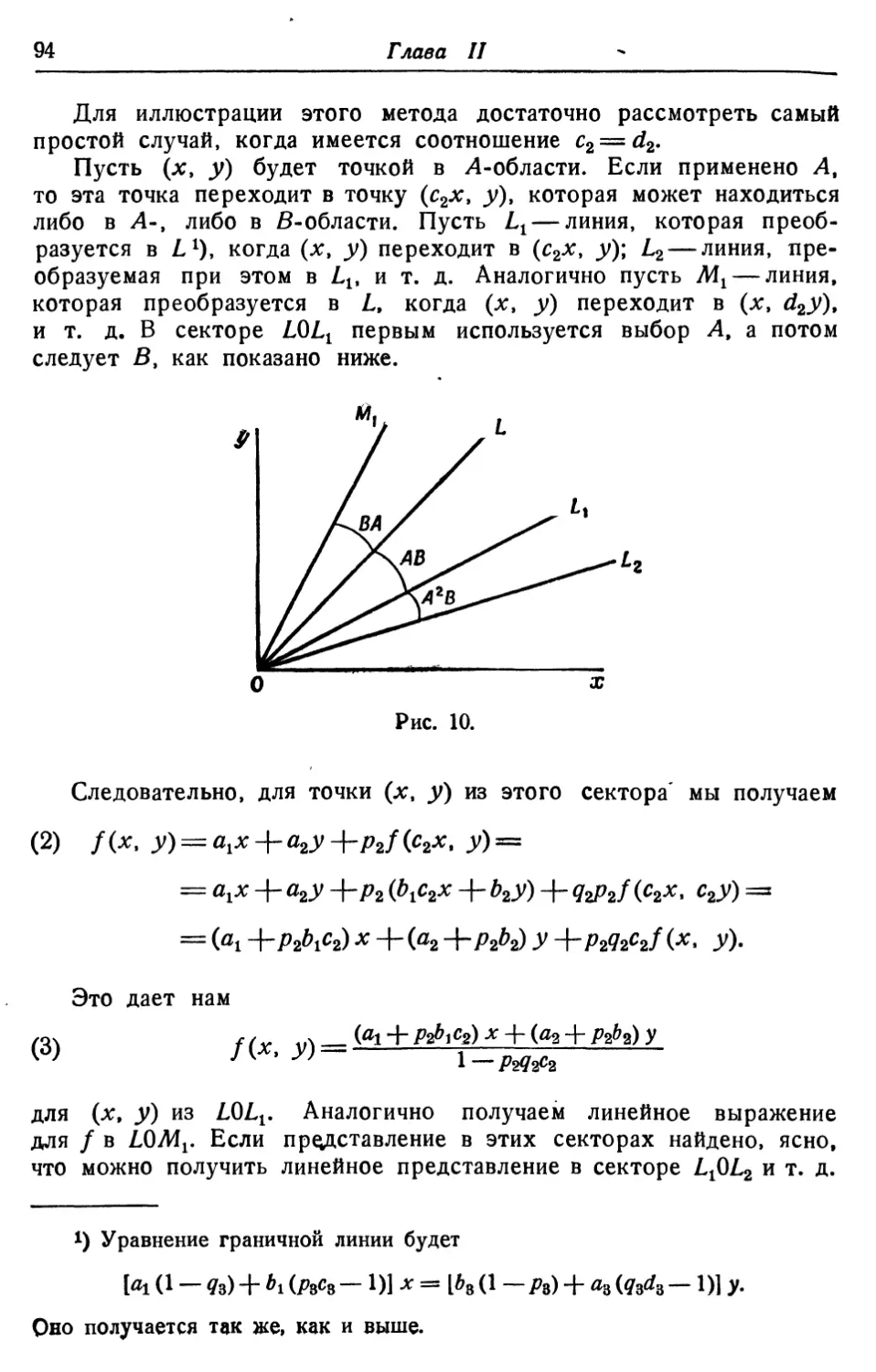
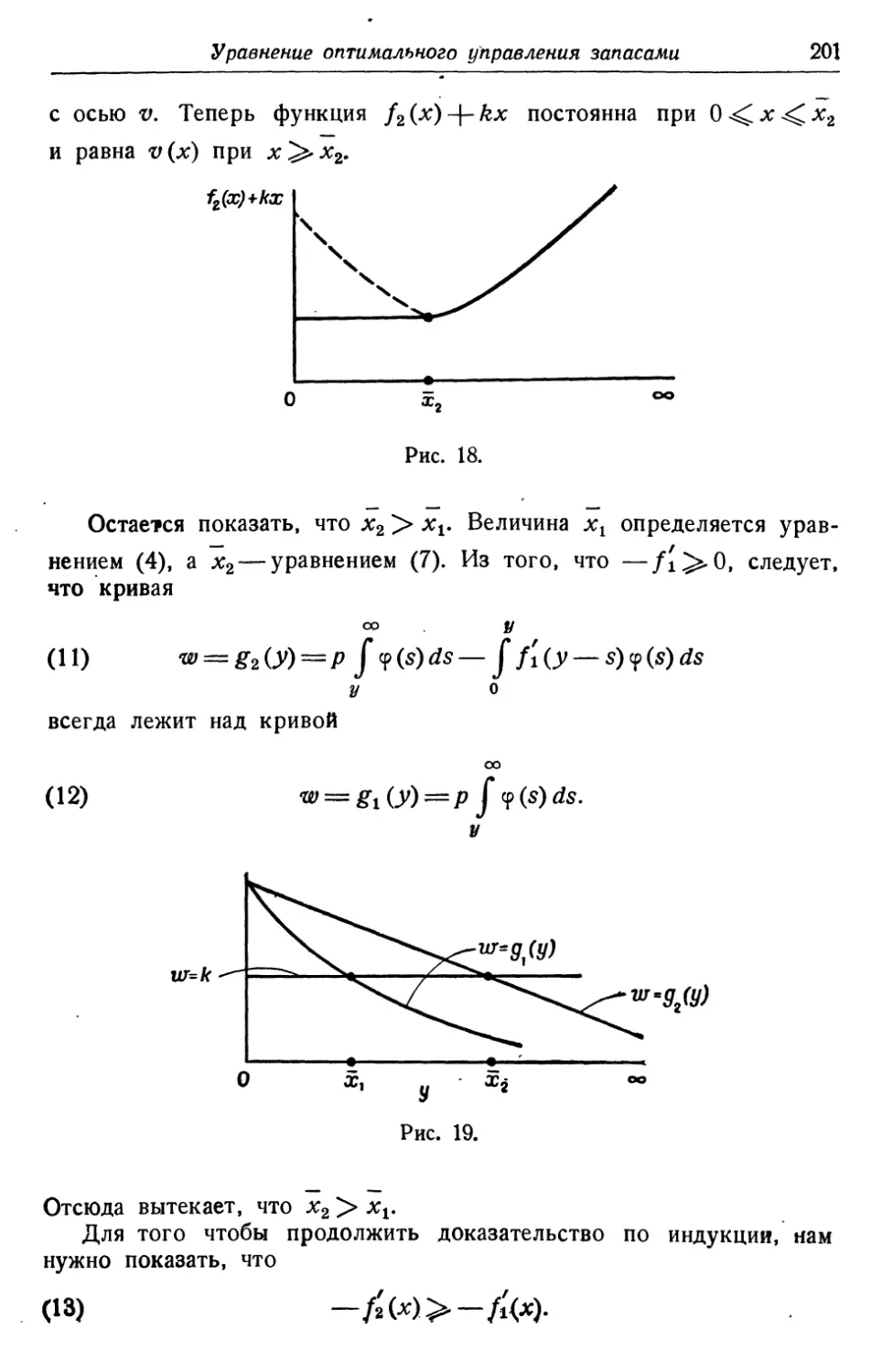
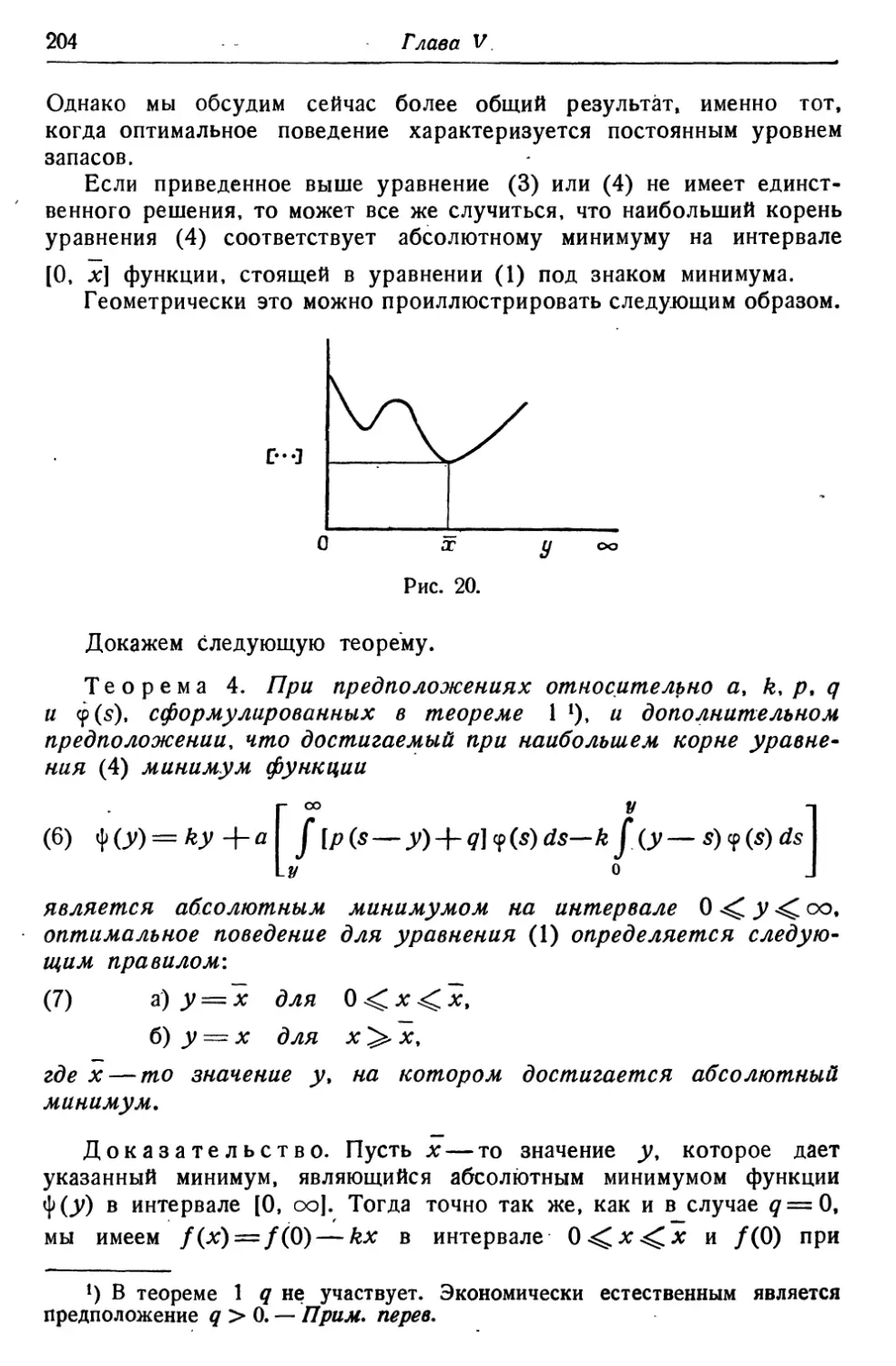
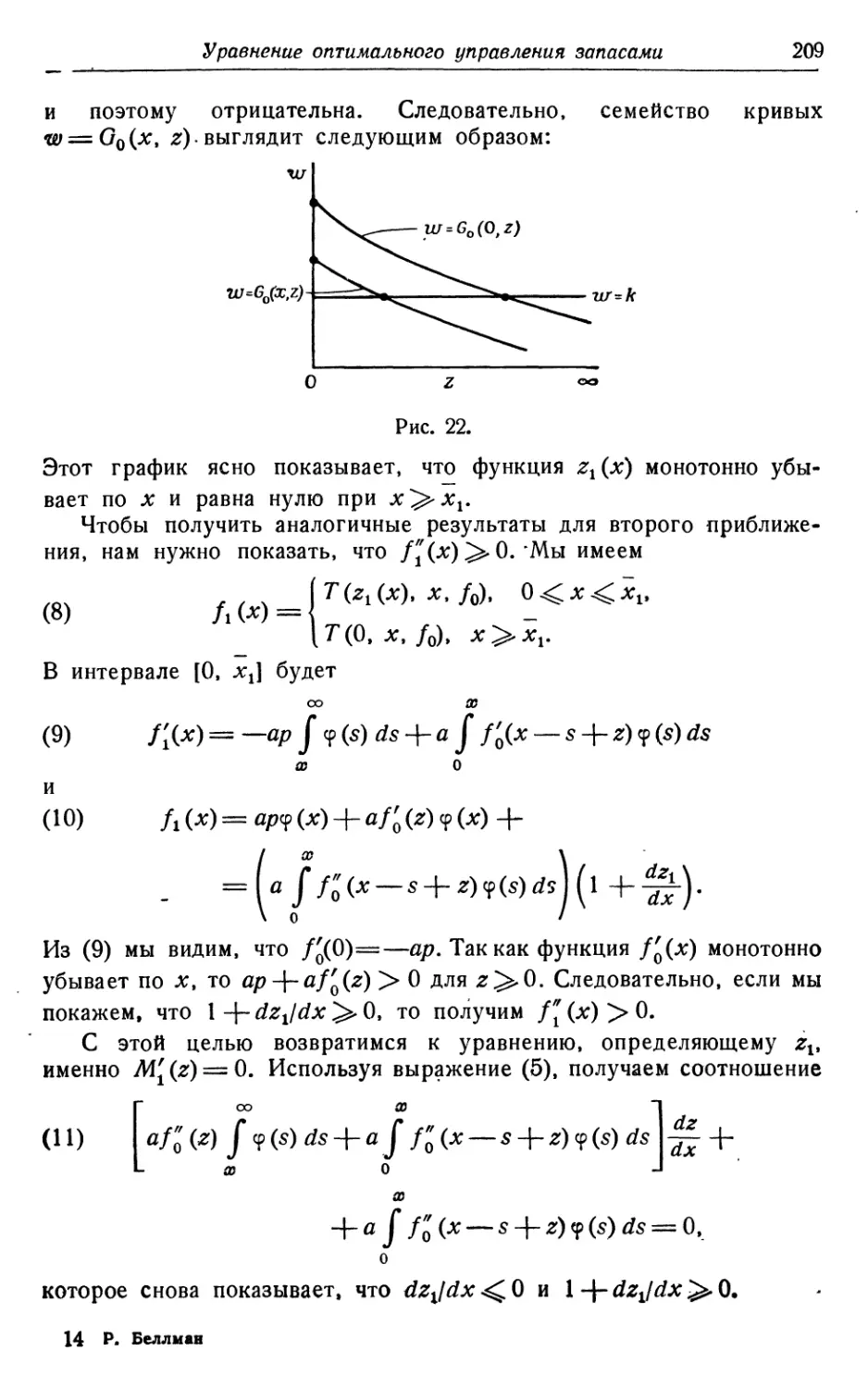
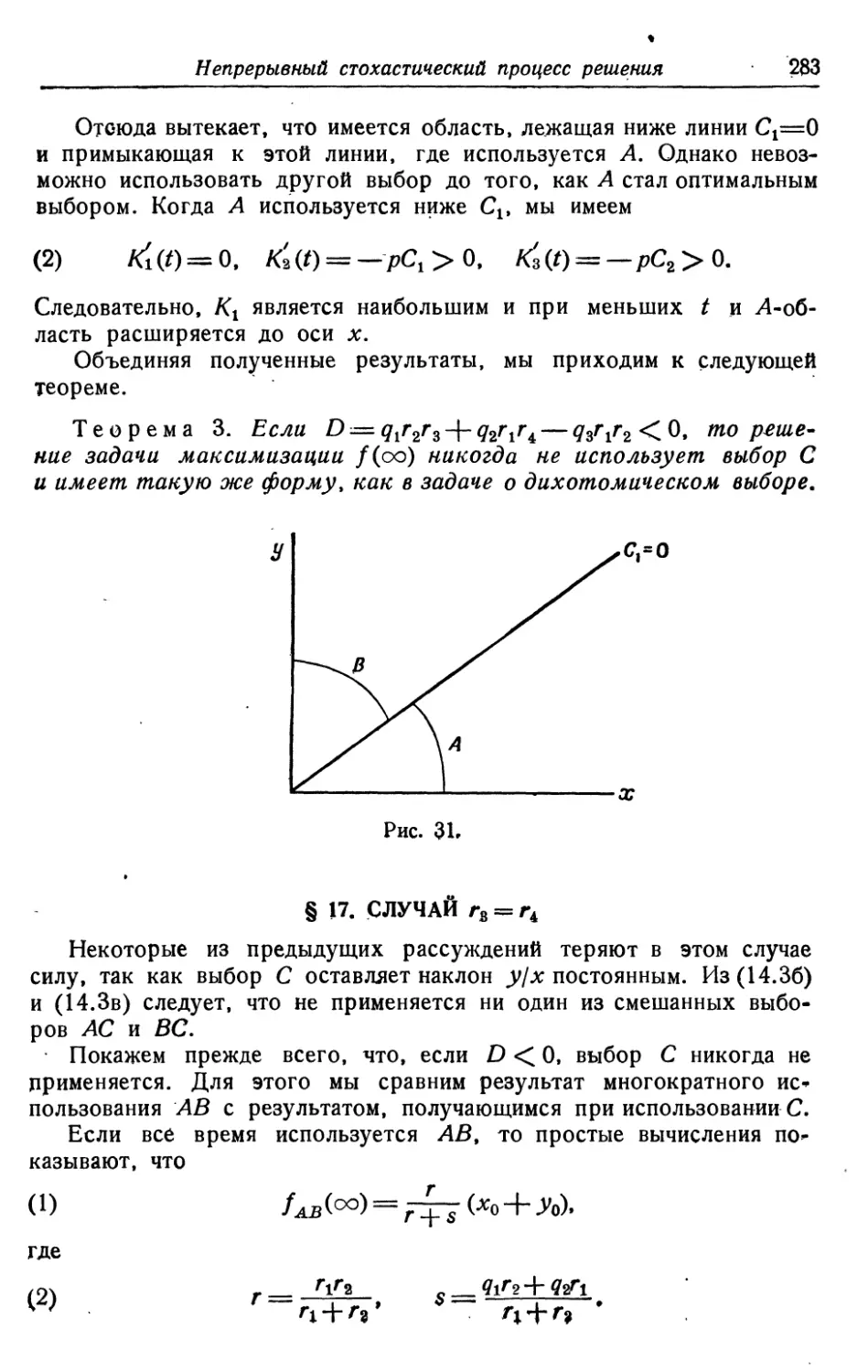
Текст
и * л
Издательство
иностранной
литературы
0УЫАМ1С РКООКАЛШШО
ьу
Ц1СНАВД)
195 7
РгШсегоп ШмегаНу Ргезз
Ргтсегоп, N610
Р. БЕЛЛМАН
Динамическое
ПРОГРАММИРОВАНИЕ
Перевод с английского
И. М. Андреевой, А. А. Корбута,
И, В, Романовского, И. Н. Соколовой
Под редакцией
Н. Н. Воробьева
ИЗДАТЕЛЬСТВО ИНОСТРАННОЙ ЛИТЕРАТУРЫ
Москва, 1960
АННОТАЦИЯ
Советский читатель уже знает автора по его монографии
„Теория устойчивости решений дифференциальных уравнений",
вышедшей в Издательстве иностранной литературы в 1954 г.
Теория динамического программирования родилась из ряда
технико-экономических задач, таких, как задача о наиболее эф-
эффективном использовании оборудования или задача о наиболее
выгодной политике закупок. По этой новой области математики
литература на русском языке отсутствует, если не считать не-
небольшой обзорной статьи автора, опубликованной в сборнике
„Современная математика для инженеров" под редакцией
Э. Ф. Беккенбаха, Издательство иностранной литературы, 1958 г.
Автор является одним из создателей теории динамического про-
программирования, подробному изложению которой и посвящена
его монография.
Книга интересна для широкого круга математиков, занимаю-
занимающихся приложениями, специалистов по регулированию, инже-
инженеров, экономистов и др.
Книга доступна студентам старших курсов и аспирантам ука-
указанных специальностей.
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
В самых разнообразных областях теоретической и практической
деятельности часто оказывается целесообразным принимать решения
не сразу, а постепенно, шаг за шагом. Принятие решения, таким
образом, рассматривается не как единичный акт, а как процесс,
состоящий из -нескольких этапов.
Такой подход использовался уже довольно давно при исследо-
исследовании некоторых частных вопросов. Наиболее полно эта идея была
воплощена А. Вальдом в его теории секвенциального статистического
анализа. Систематизация примеров подобного рода исследований пока-
показывает, что многие из них с успехом могут быть обслужены некото-
некоторым единообразным математическим аппаратом. Таким аппаратом
оказывается созданная в значительной мере трудами Р. Беллмана и его
учеников теория динамического программирования.
Предметом динамического программирования является изучение
многошаговых решений, в том или ином смысле оптимальных. Клас-
Классические методы нахождения экстремумов функций многих перемен-
переменных здесь часто оказываются неприменимыми ввиду большого числа
параметров, от которых зависит решение. Лежащий же в основе
динамического программирования принцип оптимальности часто может
быть реализован в виде такого функционального уравнения, решение
которого более доступно методам современной математики (в том
числе вычислительной математики), чем решение соответствующих
уравнений в условиях классической постановки задачи. На таком пути
обнаруживается и новый подход к решению обычных задач вариа-
вариационного исчисления. .
Оптимизационные задачи встречаются почти во всех отраслях науки,
техники и хозяйства. С ними приходится иметь дело в промышлен-
промышленной технологии, в организации производства, в экономическом пла-
планировании, в различных вопросах физики, биологии и военного дела.
Поэтому круг приложений динамического программирования исклю-
исключительно широк.
Возможности применения методов динамического программирова-
программирования для решения задач, возникающих в физике, экономике, биологии
и т. д., отнюдь не означают, что динамическое программирование
является частью одной из этих дисциплин. Теория динамического про-
программирования, подобно, например, математической физике, есть часть
математики, и в этом отношении она принципиально не отличается от
других математических теорий. При этом, разумеется, не следует
Предисловие редактора перевода*
забывать, что вопрос о правомерности использования идей и аппа-
аппарата динамического программирования при решении той или иной
конкретной прикладной задачи должен каждый раз решаться с учетом
специфики соответствующей науки.
Предлагаемая вниманию советского читателя монография предста-
представляет собой первый том задуманного автором труда и содержит изло-
изложение основных вопросов динамического программирования. В этой
книге автор сознательно ограничивается сравнительно элементарными
задачами, предполагая затронуть более глубокие проблемы во втором
томе. С методической точки зрения такое разделение вполне оправ-
оправдано, так как большое количество новых идей и*понятий, осложнен-
осложненное рассмотрением математических тонкостей» нанесло бы большой
ущерб доступности книги и сузило бы круг ее возможных читателей.
Заметим тут же, что в разных главах книги преследуются различные
цели. Так, если главы III и IV (наиболее интересная для математика
часть книги) посвящены весьма общим вопросам, то глава VII — это
подробный анализ решения некоторой конкретной задачи. Остальные
главы занимают промежуточное положение.
Почти к каждой главе прилагается большое число упражнений и
проблемных задач различного интереса и различной трудности (всего
книга содержит 370 задач). Формулировка некоторых из них (напри-
(например, задачи 29 гл. I) в нарочито легкомысленном виде лишний раз
подчеркивает разнообразие приложений динамического программиро-
программирования.
Перевод книги выполнили: И. М. Андреева (главы I и II), А. А. Кор-
бут (Введение, главы IV, V и §§ 13—25 главы IX), И. В. Романов-
Романовский (главы VIII, X, XI) и И. Н. Соколова (главы III, VI, VII и §§ 1—12
главы IX). В отношении экономической терминологии текст про-
просмотрел В. А. Маш.
И. И. Воробьев
ПРЕДИСЛОВИЕ АВТОРА
Цель настоящей книги состоит в том, чтобы дать введение
в математическую теорию многошаговых процессов решения. Так
как с этими процессами связан довольно громоздкий набор понятий,
то для наименования нашего предмета мы ввели специальный термин
„динамическое программирование". В действительности, как мы
увидим далее, специфика этих процессов заключается не только
в особой терминологии. Скорее, она заключается в определенной
идейной общности, которая дает гибкий и современный математи-
математический аппарат для рассмотрения многих новых и интересных задач
как внутри самой этой молодой дисциплины, так и в различных
разделах классического анализа. Прежде чем углубиться в эту
тему, опишем вкратце, что понимается под многошаговым про-
процессом решения.
Рассмотрим некоторую физическую систему 5, состояние которой
в любой момент времени I описывается вектором р. Если мы на-
настроены оптимистически, то мы можем представлять себе, что
компоненты этого вектора — вполне определенные величины, такие,
как декартовы координаты, или координаты вместе с проекциями
моментов, или, скажем, объем и температура, или, наконец, при-
применительно к экономической системе, предложение и спрос, либо
запасы и производственные, мощности. Находясь же в пессимисти-
пессимистическом расположении духа, мы можем предполагать, что компоненты
вектора р являются распределениями вероятностей для таких вели-
величин, как координаты и моменты или, быть может, моментами рас-
распределения.
С течением времени эта система подвергается изменениям либо
детерминированного, либо стохастического характера. Математи-
Математически это означает, что описывающие систему переменные под-
подвергаются некоторым преобразованиям. Пусть теперь, в отличие от
сказанного выше, мы имеем процесс, в котором в каждый момент
времени мы должны выбирать преобразования, которым можно под-
подвергнуть систему. Процесс такого типа мы называем процессом
решения, причем в этой терминологии понятия решения и пре-
преобразования считаются эквивалентными. Если нам нужно принять
одно решение, то мы называем процесс одношаговым; если следует
принять некоторую последовательность решений, то мы пользуемся
термином многошаговый процесс решения.
8 Предисловие автора
4
Это различие, разумеется, не является вполне четким. Так, выбор
точки в трехмерном пространстве можно рассматривать либо как
одношаговый процесс, в котором мы выбираем тройку (х, у, г),
либо же как многошаговый процесс, где последовательно выбирается
сначала х, затем у и наконец г.
Имеется целый ряд многошаговых процессов, которые нам
хорошо знакомы. Пожалуй, наиболее известными являются процессы,
встречающиеся в карточных играх, например, система торгов
в договорном бридже или система „повышение против повышения^
в покере с его тонкими оттенками блефд*1). В более серьезных
вопросах мы постоянно сталкиваемся с многошаговыми процессами
решения в нашей экономической жизни в связи с программами
капиталовложений и политикой страхования. Другими примерами,
взятыми из области науки, могут служить управляемые процессы
и планирование экспериментов.
Мы хотим подчеркнуть то обстоятельство, что в современной
жизни—в экономических, промышленных, научных и даже полити-
политических ее областях — мы со всех сторон окружены многошаговыми
процессами решения. Некоторые из них мы изучаем, основываясь
на нашем опыте, некоторые пытаемся решить „на пальцах"; некото-
некоторые же процессы настолько сложны, что нам остается лишь по-
попытаться угадать решение и смиренно уповать на удачу.
К огорчению экономистов, промышленников и инженеров, за
последние годы в экономике, промышленности и технике возникли
столь обширные по своей значимости и объему задачи, что их уже
нельзя решать изолированно, как в прежние спокойные времена.
Громадное расширение круга задач было достигнуто лишь в резуль-
результате крайней систематизации усилий.
Несмотря на то, что эти задачи возникают в самых разнообраз-
разнообразных областях, они обладают одной, общей чертой — все они исклю-
исключительно трудны. Возникают ли они при изучении оптимального управ-
управления запасами или при анализе балансов затрат и выпуска целого
комплекса взаимозависимых отраслей, в составлении графика об-
обслуживания пациентов в медицинской клинике или при обслуживании
самолетов на аэродроме, при изучении задач организации тыла или
задач о капиталовложениях, в управлении сервомеханизмами или
в последовательном (секвенциальном) статистическом анализе—всюду
они обладают определенными общими неприятными чертами, вы-
выводящими нас за рамки стандартных математических теорий.
Следовательно, для того чтобы принять вызов со стороны этих
новых задач, необходимо создать новые методы, а для математика
ничто не может быть более привлекательные. Для этой породы
*) Читатель, незнакомый с этими играми, может представить себе, на-
например, систему * торгов в преферансе или карточную игру „веришь — не
веришь". — Прим. перев.
Предисловие автора
людей вообще характерно, что ее представители никогда не бывают
так счастливы, как при встрече с задачами, которые не могут быть
решены — по крайней мере немедленно. Давно минули те дни, когда
иные всерьез беспокоились, не иссякнет ли родник математической
изобретательности, и тем не менее, испытываешь великое насла-
наслаждение, когда перед тобой внезапно открываются обширные не-
непокорные джунгли трудных и важных задач, подобных тем, которые
возникают в теории многошаговых процессов решения.
Бегло очертив этот круг вопросов, посмотрим, каким компасом
мы будем пользоваться, прокладывая путь в эту новую область.
Традиционный подход можно назвать «методом перечисления».
Каждое решение можно мыслить себе как выбор определенного
числа переменных, определяющих преобразование, которое следует
применить; каждая последовательность таких выборов, или, как мы
будем говорить, поведение, представляет собой выбор большего
числа переменных. Беря огулом все эти варианты выбора, мы
„сводим" нашу задачу к классической задаче определения максимума
некоторой заданной функции. Эта функция, возникающая в ходе изме-
измерения некоторого количественного свойства системы, и является осно-
основой для вычисления поведений.
В этот момент математик очень легко может потерять интерес
к задаче и предоставить остальное вычислительной машине. Макси-
мизация достаточно хорошо ведущей себя функции представляется
сравнительно простой задачей: стоит только взять частные произ-
производные и решить получающуюся систему уравнений для максими-
максимизирующей точки.
Однако здесь приходится считаться с некоторыми осложняющими
дело обстоятельствами. Прежде всего, эффективное аналитическое
решение систем, состоящих из большого числа даже простых урав-
уравнений (например, линейных уравнений), является весьма нелегким
делом. Омрачая наши перспективы еще более, напомним, что чис-
численное решение даже таких систем обычно наталкивается на целый
ряд трудностей — как технических, так и принципиальных. Следова-
Следовательно, когда число переменных велико, определение этого макси-
максимума отнюдь не является шаблонным.
Все это дает нам право говорить о „проклятии многомерности".
И хотя это проклятие много лет тяготело над головами физиков
и астрономов, все же не следует терять надежду на получение
вопреки ему важных результатов.
К сожалению, указанная трудность далеко не единственна. Дру-
Другая характерная черта этих задач, как мы увидим на последую-
последующих страницах, заключается в том, что классический анализ не всегда
достаточен для наших целей вследствие того упрямого факта, что
весьма часто решение является граничной точкой области изменения
переменных. Это обстоятельство отражает тот факт, что многие
процессы решения включают определенные характеристики типа „все
10 Предисловие автора
или ничего". Тогда очень часто мы приходим к определению макси-
максимума функции посредством комбинирования аналитических методов
и методов „поиска и охоты".
Каковы бы ни были трудности, возникающие в условиях детер-
детерминированного варианта (выше мы молчаливо предполагали, что
имеем дело именно с ним), эти трудности умножаются в стохасти-
стохастическом варианте, когда исход решения (т.е. преобразования) является
случайной величиной. Здесь любые поисковые или перечислительные
методы неизбежно обречены на неудачу ввиду чудовищного увели-
увеличения числа комбинаций случаев с ростом числа самих случаев.
Предположим, однако, что мы благополучно обошли все эти
трудности и достигли некоей вычислительной нирваны. Но математик
при этом еще не имеет права снимать с себя ответственность, ибо
нельзя считать, что наша задача решена в математическом
смысле, пока не выяснена структура оптимального поведения.
Довольно интересно, что это понятие математического решения
совпадает с обычным понятием решения в физическом, экономи-
экономическом или техническом смысле. Для внесения полной ясности
в этот пункт — а он чрезвычайно важен, поскольку по многим причинам
это га1$оп сГё^ге1) математической физики, математической экономики
и многих аналогичных областей, расположенных на стыке двух
наук, — сделаем краткий экскурс в философию математических
моделей.
Цель ученого состоит в познании явлений окружающего мира,
которые он наблюдает. Для того чтобы доказать, что он действи-
действительно познает эти явления, он должен уметь предсказывать их ход,
а для этого, в свою очередь, требуются количественные измерения.
Качественное предсказание, например, предсказание наступления
затмения, землетрясения или экономической депрессии где-то в не-
недалеком будущем не. столь удовлетворительно, как аналогичное
предсказание, связанное с датой и временем, и возможно поддер-
поддержанное предложением пари2).
Чтобы делать удовлетворительные количественные предсказания,
необходимо иметь аппарат для получения числа, а это в свою очередь
требует наличия математической модели. Представляется разумным
предположить, что чем точнее эта математическая модель отражает
реальный мир, тем точнее оказывается предсказание.
Однако здесь имеется оборотная сторона медали. Действительный
мир чрезвычайно сложен, и поистине, чем больше его изучаешь,
тем больше преисполняешься удивлением по поводу того, что при
объяснении происходящих сложных явлений в основном приходится
иметь дело с „оценками порядка величиныи, и гораздо реже—с со-
х) Разумное основание, смысл (фр.). — Прим. перев.
2) При заключении пари о наступлении некоторого события соотноше-
соотношение ставок является количественной оценкой уверенности в правильности
прогноза об этом событии. — Прим. ред.
Предисловие автора 11
вершенно незыблемыми „законами природы". Если мы попытаемся
включить в нашу математическую модель слишком много черт дей-
действительности, то мы захлебнемся в сложных уравнениях, содержа-
содержащих неизвестные параметры и неизвестные функции. Определение
этих функций приведет к еще более сложным уравнениям с еще
ббльшим числом неизвестных параметров и функций и т. д. Вот уж
поистине сказка про белого бычка. Если, наоборот, оробев от столь
мрачных перспектив, мы построим слишком упрощенную модель,
то мы вскоре обнаружим, что она не предсказывает дальнейший
ход явлений настолько, чтобы удовлетворить нашим требованиям.
Следовательно, Ученый, подобно Паломнику, должен идти прямой
и узкой тропой между Западнями Переупрощения и Болотом Пере-
Переусложнения *).
Отдавая себе отчет в том, что никакая математическая модель
не может дать исчерпывающего описания действительности, мы
должны в наших попытках познания реального мира примириться
с необходимостью использования последовательности моделей все
большей и большей сложности. Если в решениях некоторой после-
последовательности моделей наблюдается известное сходство их строения,
то мы можем считать, что в нашем распоряжении имеется некото-
некоторое приближение к тому, что обычно называют „законом природы".
Следовательно, с телеологической2) точки зрения конкретное
численное решение любой конкретной системы уравнений имеет
гораздо меньшую важность, чем понимание природы этого решения,
иначе говоря, влияния физических свойств системы на вид решения.
Посмотрим теперь, каким образом эта идея приводит нас к новой
трактовке процессов решения, а также ряда других процессов
анализа, которые обычно не рассматриваются как процессы реше-
решения. В традиционной трактовке мы рассматриваем весь много-
многошаговый процесс решения — ценой громадного увеличения размер-
размерности задачи — по существу как некоторый единый шаг. Так, если
мы имеем Л^-шаговый процесс, в котором на каждом шаге следует
принять М решений, то классический подход имеет дело с ЖЛ^-мер-
ным одношаговым процессом. Основной вопрос, стоящий перед нами,
заключается в следующем: как избежать этого нарастания размер-
размерности, которое подавляет исследование и сильно препятствует
вычислениям?
) Пародия на символические высказывания в романе аСтранствования
паломника" английского писателя XVII века Дж. Беньяна. — Прим. ред.
2) Телеология — идеалистическое учение, согласно которому всякое
развитие является реализацией некоторой заранее предопределенной цели.
Направленная против причинного объяснения мира, телеология является
попыткой перенесения закономерностей, присущих лишь некоторым формам
деятельности человека, на весь реальный мир.
Тем не менее замечание автора справедливо и не нуждается для своего
обоснования в привлечении каких бы то ни было идеалистических теорий
(в том числе и „телеологической точки зрения"). — Прим. перев.
12 Предисловие
Для ответа на этот вопрос обратимся к высказанному ранее
положению о том, что существенна именно структура поведения.
Каков точный смысл этого утверждения? Оно означает, что мы
желаем знать характеристики системы, определяющие решения,
которые надлежит принимать на каждом конкретном шаге процесса.
Иначе говоря, вместо определения оптимальной последовательности
решений в условиях некоторого фиксированного состояния системы
мы желаем определить оптимальныеч решения, которые следует
принимать в каждом состоянии системы. Только в этом случае мы
можем считать, что действительно понимаем внутреннюю структуру
решения.
Математическое преимущество такой постановки вопроса заклю-
заключается, во-первых, в том; что она уменьшает размерность процесса
до присущего ему уровня, именно, до размерности решения,
с которым мы сталкиваемся на любом конкретном шаге. Это делает
задачу более легко поддающейся аналитической обработке и значи-
значительно упрощает ее в вычислительном отношении. Во-вторых, как
мы увидим, принимаемый подход приводит нас к некоторому типу
приближения, именно, к „приближению в пространстве поведений",
обладающему одним существенным математическим свойством —■
монотонности сходимости, —и хорошо приспособленному к при-
приложениям. Принципиальное преимущество рассуждений в терминах
поведений также весьма велико. Этот подход дает нам возмож-
возможность ставить и рассматривать такие задачи, которые не поддаются
плодотворному изучению любыми другими методами. Если бы мы
должны были высказать предположение о том, какое направление
исследований сулит наибольшие успехи теории многомерных про-
процессов в будущем, мы без колебаний избрали бы указанное на-
направление.
Темой настоящей книги являются приложения этого понятия
решения к целому ряду процессов разных типов, которые мы будем
обсуждать ниже.
Название книги принято на основании следующих соображений.
Пользуясь популярной ныне терминологией, можно сказать, что
рассматриваемые нами задачи являются задачами программирова-
программирования1). При этом прилагательное „динамический* указывает на то,
что мы интересуемся процессами, в которых существенную роль
играет время и в которых порядок выполнения операций может
оказаться решающим. Кроме того, существенной чертой нашего
подхода будет интерпретация многих статических процессов как
динамических процессов с искусственно введенным временем.
Обратимся теперь к обзору содержания книги.
В первой главе мы рассматриваем многошаговый детерминиро-
детерминированный процесс распределения ресурсов, который является прототипом
То есть задачами принятия решений. — Прим. ред.
Предисловие авторй 13
общего класса задач, встречающихся в различных вопросах органи-
организации тыла, в многошаговых процессах инвестирования, в изучении
оптимальной политики закупок и при рассмотрении многих других
экономических процессов. С математической точки зрения эта задача
сводится к многомерным задачам максимизации и, в конечном счете,
к вариационному исчислению.
Сначала мы рассмотрим процесс общепринятым способом и от-
отметим возникающие при рассмотрении даже самых простых про-
процессов этого типа затруднения, связанные с размерностью. Затем
мы изложим основной метод всей теории, заключающейся в превра-
превращении исходной задачи максимизации в задачу решения некоторого
функционального уравнения.
Функциональные уравнения, которые встречаются нам на этом
пути, являются уравнениями совершенно нового типа и существенно
отличаются от всех функциональных уравнений, рассматриваемых
в классическом анализе. То уравнение, относительно которого будут
проведены рассуждения в этой главе, имеет вид
A) /(*)= тах
где й* и ^ — заданные функции, а и Ь—известные постоянные,
удовлетворяющие условию О^а, #<1.
Доказав теорему существования и единственности, мы установим
несколько простых свойств оптимального поведения, которые можно
вывести из простых функциональных свойств функций § и к.
В частности, мы приведем явные решения этого уравнения для не-
некоторых частных видов функций ^ и А.
Преимущество этих решений заключается в том, что их можно
использовать для получения аппроксимаций к решениям более сложных
уравнений и, что еще более важно, для получения аппроксимаций к
соответствующим оптимальным поведениям. Идея аппроксимации при-
приводит нас к весьма важному понятию приближения в пространстве
поведений, используемому в теоретических и в практических рас-
рассмотрениях, а также при изучении вопроса об устойчивости функ-
функции / при изменениях % и /г.
Во второй главе мы рассматриваем многошаговый процесс реше-
решения стохастического типа в терминах золотодобывающего пред-
предприятия, оснащенного не очень надежной машиной -для добычи
золота. Здесь нам приходится иметь дело с уравнением
,ЛЧ ,, , ^: Р\ \Г\Х -\-/(A—г\)х, У)\у
Г2/ У)\
Кроме проведения исследования, аналогичного тому, которое
было сделано в гл. I, мы находим фактическое решение этого урав-
уравнения и некоторых его обобщений. Решение имеет весьма простую
14 предисловие автора
и интуитивно ясную форму и приводит к важной идее „областей
решения".
Мы покажем, однако, что ряд других обобщений уже не имеет
такой простой структуры и ставит еще не решенные задачи. Попытка
получить приближенные решения этих задач для частной области
пространства параметров приведет нас к непрерывным вариантам,
которые рассматриваются в гл. VIII.
Глава III посвящена синтезу* этих процессов, кажущихся на
первый взгляд столь различными. В этой главе мы исследуем общие
черты двух процессов, рассмотренных в предыдущих главах, и пере-
переходим после этого к формулировке общих вариантов этих про-
процессов. На этом пути мы приходим к функциональному уравнению
C) /(Р)=тах[*(р. ?)■+-*(р.
частными случаями которого являются как оба предыдущих урав-
уравнения, так и целый ряд других уравнений более общего типа.
В этой же главе мы сформулируем в явном виде „принцип
оптимальности", математическая перефразировка которого дает
в случае любого конкретного процесса функциональное уравнение,
управляющее этим процессом. Более подробно обсуждается также
понятие о приближении в пространстве поведений.
В следующей, четвертой главе устанавливается ряд теорем
существования и единственности для некоторых часто встречаю-
встречающихся классов уравнений, имеющих указанный выше вид. Наши
доказательства основываются на простой лемме, позволяющей срав-
сравнивать два решения уравнения C). Хотя все эти уравнения имеют
резко выраженный нелинейный характер, они в некоторых отноше-
отношениях представляют собой естественное обобщение линейных урав*
нений. Уже по одной этой причине, не говоря уже об их прило-
приложениях, эти уравнения заслуживают изучения.
В главе V мы рассматриваем функциональное уравнение,
выведенное на основе задачи, представляющей в настоящее
время большой экономический интерес, — задачи об „оптимальном
управлении запасами". Здесь мы показываем, что различные методы,
рассмотренные в предыдущих главах, дают решения в некоторых
интересных частных случаях. В частности, мы убедимся, что
метод последовательных приближений является эффективным ана-
аналитическим аппаратом для обнаружения свойств решения и поведе-
поведений, а не просто набившим оскомину методом доказательства теорем
существования и единственности. Существует много различных
вариантов задачи об оптимальном управлении запасами; мы ограничи-
ограничиваемся рассмотрением математической модели, впервые предложенной
Эрроу, Харрисом и Маршаком и изучавшейся также Дворецким,
Кифером и Вольфовитцем.
Предисловие автора 15
Конкретное уравнение того типа, который мы будем рассма-
рассматривать, имеет вид
D) / (х) = гшп
У>х
е(у—
- со
со у
+/@) / а о (з) + //су
у о
Затем мы переходим к изучению процессов, которые мы назы-
называем „процессами с узким местом". Последние мы определяем как
процессы, в которых нужно объединить ряд взаимозависимых фак-
факторов для единой общей цели. Уровень интенсивности основного
процесса зависит от минимального уровня мощности компонент
процесса. Этим задачам посвящены две главы: первая из них, гл. VI,
носит теоретический характер, вторая (гл. VII) посвящена техни-
техническим деталям подробного решения одного частного процесса.
Задачи, которые мы встречаем, являются частными случаями
общей задачи, по-видимому, не рассматривавшейся ранее в матема-
математике сколько-нибудь подробно. Это задача определения максимума
по г скалярного произведения (х(Т), а), где х и г связаны посред-
посредством векторно-матричного уравнения
E)
и подчинены, кроме того, ограничению вида Сг-\- их <;/. Здесь х%
г, с и /—векторы, А, В, С и п — матрицы. Основная трудность
здесь заключается в линейности операторов и функционалов.
Мы могли бы попутно указать на распространенное мнение, что
линеаризация задачи облегчает ее решение. Однако в некоторых
случаях, особенно в вариационных задачах, линеаризация задачи
чрезвычайно усложняет дело, поскольку она делает классические
вариационные методы в значительной мере неприменимыми. Вместе
с тем численное решение в ряде частных случаев может быть полу-
получено стандартными методами.
В гл. VIII мы возвращаемся к процессу золотодобычи и рас-
рассматриваем его непрерывный вариант. Существует много задач
довольно неясной природы, связанных с описанием непрерывных
стохастических процессов решения. В рассматриваемых процессах нам
удастся эти трудности обойти. В непрерывном варианте, сочетая
классический вариационный подход с методами, использованными
в предыдущих главах, мы в состоянии полностью решить непре-
непрерывные варианты целого ряда задач, которые в дискретном случае
Оьцщ совершенно непробиваемы.
16 Предисловие автора
У
Далее, в гл. IX мЬ1 обращаемся к вариационному исчислению и
показываем, что различные его характерные задачи можно рассма-
рассматривать как процессы динамического программирования непрерывного
и притом детерминированного типа.
В геометрических терминах классическая формулировка экви-
эквивалентна рассмотрению экстремали как геометрического места точек,
в то время как в формулировке динамического программирования
экстремаль представляется как огибающая семейства своих каса-
касательных.
Становясь на эту последнюю точку зрения, мы можем получить
новую формулировку некоторых разделов классической теории.
В частности, мы показываем, как получать дифференциальные урав-
уравнения в частных производных для главного собственного значения
дифференциального уравнения
м 7\ \ // | Л О / ^А\ Г\ Х^Ч\ / < ч т\
ш ш\ 1 11 | к С*([\ I Г 1 // —"^ I I // I I I 1 "-' // I I 1 ■ I I
в терминах надлежащим образом введенных параметров состояния.
Кроме того, мы даем новый вычислительный подход к вариацион-
вариационным задачам с ограничениями.
В главе X рассматриваются процессы динамического программи-
программирования, включающие двух принимающих решения лиц, обладающих
противоположными интересами. Это приводит к изучению много-
многошаговых игр* и, в частности, к очень интересному классу игр, на-
называемых „играми на выживание". С помощью некоторых эвристи-
эвристических рассуждений мы можем получить в качестве побочного
результата новое истолкование для игр с ненулевой суммой.
Функциональные уравнения, встречающиеся в этой области, имеют
общий вид
G) /(р, //)=тах т1п1 Г Г18 (Р* Р'> <7» <7') +
о о/ I./ о
+ Ь(р> р', Ч, ?')/(Л(Р> Р'> 1. Ч'\ Т2(р% р\ д. д'))\ йО(д) йО'Ч?')}.
Их можно изучать посредством тех же общих методов, которые
применялись в гл. IV при рассмотрении приведенного выше урав-
уравнения C).
В заключительной главе мы рассматриваем класс непрерывных
процессов решения, которые приводят к системам нелинейных диф-
дифференциальных уравнений вида
(8)
г N
(9)
= 1, 2 Л/,
а также к соответствующим системам уравнений, выведенным на
дснове дискретного процесса.
Предисловие автора 17
Будет показано, что эти уравнения обладают любопытными свя-
связями с некоторыми классическими нелинейными уравнениями.
В дополнение к ряду упражнений, приведенных с педагогиче-
педагогическими целями, мы включили некоторую прослойку задач, предна-
предназначенных для иллюстрации объема приложений методов динами-
динамического программирования.
Возможно, что иной читатель нахмурится по поводу некоторых
не слишком глубоких вопросов, которые изредка рассматриваются
в упражнениях и используются для иллюстрирования различных
типов процессов. Мы готовы защититься от обвинений в 1ёзе та-
^ез^е) различными способами, но предпочитаем два следующих.
Во-первых, интересная математика встречается всюду, где мы ее
сумеем найти: в головоломке с кенигсбергскими мостами и в про-
проблеме раскраски карт,, в задаче о рассаживании школьниц и при
определении выигрывающей тактики в азартных играх, или, наконец,
в неожиданной регулярности распределения простых чисел. Во-вто-
Во-вторых, всякая мысль абстрактна, а математическая в особенности.
Следовательно, вводим ли мы наши математические величины под
респектабельными наименованиями А и В или же под более обаятель-
обаятельными— Алиса и Бетти, говорим ли мы о случайных процессах
или об искусстве ведения игры — всюду мы имеем дело с матема-
математическим анализом, т. е. с количественным изучением явлений.
Любое математическое исследование, подобное предлагаемому, сле-
следует судить в конечном счете по его внутреннему содержанию,
а не по удельному весу высокопарных псевдоабстракций, которыми
так легко пересолить любой текст.
На этом мы заканчиваем наш краткий обзор содержания этого
тома. Поскольку процессы, которые мы рассматриваем, возникаю-
возникающие из них функциональные уравнения и применяемые нами методы
в основном новы и поэтому непривычны, мы сознательно ограни-
ограничиваем себя умеренным математическим уровнем для того, чтобы
подчеркнуть некоторые лежащие в основе теории положения, не
загромождая их чисто аналитическими деталями. В соответствии
с этой целью мы не углубляемся слишком далеко ни в одну из
областей приложений теории как с математической, так и с физи-
физической или экономической стороны.
Во всех главах мы пытались избежать какого бы то ни было
обсуждения более глубоких результатов, требующих либо более
серьезной подготовки со стороны читателя, либо более мощной
аналитической аргументации. Изредка, как в гл. VI и гл. IX, мы
без колебаний вообще отказались от строгого рассмотрения и пред-
предпочли действовать откровенно эвристическим методом.
Во втором томе, задуманном нами, мы намереваемся на более
высоком математическом уровне исправить некоторые из
Оскорбление величества (фр.)- —Прим.
2 Р. Беллман
18 Предисловие автора
упущений и изложить ряд тем более тонкого характера, которые мы
либо совсем здесь не упоминали, либо упоминали мимоходом, либо
намечали лишь в общих чертах. Из текста будет видно, сколько
еще предстоит сделать.
В этой связи стоит отметить обширную, важную и относительно
неразработанную область, в которую» весь настоящий том делает лишь
небольшой экскурс. Это — общее изучение численного решения
многомерных вариационных задач. Конкретно общую задачу можно
поставить следующим образом: пусть имеется процесс и связанная
с ним вариационная задача; как использовать специфические черты
процесса для построения вычислительного алгоритма решения этой
вариационной задачи?
Динамическое программирование предназначено для изучения
многошаговых процессов, обладающих определенными свойствами
инвариантности. Теория линейного программирования предназначена
для рассмотрения процессов, обладающих определенными чертами
линейности; изящный симплекс-метод Дж. Данцига в значительной
степени решает задачи, связанные с этими процессами. Для опреде-
определенных классов задач теории расписаний1) разработан целый ряд
итеративных и релаксационных методов. В частности, отметим
методы Хичкока, Купманса и Флада для транспортной задачи Хич-
Хичкока— Купманса и метод потоков А. Болдырева для железнодо-
железнодорожных сетей. Кроме того, недавно создана теория нелинейного
программирования Г. Куна, А. У. Таккера и Э. Била. Однако изу-
изучение вычислительных методов находится еще в своем младен-
младенчестве.
Обсудим теперь вкратце некоторые педагогические аспекты
книги. Своей аудиторией йы считали всех интересующихся вариа-
вариационными задачами, включая математиков, статистиков, экономистов,
инженеров, специалистов по исследованию операций и т. д. По-
Поскольку интересы различных представителей этой аудитории пере-
перекрываются лишь в небольшой степени, некоторые части книги будут
представлять больший интерес для одной группы читателей, чем
для другой.
По уровню математической трудности настоящая книга подхо-
подходит для изучения после общего курса анализа и может изучаться
либо на математических факультетах, либо на технических или
экономических факультетах — в сочетании с курсами прикладной
математики или исследования операций.
) Обзорная статья автора по теории расписаний цитируется на стр. 180.
В этой статье автор относит к теории расписаний не только чисто комби-
комбинаторные задачи составления графиков и расписаний (типичными приме-
примерами которых являются, например, задачи 8—11 к гл. III), но и теорию транс-
транспортных задач, всевозможные проблемы сглаживания и другие задачи линей-
линейного программирования. — Прим. перев.
Предисловие автора
Для первых курсов или первых чтений мы предлагаем следую-
следующие программы.
Для математика: главы I, И, III, IV, IX» X.
„ экономиста: главы I, II, III, V, IX.
„ статистика: главы I, II, III, IX, X, XI.
„ инженера: главы I, II, III, IX.
„ специалиста по исследованию операций: главы I, II, III, V,
IX, X.
Наконец, прежде чем закончить этот пролог, я считаю своим
приятным долгом указать на целый ряд источников. Во-первых,
это теория игр фон Неймана, развитая Дж. фон Нейманом, О. Мор-
генштерном и другими авторами — теория, показывающая, как при
помощи методов математического анализа можно изучать обширные
классы задач, которые прежде были вне сферы досягаемости мате-
математиков и поэтому были сданы в архив как неподдающиеся иссле-
исследованию. Во-вторых, это теория секвенциального анализа Вальда,
развитая А.- Вальдом, Д. Блекуэллом, А. Гирщиком, Дж. Воль-
фовитцем и другими, — теория, показывающая большую экономию
усилий, которая может быть достигнута при помощи надлежащего
рассмотрения многошаговых процессов испытаний. Я признателен
также ряду коллег и друзей, обсуждавших со мной различные
вопросы излагаемой теории и содействовавших ее прояснению и раз-
развитию.
Многие результаты этой книги были получены в сотрудничестве
с коллегами математиками. Формулировка игр на выживание была
получена вместе с Дж. П, Ла-Саллем; результаты об уравнении
оптимального управления запасами получены вместе с И. Гликсбергом
и О. Гроссом; результаты о непрерывном процессе золотодобычи
в гл. VIII и результаты в гл. VII, относящиеся к конкретным про-
процессам „с узким местом", получены вместе с С. Леманом. Ряд ре-
результатов, полученных вместе с X. Осборном (о связи между ха-
характеристиками и уравнениями Эйлера и о сходимости дискретных
процессов золотодобычи к их непрерывным вариантам) не вошел
в книгу. Мы не включили также исследование о фактическом чи-
численном решении многих обсуждаемых ниже процессов, которым
мы занимались с С. Дрейфусом *).
Я хотел бы особенно поблагодарить И. Гликсберга, О. Гросса
1) См. например, В е 11 т а п Р., О г е у I и 8 5., а) Оп а 1асНса1 а1'г-
дуаг!аге тос!е1 о* Мепде!, Орегаг. Яез., 6, № 1 A958), 65—78, б) А ЪоШепеск
A958), 307—314, в) РипсП"опа1 арргох1"та(юп8 апс! дупагшс ргодгатттд, МаНъ.
ТаЫез апй оНгег Аш$ го Сотр., 13, № 68A959), 247—251, г) Ап аррИсаНоп
о^ Aупат1с ргодгатт1пд (о Ше Aе1егт1па11'оп о! ор11та1 8а1е1Н{е 1га]"ес(опез,
^. ВгИ. ЫегрЫпег. Зое, 17, № 3—4 A959), 78—83; Огеу!из 5., Сотри*а-
1юпа1 а§рес*8 о! дупапн'с рго^гатгт'п^, Орегаг. #ез., 5, № 3A957), 409—415.—
Прим. перев.
20 Предисловие автора
и А. Болдырева, которые с большой тщательностью прочли окон-
окончательную рукопись и сделали ряд полезных предложений и ис-
исправлений, и С. Карлина и X. Н. Шапиро, проделавших много
ценной работы в этой области; я извлек немало полезного из пло-
плодотворных бесед с ними.
Наконец, я хотел бы засвидетельствовать особую признатель-
признательность О. Хельмеру и Э. В. Паксону, которые давно поняли важность
многошаговых процессов и постоянно вдохновляли меня в моих
исследованиях, и, кроме того, предложили ряд пленительных
задач, естественно возникающих в различных важных прило-
приложениях.
Здесь следует особо отметить, что большинство названных выше
математиков являются либо сотрудниками корпорации КАИО, либо
ее консультантами. Наша работа проводилась по широкой про-
программе исследований для Военно-воздушных сил Соединенных
Штатов.
Санта Моника, Калифорния
Ричард Беллман
Глава I
МНОГОШАГОВЫЙ ПРОЦЕСС РАСПРЕДЕЛЕНИЯ
§ 1. ВВЕДЕНИЕ
В этой главе мы намерены познакомить читателя с задачами,
характерными для круга вопросов, являющихся предметом динами-
динамического программирования, а также с основным методом, которым
мы будем пользоваться в дальнейшем.
Сначала будет рассмотрен некоторый, довольно простой, много-
многошаговый процесс последовательного распределения, обладающий
рядом черт, общих для многих процессов, рассматриваемых
V в самой математике, — в таких ее областях, как дифференциаль-
дифференциальное, интегральное и вариационное исчисления, и в таких ее при-
приложениях, как математическая экономика и управление техни-
техническими системами.
Сначала мы сформулируем задачу в ее классической постановке.
Это мы сделаем главным образом для того, чтобы проиллюстри-
проиллюстрировать некоторые трудности такого непосредственного подхода
к вопросу. Чтобы обойти эти трудности, мы введем тот новый
основной математический метод, который будет использоваться на
протяжении всего дальнейшего изложения. В основе этого метода
лежит идея рассмотрения любой конкретной задачи как представи-
представителя семейства сходных с ней задач1). Такая точка зрения позволит
нам заменить исходную многомерную задачу о максимизации задачей
решения системы рекуррентных соотношений, включающих функции
значительно меньшего числа переменных.
В качестве первого этапа решения этой системы функциональ-
функциональных уравнений мы рассмотрим единственное функциональное урав-
уравнение
A) /(*)= шах
Для этого уравнения будут более детально изучены вопросы, свя
Один из простейших вариантов этой идеи реализуется в следующем
хорошо известном случае. Пусть нам нужно доказать справедливость
утверждения, содержащего некоторое конкретное натуральное число п0. Обо*
значая это утверждение через А (п0), рассмотрим переменное утверждение
Л (/г), зависящее от натурального аргумента. Доказав по индукции справед-
справедливость А (л) при любом /г, мы тем самым докажем и А (/г0). — Прим. ред.
22 Глава 1
занные с существованием и единственностью его решения, свойствами
этого решения, а также частными решениями этого уравнения.
Обращаясь к процессам более сложного типа, область приме-
применения которых значительно шире, мы прежде всего рассмотрим
процессы, зависящие от времени. Кроме того, будут получены не-
некоторые многомерные аналоги уравнения A), возникающие при
рассмотрении многошаговых процессов, которые требуют принятия
нескольких решений на каждом шаге. Эти многомерные уравнения
являются источником ряда трудных и до сих пор не решенных
задач численного анализа.
В заключительной части главы рассматриваются некоторые сто-
стохастические варианты описанных процессов распределения. Как мы
увидим, при рассмотрении как стохастического, так и детермини-
детерминированного процессов могут быть применены одни и те же анали-
аналитические методы.
§ 2. МНОГОШАГОВЫЙ ПРОЦЕСС РАСПРЕДЕЛЕНИЯ РЕСУРСОВ
Перейдем теперь к рассмотрению простого, но важного при-
примера многошагового процесса распределения.
Допустим, что мы имеем некоторое физическое количество х% кото-
которое разделим на две неотрицательные части у и х— у, получая от
первой доли у доход &(у), а от второй — доход Н(х— хI).
Желание выполнить это разделение' так, чтобы максимизировать
общий доход, приводит нас к аналитической задаче определения
максимума функции
A) КЛхшу) = е(У)-\-Нх — У)
по всем у$.[0,х]. Мы будем предполагать, что функции ^ и й
непрерывны при всех конечных х^О, так что интересующий нас
максимум всегда будет существовать.
Рассмотрим теперь двухшаговый процесс. Предположим, что
за счет издержек, требующихся для получения дохода @(у), пер-
первоначальное количество у уменьшается до ау, где а — некоторая
постоянная, заключенная между 0 и 1@^а<1). Пусть анало-
аналогично х — у уменьшается до Ь(х — у) @<!1#<С1) за счет издер-
) Единицы измерения дохода в этом случае отличны от единиц изме-
измерения количества х. Так, например, х может представлять собой денежную
сумму, а &(у) — количество человеко-часов, сэкономленное в результате
применения машин, приобретенных на сумму у. В других случаях, встре-
встречающихся в многошаговых задачах о капиталовложениях или в многоша-
многошаговых производственных задачах, дело может обстоять иначе: как исходные
ресурсы, так и доход могут выражаться в одних и тех же единицах. Встре-
Встречается и сочетание этих двух вариантов задачи. Пока мы рассматриваем
самый простой случай.
Многошаговый процесс распределения 23
жек для получения Н(х— у). Затем мы повторяем процесс с сум-
суммарным остатком ау\-Ь(х— у), полагая
B) ау-\-Ь(х — у) = х1 = у1 -И*! — уг),
где 0 <! ух ^ хг. В результате этого нового распределения мы на
втором шаге получим доход & (уг) -\- Н (хг — у{). Полный доход от
описанного двухшагового процесса будет
C) #2(х. у, ух) = ё(у) + Н(х — у) + ё(уг) + *(*! — уг).
Максимальный суммарный доход получается при максимизации
этой функции относительно у и ух в двумерной области, опреде-
определенной неравенствами
D)
б)
Обратимся теперь к Л/-шаговому процессу, где вышеописанная
операция распределения повторяется последовательно N раз. Тогда*
полный доход от Л/-шагового процесса будет равен
E) К„(х, у, у1
где величины, подлежащие дальнейшему разделению после первого,
второго (Л^—1)-го шагов, определяются соотношениями
F) х1 =
1 — ух), 0
"У* -
Максимальный окончательный доход будет получаться в результате
максимизации функции /?^ по Л/-мерной области в пространстве
переменных у, ух Уы-х> в КОТОРОЙ значения этих переменных
удовлетворяют соотношениям F).
§ 3. ОБСУЖДЕНИЕ
При решении этой задачи естественно возникает искушение вос-
воспользоваться аппаратом классического анализа. Если абсолютный
максимум достигается внутри области, т. е. для всех максимизи-
максимизирующих у$ выполняются строгие неравенства 0 < у\ < х$, и
24 Глава I
функции & (у) и Н(х — у) дифференцируемы, то, взяв частные
изводные по у^ мы получаем для максимизирующих у^ систему
уравнений
N -
8'(У)-Ь'(х-у)-\-(а —
Однако если мы не знаем, выполняются ли указанные условия,
и, кроме того, нас интересует не относительный, а абсолютный
максимум, то необходимо испытать на экстремальность и граничные
значения У\—0 и Уг = Хг, а также все комбинации граничных зна-
значений и внутренних максимумов. Кроме того, в случае неедин-
неединственности решения системы A) мы должны дополнительно рас-
рассмотреть большое количество условий, достаточных для наличия
именно абсолютного максимума, а не минимума и не относительного
максимума. Очевидно, что для задач большой размерности, т. е. для
процессов с большим числом шагов, совершенно необходимы некото-
некоторая систематическая процедура и постоянный контроль для дове-
доведения до конца полной программы решения.
, что как аналитики мы отступаем перед лицом этой
то^дной задачи и занимаем позицию пораженцев. Поэтому откажемся
(т аналитических методов, чтобы обратиться за помощью к совре,-
(менным вычислительным машинам. В качестве поучительного при-
[ера рассмотрим задачу о 10-шаговом процессе. Если мы хотим
определить максимум тривиальным образом, т. е. путем подсчета
значений функции /?10 = Ню (у, У\* • • •» Уд) в соответственно вы-
выбранных точках решетки, то мы можем разделить все интересую-^
щие нас интервалы 0<^<;л:, 0<з;1<;л:1, . .., 0<;.у9<;л;9,
скажем, на десять частей и подсчитать значения /?10 в каждой из
1010 полученных таким образом точек. Однако 1010 — число, вну-
внушающее* уважение. Даже самая быстродействующая современная
машина или машина недалекого будущего потребует еще довольно
много времени, чтобы определить решение таким путем.
Для того чтобы дать некоторое представление о величине 1010,
заметим, что если машине потребуется одна секунда на вычисление
/?10 в точке решетки, запоминание и сравнение его с другими зна-
значениями, то для 1010 значений потребуется 2,77 миллиона часов;
если время для одной точки составит одну миллисекунду {\0~*сек)г
то для выполнения всей работы понадобится 2,77 тысячи часов.
а если одну микросекунду (\0~6сек), то 2,77 часа. Только послед-
последняя величина может считаться достаточно приемлемой. Заметим,
однако, что если рассматривается 20-шаговый процесс, то каждую
из этих величин необходимо умножить еще на 1010. потому что
Ю20 К)Ю 10ю
Многошаговый процесс распределения 25
,*- *-— ■ » —— '■"■* ■ ■ """■"" " ^* """■*■■——■.■■И— — II ■!■■!■■ ■ 11—И.1- ■'■■■П 1-— III I. I ■!■.. -, . ||, 1...1.1..1 I II..—
Излишне говорить, что существуют различные искусственные
приемы, которые могут быть использованы для сокращения необхо-
необходимого для вычислений времени. Тем не менее описанный метод
по-прежнему является слишком громоздким и грубым для решения
данной задачи.
Кроме того, нужно отдавать себе отчет в следующем. Если мы
настолько заинтересованы в решении задачи, что готовы предпри-
предпринять описанные вычисления, то мы, вообще говоря, захотим узнать
ответ не только для одного частного значения х, но для целого
ряда его значений, не только для одного набора значений а и Ь,
но для некоторого множества таких наборов, и не только для
одной пары функций & и к, но для целого класса функций. Иначе
говоря, мы хотим провести анализ чувствительности, устойчи-
устойчивости решения. Любой такой анализ устойчивости, если только он
будет проводиться вышеописанными методами, потребует огромного
количества вычислительного времени.
Отметим, что рассмотренная нами задача есть прежде всего
лишь реализация очень простого, до смешного, варианта одной из
прикладных задач. Поэтому в создавшемся положении одна из
действительно приводящих в уныние перспектив состоит в том, что
любое приближение условий задачи к реальным (например, разде-
разделение х более чем на две части, т. е. увеличение числа отраслей,
в которые можно помещать капитал, или возрастание числа видов
ресурсов) повлечет за собой возрастание вычислительного времени
по экспоненциальному закону. .
Кроме того, как уже было отмечено в предисловии, необходимо
ясное понимание того, что основная цель при создании подобных
математических моделей космогонических, экономических, физи-
физических, биологических и т. д. процессов состоит не столько в по-
получении чисел, которые во многих случаях являются сомнительными
из-за недостаточности наших знаний относительно некоторых ос-
основных постоянных и входящих в задачи функций, сколько в опре-
определении самой структуры решения. Во многих процессах более
важны общие представления, чем конкретные значения констант.
Однако, вообще говоря, эти две задачи тесно связаны друг
с другом. Если есть полное представление о пррцессе, то благо-
благодаря различным видам идеализации мы можем определить и тре-
требуемые постоянные. К тому же в приложениях встречаются про-
процессы такой огромной сложности, что бесполезны вычисления, ос-
основанные на пробах и ошибках, и только предварительное выяснение
общей структуры решения может подать надежду на эффективное
использование вычислительных машин.
Возвращаясь к идее о внутренней структуре решения, спросим
себя, что именно мы желаем узнать при изучении процесса подобного
типа. Естественно, нам хотелось бы получить точку (у, ух у^,
в которой достигается Максимум, причем любое решение, вычисленное
26 ► Глава I
в этой точке, должно давать максимальное значение. Однако
с точки зрения лица, проводящего процесс, в действительности на
любом шаге требуется только знание у как функции имеющихся
в наличии ресурсов х и числа предстоящих шагов М, т. е. распре-
распределение определено, если известны имеющееся в наличии коли-
количество х и число оставшихся шагов N. Хотя рассматривается
многошаговый процесс, но выбор на каждом шаге делается одно-
одномерный, т. е. выбирается число у из интервала [0, х]. Отсюда сле-
следует1), что нужно так сформулировать задачу, чтобы сохранить
одномерность; это спасет нас от возможности увязнуть в сложностях
многомерного анализа задолго до завершения вычислений.
§ 4. МЕТОД ФУНКЦИОНАЛЬНЫХ УРАВНЕНИЙ
Поставив своей целью сохранение одномерности задачи, будем
действовать следующим образом. Прежде всего заметим, что макси-'
мум полного дохода от Л^-шагового процесса зависит только от
и от начальной величины х. В связи с этим определим функцию
A) /^(х) как максимум дохода, полученного от Л^-шагового
процесса, который начинается с величины х, для
Л/ = 1, 2, ... и л:>0.
Мы имеем
B) /#(х)= тах /?
и
C) Л(*)= тах
Наша ближайшая цель состоит в получении уравнения, выражаю-
выражающего /2(х) через /х(х). При рассмотрении двухшагового процесса
мы видим, что полный доход будет состоять из дохода от первого
шага плюс доход от второго шага, на котором для распределения
оставалась сумма ау-\-Ь(х — у). Отсюда ясно, что какой бы ни
была первоначально выбранная величина у, оставшаяся к следующему
шагу сумма ау-\~Ъ(х — у) должна быть использована наивыгодней-
наивыгоднейшим образом, если только мы намерены получить максимум при
двухшаговом распределении ресурсов.
Это замечание, само по себе простое, является ключом ко всему
дальнейшему математическому аппарату. Для читателя имеет смысл
заострить на нем свое внимание и удостовериться в том, что он
действительно согласен с этим замечанием, обладающим обманчивой
простотой полуистины.
1) Как приложение полезного принципа видеть все таким, как хочется.
Многошаговый процесс распределения 27
Если только уг выбрано оптимальным» то в результате началь-
начального распределения у мы получим от второго шага нашего двух-
шагового процесса полный доход }г{ау-\-Ь(х— у)). Следовательно,
для окончательного дохода от двухшагового процесса при начальном
распределяемом количестве у получается выражение
D) Яг(*. у. уг) = е(у) + Н(х — у)+/1 (ау + Ъ(х — у)).
Так как у выбиралось таким образом, чтобы максимизировать
это выражение, то можно легко установить рекуррентное соотно-
соотношение
E) /,(*)= ™х 18(У) + Чх — У)+А(ау + Ь(х — у))].
связывающее функции /х(х) и /2(х). Используя точно такую же
аргументацию для Л/-шагового процесса, мы получим основное
функциональное уравнение )
F) /*(*)= тах
для Л^^-2, где /г(х) определяется соотношением C).
Отправляясь от функции /г(х), определенной уравнением C), мы
используем F) для вычисления /2(х), которое, если процесс повто-
повторить снова, даст нам /3(лг) и т. д. При этом на каждом шаге вычи-
вычисления мы получаем не только /ъ(х), но также и Ук(х), так как
распределение исходной величины х в начале ^-шагового процесса
было оптимальным.
Отсюда видно, что процесс решения нашей задачи состоит
в табулировании последовательностей функций {Уь(х)} и {/^(х)} для
х^О, к— 1, 2
Если дана последовательность функций {Ук(х)}, то решение
конкретной задачи с заданными числом шагов /^ и величиной х
имеет вид
G)
''N-2 У N-2) )■
где (.у, ух Уя-г)— система распределений, максимизирующих
полный доход от /^-шагового процесса.
28 Глава 1
Заметим, что для цифровой вычислительной машины может быть
составлена такая программа, при которой машина не только табу-
табулировала бы последовательности {Д(л:)} и {.у* С*)}» но и печатал*
бы последовательность значений у, у±9
. 9
§ 5. ОБСУЖДЕНИЕ
Необходимо отметить тот важный факт, что мы пытались решить
задачу о максимизации для случая конкретных значений х и N путем
решения общей задачи, включающей произвольную величину х и
произвольное значение Л/. Иначе говоря, как это и было обещано
в § 1, мы рассматривали первоначальную задачу как частный случай
семейства сходных задач. Этот основной математический метод
будет развиваться на протяжении всего дальнейшего изложения.
Какая же польза от такого подхода к решению задач? Прежде
всего это позволит свести одну М-мерную задачу к последователь-
последовательности из N одномерных задач. Вычислительная выгода такой поста-
постановки задачи очевидна; кроме того, в следующих параграфах мы
покажем, что она дает значительные аналитические выгоды, которые
и следовало ожидать. Как мы увидим, для широкого класса функ-
функций @ и к нам удастся получить даже явные решения, которые
могут быть использованы для целей аппроксимации. В дальнейшем
эта точка зрения будет обсуждаться снова. Даже в тех случаях,
когда решение довести до конца не удается, окажется возможным
установить ряд его важных структурных свойств. Использование
структурных свойств решения и уменьшение числа измерений позво-
позволяет применить вычислительную технику, которая сильно сокращает
время, необходимое для решения первоначальной задачи. К этой
точке зрения мы еще вернемся в связи с некоторыми многомерными
вариантами рассмотренной задачи.
§ 6. МНОГОМЕРНАЯ ЗАДАЧА О МАКСИМИЗАЦИИ
Прежде чем перейти к более детальному изложению теории опи-
описанных выше процессов, отвлечемся на мгновение и кратко остано-
остановимся на двух следующих примерах применения общего метода.
В качестве первого примера рассмотрим задачу об определений
максимума функции
A) (г 2%) 2
в области, определенной соотношениями
B) а) хг
б) л;*
причем каждая из функций §*(.*) непрерывна для всех
Многошаговый процесс распределения
Так как максимум функции Р зависит только от с и Л/, то можно
определить последовательность функций
C) /1Г(
Ы
для с>0 иЛ/=1, 2
Тогда, рассуждая как и выше, мы получаем рекуррентное со
отношение
D) /^ (с) = тах [^ (л:) +/лг_1 (с — х)\
для N = 2, 3 где
E) Л (с) = ёг (с).
§ 7. ЗАДАЧА О „СГЛАЖИВАНИИ"
В качестве второго примера приложения общего метода рассмот-
рассмотрим задачу об определении последовательности {хк}, максимизирую-
максимизирующей функцию
N N
/1\ р (у V V ^ V /т (у г \
V1/ * 1Л1» Л2» ••• » ^м)— ^ькУ-^к 'к)
Здесь [гк] — некоторая заданная последовательность чисел, хо—с —
фиксированная постоянная, функции &к(х) и кк(х) предполагаются
непрерывными для всех конечных х, причем &к(х), кк(х)-+оо при
\х |-> оо.
С происхождением этой задачи, объясняющим ее название, мы
познакомимся в упражнениях.
Определим последовательность ПЕ (с)\, /? = 1, 2 Л/, где/Б(с)
есть минимум функции
N N
B) Рн = 2 8п (** — гк) + 2 К
ПО
C)
и
D)
Для
всем
Мы
ХЕ* ХВ+1*
имеем
"• 1 ^ +>) • « •
• X
N
*
с) = пип Г
ппп\%Е (х
X
, N—1,
а хК_х = с.
А (х — с)]
(л:
80 Глава I
—- Г =-1 ——■ 1 Г* ГП-ТЩ Щ-ЦТП II II 1~Ш1. 11Ш-111Л11. ... N. ■■ .......
§ 8. БЕСКОНЕЧНОШАГОВАЯ АППРОКСИМАЦИЯ
Обратимся вновь к процессу распределения. Приводимое здесь
изложение вопроса послужит прототипом при рассмотрении целого
ряда многошаговых процессов различного происхождения, но одина-
одинаковой аналитической структуры.
Если число шагов Л/ велико, то естественно рассмотреть в ка-
качестве аппроксимации Л^-шагового процесса бесконечношаговый про-
процесс, отличающийся от конечношагового процесса только тем, что
он продолжается сколь угодно долго. Несмотря на то, что неогра-
неограниченно продолжающийся процесс физически всегда является неко-
некоторой фикцией1), с математической точки зрения он имеет много
привлекательных черт. Одно несомненное и немедленно сказываю-
сказывающееся преимущество такой аппроксимации заключается в том, что
вместо последовательности уравнений D.6) можно рассматривать
единственное уравнение
A) /(*)= тах 1е(У) + Их — у)+Пау + Ь(х — у))]ш
0< у <а?
1
которому должна удовлетворять функция /(х) и которое определяет
полный доход от процесса вместе с единственной распределяющей
функцией у = у(х).
С другой стороны, мы сразу же сталкиваемся с обычными труд-
трудностями, связанными с бесконечными процессами. Прежде всего
далеко не ясно: будет ли существовать в соотношении A) максимум
или же следует ограничиться супремумом? Это означает, что в дан-
данном случае может и не оказаться такой политики распределений,
в результате которой получается полный доход /(х). Кроме того,
если мы хотим неограниченно пользоваться уравнением A) для уста-
установления свойств бесконечного процесса, то необходимо доказать,
что оно не имеет посторонних решений. Другими словами, мы
должны доказать для него теоремы существования и единственности,
если, конечно, мы имеем в виду использовать это уравнение обыч-
обычным образом.
§ 9. ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ
В этом параграфе будет получен результат, являющийся по
существу частным случаем более общего результата, о котором
пойдет речь в следующей главе. Однако повторение, которое
обычно шокирует нас в художественной литературе, не является
большим математическим грехом. Для нас во всяком случае более
) Мы иногда будем употреблять слово „физический" для обозначения
„действительного" мира. Его можно интерпретировать как „экономический",
„биологический''1, „технический" и т. д. в зависимости от содержания задачи
и интересов читателя.
Многошаговый процесс распределения 31
важно детально рассмотреть сначала простейший вариант, что даст
возможность выявить основные идеи, свободные от менее существен-
существенных технических деталей.
Докажем следующую теорему.
Теорема 1. Предположим, что
0) а) 8 (х) а Ь(х) — непрерывные функции от х для лг^О,
б) Если т(х)= тах. тах(|#О0|,„|/г(.У)|)> с =
то ^т(спх) <оо для всех х
в) 0<а< 1, 0<&< 1.
При этих предположениях существует единственное решение
уравнения (8.1), непрерывное при х = 0 и обращающееся в этой
точке в нуль; это решение является непрерывкой функцией от х.
Прежде чем перейти к доказательству, отвлечемся на мгновение
и рассмотрим важный частный случай, когда обе функции ^ и й
принимают только неотрицательные значения. Тогда при любом х
последовательность чисел (/^С*)}» получаемая из соотношения D.6),
является монотонно возрастающей и, как будет показано ниже, огра-
ограничена в силу условия A6). Л Следовательно, для всех х^О после-
последовательность функций /#(х) сходится к функции /(х) при Д^—>оо.
Покажем, что эта функция удовлетворяет уравнению
B) /(*)= вир [ё(у) + Н{х-у)+!{ау + Ь{х--у))].
0<У<Х
Для упрощения записи положим
C) Г(/, у) = ё(у) + Н(х-у)+/(ау + Ь(х — у)).
Тогда основное рекуррентное соотношение запишется так:
\ м> У)-
Из D), как следствие монотонности по N. получаем
/(*)> тах ТИ^ у).
Но это означает, что для любого ,у^[0, х] справедливо неравенство
F) /(х)>Т(/„, У).
Устремляя М к бесконечности, получаем
G)
32 Глава I
для всех .у^[0, х], откуда в свою очередь следует, что
(8) /(*)> 5ир 7(/, у).
Мы не можем написать здесь тах, так как ничто не гарантирует
нам непрерывности предельной функции /(х). С другой стороны,
из D) мы получаем также соотношение
(9) /*+!<*)< 8иР г(/. У)
для всех N. а отсюда и
(Ю) /(*)< вир Т(/гу).
Сравнение (8) и A0) дает нам B).
Один из недостатков проведенного, доказательства, основанного
исключительно на монотонности, заключается' в том, что непрерыв-
непрерывность предельной функции не доказывается, и тем самым не уста-
устанавливается существование оптимального поведения. Но это опти-
оптимальное поведение есть функция у(х), при которой достигается
максимум в соотношении
A1) /(*)= шах Г(/, у),
если этот максимум существует.
Как с точки зрения приложений, так и с точки зрения вычислен
ний вопрос о существовании оптимального поведения "для бесконеч-
бесконечного процесса не играет большой роли. Однако он очень важен
в связи с определением структуры оптимальных поведений беско-
бесконечно продолжающегося процесса. Таким образом, вопрос о суще-
существовании непрерывных решений косвенно является существенным
именно в той мере, в какой это связано с получением численных
результатов, так как решение задачи для бесконечного процесса
может быть использовано в качестве аппроксимации решения анало-
аналогичной задачи для конечного процесса.
Для того чтобы установить существование и единственность
непрерывного решения уравнения A1), используем метод, который
применим к широкому классу уравнений подобного типа,—метод
последовательных приближений. С монотонностью же мы встре-
встретимся снова в следующих главах.
Обратимся вновь к рекуррентным соотношениям D). Прежде
всего заметим, что благодаря сделанным предположениям относи-
относительно &(х) и к(х) функция /х(х) является непрерывной при всех
аг^-О. Отсюда, рассуждая по индукции, можно получить, что каждая
функция из последовательности {/#0*0} непрерывна. Следует заметить,
Многошаговый процесс распределения 33
однако, что максимизирующие распределения у н€ обязаны непре-
непрерывно зависеть от х; Иными словами, оптимальное поведение не
обязательно должно быть непрерывной функцией от х. Соответствую-
Соответствующий пример будет приведён в ;§ 15.
Пусть уы(х) является тем значением у, которое осуществляет
максимум в D), причем если имеется более одного значения, до-
доставляющего максимум выражений) D), то безразлично, какое именно
значение у берется. Тогда мы
*т
- Т
Как следствие максимизирующих свойств Уд мы получаем неравенства
A3) /к+1 (х) = Т (/„, ун) > Т
С другой стороны, эти неравенства дают нам
Комбинируя эти два неравенства, мы получаем важную оценку
\/м+1 (х)—/к+г(х) | < шах [ | Т(/„, у„+1) - Т
Возвращаясь к даваемому формулой C) определению Т"(/, ^), мы
видим, что
A6) У \
Положим теперь
A7)" «
Так как ау-\-Ь(х — .УХ сх Для всех У$.№> х\* то соотношение A6)
дает нам • ;. , - • -
A8) ^+1(*)<М^)-
Остается оценить и^х). Обращаясь к уравнениям для /г
и /2(х), мы имеем соотношение
A9У |/Л*) -72(л:Т| ^ тах [ 1Д (д^ +.»(л: —
где использовано определение Агг(д:), данное в A6).
3 Р. Беллман
34 Глава 1
Таким образом, мы видим, что щ (х) ^ т(сх), а используя
далее A7), получаем, что и1^(х)^т(смх). Из предположения отно-
оо
сительно т(х) следует, что ряд ^ин(х) сходится при всех х, и
притом (что является весьма существенным) равномерно в любом ко-
конечном интервале. Следовательно, предельная функция /(х) =
существует и непрерывна при всех значениях х. Кроме того, в силу
этой равномерной сходимости функция /(х) является решением
уравнения F.1).
Остается установить единственность этого решения. Пусть Р(х)
будет любое другое решение, которое существует при всех х и
непрерывно при х — 0, причем ^(О) —0.
Пусть в уравнении
B0) /(*)= ™ах Г(/, у)
= у(х) является тем значением у, при котором достигается мак-
максимум, а функция 1Ю = 1ю(х) играет аналогичную роль в соотношении
B1) Р(*)= тах
Тогда, как и выше, можно получить два неравенства
B2) /(*) = Г(/, з;)>Г(/, «г).
и это, как прежде, приводит к оценке
B3) |/(*) —/Ч*)! < тах [| Г(/, у) — Т(Р. у% \ Т(/, <»)-ГС7-
л: — ^)) — Р (ахи -\-Ь(х — чю)) \ ]
Теперь положим
B4) «(*)= вир 1/(^ —
Так как функция /(х) непрерывна при всех х^О и функция Р(х)
по предположению непрерывна при л; = 0, то отсюда видно, что
функция и(х) также непрерывна при х — 0 и обращается в этой
точке в нуль.
Из B3) мы получаем
B5) #
Многошаговый процесс распределения 35
откуда, итерируя, находим, что
B6) и (*)< и
для всех Л/^-1. Так как функция и(х) при х=0 непрерывна
и #@) = 0, то при М —> оо мы получаем и(х)^0 и, следовательно,
^(х) = Р (х). Это завершает доказательство существованиям един-
единственности решения . для функционального уравнения, связанного
с бесконечным процессом.
§ 10. ПОСЛЕДОВАТЕЛЬНЫЕ ПРИБЛИЖЕНИЯ
Рассмотрим уравнение
A) /(*)= тах Г(/, у).
0<г/<я?
Ранее нами было показано, что некоторая конкретная последователь-
последовательность последовательных приближений сходится к единственному
решению, которое непрерывно при х = 0 и равно нулю в этой
точке. Как с аналитической, так и с вычислительной точки зрения
важно знать, действительно ли любая последовательность, начальная
функция которой удовлетворяет некоторым простым условиям, схо-
сходится к решению.
Использованный выше метод может быть с успехом применен
при доказательстве следующей теоремы.
Теорема 2. Пусть функция /0(х) удовлетворяет следую-
следующим условиям:
B) а) /о0*0 непрерывна*при х^О,
б)/0@)=0.
Если выполнены все условия теоремы 1, то последовательность
функций, определенная рекуррентным соотношением
= тах Т
сходится равномерно в любом, конечном интервале к реше-
решению /(х), которое было определено ранее.
§11. ПРИБЛИЖЕНИЕ В ПРОСТРАНСТВЕ ПОВЕДЕНИЙ
Для получения решения нелинейного функционального уравнения
A) /(*)= тах Г(/, у)
0<г/<ж
выше был применен классический метод последовательных прибли-
приближений. Теперь мы намерены более детально исследовать некоторую
двойственность, которая возникает при рассмотрении этих процессов
36 Глава 1
решения. Это будет сделано главным образом для доказательства
того, что можно выбрать начальное приближение таким обраггом,
чтобы обеспечить монотонную сходимость последовательных прибли-
приближений. Последнее означает, что с каждой итерацией приближение
равномерно улучшается.
Как и прежде, будем называть последовательность распределений,
т. е. последовательность допустимых выборов у, поведением,
а поведение, дающее /(х),— оптимальным поведением.
Двойственность, которая имеет место в теории динамического
программирования, является результатом взаимной связи между
функциями /(х), измеряющими максимальный доход, и поведениями,
которые эти максимальные доходы дают. В действительности пове-
поведение также есть функция, так как каждому значению аргумента х
сопоставляется некоторое значение у(х). Тем не менее полезно
сохранить термин „поведение", ибо он дает некоторые преимущества
интуитивного порядка. Если поведение не единственно, то у не
будет однозначной функцией от х.
Из функционального уравнения A) следует, что у(х) может
быть определено, если известна /(х), и обратно: любое у(х) опре-
определяет /(х) итеративно с помощью функционального уравнения
B)
Так, например, если оптимальное поведение состоит в неизменном
выборе у = 0, то /(х) будет удовлетворять функциональному урав-
уравнению
C)
которое дает в результате
D)
оо
2
Как было упомянуто выше, цель нашего исследования состоит
не столько в определении функции /(х), которое по существу
является побочным результатом, сколько в определении структуры
оптимального поведения, т. е. у(х), что в конечном счете является
более важным.
Это приводит к важной и полезной идее. Приближения можно
осуществлять как в пространстве функций /(х), так и в простран-
пространстве поведений у(х). Последнее во многих случаях является наи-
наиболее естественной и простой формой приближения. Аналитическое
преимущество такого подхода к Бопросу состоит в том, что он
всегда приводит к монотонным приближениям. С практической же
точки зрения приближение в пространстве поведений и более есте-
естественно, тем более, что обычно это является той частью задачи,
О которой мы* получаем некоторую информацию из опыта»
Многошаговый процесс распределения 37
Пусть уо(х) — некоторое поведение, которое мы возьмем в ка-
качестве начального, а /о(х)~функция дохода, полученная на основе
этой функции поведения. Иными словами, предположим, что /0(л:)
удовлетворяет функциональному уравнению
E) /о(*) = 7Ч/о. Л(*)).
которое будем решать посредством итераций. Чтобы улучшить
поведение уо(х), определим уг(х) как функцию от х9 которая макси-
максимизирует Г(/о, у) для 0^.у^л:. Допустим на мгновение, что
функция уг(х) сама непрерывна по х (что не обязательно имеет
место) и что функция дохода /х(х)9 вычисленная при использовании
этого поведения, также непрерывна. Как будет показано ниже, при
сделанных ранее предположениях это всегда имеет место. Продол-
Продолжая точно так же действовать и дальше, мы получаем последова-
последовательность поведений {.У^(*)} и последовательность функций до-
дохода \/х(х)}.
Используя описанные в предыдущих параграфах методы, легко
показать, что при сделанных предположениях последовательность
{/н(х)\ является монотонно возрастающей. Оказывается, что строгое
доказательство существования решения, т. е. сходимости последова-
последовательностей {.У/у С*)} и {/лг^*)}» получить трудно. Следовательно,
приходится удовольствоваться следующим.
Теорема 3. Пусть /0(х) является результатом начального
приближения в пространстве поведений, т. е.
F) /о(*) = Т{/о- УоШ.
где уо(х) — произвольная непрерывная функция от х, удовлетво-
удовлетворяющая условиям
G) 0 <з>0 (*)<*.
Тогда в предположениях теоремы 1 определяемая рекуррентным
соотношением
(8) /*+!(*)= тах ТУюУ)> N = 0. 1, 2
последовательность функций сходится равномерно к получен-
полученному решению /(х), и сходимость эта монотонна.
Доказательство. Прежде всего докажем монотонность,
которая является весьма существенной. Мы имеем
(9) Л(*)= тах Г (/0, .у).
<
Сравнивая определение /0(лг) из формулы E) с этим определе-
определением /х{х), мы видим, что Д(*)^>/оС*0 Для всех значений х.
38 Глава I
Отсюда по индукции следует, чтЪ /1^+1(х)^/1^(х) для всех значе-
значений х ^ 0.
Остается доказать непрерывность функции /0(х) для лг^О.
Условия, которые мы далее наложим на функции $?(х) и к(х), пока-
показывают, что формальный ряд для /0(х)
(Ю) /оМ = ?C'о) + *(*-Л) +
полученный итерациями, сходится равномерно в любом конечном
интервале и представляет непрерывную функцию от х для всех
х^О, если только уо(х) есть непрерывная функция от х.
§ 12. СВОЙСТВА РЕШЕНИЯ. I. ВЫПУКЛОСТЬ
Покажем, что на основании ряда простых структурных свойств
функций & и И можно получить некоторые структурные характе-
характеристики оптимального поведения. Структура оптимального поведе-
поведения у(х) и структура функции дохода /(х) оказываются, таким
образом, тесно связанными.
Наш первый результат в этом направлении состоит в следующем.
Теорема 4. Если в дополнение к предположениям теоремы 1
мы наложим на % и Н еще условие, чтобы они были выпуклыми
функциями от х, то /(х) тоже будет выпуклой функцией; в этом
случае для каждого значения х соответствующее значение у
будет равно либо нулю, либо х.
Доказательство. Доказательство будем вести по индукции.
Так как
A) Л(*)= тах (ё(у) + Н(х — у))
и &(У)-\-Ь(х — у) есть выпуклая функция у для О^з7^*» то
B) Л (*)=тах (*(*). *(*)),
так как максимум выпуклой функции должен достигаться на одном
из концов интервала. Будучи максимумом двух выпуклых функций,
функция /х (х) тоже выпукла.
Из того, что 8(у)-\-к(х — У)-\-}\(аУ-\-Ъ(х — у)) есть выпуклая
функция у для у(^[0, х], следует в результате аналогичных рас-
рассуждений, что и
C) /2(х) = тах &(х) +/, (ах), к (х) +Д фх)\
является выпуклой функцией от х. Тогда, рассуждая по индукции,
мы устанавливаем выпуклость функции /ц(х). Следовательно, пре-
предельная функция /(х) также-выпукла, и.:
Многошаговый процесс распределения
Обратимся снова к уравнению /(х)= тах Г(/, у). В силу
0<г/<а?
выпуклости функции /(х) оно приводится к следующей прссгой
форме:
D)
так как для каждого значения х либо у —О, либо у==х. Неожи-
Неожиданно оказывается, что это уравнение по-прежнему трудно решить
в общем виде. Ниже будет рассмотрен один частный случай этого
уравнения.
§ 13. СВОЙСТВА РЕШЕНИЯ. II. ВОГНУТОСТЬ
Покажем, что аналогичные результаты имеют место и тогда,
когда обе функции $ и к — строго вогнутые функции от х для х
Теорема 5. Если в дополнение к условиям теоремы 1 функ*
ции &(х) и Н(х) строго вогнуты, то и /(х) будет строго вогну-
вогнутой функцией от х.
В этом случае оптимальное поведение единственно.
Доказательство. Мы рассмотрим сначала случай одно»
шагового процесса и выполним некоторые простые вычисления,
из которых будет видно, почему сформулированнаугтеорема спра*
ведлива, а затем перейдем к строгому доказательству, в котором
будет использован другой, более общий метод.
Мы имеем
A) /,(*)= тах [ё(у) + Н(х — у)].
Так как $ и Н — строго вогнутые функции, то функция &(У)-\-к(х—у)
также является строго вогнутой функцией от у. Следовательно, эта
функция для 0<!.у<;л; обладает единственным максимумом, кото-
который, впрочем, может достигаться в одной из точек ^ = 0 или у — х.
Предположим сначала, что этот максимум достигается во внутренней
точке и что функции ^ и й имеют вторые производные. Тогда
B)
где у определяется как функция от л; с помощью соотношения
C) #'О0 = Л'(*-ко-
Л'(*-кодифференцирование равенства B) дает нам
D) /; (Д?) = 1^ О — *'(* —
а отсюда
E) Г
40 Глава I
Дифференцируя соотношение C), мы получаем
F) §Г{у)*1=ьгь-я[х-*!.),
откуда
G) йу = ^и-У)
их &"(У)-\-Ь"(х — У)'
Поэтому 1 > йу\йх > 0, так что, возвращаясь к E), мы имеем
/; (*> < о.
Если максимум достигается на одном из концов интервала, то
с помощью некоторого незначительного изменения функций ^ и й
можно сделать так, что в точках у = 0 или у — х максимума уже
не будет; например, это можно сделать путем прибавления члена
е\о%у(х — у) при достаточно малом положительном е. Далее можно
перейти к индуктивным рассуждениям и установить, что все члены
последовательности {/#(-*0}— вогнутые функции. Однако такой
подход к вопросу является довольно грубым и без больших труд-
трудностей не может быть распространен на многомерные задачи. Поэтому
для доказательства теоремы будет использован элементарный, но
более тонкий метод.
Лемма 1. Если С(х, у) — вогнутая1) функция от х и у для
^, то функция
(8) /С*)— тах О(хшу)
также вогнута для х ^ 0.
Доказательство. Для произвольного 0<^Х^1 мы имеем
(9) /(Хх-Н1— >>)*)= тах О(Кх +A — X)*, У).
Заменим у величиной у^=\ух-\-{\ —V)у2, где ух и у2 изменяются
независимо друг от друга в интервалах 0 <; у1 -^ х и 0 -^ у2
Тогда
A0) /(Хлг-г-A — \)г)= тах О
0 < 2/, < х
0 < уи < г
Так как функция О(х, у) вогнута относительно х и у9 то
A1)
1) Вогнутость относительно обеих переменных х и у означает, что для
Х<1
ХО (хь уг) + A — X)
Многошаговый процесс распределения 41
Отсюда
A2) /(Хл+A—Х)*)> тах [кО(х,
О < г/, < я?
О < г/9 < г
тах (, зО+О
<я? 0<г/9<г
Применим теперь эту лемму к доказательству теоремы 5. Легко
удостовериться в том, что ё(у)-\-Ь(х— у) есть вогнутая функция от
хну, если только обе функции & и к вогнутые. Отсюда непосред-
непосредственно вытекает, что функция /г(х) также вогнутая. Точно так же
из вогнутости функции /х(ау-\-Ь(х — у)) относительно х и ^сле-
^следует вогнутость функции /2(х), которая определяется основным
рекуррентным соотношением. Таким образом, по индукции доказы-
доказывается строгая вогнутость каждой функции последовательности
{/^(х)}. Отсюда мы получаем, что предельная функция должна быть
вогнутой. Строгая же вогнутость предельной функции следует из
строгой вогнутости функций & и к, если применить лемму 1
к функциональному уравнению для /(х).
Коль скоро установлена строгая вогнутость функции/(х), единст-
единственность максимизирующего значения у, а следовательно, и единст-
единственность оптимального поведения получается непосредственно. Это
завершает доказательство теоремы 5.
§ 14. СВОЙСТВА РЕШЕНИЯ. III. ВОГНУТОСТЬ
Убедимся теперь в том, что предположение относительно вогну-
вогнутости дает нам возможность выяснить природу решения несколько
подробнее.
Теорема 6. Предположим, что
(О а) 8(х) и Ь(х) — строго вогнутые для х^О, монотонно
возрастающие и непрерывно дифференцируемые функции,
причем 8@) = к @) = 0.
*'@)> в7<оо). Ь>а.
Тогда оптимальное поведение имеет следующий вид:
B) а) у = х для О^х^х, где х есть корень уравнения
Ь'@) = ё'(х)-\-Ф — а)^(ах)-\-ф — а) а^ (а*х) + ....
б) у = у(х) для х^>х, где у(х) есть функция, удовлет-
удовлету
воряющая неравенству 0<С.У(х)<^х и являющаяся ре-
решением уравнения
42 Глава I
C)
Замечание. Мы определили здесь решение только для одной
из возможных комбинаций неравенств, связывающих $' @), Ь! @), Ъ
и а. Из следующих далее рассуждений легко усмотреть, что для
других случаев получаются аналогичные неравенства. При этом
число рассматриваемых случаев может быть уменьшено вдвое в силу
того, что перемена ролями у и х — у ведет к перемене ролями а и Ь.
Доказательство. Применим метод последовательных прибли-
приближений. Положим
D)
По предположению, &' @)> Ы @) для м.алых значений х, так что
$'(у)— Ь! (х — .У)>0 для у, лежащих в интервале [0, а:]. Поэтому
@(у)-\-к(х— у) является монотонно возрастающей функцией для
О^^у^л: и максимум достигается при у = х. Так как х возрастает,
уравнение &'(у) — Ъ!{х — ^) = 0 в конечном счете будет иметь
корень у = х, а так как х продолжает возрастать и дальше, то этот
корень окажется внутри интервала [0, х]. Критическое значение х
дается решением уравнения &'(х) — Л/@)=0. Это уравнение имеет
в точности одно решение, которое мы обозначим через хх. Пусть
для х^хх единственным решением уравнения 8'(у) = Н'(х — у)
является уг = У\(х). Единственность решения следует из предполо-
предположения о вогнутости § и к, а его существование — из непре-
непрерывности $' и К.
Таким образом, мы имеем
И
(б)
'(Уд
х >. х.
Так как ух(х1) = х1, то легко видеть, что функция /[(х) непрерывна
при х = х19 а следовательно, и для всех значений х ^ 0. Кроме того,
/г(х) является вогнутой функцией от х (ср. с рассуждениями § 11).
Перейдем теперь ко второму приближению
G) /2(*)=
Функцию В(у)=8' (У) — *' (х — у)-{-/'г(ау+Ь(х~у))(а
Многошаговый процесс распределения 43
будем называть критической. Так как ^'@)— ^ @)-\~/[@)(а— Ь) =
]
то значения функции й(у) будут положительными для всех у^[0, х]
при достаточно малых х. Из этого следует, что в G) максимум
достигается при у = х для малых х. Так как х возрастает, то най-
найдется первое значение х, для которого О(л;) = 0. Это значение х2
определяется из уравнения $' (х) = Ы @)-(-(Ь— а)/[(ах)- Из сравне-
сравнения двух уравнений
(8)
получаем- 0 < хг < хх.
Поэтому уравнение для х2 имеет следующий простой вид:
(9) & (х) = V @) + (* — а) 8' (ах).
Таким образом, в G) у = х для 0^л;<;л;2 и у = у2(х) для
л:2, где У2(х) является единственным решением уравнения
(Ю)
Кроме того,
и /'2(х) непрерывна в точке х = х2.
Сравнивая A0) с уравнением ^(у)==: Ы(х — у), определяющим уг,
получаем у2(х) < уг(х). Для того чтобы провести индукцию до конца
и получить соответствующие результаты для всех членов последо-
последовательности {/п}, рекуррентно определяемых соотношением
/п+1(*)=
потребуется весьма важное неравенство /'2 (х) ^> /[ (х). Нам пред-
предстоит исследовать поведение этих функций в трех интервалах
[0, лг2]> [#2» Х1]у \Х1> °°]- При рассмотрении каждого из них будут
применяться различные методы доказательства. Для х^х2 мы,
используя A0) и A1), имеем
A2)
Сопоставляя F) с уравнением для уг, получаем
A3) ГЛх)= Ьё'{ь)~аН
44
Глава
-1
Выражение \Ь(г'(у) — ак'(х — У)\(Ъ — а) является монотонно
убывающей функцией у для О^^^х. Из того, что у2 < У\, сле-
следует, что /'2(х) > /[(х), и доказательство для интервала [хх, оо]
завершено. В интервале [0, х2] имеет место равенство. Осталось
рассмотреть интервал [лг2, хг]. В этом интервале мы имеем
A4)
/[(*) =
/о (X)
а
При
{*' (х) ^> Ы @).
интервале
A5)
и
из
Поэтому, так как
' (х — у) следует
в рассматриваемом
Это завершает доказательство того, что 2[
Мы имеем теперь все составные части доказательства по индук-
индукции, из которого следует, что
A6) а) *, >*2> • • • > хп> • • • > О,
в)
Так как /п(х) сходится к /(х), /п(х) к /'(х), уп(х) к у(х) и хп
к х, то мы видим, что решение имеет указанную форму.
§ 15. ПРИЧУДЛИВЫЙ ПРИМЕР
Успешно воспользовавшись предположением об одновременной
выпуклости или вогнутости функций $ и /г, мы сейчас убедимся
/О
9
8
7
6
5
3
2
I
20
30
Рис. 1.
40
50
на примере, что решение может стать чрезвычайно сложным, если
брать более <5бщие функции, обладающие точками перегиба.
Многошаговый процесс распределения
45
Рассмотрим уравнение
A)
тах
у))]
Функция е*0!00 используется здесь потому, что она является одной
из простейших функций, имеющих точку перегиба. Определяя /(х)
при помощи метода последовательных приближений, мы получим
гладкую кривую, изображенную на рис. 1.
Отметим, однако, что у(х) ведет себя очень странно (см. рис. 2).
20
Ю
О
20
30
40
5Г
Рис. 2.
Как только допускается изменение знака со стороны &"(х) или
к"(х), сразу получается функциональное уравнение, не поддающееся
точному анализу.
§ \в. ОБЫЧНЫЙ ПРИМЕР. I
Рис. 1 и 2 указывают на трудности, которые могут встретиться
при отыскании общих «решений. Рассмотрим поэтому некоторые
простые уравнения, которые могут быть использованы в целях ап-
аппроксимации.
Теорема 7. Непрерывное решение уравнения
A) /(х) = тах[сх*+/(ах), ех* + /(Ьх)], /@) = 0
при выполнении условий
B) а) 0 < а, Ь< 1;
имеет вид
C)
О,
/(*)=
сх1
, 0
х,
46 N Глава 1.
где
D) х
0<#<1, то /(х) может быть получена в явном виде
в интервалах
I Л Я ЛЯ
?Ар „ О 1 О
\.П *
Доказательство. Обозначим через А операцию выбора
сха-{-/(ах), а через В — операцию выбора ехв -{-/(Ьх). Тогда ре-
решение 5, соответствующее оптимальной последовательности выборов,
можно символически представить как
E) 5 = Аа1Вь>Аа*Вь* ... ,
г
где пц и Ъ$ — целые неотрицательные числа, причем Аа* означает,
что выбор А повторяется аг- раз; В *> имеет аналогичное значение.
Предположим, что решение имеет указанную форму, и покажем,
как можно получить х. В точке х либо А, либо В является опти-
оптимальным решением, в то время как для значений, меньших хУ опти-
оптимальным решением является только А. Следовательно, х есть точка,
для которой имеет место символическое равенство
|ОО
СХй
-аа
F) ВАГ = А
Для выражения Л°° напишем
G) 1{х)=схй+1(ах) = схй+
Аналогично ВЛ°° дает
(8) /(*)=**,+
Приравнивая эти два выражения, находим, что х имеет указанное
в D) значение.
Остается доказать, что решение имеет вид C). Прежде всего
докажем, что для малых значений х всегда используется А. Для
этого достаточно показать, что /(х)= сха/(\ —а<*)для этих х является
решением, а затем призвать на помощь теорему единственности1).
) Строго говоря, эта теорема единственности нами еще не доказыва-
доказывалась. Однако легко видеть, что примененный для доказательства теоремы 1
метод действует* хорошо и в этом случае.
Многошаговый процесс распределения , 4?
Кроме того, необходимо, чтобы для малых х
(9) [
Это очевидно при ^ > ^ > О и 0 < # < 1.
Теперь будем рассуждать по индукции. Пусть г означает самое
малое значение х> для которого выбор В является оптимальным.
В этой точке &А°°= Л°°. Это значит, что г — х. Рассмотрим теперь
интервал х^>х и определим точку /?, в которой ^4Б и В А дейст-
действительно равны как совокупность первых двух выборов.
Мы имеем в очевидных обозначениях
A0)
/ва (*) = ехя + сЪахй-\-$(аЪх).
Отсюда для искомой точки р можно получить уравнение
00 р~
Так как $ > й, то р < х.
Из того, что /лв (л:)< /Б^ (х) для л:>/?, следует, что длял:>л:
выбор ^4В плюс оптимальное продолжение хуже, чем выбор БЛ плюс
оптимальное продолжение. Отсюда мы видим, что выбор А не может
быть использован для х > х, если за ним не следует ^4°°, что, как
нам известно, также невозможно. ^Следовательно, теорема доказана
полностью.
§ 17. ОБЫЧНЫЙ ПРИМЕР. II
Другим интересным случаем является тот, когда функции &(х)
и к (х) являются квадратичными. Следующая теорема дается в ка-
качестве упражнения.
Теорема 8. Пусть с, ^>0, 0<#^а<1 а
A) /(*)= тах [су—у*-\-а(х—у)—(х—уу*+/(ау + Ь(х — у))]ш
Тогда в интервале1) О^лг^тт (с/2, с?/2) функция /(х) имеет
указанную ниже форму, которая зависит от знака разности
Это наибольший интервал, в котором обе функции § л Н возрастают.
48 Глава I
Случай 1. с/A — а)^=Щ\—
V) ^Уx)-^x^.ь^^(ь_а)аx \ — [(а — Ь)а + Ъ]*х '
где
Случай И. с/(\— а)<(ЦA— Ь).
^ й/2),
Х- 2A-0*) *
X < т!п (с/2, й?/2), то в качестве рекуррентной формулы
используется A), которая дает возможность получать /(х)
во всем интересующем нас интервале.
Случай Ш. с/(\— а)>с11(\— Ъ).
для О <С л: <[ т!п (|х, с/2, Щ2), где
— ~ 2A-оА) *,
§ 18. ПРИБЛИЖЕНИЕ И УСТОЙЧИВОСТЬ
Разумеется, было бы весьма интересно иметь явные решения
для возможно большего числа уравнений. Однако подлинное значе-
значение явных решений простых уравнений заключается в использова-
использовании их в качестве приближенных решений для более сложных урав-
уравнений, а также в том, что они являются ключом к природе опти-
оптимальных поведений в более сложных процессах.
В предыдущих параграфах были получены явные решения в двух
случаях: когда ^ и й имеют форму одночленов вида сха и когда
они являются квадратичными функциями. Обратим внимание на то,
что аппроксимация функции §(х) функцией вида схй эквивалентна
аппроксимации Хо^^^е00) функцией вида \о%с-\-A\о%ху т. е. прямой
линией, построить которую нетрудно.
Отметим, что при изменении х мы можем изменить наши ап-
аппроксимирующие кривые таким образом, чтобы получить бол^е под-
подходящие, если» мы добиваемся лучшей аппроксимации. Кроме того,
Многошаговый процесс распределения 49
заметим, что, вообще говоря, аппроксимация в пространстве пове-
поведений более полезна, чем аппроксимация в пространстве функций.
Для использования аппарата аппроксимации оценим разность между
решениями*) двух уравнений
A) /(*)= тах [и(хш у) + /(ау + Ь(х — у))]ш /@) = 0.
Р(х) = тах
по разности между и(х, у) и ф(х, у), т. е. докажем теорему устой-
чивости в классическом смысле.
Теорема 9. Пусть /(х) и Р (х)— непрерывные решения урав-
уравнений A), причем и(х, у) и V(x, у) являются непрерывными функ-
функциями х и у для всех х, у^-0, 0 < я, &<1, и пусть
оо
2 т(спг) < со, где
т(г)= тах { тах тах[|и(л;, ^)|, \^(х9 у)\\).
0< < 0<
B) тах { тах \и(х, у) — у(х, у)\}=п(г)
0<а; < г 0 < у <аз
оо
2 О (спг) < оо, с = тах (а, Ъ),
то
оо
C) !/(*)—/>(*) К 2 о (Л).
Доказательство. Положим
тах
0<
= тах у(х, у),
0<2/<а
= тах
Используя изложенные ранее методы, получаем, что /# (л:) сходится
к /(л:), а рN(x) сходится к ^(х) при N —>-оо.
1) Существование и единственность этих решений обеспечивается есте-
естественным изменением доказательства теоремы 1. Под словом „решение"
будет пониматься непрерывное решение или решение, конструируемое при
доказательстве теоремы существования,
4 Р.
50 ' Глава I
Оценим разность между /х и Рх. Ясно, что
E) 1Л(*) — Рх(*)|< шах \и(*. у) — ч(*. у)|<В(*).
0<<
Поступая, как в § 7, мы получаем
F) | /#+1 (х) — ^N+1 (х) |< тах | {к {а у + Ь(х — у))
0<<
* С* — У))\+ тах
Отсюда по индукции следует, что
N
G) I /лг+1 (л:) — /7^+1(х)|< 2
Полагая Л^->оо, получаем C).
§ 19. ПРОЦЕССЫ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ
До сих пор мы молчаливо предполагали, что рассматриваемые
процессы не зависят от времени, а полный доход зависел только
от начального количества х и продолжительности процесса Л/,
но не от времени начала процесса. Посмотрим, что можно сделать,
если это не так.
Допустим, что в результате разделения х на у и х — у на к-и
шаге мы получаем доход §"&(*, у) и для распределения остается
величина ак(х, у). Необходимо определить поведение, которое
максимизирует полный доход от Л/-шагового процесса.
Предположим, что функции ёк(х, у) и ак(х, у) непрерывны
как функции от х и у для х^О н 0^.у^х, причем ак(х, у) в этой
области удовлетворяет неравенству 0^%(л:, у)^ах, #<1, для
А= 1. 2
Определим
A) /л,лг(#) как полный доход, который получится от Л^-шаго-
вого процесса, начинающегося с величины х на к-и
шаге, если придерживаться оптимального поведения.
Мы имеем
B) /А, 1 (х) = тах #А (х. у),
0<<
а для N^2, рассуждая, как прежде, получаем
C) Л, N (х) = тах [#А (х, ^>+/л+1, лг-1 (яЛ (*. Я)].
0<<
Так как двойные индексы неудобны с аналитической, эстети-
эстетической и прежде всего вычислительной точек зрения, посмотрим, нельзя
Многошаговый процесс распределения 51
ли восстановить запись с одним индексом. Памятуя о том, что нас
в конечном счете интересует Л/-шаговый процесс, начиная с пер-
первого шага, определим
D) /н(х) Для всех А == 1, 2 N как полный доход, который
получится от процесса, начинающегося с величины х
на к-м шаге и кончающийся на Л/"-м шаге, если при-
придерживаться оптимального поведения.
Тогда
E) /И*)= тах $х(х, у\
/*(*)= тах [Л(*О0-|-Л+1(я*(*. У)I Ь=\ш 2,
Это упрощение существенно, поскольку нас интересует полу-
получение численного решения, ибо если разница между трудностью,
которая возникает при табулировании функций одной переменной,
и трудностью при табулировании функций двух переменных огромна,
то разница между табулированием функций двух переменных и
функций трех переменных "может стать разницей между осуществи-
осуществимым и неосуществимым подходом к решению задачи.
Случай неограниченно продолжающегося процесса, т. е. тот
случай, кргда Л/=оо, приводит к системе функциональных урав-
уравнений
F) /*(*)= тах 1ек(хш .У)+Л+1 (<**(*. у))].
Для этих систем уравнений нетрудно получить теоремы, аналогич-
аналогичные теореме 1.
§ 20. ПРОЦЕССЫ С НЕСКОЛЬКИМИ ВИДАМИ РЕСУРСОВ
Процесс, который был использован с целью выяснения сущности
задач, является простейшим среди всех процессов такого типа, так
как в нем учитывался только один тип ресурсов и на каждом шаге
требовалось только одно распределение. Теперь посмотрим, как
ставится задача для более общих и более близких к реальным про-
процессов.
Пусть М означает различные виды ресурсов соответственно
в количествах х19 х2 х^. На каждом шаге количество Хц
/-го ресурса используется таким образом, чтобы произвести доба-
добавочно некоторое количество у-го ресурса. Отсюда можно полу-
получить уравнения, связываюдие ресурсы на (А'4-1)-м шаге с ресур-
52 . Глава 1
■ - —щ --— ■ ГГ1 Т— -II *~ ■ 1ГЧМ1 Т~1 М-"И1 I
сами на к-ы шаге:
м
A) . ^
' Х2г
для /= 1, 2 М, где
B) а) *<,(*)> 0.
б) у
При этом предполагается, что известны как производственные
функции §"|, так и начальные величины л;$@) = с$.
Количества хц(к) выбираются так, чтобы максимизировать
значение некоторой заранее определенной функции конечных ре-
ресурсов
C) КК = Р (хх (АО, х2 (АО хм (АО).
Как будет показано в гл. VI, во многих случаях, кроме огра-
ограничений B), могут быть и другие ограничения.
Если положить
D) /# (сг, сг см) = тах
то, как и прежде, для N^2 мы получим рекуррентные соот-
соотношения
E) /# (си с2 см) = тах /#-1(^—2 Ун + 5*1 (^и* 3^21
где уц ограничены следующими соотношениями:
F) а) уц > О,
м
с«- /=1,2 А!,
И
G) Л(С1» сг См) = Р(сх> с2 См)-
Теоремы существования и единственности, охватывающие все
неограниченные варианты этих общих процессов, будут даны в гл. IV
вместе с более удобными обозначениями. В дальнейшем мы встре-
встретимся с -частным случаем этого уравнения в связи с задачами
„об узком месте" в гл. VI. В настоящей же главе будут кратко
рассмотрены некоторые из задач, в которых вычислительные труд-
кости возникают в связи с максимизацией по многомерным областям.
Многошаговый процесс распределения 63
§ 21. ТЕОРЕМЫ О СТРУКТУРЕ РЕШЕНИЯ
ДЛЯ МНОГОМЕРНЫХ ЗАДАЧ
Не представляет никакого труда распространить полученные
для одномерного случая результаты относительно выпуклости и
вогнутости решений функционального уравнения (8.1) на уравнения
§ 20 для многомерных задач.
Пусть О(х)—скалярная функция векторного переменного х.
Говорят, что эта функция выпукла, если для всех Х^[0, 1]
— \)С(у).
Функция называется вогнутой, если имеет место противоположное
неравенство.
Многомерный аналог леммы 1, доказанной в § 13, справедлив,
и доказательство его совершенно такое же, как и доказательство
этой леммы. С 'помощью- этого предложения можно установить
результат, который будет приведен ниже.
Прежде чем сформулировать этот результат, введем более
подходящие обозначения. Обозначим через х вектор с компонентами хгу
а через У*) — вектор с компонентами у^, где 1^/, у^Ж. Тогда
в терминах описанного выше процесса мы имеем
B) а) х =
г
б) У«>>0.
где запись у^-0 означает, что все компоненты вектора у неотри-
неотрицательны. Пусть п (х, у) означает область, определенную соотно-
соотношениями B).
Теорема 10. Если г(х, у) и а(х, у)— непрерывные вогну-
вогнутые функции относительно х и у для всех х, у^О, моно-
монотонно возрастающие относительно компонент х, то все функ-
функции /лг(л:), определенные уравнениями
х (х) = тах г (х, у),
Р С», у)
C) /лг+1 (х) = тах [г (х, у) -[-Дг (а (х, у))],
^ (а?, у)
также являются вогнутыми функциями относительно х для
Если г(х, у) является строго вогнутой функцией, то опти-
оптимальное поведение будет единственным для каждого N.
Ценность этого результата состоит в следующем. Если мы
имеем /^-шаговый процесс, где на каждом шаге должно быть
выбрано к решений, то метод функциональных уравнений сводит
54 Глава I
Л/&-мерную задачу максимизации к системе из N ^-мерных задач.
Хотя это и является существенным уменьшением числа измерений,
но &-мерные задачи максимизации сами по себе являются чрезвы-
чрезвычайно трудными.
Однако если функция к переменных, которую необходимо
максимизировать, является строго вогнутой, то, как мы знаем,
уже одно это влечет существование единственного относительного
максимума, который в то же время является и абсолютным макси-
максимумом. Эта дополнительная информация относительно того, что
исследуемая функция имеет единственный относительный макси-
максимум, дает нам возможность наметить поисковую процедуру для
отыскания местоположения этого максимума, которая, несомненно,
является более эффективной, чем процедура, которая использовалась
для произвольной функции.
§ 22. РАЗЫСКАНИЕ ЕДИНСТВЕННОГО МАКСИМУМА
ВОГНУТОЙ ФУНКЦИИ
Определение оптимальных процедурх) для обнаружения макси-
максимума вогнутой функции или соответственно для определения минимума
выпуклой функции является чрезвычайно важной и трудной задачей,
которая не была разрешена до настоящего времени. Тем не менее
в одномерном случае решение может быть получено даже для
более общих задач, в которых функция лишь унимодальна, т. е.
обладает единственным относительным максимумом.
Сформулируем задачу следующим образом. Пусть У = /(х)—
строго унимодальная, определенная в интервале [0, Ьп\ функция. Мы
хотим определить максимальное из чисел Сп, обладающих тем свойст-
свойством, чтобы всегда можно было указать подынтервал единичной длины
интервала [0, Ьп], содержащий точку максимума у = /(х), путем
вычисления не более чем п значений функции /(х). Так как мак-
максимум может не существовать, то безопаснее будет написать
A) Рп =
Имеет место следующая теорема.
Теорема И. Рп есть п-е число Фибоначчи, т. е. Р0 = Р1=\
и для п^-2
B) * п:== * м-1 т 'п-2-
Доказательство. Задание Ро является в какой-то мере
условием, но значение Рг уже определяется процессом.
1) В действительности нелегко точно установить, что следует понимать
прд оптимальной процедурой. Ясно, что это зависит от имеющегося в нашем
распоряжении оборудования, от характера допустимых операций, от „стои-
„стоимости" проведения этих операций и т. д. Следовательно, может быть поста-
поставлено множесчво задач об отыскании такого рода процедур. Но этот во-
вопрос в сколько-нибудь общей постановке не изучался.
Многошаговый процесс распределения
Дальше будем вести доказательство по индукции. Зафиксируем п
и вычислим значения у1 = /(х1), У2 — /(Х2)> где 0 < ^ < лг2 < Ап.
Если Ух^ У2> т0 максимум достигается в @, х2), так как функ-
функция /(х) строго унимодальна. Если уг > уг, то максимум будет
в (аг1§ Ьп). Если ух = у2, то выбирается один из этих интервалов,
если даже известно, что максимум достигается в (хх, х2). Таким
образом, после описанного первого шага мы имеем подинтервал
интервала @, Ьп) и значение /(х) в некоторой его внутренней
точке х. Так как значения функции на концах интервала сами по
себе не доставляют никакой информации, то мы сосредоточим свое
внимание на внутренних точках.
Для /г =2 можно взять /,п=2—е, хх = 1—е, д;2=^1, где
е>0 — некоторая произвольно малая величина. Из предыдущих
рассуждений следует, что
рг = 2 =
Рассмотрим случай я>2. Предположим, что Рк=
для к =2, ..., п—1. Начнем с доказательства того, что
C) ^П< ^-1 + ^-2.
Если мы вычислим значения /(х) в точках хх и хг из (О,
получим
, то
о
X.
'Л
Если
Рис. 3.
у2, то получим другую картину:
Рис. 4,
56 Глава I
В этом случае х2 < Рп-\* так как в нашем распоряжении остается
только п — 2 дополнительных вычислений с первым выбором хх
для случая, когда к = п—1. Кроме того, хг < Рп-1, так как мак-
максимум может встретиться в [0, хг], где уже было взято два значе-
значения х.
Аналогично, если у2 > ух, то Ьп — х1<С,Рп^1.
Таким образом, в любом случае /,п < Рп-х-\-Рп-2> что дает C).
Выбирая Ьп, хг и хг произвольно близкими к своим верхним гра-
границам, т. е. соответственно к числам Рп-\-\~Рп-2* ^п-1 и ^п-2»
мы в пределе получаем Рп = Рп-\ -\-Рп-г* и теорема 11 доказана.
Кроме того, из проведенных рассуждений мы получаем и оптималь-
оптимальное поведение, так как каждое хг либо отбрасывается, либо ока-
оказывается оптимальным первым выбором для оставшегося подинтервала.
Первыми членами последовательности. {Рп} являются числа
D) 1, 1, 2, 3, 5, 8, 13, 21, 34, 55
причем ^ > 10 000. Отсюда видно, что максимум строго унимо-
унимодальной функции всегда может быть локализован в 10~4 первона-
первоначального интервала в результате вычисления не более 20 значений
функции.
Легко получить и явное выражение для Рп, а именно:
п
Г2—Г± '
где
F) Г1 = Ш^-^
Г2 — —§ = — • '
Отсюда видно, что Рп+11Рп-+ гг= 1,61 прид->оо. Таким образом,
для больших значений п процедура равномерного приближения со-
состоит в выборе двух первых значений аргумента на расстоянии Цгх
от каждого из концов отрезка длины /,. Такая постановка задачи
является полезной с точки зрения применения вычислительных машин.
Рассмотрим теперь сходную задачу, в которой унимодальная
функция определена только для дискретного множества значений х.
Пусть Кп обозначает максимальное число точек, для которого ма-
максимум функции может быть всегда точно установлен после п вычи-
вычислений. Рассуждения, проведенные по той же схеме, позволяют
доказать следующую теорему.
Теорема 12. Ко= 1. Кг=\, /С2 = 2, /С3 = 4 и
Многошаговый процесс распределения
57
§ 23. НЕПРЕРЫВНОСТЬ И ПАМЯТЬ
Предположим, что имеется функция двух переменных /(х, у),
непрерывно зависящая от х и у при х^О и 0^^-^л:. Опреде-
Определим функцию
A) В(х) = тах /(*, у).
Ясно, что &(х) будет непрерывной функцией, в то время как функ-
функция у = у(х), дающая максимум функции /(х, у), быть непрерыв-
непрерывной не обязана. Пример этого мы уже видели в связи с функцио-
функциональным уравнением § 15.
Однако если /(х, у) будет строго вогнутой функцией у для
всех у^[0, х] при х^>0, то при изменении х максимизирующее у
будет непрерывной функцией от х.
Л*. У)
О
У
х
Рис. 5.
Посмотрим, как можно воспользоваться этим обстоятельством,
чтобы упростить решение проблемы памяти для вычислительных
машин. Рассмотрим уравнения
B)
= 1, 2
Если нам ничего неизвестно относительно расположения максимизи-
максимизирующих у, то для определения/^+1 (х) необходимо располагать всеми
значениями /^ B), 0 <; г ^ ах. Теперь предположим, что функции §" (х)
и к (х) являются строго вогнутыми и непрерывными. В этом случае
строго вогнутыми будут и функции /#(х) для каждого /V, а также
функция ё(у) + Н(х— У)+/М(ау + Ь(х — у)) для 0<^<дг.
Кроме того — и это самое важное — функция уы(х), дающая максимум
в соотношении B), является непрерывной функцией и определяется
однозначно.
Отсюда следует, что если для вычисления /(л:) используется
сетка значений х: О, Д, 2Д, ... , — то нет необходимости знать
58 Глава I
полное множество значений }и(г), Ъ^г^ах, для того чтобы вы-
вычислить /ЛГ+1 (х), а достаточно знать только значения /^(я) в срав*
нительно малой окрестности точки г = ун(х — Д).
Эта идея, распространенная на многомерные уравнения, может
привести к значительному упрощению запоминающего устройства
в вычислительных машинах. Наоборот, представляется возможность
решать некоторые задачи, используя существующие машины, кото-
которые, в противном случае, на этих машинах не могли быть решены.
В любом случае результатом будет большая экономия во времени
и значительное увеличение возможностей решения задач этими сред-
средствами.
§ 24. СТОХАСТИЧЕСКИЕ ПРОЦЕССЫ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ
На предыдущих страницах главы были более или менее подробно
рассмотрены разнообразные многошаговые процессы распределения,
характеризуемые тем свойством, что результат любого решения
однозначно определялся выбором этого решения. Процессы такого
типа мы будем называть детерминированными.
Однако не все многошаговые процессы обладают этим свойст-
свойством. Многие из наиболее интересных процессов вовсе не являются
процессами такого типа. Здесь мы рассмотрим один важный класс
недетерминированных процессов, в которых результатом решения
является определение некоторого распределения исходов в смысле
теории вероятностей. Процессы такого типа мы будем называть
Стохастическими.
В этой главе мы ограничимся процессами этих двух типов.
Обсуждение происхождения процессов более сложной природы
и их подробное рассмотрение мы проведем в другом месте.
С математической точки зрения стохастические процессы приводят
к ряду пленительных аналитических задач и проливают неожидан-
неожиданный свет на многие на первый взгляд детерминированные процессы.
Приложения этой теории представлены множеством примеров из
области биологии, экономики, техники и физики.
Обратимся вновь к процессам решения. Основной задачей, кото-
которая непосредственно стоит перед нами, является определение того,
что мы понимаем под оптимальным поведением в условиях неоп-
неопределенности его результатов. Кристально ясным является тот факт,
на который так часто не обращают внимания, что в действитель-
действительности недостаточность контроля над процессом не позволяет гаран-
гарантировать получение максимального дохода.
С другой стороны, несмотря на этот дамоклов меч неопределен*
ности, должная существовать некоторые средства для сравнения по-
поведений с учетом возможных флуктуации результатов.
Многошаговый процесс распределения 59
Основной трудностью в приложениях является не то, что трудно
найти такую меру, а скорее то, что трудно найти единую меру.
Короче говоря, необходимо подчеркнуть, что имеется далеко не
единственный метод, который имеет какие-то претензии на звание
„лучшего". Любой применяемый метод в большой степени зависит
от различных аналитических и арифметических сторон процесса,
а также от философских и психологических установок принимаю-
принимающего решение лица.
Остановившись столь подробно на печальной стороне дела, мы,
чтобы успокоить свою совесть, перейдем к конструктивным во-
вопросам.
Общая идея — и это совершенно единодушно принимается всеми —
состоит в использовании некоторой средней характеристики воз-
возможных результатов в роли меры качества поведения. Именно при
выборе этой характеристики и возникают трудности.
Заметим вскользь, что не существует определенного единодушия
относительно использования средних характеристик при определении
поведений для стохастических процессов, которые могут быть вы-
выполнены до конца за один шаг или по крайней мере за небольшое
число шагов. В некоторых случаях могут быть получены поведе-
поведения, „не зависящие от распределений". Однако, по-видимому, нет
иного подхода к этим вопросам, чем обычный подход, который
будет изложен ниже.
Первой такой характеристикой (критерием), которая будет при-
применяться в дальнейшем, является обычное среднее, т. е. матема-
математическое ожидание. В силу своей линейности математическое ожи-
ожидание обладает важным свойством инвариантности, которое сильно
упрощает функциональные уравнения, описывающие процесс. Из этого
свойства инвариантности следует, что будущие решения основы-
основываются только на состоянии системы в данный момент и не зависят
от ее предыстории.
В качестве второго, реже используемого критерия применяется
вероятность достижения некоторого фиксированного уровня дохода.
Этот второй критерий также обладает подходящим свойством инва-
инвариантности в той мере, в какой это необходимо при рассмотрении
многошаговых процессов. В следующей главе мы обсудим эти кри-
критерии более подробно.
§ 25. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ
#
Рассмотрим простой стохастический вариант детерминированного
процесса, который обсуждался в § 2, и покажем, что к нему при-
применим тот же метод функциональных уравнений.
Ранее нами предполагалось, что в результате разделения коли-
количества х на у и х — у получается доход 8(у)-\-к(х1—у), после
Чего для распределения остается количество ресурса хх = ау .-[-
60 Глава I
-\-Ь(х— у). Допустим теперь, что в результате разделения с ве-
вероятностью рг будет получен доход ё\{У)-^г^Лх — У) и Для Рас*
пределения останется количество аху-\-Ъ1(х — у), а с вероятностью
А—1—А будет получен доход Я'гОО + М*— У) и останется
количество а2у -+- Ь2 (х ~ У)-
Определим
A) /#(х) как математическое ожидание полного дохода, кото-
рый получится от Ы-шагового процесса, начинающегося
с исходного количества х, если придерживаться опти-
мального поведения.
В этом случае, как и раньше, мы получим уравнения
B) /х(х)= тах {аЙ*!СУ) + *1 (* — ^I+Р2[5*2(З') + ^2(^ — У)]}.
0<<
= тах
\ (У) + Н2 (Х — У)
для N^1
Эти уравнения имеют ту же аналитическую природу, что и урав-
уравнения, полученные для детерминированного процесса. Употребляя
математическое ожидание как меру качества поведения, мы тем са-
самым устраняем стохастические стороны процесса, по крайней мере
настолько, чтобы провести анализ решения.
§ 26. ИНТЕГРАЛЫ СТИЛЬТЬЕСА
Те, кто хорошо знаком с интегралом Римана — Стильтьеса, мо-
могут воспбльзоваться весьма компактным способом записи всех при-
приведенных выше уравнений. Пусть
A) О (и, V, х, у) есть функция распределения дохода и и остав-
оставшегося количества V, если начальное коли-
количество ресурса равнялось х и разделялось на у
их — у.
Определяя /м(х), как это делалось выше, мы получаем уравнения
B) Л (х) = тах Г ийО (и, V] х, у),
0< у <а? •'
у
= тах
Использование такого „стенографического" обозначения поз-
позволяет проще всего описать процессы для соответствующих фунн-
Многошаговый процесс распределения 61
циональных уравнений, доказать для них теоремы существования
и единственности, а также вывести аналитические свойства их ре-
решений. Основные математические идеи при этом остаются теми же.
Уравнения такого типа будут рассмотрены снова в гл. III среди
уравнений более общего вида.
УПРАЖНЕНИЯ И ПРОБЛЕМНЫЕ ЗАДАЧИ
К ГЛАВЕ I
1. Определим функцию
= шах
где /? есть область, определяемая условиями
а) хх-\-х2-\- ... -\-хк = а,
б) ^>0.
Доказать, что /^(я) удовлетворяет рекуррентному соотношению
х = шах х^
О <а? < а
И
Л (я) = а.
2. Доказать по индукции, что /к(а) = ак1Ык, а потом показать,
что справедливо следующее неравенство между арифметическим
и геометрическим средними:
+XN\N
)
ХХХ2 • • •
для X} ^ 0, причем равенство имеет место только в случае, когда
3. Определим функцию
Е
где /? есть область, определенная неравенствами
N
а) 2 хг ;> а, а > О,
г<=1
б) ^
62 Глава 1
Показать, что /^(#) удовлетворяет рекуррентному соотношению
„ (а) ~ т!п \хР +Лг-.1 (я — *I. N > 2,
о<<а1 ^
4. Показать, что /у(а) — арСу, где с^ зависит только от N и р9
причем
= тт [лгр + A — х)рснЛ.
0<а<1
Определить г^ отдельно для областей О^р^ 1 и 1
5. Рассмотреть задачу о максимизации функции
* Х2 Хк) ==
N
где параметры р{ и ^ подчинены следующим условиям:
2р<== 1, $$>0, а^ изменяются в области, определенной соотно-
г N
шениями хг ^ 0, 2 -^г = а-
Вывести соответствующие рекуррентные соотношения и показать,
что решение имеет вид
при соответствующем упорядочении переменных х$
6. Рассмотреть задачу о максимизации функции
при условиях хг^0, ^хг = с. Показать, что если функция ср(л:)
г=1
является выпуклой, то максимум равен ср (с).
7. Рассмотреть случай, когда ср(л:) — монотонно возрастающая
и строго вогнутая функция. Показать, что решение соответствую-
соответствующего функционального уравнения
/я(с)= шах [9(у)-\-/(с — у)), Л/>2,
0<г/<е
Многошаговый процесс распределения 63
имеет вид
(О, О < с <
Ук =
г Ос
где г^ — единственное решение уравнения
для N^2. Выяснить, как определить последовательность [см\.
8. Получить явные рекуррентные соотношения и аналитическую
форму последовательности для случая, когда
9. Какие результаты, аналогичные предыдущим, можно получить
для случая, когда функция Р имеет вид 2 ?»(**)» где каждая
функция сргС*) удовлетворяет тем же условиям, что и выше?
10. Довести до конца соответствующий анализ для случая задачи
о минимизации функции Р(хг,х2 х^Л = 2?(л:г)» ПРИ условиях
N
Х1 = а в случае, когдз у(х) есть неотрицательная моно-
тонно возрастающая и строго выпуклая функция. В частности, рас-
рассмотреть случай, когда
ср (а:) = х + Ьх2>
11. Рассмотреть задачу о максимизации функции
! 2Ю Л Лн)ь Уг)
при условиях
N N
*г> Уг > 0, 2 Х1 = С1> 2 Уг = С2*
где у(х, у) — строго вогнутая, монотонно возрастающая относи
тельно х и у функция.
Показать, что соответствующее функциональное уравнение
*(С1* С2) = тах [<р(х, у) + /у-1 (сх — х,с%— у)]
о -^ со -^. с^
64
Глава I
для каждого N ^> 2 имеет решение следующего вида
0<х<с,
0<у<сг
О
Рис. 6.
Выяснить, как определяются граничные кривые.
Рассмотреть, в честности, случай
4- и2*
ср (*. у) = ахх
12. Определить максимум функции
по области, определенной следующим образом:
а)
О,
б)
Х1 < ^2»
соответственно для двух различных случаев р> 1 и /?<^1, если
функция ср(х) — строго вогнутая и монотонно возрастающая.
13. Получить рекуррентные соотношения для задачи о мини-
мизации функции
хг) при условиях
-а) 0 < хл < гх,
где каждая функция
неотрицательна, мойотонно вшрастает
Многошаговый процесс распределения 65
14. При соответствующих предположениях относительно после-
последовательности {ф|} рассмотреть аналогичную многомерную задач-
о минимизации функции 2сР*(Лч» Уд ПРИ условиях
а) 0 < ** О* 0
б)
15. Определить максимум функции ххх2 ... х^ по области, опре-
определенной соотношениями
б) *лгй<]л:й+1, ^> 1, ^=1,2 Л^—1.
N
Рассмотреть эту же задачу для случая функции 2 х' Фи раз
1-1 1
личных областях изменения р.
16. Рассмотреть рекуррентные соотношения
= тах
х— у))\
где 5>C;) = ^13;й» Ь(У) — с2Уа, с19 с2, с?>0. Показать, что
= тах
— тах
Показать, что
Нт «дг= тах ||-~
17* Описанный в § 2 процесс рассмотреть в предположении,
что не обязательно на каждом шаге использовать все доступные
ресурсы. Показать, что полученное при этом функциональное урав-
уравнение имеет вид
/(х) = тах
5 Р. Беллман
Глава I
Имеет ли это уравнение решение, если функции 8(х) и к(х)
являются вогнутыми функциями х? Имеет ли оно решение, если
обе эти функции выпуклы? При каких условиях, наложенных на &(х)
и к (х), имеется решение с соответствующим оптимальным пове-
поведением?
18. Показать, что если существует решение для У\-\-У% <С х>
У\> ^2>0, то ^'СуО/О—#) =/*'СУгИ 1—Ь) при надлежащих пред-
предположениях относительно & и к. Какова интерпретация этого
решения?
19. Рассмотреть процесс, описанный в § 2, в предположении,
что на каждом шаге присоединяются дополнительные ресурсы либо
извне, либо за счет превращения в ресурсы всего или части уже
полученного дохода & (у) -|~ к (х — у). Получить соответствующие
рекуррентные соотношения.
20. Рассмотреть процесс, описанный в § 2. Определим
как минимальные издержки, необходимые для получения полного
дохода, равного 2, после N шагов. Показать, что
= йИп 1(\—а)у1-+-A—Ь)у21
Ух* У* > О
= т1п [О— °)^ + О— Ь)У^ём{г-
Ух* 2/а > О
21. Пусть имеется N различных видов предметов, причем вес
предмета /-го вида равен щ, а стоимость ^. Требуется нагрузить
судно грузоподъемностью -до фунтов максимально ценным грузом.
Показать, что эта задача приводит к задаче определения максимума
линейной формы Ь= 2 п^ по щ при условии, что пг = 0, 1,2 Л^
г-1
2 п%Щ -^ ^, а затем показать, что эта задача приводит к рекур-
рентным соотношениям
([а] обозначает целую часть числа а),
где л: может принимать целые неотрицательные значения.
22. Предположим, что мы имеем стадо крупного рогатого скота
и располагаем возможностью отправлять в конце года некоторую
часть стада (у) на рынок, сохраняя оставшуюся часть {г) для раз-
Многошаговый процесс распределения 67
ведения. Допустим, что стоимость посылаемого на рынок скота
выражается функцией срОО» а оставшаяся часть стада за год увели-
увеличивается до аг, а > 1.
Показать, что задача определения такого поведения, при кото-
котором максимизируется полный доход скотоводческой фермы за Л^-лет-
ний период, приводит к рекуррентному соотношению
= тах
— у))]
23. Определить структуру оптимальных поведений в следующих
случаях:
а) ?О0 = *У. "*>0;
б) у (у)— квадратичная функция;
в) ср(з>) — строго выпуклая функция;
г) срОО — строго вогнутая функция.
24. Вывести уравнение при дополнительном ограничении: возраст
направляемого на продажу скота должен быть не менее двух лет.
Учесть затраты на покупку кормов для скота и убытки от падежа.
25. Рассмотреть случай, когда цены и спрос случайны и рас-
распределения их известны.
26. Пусть в условиях задачи 22 у(х)=сха, с, й > 0. Показать,
что /дг(л:) = СдХа, где сх = с и с# = тах \га -\- с^ай{\ — г)а]
0<Г<1 ь Л
для УУ= 1, 2, . .. . Выяснить асимптотическое поведение отношений
И
27. Предположим, что имеется некоторое количество денег х
и некоторая часть этих денег может быть использована на приобре-
приобретение ценных бумаг — облигаций или акций. Пусть сумма у, поме-
помещенная в облигации, по истечении года превращается в ау (а > 1),
а сумма г, помещенная в акции, — в Ьг ф > 1). Через <р(-о>) обо-
обозначим полный доход при общих затратах на покупку ценных бумаг
*ш долларов. Как должен использоваться капитал, чтобы за N лет
получить максимум дохода?
28. Рассмотреть эту же задачу в предположении, что доход
от акций является случайной величиной.
29. У студента-второкурсника есть три приятельницы: блондинка,
брюнетка и шатенка. Если он пригласит одну из них в субботу на
вечер танцев, то две другие обидятся. В результате этого возрастает
6*
68 Глава I
вероятность того, что на следующей неделе они отвергнут его
приглашение на танцы. Кроме того, в результате приглашения по-
появляется некоторая вероятность того, что девушка, которую он
пригласил в первый раз, примет второе приглашение с большей
готовностью, а также и некоторая' вероятность того, что она примет
его менее охотно.
Предполагая, что девичья память не способна удерживать обиду
дольше, чем одну неделю, определить, какое "поведение в пригла-
приглашениях максимизирует среднее число танцев, на которые студент-
второкурсник пойдет с девушкой?
30. Получить последовательность рекуррентных соотношений,
N
эквивалентных определению минимума линейной формы /*=
при условиях л^^.0, лчН~ЛЧ+1 > а1* *= 1. 2, ..., N—1. Пока-
Показать, кроме того, что ппп/,= таха4, если хотя бы одно из чисел а$
положительно.
31. Решить аналогичную задачу для случая, когда ограничения
следующие:
32. Определить рекуррентные соотношения для задачи о мини-
мизации линейной формы ^=2с*-*:*» СС&*§ ПРИ условиях
ш Ьгхг-\-йгхих^аг, /=1, 2 N
33. Решить предыдущую задачу для случая, когда ограничения
такие:
а) хг-{-х1+1^а1з 1= 1, 2, ..., Л/— 1, хм=аю или
б) *<-г-**+1>я*- '=1. 2 Л/—1, ^
или
в) хг-\~хих-\~х{^г^аь /=1, 2, .... N—2,
XN ^ аN
вместе с обычным ограничением
34. Выяснить, насколько точно можно аппроксимировать функ-
функцию /(х) в интервале [а, Ь\ линейной функцией их-\-у при еле-
Многошаговый процесс распределения 69
дующих мерах отклонения:
ь
а) /(/(*) — их — юJйх,
а
б) тах |/(х) —их — г>|.
35. Предположим, что необходимо пройти расстояние х. Если
мы движемся со скоростью г>, то имеется вероятность/? (г>) д?$ быть
остановленным в интервале E, 8-\-с18) и подвергнуться задержке
на й минут. С какой скоростью мы должны двигаться, чтобы мини-
минимизировать среднее время, необходимое для прохождения рас-
расстояния х?
{Гринспан)
36. Определить в условиях предыдущей задачи скорость, с ко-
которой следует двигаться для минимизации вероятности того, что
для прохождения расстояния х потребуется большее время, чем Т.
37. Предположим, что в условиях предыдущих задач за оста-
остановку в пути взимается штраф в сумме р долларов, а чистое время
передвижения стоит с долларов за единицу времени. Как следует
поступить, чтобы минимизировать математическое ожидание издержек?
38. Получить рекуррентное соотношение для задачи о мини-
N
мизации квадратичной формы (^# = 2 (*&— хк-д2 по всему мно-
N
жеству значений хЛ, которые удовлетворяют условиям ^ х& = 1,
39. Известно, что частица находится в одном из двух состояний,
которые мы обозначим через 5 и Г. Задается начальная вероят-
вероятность х того, что она находится в состоянии Т. Применение опе-
операции А уменьшает начальную вероятность х до величины ах, где
0-^а<1. Операция Ь, которая состоит в наблюдении частицы,
может точно установить, в каком из двух состояний, она находится.
Желательно с достаточной уверенностью перевести частицу в со-
состояние 5 за минимальное время.
Пусть /(х) обозначает среднее число операций, которые потре-
потребуются для перевода частицы в состояние 5. Показать, что /(х)
удовлетворяет уравнению
I: ]
70 Глава I
40. Показать, что в интервале @, 1) имеется число х0, такое, что
Показать, кроме того, что
/г=1, 2
1-я*
" (\-а)(к+\)
при минимизирующем значении /г.
41. На каждом шаге последовательности некоторых выборов
допускается одна из двух, операций. В результате первой операции
с вероятностью рх получается единица чего-то, с вероятностью р2
получаются две единицы и с вероятностью р3 ничего не получается
и процесс заканчивается. Результат второй операции связан с анало-
аналогичным набором вероятностей: р'±, р'2, р^. Желательно определить
такую последовательность выборов операций, которая бы макси-
максимизировала вероятность р(п), п— 1, 2, 3, ... , получить по крайней
мере п единиц, прежде чем процесс оборвется.
Показать, что р(п) удовлетворяет уравнению
Р\Р(п— \) + р2р(п — 2),
У±Р(п — О + Р2Р (п — 2)
при п = 2, 3, 4, .... р @) = 1 и р A) = тах {р1% р[у
42. Ссылаясь на § 7, показать, что для случая, когда &(х) и к(х)
квадратичны, имеем /л (<0 = а# + Р#с + Т^2* пРичем а#» Р#» 7^ не
зависят от с.
43. Показать, что имеют место рекуррентные соотношения сле-
следующего вида:
где /?^ — рациональные функции,
*
Многошаговый процесс распределения 71
44. Рассмотреть аналогичным образом задачу о минимизации
функции
N
18(хк—
где §■(*), Н(х) и т(х) квадратичны.
45. Предположим, что имеется некоторая машина, производи-
производительность которой в единицу времени есть функция времени г(г)у
а срок службы ее выражается в тех же единицах времени. Издержки
на содержание машины в единицу времени представляют собой функ-
функцию времени и (г)у а цена, по которой ее можно продать в момент Л
равна 8A:). Цена приобретения р новой машины больше, чем 5@).
В любой момент времени ^ = 0, I, 2, ... представляются две воз-
возможности: либо продолжать пользоваться старой машиной, либо при-
приобрести новую. Рассмотреть неограниченно продолжающийся процесс,
когда доход от каждого следующего шага уменьшается в а раз,
0 < а < 1, по сравнению с доходом от предыдущего шага. Пусть /(^)
обозначает полный доход, получаемый при использовании оптималь-
оптимального поведения,
Показать, что /(() удовлетворяет уравнению
46. Пусть оптимальное поведение состоит в том, чтобы исполь-
использовать новую машину в течение некоторого периода времени, а затем
заменять ее новой машиной. Определить в этих условиях решение
приведенного выше уравнения.
47. Всегда ли верно, что при наличии машины, срок службы
которой превысил норму, оптимальное поведение состоит в немед-
немедленной замене ее новой?
48. Как сформулировать, задачу, в которой принимается в расчет
технологическое усовершенствование в машинах и в осуществляемых
с их помощью операциях?
49. Секретарь ищет некоторый листок из корреспонденции (обычно
копию на тонкой бумаге). Пусть у него имеется 6 мест, где этот
листок может лежать:
Папка № к
Три папки по 30 листов каждая .... 1, 2, 3
Одна папка в 50 листов 4
Одна папка в 100 листов 5
Еще какая-нибудь папка 6
72 Глава I
Пусть начальные вероятности того, что письмо находится в одном
из указанных мест, взяты такими:
к
1
2
3
4
5
б
Рк
Вероятность того,
что письмо в пап-
папке к
0,11
0,11
0,11
0,20
0,37
0,10
1 — ?к
Вероятность того, что
оно будет обнаружено
при одном просмотре,
если оно действительно
в папке
0,95
0,95
0,95
0,85
0,70
0,10
Время, необходимое
для одного просмотра
1
1
1
2
3
100
Как должен секретарь просматривать папки, чтобы
а) минимизировать среднее время, необходимое для обнаружения
данного письма,
б) максимизировать вероятность его обнаружения за данное
время?
(Ф. Мостеллер)
50. Пусть функция а(х) удовлетворяет условию а
при всех х. Показать, что решение уравнения
и — тах [Ь(х)-\- а(х)и],
X
если только оно существует, единственно и задается выражением
Ь(х)
А з
X
и = тах -л . ч .
1 — а(х)
При каких условиях это решение существует?
Если а(х) не удовлетворяет указанному условию, то показать, что
уравнение может иметь 0, 1,2 или даже целый континуум реше-
решений. Привести пример на каждый из этих случаев.
51. Пусть нам дано некоторое количество х > 0, которое должно
быть использовано при выполнении некоторой задачи. Если при
каждой из попыток выполнения используется количество у, О^у^х,
то вероятность успеха опыта равна а (у). Если после первой по-
попытки задача остается невыполненной, то испытания продолжаются
с оставшимся количеством х — у. Показать, что если обозначить
через /(х) полную вероятность успеха и придерживаться оптималь-
оптимального поведения, то /(х) удовлетворяет функциональному уравнению
■/(*)= 8иР [вО0 + A— а(У))/(х — У)Ъ
<
Многошаговый процесс распределения 73
52. Вывести аналогичное уравнение для 1 —/(х), т. е. для ве-
вероятности неудачи.
53. Рассмотреть два случая, когда а (у) есть выпуклая или во-
вогнутая функция, и получить для этих случаев явные решения. Обра-
Обратить внимание на то, что в одном из этих случаев нет оптималь-
оптимального поведения.
54. Рассмотреть описанный в § 2 процесс в предположении, что
полный доход от Л^-шагового процесса равен
где к(х) — заданная функция.
55. Рассмотреть функциональное уравнение
шах
в предположениях, что
а) вгСу)~<Ч-уй, Н(у)^с2уа, с19с29а>0 при у-юо
или
б) в(у) ~ схуа\ к (у) — с2уа\ с19 съ йх, а2>0 при у -+ эо.
В обоих случаях определить асимптотическое поведение /(х) пр
56. Определить рекуррентное соотношение для
[V V V
•Л1 ■ Ло I • -^71 — 1 I
^ ^ Ь ... ^ ™__^__^.
•^2 "|" 3 *^3 " г 4 ТЬ " Г 1
введя подходящие дополнительные параметры.
57. Рассмотреть задачу об определении минимума функции
2
где Гд+1 = гг, а числа гк удовлетворяют условиям
а) 0 < гк < Ък,
N
74 Глава I
причем каждая <рл(х) — известная, монотонно возрастающая функ
ция х и срл(О)— 0.
Введем вспомогательную задачу: минимизировать функцию
где г2, г3 гЛ удовлетворяют условиям
а)
(гк) > с.
к~2
Показать, что если обозначить указанный выше минимум через
Р(и, V, с), то в исходной задаче этот минимум дается выражением
т1п Р
О < г, < Ьг
58. Введем для /? = 2, 3, ..., N—1 последовательность функ-
функций
гк
N
Для каждого /? допускается только с значений, удовлетворяющих
условию 2СР&(^&)^'С> где Ъч—фиксированные положительные по-
стоянные.
Показать, что имеет место рекуррентное соотношение
, г/, с —
где гд изменяется в интервале, определяемом одним из следующих
неравенств:
а)
б)
59. Рассмотреть аналогичным образом задачу о минимизации
функции
П (г, г2, г3) + ^-(г2, г3,
Многошаговый процесс распределения
75
60. Пусть имеется капитал х и возможность производить в пере-
переменных количествах N различных видов продукции. Предположим
сначала, что имеется неограниченное предложение рабочей силы и
мащин для производства продукции в любом выбранном нами ассор-
ассортименте и в любом объеме. Пусть производство количества хг /-го
вида продукции связано со следующими издержками на единицу
/-го вида продукции:
а) щ — стоимость основных материалов;
б) Ь\—расходы по работе оборудования;
в) Сх — заработная плата;
г) С{ — постоянные расходы (при х
производства).
Тогда издержки на производство количества х$ /-го вида продукции
составляют
не зависят от объема
Обозначим через р\ реализационную цену единицы /-го вида про-
продукции. Задача состоит в выборе таких Х\, которые максимизируют
чистую прибыль
N
при условиях
N
а)
С**) <
Пусть
Показать, что
г=1
б) Хг > 0.
«■•
I о,
И
(х)
_ ± (х —
х
Показать, что неравенство
ством
может быть заменено неравен-
неравен76 Глава I
61. Допустим, что спрос на каждый вид продукции является
случайной величиной. Пусть Ок{г) есть функция распределения
спроса г на &-й вид продукции. Показать, что математическое ожи-
ожидание дохода от произведенного количества хк к-го вида продукции
определяется выражением
хк °°
о хк
хк
= Рк / гЛОк (г) + ркхк (\ — Ок (хк)),
о
и получить рекуррентное соотношение, соответствующее задаче
о максимизации полного ожидаемого дохода.
62. Рассмотреть задачу о максимизации вероятности того, что
доход превзойдет величину г.
63. Рассмотреть эту же' задачу в детерминированном и стоха-
стохастическом вариантах, где наложены ограничения на количество
имеющихся в распоряжении машин и рабочих.
64. Получить рекуррентные соотношения при следующих допол-
дополнительных ограничениях;
О.) Л1Л9 ' \) • ХггХс± — V/, Л<лЛ\лЛ\ 1 ^^^ V/
' X ш 4О »/ Х\/ X X
И Т. Д. ИЛИ
111 V/ ) М/ ——— X у & у • • • у IV ' X •
65. Предположим, что имеется сложный механизм, состоящий
из N взаимодействующих деталей. Пусть 1-я деталь имеет вес УУг
и объем 5^. Допустим, что известна плотность распределения про-
продолжительности времени, в течение которого эта деталь механизма
будет работать без поломки, ставящей нас перед необходимостью
заменить ее новой деталью. Предположим далее, что известно время
и издержки, необходимые для замены детали, а также общий раз-
размер убытков, вызываемых одной поломкой. Примем, наконец, что
общее количество запасных деталей ограничено по весу и объему.
Какие детали и в каких количествах следует хранить, чтобы мини-
минимизировать
а) ожидаемую потерю времени, вызванную поломками механизма
машины;
б) убытки от ожидаемых поломок;
в) некоторую заданную функцию от двух переменных, времени
и убытков;
Многошаговый процесс распределения 77
г) вероятность того, что потерянное из-за поломок время пре-
превысит величину Г;
д) вероятность того, что убытки из-за поломок превысят сумму С?
66. Определить возможные случаи асимптотического поведения
последовательности {ип}, которая определяется рекуррентным соот-
соотношением
или более общим рекуррентным соотношением
(ср. с задачей 50).
67. Определить минимум функции
Л"
Г (Хг Х2, . . . , ХИ) = 2 8г (Хг) ~\~ тах
где лг^^
68. Предположим, что имеется N различных отраслей произ-
производства, в которые можно помещать капитал. Через 8{(хг) обозначим
доход от /-й отрасли производства, в которую вложена сумма хг.
Если дано начальное количество капитала х, то как следует поме-
поместить его не более чем в к отраслей производства, чтобы макси-
максимизировать полный доход?
Обозначим максимальный доход через Д ы(х). Показать, что
имеет место рекуррентное соотношение
Л, * (*>=
тах
тах
для 1</г<ЛГ— I.
69. Двум корпорациям, в состав правлений которых входят одни
и те же лица, на основании законов о трестах запрещено помещать
деньги в одни и те же предприятия. Первая корпорация намерена
поместить капитал х, а вторая — капитал у. Пусть ^{(г) — доходы
от помещения капитала % в 1-е предприятие из N различных пред-
предприятий.
Показать, что если руководители хотят максимизировать полный
доход по двум корпорациям, то необходимо максимизировать функцию
у-) = 2 8г {*%) + 2 8г (Уг)
78
Глава I
при условиях:
N
а)
2 х% — х>
N
г-1
в)
*Л = 0.
Пусть
Показать, что
х, у) =
У)= тах РN(x^9
тах
Рассмотреть случай, когда различные корпорации от одного и
того же предприятия получают различные доходы.
70. Пусть решено одновременно заменить все осветительные
электрические лампочки в рабочем помещении. Обозначим через а
издержки от замены электролампочек, а через ^(х)—-потери,
которые вызваны недостаточностью освещения, когда между двумя
заменами проходит время х. Пусть принято решение заменять лам-
лампочки в течение интервала Т в следующие моменты времени:
х\* ^1 + ^2» •••» хх-\-х2-\- ... -\-хп — Т, где число п определено
заранее.
Эффективность такой программы действий измеряется средней
суммой потерь
п
I \Лц, Л^2» • • », лп/
Д
Каким должно быть оптимальное поведение?
71. Пусть функции
(//. Р. Савидж)
N VI1 ^
таковы, что максимум выражения
N
:=:= ~ ^*
N
по области
=.с может быть определен с помощью
Многошаговый процесс распределения 79
множителя Лагранжа X при рассмотрении выражения
= 2?г (хг) —
С другой стороны, пусть /^ (с) = тах Т7^. Показать, что
{}
Получить аналогичный результат для максимума выражения
N
^ёг(хи .Уг) ПРИ УСЛОВИЯХ
г-1
1
72. Пусть
есть г"е наибольшее число среди чисел
1' 2' • • • » М9
тг(х1' Х2* ###' х,г\г) есть г"е наименьшее число среди чисел
для г=1, 2, ..., N. Получить рекуррентные соотношения, связы-
связывающие члены последовательностей
73. Рассмотреть задачу о максимизации выражения 2 2"^* при
1=1
условиях
г-1
(Дж. В. Уиттекер)
74. Игрок имеет сумму денег х и хочет держать пари в N раз-
различных случаях. Существует вероятность рп того, что он может
правильно предсказать исход в к-и случае. Ограничивается лишь
ставка пари; это необходимо для того, чтобы игрок мог оплатить
все свои проигрыши.
Показать, что задачу максимизации ожидаемого им дохода можно
свести к задаче максимизации линейной функций
^
1дг (х) = 2 Ркхн
*4
80 Глава 1
при условиях
а) хг > 0,
N
б) 2 *! <* + •*/» 7=1. 2 N.
75. Рассмотреть задачу о максимизации линейной формы
N
= 2^ Ркхк
при следующих ограничениях:
а) х*
а
б)
В)
г-=1
Пусть /м(и, у)=тъх1п(х). Показать, что
у — х„, и))].
76. Проблема проектирования эффективного перегонного устрой-
устройства для производства тяжелой воды включает задачу о минимизации
выражения
где а^ подчинены следующим ограничениям:
а) аг > 1,
Показать, что эта задача может быть сведена к функциональному
уравнению
а, > 1 Ь
и получить решение в случае ^C;) = ^. Ь > 0.
77. Рассмотреть случай
[СегП Е., 511 V е з 1 г 1 М., VI Пап 5., ТЬе сазсасПп^ ргоЫет
а ^а!ег ШзШШюп р1ап! ап<1 Ьеауу \уа!ег ргойисИоп, 2. Ыагиг-
., Па A956), 694.]
Многошаговый процесс распределения 81
78 Рассмотреть задачу распределения ресурсов ло N различным
отраслям производства, которая приводит к задаче о максимизации
функции ^ёг(хг) ПРИ условиях хг ^> 0, 2х%== с* Показать, что
функция /м(с), которая получается посредством обычного рекур-
рекуррентного соотношения, не зависит от порядка, в котором перену-
перенумерованы отрасли производства.
БИБЛИОГРАФИЯ И КОММЕНТАРИИ
К ГЛАВЕ 1
§ 1. Весьма полный указатель статей до 1954 г. включительно, а также
некоторые замечания, дополняющие тему, могут быть найдены в работе Белл-
мана [В е 11 т а п Р., Тпе 1пеогу о! йупагшс рго^гаттт^, ВиМ. Атег.
МШ. 8ос, 60 A954), 503—516].
§ 2. Впервые этот процесс был рассмотрен в журнале „Эконометрика"
[ЕсопотеШса, 22 A954), 37—48].
§ 7. Дальнейшее обсуждение этой задачи может быть найдено в работе
Беллмана [ВеПтап Р., А с1а88 о! уапаНопа1 ргоЫетз, (}иаг(. о/ Арр1.
Ма(Н. A956)]. Интересное изложение общих задач „о сглаживании" можно
найти в работе Шёнберга, где приведены дополнительные ссылки на другие
работы [5 с п о е п Ъ е г § I. .К, Оп 8тоо1птд !ипс!юпз апс! Шен* депега1т§
{ипс1юп8, Ви11. Атег. МаИг. Зое, 59 A953), 199—230].
§ 11. Важность понятия „приближение в пространстве поведений" была
подчеркнута в работе Беллмана (В е 11 т а п Р., Оп сотри1а1юпа1 ргоЫетз
т 1пе 1пеогу о! йупагше рго^гаттш^, Зутрозшт оп Китегк;а1 МеШойз,
Атег. Ма1п. Зое. 5ап1а Мопка, 1953).
§ 12. Изящное доказательство леммы 1 было получено независимо от
автора Гликсбергом и Флемингом, перед которыми автор поставил задачу
получить лучшее доказательство, чем то, которое изложено на страницах
этого параграфа.
§ 17. Результаты этого параграфа были установлены Д. Андерсоном.
§ 18. Более полное изложение понятия устойчивости решений функцио-
4 нальных уравнений можно найти в книге Беллмана „Теория устойчивости
дифференциальных уравнений", ИЛ, М., 1955.
§ 19. Сведение последовательности {Д у(х)\ к последовательности {/^(х)}
является важной частью математического приема, поскольку это касается
численных решений (ср. § 6 и § 7). Ограниченная емкость запоминающего
устройства вычислительной машины делает ее чрезвычайно капризной по
отношению к индексам и параметрам.
§ 22. Доказательство в тексте следует статье Джонсона (Л о п п 8 о п 5.,
ОрИта1 зеагеп 18 РФопасаап, 1955).
Эквивалентный результат, оставшийся Джонсону неизвестным, был
получен ранее Кифером, использовавшим более сложную аргументацию
[К^еГег X, 5е^иеп^^аI гшштах зеагеп !ог а тах1тит, Ргос. Атег. МаШ.
8ос> 4, № 3 A953), 502—506].
Р., Белл мав
82 Глава Г
Получение соответствующего результата для задачи с большим числом
измерений является чрезвычайно трудным делом, и в настоящее время в этом
направлении ничего не сделано.
§ 24. Превосходное введение в теорию стохастических процессов дано
в книге Феллера „Теория вероятностей", ИЛ, М., 1948. Целый ряд важных
физических процессов рассмотрен в книге Бартлетта „Введение в теорию
случайных процессов", ИЛ, М., 1958.
Упражнение 76. См. В е 11 ш а п К., ИисЬеаг Еп%1пеепп& 1957.
Глава II
СТОХАСТИЧЕСКИЙ МНОГОШАГОВЫЙ ПРОЦЕСС РЕШЕНИЯ
§ 1. ВВЕДЕНИЕ
В предыдущей главе мы детально рассмотрели некоторый много-
многошаговый процесс решения как в детерминированном, так и в сто-
стохастическом вариантах. В этой главе мы займемся изучением
стохастического многошагового процесса решения совершенно иного
типа, который обладает рядом интересных особенностей. В част-
частности, при получении решения для некоторых простых вариантов
процессов этого типа мы встретимся с важным понятием „области
решения".
Мы по существу будем следовать тому же пути рассужде-
рассуждений, который был намечен в предыдущей главе: сначала по-
постановка задачи, а затем краткое обсуждение ее в классических
терминах. Придерживаясь этого плана, мы сначала сформули-
сформулируем задачу в терминах функциональных уравнений, а затем дока-,
жем требуемые теоремы существования и единственности. Остальная
часть главы посвящается обсуждению различных свойств решения,
таких, как устойчивость и аналитическая структура.
Для одного простого процесса, используемого в качестве мо-
модели, нам удастся получить решение, которое имеет весьма инте-
интересную интерпретацию. С математической точки зрения не менее
удачным является также то, что это решение не распространяется
на более общие процессы того же типа. Это заставляет нас приме-
применить совершенно другие методы, которые будут рассматриваться
в одной из дальнейших глав (именно в гл. VIII).
Отсутствие элементарного решения обусловлено не только недо-
недостаточностью анализа. Был построен опровергающий пример, кото-
который показывает, что. решение многошагового процесса этого
класса не всегда может иметь простую форму, приводимую ниже
в § 8. Другое доказательство этого факта следует из леммы
8 гл. VIII.
Ряд интересных результатов, которые здесь не будут деталь-
детально рассматриваться, приводится в качестве упражнений в конце
главы.
84 Глава И
§ 2. СТОХАСТИЧЕСКИЙ ПРОЦЕСС ЗОЛОТОДОБЫЧИ
Перенесемся теперь в область процессов золотодобычи.
Предположим, что мы настолько удачливы, что владеем двумя
золотыми приисками, Анаконда и Бонанца, первый из которых со-
содержит в своих недрах количество золота х, а второй — количе-
количество у. Кроме того, мы имеем единственную, довольно чувстви-
чувствительную к повреждениям, машину для добычи золота. Если эта
машина работает на прииске Анаконда, то с вероятностью рх она
добудет долю гх находящегося там золота и не выйдет из строя,
а с вероятностью 1 —рх она не добудет золота и будет приведена
в полную негодность. Аналогично прииску Бонанца приписываются
вероятности р2 и 1 —р2 и доля г2.
Начнем процесс с использования машины либо на прииске Ана-
Анаконда, либо на прииске Бонанца. Если машина не вышла из строя
после этого первого этапа работы, то мы должны решить, на каком
из наших приисков снова использовать машину. Будем поступать
так после каждого этапа до тех пор, пока машина не сломается.
Как только машина выходит из строя, работа кончается, а это озна-
означает, что ни один прииск не даст больше золота.
Какая последовательность выборов максимизирует общее коли-
количество золота, добытого до того, как машина выйдет из строя?
§ 3. МЕТОД ПЕРЕЧИСЛЕНИЯ
Так как мы имеем дело со стохастическим процессом, то
нельзя говорить о каком-то определенном доходе от поведения,
о чем уже упоминалось в § 24 предыдущей главы. В соответствии
с этим нельзя выбрать и поведение, которое бы гарантировало
максимальный доход. Остается утешиться измерением качества по-
поведения при помощи среднего дохода и выбирать оптимальное
поведение именно на этом основании. Как и прежде, наиболее про-
простой средней характеристикой является математическое ожи-
ожидание.
Условимся, что нас интересуют такие поведения (их может быть
и много), которые максимизируют ожидаемое количество золота,
добытого до того, как машина выйдет из строя. В этом случае
поведение будет состоять из выбора А или В {А означает Ана-
Анаконда, а В — Бонанца) и может быть записано в виде последова-
последовательности
A) 8 = ААВВВАВВ
которая должна читаться так: сначала Л, затем снова Л, если ма-
машина не сломана, потом В, если машина все еще не вышла из
строя, и т. д.
Стохастический многошаговый процесс решения 85
».— ■
Для начала, чтобы избежать трудностей общего порядка, при-
присущих неограниченно продолжающимся процессам, рассмотрим опе-
операции золотодобычи, которые автоматически заканчиваются после N
шагов, независимо от того, сломалась ли машина или нет. В этом
случае по идее легко перечислить все доступные нам поведения и
подсчитать все возможные значения дохода *). Эту идею удается
в определенной мере использовать при решении некоторых задач.
Однако вообще этот метод имеет довольно ограниченные приложе-
приложения, так как он не раскрывает структуры оптимального поведения
и, будучи грубым силовым методом, является изменой математике,
как науке, упрощающей вычисления.
§ 4. МЕТОД ФУНКЦИОНАЛЬНЫХ УРАВНЕНИЙ
Вместо подхода, основанного на прямом перечислении возмож-
возможностей, применим еще раз метод функциональных уравнений.
Определим
A) /^(л:, у) как ожидаемое количество золота, которое будет
добыто до того, как машина выйдет из строя,
когда Л имеет х, В имеет у и применяется опти-
оптимальное поведение, причем процесс может продол-
продолжаться не более чем N шагов.
Рассматривая одношаговый процесс, мы видим, что выбор Л
дает среднее количество золота рхгхх, в то время как выбор В
дает РчГгу. Следовательно,
B) и (х, у) = шах [р^х, р2г2у].
Рассмотрим теперь (N-4- 1)-шаговый процесс общего вида.
Каким бы ни был первый выбор, его продолжение на оставшихся N
шагах должно быть оптимальным, если мы намерены получить оп-
оптимальное (Л/*-)- 1)-шаговое поведение. Значит, полный ожидаемый
доход при первом выборе Л можно записать как
C) /А(х, У) = РЛг1х+/м(A—г1)х' У)]
а полный ожидаемый доход при выборе В
D)
Желание максимизировать полный доход от (Л[-[-1)-шагового
процесса приводит нас к следующему основному рекуррентному
) Сошлемся опять на числа. Мы видим, что для 10-шагового процесса
потребуется перечислить 210 = 1024 возможных поведения; если же на каждом
шаге возможны три выбора, то целых 59049.
86 Глава П
соотношению:
E) /к+Лх' У) = тах[/А(х, у),
[р± (гхх 4-/^ ( A — гх) х, у) ),
§ 5. АППРОКСИМАЦИЯ БЕСКОНЕЧНОШАГОВЫМ ПРОЦЕССОМ
Аналогичные рассуждения показывают, что доход от неограниченно
продолжающегося процесса, который мы обозначаем через /(л:, у)
(предполагая, что он существует), удовлетворяет функциональному
уравнению
A) /(*. у) = тах[р1(г1х-\-/(A—г1)х9 у)),
Отметим еще раз, что бесконечный процесс рассматривается
здесь как аппроксимация конечного процесса с большим N. Здесь
мы можем рассматривать единственную функцию, но зато сталки-
сталкиваемся с необходимостью установления существования и единствен-
единственности решения уравнения A). К этому мы и перейдем в следующем
параграфе.
§ 6. СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ
Докажем следующую теорему.
Теорема 1. Пусть г
A) а)
б) 0<г1§г2<1.
Тогда существует единственное решение уравнения E.1), огра-
ограниченное в любом прямоугольнике
Это решение /(х, у) непрерывно в любой ограниченной части
области х,
Доказательство. Для упрощения обозначений положим
B) 7\(/) = р1[г1х+/(A-г1)х, УI
Т2(/)=Р2[г2У+/(х, A— г2)у)].
Тогда функциональное уравнение E.1) примет вид
C) /(х, у) = тах [7\ (/), Т2 (/)].
) В уравнениях, которые получались для рассмотренных ранее процес-
процессов, все числа /?$ были неотрицательными. Приводимое здесь доказательство
охватывает и более общие уравнения.
Стохастический многошаговый процесс решения 87
Определим точно такую же, как в рекуррентном соотноше-
соотношении D.5), последовательность функций
D) Л (*, У) = тах [рхгхх, р2г2УЪ
/*+!<*- >0= тах [7, (/,,), Г2 (/„)] = тах [Т,(/,,)].
1 = 1, л
Пусть / = / (ЛО = / (М, хУ у) — индекс, при котором достигается
максимум в выражении тах [7\(/#I Для N=1, 2, .... Тогда,
используя ту же схему доказательства, которая была применена
при доказательстве теоремы о существовании и единственности ре-
решения функционального уравнения в (9.1) гл. I, получаем
Тг (N+1)
Отсюда мы имеем
F)
г)х. у) —
Положим
G) % (х, .у) = тах I /м E, Г) — /^
Из F) мы получаем
(8) N+1 лг
оо
где ^=тах(|р1|, |р2|)« Так как 0<^<1, то ряд 2 аА** У)
сходится равномерно в любом ограниченном прямоугольнике
О^х^А', 0<^.у<;К. Следовательно, и /М(х, у) сходится равно-
равномерно к функции /(х, у), которая удовлетворяет уравнению E.1)
и непрерывна в любом ограниченном прямоугольнике пло-
плоскости (х, у).
Единственность доказывается точно так же, как в теореме 1
гл. I; проведение доказательства предоставляется читателю в каче-
качестве упражнения.
Как видно из только что проведенного доказательства, функ-
функция /г(х, у) выбирается произвольно и подчиняется лишь тому ус-
условию, что она должна быть ограниченной в любом конечном
Глава II
прямоугольнике. Интересно отметить, что вследствие единственности
решения предельная функция будет непрерывной, даже если на-
начальная функция таковой не является.
§ 7. ПРИБЛИЖЕНИЕ В ПРОСТРАНСТВЕ ПОВЕДЕНИЙ
И МОНОТОННАЯ СХОДИМОСТЬ
Как и прежде, легко видеть, что в случае р1% р2^>0 можно обес-
обеспечить монотонную сходимость посредством приближения в про-
пространстве поведений. В качестве двух простейших приближений
можно взять приближения, соответствующие поведениям Л°° и Ял *).
От первого из этих поведений мы получаем следующий средний
доход:
а от второго
Как будет показано ниже, в § 8 и 9, при рассмотрении сложных
процессов мы фактически располагаем гораздо более изощренным
методом для получения первого приближения, но за счет утраты
имевшейся простоты выражений. Основной принцип, однако, совсем
прост.
§ 8. РЕШЕНИЕ
Вернемся теперь к решению уравнения E.1) для случая, когда
Рх и Р2 — вещественные числа, удовлетворяющие неравенствам
О-^А» Р2<^1* Интуитивно ясно, что выбор А делается в том слу-
случае, если х/у^>1, а выбор Б — в случае, когда у/х^> I2).
Также легко видеть, что на каждом шаге выбор зависит только
от отношения х/у, так как /(кх, ку)= к/(х, у) для к > 0. Веро-
Вероятно, проще всего это можно доказать, если призвать на помощь
теорему единственности, хотя все это интуитивно ясно из самого
описания процесса.
Отсюда следует, что если рассматривать положительный квад-
квадрант плоскости (х, у) и разделить его на Л-область и Б-область
(т. е. на множество тех пар значений хну, для которых опти--
мальным первым выбором является Л, и множество тех пар, для
которых оптимален выбор в), то из того, что точка (х, у) лежит
в Л-области, будет вытекать, что точка (кх, к у) также находится
в Л-области для всех к > 0, и аналогично для Б-области.
) Небезынтересно отметить следующее различие между процессом и
полученным из него функциональным уравнением. По отношению к процессу
последовательность А°° является условной, но с точки зрения уравнения она
является детерминированной.
2) Запись а ^> 1 означает, что а значительно больше единицы.
Стохастический многошаговый процесс решения
89
Если эти области устроены достаточно хорошо, то их границы
должны быть прямыми линиями, как это показано на рис. 7. Обла-
Области, где используются А или В, называются областями решения.
Рис. 7.
Смело предположим теперь, что имеются только две области, как
это изображено на рис. 8, и посмотрим, как можно определить
в этом случае граничную линию Ь.
Что является тем существенным признаком граничной линии,
опираясь на который можно было бы определить ее уравнение?
О
Рис. 8.
Он таков: граничная линия — это линия, на которой оба выбора А
и В оптимальны в одинаковой мере.
Если в точке (х, у) сначала используется выбор Д а затем
после первого шага следует оптимальное продолжение, то мы по-
получаем
A) /а(х, У)=р1г1х+рУ((\—г1)х9 у),
тогда как применение выбора В в (х, у) с последующим опти-
оптимальным продолжением дает
— г2) У)-
B)
/в (х, у) = р2г2у -\- р2/ (х,
90 Глава II
Приравняв эти два выражения, мы получаем уравнение для /,.
К сожалению, это уравнение в том виде, в каком оно нами по-
получено, мало применимо, так как содержит неизвестную функцию /.
Для того чтобы успешно завершить анализ, необходимо отметить
дополнительно следующее обстоятельство. Если в некоторой точке
на Ь мы применяем Л, то х уменьшается, в то время как у оста-
остается постоянным, после чего происходит переход в в-область;
аналогично если используется В в точке на /,, то мы проникаем
в Л-область (см. рис. 8). Отсюда следует, что для всякой точки
на Ъ первоначальный выбор А означает, что вторым выбором будет В,
тогда как первоначальный выбор В означает, что вторым выбором
будет А.
Если, сначала применить А, а потом В и воспользоваться опти-
оптимальным продолжением, то
и аналогично
D) /ва(х, У)=Р2Г2У±р1р2Г1Х+р1р2Ш1—г1)х, A— г2)у).
Если приравнять /ав и /ва* то неизвестная функция исчезает1)
и мы получаем для Ь уравнение
E)
р2г2у
1— рх 1—р?'
Остается вывести это уравнение строго. Начнем с доказательства
того, что вблизи оси х имеется область, где А всегда является
оптимальным первым выбором.
Если ,у= 0, то
У) /* V* I *-* т § / I _ «• \ ^/» 111
F) /(х, 0) = тах * \, *
1Р2/(х> 0)
= /?1г1х-(-/?1/(A—г^х, 0).
Из непрерывности /(х, ^/) по ,у следует, что
G) /(х, .У)>/?2(г2.У+/(х, "
для 0^^-^/гх, где к — некоторая малая положительная постоян-
постоянная, в то время как при у=0 имеет место строгое неравенство.
Таким образом, мы имеем область (см. рис. 9), в которой в ка-
качестве первого выбора используется А.
Теперь возьмем точку Р — Р(х, у) в области между Ь и у = кх,
такую, что точка (х, A—гг)у) находится уже в заштрихованной
1) Значение этого факта состоит в том, что как только сделаны как
выбор Д так и выбор В, для продолжения процесса первоначальный по-
порядок этих выборов больше не важен.
Стохастический многошаговый процесс решения
91
области. Иначе говоря, применение выбора В в точке Р должно
привести к тому, что следующим выбором будет А, если только
после первой операции машина не вышла из строя (как уже от-
отмечалось раньше, это условие необходимо при рассмотрении про-
процесса, но не при рассмотрении уравнения).
Если выбор В оптимален в точке Р, то мы получаем
(8)
У)=Ьа(х% у).
как это следует из D). Однако мы знаем, что ниже
/ва(х, уХ/ав(х, у), так что В не может быть оптимальным в Р.
Рассуждая по индукции, мы распространяем заштрихованную область
вверх вплоть до Ь. Точно так же доказывается, что область
Рис. 9.
между Ь и осью у является Б-областью. Итак, мы завершили до-
доказательство следующей теоремы.
Теорема 2. Рассмотрим уравнение
х, у)= тах
(9)
где 0</?1э р2< 1. 0<г1в г2< 1.
Его решение дается формулой
A0)
, *, .У>0,
для
Для
малъным.
—р1) = р2г2у1A—Рг) любой выбор является опта-
92
Глава II
§ 9. ОБСУЖДЕНИЕ
Полученное решение имеет очень интересную интерпретацию.
Можно рассматривать рхгхх как непосредственно ожидаемую при-
прибыль, а A—Р\)Г\Х— как непосредственно ожидаемый убыток.
Тогда теорема утверждает следующее: решение состоит в осуще-
осуществлении такой последовательности выборов, которая в каждое
мгновение максимизирует отношение непосредственно ожидаемой
прибыли к непосредственно ожидаемому убытку. Как мы увидим
дальше, этот интригующий критерий время от времени появ-
появляется почти во всех вопросах теории динамического программиро-
программирования.
§ 10. НЕКОТОРЫЕ ОБОБЩЕНИЯ
Аналогичные методы применимы для доказательства двух сле-
следующих результатов.
Теорема 3. Рассмотрим уравнение
@
где х,
B)
, у) = тах
&=1
N
Рк
\*. У)]-
' «нУ)\
и
N
N
а) рй>0.
б) 1
Оптимальный выбор операций определяется следующим образом:
если
N
N
C)
У>
то выбирается А\ если же имеет место обратное неравенство,
то выбирается В, В случае равенства любой выбор является
оптимальным.
Теорема 4. Рассмотрим функциональное уравнение
D)
Х2,
Стохастический многошаговый процесс решения
93
к
где Ха^-0 и
E)
Функции решения имеют вид
А-У^ \Х )
1 1 9
к
1- 2 Л*
X,,
в том смысле, что максимум О\ (х) достигается при том же
значении индекса /, при котором достигается максимум в D).
В случае равенства безразлично, что использовать.
Ясно, что теоремы 3 и 4 можно объединить в один всеобъем-
всеобъемлющий результат, который в свою очередь может быть обобщен
при помощи интеграла Стильтьеса. Так, вариантом уравнения A),
соответствующим непрерывному распределению доходов, является
уравнение
о
л.
/
[1Уу-{-/(Х, A IV) У)] йИ A0)
О
Предоставляем читателю в качестве упражнения вывод обобщений
теорем 3 и 4, а также формулировку и доказательство соответст-
соответствующих теорем существования и единственности.
§ 11. ВИД ФУНКЦИИ /(*, у)
Получив достаточно простую характеристику оптимального по-
поведения, обратим внимание на функцию /(х, у). Вообще говоря,
не существует простого аналитического представления решения.
Однако если мы будем рассматривать уравнение
а2у-\-р2/(с2х, у),
A)
/С*. .У)=тах
ахх
то можно показать, что /(х, у) может быть представлена в виде
кусочно-линейной функции, если с2 и й2 связаны соотношением
типа с™—а1™, где тип— положительные целые числа, 1
94
Глава II
Для иллюстрации этого метода достаточно рассмотреть самый
простой случай, когда имеется соотношение с2 = й2.
Пусть (х, у) будет точкой в Л-области. Если применено А,
то эта точка переходит в точку (с2х, у), которая может находиться
либо в Л-, либо в в-области. Пусть Ьг — линия, которая преоб-
преобразуется в /,*), когда (х, у) переходит в (с2х, у)\ Ь2— линия, пре-
преобразуемая при этом в Ьг, и т. д. Аналогично пусть Мх — линия,
которая преобразуется в /,, когда (х, у) переходит в (х, й2у)%
и т. д. В секторе Ь0Ьг первым используется выбор Л, а потом
следует В, как показано ниже.
х
Рис. 10.
Следовательно, для точки (х, у) из этого сектора' мы получаем
B) /(х, у) = а1х-\-агу-\-р2/(с2х9 у) =
= ахх -+- а2у
гс2х + Ъ2у)
У
. с2у)
х, у).
Это дает нам
1—Р2Я2Р2
для (х, .у) из АОАХ. Аналогично получаем линейное выражение
для / в Ь0Мх. Если представление в этих секторах найдено, ясно,
что можно получить линейное представление в секторе Ьг0Ь2 и т. д.
1) Уравнение граничной линии будет
[а± A — ?3) + Ьх (р3с3 — 1)] х =
Оно получается так же, как и выше.
1)]
Стохастический многошаговый процесс решения
95
§ 12. ЗАДАЧА ДЛЯ ПРОЦЕССА С КОНЕЧНЫМ
ЧИСЛОМ ШАГОВ
Прежде всего установим теорему.
Теорема 5. Рассмотрим рекуррентное соотношение
A) /х (х, у) = тах [рхгххш р2г2у),
[г2.У+7И*. A— гъ)У)\_
/N+1
N=1, 2
= тах
Для каждого N имеется две области решения.
Доказательство. Для каждого N^2 точки, для которых
АВ с последующим оптимальным продолжением на оставшихся N— 2
шагах эквивалентно В А с оптимальным продолжением на этих N — 2
шагах, лежат на той же самой линии /,, которая была определена
раньше, а именно:
B) Ь:РЦ^ =
Рис. И.
Для Л/-шагового процесса любое поведение, а следовательно,
и любое оптимальное поведение имеет вид
C)
где
неотрицательные целые числа, причем
N.
Рассмотрим теперь точку Р = Р(х, у), лежащую выше /,. Если
в точке Р использовано Л, то дальше представляется две возмож-
возможности: либо А используется к раз подряд, и только затем следует В:
D)
либо 5^ = А
пользуется к-
Рассмотрим первый из этих случаев. Если А ис-
1 раз подряд, то мы дойдем до точки Р\ лежащей
96
Глава II
все еще выше /,. В точке Р' выборы ЛВ не могут быть первыми
двумя выборами при оптимальном (Л/ — к~\- 10-шаговом поведении,
так как В А с оптимальным продолжением лучше.
Следовательно, выше Ь либо В используется первым, либо
оптимальным поведением является А . Теперь покажем, что если
А1 является оптимальным поведением в Р, то оно является опти-
оптимальным и в области между ОР и осью х.
Доказательство начнем с замечания, что можно предположить,
что х-{-у=\, О^х, у*С1, так как функция /^(х, у) однородна
относительно х и у. Рассматривая Л/-шаговый процесс, мы видим,
что имеется 2 возможных поведений, скажем, Р1э Р2, ..., Р я-
При использовании каждого из этих поведений в точке (х, у) по-
получаем доход от Л/"-шагового процесса, который является линейной
функцией от х и у\ обозначим его Ьк(х, у). Для х-+-у~ 1 можно
вычертить графики этих функций; это будут 2^ прямых линий (см.
рис. 12).
■к
О
X
Рис. 12.
Если N = 2, то имеется всего четыре поведения АА% АВ%
ВА, ВВЛ которые дают четыре линии. График максимального дохода
как функции от х изображен на рис. 13.
О
X
Рис. 13.
Ясно, что А является оптимальным поведением для у — О,
х= 1. Отсюда следует, что если А оптимально в точке (х, у),
Стохастический многошаговый процесс решения
0<.у<1, то линия, соответствующая Л , будет расположена над
всеми другими линиями для х^х<^1.
Объединяя полученные результаты, мы видим, что для любого N
границей между Л-облзстью и Б-областью будет либо АВ = В А,
либо А = Мх, где Мх — поведение более сложной формы, либо,
наконец, В = М2 — тоже довольно сложное поведение..
Теперь мы можем установить более точный результат.
Теорема 6. Области решения для /^ монотонно сходятся
к областям решения для / при Л/"—>оо. Кроме того, всегда
найдется такое целое число Ыо% что для N ^ Ыо области реше-
решения для /^ совпадают с областями решения для /.
Доказательство. Рассмотрим случай Д/ = 3. Через Ьг обо-
обозначим граничную линию для двухшагового процесса и допустим,
что Ь2 и Ь расположены друг относительно друга так, как это по-
показано на рис. 14.
Рис. 14.
Пусть Ь2 (Л~ ) — линия, которая преобразуется в /,2, когда
в точке на А2(Л~ ) используется Л, т. е. когда (х, у) преобразуется
в (сх, у). Пусть точка <2 находится в секторе между Ь2 и /^(Л).
Если в точке <2 в качестве первого выбора трехшагового поведения
используется Л, то на следующем шаге используется В, так как
для двухшагового процесса преобразованная точка находится
в В-области. Однако если <2 расположено выше Ь, то (как мы уже
знаем) АВ не может быть первой парой выборов в оптимальном
поведении. Отсюда следует, что в точке ф используется В. Таким
образом, мы показали, что ^-область для трехшагового процесса
во всяком случае содержит область, лежащую выше /^(Л). Этот
процесс может быть распространен на все ббльшие N до тех пор,
пока /*&(Л~ ) для некоторого конечного к не будет лежать ниже /..
В этой точке граничной линией становится линия АВ = ВА, и она
остается граничной для всех ббльших
7 Р. Беллман
Глава II
§ 13. ТРИХОТОМИЧЕСКАЯ ЗАДАЧА
Предположим теперь, что, кроме двух уже рассмотренных выбо-
выборов Л и Б, мы имеем третий выбор С, который является проме-
промежуточным между выборами А и В. Уравнение, которое в этом
случае получается, имеет вид
А: Р1[Г1х-+■/(({— гх)х, у)],
A)
где 0<>3, г4<!1, 0^/?3<1 и величины /?х, /?2, г19 г2 удовлетво-
удовлетворяют предыдущим неравенствам, т. е. те же, что и раньше.
Основываясь на том, что уже известно относительно решения
уравнения, где отсутствует член, соответствующий С, можно пред-
предполагать, что решение этого уравнения будет определяться следую-
следующим образом: имеются три области решения, как показано на рис. 15,
Рис. 15.
Рис. 16.
аричем каждый из выборов А, В и С является оптимальным первым
пыбором в соответствующей области.
К сожалению, имеется пример, показывающий, что в общем случае
это не так. Посредством довольно сложного, хотя и непосредствен-
непосредственного вычисления можно показать, что при подходящих значениях
параметров решение может иметь вид, изображенный на рис. 16.
Решение уравнения A), по-видимому, является чрезвычайно
трудной задачей, и относительно характера этого решения известно
очень мало.
Неизвестно даже, всегда ли конечно число областей решения,
а если конечно, то является ли оно равномерно ограниченным. Чтобы
получить некоторую информацию об этой задаче в некоторой области
пространства параметров, мы в гл. VIII рассмотрим ее непрерыв-
непрерывный вариант, где с помощью вариационных методов могут быть
определены области решения.
Для непрерывного варианта необходимо будет предположить
простое расположение областей решения, подобное показанному на
рис. 15.
Стохастический многошаговый процесс решения
99
A)
/(х, у)= тах
§ 14. ТЕОРЕМА УСТОЙЧИВОСТИ
Теперь докажем теорему устойчивости решения1) уравнения
^: Р21г2У-\-/(х> О—гт)У)\
Теорема 7. Пусть &(х, у) будет решением уравнения
А: ^[^ + ^(A—гх)х, у)],
B)
Тогда в любом прямоугольнике /?:
в
C)
где #=гшп[A —рг)ш A— р2)\.
Доказательство. Доказательство проводится методом после-
последовательных приближений, как в § 18 гл. I. Поэтому здесь доста-
достаточно отметить лишь некоторые детали. Положим
D)
и, вообще,
E)
Л (*. У)
. р2г2У\.
у)=ты[р1г1х9
Л:
, у)
г^аг,
З' + /
А:
— гг)х> У)Ъ
ш у).
Ясно, что
F)
в
, у)\.
Применяя уже не раз использованные методы, мы видим, что
G) тах | /я+1 (хш у) — ^п+1 (х, у) \ <
тах|/я+1(АГ. .у)
в
где р3=тах(А' Рг)- Итерация этого неравенства дает
(8) тах !/„(*. .у) —
для м=2, .... Полагая Аг->оо, получаем требуемый результат.
) Под решением здесь и в дальнейшем будет подразумеваться един-
единственное решение в соответствующем классе функций.
7*
100 Глава II
УПРАЖНЕНИЯ И ПРОБЛЕМНЫЕ ЗАДАЧИ
К ГЛАВЕ II
1. Для описанного в § 2 процесса рассмотреть случай, в кото-
котором целью процесса является максимизация математического ожи-
ожидания ср(/?), где /?—полный доход, а ср(г) — некоторая фиксиро-
фиксированная функция г. Определим функцию
/(х, у, а) как математическое ожидание <р(/?), полученное в условиях
оптимального поведения, когда начальные запасы золота
соответствующих приисков равны х и у, а количество а
уже добыто.
Показать, что /(х, у, а) удовлетворяет следующему функциональ-
функциональному уравнению:
/(х, у, а) — тах
г±х, у, а
В:
/(О, 0, о) = <р(в).
. У>0,
Здесь
/ ,_ 1 п -У ^.^ 1 п у.' __^ 1 - ~' 1 -.
НЛ ——— // ^ /'о -^ г О* 1 1' 9 ' • оф
ДХ Ха ^Х Хи "й
2. Доказать для этого уравнения теоремы существования и един-
единственности.
3. Рассмотреть случай, когда ср(#) определяется следующим
образом: ср(^)==О, 0<^2^ и, срB)=1, г^и% где и <^х-{-у.
4. Пусть #(х, ^)= тах Е(^Ьг), ^ > 0, где Е означает матема-
р
тическое ожидание и максимизация производится по всем поведе-
поведениям Р. Показать, что #(х, у) удовлетворяет уравнению
А: пАеЪг*
5. Показать, что решение уравнения из предыдущей задачи свя-
связано с отношением функций
7 И 7 .
Рг Р2
6. Показать, что теорема 2 является предельным случаем этого
результата, когда #->0.
7. Функция §*(х, 0) удовлетворяет уравнению
В(х. 0)=р1е»*>е(г'1х9 0)-\-р[.
Изучить ее асимптотическое поведение при х —> оо.
Стохастический многошаговый процесс решения
101
8. Для задачи 1 получить некоторые достаточные условия, кото-
которые бы обеспечивали в точности две области решения.
9. Решить уравнение
, у) = тах
10. Решить уравнение
А:
1*. у)].
1С: ръ [гъх
+ / (гх, гу)\1
А: х-\-/(ах, Ъу),
В: у-{-/(су, ах)
где 0 О, Ь, с, й < 1.
(О. Гросс — X. Н. Шапиро)
11. Рассмотреть описанный в § 2 процесс в предположении,
что имеется вероятность рг получения величины гхх и продолже-
продолжения процесса, вероятность р2 ничего не получить, но продолжать
процесс, и вероятность ръ ничего не получить и прекратить добычу,
если выбрано Л, причем рх -\~Р2-\-Рг— 1; и аналогичные вероят-
вероятности <71э #2» #3* если выбрано В. Показать, что соответствующее
функциональное уравнение имеет вид
А:
, у),
В: д1[81у-\-/(х, A—51)у)\-\-д2/(х9 у)
и что оно может быть записано в более простой форме
/С*. ^)==
Ч\
■+■/(*, A —
А:
В:
12. Рассмотреть процесс, описанный в § 2, в котором после
его начала невозможно наблюдать результаты выборов на каждом
шаге. Определить поведения, максимизирующие средний доход
в следующих случаях:
а) когда машина исправна, она на любом прииске добывает фик-
фиксированную долю золота;
б) когда машина исправна, существует распределение дохода*.
Предполагается, что мы намерены максимизировать вероятность
того, что доход превысит фиксированную величину /?0.
13. Описанный в § 2 процесс рассмотреть в предположении,
что для каждого из приисков задается не извлекаемая доля запасов
в месторождении, а абсолютное количество золота, добываемое на
прииске за единицу времени, пока неизвлеченная часть запасов.пре-
запасов.превосходит установленную заранее величину. . . . . I
102 Глава //
14. Показать, что уравнение в E.1) эквивалентно уравнению
/м—х
[В: рг\ггг + т\~г2)г)\
для 0 <; х < оо.
15. Рассмотреть уравнение
*: г* + /(A—г)*, .у).
в:
х, у) = шах
для л:, у^>0, 0<г, 5,
Показать, что это уравнение имеет решение
/(*. у) — х
16. Показать, что процесс золотодобычи, приводящий к этому
уравнению, не имеет оптимального поведения, т. е. поведения,
обеспечивающего в точности этот доход, но что имеется много
поведений, при которых доход превышает величину
х-\--л ^тт г — ^ для любого 8 > 0.
1 1 — 0A — $) ^
17. Доказать, что приведенное в задаче 15 решение уравнения
не единственно в классе функций, ограниченных в любом ограни-
ограниченном прямоугольнике, но что оно единственно в классе функ*
ций /(л:, у), для которых /@, 0) = 0 и /(х, у) непрерывна при
БИБЛИОГРАФИЯ И КОММЕНТАРИИ
К ГЛАВЕ II
§ 1. Понятие „областей решения" является очень важным в изучении
процессов решения. Мы встретимся с ним снова в гл. VIII, где оно при-
приведет нас к решению рассматриваемых в этой главе вариационных задач,
и далее в гл. IX в связи с вариационными задачами с ограничениями.
По этому вопросу имеется интересная статья Эрроу, Блекуэлла и Гиршика
[Аггом К. 3., ЫаскшеП Б., О1Г§п1ск М., Вауез ап<1 лиштах 8о1и-
1ЮП8 о! 8е^иет^а1 <1ес18юп ргоЫетз, ЕсопотеМса, 17 A949), 213—214].
§ 8. Результат § 8 был получен совместно с М. Шифманом летом 1950 г.
§ 12. Типичный образец использованного здесь геометрического приема
был детально разработан Карлином и Шапиро для получения другого
доказательства теоремы 2, а также других результатов.
§ 13. Первый опровергающий пример был построен Карлином и Шапиро
после долгих бесплодных поисков, направленных на получение результата,
основанного на рис,. 15. (См. К а г П п 5., 5 Н а р 1 г о Н. N.. БеЫзюп ргосез-
апй 1ипс1юпа1 еяиа!к>пз, КМ-933, 5ер1. 1952, ТНе КАШ СогрогаНоп.)
Глава III
СТРУКТУРА ПРОЦЕССОВ
ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
§ 1. ВВЕДЕНИЕ
В этой главе мы хотим исследовать и сопоставить наиболее
существенные черты двух процессов, которые уже были детально
рассмотрены в первых двух главах. "Хотя на первый взгляд может
показаться, что эти процессы несопоставимы, так как один из них
является процессом детерминированного типа со стохастическим
вариантом, а другой — процессом стохастического типа без детер-
детерминированного варианта, мы тем не менее увидим, что с абстрактной
точки зрения оба они являются частными случаями одного и того же
процесса общего типа. Естественно поэтому, что они описываются
функциональными уравнениями сходного вида.
После изложения общих соображений и анализа сходных черт
процессов мы перейдем к описанию более общих процессов решения
и получим для них ряд функциональных уравнений, обладающих
единой структурой. При желании мы могли бы свести их в одно
функциональное уравнение, охватывающее все случаи. Однако так
как крайняя общность достигается только ценой утраты некоторых
тонкостей, то как с принципиальной, так и с аналитической точки
зрения несомненно представляется более целесообразным рассмо-
рассмотреть отдельно ряд важных классов процессов, каждый из которых
обладает определенными характерными математическими и физиче-
физическими свойствами.
Мы закончим эту главу дальнейшим рассмотрением понятия при-
приближения в пространстве функций, с которым мы уже встречались
в предыдущих главах, и доказательством его важнейшего свой-
свойства—монотонной сходимости.
§ 2. ОБСУЖДЕНИЕ ДВУХ ПРОЦЕССОВ,
РАССМОТРЕННЫХ РАНЕЕ
Начнем с констатации того факта, что процессы, рассмотренные
в гл. I и II, имеют следующие общие черты:
а) в обоих случаях мы имеем физическую систему, которая на
любом шаге характеризуется небольшим числом параметров, назы-
называемых параметрами состояния;
б) на каждом шаге как одного, так и другого процесса мы
должны принять одно из нескольких решений;
104 Глава III
в) результатом принятия решения является преобразование пара-
параметров состояния;
г) предыстория системы не имеет никакого значения при опре-
определении будущих действий;
д) целью процесса является максимизация некоторой функции
параметров состояния.
Мы намеренно оставили это описание несколько неопределенным,
так как именно сам дух подхода к рассматриваемым процессам
является более важным, чем буква какой-нибудь строгой формули-
формулировки.
Крайне важно отдать себе отчет в том, что мы не можем
йй аксиоматизировать математическую формулировку процесса,
ни узаконить отсутствие изобретательности. В некоторых за4ачах
параметры состояния и преобразования навязываются нам существом
дела; в других случаях остается возможность некоторого выбора,
в зависимости от которого возникает или не возникает возможность
аналитического решения. Наконец, может случиться так, что пара-
параметры состояния, а иногда и преобразования должны быть построены
искусственно. Только опыт в сочетании с зачастую трудоемким
методом проб и ошибок приводит к подходящим формулировкам
для каждого из исследуемых процессов.
Рассмотрим теперь конкретное содержание указанных выше
общих свойств для каждого из двух процессов, описанных в пре-
предыдущих главах.
В неограниченно продолжающемся многошаговом процессе рас-
распределения параметрами состояния являются наличное количество
ресурсов х и доход 2, полученный к данному моменту. На любом
Шаге решение состоит во вложении количества у в первый техно-
технологический процесс, где О^^у^л;. Результатом принятия этого
решения является преобразование х в ау -\- Ь(х — у), а г
в г-\- §(у)-\-к(х — у). Цель этого процесса состоит в максимизации
Окончательной величины дохода г.
В стохастическом процессе золотодобычи параметрами состояния
Являются наличные 'запасы х и у двух приисков и количество
золота г, добытого к данному моменту. Решение на любом шаге
состоит в выборе прииска Анаконда или прииска Бонанца. Если
выбирается Анаконда, то пара (х, у} переходит в пару (A—г^х, у)
и г в г-\-гхх, а если Бонанца, то пара (х, у) переходит в пару
(х, A—г?) у) и г в г-\-г2у. Целью этого процесса является
максимизация математического ожидания количества золота я, полу-
полученного до момента выхода машины из строя.
В конечных вариантах обоих процессов мы имеем дополнительно
Параметр времени, проявляющий себя в виде числа шагов, остаю-
остающихся до конца процесса. Однако очень полезно все время отличать
этот параметр состояния от остальных, так как обычно время играет
особую роль.
Структура процессов динамического программирования 105
Условимся теперь о следующей терминологии: будем называть
поведением любое правило для принятия решений, которое дает
допустимую последовательность решений; оптимальным поведением
назовем поведение, максимизирующее некоторую заранее заданную
функцию параметров окончательного состояния. Более точное опре-
определение поведения получить не так легко, как это можно было бы
предполагать. Хотя его не очень трудно дать для случая детерми-
детерминированных процессов, стохастические процессы доставляют больше
забот. Однако для любого конкретного процесса нетрудно сформу-
сформулировать это понятие вполне точно. Магическим словЪм является
здесь, конечно, словечко „допустимый".
Удобным термином для этой заранее заданной функции пере-
переменных окончательного состояния является термин „функция кри*
терияа. Во многих приложениях определение надлежащей функции
критерия представляет известную трудность. Может случиться, что
с аналитической точки зрения решение совсем легко получается
для одной функции критерия и лишь с большим трудом для очень
близкой к ней другой. Поэтому в выборе таких функций желательно
сохранить некоторую свободу.
§ 3. ПРИНЦИП ОПТИМАЛЬНОСТИ
Для каждого процесса управляющее им функциональное урав-
уравнение было получено путем применения следующего интуитивного
принципа оптимальности.
Принцип оптимальности. Оптимальное поведение обла-
обладает тем свойством, что, каковы бы ни были первоначальное
состояние и решение в начальный момент, последующие решения
должны составлять оптимальное поведение относительно со-
состояния, получающегося в результате первого решения.
Математическая перефразировка этого простого принципа дает
все функциональные уравнения, с которыми мы будем встречаться
в оставшейся части книги. Высказанный принцип легко можно про-
проверить доказательством от противного.
§ 4. ПОСТАНОВКА ЗАДАЧИ.
I. ДИСКРЕТНЫЙ ДЕТЕРМИНИРОВАННЫЙ ПРОЦЕСС
Рассмотрим теперь детерминированный процесс, понимая под
ним процесс, у которого результат принятия любого решения опре-
определяется этим решением однозначно. Допустим, что состояние
системы, если не считать зависимости его от времени, описывается
на каждом шаге Л1-мерным вектором р = (рГ р2, ..., рм\ принад-
принадлежащим некоторой области п. Пусть Г—{Г„}, где; индекс ц про-
106 Глава III
бегает некоторое множество 5 E может быть конечным, счетным,
непрерывным или комбинацией множеств этих типов), представляет
собой множество преобразований, обладающих тем свойством, что
если /?^А то Тя(р)^п для всех #^5 (т. е. любое преобразо-
преобразование Тд переводит множество О в себя).
Термин „дискретный" означает здесь, что мы имеем дело с про-
процессом, состоящим из конечного или счетного числа шагов.
Для конечного процесса, который мы рассмотрим сначала,
каждое поведение состоит в последовательном выборе N преобра-
преобразований Р = G\, Г2, ..., Т^I)» дающих одно за другим последо-
последовательность состояний:
A)
Р2 =
Эти преобразования должны быть выбраны так, чтобы максими-
максимизировать значение заданной функции /? окончательного состояния рм.
В целом ряде случаев нетрудно установить существование "этого
максимума, а следовательно, и существование оптимального пове-
поведения. Простейшим из них является тот случай, когда на каждом
шаге процесса выбор индекса # производится только из конечного
числа допустимых альтернатив. Вероятно, следующим по сложности
является случай, где мы предполагаем, что С — ограниченная
замкнутая область, /?(р) — функция, непрерывная по р для р^ О,
Тд(р)—преобразование, непрерывное по совокупности р и # для
всех р ^ О и всех ц из ограниченной замкнутой области 5.
.Этими двумя случаями охватываются наиболее важные конечные
процессы, причем неограниченно продолжающиеся процессы можно
рассматривать как предельные по отношению к конечным.
Отметим, что максимальное значение функции ^?(рА опреде-
определяемое с помощью оптимального поведения, будет зависеть только
от начального вектора р и числа шагов N. Введем теперь основные
вспомогательные функции
B) /# (р) = тах К (рА равные доходу, получаемому при осу-
р
р ществлении А/-шагового процесса, если
его начальное состояние описывается век-
вектором р и используется оптимальное
поведение.
Мы пишем Тх вместо Тя , Т2 вместо Т^ и т. д.
Структура процессов динамического программирования 107
Эта последовательность определяется для N=1, 2, ... и для
Подобный подход к вопросу является проявлением основного
принципа анализа — принципа непрерывности. Для того чтобы
решить интересующую нас задачу для процесса с фиксированным
числом* шагов N и с единственным начальным вектором /?, мы рас-
рассматриваем все множество задач о максимизации, возникающих при
рассмотрении процессов с произвольным числом шагов и произ-
произвольным начальным вектором р.
Первоначальный процесс оказывается, таким образом, вложенным
в семейство подобных ему процессов. Вместо того чтобы пытаться
определить характеристики оптимального поведения для отдельного
процесса, мы будем исследовать общие свойства всего множества
оптимальных поведений, соответствующих различным процессам
из этого семейства.
Такой подход к вопросу даст нам возможность решить перво-
первоначальную задачу в ряде случаев, где применение прямых методов
к успеху не приводит.
Для получения рекуррентного соотношения, связывающего члены
последовательности {/дг (/?)}» воспользуемся принципом оптималь-
оптимальности, сформулированным в § 3. Предположим, что в качестве
первого решения мы выбираем некоторое преобразование Тд, полу-
получая таким образом новый вектор состояния Тй(р). Максимальный
„доход" *), получаемый после осуществления следующих N—1 ша-
шагов процесса, равен по определению /^-1 (Тд(/?)). Следовательно,
если мы хотим максимизировать полный доход от осуществления
всех N шагов процесса, ТР индекс ц следует выбрать так, чтобы
максимизировать доход, получаемый на последних N—1 шагах.
В результате мы приходим к основному рекуррентному соотноше-
соотношению
/*(/>)== «пах/^ (Г, (/>)) для
И
D) Л (/>)== тах
Заметим, что величина /м(р) определяется однозначно, в то
время как элемент д^8У на котором достигается максимум, может
единственным и не быть. Таким образом, максимальный доход опреде-
определяется однозначно, но может существовать много оптимальных по-
поведений, которые обеспечивают получение этого дохода.
То есть значение функции критерия.
108 Глава Ш
В случае неограниченно продолжающегося процесса последова-
последовательность функций \/ы(р)\ заменяется единственной функцией /(р),
равной полному доходу, получаемому при использовании оптималь-
оптимального поведения, если начальное состояние процесса описывается век-
вектором /?. Первоначальное рекуррентное соотношение заменяется при
этом функциональным уравнением *
E) /(р)=тах/G^ (/?)).
§ 5. ПОСТАНОВКА ЗАДАЧИ.
П. ДИСКРЕТНЫЙ СТОХАСТИЧЕСКИЙ ПРОЦЕСС
Продолжим рассмотрение дискретных процессов, считая на этот
раз имеющиеся преобразования не детерминированными, а стоха-
стохастическими.
В этом случае любое решение приводит уже не к какому-то
определенному преобразованию, а к некоторому распределению пре-
преобразований. Начальный вектор р преобразуется при этом в слу-
случайный вектор х с соответствующей функцией распределения
с1Од(р, 2), зависящей от вектора р и от выбора индекса ^.
Процесс может принадлежать одному из двух различных типов,
в зависимости от того, предполагаем ли мы, что сам вектор г из-
известен после того, как некоторое решение принято, а следующее —
только должно быть принято, или же мы предполагаем, что известна
лишь функция распределения этого вектора. В настоящей книге мы
рассмотрим только процессы первого типа, так как процессы вто-
второго типа, вообще говоря, требуют введения понятия функции от
функции, т. е. функционала.
Как неоднократно указывалось ранее, теперь, очевидно, ста-
становится уже бессмысленным говорить о максимизации определен-
определенного дохода. Поэтому мы должны условиться измерять качество
поведения посредством некоторого усреднения функции окончатель-
окончательного состояния. Будем называть это математическое ожидание
доходом.
Начиная со случая конечного процесса, мы определяем функции
/^(/?) в соответствии с формулой D.2). Если вектор г описывает
состояние, получающееся в результате начального преобразования Тй%
то при использовании оптимального поведения доход от последних
N— 1 шагов будет равен /^-1(^). Математическое ожидание дохода,
получающегося в результате первоначального выбора преобразова-
преобразования 7^, равно,. следовательно,
A) / /*.! (*) ао9 (р. г).
«€■0
Структура процессов динамического программирования 109
Поэтому для последовательности (/#(/01 справедлива следующая
рекуррентная формула:
B) /к (Р) = тах Г / (г) йОч (р, г), Л/> 2,
где
C) /1(р)=тах
В случае неограниченно продолжающегося процесса мы прихо
дим к функциональному уравнению
D) /(/0 = тах (
§ 6. ПОСТАНОВКА ЗАДАЧИ.
III. НЕПРЕРЫВНЫЙ ДЕТЕРМИНИРОВАННЫЙ ПРОЦЕСС
Имеется целый ряд интересных процессов, в которых требуется
принимать решения в каждой точке некоторого непрерывного мно-
множества, например интервала времени. Простейшие примеры процес-
процессов этого типа приводятся в вариационном исчислении. Как мы
увидим ниже (см. гл. IX), такое понимание вариационного исчисле-
исчисления приводит к новому взгляду на различные разделы этой клас-
классической теории.
Определим
О) /С/7'» Т) как доход, получаемый за промежуток времени [0, Г],
если исходить из начального состояния р при исполь-
использовании оптимального поведения.
Хотя мы и считаем, что процесс состоит из выборов, произво-
производимых в каждой точке г интервала [0, Г], но лучше начать с поня-
понятия выбирающих поведений, т. е. функций, определенных на интер-
интервалах, и затем уже перейти к пределу, когда эти интервалы стяги-
стягиваются в точки. Аналогом формулы D.3) является
B) ПР\ 5 + 7)= шах/(/^ Г),
Я [0, 5] Ч '
где максимум берется по всем допустимым решениям, принимаемым
в интервале [0, 5].
Когда мы рассматриваем бесконечные процессы, являющиеся ре-
результатом либо бесконечных последовательностей операций, либо
выборов, сделанных в каждой точке непрерывного множества, мы
встречаемся с трудностью доказательства существования достигае-
достигаемого максимума, а не просто супремума. Поэтому при рассмо-
ПО Глава 111
трении процессов непрерывного типа, вообще говоря, лучше начать
с уравнения
C) ПР\ 5 + Г) = 8ир/(/^; Г),
которое обычно легко, выводится, а затем уже показать, что при
надлежащих предположениях супремум фактически достигается и
поэтому может быть заменен максимумом.
Как мы увидим в гл. IX, предельный случай уравнения B) при
5->0 представляет собой нелинейное дифференциальное уравнение
в частных производных. Оно играет важную роль при аналитическом
исследовании вопроса. При численном же решении 5 можно при-
принять малым, но положительным 1).
§ 7. НЕПРЕРЫВНЫЕ СТОХАСТИЧЕСКИЕ ПРОЦЕССЫ
Интересным и спорным вопросом, еще ожидающим своего иссле-
исследования в дальнейшем, является строгая формулировка и решение
достаточно общих классов непрерывных стохастических процессов
решения для случаев с одним и двумя заинтересованными лицами.
Хотя в гл. VIII и будет рассмотрен один частный процесс такого
типа, мы не будем здесь останавливаться на общей формулировке
непрерывных стохастических процессов .решения, так как строгое
исследование требует тонких и хитроумных соображений, основан-
основанных на сложных понятиях.
§ 8. ОБОБЩЕНИЯ
Читатель увидит, что функциональные уравнения, которые мы вы-
вывели выше для случая, когда параметры состояния и решения при-
принимали значения в конечномерных эвклидовых пространствах, мо-
могут быть распространены на случай, в котором как параметры со-
состояния, так и решения являются элементами более общих пространств
(например, банаховых пространств).
Вместо того чтобы рассматривать здесь это обобщение абстрактно,
мы предпочитаем отложить вопрос до второго тома, в котором бу-
будут рассматриваться примеры этих более общих процессов. Теория
интегральных уравнений и вариационные задачи, в которых участвуют
функции нескольких переменных, так же как и более общие стоха-
стохастические процессы — все это дает нам примеры процессов, выхо-
выходящих за рамки конечномерной формулировки, которой мы ограь
ничились в этой книге, и требующих для своего определения теории
функционалов и операторов.
1) В гл. IX мы покажем, что можно избежать многих трудностей, свя-
связанных с требованиями строгости и возникающих в процессе нахождения
предела, если интересоваться только численным решением вариационных
процессов.
Структура процессов динамического программирования 111
§ 9. ПРИЧИННОСТЬ И ОПТИМАЛЬНОСТЬ
Рассмотрим многошаговый процесс, не сопровождающийся при
нятием решений, скажем» процесс, порожденный системой диффе
ренциальных уравнений
A) -^ = 8г(х1>х2 х^), хг@) = сг, /==1,2
которую можно записать короче в векторной форме
Ах
B) ЧГ = 8(Х>>> *@) = '-
Если считать, что решение системы существует и единственно, то
ее состояние в момент г есть функция только от с и г\ таким обра-
образом,
C) *(')=/(*.*).
Требование единственности решения приводит к функциональ-
функциональному уравнению
D)
для 5, ^^0, которое представляет собой аналитическую перефор-
переформулировку закона причинности. Это уравнение выражает основное
полугрупповое свойство процессов такого типа.
Сравнивая уравнения D) и F.2), мы видим, что многошаговые
процессы решения можно рассматривать как естественное обобще-
обобщение теории полугрупп. Всякие дальнейшие рассуждения в этом на-
направлении неизбежно вывели бы нас за те пределы, которыми мы
себя ограничили; поэтому мы удовлетворимся приведенным выше
замечанием.
§ 10. ПРИБЛИЖЕНИЕ В ПРОСТРАНСТВЕ ПОВЕДЕНИЙ
В гл. IV для решения функциональных уравнений типа D.5) и
E.4) мы используем общий прием анализа, метод последовательных
приближений. Этот метод вкратце состоит в выборе начальной функ-
функции /0(р) и последующем определении последовательности функций
\/х(р)\ с помощью алгоритма, который, например, для уравне-
уравнения D.5) имеет следующий вид:
A) /*00 = шах/^(Гд(/?)), N=1. 2
Этим методом мы уже пользовались для решения уравнений в гл. I
и II.
Во многих важных случаях после надлежащего предварительного
преобразования функционального уравнения применение §того
112 Глава 111
метода приводит к сходящейся последовательности, предел которой
является решением рассматриваемого функционального уравнения *).
Мы будем широко пользоваться этим обстоятельством в следующей
главе.
Однако в теории динамического программирования имеется еще
один, столь же важный метод приближения, который называется
„приближением в пространстве поведений".
Прежде чем перейти к его рассмотрению, отметим, что в про-
процессах динамического программирования существует естественная
двойственность между функцией /(/?), описывающей максимальный
доход, и оптимальным поведением (или поведениями), которое обес-
обеспечивает получение этого дохода. Каждый из этих двойственных
элементов может быть использован для определения другого, с той
только особенностью, что знание функции /(/?) дает возможность
найти все оптимальные поведения, так как можно указать все ин-
индексы #, которые максимизируют правую часть уравнения [напри-
[например, уравнения D.5)], в то время как знание какого-нибудь одного
частного оптимального поведения позволяет определить значение /(/?).
Можно считать, что индекс ^, при котором достигается макси-
максимум, является функцией от/?. Эта функция будет многозначной, если
существует более одного такого индекса. Поскольку /(/?) называется
элементом пространства функций, назовем д = д(р) элементом про-
пространства поведений. Хотя оба эти пространства являются простран-
пространствами функций, их целесообразно отличать друг от друга, так
как элементы этих пространств имеют совершенно различный смысл.
Таким образом, мы имеем два способа выбора начального при-
приближения. Мы можем аппроксимировать саму функцию /(/?), как
это обычно делается в методе последовательных приближений, или
же можем построить первое приближение в пространстве поведе-
поведений, и это является особенностью функциональных уравнений, опи-
описывающих процессы динамического программирования 2).
Выбирая в качестве начального приближения до-до(р), мы опре-
определяем доход, соответствующий этому поведению, из функциональ-
функционального уравнения
B) /о(/0 = /оG«о(/0).
Пример такого типа мы уже приводили в § 11 гл. I.
) Интересно отметить, что во многих теориях, например в теории диф-
дифференциальных уравнений в Устных производных, предварительное преоб-
преобразование уравнения носит такой характер, что главная трудность при до-
доказательстве существования решения заключается в установлении того, что
предельная функция действительно удовлетворяет рассматриваемому урав-
уравнению.
2) На самом деле этот метод приближения молчаливо используется и
в других областях анализа, как, например, в теории дифференциальных
уравнений, где дифференциальное уравнение часто заменяется разностным
с целью получения приближенного решения. При этом пространство всех
функций заменяется подпространством ступенчатых функций.
Структура процессов динамического программирования 113
Далее мы можем вступить на один из двух путей. Рассматривая
функцию от ^\ /0(Тд (/?)), мы можем, исходя из требования макси-
максимальности, определить функцию д(р), обозначая ее через ^(р).
Используя это новое поведение, мы определяем новый доход /х(р)
из функционального уравнения
C)
Это уравнение решается итерациями, так же как и уравнения D.6)
и (8.1) в гл. I.
Продолжая рассуждать аналогично, мы получим две последова-
последовательности функций: {Дг(р)} и [ям(р)).
Другой путь состоит в определении /х (/?),
D) Л(р) = п1ах/о(ЗД).
я.
и последующем индуктивном построении последовательности
с помощью обычного метода последовательных приближений:
Ф) ^+1
Очевидно, что Л^/о» и, таким образом, последовательность
Л — монотонно возрастающая. Вопрос о сходимости этого про-
процесса мы рассмотрим в следующей главе.
Первый метод, хотя и является более естественным, представ-
представляется более трудным для строгого изложения и не будет здесь
рассматриваться. Однако при исследовании различных типов непре-
непрерывных процессов, например, таких, к которым приводят задачи
вариационного исчисления, им приходится пользоваться для построе-
построения последовательных приближений. Мы снова вернемся к этому
вопросу в гл. IX.
УПРАЖНЕНИЯ И ПРОБЛЕМНЫЕ ЗАДАЧИ
и ° К ГЛАВЕ III
1. Пусть нам известно, что в одной из N урн находится шар,
причем априорная вероятность того, что он содержится в &-й урне,
равна рк. Показать, что процедура, минимизирующая среднее время,
необходимое для отыскания шара, состоит в том, чтобы в первую
очередь обследовать урну, которой соответствует наибольшая априор-
априорная вероятность рк.
2. Рассмотрим более общий процесс, в котором для исследова-
исследования содержимого &-й урны требуется время гк и, кроме того, задана
вероятность #& того, что любой отдельный просмотр &-й урны не
дает никакой информации относительно ее содержания. Когда это
Р.
114 Глава III
случается, мы продолжаем процесс исследования с той информацией,
которая у нас уже имелась.
Пусть /(рх, р%> ..., р^ — среднее время, которое приходится
тратить, чтобы извлечь .шар, при использовании оптимального по-
поведения. Показать, что эта функция удовлетворяет уравнению
/(А. Л. • • •. Ри) = ™п [(Т=^) + {У^) ^(/?*' Р*2'
к
где /?* = /?*/A—рк), а 0 стоит на к-ы месте.
3. Показать, что если мы хотим извлечь шар, то оптималь-
оптимальное поведение состоит в том, чтобы в первую очередь обследовать
ТУ УРНУ» Для которой величина рк(\ —%)/** будет наибольшей.
С другой стороны, если мы ставим задачей только обнаружить со-
содержащую шар урну в минимальное среднее время, то в этом слу-
случае урна, для которой указанная величина наибольшая, должна или
исследоваться в первую очередь, или не исследоваться совсем.
4. Рассмотреть случай, когда мы можем осуществлять поиски
шара одновременно в нескольких урнах.
5. Имеется несколько монет, причем все монеты, за исклю-
исключением одной, одинакового веса, и чашечные весы без гирь. Ука-
Указать процедуры взвешивания, которые минимизируют максимальное
время, необходимое для обнаружения этой отличающейся по весу
монеты, в следующих случаях:
а) известно, что эта монета тяжелее остальных,
б) неизвестно, тяжелее эта монета или легче, чем остальные.
6. Определить процедуры взвешивания, которые минимизируют
среднее время, необходимое для обнаружения этой монеты.
7. Рассмотреть более общую задачу, где таких особых монет
две или больше, при различных предположениях относительно
свойств этих монет.
(Кэрнс)
8. Имеется м, вообще говоря, не одинаковых изделий, которые
должны быть обработаны на ряде установок различных типов
(числом т). Порядок, в котором эти установки должны использо-
использоваться, имеет существенное значение, так как некоторые процессы
обработки должны быть выполнены раньше других. При заданном
времени ац (/— 1, 2, . . ., п\ у = 1, 2, . .., т)У необходимом для
обработки /-го изделия на у'-й установке, требуется так определить
порядок, в котором эти изделия должны запускаться в обработку,
чтобы общее время, необходимое для выпуска готовой продукции,
было минимальным
) По поводу задач 8—11 см. статью автора, цитированную на стр. 180,—
Прим. ред.
Структура процессов динамического программирования 115
Рассмотрим случай, когда обработка состоит только из двух
операций, причем п\х = щ и я?2 = Ь\ и обрабатывающие установки
должны использоваться именно в этом порядке. Обозначим через
/(л1, Ьг, а2, Ъг ..., аю Ьк\ С) время, необходимое для обработки N
изделий при условии, что вторая установка начинает работать на I
часов позже и используется оптимальное распределение изделий по
установкам; а^Ъх— время, необходимое для обработки /-го изделия
соответственно на первой и второй установках.
Доказать, что функция / удовлетворяет функциональному урав-
уравнению
= пип [%-(-/(я^, Ьи агЛг О, 0, •. ., аю Ьы\ ^.Ц-тах^ — а{, 0))],
где пара @, 0) стоит на месте пары (а*, ^).
9. Показать, что оптимальный порядок обработки определяется
по следующему правилу: /-й вид изделий предшествует у-му виду
изделий, если т1п(^, ^)<т1п(а^, ^). В случае равенства любое
упорядочение будет оптимальным при условии, что оно является
предпочтительным и во всех других отношениях.
(С. Джонсон)
Каково будет решение, если процесс может быть начат с обра-
обработки сырья на любой из обрабатывающих установок?
10. Пусть хг есть время простоя второй установки непосред-
непосредственно перед обработкой на ней /-го вида изделий. Пусть далее
а\* &г — соответственно время обработки /-го вида изделий на первой
и второй установках, причем виды изделий подвергаются обработке
в порядке их нумерации. Тогда
п
1 Х;= тах
и и-1
(С. Джонсон)
11. Если процесс обработки состоит из трех операций, то пол-
полное время простоя третьей установки есть
и и—1 V ь—1
аг— 2 ^г+ 2 ^г— 2 сг
г-=1 г«=1 г=1
(С. Джонсон)
12. Рассмотрим следующую задачу, возникающую при производ-
производстве агрегата, состоящего из многих деталей, а также при эксплу-
эксплуатации сложной производственной системы. Имеется N различных
стадий производства, участвующих в выпуске готового продукта.
8*
116 Глава 111
Вероятность того, что на /-3 стадии обработка выполнена правильно,
равна /?$.
Пусть в нашем распоряжении имеется к устройств, которые могут
быть использованы для увеличения точности обработки на любой
отдельной стадии производственного процесса следующим образом.
Если на 1-й стадии производства применяется одно устройство, то
вероятность /?$ изменяется, делаясь равной р^; если используются
два устройства, то она становится равной /?$а, и т. д.
Как следует распределить имеющиеся устройства для максими-
максимизации общей точности процесса? Рассмотреть эту же задачу при
следующих альтернативных предположениях:
а) на 1-й стадии допускается использование не более чем тг
устройств;
б) устройство, которое может быть использовано на /-й стадии,
стоит их долларов, а на все используемые устройства мы можем
затратить не более й долларов;
в) для обслуживания устройства, используемого на /-й стадии
процесса, требуется Н{ человек, а для обслуживания всех устройств
имеется не более к человек.
13. Для исправления ошибки, обнаруженной на /-й стадии про-
производственного процесса, требуется время ^, а связанные с этим
исправлением расходы равны сг. Определить сумму, которую целе-
целесообразно выделить на приобретение контрольной аппаратуры, а также
распределение последней между операциями, если известны величина
заработной платы и стоимость работы оборудования, приходящиеся
на одно изделие, а также убытки от выработки дефектного изделия
(скажем, г).
п
14. Рассмотреть задачу максимизации функции 2 9%(хг) ПРИ
следующих ограничениях:
а)
п
б)
в) Х1кх%к+1 — 0 для некоторого множества целых чисел 1Х < 1
Рассмотреть, в частности, случаи
Ю ^^+1 = 0» /=1,2 п — 1,
Рассмотреть обратную ситуацию, когда ограничения имеют вид
Структура процессов динамического программирования 117
Исследовать, в частности, случаи:
б) Х$
«
15. Владелец ресторана располагает двумя различными способами
стирки салфеток; при быстром способе стирка занимает ц дней и
обходится в с центов за штуку; медленный же способ стирки
требует р > ц дней и обходится в й < с центов за штуку. Пред-
Предполагая, что владелец ресторана заранее знает число посетителей,
которых он должен будет обслужить в любой из дней Л^-дневного
периода, и что он должен обеспечить салфеткой каждого посетителя,
определить, сколько салфеток он должен купить и как должен от-
отдавать их в стирку, чтобы минимизировать общие расходы в тече-
течение Л^-дневного периода. Рассмотреть сначала случаи, когда
16. Рассмотреть аналогичную задачу в предположении, что сал-
салфетка выдерживает лишь к стирок.
17. Рассмотреть эту задачу в предположении, что число посети-
посетителей в каждый из дней является случайной величиной.
18. Имеется некоторый ресурс х, который может быть исполь-
использован несколькими способами. Пусть у— параметр, характеризую-
характеризующий способ использования ресурса, /?(х, у) — получаемый при этом
способе доход, а О(х, у)— истраченный ресурс. Обозначив через/(х)
общий доход от многократного использования первоначального ре-
ресурса х, получаемый при оптимальном поведении, мы приходим
к функциональному уравнению
ш у))].
у
Предполагая, что величина п(х, у) мала по сравнению с х для всех
значений у, показать, что мы получаем формальное приближенное
уравнение
в дать интерпретацию этого результата.
19. Рассмотреть стохастический случай. Показать, что соответ
ствующее этому случаю функциональное уравнение имеет вид
= тах
-о
оо / оо
ГгйН(у, г, хL-/[ х— Г чю(Ю(у> чю> х)
118 Глава III
а приближенное уравнение —
оо
Г гЛН (у, г, л:)
тах
оо
У
| чюЛй (у, и/, л:)
о
дать интерпретацию результата.
20. Рассмотрим применение метода аппроксимации в пространстве
поведений к функциональному уравнению
/(*)= тах
Мы выбираем начальное приближение уо(х) и вычисляем /0(х).
Затем определяем первое приближение ух (х) из того условия, что уг
максимизирует функцию % (у) -\- к (х — у)-\-/о(ау-\-Ь(х — У))* и по
нему находим /х(х) и т. д. При каких условиях элементы последо-
последовательностей {уп(х)} и {/п(х)} являются непрерывными функциями
по х и когда эти последовательности сходятся? В частности, рас-
рассмотреть случаи, когда функции & и к являются одновременно
выпуклыми или вогнутыми.
21. Пусть в нашем распоряжении имеются две машины (будем
называть их просто машина I и машина II) со следующими свой-
свойствами. Если используется машина I, то с вероятностью г мы по-
получим единицу прибыли. Если же используется машина II, то вероят-
вероятность получения этой единицы прибыли равна 5. Будем предпо-
предполагать, что значение 5 известно, а для г задано только некоторое
априорное распределение. Задача состоит в определении поведения
выбора, которое максимизирует средний доход, получаемый после Л/
испытаний, а также поведения, максимизирующего урезанный доход
от неограниченно продолжающегося процесса (урезывание дохода
производится на каждом шаге умножением его на а < 1).
Предположим, что функция распределения случайной величины г
при условии, что на машине I т испытаний были успешными, а п —
нет, определяется соотношением
п
о
Обозначим через /туП средний доход, получаемый от неограниченно
продолжающегося процесса, если используется оптимальное поведе-
поведение и выполняется приведенное выше условие относительно исходов
Структура процессов динамического программирования
119
испытаний на машине I. Показать, что /т%п удовлетворяет рекур-
рекуррентному соотношению
1
/ гс1Гтг п (г) [ 1 + а/т+и п]
о
1 .
п
тах
о
II:
1— а
22. Доказать, что существует единственное ограниченное реше-
решение этого уравнения, которое может быть получено методом после-
последовательных приближений.
23. Доказать, что для каждой пары целых чисел т, п ^> 0 суще-
существует единственное значение $(т, п), при котором последователь-
последовательность {/тгП\ определяется из уравнений
1 % п),
л.
/т, п =* /
о
1
Последовательность {5{т, Аг)} обладает следующими свойствами:
«
б) 8(т-{-19 Аг)>5(т, Аг)>5(т, лг —|—
и
Как вычислять члены последовательности {$(т, Аг
24. Получить соответствующие результаты для процесса, допу-
допускающего только конечное*число испытаний.
25. Рассмотрим следующую ситуацию. Имеется склад товаров
с заданной вместимостью и некоторым начальным запасом товара,
для которого известна закономерность сезонного изменения реали-
реализационной цены, а также издержек производства. Задача состоит в
определении оптимальной модели закупки (или производства), хра-
хранения и продажи.
Обозначим через В заданную вместимость склада, а через А—
начальный запас товара на складе. Предположим, что наш сезонный
120 Глава III
товар покупается (или производится) и продается в каждый /-й
период, /= 1, 2 я. Пусть для /-го периода
A) сг — издержки производства на единицу товара,
Рг — реализационная цена единицы товара,
хг — купленное (или произведенное) количество товара,
У % — проданное количество товара.
Вводятся следующие ограничения:
B) а) ограничение на покупку: запас товара в конце /-го периода
не может превышать вместимость склада,
б) ограничения на продажу: количество товара, проданное за
1-Й период, не может превышать количества его в конце (/—1)-го
периода,
в) неотрицательность: покупаются (производятся) и продаются
лишь неотрицательные количества товара.
Задача состоит в определении поведения, максимизирующего
полную прибыль.
Показать, что ее можно свести к задаче определения значений
хг и з>г» максимизирующих линейную форму
п
C)
при условиях
г
D) а) Л 4-2 (*/—-V./)< В, *=1. 2 я,
4-1
б) Л<^4- 2 (*> — Уэ)> 1— Ь 2 п,
.7=1
в) лч, ^>0.
26. Для фиксированного значения В определяем последователь-
последовательность
/п (А) = тах Р, я = 1, 2, ... .
Показать, что /1(А)=р1А и что
A) /пИ)= тах
»1, 2/1
для я ^ 2, где максимум берется по области
B)
0) х; —>»1<В —Л,
Структура процессов динамического программирования 121
27. Доказать, что функция /^ (г/) линейна относительно г/, именно
С1» С2» * • • » С#) I
и, следовательно, оптимальное поведение не зависит от V.
(С. Дрейфус)
28. Рассмотреть следующую идеализированную транспортную
систему:
ш щ
На каждом шаге имеются две конечные станции Тк и 5Л. Из
пунктов Тк и 5Л можно перевозить материал в пункты Тк+1 и 5Л+1.
. Максимальные количества, которые можно перевезти по этим
участкам, следующие:
а)
б)
в)
г)
Обозначим через Ръ(х, у) количество материала, доставляемое
в пункт /\ при условии, что перевозки начинаются с начальных ко-
количеств х в пункте Тк и у в 5Л и при перевозках используется
оптимальное поведение. Показать, что
= т\п(х,
где максимум берется по области
Р -^ *1 ^ ^й, й+1» 0
О < щ < 5Л, Л+1, 0 < щ < 8кг к+1.
29. Сформулировать соответствующую задачу для случая, когда
конечные станции обладают ограниченной вместимостью.
122 Глава ///
30. Рассмотреть стохастический случай, когда упомянутые вме-
вместимости являются случайными величинами с известными функциями
распределения. Получить рекуррентное соотношение для максималь-
максимального среднего количества материала, доставляемого в пункт /\ при
различных предположениях относительно имеющейся информации.
31. Рассмотрим следующую транспортную задачу. Имеется ряд
„источников", или „пунктов отправления", 5Х, 52, .... 8м и ряд
„стоков", или „пунктов назначения", 7\, Г2, ..., Г#. В каждом
источнике 5^ имеется некоторое количество материала хг, кото-
которое должно быть перевезено в различные пункты назначения,
причем так, чтобы общее количество материала, доставляемое
в пункт 7^, равнялось заданному требованию у$ на него в этом
пункте. Предполагается, что 2ЛГ*==2-У/- При данных расстоя-
ниях йц между пунктами отправления и пунктами назначения
и в предположении, что стоимость перевозки единицы количества ма-
материала между пунктами 5^ и Т$ равна йц, определить план перевозок,
минимизирующий общую стоимость удовлетворения требований.
Показать, что рассмотренная выше задача эквивалентна миними-
минимизации линейной формы
при ограничениях
-..— г. У г.
0
(Хичкок —Купманс)
32. Положим для фиксированных у19 у2 у1Г
Показать, что
'
Ж
= тш
где минимум берется по области
ж
^ хг\ == У\* 0 ^ Хц ^ X},
г-1
ХМ\)
Структура процессов динамического программирования 123
М N
33. Показать, что при выполнении соотношения 2*1 =
мы можем всегда уменьшить на единицу размерность задачи, рас
сматривая вместо/к(хг, х2 хм) функцию/^(хи х2,
..,
34. Рассмотреть стохастический случай, когда расстояния й
являются случайными величинами с заданными функциями распре
деления.
35. Предполагая, что стоимость транспортировки из /-го пункта
о
в /-й есть квадратичная функция йуХц-\-ецХ\$% #^>0, показать,
что в этом случае существует единственный план перевозок, обес-
обеспечивающий минимум затрат.
(В. Прагер)
36. Рассмотреть аналогичный многошаговый процесс, при кото-
котором масса из пунктов (А$, Д$, С$) должна быть перевезена в пункты
(А$+1, В|+1, Сг+1) и т. д., причем перевозки продолжаются до тех
пор, пока масса не достигнет мест назначения Т19. Т2, Г3, как пока-
показано ниже
7\
. ^N Т2
• т
Ск Т3
37. Рассмотрим задачу о минимизации линейной формы
N
при условиях
N
— 2 сгхг
2 аЦхо ^ ^г» / = 1, 2,
1
причем будем предполагать, что а
Обозначим т[пЬ(х) через /К(ЬХ, Ъг> ••-. ЪЛ. Показать, что
X
Ьм) = ш1п
где а:^ удовлетворяет условиям
124 Глава III
38. Пусть имеется два пустых сосуда Ух и У2 емкостью соответ-
соответственно в пять и в два галлона и, кроме того, виски и вода в не-
неограниченных количествах. Будем допускать следующие операции:
Ах— наполнение
А2 — полное опорожнение
Ав—наполнение У2,
А4 — полное опорожнение У2,
Аь— переливание содержимого из ^x в У2 Д° ег0 наполнения,
Л6 — переливание содержимого из У2 в Л Д° наполнения последнего.
После выполнения конечного числа допустимых операций состоя-
состояние системы может быть описано следующим образом:
1. В сосуде У2 имеется / = 0, 1, 2 галлонов жидкости с про-
процентным соотношением г : A—г) виски и воды.
2. В сосуде Ух имеется у = 0, 1, 2, 3, 4, 5 галлонов жидкости
с процентным соотношением 5 : A—5) виски и воды.
Обозначим через /(/, у; г, 5) минимальное число операций, необ-
необходимое для достижения системой с начальным состоянием (/, у; г, *)
заданного состояния, например для получения в У2 смеси с одина-
одинаковым процентным содержанием воды и виски.
Показать, что
/(/, У; г, $) = 1 + пнп Ак/.
Будет ли функция /(/, у; г, 5) конечной для всех рациональных
значений г при у = 0 и для всех рациональных значений 5 при
/?=0? В противном случае указать, какие смеси воды и виски можно
получить в У2 после конечного числа операций.
39. Рассмотрим следующую задачу. Пусть на каждом шаге неко-
некоторой последовательности действий мы вправе выбрать один из двух
вариантов возможных образов действий. При выборе первого ва-
варианта мы с вероятностью рх получаем единицу прибыли, с вероят-
вероятностью р2 — две единицы прибыли и с вероятностью /?3 процесс
заканчивается. При втором варианте эти вероятности соответственно
равны р[, /?2» /V Указать последовательность выборов, максимизирую-
максимизирующую вероятность получения по крайней мере п единиц прибыли до
завершения процесса.
Обозначим максимальную вероятность через и(п). Тогда
и (п) = тах
Структура процессов динамического программирования
125
A)
40. Доказать, что если
и(п)= тах
в
2 аци (п — У)
• <4
= 0, 1, 2, .... /? — 1,
и, кроме того,
а) а{л > 0,
в
б) существует одно уравнение вида гп =
п~*> наибольший
положительный корень которого превосходит по величине
соответствующие корни остальных уравнений этого же вида,
в) для этого индекса к имеем ам ф 0,
то решение уравнения A) для достаточно большого п представится
в виде
в
Рассмотреть случай, когда по крайней мере два характеристиче-
характеристических уравнения имеют одинаковый наибольший корень.
41. Рассмотреть уравнение
и (п)
тах
в
В
где
, / = 0, 1, 2 # —1.
В

Пусть тах^/2УЛн:==с достигается при единственном значе-
нии 1 = $. Если а81 > 0, то для м^м0 решение представляется в виде
где п0 зависит от начальных условий и коэффициентов.
42. Остается ли это утверждение в силе, если а81 = 0? Построить
пример, когда оно перестает быть верным.
43. Дано конечное множество [А^ неотрицательных квадратных
матриц. Обозначим через С# ту из матриц ВХВ2 . .. В# (каждое
Вг — это некоторая матрица А-), которая обладает наибольшим по
абсолютной величине характеристическим числом. Пусть это характе-
характеристическое число равно г#. Доказать, что существует ^ = Ит /--л1/
126 Глава III
Обозначим через Мы минимальную мажоранту произведений Р# =
= ВхВг ... В#, т. е. такую матрицу М#, что ее //-й элемент не
меньше соответствующего //-го элемента любой из матриц Рдг.
Пусть тн — наибольшее по абсолютной величине характеристическое
число матрицы М^- Доказать, что существует Х= Ит.
44. Доказать или опровергнуть равенство [х =
45. Рассмотрим следующую задачу. Пусть мы располагаем в неко-
некоторый начальный момент х долларами и сывороткой в количестве у,
а также возможностью покупки добавочных количеств сыворотки
в точно установленные моменты времени: Ьх < Ьг < .... За г долла-
долларов в каждый из моментов гк можно купить сыворотку в количе-
количестве скг, где ск— монотонно возрастающая функция к. Задана ве-
вероятность вспышки эпидемии в период между моментами гк и ^+1,
причем в случае ее возникновения мы можем использовать только
то количество сыворотки, которое уже имеется у нас на руках. За-
Задача состоит в определении поведения закупки сыворотки, максими-
максимизирующего полную вероятность успешности борьбы с эпидемией.
Вероятность успешного исхода этой борьбы при наличии сыво-
сыворотки в количестве ~*ш считается известной.
Условие ск > ск_х означает, что стоимость сыворотки уменьшается
со временем вследствие совершенствования технологии производства.
Пусть
рк — вероятность возникновения эпидемии в период между
моментами гк и 1к+1 при условии, что до момента гк
ее не было,
ср(^) — вероятность успешного исхода борьбы с эпидемией
при наличии количества чю сыворотки,
/к(х* У) — полная вероятность успешного исхода при использо-
использовании оптимального поведения закупки сыворотки, на-
начиная с момента Ьк, когда в распоряжении имеется х
долларов и количество у сыворотки.
Показать, что /к(х, у) удовлетворяет функциональному уравнению
/*(*. У)= тах
< <
46. Показать, что если функция ср(^) — выпуклая на всем мно-
множестве значений -о/, то оптимальное поведение состоит в том, чтобы
не производить закупку сыворотки в моменты ^, 12, .. ., ^_1§ а израс-
израсходовать на нее все имеющиеся деньги в момент 1к. Индекс к нахо-
находится из условия максимальности функции
Структура процессов динамического программирования
127
если ркЕЕ=р. Найти соответствующее выражение при общих предпо
ложениях относительно рк.
47. Пусть
о
N
П
их.
Показать, что
аы
48. Пусть т(х1У х2, ..., ад) означает минимум Л/ величин
хг, хъ ..., х^. Показать, что имеет место функциональное уравнение
т(т(х1, х2, ...,
и аналогично для максимума N величин М(х1% х2,
49. Показать, что
тах[A—л
где ^х = е, е^ =
50. Положим
Г
== ГШП ^
«„• I
Показать, что
= ГП1П
, Л)=т1П С
а у
(х).
51. Получить рекуррентные соотношения для задачи определения
минимума и максимума следующих функций:
а) ^N =
при условии х\-\-х\-\- ...
ах2J
б) д# = х\
при условии
128 Глава Ш
в) <2# == х\ + (хг + ах2J ■+- (хг + ЛАГгтЬ (а + ь) хгJ
... +(х14-ах2 + (а+^)л:з~+" • • • 4-(я-+-(^ — 2) #)
при условии х2|2[ 4^1
52. Конфету надо поделить между двумя детьми. Показать, что
оптимальная процедура состоит в том, чтобы разрешить одному
ребенку поделить конфету, а другому выбрать тот кусок, который
он хочет. Показать, что при этом доля первого ребенка опреде-
определяется из уравнений
г== тах пнп(_у, х—у) = —.
53. В чем будет состоять аналогичная процедура в задаче с N
детьми?
(Г. Штейнгауз)
54. Известно, что автомашина может взять с собой бензина в ко-
количестве, достаточном для прохождения расстояния в й миль. Чтобы
она могла пройти расстояние в 2й миль по пустынной местности,
ей необходимо создать на своем пути промежуточные заправочные
пункты, завезя на них запасы бензина. Как следует их разместить,
чтобы общие расходы бензина, необходимые для достижения пункта
назначения, были минимальными, и чему равно общее расстояние,
которое при этом придется пройти машине? [Р1пе N. Л., ТНе ]еер
ргоЫет, Атег. Ма1к. МопгЫу, 54, № 1 A947).]
55. Рассмотреть следующие более реальные случаи:
а) используется более одной машины,
б) перевозится дополнительный груз,
в) используются несколько ранее созданных постоянных запра-
заправочных пунктов с запасом бензина,
г) задано несколько пунктов доставки груза,
д) задан срок прибытия,
е) минимизируется общая стоимость, включая стоимость бензина,
стоимость приобретения автомашин, а также стоимость созда-
создания запасов бензина,
ж) произвольное расстояние х > 2й. /^ Хельмеп)
56. Доказать, что в общем случае задача определения
тах пил
N
Ук)
при условиях
N N
&-1
Структура процессов динамического программирования
129
не может быть сведена к рекуррентному соотношению вида
57. В каждый момент времени п к системе предъявляется тре-
требование гп. Обозначим через хп действительный уровень произво-
производительности системы, тогда для всех значений п должно выполняться
неравенство хп ^ гп.
Пусть, далее, имеется ограничение на изменение уровня произ-
производительности системы в любой момент
^П + 1 ^п ^> \^П ХП — 1/> ^ -^ * *
Мы хотим выбрать хг так, чтобы минимизировать форму
N
Показать, что искомые значения х$ определяются следующим обра
зом:
Х
= ГП1П [Х(рх, Х(р2] = Ш1П [Ххх, Ср2]«
хг), ср3].
где
х
п
гя„1 —агя_2),
срл = тах
гЭ~~г
К г
58. Определить максимум линейной формы
N
1=1
ниях
2л XI = 1, 0
ограниче-
, где числа аг неотрицательны
59. Рассмотрим • задачу определения максимума произведения
Д(хг — а) при ограничениях
, где
и
казать, что для получения функционального уравнения необходимо
рассмотреть также задачу определения минимума произведения
N
| — а) и вывести для нее функциональные уравнения.
9 Р. Беллман
130 Глава III
Показать, что в этом нет необходимости, если мы рассматриваем
N
произведение XII-^г — а\-
11
1=1
60. Предположим, что мы участвуем в викторине и имеем воз-
возможность получить в качестве приза значительную сумму денег, если
ответим правильно на ряд вопросов.
Обозначим через гк количество денег, получаемое при правиль-
правильном ответе на &-й (к— 1, 2, ..., Л0 вопрос, и через рк априорную
вероятность того, что мы сможем правильно на него ответить.
Пусть ср(х) —функция полезности, определяющая ценность выигрыша
для нас суммы х. ,
Допустим, что после каждого вопроса мы можем принять одно
из двух решений: пытаться ответить на следующий вопрос или пре-
прекратить участие в викторине с той суммой денег, которую мы уже
получили. Определить оптимальные поведения, которым надо следо-
следовать, при следующих условиях:
а) при первом неправильном ответе процесс заканчивается с общим
нулевцм выигрышем,
б) допускается два неправильных ответа,
в) ответив правильно на к0 вопросов, мы должны получить по
крайней мере сумму 2Г&« независимо от того, что произой-
#дет позже,
г) мы соревнуемся с другими участниками викторины; участнику,
который получает наибольшую сумму, предоставляется право
попытаться, правильно ответив на вопрос, получить „главный
N
приз", который значительно превышает
1
д) на каждом шаге процесса опроса мы можем сделать выбор
между трудным и легким вопросом с условием, что при ошибке
в ответе на легкий вопрос процесс заканчивается с нулевым
выигрышем, а при неправильном ответе на трудный вопрос
процесс заканчивается с общим выигрышем, равным половине
суммы, полученной к этому моменту.
61. Пусть Ь{ и йц — случайные величины с заданными функциями
распределения. Получить рекуррентное соотношение для последо-
последовательности функций
определяемой следующим образом:
N
> ■ ■ ■ • ст)
е
г
Структура процессов динамического программирования
131
где минимум берется по области
а) х*>0,
N
б) 2 аг5хъ5 < С|, /
*1
1,2 т
Сделать то же для случая последовательности функций
N
, . .., ст)= гшпЕ
2Л
г=1
В обоих случаях Е означает математическое ожидание соответствую-
соответствующей случайной величины.
62. Рассмотрим форму Сельберга
к\п
считая х1=1, а остальные хк — пока произвольными. Запись
к\п
\
означает, что сумма берется по всем целым числам к, являющимся
делителями числа м, например ^хк = х1-\-х2-^х3-{'Х6. Вводя
надлежащие параметры состояния, получить рекуррентные соотно-
соотношения для
со
63. Задача определения минимального и максимального характе-
характеристических чисел матрицы Якоби
Ъ\ а2 Ь2
где точки означают, что все остальные элементы равны нулю, экви-
эквивалентна нахождению минимума и максимума квадратичной формы
N N-1
N
на сфере 2 лг?= !•
Рассмотреть две последовательности:
(с) = тах
8
тт
132 Глава ///
где через 5 обозначена Л/'-мерная сфера. Показать, что можно по
лучить рекуррентные соотношения, связывающие /дг(с) с
и §>(<0 с ()
64. Получить аналогичные результаты для квадратичной формы
N N-1 N-2
65. Обозначим через А— \\а^\\ положительно определенную сим-
симметричную матрицу. Показать, что задача решения системы линейных
уравнений
N
У> пхаХа = С--, / = 1, 2, . .., N %
эквивалентна задаче отыскания абсолютного минимума формы
# N
ачХгХл — 2 2 сг^г-
,^ г=1
66. Обозначим упомянутый в предыдущей задаче минимум через
г С2' •••» с#)- Получить рекуррентное соотношение, связываю-
связывающее /„ и //__1.
Показать, что /^ представляет собой квадратичную форму отно-
относительно переменных сг:
N
Выяснить, как рекуррентное соотношение, связывающее /^ и /ЛГ_1|
может быть использовано для получения рекуррентных соотношений,
связывающих члены последовательностей
67. Телевизионная компания намерена арендовать телевизионные
линии связи для объединения части своих станций в единую сеть. Теле-
Телевизионные линии связи существуют между любыми двумя станциями,
и известна стоимость их аренды, которая, вообще говоря, различна для
различных пар станций.. Показать, что для создания сети с мини-
минимальными затратами следует среди еще не включенных в сеть линий
связи выбирать ту, арендная плата за которую минимальна и кото-
которая не замыкает кольца уже работающих линий.
(Р. Калаба)
п
68. Рассмотрим задачу минимизации функции ^^(хА на мно-
жестве всех м-мерных векторов х = {хх, х2, ..., хп) с целочислен-
целочисленными неотрицательными компонентами, удовлетворяющими условию
Структура процессов динамического программирования 133
п
^=т, причем функции срх, ср2» •••> ?п выпуклые для л^^.0
Пусть /={1, 2, ..., м}. Обозначим для любого допустимого мно-
множества {хх, х2, .... хп} через 5+ (х) множество индексов У^/,
для которых х$ > 0. Показать, что, для того чтобы минимум дости-
достигался на допустимом множестве х^ необходимо и достаточно выпол-
выполнение условия
() (^]^ тах
Получить соответствующее условие, когда переменные хг ограничены
только требованием неотрицательности и выполнения равенства
п
т.
(О. Гросс)
69. Дана прямоугольная матрица А = ||а^||. Требуется перейти от
клетки A,1) к клетке (т, п), сдвигаясь на каждом шаге либо на одну
клетку вправо, либо на одну клетку вниз, таким образом, чтобы
минимизировать сумму встречающихся при этом элементов а^. По-
Показать, как определить оптимальные траектории.
(С. Дрейфус)
70. На тостере (приборе для поджаривания гренков) можно одно-
одновременно поджарить два ломтика хлеба, каждый с одной стороны.
Какая процедура приготовления гренков минимизирует время, необ-
необходимое для поджаривания трех ломтиков хлеба, каждого с Двух
сторон?
(Дж. Э. Литтлвуд)
Решить общую задачу, когда надо обработать Л/ й-сторонних
предметов на М машинах, причем каждая машина может обрабаты-
обрабатывать одновременно /? предметов с 5 сторон.
71. Рассмотрим систему связи, соединяющую три пункта:
134 Глава 111
Из каждого пункта можно посылать сигналы в остальные.
Обозначим через г^ максимальное число сигналов, которое может
быть послано из пункта Тг в пункт Т$ в единицу времени, и рас-
рассмотрим два случая: первый — когда передача сигнала из 7^ в Т$
не мешает передаче другого сигнала в обратном направлении, и
второй — когда общее число сигналов в обоих направлениях не может
превышать г^.
Обозначим через х{$, /, /=1, 2, 3, 1Ф]% количество сигналов
в пункте Тг, которые предназначаются для передачи в пункт Т$%
и предположим, что для передачи сигнала из любого пункта 71$
в любой пункт Т^ тратится единица времени. Обозначая через/п(х^)
максимальное число сигналов, которое может быть передано за
п единиц времени, получить рекуррентное соотношение для после-
последовательности {/п (*$,/)}•
(Хункоса — Калаба)
72. Газеты доставляются для продажи в ряд киосков. Предпола-
Предполагая, что функция распределения количества продаваемых в каждом
из киосков газет известна и что определенное количество непродан-
непроданных газет может быть возвращено с соответствующей уценкой,
определить, сколько должно быть отпечатано экземпляров газеты
и как они должны быть распределены по киоскам.
73. Рассмотрим задачу о минимизации суммы
где каждая функция §\$ выпуклая, а переменные должны удовле-
удовлетворять условию а ^ хх <^ х2 ^ ... <^ хы <^ Ь. Определим
для N=1, 2, ...
и — оо<а<#< оо. Показать, что
74. Пусть &(х) — непрерывная и выпуклая функция для
Положим
, 5)= ПИП
Г <Я?<8
Показать, что для й ^ а ^ Ь ^ с справедливо равенство
ш с) — е(Ь. Ь).
Показать, кроме того, что &(а, х) как функция от х является
непрерывной и выпуклой для х ^> а,
(Каруш)
Структура процессов динамического программирования
135
75. При указанных выше предположениях доказать, что
оо
оо.
76. Пусть §^00— ограниченные снизу выпуклые функции в ин-
интервале — со < у < оо. Тогда /д(а, Ь) может быть представлена
в виде
= ик(а) + ^(*), а < Ь,
где ик(х) и VN(x) — соответственно возрастающая и убывающая
выпуклые функции на интервале — оо < х < оо.
(Каруш)
77. Пусть
м
Показать, что
п
78. Получить аналогичное выражение для функции
N / М \ 2
и вывести на его основе рекуррентные соотношения для коэффи-
коэффициентов в выражении
N
к (ао> аг а
79. Следователь, устанавливающий личность убийцы, имеет N
свидетелей различной степени надежности, причем один из них
является убийцей. Обозначим через р{ вероятность того, что /-й сви-
свидетель ответит правду в любой момент на любой обращенный к нему
вопрос. Следователь допрашивает свидетелей в некотором порядке.
При этом первому из допрашиваемых он задает некоторый во-
вопрос, а каждому следующему задает либо прямой вопрос, либо
вопрос относительно истинности показаний предыдущих свидетелей.
Предполагая, что следователю разрешается при каждом допросе
задавать один вопрос и что /-му свидетелю для ответа на вопрос
требуется время ^, указать, в каком порядке свидетели должны
допрашиваться и какие вопросы им следует задать, чтобы макси-
максимизировать вероятность обнаружения убийцы в течение заданного
промежутка времени 7\
136 Глава III
80. Рассмотрим задачу о минимизации функции
, х2, ...,
по всем значениям х^ из области
а) х*>0,
Х± I Л2 <^* '2»
Х\ 1~ Х2 I" * * * "I ^ <^ ГЛГ*
Введем в рассмотрение последовательность функций
N
х
где минимум берется по области, в которой
а)
б)
Хк~Т~Хк + 1 <^ Гк\-1
Получить отсюда, что
х
для значений 2^>0, Л=1, 2, ..., А/. Показать, что
= Ш1П [%(^ЛL-/Л + 1(^ + ГйI ДЛЯ /5=1, 2, ..., ЛЛ
81. Показать, что рассмотренная выше задача при дополнитель
ном условии х$+1 — хг^^г+1 может быть сведена к задаче опре
деления последовательности {/&0г, с)} из уравнений
[Мапа^етепЬ 8с1епсе, 3 A956), 111 — 113]
82. Рассмотреть также ограничение ^+1^Хх^.
83. Определить структуру оптимального поведения в случае,
когда уъ(х) являются линейными функциями от х, ср& (х) = гкх,
причем предполагается, что
а)
Структура процессов динамического программирования 137
в) г{ монотонно возрастают до некоторого момента, а потом
убывают,
г) гг монотонно убывают до некоторого момента, а потом
возрастают.
(Лнпгосевич — Гофман)
84. Для данной выпуклой непрерывной функции /(х) известны
два ее значения — положительное /(х^^ О и отрицательное/(х2)<О,
х\ < Х2- Требуется определить положение нуля функции в интер-
интервале [х19 х2]. Задача состоит в том, чтобы минимизировать макси-
максимальную длину интервала, содержащего отыскиваемый нуль и полу-
получающегося после п-кратного последовательно осуществляемого вычи-
вычисления значений функции /(х).
Рассмотрим множество выпуклых функций /, определенных
в интервале [0, 1], со значениями /@)= 1, /A) = — у. Обозначим
через /?п($, у) минимальную длину интервала, на котором можно
гарантировать существование нуля для любой функции этого мно-
множества после д-кратного вычисления ее значений, если известно,
что нуль расположен между 5 и 1. Показать, что
1
У)— Ш1П тах
тах х/?,
, / У&-8)
1-8
X V
/1
тах A
(О. Гросс — С. Джонсон)
85. Человек стоит в очереди в ожидании обслуживания, причем
перед ним стоят N человек. Ему известна полезность г от выстаива-
выстаивания очереди и вероятность р того, что за единицу времени будет
обслужен один человек. С другой стороны, он терпит убюток вели-
величиной с, за каждую единицу времени, потраченную на ожидание.
Задача состоит в определении такого поведения ожидания, которому
соответствует максимальный средний доход.
Обозначим через {у средний доход, получаемый при использова-
использовании оптимального поведения ожидания в случае, когда впереди
стоят N человек. Показать, что
— р)/ю 0], Ы—19 2,... и/0 = г.
138 Глава III
Вывести из этого, что
и определить таким образом оптимальное поведение ожидания.
(Хейт)
86. Рассмотреть эту же задачу при условии, что ожидающий
может стоять в очереди не более чем время Г.
(Хейт)
87. Какое поведение ожидания выбрал бы человек, если бы
он знал, что событие, состоящее в обслуживании одного человека
в каждую единицу времени, — случайное, но не знал бы соответ-
соответствующее ему значение вероятности (/?)?
88. Лесопромышленная фирма обладает некоторым начальным
заданным денежным капиталом, а также лесным массивом. Делаются
следующие допущения:
1. Имеется заданная начальная сумма наличных денег, а доход
поступает как от продажи леса, так и в виде процентов
на наличные деньги. Никакого кредита не допускается, и все
текущие расходы должны быть покрыты наличными или за счет
продажи леса.
2. Деревья можно выращивать только из семян, и нет возмож-
возможности купить молодые деревья вне хозяйства фирмы.
5 3. Годовой прирост древесины зависит от возраста дерева (ско-
(скорость роста не обязательно монотонная функция).
' 4. Стоимость выращивания растущего дерева в течение года
I 1 зависит от возраста дерева.
5. Реализационная цена дерева зависит только от количества
содержащейся в нем древесины, т. е. от его возраста.
6. Цель процесса состоит в максимизации суммы наличных денег
по прошествии заданного количества лет.
Пусть фирма может осуществлять 4 вида деятельности: пускать
деньги в оборот, сажать деревья, выращивать их и рубить лес, причем
1. Деньги можно пускать в оборот на год с доходом г про-
процентов.
2. Деньги можно расходовать на посадку деревьев.
3* Деньги и деревья могут быть использованы для выращивания
более старых деревьев.
4. Деревья данного возраста могут быть срублены на продажу.
,,,. К^к следует поступать в течение заданного периода времени,
чтобы максимизировать полное достояние фирмы, т. е. денежный
капитал и лес?
(МоПоп, Бупагшс рго&гатгшщг, РгосеесИп&з о! ап 1п*егпаИопа1
СоЪГегепсе оп 1при*-Ои{ри{ Апа1у815, Л. АЙШеу апс! 5оп$, 1956).
Структура процессов динамического программирования 139
•9
89. Рассмотрим многокомпонентную электрическую систему,
надежность которой может рассматриваться как произведение на-
дежностей отдельных компонент.
/V-/ N
Для повышения надежности каждого отдельного участка можно
присоединить к системе параллельно ряд элементов. Обозначим
через рк(хк) надежность к-то участка после* параллельного присо-
присоединения к нему хк элементов, а через &ь(хк)— стоимость парал-
параллельного включения хк элементов.
Задача состоит в максимизации общей надежности
при ограничениях
3.) Хк==^ 1, Лу о, ... ,
N
б) 2л(**)<*.
Полагая /^(с) = тахРм(х), показать, что
Г-1 (с — 8 ц (х))]
где максимум берется по области
а) X • ■■ 1,
б) ^(л:)
(Иадель)
90. Предположить, что имеются две „стоимости", одна выра-
выражается в денежной форме, а другая в единицах веса.
91. Изучить связь между следующими задачами:
N ■ N
а) максимизировать Х1л(хй) пРи условиях
N
:2 и хк= 1, 2, ... ,
«1
N N N
б) максимизировать Ц/7Л(л:й)—Хг 2 8и(хк) — \*^Ьк(хк) при
условии хк=\, 2, ... ,
140 Глава III
N N
в) максимизировать Л Рк(хк)— ^1 2и 8к(хк) ПРИ условиях
N
Ъ &к (хк) ^С2 и Хк —
г) минимизировать 2 8лС*»)Ч~*« 2 Ьк(хк) при условиях
=1. 2, ... .
92. Получить соответствующие функциональные уравнения и рас-
рассмотреть вопрос о наиболее удобном способе нахождения числен-
численного решения.
93. Потребность в машинах данного типа задается в виде не-
некоторой функции времени. Требуется определить порядок их при-
приобретения, при котором эта потребность удовлетворяется с мини-
минимальными расходами, в следующих условиях:
1. Покупка одной новой машины обходится в р долларов.
2. Эксплуатация машины в течение рассматриваемого периода
стоит т долларов.
3. Стоимость содержания и ремонта машин в течение рассматри-
рассматриваемого периода является известной функцией имеющегося
в распоряжении числа машин и требуемого числа машин.
Показать, что соответствующее функциональное уравнение имеет
вид
(х)= Ш1П
где гг может принимать только целые неотрицательные значе-
значения 0, 1, 2, ....
Получить решение этого уравнения в случае, когда график
каждой из функций Ьк(х) имеет следующий вид:
оо
и, в частности, рассмотреть случай, когда эти графики представ-
представляют собой параболы, т. е. функции Ь^(х) квадратичны относи-
относительно х.
Структура процессов динамического программирования 141
94. Рассмотреть ту же задачу при условии, что приобретаются
машины двух различных типов с общим вспомогательным обору-
оборудованием, причем потребности в этих машинах независимы.
БИБЛИОГРАФИЯ И КОММЕНТАРИИ
К ГЛАВЕ Ш
§ 1. Основные идеи этой главы вместе с „принципом оптимальности"
были впервые изложены в монографии „Введение в теорию динамического
программирования" (Ап 1Щгос1ис1юп Ю 1пе 1пеогу о! йупаггпс рго^гаттт^,
НАИБ СогрогаИоп, 1953), написанной на основе другой более короткой
работы, выполненной в 1952 г., но не опубликованной тогда. Последняя,
в свою очередь, появилась в результате исследований, проделанных в 1949,
1950 и 1951 гг., и содержалась в ряде неопубликованных статей.
§ 3. Как мы показали недавно в связи с одной совместной работой
[ВеПтап К., Ка1аЬа К., Оп 1пе рппс1р1е о! туаНапЫтЬесЫт^ апс1
ргора^аНоп 1пгои§п тпото^епеоиз тесИа, Ргос. Иаг. АсаЛ. 8с1. [/8А A956)],
„принцип оптимальности" является частным применением того, что мы
назвали „принципом инвариантного погружения".
Частный случай принципа инвариантности был применен В. А. Амбарцу-
мяном в статье „К вопросу о диффузном отражении света мутной средой",
ДАН СССР, 38 A943), 257, и широко развит Чандрасекаром (Чанд-ра-
с е к а р С, Перенос лучистой энергии, ИЛ, М„ 1953). Более раннее, исполь-
использование этого метода восходит к Стоксу E1 о к е 8 О., Ма1петаиса1 апс1
рпузк:а1 рарегз, V. IV, Оп Иле т1еп8.;гу оТ 1пе Н§Ы геИес1ес1 Ггот ог
{гапзтШесЗ 1пгои§п а рПе о! р1а1е8, р. 145—156).
Применяемый повсюду метод функциональных уравнений тесно связан
с методом „точки регенерации", используемым при изучении ветвящихся
процессов [ВеПтап К., Н а г г 18 Т. Е., Оп а§е-Aерепс1еп1 Ыпагу Ьгап-
сЫщ* ргосеззез, Апп. Маш., 55 A952), 280—295].
Мы не пытались здесь систематически проследить происхождение и при-
применение принципов инвариантности, и приведенные выше ссылки составляют
небольшую часть того, что можно было бы привести. Однако нельзя не
упомянуть одной работы Адамара [Нас1атагс1 Л., Ье рпшмре <1е Ниу^епз,
Ви11. 8ос. МаИг. Ггапсе, 52 A924), 610—640), где имеется интересное изло-
изложение, касающееся причинности, функциональных уравнений и принципа
Гюйгенса.
Классическое изложение теории полугрупп имеется в книге Хилла
„Функциональный анализ и полугруппы", ИЛ, М., 1951.
§ 6. Вопрос о представлении задач вариационного исчисления как
непрерывных процессов решения будет детально рассмотрен в гл. IX.
§ 9. Детальное рассмотрение вопроса причинности и оптимальности и
связь его с теорией полугрупп можно найти у Беллмана [ВеПтап К.,
Оупагшс рго^гаттт^ апй а пеш РогтаНзт т 1пе 1пеогу о! т1е§га1 е^иа-
иопз, Ргос. Иа1. Асай. 8с1. Ц8А, 41 A955), 31—34].
Задача 92. См. В е 11 т а п К., Оупатк рго^гаттт^ апс1
тиШрНегз, Ргос Иаи Асай. 8с1. Ц8А, 42 A956), 767—769.
Глава IV
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ
§ 1. ВВЕДЕНИЕ
В предыдущих главах мы описали в общих чертах схематическое
строение процессов динамического программирования и вывели
некоторые общие классы функциональных уравнений. В настоящей
главе мы обобщим частные методы, использованные в гл. I и II при
рассмотрении встречающихся в этих главах уравнений, и докажем
некоторые теоремы существования и единственности для более общих
уравнений гл. III. Нашим основным аппаратом будет восходящий
к Пикару метод последовательных приближений.
Хотя все доказательства по существу проводятся по единой
схеме, но вместе с тем каждое из них в соответствующий момент
требует своего индивидуального обходного маневра. Можно было бы
попытаться объединить все сделанные нами предположения в столь
общих' терминах, чтобы все наши результаты было возможно сфор-
сформулировать в единой теореме. Результатом явилась бы меньшая
ясность и затруднение понимания лежащих в ее основе простых
построений. Вместо этого мы разбили наши результаты на ряд
теорем, относящихся к частным классам уравнений. Однако общий
метод доказательства повсюду остается одним и тем же.
Наш первый шаг состоит в формализации схемы, уже исполь-
использованной ранее для сравнения решений двух уравнений (ср. § 9
гл. I и § 6 гл. II). Получающееся неравенство существенно исполь-
используется в наших доказательствах в этой главе; оно будет применено
снова при рассмотрении многошаговых игр в одной из последующих
глав, а также в теоремах сравнения в вариационном исчислении
(гл. IX).
Первый класс уравнений, который мы рассматриваем, состоит
из уравнений, в которых каждая операция имеет результатом сокра-
сокращение ресурсов; иначе говоря, встречающиеся в них точечные
преобразования являются преобразованиями сжатия в смысле Кач-
чиополи *). Уравнения этого типа мы довольно прозаически назовем
уравнениями первого типа.
Следующий класс уравнений, который мы рассматриваем, состоит
из уравнений, в которых вероятность выживания равномерно убывает
Речь идет об известной теореме Каччиополи — Тихонова (см., на-
з, Петровский И. Г., Лекции по теории обыкновенных дифферен-
[ых уравнений, М.. 1952\ — Прим. ред.
пример, петровский у\. 1 ., лекции ни
циальных уравнений, М., 1952). — Прим. ред
Теоремы существования и единственности 143
с каждой операцией. Это равносильно тому» что соответствующее
функциональное преобразование является преобразованием сжатия.
Такие уравнения мы будем называть уравнениями второго типа.
Уравнения обоих типов имеют в частных случаях вид
A) /(/>) = вир [#(/7, д)-\-Н(р, ?)/(Г(р. Я))\
я.
(все величины, входящие в уравнение, были определены в преды-
предыдущей главе). Как мы увидим, эти уравнения довольно легко под-
поддаются обычным итеративным методам с использованием нашего
основного неравенства. Уравнения, не принадлежащие ни одному
из указанных классов, обычно требуют для своего изучения более
тонких методов, в чем мы убедимся при рассмотрении одного такого
уравнения в § 8. Уравнения, не принадлежащие к первому или
второму типу, мы беззаботно сваливаем в одну кучу, именуя их
уравнениями третьего типа.
Вслед за результатами, касающимися существования и единствен-
единственности, мы обсудим в общей постановке вопрос о монотонной схо-
сходимости и сформулируем некоторые общие теоремы устойчивости,
доказываемые точно таким же образом, как и прежде.
Указав некоторые направления обобщений, которые можно про-
провести довольно далеко, мы, как уже было сказано, изучим
одно частное уравнение третьего типа. Здесь мы имеем комбинацию
двух типов преобразований сжатия, и рассмотрение несколько
усложняется.
Мы завершим главу рассмотрением одного интересного инте-
интегрального уравнения, возникающего в теории „оптимального управ-
управления запасами". Эта тема будет более детально изучена в следую-
следующей главе, где будут получены также конкретные решения.
Рассматриваемые нами уравнения, даже если отвлечься от того
интереса, который они представляют в связи с многошаговыми
процессами решения, обладают тем аналитическим преимуществом,
что они в некоторых отношениях являются естественными обобще-
обобщениями линейных уравнений. Их изучение заслуживает особого вни-
внимания, поскольку они служат мостом между содержащимся в образ-
образцовом порядке заповедником линейных уравнений и до сих пор
непокоренными джунглями нелинейных уравнений.
§ 2. ОСНОВНОЕ НЕРАВЕНСТВО
Рассмотрим два функциональных преобразования:
A) МЛ р. Я)^8(Р> <7)+ }/(г)аО(р, д, г),
, д, г),
144 Глава IV
где сЮ(р, #, г)^>0; определим два других преобразования следую-
следующим образом:
B) а) /2(р)=зир51(/1, р. д\
я
б) /72(р)=8иР52(/71, Р, Я).
я .
Нет нужды входить здесь в обсуждение того, что мы понимаем
при этом под интегралом Стильтьеса, поскольку мы используем его
чисто формальным образом. Фактически все наши результаты будут
использованы для случая, когда
/ 9 д)).
и читатель, не знакомый с интегралом Стильтьеса, должен попросту
совершить это преобразование для того, чтобы свести все уравне-
уравнения к привычному виду, или же он может считать, что с1О(р, #, г)
имеет вид Я(/?, #, т)йг, где Н^>0.
Неравенство, которое мы хотим доказать, составляет содержание
следующей леммы.
Лемма 1.
C) \\
+ / |Л(г)—^(г) |<Ю (р. д. г)]
Л
Доказательство. Сначала упростим обозначения, предположив,
что оба преобразования B) обладают тем свойством, что супремум
в действительности является максимумом. Пусть ^ = ^(р)—то
значение #, при котором достигается максимум в Bа), и ^ = ^(р)—
значение #, ПРИ котором достигается максимум в B6). Тогда, как
и в § 9 гл. I и в § 6 гл. II, мы имеем следующий набор равенств
и неравенств:
D) а) /2 (/?) = 5, (/,. р. я) > 5, (/„ р, д).
б) /%(/>) = *$, С7!. Р' 9)>52(/71, р. я),
из которых непосредственно вытекает
E)
$\ \,д. г)
Теоремы существования и единственности 145
и
1% (р)—Рг 0>Х \ё (р. ч) — л (р. я)} +
В свою очередь эти неравенства приводят к единому неравенству
Я. г),
% г)
из которого непосредственно вытекает неравенство C) *).
Для получения результата в его первоначальной формулировке,
т. е. в терминах супремума, нам остается только заметить, что,
выбрав соответствующим образом д = ^(р), мы можем сколь угодно
точно приблизить значение нашей функции к ее супремуму. Даль-
Дальнейшее осуществляется путем предельного перехода.
§ 3. УРАВНЕНИЯ ПЕРВОГО ТИПА
Наложим теперь следующие условия на функции, входящие
в уравнение A.1):
A) а) функция #(р, с[) равномерно ограничена для всех #^5
и всех р^Ь, удовлетворяющих ограничению ||р || -^ с1э
где И/? ||=( 2^Ри • ^ есть область /?, содержащая нуле-
вой вектор р = 0, и Т (/?, ^) ^ О для всех р ^ О;
б) #F, <7) = 0 для всех ^^5;
в) I А (р. Я)\ < 1 ^-^^ в^х р€® и я€
г) || Г (р. ?)||"<я||р|| &ля некоторого
сю
д) есля ^(с)= зир 5ир|^-(р, у)|, то
||Ц< ^ п-0
Уравнения, которые удовлетворяют этим условиям, называются
уравнениями первого типа. Во многих случаях может оказаться
более удобным и естественным использовать иную норму: ||р|| =
) Мы опираемся на тот простой факт, что из а ■< х -^ Ь следует
х I < шах (| а |, |6|)
10 Р.
146 Глава IV
N
= 2 \рЛ* Впрочем, из последующих рассуждений будет ясно, что
г—1
конкретный способ задания нормы не играет большой роли.
Наш основной результат, относящийся к этим уравнениям, состоит
в следующем.
Теорема 1. Рассмотрим уравнение
B) /(/>) = 81ф [*(/>. ?) + *(/>, я)/(Т(р.
предполагая^ что оно первого типа.
Существует в точности одно решение уравнения B), непре-
непрерывное при /? = 0, обращающееся в этой точке в нуль и опре-
определенное во всей области п.
Это решение может быть получено как предел последова-
последовательности {/п(р)}, определенной следующим образом:
C) а) /о(р)=мР8(р, Я\
я
б)/»+!(/>)= вир
я
Обратно, любая исходная функция /0(р), непрерывная при
/?=0, равная в этой точке нулю и ограниченная для \\р\\^.сг
при любом сг > 0 и р ^ О, может быть использована в C6) для
получения сходящейся последовательности.
Если &(р, я). Ь(р* я) и Т(р, я) непрерывны по р в любой
ограниченной части области П> равностепенно для всех ц ^ 5,
то /(/?) непрерывна в любой ограниченной части области О.
Доказательство. Рассмотрим последовательность, опреде-
определяемую соотношениями C). Используя лемму 1, доказанную в § 2,
имеем для ^\
D) \/п+1(Р) — /»(/>) К вир |*(р. д)\\/„(Т(р, ?) )-/„_, G1 (р.
<зир|/пG(/7> ?))—/„_!(Г(р, д))\
в
и
E) |Л (Р) — /о (Р) | < вир | /о (Г (р, д)) | = зир | * (р.
Определим теперь новую последовательность
ы\<с. р
V
Используя функцию, определенную в пункте Aд), мы видим, что
= V(с). Обращаясь к соотношению D), имеем для р^ О и
Теоремы существования и единственности 147
G) зир|/„+1(р)—
Я V
\/п(р)
\\р\\<ас
в силу нашего предположения относительно Т(р, #)- Следовательно,
л = 0. 1, 2 или Vп(с)^.V0(апс). Поэтому
оо
ряд 2 \1п+\(Р) — /п(Р)\ сходится равномерно при ||/?||<^ с и, зна-
чит, последовательность {/п(р)} при ||/?||^с равномерно сходится
к некоторой предельной функции /(/?).
Это завершает доказательство существования и доказательство
утверждений, связанных со сходимостью и непрерывностью.
Для установления единственности рассмотрим два решения урав-
уравнения A.1) /(/?) и Р (/?), оба непрерывные при. р = Ь и, следова-
следовательно, определенные для всех р^О. Положим
(8) *{с)=ви1р\/(р) — Р(р)\. \\р\\<с,
Применяя лемму 1, имеем
(9) |/(р) — /'(/ОК вир |/(Г(р. я)) — Р(Пр. я))\.
я.
откуда
A0) V(с) ^.V(ас) < ... < ю(апс).
Так как функции /(/?) и Р (/?) при р = в непрерывны, то V(апс) -> 0
при /г->оо. Следовательно, г;(с)^О и /(р) = Р(/?).
Роль леммы 1 состоит в том, что она дает нам возможность
уклониться от рассмотрения поведения, максимизирующего #, как
функции от р. (Это тема большой сложности, о которой вообще
мало что известно.)
§ 4. УРАВНЕНИЯ ВТОРОГО ТИПА
Рассмотрим теперь уравнение A.1), сделав следующие пред-
предположения:
A) а) \ё(р, #)| равномерно ограничена для всех
I Ь(Р> Я)\ "С^ <1 1 &ля 6Сех Я^.$ равномерно в любой
области \\\
в) \\Т(р, <7)||^||р|| для всех р или же п — ограниченная
область, а на Т не накладывается никаких условий,
кроме того, что Т(р, #)^О для всех
10*
148 Глава IV
Уравнения, удовлетворяющие этим условиям, мы будем называть
уравнениями второго типа. Нами будет доказана
Теорема 2. Если
B) /Ы=зир[^(/7, 0 + Л(р, д)/(Т(р, д))]
я
—уравнение второго типа, то оно имеет единственное решение,
ограниченное в любой конечной части области О.
Как и выше, это решение может быть найдено методом
последовательных приближений. Предыдущие утверждения отно-
относительно непрерывности решения остаются справедливыми.
Доказательство. Положим
р1ё(Р Я) + (Р Я)/п((Р ЧI п = 0, 1,2
я
Используя лемму 1, имеем
D)
<а*ир\/п(Т(р, ^))_/п_1
я.
где а < 1, Начиная с этого места, доказательство очевидным обра-
образом повторяет доказательство теоремы 1. Обращение решения в нуль
при р = б теперь является следствием самого уравнения.
§ 5. МОНОТОННАЯ СХОДИМОСТЬ
В предыдущих параграфах мы доказали сходимость процесса
последовательных приближений в предположениях, которые давали
по существу геометрическую сходимость. Покажем теперь, что
в предположении /г(/?, <7)^>0 (справедливом во всех известных
сейчас приложениях) мы имеем в нашем распоряжении такой метод
выбора начального приближения, который вдобавок даст нам моно-
монотонную сходимость.
В некоторых уравнениях третьего типа, в которых сходимость
геометрического типа либо устанавливается с трудом, либо вообще
не имеет места, этот метод весьма ценен.
Рассмотрим наше уравнение в виде
A) /(/7) = шах[#(/7, ^) + /г(/7, Я)ППр. я))].
я
Пусть до = %(р) — начальное приближение к д(р), и пусть функ-
ц-ия /о(Р) определена при помощи этого поведения, т. е.
B) /о(Р) = 8(р. Яо)-\-Ь(Р. Яо)/о(Т(Р. Яо)У>
Теоремы существования и единственности 149
пусть, далее, последовательность {/п(р)}, /1=1, 2 построена
рекуррентно:
. л = 0. 1. 2
(Теперь, после того как введено понятие приближения в про-
пространстве поведений, удобно снова использовать супремум, чтобы
обойти весьма нелегкие вопросы относительно непрерывности по #.)
Предположим, как и в случае уравнений первого и второго типов,
что наложены достаточные условия для того, чтобы последователь-
последовательность \/п(р)} была равномерно ограничена в любой конечной части
области Ь.
Непосредственно убеждаемся в том, что Л(/?)>-/о(р); поэтому
в силу неотрицательности к(р, #) имеем }п+\{р)'^}п{р) для всех п.
Следовательно, \/п(р)} сходится к некоторой функции /(/?) при п-^оо
в любой конечной области И.
Если ^ является элементом некоторого конечного множества 5,
то вопрос о сходимости последовательности {/п(р)} к фактическому
решению уравнения A) не возникает, а супремум в этом случае
будет максимумом. Если 5 содержит континуум, то, возможно, нам
и не удастся доказать непосредственно, что /(р) является ограни-
ограниченным решением уравнения
D)
я
Для того чтобы это установить, заметим, что в силу монотонной
сходимости мы имеем
E) Л,+1(р)<*ир[йЧ/?, 0 + Л(р. д)/(Т(р.
я.
откуда
F) /(РХзирйЧл ?) + Л(р. д)ПТ(р.
С другой стороны, имеем
G) /(/>)>8"Р!*(/>. ?) + А(Р. д)Гп(Т(Р. Ч))\>
К . д))
для всех ^5 и всех п. Устремляя я к бесконечности, мы полу-
получаем неравенство, противоположное неравенству F), а следовав
тельно, и равенство.
Это свойство монотонной сходимости или, в худшем случае,
монотонного приближения особенно полезно в других разделах
теории динамического программирования и, в частности, как мы
увидим в одной из последующих глав, в его приложениях к вариа-
вариационному исчислению.
150 Глава IV
§ 6. ТЕОРЕМЫ УСТОЙЧИВОСТИ
В теории функциональных уравнений проблемой, представляю-
представляющей большой теоретический интерес и имеющей важные физические
приложения, является вопрос о зависимости решения от вида урав-
уравнения. В частности, немало усилий было посвящено определению
уравнений, обладающих тем свойством, что небольшие изменения
вида уравнения вызывают соответственно малые изменения вида
решения. Уравнения, не обладающие этим свойством, как правило,
не представляют большого физического интереса.
Рассмотрим два уравнения
A) а) /(/?) = зир [§•(/?, д)-\-И(р, д)/(Т(р, д))],
я
б) Г(р)=вир[О(р, д)+Н(р,д)Г(Т(р,д))}
й предположим для начала, что оба эти уравнения первого типа.
Мы желаем получить неравенство, оценивающее зир|/(/?) — Р(р)\*
р
/?^О, ||р || <С с, где / и Р — единственные, обращающиеся в нуль
при р — б и непрерывные в этой точке решения соответствующих
уравнений.
Для вывода этого неравенства применим к обоим уравнениям
метод последовательных приближений, полагая
B)
я
я
= 5ир[О(/7, ?) + *(/>. д)Гп(Т(р, д))}.
я
Мы имеем
C) \РЛР)— Л(р)|<8ир|О(р. ?) — *(/>. Я)\
и
D) |/7»+1(р)—/л+1 (Р) I
ч
+ *'(/>. д)\Рп(Т(р. д))-/п(Т(р, д))\Ъ
Положим
E) и(с)= зир зир| О(р, д) — ^(р, д)\.
Ы<е я
Тогда имеет место
Теоремы существования и единственности
151
Теорема 3. Для уравнений первого типа при введенных
выше обозначениях справедливо неравенство
со
F)
8ир \Г(р)—
П—О
Доказательство. Положим
G)
*ир\Рп(р)
Ш<е Я.
Используя неравенство D) и предположения относительно урав-
уравнений первого типа, можно показать по индукции, что
П-1
Устремляя п к бесконечности, получаем F), поскольку Рп (/?)-
Аналогично справедлива
Теорема 4. Для уравнений второго типа при введенных
выше обозначениях имеет место неравенство
(8)
-/("Ж 1^
Доказательство следует по тому же пути, что и выше, и по-
поэтому опускается.
Аналогичные оценки можно получить в случае, когда варьируются
Н (/?, д) и Т (/7,
§ 7. НЕКОТОРЫЕ НАПРАВЛЕНИЯ ОБОБЩЕНИЙ
Первым обобщением уравнения A.1) является уравнение
A)
/(/?)= зир
ч
N
(Р.
г-1
которое в свою очередь представляет собой частный случай урав-
уравнения
B)
/(/?) = 811 р
Я.
Используя" уже известные методы, можно получить аналоги преды-
предыдущих теорем, относящиеся к существованию, единственности и
152
Глава IV
устойчивости для всех этих уравнений, а также для систем вида
C)
/*(/>)= вир
я.
N
%${р* я*г)
1=1. 2 N.
Если исподьзовать векторно-матричные обозначения, то система C)
будет эквивалентна уравнению B).
Примером уравнения вида B) является уравнение „оптимального
управления запасами"
D) /(х)- на
*Ч*. У)+а
У
О—осу))/@)+ { / (у—и) ао <з)
О
которое мы подробно изучим в следующей главе.
§ 8. ПРИМЕР УРАВНЕНИЯ ТРЕТЬЕГО ТИПА
Метод приближения в пространстве поведений, который дает
монотонную сходимость, рассмотренную выше, в § 5, оказывается
весьма полезным при установлении существования решений уравне-
уравнений третьего типа. Напомним, что мы определили этот класс весьма
просто — как дополнительный класс к уравнениям первого и вто-
второго типа.
Установление единственности решения уравнений третьего типа
является, вообще говоря, задачей более высокого уровня трудности.
В этом мы убедимся как в настоящем параграфе, так и в одной из
последующих глав, где рассматриваются „игры на выживание".
В качестве иллюстрации этих замечаний рассмотрим функци-
функциональное уравнение
A) /(р)= ппп
П
7с==0
тш[1+/(Ггр)]
I
• Р Ф
г
де / принимает значения 1, 2 М. Здесь мы полагаем
п
B)
Р = КРо> Р\
г«=0
п
тгР =
Ри =
Теоремы существования и единственности 153
где
1= 1. 2, .. ., М;
= @, ..., 1, .. ., 0), где 1 стоит на к-м месте, к = 0, 1 п.
Здесь /(р) — скалярная функция р.
Это уравнение является весьма широким обобщением уравне-
уравнения, приведенного в упражнении 39 гл. I.
Можно считать, что это уравнение возникает следующим обра-
образом. Известно, что некоторая система находится в одном из Л/' —|— 1
различных состояний, которые мы обозначаем через 0, 1, 2, ..., Л/",
причем априорная вероятность того, что она находится в к-м
состоянии, равна рк. Пусть мы желаем привести нашу систему
к нулевому состоянию с полной уверенностью в том, что это сде-
сделано, посредством некоторой комбинации следующих операций
(каждая из которых совершается за единицу времени) за минималь-
минимальное среднее время:
Ь: мы наблюдаем фактическое состояние системы и продол-
продолжаем наши действия, уже обладая этой информацией;
А: * мы совершаем операцию Аг, которая переводит первона-
первоначальное распределение вероятностей {рк} в некоторое новое
распределение {ркг}.
Пусть р = (р0, рх рн)\ обозначим через /(/?) среднее время,
необходимое для приведения системы к нулевому состоянию при
использовании оптимального поведения, если система находится
вначале в состоянии р. Тогда /(р) удовлетворяет приведенному
выше уравнению A).
Докажем следующую теорему.
Теорема 5. Если для любого преобразования Тг и для всехр
справедливо неравенство
п
C) 2Ри<'!. 0<^<1,
то существует единственное, ограниченное решение уравнения A).
Эта функция положительна при р Ф х0.
Доказательство. Применим метод последовательных при-
приближений, используя в качестве первого приближения некоторое
приближение в пространстве поведений. Обозначим через Ь выбор
п
Л-0
а через 7\ выбор /=1 в уравнении A). Рассмотрим функ-
функцию Ру(р), определяемую поведением, которое мы изобразим
символически ЬТ1ЬТ1 . . . , и функцию Р2(Р)* определяемую
154 Глава IV
поведением ТХ1ТХЬ .... Ясно, что
D) Рг(р)=1+Р2(Т1Р)9 рфхо,
п
(Р) = 1 + 2 РШ ?\ (*к)> Р Ф
й-0
Следовательно, для /= 1, 2, . .., п мы имеем
п
E) РЛх1)=2-\-2$рыРг(хд, 1=1. 2 п.
п
Поскольку, по предположению, 2рй1^*ч <С 1. то определитель
этой системы отличен от нуля и система имеет единственное реше-
решение, обязательно положительное (в этом легко убедиться,* решая
систему с помощью итераций). После определения Рх (хг) функ-
функция Р2(р) и, следовательно, функция Рх(р) для любых р опреде-
определяются непосредственно.
Для того чтобы начать процесс последовательных приближений,
положим
F) /о(р) = т1п[/71(р). Р2(р)],
Л=1
Легко видеть, что /0(/?)^/г(р)>. ... /п(р)^1, р ф Не-
Непоследовательность /п(р) монотонно сходится к некоторой функ-
функции /(/?)» которая, очевидно, удовлетворяет нашему функциональ-
функциональному уравнению. Тем самым существование ограниченного решения
установлено.
Доказательство единственности значительно более сложно и про-
проводится в несколько шагов. Пусть /(/?) и &(р) — два ограничен-
ограниченных решения уравнения A). Нашим первым шагом явится
Лемма 2. зир|/(р) — #(/?)| = тах|/(л:л) —
р к
Доказательство. Неравенство
G)
Теоремы существования и единственности 155
очевидно. Для доказательства обратного неравенства рассмотрим
четыре случая:
(8) а) /0>)=1+2
п
Л-1
б)
в) /(/»)= 1+/G'1/>).
Й-1
Рассмотрим сначала случай, соответствующий (а). Мы имеем
П
откуда
(Ю) |/(Р)-вГ(Р)К«пах|/(*Л)—«Г
Поэтому лемма справедлива для всех /?, для которых имеет
место (8а). Уравнение (8а) будет удовлетворяться, когда р близко
п
к х0, так как в этом случае 1 -+- 2 Рп! (хк) < 2, а 1 -}-/
Л1
Таким образом, 1+/(Тгр)и 1+^(Ггр)при/= 1, 2, .... Ж превзой-
превзойдут результат „хода 1а 1) для р, близких к л:0.
Это — важный момент, так как трудность нашего доказательства
заключается в том факте, что (8а) в силу условия C) всегда будет
иметь место после конечного числа шагов.
Теперь рассмотрим случай (86)". Имеем
A1)
2
*) То есть выбора преобразования
156 Глава IV
Следовательно,
A2) |/(Р> — *(/>)!< тах { шах
Аналогично рассматривается случай (8в).
Из (8г) выводим #
A3)
Теперь будем применять к этим неравенствам процесс после-
последовательных приближений. Для любого фиксированного р вектор
ТггТи • • • Т\ р при достаточно больших п будет лежать в области,
описываемой равенствами (8а). Следовательно, мы получаем
(Н) | |
р к
Этим завершается доказательство леммы.
Остается показать, что тах | / (хк) — § (хк) | = 0. Пусть к — то
к
значение индекса, при котором достигается максимум. Из функ-
функциональных уравнений для /и ^ следует, что
A5)
Как и выше, мы имеем
A6) /(**)= 1
Если оба неравенства являются строгими, то
A7) |/(*Л) —*(**)!<
| — е(Тгхк)\.
р
Получено противоречие.
Таким образом, как для /, так и для V должно быть
A8) /(**)=
или
Это означает, что первые выборы преобразований в позиции хк
могут быть одинаковыми для обеих функций.
Теоремы существования и единственности 157
Теперь рассмотрим ситуацию для вторых ходов. Используя те же
соображения, мы видим, что вторые ходы [т. е. уравнения для
/(Тгхк) и 8(Тгхк)] также могут быть одинаковыми, и т. д. по
индукции.
Пусть рп = рп(хк)—распределение, достигнутое после п ходов,
где (п-\- 1)-й ход переводит хк в область, определенную равен-
равенствами (8а). Приведенное выше рассуждение показывает, что / и ^
попадут в эту область на одном и том же ходе. Таким образом,
п
A9) /(**) = я + 1 + 2 Рьп/(**>>
п
8(хк) = п+\ + ^ ркп8(хк)
и, следовательно,
п
B0) \/{хк) — е (хк) |< 2 Рнп I / (•**) - В (Ч) I
7
7е-\
— РопI 5"р |/(хк) — ё (хк) |.
к
к
Так как 1>рОп>0, то это дает \/(хк) — ё(хк)\==^- Следова-
Следовательно, зир |/(/7) — ^-(/7I = 0, чем завершается наше доказательство
V
единственности.
§ 9. УРАВНЕНИЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ЗАПАСАМИ
В этом параграфе мы рассмотрим уравнение
A)
ь>
к(у — х)-\-а
— У)
оо
+ /@)/
У
оо у
/ /СУ —
у о*
для х^-0, которое уже фигурировало ранее в более общем виде,
содержащем интеграл Стильтьеса. Как мы увидим в следующей
главе, это уравнение встречается при изучении оптимального управле-
управления запасами, или регулирования уровня запасов. Доказательство
существования и единственности решения естественно провести здесь,
так как в нем мы используем те же методы, что и в предыдущих
параграфах.
В соответствии с нашим образом действий, которого мы все
время придерживались, мы не будем рассматривать общего урав-
уравнения, содержащего интеграл Стильтьеса,
158 Глава IV
Для упрощения последующих обозначений положим
г- оо
I- V
оо у
+ /@) \Ч(8)й8-\-\
У 0
Тогда уравнение A) примет вид
C) /(*)= 1ШТ(уш х, /).
Сделаем следующие предположения:
оо
D) а) ср (^) ^> 0, I ср E) из = 1;
о
б) функция /7E) монотонно возрастает, непрерывна и
оо
о
в) функция к (у) непрерывна при у^О; к(оо) = оо;
г) 0<а<1.
В этих условиях имеет место следующий результат.
Теорема 6. Существует единственное решение уравнения A),
ограниченное по х в любом конечном интервале. Это решение /(х)
непрерывно.
Пусть /0(х) — любая неотрицательная непрерывная функция,
определенная для х^О.
Определим последовательность {/п(х)} следующим образом:
E) /п+1С*0= т*п Т(У. х. /п), л = 0, 1, 2
Тогда /(*)= ^т /п(х) существует для ^>0и является реше-
П->СО
нием уравнения
F) /М= т!п Т(у9 х,/).
Доказательство. Доказательство идет хорошо знакомыми
путями. Для любого п^1 рассмотрим Уп = Уп(х) — тб значение у,
при котором Т (у, х, /п) достигает минимума. Поскольку функ»
ция /г(х) по предположению непрерывна, убеждаемся по индукции
в том, что каждый член нашей последовательности также непре*
рывен. Так как Г(оо, х,/п)~оо, то минимум достигается,*
Теоремы существования и единственности
15Ф
Мы имеем
G)
/п+1 = Т(уп, х, /п) < Т(уп_1% х, /п),
х,
(8)
Комбинируя обычным образом эти неравенства, получаем
— /п1<тах{|Г(.уя, х.
х./п_д\.
или
(9) 1/я+1 —
о
оо
-! Су»
* 4-
оо
Следовательно,
A0) тах
оо
оо
тах
0<а?<оо
тах
0<а?<оо
сходится равномерно
Таким образом, ряд 2[/п+1(л:)
в любом конечном интервале для всех х^О, и /п(х) сходится
к /(х) для всех х^О. Так как все /п(х) непрерывны, /(х) также
непрерывна.
Для доказательства единственности рассмотрим другое реше-
решение Р(х), равномерно ограниченное при х^>0. Используя те же
методы, что и выше, применительно к двум уравнениям
A1)
й1 70/, х. Г),
у>х
/(*)= т!п Т(у. л:,/),
160 Глава IV
мы легко убеждаемся в том, что разность Р(х)—/(х) тождественно
равна нулю. Случай, когда в уравнении A) тт заменяется на т!,
снова исчерпывается процессом приближения.
Отметим, наконец, что, полагая
оо
Ь(У — х) + а §р(8 — у)
A2) Л(*)= пНп
/2(х) = тт [ГСу, х9 Д
и т. д., мы получаем монотонно возрастающую сходящуюся после-
последовательность, так как /2 (х) ^Д (х) и, следовательно, по индукции
С другой стороны, мы можем получить монотонную сходимость
также и приближением в пространстве поведений. Можно положить
у = х для всех ^>0 и получить в качестве первого приближения
СО X
Г I Г
A о) /1 (х) — а | р (8 — х) ср E) аз -\- а I
о о
оо
для х>
Это уравнение представляет собой „уравнение восстановления";
его решение мы исследуем в добавлении к следующей главе.
Определим /2(лг) посредством уравнения
A4) /2(*)= тт
у>х
оо
к (у —.х) + а { р(8—у)у(8)а8-)г
оо г/
у о
Отсюда следует, что /2(Х)^С/\(Х)- Таким образом, полагая
= т!п Т(уу х,
мы получаем монотонно убывающую сходящуюся последовательность.
УПРАЖНЕНИЯ И ПРОБЛЕМНЫЕ ЗАДАЧИ
К ГЛАВЕ IV
1. Определить структуру оптимальных поведений, соответствую-
соответствующих функциональному уравнению
= тах
я.
Теоремы существования и единственности
161
в предположении, что /?(/?, я) и Т(р, я)— выпуклые функции от р
и # и что /?(/?, й и Г(/?, #)— монотонно возрастающие функции отр
при любом я-
2. Провести подробное доказательство теоремы существования
и единственности для системы уравнений
тах
я
N
, г)
=1, 2, • • •, N,
3. Показать, что мы получим уравнение, принадлежащее к этому
классу, если в задачу 45 гл. I ввести дополнительное условие: на
каждом шаге известна вероятность рг того, что реализационная цена
будет описываться функцией 8гA)9 и вероятность р2— I—Р\ того,
что она будет описываться функцией $
4. Рассмотрим многомерный процесс, в котором ресурсы на
каждом шаге измеряются неотрицательным вектором р. На каждом
шаге вектор р разделяется на г неотрицательных векторов ц^ т. е.
г
В результате такого распределения мы получаем доход
К {я) = /? (^), издержки, при этом составляют 2@'» ?/)• [ЗДесь (^. Я)
1
3
обозначает скалярное произведение двух векторов.]
Обозначим через Рм(г) издержки, которые имели место при
получении общего дохода г за N шагов при использовании опти-
оптимального поведения. Показать, что
N
Рх(г)= гшп
П+1
Ш1П
5. При каких условиях предельное уравнение
Ш1П
имеет решение?
6. Как можно сформулировать математически следующую задачу?
Мы заблудились в лесу, форма и размеры которого точно нам
известны. Как выбраться из леса в кратчайшее время?
И Р. Беллман
162 Глава IV
7. Рассмотреть случай, когда „лес" представляет собой область,
заключенную между двумя параллельными прямыми.
(О. Гросс)
: 8. Обобщить результат теоремы 5, рассматривая процессы,
в которых на каждом шаге имеется либо счетное множество, либо
континуум различных преобразований.
9. Рассмотреть еше более общий процесс, в котором имеется
счетное множество или континуум состояний.
10. Вывести функциональные уравнения, отвечающие нелинейным
критериям, и установить соответствующие теоремы существования
и единственности.
11. В частности, рассмотреть для стохастических процессов кри-
критерий максимизации вероятности получения дохода, не меньшего,
чем /?0.
12. Рассмотрим уравнение
х2-{-ах — Ь, а, Ъ > 0.
Поскольку для х ^> 0
х2= тгх[2хи— а2],
и > 0
это уравнение можне записать в виде
тах [2хи -{-ах — и2] = Ь.
Отсюда для положительного корня имеем
С другой стороны, полагая х2 — у, мы можем написать
П>0
получая
"~ аи
у= тах
Таким образом, для 0^и^2Ь1а имеем
Теоремы существования и единственности 163
13. Распространить эти результаты на уравнение хп -\- ах = Ь.
Показать, что для подходящим образом выбранных функций
и Н{и)
хп = тах [хи — § (и)], п > 1,
хп = т1п[хи-{~к(и)], О
откуда для #> 1 будет
х = пип
а для 0 < гс < 1
14. Показать, что если функция ср(х) строго выпукла и диф-
дифференцируема, то
ср (х) = тах [ср (и) — (а — х) ср' («)];
и
если же она вогнута, то
ср(х)= Ш1П [ср(«) — {а—х)у' (и)]*
и
Дать два доказательства — аналитическое и геометрическое.
15. Рассмотреть многомерный аналог предыдущей задачи:
ср (хг, х2) = тах ^ (аг, и2) — (иг — х
для выпуклых функций. Получить соответствующий результат для
вогнутых функции.
16. Изучить возможность использования этих результатов для
получения явных решений нелинейных систем вида
где функции срх и ср2 обе вогнутые или же обе выпуклые.
17. В методе Ньютсна строится последовательность приближений
к решению уравнения /(х) = 0. Показать, что если //(х)у>0 и
///(х)>0 в интервале [а, Ь], то для корня в этом интервале имеем
х = тш \у тпгА*
Полуяить соответствующие выражения для многомерного случая,
11*
164
Глава IV
18. Рассмотрим два уравнения:
а) V(р) = ^(V, р,
б) я(/?) =
, д\
, д)],
где и (/?) — скалярная функция вектора р, принадлежащего некото-
некоторой области /?, а д—векторная переменная, принадлежащая мно-
множеству 5, которое может зависеть, а может и не зависеть от /?.
Предположим, что
(.1) для любого фиксированного д = д(р) существует единствен-
единственное решение уравнения (а), обозначаемое через V(р, д), где р^Н;
B) для р^Н существует единственное решение уравнения (б);
C) если <ш(р)^Цуй, р, д)-{-а(р, д) для некоторого фиксиро-
фиксированного д = д(р)9 то '0^(р)'^'V(р9 д).
Доказать, что при этих предположениях
, д).
19. При каких предположениях относительно матрицы А(р, д) —
= \\а^(р, д)\\ решения систем
N
= тах
я.
/=1. 2 А/,
или
тах
N
Щ (Р> Я) Щ (/?) + 2 а%з (Р> Я)
/=1, 2 N.
можно определить таким же способом, как и выше?
20. Пусть Рх (х) = Ог (х) = х и
Доказать, что
1 1
Ит Г ... Г Р
1Ш I ... I
Ит
= 1 тс/3
О
[Гросс—Ван, Атег, Ма1Н. МопШу, 63, Яз 8 A956), 589.1
Теоремы существования и единственности
165
21. Пусть уь—независимые случайные величины, принимающие
значение 1 с вероятностью р и значение 0 с вероятностью 1 —р.
Пусть XI — некоторый набор положительных величин. Положим
хг)
N
Показать, что
и, таким образом, получить некоторую нетривиальную равномерную
оценку снизу для
22. При каких условиях существует единственное решение урав
нения
и (х) = гшп
й (х + ду). О < л: < С,
= 0, л:<0,
(л:) = 1, х >- С,
где для 0 < * < С
а)
б)
О,
Рассмотреть случай, когда х принимает только дискретное мно-
множество значений {&Д} и а^ = т^Д, где т^ — целые числа, отлич-
отличные от нуля.
23. Вернемся к задаче 15 из упражнений в конце гл. III. Пока-
Показать, что задача определения минимальных расходов эквивалентна
N
задаче нахождения минимума линейной формы
2
г=1
г ПРИ
условиях
а) х,
б) Хк~\~Хк+1 Н" • • •
где Хлг,,'=х1^,
= 1, 2, .... N.
8с1епсе9 1957)
166 Глава IV
24. Рассмотреть более общую задачу определения минимума
линейной формы ^О0 = .У1 + .Уа+ ••• Л'Уц ПРИ условиях
Для фиксированного г положим /^ E) = пип I (у) (N^2). Пока-
Показать, что
где 5*= тахE, 0).
Показать, что
/к(8) = тгх(8-\-ик, VII), Л = 1. 2, ...,
где #Л и т^Л — функции от г.
25. Показать, чтб для
где
26. Рассмотреть сходным образом задачу о минимизации линей
N
N
ной формы Ьк(х)= 2^хг при условиях
г—1
а) х
б) хх
в) лг1
г) х1
%2 I
Теоремы существования и единственности 167
27. Рассмотреть задачу о минимизации линейной формы
N
при условиях
а)
б)
2*^2 I* ^23-^3
-1, N-1XN-1 I *Л"-1,
В) Х Ш
При подходящих предположениях относительно коэффициентов ^
получить соответствующее функциональное уравнение и аналоги при-
приведенных выше результатов.
28. Предположим, что мы имеем карту, на которую нанесено
различных пунктов, перенумерованных в некотором порядке числами
от 1 до N. Пусть гц (/, у=1, ..., Л^) — время, необходимое для
переезда из пункта / в пункт у, причем ^ = 0. Мы хотим, затра-
затратив минимальное время, переместиться из пункта 1 в пункт Ы, про-
проходя при этом каждый из остальных пунктов (и только их) в ка-
качестве промежуточных остановок.
Пусть /^ обозначает время, необходимое для того, чтобы попасть
из пункта / в пункт NA= 1, 2, ..., N—1, /# = 0) при исполь-
использовании оптимального поведения, Показать, что
/=1,2 N—1.
29. Показать, что это уравнение имеет решение {/$}, единствен-
единственное с точностью до постоянного слагаемого.
30. Показать, что любого из этих решений достаточно для того,
чтобы определить оптимальное поведение.
31. Рассмотрим следующую аппроксимацию в пространстве пове-
поведений:
при /== 1, 2, ..., М— 1. Определим последовательность {/|Л)} сле-
следующим образом:
1=1, 2 ЛГ— 1; к^\,
168 Глава IV
Показать, что векторы У\к)] сходятся к решению указанного выше
функционального уравнения и, следовательно, могут быть исполь-
использованы для определения оптимальных поведений.
(ВеИтап К., А гои{т& ргоЫет, С}иаг{ег1у о/ АррИей
МаШетаИсз, 2, № 4 A957), 523—525.)
2N
32, Рассмотреть задачу о максимизации суммы ^й'гС**) ПРИ
2Ы
условиях 2*1^^» Х1^>0. Показать, что эта задача эквивалентна
задаче максимизации выражения /# (.УО + й# О>2) ПРИ условиях
=с. где
N
2
1=1
2N
= таХ
а области /?х и /?2 определены следующим образом:
N
2N
/?2: ^ > 0, 2 хг <
Какими вычислительными преимуществами обладают этот прием
и его естественное обобщение? Рассмотреть многомерный случай.
33. Игрок получает по каналу связи с шумом предварительную
информацию об исходах последовательности независимых спортив-
спортивных встреч. Будем предполагать, что исход каждой встречи является
результатом игры между двумя одинаково искусными командами и
что вероятность правильной передачи равна /?, а вероятность непра-
неправильной передачи равна ц = 1 —р.
Предполагая, что игрок имеет начальный капитал х и держит
пари об исходе каждого состязания, чтобы максимизировать свой
ожидаемый капитал после /V шагов игры, показать, что он ставит
весь свой капитал на каждом шаге при условии р > 1/2 и не ста-
ставит ничего, если р < 1/2.
34. Предположим, что наш игрок играет так, чтобы максимизи-
максимизировать математическое ожидание логарифма своего капитала после
Л/ шагов. Предполагая, что на каждом шаге он применяет одну и
Теоремы существования и единственности 169
ту же тактику заключения пари, определить отношение каждой его
ставки к общему капиталу.
(КеПу Л., А пе>у т^егргеЫюп о! ттогтаиоп га!е, 1956,
Зутрозшт оп ШогтаИоп Тпеогу, Тгапз. /. /?. Е. A956),
185—189.)
35. Предположим, что игрок играет так, чтобы максимизировать
математическое ожидание логарифма своего капитала после N шагов.
Пусть /лг(х) обозначает эту ожидаемую величину, получаемую при
использовании оптимального поведения. Показать, что в предполо-
предположении равенства шансов
Лч-1( тах [Р/л(* + -У) + «М* — УI N=1,2
где
/()= тах
[По поводу этого и следующих результатов см. ВеПтап К., Ка-
1а Ь а К., Оп Ше го1е о! (Зупагшс рго^гатт1п^ 1п 5Ш15иса1 сотти-
П1саИоп 1Ьеогу, ТгапзасНопз /. /?. Е. оп 1п/огтаНоп ТНеогу, 3,
3 A957), 197—203.]
36. Доказать по индукции, что
/м (х) = 1ое х + Мк,
где
к= тах [р 1оеA + г) + ?1оеA—г)],
0<г<1
и, следовательно, существует такое число г0, что оптимальное пове-
поведение на каждом шаге определяется соотношением у = гох.
37. Рассмотреть нестационарный случай, где вероятность пра*
вильной передачи зависит от номера шага. Установить соответствую-
соответствующее функциональное уравнение и выяснить структуру оптимального
поведения.
38. В случае, когда целью процесса является максимизация мате-
математического ожидания дохода или логарифма дохода после N шагов,
проведенный выше анализ показывает, что оптимальное поведение
не зависит от количества ресурсов, имеющихся на каждом шаге.
Рассмотреть задачу нахождения класса функций критерия, обла-
обладающих следующим свойством. Пусть ср(х)—монотонно возрастаю-
возрастающая вогнутая функция, определенная для 0<^л;<оо и нормализо-
нормализованная условием ср'A)=1. Рассмотрим одношаговый процесс,
в котором мы желаем максимизировать
— Р)9(х — У)
170 Глава IV
по всем у^[0, х], где 1]>/?>1/2. Показать, что если для всех
лг>0 существует максимум вида у = г(р)х, то мы должны иметь
уй + 1
=
или, как предельный случай,
ср (у)
39. Рассмотрим случай, когда последовательные сигналы не
являются независимыми. Пусть вероятность правильной передачи
на к-м шаге зависит от правильности передачи сигнала на (к—1)-м
шаге. Для х>0 и й=1,2 N определим
/к(х) как математическое ожидание логарифма конечного капи-
капитала, получаемого на остающихся к шагах исходного
Л^-шагового процесса при использовании оптимального
поведения, если начальный капитал равен х и (к—1)-й
сигнал был передан правильно,
ёк(х) как соответствующую функцию в случае, когда (к—1)-й
Сигнал был передан неправильно.
Тогда
/*(*)= шах
ёк(х) =^ тах [?^.Л+1Д.,^ + у)^A—д^к^)ек^{х — у)].
где
рк — вероятность правильной передачи к-го сигнала, если (к— 1)-й
сигнал был передан правильно,
<7&— вероятность правильной передачи к-го сигнала, если (к— 1)-й
сигнал был передан неправильно.
Показать, что /к(х)= \о%х-{-акш 8к(х) — \о%х-\-Ьк. Определить ак
и Ьк и выяснить структуру оптимального поведения.
40. Рассмотрим случай, когда канал передает любой из М раз-
различных символов. После получения символа игрок должен заклю-
заключить пари о том, какой, по его мнению, сигнал был в действитель-
действительности передан. Пусть игрок обладает следующей информацией:
— условная вероятность того, что был послан сигнал у, если
принят сигнал /;
— вероятность приема сигнала /;
Гу —доход от единицы ставки при выигрыше пари о сигнале/.
Пусть игрок вправе поставить сумму х\ относительно сигнала /
при условии 2^<Сл;. Определяя последовательность {/#00}. как
Теоремы существования и единственности
171
и выше, показать, что
м
= 2 Яг
тах
м
Л (*) = 2 Яг
2 Рц
^'1
м
8=1
л:
8-1
Доказать, как и выше, что /^(л;) — 1о^ х~\-Мак% определить яй и
выяснить структуру оптимального поведения. Показать, что опти-
оптимальное поведение не зависит от ^.
41. Рассмотреть случай, когда имеется непрерывное множество
различных сигналов. Пусть йО{а, V) — условная вероятность того,
что послан сигнал, лежащий между V п ъ-\-йю при условии, что
принят сигнал и.
йН(и) — вероятность того, что на некотором шаге принят сиг-
сигнал, лежащий между и и и-\-йи.
Показать, что соответствующие функциональные уравнения имеют
вид
ос
Г
тах
—оо _
оо
оо
—со
оо
аН(и),
Л(*) = Г тах Г \ъ%{2г(р))йО(и, V)
% (ь)
—оо _ —оо
аН(и),
где для простоты предположено, что шансы равны и что должны
ставиться все деньги. Максимизация производится по всем функциям,
удовлетворяющим условиям
оо
а) х (V) ;> 0, б) Г г (у) (IV = х.
—оо
Выяснить вид /д(х) и структуру оптимального поведения.
42. Рассмотреть случай, когда р само является случайной вели-
величиной, подчиненной известному распределению вероятностей.
43. Рассмотреть случай, когда распределение вероятностей не-
неизвестно. Однако мы располагаем априорной оценкой (Ю(р) и при-
принимаем, что после к верных передач и / неверных новая априорная
172 Глава IV
оценка должна быть
Лр)-
-а.
/
рК{\-р)ЫО(р)
О
44. Несколько промышленных предприятий, расположенных вдоль
реки, перенумерованы с севера на юг: 1, 2 N. Вниз по реке
протекает определенное,количество воды, которое по пути следует
распределить между этими предприятиями. Предположим для начала,
что вода, потребленная одним предприятием, не может быть исполь-
использована остальными. Определить распределение воды, максимизирую-
максимизирующее общий доход всего комплекса предприятий.
(У. Холл)
45. Рассмотреть ту же задачу в предположении, что определен-
определенное количество воды, использованной каждым предприятием, воз-
возвращается в реку — либо в том же месте берега, либо на несколько
„шагов" ниже по течению.
(У. Холл)
46. 'Пусть производственные отходы каждого предприятия загряз-
загрязняют воду, причём стоимость использования этой воды зависит от
Степени загрязненности. Определить оптимальную политику рас-
распределения для этого случая.
(У. Холл)
47. Пусть количество имеющейся воды, а также спрос на нее
являются сезонными. В различных местах вдоль реки имеются пло-
плотины, с помощью которых могут создаваться запасы воды. Опре-
Определить оптимальную политику распределения.
(У. Холл)
48. Рассматривается задача о строительстве вдоль реки п раз-
различных промышленных предприятий, /-е предприятие обладает объ-
объемом производства т^, сбрасывает в реку производственные отходы
в количестве щ и может использовать воду со степенью загрязнен*
ности ^, которая должна быть выше суммарного загрязнения воды
предприятиями, расположенными выше по течению. Нужно выбрать
некоторое подмножество из этих п предприятий для их строитель-
строительства вдоль реки так, чтобы максимизировать общий доход пред-
предприятий.
(Л. М. К. Бёлътер)
Показать, что это задача о максимизации по 2пп\ выборам и что
последнее число можно снизить д.01) [п\* е]—1.
(О. Гросс — С. Джонсон)
*) [а] здесь обозначает целую часть а. — Прим. перев.
Теоремы существования и единственности 173
49. Показать, что всякое оптимальное решение может быть без на-
нарушения оптимальности переупорядочено в порядке возрастания вели-
величин 1{-\-щ и что поэтому подлежат рассмотрению менее чем 2п случаев.
(О. Гросс — С. Джонсон)
50. Пусть V^=\ для 1=1, 2 п. Показать, что в этом
случае оптимальное решение может быть найдено при помощи сле-
следующего процесса:
а) упорядочить и перенумеровать все предприятия в порядке
возрастания величин ^
б) вычислить $$ = 2 щ и
*1
в) если йк < 0 является первым нарушением *), то вычеркнуть
в множестве /^й то предприятие, для которого чю{ наибольшее;
г) выполнить вычисления шага (б) для нового множества и по-
повторять шаги (б) и (в), пока все нарушения не будут удалены.
(О. Гросс — С. Джонсон)
51. Показать, что в общем случае оптимальное решение содер-
содержит не больше предприятий, чем содержится в оптимальном реше-
решении для той же задачи, когда все т^ равны между собой.
(О. Гросс — С. Джонсон)
52. Рассмотрим задачу нахождения приближенного решения си-
системы уравнений /(х, у) = а, $(х, у)==Ь. Пусть {хк, ук] (& —0,
1, 2, ...) — некоторая последовательность предполагаемых реше-
решений и
Принимая, что хо=с19 уо = с2 и (х{+1 — х{J-+-(уш-\-угJ <г3
при / = 0, 1, 2 положим для N = 0, 1, 2, ...
/#(^1. С2)= Ш1П
Показать, что
а
где область /? определяется соотношением (хг — сгJ + (уг — с2J ^ г2.
53. Пусть х1 = с1-\-гсо$в, у1 = с2-\-г$[пв, где 6 — малая вели-
величина. Тогда
Имеется в виду первый индекс к, для которого йъ<Ч).—Прим. перев.
174
Глава IV
Определить отсюда приближенные значения соз б и $шб. В чем за-
заключается связь с классическим градиентным методом?
54. Рассмотрим задачу определения чебышевской нормы
— гшп шах
N
-2 V
*
Выяснить сходимость следующей схемы,
приближение; определим с'о как минимум
N
тах
Пусть
начальное
затем определим сх как минимум
тах
N
И Т. Д.
55. Предположим, что мы хотим направить ракету к Луне.
Ввиду сложностей в постройке и значительной цены ракеты, вызван-
вызванных необходимостью нести большие количества топлива и топливные
баки, мы пытаемся сократить количество требуемого топлива и
размеры ракеты путем создания многоступенчатой ракеты следую-
следующего типа1):
«—Головной—■
конус
Вторая
ступень
Первая
ступень
Лодракета V
Подракета 2
После того как топливо, имеющееся в последней (&-й) ступени,
будет израсходовано, эта ступень отделяется, оставляя (к—1)-
ступенчатую ракету и т. д.
Задача заключается в том, чтобы построить /г-ступенчатую
ракету минимального веса, которая достигла бы окончательной
скорости V. Введем обозначения:
1) Мы сохраняем терминологию оригинала. Обычно ступени ракеты
нумеруются в обратном порядке. — Прим. перев.
Теоремы существования и единственности 175
— начальный брутто-вес подракеты к;
чюк—начальный брутто-вес ступени к\
рк — начальный вес горючего в ступени к\
юк—изменение скорости ракеты во время горения ступени к.
Предположим, что изменение скорости Vк является известной
функцией от Шк и рк, т. е. <ок = у(урк, рк) и, следовательно,
рк=р(№к,^к). Поскольку №уй = №й_1-|-«0*» а вес &-й ступени
есть известная функция &(рк) количества горючего, находящегося
в этой ступени, мы имеем
откуда, разрешая это уравнение относительно *№к> получаем
Пусть /й(г>) обозначает минимальный вес подракеты к, дости
гающей окончательной скорости V. Тогда для к^>2 мы имеем
причем
/0(«у) = \^0 (У70—вес головного конуса),
= тт о
О < ^ < V
(Р. Я.
56. Рассмотрим задачу о минимизации линейной формы /,>(л;) =
= 2 х* по всем неотрицательным л:^, удовлетворяющим следую-
щим ограничениям:
^11-^1 I ^12-^2 I ^13-^3
^21'^'1 I* ^22-^2 I* ^23-^3
^31-^1 I ^32-^2 [ ^33-^3 "I Х 4
аиХ* I а4ЬХЬ \ ^46-^
-2, 3#-2 -^3^-2 + ^3^-2, 3^-1 #3#-1 + ^3^-2,
Г, 3^-2 -^3^-2 + ЯЗДГ, 3^-1 ^3^-1 +
и хг > 0, где ^ > 0, ^ > 0,
176
Глава IV
Определим последовательность функций
г (г) = тах Ъ^ (х),
где хг удовлетворяют всем приведенным выше ограничениям, за
исключением последнего, которое теперь принимает вид
Показать, что при
где
^-1 (^3^-3 ##-.
подчинены ограничениям:
ЗЛ"-2, ЗЛ"-
3^-2-^3^-2 + ^3^-1, 3^-1-^3^-1+^3^-1, ЗЛТ
-2 +
-1 +
0.
Функцию
принимаем тождественно равной нулю.
57. Получить соответствующие результаты для случая, когда
рассматриваются матрицы различных порядков1).
58. Рассмотреть случай, когда неравенство с номером Ък (к =
= 1, 2, ...) имеет вид
Матрица ограничений в предыдущей задаче имела вид
аЬЪ
аТ1
(Такого рода матрицы в зарубежной литературе иногда называются квази-
блочнодиагональными.) По-видимому, автор предлагает для исследования
случай, когда квадратные диагональные блоки матрицы ограничений имеют
различные порядки. — Прим. перев.
Теоремы существования и единственности 177
59. Показать, что указанное выше функциональное уравнение можно
привести к виду
где Хън-2 удовлетворяет неравенству
60. Рассмотрим задачу о решении системы линейных уравнений
вида
а\\Х1 I ^12-^2 I ^13-^3 == ^1»
^21^1 1~ ^22*^2 I" ^23-^3 ^2»
^31-^1 I ^32-^2 I ^33-^3 I ^1-^4 == ^3»
ЬХХЪ + «44X4 + «45-^5 + «46^6 = ^
аЬ4Х4 \ аЬЬХЬ I ^56-^6 == ^5»
где \\ау\\—симметрическая положительно определенная матрица.
Линейные системы такого типа возникают при изучении много-
многокомпонентных систем, в которых имеется слабое взаимодействие
между отдельными компонентами.
Задача решения этой системы эквивалентна задаче нахождения
минимума неоднородной квадратичной формы
;2, Л2х2)+ ...
— 2(с\ х1) — 2(с2, х?)— ... —
где векторы хк и ск определяются следующим образом:
к =
Х
а Лк= ||«г+зл,;+зй||» /, 7=1, 2, 3.
Показать, что эта задача может быть сведена к задаче на-
нахождения последовательности {/#(<г)}. определяемой рекуррентным
12 Р. Беллман
178 Глава IV
соотношением
= тш [(х* Амх*) — 2гхъы — 2
(а?зЛГ,
AШпо18 ЗопгпаЬ о/ МаЫгегпаНсз, 1957)
61. Показать, что.рекуррентное соотношение предыдущей задачи
можно привести к виду
{г) = гшп [$ы (г, у) +/лг_1 Фы-1У)\.
У
где
62. Показать, что/^(^) = ^ + г;Аг'г:-|-'а;^^2. где и^, ъх, 10^ не
зависят от г, определить рекуррентные соотношения, связывающие
(Цн* ^у. ^1\) и (йлг-1. ЗД-1. ^у-1), и найти отсюда решение линей-
линейной системы задачи 60.
63. Рассмотреть задачу нахождения максимума выражения
N N-1
Як (X) = 2 (** ■ Агх1) + 2 2 МЛ+3г
сфере 5^: 2
на
Рассмотреть соответствующие функции от хъ определяемые
соотношением
С?) = тах [<Эн (х
и. получить рекуррентное соотношение, связывающее /#B) и
ч
64. Обобщить предыдущие результаты на случай, когда мат
рицы Ак могут иметь различные порядки1).
65. При надлежащих предположениях получить теоремы суще
ствования и единственности для следующих функциональных урав
нений:
а) /(р) = гшп тах [#(/?, ч). /(Г(рш д))]ш
ч
б) /(р) = т!п тах [§{р% Я\ Н(р, ^)/(Г(р, д))].
д.
/(р)=т\пт&х[8(р. д), г(р, д)+ [/(г)AО(г, р. д)}.
а •*
4
а
4 Е
Ср. примечание на стр. 176. — Прим перев.
Георемы существования и единственности 179
66. Рассмотрим задачу распределения п различных работ по ш
различным типам машин. Пусть А^^О— количество работы у,
выполняемое при однократном использовании машины /. Пред-
Предположим, что
а) если Ац > 0 и V < /, то Ащ > 0;
б) если Ац > 0 и/> у, то Ац> > 0;
в) если / < Г, у < у", Ап > 0, то 4^ <
Э г 3
Пусть Хц—количество машин типа I, которое используется
на работе у. Матрицу х= 11-Хг^Ц, /=1,2 т; у = 1, 2 л,
назовем допустимой, если
га м
Хц > 0, 2 ^-^У = Тр ) = !» 2. • • • • Л- и 2 х^ < ^г.
/ = 1 , 2, • « « » /%.
Рассмотрим следующее поведение. Возьмем в качестве хп
минимум 7\ и Мх. Если хп= 7^ то определим дг12=п11пG2, Мх—хп)
и т. д. Когда Мх будет в результате использовано целиком на у-й
работе для некоторого у, распределим х2^ таким образом, чтобы
либо вся работа у была выполнена, либо все машины типа 2 были
распределены. Аналогично закончим все распределение.
Показать, что если это поведение не приводит к допустимому
размещению, то допустимого поведения не существует.
(/С. Эрроу — Г. Марковиц — С. Джонсон)
67. Показать, что описанное выше поведение дает решение задачи
т
о максимизации Тп= 2 ^гпхгп ПРИ условиях.
п
т
лч "V А V Т / 1 9 и
где Ац удовлетворяют приведенным выше условиям.
(С. Джонсон)
N
68. Показать, что задача максимизации суммы 2 ёъ(хг> Уд ПРИ
ограничениях
N
а) х> 0 2 х' *
б) л<о. 2 л=
12*
180 Глава IV
при надлежащих предположениях относительно функций ^(х, у)
может быть сведена к задаче максимизации выражения
N N
Уг
при условиях
N
а) хг !> 0, 2 хг = *•
б) Л > 0.
Эта последняя задача приводит к рекуррентным соотношениям
= шах
определяющим для каждого фиксированного X некоторую последова-
последовательность функций одной переменной.
Как использовать решение этой второй задачи для решения
исходной?
(Ргос. Ыа{. Асай. За. ЦЗА, 1956)
69. Каждый год урожай грецких орехов состоит из орехов
различных сортов, скажем О19 О2, . .., Оъ в количествах цх% цг% ...
.... ^Л. Для коммерческой продажи по различным ценам со-
составляют ассортиментные наборы орехов, используя различные
количества орехов каждого сорта. Пусть нам известны фиксирован-
фиксированный спрос 6.1 на /-й набор и фиксированное количественное со-
соотношение орехов различных сортов для каждого набора. Сколько
пакетов каждого набора нужно изготовить, с тем чтобы максими-
максимизировать общую выручку?
70. Рассмотреть случай стохастического спроса с известными
распределениями спроса для каждого типа пакета1).
БИБЛИОГРАФИЯ И КОММЕНТАРИИ
К ГЛАВЕ IV
§ 1. Эта глава следует изложению Беллмана (В е 11 ш а п К., Рипс1юпа1
е^иаиопз т 1Ье 1Ьеогу о! дупапис рго^гатпип^. I, РипсНопз о! р01п!з апс1
рот! 1гап8!огта1юп8, Тгапз. Атег. МаНг. Зое, 80, № 1 A955), 51—77).
Совершенно иное, более абстрактное рассмотрение, использующее тео-
теорему Тихонова, содержится в неопубликованной работе Карлина и Шапиро
1) См. В е 11 т а п К., Ма1Ьета11са1 азрес!з о! зсЬес!и1т§ 1Ьеогу, /. Зое.
Ш. Арр1. Маш., 4, № 3A956), 168—205. — Прим. перев.
Теоремы существования и единственности 181
(КагПп 5., 5 Н а р 1 г о Н. N.. Оес181оп _ргосе88в8 апс! 1ипс1юпа1
ТНе КАШ СогрогаНоп, КМ-933, 5ер*. 1952).
См. также К а г И п 5., ТНе 81гис1иге о! йупаппс рго^гаттт^
1 НезеагсН 1о§Ш1сз (^иаНеНу, 2 A955), 285—294.
§ 6. Обсуждение важности теории устойчивости в области дифферен-
дифференциальных уравнений можно найти в книге Беллмана „Теория устойчивости
дифференциальных уравнений", ИЛ, М., 1954.
§ 8. Выбор /0 (/?) в формуле (8.6) предложен X. Н. Шапиро.
§ 9. Это уравнение будет подробно рассмотрено в следующей главе.
Глава V
УРАВНЕНИЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ЗАПАСАМИ
§ 1. ВВЕДЕНИЕ
В этой главе мы изучим один класс аналитических задач, возни-
возникающих в связи с интересным стохастическим процессом распреде-
распределения, встречающимся при изучении проблем управления запасами.
Изучение общего уравнения представляется весьма нелегким делом.
Однако мы можем при некоторых простых и не слишком далеких
от реальной действительности предположениях получить в явном виде
решение для одного частного случая, а также определить структуру
оптимального поведения в некоторых других случаях.
Эти явные решения весьма полезны, так как они выявляют пол-
полные внутреннего смысла сочетания существенных параметров. Эта
особенность может сыграть важную роль, поскольку обратная за-
задача— оценка параметров на основе наблюдаемых данных — играет
решающую роль во всей этой теории.
Кроме того — и это замечание относится ко всем процессам ре-
решения вообще — аналитическая форма решения будет иногда обла-
обладать простой экономической интерпретацией, которая после ее сло-
словесной формулировки открывает путь к аппроксимации оптимальных
поведений для случая более сложных процессов1).
Помимо получаемых нами результатов, представляют определен-
определенный интерес и сами методы, которые мы применяем для исследо-
исследования структуры оптимальных поведений. Читатель уже встречался
с ними, в частности, в § 12 гл. I и встретится вновь в одной
из последующих глав, посвященной вариационному исчислению. Весьма
ярко здесь проявляется тот факт, что метод последовательных при-
приближений не только полезен при доказательстве теорем существо-
существования и единственности (он обычно применяется именно для этой
скучной работы), но, кроме того, является мощным аналитическим
средством для обнаружения и доказательства различных свойств ре-
решений функциональных уравнений, в нашем случае — для опреде-
определения оптимального поведения.
Мы начнем с формулировки одного класса сходных между собой
задач, возникающих при изучении оптимального управления запасами.
После этого мы посвятим один параграф простым общим сообра-
Разумеется, эта идея широко используется в физике и технике.
Уравнение опъимального управления запасами 183
жениям, которые лежат в основе всех исследований в настоящей
главе.
Далее мы рассмотрим ряд случаев, в которых оптимальное по-
поведение характеризуется особенно просто и интуитивно ясно, именно
поддержанием постоянного „уровня запасов". В частности, это имеет
место как в одномерном, так и в многомерном случаях, если стоимость
заказываемой партии товаров прямо пропорциональна размеру этой
партии.
Если в стоимость заказанной партии входит некоторая сумма
постоянных расходов, величина которой не зависит от размера
партии, то задача намного усложняется. Эти постоянные расходы
могут представлять собой либо затраты на управленческий аппарат,
либо — для производственных процессов — затраты на организа-
организацию производства. Здесь мы не будем рассматривать задачи этого
типа, поскольку в настоящее время решения соответствующих функ-
функциональных уравнений практически неизвестны; кроме того, по-ви-
по-видимому, очень мало известно о характере оптимальных поведений,
возникающих из этих значительно более близких к действительности
процессов.
С целью дальнейшей иллюстрации метода последовательных при-
приближений мы рассмотрим два процесса, каждый из которых является
вариантом сравнительно простого процесса, описанного выше. В пер-
первом из них мы отказываемся от предположения линейности и счи-
считаем, что функция величины издержек является выпуклой функцией
размера партии; во втором мы снимаем требование одновременности»
предполагая, что каждый заказ удовлетворяется с некоторым запаз-
запаздыванием во времени. Хотя оптимальные поведения здесь не под-
поддаются простому описанию, мы все же можем выяснить их общую
структуру.
С математической точки зрения нам предстоит иметь дело с весьма
интересным классом квазилинейных интегральных уравнений, явля-
являющихся нелинейными вариантами уравнения восстановления, которое
рассмотрено в добавлении к этой главе. Как обычно, эти- нелинейные
уравнения обладают определенными чертами квазилинейности, кото-
которые мы время от времени будем использовать в качестве крючьев
и веревок в нашем продвижении по этим труднопроходимым местам.
§ 2. ПОСТАНОВКА ОБЩЕЙ ЗАДАЧИ
Задача, которую -мы будем здесь рассматривать в самых различ-
различных облачениях, является частным случаем общей задачи принятия
решений в условиях неопределенного будущего. Рассматриваемый
нами вариант относится к проблеме создания материальных запасов
при неопределенном спросе, причем создание как избыточных, так
и недостаточных запасов ведет к убыткам.
184 Глава V
Положение дел можно описать следующим образом: в различные
моменты времени (определяемые заранее или же зависящие от хода са-
самого процесса) мы имеем возможность заказать партии предметов
снабжения в некотором ассортименте, причем стоимость заказа, есте-
естественно, зависит от количества каждого из заказываемых нами пред-
предметов. Кроме того, могут иметься (а могут и не иметься) неко-
некоторые постоянные расходы — административные и т. п., — не зави-
зависящие от размера заказываемой партии. В различные другие моменты
времени возникает спрос на предметы, запасы которых созданы.
Интересен случай, когда величина этого спроса заранее не установ-
установлена, но мы знаем совместное распределение величины спроса, ко-
который может возникнуть в любой отдельный момент времени. По-
Побудительной причиной создания запасов являются убытки, возникаю-
возникающие в том случае, когда спрос на некоторый предмет превышает
его запасы. В различных областях деятельности характер таких
убытков может быть неодинаковым. Мы весьма подробно рассмот-
рассмотрим случай, когда эти убытки прямо пропорциональны величине
неудовлетворенного спроса. Важность этого случая состоит в том,
что мы можем решить функциональные уравнения, возникающие
из этого процесса, в явном виде. При этом решающим оказывается
предположение о том, что стоимость первоначально заказываемой
партии зависит только от ее размера и является либо линейной,
либо в более общем случае выпуклой функцией.
Выражаясь. несколько вольно, мы хотим определить такую по-
политику заказов на каждом шаге, которая минимизировала бы неко-
некоторую среднюю функцию общей величины издержек на создание за-
запасов. В практических приложениях важной стороной задачи является
определение подходящих критериев для различных видов издержек,
которые были бы реалистичными и вместе с тем поддающимися
анализу. Однако здесь мы не будем касаться этой стороны вопроса.
В следующих разделах данного параграфа мы рассмотрим раз-
различные системы предположений, которые приводят к различным
функциональным уравнениям, принадлежащим некоторому общему
семейству. Ряд других процессов будет рассмотрен в упражнениях.
А. Конечный период времени
Первый из рассматриваемых нами процессов включает образо-
образование запасов только одного предмета снабжения. Будем предпо-
предполагать, что заказы делаются в каждый из конечного числа равных
промежутков времени и немедленно выполняются. Величина спроса
становится известной после осуществления заказа и получения за-
заказанной партии товара; этот спрос по возможности удовлетворяют
за счет созданных запасов, причем неудовлетворенный спрос приво-
приводит к убыткам.
Уравнение оптимального управления запасами 185
Пусть нам полностью известны следующие функции:
A) а) ср($)б?$ — вероятность того, что величина спроса будет нахо-
находиться между 5 и 8-\-й81)\
б) к(х) — стоимость первоначального заказа партии размером
х единиц для пополнения уровня запасов;
в) р (г) — стоимость заказа партии размером г единиц для покры-
покрытия неудовлетворенного спроса, или дополнительные
расходы.
Заметим, что эти функции предполагаются не зависящими от вре-
времени. Предположим, кроме того, что все заказы, о которых идет
речь, могут быть выполнены немедленно.
Обозначим через х уровень запасов в начале процесса. Пусть
процесс состоит из га шагов, причем на первом шаге заказывается уг
предметов, на втором у2 предметов и т. д.
Будем называть поведением набор функций (у19 у2,..., уп),
ук = ук (х), определяющий для каждого к то количество, которое
нужно заказать на к-м шаге, если имеющийся уровень запасов ра-
равен х. Каждому поведению будет соответствовать определенное мате-
математическое ожидание суммарных издержек для этого га-шагового
процесса, включающих стоимость первоначального заказа и „допол-
„дополнительные .расходы".
Мы ставим перед собой задачу определения поведения или по-
поведений, минимизирующих ожидаемые суммарные издержки. Пове-
Поведение, дающее минимум ожидаемых издержек, называется оптималь-
оптимальным. Все это соответствует введенной ранее терминологии.
Не менее интересный, но более трудный класс задач мы получим,
если будем пытаться минимизировать вероятность того, что издержки
превзойдут некоторый заданный уровень.
На любом шаге задача полностью характеризуется двумя пара-
параметрами состояния: величиной запасов х и числом остающихся ша-
шагов га. Поэтому определим
B) /п(х) как математическое ожидание общих издержек для га-шаго-
га-шагового процесса при начальном запасе х и оптимальном
поведении в области заказов.
ГГерейдем к выводу функционального уравнения для /п(х). Если
заказано количество у — х^>0, то мы имеем
оо
C)
У
1)Для упрощения наших рассмотрений мы повсюду будем избегать ин-
интегралов Стильтьеса. Легко видеть, что большинство наших результатов
переносится и на более общий случай, если уделять должное внимание воз-
возможной неединственности решений уравнений. Предоставляем это читателю
как ряд упражнений нетривиального характера.
186
Глава V
Хотя может показаться странным заказывать количество у— х
вместо, скажем, у, однако оказывается, что проще представлять себе
заказ, пополняющий величину запасов до определенного уровня у.
Оптимальный уровень запасов оказывается более существенной вели-
величиной, чем размер заказа.
Поскольку у выбирается так, чтобы минимизировать ожидаемые
издержки-, Л (л:) определяется формулой
D)
у>х
оо
к(у — х)-+-
.У)
У
Вообще, для и^>2 мы имеем (перечисляя различные случаи, соот-
соответствующие возможности превышения спроса над предложением,
а также возможности удовлетворения спроса)
/»(*)
тт
У>х
со
Ну
.у) ?(*)<& Ч-
У
со
-1 @)
У
+ //»-! СУ
о
Б. Бесконечный промежуток времени,
скидка с издержек
При рассмотрении неограниченного промежутка времени, в те-
течение которого развертывается процесс, необходимо ввести какой-
нибудь прием для предотвращения бесконечного роста издержек.
Наиболее естественным приемом служит введение скидки на
будущие издержки, определяемой для каждого периода заданным
коэффициентом скидки а @ < а < 1). Этот метод в значительной
мере экономически оправдан, и обладает, кроме того, немалыми
математическими преимуществами, в особенности в том случае, когда
коэффициент скидки постоянен.
Если определить
F) /(х) как математическое ожидание общей суммы издержек
со скидкой, если начальный запас равен х и приме-
применяется оптимальное поведение,
то вместо уравнения E) мы получим, после такого же перечисления
возможностей, следующее уравнение:
G) /(*) = тт
со
У
со
у
а/@)
в //СУ
V
Уравнение оптимального управления запасами 187
Уравнение G) обладает уже хорошо известным нам преимуще-
преимуществом по сравнению с уравнением E) — оно содержит только одну
функцию одной переменной /(х) вместо последовательности функций
В. Бесконечный промежуток времени,
частичный возврат предметов
Предположим, что некоторые предметы, поставленные для удо-
удовлетворения спроса на них, подлежат частичному возврату, так что
спрос на 5 единиц имеет результатом возвращение Ьз единиц @^#<^1),
пригодных к повторному использованию. Тогда аналогом уравне-
уравнения G) будет уравнение
(8) /(*)= гшп
оо
к (у — х)-\-а С р E — .у) ср E) из -\-
V
оо у
/(Ь'$) у($) A$-\-а I /(у — *
у о
Г. Бесконечный промежуток времени,
задержка поставки на один период
Предположим теперь, что когда мы заказываем партию разме-
размером г, она поступает в наше распоряжение не сразу, а на один период
позже. Если наличный запас равен х% а в предыдущем периоде было
заказано у, то для удовлетворения спроса в следующем периоде
в нашем распоряжении будет запас х-\-у. Функциональное уравне-
уравнение, соответствующее уравнению G), имеет теперь более сложный вид
(9) /(*)=
2>0
ОО ОО
кг-\-а \ р{з — х)срE)й$ + а/(г) Г ср($)</$-[-
X X
X
-}- а С /(х — 5
Величина х теперь представляет собой общее количество, имею-
имеющееся в нашем распоряжении на каждом шаге для удовлетворения
спроса.
Д. Бесконечный промежуток времени,
задержка поставки на два периода
При задержке поставки на два периода для описания хода про-
процесса требуются два параметра состояния, именно;
188 Глава V
A0) х— величина запаса, имеющегося в распоряжении для того,
чтобы удовлетворить спрос в очередном периоде,
у— количество, которое нужно поставить через один период
после удовлетворения этого спроса.
Поэтому определим
A1) /(л:, у) как математическое ожидание общей суммы издер-
издержек при оптимальном поведении (величины х и у
определены выше).
Тогда функция /(х, у) удовлетворяет уравнению
A2) /(*, у) = т\п
2>0
оо
кг + а Г р{8 — х) ср E)
X
оо аз
я/О>. г) ^
а /
X О
Здесь мы не будем рассматривать уравнения (8), (9) и A2), хотя
они поддаются тому же методу последовательных приближений,
который мы будем применять к другим уравнениям. Для уравнений
этого типа, по-видимому, нельзя получить явных решений, срав-
сравнимых по простоте с решением, которое можно получить для урав-
уравнения G).
§ 3. ОДНО ПРОСТОЕ ЗАМЕЧАНИЕ
В этом параграфе мы намерены изложить в наиболее простой
форме основное аналитическое свойство функциональных уравнений
вида
A) и (х) = гшп V (х, .у), у ^ /? (х).
У
На этом свойстве основывается все дальнейшее рассмотрение
в настоящей главе !).
Вообще говоря, у будет пробегать некоторую область /?(х),
в данном случае являющуюся некоторым множеством интервалов,
зависящих от х. Предположим, что на некотором интервале зна-
значений х9 а^х^Ь, минимум функции V достигается внутри обла-
области лК(х) и что эта функция дифференцируема. Тогда для миними-
минимизирующего значения у мы получаем
B) 0 = юу.
Это определяет функцию у(х), которая уже не обязана быть
однозначной, но которую мы, однако, предполагаем дифференци-
дифференцируемой.
1) Это свойство мы уже использовали, не оговаривая этого явно, в § Ц
гл. I.
Уравнение оптимального управления запасами , 189
На любой конкретной ветви этой функции у(х) будет
C) и(х) = ъ(х, у).
Решающим здесь является то, что для а^х^б мы имеем
D) и' (х) = V
поскольку в силу B) <оу = 0.
Аналогично, если
E) и(хг. х2)= Ш1п[т;(л:1, х2, у19 у2)], (у19 у2)€К(х1, х2).
Уху Уи
то в предположении, что минимум всегда достигается внутри обла-
области, в минимизирующих точках мы будем иметь
F) иХх = Vx^
Применим теперь сделанные замечания к функциональному урав-
уравнению B.7) в предположении, что к(г) и р(г) являются линейными
функциями 2, т. е. к(г) = кг% к > 0, р(г)—рг. Мы получим
оо
G)
У
ку — кх-\-а Г /7E
оо у
/
у о
Если минимум достигается в некоторой точке у > х, то в этой
точке
оо у
(8) & — ар ^ ср($)Ж?4-а Г /'(у —
2/ О
Получено уравнение, не зависящее от х\
Кроме того, для указанного значения у имеем
(9) Г
Правильная интерпретация двух последних результатов, должным
образом скомбинированных, дает ключ к решению задач, содер-
содержащих издержки, пропорциональные размеру заказываемой партии.
В последующих параграфах мы обсудим эти задачи более детально,
а также используем их многомерные аналоги.
§ 4. ПОСТОЯННЫЙ УРОВЕНЬ ЗАПАСОВ,
ПРЕДВАРИТЕЛЬНОЕ ОБСУЖДЕНИЕ
В этом и в нескольких следующих параграфах мы рассмотрим
некоторые процессы, характеризующиеся принципом „постоянства
уровня запасов". Общей чертой моделей такого рода является
190 Глава V
предположение о том, что стоимость первоначально заказываемой пар-
партии прямо пропорциональна ее размеру и что распределение величины
спроса от шага к шагу не изменяется. Добавление постоянных адми-
административных расходов (затрат на управленческий аппарат) сущест-
существенным образом изменяет природу оптимального поведения 1). Для
производственных процессов эти расходы могут также соответство-
соответствовать издержкам на организацию производства.
В § 5 мы получим полное решение для произвольного распре-
распределения ср($) в случае, когда „дополнительные расходы" также
прямо пропорциональны размеру заказа. В § 6 мы распространим
этот результат на многомерный случай и покажем, что решение
в случае, когда имеется много изделий, подчиненных совместному
распределению спроса, обладает весьма важным свойством частичной
оптимальности.
Переходя от изучения этих процессов, происходящих в течение
неограниченных промежутков времени, к рассмотрению конечных
процессов, описанных в § 2, мы покажем, что предположение пря-
прямой пропорциональности требует на каждом шаге соблюдения прин-
принципа постоянства уровня запасов. Этот уровень, разумеется, меняется
от шага к шагу.
Этот параграф служит отличным введением в использование метода
последовательных приближений как аналитического средства изуче-
изучения этих функциональных уравнений.
Если рассмотреть случай, когда „дополнительные расходы"
включают „административное слагаемое", не зависящее от размера
партии, мы вступаем на гораздо более тернистый путь. В этом
случае, как нам представляется, вид решения зависит, вообще
говоря, от функции спроса2). Тем не менее несколько важных
классов распределений попадают в те категории, которые мы можем
рассмотреть точно.
Наконец, мы вкратце опишем вид общего решения, не будучи,
однако, в * состоянии извлечь из этого какие-либо конструктивные
результаты.
§ 5. ПРОПОРЦИОНАЛЬНЫЕ ИЗДЕРЖКИ, ОДНОМЕРНЫЙ СЛУЧАЙ
В этом параграфе мы приводим решение для того случая, когда
функции издержек для обеих партий — первоначальной и заказы-
заказываемой для покрытия неудовлетворенного спроса — прямо пропор-
пропорциональны размеру этих партий.
В том смысле, что оно превращает поведение известного вида в пове-
поведение неизвестного вида.
2) По-видимому, имеется в виду плотность распределения спроса
у, —Прим. перев.
Уравнение оптимального управления запасами
191
Теорема 1. Рассмотрим уравнение
A) /(*) = шШ
оо
—х)-\-а ^
У
со
у
^
г/
при следующих условиях:
B) а) к и р — положительные постоянные,
со
со
ОО,
О
О
г) ар > /г.
Пусть х — единственное решение уравнения 1)
со
C)
= ар Г
/
Тогда оптимальное поведение имеет вид
D) а) _у = * для 0
б) у — х для х
Иными словами, оптимальный уровень запасов равен х.
Если ар^к, то для х^О решение дается формулой у
т. е. предпочтительнее всего воздерживаться от заказов.
— х,
Доказательство. Для того чтобы понять сущность этого
решения, будем рассуждать эвристически. Если мы при помощи
каких-либо формальных средств сможем получить правдоподобное
решение и затем докажем непосредственно, что оно удовлетворяет
уравнению A), то доказанная в § 9 гл. IV теорема единственности
гарантирует, что получено именно нужное нам решение. Отметим,
однако, что метод последовательных приближений неизбежно привел
бы нас к этому решению.
х) Этому уравнению можно дать следующую интерпретацию: вероятность
исчерпания запасов должна быть установлена на таком уровне, при котором
приращение затрат по хранению запасов (маргинальные издержки) равно при-
приращению издержек при дополнительном заказе*
192
Глава V
Как отмечено в § 3, если минимум достигается в точке у > х,
то минимизирующие значения у должны быть решениями уравнения
E)
к-\-а
со
у
— р
/'(У
о
О,
и для этого значения у будет
F) '
Теперь нам придется вытаскивать себя за волосы. Если решение
у
имеет предполагаемый вид, то сложное слагаемое I/'(у —
у
можно заменить более простым: —к Гср($)б?$. Поэтому уравнение E)
о
заменится уравнением
оо
у
G)
к — ар
ак
у - О
которое как раз представляет собой уравнение C).
оо
Так как | ср($)с?$=1, это уравнение сводится к следующему:
о
У
(8)
о
ар — к
а(р — к)'
Последнее уравнение, в предположении, что ср($)>0, имеет в точ-
точности одно решение. Отметим, что предельные случаи ведут себя
подобающим образом: если ар — & = 0, то у=0\ если а=\,
то ^/ = оо; наконец, если р — оо, то у = оо.
Определив х, перейдем к определению /(х) следующим образом.
Для 0 ^ х ^ х мы имеем
(9)
= к(х — х)-\-а
- оо
со
х
/(X—
5
и /' (х)
(Ю)
к, или
/(*) = /(<>)-Л*.
Уравнение оптимального управления запасами 193
* "II ■■ "п ■■ ^ ' " ■ """ ■ "■ "■■•"■* "^ '■ "■■■■ ■ ■|1~ >
Подставляя A0) в (9) и полагая л; = 0, получаем для /@) следую-
следующее выражение 1):
ОО X
из
о
кх-\-ра\ (8— х)у(8)с18 — ак I (х — 8)у(з)
(П) /@) = *
Для определения функции /(лг) при лг^-лг2) имеем уравнение
A2)
ОО
а? х
х
о
которое мы запишем в виде
х
Aо) /(х) = и(х)-\-а I
о
где #(х) — известная функция от х. Последнее уравнение в свою
очередь перепишем так:
а?—а? х
A4) /(х) = к (х) + « ^ /(х — 5) ср E) ^5 + а ^ /(а: — 5) ср E) Л.
0 х-х
В интервале [л: — х, х] функция /(х — 5) известна; следовательно,
объединяя и(х) и второй интеграл, можно написать
A5) /(х) = ъ(х)+-а С /(
х—х
о
Если теперь положить х — х = г и $(х-\-г) — &(г), то легко видеть,
что функция % (г) удовлетворяет уравнению
A6) в (*) = V (х + ^ + а / 8" (^ — 5) ср E) <&, ^ > 0.
Отметим, что значение лг, полученное из G), минимизирует это выра-
выражение для /@).
3) В прикладном отношении эта часть решения представляет весьма
незначительный интерес, так как х будет превосходить х разве только
в одном начальном интервале.
13 Р. Беллман
194 Глава V
Это—простое уравнение восстановления; его свойства рассмотрены
в добавлении к этой главе.
Фактически гораздо проще сначала продифференцировать уравне-
уравнение A2), а затем уже действовать, как описано выше. Отметим
мимоходом, что важная роль производных и простота уравнений,
которым они удовлетворяют, является, по-видимому, общей чертой
функциональных уравнений теории динамического программирования.
Причина этого заключается в том, что они представляют собой
„маргинальные приращения" издержек или цены; с математической
точки зрения они представляют собой множители Лагранжа1). Это,
в свою очередь, связано с общей проблемой построения двойствен-
двойственных процессов; здесь мы этим вопросом заниматься не будем.
Теперь перейдем к доказательству того, что наше гипотетическое
решение действительно является решением. Обозначим полученную
выше функцию через Р(х), а постоянную /@), определенную фор-
формулой A1), —через С. Тогда функция Р(х) полностью определяется
следующими уравнениями:
A7) а) Р(х) = С — кх,
б) Р(х) = а
ОО ' ОО
^ р(8—
х
X
X ^^ Хт
о
В нашей проверке решения существенным является строгое воз-
возрастание функции Р{х)-\-кх при х ^> 0. Последнее устанавливается
следующим образом. Из A76) мы видим, что для х > х
ОО X
A8) р/(х) = — ар Г у(з)A8-{-п I Рг (х — $)ср($)б?$.
х о
В интервале [х — х, х] мы имеем О^х — $<^л: и, следовательно,
Р' (х — 5) = — к, как видно из A7а). Итак, для х > х получаем
е
со х
\ 1 \У) Л |Л I —— ~~~~ ш/ I Ч' 1о г НО ' гСС1 I у^о I НО |
Х Х-Х
х-х
-\-п С Р'(Х
1) Ср. задачу 71 гл. I. — Прим. перев.
Уравнение оптимального управления запасами
195
или
B0)
р' (х) 4- к =
со
к — ар Г
х
X
ак ^ срE)
о
х—х
-\-а
+- /г] ср
О
Выражение
B1) и(х) = к-
равно нулю при х = х и
х — х = г и Р'(х-\-г)-\-к
воряет уравнению
B2)
оо
X
ар Г
х
ак Г ср
о
положительно при х > х
= §"(^), убеждаемся, что
Полагая
удовлет-
удовлетг
о
Следовательно, #Сг)>0 при г > О (ср. добавление к этой главе).
Итак, Р' (х) -+- к > 0 при х > х\ поэтому функция Р(х)-\-кх
при х > х является строго возрастающей.
Возвратимся теперь к доказательству того, что функция Р(х)
удовлетворяет уравнению A). Рассмотрим сначала случай х > х.
Используя представление A76), мы имеем
B3)
у>х
у>х
Поскольку при у^-х должно быть ку-\-Р(у)^ кх-{-р{х), то
ясно, что минимум достигается при у = х. В результате мы полу-
получаем Р(х), что и требовалось.
■ Теперь рассмотрим интервал 0 <; х < х. Напишем
B4)
Как и выше,
вательно,
B5)
ГП1П= 1ШП
пип[
у>х
Ш1П [ ]
> у>х
минимум по
Ш1П [...]
у > х
х достигается при у=^х. Следо-
тт [...].
а>~> у > х
13*
196 Глава V
Так как Г{х) = С— кх для 0<^л;^;с, то отсюда следует, что
минимум достигается при у = х, как в первоначальном определении
значения х.
ЕГ случае ар^.к, полагая в A7) # = 0, мы получим функцию/7,
которая, как легко видеть, удовлетворяет B3), поскольку функция
Р(У)-\-ку* как и прежде, является неубывающей.
Это завершает доказательство. Интересно отметить, что реше-
решение в интервале О^лг^лг, т. е. наиболее важная часть решения,
может быть найдено безотносительно к виду решения для л:>лг.
Этим завершена проверка того факта, что Р(х) является неко-
некоторым решением уравнения A) и, следовательно, нужным нам
решением в классе равномерно ограниченных функций, определен-
определенных для л
§ 6. ПРОПОРЦИОНАЛЬНЫЕ ИЗДЕРЖКИ,
МНОГОМЕРНЫЙ СЛУЧАЙ
Рассмотрим теперь многомерный вариант задачи. Здесь мы имеем
А/ предметов снабжения, уровни запасов которых обозначим через
х1% х2 хп. Пусть спрос EР $2, . .., 8п) на эти предметы в любой
момент времени имеет совместное распределение с плотностью
1 2 п
При выводе функционального уравнения для функции
/С#1. Х2> • • • • хп)> представляющей собой минимальные ожидаемые
суммарные издержки со скидкой, будем для простоты рассматривать
только двумерный случай.
Выясняется замечательный факт: вид решения оказывается точно
таким же, как если бы функция срEг, 82 §п) имела вид
?1 E1)?2E2) • • • Уп(8п)> т- е- потребности в различных предметах
были независимыми. Именно это обстоятельство порождает важное
свойство частичной оптимальности, обсуждаемое ниже. Перечисле-
Перечисление всех возможных случаев приводит к следующему функцио-
функциональному уравнению, которому удовлетворяет функция /(хх, х2):
A) /(хх, х2\= гшп
К (Ух — *1> + К (У2 ~
г- ОО ОО
С / 1РгC1—Уг)+Р2
I У%
оо оо
Ух У%
оо г/а
-\- I I [Рг E1 — Уг) -(- / @, ^2 —
Ух о
Уравнение оптимального управления'запасами
197
Ул оо
/[/(.VI —^1.
О
. У2 — 82) ф E,,
о о
Упростим немного наши обозначения, полагая срEр 8
^=^AО(81, $2), и обозначим выражение, стоящее в фигурных скобках,
через К(Уг, У2)- Тогда мы будем иметь
B)
кх-\-а
ОО I СО
/ /
/, \8а=0
1, 52)
2/1
ОО
0
1. 0)
Ух У*
О О
оо
оо
оо
О
л
2/з
О О
19 82)
Кроме того, как и выше, при .У! > х{, у2 > а:2 получаем
C)
дхх
к2.
Следовательно, если предположить, что решение здесь имеет
тот же вид, что и в одномерном случае, критические уровни хх и х2
будут решениями уравнений
D) а) /г, + а
СО / СО
а?, / со
о
=0.
б) к2-{-а
СО
— Рг
со
—*2 / ( / 40 (Яр 52)
198 Глава V
Эти решения существуют и единственны, если сделать такие же
предположения, как и выше, именно ар1> к{, ар2 > &2 и АО > 0.
• Мы видим, что хх зависит только от условного распределения
оо
\ <Ю(зх, 82)', аналогично для определения х2 требуется только
ОО
Г
В этом и заключается важное свойство частичной оптималь-
оптимальности, упомянутое выше.
Проверка решения проводится точно по такой же схеме, как и
для одномерного случая. Поэтому мы ее опустим, так как выкладки,
разумеется, здесь гораздо более утомительны.
Сформулируем наши выводы в виде теоремы.
Теорема 2. Пусть уравнение A) удовлетворяет следующим
условиям:
E) а) к\ и р{ — положительные постоянные,
сю оо оо оо
б) ср > 0, I I ср ^8Х й8г = 1, \ \ 8^ й8х й82 < оо,
ОО 0 0
в) 0<а<1.
г) ар{ > к{.
Пусть далее х^ — единственное решение уравнения
оо г оо \ у , со
3 \ 3 I 3 3
\.^=о
\у \«.=0 / 0
г
8,
Тогда оптимальное поведение имеет следующий вид:
G) а) Уъ~хг для 0<л:|<л:|,
б) Уг = хг' для х{>.хг.
Иными словами, оптимальный уровень запасов для 1-го вида
предметов равен х-х. ' .
Если ар1^кг для некоторого /, мы полагаем х$ = 0 (/= 1, 2).
Ясно, что решение в этом виде непосредственно обобщается на
Л/-мерный случай.
§ 7. КОНЕЧНЫЙ ПРОМЕЖУТОК ВРЕМЕНИ
Рассмотрим соответствующую задачу для конечного процесса,
в котором будущие издержки учитываются целиком. Теперь мы хотим
минимизировать математическое ожидание суммарных издержек.
Уравнение оптимального управления запасами
199
Определим
A)
— как математическое ожидание суммарных издержек
за Л^-шаговый период при начальном количестве х
и оптимальном Л/^шаговом поведении.
Тогда
B)
/г (X) = ГШП
У>х
оо
у
у>х
со
V
оо
V
• V ~~~~
«/ о
При естественном предположении р^> к нами будет доказана
1
Теорема 3. Для каждого п оптимальное поведение имеет
вид
C).
а) у = хп для л:<л:п,
б) у = х для х ^ хп%
где последовательность хп — монотонно возрастающая по п.
Доказательство. Доказательство будем вести по индукции.
Если функция /г(х) определена согласно B), то критическим уровнем
запасов будет служить решение уравнения
оо
D)
Г
Если это решение существует, то оно единственно. При естествен-
естественном предположении /? > к это решение всегда существует. Обозна-
Обозначим его через хг. Ясно, что для п = 1 оптимальное поведение имеет
=хг для х^Х!; у = х для х^>хг. При
— к\ при х
вид
получаем
оо
E)
/1(Х)=р §(8 —
X
— к.
X
.гг
Следовательно,
/,(*)=??(*) >0.
для всех
200
Глава V
Рассмотрим случай п — 2. Мы имеем
F)
= ГП1П
У>х
оо
(8) Л8
оо
+Л.@) /?(*)<& + / Л Су—5) 9 E) аз
У 0
Критическое значение у мы получим, полагая частную производ-
производную по у равной нулю, или
оо у
G) ({1
у
Производная функции Р±(у) равна
У
(8)
Су)
р<р(у)—МО)
/Г Су
0
Так как /1 > 0 и р + /г @) > А; + /\ @) = 0, функция Т7! (^) является
монотонно убывающей и уравнение G) может иметь не более одного
решения. Однако /71(.0)==р>А, Р{(оо) = 0. Следовательно, суще-
существует в точности одно решение. Обозначим его через х2.
Тогда поведение имеет вид
Геометрическая иллюстрация оказывается весьма наглядной.
Запишем F) в виде
A0) /г С*) + й* — пип^Су),
где V(у) — известная функция. Из доказанного выше ясно, что
график 1>(у) выглядит следующим образом.
V
>г У
Рис. 17.
©о
Функцию {2(х)-\-кх мы получаем, проводя касательную к кри-
вой V(у) в точке у = х2 и продолжая ее влево до пересечения
Уравнение оптимального управления запасами
201
с осью V. Теперь функция /2(х)-\-кх постоянна при
и равна V (х) при х
Рис. 18.
оо
Остается показать, что х2 > хг. Величина хг определяется урав-
уравнением D), а х2 — уравнением G). Из того, что —/1^-0, следует,
что кривая
со . у
(И) ™ = 82(У) — Р Гф($)^5— Г
у о
всегда лежит над кривой
A2)
оо
У
Отсюда вытекает, что х2 > хх.
Для того чтобы продолжить доказательство по индукции, нам
нужно показать, что
A3)
•/•(*) >—/!<*)•
202 Глава V
Мы имеем
к,
A4) -П(х)
со
р Гер
а?
И
( /2, 0 < * < Х2%
A5) -/!(*)= | л г /
I Р I <?($)*/$ I /1 (Л: — 5) ср E) */$, ЛГ > Х2.
\ х О
В интервалах [0, л^] и [лг2, оо] доказываемое неравенство оче-
очевидно. В интервале [хх, х2] оно следует из монотонности функции'
со
к—р Гср($)г/$, обращающейся в нуль при х = хх.
х
Наконец, остается установить выпуклость функции /2(л0-
интервала [0, х2] это очевидно. В интервале [х2, оо] в силу A5)
х
A6) /2(^) = рср(д:)+/1/@)ср(д:) + //Г(л: — *)?(*)*•
о
Из /1@)+р>0 и /Г>-0 вытекает, что /г (*) > 0:
Теперь мы располагаем всеми составными частями индуктивного
доказательства.
§ 8. КОНЕЧНЫЙ ПРОМЕЖУТОК ВРЕМЕНИ,
МНОГОМЕРНЫЙ СЛУЧАЙ
Настойчивый читатель может проверить, что решение и в много-
многомерном случае имеет в общих чертах точно такой же характер.
§ 9. НЕПРОПОРЦИОНАЛЬНЫЕ „ДОПОЛНИТЕЛЬНЫЕ РАСХОДЫ" —
АДМИНИСТРАТИВНЫЕ РАСХОДЫ
Как только мы начинаем рассматривать случаи, в которых „допол-
„дополнительные расходы" не являются прямо пропорциональными величине
неудовлетворенного спроса, мы наталкиваемся на различные труд-
трудности. Похоже, что простое и изящное решение, полученное для
случая пропорциональных издержек, в общем случае перестает быть
верным.
Однако в ряде интересных случаев мы еще можем получить
решение, включающее постоянный уровень запасов. Наиболее инте-
Уравнение отимального управления запасами
203
ресные случаи возникают, когда мы принимаем стоимость заказа
партии размером E — у) равной р E — У)-\-д. Здесь д— постоян-
постоянные административные расходы, которые не зависят от величины
спроса, но появляются каждый раз. когда ввиду неудовлетворенности
спроса приходится заказывать дополнительную партию. Стоимость
первоначально заказываемой партии, однако, принимается пока про-
пропорциональной ее размеру.
Рассмотрим уравнение
A)
ГП1П
У>х
г со
I У
оо
У
+/@)
У
О
отличающееся от уравнения, которое мы рассмотрели выше, только
оо
добавочным членом ад I ср($)с?$. Поистине удивительно, какое зна-
у
чительное усложнение вносит это столь безобидное на первый взгляд
выражение.
Для начала мы. будем формально исходить из предположения
о существовании решения с постоянным уровнем запасов. Тогда кри-
критический уровень определяется решением уравнения
B) 0 =
со
У
р
у О
при у > х имеем /г(х) — — к.
Следовательно, х должно быть решением уравнения
у
C)
ОО
^
У
о
К сожалению, неверно, что это уравнение имеет единственное
решение при любых плотностях ср($). Перепишем его в виде
со
D)
A — а) к = а(р — к) Г ср E) й8 -\- аду (у).
у
Простым условием, при котором решение этого уравнения един-
единственно, является ср'(^/)^О.
Если предположить, что это уравнение имеет единственное реше-
решение, то доказательство'будет почти дословно таким же, как и прежде.
204
Глава V
Однако мы обсудим сейчас более общий результат, именно тот,
когда оптимальное поведение характеризуется постоянным уровнем
запасов.
Если приведенное выше уравнение C) или D) не имеет единст-
единственного решения, то может все же случиться, что наибольший корень
уравнения D) соответствует абсолютному минимуму на интервале
[0, х] функции, стоящей в уравнении A) под знаком минимума.
Геометрически это можно проиллюстрировать следующим образом.
0 X у оо
Рис. 20.
Докажем следующую теорему.
Теорема 4. При предположениях относительно я, к, р, 7
и ср($), сформулированных в теореме 1 *), и дополнительном
предположении, что достигаемый при наибольшем корне уравне-
уравнения D) минимум функции
F)
г оо
-V
У
о
является абсолютным минимумом на интервале 0 ^ у ^ оо,
оптимальное поведение для уравнения A) определяется следую-
следующим правилом:
G) а) у = х для 0 < х < лг,
б) у = х для х > лг,
где х — то значение у, на котором достигается абсолютный
минимум.
Доказательство. Пусть х — то значение у, которое дает
указанный минимум, являющийся абсолютным минимумом функции
фОО в интервале [0, оо]. Тогда точно так же, как и в случае <7=0,
мы имеем /(х) = /@) — кх в интервале 0 <;*<;.*: и /@) при
) В теореме 1 д не участвует. Экономически естественным является
предположение д > 0. — Прим* перев.
Уравнение оптимального управления запасами
205
г определяется подстановкой этого результата в A). В ин-
интервале [лг, оо] функцию /(лг) определяем, полагая в уравнении A)
у = х.
Доказательство того, что /(х) действительно удовлетворяет урав-
уравнению, продолжается теперь точно таким же образом, как и в слу-
случае <7= 0.
§ 10. ЧАСТНЫЕ СЛУЧАИ
Укажем некоторые частные случаи, когда приведенные выше
условия выполняются:
A)
а) <р(дг) =
е-(х-а)>
ОО
—а
б) у(х) =
Проверку мы предоставляем читателю в качестве упражнения.
§11. ВИД ОБЩЕГО РЕШЕНИЯ
Пусть /(лг) представляет собой решение уравнения (9.1), т. е.
A)
где
B)
ОО
ОО
I У
У
У
//Су —
о
Пусть функция Р(у) имеет следующий график:
X оо
Рис. 21.
206
Глава V
Тогда оптимальное поведение имеет вид
D)
а)
б)
в)
г)
— Хл, и -^ X -^-
X
и
E)
л:
л:
оо.
Однако задача нахождения числа различных областей при задан-
заданных функциях издержек и спроса представляется весьма сложной.
До настоящего времени эта задача не решена; неясно также, каким
образом связать эти данные воедино.
§ 12. ПОСТОЯННЫЕ РАСХОДЫ
Рассмотрим теперь случай, когда в стоимость начального заказа
включены постоянные административные расходы. Эта задача также
не решена до сих пор.
В данном случае уравнение принимает вид
A) /(х)= тШ
г оо
оо
У
+ /@)
У
о
где
B)
0, х = 0.
Здесь § обозначает постоянные расходы.
Трудно удержаться от соблазна рассмотреть решение следующего
вида:
E для 0<лг<5,
У = { _
I х для х > 5,
где 0 < 5 < 5 < со. Поведение такого, типа называется „$5-поведе-
нием".
Уравнение оптимального управления запасами 207
Поведения этого типа, имеющие четкий интуитивный смысл,
нередко используются на практике. Однако вся беда в том, что
легко построить относительно простые примеры, показывающие,
что это поведение не может быть оптимальным во всех случаях.
§ 13. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
К ОБСУЖДЕНИЮ БОЛЕЕ СЛОЖНЫХ ПОВЕДЕНИЙ
В предыдущих параграфах мы рассмотрели ряд процессов, обла-
обладающих решениями довольно простого и интуитивно ясного вида.
Теперь мы намерены рассмотреть два случая, в которых решения
будут иметь более сложную природу. Первый из них содержит
запаздывание в выполнении заказов на один период; вторым мы рас-
рассмотрим случай, когда функция стоимости первоначально заказывае-
заказываемой партии является нелинейной выпуклой функцией ее размера.
Как в одном, так и в другом случаях постоянные административные
расходы отсутствуют. #
В обоих случаях для установления свойств решения мы приме-
применим метод последовательных приближений.
§ 14. НЕОГРАНИЧЕННО ПРОДОЛЖАЮЩИЙСЯ ПРОЦЕСС,
ЗАПАЗДЫВАНИЕ НА ОДИН ПЕРИОД
Функциональное уравнение, которое мы будем рассматривать,
было выведено в § 2:
A) /()
оо
\- х
оо х
X
Нами будет доказана
Теорема 5. Оптимальное поведение определяется следую-
следующим правилом:
B) г = г (х) для
2 = 0 для
где г(х)^>0 и г (л:) = 0.
Функция г(х) монотонно убывает по х.
208 Глава V
Доказательство будет проведено по индукции, основанной на
последовательности приближений
C)
оо оо
<рE) аз -\-и @) / <?(«)
1- X X
X
//о (* —
о
(эту функцию мы уже несколько раз встречали раньше) и для
лг = 0, 1, 2, ...
D) /п+1 (*) = Ш1П Г B:. лг,
г>0
где Т(г,х,/п) — выражение, стоящее в формуле A) под знаком
минимума.
Рассмотрим теперь Т(г,х,/0) как функцию от г, обозначив ее
через Мх (г). Мы имеем
оо х
E) Ж; (г) = к + а/'0(г) ]* ср E) ав + а | /;(лг — 5 + г) ср E) а$,
X 0
а для втррой производной —
оо х
F) М'[ (г) = а/'; (г) / ср E) Й5 + с ^ /^ (х — 8 -(- г) ср (я) Л?.
я? о
Поскольку /^ > 0, мы видим, что М^(г)>0 для всех х^О.
Следовательно, уравнение М[(г)=0 имеет не более одного реше-
решения г при любом х. Ясно, что для больших значений х решения
вообще не будет, а для малых х (скажем, при лг = О) решение бу-
будет существовать, если только а, р и к связаны между собой должньш
образом. Это обстоятельство мы проверим позже; пока же убедимся
в том, что это решение, которое мы обозначим через ^(лг), является
монотонно убывающей функцией от х.
оо
Для этого рассмотрим выражение О0(лг, г) = — аГ0(%) Г
X
X
—а Г/о(* — 8-\-г)у(8)<18 как функцию от х при фиксированном г.
о
Ее производная по х имеет вид
X
Уравнение оптимального управления запасами
209
и
12)
поэтому отрицательна. Следовательно,
= О0(лг, г)-выглядит следующим образом:
семейство кривых
Ш
©о
Рис. 22.
Этот график ясно показывает, что функция хх (х) монотонно убы-
убывает по л; и равна нулю при х^> хх.
Чтобы получить аналогичные результаты для второго приближе-
приближения, нам нужно показать, что /''(л;)^>0. *Мы имеем
(8)
1 | \т™ / ■■
то
0
х
/о).
В интервале [0, хх] будет
оо
(9)
И
A0)
/[(х) = -ар {ср
«/ их -
12!
= ар<р (лг) + а/; (г)
о
Из (9) мы видим, что /^@)=—ар. Так как функция /^(х) монотонно
убывает по х, то ар -\~а/'0(г) > 0 для 2:^0. Следовательно, если мы
покажем, что \-\-йгх1йх^0ш то получим /[(х)>0.
С этой целью возвратимся к уравнению, определяющему гХш
именно М'1(г) = §. Используя выражение E), получаем соотношение
(Н)
ОО
X
X
_
их
х
о
которое снова показывает, что 4гх1с1х^.О и
14 Р. Беллман
210 Глава V
Наконец нам требуется соотношение между /'0(х) и/^(лг). Имеем
оо х
X О
Таким образом, мы видим, что в интервале [0, х\ будет /^
, так как функция /'0(х) монотонно возрастает. Поскольку
Д /0 (лг) для лг>лг, то
A3) /о (*)</!(*)
для всех л^
Продолжая точно так же, как и на предыдущих страницах, мы
получим для каждого п функцию гп(х\ обладающую следующим
свойством:
A4) а) гп(х)>0 для 0<лг<лгп,
б) гп(х) — 0 для лг>лгм,
причем гп(х) монотонно убывают по х. Кроме того, последователь-
последовательность [хп\ является монотонно убывающей и имеет предел х.
Остается показать, что лг==О, если только я, р и к подобраны
надлежащим образом. Это эквивалентно проверке того обстоятель-
обстоятельства, является ли /0(х) решением или нет. Возвращаясь к E), пола-
полагаем лг —0 и рассматриваем уравнение
A5) к + а/'о{г) = 0.
Если /г + с/^@)<0, то это уравнение будет иметь решение. Обра-
Обращаясь к A2), видим, что /о@) = — ар. Следовательно, мы должны
требовать, чтобы
A6) к<а2р.
Для процесса с запаздыванием на один период именно этого
интуитивно ясного условия и следовало ожидать.
§ 15. ВЫПУКЛАЯ ФУНКЦИЯ ИЗДЕРЖЕК,
НЕОГРАНИЧЕННО ПРОДОЛЖАЮЩИЙСЯ ПРОЦЕСС
В качестве другой иллюстрации эффективности метода последо-
последовательных приближений рассмотрим случай, когда стоимость зака-
заказываемой партии §{у — х) является строго выпуклой функцией
Уравнение оптимального управления запасами
211
размера партии у— л:. В этом случае уравнение принимает вид
/(*)
у>*\
у—х)-\-а
со
оо
У
Ну-
У
о
Как обычно, полагаем
B)
/0 (х) = а
ОО
оо
р (8 — X) ср (в) йВ Ч- /о @) I ср E) й8
О
и для п = О, 1, 2,
C)
Рассмотрим сначала функцию /, (х), предполагая, что
прерывную производную при х^О.
Если у > х, то у определяется из уравнения
D)
ОО
У
ь 2/
О
имеет не-
Из предположения о выпуклости функции ^(л;) [это значит, что
&""(*)> 0] следует, что это уравнение может иметь не более одного
решения, так как его левая часть монотонно возрастает, а правая —
монотонно убывает.
При х = 0 решение существует, если
E)
' @) < ар.
При больших х решения не существует, если §"'@)>0.
Для _у> х мы имеем
F)
И
G)
-*" Су—
14*
212
Глава V
Для определения величины йу\йх — 1 обратимся к уравнению D).
Оно дает нам
(8)
V
/о" (У — «) 9 («)
О
ау
Отсюда уже можно заключить, что йу\йх > 0 и йу\йх — 1 < 0.
Следовательно, /" (х) > 0.
Кроме того, легко видеть, что —/[<^- — /о* Теперь мы распо-
располагаем всеми элементами индуктивного доказательства следующей
теоремы.
Теорема 6. Существует функция у (х) и число х, обладаю-
обладающие следующими свойствами:
(9) а) у (х) ;> х; функция у (х) монотонно возрастает;
б)У(х)>х пРи Х^СХ'> у(х) = х при х
в) х > 0, если ар > &' @).
дта функция у(х) описывает оптимальное поведение для урав-
уравнения A).
ДОБАВЛЕНИЕ К ГЛАВЕ V.
УРАВНЕНИЕ ВОССТАНОВЛЕНИЯ
Уравнение
х
A)
и (х) = /(х) + I и (х — 5) ср E)
•/
о
которое встречается в самых различных областях математического
анализа, обычно называется уравнением восстановления.
Для выяснения свойств его решений имеются два основных
метода — метод преобразования Лапласа и метод последовательных
приближений Лиувилля — Неймана.
Метод преобразования Лапласа обязан своим успехом тому
X
обстоятельству, что выражение Г и (х — 5) ср E) из является сверткой,
о
обладающей следующим формальным свойством:
х
со Г а? "I / оо
B) Ге~гх Си(х—8)у(8)с18ах=1Се-*хи
о 1-о 1 \о
(х)йх
Ср E) С18
Уравнение оптимального управления запасами 213
Действуя совершенно формально, получаем из A)
оо
C) / е-**и (х) ах = -2-^ .
0 1— Г е~гху (х) ах
о
Отсюда при соответствующих предположениях относительно / и ср
можно вывести многое относительно асимптотического поведения и(х)
при х —> оо (используя тауберовы теоремы или же теорию функций
комплексного переменного).
Однако наиболее интересные для нас в данном случае свойства:
положительность, выпуклость и пр. — удобнее устанавливать, рас-
рассматривая следующую последовательность приближений:
D) «о = /(*).
х
ип+1 = /(*) + / ип (х — 8) ср E) аз
о
и показывая, что каждая функция ип(х) обладает требуемым свой-
свойством.
Этот подход оправдывается следующим результатом.
Теорема 7. Пусть
E) а) функция /(х) ограничена в любом конечном интервале
[О, х0];
оо
О
Тогда существует единственное решение уравнения A), ограни-
ограниченное в любом интервале [0, лг0].
Это решение может быть получено как предел последова-
последовательности D).
Если функция /(х) дифференцируема, а функция ср(-*О непре-
непрерывна, то
X
F) и' (х) = /' (*) + и @) ср (х) +1 и' (х — в) ср E) йа.
о
Если /(д:)>0 и ср(*)>0, то и(лг)>0.
Можно дать целый ряд других комбинаций условий, соответ-
соответствующих условиям Eа) и E6), которые также обеспечивают суще-
существование и единственность.
214 Глава V
Доказательство этой теоремы легко получить, следуя тем мето-
методам, которые мы уже многократно использовали.
УПРАЖНЕНИЯ И ПРОБЛЕМНЫЕ ЗАДАЧИ
К ГЛАВЕ V
1. Получить аналог теоремы 3 для того случая, когда функция
распределения спроса от шага к шагу изменяется.
2. Рассмотреть случай, когда как в стоимость первоначально
заказываемой партии, так и в „дополнительные расходы" включены
постоянные расходы, а распределение спроса имеет вид
ср(х) = \\к при 0 <; х <; к\ ср (лг) = 0 при х > к.
3. Рассмотреть процесс с постоянными расходами в случае,
когда возможны только два уровня спроса — низкий и высокий.
Можно ли обобщить полученный результат на случай, когда имеется
произвольное конечное число уровней спроса?
4. Получить аналоги теорем 1, 2 и 3 для случая, когда на каж-
каждом шаге имеются некоторые издержки на хранение, пропорциональ-
пропорциональные количеству изделий, сохранившихся с предыдущего периода.
*
5. Получить функциональные уравнения, описывающие процесс,
в котором как величина спроса, так и моменты времени, в которые
он предъявляется,. — случайные величины. Рассмотреть случаи, когда
моменты времени, в которые предъявляется спрос, имеют непре-
непрерывное распределение и дискретное распределение.
6. Получить аналог теоремы 5 для процессов с произвольными
запаздываниями во времени.
7. Рассмотреть случай постоянных расходов и определить:
а) поведение „постоянного уровня запасов", минимизирующее
ожидаемые издержки;
б) „55-поведение", минимизирующее ожидаемые издержки.
8. Мы хотим производить единственный вид товара в течение
заданного ряда промежутков времени, с тем чтобы удовлетворить
известный будущий спрос. Это следует делать таким образом, чтобы
минимизировать суммарные издержки, зная издержки на производство
и хранение и функцию изменения уровня производства во времени.
Рассмотрим сначала дискретный вариант. Пусть
Т—число периодов,
гг — величина спроса в момент I,
х* — количество, произведенное в промежуток времени [I—1, (],
Уравнение оптимального управления запасами 215
х0 — заданный объем производства в единицу времени (произ-
(производительность) начального этапа,
у^ = х^+1— хг^0—увеличение производительности в момент/,
щ — превышение предложения над спросом в момент Ь.
Издержки:
С} — издержки на производство единицы товара за период [/—1, /],
их — издержки на хранение избыточной единицы товара в тече-
течение одного периода,
в\ — издержки на увеличение производительности на одну еди-
единицу за единицу времени.
Нужно минимизировать общие издержки процесса, состоящего
из Т периодов, при условии, что предложение всегда должно пре-
превосходить спрос.
9. Рассмотреть поставленную выше задачу при условии, что
производительность нельзя увеличивать произвольным образом.
В частности, рассмотреть два случая1):
•
а) хг ^ хг+\ *С ахр 1 < а < оо;
10. Рассмотреть вариант, когда спрос случаен, при следующих
двух различных предположениях:
а) спрос должен всегда удовлетворяться;
б) удовлетворение спроса может быть отложено на один шаг.
11. Получить функциональное уравнение, соответствующее про-
процессу, описанному в § 2, в предположении, что мы стремимся мини-
минимизировать вероятность того, что издержки превзойдут заданную
величину с.
12. Рассмотреть функциональные уравнения, изучавшиеся в этой
главе, в предположении, что распределение с плотностью ср($)с?$
заменено более общим стильтьесовским распределением кО(&).
Получить относящиеся к этому случаю теоремы существования и
единственности и выяснить, каким образом следует видоизменить
установленные выше теоремы для того, чтобы они оставались спра-
справедливыми.
13. Чем отличается задача производства заказов для военного
склада от задачи производства заказов товаров для универсального
магазина?
14. Пусть за невыполнение заявки на товар мы не платим штрафа,
но с каждой единицы товара, которая была заказана и поставлена,
имеем прибыль в Ь долларов. Пусть этот доход можно использовать
Ср. задачу 57 к гл. III. — Прим. перев.
216 Глава V
для увеличения количества товаров на следующем шаге. Если
задан начальный запас х и запас денег у, то какую политику зака-
заказов следует применить, чтобы максимизировать общий ожидаемый
доход? Рассмотреть конечный и бесконечный процессы в предполо-
предположении пропорциональности издержек размерам заказываемых партий.
15. Рассмотрим уравнение
у
/(х)= тах
где
б)8г/СУ)>0. *'СУ)>0.
в) &($)>• О,
г) & (у) > 0, к" (у) > О,
д) функция к (у) — $(у) монотонно возрастает по у.
Показать, что решение этого уравнения дается формулой
к (х), О <! х ^ х,
/(*) =
84*)+ //С*
где д: определяется как ненулевое решение уравнения
X
Н{х) =^(*)+Га(д: — 8)к($) из.
о
16. Рассмотрим случай, когда нужно заказывать подлежащие
продаже товары в ожидании неопределенного спроса, который
можно считать известной случайной величиной. Пусть равные по
длительности периоды заказов занумерованы числами 0, 1,2
а спрос описывается распределением Р%{х)% где
Р\(х) — вероятность того, что в период / спрос будет меньше
или равен х.
Пусть р—реализационная цена единицы товара, С (у) — общая
стоимость заказа у единиц в любой период [функция С (у) пред-
предполагается дифференцируемой], / — запас в начале текущего периода
(периода с номером 0). Пусть все товары, заказанные в начале
периода, предоставляются немедленно и могут расходоваться только
путем продажи по цене р по требованию.
При политике заказов уг на каждом шаге наличный доход
составит
Уравнение оптимального управления запасами 217
1 ■ ..... ■—I
Пусть целью процесса является максимизация математического ожи-
ожидания
оо
>г. Л. Л). 0<а< 1.
Показать, что получающаяся система рекуррентных соотношений
имеет вид
-\-а/к+1 (тах @, / ■+■ у — х))] йРк (*) .
Решить задачу в случае С (у) = су.
(X. Д. Миле)
17. Рассмотрим уравнение
= тш
х
оо оо
кг-\-а Г р(& — х) ср E) из -}- а/ (г) Г ср (
а? х
X 5 -|- X) ср E) С?5
о
соответствующее случаю запаздывания в поставке на один период.
Предполагая, что оптимальное поведение состоит в выборе
такого г, чтобы х-\-г = Ь для 0<;л;<С/, И г = 0 для *>/.,
определить /,.
18. Доказать, что описанное выше поведение является оптималь-
оптимальным, или опровергнуть это.
19. Изучить предположение о том, что в общем случае запазды-
запаздывания на к периодов оптимальное поведение заключается в следую-
следующем: не заказывать ничего, если количество заказанных и имею-
имеющихся в наличии товаров превышает определенную величину /,, и
заказывать разность, если /, превышает это количество.
БИБЛИОГРАФИЯ И КОММЕНТАРИИ
К ГЛАВЕ V
§ 1. Рассматриваемая нами математическая модель задачи об управле-
управлении запасами берет начало от основополагающей статьи Эрроу, Харриса и
Маршака [А г го ш К. О., Н а г г 1 8 Т. Е., Магзс Ь а к Л., ОрИта1 игуеШогу
роПсу, ЕсопотеШса, 19, № 3 A951)]. Вскоре появились еще две статьи,
стимулированные этим исследованием [Оуоге1гку А., К1е1ег X, \Уо 1-
1ошПг X, ТЬе шуепюгу ргоЫет, I, II, Есопсте(г1са, 20, № 2—3. A952)
187—222].
218 Глава V
Первая из этих статей посвящена исследованию существования и един-
единственности решения основного функционального уравнения и обсуждению
некоторых частных процессов. Вторая статья — по своему характеру более
статистическая — посвящена вопросу нахаждения распределения функций
спроса в течение процесса.
Результаты настоящей главы были получены в сотрудничестве
с И. Гликсбергом и О. Гроссом [В е 11 ш а п Р., ОМскзЬег^ I., О г о 8 8 О.,
Оп 1Не орита1 туеШогу е^иа^^оп, Мапа^етепг 8с1епсе, 2 A955), 83—104].
Со времени выхода этих^ статей появилось большое число работ,
посвященных управлению запасами, — как опубликованных, так и находя-
находящихся в частном пользовании. Мы полагаем, что интересующийся этими
вопросами читатель перелистает страницы журналов Есопотегг1са,
/. Зое. 1пйи81г. Арр1. МаНг., /. Орегапопв Ш§. 8ос. Атег., Мапа^етепг
8с1епсе, Иауа1 НезеагсН Ьо§Ш1С8 ($иаг1ег1у% где он найдет дальнейшие
результаты и библиографические ссылки.
§ 3. Обсуждаемые здесь результаты находятся в соответствии с замеча-
замечанием в одной из предыдущих глав о том, что производные функций дохода,
или „маргинальные доходы", во многих случаях обладают более простой
структурой, чем сами функции дохода.
Добавление. Дальнейшие результаты относительно уравнений вос-
восстановления и функций подобного типа можно найти в статьях Феллера
[Р е 1 I е г \У., Оп 1Не 1Шедга1 е^иа^^оп о! гепеша1 1Неогу, Лпп. Маш. 8Ш1-
зНсз, 12 A941)] и Беллмана и Данскина (В е 11 ш а п К„ О а п з к 1 п 3. М.,
А зигуеу о! 1Не 1Неогу о! Нте-1а^, ге1агс1ес1 соп(го1 апс! ЬегесШагу ргосеззез,
РАШ СогрогаНоп, Р-271, 1954).
Г л а в а VI
ЗАДАЧИ „НА УЗКИЕ МЕСТА"
В МНОГОШАГОВЫХ ПРОЦЕССАХ ПРОИЗВОДСТВА
§ 1. ВВЕДЕНИЕ
В этой главе мы рассмотрим некоторый частный класс важных
и трудных вариационных задач, возникающих при изучении много-
многошаговых производственных процессов.
Прежде всего мы опишем дискретный вариант этого процесса,
который при некоторых предположениях относительно пропорцио-
пропорциональности выпуска продукта затратам производства приводит нас
к задаче определения максимума линейной . формы, подчиненной
линейным ограничениям, — важнейшей задаче, в решение которой зна-
значительный вклад за последние годы внесла теория линейного про-
программирования. Хотя аналитическое исследование этой основной
задачи находится еще в своей начальной стадии, тем не менее
широкий класс задач, возникающих в приложениях, может быть
успешно решен численно с помощью современных вычислительных
машин и различных итеративных методов, таких, как, например,
симплекс-метод.
Однако если пользоваться стандартными вычислительными мето-
методами, то при изучении процессов „с узкими местами", характеризую-
характеризующихся небольшим числом технологических способов на каждом шаге
процесса и одновременно большим числом шагов, мы сталкиваемся
с обычной трудностью размерности. Как и при рассмотрении про-
процессов в предыдущих главах, это препятствие можно до известной
степени обойти, описывая процесс при помощи функциональных
уравнений. Поскольку, однако, мы в целях изучения характера
оптимальных поведений интересуемся аналитическими решениями
в явном виде, мы дадим формулировку непрерывного варианта этих
процессов. Следует подчеркнуть, что во многих случаях непрерыв-
непрерывная модель процесса может дать на самом деле более точное опи-
описание действительности, чем дискретная. Весьма важным оружием
в нашем математическом арсенале является применение двойственного
непрерывного процесса; таким образом используется линейность рас-
рассматриваемого процесса. •
Чтобы проиллюстрировать этот метод, мы в настоящей главе
детально изучим один простой процесс, оставляя рассмотрение более
сложного процесса до следующей главы. Во многих случаях эти
аналитические методы, примененные с аккуратностью и старанием, по-
позволяют нам получить в явном виде аналитические решения задачи
220 Глава VI
максимизации вместе с явным описанием оптимальных поведений.
Много трудностей остается, однако, непреодоленными, когда дело
доходит до построения общей теории. Изучая следующие страницы,
читатель быстро убедится в том, что математическая теория задач
этого типа находится еще в зачаточном состоянии.
Будем рассматривать вариационную задачу, состоящую в*опре-
в*определении максимума скалярного произведения (х(Т), а) по вектор-
функции г {г), где вектор-функции х и г связаны векторно-матрич-
ным дифференциальным уравнением
A) ^ = Ах + Вг, х@)
а г удовлетворяет ограничению
B) Сг < Ох
для
Методы, которые мы используем для решения этой задачи, будут
развиты дальше и применены к классическим задачам вариационного
исчисления в гл. IX.
§ 2. ОБЩИЙ КЛАСС ЗАДАЧ, ВОЗНИКАЮЩИХ ПРИ ИЗУЧЕНИИ
МНОГОШАГОВОГО ПРОЦЕССА ПРОИЗВОДСТВА
Центральной задачей в теории и в приложениях математической
экономики является задача комбинирования одинаковых или различ-
различных отраслей промышленности с целью изготовления какого-либо
конкретного вида продукции наиболее эффективным образом. Кри-
Критериями эффективности при этом могут быть либо минимальная про-
продолжительность процесса изготовления или максимальная прибыль,
либо же некоторая комбинация этих двух характеристик процесса.
В качестве примера, который совершенно элементарен с эконо-
экономической точки зрения, но достаточно сложен математически и при-
приводит к задачам, которые мы не можем решить так легко, как нам
этого хотелось бы, рассмотрим простую модель трехотраслевого
производства, где в качестве составляющих взяты „автомобильная",
„сталелитейная" и „инструментальная" отрасли промышленности1)»
В этой чрезвычайно сжатой, „огрубленной" экономической модели
межотраслевых связей2) мы будем предполагать, что состояние каж-
каждой отрасли в любой момент времени полностью определяется со-
созданными в ней запасами материалов и мощностью производства при
) Излишне говорить, что эти названия используются только чтобы на-
направлять должным образом нашу интуицию. Здесь не предполагается, что
этим терминам приписывается какой-либо глубокий содержательный смысл.
2) Это огрубление совершенно аналогично тому, которое делается при
изучении электрических токов низкой частоты, где вводятся понятия „сопро-
„сопротивления", „индуктивности* и цемкости".
Задачи «на узкие места» в многошаговых процессах производства 221
изготовлении новой продукции из этих материалов. Кроме того, мы
начнем с предположения, что изменения в этих основных количе-
количествах, запасе сырья и производственной мощности, происходят только
в дискретные моменты времени: * = 0, 1, 2, .... Г.
Определим следующие параметры состояния:
A) хх(г)—число автомобилей, выпущенных к моменту г,
лг2(О — производственная мощность автомобильных заводов в мо-
момент Ь,
х$(Ь) — з'апас стали в момент Ь,
хАA)—производственная мощность сталелитейных заводов в мо-
момент I,
хь @ — запас инструмента в момент Л
х%(Ь)— производственная мощность инструментальных заводов
в момент Ь.
Введем следующие предположения относительно взаимосвязи этих
трех отраслей:
B) а) для увеличения производственной мощности автомобиль-
автомобильной, сталелитейной или инструментальной отраслей тре-
требуются только сталь и инструмент,
б) для производства автомобилей требуется только произ-
производственная мощность автомобильной отрасли и сталь,
в) для производства стали требуется только производствен-
производственная мощность сталелитейной отрасли,
г) для производства инструмента требуются только произ-
производственная мощность инструментальной отрасли и сталь.
Динамика этого процесса производства может быть описана сле-
следующим образом: в начале каждого единичного периода времени,
скажем, от Ь до Ь-\- 1, мы выделяем различные количества стали и
инструмента, взятые соответственно из их запасов, для производ-
производства автомобилей, стали и инструмента, —т. е. для пополнения запа-
запасов последних, — и для увеличения производственных мощностей
автомобильной, сталелитейной и инструментальной отраслей.
Пусть для / = 1, 2, ...
C) а) гг(г) есть количество стали, выделенное в момент Ь
на увеличение л;$@.
6) Щ({) есть количество инструмента, выделенное в мо-
момент г на увеличение Х
Учитывая предположения B), мы видим, что
D) а) 2,@=0.
б) щ (I) = да3 (О = Щ @ = 0.
Чтобы получить соотношения, связывающие величины л:{
я»@ и щ(()> мы должны сделать еще несколько дальнейших
222 Глава VI
предположений относительно связи между выпуском продукта и
затратами производства. Самое простое допущение, которое может
быть сделано, состоит в тохМ, что мы имеем линейный производ-
производственный процесс, в котором выпуск продукта всегда прямо про-
пропорционален объему затрат наиболее дефицитного из требуемых
ресурсов1). Таким образом, объем производства при обилии сырья
прямо пропорционален производственной мощности, а при избытке
соответствующих производственных мощностей прямо пропорцио-
пропорционален количеству дефицитного сырья.
Именно эта зависимость от количества наиболее дефицитного
ресурса и приводит к термину „задачи на узкие места".
Проиллюстрируем сказанное: объем производства автомобилей
за период от I до г-\- 1 будет зависеть от производственной мощ-
мощности автомобильных заводов в момент Ьь т. е. от хг (() и от коли-
количества стали гг (I), определенного в (За). Так как объем производ-
производства зависит от минимальной из двух величин: производственной
мощности и запаса сырья, то мы получаем уравнение
E) хх {I + 1) = хх (О + гшп (ТЛ (*). а а (*)),
где ^1 и а1 — положительные постоянные, которые предполагаются
известными.
Аналогично на основании этого предположения, а также пред-
предположений B) мы получаем следующие уравнения, связывающие
величины хг(г-\-\) с **(*). **@ и Щ(*JУ-
F) А?
= Х2 @ + т[П («2*2 (О- Р2^2 @ ).
= ^3 @ — *1 @ — *2 @ — ** @
(О )•
аьгь(*)]9
где а^, р^ и ^г — постоянные.
) Как мы уже отмечали в введении, это допущение в действительности
может и не быть с математической точки зрения самым простым. Более
реальное предположение, основанное на законе уменьшающегося дохода и
связанное с нелинейными функциями, может на самом деле привести к более
простой математической задаче. Это объясняется тем, что нелинейные функ-
функции более удобны при вариационном подходе. С другой стороны, линейные
задачи в некоторых случаях гораздо легче решать численно.
2) Все эти уравнения являются „уравнениями сохранения", которые
утверждают, что количество ресурса в момент г -\- 1 равно количеству его
в момент г минус то, что было использовано за период [/, г -\-1], и плюс
то, что было произведено за период [/, / + 1].
Задачи «на узкие места» в многошаговых процессах производства 223
Ограничения, которые должны быть наложены на г\ и щ, оче-
очевидны:
G) а) {
б) гг + г2 -+- *4 + гь
в)
Здравый смысл подсказывает также ограничения:
а) а1г1
б) а2г
в) а4г4
г) а52:
д) аб2
Смысл последних соотношений состоит в том, что, во-первых,
выделение сырья сверх того количества, которое может быть освоено
производственной мощностью, никакого прироста производства не
даст, и, во-вторых, что объем производства определяется запасами
наиболее дефицитного ресурса.
Пользуясь этими дополнительными ограничениями, мы можем
полностью исключить переменные чю{ и вместо соотношений F)
получить систему уравнений
(9) хх {I + 1) = хх (I) ■+- аггх (О, х, @) = си
= х2 @ + Ч*г @> х2 @) = с2,
= *3 @ — г, (О — *2 (/) — гА @ — ^ @ — *б @ 4- Тз*4 @.
л:4 (/ -+-1) = х4 @ -+- а4<г4 @, х4 @) = сА,
— е2г2 (() — е4<г4 (О — еб2е (О -+-*ьЧ @. 5г =
= *6 @ 4- аб26 @, л:6 @) = с6.
Теперь для каждого I ограничения на гг{1) принимают вид
A0) а) ^
б) гх 4- г2
в)
Г)
Мы должны выбрать ^@ для / — 0, 1, 2, ..., Т — \ с учетом
указанных выше ограничений и притом так, чтобы максимизировать
величину хх(Т).
224 Глава VI
§ 3. ОБСУЖДЕНИЕ РАССМОТРЕННОЙ ВЫШЕ МОДЕЛИ
Легко видеть, что величина хх (Г), равная общему объему произ-
производства автомобилей за период [О, Т], может быть линейно выражена
через величины г{{1), ( = 0, 1, 2, .... Т—1, 1=1, 2, .... 6.
Поэтому задача максимизации величины хх (Т) при линейных ограни-
ограничениях B.10) является задачей линейного программирования. При
заданных значениях коэффициентов и времени Т ее можно решить
численно с помощью различных итеративных методов, если только Т
не слишком велико. В частности, для динамических процессов рас-
рассмотренного здесь типа возможен ряд важных упрощений.
Однако обычно в анализе, подобном тому, который здесь про-
проводится, мы не столько интересуемся численным решением, соответ-
соответствующим некоторому конкретному набору постоянных, сколько
всем множеством числовых значений, соответствующих ряду зна-
значений параметров. Иными словами, в большинстве случаев цель
исследования состоит в „анализе чувствительности", „устойчивости"
решения.
Такой анализ чувствительности необходим, поскольку мы сделали
много допущений, например о линейности процесса производства
продукта, об отсутствии времени запаздывания и „времени опереже-
опережения" в производстве, пользовались упрощенным описанием отраслей
при помощи огрубленных понятий производственной мощности и
запасов сырья и т. д. Любые выводы относительно структуры опти-
оптимальных поведений, которые делаются на основании этой упрощен-
упрощенной математической модели, могут быть признаны обоснованными
только в том случае, когда они сравнительно нечувствительны к точ-
точности определения значений различных описывающих эту модель
параметров.
Из сказанного выше ясно, что вычислительная работа, связанная
с выполнением любого надежного анализа чувствительности, при
использовании только чисто вычислительных методов (когда прихо-
приходится исследовать многомерное пространство) будет утомительной,
требующей много времени, а анализ неизбежно неполным.
Встает вопрос, можно ли определить внутреннюю структуру
оптимального поведения, не зависящую от тех численных значений,
которые мы можем последовательно приписывать параметрам. Знание
этого факта важно не только само по себе (оно позволяет нам
осуществить полный анализ чувствительности решения), но и чрезвы-
чрезвычайно полезно при отыскании приближенных решений в тех
случаях, где точный анализ оказывается неосуществимым, а также
при отыскании способов аналитического решения сложных про-
процессов.
В качестве первого шага на пути к получению аналитического
и численного решений мы переформулируем задачу в терминах
функциональных уравнений.
Задачи «на узкие места» в многошаговых процессах производства 225
§ 4. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Ясно, что общий объем производства автомобилей при оптималь-
оптимальном поведении распределения зависит только от начальных ресур-
ресурсов (?!,..., с6 и продолжительности процесса 7. При этом вели-
величину сх можно точно и не указывать.
Определим тогда для 7=1, 2, ...
A) /(с2, сг> • • •» съ> Т) как общий объем производства автомоби-
автомобилей за период 7 при начальных ресурсах с{,
1 = 2, 3, ..., 6 и использовании опти-
оптимального поведения.
На основании принципа оптимальности мы получаем следующее
функциональное уравнение для функции /(с2, с3, .... с6; 7):
B) /(е2, съ с6; Т-\-\) = тах[а1г1-{--/(с'г с'д, . .., ^; 7I
где
у _____ V _____ у 9 9 I
1 *2 ^4 ^5 ^6 I
4 ■ 4 4'
СЪ ===
а через 2 обозначена область в пространстве векторов (гх, г2, ^4, гь%
определяемая следующими неравенствами:
D) а)
б)
г) ^ < /&>
Аналитическая задача определения функции / и, что, еще более
важно, природы оптимального поведения все еще связана с боль-
большими трудностями. Вычислительная задача также громоздка, так как
для каждого значения Т приходится табулировать функцию пяти
переменных. Однородность рассматриваемого процесса позволяет нам
свести эту задачу к другой, содержащей четыре переменных;
этим замечанием мы воспользуемся в следующих параграфах.
Вычислительную задачу, связанную с определением максимума
в многогранной области 2, можно значительно упроетить, если
учесть, что отыскиваемый максимум достигается на ее вершинах.
15 Р. Беллман
Глава VI
§ 5. НЕПРЕРЫВНЫЙ ВАРИАНТ^)
Чтобы упростить аналитическую задачу, мы перейдем от дискрет-
дискретной модели процесса к непрерывной. При этом мы преследуем
цель использования мощных методов анализа и линейной алгебры.
Очень часто при рассмотрении физических явлений непрерывные
модели значительно проще для изучения, чем дискретные.
Для построения непрерывного варианта задачи мы предположим,
что решения принимаются в моменты О, А^, 2А^ и т. д., а коли-
количества материалов ^(^), щ([), выделенные в интервале времени
У;*-г-11, заменяются количествами гД^)Д/, до{A)Д1, выделенными
в интервале времени [*, 1-\-Ы]. Величины Х\{$) и щA) являются
теперь плотностями распределений ресурсов.
Возвращаясь к уравнениям B.9), описывающим дискретный про-
процесс, и устремляя А* к нулю, получаем новые уравнения:
A) ^ А х
х2 @ = а2г2 @, х2 @) = с2ш
*з @ — — гг @ — г3 @ — гА (() — гь (г) — г6 @ + Тз*4 @.
^4 @ = «4^4 @. ^4 @) = С4•
^5 @ = — е2*2 @ — Ч *4 @ — 86^6 (О + а5*5 @. ^5 @) =
^б@ = «6^6 @. ^6@) = ^6
(здесь точкой обозначается дифференцирование по О-
Ограничения, накладываемые на г^ теперь таковы:
B) а) ^
б) ^
в) г2г2 + е4г4 + *еге < сю,
г) *
Это означает, что ограничения B6) и Bв) отпадают. Однако
теперь должны быть добавлены два условия, смысл которых состоит
в том, что в любой рассматриваемый момент величины запаса сырья
должны быть неотрицательными:
(в дискретном варианте эти условия выполнялись автоматически).
) Гл. VIII посвящена изучению аналогичного непрерывного варианта
дискретного процесса, рассмотренного в гл. П.
Задачи *на узкие места» в многошаговых процессах производства 227
Из этих ограничений видно, что всякий раз, когда лг3 = О, должно
выполняться неравенство
D) ^
и аналогично, когда хъ — 0, мы должны иметь
E)
Следовательно, величины г2, я3, ^4 и г6 неограниченно возра-
возрастают, как только хъ и д:5 становятся положительными. Это означает,
что нам могут встретиться, решения типа дельта-функции. Более
детально это обстоятельство будет рассмотрено в следующей главе,
где исследуется пример с решением именно этого типа. Однако
строгое изучение этой особенности решения будет отложено до сле-
следующей книги. В этой и следующей главах мы будем поступать
по существу формально в тех случаях, где строгое рассмотрение
увело бы нас слишком далеко в сторону1).
Теперь задача состоит в том, чтобы максимизировать вели»
чину хх (Г) с учетом приведенных выше ограничений.
Остановившись на некоторое время на системе обозначений, мы
перейдем к решению этой задачи, используя рассматриваемый в дина-
динамическом программировании метод функциональных уравнений.
§ 6. СИСТЕМА ОБОЗНАЧЕНИЙ
Введем векторно-матричную систему записи, которая значительно
упростит обозначения и таким образом поможет при изложении
общего теоретического подхода, избавляя нас от обилия различных
индексов. Одновременно с изучением основных понятий мы рас-
рассмотрим один частный пример, чтобы проиллюстрировать нетривиаль-
нетривиальные аналитические детали.
Пусть символы х(г), гA) и с обозначают соответственно д-мёр-
ные векторы-столбцы:
х{0 —
с ^^
а символы Аг, В$ (для встречающихся далее значений /и у) обозна«
чают (п X яг)-матрицы.
1) Важно отметить, что непрерывный процесс действительно описы-
описывается приведенными выше уравнениями. Детальное рассмотрение этого
вопроса дано в гл. VIII, где также исследуется связь между дискретным
и непрерывным процессами. -' - * ■ , - : ^: л
228 Глава VI
Мы будем рассматривать векторы х и г только с неотрицатель-
неотрицательными компонентами. Чтобы указать на это, мы будем использовать
запись дг^О, которая означает, что л^^О для /=1, 2 п.
Неравенство х^>у равносильно неравенству х — У^О.
Возвращаясь к системе уравнений E.1), мы видим, что ее можно
записать в виде
A)
где Ах и А2 — матрицы, составленные из коэффициентов системы E.1).
Аналогично ограничения E*2) — E.5) принимают вид
B)
Вхг <! В2х.
Задача максимизации величины Х1(Т) является частным случаем
п
задачи максимизации линейной формы 2ГЛ(^)- Чтобы представить
это выражение в более простой форме, мы вводим скалярное произ-
произведение двух векторов х и у, именно
п
Общая задача состоит тогда в выборе функции г (г), максимизи-
максимизирующей скалярное произведение (х(Т), а) (а—данный вектор) при
выполнении приведенных выше ограничений A) и B).
Одна из трудностей, которая не возникает при рассмотрении
дискретного процесса и появляется при изучении его непрерывного
варианта, состоит в том, что если в качестве г (О рассматриваются
только функции в обычном смысле, то отыскиваемый максимум
может и не Существовать. В дальнейшем мы будем предполагать,
что ограничения D.4) обеспечивают существование максимизирующей
функции. Так действительно и будет, если условия D.4) имеют
вид г^Въх, где матрица Вв — положительная. Для полного иссле-
исследования задачи необходимо использовать интегралы Стильтьеса.
I
§ 7. ПОСТАНОВКА ЗАДАЧИ С ТОЧКИ ЗРЕНИЯ
ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
Так как вид уравнений D.1) и D.2) не зависит от времени,
то тах(хG1), а) (мы будем предполагать всюду в оставшейся части
этой иллюстративной главы, что рассматриваемый максимум действи-
действительно существует) является функцией только времени Т и компо-
компонент вектора с (начальных запасов сырья и производственных
Задачи «на узкие места» в многошаговых процессах производства 229:
мощностей), т. е. только параметров состояния и продолжительности
процесса.
Напишем поэтому
A) шах (л? (Г). а) = /(с, Т)з*/(с1ш с2. .... сп; Т).
г
§ 8. ОСНОВНОЕ ФУНКЦИОНАЛЬНОЕ УРАВНЕНИЕ
Мы хотим получить функциональное уравнение для функции /
на. основе использования принципа оптимальности *), который в дан-
данном случае утверждает, что природа произвольного оптимального
поведения в вопросах распределения ресурсов на интервале [О, Т]
[т. е. поведения, максимизирующего скалярное произведение (л: (Г), а)]
такова, что его продолжение в любом конечном подинтервале [5, Т]
должно быть оптимальным поведением для процесса продолжитель-
продолжительности Т — 5 с начальным состоянием с (8).
Здесь через с (8) обозначен вектор х E), определяемый из урав-
уравнения F.1) при некотором поведении в вопросах распределения
ресурсов на интервале [0, 5].
Математическая формулировка этого принципа приводит к функ-
функциональному уравнению
О) /(с, 3 + Т) = / (сE), Т)
для оптимального поведения на интервале [О, 5-|-Т].
Следовательно, оптимальное поведение на интервале [0, 5] опре-
определяется уравнением
B) /(с, 5.4-Л = тах/(сE). Т),
[о/Я
где максимум ищется на множестве всех допустимых поведений
на интервале [0, 5], т. е. по всем функциям гA), удовлетворяющим
соответствующим ограничениям.
Уравнение B) вместе с начальным условием /(с, 0) = (с, а)
является основным функциональным уравнением, описывающим этот
процесс.
§ 9. НЕЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
Используем теперь основное уравнение (8.2) для получения диф-
дифференциального уравнения в частных производных для функции /
(в предположении, что функции /их обладают всеми необходимыми
свойствами дифференцируемости). Как мы увидим далее, в этом
месте мы вправе действовать совершенно формально, т#к как
Гл. Ш, § 3; - . , .
230
Глава VI
в.дальнейшем мы построим метод для обоснования того» что любая
функция, полученная таким несколько вольным путем, действительно
является решением данного уравнения.
Пусть 5 является бесконечно малой величиной. Тогда мы имеем
A)
а) /(с,
0) с E) == с
в)/(сE). Т) =
= /(с,
[А.с
гг @)Ц- о E),
где через д//дс обозначен вектор
B)
К.
дс
дс
Л
\дсп
Когда «Ъ стремится к нулю, максимум на интервале [0, 5] при
наших предположениях о непрерывности сходится к максимуму
в точке 5 = 0, т. е. к максимуму по значениям величины г@).
Учитывая рассмотренные выше соотношения A), мы убеждаемся
в том, что для уравнения (8.2) аналогом в бесконечно малом является
нелинейное дифференциальное уравнение в частных производных
C)
*@)
причем величина г@) должна удовлетворять условиям F.2).
§ 10. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
Важность уравнения (9.3) состоит в том, что оно позволяет нам
определить решение в интервале [0, Г-^ДГ], если оно уже опре-
определено в интервале [0, Т] для всех начальных состояний»
Оказывается, для большинства задач этого типа многие трудности
легко преодолеваются в случае малого Т, так как для процессов
малой продолжительности оптимальными являются очевидные грубо
приближенные поведения. Поэтому теоретически мы имеем система-
систематический метод продолжения* решения вплоть до любого желаемого
значения Г, Однако в следующей главе мы увидим, что, -хотя рот
Задачи «на узкие места» в многошаговых процессах производства'231
метод является систематическим, детали, связанные с его примене*-
нием, никоим образом не тривиальны.
В следующем параграфе мы остановимся на анализе решения
одной сравнительно простой задачи. Многое в этом анализе может
быть опущено, если только определить структуру решения, которая
во многих случаях подсказывается экономическими соображениями.
§ 11. ЧАСТНЫЙ ПРИМЕР
Для иллюстрации описанного выше общего подхода рассмотрим
задачу максимизации величины х2(Т), где
A)
——
и плотности распределений гХУ г2, как функции от /, удовлетворяют
в интервале 0^/^Г следующим ограничениям:
B) а) ги *2>0,
б)
в)
г) *2>0.
В этом случае плотности гх и г2 равномерно ограничены, и,
используя свойство слабой сходимости или основываясь на клас-
классических теоремах вариационного исчисления, легко убедиться, что
в данном случае максимум достигается. Следовательно, мы вполне
обоснованно можем написать
C) /(с1§ с2, Т) = тах х2 (Т).
[О, Г]
Как и в общем случае, функция / удовлетворяет функциональ-
функциональному уравнению
D) /(*!. с2. 5 + Г) = тах/(х1E),,х2E), Г),
[О, 5]
которое в пределе при 5—► 0 приводит к дифференциальному урав-
уравнению в частных производных:
E) -^ = тах [ад *- + (в^ - г,)
Мы напоминаем, что пока это уравнение является чисто формальным,
так как нам не известно, обладает* ли функция / необходимыми
свойствами непрерывности. - '.
232 ГЛавй VI
Максимум берется по области, определяемой неравенствами
F) а) ОО^ г2,
б) г1+
в) г2
при дополнительном ограничении
G) я2г2 —
если х2 = 0. Переменными являются ^ = ^ @), г2 = г2 @).
Обрисуем теперь в общих чертах схему аналитических преобра-
преобразований, которая позволит нам получить решение. Мы начнем
с наиболее сложного случая, когда с2 <С сх. Для процесса с малой
продолжительностью решение тривиально. Именно, мы имеем
(8) гх = 0, г2 = х2,
/=С2еа*т.
Этого поведения придерживаются до тех пор, пока не возникнет
„узкое место", т. е. пока с2 не превысит сх. Используя оптимальное
поведение, определяемое формулой (8), мы убеждаемся, что этот
случай имеет место, когда Т больше, чем Т1 = \о%(с1/с2)/а2.
Чтобы получить решение, для значений Т > Тх, мы перепишем
уравнение E) в виде
(9) -^ = тах \гх[ах-^-^- -/-) + а2 -^- г2 .
Точка (^(О), -г:2@)), где достигается максимум, зависит от знака
Й от величины коэффициентов при гх и г2. Для Т < 7\ мы имеем:
(Ю) ах
х 2 г дс2
Пользуясь условием непрерывности производных д//дс1 и д//дс2,
мы можем подозревать, что для значений Г, ненамного превосходя-
превосходящих Ти решение будет иметь вид
A1) а) гх = 0ш г2 = х2 для
б) гх = 0, г2 = а:! для Гг < 5 <; Т.
Этому поведению соответствует функция / следующего вида:
A2) /=Ь2с2 + (Г —
где значение Г!—^-то же, что и выше. Чтобы определить, при каких
значениях Т (Т^> Тг) это поведение остается оптимальным, допустим,
что рассматриваемый процесс начинается с момента 5==^. Полагая
^ = с1(ГЛ, с'2 = 'с2(ТЛ, записываем /в виде
A3)
Задачи «на узкие места» в многошаговых процессах производства 233
Уравнение, заменяющее уравнение (9), имеет точно такой же вид,
только вместо сх, с2 в него входят с[, с'г именно,
A4)
= шах
1/7
д/
п2~дсТ
Используя формулу A3), мы находим
A5)
дс<
? —
а2 —у — #2*
Коэффициент при гх отрицателен для значений Т<Т* = Тх-\- ^
равен нулю в точке Т* и положителен для всех остальных значе-
значений Т. : . .
Следовательно, новое поведение, определяемое формулами A1),
остается оптимальным для Т в интервале 7\ ^ Т ^ Г*.
Кроме того, так как величина Т* — Тх не зависит от сх и с2,
то нам известен вид оптимального поведения и в остальной части
интервала.
Теперь остается определить вид оптимального поведения внутри
интервала [0, Т] в общем случае, когда Т превосходит Т*. Рас-
Рассматривая вершины на приведенном ниже рисунке, мы можем предпо-
предположить, что оно имеет вид
A6) гх = х2 — хХш г2 =
Поучительно рассмотреть область, определяемую ограничениями F),
при с2
При максимизации гасн# тремя критическими точками являются
вершины Р. <2- и. /& где Р = @, сх)ш Я = (с2 — сх, сх), /? = (г2, 0).
В случае, Кчогда с2 превосходит сх% принцип непрерывности приводит
к. выбору ф как максимизирующей вершины^
?34 Глава VI
Вместо непосредственной проверки этого утверждения (которую
можно фактически осуществить), мы опишем в следующем параграфе
более изящный метод, использующий линейность рассматриваемого
процесса. Этот метод можно использовать не только для проверки
предлагаемых решений, но и в качестве теоретического аппарата
для определения природы оптимальных поведений.
§ 12. ДВОЙСТВЕННАЯ ЗАДАЧА
Для иллюстрации принципов, которыми мы будем пользоваться,
возьмем наше основное уравнение в виде
A)
со следующими ограничениями:
B) а)
б)
Заметим, что уравнение F.1) всегда может быть записано в виде A)
при Ах ^ 0, если переписать его сначала следующим образом:
C)
с ограничениями
D) а)
б)
в) 1ю <; х,
и затем объединить векторы чю и г в некоторый единый вектор.
Следовательно, к уравнению типа F.1) эти методы также непосред-
непосредственно применимы.
Так как х = с-\- Г АгсН* то ограничение B6) можно переписать
о
следующим образом:
E) • Вг+ $ СгМ^с (С = — А).
о
Задача максимизации величины (х(Т), а) равносильна задаче макси-
т т
мизации выражения Г (Аг, а)сМ= Г (г, а') Л, где а7 = А а. Здесь
о
через А обозначена матрица, транспонированная к А.
Задачи «на узкие места» в 'многошаговых процессах производства <*235
Возвращаясь опять к началу, мы рассмотрим задачу максимизации
т
функционала У= Г (г, а!)си на множестве всех функций г, удовле*
о
творяющих ограничениям
F) а) 2>0,
г
О
Обозначим через ад(^) некоторый неотрицательный вектор той же
размерности, что и вектор с. Тогда, используя условие F6), мы
получаем
Л г \ т
ад, Вг-\- Г С%A1Х ] йЬ < Г (ад, с) М.
о / о
Пусть, как и выше, через В' обозначена матрица, транспонированная
к В. Легко видеть, что (Вгъ ад) = {г, Вгчю\ Для произвольной по-
постоянной матрицы С интегрирование по частям дает
т I г \
т/ т
(8)
О V О
Пользуясь этими двумя равенствами, находим
т/ г \ т I т \
() ^ 1^' *+) г и .~.М ™~^) т 1ш гI
о \ о . / о \ г I
Предположим, что можно найти неотрицательный вектор ад =
удовлетворяющий неравенству
г
A0) Б'ад+/С'адг#1>а'.
Тогда мы приходим к следующей цепочке равенств и неравенств:
т т
A1) ]>, с)
о о \ о
ЛТ \ Т
ВГ . С ПГ Л4. \ ^/^ Г/ Г Ч ЛА
Г\ Т0\ I I (■, <ТО\ ПТ- У I ПТ ^^> I 1п 9\ ПТ
3 } ^3 ч '
г 'о
Отсюда ясно, что
т т
.г
02) 1Ш Г («г,
', а
о
236 Глава VI
где точные нижняя и верхняя границы ищутся на множестве всех
функций 1Л) и г, удовлетворяющих неравенствам A0) и F6). В слу-
случае существования минимума и максимума приведенные рассуждения
остаются в силе. Если, однако, их существование предполагать
нельзя, то появятся дельта-функции, и мы должны переформулиро-
переформулировать эти задачи с помощью интегралов Стильтьеса. При этом возни*
кает ряд интересных и трудных задач, которые мы не будем здесь
рассматривать *).
Если оба экстремума в неравенстве A2) равны, то, очевидно,
должны выполняться следующие соотношения2):
A3) щ = 0, если ск > I Вг + / Сг й1
^ = 0, если о!. <
О /г
Т \
В'<ш 4- I Сгт йг
3
3
Установим теперь то важное обстоятельство, что справедливо
и обратное утверждение: любая пара неотрицательных гида, удовле-
удовлетворяющих условиям A3) и первоначальным ограничениям, является
решением рассматриваемых задач на максимум и минимум.
Для доказательства заметим, что если выполняются условия A3),
то все соотношения A1) превращаются в равенства. Предположим,
что какой-то другой вектор г удовлетворяет всем ограничениям
и что для него
т т
A4) {(г, а')сН<{(г, с/)Л-
о о
Тогда, используя вектор 'ДО, соответствующий вектору г, мы прихо-
приходим к противоречию:
т т 1 т
A5)
о о V г
т I г \ т
(с,
о \ о
т
= ^ (г, а') йи
о
В частности,. мы не будем рассматривать связь с теоремами о мини-
максе в теории игр, соответствующими известным результатам для дискрет*
ной задачи.
*) С точностью до множеств меры нуль.
Задачи «на узкие места» в многошаговых процессах производства 237
Следовательно, мы нашли метод для проверки справедливо-
справедливости угаданного решения. По данному г мы определяем вектор %ю
с помощью неравенств A3). Получив чю% мы проверяем, удовлетво-
удовлетворяет или не удовлетворяет *ш заданным ограничениям. (В следующем
параграфе мы подробно рассмотрим это на примере задачи из § 11.)
При использовании этого метода возникают трудности, если век-
вектор *ш не определяется однозначно из условий A3). В этом случае
должны быть рассмотрены различные альтернативные решения.
§ 13. ПРОВЕРКА РЕШЕНИЯ, ПОСТРОЕННОГО В § 11
Используя описанный выше метод, мы находим, что для задачи,
рассмотренной в § 11, двойственной является задача минимизации
т
функционала Г {сх1Юх -\- с2щ) сН по всем функциям щ (*) и щ (/).
о
где у и т связаны уравнениями*)
A)
У г СП = а2,
а ограничения таковы:
B) а)
б)
В)
Уравнения A2.13) приобретают теперь следующий вид:
C) а) если г2 < х1ш то щ = О,
б) если хх-\-г2 < х2, то
т в) есл'и ю2 > Ух* то г\ = О»
г) если щ -\- т> > у2, то Х2 = 0.
Мы опустили условия, соответствующие неравенству х2^0, так
как мы предполагаем, что предложенное оптимальное поведение рас-
распределения автоматически удовлетворяет условию х2^0. В дей-
действительности это так и есть.
1) Заметим, что двойственный процесс протекает в обратном направле-
направлении во времени.
23& Глава VI
Мы хотим проверить, что поведение, максимизирующее вели-
величину х2(Т), задается следующим образом:
D) а) гх @ = 0, г2 = гшп (х1ш х2) для Т—1/(аха2) < г <! Т;
A)если х2<д:1, то ^ = 0, г2 = х2, }
б) } для
B) если х2 ]> хх, то гх = х2 — хх, г2 = хх )
Легко видеть, что это допустимое поведение, при котором век-
вектор гх = х2— хх действительно неотрицателен, когда гх и г2 имеют
указанные выше значения.
По данному вектору г мы можем с помощью условий C) опре-
определить вектор -ш, а затем проверить согласованность. При этом при*
ходится рассматривать два случая в зависимости от того, превос-
превосходит ли функция х2 в какой-либо точке функцию хх или нет.
Предположим, что Т^ТХ; в этом случае, если используются со-
соответствующие поведения, функция х2 может превосходить функцию хх.
Случай I: Т—1/(аха2) < 7\ <^ 7\ Решение дается в следующем
ниде:
E) для г < Тх гх = О, г2 = х2,
для / ^ Г, ^ = О,
Для значений / < Тх эти результаты вместе с условиями C) при-
приводят к следующему:
F) для 7\ < Т щ (О = 0, щ (О = у2 (О,
для
Используя уравнения A), мы получаем для значений
G) У2(*)
тогда как для Ь << Тх имеем
(8) у2(*) = а2еа>(т*-
Ух @ = — 1 + аха2 (Т — 7\) — е°* ^ -*> < 0.
Следовательно, неравенства тх, т2^0, Щ^-Ух. *№х-\-щ&J
в соответствующих интервалах выполняются.
Случай II: Т, < Т—\/(аха2). Этот случай наиболее интересен.
Векторы г и чю определяются здесь следующим образом:
(9) для Г 1
ДЛЯ Г
для
Задачи «на узкие места» в многошаговых процессах производства
В интервале Т—1/@^2) <С*<>^ мы имеем
A0) у2 @ = а2, ух @ = — 1. + в А (Т —
Следовательно, в этом интервале :ух (Ь) <^ 0 = щ. Заметим, что,
ух[Т—1/(я1я2)] = 0. При 7\<^^Г—\1(ахаг) мы имеем уравнения
A1)
Покажем, что в этом интервале ух ^0, у2^У\- Беря за началь-
начальную точку г — Т—\1{аха2)ъ в которой эти неравенства соблюдаются,
будем считать, что время изменяется в обратном направлении. При.
этом наши уравнения примут вид
012)
Отсюда получаем
A3) й
Следовательно, если функция ух неотрицательна, то выполняется
неравенство у2—З^^-О. Ясно, что производная йу^йг, будучи по-
положительной в начальной точке, сохраняет свой знак все время, пока
точка (ух, ^находится над прямой а2у2 — A -+-л^) ^ = 0. Когда же
она попадает на эту прямую, мы имеем йух\й1 = 0, т. е. эта точка
является для функции ух либо точкой максимума, либо точкой пере-
перегиба. Обе эти возможности исключены, так как
0.
Последнее показывает нам, что в рассматриваемом интервале функ-
функции 1ЮХ и чйJ неотрицательны.
Наконец, для значений Ь <ТХ имеем
У 2* аг — «2^2-
При уменьшении Ь функция у2 возрастает, а функция ух убывает.
Следовательно, неравенство у2 ^ ух остается справедливым.
Это завершает проверку, . .,
240 Глава VI
§ 14. ЧИСЛЕННОЕ РЕШЕНИЕ
Задача максимизации величины х#9 где
A) хк+1 = апхк + а12^ +- *п** + Ью™* хо = *1.
= С2>
на множестве всех последовательностей [гк] и {^}» удовлетворяю-
удовлетворяющих условиям вида
B) аигк + Лг2щ < ^3*й + **<4Л. ' = 1. 2
как известно, может быть сведена к вычислению членов последова-
последовательности {/к(си с2)}, Л=1, 2 N. где
C) Л(^, с2)=с1§
/ ( > 1/ ( + + Ь + *^ + «22^2
1 * 11
а область /? определяется неравенствами
D) й1хг + й?^^ < ^з^1 + ^и^2» ' = 1. 2. • • •.
Хотя нетрудно доказать, что этот максимум достигается в неко-
некоторой вершине области, определенной неравенствами D) (мы реко-
рекомендуем это читателю в качестве упражнения), и, значит, вычисление его
на каждом шаге тривиально, однако нам приходится все-таки табу-
табулировать последовательность функций двух переменных. Оказывается,
что в этом случае решение задачи особенно затрудняется тем фактом,
что решетка в плоскости (си с2) может увеличиваться. Другими сло-
словами, если мы хотим найти значение /м(сх, с2) в области 0^^^^,
0<Сс2<^с2, то, возможно, нам придется вычислять значения функ-
функции /н_г в большей области, /^_2 в еще большей и т. д.
Ясно, что каждый раз, когда возникает подобная ситуация, вы-
вычисления требуют много времени и средств.
Покажем теперь, что вычисление членов последовательности
[/#(сх, с2)} можно одновременно свести, во-первых, к вычислению
членов двух последовательностей функций одной переменной и, во-
вторых, к случаю, когда решетка фиксированная.
Нашим основным орудием является следующее свойство однород-
однородности функции /^ (сх, с2): для всех с1% с2 > 0
Задачи <ма узкие места» в многошаговых процессах производства 241
Мы можем, таким образом, переписать уравнение C) в виде
- тах
= тах
, 1 \]
Мы видим, что вычисление значений функции /^+1(^, сЛ можно
осуществить, если известны две функции:
G) 11
= /^A, а:),
Следовательно, нахождение последовательности
быть сведено к вычислению членов двух последовательностей
может
§ 15. НЕЛИНЕЙНЫЕ ЗАДАЧИ
Ряд задач в математическом анализе и в его приложениях к про-
проблемам управления, возникающим в инженерном деле и в математи-
математической экономике, сводятся к максимизации или минимизации инте-
интеграла вида
г
о
на множестве всех функций *$(/). удовлетворяющих следующим огра-
ограничениям:
B) а) ^ = О<(*.*). *=1, -.., А.
б) ^(д:, г)<0, У==Ь 2
В некоторых случаях нелинейность задачи приводит к более пол-
полному анализу, позволяя нам определить экстремаль с помощью класси-
классических вариационных методов, а не путем испытания вершин, как это
приходилось делать в линейных задачах. В тех случаях, когда в^задаче
имеются ограничения указанного выше типа, мы должны одновременно
сочетать оба этих подхода. Во всех случаях метод функциональных
уравнений может быть использован как для аналитических, так и для
вычислительных целей.
Задачи этого типа будут рассмотрены в гл. IX.
А>- Ьеллман
242 Глава VI
УПРАЖНЕНИЯ И ПРОБЛЕМНЫЕ ЗАДАЧИ
1.
К ГЛАВЕ VI
1. Рассмотреть задачу о максимизации линейной формы
п
п
при ограничениях Х{^0 и ^сц^ ^Сс^ /== 1, 2 М. Пред-
полагается, что коэффициенты ац и Ъ\ положительны. Пусть
/п(сх. с2 ^)=тах
Показать, что
А(сл» С2> ♦ • •» сг
1 г яц
ч Г > I /• Г
, С2, .... С,
00
где
2. Показать, что /п(с19 с2 сп) является вогнутой функцией
переменных с$ при с\ = 0.
3. Какой вывод о числе ненулевых максимизирующих последова-
последовательностей XI может быть сделан на основании этого результата?
- 4. Рассмотреть приведенную выше задачу для случаев, когда
М= 1, 2 или 3, и определить зависимость максимизирующей после-
последовательности Х\ от параметров с^ а также аналитический вид функ-
функции /п.
5. Показать, что табулирование функции /п(с19 с2 см) всегда
можно свести к табулированию функции /п(сх, с2 1). Устано-
Установить соответствующий результат для рассмотренного выше процесса
*с узким местом".
6. Рассмотреть задачу о максимизации величины и(Т) по всем
функциям г;(/), удовлетворяющим условию 0^г>^# в интервале
0 ^ I <; Т, если
Здесь все рассматриваемые величины -^скаляры.
Задачи «на узкие места» в многошаговых процессах производства 243
7. Решить общую задачу о максимизации скалярного произведе-
произведения (х (Г), а) по всем векторам .у @» удовлетворяющим условию
У ^ х в интервале 0 <^ г <^ Г, если
— = Ах -\- Ву% х @) = с.
Здесь х% у% с и а — векторы, а Л и В — матрицы.
8. Показать, что задача максимизации величины х2(Т) при усло-
условиях
^^З Т2^2» "^3 @) == ^3»
где г2 и 2г3 — функции от Ь, подчиненные ограничениям
б) 1. г2-\-гв
2. ^2 т
при соответствующих предположениях о непрерывности равносильна
решению дифференциального уравнения в частных производных
В) -37" = таХ I а2 3^ Т2 -Т~ I ^2 + *ЗТЗ 1Г "л^ ^3 »
^ х>(^ Ь\ ^з п дсь) 21Г 3*3 дсв дс2 3У
где О (г) — область, определяемая неравенствами (б).
Предполагается, «что все входящие в задачу параметры — неот-
неотрицательные и что / = /(с2, с3,
9. Показать, что оптимальные поведения зависят только от вели-
величины отношения г = с2/св, т. е. х2/хв, и от остающегося времени Т.
10. Определить вид решения для малых значений Т.
11. Решить рассматриваемую задачу для частного случая Ьг=0.
БИБЛИОГРАФИЯ И КОММЕНТАРИИ
К ГЛАВЕ VI
§ 1. Изложение теории линейного программирования можно найти
в сборнике под редакцией Купманса (АсПуку апа1у818 о! ргос1ис1юп апс!
\11оса*юп, ей. Ьу Т. С. Коортапз, Сош1ез Сотпиззюп, II. о! СЫсадо, 1951),
где имеется описание симплекс-метода Данцига и рассмотрен ряд приложе-
приложений1). Изложение итеративного метода другого типа, метода „потока" Бол-
1) См. также сборник „Линейные неравенства и смежные вопросы", ИЛ»
М., 1959. — Прим. ред.
16* '
244 Глава VI
дырева, можно найти в его работе [В о 1 дуге!! А., 0е1егтша1юп о! Ше
тах1та1 81еас1у !1ош о! 1га№с Шгои^Н а гаПгоас! пе*шогк, КАШ СогрогаНоп,
1955, Р-687]. Оба они являются „релаксационными" методами, на важность
которых впервые указал Р. Саусвелл.
§ 5. Методы и результаты этого и следующего параграфов были опубли-
опубликованы в работе Беллмана [В е 11 т а п К., ВоШепеск ргоЫетз апс! дупаппс
рго^гаттт^, Ргос. Мя/. Асай. 8с1. [/8А 39 A953)] и подробно изложены
Беллманом в статье: В е 11 т а п Р., ВоШепеск ргоЫетз, !ипс1юпа1 е^иа^^опз
апс! дупат^с рго^гаттт^, ЕсопотеМса, 23 A955), 73—87.
§ 9. Строгая теория этих вариационных задач будет во всяком случае
опираться на интегралы Лебега — Стильтьеса и, вероятнее всего, на теорию
обобщенных функций Шварца. Очень может быть, что это послужит пово-
поводом к изучению вариационных задач, содержащих обобщенные функции.
§ 12. Как и в дискретном случае, эту двойственную задачу можно
изучить наиболее последовательным образом, если рассмотреть задачу на
минимакс, содержащую как первоначальный, так и двойственный процессы.
В случае, когда функции, описывающие поведения, равномерно ограничены
в силу имеющихся в задаче условий, можно установить ряд результатов
о существовании значения соответствующей игры и об эквивалентности,
тт-тах = тах-тт, используя сведения из теории непрерывных игр. Общий
случай, однако, требует уже использования теории игр в пространстве
обобщенных функций Шварца.
Примечательно, что так много выводов можно сделать только на
основании легко получаемого результата A2.12).
§ 13. Леман построил непрерывный аналог симплекс-метода Данцига,
который можно использовать как систематическую процедуру для получе-
получения решений вариационных задач этого типа. Предварительное изложение
его результатов можно найти в работе Ь е Ь т а п Я 5., Оп Ше соШШиоиз
81тр1ех теШос1, КМ-1386, КАШ СогрогаИоп, 1954.
Глава VII
ЗАДАЧИ «НА УЗКИЕ МЕСТА». ПРИМЕРЫ
§ 1. ВВЕДЕНИЕ
В предыдущей главе мы рассмотрели многошаговый процесс про-
производства, включающего три отрасли промышленности, которые мы
назвали автомобильной, сталелитейной и инструментальной отраслями.
Исходя из этой задачи, мы пришли к некоторой общей теоретиче-
теоретической формулировке одного класса непрерывных многошаговых про-
процессов производства в терминах понятий и методов теории динами-
динамического программирования.
Цель настоящей главы состоит в том, чтобы на примере деталь-
детального изучения некоторого частного случая показать, что с помощью
нашего нового подхода можно получить явные аналитические решения
для задач этого более общего типа. Математическая сторона таких
задач доставляет много трудностей, так что эти задачи ни в каком
смысле нельзя еще считать освоенными.
Мы рассмотрим упрощенный двухотраслевой процесс, включаю-
включающий автомобильную и сталелитейную отрасли. О высокой степени
огрубления или, выражаясь более педантично, укрупнения (соп^1отега-
(юп) свидетельствует наше предположение о том, что в любой мо-
момент времени I состояние этой системы отраслей полностью опре-
определяется следующими величинами:
A) хг(() — запас автомобилей в момент {,
—производственная мощность автомобильной отрасли в мо-
момент I,
— запас стали в момент 1>
— производственная мощность сталелитейной отрасли в мо-
момент г.
Считая, что / изменяется непрерывно, мы должны в каждый
момент определить плотности распределения запаса стали для трех
различных целей:
B) а) производство автомобилей,
б) строительство автомобильных заводов, т. е. увеличение
производственной мощности автомобильной отрасли,
в) строительство сталелитейных заводов, т. е. увеличение про-
производственной мощности сталелитейной отрасли.
246 Глава VII
Последние две из этих трех целей должны быть подчинены
основной задаче максимизации общего числа автомобилей, выпускае-
выпускаемых за период времени Г, т. е. максимизации величины хх(Т).
Основные предположения, положенные в основу нашей модели,
состоят в следующем: единицы измерения запаса и производственной
мощности выбраны так, что и в сталелитейной и в автомобильной
отраслях для производства единицы запаса за единицу времени тре-
требуется единица соответствующей производственной мощности. Пусть
для выпуска одного автомобиля требуется Ьх единиц стали, а для
увеличения на одну единицу автомобильной и сталелитейной произ-
производственных мощностей-—соответственно Ь2 и Ь4 единиц стали. При
этом предполагается, что не требуется стали для производства до-
дополнительного ее количества.
Очень важным является допущение об отсутствии отставания во
времени между выделением ресурса и увеличением производственной
мощности. Задачи, возникающие при учете этого времени запазды-
запаздывания, являются значительно более трудными и рассматриваться
здесь не будут.
Пусть
C) а) хх{Г) — скорость производства автомобилей,
б) ^2 @ — скорость роста производственной мощности авто-
автомобильной отрасли,
в) ^з@ — скорость производства стали,
г) г4 (г) — скорость роста производственной мощности стале-
сталелитейной отрасли.
Рассуждая так же, как и в предыдущей главе, мы получаем сле-
следующую систему уравнений:
D) —гг- = гх (Л, х< @) = сх,
-^■ = ^@. *2@) = г2.
— ^2^2 @ — #4*4 @» *3 @) = С3,
иХл. /1ч ^
в которой функции %1 и XI должны удовлетворять ограничениям
вида
E) а) г, @ < х2 (/),
б) *,@<*4(').
в) *{(*)>0, /=1. 2, 3, 4.
г)
Задачи «на узкие места». Примеры 247
Из этих условий первые два связаны с ограниченностью произ-
производственных мощностей, т. е. являются ограничениями типа „узкого
места", третье требует, чтобы скорости производства были неотри-
неотрицательными, т. е. чтобы не было разрушения или „каннибализма",
и, наконец, четвертое условие утверждает, что величина запаса стали
должна быть неотрицательной, что означает невозможность брать
металл в долг.
Наша задача состоит в определении функций ц((;)ш удовлетворяю-
удовлетворяющих условиям E) и максимизирующих величину хг(Т). Благодаря
отсутствию явного ограничения функций г2 и г4 сверху возникают
различные трудности, которые должны быть преодолены с помощью
дельта-функций.
§ 2. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
В § 1 мы математически сформулировали задачу использования
сталелитейной и автомобильной отраслей промышленности для макси-
максимизации выпуска автомобилей. Будем исходить из уравнений A.4)
и A.6).
Эти уравнения можно объединить в равносильную им систему
интегральных неравенств;
I
A) гх < х2, гх @ — ^ гг {в) й$ < с2,
о
г
о
г
о
Наша задача является частным случаем следующей более общей
вадачи. Обозначим через 2 множество всех векторных функций гA),
удовлетворяющих условиям
B) а) г @ > 0.
г
б)
где В и С—матрицы, а с — постоянный вектор. Мы хотим найтц
в множестве 2. векторную функцию г{$), которая максимизирует
248 Глава VII
функционал
1
C) Г B (О. а)^-
о
Эту задачу мы рассматривали в предыдущей главе. Там было
показано, что имеется двойственная задача, которая дает достаточное
условие того, чтобы функция г {г) из множества 7, являлась макси-
максимизирующим вектором, или, другими словами, допустимое решение
было оптимальным.
Обозначим через № множество векторных функций <и)(г), для
которых
D) <т @ > О,
т
С I IV (8) й8 ^ а,
I
где В' и С — матрицы, транспонированные к В и С. Двойственная
т
задача состоит в определении минимума интеграла Г (уиA), с) сН на:
о
множестве функций <ш ^ №.
Как было показано в § 12 гл. VI, для всех функций г и чю из
соответственных классов 2, и № выполняется неравенство
E) I B@." а)
о о
Если мы сможем найти две векторные функции г и гю, для кото-
которых соотношения E) выполняются со знаком равенства, то на них
будет достигаться соответственно максимум и минимум в двух рас-
рассматриваемых задачах. Такие две векторные функции, для которых
в выражении E) имеет место равенство, будем называть двойствен-
двойственными по отношению друг к Лругу. Таким образом, достаточное
условие того, чтобы функция г ^2 была оптимальным решением,
состоит в том, чтобы для нее нашелся двойственный элемент чю ^ №.
Для рассмотренной выше задачи со сталелитейной и автомобиль-
автомобильной отраслями мы имеем:
A 0 0 0\ /0—1 О О
0 0 0 01, С=[ЬХ Ь2 -1 Ь4
0 0 10/ \0 0 0—1
Задачи «на узкие места». Примеры 249
Поэтому двойственная система неравенств имеет вид
т
G) /^^(О + ^/^зС*)^—1>0.
т
/2 = — Г <ш2 ($) йз-\-Ь2 Г
г г
т
I
Т Т
1.^о4 I <хюъ ($) из — I ^ ($) ^8 ^> 0.
Мы обозначим компоненты вектора чю через ^2» ^з и ^4» чтобы была
ясной их связь с неравенствами хх^х2, 0^лг3, ^з^^-
Условия оптимальности, т. е. условия того, чтобы соотношение E)
выполнялось со знаком равенства, состоят в следующем:
(8) если г{ {г) > 0, то /«@ = 0 (/=1,2,3, 4),
если гх (г) < х2 A), то чю2 @ = 0,
если 0 < лг3@. то чюъ(() = О,
если г3 (() < х4 ((), то ^4 @ = 0.
Условия оптимальности эквивалентны следующим условиям:
(9) если /ДО > 0, то г1 (() = 0 (/ = 1, 2, 3, 4),
если чзJ @ > 0, то гг @ = лт2
если <пу3(О>0, то д:
если т^ @ > 0, то гъ (() = л:4 (О-
§ 3. ДЕЛЬТА-ФУНКЦИИ
Прежде чем перейти к нахождению решения, рассмотрим пред-
предстоящее использование „дельта-функции". Вполне может случиться так,
что рассмотренные выше общие задачи не имеют решений, если
множества 2, и \Р состоят только из векторов, компоненты которых
являются интегрируемыми функциями. Фактически, как мы позже
увидим, так обычно и бывает в задаче с автомобильной и сталели-
сталелитейной отраслями. Этой трудности можно, однако, избежать, если
расширить множества 2 и ^ так, чтобы они содержали векторные
„функции", компоненты которых являются суммами интегрируемых
функций и „дельта-функций". В этих расширенных классах рассмат-
рассматриваемые задачи уже имеют решения. Под дельта-функцией,
250 Глава VII
сконцентрированной в точке @, с весом со, которую мы обозначим
через о)8(^ — ^0), мы понимаем такую обобщенную функцию, что для
каждой функции ср. непрерывной в точке *0,
г
(о о E — г0) ср ($) аз =
С
если г < 'о.
о 1«>?(^о). если
[Для 1 = 10 этот интеграл не определен, за исключением того слу-
случая, когда ср(^о) = О; в этом случае интеграл полагается равным нулю.]
Использование дельта-функций может быть строго обосновано
при помощи теории интегралов Стильтьеса. Другой подход заклю-
заключается в том, что дельта-функции рассматриваются как расширение
пространства интегрируемых функций с помощью предельного про-
процесса, аналогичного тому, который применяется для получения веще-
вещественных чисел из рациональных х).
Условия оптимальности остаются прежними даже в тех случаях,
когда классы 7. и 1^ расширены описанным способом. Заметим,
что если в качестве компонент векторов г и т допускаются только
измеримые функции, условия олтимальности могут нарушаться в изо-
изолированных точках и даже на множествах меры нуль. Но если один
из векторов, например т3 имеет в качестве компоненты щ дельта-
функцию в точке @, то для вектора г, двойственного вектору *ш9
в точке @ соответствующие условия оптимальности должны выпол-
выполняться.
Мы увидим далее, что для нахождения оптимального вектора нам
никогда не придется пользоваться дельта-функциями, сконцентриро-
сконцентрированными в точках, отличных от нуля. Интуитивно это означает, что
в точках, отличных от начала отсчета, скачкообразные изменения не
являются необходимыми.
§ 4. РЕШЕНИЕ
Мы будем применять метод, состоящий в построении ряда ^-ре-
^-решений, для которых можно найти двойственные элементы г из
класса 7. и, следовательно, получить решения нашей задачи. Главную
трудность представляет построение <ш-решений с нужными свойст-
свойствами. При этом мы будем сочетать догадки с использованием тех
свойств, которыми должен обладать оптимальный вектор г. Догад-
Догадками здесь можно пренебречь только ценой рассмотрения гораздо
большего числа случаев.
Прежде всего ясно, что всегда должно выполняться равенство
= лг4. Произведя слишком много стали, мы во всяком случае не
) Изучение получаемых таким образом обобщенных функций в настоя-
настоящее время разрослось в целую математическую дисциплину. См., например,
Г е л ь ф а н д И. М., Шилов Г. Е., Обобщенные функции и действия над
ними, Физматгиз, 1958. —Прим. ред.
Задачи «на узкие места». Примеры 251
причиним вреда. Это означает, что для всех значений / должно быть
т
13({) = 0, т. е. зд4(О = Г ^з($) &8- Остальные неравенства B.7) при-
г
нимают вид
т
/•
—— I ТО) (*1\ //С "^ С\
^^^ I СК/о XV/ 1^» -^^ V/»
Ясно, что непосредственно перед моментом Т автомобили должны
производиться, так как мы хотим максимизировать величину хг
в момент Т. Следовательно, гх > 0, откуда следует, что /1 = 0,
Однако один только этот факт не дает еще нам достаточной инфор-
информации для нахождения функций щ и тА-
Построим сначала ^-решение с тем свойством, что /2 = 0 вблизи
точки Т. (Это решение назовем базисным ^-решением.) Это озна-
означает, что ^4 G")— О- Тогда на основании A) мы имеем
B) ^4 (О = -1A
Мы видим, что все функции ^2, ^3 и Щ остаются положительными
при убывании I. Следует проверить, выполняется ли неравенство
/^0 В соответствии с выбором вектора но находим
C) /4=-М1 — е-) +
Правая часть этого равенства положительна для малых значений
Т — / и отрицательна, когда разность Т — I велика. Обозначим
через 10 то значение 1% при котором правая часть равна нулю. Тогда
разность Т — @ будет решением уравнения
D) Т — *0 =
Таким образом, в точке 10 мы должны отбросить одно из урав*
нений: 1г = 0 или /2=0. Попытаемся теперь выбрать функцию *ш
так, чтобы для значений и мен|?щих г^ было./4 = 0 и /4 = 0. Мы
252 Глава VII
имеем
E)
Щ(()=1 — Ь^{*0)е{г°-гIЬ'.
Для проверки того, что /2 ^- 0, найдем производную этой функции.
Мы получаем
F)
Для того чтобы /2^0, достаточно выполнение неравенства й1г\(И <^ О
для всех значений / <^0. Последнее будет иметь место, если
что на основании B) и D) равносильно условию Т — ^^ЬА. Это
неравенство можно проверить, если подставить Ъ± вместо Т — г
в формулу C) и затем убедиться, что полученная при этом величина
является положительной. Мы имеем
(8) ^ [(*4 + %) 0 - е~Ь^Ь>)- Ь] =
(^)] 0.
\ е
Следовательно, /2^>0 для всех значений /^^ при указанном выше
выборе функции чю.
Из формул E) видно, что функции ^4 и 1й)ъ остаются положи-
положительными. Таким образом, выбор векторной функции чю в соответ-
соответствии с формулами E) будет удовлетворительным до тех пор, пока
функция чюг не. обратится в нуль. Предположим, что это произойдет
при ^ = ^. Тогда на основании B) и D) мы получаем
Посмотрим, можно ли для значений (, меньших^ чем 11$ выбрать
= 0 и при этом иметь /4 = 0. Мы видим, что щ > 0 и Щ^> 0.
Кроме того, сИ2/сН = &2йщ/<И <0*0, т. е. /2>0, и й1х\йг~
^Ъ^йщ/сМ < 0, так что 1Х > 0. Следовательно, сделанный выбор
векторной функции т будет верным для всех значений ^^^.
Наше базисное решение может быть сведено в помещаемую ниже
таблицу. В этой таблице перечислены также те свойства, которыми
должна обладать векторная функция г, двойственная этому -пу-реше-
нию. Если поведение, описываемое любым вектором г с этими
свойствами, является допустимом (т. е. удовлетворяет налагаемым
да # ограничениям),, то оно „будет и
Задачи «на узкие места». Примеры
253
к>
/
/3 —
/4 =
^2 =
ЧЮ ^>
0
0
0
0
? — о
лз ^
•о>2
1
>
" ——
>
>
0
0
0
0
0
г —0
в
хх = х2
у Л
к
к
к
1Юо
ЧЮл
X
=
>
>
>
Та
1
0
0
0
10 Л
г.
г
К
<
ица
1 = 0
^ ='Х
1
2
Посмотрим, как можно использовать эту таблицу для нахождения
частного решения задачи с автомобильной и сталелитейной отраслями.
Предположим на время, что г3 = 0. Для значений I <^(х мы должны
иметь
A0) х = 0 х = О X = х х
В интервале ^1 < ^ < ^0 нам следует выбрать
(Л 1V 2 = г 7 —
т —
Такой выбор можно произвести в том и только в том случае, когда
#4(^1)—-#1*2(^1)^ 0- Предположим, что это неравенство справедливо^
Тогда в интервале /0 < г < Г мы должны иметь
A2)
Ао, <Со ——
О,
что возможно, если дг4(^1) — ^1^2(^1)^^- Таким образом, мы видим,
что при некоторых начальных условиях мы можем найти опти-
оптимальное решение.
§ 5. МОДИФИЦИРОВАННОЕ «^-РЕШЕНИЕ
Как уже отмечалось» если х±{г^ — ^1Л:2(^1)<О, то задача ослож-
осложняется. Для успешной работы над этим случаем рассмотрим моди-
модификацию базисного ^-решения (табл. 1). Обозначим через и0
некоторую точку из интервала [^, Г]. Для каждой такой точки и0
мы определяем решение следующим образом.
В интервале и0 < I < Т пусть /до(^) совпадает с базисным реше-
решением. Для значений г < й0 выбираем щA) = 0. Для значений I <^ иОщ
но близких к и0, полагаем/ш4 @=1/*;» так что /; = 0. При таком
254
Глава VII
выборе в некотором интервале слева от а0 должно быть /4 ]> 0.
Обозначим через ах точку, в которой функция /4 обращается в нуль
при данном выборе т. Для значений I < ах определяем т так,
чтобы /4 = 0. Легко видеть, что при таком выборе 1Х > 0, /2 > 0,
1ЮЪ > 0 и щ > 0 для всех значений / <^их. В результате описанного
построения мы получаем некоторое ^-решение для каждого и0 из
интервала [1Х% Т]. Заметим, что если ио=х119 тои1 — 2х, и это реше-
решение тождественно совпадает с нашим базисным решением (табл. 1).
Отметим также, что их непрерывно зависит от а0. Так как
их = Т — Ь4 при ио—Т, то ^-решение существует для каждого
значения их в интервале [1Х9 Т — Ь4].
Построенные -^-решения, а также свойства соответствующих
г-решений сведены в следующую таблицу.
Таблица 2
к>
к>
к=
/4 =
^3>
Щ>
г<их
0
0
0
0
0
0
0
■ гх = 0
22 — 0
г3 = х.
к>о
к=о
к>о
Ш2 = 0
«/3 = 0
хе>*>°
( <а0
■
гл = 0
*г = х*
к
к
к
к
™*
<< т
= 0
>о
= 0
= 0
>о
>о
>о
г1 — х2
х3 = 0
г3 = хА
/,=
/2 =
к =
к>
Щ>
Щ>
т
0
0
0
0
0
0
0
гА
гх
лг3
ч
= 0
= хг
= 0
= лг4
Так как мв есть дельта-функция в точке и0, должно быть хъ (и0) = 0.
Заметим, что при и0 > г0 не существует /, удовлетворяющего
условиям, указанным в третьем столбце таблицы; если же ио=Т,
то не найдется {, удовлетворяющего условиям, приведенным в по-
последнем столбце.
§ 6. РАВНОВЕСНОЕ РЕШЕНИЕ
В ряде случаев представляется естественным выбор следующего
поведения: израсходовать начальный запас стали (т. е. уменьшить лг3
до нуля) таким образом, чтобы в результате стало л?4 = #1лт2. После
этого увеличение производственных мощностей уже не является
необходимым, и вся имеющаяся сталь может быть использована дли
производства автомобилей. Так как и г2, и г± в общем случае
должны быть дельта-функциями, то выбор такого поведения требует,
чтобы для двойственной" ему функции чи было /2@) = 0 и /4@)=0.
Йострош4 ш-решение; обладающее этим свойством, ~
Задачи «на узкие места». Примеры
255
Прежде всего заметим, что наше базисное решение имеет указан-
указанное свойство, если Т таково, что ^0 = 0. Это наводит на мысль,
что можно попробовать вЗять
A) $
где а и р—постоянные. Если щ выбрано так, что
равенства D.1) принимают вид
= 0, то не-
нет
B)
(Г-
т
!■
о.
Если /2@) = /4@) = 0, то
C)
Полагая Е = е-ь*т/ь*, мы получаем из формул A) — C) следую*
щие два уравнения для а и C
D) *2 + B + ^)р
А) е*+(»2 + * А) Р =^ т.
Решение этих уравнений позволит найти чю, для которого /2@)
/4@) = 0. Мы имеем
(б)
а
= 4:1»1(*4— Г)].
д
р
где
F) А =
Таким образом,
G) А = (Ь2
1 =
Г — й2 — ЬХТ) = б.
Предположим теперь, что Т — г^^Т^Ь^, Тогда из формулы E)
видно, что а^О. Проверим теперь, что построенная нами векторная
функция *ш в интервале 0 <! Ь ^ Т имеет неотрицательные ком-
компоненты щA), щA) и да4@% Это равносильно проверке неравенств
0О4(*)< 1/&1 и й^4/Л<0/Мы имеем й^4/Л = а*1/&
Поэтому достаточно убедиться в том, что ^СП^О и
Глава VII
Так как Т
(8)
«4@)
И
Х9)
70,
то из формул D.4) и C) мы получим, что
>0.
—Б) —г]
Наконец, мы должны проверить, что в интервале 0
/2 ^ 0 и /4 ^ 0. Так как
(Ю)
и /2 (Г) = ^2'г(У4(Г)'>0, то /2>-0 для всех значений ^ из [0, Г].
Кроме того, нам известно, что 1^(Т^=^Ь^о^(Т)^^. Поэтому, если
мы покажем, что й?2/4/^2^0, то будет доказано, что /4!^>0 для
всех значений Ь из [0, Г]. Но
ач
4
Это завершает доказательство того, что построенное нами *ш является
решением. Его свойство вместе со свойствами двойственной ему
функции г сведены в следующую таблицу:
Т а б л и ц а 3
1
к
к
=.0
= 0
= 0
/,==0
/2>о
/4>0
■ш3>0
< т
ч
= 0
= 0
1 = 0
Примечание. Это решение является верным
только при Т^Ь
§ 7. ад-РЕШЕНИЕ ДЛЯ ПРОЦЕССА МАЛОЙ ПРОДОЛЖИТЕЛЬНОСТИ
-пу-решение, которое мы теперь построим, будет полезным при
Нахождении решения нашей задачи максимизации в случае малой
продолжительности процесса, Г<^4. Это решение отличается от уже
Задачи «на узкие места». Примеры
257
построенных тем, что допускает, чтобы лг3 принимало положительные
значения, а хг было дельта-функцией, сконцентрированной в нуле.
Пусть в интервале 0<^<^Г мы имеем ^(О —1» ^@ =
= 1 — Ъп> где 0 < ^ < \1ЬХ. Тогда 1Х (!) = 0, /4@ > 0 для 0 < I < Т.
Кроме того.
= *2т— (Г
Т— (Г
A)
Если положить 1 = Т/ф2-{-&1Т), то /2@) = 0, а при *>0 и /2@>0-
Таким образом, мы получаем решение системы неравенств D.1).
Оно приводится ниже вместе со свойствами двойственного ему
вектора г.
Таблица 4
* = 0
/2 = о
■
/1 = 0
/2>0
^>°
т2 >0
7-. 0
^4 >0
*2=0
г4 = 0
Так как ш3 — дельта-функция, сконцентрирован-
сконцентрированная в Т, то лг3 (Г) = 0.
Примечание. Это решение является верным
только при Т < Ь±.
§ 8. ОПИСАНИЕ РЕШЕНИЯ И ДОКАЗАТЕЛЬСТВО
Теперь мы можем дать полное решение поставленной задачи
При этом имеется совсем немного случаев, требующих отдельных
рассмотрений. Критические значения Ьо и 11ш определяемые из D.4)
и D.9), зависят от Г, но таким образом, что при фиксирован-
фиксированных Ь1% Ь2 и #4 величины Т — Ьо и Т — 1Х постоянны.
Случай I: Т настолько велико, что ^^-0. В этом случае
мы выбираем в качестве гх дельта-функцию, сконцентрированную
в точке 0, чтобы можно было непосредственно уменьшить хг до
нуля. Это означает, что в случае, когда общая продолжительность
процесса достаточно велика, мы должны не держать сталь в запасе,
а употребить ее для строительства новых сталелитейных заводов.
17 Р. Беллман
258 Глава VII
Использование дельта-функции здесь допустимо, так как для значений
Л близких к нулю, /4 = 0. Положим в интервале О
A) гг =
сохраняя, таким образом, величину лг3 равной нулю. В точке 1Х при-
приходится рассматривать отдельно два подслучая:
1В: х4 (^) —.Ъхх2 (^) < 0.
В случае 1А мы можем выпускать автомобили, используя всю
производственную мощность и не истощая при этом запаса стали.
Поэтому положим в интервале ^<^<^0
х4 — Ьхх2
C) %1 = Х2, Х2 === 0» %ъ ==: Х4,
а в интервале ^0< г ^ Г
D) %1 = ЛГ2, 2^2 ==:: 7 , #з г*== **'4» ^4 :=:::
Это решение будет оптимальным в случае 1А, так как оно является
двойственным к базисному ^-решению, приведенному в табл. 1.
В случае 1В у нас уже нет" достаточного количества стали,
чтобы использовать для выпуска автомобилей всю производственную
мощность. Поэтому при г > 1Х мы производство автомобилей прекра-
прекращаем, т. е.
1 —— V/, %2
~~7
Мы не производим автомобилей до тех пор, пока величина х4 — Ьхх2
не обратится в нуль или же пока не окажется г = Т — Ь4 (в зависи-
зависимости от того, какое из этих событий произойдет первым). Если
величина х4 — Ьхх2 обращается в нуль в точке (', то мы после
этого момента выбираем гх — х2, г2 = 0, 2з = лг4» г4 = 0. Построен-
Построенное решение, очевидно, оптимальное, так как оно является двой-
двойственным к ^-решению, приведенному в табл. 2, если считать
и1 = ^/. Как уже отмечалось, такое решение существует при любом V\
если только }х<^{' ^*Г — Ь4. Если же, с другой стороны, хА(Т—Ь4) —
— Ъхх2(Т—Ь4) < 0, то в интервале Т — Ь4<С(^Т мы выбираем
F) хх = ^> 22 = 0, 23 = лг4, ^4 = 0-
В оптимальности этого решения можно убедиться, проверив, что
оно является двойственным к ^-решению, приведенному в табл. 2,
где ио=Т, их = Т — Ь4.
Случай И: величина Т такова, что ^^0<^0. Как и раньше,
мы выбираем в качестве г± дельта-функцию, сконцентрированную
Задачи <г«а узкие места». Примеры 259
в точке 0, чтобы сразу же уменьшить лг3 до нуля. После этого
решение находится, как и выше. Здесь также могут представиться
два подслучая:
G) IIА: х4 @) — Ьхх2 @) > 0,
ИВ: хА @) — Ьхх2 @) < 0.
В случае ПА полагаем г1 = лг2, т. е. автомобили производятся
с использованием всей производственной мощности. Остающуюся
сталь мы используем до момента @ для увеличения производствен-
производственной мощности сталелитейной отрасли, а начиная с момента ^0—для
увеличения производственной мощности автомобильной отрасли.
Таким образом, в интервале 0 < г < ^0 мы полагаем
/О\ ~ у ~ Г) ~ у ~ ..
1О1 л>* —— «^2» % ~"~~" * 3 ' •^'4' 4 ™"
а для г > 10
(9)- гг = х2ш г2 = ^±^о
Это решение будет оптимальным, так как оно является двойствен-
двойственным к базисному решению, приведенному в табл. 1.
Случай ИВ аналогичен случаю 1В. Здесь проводятся такие же
рассуждения и получаемое решение ^оказывается двойственным
к решению, данному в табл. 2.
Случай III: Т таково, что {о^0^Т — Ь4. Здесь приходится
рассмотреть три подслучая:
A0) III А: с4 —
ШВ: с^Ьхс2< ь,
з
Ьо
В случае ША мы используем наш начальный запас стали для
увеличения производственной мощности автомобильной отрасли; дру-
другими словами, мы выбираем в качестве г2 дельта-функцию, сконцент-
сконцентрированную в точке 0, уменьшая лг3 до нуля. Далее полагаем <г1 = лг2
и используем всю остающуюся сталь для увеличения производственной
мощности автомобильной отрасли, т. е.
О1\ - у. г ХА — #1*2 ~ у.
/ 1 г . г ь > з 4»
Это решение будет оптимальным, так как оно является двойствен-
двойственным к базисному -пу-решению, приведенному в табл. 1.
В случае ШВ нам не хватает производственной мощности стале-
сталелитейной отрасли. Решение и доказательство в этом случае те же,
что и в случае 1В.
17*
260 Глава VII
В случае ШС мы можем так израсходовать начальный запас
стали, что величина лг3 будет равна нулю, а х4 = Ьхх2. Мы выбираем
для этого в качестве г2 и гь дельта-функции, сконцентрированные
в точке 0. Затем полагаем гх = х2% г2 = ®> 23=.*:4, г4 = 0. Это ре-
решение— оптимальное, так как оно является двойственным к равно-
равновесному -до-решению, приведенному в табл. 3.
Случай IV: Т -^ Ъ4. В зависимости от начальных значений рас-
рассматриваются три подслучая:
A2) 1УА: с4 —
1УВ: с4 —
1УС: '^*
В случае IVА решение и доказательство те же, что и в случае ША.
В случае 1УВ мы выбираем г2 = 0 и г4 = 0 для всех значений (.
Как всегда, полагаем гъ= х4. Функция хх может быть произвольной
и подчиняется лишь условиям гх({)*Сх20) и х3(Т) = 0. Таким обра-
образом, в этом случае решение не будет единственным. В оптималь-
оптимальности каждого решения такого вида можно убедиться, проверив его
двойственность к -^-решению, приведенному в табл. 2, где ио=Т.
Случай 1УС является промежуточным, и в нем нельзя следовать
поведениям, Построенным для случаев 1УА и 1УВ. На этот раз мы
расходуем начальный запас стали до уровня Сд, используя ее для
увеличения производственной мощности автомобильной отрасли. Затем
мы выбираем г1 = х2, г2 = 09 гъ = х4 и г4 = 0. Величина с'в опреде-
определяется из условия хг(Т) = 0. Оказывается, что этим свойством
обладает
сз— Ь2+Ь±Т
Это решение будет оптимальным, так как оно является двойствен-
двойственным к -до- решению для процесса с малой продолжительностью, дан-
данному в табл. 4.
§ 9. ПЕРЕЧЕНЬ СЛУЧАЕВ РАСХОДА НАЧАЛЬНОГО ЗАПАСА СТАЛИ
После того как начальный запас стали использован, оптимальное
поведение можно определить с помощью системы очередности. До
момента гх увеличение производственной мощности сталелитейной
отрасли, т. е. г4, является первоочередным. Это положение сохра-
сохраняется и после момента 1Х до тех пор, пока не будет или х4 ^ Ьхх2%
или 1 = Ь4, в зависимости от того, какое из этих событий произойг
дет первым. В каждом из этих случаев (они могут, конечно, ветре?
Задачи «на узкие места». Примеры
261
А
В
Уменьшить х% до нуля,
увеличивая х±
Уменьшить л:3 до нуля, увеличивая х2
„Увеличить производственную мощ-
мощность автомобильной отрасли"
Увеличить производственную мощность
сталелитейной отрасли"
Начальный запас
стали не расхо-
расходуется
Уменьшить хъ до
нуля так, что-
чтобы х4 = Ь1х
1х2,
увеличивая хг
Уменьшить Лд, но
не до нуля, так
чтобы х%(Т) =
= 0; увеличить
и
титься и в точке 1Х) первоочередным становится производство авто-
автомобилей гх. На него расходуется вся имеющаяся сталь, если только
не выполняется неравенство лг4 (^) > Ьх хг {гх). В последнем случае
до момента ^0 приписывается вторая очередность увеличению произ-
производственной мощности сталелитейной отрасли. После момента ^0
вторая очередность приписывается увеличению производственной
мощности автомобильной отрасли.
БИБЛИОГРАФИЯ И КОММЕНТАРИИ
К ГЛАВЕ VII
§ 1. Результаты этой главы были получены совместно с Леманом
в неопубликованной статье: В е 11 т а п К., ЬеЬтап -К. 5., ЗШсИез оп
ЪоШепеск ргоЫетз т ргос1ис1юп ргосеззез, РаП I, КАШ Согрогайоп, 1954,
Р-492.
Подобного типа, но более сложный анализ решения вариационной задачи
из этого общего класса можно найти в работе Лемана: ЬеЬтап К. $.,
ЗшсИез т ЪоШепеск РгоЫетз т ргос1ис1юп ргосеззез, Раг! II, КАЫО Согрога-
11оп, 1954, Р-492.
ч Глава VIII
НЕПРЕРЫВНЫЙ СТОХАСТИЧЕСКИЙ ПРОЦЕСС РЕШЕНИЯ
§ 1. ВВЕДЕНИЕ
Как мы видели в гл. II, постановка задачи о золотодобыче в ее
дискретной форме приводит к ряду нерешенных задач, таких, как
задача о трихотомическом выборе, задача с нелинейной функцией выгоды
и многие другие, которые также можно было бы сформулировать.
Мы обратимся поэтому к непрерывному варианту задачи в надежде
преодолеть эти трудности путем использования более мощных средств
непрерывности. Как мы увидим, теперь мы сможем детально изучить
соответствующие вопросы и тем самым составить ясное представле-
представление 0 структуре оптимальных поведений. Получаемые нами сведе-
сведения о структуре поведений можно использовать для построения
полезных приближений к исходному дискретному процессу.
Выясняется . один очень интересный и значительный факт. В то
время как исходная дискретная задача имеет определенные черту
линейности, которые делают затруднительным ее вариационный ана-
анализ (по крайней мере в случае, когда мы рассматриваем средний
ожидаемый доход), непрерывный вариант в достаточной мере нели-
нелинеен, чтобы позволить нам использовать вариационный подход в его
классическом виде с некоторыми модификациями, которых требует
наличие ограничений. Однако при нахождении решения этим методом
наше знание формы решения для дискретного случая сослужит нам
большую службу, предсказывая, каких результатов можно ожидать.
Мы используем комбинацию двух методов, старого и нового, кото-
которая обеспечит успешное наступление на задачу.
Прежде чем обратиться к действительно применяемому нами методу,
мы рассмотрим еще два возможных подхода, каждый из которых
связан с некоторыми трудностями, делающими его неприемлемым.
Вероятно, одинаково важно знать как то, какие методы работают
с успехом, так и то, какие методы не действуют и почему. В более
общих процессах решения этого типа корректная формулировка
непрерывного варианта задачи не является тривиальной. В частности,
это так для случая многошаговых игр непрерывного типа. •
Можно предложить много различных возможных формулировок;
и о корректности подхода следует судить не только на основании
его математической строгости, но также и по аналитической трудности.
Если мы не имеем систематических средств для решения типичных
проблем, то мы не имеем и удовлетворительной теории.
Непрерывный стохастический процесс решения
63
После предварительного обсуждения мы обратимся к действи-
действительно применяемому нами подходу, который является компромис-
компромиссом между двумя предыдущими.
Обоснование, нашего подхода заключается в том, что мы можем
показать, что рассматриваемый нами непрерывный процесс является
в соответствующем смысле пределом дискретного процесса. Однако
в этом томе мы не будем обсуждать этих важных и интересных
вопросов.
§ 2. НЕПРЕРЫВНЫЙ СЛУЧАЙ.
I. ДИФФЕРЕНЦИАЛЬНЫЙ ПОДХОД
Перейдем теперь к рассмотрению некоторых возможных непре-
непрерывных аналогов функционального уравнения E.1) гл. П.
Здесь и в следующих параграфах основное наше предположение
будет заключаться в том, что при каждом нашем действии должна
иметь место высокая вероятность добычи малого количества золота
и отсутствия поломок в машине. Иными словами, мы теряем всякую
надежду на решение нашей задачи для всех возможных значений
параметров и рассматриваем вместо этого малую область изменения
параметров г19 г2, ^, ?2.
Введем в рассмотрение величины:
1—дхЬ — вероятность получения ггхЬ и отсутствия поломок
в машине, когда работы ведутся на прииске Анаконда,
1—^ — вероятность получения г2уЬ и отсутствия поломок в ма-
машине, когда работы ведутся на прииске Бонанца,
где <7Х и д2 положительны, а 8—достаточно малая положительная
величина, такая, что 1—^8 и 1—д2Ь суть вероятности, а гх8 и
г2Ь меньше единицы.
Определяя /(х, у) как и раньше, мы получаем функциональное
уравнение
A)
Это уравнение совпадает с уравнением E.1) гл. II для этих новых
параметров. Действуя формально, в предположении, что / имеет
непрерывные частные производные, для малых 8 получаем прибли-»
женное уравнение
В: /(х,
B)
264 Глава VIII
Его предельной формой при 8->0 является уравнение
Л» г V П "Р —— Г V
C) 0 = шах
Такой подход не представляется нам плодотворным из-за, труд-
трудности установления теорем существования и единственности для функ-
функциональных уравнений этого типа.
§ 3. НЕПРЕРЫВНЫЙ СЛУЧАЙ.
II. ИНТЕГРАЛЬНЫЙ ПОДХОД
Рассмотрим теперь диаметрально противоположный подход. Пусть
5г\г — обозначает некоторую последовательность, состоящую из N
выборов А (т. е. Анаконды) и В (т. е. Бонанцы). Определим
;, у) как вероятность выживания в течение N шагов и
окончания процесса в состоянии (хмс, ^л), с исполь-
использованием последовательности 5# и при начальном
состоянии (х% у)%
, у) как ожидаемый доход от N шагов с использованием
последовательности 5# при начальном состоянии (х, у).
Если 5# действительно состоит из первых N выборов некото-
некоторого оптимального поведения, то мы получим для /(х, у) функцио-
функциональное уравнение
A)
Если А/8, где 8 определяется как и ранее, выбрано так, что при
8 —>■ 0 и /V —> оо оно остается конечным и становится равным I, то
аналогом уравнения B.1) будет функциональное уравнение типа
У* *)+ I П*г* У8)аи8(г, 5, хш у,
г—0 8=-0
где 5 обозначает непрерывное поведение на интервале [0, г\, а
вероятность перехода, определяемую этим поведением.
Функциональные уравнения такого типа встречаются в общей
теории случайных процессов. Мы не будем развивать этот подход
в настоящем томе вследствие обилия трудностей, возникающих при
обосновании этого уравнения и определении общих непрерывных
поведени<|. Вместо этого мы будем использовать подход, средний
между дифференциальным и интегральным подходами, который при-
приведет к функциональному уравнению, имеющему такое же отноше-
Непрерывный стохастический процесс решения
265
ние к уравнению B), как уравнение диффузии или теплопроводности
к уравнению Чепмена — Колмогорова в теории диффузионных про-
процессов»
Обоснование этого подхода заключается в том, что можно дока-
доказать сходимость решения для дискретного процесса к решению для
непрерывного процесса при 8—>0. Однако, как указывалось выше,
здесь этот вопрос рассматриваться не будет.
§ 4. ПРЕДВАРИТЕЛЬНОЕ ОБСУЖДЕНИЕ
Продолжим использование простого уравнения B.1) в качестве
модели для дальнейшего рассмотрения. Согласно решению, рассмот-
рассмотренному ранее в .гл. Н, А- и Б-области отделены граничной линией
2, определяемой уравнением
A)
Эта линия при 8—>-0 переходит в линию Ь с уравнением
B)
Я\
Чг
Для каждого 8 > 0 оптимальное поведение имеет следующую
форму: „Находясь ниже Ц, продолжать применение выбора А до
попадания в Б-область, выше [.%. Затем применять выбор В до
попадания в Л-область, ниже Ц, и т. д.; аналогично для началь-
начального положения выше
Геометрически:
В-область
А- область
О
X
Рис. 24.
Предельная форма этого поведения при 8 -> 0 такова:
„Если (х, у) ниже ^, то использовать выбор А до попадания
на прямую ^ затем двигаться вдоль Ь\ если (х, у) лежит выше ^
то использовать выбор В до попадания на прямую Д, затем дви«%
гатьс:Я вдоль 4%
266
Глава VIII
Заметим, что поведение такого рода, требующее движения вдоль
прямой Ьш не включено ни в какое из множеств поведений, соответ-
соответствующих ненулевым В. Эти поведения, включающие только исполь-
использование А или Б, приводят к путям в виде ломаных, состоящих из
горизонтальных и вертикальных отрезков, как на рис. 24.
У
В- область
А-область
О
Рис. 25.
Однако ясно, что такой путь, как изображенный на рис. 25, мо-
может быть произвольно точно аппроксимирован оптимальным поведе-
поведением при 8—► 0.
Сказанное приводит нас к важному выводу, что непрерывный ва-
вариант исходной дискретной задачи может не обладать оптимальным
поведением, обеспечивающим максимальный доход. Вместо этого
может существовать последовательность поведений, приводящая
к супремуму, если только мы не расширим надлежащим образом
понятие поведения. Естественным путем для получения этого
расширения является допущение смешивания в некотором подход
дящем смысле решений на каждом шаге.
§ 5. СМЕШИВАНИЕ В ТОЧКЕ
Без намерения каламбурить заметим, что введение смешивания
является смешанным благодеянием, поскольку с ним приходит ряд
трудностей как математической, так и физической природы. С ма-
математической стороны мы находим, что перед нами стоят те же
трудности, которые вызвали наше желание пренебречь интегральной
формулировкой из § 3; с физической стороны мы неохотно прини-
принимаем поведение, которое допускает использование смеси решений
в задаче, где требуется определенный-выбор того или иного решения.
Чтобы избежать идейных трудностей математической и физической
природы, применим интерпретирующую схему, которая в очень похо-
похожей ситуации уже использовалась ранее. Сущность этой схемы со-
состоит в том. что при некоторых естественных предположениях
непрерывности смесь решений в точке эквивалентна смеси решений
на малых интервалах около этой точки, - . - . г
Непрерывный стохастический процесс решения 267
Начиная строить нашу математическую модель, будем предпо-
предполагать, что мы рассматриваем процесс, который в момент вре^
мени г = О, А, 2Д и т. д. требует от нас решения, какую долю сле-
следующего временнбго интервала длины А мы отводим соответственно
для Л и для В. Так, на интервале [&Д, &Д + Д] мы уделяем первую
часть [&Д, бД + ^Д] использованию Л, а в течение оставшейся
части [^А -|— ср1Д, &Д-|-Д] используем В,
А В
I !
\ 1 I
к А кА+уА (к+1)А
Рис. 26.
Выбор срх будет зависеть от к или, более точно, от х(кк) и
у(кк) и, кроме того, если процесс конечен, от самого к.
Считая А настолько малым, что процесс достаточно хорошо опи-
описывается влияниями первого порядка малости, мы получим в пределе
при А—>0 систему дифференциальных уравнений, которые мы будем
использовать для определения нашего непрерывного поведения1).
Теперь непрерывное поведение будет описываться функцией ср^/).
В настоящей главе мы выведем эти дифференциальные уравнения.
Чтобы проиллюстрировать силу этого метода, мы решим последова-
последовательно задачи, соответствующие задаче о дихотомическом выборе,
задаче о дихотомическом выборе для конечного числа шагов, задаче
о дихотомическом выборе с нелинейной функцией выгоды, изложенной
в упр. 1 гл. II, и задаче' о трихотомическом выборе из § 13 той же
главы. Хотя эти решения изобилуют подробностями, основные их
идеи просты.
Чтобы обосновать использование этой формализации, следовало бы
показать, что полученный таким путем непрерывный процесс действи-
действительно является в некотором естественном смысле пределом исходного
дискретного процесса. Этот вопрос будет рассматриваться во втором
томе.
§ 6. НОВАЯ ФОРМУЛИРОВКА ПРОЦЕССА ЗОЛОТОДОБЫЧИ
Приступим теперь к осуществлению программы, намеченной в пре-
предыдущих параграфах. Интересной чертой этих построений будет
непрерывное взаимодействие между техникой классического вариа-
вариационного исчисления и методами динамического программирования.
Для упрощения результатов переформулируем рассматриваемую
нами задачу следующим образом:
„В каждый из моментов времени ? = &А мы должны принять реше-
1) Ср. соответствующее замечание в гл. VI.
268 Глава VIII
ние-относительно того, какую долю следующего временнбго интервала
длины А машина будет использоваться на прииске Л, а какую
на прииске В. Это влечет выбор доли срх, которая зависит от коли-
количества золота на этих двух приисках в момент ^ и от самого ^,
если процесс конечен.
Условимся, что если выбрана пропорция ср1э то первую часть
интервала, [&Д, (Лг —|— срх) А], машина используется на прииске А,
а вторую часть, [(/г —|— срх) А, (/г —|— 1) Л], на прииске Б. Если х — коли-
количество золота на прииске А в момент &Д, то-с вероятностью I —Ц^А
будет добыто /^лг^Д золота и машина не испортится, а с веро-
вероятностью ^г1ср1Д золота добыто не будет и машина полностью выйдет
из строя. Если прииск В содержит золото в момент &Д в коли-
количестве у, то с вероятностью I—^Фг^ будет получено количество
и машина не испортится и с вероятностью ^Тг^ (ГДе ?2 — 1 —
эта операция прекратится.
Задача состоит в определении такой последовательности операций,
которая максимизирует ожидаемое количество золота, добытое до
поломки машины".
§ 7. ВЫВОД ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Легко видеть, что если Д мало, то перестановка порядка опера-
операций в [&Д, (&-)-1)Д] дает эффект второго порядка малости. Именно
это свойство позволяет использовать смешивание на интервалах для
получения функции смешения в точке.
Поведение состоит теперь из последовательности {срДАД)},
= 0, 1, 2 Для любого данного поведения определим
х{г) как количества золота, оставшегося на прииске А%
когда процесс продолжается до времени /,
у {г) как количество золота, оставшегося на прииске В,
когда процесс продолжается до времени /,
р (г) как вероятность того, что машина сохранится до вре-
времени Ь, т. е. что процесс продолжится до I,
/({) как ожидаемое количество золота, добытого до вре-
времени /,
где г = #Д, п = 0, 1, 2
Пренебрегая членами второго порядка малости по Д, имеем
A) *(* + *) = *(') — г1?1 @ х (О Д,
р (*) A _ дЛ (*) д —
Непрерывный стохастический процесс решения 269
Устремляя Л к нулю, получаем систему дифференциальных уравнений
Ах
B)
= ~ ?2 С) ГьУ @. .У @)
Мы рассматриваем теперь эти уравнения как определяющие уравне-
уравнения нашего процесса и забываем их формальное происхождение.
Наша цель найти срх = срх (*)• где
C) 0<?1@<1, ?2@=1-?1@>
так, чтобы максимизировать /(Г). Особенно важен случай Т=оо.
Аналогичные уравнения для случая трихотомического выбора
будут выведены ниже, в § 12.
§ 8. ВАРИАЦИОННЫЙ МЕТОД
Пусть срх и ср2 — функции, обеспечивающие максимум х), и пусть
A) ?« = ?« + «&(').
где е— малое положительное число, а (Зх и C2.—Две функции от /,
удовлетворяющие для всех ^^-0 условиям
B) 0<<р4 + вр4<1. _ р1Ч-р2 = 0
(откуда следует | фг \ ^ 1 /е), так что ср^ также допустимы в качестве
функций <р4.
Следовательно, р4 @ «< 0, если ср$ (^) = 1, р{ @ >> 0, если ср* (^) = 0,
и р$ может быть любого знака, если 0<ср$@<1э — область, где
допускается свободная вариация. Производя варьирование, без труда
найдем, что 2)
C) ху) = х @ A — егА @) + о F),
@= У @ A — «В2 @) + о (е),
@ = Р @ A — ^1^1 @ — е<72#2 @ ) + о F),
г
/
о
(Ор @ д/ @+/"А (Ор (О У @+
(Ор @ * @ + ъЪ (О Р @ > @} « + о (•).
) Легко показать, что вследствие равномерной ограниченности функ-
функции срх (/) максимум достигается.
2) Член о(е) обозначает некоторую функцию от е, стремящуюся к нулю
быстрее, чем е, для всех I из [О, Т].
270 Глава VIII
где
г
D) ВгУ)= Ы8)а8
о
и черточками помечены варьированные переменные.
Интегрируя по частям для исключения 5$ (О» МЫ получаем
т
E) /(Г) — / G) = в / [К, @ рг @ + /С2 @ р2 @1Л + о (е),
о
где
т т
F) Кг @ = — #1 Г /' E) ^5 + Г\Р (Т) Х(Т) — Г1 Г Р' E) -^ E) ^5»
т т
Так как /(Г) — /G")^0, мы видим, что при Кь{$)*>> К${$) мы
должны иметь ср$ (I) = 1, ср^- (^) = 0. Эти соотношения дают неявные
уравнения для ср$ и ср^. В следующем параграфе мы рассмотрим
более детально поведение функций К\, с тем чтобы определить (^)
в явном виде.
§ 9. ПОВЕДЕНИЕ ФУНКЦИЙ Кг
Основным соотношением является следующее:
Таким образом, „смешанное поведение" [т. е. такое поведение, для
которого более чем одна из функций ср^ положительна при задан-
заданном Ь, откуда следует, что К1(() = К2@\ может быть оптимальным
только на линии. д^гУ — Я2Г1Х- Эта линия как раз и является той
граничной линией, которая получается при переходе к пределу при
Д->0 из решения для дискретного случая, как в § 4 1).
Если смешанное поведение следует вдоль этой линии, то ср± и <р2
должны выбираться так, чтобы остаться на линии; это означает,
что наклон 8 = у/х должен оставаться постоянным. Так как
= Т" - 4 * М = ['Л - г^15-
Если в результате анализа дискретного случая появляется уверен-
уверенность, что эта линия должна появиться, ее сравнительно нетрудно опознать.
Непрерывный стохастический процесс решения 271
мы видим, что
§ 10. РЕШЕНИЕ ДЛЯ СЛУЧАЯ Т = со
После этих напутственных замечаний определим оптимальное
поведение для бесконечного процесса 7 = оо. Бесконечная задача,
как обычно, проще, чем конечный случай, по причине однородности,
порождаемой бесконечным временем: после любых начальных дей-
действий мы оказываемся перед проблемой такого же типа с другими
исходными значениями. Отметим, что вследствие этого, а также
вследствие однородности уравнений по х и у, решение в каждой
точке является функцией одного только наклона $ — у1х.
Начнем с замечания, что если выбор А применяется где-либо
на прямой ц±г2у = д2гхх в плоскости (х, у), то после этого он
применяется все время. Это следует сразу же из соотношения (9.1),
которое показывает, что при (}1г2у — Ц&\Х > 0 разность Кх — К2
возрастает. Так как использование А уменьшает л; и не изменяет у,
использование А не может нарушить неравенства К1^> К2.
Однако возле оси у непрерывное использование А не столь
прибыльно, как непрерывное использование В. Действительно, при
ср1 = 1, ср2 = 0 для г ^ 0 мы имеем
A)
У (<)
= Г
о
и, таким образом,
Однако при ^ = 0, ср2 = 1 для всех / получаем аналогично /в(оо) =
— г2.Уо/(#2-г~г2)- Для достаточно большого уо/хо мы имеем /в(схэ)>
>/а(оо). Таким образом, около оси у существует область, в кото-
которой используется В.
Эта область, где используется В, простирается вниз до прямой
д1Г2у = д2^1Х. Чтобы доказать это, заметим, что смешанный выбор
не может употребляться выше этой линии и что если выбор А
используется где-нибудь выше этой линии, он в дальнейшем упо-
употребляется все время. Однако бесконечное использование А при-
привело бы в конечном счете точку (х, у) в область, близкую к оси у,
где, как известно, оптимален выбор В, что создает противоречие.
272 Глава VIII
Следовательно, выше линии всегда применяется В. Аналогично ниже
линии всегда применяется Л.
После достижения прямой д1г2у = д2г1х точка (л;, у) должна все
время оставаться на этой линии. Действительно, если это не так,
то в В-области должно использоваться поведение АЛ а в Л-области —
поведение В, что невозможно. Следовательно, на самой линии должно
использоваться смешанное поведение (9.3).
Нами, таким образом, доказана
Теорема 1. При выполнении условий G.2) и ограниче-
ограничений G.3) максимальное значение /(оо) достигается использова-
использованием поведения
B) ?1=1 для Я1г2у<я2г1х9
ср2 = 1 для дхг2у > д2ггх,
= ~Т
Т /1 + Г2 Т
Отметим, что 91 и ?2 определены указанными соображениями
почти всюду и, следовательно, единственны с точностью до значений
на множестве меры нуль. Указанное конструктивное построение
решения дает другое доказательство существования.
§ 11. РЕШЕНИЕ ДЛЯ КОНЕЧНОГО ПОЛНОГО ВРЕМЕНИ
При определении решения для конечного Т мы будем начинать
с определения поведения, применяемого в конце процесса. Так как
оптимальное поведение обладает тем свойством, что его продолже-
продолжение после начальной части также оптимально, то сначала рассмотрим
случай, когда Т мало. Для Т, близких к нулю, мы имеем
A) I
о
т т
= Г1*0 / ?1 (^) * + Г2Уо / ?2 00 <*8+0 (Т).
о о
Отсюда следует, что для малых Т максимум достигается, если
9! E) = 1, 92 (*0 = 0 для гхх0 > г2у0 и срх E) = 0, 92 E) = ! Для
г2у0> гхх0. Как и следовало ожидать, для процессов малой про-
продолжительности определяющим фактором является ожидаемый
выигрыш, а опасения относительно остановки процесса не учиты-
учитываются.
Непрерывный стохастический процесс решения
273
Если <71 = <72» т0 линии г2у==г1х и цхг2у = ц2гхх совпадают и,
как легко проверить, оптимальное поведение будет таким же, как
и для Т = сю.
Рассмотрим общий случай, когда #1 Ф ц2. Предположим без
ограничения общности, что линия г2у = гхх лежит выше линии
Я\ггУ — Я2г\х- Положительный квадрант разделяется при этом на три
области, которые мы обозначаем через I, II, III (рис. 27).
У
III
Ч
I
X
Рис. 27.
Как и выше, если в области I хоть раз используется выбор В,
он должен использоваться все время, тогда как в областях II и III
это же относится к выбору А. Кроме того, в областях I и II, когда
остающееся время достаточно мало, используется выбор Б, а в об-
области III при тех же условиях используется выбор В. Отсюда сле-
следует, что в I всегда применяется выбор А, а в III всегда приме-
применяется выбор В.
Покажем теперь, что оптимальное поведение никогда не пере-
переходит от А к В. Предположим противное; пусть ^0 — момент, когда
наступило это изменение. Так как в ^0 выбор А прекращается,
точка (хA0), уУо)) должна лежать в области I или на гра-
границе между областями I и II. Использование В оставляет точку
С*(О» У@) в I Для всех ^ > ^о» так как мы знаем, что, если В однажды
применен в I, он должен применяться и впредь. Однако, это про-
противоречит тому, что, когда остающееся время достаточно мало,
в I используется А. Аналогично не может встретиться комбинация
использования смешанного выбора, а затем выбора В, так как пере-
переход должен произойти на границе между областями I и II, а затем
в области I должен все время применяться выбор В, что приводит
к противоречию.
Это сводит число типов решений к шести: всегда А\ всегда В;
после смешанного выбора идет А; выбор А, затем смешанный выбор
и окончательно выбор В; выбор В, затем смешанный выбор и окон-
окончательно выбор А\ после В идет А.
Пусть ^0 — значение I, при котором в оптимальном поведении
происходит последнее изменение, если такое изменение встречается.
18 Р. Беллман
274 Глава VIII
Для ?0<^^^ мы должны иметь <р, (^)=1, ср2(^) = 0. Вычислим
значение К1 (^0) — К2 (^о)- Для 'о <С I ^ Т мы имеем
B)
' @ =
и после некоторого упрощения
C)
Для любой фиксированной точки (х(@), у(@)) из области II
правая часть этого выражения положительна при малых Т — @ и
отрицательна для больших Т — @. Она равна нулю только для
одного значения Т-—@. Этот нуль определяет, когда именно проис-
происходит переход. Когда он уже произошел, в оставшееся время ис-
используется выбор Л, тогда как ранее возможно любое из шести
начал, в зависимости от положения исходной точки.
§ 12. ЗАДАЧА О ТРИХОТОМИЧЕСКОМ ВЫБОРЕ
Непрерывный вариант задачи о трихотомическом выборе, упомя-
упомянутый выше, в § 13 гл. II, тем же формальным путем, что и в § 7,
приводит к следующему. Задана система
-§■ = Р (О К?1 @ г, + Тз @ 'з) * (О +
где для всех I
B) ?1 + %+<Рз=1. ^по
требуется определить уг({) так, чтобы максимизировать /(Г).
Мы рассмотрим только случай, когда Г=оо.
Как и ранее, положим <в = ^ + 8Р* и В1(()= [
Непрерывный стохастический процесс решения 275
Получим
C) х(() = х @ A — егА @ — ег3В3 (О ) + о (е),
У @ = У (О A — ег2В2 (О — ег4В3 (О) + о (в).
(О = р (О A — в 2 <7 А @) + о (в).
=р
Следовательно, используя те же приемы, что и раньше, мы получаем
т
D) 7(Т) — /(Т) = е[ [К1Р1 + #2р2 + /СзРз1 01 + о (е),
о
где
т т
E) Л\ @ = — ^ ^ /' E) Й5 + /*1Р СП X (Г) — Гх^Р' E) * E) <*5,
I
т
г
т
3Х E) + Г4у E)] Л-
§ 13. НЕКОТОРЫЕ ЛЕММЫ И ПРЕДВАРИТЕЛЬНЫЕ РЕЗУЛЬТАТЫ
Утверждения в приводимых ниже леммах, касающиеся зависи-
зависимости ср| от К\у считаются, конечно, выполняющимися почти всюду.
Лемма 1. Если К%{$)> К${$)% то ^(() = \ или ср^(^) = 0.
Доказательство. Пусть Е — множество тех г, для которых
эти утверждения не выполняются. Пусть C$=1, р^ = —1 для г
из Еу а вне Е пусть эти р равны нулю. Для достаточно малых е
эта вариация допустима и делает разность /(Г)—/(Г) положитель-
положительной, если тез Е > 0:
Лемма 2. Если /С|@>^@ для всех ] Ф1, то ср^ = 1.
Доказательство следует непосредственно из предыдущей леммы.
18*
276
Глава VIII
Лемма 3. Если существует такое у, для которого
, то <р* =
Это снова простое следствие леммы 1.
Вычислим' теперь производные функций /С*. Непосредственное
вычисление дает симметричные результаты:
A)
где мы положили
B)
Относительное расположение трех линий
величиной
C)
определяется
Если мы допустим, что все три линии лежат в положительном
квадранте, то непосредственное вычисление показывает, что при О>0
линии имеют расположение, изображенное на рис. 28, тогда как
при Х> < 0 они лежат, как показано на рис. 29.
е,=о
С2=О
а;
Рис. 28.
Рис. 29.
Может встретиться каждый из случаев О > 0 и п < 0. Случай,
когда одна из линий С2==0, С3 = 0 лежит вне положительного
квадранта, приводит к немедленному упрощению наших рассуждений
без изменения их структуры в целом. Поэтому мы рассмотрим по-
подробно только указанные выше случаи.
§ 14. СМЕШАННЫЕ ВЫБОРЫ
Как и выше, обозначим термином „смешанный выбор" то положе-
положение, при котором некоторые из <р^ имеют значения, отличные от нуля
в единицы. Под выбором А мы будем понимать, что 91=1, под
Непрерывный стохастический процесс решения 277
пыбором В— что ср2=1, под выбором С — что ср3 == 1. Докажем
лемму.
Лемма 4. Никакое оптимальное поведение не содержит
смеси выборов А, В и С.
Доказательство. Предположим, что в некотором интервале
мы имеем одновременно срх, ср2, ср3>0. В этом интервале мы должны
иметь Кх = Кг — /С3.
Отсюда
A) <Р1 -Ь 9г Ч- <Рз =
Если Сх — С2— С3 Ф О, то решением для ср1э ср2, ср3 является
Так как ср^ должны быть в этом интервале положительны, С1э —С2
и —С3 должны иметь один и тот же знак. Обращаясь к рис. 28 и 29,
легко проверить, что этого не может произойти ни в случае Э > О,
ни в случае И < 0.
Далее, Сх — С2 — С3 = 0 только в том случае, когда линии С^^О,
С2=0, С3=0 совпадают. В этом случае задача эквивалентна задаче
о дихотомическом выборе.
Исследуем теперь возможность использования смешанных выбо*
ров, включающих только два из трех выборов Л, В, С.
Лемма 5. Допуская смешивани? двух а только двух выбо*
ров, мы получаем следующие результаты:
C) а) смесь выборов А и В допустима только на линии
^ = 0, где
Го * Г\
1 г I г » ?2 — г | ' I
Г1 "Г Г2 /Ч "Г Г2
б) сл/^сь выборов А и С допустима только на линии
С2=0, где
Г4 —
в) смесь выборов В и С допустима только на линии
С3==0, где
278 Глава VIII
Доказательство. Если ср^ ср2 > 0, ср3 = О» мы должны иметь
К2 > /Сз- В интервале, где это имеет место, выполняется соот-
соотношение
D)
Следовательно, С{ = 0. Значения ^ и ср2» которые удерживают (л;, у)
на этой линии, определяются, как и в случае дихотомического выбора.
Остальные утверждения леммы 5 доказываются аналогично.
§ 15. РЕШЕНИЕ ДЛЯ БЕСКОНЕЧНОГО ВРЕМЕНИ;
СЛУЧАЙ й>0
Получив эти предварительные результаты, мы приступим теперь
к нахождению решения для задачи максимизации /(оо). Будем пред-
предполагать, что г3 > г4, так как случай г4 > г3 может быть получен
переменой ролей х и у и А и В. Вырожденный случай гъ = г±
будет рассматриваться отдельно.
Заметим сначала, что, когда гв = г4, смешанный выбор АС ни-
никогда не употребляется, так как, согласно A4.3), в этом случае 91
и 9з не могут быть одновременно положительными. Решение прини-
принимает две разные формы в зависимости от того, будет О > 0 или
п < 0. Начнем с рассмотрения случая О > 0. Основные результаты
мы получим в ряде лемм.
Лемма 6. В оптимальном поведении около оси у исполь-
используется выбор В.
Доказательство. Около оси у имеется область, где вы-
выбор А не используется. Действительно, если Сх > 0, С2 > 0 и А
используется/ V е. уг({) =1, мы имеем К[ = 0, /Се < 0, АГз < 0.
Это означает, что Кг остается наибольшим для (г^(. Следовательно,
если 4//использУется в этой области, это должно происходить и
Вычислим результаты постоянного применения выбора Л, вы-
брра В и выбора С. Мы имеем
(О /Л°о) =
/• V
Сравнение /А(оо) и /в(оо) показывает, что для достаточно боль-
больших .уо/л;о имеет место неравенство /Б (оо) > /А (оо).
Покажем теперь, что если в области выше линии С3 = 0 выбор С
используется хоть раз, то он используется и во всем дальней-
Непрерывный стохастический процесс решения 279
шем ходе процесса. Использование С увеличивает наклон 5@ =
*=* У @/* @» так как Для ?з:== 1 мы имеем
B) *'Ю = *(*)('з — О>0.
С другой стороны, использование Б уменьшает наклон. Следова-
Следовательно, мы не можем использовать В после С, так как это возвра-
возвратило бы нас в область, где должен был применяться выбор С. Мы
уже показали, что вблизи от оси у выбор А не может использо-
использоваться после выбора С. Сравнение /Б(оо) и /с(оо) показывает, что
около оси у лучше использовать В, чем С, если /*2.У/(<72 Ч" гг) >
> г4У1(Уз-\~гд или <7зг2 — #2Г4 > 0- Это, однако, эквивалентно усло-
условию, что С3=0 лежит в положительном квадранте, что мы и пред-
предполагали.
Отсюда следует, что около оси у существует область, где не
употребляются ни Л, ни С. Так как по лемме 5 выше линии С3 = О
смешанные выборы не употребляются, мы заключаем, что суще-
существует область, прилежащая к оси у, где должен применяться вы-
выбор В.
Лемма 7. Нижняя граница В-об ласти, прилежащей к оси у,
есть линия С3 = 0. На этой линии используется смешанный
выбор ВС. Ниже линии С3 = 0 выбор В не употребляется.
Доказательство. Начнем с исходных значений (л;0, у0) около
оси у в области, где используется выбор В, и посмотрим, какую
форму может иметь оптимальное поведение. Выбор В не может ис-
использоваться все время, так - как это в конечном счете приблизит
(х, у) к оси х, где сравнение /^(оо) и /Б(оо) покажет, что вы-
выбор А лучше. Однако, ,так как и Л и С увеличивают наклон у/х;
выбор В не может предшествовать выбору А или выбору С, ибо
любой из них привел бы точку (х, у) опять в область, где нужно
использовать В. Следовательно, В может предшествовать только
Одному из смешанных выборов.
Как мы уже видели, для г%^> гА смешанный выбор АС никогда
не употребляется в оптимальном поведении. Мы утверждаем, что
если смешанный выбор применен в оптимальном поведении, то и
продолжение смешанного выбора в дальнейшем также оптимально.
Действительно, пусть (^0, /^-—.интервал, в котором употребляется
смешанный выбор. Так как точка (ху^), у(^)) лежит на том же
луче, что и точка (#(^0)» У(*о))> т0 вследствие однородности это же
поведение, продолженное на равный интервал времени, является
оптимальным. Следовательно, смешанный выбор можно продолжить
далее. Используя это замечание счетное число раз» мы можем пока*
зать, что .для О > 0 смесь АВ никогда не встретится в оптималь-
оптимальном поведении. Согласно п. (а) леммы §, выбор АВ может арименятъся
280 Глава VIII
только на линии Сх = 0. Если бы здесь употреблялся АВ, мы имели бы
=р [С3ср2 — С2?11 < 0,
так как здесь С2 > 0 и С3 < 0 (ср. рис. 28). Так как при исполь-
использовании Л мы имеем Кх (со) = К2 (со) = /С3 (со) =0 и К\ = К2 — 0,
то поэтому /С3 > А^1 = /С2, когда используется ЛВ. Отсюда, однако,
следует, что ср3 = 1 • 91 = 92 = 0» чт0 приводит к противоречию.
Остается возможность использовать после В выбор ВС на линии
С3 = 0. Выбор В вследствие приведенных рассуждений на этой ли-
линии использоваться не может.
Лемма 8. Существует такая линия /, = 0 между линией
С2 = 0 и осью х, что выбор С используется в области между
линиями С3 = 0 и /, — 0, а выбор А используется в области ниже
линии /, = 0.
Доказательство. Из уже полученных результатов мы знаем,
что единственные выборы, которые можно использовать в области
ниже линии С3 = 0, это А и С. Так как оба этих выбора экспо-
экспоненциально увеличивают наклон, в конце концов точка (х, у) до-
достигнет линии С3 = 0, где применяется смешанный выбор ВС.
Исследуем возможности переходов от А к С и от С к Л. Из
A3.1) имеем
@ — /Сз (*) = р [С1?2 + С2?3 + С2?1 - С3ср2],
и, следовательно, когда применяется только С или Л,
C) /
/
а этб выражение положительно выше линии С2=0 и отрицательно
ниже этой линии. Далее, при переходе от С к А мы должны иметь
Кг — Лз^-0. Следовательно, изменение С на Л не может встре-
встретиться ниже С2=0. Аналогично мы видим, что переход от Л к С
не может встретиться выше С2=0. Точно так же не может быть
перехода от Л к ВС, так как, когда Л применяется выше С2 = 0,
разность Кх—/С3 положительна и возрастает, следовательно, вы-
выбор ВС, который требует /С3 >/(*!, не может использоваться. Таким
образом; допущение, что Л может использоваться выше С2 = 0,
приводит к противоречию, поскольку, как мы знаем, в конце концов
должен использоваться выбор ВС.
Мы можем также доказать, что переход от Л к С не может
произойти на линии С2=0. Действительно, предположим, что та-
такой переход произошел. В момент перехода мы имели бы /С1 = /С3.
Выбор С увел бы точку выше линии С2 = 0, где к[ — /Сз>0.
Следовательно, Кх > К& откуда следует, что должен применятьря
выбор Л, а это приводит к противоречию-
Непрерывный стохастический процесс решения
281
Теперь остались две возможности:
1) С используется во всей области ниже линии С3 = 0,
2) существует такая линия /,= 0, лежащая между осью х и ли-
линией С2 = 0, что Л используется ниже Ь=0у а С—выше.
Следующее ниже доказательство от противного показывает, что
первый случай невозможен. Пусть (л:0, у0)— точка ниже С3=0.
По предположению, единственными используемыми выборами яв-
являются С и ВС, так что мы должны иметь Кз @ = 0 для всех I ^ 0.
Так как /С3(оо) = 0, мы имеем /С3@)=0. Поскольку в точке
(хо> Уо) предпочтительнее С, мы должны иметь 0 = /С3 @) ^ Кх @).
Следовательно, так как /С1(со)=0, мы получаем в силу A3.1)
г' со
D) 0 < Кг (оо) — К, @) = I р @ С2сХ+ { р (О [С1Т2 + С2ср3] Л.
о *'
где ^ — момент перехода от С к ВС, Сохраняя х0 неизменным,
устремим у0 к нулю. Это влечет *'—юо. Так как функция Сху2-\-
-+-С2ср3 равномерно ограничена, второй интеграл стремится к нулю.
Тогда, применяя выражения для х, у и р, полученные для поведе-
поведения С, имеем
V
E)
ИЛИ
F)
Нт Г
(И > 0,
ОО
о.
что противоречит предположению о том, что линия С2 = 0 проходит
через положительный квадрант.
с,=о
Рис. 30.
Это завершает рассмотрение случая О>0, когда линии С2=0
и С3==0 содержатся в положительном квадранте. Окончательным
результатом является
282 Глава VIII
Теорема 2. Если Е> = Ц\Г2гъ-\-цггхг±— <7зг1г2>0» то реше-
решением задачи максимизации функции /(оо), подчиненной ограниче-
% нию A2.1), будет решение, схематически изображенное на рис. 30.
Найти Ъ каким-нибудь простым путем, по-видимому, невозможно.
Наконец, рассмотрим . вырожденные случаи, когда линия С3 = 0
или линия С2 = 0 не лежит в положительном квадранте. Если вне
квадранта лежит С3=0, то область С расширяется до самой оси у.
§ 16. СЛУЧАЙ й < О
Рассмотрим теперь случай, когда О < 0. В этом случае оказы-
оказывается, что выбор С никогда не используется, а это означает, что
решение такое же, как в задаче о дихотомическом выборе.
Лемма 9. Выбор В используется только около оси у.
Доказательство такое же, как и раньше.
Лемма 10. Нижней границей В-области, прилежащей к оси у,
является линия С1 = 0. На этой линии используется выбор ЛВ.
Ниже этой линии выбор В не используется.
Доказательство. Как и в случае О > 0, мы находим, что
за выбором В должен следовать один из смешанных выборов ЛВ
или ВС. Однако, в настоящем случае, когда О < 0, смешанный вы-
выбор ВС не может быть использован в оптимальном поведении. Дей-
Действительно, при использовании ВС имеем
A) / К[ф = р [С1?2 + С2срз] < 0.
так как С3=0 ниже, чем С2 = 0 и Сх = 0. Кроме того, когда ис-
используется смешанный выбор ВС, имеем Кх (оо) = К2 (об) = /С3 (оо) = 0
и #<2@ = /Сз@ = 0- Следовательно, когда используется смесь ВС,
Гы имеем Кх @ > К2 @ = К$ (/). Это, однако, является противоре-
противоречием, так как отсюда вытекает, что ср4 = 1, ср^ = ср3=0. Следова-
Следовательно, выбор В должен предшествовать использованию выбора ЛВ
на линии Сх = 0. Снова такие же соображения, как и выше, пока-
показывают, что В не используется ниже Сг = 0.
Лемма 11. Выбор Л используется во всей области между
линией Сх = 0 и осью х.
Доказательство. Во-первых, С не может применяться не-
непосредственно перед смесью ЛВ. Когда применяется ЛВ, то
и /Сз@=/М—
как это можно увидеть из рис. 30. Следовательно, непосредственно
перед переходом к ЛВ мы имеем /С3 < К2 и К$ < Кх, Поэтому вы-
выбор С не используется непосредственно перед ЛВ.
Непрерывный стохастический процесс решения
283
Отсюда вытекает, что имеется область, лежащая ниже линии Сх=0
и примыкающая к этой линии, где используется А. Однако невоз-
невозможно использовать другой выбор до того, как А стал оптимальным
выбором. Когда А используется ниже С1э мы имеем
B) к[ @ = 0, К* @ = — рС, > 0, Кз @ = — рС2 > 0.
Следовательно, Кг является наибольшим и при меньших I и Л-об-
ласть расширяется до оси х.
Объединяя полученные результаты, мы приходим к следующей
теореме.
Теорема 3. Если О = Цхгггъ -\- цггхг± — Цъг\гг <С 0, то реше-
решение задачи максимизации /(оо) никогда не использует выбор С
и имеет такую же форму, как в задаче о дихотомическом выборе.
а;
Рис. ЗЬ
§ 17. СЛУЧАЙ г8 = г4
Некоторые из предыдущих рассуждений теряют в этом случае
силу, так как выбор С оставляет наклон у/х постоянным. Из A4.36)
и A4.Зв) следует, что не применяется ни один из смешанных выбо-
выборов АС и ВС.
Покажем прежде всего, что, если О < 0, выбор С никогда не
применяется. Для этого мы сравним результат многократного ис-»
пользования АВ с результатом, получающимся при использовании С.
Если все время используется АВ, то простые вычисления
казывают, что
О ) /ав(°°) = Г"Г~7 (*о ~г У о)»
где
B)
г —~
284 Глава VIII
Аналогично результатом постоянного использования выбора С
будет
C)
Неравенство /АВ(оо) >/с(оо) эквивалентно О < 0.
Если О > 0, то приведенные рассуждения показывают, что не
используется ни один из смешанных выборов. Встречаются различ-
различные случаи, зависящие от того, какие из линий С2 —0, С3
у 2 3
проходят через положительный квадрант. Как и раньше, можно уви-
увидеть, что если С3 —0 лежит в положительном квадранте, то около
оси у выбор В предпочтительнее выбора С. Определим теперь, где
может быть сделан переход от В к С. Пусть ^0—время перехода.
Для ^0 < г < оо мы имеем
D) К1(О = — С2,
Кроме того, мы должны иметь Кх (^0) -С К2(^о) = ^з (^о)- Снова, ис-
используя замечание, что/С1(оо) = /С2(оо) = К3(оо), мы видим, что для
1^@ должны иметь С3 = 0. Таким образом, нужно следовать вы-
выбору В до достижения линии С3 = 0, а затем следовать выбору С.
В этом вырожденном случае С играет роль ВС. Аналогично пере-
переход от Л к С происходит по достижении линии С2 = 0. Если ли-
линия С3—0 не |ежит в положительном квадранте, то С используется
вплоть до оси у. Если С2 = 0 не лежит внутри положительного
квадранта, то С используется вплоть до оси х.
§ 18. НЕЛИНЕЙНАЯ ФУНКЦИЯ ВЫГОДЫ,
ЗАДАЧА О ДИХОТОМИЧЕСКОМ ВЫБОРЕ
Рассмотрим коротко задачу о дихотомическом выборе, обсуждав-
обсуждавшуюся в § 6—10, при условии, что мы желаем максимизировать
ожидаемое значение некоторой функции и полного дохода /?.
Ввиду результатов, полученных для дискретной задачи, или ско-
скорее ввиду недостатка результатов, несколько неожиданным является
то, что для любой функции выгоды и, которая строго возрастает
и имеет непрерывную производную, оптимальное поведение является
в точности таким же, как для решенной выше задачи с линейной
функцией выгоды. Одного этого было бы достаточно, чтобы преду-
предупредить неосторожных, что непрерывные варианты не могли бы
использоваться без пристального внимания к характеру приближе-
приближений к ним.
Так как любая монотонно возрастающая функция выгоды может
быть произвольно близко аппроксимирована функцией указанного типа,
то это поведение оптимально для любой монотонно возрастающей
функции выгоды (хотя и не обязательно единственно). Большой тео*
Непрерывный стохастический процесс решения 285
ретический и практический интерес имеет следующая функция этого
класса:
О для 0 < Я < До,
пи*
для
о.
Ожидаемое значение и (Я) есть вероятность того, что /? больше или
равно /?0.
Пусть переменные имеют такой же смысл, как и раньше; тогда
мы получим
Р@)=1.
Пусть ^@ = ^0+^0 — л:@ — у (г) — величина, которая представляет
собой полное количество золота, добытого вплоть до времени ЬУ
если машина до этого времени не испортилась. Математическое ожи-
ожидание и {И) дается интегралом
со
C) О = — [и(г«))ар<&.
О
Это легче всего увидеть, рассматривая плату за то количество зо-
золота, которое машина добыла за время до ее поломки.
Наша цель — найти функции <р1@. ?г@» которые при выполнен
нии условий
D) 0<Т|<1. ?1 + ?2=1
максимизируют О.
Используя тот же вариационный аппарат, что и ранее, после
некоторых непосредственных вычислений получаем
оо
E) О - О = в / [Кг @ р! (О + К2 @ % (/)! Л + о (е),
О
где
F) К1 =
оо
— / [р' E) в' (г E) ) гх л: E) — дхр' (8) и {г {$))]
о
ОО
( [р' ($)«' С* E) )ггУ E) — ?2р' E)и B E) I ^
О
286 Глава VIII
Далее,
G) К[ @ — /С2 (О =р (О в'
Отсюда следует, что в предположении, что и'(,г)>0 при >,
применимы с очень небольшими модификациями все рассуждения
и результаты линейного случая.
БИБЛИОГРАФИЯ И КОММЕНТАРИИ
К ГЛАВЕ VIII
§ 1. Результаты этой главы были получены в сотрудничестве с Лема-
ном, см. ВеПтап К., ЬеЬтап Р. 5., Оп Ше соШтцоиз %о1й-фШп%
еяиа!юп, Ргос. Иа*. Асай. 8с1. С/8АУ 40 A954), 115—119; ВеПтап К.,
ЬеЬтап К. 5., Оп а ?ипс(юпа1 е^иа^^оп т 1пе 1пеогу о! сгупапнс рго^гат-
пнп§ апс! 118 §епегаП2а110П8 (не опубликовано).
§ 2. Уравнение B.3) может быть формально использовано для нахожде-
нахождения характера решения, но пока еще в изучении нелинейных дифференциаль-
дифференциальных уравнений в частных производных этого типа ничего не сделано.
§ 3. Современная теория случайных процессов в том виде, как она
изложена в книге Дуба „Вероятностные процессы" (М., 1956), дает основу
для строгой теории таких уравнений, но для этого требуется математика
бесспорно более^ высокой категории.
§ 5. Идея замены смешения в точке смешением на малом интервале
была использована в статье Беллмана и Блекуэлла [ВеПтап Р., В 1 а с к-
\у е 11 ^.у 5оте 1иго-рег8оп датез [ПУ01У{П^ Ь1и№п§, Ргос. Иа(. Асай. 8с1.
I/8А, 35 A949), 600—605] при изучении некоторых простых игр двух лиц
типа покера^ ср. также ВеПтап Р., Оп ратез туоМпд ЫиШпд, Яепй.
С1гс. Маг. Ра1егто B), 1 A952), 1—18.
Более/ общие результаты относительно сходимости дискретного про-
процесса к непрерывному содержатся в работах Осборна [О 8 Ь о г п Н., Оп 1Ье
сопуег^елсе о! с11зсге1е 81оспазис ргосеззез 1о Шен* сопНпиоиз апак^иез,
КМ-1368, РА^ СогрогаКоп, 1955; ТЬе ргоЫет о! соттиоиз рго^гатз,
Р-718, КАШ СогрогаИоп, 1955; см. также Рас1/. У. МаШ., 6 A956),
721-731.]
Глава IX
НОВАЯ ФОРМАЛИЗАЦИЯ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
§ I. ВВЕДЕНИЕ
При рассмотрении многошаговых процессов производства в гл.
VI и VII мы встретились с задачей максимизации функционала
(х(Т), а) на множестве всех функций г (г), удовлетворяющих
условиям
A) а) ^ =
б) Яг < С*,
В)
Используя тот факт, что максимум (мы предполагаем, что он
достигается) является функцией только начального вектора с и про-
продолжительности процесса 7\ мы получили функциональное уравне-
уравнение для /(с, Т) = тах(л:G), а), которое преобразовали в диффе-
ренциальное уравнение в частных прозводных. Как уже упоминалось
в конце гл. VI, подобный подход применим также и к изучению
других классов задач вариационного исчисления.
В настоящей главе мы продолжим исследование, обращая внима-
внимание на два частных типа задач. Задача первого типа состоит в опре-
определении максимума или минимума функционалов вида
т
-"= I Г \Х±, ЛГ2, ...» Хп\ 2р #2» • • •» Хць) и*
О
при наличии следующих связей и ограничений:
C) а) ^-« = О,(*. *). *4@) = с,. /=1. 2, .... л.
б) Кк(х. 2)<0, *=1, 2, .... /.
Ко второму типу относится задача отыскания собственных значе-
чений уравнения
D) и
Эта задача тесно связана с той, которая описывается уравнениями
B) и C), так как при естественных предположениях относительно
288 Глава IX
функции ср(^) она эквивалентна задаче определения относительных
минимумов функционала
1
E) ^{и) = ^ и'2
о
при ограничениях
1
F) а) ^<р@я2
о
б) и@) = й
Однако наличие граничного условия, заданного в двух точках, вно-
вносит в задачу новые особенности и трудности.
Следуя нашему обычному подходу, мы введем соответствующие
параметры состояния и получим функциональное уравнение для ми-
минимума функционала ^ (и) как функции этих параметров. Предель-
Предельной формой этого функционального уравнения будет дифференциаль-
дифференциальное уравнение в частных производных.
Затем мы перейдем к численному решению этих уравнений.
Отметив обычный способ решения с помощью уравнений в конечных
разностях, мы пркажем, как можно ввести разностные уравнения
иным путем. Значение этого нового подхода состоит в том, что он
позволяет нам обойти целый ряд аналитических трудностей, свой-
свойственных вариационному исчислению. Он также дает нам возмож-
возможность избежать/ трудностей, связанных с исследованием устойчи-
устойчивости вычислительных методов.
Используя ётот подход, мы рассмотрим также некоторые задачи,
содержащие чебышевский функционал
шах г \Х±, х^* • • •» хп$ %1* %2* • • •» 2т)*
< Т
В данной главе мы во всех случаях будем неизменно придержи-
придерживаться чисто формальной точки зрения. В этом вводном иллюстра-
иллюстративном обзоре мы прежде всего стремимся к изложению основных
идей метода функциональных уравнений. Строгое изложение, неиз-
неизбежно связанное с большими трудностями, мы откладываем до вто-
второго тома.
§ 2. НОВЫЙ ПОДХОД
Прежде чем пуститься в открытое море анализа, рассмотрим
Основную идею нашего нового подхода к решению непрерывных
вариационных задач.
Классический аппарат вариационного исчисления, точно копирую-
копирующий технику конечномерных вычислений, основывается на пред-
представлении экстремали в виде точки пространства функций и на
характеризации этой точки посредством ее вариационных свойств.
Новая формализация вариационного исчисления 289
Вместо этого мы будем рассматривать задачи вариационного
исчисления как частный класс многошаговых процессов решения
непрерывного типа. Функция, осуществляющая экстремум, может
тогда рассматриваться как непрерывное поведение.
Приведем некоторые простые примеры, которые могут проил-
проиллюстрировать эту идею более ясно, чем любое абстрактное рассуж-
рассуждение.
Пример 1. Определить кривую,, которая соединяет две
точки Р и С? и обладает тем свойством, что частица, движу-
движущаяся вдоль нее под действием силы тяжести, приходит из
точки Р в точку С} за минимальное время (классическая задача
о брахистохроне).
Рис. 32.
Ясно, что, какова бы ни была промежуточная точка /? на экстре-
экстремали, путь вдоль экстремали от /? до ф должен быть таков, чтобы
минимизировать время, требуемое для прохождения участка кри-
кривой /?B при заданной в точке /? скорости слева. •
В каждой точке на кривой мы определяем направление движе-
движения, т. е. касательную к кривой. Оптимальное поведение, или экст-
экстремаль, может быть выражено не только при помощи уравнения
для у как функции от х, как это делается обычно, но и при по-
помощи уравнения для йу\йх как функции от у и заданной в точке
(х, у) скорости слева.
Пример 2. Через точки Р и <2 (см. рис. 33) провести кри*
вую фиксированной длины Ь так, чтобы ^площадь криволинейной
трапеции, ограниченной искомой кривой, перпендикулярами РР'
и <2<2' и отрезком Р'<2' оси х была максимальной (классическая
изопериметрическая задача).
Ясно, что,, каковы бы ни были участок экстремали Р/? и огра^
ничиваёмая им заштрихованная площадь, продолжение вдоль экс??
ремали от /? к О должно максимизировать площадь трапеции
при условии, что кривая /?<2 имеет длину
19 Р* Беллман
290
Глава IX
Оптимальное поведение может быть выражено при помощи урав-
уравнения для йу\йх как функции от у и ^ — V вместо уравнения для у
как функции от х.
Оба вывода в этих двух примерах получены на основе „прин-
„принципа оптимальности", рассмотренного в гл. III и применявшегося
во всех предыдущих главах. Математическая формулировка этого
принципа позволит получить наш новый подход к задачам вариа-
вариационного исчисления.
Преимущество нового подхода состоит в том, что при нахожде-
нахождении оптимальных поведений для многошаговых процессов очень
^
/?'
Рис. 33.
о!
х
часто определение следующего хода через текущее состояние про-
процесса дает во многих отношениях более простую, естественную
и даже более важную часть информации, чем определение полной
последовательности ходов в оптимальном поведении, которые надо
осуществить, начиная с некоторого фиксированного начального по-
положения.
Если говорить в геометрических терминах, мы стремимся опре-
делить натуральные уравнения экстремальных кривых. Вместо того
чтобы рассматривать кривую как множество точек, мы считаем ее
огибающей своих касательных, что является двойственным подхо*
дом по отношению к классической трактовке1).
Обычно, как и следует ожидать, сочетание этих двух под*
ходов, локального и глобального, будет наиболее плодотворным,
так как одни свойства экстремали проще всего описываются в то*
чечных координатах, а другие — в тангенциальных.
1) Употребляя терминологию теории игр, можно сказать, что рассмотре*
ние процесса в его позиционной (ех1еп81Уе), а не в нормальной форме может
дать существенные преимущества. По существу только тогда мы и можем
Полностью использовать внутреннюю структуру процесса и таким образом
выделить его среди остальных многошаговых процессов и других многомер-
многомерных задач максимизации.
Новая формализация вариационного исчисления 291
В следующих параграфах мы применим эти идеи к ряду типич-
типичных задач и рассмотрим вопрос о применении этого подхода к на-
нахождению решений.
со
§ 3. МАКСИМИЗАЦИЯ ФУНКЦИОНАЛА $ Р (х, у)
В гл. I мы рассмотрели дискретный процесс, который описы-
описывался следующим функциональным уравнением:
Непрерывная модель этого процесса приводит к задаче макси
мизации функционала
оо
B) ЛУ)=$\ё{У) + Ь(х—у)\йЬ
о
на множестве функций у (г), удовлетворяющих условиям
*) 2?== —«.У —*(* —.У). а.Ь>09 х@) = с9
2?
б) О
Для ознакомления с нашим методом рассмотрим в качестве пер-
первого примера задачу о максимизации интеграла вида
с»
D) лу)=[р{х, у) а*
О
при условии, что хну связаны соотношением
E) % = О(х9у), х@) = с.
Для начала опустим ограничение C6).
Подчеркнем еще раз, что мы в данном случае будем рассуждать
формально, так как здесь мы ставим целью только показать схему
нашего подхода. Именно, мы всюду будем предполагать, что макси-
максимумы и минимумы существуют, а экстремали обладают всеми теми
дифференциальными свойствами, которые нам понадобятся. Строгое
установление этих свойств требует совершенно другого, отличного
от формального, подхода, и не будет здесь рассматриваться. Кроме
того, как будет указано ниже, в ряде случаев мы не будем нуж-
нуждаться в получении априорных результатов относительно природы
максимизирующей функции у.
Возвращаясь к сформулированной выше задаче о максимизации
мы замечаем, что максимальное значение функционала Лу) будет
19»
292 Глава IX
зависеть только от начального значения х, а именно от с. Напишем
поэтому
F) шах У00 =/(О
у
и перейдём к выводу функционального уравнения для функции/(с).
Обозначим через у = у({) функцию, максимизирующую функцио»
нал ^(у). Тогда для любого значения 5 > 0 можно написать
8 оо
G)- /<с)» / Р (х, уLг± / Р (*. у)
О 5
Рассмотрим второй из этих интегралов. После любого началь-
начального выбора функции у (г) для значений I из интервала [0,5] можно
по с на основании дифференциального уравнения E) определить
значение функции х в точке 5, которое мы обозначим через г E).
Следовательно, при любом начальном выборе функции у на интер-
интервале [0, 5] на остающемся интервале [5, со] мы будем иметь дело
с задачей точно такого же типа, что й первоначальная, с той только
разницей, что роль с в ней будет играть с E) = х E). Так как
пбдинтегральная функция, так же как и правая часть дифферен-
дифференциального уравнения, не зависит от г% то новый интервал можно
рассматривать как интервал [0, оо], полагая х@) = с(8).
Следовательно, на основании принципа оптимальности уравнение
G) можно переписать в виде
(8) /(с)= ) Г(х,уL.1 +/(сE)).
О
Поскольку функция у должна быть выбрана так, чтобы значение
было максимальным, то мы приходим к основному функциональному
уравнению
(9) 1(с)= шах"
//*(*. ЗОЛ+/(<:E))
для любого значения 5 > 0.
Устремляя 5 к нулю, мы из этого уравнения получим дифферен-
дифференциальное уравнение для функции /(с). Для малых значений 5 при
соответствующих предположениях о непрерывности мы имеем
(Ю)
У10» Я]
Так как интервал [0, 5] стягивается в точку 0, выбор функции у
на интервале [0, 5] сводится в конечном счете к выбору .у(О). Для
упрощения обозначений положим у@) = V. Тогда на основании фор-
Новая формализация вариационного исчисления 293
мулы A0) мы получаем
A1) /(с)=етгх[Р(с. гО $*+/(*)*+30 (*. *>)/'
V
что в результате предельного, перехода при 5->0 приводит к соОт<
ношению
A2)
V
Используя" для определения' точки максимума приемы классиче-
классического анализа, мы получаем два уравнения:
A3) 0 = Р(с9 V) + О (с, *)/' (с),
Исключение из этой системы производной /'(с) приводит к урав-
уравнению
A4)
, V)
о,
из которого можно найти V как функцию от с.
: Определив V как функцию от с, т. е. у как функцию от х, мы
возвращаемся к дифференциальному уравнению E) и, решая диффе-
дифференциальное уравнение
A5) йх
находим х, а затем и у как функции от Ь.
Из этого следует, что Относительно простое поведение у = у {X)
может привести к сравнительно сложной экстремальной функции
х = х {г).
§ 4. ОБСУЖДЕНИЕ
Будем предполагать, что О(х, у) — всюду отрицательная функ-
функция, равная —А (х, у), так что мы можем рассматривать приведен-
приведенную выше задачу как непрерывный процесс распределения ресурсов,
в котором плотность дохода описывается функцией Р(х, у), а плот-
плотность расхода ресурсов — функцией А(х, у). Исходя из основного
уравнения
A) 0 = тгх[Р(с, ю) —
V
мы получаем для всех значений V неравенство
B)
и1 следовательно.
294 Глава IX
Так как неравенство C) обращается в равенство по крайней
мере для одного значения г>, то мы получаем уравнение
D)
Это уравнение показывает, что поведение, которое максимизи-
максимизирует полный доход, одновременно локально максимизирует отно-
отношение плотности дохода к плотности расхода ресурсов; с поведе-
поведением такого рода мы уже встречались раньше (ср. упр." 18 гл. I;
§ 8 гл. II).
Возможна очень интересная интерпретация уравнения Эйлера для
вариационных задач рассмотренного выше простого типа. Мы пре-
предоставляем читателю возможность самому убедиться в том, что вы-
выражение C.14) представляет собой первый интеграл уравнения
Эйлера, полученного классическим методом.
§ 5. ДВУМЕРНЫЙ СЛУЧАЙ
Мы оставляем в качестве упражнения доказательство того факта,
что, применяя тот же самый метод к задаче определения максимума
функционала
оо
A)
на множестве всех функций ух(г) и у2У), удовлетворяющих усло-
условиям
B) —^ = О (*!, х2, уг, у2\ хх @) = с19
= #(*1. х2, ух, у2), х
можно получить уравнение
Р(сь с2, «, V) О(сь с2, и, V) Н(съ с2> и, у)
РОИ
1 у УЛу Ну
= 0,
связывающее величины Ух(О)= и(сг, с2) и У2(®) — ъ(с1, с2).
Вопрос о том, может или нет решение поставленной выше ва-
вариационной задачи быть получено в той же форме, как и в одно-
одномерном случае, т, е. в виде >у1 = ср1(л:1, х2), уг = ^{хх% х2), остается
открытым.
Новая формализация вариационного исчисления 295
т
§ 6. МАКСИМИЗАЦИЯ ФУНКЦИОНАЛА Г^Ч*, У)М
о
Перейдем к рассмотрению более общей задачи определения мак-
максимума функционала
т
A) УО0 = /'7(*. У)
о
при условии, что х и у связаны соотношением
B) Ж~0(<х> У>- *(Р) = С'
Как это будет еще раз обнаружено ниже, в рассмотрений конеч-
конечной задачи существуют определенные преимущества, несмотря на
усложнения, возникающие благодаря наличию дополнительного па-
параметра.
В этой задаче имеются два параметра состояния: С и Т. Во мно-
многих приложениях параметр С описывает начальное количество ре*
сурсов, а 71 — продолжительность процесса. Запишем это в следую*
щем виде:
C) тахУОО = /(<?, Г).
у
Рассуждая точно так же, как и в предыдущем параграфе, мы
приходим к функциональному уравнению
D) /(<?, Г)= шах
У10» 5]
ш Т—8)
из которого в процессе предельного перехода при 5 ~> 0 получается
нелинейное дифференциальное уравнение в частных производных
E) 0 = шах
V
Последнее, в свою очередь, приводит к следующей системе:
О =
Решая ее относительно /с и /г» мы находим
G) /с=
296 Глава IX
Чтобы получить уравнение для основной переменной V, мы при-
приравниваем выражения для производных /Тс и /сТ и приходим к урав-
уравнению
(в) />г — <Э^С + <2С.
Это — линейное дифференциальное уравнение в частных производ-
производных первого порядка для функции V=*=V(с, Т)\ оно может быть
решено методом характеристик (к этому вопросу мы еще раз вер-
вернемся ниже в § 14) или же численными методами, если задано зна-
значение V (О, Т) ИЛИ V (С, 0).
Именно здесь выясняется преимущество, связанное с наличием
в формулировке задачи параметра Т. Мы можем почти без труда
определить V как функцию от с при 7 = 0, так как для малых зна-
значений Т имеет место равенство
(9) /(*, Т) = шах [Р (с, V) Т + о (ТI
V
Следовательно-, при 7=0 значение <о=.-ю (с, 0) определяется из
условия максимальности Р(с, V).
т
§ 7. МАКСИМИЗАЦИЯ ФУНКЦИОНАЛА С Р(х,у)
ПРИ УСЛОВИИ 0<д><х
Рассмотрим -теперь задачу определения максимума функционала
т
=. Г Р(х,у)сН при условиях
О)
б)
При классическом подходе трудность этой задачи состоит в том,
что функция у не может быть, вообще говоря, определена на ос-
основе произвольных вариаций. Когда 0 <С У < х, мы можем варьи*
ровать совершенно свободно, и в интервалах, где это неравенство
выполняется, функция у должна удовлетворять уравнению Эйлера.
Однако, когда у есть 0 или л:, мы.имеем только неравенство Эйлера.
Основная трудность* задачи состоит в том, чтсбы решить, как сле-
следует сопрягать три типа решения:, у ==* О, -у=в*-х й функцию ^
являющуюся решением уравнения Эйлера. Эта задача эквивалентна
определению точек перехода^ в которых-, соединяются решения двуз
типов.
В настоящее время,не существует единого метода для решения
таких задач в явной аналитической, форме. Некоторые классы задач
Новая формализация вариационного исчисления 297
подобного типа решаются просто, и на этом вопросе мы коротко
остановимся ниже.
Рассмотрим теперь, как применяется для решения данной задачи
метод функциональных уравнений. Положим
B) _ /(с, Г) = шах УХУ).
у
Как и выше, мы получаем дифференциальное уравнение в ча-
частных производных
C) /г= тах [Р(с9
0< г><с
Первоначальное условие О^з7^* перешло в ограничение
О ^ V ^ с. Начальное условие имеет следующий вид:
D) /(с.0) = 0
для всех значений с.
Мы видим, что ограничение 0^1/^ с не позволяет нам сво-
свободно дифференцировать по V. В § 10 мы покажем, как при не-
некоторых предположениях относительно функций Р и О уравнение C)
можно использовать для определения структуры решения.
§ 8. ЧИСЛЕННОЕ РЕШЕНИЕ
Исследуем нелинейное дифференциальное уравнение в частных
производных
A) /г-= тах
V
при условии, что/(с, 0) = 0, и опишем, в общих чертах процесс,
который может быть использован для его численного решения.
Вместо того чтобы считать параметры Тис изменяющимися
непрерывно, ограничим область их значений дискретным множеством
B) 7 = 0, А, 2А, /гД
с = 0, ±5, ±28 ±кЬ
где А и 8 — положительные величины.
Частные производные /т и /с аппроксимируются в этом случае
разностными отношениями
Т + А)—/(с, У)
2В
298 Глава IX
в результате чего нелинейное дифференциальное уравнение A) за
меняется приближенным уравнением вида
D)
. Т) — /(с — 5,
, 0) = 0.
Начиная с известных значений /(с, 0), можно последовательно вы-
вычислять значения /(с, А), /(с, 2Д), .... и т. д.
Хотя общая идея этого метода очень проста, однако при его
фактическом применении возникают большие трудности. По суще-
существу основной вопрос заключается в выборе величин А и 8. От
правильного выбора этих параметров зависят сходимость процесса
и устойчивость численного решения. Для линейных уравнений, ко-
которые получаются, если убрать операцию взятия максимума, эти
вопросы теоретически разработаны достаточно полно и удовлетво-
удовлетворительно. Однако для нелинейных уравнений никакой теории такого
рода практически не существует и эти вопросы решаются на основе
искусства и опытах).
Интересно отметить, что уравнение с ограничением G.3) легче
поддается численному решению, чем рассмотренное выше уравне-
уравнение A), так как существование ограничения суживает ту область,
которая должна быть исследована для определения максимума. По-
Поэтому во многих случаях более реальный процесс будет и более
просто решаться численно.
В § 11 мы рассмотрим еще один метод численного решения,
также основанный на использовании разностных уравнений, который
оказывается более эффективным на практике и дает возможность
рассуждать более строгим образом, не затрагивая при этом трудных
областей вариационного исчисления.
§ 9. ОБСУЖДЕНИЕ
Выше мы ^помянули о трудностях, которые могут возникнуть
при решении царцрционной задачи с ограничениями, а также о том,
что некоторые классы этих задач могут быть исследованы полностью.
Покажем, как для получения сведений о структуре решения
данной задачу можно использовать функциональное уравнение (8.1).
Мы рассмотрим только случай, когда функция Г (с, V) для всех
1) Возникает также задача и о выборе надлежащего приближения с по-
помощью разностного отношения. В формулах C) мы рассматриваем симмет-
симметричную аппроксимацию для / и асимметричную для /т. В случае линейных
уравнений часто могут быть полезны соображения, связанные с устойчи-
устойчивостью. Для нелинейных уравнений в этом отношении практически ничего
известно.
Новая формализация вариационного исчисления 299
значений с строго вогнута по V, а функция О (с, V) зависит от V
линейно. Нелинейное дифференциальное уравнение в частных про-
производных имеет в этих условиях вид
A) /т= тах
Функция Р(с, у)-\-[@(с)-\-к(с)у]/с для всех значений с и Г яв-
является строго вогнутой по V и достигает максимума по ^ в един-
единственной точке. При этом он может достигаться в точках г> = 0,
V=с или в некоторой внутренней точке.
Предполагая, что все рассматриваемые функции непрерывны по
с и Т, мы можем сделать следующее важное замечание. Так как
функция Р (с, V)-\-[8(с)-\-к(с)V]/с непрерывно зависит от с и Т
и является стррго вогнутой по V, ее максимум по V не может пе-
переместиться из точки V=0 в точку V=сУ минуя при этом вну-
внутренние точки интервала [0, с].
Это является следствием того факта, что максимум данной функ-
функции по V зависит от с и Т непрерывно. Сделанное замечание можно
использовать для того, чтобы значительно сократить время, необхо-
необходимое для численного решения подобных процессов; кроме того,
оно делает осуществимым численное решение многомерных про-
процессов *).
Таким образом, любая экстремаль должна иметь следующую
структуру. Интервал, где у=0, должен заключаться между двумя
интервалами, в которых 0 < у < х\ аналогичное утверждение спра-
справедливо для интервала, в котором у = х.
Возникает вопрос, как часто решение может переходить из
одного типа в другой. Для ответа на него мы должны сделать
дальнейшие предположения относительно рассматриваемых функций.
Нетрудно построить примеры, показывающие, что при надлежащем
выборе функции Р таких переходов может быть сколь угодно много.
В примере, который рассматривается в следующем параграфе, этг
исследование будет выполнено более подробно.
§ 10. ПРИМЕР
Рассмотрим задачу определения максимума функционала
т
A) ЛУ)= I
о
Ср. замечания в § 22 и 23 гл. I.
300 Глава IX
при выполнении условий
B) а) § =
Основное уравнение имеет вид
C) /т= тах [с—
о<© < с
Будем предполагать, что функция Ъ(у) удовлетворяет следующим
условиям:
D)
б) й'ООХ), Ь'(у)-+О при у-+оо,
в)
Из простых функций этими свойствами обладает функция У у.
Предположим (это допущение вполне правдоподобно), что
О1)- Тогда, возвращаясь к определению максимума функции
у)=с — у-\-Ь(у)/с, мы видим, что ее производная по V, К'(у) =
= —1 4"*'0*0/с» будет положительной для малых значений ?/,
отрицательной для больших значений V и равной нулю в точности
Для одного значения V. Пусть, кроме того (это условие также
в данном случае правдоподобно), /о=0 при Т=0, а, начиная с мо*
мента Г=0, монотонно возрастает как функция от 7\
Если V изменяется в интервале 0<^г><оо, то решение урав-
уравнения /С/('У) = О существует всегда. Однако когда изменение V
ограничено условием 0 ^ V ^ с, то при большом /с, т. е. при боль-
большом Т% функция К'(у) будет положительной во всем интервале
0^г>^с. Это означает, что если Т велико по сравнению с с, то
искомый максимум будет достигаться в точке ю=с или в точке
/
/
Остается определить кривую перехода Т=Т(с)9 состоящую из
точек, в "которых в поведении происходит переход от одного типа
решений к другому. Нам известно, что решение будет иметь вид
E) *1у = х, 0
б) 0<У<х,
Первый участок кривой, где у = х; содержится в решении только
в том случае, когда значение Т достаточно велико. При малом зна-
1) В следующем параграфе мы покажем,. как можно, получить эти ре-
результаты посредством рассмотрения дискретного процесса.
Новая формализация вариационного исчисления 301
чении Т решение будет состоять только из второй части, где
0<у<х.
Рассмотрим тот случай, когда значение Т мало. Здесь мы можем
рассуждать двумя способами. Можно сначала использовать то обстоя-
обстоятельство, что максимум в формуле C) достигается внутри интер-
интервала, а это означает, что уравнение C) эквивалентно следующей
системе:
F)
Этих уравнений вместе с граничными условиями
G)
достаточно для определения функции /(с, Т) при малых значе-
значениях Т.
Есть и другой путь. Мы можем применить классические вариа-
вариационные методы, пользуясь тем, что мы вправе игнорировать усло-
условие 0 < у < х. Полагая
(8) ./О0=/
т
* Ь{у)й8 — у
о
о
мы без труда получаем в качестве вариационного уравнения сле-
следующее уравнение Эйлера:
(9) (Г—О** (.у)—1=0
С помощью однозначно определяемой этим уравнением экстремали у
мы можем вычислить соответствующее ей значение функционала 3{у)
и таким образом определить /(с, Т).
Когда Т возрастает, его критическое значение как функция от с
определяется как значение Т, при котором уравнение
(Ю) — 1-И»/с = 0
имеет решение ъ = с, т. е. критическое значение Т находится из
уравнения
Если, как это и предполагается, функция /с(с, Т) монотонно воз-
возрастает по 7\ то это уравнение имеет один корень Т(с). С нахож-
нахождением критического значения решение полностью определяется.
302 Глава IX
§11. ДИСКРЕТНАЯ МОДЕЛЬ
Один из методов, которым можно пользоваться, чтобы сделать
строгими приведенные выше рассуждения, основан на дискретной
аппроксимации непрерывной задачих). Для задачи, рассмотренной
выше в § 10, дискретная модель представляет собой задачу опре-
определения максимума функционала
A) лу)=Цу„ л. у г • • •• у^= 2 (**—Л)
на множестве всех значений у^ удовлетворяющих соотношениям
B) а) *Л+1 = ■**+■*(Л). *о = *.
б) 0 < Л < •*:*, * = 0, 1, 2
Если положить
C) «
2/
то мы получаем рекуррентные соотношения
D) а) ио(с) = с,
б) иы+1<<с)= тах
N=0, 1
Используя те же методы, которые мы применяли в § 12 гл. I,
а также при изучении уравнения оптимального управления запасами,
легко установить следующий результат.
Теоое^ма 1. Для каждого целого N^1 существует функ-
функция Ч^(с), обладающая следующими свойствами:
а) функция VN{с) монотонно убывает при возраста-
возрастании с,
б) VN+ЛС)>VN^ Ы= Ь 2, .. .,
в) уравнение юк{с)=^с имеет единственное решение-,
если его обозначить через ск, то сы > сю
г) %(О = %-1 (с + #(<0) для 0<с<с^, т. е. V = с,
Д) иN(с) = с — VN(с)-{-иN_1[с + Ь(уN(с))\ для
N=1,2 для
1) Эти результаты можно также строго установить, используя класси-
классические методы. Соответствующая ссылка имеется в библиографии в конце
этой главы.
Новая формализация вариационного исчисления 303
Доказательство этой теоремы, которое проводится обычным спо-
способом по индукции, мы предоставляем читателю.
Аналогичный результат можно получить и для более общего
случая, соответствующего задаче из § 7, если потребовать выпол-
выполнение соответствующих условий для функций Р(х% у) и О(лг, у).
При этом доказательство будет гораздо более громоздким.
Как мы видели в § 7—8, задача определения максимума функ-
т
ционала ^{у)= \ Р(х, у)йг при выполнении условий
о
F) а) ^ =
б) 0<.у<*
может быть сведена к задаче решения "нелинейного дифференциаль
ного уравнения в частных производных
G) /т=шах [Р{сш V) + О{с9V)п9 /(с, 0) = 0.
Последнее уравнение может быть численно решено, если его аппро-
аппроксимировать уравнением в конечных разностях.
Чтобы пользоваться этим методом с полной уверенностью, мы,
во-первых, должны установить, что поставленная вариационная за-
задача эквивалентна решению построенного нелинейного уравнения
(доказательство этого несколько затруднительно при наличии огра-
ограничений), и, во-вторых, должны показать, что метод конечных раз-
разностей дает приближенное решение рассматриваемого нелинейного
уравнения (это тоже сложная задача). Доказательств обоих этих
утверждений можно избежать следующим образом. Мы заменяем
первоначальную задачу задачей об определении максимума функции
N
(в) /7(Ы)=д2 /*(**. л)
по всем значениям ук, удовлетворяющим условиям
(9) а) хк+1 = хк + АО (хк9 ук)У х0 = с,
б) 0<л<лгл, & = 0, 1, 2
где хк=х
Полагая
(Ю)
804 Глава IX
мы заменяем рассмотренную выше задачу максимизации рекуррент-
рекуррентными соотношениями
A1) /о(<0 = 0.
/*+1(<0= шах
о <: V <
Во всех рассмотренных до сих пор случаях выяснилось, что
этот метод является более надежной вычислительной процедурой,
обладающей к тому же рядом других привлекательных с точки зре-
зрения численного решения черт.
Оказывается, не очень трудно показать, что
A2)
при тех же требованиях, предъявляемых к функциям Р и О, ко-
которые обычно рассматриваются в вариационном исчислении. На
самом деле эти требования могут быть значительно ослаблены, од-
однако всякое дальнейшее рассмотрение этого вопроса увело бы нас
слишком далеко в сторону.
§ 12. ДОКАЗАТЕЛЬСТВО СХОДИМОСТИ
Так как изучение вопроса о сходимости во всей общности даже
при сильных предположениях становится очень скучным делом
и в принципе не дает ничего нового, то мы ограничимся получением
одного типичного результата.
Пбложим
X
A) /(с, Т)=тах Г ^(д:,
* о
при ограничениях
B)
б)
Для удобства положим у = срл:х), так что, вводя новые функции
Р и О, мы получим
т
C) /(с, Г) == тах |
* о
1) В частности, такое преобразование независимой переменной удобно
использовать при численном решении, так как оно позволяет перейти от
максимизации по переменной области к максимизации по фиксированной
области 0<!<рд;<;1. С другой стороны, существуют случаи, когда наличие
переменной области представляется даже желательным, в частности, при
рассмотрении процессов с сокращением.
Новая формализация вариационного исчисления 305
Где
D)
б) 0-^ср^1 для всех значений
Теперь определим для л=1, 2, ... последовательность аппро-
аппроксимирующих задач: максимизировать
E)
при условии, что лгд. и срЛ связаны при помощи уравнений
F) 4+1 — хк=°(хк> ?л)-^» * = 0, 1 п — \,
хо = с,
а переменные срЛ удовлетворяют следующим ограничениям:
G)
Здесь, как и выше, хк = л: (^ А), срЛ =
Для каждого значения с и Г положим
(8) /(с, Г, л) = тах/у({<рй}| л)
Мы хотим показать, что
(9) Ит/(с. Г, л) =
оо
Прежде всего нам понадобится следующая лемма.
Лемма» Предположим, что функция О (л:, ср) удовлетворяет
условию Липшица в области т^х^М, 0^ср^1. Яр« 5тол«
пусть
A0) а) <р@ — ступенчатая функция с постоянным значением
срл, 0<срл<; 1, в интервале к/п^1 <(й + 1)/л," Л =
= 0, 1, . . ., /V,
б) последовательность {хк} определяется рекуррентно по
формуле F), причем числа т и М являются нижней
и верхней границами множества членов этой последова-
последовательности, т. е. т^хк^.М\
в) х(г) — ступенчатая функция с постоянным значением х%
в интервале к/п^.1: <(&-]- \)/п;
г) функция х({) определяется как решение дифференци*
ального уравнения D).
20 Р- Беллман
306 Глава IX
Тогда существует постоянная к, зависящая только от О и Т,
такая, что \хA)— х(()\^к/п в интервале 0<^<;ЛЛ
Эту лемму можно доказать методом Коши—Липшица, применяя
его таким же образом, как и при доказательстве теоремы существо-
существования для систем обыкновенных дифференциальных уравнений.
Докажем теперь теорему о предельном соотношении (9).
Теорема 2. Пусть
A1) а) функции Р и О имеют непрерывные вторые частные
производные,
б) существуют постоянные р, цу г, такие, что
<О(л:, .УХ?* + г для л;>0 и 0<.у<*.
в) Оу не меняет знака: либо Оу > 0, либо Оу < 0 для
всех значений л; > 0 и 0 <; у ^
Тогда
A2)
СО
для всех значений с^>0, Т > 0.
Доказательство. Пусть, как и выше, М== \Т/п] при дан-
данных значениях с>0 и Г>0. Условие A16) позволяет установить
равномерную ограниченность функций хA) в интервале О^^^Г.
Пусть т^.х{г)^М и, таким образом, т<; лгд.<; Л1 Так как по
предположению функции Р(х,у) и О (л:, ср) удовлетворяют условию
-Липшица в области т^лг^М, 0<;ср^1, то на основании дока-
доказанной выше леммы существует постоянная В', зависящая только
от с, Г, Р и О, такая, что
каковы бы ни были ср(^) и срл, удовлетворяющие условиям этой
леммы. Отсюда следует, что
(И) ?
для всех л=1, 2, ....
Обозначим через {щ} подпоследовательность последовательности {/г},
для которой Ит /(с, 7\ Л|) = Ит /(с, Г, /г). По заданному е> 0 вы-
оо п->> оо
берем функцию <р(/) так, чтобы
A5) /(с, Г)
Функция ср(^) является пределом сходящейся почти всюду после-
последовательности {<рт(/)} ступенчатых функций, для каждой из кото-
которых 0 <! срт {г) ^ 1, и при этом Ит ^(ут) = У (ср). Следовательно,
в формуле A5) в качестве функции ср можно взять ступенчатую
Новая формализация вариационного исчисления 307
функцию, постоянную в каждом интервале вида &//х^!^ < (&+ \)/п
при некотором произвольно большом числе /г = /ц. Учитывая нера-
неравенство A3), мы получаем
A6) /(с, Г>< •/*({?*}, л)-|-^ + е</(в, Т, л) + ^
Следовательно,
A7) /(с, Г)< Шп /(с, 7\ /ц) + е= Нгп /(с, Т, л
С другой стороны, используя неравенство A4), заключаем, что
A8) Шп/(с. 7\ л)</(с. Г).
оо
Так как е произвольно, мы убеждаемся в справедливости формулы A2).
Последовательность {срЛп}, которая максимизирует /# ({?&}. л),
определяет для каждого /1=1, 2, ... ступенчатую функцию <рп@»
для которой
A9) Ит
ОО
Если при этом существует подпоследовательность, которая почти
всюду сходится к предельной функции ср(^), то Нт У(срп) = У(ср)
П->ОО
и <р(^) является максимизирующей функцией.
Если эта функция обладает соответствующими свойствами моно-
монотонности, то для выделения сходящейся подпоследовательности можно
воспользоваться теоремой Хэлли. В противном случае мы должны
использовать свойство слабой сходимости или какой-нибудь подоб-
подобный метод.
т
§ 13. МАКСИМИЗАЦИЯ ФУНКЦИОНАЛА ^Г(х,у, *)<И
о
До сих пор мы рассматривали процессы, не зависящие от вре-
времени, т. е.-такие процессы, в которых функции Р и О не зависят
от г. Рассмотрим теперь более общую задачу максимизации функ-
функционала
т
A) ЛЯ =]>(*. У.
о
при условии
B) ^Ц- = О(х9 у.*)9 х@)=с.
Для того чтобы применить метод функциональных уравнений,
мы будем рассматривать эту задачу как частный случай несколько
более общей задачи о максимизации функционала
т
C) Лу) = / Р (х9 у, 0 Л
а
20*
305 Глава IX
при условии
D) % = О(х.у.*), х{а) =
(Здесь а изменяется в интервале [0, 71].)
Если зафиксировать Т, то мы будем иметь два параметра со
стояния, а и с. Поэтому можно написать
5) тахУ(зО = /(#, с).
у
Функциональное уравнение для / будет иметь вид
а+8
9 у, 0^ + /(^ + 5, сE))
F) /(а, с)= тах
V 1а, а+#]
где 0<5<Г — а.
Устремляя 5 к нулю, мы приходим к уравнению
G) 0 = тах[/?(с, V. а) + /а+О(с, V. а)/е]9
где ъ^ъ^а, с) есть значение 3;(^)-
Из уравнения G) получаем систему уравнений
(8)
0=/7г?(с, 1/, л) + О^(с, V, а)/с.
Решая ее относительно /а и /с, находим
(9) ^
« = —Ьг—=
Как и выше, приравнивая значения производных /са и /^», получаем
дифференциальное уравнение в частных производных первого порядка
Читатель, знакомый с квазилинейными уравнениями этого типа,
легко проверит, что уравнения характеристик этого уравнения
совпадают с уравнениями Эйлера, полученными классическими вариа-
вариационными методами.
§ 14. ОБОБЩЕНИЕ И ОБСУЖДЕНИЕ
При рассмотрении задачи о максимизации функционала
т
A) {
Новая формализация варийционного исчисления 809
^ ^ 1_ ■ ... . I ---- "■■ I,,.. _ II.
при условиях
B) -
где х, у, с и §*—я-мерные вектор-столбцы, а Т7 — скалярная функ-
функция от х и ух), можно действовать аналогичным образом. Положим
C) /(с, 7) = тахД.у).
у
Тогда принцип оптимальности приводит к функциональному урав-
уравнению
D) /(с, 8-\-Т) = тах
у [о, /5;
Классические условия трансверсальности оказываются частным
случаем этого уравнения; этого и следовало ожидать в силу той
двойственности между точечными и тангенциальными координатами,
которую мы отмечали выше.
Производя выкладки, аналогичные G) — (9) § 13 этой главы,
мы получим систему квазилинейных дифференциальных уравнений
в частных производных для вектора ю = ю\с, Т) = у@).
Для этого уравнения построена теория характеристик; как и
следовало ожидать, уравнения этих характеристик совпадают с урав-
уравнениями Эйлера для вариационной задачи. Строгое доказательство
этого факта довольно громоздко и здесь не приводится.
§ 15. ИНТЕГРАЛЬНЫЕ ОГРАНИЧЕНИЯ
В § 7 настоящей главы рассматривалась вариационная задача,
в которой на у было наложено ограничение О^^у^л:. Рассмотрим
эту задачу в случае, когда наложено дополнительное ограничение
т
V*) V У 0% -^ /Л.
о
г
Минимум функционала \ Р (х, у)Ш будет теперь функцией трех
о
параметров состояния: с, Тит. Обозначим его через /(с, Т, т).
Используя уже знакомые нам методы, убеждаемся, что / удовлетво-
удовлетворяет уравнению
B) /т— тах
) Любую явную зависимость от I всегда можно устранить, рассматри-
рассматривая г как зависимую переменную л:п+1, определяемую соотношениями
*/« 1 @)С
310 Глава IX
Задачи, содержащие ограничения уже известного нам по преды-
предыдущим параграфам типа, возникают при изучении многих физических
проблем, если мы накладываем реалистичные ограничения на такие
величины, как скорость, ускорение, радиус кривизны, плотности
распределения ресурсов и т. п. Интегральные ограничения, подобные
приведенному выше, или же ограничения вида \ у'2сН4^т возни-
о
кают, если мы предполагаем, что ограничены ресурсы или кинети-
кинетическая энергия и т. д.
Вообще говоря, оперировать с интегральными ограничениями
более удобно, чем с локальными. Хотя теоретически метод множи-
множителей Лагранжа применим для рассмотрения обоих типов ограни-
ограничений (равно как и ограничений более общих классов), однако на
практике мы, как уже упоминалось выше, встречаемся с трудностями
при выяснении того, когда переменная лежит внутри области изме-
изменения, а когда — на ее границе.
§ 16. ДАЛЬНЕЙШИЕ ЗАМЕЧАНИЯ
ОТНОСИТЕЛЬНО ЧИСЛЕННОГО РЕШЕНИЯ
Рассмотрим задачу определения максимума интеграла
A) ^
о
где х@) = с, причем других ограничений на х не налагается. В пред-
предположении, что Р удовлетворяет надлежащим условиям, решение
этой задачи будет определяться уравнением Эйлера
дх (И дх'
которое представляет собой уравнение второго порядка, имеющее вид
C) х"=О{х. х',
Поэтому для определения решения необходимо иметь два гра-
граничных условия. Одно условие дается* исходным ограничением
л;@)=с, другое же, возникающее в результате варьирования, таково:
<♦> ^
= 0.
Мы видим, что одно условие задано в точке ^=0, а другое —
в точке 1—Т. С другой стороны, для того чтобы достаточно удоб-
удобным образом проинтегрировать уравнение C) — либо на цифровой
Новая формализация вариационного исчисления 311
вычислительной машине, либо на машине непрерывного действия, —
нам требуются значения х и хг при / = 0 или при 1==Т. К сожа-
сожалению,, из проведенного выше исследования мы не получаем ни
одного из этих наборов условий.
Таким образом, перед нами возникает классическая трудность
двухточечного краевого условия. Если функция О линейна по ^ и
х', мы не встречаем особых трудностей; если, однако, как это имеет
место в общем случае, функция О нелинейна, то мы должны считаться
с тем фактом, что для нахождения решения уравнения C), удовлет-
удовлетворяющего условию D) и начальному условию, мьг не имеем систе-
систематических методов.
Обычная процедура заключается в следующем. Нужно начать
интегрирование при ^ = 0, задавшись некоторым промежутком зна-
значений лг'(О), и сужать этот промежуток до тех пор, пока условие D)
не будет аппроксимировано достаточно хорошо. Этот процесс весьма
трудоемок; иногда он усложняется проблемами устойчивости и
с увеличением размерности вариационной задачи быстро становится
малоэффективным.
Чтобы оправдать использование уравнения B), мы предположим,
что Р— достаточно гладкая функция. Если же мы допускаем, чтобы Р
содержала такие члены как \х — а\ или тах(л: — а, хг— Ъ, #@)
(подобные функции возникают весьма естественным образом в эко-
экономических и технических процессах), то применение обычного
вариационного подхода резко затрудняется.
Соединим перечисленные затруднения с теми затруднениями,
которые вносятся существованием ограничений, и мы увидим, что
для эффективного решения разнообразных задач, возникающих
весьма естественным путем в физическом мире, традиционные методы
должны быть обобщены.
Отметим, наконец, что замечания относительно необходимости
анализа „чувствительности", или устойчивости, которые мы сделали
в гл. VI, а также в связи с дискретными процессами решения,
разумеется, равным образом справедливы применительно к непре-
непрерывным процессам решения.
§ 17. ЗАДАЧА О СОБСТВЕННЫХ ЗНАЧЕНИЯХ
Посвятим теперь наше внимание задачам определения тех зна-
значений X, при которых возможно существование нетривиального
решения уравнения
A) а
Связь между нашими предыдущими рассмотрениями и этой задачей
(на первый взгляд они кажутся далекими друг от друга) имеет своим
источником то обстоятельство, что — при слабых ограничениях на
312, Глава IX
функцию ср(О — задача о собственных значениях эквивалентна задаче
1
отыскания относительных минимумов функционала Г а/2сИ при
о
условиях
B) ср@«2<#=1, й@) = йA) = 0
о
или задаче отыскания относительных максимумов функционала
1
о
при условиях
C)
о
То обстоятельство, что условие и@) = 0 нарушается, когда мы
пересекаем экстремаль, делает эту задачу качественно отличной
от задач, рассмотренных нами выше. Следовательно, если мы хотим
применить метод функциональных уравнений, мы должны рассма-
рассматривать эту задачу как частный случай некоторого более общего
класса задач, обладающих соответствующими свойствами инвариант-
инвариантности. К счастью, это можно осуществить несколькими путями.
Первый подход состоит в следующем. Рассматривается задача
минимизации функционала
1
D) Да)= ^и'2 (И
а
по всем #, удовлетворяющим условиям
E) а) и(а) = к,
1
Л
б)
О
Здесь новый параметр состояния а удовлетворяет условию О^а < 1.
Мы предполагаем, что функция ср(^) подчинена ограничению О
•^9@^^2 Для 0^^<^1 и непрерывна на интервале [0, 1].
Эквивалентная задача — максимизировать функционал
. 1
F)
Новая формализация, вариационного исчисления
313
при условиях
G)
а) и(а) — к,
1
■б) Ги'2й*=1
а
Вторая, менее очевидная формулировка, которая служит нашим
целям, состоит в следующем. Требуется минимизировать функционал
при условиях
(9)
А.
^(а) = ^ и'2
а
а) и(а
1
б) /
а
Положим
A)
где
B)
§ 18. ПЕРВАЯ ФОРМУЛИРОВКА
/\а, к)=т\п ( и'2сН,
а
а) и(а) = к,
1
Вдоль экстремали, с точностью до членов порядка О^I), можнЪ
написать
1
C) а) ^ ср (О и'
а+8
в) /(а, ^) = ^
а+8
Для упрощения исследования мы перейдем непосредственно к йывоДу
йрёдёльного дифференциального уравнения в частных производных. -
314 Глава IX
Теперь, для того чтобы выполнялось условие B6), произведем
замену переменной
D)
Мы имеем с точностью до членов порядка о {$)
к*
(б) а) IV (а-{- з) = к-)- 8V \ ()
б) /(а, к) = V2 §
а+з
Комбинируя полученные результаты, приходим к приближенному
функциональному уравнению
F) /(а, к) =
Устремляя 5 к нулю, в пределе получаем уравнение
7) 0 = тт [«Н- «Л! + /а + Щ^~ /* — Т (в)
V
ИЛИ
(8) /а = 4 — 9 («) Л3 ^ -Ь <Р («
Начальное условие задается в точке а = 1 и является нетри*
виальным, поскольку /(а, к)->оо при а—>1. Для| определения
этого начального условия имеются два пути, которые мы обсудим
в следующем параграфе.
§ 19. ПРИБЛИЖЕННОЕ РЕШЕНИЕ
Если а близко к единице, а функция <р@« как предполагалось
ранее, непрерывна, то вариационную задачу A7.4) и A7.5) можно
заменить следующей аппроксимирующей ее задачей: минимизировать
функционал Г и'2 (И при условиях
а
A) а) и(а) = к,
1
б) Г«2^= 1,
а
где Множитель срA) включен в функцию «(О1)-
1) Здесь аппроксимация заключается в замене у (*) на 9 A). — Прим. перев.
Новая формализация вариационного исчисления 315
К этой задаче можно подойти двумя путями. Используя класси»
ческий подход, мы получаем уравнение Эйлера
B) и" + Хн = 0,
которое может быть разрешено в явном виде. Неизвестный параметр
определяется из условий Aа) и A6).
Второй метод использует уравнение A8.8) при ср(аM=а1. Так как
для А==0 решение задачи A) известно, именно
C) /(«. 0) =
то мы можем получить решение задачи A7.8) в виде степенного
ряда по к, где к ^ 0. Поскольку нас интересует в первую очередь
решение для малых к, этот вид решения удобен для получения
численного решения.
§ 20. ВТОРАЯ ФОРМУЛИРОВКА
Вывод соответствующего дифференциального уравнения в частных
производных для вариационной задачи A7.8) и A7.9) мы предоста-
предоставляем читателю в качестве упражнения. Отметим лишь, что важным
моментом является такая нормализация функции и (^), чтобы выпол-
выполнялось начальное условие и(а) =
§ 21. ДИСКРЕТНЫЕ АППРОКСИМАЦИИ
В той мере, в какой это касается начальных значений, диффе-
дифференциальное уравнение для минимума /(а, к) обладает определен-
определенными неприятными чертами. Поэтому может оказаться полезной сле-
следующая дискретная формулировка.
Рассмотрим задачу о минимизации функции
N
/1\ Р A1 11 11 \ "V A1 // 42
V,*/ * 1**1» **2* • • •» N—1/ — ~Ь V Й ик — 1/
при условиях
N-1
B) а) 2 %а1= 1 •
б)ио = а9 иК==0.
Введем параметр состояния К и в соответствии с этим рассмо-
рассмотрим последовательность {/в(я)}. определенную следующим образом;
N
C) / (а) = т!п
316
Глава IX
где ип подчинены условиям
D)
N
для к=^\*~2, .... Л/—1.
Поскольку эти условия содержат переменные.границы для.каж*
дого ик, произведем замену переменных
(б) ЪЦк=Ъ*
предполагая, что 0 <61<срй<*2<оо для А==0, 1, 2,..., N.
Тогда
где
G)
О 2а ^1—
Задачу определения рекуррентного соотношения для последова-
последовательности 1/д(^)} мы предоставляем читателю в качестве упражнения.
A)
§ 22. ПОСЛЕДОВАТЕЛЬНЫЕ ПРИБЛИЖЕНИЯ
Вернемся к выведенному в § 3 уравнению
/(с)= тах
у [о, 5
Соблазнительно рассмотреть вопрос об испольаовании для решения
этого уравнения метода последовательных приближений. Однако
если выбрать некоторую начальную функцию /0(с) и определись
второе приближение при помощи уравнения
^
B)
1 (с) = тах
у [о, 5]
в
//>(*. ".У) <*Н-/о ('($))
мы видим, .что в пределе (при 5->0) мы должвд иметь,/4 (с) == /0
если только функция /0(с) непрерывна.
На первый взгляд может показаться, что это обстоятельство
делает невозможным • использование метода последовательных при-
приближений. В действительности это не так. Правда, теперь мы должны
Новая формализация' вариационного исчисления 317
строить приближения уже в пространстве поведений, а не в про-
пространстве функций и должны сконцентрировать наше внимание
в первую очередь на поведении V = V(с^ Г), а не на функции/(с, Т).
Тем не менее функция /(с, Т) еще играет важную вспомогатель-
вспомогательную роль.
Для иллюстрации этого положения рассмотрим задачу о макси-
максимизации функционала
C)
при условиях
D) " ~ = О(х,у), х@)=с.
Тогда, как и в § 6, получаем уравнение
E) /г=тах
Выберем теперь начальное приближение V0 = V0(с^ Т), что равно-
равносильно выбору- начальной функции уо — уо(х, Т—Л), помня соот-
соотношение между текущим временем / и временем Т, остающимся
до окончания процесса. Используя это значение у0, вычислим х0
при помощи дифференциального уравнения
а затем /0(с, Т) по формуле
G)
Эта функция /0 удовлетворяет линейному дифференциальному урав-
уравнению в частных производных
(8) /от = Р (с> «о) + ° (с- *о
Для получения следующего приближения к экстремали у (или
к оптимальному поведению V) возьмем в качестве г\{е, Т) функцию,
максимизирующую выражение
(9) Р{с^)+0{с,ъ)Гос-
Используя V^(с, Т), мы, как и выше, получим у^х* Т—^), а затем
хг и /х. Найдя /1§ выберем в качестве' ю"г функцию, максимизирующую
(Ю) г (с.
318 Глава IX
и будем продолжать в том же духе, определяя {/п} — последова-
последовательность приближений к / и ^п] — последовательность прибли-
приближений к V.
§ 23. МОНОТОННАЯ АППРОКСИМАЦИЯ
Покажем теперь, что указанная последовательность приближений
к / является монотонно возрастающей. Это обстоятельство важно
как с теоретической, так и с вычислительной точек зрения. Имеем
A)
Следовательно,
B) (Л — /о)Т >°(С> «1> (/1
Поскольку /1(с, 0) = /0(с, 0) = 0, мы видим, что /х —
для всех Т^О.
Продолжая аналогично, мы легко устанавливаем монотонность
последовательности {/п}. Если эта последовательность равномерно
ограничена, то она должна быть сходящейся. Однако существенно
знать, когда сходятся последовательности частных производных {/пс}
и {/пГ}> а также последовательность поведений {?/п}. Эта общая
проблема весьма сложна, и мы не будем здесь углубляться в нее.
Интересно отметить, однако, что мы располагаем систематиче-
систематическим методом для улучшения любого конкретного поведения.
§ 24. ЕДИНСТВЕННОСТЬ РЕШЕНИЯ
Как уже отмечалось выше, мы обходим все требующие строгого
обоснования моменты при выводе дифференциальных уравнений,
с которыми мы встречались,-а также избегаем изучения существо-
существования решения этих уравнений. Следует, однако, заметить, что
единственность решения может быть установлена весьма легко
с помощью того же приема, который мы формально изложили в виде
леммы 1 в гл. IV.
Пусть, например, / — решение уравнения
A) /Т = тгх[Р (с, V) + О(с, */)/с].
V
\
Предположим, что существует другое решение этого уравнения
@ = @ (с, Т), имеющее при всех с то же начальное значение, именно
B) /(с, 0) = ё(с, 0) = 0,
Новая формализация вариационного исчислении 319
Тогда будет справедливо также и соотношение
C) #г = шах
го
Пусть V = V(с, Т) — функция, на которой достигается максимум в A),
и 1ю = 1®(Т) — функция, на которой достигается максимум в C).
Мы имеем следующие неравенства:
D) т с
Эти неравенства дают
E) О(с, да)(/с_
Таким образом, полагая и = / — §", видим, что функция и удовле-
удовлетворяет неравенствам
F) О (с, да) ис < ит < О (с, V) ис.
Поскольку решения уравнений
G) хт— О (с, <ю)хс = 0, х(с, 0) = 0,
ут— О(с, ъ)ус = 0, у{с, 0) = 0
тождественно равны нулю, из теоремы сравнения следует, что функ*
ция а тождественно равна нулю.
§ 25. МИНИМУМ МАКСИМАЛЬНОГО ОТКЛОНЕНИЯ
Рассмотрим теперь численное решение вариационной задачи сле-
следующего типа: минимизировать
A) шах \и — а\
по всем функциям V(^)^ удовлетворяющим ограничению —
где
B)
Рассмотрим соответствующий дискретный процесс, в котором
C) икАЛ = йй + г («л. *>к)д. ио = ^1
и
Положим
/(Л^тш тах \ик —
320 Глава IX
Тогда
E) /о (*1> = 1*1 —
и
с- — а\% тш /„(сл -А-р*[сл% гЛ А^1
1 V I < 1
для N=0, 1, 2, ... .
Таким образом, мы свели решение исходной вариационной задачи
к вычислению последовательности функций одной переменной, опре-
определенной рекуррентным соотношением F).
*
УПРАЖНЕНИЯ И ПРОБЛЕМНЫЕ ЗАДАЧИ
, К ГЛАВЕ IX
1. Вывести функциональные уравнения для следующих выражений:
а) шах
Г
б) тах ]>™^, -/{0)=ьс9 {(/'Jпа* =
.. /. е- о
т т
в) тах I
'"*' б : о о
2. Вывести функциональные уравнения для следующих выражений:
т
а) тах I /&(Н, /@) = е, / — монотонно возрастающая функции.
о о
т т
о
б) тах Г 1{*йЬ, /@) = с, / — монотонно возрастающая выпуклая
о
т
(вогнутая) функция, I /2с1(= 1.
о
3. Провести исследование, намеченное в § 18, и получить не*
сколько первых членхж разложения /(а, к) в ,вйде степенного ряда
по к для а, близких к единице. :
Новая формализация вариационного исчисления
321
4. Проделать это же для второй формулировки задачи о собствен-
собственных значениях.
5. Вывести функциональное уравнение для следующего выражения:
1П1П Г [(х СJ-\-
1 о
к/2] <и,
их
Ж
= — ах-\~/, х@)
6. Получить соответствующий результат для общего случая
^ о
(*(*)_^J+/2
-л-о
X
7. Применить метод функциональных уравнений для нахождения
минимума функционала
т
A-хJ
I
О
по всем функциям /, удовлетворяющим условиям
их
, УИ>Ь
/
О
8. При тех же предположениях найти минимум функционала
т
\аТ) аи
о
9. Определить минимум функционала Г/2 й1 по всем /, удовле-
о
творяющим условиям
их
для
21 Р. Беллман
322 I Глава IX
т
10. Определить минимум функционала Г (х — у) (И по у, если
о
а)
б) Ъ'\у) непрерывна, Р'(у)<0, V (у) > 0,
в) V (+ 0) = -+- оо.
11. Рассмотреть ту же задачу в предположении, что значение
конечно.
т
12. Определить минимум функционала Г [К(у)-\-Ь(х — у)]
о
по всем у при условиях
а)
б) /С"(*)>0, */'(*) >0 для всех л:,
в) — = — а^ — ^(л: — З'). л:@) = с, ^ > а > 0.
13. Рассмотрим задачу минимизации функционала
т
| — Ьх @ J + «2 @ (*' — ^2 @ )
8
0-^5-^ Г, по всем функциям л:, для которых х(з)=с и
т
Г л/2б?/<оо. Предположим, что все входящие сюда функции непре-
8
рывны и что а$(^)>0 в интервале [0, 71].
Положим
/(с, 5)= т1пУ(л:, 5).
Показать, что
, 7)= 0, для всех с.
14. Показать, что /(с, 5)== «E)+суE) + с2'о;E), где «, V и та;
зависят только от 5.
15. Показать, что к, V и до удовлетворяют уравнениям
а) «'(*)=—<ц
б) я/ E) = 2в, E) Ьх {в) + 2Й2 E) до
Новая форнализация вариационного исчисления 323
в) ш ($) = — ах ($)
а2(8) *
причем и G1) = V (Т) =
16. Получить соответствующие результаты для функционала
т
/ — Ьх @ J + аг (о (*' -а2 @ J + «з (О (*"-А (О )
17. Рассмотрим следующий дискретный аналог задачи 12: мини-
минимизировать функцию
N
по всем возможным значениям хк, К= 1, 2, .... N. причем л;0 = л;.
Как обычно, предполагаем, что функции ук(х) и §к(х) непрерывны
и обладают надлежащими свойствами при
Показать, что эта задача приводит к последовательности {/я(^I,
определяемой следующим образом:
(х) = т1п [ср1У (х^) + ф^ (х„ — х)]9
(хв) + фд (лд — х)
18. Рассмотрим, в частности, случай, когда функции сря и
квадратичны по х% причем ^к = Ьк(х — ^#J» а ф^ = сял;2. Показать»
что в этом случае /ы(х) = иN~^ГVNx-{-'V^Nx2^ где и у, Ъц и
не зависят от л:.
19. Показать, что
2 -1ьн-1 — V2J
и
»
С/ АТ •« " *
етп)
21
324 Глава IX
20. Пусть {ХЛ — минимизирующая последовательность. Пока-
Показать, что
ХСх -|- А\Ь\ — 1^2/2
•^1 ^^ п
21. Рассмотреть соответствующим образом задачу минимизации
выражения
N
к — ак)*]>
Я-1
где 8к = х.
22. Рассмотреть стохастический случай, когда входящие пара-
параметры являются случайными величинами и нужно минимизировать
математическое ожидание ^(x).
23. Рассмотрим скалярное уравнение
йи
где 1/ выбирается так, чтобы минимизировать функционал
т
^^V)= Гк(и—с)аг.
о
Положим /(с, Т)=т^п^(V). Вывести функциональное уравнение
для /.
24. Рассмотреть задачу, в которой нужно минимизировать
т
о
25. Рассмотреть задачу, в которой нужно минимизировать
тах
о<*< г
где а @ — известная функция от ^.
26. Рассмотреть соответствующую двумерную задачу, используя
уравнение
где —
Новая формализация вариационного исчисления 325
27. Рассмотреть таким же образом задачу о максимизации
г
где
а функции /(^) и ^@ удовлетворяют условиям
/ + #=1.
28. Рассмотрим уравнение
Нужно выбрать функцию /(/), подчиненную ограничению
— 1-^/@^1» так» чтобы уменьшить и до нуля за минимальное
время. Каково соответствующее функциональное уравнение?
29. Получить методом функциональных уравнений решения задачи
о брахистохроне и изопериметрической задачи.
30. Определить путь луча света через неоднородную среду,
предполагая, что луч света проходит этот путь за минимальное время.
31. Рассмотрим задачу определения минимума
= шах
по всем последовательностям {ч®к}, удовлетворяющим условиям
где
Положим
Показать, что
32. Получить соответствующие рекуррентные соотношения для
случая, когда
/Л0 тах
326 Глава IX
33. Рассмотрим реактивный самолет, движущийся по горизон-
горизонтальной траектории. Его масса слагается из постоянной массы самого
самолета *ш и массы топлива т. Его движущая сила считается извест-
известной функцией скорости горения топлива, скорости самолета и массы
горючего. В то же время движущая сила является известной функ-
функцией тяги и лобового сопротивления, которые в свою очередь
представляют собой известные функции скорости горения топлива,
скорости самолета и массы горючего.
Пусть
A) х @ — расстояние по оси х от начала в момент 1Ч
®@ — скорость самолета,
т(г)— масса топлива,
<ш — постоянная масса самолета,
у (I)—скорость горения топлива,
Р(у, V, т) — движущая сила.
Тогда
с12х
(™ + ™)-М2- = Р(У> V, т),
или
& + т) Ж =
и
_=_ у
34. Рассмотрим дискретный вариант описанного выше процесса
и наложим ограничение на скорость горения топлива: 0 <1 .у (^) <1/?.
Пусть
/(у, т)—расстояние, пройденное при начальной скорости V,
количестве топлива т и окончательной скорости ут$
если при сжигании топлива используется оптимальное
поведение.
Показать, что
шах [>(« + Р& * т)
и выяснить зависимость /A/, т) от юТ
(Р. Беллман — С. Дрейфус, А. Картано — С. Дрейфус1))
35. Пусть аналогично
/A/, т, й) — время, необходимое для того, чтобы пройти рас-
расстояние й при начальной скорости ?/0, заданном
С а г 1 а 1 п о Н., О г е у \ и 8 5., АррНсаНоп о! йупагшс р^
Ю Ше пиштит Ише^о-сНтЬ ргоЬ1ет, АегопаиШа1 Еп$п#. Кеу., 1957,
Новая формализация вариационного исчисления
327
количестве топлива т и требуемой окончательной
скорости юТ, если при сжигании топлива применяется
оптимальное поведение.
Показать, что
;, щ, с1) =
ппп
V, т) А
-\- т
—ук, а—V^\\.
36. Рассмотрим уравнение
а2х
ах
где нам нужно определить функцию ю = ю(х, йх\й1, I), подчиненную
ограничению |#|^1, так, чтобы минимизировать математическое
ожидание величины
о
в некотором подходящем классе случайных функций г {г).
Перейдя к дискретному варианту, показать, что мы получаем
рекуррентное соотношение
со
—оо
где йО (г0) — функция распределения независимых случайных ве
личин.
37. Рассмотрим линейное уравнение
где V нужно определить так, чтобы минимизировать математическое
ожидание величины
т
328 Глава IX
Найти соответствующие рекуррентные соотношения, выяснить струк-
структуру последовательности 1/#(^1. ^2)} и определить оптимальное
поведение.
(Р. Беллман 1))
38. Возвращаясь к задаче 36, рассмотрим задачу определения
такого V, которое минимизирует вероятность
^=Р{ тах \х
<*Т
Показать, что дискретный вариант приводит к рекуррентному соот-
соотношению
оо
—ОО
39. Рассмотрим случай, когда переменные г{ не являются неза-
независимыми. Предположим для начала, что распределение гп+1 зависит
от значения гп. Определим
*г(сл> со* г) как минимальное математическое ожидание величины У„
Л1 \ л. С у /V
при начальном состоянии (с1§ с2) и информации о том,
что значение случайной величины на предыдущем шаге
было равно г.
Показать, что рекуррентное соотношение для последовательности
имеет вид
оо
г Г)= ГШП
1 2, /
—оо
0. г)
40. Рассмотрим задачу нахождения монотонно убывающей после-
последовательности приближений к первому собственному значению урав-
уравнения /г//-т-Хср(^)« = О, #@) = #A) = 0. Пусть ср — непрерывная
положительная функция от^ [0, 1]; тогда первое собственное значение
дается соотношением
) В е 11 т а п К., Пупат1с рго^гаттт^ апс1 з^осЬавИс соп!го1 ргосезвез,
Тгапз. 1КЕ, 1957.
Новая формализация вариационного исчисления 329
Хх = гшп —
и с
2 а*
Будем строить приближения в пространстве поведений, рассматри-
рассматривая функции и'A)% постоянные в интервалах [АЛ, (й-{-1)Д],
& = 0, 1, 2 М— 1, МД=1, т. е.
Пусть ХХ(АО обозначает минимум в этом пространстве. Показать, что
и вывести рекуррентный метод для вычисления
41. Рассмотреть ту же задачу для уравнения
«D) + Хер @ а = О, а @) = и' @) = а A) = а' A) = 0;
соответствующая вариационная задача заключается в определении
1
а ЛЬ
о
п —
и
1
Г
х = ГШП -у
БИБЛИОГРАФИЯ И КОММЕНТАРИИ
К ГЛАВЕ IX
§ 1. Метод, применяемый в этой главе, был впервые изложен в статье
Беллмана [В е 11 т а п К., Оупапис ргодгаттт^ апс1 а пе\^ ЕогтаНзт т Ше
са1си1и8 о! уапаНопв, Ргос. Ипг. Асай. ЪеШЗА, 39, № 9A953), 1077—1082].
§ 3. Ряд приложений метода функциональных уравнений в математи-
математической экономике можно найти у Беллмана (В е 11 ш а п К., Оп Ше аррНса1юп
о\ йупагше рго^гатгшп^ 1о уаГ1аНопа1 ргоЫетз аг181П§ 1П та1пета1юа1
есопотюб, Ргос. Зутр. оп Са1си1и8 о! Уаг!аНоп8 апс1 АррИсаНопв, Спюа^о,
1956).
§ 7. Рассмотрение задачи этого параграфа классическими вариацион-
вариационными методами можно найти в статье Беллмана, Флеминга и Уиддера
(В е 11 й1 а п К., Р 1 е ш 1 п § \У., \У 1 с1 с1 е г Э. V., Уапаиопа1 ргоЫешз шуо1-
СОП81ГЭ1П18, Апп. (II А\аг., 1956).
330 Глава IX
§ 11. Эта задача рассмотрена в статье Беллмана (В е 11 т а п Р., 1Чо1е8 оп
Ше Шеогу о! йупагшс рго^гаттт^, У. Зое. 1пйи81г. Арр1. Ма1к., 1955).
§ 12. Другое доказательство сходимости, основанное на функциональных
уравнениях, описывающих процесс, дано у Беллмана (В е 11 гп а п К., РипсИо-
па1 еяиаиопз т 1Ье Шеогу о! сгупатю рго^гаттт^ VI, А сПгес* сопуег^епсе
ргоо!, Апп. МаАк., 1957).
Приведенное здесь доказательство принадлежит Флемингу.
§ 14. Доказательство эквивалентности характеристик системы квази-
квазилинейных дифференциальных уравнений в частных производных для VI и
уравнений Эйлера, полученных обычным путем, было дано Осборном. Его
можно найти в гл, 7 монографии Беллмана (В е 11 т а п К., Эупагшс рго-
^гаттт^ о! сопНпиоиз ргосеззез, ТЬе КАИО СогрогаИоп, Н-271, 1954).
§ 21. Эта последняя формулировка кажется наиболее многообещающей
для вычислительных целей.
§ 22. Результаты этого параграфа были намечены в статье Беллмана
[ВеПшап Н., Мопо1опе арргсштаиоп т йупатю рго^гатт1П^ апс! 1Ье
са1си1из о! уапа1юпб, Ргос. Иа(. Асай. 5с/. С/8А, 40, № 9 A954), 1073—1075].
§ 25. Обсуждение приложения метода функциональных уравнений
к некоторым аналитическим задачам, возникающим при изучении управляе-
управляемых процессов, можно найти у Беллмана (В е 11 гп а п Р., Оп 1Ье аррНсаНоп
о! с1упагл1С рго&гатгшп^ ю *Ье 8Шс1у о! сопи*о1 ргосеззев, Ргос. 5утр. оп
ИопИпеаг Соп1го1 Ргосеззез, Вгоок1уп Ро1у1есЬтс 1пз1., 1956).
Глава X
МНОГОШАГОВЫЕ ИГРЫ
§ 1. ВВЕДЕНИЕ
В предыдущих главах мы рассматривали ряд процессов решения,
которые, хотя они и были разного происхождения и различной ана-
аналитической структуры, обладали важной общей "чертой — все эти
решения направлялись единой целью максимизировать значение
некоторой функции критерия. В этой главе мы будем рассматривать
многошаговые процессы решения, в которых эта общая целенапра-
целенаправленность более не сохраняется. Некоторые решения будут напра-
направлены на максимизацию, а другие на минимизацию.
Вероятно, в наиболее интересной форме эти процессы с про-
противоположными интересами предстают перед нами при изучении
действий двух одушевленных противников, которые на каждом шаге
процесса обмениваются оптимальными ходами.
В этих терминах можно успешно рассмотреть многие ситуации
экономического мира, а теория азартных игр случая и умения1)
предоставляет ряд изящных приложений общих методов.
Далее, в области физики в связи с испытаниями и эксперименти-
экспериментированием часто полезно рассматривать природу в какой-то мере
антропоморфизированной, в виде противника, стремящегося утаить
от нас истину2). Постановку экспериментов можно рассматривать
как игру, в которой мы пытаемся выудить сведения из упрямого,
но честного противника.
Развивавшаяся в последние годы математическая теория, которая
исследует задачи, характеризующиеся таким взаимодействием между
личными целями, и есть теория игр. Хотя много усилий в этом
направлении приложил Э. Борель, теория игр основывается на фундамен-
фундаментальном результате Неймана — известной теореме о минимаксе. Прежде
Игры случая и игры умения — два типа игр. К первому из них можно
отнести кости и детские игры типа „Цирк", ко второму — шахматы, пре-
преферанс и т. п. — Прим. перев.
2) Не следует придавать этой гипотезе философской окраски. Она лишь
отражает ту принятую в теории игр установку, что при отсутствии инфор-
информации о деятельности противника следует предполагать, что он действует
наихудшим для нас образом. В применении к природе это означает, что
неизвестная, но важная для нас закономерность объективного мира приводит
к наименее благоприятным для нас результатам. Как только эта закономер-
закономерность познается, она перестает быть элементом „стратегии природы",
а включается в число .правил игры". — Прим. ред.
332 Глава X
чем приступить к рассмотрению многошаговых игр, мы очень коротко
остановимся на основных понятиях теории игр.
Теорию многошаговых игр можно рассматривать не только как
обобщение теории одношаговых игр, но во многих отношениях
и как нечто более фундаментальное1). Одношаговую игру можно
рассматривать как стационарный вариант исходного динамического
процесса, именно многошагового процесса.
После этих предварительных замечаний мы рассмотрим некоторые
частные многошаговые игры, возникшие из многошаговых ггроцессов
распределения, а затем рассмотрим „игры на выживание" и игры
типа погони. Следуя этим примерам, мы по образцам гл. III пред-
представим общую формулировку, а затем, как в гл. IV, докажем ряд
теорем существования и единственности для некоторых важных спе-
специальных классов уравнений.
В основном используются те же методы, что и в исследовании
процессов с единым намерением. Однако игры на выживание содержат
особые трудности, требующие более развитого аппарата для общего
исследования. Метод, который мы употребляем, приложим только
к узкому классу уравнений.
Одним из интересных аспектов игр на выживание является при-
приложение этой концепции к изучению игр с ненулевой суммой, где
интересы игроков уже не являются прямо противоположными. Фор-
Формулировка этих игр в терминах выживания дает нам возможность
ввести для этих игр метрику так, чтобы сделать их играми с нуле-
нулевой суммой. Далее, как мы покажем ниже, достаточно разумные
аппроксимации приводят нас к нахождению новой метрики для игр
с ненулевой суммой, метрики с соответствующей теоремой о мини-
максе.
§ 2. ОДНОШАГОВАЯ ДИСКРЕТНАЯ ИГРА
Мы будем рассматривать класс процессов решения, в которых
участвуют два лица. Эти процессы мы будем называть играми. Два
действующих лица, которых мы будем называть игроками, будут
несколько прозаично именоваться А и Б2). Рассмотрим типичную
игру.
Трактовка теории многошаговых (позиционных) игр как обобщения
теории одношаговых игр (т. е. игр в нормальной форме) представляется спор-
спорной. Естественнее, пожалуй, считать, что многошаговые игры являются более
конкретным объектом, чем одношаговые, так как в многошаговых играх
стратегии являются некоторыми функциями, т. е. более конкретными и
индивидуализированными объектами, чем в одношаговых играх, где они
являются просто элементами абстрактных множеств. Важность теории
многошаговых игр определяется не ее общностью, а возможностью вос-
воспроизвести в ней больше черт изучаемого явления. — Прим. ред.
2) Преемники алгебраических А, В и С, рассмотренных С. Ликоком.
[Стефан Ликок A869—1944) — популярный в Америке канадский юморист.—
Прим. перев.].
Многошаговые игры 333
Правила этой игры состоят в следующем. Первый игрок А де-
делает выбор из М различных ходов, которые мы будем обозначать
числами 1, 2, .... /И, а второй игрок В— из N различных ходов,
обозначаемых через 1, 2, .... N. Если А выбирает свою 1-ю воз-
возможность, а В—у-ю, то А получает величину ац, а В величину Ьщ.
Если эти величины положительны, мы можем смотреть на них как
на выигрыши, если они отрицательны — как на проигрыши1).
Эти доходы, или выигрыши, удобно вводить посредством двух
матриц игры, или матриц выигрышей
A)
Рассмотрим теперь одношаговый процесс, в котором каждый
игрок делает в точности один ход. Оптимальный ход, определяемый
как ход, который обеспечивает максимальный доход, находится не-
непосредственно, если А должен ходить раньше В и В может исполь-
использовать информацию о его выборе. Если А выбирает 1-ю возможность,
то В выбирает у = /@ так, чтобы максимизировать Ъц. Следовательно
А выбирает / так, чтобы максимизировать а{^^у Такое же правило
определяет выбор у, если первым ходит В.'
Единственно интересным является случай, когда оба игрока
должны ходить одновременно и ни один из них ничего не знает
о выборе другого.
В этих условиях игроки могут защитить себя, смешивая свои
выборы, т. е. определенным образом рандомизируя их. Предположим
тогда, что А делает 1-Й выбор с вероятностью р$, а В свой у'-й
выбор с вероятностью д^ Вектор /? = (рг /?2, ..., рЛ определяет
распределение вероятностей для Л, а вектор д = (дГ д2, ..., дЛ—
распределение вероятностей для В.
Как и в нашем рассмотрении случайных процессов в предыдущих
главах, мы не можем далее говорить о самом доходе, а должны
согласиться рассматривать некоторый средний доход. Как обычно,
простейшим является ожидаемый доход. Математическое ожидание
дохода для А будет
М N
B) ЕА(р, д) = 2 2 Щ
а для В —
М N
C)
) Новые результаты по теории таких игр см. в статье Н. Н. Воробьева
.Ситуации равновесия в биматричных играх", Теория вероятностей и ее
применения, 3 A958), 318—331. — Прим. перев.
334 Глава X
Первому игроку следует выбирать р так, чтобы максимизиро
вать ЕА, тогда как второй должен выбирать ^, максимизирующее
§ 3. ТЕОРЕМА О МИНИМАКСЕ
Чтобы получить достаточно полные результаты, мы должны пред-
предположить, что интересы игроков прямо противоположны, что выра-
выражается соотношением
В этом случае игра называется игрой с нулевой суммой (или нуле'
вой игрой), и только для этого случая существует удовлетвори-
удовлетворительная общая теория. Мы имеем
B) Ев (р, ?) = — ЕА (/?,
откуда ясно, что любой выбор р и #, который увеличивает ЕА(р,
уменьшает Ев(р, д), и наоборот.
В дальнейшем нашем обсуждении достаточно рассматривать только
ЕА(р, Я)- Мы можем, используя это выражение, определить два
значения игры
C) • УА = пнп шах ЕА (р,
а р
Ув = шах тгпЕА(р,
р я.
Первое из них — это ожидаемый доход игрока Л, если В выбирает ц
до того, как А выбирает /?, второе — аналогичная величина в обрат-
обратной ситуации.
Тот замечательный факт (теорема Неймана о минимаксе), что
D) УЛ = УВш
является основным результатом в теории игр. Эта величина назы-
называется значением игры. Этим результатом мы будем пользоваться
здесь без доказательства 1).
Интерпретация этого результата такова: Л может заранее объявить
свое распределение вероятностей /?, точно так же как В может
объявить <7, так как эти дополнительные сведения не увеличат ничьего
выигрыша. Этот результат не является ни интуитивно ясным, ни три-
тривиальным, но он верен.
) Различные доказательства этой теоремы см., например, в книге Мак-
Кинси „Введение в теорию игр", Физматгиз, М. (в печати), в сборнике «Линей-
«Линейные неравенства", ИЛ, М., 1959, или в статье Воробьева Н. Н. „Конечные бес-
бескоалиционные игры", Успехи машем, наук, 14, № 4 A959), 21—56—Прим. ред.
Многошаговые игры 335
§ 4. НЕПРЕРЫВНЫЕ ИГРЫ
Предположим теперь, что вместо выбора одного хода из дискрет-
дискретного множества ходов Л (а также В) должен выбрать ход из конти-
континуума. В качестве простого, примера допустим, что Л должен выбрать
в интервале [0, 1] вещественное число х, а В — выбрать в таком же
интервале вещественное число у. Рассматривал только случай игры
с нулевой суммой, мы имеем функцию выигрыша К(х, у)у которая
оценивает значение этого набора ходов для Л, причем значение этой
функции для В равно —К (х% у).
Если В выбирает распределение Р (х) вероятностей, с которыми
он избирает л;, а В выбирает О (у), то ожидаемый выигрыш для А
будет равен
1 1
A) ЕА={ 1К(Х, у) йР (х) аО (у).
о о
Непрерывный аналог теоремы о минимаксе состоит в том, что
B) тахш1П^=п11П
& о о р
по всем Р и О, для которых
1
C) а) <*/>>0. /
о
1
б) йО ^> О, I
о
при условии, что функция К (х, у) непрерывна по х, у на единич-
единичном квадрате1). Если К(х, у) не является непрерывной функцией,
то равенство B) может и не выполняться и Ед(Р, О) может даже
существовать не для всех Р и О2).
§ 5. ОГРАНИЧЕННЫЕ РЕСУРСЫ
Во многих ситуациях, включающих многоходовые действия, при-
приведенная выше модель не является удовлетворительной. Так обстоит
дело, в частности, в многошаговых процессах, в которых каждый
Эта теорема является весьма тонкой иллюстрацией полезности инте-
интеграла Стильтьеса, так как результат неверен, если мы будем рассматривать
только функции Р(х) и О (х), являющиеся первообразными, т. е. если
йР (х) = ср (х) ах, сКЗ (у) = ф (у) йу.
2) См. по этому поводу статью Карлина (К а г И п 5., Орегаюг *геа{теп(
о! гшштах ргтар1е, СотпЪийопз 1о 1Ье Шеогу о! ^атез, уо1. I, Рппсеюп,
1950). Весьма общие условия существования и равенства минимаксов (~;)
см. в статье Фань Цзи в сборнике „Линейные неравенства". — Прим. —*
336 Глава X
игрок обладает ограниченными ресурсами. Здесь выбор ходов зависит
от того, какое количество ресурсов имеется в распоряжении, и игра
прекращается, когда какой-либо игрок исчерпает свои ресурсы.
Следовательно, мы не можем считать получающийся набор N игр со-
состоящим из N отдельных партий.
Рассмотрим простой пример. Пусть А имеет количество ресур-
ресурсов х, а В— количество у. На каждом шаге каждый игрок может
поставить на кон одну или две единицы ресурсов с выигрышем ац
для игрока Л, если А поставил /, а В поставил у, и с выигрышем — ац
для игрока Ву где /, у = 1, 2.
Здесь, чтобы упростить первоначальный пример, выигрыш изме-
измеряется в иных единицах, чем х и у, и поэтому не может превра-
превращаться в ресурсы.
Пусть процесс обрывается, когда кто-либо из игроков исчерпает
свои ресурсы, и каждый из них играет так, чтобы максимизировать
свой полный доход. Допустим, что мы можем определить функцию
A) /(х, у) как доход, ожидаемый от процесса игроком Л, если
вначале А имеет х> В имеет у и каждый использует
оптимальное поведение.
На первом шаге А делает свои выборы согласно распределению
вероятностей р ==(р1з р2)» а & — согласно распределению вероят-
вероятностей д = (дХу <72)» гДе Р и Я будут, вообще говоря, функциями
от х и у.
Перечисление всех возможностей приводит к следующему соот-
соотношению для оптимального поведения:
2 2
=2 2
причем в данный момент считается, что для многошаговых игр
выполняется принцип оптимальности. Доказательство этого будет
дано в § 9. Таким образом, мы получаем для /(х, у) функциональ-
функциональное уравнение
C) /( у) \ 2
р 3 I г=1
Ш1птах
^ р
^ —'. У—Л\\
для х, )/>0 с граничными условиями
D) /(х, у) = 0, если х^О или
Многошаговые игры 337
§ 6. ИГРЫ НА ВЫЖИВАНИЕ
Обращаясь к игре, описанной в § 2, будем считать, что А
имеет х ресурсов, В имеет у, и допустим, что доходы игроков ац
и Ь{а выражены в тех же единицах, что и х, у (например, в дол-
долларах), и что 6у = — ац (случай нулевой суммы). Предположим
теперь, что игра продолжается, пока не разорится один из игроков,
и что каждый игрок стремится разорить противника. Игру такого
типа мы назовем игрой на выживание. Она является обобщением
известной задачи о разорении игрока1).
Предполагая существование функции
A) /(х, у)—вероятности того, что А разорит В, когда А имеет х,
В имеет у и каждый игрок придерживается оптималь-
оптимального поведения,
и рассуждая, как и раньше, мы получим функциональное уравнение
B) /(*, у) = тах тт 2/С* + ац. У —
V Я г*Э
= тт тах 2/С* + а%г У —
Я V г,Э
где х, у>0, с граничными условиями
. *>о. .у<о,
Так как игра имеет нулевую сумму, количество ресурсов в игре
остается постоянным. Таким образом, состояние процесса опреде-
определяется величиной х, т. е. количеством ресурсов, принадлежащих А.
Полагая х-\- у — с и /(х, у) — /(х), получим более простое уравнение
D) /(х) = тах тт 2/О + афР\Ч} = т!п тах 2/(* + а
V Я. г>3 Я V г* 5
для 0 < х < с, где /(х) == 0 для х<0и /(х) = 1 для х^> с.
§ 7. ИГРЫ ПОГОНИ
Другой интересный класс игры составляют игры, включающие
догоню одного игрока за другим. В одних случаях ставится вопрос,
может ли один игрок поймать другого, в других случаях, где
поимка бесспорна, задача состоит в том, чтобы определить выбор
такой траектории для одного игрока, которая минимизирует время
) См., например, Г н е д е н к о Б. В., Курс теории вероятностей, ГТТИ,
М., 1954, стр. 60. — Прим. перев,
22 Р-
338 Глава X
поимки, а для другого игрока —траектории, которая максимизирует
это время.
Непрерывные варианты этих задач очень трудно строго сформу-
сформулировать, и поэтому большинство полученных результатов относится
к дискретному варианту.
Рассмотрим следующую простую задачу. Два игрока, А и В, рас-
расположены на прямой соответственно в точках йД и /Д, где Д > О,
а к и /—целые числа. На каждом шаге игры каждый игрок решает,
продвинуться ему на одну единицу вправо или влево. Ходы делаются
одновременно, причем имеется полная информация относительно
позиций каждого игрока. После каждого шага В уплачивает А коли-
количество #(<2), где <2 = |& — /|Д — расстояние между игроками. Кроме
того, на этом шаге с вероятностью 1—а (А) процесс заканчивается.
В этой многошаговой игре за полный выигрыш принимается
ожидаемое значение величины, которую В уплатит А до того, как
закончится процесс. Снова предположим, что существует функция
A)/(с?)—ожидаемый выигрыш, если вначале А и В находятся на
расстоянии б, и оба используют оптимальные стратегии.
рассуждая, как и раньше, получим функциональное уравнение
B) /(а) = а (а) тах тт [/^/(Й) +А#2/(<0 +Л?2/(^ — 2) +
V Я.
где рх и р2— соответственно вероятности того, что А пойдет влево
или вправо (для любого шага), а дх и д2— соответствующие вероят-
вероятности для В. Вообще говоря, оптимальные рг, р2, дх и д2 будут
зависеть от й.
§ 8. ОБЩАЯ ФОРМУЛИРОВКА
Опишем теперь в более или менее общем виде класс многошаго-
многошаговых игр, которые мы намерены анализировать. На каждом шаге
игры положения обоих игроков А и В будут характеризоваться
т-мерными векторами х и у, которые мы будем понимать как
„ресурсы".
Чтобы исключить на время принципиальные трудности, связанные
с рассмотрением бесконечных процессов, рассмотрим сначала конеч-
конечный процесс. В начале каждого шага Л/-шагового процесса игрок А
выделяет определенное количество своих ресурсов — вектор и и
В — определенное количество своих ресурсов — вектор V] это сим-
символически будет выражаться соотношениями 0<^#^л;, 0<^'а^>у,
где неравенства выполняются покомпонентно.
В результате этого распределения ресурсов А получает выигрыш
V, х, у), где /? — скалярная функция, а В—выигрыш
, V; х, у) (рассматривается процесс с нулевой суммой).
МногоШаёбвЫё йёрЫ 339
Кроме этого, происходит изменение их ресурсов: х преобразуется
в Т(х, у\ иу V), а у—в Г7(л:, у\ и, V). Процесс продолжается
теперь по тому же принципу еще (/V—1) шагов. Полный доход
игрока А в Л/-шаговом процессе выражается формулой
A) /?дг=:/^(й, и1§ и2, ..., ик__х\ V,
Имеется несколько способов, которыми мы можем исследовать этот
Л/-шаговый процесс. Одна крайность — рассматривать эту М-шаго-
вую игру как одношаговую игру усложненного типа, требуя, чтобы А
выбирал множество векторов (и, иГ ..., ик_^, а В — множество
векторов (уу ю±, . .., ^Л-_1), где выбор ак и юк зависит от
й, иГ .... икг V, VV ..., *ок_у Другая возможность—использо-
возможность—использовать функциональное уравнение. Для случая неограниченно продол"
жающегося процесса и для процессов, включающих случайное воз-
воздействие, единственно возможным является применение рекуррентных
соотношений. Для случая конечных детерминированных процессов
этот метод обычно проще и с аналитической и с вычислительной
точек зрения.
Мы будем предполагать, что /?(#, V] х, у) — непрерывная функ-
функция от и и V для всех конечных значений и и V, х и у, и анало-
аналогично, что Т(х, у\ и, V) и Т'(х, у\ и, V) — непрерывные функции
от х, у, и и V для всех конечных значений этих векторных переменных.
Общий случай, когда предполагается только ограниченность и
измеримость функций, можно исследовать, применяя те же принципы,
ценой введения операторов зир и т! вместо тах и тт. Интересно
также рассмотреть частный случай, когда величины х, у, и, V, Г, V
принимают лишь конечное число значений; он имеет то преимущество,
что позволяет избежать рассмотрений, основанных на непрерывности.
Одно из преимуществ рассмотрения М-шагового процесса как
одношагового, как это описано выше, состоит в том, что это по-
позволяет нам на основе известных результатов об одношаговой игре
точно определить многошаговую игру, а также значение многошаго-
многошаговой игры. Определив игру, мы можем доказать приложимость метода
рекуррентных соотношений.
Значение описанной выше Л/-шаговой игры задается выражением
B) 1^ = тахтт ^ ^Я^б,О{и, и1$ иг ..., а1Г^1) X
О О'
= тш тах
22*
340 Глава X
где О и О' — функции распределения на областях очень сложной
формы, определенных неравенствами
C) 0<и<х,
0<м1<Г,
' 0 < им_г < Тя_г 0 < VN_1
Величины Г и Г' зависят от х, у, и и V, величины 7\ и 7\ — от
х, у, и, V, и19 ъг и т. д.
§ 9. ПРИНЦИП ОПТИМАЛЬНОСТИ И ФУНКЦИОНАЛЬНЫЕ
УРАВНЕНИЯ
Изменим теперь наши обозначения, введя Р вместо х и Р' вместо у,
с тем чтобы рассмотреть более общие случаи, в которых х и у уже.
не будут обязательно векторами, элементы которых являются количе-
количествами ресурсов х).
Так как У]^ зависит только от исходных состояний, мы можем
определить последовательность функций
О) /*(Р. П = УЮ N=1. 2
Предполагая на время, что для многошаговых игр справедлив
принцип оптимальности, мы получим следующие рекуррентные соот-
соотношения 2):
B) Д(Р, Р') =
= тах Ш1П \ \ Н (и, V) АО (и) ДО' (V) = тт тах [...],
о с N ^ ^ О' о
0<ад<Р
= тах тт \ С С [/? (и, V) + !м G\ Т')\ АО (и)
О О' I «/ 3
= тт тах [. . . 1:
о
В том, что этот принцип имеет место для процессов с одним
действующим лицом, где мы стараемся максимизировать доход или
) По-видимому, в этих более общих случаях предполагается какая-то
упорядоченность элементов Р и Р'. См., например, область интегрирования
в B) и дальнейшее изложение. — Прим. перев.
*) Для простоты мы будем вместо К(и, V; Р, Р') писать Я {и, V).
Многошаговые игры 341
минимизировать „издержки", легко убедиться, рассуждая от против-
противного. Так как его выполнение для игровых процессов может ока-
оказаться не столь очевидным, мы в целях полноты предложим краткое
доказательство.
Рекуррентное соотношение B). обеспечивает последователь-
последовательность (не обязательно единственную) пар функций распределения
{Ом(и, Р, РО, 6'м(у, Р, РО}, которые определяют последователь-
последовательность {/^(Р, РО}- Чтобы показать, что функция /^(Р, РО действи-
действительно является значением М-шаговой игры, достаточно показать,
что игрок А может обеспечить себе ожидаемый выигрыш /^(Р, РО»
если он выберет и на первом шаге М-шагового процесса в соответ-
соответствии с функцией распределения Ск(и, Р, РО, когда состояния А
и В описываются соответственно точками Р и Р\ и аналогично,
что В может гарантировать, что его ожидаемый убыток будет не
больше, чем /^ (Р, РО-
Чтобы показать это, рассмотрим ЛЛшаговый процесс с одним
действующим лицом, в котором А использует заданную страте-
стратегию, представленную последовательностью функций распределения
{ОЛ(#, Р, РО}, /5=1, 2, ..., /V, а В старается минимизировать
ожидаемый доход для А за Л/ шагов. Достаточно рассмотреть этот
процесс, так как любое другое поведение, применяемое В, даст А
больший ожидаемый выигрыш. Пусть
C) ^(Р, РО—ожидаемый доход игрока А за /V шагов, когда А
использует заданную стратегию {Ой(#, Р, РО}»
В использует минимизирующую стратегию и А и В
первоначально находились в состояниях Р и Р'.
Тогда после использования принципа оптимальности для процесса
с одним действующим лицом мы получим рекуррентные соотношения
D)
Р,
ас (V),
°' 0<г><Р'
Рассматривая происхождение функции Ох, мы видим, что минимум
в выражении для щ(Р, Р') в формулах D) достигается на функции
С' — С'у которая, вообще говоря, не является единственной. Следова-
Следовательно,
E)
342 Глава X
Так как щ^У19 выражение для щ тем же путем приводит к тому,
что щ=2У2, и, таким образом, по индукции убеждаемся в том, что
F) «^(Я, Р') = УН{Р, Р').
Точно так же мы убеждаемся, что если В использует стратегию
^Оа, Р, Р')> то А не может получить больше, чем УМ(Р, Р')- Следова-
Следовательно, УН(Р, Р') является значением данной Л/-шаговой игры.
§ 10. БОЛЕЕ ОБЩИЙ ПРОЦЕСС
Прежде чем предлагать какие-либо точные утверждения о про-
процессах, которые мы рассматривали выше, рассмотрим группу более
общих процессов, которые также можно исследовать с помощью
методов, употребляемых нами ниже.
Рассмотрим сначала бесконечный процесс описанного в § 8 типа,
в котором мы считаем преобразования Т и Т', так же как и доход /?,
зависящими от номера шага.
В этом случае мы рассматриваем функции
A) /(Р, Р'\ к)— значение для А бесконечного процесса, начатого
на к-и шаге, если А и В имели на этом шаге Р
иР' и оба использовали оптимальные стратегии.
Эта последовательность с обычной оговоркой относительно суще-
существования удовлетворяет рекуррентному соотношению
B) /(Р, Р';
тахт1пГ С С [#(н, ъ,к)+/(тк, Тк; к + \)] аО (и) а<3'(V)]
0 °' 1о<кР *
тт пгах [...].
а
Перейдем теперь на следующую ступень усложнения процесса.
В предшествовавшей задаче мы предполагали, что взаимодействие
игроков вполне определено после того, как сделан выбор и и V.
В ряде процессов выбор и и V определяет распределение резуль-
результатов, что вынуждает назвать взаимодействие скорее случайным, чем
детерминированным. Пусть /С&Ог, 1Ъ 1'\ и, V) обозначает функцию
распределения, где г — значение Нк{и, V), г — значение Тк и I' — зна-
чение Тк.
Функциональное уравнение B) заменяется уравнением
, Я'; к) =
= тах
ахттГ § § [/[*+/(', ^; к + \)\ йК^йО (и)
= тттах
в1 в
Многошаговые игры 343
Наконец, рассмотрим случай, когда мы сталкиваемся не столько
с самим полным доходом /?, сколько с его нелинейной функцией.
Особенно важна ситуация, когда А стремится максимизировать вероят-
вероятность получения дохода, не меньшего, чем заданная постоянная /?0.
Другая интересная функция выгоды — это еаЕ.
Предположим, что А стремится максимизировать ожидаемое зна-
значение ср(/?), где ср — заданная функция от /?. Чтобы описать этот
нелинейный случай, мы должны ввести дополнительный параметр
состояния а, полный доход, полученный А от предыдущих шагов
процесса. Определяя функцию /(Р, Р', а; к) в основном как в A),
мы получим соответствующее функциональное уравнение
D) /(Р, Р', а- к) =
пГ
= тахгшп
° 0<ад<Р
0<г><Р'
= тт тах [...].
О' О
Здесь не будут рассматриваться вопросы единственности и суще-
существования решений ни для одного из этих функциональных уравне-
уравнений, поскольку основной подход является во всех случаях одним и
тем же.
§ И. ОСНОВНАЯ ЛЕММА
Рассмотрим простое, но крайне полезное неравенство, которое
обнаруживает квазилинейность преобразования
A) I (/) = тах тт Т (Р, Р'; /; О, О') = тт тах Т.
0 0' О' О
Оно будет играть такую же роль в доказательствах существования
и единственности в этой главе, какую в гл. IV играла лемма 1.
Лемма 1 х). Пусть
B) Ч/) =
= тахгшпГГ [[К(и> ©) + А(Р. Р'; ишю
о в' У-*/{.
= гшп тах[.. . ],
О' О
1 (П=
(П Г 1
= тах тт Г Г[/?х («, ю) + И(Р, Рл, «, V) Р (Г, Г)] АО (и) АО' (V) =
о О' IV-•{, ^
1п тах[...].
о' а
1) Предполагается, что для каждого преобразования тах тт = т!п тах.
Аналогичный результат верен для одностороннего оператора гшп тах
(см. § 18).
344 Глава X
Тогда
C) и(/) —М/01<тах шах [| Л (я. г;) —^(и, *
м € # » €
-НА(Р. Р'; й. о)|-|/(Г. Т') — Г(Т, Т')\].
Доказательство. Зааишем
D) /,(/) = тах тт Г(Р, Р'; /; О, О') = гшп тах Г(Р, Р'; /; О, (Г),
СО" в" в1
11(/7)=тахт1пГ1(Р, Р'; Т7; О, СГ) = т1п тах Гх (Р, Рг; Т7; О,
О О' О' в
Пусть (Ох, Ох) — пара функций, на которой достигается значе
ние /,(/), а (О2, О2) — пара функций, на которой достигается зна
чение ^чС/7). Тогда в силу свойств седловой точки мы имеем сле
дующую цепочку неравенств:
E) Т(Р, Р'\ /; О1Ш О0<7-(Р, Р'; /; О2, О[) =
. Р';/; Ог
Тх (Р, Р'; /?; О2) 0'2) < 7\ (Р. Р'; Р; Ои О*) = I, (Р) <
< 7\ (Р. Р'; ^. О2,
Комбинируя эти неравенства, получаем
F) Т(Р, Р'; /; О2> ОО — Л (Р. Р'; ^ О2,
<Г(Р, Р'; /; О». Оа) —^(Р, Р'; Р;
Неравенства F) дают
G) / / {Л (и, «)-/?! (а. «)+* (Р, Р'; и, г) [/(Г, Г) -
, щ} ао2 (и) ао[ (
, Т')—Г(Т, Г
Многошаговые игры 345
Используя, как и в гл. IV, тот факт, что из я^с<1# следует
тах(| а\, \Ь\), мы получим из G) следующее неравенство:
(8)
\к(Р. Р'; и, гО||/G\ Т') — Г(Т, Т')\]с1С2(и)
V €8*
из которого непосредственно вытекает C).
Легко сделать изменения, нужные для получения аналогичных
результатов в случае, когда тахтт заменяется на зирт!.
§ 12. СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ
До установления наших результатов введем некоторые обозначе-
обозначения. Пусть Р и Р' являются п- и я'-мерными векторами, определен-
определенными соответственно в областях О и п\ каждая из которых содержит
начало координат соответствующего пространства. При всех значе-
значениях й, г>, Р и Р' от преобразованных векторов Г(Р, Р'\ я, V) и
Т'(Р, Р'\ к, V) требуется, чтобы они лежали в тех же областях,
причем и и V суть соответственно к- и /^-мерные векторы выбора,
ограниченные областями 5 и 5\ которые могут зависеть или не
зависеть от Р и Р'. Так как в следующей ниже теореме мы будем
иметь дело с преобразованием сжатия, то предположение о конеч-
конечности множеств В и п' не уменьшает общности.
В каждом из этих пространств введем норму ||Р||, равную сумме
абсолютных величин компонент вектора Р:
п
п'
По существу эти нормы не должны быть обязательно идентич-
идентичными; в некоторых случаях может оказаться полезнее рассматривать
нормы, сформированные по структуре функционального уравнения,
чем стандартные нормы указанного типа.
346 Глава X
Функциональные уравнения, которые мы рассмотрим несколько
обстоятельнее, таковы:
/(Р,
, Р'\ и, ъ)](Т, Т')]AО(и) АО'(V) 1 = тттах
> в' о
где Т=Т(Р, Р'; и, V), Г = Т'(Р, Р'\ и, V).
Для упрощения наших обозначений запишем оператор в фигурных
скобках в уравнении B) как Т(Р, Р'\ /; О, О7). Тогда уравнение
в B) примет вид
C) /(Р, РО^тахяппГСР, Р'; /; О, О0 =
О О'
= тттахГ(Р, Р'\ /; О, О").
в' о
•
Возникает вопрос, следует ли относиться к этому соотношению
как к одному уравнению или как к паре уравнений. Мы будем назы-
называть C) „уравнением".
Результат, который мы будем доказывать, составляет содержание
следующей теоремы.
Теорема 1. Рассмотрим уравнение B) при следующих пред*
положениях:
D) а) функции /?(и, V), Л(Р, Р'; и, V), Г(Р, Р7; и, V) и
Г7(Р, Р'\ к, V) — непрерывные функции от Р, Р', к, V
в любой ограниченной области изменения этих пере*
менных;
б) области выбора 5(Р, Р7)* 5Г(Р, Р;) изменяются не-
непрерывно по Р и Р/#,
в) Г в Г — преобразования сжатия, т. е.
где к — заданная постоянная, меньшая единицы;
оо
г) 2 ™(кпс) < сю для всех с > 0, где
=* тах (тах
д) тах |Л(Р, Р'\ я, г>)|<1.
Щ V, Р, Р'
указанные условия выполняются, то мы можем уШёр*
Ждать, что существует единственное решение уравнения B)
Многошаговые игры 347
в классе функций /(Я, Я7), которые непрерывны для всех конеч-
конечных Я и Я' и равны нулю, когда Я и Я7— нулевые векторы.
Это решение может быть получено методом последователь-
последовательных приближений:
E) /о (Я, Я7) = шах тт Г Г Г К (и, V) йО (и) йО' (<яI =
о в' I ^ у ^
= гшп тах [...],
в1 о
/Л+1(Я, ЯО=тахттГ(Я> Я'; /п; С, 00 =
о о'
— тт тах Г (Я, Я7; /> О, С7), п >0.
Решение получается как предел /(Я, Я/)= Ит /П(Я, Я7) в любой
П>ОО
ограниченной области пространства (Я, Я7).
Далее будет доказана следующая
Теорема 2. Б предположениях теоремы 1 множество
функций {О (и), С (у)), порожденное функциональным уравнением,
образует множество оптимальных решений соответственно для
игроков А и В в описанной выше многошаговой игре.
§ 13. ДОКАЗАТЕЛЬСТВО РЕЗУЛЬТАТОВ
Приступим теперь к доказательству сформулированных выше
результатов. Пусть
A) /о(Р, Р*) = тах тт \ Г Г К (и, V) йО (и) йО' (*)
о о' I./ у
= т1П тах [.
О' О
и
B) /п+1 (р» р/) = тах т1п Г (р» р/» /п'. О- °0 = т1п тах г»
где Г определяется формулами A2.2) и A2.3).
В силу наших предположений о функциях, входящих в коэффи-
коэффициенты, и об областях X иУ мы можем получить существование
седловой точки в A) и непрерывность /0(Я, Я7). Тогда по индукции
можно показать, что все функции /П(Я, Я7) существуют и непре-
непрерывны для всех конечных Я и Р\
. Покажем теперь, что последовательность {/п) сходится равно-
равномерно в любой конечной части пространства (Я, Я7). Используя
348 Глава X
лемму 1, получаем неравенство
C) |/„«(Л П—/»(Р. П\<
<тахтахГ/ Г|/П(Г, Г)-/п^(Т. Т')\аО(.и)№'{у)\,п=*2. 3
Определим новую последовательность
D)
Тогда при использовании предположения Dв) теоремы 1 соотноше-
соотношение C) дает нам
E) ип+1 (с) < ип (кс), п = 2, 3
Кроме того, мы имеем
F) |/2(Я. Р') — /ЛР, РОК тахтах Г Г|/?(«, «) | й(О (и) йО'
О О' •* •/
О О
откуда
G) «2 (с) <
Используя наше предположение о том, что 2 ^(кпс) < оо, мы
видим, что ряд 21/п+1(^» Р')—/п(Р* Р'У\ сходится равномерно
п
в любой конечной области. Следовательно, {/П(Р, Рг)} сходится
равномерно к функции /(Р, Р'), которая удовлетворяет исходному
функциональному уравнению.
Это завершает доказательство существования. Приступим теперь
к доказательству единственности. Пусть Р(Р, Р')—другое решение,
которое непрерывно при Р —О, Р' = 0 и ограничено в любой
конечной области. Мы видим, что тогда Р(Р, Рг) действительно
непрерывно при всех конечных Р и Р', хотя этот факт и не не-
необходим для нашего доказательства. Он просто несколько упрощает
его, так как мы можем заменить вир т! на тах тт.
Мы имеем тогда два уравнения
(8) Р(Р9 РО = гаахттГ(Р, Р'; Р; О, С')=гшптах7\
О О' О' в
/(Р, Р') = тахттГ(Р, Р'; /; О, 0')== шп тах Т.
0 0' О' О
Применяя лемму 1, мы видим, что
(9) \Р(Р. РО—/(Л Р0|<
тах тах Г Г Г\Р(Т, Г)—/(Г, Г)\аоа(у]т
Многошаговые игры 349
Пусть
A0) Д(*)= шах \Г(Р, Р') —/(Р. Р')\.
Из неравенства (9) следует
(И) Д(*)<Д(*с).
что после итераций дает Д(г)^ А(Апс), я= 1, 2, ... . Так как
функции Р и / непрерывны при Р = 0, Р' = 0 и имеют общее
значение 0, мы видим, что Д(Апс)->0 при я-*оо. Следовательно,
Д(с)эО и /"=/.
Это завершает доказательство теоремы 1.
§ 14. ДРУГОЕ ДОКАЗАТЕЛЬСТВО СУЩЕСТВОВАНИЯ
При изучении функциональных уравнений этого класса доказа-
доказательство существования достается почти даром, тогда как доказа-
доказательство единственности требует различной степени усилий. Что же
касается функциональных уравнений, возникающих в вариационном
исчислении, то для них имеет место обратное: доказать существова-
существование трудно, а единственность просто.
Отметим, как мы можем получить существование решения урав-
уравнения с зирт! в случае, когда мы предполагаем, что К(и, г>)^-0
и Н(Р, Р'\ и\ у)^>>0. Рассуждая индуктивно, мы получаем, что
последовательность {/П(Р, Р')} монотонно возрастает и ограничена.
Значит, эта последовательность сходится к функции /(Р, Р').
Чтобы показать, что эта функция удовлетворяет функциональ-
функциональному уравнению
A) /(Р. Р') = 5ир Ы Т(Р, Р'\ /; О, С') = ЛхА вир Г,
0 0' О' О
поступим следующим образом. Мы имеем
B) /(Я, Р')>/п+1(Р, Р') = *ир 1Ш Т{Р, Р>; /„; О. О')
О О'
и, значит,
C) /(Р, Р0>зир 1п! Г(Р, Р'; /; О, О').
О О'
Обратно, используя положительность этого оператора, мы по-
получаем
D) /п+ЛР' Р/)<5ир1п!Г(Р, Р'; /; О, О')
для всех п и, следовательно,
E) /(Р, Р')<8ир1п1Г(Р, Р'\ /; О, О').
Сравнивая C) и E), мы видим, что достигается равенство.
350 Глава X
§ 15. ПОСЛЕДОВАТЕЛЬНЫЕ ПРИБЛИЖЕНИЯ В ОБЩЕМ СЛУЧАЕ
Последовательность приближений {/П(Я, Я7)}, используемых для
построения функции /(Я, Я'),—это последовательность, которая
получается из конечных я-шаговых процессов. Эта последователь-
последовательность не самое лучшее, что можно использовать, если интересоваться
только бесконечношаговым процессом. Как мы указывали на пре-
предыдущих страницах, приближение в „пространстве поведений" (здесь
в „пространстве стратегий") по ряду причин является более есте-
естественным и более важным типом приближения.
Чтобы обосновать этот и другие типы приближений, нам нужна
Теорема 3. В предположениях теоремы 1 последователь-
последовательность, определяемая соотношением
И + 1 » в О'
= тттахГ(Я, Я7; /й; О, СГ), я^=0, 1
О' О
сходится к решению уравнения A2.3) для любой исходной функ-
функции /о (Я, Я'), которая непрерывна в любой конечной части
области (Я, Я') и равна нулю при Я = О, Я' = О.
* Доказательство точно такое же, как данное выше.
§ 16. ЭФФЕКТИВНОСТЬ РЕШЕНИЯ
Мы установим существование и единственность для выведен-
выведенного выше функционального уравнения в предположении, что бес-
бесконечный процесс обладает значением для каждого игрока. Теперь
возникает вопрос, будет ли действительно это функциональное
уравнение давать достаточную информацию, чтобы позволить каждому
игроку достичь этого значения. Если это так, мы будем говорить,
что решение эффективно и функциональное уравнение теоретически
эквивалентно игре *).
Решение будет эффективно в предположениях теоремы 1, которые
равносильны непрерывности.
Чтобы показать эффективность в предположениях теоремы 1,
мы должны показать, что если игрок А использует функцию рас-
распределения О(и)=О(и; Я, Я'), получающуюся из пары (О, О').
1) По многим причинам это, однако, неверно. После того как функцио-
функциональное уравнение было сформулировано, а процесс снят с рассмотрения,
мы ограничили себя определенным направлением подхода, который может
и не быть оптимальным для исследования всех свойств этого процесса.
Хорошо всегда помнить, что указанное функциональное ^ уравнение — это
только однонз многих мыслимых математических описаний процесса.
Многошаговые игры 351
которая дает минимакс, то независимо от того, что может делать В,
А может гарантировать доход не меньший, чем /(Р, Р').
При использовании этой фиксированной стратегии доход игрока А
будет в наименее благоприятном случае определяться решением
функционального уравнения
A)
Ь(Р, Р'\ и, ъ)Р(Т, Г)] ав (и)
Используя аппарат предыдущих глав вместе со сделанными
предположениями, легко показать, что это уравнение имеет един-
единственное непрерывное решение, которое равно нулю при Р = 0,
р'—0. Более того, решение этого уравнения может быть получено
как предел последовательности, определенной соотношениями
B) Л) (Р. Я') = т!п [^/ /? {и, V) аО (и) йО' (*)].
и
Рп+х(Р. Р0=т1
н(Р. Р'\ и, V) ря(Т, т')\ао(и)ас(V)}.
Из происхождения О (и) ясно, что Ро^/О. Следовательно, по индук-
индукции Рп+1=/п+1> где /п определено в соответствии с A5.1). Таким
образом,
C) Р(Р, Р0= Нт Гп=
Л > ОО П> ОО
Это показывает эффективность решений.
Обращаясь к замечаниям, сделанным в § 6 гл. IV, получим теперь
следующую теорему.
Теорема 4. Пусть ,
D) Д(<?)= п1ах
ЦР11+11Р' II <с
352 Глава X
Тогда в предположениях теоремы 1 решения уравнений
E) /(Р, Р/)=тахт1п Г Г[Л(я.
о в' ^ {
Н (Р, Р'\ а, г> )()()
0 О
, Р')=тахгшп Г
,Р\ и, ) )\()()
удовлетворяют неравенству
со
F) \/(Р. Р') — Г(Р. Р')\<1,Ь(кыс).
П—0
Доказательство. Применяя лемму из § 11, мы видим, что
G) |/(Я,
I \\К — "+/('» Т')—Р(Т, Т'у
.... ^
Повторное применение этого неравенства приводит к желаемому
результату.
§ 17. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
Результаты, полученные в предыдущих параграфах, зависели
только от того, что полные ресурсы системы уменьшались вслед-
вследствие участия в игре на любом отдельном шаге игры. Аналитически
мы можем выразить это утверждением, что преобразование (Р, Р')—*
->G\ Г7) является преобразованием сжатия.
Введем теперь преобразование сжатия другим путем, предполагая,
что
A) |А(Л Р'\ и,
для всех допустимых Р, Р\ и и V. Учитывая, что сейчас мы пред-
предположили, что Р и Р/ лежат в ограниченных областях и что Т
и V при любых и и V представляют хобой преобразования этих
областей в себя, мы легко получим аналоги предыдущих теорем для
предположения A). Мы предоставляем формулировку и доказатель-
доказательство этих результатов читателю в качестве упражнения.
Многошаговые игры 353
§ 18. ОДНОСТОРОННИЙ МИНИМАКС
* Рассмотрим теперь уравнение
A) /(Р. Р') = тштах [/?(«, о) + й(Р. Р'; й. ч)/G\ Г)],
которое возникает из описанного выше процесса распределения,
если от второго игрока требуется, чтобы он перед каждой партией
сообщал первому выбранное им V.
Мы можем получить аналог основной леммы из § 11, поступив
следующим образом. Для любой функции К(и, V), для которой
написанные далее выражения имеют смысл, имеем
B) гшп тах/? (и, у) = тт тах /?(#, V),
где а {у) — функция, которая при заданном V максимизирует /?(#, V).
Пусть О (у) — такая функция.
Пусть V — значение V, которое минимизирует /?((У(г>), V).
Тогда мы имеем неравенства
C) К (и (У). 1О<Л(*/(«0. V).
A/A0. 10>Л(«00. V)
для любых других допустимых значений и и V. Из этого свойства
седловой точки следует аналог леммы 1. Получив эту лемму, мы
выводим доказательства существования и единственности уже без
всяких ухищрений.
§ 19. СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ ДЛЯ ИГР
НА ВЫЖИВАНИЕ
Мы докажем следующее предложение.
Теорема 5. Рассмотрим уравнение
A) /(*) = т1п тах
я. р
с) +/?2?2/ (х — Ь)]
= тах тт [р^/(х—1)-\-р&г1 (х + а
р я.
— Ь)\
для д:=1, 2, 3, .... й—1, соответствующее матрице игры
23 Р. Беллман
354 Глава X
где а% Ъ и с—целые положительные числа, а> 1, а /(х) удовле
творяет граничным условиям
, х < О.
Существует единственная функция /(х), удовлетворяющая
неравенствам 0<^/(лг)<^1, для которой выполняются A) и C).
Доказательство. Для упрощения обозначений будем под
V(/(х)) понимать значение игры с матрицей
\
/(*-!)
V (/(*)). х=1, 2, .... а—1.
Функциональное уравнение A) имеет вид
О
(б) /(*) = ■
1.
Определим последовательность {/п(х)} следующим образом:
О у <? г1 1
F) /о(^) 1
[О, х<
х=\ш 2, а—1, л = 0, 1, 2,
Ясно, что /г(х)^/о(х) для всех х; следовательно, по индукции
+1х^>/п(х)- Из этого и из того, что 0<;/п(л:)<;1 для всех х
и я, вытекает, что /п(х) сходится при п—>оо для всех х к функ-
функции /(х). То, что /(х) удовлетворяет E), легко проверяется. Это
завершает доказательство существования.
Так как /0(х) есть монотонно возрастающая функция от х%
каждая функция /п(х) также монотонно возрастает и, следова-
следовательно, /(х) также монотонно возрастает. Получим теперь важный
результат, состоящий в строгой монотонности этой функции. На
этом факте основано наше доказательство единственности.
Мы имеем х)
Если /(а) и /(с) положительны, мы имеем /A)>0.
Уа1Л — значение игры с матрицей А. — Прим. перев.
Многошаговые игры 355
Чтобы установить положительность /(а) и /(с), допустим про
тивное, что /(л;) = 0 при л; = 0, 1, ..., к < й, но
Тогда
\пь + ) ПкЬ)] \пь + ) о
Так как /(* + а)>/(&+ 1) > 0,/(й + с)>/(* + О> 0, отсюда
следует, что /(&)>0, что приводит к противоречию, кроме случая,
когда к=\. Таким образом, /A)> 0.
Мы имеем
Так как /A)>0, /(в + 2»/(а+1), /(с + 2)>/(с+ 1).
/B — ^)>-0, то мы должны иметь /B)>/A), кроме случая, когда
/B — #) = 0 и решением является р2 = <72= 1- Это, очевидно, не-
невозможно, так как это дает /B) = 0</A), а мы знаем, что
Таким образом, по индукции получаем, что
(Ю)
со строгим неравенством на каждом шаге.
Теперь легко получается единственность. Положим
(П)
+РгЧЛ (* + с)
Пусть / и §•—решения уравнений"
A2) /(л;)=тттахГ(/?, #, /)== тахтШ
« р V я.
—гшптах Г(р, ^, §•)= тах тт
ДЛЯ 0 < X < ^ И
@
A3) ^
с дополнительным предположением об ограниченности &(х) при
0 <л:<^.
В предположении, что /(х) ф §• (х), положим
A4) ' А=тах|/(д:)
и пусть з/ — наибольшее число из интервала [0, й\, при. котором
достигается максимум, предполагаемый отличным от нуля.
23*
356 Глава X
Если мы обозначим через Р1=Рг(у), Яг = Я1(У)> Рг=Р% 0>),
стратегии, на которых достигаются соответствующие мини-
максы, то получим
A5)
8(У)=Т(р. ?,
и, как в лемме 1,
A6) ь=\/(у)—е(у)\< тах
Так как для всех р и я
A7)
мы видим, что в A6) имеет место равенство; это означает, что
A8) Т(р9 ?, /)=Т(р. Я, /),
Рассмотрим соотношение
A9) /су)—е{у)=РгЧЛ!{у— О—$(у— 01
— *) — 8 (У — Ь)].
Так как ^РгЯэ=1> то если какие-нибудь скобки в A9) по абсо-
лютной величине меньше, чем Д, то соответствующий коэффи-
коэффициент р$2 должен равняться нулю. По предположению у является
2
наибольшим значением, для которого \/(у) — ^*(^)| = Л. Следова-
Следовательно, ргЯ\ = 0. Р\Яг — 0.
Так как р1-\-р2— ^ и» следовательно, рх и р2 не могут одно-
одновременно равняться нулю, то либо ?1 = 0, либо же <72 = 0. Обра-
Обращаясь к матрице игры
мы видим, что строгая монотонность /(х) как функции от х делает
невозможным, чтобы ^ = 0 или ^2==:0 было оптимальной страте-
стратегией при х = у. Это означает, что предположение Л > 0 приводит
к противоречию, и завершает доказательство.
Мы видим, что доказательство единственности строго возрастаю-
возрастающего решения относительно легко, и вся трудность доказательства
единственности состоит в доказательстве строгой монотонности.
Многошаговые игры
357
Использованный нами метод является достаточно общим и при-
применим к широким классам функциональных уравнений. Он непри-
неприменим, однако, к исследованию общего случая, когда относительно
элементов пц матрицы игры А предполагается только их веще-
вещественность.
§ 20. ПРИБЛИЖЕНИЕ
Вернемся теперь к общему уравнению
A)
= тах тт
V Я
= тт тах
и допустим, что .х велико в сравнении с пц.
Используемое нами ниже рассуждение, несмотря на всю фор-
формальность, обладает многими интересными чертами. Допустим, что
мы можем написать
B)
Тогда уравнение A) примет вид
C) / (х) ^ тах тт 2 РгЯз I/ (*
Р Я Ь 3
/(х + ау) ^/(х) + пцГ (х).
тах тт
р я
что ведет к
D)
0 ^ тах тт Г/' (х) ^Рг
р я I м
= тт
т тах Г/ (х)
Предположим теперь, что /'(х)>0. Тогда мы получим прибли-
приближенное уравнение для неизвестных распределений р и
E)
0
тах тт
р я * л
т1п тах 2
— уравнение, которое не зависит от
Смысл этого уравнения состоит в том, что для больших л; при
большом числе партий, остающихся до конца игры, способ действий
приближенно такой же, как в одношаговой игре, где оба игрока
стремятся просто максимизировать свой ожидаемый выигрыш за одну
партию.
Полагая а^ малым сравнительно с ху мы по существу перешли
к непрерывному варианту процесса. Как мы отмечали в § 18 гл'. VIII,
при рассмотрении нелинейной функции выгоды оптимальное поведе-
поведение не зависит от вида функции выгоды. Здесь этот общий принцип
, Отметим, что во многих случаях функция /(х) не обладает требуе-
требуемыми для этого качествами и приближенное равенство B) написать
нельзя. — Прим. перев.
358 Глава X
демонстрируется еще раз, а в § 22 мы найдем еще один пример,
посвященный аналогичному приближению для игр • с ненулевой
суммой.
§ 21. НЕНУЛЕВЫЕ ИГРЫ НА ВЫЖИВАНИЕ
Обратимся теперь к рассмотрению более общего случая, когда
Ьц Ф — пу. Здесь не излагается приемлемой теории для определе-
определения оптимальных действий в одношаговом процессе. Поэтому 1лы
обратимся непосредственно к рассмотрению многошагового процесса.
Предположим снова, что каждый из игроков стремится разорить
другого и что игра продолжается до тех пор, пока это не про-
произойдет *). Теперь их интересы прямо противоположны, и мы можем
использовать минимаксную формулировку.
Так как это игра с ненулевой суммой, состояние процесса зави-
зависит от капиталов и А и В, обозначаемых соответственно через х
и у. Определим
A) /(я, у) как вероятность того, что А разорит В, когда А
имеет ху В имеет у и оба используют оптимальные стратегии.
Тогда функция /(х, у), если только она существует, удовлетворяет
функциональному уравнению
B) /(х, у)=т^хтт^р^/(х-\-а1^
Р О. ^» 3
Я. Р
с граничными условиями
У<0.
C) _ _
— х — у = 0 (по соглашению).
Используя употреблявшиеся ранее методы, легко получить сле-
следующий результат.
Теорема 6. Если ац -|- Ьц < 0 для всех /, у, то уравне-
уравнение B) имеет единственное ограниченное решение, удовлетво-
удовлетворяющее граничным у-словиям C).
При этом игра, очевидно, становится игрой с нулевой суммой. При-
Привлечение игр с ненулевой суммой в данном случае совершенно несуще-
несущественно, так как получающиеся изменения относятся лишь к правилам
игры. — Прим- перев.
Многошаговые игры 359
§ 22. ПРИБЛИЖЕННОЕ РЕШЕНИЕ
Предположим теперь, что мы имеем дело с процессом, где
выигрыши пц и Ъц всегда отрицательны. Тогда, предполагая, что х
и у велики в сравнении с пц и Ьц и что мы можем написать
A)
мы получим приближенное уравнение
B)
Р Я г>3
= тт 2
Я Р *» Э
Отсюда мы получим приближенные уравнения
C) 0 = шах тт Г/а, 2 ацРкЧ* + /у 2 ЬцрдА =
Р Я V г, Э г*3 л
= Ш1П тах Г/а 2;^Л9> +/г/ 2 *
Я. Р V г,э г,3
Используя соображение, приведенное в § 4 гл. IX, мы видим, что
эти уравнения дают
2 ЬЦР*Я$ 2
D) — ^ = тах тт -^ = тт тах
*У V Я 2л аг1РгЯ1 Я Р
Это весьма основательный критерий. Заметим, что не представляет
разницы, пишем ли мы равенство для /х//у или для /у1/х, так как
максимизация /х!/у эквивалентна минимизации /у!/х.
В следующем параграфе мы покажем, что в формуле D) тахтт
действительно равен тт тах.
§ 23. ДОКАЗАТЕЛЬСТВО ОБОБЩЕННОЙ ТЕОРЕМЫ О МИНИМАКСЕ
В этом параграфе мы хотим доказать следующую теорему.
Теорема 7. Если ^Ьцр^^^ с? > 0 для всех векторов
вероятностей р и <7 х), то
а1}Р%Я$ 2шА
A) тах тт -^ = тт тах *'3
р я 2лицр\Ч5 я р
) То есть если Ьц !> й для всех /и ]. Очевидно, что знак элементов
матрицы (при условии их знакоопределенности) не играет роли, и поэтому
не следует придавать значения тому, что в § 22 все Ьц отрицательны,
а в § 23 положительны. — Прим. перев.
360 Глава X
Доказательство. Без ограничения общности будем в даль-
дальнейшем считать, что Ь^^т < 1 для всех /, у, так что 2 Ъцр$$ <^ т
для всех приемлемых р и #. Рассмотрим систему рекуррентных
соотношений
B) и0 = тах тт 2^ а%$РгЯ$ = т*п тах ^ а%$РгЯ$*
р я 1»з я р 1»з
= тах тт |а^РгЯз + A — 2 Ь^РгЯЛ ип\==
= тт
1п тах [2 ацРкЧз + A — 2 ^г^г^^ «Я1
\ Р И, .9 \ г,Э I Л
Используя рассмотренные выше методы, легко показать, что
последовательность {ип) сходится к значению к, удовлетворяющему
уравнению
C) и = тах тт [2 а^рщ -\-(\ — 2 ь^РгЯз\ и] =
Р Я 1г,,9 \ 1,э / ^
= тт тах [2 ЬцРгЧз + (х ~ 2 Ь
Я Р Иг .7 \ г, .9
Условие , 0 < 1 — 2 ^%з'РгЯз' ^ ^ — ^ обеспечивает геометрическую
со
сходимость ряда 2 (ип+1 — ап)-
Так как и удовлетворяет уравнению C), легко видеть, что оно
задается выражением х
2
• *
D) а = тах тт -^ == П11п тах
2ь
р я 2^ьгзРгЯз я р
из которого следует теорема
Действительно, первое из равенств C) эквивалентно следующему:
тах тт | щрщ — 2
Отсюда
— 2
т1п [2
« и,з
причем существует /?°, для которого
тш
я.
{п Г2 аЦР°гЪ - 2
1 и,$ ьз
Многошаговые игры 361
§ 24. ИСТОЛКОВАНИЕ ИГР С НЕНУЛЕВОЙ СУММОЙ
Важность полученного результата в сочетании с методом прибли-
приближения, описанным в § 22, состоит в том, что теперь мы имеем воз-
возможное естественное истолкование игры с ненулевой суммой, а именно
основывающееся на функции критерия
т
2л
Соглашаться с этим или чне соглашаться — дело вкуса. Нужно
понимать, что этот вопрос всегда должен возникать в процессах
с двумя действующими лицами, когда не очевидно а ргюп, что оба
участника имеют общую функцию критерия, или, что еще хуже,
когда они не имеют соизмеримых шкал пользы.
Значит, для любого р найдется такое #(/0. что
2 агоРгЬ (Р) — 2 ЬЦРЛ$ (Л и
°) и = О,
ИЛИ
2 ацРгЯ* (р) 2 "цр
Тогда
2 ацРЛ} 2
из
откуда
2
и в= тах тт 4==
г т 2
из
Второе равенство в C) дает
2
из
и = гшп тах
из
362 Глава X
УПРАЖНЕНИЯ И ПРОБЛЕМНЫЕ ЗАДАЧИ
К ГЛАВЕ X
1. Рассмотрим следующую игру. Два игрока, I и И, выставляют
монетки, исходя из следующих правил:
а) если обе монетки положены вверх гербом, оба проигрывают
по единице;
б) если обе монетки положены вверх решеткой, I выигрывает,
а II проигрывает единицу,
в) если монетки положены разными сторонами, I проигрывает,
а II выигрывает единицу.
Первый игрок начинает с количеством т, а второй с количеством п.
Каждый играет так, чтобы разорить другого. Пусть р(т, п; х, у)—
вероятность того, что I будет разорен раньше или вместе со И,
если первый кладет герб с вероятностью л:, а II — с вероятностью у х).
Пусть
— ху — вероятность того, что оба игрока выбирают герб,
=л;A—у)~\-уA—х) — вероятность того, что монетки поло-
положены разными сторонами,
—л;)A —у) — вероятность того, что оба игрока выби-
выбирают решетку.
Получить для т, п^> \ рекуррентное соотношение
р(т, п) — цхр(т—\, я—1) + ?2/?(т+1. п—\)-{
с граничными условиями
р(т, 0) = 0, го>1, р@, п)=1, л
(Беллман, Блекуэлл)
2. Показать, что для я ^2 мы получим конечную систему
уравнений
/?A, я) = ?1 + ?2 + ?8/?B, п— 1),
, п— 1) = Я1РA, п — 2) + ?2/>(Ь л) + ?3РC, л—2).
р(п—\, 2) =?!/>(* — 2/ \) + ЯгР(п — 2, Ъ) + яър{п. 1),
р(п, \) = д2р(п—1, 2).
Отметим неточность в постановке задачи. Здесь игрок может стре-
стремиться разорить противника, но может стремиться не разориться сам (раз-
(разница заключается в отношении игроков к случаю, когда они оба разоряются:
в первом случае он желателен, во втором — нет). Что касается обозначений,
то здесь считается, что у и х выбираются в начале игры, а потому далее
автор пишет просто р (т, п), — Прим, перев.
Многошаговые игры 363
3. Показать, что
и, следовательно, в общем случае гшптах/? (т, п\ х, у)
х у
Ф тах ттр(т, п, х, у) (интересно отметить, -что тш тах~ 0,4397,
ух х у
л:'= 0,43, у = 0,5, тах тт^ 0,4302, лг' = 0,43, /=1, где
у х
х' = 1 — л:, У = 1 — у).
4. Из теоремы о минимаксе для непрерывных игр следует, что
п\ Л, Б)= тдх
где
, я; Л, В)= I ] р(т, п; х, у)йА(х)AВ(у),
о о
а Л и Б изменяются на пространстве монотонных функций равно-
равномерно ограниченной вариации, равной единице. Показать, что реше-
решение для т = 2, п=\ дается следующим правилом:
а) II выбирает для у' такое значение у0, чтобы /?B, 1, 0, у') =
= /?B, \У 1, У), — чистая стратегия.
б) I выбирает смешанную стратегию, используя либо выбор гер-
гербов, либо выбор решеток в комбинации (а, 1—а), где а
подбирается так, чтобы величина арB, 1, 0, зО + A—о) X
Х/?B, 1. 1, У;) достигала максимума при у/ =
5. Показать, что ожидаемая вероятность разорения I игрока
равна ,уо = 0,4302, единственному вещественному корню уравне-
уравнения у' = (\— УJ/A— У
6. Доказать, что если т, п—> оо с любым фиксированным соот
ношением т'п — г, то II игрок может выбрать у так, чтобы равно
мерно по х
Нт р(т, п)=\.
т, п -> со
7. Показать, что предыдущие рассмотрения приводят к сле
дующему принципу: участвуя в игре такого типа, 1 должен стре
миться к увеличению ставок, тогда как II — к их уменьшению.
) Напомним, что х и у выбираются в начале игры и являются чистыми
стратегиями. Смешанная стратегия играется так: игрок случайно (по сме-
смешанной стратегии) определяет, с какой вероятностью ему выбирать гербы;
найдя эту вероятность, он ее уже не меняет. — Прим. перев.
364 Глава X
8. Пусть
N
2 Ч5хг
У
N N
2 «л
тах тт [...], Л^= 1, 2
х у
Найти рекуррентную формулу для
9. Рассмотрим игру на выживание, описываемую матрицей
-2 1/'
где полный капитал игроков равен 4, а к— капитал пбрвого игрока.
Показать, что /(к), вероятность выживания первого игрока, удо-
удовлетворяет уравнениям
/A) =
П }~ 1 4-/C) —/A)'
П }~ 2—/B)/A) •
(Хауснер)
10. Показать, что, следовательно,
и что соответствующие оптимальные стратегии таковы:
= 1/2—1, /72=^, /73=2 —/2
= /2.—1, ^=1—
11. Рассмотрим игру на выживание, описываемую матрицей
где а и # — положительные целые числа. Пусть ъп(к) — вероят-
вероятность выживания I игрока, когда общий капитал игроков равен п
и I имеет к. Показать, что
12. Показать, что
Многошаговые игры
365
и, следовательно,
13. Показать, что
14. Доказать теорему 7, получив непрерывность и монотонное
возрастание Уа1 (Л — В\) как функции от X. На основании этого показать,
что существует в точности одно решение уравнения Уа1 (А — В\) = О,
которое можно представить формулой B3.1).
(Карлин)
15. Рассмотрим уравнение
и связанное с ним уравнение
= тах пип
— т1Г] тах
Я.' Я.
При каких условиях мы можем написать
<#(/?) = тах тт и (р)
о. я.'
1П тах и (р)?
16. Рассмотреть, в частности, систему уравнений
хх =
тах тт
я я'
гшп тах
я' я
п
п
г (?, ?0 + 2
1,
при подходящих ограничениях, налагаемых на матрицу
(Шепли)
17. Предположим, что нам сообщили, что монета имеет фиксиро-
фиксированную, но неизвестную вероятность р выпадения герба и вероят-
вероятность ^ = 1 —р выпадения решетки и что р имеет известную
априорную функцию распределения /^(р). Монета бросается N раз,
и перед каждым бросанием мы должны угадывать, что выпадет,
зная результаты предыдущих бросаний. Какое поведение максимизи-
максимизирует ожидаемое число правильных ответов?
18. Предположим, что мы можем бросать монету столько раз,
сколько захотим, уплачивая с за каждое бросание, и требуется
366 Глава X
определить значение р, вероятности выпадения герба. Если выбрано
значение //, то за отклонение от истинного значения уплачивается
8(р—/?')» гДе 8 — известная функция. Какое поведение минимизи-
минимизирует полную ожидаемую уплату?
19. Возвращаясь к задаче 17, предположим, что противник
может выбирать Р(р), с тем чтобы уменьшить ожидаемое число
правильных ответов при использовании оптимальной стратегии.
Можно ли охарактеризовать оптимальный выбор Р(р) утвержде-
утверждением, что противник выбирает Р(р) так, чтобы минимизировать
информацию, получаемую после любого конечного числа бросаний.
В этом предположении найти минимакс.
20. Обобщить эти результаты на случаи, когда на каждом шаге
имеется много различных возможных результатов, например бро-
бросается игральная кость.
21. Игрок А имеет ресурсы в количестве х, а игрок В — в коли-
количестве у. Игрок А разделяет х на п частей: х =
Игрок В аналогично разделяет у: У = 2лУг* УС^-§- Выигрыш
г
игрока А равен
п
Р (х, у) = 2 Сг шах (хг — ул% 0),
а выигрыш игрока В противоположен ему по знаку.
Пусть
= шах Ш1П Г Г Р (л:, у) АО (х1з х2, . .., хп) АО' (ух, у2, . .., уп)] =
о о
= гшп тах [...].
О' О
Найти рекуррентное соотношение между /п и /п_!.
^ ' (Полковник Блотто *))
22. Пусть А — положительная матрица, т. е. ац > 0 для всех /, /.
Показать, что А имеет единственное наибольшее по абсолютной
величине собственное значение, которое положительно, а соответ-
соответствующий собственный вектор может быть выбран положительным.
) Эта задача является обобщением известной'„задачи Блотто" (см., на-
например, сборник „Линейные неравенства", ИЛ, М., 1959, стр. 12). Полков-
Полковник Блотто является в этой задаче действующим лицом. — Прим. пере в.
Многошаговые игры
367
Это собственное значение, называемое перроновским корнем мат-
матрицы А, обозначается через р(А).
23. Показать, что
р (А) = тах тш V а{л -— = тт тах V
т а шш * Хл „ • шт
П
X
П
где изменение происходит в области
24. Показать, что
п
р (А) = тах тт У\ау-~ =
п
тт тах
П' г
где /?' определяется условиями х^А% 2^=1, а д, можно счи-
тать заданным равенством
Ш1П
г* 3
тах /2 (НЛ '
г \ з /
25. Доказать, что р(А) есть единственное решение уравнения
п
или
п
\= тах тт
Я' г
= Ш1П тах
В' г
где /?г определено так же, как в предыдущей задаче. •
26. Рассмотрим нелинейное рекуррентное соотношение
п
ип+1 — пнп тах
2 а,
ьУ-1
с произвольным и0. Доказать, что /?(Л)= Нт ип.
П->оо
(Ргос. Атег. Ма1Н. 8ос, 1956)
368 Глава X
БИБЛИОГРАФИЯ И КОММЕНТАРИИ
К ГЛАВЕ X
§ 1. Блестящее введение в теорию игр дано в книге Вильямса (
11 а ш 8 3. О., ТЬэ сотр1еа! 8(га1е§у81, Мс Огаш-НШ, 1954 г)). Классической
работой в этой области является книга Неймана и Моргенштерна »Тео-
»Теория игр и экономическое поведение" (V о п N е и т а п п ^, Могдеп-
81 е г п О., ТЬе 1пеогу о! &атез- апA есопоггпс Ъепауюг, РппсеЮп 1]п1у.
Рге88, I ес1.1944, II ес1. 1947, III ес1. 1953). Описание приложения математической
теории игр к изучению карточных игр имеется в статье Беллмана и Блекуэлла
[ВеНтап Р., В1 ас к иге 11 О., Нес! с1о§, Ыас1фск апс1 рокег, Зс1епН/1с
АтегЬсап, 184 A951), 45—47]; см. также ссылки в примечании к § 5 гл. VIII.
Рассмотрение некоторых игр типа покера имеется в упомянутой выше книге
Неймана и Моргенштерна, а с тех пор конкретные игры изучались многими
авторами. Интересующийся читатель может за дальнейшими ссылками обра-
обратиться к СотпЬиНопз 1о 1Ье Шеогу о! Оатез, выпускаемым издательством
Принстонского университета в серии Аппа1з о! Ма1петаИс8 51исНе8 2).
Мы полностью избегали в этом томе какой-либо связи с секвенциаль-
секвенциальным анализом Вальда и общей теорией статистических решений и планиро-
планирования экспериментов. Интересующийся читатель может обратиться к книге
Вальда (\У а 1 с1 А., 51аН8Иса1 йее18юп 1ипс1юп8, №ш Уогк, 1950) и книге
Блекуэлла и Гиршика „Теория игр и статистических решений", ИЛ, М., 1959,
и вообще к статьям по этому вопросу в свежих и старых номерах жур-
журнала Аппа18 о/ МаШетаШа1 8ШШ1С8. См. также Р о Ь Ь 1 п 8 Н., 5оте
азрес18 о| 1пе 8е^иеп^^а1 с1е81дп о! ехрептешз, Ви11. Атег. МаШ. Зое, 58
A952), 527—536.
§ 3. Доказательство теоремы о минимаксе можно найти в цитированной
выше книге Неймана и Моргенштерна, равно как и в книге Блекуэлла и Гир-
Гиршика, где рассмотрены также ее обобщения.
Хотя в нашем распоряжении и имеются теории игр с ненулевой суммой
и игр N лиц (Ы > 2), ни одна из них не обладает ни изяществом, ни завер-
завершенностью теории игр двух лиц с нулевой суммой ввиду отсутствия соот-
соответствующей теоремы о минимаксе. Этим вопросам посвящена значительная
часть книги Неймана и Моргенштерна, а основной результат содержится
в статье Нэша [Ы а 8 п 3. Р., Е^иШЪ^^ит рот!8 1П Л^-регзоп датез, Ргос.
Ыа(. Асаа. 8с1. С/8А, 36 A950), 48—49].
§ 4. Абстрактное рассмотрение непрерывных игр см. в статье Карлина
[КагПп 5., ТЬе Шеогу о! 1п!!п!(е ^атез, Апп. Магк., 58 A953), 371—401],
а дальнейшие результаты — в статье Дрешера и Карлина (О г е 8 п е г М.,
К а г И п 5., 5оЫюп8 о! сопуех датез аз НхеА рот*8, Соп1пЪи*юп8 1о 1пе
ТЬеогу о! Оатез, II, Апп. Ма1п. ЗШсПез, № 28, РппсеЮп 1]ту. Ргезз, 1951,
р. 75—86).
§ 5. Насколько нам известно, первое исследование игр, в которых каж-
каждый из игроков имеет конечные рессурсы, и в частности „игр на выжи-
) Автор переоценивает достоинства этой популярной книжки, являю-
являющейся набором элементарных задач. В качестве элементарного введения
в теорию игр скорее можно рекомендовать книгу Мак-Кинси „Введение
в теорию игр", Физматгиз, М. (в печати) (МсЮпзеу «I. С. С, 1п1гос1ис-
Ноп Хо 1пе 1пеогу о! §атез, Иеш Уогк — ТогоШо — Ьопс1оп, 1952). — Прим.
ред.
3) В настоящее время вышло четыре таких сборника. См. также библио-
библиографию в сборнике „Линейные неравенства и смежные вопросы", ИЛ, М.,
1959. — Прим. перев.
Многошаговые игры 369
вание", проведено в работах Беллмана и Ла-Салля (В е 11 т а п
Ь а 5 а 11 е «I. Р., Оп поп-гего зит §атез апс1 8*осЬа8Нс ргосеззез, КМ-212,
ТЬе КАШ СогрогаНоп, 1949) и Беллмана и Блекуэлла (ВеПтап К.,
В1 ас к иге 11 О., Оп а рагИси1аг поп-гего зит &ате, КМ-250, ТЬе КАШ
СогрогаНоп, 1949).
Название „игры на выживание" было дано во время некоторых семи-
семинарских лекций в Корпорации КАМО.
§ 7. Предмет „игр погони" интенсивно исследовался Айзексом, который
решил ряд специальных игр и развил общую теорию этого класса задач.
См. 18 а а с 8 К., Оатез о! ригзиИ, Р-257, ТЬе КАШ СогрогаНоп, 1955;
ТНе ргоЫет о! а1Ш1П§ апс1 еуазюп, Р-642, ТЬе КАШ СогрогаИоп, 1955;
ОШегепНа! &ате8 I, II, III, IV, КМ-1391, 1399, 1411, 1486, ТЬе КАШ Сог-
рогаНоп, 1955.
§ 8. Результаты этого и дальнейших (9—17) параграфов излагаются
в статье Беллмана [ВеПтап К., Рипс1юпа1 е^иа^юп8 т 1Ье Шеогу о!
йупагшс рго^гатт1п§ III, МиН1-51а§е Оатез, Пепй. С1гс. Маг. Ра1егто A957)].
§ 18. Использованный здесь аппарат был предложен Флемингом. Даль-
Дальнейшие результаты в вопросах существования и единственности указаны
в статье Шепли [5 Ь а р1 е у Ь., З^осЬазНс §атез, Ргос. Ыаг. Асай. 8с1. С/8А,
39 A953), 1095—1100].
§ 19. Предложенное здесь доказательство содержится в работе Беллмана
(ВеПтап К., 1п1гос!ис1юп № 1Ье 1Ьеогу о! йупагшс рго&гаттт^, К-245,
ТЬе КАN^ СогрогаНоп, 1953, сЬ. VI). Со времени появления цитированных
выше основоположных работ эта проблема подверглась интенсивному иссле-
исследованию. Наиболее значительные результаты, полученные к настоящему
времени, содержатся в статьях Пейсакова (Ре18ако!! М., Моге оп датез
о! 8ш-У1Уа1, РМ-884, ТЬе КАШ СогрогаКоп, 1952) и Милнора и Шепли
(МПпог 1, 5Ьар1еу Ь., Оп &ате8 о! 8игу1уа1, Р-622, ТЬе КАШ Согро-
гаНоп, 1955 1))
§ 20. Содержание этого параграфа и § 21, 22 и 24 взято из статьи
Беллмана [ВеПтап К., Оеазюп так1П& т Ше !асе о! ипсегЫШу. II, Ыауа1
ЯевеагсН 1о%Ш1с& <Эааг*ег1у 1 A954) 323—332]
ап К., Оеазюп так1П& т Ше !
<Эааг*ег1у, 1 A954), 323—332].
§ 23. Это доказательство обобщенной теоремы о минимаксе было дано
Шепли в статье, цитированной в примечании к § 18. Формулировка теоремы
и первоначальное доказательство даны Нейманом.
См. также СоЩпЪшюпз го 1Ье ТЬеогу о! ^атез. III, Апп. Ма1Н.
, № 39, РппсеЮп 11п1у. Ргезз, 1957. — Прим. перев.
24 р- Беллмаж
Глава XI
МАРКОВСКИЕ ПРОЦЕССЫ РЕШЕНИЯ
§ 1. ВВЕДЕНИЕ
В этой главе мы будем изучать некоторые процессы решения,
которые отличаются от встречавшихся ранее и приводят к новому
классу функциональных уравнений.
Мы рассмотрим дискретные йроцессы, которые приводят к изу-
изучению разностного уравнения
N
A) *<(л+1)=тах2а^(?)*,(л), лг*(О) = ^, 1=1, 2, ..., Л/,
а также некоторые непрерывные процессы, которые порождают урав-
уравнение
N
B) -ж = тах
3 .7-1
в случае одного действующего лица и уравнение
C) -^ == тах т!п
= ш1птах[.. .], *4@) = с*. /=1, 2, ..., N.
р о.
в случае двух действующих лиц.
Как мы увидим, уравнения этого типа имеют связь с класси-
классической теорией дифференциальных и разностных уравнений. Мы отло-
отложим, однако, детальное рассмотрение этой связи до второго тома.
§ 2. МАРКОВСКИЕ ПРОЦЕССЫ РЕШЕНИЯ
Опишем в этом параграфе процесс решения, который побуждает
к изучению класса нелинейных разностных уравнений, представлен-
представленного уравнением A.1). Затем мы рассмотрим предельную форму,
именно A.2).
Рассмотрим физическую систему 5, которая в каждый из момен-
моментов I = О, А, 2А, ... может находиться в одном из ряда состояний,
обозначаемых нами через 5г, 52, .... 5#. Предположим, что в любой
Марковские процессы решения 371
момент г задана вероятность Хх(р) того, что система находится
в /-ом состоянии и что существуют переходные вероятности? упра-
управляющие переходом из одного состояния в-другое. Следует отда-
отдавать себе отчет в том, что это очень сильные предположения о при-
природе системы.
Пусть
A) пц — условная вероятность того, что система будет в состоя-
состоянии / в момент г-\-Ъ^ если в момент I она была в со-
состоянии у.
Соотношение между множеством вероятностей {.к$(^ + А)} и мно-
множеством {л^@} задается тогда соотношениями
N
B) *«(* + *) = 2 *<Л@. 1=1. 2. .... N.
для ^=0, А, 2А Полагая л^(яД) = .У|(я), мы можем записать
эти соотношения в более простой форме
N
C) Л(п+1) = 2ад(л)' *=1' 2
Асимптотическое поведение вектора состояния (уг у2% ...,
при Ь ~> оо определяется алгебраической природой собственных зна-
значений матрицы Л=||а^||. Процесс такого типа называется мар-
марковским процессом. Существует хорошо разработанная математи-
математическая теория этих процессов.
Рассмотрим теперь марковские процессы решения. Предположим,
что переходные вероятности ау зависят от параметра ^ (который
может быть и вектором) и что на каждом шаге процесса ц следует
выбирать так, чтобы максимизировать вероятность того, что система
перейдет в состояние 5г. Вместо уравнений C) мы получим нели-
нелинейную систему ^
N
D) ух(п-\-1)= шах2 ах§(Я)У5(л).
Я. 7 = 1
N
3, ..., N.
где ^* = ^*(м) в последних N—1 уравнениях есть одно из значе
ний #, максимизирующих ^(л+1).
Так как пц — переходные вероятности, они при всех # удовле
творяют условиям
E) Яу>0. 2««=1. У=1. 2. ....
24*
372 Глава XI
Для получения более общих уравнений рассмотрим положение,
когда имеется N различных видов продукции, причем х$(/) — коли-
количество /-ой продукции в момент Ь. Эти продукции обладают тем
свойством, что единица /-ой продукции за время \1, 1-\-к\ замещается
количеством а^ /'-ой продукции. Здесь а^ > 0 обозначает производ-
производство, обратное неравенство обозначает потребление. Пусть снова ац
зависит от параметра д, а цель процесса состоит в максимизации
в каждый момент времени количества первого вида продукции.
В этом случае мы получим уравнение D) без ограничений на вели-
величину или знак ац.
При Л->0 мы получим в пределе вместо D) систему нелиней-
нелинейных дифференциальных уравнений
N
9 - — »
F) ^ 2
N
, (О */('). *< (<>) = *<. * = 2> 3.
Для получения этой системы мы полагаем, как обычно,
G) ац = Ъф% IФ у,
и затем устремляем А к нулю. Получив эти уравнения с помощью
такого формального подхода, мы определим теперь с помощью
уравнений F) непрерывный процесс. Для этого мы должны в свою
очередь убедиться в существовании и единственности решения. Дру-
Другими словами, мы должны показать, что этот метод определения
процесса действительно обоснован.
§ 3. ОБОЗНАЧЕНИЯ
Учитывая предыдущие замечания, мы приступим сначала к рас-
рассмотрению непрерывного случая. Для упрощения записи введем
векторно-матричные обозначения
A) х
\XN
Тогда система
N
B) —тг= тах /МцСа^Хл, Ха@) = Сл, 1=1, 2,..., Л^,
Марковские процессы решения 373
примет вид
их
C)
где подразумевается, что максимум берется отдельно для каждой
компоненты. Под этим мы понимаем, что набор параметров # для
каждой строки отличен от соответствующего набора для любой дру-
другой строки. Таким образом,
01* (?) = 01
(» #22»
ЯN2*
так что взаимодействия между различными максимизациями нет1)
После рассмотрения этого случая мы обратимся к уравнениям, полу-
полученным в предыдущих параграфах, где такое взаимодействие дей-
действительно встречается.
Удобно ввести обозначения
E) N1 = 21
2.
г, *-1
Эти величины удовлетворяют обычным аксиомам нормы и, кроме
того, неравенству
F)
§ 4. ЛЕММА
Как это обычно делается в теории дифференциальных уравнений,
первый шаг доказательства существования и единственности реше-
решения состоит в превращении дифференциального уравнения в соот-
соответствующее интегральное. Это дает нам возможность использовать
сглаживающие свойства интегрирования.
Рассматривая более общее уравнение
их
A)
1) Фактически здесь разные строки матрицы зависят от разных парамет-
параметров, и максимизация производится по множеству параметров $Х»••$
Прим. перев.
374
Глава XI
мы получим интегральное уравнение
г
B) х — с-\- Г тах [А (д, 8)х-\-Ь(д,
о
ч
которое может быть записано следующим образом:
I I
с -\- Г Ь (д, з) йв -\- Г А (д, з) х
C)
х = тах
я
о
о
Так как д — функция от /, максимизация в каждой точке порождает
максимизацию в целом.
Легко доказывается следующий результат (в основном по тому же
принципу, что и лемма 1 гл. IV).
Лемма. Пусть
D)
Т1(х) = тах
я
(У)
о
тогда
E)
О
— ^2ООН <тах
я
011
о
Эта лемма будет точкой опоры в нашем доказательстве существова-
существования и единственности.
§ 5. СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ. I
Рассмотрим теперь вопрос о существовании и единственности
решения уравнения
A) йХ
Имеется ряд особенно интересных случаев, соответствующих раз-
разным допущениям, которые можно делать в отношении функций
А(д, г), Ь(д, О1) и множества допустимых функций ^@- Мы рас-
1) Напомним, что А — функция-матрица, а Ь — функция-вектор. — Прим,
перев.
Марковские процессы решения 375
смотрим один класс уравнений и на этом оставим данный вопрос,
так как применяемый метод будет в достаточной мере иллюстриро-
иллюстрировать действия, которые можно использовать в других случаях. *
Первый наш результат — это
Теорема 1. Предположим, что д есть элемент множества
функций 5, обладающих свойством
B) \\А(Ч. ОН, II*(д. 91К/Ю.
где функция /(*) интегрируема на любом конечном интервале
О ^ г ^ Т. Предположим далее, что максимум выражения
А(д, г)х-\-Ь(д, г) достигается1) для д^8 при любых фиксиро-
фиксированных значениях г и х2).
Тогда имеется единственное решение уравнения A), удовле-
удовлетворяющее уравнению почти всюду. Это решение можно полу-
получить как предел последовательных приближений
C) хо=с, »
, 8)]
/г == 0, 1, ... .
Доказательство. Покажем сначала, что функции хп равно-
равномерно ограничены в интервале [О, Т]. Именно, мы покажем, что
/ г
D)
где
E)
О
Это неравенство бесспорно верно для я = 0. Предположим, что оно
выполняется для к = О, 1, .... п. Тогда из D) мы имеем
г
((л\ \\г II <" II г II -4- I
О
О *
О
1) Имеется в виду максимум сразу по всем компонентам. — Прим. перев,
2) Цель этого предположения — учесть одновременно случай, когда д
принимает только дискретное множество значений (в этом случае максимум
всегда достигается), и случай, когда д меняется непрерывно.
376
Глава XI '
Заменяя ||л:п|| ее оценкой, имеем
G)
II *Я+1 II
о
8
яехр
о
A$
и, таким образом, получаем такую же оценку для ||+
Докажем теперь сходимость последовательности {хп}.
лемму из § 4 к двум соотношениям
Применяя
(8)
V
][А(д, 8)хп-\-Ь(д, 8)] Аз
I- О
хп = с -\-
мы получаем неравенство
(9),
, 8)]
о
, 2
о
Итерируя эти соотношения, начиная с неравенства для
мы приходим к неравенству
П+1
°
A0)
которое обеспечивает равномерную сходимость последовательности
\хп) в интервале [0, Т] к функции хA). Эта функция непрерывна
для О^^^Г, удовлетворяет интегральному уравнению
(И)
х (*) = с + Г тах [ А (д, з)х-\-Ь(д,
о
и, следовательно, удовлетворяет дифференциальному уравнению почти
всюду.
Наконец, докажем единственность. Пусть у (г) — произвольное
решение, существующее на некотором интервале [0, 5]. Тогда в этом
интервале у {г) удовлетворяет уравнению A1). Применяя лемму из § 4,
Марковские процессы решения 377
мы получим неравенство
A2) |И0 — .У@||< шах]* ||Л(«7,
о
о
Это неравенство имеет вид
A3) и(*)<|
о
где /E)^-0, #($)= ||л;($)— .УE)||^-0- Следовательно, для сколь
угодно малой положительной постоянной а мы имеем
A4) «
о
или, после деления,
A5) ^^ </(*)
о
Интегрируя от 0 до ^, находим, что
A6) й + ^ /(8)и(8)
о
Комбинируя это с A4), получаем неравенство
г
Г Г (в)
A7) 6
Так как а — произвольная постоянная, отсюда следует, что иA)
Можно дать и другое доказательство. Ясно, что существует та-
такая постоянная Ь, что Ца: — ,У||<^ на [0, 5]. Следовательно,
A8) И(О< ^//E)^/5.
о
Используя это неравенство в правой части A3), получаем
A9) а@ <*/[/(«)//(*)<&!]<& = !-1 ]
378 ч Глава XI
Продолжая таким же образом, получаем для каждого п =
= 1, 2, ... неравенство
/ г \ п+1
B0) «@<(^
Устремляя п—> со, мы снова убеждаемся в том, что иB) = 0.
§ 6. СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ. II
Рассмотрим теперь уравнение B.6). В общем случае уравнения
этого типа не обязательно имеют единственное решение ввиду мно-
множественности максимизирующих значений д. Рассмотрим, например,
уравнение
A)
ЧГ =
Так как ^* = 0 или 1, мы получим бесконечное множество решений,
представителями которого являются, например, следующие решения:
B)
В .
Мы можем, однако, получить теоремы единственности, если огра
ничим себя решениями, полученными следующим образом. Рассмот
рим сначала уравнения
N
N
N
Ш
для величин а:2, лг3, . .., х#, зависящих от функции х19 временно
считая д некоторой неизвестной функцией. Каждая величина хк,
= 2, 3, .»., Л^, будет иметь вид
D) хк — ик{д, 1) + {4ок(д. Л
Марковские процессы решения
379
Подставляя эти выражения в уравнение
N
E) —~- = тах
мы получим уравнение
F)
= тах
Это уравнение запишем в виде
г
G)
тах
я.
I- 0
I I гл
4-/1 /^(?- ^. 5)^
о
о
О * О
*1 @) =
Г ^ (д, 8) Аз + Г аи (#) X! й?5 -{-
Применяя метод, использованный в § 5, легко доказать суще-
существование единственного решения этого уравнения в предположениях
теоремы 1х).
§ 7. СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ. III
Можно, используя такие же последовательные приближения и
неравенства, получить теоремы существования и единственности для
более общих систем дифференциальных уравнений вида
их
A)
х@)=с.
Так как этот результат относится скорее к области дифференциаль-
дифференциальных уравнений, чем теории процессов решения, мы предоставим
честолюбивому читателю построить свои собственные аналоги класси-
классических теорем существования и единственности.
1) Эти рассуждения автора не являются достаточно строгими. Автор
подменяет задачу максимизации функции в каждый момент [формула F)]
максимизацией функции в конце любого промежутка времени [формула G)].
В первом случае независимо от того, какие значения имела функция ^E)
при 5 < г (так как эти значения входят лишь в не зависящее от д (г) слагае-
г
мое I V (д E), г, 8) х± (з) из), выбирается значение д ($) при 5 = г. Во втором
случае при каждом г выбирается функция #E), 0<!5<!^ вообще говоря»,
зависящая от I. Значения этой функции для одного и того же 5 при разных 4*
могут и не совпадать. — Прим. перев.
380 Глава XI
§ 8. УРАВНЕНИЕ РИККАТИ
Хотя мы и не хотим здесь глубоко вникать в изучение этого класса
нелинейных дифференциальных уравнений, следующий результат
представляется нам особо достойным упоминания.
Замена переменных
/1ч и'
(О *=-?
сводит общее линейное дифференциальное уравнение второго порядка
B) */"+/7@«'-И(/)и = 0
к нелинейному уравнению первого порядка
C) т/ -{-V2-\-р@V + ?(*) = 0.
Это уравнение называется уравнением Риккати. Из предыдущего ясно,
что общее решение уравнения C) эквивалентно общему решению
уравнения B) и, следовательно, не может быть получено в квадра-
квадратурах.
Покажем теперь, что уравнение C) можно интерпретировать как
уравнение указанного выше общего класса. Начнем с замечания,
что
D) — V* = ппп (те;2 —
го
Следовательно, C) можно переписать в виде
E) V' = гшп [<о>2 — 2<шъ — р (I) V — д (()],
го
где ч$) пробегает сейчас множество всех функций от Ь.
Для фиксированного 1Ю пусть V (<и), I) обозначает решение урав-
уравнения
F) V = т2 — 2тУ —р У)У —
удовлетворяющее условию V @) = V @) = с. Это решение имеет
явное представление
<в)+2«о аз * _ С{р (81) +
+/B ())е '
G) У = се о +/(^2 — я(8))е §
о
получаемое обычным путем с помощью интегрирующих множителей.
Покажем теперь, что
(8) ,
Марковские процессы решения 381
Для произвольной функции 1Ю = 1Ю (I) мы имеем
(9) V' < <и>2 — 2<го _р (*) г> — ?(*),
откуда следует, что г>^У('о;, ^). Следовательно, г/
го
С другой стороны, (у=1/('О/*, г) для минимизирующего значения те;*,
которое равно V(^). Следовательно, равенство (8) справедливо.
Таким образом, мы получили явное представление решения урав-
уравнения Риккати в терминах квадратур и минимизации.
§ 9. ПРИБЛИЖЕНИЕ В ПРОСТРАНСТВЕ ПОВЕДЕНИЙ
Как мы уже видели в предыдущих главах, в теории динамиче-
динамического программирования имеется два типа последовательных при-
приближений, один из них основан на приближении функций, которые
удовлетворяют функциональному уравнению, а другой — на прибли-
приближении поведений, которые к этим уравнениям приводят. Мы уже
использовали наш традиционный метод выше в § 3. Рассмотрим
теперь второй метод.
Рассмотрим скалярное уравнение
(О
Я.
где мы налагаем ограничения \а(д, /)|, |#(<7, 01*^/@ и Г
о
Мы начнем, приняв за исходное доведение функцию <7о —<7о(О»
и определим щ из уравнения
B) 1Г = * {д°- ° + а (<7°' ° > ~ м° <0) = с-
Далее определим функцию цх из условия, что она максимизирует
» О^о» и вычислим их как решение уравнения
Продолжая идти по этому пути, мы определим последователь-
5 функций \ап) и последовательность поведений {<7П}. Остается
доказать, что эта последовательность {ип) действительно сходится.
Мы имеем
в силу определения дг.
382 Глава XI
Решение уравнения
E) 2?=*@о + *(О. <Ч0) = с.
имеет вид
г %
[* д(8)Яз * § д
F) г; = 6 ^
о
это выражение можно записать в виде Ь(Н), где Ь— оператор, дей-
действующий на функцию Н.
I
^ 9 (в) ав
Из того, что е8 ^ 0, вытекает соотношение
G) /,(/*,) >/,(/*2),
если Н1(()^.Н2(О для /^.0. Следовательно1),
(8) ИоОх для
Продолжая таким же образом, мы получим по индукции, что
ип^ип+1 Для ^ = 0, 1, 2, .... Так как каждый член последова-
последовательности [ип] равномерно ограничен величиной
т
т
то последовательность {ип(()} сходится к некоторой функции и({).
Эта предельная функция удовлетворяет интегральному уравнению
г
(9) и @ = с + Г шах [Ь (#,
* а
а
и, следовательно, почти всюду удовлетворяет дифференциальному
уравнению. Мы видим, что в одномерном случае приближение в про-
пространстве поведений приводит к сходящимся последовательностям.
Обратимся теперь к соответствующему вопросу для систем вида
(Ю)
) Из G) еще не следует (8), так как у нас меняется не только /г, но
и #, а при отрицательном с увеличение § будет уменьшать 1/ [ср. F)].
Однако самый результат (8^ верен, так как в любой точке, где щ (г) = % (^)
имеет место соотношение их (г) > и0 (^). — Прим. перев.
Марковские процессы решения 383
Используя тот же метод, что и раньше, легко усмотреть, что
задача сводится к определению ограничений, наложенных на матрицу
Л(#, ^), которые гарантировали бы, что из /A)^*0 для 1^0 сле-
следует у^О для 1^0, где у—решение уравнения
(И)
Так как решение уравнения A1) дается формулой
I
A2) / 1
О
где У (г) — матричное решение уравнения
йУ
A3) ^ = А(д91)У9 К@) = /.
мы видим, что необходимое и достаточное условие состоит в том,
чтобы
A4) У(*)У~1(8)>0 для />5>0
для всех
Так как это условие проверяется с трудом, мы удовольствуемся
замечанием, что достаточным условием является ау(д% 0^-0» 1Ф]*
Если условие а>ц($, {)^0, 1Ф], выполняется для /^0 и
для всех #^5, то требуемая сходимость в пространстве поведений
имеет место.
§ 10. ДИСКРЕТНЫЕ ВАРИАНТЫ
В этом параграфе мы хотим выяснить асимптотическое поведение
последовательности {х{{п))% /=1, 2, ..., Л/, определяемой рекур-
рекуррентными соотношениями
N
A) хг(п-\- 1) = тах2 Ян(?)-^(м), / = 1, 2, .. ., /V, я>0,
при некоторых предположениях относительно начальных значений
и матрицы коэффициентов А(д).
Начнем с рассмотрения однородной системы уравнений
B) \у{ = шах 2 лу {д)у$, /=1,2
где мы налагаем следующие условия:
C) а) ^ = (^г1» Чг •-., Ч^) пробегает множество 5, обладаю-
обладающее тем свойством, чтЬ максимум в B) достигается
при любом наборе параметров (уг у2
, ...,
384 Глава XI
б) 0 < йц(#)<^т < со для д^8 и /, у = 1, 2, .. .,
в) пусть ср(#) для любого <7 обозначает наибольшее по
абсолютной величине собственное значение матрицы
А(д)=\\а^(д)\\, т. е. перроновский корень. Предпо-
Предполагается, что ср(#) достигает максимума на 5.
Докажем теперь следующую теорему.
Теорема 2. При указанных предположениях существует
единственная положительная, постоянная X, обладающая тем
свойством, что однородная система B) имеет положительное
решение у{ > 0, /= 1, 2 N. Это решение единственно с точ-
точностью до постоянного множителя, и
D) X = шах ср (?).
Доказательство. Мы начнем с доказательства существова-
существования положительного X и положительного решения [уг). Наиболее про-
простой, хотя и наименее элементарный метод доказательства использует
теорему Брауэра о неподвижной точке 1). Рассмотрим область, опре-
определяемую условиями
N
E)
г-1
Нормализованное преобразование
шах
F) [ 9
N
2
тах
2 ац (?) Уз
является непрерывным отображением этой области в себя. Отсюда
следует, что существует неподвижная точка {У{}, дающая искомое
положительное решение, поскольку ац (д) > 0. Параметр X равен
знаменателю в выражении F).
Чтобы показать, что решение единственно с точностью до по-
постоянного множителя, предположим, что [|х, г\ — другое решение
системы B), где [х>0 и г — положительный вектор. Пусть {д}—
множество значений, при которых в B) достигается максимум,
а {д}—соответствующее множество для г. Мы имеем
1) См., например, Канторович Л. В. и Акилов Г. П., Функ-
Функциональный анализ в нормированных пространствах, Физматгиз, 1959,
гл. XVI. — Прим. перев.
Марковские ' процессы решения 385
Не ограничивая общности, можно допустить, что X < \ь, так что
векторы у и г неколлинеарны. Если у к г коллинеарны, то у = г.
Пусть в — положительная постоянная, выбранная так, что по меньшей
мере одна из компонент у{ — вгг равна нулю, по меньшей мере одна
положительна, а все остальные неотрицательны. Если / — индекс рав-
равной нулю компоненты уг — е^. то мы имеем
N _
(8)' 0 ■= у {уг — ег{) > \уг — е^ > 2 ац (?) (У$ — е^) > 0.
что является противоречием, так как а^(?)>0. Следовательно, у
и г коллинеарны, откуда следует, что X = |а.
Чтобы показать, что Х=тахср(<7), поступим следующим образом.
я.
Пусть |1 = тах ср (<7). Ясно, что X как собственное значение ма-
ч
трицы Л(<7) при некотором ^ удовлетворяет неравенству Х<^{л. Пред-
Предположим, что Х< \1. Пусть г = (гх, г2, ..., г^ — положительный
собственный вектор, соответствующий [х, а ^ — набор значений </,
для которого [х = ср(<7). Тогда мы имеем
N __ N
(9) \>Х1 = 2 а15 (^) гй < шах 2
Так как каждая из компонент у$ положительна, мы можем найти
такую положительную постоянную т% что
A0) ^Ол. /=1, 2, ..., N.
Тогда (9) приводит к
A1)
Таким образом, вместо A0) мы получим неравенство г{
Повторяя приведенные рассуждения, находим, что 2г^Сту{(к1\1)к для
любого к. Так как по предположению Х/[х < 1, то из этого следует,
что ^ — О. Полученное противоречие доказывает, что Х=[а.
§11. РЕКУРРЕНТНОЕ СООТНОШЕНИЕ
Возвращаясь к рекуррентному соотношению A0.1). докажем сле-
следующее утверждение.
Теорема 3. Если в дополнение к условиям A0.3) предполо-
предположить, что существует только одно значение ^, для которого
2& К Белл май
386 Глава XI
достигается максимальное значение ср(^), и что сг^>0, то при
A)
где а — а(сг сг ....
Доказательство. Без ограничения общности можно считать,
что сг > 0. Найдутся две положительные постоянные к и /С, такие,
что кУг^.С1^Ку{ для /=1, 2, ..., N. Покажем по индукции, что
для любого п
B) куг\п < хК
Если этот результат уже получен для п, то
C) х{ (п + 1) < КХп шах
^ (л + 1) > ^ХЛ тах
9 7-1
Чтобы выяснить асимптотическое поведение, покажем, что для
достаточно больших п набор #, ПРИ которых достигается максимум
в A0.1), совпадает с набором #, максимизирующих ср(^).
Предположим противное. Это означает, что в рекуррентном со-
соотношении A0.1) мы бесконечное число раз получим набор {?}, ко-
который не совпадает с набором {?}, максимизирующим ср(^).
Тогда мы имеем
D) 2
/ = 1,2» . . . * Л/.
Для некоторого индекса / мы должны иметь
N __
Ф) 2 агз (Я) Уэ < *Л-
N _
т. е. строгое неравенство. Действительно, если 2 ау (#) .V*
для всех /, то собственное значение матрицы Л(?)= \\а^ (д)\\, наи-
наибольшее по абсолютной величине, было бы не меньше, чем X =
= тахср(<7), вопреки предположению о единственности максимума
я.
9 (?).
Здесь у — решение уравнения A0.2), ^ = тах <р (д), с^ = XI @). — Прим.
перев*
Марковские процёсёы решения $87
Следовательно, для некоторой компоненты, например для первой,
мы имеем
F) хх(п + 1) < 0/ап+1^, о < е < 1.
Так как а^(^*)>0 для всех /, у, где ц* — значение ц, для которого
=ср(^*), мы видим, что для /=1, 2, . ..,Л/"
G)
п+1
N
П+2
где б1 < 1.
Следовательно, если /? раз использовать набор {^}, отличный от
{<7*}, то для больших п мы получим1)
\р) Х\ \П) -^ VI АЛ У\ш
Так как 0 < 0! < 1, мы в конце концов нарушим нижнюю границу
для х{(п), выбрав достаточно большое /?. Следовательно, набор (^},
отличный от {<7*}, можно использовать только ограниченное число
раз, причем границы определяются числами к и К.
§ 12. МИНИМАКС
Тот же метод, который мы использовали при доказательстве тео-
теоремы 1, дает следующий результат.
Теорема 4. Рассмотрим уравнение
A)
V Я
= пип тах [..-], х @) = с,
мы предположили, что
B) а) для фиксированных значений х и г максимин в со
отношении A) равен минимаксу, когда р и ц пробе
гают некоторое множество допустимых векторов
б) тах || А (/?,
I /(*)Л<оо.
о
Это заключение автора кажется не вполне обоснованным, так как #,
в и 6Х зависят от л, а, следовательно, (8) имеет вид ^(/г)< |Т 0г (п8)
&1
и противоречие не имеет места. Доказательство этой теоремы содержится
в заметке И. В. Романовского *Об одной теореме Р. Беллмана" (Теория
вероятностей и ее применения, 4, № 4 A959), 456—458).—Прим. ре&.
25*
388; Глава XI
существует единственное решение уравнения A) при
О <^ I <^ Т, которое удовлетворяет уравнению почти всюду и ко-
которое можно получить как предел последовательности
C) х0 = с,
г
Хп+\ = с+ Г тах пип [Л (/?, ц, 8)хп-\~Ь(р, д,
V П П
о
= с+ Гпнптах[Л(р, #, 5)л:п
о « *
§ 13. ОБОБЩЕНИЕ РЕЗУЛЬТАТА НЕЙМАНА
В главе, посвященной многошаговым играм, мы нашли, что
(Ар, а)
A) тах тт ;р^ ^.7 = тт тах ;р
1 } р а (Вр, Я) ч р (Вр,
где А и В — матрицы, а р и ц — векторы вероятностей, причем
{Вр, #)>с?>0 для всех р и #.
Получим теперь обобщение этого утверждения.
Теорема 5. Рассмотрим скалярное уравнение
B) -2-= тах т!п
= тт тах [(Ар, #) — (Бр, ?)«!, и@) = с.
я. V
Если (Вр, #) >. с? > 0 для в^л: векторов вероятностей р и #, то
C) Ит н @ = тах т!п т^Щ = т!п тах ^А д\ .
^ *>оо р д (ВР> Я) а V (ВР* Я)
Доказательство. Классическая теорема Неймана о минимаксе
обеспечивает равенство максимина и минимакса величины (Ар, я) —
*—(Вр, д) и для каждого и. Остальные условия теоремы 4 также
выполняются, что обеспечивает существование и единственность иA).
Для выяснения асимптотического поведения решения рассмотрим
сначала скалярное уравнение
D) -^- = а — Ьи, и@) =
где а и Ь — постоянные и Ъ > 0. Легко видеть, что решение огра-
ограничено при I —► оо. Мы можем показать, что Нт и (г) = а\Ъ, с помощью
*->оо
следующего простого рассуждения. При йЩ61 === 0 мы должны иметь
Марковские процессы решения 389
1~ .11 1М1
и = а/д. Следовательно, функция и {I) может иметь не более одной
точки возврата при />0 и, значит, монотонна. Так как и{1) огра-
ограничена, она при Ь -> оо стремится к конечному пределу, который
должен равняться а/Ь. Рассмотрим нелинейное уравнение
E) " = тах [а (/?) — Ь(р)и],
где Ь(р)^Ь> 0 для всех р, \а(р)\ ^.М для всех р и а(р),
Ь(р) таковы, что максимум достигается. В любой точке возврата и
мы должны иметь
F) «^
Следовательно, функция а{1) должна быть монотонной и стремиться
к пределу, определяемому формулой F).
Мы видим, что в точности те же рассуждения применимы к урав-
уравнению B). В качестве точки возврата мы должны взять
G) и = шах гшп ^ ч\ = т!п шах
№ Я)
Р
\ = т!п шах \ .
. Я) д р {Вр. я)
УПРАЖНЕНИЯ И ПРОБЛЕМНЫЕ ЗАДАЧИ К ГЛАВЕ XI
1. Торговец имеет п одинаковых товаров, которые он должен
продать за период времени Ь. Товары могут продаваться в любой
из моментов 1, 2 Ь, и вероятность покупки зависит от цены1).
Пусть ср(г) — вероятность продажи товара по цене г в любой от-
отдельный момент времени.
Определим /п(?) как максимальный ожидаемый доход от про-
продажи п товаров за время г. Предполагая независимость цен, полу-
получить рекуррентное соотношение
/„@ = шах ( 2 Сип [<р (г)]й [ 1 — 7 (г)]""* [/„_* (* — 1L- кг]
где /п()
(Дарланг)
2. Предположим, что товары продаются непрерывно и что
у(г)сН — вероятность того, что товар будет продан по цене г за
время от I до 1-\-йЬ. Показать, что предельная форма предыдущего
рекуррентного соотношения такова:
Г
х) Считается, что товары, продаваемые в один момент времени, имеют
одинаковую цену и продаются независимо. — Прим. перев.
390 .. . Глава XI
3. Рассмотрим в условиях задачи 2 случай, когда N=1. Пока
вать, что*)
/г(!)=твхРA, г).
где
г
8
есть решение уравнения
0+ ?(*). /7@)=0
4. Показать, что уравнение
х = шах [— <р (г) Л @ + *<? (г)], /, @) = 0.
эквивалентно двум уравнениям
ДО = -?(*)/! (О+
0 = — ср' {г) !х (г) +
Б. Подробно рассмотреть частные случаи:
а) <р (г:) = Ье~Ьг%
0 2
6. Найти решение уравнений в задаче 2 для любого N.
7. Рассмотреть аналогичную задачу, когда цены могут назна-
назначаться лишь в некоторых пределах. Как нужно устанавливать цены
в этом случае?
8. Рассмотреть процесс из задачи 1, в котором цены за еди-
единицу товара уменьшаются при увеличении закупаемой партии. Как
следовало бы поступать, чтобы максимизировать ожидаемый доход?
9. Получить при надлежащих предположениях теоремы существо-
существования и единственности для интегральных уравнений вида
и (^) = тах
Я(?. 0+ /К(?' и 8I1(8L8
о
) Здесь максимум берется по всем неотрицательным функциям г = г (I). —
Прим. перев.
Марковские процессы решения 391
10. Получить результаты, аналогичные результатам § 8, для
уравнения
@ «
при к> 1 и 0<&< 1.
11. Рассмотреть общий случай, когда
и'=
и функция §г либо строго выпукла по и при любом {, либо строго
вогнута.
12. Рассмотреть уравнение Риккати
и последовательные приближения
аил
01;0 — г$ + а (О, «о @) =
где г>0(/) — произвольная непрерывная функция.
Показать, что этот метод эквивалентен определенным аппроксима-
аппроксимациям в пространстве поведений и что #о^ #1 ^* • *<^гс^ ... на
общем интервале определения.
13. Аналогично, в связи с уравнением с1и/сИ = ^(и, (), и@) = с,
рассмотреть последовательность
14. Какова связь между этим методом последовательных прибли
жений и ньютоновским методом решения уравнений?
15. Какова связь между указанными аппроксимационными схе
мами и идеей приближения в пространстве поведений?
БИБЛИОГРАФИЯ И КОММЕНТАРИИ
К ГЛАВЕ XI .
§ 1. Рассмотрение этих процессов и вывод соответствующих функцио-
функциональных уравнений содержится у Беллмана (В е 11 т а п К., РипсНопа1 е^иа-
1юп8 1П 1Ье 1Ьеогу о! дупагшс рго§гатгшп§. IV, МиШ-81а§е йесмзюп рго-
сеззез о! сопипиоиз 1уре, РАЫО Рарег, Липе 1955, Р-705).
392 Глава XI
§ 2. С теорией марковских процессов можно познакомиться по книге
Феллера „Введение в теорию вероятностей и ее приложения", ИЛ, М., 1952 *).
§ 5. Теоремы существования и единственности для этого типа нелиней-
нелинейных дифференциальных уравнений были получены в статье Беллмана
[В е 11 т а п Н., РипсНопа1 е^иа^юп8 т 1Ье 1Ьеогу о! дупаппс рго&гаттт^.
II, КГопНпеаг (ШегепНа1 еяиаИопз, Ргос. Ыа(. Асай. 8с1. [/8А, 41 A955),
482—485].
Следствие из неравенства E.14), указанное в E.17), является основным
неравенством при изучении ограниченности и устойчивости решений линей-
линейных дифференциальных уравнений. Впервые с этой целью оно было исполь-
использовано в статье Беллмана [В е 11 т а п Н., ТЬе 81аЫШу о! 8о1иНоп8 о! Нпеаг
(ШегепНа1 е^иаНоп8, пике МаНг. /., 10 A943), 643—647], а дальнейшие его
применения можно найти в книге Беллмана „Теория устойчивости решений
дифференциальных уравнений", ИЛ, М., 1954.
§ 8. О применении этой схемы к другим классам функциональных урав-
уравнений см. статьи Беллмана [ВеИтап Н., Рипс1юпа1 е^иа^^оп8 1п 1пе 1Ьеогу
о! йупапис рго§гаттт§. V, РозЦмЧу апй 11пеагИу, Ргос. Иаг. Асай. 8с1. Ц8А,
41 A955), 743—746, а также ВеИтап Н., Оп 1Ье ехрПсй 8о1иИоп8 о! зоте
1г1пот1а1 е^иа^^оп8 т 1егтз о! 1Ье тах1тит орегаНопз, МаНъ. Ма§., 30 A956),
41—44].
§ 10. Содержание этого параграфа первоначально опубликовано в статье
Беллмана [В е 11 ш а п Н., Оп а с1а8& о! ^иа8^-1^пеаг е^иа^^оп8, Сапай. У. МаНг.у
8 A956), 198—202] 2).
§ 13. На это обобщение было указано в статье, цитированной в приме-
примечании к § 8.
) См. также Г н е д е н к о Б. В., Курс теории вероятностей, ГТТИ, М.,
1954; С а р ы м с а к о в Т. А., Основы теории процессов Маркова, ГТТИ, М.,
1954. — Прим. пере в.
2) В этой же статье опубликовано и содержание § 11. — Прим. перев.
УКАЗАТЕЛЬ ПРИЛОЖЕНИЙ
Вариационное исчисление гл. IX
Замена оборудования 71 (упр. 45—48), 78 (упр. 70)
Использование водных ресурсов 172 (упр. 45—48), 173 (упр. 49—51)
Капиталовложения 67 (упр. 27, 28,), 77 (упр. 68, 69)
Каскадный процесс 80 (упр. 76, 77), 124 (упр. 38)
Контролируемые процессы, см. Управляемые процессы
Лесоводство 138 (упр. 88)
Максимизация и минимизация в многомерном случае 28, 29, 61
(упр. 1—3), 62 (упр. 4—7), 63 (упр. 8—11), 64 (упр. 12, 13), 65 (упр. 14, 15),
73 (упр. 56, 57), 74 (упр. 58, 59), 78 (упр. 71), 79 (упр. 72, 73), 81 (упр. 78),
116 (упр. 14), 127 (упр. 47—51),. 128 (упр. 56), 129 (упр. 58, 59), 130 (упр. 61),
132 (упр. 68), 134 (упр. 73, 74), 135 (упр. 75—78), 139 (упр. 91), 140 (упр. 92),
168 (упр. 32), 179 (упр. 68)
Максимизация и минимизация линейных функций 68 (упр. 30—32),
80 (упр. 75), 119 (упр. 25), 120 (упр. 26), 121 (упр. 27—29), 122 (упр. 31, 32),
123 (упр. 33, 37), 165 (упр. 23), 166 (упр. 24—26), 167 (упр, 27), 175 (упр. 56),
176 (упр. 57, 58), 177 (упр. 59, 60), 241 (упр. 1), 242 (упр. 2—5)
Многошаговые процесоА-Лроизводства и планирования 75 (упр. 60),
76 (упр. 61—64), 114 (упр. 8), 115 (упр. 9—12), 116 (упр. 13), 117 (упр. 15—17),
119 (упр. 25), 120 (упр. 26), 129 (упр. 57), 133 (упр. 70), 138 (упр. 88),
161 (упр. 4, 5), 179 (упр. 66), 180 (упр. 69, 70), гл. VI, VII
Надежность многокомпонентных схем 76 (упр. 65), 139 (упр. 89—91)
Оптимальные траектории 69 (упр. 35—37), 133 (упр. 69), 326 (упр. 33—35)
Оптимальная загрузка судов 66 (упр. 21)
Последовательные испытания 67 (упр. 29), 69 (упр. 39), 70 (упр. 40, 41),
71 (упр. 49), 113 (упр. 1, 2), 114 (упр. 3—7), 118 (упр. 21), 119 (упр. 22—24),
124 (упр. 39), 125 (упр. 40—42), 130 (упр. 60), 135 (упр. 79), 137 (упр. 85),
138 (упр. 86, 87), 365 (упр. 17, 18), 366 (упр. 19, 20)
Процессы поиска 54, 137 (упр. 84), 161 (упр. 6), 162 (упр. 7)
Процессы распределения ограниченных ресурсов 22, 26, 51, 58, 65, 66=
(упр. 17—20, 22), 73 (упр. 54), 77 (упр. 68), 81 (упр. 78), 117 (упр. 18, 19),
118 (упр. 20), 128 (упр. 52, 53), 134 (упр. 72), 366 (упр. 21)
Разведение скота €6 (упр. 22), 67 (упр. 23—26)
Ракетная техника 174 (упр. 55), 326 (упр. 33—35)
Решение уравнений 132 (упр. 65, 66), 162 (упр. 12), 163 (упр. 13—17),
164 (упр. 18, 19), 173 (упр. 52, 53), 177 (упр. 60), 178 (упр. 65), 365 (упр. 15, 16),
390 (упр. 9), 391 (упр. 10—15)
Сглаживание 29, 70 (упр. 42, 43), 71 (упр. 44), 119 (упр. 25), 129 (упр. 57),
136 (упр. 80—83), 165 (упр. 23), 166 (упр. 24—26), 214 (упр. 8), 215 (упр. 9, 10>
Собственные значения 125 (упр. 43), 126 (упр. 44), 131 (упр. 63).
311—316, 328 (упр. 40), 329 (упр. 41), 366 (упр. 22), 367 (упр. 23—26)
"* Стохастический процесс распределения ресурсов 57, 72Дзш&и^Ш1;
73 (упр. 52, 53), гл. И, 118 (упр. 21), 119 (упр. 22—24), 126 (упр. 45,46),
гл. VIII
Теория вероятностей 113 (упр. 1, 2), 114 (стр. 3, 4), 165 (упр. 21),
365 (упр. 17, 18), 366 (упр. 19, 20), гл. X
Теория игр, гл. X
Теория информации 133 (упр. 71), 168 (упр. 33, 34), 169 (упр. 35—38),
170 (упр. 39, 40), 171 (упр. 41—43)
Теория расписаний 18, 114 (упр. 8), 115 (упр. 9—11)
Транспортные задачи 121 (упр. 28,29), 122 (упр. 30, 31), 123 (упр. 33—36),
132 (упр. 67), 133 (упр. 69, 71), 167 (упр. 28—31)
Управление запасами гл. V, 389 (упр. 1, 2), 390 (упр. 3—8)
" Управляемые процессы 321 (упр. 5—9), 324 (упр. 23—26), 325 (упр. 27, 28),
327 Гупп. 36. 37*
327 (упр. 36, 37)
ИМЕННОЙ И ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Адамар (Нас1атагс1 Л.) 141
Айзеке Aзаасз Р. Р.) 369
Акилов Г. П. 384
Амбарцумян В. А. 141
Анализ чувствительности 25, 224,
288, 311
Андерсон (Апс1ег8оп Э.) 81
Антосевич (Ашо81емс2 Н. А.) 137
Бартлетт (ВагНеИ М. 5.) 82
Беллман (ВеИтап Р.) 19, 81, 82, 141,
168, 169, 180, 181, 218, 243, 261, 286,
328, 329, 330, 362, 368, 369, 391, 392
Бёльтер (ВоеНег Ь. М.) 172
Бил (Веа1е Е.) 18
Блекуэлл (В1аскше11 О.) 19, 102, 286,
362, 368
Болдырев (ВоМугеК А. V/.) 18, 20, 243
Борель (Воге! Е.) 331
Бальд (№а1с! А.) 19, 368
Ван (У/ап%) 164
Виллан (\УШап 5.) 80
Вильяме (АУПНат8 3. Э.) 368
Вогнутость 39, 41, 53, 54, 62
Вольфовитц (^/оИош1г 3.) 14, 19, 217
Ворооьев Н. Н. 333, 334
Выпуклость 38, 53, 62, 210
Динамическое программирование 7
18, гл. III
Дискретный детерминированный про-
процесс 105
— стохастический процесс 108
Дифференциальный подход 263
Дихотомическая задача 284
Дрейфус (Огеу!из 5.) 19, 121, 133, 326
Дрешер фгезпег М.) 368
Двойственный процесс 234, 237, 248
Дуб фооЪ 3. Ь.) 286
Игры на выживание 337, 353
— с ненулевой суммой 336, 361
нулевой суммой 334
Интегральный подход 264
Калаба (Ка1аЬа Р.) 132, 134, 141, 169
Канторович Л. В. 384
Карлин (КагИп 5.) 20, 102, 180, 181,
335, 365, 368
Картано (СаПашо Н.) 326
Каруш (Кагизп №.) 134, 135
Келли (КеИеу 3.) 169
Кифер (К1е!ег 3.) 14, 81, 217
Кун (Кипп Н.) 18
Купманс (Коортапз Т. С.) 18, 122, 243
Кэрнс (Саи-пз) 114
Гиршик (СНгбЫк А.) 19, 102, 368
Гликсберг (ОПскзЬег^ I.) 19, 81, 218
Гнеденко Б. В. 337, 392
Гофман (Нойтап А. Л.) 137
Гринспан (Огеепзрап) 69
Гросс (Ого88 О.) 19, 101, 133, 137, 162,
164, 173, 218
Данскин (Оапзкт 3. М.) 218
Данциг (ОаШ212 О.) 18, 243, 244
Дарлинг (ОагПпд) 389
Дворецкий (Эуоге12ку А.) 14, 217
Дельта-функция 236, 249
Джонсон (Лоппзоп 5.) 81, 115, 137,
173, 179
Ла-Саль (ЬаЗаПе 3. Р.) 19, 368
Леман (Ьептап 5.) 19, 244, 261, 286
Ликок (Ьеасоск 5.) 332
Линейное программирование 18, 219
Литтлвуд (ЫШешооа X Е.) 133
Мак-Кинси (МсЮпзеу 3. С.) 368
Маркович (МагкошИг Н.) 179
Маршак (Магбспак .1.) 14, 217
Метод „потока" 243
Милнор (МПпог .1.) 369
Миле (МШз Н. В.) 217
Минимакс 334, 387
Многошаговый процесс решения 7
Монотонная сходимость 148
Именной и предметный указатель
395
Моргенштерн (Мог&еп81егп О.) 19,.368
Мортон (Мопоп О.) 138
Мостеллер (Мо81е11ег Р.) 72
Надель (Ыаае1) 139
фон Нейман (уоп Ыеитапп Л.) 19, 331,
368, 369, 388
Непрерывный детерминированный
процесс 109
— стохастический процесс ПО
Нэш (Ыазп Л. Р.) 368
Область решения 102
Оптимальное поведение 105, 111
— управление запасами 157,182, гл. V
Осборн (ОбЬогп Н.) 19, 286, 330
Паксон (Рахзоп Е. №.) 20
Параметры состояния 103
Пейсаков (Ре18ако!! М.) 369
Петровский И. Г. 142
Поведение 9, 185
Последовательные приближения 32,35,
гл. IV, 350
Прагер (Рга^ег №.) 123
Приближение в пространстве пове-
поведений 35, 88, 111, 317, 381
Принцип оптимальности 105, 340
Причинность 111, 141
Пространство поведений 35, 88, 111
Процесс распределения ресурсов 22,
58
— решения 7, 370
— с „узким местом" 219
Роббинс (КоЬЫпб Н.) 368
Романовский И. В. 387
Савидж (Зауа^е I. К.) 78
Сарымсаков Т. А. 392
Саусвелл Eои(Ь\ге11 Р. V.) 243
Сглаживание 29
Сельберг Eе1Ьег§) 131
Сильвестри E11уе8(г1 М.) 80
Симплекс-метод 219, 24$, 244
Смешивание 266
Стильтьеса интеграл 60, 144, 236
Стоке Eюке8 К. АУ.) 141
Существование и единственность гл. IV
Таккер (Тискег А. №.) 18
Тен Дайк (Теп Буке Р. Р.) 175
Трихотомическая задача 98, 274
Уиддер (АУШег О. V.) 329
Уиттекер (АУЬШакег 3. V.) 79
Уравнение восстановления 212
Устойчивость 48, 99, 150
Файн (Рте N. Л.) 128
Фань Цзи (Рап Ку) 335
Феллер (РеИег №.) 82, 218, 392
Флад (Р1ооа М. М.) 18
Флеминг (Р1етт§ У/.) 81, 329, 369
Функциональное уравнение 26,59,225,
229
Функция критерия 105
Харрис (Нагп'8 Т. Е.) 14, 141, 217
Хауснер (Наизпег) 364
Хейт (НафП) 138
Хельмер (Не1тег О.) 20, 128
Хилл (НШе Е.) 141
Хичкок (НПсЬсок Р. Ь.) 18, 122
Холл (На11 М.) 172
Хункоса (Липсоза М. Ь.) 134
Чандрасекар (СЬапс1га8екЬаг 5.) 141
Черри (Сегп Е.) 80
Численное решение 44, 140, 297, 310
Шапиро EЬар1го Н. Ы.) 20» 101, 102,
180, 181
Шварц Eс11шаг2 Ь.) 244
Шеперд EЬерЬегс1) 129
Шепли Eпар1еу Ь.) 365, 369
Шёнберг (ЗсЬоепЬегд 1. Л.) 81
Шифман (ЗЬШтап М.) 102
Штейнгауз (ЗимпЬаиз Н.) 128
Эрроу (Аггош К. <1.) 14, 102, 179,
217
ОГЛАВЛЕНИЕ
Предисловие редактора перевода 5
Предисловие автора 7
Глава /. Многошаговый процесс распределения 21
§ 1. Введение 21
§ 2. Многошаговый процесс распределения ресурсов 22
§ 3. Обсуждение 23
§ 4. Метод функциональных уравнений 26
§ 5. Обсуждение 28
§ 6. Многомерная задача о максимизации 28
§ 7. Задача о „сглаживании" 29
§ 8. Бесконечношаговая аппроксимация 30
§ 9. Теоремы существования и единственности 30
§ 10. Последовательные приближения 35
§ 11. Приближение в пространстве поведений 35
§ 12. Свойства решения. I. Выпуклость 38
§ 13. Свойства решения. II. Вогнутость 39
§ 14. Свойства решения. III. Вогнутость 41
§ 15. Причудливый пример 44
§ 16. Обычный пример. I 45
§ 17. Обычный пример. II 47
§ 18. Приближение и устойчивость 48
§ 19. Процессы, зависящие от времени 50
§ 20. Процессы с несколькими видами ресурсов 5]
§ 21. Теоремы о структуре решения для многомерных задач ... 53
§ 22. Разыскание единственного максимума вогнутой функции ... 54
§ 23. Непрерывность и память 57
§ 24. Стохастические процессы распределения ресурсов 58
§ 25. Функциональные уравнения 59
§ 26. Интегралы Стильтьеса 60
Упражнения и проблемные задачи к главе I 61
Библиография и комментарии к главе I 81
Глава /Л Стохастический многошаговый процесс решения .... 83
§ 1. Введение 83
§ 2. Стохастический процесс золотодобычи 84
§ 3. Метод перечисления 84
§ 4. Метод функциональных уравнений . 85
§ 5. Аппроксимация бесконечношаговым процессом 85
§ 6. Существование и единственность • . . '86
§ 7. Приближение в пространстве поведений и монотонная сходи-
сходимость 88
§ 8. Решение 88
§ 9. Обсуждение 92
§ 10. Некоторые обобщения 92
§ 11. Вид функции /(х, у) 93
§ 12. Задача для процесса с конечным числом шагов 95
§ 13. Трихотомическая задача 93
§ 14. Теорема устойчивости 99
Упражнения и проблемные задачи к главе II 100
Библиография и комментарии к главе II 132
Оглавление 397
Глава III. Структура процессов динамического программирования 103
§ 1. Введение 103
*§ 2. Обсуждение двух процессов, рассмотренных ранее 103
§ 3. Принцип оптимальности * 105
§ 4. Постановка задачи. I. Дискретный детерминированный процесс 105
§ 5. Постановка задачи. II. Дискретный стохастический процесс . . 108
§ 6. Постановка задачи. III. Непрерывный детерминированный
процесс , . * . , * . . < 109
§ 7. Непрерывные стохастические процессы ПО
§ 8. Обобщения ПО
§ 9. Причинность и оптимальность 111
§ 10. Приближение в пространстве поведений 111
Упражнения и проблемные задачи к главе III 113
Библиография и комментарии к главз III . . , 141
Глава IV. Теоремы существования и единственности . . . . 142
§ 1. Введение . . .142
§ 2. Основное неравенство 143
§ 3. Уравнения первого типа 145
§ 4. Уравнения второго типа 147
§ 5. Монотонная сходимость 148
§ 6. Теоремы устойчивости .... 150
§ 7. Некоторые направления обобщений 151
§ 8. Пример уравнения третьего типа 152
§ 9. Уравнение оптимального управления запасами 157
Упражнения и проблемные задачи к главе IV 160
Библиография и комментарии к главе IV 180
Глава V. Уравнение оптимального управления запасами 182
§ 1. Введение 182
§ 2. Постановка общей задачи 183
А. Конечный период времени 184
Б. Бесконечный промежуток времени, скидка с издержек . . 186
В. Бесконечный промежуток времени, частичный возврат пред-
предметов „ . 187
Г. Бесконечный промежуток времени, задержка поставки на
один период 187
Д. Бесконечный промежуток времени, задержка поставки
на два периода «....". 187
§ 3. Одно простое замечание . . 188
§ 4. Постоянный уровень запасов, предварительное обсуждение . .189
§ 5. Пропорциональные издержки, одномерный случай 190
§ 6. Пропорциональные издержки, многомерный случай 196
§ 7. Конечный промежуток времени 198
§ 8. Конечный-промежуток времени, многомерный случай .... 202
§ 9. Непропорциональные „дополнительные расходы" — администра- .
тивные расходы 202
§ 10. Частные случаи 205
§ 11. Вид общего решения 205
§ 12. Постоянные расходы 206
§ 13. Предварительные замечания к обсуждению более сложных
поведений * 207
§ 14. Неограниченно продолжающийся процесс, запаздывание на один
период 207
§ 15. Выпуклая функция издержек, неограниченно продолжающийся
процесс ' , » 210
398 Оглавление
Добавление к главе V. Уравнение восстановления 212
Упражнения и проблемные задачи к глзве. V . ,. *• • 214
Библиография и комментарии к главе V 217
Глава VI. Задачи „на узкие места" в многошаговых процессах
производства *. . . 219
§ 1. Введение 219
§ 2. Общий класс задач, возникающих при изучении многошаго-
многошагового процесса производства . 220
§ 3. Обсуждение рассмотренной выше модели 224
§ 4. Функциональные уравнения 225
§ 5. Непрерывный вариант .. . 226
§ 6. Система обозначений 227
§ 7. Постановка задачи с точки^ зрения динамического программи-
программирования 228
§ 8. Основное функциональное уравнение 229
§ 9. Нелинейное дифференциальное уравнение в частных произ-
производных 229
§ 10. Приложение дифференциального уравнения в частных произ-
производных 230
§ 11. Частный пример 231
§ 12. Двойственная задача 234
§ 13. Проверка решения, построенного в § 11 237
§ 14. Численное решение ... г 240
§ 15. Нелинейные задачи 241
Упражнения и проблемные задачи к главе VI 241
Библиография и комментарии к главе VI 243
Глава VII. Задачи „на узкие места". Примеры 245
§ 1. Введение 245
§ 2. Предварительные замечания 247
§ 3. Дельта-функции ; . . . 249
§ 4. Решение 250
§ 5. Модифицированное ш-решение 253
§ 6. Равновесное решение 254
§ 7. ш-решение для процесса малой продолжительности 256
§ 8. Описание решения и доказательство 257
§ 9. Перечень случаев расхода начального запаса стали 260
Библиография и комментарии к главе VII 261
Глава VIII. Непрерывный стохастический процесс решения .... 262
§ 1. Введение 262
§ 2. Непрерывный случай. I. Дифференциальный подход 263
§ 3. Непрерывный случай. II. Интегральный подход 264
§ 4. Предварительное обсуждение • • 265'
§ 5. Смешивание в точке 266
§ 6. Новая формулировка процесса золотодобычи 267
§ 7. Вывод дифференциальных уравнений 268
§ 8. Вариационный метод 269
§ 9. Поведение функций Кг 270
§ 10. Решение для случая Т = оо 271
§11. Решение для конечного полного времени 272
§ 12. Задача о трихотомическом выборе 274
§ 13. Некоторые леммы и предварительные результаты 275
§ 14. Смешанные выборы ^ ' • • 276
§ 15. Решение для бесконечного времени; случай й > 0 278
Оглавление 399
§ 16. Случай И < 0 282
§ 17. Случай г% = Г1 283
§ 18. Нелинейная функция выгоды — задача о Дихотомическом выборе 284
Библиография и комментарии к главе VIII 286
Глава IX. Новая формализация вариационного исчисления .... 287
§ 1. Введение 287
§ 2. Новый подход 28$
оо
§ 3. Максимизация функционала I Р(х, у)йг 291
о
§ 4. Обсуждение 29&
§ 5. Двумерный случай 4 294
§ 6. Максимизация функционала I Р(х, у)<Н 295
§ 7. Максимизация функционала I Р(х, у) <Н при условии 6 <; у <; х 296
о
§ 8. Численное решение 297
§ 9. Обсуждение 298
§ 10. Пример 299
§ 11. Дискретная модель 302
§ 12. Доказательство сходимости 304
Т
§ 13. Максимизация функционала | Р(х, у, 1)сН 307
0
§ 14. Обобщение и обсуждение 308
§ 15. Интегральные ограничения 309
§ 16. Дальнейшие замечания относительно численного решения . . 310
§ 17. Задача о собственных значениях , . 311
§ 18. Первая формулировка 313
§ 19. Приближенное решение 314
§ 20. Вторая формулировка 315
§ 21. Дискретные аппроксимации 315
§ 22. Последовательные приближения .... 316
§ 23. Монотонная аппроксимация 318
§ 24. Единственность решения . . . .' 318
§ 25. Минимум максимального отклонения . . - 319
Упражнения и проблемные задачи к главе IX 320
Библиография и комментарии к главе IX 329
Глава X. Многошаговые игры 331
§ 1. Введение 331
§ 2. Одношаговая дискретная игра 332
§ 3. Теорема о минимаксе 334
§ 4. Непрерывные игры 335
| 5. Ограниченные ресурсы 335
§ 6. Игры на выживание 337
§ 7. Игры погони 337
§ 8. Общая формулировка . 338
§ 9. Принцип оптимальности и функциональные уравнения .... 340
400 Оглавление
§ 10. Более общий процесс 342
§ 11. Основная лемма 343
§ 12. Существование и единственность 345
§ 13. Доказательство результатов 347
§ 14. Другое доказательство существования 349
§ 15. Последовательные приближения в общем случае 350
§ 16. Эффективность решения . . . 350
§ 17. Дальнейшие результаты 352
§ 18. Односторонний минимакс 353
§ 19. Существование и единственность для игр на выживание . . 353
§ 20. Приближение 357
§ 21. Ненулевые игры на выживание 358.
§ 22. Приближенное решение 359
§ 23. Доказательство обобщенной теоремы о минимаксе 359
§ 24. Истолкование игр с ненулевой суммой 361
Упражнения и проблемные задачи к главе X ... .... 362
Библиография и комментарии к главе X 368
+
Глава XI. Марковские процессы решения . . . 370
§ 1. Введение 370
§ 2. Марковские процессы решения ...... . . 370
§ 3. Обозначения 372
§ 4. Лемма 373
§ 5. Существование и единственность. I 374
§ 6. Существование и единственность. II 378
§ 7. Существование и единственность. III 379
§ 8. Уравнение Риккати 380
§ 9. Приближение в пространстве поведений 381
§ 10. Дискретные варианты 383
§ 11. Рекуррентное соотношение ........ 385
§ 12. Минимакс 387
§ 13. Обобщение результата Неймана 388
Упражнения и проблемные задачи к главе XI 389
Библиография и комментарии к главе XI 391
Указатель приложений 393
Именной и предметный указатель 395
Р. Беллман
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Редактор И. В. Глатёнок Художественный редактор Е. И. Подмарькова
Технический редактор В. А. Доценко.
Сдано в производство 26/Х 1959 г. Подписано к печати 24/П 1960 г. Бумага /^
— 12,5 бум. л., 25 печ. л., Уч.-изд. л. 23,0. Изд. № 1/5111. Цена 17 р. 60 к. Зак. 834.
ИЗДАТЕЛЬСТВО ИНОСТРАННОЙ ЛИТЕРАТУРЫ
Москва, Ново-Алексеевская, 52
Типография № 2 им. Евг. Соколовой УПП Ленсовнархоза. Ленинград, Измайловский пр., 29