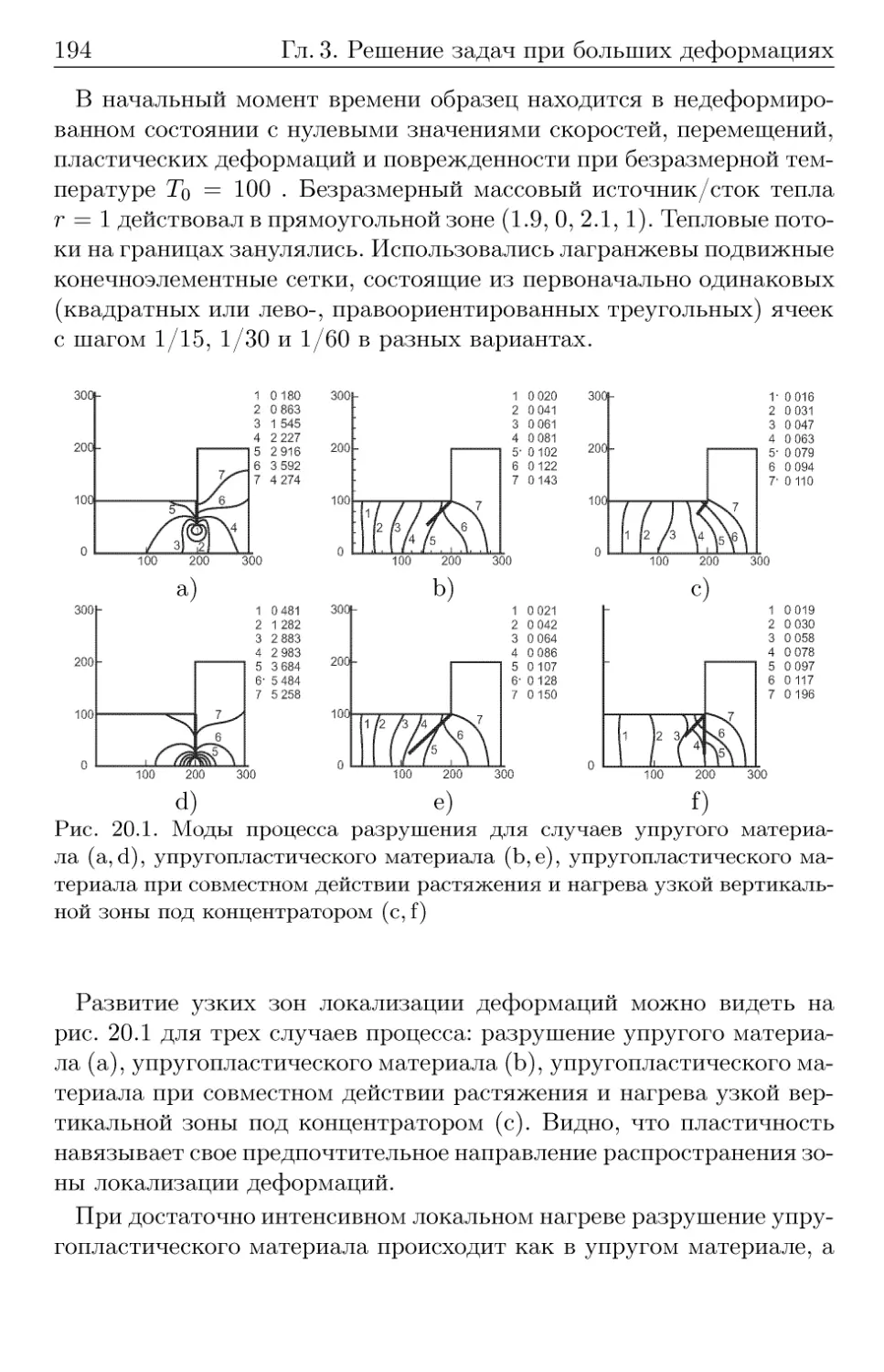
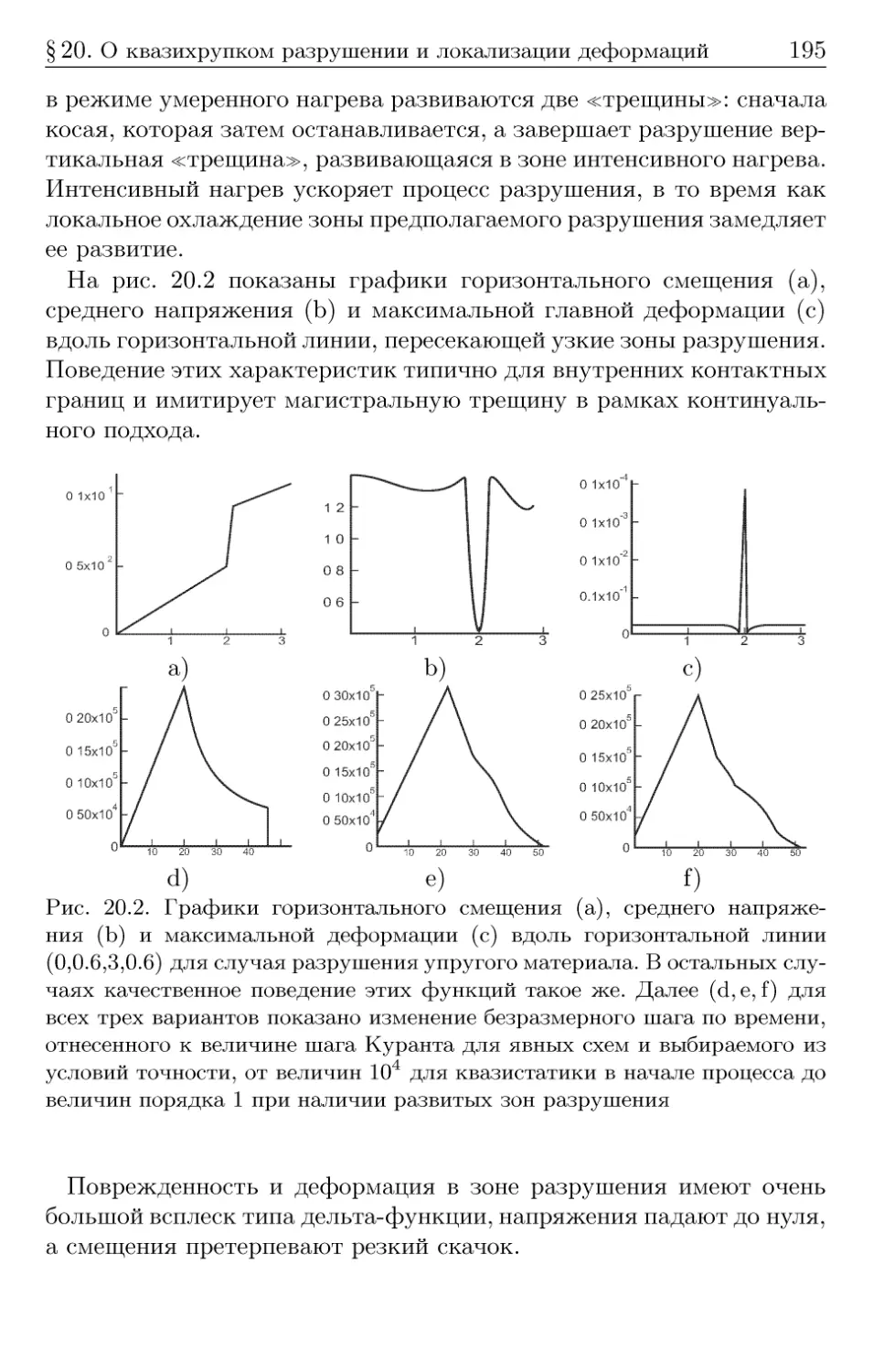
Автор: Кукуджанов В.Н.
Теги: механика деформируемых тел упругость деформация вычислительная математика численный анализ механика физика
ISBN: 978-5-7417-0238-3
Год: 2008
Текст
Московский физико-технический институт
(государственный университет)
Кафедра прикладной механики
В. Н. Кукуджанов
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
ДЕФОРМИРОВАНИЯ, ПОВРЕЖДАЕМОСТИ
И РАЗРУШЕНИЯ НЕУПРГУГИХ
МАТЕРИАЛОВ И КОНСТРУКЦИЙ
УДК 539.3:519.6(075)
ББК 22.251я73
К88
Рецензенты:
Кафедра Вычислительной математики и программирования
Московского авиационного института
(зав. кафедрой член-корреспондент РАН У. Г. Пиру мое)
Доктор физико-математических наук, профессор Н.В. Баничук
Кукуджанов В.Н.
К88 Компьютерное моделирование деформирования,
повреждаемости и разрушения неупругих материалов и
конструкций: Учебное пособие. - М.: МФТИ, 2008. - 215 с.
ISBN 978-5-7417-0238-3
Рассматривается компьютерное моделирование процессов
деформирования, поврежденности и континуального разрушения
нелинейных материалов и конструкций. Основное внимание уделяется
механике твердого деформируемого тела. Это связано с научными
интересами автора и тем обстоятельством, что на русском языке
учебников и монографий, посвященных этой области механики,
недостаточно.
Книга рассчитана на студентов старших курсов и аспирантов
механико-математических и физико-технических факультетов
университетов, знакомых с основами механики сплошной среды и с
понятиями вычислительной математики, а также представляет интерес
для специалистов в области численного моделирования задач
механики сплошных сред.
УДК 539.3:519.6(075)
ББК22.251я73
ISBN 978-5-7417-0238-3 © Кукуджанов В.Н., 2008
О Московский физико-технический институт
(государственный университет), 2008
Оглавление
Предисловие 5
Обозначения 8
Глава 1. Решение волновых задач 9
§1. Линейные колебания упругих стержней 9
§ 2. Решение задач распространения нелинейных волн
методом характеристик. Одномерные задачи 24
§ 3. Решение связных задач термомеханики 47
§ 4. Дифференциальные приближения разностной схемы.
Устойчивость 50
§ 5. Упражнения 64
Глава 2. Разностные схемы расщепления 68
§ 6. Общая схема расщепления 68
§ 7. Расщепление по направлениям 71
§ 8. Расщепление по физическим процессам. Уравнения
Навье-Стокса вязкой жидкости 77
§ 9. Расщепление по физическим процессам уравнений
теории пластичности 83
§ 10. Расчет граничных точек и точек на оси вращения при
расщеплении 96
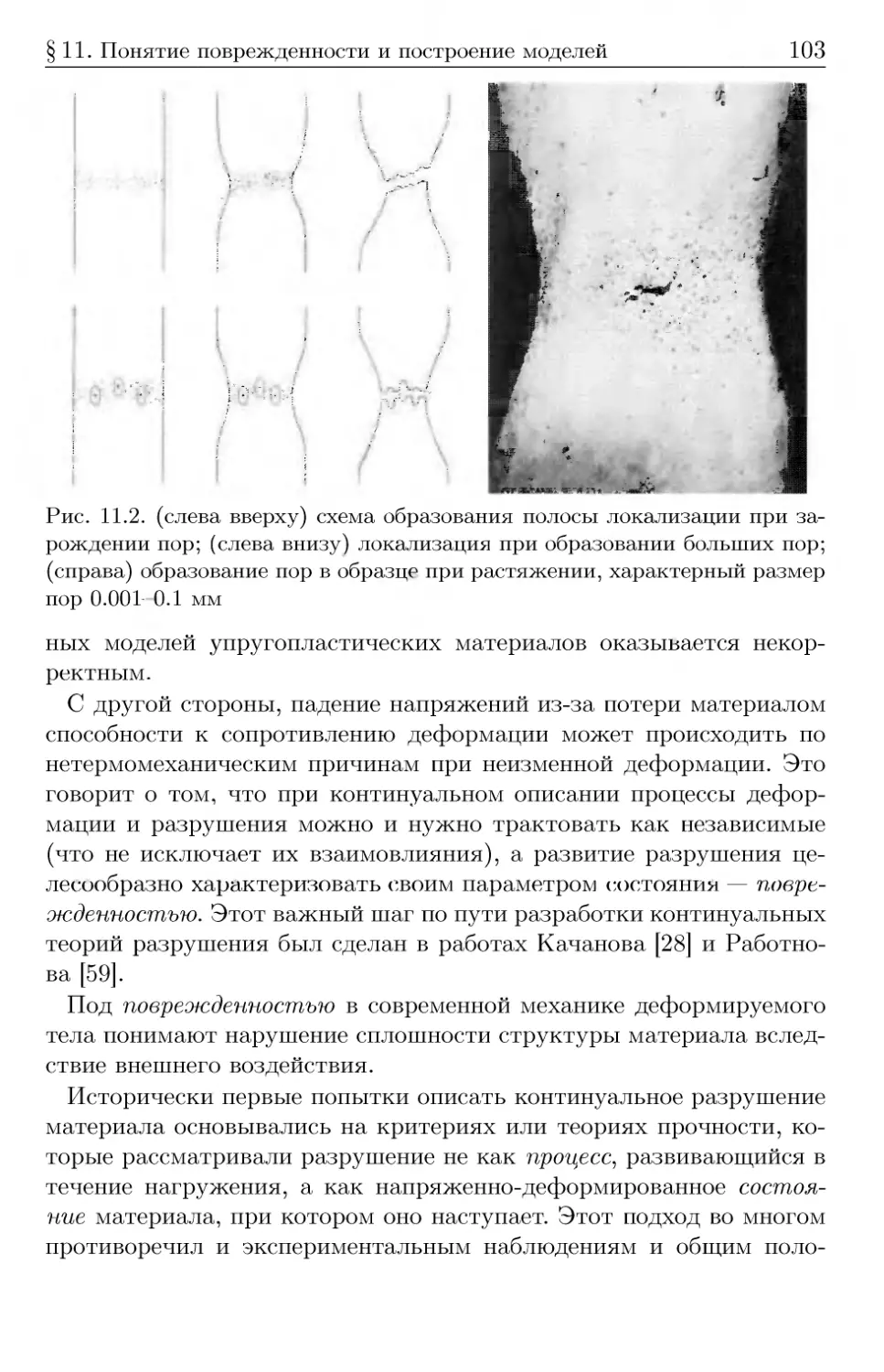
§11. Понятие поврежденности и построение моделей
повреждающихся сред 101
3
4 Оглавление
§ 12. Микромеханическая многомасштабная модель
поврежденное™ упругопластического материала 112
§ 13. Численное моделирование поврежденности упруго-
пластических материалов (вязкое и хрупкое
разрушение) 123
§ 14. Численное моделирование процессов резания упрго-
вязкопластических материалов в трехмерной
постановке 143
§ 15. Упражнения 154
Глава 3. Решение задач при больших деформациях 157
§ 16. Консервативные аппроксимации на криволинейной
лагранжевой сетке 157
§ 17. Большие упругопластические деформации 163
§18. Метод частиц в ячейках (PIC-метод) 168
§ 19. Формулировка теории течения упругопластической
среды в виде вариационного неравенства 176
§ 20. О квазихрупком разрушении и локализации
деформаций 183
§21. Упражнения 198
Список литературы 201
Предметный указатель 211
Предисловие
5
Предисловие
Численное моделирование внедряется во все более широкий круг
наук, еще недавно весьма далеких от использования математических
методов. Механика сплошной среды занимает особое место среди
них. Она по существу была и остается наукой, в которой
моделирование зародилось и стало мощным средством исследования наряду
с физическим экспериментом. Численный эксперимент стал столь
же востребованным средством исследования в технических и
естественных науках, как и эксперимент физический. Бурное развитие
численного моделирования стало возможным благодаря созданию
мощных вычислительных средств. Компьютерное моделирование не
только использует современную высокоскоростную вычислительную
технику, но и стимулирует ее развитие благодаря созданию все более
и более сложных математических моделей, реализация которых
находится на грани возможностей самой современной вычислительной
техники. Такое стремительное развитие этого нового подхода к
исследованию современных проблем естествознания и техники требует
квалифицированных специалистов, владеющих методами
математического моделирования. Хотя основы линейной теории не потеряли
своего значения, разрыв между методами моделирования сложных
нелинейных задач и строгой линейной теории численных методов
непрерывно растет. Критерием корректного решения задачи
математического моделирования в настоящее время является соответствие
между численным и физическим экспериментом. В книге делается
попытка сократить этот разрыв, дополнив традиционный материал
современными подходами к исследованию более сложных
нелинейных задач механики сплошных сред. Такими не вполне
традиционными вычислительными методами, изложенными в настоящем
пособии, являются явные и неявные разностные характеристические
схемы для решения нестационарных задач механики материалов со
сложной реологией. Разработаны новые методы расщепления
стационарных и нестационарных задач для нелинейных материалов с
учетом структурных изменений в процессе нагружения. Решение
связанных задач континуального разрушения и повреждаемости, задач
теории пластического течения с помощью вариационных неравенств.
Дано применение смешанных эйлерово-лагранжевых подходов
описания движения к исследованию больших деформаций сплошных
сред. Предложено обобщение метода частиц в ячейках и приведены
6
Предисловие
его модификации к исследованию деформаций материалов со
сложной реологией и др.
Учебное пособие написано на основе курсов лекций <Численные
методы в механике деформируемых тел» и <Численное
моделирование в задачах МСС», которые автор читает студентам
старших курсов Московского физико-технического института
(государственного университета) (http://www.mfti.ru/) и студентам МАТИ —
Российского государственного технологического университета
имени К.Э. Циолковского (http://www.mati.ru/) в течение ряда лет. В
учебное пособие вошел материал, связанный с моделированием
актуальных задач механики деформируемых тел и конструкций. Пособие
дополняет и развивает материал курса, изложенный в предыдущих
учебных пособиях автора [43, 44, 48].
В книге большое внимание уделено новым моделям и методам
решения задач микро- и мезомеханики поврежденности и разрушения,
которые бурно развиваются в последние годы и связаны с
научными интересами автора. Эти вопросы механики сплошных сред пока
не вошли в учебную литературу. В то же время существует острая
нужда в квалифицированных специалистах в связи с
необходимостью моделирования и разработки технологий для создания новых
высокопрочных материалов микро- и наномасштабной структуры.
В списке литературы приводятся ссылки не только на статьи и
книги, непосредственно использованные в процессе написания, но
и на некоторые оригинальные работы, которые помогут
заинтересованному читателю подробнее познакомиться с изучаемым
предметом. Автор надеется, что это облегчит студентам, аспирантам и
молодым ученым знакомство с перспективными задачами механики
на стыке с материаловедением и физикой твердого тела.
Текст книги разбит на главы. Параграфы имеют сквозную
нумерацию. Нумерация формул и рисунков двойная — номер параграфа
и номер формулы в параграфе. Мелким шрифтом дан углубленный
материал, который можно пропустить при первоначальном
прочтении.
Книга рассчитана на студентов старших курсов и аспирантов
механико-математических и физико-технических факультетов
университетов, знакомых с основами механики сплошной среды и
вычислительной математики в объеме стандартных курсов. Книга также
представляет интерес для специалистов в области численного
моделирования задач МСС.
Предисловие
7
Данное пособие выполнено при финансовой поддержке со
стороны Программы Отделения энергетики, машиностроения, механики
и процессов управления РАН 130Э и Российского фонда
фундаментальных исследований (0б-01-00523а).
Автор благодарен своим коллегам и ученикам, принимавшим
участие в обсуждении и подготовке материала, проф. Н.Г. Бураго,
м.н.с. А.Л. Левитину и студенту-дипломнику B.C. Синюку.
Обозначения
Обозначения
В книге используются обозначения, характерные для разных
разделов математики, вычислительной математики и физики
(механики). Приведем некоторые наиболее употребительные обозначения.
Полужирный — А или сг:
матрица или тензор соответственно
с элементами Ац или ац.
Стрелка — й или х: вектор с
элементами Щ ИЛИ Xi-
Крышка — й: фурье-образ
скаляра или вектора.
Нижний индекс
— Xi\ элемент вектора ж;
— (Гц или Dijki: элемент
матрицы/тензора сг, D;
— fx или f'x: частная
производная функции / по
переменной ж;
— f% или fL: частная
производная функции / по
вектору х.
Верхний индекс
— х2 или хп: степень;
— Рп(х): полином п-й
степени;
— й или (ui,U2j или А :
операция
транспонирования вектора или матрицы;
— й* или А*: комплексное
сопряжение вектора или
матрицы.
• Фигурные скобки - {ж}:
множество.
• Квадратные скобки
— [а, 6]: интервал;
[и] = w+ •
личины.
разрыв ве-
Круглые скобки - (и, /):
скалярное произведение
векторов/матриц.
Точка - й • f или Н • и:
произведение векторов/матриц.
Точка сверху — й или (uv)':
материальная производная по
времени.
Обозначения в разностных схемах
• /г, Ах или Ау: шаг разностной схемы по пространству;
• т или At: шаг разностной схемы по времени;
• Ар: шаг по параметру нагрузки;
• и^: значение и в узле к разностной сетки;
• Uij или Щ^: значение и в узле (i,j) разностной сетки;
• ип: значение и на п-м временном слое.
Глава
Решение волновых задач
§ 1. Линейные колебания упругих
стержней
Продольные колебания (9). Явная схема. Достаточные условия
устойчивости (10). Продольные колебания. Неявная схема (12). Поперечные
колебания (13). Поперечные колебания. Явная схема (14). Поперечные колебания.
Неявная схема (16). Продольно-поперечные колебания (17). Поперечный
изгиб пластины с учетом сдвига и инерции вращения (20). Заключение (22).
Продольные колебания. Рассмотрим задачу о продольных
колебаниях линейных сред, которые сводятся к волновому уравнению,
зависящему от одной пространственной переменной. Этим
уравнением описываются продольные колебания упругого стержня или слоя
упругой среды конечной толщины, акустические колебания газа,
колебания упруго-магнитных волн и другие многочисленные явления,
отличающиеся друг от друга физическим содержанием, но
эквивалентные математически:
д2У = с2 д2У
dt2 дх2
Пусть заданы начальные условия:
y(0,x) = f1(x) и y'(0,x) = f2(x).
9
(1.1)
10
Гл. 1. Решение волновых задач
В качестве граничных условий задано условие периодичности:
г/(0, х) = у(0,х-1).
Введем новые переменные
ду ду
dt дх
Получим вместо волнового уравнения (1.1) эквивалентную ему
систему уравнений
dv dw dw dv
dt дх' dt дх'
Явная схема. Достаточные условия устойчивости.
Разностное уравнение для волнового уравнения (1.1) запишется так:
д£-^- = с^"' (L3)
где {$2у) . — вторая центральная разность в точке tn,Xj.
Разностные уравнения для эквивалентной системы (1.2) имеют вид
п+1 _ п 1Пп _ ?..п
VJ_VJ_ _ ™3 + ^1Ъ WJ~l/2
At Ax
п+1. -и,™ я,п+1 _ vn+l
w-,/2-w-_1/2 v»
(1.4)
At Ax
Если положить
v? = (у? - уГ1) /At> <-i/2 = (у? ~ v?-i) /^
то получим (1.3).
Во втором уравнении производная по х берется с верхнего слоя, но
Г7-И
при этом схема остается явной, поскольку v ^ вычисляется по
явной формуле из первого уравнения. Спектральный радиус матрицы
перехода для системы (1.4) определяется из системы
/л ,ч Л At . . jAx Л
(Л — l)v — 2cw-— г sin = 0,
Ах 2 ' (1.)
(А — l)w — 2cv\-— г sin = 0.
v J Ax 2
§ 1. Линейные колебания упругих стержней 11
Определитель системы (1.5) должен обращаться в нуль, чтобы
система имела ненулевое решение:
/л \2 л 2 ^ jAx
(А — 1) + ла = О, где а = 2с—— sin .
При а2 ^ 4 оба корня по модулю JAi^l = 1. Откуда следует, что
необходимым условием устойчивости схемы (1.5) будет условие Ку-
cAt
ранта: —— ^ 1. Чтобы определить, будет ли признак Неймана до-
Ах
статочным условием устойчивости, необходимо найти матрицу
перехода G. В нашем случае уравнение, связывающее un+1 с йп (см. § б
в [48]), имеет вид
Hi ип = Н0 йп, ип+1 = Н^Но йп = G ип,
где и — вектор решения, преобразованный по Фурье.
Из (1.5) следует, что матрицы Но и Hi имеют следующий вид:
Матрица перехода G будет такой:
G=(L 1-"«>)■ ^
Матрица G не является нормальной матрицей, поэтому критерий
Неймана для неё не дает достаточного условия устойчивости (§6
в [48]), но в теории устойчивости разностных схем есть теорема,
дающая другое достаточное условие сходимости [60].
Теорема. Если матрица G имеет полную систему
нормированных собственных векторов Un и модуль определителя Грамма А
для них ограничен снизу некоторой положительной константой
А > с > 0; то для такой матрицы G условие Неймана достаточно
для устойчивости.
Применим эту теорему к матрице (1.6). Собственные векторы
матрицы перехода определяются из уравнения
GUi = \iUi, г = 1,2, Щ =
:
12
Гл. 1. Решение волновых задач
А
det(UuU2)
fcAty
Откуда находим, что условие Неймана является не только необходи-
/-, ^ cAt -1
мым, но и достаточным для устойчивости схемы (1.4), если —— < 1.
При —— = 1 схема неустойчива.
Ах
Продольные колебания. Неявная схема. Неявная схема для
системы (1.2) имеет вид
с At
"'Г-*? = од: ^2-^2+^1/2-^1/2 f
,„"-! ,„" _ С Д* („п+1 „п+1
Wj-l/2-W3-l/2 - 2~K^\j ~ J-1
(1.7)
Эта система эквивалентна трехслойной разностной схеме для одного
волнового уравнения второго порядка точности:
t/J"+1-2t/J" + t/J"-1 _ 262у?+1 + 2б2у? + 62у?-1
С
(At)2 4(Аж)2
Преобразование Фурье для уравнений (1.7) дает систему
(А - l)v - cig sin ifE(A + l)«; = 0,
{X - l)w-ci^ sin i^{X + l)v = 0.
Собственные значения матрицы перехода G находим, приравнивая
нулю детерминант
4 ) V 4
Оба собственных значения по модулю равны единице при любом а:
|A|i,2 = 1, (1.9)
а сама матрица G определяется в виде
tt-Itt / 1 -^-\ /1 Т _ Н«2/4 1+а2/4
Н1Н0-(_ х I I 1 ] - 1-jg c2/4
2 / \2 / \1+а2/4 1+а2/4у
§ 1. Линейные колебания упругих стержней 13
откуда ясно, что G — унитарная матрица, а значит, и нормальная,
и схема (1.7) безусловно устойчивая по Нейману.
Полученная система уравнений (1.7) приводится к системе с трех-
диагональной матрицей, решение которой эффективно находится
методом прогонки, так лее, как это делалось выше для уравнения
теплопроводности (см. § 15 в [48]).
Поперечные колебания. Уравнение изгибных колебаний
тонкого упругого стержня при малых прогибах г/, основанное на гипотезе
плоских сечений и предположении, что инерцией вращения
поперечного сечения можно пренебречь, приводится к уравнению четвертого
порядка
^ - & (-S) • <"•>
где р — линейная плотность, Е — модуль упругости материала, / —
момент инерции поперечного сечения стержня относительно его
нейтральной оси.
Если считать, что р, Е, I не зависят от ж, то (1.10) можно записать
в виде
J = -aW> a=V (1Л1)
Изгибающий момент М и перерезывающая сила Q определяются
по формулам
« = -*'&■ « = й(*'Э)- с-"»
Граничные условия могут иметь различный вид в зависимости от
закрепления концов стержня. Например, в случае свободного опира-
ния балки на концах равны нулю прогиб и изгибающий момент М:
х = 0, у = 0, д2у/дх2 = 0,
х = Z, у = 0, д2у/дх2 = 0.
Для численного решения, чтобы не иметь дело с производной
четвертого порядка, уравнение (1.11) удобнее представить в виде
системы двух уравнений второго порядка относительно переменных
ду д2у
,2../Я~2_п (1-13)
14
Гл. 1. Решение волновых задач
Граничные условия (1.13) могут быть заменены эквивалентными
условиями нечетности (косой симметрии) и периодичности с
периодом 21:
у(х, t) = -у(-х, t), у{х + 21, t) = у(х, t). (1.15)
Тогда можно считать, что решение определено на всей оси х и
рассматривать его как решение задачи Коши (рис. 1.1).
Рис. 1.1. Нечетные периодические начальные условия
Докажем, что при выполнении условий (1.15) следуют граничные
условия (1.13). Дифференцируя (1.15) по ж, находим, что вторые производные, а
следовательно, и w, также удовлетворяют условиям
w(x, i) = -w(-x, £), w(x + 21, t) = w(x, t). (1.16)
Из первых условий (1.15) - (1.16) следует, что
у = w = 0 при х = 0.
Во вторых условиях (1.15) - (1.16) сделаем замену £ = х + I, полагая затем £ = 0
и учитывая нечетность функций у и w, получим
2/(-г, i) = -y(l, i) и w(-l, i) = -w(l, t).
Откуда следует, что
у = w = 0 при х = I,
что и требовалось доказать.
Иначе говоря, краевые задачи с условиями (1.13) и краевыми условиями (1.15)
- (1.16) дают одинаковые решения. Тогда доказательство устойчивости
разностной схемы для краевой задачи (1.13) сводится к доказательству устойчивости
для задачи Коши с условиями периодичности (1.15), которое доказывается
стандартным спектральным методом.
Поперечные колебания. Явная схема. В первом уравнении
правую часть берем с нижнего (п)-го слоя, а во втором с
верхнего (п + 1)-го слоя. Тогда получаем
„п+1
Vj
At
' Ах2
wri
(Л/
n+l
At
Ax2
(1.17)
§ 1. Линейные колебания упругих стержней 15
где S2Wj = (wj+i — 2wj + Wj-i) — вторая центральная разность в
узле j. Хотя во втором уравнении вторая производная по х берется с
верхнего слоя, схема остается явной, поскольку на 1-м этапе vnJrl
вычисляется по явной схеме из первого уравнения и [о V) . уже
вычислена ко 2-му этапу, на котором вычисляется w™^ .
Матрица перехода для системы разностных уравнений (1.17) будет
иметь вид
1 ио \ _ л ^ At : fjAx
со 1
G = ( _ 1 о ) , где ии = 4,а-^-^ sin
Спектральный радиус матрицы G при |о;| < 2 будет тах|А| = 1, и
необходимое условие устойчивости фон Неймана запишется в виде
неравенства
ащ^ ^ \- (1Л8)
Матрица G не является нормальной, т.е. G G* ^ G*G. Поэтому
требуются дополнительные исследования достаточности признака
Неймана.
Прежде чем доказывать достаточное условие устойчивости
разностной схемы (1.17), заметим, что она эквивалентна разностному
уравнению
Ак~^ = -аЪ^> (1Л9)
которое аналогично более простому разностному волновому
уравнению (1.3), где вместо 4-й разности стоит вторая разность по х.
Достаточность условия Неймана для матрицы перехода (1.18)
разностной схемы (1.17) доказывается аналогично тому, как это было
сделано для системы волновых уравнений (1.4), на основании
теоремы, приведенной выше (см. с. 11). Для неё определитель Грамма
равен
det(UuU2)
и2 . . (aAt\ . 4fjAx
и условие Неймана будет достаточным при
aAt 1
А^2 < 2'
что совпадает с необходимым условием устойчивости схемы (1.17).
16
Гл. 1. Решение волновых задач
Поперечные колебания. Неявная схема. Перейдем к
исследованию неявной схемы для поперечных колебаний упругого
стержня, которую построим аналогично разностным уравнениям (1.7),
заменяя в правых частях разности соответствующими вторыми
центральными разностями:
tf+1-iff (S2w)]+1 + (S2w)]
At " ~а 2А^2 ' , ,
wl+1 ~ w? _ (^2«)"+1 + №v)? '
At 2Аж2
Матрица перехода получается из уравнений, аналогичных (1.8):
(А - l)v + к(Х + l)w = 0, _ 4а At , 2 j Ах
(А - l)v - я{\ + l)w = О, К~ Ах2 sm 2 '
Матрица перехода G имеет вид
2_/4
Гл _ \ 1+х2/4 1+х2/4 1
* 1-х2/4
\ 1+х2/4 1+х2/4/
и является унитарной. Оба собственных значения по модулю
равны единице при любом к. Кроме того, G — нормальна, т.е.
GGr = GrG, и, следовательно, условие Неймана для схемы (1.20)
достаточно для устойчивости. Таким образом, неявная схема при
любых к абсолютно устойчива и имеет второй порядок
аппроксимации по At и Ах: О (At2) + О (Ах2). Это очевидно из
эквивалентности (1.17) и (1.19).
Как видно из приведенного анализа, неявная схема (1.20)
обладает существенным преимуществом перед явной схемой (1.17), условие
устойчивости которой требует, чтобы At убывало как Аж2, что
приводит к необходимости существенного увеличения числа шагов по
времени, чем это требуется по соображениям точности решения.
Менее приятным обстоятельством является необходимость решать
систему уравнений (1.20). Эта система может быть записана как
матричное уравнение для двумерного вектора Uj с компонентами г>™+ ,
ь№ , содержащее значения в трех точках j + 1, j и j — 1:
AjUj+i +BjUj + CjUj-! =dj, j = 1,2... J, (1.21)
§ 1. Линейные колебания упругих стержней 17
к которому применима обратная матричная прогонка (см. § 19 в [48]),
где матрицы Aj, Bj, Cj имеют вид
А • - С • - , д 2 Ах2
,2Аж2 ° /
1 a At \ / a At \
л "А^2
aAt
В;
\Ах2 1 /
dj — известный вектор, зависящий от значений функций на п-ом
временном слое.
Матричная прогонка осуществляется по алгоритму, аналогично
приведенному в § 19 в [48] при решении уравнения эллиптического
типа, где матрицы А^, Bj, Cj в соотношении (1.21) имеют
размерность п х п.
В рассматриваемом случае между матричными коэффициентами
имеет место равенство
В-(А + С) = Е,
из чего следует ограниченность матричных коэффициентов Lj и fj
при прямой прогонке
иэ = ^зиз+^ + fj
и разрешимость системы уравнений на правом конце интервала, а
следовательно, корректность алгоритма матричной прогонки.
Продольно-поперечные колебания. Если в уравнение
поперечных колебаний стержня добавить член, связанный с продольной
сжимающей силой Т, то оно примет вид
д2у д2 ( д2у\ д2у
PW = d^\EJd^)+T№' (L22)
где продольная сила Т принимается постоянной по длине стержня.
Вводя новые переменные v ж w по аналогии с (1.14):
ду д2у By (EJ\1/2 1 /^1/2
at ox1 ox \ p J
получим систему уравнений
dv d2w dw dw d2v dv
dt dx2 dx' dt дх2 дх'
18
Гл. 1. Решение волновых задач
Как показано выше, неявная схема более эффективна для
решения задач поперечных колебаний, чем явная. Для рассматриваемого
случая неявная схема обобщается следующим образом:
v-' - - v- = -ai\t J J- + bAt —ГТ-
3 3 2Ax2 4Аж
w"+i -w" = aAt 3 t 0 + bAt -
3 3 2Ax2 4Аж
(1.24)
где Sv и S2v — первые и вторые пространственные разности
соответственно. Эта схема так же, как и (1.20), абсолютно устойчива.
Система алгебраических уравнений, к которым она приводит, имеет
такую же трехчленную структуру и решается методом матричной
прогонки. Однако здесь из-за дополнительного члена,
отвечающего продольной силе, возникают определенные сложности с
прогонкой, когда параметр Ъ ^> 1. Это связано с тем обстоятельством, что
при Ъ ^> 1 задача, по существу, становится гиперболической и
описывается волновым уравнением, для которого более подходящей
является явная схема (1.17). Поэтому воспользуемся явной схемой,
аналогичной разностной схеме (1.17) для поперечных колебаний стержня.
В рассматриваемой задаче она примет следующий вид:
vn+1 - vn = - — (52w)n + — (5w)n
3 3 Ax2[ )j 2Аж1 )jJ
wn+1 -wn = —(52v)n+1 + — (5v)n+1
wj wj Ах2У° uh + 2Ax[ )j
(1.25)
Во втором уравнении правые части взяты на верхнем (п + 1) слое
так же, как и раньше.
Если условие устойчивости в гиперболо-гиперболических Н — Н
задачах с модулями упругости Е\ ^> Е2, соответственно со
скоростями с\ ^> С2, выполняется для ci, то тем более будет
выполняться для С2- Иначе обстоит дело с параболо-гиперболическими Р — Н
задачами (такой является задача (1.22)), если схема явная. В этом
случае условие устойчивости
aAt/Ах2 < 1/2 при Ъ = 0 (1.26)
изменяется на
bAt/Ах < 1 при а = 0 . (1.27)
§ 1. Линейные колебания упругих стержней 19
При малом а и большом Ъ и конечных Ах и At выполнение
условия (1.26) может оказаться недостаточным для выполнения (1.27).
Тут возникает определенная проблема, связанная с
недостаточностью самого теоретического понятия устойчивости, имеющего
асимптотический характер, и приходится говорить о практической
устойчивости, т.к. нас интересует устойчивость при использовании
реальной сетки, а не при At —► 0 и Ах —► 0.
Для такой устойчивости нужно потребовать, чтобы скорость роста
амплитуды любой компоненты Фурье была бы не больше, чем
максимальная скорость роста компонент Фурье в точном решении.
Если система консервативна, то в точном решении амплитуды фурье-
компонент остаются постоянными. Потребуем, чтобы это было так
и для разностного уравнения. Это приводит к тому, что в условии
Неймана Xi(t) не должны быть возрастающими со временем, что
выполняется при условии А ^ 1 вместо Л ^ 1 + О (At) (см. § б в [48]).
Для системы продольно-поперечного изгиба (1.25) матрица
перехода получится из матрицы перехода (1.18) для поперечного изгиба
заменой а на /3, где
AaAt . 2jAx At .
а = ——— sin V г о—— sin iAx,
н Ах2 2 Ах J '
G=(-/3 i-Vl)' (L28)
Характеристическое уравнение будет иметь вид
А2 _ 2А [\ - 1^1 ]+ 1 = 0.
Чтобы выполнялось условие |А| ^ 1, должно выполняться условие
|/32К4:
/4аДЛ2 . 4 кАх [ЪМ\2 . 2, д , ,„ „ЛЧ
или, мажорируя — заменяя sin к Ах на 1, получаем простое
достаточное практическое условие устойчивости:
(2aAt\2 (hAt\ Л 2 2,
20
Гл. 1. Решение волновых задач
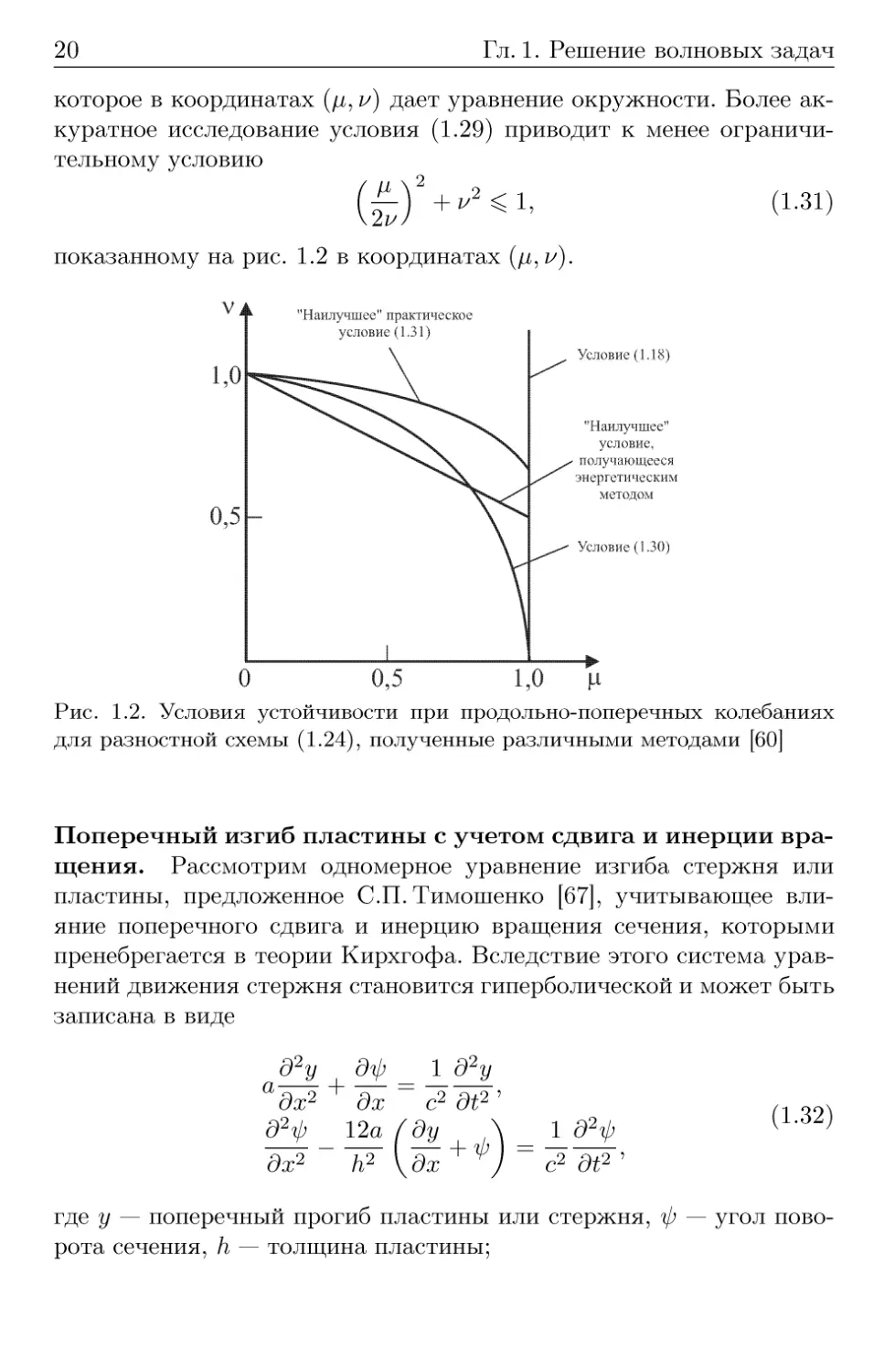
которое в координатах (/х, и) дает уравнение окружности. Более
аккуратное исследование условия (1.29) приводит к менее
ограничительному условию
показанному на рис. 1.2 в координатах (/х, и).
(1.31)
"Наилучшее" практическое
условие (1.31)
Условие (1.18)
"Наилучшее"
условие,
получающееся
энергетическим
методом
Условие (1.30)
0 0,5 1,0 \i
Рис. 1.2. Условия устойчивости при продольно-поперечных колебаниях
для разностной схемы (1.24), полученные различными методами [60]
Поперечный изгиб пластины с учетом сдвига и инерции
вращения. Рассмотрим одномерное уравнение изгиба стержня или
пластины, предложенное С.П.Тимошенко [67], учитывающее
влияние поперечного сдвига и инерцию вращения сечения, которыми
пренебрегается в теории Кирхгофа. Вследствие этого система
уравнений движения стержня становится гиперболической и может быть
записана в виде
д2у дф 1 д2у
дх2 дх с2 dt2 '
д2ф
дх2
12а
'К2
ду_
дх
■ф
1 д2ф
где у — поперечный прогиб пластины или стержня, ф
рота сечения, h — толщина пластины;
(1.32)
угол пово-
; 1. Линейные колебания упругих стержней 21
С
2
Е к2(1-1у)
(1-*V 2 '
где с — скорость распространения изгибных возмущений; к2 —
безразмерный коэффициент, зависящий от принимаемого
распределения сдвиговых напряжений по толщине пластины 2/3 ^ к2 ^ 1 [67].
Введем безразмерные переменные у = у/1, rj = h/l, x = х/1,
i = t • с/1, где I — характерный линейный размер.
Исключая ф из системы (1.32), получим уравнение четвертого
порядка относительно прогиба у:
д4у 12а^_Л Л д4у 1^_п
дх* + г]2 di2 ~ V + a) dx2di2 + а дР ~ ( '
Явная конечно-разностная аппроксимация на шаблоне крест обез-
размеренной системы (1.32) запишется в следующем виде:
a(D11y + D01il>)-Dtty = 0,
Вцф - ^ (Doi +ф)- Виу = О,
где для конечно-разностных формул введены обозначения
Аю/ = i (fi-i + 2fi + fi+i),
An/ = -Ао/ = y^= (fi+i - fi-i),
Al/ = (Ag^ (fi+1 - 2/j + /г-l) ,
At/ = I^F(/"+1-2/" + /"-1).
Если исключить ф из уравнений (1.34) и учесть, что
(Ах)2
D01D10 - Dn = ^-DnDn,
то получим
1 + За( — ) ]D11D11y + ^Duy-
1 + -)du Dtt + - Dtt Dtty = 0. (1.35)
а / а
22
Гл. 1. Решение волновых задач
Отсюда становится очевидным, что аппроксимация исходного
дифференциального уравнения (1.33) разностной схемой (1.35) условная
и при малых г) ~ Ax схема (1.35) аппроксимирует уравнение,
отличное от уравнения (1.33). Поэтому при расчете по схеме (1.35)
или (1.34) необходимо ограничивать шаг Ах <С rj ft, где rj ^ 10_3.
Следовательно, такая схема не эффективна, т.к. для аппроксимации
требуется слишком мелкое разбиение по х.
Член (Ах/г])2 появляется из-за стандартной аппроксимации
недифференциального члена, содержащего угол поворота ф, во
втором уравнении (1.34). Если стандартную аппроксимацию заменить
на усредненную по трем соседним точкам ф —► Мю^ TO придем к
безусловной аппроксимации относительно параметра (Ах/т/)2 и
получим схему
a(D11y + D01il>)-Dtty = 0,
12а , ч (1.36)
Оцф - -J- (Doiy + A)oV0 - DttV = 0.
Исключая фу получим уравнение, не содержащее членов порядка
(Ах/г])2:
DnDny + ^D00Dtty - (1 + - ) DnDtt + -DuDuy = 0. (1.37)
т\г \ а) а
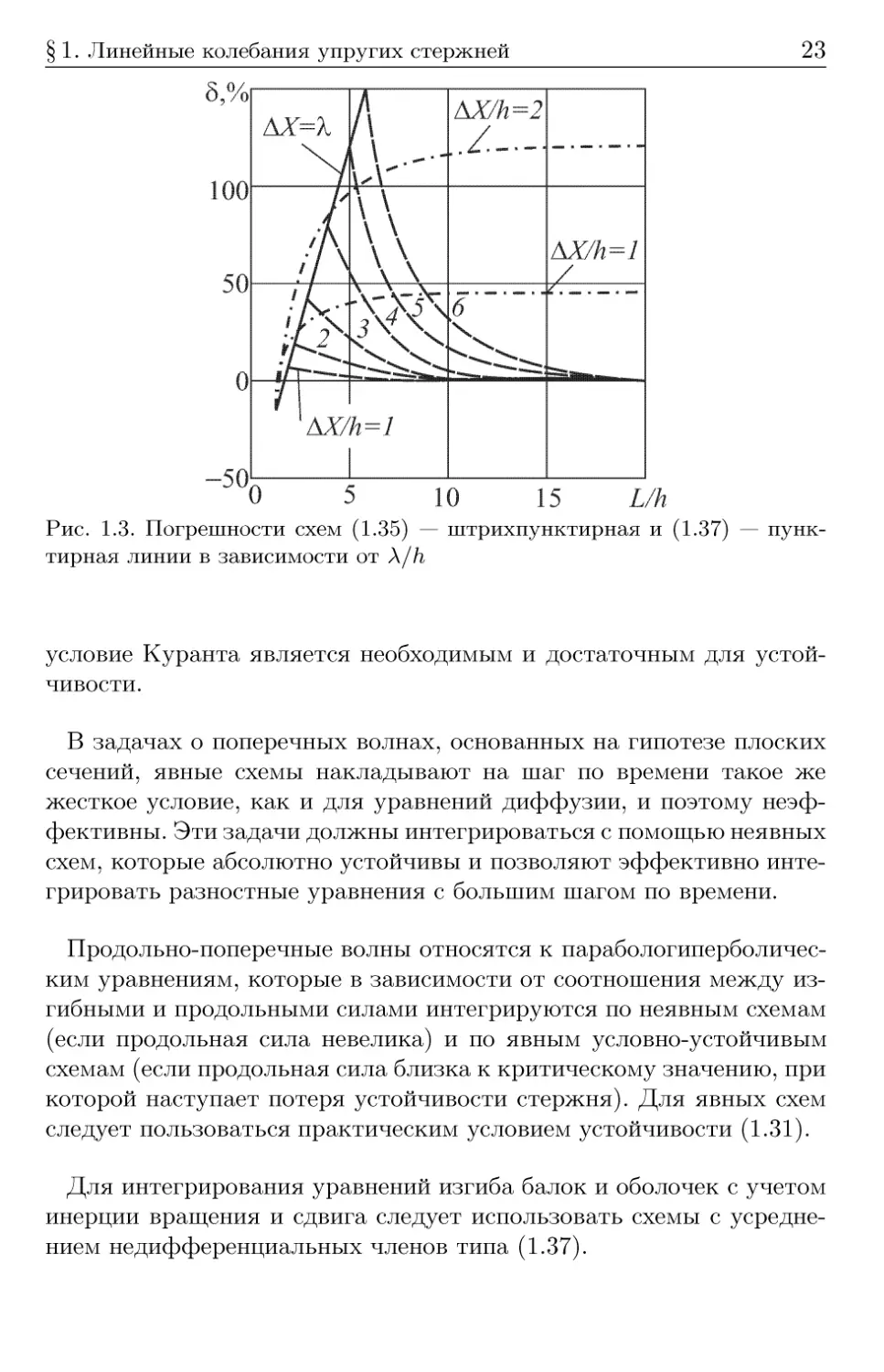
Анализ погрешности для низшей собственной частоты, наиболее
существенной в задачах изгибных колебаний, приводит к
результатам, показанным на рис. 1.3.
Видно, что схема (1.35) без усреднения дает незатухающую
ошибку при Ax/h = const, в то время как ошибка системы (1.37) быстро
затухает с ростом A/ft, при Ах —► 0 (А — длина волны).
Заметим, что теория Кирхгофа при ft —► 0 дает тот же результат,
что и теория Тимошенко. Таким образом, схема (1.37) более
адекватно отражает свойства исходной системы и позволяет вести расчет
со значительно большим шагом, чем схема без усреднения. Схемы
с усреднением можно получить вариационно-разностным способом
для общего случая уравнений поперечного изгиба пластин и
оболочек по теории Тимошенко [2].
Заключение. Для численного решения задач о продольных
волнах в стержнях эффективными являются явные схемы, для которых
; 1. Линейные колебания упругих стержней
23
О 5 Ю 15 L/h
Рис. 1.3. Погрешности схем (1.35) — штрихпунктирная и (1.37) —
пунктирная линии в зависимости от X/h
условие Куранта является необходимым и достаточным для
устойчивости.
В задачах о поперечных волнах, основанных на гипотезе плоских
сечений, явные схемы накладывают на шаг по времени такое же
жесткое условие, как и для уравнений диффузии, и поэтому
неэффективны. Эти задачи должны интегрироваться с помощью неявных
схем, которые абсолютно устойчивы и позволяют эффективно
интегрировать разностные уравнения с большим шагом по времени.
Продольно-поперечные волны относятся к парабологиперболичес-
ким уравнениям, которые в зависимости от соотношения между из-
гибными и продольными силами интегрируются по неявным схемам
(если продольная сила невелика) и по явным условно-устойчивым
схемам (если продольная сила близка к критическому значению, при
которой наступает потеря устойчивости стержня). Для явных схем
следует пользоваться практическим условием устойчивости (1.31).
Для интегрирования уравнений изгиба балок и оболочек с учетом
инерции вращения и сдвига следует использовать схемы с
усреднением недифференциальных членов типа (1.37).
24
Гл. 1. Решение волновых задач
§ 2. Решение задач распространения
нелинейных волн методом
характеристик. Одномерные задачи
Гиперболическая система уравнений и характеристики (24). Разностная
аппроксимация вдоль характеристик. Прямой и полуобратный методы (26).
Обратный метод. Сеточно-характеристическая схема Куранта, Изаксона,
Рисса (26). Неявные сеточно-характеристические схемы (28).
Распространение волн в нелинейно-упругом стержне (30). Распространение волн в стержне
из упруговязкопластического материала (33). Разрывные решения.
Уравнение с постоянными коэффициентами (37). Разрывные решения нелинейного
уравнения (39). Устойчивость разностных характеристических уравнений (40).
Устойчивость неявной сеточно-характеристической схемы (41).
Характеристические и сеточно-характеристические схемы для решения жестких задач (42).
Устойчивость характеристической и сеточно-характеристической схем в случае
жестких уравнений (44). Характеристические схемы высокого порядка
точности (45).
Гиперболическая система уравнений и характеристики.
Рассмотрим гиперболическую систему N уравнений с одной
пространственной переменной ж, разрешенную относительно вектора
временной производной:
Щ^ + А(г,х,и)Щ^ = Р^и). (2.1)
Решение U — вектор размерности iV, A — матрица N х iV, F —
вектор правых частей, который, как и матрица А, может
зависеть от решения U. По определению гиперболического
уравнения все собственные числа А^ матрицы А — действительные
числа и каждому Xi соответствует левый собственный вектор-строка
иъА = \ъиъ => (Ат - АгЕ) щ = б, г = 1... N (2.2)
Если все N собственных векторов линейно независимы и образуют
базис, то матрица приводится к диагональному виду
преобразованием
Г&АГГ1 = Л,
где Л — диагональная матрица, состоящая из собственных
значений Xi матрицы А, а Г2 — матрица, строками которой являются соб-
§ 2. Одномерные нелинейные волны. Характеристики 25
ственные векторы о^. Если А — симметричная матрица, то левые и
правые собственные векторы совпадают и ft = ft .
Умножая уравнение (2.1) скалярно на левые собственные
векторы u)i и учитывая (2.2), приведем уравнения (2.1) к каноническому
виду:
_ аи л _ аи _ - _ /ас/ л ас/\ _ -. /л оч
Ui—+ AiUi—= UiF => о;г I —+Аг-«- I =o;iF, (2.3)
здесь по повторяющемуся индексу г суммирование не производится.
Выражение в скобках представляет собой производную в
направлении кривой
dx .
-г: =К г = 1... JV,
at
называемой характеристикой. Обозначая оператор
дифференцирования в направлении г-й характеристики
—\-— А —
alt J i dt г дх'
получим, что вдоль г-й характеристики выполняется
дифференциальное соотношение
uJidiU = uJiFdt, (2.4)
где diU — полный дифференциал функции U вдоль г-ой
характеристики.
Если А — матрица с постоянными коэффициентами, то йг также
постоянны и (2.4) можно записать в инвариантах Римана ri
(суммирования по повторяющимся индексам нет):
-£) =uiF, тАегг=йги. (2.5)
Если правые части в уравнениях (2.1) равны нулю, то r^ = const
вдоль г-й характеристики. В этом случае решение элементарно
определяется в любой точке (ж, t) по значениям, заданным при t = 0.
Итак, гиперболической системе соответствуют N уравнений (2.4)
или (2.5), которые отражают направленный характер
распространения величин Ti = uiU вдоль характеристических линий.
Отметим, что гиперболическая система уравнений может быть
приведена к виду (2.5) относительно инвариантов Римана и для
26
Гл. 1. Решение волновых задач
некоторых частных случаев нелинейных уравнений (2.1), в
частности для случая двух уравнений (см. [61]).
Разностная аппроксимация вдоль характеристик. Прямой
и полуобратный методы. Чтобы это свойство гиперболических
уравнений (направленный характер распространения инвариантов
вдоль характеристик) сохранить при аппроксимации, необходимо
проводить ее на сетке, образуемой характеристиками, тогда
инварианты переносятся вдоль линии сетки. В общем случае такая сетка
будет криволинейной и неравномерной. Этот способ легко осуществим,
если мы имеем систему всего двух уравнений с двумя семействами
характеристик. Будем называть его прямым методом
характеристик.
Если характеристик больше двух,
то они не будут пересекаться по
одним и тем же узлам. Тогда
необходимо сетку строить по двум
основным характеристикам, а
остальные характеристики выпускать из
узлов этой сетки назад по
времени до пересечения с линиями ос-
Рис. 2.1. Полуобратный метод ха- НОВной сетки и использовать ин-
рактеристик терполяцию между узлами
основной сетки для вычисления величин в точках пересечения. Эти точки
отмечены крестиками на рис. 2.1. Такой метод характеристик
называется полуобратным методом.
Обратный метод. Сеточно-характеристическая схема
Куранта, Изаксона, Рисса. Можно интегрировать уравнения (2.3)
или (2.4) на регулярной нехарактеристической сетке, образуемой
линиями х = const и t = const. В этом случае используется обратный
метод: все характеристики выпускаются назад из узла (n + l,fc),
в котором ищется решение. При этом, чтобы не утратить
полностью направленный характер распространения инвариантных
комбинаций искомых величин вдоль характеристики, аппроксимация
производной dU/dxy входящей в соотношение на
характеристике (2.3), производится односторонней разностью вперед С/^+1 — U]}
(при Xi > 0) или назад Щ — Щ_1 (при А^ < 0) в зависимости от на-
ф
j 2. Одномерные нелинейные волны. Характеристики
27
правления рассматриваемой характеристики (рис. 2.2):
Ui
&п+1
т
At
ТТП
т
Ах
w,-Fn,
(2.6)
где верхний знак — (разность назад по х) отвечает характеристике с
положительным наклоном Л^ > 0, а нижний + (разность вперед) —
Лг<0.
{щ к-1)
Ш — узел регулярной сетки
О — узел, не принадлежащий
регулярной сетке
— характеристика
— направление
(п k+Y) х производных по х
Рис. 2.2. Обратный метод характеристик
Таким образом, необходимо во внутренней точке использовать на
временном слое минимум трехточечный шаблон. Правая часть F
известна и вычисляется в любой удобной для нас точке. Схема (2.6)
является простейшей обратной характеристической схемой. Она
была впервые предложена в работе Куранта, Изаксона и Рисса [79] и
носит их имя.
Можно придать этой записи единый вид, введя следующие
обозначения: |Л| = {|Аг|} — диагональная матрица модулей собственных
значений, Л+ = |(Л + |Л|) и Л~ = |(Л — |Л|) — диагональные
матрицы только положительных и только отрицательных собственных
значений. Тогда в векторном виде (2.6) примет вид
up1
и?
At
Ах
1 At
MUk+i/2 - t4n-i/2)+
+МрП + 2 д^П_11А1«(^-1 " 2t}k
+ Etf+i),
(2.7)
U,
fe±l/2
j№±i
ик),
где П — матрица, составленная из левых собственных векторов
матрицы А.
Последний член в (2.7) играет роль стабилизирующей
вязкости, обеспечивающей устойчивость при выполнении условия
Куранта [54]. Схема (2.6) явная первого порядка точности.
28
Гл. 1. Решение волновых задач
Неявные сеточно-характеристические схемы. Рассмотрим
неявные абсолютно устойчивые сеточно-характеристичекие схемы,
которые позволяют вести расчет с шагом большим, чем курантов-
ский. Такую схему первого порядка точности молено построить без
особого труда, если в схеме КИР (2.6) производные по координате х
брать не на n-м, а на (п + 1)-м слое:
и.
п+1
■т
At
1Ш
ту п+1
tfn+l
Да
w,-Fn+1.
(2.S
Если iSi зависит от решения U, то LOi в каждом слагаемом берется
как среднее значение по индексам, которые меняются, например, в
первом слагаемом как среднее в точках (п + 1, /с), (п, к) и т.д.
Схема (2.8) была предложена впервые в работе [53].
Можно построить неявную сеточно-характеристическую схему
второго порядка точности [44].
Аппроксимируем соотношения (2.4) со вторым порядком точности,
для этого необходимо использовать уже шесть точек — три на слое t
и еще три на слое t + At.
Производные в уравнениях (2.4) по х аппроксимируем полусуммой
односторонних разностей вперед на п-м и (п + 1)-м слоях при Л^ > О,
а производную по t полусуммой в точках {к — 1) и к. При Л^ < О
используем разности назад, т.е. узлы к и к + 1:
2
Ur
n+l
uv
At
\M
ffn+l _ fjn
At
fjn+l fjn _ fjn
Uk^l , Uk Uk^l
+
Aa
4
fc=Fl
, (2.9)
где верхний знак — отвечает характеристике Л^ > 0, а нижний +
отвечает Л^ < 0.
Когда уравнения (2.4) записываются в инвариантах, тогда система
уравнений распадается и достаточно рассмотреть одно уравнение,
например, для Л^ > 0:
§ 2. Одномерные нелинейные волны. Характеристики 29
{rn+l_rn) + {rn+l_rn_i) +
+ ^(rnk-rnk_1+rnk+1-rnk+11) = 2Fk, Xt>0, (2.10)
где Fk — среднее значение правой части по четырем точкам шаблона.
Аналогично (2.10) записывается уравнение для Л^ < 0, где берется
пространственная производная назад.
Полученная разностная схема, по существу, явная, т.к. имеет вид
г1+1=а1_хт^\+Щ.х, (2.11)
77,4-1
что позволяет вычислять гк через предыдущие значения,
если гп+1(0) задано при х = 0 на левом конце интервала.
В краевых физических задачах при х = 0 обычно задается
только часть компонент Ui (г = 1.../с), остальные компоненты Ui
(г = к + 1... N) задаются при х = 1 на правом конце.
Поэтому гп+1(0) неизвестно, и для решения задачи необходимо
использовать метод прогонки. Для этого выразим г о = г(0) через г&:
r0 = ai/2ri+61/2,
гп = Ьк+1/2гк+Мк+1/2, (fc = 0...iV),
где коэффициенты -ZJfc+i/2? ^fc+i/2 вычисляются по явным
формулам:
^fc+l/2 — £/с-1/2а/с+1/2>
-Mfc+1/2 = £fc-l/2&fc+l/2 + bfc_i/2bfc_i/2 H Ь ^1/2^3/2 + ^1/2-
(2.13)
Рассмотрим случай iV уравнений, следовательно, решение
содержит N инвариантов. Граничные условия на концах интервала
задаются в виде линейных комбинаций N инвариантов г^г\ Пусть на
одном конце интервала х = 0 задано М условий, тогда на другом х = 1
задаются N — М условий:
N
X = 0, ^ атгГ0 =Ьт, Ш = 1 . . . М,
N
ж = 1, ^аШг^=Ьш. m = M + l...iV,
г=1
30
Гл. 1. Решение волновых задач
где amiy Ът — заданные величины.
Выражая Гд через г^ , по формуле (2.12) получим систему N
(г)
уравнении для определения rN :
N
' - « „.« , Г (г)
7 . ат* (^JV+l/2riV + ^7V+l/2j = ^т, Ш = 1 . . . М,
г=1
1]а
ш^' = &т, Ш = М + 1 . . . TV,
где Ьдг+1/2 и ^tv+1/2 определяются по формулам (2.13).
Для обратной прогонки воспользуемся уравнением (2.11).
Таким образом, сеточно-характеристическая схема (2.9) - (2.10)
квазиявная, абсолютно устойчивая (будет показано ниже),
второго порядка точности, т.е. обладает редким сочетанием достоинств.
Она предложена в работе [44] и использовалась для решения задач
о распространении плоских волн в упруговязкопластическом
материале [6].
Распространение волн в нелинейно-упругом стержне.
Рассмотрим прямой метод характеристик на примере системы двух
уравнений распространения волн в нелинейно-упругом стержне
с произвольной диаграммой материала напряжение-деформация
а = а(е) при условии, что о'(е) > 0. Система уравнений может быть
представлена в виде двух уравнений относительно скорости v и
деформации г:
dv о / \ д£
— -а (£)— =0, -1 о
dt дх
о Гт (А л ( ° -аЧе)\
Вектор решения и = I ), матрица А = I I зависит от
решения.
Из условия |А — АЕ| = 0 находим Ai}2 = =Ьа(£).
Характеристики системы (2.14) определяются из уравнений
dx
— = ±а(е), dxTa(s)dt = 0. (2.15)
§ 2. Одномерные нелинейные волны. Характеристики 31
Находим левые собственные векторы матрицы А:
щ (А - А; Е) = 0 =>
Ai)2=±a(e)
лл ш2 ч (Та(е) -аНе)\ _ [0\ <* = (1, -а(е)) ,
Ка Ы I "I Ta(£) )-[р) => £2 = (1, +а(£)) .
Дифференциальные соотношения (2.4) вдоль характеристик (2.15),
записанные в полных дифференциалах, примут вид
LJidU = LJiF dt => dv^f a{e) de = 0 при dx = ±a(e) dt. (2.16)
Соотношения вдоль характеристик молено проинтегрировать:
£
ri,2 = vTi>(e), ф(г)= J a{e)de. (2.17)
£0
Таким образом, нелинейная система (2.14) вдоль характеристик
имеет следующие инварианты:
ri — вдоль первого семейства с положительным наклоном,
г2 — вдоль второго с отрицательным наклоном.
Рассмотрим решение задачи Коши системы (2.14) прямым методом
характеристик. При t = 0 заданы
v = vo(x) и е = ео(х). (2.18)
В прямом методе интегрирование проводится на криволинейной
сетке характеристик, которая выстраивается одновременно с
нахождением решения. Разбиваем ось t = 0 с равномерным шагом h
(рис. 2.3). В узлах сетки находим по заданным значениям £о(х)
значения -\-a(so) и из двух соседних точек (ж, t)i+ij, (ж, £)i,j+i выпускаем
характеристики с положительным и отрицательным наклоном.
Xi+i,j+i - Xi+ij = a(ei+lyj) • (ti+ij+i - U+ij),
3^+1, j+1 — xi,j+l — —a\ei,j+l) ' {4+lj+l — H,j+l)-
Здесь принята следующая нумерация узлов сетки: вдоль
положительной и отрицательной характеристических линий изменяется
индекс j к i соответственно (рис. 2.3).
32 Гл. 1. Решение волновых задач
Рис. 2.3.
Из уравнений (2.19) находим две неизвестные величины:
координаты точки пересечения (x,£)i+i,j+i. В эту точку переносятся
(1) (1) (2) (2) ' 1
ri+ij = 4+i,j+i и Чя-i =r1+i,j+i' по котоРым> используя
формулы (2.17), находим
vi+1,j+1 = (rW+rV)
Аналогичным образом определяем решение в остальных точках
пространственноподобного слоя, показанного на рис. 2.3 пунктиром.
После этого молено перейти к следующему слою и т.д., определяя
решение внутри характеристического треугольника, показанного на
рис. 2.3. Таким образом, строится решение с первым порядком
точности.
Для того чтобы получить второй порядок точности, необходимо
провести корректировку или <пересчет> решения. Тогда полученное
решение в точке (ж, £)i+i,j+i рассматривается как первое
приближение. Используя его, уточняются значения наклонов характеристик,
§ 2. Одномерные нелинейные волны. Характеристики 33
они вычисляются как средние значения:
<Ч+1,.7 + 1/2 = 2 (a*+l,J + l + a*+l,j) ?
ai+l/2,j + l = ^ (a*+l,J + l +ai,j + l)
и подставляются в формулы (2.19), в результате находятся уточ-
(1)
ненные координаты нового узла сетки, в который переносятся г\Л
(2)
Распространение волн в стержне из упруговязкопластиче-
ского материала. Рассмотрим еще один пример применения
метода характеристик при постоянной матрице А и при наличии
правой части F(U), зависящей от решения [39]:
dv 1 да
— —— =0 - уравнение движения,
Ot р ох
— —— =0 - уравнение совместности, (2.20)
at ox
да ^dv E±., ч
Ф(сг, е) - определяющее уравнение,
а < as(e),
Ф(0) = 0.
а > as(e),
Здесь последнее уравнение — определяющее уравнение упруговяз-
копластического материала; при а < as(s) оно переходит в закон
Гука, записанный в дифференциальной форме. При r<tc (tc —
характерное время рассматриваемой задачи), т.е. при малой
вязкости а ~ сг5(г), система уравнений переходит в рассмотренную выше
систему (2.14) для нелинейно-упругого материала а ~ as(s)y а при
а < as(s) — в систему для линейно-упругого материала.
Если решается начально-краевая задача для стержня конечной
длины Z, то граничные условия на концах стержня в общем виде
могут иметь следующий вид:
dv
Ai—- + А2 v + А3 а = pi(t) при х = 0,
II (2-20а)
Bi—- + В2 v + В3а = cp2(t) при х = 1,
Ot
34
Гл. 1. Решение волновых задач
где Ау В — постоянные. Начальные условия:
U = U0(x) при t = 0 (2.206).
Перейдем к безразмерным переменным (отмечены знаком черты):
_ х - t а _ а а е _ v v
х=-, t = — =t-, a = — = -^—, £=—, v= — = •
I tc i <JC tLSc £c Vc a £c
Характерные величины выбраны следующим образом: I — длина
стержня; ас — предел текучести, ес = ас/Е — упругая деформация,
соответствующая пределу текучести; а = \/Е/р — скорость
распространения звука в ненапряженном стержне; tc = l/a — время
прохождения упругой волны вдоль стержня длиной Z; vc = аес —
скорость частиц в упругом материале при напряжении ас.
Тогда система (2.20) примет более компактный вид (здесь и далее
используются только безразмерные переменные и знак черты
опущен для краткости записи):
dv да
dt дх
^-^ = 0, (2.21)
dt дх
д(Т dV Г лч/ N
где S = tc/r — безразмерный параметр, который для многих
реальных материалов может быть большим S ^> 1.
Представим систему (2.21) в матричном виде:
~ж+А^ = ^ (2-21a)
где U =
Характеристические числа Л^ определяются из уравнения
|А-А;Е|=0 => Аг(А?-1)=0,
т.е. две характеристики имеют постоянный наклон ±а и совпадают
с упругими, а третья направлена параллельно оси t (рис. 2.4).
j 2. Одномерные нелинейные волны. Характеристики
35
ti
0
к
i
ч|
1 ^1
1
/%
,2Ах,
X \
Г° Х\
ХА,>(К
=
[ *►
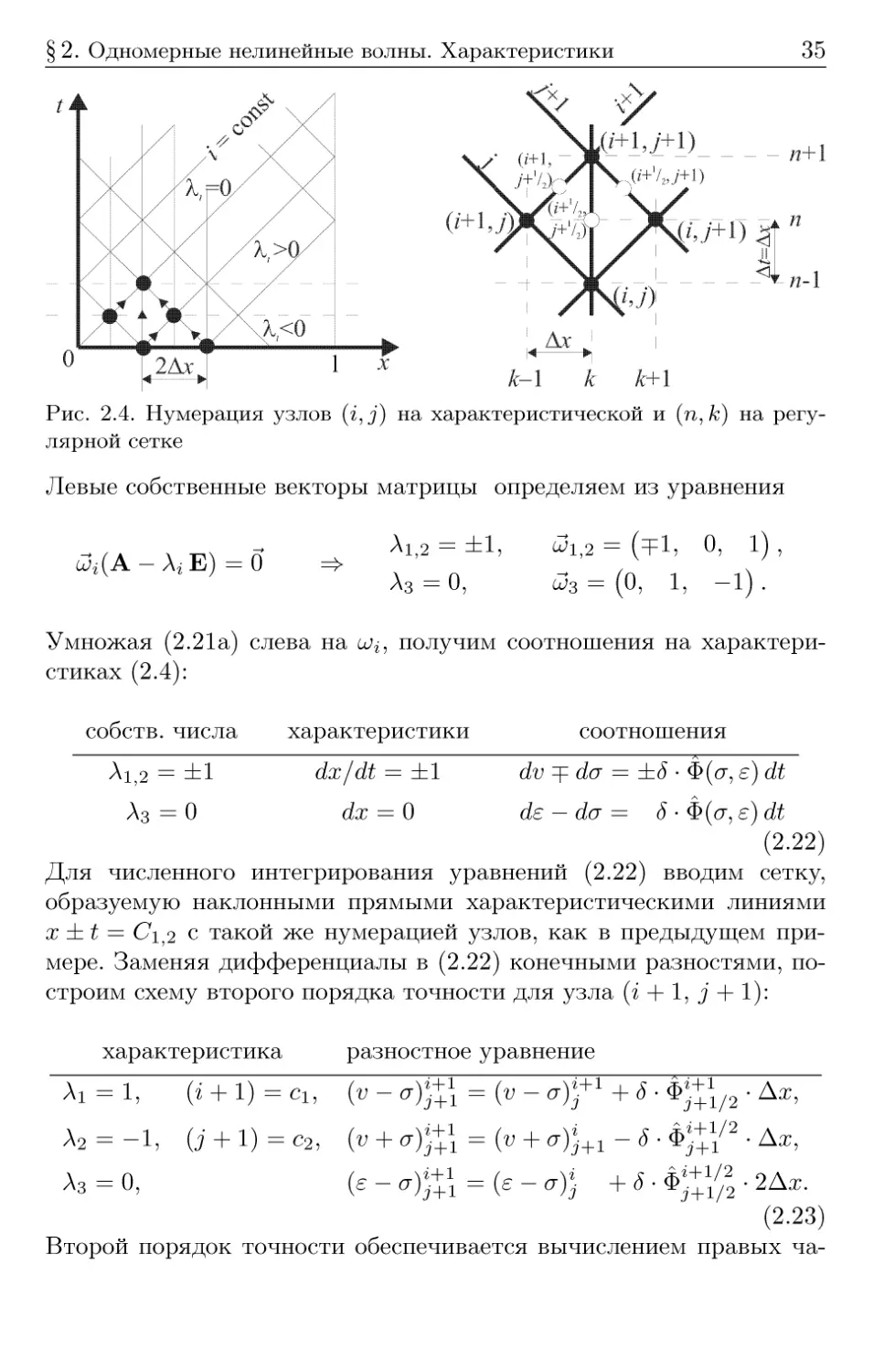
£-1 * Ш
Рис. 2.4. Нумерация узлов (i,j) на характеристической и (п, /с) на
регулярной сетке
Левые собственные векторы матрицы определяем из уравнения
Ui(A-\iE) = 0 =
Al,2 = ±1, <2i,2 = (Tl, 0, 1)
Аз=0, cJ3 = (0, I, -1).
Умножая (2.21а) слева на cj^, получим соотношения на
характеристиках (2.4):
собств. числа характеристики
соотношения
Al,2
Аз
±1 dx/dt = ±1 dv^fda = ±5 • Ф(сг, г) d£
О dx = О ds — da = 5 • Ф(сг, г) d£
(2.22)
Для численного интегрирования уравнений (2.22) вводим сетку,
образуемую наклонными прямыми характеристическими линиями
х ± £ = Ci52 с такой лее нумерацией узлов, как в предыдущем
примере. Заменяя дифференциалы в (2.22) конечными разностями,
построим схему второго порядка точности для узла (г + 1, j + 1):
характеристика
разностное уравнение
Ai = 1, (г + 1) = сь (г; - a)fi_\ = (v - a))+1 + 5 • Ф)++\/2 • Ах,
А2 = -1, 0" + 1)=с2, (г; + <т);+1 = (г; + <7);+1^
а3 = о, (г-*)5li = (*-*)} +д.ф;;а//2.2Дх.
(2.23)
Второй порядок точности обеспечивается вычислением правых ча-
36
Гл. 1. Решение волновых задач
стей в промежуточных точках с дробными индексами (рис. 2.4)
на этапе корректора после того, как вычислены на этапе
предиктор по схеме первого порядка точности Ut+i при известных правых
частях с целыми индексами.
В этом примере а = const = ±1, т.е. характеристики постоянны и
идут под углом 45°. Следовательно, узлы характеристической
сетки (i,j) легко сопоставить узлам регулярной сетки (fc,n) (рис. 2.4).
Чтобы узлы регулярной сетки совпадали с характеристическими,
необходимо брать одинаковые шаги At по времени и Ах по
пространству: At = Ах (рис. 2.4). Перепишем разностные соотношения
на характеристиках (2.23) в терминах узлов регулярной сетки:
характеристика разностное уравнение (регулярная сетка)
Ai = l, (г + 1) = ci, (v - а)^1 = (v - а)^ + 6 • Ф^2 • Ах,
А2 = -1, С? + 1)=с2, (Н^^Н^-^Ф^-Ах,
Аз = 0, (е- а)^1 = (в - а)^1 + 5- Щ • 2Ах.
(2.23а)
Граничные условия (2.20а) в разностном виде при х = 0 примут
вид соответственно для характеристической и регулярной сетки:
a Uj+l Uj , л г+1/2 , , г+1/2 г+1/2
Al " 2Ах" +-42< + A3afc"=^.
Аналогично записывается условие на правом конце х = Z, но
при к = п.
Решение во внутренних точках вычисляем по формулам (2.23), а в
граничной точке на левом конце используем уравнение (2.24) и
второе и третье уравнения (2.23), а на правом конце — первое и третье.
Правило выбора трех соотношений из четырех возможных
уравнений (2.23) и (2.24) при использовании характеристических
соотношений очевидно: отбрасывается уравнение, которое в граничной точке
соответствует характеристике, лежащей вне тела.
§ 2. Одномерные нелинейные волны. Характеристики 37
При использовании в разностном виде исходных уравнений (2.21)
без учета характеристик задача определения решения в граничной
точке переопределена и выбор правильной аппроксимации
затруднен. Неправильный выбор уравнений при построении разностной
схемы в граничных точках может привести к неустойчивым
решениям. То же самое и даже в большей степени относится к расчету
разрывов, если они имеются в задаче и не выделяются при
численном решении. Точно выделить разрывы можно, только используя
характеристические методы расчета.
Приведенные замечания имеют общий характер и относятся к
построению алгоритмов для любых уравнений гиперболического типа
вида (2.1).
Разрывные решения. Уравнение с постоянными
коэффициентами. Рассмотрим расчет разрывных решений на примере
уравнений (2.21). Будем для простоты считать, что массовые скорости
частиц материала и<Са — скорости упругих волн, тогда закон
сохранения импульса и условия совместности на разрывах примут вид
[a}=pD[v], [v]=D[e], (2.25)
квадратные скобки обозначают скачок величины при переходе через
линию разрыва [а] = а+ — а~, D — скорость распространения
разрыва. Для системы уравнений (2.21) с постоянной матрицей скорость
распространения разрыва известна: D = а = Е/р, а для контактного
разрыва D = 0. Поэтому вычисление U~ за разрывом
осуществляется чрезвычайно просто, если известно решение U+ перед ним.
Контактный разрыв. На контактном (неподвижном)
разрыве х = const, подставляя D = 0 в (2.25), получим условия на разрыве:
сг+ = сг-, v+=v~, е+^е~. (2.26)
Для расчета решения в точке п + 1, к необходимо к этим условиям
добавить справа от разрыва второе и третье соотношения на
характеристиках (2.23):
(v+ + а*)?1 = (v+ + а+Тк+1 + 5 . Ф^2 • А,,
(е+-*+)2+1 = (е+-"+)г +<ЬФГ+1/2-2Л*,
38
Гл. 1. Решение волновых задач
а слева — первое и третье уравнения (рис. 2.5а):
г+1/2
{v+ + v+)nk+L = (v+ + <t+)£_i + S • Ф^'ТГ ' Ax,
/2
n+1/2
(a' - ОГ1 = (a' - a^)t + 5- Ф" "^" • 2Ax.
(2.28)
Здесь уже использованы соотношения (2.26). Для определения
четырех величин сг+, г>+, £+ и е~ имеем систему четырех
уравнений (2.27) - (2.28), определитель которой отличен от нуля.
(п+1,к)
п^5^ ^Д) ^ j^
(«Д-1) (иД) (w,£+l) х
(а) (Ъ)
Рис. 2.5. Схема решения на (а) контактном, (Ь) движущемся разрывах.
Постоянные характеристики
Движущийся разрыв. Для расчета решения на разрыве,
перемещающемся с постоянной скоростью D = 1 (в безразмерных
переменных), кроме двух уравнений на разрыве (2.25) нужно справа
взять все три соотношения на характеристиках (2.23), а слева только
первое (рис. 2.5Ь). По соотношениям справа находим решение перед
фронтом волны г>+, £+, а^', а затем по остальным трем уравнениям
с определителем, необращающимся в нуль, находим v~, £_, а~ —
решение за фронтом волны. Решения этих уравнений так же, как и
(2.27) - (2.28), легко записываются в явном виде, если правые части
считать известными. Они действительно известны, когда
разностные уравнения (2.25) - (2.27) решаются итерациями или с
использованием пересчета. Первое приближение вычисляется при известной
правой части
Ф
п+1/2
П,
и только на втором этапе — корректоре, когда решение в точке
(г + 1, j + 1) в первом приближении найдено, используется форму-
2. Одномерные нелинейные волны. Характеристики
39
л а осреднения:
фГ 1/2 = \ (П + П+1) ■
Таким образом, на первом этапе — предикторе — расчет ведется по
схеме первого порядка точности, а на втором — по схеме второго
порядка, и правые части на обоих этапах известны.
Разрывные решения нелинейного уравнения. Обратимся
теперь к примеру нелинейной системы (2.14), когда матрица А = A(U)
зависит от решения U. В этом случае расчет подвижного разрыва
несколько отличается от случая матрицы А с постоянными
элементами, здесь скорость ударной волны заранее неизвестна и находится
из соотношений (2.25) одновременно с решением за фронтом
ударной волны. Из условия устойчивости ударной волны известно, что
должно выполняться неравенство [61]
а+ ^ D ^ а~,
где а+ и а~ — скорости распространения возмущений (углы наклона
характеристик) перед и за фронтом волны.
Тогда конфигурация характеристик перед и за ударной волной
будет такой, как показано на рис. 2.6. Расчет начинается с определе-
(-У(+)
Рис. 2.6. Схема решения на ударной волне. Переменные характеристики
ния координат точки 0\ — точки пересечения ударной волны 00\ с
новым n-м пространственноподобным слоем. Координаты этой
точки находятся как точка пересечения характеристики АО\ с ударной
волной 00\ по известным значениям Dn и qPl на n-м слое. После
этого находим координаты точек В и С. Для этого проводим
положительные характеристики ВО\ и СО\ с наклоном, взятым на n-м слое:
40
Гл. 1. Решение волновых задач
ав = \{о>к + ак+\) и &с = |(ttfc+i + dk+2)- Индексом к обозначаются
точки характеристической сетки вдоль n-го пространственноподоб-
ного слоя. Интерполяцией по слою п (точки сетки с индексами к)
находим значения £в, ^ и £с, vc и, используя соотношения вдоль
характеристик ВО\ и СО\ (2.17) перед ударной волной, находим Eq,
Vq. Далее, применяя соотношения (2.25) на ударной волне, получим
a(e+)-(j(e-)=D2(e+-e~), v~ = v+ + D (e+ - е~). (2.29)
Из соотношения вдоль характеристики положительного
наклона АО\ слева от ударной волны, пересекающей п-й пространственно-
подобный слой в точке А, находим величину
v~ — ф(е~) = va — Ф(£а) = const, (2.30)
Исключая из соотношений (2.29) D и подставляя v~ в (2.30),
находим уравнение для определения е~:
[а(е+) - а{е-)\ (е+ - г~) = (ф{г~) - ф{гА) +vA- v+f . (2.31)
Нелинейное уравнение (2.31) решается относительно е~ методом
Ньютона, после чего находим Dn+1 и v~ из уравнений (2.29).
Далее полученное решение может быть еще раз уточнено по тому же
алгоритму с помощью осреднения всех величин в найденной точке
(п + 1)-го слоя и точках n-го пространственноподобного слоя, на
котором решение известно (рис. 2.6).
Расчет контактного слоя в нелинейном случае осуществляется с
использованием тех же уравнений по алгоритму, мало отличающемуся
от случая, когда матрица А постоянна.
Устойчивость разностных характеристических уравнений.
Для линейных или линеаризованных характеристических уравнений
устойчивость доказывается проще, чем для не характеристических
схем, т.к. соотношение между шагами по пространственной и
временной координатам здесь жестко определено самой
характеристической сеткой, а системы уравнений получаются с матрицей перехода
диагонального вида.
Покажем это на примере разностной схемы (2.23). Поскольку, как
указывалось в § б в [48], правые части уравнений не влияют на устой-
§ 2. Одномерные нелинейные волны. Характеристики 41
чивость, их можно не рассматривать. Применяя преобразование
Фурье по ж и Лапласа по £, находим
(Л - e-ikAx) (v - а)0 = 0, (А - eihAx) (v + a)0 = 0,
(л - £) (е - а)0 = 0, (2'32)
откуда ясно, что |А^| = 1, т.е. условие устойчивости Неймана
выполняется и является не только необходимым, но и достаточным
условием, т.к. матрица перехода диагональная. Более того, из того факта,
что все |Аг| строго равны единице, следует, что в случае однородной
системы уравнений, когда Ф(<т, s) = 0 (упругий случай), схема не
обладает аппроксимационной вязкостью и у нее отсутствует дисперсия
(см. §4). Она имеет бесконечный порядок аппроксимации, т.е. дает
точное решение задачи.
Устойчивость неявной сеточно-характеристической схемы.
Исследуем аппроксимацию и устойчивость схемы (2.9). Для этого
применим преобразование Фурье по х и £, тогда получим
уравнение (2.9) в изображениях г (к):
(1-егшАг) (1 + е~гкАх)г+
+ (1 + elujAt) (1 - егкАх) кг = 2F, (2.33)
где к = A At/h — число Куранта.
Разлагая по степеням г и At и г к Дх, получим с точностью до
второго порядка малости:
{гш + ягк) r = F + 0 (At3 + Ах3) . (2.34)
Уравнение (2.34) есть фурье-изображение дифференциального
уравнения (2.10). Члены второго порядка малости при разложении (2.10)
в ряд обращаются в нуль, если учесть (2.34), отличны от нуля
только члены 0(At3)y 0(Ах3)у т.е. схема (2.10) имеет второй порядок
точности.
Исследуем устойчивость предложенной схемы. Обозначая
exp(icj At) = Л, находим из (2.33) следующее выражение для
множителя перехода на (п + 1)-й слой:
(1 + cos ср) — к(\ — cos ср) + г sin ср (1 + к)
(1 + cos ср) + к(\ — cos ср) + г sin ср (1 — к)'
42
Гл. 1. Решение волновых задач
где введены обозначения ср = к Ах, к = (a At)/ Ax. Нетрудно
показать, что |Л| = 1 при любых к, т.е. условие устойчивости Неймана
выполняется и предложенная схема абсолютно устойчива.
Характеристические и сеточно-характеристические схемы
для решения жестких задач. Для многих реальных
материалов в уравнении (2.21) параметр S ^> 1, а для упругопластического
материала S —► сю. Это следует из последнего уравнения (2.21) при
Ф (а,е) = Ф (а — as(s)) и S —► оо, т.е. а —► os(e). Тогда система
уравнений для упруговязкопластического материала (2.21) переходит в
систему (2.14). Упруговязкопластическую модель молено
рассматривать как регуляризирующую по отношению к упругопластической
модели.
Таким образом, система (2.21) является сингулярно возмущенной
системой гиперболических уравнений и начально-краевые задачи
для нее являются жесткими. В § 4 в [48] рассматривалось решение
сингулярно возмущенных систем обыкновенных дифференциальных
уравнений (ОДУ). Интегрирование таких уравнений должно
проводиться с достаточно большим шагом SAt по неявным или явно-
неявным схемам, если целью является получение
квазистационарного решения, отвечающего упругопластической модели (но не
исследование переходной структуры или погранслоя). Поэтому требуются
А-устойчивые схемы (абсолютно устойчивые при любом SAt).
Вследствие того, что метод характеристик сводит интегрирование
гиперболических систем уравнений (2.1) к интегрированию ОДУ, то
и для этого случая возможно применение методов, схожих с
развитыми в § 19 в [48].
Поскольку схема интегрирования уравнений, содержащих большой
параметр, должна быть неявной, то для характеристических
уравнений (2.23а) построим неявные схемы второго порядка точности:
(v - a)nk+l = (v- <t)£_i + ^ [П+1 + *fc-i] A*,
(г; + <r)£+1 = (v + a)nk+l - 5- [Ф%+1 + Ф£+1] At, (2'35)
(e - a)l+l = (s- а)Г_\ + 5 [Фпк+1 + Фпк~'] At.
Здесь нумерация приведена для узлов регулярной сетки (рис. 2.4).
В системе (2.35) нелинейные члены того же порядка, что и
линейные, поэтому решение итерационным методом по схеме предиктор-
j 2. Одномерные нелинейные волны. Характеристики
43
корректор (в качестве первого приближения используется явная
схема) эффективно только тогда, когда S At мало. При S At ^> 1 следует
применять линеаризацию правой части, раскладывая Ф^+ с
точностью до членов второго порядка (Асг^ ) , иначе схема будет плохо
обусловленной.
Использование явной схемы даже в первом приближении при
решении уравнений (2.35) при S At ^> 1 приводит к плохой
обусловленности.
Напряжение а7] определяется из разности двух первых
уравнений (2.35):
2а
п+1
5 At
0> + °)k+i ~ (" - °)k-i + ^Г №+i - П-i)
или для приращения Аа7} = а7^ — а7}:
Aafe" =^ + \(v + a)nk+1 -\{v- а)пк_, + ^ (Ф£+1 - Ф£_0 .
Нелинейные члены в точке (п + 1,/с) уничтожаются и Аа7]
определяются в явном виде.
Разлагая в третьем уравнении (2.35)
ф»+1 = фп+ф^(Д<т«+1-(ТвПДе»+1),
получим
5 At
Аепк = Аапк + —- Ф'Ц (Aafe"+1 - а^Ае?1),
Ael
1 + ^ф'1^Л4)
Aal
i + ^ ф'1Г
Откуда находим Ае7^. Подставляя найденные значения а7^ и е7^
во второе уравнение системы (2.35), определяем v7^ в явном виде
7,™+! Л,, i лЛп л-w+l I "^ Гфп+! _l ф™ 1
Предложенная схема является локально явно-неявной схемой.
Первые два уравнения — явные. Неявным является лишь третье
уравнение, из которого определяется е7^ . Этого оказывается
достаточным, чтобы сделать расчет устойчивым. Доказательство
приведено в следующем пункте.
44
Гл. 1. Решение волновых задач
Устойчивость характеристической и
сеточно-характеристической схем в случае жестких уравнений. Предположение,
что правые части (2.1) не влияют на устойчивость верно, если
только параметр S ~ O(l). Если S ~ О (Дж-1), т.е. Ах 5 ~ O(l), то тогда
правые части будут влиять на устойчивость. Поскольку, как
упоминалось, этот случай является практически важным, исследуем его
отдельно.
Доказательство устойчивости для явно-неявной схемы (2.35)
проведем на модельной задаче. Примем для упрощения Ф(г) —
линейной функцией, a crs(e) = сто, т.е. исследуем модель идеально вязко-
пластического материала. Тогда третье уравнение в (2.23) можно
отбросить, т.к. е больше не входит в систему уравнений, и после
преобразования (2.23) по Фурье и Лапласу получим
(А-
(А-
= V
i к Ах\
— гкАх\ _
- (a -do),
*^(А + е-<*д*
) (Р2 -Pi),
4 (A + e^fo-px),
р2 = v+ (а -сг0).
5 Ах
(2.36)
А определяем из условия равенства нулю определителя
системы (2.36):
А
i к Ах
-А(Х +
+ А (А + е
-г к Ах\
Л к Ах\
А2 +
Al,2
1) при
2А
1 + 2А
cos(/c Ax)
1
А-е
2А
-А (А +,
-г к Ах\
кАх + А(\ + егкАх]
5 Ах
О,
1 + 2А
О,
где 2А
1
1
5 Ах
■2 А
cos(fc Дж) ± J4A2 - sin2(kAx) ,
(2.37)
^ 1 подкоренное выражение АА2 — sin2 (/с Ах) > 0 и
А — действительное число.
Если cos (к Ах) > 0, то
|Ai|
— (cos(kAx) ± ^Ы2 -sin2(кАх) ]
(cos(k Ax) + 2А)
1
1 + 2А
^ 1.
j 2. Одномерные нелинейные волны. Характеристики 45
Если cos(/c Ax) < О, то |Ai|
5 Ах
1
1 + 2А
<1;
2) при < 1 тах(4А2 — sm2(k Ах)) < 0 и Л —
комплексное,
1т л/АА2 — sin2{к Ах) < 1т у — sin2(к Ах) = г sin(fc Ax),
|Л| < |cos(fc Ах) ±г sin(kAx)\ = 1,
откуда следует, что схема устойчива при условии S Ах = const или
по терминологии, принятой для жестких систем уравнений — А-
устойчивая. Отметим, что явная схема будет устойчивой только при
^ 1, т.е. не является А-устойчивой. Это не позволяет
использовать ее при S ^> 1.
Для интегрирования жестких задач полулинейной системы
уравнений целесообразно использовать неявную сеточно-характеристичес-
кую схему (2.10), т.к. для нее шаг At не связан с Ах условием
Куранта, как для явной характеристической схемы, и может быть
большим, чем Ах/с. Устойчивость схемы (2.10) для жестких задач
доказывается тем же методом на том же примере линеаризованной
системы уравнений идеально упруговязкопластического стержня.
Доказательство здесь не приводится в силу его громоздкости.
Характеристические схемы высокого порядка точности.
Для неоднородных систем уравнений с постоянной матрицей А
можно построить характеристические схемы не только первого или
второго, но и более высокого порядка точности по аналогии со
схемами Адамса и Рунге-Кутты для ОДУ, описанных в § 3 в [48].
Покажем это для системы (2.21), точнее для ее характеристических
уравнений (2.22), которые запишем через инварианты р\^ = v T с?
р3 = е - а:
ds л д1 (2.38)
— =6Ф(рЪр2,Рз),
где -— = — + -— — оператор дифференцирования вдоль dx = dt;
ds dt dx
d d d TT
— = — вдоль характеристики dx = —dt. Интегрируя урав-
dl dt dx
46
Гл. 1. Решение волновых задач
нения (2.38) на шаге длиной Ах от sn до sn + Дх, получаем
Pl(sn + Дх) -Pl(sn) = (5 / Фбк.
Если на интервале [sn, sn + Дх] известны значения
подынтегральной функции Фп ... Фп_/с, то в (к + 1)-й точке по ним молено
построить интерполяционный многочлен fc-й степени Rk(s), приближаю-
щий функцию Ф(з) на интервале [sn, sn + Дх] с порядком (9(Дх/с+1),
если она достаточно гладкая. Тогда
pi(s„ + Дх) = pi(s„) + / i?fc(s)ds + 0(Aa;fe+2). (2.39)
Если точки 5П ... 5п_/с расположены с равномерным шагом, то после
интегрирования в (2.39) получаем формулы, аналогичные формулам
Адамса, которые используются при интегрировании обыкновенных
дифференциальных уравнений:
при к = 1 р}+1 = р}+1 + (ф}+1 + ^Ф}+1) Ах = L'1>i+1,
^+1 _ Г* . /^Av72r
при к = 2 р5+х = Lb-+i + ( иV Ф ) Аж = Я>+1>
j'+i
при к = 3 ^+1 = L»2>i+1 + ( |У3Ф ) Ах = Llj+1
j'+i
и т.д.,
(2.40)
где
уф* = ф* - ф*-1, У2Ф* = Ф* - 2Ф*-1 + Ф*-2,
у3Ф* = Ф* - ЗФ*-1 + ЗФ*-2 - Ф*_3.
Аналогичные формулы получаем, интегрируя два других
уравнения (2.38). Из формул (2.40) ясно, что для получения разностной
схемы порядка 0(Ахк) необходимо использовать данные на к
предыдущих слоях. Чтобы получить их на к первых слоях, необходимо
начинать расчет со схемы первого порядка точности, последовательно
3. Решение связных задач термомеханики
47
увеличивая порядок от г = 1 до г = к. При этом нет необходимости
помнить всё решение на к слоях, достаточно запомнить лишь
значения Ф^.
Аналогичным образом молено построить характеристическую
схему, обобщающую метод Рунге-Кутты.
§ 3. Решение связных задач
термомеханики
При движении теплопроводного сжимаемого газа происходит
изменение температуры и перенос энергии за счет теплопроводности,
которая оказывает существенное влияние на распространение
колебаний. Поэтому приходится одновременно рассматривать два
взаимосвязанных процесса: 1) движение газа или деформируемого
твердого тела под действием приложенного давления, которое
описывается гиперболическими уравнениями, и 2) процесса
теплопроводности, описываемого параболическими уравнениями. Учет
теплопроводности приводит к поглощению высокочастотных составляющих
механического импульса.
Рассмотрим малые возмущения давления р <С Ро? объема V <С Vb
и удельной внутренней энергии Е <С Ео, где величины с индексом о
относятся к невозмущенному состоянию.
Уравнение состояние газа возьмем в виде
(7 - 1)(Ео +Е) = (ро + p)(V0 + V).
Полную систему уравнений с точностью до малых величин первого
порядка можно записать в виде
ди д
_ = c_(w_(7_1)e),
(3.1)
dv ди
dt дх^
де д2е
dt дх2
с — скорость частиц газа,
ди
дх
7 -
где и — скорость частиц газа, j — материальная постоянная,
с = л/poVo — изотермическая скорость звука. Введены переменные
v = cV/Vo, е = Е/с, к = а/су — отношение коэффициента
теплопроводности а к удельной теплоемкости при постоянном объеме су.
48
Гл. 1. Решение волновых задач
Явную разностную схему для системы (3.1) возьмем в следующем
виде:
п+1 п 7,п _ 7,п п _ рп
U3 - U3 _ . ^J + l/2 Vj-l/2 _ ( _ , ej+l/2 ^-1/2
At Ах [1 } Ax
п+1 _ 1)П „,п+1 _ „,п+1
^J + l/2 ^J + l/2 _ ^j+1 ^
At Аж
п+1 _ п п _рп _|_ п „,п+1 ^/п+1
ej + l/2 ej + l/2 _ ej+3/2 ej + l/2^ej-l/2 ^ ~ Uj
>t —— — — С
At (Ax)2 Ax
(3.2)
Система уравнений (3.2) явная, т.к. сначала из первого уравнения на-
77-1-1
ходится значение и- , затем оно используется во втором и третьем
уравнениях. Сетка для термодинамических величин берется
сдвинутой на полшага по отношению к сетке для кинематических величин.
Это дает аппроксимацию второго порядка по пространственной
переменной.
Если в системе (3.2) пренебречь связностью двух процессов, то
система распадется на две независимых: два первых уравнения
описывают распространение звуковых возмущений, а третье —
распространение тепла.
Условия устойчивости для независимых подсистем:
г- At At 1 . ч
^СА~Х<1> "(А^<2- (3'3)
При At —► 0 и Ах —► 0 выполнение второго условия обеспечивает
выполнение первого. Однако на реальной сетке при конечных Ах и At
необходимо выполнять оба условия (3.3).
Чтобы расчет по явной схеме сделать более эффективным, третье
уравнение следует решать с более мелким шагом At /к, чем первые
два, так, чтобы каждый шаг решения волновых уравнений At
сопровождался к шагами решения уравнения теплопроводности. В этом
случае условия (3.3) заменяются условиями
г- ^ At к . п ч
^СА~х<1^ "(А^<2- (3'3а)
Выполнение второго условия (3.3), как отмечалось в §6 в [48],
приводит в случаях гладких решений к неоправданной малости ша-
3. Решение связных задач термомеханики
49
га At. Поэтому в этих случаях эффективнее применять при
аппроксимации параболического уравнения теплопроводности неявную
схему, вычисляя правую часть в последнем уравнении системы (3.2)
на (п + 1)-м слое, оставляя первые два уравнения без изменения.
Тогда третье уравнение будет абсолютно устойчивым и достаточно
выполнения только первого условия устойчивости (3.3). Из
физических соображений ясно, что неустойчивость обычно развивается
из-за высокочастотных составляющих волны, а для них
температура не успевает измениться, поэтому при конечной величине к ^ 0(1)
адиабатическую скорость распространения звука у^ус молено
заменить в первом условии (3.3) на изотермическую скорость с, ослабив
этим требование к At.
В случае, когда к <С 1, нельзя считать, что Ах <С я/с и
должно выполняться практическое условие устойчивости для сср,
которое находится между адиабатической и изотермической скоростями
звука с < сср < у/7 с- Условие устойчивости должно зависеть в этом
случае от двух параметров:
At At
Это практическое условие устойчивости может быть получено
на основании признака устойчивости Неймана: |Лтах| ^ 1 + (9(At),
где О (At) можно отбросить, т.к. степень роста компоненты Фурье
приближенного решения не должна превышать степень роста
точного решения, а оно затухает по t. Применяя спектральный анализ
(см. §6 в [48]) к исследованию системы (3.2), найдем, что
собственные числа матрицы перехода определяются из условия
Л —1 2гь> since 2iu(j — 1) since
2i\i/ since Л — 1 О
2i\i/ sin се О Л - 1 + 2/iA(l - cos(2ce))
се = ^k Ax.
Можно показать, что условие (3.4) выполняется при
о,
(3.4)
»<ХГ-^Г- (3-5)
V 7 + 2м V ;
При /i<l условие (3.5) дает ограничение на шаг v < 1/y/j,
совпадающее с условием Куранта при адиабатической скорости распро-
50
Гл. 1. Решение волновых задач
странения возмущений, а при \± ^> 1 при изотермической скорости.
При \± ~ 1 средняя скорость с < сср < y/j с.
Численные расчеты показали, что устойчивость решения по
схеме (3.2) выполняется далее при знаке равенства в условии (3.5) [60].
§ 4. Дифференциальные приближения
разностной схемы. Устойчивость
Гиперболическая и параболическая формы (50). Пример (52).
Устойчивость (53). Анализ диссипативных и дисперсионных свойств (53).
Пример (56). Исследование свойств разностных схем при разрывных
решениях (57). Сглаживание нефизических возмущений при расчете на реальной
сетке (62).
Гиперболическая и параболическая формы. Рассмотрим
дифференциальное уравнение
£-А* <4Л,
где А — матрично-дифференциальный оператор по
пространственным переменным л^.
Аппроксимируем (4.1) двухслойной разностной схемой с матрицей
перехода G с n-го временного слоя на (п + 1)-й.
уГ+1{х) =Gun(x). (4.2)
При этом, как уже отмечалось (см. § 1 в [48]), совершается переход от
бесконечномерного функционального пространства к
конечномерному векторному пространству. Хотя решения (4.1) и (4.2) определены
в разных пространствах, молено считать, что разностные уравнения
удовлетворяются функциями непрерывного аргумента в каждой
точке области. Тогда разностные операторы можно представить через
дифференциальные, используя разложения в ряд Тейлора. Нетрудно
получить, разлагая в ряд по параметру т, что для оператора сдвига
на шаг т по времени То (г?) = u(t + т) будет справедливо операторное
представление
Тп — ptD° — V^ — Dn
0 ~ ^ п\ °'
дп
lnerD° =тД),
где D% = —. (4.3)
§ 4. Дифференциальные приближения схемы. Устойчивость 51
Аналогичная формула верна и для оператора сдвига на hi по
пространственной переменной Ti(u) = u(xi + hi):
оо
0hiDi
h? _ _ дп
«- = EiB". гда д? = я^. < = 1'2'3-
п! г' " г <9х"
п=0 *
(4.4)
Из (4.3) и (4.4) следует, что разностная схема (4.2)
эквивалентна дифференциальному уравнению бесконечно большого порядка с
быстро убывающими коэффициентами, если г и hi малы
дй sr^ тп х дпй А _ ^г^ dni
^ п\ dtn ^
= 2 /С1+/С2+/Сз
UU \Г~^ I U U ._> ^-^ U U , >
Г7, = 2 t.1^fcn4-fco=«. 1 2 d
и ряды (4.5) сходятся. Коэффициенты ряда в правой части
имеют порядок с/С1 &2 ^3 = О (/^i, /г 2 •> ^з)> ^ — целые числа,
fci + /ь2 + ^з — ^ ^ 1- Первые члены в левой и правой частях
уравнения (4.5) имеют выписанный вид в силу условия аппроксимации
уравнения (4.1).
Уравнение (4.5) есть гиперболическая или Г-форма
дифференциального приближения разностного уравнения (4.2).
Заметим, что если к (4.4) и (4.5) применить преобразование Фурье
по t и Xi, то оператор Do можно трактовать как s-параметр
преобразования по t, a Di как /с-параметр преобразования по х^.
оо
/ f(x — г) exp(ikx) dx =
—00
00
= ехр(г/ст) / /(£) ехр(г/с<^) d£ = f(k) ехр(г/ст),
оо
где/»= J /(Oexp(ifcO^-
Можно получить параболическую или U-форму для того же
разностного уравнения, если производные по £ n-го порядка (n ^ 2) в
уравнении (4.5) выразить через производные по ж, используя
уравнение (4.1). Другими словами, если рассматривать
дифференциальное приближение (4.5) на решениях дифференциального
уравнения (4.1), тогда получим П-форму, которая не содержит высших
52
Гл. 1. Решение волновых задач
производных по t:
ди _> v-^ дпй
m=Au + h Ph dk^k^x^dxfdxf (46)
к1+к2+к3=п 12 6
Пример. Рассмотрим дифференциальные приближения на
простом примере уравнения переноса:
ди ди _
— а —— = О, а = const. (4.7)
at ox
Аппроксимируем это уравнение трехточечной разностной схемой
т
А0ип(х) =ахА1ип(х), к= - = const, (4.8)
где введены обозначения
0 _ и • —щ, Ai — ui+1 - ui, z\_i —щ— ui_1.
Разлагая разности Ао и Ai в ряд Тейлора, получим Г-форму
разностного уравнения (4.8):
ди ди ^л/гп_1 / дпи п-лдпи\ ,t ч
т=ад-х + ^>^г{ад^->(~ a^J' (4'9)
n=2 v /
а П-форма запишется так:
-=а-+) а—— (1-хп 1ап М-—. (4.10)
dt дх ^ п\ v ; джп v J
n=2^ v /
Коэффициент при старшем члене в (4.10): «2 = ah(l — ка)/2у а
остальные члены имеют более высокий порядок: ап = О (/in_1),
n ^ 3. Ограничиваясь главным членом в разложении (4.10),
получим первое дифференциальное П-приближение:
ди ди ah. .д2и ^/7оч , л ,, ч
^=«^ + Y(l--)^ + 0(/l2), (4.11)
§ 4. Дифференциальные приближения схемы. Устойчивость 53
Устойчивость. Исследуя свойства первого дифференциального
П-приближения, можно сделать важные заключения о свойствах
разностного уравнения. В частности, можно определить его
устойчивость.
_ дй дй
Простой разностной схемой системы уравнений —- = А—— назы-
ot ох
вается схема вида
2
^+\х) = J2 вк^ (х + h£k), (4.12)
к=1
включающая только два узла на п-м слое. Здесь В к — матрицы, h —
шаг сетки, £& — целые числа.
Теорема. Простая разностная схема (4-12) аппроксимирует
систему уравнений (4-1), если выполняются условия
Вг+В2 = Е, £i£i + &В2 = А.
Кроме того, если первое дифференциальное приближение И-формы
(4-^2) является неполной параболической системой, то это
условие является необходимым для устойчивости схемы (4-12), а при
симметричной матрице А и достаточным.
Доказательство этой теоремы приведено в монографии [72], где
исследование разностных схем с помощью дифференциальных
приближений используется систематически.
Система дифференциальных уравнений будет неполной
параболической, если матрица коэффициентов при производных второго
порядка будет неотрицательной, D ^ 0.
Например, схема (4.8) является простой. Ее первое
дифференциальное приближение (4.11) имеет коэффициент при второй
производной ^(1 — ха) ^ 0, если яо ^ 1 и, следовательно, на основании
приведенной теоремы схема устойчива при выполнении условия
Куранта. Это согласуется с выводами, полученными ранее (см. §6 в [48]).
Анализ диссипативных и дисперсионных свойств. По
первому дифференциальному приближению можно судить не только об
устойчивости схемы, но и о ее диссипативных и дисперсионных
свойствах [72].
Рассмотрим эти свойства на простых примерах.
54
Гл. 1. Решение волновых задач
Решение системы гиперболических уравнений с постоянной
матрицей А
ди ди
dt дх
как было показано в § 2, может быть сведено к интегрированию п
независимых уравнений для инвариантов г^ вида
дт' дт'
ef+^ = 0, < = !...», (4.13)
по г нет суммирования, п — порядок матрицы А.
Поэтому молено ограничиться исследованием расчетных схем и их
диссипативных свойств только для одного скалярного уравнения ви-
да (4.13).
Рассмотрим для него произвольную двухслойную схему:
гп+1
(х) = J2 birn(x + lh), (4.14)
где 2L — число точек на п-м слое используемого шаблона схемы.
Параболическая форма разностного уравнения (4.14) может быть
записана в виде
оо
дт дт v-^ 9mr
Ы+ад-х = Т,С^> (4-15)
га=2
где cm — коэффициенты, зависящие от Ь&, т и h.
Импульс произвольного вида, задаваемый при t = 0 в виде
г (0, ж) = го (ж), может быть разложен в ряд Фурье:
г0 (ж) = ^ап
2шх/\п
Каждой гармонике с волновым числом к = 27г/Л этого ряда в
решении (4.13) будет соответствовать бегущая гармоническая волна вида
ехрг (кх — out),
где Л — длина волны, и — частота. Скорость, с которой
распространяется в пространстве фиксированная интенсивность волны или
фаза каждой гармоники, равна
2тг ,
(р = кх — out = —- [х — ар t),
Л
§ 4. Дифференциальные приближения схемы. Устойчивость 55
где ар = и/к — фазовая скорость.
В общем случае в среде отдельные гармоники импульса
распространяются с разными фазовыми скоростями ар, что приводит к
искажению первоначальной формы импульса. Зависимость ар(Х)
характеризует дисперсию импульса. Если dap/d\ > О, т.е. гармоники
с большей длиной волны распространяются быстрее, чем с
меньшей длиной волны, то дисперсия называется нормальной. Импульс
при этом расплывается в пространстве. Если же dap/d\ < 0, то
дисперсия называется аномальной, импульс в пространстве искажается.
Фурье-компонента ехр(г/сж) в решении уравнения (4.13) за время т
изменяется на величину ft = ехр(—гит) = ехр(—гна^), где для
удобства сравнения решений дифференциального уравнения (4.13) и
разностной схемы (4.14), аппроксимирующей его, введены обозначения
к = г/(ah), £ = kh. Если \ft\ = 1, то диссипации не происходит, а
аргумент изменяется на
Ф = argO = —на^.
Величину ft можно трактовать как образ оператора сдвига на
величину т решения уравнения (4.13).
Применяя преобразования Лапласа по времени и Фурье по
пространству к уравнению (4.3), получим образ оператора шага по t:
То —► ехр(т s) и по х: Do —► г к, где s — комплексный параметр
преобразования Лапласа по t. Для разностной схемы (4.14) получим
Р
exp(rs) = ^frmexp(-im^),
Преобразуя по Фурье П-форму (4.15), получим
£ ОО
Т z—'
га=2
откуда нетрудно найти \р\ и <I>/l = argp и сравнить их с \ft\ и
Ф = arg£l, характеризующих точное решение исходного
дифференциального уравнения (4.13):
_ /Imp
Фн = argp = arg tg-—
\ Repy
ОО
= т Im s = -ка^ + т ^ ЫГ k2m+l c2m+l,
ra=l
56
Гл. 1. Решение волновых задач
АФ = Фк-Ф = т^2(-1)тк2т+1С2т+1 (4.16)
га=1
величина АФ определяет дисперсию разностной схемы или ее
фазовую ошибку.
Диссипация разностной схемы определяется величиной разности
D = \Sl\-\p\,
D = 1 - exp (r Re s) = 1 - exp ( -т ]Г (-l)m/c2mc2m J . (4.17)
Элементарное волновое решение дифференциального
представления (4.15) разностной схемы (4.14) имеет вид
exp [—fiek2t + ik(x — aet)
(1 - D)nexp I Щж - at) + —- АФ,^
1 rk
(4.18)
где
Me = -^(-irfc2m"2C2m,
ra=2
oo
ае=а-^(-1ГЛ2га+1.
ra=2
Если для какого-либо волнового числа к коэффициент аппрокси-
мационной вязкости будет \хе < 0, то тогда схема некорректна и
вычислительный процесс неустойчив. Величина ае есть эффективная
скорость распространения волны. Если для некоторого волнового
числа к эффективная скорость ае < 0, то уравнение (4.15)
некорректно и разностная схема неустойчива. Видно, что главный член ае
определяется коэффициентом сз, который не связан с диссипатив-
ными свойствами.
т-г т^ ди ди
Пример. Рассмотрим для уравнения ——\- а—— = 0 двухслойную
at ах
разностную схему
До п/ ч , Ai + A_i n z//i2AiA_i n
—ип(х) + а ип(х) = — ——ип(х) (4.19)
т т 2т а1
4. Дифференциальные приближения схемы. Устойчивость 57
вида (4.14) при L = 1, тогда / = —1, 0,1, что соответствует bo = 1 — v
и b=pi = \{у ± ха), z/ > 0 — параметр разностной схемы.
При z/ = 1 получаем схему Лакса, при v = х2а2 — Лакса-
Вендроффа второго порядка аппроксимации, а при v = ка — схему
Годунова. Схемы Лакса и Годунова имеют первый порядок
аппроксимации. Условие устойчивости для (4.19) имеет вид
н2а2 < v < 1.
При малых ^ = kh находим выражение для диссипации:
( I {v - я2а2) i2 + 0(Ц4) при оА2,
D=\ \
-(l-A2)AY + OK6) при v = ^a2.
v 8
Дисперсия или фазовая ошибка равна
АФ/, = - (1 + 2xV - Зи) ка^ + (9(^5).
Отсюда ясно, что 2/ схем первого порядка точности диссипативный
эффект преобладает над дисперсионным, он второго порядка
малости, а дисперсионный — третьего. Для схем второго порядка
точности картина обратная: диссипативность имеет четвертый
порядок, а дисперсия — третий, и, следовательно, преобладает
последний эффект. Следствием этого факта является, что в схемах
первого порядка эффекты диссипации проявляются достаточно сильно
и паразитные колебания, возникающие на разрывах, очень быстро
затухают, профиль волны получается гладким. У схем второго
порядка возникающие паразитные колебания слабо затухают и
сказываются во всей области движения. Такие колебания характерны
для ударных волн в схемах второго порядка. Более детально этот
вопрос может быть рассмотрен, если, следуя работам [72, 86],
применить к исследованию разрывных решений асимптотический метод.
Исследование свойств разностных схем при разрывных
решениях. Дифференциальные приближения позволяют судить о
свойствах разностной схемы не только на гладких, но и на
разрывных решениях [86]. Например, уравнение (4.7) допускает разрывные
решения. Возникает вопрос: как ведут себя решения разностного
уравнения (4.8) при решении задач с разрывами?
58
Гл. 1. Решение волновых задач
Исследуем этот вопрос для семейства трехточечных разностных
схем предиктор-корректор уравнения (4.7). Предиктор выполняется
по схеме Лакса:
W/2 =1Ы+ <+0 - "* (< + <+0 >
О < z/< 1,
Ui-l/2
1
и? -и?_л) - ук{г
H-i
-О
(4.20)
Обозначения показаны на рис. 4.1. Основные узлы обозначены
-—Ь и+1/2
/-1 /-1/2
i i+l/2 i+l
Рис. 4.1.
сплошными кружками, а промежуточные с полуцелыми
индексами — незакрашенными кружками. Корректор выполняется по
схеме крест. Для вычисления пространственной производной
используются значения функций с полуцелыми индексами, полученными на
промежуточном шаге:
v?+1 =*?-*(*%$-,£$). (4.21)
После исключения величин с полуцелыми индексами находим
,п+1
"УС U УС
при z/ = 1/2 разностная схема (4.22) совпадает со схемой Лакса-
Вендроффа. Разлагая все члены уравнения (4.13) в точке с
индексами (п, г) по степеням г и /г, получим эквивалентное ему дифферен-
§ 4. Дифференциальные приближения схемы. Устойчивость 59
циальное уравнение
dt + адх + ^ {2к + 1)! \ dt2^1 + К дх2^1) +
~ 2fc-l /Л 2k+2d2ku\ /лп^
+ E^r(^F+^-^^=0. (4.23)
k=l v 7
Поскольку для любой явной схемы параметры v и к —
фиксированные конечные величины 0 < к ^ 1, то (4.23) содержит один малый
параметр т, степени которого возрастают в коэффициентах с ростом
порядка производных. Будем искать решение (4.23) в виде
разложения в ряд по степеням малого параметра т:
и = и0 + та(1) + т V2) + ...
Предполагая, что решение изменяется плавно: и ~ ди/dt ~ ди/дх
одного порядка, получаем для нулевого приближения уравнение
{du/dtf + а (ди/дх)° = О,
совпадающее с аппроксимируемым уравнением (4.7). В отличие от
параболического приближения уравнения (4.23), решение которого
ищется и которое не допускает разрывов, это уравнение допускает
разрывные решения. Поэтому в окрестности разрыва решение и0
отличается от и на величину O(l), а не на О (г), как в области гладкого
решения. Происходит это из-за того, что в окрестности линии
разрыва х = at предположение о равенстве порядков и и ди/dt неверно.
В направлении /3, ортогональном этой линии, производные велики и
это необходимо учитывать при разложении и приравнивании членов
одного порядка малости. Для этого перейдем к новым переменным /3
и се, введем неизвестный малый параметр Л, который характеризует
скорость роста решения в направлении /3, нормальном фронту
волны:
{ a = t,
за вторую переменную оставляем время t. Тогда уравнение (4.23)
60
Гл. 1. Решение волновых задач
примет вид
ди ^
Jim
да
га=1
' (2т
2га-1
2т!
+ 1)!
(д2ши
\да2т
fd2m+1u 1 д2т+1и
уда2т+1
1 д2п
+
я-2т Q2m+lu
Хдр
2m
+ 2z/-
Д2т+1 0р2т+1
я-2т+2 Q2m,
x2m dp
2m
0. (4.24)
В это уравнение входят два малых параметра г и Л, которые
связаны между собой. Эту связь можно найти, если и разложить по
степеням Л:
и = щ + Xui + ... (4.25)
Подставляя (4.25) в уравнение (4.24), находим, что главным членом
при v ^ 1/2 будет первый член второй суммы, при этом должно
выполняться условие Л = т1'2 так, чтобы его порядок был бы O(l). Для
нулевого приближения в окрестности разрыва получаем
дщ , 2 92щ , 2 2ь> — 1
При и = 1/2 разностная схема имеет второй порядок точности,
член в правой части (4.26) обращается в нуль, главным членом
разложения в (4.24) становится первый член в первой сумме. Поэтому
(4.26)
Л
г2/3
а уравнение для щ принимает вид:
да
>д3
щ
Ь\
1
(4.27)
1 д(3* ' -1 б
Как видно из (4.26) и (4.27), в окрестности разрыва поведение
решения описывается разными уравнениями для разностных схем
первого и второго порядков точности. Решение уравнения (4.26) должно
удовлетворять условиям сопряжения с медленноменяющимся
решением и0 при /3 = ±оо:
при
при
р-
р-
+оо,
— оо,
(4.28)
где uf± — значения и0 перед и за фронтом волны разрыва.
Это решение можно получить в аналитическом виде через
интеграл ошибок:
щ = и_ +
— I e~z dz
(4.29)
\ 4. Дифференциальные приближения схемы. Устойчивость
61
где (3
х — at
1/2
2 \tb;
Профиль решения показан на рис. 4.2а в масштабе т. Хотя
теоретически ширина переходного профиля бесконечна, эффективная
ширина Дх, вычисляемая по формуле (4.30), оказывается конечной
величиной при фиксированном t и растет со временем по степенному
закону одной второй
Ах-
max
ди I
дх I
ыг1'2.
(4.30)
Решение уравнения (4.22), удовлетворяющее условиям (4.28), ЗаПИ-
£+ ^
и »
£А
л
р
(а)
(Ъ)
Рис. 4.2.
сывается через функцию Эйри Ai(z) и имеет вид
3 ~
щ = и_ +
и°+-и°_ l it
Ai(z) dz ,
£ = (3а~1/3. (4.31)
Здесь эффективная ширина ударной волны определяется
формулой
Да
Аг(0)
Профиль волны имеет осциллирующий характер, затухающий на
бесконечности рис. 4.2Ь, а эффективная ширина ударной волны
растет со временем по закону одной трети. Таким образом, решения
вблизи разрыва по схеме первого и второго порядков качественно
62
Гл. 1. Решение волновых задач
отличаются. Для схем первого порядка профиль гладкий с
эффективной шириной, растущей по степенному закону одной второй, а
для схемы второго порядка осциллирующий с эффективной
шириной, растущей медленнее, по закону одной трети. Следует отметить,
что эти свойства являются общими для всех схем первого и
второго порядков точности при постоянной матрице А. Различие состоит
лишь в коэффициенте 6, который зависит от конкретного вида
схемы. Минимизируя его выбором схемы, изменяя параметр z/, можно
найти схему с минимальной шириной ударного перехода.
Интересно отметить, что для линейных уравнений с постоянными
коэффициентами схема, обладающая минимальной шириной
ударного перехода, является одновременно и схемой минимальной вязкости
на гладких решениях. Это легко показать на примере
рассмотренного нами семейства схем (4.22).
Запишем для этого первое дифференциальное приближение (4.23)
в П-форме. Оставляя в уравнении (4.23) только члены порядка т,
полагая, что г = /г/а, и заменяя производные по t производными
по ж в силу уравнения (4.7), получим
ди ди т , ч д2и
ПРИ V>1'2 Tt-aTx = 2{2v-1)^
. ди ди т2 _о ч д3и
при v = l'2 -ш-атх = ^и~ "1}^з-
Отсюда видно, что коэффициенты в правых частях те же, что и в
уравнениях (4.26) и (4.27) соответственно. Рассмотренное семейство
схем устойчиво при v ^ 1/2 и неустойчиво при v < 1/2, а схема с
минимальной шириной ударной волны является одновременно и схемой
минимальной вязкости.
Отметим, что это свойство, строго говоря, верно только для
линейных уравнений. Для нелинейных волн положение сложнее: схемы,
устойчивые на гладких решениях, могут оказаться неустойчивыми
на разрывных решениях. Это показано на примерах. Общих
результатов пока получить не удалось [72, 86].
Сглаживание нефизических возмущений при расчете на
реальной сетке. В заключение приведем некоторые общие
соображения по практическому использованию результатов исследования
устойчивости по дифференциальным приближениям на реальной
сетке с конечным шагом интегрирования.
§ 4. Дифференциальные приближения схемы. Устойчивость 63
Из уравнения (4.5) видно, что разностное уравнение при
конечных г и h эквивалентно дифференциальному уравнению бесконечно
высокого порядка с малыми коэффициентами при старших
производных, а вовсе не уравнению первого порядка (4.1), для которого
аппроксимация имеет место только при т^О и h —► 0. В
действительности расчет всегда ведется с конечными шагами, и решение
разностного уравнения будет отличаться от решения исходного
дифференциального уравнения так же, как решение последнего
отличается от решения дифференциального уравнения высокого порядка
или в первом приближении от своего первого дифференциального
приближения. Различие в решении этих дифференциальных
уравнений изучается в теории дифференциальных уравнений с малыми
коэффициентами при старших производных. Из нее известно, что
решение для нулевого приближения, которое соответствует
аппроксимируемому уравнению (4.1), передает поведение только
медленно меняющейся части решения, а быстро меняющиеся гармоники у
этих решений совершенно разные. Следовательно, и результаты
решения разностного и дифференциального уравнений при конечном
шаге интегрирования близки только для гладких решений, а для
быстроизменяющихся решений такой близости нет. Это зависит, с
одной стороны, от гладкости решения исходной задачи, а с другой —
от согласованности граничных условий разностных и
дифференциальных уравнений. Необходимо, чтобы аппроксимация граничных
условий была такой, при которой не возникало бы псевдокраевого
эффекта, т.е. граничные условия для высших дифференциальных
приближений должны быть такими, чтобы решение стремилось на
границе к нулю при г —► 0 и h —► 0.
Исследование устойчивости, корректности и сходимости краевых
задач для разностных уравнений — наиболее трудные и слабоизу-
ченные вопросы теории вычислительных методов. Читатель, по-
видимому, обратил внимание на тот факт, что теоретические
вопросы исследования устойчивости дифференциальных приближений и
др. касаются почти исключительно задач с начальными условиями
и только в очень слабой степени краевых задач.
Из сказанного следует, что вероятным источником всевозможных
неприятностей являются границы тела и линии разрывов решений.
Именно здесь возникают незатухающие, а в случае неустойчивой
схемы — растущие во времени по амплитуде колебания, которые в
дальнейшем распространяются на всю область решения.
64
Гл. 1. Решение волновых задач
Отсюда ясно, что быстроменяющиеся компоненты решения
разностного уравнения при конечных размерах сетки не несут никакой
объективной информации о реальном решении и являются
паразитными, связанными с чисто вычислительным аспектом. Поэтому от
них молено и нужно избавляться по ходу вычислений. Это улучшит
качество получаемого решения, если сетка недостаточно мелкая.
Когда в решении появляются высокочастотные колебания явно
нефизической природы, следует после каждой серии из нескольких
шагов по времени производить искусственное сглаживание решения,
т.е. отфильтровывать паразитную негладкую компоненту
разностного решения. Более того, такой прием можно применять даже при
расчете по неустойчивой схеме. Сглаживание будет каждый раз
стабилизировать решение, устраняя высокочастотные колебания,
которые являются причиной неустойчивости. Именно такое сглаживание
и производят абсолютно устойчивые разностные схемы, только
происходит это автоматически без вмешательства вычислителя.
§ 5. Упражнения
1. Привести к характеристическому виду систему уравнений
одномерного нестационарного движения идеального баротропно-
го газа и записать для нее сеточно-характеристическую схему
Куранта-Изаксона-Риса.
2. Решить задачу Коши на интервале времени 0 ^ t ^ to = 1/соУ
со = Е/р с помощью прямой характеристической схемы
интегрирования уравнений для бесконечно длинного нелинейно-
упругого начально напряженного стержня:
при t = to: cr = его sin(7r x/l), v = 0.
Материал стержня сталь Е = 2 • 105 МПа, I = 0.5 м.
Диаграмма материала степенная:
а ( е
о~о \£о
сг0 = 2 • 102 МПа, е0 = сго/Е, п = 1/2.
5. Упражнения
65
3. Решить задачу (плоская деформация) о вдавливании
жесткого эллиптического штампа в идеальнопластическую
полуплоскость. Штамп наполовину погружен в плоскость и движется с
постоянной скоростью v = Vo (рис. 5.1). Уравнения жесткопла-
стической среды см., например, в [27]. Уравнение для
эллиптического штампа
а2 + б2 '
а = 5 см, b = 1 см. В безразмерных переменных скорость
^о = 1, предел текучести as = 1.
b
л х
Т77777777777?
— — —•— — — ^77777777777777777*
4. Решить задачу о продольном ударе по упругому
стержню с постоянной скоростью v = г>о, используя сеточно-
характеристическую неявную схему первого порядка
точности. Упругая скорость с = 5 • 103 м/с, приложенная скорость
^о = 1 м/с.
5. Исследовать с помощью П-формы устойчивость схемы Лакса-
Вендроффа второго порядка точности для одномерного
волнового уравнения.
6. Определить П-форму (параболическая форма) первого
дифференциального приближения схемы Лакса для волнового
уравнения. Доказать устойчивость схемы по П-форме.
7. Сеточно-характеристическим методом Куранта-Изаксона-Ри-
са решить одномерную задачу о распространении плоской
волны сдвига в бесконечном слое толщины h из нелинейно-
упругого материала. На поверхности слоя х = 0 в момент
времени t = 0 прикладывается постоянная нагрузка а\2 = его H(t),
66
Гл. 1. Решение волновых задач
тыльная сторона х = h свободна от напряжений. Модуль
сдвига G = 105 МПа. Определяющее уравнение материала в
безразмерных переменных имеет вид
/ \ 1/2
*1 = а(£л) ,
^о V £о J
h = 5 см, ао = 102 МПа, £0 = &o/G, a = 0.1.
8. В задаче из упражнения 7 для упруговязкопластического слоя
аналитически определить интенсивность напряжений сдвига на
фронте волны, используя соотношения на характеристиках и
условия на сильном разрыве. Уравнения приведены в § 2.
Вязкость линейная.
9. Решить одномерную задачу распространения волн в
упругом стержне по неявной трехточечной схеме. На левой
границе х = 0 задано напряжение сгц = aoH(t). Правая граница
свободна: ац(х = I) = 0.
Для решения полученной системы использовать метод
прогонки. Материал стержня: сталь Е = 2 • 105 МПа, его = 3 • 102 МПа.
10. Решить задачу о распространении одномерных упругих волн в
слое толщины h при ударе по границе слоя с постоянной
скоростью v(x = 0) = vo H(t), приложенной под углом 30° к
нормали. Тыльная сторона свободна от напряжений. Использовать
неявную сеточно-характеристическую схему второго порядка
точности на четырехточечном шаблоне (см. (2.10)). Систему
уравнений привести к инвариантам Римана. Упругие
константы Е = 2 • 105 МПа, v = 0.3.
11. Провести исследование диссипативных и дисперсионных
свойств схемы Лакса методом 1-го дифференциального
приближения для задачи распространения упругих волн сдвига.
12. Провести исследование диссипативных и дисперсионных
свойств схемы Лакса-Вендроффа методом 1-го
дифференциального приближения для задач о продольных упругих волнах.
13. Методом конечных разностей решить неустановившуюся
задачу о расширении сферической полости радиуса г о = 1 см, на-
5. Упражнения
67
ходящейся в безграничной упруговязкой среде. К границе
полости приложено внутреннее давление аг = ро е~г^°.
Начальное состояние среды невозмущенное. Используя схему крест,
определить напряженно-деформируемое состояние до
момента t = 2 to. Принять ро = 20 МПа, to = Зт, модуль упругости
Е = 2 • 105 МПа, коэффициент Пуассона и = 0.3, время
релаксации т = Ю-4 с.
14. Решить задачу распространения продольных волн в нелинейно-
упругом стержне с билинейной диаграммой с модулем
Е\ = 0.1 Е. По концу стержня х = 0 наносится удар v = vo • H(t).
Конец х = I жестко закреплен. Использовать неявную
характеристическую схему 2-го порядка точности.
Глава
2
Разностные схемы
расщепления
§ 6. Общая схема расщепления
Явная схема расщепления (68). Неявная схема расщепления (70).
Устойчивость (70).
Разностные схемы расщепления являются одним из
эффективнейших способов решения многомерных эволюционных задач механики
сплошных сред. Они позволяют сводить решение сложной системы
уравнений к последовательному решению более простых задач и
получать за счет этого более высокую скорость решения, чем без их
применения.
Явная схема расщепления. Рассмотрим задачу Коши для
эволюционного уравнения вида
где А — некоторый матрично-дифференциальный оператор по
пространственным переменным, который представим в виде суммы двух
операторов:
А = Ai + A2.
§ 6. Общая схема расщепления 69
Тогда задачу (6.1) можно представить в виде последовательного
решения двух следующих задач Коши на интервале tn ^ t ^ £n+i:
dv ^
Ж = MV' (6.2)
v(tn) = u(tn),
dw ^
Ж = A2W' (6.3)
в результате получим решение задачи (6.1):
u(tn+1) = w(tn+1) + 0(At2). (6.4)
Докажем это для явной схемы, когда правая часть в
уравнениях (6.2), (6.3) берется с нижнего слоя:
Ai^1, = A2uf\
At x ' At
^+1 = (E + AtAiK, wn+1 = (E + AtA2)wn.
Учитывая, что начальные условия для второй задачи есть решения
первой wn = v71^1 и Vй = ип, получаем
^+1 = (Е + Д£А2)(Е + AtA^u" =
= [Е + At(Ai + А2) + At2A2Ai] Й" =
= (E + rA)ixn + 0(At2).
Это совпадает с решением разностного уравнения задачи (6.1) с
точностью до О (At):
ixn+1 = (E + AtA)i2n,
что и требовалось доказать: Йп+1 = уоп+1 + (Э(А£2).
Это позволяет на каждом временном шаге At решать вместо
задачи (6.1) последовательность задач (6.2)-(6.3). Можно рассматривать
процесс расщепления как приближенную факторизацию оператора
Е + AtA = (Е + AtAi) (E + AtA2) + 0(At2)
на произведение двух операторов.
70
Гл. 2. Разностные схемы расщепления
Очевидно, что если оператор А представим в виде п слагаемых,
А = Ai + А2 + ... Ап, то на интервале tn ^ t ^ £n+i его можно
представить в виде произведения п множителей:
Е + AtA = (Е + AtAi) (Е + А£А2)... (Е + AtAn) + 0(At2),
и решение (6.1) заменить последовательным решением п задач.
Неявная схема расщепления. Нетрудно показать
правомерность расщепления и для неявной схемы. Решение разностного
уравнения (6.1) по неявной схеме имеет следующий вид:
,-тп-ы
(A1+A2)«"+i,
At y L z' ' (6.5)
un+1 = [E-At(A1+A2)]-1un,
проводя расщепление, аналогичное (6.2)-(6.3), и используя для
каждого из них неявную схему
Ai At (6.6)
vn+l = (Е - AtAi)"1^1, wn+l = (E - AtAa)"1^",
получаем с точностью до 0(At2) решение исходной задачи (6.1):
vln+1 = (Е - AiA2)"1(E - AtAi)"1^ =
= [(Е - AtA2)(E - AiAi)]-1 Vй =
= [Е - At(Ai + А2) + 0(At2)} ~l tT,
что совпадает с решением (6.5) с точностью до 0(At2).
Устойчивость. Легко видеть, что если на каждом шаге
разностные схемы расщепления удовлетворяют условию устойчивости, т.е.
нормы матриц перехода у них ограничены, то будет ограничена и
норма их произведения. Пусть
||E + AtAi|| <Ci и ||Е + Д*А2|| <С2.
7. Расщепление по направлениям
71
Тогда получим
||Е + Д*А|| = ||(Е + AtAi)(E + AtA2) + 0(Ai2)|| <
< ||(Е + AtAi)|| || (E + AtA2)|| < d C2,
и, следовательно, схема расщепления (6.2) - (6.3) будет устойчивой.
Таким образом, доказан достаточный признак устойчивости для
разностных схем расщепления.
Замечание. Расщепление применимо и в случае нелинейных
уравнений, когда матрицы АДгГ) зависят от решения й.
Доказательство аналогично приведенному при замороженных коэффициентах
в уравнении (6.1).
§ 7. Расщепление по направлениям
Расщепление по направлениям начально-краевых задач для уравнения
теплопроводности (71). Схемы расщепления волнового уравнения (74).
Расщепление по направлениям начально-краевых задач для
уравнения теплопроводности. При решении начально-краевых
задач для получения окончательной разностной схемы расщепления
необходимо конкретизировать вид операторов А^ в уравнении (6.1)
и аппроксимировать их по пространственным переменным
разностными соотношениями.
Рассмотрим начально-краевую задачу для двумерного уравнения
теплопроводности в прямоугольнике О^ж^а, 0 ^ у ^ b
(7.1)
ди
~di~~
= Аи =
д2и д2и
дх2 ду2'
Ai
д2и
дх2'
А2 =
д2и
ду2
при начальных условиях
Ч=о = ио(х,у)
и краевых условиях
a) U\x=0 = MV>t) U\x=a = MV>t)
b) u\ 0 = u3(x, t) и\у=ъ = щ(х, t)
(7.2)
72
Гл. 2. Разностные схемы расщепления
Используем неявную схему расщепления и аппроксимируем
пространственные производные на (п + 1)-м слое центральными
разностями второго порядка Ахх и Ауу:
Axxv"+1
V,
П+1
т-\-1,к
9 п+1 | п+1
Z(7m,/c ^ ит-1,к
ит,к
п+1
/с
Тогда (6.6) примет вид
п+1
ит,к+1
Ах2
Um,k
п+1
ит,к-1
Ау2
„п+1
^m,fc
а)
Ь)
At
Л
T.V.
п+1
ит,к ~
и,
п
т,к
т,к
W*
At
■ = v,
п+1
т,к '
■хх ^т к
Л ?/;п+1
2^УУШт,к
т
к
1,.
1,-
,М,
,iV.
(7.3)
.п+1
1т,к
Первая система (7.3) решается методом скалярной прогонки при
краевых условиях (7.2а), вторая — при (7.2Ь).
Расщепление двумерного уравнения на два одномерных физически
можно трактовать как разбиение процесса теплопереноса сначала в
направлении х при теплоизолированных стенках в направлении г/,
а затем в направлении у при теплоизоляции в направлении х.
Таким образом, переход на следующий слой требует решения (N + М)
одномерных задач. Такое расщепление называется расщеплением по
направлениям. Отметим, что каждая из этих разностных схем, как
было показано в §6 в [48], устойчива, следовательно, устойчива и
разностная схема для двумерного уравнения (7.1).
Ясно, что даже в рассматриваемом простейшем примере
расщепление можно провести многими другими способами. Например, так:
,.п+1
ит,к
ит,к
At
А
r.V,
п+1
■хх ^mk
■А.
ит,к
(7.4а)
Jm,k
lm,k
при краевых условиях (7.2а);
п+1
ит,к
ит,к
At
i(A,
хх^гп к
+ avvw,
т,к J
Jm,k '
(7.4b)
„П+1
.n+1
7. Расщепление по направлениям
73
при краевых условиях (7.2Ь)
Это схема расщепления по
переменным направлениям.
Рис. 7.1а показывает,
какие шаблоны используются
в схеме (7.3), а рис. 7.16
соответствует схеме (7.4).
Хотя в схеме (7.4) каждая из
расщепленных задач
остается двумерной, тем не
менее на каждом этапе схема
неявная только в одном
направлении, и
соответствующая алгебраическая
система уравнений будет трехдиа-
гональной. К ней применим
метод скалярной прогонки,
а не матричной, как это
было бы, если решать
исходную задачу без расщепления
по неявной схеме.
Нетрудно убедиться, что схемы расщепления позволяют сильно
сократить число арифметических операций, необходимых для решения
многомерных задач.
Разностные схемы называются экономичными, если число
арифметических действий для перехода от ип к гГп+1 пропорционально
числу неизвестных. Этому свойству удовлетворяют в первую
очередь явные схемы, но, как мы видели в §6 в [48], явные схемы при
решении уравнения теплопроводности условно устойчивы при
жестком ограничении на шаг по времени At ^ Ах2 /А. Поэтому от них
приходится отказываться.
Неявная схема без расщепления для уравнения (7.1) приводит на
каждом шаге по At к решению уравнения Пуассона. Эта задача
даже при использовании матричной прогонки требует числа операций
К\ г^> М • iV2, где N — число неизвестных по короткой стороне
прямоугольника N < М.
Применение же скалярной прогонки по каждому из направлений
пропорционально числу неизвестных на слое, поэтому неявные схе-
т+1
т—\ к 1
т+1
Ш
т—\
М
Jmjc k-ц
(а) (Ъ)
Рис. 7.1. Расщепление (а) по
направлениям, (Ь) по переменным направлениям
74
Гл. 2. Разностные схемы расщепления
мы расщепления как (7.3), так и (7.4) являются экономичными.
Число арифметических операций для их решения — К2 ~ 2 • М • iV, что
существенно меньше, чем К\. Нетрудно убедиться в том, что эти
схемы абсолютно устойчивы, т.е. обладают преимуществами по
сравнению как с явными схемами, так и неявными схемами без
расщепления. Эти преимущества тем больше, чем больше независимых
переменных в задаче и чем больше число разбиений, а следовательно, и
число неизвестных.
Схемы расщепления волнового уравнения. Так же просто
построить схему расщепления для гиперболических уравнений,
зависящих от нескольких пространственных переменных. Рассмотрим
волновое уравнение вида
д2и _ 2 /д2и д2и\
W = a {dx^ + w)' (7-5)
Чтобы использовать общую схему решения (6.1) - (6.3), это
уравнение следует привести к системе уравнений первого порядка. Для
этого введем новые независимые переменные:
ди ди ди
-di = V> Tx=£' %=7' (7'6)
Тогда из (7.5) получим
dv 2 f де dj
dt \ дх ду
Дифференцируя первое уравнение (7.6) по х и по г/, а второе и третье
по £, получим
д2и dv де д2и dv dj
dt дх дх dt' dt ду ду dt'
В результате получим систему трех уравнений первого порядка,
эквивалентную уравнению (7.5):
де dj
дх ду
dv
~di =
де
dt "
д-у
dt
= а2(
dv
дх'
dv
ду'
(7.7)
7. Расщепление по направлениям
75
Вектор решения U и дифференциально-матричные операторы Ai,
А2 равны
U ■■
Л
А
1
Ai =
(°
1
\о
о2
0
0
0
0
0
_д_
дх'
'О 0 а2^
0 0 0
,0 1 0
д_
ду'
Начальные значения для (7.6) имеют вид
ди
и = и0(х,у),
dt
v = v0(x,y)
при t = 0.
(7.8)
Кроме того, зададим краевые условия на сторонах прямоугольника
О^х^а, О^у^Ь, например, в следующем виде:
х = 0
х = а
у = 0
у = Ъ
ди . ч
— =v = v0(t,y),
ди
-=s = e0(t,y),
ди
~т
ди
ду
v = v0(t,x),
j = jo(t,x).
(7.9)
(7.10)
Применяя явную схему расщепления, получим следующие две
задачи:
1)
dv
, дё
dt дх
дё dv
dt дх
2)
^ at
( ду_
dt
дё п
dj dv
{ dt dy
At
2Аж
2Vm+l ~ Vm-1
>^7
dy
At
, ^n+l = n
\ Im i mi
-n+1 -n
At
-n+l _ ~n+l
2Аж
AVA4 _ '71
2Ay
vn =vn
um umi
Im I mi
fin _ r.n+1
Vk - vk '
4
-n+1
At
Lfe. = a2Vk+l Vk-1
2Ay
lt=lnk+l-
Здесь по каждому из направлений применяется явная одномерная
схема Лакса на трехточечном шаблоне, где Uk = ^(uk+i + Uk-i).
76
Гл. 2. Разностные схемы расщепления
На начальном слое п = 0 для первой задачи используются условия
v^n = v0(x,ym), £0m = £o(x,ym), т = 0...М, МАу = Ь
и решается на каждом временном слое М одномерных задач при
фиксированном ут с граничными условиями (7.9).
Во второй задаче на начальном слое п = 0 используем условия
v%=v0(xk,y), £°к=£0(хк,у), k = 0,...,K, КАх = а
и решаем К одномерных задач при фиксированном хк с граничными
условиями (7.10).
Построенная схема расщепления условно устойчивая при
выполнении условия Куранта по каждому из направлений х и у на основании
достаточного признака устойчивости (см. §6 в [48]).
Таким образом, чтобы перейти на (п + 1)-й слой по времени на
каждом временном слое необходимо решить К + М одномерных
задач.
Аналогичным образом для решения задачи (7.6)-(7.8) можно
применить неявную схему расщепления и использовать для решения
полученных систем уравнений скалярную прогонку.
Расщепление может производиться не только по направлениям для
уменьшения размерности задачи. Его часто оказывается
целесообразно применять для систем уравнений, описывающих комплексные
физические процессы в сложных реологических средах. В этом
случае процесс можно расщепить на последовательность более
простых процессов, которые уже изучены или которые поддаются более
простому исследованию. Например, сложные механические свойства
среды могут быть расщеплены на совокупность простейших свойств.
Такое расщепление во многих случаях позволяет использовать
физическую интуицию и ранее накопленный опыт по решению более
простых задач. Приведем примеры эффективного применения схем
расщепления уравнений вязкой жидкости, уравнений упруговязко-
пластичности и других реологически сложных сред.
§ 8. Расщепление по физическим процессам. Уравнения Навье-Стокса 77
§ 8. Расщепление по физическим
процессам. Уравнения Навье—Стокса
вязкой жидкости
Дивергентная форма уравнений (77). Недивергентная форма уравнений (78).
Одномерные уравнения. Идеальный газ (79). Реализация схемы (81).
Дивергентная форма уравнений. Уравнения Навье-Стокса
для сжимаемого теплопроводного вязкого газа запишем в
матричной форме:
dt dxi
U, Wi, F — пятимерные векторы:
/
1,2,3,
(8.1)
U
//Л
PV2
PV3
\рЕ)
Wi
PVi
pviVi + ац
pV2Vi + Gi2
pv3Vi + ai3
,dT
\pvxViE + VjCTij - k%^J
Для вязкой жидкости напряжения выражаются так:
Oij = (р - XVv)Sij - fi(vij + Vjj) = pSij -
( 0 \
P9i
P92
РЯъ
\pVi9i)
D
1.2)
(8.3)
где р = p(p, T) — давление, U — вектор неизвестных величин, Wi —
вектор гидродинамических потоков в направлении л^, F — вектор
правых частей, g — вектор массовых сил, Е — полная энергия, Л,
/i — коэффициенты вязкости, к — коэффициент теплопроводности,
сг^ — диссипативная составляющая напряжения.
Гидродинамические силы определяются градиентами вектора
потоков и их можно разбить на три вида: 1) инерционные или
конвективные силы, 2) силы за счет градиента давления р или в общем
случае консервативные силы, см. [32], 3) силы, обусловленные
вязкостью и теплопроводностью, или диссипативные силы.
Расщепление удобно проводить в дифференциальном
представлении уравнений, а затем переходить к дискретной форме расщепления
уравнений.
В соответствии с этим можно разбить матрицу W размером (3 х 5)
на три составляющих: W = W^ + W(2) + W(3). Матрицам W^)
78
Гл. 2. Разностные схемы расщепления
(к = 1,2,3) соответствуют процессы, при которых обращаются в
нуль следующие величины:
W
W
W
w
w
w
7(1)
7ik
о,
РЩ
(2)
(рщ
(3)
т(1) =
D{2)
о,
О, v
(3)
О, Т<2> = 0),
0).
Эти матрицы называются: W^1) — конвективная, W^ —
акустическая или консервативная, W^ — диссипативная.
При замене в уравнении (8.1) матрицы W на W^1) получаем
модель свободного течения (при F = 0), при замене W —► W^
получаем уравнения акустики гиперболического типа, наконец, при
W —► W^3) получим систему уравнений параболического типа,
описывающих диссипативные процессы вязкого течения и
теплопроводности:
1)
dpw др^\
(i)
dt
dpWyV
dt
дрУ>ЕУ>
dt
+
dxk
dpWy^vj =
dxk
dxk
2) {
0;
,(2)
.(2:
0,
dpW
dPw
dt
dt
dE&
dt ' dxi
p = p(p,0);
0,
dxi
dp^v\ '
(8.4)
3) \
dp(3)
dt
0,
dv
(3)
P
P-
dt
de^
~dt~
d
d2v(3)
dxkdx,
dxi dxi
+ vAvk + X,iVv^ Sik + ^i(v(k3> + vfl)
где D = A(VtT)2 + ^/iVijVij ^ 0 — диссипативная функция,
e = E — \{v)2 — массовая плотность внутренней энергии, (v)2 = ^2v?.
Недивергентная форма уравнений. Уравнения Навье-Стокса
(8.1) имеют дивергентную форму, но их можно записать и в неди-
§ 8. Расщепление по физическим процессам. Уравнения Навье-Стокса 79
вергентной форме, если в качестве вектора неизвестных принять
h(u)
либо f2(U) = I Vi I , либо f3(U)
Уравнение (8.1) при отсутствии внешних сил принимает вид [32]
з
Ri) f = 0, (8.5)
Э/ + Е(" э
dt
dxi
где £li и Hi — матрично-дифференциальные операторы. Например,
при /= h
П7
Vi
a25u
a252i
a2S3i
0
phi
Vi
0
0
c2hi
phi
0
Vi
0
c2hi
phi
0
0
Vi
c2hi
0
b2Su
Ь262г
Ь263г
Vi
R?
0
дх^
dxi 2г
A
дх,
д ОТ
.dxi дх^
<&
здесь по г нет суммирования;
ldp
62 = I^
РдГ
p де\ I де
~р~Р~др) / ~дТ"
Ф = 2//
dvk_Y
,-?\2
дхк)
■ A(W)
dvi dv2
дх2 дх\
дхз дх\
+
<%2 dv3
дхз дх2
Одномерные уравнения. Идеальный газ. Рассмотрим более
детально случай одномерного уравнения изотермического невязкого
газа. Уравнения запишем в недивергентной форме:
df_ df_ _
dt дх
(8.6)
80
Гл. 2. Разностные схемы расщепления
V
а2
0
Р
V
с?
0
ь2
V
р
р
Введем операторы с диагональной матрицей Ai = А (р = 0) и с
несимметричной матрицей А2 = A (v = 0) и заменим систему (8.6)
расщепленной системой уравнений:
is/i
дк
2 dt l дх
Idfr A аЛ
2 at 2 &r
и, ъп ^ t ^ tn
0, *„ + - < t < t„ + г.
На первом полушаге в уравнении (8.6) учитываются конвективные
члены, что соответствует переносу вектора состояния вдоль
траектории без изменения, а на втором полушаге — изменение состояния
в ячейке за счет градиента давления в уравнении движения и
градиента скорости в уравнениях неразрывности и энергии.
Введем матрично-разностные операторы А^ , аппроксимирующие
д
дифференциальные операторы А^ ^— с порядком к = 1, 2 в узлах сет-
дх
: и?АкЕ,
Лк)
V2h
о
(а2)пАк
0
рпАк
0
(с2)пАк
0
(Ъ2)пАк
о
где Е — единичная матрица, Л — разностный оператор первой
производной с порядком к, Ак — сопряженный к нему оператор
при к = 1 и к = 2. Выполняются соответственно равенства Л^ = Л^
и Л2 = Л2. Здесь Л^ — разность вперед, Al_ — разность назад, Л2 —
симметричный разностный оператор.
Л^
несимметричный
оператор (к = 1,2).
Примем неявную разностную схему расщепления вида
Тп-\-1/2 _ In
Т
Гп+1 _ рН-1/2
Ми
A%h
'afn+l/2 + ^ _ ajjh
afn+i + (1 _ a)/»+i/2'
0,
(8.7)
§ 8. Расщепление по физическим процессам. Уравнения Навье-Стокса 81
перепишем (8.7) в виде
(Е + raAkh) Г+1/2 = (Е _ т(1 _ a)Akh) Д
(Е + таАк21г) Г+1 = (Е - т(1 - a)Ak2h) fn+l/\
где 0 < а < 1.
Умножая первое уравнение на оператор Е — т(1 — се)А^, а второе
на Е — т(1 — a)A.\h и складывая, получим
/
П+1
■/"
■£а*л [а/^1 + (1 - а)/*1
+
+ г [А*ЛА^а2/**+1 - А*„А*Л(1 - а2)/"
r(l - a)a (AklhAk2h - А*„А*„) Г+1/2,
откуда ясно, что значение /'
71+1/2
исключается, если только а = О
или а = 1, либо когда А^; и А^ коммутативны, но это условие
выполняется, если только коэффициенты в уравнении приняты
постоянными. В этом случае схема (8.7) будет строго порядка
аппроксимации по t при а = 1/2. В нелинейном случае разностная схема
имеет первый порядок по t и к-й по пространственной переменной.
Реализация схемы. На первом шаге решение разностных
уравнений (8.7) осуществляется независимо для каждого уравнения, т.к.
оператор А^ диагональный. Если Л^ = Л* т.е. разность первого
порядка вперед либо назад, то уравнения двухточечные, и их
решение может быть найдено по неявной схеме бегущего счета:
/"
"п+1/2
1-т(1-«КЧ
fn +
Лг+1/2
Лп+1
i + ^tel
где к = т/h. Когда v7^ > 0 — счет идет слева направо (формула (8.8)
берется со знаком —) и в обратном направлении, если v7^ ^ 0 (в
формуле (8.8) знак +). При знакопеременной скорости удобнее
применять скалярную трехточечную прогонку для каждой компоненты /,
82
Гл. 2. Разностные схемы расщепления
записав разностное уравнение (о. о J в виде
) mi
Рп+1/2 , fn+1/2 , ^г+1/2 _ п Л
^mJm-i ^umJm * urnJm+i — 4mJn
где am = x(|<J+<J, Ьго = 1 + 2^К|, cm = x(^-|^|),
^=(l-r(l-a)<A^;
в зависимости от знака v либо am, либо ст обращается в нуль.
Если Л^ = Л?-, тогда используется трехточечный шаблон и схема
бегущего счета, а при знакопеременном v — пятиточечная скалярная
прогонка (см. [32]).
На втором дробном шаге систему (8.7) в скалярной форме можно
записать так:
pn+1 = рп+1/2 - rpnAkv,
vn+1 + г [(а2)пАкр + (Ъ2)пАкё\ = О,
v = avn+1 + (1 - a)vn, ё = аеп+1 + (1 - се)еп
(индекс тп для упрощения записи в этих уравнениях опущен).
Исключая рпЛ
уравнение:
ключая pn+1 и en+1 из последнего уравнения, находим разностное
{1 - т2а2 [{а2)пАкрпАк + (62)пЛ/с(с2)пЛ/с] } ^n+1 =
= {1 + т2а(1 - а) [(а2)пАкрпАк + (62)пЛ/с(с2)пЛ/с] } vn+1/2-
[(a2)nAV+1/2 + (b2)nAken^2} .
г
Решение этого уравнения на шаблоне из (2fc + 1) точек находим
при к = 1 трехточечной, а при к = 2 — пятиточечной прогонками,
которые хорошо обусловлены. Значения pn+1 и en+1 получим из
первых двух уравнений при уже найденном v™ . Этим завершается
расчет.
Систематическое применение метода расщепления в задачах
газовой динамики дано в монографии [32].
9. Расщепление уравнений теории пластичности
83
§ 9. Расщепление по физическим
процессам уравнений теории
пластичности
Определяющие уравнения упругопластической среды (83). Некоторые подходы
к решению упругопластических уравнений (85). Расщепление определяющих
уравнений (87). Теория течения типа Мизеса. Изотропное упрочнение (90).
Теория пластичности Прагера-Дракера (93). Упруговязкопластические ере-
ды (94).
Расщепление уравнений твердых деформируемых тел отличается
от уравнений механики жидкости. В вязкой жидкости напряжения
непосредственно выражаются через скорости деформаций и могут
быть исключены из уравнений. Для твердых тел, которые
обладают наряду с вязкопластическими свойствами свойством упругости,
в определяющие уравнения входят не только сами напряжения, но
и их производные по времени. Поэтому напряжения не могут быть
исключены из полной системы уравнений, как для вязкой
жидкости, а должны входить в вектор основных неизвестных величин:
и = (р, pvi, pE, cr^j), размерность которого в пространственном
случае равна одиннадцати. В системе (8.1) - (8.3) уравнение (8.3)
необходимо заменить определяющими уравнениями
упругопластической среды.
Определяющие уравнения упругопластической среды.
Исходная формулировка состоит из следующих основных положений
теории пластического течения [7, 44].
1. Аддитивность упругих и пластических скоростей деформаций:
<Ьз=<Гц+<Рц, (9.1)
где dij = \ (vij + Vjj) — полная, df • — упругая, dp- — пластическая
скорости деформации.
2. Область упругой деформации ограничена условием, которое
представляет собой конечное соотношение между инвариантами
тензоров напряжения J^, скоростей деформаций Di и внутренних
параметров среды Хк'-
F(JU А, Хк) = 0 (г = 1, 2, 3; к = 1, 2,..., п). (9.2)
84
Гл. 2. Разностные схемы расщепления
3. Упругая деформация е\, связана с тензором напряжения g^i
законом Гука:
de% = D-^dau, (9.3)
где D~-kl — тензор упругой податливости, который для изотропного
материала равен
D
-1
ijkl
1
2/1
SkiSij - ( 1 - — j SijSki
где /i — модуль сдвига, К — модуль объемного расширения.
При выполнении условия (9.2) в материале появляются
пластические деформации, которые описываются ассоциированным законом
пластического течения, согласно которому скорость или приращение
пластической деформации Ае^- направлена по нормали к
поверхности (9.2),
<Ц,=<£\|^-, (9.4)
O&ij
где d\ — безразмерная скалярная величина, определяемая в
процессе решения. При выполнении условия активного нагружения
OF 8F
——Soij > 0 и F = 0. При ——Soij = 0 происходит <нейтральное
OGij OGij
dF
нагружение». Если ——Sg^ < 0, то догрузка Sg^ не вызывает пла-
OGij
стических деформаций и de^- = 0.
4. Внутренние параметры Хк, характеризующие внутреннюю
структуру материала, изменяющуюся при деформировании,
определяются эволюционными уравнениями:
Хк = Xk(Ji,Xk). (9.5)
В качестве примеров таких параметров могут использоваться
параметр упрочнения материала, остаточные напряжения, пористость,
поврежденность и другие параметры.
В случае, когда условие пластичности (9.2) и эволюционные
уравнения (9.5) не зависят от изменяющихся во времени переменных Dvk
или Хку а только от их приращений, то свойства пластической среды
не зависят от изменения масштаба времени. Будем называть такие
среды упругопластическими или классическими, а среды,
зависящие от изменения масштаба времени, - упруговязкопластическими.
§ 9. Расщепление уравнений теории пластичности 85
Уравнения (9.1) - (9.5) полностью определяют модель среды и
совместно с законами сохранения (8.1) и (8.2) дают замкнутую систему
уравнений.
Некоторые подходы к решению упругопластических
уравнений. Математическая формулировка уравнений теории
пластического течения отличается тем, что для нее определяющие
уравнения формулируются в виде дифференциальных соотношений и
условия пластичности, которое является конечным соотношением,
ограничивающим инварианты тензора напряжений. Например, условие
пластичности Мизеса является ограничением на второй инвариант
тензора напряжений.
Это обстоятельство вносит определенные особенности в
формулировку замкнутой системы уравнений теории пластичности.
Появляются различные возможности в представлении системы
определяющих уравнений и, как следствие, различия в методах ее решения.
1. Одна из возможностей состоит в тождественном
удовлетворении условия пластичности введением новых переменных и
сведении уравнений к системе дифференциальных
соотношений [27, 64].
2. Другая возможность, которая используется в большинстве
работ по численному моделированию упругопластических
процессов, заключается в формулировке уравнений в виде
системы дифференциальных уравнений, которая получается после
дифференцирования условия пластичности (9.2) и
исключения d\ на основании (9.4) при дополнительном начальном
условии в виде исходного условия пластичности (9.2).
Определяющие уравнения после этих преобразований имеют вид
de%3 = de% + de% = (d'^ + HFi5Fk^ dakl = A^kldakh
8F „ „ dF
Fij = t;—> H = cfkiFki- ■
(9.6)
86
Гл. 2. Разностные схемы расщепления
Уравнения (9.6) можно представить в обращенной форме:
doij = Dijki
i
deki — Н [ h HFmnFmn J FkiFpq dsp
= Aijkideku (9.7)
где Dijki — матрица упругих модулей, Aijki — матрица
упругой л астических модулей.
Добавляя уравнения (9.7) к (8.1) - (8.2), получим замкнутую
систему уравнений гиперболического типа в гипоупругой
форме. Эта форма уравнений применяется обычно при решении
упругопластических задач МКЭ [21, 95].
Нежелательным моментом при таком подходе является
дифференцирование условия пластичности (9.2).
Искусственное дифференцирование условий пластичности
приводит к возрастанию порядка системы дифференциальных
уравнений, а следовательно, к ее усложнению и
дополнительным трудностям при интегрировании.
3. Еще одна возможность состоит в сведении задачи к
минимизации функционала теории упругости при дополнительном
ограничении, налагаемом на решение во всей области в виде
неравенства пластичности F ^ 0 (см. [18]).
Эти различия в формулировке исходных уравнений требуют
существенно разных методов численного решения задачи, которые
существенно различаются.
В первом случае происходит сокращение числа неизвестных и
соответственно понижение порядка системы дифференциальных
уравнений на единицу. Этот подход можно было бы считать наиболее
удачным, если бы эта замена осуществлялась так же просто, как
в случае плоской задачи для идеального жесткопластического
материала. Но в более общих случаях это усложнение существенно,
особенно в трехмерном случае.
При третьем подходе задача может быть сведена к решению
вариационного неравенства специальными методами, которые имеют
свои особенности и преимущества и будут рассмотрены в главе 3.
§ 9. Расщепление уравнений теории пластичности 87
4. Наконец, существует еще одна возможность решения задачи
в исходной, естественной постановке уравнений (9.1) - (9.5),
если воспользоваться численным методом, основанном на
расщеплении уравнений по физическим процессам, не прибегая к
дифференцированию условия пластичности (9.2).
Такой подход, использующий исходную формулировку уравнений,
оказывается проще и потому предпочтительнее тех, которые
основываются на различного рода преобразованиях условия пластичности.
Расщепление определяющих уравнений. Полная система
уравнений для гипоупругопластической среды при конечной
деформации состоит из законов сохранения массы, импульса и энергии,
которые в переменных Эйлера могут быть записаны в следующем
дивергентном виде:
др д(рУк) =()
dt dxk
d(pVj) д(рУгУк) _ daik _ dsik dp
dt dxk dxk dxk dxi'
д(рЕ) д(рукЕ) д(у3акз) д( дТ_\
dt дхк dxk ' dxk V &xk)
К этим уравнениям следует добавить определяющие
уравнения (9.1) - (9.5) гипоупругопластической среды, записанные в
переменных Эйлера.
Условие аддитивности деформаций совместно с законом Гука для
гипоупругого материала [44, 58] дает уравнения для определения
напряжения:
Df = —тг + QikVkj + QkiVjk = Dijki (dki - dpkl), (9.9)
где D<Jij/Dt — производная Яуманна, исключающая изменение во
времени тензора ov/ за счет поворота частицы как жесткого
целого, D^ki — тензор упругих модулей материала, flij = \ (vij — Vj^) —
тензор скоростей поворота (см. [58]).
Система уравнений (9.2) - (9.5), (9.9) представлена в виде,
разрешенном относительно производных по временной переменной,
как это необходимо для применения расщепления. Основной нашей
Гл. 2. Разностные схемы расщепления
целью будет интегрирование методом расщепления определяющих
уравнений (9.2) - (9.5), (9.9) упругопластической среды, так как
именно этим полная система уравнений отличается от других
моделей сплошной среды, а расщепление законов сохранения молено
осуществить по схемам, которые используются, например, в
механике жидкости и газа [32] с малосущественными изменениями и
независимо от того, в какой форме — слабой или в дифференциальной —
формулируются законы сохранения.
Рассмотрим общую схему расщепления для динамической задачи
на уровне дифференциальных уравнений, а дискретизацию будем
проводить позже. Расщеплению подвергается уравнение (9.9).
1. Предиктор берется при dp- = 0, тогда материал среды — гипо-
упругий, и совместно с уравнениями движения на шаге At
необходимо решить систему уравнений (9.8) в изотермическом случае:
др д(рУк) =()
dt dxk
д(т) , d(pVjVk) = др-jk ,g щ
dt dxk dxk '
—— + QikO~kj + o~kiQjk = TjDijki (vij + Vjyi)
при начальных условиях, полученных на предыдущем шаге для
полной упругопластической задачи. В случае малых изотермических
деформаций получим более простую систему:
dvi daik doij 1
Р0Ж = to? ~Ж = 2^W ^ + V^ ■ (9Л1)
Таким образом, предиктор представляет собой хорошо известную
задачу для упругого материала, для решения которой можно
предложить одну из известных устойчивых разностных схем, например
явную характеристическую схему (§2).
2. Корректор вычисляется при dij = 0 в уравнении (9.9). Тогда
из (9.9) и (9.4) следует уравнение релаксации напряжений:
dt dt %зЫдаы V ;
Релаксация происходит до момента выполнения стационарного
условия пластичности F(Jj, Ji,Xi). = О, если среда упруговязкопла-
9. Расщепление уравнений теории пластичности
89
стическая, или до наступления условия упругой разгрузки, если
среда классического упругопластического типа.
Следует заметить, что задача интегрирования определяющих
уравнений для нахождения напряжений и внутренних параметров
среды при фиксированных деформациях представляет задачу о
релаксации напряжений и внутренних параметров, имеющую
самостоятельный интерес.
В случае классической или равновесной упругопластической
среды, свойства которой не зависят от изменения масштаба времени,
из уравнений (9.5) и (9.12) можно исключить время t и перейти к
зависимости процесса от переменной Л:
do^_ = _D dF_
Решая уравнения (9.13) и (9.5) при начальном условии Л = Ло,
Oij = erf- и Хг — Хл-> полученном на предыдущем шаге полной
задачи1, найдем решение на этапе корректора, как функции параметра Л
°ij = <rij(\<Tij,Xi), Хгз = Xij(\<Tij,Xi)- (9-14)
Подставляя найденные решения в условие пластичности (9.4),
получим уравнение для определения параметра Л:
F(Ji(X),XiW,Jf,Xi)=0. (9.15)
Найденное Л подставляем в (9.14) и получаем окончательное
решение полной упругопластической задачи через скорректированное
решение упругой задачи.
Если условие пластичности дифференциального типа, т.е. среда
упруговязкопластическая, то условие (9.2) для определения Л
приводится к дифференциальному уравнению вида
Fi(4,X,?,A,A)=0, (9.16)
где
F1(atj,xt,X,0)=F(afj,xt,X).
1 Здесь и далее индексом е обозначаются величины, полученные на этапе
предиктора для упругой задачи.
(9.13)
90
Гл. 2. Разностные схемы расщепления
Разрешая (9.16) относительно Л, получим
T^=^lF(Jt(X),Xl(\))}=v(F), (9.17)
где функция ср характеризует зависимость от скорости деформации
(тип вязкости), a F(Ji(X) — стационарное условие пластичности при
Л = 0, (р(0) = 0, т — время релаксации — материальный параметр
размерности [с], который входит в условие пластичности, зависящее
от времени.
В правой части (9.17) функция F = F(J^(A), XiW) отвечает
равновесному условию пластичности (9.15). Функция <p(F)
определяется типом вязкости упруговязкопластического материала.
Уравнение (9.17) может быть проинтегрировано в аналитическом виде, что
позволяет проанализировать свойства полученной разностной схемы
для разных функций (/?, F и параметра т.
Очевидно, что предлагаемая схема расщепления устойчива, если
устойчива разностная схема предиктора для решения упругой
задачи, и существуют решения уравнений (9.15) и (9.17).
Применим эту общую схему метода расщепления к конкретным
типам уравнений пластического течения.
Теория течения типа Мизеса. Изотропное упрочнение.
Рассмотрим упругопластические среды классического типа. Начнем с
теории течения Мизеса, зависящей от второго инварианта девиато-
ра напряжения J^ и деформационного упрочнения степенного вида:
J2 = (\ sljSlJ)1/2 = ко + 2/xix^, (9-18)
где /ii — модуль упрочнения.
Ассоциированный закон (9.4) примет вид
4 = if = A»„, A = A. (,.,„
Для параметра упрочнения \ эволюционное уравнение примем в
степенном виде:
! = аА№Г) || = a(J2)«. (9.20)
§ 9. Расщепление уравнений теории пластичности 91
Если в качестве параметра упрочнения принимается работа
пластической деформации
1 v Asa 2Л. _ ч2 2
Х = ¥^ = 1^^ = Т,Ш> то а = 2' a=V
если параметр Одквиста
X=(k ё%ё%) V2 = А (\ SijSij)1'2 = AJ2, то а = 1, а = 1.
Уравнение релаксации напряжений (9.12) примет вид
dsij = —2fidAsij.
Интегрируя при начальном условии, полученном на n-м шаге на
этапе предиктора Л = Лп, Sij = s^ , находим
лп <л<лп+ь
п+1 _ е(п+1) -2/х(Л-ЛТ1)
тп+1 _ те(п+1) -2»(An+1-An) _ те(п+1)
^2 — ^2 е — ^2 •Ln+1-
индекс е относится к упругому предиктору.
Поскольку все формулы в дальнейшем относятся к указанному
интервалу Л, индексы (п + 1) для упрощения записи будем опускать,
сохраняя их только там, где это необходимо.
Интегрируя уравнение (9.20) для параметра упрочнения %,
находим
„+i= n + ^D!(1_n ж = е_2м(л-л„)^
2ce/i
Подставляя \ в условие пластичности (9.18), получим степенное
нелинейное уравнение относительно параметра х:
J%x — ко — 2/ii
^^-*•>]'
0, (9.21)
которое можно решить любым итерационным методом с нужной
точностью. Начальное приближение х = хп берется с предыдущего
шага. Аналитическое решение легко получить и для общего вида
условия пластичности, если уравнение (9.21) линиаризовать около хп.
92
Гл. 2. Разностные схемы расщепления
При а = 1 и линейном упрочнении материала /3
сывается в явном виде:
fco + f Jj + 2/xiXe
В случае идеальной пластичности /ii = 0 получим
т _ *° яп+1 _ е *0
Х _ те > "^j _ "^j те '
J2 J2
т.е. решение упругопластической задачи получается из решения
упругой задачи простым умножением на коэффициент
корректировки ж, что означает нормировку вектора напряжения sf7-/Jf и
привидение его на поверхность текучести (9.18) в пространстве
напряжений. Это и есть известное правило корректировки Уилкин-
са [68], которое верно только для случая идеально пластической
среды (рис. 9.1).
Рис. 9.1. Корректировка по Уилкинсу при условии текучести Мизиса
В случае упрочнения из формулы (9.22) видно, что если это
правило формально распространить на случай упрочняющейся среды,
полагая х = (fco + 2/iixe)/</f •> то получим результат, отличный от (9.22).
1 решение запи-
(9.22)
§ 9. Расщепление уравнений теории пластичности 93
Теория пластичности Прагера—Дракера. Другой широко
используемой теорией пластичности является теория Прагера-
Дракера, которая применяется для сжимаемых сред, таких, как
грунты, пористые материалы. Условие пластичности Прагера -
Дракера зависит от двух инвариантов тензора напряжений:
F(Jb J2, к) = J2 + aJi - к = 0, (9.23)
тогда ассоциированный закон (9.4) примет вид уравнения
^'хщ = к(й+""•')■ ("4)
которое запишем отдельно для шаровой и девиаторной частей
тензоров:
4=3Aa, ^=4-KA=Ag, (9.25)
откуда, используя закон Гука, находим соотношение для компонент
скоростей полной деформации:
-ЪК (ska + Ё«) , ^ = 2ц [iij - ё\) = 2ц U
После расщепления получим релаксационные уравнения для этапа
коррекции:
dX ' dX J2
Переходя во втором уравнении к новой переменной dA = /idA/J2,
получим после интегрирования
s---s--e<A-Ao) dA- ^ ^ (l-e-(A-AoA - А-Ап
ъз~ ^ ' Лее-(Л-Ло)' /i
9Ка
Подставляя эти соотношения в условие пластичности, находим
аи - ol = -Ша{\ - Ао) = - —Jf (l - е-(Л"Л°)) .
ЯКа
Цх + a[Jf J|(l -x))-ko=0, (9.26)
ko-aJf + ^Ji
Д 1 +
ж«:
(a < 1), (9.27)
94
Гл. 2. Разностные схемы расщепления
9К7/
si:i = stjX, Л = J{ Jf (1 - x). (9.28)
/i
Коэффициент корректировки получается с поправкой, вызванной
влиянием первого инварианта. Из (9.27) видно, что правило
корректировки Уилкинса здесь не применимо. Оно выполняется для деви-
аторных компонент только в случае, когда объемный модуль К = О,
а для вычисления J\ формула имеет более сложный вид (9.28).
Упруговязкопластические среды. Среда называется упруго-
вязкопластической, когда условие пластичности (9.2) зависит от
инвариантов девиатора скоростей пластической деформации.
Рассмотрим случай, когда уравнение (9.2) и соответственно (9.16) зависят
только от второго инварианта D%. В результате получим
тЩ = <р [F(Ji, Xi) ~ fco], Ф) = О- (9.29)
Это условие неоднородно относительно времени t и содержит
константу г размерности [с] (время релаксации). Уравнение (9.29) при
т —► 0 дает равновесное условие пластичности (9.15).
При условии (9.15) типа Мизеса из ассоциированного закона имеем
соотношение (9.20) <Й = Asij, откуда находим
d'I= (i«)1/2 = A(iSlJ%)1/2 = Aj2) (9.30)
где d\, — девиатор скорости деформаций.
Перейдем от Л к параметру корректировки х = ехр[—2/х(Л — Лп)],
тогда дифференциальное уравнение (9.29), записанное относительно
параметра ж, будет иметь следующий вид:
dx 2u
-^ = -^ V №)), tn^t^ tn+u (9.31)
где через F(x) обозначена функция F( Ji, Хг) после подстановки в нее
скорректированных значений инвариантов, вычисленных на этапе
предиктора.
Интегрируя при начальном условии t = tny Sij = sf •, x = xny
находим
1—^ = "? / \tXf м' tn^t^ tn+u (9.32)
r 2ц J (f[F(x)]
§ 9. Расщепление уравнений теории пластичности 95
Рассмотрим случай степенной зависимости условия пластичности
типа Мизеса от D'J//:
T(D'2py=F(J2,Xi)-ko. (9.33)
Тогда, используя (9.31) и (9.32) и учитывая, что правая часть
уравнения (9.33) есть условие пластичности Мизеса с изотропным
упрочнением, воспользуемся (9.21). В результате получаем
дифференциальное уравнение для определения параметра корректировки х:
1=-^(*-*»+ч*"+й(1-*,>]Т- <аз4)
которое легко интегрируется. Подынтегральная функция в (9.32)
имеет особенность при х = х*, отвечающую равновесному значению
коэффициента корректировки, при котором F(x%) = 0. Так как х* —
простой корень, то сходимость интеграла будет зависеть от
показателя степени j. При j > 1 интеграл сходится, а при 7^1 расходится.
Соответственно интервал изменения At/т при 7 > 1 ограничен
значением правой части (9.32), при 7 ^ 1 он неограничен:
0 < nAt/т ^ n^At/т, (7 > 1), х —► х* при nAt/т —► n^At/т,
0 < nAt/т < сю, (7 ^ 1)? х ~^ х* ПРИ nAt/т —► оо.
Решение записывается особенно просто в явном виде, если F(X) -
линейная функция и j = 1. Например, для идеальной упруговязко-
пластической среды из (9.34) при ji\ = 0 получим
(9.35)
Шаг At определяется на этапе предиктора из условия устойчивости
явной схемы или из условия точности при использовании неявной
схемы.
При г —► 0 выполняется предельный переход к коэффициенту
корректировки Уилкинса:
х^х% = — при г -► 0.
J2
t tn
т
^n+1 ^0 _
Iе ~
J2
Jf /" dx
2fiJ (x-k0/J$Y
(Xn _ ^Л e-(nAt/r)(2M/J2e)
96
Гл. 2. Разностные схемы расщепления
Отсюда следует, что при (nAt/r)(2/i/J|) ^> 1 решение будет
стремиться к равновесному и, следовательно, разностная схема на этапе
корректора асимптотически абсолютно устойчива при любом At.
Таким образом, решение упруговязкопластической задачи методом
расщепления на этапе корректора сводится к решению одного
дифференциального уравнения, которое интегрируется в аналитическом
виде. Коэффициент корректировки при этом зависит от величины
шага интегрирования At, который определяется на этапе
предиктора.
Если решение упруговязкопластической задачи при t ^> r
стремится к упругопластическому решению, то и схема расщепления
гарантирует такое стремление без ограничения на величину At.
§10. Расчет граничных точек и точек на
оси вращения при расщеплении
Расчет точек на границе (96). Расчет точек на оси вращения (98).
Расчет точек на границе. Рассмотрим расчет граничных точек
при расщеплении определяющих уравнений в динамической задаче.
Очевидно, что граничные условия должны использоваться в первую
очередь на этапе предиктора при решении упругой задачи. При
этом ставятся те же условия, что и для полной упругопластической
задачи. Поэтому расчет граничных точек на этапе предиктора
ничем не отличается от расчета в случае упругой задачи, например
методом характеристик.
Граничные точки, как отмечалось выше (§2), корректно
рассчитываются приведением уравнений к характеристическому виду и
отбрасыванием в расчете тех соотношений, для которых
соответствующая им бихарактеристика оказывается за пределами
рассматриваемой области.
В сеточных методах, неиспользующих приведение уравнений к
характеристической форме, алгоритм расчета граничных условий
получают из физических соображений, а не из математической
формулировки условий. Например, гладкую жесткую стенку моделируют
с помощью дополнительных фиктивных ячеек, задавая в них
зеркальное отображение смещения в реальной ячейке, симметричной
относительно границы [68]. Для тензора напряжения нормальные
10. Расчет граничных точек и точек на оси вращения
97
компоненты в локальных координатах, связанных с границей,
отражаются симметрично, а касательные компоненты кососимметрично.
После этого узлы, находящиеся на границе, молено рассчитывать по
тем же формулам, которые используются для расчета внутренних
узлов. Свободная поверхность моделируется с помощью фиктивных
ячеек, не обладающих массой. Если на границе задано давление,
зависящее от времени, то в такой ячейке задается давление, а все
компоненты девиатора полагаются равными нулю. Можно моделировать
и более сложные условия на контактных границах с трением [68].
Такие расчетные модели не всегда можно выбрать однозначно, их
выбор основывается на физической интуиции вычислителя. Обзор
этих моделей и методов приведен в [41].
В методе расщепления на этапе корректора при вычислении
коэффициента корректировки в граничных точках необходимо
учитывать вид граничных условий (ГУ). Если ГУ заданы в
напряжениях, то заданные компоненты тензора напряжений не
корректируются. Корректировке подлежат лишь остальные компоненты девиатора
напряжений.
Если же ГУ заданы в перемещениях или в скоростях, то в этом
случае корректируются все компоненты девиатора напряжений
точно так же, как во внутренних точках области.
Если ГУ задаются смешанного типа, т.е. представляют собой
некоторую комбинацию кинематических величин и напряжений, то и в
этом случае корректируются все компоненты.
Рассмотрим, например, как определяется коэффициент
корректировки в простейшем случае плоской задачи для идеально
пластического условия пластичности, когда на границе тела заданы
нормальное <тц = сг^ и касательное а\2 — ^12 напряжения. В этом случае
корректируется только компонента девиатора напряжений 522-
Коэффициент корректировки определяется из условия пластичности,
которое принимает вид
(s?i-s!2-*)2+4<7?2]12 = 2fc, (10.1)
где s\x = а\х — \J\, s\2 — cri2? J\ — Ga ~ известные величины.
Откуда
98
Гл. 2. Разностные схемы расщепления
При извлечении корня взят знак минус, т.к. х* < 1.
Для упруговязкопластической среды коэффициент
корректировки х определяется из уравнения
At _ Jf f dx
I Zj LI J X X ■%
1
откуда
(10.3)
x - x* = (1 - x*) exp ( — ) , (Ю-4)
т ^
где x* определяется формулой (10.2).
Формула (10.4) аналогична формуле (9.35).
Расчет точек на оси вращения. В осесимметричных задачах
важным моментом является корректный расчет точек на оси
вращения г = 0. В этом вопросе не все ясно. Ось симметрии при
математической формулировке осесимметричных задач часто
рассматривается как граница области, хотя физически точки оси являются
внутренними точками тела. Это часто приводит к неудачным расчетным
схемам. Ключ к корректному построению алгоритма заключается в
рассмотрении точек оси как внутренних точек тела, для которых все
условия должны следовать из самой системы уравнений при г^Ои
соображений симметрии при замене г на —г, а не из каких-либо
дополнительных <граничных> условий, как это делается в некоторых
работах [68].
Приведем детальный вывод расчетной схемы на оси вращения,
поскольку в литературе нет ясности в отношении нее.
Рассмотрим упругопластическую осесимметричную задачу
методом расщепления. На этапе предиктор полагаем Л = 0 и решаем
упругую задачу. Уравнения движения, записанные в
цилиндрической системе координат, имеют вид
do~rr do~rz o~rr — o~qq
dr dz г /105ч
do~zz darz arz
PVz = ~^~ + ~^~ + •
oz or r
Предполагая, что напряженно-деформированное состояние на оси
г = 0 остается ограниченным, предельным переходом при г —► 0 из
10. Расчет граничных точек и точек на оси вращения
99
первого уравнения получаем
lim (arr — аев) = 0 => arr = Gee ПРИ г = 0.
Используя условия симметрии, из которых следует, что vr = 0 и
Grz = 0 при г = 0, получим из первого уравнения (10.5)
&Grr dGee n ^ о л/ +ч п
2— Ь -г— =0 => 2crrr - Gee = &rr = f{z, t) при г = 0.
Из второго уравнения получаем
dcrzz ^dGrz .п .
^ = — +2 —. (10.6)
Здесь не делается предположения, что —-— = 0 при г = 0, т.е.
досуг
пускается существования разрыва производных.
При рассмотрении определяющих уравнений, руководствуемся
теми же соображениями, что и выше. Рассмотрим уравнения упруго-
вязкопластической среды как более общие. Уравнения упругопла-
стической среды, как указывалось в предыдущем параграфе, могут
быть получены из них предельным переходом при г —► 0. Поскольку
применяется расщепление, то на этапе предиктора получим
уравнения гипоупругой среды, записанные в цилиндрической системе
координат для осесимметричной задачи следующего вида:
/ „ 2 \dvr / 2 \ dvz
оее = огг = 2 \^ + К- -^ — + [К - -^ — =
-»Н*)£+Н*)£- <->
7Л 4 \ dvz / 2 \ dvr
где учтено, что lim ir = lim — = -^-.
r^0 r^0 Г Or
Таким образом, все величины, кроме gzz и vZy в окрестности
оси г = 0 определены. Для их определения осталось два
уравнения: (10.6), третье уравнение в (10.7):
dvz 8gzz _ dGrz
dt dz dr ' qq g\
d(Tzz dvz dvr
— -—(\ + 2ц) = 2\—,
100
Гл. 2. Разностные схемы расщепления
где учтено, что (К + |/х) = (Л + 2/х) и (К — |/х) = Л.
Правые части в этих уравнениях известны, они определяются с
помощью односторонних разностей:
дгг \n+1 (rr \п+1-(гг \n+1
UOrz \ _ \Vrz)l k \UrzjQ k
dr Jok Ar
drj0k Ar
Здесь нижние индексы соответствуют пространственному
разбиению по г и z. Индекс 0 отвечает точкам оси г = 0, где
(crz)o^1 = (vr)o~^ = 0 по соображениям симметрии, а величины с
индексами 1 отвечают внутренним токам тела, которые
рассчитываются по формулам для внутренних точек.
Напряжение (<тГг)о к определяется интегрированием первого
уравнения (10.7) после того, как вычислено (vz)o~^ из (Ю.8):
г ) ~ 2(А + ^-дГ" + А A~z '
Таким образом, алгоритм определения в точках оси г = 0 на
этапе предиктора полностью замыкается из рассмотрения только самой
системы уравнений без привлечения каких-либо <граничных>
условий или дополнительных предположений.
Этап корректора выполняется так же, как и в любой внутренней
точке, без всяких изменений. Окончательное выражение для ^n+1
находим из разностной аппроксимации первого уравнения (10.8).
11. Понятие поврежденности и построение моделей
101
§11. Понятие поврежденности и
построение моделей
повреждающихся сред
Понятие о континуальном разрушении материала и его поврежденности (101).
Построение моделей поврежденности (102). Определяющие уравнения GTN-
модели (109).
Понятие о континуальном разрушении материала и его
поврежденности. Описание процессов разрушения основывается на
представлениях о разрушении как о потере способности материала к
сопротивлению деформации вследствие нарушения внутренних
связей. Потеря способности материала к сопротивлению деформации
может вызываться как внешними воздействиями нетермомеханиче-
ской природы (химические реакции, облучение), так и термомеха-
нически при достижении напряженно-деформированным
состоянием некоторых пределов, определяемых критериями разрушения.
Эксперименты по деформированию и разрушению стандартных
образцов при растяжении и сдвиге (кручении полых цилиндров)
демонстрируют на диаграммах деформирования участки
разупрочнения, на которых напряжения падают с ростом деформаций. При
трактовках таких зависимостей надо учитывать, что напряжение и
деформация являются не единственными параметрами состояния, и
поэтому такие диаграммы показывают лишь срез
многопараметрического процесса.
Поврежденность можно разделить на два основных типа — это по-
врежденность хрупких упругих материалов и поврежденность
вязких упругопластических материалов за пределом упругости.
Характерные картины разрушения для вязких и хрупких материалов
приведены на рис. 11.1.
Основные типы экспериментов по исследованию разрушения — это
сдвиг (растяжение) при постоянной скорости деформации в
квазистатике и соударение пластин (стержней) в динамике.
При сдвиге происходит сильный локальный разогрев и
термическое разупрочнение, которое часто сопровождается фазовым
превращением в полосе сдвига, т.е. это локальное явление (микротрещины
и микропоры сливаются в одну полосу адиабатического сдвига, по
котором в дальнейшем происходит разрушение материала). Полосы
102
Гл. 2. Разностные схемы расщепления
Рис. 11.1. Характер разрушения на микроуровне для вязких (а) и хрупких
(Ь) материалов
локализации могут наблюдаться не только в пластических, но и в
хрупких материалах, что возможно вследствие сильного
локального разогрева и разупрочнения. На рис. 11.2 изображено образование
пор в образце при растяжении [96].
Другой тип экспериментов — это разрушение отколом при
соударении пластин. Это разрушение растяжением при взаимодействии волн
растяжения, отраженных от свободной поверхности. Опыты
Курана Д.Р., Симана Л., Шоки Д.А. [77], [78]; Каннеля Г.И.,
Разоренова СВ., Уткина А.В. Фортова В.Е. [26] и др. многократно
подтвердили этот факт. Для пластических материалов здесь наблюдается
вязкий откол с образованием сферических пор вследствие
всестороннего растяжения. Для разрушения требуется достаточная скорость
соударения и продолжительность растягивающего импульса,
чтобы механизм зарождения, роста и слияния микропор привел бы к
образованию трещины. На рис. 11.3 изображено образование
макротрещины вследствие слияния микропор.
Построение моделей поврежденности. Применение
инкрементальных теорий пластичности типа Прандтля-Рейсса при описании
разупрочнения (падение предела текучести с ростом деформации)
приводит к некорректным краевым задачам из-за нарушения
постулата Драккера или его математического аналога — критерия Ада-
мара. В квазистатике это связано с утратой уравнениями свойств
эллиптичности, а в динамике — с нарушениями гиперболичности.
Поэтому прямое описание процесса разрушения в рамках стандарт-
§11. Понятие поврежденности и построение моделей
103
Ж
■ ,,г^
Рис. 11.2. (слева вверху) схема образования полосы локализации при
зарождении пор; (слева внизу) локализация при образовании больших пор;
(справа) образование пор в образце при растяжении, характерный размер
пор 0.001-0.1 мм
ных моделей упругопластических материалов оказывается
некорректным.
С другой стороны, падение напряжений из-за потери материалом
способности к сопротивлению деформации может происходить по
нетермомеханическим причинам при неизменной деформации. Это
говорит о том, что при континуальном описании процессы
деформации и разрушения можно и нужно трактовать как независимые
(что не исключает их взаимовлияния), а развитие разрушения
целесообразно характеризовать своим параметром состояния — повре-
жденностъю. Этот важный шаг по пути разработки континуальных
теорий разрушения был сделан в работах Качанова [28] и Работно-
ва [59].
Под поврежденностъю в современной механике деформируемого
тела понимают нарушение сплошности структуры материала
вследствие внешнего воздействия.
Исторически первые попытки описать континуальное разрушение
материала основывались на критериях или теориях прочности,
которые рассматривали разрушение не как процесс, развивающийся в
течение нагружения, а как напряженно-деформированное
состояние материала, при котором оно наступает. Этот подход во многом
противоречил и экспериментальным наблюдениям и общим поло-
104
Гл. 2. Разностные схемы расщепления
Рис. 11.3. Образование макротрещины (слева) при слиянии микропор
(справа) в экспериментах по соударению пластин
жениям механики сплошных сред. В шестидесятые годы
прошлого века в работах советской школы механиков оформился новый
подход, в котором разрушение стало рассматриваться как процесс,
связанный с нагружением. Такая точка зрения очень быстро
завоевала признание, и в течение короткого времени сложилось
новое направление в механике сплошных сред — механика
повреждающихся среду или механика континуального разрушения:
Ильюшин А.А., Победря Б.Е. [25]; Качанов Л.М. [28]; Работнов Ю.Н. [59];
Кукуджанов В.Н. [42]; Curran D.R., Seaman L., Shockey D.A. [77];
Gurson A.L. [14], Tvergaard V. [103], Chu C.C., Nedelman A. [76] и
многие другие.
Континуальный подход к описанию процессов разрушения
предполагает построение теоретических моделей сплошной среды,
описывающих разрушение как процесс на основе единых уравнений для
деформирования разрушенного и неразрушенного состояний
материала. Этот подход описывает появление и развитие поверхностей и
зон разрушения без явного их выделения.
В первых работах по теории поврежденности на основе
представления о разрушении как о процессе развития в материале
микродефектов в виде микротрещин и микропор поврежденность
ассоциировалась с образованием пустот (пористостью), что приводит к
уменьшению площади, по которой действует напряжение и, следовательно,
к уменьшению упругих эффективных модулей материала,
изменение которых легко поддается измерению в эксперименте. Влияние
§11. Понятие поврежденности и построение моделей 105
микродефектов на несущую способность стержня при растяжении
проявляется в уменьшении эффективного модуля Юнга: а = Ее, где
Е = Е(1 — D) - эффективный модуль, уменьшающийся с ростом
поврежденности D.
Поясним на простом примере одномерного динамического
растяжения стержня, в чем смысл введения параметра поврежденности.
Рассмотрим упрощенную систему уравнений нелинейной упруго-
пластической модели Прандтля-Рейсса:
dv да
рт
дер
~дГ ~
дх '
ди
дх1
Н(Фр)\ра,
а -
V
= СГ{£ -
ди
&>(е,
-е%
ер)
0.
Для приращений напряжений и деформаций на шаге по времени
получаются следующие соотношения:
да де да
-dt=Etm> Et = ^>
где Et зависит от полных и пластических деформаций и от режима
нагружения (активное или разгрузка).
Получается следующая система уравнений:
dv да де де dv
dt де cbc' dt дх'
Корректность этой гиперболической системы уравнений в динамике
или эллиптической — в статике (если инерцией пренебречь),
определяется условием Адамара:
де
или его физическим эквивалентом, известным как условие Дракке-
ра:
da • de > 0.
Разрушение (участок 2-3 на диаграмме а — £, показанной на
рис. 11.4а) сопровождается разупрочнением Et < 0 и приводит в
рамках классической теории к потере корректности задачи.
106
Гл. 2. Разностные схемы расщепления
х
(а) (Ъ) (с)
Рис. 11.4. Типичная диаграмма деформирования материала: 0-1 —
упругое деформирование, 1-2 — пластическое деформирование, 2-3 —
разупрочнение (разрушение) (а). Поведение точного решения для
растягиваемого стержня с ослабленной центральной частью: показаны качественные
графики изменения деформации (Ь) и смещения или скорости (с)
С другой стороны, можно смоделировать явление разрушения с
помощью следующей упругой модельной задачи для неоднородного
растягиваемого стержня, имеющего в средней части участок
ослабленного сопротивления (<зону разрушения») Е\ « Е. Точное
решение показывает, что в <зоне разрушения» имеется всплеск
деформаций (рис. 11.4Ь), а скорость и перемещения меняются
скачкообразно (рис. 11.4с).
Возникает вопрос: можно ли построить физически и
математически корректную модель упругопластического материала,
описывающую появление зон пониженного сопротивления материала,
подобных <зоне разрушения» из рассмотренной модельной задачи?
Теории повреждаемости (поврежденности) дают утвердительный
ответ. Действительно, для повреждающейся упруго-пластической
среды система уравнений принимает следующий вид:
dv да
ди ди
а- = a(s -sp,f),
дхУ
dt
v,
де
~dt
f = Н(Фр)\р(Т, Фр(£,£р)=0,
dt
Я(Ф/)А/(е,еР)/)^0, <bf(e,ep,f) = 0,
где / — внутренняя переменная, характеризующая поврежденность
11. Понятие поврежденности и построение моделей
107
материала в процессе нагружения.
Откуда получаем
да д{е - ер) df да да
Ж = Et^dT~ + EfW Et = Те ' Ef= df'
В теории поврежденности ответственность за разупрочнение не
возлагается более на пластическую деформацию или на условие
активного нагружения, а относится к уравнению поврежденности.
Разупрочнение или, в более общем смысле, разрушение
рассматривается как потеря материалом способности к сопротивлению
деформации, выражающаяся в уменьшении значений модулей сопротивления
из-за разрыва связей или, что то же самое из-за появления
микротрещин. Разрушение описывается как независимый от деформации
процесс (именно независимый, это важно), поэтому характеристика
разрушения, называемая параметром поврежденности, связана не с
деформацией, а со структурой материала, её способностью к
сопротивлению нагружению и с другими параметрами состояния лишь
постольку, поскольку они все вместе участвуют в общей системе
уравнений и начально-краевых условиях термомеханики. Спад
напряжений независимо от изменения деформации обеспечивается вторым
слагаемым в приведенном выше выражении для скоростей
напряжений. Коэффициент Ef < 0, что отражает тот факт, что при модуле
Et(f) > 0 напряжения убывают с ростом поврежденности.
Положительность модулей упругости обеспечивает выполнение необходимых
условий корректности начально-краевых задач по Адамару и Драк-
керу.
В данном комментарии формулировка теорий и рассуждения
намеренно огрублены, например, температура не участвовала в
рассуждениях, параметры упрочнения не рассматривались, скоростное
упрочнение не фигурировало. Это сделано для более отчетливого
описания основной идеи теорий поврежденности. В дальнейшем эти
упрощения не используются.
Следует подчеркнуть еще один существенный момент: до
появления теории поврежденности в теориях прочности критерий
разрушения, как правило, не был связан с законами деформирования
материала и предлагался независимо. В большинстве моделей
поврежденности деформация и континуальное разрушение описываются
как единый процесс, то есть тело разрушается в результате своего
деформирования.
108
Гл. 2. Разностные схемы расщепления
Поврежденность моделируется зарождением и ростом
определенных микродефектов: дислокаций, микротрещин, микропор и т.д.
вплоть до образования макротрещин. Такой подход
подразумевает на определенном этапе усреднение или гомогенизацию свойств
материала в микрообъеме (размеры микродефектов составляют
Ю-15—Ю-10 см) и определение его эффективных свойств,
рассматриваемых уже в рамках сплошной среды (характерный мезомасштаб
носителей поврежденности — 10-4-10-2 см).
Это физический подход к построению моделей повреждающихся
материалов, когда в основу модели закладывается определенный
микромеханизм образования и развития неупругой деформации и
континуального разрушения материала.
Альтернативным ему является термодинамический подход к
построению континуального разрушения или поврежденности
материала. Здесь поврежденный материал изначально предполагается
сплошным, обладающим определенной внутренней структурой,
которая характеризуется некоторым набором внутренних переменных
(в частности поврежденностью, пластической необратимой
деформацией и т.п.), связанных с напряженно-деформируемым состоянием
материала. Для определения внутренних переменных
постулируются кинетические уравнения, согласованные с основными
принципами термодинамики и теории определяющих соотношений. Система
определяющих уравнений совместно с законами сохранения
образует замкнутую систему уравнений термомеханики, которая описывает
поведение материала вплоть до разрушения. Этот подход описан в
работах Кондаурова В.И. и Фортова В.Е. [35], Можена [90] и других
авторов.
В промежуточных подходах вводятся объекты различной
природы, из которых состоит материал промежуточного мезомасштаба
(зерна, поликристаллы, макротрещины, молекулярные цепи,
многофазные смеси и т.д.). Постулируется определенный механизм
образования обратимых и необратимых деформаций материала. Разделы
механики, развивающие такие подходы построения определяющих
уравнений, объединяются под названиями <мезомеханика>,
<молекулярная механика», <механика трещин» и т.д.
Поврежденность может быть изначальной, может возникать
только вследствие нагружения (зарождение пор) и иметь пороговое
условие аналогичное условию пластичности.
Физически механизмом нелинейной деформации является зарож-
11. Понятие поврежденности и построение моделей
109
дение и развитие в материале дефектов кристаллической решетки
под действием термомеханической нагрузки. Механизмы развития
дефектов, как и их природа, многообразны и исследуются в физике
твердого тела. В настоящее время хорошо изучены на микроуровне
природа дислокаций и их связь с пластической деформацией.
В работах Гарсона и Твергаарда [14], [103] предложено условие
пластичности для среды с периодическим расположением
сферических пор, полученное из теоретического решения. На его основе
Гарсоном, Твергардом и Нидельманом (Gurson, Tvergaard, Nedelman)
была предложена модель (GTN-модель) поврежденности
эффективного упругопластического материала, независящего от скорости
деформации, со скалярной мерой поврежденности — пористостью.
Модель учитывает зарождение и рост пор в процессе пластической
деформации, описывает пластическую сжимаемость материала и
эффект дилатансии. В качестве критерия разрушения принимается
критическая величина пористости.
GTN-модель получила достаточно широкое распространение и
использовалась при решении конкретных задач. Она хорошо
описывает влияние первого инварианта на пластические свойства и
сжимаемость разупрочняющегося пластического материала.
Определяющие уравнения GTN-модели. Гарсоном,
Твергардом и Нидельманом [14, 76, 103] была предложена связная модель
повреждаемости упругопластического материала, которая известна
в литературе как GTN-модель. В упругой области материал
подчиняется закону Гука:
<r = D:se/. (11.1)
Скорости упругих и пластических деформаций аддитивны:
e = eel+epl. (11.2)
Условие пластичности пористого материала получено Гарсоном,
исходя из решения задачи о сферически-симметричном
деформировании сферической поры в идеальнопластическом материале в
виде [14]:
•=Ш1+2п/А(-1^)-(1-(й/>а)=о- (пл)
по
Гл. 2. Разностные схемы расщепления
где s = pi + а — девиатор тензора напряжений Коши; S
tS : s —
интенсивность касательных напряжении; р = — ±сг : 1 —
гидростатическое давление; оу (ё?п) ~ предел текучести сплошного материала
(материала матрицы), зависящий от интенсивности пластических
деформаций; / — пористость (объемная доля пор в материале).
Твергард [103] ввел в это условие константы gi, q<i (как
коэффициенты корректировки пористости и давления) для того, чтобы
модель Гарсона давала согласие с численным расчетом модельной
задачи о растяжении материала, с периодической пористой структурой,
в случае плоской деформации. Твергард получил q\ = 1.5, q^ = 1.0.
Варьируя эти параметры, можно приблизить результаты численного
расчета к экспериментальным данным.
На рис. 11.5 приведена зависимость а(е) для материала с
начальной пористостью /о ПРИ одноосном растяжении и сжатии. При
сжатии материал упрочняется, так как пористость уменьшается, а при
растяжении разупрочняется из-за зарождения и роста пор.
а >
° г
_—^7 "'
Материал матрицы
/ Пористый материал
-cv
8
Рис. 11.5.
Рассматриваемая модель описывает поведения металлов с не
слишком большой долей пор. Хотя материал матрицы, содержащий поры,
предполагается пластически несжимаемым, поведение
эффективного материала зависит от давления из-за наличия пор.
В качестве пластического потенциала принимается условие
пластичности. Пластическая деформация представляется в виде (ассо-
11. Понятие поврежденности и построение моделей
111
циированный закон)
^ = xto=x{-libI + uas*)> (1L4)
где А — неотрицательный скалярный множитель.
Эволюция интенсивности пластической деформации и
пористости. Упрочнение-разупрочнение материала матрицы описывается
зависимостью о~у (^т) • Исходя из того, что работа пластических
деформаций выполняется только материалом матрицы, получим
уравнение, описывающее эволюцию е^:
(1-/)ауё£=*:ё?1, ё* = у/let : e£, (11.5)
где е9^ — пластическая деформация материала матрицы.
Изменение пористости материала происходит вследствие роста
существующих пор и зарождения новых:
/ — /gr ~г /nucl
Из уравнения неразрывности, считая материал матрицы
пластически несжимаемым, получим уравнение для роста пор:
fgI = (l-f)ipl:I. (11.6)
Зарождение пор происходит вследствие относительного движения
зерен и зависит от интенсивности пластических деформаций, в [76]
было предложено соотношение
/nUcl = ^, А(Р)=-Щ=еХр(-±£^)- (П.7)
5дгл/27Г \ Z Sn J
Интенсивность деформаций, при которой зарождаются поры,
подчиняется нормальному распределению со средней величиной £дг, с
дисперсией 5дг. Объемная доля зарождающихся пор равна /дг.
Поры зарождаются только при растяжении (объемная пластическая
деформация е\ > 0).
112
Гл. 2. Разностные схемы расщепления
§12. Микромеханическая
многомасштабная модель
поврежденности
упругопластического материала
Микромодель. Стадия пластического течения и упрочнения материала (112).
Стадия появления пор и поврежденности (113). Макромодель (115).
Растяжение тонкого стержня с постоянной скоростью деформации (120).
Заключение (122).
Рассмотрим уравнения микромодели упруговязкопластической
среды, в процессе деформирования которой зарождаются и растут
микродефекты, приводящие к интенсификации пластического
течения в локализованных областях типа полос скольжения и
постепенному разрушению материала.
Микромодель. Стадия пластического течения и упрочнения
материала. Начальный этап пластического течения описывается
на микроуровне движением дислокаций. Скорость вязкопластиче-
ской деформации jp пропорциональна потоку движущихся
дислокаций [22, 82]:
f = abNmV, (12.1)
где а — вектор Бюргерса, Ъ — коэффициент ориентации. Средняя
скорость дислокаций V определяется термофлуктуационным
движением и действующим активным напряжением s". = Sij — s[- [38, 82]:
V = V0 exp U°~^l~Sr\ s > sr, (12.2)
где Uo — энергия активации, к — постоянная Больцмана, в —
абсолютная температура, sr — остаточное напряжение.
Число подвижных дислокаций Nm растет пропорционально
степени пластической деформации jp и падает с увеличением общего
числа дислокаций N вследствие их запирания на межзеренных
границах [66]:
Nm = (No + crf)n exp (-N/N*), (12.3)
где iVo? iV*, a — постоянные материала.
Чтобы описать процесс зарождения микродефектов и их развития,
необходимо рассмотреть баланс потоков дислокаций в материале. В
§12. Микромеханическая многомасштабная модель поврежденности 113
соответствии с формулами (12.1) - (12.3) полный поток дислокаций
pij на первой стадии пластической деформации распадается на два:
поток подвижных дислокаций jf-, идущий на образование
собственно пластической деформации, и на поток дислокаций а;^/, который
скапливается около изолированных препятствий и на границах
зерен.
Обозначая через т\ часть потока р^', которая связана с подвижными
дислокациями, а через 1 — rj поток, скапливающийся на границах
зерен, можно записать:
откуда получим ш^ = (1 - 77)7^/77.
Стадия появления пор и поврежденности. При достаточном
скоплении дислокаций на межзеренных границах происходит
частичная аннигиляция накопившихся дислокаций и движение зерен
друг относительно друга, возникают дисклинации, образуются
микропоры и микротрещины [66]. Эта вторая стадия деформации
характеризуется постепенным разрушением материала, которое приводит
к дополнительной деформации. Пластическая деформация
сосредотачивается в областях наибольшего макроразрушения и приводит к
развитию полос скольжения.
На второй стадии баланс потоков запишется так:
(1 -v)Pij =Vij +bij,
где bij — тензор потока аннигилирующихся дислокаций.
Образование пор также часто связывают с образованием таких дефектов, как
вакансии в узлах кристаллической решетки, и с их перемещением к
границам кристалла, где происходит их коагуляция и образование
пор [66, 71]. Заметим, что на первой стадии пластической
деформации шаровая часть тензора пластической деформации рц = О,
поэтому соц = 0, на второй стадии появляется объемная пластическая
сжимаемость рц ф 0 и Ьц Ф 0.
Естественно предположить, что поток аннигилирующихся
дислокаций Ь^ пропорционален накопившимся на препятствиях
дислокациям UUijl
bij = Xouij, (12-5)
114
Гл. 2. Разностные схемы расщепления
где Л — неизвестный скалярный множитель.
Процесс стока начинается только после того, как интенсивность
~ гл /Я \1/2
тензора накопившихся на препятствиях дислокации У = y^ij^ij)
достигает критического значения Qq. При этом интенсивность
стока Вц будет монотонной функцией избыточной интенсивности
(Ojj-По):
где Q(z) безразмерная функция своего аргумента, атр- параметр
размерности [с], связанный с масштабом пор. Условие (12.6)
позволяет определить параметр Л:
А=3(""-Ч (12.7)
Tpilii
Окончательное уравнение для определения потока Uij на
основании (12.4) - (12.7) можно записать в виде
ckjjj Q(Sln-Slo) =1^^
dt трПп г° г) dt [ ' }
Макрофизический смысл тензора Uij соответствует тензору
микронапряжений и следует из хорошо известного экспериментального
факта, что величина микронапряжения пропорциональна плотности
скопления дислокаций на границах зерен [66, 82].
Критическая плотность дислокации ^о? ПРИ которой появляются
микротрещины на межзеренных границах или других
препятствиях и соответствующая ей критическая интенсивность остаточных
напряжений Sq, может быть определена на микроуровне на основе
дислокационных моделей разрушения (см. [63] 67-68).
Условие £1ц = ^о в пространстве компонент тензора напряжений
имеет смысл поверхности начала разрушения.
Характеристики тензора аннигиляции Ь^ корелирируют с
тензором повреждаемости среды Dij. Девиаторная часть тензора Ь'ц
связана с девиатором повреждаемости D[a, которая приводит к
релаксации остаточных напряжений (второе слагаемое в уравнении (12.8)).
12. Микромеханическая многомасштабная модель поврежденности 115
Шаровая часть Ьц корелирует с объемной деформацией
повреждаемости Ьц —► Da и связана со скоростью роста пористости /, которая
определяется уравнением неразрывности.
Макромодель. Переходя от микропараметров к
макропараметрам, запишем уравнения (12.1) - (12.3) для трехмерного
напряженно-деформированного состояния в обобщенной форме в
виде соотношения между вторыми инвариантами тензора скорости
пластической деформации jp и тензора активных напряжений Sa:
(12.9)
Ъ = /Ы
са _ (3Qa а Л1/2
— ^-А
1>(sa-ss)
i
~p - (Ча.Ра.рЛ1/2
1 V3 hj hj) •>
P 1 Г
где Td — время релаксации активных напряжений, связанное с
масштабом дислокаций.
Принимая гипотезы теории течения [27], получим из уравнений
(12.1) - (12.3) на первой стадии деформирования при £1ц < ^о УПРУ_
говязкопластические уравнения для общего трехмерного
деформируемого состояния:
1
/(7р^(*а sS) (12ло)
Ъэ- 2j3*ij ' ,V/ / TdT ~г3
Считая материал для простоты пластически несжимаемым: evkk = О,
для шаровых частей тензора оц получим упругий закон.
Принимая, что для девиаторов остаточных напряжений и
накопившегося потока дислокаций выполняется соотношение
4=2М*Ч'я (12-11)
получим, что условию ftц < fto Для остаточных напряжений s[
отвечает макроусловие Sr ^ fig, здесь /х* — константа
размерности [Н/м2]. Эволюционное уравнение (12.4) для s[ на первой стадии
пластического деформирования примет вид
2ц* tJ « lij'
$ = —^%- (12Л2)
116
Гл. 2. Разностные схемы расщепления
Интегрируя (12.12) по t при постоянном /х*, получим известный
закон кинематического упрочнения:
4 = 2а7£, а = М*^- (12.13)
Модуль упрочнения а определяется из экспериментальных данных
по эффекту Баушингера.
Таким образом, для Sr < Sq , т.е. до начала образования микропор,
материал матрицы описывается в соответствии с теорией
дислокаций уравнениями (12.10) - (12.13) упруговязкопластической среды с
кинематическим упрочнением. При Sr ^ Sq для тензора s[
получаем релаксационное уравнение:
2^(У-ЗД)) (]214)
Тр о
Уравнения (12.12) - (12.14) молено записать в виде единого
уравнения, если ввести функцию Q(z) в соответствии с формулой (12.6).
Это уравнение описывает релаксацию остаточных напряжений в
материале после того как начался процесс образования микропор, а
следовательно, разупрочнение материала. До этого в материале
происходило упрочнение в соответствии с уравнением (12.13).
Уравнение (12.14) показывает, что релаксация происходит до некоторого
стационарного значения Sq(/), отличного от нуля. В дальнейшем
при t ^> тр остаточные напряжения будут изменяться по закону
пластического течения, ассоциированного с поверхностью текучести с
пределом текучести, зависящим от пористости Sr = #о(/), которое
следует из (12.14) при тр —► 0:
ds\3 + Н {s^deU) T^TTTTf 4 = 2c<-> (12.15)
где H(z) — функция Хевисайда.
С появлением пор ситуация существенно меняется. Теперь
материал состоит из матрицы и пустот, т.е. является двухфазным
материалом. Зная свойства матрицы, которые описываются уравнениями
(12.10), (12.13), можно найти эффективные характеристики
пластического материала. С появлением пор изменяется условие
пластичности материала, кроме того, нужны уравнения, описывающие
зарождение и эволюцию дефектов. Трудность решения этой задачи
12. Микромеханическая многомасштабная модель поврежденности 117
существенно зависит от формы пор. Теоретическое решение
проблемы возможно на основе решения задачи о единичной поре в среде под
действием сил, приложенных на бесконечности, и последующем
суммировании этого решения для некоторого известного распределения
пор по размерам и ориентации. Ясно, что решение в аналитической
форме, если и возможно, то только для простых линейных сред. Для
нелинейных сред решение можно получить только численно и
постараться аппроксимировать его простым аналитическим выражением,
выделив наиболее существенные факторы, либо сделать это,
основываясь на экспериментальных данных.
Полагая, что поры имеют сферическую форму, примем, что для
идеально упругопластического пористого материала справедливо
условие пластичности Гарсона. Обобщим его на пористый материал,
матрица которого описывается упруговязкопластическими
уравнениями с кинематическим упрочнением:
$(a?jJ,aY) = l^+2qifchZf^-(l + (qiff) =0,(12.16)
где sfj — девиатор тензора активных напряжений, а а у есть предел
текучести матрицы упруговязкопластического материала, который
определяется из условия равенства пластичной работы для матрицы
и эффективного материала:
а ~Р
(ТТо?
(1-/)7р[^у(7р)+^-1Ир)],
Из первого уравнения определяется 7Р, после чего из второго
находим оу. Напряжение а^ и скорости диссипативных деформаций ё\-
в эффективном материале связаны ассоциированным законом
пластического течения:
4=^, (12.18)
если ассоциативный закон имеет место для материала матрицы [83].
Параметр Л определяется из второго уравнения: (12.17):
118
Гл. 2. Разностные схемы расщепления
Из уравнения неразрывности следует уравнение роста пор:
fgr = (1 - f)4k = Л ^1^2 sh — . (12.19)
О у ZtJy
Уравнения зарождения и эволюции пор остаются такими лее, как
для GTN-модели и описываются формулами (11.5) - (И-7) и
замыкают полную систему определяющих уравнений (12.16) - (12.19). Из
них находятся напряжения и внутренние параметры материала при
заданном поле скоростей, которое определятся из законов
сохранения.
Критерием разрушения материала для предполагаемой модели
является условие критического накопления пор. Поскольку
кристаллиты находятся в стесненном состоянии и не могут деформироваться
свободно, то на межкристаллитных границах образуются межкри-
сталлитные поры. Они накапливаются до некоторого критического
значения пористости / = /сг, при котором происходит их
катастрофическое распространение, что ведет к полному межкристаллитно-
му разрушению материала. Это критическое значение пористости fcr
зависит от многих внешних факторов температуры, скорости нагру-
жения и других, а также от структуры материала, и, как показывают
эксперименты, изменяется в пределах (0,05-0,50) [66].
Введем в модель эффекты, учитывающие некоторые особенности
поведения материала в поврежденном состоянии. Они касаются
влияния пористости на упругие модули среды и поверхность
поврежденное™ материала Sr = Sq(/).
Учитывая, что внутренняя упругая энергия поврежденного
материала зависит от пористости и не зависит от пластических
деформаций: Uel(f,efj), получим, что упругие модули Е, ц
изменяются в соответствии с формулой, предложенной Л.М. Качановым:
Е = Е(1 — /), Д = /х(1 — /), где / — пористость, определяемая
формулой (12.19).
Считая, что влияние пористости на поверхность поврежденности
подобно ее влиянию на поверхность пластического течения для
активных напряжений, примем следующее приближенное
соотношение:
W) = ^^, W) = °у (1 + «?/а)1/а ■
Учет обоих эффектов приводит к более интенсивному
разупрочнению, следовательно, и более резкой локализации. Как показали рас-
12. Микромеханическая многомасштабная модель поврежденности 119
четы по начальной версии модели (без перечисленных добавлений),
эти эффекты были недостаточно выраженными вследствие большой
мезовязкости материала: тр^> т&.
Подчеркнем, что предложенная модель поврежденности в
отличии от GTN-модели многомасштабная. Она содержит три
временных масштаба: to — характерное время задачи, тр — время
релаксации напряжения в поврежденном материале, т^ — время
релаксации в исходном вязкопластическом материале, которые отвечают
трем разным пространственным масштабам: макро-, мезо- и
микромасштабам, которые отвечают соответственно размерам
макрообъекта, размерам поры и дислокации и удовлетворяют неравенствам
to > тр > rd.
На стадии упрочнения масштабный эффект определяется малым
параметром Sd = т^/£о, а на стадии разупрочнения Sp = rp/to ^> $d-
При стремлении 5Р и Sd к нулю модель переходит в GTN-модель с
кинематическим упрочнением, не зависящую от масштабных
факторов.
Приведем геометрическую
интерпретацию поверхности
пластичности и поврежденности для
предложенной модели в пространстве
напряжений, которая широко
используется при описании теории
пластического течения. Модель
имеет две критические
поверхности, зависящие от интенсивности
скоростей пластической
деформации и пористости /, которые
определяют поведение материала. Они
показаны на рис. 12.1
штриховыми линиями. Поверхность
пластичности активных напряжений
Sa = сгу(/) определяет переход из Рис- 12-1-
упругого состояния в пластическое, поверхность Sr = Sq(/)
определяет начало образования пор. Сплошными линиями показаны
стационарные положения этих поверхностей.
В модель нетрудно включить температурные эффекты, если к
деформации е добавить температурную составляющую £?• = aOSij, a
SQ=aY(f)
Sr = Sr0(f)
120
Гл. 2. Разностные схемы расщепления
температуру в определять из уравнения
ВО
PCV=-Qt= X°aA (12'20)
которое следует из предположения об адиабатичности
процесса. Здесь ср — теплоемкость при постоянном напряжении,
X = 0.8 -!- 0.9 — тепловой коэффициент конвертируемости, а —
коэффициент теплового расширения, р — плотность эффективного
материала.
В заключение отметим, что численное моделирование процессов
разупрочнения и локализации деформаций на основе уравнений
(12.16) - (12.20) предложенной микромодели было рассмотрено в [31],
где приведено решение задачи о разрушении осесимметричного
цилиндра при квазистатическом растяжении с постоянной скоростью, а
в работе [45] рассмотрена задача о динамическом разрушении
стержня при высоких скоростях нагружения.
В литературе имеются и другие мезомодели связанных вязкопла-
стических повреждающихся сред, построенных в более упрощенных
предположениях, чем приведенная в настоящей работе, как для
описания вязкого континуального разрушения [105], так и для хрупкого
разрушения под действием циклического нагружения [80].
Растяжение тонкого стержня с постоянной скоростью
деформации. Рассмотрим наиболее распространенный вид
испытания материалов на одноосное растяжение-сжатие тонкого стержня с
постоянной скоростью деформаций. Решение этой задачи позволит
оценить, насколько хорошо предложенная модель описывает
диаграмму материалов с разупрочнением. Подчеркнем, что вид кривой
а — е в модель явно не закладывается, а является следствием
принятой модели разрушения материала. На стадии упрочнения
принимается простейшая гипотеза о линейном упрочнении материала.
Результаты интегрирования определяющих уравнений
представлены в виде кривых а — е при постоянной скорости деформации ё = ёо •
На рис. 12.2 приведены четыре характерные кривые для
различного типа материалов. Первые три кривые получены при So = 1,5
и разных значениях параметра упрочнения а (см. табл.), q\ = 1.0,
<22 = 1.0, Td/to = 0.01, Tp/to = 1.0, a, So — безразмерные величины,
отнесенные к пределу текучести.
§12. Микромеханическая многомасштабная модель поврежденности 121
Таблица
№
So
а
1
1.5
0.01
2
1.5
0.1
3
1.5
0.9
4
0.2
0.1
Как видно из рис. 12.2, кривые при переходе во вторую стадию
деформирования при появлении пор имеют излом, после которого
следует разупрочнение.
Для кривой 1 при малых а = 0.01 характерны большие
пластические деформации в стадии упрочнения и резкий спад напряжений
при разупрочнении, которое затем выходит на стационарное
значение.
Кривая 2 получена при сё = 0.1 и
So = 1-5 в этом случае диаграмма
имеет «зуб» текучести, после
которого происходит частичное
разупрочнение материала с
последующим упрочнением. Такое
поведение характерно для мягких сталей,
железа и некоторых других
материалов, в которых происходят фа- " J0 ^ J^
зовые превращения. рис -^ 2
Кривая 3 соответствует большим
значениям параметра кинематического упрочнения а = 0.9,
остальные параметры приведены в табл. Видно, что в этом случае
участок разупрочнения невелик критическое значение /* достигается
при сравнительно небольших деформациях. Кривые такого типа
характерны для высокопрочных материалов.
Кривой 4 соответствуют значения So < 1 (а = 0.1, 5 = 0.2). В этом
случае диаграмма а — е получается гладкой без излома,
характерного для предыдущего случая (So > 1), с длительным участком
разупрочнения, предшествующим полному разрушению материала при
Д = 0.5. Подобные диаграммы характерны для таких материалов,
как некоторые грунты, глина.
Таким образом, при сравнительно небольшом произволе в четыре
параметра, модель позволяет описать, по крайней мере
качественно, широкий спектр свойств различных материалов. При
феноменологическом количественном описании реальных материалов
дополнительно для согласования с экспериментальными данными может
/GT
к
\
- -»
ч-—
\\
Л
122
Гл. 2. Разностные схемы расщепления
быть использован произвол в выборе функций Q(z), Ф(^), So(/),
a(sp)y E(f)y которые фигурируют в модели и в приведенных
расчетах, принимались линейными или постоянными.
Заключение. Предложенная модель является многомасштабной
моделью, она качественно отличается от GTN-модели. Как видно из
текста, предложенная модель построена на основе дислокационных
представлений о пластической деформации при термомеханическом
нагружении поликристаллических материалах при умеренных
пластических деформациях. При больших деформациях — на
представлениях о зарождении и росте мезодефектов типа пор и микротрещин.
На конечной стадии разрушения происходит за счет слияния пор в
макротрещину и её распространения вплоть до фрагментации
конструкции. Постулирование кореляции между микро- и
макропараметрами позволяет осуществить переход от микроуравнений к
определяющим макроуравнениям механики сплошных сред и получить
кинетические уравнения связной модели упруговязкопластичности
с поврежденностью. В результате такого подхода поврежденность
описывается тензором, шаровая часть которого — пористость, а де-
виаторная — связана с релаксацией остаточных напряжений.
Изменение упругих модулей происходит на стадии появления пористости.
Материал матрицы учитывает кинетическое упрочнение и,
следовательно, остаточные напряжения, а также описывает эффект Бау-
шингера.
13. Численное моделирование поврежденности
123
§13. Численное моделирование
поврежденности
упругопластических материалов
(вязкое и хрупкое разрушение)
О регуляризации уравнений упругопластических материалов при
разупрочнении (123). Решение задач повреждаемости (125). Обратный метод
Эйлера (125). Решение краевой задачи. Вычисление якобиана (127).
Метод расщепления (128). Интегрирование определяющих соотношений GTN-
модели (131). Одноосное растяжение. Результаты расчета (135). Изгиб
пластины (137). Модель квазихрупкого разрушения с учетом
повреждаемости (139).
О регуляризации уравнений упругопластических
материалов при разупрочнении. Для моделирования процессов
поврежденности, кроме определяющих уравнений модели, необходимы
специальные численные методы их решения. Поврежденность
материала связана с разупрочнением, локализацией пластических
деформаций и с фазовыми превращениями. Это создает определенные
трудности при интегрировании определяющих уравнений и решении
начально-краевых задач. Модели повреждающихся сред, неучиты-
вающие многомасштабный эффект в процессе разрушения,
требуют регуляризации. Например, как уже отмечалось, первые попытки
описать поврежденность в рамках теории течения с падающей
диаграммой материала оказались неудачными, т.к. при этом
нарушается условие реологической устойчивости Дракера (квазистатическое
нагружение), а в динамике условие Адамара [12, 19]:
det (Cijkinifij) > 0 Утц,
где Cijki — матрица модулей материала d<Jij = Cijkideki-
Введение в модель регуляризирующих операторов возможно как
на основе учета дополнительных физических процессов (неучтенных
основной моделью), так и на основе математических соображений
введением в уравнения искусственных членов с малыми
параметрами, регуляризирующими уравнения более низкого порядка.
Вводимые операторы высокого порядка могут быть связаны с временным
либо с пространственным масштабными факторами.
Например, в теории течения при условии пластичности, не
зависящим от изменения масштаба времени, при падающей диаграмме
124
Гл. 2. Разностные схемы расщепления
материала: а = оу(е\ day jde < О, задача оказывается
некорректной. Регуляризация достигается переходом к упруговязкопластиче-
ской модели:
dt Edt] оу(0) ' l }
где т — время релаксации, Е — модуль упругости. Оператор в левой
части уравнения, отвечающий скорости пластической деформации,
повышает порядок определяющего уравнения по времени t.
Другой способ регуляризации заключается в переходе к
градиентным или нелокальным соотношениями между напряжениями и
деформациями (повышение порядка производных по пространству)
также регуляризирует задачу:
ди д3и
дх дх3'
Тогда уравнение движения примет вид
h2^u д2и _ д2и т2
дх4 дх2 dt2 '
Однако введение в определяющие уравнения операторов высшего
порядка с малым параметром S неединственны и не лучший способ
регуляризации задачи. Будем называть его математическим. Болле
простой и естественный физический способ заключается в
расширении числа определяющих параметров, например, как это сделано в
вышеприведенных моделях введением параметра поврежденности /.
При повышении порядка уравнений предельная задача при малом
параметре S = 0 не имеет решения в классическом смысле. Решение
жесткой задачи существует в лучшем случае только в
асимптотическом смысле. В то время как при физическом способе предельная
задача остается корректной и её решение существует в
классическом смысле. Численное решение при <5<1 проще, чем в случае
математического способа регуляризации. Математическая
регуляризация дифференциальных уравнений не снимает полностью проблему
численной корректности решения дискретной задачи и требует
специальных методов решения жестких задач, а также различного рода
искусственных вычислительных приемов для получения адекватных
результатов, подавляющих чувствительность решения к
дискретизации задачи [12].
13. Численное моделирование поврежденности
125
Решение задач повреждаемости. В настоящее время метод
конечных элементов успешно применяется для решения широкого
круга нелинейных задач, в частности для решения упругопластических
и упруговязкопластических задач. В большинстве работ
интегрирование определяющих уравнений выполняется пошаговыми
методами по параметру нагружения. При этом приходится численно
интегрировать определяющие уравнения и полную систему уравнений
краевой задачи. Выбор схемы интегрирования чрезвычайно важен
для решения, особенно при больших деформациях, на порядки
превосходящих упругие. В литературе предложено несколько методов
интегрирования определяющих уравнений [97, 94, 100].
Использование явных методов приводит к условно устойчивым схемам [93].
При больших деформациях и при решении многомасштабных
жестких задач необходимо использовать неявные безусловно устойчивые
схемы [46, 93]. Как показано в [94], обратный метод Эйлера дает
хорошие результаты при условии пластичности Мизеса. В работе [73]
этот метод был обобщен на уравнения с условием пластичности,
зависящим от двух первых инвариантов тензора напряжений и
внутренних переменных модели и применен к решению задач для
упругопластических пористых материалов.
Обратный метод Эйлера. Проведем интегрирование
определяющих уравнений упругопластической среды с условием
пластичности общего вида, зависящим от двух первых инвариантов тензора
напряжений и со структурными переменными. Свойства материала
примем не зависящими от изменения масштаба времени, имея в виду
интегрирование уравнений GTN-модели.
Уравнения GTN представляют собой систему дифференциальных
уравнений, которая не зависит от изменения масштаба времени и
может быть записана в приращениях. Интегрирование выполняется
по шагам по условному параметру нагружения, который обозначим
через t. Состояние материала в момент времени t известно, кроме
того, при t + At задается приращение полной деформации As.
Требуется определить напряжение и внутренние переменные,
удовлетворяющие всем уравнениям системы, включая условие пластичности
при t + At.
Для этого запишем закон Гука при t + At в следующем виде:
<r = De/ : se/|t+At = De/ : (se/|t + Ase/) = ael - De/ : Ase/, (13.3)
126
Гл. 2. Разностные схемы расщепления
где
ael =De/ : (se/|t + As)
ael молено рассматривать как упругий предиктор, где
BeL = 2GI(g)I+ [K--G)I-I
— линейный изотропный тензор упругости. Здесь G — модуль
сдвига, К — модуль объемного сжатия, I ® I и I — соответственно
единичные тензоры четвертого и второго порядка. Предполагается
разложение полной деформации на сумму упругой и пластической частей.
Условие пластичности, закон течения и эволюционное уравнение
для внутренних переменных записывается в следующем виде:
Ф(<т,На) = 0,
Aepl = ^AspI + Asgn,
AHa = Да (д^ А(7 н^ ;
дФ
Аер = -ДА—, Д£д =
_ дФ
dq '
(13.4)
(13.5)
где
3
п = —s,
2q
Здесь На — внутренние переменные. Для GTN-модели а = 2:
Н1 = Щ^ — интенсивность деформаций в пластической матрице и
Н2 = f — пористость.
Приращение параметра АЛ исключается из двух последних
уравнений. В результате получаем
дФ Л дФ
Уравнение (13.4) подставляем в (13.3):
а = ael - KAepI - 2GAeqn, (13.6)
se^ и п коаксиальны, поэтому
3 м
п=—-,8е'. (13.7)
2qel х '
13. Численное моделирование поврежденности
127
Т.к. п известно, то согласованное определение скалярных величин
Аер и Aeq замыкает решение задачи. Таким образом, задача
интегрирования упругопластических определяющих уравнений,
зависящих от давления, сводится к решению двух следующих нелинейных
уравнений для скалярных величин Аер и Aeq:
Ф(р,д,На)=0, (13.S
дФ дФ
dq q dp
A£p—+A£q—=0. (13.9)
В (13.8) - (13.9) p, q, Ha определяются по формулам
p = pel+KAep, (13.10)
q = qel -3GAeq, (13.11)
AHa = ha(Asp,Asq,p,q,H^. (13.12)
Уравнения (13.10) - (13.11) получены умножением уравнения (13.8)
на I и п соответственно. Уравнение (13.12) — альтернативное
выражение уравнения (13.5).
Разрешая эту систему уравнений относительно неизвестных р, q,
Aepi Aeq и Нау замыкаем алгоритм интегрирования для пористого
пластического материала.
Уравнения (13.8) и (13.9) решаются относительно Аер и Aeq
обратным методом Ньютона. Затем с помощью (13.10) - (13.12)
определяются р, q и На на следующем слое.
Решение краевой задачи. Вычисление якобиана. При
использовании неявной схемы для решения нелинейных задач
дискретное уравнение равновесия приводит к нелинейной системе уравнений
относительно узловых переменных, для решения которой
используется метод Ньютона с квадратичной скоростью сходимости. Этот
метод требует вычисления линеаризованного модуля
дАе \de)t+M
Для вычисления якобиана 3 используется (13.6), переписанное в виде
сг = 2G (eel\t + Ае - Aegn) + К (eeklk\t + Askk - Аер) I,
128
Гл. 2. Разностные схемы расщепления
где 6 = 6 — \ек]Л — девиаторная часть тензора дееформаций е.
После дифференцирования получим:
да = 2G (де - dAsqii - Asqdn) + К (декк - дАер) I. (13.13)
Вариации dAeq и дАер вычисляются с помощью (13.8) и (13.9).
После достаточно трудоемких алгебраических вычислений
получаем систему линейных уравнений для определения вариаций dAeq
и dAsp. Подставляя найденные величины в (13.13), получаем
линеаризованный модуль.
В общем случае линеаризованный модуль оказывается
несимметричным, но несимметрия, как правило, мала и ей молено пренебречь
при решении системы уравнений.
Метод расщепления. Общая схема расщепления определяющих
уравнений упругопластического материала была изложена в § 9 для
решения задачи динамики по явной схеме. Здесь же мы рассмотрим
применение метода расщепления для решения краевых задач в
слабой формулировке по неявной схеме. Как уже отмечалось выше,
расщепление определяющих уравнений при этом никак не изменится.
Изменения касаются решения системы уравнений краевой задачи по
неявной схеме. При это необходимо вычислять якобиан для полной
системы уравнений. Расщеплению подвергается только уравнение:
f=D :(«-*-). (13.14)
где D — тензор упругих модулей материала, dcr/dt — объективная
производная от тензора напряжений Коши.
Предиктор берется при ер = О, тогда материал среды упругий:
£=»■■*> (13Л5)
совместно с уравнениями движения на шаге At необходимо решать
упругую задачу при начальных условиях, полученных на
предыдущем шаге для полной упругопластической задачи.
После этого на этапе корректор решаются уравнения релаксации
напряжений (13.14) при е = 0 совместно с уравнениями,
описывающими внутреннюю структуру материала (упрочнение,
повреждаемость и т.д.) при начальных условиях, полученных на этапе
предиктор.
13. Численное моделирование поврежденности
129
Используя закон ассоциированного течения, получим уравнение
релаксации напряжений:
da (1\^дФ , п
-J7 = --jrV —, 13.16
at at да
Щ = ^{а,Н^, (13.17)
где Hi — параметры, описывающие внутреннюю структуру
материала.
Задача интегрирования определяющих уравнений для нахождения
напряжений и внутренних параметров среды при фиксированной
деформации представляет задачу релаксации напряжений, имеющую
самостоятельное значение.
В случае классической или равновесной упругопластической
среды, свойства которой не зависят от изменения масштаба времени, в
уравнениях (13.16) и (13.17) можно исключить время t и перейти к
дифференцированию по переменной Л:
da
d\
ВФ
-D—
да
(13.18)
\ ии
нн
-^=рг(ст,Н3). (13.19)
Решая уравнения (13.18) и (13.19) при начальных условиях
сг(Ло) = сгп, Щ(Хо) = Hf\ полученных из решения упругой задачи
на этапе предиктора, найдем решение как функции Л, ael и Hf:
а = а (\ае\Щ) , Нг = Нг (\ае\Щ) (13.20)
Подставляя найденные решения в условие пластичности, получаем
уравнение для определения параметра Л = Л*, отвечающего
коэффициенту корректировки:
Ф(А,р(А),5(А),Я<(А)) = 0. (13.21)
Решая это уравнение, находим Л = А*(сгп, Hf) и, подставляя Л*
в (13.20), получаем окончательное решение определяющих
уравнений на рассматриваемом шаге нагружения, после чего переходим к
решению полной краевой задачи при заданном шаге по параметру
нагружения.
130
Гл. 2. Разностные схемы расщепления
Решение краевой задачи. Вычисление якобиана. Решение краевых
задач на основе принцип возможных перемещений методом
конечных элементов сводится к системе нелинейных алгебраических
уравнений относительно узловых перемещений. Для решения этой
системы уравнений методом Ньютона нужно вычислять якобиан дет /да
(а — полная деформация). Вычисление якобиана зависит от
алгоритма интегрирования определяющих уравнений. Стандартным
методом это удается сделать только в численном виде. При
интегрировании определяющих соотношений методом расщепления
достигается существенное упрощение этой задачи, и она может быть решена
в аналитическом виде.
Покажем это на примере упругопластической среды с линейным
упрочнением. На этапе предиктора полная деформация а
считается упругой и решение для напряжений полной задачи выражается
только через ael, поэтому
а
сг
да дае1'
(13.22)
Продифференцируем уравнение для напряжения по а с
учетом (13.22):
да fdpel\ /dse/N
да \ да ) \ да /
dpel dsel
да ' да
модуль объемного сжатия,
)--(!)■
= 2GI- -GI(g)I,
о
G = /i — модуль
(13.23)
(13.24)
сдвига, I —
где К
единичный тензор второго ранга.
Так как выражение для коэффициента корректировки х находим
в явном виде [46], то, дифференцируя его по s, получаем
окончательный результат:
— =Жх1+[К--Сх\1®1 + ——^®^, (13.25)
где учтено Sel = A/|se/ : se/.
Результаты расчёта. В качестве примера рассмотрим задачу
о сдвиге бруска в 3-мерном случае. Стальной брусок размерами
5x2x1 мм жестко закреплен на торцах. Верхняя грань как жесткое
13. Численное моделирование поврежденности
131
целое перемещается в направлении, показанном на рис. 13.1а
стрелкой. Перемещение сдвига равно толщине бруска 2 мм.
Безразмерные константы материала, отнесенные к пределу текучести Е = 500,
v = 0.3, модуль пластического упрочнения \±\ = 0.1.
На рис. 13.1 показаны деформация бруска, деформация лагран-
жевой сетки и изолинии интенсивности касательных напряжений в
материале. Задача решалась двумя разными методами: методом
расщепления и обратным методом Эйлера второго порядка точности,
предложенным в работе [73].
а)
На рис. 13.2 изображены зависимости интенсивности касательных
напряжений S и давления р от параметра нагружения в элементе,
выделенном стрелкой на рис. 13.16. На рис. 13.2 сплошная линия
соответствует расчету по методу [73], а крестики — расчету по методу
расщепления.
Были получены следующие результаты: шаг по времени в точности
совпадает в обоих методах; количество итераций в методе Ньютона
одинаковое в обоих случаях; время расчета методом расщепления
меньше (12 мин 18 с по сравнению с 13 мин 26 с); значения для
интенсивности и давления совпали с хорошей точностью.
Относительная погрешность не превышает Ю-5.
Интегрирование определяющих соотношений GTN—модели.
Применим численно-аналитический метод к более сложным уравне-
- +1
- +1
- +5
430е+00
180е+00
OZSe+00
lS9e-01
61Ze-01
06Se-01
Рис. 13.1.
6)
132
Гл. 2. Разностные схемы расщепления
а) б)
Рис. 13.2.
ниям упругопластической среды с пористостью. Для простоты
примем, что зарождение пор отсутствует и материал матрицы идеально
пластический, тогда уравнение для роста пор будет / = fgr.
Преобразование системы определяющих соотношений. Запишем
уравнение для напряжения в следующей форме:
da = D : (de - deel) ,
_ , d\d<S>^ x
da = T> : ds+ — — D : I
3 op
3d\d<S>
где
D : s = 2Gs,
Уравнение для давления имеет вид
25 dS
D : I = SKI.
D : s,
dp= -K(de:I)-dXK
дФ
dp'
Уравнение для девиатора напряжений:
ds = 2Gde-6Gsd\.
Преобразуя уравнение для пористости, получим
df
с1Ф
(13.26)
(13.27)
(13.28)
Приведем для сравнения систему определяющих уравнений
полной задачи при решении методом [73] и уравнений в методе
расщепления на этапе корректора.
13. Численное моделирование поврежденности
133
Полная задача
дФ
dp=-K(de:I)-dXK—
ар
ds = 2Gde-6GsdX
df = -d\(l-f)^
начальные условия берутся с
предыдущего шага
Метод расщепления
дФ
dp = dXK—
op
ds = — 6Gsd\
df = -d\(l-f)^
в качестве начальных условии
берется упругое решение
-(£)"+W-i^)-<i+«"'>-
Этап корректор. Решаем задачу релаксации напряжений.
Система уравнений в безразмерных переменных, отнесенных к о~уу имеет
вид
dp „9Ф _ . , /3
d\ dp
ds
d[_
d\
-^Kq1q2f sh I -q2p
—6Gsd\,
d<$>
(i-Л
dp '
Ф
S'z + 2Qlf ch ( --q2p ) - (1 + qsf) = 0.
(13.29)
(13.30)
(13.31)
(13.32)
Начальные условия берутся из решения упругой задачи,
полученном при Л = Лп и помечены снизу нулем: ро, so, So, /о.
Всю систему уравнений полностью не удается проинтегрировать в
аналитическом виде, как в случае условия текучести Мизеса. Точно
интегрируются уравнения для компонент девиатора (13.30) и
давления (13.31). Для интенсивности касательных напряжений получим
dS^
Т
-6GdX.
(13.33)
Интегрируя уравнение для безразмерного давления р при начальном
условии р = ро, получим
1-/
р = Ро-КЫ-
1-/о
Из (13.31) находим пористость через давление:
Р-Ро
К
/ = 1-(1-/о)ехр
(13.34)
(13.35)
134
Гл. 2. Разностные схемы расщепления
Исключая пористость / из (13.29), получаем дифференциальное
уравнение для р:
U = 3Kqiq28b(lq2p
(л s\ iP-Po
(1-/о)ехр( —-=£-
(13.36)
Это уравнение интегрируется численно на отрезке АЛ по неявной
схеме и может быть легко найдено с любой требуемой точностью.
Найденные р(Х) и /(А) подставляются в условие пластичности
Гарсона (13.32), из которого численно определяется значение Л = Л*,
отвечающее коэффициенту корректировки. В этом случае все
дальнейшее решение краевой задачи должно также выполняться в
численном виде.
Целесообразно использовать на малом шаге АЛ линеаризацию
уравнений (13.34) - (13.36) и найти простые приближенные
аналитические выражения для р(Х) и /(А) с достаточной точностью.
Такой подход, основанный на линеаризации уравнений, применен
ниже. Функция Ф(Х) определяется в аналитическом виде, и все
последующие выкладки также проводятся аналитически, что существенно
упрощает вычисление якобиана и дальнейшее интегрирование
уравнений краевой задачи.
В результате линеаризации получим
dp
Ж
С% + С*р, (13.37)
где С$ и С1? — константы разложения правой части
уравнения (13.36).
Интегрируя (13.37) с учетом начального условия р(Ао) = Ро,
найдем зависимость р(Х) в явном виде:
Р
(ро + Щ) ехр (с*(\ - Ао)) - Щ. (13.38)
Подставляя (13.38) в (13.35), получим явное выражение для
пористости:
f = c£ + C{pAp. (13.39)
Введем коэффициент корректировки X = ехр (—103 • (А — Ао)).
Множитель 103 введен, чтобы не было высоких степеней в
выражениях для давления и интенсивностей.
13. Численное моделирование поврежденности
135
Представим линеаризованные выражения
S = S0Xa, р = а + ЪХа, f = c + dXa, (13.40)
где а = -1(Г3С£, (3 = 6- КГ3С, а = -СЦС*, Ь - р0 - а,
с = С$- CfApa, d = CfApb. Подставляя (13.40) в условие
пластичности (13.32), получим обыкновенное нелинейное уравнение Ф(Х) = 0,
которое решаем методом Ньютона относительно коэффициента
корректировки X:
Xn+i = Хп _ Ф(*та) (13>41)
Ф'(ХП)' v )
Ф/(Х) = 2/З^Х2/3-1+
+ аХ*'1 [2Qld ch (У2р) + 3qiq2bf sh (f g2p) - 2g3/d] .
В качестве начального приближения берется Хо = 1.
Итерационный процесс (13.41) продолжается до тех пор, пока относительная
погрешность £ в определении X не станет меньше, чем £о = Ю-7.
Якобиан дет j де вычисляется аналогично тому, как было сделано
в предыдущем пункте для условия пластичности Мизеса.
Окончательное выражение для якобиана имеет вид
-^- = CiI + CnI(g)I+ \ (Cni + Cin) (n ® I + I ® n) + Cnnn(g)n. (13.42)
Вид коэффициентов Сп приведен в работе [47].
Одноосное растяжение. Результаты расчета. В качестве
модельной задачи рассмотрим одноосное растяжение квадратного
элемента, изображенного на рис. 13.3 для случая плоской деформации.
Здесь использовалась логарифмическая мера деформаций:
£ = ln/l + ^p), u(t) = 0M. (13.43)
Начальная пористость материала / = 0.001.
Эта тестовая задача была решена двумя методами: методом,
предложенным в [73] и заложенным в пакете ABAQUS, и методом
расщепления.
136
Гл. 2. Разностные схемы расщепления
2А
Рис. 13.3.
а)
б)
Рис. 13.4.
На рис. 13.4 изображены зависимость давления и пористости / от
параметра нагружения, где сплошной линией показано точное
решение [73] (рассчитанное с очень малым шагом), крестиками — по
методу расщепления.
Как видно из рис. 13.4Ь, материал разупрочняется и пористость
растет. Совпадение результатов достаточно хорошее.
Хотя материал матрицы пластически несжимаем, пластическая
сжимаемость эффективного материала происходит за счет
изменения пористости, тело увеличивает объем в 1.5 раза, упругая
деформация при этом составляет всего eel = 0.002.
Краевая задача. Рассмотрим задачу о сдвиге бруска в 3-мерном
случае (рис. 13.1). Выше эта задача была решена для упругопласти-
ческого материала при условии пластичности Мизеса.
Как показали расчеты при фиксированном шаге, для решения
задачи методом расщепления требуется выполнить в 2.4 раза больше
итераций, чем при решении этой же задачи методом [73], тогда как
13. Численное моделирование поврежденности
137
время решения полной задачи примерно одинаковое (MP — 1 час
31 мин, a ABAQUS — 1 час 27 мин).
Таким образом, метод расщепления для интегрирования
определяющих соотношений оказался в два с половиной раза быстрее, чем
стандартный.
Сравнение результатов, полученных при условии пластичности
Мизеса и при условии пластичности Гарсона, в рассмотренных
примерах показывает существенное влияние пористости на напряженно-
деформируемое состояние, которое приводит к разупрочнению
материала и разрушению конструкции.
Изгиб пластины. Рассмотрим пример, показывающий
существенное различие в характере разрушения конструкции при
учете повреждаемости и при ее отсутствии. Рассмотрим задачу
изгиба пластины, свободно опертой на концах и нагруженной посредине
жестким цилиндрическим штампом (плоская деформация), с
учетом повреждаемости материала и без нее. В силу симметрии задачи
будем рассматривать только правую часть пластины. На рис. 13.5а
приведена геометрия задачи, где h = 0.25 мм. Константы материала
Е = 1 • 105 МПа, v = 0.3, gy = 400 МПа, q1 = 1.5, q2 = 1.0, /0 = 0.05,
fN = 0.04, eN = 0.3, sN = 0.1.
12h
a)
( i-6hA
/
Рис. 13.5.
сетка
Между пластиной и штампом, а также между пластиной и опорами
отсутствует трение. Так как наибольшие деформации пластины
возникают в области под штампом, то введем в этой области более
мелкую сетку. При больших деформациях элементы лагранжевой сетки
сильно искажаются, при этом точность расчета падает. Поэтому
полуширина пластины разделена на 4 области (рис. 13.5Ь). Переход в
138
Гл. 2. Разностные схемы расщепления
область с более мелким разбиением осуществляется через
треугольные элементы (при этом шаг разбиения изменяется в два раза). В
области 1 используется адаптивная сетка, которая перестраивается на
каждом временном шаге (время здесь фигурирует как параметр на-
гружения). В областях 2-4 используется обычная лагранжева сетка.
Разбиение расчетной области приведено на рис. 13.5Ь. Количество
элементов — 28 977, а количество узлов — 29 380.
На рис. 13.6 приведена сила реакции на штамп со стороны
пластины. На графике видно, что для пористого материала потеря
устойчивости пластины или образование пластического шарнира
(горизонтальный участок кривой) наступает раньше, чем в случае идеально-
пластического материала. Это обусловлено тем, что предел
текучести сгуо для материала с поврежденностью падает при зарождении
и росте пор и становится ниже, чем для материала матрицы ауо-
Снижение предела текучести связано с начальной пористостью
материала, /о = 5%. Такое значение /о выбрано с целью проследить
процесс образования полос скольжения более детально. В случае,
когда /о = 0? начальной пористости нет, а есть только зарождение,
то также наблюдается образование полос сдвига, но этот процесс
начинается позднее.
Скачок контактной силы (рис. 13.6) обусловлен появлением зазора
между штампом и пластиной при образовании пластического
шарнира (см. рис. 13.7).
—-—-модель с пористостью
3 5 —«—идеальная пластичность
с
S
(О
н
Н
СП
I
"ч
-г
^
го
ф
о.
го
О
3.0
?5
2.0
1 Ь
1 0
0.5
0.0
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5
Перемещение штампа, h
Рис. 13.6.
§13. Численное моделирование поврежденности 139
Рис. 13.7.
Из графика (рис. 13.6) видно, что в модели с повреждаемостью
(пористостью) наблюдается резкое падение контактной силы, чего нет
в случае идеальной пластичности. Такое резкое падение контактной
силы свидетельствует о разупрочнении материала, которому
предшествует локализация пластических деформаций (см. рис. 13.8).
На рис. 13.7а видно образование полос локализации при
образовании пластического шарнира, на 13.7Ь показано образование зазора
между штампом и пластиной (плоская деформация).
На рис. 13.8 показан изгиб пластины при перемещении штампа:
d = 2.2/г, е — логарифмическая деформация, в одномерном
случае е = In (L/l) = In (1 + и/I), где и = L — I. В случае GTN-модели
(рис. 13.8Ь) наблюдается четкое образование квазипериодической
структуры полос локализации больших пластических деформаций,
разделенных разгруженными областями. В полосах локализации
существенно повышена концентрация пор. Такая картина полос
локализации пластических деформаций соответствует наблюдаемой в
экспериментах. В случае идеальной пластичности структуры полос
локализации не наблюдается, переход между линиями уровня
деформаций монотонный (рис. 13.8а).
Модель квазихрупкого разрушения с учетом
повреждаемости. Для решения задач квазихрупкого разрушения сплошных
сред и конструкций можно применять модифицированную модель
пористого упругопластического материала, основанную на условии
пластичности Гарсона и критерии критической пористости, при
выполнении которого образуется трещина и происходит разрушение.
Образование трещины моделируется появлением в точке элемента
свободной (от напряжений) поверхности. Т.к. квазихрупкое
разрушение происходит при небольших пластических деформациях, а по-
140
Гл. 2. Разностные схемы расщепления
(а) * ^ (Ъ)
с = 0.15 с = 0.24
Рис. 13.8.
ристость связана с объемной растягивающей деформацией (11.6),
(11.7), то величина критической пористости для квазихрупкого
материала на порядок меньше, чем при вязком разрушении. Большие
пластические деформации не успевают развиться, материал
разрушается раньше из-за низкой критической пористости на растяжение.
Зарождением новых дефектов можно пренебречь. Подводимая
внешняя энергия идет не на вязкопластическую деформацию, а на
образование свободной поверхности и разрушение сплошной среды. Эти
затраты энергии существенно меньше, чем при вязкопластическом
разрушении. Механизм квазихрупкого разрушения кардинально
отличается от вязкопластического механизма. До появления трещины
математическая система уравнений формально практически не
отличается от вязкопластических уравнений. Вопрос о критерии
образования свободной поверхности в сплошной среде при
квазихрупком разрушении не столь важен, как в механике хрупкого
разрушения, но преимущество деформационных критериев перед силовыми
(энергетическими) при квазихрупком и вязком разрушении
очевидно. Для расчета квазихрупкого разрушения предлагается использо-
§13. Численное моделирование поврежденности
141
вать модель пористого упругопластического материала, а при
достижении критического значения пористости дополнительно ввести
модель разрушения сплошной среды.
(а) (Ъ)
Рис. 13.9. Повреждаемость материала (распределение пористости) и
распространение трещины для различных типов разрушения: а) хрупкое
разрушение, критическая пористость /с = 1 • 10_ , скорость нагружения
v = 1 м/с, время t = 1.35 • Ю-4 с; Ь) пластическое разрушение, скорость
нагружения v = 2 м/с, время t = 3.00 • Ю-4 с
Наиболее простой моделью разрушения является модель Майнчена-
Сака, которая была описана выше и по которой разрушение
происходит скачком, а напряжение в разрушенной частице падает до нуля.
Более сложная модель связана с плавным переходом к
разрушенному состоянию — релаксацией до нуля напряжений и образованием
поверхности свободной от напряжения. Ниже используется простая
модель для исследования перехода от квазихрупкого разрушения к
вязкому при изменении свойств материала в плоском образце с
симметричными двумя V-образными вырезами или в осесимметричном
образце с кольцевым V-образным вырезом.
При решении задач квазихрупкого разрушения меняется не
только модель, но и метод решения. Задача решается в динамической
постановке (с учетом инерционных сил) методом установления, с ис-
Is
11
1
ЭЭЭе-06 |
l;[ll;;ii'
j jjjj|j;
;!!<;!!
jtrt4
inj;
ui-L
£
33
;i
1-j-j-h-
■pTT
шн
n
■■И
[[Si
w^__L_- — ■'■1!:К". --LLiJ
'■....„ill
, 1 ijjjjj
iHjjij;!'
|2джжщ
ШШшНИПШЩЙ
:l !NfH-| !!Итгпм'м1
1: !!;:!!
ji iijij:
^
s
■
■fi
t
!;■
Тт
фЕ
w
, ;|i|;|'
■ ■ :
4444-
i|i[ |[
Щ:
35
44-
44-
, '|i|.j:|.j.|.j'.j=f
142
Гл. 2. Разностные схемы расщепления
пользованием явной схемы интегрирования.
Плоский образец (плоско деформируемое состояние) с
симметричными 2-мя V-образными вырезами, показан на рис. 13.9а. Такие
образцы являются объектом многочисленных как
экспериментальных, так и теоретических исследований механизма перехода от
квазихрупкого к вязкому разрушению. На рис. 13.9а показана картина
квазихрупкого разрушения. Пластические деформации имеют место
только в окрестности кончиков вырезов, от которых
распространяется трещина, соединяющая вырезы.
Разрушение упругопластического образца показано на рис. 13.9Ь.
Упругопластический материал выдерживает гораздо большие
деформации не разрушаясь, критическое значение пористости для него
на порядки больше, чем для хрупкого, поэтому достигаемая в
кончике выреза пористость при умеренных пластических деформациях
недостаточна для образования свободной поверхности и трещина не
образуется. В то же время в пластическом материале появляются
линии скольжения, в которых пористость достигает больших значений,
чем в кончике выреза, и тогда вся деформация сосредотачивается в
окрестности поверхностей скольжения, а в окрестности выреза
происходит разгрузка. Трещина распространяется не нормально, а под
углом к направлению растяжения вдоль линий максимальной
локализации пористости (рис. 13.9Ь). Когда материал квазихрупкий, то
есть такой, для которого критическая пористость невелика,
разрушение происходит по трещине, соединяющей кончики вырезов, если
же материал упругопластический, для которого критическая
пористость на порядок больше, разрушение происходит за счет сдвига по
полосам локализации под углом к оси растяжения (как показано на
рис. 13.9Ь) Таким образом, показано, что модель, учитывающая
зарождение и рост мезодефектов в виде сферических пор, правильно
описывает оба типа разрушения и переход от квазихрупкого к вяз-
копластическому благодаря разной сопротивляемости материала и
разному механизму разрушения. Таким образом, модель позволяет
объяснить изменение картины разрушения в образце с V-образными
выточками, наблюдаемое экспериментально.
14. Численное моделирование процессов резания
143
Численное моделирование
процессов резания
упрговязкопластических материалов
в трехмерной постановке
Введение (144). Постановка задачи (145). Результаты расчета (149).
Заключение (153).
В качестве примера разработанных методов моделирования
трехмерных задач для упруговязкопластических материалов приведем
решение методом конечных элементов неустановившегося процесса
резания упруговязкопластической пластины (заготовки) абсолютно
жестким резцом, движущимся с горизонтальной постоянной
скоростью Vo при различных наклонах грани резца а (рис. 14.1).
Моделирование проводилось на основе связанной термомеханической
модели упруговязкопластического материала. Приводится сравнение
адиабатического процесса резания и режима с учетом
теплопроводности материала заготовки. Проведено параметрическое
исследование процесса резания при изменении геометрии заготовки и
режущего инструмента, скорости и глубины резания, а также свойств
обрабатываемого материала. Варьировался размер толщины
заготовки в направлении оси z. Напряженное состояние изменялось от
плосконапряженного — Н = H/L <С 1 (тонкая пластина) до плоско-
деформируемого — Й ^> 1 (широкая пластина), где Н - толщина,
L - длина заготовки. Задача решалась на подвижной адаптивной
лагранжево-эйлеровой сетке методом конечных элементов с
расщеплением и использованием явно-неявных схем интегрирования
определяющих уравнений, развитых в параграфе 9. Показано, что
численное моделирование задачи в трехмерной постановке позволяет
исследовать процессы резания с образованием непрерывной
стружки, а также с разрушением стружки на отдельные куски. Механизм
этого явления в случае ортогонального резания (а = 0) может быть
объяснен термическим разупрочнением с образованием
адиабатических полос сдвига без привлечения моделей поврежденности. При
резании более острым резцом (угол а велик) необходимо
привлечение связанной модели термического и структурного разупрочнения с
учетом поврежденности. Получены зависимости силы, действующей
на резец при разных геометрических и физических параметрах
задачи. Показано, что возможны квазимонотонный и осциллирующий
14.
144
Гл. 2. Разностные схемы расщепления
режимы и дано физическое объяснение этого явления.
Введение. Процессы резания играют важную роль в обработке
труднодеформируемых материалов на токарных и фрезерных
станках. Машинная обработка является основной ценообразующей
операцией при изготовлении деталей сложного профиля из
труднодеформируемых материалов, таких как титаново-алюминиевые и
молибденовые сплавы. При их резании образуется стружка, которая
может разрушаться на отдельные куски (чипы), что приводит к
негладкой поверхности срезаемого материала и сильно
неравномерному давлению на резец. Экспериментальное определение
параметров температурного и напряженно-деформируемого состояний
обрабатываемого материала при высокоскоростном резании
чрезвычайно затруднено. Альтернативным является численное моделирование
процесса, которое позволяет объяснить основные особенности
процесса и детально исследовать механизм резания. Фундаментальное
понимание механизма образования и разрушения стружки важно
для эффективного резания. Математическое моделирование
процесса резания требует учета больших деформаций, скоростей
деформаций и нагрева вследствие диссипации пластической деформации,
приводящих к температурному разупрочнению и разрушению
материала.
Полноценного исследования этих процессов до настоящего
времени не получено, хотя интенсивные усилия предпринимаются с
середины XX века. Первые работы основывались на простейшей жест-
копластической схеме расчета [91, 70, 101, 102]. Однако результаты,
полученные на основе жесткопластического анализа, не могли
удовлетворить ни обработчиков материалов, ни теоретиков, так как
такая упрощенная модель не дает ответов на поставленные вопросы.
В литературе отсутствует решение этой задачи в пространственной
постановке, учитывающей нелинейные эффекты образования,
разрушения и фрагментации стружки, связанные с трехмерным
термомеханическим поведением материала.
Только в последние несколько лет благодаря численному
моделированию были получены определенные сдвиги в исследовании этих
процессов. Проведены исследования влияния на образование и
разрушение стружки угла резания, термомеханических свойств детали
и резца, механизма разрушения [88, 92, 74]. Однако в большинстве
работ процесс резания рассматривался при существенных ограниче-
14. Численное моделирование процессов резания
145
ниях: принималась двумерная постановка задачи (плоская
деформация); не рассматривалось влияние начального этапа
неустановившегося процесса на силу, действующую на резец; разрушение
полагалось происходящим по заранее заданным поверхностям. Все эти
ограничения не позволяли исследовать резание в полном объеме, а
в некоторых случаях приводили к неправильному пониманию
механизма самого процесса.
Кроме того, как показывают экспериментальные исследования
последних лет [99, 85], при высоких скоростях деформирования:
ё > 105 — 106 с-1 многие материалы обнаруживают аномальную
температурную зависимость, связанную с перестройкой механизма
движения дислокаций. Термофлуктуационный механизм сменяется
на механизм фононного сопротивления, в результате которого
зависимость сопротивления материала от температуры становится прямо
противоположной: с увеличением температуры возрастает
упрочнение материала. Такие эффекты могут привести к большим
неприятностям при высокоскоростном резании. Эти проблемы в
литературе до настоящего времени совершенно не изучены. Моделирование
высокоскоростного процесса требует развития моделей,
учитывающих сложные зависимости вязкопластического поведения
материалов и в первую очередь учета поврежденности и разрушения с
образованием трещин и фрагментацией частиц и кусков
деформируемого материала. Чтобы учесть все перечисленные эффекты,
требуются не только сложные термофизические модели, но и
современные вычислительные методы, позволяющие рассчитывать большие
деформации, не допускающие предельных искажений сетки и
учитывающие разрушение и появление нарушения сплошности
материала [89, 69, 12]. Рассматриваемые задачи требуют огромного
объема вычислений. Необходима разработка высокоскоростных
алгоритмов решения многомасштабных задач для упруговязкопластических
уравнений с внутренними переменными [46, 47, 49, 73].
Постановка задачи.
Геометрия. Принимается трехмерная постановка задачи. На
рис. 14.1 изображены область и граничные условия в плоскости
резания. В направлении, перпендикулярном плоскости, заготовка
имеет конечную толщину: Н = H/L (L — длина заготовки), которая
варьировалась в широком диапазоне. Пространственная постановка
146
Гл. 2. Разностные схемы расщепления
допускает свободу движения обрабатываемого материала из
плоскости резания и более плавный выход стружки, что обеспечивает
благоприятные условия резания.
1.0
A ЖЖЖЖЖ ЖГ
и2=0
Рис. 14.1. Геометрия задачи и граничные условия
Основные уравнения. Полная связанная система уравнений
термоупруговязкопластичности состоит из уравнения сохранения
импульса:
dv
закона Гука с температурными напряжениями:
da-
ч
,. Щы (е'ы ~ £Ры ~ otSkiO),
уравнения притока тепла:
dO
рСе
dt
K0yii - (ЗА + 2{1)а60е'ц + ^-^,
(14.1)
(14.2)
(14.3)
где Се — теплоёмкость, К — коэффициент теплопроводности, к —
коэффициент Куини-Тейлора, учитывающий разогрев материала за
счет пластической диссипации. Имеем также ассоциированный закон
пластического течения:
dF
А-
и условия пластичности:
F(Ji,E?,Xi,e) = Ъ-<туЫиЩ,Хг,0) < 0, (14.5)
14. Численное моделирование процессов резания
147
где Ji — инварианты тензора напряжений, Ei — тензора
пластической деформации. Эволюционные уравнения для внутренних
переменных имеют вид
^ = fi(Jk,Xi,0). (14.6)
Модель материала. Принимается термоупруговязкопластиче-
ская модель типа Мизеса — модель пластичности с пределом
текучести в виде мультипликативной зависимости (14.7),включающая
деформационное вязкопластическое упрочнение и термическое
разупрочнение [84]:
ау(Ер,Ёр,в) = [А + В(Ер)п]
где а у — предел текучести, ёр — интенсивность пластических
деформаций, 6 — относительная температура, отнесенная к температуре
плавления вш:
в = {в-в*)/{вт-в*). (14.8)
При в < 6>* в = 0, при <9 > 0* в = 1.
Материал детали принят однородным. В расчетах
использовался относительно мягкий материал А12024-ТЗ (упругие постоянные:
Е = 73 ГПа, v = 0.33; пластические: А = 369 МПа, В = 684 МПа,
п = 0.73, ё0 = 5.77 • 10~4, С = 0.0083, т = 1.7, 9* = 300 К,
вш = 775 К, (3 = 0.9) и более жесткий 42CrMo4 (E = 202 ГПа,
v = 0.3, А = 612 МПа, В = 436 МПа, п = 0.15, ё0 = 5.77 • 10~4,
С = 0.008, т = 1.46, 0* = 300 К, 0Ш = 600 К, (3 = 0.9). Производится
сравнение адиабатического процесса резки с решением полной
термомеханической задачи.
Разрушение. Модель разрушения материала основывается на
континуальном подходе Майнчена-Сака [89], основанном на
моделировании зон разрушения дискретными частицами. В качестве
критерия разрушения принимается критическая величина интенсивности
пластических деформаций ер.\
гр = [di + d2 exp (d3 Ji/J2)] [1 + d4 \nip/e0] (l + d5#) , (14.9)
\l + Cln
Ep
(14.7)
148
Гл. 2. Разностные схемы расщепления
где di — константы материала, определяемые из эксперимента. Если
в лагранжевой ячейке выполняется критерий разрушения, то связи
между узлами в таких ячейках освобождаются и напряжения
либо релаксируют к нулю, либо сопротивление сохраняется только по
отношению к сжатию. Лагранжевы узловые массы при разрушении
превращаются в самостоятельные частицы, уносящие массу, импульс
и энергию, движущиеся как жесткое целое и не взаимодействующие
с неразрушенными частицами. Подробный обзор этих алгоритмов
приведен в [69, 12]. В настоящей работе разрушение определяется
достижением критической интенсивности пластической деформации
еК и поверхность разрушения не задается заранее. В приведенных
расчетах еК = 1,0, скорость движения резца принималась равной
2 м/с и 20 м/с.
Метод интегрирования уравнений. Для интегрирования
приведенной связанной системы уравнений термопластичности
(14.1) - (14.9) целесообразно применить метод расщепления,
развитый в работе [46]. Схема расщеплений упругопластических
уравнений заключается в расщеплении полного процесса на 1) предиктор —
термоупругий процесс, в котором ер = 0 и все связанные с
пластической деформацией операторы обращаются в нуль, и 2) корректор —
при котором полная скорость деформаций е = 0. На стадии
предиктора система (14.1) - (14.6)относительно переменных, обозначенных
знаком ^, примет вид
dv_ _ ~ .
V dt — ° WJi
^f = Dijkl(ekl - а5к1в),
рСе^ = Квугг - (ЗА + 2^)ав0е'гг + ^-^,
Система (14.10) интегрируется просто, так как последний член в
уравнении притока тепла, связанный с упругой диссипацией — малая
величина даже при высоких температурах [4] и может быть
отброшен. Тогда уравнение теплопроводности проинтегрируется отдельно
от остальных (по явной условно устойчивой или по неявной
абсолютно устойчивой схеме с расщеплением по направлениям). Затем
решается изотермическая динамическая задача по явной центрально-
разностной схеме относительно v и д^. Полученные значения
используются в качестве начальных значений на этапе корректора для
14. Численное моделирование процессов резания
149
следующей системы уравнении относительно величин, отмеченных
значком Л:
dv
р-=0,^=4+^ =0. (14.11)
dt
Закон Гука и ассоциированный закон (2.4) приводят к уравнению
релаксации:
da».
dt dt
d\^ OF
' d&a
Уравнение притока тепла принимает вид
pCedO/dt = K(7ijipkl.
(14.12)
(14.13)
Уравнения (14.4) - (14.6) относительно величин с Л остаются без
изменений.
Результаты расчета. Вначале рассмотрим плоскую постановку
задачи при Н ^> 1 (плоская деформация). При большой толщине
пластины Н ^> 1 материал находится в стесненном состоянии и под
действием движущегося резца вынужден двигаться в сторону
свободной поверхности (рис. 14.2а, Ь). На рис. 14.2 показано
образование полос локализации сдвига и развитие поверхностей разрушения
при резании толстой пластины из сплава 42CrMo4: a - образование
начального куска, Ъ - второго фрагмента, с - отрыв серии
фрагментов (а = 90°, V = 2 м/с, адиабатический процесс).
»
'М&
%,
(а) (Ь) (с)
Рис. 14.2. Образование полос локализации и разрушение при резке толстой
пластины из 42СгМо4, угол наклона верхней грани резца при
ортогональной резке а = 0°, адиабатическая модель, V = 2 м/с, (а) отрыв начального
куска; (Ь) отрыв второго куска; (с) отрыв серии кусков
150
Гл. 2. Разностные схемы расщепления
Разрушение в полосе сдвига происходит по следующей схеме.
Выдавливаемый материал образует бугор, который растет по мере
движения резца. При ортогональном резании зарождаются две полосы
сдвига — вблизи кончика резца и на поверхности бугра (вследствие
потери устойчивости поверхности). При продвижении резца они
двигаются навстречу друг другу и разрушение происходит при их
слиянии (рис. 14.2Ь). Часть материала в виде чипа отделяется от
обрабатываемой детали. После этого образуется новый бугор и новая
полоса сдвига в уже нагретом и разупрочненном материале. Процесс
приобретает немонотонный квазипериодичский характер,
определяемый скоростью движения резца.
Показано, что при ортогональной резке разрушение происходит
по полосам локализации сдвига и связано с термическим
разупрочнением вследствие диссипации. После откалывания первого куска
процесс выходит на квазистационарный режим. Образуется
непрерывная стружка или стружка в виде последовательности отдельных
фрагментов (рис. 14.2с). Это зависит от соотношения прочностных и
термомеханических свойств материала заготовки. Более гладкая
поверхность резания и непрерывная стружка образуются при малых
скоростях и острых углах резания, а также при учете
теплопроводности.
В условиях плоской деформации (относительная толщина Н ^> 1)
материал стеснен в боковом направлении и стружка выходит вверх
в плоскости резца. В пространственной постановке для тонких
пластин (Н < 1) характерен выход стружки вбок из плоскости
движения резца. При этом образование непрерывной стружки происходит
в более широком диапазоне скоростей и теплопроводности
материала.
На рис. 14.3а показано распределение интенсивности пластических
деформаций и образование спиралевидной непрерывной стружки,
На рис. 14.3Ь — изменение суммарной силы, действующей на резец
во времени. Материал заготовки 42СгМо4, а = 90° , V = 2 м/с,
процесс резания с учетом теплопроводности.
Образование непрерывной стружки дает монотонную силу
реакции резца. При разрушении стружки на фрагменты сила реакции
имеет пилообразный вид (рис. 14.5), что отрицательно сказывается
на технологическом процессе резки.
При небольшой толщине пластины сначала, пока материал не
успел разогреться под действием резца, образуется полоса сдвига,
14. Численное моделирование процессов резания
151
(а) (Ь)
Рис. 14.3. Образование стружки и распределение интенсивности
пластических деформаций (а) и суммарная сила реакции резца (Ь) при резке
тонкой пластины (термомеханическая модель, деталь 42СгМо4, резец а = 0°,
V = 2 м/с)
по которой происходит разрушение и отделение первого чипа от
основного материала. После этого резец движется вдоль образца по
разогретому и разупрочненному материалу, расплющивая его и
срезая материал, вытекающий в боковом направлении с образованием
непрерывно сворачивающейся спиралевидной стружки (рис. 14.3а).
Сила, действующая на резец после начального неустановившегося
участка, на котором она максимальна, падает и выходит на
стационарное значение и процесс резания происходит квазимонотонно.
Высокочастотные колебания около этого значения связаны с
разрушением материала на контактной поверхности и фрагментацией
мелких частиц (рис. 14.3Ь).
у
Й\
(а) (Ь)
Рис. 14.4. Термомеханическая модель резки, образование стружки, (а)
деталь 42СгМо4, резец а = 0°; (Ь) детель А12024-ТЗ, резец а = 30°
152
Гл. 2. Разностные схемы расщепления
На рис. 14.4а показано разрушение стружки при ортогональном
резании труднодеформируемого материала 42СгМо4, на рис. 14.4Ь —
непрерывное резание мягкого материала А12024-ТЗ под углом
а = 30°.
При малой скорости резки и учете теплопроводности или
уменьшении угла наклона резца и/или увеличении пластичности детали
(дюралюминий) не образуются полосы локализации и слой срезается
однородно без образования чипов (рис. 14.4Ь). При малой скорости
резки, близкой к ортогональной (а « 90° -!- 80°), разрушение
происходит только в первичной полосе сдвига и образуется единственный
чип (рис. 14.4а).
'фМйШ^И^ЦУЦ/^*^^
(а) (Ъ)
Рис. 14.5. (а) Сила, действующая на резец при резке толстой пластины.
Материал 42СгМо4, резец а = 0°. 1 - адиабатическая модель, 2 - модель
с учетом теплопроводности. (Ь) Сила, действующая на резец при резке
толстой пластины. Материал А12024-ТЗ. Различные углы наклона резца а
На рис. 14.5а, Ь) приведены результаты расчета силы
сопротивления резанию, действующей на инструмент во времени. На рис. 14.5
для толстой пластины видно, что имеется начальный участок
неустановившегося процесса, связанный с образованием первичной полосы
сдвига, при котором сила сопротивления максимальна. Для
ортогональной резки тонкой пластины (рис. 14.3Ь) после разрушения и
отделения куска пластины происходит резкий спад, величина которого
зависит от скорости резания, после чего наступает этап установления
и выход на квазиустановившееся стационарное значение силы
сопротивления. Аналогичные спады происходят при отколе последующих
кусков (кривая 1 на рис. 14.5). Отметим, что падение силы реакции
связано с тем, что после откола первого куска резец давит на
нагретый и разупрочненный в полосе сдвига ослабленный материал,
14. Численное моделирование процессов резания
153
который легче разрушается. При учете теплопроводности
материала в полосе сдвига разупрочнение слабее и разрушение по вторичной
полосе сдвига не происходит (рис. 14.5, кривая 2).
Для более острого угла резания и мягкого материала А12024-ТЗ
(рис. 14.5Ь) не происходит разрушение стружки по первичной полосе
сдвига и, как следствие, отсутствует падение силы реакции.
Характерно образование непрерывной стружки, которая дает монотонно
возрастающую силу реакции резца с выходом на
квазистационарный режим. При кусковой стружке сила реакции имеет
пилообразный вид, что отрицательно сказывается на технологическом
процессе резки (рис. 14.5).
На рис. 14.5Ь) видно, что с уменьшением угла наклона резца сила
сопротивления падает и изменяется монотонно с выходом на
стационарное значение. Изменяется и механизм резания и разрушения
стружки. Разрушение по полосам адиабатического сдвига не
происходит. Резец внедряется в материал и разрушение происходит по
типу расклинивания. Перед резцом возникает зона сдвига с
всесторонним растяжением, в которой следует учитывать не только
термическое, но и структурное разупрочнение. Эта зона связана с
зарождением и ростом микродефектов.
Заключение. Показано, что процесс резания с постоянной
скоростью на начальном этапе носит неустановившийся характер и ему
отвечает максимальная сила сопротивления, после падения которой
устанавливается либо осциллирующий, либо монотонный режим
изменения силы сопротивления в зависимости от того разрушается
срезаемый слой (стружка) на дискретные фрагменты или остается
непрерывным. Для моделирования этого процесса необходимы учет
термического разупрочнения, разрушения и фрагментации
материала.
Процесс резания в зависимости от геометрии резца и напряженно-
деформируемого состояния в окрестности кончика резца может
происходить с образованием дефектов типа пор либо без них. При
резании, близком к ортогональному, поры не образуются, и причиной
разрушения стружки является термическое разупрочнение.
154
Гл. 2. Разностные схемы расщепления
15. Упражнения
1. Произвести расщепление по направлениям явной разностной
схемы для двухмерного волнового уравнения (предварительно
сведя ее к системе уравнений 1-го порядка), шаблон которой
показан на рис. 15.1а при начально-краевых условиях
t = 0: гх(0, ж, у) = и0(х, у), u>t(0, ж, у) = v0(x, у),
х = 0: uiX=e1(t,y), x = a: uiX = e2(t,y),
у = 0: uit = v1(t,x), y = b: Uj = v2(t,x).
(15.1)
4
I
p
4—21
ft
^Cy
tytti
J At
\i X
jAt
\x—►
i >
*K
At (корректор)
" У
I At (предиктор)
~H— 2Ax H X
(a) (b) (c)
Рис. 15.1. Шаблоны явной (а) и неявной (Ь) схем расщепления по
направлениям, (с) — шаблон неявной схемы по переменным направлениям. О —
узлы, используемые на стадии предиктор, 0 — на стадии корректор
2. Провести расщепление по направлениям для неявной схемы
двумерного волнового уравнения, шаблон которой изображен
на рис. 15.lb, при тех же начально-краевых условиях (15.1).
Доказать ее устойчивость.
3. Построить явную схему расщепления по направлениям для
динамической плоской задачи теории упругости1 в
прямоугольнике, на контуре которого на двух противоположных сторонах
1 Система уравнений состоит из двух уравнений движения и трех уравнений
продифференцированного по времени закона Гука для трех компонент
напряжений
15. Упражнения
155
заданы граничные условия в напряжениях, а на двух других
скорости равны нулю:
х = 0
х = а
у = 0
у = Ь:
: <Гуу = <п(у),
: <7уу = <72(у),
й = б]
й = 0.
7~ху — U 5
Т~ху = ^5
При t = 0 задан полный вектор неизвестных:
[и, V, (Txxi Oyyi Oxy)
4. Построить разностную схему расщепления по физическим
процессам для термоупругой связанной одномерной динамической
задачи:
^(T)|^+G0M), Q(x,t)=jjai.
dv_Ede_ aT (15.2)
dt дх дх'
де dv
dt дх'
Исследовать полученную схему на устойчивость.
5. Провести расщепление определяющих уравнений гипоупруго-
пластической среды с кинематическим упрочнением.
Определить коэффициент корректировки численно-аналитическим
методом (см. § 9).
6. Провести расщепление одномерных нестационарных
уравнений (2.20) для упруговязкопластических стержней на упругий
предиктор и релаксационный корректор напряжения. Доказать
устойчивость схемы расщепления.
7. Провести расщепление волнового двумерного уравнения по
переменным направлениям. Шаблон схемы приведен на
рис. 15.1с.
8. Построить схему расщепления закона сохранения энергии
для термоупругопластической среды (третье уравнение
системы (17.5)), состоящую из предиктора (без учета конвективных
156
Гл. 2. Разностные схемы расщепления
членов) и корректора (только конвективный перенос). На
стадии корректора использовать формулы метода потоков (18.11),
см. главу 3.
9. Для уравнения теплопроводности с распределенным
источником, зависящим от двух переменных Q(x,y) = Qi(x) -Q2(y),
предложить схему расщепления по направлениям.
Глава wx I
Решение задач при больших
деформациях
§16. Консервативные аппроксимации на
криволинейной лагранжевой сетке
Формулы естественной аппроксимации пространственных производных (157).
Аппроксимация на лагранжевой сетке (158). Консервативные разностные
схемы (161).
Формулы естественной аппроксимации пространственных
производных. Рассмотрим интегрирование законов сохранения,
записанных в дивергентной форме в эйлеровых координатах, но на
криволинейной лагранжевой сетке. Это означает, что Хк в
уравнениях (9.8) не будут независимыми переменными, а меняются со
временем и являются функциями времени и начального
состояния Xi = Xi(t,X®).
Будем рассматривать общий случай, когда сетка образуется из
криволинейных многоугольных ячеек и на такой сетке требуется
аппроксимировать законы сохранения. Для этого прежде всего
необходимо правильно выбрать аппроксимацию пространственных
производных функции f(x,y). Ограничимся ради простоты двухмерным
случаем. Докажем следующую теорему.
157
158
Гл. 3. Решение задач при больших деформациях
Теорема. Пусть дана замкнутая односвязанная область R,
ограниченная контуром Y, в которой заданы дифференцируемые в R
функции f, и, v. Тогда существуют такие точки (х^, У г) £ R, в которых
выполняются следующие равенства:
' fdy § fdx
г
fAx(hyo) = j^> ^(a;o'yo) = -j^' (16Л)
г г
соответственно для дивергенции вектора fU с компонентами
(fu, fv) справедлива формула
§{fu)dy- §{fv)dx
Vfu) I = ^ ^-f , (16.2)
'\xi,yi fxdy
г
где V = г д/дх + jd/ду.
Доказательство. Из формулы Грина находим
Л VfUdxdy = II [(fu)jX + (fv),y] dxdy = j>(fu) dy - (fv) dx,
R R Г
а из теоремы о среднем следует
II(VfU) dS = (VfU)\x J! dxdy,
откуда
§(fu)dy- (fv)dx
(УД/)1 Г
xi,yi J J dxdy
R
При г£=1,г; = 0иг£ = 0,г; = 1 получаем соответственно
§ f dV ^ , ■ § j dx
3/
dx
r
J J dx dy' dy
J J dx dy
R
> / / dxdy = (b
Учитывая, что / / dxdy = Ф x dy при обходе контура против часовой стрелки,
R г
получаем формулы (16.1) - (16.2), что требовалось доказать.
Аппроксимация на лагранжевой сетке. Используем
формулы (16.1) - (16.2) для аппроксимации производных функции внутри
16. Консервативные аппроксимации на лагранжевой сетке 159
ячейки, контур которой представляет собой многоугольник с п
вершинами с координатами (xi,tji) (рис. 16.1а). Используя линейную
интерполяцию для функции f(x,y) между вершинами или узлами
сетки, при вычислении контурных интегралов в (16.1)—(16.2),
получим формулы для аппроксимации производных внутри ячейки:
df
дх
df
ду
Х3
х0
,Уз
,Уз
L^i иг+1
п
Е (Яг+1
г=1
п
Е(Л+1
п
Е (Яг+1
i jij\yi-\-L
+ Хг)(2/г+1 "
+ fi){Xi+l ~
+ Яг)(2/г+1 "
уг;
-Уг)
-Xi)
~Уг)
(16.3)
Индекс г пробегает по п вершинам многоугольной ячейки.
у-
л
(а) (Ь)
Рис. 16.1. Многоугольная ячейка
И аналогичное выражение для VfU в точке (xj,yj):
Е [(/^)г+1 + (fu)i] (г/г+1 - Уг) ~ [(/^)г+1 + (fv)i] {xi+1 ~ Xi)
г=1
п
Е(^г+1+а;г)(2/г+1 ~ Уг)
г=1
VfU
Формулы (16.3) носят название формул естественной
аппроксимации производных для нерегулярных многоугольных ячеек. Эта
аппроксимация обладает рядом замечательных свойств, важных при
160
Гл. 3. Решение задач при больших деформациях
применении численного анализа к решению задач механики
сплошных сред.
Прежде всего покажем, что для четырехугольной криволинейной
ячейки аппроксимация (16.3) эквивалентна центрально-разностной
аппроксимации после отображения на прямоугольную лагранжеву
сетку с координатами rj£. Пусть криволинейная ячейка в
плоскости ху отображается на правильный прямоугольник в плоскости rj£
преобразованием
Производные функции fyX(x,y) и /уУ(х,у) выражаются через
производные /)7? и /}£ по известным формулам замены переменных:
f,y = J-i (/,**,„ - /l4x,c), ' = *"* - ^ = Щ)- (16'4)
Используя центральные разности на прямоугольнике с
координатами узлов (di,bi) г = 1,2 (рис. 16.lb), получим
, (/2 + /3) ~ (/1 + к) , (/4 + /з) ~ (/2 + /l) ,1R_.
Л"- 2(^1) ' '*- WTW) • (16'5)
Аналогичные выражения для х)77, х^ и т.д.
Подставляя (16.5) в (16.4), как нетрудно проверить, получим
формулу, совпадающую с (16.3):
fx= (Л + /2X2/2 - 2/i) + (/2 + /з)(2/з - 1/2) +
(xi + х2)(г/2 - 2/1) + (^2 + я3)(г/з ~ 2/2) +
+ (/з + Л)(2/4 - 2/з) + (Л + /i)(2/i - 2/4)
+ (ж3 + х4)(2/4 - 2/з) + (#4 + ^i)(2/i - 2/4)'
Отсюда следует, что при аппроксимации уравнений механики
сплошной среды на лагранжевой сетке в уравнениях (9.8) можно не
переходить к лагранжевым координатам, а непосредственно
использовать формулы (16.3), вычисляя в процессе движения переменные
координаты сетки л^, У г по полю скоростей Vi.
На треугольной сетке аппроксимация (16.3) эквивалентна
линейному конечному элементу (см. [21]). Для треугольного элемента имеет
место линейная аппроксимация:
/ = а\ + а2х + азу, f,x = «2, fiV = as,
§ 16. Консервативные аппроксимации на лагранжевой сетке 161
коэффициенты щ выражаются через узловые значения fi по
формулам
3 3
г=1
где
b1=2J-1(y2-y3),
с\ = 2J~1(x2 -ж3),
J = det(A), A
где Xi, уi (г = 1, 2, 3) — координаты вершин треугольника.
Остальные коэффициенты Ь^, Q получаются круговой
перестановкой индексов. Подставляя и производя сокращения подобных
членов, найдем
f = А (2/2 ~ Уз) + /2(1/3 ~ 2/1) + /з(г/1 - 1/2)
J> 2J
Эта формула совпадает с формулой (16.3) при п = 3, здесь 2 J = S —
площадь треугольника. Однако уже для билинейного элемента
аппроксимация отличается от аппроксимации по формулам (16.1) для
прямоугольника. Многоугольная ячейка соответствует
аппроксимации треугольными элементами, на которые разбивается
многоугольник с центром в точке (хо?2/о)? в которой вычисляется производная
(рис. 16.1а), т.е. производные внутри многоугольника не будут
непрерывными, если п > 3.
Консервативные разностные схемы. Другим очень важным
свойством формул естественной аппроксимации является свойство
точно аппроксимировать законы сохранения на любой, как угодно
грубой сетке.
Другими словами, это означает, что если в некоторой области Dy
ограниченной контуром Г, имеет место локальный закон сохранения
для /(х, г/), т.е. внутри области выполняется
df d(fu) d(fv) л ,_ч
162 Гл. 3. Решение задач при больших деформациях
а / = 0 на границе Г, то в любой момент времени t справедлив
интегральный закон сохранения:
/ dxdy = const. (16.7)
D
Теорема. Если в уравнении (16.6) пространственные
производные аппроксимируются по формулам естественной
аппроксимации (16.3)
/;+1=/; + (V/^, (16.8)
то закон сохранения (16.7) выполняется точно на любой
нерегулярной сетке Fh, покрывающей область D:
£/ГЧ- = £Я^- (16-9)
Действительно, умножая (16.8) на Aj (площадь j-й ячейки) и
суммируя по всем ячейкам, получим
£ /;+ч- = £ t?Ai + £(v/tf)?A,-- (16.Ю)
Последняя сумма в правой части (16.10) на любой сетке Fh состоит
из интегралов по контуру каждой ячейки, при этом каждая
сторона принадлежит двум смежным ячейкам и проходится дважды
в разных направлениях, так что по всем линиям сетки, лежащих
внутри D, эта сумма равна нулю. На сторонах ячеек, составляющих
внешнюю границу области D, выполняется условие /n+1 = 0. Тогда
последняя сумма в (16.10) равна нулю и верно (16.9), т.е. закон
сохранения величины / в области D выполняется точно.
Схемы, обладающие свойством (16.9), называются
консервативными.
//
17. Большие упругопластические деформации
163
dv
>Jdt~
да
дх'
де
dt ~
dv
dx'
да
dt
§17. Большие упругопластические
деформации
Консервативные схемы в одномерном случае (163). Консервативная двумерная
схема упругопластической среды (165). Расщепление уравнений гипоупругого
материала (166).
Консервативные схемы в одномерном случае. Прежде чем
применить консервативную разностную схему к уравнениям упруго-
пластической среды (9.8) в многомерном случае, рассмотрим ее
особенности в одномерном случае на примере системы уравнений (2.20)
упруговязкопластического стержня:
ВД|+ *&*(„). („.,)
При естественной аппроксимации уравнений механики
неизвестные величины определяются в разных точках ячейки в соответствии
с их физическим смыслом: напряжения и деформации определяются
на границах, а скорости, плотность и термодинамические
переменные — внутри ячейки.
В случае равномерной одномерной сетки узлы, в которых
определяются напряжения, сдвинуты на полшага как по пространству,
так и по времени по отношению к узлам, в которых определяется
скорость. Поэтому сетка состоит из двух типов узлов,
расположенных по отношению друг к другу в шахматном порядке (рис. 17.1а).
Крестиками отмечены узлы, расположенные на границах ячейки, а
кружочками — внутренние узлы. Уравнения (17.1) в разностном
виде запишутся так:
п+1/2 п-1/2
Vl/2 Vl/2 _ <7j+l ~ °j
р1+1'2 At " Ax '
_n+l _ pn „«+1/2 _ „n+1/2
-\7 J_
е'Г^-еЧ уi/2 -уi/2 (17.2)
At Ax
Разностная схема (17.2) представляет собой схему <крест>. Первые
два уравнения имеют второй порядок аппроксимации О (At2 + Ax2)
164
Гл. 3. Решение задач при больших деформациях
1 I 1
ф I ф 1 та 1
ф i ф i Ф i
-е-
J
i
t
-Ф-
I
У'
п+1/2
п
7+1
(а)
X
Рис. 17.1. Лагранжева сетка
/+1/2
х
(Ь)
и решаются явно, а в последнем определяющем уравнении
используется неявная схема первого порядка точности в соответствии с § 9.
Чтобы получить второй порядок и в третьем уравнении, функцию Ф
нужно взять в точке (n + 1/2, j):
фП+1/2 = 1 /фп+l
(Ф-+1 + ф»).
Начальные условия при t = 0 задаются на слоях п = 0 и п = 1/2
одновременно.
Граничные условия, например (2.20а), при х = 0
аппроксимируются так:
А1
п+1/2
^1/2
■ V
п-1/2
1/2
At
+ А2</+21/2 + Аз^ = (^(Г).
(17.3)
В этих уравнениях величины с пространственными индексами 0
и 1/2 следует трактовать как принадлежащие одной ячейке,
находящейся на границе стержня.
Для расчета граничных точек используем приведение системы к
характеристическому виду.
К этому уравнению для расчета граничных точек необходимо
добавить уравнение вдоль отрицательной характеристики:
чп+1/2
(v + a)™" = (v + <T)Z/2 + *l
3/2-
Выражение в правой части характеристического соотношения в
общем случае при переменной скорости распространения вычисляется
17. Большие упругопластические деформации
165
с использованием линейной интерполяции в точке пересечения
характеристики с предыдущим временным слоем.
В случае, когда деформации стержня велики, в уравнениях (17.1)
координата х не остается постоянной, как в случае малых
деформаций. Ее следует рассматривать как функцию х = x(xo,t) и
вычислять по полю скоростей:
dx Xj Xj n+l/2 n+l/2 1 / n+l/2 . n+1/2
Первые два разностных уравнения (17.2) в этом случае запишутся
п+1/2 п-1/2
Vl/2 Vl/2 = Pj+1 ~ ^j
^'+1/2 At жп+1 - ж?
рп+1 рП ?;«+1/2 _ п+1/2
At n+l/2 _ n+l/2 '
Xj + l/2 x j-1/2
(17.4)
третье уравнение остается без изменений. Формулы (17.4) есть
одномерный аналог формул естественной аппроксимации, приведенных
в § 16. Сетка интегрирования показана на рис 17.lb.
Консервативная двумерная схема упругопластической
среды. Перейдем к рассмотрению двухмерного случая численного
интегрирования уравнений (9.8) на четырехугольной
криволинейной сетке с шахматным расположением узлов в пространстве ж, у
(рис. 17.lb) со сдвигом на At/2 по времени для узлов с
дробными пространственными индексами, которые находятся в центре масс
ячейки, образованной узлами с целыми индексами.
Запишем систему уравнений (9.8) в эйлеровых переменных в
недивергентном виде, она имеет более простую форму и удобна при ис-
166
Гл. 3. Решение задач при больших деформациях
пользовании метода естественной аппроксимации:
+ pVv = О,
9sik
dp
dt
dvi
дЕ
~dt
Dsjj
дхк
dp
dxi
0,
— (va- —
дхк % % дхк
дхк)
0,
(17.5)
/i
Dt
P = p(p, e)
dvi dvj
dxj dxi
2/i
VvSn + Asa
b — \sijsij)
1/2
j%3 -r ^«^j?
if(x,£>P),
где DP = [i^i]
p -p \V2 &
dt
материальная производная для
фиксированной частицы, £ — лагранжева координата, е — внутренняя
энергия, Е = е -\- ^v2 — сумма внутренних и кинетических энергий
Ds ds-
(маССОВаЯ ПЛОТНОСТЬ ПОЛНОЙ Энергии), г3 = —р~ + QikSkj + ^jk^ki ~
яуманновская производная, Г^' — кососимметричный тензор
поворота.
В разностном виде систему (17.5) можно представить следующим
образом:
pn+1
Рг
1+1/2
At
Д£ +^'V^+l/2,j + l/2
(^)П+1/2 - (^)П"1/2
• • • • и т.д.
о,
+ l/2,j + l/2
dskr)
dXrr,
+
^+i,j
^-i,j
Aa:fc
(17.6)
После того как вычислены рие, находим р = р(р, е).
Подробные формулы аппроксимации уравнений (17.5)
достаточно громоздки, поэтому мы ограничились основными принципами их
составления и отсылаем заинтересованного читателя к работе Уил-
кинса [68], где эти формулы приведены подробно.
Расщепление уравнений гипоупругого материала.
Определяющее уравнение гипоупругого материала для определения Sij
(последнее уравнение системы (17.5)) в случае больших деформаций
17. Большие упругопластические деформации
167
подвергается расщеплению на три оператора: упругий, пластический
и кинематический, состоящий из яуманновских членов, связанных с
вращением частицы.
На первом этапе отбрасываются кинематический и пластический
операторы и интегрируется лишь упругий:
\\Skl)ij y^klHj) _
At
fdvk dvi\nJrl/2 2/i _^n+i/2
где Ski — символы Кронекера.
На втором этапе отличен от нуля только пластический оператор.
Интегрирование на этом этапе ничем не отличается от того, которое
описано в § 9, так как оно выполняется только по времени t и не
связано с пространственными переменными.
На последнем этапе учитывается только кинематический оператор,
связанный с поворотом частицы как жесткого целого на угол QikAt:
\sml)jj ~ \Sml)ij ,
At
№mk)i+1/2j+i/2(Skl)7ij + (^*™)г+1/2,.7 + 1/2 (Slk )ij
о,
где 5^ — компоненты упругопластического девиатора, вычисленные
на втором этапе. В плоском случае кососимметричный тензор flmk
имеет только одну компоненту 0,ху:
/ д д \ п+1/2
(я ^ln+1 - fVp\n+l | /Q ерчп+1д, ( t±vx _ ^Щ \
\ ^1/ ZAX у ;+l/2,j+l/2
/A A \ n+1/2
/Q \n+l _ / ep\n+l _ /Q ерчп+1д, ( ^s _ ^VV \
\byy)ij - \byy)ij \bxy)ij ^l l д д J '
\ ^1/ L\X J i+1/2,j+l/2
/ ep _ ep\ n+1 /д д чп+1/2
м« -(««„)« +{ 2 jy д^Ду Aa;;i+i/2j+i/2-
(17.7)
Заметим, что здесь для получения значений компонент девиатора
тензора напряжений использовано выражение объективной
производной Яуманна, возможен и другой способ их получения, который
будет приведен в следующем параграфе.
168
Гл. 3. Решение задач при больших деформациях
§ 18. Метод частиц в ячейках (Р1С-метод)
Недостатки лагранжевой и эйлеровой сеток (168). Р1С-метод (168).
Метод крупных частиц (172). Ограничения PIC-метода и его
усовершенствование (173). ПИЧ-метод (174). Метод маркеров и потоков (175).
Недостатки лагранжевой и эйлеровой сеток. Решения задач
механики сплошных сред при больших деформациях с
использованием классических подходов как на эйлеровой, так и на
лагранжевой сетках (рассмотренные в предыдущих параграфах) приводят к
определенным сложностям. При достаточно грубых сетках, которые
используются в реальных расчетах, начиная с некоторой степени
деформации среды, расчет становится практически неосуществимым.
На лагранжевой сетке при использовании явных схем это происходит
из-за сильных искажений ячейки, и условия устойчивости Куранта
приводят к сильному ограничению на шаг вместе с диаметром
основания характеристического конуса d —► 0, вписанного в ячейку в
физическом пространстве xf. At ^ - —► 0. При использовании
эйлеровых сеток среда движется относительно фиксированной сетки и,
переходя на границах тела в новые незаполненные ранее средой
ячейки, образует частично заполненные так называемые дробные ячейки
самого причудливого вида, расчет которых связан с определенными
трудностями и потерей точности. Поэтому предпринимаются
попытки как-то преодолеть эти трудности, используя новые
неклассические подходы для решения указанной проблемы.
Остановимся на двух основных подходах, которые были развиты
в механике сплошных сред. Первый основан на
усовершенствовании описания движения сплошной среды на эйлеровой сетке. Это
метод частиц в ячейках, или сокращенно — метод PIC (по
заглавным буквам Particles In Cells). Второй — метод адаптирующихся
подвижных сеток, в котором сделана попытка объединить
достоинства эйлерова и лагранжевого подходов и устранить их недостатки.
PIC-метод. Основная идея этого метода заключается в
совмещении описания сплошной среды, с одной стороны, как континуума, а с
другой — как совокупности большого числа отдельных частиц,
движущихся на эйлеровой пространственной сетке. В отличие от
моделей таких сред, как плазма или галактическая среда, где соударения
между частицами среды сравнительно редки и возможно примене-
§ 18. Метод частиц в ячейках (Р1С-метод) 169
ние бесстолкновительной модели многих частиц [57], в жидких или
твердых средах, где число частиц несравненно больше, такая модель
неприменима. Благодаря непрерывным столкновениям соседних
молекул импульс и энергия отдельных частиц не сохраняются, а
непрерывно распределяются между соседями, это означает, что
молекулы в некотором небольшом объеме можно считать находящимися в
тепловом равновесии. Эти соображения позволили создать
комбинированную модель, объединяющую движения отдельных частиц с
движением континуума.
Рассмотрим этот метод на примере идеального газа. Законы
сохранения вещества и импульса в эйлеровых переменных могут быть
записаны в такой форме:
дпт
— V div(mnv) = О,
я (18Л)
UTiTflV
— Ь div(mm7(g) v) = — gradp,
где n(x, t) — значение плотности частиц в точке пространства х, г/,
т — масса частицы в ячейке, v — усредненная скорость частиц в
ячейке, р — давление, гГ ® v — диадное произведение.
Уравнение для идеального газа возьмем в виде рр~7 = const или в
дифференциальном виде:
Jt(PP"1)=0> (18'2)
где d/dt — полная или лагранжева производная. Уравнение (18.2)
удобно также представить в виде закона сохранения в эйлеровой
форме, используя первое уравнение (18.1), получим
д
— (рр'1) + div (pp-^v) = 0. (18.3)
Изложим метод PIC для простоты в двухмерном случае, обобщение
на трехмерный случай очевидно.
Рассматриваемая область пространства покрывается эйлеровой
сеткой. В каждой ячейке сетки, которая определяется индексами г/,
распределяется достаточно большое число частиц,
характеризующихся номером а и координатами ж™, г/™ в момент времени tn.
Координаты частицы в процессе движения определяются по скоростям
~^=иа, — = va, (18.4)
170
Гл. 3. Решение задач при больших деформациях
где (u,v) — компоненты вектора скорости v = (u,v).
Каждой частице, кроме координат, приписывается значение
массы та, импульса (таи%, mav^) и адиабатического инварианта
е2 = (РР_7)а? связанного с уравнением состояния частицы. Таким
образом, вектор неизвестных [/, характеризующий частицу,
определяется шестью компонентами:
&а = (ж£, г/£, ma, mau™, mav™, е£) , 1 < а < N.
Т.к. внутри ячейки частицы испытывают большое число
столкновений, то их импульсы и инварианты выравниваются в течение малого
промежутка времени и их можно определить как средние значения
по всем частицам в ячейке, т.е. щ^ — плотность числа частиц в
ячейке г/, pij — плотность газа, импульс (pv)ij и адиабатический
инвариант eij определяются для данной ячейки ij в момент tn. Введем
обозначение
A; = .(int(f)-.).(i».(f)-i
где Int(z) — целая часть аргумента z:
1, если к = т.
г) ( /с 7Т7 1
v ' * 0, если к ф т.
Тогда А™ = 1, когда частица находится в ячейке, Д™ = 0, когда
частица вне ячейки. Здесь h — шаг эйлеровой сетки.
Усредненные значения в ячейке можно записать в виде
— Удп
h2
1 _ 1 _ <18'5)
рЪ = ^ Е Л>«> (^)« = й2 Е А>«с
а а
После этого можно вычислить давление в ячейке р™- = (ер7)", и
определить новые мгновенные значения скорости частиц (й, г;) в
ячейке ij по уравнениям движения (18.1), в которых отбрасывается
член, связанный с дивергенцией, т.е. без учета переноса:
At
и
Г/п+1 _ „,п _ ^ь ( п _ п \
At
13 lJ 2pf, h
HlJ (18.6)
vn+1
2plh
[Pi,j+i -Pi,j-i)
; 18. Метод частиц в ячейках (Р1С-метод)
171
где шаг по времени At выбирается с учетом условия Куранта.
Для того чтобы найти скорости частиц Vй = (u%,v™) по (й™,г)2),
предлагается алгоритм интерполирования по пространству по
четырем соседним ячейкам, прилегающим к узлу, ближайшему к
частице а (рис. 18.1).
V/,.
•У'+1
/,J / /
М/ / /
V/+1J+1
®
3/W1/+1
'3/^11"
V.
/+ij
Рис. 18.1. Алгоритм нахождения скорости частицы по 4-м соседним
ячейкам
Для определения скорости частицы а вводится фиктивная
площадь (объем) частицы, равная площади ячейки с центром в этой
частице (рис. 18.1, заштрихованный квадрат). Это позволяет
вычислить весовые коэффициенты а^ в (18.7), которые принимаются
равными тем частям площади, которые приходятся на каждую из 4-х
ячеек:
<+1 = ^з [(aU)i+i,j + (atyi+ij+i + (au)iij+1 + (au)ij] , (18.7)
где й = \ (ип+1
По определенным в (18.7) скоростям (г^+1,г>2+1) находим новое
+ ип).
положение частицы:
,п+1
^ ' *=х^ + и^ At, j/S+1 = Уа + <+1 At, (18.8)
и находим ячейку г/, в которую попадает частица а. Если она
попадает в фиктивную ячейку, находящуюся за жесткой стенкой или
осью вращения, то осуществляется ее зеркальное отображение.
172
Гл. 3. Решение задач при больших деформациях
Частицы с полученными скоростями v7^1 переносят
пропорционально своей массе импульс (rm7)™+1 и адиабатический инвари-
Г7-И
ант е^ , что соответствует интегрированию уравнении переноса, т.е.
уравнениям (18.1) - (18.3) без правых частей. Шаг по времени At на
этом заканчивается, т.к. найден весь вектор решения U.
Метод PIC можно рассматривать так же, как метод расщепления
законов сохранения (18.1), на первом этапе которого
отбрасываются конвективные члены. На втором этапе отбрасывается градиент
давления, а интегрирование уравнений переноса заменяется
перемещением отдельных частиц и переносом ими массы т, импульса mv
и адиабатического инварианта е. Метод PIC будет полностью
эквивалентен методу расщепления, если каждая ячейка содержит одну
единственную частицу, полностью заполняющую ее.
Метод крупных частиц. Если считать, что в каждой ячейке
имеется только одна частица, PIC-метод совпадает с расщеплением
уравнений для идеального газа по физическим процессам. Перенос
частицами заменяется перетоком жидкости или газа через границы
ячеек и вычислением плотности этих потоков [3].
Первый этап состоит в вычислении (й™+ , г)™+ ) по
формулам (18.6). На втором этапе осуществляется перенос величины Q
через стенки ячейки потоком массы в соответствии с законом
сохранения
dQp
dt
+ div(Qpv) = 0. (18.9)
Поток массы через одну грань ячейки (г + 1/2, j) с центром в узле ij
за время At будет равен
ЛМП+1
LXN1i+l/2,j
uij т Мг+1,.7 Ля1 ллтттх ~п+1 , ~п+1
Pij J 2 ^ ^ли й^ + й^\3 > 0,
Pi+U Ъ3 9 *+1,'Ау, если й^1 + й?+Ъ < 0.
(18.10)
Плотность берется из той ячейки, из которой вытекает среда
(рис. 18.2). Изменение величины Q™+1 за счет переноса потоком
массы через все стороны ячейки вычисляется по формуле
; 18. Метод частиц в ячейках (Р1С-метод)
173
AQ
п+1
)П+1
At
Pij Ах Ay
(qpl
AM'
■n+l
+ОД
n+1 AMn+1
i,r
+ 1/2,J
Sn+1
,AMn+1
1 *,j
1/2
CA«- (18-n)
J4
7+1
H
r
p
i
4
P
3
6
« 5 ^e
^A ^
1
"a
2
J*i
' ^1
С Pc
▼ "с 8
£> Рд
9|
i-\
l+l
Рис. 18.2. Переток среды между соседними ячейками
Эта формула соответствует вычислению дивергенции в
уравнении (18.9) по формуле естественной аппроксимации (16.3) для
фиксированной эйлеровой ячейки. Из приведенного алгоритма следует,
что масса, импульс и адиабатический инвариант е для всего тела
сохраняются, т.е. схема консервативна.
В методе PIC просто визуализируется движение границ тела,
контактных границ между средами с различными плотностями при
больших перемещениях и деформациях, образование вихрей и
других тонких структур.
Ограничения PIC-метода и его усовершенствование. PIC-
метод не лишен недостатков. Для его реализации требуются
высокомощные вычислительные машины, так как число частиц в ячейке
должно быть достаточно велико. Требуется большая память,
необходимо помнить не только сеточные функции, но и все характеристики
174
Гл. 3. Решение задач при больших деформациях
частиц, кроме того, существенно возрастает время счета. Если
число частиц невелико, то из-за дискретного характера переноса при
пересечении частицами границ ячеек возникают флуктуации
основных физических величин, что может привести к развитию
неустойчивости. Исследование устойчивости численной схемы Р1С-метода
показало, что она условно устойчива при ограничении на шаг по
времени At [44]:
At
~h
^
\v\2 + ас2'
(18.12)
где а — константа, зависящая от свойств среды, с — скорость звука.
Численные эксперименты дают условие на минимальное число
частиц в ячейке, при котором флуктуации еще не приводят к
неустойчивости:
N>
pvz
dp
дх
Из условий (18.12) - (18.13) следует оценка:
с2
7V>l + a—.
(18.13)
(18.14)
Здесь использована оценка
др
дх
dv
At
Из (18.12) - (18.14) следует, что при уменьшении скорости
движения среды для устойчивости требуется малый шаг At и большое
число частиц в ячейке. Поэтому, если в области решения
появляются ячейки с небольшой скоростью, возрастают требования к методу
в отношении числа частиц, при этом метод становится мало
эффективным.
ПИЧ-метод. Для того чтобы уменьшить число вводимых частиц
и сократить время счета, в [16] был предложен гибридный ПИЧ-
метод (совместный метод потоков и частиц в ячейках). Этот метод
заключается в том, что везде в расчетной области, кроме
окрестностей контактных и свободных границ, применяется метод
потоков (<крупных частиц»), а в окрестностях свободных и контактных
границ расчет проводится по методу частиц в ячейках. Если среда
18. Метод частиц в ячейках (Р1С-метод)
175
перетекает в ячейку, содержащую другой материал, то перетекший
материал и материал ячейки представляется в виде частиц. Если
частица переходит в ячейку с крупной частицей и материал
одинаков, то частица исчезает, а её масса, импульс и энергия передаются
ячейке, куда она пришла. В случае, когда частица переходит в
ячейку со сплошной средой другого материала, материал этой ячейки
представляется частицами.
В этом методе переток массы дискретный, поэтому он не
устраняет, а лишь ослабляет недостатки PIC-метода. При малых скоростях
движения может образоваться очень большое количество частиц,
при этом из-за дискретности перетока на контактных и свободных
границах также возникают флуктуации массы, импульса, энергии,
хотя, как отмечается в [16], эти флуктуации слабее флуктуации в
Р1С-методе.
Метод маркеров и потоков. Наконец, чтобы полностью
устранить колебания, возникающие на границе тела или на границе двух
разных сред, составляющих тело, в [3] было предложено вообще
отказаться от рассмотрения движения лагранжевых частиц, заменив
его перетеканием среды на эйлеровой сетке. Задача интегрируется
на эйлеровой сетке методом потоков, а движение границы
отслеживается с помощью специальных маркеров [30]. Маркеры
представляют собой частицу, неимеющую массу и каких-либо других свойств
сплошной среды, но ей приписывается скорость, равная средней
скорости жидкости в той окрестности пространства, в которой в
данный момент находится маркер. Каждой среде соответствует свой тип
маркеров. Маркеры, помещенные на границе, теоретически должны
были бы перемещаться вместе с ней и отслеживать ее положение
в пространстве. Но из-за грубой сетки это соответствие может
нарушаться и для его устранения вводится процедура периодической
корректировки. Корректировка, грубо говоря, состоит в том, что
если в некоторой эйлеровой ячейке вблизи границы оказывается, что
есть масса среды М > Mq (Mq — некоторое предельное значение), но
нет маркеров, то в нее перетаскивается ближайший маркер. Если же
М < Мо и нет маркеров, то масса М возвращается назад, т.е. переток
зануляется. В остальных ситуациях считается, что есть соответствие
между движением среды и маркеров и коррекции не производится.
Расчет методом потоков обеспечивает достаточно плавный переток
среды на границах, что снижает колебания и делает решение более
176
Гл. 3. Решение задач при больших деформациях
устойчивым, чем в методах частиц. Маркеры же позволяют остле-
живать границы, и благодаря этому устраняется нефизическая
диффузия и перемешивание составляющих тела.
Во всех приведенных выше методах используется расщепление
уравнений гидродинамики: на первом (эйлеровом) этапе уравнения
отбрасываются конвективные члены, а второй этап (лагранжев)
отвечает переносу частицами либо потоками свойств среды в новое
положение.
Таким образом, хотя PIC-метод и его модификации позволяют
производить расчет больших деформаций, он требует дальнейших
усовершенствований и сочетания с другими методами, особенно в
области дозвуковых скоростей. Одним из таких методов может быть
метод адаптирующихся сеток, который в силу своей общности может
легко сочетаться с другими численными методами.
§19. Формулировка теории течения
упругопластической среды в виде
вариационного неравенства
Вариационное неравенство (176). Диссипативные схемы (179).
Вариационное неравенство. Уравнения упругопластического
течения кроме традиционной дифференциальной формулировки
могут быть сформулированы в виде единого вариационного
неравенства как в упругой, так и в пластической областях. Полная система
уравнений теории течения Прандтля-Рейса в случае малой
деформации состоит из дифференциального уравнения движения:
m,t =<7ijj, (19.1)
закона Гука:
£ij =aijki&ki (19.2)
и определяющих уравнений упругопластического деформирования,
которые могут быть сформулированы в виде принципа максимума
скорости диссипации энергии:
К - *аК < 0, аЩ < щЖ, (19.3)
19. Вариационное неравенство теории течения
177
4+4 = oKj+^i),
ющее условию пластичности также как и оц\
F(°*tj) ^ т„ (19.4)
где rs — предел текучести материала на сдвиг, F((Jij) — выпуклая
поверхность в пространстве напряжений ov/, которая может быть
кусочно гладкой. Например, для уравнений пластичности Треска-
Сен-Венана она представляет собой призму шестиугольного сечения,
описанную около цилиндра эллиптического сечения, которым
задается условием пластичности Мизеса [64, 27].
Уравнение (19.3), по существу, представляет собой вариационное
неравенство для произвольной вариации 5<Jij = о*, — <Jij,
удовлетворяющее условию (19.4)
5a%je% < О,
Если еще ввести произвольную вариацию вектора скорости Svi, то
можно всю систему уравнений (19.1)—(19.4) записать в виде
вариационного неравенства
5vi(pvi - (Tijj) + 6<Tij(aijki&ki ~ Vij) > 0, (19.5)
которое сформулировано относительно вектора скорости Vi и тензора
напряжений сг^-.
Неравенство (19.5) удобно записать в матричном виде:
к=1 J
5й Auyt - У Вкй,к > 0, (19.6)
вводя 9-мерный вектор и, состоящий из 3-х подвекторов (блоков):
0"13
Матрицы А и Т5к имеют блочную структуру:
/о в* в*>
Bfc = В£ О О
\в* о о
J\v
0
0
0
Аа
■^as
0
■^as
А„
178
Гл. 3. Решение задач при больших деформациях
Матрицы Av = pi, Act, Aas размерности (3 x 3) легко выразить
через упругие постоянные a^/cb а матрицы В^ имеют вид:
В*
<&
0
0
0
<*?я
0
0
0
&Ъ
в
1 k3i,j,
О к = г или
Функция текучести F(sijSij) = у f s^-s^, где s^- - .tJ - uuy.
Покажем, что формулировка задачи в виде (19.5) или (19.6)
эквивалентна формулировке, которая следует из ассоциированного
закона пластического течения.
Запишем вариационное неравенство в общем виде:
(бй, Ь(й)\ > О,
где и и 5и G К.
(19.7)
Здесь К — выпуклое замкнутое множество, удовлетворяющее
условию (19.5), 5и — произвольный элемент этого множества.
Геометрическая интерпретация неравенства (19.7) приведена на
рис. 19.1. Угол а в силу (19.7) не может быть тупым. Если и на-
Рис. 19.1. Геометрическая интерпретация неравенства (19.7)
ходится внутри поверхности, то должно выполняться Ь(и) = б,
если и на границе (как показано на рисунке), то вектор L(u) должен
быть направлен по нормали п к поверхности F(u) = rs, иначе угол а
будет тупым. Тогда в случае непрерывно дифференцируемой функ-
19. Вариационное неравенство теории течения
179
ции F(u)
т dF(u)
А > О, если F(u) = 1,
Л = 0, если F(u) < 1,
где Л определено из условия текучести (см. § 9).
В случае уравнений упругопластической среды эта запись
совпадает с ассоциированным законом текучести, т.к. L(u) = £\.-, а
г \%1) = \~2^ijSij) = Ts,
.р H(S-rs)
£ij = 2 sklVk,lSij,
где Н(х) — функция Хевисайда.
Диссипативные схемы. На основе дискретного представления
вариационных неравенств в работе [62] предложен метод
построения диссипативных разностных схем. Неравенство (19.7) заменяем
на
(u*h - uh)Lh{uh) > О, uh = h(uh), К G К, (19.8)
где Lh(uh) — аппроксимация дифференциального оператора для
сеточной функции Uh, Ih(uh) — аппроксимация тождественного
оператора, который аппроксимирует ограничения и, по существу,
указывает в каком смысле следует понимать включение Uh в множество К.
Рассмотрим задачу Коши для вариационного неравенства с
линейным одномерным оператором гиперболического типа:
L(u) = Аг?£ — Вг?ж.
Аппроксимация L^(u^) строится на основе консервативного
представления
Й*ВД = Й*(АЙ,* - Ви,х) > -(йАЙ),* - -(йВЙ),я, (19.9)
которое интегрируется по области решения задачи и после
интегрирования по частям позволяет сформулировать понятие
обобщенного решения, допускающего сильные разрывы [62]. Это дает
возможность интегрировать уравнения, не выделяя разрывов, по схеме
180
Гл. 3. Решение задач при больших деформациях
сквозного счета. Аппроксимация (19.9) записывается в виде
W = {UAU)k ~2£Ай)к~1 - ^ ((9ЙВЙГ-1'2), > 0, (19.10)
где A{uh) = {uj - Uj-!)/Ax.
Т.к. матрицы А и В симметричны, требование консервативности
можно представить в виде
/ ик-\-ик~1\ ик^ик~г
dh= [uh А
At
йк - A0(un-1/2))BA(un-1/2)
где A°(uh) = \(uj + uj-i)t uh = Ih < uh > — аппроксимация
тождественного оператора, dh — погрешность аппроксимации для
выражения в формуле (19.9):
d = uL(u) — - [(uAu)j + (иВи),х] = 0,
которая равна нулю для любой непрерывно дифференцируемой
функции и = u(t,x) и, следовательно, 4^0 в упругопластических
задачах имеет смысл скорости диссипации энергии, вносимой за счет
аппроксимации вариационного неравенства, а условие dh ^ 0
является условием диссипативности разностной схемы (19.10).
Введем вспомогательную сеточную вектор-функцию й^,
удовлетворяющую разностному уравнению
АФ ~^~Х = В А(ип~1/2). (19.11)
Тогда выражение для dh можно представить в виде следующей
квадратичной формы:
{~ь ик + ик\ ик -ик
dh = (V - _^_ j A^^+
+ (aV"-1/2) - ик-^~1\ ВАК"1/2). (19.12)
Это можно проверить преобразованием выражения (19.12) с учетом
симметрии матриц А и В.
19. Вариационное неравенство теории течения
181
Для выполнения условия dh ^ 0 необходимо и достаточно, чтобы
между введенной функцией uh и неизвестными функциями Uh и uh
существовала связь
2йк-ик-йк \_ъ( А(ик-йк) \.0A.f О
2Л0(|хп-1/2) _йк_ uk-lJ -U[AtB A(un-W)J + Zm \Хъ-1/2
(19.13)
тл / Doo Doi \ . п
где и = \ тл тл ^ 0 — неотрицательно определенная матрица
\-Lho -^11/
размерности 2т х 2m; x/i ~~ произвольная вектор-функция,
удовлетворяющая условию
п-1/2-d _ п
Тогда
dh = -UhDUh > 0, ^ = ( в Л(ы„-1/2) J •
Система уравнений (19.13), связывающая г^ и й^, совместно
с (19.10), составляет семейство диссипативных разностных схем со
схемной вязкостью, зависящей от выбора матриц D^j (i,j = 0,1).
Наиболее простой вариант, когда блок Dio = 0 и Doo = Doo- Тогда,
исключая из (19.13) й^, получим уравнение, которое определяет
решение на промежуточном слое (предиктор):
п-1/2 . п-1/2 Л п-1/2 . п-1/2
-1 э- (А-1 + Бц)В^ —э- =
2 2 v ш Ах
= ukzl/2 + AtX]:11//l (19.14)
Эту систему уравнений можно рассматривать как систему ОДУ
первого порядка по переменной ж, если положить
п-1/2 п-1/2 , N п-1/2
Аж \dx
К (19.14) необходимо добавить произвольное диссипативное
граничное условие на достаточном удалении от области решения
(условие <на бесконечности») [62].
182 Гл. 3. Решение задач при больших деформациях
Второе уравнение (19.13) можно представить в виде
йк = ц*+2Ц*~1+ВооАЦ*-2Ц*~1+^ (А"1 - Doo + Doi) BA(un~^y
Это соотношение дает конкретное выражение для тождественного
оператора Ih(uh)-
Таким образом, алгоритм разностной схемы состоит в решении
системы (19.13) - (19.14) (предиктор) и вычислении решения для
нового временного слоя (корректор) по формулам
Uj-l/2 ~ Uj-l/2 + Ах А а \из Uj-1 ) '
4-1/2 = 4-1/2 + Ь01А (йк_1/2 - йкг{/2) , (19«15)
4-1/2 = 4-1/2 + 2(1 + DooA)-1 (йк_\/2 - 4-i/2) ,
здесь ик * = тг(ик) — означает проектирование на поверхность
текучести.
При задании произвольных матриц Doo — А-1 и Doi = 0
последнее уравнение совпадает с корректировкой напряжений по Уилкин-
су [68]:
4-1/2 =КА (4-1/2 )'
Оператор тга вычисляет проекцию по норме матрицы А:
\\и\\А = VA.uA.
Хотя рассмотренный численный алгоритм диссипативных схем
внешне отличается от метода расщепления в § 9, но по существу
близок к нему. На этапе предиктор ищется решение,
удовлетворяющее в обобщенном смысле линейным дифференциальным
уравнениям и начальным условиям задачи. После чего на этапе
корректор полученные решения проектируются на поверхность
текучести. Для практического выполнения этой операции в общем случае
кусочно-гладкой поверхности привлекаются математические методы
<выпуклого> анализа [62]. Для решения многомерных задач
изложенная диссипативная схема (для одномерной задачи) применяется
после расщепления задачи по направлениям.
§ 20. О квазихрупком разрушении и локализации деформаций 183
§20. О квазихрупком разрушении и
локализации деформаций
Введение (183). Квазихрупкая термоупругопластическая повреждающаяся
среда при конечных деформациях (187). Численный метод (191).
Разрушение плоского стандартного образца при растяжении (193). Задача об оползне
склона под действием веса сооружения (196). Выводы (198).
Введение. Описание процессов разрушения основывается на
представлениях о разрушении как о потере способности
материала к сопротивлению деформации вследствие нарушения внутренних
связей с ростом концентрации микротрещин.
Для хрупких материалов считается, что разрушение происходит
мгновенно при выполнении критерия разрушения. Такие модели
рассматриваются в рамках механики хрупкого разрушения путем
явного выделения поверхностей разрушения как контактных
разрывов типа магистральных трещин. Подход механики хрупкого
разрушения сталкивается с непреодолимыми или во всяком случае со
значительными трудностями при описании зарождения и развития
трещин, особенно при нарастании их числа. Поэтому подобно тому,
как в газовой динамике для расчета множественных разрывов
прибегают к схемам сквозного счета, в механике деформируемых сред
для расчета общих случаев разрушения также вводят континуальное
описание разрушения.
Континуальный подход к описанию процессов разрушения
предполагает построение теоретических моделей сплошной среды,
описывающих разрушение как процесс на основе определяющих уравнений,
записанных в единой форме для разрушенного и неразрушенного
состояний материала. Континуальный подход описывает появление и
развитие поверхностей и зон разрушения без явного их выделения,
что при численной реализации отвечает методам сквозного счета.
Пионерской работой по сквозному счету процессов разрушения по
праву следует считать исследование Майнчена и Сака [55], не
утратившее актуальности и по сей день. В этой работе кинетика
разрушения не учитывается, то есть при выполнении критерия
разрушения напряженно-деформированное состояние в малом объеме
ячейки подвижной лагранжевой расчетной сетки происходит скачком.
Такой подход в принципе позволяет прослеживать развитие зон
разрушения, но оставляет открытыми множество вопросов, связанных с
184 Гл. 3. Решение задач при больших деформациях
выполнением законов термодинамики, соответствием эксперименту,
выбором критерия разрушения, влиянием кинетики процесса
разрушения и так далее.
Эксперименты по деформированию и разрушению стандартных
образцов при растяжении и сдвиге (кручении полых цилиндров)
демонстрируют на диаграммах деформирования участки
разупрочнения, на которых напряжения падают с ростом деформаций. При
трактовках этих зависимостей надо учитывать, что напряжение и
деформация являются не единственными параметрами состояния, и
поэтому такие диаграммы показывают лишь срез
многопараметрического процесса на плоскость а — е.
Как уже отмечалось, применение инкрементальных теорий
пластичности типа Прандтля-Рейсса при описании разупрочнения
(падение предела текучести с ростом деформации) приводит к
некорректным краевым задачам из-за нарушения постулата Драккера [45]
или в динамике критерия Адамара. В квазистатике это связано с
утратой уравнениями свойств эллиптичности, а в динамике — с
нарушениями гиперболичности. Поэтому бесхитростное описание
процесса разрушения в рамках стандартных моделей упругопластиче-
ских материалов оказывается несостоятельным.
Чтобы получить математически корректное описание процессов
разрушения, в определяющие уравнения инкрементальной
пластичности вводятся разного рода регуляризаторы как физического, так
и вычислительного плана: искусственная или физическая
вязкости (теории упруговязкопластичности), пространственное
осреднение или нелокальные меры деформации, градиентные теории и так
далее.
С другой стороны, как уже упоминалось, падение напряжений из-
за потери материалом способности к сопротивлению деформации
может происходить по нетермомеханическим причинам при
неизменной деформации. Это говорит о том, что при континуальном
описании процессы деформации и разрушения можно и нужно трактовать
как независимые (что не исключает взаимовлияния), а развитие
разрушения целесообразно характеризовать не деформацией, а своим
параметром состояния — поврежденностью.
Параметр разрушения, или поврежденность, подчиняется
кинетическому уравнению, является скаляром или тензором второго ранга
[45, 35, 75] и отвечает за способность среды к сопротивлению
деформации. С ростом поврежденности, который происходит при вы-
§ 20. О квазихрупком разрушении и локализации деформаций 185
полнении критерия начала разрушения, сопротивление среды
падает: уменьшаются эффективные модули упругости с ростом повре-
жденности, о чем свидетельствует экспериментально фиксируемое
падение скоростей распространения малых возмущений, и в
особенности падает сопротивление материала за пределами упругости в
состоянии предшествующем разрушению, изменяется характер
деформации материала — происходит локализация пластических
деформаций в узких полосах сдвига, разделенных полосами частично
разгруженного материала.
Разупрочнение и разрушение хрупких и квазихрупких материалов
сопровождается явлением локализации деформаций в зонах
ослабленного сопротивления материала. Для хрупких материалов такие
зоны очень узки и представляют контактные разрывы, на которых
скорости и перемещения меняются чрезвычайно резко,
скачкообразно. При континуальном (непрерывном) описании таких разрывов
деформация имеет вид скачка типа дельта-функций, нормальные и
касательные к поверхности скачка напряжения стремятся к нулю при
нормальных деформациях растяжения или моделируют контактное
взаимодействие берегов трещины, включая силы трения и
контактное давление.
В подавляющем большинстве используемых численных моделей
континуального разрушения (см., например, [55, 69]) расчетные
зоны квазихрупкого разрушения неправдоподобно обширны, а
локализация деформаций часто выражена настолько слабо, что
интерпретация результатов расчета процессов разрушения зависит от
воображения расчетчика. При уменьшении влияния регуляризирующих
членов при попытках смоделировать более сильную локализацию
деформаций может появляться аномальная зависимость решения от
размера и формы ячеек сетки, означающая потерю сходимости.
Поэтому построение численных алгоритмов для аккуратной
реализации континуальных моделей разрушения представляет важную
самостоятельную проблему.
Отметим, что картины обширных зон рассеянного разрушения
наблюдаются в экспериментах и свойственны материалам с вязким
типом разрушения со сравнительно медленным ростом накопления
плотности микротрещин (поврежденности). Для стандартных
образцов разрушение при растяжении сопровождается для таких
материалов образованием шейки. Еще более медленное накопление
повреждений определяется как усталостное разрушение.
186 Гл. 3. Решение задач при больших деформациях
Во многих современных работах теоретические модели
континуального разрушения неизбежно сращиваются с численными
алгоритмами их реализации в единое целое, то есть непрерывность решения
в зонах разрушения и моделирование разрывов обеспечиваются ре-
гуляризаторами нефизической природы. Отметим ниже некоторые
типичные работы такого типа.
Развитием идей Майнчена-Сака является подход, основанный на
моделировании зон разрушения дискретными частицами,
предлагавшийся в работах [16, 17] ив ряде других. Если в лагранжевой ячейке
выполняется условие разрушения (по предельному значению
деформации, пластической деформации, максимальному главному
напряжению и т.д.), то связи между узлами в таких ячейках
освобождаются, напряжения релаксируют к нулю и сопротивление сохраняется
только по отношению к всестороннему сжатию. Лагранжевы
узловые массы при разрушении превращаются в самостоятельные
частицы, способные к контактному взаимодействию с деформируемой
средой и уносящими массу, импульс и энергию. Подробный обзор и
описание такого типа алгоритмов сквозного счета есть в книге [69].
Имеется направление работ по моделированию разрушения, в
которых контактные разрывы, отвечающие магистральным трещинам,
выделяются явно.
В общем случае такое выделение производится сдвоенными
узлами, которые вводятся в процессе решения с локальной перестройкой
сетки.
Способ явного выделения вновь образующихся контактных
разрывов, не требующий введения новых узлов и основанный на локальной
перестройке сетки путем <схлопывания> разрушенной ячейки
(путем сдвига ее узлов на поверхность разрушения), предложен в работе
[16].
Отметим ряд алгоритмов, в которых нарушения сплошности типа
трещин моделируются на уровне элементов без перестройки сетки, с
использованием техники подвижных сеток с дополнительными
степенями свободы в элементах, содержащих контактный разрыв,
которые отвечают разрывным функциям формы.
Два основных дефекта свойственны большинству имеющихся
моделей разрушения: 1) недостаточная количественная связь с
результатами физических экспериментов и 2) неуверенное поведение
численных моделей разрушения из-за сильной чувствительности к
параметрам дискретизации. И в физических, и в вычислительных экспе-
§ 20. О квазихрупком разрушении и локализации деформаций 187
риментах результаты сильно меняются при малых изменениях
входных данных, что отвечает физике явления разрушения. Отметим
также естественный для переходного явления разброс результатов:
молено разбить 100 стаканов и каждый при этом разобьется по
индивидуальному сценарию, несмотря на все меры по выравниванию
условий проведения испытаний (фиксация начального положения
стакана и его скорости, обеспечение сходности свойств материала
и так далее). Поэтому реально согласование теории и эксперимента
может ожидаться только для основных интегральных характеристик
процесса.
Помимо этого, сложности физического и численного
экспериментов обусловлены еще и тем, что явление разрушения имеет очень
медленные и очень быстрые этапы при общем нелинейном
поведении сплошной среды, поэтому моделирование квазихрупкого
разрушения требует значительных усилий и для расчета, и для измерения
характеристик общего термомеханического процесса, на фоне
которого происходит разрушение. Это делает проведение
параметрических исследований очень трудоемким.
Способы описания явления разрушения (разупрочнения),
сохраняющие корректность задачи, до конца не ясны, и вопрос о том, какими
свойствами должны обладать математические модели
континуальной механики для эффективного описания локализации
деформаций и эволюции зон разрушения, остается до сих пор открытым и
актуальным.
Квазихрупкая термоупругопластическая повреждающаяся
среда при конечных деформациях. Перейдем к
моделированию повреждаемости квазихрупких упругопластических
материалов. На основе термодинамически корректной теории повреждаемой
упругопластической среды формулируется феноменологическая
модель и предлагается методика численного решения. Таким образом,
делается попытка преодоления отмеченных выше недостатков при
решении задач разрушения, позволяющая проследить развитие
магистральных трещин в виде узких полос квазихрупкого разрушения,
представляющих скачки скорости и всплески деформаций. Модель
справедлива для случая конечных пластических деформаций и
учитывает то обстоятельство, что разрушение сопровождается сменой
режима деформирования от квазистатического при отсутствии
разрушения к ярко выраженному динамическому при развитии узких
188
Гл. 3. Решение задач при больших деформациях
зон локализации деформаций. Численная методика, учитывающая
данные особенности, реализована в рамках пакета программ <АСТ-
РА> и описана в [7, 8].
Проведены параметрические расчеты процессов разрушения
типовых растягиваемых образцов, испытаны ряд критериев разрушения
и ряд режимов кинетики повреждаемости. Исследовано так же
влияние пластических деформаций и локального интенсивного нагрева
(охлаждения) на разрушение, прослежено развитие зон
локализации деформаций. Выработаны рекомендации по численной
реализации моделей континуального разрушения, которые повышают их
эффективность.
Система уравнений, описывающая поведение термоупругопласти-
ческой повреждающейся среды разрабатывается на основе
термодинамического подхода и используется здесь в варианте, описанном в
работах [9, 10, 11]. Система уравнений содержит законы сохранения
массы, импульса и энергии, а также кинематические соотношения:
dU _
= 0, р— = а : е + Vq + pr = 0,
•Г"1), e=i(L + LT), (20.1)
de _ т _ dx
е = —- + £ • L + L • е, L = Vu, —- = u
dt dt
и определяющие соотношения, которые заслуживают более
подробного рассмотрения, приводимого ниже. Здесь использованы
традиционные обозначения: р — плотность, и — скорость материальной
сплошной среды, t — время, х — эйлеров радиус-вектор (актуальная
конфигурация), х — лагранжев радиус-вектор (начальная
конфигурация), F — градиент деформации, L — градиент скорости, е —
тензор деформации Альманси, е — эйлеров тензор скорости
деформации, а — тензор напряжений Коши, U — внутренняя энергия
единицы массы, q — вектор теплового потока, Т — температура, г —
массовый источник тепла, djdt — материальная временная
производная, V — оператор пространственного дифференцирования в
актуальной конфигурации, I — единичный тензор.
Определяющие соотношения представляют связи между
характеристиками состояния бесконечно малого объема сплошной среды,
накладываемые законами термодинамики. Образуем минимальный
набор взаимно независимых параметров состояния бесконечно малого
dp
~dl
+ ре :
F"^
:I = 0,
= v5,
du „
*=i(i-F--
§ 20. О квазихрупком разрушении и локализации деформаций 189
объема сплошной среды: Т, s, X, ^, е, -^, VT, где % = (ер,0) —
структурные параметры: тензор пластической деформации ер и
повреждаемость #, определяемые далее и ответственные за изменение
внутренней структуры сплошной среды, то есть за развитие
дислокаций и микротрещин соответственно. Нулями отмечают
материальные тензоры, связанные с пространственными тензорами
соотношениями
s=FT-s-F, e = FT e F, a= F"1 • а • F"T.
Из первого закона термодинамики, утверждающего закон
сохранения энергии, и второго закона термодинамики, закона возрастания
энтропии
dr] /q\ pr
следует неравенство скорости диссипации:
/ дср\ dT fo дср\ о дер о VT
D=-4r?+^)^+r"^J:e"^:Xt+4'^^°-
Здесь ср = U — Тг] — свободная энергия единицы массы.
Свободная энергия и скорость диссипации принимаются такими:
V=^(ln^+f3(T-T0)))\^(e>-ep):(e>-e>p),
Лро \ Ро ) Р
I /d0\2 к
D = Н(Фр)кр^/е'р : е'р + Н(Фв)кв [-) + -^VT • VT,
то есть полагается, что упругие составляющие девиатора
деформации малы по сравнению с единицей. Эффект температурного
расширения учитывается членом с коэффициентом (3. Составляющая
скорости диссипации, отвечающая за пластическое течение,
полагается однородной функцией первого порядка от скорости
пластической деформации, что соответствует случаю упругопластической
среды, независящей от изменения масштаба времени. Пластическая
деформация растет при выполнении условия активного нагружения
Фр(Т,е,ер,0,е) ^ 0. Полагается также, что материал пластически
несжимаем (скорость диссипации зависит только от девиатора
скорости пластической деформации, что обычно хорошо выполняется
190
Гл. 3. Решение задач при больших деформациях
для металлов). Сопротивляемость среды, представленная
модулями упругости и пределом текучести, помимо температуры,
деформации и пластической деформации зависит также от дополнительного
структурного параметра состояния в поврежденности: /i = ^од^(О),
К = К0дк(в), кр = крОдр(0), где /i0, К0 — модули упругости, кр0 —
предел текучести, для неповрежденной сплошной среды.
Убывающие функции дм, дкУ дР обеспечивают спад сопротивления среды с
ростом поврежденности, который происходит при выполнении
условия разрушения Ф#(Т, s, ер, #, е) ^ 0. Кинетика процесса разрушения
определяется зависимостью скорости диссипации от скорости роста
поврежденности. Неотрицательные функции /io, -Ко? кро, ко и kq
Залп ° °
висят от 1 , е и ер.
В результате определяющие соотношения принимают следующий
вид:
а' = 2/х(е' - е;), р = К^ (ln^- + /?(Т - Т0)) , (20.2)
Ро \ Ро )
е'р = Н(Фр)у/^4рег'/кр, ft = -Н(Фв)к^.
Граничные условия следующие:
X t ^>ип->
X G о\оип.
X G *bnQ;,
£>0
£>0 :
t >0 :
: G S\Sua, £ > 0 :
x€ST
х G ^\^т.
^, £ >0
, £ > 0
: un = <,
(<т-п)-п = р;,
u • та = ита,
(<т • п) • та = р*т(Х
: Т = Т*,
: (q-n) = g£,
(20.3)
где а = 1,2. Начальные условия имеют следующий вид
xGV, t = 0: x = x, u = u0, T = To, ep, 0 = 0 (20.4)
Таким образом, требуется решить начально-краевую задачу для
системы уравнений (20.1) - (20.2) с граничными (20.3) и
начальными (20.4) условиями.
§ 20. О квазихрупком разрушении и локализации деформаций 191
Численный метод. Алгоритм решения основан на модификации
неявной конечно-элементной схемы, построенной в работах [7, 8], и
реализован в рамках пакета прикладных программ <АСТРА».
Основные черты этого алгоритма заключаются в следующем. Исходные
уравнения задачи, включая определяющие и кинематические
дифференциальные соотношения, применяются в интегральной
вариационной форме Бубнова-Галеркина. По пространственным
переменным вводится простейшая кусочно-линейная конечно-элементная
аппроксимация решения на лагранжевой подвижной сетке,
содержащей треугольные и четырехугольные ячейки. Кусочно-линейная
аппроксимация применяется для всех искомых функций, включая
перемещения, скорости, температуру, тепловые потоки, деформации,
пластические деформации, напряжения, параметры упрочнения и
поврежденность, дискретные значения которых представлены
узловыми значениями.
Основными искомыми функциями являются те, которые
дифференцируются по времени в исходной системе уравнений:
перемещения, скорости, температура, пластические деформации,
пластическая работа (параметр упрочнения) и поврежденность. Остальные
искомые функции всегда можно определить для данного момента
времени по основным с помощью дифференцирования по
пространству и недифференциальных по времени соотношений.
Точки численного интегрирования расположены в узлах сетки,
таким образом, матрица масс диагональна. На шаге по времени
нелинейные члены уравнений линеаризованы по методу Ньютона
относительно малых приращений искомых функций на временном шаге.
Для решения вспомогательных линеаризованных алгебраических
задач применен итерационный метод сопряженных градиентов,
реализуемый без матричных операций и работающий на каждой итерации
как явная схема [7]. При уменьшении величины шага по времени
число итераций метода сопряженных градиентов для решения
вспомогательных задач уменьшается, и для временных шагов в пределах
курантовского ограничения неявная схема работает асимптотически
так же быстро, как обычные явные схемы. Шаг по времени
выбирается из условия точности с тем, чтобы ограничить максимальное
приращение деформации величиной порядка одной десятой
деформации, отвечающей пределу текучести, или для упругих материалов,
величиной много меньшей единицы.
Для преобусловливания алгебраических задач (умножения систе-
192 Гл. 3. Решение задач при больших деформациях
мы уравнений на приближенную обратную матрицу), необходимого
для подавления случайных ошибок при численном счете,
использовалась диагональная матрица преобусловливания, составленная из
диагональных элементов матрицы жесткости, что соответствует
масштабированию неизвестных. Этого вполне достаточно для
обеспечения устойчивости итерационного процесса метода сопряженных
градиентов даже при учете ухудшающих обусловленность задачи
штрафных членов, включающих контактные условия или условия
несжимаемости.
Вследствие погрешностей дискретизации численные решения
нелинейных задач могут содержать нефизические осцилляции,
характерным признаком которых является их длина волны,
совпадающая с шагами сетки (размерами ячеек), и частота с полупериодом,
равным шагу по времени. Для подавления таких возмущений
известно большое количество разнообразных рецептов, отражающих
различные способы введения явных или аппроксимационных вязкостей,
монотонизирующих решение. Для задач о разрушении такие
способы сглаживания должны вводиться очень осторожно, поскольку по
физике явления разрушения оно очень чувствительно к малым
возмущениям, и, следовательно, слишком грубая монотонизация или,
наоборот, ее отсутствие могут сильно искажать решение:
локализация деформаций не состоится, если нефизическая вязкость схемы
велика или, наоборот, расположение зон разрушения окажется сильно
зависимым от шагов сетки по времени и пространству, если
нефизическая вязкость мала и не обеспечивает устойчивости и сходимости
приближенного решения.
Заметим еще, что покоординатное расщепление процедуры
монотонизации позволяет сделать ее более точной. Применение
упрощенных процедур, основанных на некоторых более грубых индикаторах
немонотонности (например, по выходу узлового значения функции
за границы диапазона ее изменения в соседних узлах) и на
осреднении по всей окрестности, приводит к пропусканию немонотонностей
и к сглаживанию физических минимумов и максимумов.
Комментируя выбор единого способа аппроксимации для всех
искомых функций, отметим следующее. Традиционно в лагранжевых
схемах деформации и напряжения относятся к гауссовым точкам
численного интегрирования, расположенным внутри ячеек,
например, в центрах треугольных симплекс-элементов. Такой способ
аппроксимации затрудняет обобщение схем на случай нелагранжевых
20. О квазихрупком разрушении и локализации деформаций 193
сеток, в которых надо учитывать конвекцию, то есть движение
сплошной среды относительно системы координат и
соответствующей сетки. Поэтому, хотя в данной работе сетки являются лагран-
жевыми, предпочтение отдано единообразной аппроксимации всех
искомых функций. Необходимые изменения в эволюционных
уравнениях, которые при этом надо сделать для получения устойчивых
алгоритмов, подсказываются анализом первых дифференциальных
приближений: просто надо добавить малую искусственную вязкость
с коэффициентом 0.5с2At в случае явных схем или применить
неявную схему, что и сделано в нашем случае.
Разрушение плоского стандартного образца при
растяжении. Расчетная область показана на рис. 20.1 и представляет
собой 1/4 часть стандартного образца, на нижней и левой границах
ставятся условия симметрии. Начальная безразмерная длина
расчетной области равна 3.0, высота — 2.0. Правая граница движется
вправо с постоянной скоростью Vb, верхние горизонтальные и
вертикальные границы свободны. Для обезразмеривания использованы
следующие характерные значения переменных, помеченные
индексом s:
х
xs = /i, us = /г, vs = O.OOlco, ts = —,
vs
as = ps = Ks = ps = kpo, ps = kp0v~2, Ts = v2CyX, (3S = Ts_1,
U3 = cp3= v2, T]8 = vlT'1, rs = v^tj1, qs = psvlt^Xs,
£s = (ep)s = 1, es = (ep)s = t'1, 03 = 1, (ke)s = xsvs.
Уравнения задачи, начальные и граничные условия в
безразмерных переменных сохраняют свой вид. Безразмерные входные данные
приведены ниже:
Ко = 975, /i0 = 369, fcpo = l, с0 = Жо + 4^°? ко = 103,
бро
Фр = а' :а' - к2р, Фв = етах - 10~2, U « cvT, cv = l,
kq = l, дк = д» = дР = е-1о3в, /3 = 0.0001, Уо = Ю-4, со = Ю3,
где £тах — максимальная главная деформация, со — безразмерная
скорость звука.
194
Гл. 3. Решение задач при больших деформациях
В начальный момент времени образец находится в недеформиро-
ванном состоянии с нулевыми значениями скоростей, перемещений,
пластических деформаций и поврежденности при безразмерной
температуре То = 100 . Безразмерный массовый источник/сток тепла
г = 1 действовал в прямоугольной зоне (1.9, 0, 2.1, 1). Тепловые
потоки на границах занулялись. Использовались лагранжевы подвижные
конечноэлементные сетки, состоящие из первоначально одинаковых
(квадратных или лево-, правоориентированных треугольных) ячеек
с шагом 1/15, 1/30 и 1/60 в разных вариантах.
шш
Ь)
ъ
е)
1: 0.020
2: 0.041
3: 0.061
4: 0.081
5: 0.102
6: 0.122
7: 0.143
0.021
0.042
0.064
0.086
0.107
0.128
0.150
с)
f)
I1 )Ш
0.016
0.031
0.047
0.063
0.079
0.094
0.110
1: 0.019
2: 0.030
3: 0.058
4: 0.078
5: 0.097
6: 0.117
7: 0.196
Рис. 20.1. Моды процесса разрушения для случаев упругого
материала (a, d), упругопластического материала (Ь,е), упругопластического
материала при совместном действии растяжения и нагрева узкой
вертикальной зоны под концентратором (с, f)
Развитие узких зон локализации деформаций можно видеть на
рис. 20.1 для трех случаев процесса: разрушение упругого
материала (а), упругопластического материала (Ь), упругопластического
материала при совместном действии растяжения и нагрева узкой
вертикальной зоны под концентратором (с). Видно, что пластичность
навязывает свое предпочтительное направление распространения
зоны локализации деформаций.
При достаточно интенсивном локальном нагреве разрушение
упругопластического материала происходит как в упругом материале, а
j 20. О квазихрупком разрушении и локализации деформаций
195
в режиме умеренного нагрева развиваются две <трещины>: сначала
косая, которая затем останавливается, а завершает разрушение
вертикальная <трещина>, развивающаяся в зоне интенсивного нагрева.
Интенсивный нагрев ускоряет процесс разрушения, в то время как
локальное охлаждение зоны предполагаемого разрушения замедляет
ее развитие.
На рис. 20.2 показаны графики горизонтального смещения (а),
среднего напряжения (Ь) и максимальной главной деформации (с)
вдоль горизонтальной линии, пересекающей узкие зоны разрушения.
Поведение этих характеристик типично для внутренних контактных
границ и имитирует магистральную трещину в рамках
континуального подхода.
0.20x105
0.15x105
0.10x105
0.50x104
а)
' I ! ! II
10 20 30
0.30x105
0.25x105
0.20x105
0.15x105
0.10x105
0.50x104
20 30 40 50
0.1x10
0.1x10"3
0.1x10"2
0.1х10"1
0
0.25х105
0.20х105
0.15x105
0.10x105
0.50x104
0
1
с)
Г Л
г /\
г /
\ 1
у
г
.
1
ik- i
2 3
i V^
d) e) f)
Рис. 20.2. Графики горизонтального смещения (а), среднего
напряжения (Ь) и максимальной деформации (с) вдоль горизонтальной линии
(0,0.6,3,0.6) для случая разрушения упругого материала. В остальных
случаях качественное поведение этих функций такое же. Далее (d,e, f) для
всех трех вариантов показано изменение безразмерного шага по времени,
отнесенного к величине шага Куранта для явных схем и выбираемого из
условий точности, от величин 104 для квазистатики в начале процесса до
величин порядка 1 при наличии развитых зон разрушения
Поврежденность и деформация в зоне разрушения имеют очень
большой всплеск типа дельта-функции, напряжения падают до нуля,
а смещения претерпевают резкий скачок.
196 Гл. 3. Решение задач при больших деформациях
С ростом зон разрушения приложенные нагрузки вызывают все
большие деформации, и поэтому шаг по времени уменьшается из-
за ограничения приращения деформации в связи с требованиями
к точности расчета. Процесс развития зон разрушения постепенно
становится динамическим.
Моды разрушения сохраняются при измельчении шага сетки и
смене формы ячеек. Но надо отметить, что при отключении или
уменьшении регуляризации, например, за счет отключения
инерционных членов или за счет проведения расчета с увеличенными
шагами по времени, появляется аномальная зависимость решения от
малых возмущений, в том числе и от сетки.
Задача об оползне склона под действием веса сооружения.
Пусть на крутом склоне строится некоторое сооружение. По
мере возрастания нагрузки деформации максимального растяжения
концентрируются у дальней от края склона границы
строящегося сооружения, где и возникают зоны разрушения и локализации
деформаций. По мере их роста такие зоны занимают некоторую
окрестность наклонной поверхности, эволюция которой показана на
рис. 20.3. С выходом зон разрушения на свободную поверхность
склона процесс деформации ускоряется и становится динамическим.
Часть грунта между дневной поверхностью и зоной разрушения
приходит в движение как жесткое целое и сползает вниз под действием
сил тяжести. Полученная картина разрушения хорошо
подтверждается имеющимися экспериментальными данными [81].
Рассматривались и многие другие задачи о разрушении частей
конструкций при квазистатических и динамических нагружениях.
Общие выводы таковы: критерии максимальной деформации
сдвига работают удовлетворительно в подавляющем числе различных
случаев напряжено-деформированного состояния. Узкие зоны
разрушения образуются в условиях квазихрупкого разрушения, когда
предельная деформация достигается ранее, чем зоны
пластичности охватывают значительную часть конструкции. Во многих
случаях первоначально квазистатический режим деформации
сменяется быстрым динамическим процессом деформации и ростом узких
зон разрушения. Алгоритмы расчета, реализующие модели
континуального разрушения, должны иметь контроль точности по
максимальному приращению деформации на шаге по времени и
учитывать инерционные члены даже для первоначально квазистатиче-
j 20. О квазихрупком разрушении и локализации деформаций
197
0 0.5 1 1.5 2.0
(а)
■ I
J-
J-
-L
0 0.5 1 1.5 2.0
(Ъ)
Рис. 20.3. Оползень склона от действия веса сооружения. Показано
распределение изолиний горизонтального смещения (а) и максимальной
деформации (Ь) для конечной стадий процесса
ских процессов деформации, иначе сходимость решений теряется
при появлении зон разрушения и появляется аномальная
зависимость решения от особенностей дискретизации.
Размывание зон разрушения и искажение решений может
происходить также в схемах с повышенной вязкостью. Схемная вязкость
должна быть минимизирована в окрестности зон разрушения.
Резкая потеря способности сопротивления деформации также
является необходимым условием возникновения узких зон локализации
деформаций.
Для обеспечения сходимости результатов при дроблении
временных и пространственных шагов критерий разрушения должен
содержать масштабный множитель, вид которого подсказывается теорией
трещин и механикой хрупкого разрушения. Известно, что в
кончике трещины теория упругости предсказывает корневую особенность
решения и неограниченный рост напряжений и деформаций.
Поэтому критерий разрушения должен формулироваться в терминах ко-
эффициетов концентрации напряжений и деформаций. В численной
реализации настоящей работы удовлетворительные результаты для
сходимости предельных значений средней деформации разрушения
растягиваемых образцов были получены с модификациями критерия
разрушения следующего вида:
£i\/mm(hx, hy)/ тах(ж
х
Уп
mm 7 i/max
Ут'т) -1 &п
где множитель с корнем как раз и учитывает асимптотику,
подсказываемую теорией упругости.
198 Гл. 3. Решение задач при больших деформациях
Представленное исследование локализации деформаций позволило
реализовать континуальный подход к численному описанию
распространения узких зон разрушения в квазихрупких материалах,
имитирующих магистральные трещины. Это исследование показывает
результаты, обобщающие детальное моделирование явлений,
сопутствующих фрагментации разрушающихся тел.
Выводы. Численные эксперименты показали, что критерии
разрушения по предельным деформациям для упругопластических
материалов работают лучше, чем критерии по предельным
напряжениям. Для получения зон локализации в виде узких трещиноподобных
лент важную роль играют также следующие свойства теоретической
модели.
• Резкий спад сопротивления среды с ростом поврежденности.
• Контролируемая по приращениям деформаций точность расчета.
• Учет сил инерции (естественная регуляризация задачи).
• Минимальное сглаживание (особенно в зонах разрушения).
• Сопротивление разрушенного материала сжатию (для
обеспечения невырожденности закона движения).
Показано, что благодаря указанным выше свойствам модель
повреждающейся упругопластической [9] среды хорошо описывает
резкую локализацию деформаций вдоль тонких полос больших
градиентов смещений и всплесков деформаций и поддерживает сходимость
решения в процессе развития узких зон разрушения.
Вопросы приведения модели повреждающейся
упругопластической среды в соответствии с данными физических экспериментов
остаются открытыми и актуальными.
Используемая методика без принципиальных изменений может
быть обобщена на пространственные трехмерные задачи.
§21. Упражнения
1. Показать, что если закон сохранения записан в не
дивергентном виде, то при применении формул естественной
аппроксимации (16.3) разностная схема будет неконсервативной.
2. Записать систему уравнений движения в двумерном случае для
гиперупругого материала в консервативной форме. Аппрок-
21. Упражнения
199
симировать ее с помощью формул естественной
аппроксимации (16.3).
3. Привести обобщение формул естественной аппроксимации (16.3)
для трехмерного случая.
4. Провести сравнение формулы естественной аппроксимации
производных от двух переменных на регулярной
четырехугольной сетке с формулами аппроксимации для билинейного
конечного элемента (формулы для билинейного конечного элемента
см. в [43], с. 47.
5. Исследовать систему разностных волновых уравнений для
схемы Лакса на консервативность.
6. Записать систему уравнений распространения одномерных
волн в эйлеровых переменных в дивергентном виде для
нелинейно-упругой среды при больших перемещениях.
Получить для нее консервативную разностную схему.
7. Доказать, что в подвижной системе координат щ, закон
движения которой относительно системы отсчета Хк = Xk(T]i,t),
полная производная функции f(xi,X2,t) запишется в виде
dt dt
~ s df
+ (Vt - Wi) —,
где Vi — скорость частиц, Wi — скорость узлов сетки щ в базисе,
связанном с подвижной сеткой тц.
8. Получить выражение для дифференциальных законов
сохранения в системе подвижных координат т^, в компонентах
векторов, отнесенных к базису подвижной системы координат ё^.
9. Записать уравнение движения в смешанной лагранжево-
эйлеровой системе координат, у которой одна координата щ
лагранжева, а щ — эйлерова.
10. Получить схему расщепления определяющих уравнений для
изотропной несжимаемой гиперупруговязкой среды с упругим
потенциалом, зависящим от второго инварианта тензора
деформаций Ф(/|) и вязким потенциалом, зависящим от второго
инварианта скорости вязкой деформации Ф^ )•
200 Гл. 3. Решение задач при больших деформациях
11. Решить задачу о распространении пластических волн в
полубесконечном стержне из упруговязкопластического материала
с определяющим уравнением
де Ida 1 fa ^ (Е\2\ /ч f za z > 0
т = Ёт+т*[ъ-Е{та) )> где ^) = {о *<о
на адаптирующейся сетке при нулевых начальных условиях и
при граничном условии а(х = 0, t) = aoH(t). Здесь ао = 1.5<rs,
г = Ю-5 с, as = 103 МПа, Е = 2 • 106 МПа, Я(£) - функция Хе-
висайда.
12. Построить неравномерную сетку на отрезке — 1 ^ х ^ 1,
минимизирующую градиенты функции у = С • е~ах . Здесь С = 102,
а = 103. Число разбиений отрезка п = 102.
13. Решить осесимметричную задачу неустановившейся
теплопроводности с точечным источником на оси цилиндра на
неравномерной сетке, минимизирующей градиент
температуры. Интенсивность источника q = qo (T/T*)a. Граничное
условие при Т(г = 1) = Т*. Начальная температура во всем теле
T(t = 0) = Т0. Положить Т0 = Т* = 20 °С, а = 5.
14. Идеальнопластический материал сжимается системой
идеальных жесткопластических штампов без трения. Верхний штамп
синусоидального профиля движется вертикально с постоянной
скоростью v = Vo. Нижний штамп неподвижен. Боковые
штампы могут перемешаться в горизонтальном направлении.
Ввести эйлерово-лагранжеву систему координат. Записать систему
уравнений плоской задачи теории пластичности в этой системе
координат (см. рис. 18.2).
Список литературы
1. Аптуков В.Н. Модель термоупругопластической
поврежденной среды. Приложение к откольному разрушению // ФГВ. —
1986. - Т. 22. N. 6. - С. 120-130.
2. Баженов В.Г., Чекмарев Д.Т. Вариационно-разностные схемы в
нестационарных волновых задачах динамики пластин и
оболочек. - Н. Новгород: Изд-во ННГУ, 1992. - 159 с.
3. Белоцерковский О.М., Давыдов Ю.М. Метод крупных частиц. —
М.: Наука. 1982. — 392 с.
4. Боли Б.А.У Уэйнер Дж.Х. Теория температурных
напряжений. — М.: Мир, 1964. — 517 с.
5. Борис Дж.П., Бук Д. Л. Решение уравнений непрерывности
методом коррекции потоков // Вычислительные методы в физике.
Управляемый термоядерный синтез. — М.: Мир, 1980. — С. 92-
141.
6. Брызгалов Ю.Б., Кукуджанов В.Н. Численное моделирование
разрушения и локализации деформаций при импульсном разру-
шениии стрежней // Математическое моделирование. — 2001. —
Т. 13, № 6. - С. 99-103.
7. Бураго Н.Г.У Кукуджанов В.Н. Решение упругопластических
задач методом конечных элементов. Пакет прикладных программ
«АСТРА»: Препринт /ИПМ. — М., 1988. — 68 с.
201
202
Список литературы
8. Бураго Н.ГУ Кукуджанов В.Н. Решение упругопластических
задач методом конечных элементов // Вычислительная
механика деформируемого твердого тела. — М.: Наука, 1991. —
Вып. 2. - С. 78-122.
9. Бураго Н.Г., Глушко А.И., Ковшов А.Н. Термодинамический
метод получения определяющих уравнений для моделей сплошных
сред // Изв. РАН. МТТ. - 2000. - N. 6. - С. 4-15.
10. Бураго Н.ГУ Кукуджанов В.Н. О континуальном разрушении и
локализации деформаций // Прикладные проблемы прочности
и пластичности. — Нижний Новгород: Изд-во Нижегородского
ун-та, 2001. — Вып. 63. — С. 41-48.
11. Бураго Н.Г., Кондауров В.И., Кукуджанов В.Н. Численное
моделирование континуального разрушения упругопластических
тел // Науч. сессия МИФИ-2002. Науч.-техн. конф. <Науч.-
инновац. сотрудничество». Сб. науч. трудов. — М.: МИФИ, 2002.
Ч. 1. С. 95-96.
12. Бураго Н.Г., Кукуджанов В.Н. Численное решение задач
континуального разрушения: Препринт/ИПМ РАН. — М., 2004. —
№ 746. - 40 с.
13. Вакуленко А.А., Качанов Л.М. Континуальная теория среды с
трещинами // Изв. АН СССР. МТТ. - 1971. - Ж 4. - С. 159-
166.
14. Гарсон А.Л. Континуальная теория вязкого разрушения,
обусловленного образованием и ростом пор // Тр. Амер. о-ва инж.-
мех. Теорет. осн. инж. расчетов. — 1977. — Ж 1. — С. 182-201.
15. Годунов С.К. Разностный метод численного расчета разрывных
решений уравнений гидродинамики // Матем. сб. — 1959. —
Т. 47. Вып. 3. - С. 271-306.
16. Гулидов А.И.У Фомин В.М.У Шабалин И.И. Алгоритм
перестройки разностной сетки при численном решении задач соударения с
образованием трещин // Численные методы решения задач
теории упругости и пластичности, Материалы 7-й Всес. конф. —
Новосибирск: ИТПМ СО АН СССР, 1982. С. 182-192.
Список литературы
203
17. Гулидов А.И.У Шабалин И. И. Метод свободных элементов: Пре-
принт/ИТПМ СО РАН. - Новосибирск, 1994. - N. 9-94. - 32 с.
18. Дюво Г., Лионе Н. Неравенства в механике и физике. — М.:
Наука., 1980. — 384 с.
19. Ежов Г.П., Кондауров В. И. О волнах разрушения в начально
напряженном слое пористого материала // ПММ. — 2006. — Т. 70.
Вып. 3. - С. 515-530.
20. Заппаров К.И.У Кукуджанов В.И. Математическое
моделирование задач импульсного деформирования, взаимодействия и
разрушения упругопластических тел: Препринт/ИПМ АН СССР. —
М., 1986 - № 280. - 68 с.
21. Зенкевич О. Метод конечных элементов в технике. — М.: Мир. —
1975. - 541 с.
22. Зегер А. Механизм скольжения и упрочнения в кубических
гранецентрированных и гексагональных плотноупакованных
металлах. Дислокации и механические свойства кристаллов. —
М.: Изд-во иностр. лит., I960. — С. 179-268.
23. Иванов Г.В.У Волчков Ю.М.У Вогульский И.О., Анисимов С.А.У
Кургузое В.Д. Численное решение динамических задач упруго-
пластического деформирования твердых тел. — Неб.: Сибирское
унив. изд-во., 2002. — 350 с.
24. Ильюшин А.А. Об одной теории длительной прочности. — Изв.
АН СССР МТТ. 1967. - Ж 3. - С. 21-35.
25. Ильюшин Ф.Ф.У Победря В.Е. Основы математической теории
термо-вязко-упругости. — М.: Наука, 1970. — 280 с.
26. Каннель Г.И., Разоренов СВ., Уткин А.В., Фортов В.Е.
Ударно-волновые явления в конденсированных средах. — М.:
Янус-К, 1996. - 408 с.
27. Качанов Л.М. Основы теории пластичности. — М.: Изд-во Тех-
теор лит., 1956. — 324 с.
28. Качанов Л.М. О времени до разрушения в условиях
ползучести // Изв. АН СССР, ОТН. - 1958. - Ж 8. - С. 26-31.
204
Список литературы
29. Качанов Л.М. Основы механики разрушения. — М.:Наука,
1974. - 311 с.
30. Калмыков С.Г.У Кукуджанов В.Н. Метод потоков и
корректирующих маркеров (ПИКМ-метод) для моделирования
высокоскоростных соударений: Препринт/ИПМ РАН. — М., 1993 —
№ 529. - 39 с.
31. Кибардин В.Ю., Кукуджанов В.Н. Численное моделирование
локализации деформаций и разрушения упруговязкопластических
материалов // Известия РАН МТТ. - 2001. - № 1. - С. 113-123.
32. Ковеня В.М., Яненко Н.Н. Метод расщепления в задачах газовой
динамики. — Новосибирск. Изд-во Наука СО АН СССР., 1981. —
304 с.
33. Колган В.П. Применение оператора сглаживания в разностных
схемах высокого порядка точности // Журнал вычислительной
матемитики и математической физики. — 1978. — Т. 18, № 5. —
С. 1340-1345.
34. Кондауров В.И., Мухамедиев Ш.А., Никитин Л.В., Рыжак Е.И.
Механика разрушения горных пород. — М.: Наука, 1987. — 218 с.
35. Кондауров В.И., Фортов В.Е. Основы термомеханики
конденсированной среды. — М.: Изд-во МФТИ, 2002. — 336 с.
36. Кондауров В.И., Петров И.Б. Расчет процессов динамического
деформирования упругопластических тел с учетом
континуального разрушения // Доклады АН СССР. - 1985. - Т. 285. Ж 6. -
С. 1344-1347.
37. Кортков П.Ф. Полосы сдвига при разрушении склонов //
Доклады АН СССР. - 1982. - Т. 267. Ж 4. - С. 818-822.
38. Коттрел А.Х. Дислокации и пластическое течение в
кристаллах. — М.: Металургиздат., 1958. — 267 с.
39. Кукуджанов В.Н. Распространение упругопластических волн в
стержне с учетом влияния скорости деформации. — М.: ВЦ
АН СССР. 1967. - 48 с.
Список литературы
205
40. Кукуджанов В.Н. Одномерные задачи распространения волн
напряжений в стержнях // Сообщение по прикладной
математике ВЦ. - 1977. - Вып. 7. - 55 с.
41. Кукуджанов В.Н. Численное моделирование динамических
процессов деформирования и разрушения упругопластических
сред // Успехи механики. — 1985. — Т. 8, Вып. 4. — С. 21-65.
42. Кукуджанов В.Н. К численному моделированию процессов
деформирования и разрушения упругопластических тел при
больших деформациях. Математические методы в механике
деформируемого твердого тела. — М.: Наука, 1986. — С. 75-85.
43. Кукуджанов В.Н. Численные методы решения нелинейных
задач механики деформируемого твердого тела: Учебн. пособие. —
М.: МФТИ, 1990. - 95 с.
44. Кукуджанов В.Н. Разностные методы решения задач механики
деформируемых тел: Учебн. пособие. — М.: МФТИ, 1992. — 123 с.
45. Кукуджанов В.Н. Микромеханическая модель разрушения
неупругого материала и ее применение к исследованию
локализации деформаций // Изв. РАН. МТТ. — 1999. — № 5. — С. 72-87.
46. Кукуджанов В.Н. Метод расщепления упругопластических
уравнений // Механика твердого тела. — 2004. — Ж 1. — С. 98-
107.
47. Кукуджанов В.Н., Левитин А.Л., Синюк B.C. Численное
моделирование повреждающихся упругопластических материалов:
Препринт/ИПМех РАН. - М., 2006. - № 807. - 54 с.
48. Кукуджанов В.Н. Введение в численные методы в механике
сплошных сред: Учебн. пособие. — М.: МАТИ-РГТУ 2006. —
157 с.
49. Кукуджанов В.Н. Связанные модели упругопластичности и
поврежденное™ и их интегрирование // Изв. РАН. МТТ. — 2006. —
№ 6. - С. 103-135.
50. Куликовский А.Г.У Погорелое Н.В.У Семенов А.Ю.
Математические методы численного решения гиперболических уравнений. —
М.: Изд-во Физматлит, 2001. — 607 с.
206
Список литературы
51. Курант Р. Уравнения с частными производными. — М.: Мир.
1964. - 830 с.
52. Курант Р., Фридрихе К., Леей Г. О разностных уравнениях
математической физики // Успехи математических наук. — 1940. —
Т. 8. - С. 125-160.
53. Ландау Л.Д., Мейман Н.Н., Халатников ИМ. Численные
методы интегрирования уравнений в частных производных
методом сеток: Труды Зего Всесоюзного математического съезда. —
Т. 3. - С. 92-100.
54. Магомедов К.М.У Холодов А. С Сеточно-характеристические
методы. — М.: Наука., 1988. — 287 с.
55. Майнчен Дж., Сак С Метод расчета < Тензор»,
Вычислительные методы в гидродинамике/ Под ред. Б. Олдера, С. Фернбаха,
М. Ротенберга. - М.: Мир, 1967. - С. 185-211.
56. Марчук Г.И. Методы расщепления. — М.: Наука., 1988. — 263 с.
57. Поттер Д. Вычислительные методы в физике. — М.: Мир,
1975. - 392 с.
58. Прагер В. Введение в механику сплошных сред. — М.: Изд-во
Инлит., 1963. — 311 с.
59. Работное Ю.Н. Механизм длительного разрушения: Сб. <Во-
просы прочности материалов и конструкций». — М.: Изд-во АН
СССР, 1959. - С. 5-7.
60. Рихтмайер Р., Мортон К. Разностные методы решения краевых
задач. — М.: Мир., 1972. — 418 с.
61. Рождественский Б.Л.У Яненко Н.Н. Системы квазилинейных
уравнений. — 2-е изд. — М.: Наука, 1978. — 688 с.
62. Садовский В.М. Разрывные решения в задачах динамики упру-
гопластических сред. — М.: Наука, 1997. — 208 с.
63. Селективное разрушение минералов / Под. ред. В.И. Ревнивце-
ва. — М.: Недра, 1988. — 286 с.
Список литературы
207
64. Соколовский В.В. Теория пластичности. — М.: Высшая школа,
1969. - 608 с.
65. Соколовский В.В. Статика сыпучих сред. — 4-е изд. — М.: Наука,
1990. - 272 с.
66. Судзуки Г., Есинага X, Такеуки С Динамика дислокаций и
пластичность. — М.: Мир, 1989. — 294 с.
67. Тимошенко СП. Колебания в инженерном деле. — М.: Наука,
1967. - 444 с.
68. Уилкинс М.Л. Расчет упругопластических течений. //
Вычислительные методы в гидродинамике. — М.: Мир. 1967. — С. 212-263.
69. Фомин В.М.У Гулидов А.И.У Сапожников Г.А. и др.
Высокоскоростное взаимодействие тел. — Новосибирск: Изд-во СО РАН,
1999. - 600 с.
70. Хилл Р. Математическая теория пластичности. — М.: Гостехиз-
дат, 1956. - 407 с.
71. Хоникомб Р. Пластическая деформация металлов. — М.: Мир,
1972. - 408 с.
72. Шокин Ю.И., Яненко Н.Н. Метод дифференциального
приближения. Приложения к газовой динамике. — Нск.: Наука СибОт.,
1985. - 357 с.
73. Aravas N. On the Numerical Integration of a Class of Pressure-
Dependent Plasticity Models // International Journal for Numerical
Methods in Engineering. — 1987. — V. 24. — P. 1395-1416.
74. Baker M. Does chip formation minimize the energy? // Comput.
Mat. Sci. - 2005. - V. 33. - P. 407-418.
75. Bazant Z.P. Reminiscences on four decades of struggle and progress
in softening damage and size effect // Concr. J. (Japan Concr.
Inst.). - 2002. - V. 40. - P. 16-28.
76. Chu C, Needleman A. Void nucleation Effects in Biaxially Stretched
Sheets. J. Eng. Mater. Tech. - 1980. - V. 102. - P. 249-256.
208
Список литературы
77. Curran D.R.y Seaman L.y Shockey D.A. Dynamic failure in solids //
Physics Today. January. — 1977. — P. 46-55.
78. Curran D.R.y Seaman L.y Shockey D.A. Dynamic failure of solids //
Physics Reports. - 1987. - Ж 147. - P. 253-388.
79. Courant R., Isaacson E., Rees M. On the solutions of nonlinear
hyperbolic differential equations by finite differences Comm. Pure
Apll. Math. - 1952. - V. 5. - 243 p.
80. Dirnovski W., Perzyna P. Localization and localized fracture
phenomena in inelastic solids under cyclic dynamic loadings //
Foundation of Civil and Enviromental Eng. — 2002. — Ж 1. — P. 41-
86.
81. Drucker D.C., Prager W. Soil mechanics and plastic analysis on
design // Quart. Appl. Math. - 1962. - V. 10. - P. 157-165.
82. Gillman J.J. Dislocation dynamicss and the responce of material to
impact // Appl. Mech. Rev. - 1968. - V. 21. - Ж 8. - P. 767-783.
83. Hill R. The essential structure of constitutive laws for metal
composites and polycrystals // J. Mech. and Phys. of Solids. —
1967. - V. 15., Ж 2. - P. 79-97.
84. Johnson G.R.y Cook W.H. A constitutive model and data for metals
subjected to large strains, high strain rates and high temperatures //
Proc. 7th Intern. Symp. Ballistics. — 1983. — P. 541-547.
85. Kanel G.I., Razorenov S.V., Fortov V.E. Shock-wave compression
and tension of solids at elevated temperatures: superheated crystal
states, pre-melting, and anomalous growth of the yield strength //
J. Phys. Condens. Matter. - 2004. - V. 16., Ж 14. - P. 1007-1016.
86. Kukudzhanov V.N. Investigation of shock wave structure in elasto-
visco-palstic bars using the asymptotic method // Archives of
Mechanics. - 1981. - V. 33., Ж 5. - P. 739-751.
87. Continuum Damage Mechanics. Theory and Application. CISM.
Lectures / Eds. 0. Krajcinovic, J. Lemaitre. Vien: Springer. — 1987.
88. Liu K., Melkote S.N. Material strengthening mechanisms and their
contribution to size effect in micro-cutting // Trans. ASME J.
Manufact. Sci. and Eng-ng. - 2006. - V. 128., Ж 3. - P. 730-7-38.
Список литературы
209
89. Maenchen G., Sack S. The "Tensor" code // Methods Comput. Phys.
N.Y.: Acad. Press. - 1964. - V. 3. - P. 188-210.
90. Maugin G.A. The Thermodynamics of Plasticity and Fracture
Cambridge Texts in Applied Mathematics, Cambridge University
Press. — 1992. — 350 p.
91. Merchant M.E. Mechanics of the metal cutting process. I.
Orthogonal cutting // J. Appl. Phys. — 1945. — V. 16. — P. 267-275;
II. Plasticity conductions in orthogonal cutting // J. Appl. Phys. —
1945. - V. 16. - P. 318-324.
92. Miguelez H., Zaera R., Rusinek A., Moufki A., Molinari A.
Numerical modeling of orthogonal cutting: Influence of cutting
conductions and separation criterion // J. Phys. IV France. —
2006. - V. 134. - P. 417-422.
93. Nagteggal J.С On the implementation of inelastic constitutive
equations with special reference to large deformation problems //
Сотр. Method. Appl, Mech. Eng. - 1082. - V. 33. - P. 469-484.
94. Ortiz M., Popov E.P. Accuracy and stability of integration
algorithms for elastoplastic constitutive relations // Int. J. Numer.
Methodds Eng. - 1985. - V. 21. - P. 1561-1576.
95. Owen D., Hinton E. Finite elements in plasticity. Swansea. U.K. —
1984.
96. Puttick K.E. Phil. Mag. - 1959. - V. 4. - 964 p.
97. Rice J.R., Tracey DM. Computational fracture mechanics // in
S.J.Fenvaes et al. (ed) Proc Symp Numerical Methods in Structural
Mechanics, Urbana, Illinois. — 1971, Academic Press, New York. —
1973.
98. Seaman L.y Curran D.R.y Shackey D.H. Computational models for
ductile and brittle fracture // J. Appl. Phys. — 1976. — V. 47.,
Ж 11. — P. 814-4826.
99. Sakino E. Transition in rate controlling mechanics of FFC metals
at very high strain rates and high temperatures // J. Phys. IV.
France. - 2000. - V. 10. - P. 57-64.
210
Список литературы
100. Simo К.у Taylor R.L. Consistent tangent operators for rate-
independend elastoplasticity // Сотр. Methods Appl. Mech. Eng. —
1985. - V. 48. - P. 101-118.
101. Shaw M.C. A quantized theory of strain hardening as spplied to
cutting of metals // J. Appl. Phys. — 1950. — V. 21., Ж 6. —
P. 599-606.
102. Shaw M.C. Metal Cutting Principles. New York: Oxford Sci.
Publ. - 1986. - 594 p.
103. Tvergaard V. Influence of Voids on Shear Band Instabilities under
Plane Strain Condition // Int. J. Fract. — 1981. — V. 17. — P. 389-
407.
104. Tvergaard V., Needleman A. Analysis of the cup-cone fracture in a
round tensile bar. Acta Metall. — V. 32. — P. 157-169.
105. Tvergaard V., Needleman A. Elastic-Viscoplastic Analysis of
Ductile Fracture. In Finite Inelastic Deformations — Theory of
Applications. Eds. D.Besdo, E.Stain. Springer-Verlag. — 1991. —
P. 3-14.
106. Zienkievicz 0., Nayak G.C. Elastoplastic stress analysis: a
generalization for strain softening // Intern. J. Numer. Meth.
Engng. - 1972. - V. 5. - P. 113-135.
Предметный указатель
аддитивный оператор, 70
адиабатический инвариант, 170
алгоритм
интерполирования, 171
расчета точек
граничных, 96
осевых, 98
аппроксимация
безусловная, 22
естественная, 157
условная, 22
усредненная, 22
формулы естественной
аппроксимации, 159
ассоциированный закон, 94
вариационная форма Бубнова-
Галеркина, 191
вязкость
аппроксимационная, 192
стабилизирующая, 27
дискретный переток массы, 175
дислокации
аннигиляция,113
поток движущихся, 112
дисперсия
аномальная, 55
нормальная, 55
фазовая ошибка, 56
зависимость решения от сетки,
185
изгиб
поперечный, 20
продольно-поперечный, 17
инвариант Римана, 25
колебания
поперечные, 13, 20
продольно-поперечные, 17
продольные, 9
корректировка по Уилкинсу, 92
критерий
Адамара, 184
разрушения, 107
критические поверхности, 119
маркер, 175
масштабный эффект, 119
матрица
акустическая, 78
диссипативная, 78
конвективная, 78
консервативная, 78
нормальная, 15, 16
перехода, 12
211
212
Предметный указатель
метод
адаптирующихся подвижных
сеток, 168
крупных частиц, 172, 174
маркеров и потоков, 175
обратный Эйлера, 125
ПИЧ, 174
потоков, 174
расщепления, 128
характеристик
обратный, 26
полуобратный, 26
прямой, 26
частиц в ячейках (PIC), 168
устойчивость, 174
модель
Майнчена-Сака, 141, 147
микромеханическая
многомасштабная поврежден-
ности, 112
пористая упругопластическая
(GTN), 109
разрушения, 141, 147, 183,
185
термоу пру говязкопл астическая,
147
монотонизация, 192
неравенство
вариационное
упругопластическое, 176
нефизические осцилляции, 192
определитель
Грамма, 11
первое дифференциальное
приближение, 53
Г-форма, 51
П-форма, 51
поврежденность, 101
полосы локализации, 139
полосы сдвига
адиабатические, 143
поры
зарождение, 111
начало образования, 119
рост, 111
постулат Дракера, 184
принцип
максимума скорости
диссипации энергии, 176
прогонка, 17, 29
пятиточечная, 82
трехточечная, 82
производная
Яумана, 166
псевдокраевой эффект, 63
разностные схемы
диссипативные, 179
условие диссипативности,
180
консервативные, 161
разрушение
вязкое, 140
дискретными частицами, 186
квазихрупкое, 139
разрыв
движущийся, 38
контактный, 37
неподвижный, 37
разупрочнение
деформационное, 123
термическое, 147
расщепление
покоординатное, 192
уравнений
определяющих, 87
расщепление уравнений
волнового, 74
гипоупругого материала, 166
по направлениям, 71, 72
по переменным
направлениям, 73
по физическим процессам
Предметный указатель
213
вязкой жидкости, 77
пластичность, 83
у пру говязкопл астичность,
94
регуляризаторы
вычислительные, 184
физические, 184
регуляризация
способ
математический, 124
физический, 124
регуляризация уравнений, 123
резание, 143
релаксация остаточных
напряжений, 114
решение
сглаживание, 64
свойства схемы
дисперсионные, 53
диссипативные, 53
связные задачи
термомеханика, 47
сглаживание
аппроксимационное, 63
искусственное, 64
сглаживание нефизических
возмущений, 62
сетка
адаптивная, 183
лагранжева, 168
подвижная, 183
эйлерова, 168
система
гиперболическая, 24
скорость звука
адиабатическая, 49
изотермическая, 49
спектральный радиус, 15
среда
гипоупругопластическая, 87
классическая, 84
комбинированная, 169
повреждающаяся, 101
у пру говязкопл астическая, 84,
94
у пру гопл астическая, 83, 84
схема
консервативная, 162
Лакса-Вендроффа, 58
разностная
двухслойная,12
дисперсия, 56
диссипация, 56
простая, 53
трехслойная, 12
расщепления, 68
неявная, 70
явная, 68
сеточно-характеристическая,
44
КИР, 26
неявная, 28
характеристическая
высокого порядка, 45
квазиявная, 29
экономичная, 73
явно-неявная, 43
схемы
разностные
при разрывных
решениях, 57
тензор
повреждаемости, 114
теория пластичности
Мизеса, 90
Прагера-Дракера, 93
уравнение
гиперболическое, 51
Навье-Стокса, 77
параболическое, 51
уравнения
в инвариантах, 28
парабологиперболические, 23
214
Предметный указатель
расщепление
дискретная форма, 77
дифференциальная
форма, 77
форма
дивергентная, 77
недивергентная, 78
условие
Куранта, 11, 27
Неймана, 11, 12, 19
неполной параболичности,
53
практической устойчивости,
19, 49
устойчивости
достаточное, 10
устойчивость, 40
А-устойчивость, 42
жесткие уравнения, 44
метода PIC, 174
по Рг-форме, 53
схемы расщепления, 70
факторизация оператора, 69
формула
Грина, 158
формы дифференциальных
приближений
гиперболическая, 50
параболическая, 50
фрагментация, 149
характеристика, 25
характеристическая линия, 25
ячейка
дробные, 168
фиктивная, 171
Учебное издание
КУКУДЖАНОВ Владимир Николаевич
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
ДЕФОРМИРОВАНИЯ, ПОВРЕЖДАЕМОСТИ
И РАЗРУШЕНИЯ НЕУПРУГИХ МАТЕРИАЛОВ
и конструкций
Редактор О. П. Котова
Корректор И.А. Волкова
Подписано в печать 03.06.2008. Формат 60 х 84 V|6. Бумага офсетная.
Печать офсетная. Усл. печ. л. 13,5. Уч.- изд. л. 12,8. Тираж 150 экз. Заказ № ф-086
Государственное образовательное учреждение
высшего профессионального образования
Московский физико-технический институт
(государственный университет)
Отдел автоматизированных издательских систем "физтех-полиграф"
141700, Московская обл., г. Долгопрудный, Институтский пер., 9
Кукуджанов Владимир Николаевич - доктор физико-
математических наук, профессор кафедры прикладной
механики Московского физико-технического института
(государственного университета), заслуженный деятель науки
РФ, лауреат премии Совмина СССР. Автор более двухсот
пятидесяти научных работ, семи монографий и учебных
пособий, работает в МФТИ с 1956 года после окончания
аспирантуры. Читал различные курсы по механике студентам
старших курсе МФТИ и М АТИ.
Область научных интересов: численные методы в механике
нелинейных сплошных сред, теория пластичности,
распространение волн напряжений неупругих материалах,
микро и мезо механика разрушения деформируемых тел. В.Н.
Кукудджанов: Член Национального комитета по
теоретической и прикладной механике, член нескольких
международных комитетов научных обществ журналов по
механике.