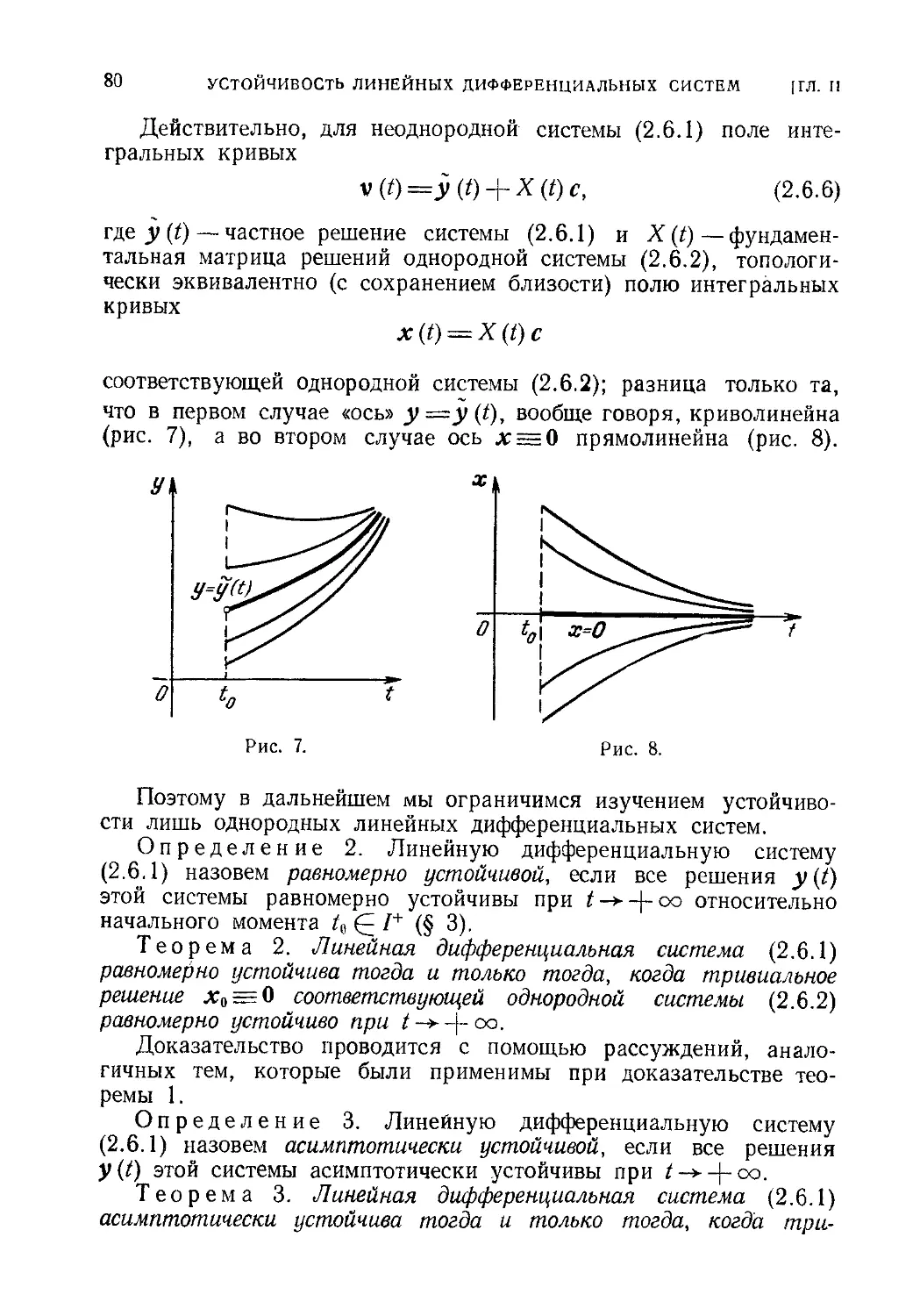
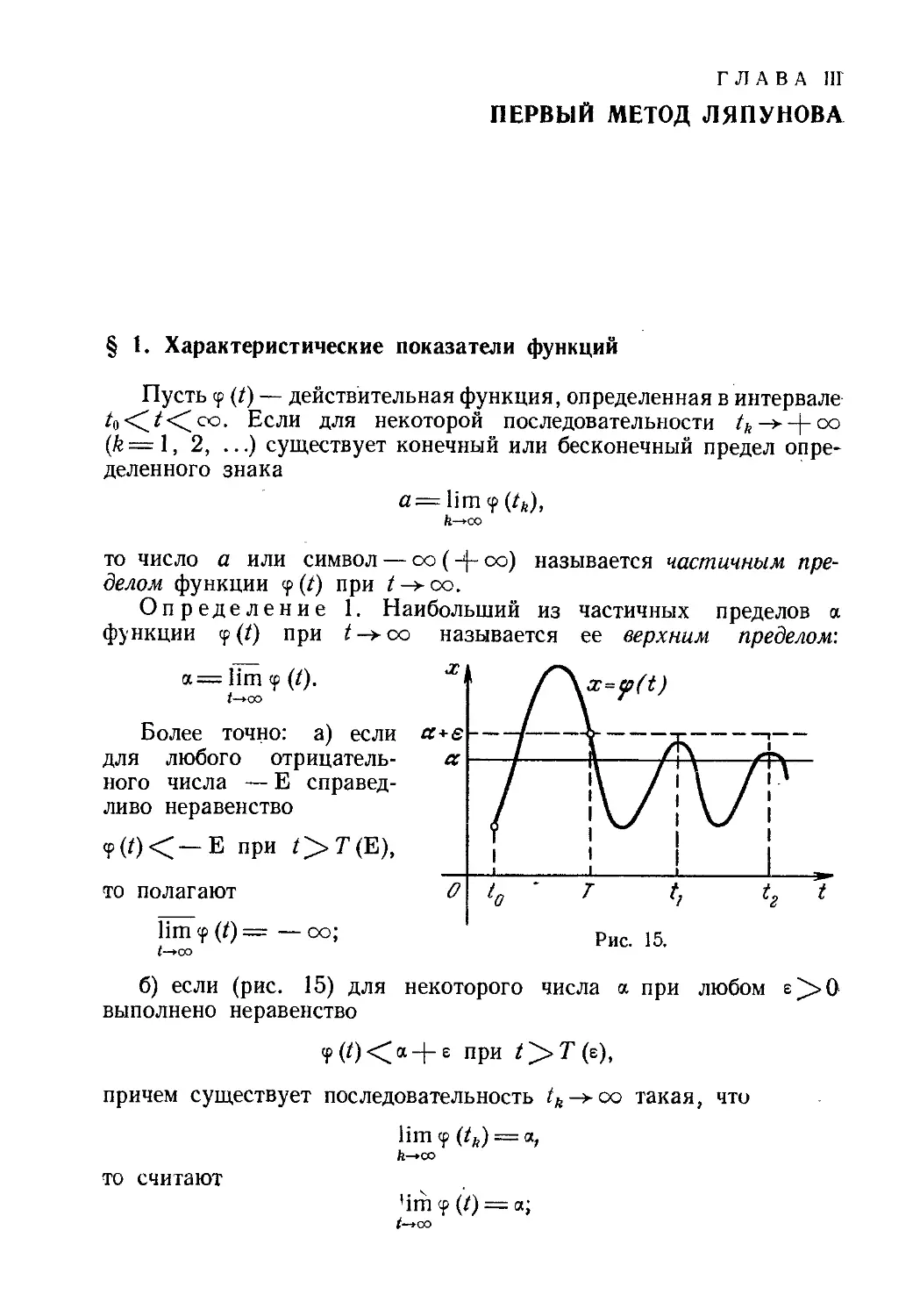
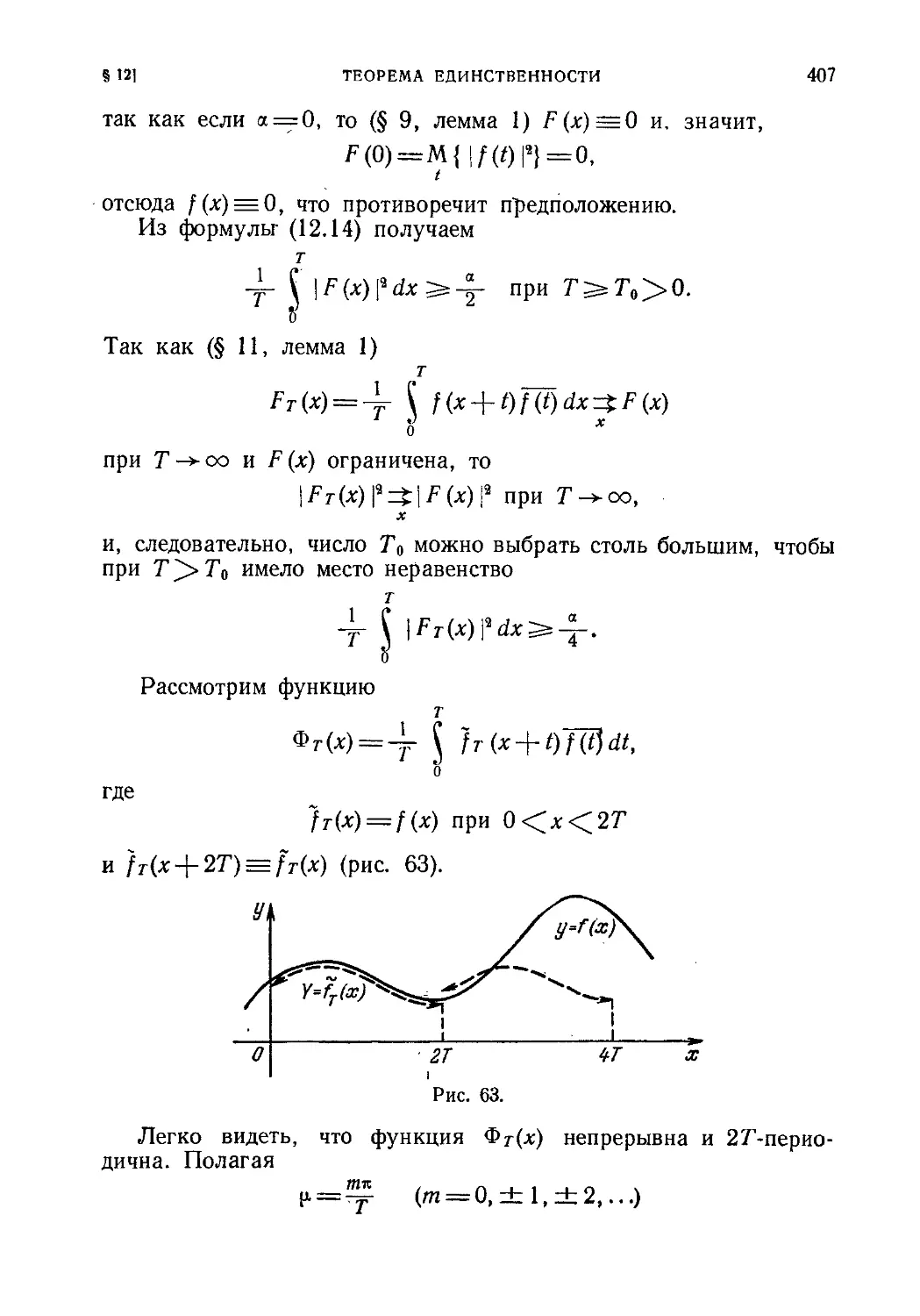
Текст
Б. П. ДЕМИДОВИЧ
ЛЕКЦИИ
по
МАТЕМАТИЧЕСКОЙ
ТЕОРИИ
УСТОЙЧИВОСТИ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1967
517.2
ДЗО
УДК" 317. 91
Лекции по математической теории
устойчивости. Д е м и д о в и ч Б. П., 1967 г.
Систематически излагаются основы теории
устойчивости решений обыкновенных дифференци-
дифференциальных уравнений и некоторые смежные вопросы.
В дополнении излагаются основы теории почти пе-
периодических функций и их приложения к дифферен-
дифференциальным уравнениям. Включены дополнительные
сведения к втузовскому курсу высшей математики.
Рисунков 66. Библиографических ссылок 82.
Борис Павлович Демидович
Лекции по математической теории устойчивости
М., 1967 г., 472 стр. с илл.
Редактор И. П. Купцов
Теки, редактор К. Ф. Брудно Корректоры С. Н. Емельянова и Е. #. Строева
Сдано в набор 11/VII 1967 г. Подписано к печати 5/XI 1967 г. Бумага 60X90 Vie- Физ. печ.
л. 29,5. Услови. печ. л. 29,5. Уч.-изд. л. 23,99. Тираж 35 000 экз. Т-12589. Цена книги 94 коп.
Заказ № 1103.
Издательство «Наука»
Главная редакция физико-математической литературы
Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени Ленинградская типография № 1 «Печатный Двор>
имени А. М. Горького Главполиграфпрома Комитета по печати нри Совете Министров СССР,
г. Ленинград, Гатчинская ул., 26.
2-2-3
49-67
ОГЛАВЛЕНИЕ
Предисловие в
Обозначения 9
Глава I
Некоторые сведения из матричного исчисления 11
§ 1. Арифметические действия над матрицами 11
§ 2. Степень матрицы 18
§ 3. Клеточные матрицы 19
§ 4. Норма матрицы 20
§ 5. Векторное пространство 22
§ 6. Жорданова форма матрицы 35
§ 7. Функции матрицы 41
§ 8. Матричные ряды 42
§ 9. Матричные степенные ряды 44
§ 10. Тождество Кейли и формула Сильвестра 48
§ 11. Производная и интеграл матрицы 50
§ 12. Экспоненциал матрицы 54
§ 13. Нормальная форма экспоненциала матрицы 55
§ 14. Некоторые свойства экспоненциала матрицы 57
§ 15. Логарифм матрицы 59
Упражнение к главе I 62
Глава 11
Устойчивость линейных дифференциальных систем 64
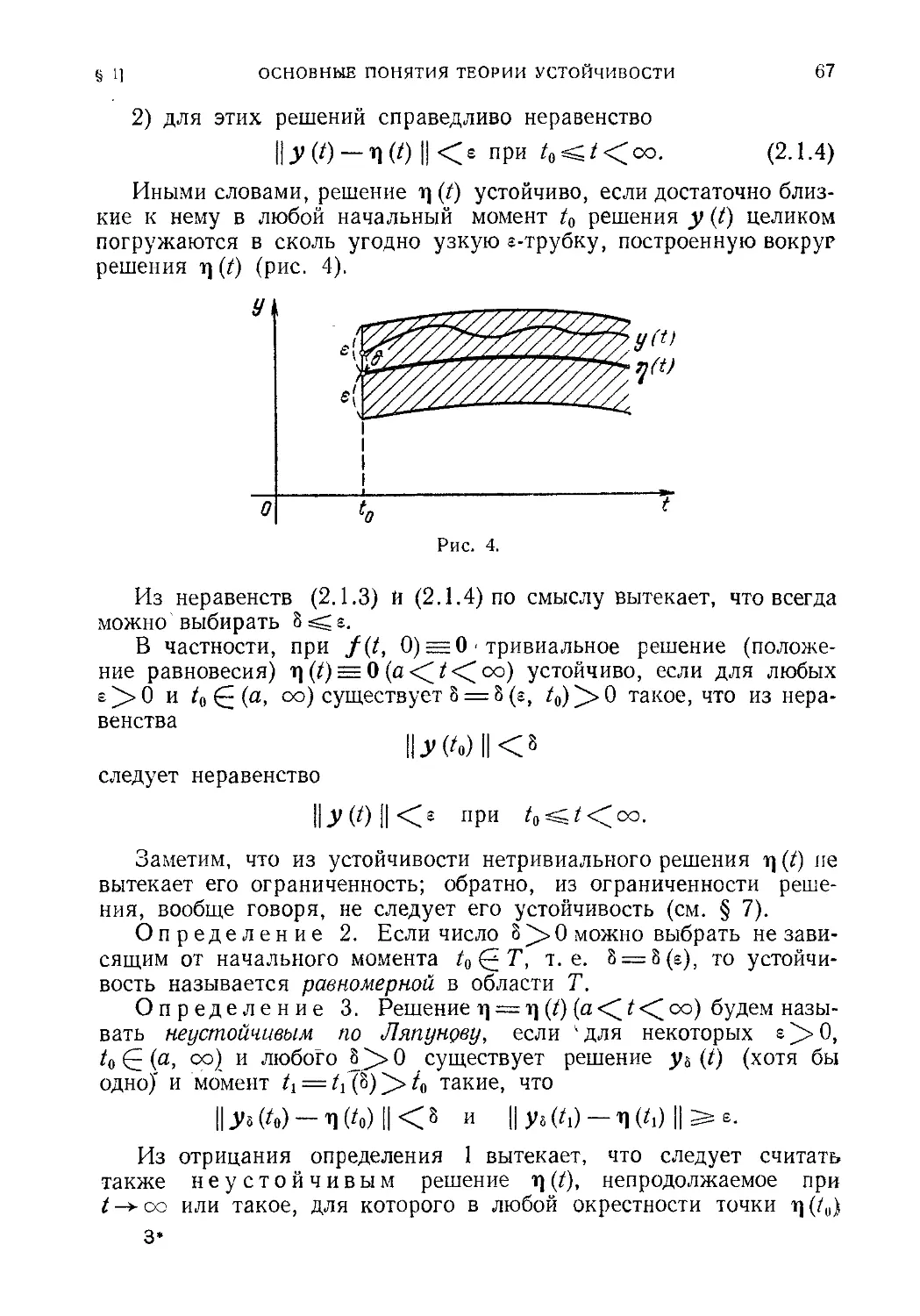
§ 1. Основные понятия теории устойчивости 64
§ 2 Общие свойства решений линейной дифференциальной си-
системы 70
§ 3. Формула Остроградского — Лиувилля 73
§ 4. Матрицант 74
§ 5. Метод вариации произвольных постоянных Лагранжа .... 76
§ 6. Общие теоремы об устойчивости линейных дифференциаль-
дифференциальных систем 78
§ 7. Устойчивость линейных однородных дифференциальных
систем 81
§ 8. Устойчивость линейной дифференциальной системы с посто-
постоянной матрицей 85
§ 9. Критерий Гурвица 90
§ 10. Критерий Михайлова 102
§ 11. Леммы Гронуолла — Беллмана и Бихари 108
§ 12. Устойчивость линейной дифференциальной системы с почти
постоянной матрицей 112
§ 13. Случай Лаппо-Данилевского 117
Упражнения к главе II 119
1*
4 ОГЛАВЛЕНИЕ
Глава ИГ
Первый метод Ляпунова 123
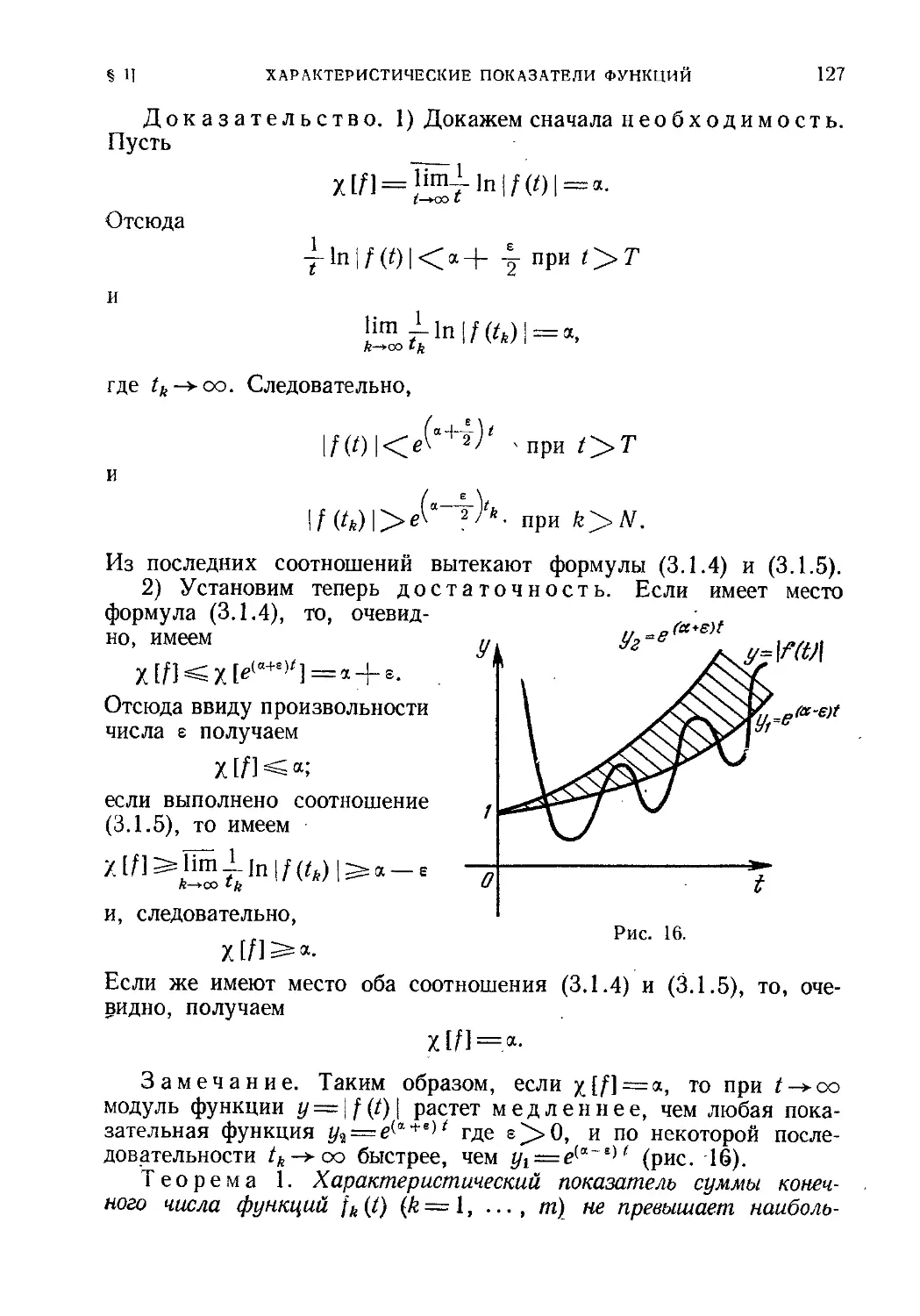
§ 1. Характеристические показатели функций 123
§ 2. Характеристические показатели функциональных матриц . . 132
§ 3. Спектр линейной однородной системы 135
§ 4. Нормальные фундаментальные системы 138
§ 5. Достаточное условие асимптотической устойчивости линей-
линейной дифференциальной системы 147
§ 6. Неравенство Важевского 149
§ 7. Неравенство Ляпунова 150
§ 8. Приводимые системы. Теорема Н. П. Еругина 153
§ 9. Приводимость к системе с нулевой матрицей 156
§ 10. Асимптотически эквивалентные системы 159
§ 11. Правильные системы 165
§ 12. Теорема Перрона 168
§ 13. Правильность треугольной линейной системы 174
§ 14. Теорема Перрона о триангуляции линейной системы 178
§ 15. Теория Флоке 183
§ 16. Приводимость периодической линейной системы 188
§ 17. Нормальная форма решений линейной периодической системы« 190
§ 18. Приближенное вычисление мультипликаторов 193
§ 19. Линейное дифференциальное уравнение второго порядка с
периодическими коэффициентами 197
§ 20. Гамильтонова система дифференциальных уравнений 208
§ 21. Возвратные уравнения 211
§ 22. Теорема Ляпунова — Пуанкаре 213
§ 23. Неоднородная периодическая система 215
§ 24. Метод малого параметра 222
Упражнения к главе III 225
Глава IV
Второй метод Ляпунова 234
§ 1: Приведенная система 234
§ 2. Знакоопределенные функции 235
§ 3.; Первая теорема Ляпунова (теорема об устойчивости) .... 237
§ 4. .Вторая теорема Ляпунова (теорема об асимптотической устой-
устойчивости) 240
§ 5. Третья теорема Ляпунова (теорема об неустойчивости) . . . 244
§ 6. Теорема Четаева . . 246
§ 7. Асимптотическая устойчивость в целом 248
§ 8. Экспоненциальная устойчивость 251
§ 9. Теорема Персидского 254
§ Ю. Устойчивость квазилинейных систем 257
§ 11. Оценка матрицы Коши для правильной системы . 265
§ 12. Теорема Ляпунова об устойчивости по первому приближению 266
§ 13. Признак устойчивости для нелинейных систем с неправиль-
неправильной линейной частью 271
§ 14. Неограниченная продолжаемость решений 274
§ 15. Устойчивость по Лагранжу 278
§ 16. Системы с конвергенцией 281
§ 17. Диссипативные системы 289
§ 18. Уравнения в вариациях 293
§ 19. Орбитальная устойчивость 295
-§ 20. Аналог теоремы Андронова — Витта . 299
ОГЛАВЛЕНИЕ 5
§ 21. Признак Пуанкаре 312
§ 22. Условная устойчивость - 314
Упражнения к главе IV 319
Глава V
Асимптотическое интегрирование дифференциальных уравнений 324
§ 1. Равномерная сходимость семейства функций 324
§ 2. Теорема Арцеля 325
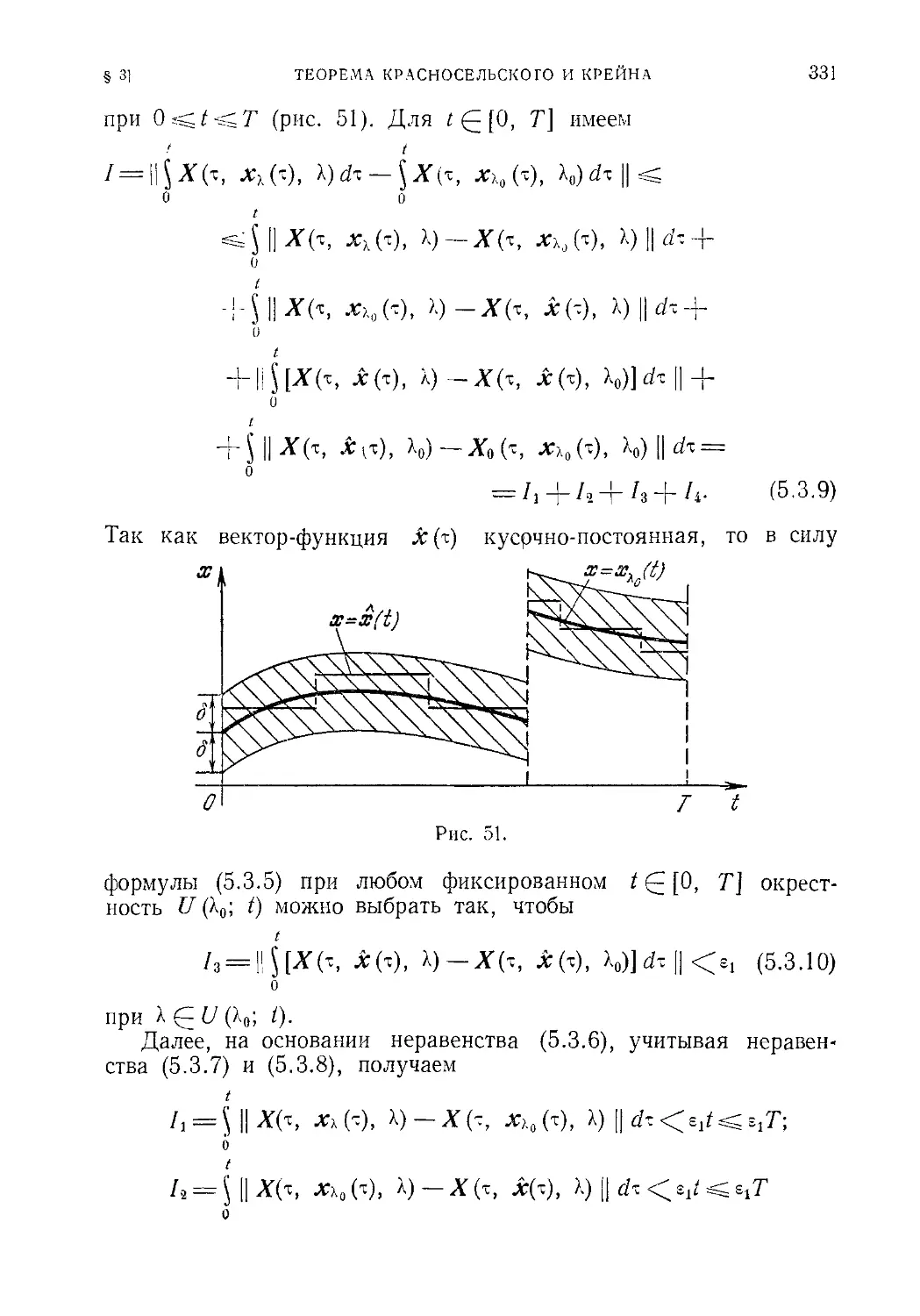
§ 3. Теорема Красносельского и Крейна 328
§ 4. Теорема Н. Н. Боголюбова 332
§ 5. Принцип сжатых отображений 335
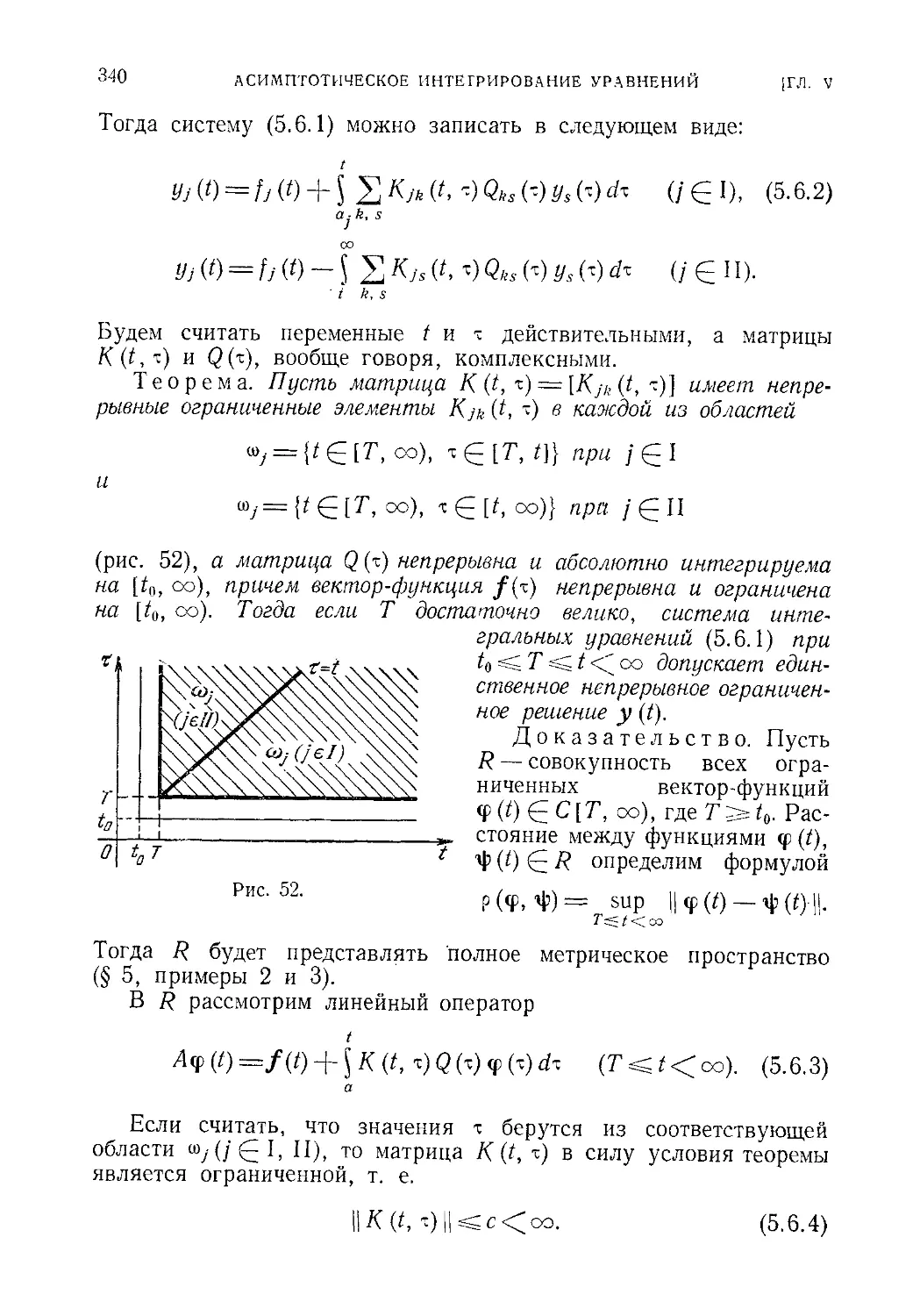
§ 6. Сингулярные интегральные уравнения типа Вольтерра.... 339
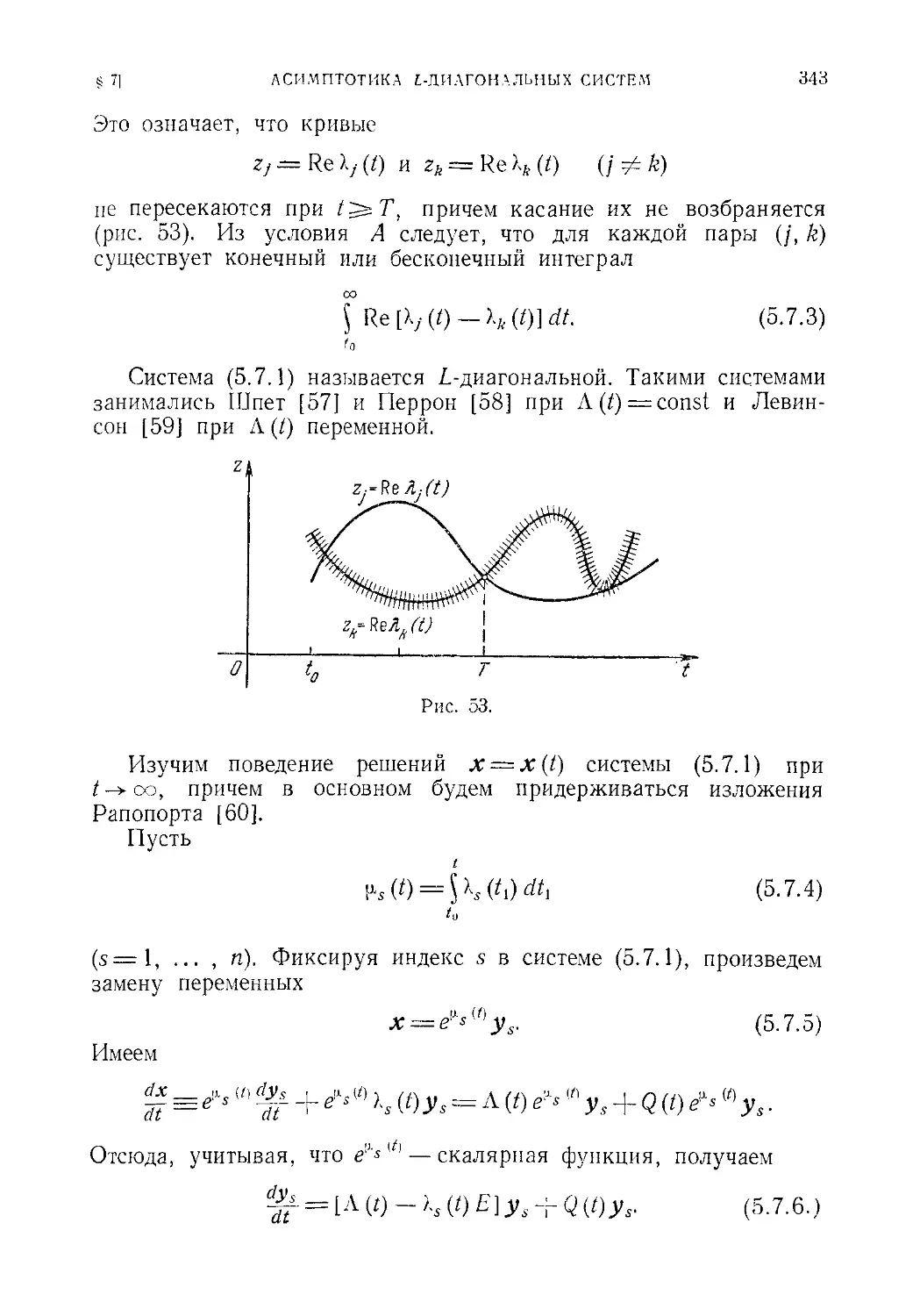
§ 7. Асимптотика /.-диагональных систем 342
§ 8. Лемма о диагонализации переменной матрицы 349
§ 9. Приведение линейной системы к /.-диагональному виду . . . 353
§ 10. Теорема Боля 358
Упражнения к главе У 365
Дополнение
Почти периодические функции 367
§ 1. Почти периодические функции в смысле Бора 367
§ 2. Основные свойства почти периодических функций 369
§ 3. Арифметические действия с почти периодическими функ-
функциями 371
§ 4. Равномерно сходящаяся последовательность почти периоди-
периодических функций . . ; 374
§ 5. Интеграл почти периодической функции 376
§ 6. Теорема о среднем значении почти периодической функции 379
§ 7. Пространство почти периодических функций 387
§ 8. Неравенство Бесселя 389
§ 9. Понятие о ряде Фурье почти периодической функции .... 391
§ 10. Формальные операции над рядами Фурье почти периодичес-
периодических функций 395
§ 11. Свертка почти периодической функции 397
§ 12. Теорема единственности 402
§ 13. Равенство Парсеваля 410
§ 14. Теорема аппроксимации 412
§ 15. Теорема компактности Бохнера 415
§ 16. Почти периодические матрицы .- 418
§ 17. Линейная система с постоянной матрицей и свободным почти
периодическим членом 421
§ 18. Квазилинейная почти периодическая система 425
§ 19. //-класс почти периодической системы • 428
§ 20. Ограниченные решения почти периодических систем 431
§ 21. Теоремы Америо и Фавара 437
Упражнения 442
Приложение. Жорданова форма матрицы 445
Цитированная литература -466
Предметный указатель 470
ПРЕДИСЛОВИЕ
Книга представляет собой обработанный и дополненный курс
лекций по теории устойчивости решений дифференциальных урав-
уравнений, читанный автором в течение ряда лет на механико-матема-
механико-математическом факультете Московского университета. Книга в основ-
основном рассчитана на студентов физико-математических факультетов
университетов и педагогических институтов, прослушавших обыч-
обычный курс теории обыкновенных дифференциальных уравнений, но
она будет также доступна и инженерам механического профиля, так
как необходимые дополнительные сведения по математике приве-
приведены в курсе. Большое внимание обращено на точность форму-
формулировок и строгость доказательств. Механические и физические
приложения затронуты незначительно; интересующийся этими воп-
вопросами читатель может обратиться к сочинениям: А. А. Андро-
Андронов, А. В. Витт, Э. С. Хайкин, Теория колебаний, Физмат-
гиз, 1959; Б. В. Булгаков, Колебания, ГИТТЛ, 1954;
И. Г. Малкин, Теория устойчивости движения, ГИТТЛ, 1952;
Н. Г. Четаев, Устойчивость движения, ГИТТЛ, 1946 и др.
Содержание книги посвящено классическому понятию устой-
устойчивости движения в смысле Ляпунова и некоторым связанным с ним
проблемам. В основу положена матрично-векторная трактовка систем
дифференциальных уравнений, в частности, широко использована
жорданова форма матрицы. Это позволяет избегать излишних техни-
технических подробностей при вычислениях и более отчетливо выяв-
выявлять суть дела. Решения линейных дифференциальных систем в
большинстве случаев рассматриваются как комплекснозначные
векторы-столбцы без перехода в действительную область; это
выгодно при записи многих формул. Что касается нелинейных
систем, то они, как правило, изучаются в действительной области.
Необходимые сведения по матричному исчислению приведены
в первой главе и в приложении.
ПРЕДИСЛОВИЕ 7
Чтобы не усложнять изложение техническими подробностями,
в книге рассматриваются системы дифференциальных уравнений,
правые части которых непрерывны (или кусочно непрерывны) от-
относительно независимой переменной и дифференцируемы по зави-
зависимой переменной.
Первая глава книги содержит элементы матричного ис-
исчисления. Здесь излагаются алгебра матриц и теория матрич-
матричных рядов. Дается понятие об экспоненциале и логарифме
матрицы.
В главе второй изучается устойчивость линейных дифферен-
дифференциальных систем. Доказывается критерий Гурвица. На основе
леммы Гронуолла — Беллмана исследуется устойчивость линейных
систем с почти постоянной матрицей.
Глава третья посвящена первому методу Ляпунова. Проводится
теория характеристических чисел функций и матриц. Рассматрива-
Рассматриваются правильные и приводимые системы, включая теоремы Ляпу-
Ляпунова, Перрона и Еругина. Излагается теория Флоке и теорема
Ляпунова — Пуанкаре для линейных гамильтоновых систем. Да-
Дается понятие о методе малого параметра для разыскания перио-
периодических решений.
В главе четвертой для систем в действительном пространстве
изучаются основы второго метода Ляпунова. Доказываются клас-
классические теоремы Ляпунова, теорема Четаева и теорема обраще-
обращения Персидского. С помощью метода функций Ляпунова устанав-
устанавливаются необходимые и достаточные условия ограниченности
решений дифференциальных систем (устойчивость в смысле Лаг-
ранжа). Дается понятие о диссипативных системах.
Глава пятая содержит теоремы Красносельского — Крейна,
теорему усреднения Боголюбова и асимптотику L-диагональных
систем.
В дополнении изложены основные сведения по теории почти
периодических функций в смысле Бора и теорема Америо для
почти периодических дифференциальных систем.
В приложении дается понятие о жордановой форме матрицы.
Приведенные рисунки носят приблизительный характер и яв-
являются лишь схемами, облегчающими понимание определений и
доказательств.
8 ПРЕДИСЛОВИЕ
Заметим, что отбор теоретического материала для курса лек-
лекций ввиду ограниченности времени является, естественно, непол-
неполным. Книга носит учебный характер и представляет собой введе-
введение в современную теорию устойчивости. Поэтому многие замеча-
замечательные результаты наших и заграничных ученых не нашли здесь
отражения. Часть теорем приведена в упражнениях.
В конце книги помещен список цитированной литературы, ко-
который ни в коей мере не претендует на полноту.
Отметим, что нумерация формул дается по трехступенчатой си-
системе (а • р - -у), где первое число я обозначает номер главы, второе
р — номер параграфа и третье f — номер формулы.
Приношу благодарность проф. j В. В. Немыцкому | за неизмен-
неизменный интерес к этой работе. Выражаю свою признательность проф.
¦Л. Э. Эльсгольцу за обстоятельную рецензию на рукопись книги.
Считаю своим долгом поблагодарить доц. Н. П. Купцова, осу-
осуществившего компетентное научное редактирование рукописи книги
и внесшего в нее ряд ценных дополнений и существенных испра-
исправлений.
Приношу благодарность также И. Е. Морозовой, проделавшей
большую работу по редактированию книги.
Б. П. Демидович
Москва, 1967 г.
ОБОЗНАЧЕНИЯ
х 6 X — х есть элемент множества X;
х?Х(х(?Х)—л; не является элементом множества X;
ХС^ — множество X составляет часть или совпадает
с множеством Y, т. е. каждый элемент х ? X есть также элемент
множества Y;
X(JZY — множество X не является частью множества Y,
т. е. существует элемент х* ? X такой, что х* ? Y;
3* ? X — существует элемент х множества X;
V*?X —все элементы х множества X;
\JXa — объединение (сумма) множества Ха;
а
Р)Ха — общая часть (произведение) множеств Ха;
а
X\Y — разность множеств X и У, т. е. совокупность всех
элементов х?Х таких, что x?Y;
{ х: f(x)<^a \—множество всех точек х, для которых выпол-
выполнено неравенство f(x)<^a;
(а, Ь) — интервал а<^^
[а, Ь] — сегмент (отрезок)
[а, Ь) и (а, Ь] —полусегменты а^х<^Ь и ^;
Rez = *, lmz=y — действительная и мнимая ча.сти ком-
комплексного числа 2 = х-\-iy- (t = l/"— 1);
z — x—iy — сопряженная величина для числа z;
| z | i= У'(Re zK -f (Im zf — модуль числа z;
A = (ayft) — матрица с элементами o,-ft;
AT — (dkj) — транспонированная матрица А;
A* = (akj) — эрмитово-транспонированная матрица А;
det Л — определитель матрицы Л;
\\A\\ — норма матрицы А;
Sp А = Ц а/7 — след квадратной матрицы Л;
Ap) =
Ai
0
0
Ap
J
— квазидиагональная матрица;
10 ОБОЗНАЧЕНИЯ
colon (xit..., хп) — \ • —матрица-столбец;
X\Y—декартово произведение' множеств X и Y, т. е.
совокупность всех пар (х, у), где х?Х и y?Y;
3R" — комплексное n-мерное векторное пространство 0*i ... хп,
т. е. множество всех упорядоченных n-мерных комплексов х =
= (хи..., хп) (точки или радиусы-векторы пространства), где
Xj = \j ~\- it\j (j = 1,..., п) — комплексные числа (координаты
вектора х);
{х, y) = ^Xjyj — скалярное произведение векторов х и у;
<fflnx — действительное n-мерное пространство 0*1...*„;
|| дг|| = 1/"(д:, дг) — евклидова норма вектора х;
р (х, у) = |! х—у || — евклидово расстояние векторов х и у;
f(x)?C (D) — функция f (x) = f (*! хп) непрерывна в области
D СЮ»;
f (х) ? Ст (D) — функция f(x) = f (xu ..., хп) непрерывна
в действительной области DCI^x вместе со своими частными
производными
0,.... а. ^ 0)
до порядка а1~\-...-\-ап = т включительно (С0 = С);
/ (хи..., хп) ? С{™1' ¦" •;m«)(D)—функция / (хи.. .,хп) имеет в области
непрерывные частные производные
да!+ • ¦ • +anf
где О^Я1^ть ...,
/ (х) $ Lip — функция f (x) удовлетворяет условию Липшица.
ГЛАВА I
НЕКОТОРЫЕ СВЕДЕНИЯ
ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ
§ 1. Арифметические действия над матрицами
Определение 1. Под матрицей A = (ajk) типа nC/ji (или,
короче, (т>(п)-матрицей) понимается система действительных
или комплексных чисел (или функций), записанная в виде прямо-
прямоугольной таблицы:
ап... а1п
A.1.1)
Числа (функции) aJk называются элементами матрицы А, при-
причем первый индекс / есть номер строки, а второй k — номер
столбца (см. [1]).
Матрицы
х==
= colon(xi, ...,хт)
типа mXl и IX" называются, соответственно, вектором-столбцом
и вектором-строкой.
Матрицу А = (ап) типа 1X1 принято отождествлять с числом
(скаляром) ап.
Если А — квадратная матрица, то под det А будем понимать
ее определитель.
Определение 2. Матрица A.1.1) называется нулевой и
обозначается
А=0,
если ajk = 0 для всех допустимых / и k (/ = 1,...,m; k=l,...,n).
Две матрицы А = (aJk) типа m X « и 5 = Fyfe) типа т' X п'
считаются равными:
А = В,
12 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ |ГЛ. Г
если 1) они имеют одинаковые типы, т. е. т' = т и п' = п, и
2) V ') Д/ft = bjk, т. е. каждый элемент матрицы А равен соответ-
соответствующему элементу матрицы В.
Определение 3. Сумма и, соответственно, разность двух
матриц А = (ajk) и В = (bjk) одинаковых типов определяется
формулой
Очевидно, имеет место переместительное свойство
А-\-В = В-\-А.
Если А, В и С — матрицы одинаковых типов, то по определе-
определению полагаем
причем
По индукции можно определить сумму любого конечного числа
матриц одинаковых типов.
Определение 4. Под произведением матрицы A = (aJk) на
число а понимается матрица
Ал = а.А = (оду*).
Если А и В — матрицы, а я и р — числа, вообще говоря,
комплексные, то очевидны свойства:
3) а
4) \А —А;
5) ОЛ = О.
Матрица
называется противоположной для матрицы В.= (Ь/к). Очевидно»
имеем В-\-(—fi) = 0 и
А -5 = А + (—5).
Заметим, что если А — квадратная матрица порядка п, то
1) Символ у обозначает «все».
§ ч
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД МАТРИЦАМИ
3
Определение 5. Под произведением матриц A = (aJk) типа
mXn и B = (bJh) типа т'Хп', где га = т', понимается матрица
ЛВ = (? а,-А*)
5=1
типа т X п'.
Аналогично, если т = п', то
есть матрица типа п X гп'¦
Пример.
я, t>, с
а3х-\-Ьау-\-сяг
В общем случае даже для квадратных матриц
АВ^ВА.
Пример.
[о oj[i oj [о oj'
[ioJLooJ Loir
Если А, В, С — матрицы и я — число, то справедливы следую-
следующие свойства:
2) А (ВС) = (АВ) С;
3) а (А В) = (аА) В = А (аВ).
Из определения 5 следует, что квадратные матрицы А = (ajk)
и S = (bJk) допускают перемножение друг на друга в любом по-
порядке тогда и только тогда, когда они одинакового порядка.
В этом случае
det (АВ) = det (ВА) = det A ¦ det В.
Единичная (п X п)-матрица
где 8;fe — символ Кронекера, т. е.
A, если j = k,
[О, если у Ф k,
Не
14
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. I
играет роль единицы при умножении:
ЕА=-~АЕ = А,
где А — любая квадратная матрица, одинакового с Е порядка.
Определение 6. Матрицу
0...1 0...0
о:..о 1 ...о
0...0 0...1
п — р,
где
и
_О...О 0...0
=1 (/ = 1,...,я — Р)
— 0 при k — j^p @ s=? p «S га — 1),
будем называть р-и единичным косым рядом (верхним) порядка
л (см. [1]).
Очевидно,
/„ = ?.
Лемма. Если 1р и Iq — единичные косые ряды одного и того же
порядка п, то
IpI9 = ip + 9 nPu 0
(C/k)¦
IPJ9 = и при
Доказательство. Пусть
Ip—(fljh), Iq = (b]h)>
Имеем
Из определения 6 следует, что c1k равно 0 или 1, причем c/k= 1
тогда и только тогда, когда для некоторого s имеем
8—i = p, k — s = q. A.1.2)
Отсюда при p-\-q<^n получаем
§ 1) АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД МАТРИЦАМИ 15
Следовательно,
V? = /p+? ПРИ О^р-\-Ч<п.
Если же p-\-q^n, то равенства A.1.2) не могут быть выпол-
выполнены одновременно. Поэтому
1р1д = 0 при p-^-q^n.
Замечание. Если условно полагать /р = О при р 3= я, то
всегда
Следствие. Если р — натуральное число, то
Л^! = /* = /,. A.1.3)
р раз
Определение 7. Если А = (ajk) есть матрица типа тX п,
то матрица
AT=(ahJ)
типа п~Х_т называется транспонированной по отношению к мат-
матрице А.
Матрица А называется симметрической, если
АГ=А;
и кососимметрической, если
Для матриц А и В, допускающих указанные действия, спра-
справедливы соотношения:
(АТ)Т=А;
Т
) ()
2) (*А + ЩТ =аАт-!г$В7 (а и р — числа);
3) (АВ)Т = ВТАТ.
Если Л — квадратная матрица, то
det AT=detA.
Определение 8. Если A = (a/k), то матрица
(где aJk — сопряженные величины для a/k) называется комплек-
комплексно-сопряженной для матрицы А.
Если А—квадратная матрица, то, очевидно,
det A = det A.
16 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ | ГЛ. I
Матрица
A* = AT=(akf)
называется эрмитово-сопряженнои или просто сопряженной для
матрицы А.
Очевидно, выполнены соотношения:
1) (Л*)* = Л;
2) (А-{-В)* = А*-\-В*;
3) (АВ)*=В*А*.
Если
то матрица А называется эрмитовой или самосопряженной.
Действительная матрица А является самосопряженной тогда
и только тогда, когда она симметрическая:
АТ=А.
Определение 9. Матрица А'1 называется обратной данной
матрице А, если
А^А = ААЛ — Е, A.1.4)
где Е — единичная матрица соответствующего порядка.
Из условия A.1.4) следует, что если матрица А имеет обрат-
обратную А'1, то матрицы А и А — квадратные и одного и того же
порядка.
Обратная матрица для данной матрицы А единственна. Дей-
Действительно, если, кроме Л~\ существует обратная матрица В,
т. е. ВА = АВ = Е, то
ВА = А~1А.
Отсюда, умножая последнее равенство справа на Л, получим
т. е.
Определение 10. Матрица Л называется неособенной (несин-
(несингулярной), если она квадратная и
det A ^ 0.
В противном случае матрица А называется особенной (сингу-
(сингулярной).
Теорема. Всякая неособенная матрица имеет обратную.
11 АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД МАТРИЦАМИ 17
Доказательство. Пусть А = [а/к] — неособенная матрица и
— союзная матрица, представляющая собой транспонированную
матрицу \Ajk\, элементами которой служат алгебраические дополне-
дополнения А]ь элементов а/к.
Рассмотрим матрицу
о_ As
det A •
Согласно известному свойству (см. [2]) имеем
Следовательно, на основании формулы A.1.4) получаем
В = А~1.
Таким образом,
det
Замечание. Из формулы A.1.4) вытекает
1) det А'1 = (det' A)~u,
2) (А~*)Т = (АТГ\
3) если А и В — неособенные матрицы одинакового порядка, то
Определение 11. Действительная квадратная матрица S,
удовлетворяющая условию:
Sl = ST, A.1.5)
называется ортогональной.
Из соотношения A.1.5) получаем
detS = ±l.
Пример. Если а действительно, то матрица
' COS я — !
А =
I sin I cos
sin * "I
L-OS at J'
как нетрудно проверить, является ортогональной.
18 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ ! ГЛ. I
Заметим, что матрица, обратная ортогональной матрице 5,
есть матрица ортогональная. Действительно,
Таким образом,
Определение 12. Квадратная матрица б', обладающая
свойством
U~l = U*, A.1.6)
называется унитарной.
Очевидно, имеем
На основании A.1.6) выводим
|detf/| = l.
Заметим, что если U унитарна, то U~l также унитарна и, сле-
следовательно,
1 det t/-11 == 1.
Определение 13. Под следом SpA квадратной матрицы
А = [afk] понимается сумма всех ее диагональных элементов:
Очевидно, имеем
SpAT=SpA
и
Sp (а.А) = a Sp А (а — скаляр).
Если А и В — квадратные матрицы одного и того же порядкаг
то справедливы следующие соотношения:
1) Sp(a/4-f pB)=aSp A +pSp5 (а и J3 — числа);
2) S(AB) S(BA)
§ 2. Степень матрицы
Если А — квадратная матрица и р — натуральное число, то по
определению полагают
АР = А ...А.
р раз
§ 3] КЛЕТОЧНЫЕ МАТРИЦЫ
Кроме того, имеет место соглашение
19
где Е — единичная матрица того же порядка, что и А.
Если А — неособенная матрица, то по определению имеем
В этом случае для любых целых р и q справедливо правило
перемножения степеней
ApA" = A^q. A.2.1)
В случае особенной матрицы А формула A.2.1) имеет место
лишь для неотрицательных р и q.
Если А и В — квадратные матрицы одного и того же порядка,
перестановочные между собой, т. е.
АВ = ВА,
то для натурального р справедлива формула бинома Ньютона
где
(А+В)' =
<7> (Р — ЯУ-
— число сочетаний из р элементов по q.
§ 3. Клеточные матрицы
В приложениях приходится рассматривать матрицы
А =
Кп
КгМ
...
...
Kln
Ктп
\p?j.
A.3.1)
элементы которых ajk объединены в клетки (блоки) Крд. Такие
матрицы называются клеточными или блочными.
Если
— клеточная матрица, имеющая одинаковое с матрицей А раз-
разбиение на блоки, то
A±B = [Kpq±Lpq].
20
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ [ГЛ. Г
Если клетки Крг и Lrq допускают перемножение для любых
р, q и г, то
В частности, пусть
0 1
Г
diag(L,, ..., Ls) =
0 i
L о
— квазидиагональные матрицы (клеточно-диагональныё), содержа-
содержащие квадратные клетки К\, • ••, Ks и Lu ..., ^.расположенные
по главной диагонали, причем все остальные элементы матриц.
А и В равны нулю. Тогда, если порядки клеток Kj и1;- (/= 1, ...
..., s) одинаковы, то
Отсюда
§ 4. Норма матрицы
i±bu ..., KS±LS)
ibu .... Ksbs).
e, .-., К?) (р^О).
Определение. Под нормой матрицы A — [aJk~\ понимается
неотрицательное число || А ||, удовлетворяющее следующим усло-
условиям (аксиомам):
1) О ||=0, и обратно, если ||Л||=0, то А = О;
2) яА || =|а| || А || , где а —любое комплексное число;
3) А -\- В || sg || А || -f- || В || , где А и В — любые матрицы,
допускающие сложение;
4) || АВ || < || А || || В
пускающие умножение.
Из 2) и 3) вытекает
где А я В — любые матрицы, до-
до§ 41 НОРМА МАТРИЦЫ 2!
В дальнейшем мы будем использовать три нормы:
i k
{евклидова норма).
Для вектора-столбца
эти нормы имеют, соответственно, следующие значения:
В дальнейшем, если некоторое соотношение окажется выпол-
выполненным для любой нормы I — III, то значок при норме будет
опускаться.
Нетрудно проверить [3], что для приведенных норм выполнены
аксиомы 1) — 4). Кроме того, имеет место следующее свойство:
5) V\aJk\^\\A\\.
Отметим, что если Л = [ои] есть A X 1)-матрица, то
Отметим еще одно полезное свойство нормы:
||И||_||дц|^||Д_д||. A.4.1)
Действительно,
И1|-||Я||«;||Л-Д|1. A.4.2)
Аналогично имеем
•\В\\ — \\А\\^\\В-А\\ = \\А~В%, A.4.3)
Из нераьенств A.4.2) и A.4.3) вытекает неравенство A.4.1).
22
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ
(ГЛ. I
Введем понятие абсолютной величины (модуля) матрицы А =
= [ау*]. полагая
\A\ = modA = [\aJk\].
Для норм I — III, очевидно, имеем
\\А || = || mod А ||.
Для матриц A = [aJk] и B = [bjk] одинакового типа можно
ввести понятие неравенства
A.4.4)
\В
в том случае, если Vay*^^y*; в частности, А^О, если \//*
Из формул для норм I — III вытекает: если выполнено нера-
неравенство A.4.4)
mod A ^ mod В,
то справедливо свойство монотонности нормы
\\А\\^\\В\\.
§ 5. Векторное пространство
Определение 1. Упорядоченная совокупность чисел (вообще
говоря, комплексных)
x={xlt..., хп\
называется п-мерным вектором, а числа xt xn называются
координатами (компонентами) вектора аг.
В дальнейшем мы будем интерпретировать л-мерный вектор аг
как (л X 1)-матрицу (матрица-столбец)
Транспонированный вектор
хТ = [хи ..., хп]
представляет собой A X л)-матрицу (матрица-строка).
Если
х —
и у =
Уп
ВЕКТОРНОЕ ПРОСТРАНСТВО
— векторы и а — произвольное комплексное число, то естественна
определяются операции сложения векторов
х-\-у=
и умножения вектора на число (скаляр)
алг = лга =
о.х„
Эти операции обладают обычными свойствами.
Определение 2. Совокупность всех л-мерных векторов х
с определенными операциями сложения и умножения на числа
называется п-мерным векторным пространством (комплексным) от™,
а сами векторы лг— точками этого пространства.
Для векторов лг, у G эти определим скалярное произведение:
A.5.1)
Если ввести эрми-
У=1
где у~] — число, комплексно-сопряженное с
тово-сопряженный вектор
У*=УТ,
где
У =
Уп
то формулу A.5.1) можно записать в виде
(х,у)=у*х.
A.5.2)
Легко проверить, что скалярное произведение обладает следу-
следующими свойствами:
1) (лг, дс)>0, если хфО, и (лг, лг) = О, если лг = О;
2) (х,у) = {у, х);
3) (алг, з') = а(лг, у), (лг, ау) = а(х, у), где а — произвольное
комплексное число;
4) (х+у, z) = (x, z) + {y, z), (г, х+у) = (г, x) + (z, у).
Число
называется длиной или модулем вектора х (ср. § 4).
21 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ [ГЛ. I
Заметим, что если вектор х рассматривать как матрицу-стол-
матрицу-столбец, то длина вектора |дг| совпадает с его нормой ;jjej|in, т. е.
евклидова норма вектора согласована с его длиной.
Из формулы A.5.2) имеем неравенство Коши
К*. jOKIIj>*IIII*II = II*II||jM|.
Векторное пространство Шп, в котором определено скалярное
произведение со свойствами 1) — 4), будем называть комплексным
евклидовым или унитарным пространством (см. [4]).
Иногда будем рассматривать вещественное п-мерное векторное
пространство <Мп, точки которого представляют собой векторы *х
с действительными координатами xt (J = l, ..., я). Для таких
пространств операция умножения на скаляр определена лишь для
действительных чисел.
Для вещественного пространства <Мп свойства 1) — 4) прини-
принимают вид:
Г) (аг, лг)>0 при лг^О и (х, лг) = О при х = 0;
2') (х,у) = (у, х);
3') (ах, у) = а(х, у) (а — вещественное число),
4') (х+у, г) = (х, *) + (у, г).
В этом случае норму вектора
i
будем называть евклидовой, а само пространство <Мп — евклидовым
я-мерным пространством.
Векторное пространство $\п является частным случаем линей-
линейного пространства 2, под которым понимается совокупность эле-
элементов х, у, z, ..., произвольной природы, с двумя определен-
определенными операциями: а) сложением х-\-у и б) умножением ах на
комплексное число а, не выводящими за пределы 2. Предпола-
Предполагается, что эти операции удовлетворяют обычным аксиомам
алгебры.
Вектор
5] . A5.3)
где сi — постоянные, называется линейной комбинацией векторов
Определение 3. Векторы дгA), .... хЫ) называются линей-
линейно зависимыми, если некоторая нетривиальная линейная комби-
комбинация их представляет нуль-вектор, т. е.
В противном случае векторы называются линейно независимыми.
§ 51 ВЕКТОРНОЕ ПРОСТРАНСТВО 25
Определение 4. Совокупность л линейно независимых век-
векторов еь ..., ея образует базис векторного пространства Ып (см. [4]),
если каждый вектор х? SR" можно представить единственным спо-
способом в виде линейной комбинации
где \j — некоторые числа, называемые координатами вектора х
в данном базисе.
Вектор
п г
отнесенный к данному базису е = {е,, ... ,е„}, будем называть
представлением вектора х в этом базисе. Очевидно, для вектора
х—{хи ..., хп) числа хи ..., хп являются его координатами в
каноническом базисе ортов:
в, = {1, 0, ..., 0},.
е, = {0, 1, .... 0},
еп = \0, 0, ..., 1}.
Базис еь ..., е„ называется ортогональным, если векторы его
попарно ортогональны, т. е.
(8/, «У = 0 при /^*.
Если, кроме того,
то базис называется нормированным. В этом случае имеем
(«V, е») = 8у»,
где 8;А — символ Кронекера.
Пусть х{1\ ..., аг(*' — линейно независимые векторы в Ш" и
сь • • •, с* — произвольные числа. Совокупность всех векторов
3=1
представляет собой линейное пространство ?А С $Rn (так называ-
называемое линейное подпространство в 91", порожденное k векторами
26 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ (ГЛ. I
Обратно, пусть некоторое множество 2 является линейным про-
пространством в Ып относительно введенных там операций сложения
векторов и умножения векторов на числа, т. е. 2 есть линейное под-
подпространство в Шп. Тогда любая максимальная система дг111, ...
..., x^k) линейно независимых векторов из 2 образует его базис,
т. е. для каждого элемента у ? 2 справедливо представление
A.5.3), а число k@^k^n) называется размерностью подпро-
подпространства 8:
Введем понятие ранга матрицы.
Определение 5. Под рангом г —г (А) матрицы A = [a/tl]
понимается максимальный порядок ее минора, отличного от нуля.
Если матрица А имеет тип п X tn, то, очевидно,
г (A) sgmin (n, т).
Если столбцы матрицы А рассматривать как векторы простран-
пространства 5Г, то ее ранг г (А) представляет собой максимальное число
линейно независимых столбцов и, следовательно, совпадает с раз-
размерностью подпространства 2Г, порожденного этими векторами:
г (Л) = dim ?,..
Заметим, что матрица Л и ее эрмитово-сопряженная матрица
А* имеют одинаковые ранги:
Рассмотрим систему линейных уравнений
п
^xk = b] (У=1, ..., п). A.5.4)
Введя матрицу системы А = [aJk] и векторы-столбцы х =
= colon (xu ..., хп), 6 = colony, ...,#„), систему A.5.4) можно
записать в виде векторно-матричного уравнения
Ах = Ь. A.5.5)
Теорема Кронекера — Капелли (см. [2]). Система
A.5.5) имеет решения тогда и только тогда, когда ранг г = г{А)
матрицы А системы совпадает с рангом г' — г (В) расширенной
матрицы
В = [\ А 1 Ъ 1].
В частности, если det^^O, то, очевидно, г(А) = г(В)~п и
для системы A.5.5) существует единственное решение
дг = А'1 Ь,
§ 5] ВЕКТОРНОЕ ПРОСТРАНСТВО 27
Если detA = O и k~n — г — дефект матрицы А, то каждая
из однородных линейных систем
Л§ = 0 и Л*т] = 0 A.5.6)
имеет k линейно независимых нетривиальных решений соответ-
соответственно: |A), ..., §(*> и tjA), ..., т]'*'. В этом случае линейная
неоднородная система A.5.5) совместна тогда и только тогда,
когда выполнены условия ортогональности:
(т,1р), Ь) = 0 (р = 1, ..., k).
При соблюдении этих условий система A.5.5) допускает оо* ре-
решений:
3=1
где лг0 — некоторое частное решение системы A.5.5) и с,, ...,
ch — произвольные постоянные.
Определение 6. Пусть каждому вектору х ? <йл ставится
в соответствие вектору 6 Sffm. Тогда говорят, что в Ып определено
преобразование
У = Ах, A.5.7)
действующее из Ып в 5Ят.
Естественно определяются операции над преобразованиями А
и /3:
=а(Л jc) (а —число);
= Л (Бх).
Отметим еще нулевое преобразование
дх = о
и единичное преобразование
Ёх~х.
Если для преобразования А существует преобразование А'1,
удовлетворяющее условию:
то оно называется обратным преобразованием для А.
28
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. !
Преобразование А называется линейным, если выполнены сле-
следующие условия:
1) А (з.х) = у- Ах (а — число);
Пусть А — линейное преобразование, действующее из 9Г в ?Я"
и е = {8ь ..., е„} — некоторый базис пространства Шп. Тогда век-
векторы Авк (& = 1, ..., п) допускают разложения
Ч =
A.5.8)
Матрица А = (а,/;) называется матрицей преобразования А (в дан-
данном базисе). Заметим, что первый индекс j элемента а1Ь обозна-
обозначает номер координаты и таким образом aiu есть /-я координата
k-vo преобразованного базисного вектора ек, т. е. ajk = (Aztl)j.
Пусть
— произвольный вектор из Я" и ^(fc=l, ..., п) — его коорди-
координаты. В силу линейности преобразования А имеем
к k
Отсюда на основании формул (Г.5.8) получим
У ~ ii ** JLi aJ'k zi === 2-i B-i aiu ;*^ s'- A.5,9)
и j i и
Следовательно, координаты вектора у в данном базисе еь ... , е„
суть
^ = Sa^* (/=1. •¦-. ")¦ A.5.10)
Если для векторов л: и у ввести представления
то соотношения A.5.10) эквивалентны матричной формуле
у = Ах. A.5.11)
Таким образом, линейно преобразованный вектор равен про-
произведению матрицы преобразования на исходный вектор.
§ V ВЕКТОРНОЕ ПРОСТРАНСТВО 29
Нетрудно убедиться, что арифметическим операциям над ли-
линейными преобразованиями отвечают такие же операции над их
матрицами.
Пусть е = {в\, ..., е„\ и е = {еь ..., еа\ — два базиса про-
пространства Ып. Установим связь между ними, причем, следуя
традиции аналитической геометрии, будем выражать элементы пер-
первого базиса (старого) через элементы второго (нового). Имеем
ek=y^sjk&j (k=l,...,n), A.5.12)
i
где Sjk — некоторые постоянные, причем, как обычно, первый ин-
индекс j представляет собой номер координаты вектора ек в базисе е.
Неособенную матрицу S = [s,/(] будем называть матрицей пере-
перехода (от второго базиса к первому).
Заметим, что если базисы е и е ортонормированы (ортогональ-
(ортогональны и нормированы), т. е.
то матрица перехода 5— унитарная (в частности, в действительном
пространстве (Мп— ортогональная). Действительно, в этом случае
в силу формулы A.5.9) имеем
т. e.
Таким образом, матрица S — унитарная.
Пусть
где л-], ..., хп — координаты вектора х в базисе е. На основа-
основании формулы A.5.12) имеем
= 28/2 *./»**• A.5.13)
з !<
Отсюда координаты вектора х во втором базисе суть
30 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ [ГЛ. I
Полагая | = colon(?ь ..., ?„), будем иметь
т. е. новый координатный столбец вектора равен матрице пере-
перехода (от нового базиса к старому), умноженной справа на его ста-
старый координатный столбец.
Пусть еи ..., еп и еь ..., е„ — два базиса в Шп и S (det S ^=0)
— неособенная матрица, устанавливающая связь между коорди-
координатами вектора в первом и во втором базисах. Предположим,
что А — линейное преобразование в Шп, имеющее матрицу преоб-
преобразования А в первом базисе и матрицу В — во втором. Пусть
х={хи ..., хп} иу = {уи ..., уп)—два вектора, отнесенных к
первому базису, такие, что
у = Ах. A.5.15)
Во втором базисе эти векторы будут иметь, соответственно, новые
координаты {?1( ..., \п] и {?],, ..., %}, и наборы этих координат
можно интерпретировать как некоторые векторы
" «1
'л
I
И
Т] =
ъ
в первом базисе, причем
Кроме того, в силу A.5.14), имеем
Из соотношений A.5.15), A.5.17) получаем
A.5.16)
A.5.17)
Сравнивая с A.5.16), находим
B = SAS'\ A.5.18)
Матрицы, связанные соотношением A.5.18), называются подобными.
Таким образом, линейное преобразование в различных базисах
описывается подобными матрицами. Для краткости говорят, что
В получается из А с помощью матрицы S.
Отношение подобия A.5.18) между (п ><^-матрицами А и В
обычно коротко обозначается так: ВстгЛ. Легко проверить следу-
следующие свойства: 1) А суз А (рефлексивность); 2) если А с/г Б, то В га А
(симметрия); 3) если ЛсугВ иВстгС, то ЛстгС (транзитивность);
4) если АагВ, то, очевидно, имеем det A = det В.
§ 5] ВЕКТОРНОЕ ПРОСТРАНСТВО 31
Определение 7. Вектор х Ф 0 называется собственным для
линейного преобразования А, если
1х, A.5.19)
где число X называется собственным значением или характеристи-
характеристическим числом (характеристическим корнем) преобразования А
(см. [4]).
Пусть Л — матрица преобразования А в некотором базисе.
Из формулы A.5.19) имеем Ах = Кх и, следовательно,
(А — \Е)х = 0. A.5.20)
Линейная однородная система A.5.20) может иметь ненулевые
решения только в том случае, когда
det (Л — Щ=0. A.5.21)
Корни Хь ..., Х„ векового уравнения A.5.21) называются
характеристическими числами (характеристическими корнями)
или собственными значениями матрицы Л, а соответствующие
нетривиальные решения однородной системы A.5.20), получающи-
получающиеся при А = Х/,— отвечающими ему собственными векторами мат-
матрицы Л.
Корни векового уравнения A.5.21) не зависят от выбора ба-
базиса и представляют собственные значения преобразования А.
Действительно, если преобразование А в другом базисе опи-
описывается матрицей В, то имеем
отсюда
det (В — Щ = det (SAS^1 — k SES~l) =
= det S det (Л — IE) det S = det (A — Щ.
Аналогично, если х есть собственный вектор матрицы А, от-
отвечающий ее характеристическому числу X, т. е. х есть нетри-
нетривиальный вектор, удовлетворяющий уравнению A.5.20), то | =
= Sx т^Ои является собственным вектором подобной матрицы В,
отвечающим тому же характеристическому числу X, так как
(В — Щ % == S (А — ХЕ) S Sx = 0.
Таким образом, свойство собственности вектора преобразования А
также не зависит от выбора базиса.
Определение 8. Преобразование А называется эрмитовым
или самосопряженным, если в любом ортонормированном базисе
ему соответствует эрмитова матрица
Л = Л*, где А*=.АГ .
32 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ Г ГЛ. Т
Как было показано выше, переход от одного ортонормиро-
ванного базиса к другому осуществляется с помощью унитарной
матрицы U:
Поэтому, полагая
В--= U Аи~* = и AU*,
будем иметь
A
т. е. если преобразование А эрмитово в одном ортонормированием
базисе, то оно будет эрмитово и в любом другом ортонормирован-
ном базисе.
В случае, когда эрмитова матрица действительная, она явля-
является симметрической.
Для эрмитова преобразования справедливы следующие пред-
предложения (см. [4]).
Теорема 1. Все собственные значения эрмитова преобразо-
преобразования действительны.
Теорема 2. Собственные векторы эрмитова преобразования,
соответствующие различным собственным значениям его, ортого-
ортогональны между собой.
Теорема 3. Для всякого эрмитова преобразования сущест-
существует естественный ортонормированный базис, состоящий из соб-
собственных векторов, в котором матрица преобразования диагонально
и вещественна.
Пусть х, у к. 2ftn и A=-[aJk] — матрица типа л X "• Скалярное
произведение
(Ах, y)='El(Ax)jy, = J^a}kX-f, A.5.22)
7 ». ft
называется билинейной формой с матрицей А. Выражение A.5.22),
учитывая независимость суммы от обозначения индексов, можно
записать в виде
(Ах, у) = У\ a*/ xj Уь = Х а'</ У" XJ =(А *У' *)>
з, ft s. I'
где A* — [akj]—эрмитово-сопряженная с А матрица. Следова-
Следовательно,
(Ах,у) = (х, А*у), A.5.23)
т. е. в скалярном произведении A.5.23) матрицу А можно пере-
перебрасывать с первого места на второе, заменяя ее эрмитово-сопря-
§ 5) ВЕКТОРНОЕ ПРОСТРАНСТВО 33
женной А*. Отсюда, если матрица А эрмитова (в действительном
случае — симметрическая), то имеем
{Ах, у) = {х, Ау). A.5.24)
В этом случае
V (х) = (Ах, х) — х*Ах =
называется эрмитовой квадратичной формой. Так как
V (х) = 2 ajk Ч xj = 2 akJXjXk — V(x),
f, k k, j
то эрмитова квадратичная форма имеет вещественные значения.
Если х^е^п и Л — вещественная симметрическая матрица
(Лг—Л), то эрмитова форма V (х) представляет собой действи-
действительную квадратичную форму (т. е. однородный полином второй
степени):
V (х)~х ТАх = 2 ajkXjXk (aIk = akJ)
i.k
с матрицей A — [ajk],
Найдем оценку для функции V (х). Пусть >.,- —Х7- (А) (/=1, •••
... , п) собственные значения матрицы А и
X (А) = min X/ (Л), А (Л) = max Xy- (Л).
/
Для эрмитовой матрицы .4 существует унитарная матрица U,
переводящая ее в диагональную D = (X,, ..., Х„), т. е.
Полагая
и
имеем
V (х) =y*UAU*y =y*Dy
Отсюда
Х(Л)|у|'2^
где
2 Б, П, Демидович
34 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ IW1. 1
Используя формулу A.5.23), будем иметь
(У. y) = (Ux, Ux) = (x, U*Ux) = {x,-x),
т. е.
\у\ = \х\.
Таким образом, окончательно получаем
\(A)\x\9^V{x)^A(A)\x\\ A.5.25)
причем равенства слева и справа достигаются при собственном
векторе х, отвечающем, соответственно, наименьшему характе-
характеристическому числу X (А) и наибольшему характеристическому
числу А (А) матрицы А.
Неравенство A.5.25) имеет место также для действительной
квадратичной формы V (х).
Определение 9. Действительная квадратичная форма
V(x) — (Ax, х) (АГ=А)
называется положительно или отрицательно определенной, если,
соответственно,
V (X) > 0 при х ?? О
или
V(je)<0 при Х^О,
причем, очевидно, V@) = 0.
В этом случае поверхности уровня
V (х) = const
представляют собой (п— 1)-мерные эллипсоиды пространства е^.
Из неравенства A.5.25) вытекает, что квадратичная форма V (х)
является положительно определенной тогда и только тогда, когда
все собственные значения ее матрицы Л положительны, т. е.
Аналогично V (х) представляет собой отрицательно определен-
определенную квадратичную форму тогда и только тогда, когда все соб-
собственные значения ее матрицы А отрицательны, т. е.
Если Л — произвольная матрица, то матрица А*А, очевидно,
эрмитова, и так как
{А*Ах, х) = (Ах, Ах<=[Ах\\
ЖОРДАНОВА ФОРМА МАТРИЦЫ
35
то при А =? 0 все ее собственные значения Xj (А*А) положительны;
если же Л=0, то они равны нулю. В функциональном анализе
показывается, что за норму матрицы А можно принять число
i| А || = Va(A*A),
где A(A*A)==maxXj(A*A).
i
В частности, если вектор х рассматривать как вектор-столбец:
X — colon(xi, ..., х„), то имеем
и, следовательно,
Х*Х = | X |
I v II 1 v I
Таким образом, введенная выше норма вектора согласована с его
длиной.
Отметим, что из соотношения A.5.25) имеем
| А || = max {-~> = max (Ax).
хфО
§ 6. Жорданова форма матрицы
Пусть A — [a/ti] — квадратная матрица порядка п и
— ее характеристическое или вековое уравнение [4], [5J. В рас-
раскрытом виде имеем
Х-
аи —а12
— а.2. К—а22
— а1п
— ain
Обозначим через Хр (р = 1, ..., я) корни характеристического
уравнения A.6.1) (характеристические корни или собственные
значения матрицы А). Можно доказать (см. приложение), что с по-
помощью преобразования подобия
A.6.2)
') Иногда характеристическое уравнение матрицы записывают в эквива-
эквивалентном виде det (А — \Е) = 0.
2*
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ
| ГЛ. I
(det S Ф 0) матрица А может быть приведена к квазидиагональ-
квазидиагональной форме Жордана
j = diag[J] (Xj), ..., JmQ~m)] (m^n),
где
- хр
0
0
_ 0
0>=1
1
К
0
0
0 ...
1 ...
0 ...
0 ...
., т; ег
0~
0
1
=э1
— так называемые клетки Жордана, причем каждому характери-
характеристическому корню \р кратности а.р соответствует одна или несколько
\ (
\
клеток Жордаиа размерами ер\ ..., е(р такие, что
„(П
е? +
4- е(г) —'
Легко убедиться, что каждой клетке Жордана Jp(kp) порядка ер
с точностью до нулевого скалярного множителя отвечает один
и только один собственный вектор матрицы А, имеющий в над-
надлежащем базисе вид
) О,
где
0, ..., 0),
(h ^ о).
причем различным клеткам Жордана соответствуют линейно неза-
независимые собственные векторы. Поэтому постоянная г, так назы-
называемая степень вырождения соответствующего собственного значе-
значения Хр, представляет собой максимальное число линейно независимых
собственных векторов матрицы Л, соответствующих ).р.
В общем случае г ==s a.p. Если степень вырождения характе-
характеристического корня X равна его кратности, т. е. г = ар, то, оче-
очевидно, вр}— ... =ер—\. Таким образом, в этом случае все
соответствующие клетки Жордана будут содержать по одному
элементу (простые клетки).
Так как
lE = S'lkS и A = S~lJS,
то характеристический полином А (X) A.6.1) может быть представ-
представлен в виде
§ 6] ЖОРДЛНОВЛ ФОРМА МАТРИЦЫ 37
где X], ..., ).т — характеристические числа матрицы А, соответ-
соответствующие различным клеткам Жордана (не обязательно различные
между собой).
Множители (X— 1р)ер (р = 1, ..., т) называются элементар-
элементарными делителями матрицы А, а натуральные числа ер (т. е, раз-
размеры (порядки) клеток Жордана) — показателями элементарных
делителей, соответствующих характеристическому числу Х„ или
линейному множителю X — Хр.
Если все характеристические числа Хр имеют простые элемен-
элементарные делители (ер=1), то матрица Жордана J будет чисто
диагонального вида:
J =
= diag (Xlf
причем числа Хр (p=l п) не обязательно различны. Это
обстоятельство, например, имеет место для симметрической мат-
матрицы (см. [4]).
Заметим, что, вообще говоря, характеристические числа Хр —
комплексные и, следовательно, в общем случае как матрица пре-
преобразования S, так и матрица Жордана J имеют комплексные
элементы. Если ограничиться действительными преобразованиями,
то соответствующая модифицированная матрица Жордана имеет
более сложный вид (см. [4]).
Можно доказать, что форма Жордана обладает свойством
единственности, т. е. данную матрицу с помощью преобра-
преобразования подобия A.6.2) можно привести только к единственной
форме Жордана, с точностью до порядка клеток, и, в частности,
размеры набора клеток Жордана не зависят от выбора матрицы 5
(см. [4], [5]). Например, форма Жордана матрицы А будет пол-
полностью определена, если упорядочить ее характеристические
числа Хр (р=1, ..., т), а клетки Жордана, соответствующие
одному и тому же характеристическому числу, расположить в по-
порядке возрастания их размеров.
Пусть В z/z А, т.е. существует неособенная матрица Т (det T Ф 0)
такая, что
Отсюда
А = Т~1ВТ, A.6.3)
Теорема 1. Подобные матрицы имеют одинаковые формы
Жордана (с точностью до порядка клеток).
38
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
Доказательство. Действительно, из формулы A.6.3) имеем
ХЕ — А = Т'1 (ХЕ — В) Т,
отсюда
det (IE — А) = det T'1 det (IE — В) det Г = det (IE— В)
и, следовательно, характеристические полиномы матриц А и В,
а значит, и их собственные значения Хр (р = 1, ..., п), совпадают
между собой.
Кроме того, если
А = S-VS,
где J — форма Жордана, то
В = ТАТ'1 = TS-4ST-1 = (ST-1)-1 J (ST'1).
Таким образом, J есть также форма Жордана матрицы В.
Следствие. Собственные значения Хр (р = 1, ..., п)
рц Л и ее элементарные делители (к — \р)ер (р = 1, ..., т)
являются инвариантами для преобразований подобия A.6.3).
Отметим еще один полезный результат.
Теорема 2. Верхняя треугольная (л X л)-матрица
О
Ъп
oo ... т„_,.„
Lo о ... х
где петый косой ряд отличен от нуля, т. е.
TiaTM • • • 7n-i,n ^ 0,
подобна соответствующей клетке Жордана
"К 1 ... 0"
0 X ... 0
О 0 ... 1
О 0 ... X J
A.6.4)
A.6.5)
A.6.6)
Доказательство. Покажем, что существует неособенная
матрица S = [s/A,] такая, что
A.6.7)
где 1Х — первый единичный косой ряд (см. § 1), или
§ 6]
Положим
ЖОРДАНОВА ФОРМА МАТРИЦЫ
39
Тогда
s/,=
0
0
0
0
0
0
-°
0
0
0
U Sjj
0 0
0 0
_ о о
Sla
«22
0
0
...
• • •
...
S12
S»
0
0
••• «1. n-l
• • • S2, n-l
I
• • ¦ sn-l. n-l
... о
Zj Ъ psp.
,'s ^
0
0
• • • Sl. Л-2
и
0
0
1 _
n-l
(
*.,
&П-1, П-i an-
... 0
0
fin
fan
Tn-l.;
)
,-ll
1
'• ' l
Приравнивая в силу A.6.7) соответствующие элементы вторых
диагоналей матриц 5/t и YS, будем иметь
Sn-l, n-l :== Тл-1, л-
Отсюда, учитывая условие A.6.5), получим
S22 == T23 • • • Tn-1, n Ф 0,
-1. n-l
[1.6.8)
40
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[[Л. ?
Приравнивая соответствующие элементы третьих диагоналей мат-
матриц S/i и FS, находим
S12— 7l2S23~j~ Tl3S33, 1
S-23 = T23S34 + T24S44, 1 A.6.9)
$п-1. п-Л = Tn-a. n-isn-l, n Л~ ЛпЛ, n, I
где sn_i-n = 0. Отсюда последовательно определяются элементы
Аналогично находятся все остальные элементы матрицы S.
Так как на основании A.6.8) имеем detS = SuSaa ... sn_iin_j ^ О,
то матрица — неособенная и, следовательно, теорема доказана.
Следствие 1. Если матрица А имеет вид
4 = S-Idiag[Ki(XI), .... Km(lm)]S
где det S ф 0 и KPQ-P) (p=l, ..., /п) — верхние треугольные
матрицы специальной формы
L° о
X
Р -I
то числа кр (р = 1 т) суть собственные значения матрицы А Т
причем если
mo размеры клеток Кр (лр) представляют собой показатели эле-
элементарных делителей матрицы А.
Следствие 2. Всякую квадратную матрицу А с помощью
преобразования подобия
B = SAS'1
можно привести к почти диагональному виду
'К ь12 ... ьы
b л Ь
ь ' ь ' Y
\_ип1 ип2 ••• Лл .
где \
при jy^k и е — сколь угодно мало -;см. S6]).
5 7] ФУНКЦИИ МАТРИЦЫ 41
Действительно, матрица А подобна матрице
J = diag[J1(kl), ..., Jm(lm)],
где Хь .... >.т (т^п) — характеристические корни матрицы А
и Jpftp) (/? = !, •••, /^ — соответствующие клетки Жордана. Так
как в силу теоремы 2 имеем
где
0
0
0
(p=
К ¦
0 .
0 .
1,
¦•
0 '
0
m).
то, очевидно, матрица А подобна матрице
S==diag[/(, (X,) Km(km)}.,
обладающей нужным свойством,
§ 7. Функции матрицы
Пусть" X — квадратная матрица. Тогда, используя действия
над матрицами, можно определить матричные полиномы
(правый) и
(левый), где постоянные матрицы Ло, ... , Лр и Во, ... , В9 та-
таковы, что указанные действия возможны. В частности, это могут
быть квадратные матрицы одинакового с X порядка или числа
(скаляры).
Если Q (X) — неособенная матрица, то можно определить ра-
рациональные функции матриц
(правое частное) и
(левое частное).
Пусть
%> (р=\, 2, ...) A.7.1)
42 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ |ГЛ. F
— последовательность матриц одного и того же типа. В таком
случае матрица
С= lim Cp==( lim С'Д'),
р —* со о -* аэ
если она имеет смысл, называется пределом последовательности
A.7.1). Отсюда, естественно, вводится сходимость матричных
рядов
+ ... A.7.2)
А именно, матричный ряд A.7.2) называется сходящимся, если
существует предел последовательности его частичных сумм
S= lim (i/, + t/, + ... + i/p).
р -• со
Предельная матрица S называется суммой ряда A.7.2), т. е.
Заметим, что из определений нормы матрицы вытекает, что
если Ср-+С, то 1) ,|С — СрЦ->0 и 2) j| Cp || -+ \\ С \\ при р-+оо.
Если функция F (X) в некоторой области {X} = D представ-
представляет собой сумму степенного ряда
F (X) = 2 ЛрХР
р = 0
или
где Лр, Вр (р = 0, 1, 2, ...) — постоянные матрицы, то F (X) на-
называется аналитической функцией от X в области Ь.
§ 8. Матричные ряды
Определение 1. Матричный ряд
?/, + ?/, + ...+ <;„ + ... A.8.1>
будем называть абсолютно сходящимся, если сходится ряд норм
его членов
где норма понимается в смысле 1—111 норм (см. § 4).
§ 8] МАТРИЧНЫЕ РЯДЫ 43
Теорема. Абсолютно сходящийся матричный ряд есть ряд
сходящийся.
Доказательство. Пусть
Up = (U%}) (p=\, 2, ...)
Из определения сходимости матричного ряда следует, что
оо со
р = 1 р = 1
Так как для всех / и k справедливы неравенства
то на основании признака сравнения скалярных рядов все ряды
со
2 U%' абсолютно сходящиеся. Следовательно, матричный ряд
A.8.1) также сходится.
Следствие (признак сравнения). Если матричный
ряд A.8.1) абсолютно сходящийся и выполнены неравенства
Iivy;^li?/Pn (р = \, 2, ...),
то матричный ряд
v, + v, + ...+ vp + ...
также абсолютно сходящийся.
Пусть
% (p=l, 2, ...)
— матричные функции одного и того же типа т X п, где пере-
переменная матрица X ^ D.
Определение 2. Функциональный матричный ряд
2 FP(X) A-8.2)
p = i
называется равномерно сходящимся в области D, если в этой
области сходятся равномерно все скалярные ряды
со
2 $'(*) (/ = 1. •••• т; й=1 л).
Р=Д
Нетрудно убедиться, что справедлив обобщенный при-
признак Вейерштрасса: если ряд норм
2 i'^
44 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ Л1АТРИЧН0Ю ИСЧИСЛЕНИЯ |1Л. I
мажорируется в области D сходящимся числовым рядом
(т. е. \\FP(X ;|=??cp> р=\, 2, ...), то ряд A.6.2; сходится аб-
абсолютно и равномерно в области D.
§ 9. Матричные степенные ряды
Рассмотрим степенной ряд
2 прхр< о-9-1)
где X — (п X я)-матрица, причем для простоты будем считать,
что коэффициенты ар(р = 0, 1, 2, ...) — числа, вообще говоря,
комплексные. Наряду с матричным рядом A.9.1) рассмотрим ска-
скалярный степенной ряд
со
2 а/- A-9.2)
где х — 1-\-щ, и пусть /? — его радиус сходимости.
Теорема 1. Матричный степенной ряд A.9.1) сходится абсо-
абсолютно для каждой матрицы X, для которой выполнено неравенство
\\X\\<R. A.9.3)
Доказательство. Так как внутри круга сходимости
;xi<^R степенной ряд A.9.2) сходится абсолютно (см. [7]), то из
неравенства A.9.3,) вытекает сходимость ряда
J] |а„!1!Х||р.
р = 0
Но (з силу свойств нормы
\\арХР\\^\ар\\\Х\\Р (р = 0, 1, 2, ...).
Поэтому на основании признака сравнения степенной ряд A.9.1)
сходится абсолютно в данной точке X.
Следствие. Если скалярный степенной ряд A.9.2) сходится
для любого х (т. е. R — co), то соответствующий матричный
ряд также сходится для любой квадратной матрицы X.
Пусть
СО
f (Х)= ]] а/' A.9.4)
р = 0
— функция, аналитическая в области <\
«> 9]
МАТРИЧНЫЕ СТЕПЕННЫЕ РЯДЫ
45
Теорема 2. Если F (X) определена для матрицы X, то она
определена также для любой подобной матрицы SXS~l (det S Ф 0),
причем справедлива формула
) = SF(X)S-\ A.9.5)
Доказательство. Пусть
p=i
Используя очевидные свойства подобных матриц
S (X -f- Y) S-1 = SXS + SYS'1
и
имеем
B
р = 0
Отсюда, переходя к пределу при N-±co и учитывая, что
п
Mm
.V—> со
получаем формулу A.9.5). Теорема
доказана,
Теорема 3. Матричный степен-
степенной ряд
СО
? ааХ" A.9.6)
(ар — скаляры) сходится, если все соб- рис j
ственные значения Хь ... , \п матри-
матрицы X находятся внутри круга сходимости соответствующего
скалярного ряда
A.9.7)
1 =0
т. е. если выполнены неравенства
\h\<R (*=l, .... л),
гбе R —радиус сходимости ряда A.9.7) (рис. 1).
46 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ [ГЛ. I
Если же хотя бы одно собственное значение матрицы X -:е-
жит вне замкнутого круга сходимости \\x\\^R, то ряд A.9.6)
расходится (см. [8]).
Доказательство. 1) Пусть
— отрезок матричного ряда A.9.6). Приводя матрицу X к жор-
дановой форме (§ 5), будем иметь
где Хь ..., 1т (т^_п) — характеристические корни матрицы X,
отвечающие различным элементарным делителям,
— соответствующие клетки Жордана и det S ^ 0. Отсюда, исполь-
используя теорему 2 и свойства квазидиагональных матриц, получим
), .... Jm(\J])S =
iJAK)), ... , /v(./m(v))]S. A.9.8)
Далее, применяя бином Ньютона и правило возведения единич-
единичного косого ряда в степень A.1.3), имеем
2 ар(\Еч+1?)>= 2 2 арС;
р = 0 t=f)f = »
Так как
то
= 2 «pp(p-i)...(p-
р'= с
^(^I^ (^0,1,2,...).
§ 9] МАТРИЧНЫЕ СТЕПЕННЫЕ РЯДЫ 47
Поэтому
N
<?> V /{rq)
и, следовательно,
Л'
VI /'9) "VI 'г
г = О г — О
где eq — порядок клетки Жордана Jq(\), так как
/<?) = 0 при г S= e9.
Отсюда при N -»¦ оо, учитывая сходимость рядов (см. [6])
со
^^ (Ч) = 21 sp (р - о • • • (р -г +1) Н"г
(г = 0, 1, 2, ...; 9 = 1, .... т),
будем иметь
Поэтому на основании формулы A.9.8) находим, что существует
предел
-=S^1diag[F(/1(X1)),...,F(ym(Xm))]S A.9.10)
и, значит, матричный степенной ряд A.9.6) сходится.
2) Если некоторое Х? лежит вне замкнутого круга сходимости
\x\5sR, то
N->co
не существует и поэтому ряд A.9.6) расходится.
Следствие. Если собственные значения Xk (k = 1,..., п) мат-
матрицы X лежат внутри круга сходимости |х|<^R скалярного
ряда A.9.7), то характеристическими корнями матрицы
со
р—о
являются числа f (kk) (k = 1,..., п).
48 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ | ГЛ.
Если, сверх того,
то порядки соответствующих клеток Жордана матриц X и F (X)
совпадают между собой (теорема Лаппо-Данилевского).
Этот результат непосредственно вытекает из формул A.9.9),
A.9.10), а также из следствия 1 к теореме 2.
§ 10. Тождество Кейли и формула Сильвестра
Пусть X — (л X «)-матрица и
Д (к) = det (кЕ — X) A.10.1)
— ее характеристический полином.
Теорема. Всякая квадратная матрица X удовлетворяет
своему характеристическому уравнению, т. е.
Д(Х) = 0 A.10.2)
(тождество Кейли).
Доказательство. Действительно, пусть
где Jq (kg) (q = 1,..., tri) — клетки Жордана и det S Ф 0. Так как
А (X) — аналитическая функция, то на основании формулы A.9.10)
имеем
Д (X) = S-1 diag [Д (J1 (X,)) A (-UU)l S.
Если kg — характеристический корень матрицы X кратности a.q, то
(q=\,...,m). Поэтому, учитывая, что порядок соответствующей
клетки Жордана eq^a.q, в силу формулы A.9.9) будем иметь
г=п
(q = 1,..., т)
и, следовательно,
Д(Х) = О.
Теорема доказана.
Пусть
г (X) = 2j арх \ х ' ---¦. К)
— аналитическая функция, определяемая степенным рядом со ска-
скалярными коэффициентами ар (р = 0, 1,...).
КГ ТОЖДЕСТВО КЕЙЛИ И ФОРМУЛА СИЛЬВЕСТРА 49
Рассмотрим соответствующую матричную функцию
Положим, что собственные значения ХЛ (k=l,...,n) матрицы X
различны и удовлетворяют условию
1ч1<С# (k=l,..., п).
Построим интерполяционный полином Лагранжа
п
такой, что
Тогда разность F (л;) — P (x) есть аналитическая функция, имеющая
нули X, Х„ и, следовательно, ее можно представить в виде
F (х) — Р (х) = (jc — X,)... (х — Xл) G (х),
где G (*) — аналитическая функция в круге \x\<^R. Отсюда
получаем
F(x) = P(x) + \(x)G(x), A.10.3)
где
Д (х) = (х — л,)... (х — XJ = det (*Я - X).
Так как матрицы Д (X) и G (X) содержат степени только одной
матрицы X, то они коммутируют между собой и, следовательно,
тождество A.10.3) останется в силе, если вместо скаляра х под-
подставим матрицу X. Таким образом, имеем
F (Х) = Р(Х) + Д(Х)О(Х). A.10.4)
Но в силу тождества Кейли
Д(Х)=0.
Поэтому из равенства A.10.4) получаем формулу Сильвестра
(см. [8])
и
Г (Л) = / -р; 7—г гт -ут ~^- ^ ^—- Г \ки) , (I . IU.D)
v ; Li ^ —X!)...(xft —xft_,)(x* —xft+1)...(Xft —xn) ft/> v ;
причем предполагается, что характеристические корни \k(k =
= 1,..., п) матрицы X различны. Формула Сильвестра дает
50 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ [ГЛ. I
представление аналитической функции/7^) в виде полинома
от матрицы X.
Замечание. Если среди собственных значений \k матрицы
X имеются кратные, то формула Сильвестра имеет более сложный
еид (см. [1], [8]), который может быть получен соответствующим
предельным переходом из формулы A.10.5).
§11. Производная и интеграл матрицы
Пусть F (t) = [fjk (t)] — функциональная матрица типа т X п
класса С1 (а, Ь), т. е. функции ffk(t) непрерывно дифференцируемы
в некотором интервале a<^t<^b. Тогда под производной (см. [1])
понимается матрица
Употребляется также обозначение -гг = F (t).
Если соответствующие матричные действия имеют смысл, то
справедливы следующие соотношения:
1) если С — постоянная матрица, то
dt ~u'
2) ?t[F(t) + G(t)] = F(t) + G'(t);
3) | [CF @1 -= CF' (t), | [F (t) C) = F' (t) C;
4) | [F (/) G (t)] = F(t) G (t)+F(t) G' (t).
Далее, пусть F (t) — неособенная матрица и F~l (t) — ее обратная
матрица, Имеем
F(t)F~1(t) = E.
Дифференцируя это равенство, получаем
Отсюда
Приведем еще одну формулу дифференцирования. Пусть V —
скалярное произведение
§ 11] ПРОИЗВОДНАЯ И ИНТЕГРАЛ МАТРИЦЫ 51
Учитывая, что
dt \dt J '
имеем
Укажем еще один результат. Пусть (п X «)-матрица X (t) ? С1 и
•• т раз
Имеем
У (t) = "l![X (t)rx' (t) [X (t)y—'
v=o
В частности, если X (t) коммутирует со своей производной X' (t),
X{t)X'(t) = X'{t)X(t),
то получаем
^ [X (t)]m = m[X (тт~'Х' {t) = mXr (t) [X (t)]m~l.
Пусть
Fp(f) = (f%4t))eC4a, b) (p=l, 2,...)
и матричный ряд
S Fp(t)
p=i
сходится при t 6 (a, b), а ряд производных
со
2 F'p (О
P=I
сходится равномерно на (а, Ь), т. е. все функциональные ряды
p=i
равномерно сходятся на (а, Ь). Тогда при t ? (а, Ь) справедлива
формула
р=Л
Доказательство проводится аналогично скалярному случаю.
В частности' формула A.11.1) верна, если
\\FpV)\\^cp (p=l, 2,...),
ос
где ряд ? сР сходится.
р=\
Если матрица F(t) ? С [а, Ь], то при to?[a, b] и t ?'[a, b]
определяется ее интеграл (см. [1])
S F (т) d-r = E/УА (т) dx).
'о h
Используя понятие предела матрицы, интеграл матрицы можно
определить через предельный переход
\F(x)d-= lim ?
max I
где /o<*i<.••<'» = t и
Д^, = ^ + 1 — /, (v = 0, \,...,n — 1).
Справедливы следующие свойства:
1) если F(t) = <fy(t), то
2) если С—постоянная матрица, то
'о h
t t
\F(x)Cdi = \F{-z)dT.-C\
to to
3) если F(x), G(t)? С [/o, /], то
\[F(x)-\-G (т)] й!т = J F (t) dx + \ G (x) dT;
4) если F(t), G^KC'tfo. 0, то
^ f (t) G' (t) dx = F (t) G(t)-F (t0) G (g - ( F (t) G (t) dx
(формула интегрирования по частям);
5)
||Sf(T)dT||^J |! F (т) || ! d, \. A.11,2)
'o 'o
111
ПРОИЗВОДНАЯ И ИНТЕГРАЛ МАТРИЦЫ
53
Действительно, в силу свойства 3) нормы матрицы для любой
конечной суммы имеем
га—1
м=0
0 и учитывая непре-
непреОтсюда, переходя к пределу при max | A
рывность нормы, получаем формулу A.11.2).
В дальнейшем иногда придется рассматривать вектор-функции
/(*) =
П{х)
fm(X)
компоненты которых /у (х) = fj (хи ..., хп) зависят от нескольких
переменных x = (xlt..., хп). Если fj(x)^Cl (/=1, ••-, т),
то под производной такой функции по вектору х понимается
матрица Якоби
dx'
\ dxk
¦1 ¦ ¦" дхп
где
Если мы имеем сложную функцию
u=f(x) (« = («ь ...,' ит); х = (хи ..., хп)),
X = <f(t), t=(tu .... tp),
причем f(x) и ф (t) непрерывно дифференцируемы, то согласно
правилу дифференцирования сложной функции получаем (см. [7])
р.
dxs
— 1, ..., т; k = \, .... п).
Отсюда, используя правило умножения матриц, будем иметь
du
~dt~
т.
dt '
54 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ I ГЛ. I
§ 12. Экспоненциал матрицы
Пусть Х = (Х]ь) — квадратная матрица порядка п.
Определение. Под экспоненциалом квадратной матрицы X
понимается матричная функция
Матричный ряд A.12.1) сходится для любой квадратной мат-
матрицы X и притом абсолютно. Действительно, составляя соответ-
соответствующий ряд норм, будем иметь
i^ A.12.2)
что и доказывает наше утверждение.
В частности, на основании формулы A.12.2), используя 1 или
II нормы, где || Я || = 1, имеем
lie* ц^ У Ш! = влх«.
р = 0
Пусть матрицы X и Y перестановочны, т. е.
Докажем основное свойство экспоненциала матрицы
Действительно, в силу абсолютной сходимости разложения
A.12.1) имеем
пл со со со
хр vi Yi "V V хрУд
р\ Li ц\ Li L. pi?!
Положим
I / ^ 0 10 \ •
тогда
и, следовательно,
СО S СО S
ехе>'= У У ^VS'\.= У ~ У CpsX"Ys'p, (i.12.4)
La La p! (s—р)\ » s! La s
где
§ 13| НОРМАЛЬНАЯ ФОРМА ЭКСПОНЕНЦИАЛА МАТРИЦЫ 55
— число сочетаний из 5 элементов по р. Так как матрицы X и
Y перестановочны, то
Отсюда на основании формул A.12.4) и A.12.1) получаем
5 = 0
что и требовалось доказать.
Из формулы A.12.3), в частности, находим
A.12.5)
Отметим еще одно свойство экспоненциала матрицы. Если Xt —
квадратная матрица, подобная матрице X, т. е.
то имеем
00
eXl = 2 J\ (SXS-1)" = S (
p=0 p=0
т. e.
exp (SXS~X) = S (exp X) S'K A.12.6)
(cp. § 9).
§ 13. Нормальная форма экспоненциала матрицы
Пусть А — квадратная матрица. Рассмотрим экспоненциал
более общего вида
eAt, A.13.1)
где t — числовой множитель (параметр). Обозначим через
собственные значения матрицы А, отвечающие различным клет-
клеткам Ji(Xi), ..., Ут(Ат) ее канонической формы Жордана, и пусть
еъ ..., ет, соответственно, порядки этих клеток. Тогда
где S — некоторая неособенная матрица
•" НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ [ГЛ. I
Воспользовавшись формулой A.12.1) и учитывая известные
свойства квазидиагональных матриц, имеем
= 5 (diag(ef/i'x", .... e'W ]S. A.13.2)
Так как
где Eq — единичная матрица порядка q и /<?> — ее первый единич-
единичный косой ряд, то
о? со р
/- = 0
г! (/»— г)! д ' г
Как известно,
причем
—»' rl ^j (р — г)'.
при
A.13.3)
^ (р—г)! ~ *
Поэтому из формулы A.13.3) окончательно получаем
.13.4)
где
Формулы A.13.2) и A.13.4) и дают нормальную форму матрицы.
Заметим, что формулу A.13.4) можно было непосредственно
получить из общих формул A.9.9) и A.9.10).
Замечание. Из формул A.13.2) и A.13.4) при /==1 выте-
вытекает, что если ).q(q—-\, ..., т) -- собственные значения матрицы
А, то e'i являются собственными значениями матрицы еА, при-
причем, так как е'я Ф 0, порядки соответствующих клеток Жордана
матриц А и еА одинаковы (§ 9, теорема 3, следствие).
Прим о р. Написать нормальный вил матрицы е , где
1 0"
А—
0 2 1
0 0 2
§ 141 НЕКОТОРЫЕ СВОЙСТВА ЭКСПОНЕНЦИАЛА МАТРИЦЫ 57
Гак как матрица А в данном случае есть клетка Жордана, го на осно-
основании формулы A.12,4) получаем
г , t t*
1 ГГ 9i
e2!
1! 2!
-00 ; -
Замечание. Из формул A.13.2) и A.13.4) можно получить
оценку нормы матрицы eAt.
Пусть
а = max Re л, (Л).
Используя I норму или II норму, на основании формулы A.13.2)
при /ЗгО получаем
max|eY', У % ==?с е"л Р (t), A.13.5)
где Р (/) — некоторый целый полином степени fe = max(e9 — 1).
Так как при любом г ^> 0 имеем
lim ^ = 0,
то из формулы A.13.5) находим
||ел'||<«?<а+г)' при 0s?/<oo, A.13.6)
где c = c(s) — некоторая положительная постоянная.
Оценка вида A.13.6) имеет место также и для III нормы.
Отметим, что если характеристические числа матрицы А, об-
обладающие наибольшими вещественными частями а, имеют простые
элементарные делители, то при ^5=0 справедлива улучшенная
оценка:
||e*'||<ce"'. A.13.7)
§ 14. Некоторые свойства экспоненциала матрицы
Найдем dete^. На основании формулы A.13.2) получаем
det eAl — det 5 ' det eu>- a*>.,. det e""> (>'m' det S = Ц det e ui{1ч}.
58 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ
Так как в силу формулы A.13.4), очевидно, имеем
dete'W=eW (q = l, ..., т),
го
(ГЛ. I
9=1
где
Собственные значения Хд являются корнями векового уравне-
уравнения
или
— an
— a«i
det
X-
(kE —
— &\% . .
— u^'2 • ¦
Л) = 0,
• — «i»
• -a*,
• X—ап„
= 0.
Отсюда получаем
=0. A.14.2)
Так как выражение ^1 ед\> очевидно, представляет собой сумму
9=1
всех корней уравнения A.14.2), где каждый корень берется сла-
слагаемым столько раз, какова его кратность, то
... + ann = Sp A.
Таким образом, из формулы A.14.1) имеем
где
i = >, a,
матрицы А.
Найдем производную матричной функции еА' по параметру t.
Так как элементы матрицы
A.14.3)
§ 151 ЛОГАРИФМ МАТРИЦЫ 59
представляют собой целые функции от /, то законно почленное
дифференцирование ряда A.14.3) по t и. следовательно, имеем
TteA!= 2 ^^-> = Ае* = е*>А. A.14.4)
Из формулы A.14.4) вытекает, что матрица
удовлетворяет дифференциальному уравнению
— = АХ
причем X @) = Е.
В более общем случае, если (п X «)-матрица X (t) ? С1 ком-
коммутирует со своей производной X' (t), получаем
[Х ^K' Х'{t) = eX U)X' W = X>
§ 15. Логарифм матрицы
Определение. Пусть X — квадратная матрица. Матрица У,
удовлетворяющая условию
называется логарифмом матрицы X и обозначается следующим
образом:
К = Ln X.
Теорема. Всякая неособенная матрица X имеет логарифм.
Доказательство (см. [6]). 1) Пусть сначала X = J(kx)~
клетка Жордана порядка еь соответствующая собственному зна-
значению А,, причем X] ф 0, так как предполагается, что матрица не-
неособенная. Имеем
где Л — первый единичный косой ряд.
По аналогии с известным логарифмическим разложением
60 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ |1Л I
рассмотрим матрицу
У = ?1пХ1-|- ^У ^-^—(~) , A.15.2)
p=i
где
Ln X, = In j X, | -j- i (arg lt -f- 2Ы)
(k = 0, ±1, ±2, ...).
Так как /р = 0 при р^ех, то ряд A.15.2) сходящийся и матри-
матрица Y всегда имеет смысл.
На основании формулы A.15.1) при jz|<^l справедливо то-
тождество
со
~'=^2' = 1+г, A.15.3)
из которого вытекает, что коэффициенты при одинаковых степе-
степенях г степенных разложений левой и правой частей равенства
A.15.3) совпадают между собой. Так как квадратная матрица Z
коммутирует со своими степенями, то степенное разложение левой
части равенства A.15.3) формально совпадает с соответствующим
матричным степенным разложением
аз
где принято Zn = E. Поэтому, если матричный ряд \ ^--—Zp
сходится, то имеет место тождество
ехР
со
2 —pZ'^E + Z A.15.4)
Отсюда, учитывая, что матрица Е перестановочна с любой матри-
матрицей того же порядка, и используя основное свойство экспонен-
экспоненциала матрицы, будем иметь
со
P=i
Следовательно.
§ is;
ЛОГАРИФМ МАТРИЦЫ
6!
Таким образом, принимая во внимание, что /f = Ip при р <^es
и JP — O при /?32еь окончательно получим
?! - I
Г V Г I Г \ С Г 1 ! V (—1)Р"' , /t ГС С\
Ln л = Ln J1 (/.j) = c Ln Xj -[- > i—-—/ A.15.5)
*^ Pi
2) Пусть теперь X — произвольная неособенная матрица. При-
Приводя X к канонической-форме Жордана, будем иметь
где S — неособенная матрица и Jg (kQ) (q=lt ..., tn) — соответ-
соответствующие клетки Жордана. Можно принять
LnX = 5-Idiag[Ln/1(X,), ..., Ln Jm(km)]S, A.15.6)
где Ln Jq (Х?) определяются по формуле A.15.5).
Действительно, аналогично формуле A.13.2) имеем
eLn
5 =
что и подтверждает формулу A.15.6).
Теорема доказана.
Замечание 1. Из формул A.15.6) и A.15.5) следует, что
Ln X есть функция многозначная.
Замечание 2. На основании следствия теоремы 2 из § 6 и
из формул A.15.5) и A.15.6) вытекает, что если lq(q=l,..., m)
суть собственные значения неособенной матрицы X, то Ln;.?
(<7- 1, ..., т) являются собственными значениями матрицы LnX,
причем X и Ln X имеют одинаковые порядки eq соответствующих
клеток Жордана.
Замечание 3. Если (п X п)-матрица X действительная и по-
положительно определенная, т. е. все собственные значения ее
Ху (X) (/—1, ..., п) положительны, то имеется вещественная ма-
матрица 5, приводящая ее к жордановой форме. В этом случае,
как видно из формулы A.15.6), для матрицы X существует дей-
действительный In X.
Пример. Найти Ln X, где
1 1 О'
О 1 1
_0 0 1
Используя формулу A.15.5), получаем
Ln Л = ? Ln I -i—/г — ^ /а:
1 -у
О 2/Ы 1
О 0 2ft7i«.
(k — целое;
62
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОГО ИСЧИСЛЕНИЯ
1ГЛ. I
Нетрудно убедиться, что если неособенные матрицы X и Y
коммутируют между собой, т. е.
= YX,
то
где ветви логарифмов выбираются соответствующим образом.
Упражнения к главе I
1. Показать, что верхняя треугольная матрица
Г —
0 Ъг ¦•• Tin
О 0 ... Лш
О 0 ... ¦,„_,, „
Lo о ... о
с нулевой диагональю нилъпотентна, т. е.
где п — порядок матрицы.
2. Пусть Г— верхняя треугольная матрица вида
где Г — сумма косых рядов от 1-го до (п — 1)-го.
Показать, что
Г = сГ'? — сГ2Г + аГ2 -f ¦.. + (—1 )п-1а-™Гп-1
3. Пусть Е—А — неособенная матрица. Показать, что
[Е — А)'1А = А{Е — А)-К
4. Показать, что если
JAK), -, Jmi^rn)],
4-i = diag|_y /_ 1) __у (__L^1
О, 9=1, ..., т).
то
5. Доказать, что для всех квадратных матриц X определены аналитичес^
кие функции
2! " ^4! "
Найти sin У (а), где /(а) —клетка Жордана.
УПРАЖНЕНИЯ К ГЛАВЕ I
63
6. Пусть Г — сумма косых рядов от 1-го до (п — 1)-го.
Показать, что
7. Пусть
/4 =
-S ?2 О ... О 0-1
О S ?s ... О О
0 0 0 ... S Е<
L0 О О ...OS J
— матрица типа 2р х 2р, где
и Es — единичная матрица второго порядка. Показать, что
V5 — ets tV~l с1'
1! ¦'¦ (р — 1I
еА' =
tP-
где
О ets
О О
efS=tfit\a*P -sinl
I sin E
ets
'}¦
cosp*.
8. Пользуясь формулой Сильвестра, найти ех, если
Г2 1-
14
X
L4
9. Для матриц второго порядка X найти представление аналитической
функции F(X) в виде полинома в следующих случаях: 1) неравных харак-
характеристических корней X; -ф >.2 и 2) равных X, = \%.
10. Найти Ln А, если
fcos а — sin otl
[sin а cos а
(ot действительно).
ГЛАВА II
УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ
ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ
§ 1. Основные понятия теории устойчивости
Рассмотрим нормальную систему обыкновенных дифференциаль-
дифференциальных уравнений
#=/,(', Ух Уп) (/=1, •¦¦, п), B.1.1)
где t — независимое переменное (время); ух, ..., уп— искомые
функции; /;- — функции (в общем случае комплекснозначные), опре-
определенные в некотором полуцилиндре:
причем t — число или символ — оо и Dy — открытая об-
область действительного <Мпу или комплексного ffiy «-мерного век-
векторного пространства. В дальнейшем для краткости систему B.1,1)
будем называть дифференциальной.
Переходя к матрично-векторным обозначениям
= \ i =со1оп(г/ь ..., уп),
f(t, У) — colon [ft (t, y), ..., fn(t, y)]
и учитывая, что
-? = colony yn),
систему B.1.1) можно записать в виде матрично-векторного урав-
уравнения
%=f(t, У). B.1.2)
Действительную или комплекснозначную вектор-функцию у =
=у (t)czCx, определенную в некотором интервале (a, b)czt-
ч В тех случаях, когда это нр вызывает неясностей, мы ьместо сим-
символа -i-oc будем писать символ со.
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ УСТОЙЧИВОСТИ
65
и удовлетворяющую при a<^t <^b уравнению B.1.2), будем назы-
называть его решением.
В дальнейшем будем обычно предполагать, что
f(t, У) Е с?'у (z),
т. е. вектор-функция f(t, у) в области Z непрерывна по незави-
независимой переменной t и имеет непрерывные частные производные
первого порядка по зависимым переменным уи ..., уп. Если
система B.1.1) рассматривается в действительном пространстве
¦а%п т0 производные правой части ее трактуются в обычном
смысле. В том случае, когда у может принимать комплекс-
комплексные значения, функцию/^, у) будем предполагать аналитической
относительно совокупности комплексных переменных уи ..., уп
(в простейшем варианте — многочленом от этих переменных). При
этом под производными f'jVk(t, уи .-., у„)(], k=l, ..., п) пони-
понимаются производные с точки зрения теории аналитических функ-
функций (см., например, Гурса, Курс математического анализа, Гос-
техиздат, 1933, т. II, ч. 1, гл. XVII).
При этих условиях справедлива теорема Коши (см. [9], [10],
[11]): для каждой системы значений (tu, у„) ? Z существует
единственное решение системы и
B.1.2): п
y=y{t) (t0 — А </</„^В;
Л>0, Я>0),
определенное в некотором ин-
интервале (t0 — Л, /0 -г В) cz (t, со)
и удовлетворяющее начальному
условию: y(to)=yo, т. е. одно-
однозначно разрешима соответствую-
соответствующая задача Коши. Иначе говоря,
в области Z cz If X Щ суще-
существует единственная интеграль-
интегральная кривая y~=y(t) системы
B.1.2), проходящая через точку
Рис. 2.
Мо, Уо)
Заметим, что если для любого t (^ [/0, 1Л-'Г В) точка у (t) ^ KczDv,
причем расстояние d ограниченного замкнутого множества (ком-
(компакта) К до границы области Dy положительно (рис. 2), то можно
принять В = оо, т. е. решение у (I) имеет смысл при /0=ss/<^co
(бесконечно продолжаемо вправо). Аналогично при t = — оо фор-
формулируются условия бесконечной продолжаемости влево (Л = — оо).
3 Б. П. Демидович
66
УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ
[ГЛ. II
В дальнейшем мы ограничимся рассмотрением дифференциаль-
дифференциальных систем вида B.1.2), обладающих свойством единственности,
т. е. таких, для которых задача Коши при начальных данных
D. У о) ? Z имеет единственное решение. Иными словами, если
y(t) (a</<6)
есть решение системы B.1.2), то оно тождественно при a<^t<^b
с решением этой системы у (t), определяемым начальными усло-
условиями: у (t9) =y (to), где to — любая точка интервала (а, Ь).
Решение у =у (t) можно рассматривать как траекторию фазо-
фазового пространства %, гДе t играет роль параметра.
Для дифференциальных систем с непрерывной правой частью
и свойством единственности имеет место интегральная непрерыв-
непрерывность решений (см. [9] — [12]), а именно: если у (t) (a<^t<^b) есть
Рис. 3.
решение системы B.1.2), то для любых е]>0 и [a, $]cz(a, b)
существует 8]>0 такое, что решение z(t), определяемое началь-
начальным условием z(i)=z0, где tGI*. PI и II ^(т)— y(l) ll<8>
будет иметь смысл при asg:^^p, причем \\ z (t)—.У(О||<Се Для
^G[«, PI (см. рис. 3).
Определение 1. Решение ч\ = t] (t) (a <^ t<^ oo) системы
B.1.2) называется устойчивым по Ляпунову (см. [13]) при t-*--\-oo
(или, короче, устойчивым), если для любых ?^>0и/0^(а, оо)
существует 8 = 8 (е, 4)^>0 такое, что
1) все решения y=y(i) системы B.1.2) (включая решение
т) (t)), удовлетворяющие условию
определены в промежутке
т.е.
при
§ ч
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ УСТОЙЧИВОСТИ
67
2) для этих решений справедливо неравенство
Н.У(')-Ч('I1<* ПРИ to^t<co. B.1.4)
Иными словами, решение ц (t) устойчиво, если достаточно близ-
близкие к нему в любой начальный момент t0 решения у (t) целиком
погружаются в сколь угодно узкую s-трубку, построенную вокруг
решения т) (t) (рис. 4).
У
Рис. 4.
Из неравенств B.1.3) И B.1.4) по смыслу вытекает, что всегда
можно выбирать 8 ^ е.
В частности, при f(t, 0) = 0 ¦ тривиальное решение (положе-
(положение равновесия) r\ (t) = 0 (а <^ t <^ оо) устойчиво, если для любых
е^>0 и /0 G (а> °о) существует 8 = 8(е, t^^O такое, что из нера-
неравенства
следует неравенство
<s при t0^t<oo.
Заметим, что из устойчивости нетривиального решения т) (t) не
вытекает его ограниченность; обратно, из ограниченности реше-
решения, вообще говоря, не следует его устойчивость (см. § 7).
Определение 2. Если число 8 ^> 0 можно выбрать незави-
независящим от начального момента to?T, т.е. 8 = 8(г), то устойчи-
устойчивость называется равномерной в области Т.
Определение 3. Решение т) = т) (/) (а <[^<[оо) будем назы-
называть неустойчивым по Ляпунову, если v для некоторых s ^> О,
t0 ? (а, со) и любого _8J> 0 существует решение уь (t) (хотя бы
одно/ и момент tt = tjb) ^> /0 такие, что
Из отрицания определения 1 вытекает, что следует считать
также неустойчивым решение r\(t), непродолжаемое при
t-*-oo или такое, для которого в любой окрестности точки т)(/„)
3*
68
УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ
[ГЛ. И
найдется точка у0, порождающая в момент времени /0 решение у (/),
непродолжаемое при 6,*---. /<^со.
Аналогично, тривиальное решение (положение равновесия) г} = 0
неустойчиво (рис. 5), если для некоторых е_~>0, t0 ?j (а, оо) и лю-
любого 8^>0 существуют реше-
решение у г, (t) и момент tt'
такие, что
Определение 4. Реше-
Решение т) = т) (t) {а <^ / <^ оо) на-
называется асимптотически ус-
устойчивым при *->--)-ос, если:
1) это решение устойчиво по
Рис. 5. Ляпунову и 2) для любого
t0 (^ (а, оо) существует Д =
= ДD)^>0 такое, что все решения у —у (/) (/0 ==s/<^oo), удовле-
удовлетворяющие условию || _у (/0) — т) D) || <С ^> обладают свойством
lim
B.1.5)
Таким образом, асимптотическая устойчивость есть «устойчи-
«устойчивость с нагрузкой», т.е. устойчивость при наличии допол-
дополнительных условий. В частности, тривиальное решение т)(/) = 0
асимптотически устойчиво, если оно устойчиво и
Шп.у(/) = 0
Шар |! у || <^А D) при фиксированном t0 является областью
притяжения положения равновесия О.
Определение 5. Пусть система B.1.2) определена в полу-
полупространстве i2 = {t_<^t<dco\ х {||jc||<^oo}.
Если решение т) = т) (/) (а <^ t <^ ос^) асимптотически устойчиво
при /->оо и все решения у —у (t) (t№^t<^oo, to^>a) обладают
свойством B.1.5), т. е. Д = со, то решение ц (t) называется асимп-
асимптотически устойчивым в целом.
Иными словами, в случае асимптотической устойчивости в целом
решения ц (t) его областью притяжения в любой началь-
начальный момент t = t0 является асе пространство ЗЯ^(Д = оо).
Пусть наряду с системой B.1.2) имеется возмущенная система
B.1.6)
где
г=ср1оп(гь
$ I] ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ УСТОЙЧИВОСТИ 69
Определение 6. Решение ц — ц (t) (a <^ t <^ оо) системы
B.1.2) называется устойчивым при постоянно действующих воз-
возмущениях <p(t, z) (см. [14]), если для любых е^>0 и t0 ^ (а, оо)
существует 5 = 8 (s, /0)^>0 такое, что при || <p(t, z) || <^S все реше-
решения z=z (/) системы B.1.6), удовлетворяющие условию || z (ta) || ^S
определены на промежутке [t0, оо), причем
Замечание. Если решение ц = ц (t) (a<^t<^сю) системы
B.1.1) с непрерывной правой частью устойчиво для какого-нибудь
фиксированного момента t9 ? (а, со), то оно будет устойчиво для
любого другого момента t'u ? (а, оо), т. е. является устойчивым
в смысле определения 1.
Действительно, пусть при
имеем
1|У(')-Ч(')||<е для ^о«=;/<оо. B.1.8)
В силу свойства интегральной непрерывности существует 8' =
Q такое, что если
\\y{Q-4{Q\\<b', B.1.9)
то
1|У@—4(')ll<8(s, h) = b при t?[tl Г«|.
Поэтому на основании формул B.1.7) и B.1.8) из неравен-
неравенства B.1.9) вытекает неравенство
||У(')-Л(')Ц<в при /i </<сзо.
Таким образом, можно ограничиваться проверкой устойчивости
решения, а также его асимптотической устойчивости, лишь для
некоторого заданного начального момента t9.
Отсюда также получаем, что если решение t\(t) (a<7<^oo)
неустойчиво при t = t9, то оно является неустойчивым для любого
другого момента t'o ? (а, оо).
В дальнейшем для теорем устойчивости мы, как правило,
начальный момент t0 будем считать фиксированным (см. [14]
115], l!6j).
70 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. II
§ 2. Общие свойства решений линейной дифференциальной
системы
Рассмотрим линейную дифференциальную систему
п
4t = 2 а»(/)У* + Ь® (/ = 1. • • •. п). B-2.1)
* = 1
где ajk(t), f/ (t) ? С (/+), т. е. коэффициенты системы и свободные
члены ее непрерывны в интервале /+ = (а<^<^оо), причем а —
число или символ — со. Если не оговорено противное, то функции
ajk(t) и fjif) предполагаются действительными. Что касается ре-
решений yj = yj(t)(j—l, ..., я), то, вообще говоря, мы будем
считать их комплекснозначными.
Можно также предполагать функции aJk(t) (/, &=1, ..., п)
и fj(t)(j—l, ... , п) кусочно непрерывными на /+. В этом слу-
случае под решением yj{t)(j=\, ..., п) понимаются непрерывные
на /+ функции, удовлетворяющие уравнениям B.2.1) в инте-
интегральной форме
yj (t) = Cj+§ |2 fly* (т) yk (т) + fj (
'о *= 1
(/=1, ..., n; l0 ^ /+; Cj — постоянные).
Введя векторно-матричные обозначения
у = со\оп[уи ..., у„], A{l) = [aJk(t)},
/(/) = colon[/,(/), .... fn(t)),
систему B.2.1) можно записать более просто:
% B.2.2)
где A(t)ec(n, /(t) ее (п.
Для линейной системы B.2.2) справедлива следующая теорема
существования и единственности решений (см.
[9] — [П.]): ддялюбой системы чисел t0 ? /+, уо = colon [y9t, ..., уы]
существует решение y=y{t) системы B.2.2), определенное для
всех t ^ /+ и удовлетворяющее начальному условию:
y{U)=yu, B.2.3)
причем решение с такими свойствами единственно в /+.
Пусть
X @ = [xJk (/)] (det X (t) ф 0) B.2.4)
— фундаментальная матрица (иными словами, фундаментальная
система решений, записанная в виде (п X п) -матрицы) соответствую-
§ 2] ОБЩИЕ СВОЙСТВА РЕШЕНИЙ -71
щей однородной дифференциальной системы
d-?t = A(f)x, B.2.5)
т. е. матрица, состоящая из п линейно независимых ее решений:
xw(t) = colon [*„(/), .... xnl(t)];
*<»>(/) = colon [*,„('), ..., xnn(t)].
В записи {xjk{t)\ первый индекс / обозначает номер коорди-
координаты, а второй k — номер решения, так что в фундамен-
фундаментальной матрице B.2.4) решения располагаются по столбцам.
Покажем, что матрица X (t) удовлетворяет матричному урав-
уравнению
X(t) = A(t)X(t). B.2.6)
Действительно, так как функция xjtl (t) удовлетворяет /-му урав-
уравнению системы B.2.5), то имеем
ауЛ0*,*@. B-2.7)
5=1
Следовательно, вспоминая правило перемножения матриц, получаем
что и требовалось доказать.
Заметим, что при нашем доказательстве не понадобилась нео-
неособенность матрицы X(t). Поэтому любая матрица X(t), столбцы
которой представляют собой решения линейной однородной системы
B.2.5), удовлетворяет матричному уравнению B.2.6).
Обратно, если (п X и)-матрица X (t) = [xjk (t)] удовлетворяет
матричному уравнению B.2.6), то столбцы ее
*<*> = colon[*„(*), ..., xnk(t)] (k=\, ..., п)
представляют решения линейной однородной системы B.2.5).
Если при этом det X (t) ф 0, то матрица X (t) является фундамен-
фундаментальной.
Действительно, очевидно, имеем
x^(t) = X{t)ek>
где eft = colon[0, ..., 1, ..., 0]. Умножая справа на ек уравне-
уравнение B.2.6), получим
72 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. II
т. е.
^ = A(t)x^ (k=l, .... п).
Если X (t) — фундаментальная матрица системы B.2.5), то, как
известно (см. [9] — [12]), каждое решение этой системы может быть
записано в виде
x(t) = X(t)c, B.2.8)
где с = colon [сь ... , сп] — некоторая постоянная матрица-столбец.
Пусть решение x = x(t) удовлетворяет начальному условию
x(tt)) — X0. Полагая в тождестве B.2.8) t = t0, будем иметь
х U) = K{U)c\
отсюда с = Х ' (to)x (t0). Следовательно,
x(t) = X(t)X~1(to)x(to).
Вводя матрицу Коши
K(t, to) = X(t)X-1(t0),
получим
x(t) = K(t, h)x(t,). B.2.9)
В частности, если фундаментальная матрица X (t) нормирована
при t = t,]t т. е. X(to) = E, где Е— единичная матрица, то фор-
формула B.2.9) принимает вид
x(t) = X{t)x{U). B.2.10)
Заметим, что матрица Коши не зависит от выбора фундамен-
фундаментальной матрицы X (t). Действительно, если X (t) есть другая
фундаментальная матрица системы B.2.1), то имеем X (t) — X (t) С,
где С — постоянная неособенная матрица. Отсюда X (t) = C~[X^ (t)
и, следовательно,
К if, /0) = X (t) X (t0) = X (t) СС-'Х-1 (/о) = К it, t0).
Любое решение y=y(t) неоднородной системы может быть
записано в виде
У (t) =У (t) + X (t) с,
где у (/) — некоторое фиксированное решение ее и с — постоянный
(а? X 1)-вектор. Если у (t) таково, что у (t0) = 0, то, очевидно,
и, следовательно,
y{t)=-y{t)^rKit, to)у (h).
§ 3] ФОРМУЛА ОСТРОГРАДСКОГО - ЛИУВИЛЛЯ 73
§ 3. Формула Остро градского—Лиувилля
Пусть
X(t) = [x,k(t)]
— фундаментальная матрица однородной дифференциальной си-
системы B.2.5) и
W(t) = detX(t) B.3.1)
— определитель Вронского.
Используя правило дифференцирования определителя, находим
dW
dt
хп (t) ... xlk{t) ... xln (t)
Х'л (t) ... X'jk (t) ... X;n (t)
XnX (t) ... Xnk (t) ... Xnn (t)
Отсюда, так как
x'-k (t) = ^ au (t) xsk (t) (/, k = 1, ... , n).
в силу известных свойств определителя получаем
хп (t) ... xlk (t) ... xin (t
dt
aJs (t)
XS1
@ • • • *sn Ф j =
xni (t) ... xnk(t) ... xnn(t)
r. e.
^ = Sp A (t)W(t).
SAMdt
Следовательно,
Интегрируя последнее уравнение в пределах от tn до I, где t0 ? /+
и t f- I , приходим к формуле Остроградского—Лиувилля (см.
[9] -~[llj)
W (t) = W (t0) exp \ Sp Л
B.3.2)
74 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. Ц
§ 4. Матрицант
Рассмотрим линейную однородную дифференциальную систему
^- = A(t)x, B.4.1)
где Л(/)?С(/+). Пусть /0 ? 1+ и x = x{t) — решение системы
B.4.1), определяемое начальным условием
*('о) = *о, B.4.2)
где х0 — некоторый вектор-столбец. Для аналитического представ-
представления решения jc (t) применим метод последовательных приближе-
приближений в специальной форме. Из уравнения B.4.1) с учетом B.4.2)
получаем интегральное уравнение
t
x(t) = x{h)-\-\A(h)x{tl) dt,.
to
Заменяя в последнем интеграле jc (ti) суммой
h
х (t0) + $ A (t2) x (U) dt,,
будем иметь
x{t) = x (U) + \ A (U) x (t0) dU + \A (U) dh \ A (tt) x (/,) dU.
Повторяя этот процесс неограниченное число раз,' получим фор-
формальное представление решения
x(t) = x (t0) + $ A (h) x (h)dU + j A (/,) dty ( A (L) x (/2) dt, + ...
to to tQ
ИЛИ
*(*)=^',*(*o), B.4.3)
где
$e = E+[A{t1)dtl+\A(ti)dtl)A(ti)dti-\- ... B.4.4)
to to 'o
Матрица Sj0 называется матрицантом дифференциальной системы
B.4.1). Покажем, что ряд B.4.4) сходится абсолютно для всякого
/? /+, причем сходимость равномерна на каждом конечном от-
отрезке [а, р] d /+.
§ 4] МАТРИЦАНТ 75
Действительно, оценивая члены ряда B.4.4) по первой норме
(см. формулу A.11.2)), получим ряд
Е |j + J |! А (/,) || | Л, | -|- 5 || Л (/,) || | dtx \\\А ((.г) || | Л,! +.. .B.4.5)
t» to tt,
Пусть [а, 8] С \h — A, U-\-B\C.l* (Л>0, В>0) (рис. 6),
С = тах(А, В) и М= max ||Л@||.
1„ - A^St^to + B
При ? (^ [а, [3] последовательно имеем
\\\АШ\<ил\\\А1
to ta
Так как \t — ta I <; С, то, следовательно, ряд B.4.5) мажорируется
сходящимся знакоположительным рядом
|! Е || + МС -|- ~~ +... = || Е || — 14-ехр (МС). B.4.6)
Отсюда на основании известного признака Вейерштрасса получаем,
что знакоположительный функциональный ряд B.4.5) сходится
to-A t0 ос t fi to*B
I,
Рис. 6.
t'
равномерно на любом отрезке [а, ^] (I /+. Следовательно, матрич-
матричный ряд B.4.4) также сходится абсолютно и равномерно на [а, р].
Дифференцируя почленно ряд B.4.4), получаем равномерно
сходящийся на [а, р] ряд
+ A{t)\A {U) dt, \ A (tt) dta + ... = А @
кроме того,
76 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. 'Т
Следовательно, матрицант Q't(l представляет собой нормированную
фундаментальную матрицу однородной дифференциальной системы
B.4.1), причем любое решение этой системы хA) выражается по
формуле B.4.3).
В силу свойства единственности решений линейной дифферен-
дифференциальной системы имеет место тождество
Qto^K(t, /0),
где K(t, r0) — матрица Коши.
Формулы B.4.3) и B.4.4) впервые были получены итальянским
математиком Пеано. На основании теоремы единственности полу-
получаем основное свойство матрицанта
§ 5. Метод вариации произвольных постоянных Лагранжа
Для неоднородной дифференциальной системы
i?t = A(t)y-j-f(t) B.5.1)
будем искать решение в виде
y = X(t)u, B.5.2)
где X (I) — фундаментальная матрица соответствующей однородной
системы
^ = A(t)x B.5.3)
и u = u(t) — новая неизвестная вектор-функция. Подставляя вы-
выражение B.5.2) в уравнение B.5.1), получим
X @ ^ + X(t)a = A (О X @ и -4-/@,
или так как
X(t) = A{t)X(t),
то отсюда будем иметь
X(t)^=f(t).
Следовательно,
§ 51 МЕТОД ВАРИАЦИИ ПРОИЗВОЛЬНЫХ ПОСТОЯННЫХ ЛАГРЛНЖА 77
Поэтому на основании формулы B.5.2) находим (см. [6], [12])
\ d'i, B-5.4)
'о
где
K(t, tl) = X(t)X^(tl)
—матрица Коши. Для определения произвольного постоянного
вектора с в формуле B.5.4) положим t = t0. Тогда будем иметь
c = X-l(tB)y(t0)
и, следовательно,
y(t) = K (t, to)y (*„) -f $ К (t, k)f{tx) dty. B.5.5)
'o
В частности, если фундаментальная матрица X (t) нормирована
при t — U, т. е. X(to) = E, то из формулы B.5.5) получим
o) + [ K(t,
h
Из формулы B.5.5) вытекает, что неоднородная система B.5.1)
имеет частное решение
t
у (о=$ Kit, tofitjdtu
h
удовлетворяющее условию у (to) = 0.
Заметим, что если матрица A(t) = A постоянна и Х(^) = Е,
то
X(t)Xl(t0 и Xit — U + t»)
представляют собой фундаментальные матрицы однородной си-
системы B.5.3), совпадающие при ^ = ^. Поэтому
X{t)X '(«sX^-dig.'
Следовательно, полагая to = O, получаем, что дифференциаль-
дифференциальная система
d?t = Ay-\-f(t), B.5.6)
где А = const, имеет общее решение
t
у @ — X it) у ф)-\-\Х (t-tJfVJdh. B.5.7)
78 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. II
В частности, при_у@)==0 получим, что неоднородная систе-
система B.5.6) обладает частным решением
§ 6. Общие теоремы об устойчивости линейных
дифференциальных систем
Рассмотрим линейную дифференциальную систему
% = A(t)y+f(t), B.6.1)
где A{t), /(ОеС(П, и пусть
§ = Л@* B.6.2)
— соответствующая однородная система.
Определение 1. Линейную систему B.6.1) будем называть
устойчивой (или вполне неустойчивой), если все ее решения у =
=у (t) соответственно устойчивы (или неустойчивы) по Ляпунову
при t-*-\-oo.
Замечание. Как мы увидим ниже, решения линейных диф-
дифференциальных систем либо все одновременно устойчивы, либо
неустойчивы. Подобная терминология не применима к нелинейным
дифференциальным системам, некоторые решения которых могут
быть устойчивыми, а другие — неустойчивыми.
Теорема 1. Для устойчивости линейной системы B.6.1) при
любом свободном члене f(t) необходимо и достаточна, чтобы было
устойчивым тривиальное решение хо = О D<^<С°о, t0 ? /+) со-
соответствующей однородной системы B.6.2).
Доказательство. 1) Докажем сначала необходимость
условия теоремы. Пусть т] = ц (t) (t0 eg t<^ со) есть некоторое
устойчивое решение неоднородной системы B.6.1). Это значит, что
для каждого е >> 0 существует 8 ^> 0 такое, что для любого реше-
решения y=y{t) системы B.6.1) при <0==s*<^oo справедливо неравен-
неравенство
Н.У(')-Ч@1Ке. B.6.3)
если только
11У('в)-Ч(*о)||<8. B-6.4)
Но, как известно,
*(').=.У@ —1(9 B-6.5)
является решением линейной однородной системы B.6.2), причем
любое ее решение x(t) может быть представлено в виде B.6.5).
§ 6] ОБЩИЕ ТЕОРЕМЫ ОБ УСТОЙЧИВОСТИ 79
Таким образом, неравенства B.6.3) и B.6.4) эквивалентны
следующим:
||*(911<в при /,а
если только \\ jc (?„) || <[ &.
Отсюда вытекает, что тривиальное решение jco = O соответ-
соответствующей однородной системы B.6.2) устойчиво по Ляпунову при
t -*¦ сю.
Замечание 1. Из доказательства следует, что устойчивость
тривиального решения jto = Q однородной системы B.6.2) вытекает
из устойчивости хотя бы одного решения линейной систе-
системы B.6.1) при каком-нибудь свободном члене f(t) (может быть,
/ !
0 )
2) Докажем теперь достаточность условия теоремы. Пусть
тривиальное решение jro = O однородной системы B.6.2) устойчиво
по Ляпунову при t -у оо. Тогда, если x = x(t) (t0 sg t <^оо) — про-
произвольное решение однородной системы такое, что
11*(911<Ч*. 'о),
то
11*(*I1<Се при t<,^t <^со.
Следовательно, если ц (t) — некоторое решение линейной неодно-
неоднородной системы B.6.1) и у (t) — произвольное решение этой си-
системы, то из неравенства
будет вытекать неравенство
\\y(t)-4(t)\\<t при
А это и значит, что решение r\(t) устойчиво при t-+oo.
Следствие 1. Линейная дифференциальная система устой-
устойчива, когда устойчиво хотя бы одно решение этой системы, и
вполне неустойчива, если неустойчиво некоторое решение ее.
Это утверждение непосредственно вытекает из теоремы 1 и за-
замечания 1 к. ней.
Следствие 2. Линейная неоднородная дифференциальная си-
система устойчива тогда и только тогда, когда устойчива соответ-
соответствующая однородная дифференциальная система.
Замечание 2. Таким образом, поведение решений линейной
неоднородной системы B.6.1) с любым свободным членом /(/)
в смысле устойчивости такое же, как поведение решений соответ-
соответствующей однородной системы B.6.2).
80
УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. I!
Действительно, для неоднородной системы B.6.1) поле инте-
интегральных кривых
v(i)=y(t) + X(t)c, B.6.6)
где у (t) — частное решение системы B.6.1) и X (t)—фундамен-
(t)—фундаментальная матрица решений однородной системы B.6.2), топологи-
топологически эквивалентно (с сохранением близости) полю интегральных
кривых
x(t) = X(t)c
соответствующей однородной системы B.6.2); разница только та,
что в первом случае «ось» y—y(t), вообще говоря, криволинейна
(рис. 7), а во втором случае ось л: = 0 прямолинейна (рис. 8).
о
Рис. 7.
Рис. 8.
Поэтому в дальнейшем мы ограничимся изучением устойчиво-
устойчивости лишь однородных линейных дифференциальных систем.
Определение 2. Линейную дифференциальную систему
B.6.1) назовем равномерно устойчивой, если все решения у(()
этой системы равномерно устойчивы при t-*¦-{- оо относительно
начального момента t9 (^ /+ (§ 3).
Теорема 2. Линейная дифференциальная система B.6.1)
равномерно устойчива тогда и только тогда, когда тривиальное
решение jco = O соответствующей однородной системы B.6.2)
равномерно устойчиво при t-*--\-oo.
Доказательство проводится с помощью рассуждений, анало-
аналогичных тем, которые были применимы при доказательстве тео-
теоремы 1.
Определение 3. Линейную дифференциальную систему
B.6.1) назовем асимптотически устойчивой, если все решения
y(t) этой системы асимптотически устойчивы при t-+-\-oo.
Теорема 3. Линейная дифференциальная система B.6.1)
асимптотически устойчива тогда и только тогда, когда три-
§ 7] УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ОДНОРОДНЫХ СИСТЕМ 81
виальное решение л;0 = 0 соответствующей однородной системы
B.6.2) асимптотически устойчиво при t->-\-co.
Доказательство этой теоремы непосредственно вытекает из того
обстоятельства, что разность двух решений линейной неоднород-
неоднородной системы есть решение соответствующей однородной системы
(формула B.6.5)).
Следствие. Для асимптотической устойчивости линейной
неоднородной дифференциальной системы B.6.1) при любом сво-
свободном члене f{t) необходимо и достаточно, чтобы была асимпто-
асимптотически устойчивой соответствующая однородная система B.6.2).
§ 7. Устойчивость линейных однородных
дифференциальных систем
Рассмотрим однородную систему
^ = A(t)x, B.7.1)
где A(t)eC(n.
Покажем, что устойчивость системы B.7.1) эквивалентна
ограниченности всех ее решений.
Теорема 1. Линейная однородная дифференциальная система
B.7.1) устойчива по Ляпунову тогда и только тогда, когда
каждое решение x = x(t)(t0s^st<^co, ^о G ^+) этой системы огра-
ограничено на полуоси t0^t<^co.
Доказательство. 1) Докажем сначала, что ограничен-
ограниченность решений линейной однородной системы достаточна для
ее устойчивости.
Пусть любое решение системы B.7.1) ограничено на [/0, оо) С1+
Рассмотрим нормированную фундаментальную матрицу
где X(t<)) = E. Так как матрица X(t) состоит из ограниченных
функций x)k(t), то она ограничена, т. е.
||Х(/)||<М при /,
где М — некоторая положительная постоянная, зависящая, вообще
ГОВОРЯ, ОТ tfj.
Как известно B.2.10), каждое решение x = x(t) системы B.7.1)
может быть представлено в виде произведения
x(t) = X(t)x(t,).
Отсюда получаем
если только
82 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. II
Следовательно, тривиальное решение лго = О, а значит, в силу
теоремы 1 из § 6 и любое решение системы B.7.1) устойчиво по
Ляпунову при ^->--|~оо.
Таким образом, система B.7.1) устойчива.
2) Докажем теперь, что ограниченность решений линейной
однородной системы нербходима для ее устойчивости.
Пусть система B.7.1) допускает неограниченное на [t0, со)
решение z{t), где,, очевидно, z{tu)^0. Фиксируя два положи-
положительных числа е)>0и 8^>0,-рассмотрим решение
II* С.) I
Очевидно,
причем в силу неограниченности z(t) для некоторого момента
t^t имеем
Таким образом, тривиальное решение лг0 = О системы B.7.1)
неустойчиво по Ляпунову при t-*--\-oo, а следовательно, на
основании теоремы 1 из § 6, система B.7.1) также вполне не-
неустойчива.
Заметим, что здесь неустойчивость системы обнаруживается
в усиленной форме, так как положительное число е про-
произвольно.
Следствие. Если неоднородная линейная дифференциальная
система устойчива, то все ее решения или ограничены, или не
ограничены при t-*--\-oo.
Пример. Скалярное уравнение
допускает неограниченное решение у0 = t. Так как
то решение у0, очевидно, устойчиво и даже асимптотически.
Замечание. Для нелинейной дифференциальной системы из
ограниченности ее решений, вообще говоря, не следует устой-
устойчивость их.
Пример. Рассмотрим скалярное уравнение
dx . .
smx
§ 7] УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ОДНОРОДНЫХ СИСТЕМ 83
Интегрируя, будем иметь (рис. 9)
х — Arcctg (ctg х0 — t) при х0 ф Ы B.7.2)
и
х — кк при х0 = k-к (k = 0, ± 1, ± 2, ...). B.7.3)
Все решения B.7.2) и B.7.3), очевидно, ограничены на (—оо, -)-оо).
х
Однако решение хо =
хо € @> я) имеем
oo, так как при любом
Теорема 2. Линейная однородная дифференциальная система
B.7.1) асимптотически устойчива тогда и только тогда, когда
все ее решения x = x(t) стремятся к нулю при t-*--\-oo, т. е.
lim л: @ = 0.
B.7.4)
Доказательство. 1) Пусть система B.7.1) асимптотически
устойчива при t-*--\-oo. Тогда все ее решения, в том числе
тривиальное х0 = 0, асимптотически устойчивы при t -v -\~ оо.
Следовательно (см. § 1, определение 4), для любого решения %(t)
системы B.7.1) имеем
lim 1@ = 0,
если только || !(/0I!<Сд> гДе 4G/+ произвольно.
Рассмотрим произвольное решение x(t), определяемое началь-
начальным условием x(to) = Xo фО. Положим
где
lit)— *w
6W~ II *('.)!
84 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. II
Так как решение | (t), очевидно, удовлетворяет условию
то для него справедливо соотношение B.7.5). Следовательно,
lim x(t)==0.
Таким образом, необходимость условия теоремы доказана.
2) Пусть условие B.7.4) выполнено. Тогда для каждого ре-
решения х (t)(t0 ==? / < оо) будем иметь
||лг(/)||<^1 при Т<^t<^оо.
Так как на конечном отрезке [t0, Т] непрерывная векгор-функ-
ция x(t) ограничена, то любое решение x(t) ограничено на полу-
полупрямой [/0, со) и, следовательно, на основании теоремы 1 система
B.7.1) устойчива, причем ее тривиальное решение асимптотически
устойчиво. Отсюда в силу теоремы 3 из § 6 вытекает асимптоти-
асимптотическая устойчивость системы B.7.1).
Следствие. Асимптотически устойчивая линейная диффе-
дифференциальная система асимптотически устойчива в целом (§ 1,
определение 5).
Замечание. Для нелинейной дифференциальной системы
стремление к нулю всех решений, вообще говоря, не является
достаточным условием для асимптотической устойчивости триви-
тривиального решения ее.
Пример. Рассмотрим систему
dx _ х s
dt ~Т У
dy У
dt t
допускающую тривиальное решение х = 0, у = 0. Интегрируя, получим
или, полагая <0=1, будем иметь
x(t) = x(to)te-* «•>«-",
Очевидно,
х (t) — 0 и у (t) -* 0 при t -* -j- со.
<5 8] УСТОЙЧИВОСТЬ СИСТЕМЫ С ПОСТОЯННОЙ МАТРИЦЕЙ 85
Однако для любого 8 > О при х (t0) — V1, y(to)=^b будем иметь
Рис. 10.
Следовательно, решение х = 0, у = 0 не является устойчивым, а тем более
асимптотически устойчивым при t—*-\-co (рис. 10).
§ 8. Устойчивость линейной дифференциальной системы
с постоянной матрицей
Рассмотрим систему
dx
'° 8.1)
где A — [aJk] — постоянная (п X п)-матрица.
Положим
= eAtu;
тогда, учитывая свойства экспоненциала матрицы (гл. I, § 14),
будем иметь
или
¦§- = е" ~ + Ае"и = АеА<и,
«"-^ = 0.
B.8.2)
Так как deteAf = etsv л -^ Q; то матрица еА' неособенная. Поэтому
из B.8.2) получаем
du
dt
= 0
и, следовательно,
где с — постоянная («X 1)-матрица.
86 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. II
Таким образом, общее решение системы B.8.1) с постоянной
матрицей А есть
x = eAtc. B.8.3)
Пусть x(tu) = x6. Из формулы B.8.3) имеем
т. е.
и, значит,
B.8.4)
Пусть X,,..., Хт (т^п) — собственные значения матрицы А,
отвечающие различным клеткам Жордана, и еъ ..., ет — соот-
соответствующие им порядки клеток Жордана. Обозначим через 5
неособенную матрицу, приводящую матрицу А к жордановой
форме:
S1dXI),..., /m(Xm)]5,
где Jp(Xp)(p = I, ... , т) — соответствующие клетки Жордана,
Тогда на. основании свойств экспоненциала (гл. I, § 13) из фор-
формулы B.8.4) получаем
X @ = S1 diag [ехр (/ - *,) /, (ХО, ...
... , exp (t -1,) Jm (Xm)] Sx (/,), B.8.5)
где
exp[(t-to)Jp(Xp)] =
"^ 2i '• +--H
2i
где //'(/= 1,..., ep — 1) — соответствующие единичные косые
ряды.
Теорема 1. Линейная однородная система B.8.1) с постоян-
постоянной матрицей А устойчива тогда и только тогда, когда все
характеристические корми Ху = Ху(Л) матрицы А обладают непо-
неположительными вещественными частями
ReXy(i4)<0 (/=1,..., п),
причем характеристические корни, имеющие нулевые вещественные
части, допускают лишь простые элементарные делители (т. е. со-
соответствующие клетки Жордана сводятся к одному элементу).
Доказательство. 1) Докажем сначала достаточность
условий теоремы.
§ 8] УСТОЙЧИВОСТЬ СИСТЕМЫ С ПОСТОЯННОЙ МАТРИЦЕЙ 87
Пусть Ху = а; 4- % (у = 1,..., р; i—V— 1) — все характеристи-
характеристические корни матрицы А с отрицательными вещественными ча-
частями о,-, отвечающие различным клеткам Жордана, и ХА =
— q-A(?=l (?) — все характеристические корни матрицы А
с нулевыми вещественными частями, причем p-\-q = m — общее
число клеток Жордана в нормальной форме матрицы А. Тогда
в силу формулы B.8.5) любое решение системы B.8.1) имеет вид
* @ = 2 e'f (cos у + i sin py0 P, (О +
? fsinT*Oc*, B-8.6)
* = i
где P;@ — некоторые полиномиальные вектор-функции, степень
которых ниже кратности корня Ху, и ck — постоянные вектор-
столбцы. Так как ау-<^0, то
е*/'Pj(t)-*O при /->-f-oo.
Кроме того,
Поэтому из формулы B.8.6) вытекает, что каждое решение x(t)
ограничено на полурси /0 sg t <^ оо.
Следовательно, на основании теоремы 1 из § 7 система B.8.1)
устойчива.
2) Докажем теперь необходимость условий теоремы
(см. [17]).
Пусть система B.8.1) устойчива. Покажем сначала, что все
характеристические корни ^ матрицы А имеют неположительные
вещественные части. Действительно, предположим, что найдется
собственное значение ls = a-\~h матрицы А такое, что
Тогда, как известно, система B.8.1) имеет нетривиальное реше-
решение вида
где || с || 9^ 0. Отсюда
Ш = |Л'1|И|==ео'!И!-*схэ при t-^oo
и, таким образом, решение неограниченно, что противоречит ус-
устойчивости системы. Поэтому
ReA,<0 (/¦=!,..., л). B.8.7)
88
УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ
[ГЛ. II
Покажем теперь, что каждый характеристический корень Xj с ну-
нулевой вещественной частью Re>-y = 0 имеет простые элементарные
делители.
В самом деле, предположим, что матрица А приведена к жор-
дановой форме
где det S Ф 0, причем некоторому характеристическому корню
Х^ = /;i.s (Re Xs = 0) соответствует клетка Жордана
ГХХ 1 ...00"
О 1...0 0
о о ... к 1
о о ... о к
типа е$Хе.$' гДе
Тогда
..., /W, ..., 0]5 B.8.8)
будет являться матричным решением системы B.8.1), так как
/л ч tj (А ) А1 О
;(\)е sv *,..., 0] S =
Из формулы B.8.8) получаем
diag[0, .... Л11'1, .... 0]= S3 @
Отсюда, оценивая по норме, будем иметь
||diag[0, ..., e'W, ..^, 0]|| =
= || е"*У |К ;| 51| || S (^
Так как
t
B.8.9)
Л
II "• (es —1
0 1 ...
(es-2)!
i_0 0 ... 1 J
то, воспользовавшись, например, первой нормой при
чаем
полу-
полу§ 8] УСТОЙЧИВОСТЬ СИСТЕМЫ С ПОСТОЯННОЙ МАТРИЦЕЙ 89
где a = ReX5 = 0. Из неравенства B.8.9) выводим
при /=гО.
Таким образом, || S (t) j|->-oo при /~>оо, что невозможно для
устойчивой системы.
Теорема доказана.
Замечание. Устойчивая линейная однородная система с по-
постоянной матрицей А равномерно устойчива относительно началь-
начального момента t0 ? (— оо, -\- оо).
Действительно, так как решения устойчивой линейной системы
ограничены, то имеем
;|ел'||«?е при /5гО.
Пусть х (t) — произвольное решение нашей системы. Тогда
и, следовательно, при t^t0 получаем
если
причем число 8 не зависит от начального момента /0. Таким об-
образом, тривиальное решение х = 0 равномерно устойчиво при
/->оо, а значит, и все решения этой системы также равномерно
устойчивы при t-+oo (§ 6, теорема 2).
Теорема 2. Линейная однородная дифференциальная система
B.8.1) с постоянной матрицей А асимптотически устойчива тогда
и только тогда, когда все характеристические корни \j = \j{A)
матрицы А имеют отрицательные вещественные части, т. е.
ReX;.(^)<0 (/=1, ...,«).
Доказательство. 1) Докажем сначала достаточность
условия теоремы. Пусть X,, ..., \т(т ==gn) — все характеристи-
характеристические корни матрицы А, отвечающие различным клеткам Жор-
дана, причем
ReXy<0 (/=1, ..., т). B.8.10)
Из формулы B.8.5) вытекает, что каждое решение системы B.8.1)
имеет вид
90 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. II
где Pj (t) — полиномиальные матрицы. Отсюда на основании ус-
условия B.8.10) получаем
lim х @ = 0
и, следовательно, в силу теоремы 2 из § 7 система B.8.1) асимп-
асимптотически устойчива.
2) Докажем теперь необходимость условия B.8.10). Пусть
система B.8.1) асимптотически устойчива. Тогда эта система ус-
устойчива по Ляпунову при t-+oo, и, следовательно, на основании
теоремы 1 имеем
(/=1, .... т). B.8.11)
Допустим, что найдется хотя бы один характеристический корень
X (l) такой, что
Тогда система B.8.1) имеет решение вида
| = ех*'с== (cos fi^ + isin
где с — ненулевой вектор-столбец. Поэтому
и, значит, | ¦/> 0 при t-*-oo, что противоречит асимптотической ус-
устойчивости системы B.8.1). Следовательно,
ReXy<0 (/=1 т).
Теорема доказана полностью.
Замечание. Таким образом, чтобы доказать асимптотиче-
асимптотическую устойчивость линейной однородной 'системы B.8.1), доста-
достаточно убедиться, что все корни Хи ..., Хп ее векового уравнений
обладают отрицательными вещественными частями. В следующем
параграфе мы дадим необходимые и достаточные условия, при
которых алгебраическое уравнение с действительными коэффи-
коэффициентами имеет корни лишь с отрицательными вещественными
частями.
§ 9. Критерий Гурвица
Рассмотрим полином
f(z) = o,-f alZ + ... + an2n (n^l), B.9.1)
где z = x-\-iy — комплексное число и а0, аи ..., а„ — действитель-
действительные или комплексные коэффициенты.
§ 9]
КРИТЕРИЙ ГУРВИЦА 91
Определение. Полином f(г) степени п;э= 1 называется
полиномом Гурвица, если все его корни (нули) zu z, г„ обла-
обладают отрицательными вещественными частями
Rez,<0 (/ = 1, .... л),
Т. е. все корни г;- расположены в левой комплексной полуплоскости.
В дальнейшем мы будем предполагать, что коэффициенты а0,
аи ..., ап полинома f(z) B.9.1) действительны, причем
ао>О, ап^0. B.9.3)
Такой, очевидно, не имеющий нулевых корней полином для крат-
краткости будем называть стандартным полиномом степени п(«^=1).
Установим простое необходимое условие для полинома Гурвица.
Теорема. Если стандартный полином является полиномом
Гурвица, то все его коэффициенты положительны.
Доказательство. Пусть
Zj = — aj±i$j (j = \ р)
— комплексные корни (Ру^О) полинома Гурвица /(г) B.9.1) и
zft = -T* (*=1, .... Я)
— действительные корни этого полинома. В силу определения
полинома Гурвица имеем
Т*>0. B.9.4)
Обозначим через оу- (/ = 1, ..., р) кратность корня Zj = — ау- -\- ify;
тогда, так как коэффициенты полинома B.9.1) действительны, то
сопряженный корень Zj = — а;- — /р^ имеет ту же кратность о/#
Пусть кратность действительного корня 7* (k = 1, ..., q) есть sft.
Очевидно,
Пользуясь известным разложением полинома /(z) на линейные
множители, имеем следующее тождество:
/(г) =а„[[(г + а, - ipy)e/(z + «у + ipy)'/П (г + 7*)Ч
У = 1 ft=l
или
/ B) = а„П(za + 2ауг + «? 4- Р7)°'П (г + 7а)'*. B.9.5)
Сравнивая коэффициенты при одинаковых степенях переменной z
в правой и левой частях тождества B.9.5), получаем, что все
32 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [1Л. II
коэффициенты полинома f (г) имеют одинаковые знаки. А так как
в силу условия B.9.2) aoj>O, то
flt>0, a3>0, .... а„>0. B.9.6)
Теорема доказана.
Замечание. Легко показать, что для стандартного полинома
второй степени
f + ^ B.9.7)
условие теоремы является достаточным, т. е. если
a.>0, a,>0,
то полином B.9.7) будет полиномом Гурвица.
Для стандартного полинома степени выше второй из положи-
положительности его коэффициентов в общем случае не вытекает, что
этот полином есть полином Гурвица.
П d и м е р. Полином
имеет лишь положительные коэффициенты, но не является полиномом Гур-
Гурвица, так как его корни есть zt = — 3, 22 = l-f-3(, z3 = 1—Ы.
Обозначим для краткости через Я„(и = 1, 2,...) совокупность
всех стандартных полиномов Гурвица степени п, и пусть
— множество всех стандартных полиномов Гурвица.
Для вывода необходимых и достаточных условий для отно-
отношения f (z) (? Н введем понятие присоединенных полино-
полиномов (ср. [15]).
Определение. Полином
F(z) = Sf(z),
где
будем называть присоединенным к полиному f(z).
Лемма 1. Полином, присоединенный к стандартному поли-
полиному Гурвица, есть стандартный полином Гурвица, т. е. если
Ha, то F(z)
Доказательство. Рассмотрим полином
% B) = A + w) f (z) + tf (- г), B.9.8)
где действительный параметр ц пробегает отрезок 0 ^ р <g 1 г причем
« 9]
КРИТЕРИЙ ГУРВИЦА
93
Покажем, что корни Zy(p.) (/=1, 2, ..., п-\-1) полинома
при [1 ^ [0, 1] расположены в левой полуплоскости R
т. е. полином Фц (г) есть полином Гурвица.
Действительно, прежде всего, полагая
где
будем иметь
ao-\ra1z-\- ...
, а,>0, ..., а„
(г) = bQ
г +...
где fev([j.) (v = 0, 1, ..., n) — линейные функции параметра jj..
Отсюда, учитывая, что аа„^>0, получаем
'!ф1*(гI>° при ,z\^sR, р,?[0, 1],
где R достаточно велико и не зависит от ц.
Следовательно, корни Zj (jj.) заключены внутри достаточно
большого конечного круга \z\<^R (рис. 11) и, значит, являются
ограниченными непрерывными функ-
функциями параметра jj.. При р. = 0 поли-
полином Ф^ (г) имеет корни, лежащие в
левой полуплоскости, т. е.
Пусть теперь при некотором р. ? [0, 1 ]
полином Ф* (г) не является полино-
полиномом Гурвица. Тогда по меньшей
мере одна из кривых Zj = Zj (p.) по-
покинет левую полуплоскость и, сле-
следовательно, при некотором значе-
значении и. пересечет отрезок мнимой оси
{— Ri, Ri] (рис. 11). Иными слова-
словами, при р. ? @, 1] полином Ф' (г) имеет мнимый корень р«, т. е.
Отсюда
О = A + а
») + (,[ (_ р/) = 0.
B.9.9)
Так как значения полинома f(z) с действительными коэффициен-
коэффициентами в сопряженных точках гиг комплексно сопряжены, т. е.
то, учитывая, что коэффициенты полинома /(г) действительны
и что полином /(г) есть полином Гурвица, будем иметь
94 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. II
Сокращая равенство B.9.9) на равные, отличные от нуля вели-
величины | / (J3i) | и | / (— РО It получим
т. е.
l+a8P'=fi". B.9.10)
Так как
то р^О и поэтому равенство B.9.10) невозможно при jl ? [0, 1].
Итак,
Лемма 2. Для всякого стандартного, полинома Гурвица сте-
степени п-\-1 существует стандартный полином Гурвцца степени
п (л^Э=1), по отношению к которому данный полином является
присоединенным, т. е. если F(z) ? #„+1, то существуют а^>0
a / B) ? #л такие, что
F (z) = Sf (г) ~ A + «) / (г) + / (- г). B.9.11)
Доказательство. Из функционального уравнения B.9.11)
имеем
Исключая f(—z) из уравнений B.9.11) и B.9.12), получил
«V/ (г) = - A - ог) F (г) + F (- г). B.9.13)
Пусть
FB) = ^0+^z + ...+ ^n+l2n+'
F (- г) = Ао - Ахг +... + (- l)"+Mn1z"+1
n+1z+1,
где Л*>0 (fe = 0, I,..., n+1).
Если выбрать
B.9.14)
то функция f(z), определяемая формулой B.9.13), очевидно, бу-.
дет полиномом м-й степени. Легко проверить, что
Докажем, что / (г) ? #„. Рассмотрим полином
(- z)==- (I ~р) Ао-\-A -
B.9.15),
§ 9] КРИТЕРИЙ ГУРВИЦА 95
где постоянная а определяется по формуле B.9.14) и параметр jj.
пробегает отрезок [0,1]. Корни этого полинома Zj = Zj(i>,) (/=1,
2,..., п-\~2) являются ограниченными непрерывными функциями
параметра jx на отрезке [0,1]. При [* = 0 один из корней г„+3 =
= — находится в правой полуплоскости Re z^>0, а все осталь-
остальные корни Zj (j<^n-\-2) — в левой Re z<^0. Такое расположе-
расположение корней сохраняется при jx ? [0, 1). Действительно, если бы
один из корней z,- перешел из одной полуплоскости в другую,
то кривая Zj = Zj ([*) должна была бы пересечь мнимую ось и при не-
некотором [j. ? @, 1) полином Ф|Г (z) имел бы мнимый корень |3/, т. е.
и, следовательно,
\\-^i\\FW)\ = ^\F -Щ\, B.9.16)
причем р 9^ 0, так как
ФД0) = -Л0A-[А)^0 при |х^1.
Отсюда, учитывая, что F(z) — полином Гурвица, и рассуждая
аналогично тому, как в лемме 1, будем иметь
Поэтому из неравенства B.9.16) выводим
т. е.
что невозможно при а^>0 и действительном C т^ 0.
Из формулы B.9.15) вытекает, что при ц=1 полином Ф,,.B)
имеет двукратный нулевой корень. Пусть корни zp (\>.) -*¦ 0 и
Zqi?)-*-® ПРИ (а-*¦ 1—0. На основании известных соотношений
между корнями и коэффициентами полинома при 0«=?ц<Ч по-
получаем
п+2
1 А
или, переходя к действительным частям, находим
п+2
2 КеМЙГ = ^7' B.9.17)
J—1
Отсюда следует, что один из корней zp (jj.) и z?(jj.) при
0s^[a<4 должен иметь положительную вещественную часть, так
96 устойчивость линейных дифференциальных систем /гл. и
как в противном случае, при jx ->¦ 1 — 0, левая часть равенства
B.9.17) стремилась бы к — оо, а правая оставалась ограниченной
и положительной, что, очевидно, невозможно. А так как гл+5([х)
есть единственный корень с положительной вещественной
частью при Os^jj.<4, то, полагая
Re г»>0, lim
получаем р — п-\-2. Без нарушения общности рассуждения мож-
можно принять q — n-\-\ и, следовательно,
lim г„+, (jj.) = O.
Тогда, учитывая, что
аА^ — A — jj.) А2 -+ aAi -Ф О
при [j, -»-1 — 0, будем иметь
lim zj{v) = cJ, Re cy<0 (/=1,...,«). B.9.18)
Так как на основании формул B.9.13) и B.9.15) при jj. = 1 имеем
то Cj (/=!,..., п) являются корнями многочлена / (z) и, следо-
следовательно,
Замечание. Если
есть стандартный полином степени п-\- 1, причем Л0^>0 и ^
то на основании формул B.9.13) и B.9.14) получаем, что су-
существует стандартный полином / (z) степени п такой, что
Из лемм 1 и 2 следует, что множество всех стандартных по-
полиномов Гурвица Н можно построить, исходя из совокупности
стандартных полиномов Ht первой степени и последовательного
применения операции присоединения 5. А именно
J
р=0
§ 91 КРИТЕРИЙ ГУь-ВИЦА
Рассмотрим стандартный полином
/ (z) = а0
97
B.9.19)
где ао>О, ап=?0 (яё=1).
Составим (я X п)-матрицу Гурвица
О] о0 О О
CL§ Ct% CL\ Ct$
... 0-
... О
-агп-\
а
2п 3
B.9.20)
где принято as = 0 при s<^0 и s^>«.
Теорема Гурвица. Для того чтобы стандартный поли-
полином B.9.19) являлся полиномом Гурвица, необходимо и достаточ-
достаточно, чтобы были положительны все главные диагональные миноры
а0
«3
B.9.21)
его матрицы Гурвица Mf (условие Гурвица).
Доказательство. 1) Докажем сначала необходи-
необходимость условий Гурвица B.9.21), т. е. покажем, что если
f (z) ? Нп, то условия Гурвица B.9.21) выполнены. Для доказа-
доказательства применим метод математической индукции (см. также
[15]).
При п = 1 имеем
f{z) = ao-f-a1z,
причем если /(г) $ Ни то ао~^>О и at
— — ac/ai<^0, то условие Гурвица
0. Так как коиень zx =
выполнено.
Пусть теперь для всех полиномов / (г) ? #„ теорема справед-
справедлива и F (г) ? Я„+1. На основании леммы 2 полином F (г) можно
рассматривать как присоединенный для некоторого стандартного
полинома / (z) ? Нп, т. е.
B.9.22)
где
4 Б,. П. Демидович
УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ
[ГЛ. II
Положим
где
тогда
f(z) — a0
flo>O,
fc=0
где a_i = an+1 = 0.
Составляя главный диагональный минор ?-го порядка матрицы
Гурвица полинома F(z), будем иметь
са9
со,
Щ О
(k=l,..., п).
Отсюда, вынося за знак определителя общие множители с эле-
элементов нечетных столбцов (первого, третьего и т. д.), а затем
вычитая из элементов четных столбцов (второго, четвертого и т. д.)
соответствующие оставшиеся элементы нечетных и вынося за
знак определителя общие множители с преобразованных элемен-
элементов четных столбцов, находим
0 0 0..
a0
0
(&= 1 п),
где ДА — главные диагональные миноры матрицы Гурвица М; по-
полинома / (г).
Так как для полинома / (г) ? #„ согласно индукционному
предположению выполнены условия Гурвица, то
Поэтому, учитывая, что а„>0, имеем
#*+1>0 (А = 0, 1,..., п),
что и требовалось доказать.
§ 9] КРИТЕРИЙ ГУРВИЦА 99
2) Докажем теперь достаточность условий Гурвица, т.е.
покажем, что если для стандартного полинома f{z) выполнены
условия Гурвица, то /(*)?#„.
Для п—1 теорема, очевидно, справедлива, так как если
f(z) = ao-{-a1z,
где ао^>О и Д, =rai>0, то корень полинома
«—SL<0.
Пусть теперь теорема верна для всех полиномов f (г) ? #„ и
F (г) = Л „ + Л 1г-{-... + А^г™
— некоторый стандартный полином степени п-\-1, для которого
выполнены условия Гурвица:
В силу замечания к лемме 2 этот полином можно рассматривать
как присоединенный к некоторому стандартному полиному
, ап^.О) степени п. Так же как при доказательстве
первой части теоремы, получаем, что главные диагональные ми-
миноры Дл матрицы Гурвица Mf удовлетворяют соотношениям
Dk+1 = a*«a0Aft > 0 (k = 1, 2,.... л),
где а>0. Отсюда
Д*>0 (k=\, 2,..., п),
т. е. для полинома f (г) выполнены условия Гурвица. А так как
по предположению теорема верна для всех стандартных поли-
полиномов степени п, то /(г)?#„. Таким образом, полином .Р(г)
является присоединенным к стандартному полиному Гурвица /(г),
и, следовательно, на основании леммы 1 имеем
Теорема доказана полностью.
Замечание 1. Если
/(z) = a, + fliZ + ... + aBz* B.9.23)
есть стандартный полином Гурвица, то имеем
где
g(z) — a()zn-\-alzn~l-\-...-lran B.9.24>
— также стандартный полином Гурвица, и обратно.
4*
100
УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. II
Действительно, если Zj (/=1,..., п) — корни полинома
B.9.23) и Rezy<0, то j- (/=1 п)~ корни полинома B.9.24)
и
(рис. 12). Поэтому условия Гурвица для
полинома можно записывать также в виде
B.9.25)
Рис. 12.
Замечание 2. Пусть
л.*
- = Л*
-dJ — «* B.9.26)
— линейная однородная система с постоянной действительной
матрицей Л = [а,-А] и
det(X? — Л)=0 B.9.27)
— характеристическое уравнение матрицы Л. В раскрытом виде
уравнение B.9.27) имеет вид
Х« _ А ,ХП-
- 1)М„ = 0,
где
a», a.
Для асимптотической устойчивости системы B.9.26) необходимо
выполнение следующих условий:
, А>0 (_1)»л
В частности, должно быть
Sp4<0, (— l)"det4>0. B.9.28)
tLcm система B.9.26) — второго порядка (л = 2), то условия
B.9.28) также достаточны для ее асимптотической устойчивости.
КРИТЕРИЙ ГУРВИЦА
101
В общем случае для асимптотической устойчивости системы
B.9.26) необходимо и достаточно выполнение условий Гурвица:
— Л, 1
A A
/13 /12
Пример 1. Для полинома
где р, д, г действительны, условия Гурвица суть
г>0
>0>
т. е.
Таким образом, в пространстве коэффициентов область Opqr полиномов
Гурвица ограничена положительной частью координатной плоскости г = 0 и
гиперболическим параболоидом r = pq (рис. 13).
У
IP
, 0<zr<pq.
/"/V
Ч
9
Рис. 13.
Рис. 14.
Пример 2. Определить область асимптотической устойчивости для
системы
^
где а и р — действительные параметры.
B.9.29)
102 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. II
Характеристическое уравнение для системы B.9.29) имеет вид
X-J-1 —а ,0
_р X —{— 1 — а =0,
0 — р х+1
или
(Х + 1)[Х*+2Х+A-2ар)]=а
Отсюда асимптотическая устойчивость будет иметь место, если
1 — 2сф>0,
т. е. (рис. 14)
Замечание. Чтобы стандартный полином
имел нули, лежащие лишь в- замкнутой левой полуплоскости
Rez^O, необходимо и достаточно, чтобы все главные диагональ-
диагональные миноры Аь ..., Д„его матрицы Гурвица были-бы неотрица-
неотрицательны:
Д^О (/=1, .... л).
Пусть А = [ajk\ — постоянная действительная матрица и G —
область асимптотической устойчивости системы
% = Ах B.9.30)
в пространстве коэффициентов ajk. Область G* = G{JT* простой
устойчивости системы B.9.30) содержится в замкнутой области
G = G\JT, причем Г* представляет собой часть границы Г, состоя-
состоящую из точек (а1к), для которых характеристические корни с ну-
нулевой вещественной частью матрицы А имеют лишь простые эле-
элементарные делители («безопасная граница-»). Дополнительная часть
границы Г\Г* не входит в область G* (тпасная граница»).
§ 10. Критерий Михайлова
Если степень полинома /(г) сравнительно большая, то приме-
применение критерия Гурвица становится затруднительным ввиду необ-
необходимости подсчета определителей высоких порядков. В этом
случае для определения расположения корней гь ..., гп полинома
^(г) на комплексной плоскости иногда оказываются более удоб-
удобными геометрические признаки, эквивалентные критерию Гурвица.
Мы здесь изложим один из них, так называемый частотный кри-
критерий А. В. Михайлова.
§ 101 КРИТЕРИЙ МИХАЙЛОВА 103
Пусть
f(z) = ao-\-alZ + ... + anzn B.10.1)
— стандартный полином степени п(п^\), т. е. коэффициенты
а0, •••, ап действительны, ао>О и ап Ф 0. Кривая
(Г)
где <о — действительный положительный параметр @ =^ <о =^ -|_ оо)
и i = Y—\, называется годографом Михайлова функции /(г).
Докажем одну лемму, из которой непосредственно следует
принцип Михайлова.
Лемма. Пусть /(г) — стандартный полином степени п, не
имеющий чисто мнимых корней. Тогда угол поворота против хода
часовой стрелки ненулевого вектора f (t<o) при 0 ^ ш ^ -j- °°
Ф = у(п —2m), B.10.2)
где т — число корней полинома f (г) с положительной веществен-
вещественной частью (О^т^п), с учетом их кратностей.
Обратно, если справедлива формула B.10.2), то на положи-
положительной полуплоскости Ree^>0 расположено точно т корней
полинома /(г), где каждый корень считается столько раз, какова
его кратность.
Доказательство. Доказательство леммы проведем, следуя
в основном А. А. Фельдбауму (см. А. А. Ф е л ь д б а у м, Элек-
Электрические системы автоматического регулирования, Оборонгиз,
1954, гл. VII).
1) Пусть стандартный полином /(г) B.10.1) степени п имеет
всего 2р комплексно-сопряженных корней a.j-qzi$j (/=1, ..., р;
a.j ф 0, Ру]>0) и q действительных корней 7* (k—l, •_•-. q\
¦yft^?0), где каждый корень считается столько раз, какова его
кратность, т. е.
В частном случае, возможно р = 0 или q = 0.
Разлагая полином f(z) на линейные множители и учитывая,
что ввиду действительности его коэффициентов комплексно-сопря-
комплексно-сопряженные множители могут быть попарно объединены, получим
/ (г) = ап П {г - *, + %) (г - а, - Ifr) Д (г - Тл).
/=i ft=i
Отсюда
« - «у - %) П (»"» - Т*). B-10-3)
ft = 1
104 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. II
Интересующий нас угол поворота вектора f(i®), очевидно,
равен
где Аг обозначает приращение соответствующей функции ьдоль
годографа Михайлова Г, когда параметр <о изменяется от 0 до
-f-oo. Так как при 0=^<o^-j-°° все множители произведения
B.10.3) ненулевые, то в силу известных теорем об аргументе про-
произведения имеем
р
Фр = Дг Arg ап + Д] дг [Arg (»» — cj -f Щ +
/ = i
+ Arg (fco - а, ~ %)] + ^ Аг Arg (fco - Tft), B.10.4)
где под Argz понимается некоторая непрерывная ветвь
многозначной функции argz-j-2/гх (& = 0, ±1,±2, .<. и arg г —
главное значение аргумента: —x<^arg0=^ic). Для определенно-
определенности будем считать, что при со = 0 аргументы всех слагаемых фор-
формулы B.10.4) равны их главным значениям.
Очевидно,
ArArgara = 0. B.10.5)
Пусть
Arg (ice — olj -f- Щ |ш_0 = arg (—о, + *Эу) = еру @ < 9/ < -к).
Тогда
Arg (j<o — a.j — j-py) |ю„0 = arg (-ау — »ру) = arg (— а, + ф,) = - ?/.
Поэтому
{Arg (ico - ау+ %)+Arg («со-ау-»ру)} |eJ = 0 (/=1, .... р),
B.10.6)
Так как Р/>0, то при увеличении параметра <о, как ясно из
геометрических соображений, Arg (i<e — ay-j- %), оставаясь в пре-
пределах от 0 до х, будет монотонно возрастать, если а/<0, и мо-
монотонно убывать, если ау-^>0; при этом
Arg (tco — а/ + i$j) U=+co = Hm arg (ico — ay -f-1^) =
o>—»-|-co
rg/(o + arg(l-2rf^] = -J (/=1, .... p) B.10.7).
при ау- ^ 0.
§ 10] КРИТЕРИЙ МИХАЙЛОВА . 105
Рассмотрим, теперь поведение Arg (/со—ау—/|3У) при <о]>0.
Если to = Ру — 0^>0, то получаем
Arg (/со — °-j — t'Py) U=p .-о .= lim arg (—ay — /eco) =
О при ay
it при <*y
Если же ^Sspz + O, то в силу свойства непрерывности Arg г
следует положить
Arg (/со - ау %) = (
6 7 у I — 2к-\-arg (iu —о., —Qj) при ау>0.
Отсюда
у, если о
B.10.8)
Arg (/") — ay — %) |m==+00 =
— у, если a,-
Таким образом, из формул B.10.7) и B.10.8) находим
{ Arg (/со — o.j + /ру) -f Arg (/со — ay — $у)} |ш==+оэ =
тс, если a
тс, если a
Следовательно,
Дг [Arg (/со — a.j + фу) -f Arg (/со — ay — фу)] =
= {Arg (/» — ay + %) + Arg (/со — ay — фу)} |™ =+ °° =
тс, если a/^0,
4^n (/=!,•••, P)- B.Ю.9)
я, если •- ^ n
Пусть теверь zk = ~\k — ненулевой действительный корень по-
полинома f(z). Имеем
[ 0, если rfe <С 0,
Arg(f<o —T*)U-o = arg ( —т*)=
[ тс, если
и
Arg (/со — fft) |m==+o3= lim arg (fco — ^k) = ?L.
Поэтому
7C
Ar Arg (/со — -\k) =
2 , если
¦ у, если
(ft=l,..., ?). B.10.10)
106 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. II
Из формул B.10.9) и B.10.10) вытекает, что каждый корень
с отрицательной вещественной частью стандартного полинома / (г)
обеспечивает при 0 «S <» «g -f- со поворот вектора / (»о>) «в среднем»
на -I--S-, а каждый корень этого полинома с положительной ве-
вещественной частью создает при 0 ^ w ^ -f- oo поворот вектора
/(iw)«b среднем» на —у.
Пусть m — число корней нашего стандартного полинома f{z)
с положительной вещественной частью. Тогда число корней этого
полинома с отрицательной вещественной частью ввиду отсутствия
чисто мнимых корней равно п — т. Поэтому для суммарного по-
поворота вектора /(/<») при О^ш^оо получаем следующее выра-
выражение:
что и требовалось доказать.
2) Пусть теперь для стандартного полинома /(г) степени п
без чисто мнимых корней угол поворота при Osgwsgoo вектора
/(««>) определяется формулой B.10.2) и т—число его корней
с положительной вещественной частью. Тогда согласно доказан-
доказанному имеем
^ B.10.11)
Сравнивая формулы B.10.11) и B.10.2), получаем
т = т,
т. е. в этом случае полином f (г) имеет в точности т корней на
положительной полуплоскости 4?ег^>0.
Лемма доказана полностью.
Критерий Михайлова. Для того чтобы стандартный
полином f (г) B.10.1), не имеющий чисто мнимых корней, являлся
полиномом Гурвица, необходимо и достаточно, чтобы угол пово-
поворота против хода часовой стрелки вектора /(г«>) при О^ш^оо
был бы равен
Ф = у«, B.10.12)
где п — степень полинома (n^sl).
Действительно, полагая /п = 0 в формуле B.10.2), получим
соотношение B.10.12).
5 101 КРИТЕРИЙ. МИХАЙЛОВА 107
Следствие. Если для стандартного полинома степени п
имеет место неравенство
то f(z) не колется полиномом Гурвица.
Замечание. Если стандартный полином /(г) есть полином
Гурвица степени п, то, как следует из формулы B.10.4), вектор
/(i'(o) при 0=s?u>sgoo монотонно поворачивается против хода
часовой стрелки на угол -?¦, Так как / @) = а0 ]> 0, то годо-
годограф Г Михайлова полинома /(г), выходя из точки а0 положи-
положительной полуоси Rez^>0, при O^wsgoo будет последовательно
пересекать полуоси 1тг^>0, Rez<^0, Imz<^0, ..., проходя
через п квадрантов.
Обратно, если годограф Г Михайлова стандартного полинома
f(z) степени п без чисто мнимых корней, выходя из точки
/@) = а0^>0 положительной полуоси Rez^>0, при 0<^м=^оо
последовательно по одному разу пересекает п — 1 полуосей Im г^>0,
Rez<^0, Imz<^0 асимптотически стремясь к n-й по счету
полуоси, то угол поворота вектора f(i">), очевидно, равен Щ-и,
следовательно, полином /(г) есть полином Гурвица. На практике
это обстоятельство можно проверить, построив граФчк годографа
Г полинома f(z).
Пример. Пользуясь, критерием Михайлова, получить условия Гурвица
для полинома
f(z) = z3+pz* + qz-\-r B.10.13)
{р, q, r действительны). Имеем
/(И = (— Р^-\~ г) + '»(—
Отсюда точки пересечения годографа Г @ ;g <¦> ^со) полинома /(г) с полу-
полуосями Re г >¦ 0, Imz;>0, Rez<0 последовательно суть iu>k (k = O, 1,2), где
Так как «, и «2 должны быть действительны, то
->О и ?>0. B.10.14)
Далее, имеем
Отсюда, учитывая направления векторов / (tw^) (ft = 0, 1, 2, ...) для случая
полинома Гурвица, находим
г>0, 9 —->0, pq — r>0. B.10.15)
108 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. II
Сверх того, полагая Arg/(im) = 0 при и = 0, очевидно, получаем
Зтс
lim Arg/(»(o) = -^-.
Объединяя неравенства B.10.14) и B.10.15), получим искомые условия Гур-
вица:
р>0, q>0, 0<r<pq, B.10.16)
что согласуется с результатами, полученными ранее (см. § 9, пример 1).
§ 11. Леммы Гронуолла — Беллмана и Бихар и
В дальнейшем будет выгодно использовать две леммы об инте-
интегральных неравенствах (см. [6], [18]).
Лемма Гронуолла — Беллмана. Пусть u(t)^sO и
/(ОЗгО при t^tf, и u(t), f(t)^C[t0,co), причем при t^tu
выполнено неравенство
i
u(/)<c+5 f{h)u(ti)dtu B.11.1)
h
где с — положительная постоянная. В таком случае при t^U
имеем
t
u{t)^cexp\ f (ti)dt}. B.11.2)
Доказательство. Из неравенства B.11.1; получаем
и (t) ^ ,
/{t)a{t) <f@. B.11.3)
cJr\f(tx)u(ti)dtl
Так как
t
d Г .
h
то, интегрируя неравенство B.11.3) в пределах от tu до t, будем
иметь
t t
In [с + \ f (h) и (U) dtt] - In c< \ f (h) и (tt) dh.
§ П] ЛЕММЫ ГРОНУОЛЛА - БЕЛЛМАНА И БИХАРИ 109
Отсюда, используя неравенство B.11.1), получаем
t t
иЦ)<*с + \ f (/,) и (/,) dti ^ с exp \ f (tt) и (/,) dtu
что и требовалось доказать.
Замечание. Переходя в формулах B.11.1) и B.11.2) к пре-
пределу при с-> + 0, убеждаемся, что лемма остается верной, если
постоянная с = 0.
Обобщение леммы Гронуолла —Беллмана. Пусть
непрерывная положительная функция и (t) для любых значений
U T G (а> ^) удовлетворяет интегральному неравенству
tx\, B.11.4)
где f(t)?C(a,b) и f(t)^sO при а</<6. Тогда при а
^b справедлива двусторонняя оценка
t t
ы@<" (<о) exp [J / (/,) dt\ B.11.5)
Доказательство. Из неравенства B.11.4) при t^i имеем
Отсюда на основании леммы Гронуолла — Беллмана получаем
u^^u^exp^f^dh]. B.11.6)
Аналогично из неравенства B.11.4) при t^-z находим
Отсюда, используя метод доказательства леммы Гронуолла — Бел-
лмана, будем иметь
«19 ^i
—/(О " (О
110 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. II
Интегрируя последнее неравенство в пределах от t до т, получим
In и (т) - In [и (т) + ] f (*,) и (h) dh] ^-\f (tt) dtu
t t
т. e.
u(()^u(xL-\ f (f,)и(/,)dh =Sи(z)exp^/(*,)Л,
Заменяя теперь t на х и т на /, из последнего неравенства при
/находим
и, следовательно,
[5] B.11.7)
Полагая x = f0 в неравенствах B.11.6) и B.11.7), получим оценку
B.11.5).
Приведем еще одну лемму, обобщающую лемму Гронуолла —
Беллмана.
Лемма Бихари (см. [18]). Пусть u(t)^Q и f(t)^O при
fSzt0, причем u(t), f(t)^C[t0, со) и имеет место неравенство
t
u(t)^c+\ /(*,)*(«№))Ль B.11.8)
к .
где с — положительная постоянная и Ф (и) — положительная не-
непрерывная неубывающая функция при 0<^и<^п (й^оо), и пусть
Тогда, если
t
J/(y<tti<4T(fl-0) (<e^f<oo), B.11.10)
и
то при tusSLt<^oo справедливо неравенство
u(f)^W-i[{f(t1)dt1], B.11.11)
/о
где Ч1" (ы) — функция, обратная W (и).
В частности, если п = оо и ЧГ (оо) = оо, то неравенство B.11.11)
выполнено без всяких ограничений.
§ П| ЛЕММЫ ГРОНУОЛЛА - БЕЛЛМАНА И БИХАРИ 111
Доказательство. В силу возрастания функции Ф(«) из
неравенства B.11.8) получаем
[ 5 ] B.11.12)
Отсюда
Интегрируя неравенство B.11.12) по t в пределах от t0 до t, при
t^t0 будем иметь
t /
\ ^т 1J ^\/Ui)afi. B.11.13)
[ С
Пусть
тогда
ш'@-/@ Ф(«@) •
Следовательно, формула B.11.13) принимает вид
( wit) t
3 ф[«@]
Отсюда на основании формулы B.11.9), учитывая, что w(t0) —
= с>0 и w(t)^c^>0, будем иметь
W (w @) — Т (w (t0)) =?S J / (h) dtu
to
или, так как W (w(i0)) = W (с) =0, то
T(»@)<i/W*i. B.11.14)
Ввиду того, что
функция v = W (и) имеет однозначную непрерывную монотонно
возрастающую обратную функцию и — ЧГ1 (и), определенную в об-
области ФD-0)<><?(й — 0), где W(-f0)<0. Поэтому, если
112 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ (ГЛ. II
выполнено неравенство B.11.10), то из неравенства B.11.14)
получаем
Отсюда в силу неравенства B.11.8) вытекает искомое неравенство
B.11.11).
Следствие 1. Если Ф(и) = и, то имеем неравенство Гро-
нуолла — Беллмана B.11.2).
Следствие 2. Если Ф(и) = ит (т^>0, m^\), т. е. выпол-
выполнено неравенство
5(y[«(yr^ при t
то
t __i
— m)\ f(t1)dt1]1-"' при
, —t -г- B.11.15)
[\ — (m — l) с'1 ^ /(*i)<tf,]n>-i
to
при т>1 и
§ 12. Устойчивость линейной дифференциальной системы
с почти постоянной матрицей
Теорема 1 (см. [6]). Пусть система
^ = Ах, B.12.1)
где А — постоянная (п X п)-матрица, устойчива при t -v oo. Тогда
система
% B.12.2)
где B(t)?C[t0, oo) и
f||B(/)||^<oo, B.12.3)
to
также устойчива при t -> oo.
§ 121 УСТОЙЧИВОСТЬ СИСТЕМЫ С ПОЧТИ ПОСТОЯННОЙ МАТРИЦЕЙ 113
Доказательство. Без нарушения общности рассуждения
можно считать, что to = O.
Пусть X (t) — фундаментальная матрица системы B.12.1) такая,
что Х@) = Е.
Рассматривая B(t)y как свободный член в уравнении B.12.2)
и применяя метод вариации произвольных постоянных Лагранжа,
получим, что каждое решение у (/) удовлетворяет интегральному
уравнению
\ dt1 (fssO). B.12.4)
о
Отсюда
\\У (t)\\^\\ X (t)\\\\y @)\\ + {\\ X(t -tJM В (Ъ)\\\\у (tJWd^.
Так как система B.12.1) устойчива, то матрица X (t) ограничена,
т. е.
с/г при
Таким образом,
t
IIУ (О II ^* НУ @) || + J А II В ft) IIIIУ ft) II dt,.
о
Используя лемму Гронуолла — Беллмана, будем иметь
t
\\У @1Г*? k || у @) || ехр [Л J || 5 ft) || dtA ^
О
=?S А ||У @) 1| ехр \k \ I! В ft) || Л,] < оо.
о
Следовательно (? 7, теорема 1), система B.12.2) устойчива при
*->ср.
Пример. Пусть
V I / л2 t \ х- Г) (ft \ А\ /О 1 О К\
В силу теоремы 1 все решения лг (<) уравнения B.12.5) вместе с их произ-
производными х (t) ограничены на полуоси 0 <; t0 =g t <: оо.
Замечание. Если матрица A = A(t) переменная, то, как
показал Перрон, теорема 1 в общем случае неверна.
114 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. II
Теорема 2 (см. [6]). Если матрица A = [aJk] постоянна и
система
% = Ах B.12.6)
асимптотически устойчива при t->co, то возмущенная линейная
система
% = [А+В(Щу, B.12.7)
где В (t) ? C[t9, оо) и B(t)-*-Q при t-yco, также асимптоти-
асимптотически устойчива.
Доказательство. Из асимптотической устойчивости си-
системы B.12.6) в силу теоремы 2 из § 8 следует, что характери-
характеристические корни ^j(A) матрицы А обладают отрицательными
вещественными частями. Положим
<x = maxReXy(/l)<0 B.12.8)
/
и выберем число г^>0 столь малым, чтобы имело место неравенство
a + 2s<0. B.12.9)
В уравнении B.12.7) сделаем замену переменных
y = eAtz. B.12.10)
Тогда
и, следовательно,
Переходя к интегральному уравнению, будем иметь
t
z (*)=*(*,) + \ е~А-В (х) е*г (х) rfx.
Отсюда, так как y{t^) = eAt»z(tu), на основании формулы B.12.10)
для решения y(t) (to^t<^oo) получаем интегральное уравнение
у (t) = eA«-'tiy (U) -f \ eA«~^B (t)j; (x) di.
to
Производя оценку по норме, при t^t0 найдем
\\У V) || ^ || е* *-'.) || \\у (t0) || + \ || еА V—) || i| В (т) || \\у (х) Ц dt.
§12] УСТОЙЧИВОСТЬ СИСТЕМЫ С ПОЧТИ ПОСТОЯННОЙ МАТРИЦЕЙ 115
Как известно (см. гл. I, § 13),
iSeMi|==Sce(a+?>< при t^-0,
где с = с(&) — некоторая положительная постоянная. Поэтому
t
\\У (О II =?Sc i|jv (/,) у ^+«)('-'.> + \ а*'+м-*>!! В (т)
ИЛИ
Отсюда, применяя лемму Гронуолла — Беллмана, будем иметь
e-("+t)' \\y (t) || =?SC \\y (/0) II e-««+•)'« exp [\ с || В (t) || <
следовательно,
|| J' @ II =?SC||_y (to) || e(a + ?)('~ 'o) + cj ||B(T)|ldT B.12.11)
h
На основании обобщенного правила Лопиталя (см. [19]I) и
условия теоремы получаем
$ 1!ЯС0 II *=
lim J . ^ =Iim —j = 0.
Поэтому
при /^Г. Отсюда неравенство B.12.11) принимает вид
') Здесь применяется правило Лопиталя в форме Штольца: если
для функций и (t) и v (t) в условиях формулы Коши существует предел
частного
~г~ при t-~ а и w (?) —¦ ± оо при t — а,
то
hm —~ = lim ^ v .
Отметим, что предположение о пределе и (t) при i-»a не делается.
116 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. II
при t^>T, и значит, в силу B.12.7) для любого решения у (t)
системы B.11.7) справедливо равенство
lim y(t) = O.
t—>oo
Таким образом, система B.12.7) асимптотически устойчива.
Замечание. Теорема 2 остается верной, если \\B(t)\\<^k
при t^T, где положительное число k достаточно мало.
Следствие. Линейная система с полиномиальными коэф-
коэффициентами
где Ak (k=,0, I,..., m) — постоянные (пУ^п)-матрицы, асимпто-
асимптотически устойчива, если все корни lj (j = 1,..., п) векового урав-
уравнения
имеют отрицательные вещественные части: Re Ху<^ 0 (/ = 1,..., я).
Действительно, полагая
т-\-\
будем иметь
где
Так как В(т)^-0 при.т^-оо, причем т^-оо при /-»-оо, то наше
утверждение непосредственно вытекает из теоремы 2.
Замечание. Для линейной дифференциальной системы с
переменной матрицей теорема 2, вообще говоря, неверна.
Пример. Скалярное уравнение
Ч—т «><*
имеющее общее решение
очевидно, асимптотически устойчиво при t —<¦ со. Тем не менее скалярное
уравнение
dt t'
коэффициент которого
1А
g 13] СЛУЧАЙ ЛАППО-ДАНИЛЕПСКОГО 11Т
отличается от коэффициента первого уравнения на функцию, бесконечно-
малую при t —> оо, неустойчиво при t —* оэ. Действительно, его общее решение
не ограничено на интервале
§ 13. Случай Лаппо-Данилевского
Рассмотрим один случай линейной системы с переменной матри-
матрицей, для которого нетрудно провести исследование устойчивости.
Положим
dft = P{t)x, B.13.1)
где P{t)^C[/„, оо).
Пусть матрица Р (t) перестановочна со своим интегралом, т. е.
t t
P(t)\P (h) dtt = \P (t}) dh • P (t) B.13.2)
B.13.3)
при t^t0 (условие Лаппо-Данилевского). Тогда
представляет собой матрицант системы B.13.1) (см. [20]). Действи-
Действительно, учитывая, что
d
di
'о
на основании условия B.13.2) имеем (гл. I, § 14)
Q (t) = е(» P(t) = P (t) e1» =P {t) Q (t).
Кроме того,
Q(to) = E.
Таким образом, общее решение системы B.13.1) есть
5jc(/o). B.13.4)
to
Пример. Если B х 2)-матрица имеет вид (см. [20])
H(t)-[q(t) p{t)\>
то условие B.13.2), очевидно, выполнено.
118 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. И
Теорема. Пусть для любой пары (t0, t) ? (а, со) выполнено
условие B.13.2) и существует предел
t
A = Um±- [P{h)dtu B.13.5)
<->-00 l J
'о
"Тогда, если все собственные значения \j — \f(A) (/ = 1,..., п)
предельной матрицы А расположены в левой полуплоскости, т. е.
НеХу(Л)<0 (/=1,...,п), B.13.6)
то линейная система B.13.1) асимптотически устойчива при
t ->оо.
Доказательство. 1) Из условия B.13.2) при (t, s) ?
^ (а, оо) имеем
Р (t) \ Р( Ь) dt, = \P {t,) dh -P (t). B.13.7)
s s
Дифференцируя равенство B.13.7) по переменной s, получим
P(t)P(s) = P(s)P(t).
Отсюда находим
t s t s
P (h) dtt -1 J P (tt) dtt = | \ dh J P ft) P ft) Л, =
/5 * t
\ J P ft) P ft) Л, = | С P ft) dU j P ft) Л,.
Переходя в последнем равенстве к пределу при s-+oo, будем
иметь
t (
] Р ft) dtt ¦ А = А ¦ J P ft) Л,; B.13.8)
таким образом, предельная матрица А перестановочна с интегралом
2) Положим
t
где B(t)-+O при t-+oo.
УПРАЖНЕНИЯ К ГЛАВЕ II
Докажем, что матрицы А и В (t) перестановочны. Действительно,
учитывая соотношение B.13.8), имеем
t
-A* = B(t)A. B.13.9)
На основании формулы B.13.4) выводим, что любое решение
х(/) системы B.13.1) имеет вид
Отсюда в силу перестановочности матриц А и В (t) получаем
x(t) = e'A-e'B^-x(t9). ?2.13.10}
Пусть
и е>0 таково, что
<х-|-2е<0.
Выберем Т столь большим, чтобы выполнялось неравенство
||В@1|<в при t^T>0.
Из формулы B.13.10), учитывая оценку A.13.6) и используя
первую норму, находим
II х (t) || < ||в" || • ||е<* «> || || х (t0) || =s: с ¦ <*•+'>' • ё п в w и || х (,о) || ^
^с\\х(и)\\е*+*^ при t^T.
Следовательно,
\\mx(t) = 0
/-.00
и, значит, линейная система B.13.1) асимптотически устойчива
при /->-оо.
Упражнения к главе II
1. Методом вариации произвольных постоянных Лагранжа найти частное
решение уравнения
(р, q — постоянные; / (t) ? С [0, оо)), удовлетворяющее условиям:
^0, у@)=0.
120 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ
2. Доказать, что полином
|ГЛ. II
ip, q действительны) есть полином Гурвица тогда и только тогда, когда
р>0 и <7>0.
Вывести условия Гурвица для полинома /(z), если его коэффициенты
р и q — комплексные числа.
3. Пусть/(z) — стандартный полином и/(—в) > О F>0), причем для
полинома
g(z)=f(z-h)
выполнены условия Гурвица.
Доказать, что корни Z/ полинома /(z) удовлетворяют усиленному условию:
Rezy< — Ъ.
4. Написать условия Гурвица для возвратного уравнения
z4 -\-pz% -\-qz* -\-pz-{-1 = О
<р и q действительны).
5. Найти область асимптотической устойчивости для скалярной системы
dy
--ft— —<*x—
dz 0
{а и р — действительные постоянные).
6. Используя следствие теоремы 2, указать достаточные условия асимп-
асимптотической устойчивости линейной скалярной системы
{а, Ь, с, d, a, fi, к, Ь — действительные постоянные).
7. Определить область устойчивости системы
dx
(а, Ь, с, и d — действительные постоянные).
8. Построить годограф Михайлова для полинома
и определить расположение его корней на комплексной плоскости.
9. Методом Михайлова вывести условия Гурвица для полинома
(р и q действительны).
УПРАЖНЕНИЯ К ГЛАВЕ II 12Г
10. Доказать аналог леммы Гронуолла. Пусть <р (t), ф (t\i W € С [а, Ь]
и X{t)> 0, при asg^sgj, причем
Тогда
/ t
<р @ ==? ф @ + 5 <|/ (s) ехр Ц
при a
И. Пусть
где A (t) ? С [*„, оо).
Доказать, что
t t
\\x\tb) || ехр [—^ || A (ti) || dtt] t^\\x (t) || «g || x (t0) || exp j || A (tt) || dtt
при t^t0.
12. Доказать, что если
00
I \\ A (t1) + AT(tl)\\dtl<:со,
h
то все решения действительной системы (*) из 11 ограничены на [^0, оо).
13. Доказать, что если о>0и
то все решения скалярного уравнения
ограничены на [t0, оо).
14. Доказать, что линейная система
равномерно устойчива в области Г<^0<со тогда и только тогда, когда ее
матрица Коши
Kit, t^^X^X-Ht^
ограничена в области Z{t^^t < со, Т<tb < ее) (К о н т и).
15. Пусть система
— — Л
(Л = const) устойчива.
122 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ [ГЛ. И
Показать, что если
оо
B(t)?C [0, оо) и J ||Я (t) || dt <со,
то система
равномерно устойчива в области [0, со).
16. Показать, что все решения скалярной системы
dx_ dy 2у
ограничены на [1, оо); однако эта система не является равномерно устой-
устойчивой в облаети 1 sg t, t0 < оо.
17. Пусть система
где A (t) ? С [<0, со), устойчива при < — оо и
/ оо
Hm J Sp Л (/!>*!> — оо, ^ II/(Mi
Доказать,/что все решения неоднородной системы
ограничены на [t, со).
18. Пусть A(t)? С [t0, со) и все решения системы
ограничены на [t0, оо), причем
Urn ^ Sp A (t) dt> — со.
(-•оо <о
Тогда, если
j ||Я@||Л<оо,
'о
то все решения системы
Л
также ограничены на [?0, оо) (см. [6]).
Рассмотреть случай скалярного уравнения
a (t) x = 0.
ГЛАВА ИГ
ПЕРВЫЙ МЕТОД ЛЯПУНОВА
§ 1. Характеристические показатели функций
Пусть <р (/) — действительная функция, определенная в интервале
te<^t<^co. Если для некоторой последовательности tk-*--\-oo
(k=l, 2, ...) существует конечный или бесконечный предел опре-
определенного знака
a=lim<p(/*),
fe-»co
то число а или символ — со (-f- со) называется частичным пре-
пределом функции <р (/) при /->оо.
Определение 1. Наибольший из частичных пределов a
функции <р (/) при ^->оо называется ее верхним пределом:
a= lim <p
Более точно: а) если сс+е
для любого отрицатель- а
ного числа — Е справед-
справедливо неравенство
Т(О<-Е при
то полагают
lim cp (t)— — оо;
t
б) если (рис. 15) для некоторого числа а при любом
выполнено неравенство
cp(/)<a + s при />Т(в),
причем существует последовательность tk->oo такая, что
то считают
p(^) ,
fe-»co
4m tp ('/) = «;
124 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. Ml
в) наконец, если функция у (t) не ограничена сверху на любом
интервале (Т, оо), то принимают
lim <р@= +оо.
Аналогично определяется нижний предел функции <?(/) при
/ ->¦ -{- оо как наименьший из ее частичных пределов 8 при / -> оо:
-Можно также положить
Hm<p@=—Ifinl
Очевидно,
lim tp (t) ^ lim cp (^),
t-fCO t-*QD
причем равенство имеет место тогда и только тогда, когда суще-
существует конечный или бесконечный \imy(t). В этом случае
t-KO
lim cp (t) = lim 9 (^) = lim 9 (/).
Легко убедиться, что 1) верхний предел функции обладает
свойством монотонности, т. е. если
то
р(О
t-KO t—KX>
2) справедливо неравенство
lim [? (t) + <!» @1 «s lim ? @ + lim <|> @,
причем это неравенство превращается в равенство, если сущест-
существует конечный предел при t -»--(- 00 хотя бы одной из функций <р @
лли ([»@;
3) если <p@5s° и ф(/)^0, то
lim [cp @ ф @1 *=? lim cp (/) lim ф (t)
t—*OQ t—ЮЭ t—+ОЭ
в предположении, что правая часть неравенства имеет смысл,
причем, если существует limcp(/) или Нптф@, последнее нера-
венство превращается в равенство.
§ 1] ХАРАКТЕРИСТИЧЕСКИЕ ПОКАЗАТЕЛИ ФУНКЦИЙ 125
Пример 1. Имеем
lira sirrt = lim cos2? = l.
i-»co t->co
Здесь
Urn (sin2* + cosH) — 1 < Urn sirrt -f- flm" cos^ = 2.
Рассмотрим показательную функцию
где а действительно. Множитель а характеризует рост функции
eat; если а^>0, то, очевидно, е^->оо при t->oo; если же а<^0,
то е*'->0 при ^->- + оо. Число а будем называть характеристи-
характеристическим показателем функции ё4.
В общем случае рассмотрим комплекснозначную функцию
действительного переменного t, определенную в интервале (^„, оо).
Модуль этой функции можно представить в показательном виде
где
= 7-In
играет роль множителя при t. Изучая рост функции |/@1, есте-
естественно рассматривать максимальные значения функции а (г1).
Определение 2. Число (или символ —оо или -|-оо), опре-
определяемое формулой
будем называть характеристическим показателем Ляпунова (короче,
характеристическим показателем).
Это — функционал, определенный на множестве функций {f (/)},
заданных на полуоси (t0, оо). Для показательной функции ел1,
очевидно, имеем
X [<>«'] = а.
Характеристический показатель а равен взятому с обратным
знаком характеристическому чмслг/функции / (t), введенному Ляпу-
Ляпуновым. Изложенные ниже теоремы о характеристических показа-
показателях функций аналогичны соответствующим теоремам Ляпунова
(см. [15]).
126 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. III
Очевидно, имеем:
Пример 2. На основании формулы C.1.1) получаем
i[tm]=0 (m—любая постоянная);
sin / j — 1; i [et~] = -}_ CO И Т. П.
Из формулы C.1.1) вытекает, что характеристический пока-
показатель обладает свойством монотонности: если
\f(t)\^\F(t)\ при t>T,
то
Х1П*?Х1П . C.1.2)
Заметим, что для любой последовательности /ft-»--j-oo имеем
А->оо
Лемма, ?с^ы
Х[/] = «^±оо, C.1.3)
/по 1) 5ля любого е^>0 справедлива формула
т. е.
1Sjf^=°; (зл-4>
2)
11^ 1/@1 _ | со
/п. е. существует последовательность /ft->oo такая, что
Hm p*U=+oo. C.1.5)
А е *
Обратно, если 5ля некоторого а при любом е ^> 0 выполнено
соотношение C.1.4), /по
х [
еслы же имеет место соотношение C.1.5), /по
наконец, если выполнены оба соотношения C.1.4) и C.1.5), /по
X [/] = *¦
ХАРАКТЕРИСТИЧЕСКИЕ ПОКАЗАТЕЛИ ФУНКЦИЙ
127
Доказательство. 1) Докажем сначала необходимость.
Пусть
Отсюда
lirnl
где /ft->-oo. Следовательно,
- при
• при
N.
„№-e)t
Из последних соотношений вытекают формулы C.1.4) и C.1.5).
2) Установим теперь достаточность. Если имеет место
формула C.1.4), то, очевид-
очевидно, имеем
Отсюда ввиду произвольности
числа е получаем
хШ«?а;
если выполнено соотношение
C.1.5), то имеем
и, следовательно,
у\
1
О
Уг
Г
t
Рис. 16.
Если же имеют место оба соотношения C.1.4) и C.1.5), то, оче-
очевидно, получаем
Замечание. Таким образом, если i[f] = a, то при ?->оо
модуль функции y = \f(t)\ растет медленнее, чем любая пока-
показательная функция г/а = е(а+е>/ где г]>0, и по некоторой после-
последовательности 4->-оо быстрее, чем yl = e(-*~*'>t (рис. 16).
Теорема 1. Характеристический показатель суммы конеч-
конечного числа функций jk (t) (k = 1, ... , т) не превышает наиболь-
128
ПЕРВЫЙ МЕТОД ЛЯПУНОВА
[ГЛ. III
шего из характеристических показателей этих функций (в случае
их конечности) и совпадает с ним, если наибольшим характери-
характеристическим показателем обладает лишь одно из слагаемых, т. е.
C-1.6)
Доказательство. 1) Пусть
max х [/*(')] = а
к
В силу леммы при любом s^>0 имеем
НтЦ||е,\ = 0 (k=\, ...,m).
/—со е
Отсюда
т
12л(о| »(,,Л|
Следовательно, на основании второй части леммы имеем
2) Пусть
C-1.7)
'max
Допустим, что последовательность tg->oo такова, что
При
— оо имеем
т
aTaft
Отсюда при 0 <^ e <^ min aTaft получаем
§ 11 ХАРАКТЕРИСТИЧЕСКИЕ ПОКАЗАТЕЛИ ФУНКЦИЙ 129
Поэтому
В сочетании с неравенством C.1.7) это дает
X [2/*(*)] = « = maxх[М01.
к *
Замечание. Неравенство C.1.6) формально остается вер-
верным, если все или некоторые aft= +оо или —оо.
Теорема 2. Характеристический показатель произведения
конечного числа функций fk(t) (k—\ т) не превышает суммы
характеристических показателей этих функций, т. е.
т
')]<2х[Ы')П. (зл.8)
ft=l
Доказательство. Очевидно, имеем
'-><»
/-»OO
Следствие. Характеристический показатель конечной линей-
линейной комбинации функций fk(t) (k = \, ..., т) с ограниченными
коэффициентами ck (t) не превышает наибольшего из характера
стических показателей комбинируемых функций, т. е.
Действительно, учитывая, что
Х[с*@1<0,
на основании теорем 1 и 2 имеем
X [ 2 с* @ /* (/)] ^ max х [с* (t) fk (t)] <
[ck @1 + X[/*(O1} <max z [/ft @].
') Формула C.1.8) становится неопределенной, если среди функций fk(t)
имеются функции fp(t) и fq(t) такие, что \\fp{t)\ = — с» и х|/?@] = + оэ.
5 Б. П, Демидович
130 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. III
Замечание. Если линейная комбинация функций
где ck постоянны, содержит лишь одну функцию с наибольшим
характеристическим показателем, то
т
= max x [/*(/)].
к
Определение 3. Назовем характеристический показатель
функции f(t) (t^>t0) строгим, если существует конечный предел
^[/] = limy 1п|/(/)|. C.1.9)
В этом случае, очевидно, f(t)^O при t^>T.
Если функция f (t) имеет строгий характеристический показа-
показатель, то из формулы C.1.9) получаем
т. е.
Обратно, если выполнено равенство C.1.10), то, учитывая,
что
будем иметь-
т. е. существует предел C.1.9).
Теорема 3. Если функция f (t) имеет строгий характери-
характеристический показатель, то характеристический показатель произ-
произведения функций f{t) и g(t) равен сумме характеристических
показателей этих функций, т. е.
§ 1] ХАРАКТЕРИСТИЧЕСКИЕ ПОКАЗАТЕЛИ ФУНКЦИЙ 131
Доказательство. На основании теоремы 2 имеем
C.1.12)
С другой стороны, учитывая формулу C.1.10), получаем
Y.lfg}^xm+Xlgl C.1.13)
Из формул C.1.12) и C.1.13) вытекает формула C.1.11). .
Следствие. x[e"ty] = «--Jri[y].
Определение 4. Под интегралом функции f{t) (t0^t<^oo),
следуя Ляпунову (см. [13]), будем понимать
F{D = \f(h)dtu если хШ^О, C.1.14)
к
и
F (t) = \f V0 dtlK если x if) < 0. C.1.15)
t
Теорема 4. Характеристический показатель интеграла не
превышает характеристического показателя подинтегральной
функции.
Доказательство. Пусть
¦х [/(*)] = « 9* ±оо;
тогда Для любого е^>0 будем иметь
^+?>'-*0 при
Отсюда
где М — некоторая положительная постоянная.
1) Если а^О, то из C.1.14) имеем
to t0
Таким образом,
а так как е]>0 произвольно, то
= X I/@J.
132 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. III
2) Если а<[0, то из C.1.15) при 0 <[ е < | а Г получаем
IF (t) |< 11 / (/,) | Л, ^ М f е^^ = ^^-.
< < - i -г i
Отсюда аналогично предыдущему выводив
3) Утверждения теоремы, очевидно, остаются в силе, если
= — оо или а = -)^оо.
Следствие. Если
то
[^] C.1.16)
Действительно, используя свойство монотонности характери-
характеристических чисел и теорему 4, имеем
X [I <Р d) Ф 00 ^i] ^ X В
А так как е^>0 пpoизвoльнot то отсюда вытекает неравенство
C.1.16).
§ 2. Характеристические показатели функциональных матриц
.Определение. Назовём характеристическим показателем
матрицы F{t) = [fjk(t)\ определенно,й на [/0, °°), число или сим-
символ -j- оо (— оо):
Z[^0)] = maxz[/y*0)]. C.2.1)
Заметим, что если
— транспонированная матрица, то из формулы C.2.1) вытекает
Лемма. Характеристический показатель конечномерной мат-
матрицы F (t) совпадает с характеристическим показателем ее нормы,
т. е.
5 2] ПОКАЗАТЕЛИ ФУНКЦИОНАЛЬНЫХ МАТРИЦ 133
где под нормой матрицы понимается одна из трех рассмотрен-
рассмотренных выше норм (гл. I, § 4).
Доказательство. Так как
то
и, следовательно,
С другой стороны, очевидно, имеем
у. ft
Поэтому на основании теоремы 1 из § 1 получаем
/.ft
Таким образом,
Теорема 1. Характеристический показатель суммы конеч-
конечного числа матриц не превышает наибольшего из характеристи-
характеристических показателей этих матриц.
Доказательство. Пусть Fs(t) (s=l, ..., Л/) —матрицы
одного и того же типа т X п и
s=l
Отсюда
и, следовательно,
XIF (t)] = x[\\F(t)\\}^i\i\\Fs(t)
= maxx[\\Fs(t)\\]= max x 1^@], C.2.2)
s s
что и требовалось доказать.
Замечание. Если среди матриц Fs(t) (s = 1, ... , N) имеется
лишь одна обладающая наибольшим характеристическим показа-
показателем, то характеристический показатель суммы этих матриц
равен сумме их характеристических показателей.
134 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. lit
Действительно, пусть
Допустим, что
х [Ft @] = max у [/<'.' (t)] = y f/L1' @].
], К
На основании теоремы 1 из § 1, учитывая, что
y,\ffq(t)]^xU
при s^> 1, имеем
Следовательно,
X I/7 @1 ^ t \Р\ Ш = max х [Fs (t)].
s
Сопоставляя это неравенство с неравенством C.2.2), получим
окончательно
х[/г@] = тахх[/гЛО],
S
что и требовалось доказать.
Теорема 2. Характеристический показатель произведения
конечного числа матриц не превышает суммы характеристических
показателей этих матриц.
Доказательство. Пусть Fs(t) (s=l, ..., N) — матрицы,
допускающие последовательное умножение, и
П
Отсюда
и, следовательно,
что и требовалось доказать.
§ 3] СПЕКТР ЛИНЕЙНОЙ ОДНОРОДНОЙ СИСТЕМЫ 135
Следствие. Характеристический показатель линейной ком-
комбинации
нескольких матриц не превышает наибольшего из характеристи-
характеристических показателей этих матриц и совпадает с ним, если наи-
наибольший характеристический показатель имеет лишь одна из
матриц.
§ 3. Спектр линейной однородной системы
Пусть
dt
dx=,A(t)x C.3.1)
— линейная дифференциальная система, где A(t)?C(a, со).
Теорема Ляпунова (о характеристических пока-
показателях решений линейной системы). Если матрица
линейной системы C.3.1) ограничена,
|| Л @ || <: с < со, C.3.2)
то каждое действительное или комплексное нетривиальное ее
решение x — x(t) (a<^t0^t<^oo) имеет конечный характеристи-
характеристический показатель.
Доказательство. Пусть
[хи ..., хп]ф0
и t0, t ? (а, со). Из уравнения C.3.1) получаем
t
Отсюда
х (t) \\^\\х (U) || + { || A ft) || || х
to
Применяя обобщение леммы Гронуолла — Беллмана (гл. II,
§11), при t^t0 будем иметь
A ft) || dh].
136 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. Ill
Следовательно, учитывая, что
получим
X {exp [-{\\A (*,) || dtt]} < x [ X (t)] < x {exp ( || A (*,) || dt,} ,
т. e.
— d < X [* @] ^ Л C.3.3)
где
t
T
to
t
A =U^±r
<-»oo
Таким образом, все характеристические числа нетривиальных
решений x(t) линейной системы C.3.1) содержатся в конечном
отрезке [—А, Л"] С [—с, о].
Теорема Ляпунова доказана.
Замечание. Если матрица A (t) линейной системы C.3.1)
действительна и некоторое комплексное решение ее
(%ь (t) действительны; k — 1, 2) имеет характеристический пока-
показатель
то существует действительное решение x = x(t) этой системы,
имеющее тот же характеристический показатель: х [•*] = а.
В самом деле, так как
Tt [Ь @ + ih (t)] = A @ [g, @ + ih (t)},
то
т. е. действительная и мнимая части комплексного решения г
являются решениями системы C.3.1). Положим x — %s(t), где
X IS*(O] = max x[g*(OJ.
§ 3] СПЕКТР ЛИНЕЙНОЙ ОДНОРОДНОЙ СИСТЕМЫ 137
Так как
Xll* @] <;*[*]< max Х[ЫО1 (Л=1, 2),
k
то, очевидно, имеем
х & @1=х [*]=«.
что и требовалось доказать.
Без нарушения общности рассуждения можно предполагать,
что
так как в случае необходимости можно использовать решение
Изучим более точно структуру множества характеристических
показателей решений линейной дифференциальной системы с огра-
ограниченной матрицей A (t).
Лемма. Вектор-функции x(h) (t) (k—1, ..., т), определен-
определенные на [U, оо) и обладающие различными характеристическими
показателями, линейно независимы.
Доказательство. Пусть
*[*<*> @1 =«* (k = l, .... т)
и для определенности
«1<<Ч <••..<«». C.3.4)
Предположим, что
т
{t) = 0 при *0=ss*<oo, C.3.5)
причем с„ 9^ 0, где Is^p^m, ncq = 0 при q^> p. Тогда из соотно-,
шения C.3.5) имеем
и, следовательно, на основании следствия теоремы 2 из § 1 по-
получаем
*р = X [*(р) @1 < max х [х^ @1 = лр-и
что противоречит условию C.3.4).
Таким образом, jcA) (t),..., Jf(m) (t) линейно независимы.
Определение. Множество всех собственных характеристи-
характеристических показателей (т. е. отличных от — оо и -j- оо) решений
дифференциальной системы будем называть ее спектром.
138 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. III
Из приведенного выше замечания следует, что если матрица
A (t) линейной однородной системы действительна, то спектр ее
может быть реализован на множестве действительных решений.
Теорема. Спектр линейной однородной дифференциальной
системы с непрерывной ограниченной матрицей состоит из конеч-
конечного числа элементов
Доказательство теоремы непосредственно вытекает из леммы
и того обстоятельства, что линейная дифференциальная система
порядка п имеет самое большее п линейно независимых решений.
Заметим, что характеристические показатели а,- (/ = 1,..., т)
нетривиальных решений линейной системы
dx— Ax
с постоянной матрицей А являются вещественными частями
характеристических корней матрицы А, т. е.
А) (/= 1, .., т),
где \j — kj (A) — корни векового уравнения
det(A — Щ = 0
с различными вещественными частями (гл. II, § 8).
Замечание. Нелинейная дифференциальная система может
иметь спектр произвольной природы, например, содержащий бес-
бесконечное множество элементов.
Пример. Скалярное дифференциальное уравнение
^ f>0, x>0)
имеет общее решение
и, следовательно, это уравнение обладает сплошным.спектром —со < а < оо.
§ 4. Нормальные фундаментальные системы
Пусть в n-мерном пространстве 9?" задана линейная однород-
однородная система
^ = Л(/)*, C.4.1)
где А (/) g С [t0, оо), sup || Л @ ||< оо и — оо<а, <оц< ... <
<С am <С ~Ь °° (т ^ ") — ее спектр, расположенный в порядке воз-
возрастания.
§ 4j НОРМАЛЬНЫЕ ФУНДАМЕНТАЛЬНЫЕ СИСТЕМЫ 139
Как известно (см. [9], [10]), совокупность всех решений
x = x(t) (tu^t<^co) системы C.4.1) представляет собой линейное
пространство Ш1 (пространство решений), точками которого
являются отдельные решения, а любая фундаментальная система
состоящая из максимального числа линейно независимых решений
xs (t) (s= 1, ..., п), служит базисом.
Пусть фундаментальная система X (t) содержит ns решений
с характеристическим показателем zs E=1,..., т), причем не-
некоторые ns могут быть и нулями. Величину
т л
°* = S nsas, C.4.2)
s=l
где y^ns = n, будем называть суммой характеристических показа-
5=1
телей системы X (t). Так как число характеристических показа-
показателей линейной системы конечно, то существуют фундаментальные
системы X (t) с наименьшей суммой характеристических показа-
показателей, т. е.
ах =rrnina^. C.4.3)
Я
Такие фундаментальные системы и соответствующие им фундамен-
фундаментальные матрицы будем называть нормальными (в смысле Ляпу-
Ляпунова).
Определение 1. Фундаментальная система называется нор-
нормальной, если сумма ее характеристических показателей есть
наименьшая по сравнению с другими фундаментальными системами.
Если матрица A (t) действительна, то для каждого характери-
характеристического показателя a.s существуют действительные решения
с таким показателем, и в этом случае нормальную фундаменталь-
фундаментальную систему можно также полагать действительной.
Пусть Ns(s—l,...,m) — максимальное число линейно незави-
независимых решений системы C.4.1), обладающих характеристическим
показателем zs. Рассмотрим совокупность SMS всех решений x(t),
включая тривиальное, характеристические показатели которых
не превышают числа n.s, т. е.
В частности, имеем Шй — О, Шп = Ш". Из теорем о характеристи-
характеристических показателях следует, что если x(t)? Ша и у ({)?Ш3, то
ex (f) ? Wls (с — постоянная) и х (t) -\-y (t) 6 Ш5. Поэтому Шх
140 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. ИГ
является линейным подпространством (см. приложение)
пространства решений Щ".
Лемма 1. Число Ns совпадает с размерностью линейного под-
подпространства Ш3, т. е.
Ns = dimWs(s=l m). C.4.4)
Доказательство. В самом деле, по определению каждое
решение с характеристическим показателем л3 входит в ffls, т. е.
dimms^Ns. C.4.5)
С другой стороны, пусть { jc(p) (t), y(q) (t) } — некоторый базис
пространства Ш3, где
Этот базис обязательно должен содержать решение с наиболь-
наибольшим характеристическим показателем a.s> так • как в противном
случае существовали бы решения системы C.4.1), которые нельзя
представить в виде линейной комбинации базисных решений.
Пусть у1-1 (t) — решение системы C.4.1) такое, что -/_ [y(r\t)] =я4..
Система решений { xlP) (t) -^y{r) (t), y(q) (t) } образует новый базис
подпространства 9Д,. Действительно, если
? ар [*<*> @ + у& (ОЦ-2 ЬУ" @ = 0,
я
р
то
ар + К)у^ (t) + S bqyW (t) = 0
Отсюда в силу линейной независимости решений jcip) (/) и y(q) (t)
получим
ар = 0, Zap-\-br = 0, bq = 0 при g ф г,
р
и, значит, все Ь9 —0. Таким образом, система решений
есть базис подпространства Ш3, причем, очевидно, каждый элемент
его обладает характеристическим показателем o.s. Следовательно,
dimS№4<JV4. C.4.6)
Из неравенств C.4.5) и C.4.6) следует равенство C.4.4).
Следствие 1. Имеет место строгое неравенство
где yVm = n.
НОРМАЛЬНЫЕ ФУНДАМЕНТАЛЬНЫЕ СИСТЕМЫ
141
Следствие 2. Если ns(s—l,...,m) — число решений с ха-
характеристическим показателем as, входяищх в произвольную фун-
фундаментальную систему X(t), то справедливы неравенства
ni-\-ni-\-...^rhs?SzNs{s = \,..., m). C.4.7)
Действительно, каждая часть фундаментальной системы X (/),
включающая все линейно независимые решения с характеристи-
характеристическими показателями, не превосходящими as, очевидно, содер-
содержится в подпространстве -Df5.
Замечание. Число элементов (в обобщенном понимании)
линейного пространства размерности р будем условно обозначать
символом оор.
В этом смысле можно сказать, что линейная система C.4.1)
имеет
решений с характеристическим показателем as (s=l, ..'., tn;
No = 0). Таким образом, почти все решения линейной однород-
однородной дифференциальной системы обла-
облаб
дают наибольшим характеристическим
показателем
а = max o.s.
s
Пример. Пусть общее решение линей-
линейной дифференциальной системы имеет вид
х = с&е* -f- c2be2t -f- сгсеы,
где ct, c2, cz — действительные произволь-
произвольные постоянные и а, Ь, с — постоянные
ненулевые векторы. Тогда каждое решение
в пространстве 0 сг с3 с3 будет характери-
характеризоваться вектором с = (сц с2, с3) (рис. 17).
Спектр системы, очевидно, {1,2,3}.
Решениям х таким, что
(Ш3)
Рис. 17.
соответствует прямая е^1=={ cs = 0, с, =0 } с исключенным пулевым век-
вектором (рис. 17). Решениям х с характеристическим показателем
отвечает плоскость
с исключенной прямой е^1. Наконец, решениям х с максимальным характе-
характеристическим числом
соответствует трехмерное пространство <ffi3 = 0 су с2 с3 с исключенной пло-
плоскостью <М'*.
142 ПЕРВЫЙ МЕТОЛ ЛЯПУНОВА [ Г Л III
Чтобы охарактеризовать нормальные фундаментальные системы
решений, введем понятие несжимаемости системы функ-
функций.
Определение 2. Мы скажем, что система ненулевых вектор-
функций л:A) (/)»•••> х(к) (t) (k sg; п) обладает свойством несжимае-
несжимаемости, если характеристический показатель любой существенной
их линейной комбинации
где Cj постоянны, совпадает с наибольшим из характеристических
показателей комбинируемых решений, т. е. для всякой комбинации
у имеем
X foM = max z [*''>(')]¦
Очевидно, если ненулевые вектор-функции обладают свойством
несжимаемости и характеристические числа их отличны от — со,
то эти вектор-функции линейно независимы. Обратное неверно.
Заметим, что совокупность вектор-функций с различными
характеристическими числами, очевидно, обладает свойством не-
несжимаемости.
Лемма 2. Если фундаментальная система X (() обладает
свойством несжимаемости и ns (s=l,...,m) — число ее решений
с характеристическим показателем as, a Ns — максимальное число
линейно независимых решений системы с характеристическим пока-
показателем as, то справедливы равенства
ni+ni + ... + ns = Ns E=1 т), C.4.8)
т. е. в этом случае суммы2 nk(s=l, ..., т) достигают своих
k=\
наибольших значений.
Доказательство. Действительно, по свойству несжимаемо-
несжимаемости решение х (f), обладающее характеристическим показателем
as, может быть линейной комбинацией лишь тех решений из фун-
фундаментальной системы X (t), характеристические показатели кото-
которых не превышают as, т. е.
Ms^n, -j-nj + ... + л,. C.4.9)
С другой стороны, всегда
n,-\-ni-\-...r}-ns^Ns. C.4.10)
Сопоставляя неравенства C.4.9) и C.4.10), получаем равенства
C.4.8).
Теорема Ляпунова (о нормальности фундамен-
фундаментальной системы). Фундаментальная система линейной си-
§ 41 НОРМАЛЬНЫЕ ФУНДАМЕНТАЛЬНЫЕ СИСТЕМЫ 143
стемы C.4.1) является нормальной тогда и только тогда, когда
она обладает свойством несжимаемости.
Доказательство. 1) Докажем сначала необходимость
условий теоремы, т. е. допустим, что система обладает свойством
несжимаемости, и докажем, что она нормальная.
Предположим противное: пусть существует фундаментальная
система Y (t) = {yw (t), .. .,у{п) (t) } такая, что
°у<°х, C-4.11)
где
т
ах= 2"А B
• S=l 5=1
a, — характеристические показатели нетривиальных решений си-
системы C.4.1) и 4S, ns(s=l,..., т) — числа линейно независимых
решений с характеристическим показателем aS) содержащихся,
соответственно, в фундаментальных системах Y (t) я X (t). Для
определенности в матрицах Y (/) и X (t) решения расположим
в порядке возрастания их характеристических показателей.
S
Пусть Л^= ?nk(s=l, ..., т) — максимальное число линейно
независимых решений системы с характеристическим показателем
а5. Вводя обозначение
N's=?vk (s=l m),
в силу лемм 1 и 2 получаем
^Vi ^ Nu N2 ^N2,..., Nm^ < Nm_u
Nm = Nm = n,
причем
v, = A^; — N's-i , ns = Ns — Ns-i (s=l,...,m; N'0 = N0 = 0).
Имеем
m—\
2sA>m- 2Ns(*s«-*s) =
'¦= I>nsa.s = <:x, C.4.12)
что противоречит неравенству C.4.11).
144 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. III
Итак, несжимаемая система X нормальная.
2) Докажем теперь достаточность условия теоремы, т. е.
предположим, что система X нормальная, и докажем, что она
обладает свойством несжимаемости.
Предположим противное: пусть существует линейная комби-
комбинация
y=ic,^(f) (cp^0) C.4.13)
такая, что
у [у] <^тах%[х{ > (t)] = x[x(p) (t)]. C.4.14)
Рассмотрим систему решений
I \ X {I), . . ., X (l), у (I), X (I), . . ., X^ (I) \.
Система Y является фундаментальной. В самом деле, пусть
S ajX{J) (t) -j- apy (t) ^0, C.4.15)
где
? ! af | Ф 0.
Отсюда в силу линейной независимости решений лт(/) (t) имеем
арф0. C.4.16)
Подставляя в тождество C.4.15) выражение для у (t) C.4.13),
будем иметь
J (с, + apcf) x^ (t) + apcpx^ (t) + 2] a,*(^ @ = 0.
Из последнего тождества, очевидно, получаем
что невозможно в силу условий C.4.13) и C.4.16). Следовательно,
система Y фундаментальная.
На основании неравенства C.4.14) находим
что противоречит нормальности системы X.
Таким образом, всякая нормальная система X обладает свойст-
свойством несжимаемости.
Следствие 1. Во всех нормальных фундаментальных систе-
системах X (t) количество ns решений с характеристическим показа-
показателем y.s(s= 1,..., т) одно и то же.
§ 4] НОРМАЛЬНЫЕ ФУНДАМЕНТАЛЬНЫЕ СИСТЕМЫ 145
Действительно, в силу леммы 2 получаем
ns 1\s 1\ ?_] (S — i,..., т, 1\ ^ — и),
где
Ns = dim Ws.
Следствие 2. Всякая нормальная фундаментальная система
реализует весь спектр линейной системы.
Действительно, так как
то
ns = Ns — Ns_x^l (s=l.,..., т).
Свойство несжимаемости Ляпунов положил в основу понятия
нормальности фундаментальной системы (см. [13]).
Определение 3. Совокупность всех характеристических по-
показателей аь ..., <х„ нетривиальных решений линейной однородной
системы C.4.1), где каждый повторяется столько раз, сколько ns
E= 1, ..., т) линейно независимых решений с характеристическим
показателем a.s содержится в некоторой ее нормальной фундамен-
фундаментальной системе Xt, будем называть полным спектром системы
C.4.1), а сумму
п т
— суммой характеристических показателей линейной системы
(ns — кратности элементов спектра).
Теорема Ляпунова (о построении нормальной
фундаментальной системы решений). Пусть дана ли-
линейная дифференциальная система
ft = A(f)x, C.4.17)
где х = (хь ..., хп), A (t) ? С (а, оо), sup || A (t) || < 00, и пусть
Z (t) = {гA) @ z(n) (t)} — ее фундаментальная матрица. Тогда
существует постоянная треугольная матрица.
1 0 ... 0-
Рп\ Сщ ... 1_
такая, что
X(t) = Z{t)C C.4.19)
есть нормальная фундаментальная матрица системы C.4.17).
146 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. Ill
Доказательство. 1) Пусть
Подберем числа cjk(k<^j) так, чтобы
*-A) /А ?(Х) /Л 4- Г ^t2) (f\ _1 _J_ /¦> *(«) /Л
jk"t'2) /А —-_ >( -) /А ,., 1 „. . | /^ ^^Л^ ("А
причем
(S=l, .... Л).
Очевидно, справедлива формула C.4.18). Кр'оме того, так как
det С = 1, то
det X (t) = det Z (t) ¦ det С = det Z(t)^O
и, следовательно, X (t) есть фундаментальная матрица системы
C.4.17).
2) Докажем теперь, что так построенная матрица X (t) явля-
является нормальной фундаментальной матрицей системы C.4.17).
Пусть а,, ..., ат (ms^ti) — полная совокупность различных
характеристических показателей системы X, Рассмотрим произ-
произвольную группу решений x{rlls) (t), ..., xlr>ks) (t) из X(t), обладаю-
обладающих одним и тем же характепистическим показателем
Для любой их линейной комбинации
имеем
zUK01«s:<V C.4.21)
С другой стороны, полагая
nps = minnJs,
i
на основании структуры формул C.4.20) получаем
у (t) = upX^pJ (t) -f 2 cijX{nJs] @ = ap [z"W (t) -f У] b'jz0'(t)],
§ 51 ДОСТАТОЧНОЕ УСЛОВИЕ АСИМПТОТИЧЕСКОЙ УСТОЙЧИВОСТИ 147
где ар 9= 0 и Ь) — некоторые постоянные, не обязательно отличные
от нуля. Отсюда, учитывая способ комплектования функций
хЩг), находим
7Ay(t)]^x[X{V(t)]=o.s.
Таким образом,
х
Рассмотрим теперь произвольную линейную комбинацию
решений из фундаментальной матрицы Х(^). Выделяя из них
максимальные совокупности решений x(nis) (t), обладающих одина-
одинаковыми характеристическими показателями as, и учитывая фор-
формулу C.4.22); будем иметь
Z [2 Mr'* @] = Z Е Е ^*'V @] = max x [^ ^Jt*1 (О] =
/ s / s I
= max as = max x [•*:'"/ (/)].
* i
Следовательно, система Х обладает свойством несжимаемости и в
силу теоремы Ляпунова является нормальной.
Следствие. Если линейная система C.4.17) имеет треуголь-
треугольную фундаментальную матрицу
\гп(() 0 ... О -|
7 (Л I z« (/) г« @ • • • 0
2„, @ г„2 @ • • • глл @
зтой системы существует нормальная треугольная мат-
матрица X{t) = {xik(t)),, где xJk(t) = O при ?>/, причем xu{t)~
= 2jj (t).
Этот результат непосредственно вытекает из формулы C.4.19).
§ 5. Достаточное условие асимптотической устойчивости
линейной дифференциальной системы
Пусть
§ = A(t)x, C.5.1)
где Л (t) ?= С (а, со), sup || А (I) [|< со, и {^ ят} — спектр
системы C.5.1), причем т^п.
148
ПЕРВЫЙ МЕТОД ЛЯПУНОВА
|ГЛ. III
Теорема. Для асимптотической устойчивости линейной од-
однородной системы C.5.1) достаточно¦, чтобы наибольший харак-
характеристический ее показатель был бы отрицательным, т. е.
C.5.2)
Доказательство. Пусть x(t)y?Q—произвольное нетри-
нетривиальное решение системы C.5.1). Выберем е^>0 столь малым,
чтобы имело место неравенство
Так как
то имеем
т. е.
x(t)= o(e(a+E)') при /->оо
и, следовательно, x(t)-*-0 при t->oo. Отсюда следует (§ 7, тео-
теорема 2), что система C.5.1) (т. е. все ее решения) асимптотически
устойчива при t-+oo.
Замечание. Пусть X(t) = {Xi, ..., хп} — нормальная фунда-
фундаментальная система решений и
x[Xj] = Zj (/=1 П).
Положим
имеем (см. § 1, теорема 3, следствие)
т. е.
Таким образом, общее решение системы C.5.1) может быть
записано в виде
x^Xcjlj(t)eai', C.5.3)
где cj — произвольные постоянные, X t§y @1 = 0» ЯУ — точки спек-
спектра, %j(t)e'Jt—линейно независимые частные решения; при этом
а,- повторяется столько раз, сколько раз встречается частное ре-
решение с характеристическим показателем a.j в нормальной фун-
фундаментальной системе решений.
§ 6] НЕРАВЕНСТВО ВАЖЕВСКОГО 149
§ 6. Неравенство Важевского
Теорема (см. [22]). Для любого решения линейной диффе-
дифференциальной системы
^ C[t0, oo)) C.6.1)
при ta^t<^co справедливо неравенство
t t
I x D) I exp \ л (/,) dtx^\x{t)\^\x (^o)|exp \ A (/,) dtu C.6.2)
где \ x (t) | — евклидова норма вектора x (t); X (t) и Л (t) — наимень-
наименьший и наибольший характеристические корни эрмитово-симмет-
ризованной матрицы:
U A*(t)], C.6.3)
причем A(i) — [ajk(t)\ и A* (t) = [akj (t)]—ее эрнитово-сопряжен-
ная матрица,
Доказате льство. Пусть
х = colon [хи ..., хп]
— нетривиальное решение системы C.6.1) и
х = (Xi, ..., хп)
— эрмитово сопряженный вектор-строка. Очевидно,
|*|2 = ***.
В силу системы C.6.1), учитывая, что
получаем
^x?)
C.6.4).
Так как матрица АИ\t) эрмитова, то при любом
будем иметь (гл. I, § 5)
X (t) x*x^x*AH(t) x < A (t) x*x,
где X (I) и А (/) — соответственно наименьший и наибольший корни
векового уравнения
det [A"(t)
150 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. III
Поэтому на основании формулы C.6.4) находим
2Х (/) | х ? ^ ~ (| х S2) sg 2A (/) | х f. C.6.5)
Интегрируя неравенство C.6.5) в пределах от t0 до t, получим
формулу C.6.2).
Формула C.6.2), очевидно, справедлива также и для триви-
тривиального решения х~0.
Следствие 1. Для асимптотической устойчивости линей-
линейной однородной системы C.6.1) достаточно выполнения условия
Л@=С -Л<0 при t?[t0, сю),
где h — положительная постоянная.
Следствие 2. Спектр линейной системы C.6.1) целиком
расположен на отрезке [I, L], где
Для асимптотической устойчивости системы C.6.1) достаточно,
чтобы было
§ 7. Неравенство Ляпунова
Пусть линейная дифференциальная система
§ = A(t)x C.7.1)
с ограниченной действительной матрицей A(t) <^C[t0, оо) имеет
спектр
— oo<a1<...<am<-foo (m^n).
Обозначим через X (t) = (xjk (t)) ее фундаментальную матрицу,
где первый индекс /, как всегда, обозначает номер координаты,
а второй k — номер решения, и пусть
п т
^=2/Л^1= Zns*s C.7.2)
— сумма характеристических показателей всех решений из X (/),
где число ns(ns^s\) показывает, сколько решений с характери-
характеристическим показателем a.s содержится в системе X (t).
§ 7] НЕРАВЕНСТВО ЛЯПУНОВА 151
Рассмотрим определитель Вронского
W(t) = detX(t).
Развертывая определитель W (t), согласно обычным правилам,
будем иметь
W(t)= 2 (-l)xxPii(t)...xPnn(t), C.7.3)
<Pi V
где'сумма C.7.2) распространена на все перестановки (pi, ..., рп)
из п элементов 1, ..., п и (— 1)* — сигнатура перестановки, рав-
равная -}-1, если перестановка четная, и —1, если перестановка
нечетная. Используя теоремы о характеристических показателях
суммы и произведения (§ 1) и учитывая равенство C.7.2), по-
получим
ХППОК max {xl*Pji @1+ .-- + Х [*,„>. (91}^°*- C-7.4)
{Pi V
С другой стороны, на основании формулы Остроградского — Лиу-
вилля (гл. II, § 3) имеем
поэтому
i.= ШтГ 4- \
Отсюда на основании неравенства C.7.4) получаем неравенство Ля-
Ляпунова
m t
°y= / nk<xk^ lim — \ Sp A (t,)dt,. C.7.5)
Так как матрица Л (/) ограничена, то, очевидно,
t t
lim -г \ Sp Л (<i) cf^i = lim V Sp Л (^) Лх.
/-»oo * J /->co * *o J
«'
'о
Следовательно,
ax^ ^m
Таким образом, «Эля линейной однородной дифференциальной
системы с непрерывной ограниченной матрицей сумма характе-
152 ПЕРВЫЙ МЕТОД ЛЯПУНОВА ш
ристических показателей решений из любой ее фундажнтальной
системы X не меньше верхнего предела от саднею значения следа
матрицы системы. В частности неравенству CJ.5) справедливо
для нормальной фундаментальной системы X J. е ' , имеет
наименьшее значение. ' у х
ство
Замечание Если матрица A(t) комцлексн то ен.
э Ляпунова C.7.5), очевидно, шеет вид
T \ ReSp A {k) d\- C.7.6)
о
Приведем достаточное условие нормально^ фуНдаментальной
системы решении. ^
Теорема. Если для фундаментальной сЧстет ий Щ)
линейной однородной дифференциальной сист^м матоиией A (t)
выполнено равенство Ляпунова мы с матРииеи л \ч
W*1, C.7.7)
то эта система нормальная.
Доказательство. Действительно, ео,и система х не яв.
ляется нормальной, то существует фундаме^тальная си z
для которой '
t
Ъ<°х = Ш г \ ReSp A (tK) dtu CJ#8)
'о
что противоречит неравенству Ляпунова C.7 q\
Замечание. Существуют нормальные фундаментальные си-
системы, для которых не выполнено равенство Ляпунова.
Пример. Пусть
^=.У [sin (In 0 4-cos (In 01,
dv
Тогда получаем
где Ci и с3—произвольные постоянные. Отсюда
х = cXsin Aп<) + с„е~ 'sin (m " >
§ 8] ПРИВОДИМЫЕ СИСТЕМЫ. ТЕОРЕМА Н. П. ЕРУГИНА 153
Так как при | ct \ + | с2 [ ф. О имеем
то любая фундаментальная система Х={х, у} является нормальной и
Однако для матрицы A (t) системы C.7.9), очевидно, имеем
Г 0 sin (In 0 + cos (In 0]
(> Lsin (In t) + cos (In t) 0 ]•
Отсюда
Sp A @=0
и, следовательно,
t
с > Urn ~
§ 8. Приводимые системы. Теорема Н. П. Еругина
Определение 1. Матрица h(t) ? С1 [t0, оэ), вообще говоря,
комплексная, называется матрицей 'Ляпунова, если выполнены
следующие условия (см. [13], [20]):
1) L(t) и L(t) ограничены на промежутке [^0, оо), т. е.
o, sup||L(OI|<oo
t
t
при /0« C
2) |detb@|S&m>0,
где m — некоторая положительная постоянная.
Очевидно,
|detL@l<s2Af<oo.
Заметим, что матрица L'1 (t), обратная матрице Ляпунова L (t),
есть также матрица Ляпунова.
Действительно, если L (t) = [ljk {t)\—матрица Ляпунова и
Ljk(t) — алгебраическое дополнение элемента ljk(t), то
l (t)
Ь [l> ~ det L (t) ¦
Отсюда, учитывая условия 1) и 2), будем иметь
sup \\L-'{t) |< оо,
причем, очевидно, L'1 (t) ^ С1 [t0, оо) и ^ [L~l (t)] ограничена.
Кроме того,
Таким образом, L (/) — матрица Ляпунова.
154 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. Ill
Определение 2. Линейное преобразование
y = h{t)x C.8.1)
с (л X «)-матрицей Ляпунова L(t), где х и у — (п X 1)-векторы,
называется преобразованием Ляпунова.
Лемма. При преобразовании Ляпунова C.8.1), произведенном
над линейной дифференциальной системой
C.8.2)
характеристические показатели ее решений х сохраняются.
Действительно, из C.8.1) имеем
Следовательно,
\\y\\^\\L(t)\\\\x\\
||*|| <:|| А-(О «М-
Отсюда, учитывая, что \\b(t)\\ и Ц/г1^)! ограничены, получаем
и
Таким образом,
Определение 3. Согласно Ляпунову, однородная линейная
дифференциальная система C.8.2) называется приводимой, если с
помощью некоторого преобразования Ляпунова она может быть
преобразована в линейную систему
ш = ву ^3-8-3)
с постоянной матрицей В.
Н. П. Еругиным получены необходимые и достаточные усло-
условия приводимости линейной системы (см. [20]).
Теорема Еругина. Линейная дифференциальная система
C.8.2) приводима тогда и только тогда, когда некоторая ее фун-
фундаментальная матрица X (t) может быть представлена в виде
матрицы Ляпунова L(t), умноженной на экспоненциал произведе-
произведения независимой переменной t на постоянную матрицу В, т. е.
X{t) = L(t)efB. C.8.4)
§ 8] ПРИВОДИМЫЕ СИСТЕМЫ. ТЕОРЕМА Н. П. ЕРУГИНА 155
Доказательство. 1) Докажем сначала необходимость
условия теоремы. Пусть система C.8.2) приводима. Тогда с по-
помощью преобразования Ляпунова
x = L(t)y C.8.5)
ее можно преобразовать в линейную систему
% = Ву C.8.6)
с некоторой постоянной матрицей В. Фундаментальная матрица
Y = Y(t) системы C.8.6) удовлетворяет матричному уравнению
(гл. II, § 2)
Y = BY. C.8.7)
Отсюда получаем (ср. гл. II, § 8)
Y(t) — <*BC, C.8.8)
где С — произвольная неособенная постоянная матрица (det С ^ 0).
В силу формулы C.8.5) фундаментальная матрица системы C.8.2)
будет иметь вид
X{t) = L{t)Y {t) = L{t)e?*C.
Выбрав С = Е, мы и получим формулу C.8.4).
2) Докажем теперь достаточность условия теоремы. Пусть
имеет место формула C.8.4). Отсюда
L(t) = X(t)e-»>.
В уравнении C.8.2) произведем преобразование Ляпунова:
x = X(t)e~tBy.
Тогда
Так как
X(t) = A(t)X(t),
то в формуле C.8.9) два члена сокращаются и мы имеем
т. е.
Таким образом, система C.8.2) приводима.
156 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. III
Замечание. В формуле C.8.4) матрица В может быть взята
в жордановой форме.
Нетрудно сформулировать условия устойчивости приводимой
системы.
Теорема. 1) Приводимая линейная однородная система устой-
устойчива тогда и только тогда, когда все характеристические пока-
показатели ее неположительны, причем нулевым характеристическим
показателям отвечают простые элементарные делители, если их
рассматривать как вещественные части собственных значений со-
соответствующей постоянной матрицы.
2) Приводимая линейная однородная система асимптотически
устойчива тогда и только тогда, когда все характеристические
показатели ее отрицательны.
Доказательство непосредственно вытекает из того обстоятель-
обстоятельства, что характеристические показатели приводимой системы
C.8.2) равны действительным частям корней- соответствующего
векового уравнения
det(B —Х?) = 0,
где система
^ = Sv
dt Dy
устойчива или неустойчива одновременно с данной системой.
§ 9. Приводимость к системе с нулевой матрицей
Пусть линейная система
d? = A(f)x C.9.1)
(где A (t) — ограниченная непрерывная действительная матрица)
с помощью преобразования Ляпунова
x — h(t)y C.9.2)
преобразуется в систему
f = 0 C.9.3)
с нулевой матрицей. Так как общее решение системы C.9.3)
есть
У = с, C.9.4)
то в этом случае семейство интегральных кривых линейной си-
системы C.9.1) в пространстве /;+Xe?J (рис. 18) может быть вза-
взаимно однозначно и непрерывно отображено на семейство парал-
91
ПРИВОДИМОСТЬ К СИСТЕМЕ С НУЛЕВОЙ МАТРИЦЕЙ
157
лельных прямых в пространстве ItyC_<Mny (рис. 19), т. е. при
отображении C.9.2) различным интегральным ^кривым x = x(t)
соответствуют различные прямые у —с и обратно.
Заметим, что если линейная система C.9.1) преобразуется в
систему с нулевой матрицей, то в силу формул C.9.2) и C.9.4)
все ее решения ограничены.
У,
0
i
0
У=с
t
Рис. 18.
Рис. 19.
Теорема. Если 1) все решения x{t) линейной однородной
дифференциальной системы C.9.1) ограничены в промежутке [^0, оо);
2) интеграл от следа матрицы системы ограничен снизу, т. е.
Sp A
— сх>,
где а — постоянная, то система C.9.1) с помощью преобразова-
преобразования Ляпунова может быть преобразована в систему с нулевой
матрицей.
Доказательство (см. [12]). Пусть X (t) — фундаменталь-
фундаментальная матрица системы C.9.1). Покажем, что X (t) есть матрица
Ляпунова. Действительно, очевидно, X (t) ? С1 [ta, оо). Далее,
на основании условия 1) имеем
\\X(t)\\^c, \\X(t)\\^\\A{t)\\\\X(t)\\^Cl,
где с и сх — некоторые положительные постоянные. Кроме того,
используя формулу Остроградского — Лиувилля (гл. II, § 3)
t
det X (t) = det X (t0) exp J Sp A ft) dtu
to
в силу условия B) получаем
, det
| = i det
| exp
det X (to)[
158 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. ГЦ
при t^h, где Сч — постоянная. Таким образом, X (t) — матрица
Ляпунова.
В уравнении C.9.1) положим
x = X(t)y,
тогда
или так как
X(t) = A{t)X(t),
то
Х(*)§? = 0. C.9.5)
Так как X (t) — неособенная матрица, то, умножая на X (t) обе
части уравнения C.9.5), окончательно будем иметь
Теорема доказана.
Следствие. Если матрица A (t) системы C.9.1) абсолютно
интегрируема, т. е.
C.9.6)
то эта система приводима к системе с нулевой матрицей.
Действительно, из уравнения C.9.1) при t^t0 имеем
Отсюда
Используя лемму Гронуолла—Беллмана (гл. II, § 10) и условие
C.9.6), получаем
t
|| х (t) || =ss || х (f0) || exp J S| A (/,) [| dtt =sS I x (t0) || ek.
to
Следовательно, все решения системы C.9.1) ограничены в проме-
промежутке [t0, оо).
АСИМПТОТИЧЕСКИ ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ 159
Кроме того, если A(t) = [ajk(t)\, то, очевидно, имеем
(Sp A (h) db | *s $1 Sp A (to i dtx <s \ 2 j ajj (*,) j dtx <
h *<> (o J
Отсюда
t t
$Sp A (tx)dt^ — | J Sp Л ft)<#! |Ss — n/C.
Таким образом, все условия теоремы выполнены и система
C.9.1) приводима к системе с нулевой матрицей.
§ 10. Асимптотически эквивалентные системы
Определение. Будем говорить, что дифференциальные си-
системы
dft=g(t, у) C.10.2)
асимптотически эквивалентны, если между решениями их x(t)
и у (t) можно установить взаимно однозначное соответствие такое,
что
lim [X (t) —у @1 -----0. C.10.3)
Укажем простой признак асимптотической эквивалентности
линейных дифференциальных систем.
Теорема Левинсона (см. [23]). Пусть решения систелш
^ = Ах> C.10.4)
где А—постоянная (пу(п)-матрица, ограничены на [0, оо).
Тогда система
% C.10.5)
B(t)?C [0, оо) и
СО
J C.10.6)
о
асимптотически эквивалентна системе C.10.4).
160 ПЕРВЫЙ МЕТОД ЛЯПУНОВА |1Л И!
Доказательство. Изложим доказательство, идея которого
принадлежит Брауеру [24]. Прежде всего, так как решения си-
системы C.10.4) ограничены, то характеристические корни )-(А)
матрицы А удовлетворяют неравенству
причем характеристические корни с нулевыми вещественными
частями имеют простые элементарные делители (см. гл. II, § 8).
Без нарушения общности рассуждения мы предположим, что
матрица А имеет квазидиагональный вид
A = diag(Au A,), C.10.7)
где Аг и А2 — соответственно, (р X РУ и 07 X <7)-матрицы
(p-\-q=.n) такие, что
ReX(i4,)< — a<0, ReX(A2) = 0. C.10.8)
Действительно, в случае надобности этого можно добиться с по-
помощью неособенных преобразований
где S — постоянная (я X я)-матрица, причем взаимно однозначное
соответствие между новыми интегральными кривыми | (t) С=> ц (t)
индуцирует взаимно однозначное соответствие между старыми ин-
интегральными кривыми x(t) = S~1%(t)<?z$> S'lir\(t)=y (t). Кроме
того, из предельного соотношения | (/) — tj(?)->-0 при ^-^оо,
очевидно, вытекает предельное соотношение x(t)—у (t) -»- 0
при t-*ao.
1) Пусть
X@==diag(eM", etA")
— фундаментальная матрица системы C.10.4), нормированная в
нуле: Х@) = Е, и
/, = diag(?;)f О), /4 = diag(O, Eq),
где Ер и Eq — единичные матрицы соответствующих порядков р
и <7, при этом, очевидно, /i-J-/.2 = ?„. Положим
где
X1@ = X@/i = diag(^«, 0)
Отсюда матрицу Коши
K(t, T
§ i)| АСИМПТОТИЧЕСКИ ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ 16!
можно представить в виде
K(t, ->) = Xl(t — ':) + Xi(t — ?),
причем на основании условий C.10.8) имеем
!;Х, @!| = ||ем'|^ае"J при 0</<оо C.10.9)
и
¦X.. (O!i = ||eM-i=^b при — оо</<со, C.10.10)
где а и b — некоторые положительные постоянные.
Используя метод вариации произвольных постоянных (гл. 11,
*> 5), дифференциальное уравнение C.10.5) можно записать в ин-
интегральной форме
y(t) = X(t-ta)y(t0) +
-{- $*,(* — *) В (*)Я*)ь- Jr jX4(f —T)B(x)
где ?0 ? [0, о°) произвольно. Ввиду абсолютной интегрируемости
матрицы В @ на [0, со) все решения у (t) системы C.10.5) огра-
ограничены на [0, со) (гл. II, § 12), и поэтому несобственный интеграл
СО
\Х.,A—т) В {t)y (z)d-z является сходящимся. Отсюда, учитывая,
t,i
что
X, (t — z) = X(t — т)/.3 =
= X (t — t0) X (t0 — -с) /, = X(t — to) X, (t0 ~ x),
наше интегральное уравнение можно представить в виде
СО
У (t) = X(t- to) | у (to) + I X, (to ~-)B (z) у (x) ch\ +
'0
/ en
-f- \Xi(t — i) B(i)y (T)dx — \Xt(t- i)B (x)y (i)dx. C.10.11)
Решению у (t) системы C.10.5) с начальным условием y(t{t)=y0
сопоставим решение x{t) системы C.10.4) с начальным условием
сю
X{to)=y(tu)-\-\ ХчAо — п)ВA)у(-:)Aч. C.10.12)
h
Так как решения х (t) и у (t) полностью определяются своими
начальными условиями, то формула C.10.12) устанавливает одно-
однозначное соответствие между множеством всех решений \у (t)\ си-
системы C.10.5) и множеством решений [х (t)\ (или его частью)
6 Б- П. Демпдович
162 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. III
системы C.10.4). Заметим, что соотношение C.10.12) непрерывно
относительно начального значения y(to)=yo.
2) Покажем, что соответствие между решениями х (/) и у [t);
определяемое формулой C.10.12), является взаимно однозначным
и распространяется на все множество решений {x(t)}.
Пусть У (t) — фундаментальная матрица системы C.10.5) такая,
что Y(to) = E. Имеем
Отсюда на основании метода вариации произвольных постоянных
получим
t
K(/) = .X(f-fo)-f- [X(t— т) В (т) У (т) dx.
to
Но из неравенств C.10.9) и C.10.10) вытекает
\\X(t— 4) Ц =s? max (a, b) — c при /=э^0;
поэтому
и, следовательно, в силу леммы Гронуолла — Беллмана (гл. II,
§11) находим
= k при tns^t<^co, C.10.13)
причем постоянная k в оценке C.10.13) не зависит от выбора
начального'момента t0 D^=0).
Очевидно, имеем
Поэтому из формулы C.10.12) получаем
b), C.10.14)
где
'о
причем на основании C.10.10) и C.10.13) выводим
Uflk C.10.15)
§ 101 АСИМПТОТИЧЕСКИ ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ 163
Так как матрица В (t) абсолютно интегрируема на [0, со), то
от
\ \B(x)\dx^Q при *0->оо
'о
и, следовательно, в силу C.10.15) начальный момент t№ можно
выбрать столь большим, чтобы имело место неравенство
det[?-r-Z(/o)]>O. C.10.16)
В дальнейшем /„ будем считать фиксированным и предполагать
наличие неравенства C.10.16). Отсюда и из формулы C.10.14)
выводим
y(fo) = [? + Z(f.)] '*(/,). C.10.17)
Так как формулы C.10.14) и C.10.17) равносильны, то для ка-
каждого решения x(t) системы C.10.4) с начальным условием
хAA) = Хо найдется одно и только одно решение у (t) системы
C.10.5), отвечающее установленному выше соответствию, а именно,
это решение, начальное условие у (tu) которого определяется фор-
формулой C.10.17). Соответствие между решениями у (t) и х (t), уста-
устанавливаемое формулами C.10.14) и \3.10.17), —- взаимно однознач-
однозначное, т. е. каждому решению у (/) соответствует одно и только
одно решение x(t) и обратно. Отметим, что тривиальному реше-
решению у = 0 соответствует тривиальное решение jc = O и в силу
линейности соотношений C.10.14) и C.10.17) различным реше-
решениям yi(t) и _)ь (/) системы C.10.5) соответствуют различные ре-
решения Х\ (t) n'Xi(t) системы C.10.4) и наоборот.
3) Для соответствующих решений х (t) и у (t) оценим норму
их разности. Так как, очевидно,
x(t) = X(t-to)x(to),
где х (t0) определяется формулой C.10.12), то из формулы C.10.11)
имеем
У (/) - x(t) = \ X, {t-~) В (z)y (т) dx - \ X, (t — i)B (-)у (т) dx.
t0 t
Отсюда, учитывая, что
11^@11 = 1] v (o^(W|| <
^ \\Ут\\\\у&)\\^к\\уЦо)\\ при
164 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. Ш
на основании оценок C.10.9) и C.10.10) при t^tq получаем
\\y(t) — x(t) || ^J || Xi(t — x)||liB(T)|i||_y(x) || dx-j-
ta
со
t
CO
+6/e || у (tQ) || jj || В (x) || d-. C.10.18)
Ввиду' абсолютной интегрируемости матрицы В (t) при t^2t0
имеем
i
[ g-a('-T> || B(x) || dT =
= \ е а('-т) || В (х) || rfT + J е ""- т> || В (т)
о t
если t~^>T. Следовательно,
t
lim ?«-•<'-') ||B(t)||dT = 0.
Таким образом, из неравенства C.10.18) выводим
lim [y@--«@] = 0,
< -» оо
т е. системы C.10.4) и C.10.5) асимптотически эквивалентны.
Замечание. Если Д., = 0, то Х2(/) —0 и, следовательно,
X (to)=y (t0). В этом случае теорема тривиальна.
Следствие. Пусть
§ = B(t)y, C.10.19)
где В (t) абсолютно интегрируема на [0, со). Тогда для каждого
решения у (t) существует
\\my(t) = c, C.10.20)
t-> CD
§ 41
ПРАВИЛЬНЫЕ СИСТЕМЫ
165
т. е. все интегральные кривые у =у (t) имеют горизонтальные
асимптоты (рис. 20), причем различные интегральные кривые
у =У\ (/) и у =у-1 (t) имеют различные горизонтальные асимптоты
у = с, и у = Съ и, сверх того, „
для каждой горизонтальной
прямой у = с существует ин-
интегральная кривая y—y(t),
имеющая эту прямую своей
асимптотой.
Действительно, в силу тео-
теоремы система C.10.19) асимп-
асимптотически эквивалентна системе
о
i
^=0 C.10.21) Рис. 20.
с матрицей Л=0. Так как система C.10.21) имеет решения
X —- С,
то отсюда вытекает предельное соотношение C.10.20).
§ 11. Правильные системы
Рассмотрим линейную дифференциальную систему
^ = A(t)x C.11.1)
с ограниченной действительной непрерывной матрицей A {t):
Пусть
A(t)eC[tn, сю) и sup || Л @ || <оо.
t
°= X пк4
C.11.2)
— сумма характеристических показателей (с учетом их кратно-
стей nk) решений системы C.11.1), входящих в некоторую ее нор-
нормальную фундаментальную систему.
Определение. Действительная линейная.система называется
правильной по Ляпунову (см. [13]), если сумма характеристиче-
характеристических показателей ее совпадает с нижним пределом среднего зна-
значения следа матрицы системы, т. е. если имеет место равенство
^ Ит |
|A Sp
A (ti) dtr.
C.11.3)
166 ПЕРРЫЙ МЕТОД ЛЯПУНОВА [ГЛ. ИГ
Замечание. Если матрица АA) комплексная, то условие
правильности линейной системы записывается следующим образом:
o=jirny { ReSpA(t,)dU.
'^Ю to
Лемма. Линейная дифференциальная система C.11.1) является
правильной тогда и только тогда, когда 1) существует предел
среднего значения вещественной части следа матрицы системы
S= lim-И Re Sp Л (/,)</*,; C.11.4)
2) выполнено равенство Ляпунова
o = S. C.11.5)
Достаточность леммы очевидна. Докажем необходи-
необходимость ее.
Действительно, если система правильная и
t
S= lim -у [ ReSp A (U)dtu
~ '"^ ti
t _> со l
то, используя формулу C.11.3) и неравенство Ляпунова (§ 7),
имеем
С другой стороны, очевидно,
Отсюда получаем
что и доказывает лемму.
Связь между правильными и приводимыми системами устано-
установлена Ляпуновым.
Теорема. Всякая приводимая линейная дифференциальная
система является правильной.
Доказательство. Пусть система C.11.1) приводима (§ 8)
и X (t) — ее нормальная фундаментальная матрица. Согласно опре-
определению приводимости существует матрица Ляпунова L (t) такая,
что
Л @ = МО МО, C.11.6)
§ 111 ПРАВИЛЬНЫЕ СИСТЕМЫ 167
где Y (t) — фундаментальная матрица некоторой системы
^ = Ву
dt y
с постоянной матрицей В. Из соотношения C.11.6) имеем
det X @ = det L (t) ¦ det Y (t).
Используя формулу Остроградского — Лиувилля (гл. II, § 3),
получим
t
J Sp A (/ii dti
det X (t0) e(o = det L (t) ¦ det Y (t0) e« ~ f»> sp a.
Отсюда
\ Sp A itt) dti
\е1» \ = c (t9) | det L (
где
т. e.
^ Re Sp A (CO c«i
e l° =c (t0) | det h (t) | e^ - '<» Re sP s
Следовательно,
C.11.7)
Так как In | det h (t) \ есть величина, ограниченная на промежутке
[?о, оо), то из формулы C.11.7) вытекает, что существует предел
t
S = lim ~ [ ReSp/1 (*,) d*i = Re Sp fi. C.11.8)
'0
Кроме того, пусть ох и ау — суммы характеристических показа-
показателей решений фундаментальных матриц X и К„ соответственно.
Так как при преобразовании Ляпунова характеристические пока-
показатели сохраняются, то, очевидно, имеем
ох = °г. C.11.9)
причем, если матрица X нормальная, то матрица Y также нор-
нормальная. Но для нормальной матрицы Y характеристическими
168 ПЕРВЫЙ МЕТОД ЛЯПУНОВА |1Л. Ml
показателями являются вещественные части корней lf векового
уравнения
det (В — Х?) = О,
где каждый корень повторяется столько раз, какова его кратность.
Поэтому
°y — S Re ~Kj = Re 2 X; = Re SP B-
i i
Таким образом, справедливо равенство Ляпунова
и, значит, на основании леммы система C.10.2) правильная.
Замечание. Если матрица А (I) действительная, то матрицы
L(t) и В можно полагать также действительными.
Покажем на примере, что правильная система может быть не-
неприводимой.
Пример. Скалярное уравнение
dx х
является правильным в смысле определения этого параграфа, так как общее
решение его есть
x = ceVJ C.11.10)
и при сфО имеем
Однако это уравнение не будет приводимым, так как его общее решение
C.11.10) не имеет вида, предписываемого теоремой Еругина(§ 8).
§ 12. Теорема Перрона
Пусть
dt
~ = A(t)x C.12.1)
— линейная система с действительной или комплексной непре-
непрерывной матрицей A (t).
Определение. Система
% C.12.2)
где A*(t) = AT(t) — эрмитово-сопряженная матрица для A (t), на-
называется сопряженной для системы C.12.1). Если матрица A (t)
§ 121 ТЕОРЕМА ПЕРРОНА 169
действительная, то Л* @ = Л (/), и, следовательно, для действи-
действительной системы C.12.1) ее сопряженная система имеет вид
Очевидно, систему C.12.1) можно рассматривать как сопря-
сопряженную для системы C.12.2), т. е. системы C.12.1) и C.12,2)
взаимно сопряженные.
Лемма. Для любых решений х и у взаимно сопряженных
систем C.12.1) и C.12.2) справедливо тождество
у *х = (х, у) = с, C.12.3)
где у* — эрмитово-сопряженныи ' вектор для у и с — некоторая
постоянная.
Аналогично для фундаментальных матриц решений X = X (t)
и Y = Y (t) этих систем имеет место соотношение
Y*X = C, C.12.4)
где Y* — эрмитово-сопряженная матрица для Y и С — постоянная
матрица.
Обратно, если выполнено соотношение C.12.4), где С — неосо-
неособенная постоянная матрица (det С =? 0) и X — фундаментальная
матрица системы C.12.1), то Y есть фундаментальная матрица
сопряженной системы C.12.2).
Доказательство. 1) Пусть вектор-столбец
является решением системы C.12.2). Тогда вектор-строка
У* = [У\, ¦¦¦, Уп\,
очевидно, есть решение системы
*g.= -y*A(t). C.12.5)
Из уравнений C.12.2) и C.12.5) получаем
V*-di = y*A(t)x
170 ПЕРВЫЙ МЕТОД ЛЯПУНОВА (ГЛ. Ill
Складывая последние равенства, будем иметь
± dx , dy* A
или
d
Следовательно,
2) Так как фундаментальные матрицы X и Y удовлетворяют
уравнениям
X = A(t)X C.12.6)
и
Y = — A*(t)Y, C.12.7)
то аналогично доказанному выше имеем тождество C.12.4).
3) Пусть справедливо тождество C.12.4). Тогда
)* = (X*)'iC*, C.12.8)
где X* удовлетворяет дифференциальному уравнению
Х* = Х*Л*(/). C.12.9)
Из формулы C.12.8), используя формулу для производной обрат-
обратной матрицы (гл. I, § 7), имеем
причем
det Y = det (X*) • det С* = (det X)-1 ¦ det С Ф 0.
Следовательно, У есть фундаментальная матрица сопряженной
системы C.12.2) (гл. I, § 2).
Теорема Перрона (см. [25], [14]). Для правильности
линейной однородной дифференциальной системы необходимо и
достаточно, чтобы полный спектра) данной системы
а,^а.2^ ... =г?а„ C.12.10)
и полный спектр ее сопряженной системы
P,5sj32:&...S,j3n C.12.11)
'} Иными словами, спектр с учетом кратностей харашеристических пока-
показателей (см. § 4).
§ 12] ТЕОРЕМА ПЕРРОНА 171
были бы симметричны относительно нуля, т. е. должны иметь
место равенства
я, + Р, = 0 (s=l, .... я). C.12.12)
Доказательство. 1) Докажем сначала необходимость
условий теоремы. Пусть система C.12.1) правильная и X(t) =
=- [xJk {t)\ — ее нормальная фундаментальная матрица, состоящая
из решений
х{к) = colon [xVl{t), ..., xnk(t)} (k~l, ..., n)
таких, что
где числа %k удовлетворяют неравенствам C.12.30). Тогда в силу
леммы
Y(t) = [X-l(t)r~[yfll(t)] C.12.13)
является фундаментальной матрицей решений сопряженной системы
C.12.2). Пусть, далее,
у<*> = colon [yik (t) уп> (/)] (k = 1, ..., л),
где
Xlyw] = h- C.12.14)
Из формулы C.12.13) вытекает, что
Y*(t)X(t)=--E.
Отсюда на основании правила умножения матриц будем иметь
yW*.x(s) = l (s==1; f п)
Воспользовавшись теперь теоремой о характеристическом показа-
показателе произведения двух матриц (§ 2), находим
а. + ^3=0. C.12.15)
С другой стороны, если Xjk(t) — алгебраическое дополнение
элемента xjk (t) определителя det X (t), то на основании известного
правила обращения матрицы получаем
и. <t)= \-*иЩ * =^§iL-
J LdetX(^)J delX(t) '
где
det X (t) = det X (t0) ¦ exp \ Sp A (/,) dtv ф 0.
172 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. III
Отсюда
Очевидно,
f]=a
det
Далее, так как система C.12.1) правильная, то выполнено равен-
равенство Ляпунова
а=УХ= lim ~ \ReSp4
и поэтому
X [ехр {-
Наконец, учитывая, что при составлении алгебраического допол-
дополнения Xjs (t) вычеркивается s-й столбец, содержащий координат!.!
решения х^\ будем иметь
Таким образом,
г UJjs (Щ ^ 0 + (- о) + (о - *,) =
и, следовательно,
Р, = max xto (*)]
<0. C.12.16)
Сопоставляя эти неравенства с неравенствами C.12.15), получаем
°-s + h = 0 (s=l, ..., п). C.12.17)
Остается показать, что фундаментальная матрица У (?) нормаль-
нормальная и, следовательно, числа р,, ?.2> ..., |3Я реализуют весь спектр
сопряженной системы. Действительно, на основании равенств
C.12.17) имеем
cy=Ei3s = -IX=- limT ^ Re Sp .4 (/,) ^ ^=
t
= lim I \ Re Sp[-i4*(/,)]«//!.
§ 12] ТЕОРЕМА ПЕРРОНА 173
Таким образом, для фундаментальной матрицы Y (t) сопряженной
системы C.12.2) выполнено равенство Ляпунова и, следовательно,
эта матрица нормальная (§ 7).
2) Докажем теперь достаточность условий теоремы. Пусть
C.12.10) и C.12.11) — спектры сопряженных систем и выполнены
равенства C.12.12).
На основании неравенства Ляпунова имеем
t
У as 5= Игл \ \ Re Sp A (/,) dti = S
^^ t -» со ' iJ
s
И
t
У 3, 5s lim -г
** * — со Г
1 С
= — lim — \ ReSp Л С/,) dt, — — S.
г~^Гсо f^
Складывая последние неравенства, в силу неравенства C.12.12)
получим
S
Но так как, очевидно,
то
S = S.
Следовательно, существует предел
t
5= lim ~ [ ReSp
t — со Г J
Кроме того, выполнено равенство
Действительно, если бы
то, учитывая, что
мы бы имели
S
что, очевидно, невозможно.
174 ПЕРВЫЙ МЕТОД ЛЯПУНОВА | Г Л 41
Таким образом, на основании леммы из § 11 система C.11.1)
правильная.
Теорема доказана.
Следствие 1. Сопряженная система для правильной линей-
линейной системы есть также правильная линейная система.
Следствие 2. Если система C.11.1) — правильная и X (/) —
ее нормальная фундаментальная матрица, то
есть нормальная фундаментальная матрица сопряженной системы
C.11.2).
§ 13. Правильность треугольной линейной системы
В этом параграфе будет исследована дифференциальная си-
система с ограниченной треугольной матрицей. Не уменьшая общ-
общности, можно ограничиться рассмотрением системы с нижней
треугольной матрицей.
C.13.1)
21 — a-2i (t) Xi -f а,г (t) хъ
~^ = anl (t)xt -j-aai (t) л-, + ...+aM (/)xn.
Положим A @ = \ajk (t)] ^ С [t0, oo), где ауА(/)^0 при k^> j.
Теорема Ляпунова. Действительная треугольная одно-
однородная линейная система с ограниченными коэффициентами яв-
является правильной тогда и только тогда, когда ее диагональные
коэффициенты akk(t) (k—1, ... , п) имеют конечные средние зна-
значения
akk(ti)dti. C.13.2)
и
Доказательство. 1) Докажем сначала необходимость
условий теоремы. Пусть система C.13.1) правильная. Положим
jxft= lim -j \ akk (ti)dt,
t — от •,
t
1 f
§ 13] ПРАВИЛЬНОСТЬ ТРЕУГОЛЬНОЙ ЛИНЕЙНОЙ СИСТЕМЫ 175
и пусть
S = lim у \ Sp A (to dti = Mm J- [ У akk (to dtx.
Введем сокращенные обозначения
t0dti (k=l, ... , n).
Последовательно интегрируя уравнения системы C.13.1), убеж-
убеждаемся, что эта система имеет нормированную фундаментальную
систему X (t) = [x/b(t)] вида
t ! — 1
f (tO 2
a/s (to xsl! (to dtt (j > k),
C.13.3)
*у* @ = A, {t) \ Af
to s = k
J, k=l, ..., П,
где X (^0) = E. Умножая справа матрицу X (t) на подходящую
постоянную матрицу
- 1 0 ... Ol
с,, 1 ... О
С =
можно получить нормальную фундаментальную матрицу (см. § 4)
X(t) = X(t)C (X(t) = lx/k(t)]),
причем, очевидно,
xkk(t) = Ak(t) (k=l, ..., п).
Транспонированная обратная матрица
является нормальной фундаментальной матрицей для сопряженной
системы
Нетрудно видеть, что
C.13.4)
176 ПЕРВЫЙ МЕТ01 ЛЯПУНОВА (ГЛ. Ill
Пусть
и
У. [*(АI = max х [х/к (t)\ = г„
(/?=1, ..., п), где в силу теоремы Перрона (§ 12)
a/f-f3A, = 0 (/,>=!, .... п). C.13.5)
Так как в состав решения х{1<) входит координата хккA)=г- АкA), то
**^/ЛЛ@] = :^ (А=1. ...,л). C.13.6)
Аналогично в силу формулы C.13.4) имеем
%^y.[Ai:Ut)l = -H (*=1 «)¦ C.13.7)
Складывая равенства C.12.6) и C.12.7) и учитывая формулу
C.12.5), получим
=1, ... я),
т. е.
еде
•i;= lim -,- \ akk (tx) dtu
что и требовалось доказать.
2) Докажем теперь достаточность условий теоремы. Пред-
Предположим, что условия C.12.2) выполнены.
Пусть Z (t) = \Zjk(t)] — система функций таких, что
*„,(()= 0 (/</г),
@ — >4у
где
и
/ — 1
V a/s(tt) zsk (ti) dti
t ,> — ?„, если tA
yft = -f-oo, если
k),
C.13.8)
§131 ПРАВИЛЬНОСТЬ ТРЕУГОЛЬНОЙ ЛИНЕЙНОЙ СИСТЕМЫ 177
Очевидно,
detZ(ro)=l.
Так как
то система функций Z (t) отличается от фундаментальной системы
X (/) тем, что к входящим в нее интегралам прибавлены некото-
некоторые постоянные. Поэтому Z (t) является также фундаментальной
матрицей нашей дифференциальной системы C.12.1). Отсюда сле-
следует, что
Z{t) = X(t)B,
где
— постоянная матрица. Имеем
l[Zuk(t)'\ = l[Ak(t)]=V-k (k=l п).
Далее, по индукции выводим, если
то из формул C.13.8), используя теорему о характеристическом
показателе интеграла и ее следствие (§ 1), получаем
7[2jk(t)]^yL[A,(t)] + y[ATl @1 +max fek,@] + /J
Следовательно,
** = 1 !>'*'] =rnax У. [2/* V)] -s= i** (k=l, .... n).
Отсюда, полагая
t n n
\ .l)^l= У «.ft,
T
* = 1
1'8 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. Ш
в силу неравенства Ляпунова получим
* к
т. е. ль = рк (k=l, ..., п) и
Таким образом, построенная фундаментальная система Z (/) нор-
нормальная, а значит, система C.13.1) правильная.
Следствие. Если система C.13.1) с действительной огра-
ограниченной треугольной матрицей правильная, то средние значения
ее диагональных коэффициентов akk(t) дают спектр |жь ..., т.п\
этой системы, т. е.
1 ?
т.и ^^ Jim —г \ аьь (ч) "м (& -— 11 * • • ¦ л).
,_со t }
'о
§ 14. Теорема Перрона о триангуляции линейной системы
Пусть
% = A{t)x C.14.1)
— однородная система, где A(t)(^-C[t0, с»). Рассмотрим фунда-
фундаментальную матрицу X (t) = \Xjk{t)\, элементы которой, вообще
говоря, комплексные.
Лемм а. Всякую фундаментальную матрицу X (t) можно
представить в виде произведения ¦ непрерывно дифференцируемых
унитарной матрицы 0 (t) и верхней треугольной матрицы R (t)
с положительными диагональными элементами, т. е.
X(t) = U(t)R(t), C.14.2)
где
U*(t)U(t) = E,
R(t) = [rjk(t)], rj;-(t)^>0, rjk(t) = O при k^> j.
Доказательство. Для доказательства применим известный
метод ортогонализации Шмидта.
Пусть
*¦<*> = colon [xUl @, ¦ • • , xnk (t)] (k=\, ..., n)
— решения, входящие в фундаментальную матрицу X (t).
HI ТЕОРЕМА ПЕРРОНА О ТРИАНГУЛЯЦИИ ЛИНЕЙНОЙ СИСТЕМЫ
Положим
179
C.14.3)
n - 1
gm.
Так как решения х{к) (k=l, ... , п) линейно независимы, то
приведенная конструкция всегда возможна. Нетрудно проверить,
что вектор-функции e(s) образуют ортонормированную систему
(e{s\ e^) = bsr. C.14.4)
Из соотношений C.14.3) получаем
х = i
п — I
Следовательно,
где
Пусть
О
О
1ГМ1
@ = [ё„
— эрмитово-сопряженная матрица для U (t). Учитывая соотноше-
соотношения C.14.4), имеем
U(t)U* (t) = [J] ej ] = [в,,] =?.
180 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ ГЛ III
Таким образом, матрица U (t) унитарная. Кроме того, из вида,
треугольной матрицы R(i) непосредственно вытекает, что ее диаго-
диагональные элементы положительны: ''//= || li;) у. Очевидно,
U {t), R(t)eO[t№, oo).
Лемма доказана.
Замечание. Если матрица X (t) вещественная, то матрица
U (t) действительная и ортогональная, а треугольная матрица
R(t) действительная.
Теорема Перрона (см. [26]). Всякую линейную однород-
однородную систему C.14.1) с помощью унитарного преобразования
x = U(t)y можно привести к системе с верхней треугольной
матрицей, диагональные коэффициенты которой вещественны:
%=B(t)y, C.14.5)
где B(t) = {bJk(t)}, bJk(t) = O при />& и lmbjj(t) = 0.
Если матрица А (/) ограничена на [/,,, со), то треугольные
матрицы В (t) и О (t) также ограничены на [tt), сю).
Доказательство. Для доказательства используем способ
Винограда (см. [27]). Положим
x = U(t)y, C.14.6)
где U (t) — унитарная матрица, определяемая формулой C.14.2).
Имеем
Следовательно, система C.14.1) примет вид
где
B(t) = U-1(t)A(t) U (t) — U~l @ О (/). C.14.7)
С другой стороны, на основании формулы C.14.6) для фунда-
фундаментальной матрицы X (t) однородной системы C.14.1) имеем
X(t) = U(t)Y(t), C.14.8)
где Y (t) — фундаментальная матрица системы C.14.7), т. е.
у (t) = В (t)Y(t). C.14.9)
Сопоставляя формулы C.14.2) и C.14.8), находим
§ 14] ТЕОРЕМА ПЕРРОНА О ТРИАНГУЛЯЦИИ ЛИНЕЙНОЙ СИСТЕМЫ !81
где R(t)— верхняя треугольная матрица. Из формулы C.14.9),
учитывая, что производная и обратная матрицы треугольной суть
также треугольные матрицы того же типа, выводим:
B(t) = Y (t) Y1 (t) = R (t) RT'1 (t) = Ri @, C-14.10)
где Ri(t) — верхняя треугольная матрица.
Так как
(см. лемму), то из формулы C.14.10) следует вещественность
диагональных коэффициентов
4J)\\-J%JiJ = Ttln№J)\\ (/=1, •¦-,«)• C-14.11)
Выразим теперь матрицу В (t) через матрицу A (t). Прежде
всего, заметим, что матрица U~l (t) 0 (t) эрмитово-кососимметри-
ческая. Действительно, учитывая унитарность матрицы U (t),
имеем
= - U-1 (t) 0 (t) Ul (t) U(t) = — U x(tH (t).
Отсюда следует, что диагональные элементы матрицы U'i (t) U (t)
чисто мнимые. Пусть
Так как матрица В (t) — [bik (t)] ¦—верхняя треугольная с вещест-
вещественной диагональю, то, полагая V (t) = U~l (t) 0 @= [vjk (/)], из
формулы C.14.7) будем иметь
vjk(t) = ajk^ при />*, } C/14.12)
vJk(t) = — akj при
Следовательно,
C.14.13)
при j<^k.
Если матрица A (t) ограничена, то матрица A (t), очевидно,
также ограничена; отсюда на основании формул C.14.12) и C.14.13)
вытекает ограниченность матриц О (t) и В (t).
182 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ III
Замечание. Если матрица A (t) действительная, то матрицу
U(t) можно выбрать действительной и ортогональной.
Следствие 1. Если система C.14.1) правильная, то тре-
треугольная система C.14.5) также правильная.
Действительно, пусть аь ..., а„ — спектр системы C.14.1) и
t
>Г з./= lim i. jj Re Sp A (it) dtx.
Из формулы C.14.7) получаем
Re Sp В (t) =
= Re Sp [U-f (t) A {t) U(t))~ Re Sp [U~l (t) O(t)] = Re Sp A (t).
Отсюда, учитывая, что при унитарном преобразовании характе-
характеристические числа решений сохраняются, будем иметь
= Jim ~ [ ReSp В (U)dtu
/ —У ОО
'о
что и доказывает правильность системы C.14.7).
Следствие 2. Если линейная система C.14.1) правильная,
то для каждого ее нетривиального решения x — x(t) существует
строгий характеристический показатель ([26])
а= lim -7- In ji jc(^)!,.
/ — 00 l
Пусть решение л; (t) включено в фундаментальную систему
X (t) и х (t) = xw (t). Тогда на основании теоремы Ляпунова о
правильности треугольной системы (§ 13) и формулы C.14.11)
имеем
t -» 00 ' J
'0
ti= lim I \4-\n\\lw(tl)\\dti =
= lim
Но по способу построения функций |(ft) (t) (см. лемму)
= х{'' (/) = х (/). Следовательно, существует
а= lim у In \\.x(t) \\,
что и требовалось доказать.
5 15] ТЕОРИЯ ФЛОКЕ 183
§ 15. Теория Флоке
Рассмотрим линейную систему
™=A(t)x C.15.1)
с непрерывной (или кусочно-непрерывной) на (— со, -f- oo) пе-
периодической матрицей A (t):
A{t-\-*) = A{t) («o>0). C.15.2)
Теорема Флоке. Для линейной системы C.15.1) с ^-пе-
^-периодической матрицей нормированная nput = 0 фундаментальная
матрица решений (матрицант) имеет вид
Х(()=:Фу)еА>, C.15.3)
где Ф (t) — класса С1 (или кусочно-гладкая) ^-периодическая неосо-
неособенная матрица, причем Ф@) = ?, и А— постоянная матрица.
Доказательство (см. также [28]). Пусть X.{t)— нормиро-
нормированная фундаментальная матрица решений системы C.15.1), где
Х@) = ?. C.15.4)
Матрица X (/ -f- ш) также является фундаментальной. Действи-
Действительно, на основании тождества
X{t)~A(t)X{t)
имеем
J- [X (t + со)] = X (t -f ш) |- (/ + «») =
= A(t + u>)X(t-}-<i>) = A(t)X(t + ш).
Следовательно, X (/ -)- ш) есть фундаментальная матрица решений
для системы C.15.1).
Отсюда получаем
X(/-feo)==X(/)C, C.15.5)
где С — постоянная неособенная матрица. Полагая t = 0 в тож-
тождестве C.15.5) и учитывая условие C.15.4), находим
С = Х(со).
Таким образом,
X(t + ш) = X (О X (ш). C.15.6)
Матрица X (ш) носит название матрицы монодромии.
Очевидно,
det А' (и; ^ 0.
184 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ III
Положим
-i Ln X (<о) = Л; C.15.7)
отсюда
Х(ш) = еА">. C.15.8)
Напишем тождество
X(t)==X (t) e-At- eAt = Ф (t) eAt, C.15.9)
где
O(t) = X(t)e At.
Имеем
Ф(l-f- ш) = X (t-f со)е-Л <• +m) =X(/ + m)r Лю • e'Al.
Отсюда, учитывая C.15.6) и C.15.8), получаем
Ф (/ -f ">) = X (t) е4ш • е- Лш е~ А' = X (t) e~ At = Ф (t),
т. е. матрица Ф (t) — периодическая с периодом ш. Кроме того,
если A (t) ?С(~ оо, -j0). то из C.15.9) выводим
причем
Ф@) = ? и det
Теорема доказана.
Замечание. Матрицы
Ф (t) = X (t) e' Л',
вообще говоря, комплексные. Можно ограничиться действи-
действительными преобразованиями, если воспользоваться матрицей
Однако при этом рассуждения значительно усложняются (см. [28]).
Собственные значения >7 матрицы Л, т. е. корпи векового
уравнения
det (Л — Щ = О,
называются характеристическими показателями системы C.15.1).
Отметим, что матрица Л не является строго определенной, так
как значение Ln X (ш) многозначно (гл. I, § 15).
Во избежание недоразумений следует иметь в виду, что ха-
характеристические показатели линейной периодической системы
§ 15] ТЕОРИЯ ФЛОКЕ 185
не идентичны с характеристическими показателями Ляпунова
нетривиальных решений этой системы: первые, вообще говоря,
являются комплексными числами, а вторые — действительными чис-
числами, представляющими вещественные части первых.
Собственные значения ру (/=1, •.., п) матрицы С = Х(<о),
т. е. корни векового уравнения (характеристического уравнения)
det[X(a))-P?] = 0, C.15.10)
называются мультипликаторами. Из формулы C.15.10) выводим.
y jj (t)dt.
f= 1 0
Так как detX(i»)^O, то р; Ф 0. Из формулы C.15.7) на ос-
основании известных свойств собственных значений логарифма мат-
матрицы (см. замечание 2 к теореме § 15 гл. I) получаем
^ -j--2toc)] C.15.11)
(/=1, 2, ..., п; k — 0, ±1, ±2, ...),
где целое число k подбирается надлежащим образом. Поэтому
характеристические показатели определяются с точностью до мни-
мнимых слагаемых 2ftiw'/w.
Обобщение. Нетрудно получить более общие формулы для
матричного решения линейной периодической системы C.15.1).
Пусть X (t) (Х@) = Е)— нормированная фундаментальная мат-
матрица системы C.15.1) и Хх (t) — произвольная фундаментальная
матрица той же системы.
Очевидно, имеем
Так как X] (/ -\- ю) снова является решением периодической
системы C.15.1), то справедливо тождество
где С\ — постоянная матрица. Отсюда, полагая / = 0, получим
С, = X, @) Хг И = X, ¦ @) X (ю) Хг @).
186 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. Ш
Матрицу С], подобную матрице монодромии X («), будем назы-
называть основной для матрицы X, (/) (см. [10]). Положим
А = - LnX(w)
A,=-LnC,.
(О
Конкретизируя выбор Л, нетрудно убедиться, что можно взять
0). C.15.12)
Действительно, используя известное свойство экспоненциала мат-
матрицы (гл. I, § 6), имеем
ел1Ш = х-1 @) е^х^ @) = х-1 @) х (ш) Xi @) = Ci
Из формулы C.15.12) имеем
А = Х1@)Л,Х1-'@).
Применяя основную формулу C.15.3), получаем
X, @ = X (/) X, @) = Ф (/) еиХ1 @) =
= Ф (/) ^«"^«^"'«"'Х, @) = Ф (/) X, @) еЛ1/.
Таким образом,
X,@ = *i(*)eAl', C.15.13)
где Ф, (/) = Ф (/) Xj @) — ю-периодическая матрица и
А, = 1 Ln С, = 1 Ln [X,' @) X, (ш)].
Теорема. Для всякого мультипликатора (множителя) р сг/-
ществует нетривиальное решение % (t) периодической системы
C.15.1), удовлетворяющее условию
S(' + ">) = pS(Q C.15.14)
(так называемое нормальное решение).
Обратно, если для некоторого нетривиального решения § (/) вы-
выполнено условие C.15.14), то число р является мультипликатором
данной системы.
Доказательство (см. [29]). 1) В качестве начального век-
вектора | @) выберем собственный вектор матрицы монодромии X (is),
отвечающий собственному значению р. Имеем
в 15] ТЕОРИЯ ФЛОКЕ 187
Отсюда
! (/ + «о) = X (t + ш) 1 @) = X @ X (ш) | @) = X (/) Р$ @) = р! (t),
следовательно, условие C.15.14) выполнено.
2) Обратно, пусть для некоторого нетривиального решения
! (г) = X (/) ! @) выполнено условие C.15.14). Тогда, положив
/ = 0, из C.15.14) получим
Таким образом, | @) является собственным вектором матрицы
монодромии Х(«>), а число р есть корень векового уравнения
det[X(co) —Р?] = 0
и, значит, р—мультипликатор.
Следствие. Линейная периодическая система C.15.1) имеет
нетривиальное решение периода ш тогда и только тогда, когда по
меньшей мере один из мультипликаторов ее р равен единице.
Действительно, если р= 1, то для некоторого решения §(/) ф 0
имеет место соотношение
l(t + ») = !(/) C.15.15)
и, следовательно, |(/) — ю-периодическое решение системы C.15.1).
Обратно, из тождества C.15.15) вытекает, что существует
мультипликатор р, равный единице.
Замечание 1. Полагая
5(/) = ^Ф^, C.15.16)
из формулы C.15.14) будем иметь
т. е.
ф (* + <•>) = ф@-
Следовательно, нормальное решение периодической системы имеет
вид C.15.16), где ф(/) — ю-периодическая вектор-функция класса С1 и
А = — Ln p
~ характеристический показатель системы,
1^8 ПЕРПЫЙ МЕТОД ЛЯПУНОВА [ ГЛ III
Замечание 2. Мультипликатору р.— — 1, если он суа1,ест-
вует, соответствует так называемое антипериодическое решение
g(/)s?O периодам, т. е.
|(/-;-"») =-КО-
Отсюда имеем
|(Н-2«>) = _g(/-f со) = |@,
и, таким образом, g (/) есть периодическое решение с периодом 2«.
Аналогично, если р = exp ~T~- (p, q — целые; q :j^\), то периоди-
периодическая система имеет периодическое решение с периодом
§ 16. Приводимость периодической линейной системы
Теорема Ляпунова. Линейная система с непрерывной
периодической матрицей приводима.
Доказательство. Согласно формуле C.15.3) нормирован-
нормированная матрица решений периодической системы C.15.1) имеет вид
Х@ = Ф@^,
где Ф (t) ^ С (— со, -j- оо), причем
Ф (/ + «>) = Ф (О-
В силу периодичности Ф (/) и Ф (/) ограничены на (—со, -{-со).
Кроме того, так как
<b(t)==X(t)e-At
и X (t) — неособенная матрица, то Ф (t) — также неособенная мат-
матрица. Учитывая периодичность Ф(?), получим
inf j det Ф (О I > О
при -- оо<^t <^-|-оо.
Следовательно, Ф(() есть матрица Ляпунова. В силу теоремы
Еругина (§ 5) периодическая система C.15.1) приводима.
Замечание. Производя в уравнении C.15.1) замену пере-
переменных
получим
Таким образом, характеристические показатели t.j являются кор-
корнями векового уравнения матрицы системы C.16.1).
Отсюда имеем следующие условия устойчивости периодической
системы (ср. § Ь)-
$ 16]
ПРИВОДИМОСТЬ ПЕРИОДИЧЕСКОЙ ЛИНЕЙНОЙ СИСТЕМЫ
189
Теорема, 1) Линейная однородная периодическая система с
непрерывной матрицей устойчива тогда и только тогда, когда
все ее мультипликаторы р;- расположены внутри замкнутого еди-
единичного круга ; р j sg 1, причем мультипликаторы, лежащие на ок-
окружности р ', = 1, имеют простые элементарные делители, если
их рассматривать как собственные значения соответствующей
матрицы монодромии.
2) Для асимптотической устойчивости периодической системы
необходимо и достаточно, чтобы все мультипликаторы ее нахо-
находились внутри единичного круга pj<^l.
Действительно, так как характеристические показатели Ху-
связаны с мультипликаторами ру- соотношениями (см. § 15)
\i= -(ln|P,-|-HArgp;),
то при
IP/
1
имеем XysgO. Отсюда непосредственно вытекает наша теорема.
Для определения области асимптотической устойчивости выве-
выведем условия (см. [И]), обеспечивающие принадлежность корней
полинома
/(p) = det[p? —Х(«о)] C.16.2)
единичному кругу |р|<С1. предполагая, что матрица X (ш) дей-
действительная.
Г
Рис. 21.
Нетрудно проверить, что дробно-линейное преобразование
>2±±
-—
единичный круг | р | <^ 1 плоскости р (р = о -4- гЧ) переводит в ле-
левую полуплоскость ReX<^0 плоскости X (рис. 21, а, б). Таким
190 ПЕРВЫЙ МЕТОЛ ЛЯПУНОВА [ГЛ. III
образом, уравнение C.16.2) заменяется следующим:
или
C.16.3)
где полином F(к) должен быть полиномом Гурвица (гл. II, § 9),
причем знак в формуле C.16.3)
нужно выбрать так, чтобы полином
F (X) был стандартным, т. е. должно
быть
-2
При м е р. При каком условии корни
полинома
(р и q действительны) лежат внутри круга | z
Положим
2+1 , I
1?
1=±(г-1)Ч|-^| +р
C.16.4V
Так как F(z) должен быть полиномом Гурвица, то отсюда получаем искомые
условия:
]
1—<7>0, !• или 1—<?<0,
/> + (?> 0, ] 1 — р + g < 0.
Вторая система неравенств противоречива и, следовательно, окончательно
имеем (рис. 22) — 1 -\- \ р , < q < 1.
§ 17. Нормальная форма решений линейной
периодической системы
Согласно теории Флоке для («-периодической системы C.15.1)
существует фундаментальная матрица вида
X (/) = Ф @ *-", C.17.1)
где Ф (t) ¦— ш-периодическая матрица и Л — постоянная матрица.
Пусть X,, ..., \т (т^п) — характеристические показатели сн-
стемы, т. е. собственные значения матрицы А. Приведем мат-,
рицу А к канонической форме Жордана
6 17]
НОРМАЛЬНАЯ ФОРМА РЕШЕНИЙ СИСТЕМЫ
191
где S — неособенная постоянная матрица и Jр (лр) (р = 1, ..., т) —
соответствующие клетки Жордана. Из формулы C.17.1) получаем
X (^) = Ф (t) S'1 diag [e , ..., е "»( т ] S. C.17.2)
Так как произведение фундаментальной матрицы на неособенную по-
постоянную матрицу есть также фундаментальная матрица, то перио-
периодическая система C.15.1) допускает фундаментальную матрицу вида
где
— неособенная непрерывная матрица периода ю.
Пусть Y(t) = \yjk(t)\ й ЧГ(/) = [<Ы*I- Полагая
где
JA\) =
О
1
), 0,...; 01,
... 0
... о
о о
еЧ' гг'
О ??^1^
-I
о о
получим соответствующие корню
"т
(«1-1)!
'(е, —2)!
частные решения;
192 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. 'II
Систему решений у{[>, ..., у|<г»> можно записать более просто.
Пусть
Обозначим через D операцию дифференцирования по t при усло-
условии, что фу* (/) постоянные, т. е.
Тогда группу частных решений, соответствующих клетке Жор-
дана JiO-i), можно записать следующим образом (ср. [14]):
), C.i7.5)
учч) = еА''Р[и (t),
где РЛШ) — матричный полином типа «XI от t степени е\ — 1,
коэффициенты которого ш-периодические матрицы-столбцы.
Аналогичную форму имеют группы частных решений, соот-
соответствующие остальным клеткам Жордана JpQ.p)(p = 2, ... , in).
Из формулы C.17.5) вытекает, что для каждого характери-
характеристического показателя X однородной периодической системы суще-
существует ее нормальное решение вида
у = е''Ц- (t),
где if @ — непрерывно дифференцируемая «-периодическая вектор-
функция.
В частности, если все мультипликаторы pi, ..., р„ периодиче-
периодической системы простые, то существует ее фундаментальная система
нормальных решений, имеющая вид
у,, =
18] ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ МУЛЬТИПЛИКАТОРОВ 193
где фу- (t) (j= 1, ... , п) — непрерывно дифференцируемые ш-перио-
дические вектор-функции и ~kf — — Lnp7- (/=1,..., п).
Пример. Рассмотрим скалярное уравнение
-q(t)x — O, C.17.6)
где p it) и q (t) — непрерывные ш-периодические функции. Полагая у = х,
получим линейную периодическую систему
dx _ 1
C.17.7)
dt
Пусть р! и р2 — мультипликаторы системы C.17.7) и
Так как
PiPa = ехр [— 5
о
то можно принять
1 ш
= -^i \p(t)dt.
03 о
03 о
Если р! ф р2 или же pj = р2, но им отвечают простые элементарные
делители, то уравнение C.17.6) будет иметь фундаментальную систему решений:
*i = +1 @ *Xl'. xt = +2 @ е'12',
где Фч(О и фз(^) — непрерывно дифференцируемые ш-периодические функции.
Если pi = Рз и соответствующий элементарный делитель не является
простым, то уравнение C.17.6) допускает фундаментальную систему решений:
Xl = ф, (О *x'', xt = [«ф, @ + <Ь (/)] еЛ1<,
где ^i (О и 4"s W—«-периодические функции класса С1 и
§ 18. Приближенное вычисление мультипликаторов
Пусть Л (f) — непрерывная ш-периодическая матрица. Основной
промежуток [0, ш] с помощью точек
разобьем на т равных частей, и пусть
7 Б. П. Демидович
194 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. II!
В дифференциальном уравнении
^- = A(t)X, C.18.1)
где Х@) = Е, следуя [30], заменим матрицу A (t) кусочно-по-
кусочно-постоянной матрицей:
Ah{t) = Ak при tk^t<^tk+1 C.18.2)
(k = 0, I,..., m—1),
где
min A(t)s^Aks^ max A (t),
например,
Обозначим через Хд = Хл (t) непрерывную матрицу, удовле-
удовлетворяющую в точках непрерывности коэффициента Ah (t) дифферен-
дифференциальному уравнению
ру
циальному уравнению
§ = Ah(t)Xh, C.18.3)
где 0<(«;«) и Xh@) = E. Обобщенное решение Xh легко по-
построить. На основании формул C.18.2) имеем
^ = AkXh при 4
и
^§L = Ak+lXh при ^
где Лй(й = 0, 1,..., /п—1) — постоянные матрицы. Отсюда
XA = e('-'*»a*Cft при
и
Хд = е('-'*+')Я*+'Сл+1 при
Используя непрерывность решения Хд в точке t — tk+u будем
иметь
Сш=(ГАкСк (А = 0,-1 т-1). C.18.4)
Кроме того, при ? = 0 и t=to — O получаем
§ 181 ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ МУЛЬТИПЛИКАТОРОВ 195
Из формулы C.18.4) последовательно выводим
C.18.5)
причем, так как матрицы Ао, Л,,..., Ат^ в общем случае не-
неперестановочны, то в формуле C.18.5) нельзя применить правило
перемножения экспоненциалов. Следовательно,
Xh @ = e(t ~ '*' л* • елл"*-> ... е^0 fe < t < t^ C. j 8.6)
h
Таким образом, для последнего промежутка (tm_u tm) будем
иметь
Отсюда, полагая, что t~>tm — 0 = и — 0, получим
Xh (ш) = #*т-х. ehAm-i ... eh\ C.18.7)
Используя первую норму матрицы (см. § 8 из гл. I), оценим
ХЛ(ш) — Х(ш)\\. Из дифференциальных уравнений C.18.1) и
C.18.3) имеем
X(t) = E+]A(t1)X(tl)dt1
а
Отсюда
Лй @ - X @ = \[Ah (U) - .4
о
о
Переходя к^орме при 0^/^«>, получим
+ \ \\ А {к) \\ ii Х„ (^ - X (/,) || Л,. C.18.8)
о
7*
196 ПЕРВЫЙ МЕТОЛ ЛЯПУНОВА (ГЛ. [II
Пусть
\}A(t)\\^M при O^J^w;
тогда
\\Ak\\*zzM (k = Q, 1, ... , т— 1).
Из формулы C.18.6) при / ? [0, ш] находим
Так как матрица A (t) (^ С [0, ш], то для каждого s.^>0 суще-
существует е ^> 0 такое, что
\\А(Г)-А(П\\<*.
если f, Г^[0, со] и !/'--- Г!<8. Отсюда при /г<8 и f ? [0, ш]
будем иметь
'| Лй (9 - Л С)!! о
Следовательно, ич формулы C.18.8) получаем
!! Xh (t) - X (/) . <.е«ое-л + $ Ж !| ЛА (/,) - X (f,) || dtb
о
Применяя лемму Гронуолла — Беллмана (гл. II, § 11), получим
\\ Xh (I) — X @ :| ==S тешМ+т при 0 sg ^ «=? т
и, следовательно,
!| Хл (ш) — X (ш) || й? гше^м, C.18.9)
если 0<^/z<^§ (s).
Так как число ?^>0 может быть взято произвольно малым,
то из неравенства C.18.9) будем иметь
Л->0
т. е.
lim XA(u)) = X((o). C.18.10)
Рассмотрим характеристические уравнения
det[X(u>) —р?]=0
и
= 0, C.18.11)
s 19] УРАВНЕНИЕ ВТОРОГО ПОРЯДКА 197
п пусть ру, Pf(h) (/=1,..., п) — соответственно, корни этих
уравнений. Так как корни ру (h) являются непрерывными функ-
функциями параметра h, то в силу соотношения C.18.10) имеем
lim p,(/z) = р, (/=1, .... и). C.18.12)
Таким образом, выбрав h достаточно малым, из уравнения
C.18.11) можно определить мультипликаторы р/ с любой степенью
точности.
§ 19. Линейное дифференциальное уравнение второго порядка
с периодическими коэффициентами
Рассмотрим скалярное дифференциальное уравнение
где a(t) <~ С1 (—оо, -(-со), b(t)(^C(—оо, -)--00) и
Полагая
z = e ° x,
будем иметь
X + p(t)x = 0, C.19.1)
где
Для исследования устойчивости приведенного уравнения
C.19.1) заменим его эквивалентной системой
dx
матрица которой есть
Заметим, что
198 ПЕРВЫЙ МЕТОД ЛЯПУНОВА |ГЛ. Ill
Будем говорить, что уравнение C.19.1) устойчиво или неустой-
неустойчиво, если устойчива или, соответственно, неустойчива система
C.19.2). Таким образом, все решения x(t) устойчивого уравнения
C.19.1) ограничены на [t0, со) вместе с их производными x(t).
Из теории Флоке следует (см. § 17, пример), что если решение
x{t) уравнения C.19.1) ограничено на [/0, со), то его производ-
производная x(t) также ограничена на [t0, со). Таким образом, уравнение
C..19.1) неустойчиво только в том случае, если оно имеет неогра-
неограниченные на [ta, со) решения.
Построим фундаментальную матрицу решений
¦(О
где tp @ и ф (/) — линейно независимые решения уравнения C.19.1)^
удовлетворяющие начальным условиям:
9@)= 1, ф@) = 0 C.19.3)
и
= 3. C.19.4)
Следуя Ляпунову, решения y(t) и ф(/) можно получить в виде
сходящихся рядов. Действительно, вводя в уравнение C.19.1)
числовой параметр [л (см. [13]), будем иметь
x = y.p(t)x, C.19.5)
где в окончательном результате следует положить р. = — 1. Пусть
решение уравнения C.19.5) имеет вид
Подставляя это выражение в дифференциальное уравнение C.19.3)
и предполагая возможность двукратного почленного дифферен-
дифференцирования, получим
Отсюда
v ?*@i**=Sp(Ot*@[**+1.
То @ = 0 C.19.7)
>==р (/) ?*_,(*) (Л=1, 2, ...). C.19.8)
s 19! УРАВНЕНИЕ ВТОРОГО ПОРЯДКА 199
Введем начальные условия:
?*@) = Ф*@) = 0 при k^l;
тогда начальные условия C.19.3) для функции <p(?) = cp(f, —1)
на основании C.19.6), очевидно, будут выполнены. Из уравнений
C.19.7) и C.19.8) находим
ср0 @=1
и
<р* @ = ]dtt j p {к) %_! (ti)dtt (k^l).
о и
Последний интеграл можно заменить однократным. Действительно,
меняя порядок интегрирования в этом интеграле, будем иметь
Ъ @ = \dt, \ р (*,) cpfe_± (t,) dh = \(t-h)p (ti) ?ft_, (t9) dtt =
о t2 о
= \ (t ~ к) р (/,) cpftJ ft) Л,. C.19.9)
о
Итак,
о
о о
Исследуем сходимость'ряда C.19.10). Пусть
\p(t)\s^M При — OO<^<^-|-Q3.
На основании формулы C.19.9), учитывая, что ср0 (t) = 1 при любом
t?(—со, -f-oo), последовательно имеем
: 41
к т. д.
200 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. lit
Таким образом, функциональный ряд C.19.10) мажорируется
рядом
который сходится для любой системы значений (\х, t). В i лу
признака Вейерштрасса ряд C.19.10) сходится абсолютно и равно-
равномерно в любой конечной области G {| ;* |<^о, |^1<СП- Легко
также убедиться, что ряды, полученные в результате почленного
дифференцирования ряда C.19.10) по переменной t, также абсо-
абсолютно и равномерно сходятся в любой конечной области G. Сле-
Следовательно, сумма ср(?,[л) ряда C.19.10) представляет собой реше-
решение дифференциального уравнения C.19.5).
Полагая (i = —1, получим окончательно
<р (о = 1 - S (* - /,) р (h) dtx + \(t - h) p (tt) dtx \ (t, ~ h) p (h)du -I...
о и о
со). C.19.11)
Аналогично для дифференциального уравнения C.19.5) строится
второе решение
со
ф if U-) —тг у фь (t) U,
где
и
tj)ft (/) = ^ (/ — /j) p (/j) ^k_1 (^i) dtx (k^l).
о
Отсюда
и, следовательно,
о ¦ о
§ 19] УРАВНЕНИЕ ВТОРОГО ПОРЯДКА
Характеристическое уравнение имеет вид
det [X(ш)_ Р?] = ?^~р , ^(U))
Отсюда, учитывая, что
со
J Sp P Ц) (It
det X (ю) = det X @) е° =1,
201
= 0.
получим
где
Р2 — ар + 1 = О,
а = ср (w) -f- ф (<») = Sp X
C.19.13)
C.19.14)
— так называемая константа Ляпунова. Из формулы C.19.12)
имеем
Ф @ = 1 - J ар &) rf^ + J р (/,) л, (№ - *.) kP (tt) л, +...
О 0 0
Поэтому для константы Ляпунова а получаем выражение
а = 2 - со \ р ft) rf/, -I- J Л, J cf/, (
+ U) ft - 4) P
0 0
- j Л, ^ dtt \ Л, («>-*,+ /,) & - *,) (^ — к) р ft) р (у р ft) +...
C.19.15)
oo
Будем предполагать, что коэффициент p(t) веществен; тогда
константа а также вещественная. ^
Из уравнения C.19.13) имеем
1
Возможны три случая: 1) | а \
А) а | <^ Z И о) |ы| = л.
Если ]а|^>2, то характери-
характеристическое уравнение C.19.13)
имеет два действительных кор-
корня р, и р4, из которых один по Рис. 23.
модулю меньше единицы, а дру-
другой— больше. Таким образом, мультипликатор pt лежит внутри
единичного круга |р!< 1 (jpi I <С 1), а мультипликатор р2 —вне
этого круга (| ра I ^> 1) (рис.. 23). Следовательно, уравнение C.19.1)
неустойчиво.
202
ПЕРВЫЙ МЕТОД ЛЯПУНОВА
[ГЛ. !П
Если \а\<^2, то корни pi и р.2 характеристического уравнения
комплексно-сопряжены и их модули равны 1, причем pi^p2. Сле-
Следовательно, мультипликаторы р! и р.г расположены на окружности
| р | = 1 и не совпадают между собой (рис. 24). В силу теоремы из
§ 16 уравнение C.19.1) устойчиво, т. е. все
решения его ограничены.
Случай |а| = 2, когда pi=pi, требует
более детального рассмотрения.
Отсюда на основании формулы C.19.15)
имеем следующий признак неустойчивости
уравнения C.19.1).
Теорема 1. Если непрерывный пе-
периодический коэффициент p(t) мажет
принимать лишь отрицательные или ну-
нулевые значения, не будучи тождественно
равным нулю, то линейное уравнение C.19.1)
неустойчиво, причем мультипликаторы положительны и один из
них больше единицы, а другой — меньше.
Действительно, так как
б
0 0 0
•••D-1 — tn)p(ti)...p(ta) 52=0 (л=1, 2, ...),
то из формулы C.19.15) имеем
а>2.
Рассмотрим теперь случай неотрицательного коэффициента
p(t)^O в уравнении C.19.1).
Теорема 2 (Интегральный признак устойчиво-
устойчивости Ляпунова). Если непрерывная ^-периодическая функция
р (t) может принимать лишь положительные или нулевые значения,
не будучи тождественно равной нулю, и выполнено неравенство
C.19.16)
то все решения x(t) уравнения C.19.1) ограничены вместе с их
производными первого порядка на {— оо, -]-оо), т. е. уравне-
уравнение C.19.1) устойчиво.
§ 19] УРАВНЕНИЕ ВТОРОГО ПОРЯДКА 203
Доказательство. На основании формулы C.19.15) для
константы Ляпунова имеем следующее выражение:
a = 2-/2 + /s + ... + (-l)*-'/ft + ..., C.19.17)
где
5$ $
(A==1, 2, -..). C.19.18)
Имеем
1
*+i — j dt% ^ dti... ^ dtk(ti — к)...(tk^i — tk)p i
oo о
• • • Р (**) J (»-
Используя очевидное неравенство
получим
(«"-/.+4+1) (^ - <*
при 0
Таким образом,
(Od/-/* (А=1, 2,
Отсюда в силу условия C.19.16) находим
Из сходимости ряда C.19.17) вытекает
lim Ik — 0,
'204 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. III
Следовательно, ряд C.19.17) представляет собой ряд Лейбница и,
(О
значит, справедливы оценки 2 — ш Jp (t)dt<^a<^2, или в силу
о
неравенства C.19.16)
— 2<а<2.
Отсюда в силу уравнения C.19.13) мультипликаторы рг и р3 комп-
комплексно-сопряженные, причем ]pi | = |рз | = 1, pi Ф н- Значит, урав-
уравнение C.19.1) устойчиво и каждое решение его x(t) ограничено
вместе с производной х (t).
Следствие. Если линейное дифференциальное уравнение
C.19.1) с непрерывным положительным ^-периодическим коэффициен-
коэффициентом р (t) имеет неограниченное решение, то выполнено неравенство
Замечание. Изложенная выше теория Ляпунова об устойчи-
устойчивости приведенного дифференциального уравнения C.19.1) остается
в силе, если его («-периодический коэффициент р (t) ограничен при
Os?^sgu> и является кусочно-непрерывным на [0, ">].
Действительно, в этом случае решения <р(?)иф(/), определяе-
определяемые начальными условиями C.19.3) и C.19.4), также изобража-
изображаются функциональными рядами C.19.11) и C.19.12), сходящи-
сходящимися на (— оо, -\- оо) и допускающими почленное дифференци-
дифференцирование. Сходимость всех этих рядов, как следует из неслож-
несложных оценок их членов, равномерна на любом конечном интервале
(a, b)d(—со, -|-со). Следовательно, y(t) и ty(t) суть функции
класса С1 (—оо, -f-oo), удовлетворяющие дифференциальному
уравнению C.19.1) всюду, за исключением, быть может, точек
разрыва коэффициента p(t), число которых конечно на каждом
промежутке [&», (A-J- 1)ш] (? = 0, ±1, ±2, ...), т. е. ^ (/) и ф@
являются обобщенными решениями (см. § 18) уравнения C.19.1).
Иначе говоря, y(t) и (])(/.) суть решения дифференциального урав-
уравнения C.19.1), записанного в интегральной форме:
Так как
detX(*) =
, . 1
при t (^ (—оо, -f-oo), то <f(t) и ф(^) представляют собой фунда-
фундаментальную систему решений дифференциального уравнения C.19.1)
на каждом интервале непрерывности его коэффициента p(t). Отсюда,
используя непрерывность функций <p(t), ty(t), $ (t), ф(^) и переходя
УРАВНЕНИЕ ВТОРОГО ПОРЯДКА
205
к пределам, получаем, что ? (t) и <j> (/) образуют фундаментальную
систему решений уравнения C.19.1) навеем промежутке(—оо, -р со).
Тем самым константа Ляпунова а имеет выражение C.19.15) и
приведенные выше признаки неустойчивости и устойчивости урав-
уравнения вида C.19.1) полностью переносятся я.
на наш случай. *
Пример 1. Рассмотрим уравнение Матье
Здесь
р (t) = а
Следовательно,
(а>0,
|3 COS t
И а) = 2г..
р (t) dt = 2- \ (а 4- p cos О Л = 4А.
о
Отсюда в силу признака Ляпунова область устойчи-
устойчивости (рис. 25) характеризуется неравенствами
и 0<asS?.
Рис. 25.
Более подробно этот вопрос разобран у Стокера (см. [31J), где построена
область устойчивости, полученная численным методом.
Отметим, что наличие неравенства 0 <[ а2 ^ р (t) =<; rf* <^ оо,
где а и C — положительные постоянные, не гарантирует ограни-
ограниченности решений уравнения C.19.1).
Пример 2. Пусть
где
!а2 при 0 < t < с,
fl2 При С< f <co
C.19.19)
C.19.20)
а р (t-j-т) = р (t) (рис. 26). Под решениями x = x(t) дифференциального
\ равнения C.19.19) будем понимать функции класса С1 (— со, -|-со), удов-
-л
0 Я
Рис. 26.
ЗЛ
летворяющие этому уравнению всюду, за исключением, быть может, точек
разрыва km, ku>-\~c (й = 0, ±\, ±2, ...) коэффициента/?^).
206 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [П1. Ill
Заменим уравнение C.19.19) системой
dx
и пусть X(t)—нормированная фундаментальная матрица такая, что Х@)—Е.
На основании C.19.20), используя прием, примененный в § 18, имеем
[cos at — sin at
a np
— a sin at COS at J
Г Acds$(t —c) + B sin? (t —с) Ccos P (i — c) + Dsin$(t— c)~l
( ' ~~ I — ДЗ sin 3 (it — e) -f fig cos p (* — c) —C3 sin g (i — c) + fi3 cos 3 (t — c)\
при с^<^и.
Отсюда из требования непрерывности при t — c матрицы X{t) находим
А = cos ас, В — —г- sin ас,
Таким образом, матрица монодромии имеет вид
cos ас cos 3 (со — с) — — sin. ас sin 3 (a — с)
Л(и)== р
L— Р cos ас sin 3 (со — с) — а sin ас cos 3 (<о — с)
— sin ас cos 3 (со — с) + -о- cos ас sin 3 (со — с)
а р
а
— sin ас sin 3 (<о — с) -f- cos ас cos 3 (<о — с)
Следовательно, константа Ляпунова для уравнения C.19.19) есть
а2 ' В2
а = Sp X (со) = 2 cos ac cos 3 (со — с) LJ- sin ас sin 3 (со — с). C.19.21)
Очевидно,
Отсюда следует, что уравнение C.19.19), коэффициент которого р (t)
положителен, может быть как устойчивым, так и неустойчивым. Полагая,
например, а = 7г иВ = —^—-, будем иметь « = 0 и, следовательно,
s- 191 УРАВНЕНИЕ ВТОРОГО ПОРЯДКА 207
уравнение C.19.19) устойчиво. Если жеа = — и 3 = ^-7—-—г, то приезд —
2с 2 (<о — с) 4 '
1. е. при о-ф^,, получим
и, таким образом, уравнение C.19.19) неустойчиво.
Замечание. Н. Е. Жуковский доказал, что постоянную-4
в признаке Ляпунова C.19.16) нельзя заменить большей, т. е.
в этом смысле она является наилучшей. Приведем простой при-
пример системы вида C.19.1) с кусочно-постоянным коэффициентом,
иллюстрирующий это обстоятельство, идея которого принадлежит
Н. П. Купцову.
Пример 3. Пусть 5 — произвольно малое положительное число
@<Ь<1). В «-периодическом уравнении
X-\-p(t)x = 0 C.19.22)
положим
4
р (t) = а2 = —- при 0 < t < С
р (t) = З2 = —; при с < t < a.
ч,(ч, — с)
Очевидно, имеем
[ р (t) dt = и [ { — Л + [ —А
оЗ LflJ «с J «(«
Покажем, что при достаточно малом S и надлежащем выборе параметра с
уравнение C.19.22) неустойчиво. Для этого достаточно убедиться, что соот-
соответствующая константа Ляпунова а [см. C.19.21)] удовлетворяет неравенству
а | > 2.
Действительно, положим
Тогда
2
а = ——
и, следовательно,
> ? У «(со — с)
Отсюда
1 _ 1
а? - р ' а - » V 16; ' 8 \' 16/
8 ¦ ¦ - ¦ при
208 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. III
Используя известные асимптотические разложения тригонометрических
функций:
cos х = 1 =- + о (.V2), sin х = х A =-) + о (х3) при х —*- О,
на основании формулы C.19.21) для константы Ляпунова а получаем следую-
следующее выражение:
а — 2 cos ас cos |5 (ш — с) i sin ас sin C (ш — с) =
s
-|— о (Ь) = — 2 ^—Ь о (S) при Ь —*- 0.
о
Следовательно, при достаточно малом положительном S выполнено неравен-
неравенство а< — 2, и таким образом, уравнение C.19.22) является неустойчивым.
§ 20. Гамильтонова система дифференциальных уравнений
Пусть
H = H(t, qu ..., qn, pu ..., Pn)~H(t, q, /ХбС'"
действительна и
дН\ дН , (дН дН\
Система
называется гамияыпоновой или канонической с функцией Гамиль-
Гамильтона Я. Такие системы играют важную роль в теоретической
механике (см. [32], [33]). Заметим, что если Н не зависит от t:
H = H{q, p),
токаноническая система C.20.1) допускает первый интеграл
Положим
-[;]¦
и пусть
J ==¦ Jo =
5 20]
ГАМИЛЬТОНОВА СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
209
— так называемая симплектическая единица. Тогда каноническую
систему C.20.1) можно записать в виде
dx_ ,дЛ
dt дх'
где
гдН
C.20.2)
дН
дх :
dq
д_Н
1др
(xu .... хп),
¦ Для единообразия введем обозначения:
= (хп+1, ¦¦¦ , xin). Тогда
H = H{t, х).
Пусть функция Гамильтона Н есть квадратичная форма пере-
переxin, т. е.
менных
где
н & *)=i 2ajk {t) XjXkt
C-20>3)
Из формулы C.20.3) имеем
= A(t)x,
где a (t) = [aJk (t)] — симметрическая матрица. Отсюда получаем
линейную гамильтонову систему
C.20.4)
с функцией Гамильтона
Н (f Х) i_ I
Заметим, что
, x].
Действительно, если
Sp[jA(t)]=O.
A(t)-[Q(t) R(t)\'
то
@ Q{t4-\ Q(t) *
Q(t) R(t)\ [~P(t) — Q @
210 ПЕРВЫЙ ME ГОД ЛЯПУНОВА [1Л, III
и, следовательно, ¦
Sp [JA (t)] = 0.
Пусть
х = colon(xu ... , х.1п), .у = colon (г/,, ... , yin)
— любые решения гамильтоновой системы C.20.4) (векторы-
столбцы). Через хг обозначим транспонированное решение
(вектор-строку)
X — \-м» • * • , Х^п).
Лемма. Для любых двух решений х и у линейной гамильто-
гамильтоновой системы C.20.4) остается постоянным их симплектическое
произведение
u = xTJy. C.20.5)
Доказательство. Дифференцируя функцию и, получим
Так как х и у — решения системы C.20.4), то
% = JA(t)x и ft=JA{t)y.
Отсюда, учитывая симметричность матрицы A (t) и то, что
JT=-J,
получаем
d-?=[%)T=xTAT(f)JT=-xrA(f)J.
Следовательно, принимая во внимание, что
J J J '-'in,
из формулы C.20.5) имеем
d? = — xTA(t)JJy-\-xTJJA(t)y=xTA(t)y-xTA(t)y = O.
Поэтому
и = X TJy ^ cOnst.
Замечание. Лемма остается верной для Bп X2«)-матрич-
ных решений X (t) и У (/) гамильтоновой системы C.20.4), т. е.
XT(t)JY(t) = C,
где С — постоянная Bл X 2л)-матрица.
$ 211 ВОЗВРАТНЫЕ УРАВНЕНИЯ 21 1
§ 21. Возвратные уравнения
Определение. Алгебраический полином
f(z) = aiz -j-ai2 -f"...-\-an C.21.1)
(а0^0, 2 = х+/г/)
называется возвратным, если коэффициенты его, симметричные
относительно крайних членов полинома, равны между собой, т. е.
C.21.2)
Отсюда вытекает, что для возвратного полинома f (г) степени п
справедливо тождество
/(¦М=-^B) (г^О). C.21.3)
Обратно, если для полинома f(z) выполнено тождество C.21.3),
то этот полином возвратный.
Приравняв нулю возвратный полином, получим возвратное
уравнение
). C.21.4)
Если степень п возвратного уравнения четная, то с помощью
подстановки
<'+
его можно свести к уравнению степени у относительно неизве-
неизвестного t.
Возвратное уравнение нечетной степени п имеет корень zt =
= — 1, выделив который получим возвратное уравнение четной
степени п—-1. Таким образом, указанная выше подстановка по-
позволяет привести возвратное уравнение нечетной степени п к ал-
алгебраическому уравнению степени —=—•
Лемма. Если уравнение C.21.4) возвратное, то каждому
корню его zs Ф ± 1 соответствует взаимно обратный корень
z* = 17 C.21.5)
той же кратности. Если, сверх того, данное уравнение имеет
корень г = 1 j то кратность этого корня четная; если же оно
212
ПЕРВЫЙ МЕТОД ЛЯПУНОВА
[ГЛ. III
имеет корень z= — 1, то кратность последнего сравнима со сте-
степенью уравнения п по модулю два1).
Доказательство. Действительно, корни возвратного урав-
уравнения удовлетворяют условию C.21.5), так как, если
f(Zs) = О (г,фО),
то на основании тождества C.21.3) имеем
Таким образом, - — = zt есть также корень уравнения (рис. 27).
Заметим, что в случае zs = ± 1 полу-
получаем очевидный результат zt = db 1.
Покажем теперь, что кратности
взаимно обратных корней возвратного
уравнения одинаковы.
Обозначим через as кратности кор-
корней zs (s=l, ..., т), расположенных
внутри единичного круга i 2 J <Ч и
на верхней полуокружности |z| = l,
Im г ^> 0, а через Ъ3 кратности соответ-
соответствующих взаимно обратных корней -—,
расположенных, очевидно, вне единич-
Рис. 27. ного круга | z | ^> 1 и на нижней полу-
полуокружности |z| = l, 1гп2<^0. Кроме
того, кратности возможных корней 2=1 и 2 = —1, лежащих
на окружности |zj = l (Imz = 0), обозначим, соответственно,
через у и 8. Если какие-нибудь из указанных корней отсутствуют,
то мы условно считаем, что кратность их равна нулю. Отсюда
разложение многочлена / (г) на множители будет иметь вид
/(г) = «0
где
' ... (г~гт)'т{г- ?f* ...
г._ ^_)"». (г _ 1)т (г
(з.21.6)
C.21.7)
') То есть кратность корня z = — 1 четная, если п четно, и нечетная,
если п нечетно.
? 22] ТЕОРЕМА ЛЯПУНОВА - ПУАНКАРЕ 213
Так как полином f (г) возвратный, то в силу тождества C.21.3)
имеем
aaz [т—гг) ... (- - ги, j- - -j ...
)"«-f» (- iI (г - г,/1 ... (г - гт/« (г - ^j ...
(z-lO(z+l)'- C-21.8)
В силу свойства единственности разложения C.21.6) и C.21.8)
должны совпадать между собой; поэтому
и т четно.
Кроме того, из соотношения C.21.7) получаем
S = n(mod2)!).
Лемма доказана.
Следствие. Если возвратное уравнение четной степени
имеет корень z = 1 или корень z = — 1, то эти корни четной
кратности.
§ 22. Теорема Ляпунова—Пуанкаре
Теорема Л япунова—Пу анка ре. Если матрица A(t)
линейной гамильтоновой системы
% = JA(t)x C.22.1)
^-периодическая, то характеристическое уравнение
/(p)==det[p? —Х(ю)) = 0, C.22.2)
где X (а>) — матрица монодромии, является возвратным.
Доказательство. Приведем простое доказательство тео-
теоремы, принадлежащее Гельфанду и Лидскому (см. [34]).
На основании леммы и замечания к ней (§ 20) для фундамен-
фундаментальной матрицы X (t) (X @) = Е) справедливо соотношение
XT(t)JX(t) = C.
Полагая < = 0 и учитывая, что ХТ@) = Х @) = ?, получим
C = J.
х) То есть разность п — 5 делится без остатка на 2,
214 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. Ш
Таким образом,
Xr(t)JX(t) = J
и, следовательно,
XT(t) = JX~l(t)J~l.
В частности,
Хг(ш)=УХ"'((о)^.
Отсюда, учитывая, что
detJ = detJ'i = l,
при р Ф О имеем
= ~ det iE — Р*Г ("Ol =4r det [JEJ-1 — qJX'1 (u>) /"»] ==
= 4й det J ¦ det ffi — pX'1 (to)] • det J'1 =
= -m det X (<e) • det \oE — X (to)].
Ho
det X (to) = det X @) • exp $ Sp JA (t)dt=l,
о
поэтому
Таким образом,
C.22.3)
и, значит (§ 21), характеристическое уравнение C.22.2) является
возвратным.
Следствие 1. Для гамильтоновой системы C.22.1) мульти-
мультипликаторы р$ и — (jps|9^ 1) имеют одинаковую кратность.
Следствие 2. Если характеристическое уравнение C.22.2)
имеет корень р = 1 или р = — 1, то эти корни четной крат-
кратности.
Из теоремы Ляпунова—Пуанкаре вытекает, что гамильтонова
линейная система не может быть асимптотически устойчивой (§ 15).
Теорема. Линейная гамильтонова система с периодическими
коэффициентами устойчива тогда и только тогда, когда все ее
мультипликаторы р,- расположены на единичной окружности
| р | = 1 и имеют простые элементарные делители.
23] НЕОДНОРОДНАЯ ПЕРИОДИЧЕСКАЯ СИСТЕМА 215
Рассмотрим систему (см. [29]):
^ = 0, C.22.4)
где B(t)— (я X я)-матрица периодическая и симметрическая:
В (* + «>) = Я @, Br(t) = B(t) (<о>0).
Запишем матричное уравнение C.22.4) в виде системы:
dt
C-22.5)
или
It уу
где
'(О о
Так как матрица A(t) симметрическая, т. е. AT(t) = A (t),
имеем теорему: характеристическое уравнение для периодической
системы C.22.5) возвратное.
§ 23. Неоднородная периодическая система
Пусть
% C.23.1)
где A (t) и f(t) — непрерывные (п X ")- и (л X 1)- матрицы с общим
периодом и) . ("»^>0).
Теорема 1. Если однородная периодическая система
~ = A(t)x C.23.2)
не имеет нетривиальных ^-периодических решений, т. е. все муль-
мультипликаторы ее отличны от единицы (pj Ф ]), то соответствую-
соответствующая неоднородная периодическая система имеет единственное пе-
периодическое решение периода <».
Доказательство (см. [29]). Используя метод Лагранжа,
из уравнения C.23.1) имеем
y(t) = X (t)y @) + J X (/) X~l (т)/(т) rfx, C.23.3)
216 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. Ш
где X (t) — нормированная при / = 0 фундаментальная матрица
однородной системы C.23.2). В силу теоремы единственности ре-
решение у (t) будет io-периодическим тогда и только тогда, когда
Отсюда на основании формулы C.23.3) для ««-периодического ре-
решения у (t) будем иметь
у @) = X (ш)у @) + X (со) $ X-> (t)f(t) dt,
о
или
[Е~Х(ш)]у @) = Х (ш) $ X (t)f(t) dt. C.23.4)
о
Так как в силу условия теоремы вековое уравнение
det[pE — X («о)] = О
не имеет корня р = 1, то
det[? — X (<*>)] ф О
и, следовательно, существует
[Е-Х(Ш)]\
Таким образом, получаем
у@) = [Е-Х(а)]-1 X И $Х '@/@ Л-
о
На основании формулы C.23.3) находим периодическое решение
y(t) = X @ [Е-Х ((о)] ' {J X (,)/(,) d, + Х (ю) J Х-1
о t
C.23.5)
То, что («-периодическое решение ш единственно, вытекает из
того обстоятельства, что разность двух различных («-периодиче-
(«-периодических решений неоднородного уравнения C.23.1) является нетриви-
нетривиальным ш-периодическим решением однородного уравнения C.23.2),
а последнее в нашем случае исключается.
Замечание. Периодическое решение у (t) неоднородной си-
системы C.23.1) может быть записано в виде (см. [2_9])
y{t)~\G(t, x)/(,)dx, C.23.6)
о
где
G (t, z) = X (t) [Е — Х («о)] 'Х-1 (-с) C.23.7)
§ 23\ НЕОДНОРОДНАЯ ПЕРИОДИЧЕСКАЯ СИСТЕМА 21 Т
ПрИ Os?tsg/=^U)H
G(t, x)=-X(t-}-m)[E~XM]~1X-1(x) C.23.7)
при Os^
Действительно, из формулы C.23.5) получаем
у (/) = \ X (/) [Е-Х
о
Отсюда, учитывая, что
[?¦ — X (и))]-1^ («») = X («о) [? — X
будем иметь формулу C.23.6).
Нетрудно проверить, что функция G (t, т), определяемая фор-
формулами C.23.7) и C.23.7'), обладает следующими свойствами:
1) G(t + 0, t)-G(t-0, t) = ?;
2) G@, i) = GK т);
3) G,^, i) = ^(/)G(/, т) (t^-z)
при 0^;^=^/^;<». Эти свойства однозначно определяют функцию
G(t, x),
Если однородная система C.23.2) имеет нетривиальные ю-перио-
дические решения (резонансный случай), то соответствую-
соответствующая неоднородная система C.23.1) допускает <»-периодическое
решение не всегда.
Теорема 2. Пусть линейная однородная ^-периодическая
система C.23.1) допускает k линейно 'Независимых ^-периодиче-
^-периодических решений <Pi@, •••, <Р*@ (l^ks^n). Тогда
1) сопряженная система
?
C.23.8)
имеет также k линейно независимых ^-периодических решений
*i @, •••¦** @;
2) соответствующая неоднородная система C.23.1) имеет
^-периодические решения тогда и только тогда, когда выполнены
условия ортогональности
to
J t = O (s=l, .... *), C.23.9)
§ 23] НЕОДНОРОДНАЯ ПЕРИОДИЧЕСКАЯ СИСТЕМА 219
независимых «-периодических решений ф, (/), ... , г|зк (t) сопря-
сопряженной системы C.23.8).
2) Докажем сначала необходимость условий C.23.9).
Пусть у (t) — некоторое («-периодическое решение неоднородной
системы C.23.1). Из условий ш-периодичнести (см. формулу C.23.4))
следует, что начальное значение уй =у @) удовлетворяет условию
[?-А(«)]Л=Х(»)| X-*(t)f(t)dt. C.23.12)
о
Пусть tys(t) (s=l, ••-,«) — некоторое ш-периодическое нетри-
нетривиальное решение сопряженной системы C.23.8). Тогда
и, следовательно,
0=([?-Х(ш)]*Ц,,@), ув) =
= ([х(«.)]* ^@), I х-1 (о f{t) dt) = {%@), Iх-'@/@dt) =
о о
t = l([X-1(t)]*^l(O), f(t))dt.
Но
поэтому
3) Докажем теперь достаточность условий C.23.9). Пусть
условия C.23.9) выполнены. Тогда, если ?0 — собственный вектор
матрицы [Х(о>)]*( отвечающий единичному мультипликатору
Р = 1, т. е.
[X Н]* So = So,
то
220 ПЕРВЫЙ МЕТОД ЛЯПУНОВА
и, следовательно,
0 = 5C@ So, /(О)Л=5Aо, з*(о/(О)Л =
о о
со со
О
со
— ) (So, ^ (W)X '
О
Таким образом, система
эквивалентна системе
[ГЛ. III
C.23.13)
C.23.14)
и, значит, ранги матриц этих систем одинаковы. Отсюда, учиты-
учитывая, что матрица системы C.23.14) отличается от матрицы системы
to
C.23.13) лишь на вектор-строку [$ X ИХ (t)f(t)di\*, для
о
ранга системы C.23.12) будем иметь следующее выражение:
ранг
X Н — ?
О)
5 х и х-1 @/@ *
0
= ранг 1
[А" (<¦>) — ?]*
Л» Л" (<)/(')««]*
= ранг ([X («>) — ?]*) =
= ранг (X (и>) — Е) = п — k.
Следовательно, в силу теоремы Кронекера — Капелли (гл. I,
§ 5) система C.23.12), определяющая начальные условия («-перио-
(«-периодических решений неоднородной системы C.23.1), совместна и
имеет k линейно независимых решений.
« 23] НЕОДНОРОДНАЯ ПЕРИОДИЧЕСКАЯ СИСТЕМА 221
Теорема доказана.
Существование со-периодических решений линейной периоди-
периодической системы связано с наличием ограниченных решений ее.
Теорема Массера. Если линейная неоднородная ^-перио-
^-периодическая система C.23.1) имеет ограниченное решение у (t) (t>?0),
то у этой системы существует ^-периодическое решение.
Доказательство. Используя метод вариации произволь-
произвольной постоянной, ограниченное решение у (t) неоднородной системы
C.23.1) можно представить в следующем виде:
у (t) = X (t)y0 +{x(t) X~L (z)f(z) dz,
0
где у о ==у @) и X (t) (X (t) — Е) — нормированная фундаменталь-
фундаментальная матрица однородной системы C.23.2). Отсюда
P((o) = X(«>)j>e + &, C.23.15)
где
Так как ввиду периодичности системы C.23.1) у (t -\-ш) есть
также решение этой системы, то, используя начальное условие
будем иметь
у Bо>) = X (ш)у (со) + b = X* (о)у0 + [X (ш) + Е] Ъ
пли, в более общем виде,
т—1
у (Отш) = Хт (a))J?e + 2 X" (u>) Ъ
(т=1, 2, ...). C.23.16)
Пусть система C.23.1) не имеет ««-периодического решения.
Тогда линейная алгебраическая система
= Ь, C.23.17)
реализующая условие периодичности, несовместна и, в частности,
det[? — Х(ш)]=0.
Отсюда в силу известной теоремы алгебры выводим, что сущест-
существует ненулевой вектор с, являющийся решением сопряженной
алгебраической системы
[? —*(«>)]* с = 0, C.23.18)
222 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. Ill
причем этот вектор не ортогонален к правой части системы
C.23.17), т. е.
ф, с)^0. C.23.19)
Из уравнения C.23.18) получаем
с = [Х («>)]* с
и, значит,
с=[Х"(ч>)]*с (k = 0, 1, 2, ...). C.23.20)
Умножая равенство C.23.16) справа на с, будем иметь
ш), с) = (Хт(ш)у0, с)+ Ц(Х*(Ш)«>, с).
Отсюда, учитывая соотношение C.23.20), находим
т—1
(у (т»), С) = (у,, [Хт И]* Г) + 2 (&, [ХА (со)]* с) =
= (уо, с)-\-тф, с)-^-оо при т-^-уэ,
что противоречит ограниченности решения у (/).
Следовательно, в наших условиях система C.23.17) совместна
и, таким образом, -существует по меньшей мере одно <«-периоди-
ческое решение неоднородной системы C.23.1).
Следствие. Если неоднородная линейная ^-периодическая
система не имеет ^-периодических решений, то все решения этой
системы не ограничены как на полуоси /;з=0, так и на полуоси
0
§ 24. Метод малого параметра
Рассмотрим слабо нелинейную (квазилинейную) периодическую*
систему
% y), C.24.1)
где A (t) и f(t) — и-периодичны,
/, Ж OS11, ф(' + ш, зО = ф(', у)
и ц — малый параметр, причем при ;i = 0 система C.24.1) совпа*.
дает с линейной системой (порождающей системой):
§ C.24.2).
241
МЕТОД МАЛОГО ПАРАМЕТРА
223
Для доказательства существования ю-периодических решений
нелинейной системы C.24.1) изложим принадлежащий Пуанкаре
«метод малого параметра» (см. [35], [14], [36]).
Теорема. Если все мультипликаторы однородной системы
C.24.2) отличны от единицы, то при достаточно малых \ р. | нели-
нелинейная система C.24.1) имеет единственное ^-периодическое реше-
решение у (t, [л) такое, что
, v)=y«{t), C.24.3)
где >'о(О — ^-периодическое решение порождающей системы C.24.2).
Доказательство. Обозначим через у (t; r\, ц) ? С^01 ре-
решение системы C.24.1), определяемое начальным условием:
у@; % р) = г\. C.24.4)
Так как правая часть системы C.24.1) («-периодична по / и удо-
удовлетворяет условиям единственности решений, то для существо-
существования ш-периодического решения этой системы необходимо и
достаточно, чтобы для некоторого г\ было бы обеспечено условие:
Ф(т), р)==у(ш; Ц, v)—y@; % р)=у(«>; Ц, (*) — Ч = 0. C.24.5)
Пусть периодическое решение у0 (i) порождающей системы
C.24.2), которое существует в силу теоремы § 23, определяется
начальным условием: Уо(О = т1о- Тогда имеем
Ф(Чо, 0) = 0.
Из теории неявных функций известно, что (см. [7]) для того,
чтобы уравнение C.24.5) имело единственное непрерывное реше-
нне в окрестности то'чки т] = т]0, (а = 0, достаточно, чтобы опре-
определитель Якоби
где 11 = (%, ... , Чп) и
Ф(Ч, f*)=
Отсюда, полагая, что
y(t; ч. (*) =
yi(t; % ia
з.24.6)
получаем
A=0
= det
C.24.7)
224 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. II!
Из теории дифференциальных уравнений следует (см. [9],
[10], [11]), что решение у (/; г\, ц) имеет непрерывные частные
производные по начальным данным г\. Введя обозначения
и дифференцируя по ц систему C.24.1), будем иметь
ИЛИ
Отсюда при (а = 0 получаем
Кроме того, при ^ = 0 имеем
У @; ц, и) = л>
поэтому
Z@) = E.
Таким образом, Z = Z(t; ц, 0) является нормированной фун-
фундаментальной матрицей однородной системы C.24.2) и интересую-
интересующий нас якобиан имеет вид
Так как для однородной системы C.24.2) ее мультипликаторы
Pj^l, то для векового уравнения
det [ZK ц, 0) —Р?] = 0
число р = 1 не является корнем. Поэтому
Д ^0
и, следовательно, нелинейная система C.24.1) при | ^ | <С Р-о имеет
единственное w-периодическое решение у (t, [i), непрерывное по
параметру ц и такое, что y(t, !^)->Уи@ ПРИ ^->0.
Теорема доказана.
Замечание. В этой формулировке период ш не обязательно
наименьший, он может быть кратен некоторому наименьшему пе-
периоду ю0, т. е. теорема остается верной, если
где ю0 — период системы C.24.1) и т— целое число, отличное от
нуля.
УПРАЖНЕНИЯ К ГЛАВЕ III 225
Упражнения к главе III
1. Доказать, что
lim <p (t) — Tim <\> (t) sc 1ШГfo> (t) — ф (t)\ -g lim ? (^) _Jimф (t)i
t—*OD t ~> CO ^-*OO t-~*-OO t—> CC
предполагая, что <j (г!) и 6 Ш определены и ограничены в имервале (t0, со).
2. Пусть
где A(t)?C[tw оо). Доказать, что
t
II х (t) || =<: у х (t0) || exp $ || А (x) || Л
'о
и
\ || x (t) [| rfi ^ || x (t0) || • [exp ^ || Л (т) ll dz — 1]
при t 3= t0.
Вывести отсюда, что если
со
\\\A(x)\\dt<co,
h
то для каждого решения х (t) существует limjc(/).
t—>OO
3. Пусть нелинейная система
dx-f(t *\
такова, что f(t, x)^Ct(Z), где Z=\tos^t <с», \\х\\<сН] и в Z выпол-
выполнено условие Липшица:
II f tf у'\ f it y\ 11 '=^L / 11 v' V 11
где L—положительная постоянная.
Доказать, что каждое решение системы х (t) (t0 ^t <z соI имеет конеч-
конечный ^характеристический показатель х [х].
4. Пользуясь неравенством Важевского, исследовать на устойчивость
скалярную систему
, 2Ь\
-~ = — ах — у cos21,
где а и Ъ—действительные постоянные.
5. Пусть
8 Б. П. Демидович
2?'") ПЕРВЫЙ МЕТОД ЛЯПУПОГП
где A (t) =--\аffr (t)] — действительная (я X и)-матрица и
[ГЛ. П[
R(t) = max djj(t) -j- 7
к A
Доказан., что
x (tlt) exp ^ r (tt) dty <; \ x
| x (t0) cxp \' R
при t~:-tm еде jc (f) |—евклидова норма решения x(t).
6. П\сгь
/,•— i
[де P/ii (t)QC \tm со), причем limpf/, (t) =0 при /=?& и
с — постоянная.
Доказать, что
t
,. = 1 im — \ Re ; /;/;/, (х) dx (k = 1, ..., п)
являются характеристическими показателями Ляпунова данной системы (см.
[25], [12|).
7. Доказать, что для линейной системы
dx
с постоянной матрицей Жордана J ее фундаментальная система
является нормальной.
8. Доказать, ч:ч фундаментальная матрица X{t) действительной приво-
приводимой системы
является нормальной тогда и только тогда, когда для суммы характеристи-
характеристических показателей с^ ее решений выполнено равенство Ляпунова
t
g =lim - V SpA(-:)dx.
УПРАЖНЕНИЯ К ГЛАВЕ III 227
В частности, для системы
их
~dt ~~ '
где А—действительная постоянная матрица, ее фундаментальная система
А'(^) нормальна лишь тогда, когда
9. Пусть для линейной системы
X(t) = {хк (t)} — нормальная фундаментальная система и Z (t) = {2'*' (t)}
какая-нибудь фундаментальная система, причем
Доказать, что
«t<«t (*=1, .... л).
10. Пусть линейная система
где A (t) ?С [?„, со), sup ]| Л (<) || < со, приводима к системе
dz _
С
матрица которой С постоянна и имеет собственные значения с простыми
элементарными делителями. Тогда система
= \A(
00
где В (t)?C [t0, 00) и \ || В (Y) || <Л < со, также приводима.
«о
11. Показать, что линейная система
с матрицей
0 1
Alt)== ? °
неприводима (ср. 10).
12. Пусть действительная линейная система
dx
228 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. HI
(A(t)?C\0, со) и sup [| A (t) || <оо), имеющая спектр Х1; ..., >.„, обладает
t
нормальной фундаментальной матрицей X(t) такой, что
sup \\X(t)e-At \\ <со
t
и
t
sup I exp \t V ) ft — ^ Sp Л (т) rf-] , < со,
t it о
где A = diag (lu ..., Xn).
Доказать, что система (*) приводима (см. [13]).
Указание. Использовать подстановку
13. Доказать, что если линейная система
где A(t)?C \t0, oo), устойчива и приводима, то она равномерно устойчива
(см. [37]).
14. Действительная линейная система
~=A(t)x (*»)
(Л (t) ^ С [t0, со)) называется ограниченно устойчивой (см. [37]), если она
устойчива одновременно с сопряженной системой
Доказать, что система (**) ограниченно устойчива тогда и только тогда,
когда она приводима к системе с нулевой матрицей.
15. Доказать, что если система (**) ограниченно устойчива и
оо
$ || В (t) || dt < со,
h
то система
также ограниченно устойчива (К о н т и).
16. Две матрицы A (t) и В (t), непрерывные и ограниченные на [t0, со),
называются кинематически подобными [13], если существует матрица Ляпу-
Ляпунова L (t) такая, что
L'1 (t) A {t) L (t) — L~'- (t) Lit) —В (t).
Доказать, что если матрицы систем
? = A(t)x и ^ =
ограничены на [t0, со) и кинематически подобны, то эти системы обладают
одинаковыми спектрами, причем одновременно являются правильными или
неправильными (Ляпунов).
УПРАЖНЕНИЯ К ГЛАВЕ Ш 229
17. Доказать, что если система
с непрерывной и ограниченной матрицей A (t) правильная, то ее с помощью
сохраняющего характеристические числа линейного непрерывного преобразо-
преобразования
X = 6' (t) у
можно привести к системе с постоянной матрицей
(В = const).
18. Пусть A (t) = [a/b(t)]?C (If) —ограниченная треугольная матрица и
система
правильная.
Доказать,- что существует ее нормальная фундаментальная матрица
J
ХЦ) = Ф (t) е'а
где D(t) —u.iug[an (t), ..., ann(t)\ и
19. Доказать, что если р (t) — непрерывная «-периодическая функция
такая, что
О)
Р«)фО, W) = ~ ^
о
и выполнено условие
ш
' | р (t) | dt =? 4,
то все решения скалярного уравнения
ограничены (см. [39]).
20. Пусть для «-периодической системы
где Л (t -f-и) = A (t), все мультипликаторы по модулю отличны от единицы.
Доказать, что неоднородная система
230 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. 11!
[де а = const и f(t) — сй-иериодическая вектор-функция, имеет единственное
ограниченное решение у {t), обладающее свойством
у (t 4- <¦>) = exp (ia.u>)y(t)
(см. [40J).
21. Характеристические показатели Ляпунова <*„ ..., ап линейной си-
системы
% = A(t)x (***>
называются устойчивыми, если для всякого е>0 существует 5 = 5(е)>0
такое, что при
,\B(t)\\<b
соответствующие характеристические показатели Зц ••¦. Рл возмущенной си-
системы
удовлетворяют неравенствам
\h — ч\<* (*=1, •••, п).
Доказать, что если A(t) = const и собственные значения ее имеют про-
простые элементарные делители, то характеристические показатели системы (***)
устойчивы.
Замечание. Теорема для постоянной матрицы А верна в общем слу-
случае (Персидский), однако доказательство ее значительно сложнее.
22. Показать, что характеристические показатели скалярной системы
dx
аУ- = [sin (In t) -j- cos (In t) — 2]y
не являются устойчивыми (см. [21]).
23. Пусть нелинейная система
где А — постоянная матрица и f(t, у) — непрерывный нелинейный член,
такова, что: a) ReXy(/4)^0 (/=1, ..., п), причем корни Ау-(Л) с нулевой
вещественной частью имеют простые элементарные делители; б) \\f(t, JO || =Si
^k(t)\\y\\, где
оо
\ k (t) dt < с».
>о
Доказать, что эта система асимптотически эквивалентна соответствующей
линейной системе
dx -Ах
(см. [24J).
УПРАЖНЕНИЯ К ГЛАВЕ Ш 231
24. . <усть постоянная матрица А имеет характеристические корни
ХДЛ) (У=1, •¦•, п) с простыми элементарными делителями и
где
Доказать, что существует фундаментальная система решений y:-(t)
{/=1, ... , п) таких, что
lim yj(t)e I = Cj,
t-.co
где су —соответствующие собственные векторы матрицы Л (см. [28]).
25. Доказать теорему: Пусть X(t) (Х@) = Е)— нормированная фунда-
фундаментальная матрица системы
— — A (t
dt '
•где A (t) ? С [О, оо), и пусть В (t) ? С [0, оо) — (л X «(-матрица такая, что
сю
f \\ X~l (t) В (t)X(t)\\dt< со.
о
Тогда решения системы
~-у- = [Л (^) -|- В (t)\у
at
представимы в виде
y = X(t)c(t),
где существует \imc(t) = c , причем {c^ — i — со, -\-со) (Б е б е р н е с)
/->оо
26. Доказать теорему Беллмана: Если
dx . ... dy г, ,л
— = A(t)x, ~ = B(t)y
и
сю
^ || В (t) — А (В) || 11^@11 l|X-1@i!^<oo,
о
где X(t) = A(t)X(t), X@) = E, то
(с — постоянный вектор).
27. Пусть
— действительная ш-периодическая система и р;- (у=1, ... , п) — ее муль-
мультипликаторы.
232 ПЕРВЫЙ МЕТОД ЛЯПУНОВА [ГЛ. Ill
Показать, что мультипликаторами сопряженной системы
1 . , .
являются числа — (/=1, ... , я).
28. Доказать, чю если действительное скалярное уравнение
^=f(t,x), (****)
где f{t, х) ? С (If х <Мх), /(^Н-05, x)=f(t, x), имеет положительно .огра-
.ограниченное решение ? = с(?) (t0 sg t < с»), то существует ш-иериодическое
решение уравнения (****) (М а с с е р а).
29. Пусть
x=F(t, х),
где F d С (// X i| х || < И), причем
\ у (г) at < со.
h
Доказать, что если x(t0) достаточно мало по норме, то: 1) решение х (t)
определено при t ? [t0, со) и 2) существует
lim x(t) = x^.
отличный от нуля, если (
30. Показать, что уравнение
где f (t) ? С( — со, -|~°°) и / (^ + м) ^/(')i имеет «-периодическое общее
решение тогда и только тогда, когда
о
31. Пусть J (X) — (п X л)-клетка Жордана, имеющая собственное значе-
значение X, и
— непрерывная «-периодическая вектор-функция.
Доказать, что уравнение
имеет решение вида
где (р (t) — ш-периодическая вектор-функция, тогда и только тогда, когда
\fn(t)dt = Q.
УПРАЖНЕНИЯ К ГЛАВЕ III 233
32. Пусть линейная однородная система
с!х . ...
Ж = АХ A)
с постоянной матрицей А асимптотически устойчива, а неоднородная возму-
возмущенная система
ft=[A + B(t)]y+f(t) (II)
от
такова, что: 1) B(t),f(t) ? С [t0, со) и 2) j \\B(t)\ dt <oo, /(О—0 при
i—> со, или же 2') B{t)—*0 при ?—-оо и j \\f (t)\\dt <. со. Тогда вес реше-
решено
ния у (t) системы (II) имеют предел
lim v(t) = O.
ГЛАВА IV
ВТОРОЙ МЕТОД ЛЯПУНОВА
§ 1. Приведенная система
Пусть дана действительная нелинейная дифференциальная
система
ft=y(t,y), D.1.1)
где y?;Qy"(Q) и Q = {a<^t<^oo, у ?j G\ (а-число или символ
— оо, G — открытое множество действительного евклидова л-мер-
ного пространства е^1"). Тогда для каждой точки (t0, у0) ? Q
справедлива локальная теорема существования и единственности
решения у —у (t; t0, _у0) системы D.1.1) с начальными условиями:
у (t0; t0, у а) —у<>. В этой главе мы ограничимся рассмотрением
лишь действительных решений.
Пусть i\ = i\(t) (tQf<ct<^oo; to^>a) — решение системы D.1.1)
(невозмущенное движение), устойчивость которого требуется иссле-
исследовать, причем Я-окрестность этого решения такова, что UH{i\(t))CL
(ZG при G )
Положим
х=У-М*), D-1.2)
т. е. х есть отклонение решения у от решения r\(t). Так как
то для х получаем дифференциальное уравнение
d? = X{t, х), D.1.3)
где
X(t, x) = [Y(t, х-\-ц @) - Y(t, ч @I е СИ1 (Z),
причем, очевидно,
S 2]
ЗНЛКООПРЕДЕЛЕННЫЕ ФУНКЦИИ
235
Следовательно, система D.1.3) имеет тривиальное решение дг = О,
которое в пространстве <М^ соответствует данному решению
11 = 4@ (Рис- 28, а и б). Систему D.1.3) будем называть приве-
приведенной (по Ляпунову она называется системой уравнений возму-
возмущенного движения).
о
Рис. 28.
Таким образом, исследование устойчивости решения i\ = r\(t)
в пространстве <М^ сводится к исследованию устойчивости три-
тривиального решения (положения равновесия) л; —О в простран-
пространстве <Мп.
§ 2. Знакоопределенные функции
Рассмотрим функцию
V = V(t, x)?Ctx(Zt),
где Zo = {
Введем основные определения о знакопостоянных и з н а -
кооп реде ле н ных функциях (см. [13], [14]).
Определение 1. Действительная непрерывная скалярная
функция V (t, x) называется знакопостоянной (знакоположительной
или знакоотрицательной) в Zo, если
V{t,x)SzO (или V (t, х) s=s0)
при (t, x) (= Zo.
Определение 2. Функция V (t, x) называется положительно
определенной (определенно положительной) в Zo, если существует
скалярная функция W (х) ? С( |j x\\ <^h) такая, что
V (t, х) 5г W (х) > 0 npHJljeli^O, D.2.1)
2,'jo ВТОРОЙ МЕТОД ЛЯПУНОВА [1Л. IV
Аналогично функция V (/, х) называется отрицательно опре-
определенной (определенно отрицательной) в Zo; если найдется
W (х) ?= С( || х ||<й) такая, что
V(t, x)^ — W (х)<0 при Цлс^О
Положительно или отрицательно определенная функция назы-
называется знакоопределенной.
В качестве W (х) иногда можно брать
W (X) = inf! V (t, х)].
t
В частности, V = V(x) есть знакоопределенная функция, если
(—lfV(x)^>0 при :'\ х )--^ О и V@) = 0, где для положительно
определенной функции з = 0, а для отри-
отрицательно определенной функции о = 1.
Пример 1. В действительном простран-
пространстве (Jfi?2 = 0xy функция
V= х2 -{-у2 — 2я ху cos i D.2.2)
при | о | < 1 является положительно опреде-
ленной, так как
Vlt, X, у)^Х2-1гу- — 2< а \Х}\у}>:
Ss= A — I a i) (х2 +у-) = W(х, у) > О
при Xs -\-у2 > 0; У=0 при x=jv = 0.
При | о ! = 1 функция V лишь знаконоло-
жительна.
Рис. 29. Нетрудно дать геометрическую ил-
иллюстрацию знакоопределенной функции
V it, х). Пусть V (t, х) — положительно определенная функция
такая, что
V (t, x)^sW(x),
где №'(,y)^>0 при X 9=- 0 и W@) = 0. Предположим, что поверх-
поверхности уровня
W(x) = C (С2г0)
в пространстве Оху, ... , хп представляют собой семейство непре-
непрерывных замкнутых поверхностей, окружающих начало координат О
и монотонно расширяющихся при росте параметра С (рис. 29).
Тогда, очевидно, каждая поверхность уровня
V(t, x) = Ct
для любого значения параметра / будет целиком расположена
внутри соответствующей поверхности W (лг)==С1.
§ 3| ПЕРВАЯ ТЕОРЕМА ЛЯПУНОВА 2Н7
Определение 3. Говорят, что функция V(t, x) имеет бес-
бесконечно малый высший предел при х->-0 (см. [13], [14]), если
при некотором tn ^> а имеем
V (t, х) Ij О
t
на [t0, со) при х -у 0, т. е. для любого е^>0 существует 8 = 8 (е)^>0
такое, что
iV(/, jc)!<s D.2.3)
при Г|Д:||<;8 и t ?j [/„, сю).
В силу неравенства D.2.3) заключаем, что функция V (t, х),
допускающая бесконечно малый высший предел при дг^-О, огра-
ограничена в некотором полуцилиндре
Отметим, что если V (х) — непрерывная функция, не завися-
зависящая от времени t и такая, что 1/@) = 0, то, очевидно, V (х)
допускает бесконечно малый высший предел при х^-0.
Пример 2. Функция D.2,2) при | о | < 1 допускает бесконечно малый
высший предел, когда
г = |/лгг+/ — 0.
Функция
не допускает бесконечно малого высшего предела при || .
= (¦''xj-j-x|-f- ...-(- х2п —> О, несмотря на то, что эта функция ограничена и
V— 0 при jc п —0.
§ 3. Первая теорема Ляпунова (теорема об устойчивости)
Пусть X(t,x)?C&ll(Z), Z = {a<?< со, \\х\<Н\ и
х), D.3.1)
есть приведенная система, т. е.
X G, 0) = 0,
очевидно, допускающая тривиальное решение: 1 = С.
Положим
<?<co; ||л; i| *=:/г<Н) СZ)
= colon[Xl(t, х) Xa(tlx)l
2,48 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. IV
Функцию
п
V (t. х) = д~г + У ^- X/ (t, Х) = д^ +-(grad V, X) D.3.2)
называют производной (полной) по времени t функции V (t, x)
в силу системы D.3.1).
Если x = x(t) есть решение системы D.3.1), то V (t, х) пред-
представляет собой полную производную по времени t сложной функ-
функции V (t, x(t)), т. е.
V(t,x)=~V(t,x(t)).
Более точно, пусть (t, х) (^ Zo и x(x;t,x) есть решение си-
системы D.3.1), определяемое начальными условиями: x(t; t, x) = x.
Тогда
V(t, х) = \? V (z, X(z; t, x))]^t. D.3.3)
Заметим, что если V(t,x)(^Cl, то из формулы D.3.3) может
не следовать формула D.3.2). В дальнейшем, если явно не ука-
указано противное, мы будем предпола-
предполагать, что
v а, х) G сл1' (za).
Если V (t, х) > 0 при V (t, х) = С,
^xft) то интегральные кривые x = x(t) в
точках (t, х) поверхности V (t, x) — C
переходят с отрицательной стороны
поверхности, характеризуемой нор-
Рпс- 30. малью—gradl/, на положительную
ее сторону, определяемую нормалью
-fgrad V (рис. 30). При V (t, д:)<^0 имеет место обратная картина.
Такого рода поверхности V(t,x) = C называются поверхностями
без контакта для поля интегральных кривых системы D.3.1).
Замечание. Понятие производной V (t, x) в силу системы
D.3.1) можно обобщить (см. [41]). А именно, иногда полагают
V (t, х)— lim :{V(t-\-h, x-f-hX (t, x)) — V it, x)}.
Если V it, X) ?j Qx" (Zc), то, очевидно, имеем формулу D.3.2).
Теорема (первая теорема Ляпунова). Если для при-
приведенной системы D.3.1) существует положительно определенная
скалярная функция
ПЕРВАЯ ТЕОРЕМА ЛЯПУНОВА
239
допускающая знакоотрицапгельную производную по времени V (t, х)
в силу системы, то тривиальное решение | = 0 (а<^/<^оо) дан-
данной системы устойчиво по Ляпунову при t -*¦ -f- oo.
Доказательство. На основании условия теоремы имеется
непрерывная положительно определенная функция W (х) такая, что
V(t,
придг^О
D.3.4)
В пространстве e^J рассмотрим сферу S5:
:|Jf|l=s, D.3.5)
целиком лежащую в Zo, где 0<^е^Л<^Я.
Так как сфера Se — компактное множество и функция № (jt)
непрерывна и положительна на S?, то в силу теоремы Вейер-
штрасса нижняя грань этой функции достигается в некоторой точке
х* ?jj Se и, следовательно,
inf W(x)=W (лг*) = а>0.
D.3.6)
Пусть t0 (^ (а, со) произвольно.
Функция V (t0, x) непрерывна по д:,
причем V (t0, 0) = 0. Следова-
Следовательно, существует окрестность
||jc||^8<^s такая, что
O^V(t0, лг)<а при ||дг||<8.
D.3.7)
Рассмотрим любое нетривиаль-
нетривиальное решение
x = x(t) D.3.8)
с начальным условием: \\ дг0 (^0) II <С ^ (рис. 31). Докажем, что тра-
траектория этого решения целиком остается внутри сферы S., т. е.
||дг(/)||<е при t0^t<co. D.3.9)
Действительно, при t = t0 имеем
Рис. 31.
Пусть неравенство D.3.9) выполнено не для всех t?[t0joo) и
h ^> U — первая точка выхода решения х (t) на границу S=, т. е.
;|х@1!<Се ПРИ to^t<^ti и |JA;(^)|i = e. Изучим поведение
функции
v(l) = V(t,x(t))
240 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. IV
вдоль решения х (t). Так как в силу условия теоремы
то функция v (t) невозрастающая. Следовательно, учитывая фор-
формулы D.3.7) и D.3.6), имеем
*> V (/„, л: (*„)) S2r V(t,,x (f,)) ^ W (х (*,)) =а я,
что невозможно.
Таким образом, решение x = x{t) при любом конечном t (^
?[t0, со) остается внутри сферы Ss и, так как е<^Я, это реше-
решение определено при tas^t <^оо (бесконечно продолжаемо вправо),
причем
llAr(O;<s при t0^t<oo,
если только || л: (/0) I1 <Л А это и значит (гл. II, § 1, определе-
определение 1), что тривиальное решение 1 = 0 устойчиво по Ляпунову
при /->-р со-
Следствие 1. При наличии условий первой теоремы Ляпу-
Ляпунова все решения x(t) системы D.3.1) с достаточно малыми по
норме начальными значениями x(t0) (^ G (а> °°)) бесконечно про-
продолжаемы вправо и ограничены на полуоси [td, со).
Следствие 2. Если для линейной однородной системы
d± = A(t)x (A(t)?C[tu,oo)) D.3.10)
существует положительно определенная функция V (t, x), для
которой производная в силу системы V (t, x)^0, то все решения
x(t) системы D.3.10) определены и ограничены на полуоси [tu, со).
§ 4. Вторая теорема Ляпунова
(теорема об асимптотической устойчивости)
Теорема (вторая теорема Ляпунова). Пусть для
приведенной систгмы D.3.1) существует положительно определенная
функция V (/, х) G С'^1' (Zo), допускающая бесконечно малый высший
предел при х —>- 0 и имеющая отрицательно определенную произ-
производную по времени V (t, x) в силу этой системы. Тогда тривиаль-
тривиальное решение 1 = 0 системы асимптотически устойчиво по Ляпунову
при t —> со.
Д о к аз а те л-ьство. Так как условия теоремы являются уси-
усилением условий теоремы из § 3, то тривиальное решение 1 = 0
приведенной системы D.3.1) устойчиво.
ВТОРАЯ ТЕОРЕМА ЛЯПУНОВА
241
Согласно определению асимптотической устойчивости (гл. II,
§ 1, определение 4) остается доказать, что для каждого нетри-
нетривиального решения
где х (t0) jj «s h <^ Н и h достаточно мало, справедливо равенство
lim x(t) = 0. D.4.1)
Рассмотрим функцию
Так как в силу условия теоремы
то функция v (t) монотонно убывающая и, будучи ограниченной
снизу, имеет конечный предел
limy@ = inf v(t) — a.^O. D.4.2)
t-*oa t
Покажем, что число а не может
быть положительным. Действительно,
предположим, что а^>0. Тогда наше
нетривиальное решение л:(/) удовле-
удовлетворяет неравенству
при
D.4.3)
где В — положительная постоянная,
т. е. траектория этого решения ос- Рис. 32.
тается вне сферы радиуса В (рис. 32).
В самом деле, если это так, то найдется последовательность
/i, ?а,..., tk, ...->--[- со1) такая, что
lim л; (/А) = 0.
Отсюда в силу существования бесконечно малого высшего пре-
предела функции V (t, х) при д: -*¦ 0 имеем
lim v (tk) = lim V D, X (th)) = 0.
'; Если бы t^-^ Г<Ссо, то
k—*<x>
Отсюда в силу теоремы единственности получим jk(^)=O, что проти-
противоречит нашему предположению.
242 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. IV
А это противоречит при а^>0 формуле D.4.2), так как если а есть
предел функции v if) при ^->-f-oo, то для любой последова-
последовательности tk -> -|- оо должно быть выполнено условие v (tk) -*¦ а.
Итак, в случае а^>0 имеет место неравенство D.4.3) и, кроме
того, можно предполагать, что \\x(t)\\^h<^H (в силу устойчи-
устойчивости тривиального решения | = 0).
Пусть W\ (х) — непрерывная положительно определенная функ-
функция, удовлетворяющая неравенству
&(t) = V(t, x)^-Wi(x). (АЛА)
Такая функция существует, так как согласно условию теоремы
V (/, x) — отрицательно определенная функция..
Введем обозначение:
т= inf W1(x)y0. D.4.5)
Тогда, интегрируя неравенство D.4.4) в пределах от t0 до t и учи-
учитывая, что p=sc |: jc(t) || ^h при /о^'1^^. будем иметь
или, так как
— Wt (x) ==S — т при
TO
=l)^) —T(^ —^o)- D.4.6)
Из неравенства D.4.6) получаем, что при t достаточно большом
что противоречит положительности функции V (t, x).
Итак,
a=limV(^ jc(*)) = O. D.4.7)
Покажем теперь, что д:(/)->0 при ? —v —J- оо. Действительно,
пусть ?^>0 произвольно мало и
l=MW (д:)>0 при e^|:jcji</i. D.4.8)
Из формулы D.4.7) следует, что существует момент T^>t0 такой,
что
V(T, *(Г)
<$ i ВТОРАЯ ТЕОРЕМА ЛЯПУНОПА 243
Отсюда в силу монотонного убывания функции V (х, x(t)) по-
получаем
V(t, л:@)</ при /5>Г D.4.9)
и, следовательно,
| л: (/)ii< e при >>7\ D.4.10)
Действительно, если для некоторого момента ti^>T выполняется
противоположное неравенство
II x\lv \\ =5=с.
то. учитывая формулы D.4.9) и D.4.8), мы имели бы
l>V(tu x(ti)O^W(x{ti)O^l,
что, очевидно, невозможно.
Итак, на основании неравенства D.4.10) имеем
что и требовалось доказать.
Следствие 1. В условиях второй теоремы Ляпунова мно-
множество \\ х \\ ss^ h <^ H s^ со принадлежит области притяжения
тривиального решения § = 0.
Следствие 2. Если для линейной однородной системы
существует положительно определенная функция V (I, х), удов-
удовлетворяющая условиям второй теоремы Ляпунова, то каждое ре-
решение этой системы асимптотически устойчиво в целом.
Пример. Пусть
V=V(x,,..., х„)
— положительно определенная функция класса С2 такая, что V@) =
Рассмотрим систему уравнений (см. [13])
d_x, _ _ dV_
dt dxt
D.4.11)
dx^ ___dV_
lit ~ dx^'
имеющую, очевидно, тривиальное решение: Xl=0, ..., хп=0.
Принимая V за функцию Ляпунова для производной 'V по t, в силу
системы D.4.11) получим такое выражение:
244 ВТОРОЙ МЕТОД ЛЯПУНОВА [1,ч. IV
Следовательно в силу теоремы из § 3 тривиальное решение д; = 0 системы
D.4.11) устойчиво по Ляпунову при t —> -f- со.
Устойчивость будет асимптотической, если V представляет собой отри-
отрицательно определенную функцию. Для этого необходимо и достаточно, чтобы
система
дх, дх„
имела единственное нулевое решение х, =0,..., хп = 0 в некоторой
окрестности ]|jtj|<;A. На основании теории неявных функций для этого
достаточно, чтобы гессиан
А ,
det
был отличен от нуля в точке О.
§ 5. Третья теорема Ляпунова (теорема о неустойчивости)
Теорема 3 (третья теорема Ляпунова). Пусть для
приведенной системы D.3.1) существует функция V (t, х) ? О^}1 (Zo),
допускающая бесконечно малый высший предел при х-*-0 и
обладающая знакоопределенной производной V (t, x) no t в силу
системы. Если при некотором to^>a в любой окрестности
||д:!|<^Д (Д=^/г<^//) найдется точка (t9, л:0), для которой знак
функции V одинаков со знаком производной V, т. е. такая, что
V{h, xo) V(t0, jco)>O, D.5.1)
то тривиальное решение g = 0 системы D.3.1) неустойчиво в
емысле Ляпунова при t—>-oo.
Доказательство. Пусть для определенности V (t, X) — поло-
положительно определенная функция, т. е.
V(t, л;) Ss №!(*)> 0 D.5.2)
при tn^t<^oo и 0<^\\x''\<^h, где Wt(x) — непрерывная знако-
знакоположительная функция. Так как в силу условия теоремы функ-
функция V (/, х) допускает бесконечно малый высший предел при
х-^-0, то V (t, x) ограничена в достаточно узком цилиндре,
т. е.
| V (t, х) 1 ^ М, D.5.3)
при /п=?5^<С.со, || х \\ sS \<С/г, где М и Ао — некоторые положи-
положительные числа.
Пусть о^>0 (8<^Д0) произвольно мало. В силу условия
теоремы существует точка (t0, лг0), где 0<^|| jc0 j; <^§, такая, что
V (/0, Хо)
§ 5) ТРЕТЬЯ ТЕОРЕМА ЛЯПУНОВА 245
Положим
где х(ЦфО — решение, определяемое начальным условием:
x{tlt) — x<s, причем
8- D.5.4)
В силу неравенства D.5.2) функция v(t) монотонно возрастает
вместе с t, и, следовательно, при t^t0 имеем
V(t, x(t))^V(t, X(t9)) = *>0. D.5.5)
Покажем, что при некотором значении t = t1 (ti^>t(,) будет
выполнено неравенство
o- D-5.6)
Действительно, пусть ]|д:(/)!|^Д0 при t^t0; тогда решение
x(t) бесконечно продолжаемо вправо. Так как функция V (t, x)
имеет бесконечно малый высший предел при х-*0, то из нера-
неравенства D.5.5) на основании рассуждений, приведенных при
доказательстве второй теоремы Ляпунова, следует, что
До при *0<*<
где р — некоторое положительное число. Пусть
Т= inf Н
тогда, учитывая неравенство !| х (t) '| eg До, получаем
V(t, *(*))>Т при /0<^<оо.
Следовательно, при ^Os^/<^co имеем
t
V(t, x(t)) = V(t0, *(*«))+$V(t, je(T))dT>V(/,,JCe)+7(f-r0),
D.5.7)
что противоречит ограниченности функции V (t, x) в области
Так как §^>0 любое и Д0^>0 фиксировано, то на основании
неравенств D.5.4) и D.5.6) заключаем, что тривиальное решение
| = 0 неустойчиво по Ляпунову при t -> ее (см. гл. II, § 1, опре-
определение 3).
Теорема доказана.
Замечание 1. В третьей теореме функция V (t, x) не обя-
обязательно является знакоопределенной.
Замечание 2. Функции V (t, x), удовлетворяющие усло-
условиям первой, второй и третьей теорем Ляпунова, будем назы-
называть соответственно функциями Ляпунова 1-го, 2-го и 3-го рода.
2 К) ВТОРОЙ МЕТОД ЛЯПУНОВА |ГЛ. 'V
Следствие. Если для приведенной системы дифференциаль-
дифференциальных уравнений существует функция Ляпунова 1-го или 2-го, или
3-го рода, то тривиальное решение этой системы, соответст-
соответственно, устойчиво, асимптотически устойчиво, неустойчиво по Ля-
Ляпунову при t -> 4- so-
§ 6. Теорема Четаева
При формулировке третьей теоремы Ляпунова о неустойчи-
неустойчивости (§ 5) предполагается, что производная V (t, х) в силу
системы знакоположительна в некоторой полной окрестности
начала координат О. Однако для доказательства неустойчивости
тривиального решения системы достаточно обнаружить сущест-.
вование хотя бы одной траектории, исходящей из каждой, сколь
угодно малой, окрестности точки О и выходящей за пределы фик-
фиксированной окрестности. А для этого нет необходимости рассмат-
рассматривать полную окрестность начала координат и, следовательно,
условия третьей теоремы Ляпунова можно значительно ослабить.
Соответствующее обобщение было произведено Н. Г. Четаевым
(см. [15]).
Теорема Четаева. Пусть для приведенной системы D.3.1)
в области Z = {to^t <^~- со, \\x^^h<^H] существует непрерывно
дифференцируемая функция V (t, x), область положительности
которой П = {V (t, x)^>0, (t, x) ? Z\ имеет ненулевое открытое
сечение Dt, примыкающее к началу координат О, для каждого
t с [^>> °°). причем на части границы области П, лежащей внутри
цилиндра Z, включая ось Ot, выполнено равенство
V(t, x) = 01).
Тогда, если: 1) функция V (t, x) ограничена в области П,
2) имеет в этой области положительную производную V (t, x)
в силу системы D.3.1), 3) в каждой подобласти {V (t, x)^o.^>0}
справедливо неравенство V (t, x)^^^>Q, где р = р(я) — некоторое
положительное число, зависящее от положительного числа а, то
тривиальное решение системы D.3.1) неустойчиво в смысле Ляпу-
Ляпунова при t —>¦ оо.
Доказательство. Пусть S]>0 произвольно мало. Так
как точка О является граничной для открытого сечения Dta = D,
то в гиперплоскости t=t№ существует внутренняя точка Xq ? D
такая, что О <С |; хп" <С8<^г, причем V (t0, хо) = у.^>О (рис. 33).
') В сл}час положительно определенной функции V(t, x) эта часть
1раницы для каждого t? [t0, оо) сводится к единственной точке О.
§ 6]
ТЕОРЕМА ЧЕТАЕВА
247
Докажем, что решение x(t), определяемое начальным усло-
условием: x(t9) = x0, при возрастающем t выйдет за пределы шара
\\x\\<C.h- Действительно, пусть \\x(t)\\<^h при t^t0. В силу
условия 2) теоремы
V(t, x(t))>0 при V(t, x
отсюда при
: t0 получаем
v(t, jc(O)
V(tt, *(*,)) = a,
D.6.1)
если только V (t, x(t))^>0. Так как решение х(t) может по-
покинуть область TL — {V(t, x)^>0], лишь проходя при некото-
некотором ti~^>t0 внутреннюю часть границы, где V (tu x(ti)) = 0,
причем
V(t, х@)^
то, переходя в этом неравенстве к
пределу При t-*¦ tt — 0, будем иметь
V(tu *(/,)) 3* a> О,
что невозможно. Следовательно, ре-
решение x(t) при t^t0 целиком лежит
в подобласти {V(t, х)^а~^>0} обла-
области П. Отсюда, на основании условия
3) теоремы, получим
Рис. 33.
V(t, jc@)>P>0. D.6.2)
Интегрируя почленно неравенство D.6.2), при t^t0 будем иметь
V(t, x(t))^V(tQ, * (/,)) + ?(/ —/о). D.6.3)
Последнее неравенство невозможно, так как в силу условия 1)
теоремы функция V (t, x) ограничена в области П.
Итак, в любой 8-окрестности точки 0 при t = tn найдется
некоторое решение x(t), покидающее при t ->~Ь оо внутренность
шара \\x\\<^_h. Таким образом, тривиальное решение 1 = 0 не-
неустойчиво по Ляпунову (гл. II, § 1).
Теорема доказана. *
Замечание. Легко проверить, что для случая Ляпунова (§5)
при V (t, x)~^>0 ввиду наличия бесконечно малого высшего предела
функции V (t, X) множество П = {/, х: V (t, x) > 0} обладает
всеми указанными выше свойствами.
248 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. IV
§ 7. Асимптотическая устойчивость в целом
Рассмотрим приведенную систему
*df = X(t, х) (X(t, 0) = 0), D.7.1)
где X(t, x)?Cfx({<<}
Определение 1. Говорят, что тривиальное решение | = 0
системы D.7.1) асимптотически устойчиво в целом (см. [16]),
если: 1) оно асимптотически устойчиво по Ляпунову и 2) для
каждого решения x = x(t; /„, Xo){t№(^It) выполнено условие:
\imx(t; t0, xa) = 0 D.7.2)
(т, е. область притяжения представляет собой все пространство <М^
(см. гл. II, § 1)). Аналогично определяется асимптотическая устой-
устойчивость в целом нетривиального решения \. "
Определение 2. Будем говорить, что V (t,x) ? Q%v {ITX^i)
допускает бесконечно большой низший предел при х -*¦ со, если
V (t, х)^?оо при !|лМ1-»оэ, D.7.3)
т. е. для любого М^>0 существует R=R(M) такое, что
\V(t,x)\>M при t?[to,<x>) и \\X\\^R.
Определение 3. Будем говорить, что V (t, х) ? Ctx (If X е%1)
допускает в <М"Х сильный бесконечно малый высший предел
при JC->0, если существует функция U(x)<^C(^%) такая, что
\V(t, x)\^U(x) D.7.4)
при (t, x)?{ltx<&%) и 6/ @) = 0 (ср. § 3, определение 3).
Теорема Барбашина — Красовского (см. [42]). Если
для системы D.7.1) существует положительно определенная ска-
скалярная функция V (t, x) ^ Cfxh {if X s%x), допускающая в cfflnx силь-
сильный бесконечно малый высший предел при х -»- 0 и бесконечно боль-
большой низший предел при х-+зо, причем производная V (/, х)
в силу системы отрицательно определенна в <Мпх, то тривиальное
решение ?, = 0 асимптотически устойчиво в целом.
Доказательство. Так как условия этой теоремы, очевидно,
включают условия первой теоремы Ляпунова (§ 3), то тривиаль-
тривиальное решение |==0 устойчиво по Ляпунову при t-*--{-oo.
Пусть х = х {t; t0, x0) — нетривиальное решение системы D.7.1),
определяемое начальными условиями: х (/„; t0, х<,) — Х0 Ф 0, где
4 ^ It и х{, ^ о%1 — произвольно.
«s '1
АСИМПТОТИЧЕСКАЯ УСТОЙЧИВОСТЬ В ЦЕЛОМ
249
Обозначим через Кх некоторый компакт (т. е. ограниченное
замкнутое множество пространства effii), содержащий точку jc:
и пусть
M = supV(t, х) на ПХКХ.
В силу неравенства D.7.4) имеем
М< +оо.
Так как функция V (t, х) обладает в <Мпх бесконечно большим
пределом при л:->со, то существует шар S { \\-х \\<CR } ^ Кх та-
такой, что
V(t, x)>M при Hjclj^fl. D.7.5)
По условию теоремы вдоль траектории х (/; t0, х0) выполнено
неравенство
V(t, X(t; t0,
поэтому при t^tu имеем
V(t, x(t- U,xu))^V(t0,
и, следовательно,
\\x(t; 4, J
Рис.34.
т. е. все решения системы D.7.1)
ограничены.
Покажем теперь, что
V (t,x(t;t0,
при
Пусть s^>0 произвольно и г^>0 таково, что функция U (х),.
определяемая формулой D.7.4), удовлетворяет неравенству
О =s?
при \\х\
D.7.6)
Покажем, что решение x(t; 4, лг0) при /->-)-с» обязательно
войдет внутрь замкнутого шара ЦдгЦ^г.
Действительно, допустим, что
0<><||.*(/; 4, ^o)il<^ при t^t0
(рис. 34). Тогда V (t, x), будучи отрицательно определенной,
имеет в области It X {г ^ \\x\\^R) отрицательную верхнюю
250 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. IV
грань — т(Т^>0) и, значит, при t~^to справедливо неравенство
V{t, x(t; t0, л:0))^ — т-
Интегрируя это неравенство в пределах от ^0 до t (t^>t0), получим
V (t, х (t; tt, Xo)) <: V (tt, хл) - т С — *
если только
~\
что противоречит положительности функции V (t, x). Следова-
Следовательно, существует момент T^>t0 такой, что
||Х (Г; /о, Х0)\\^г,
U(x(T; t0, je,))<e.
Отсюда ввиду монотонного убывания функции V (t, x(t; ta, Хц))
при t^>T будем иметь
V(t, x(t; U, xo))<V(T, x(T; h, xo))^U(x(T; t0, л:„))<е
и, таким образом,
UmV(t, x(t; t0, Jfo)) = O. D.7.7)
Из последнего равенства выводим, что
\imx(t; t0, xo) = O,
/->со
так как в противном случае существовала бы последовательность
x(tk; t9, x0) {k=l, 2 tk-*oo) такая, что
lim V (tk, x(tk; t0, хл))ф0,
ft—»-oo
вопреки равенству D.7.7).
Теорема доказана.
Замечание. Из доказательства следует, что при условии
теоремы Барбашина — Красовского асимптотическая устойчивость
в целом равномерна по Хо на любом компакте Кх, т. е. можно
гарантировать, что (см. [16])
||л;(/; to, Лм>IКе
при /> Т (е, Кх), где х0 ^ Кх.
5, S] ЭКСПОНЕНЦИАЛЬНАЯ УСТОЙЧИВОСТЬ 251
§ 8. Экспоненциальная устойчивость
Определение. Тривиальное решение § = 0 системы D.7.1)
называется экспоненциально устойчивым при t->-\~co (см. [16]),
если для каждого решения x(t) = x(t; t0, x0) этой системы в не-
некоторой области tf)^t<^oo, \\x:\\^h<^H справедливо неравенство
\\x(i)\\^N\\x(ta)\\e-^-'o) (fz*t0), D.8.1)
где N я а — положительные постоянные, не зависящие от выбора
решения x{t).
Легко видеть, что из экспоненциальной устойчивости реше-
решения | = 0 следует его асимптотическая устойчивость. Действи-
Действительно, полагая
где е^>0 произвольно, из неравенства D.8.1) имеем
II* @11 О ПРИ /Si/о,
т. е. решение | = 0 устойчиво по Ляпунову. Кроме того, очевидно,
lim л:@ = 0,
если только || х D) II <С п-
Если неравенство D.8.1) справедливо для всех точек x(tt)?
(^ <Мпх, то имеет место асимптотическая устойчивость в целом.
Из неравенства D.8.1) следует, что если тривиальное решение
| = 0 системы D.7.1) экспоненциально устойчиво, то близкие
к нему решения X (t) этой системы имеют характеристические
показатели yt[x(t)\, удовлетворяющие неравенству
Аналогично определяется экспоненциальная устойчивость не-
нетривиального решения. А именно, решение § @ экспоненциально
устойчиво, если близкие к нему при t — tt решения x(t) удов-
удовлетворяют неравенству
где N и о. — некоторые положительные постоянные.
Лемма. Если тривиальное решение однородной линейной си-
системы
йШ-Ах D.8.2)
с постоянной матрицей А асимптотически устойчиво при
t ->• -)- оо, то эта система экспоненциально устойчива, т. е. каж-
каждое ее решение экспоненциально устойчиво при t-+-\-oo.
252
ВТОРОЙ МЕТОД ЛЯПУНОВА
[ГЛ IV
Доказательство. Как известно (гл. II, § 8), тривиальное
решение | = 0 системы D.8.2) асимптотически устойчиво тогда
и только тогда, когда все характеристические корни Хр(/4) мат-
матрицы А имеют отрицательные вещественные части:
ReXp04)<0
= l, ..., л).
Положим
minReXp04)< —а<0.
Тогда при /52 0 получим (гл. I, § 13)
D.8.3)
где N — некоторая положительная постоянная. Из уравнения
D.8.2) для любого решения x(t) находим
получаем
где начальный момент /0 произволен.
Следовательно, на основании D.8.3) при
Отсюда для любого решения \(t) однородной системы D.8.2),
учитывая, что разность x(t) — %(t) есть решение этой системы,
при t^t0 будем иметь
II x(t)~l (t) \\^NU (t0) -1 (t0)!! e-«('-^),
что и требовалось доказать.
Замечание. Для линейной системы с переменными коэффи-
коэффициентами из асимптотической устойчивости ее тривиального ре-
решения, вообще говоря, не следует экспоненциальная устой-
устойчивость.
Пример. Для скалярного уравнения
dx х ,,
о
его общее решение имеет вид
Таким образом, решение ? = 0 этого уравнения асимптотически устойчиво
при t— *co, однако не является экспоненциально устойчивым.
Теорема. Если существует положительно определенная квад-
квадратичная форма
V(x) = {Ax, X), D.8.4)
5 <;• ЭКСПОНЕНЦИАЛЬНАЯ УСТОЙЧИВОСТЬ 253
производная которой V (х) в силу приведенной системы D.7.1)
% = X(t, х) (X(t, 0) = 0)
удовлетворяет неравенству
V(X)^W (x) D.8.5)
где
W(x) = — (Bx, х) D.8.6)
— отрицательно определенная квадратичная форма (А и В —
постоянные симметрические матрицы), то тривиальное решение
| = 0 этой системы экспоненциально устойчиво при t-*--\-<x>.
Доказательство (см. [16]). На основании формул D.8.4) и
D.8.6) получаем
а (х, х) «S V (х) й? at (x, х)
п
b(x, x)^! — W(x)^bl(x, х),
где
a = minXp(/4), ал^
р
и, соответственно,
р
причем 0<^as^at и ^
Отсюда на основании неравенства D.8.5) выводим
Интегрируя это неравенство, будем иметь при
где a = s—. Далее, используя евклидову норму
Х\Х\\ =(JC, X),
при t^i0 находим
т. е. при t^ t0,
где
и || х (t9) || достаточно мала.
254 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. IV
§ 9. Теорема Персидского
Имеются многочисленные работы (см. [16]), посвященные
обращению теорем Ляпунова, т. е. выяснению необходимости
условий этих теорем. Мы изложим здесь один старый результат
в этой области, принадлежащий К. П. Персидскому (см. [43]).
Теорема Персидского. Пусть приведенная система
f = X(t, х) (X(t, 0) = 0), (a)
где
допускает тривиальное решение | = 0, устойчивое по Ляпунову-
при t ->-f- со. Тогда для системы (а) в области
существует функция Ляпунова V (t, x)^C^u 1-го рода, т. е.
удовлетворяющая условиям первой теоремы Ляпунова об устойчи-
устойчивости.
Доказательство. Рассмотрим вспомогательную систему
f = Y(t,y), (b)
где Y(t, y) = X (t, у) <р (у), причем ср (у) ? С1 {<Mty — скалярная
функция, удовлетворяющая условиям:
1 при II у II «?/г,
' D9П
О при \\у\\^Н. D'УЛ)
Пусть x(t; t0, х0) и у (t; t0, y0)— решения, соответственно, систем
(а) и (Ь), определяемые начальными условиями: jc(/0; ^o. х<,)=Хо
и y(tol t0, Уо) = Уо-
Из условий D.9.1) вытекает, что решения у (t; t0, ya) можно
считать определенными на полуоси to^t^оо и обладающими
свойством единственности.
Фиксируя t0, рассмотрим функцию
V(t, лг) = A+е-')Н.У(^; t, x)f D.9.2)
где норма вектора у — (уи ..., уп) понимается в смысле евклидовой
нормы:
ТЕОРЕМА ПЕРСИДСКОГО
255
Пусть t^t0 и ||лг||<[Л. Тогда на основании условия D.9. П
правые части систем (а) и (Ь) совпадают и, следовательно, для
полных производных функции V (t, х) в силу систем (а) и (Ь)
имеем
Va(t, x) = Vb(t, x) =
=,, D-9.3)
где у^—у(%; t, х). Но точка у (t0; . т, у,) лежит на траектории Г,
x,
0
, ^
|
1
1
h
(Г)
_Jy
1
1
i
r
i
i
i
1
I
i
i
t
t,x)
t
Рис. 35.
проходящей через точку (/, х), и йследствие теоремы единст-
единственности точка ее выхода на гиперплоскость t — ta совпадает
со следом у (U; t, х) траектории Г (рис. 35), т. е.
при
>; s ут) = У (to, t, x)
Таким образом, из формулы D.9.3) получаем
t, x)= \\yih; t, X)
D.9.4)
D.9.5)
при x^zO и Va(t, 0) = 0, т. е. производная V (t, x) в силу
системы (а) знакоотрицательна.
Покажем, что функция V (t, x) — положительно определенная
в области t0^t<^oo, ||jp||<^ft. Так как тривиальное решение
§ = 0 как системы (а), так и системы (Ь) устойчиво по Ляпунову,
то существует 8 ^> 0 (8 <; s <; К) такое, что при U ^ t ¦< оо имеем
||jc(/; U, x,)\\ = \\y{t; t0, Jf»)IKs. D-9.6)
если только ||лго||<8. Тогда, если 0<е< || ха || </г, то
\\У(Ь; t, хй)\\^Ь при t?zt0. D.9.7)
2Г;6 ВТОРОЙ МЕТОД ЛЯПУНОВА [Г.1. IV
Действительно, если бы
\\y(tn; t, jcn)||<8 для некоторого 7=%/,,,'
то
\\y(t; t, X») ||< г при t^h.
Отсюда, полагая i=t, мы бы имели
\\y(l, t, *o)|| = ||*o||<s,
что противоречит выбору х0 (рис. 36).
Кроме того, на основании формулы D.9.1) в силу свойства
единственности решений системы (Ь) имеем
IIУ (/0; *, х0) || < Н при
Из формулы D.9.2) получаем
V(t, x,,)>S- = 7] при s
D.9.8)
D.9.9)
n h h
1 юлагая е = ~y•, ..., pxy получим последовательность по-
положительных чисел
V(t,
таких, что
при
(п—1, 2,...). Отсюда следует, что существует непрерывная
Рис. 36.
положительно определенная функция W (х), удовлетворяющая
неравенству
V (t, x)Z^W (JC)>0 при лг^О.
Например, можно положить
п + 1
при -
Si tn] УСТОЙЧИВОСТЬ КВАЗИЛИНЕЙНЫХ СИСТЕМ 257
Следовательно, функция V (t, x) — положительно определенная.
На основании известной теоремы о гладкости решения у (t; tn,y0)
по начальным данным tn, у0 (см. [9]) функция V (t, x) непрерывна
по совокупности переменных t и х и имеет непрерывные частные
dV dV ,.
производные зг- и ^— (/ = !,...,«), причем
при /? [t0, со) и || jr
Теорема доказана.
§ Ю. Устойчивость квазилинейных систем
Рассмотрим действительную дифференциальную систему
§ (t, х), (а)
где А — постоянная матрица и ср(?, х) ? С (Q^t<^co,
Ц^Я1), причем <р (t, x) = o(\\x ||) равномерно по t, т. е.
^^#^0 при х-+0 D.10.1)
('х ||—евклидова норма вектора л:).
Систему (а) будем называть квазилинейной; очевидно, эта си-
система допускает тривиальное решение х = 0.
Теорема Ляпунова. Если все собственные значения ^;-(А)
(/=1,..., п) матрицы А имеют отрицательные вещественные
части:
ReX^^XO (;=rl,...,n), D.10.2)
то тривиальное решение х — 0 квазилинейной системы (а) асим-
асимптотически устойчиво по Ляпунову при t-*¦-{-со.
Доказательство (см. [10]). Пусть §(/, х) — действитель-
действительное решение соответствующей линейной системы
определяемое начальным условием:
1@, х)
') Для простоты принимаем to =
9 Б. П. Демидович
258 ВТОРОЙ МЕТОД ЛЯПУНОВА [Г.п. IV
Если Е (t) — нормированная фундаментальная матрица (матри-
цант) системы (Ь) такая, что
то, очевидно, имеем
lit, x) = E{t)x. D.10.3)
Из условия D.10.2) вытекает (см. гл. I, § 13), что
(| Z(t) || «sM?-M при г=эО,
где max Re \/ (А) <^ — а<^0 и N — некоторая положительная по-
постоянная. Отсюда
|| § (t, х) || «s Ne-" || х || при г 3=0. D.10.4)
Рассмотрим функцию
со
V(jO = J|IS(t, jc)||j^. D.10.5)
о
Из D.10.3), используя известные свойства скалярного произве-
произведения , имеем
о
со
= J (Е1 (х) S (т) л:, л) dx =(Sx, x), D.10.6)
где
а 27 (г) — транспонированная матрица относительно матрицы Е (Ч).
Таким образом, V (jc) представляет собой квадратичную форму
относительно переменных хи...,хп с действительной симметри-
симметрической матрицей S.
На основании неравенства D.10.4) интеграл в правой части
равенства D.10.6) сходится и, следовательно, функция V (х) опре-
определена и конечна для каждой точки х ?j cMnx, причем в силу
свойства единственности решений системы (Ь) имеем
1/(л;)>0 при х^0
УСТОЙЧИВОСТЬ КВАЗИЛИНЕЙНЫХ СИСТЕМ
259
Используя так называемое групповое свойство решений авто-
автономной системы (Ь) (рис. 37)
= i(t + -:, X),
получим
V (| (t, X)) :
= \ ||
0
x, x
Отсюда производная по времени t функции V (х) в точке х в силу
системы (Ь) будет равна
Уп,
D.10.7) ¦ У1
Рис. 37.
Найдем теперь производную по
времени t функции V (х) в точке х в силу системы (а). Имеем
V, Ax)->r(gvadV, ф (t, x)) =
', <?(*, х)). D.Ю.8)
Полагая
5 = fsjk] и JC = colon (*ь..., xn),
из формулы D.10.6) находим
Отсюда
grad V = colon
[dV
\
\
J
[_ _
\dxt '¦¦¦' dx'J
= 2 colon B S,kxk,..
Кроме того, из условия D.10.1) получаем
II? (Л *)il<s II х |!
9*
Snlixk) = 2Sx.
D.10.9)
260 ВТОРОЙ МЕТОЛ ЛЯПУНОВА (ГЛ. IV
при \\ х \\-^ h= <^ Н, где s^>0 произвольно мало. Следовательно,
из формулы D.10.8), учитывая соотношение D.10.7) и используя
неравенство Коши, имеем
V, (х) ^ - || х If2 +! (grad V, о (t, x)) | =ss
= - || д:||»A — 2s || S||)<- ~ || д:!1»<0, D.10.10)
если только 0<^s<^ и 0<^ || JC || <^ft=, причем V',,@) = 0.
Таким образом, для системы (а) в некоторой окрестности
точки О существует положительно определенная функция V (х),
не зависящая от времени t и допускающая отрицательно опре-
определенную производную Va(x), в силу этой системы.
На основании ^второй теоремы Ляпунова (§ 4) тривиальное
решение х = 0 системы (а) асимптотически устойчиво в смысле
Ляпунова при /->-{-оо.
Следствие. В условиях теоремы тривиальное решение лс = О
экспоненциально устойчиво при t-*-oo (см. теорему из § 8).
Замечание. Доказательство теоремы можно получить также
с помощью метода вариации произвольной постоянной, исходя из
формулы
X (t) = 3 (t) X @) + j S (/ - т) 9 (г, X (т)) d,
и применяя неравенство Гронуолла—Беллмана (ср. с теоремой 2
из § 12 гл. II).
Из теоремы Ляпунова, в частности, вытекают достаточные
условия устойчивости состояния равновесия.
Пусть нелинейная автономная система имеет вид
% D.10.11)
где
Если
то у—Уо есть состояние равновесия системы D.10.11). Положим
У =Уо + X.
УСТОЙЧИВОСТЬ КВАЗИЛИНЕЙНЫХ СИСТЕМ
261
Тогда
где
— матрица Якоби.
Принимая х — отклонение вектора у от положения равновесия
_у0 — за новую переменную, будем иметь
dx
dt
= Ах + о
\х\\).
D.10.12)
На основании теоремы Ляпунова имеем следующий результат.
Теорема. Если все собственные значения матрицы Якоби
f (уй) имеют отрицательные вещественные части, то состояние
равновесия у =у0 нелинейной автономной
системы D.10.11) асимптотически устойчиво
по Ляпунову при t -> оо.
Прим ер. Уравнение нелинейных колебаний
маятника в сопротивляющейся среде имеет вид
'6 + ей* + * sin в = 0,
где 9 — угловая координата (рис. 38), a a, b — по-
положительные постоянные. Отсюда получаем систему
d<" j. ¦ i
zr = — aw —¦ b sin I
dt
D.10.13)
Рис. 38.
Исследуем устойчивость состояния равновесия: 80 = 0, а>0 = 0 системы D.10.13).
Вводя обозначения
будем иметь
y0 = (B0, о>0),
— Г ш
[ — аш — b sin
- b cos 6
Следовательно,
f(yo)
-Г ° Ч
"I-* -а\-
Отсюда получаем характеристическое уравнение
— X 1
262 ВТОРОЙ МЕТОД ЛЯПУНОВА II.П. 'V
Так как «> О и 6 :> 0, то для характеристического уравнения выполнено
условие Г\рвица и, следовательно, исследуемое состояние равновесия
асимптотически устойчиво.
Теорема неустойчивости. Пусть квазилинейная система
fl? = Ax + ?(t,x), D.10.14)
где А — [оу7,] — постоянная матрица и ср (t, х) ? С (//' X || х [| < Н)
такова, что
^ЩН_>0 при ^.^0
Если хотя бы одно собственное значение Х/ = Ху(Л) G = 1,..., п)
матрицы А обладает положительной вещественной частью, то
тривиальное решение х = 0 этой системы неустойчиво по Ляпу-
Ляпунову при t -* ос.
Доказательство (см. [6]). Без нарушения общности рас-
рассуждения можно положить
ReX,(^)>0 (j=l, ..., m)
и
ReAm+t(y4)*s0 (k=l, ..., п-т),
где \-<:т^п у). Пусть S — постоянная неособенная матрица,
приводящая матрицу А к почти треугольному виду (см. следст-
следствие 2 теоремы 2 из § 6 гл. I), т. е.
где A = diag(X,, ..., Х„), B = \bJk], bjk — 0 при /^ k и || В \\ =s=e0,
причем положительное число г0 может быть выбрано сколь угодно
малым.
Произведем в системе D.10.14) замену переменной:
x = e"'Sy, D.10.15)
где а — положительное число такое, что
0<а< min Relj(A),
а матрица 5 и вектор у, вообще говоря, комплексные. Тогда
будем иметь
ea'S df( + e"aSy == euy
т. е.
Cjt = (\ -*E)y + By-\-<b{t,y), D.10.16)
') В дальнейших рассуждениях мы предполагаем, что т <; п, так как
при т=п доказательство теоремы очевидным образом упрощается.
§ 101
устойчивость квазилинейных систем
263
где матрица Л — яЕ не имеет собственных значений с нулевой
вещественной частью и
Так как
t, y) = e atS ^(t, e^Sy).
при ||JC||^AF)
то
, У)
'¦' II ?-l II ,o*
S ' || ге« || S
если || X || s^e || S || \{y || й^/г(е), т. е. если
Г* || S || ~4i (e),
D.10.17)
где sj>0 произвольно мало.
Полагая у = colon (г/,, ..., г/„),
ф(^ у) = colon [ф] (t, у), ..., фя (^, у)]
и
[х5 = Х5(Л)~а (s=l, ..., «),
систему D.10.16) можно записать в координатной форме
dt
v-пУп + % U, у),
D.10.18)
где Rea;->0 (/=1, ..., т) и Re[im+/, <0 (k—l, ..., п — т).
Отсюда, переходя к комплексно-сопряженным величинам, полу-
получим
rf<
= |iiPi
Л
• • • + hnBn
>yh \ D.10.19)
dt
ыЗп + ^пИ, у)
Пусть
=~{2'-y?- I
264 ВТОРОЙ МЕТОД ЛЯГО'НОВА [ГЛ. IV
Так как
±\У,? = ?(У,9,) = 9г% + У.% (s=l...,n),
то из уравнений D.10.18) и D.10.19) будем иметь
т п — т
V (у) = Ц Re ъ | yt ? + 2 ( - Re pm+k), ут,к г + Р (Л У) || У Л
где р(/, г/) = О(е) (т.е. р (/, у) — величина порядка е, равномерно
относительно t и у) в области D.10.17). Полагая
р = min (Re p.,, — Re [хш+Л),
/.*
при достаточно малом е ^> 0 находим
v(y)^[$-\p(t, y)\]\\y\?^^\)yr.^?V(y).
Следовательно, при ?0 = 0 и V (у @))^>0 получаем
\\y(t)\f^2V(y@))eV, D.10.20)
если только
Пусть 8]>0 произвольно мало. Выберем у @) так, чтобы вы-
выполнялись неравенства
0<||«/@)||<8, V(y@))>0
(этого можно добиться, положив, например, утлк = 0 (k=l, ...
..., п — т)). Тогда из неравенства D.10.20) вытекает, что суще-
существует момент t1 ^> 0 такой, что
Возвращаясь к прежней переменной x = x(t), в силу формулы
D.10.15) будем иметь || лг(О) || ^ || 5 || || у @) || < || 5 || 8 и
II X [tO || ^ гСг^ || У (h) II 22= ||Jb Л (е),
!|S
где e>0 фиксировано. Так как 8>-0 произвольно мало, то от-
отсюда следует, что тривиальное решение Jt = O квазилинейной
системы D.10.14) неустойчиво по Ляпунову при /->оо.
Теорема доказана.
§ 111 ОЦЕНКА МАТРИЦЫ КОШИ ДЛЯ ПРАВИЛЬНОЙ СИСТЕМЫ 265
§ 11. Оценка матрицы Коши для правильной системы
Пусть действительная линейная система
,де d? = A(t)x, D.11.1)
A (t) e С [to, oo), sup || A (t) [| <^ со,
есть правильная (гл. III, § 10) и
X(t) = [xJk(t)] D.11.2)
— ее нормальная фундаментальная матрица. Обозначим через
аь ..., а„ характеристические показатели решений
лг(*' = colon [xUl(t), ..., xnk{t)\ (k=\, ..., n),
входящих в фундаментальную систему A). Полагая
A==diag(a, а„),
будем иметь
Отсюда
4* ...хаа(Це-'«'_
у [Ф (t)] = max i [xJk (t) g-V ] = 0.
D.11.3)
Аналогично, учитывая, что в силу теоремы Перрона (гл. II!,
§11) для обратной матрицы
-* С) = [«//*(')]
ее векторы-строки
имеют характеристические показатели у[_у(/'] = — ау, находим
X [ф ' @1 = max у. [еа11у}к (t)] =0.
f."
D.11.4)
Рассмотрим теперь матрицу Коши
266 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. !V
в области ?0 -=с т й? t (рис. 39). Очевидно имеем
К (t, х) = A' (t)e-/Д е ' - -¦<д е^Х'1 (т) = Ф U) ел —¦¦ д Ф1 (%). D.11.5)
Отсюда, учитывая равенства D.11.3) и D.11.4), получаем
|| к а, 1) || =sc || ф (о || || е" --'д || ;| ф-1 (т) || ^
=s;ce 2 е'\а 2/ "'е2 т =се1в~+Е)" ~т!еет, D.11.6)
где a = max aft,
к
произвольно и с — положительная посто-
постоянная, зависящая только от е и t0.
Пусть
О
Тогда е^>0 можно выбрать столь
малым, чтобы имело место неравен-
неравенство
S-f е<«,
и из неравенства D.11.6) при t^^z^t
получаем
Следствие. Если все характеристические показатели ak
правильной линейной системы D.11.1) отрицательны, то для ее
матрицы Коши при /0 ^ t ^; / справедлива оценка:
\\К((, т)||^с(/0)е« D.11.7)
где е — любое положительное число.
§ 12. Теорема Ляпунова об устойчивости
по первому приближению
Рассмотрим действительную нелинейную систему
U х), D.12.1)
где
A(t)?C\ln, ос.), sup || Л (О
со, и /(*, х)
D,12.2)
ij 12] УСТОЙЧИВОСТЬ ПО ПЕРВЛМУ ПРИБЛИЖЕНИЮ 267
и <^(t)— непрерывная положительная функция при t(t -^! <^ сю
1
такая, что1)
Норма матрицы /4=[a7ft] здесь понимается в смысле I нормы
(гл. I, § 4):
|| Л || = max ?! а1к ;.
к
Теорема (критерий Ляпунова). Если система первого
приближения
§ = АAI D.12.3)
правильная (см. гл. III, § II) и все ее характеристические пока-
показатели y.k (k=l, ... , п) отрицательны, причем выполнено условие
нелинейности D.12.2), то тривиальное решение jc = O полной
нелинейной системы D.12.1) экспоненциально устойчиво по Ляпу-
Ляпунову при t -> 4- эо-
* « -« 0
-г
Рис. 40.
Доказательство (см. [14]). Пусть
aft=S —a<0 (k=l,...,n). D.12.4)
В системе D.12.1) выполним преобразование
X =уе- т« - t0-, t D.12.5)
где 0 <^ т <Са (Рис- 40). Тогда будем иметь
ft = B(t)y + g(t, у), D.12.6)
где
A(t)-\-iE D.12.7)
g(t, y) = ei{t-^f(t, уе-1«-Ы), D.12.8)
1) При формулировке Ляпунова f(t) — иоложшельная постоянная.
268 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. IV
причем
Легко видеть, что для системы D.12.6) система первого при-
приближения
правильная. Действительно, пусть C4(&=1, ..., и) —характе-
—характеристические показатели линейной системы D.12.9). Очевидно,
рА = аА-4-т<0 (k=\, ... , п).
Учитывая правильность системы D.12.3) и формулу D.12.7),
имеем
lim | [ Sp В (ti). dtt =
= lim
Следовательно, система D.12.9) правильная.
Пусть Н (/) (Н(/о) = ?') — нормированная фундаментальная
матрица системы D.12.9) Используя метод вариаций произволь-
произвольных постоянных, нелинейное дифференциальное уравнение D.12.6)
при начальных условиях: y(tf) = xu — можно заменить равно-
равносильным интегральным уравнением
\{l, v)g(->, y('))dz, D.12.10)
'о
где
Kit, т) = Н(/)И-'(:).
Согласно локальной теореме существования ранений, для лю-
любой пары (/„, jc0), где || jc0 || <^h, существует решение у (t) диф-
дифференциального уравнения D.12.6), а следовательно, и интеграль-
интегрального уравнения D.12.10), удовлетворяющее начальному условию:.
у (t<>) — x(ta) = x0,
определенное в некотором интервале ^о5^<Оо-М, причем
1!.у (/) || <^ h при t?[t0, to-\-i] и число /, вообще говоря, зависит
от решения у (t).
§ 12] УСТОЙЧИВОСТЬ ПП ПЕРВОМУ ПРИБЛИЖЕНИЮ 269
Так как все характеристические показатели '¦',., (к = 1, ..., п)
линейной системы D.12.9) отрицательны, то существует положи-
положительная постоянная сх такая, что
|| II (/) || <с, при /0<*<оо (с, 3*1). D.12.11)
Кроме того, на основании оценки матрицы Коши К 't, т) для
правильной системы с отрицательными характеристическими пока-
показателями (§11, следствие) имеем
II K(t, т)||<Сое'^-"> D.12.12)
при tu йс; т ssc t <^ со.
Далее, на основании формул D.12.8) и D.12.2) при /„ -г-,/<^tu -|- /
получаем
\\g(t, y)||=gir«-'o) \\f(t, ye-^-wjii^cgei'-"»-1^."-^ || у f,
где с3 — достаточно большая положительная постоянная. Отсюда,
оценивая по норме при /1nsC:^\4 + ^ левую и правую части
интегрального уравнения D.12.10), будем иметь
у @ || ^ || Н (t) || || у (t0) || + 5 || К (*, т) || || g (т, у (г)) И rf,,
ИЛИ
||^(О||^с1||у(М11+$еде[2-<т-1)т1(т-'«)||3'(-IГ^- D.12.13)
I о
Выберем положительное число е столь мальш, чтобы имело место
неравенство
Ь = (т~ 1)т — 2г>0.
Тогда из неравенства D.12.13) при *о-tS ? <Оо-|-<•' выводим
II У @ II <ct || у (/0) || + $ с4е- s<^-'o) || j, (,) |р rf-г, D.12.14)
где
Из неравенства D.12.14), используя лемму Бихари (следствие 2
из § 2 гл. II), находим
I! У (О II ^ ?l!!ZL<hUL_ _ _ l4.12.15)
[1_ (от — l) с,-1 И .у Со)
270 ПТОРОЙ МПТОД ЛЯПУНОВА [ IЛ 'V
если только
t
(in — I)с;1 -' \\y(ta)},m-] $c4e-SlT -'^d'<il. D.12.16)
'о
Так как
je-8"-' d-<y<oo,
то неравенство D.12.16) всегда можно считать выполненным за
счет выбора окрестности начальных данных x(tu)=y (tit). Из
формулы D.12.15) следует, что если >К4) || достаточно мало,
то при любом t ?\t.)t to-\-/) точка у (t) является внутренней точ-
точкой области Z = -/o й?/<Ссо, Ц.У || =^-s-<[M и, следовательно,
решение у (f) бесконечно продолжаемо вправо, т. е. можно поло-
положить / = оо. Таким образом, в бесконечном промежутке tos^t<^co
выполнено неравенство
\\y«)\\^'V\\y(h)\\<i, D.12.17)
где N — некоторая постоянная, зависящая от начального мо-
момента tn.
Возвращаясь к переменной х, в силу формулы D.12.5) при
t(l -=s t <^ схэ и || X (t0) j| <[ А <^ h будем иметь
I) jc(O || ^N \\x(t0) ||в-т('-Ч D.12.18)
где постоянная А достаточно мала.
Отсюда следует, что тривиальное решение л: = 0 нелинейной
системы D.12.1) экспоненциально устойчиво по Ляпунову при
t-*¦ею.
Теорема доказана.
Следствие. Любое решение x(t) нелинейной дифференциаль-
дифференциальной системы - D.12.1) с начальными данными x(t0), принадлежа-
принадлежащими достаточно малой окрестности || x(t(,) || <С^, имеет харак-
характеристический показатель, удовлетворяющий неравенству
>. DЛ2Л9)
где y.k — характеристические показатели соответствующей линей-
линейной системы D.12.3).
Действительно, из неравенства D.12.18) получаем
а так как число — f может быть выбрано сколь угодно близким
к max %k, то отсюда следует неравенство D.12.19).
(j 13] ПРИЗНАК УСТОЙЧИВОСТИ ДЛЯ НЕЛИНЕЙНЫХ СИСТЕМ 271
§ 13. Признак устойчивости для нелинейных систем
с неправильной линейной частью
Рассмотрим действительную линейную однородную систему
ft = A{t)x, D.13.1)
где A(t)?C[tn, со), sup |j A (t) || < со, и пусть а,,..., а„ —ее
t
характеристические показатели.
Определение. Число
•I t
х = 2]я* —lim \ Sp A (tx)dU D.13.2)
называется мерой неправильности системы D.13.1) (см. [15]).
В силу неравенства Ляпунова (гл. III, § 7)
/ ik 52 lim -T- \ Sp /4 (г1)) dty
ft 4)
из формулы D.13.2) получаем
у- 5э 1 im у \ Sp A iti) dt, — Hrn -- ^ Sp Л И{) dtt 7^ 0.
Очевидно, что система D.13.1) правильная тогда и только тогда,
когда -/.==0.
Обобщением критерия Ляпунова для неправильных систем
занимался Н. Г. Четаев. Мы приведем результат Массера (см. [44J),
обобщающий теорему Ляпунова (§ 12) и Четаева (см. [15]).
Теорема Массера. Пусть дана нелинейная система
у), D.13.3)
где А (Ос С [I, оо), sup \\ A (t) || <оо и /(/, у) С С# " (/0 ^/<оо,
j' || <С^). причем f(t, 0)^0.
Если
1) 1!/С, ЯИ«М01!.У1Г ('«>1),
гс*е 0(/) — положительная функция такая, что /[0(/)] = 0,
2) Эля характеристических показателей i.x, ..,, ал линейного
приближения D.13.1) выполнено неравенство
max ал< — —^ к- 0,
272 ВТОРОЙ МЕТОД ЛЯПУНОВА !ГЛ. IV
где ¦/ — мера неправильности соответствующей линейной систе-
системы D.13.1),
то тривиальное решение _у=0 нелинейной системы D.13.3) асимпто-
асимптотически устойчиво по Ляпунову при t —>- оо.
Доказательство. Пусть
D = diag (я, -т--у, •¦•, <*Я + Т[).
где (рис. 41)
—^-т<Ст<С~а. а = max а*. D.13.4)
Положим
y = X(t)e~Dlz, D.13.5)
где X (t) = [xik(t)] — нормированная фундаментальная матрица
а. &ггЯ - ¦ а
Г
Рис. 41.
d*^-X{t)e-Dlz-X{t)e-DtDz--
линейной системы D:13.1) (X(to) — E). В силу D.13.3) имеем
-f{t, X(t)e~D!z).
D.13.6)
z). D.13.7)
Отсюда,
получим
где
Как
где
учитывая,
git.
известно,
что
X
dz
dt
Z) = e
utx-\
Д(/) =
4 (OX (Oe""
A A) X (t),
'.-rg(t, z),
(l)f(i, X[L)
t
= det X (t)
и Д/7г (t) — соответствующие алгебраические дополнения определи-
определителя Д (/). На основании формулы Остроградского —Лиувилля,
учитывая, чго Д(го)=1, находим
t
I Sp A Uii itti
A(t)=e'°
« 13] ПРИЗНАК УСТОЙЧИВОСТИ ДЛЯ НЕЛИНЕЙНЫХ СИСТЕМ 273
Следовательно,
— J Sp А (/,) dtv
X^{t) = [bUj{t)e '» ].
Отсюда
- J SpAit^dtt
1>/)| т D-13.8)
и
aA-(aA + T)] = -T. D.13.9)
/, *
Так как
/[Х@е-°']<0,
то
X@e-D'-*0 при ^ —-L-oo. D.13.10)
Следовательно,
\\X(t)e-Dt\\^M<_oo при 4<*<oo.
Положим
Тогда на основании формулы D.13.5) получим
Оценим нелинейный член в правой части уравнения D.13.6)
при ]',z\\<^ ,,-. Используя условие 1), имеем
где в силу неравенств D.13.8) и D.13.9) и свойств характери-
характеристических показателей справедлива оценка:
у [? @1 = z f!I e0' X-1 @ и |! ф @ |] || X (/) е-о^ ц»] ^
274 ВТОРОЙ МЕТОД ЛЯПУНОВА 11Л. IV
Отсюда на основании неравенства D.13.4) получаем
/Л? @1<0.
Следовательно,
\\g(t, г)\\^с \z :т (/п>1) при 4^К — оо и ;|*'|<А.
D.13.12)
Таким образом, нелинейная система D.13.6) удовлетворяет
условиям теоремы Ляпунова об устойчивости квазилинейных си-
систем (§ 10) и, следовательно, тривиальное решение ее z = 0
асимптотически устойчиво при ^—*- — оо. В силу формулы D.13.5)
и неравенства D.13.9) это будет верно также для тривиального
решения v = 0 исходной нелинейной системы D.13.3).
Следствие. Для характеристических показателей решений
y(t), где \]-y(t0)\\ достаточно мала, справедлива оценка:
у_[у ({)]^таху.к. D.13.13)
Действительно, из формулы D.13.5), учитывая неравенство
D.13.9) и ограниченность функции г (г), получаем
А так как число — у можно брать сколь угодно близким к max гк>
то справедливо неравенство D.13.13).
§ 14. Неограниченная продолжаемость решений
Рассмотрим действительную систему
§ =/(>, У), D.14.1)
где
fit у) СО». !!(/¦- \- rjgl)
J \ ' ¦? ' ч— fy \ ;¦ / \ у'
Для произвольного решения _уG)=_у(г; ^„, _у„) (tn?lj) спра-
справедливы две возможности: 1) либо у (t) имеет смысл на беско-
бесконечном промежутке \tlt, оо); тогда оно будет неограниченно про-
продолжаемым вправо; 2) либо у (г) определено лишь па некотором
конечном промежутке tn-^J <^T<^со.
Лемма. Если решение у (t) имеет конечное время определе-
определения tn =s; t <^ T <^ оо, то
|lj;(/)!|->oo при t^-T — 0.
Доказательство. Пусть '!_у (/) Ij т4оо при t->T - 0. Тогда
существует последовательность <А -> Т — 0 такая, что_у (/;,) ->¦ 2 =^ j-э
5> П|
НЕОГРАНИЧЕННАЯ ПРОДОЛЖАЕМОСТЬ РЕШЕНИЙ
275
при &->оо. Рассмотрим решение z (t) = z (t; 7, z) (рис. 42), опре-
определенное, согласно локальной теореме существования решений
'см. [11]), в некотором интервале
G —а, 7 4-а) (*>0).
В силу свойства единственности решений, при tk^>T ~
имеем
У(*; h, y(tk))~y(t; t0, y0)
z(f, tk, z(tk))==z(t; 7, z).
Так как у (tk) может быть выбрано сколь угодно близко к z и
tk->T, то при достаточно большом k точки у (tk) и z{tk) сколь
Z(t)
угодно близки между собой (см. рис. 42). А тогда на оснований
свойства интегральной непрерывности (гл. II, § 1) получим, что
решение у (t; t0, y0) определено во всяком случае на промежутке
-2I)[T, T-~-j). А это противоречит максимальности
. Та-
Таtk
промежутка [/0, 7) существования решения у (t) при 0
ким образом, \\у (t) -,\ -у сю при t-*-T — 0.
Лемма доказана.
Следствие. Если решение у =¦ у (t; t0, y{)) ограничено в своем
максимальном промежутке существования t0 ^ t <^ t0 -\~ T, то оно
бесконечно продолжаемо вправо, т. е. 7 = оо.
Неограниченная продолжаемость вправо решений системы
D.14.1) является необходимым условием устойчивости по
Ляпунову решений этой системы. Используя функции, аналогич-
аналогичные функциям Ляпунова (§ 5, замечание 2), можно получить
л оста т о ч н ы е условия неограниченной продолжаемости
при t-±-{-co решений системы D.14.1).
276
ВТОРОЙ МЕТОД ЛЯПУНОВА
[ГЛ. IV
Следуя Ла-Саллю [45], рассмотрим дифференциальное нера-
неравенство
v^G(t, v) (t^h), D.14.2)
где G(t, v) — некоторая непрерывная скалярная функция, опре-
определенная при t^tn и и(^еЯ", a v = v(t) — непрерывно диффе-
дифференцируемая положительная скалярная функция.
Будем говорить, что решение v(t)(^Cl неравенства D.14.2)
имеет конечное время определения t№^t<^T, если: 1) v(t)^
^G(t, v) при tv^t<^T и
Тео р.ем а
Пусть
; = {i'^
при t^-T — O.
Л а -Са л л я.
Рис. 43.
внешность сферы радиуса р и
•оо, равномерно на каждом ко-
причем V (/, y)ljoo при \\у
t
нечном промежутке (a, b) (Z /J".
Тогда, если
1) производная V (t, у) по t в силу системы D.14.1) при 0
11 У €; 5р удовлетворяет неравенству
V(t, y)^G(t, V.(t, у)), D.14.3)
где G (t, v) — непрерывная скалярная функция;
2) соответствующее скалярное неравенство D.14.2) не имеет
положительных решений v (/) с конечным временем определения,
то каждое решение у = у (t) системы D.14.1) неограниченно про-
продолжаемо вправо.
Доказательство. Допустим, что некоторое решение у(t)
системы D.14.1) имеет конечное время определения tn scj<^ Г<^оо.
Тогда в силу леммы у (!)'! —> со при 1-±Т — 0 и, следовательно,
при t?(tu Г), где ^1^>^>, решение у (t) целиком будет содер-
содержаться в некоторой области Sr?t (рис. 43), где р. ^> р. Кроме того,
можно предполагать, что V (t, у)^>0 при (t, у) ^ [/0, Т] X Sc9r Но
тогда на основании неравенства D.14.3) функция
v(t) = V(t, y(t))
является положительным решением скалярного неравенства D.14.2)
6 Н) НЕОГРАНИЧЕННАЯ ПРОДОЛЖАЕМОСТЬ РЕШЕНИЙ 277
с конечным временем определения tn^t<^T (v{T) = oo). А-это
невозможно в силу условия 2) теорег-ы.
Теорема доказана.
Следствие. Пусть
G(t, v) = k(t)L(v),
где k(t)^O и L(v)^>0 — скалярные функции, непрерывные при
Если
со
dv ,
то неравенство D.14.2) не имеет положительных решений v(t)
с конечным временем определения.
Действительно, пусть существует положительное решение
v (t) (t(i^t <^ T) неравенства
^{v) D.14.4)
такое, что \\v(T)\\=co. Из неравенства D.14.4) находим
Отсюда при t^rT — 0 получаем, что левая часть неравенства
D.14.5) стремится к -)- оо, а правая — ограничена, что, очевидно,
невозможно. Следовательно, каждое положительное решение v(i)
неравенства D.14.4) или имеет смысл лишь на некотором конеч-
конечном промежутке [^0, Т), причем || v (t) \\-/*oo при t^-T — Q, или
же оно определено на бесконечном промежутке tn^t<^co.
Пример. Рассмотрим действительную систему (см. [45])
|~ =*(*,*), D.14.6)
где
Если
|| X (t, х) ,'| =S k (t) \\ x || D.14.7)
при | х !| 5^ р, где k (t) ^C(/t) — неотрицательная скалярная функция, тс>
все решения х it) системы D.14.6) неограниченно продолжаемы вправо.
Действительно, положим
V(X) = -\X\';U ~(Х, X).
Ои;юда
174 ВТОРОЙ METl ЛЯПУНОВА [ГЛ IV
Используя неравенство Коши (гл. 1, § 5) и неравенство D.14.7), будем
иметь
V(x)-s:2\\xr\:>lX(t, x)\\iz-2k(t) V(x) = G(t, V(х))
при t^t0 и : jc i.1 7=2 р. Но неравенство
v (t) й? 2 к (t) v (t)
в силу следствия (Z.(t>) = 2o) не имеет положительных реи1ений с конечным
временем определения. Следовательно, на основании теоремы Ла-Салля
каждое решение х (t) системы D.14.6) имеет смысл при t0 <c t ¦< оо.
§ 15. Устойчивость по .Лагранжу
Рассмотрим систему
^=f(t,y), D.15.1)
где fit, у) (= С% l| (it X <Щ) и /Г = {«<*< do}. Очевидно, си-
система D.15.1) обладает свойством единственности решений
У (t; ta, yt), где tn ^ /^ иуо(= Ж,-
Определение. Будем говорить, что система D.15.1) устой-
устойчива по Лагранжу (см. [12], [45]), если: 1) каждое решение
У (t\ to, у а), где („ ? It, неограниченно продолжаемо вправо-, -т. е.
имеет смысл при ^«^<^сю; 2) |Г.у(/; /0, У о) I ограничена на
['о, оо).
Например, если система D.15.1) имеет ограниченное решение
к] @; асимптотически устойчивое в целом (§ 7), то эта система
устойчива по Лагранжу.
Используя функции Ляпунова, нетрудно сформулировать необ-
необходимые и достаточные условия устойчивости системы D.15.1) по
Лагранжу (см. [41], [46]).
Теорема. Для того чтобы система D.15.1) была устойчива
по Лагранжу, необходимо и достаточно, чтобы в It X e^y сущест-
существовала функция V (I, у) такая, что
1) V(t, y)^W(y), где W(y)-+oo при 1\у[ ->оо;
2) для каждого решения у (t; ta, у„) функция V (t, у (t; t0, ya))
была невозрастающей относите who переменной L
Замечание. Для случая достаточности условие' 2) можно
заменить следующим:
2') V U, у) <,0 в силу системы D.15.1).
Доказательство. 1) Докажем сначала достаточность
условий теоремы. Пусть для системы D.15.1) существует функция
V1', у), обладающая свойствам:! 1) и 2). Для всякого решения
У{'\ t«, Уп) itn^>a, !:Уо'!:<С°°) в силу условия 2) при t^t0 имеем
V'(¦', y(t\ 'о, Уо)) '- V'Со, У Со; ^о, yo))=V(t0, у0).
151
УСТОЙЧИВОСТЬ ПО ЛЛГРАНЖУ
279
Отсюда на основании условия 1) получаем
W (У (t; /„, у»)) *? V (t, у (t; *„, у0)) < V (t0, у,) при t>-tn.
D.15.2)
Из последнего неравенства следует, что решение у (t; tn, у„) ог-
ограничено. Действительно, если это не так, то нашлась бы по-
последовательность моментов времени tk —>- со (?=1, 2, ...; tk^t0)
такая, что
'.\y(tk> 'о, Уо)!!-»-00 при k
¦ со
и, следовательно,
k\ to,
-f-co при
вопреки неравенству D.15.2). Таким образом, решение у (t; *e,j/0)
неограниченно продолжаемо вправо и
supii>'(^; /fl, yc)j|<oo D.15.3)
t
при t? [to, со).
Замечание. Для этой части теоремы не требуется выпол-
выполнения свойства единственности решений.
2) Докажем теперь необходимость условий теоремы. Пусть
любое решение у (t; tlb yfl) системы D.15.1) существует и ограни-
ограничено на промежутке
и, следовательно, бесконечно
продолжаемо при t —>- -|- со.
Положим
V(t, у) =
D.15.4)
где
Из формулы D.15.4) имеем
V(t,
Рис. 44.
схэ, т. е. условие 1) вы-
причем, очевидно, W(y)—>¦ со при ijy
полнено.
Далее, при a<^i<^a, учитывая, что в силу свойства един-
единственности решение у (t; tit у (t,2; tOl у„)) является продолжением
решения у (t; tu y(tx; t0, y0)) (рис. 44), получаем
V(tu y(tu t0, yo))= sup Hy^.+t; /,, y(/,; t0, yo))li*^
T > 0
Sssupjlj^ |--c; ?,, y(^a; /0, y0)) :p = I/ (/4> у (f4; f0> _y0)).
5d
280 ВТОРОЙ МЕТОД ЛЯПУ.'ГОЗА [ГЛ. IV
Таким образом, условие 2) также выполнено,
Теорема доказана полностью.
Замечание. Непрерывность функции V (t, у) здесь не га-
гарантируется.
Пример. Рассмотрим скалярное дифференциальное уравнение (см. [46J)
) = u, D.15.5)
где p(t) с С [0, со), q (t) ? С\ [0, со) и / (х) ? С (— со, со).
Если выполнены условия:
1) 0 < q @ -с М;
-I оз
3) \ f(x)dx = + со,
то решения х (t) уравнения D.15.5) ограничены на [0, со) вместе со своими
производными х (t).
Действительно, запишем уравнение D.15.5) в виде системы
dx ___
D.15.6)
Положим
X
V(t, х, у) =
о
На основании неравенства 1) имеем
X
V(t, х, ,уK=
О
причем W (х, у) —>- -4- со при х% -\-у% —> со.
Далее,
x(t)
Отсюда
=f(x (t))y(t) -~щ\Р it) у (t) -f- ? (t)f(x (/))] -
Таким образом, условия теоремы выполнены и, следовательно, х (t) и
y(t) = jt(<) ограничены иа промежутке 0 s^ t < со.
§ |61 СИСТЕМЫ С КОНВЕРГЕНЦИЕЙ 281
§ 16. Системы с конвергенцией
Рассмотрим систему
if
if = fit. у), я i6.i)
тле f(t, y)?C?yl)(ItXe%ny) и /, = {-с<< + }
Определение. Обобщая определение В. А. Плисса (см. [47]),
будем говорить, что система D.16.1) обладает свойством конвер-
конвергенции, если
1) все решения у (t; t0, yit) определены при t0^t<^co;
2) существует единственное решение ц (t) (t ? /(), определен-
определенное и ограниченное на всей оси, т. е.
sup !! tj (t) |! < оо;
t
3) решение tj (t) асимптотически устойчиво в целом при
t-+-\-oo (см. § 7), т. е. для любого решения у (t; t9, уь) имеем
V™{y(t; t0, yo)-r\(t)] = O.
/-* со
Можно сказать, что в некотором смысле ц (/) является пре-
предельным режимом системы D.16.1).
Очевидно, если система D.16.1) обладает свойством конвер-
конвергенции, то все ее решения у (/; /0, _у0) предельно (финально)
ограничены при ^->-}-оо (см. § 17), т. е. существует поло-
положительное число R такое, что
\y(t\ to,yo)\\< R при
В частности, например, можно принять
Замечание. Если правая часть f(t, у) конвергентной си-
системы D.16.1) w-периодична по t, то ограниченное решение i\(t),
также («-периодично по t.
Действительно, пусть
«, y)=f(t, у).
Рассмотрим вектор-функцию т| (/ —j— и). Имеем
И С+ ш)] = *К'-т-«О =
Таким образом, ^(^Н-1») также является решением системы
D.16.1) и притом ограниченным на It. А так как система
Ж ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ 'V
с конвергенцией обладает единственным ограниченным на lt
решением, то
r\(t-\ -f»)=i\(t),
т, е. ц(() есть ш-периодическое решение системы D.16.1).
Лемма 1. Пусть
%=Ay-\-f(t), D.16.2)
где А — постоянная (пУ\п)-матрица и (п X \)-матрица f(t)(~
(^ С ( ¦ - СЮ, -| - СЮ).
Если
1) «се характеристические корни Х,-(Л) матрицы А имеют
отрицательные действительные части
ReX,(/l)<0 (/=1, .... л); D.16.3)
2) вектор-функция f(t) ограничена на It = (— ээ, -f- со):
то система D.16.2) обладает свойством конвергенции, причем
4@= $ И"-х7(^ D.16.4)
представляет собой единственное ограниченное на 11 решение си-
системы D.16.2).
Доказательство. Из условия D.16.3) имеем
|! еА< || s;; Ne- al при 15- 0,
где N^>0 и 0<^я<^—max ReXy (Л). Отсюда получаем
I. Ч @ II ¦<- ^ $ е" {' Т) ii/(x) И dx <= Л1 /Ve " ~ = ^ < сю.
- о")
Следовательно, интеграл D.16.4) сходится и функция ц(^) огра-
ограничена, причем
sup||ii@ j! «s— sup :\f(t) ii.
Дифференцируя формулу D.16.4) по параметру t, получим
t
и, таким образом, ц(() является решением системы D.16.2).
s 16] СИСТЕМЫ С КОНВЕРГЕНЦИЕЙ 283
То, что ограниченное решение системы D.16.2) единственно,
следует из того обстоятельства, что разность двух ограниченных
решенШ] неоднородной системы D.36.2) является ограниченным
решением соответствующей однородной системы
не имеклщей нетривиальных решений, ограниченных на всей оси /,.
Действительно, если ти (t) — другое решение неоднородной си-
системы D.16.2), ограниченное на оси /,, то при любом tv(^It
имеем
4i (V - Ц @ = еА ¦' - '<-> (ч, (U) - ц (*„)].
Отсюда
I] Л1 С) - Ч @ il -- Nea i'-'.) ;i 4l (f0) - ц (tt) |l. D.16.5)
Так как
sup !!л1('о) — Л(*о)||<°°,
'о
то, фиксируя /" и переходя к пределу при tn -> — со в неравенстве
D.16.5), получим
ИЛ1(О-Л(О11*?О,
т. е.
Till @ = Л (О,
и, таким, образом, других, кроме ч@. ограниченных на /< ре-
решений система D.16.2) не имеет.
Если у (t)—любое решение неоднородной системы A4.6.2), то,
учитывая, что разность у (t) — ц (/) удовлетворяет однородной
системе iD.16.4), получим
у @ — л @ =еА" ~ '0) [^ Со)
отсюда
\\у (t) - ц @ il ^ /Ve-««-'.) Hj, (
при ^S^i/o и, следовательно,
iim ¦\y(t) — r\(t)V = O
t
Таким образом, r\(t) устойчива в целом при t-+-{-po и, значит,
система |D.16.2) коивергентна.
Приведем одно достаточное условие конвергентное™ нелиней-
нелинейной системы. Для этого нам понадобятся две леммы, представляю-
представляющие также самостоятельный интерес.
ВТОРОЙ МЕТОД ЛЯПУНОВА (ГЛ.
Лемма 2 (см. [48]). /7усть f (х) ? С (е^)—действительная
вектор-функция,
— симметризованная матрица Якоби (см. гл. 1, § 10), а ).(х) и
А (х) — ее наименьший и наибольший характеристические корни.
Тогда для скалярного произведения {f{x-\-h)~-f(x), h) спра-
справедлива оценка:
КФ, h)^{f{x + h)~f{x), h)^AM(h, h), D.16.6)
где
Xm= inf Цх + th)
I 6 10. 1]
AM= sup A(x-\-th).
t 6 [o. i|
Доказательство. Полагая
имеем
—f{x)= J ~ [/(!)] dt= J /' (l)hdt.
dt
о о
Отсюда
1 i
(f(x-{-h)—f(x), h) = (\f{l)hdt, h)=\{f (Dh, h)dt. D.16.7)
U II
Так как
(f(l)h, h) = (Js(l)fi, h),
то, очевидно (гл. I, § 5), имеем
(f(l)h, h)^k(c,)(h, h)^>.m(h, h)
и
Поэтому'из формулы D.16.7) вытекает неравенство D.16.6).
Лемма 3 (см. [48], [49]). Пусть
%=t{t> )>), D.16.8)
& 18]
СИСТЕМЫ С КОНВЕРГЕНЦИЕЙ
285
где fit, у)^С% ''(/(Хе^у) и выполнено свойство единственности
решений, причем при \\у0 \\=R и любому ? It все решения у (t; tn, _y0)
входят внутрь цилиндра Z{—oo<^t<^-\-oo; \\y\\^R} при воз-
возрастающем t (рис. 45), т. е.
-^-A1зН12)<0 при |iy|!=#,
s силу системы D.16.8). Тогда существует по меньшей мере одно
л
Рис. 45.
решение ц = ц@ системы D.16.8), определенное для всех
и целиком содержащееся в цилиндре Z:
т. е. ограниченное на всей оси —оо <^ t <^ -(- оо.
Доказательство. Рассмотрим последовательность трубок
Тр решений y(t; tp, у0), определяемых начальными условиями:
tp = — р (р = 0, 1, 2, ...), З'о G So, где So== {Ij-У || *^/? }. Так как
решения у (t; tp, уо)(~Тр при tp = — р входят в цилиндр Z и
остаются в нем, то они бесконечно продолжаемы вправо, т. е.
имеют смысл при —psg^<^oo.
Пусть Sp == {у @; — р, у„)} (р = 0, 1,2,...) — сечение трубки Тр
начальной гиперплоскостью ? = 0. В силу свойства интегральной
непрерывности (гл. II, § 1) множества Sp замкнуты. Так как ре-
решения у (t; —р, ул) при t^z — р содержатся внутри цилиндра Z,
то
и, следовательно, на основании свойства единственности, значения
у{—р-\-1\ —р, у о) составляют часть начальных значений
к = — (р — 1), \\уй || s? R трубки Tp_v Поэтому для каждого р S= 1
286 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. IV
трубка Тп целиком содержится в трубке Гр._и и поэтому для си-
системы замкнутых множеств {Sp} будем иметь
•So D Si D... Э 5Р_, D 5P D • • ¦
Следовательно, на основании принципа вложенных сфер для си-
системы {Sp} существует общая точка
Ло? П 5Р,
где Ji tj0 j! <^/?. Рассмотрим решение
ti(O=j»(^; О, Л(р).
Так как % (^ 5Р (р=1, 2,...), то существует решение
У(*\ —Р, Цр) (Uss — p, ',\Цр'\^Я) такое, что j; @; — р, цр) = цк.
В силу свойства единственности имеем
y(t\ 0, irio)=jv(^; —p, цр)
и, следовательно, _у (/; 0, i]0) определено при — р sc t <^oo. Отсюда
ввиду произвольности натурального числа р получаем, что реше-
решение r\(t)=y(t; 0, т]0) имеет смысл на всей оси —co<^t<^^- со,
причем
sup !i ii@ll=^ #•
Лемма доказана.
Теорема (см. [48]). Пусть дана действительная система
еде
f(t,y)€
причем
— сим метризованная матрица Якоби.
Если
1) sup,|/(*. 0)|[ = ^<oo;
2) наибольший характеристический корень A (t, у) симметри-
симметрической матрицы Ji (t, у) для всех t и у удовлетворяет неравенству
', D. Ю. 10)
где % — положительное число,
то система D.16.9) обладает свойством конвергенции.
s к;; системы с конвергенцией 287
Доказательство. Положим
У(у) = ^\\у'^=^(у,у).
На основании системы D.16.9) имеем
-SH1. *)=(/('.». у).
Отсюда
4г= № У)-/С 0). >) + (/(/, 0). у).
Применяя лемму 2 и используя неравенство D.16.10), получим
<СУ ) +
Далее, в силу неравенства Коши (гл. I, § 5) и условия 1) имеем
!(/
Таким образом,
если
Следовательно, все решения у (t; t0, y0) при \\yo\\=R входят
внутрь цилиндра Z = {—co<^t<^^- oo, |!j;||^/?} и по лемме 3
существует решение t\ = r\(t) системы D.1-6.^), определенное и
ограниченное на lt = {—осхС^^Ч0}' причем
sup И л (>) IK Я-
Пусть у (t) — любое решение системы D.16.9), определяемое
начальным условием: _у(?0)=_у0. Положим
*=y(t)-4(t)
и
V(x)=\\\x\\1 = \{x, х).
Так как
¦^г=/С. У)-fit, ч),
то на основании леммы 2 имеем
dV
dt
— f{t, 4), X) ==? — а (х, X) = —
288 ВТОРОЙ МЕТОД ЛЯПУНОВА. [гл. IV
Отсюда при t^tn получаем
т. е.
ШО —Л(О*1Х:1.У('о) —л('о)!|е-"('-'01 при t^t0. D.16.11)
Следовательно, ц (t) асимптотически устойчиво в целом (§ 7),
причем устойчивость экспоненциальная (§ 8). Из неравенства
D.16.11) следует также единственность ограниченного на оси It
решения ц (t) (ср. конец доказательства леммы). Таким образом,
система D.J6.9) — конвергентна.
Следствие 1. Пусть
¦%-=№ + g(y), D.16.12)
еде f(t)^C(It) и g(y)^e%y, причем J (у) = g' (у) — матрица
Якоби.
Если
1) sup ||/@ il<oo;
2) наибольший из характеристических корней А (у) симмет-
ризованной матрицы Я
удовлетворяет неравенству
A(y)^-«<0 (у €*%$),
где а. — положительная постоянная,
то система D.16.12) обладает свойством конвергенции.
Следствие 2. Пусть
% D.16.13)
где A (t), f(t)?C(It).
Если
1) supil/(OII<oo;
2) наибольший из характеристических корней А @ симметри-
зованной матрицы
удовлетворяет неравенству
A@=sS —а<0 (*?/,),
где о. — положительная постоянная,
то система D.16.13) обладает свойством конвергенции.
s 17] ДИССИПЛТИВНЫЕ СИСТЕМЫ 289
§ 17. Диссипативные системы
Рассмотрим действительную нелинейную систему
^y), D.17.1)
где f{t, у) ^ С (/( X ^), причем обеспечено свойство единствен-
единственности решений у (/; tlh >>„).
Определение 1. Следуя Левинсону (см. [50]), систему
D.17.1) будем называть D-системой или диссипативной, если все
решения ее у (t; t0, у„) бесконечно продолжаемы вправо и суще-
существует число R^>0 такое, что
"Пт||;У(*; 'о. Уо)\\<Я- D.17.2)
Иными словами, для каждого решения у (t; t№, y0) существует
момент t1 = tlt-\-T(t,,, yo)^to, после которого оно навсегда по-
погружается в фиксированную сферу |1.у|К#, т. е.
Заметим, что если система обладает свойством конверген-
конвергенции (§ 16), то она диссипативна. Здесь за сферу ',|j;||<C^ можно
принять любую сферу, содержащую единственное ограниченное
решение ц (t).
Решения диссипативной системы иногда называются предельно
(финально) ограниченными (см. [41]).
Пусть
где Z = {t?ty€y}
Определение 2. Будем говорить (см. [41]), что V (t, у)
обладает свойством А в области Z, если, существует положитель-
положительная непрерывная возрастающая функция а (г) (r^sO) такая, что'
V(t, y)^a(\\y\\) npn(t,y)?Z. D.17.3)
Говорят, что V (t, у) обладает свойством В в области Z, если
существует непрерывная неубывающая функция b(r)' (г^О) та-
такая, что
V(t, y)^b(\\y\\) при(/, y)?Z, D.17.4)
причем fc(r)->-j-oo при г->-оо.
Наконец, будем говорить, что V (t, у) обладает в области Z
свойством С относительно данной системы D.17.1), если суще-
существует положительная непрерывная функция с(/¦)"(r ^ 0) такая, что
V (t, У) ^ - с (iiyji) при- (/, у) ^ 2, D.17.5)
10 Б. П. Демидович
290 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. IV
где У (/, у)— полная производная по t функции V(t, у) в силу
системы D.17.1).
Теорема Йосидзавы (см. [41]). Пусть во внешности не-
некоторого цилиндра j_.
х
где Scf = {j| у \\ Эг р}, для системы D.17.1) существует функция
Ляпунова V (t, у) (^ C't'i'y (Zc), обладающая свойствами А, В и С.
Тогда система D.17.1) равномерно диссипативна относительно
начального момента t0, т. е. число Т (tQ,y0) можно выбрать зави-
зависящим только от г/0.
Доказательство. Из условия В вытекает, что при 'j/ijSspi,
где pj 5= р достаточно велико, функция V (t, у) является поло-
положительной. Так как по смыслу теоремы вместо числа р, очевидно,
можно взять число рь то в дальнейшем мы будем предполагать
функцию V (t, у) положительной, в Zc.
Рассмотрим решения у (I) =у (/; t0, y0) с начальными усло-
условиями t? It и |j;(^)|<p.'
Покажем, что эти решения равномерно ограничены в сово-
совокупности. Действительно, промежуток существования [t0, T) ре-
решения у (t) можно разбить на два множества:
где Tl (i'=l, 2) — совокупность всех моментов из [ta, T), для
которых решение y(t), соответственно, принадлежит области
||_yi|=sSp при t=l и области |^|>р при 1 = 2. Если t(^Tu то,
очевидно, имеем
ИЯОИр- D-17.6)
Если множество Тг пусто, то тем самым наше утверждение
доказано. Пусть Т.2 не пусто. Тогда, так как область |^|^>р
есть открытое множество, то в силу свойства интегральной не-
непрерывности (гл. II, § 1) Т., является также открытым множест-
множеством и, следовательно (см. [51]), представляет собой конечную или
счетную сумму интервалов
rt= у D, 9'
где \\y(ta)\\ = p, (|_У(^)|! = Р и р = р (а). Отсюда, если t^T,, то
t E (К, t-) ДлЯ некоторого а (рис. 46) и, учитывая монотонное
убывание'функции V (t, у (t)) при возрастании t, а также свойства
В я А, будем иметь
V(t, у (t)) ^V(ta, у (О) ^ а (|| у (ta) |) = а (Р). D.17.7)
Так как 6(г)->оо при г-»-сю, то существует R^p^>0 такое, что
(р) при R
fj 17! ДИССИПАТИВНЫЕ СИСТЕМЫ 291
В таком случае на основании неравенства D.17.7) получаем
\\y(t)\\<R приг?Т*. D.17.8)
Из неравенств D.17.6) и D.17.8) вытекает, что
ly(t)\\<R при *„<*<*, +Г. D.17.9)
Отсюда следует, что решение у (t) —у (t; 1„, у0) бесконечно про-
продолжаемо вправо, т. е. Т — оо, причем для всех to?ft HJj_yo||sgp
имеет место неравенство D.17.9), где R зависит только от р.
Рис. 46.
Рассмотрим теперь произвольное решение y(t)=y(t; t0, у„),
где j!j>(^o)ll>P (Рис- 46)- Покажем, что и в этом случае при
* Эг *i (*i !> *о) неизменно обеспечено неравенство D.17.9).
Прежде всего, заметим, что если для некоторого момента вре-
времени tx ^> ^о будет выполнено неравенство
\\y(tu t0, Уо)||<Р,
то в силу свойства единственности имеем
y(t\ t0, yo)=y(t; tu y{U; to, Уо)).
Отсюда на основании неравенства D.17.9) получаем
\y(t; Ц, УоУКЯ при i^tx. D.17.10)
10*
292 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. IV
Поэтому достаточно предположить, что iy(t)\\^>p при t^t0.
Но тогда в силу свойств А, В я С имеем
Ь Цу @1|) ^ V (t, у @) < V (t0, у0) ^ а (У о ||) при t ss t0
и
b(r)>a(lyo\\) при r^R^R,
где Rt достаточно велико. Отсюда получаем
где Ri зависит только от у0, т. е. любое решение у (t; t0, y0)
ограничено на [tn, oo), равномерно относительно начального мо-
момента 4 и, следовательно, бесконечно продолжаемо вправо.
Покажем, что для некоторого момента ti^>t0 будет справед-
справедливо равенство
\)y(tu /о, j>o)|| = p. D.17.11)
Действительно, пусть
?<\y(t; t0, yo)l<Rt при t-^U. D.17.12)
Положим
inf с(л)
Тогда, учитывая неравенство D.17.12), в силу свойства С будем
иметь
V(t, y(t; t,- yo))< —T при t^U.
Следовательно,
V (t; у (t; t0, jvo)) =sS V (f,, j;0) — i(t~ t0) при f ^ f0. D.17.13)
Из неравенства D.17.13) вытекает, что при достаточно большом t
функция V (t, у @) становится отрицательной, причем (t, у (/))^ Sce,
что противоречит предположению. Таким образом, решение
У {t'> tu, у о) не может для всех t^t0 удовлетворять неравенству
D.17.12) и, следовательно, при некотором t, ^> /0 выполнено ра-
равенство D.17.11). Отсюда на основании приведенных выше рас-
рассуждений вытекает наличие неравенства D.17.10). Итак, система
D.17.1) диссипативна.
Оценим момент tx. Полагая
?<\\y(t; to,
из неравенства D.17.13) выводим
$ 18] УРАВНЕНИЯ В ВАРИАЦИЯХ 293
В силу свойства А имеем
Кроме того, на основании свойства В получаем
V {t, у (t))^b{\y (t)\)^b{?).
Поэтому
*,<*„ +г о»,),
где
T(yu)<a{Ri)-b^- и R^R.qyA)-
Так как число Т(уа) не зависит от начального момента t0,
то диссипативность системы D.17.1) равномерна по t0,
3 амеча ние. Можно ослабить условия гладкости для функ-
функции Ляпунова V (t, у). А именно, для справедливости теоремы
достаточно требовать, чтобы
V(t, у) ?Ct(Zc9) ft Lip у (Zcp).
В этом случае производную V (t, у) в силу системы D.16.1) можно
определить формулой
V(t,y)= Ш 1[У(* + А, y + hf(t,y))-V(t,y)].
Л-. + 0 "
Легко проверить, нто V (t^, уй) представляет собой верхнюю пра-
правую производную по t функции V (t, у (t; t(,, ya)) в точке t = t0.
§ 18. Уравнения в вариациях
Рассмотрим систему дифференциальных уравнений
%=f(*,y), D-18.1)
где/(* O6Cg»>(Z) гй<К 1!11<я}
Пусть it\ = y\(t) (tn^t^oo) — решение системы D.18.1), удов-
удовлетворяющее условию: !t)(*)||s=sA<^#. Положим
Тогда будем иметь
Отсюда, применяя теорему о среднем, получим
< Л @+ *)-/(*, 4@). D-18.2)
лучим
, x), D.18.3)
294 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. IV
где r(t, Jt) = o(!;jc||) при л:-*0 равномерно по t на каждом ко-
конечном отрезке [/0, to~\-T] (T^>0). Линейная система
d^=fy(t,r\(t))X, D.18.4)
представляющая линеаризированную систему D.18.3), называется
уравнениями в вариациях (см. [35], [28]) для системы D.18.1)
относительно ее решения ц (t) (система первого приближения).
Заметим, что если данная система линейная
то ее уравнения в вариациях совпадают с соответствующей одно-
однородной системой
Лемма. Если система D.18.1) автономная
и к) = к) (/) есть ее решение, то
является решением ее уравнений в вариациях.
Доказательство. Дифференцируя по t тождество
будем иметь
ш й (OJ =/i (л @) ч @,
что и доказывает утверждение леммы.
Предположим теперь, что f(t, у) w-периодична по t и иссле-
исследуемое решение ц (t) также периодично и имеет период ч>. Тогда
уравнения в вариациях D.18.4) представляют собой линейную
систему с периодическими коэффициентами.
Теорема Ляпунова. Если все характеристические пока-
показатели Ху уравнения в вариациях для данного периодического ре-
решения ц (t) имеют отрицательные вещественные части, то это
периодическое решение асимптотически устойчиво при t->oo.
Доказательство (см. [28]). Согласно теории Флоке (гл. Ill,
§ 15) система D.18.4) имеет нормированную фундаментальную
матрицу вида
Х(*) = Ф(/)ел', D.18.5)
« 14] ОРБИТАЛЬНАЯ УСТОЙЧИВОСТЬ 295
где Ф (t) — ш-периодическая матрица и Л — постоянная матрица,
причем характеристические показатели Хь ..., Х„ являются собст-
собственными значениями матрицы Л.
В нелинейной системе D.18.3) сделаем замену переменной
х=ву — ч(*) = Ф@*. D.18.6)
Тогда, учитывая, что
Ф (t) = ~ [X (t)e~A/] = X (t)e~At — X (t) е~мА =
=/; (t, ц (t)) X (t) e-^-X (t) e-u A =fy (t, ц (t)) Ф (t) - Ф (t) A,
будем иметь
ф (t) ft +1/; (t, т, (о) ф (t) - ф (о Л] z ==
или
^ = Лг + Ф-1@г(<, Ф@«), D-18.7)
где
*-@M«.*W«)^0 приг->0.
Отсюда на основании теоремы Ляпунова для квазилинейных
систем (§ 10) заключаем, что тривиальное решение z = 0 системы
D.18.7) асимптотически устойчиво, что в силу формулы D.18.6)
эквивалентно асимптотической устойчивости периодического ре-
решения T\ = X\(t).
§ 19. Орбитальная устойчивость
Рассмотрим действительную автономную систему
§ D-19.1)
/0)е (fljMK
Определение l.-Если _у =У @ (а<С^<С^) есть решение
системы D.19.1), то совокупность точек L = {y{t): t(^(a, b)\
фазового пространства <М^ называется траекторией решения.
Траектория Ь представляет собой проекцию интегральной
кривой у =у (t) пространства /(Х^ в пространство <Мпу, где
время t играет роль параметра.
Так как система D.19.1) автономна, то наряду с решением
у = у (t) она допускает семейство решений ус = у (t-\-c)
(—oo<^c<^-j-oo), которые, очевидно, обладают одной и той же
траекторией.
296
ВТОРОЙ МЕТОД ЛЯПУНОВА
[ГЛ. IV
Под р (z, L), как обычно, будем понимать расстояние точки
г ?j effly до множества L с= <Щ, т. е.
р(г, L)= inf \\z—y\\.
УН
В дальнейшем для решения у —ylt) (t0 ==? t < 00) иногда при-
придется рассматривать множество точек L+={y(t): t0s^t<^oo}t
которые будем называть положительной полутраекторией. Ана-
Аналогично определяется отрицательная полутраектория [~ =
Определение 2. Решение ц = ц(() (t0^t<^oo) системы
D.19.1) называется (см. [52]) орбитально устойчивым при *->- со,
если положительные траектории ?+ всех решений y=y(t)
Ds5*<Cco), достаточно близких в начальный момент t0 к ре-
решению ц (t), в дальнейшем целиком содержатся в s-окрестности
положительной полутраектории Ц данного -решения r\ = i\(t)t
Уп
Рис. 47.
где е>0 произвольно мало (рис. 47), т. е. для любого е]> 0 су-
существует 5:^8(е, /0)]> 0 такое, что если
то
при
D.19.2)
D.19.3)
Замечание. В силу свойства интегральной непрерывности
наличие орбитальной устойчивости решения r\(t) (a<^t<^со) не
зависит от выбора начального момента t0 (= (а, со), поэтому она
эквивалентна орбитальной устойчивости траектории.
Более того, если решение r\(t) орбитально устойчиво и для
решения у (t) при t = t1?(a, со) выполнено неравенство
$ 19] ОРБИТАЛЬНАЯ УСТОЙЧИВОСТЬ 297
где 8 — число, определяемое неравенством D.19.2), то при t^t1
имеет место неравенство D.19.3).
Действительно, полагая
и учитывая, что _у (t) — также решение автономной системы D.19.1),
будем иметь
\\У (to) - Ч (to) I! = \\У (*i) - Ц (to) II ^ 8;
отсюда
p(y(t), Lt) = P(y(t-t() + tl), Zi+)<e при t^t0,
т. е.
Р(У((), U)O при *:&*,.
Определение 3. Орбитально устойчивое решение r\(t) на-
называется асимптотически орбитально устойчивым, если сущест-
существует Д0]>0 такое, что для всех решений у (t), удовлетворяющих
неравенству
D.19.4)
выполнено предельное соотношение
p(y(t), Ы)-+0 при t->co.
Таким образом, если Ц — замкнутая орбитально устойчивая
траектория, то достаточно близкие к ней при t = t0 траектории h+
навиваются на нее при ?->оо.
Замечание. Из устойчивЪсти решения, очевидно, следует
его орбитальная устойчивость. Но из орбитальной устойчивости
решения, вообще говоря, не вытекает устойчивость его по Ляпу-
Ляпунову, а тем более асимптотическая устойчивость.
Пример 1. Рассмотрим скалярную систему
Полагая ха = х @), уо=у @), будем иметь
х = хое<, у = у0 ( — oo<i< + oo).
Траекториями на плоскости Оху здесь являются:
а) правые полупрямые у—у0, х >¦ 0 при х0 > 0;
б) левые полупрямые _v=_y0, х < 0 при х0 < 0;
в) точки х = 0, у=у0 при дго = О.
Очевидно, любое решение x = x(t), y=y{t) данной системы неустой-
неустойчиво по Ляпунову при"<-*оо. Однако траектории типов а) и б) орбитально
устойчивы.
Пример 2. Пусть x\(t) — периодическое решение с периодом ш(ш>0)
автономной системы D.19.1), не сводящейся к постоянной (г\A)ф0). Тогда
такое решение не может быть асимптотически устойчивым.
298 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. IV
Действительно, полагая, что
так как r\'(to)^tO, то при любом достаточно малом 8 > 0 будем иметь
\[Уи(*о) — Ц (*„)]| = Л >0.
Отсюда, учитывая «-периодичность решения r\(t) при произвольном Г>0,
получаем
t>f
и, следовательно, у& (t) — т) (<)-/> О при t—*co. Однако' орбитальная устойчи-
устойчивость периодического решения т) (t) и даже асимптотическая орбитальная
устойчивость могут иметь место.
Лемма 1. Если автономная система D.19.1) имеет нетри-
нетривиальное со-периодическое решение r\ (t), то для соответствующих
уравнений в вариациях
ft=f*(n(t))-x, D.19.5)
представляющих собой линейную периодическую систему, по мень-
меньшей мере один из ее мультипликаторов р = 1, т. е. по крайней
мере один из характеристических показателей системы D.19.5)
является нулевым.
Доказательство. Согласно лемме из §18 система D.19.5)
допускает ю-периодическое решение
л: ^ ц @ ф 0.
Поэтому периодическая система D.19.5) имеет по крайней мере
один мультипликатор
(гл. III, § 15). Отсюда, беря главное значение логарифма, полу-
получаем, что соответствующий характеристический показатель л бу-
будет нулевым:
Определение 4. Будем говорить, что решение т| (/) имеет
свойство асимптотической фазы (см. [52], [28]), если для каж-
каждого решения y(t), удовлетворяющего начальному неравен-
неравенству D.19.4), где До]>0 достаточно мало, существует число
с = с[у] (асимптотическая фаза) такое, что1)
!!.У(Н-с) — Л@!!->0 при t->oo. D.19.6)
') Для удобства записи некоторых дальнейших формул знак фазы изме-
изменен на обратный по сравнению с [52].
§ 201 АНАЛОГ ТЕОРЕМЫ АНДРОНОВА - ВИТТА 299
Лемма 2. Орбитально устойчивое решение ц (() с асимпто-
асимптотической фазой асимптотически орбитально устойчиво.
Доказательство. Действительно, при t'^to-}-\c\ имеем
р(у(о, Ц) == inf \\у (о-TJ(to!|^из,(t)- ч (* -с)\\.
Отсюда на основании условия D.19.6) получаем
lim p(y(t), Ц) = 0,
что и требовалось доказать.
§ 20. Аналог теоремы Андронова—Витта
В этом параграфе будут установлены достаточные условия
орбитальной устойчивости периодического решения автономной
системы. Предварительно докажем три леммы (см. [28]).
Лемма 1. Пусть действительная периодическая система
dft=P(t)x, D.20.1)
где P(t)?C( — oo, -foo) и Р(t-{-'u>) = P(t) (ш>0) имеет один
мультипликатор pi = 1, а модули всех остальных ее мультипли-
мультипликаторов ру(/ == 2, ... , п) меньше единицы:
|ру|<1 при \ф\.
Тогда для системы D.20.1) существует фундаментальная мат-
матрица специального вида
X(t) = <!>(t)diag(Eu <*•'), D.20.2)
где Ф (t) — действительная неособенная ^-периодическая непрерывно
дифференцируемая (п X п)-матрица, Ех — \ и Ct — действитель-
действительная постоянная (п — 1) X (п — 1)-матрица, все характеристические
корни которой имеют отрицательные действительные части:
ReMCX0 (/ = 1, ..., п-1).
Доказательство. Пусть X (t) (X @) = Е) — нормирован-
нормированная фундаментальная матрица системы D.20.1). Так как матрица
Р (t) — ш-периодическая, то справедливо соотношение
X (t + со) = X @ X (ш). D.20.3)
В силу условия теоремы для матрицы монодромии X (<о) одно из
ее собственных значений равно 1, а все другие по модулю мень-
меньше 1. Поэтому существует действительная неособенная матрица А
такая, что
A lX(u)A = diag(Eu B0 = B, D.20.4)
300 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ IV
где В,—действительная матрица типа (п — 1)Х(я — II), все
характеристические числа которой по модулю меньше 1. Тогда,
вводя действительную фундаментальную матрицу
X(t) = X(t)A, D.20.5)
на основании соотношений D.20.3) и D.20.4) будем иметь
X (t -\-M) = X(t + w)A = X (f) X (со) А = X (t) В.
Для матрицы X (t) из D.20.5) построим основную матрицу
(обобщение, § 15 гл. III)
C=X'i @) X (со) = А' «Х-' @)Х(т)А = В,
и пусть
A = -^LnJ3 = diag@, С,), D.20.6)
где
Согласно теореме Флоке имеем
X(t) = O(t)eAt, D.20.7)
где Ф (/) — неособенная «-периодическая матрица. Отсюда на осно-
основании формулы D.20.6) получим
где
Re aj (C5) = Re [!¦ Ln X, (В,)] < 0.
Лемма 1 доказана.
Л е м м а 2. Пусть X (t) — действительная фундаментальная
матрица системы D.20.1) вида D.20.2) и
X@diag@, /•„_,)*-4s) при
-XWdiagf^, 0)X-(s) при
где Ep(p=\, ¦ ¦¦ , n) — единичная матрица соответствующего по-
порядка. Тогда матрица G (t, s) обладает следующими свойствами:
1) G(t, t-O)-G(t, t + O) = En;
2) G,{t, s) = P(t)G(t, s) при t^s;
{ ke-*^ при
3) \G(i, s)\\ =s={ ,
| fe при
где <х^>0 и k^>0 — постоянные;
') Можно, например, воспользоваться приведением матрицы X(<.о) к нор-
нормальной форме Жордана в поле действительных чисел (см. [4]).
§20] АНАЛОГ ТЕОРЕМЫ АНДРОНОВА - ВИТТА 301
4) вектор-функция
О)
\ ds> D-20-9)
где а — произвольный постоянный вектор с нулевой первой коор-
координатой, т. е.
(а, ?0 = 0, <?) = colon A, 0, ..., 0)
и
оо
/(оес[о, oo)t j ц/(оцл<оо,
о
является решением неоднородной системы
ft=P{t)y+f(t), D.20.10)
стремящимся к нулю при t—>co:
_у(оо)= lim y(t) — O.
Доказательство. Свойства 1) и 2) непосредственно выте-
вытекают из формулы D.20.8).
В силу структуры матрицы X (t) имеем
где Ф (t) — «-периодическая матрица. Следовательно,
G(t, s) = <&(t)diag(O, ес> «-«)ф-« (s) при ^>s
и
G(t, s) = —4>@diag(?,, 0)ф-'B) пРи *<s.
Так как все характеристические корни матрицы Cj имеют
отрицательные действительные части, а матрица Ф(/) ограничена
вместе с матрицей Ф~'@' го, полагая
0<a<min[-ReXy(C1)],
получим оценки 3).
Рассмотрим теперь функцию у (t), определяемую формулой
D.20.9). Так как \\G(t, s)\\^k при t, s^O, то имеем
СО СО
S \\G(t, s)||||/(s)||rfs<A!S ||/(s)||ds<oo
с о
302 ВТОРОЙ МЕТОД ЛЯПУНОВА (ГЛ. IV
и, следовательно, несобственный интеграл, стоящий в правой
части равенства D.20.9), является абсолютно сходящимся.
Записав формулу D,20.9) в виде
г со
y(t) = X(t)a-\-\G(t, s)f(s)ds + \G(t, s)f(s)ds
и дифференцируя по параметру t, используя свойства 1) и 2),
находим
t, t~O)-G(t, t + 0)]/@+ \ Gt(t, s)f(s)ds =
S P(t)G(t, s)f(s)ds,
т. е.
y(t) = P(t)y(t)+f(t)
и, таким образом, у (t) является решением неоднородной системы
D.20.10). Законность дифференцирования под знаком интеграла
легко проверить.
Учитывая структуру матрицы X (/), будем иметь
X(t)a-+0 при *->оо.
Кроме того, на основании неравенства 3) получаем
\\G(t,
i
2 со
a/ CO
О г
если t^>T(e). Поэтому
CO
lim \ G(t, s)f(s)ds = O.
Следовательно, lim у (t) = 0.
t-юо
Лемма 2 полностью доказана.
§ 20] АНАЛОГ ТЕОРЕМЫ АНДРОНОВА - ВИТТА 303
Лемма 3. Пусть дана нелинейная система
§ = P(O* + q>(f, *), D.20.11)
где ^-периодическая матрица Р (t) удовлетворяет условиям леммы 1,
а нелинейная вектор-функция ц> (t, z) ^-периодична по t и удов-
удовлетворяет условию Липшица по z:
'~y(t, z') — y(t, z)l^N^z'— z\\
(t?[0, со), ;2!:<Д, ^'!;<л), D.20.12)
причем (f>(t, 0) —G.
Рассмотрим интегральное уравнение
со
zit, a) = X(t)a+[G(t, s)q>(s, z(s, a))ds, D.20.13)
0
где X (t) — фундаментальная матрица соответствующей однород-
однородной системы D. 20.1), имеющая специальный вид D.20.2), G(t, s)
определяется формулой D.20.8) и а — произвольный постоянный
вектор такой, что
{а, е,) = 0.
Тогда, если константа Липшица N достаточно мала, то при
;; а;1 <^а0 интегральное уравнение D.20.13) имеет решение z(t, a),
представляющее собой (п — 1 )-параметрическое семейство решений
дифференциальной системы D.20.11), обращающихся в нуль на
бесконечности:*
lim z(t, а) = 0. D.20.14)
t->ca
Доказательство. В силу формулы D.20.2) при t^0
справедлива оценка
.iXWaH^ilaile-", D.20.15)
где kx (ki^l) — некоторая положительная постоянная и
0<a<minRe[ —X7.(C,)].
Предположим, что k — постоянная из леммы 2 и константа
Липшица /V удовлетворяет условию
Af<-^. D.20.16)
Применяя метод последовательных приближений, покажем,
что если
,. д
-п <2k1==a»'
то интегральное уравнение D.20.13) при t^0 имеет решение
304 ВТОРОЙ МЕТОП ЛЯПУНОВА |1.Ч IV
z(t, а), причем
iz(t, a) -:2kt о|;е'<Д. D.20.17)
За начальное приближение примем z0 (t, а) = 0 и, как обычно,
положим
оэ
zp(t, a) = X(t)a-\-\ G(l, s)^(s, zpA(s, a))ds (p=l, 2, ...).
D.20.18)
Так как qi(s, 0) = 0, то в силу неравенства D.20.15) при t^O
имеем
а.
; zx (t, a) — zn (t, a) "\ =!! X (t) а \\ «с kx || а !! e~vt «с kL \\ а ц е ~ й'.
Пусть теперь
\\z,{t, a) — zp.x(t, aJil^^illelie"' при t^-0; D.20.19)
тогда в силу D.20.18), учитывая неравенство D.20.16) и оценку 3)
для !| G (t, s): (см. лемму 2), будем иметь
\\zpU(t, a)~zp(i, a)!| ^
оэ
<$ \}G(t, s) !| И ф (s, zp(s, a)) — tf(s, zpl(s, a))!!dsss
6
о
t
при t^0
(P=l, 2, ...).
Таким образом, на основании принципа математической индук-
индукции заключаем, что все приближения zp(t, a) (р = 1, 2, ...) имеют
смысл и для них справедлива оценка D.20.19). Отсюда, так как
г pit, a) = %[zq(t, в)-г,_|(/, в)],
то существует
lim zp(t, a) = z(t, a),
§21)! АН \ЛОГ ТЕОРЕМЫ АНДРОНОВА— ПИТТ А ЗОГ)
причем сходимость последовательности равномерна в области
и, значит, предельная функция z(t, а) непрерывна по совокуп-
совокупности переменных t и а при достаточно малой ; а \\.
Переходя к пределу при р->сх> в равенстве D.20.18), полу-
получаем
со
z(t, a) = X(t)a-\-\G(t, s)q>(s, z{t, a))ds,
u
т. e. z(t, а) в области Z является решением интегрального урав-
уравнения D.20.13). Отсюда, дифференцируя по t последнее соотно-
соотношение и используя свойства функции G (t, s), будем иметь
z(t, a) = P(t)z(t, а)-г-ч>(г, z(t, а)),
т. е. z (t, а) в области Z есть решение нелинейной дифференци-
дифференциальной системы D.20.11).
Далее, из неравенств D.20.19) выводим
i\z(t, а)!!<||*„(*, a)ii -fS'l^^ a)-z^(t, a)||<
2^ *' при t^O. D.20.20)
Следовательно,
lim z(t, a) = 0, если Ца||< А-;
в частности, при а = 0 имеем
г-(^, 0) =0.
Лемма 3 доказана.
Рассмотрим теперь действительную автономную систему
i=/O0. D.20.21)
где f{y) ^ С1 (j!.y|!<[#), и пусть т] = r\ (t) — w-периодическое
ее решение такое, что \\i\(l)\\s^h<^H. Уравнения в вариациях
здесь имеют вид
$ = /;(Л(О)лР- D.20.22)
Аналог теоремы Ан д р он о в а—В итта (см. [52], [28]).
Пусть автономная система D.20.21) допускает ^-периодическое
306
ВТОРОЙ МЕТОД ЛЯПУНОВА
[гл. iv
решение ц (t), не являющееся тождественной постоянной (г\ (/) Ф 0),
причем уравнения в вариациях D.20.22) для этого решения имеют
один простой нулевой характеристический показатель, а все ос-
остальные— с отрицательными действительными частями. Тогда
периодическое решение r\ (t) асимптотически орбитально устойчиво
при t-+oc.
Более того, для каждого близкого к ц (/) решения у (t) суще-
существует асимптотическая фаза, т. е. если А^>0 достаточно мало и
для некоторых t0 и tu то найдется постоянная с = с [у] такая, что
lira [y(t-i-c)--r\(t)] = O. D.20.23)
/ -» 00
Доказательство (см. [28]). 1) Выберем новую прямо-
прямоугольную систему координат 0'vx ... vn, начало которой О' нахо-
находится в точке т| @), а первая ось O'vt икеет направление,
Уп
\z(t,a)
(D
Рис. 48.
определяемое вектором г\ @) (рис. 48). Тогда система D.20.21)
примет вид
d? = g(v), D.20.24)
где снова g{v)^Cl.
Периодическое решение r\ (t) при этом перейдет в периодиче-
периодическое решение <o0 = p(t), обладающее следующими свойствами:
р@) = 0, p@) = ei ilp@),;, D.20.25)
где
0
L 6 j
(i 20] АНАЛОГ ТЕОРЕМЫ АНДРОНОВА - ВИТТА 307
Уравнения в вариациях, соответственно, будут иметь вид
d? = g«(p{t))u, D.20.26)
причем, очевидно, характеристические показатели периодический
системы D.20.26) совпадают с характеристическими показателями
системы в вариациях D.20.22). Согласно лемме 1 для системы
D.20.26) существует действительная фундаментальная матрица
вида
U(t) = ®{t)&\ag(Eu ec'O, D.20.27)
где Ф(* + и>) = Ф (/) и ReAy(Ci)<0. Из формулы D.20.27) выте-
вытекает, что первый столбец матрицы U (t) представляет собой
«-периодическое решение уравнения D.20.26). Так как p(t) яв-
является w-периодическим решением уравнений в вариациях D.20.26)
(см. § 18) и в силу условия теоремы это решение единственно,
с точностью до скалярного постоянного множителя, то можно
принять
где Ux (t) — матрица типа п X (п — 1), причем
?/@) = [е„ U,@)]. D.20.29)
Положим
v=p(t) + z.
Тогда уравнение D.20.24) примет вид
% = g*(p{t))z + 4{t, z), D.20.30)
где
V(t, z) = [g(p{t) + z)~g(p @I -gvip @)z.
Так как
то
ф(<, 0) = ф;^, 0) = 0 D.20.31)
и
4 X ^
t t
Отсюда следует, что ф (t, z) удовлетворяет условию Липшица:
||Ф(«, z') -<f(t, z)\\^NU'~-z\\
(t?io, оо), !|г[Кд. It ^ IK Д),
308
ВТОРОЙ МЕТОД ЛЯПУНОВА
[ГЛ. IV
где константа Липшица N сколь угодно мала, если число Д до-
достаточно мало.
Пусть
Г 0 -
(X ~~~
а.2
— любой вектор, перпендикулярный орту е{.
В силу леммы 3 при ||а|'-<^а0 нелинейная система D.20.30)
допускает непрерывное по а многообразие решений
z(t, a)-»-0 при t-*oo,
норма которых подчинена неравенству D.20.20). Эти решения
удовлетворяют интегральному уравнению
со
z{t, a) = U{t)a-\-\ G(t, S)q>(s, z(s, a))ds, D.20.32)
0
где аналогично D.20.2) имеем
i/(Odiag(O, ?„..,) f/ («)
причем
D-20-33)
при
, s) S
при
2) Установим связь между начальными значениями г(о! =
= z@, а) решения z(t, а) и параметром а. Из уравнения D.20.32),
полагая 1 = 0 и учитывая формулы D.20.33), имеем
со
i, 0)\
s, z(s, a))ds, D.20.34)
где интеграл справа сходится абсолютно и равномерно по пара-
параметру а при || а || <^ а0.
Используя формулу D.20.29), получаем
diag(?i, 0).
Отсюда, полагая
S 201
АНАЛОГ ТЕОРЕМЫ АНДРОНОВА - ВИТТА
30?
и переходя в векторном уравнении D.20.34)к координатам, будем
иметь систему скалярных уравнений
D.20.35)
/=2
„(*)
где с) — соответствующие элементы матрицы 6^ @) и
со
ф(о.2, .... an) = [l G@, s)(p(s, г(в, «))
(символ [ ]j обозначает первую компоненту соответствующего
вектора), причем ф(а2, ..., ап) непрерывна при ||а||<^ао. Так
как матрица U @) неособенная, то из структуры формулы D.20.29)
следует, что
где
/, * = 2, .... л).
Поэтому последние (п — 1) уравнений системы D.20.35) можно
разрешить относительно координат аа, ..., ап, и мы будем иметь
(А = 2, .... л),
D.20.36)
где dj ' — некоторые постоянные.
Подставляя эти выражения в первое уравнение системы D.20.35),
находим
г'Г=
D.20.37)
где kj — некоторые постоянные и ^(гг", ..., zT) — результат под-
подстановки параметров а,, ..., ап в функцию ф (а2, ..., ап). В силу
формулы D.20.20) имеем:
|| *(s, в) || «ss2*, || а || <Гт' при
Кроме того, из соотношений D.20.31) вытекает неравенство
310
ВТОРОЙ МЕТОД ЛЯПУНОВА
[ГЛ. !V
где 7 (#)->¦ 0 при z->0. Поэтому, учитывая ограниченность мат-
матрицы G@, s), получаем
ф(а2, ..., а„) = о( || а || )
и, следовательно, на основании D.20.36) будем иметь
фф01, ..., zioi) = o(r), D.20.38)
где
Пусть
— начальные значения некоторого решения v (t) преобразованной
автономной системы D.20.24). Так как
то уравнение D.20.37) имеет вид
где функция ф непрерывна, если г = j U2" I +
мало, причем
0 0
iC), D.20.39)
.. -f- | v'n' \ достаточно
В пространстве O'vl ... vn уравнение D.20.39) представляет
собой некоторую непрерывную поверхность 5 (рис. 48), опреде-
определенную в окрестности точки О' и однозначную относительно коор-
координаты v'{'\ обладающую тем свойством, что из ее точек при ^ = 0
выходят траектории v = v(t) системы D.20.24), неограниченно
приближающиеся к замкнутой периодической траектории v0 =p (t),
т. е. такие, что
lim [v (()—p(t)] = O.
t —* со
Заметим, что из уравнения D.20.39) и формулы D.20.38) выте-
вытекает, что функция v'{" дифференцируема в точке v'i'=...=
= Vn' =0, причем уравнение касательной плоскости Q в этой точке
выражается линейной частью:
п
v'i(ll=y\kjV'/: D.20.40)
§ 201 АНАЛОГ ТЕОРЕМЫ АНДРОНОВА - ВИТТА 311
Обозначая через ? угол между единичным вектором п нормали
к плоскости Q в точке О' и вектором р @) = ву\р @) || , из урав-
уравнения D.20.40) будем иметь
cos ф = ц? 0.
Kl+ *!+•• +*'„
Следовательно, периодическая траектория vQ=p(t) пересекает по-
поверхность S, не касаясь ее, и, значит, переходит с одной стороны
поверхности на другую. А так как поверхность 5 непрерывна и
задана явным уравнением D.20.39), то близкие к ней траектории
4> — v(t) при возрастании или убывании / имеют с поверхностью S
общие точки.
3) Пусть для некоторых tt и ^ решение v(t) системы D.20.21)
в системе координат O'vt ... vn удовлетворяет неравенству
где А — некоторое достаточно малое положительное число. В силу
автономности системы D.20.21) вектор-функции
также являются ее решениями, причем, очевидно, выполнено не-
неравенство
И,(О)-ро(О)||<Д. D.20.41)
Для периодической траектории va=p9(t) Фо) в точке / = 0
построим непрерывную поверхность 50 со свойствами, аналогич-
аналогичными свойствам поверхности S, которую траектория La пересекает
без касания при t = 0. Следовательно, близкие к ней при ^ = 0
траектории vt = vt (t), удовлетворяющие неравенству D.20.41), где Д
достаточно мало, также пересекают поверхность So при t возра-
возрастающем или при / убывающем в некоторый момент t. Так как
траектория vo—po(t) не вырождается в точку, то момент i можно
выбрать равномерно ограниченным для траекторий, подчиненных
начальному условию D.20.41), т. е.
где Т (Д) — некоторое положительное число.
Отсюда, полагая
v(t) = vi(t-\-t) = v(t-'\-tl-
получаем
312 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. IV
В силу свойства поверхности So имеем
т. е.
lim
Отсюда находим
где
— предельная
фаза
lim || v
I -> со
lim || v 0
решения
@-
V
-Ро
с)~
it).
it)
Pi
В
ll=o.
t) II =°-
частности.
если /,
то
Возвращаясь к старым координатам уи ..., у„, получим, что
соответствующее решение y=y(t) системы D.20.21) удовлетворяет
условию D.20.23).
Так как величина t может быть выбрана равномерно ограничен-
ной в каждой начальной окрестности D.20.41), то решение i\(t)
является орбитально устойчивым, причем в силу наличия предель-
предельной фазы эта устойчивость асимптотическая (см. лемму 2 из §19).
Теорема доказана полностью.
Для сравнения приводим формулировку теоремы Андронова —
Витта (см. [52а], [10]).
Теорема Андронова — Витта.. Пусть ^-периодическое
решение ц(г) автономной системы D.20.21) не сводится к тож-
тождественной постоянной (щ (/) ф 0), причем уравнения в вариациях
для этого решения имеют один простой нулевой характеристиче-
характеристический показатель, а все остальные характеристические показатели
обладают отрицательными действительными частями. Тогда реше-
решение r\ (t) устойчиво в смысле Ляпунова при t->oo.
§ 21. Признак Пуанкаре
Рассмотрим автономную скалярную систему
dx
= Г{Х, У),
D.21.1)
%=Q(x. у),
dt
где Р(х, у), Q(x, y)?Cl. Пусть система D.21.1) имеет ш-перио-
дическое решение
5 = е</), тч = т)(О, D-21.2)
§ 21] ПРИЗНАК ПУАНКАРЕ 313
траектория которого на плоскости Оху не сводится в точку:
l'^(?)! + I tj@ i 9^ 0. Тогда соответствующая система в вариациях
ш=р'х (* (о, -ч и)) и+^; («(о. "ч @) v, )
, D.21.3)
g = q; (? (г), т) (/» и + Qy (? (/), г, @) и J
допускает нетривиальное ш-периодическое решение
u = \(t), v = Ti(t).
Пусть X (t) (X @) = Е) — нормированная фундаментальная мат-
матрица линейной системы D.21.3). Мультипликаторы pt и р2 этой
системы являются корнями уравнения
det[X(<o) —р?] = 0.
Отсюда
Р2 — Р Sp X (<») + det X (со) = 0.
Так как система в вариациях D.21.3) имеет нетривиальное
(«-периодическое решение, то в силу леммы 1 (§ 19) один из ее
мультипликаторов
Pi = l.
Отсюда по свойству корней квадратного уравнения имеем
P2 = detX(u>).
Но в силу формулы Остроградского — Лиувилля, обозначая через
A (t) матрицу системы D.21.3), получим
det X (со) = det X @) exp \ Sp Л (t) dt ==
о
= exp J [Pi (?(/), ri(t)) + Q'y(i(t), yi(t))]dt.
о
Поэтому справедлив признак Пуанкаре: если
X = "i§lP*^)> Ч(')) + <&(*('), Mt))]dt<0, D.21.4)
о
то
и периодическое решение 1 = 1 (t), ri = -q(t) асимптотически орби-
тально устойчиво, т. е. траектория его является устойчивым
предельным циклом (см. [52]) и близкие к нему решения обладают
асимптотической фазой.
314 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. IV
§ 22. Условная устойчивость
Определение. Говорят, что решение | = ; (t) я-мерной диф-
дифференциальной системы
§=/(', X) D.22.1)
условно устойчиво при t~*-oo, если в в%х существует fe-мерное
многообразие Sft =>§(?<,) начальных значений A ^k<^n) такое, что
для всякого решения x = x(t), подчиненного условию:
x(U)€Sk, WxW-KtJIKbi*),
будет выполнено неравенство
\\x(t)-l(t)\\<t при t^U.
Условная устойчивость называется асимптотической, если, сверх
того,
|| х @ — l(t) || ->0 при f-*oo,
где
(Д — некоторая положительная постоянная).
Рассмотрим квазилинейную систему
x), D.22.2)
где А — постоянная матрица, имеющая k(l^k<^n) характери-
характеристических корней с отрицательными действительными частями,
причем ф (t, x) = o{x) равномерно по t.
Обобщенная теорема Ляпунова (см. [13], [28]).
Пусть матрица А имеет k характеристических корней с отри-
отрицательными действительными частями и (п — k) характеристи-
характеристических корней с неотрицательными действительными частями, при-
причем вектор-функция ф (t, х) непрерывна по t при t ^ 0 и удов-
удовлетворяет по х условию Липшица:
||
D.22.3)
),
где L = L(A) и L->0 при Д-^01). Тогда тривиальное решение
л: = 0 системы D.22.2) условно асимптотически устойчиво от-
относительно некоторого k-мерного многообразия S,, начальных
значений.
') Для дальнейших рассуждений существенно, что константа Липшица L
может быть выбрана достаточно малой.
§ 52] УСЛОВНАЯ УСТОЙЧИВОСТЬ 315
Доказательство. Без нарушения общности рассуждения
можно принять t0 = 0. Положим
х = Су,
где действительная неособенная матрица С такова, что
С-1 АС == В = diag(N, P),
причем
Relj(N)<0 (/=1, .... k)
Relj(P)^0 (j = k+l, ..-, я).
Тогда система D.22.2) примет вид
% = By-\-W,y), D.22.4)
где
Ъ«, y) = C-ltf(t, Су).
Полагая
L,= ||C-4| || С || L,
очевидно, имеем
\\V(t, y')-V(t, у)\)^Ь1\]у-у\\ для ^0, D.22.5)
если только \\у ||<Д, и ||/ || <Ab где Д4 = Д/1| С ||.
Пусть р^>0 произвольно мало и i)>0 таково, что
a + p<min[-Re>.,(#)].
Тогда, очевидно, справедливы неравенства
=s0 j
D.22.6)
ет || < Ке-^' при
при fssO
где /(— некоторая достаточно большая положительная постоян-
постоянная.
Положим
eBldiag(Ek, 0) при
где Ер — единичные матрицы соответствующих порядков. Очевидно,
316 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. IV
Из неравенств D.22.6), учитывая, что
, ept),
получаем
Кроме того, очевидно, имеем
G{t) = BG(t) при гфО.
Рассмотрим сингулярное интегральное уравнение
y(t, a) = Z{t)a + \ G(t — s)$(s, y(s, a))ds, D.22.9)
о
где
Z (t) = eBt diag (Ek, 0) == diag (e™, 0)
и a — постоянный вектор, (п — k) последних координат которого
равны нулю. Для решения интегрального уравнения D.22.9) при-
применим метод последовательных приближений, полагая
ylo)(t, а) = 0
и
yp(t, a) = Z(t)a + lG(t-s)y(s, y^is, a))ds (p = l,2, ...).
0
D.22.10)
Выберем число Д столь малым, чтобы было выполнено неравен-
неравенство
и пусть
Тогда, учитывая первое из неравенств D.22.6) при ^^0, будем
иметь
\\у (t, а) || ^ || Z @ || || а || < Ke-^]t \\ а \\ ^ К || а \\ е~«.
Пусть
\\Ур(*. «)-Ур-1(Л аЛК-^гНаНе"* при t^0 (р=э 1). D.22.11)
§ 22] УСЛОВНАЯ УСТОЙЧИВОСТЬ 317
Из формулы D.22.10), используя неравенства D.22.8), выводим
yP+l(t, a)—yP(t, a) Use:
СО
==S $ || G (t — s) || • || i|> (s, yp(s, a))~ty(s, урЛ (s, a)
^lia!l^w при ^0.
Отсюда заключаем, что все приближения yp(t, а) имеют смысл,
причем неравенство D.22.11) выполнено для всех натуральных р.
Следовательно,
уp{t, a)^y{t, a)
на [0, оо) при р->-оо, причем предельная вектор-функция у (t, a)
непрерывна по совокупности переменных t и а при 0 ==? t <] оо и
||а;<а0.
Переходя к пределу при р-^-оо в формуле D.22.10), будем
иметь
со
у (t, a) = Z (t) a + ^ G (t - s) ф (s, ^ (s, а)) rfs, D.22.12)
т. е. предельная функция у (t, а) является решением интеграль-
интегрального уравнения D.22.9). Дифференцируя последнее равенство по
параметру t, находим
t
yt(t, a) = BZ(t)a + lBG(t — s№(s,y(s, a))rfs +
0
CO
s, y(s, a))rfs +
/, y(t, a)),
т. e.
yt(t, a) = By(t, a) + W, y(t, a))
и, значит, y(t, а) является решением системы дифференциальных
уравнений D.22.4).
318 ВТОРОЙ МЕТОД ЛЯПУНОВА
Используя неравенства D.22.11), получаем
то
\\y(t, a)\\^\\yu(t, a)\\-\- У \\yp(t,-a)— yv^(t, о)
[ ГЛ. IV
Отсюда
limy(t, a) =
Таким образом, y(t, а) при \\а\\<^а0 представляет собой мно-
многообразие решений дифференциальной системы D.22.4), непре-
непрерывно зависящее от k параметров аи ..., ak — первых k коорди-
координат вектора а и стремящихся к нулю при t->oo.
Из уравнения D.22.12), учитывая структуру D.22.7) матрицы
G(t), для координат yj(t, a) (/=1, •••, п) решения y(t, а) при
? = 0 будут иметь следующие выражения:
yj(O, a)
(/=1, ...,
= * + !, .... я),
где [ ]у обозначает /-ю компоненту соответствующего вектора.
Поэтому в окрестности начала координат О эти начальные значения
Рис. 49.
/'/' = [)>@, a)]y удовлетворяют системе уравнений
у = Ь(у'Г, ..., уТ) (/= 1, ..., п
которые определяют в пространстве s^y некоторое ^-мерное мно-
многообразие Sh начальных значений, порождающее решения у (t) -*¦ 0
при t —*¦ ос.
УПРАЖНЕНИЯ К ГЛАВЕ IV 319
Возвращаясь к прежним переменным
х = Су,
получим, что аналогичное утверждение справедливо для решений
x = x(t) исходной системы D.22.2).
Следствие. Пусть матрица А имеет k характеристических
корней с отрицательной действительной частью и (п — k) харак-
характеристических корней с положительной действительной частью,
причем условие Липшица D.22.3) дляу(г,х) выполнено для всех
?G(—°°> "Ь00) и константа Липшица достаточно мала. Тогда
в некоторой окрестности точки О пространства <МЧХ существуют
многообразия S% и Sn_fe (рис. 49), соответственно, измерений k
и (п — k) такие, что для решений x(t) системы, D.22.2) справед-
справедливы предельные соотношения:
x{f)-*Q при t->-\-oo, если
X(t)-^>-0 при t->* — со, если
Упражнения к главе IV
1. Пусть для приведенной системы
~f = X(t,x) (X(t,0)=0)
существует ограниченная функция
lx\><H},
имеющая полную производную в силу системы (*):
V (t, х) = aV (t, х) + W (t, x),
где a — положительное число и W (t, x) — знакопостоянная функция, причем
функция V такова, что в любой окрестности t = t0, ltx\\<.b существует
точка х0, для которой выполнено неравенство
V(t0,x0)W(t0, хо)>О.
Тогда тривиальное решение х = 0 неустойчиво (см. [13]).
2. Пусть для системы (*) (см. 1) существует ограниченная положительно
определенная функция V(t, Jt) ?С^1'(Z), производная которой V(t, x) в силу
системы (*) отрицательно определенная. Тогда для любого е>0 суммарное
время пребывания нетривиального решения x — x(t) (t0 =s; t < со) вне
Е-окрестности центра притяжения О ограничено.
3. Пусть 1) А = [aju] — постоянная (п х ге)-матрица и все решения си-
системы
dx .
Ж = Ах
ограничены на полуоси t0 -с t < оо; 2) f(t, x)^C(l[t x jj X \\ ^ h), причем
320 ВТОРОЙ МЕТОД ЛЯПУНОВА [ГЛ. IV
1 де
со
\" g (t) dt < CO.
k
Тогда тривиальное решение .у = 0 системы
устойчиво по Ляпунову при t —* со.
4. Пусть для приведенной системы
t\^ = X(t, х) (X (t, 0) = 0), ia)
где х = (х1, ..., хп), X{t,x) ? C'fa"' (t d It X ;! x [[ <H), существует поло-
положительно определенная квадратичная форма
полная производная которой Йа (г, x) в силу системы (а) удовлетворяет
неравенству
Va (t, х) s? — (В х, х),
причем — (В х, х) — отрицательно определенная квадратичная форма (.4 и
В — постоянные симметрические (га х га) — матрицы). Тогда для возмущен-
возмущенной системы
-f- = X (t, у) -]- К (t, у), (в)
где
Y(t, у) 6 С'0-01 (t € // х \[у \<н) и ;; V(t, у) \\^N\\у \i,
если постоянная Липшица N — достаточно мала, то ее тривиальное решение
3> = 0—асимптотически устойчиво при t —¦ со. Доказать.
5. Пусть
-*t=Ax-xrf(t, х), О»)
где А — постоянная (п X га)-матрпца, Re).;(/5)s? — а<0 (/=1, ..., и) и
f(t, х)?С {1} х ,| х j < И), причем
(а > О, Э>0, М > 0 — постоянные). Тогда, если х < Мч, то тривиальное ре-
решение д: = 0 системы (**) асимптотически устойчиво (R a m a r k i s с h п а).
6. Пусть
dx — A(t)x-\-f(t
где л (t)ее [t0, со) и f{t, х)?С (/•; х ;| х у <Н).
Если а) [;/(*, х) \\ ==S X (<) |] х \\;
б) Х;-[Л5 (t)] sg:(л (i) (y'==l, ..., га), где
1
в)
УПРАЖНЕНИЯ К ГЛАЗЕ IV
321
то тривиальное решение х = 0 системы (**s) асимптотически устойчиво
в целом (W о п g).
7. Пусть
dx
(Л-(О,лс) =
= X(t, x)+R(t, x),
(А)
(B)
где X(t, x), R (t, x) g Cf*\Z) и Z = // x (|| x \\ < h).
Если существует положительно . определенная скалярная функция
V (t, х) ? С\х (Z), удовлетворяющая в Z условиям:
а)
Wi (х) < V (t, x) =S Wt (x), V (t, x)^z-W.i (x),
где Wit (x) (k = \, 2, 3) — положительно определенные функции;
б)
dv
sup
dxf
:co (y'=l, ..., re),
то тривиальное решение х = 0 системы (А) устойчиво при постоянно дей-
действующих возмущениях R(t, х), т. е. для любого е>0 @<е<Л) сущест-
существует 5 = 8(е)>0 такое, что из неравенств
\\x(to)\\<b, \\R(t, х)\\ <5 при t^st0, ||x||<s
вытекает неравенство
|| х (t) || < е для всех t^>t0
(Малки н).
8. Пусть
dt
X
причем
где I (t)
ковы, что
\\f(t, x)||<X@<p(||x|i),
и ср (г) @<г<оо) положительны, непрерывны и та-
таТогда решение .г (t; t0, xa) равномерно ограничено, т. е. sup || x (t; t0, x0) []s
С (r0) < оо при 0 s? t < со и
9. Пусть
со (Винте р).
где f(x, х), g(x)^C(c^i) и e(t)?C[O, coj.
11 Б. П. Демидович
322 ВТОРОЙ МЕТОД ЛЯПУНОВА (ГЛ. IV
X
Если а) / (х, х) =s 0; б) G(x) = \g E) (К > 0 при х ф 0 и G (л-) — оэ при
о
оо
| х [ —> со; в) \ | е (t) \ dt < со, то каждое решение х it) предельно ограни-
ограничено вместе со своей производной х (t) при t—¦> со (см. § 17) (А н т о с и е в и ч).
Указание. Рассмотреть функцию Ляпунова
t
I e (*,)! dt,.
и
10. Пусть для автономной системы
~ = Х{х) (ДГ(О) = О), (¦*«)
где X (х) ? С {(Мпх), существует скалярная функция V (х) ?СA> (<$%), удовле-
удовлетворяющая в ограниченной области Ql={x ^ е%х '¦ V(х)<!} условиям:
a) V(x)>0 при хфО; б) l/(x)sg0. Далее, пусть уИ — максимальное
непустое инвариантное множество (т. е. множество, содержащее вместе с точ-
точкой х0 всю траекторию {x{t, лс0), —оэ <f <-{-аэ}) такое, что
Тогда каждое решение x(t) системы (****), начинающееся в Q;, неограни-
неограниченно приближается к М при г-»ю (Лефшец и Л а-С а л л ь [45]).
11. Пусть x = (xi xp), y = (yit ..., уд) и
^ = f{t,x,y), (a)
где /, g- e Cf'Jy l) (It Xe%pxX <s%p, причем /@, *, у) = g @, х,у)=0 при
I оворят, что начало координат Ох системы (а) квазиустойчиво, если
для всякого е>0 существует 6 = 8 (е, t0) > 0 такое, что любое решение
х (t) вспомогательной системы
d х
где i\(t) — непрерывный ^-мерный вектор, при \\x(to)\\<:b и || Ц (^о) !! < *
удовлетворяет неравенству
на любом отрезке to^t^tlt для которого || ц (t) \\ s; e.
Доказать теорему Персидского (см. [21]): если начала координат как
Ох, так и Оу, систем (а) и (Ь), соответственно, квазиустойчивы, то начало
координат О полной системы ((а), (Ь)) также устойчиво.
УПРАЖНЕНИЯ К ГЛАВЕ IV
323
12. Исследовать на устойчивость тривиальное решение х = 0 скаляр-
скалярного уравнения
Л + х = fi.i (ах2 + 2Ьхх + cxs)
(а > О, ас — Ь2 > 0),
где а, Ь, с — постоянные и (х — действительный скалярный параметр (см. [21]).
13. Исследовать на орбитальную устойчивость периодическое решение
i = smt скалярного уравнения
(х2 -\- х2 — 1) -j- х — 0,
где р. — действительный скалярный параметр.
14. Для треугольной нелинейной системы
ЧТ
dx,
dt
I —fn (xl> xii
гДе //6С1 (effi"x) (/ — I) •¦•> n)> получить достаточные условия асимптоти-
асимптотической орбитальной устойчивости ее ю-периодического решения
Xj=Pj{t) G = 1, .... п).
ГЛАВА V
АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 1. Равномерная сходимость семейства функций
Пусть имеется бесконечное семейство комплекснозначных век-
вектор-функций действительной переменной t
Ух=/(*. *), E.1.1)
зависящих от действительного параметра X и, определенное на не-
некотором множестве ш = {/ ? Т CZ. <& К X^ACIefi}, причем значе-
значения функции f(t, А) ? ЭТ у-
Определение. Говорят (см. [7]), что при А->Д0 ? Л се-
семейство E.1.1) равномерно по t сходится к предельной вектор-
функции <р (t), т. е.
/(/, \)ztq>(t) на Т при Х->Х0, E.1.2)
если для V ? ^> 0 существует В = S (e) j> 0 такое, что
И/С, ^)-ф@11<в E.1.3)
при *(=:г и |х — xo|<s.
Теорема. Для того чтобы семейство функций E.1.1) при
X ->- Хо равномерно на множестве Т сходилось к предельной вектор-
функции q>(t), необходимо и достаточно, чтобы из каждой после-
последовательности f(t, \k) (k—l, 2,...), где \k-*-\0, можно было бы
выделить равномерно сходящуюся подпоследовательность
i(t,Kk)^<v(t) (ten E.1.4)
Доказательство. Необходимость условий теоремы
ясна, так как в случае равномерной сходимости семейства f(t, X)
при X -> Хо к предельной вектор-функции <р (t) каждая последова-
последовательность f(t, ).k), где kk-*-X0, очевидно, также будет равномерно
сходиться к <р (i).
Докажем достаточность условий теоремы. Пусть семей-
семейство f(l, X) не является равномерно сходящимся при Х->-Хо к общей
предельной вектор-функции <р (t) всех последовательностей f(t, XA),
где Хй -> Х„. Тогда существует s^>0 такое, что для любого bk <^ j-
5 21 ТЕОРЕМА АРЦЕЛЯ 325
(/?—1, 2, ...) найдется значение параметра lk^A, обладающее
следующими свойствами:
|^-М<| (*=1, 2, ...) E.1.5)
SUP || f{t, Aft) — <Р (О I! =S ?. E.1.6)
Из неравенств E.1.5) и E.1.6) вытекает, что из последовательно-
последовательности f(t, А;,) (k=l, 2,...) нельзя выделить подпоследовательность,
равномерно сходящуюся к вектор-функции <р (t), и мы приходим
к противоречию.
Теорема доказана.
§ 2. Теорема Арцеля
Определение 1. Семейство вектор-функций f(t, X) (t^T,
X (^ Л) называется равномерно ограниченным, если существует по-
постоянная М такая, что
\\f(t,X)\\^M, E.2.1)
где / (t, А)— любая функция семейства.
Определение 2. Семейство вектор-функций f(t, X) назы-
называется равностепенно непрерывным на множестве Т, если для
Vs^>0 38^>0 общее для всего семейства, т. е. такое, что
для каждой вектор-функции f(t, X) семейства выполнено неравен-
неравенство
*", Х)||<е, E.2.2)
если только
|Г_Г|<8, f'?T, t" Z-T.
Пример. Вектор-функции f(t, X), обладающие равномерно ограничен-
ограниченными производными f't (t, к) (\\f'( (t, к) || si Mt) на промежутке a <t < й, об-
образуют равностепенно непрерывное семейство.
Действительно, предполагая, например, что норма вектора — евклидова,
на основании теоремы Лагранжа, примененной к каждой компоненте, имеем
\\f(t; i)-f(t", \)i\ = \\(t'-nft(z, x)\\^ybMl\r-f[<t,
если только
\е — Г\<-7±—=Ъ (Г, Г?(а, Ь), f<z<t").
У nMt
Теорема Арцеля. Из каждого бесконечного семейства век-
вектор-функций f (t, к) (X ?j Л), равномерно ограниченного и равносте-
326 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ [ГЛ. V
пенно непрерывного на конечном промежутке (а, Ь), можно выделить
равномерно сходящуюся на (а, Ь) последовательность
f(t, У (k=\, 2, ...; Х*?Л).
Доказательство (см. [9], [51]). Рассмотрим счетное всюду
плотное множество точек tu t.,, ..., tk, ... на промежутке (а, Ь),
например множество рациональных точек. Множество значений
/(/ь X) ^ ЭЯ" (X ^ Л) бесконечно и ограничено и, следовательно,
.из него можно выделить сходящуюся последовательность f(ti,l'm)
(т=1, 2, ...). Далее, множество значений f(t,, Х^) (т= 1, 2, ...)
также бесконечно и ограничено и, значит, допускает сходящуюся
последовательность f [tit Х^'), где числа Х^1 являются частью чи-
чисел Х^1. Продолжая рассуждение, получим счетное множество вло-
вложенных последовательностей
f(t, K'hfV, К11), •••;
f(t, K}), f(t, К"), ••¦>
из которых первая сходится в точке tlt вторая — в точках tx и
и т. д.
Рассмотрим диагональную последовательность
Mt)=f(t, К1'), Mt)=f{t, К"), ••¦, fk{t)=f(t, №), ... E.2.3)
Так как для любого т, при k ^ т, члены диагональной после-
последовательности fk (t) образуют подпоследовательность последова-
последовательности {f(t, X^')} (k = l, 2, ...), сходящейся в точке tm, то
диагональная последовательность сходится в каждой точке tm(m =
= 1, 2, ...).
Докажем теперь, что диагональная последовательность \fk (t)\
сходится равномерно на всем промежутке (а, Ь).
Пусть г^>0 произвольно. На основании равностепенной не-
непрерывности семейства вектор-функций / (t, X) можно определить
число o = 8fy|^>0, соответствующее числу у. Так как проме-
промежуток (а, Ь) конечен и множество {tm} всюду плотно на (а, Ь), то
найдется конечная система точек tai, tas, ..., ta , представляющая
собой 3-сеть на (а, Ь), т. е. такая, что каждая точка t (? (а, Ь)
будет содержаться в 8-окрестности одной из точек ta, (i=l, 2,...
..., р). На этой конечной системе точек диагональная последова-
последовательность E.2.3) сходится и, следовательно, для нее выполнен
критерий Коши, причем, ввиду конечности числа точек, равно-
§ 21 ТЕОРЕМА АРЦЕЛЯ 327
мерно относительно данных точек. Иными словами, найдется
число Л/ = Ам4-) такое, что при m^sN и k^N,
II/m ('«,)-/*('«,) И< Т (* = 1, 2, .... р). E.2.4)
Пусть t — произвольная точка промежутка (а, Ь) и ta.— бли-
ближайшая точка 8-сети, т. е.
\t-ta/\<b. E.2.5)
Тогда в силу равностепенной непрерывности функций {fk (/)} и
выбора числа Ь имеем
\\fm(t)-tm(ta)\\<~ E.2.6)
И
НЛ@-Л(^)||<|. E-2.7)
Далее, при т^ N и k^N получаем
11/т(/сс.)-ЛD;.)||<у. E.2.8)
Следовательно,
и (О -Л (о II < II /т @ -/»(и II +1| л, (9 -л (у || +
Таким образом, для последовательности {/ft (/)} на (а, Ь) вы-
выполнено условие критерия Коши и, значит, эта последователь-
последовательность равномерно на (а, Ь) сходится к некоторой предельной век-
вектор-функции <р (t), т. е.
fk(*)=f(t, №)?4>V) «a (а, Ъ).
Так как члены последовательности \fh {t)\ непрерывны, то пре-
предельная функция (р (t) непрерывна на промежутке (а, Ь).
Теорема доказана.
Следствие. Пусть семейство вектор-функций f (t, X) (X ? Л)
равномерно ограничено и равностепенно непрерывно на бесконечном
интервале (/„, сю). Тогда из этого семейства можно выделить по-
последовательность fk(t)=f(t, К) (k=U 2, ...; Ll ?j Л), сходя-
сходящуюся на интервале (t0, схэ) к непрерывной вектор-функции у (t)
равномерно на каждом конечном промежутке (а, Ъ) d (/0, со).
328 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИИ [ГЛ. V
Это проверяется непосредственно путем последовательного при-
применения теоремы Арцеля к системе расширяющихся конечных
промежутков
(аи 6,)С(а«, bj)C(fl8. *з)С---.
исчерпывающей весь интервал (t0, оо):
со
U («Ь 6*) = ('о, С»)-
А = 1
Замечание. Равномерной сходимости выделенной последо-
последовательности \fk (t)\ на всем интервале (t0, оо) в общем случае га-
гарантировать нельзя.
§ 3. Теорема Красносельского и Крейна
Пусть
X(t, х, X) E.3.1)
— вектор-функция, определенная в области
и имеющая значения X(t, х, X) (^ 94".
Определение. Будем говорить, что данная вектор-функ-
вектор-функция X(t, X, X) интегрально непрерывна в Q по параметру А в
точке сгущения Х0(^А, если для любых ^^[0, Т] и х ^ D
имеет место предельное соотношение
lim \Х(-., х, l)dx = \X(z, х, ).0)dt. E.3.2)
Замечание. Условие интегральной непрерывности не экви-
эквивалентно обычной непрерывности. Например, функция
sin-г- при X ^z 0,
X(t, Х)= ^
0 при Х = 0
не является в области {O^t^T, —оо<^Х<^со} непрерывной
по X при X = 0. Однако эта функция интегрально непрерывна
по X при Х = 0, так как для каждого отрезка [0, t] С [0, Т] имеем
t
lim \
:== nm
sin ^ dx = lim Л (l—cos^—' =
§ 31
ТЕОРЕМА КРАСНОСЕЛЬСКОГО И КРЕЙНА
329
Теорема Красносельского и Крейна (см. [55]).
(Обобщение теоремы о переходе к пределу под знаком интеграла.)
Пусть
1) X(t, х, Х)?С,B), где 2 = [О, ЛХ^ХА;
2) X(t, X, ^)^zCx(Q) равномерно по совокупности перемен-
переменных t, х, X в 2, т. е. для VsJ>0 3& = Че)^>0 такое, что
для любых t?[0, Т], X^D, x'^D и X ? Л справедливо нера-
неравенство
, х,
если только
*-' r
3) X(t, x, X) в 2 интегрально непрерывна по параметру X в
точке сгущения Хо (^ А, т. е. при любых t?[O,T] и X (^ D спра-
справедлива формула E.3.2).
Тогда, если xx(t) = x{t, X) — семейство вектор-функций, ку-
кусочно-непрерывных по t на [О, Т] со значениями xx(t)(^D при
t G [О, Т] и X ^ Л, причем
Xxify^tx^il) при Х-^Х0
, П,
E.3.3)
lim
, хх (х), X)dt =
о о
E.3.4)
Доказательство (см. [55]). 1) Докажем сначала, что фор-
формула E.3.2) справедлива для любой кусочно-постоянной вектор-
tm-r
Рис. 50.
функции х — х(т), где х(^)=х, = const при t.i
(n = 1, 2, ...,m; O = fe<'i<'i<-..<<m = r), причем
(v = l, 2, ..., m) (рис. 50).
330
Пусть
Имеем
0
АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ
tk<Ct^ tb,.
"й ^s. ^~— л+J
t), Х)Л=2 f АГ(х, л
* '
1— 1 0
0
(fesgffl- 1).
;„ X)dt+ $*(^,лг,+
'*
'»-!
(* Ж/1 / 1 \ • 1
- \ ДГ(т, лг„ X)rfd
0
'ft
JfA+1, X)dx —5 ДГ(х,
0
[ГЛ. V
Переходя к пределу при X ->- Хо в этом равенстве и учитывая усло-
условие E.3.2), при Oss/ssr получаем
t
lim \X{t, x{i), l)dx =
',-.
v = l 0
X{\ xk+1, X0)dx — J A"(x, jcft+), X0)dt{ =
о о
= JA"(x, jfc(x), X0)rfx. E.3.5)
о
2) Пусть теперь для вектор-функции xx(i) выполнено условие
E.3.3). Рассмотрим произвольно малое число г^>0 и выберем
0<^Sj<^s. Так как X(t, х, X) равномерно непрерывна по х в об-
области ш, то существует §^>0 такое, что
X(t, xu l)-X(t, х,, X)||<s, E.3.6)
при ||^1 —Х2||<8, если только * ? [0, Г], Xj ?D, x2 ? D и
X ? Л. Из равномерной сходимости семейства д;х (/) к вектор-функ-
вектор-функции Х\а (t) следует, что
||лга(/)-лгх0@||<8 E.3.7)
при 0<г<Г и X?L'(Xo).
Наконец, ввиду кусочной непрерывности предельной вектор-
функции X\a(t) найдется кусочно-постоянная вектор-функция x(t)
такая, что
ll-«xo(O--*(OII<8 E.3.8)
3]
ТЕОРЕМА КРАСНОСЕЛЬСКОГО И КРЕЙНА
331
при O^t-s^T (рис. 51). Для г?[0, Т] имеем
ДГ(т, *>
= Л-I-/j +/8 +/4. E.3.9)
Так как вектор-функция X (г) кусрчно-постоянная, то в силу
X
/ г1
Рис. 51.
формулы E.3.5) при любом фиксированном / ? [О, Г] окрест-
окрестность U (Хо; /) можно выбрать так, чтобы
), l)~X(x, x(x),
E.3.10)
при АСс/(Х0; I).
Далее, на основании неравенства E.3.6), учитывая неравен-
неравенства E.3.7) и E.3.8), получаем
332 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ [ГЛ. V
И
h = \ || X (т, ЛГ (т), Хо) - * (т, ЛГх0 (т), Хо) || dx < е,* ===: е, Г.
о
Таким образом, из E.3.9) и E.3.10) имеем
если принять ?)<"¦ ,% где Х^^/(Х0; г1). Следовательно,
1 —|— о i
для любого /?[0, Т1].
§ 4. Теорема Н. Н. Боголюбова
Пусть в области 2 = {0</<со, JtgDCe^! (D-область)
определена нелинейная система
Yt=tX{t, х), E.4.1)
зависящая от малого положительного параметра е, где
X(t, x)?Ct(Q) П Lip, B),
причем X(t, X) равномерно ограничена в Q:
|| *(/,*) || <Л1 E.4.2)
(||X [| — евклидова норма).
Теорема Боголюбова (см. [56]). Пусть 1) для каждого
X G D существует равномерный по х конечный предел
\ x)dteC(D); E.4.3)
2) усредненное уравнение
ft = zY(y), y@, г) = х0аО, E.4.4)
имеет единственное решение у =у (t, e) d D, определенное при
е = 1 на сегменте [0, Ту]. Тогда для каждого ~ц^>0 существует
е0 = е0 (tj) ^> 0 такое, что решение x = x(t, e) данного уравнения
E.4.1) и решение усредненного уравнения E.4.4) с одинаковыми
§ 41 ТЕОРЕМА Н. Н. БОГОЛЮБОВА 333
начальными условиями: Х@, е)=у@, е)=Х0 при 0sge<;s0)
будут удовлетворять неравенству
цху, e)-y(t, s)||<7i E.4.5)
на некотором отрезке Os^t^ —, где 0<^Т^Ти
Доказательство. Пусть р^>0 — расстояние начальной
точки х0 от границы области D. Тогда в силу неравенства E.4.2)
решение x(t, e) уравнения E.4.1) с начальным условием:
л: @, s) = x0, будет определено по меньшей мере в промежутке
(см. [12]). Примем
п
Введем «медленное время
¦ / т*
В таком случае уравнения E.4.1) и E.4>4) при е^>0 можно
записать следующим образом:
% = Х[т,х) = Г(х, х, в) E.4.6)
E.4.7)
Если положить
Y{t, X, 0) = Y(x),
то функция Y(t, х, е) будет в Q интегрально непрерывна по
параметру s при s = 0. Действительно, на основании условия
E.4.3) при Os^t<^co и х ? D имеем
i t
lim \ Y(%, х, e)dx=lim ix(-, x) dx ==
о о
t_
г t
= lims \
= f lim
г
= 5к('с1 х,
334 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ [ГЛ. V
Записывая уравнения E.4.6) и E.4.7) в интегральной форме
при O^TsgT и s^>0, получим
X (х, s) = х0 + j К (в, X (9, s), в) db E.4.8)
8. E.4.9)
Отсюда, полагая
Х(х, 0)=y(z),
будем иметь, что уравнение E.4.8) справедливо при е^О и
т?[0, Л-
Рассмотрим семейство решений {х(х, s)},_ где OsgtsgT и
0. Это семейство равномерно ограничено на [О, Т], так как
в силу неравенства E.4.2), учитывая, что У (в, х, е) = AT I —, х
при е^>0, из уравнения E.4.8) получаем
II* К е) II < || ЛГ0 || +] || У (в, лгF, s), е) || d6 < || лго |
Кроме того, данное семейство является равностепенно непрерыв-
непрерывным по х на [О, Т] ввиду того, что на основании уравнений
dx
E.4.6) и E.4.7) производная -г- равномерно ограничена на [О, Т]
(см. пример из § 2).
В силу теоремы Арцеля из каждой последовательности
х{%, ?*)(^=1, 2,...), где ??-*¦ + ()> можно выделить равномерно
сходящуюся на [О, Т] подпоследовательность
х(х, sPj)zty(x) (O^x^T) при \-+0. E.4.10)
Очевидно, имеем
Х(х, Spk) = xu + ly(e, x(B, вч), вр))йЬ (k=l, 2, ...).
Переходя к пределу при k -*¦ сю в этом равенстве и используя
теорему Красносельского — Крейна, получим
, у (в), O)dQ = xol
S 5] ПРИНЦИП СЖАТЫХ ОТОБРАЖЕНИЙ 335
Отсюда
и_у@) = лг0. Так как уравнение E.4.7) в силу условия теоремы
при Ог^т^Г имеет единственное решение у (%), удовлетворяющее
начальному условию: у@)=х0, то
у (т) =_у (т) при OsSxs^r.
Следовательно, из любой последовательности
лс(т, eft) (k = l, 2, ...), где 6ft->4-0, можно выбрать
подпоследовательность jf(t, sp ) (? = 1, 2, ...), равномерно схо-
сходящуюся на [О, Т] к одной и той же предельной вектор-функции
у (т). На основании теоремы § 1 отсюда следует, что семейство
решений д;(т, s) при s -*¦-]- 0 равномерно на [О, Т] сходится
к решению у (т) усредненного уравнения E.4.7), т. е.
||*К *)—У(*)\\<т\ при 0<т<7\ О^е<го(т)).
Возвращаясь к прежней переменной t, окончательно получим
что и требовалось доказать.
§ 5. Принцип сжатых отображений
Пусть R = {х\ есть совокупность элементов (точек) произволь-
произвольной природы (абстрактное пространство).
Определение 1. Множество R = \х) называется метриче-
метрическим пространством (см. [51]), если для любой пары точек
х, У ?R определена числовая функция р (х, у) (расстояние) со сле-
следующими свойствами (аксиомами):
1) Р(Х #MгО> причем р(х, у) = 0 тогда и только тогда,
когда х = у;
2) р (х, у) = р (у, х) (симметрия);
3) если х, у, z g R, то
Р(х, У)^р(х, г) + рB, у)
(неравенство треугольника).
Пример 1. Совокупность действительных упорядоченных и-мерных
комплексов х = (хи ... , х„), у = (уи ... , уп), где
является метрическим пространством (n-мерное евклидово пространство в%п).
336 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ [ГЛ. V
Пример 2. Пусть R={o(t)\— совокупность ограниченных вектор-
функций o(t)?C(a, Ь), sup || о (t) || < со, где (а, Ъ) — конечный или бесконеч-
бесконечный промежуток. Для любых о, ^^R положим
Р(?> Ф) = зир || ? (t) — ф@ || ,
где || 9 II — одна из рассмотренных выше норм (гл. I, §4). Тогда простран-
пространство R метрическое.
Действительно, выполнение аксиом 1) и 2) очевидно. Пусть теперь
?i Ф> X.€-ft- Для любого t? (a, b) имеем
II ?@-Ф@ =?II ? @-х(О II + II х (О-Ф (О II <
Отсюда
^ sup || cf (?) — -/ (t) || —j-sup || x(t) — ф (t) || ^ p (», x) ~b P ("Л
Р (?, ф) = sup || 9 @ - ф @ || < р (Т, х) +Р (X. Ф),
и, таким образом, третья аксиома также выполнена.
Определение 2. Последовательность хи хг, ..., х„, ...
точек метрического пространства R называется фундаментальной,
если для нее выполнен критерий Коши, т. е. для Vе^> О BN =
= N (е) такое, что при \/ т, п^> N имеем
?(хт, хп)<С*. E.5.1)
Очевидно, неравенство E.5.1) эквивалентно следующему:
Р(хп±р, ХпХ* при n>A/(s) и /?>0.
Пространство R называется полным, если любая фундамен-
фундаментальная последовательность {хп} его является сходящейся в ?>,
т. е. из условия E.5.1) следует, что 3?6 R такая, что
В этом случае пишут хп-+? и точку ? называют пределом после-
последовательности \хп).
Пример 3. Пространство R функций и?С (а, Ь) из примера 2 является
полным.
Действительно, пусть <?i @> ••• > ?л@>--« —фундаментальная последо-
последовательность из 7?, т. е.
Р (?л+р. <?л) < Е при я > Я (е) и р > 0.
Отсюда
1!<Рл(-р@ —?л@11<е Для <6(fl, *), E.5.2)
если только и>Л/*(е) и р>0. Таким образом, для последовательности
вектор-функций {^n(t)\ на (а, Ь) выполнен критерий Коши. Следовательно,
эта последовательность сходится на (а, Ь), т. е. существует
<Р (t) = lim ?n @-
п~юэ
§ '¦>]
ПРИНЦИП СЖАТЫХ ОТОБРАЖЕНИЙ 337
Переходя к пределу при р—>оо в неравенстве E.5.2), получаем
I! «р @ - ?„ it) II < « E-5.3)
при л ()
Отсюда следует, что сходимость равномерная:
и так как вектор-функции <рл (О непрерывны на (а, 6), то у (t)?C (a, b).
Кроме того, учитывая, что вектор-функции <?я (О ограничены:
Н?я@1Кся (п = 1, 2, ...),
из неравенства E.5.3) при фиксированном «i>jVA) находим
I! ? С) II < II <рЯ1 (О II + II <? (О — <?», (О II <s+L
Поэтому tp (tf) также ограничена и, значит, <?(]./?, что и доказывает полноту
пространства У?.
Определение 3. Пусть любому элементу х ? X по опре-
определенному правилу А ставится в соответствие элемент Ax — y(^Y.
Тогда говорят, что
у = Ах
есть оператор, определенный на множестве X со значениями из Y
(действующий из X в Y).
Множество X называется линейным пространством (см. [51]),
если для любых х, х11X определены операции: 1) 'сложения
х-\-х'^Х и 2) умножения на скаляр «f]X с обычными свой-
свойствами. Например, таковым является векторное пространство
(гл. I, § 5).
Оператор А называется линейным, если он определен в линей-
линейном пространстве X и имеет значения, принадлежащие также
линейному пространству У', причем для любых х, х' ? X имеем
\ A Atf
) \) +
2) А (ах) = о.Ах (а —число).
Пример 4. Оператор -j ставящий в соответствие каждой функции
^^ (а, Ь) ее производную у (t) = x' (t) ? С (а, Ь), называется операто-
оператором дифференцирования. Легко проверить, что этот оператор линейный.
Пусть х ?R, где R — метрическое пространство и у — Ах —
оператор, не обязательно линейный, действующий из R в R.
Определение 4. Оператор А называется непрерывным,
если для любого е^>0 существует 8^>0 такое, что из неравен-
неравенства р (х', х)<^Ь (х, х1 ? R) следует неравенство
р(Ах',
Определение 5. Отображение
у= Ах
33S АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИИ [ГЛ. V
называется сжатым (или сжимающим) в R, если для любых
точек х, х' С R выполнено условие:
р(Ах, Ax')^qp{x, х'), E.5.4)
где число q удовлетворяет неравенству 0 scq <^\.
Замечание. Сжатое отображение у = Ах непрерывно.
Действительно, для данного s^>0, выбирая 8 = — ^>0 из не-
неравенства E.5.4), будем иметь: если
р(х, x')<b=j, то р(Ах, Ax')^qp(x, x')<e.
А это и означает, что^ у = Ах непрерывно.
Теорема (принцип сжатых отображений). Всякое
сжатое отображение
у = Ах E.5.5)
в полном метрическом пространстве R имеет одну и только одну
неподвижную точку, т. е. для сжатого отображения А суще-
существует единственная тонка ?? R такая, что
Ai = l E.5.6)
Доказательство 151]. Пусть л:0? R. Рассмотрим последо-
последовательность
хп = Ахп_1 (п=\, 2, ...), E.5.7)
где xn(~z. R. Из формулы E.5.6) вытекает, что
Р(*л+ь хп) = р(Ахп, Axn_x)^qp{xn, y<(/"p(xi, x0). E.5.8)
Отсюда при любом р^>0 имеем
Р(хп±р, xn)^p(xnJrP, *л+р_1) + р(л:л+р_1, хп+рЛ)-\-...-\-р(хп+и х„)<
«?=<? Р№, ЗДтч f№, x0)-f-...-\-q p(Xy, ха) —
если n^>N(e), где /V достаточно велико. Следовательно, после-
последовательность \хп) фундаментальная, а так как пространство R
полное, то существует
Игл хп = %.
§6] СИНГУЛЯРНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ТИПА ВОЛЬТЕРРА 339
Переходя к пределу при п-*-со в равенстве E.5.7) и учиты-
учитывая непрерывность оператора А, будем иметь
\\mxn — А \\тхп_и
я—юо п—>оо
ИЛИ
Таким образом, \ есть неподвижная точка отображения E.5.5).
Эта неподвижная точка единственная. Действительно, пусть
AV = V, E.5.9)
где %'^%. Из равенств E.5.5) и E.5.9) получаем
РE, V) = P(Ai, Ж')<<и>E, V).
Отсюда
что невозможно.
Теорема доказана.
Замечание. В условиях теоремы неподвижная точка ? пре-
преобразования E.5.5), т. е. решение операторного уравнения E.5.6),
может быть найдена методом последовательных приближений E.5.7),
исходя из произв.Ш1ьного начального значения хй? R.
§ 6. Сингулярные интегральные уравнения
типа Вольтерра
Рассмотрим систему сингулярных интегральных уравнений
У (t) =/ (t) + \К (t, -О Q (х)у (х) dz (t ^ tQ), E.6.1)
а
где
~ искомый п-вектор;
/(О = colon [/, @ M*)]6C[fo, то)
— известный п-вектор; K(t, x) = [KJk(t, t)], Q(x) = [Qyft (тI —
непрерывные (n X я)-матрицы;
a = colon (a1( ... , an)
— постоянный п-вектор с координатами t0 s^ T ^ ay- «^ -j~ oo
(/ = 1, ¦•• , я), T1 — некоторое достаточно большое число.
Для краткости положим,
/6 I, если ау<4-оо,
и
/^ II, если cij = -\-оэ.
340 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ [ГЛ. V
Тогда систему E.6.1) можно записать в следующем виде:
@ = fj (9
V, -¦) Qks (-¦) ys b) dx (/ G I), E.6.2)
a • *, s
У) @ = fi @ ~ \ 2 Kjs (t, x) Qks (.) ys (x) dt (/ ^11).
• / k,s
Будем считать переменные t и z действительными, а матрицы
K(t,i) и Q(t), вообще говоря, комплексными.
Теорема. Пусть матрица К (t, t) = [/C7-ft (t, -z)] имеет непре-
непрерывные ограниченные элементы Kjk (t, T) в каждой из областей
"j = {teiT,co), i?[T,t]} при /GI
-^)} npa j?U
(рис. 52), а матрица Q (т) непрерывна и абсолютно интегрируема
на [t9, оо), причем вектор-функция /(г) непрерывна и ограничена
на [to, оо). Тогда если Т достаточно велико, система инте-
интегральных уравнений E.6.1) при
t0 s^ T ^ t <Соэ допускает един-
единственное непрерывное ограничен-
ограниченное решение у (t).
Доказательство. Пусть
R — совокупность всех огра-
ограниченных вектор-функций
<р (t) ? С [Т, сю), где Т 5= t0. Рас-
Расстояние между функциями <р (t),
Ф @ G R определим формулой
Рис'52- р(ф,*)= sup ||<р@-Ч>(9-11-
Тогда /? будет представлять полное метрическое пространство
(§ 5, примеры 2 и 3).
В R рассмотрим линейный оператор
г,
г
to
0
tQ7 t
E.6.3)
Если считать, что значения % берутся из соответствующей
области щ/(/^1, II), то матрица К (t, т) в силу условия теоремы
является ограниченной, т. е.
Coo. E.6.4)
8 b] СИНГУЛЯРНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ТИПА ВОЛЬТЕРРА 341
Поэтому для i/|i «ccj <^оо и [\(f>\\-sQc.2<^oo, учитывая, что
1я/, П С [Г, со], в силу формулы E.6.3) и абсолютной интегри-
интегрируемости матрицы Q (х) имеем
со
+ \\\K (t, •=) || || Q (-) || || ф @1| dx <;
Нетрудно убедиться также, что Л <р (/) (^ С [ Т, ос). Следова-
Следовательно, если (f^R, то Л<р(^/?.
Покажем, что отображение Ац> сжатое. В самом деле, для
<р (^ /? и 'ф ^ /? имеем
Лф @ =/@ + \К (t, т) Q (т) <р (.) ^
==/(/) -f \K (t, -z) Q (-) ^ (т)
а
Отсюда
со
Aif @ - Лг|) (/) = \-К (t, т) Q (т) [Ф (т) _
и, следовательно,
со
IIЛф @ \
ц Q (т) ||
^ с sup Ц qs @ — -ф @ 1| $ ||Q(x)i|dt. E.6.5)
t T
В силу абсолютной интегрируемости матрицы Q(%) число Т
можно выбрать столь большим, чтобы имело место неравенство
со
E.6.6)
т
Тогда из неравенства E.6.5) получим
sup || Лф@ - Лг|)(О |! ^qsup '! <р(/) -
< t
т. е.
р(Л<р, ^)^?р(?, ф), E.6.7)
где 0^<7<С1- Таким образом, отображение является сжатым.
342 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ [ГЛ. V
Согласно принципу сжатых отображений (§ 5) в R существует
единственное решение у (t) (Ts^t<^oo) уравнения
т. е. система интегральных уравнений E.6.1) допускает един-
единственное непрерывное решение y(t), ограниченное на промежутке
[Т, со).
Теорема доказана.
Замечание. Решение у (t) может быть найдено обычным
методом последовательных приближений:
yo(t)=f(t),
УР @ =/@ + { К (t, т) Q Юу^ (х) dx
а
(Р=1, 2, ...),
где
yp(t)zty(t) на [Г, со).
§ 7. Асимптотика L-диагональных систем
Рассмотрим систему линейных дифференциальных уравнений
§ = [A(t) + Q(t)]x, E.7.1)
где х = colon (хи ... , хп),
A(/) = diag[X1(f), ... , KimeClU, со)
и Q(t) ^ L [ta, ею), т. е. Q(t) измерима (например, кусочно-непре-
кусочно-непрерывна) и
оо
5d/<oo, E.7.2)
причем интеграл E.7.2) понимается или в элементарном смысле,
или в смысле интеграла Лебега. В уравнении E.7.1) искомый
вектор х и матрицы А(^) и Q(t) будем считать, вообще говоря,
комплексными.
Будем предполагать, что элементы диагональной матрицы Л (t)
асимптотически разделены, т. е. выполнено условие А:
величина
для всех / и k не меняет знака на Т ^t<^co, где T^t0 — не-
некоторое число, которое можно предполагать произвольно большим.
§ 7| АСИМПТОТИКА ?-ДИАГОНАЛЬНЫХ СИСТЕМ 343
Это означает, что кривые
не пересекаются при t^T, причем касание их не возбраняется
(рис. 53). Из условия А следует, что для каждой пары (/, k)
существует конечный или бесконечный интеграл
Re [МО-МО! Л-
E.7.3)
Система E.7.1) называется L-диагональной. Такими системами
занимались Шпет [57] и Перрон [58] при Л @ = const и Левин-
сон [59] при Л @ переменной.
Изучим поведение решений x = x(t) системы E.7.1) при
t ->• оо, причем в основном будем придерживаться изложения
Рапопорта [60].
Пусть
t
\>.s(t) = \),s(t1)dtl E.7.4)
(s=l, ... , п). Фиксируя индекс s в системе E.7.1), произведем
замену переменных
x = e"sif)ys. E.7.5)
Имеем
s = А @ е>*
+ Q @ ^.
Отсюда, учитывая, что e|J'*[t] — скалярная функция, получаем
E.7.6.)
344 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ [ГЛ. V
Введем матричную функцию
/((*>(*, т) = ехр$ [А (*,)-*,(*!)?]Ль E.7.7)
являющуюся нормированным при t = i решением однородной
системы
где
го-
1
Кр (/, т) = [А @ - Xs (/) Е] K{s) (t, т), E.7.8)
удовлетворяющим начальному условию:
Рассмотрим систему сингулярных интегральных уравнений
У* @ = es + l Kw (t, x) Q (x)ys (т) dz, E.7.9)
а= м,
причем координаты вектора а выбираются следующим образом:
1) если
оо
$ Re [\j(t) — ks(t)] dt — — oo E.7.10)
(коротко, / ? I), то полагают а}-==Т, где T^t0 конечно;
2) если же
со
\ Re[X;-(O — М*)]Л> — °° E.7.11)
(коротко, /?П), то принимают ау- —оо.
Непрерывное решение _Vs @ системы интегральных уравнений
E.7.9) удовлетворяет дифференциальному уравнению E.7.6). Дей-
Действительно, дифференцируя равенство E.7.9) по параметру / и
учитывая формулу E.7.8), будем иметь
$[ А (/) -
а
-KV)E] lys(t)-es]. E.7.12)
§7] АСИМПТОТИКА-i-ДИАГОНАЛЬНЫХ СИСТЕМ 345
Так как
[\(t)~K(t)E]es = diag[).i(t), ... , K-i(t),O,\s+i(t), •••
... , X,,(O]-diag(O, ... , 0, 1, 0, ... , 0) = 0,
то уравнение E.7.12) совпадает с дифференциальным уравнением
E.7.6).
Докажем, что система интегральных уравнений E.7.9) удов-
удовлетворяет условиям теоремы из § 6. Для этого достаточно пока-
показать, что элементы строк матрицы
ограничены в областях: о>у = {T^t<^co, t(^[T,t] при / ? I и
wJ = {T^t<oo}, z?[t,oo) при /?11.
Действительно, если / ? I, то из E.7.10) имеем
Re [МО —МОК 0 при t^T,
причем "с ==g t. Следовательно,
] К? (t, -г) | = ехр E Re [Xy (tj ~ }.s (tt)) dt^l.
т
Пусть теперь /?П, тогда т$=/, и, значит,
| Kf (t, т) | = ехр {- \ Re [X, (tt) - X, (tt)] dty}.
t
Если
Re [MO-M01 S* 0 при
то, очевидно,
\Kf(t,x)\^\.
Если же
то в силу неравенства E.7.11) получаем
со
| Kf (t, ~)' < ехр {— I Re ]X, (/,) - \s (/,)]
Таким образом,
в каждой из областей ш;-.
346 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ (ГЛ. V
Следовательно, если Т таково, что выполнено неравенство
со
$ E.7.13)
то при t^T существует непрерывное ограниченное решение ин-
интегрального уравнения E.7.9), которое (см. замечание к теореме
из § 6) можно, согласно методу последовательных приближений,
изобразить в виде абсолютно и равномерно сходящегося ряда
оэ
ys (t) = es + 2 \yf (t) - yf- 4 (/)),
P=i
где
Т
УТ(t) = es + lKis)(t,z)Q(z)yf-^(z)dz (/7=1, 2, ...
у ?'(') =
Из уравнения E.7.9), учитывая, что [ajt t] С [Т, оо], имеем
оценку:
отсюда, используя неравенство E.7.13), получаем
и, поэтому
5ир||уЛ01!<п=^ (ьл.щ
при Т^t<^oo.
Докажем, что
ys(oo)= limys(t) = es. E.7.15)
Полагая
Уs(t) —colon [yis{t), ... , yns(t)],
из уравнения E.7.9) получаем
/ t
t/js(t) = bjs-\- ^ exp^ [kj(ti) — Xs(?i)j dtt 2*3/* (x)yi<s ix)d", E.7.16)
a- " ft
где bJs — символ Кронекера.
§ 7] АСИМПТОТИКА ^-ДИАГОНАЛЬНЫХ СИСТЕМ 347
Если /GI, то, очевидно, j^s и, значит, 5/5 = 0. При
Т sS f ==S t будем иметь
v r t
y]s (t) = \ exp \ [lj (h) — Xs (*,)] dh ¦ exp ] [Xj (tL) - \s (Щ dtx X
= exp ^ [Xy (/,) _ X, (ty)] dh ¦ yjs (Г)
v
+ \Kf V, •=) S Q>* (т) ^ь (-) dr. E.7.17)
Так как для /?1, как указано выше, выполнено неравенство
то, выбирая f достаточно большим, при t^f имеем
?
к? (t,
Фиксируя f и учитывая, что
при t-+oo, получаем
sup 1^@1-
если
Следовательно, из формулы E.7.17) находим
\yjs(t)\<iz при t^>max{t',t")
и, значит,
lim yjs(f) = O = bjs.
t-*<x
Если же /?|П, то на основании формулы E.7.16), учиты-
учитывая ограниченность подинтегральнои функции при t -> оо, имеем
оэ Г
yjs (t) = bjs — jj exp J [Xy- (^) — Xs
348 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ [ГЛ. V
Таким образом, равенство E.7.15) доказано. Следовательно,
где r\s (t) -*¦ 0 при t -> оо.
Возвращаясь к переменной х, в силу формулы E.7.5) полу-
получаем, что L-диагональная система E.7.1) имеет систему решений
вида
A, (*i)fi«i •[*,-{-% @1 (s = l n-t^T). E.7.18)
Эта система будет фундаментальной, так как при достаточно
большом t, очевидно, детерминант Вронского
W @ = det [xJs (/)] = exp ^2 Х5 (*,) dt, ¦ det [%u + Vs (t)] ф 0.
t0 s
Ввиду того, что линейная система E.7.1) для каждого началь-
начального условия xs (Т) = cs допускает единственное решение, опре-
определенное в промежутке [t0, оо), фундаментальную систему E.7.18)
можно однозначно продолжить на промежуток [t0, оо).
Следствие. Если для L-диагональной системы E.7.1) суще-
существуют пределы
t
as= lim H ReX4(*i)dfi (s=l га), E.7.19)
mo эта система является правильной, причем совокупность чисел
<xs представляет собой ее полный спектр.
Действительно, на основании формулы E.7.18) будем иметь
eAs(*i)d*i = a, (s=l п).
l J
'о
Кроме того, так как
t t
lim 1? ReSp[Aft) + Q(*,)]fiKi= lim-J-? У ReXi(/1)d
/->00 ' J ^->CO ' J -^"
< t s
то система E.7.1) правильная (гл. III, §§7 и 11) и {a.s) есть ее
спектр.
§ S] ЛЕММА О ДИАГОНАЛИЗЛЦИИ ПЕРЕМЕННОЙ МАТРИЦЫ 349
§ 8. Лемма о диагонализации переменной матрицы
Лемма. Пусть для квадратной (п X ч)-матрицы A (t) (^
?C[td, со) существует конечный предел на бесконечности
A(co) = \\mA(t), E.8.1)
причем характеристические числа предельной матрицы А (со)
простые. Тогда при t^T, где Т достаточно велико, существует,
ограниченная матрица СA)(^С[Т, со), имеющая ограниченную
обратную матрицу С1 (/) (^ С [Т, со), с помощью которой мат-
матрица A (t) (t^t<^ со) приводится к диагональному виду
Л@ = С1@сНа§[Х1@. ¦¦-, K(t)]C(t).
Если, сверх того, матрица A (t) ?j С1 [t0, оо) и A (t) абсолютно
интегрируема на [t0, со), т. е. A(t)(^L [t0, со), то С (t), С'1 (t) ?j
? СЧТ, оо) и C(t),^t[C-'{t)]^L[T, оо).
Доказательство (см. 6). 1) Для матрицы A (t) рассмотрим
ее характеристическое уравнение
Д(Х, O = det [El — A @1 = 0, E.8.2)
и пусть \k = \k(t) (k = \, ..., п) — корни этого уравнения. Так
как собственные числа предельной матрицы А (со) различны, то
при t^zT функции \k (t) также будут различны, т. е. уравнение
E.8.2) в области t0 s=j T s^ t <^ со не имеет кратных корней. Даль-
Дальнейшее рассмотрение мы будем проводить в области t ^ Т. Функ-
Функции \k(t) (k=l, ..., п) будем считать непрерывными вет-
ветвями многозначной функции, определяемой уравнением E.8.2).
Пусть C=[Cjk{t)\ — неособенная матрица, приводящая мат-
матрицу A (t) к диагональному виду, т. е.
C-1(t)A(t)C(t) = A(t), E.8.3)
где
A(/) = diag[X1@, ..., K(t)].
Так как
A(t)C(t) = C(t)A(t),
то элементы матрицы С (t) определяются из системы уравнений
ИЛИ
Е Гhs h V) — aJs (t) 1 csk (t) = 0 E.8.4)
s
A = 1, ..., n; k = l, ..., n),
где bfs — символ Кронекера.
350 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ [ГЛ. V
Если через
с^> = colon [cik (t), ..., cnk (t)] (k=l, ..., n)
обозначить собственные векторы матрицы A (t), то систему E.8.4)
сокращенно можно записать следующим образом:
[Eh(t)-A(t)]c^(t) = O, E.8.5)
где det [?Xft (t) — A (t)\ — Д[ХА (t), t] = 0. Таким образом, собствен-
собственные векторы c(k) (t) ортогональны к матрице E\k (t) — A (t).
Легко видеть, что каждая из матриц Elk (t) — A (t) (k = 1,..., п)
при Т sg;/<^c» имеет ранг г = я — 1.
Действительно, обозначим через Дд (X, t) алгебраические до-
дополнения характеристического определителя Д (X, t), полученные
в результате вычеркивания /-й строки и k-то столбца его. При-
Применяя известное правило дифференцирования определителя, бу-
будем иметь
Так как корни \k (t) простые, то ^ ^ 0 при X = lk (k) (k = I, ..., n).
Следовательно, для каждого корня \k (t) найдется диагональный
минор
bppihV), t]^0 при Г^<оо, E.8.6)
где номер р, вообще говоря, зависит от k. Число р, для кото-
которого выполнено неравенство E.8.6), можно выбрать не зависящим
от I. Действительно в силу непрерывности алгебраических допол-
дополнений Ду7, (X, г!) и корней Xft (t), если для некоторого р выполнено
неравенство
Арр [\k (со), оо] = lim Дрр [X, (/), t] Ф 0,
t о
t-* со
то при этом же р будут справедливы также неравенства
bpplh(t),t]^O для T^t<оэ,
где Т достаточно велико. Но определитель App[Xft(?), t] явля-
является минором (п — 1)-го порядка матрицы Elk(t) — A(t), и, зна-
значит, эта матрица имеет ранг п—1 (k = \, ..., п).
Из линейной алгебры известно, что тогда ненулевые решения
системы E.8.5) пропорциональны соответствующим алгебраиче-
алгебраическим дополнениям:
Сlk V) ««ft (t) «„ft (()
Apl\\tl(t),t]
§ SI
ЛЕММЛ О ДИАГОНАЛИЗАЦИИ ПЕРЕМЕННОЙ МАТРИЦЫ
351
где р = рк. Выбрав равным единице коэффициент пропорциональ-
пропорциональности в этих отношениях, получим
cjk(t) = \jlh(t), t] E.8.7)
(/=1, ..., п; k=l, ..., п), причем построенные таким образом
векторы с{к] (k—l, ..., п) линейно независимы при Г=сга<се.
Таким образом, в качестве элементов матрицы C(t), приводя-
приводящей матрицу A (t) к диагональному виду, можно взять целые
рациональные функции характеристических корней Xj ((), ..., 1п (/)
и элементов asr(t) матрицы А (/):
CjAt) = PJk[h{t), asr(t)] E.8.8)
и, следовательно,
C(t)?C[T, оо].
Пусть А (со) = [djk (oo)] и hk (oo) — ее характеристические корни.
При t -> оо имеем
«д @
и, следовательно,
«у»
Так как корни Х^(оо) простые, то при t^T, где Т достаточ-
достаточно велико, корни ХА (t) будут содержаться внутри кругов
! X — Xft (oo) I ==? pk <^ со (к = 1,..., п) комплексной плоскости X
(рис. 54), попарно распо-
расположенных вне друг друга. г
Отсюда при t^T имеем
E.8.9)
и, следоватетьно, из фор-
формулы E.8.8) выводим
\C(t)\\^ca, E.8.10)
Рис. 54.
где через ср (р= 1, 2, 3,...)
здесь и в дальнейшем обо-
обозначены некоторые положительные постоянные. Далее, предельные
значения собственных векторов
являются, очевидно, собственными векторами предельной мат-
матрицы А (со), причем ввиду их линейной независимости имеем
] det С (со) ; = mod \
сп (ос) ... с]л (ее)
сл! (ос) ... е„„(се) \
352 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ
Отсюда
|detC@|Ssc8 при t^T.
Так как
; с[т, оо),
[ГЛ. V
E.8.11)
^ кч~ &z\C(t)
то из неравенств E.8.10) и E.8.11) получаем
при t^T.
¦Т. E.8.12)
2) Пусть теперь A (t) ? С1 [/„, оо). Так как корни Хк (t) про-
простые, то существуют непрерывные производные Ук {t)JJk = 1,..., га),
которые можно определить из уравнений
E.8.13)
Ввиду того, что к[[\к{со), оо] ^t 0,
Кроме того, имеем
> 0 =-5
при
ч — Ян @ ~~ °ч @ • • • — а\п @
— поЛ @ X — а>.2 @ • • • — я2п @
— anl(t) —an%
ann{t)
Отсюда, учитывая формулу E.8.8) и неравенства E.8.9), из фор-
формулы E.8.13) получаем
dt
lair (O
'@11-
Следовательно, если Л' @ 6 ^ [*о, °°). то
E-8.14)
E.8.15)
т. е. АИО€ ^[7, оо) (* = 1,..., га).
На основании формулы E.8.8) при
будем иметь
/, /г=Л,..., га).
S 9] ПРИВЕДЕНИЕ ЛИНЕЙНОЙ СИСТЕМЫ К L-ДИАГОНАЛЬНОМУ ВИДУ 353
Поэтому
и С(/) ? L\T, со). Наконец, в силу неравенства E.8.11), мы
получаем также
(Г1 @ еС1 [Г, оо) и §( lC4t)l?L[T,oo).
Лемма доказана.
Замечание. Из доказательства следует, что если матрица
A (t) имеет абсолютно интегрируемую на [/„, оо) производную A'(t),
то ее характеристические корни ХА (t) (k = l,..., n) обладают
также абсолютно интегрируемыми на [Г, оо) производными Х^ (/).
Ограниченную неособенную матрицу C(t)?Cl[T, оо), имею-
имеющую обратную матрицу С ' (t) с теми же свойствами для крат-
краткости, будем называть регулярной на [Г, оо)
Следствие. Переменную матрицу A (t) ? С1 [/„, оо), имею-
имеющую предел на бесконечности с простыми собственными значе-
значениями, с помощью регулярной матрицы С(t) в области t^T^t0
(где Т достаточно велико) можно привести к диагональному виду.
Если матрица А (() абсолютно интегрируема на [t0, оо), то
матрицы С (t) и -г [С'1 (t)\ также, абсолютно интегрируемы на
[Т, оо).
§ 9. Приведение линейной системы к L-диагональному виду
Рассмотрим линейную систему
? = [A(t) + B(t)]x, E.9.1)
где А @ 6 С1 ['о, оо) и B(f)?C[t0, оо).
Теорема. Пусть 1) матрица A(t) допускает конечный пре-
предел на бесконечности
Л(оо) = ПтЛ@, E.9.2)
причем предельная матрица А (со) имеет различные собственные
значения-. 2) производная A (t) и матрица В (/) абсолютно инте-
интегрируемы на [t0, со), т. е.
со со
51| Л (t) :| dt <оо, \ || В @ || dt <oo. E.9.3)
to h
12 Б. П. Демидович
354 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ [ГЛ. V
Тогда система E.9.1) в области t^'f^>t0 с помощью регу-
регулярного линейного преобразования
x = C(t)y E.9.4)
может быть приведена к L-диагоналоному виду
d^ E.9.5)
где
A(O = diagfXI(O,..., K(t))?Cl[T, сю), supliA(/)||<oo
t
Q(t)?C[T, oo) [\L[T, oo).
Замечание. Если производная A (t) абсолютно интегрируема
на [/„, сю), то существует предел E.9.2).
Действительно, имеем
|| A (tt) ~ A ft) 1| = || I А @ dt\\^\ || A (t) || Л<е при О t^T^to.
h h .
Отсюда в силу критерия Коши существует
lim A(t) = A (oo).
t—*оэ
Таким образом, условия 1) и 2) не являются вполне незави-
независимыми.
Доказательство (см. [60]). Пусть С(t) — регулярная мат-
матрица, приводящая матрицу A (t) к диагональному виду:
С'1 (t) A (t) С (t) = A (t) (T=s:/<oo). E.9.6)
Такая матрица существует на основании леммы о диагонализации
переменной матрицы (см. § 8). Положим
x = C(t)y.
Из уравнения E.9.1) имеем
Отсюда
§=A(tjy-\-Q(t)y,
где Л (t) — диагональная матрица E.9.6) и
Q (t) = - С @ С @ -f С @ В (t) С @ 6 С \Т, оо). E.9.7)
ПРИВЕДЕНИЕ ЛИНЕЙНОЙ СИСТЕМЫ К Г.-ДИАТОНАЛЬНОМУ ВИДУ
355
Так как матрицы С (t) и С ' (t) ограничены, то из формулы
E.9.7) вытекает, что
IQ (О II
| С (911+с, IIЯ (О II,
где с{ и с2 — положительные постоянные.
Если матрицы A (t) и В (t) абсолютно интегрируемы на \tn,oo),
то C(t) абсолютно интегрируема на [Т, оо) (см. § 8) и, следова-
следовательно,
со со оз
\ ||<3(ОЦЛ=??С1 \\\C(t)\\dt~\-c.A \\ В (t)\\ dt <oo.
т т т
Таким образом, Q@€ L[T, со).
Так как матрица A (t) ограничена, то из формулы E.9.6)
следует, что Л (t) также ограничена.
Теорема доказана полностью.
Пример [60]. Рассмотрим скалярное уравнение
)х = 0, E.9.8)
E.9.9)
E.9.10)
где р (О 6 С1 [t0, со), p(t)?L [t0, оо), причем р (t) > 0, р (оо)
Уравнение E.9.8) можно записать в виде системы
dx
где р (t)=z<*>s (t). Рассмотрим характеристическое уравнение
X —1
Д(Х, 0 =
= t<° (t),
его корни будут
I
Построим матрицу
приводящую матрицу системы E.9.9)
(t)
= 0;
0
А (О=|
к диагональному виду. Так как собственные векторы
<*== 1, 2>
12*
356 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ [ГЛ. V
ортогональны к матрице Д [Хд. (t), t\, то при k=l имеем
Отсюда можно принять
е1{ (t) = 1, c2i (t) = /w (t).
Аналогично при й = 2 получаем
[~t% iLw] C"w]=o
и, значит, можно положить
Следовательно, матрица С (t) имеет вид
Обычным способом находим обратную матрицу
c-,(t) *_Г-'ш<0
Кроме того,
ГО О
C(t)= .
| /о, (t) — Ы (t) J •
Записав систему E.9.9) в виде
положим
Отсюда
1Р 1 \]
У] \i<»{t) —i*(t)\ [у\'
1x0 -i<*(t)\ У"
1 Г ' 1 П
или, после упрощений,
Имеем
О —w(t)\ Uj 2M@ L-l IJ
Система E.9.11) является /.-диагональной, причем выполнено свойство А:
Re [X, (t) — la (t)\ — Re [2/ю (*)J =0.
^ Pit)
' @ k> @ 2/7 (t)
5 9] ПРИВЕДЕНИЕ ЛИНЕЙНОЙ СИСТЕМЫ К ^.-ДИАГОНАЛЬНОМУ ВИДУ 357
Так как р (t) =г с > 0, то
1
2с
I dt < оо.
h
Следовательно, для фундаментальной матрицы системы E.9.11) справедлива
асимптотическая формула
3@ =
exp [i S»
ехр[—f
где ey(O-*0 (j— 1, 2, 3, 4) при ^-*co.
Возвращаясь к прежним переменным х и у и учитывая ограниченность
функции (о @, для системы E.9.9) получим фундаментальную матрицу
exp
е, @
exp [- i
12 (О
где 1/@—0 С/=1, 2, 3, 4) при г — со.
Полагая
Г 1_
2
LT
получим фундаментальную матрицу вида
cos
):
Sill \ ю
(¦о
i + la @
— 0) @ Sill $ О (^) Л, + 7|, (О И @ COS J Ш ((,) Л; + Y,4 @
где 7[^@—"О (/=1, 2, 3, 4) при <—>оо, причем в силу первого из уравне-
уравнений (о.9.9) имеем
4,@ = }, @ и iL@ = ii (О-
Таким образом, уравнение E.9.8) имеет при t—«-co общее решение асимп-
асимптотического вида
х = с, cos
c2 sin
ti) dtl -f tq @,
где ct и cs—произвольные постоянные и t\(t), r( (<) —> 0 при i —» со.
358 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ [ГЛ. V
§ 10. Теорема Боля
В этом параграфе мы установим некоторые достаточные усло-
условия существования ограниченного на всей оси It= {—co<7<^-j-oo}
решения дифференциальной системы.
Предварительно докажем одну лемму (см. [61]).
Лемма. Пусть
= A
где у = (уи ..., уп), А = [ajk\ — постоянная (п X п)-матрица,
fit) ? С (—со, -f-oo), причем ReXy(i4)^0 (/ = 1, .... п) и
sup ||/@ || =Г<оо.
Тогда существует матрица G(t)^Cx @<^j t\ <Coo), имеющая
следующие свойства:
1) G (-f- 0) — G (— 0) = Еп, где Еп — единичная (п\п)-матрица;
2) \\G(t)\\sS:Ce-a't] (t^O), где с и z — положительные по-
постоянные;
3) G(t)^=AG(t) при /^0;
-}-оэ
4) ч@= \ G{t-U)f(tx)dU E.10.2)
—со
представляет собой единственное ограниченное на It решение
системы E.10.1).
Доказательство. С помощью' неособенной постоянной
(п X я)-матрицы S матрицу А можно привести к следующему
виду:
Л = S-1diag(P, N)S,
где характеристические числа матрицы Р имеют положительные
вещественные части:
Re А;(Р)>0 (/ = 1, .... т),
а характеристические числа матрицы N имеют отрицательные
вещественные части:
Re Ay(tf)<0 (/ = m + l, ..., n). E.10.3)
Положим
, 0) S при <,
= S-'diag(O, e-v') S при <>0 E-10.4)
§ 10] ТЕОРЕМА БОЛЯ 359
Очевидно, имеем G (t) ? 0е0 @ <[ | / \ <^ оо). Кроме того,
G(+0)-G(-0) = ?B
и, таким образом, свойство 1) выполнено.
Далее, полагая
0<a,<min Х,(Р)
и
0<a.2<min[—X^AOl,
получим
|| ept || sgc^i' при /s?0
и
II е№ || sSCae-' при <Ss=O,
где Cj и с2 — некоторые положительные постоянные. Отсюда
вытекает свойство 2):
||G(/)||*?ar-«:" (/^ 0), E.10.5)
где a = min(aj, a3) и с—положительная постоянная.
Дифференцируя по t формулу E.10.3), будем иметь
G(t) = -S^diag(PePt, 0)S =
= — S]d\ag(P, N)S-S'i diag(en, O)S = AG(t) при f<0.
Аналогично из формулы E.10.4) получим
G(t) = AG(t) при ^>0.
Следовательно, имеет место свойство 3).
Наконец, из неравенства E.10.5) выводим
$ ||G(/)||<ftss2c$e-»'d/ = ^. E.10.6)
-оо 0
Поэтому интеграл E.10.2) сходится для любого /? (—со, -|-оо),
причем сходимость равномерна на каждом конечном интервале
a<^t<^b. Так как
t оо
Ч @ = $ G (t - /,)/(/,) Л, + $ G (f - f,)/(^) dtu
—со I
то, формально дифференцируя по параметру t, будем иметь
i@ = [G(+0)-G(-0)]/@ +
/' оо
при — оо<Г<+со.
360 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ [ГЛ. V
Дифференцирование законно, так как несобственные интегралы,
полученные в результате формального дифференцирования, схо-
сходятся равномерно на каждом конечном интервале (а, Ь) ? It.
Итак, n\(t) является решением системы E.10.1). Оценивая т\ (t)
по норме, на основании E.10.6) будем иметь
E.10.7)
Следовательно, решение т] (t) ограничено на действительной оси
— оо <^ t <^ -j- оо.
То, что ограниченное решение r\(t) единственно, следует из
того, что для двух ограниченных на 11 решений r\ (t) и t|j (t) их
разность
является решением однородной системы
— — Ах
единственным ограниченным на /^-решением которой является
тривиальное решение х = 0.
Таким образом, свойство 4) также выполнено.
Следствие. Для ограниченного решения t\(t) системы E.10.1)
справедлива оценка
sup || Ч@ ||^ A sup ||/@||,
где постоянная k зависит только от матрицы А (см. E.10.7)).
Замечание. Если свободный член f(t) системы E.10.1)
есть («-периодическая вектор-функция:
то ограниченное решение т] @ также ш-периодично.
Действительно, на основании формулы E.10.2) имеем
-j-oo
Теорема Боля (см. [62]). Пусть дана действительная
система
% У,У), E.Ю.8)
§ 10) ТЕОРЕМА БОЛЯ 361
где у==(уи ..., уп), A = [ajk] — постоянная (га X «)-матрица,
ф(/, ЖС„(/,^||.у||<ос).
Если
1) Re Ху (Л) ^ 0 (/=1, ...,га), причем Re>vD)>0 при
1=1, -.., т, Re Х;(Л)<0 при j = mJrl, ... , n @«=m ==?«);
2) sup||q>(/, 0)||=Г<оо;
3) выполнено условие Липшица
II Ф(<, У)-ф(<, г)||<Л^||^-г|| гари у €^, г € ^,
то гары достаточно малой константе Липшица N
Г) существует решение tj = t|(/) системы E.10.8), определен-
определенное и ограниченное на всей оси Itl);
2') в пространстве $Zn имеются многообразия SYm и Sn_OT, со-
соответственно, измерений тип — т такие, что решения у (t; 0, уа)
системы E.10.8) обладают свойствами:
Hm[y(t; 0, .у») —4@1=0, если yo?SL E.10.9)
И
\im[y(t; 0, Уо) —4@1 = 0, если у0 6 S* _„. E.10.10)
Доказательство. 1) Принимая ф(?, у) за свободный член,
по аналогии с формулой E.10.2), рассмотрим интегральное урав-
уравнение
со
y(t)= \ G(t-tt)<p(tu yit^dty, E.10.11)
—со
где G(t) — функция, определенная в лемме. В силу свойств 1),
2), 3) и 4) функции G(t) непрерывное ограниченное решение x\(t)
интегрального уравнения E.10.11) является также решением
дифференциального уравнения E.10.8).
Пусть
с,= \ || G @|| dt (c,<oo)
°°
') Сл)чаи т = 0 и т — п не исключаются.
362 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ [ГЛ. V
На основании условия 2) имеем
||/01 @ 11*5 f || <?(*-*,) II ||<Р(*ь 0)||Л,<
—СО
<sup||<p(/b 0I1 $ 110(^-^I1^ = ^, = ^.
Выберем число Н такое, что
Я>2Г,. E.10.12)
В пространстве R непрерывных и ограниченных на It вектор-
функций у (t), где
рассмотрим оператор Т, определяемый правой- частью интеграль-
интегрального уравнения E.10.11):
Ty(f) = ] G (t - tO ф (tu y(t,))dtx. E.10.13)
— CO
Так как при || у \\<^Н имеем
sup||<p(*, y)||<sup||<p(<, 0I1 4-/Vsup И у !| <Г + Л^//,
t. у t v
то при у (t)?R интеграл E.10.13) сходится, причем равномерно
на каждом конечном промежутке a<^t<^b. Отсюда легко убе-
убедиться, что если у (t)?R, то Ty(t) имеет смысл для любого t?lt
и Ту (/) ? С (/,). Далее, при y(t)?R будем иметь
Отсюда
-\- N sup || у (t) || \']\G(tx)\\dtl^:Ti^rMHcl. E.10.14)
Если выбрать константу Липшица Л/ столь малой, чтобы
N<-%-> E.10.15)
то из неравенства E.10.14), учитывая, что Г,^-^-, получим
sup || 7} (/) || *s Г, + 5-<fi.
§ 10] ТЕОРЕМА БОЛЯ 363
Таким образом, при N, удовлетворяющем неравенству E.10.15),
получаем, что если v (/) с R, то Ту (t)? R. В дальнейшем мы будем
предполагать, что условие E.10.15) выполнено.
Для функций y(t), z(t)? R введем расстояние р(у, z), полагая
Тогда R будет являться метрическим пространством (см. § 5),
причем это пространство полное.
Убедимся теперь, что при условии E.10.15) отображение Ту (t)
будет сжатым (§5). Действительно, если у (/), z{t)^R, то из
формул
uy<p(tu y{h))dtx
Tz(t) = \G{t-hL{tu y{h))dtu
— CO
используя условие Липшица 3), получим
\\Ty{t)-Tz(t)\\^
<; N sup || y{t)-z @ || \ || G (t ~ tt) || dh = NclP (y, z).
Отсюда
9{Ту, Tz)^q9(y, z),
где
в силу неравенства E.10.15).
Таким образом, выполнены все условия принципа сжатых
отображений (§ 5) и, следовательно, существует непрерывное
ограниченное на It решение х\ (t) интегрального уравнения E.10.11),
а значит, и дифференциального уравнения E.10.8), причем
Решение ц (t) может быть найдено методом последовательных
приближений
СО
J G(/ —*,)ф(*„ O)dtu
1, 2, ...).
364 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ [ГЛ. V
2) В системе E.10.8) положим
Тогда будем иметь
^ = Ллг + г|5(*, л:), E.10.16)
где
Ч>(/, x) = <p(t, ц@ + *)-ф(^ 4@)-
Очевидно, имеем
y(t, 0) = 0
и
||4>(f, x')-^(t, x)\\^N\\x'~x\\ (x, JtQ&i),
причем
(f(t, л:)=>0 при лс->-0.
Отсюда на основании теоремы об условной устойчивости (гл. IV,
§ 22) заключаем о существовании многообразий Sm и Sn_m, обла-
обладающих, соответственно, свойствами E.10.9) и E.10.10).
Замечание. Теорема остается в силе, если предположить,
что условие Липшица выполнено лишь в области: ||.у||<С^>
|J2||<^#, где постоянная Н удовлетворяет неравенству E.10.12).
Следствие 1. Если q>(t, у) ^-периодична по t, то ограни-
ограниченное решение r\ (t) также ^-периодично.
Действительно, в этом случае из равенства
—со
noлJ7чaeм
Отсюда
УПРАЖНЕНИЯ К ГЛАВЕ V 365
где
с, = f || G @ [| dt.
— со
Следовательно,
sup || т) (t + со) - ц @ || < с, Л/ sup || т) (t + со) -1] @ || ,
а так как cxN <^\, то
что и требовалось доказать.
Следствие 2. ?oi« для всех характеристических чисел lj (A)
матрицы А выполнено условие:
Re >7(Л)<0,
то система E.10.8) конвергентна (гл. IV, § 16).
Действительно, в этом случае ограниченное решение ц (t) един-
единственно (ср. гл. IV, § 16, лемма 1) и для любого решения
У {t\ U, У о) системы E.10.8) имеем
lim Из? (/; t0, г/0)-t] @|| = 0.
t ->co
Упражнения к главе V
1. Пусть
%- = А. (*)*«, (*)
— семейство ш-периодических (ш > 0) линейных систем и существует пре-
предел
= lim — \
<„_>4-0 ш J
Am (t) dt.
о
Тогда характеристические показатели Ху(ш) (/=1 п) системы (*) при
надлежащем выборе их мнимых частей имеют пределы:
\Х4= lim Х,-(ш) (У=1, ..., ге),
ш-> + 0
где (х/ = (а,-(Л) — характеристические корни предельной матрицы А (см. [63),
[64]).
366 АСИМПТОТИЧЕСКОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ [ГЛ. V
2. Вывести асимптотические формулы для решений уравнения
где р @ ? С1 [t0, со,) p(t)?L[t0, со), причем p(t)>0, p(co) = a2>0
Пусть
(см. [60]).
3. Пус
(x=(xt, ..., хп) и P(t) — \pjk (t)})—правильная треугольная система
(/>/*(*) = 0 ПРИ *>У') с непрерывной ограниченной на /, матрицей Р(/),
причем
t
а,= lira -i- \ pjjVJ dt,^O (y= 1, ..., я).
Доказать, что в таком случае неоднородная система
где f(t) ? C(It) и sup |1/(О || <со, имеет единственное ограниченное на //
решение.
4. Пусть Р (t) = [pjk (t)\ ? С (If) и sup l| P (t) || < со. Говорят, что система
удовлетворяет условиям Перрона [29], если для любой непрерывной и огра-
ограниченной на If вектор-функции f(t) соответствующая неоднородная система
имеет решение y=zy(f), у (t0) = 0, ограниченное на Ц — [t0 г? t < со).
Доказать (см. [65]), что система (*•*) удовлетворяет условиям Перрона
тогда и только тогда, когда для ее матрицы Коши Kit, x)=X (t) X'1 (т)
справедлива оценка:
где а и о — некоторые положительные постоянные.
ДОПОЛНЕНИЕ
ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
§ 1. Почти периодические функции в смысле Бора
Определение 1. Числовое множество Е — \Ц называется
относительно плотным на действительной оси — со <^ х<^-\-оо, если
существует число /^>0 такое, что каждый отрезок') а^х^а-\-1
длины / содержит хотя бы один элемент нашего множества, т. е.
при любом а имеем
[a, a + l] (I S^O.
П р и м е р. Множество 0, ±1, ±2, ..., очевидно, является относительно
плотным множеством. Здесь можно принять /=1.
Множество 0, ± I2, ± 22, ... не является относительно плотным, так как
sup[(?-{-lJ — ?2| = оа
к
Рассмотрим комплекснозначную функцию
f (х) = ф (х) + *{. (х) е С (- оо, оо),
где <?(x) = Ref(x), ty(x)=lmf(x).
Определение 2. Число t==t/(s) называется почти
периодом функции / (х) с точностью до ? (короче: ее г-почти
периодом или ^-смещением), если для любого х?( — оо, со)
имеет место неравенство
Очевидно, период функции есть ее почти период для любого
0 Нетрудно показать, что 1) 0 есть почти период для любого
^ 2) если t есть е-почти период функции f(x), то —т есть
также s- почти период этой функции; 3) сумма и разность
s-почти периодов этой функции есть также почти период ее с точ-
точностью до 2б.
') В определении 1 вместо замкнутого отрезка можно брать открытый
инк-рвал.
368 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
Определение 3 (см. [66]). Комплекскочначная функция
/ (х) (^ С ( — со, со) называется почти периодической в смысле Бора'),
если для любого е ^> 0 существует относительно плотное множе-
множество почти периодов т функции / (х) с точностью до г, т. е. су-
существует положительное число 1 = 1 (г) такое, что любой отрезок
[а, а-\-1] содержит по меньшей мере одно число т, для которого
выполнено неравенство
е при — оо<ж< + оо. A.1)
Основы теории почти периодических функций были заложены
датским математиком Г. Бором [66]. Основные теоремы о почти
периодических функциях изложены, например, в [66] и [67].
Из определения следует, что всякая непрерывная периодиче-
периодическая функция, определенная на оси, является почти периодической.
Обратное утверждение не верно, почти периодическая функ-
функция может не быть периодической (см. дальше).
Замечание. Две точки
х и х' = х -\- т,
отличающиеся на е-почти период функции f (х), назовем г-конгру-
энтными.
Если функция f (х) почти периодическая, то для каждой точки
х(^( — со, со) на любом отрезке [а, а-\-1], где / = /(е), най-
найдется е-конгруэнтная ей точка х'(^[а, а-\-1].
Действительно, в силу определения почти периодической
функции f (х) на отрезке [—х-\-а, —х-{-а-\-1] существует ее
е-почти период -с, т. е.
— х-|-а^хе=; — х-\-а-\-1.
Отсюда, полагая х' = х-\-х, получим
Отметим некоторые элементарные свойства почти периоди-
периодических функций (сокращенно — п. п. функций).
1. Если /(*)— п. п. функция, то я/ (л:) -f- p (a, S — комплексные
числа) и f(ax-\-b) {a, b — действительные числа) также п. п.
функции.
2. Если f(x) — п. п. функция, то Ref(x), lmf(x), \f(x)\ и
f (x) также почти периодические функции.
1) Нскпторыр авторы здесь придерживаются терминологии «равномер-
«равномерная почти периодическая функция» (см. [67]), чтобы отличить почти пе-
периодические функции от обобщенных почти периодических функций. Так
как в нашем курсе обобщенные почти периодические функции не затра-
затрагиваются, то мы сохраним термин «почти периодическая функция».
§ 2] ОСНОВНЫЕ СВОЙСТВА ПОЧТИ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ 369
Например, если х есть'е-почти период п. п. функции f (х), то
для ее модуля (/(*)!, очевидно, справедливо неравенство
! | / (х + г) j - j / (х) i ! ^ ! / (дН- т) - / W I < s
и, следовательно, '/(*)' есть также п. п. функция.
Укажем более общее свойство.
Теорема. Если Е— множество значений почти периодической
функции f (х) и F (у) —функция, равномерно непрерывная на Е, то
функция F (/ (х)) — почти периодическая.
Доказательство. Пусть г ^> О произвольно и 8 ^> 0 таково,
что
\F{y")-F{y")\<* при |^-Л<8
(if, </"??)¦ ( }
Тогда, если х = х/(8), то в силу A.2) имеем
г при -0О<><00.
Таким образом, х есть s-почти период функции F(f(x)), что и
доказывает ее почти периодичность.
§ 2. Основные свойства почти периодических функций
Теорема 1. Почти периодическая функция равномерно огра-
ограничена на действительной оси.
Доказательство. Пусть /(х) — п. п. функция и /, = /A) —
соответствующее число из определения 3 (§ 1) для е=1. Так
как f (х) непрерывна на отрезке [0, /,], то
sup !/(*) | = Л1<;оо.
В силу замечания (§ 1) для любой точки х(?( — со, со) и г = 1
существует е-конгруэнтная ей точка x'=x-\-z ^ [0, /]]. Отсюда
I/ (х) | <: \f{x!) \ + \f(x) - / (х') | < М + 1 <оо.
Следовательно, f (х) ограничена на (— со, со).
Теорема 2. Почти периодическая функция равномерно не-
непрерывна на действительной оси.
Доказательство. Пусть / (х) — п. п. функция и l = lf[-^),
где е^>0, произвольно.
Рассмотрим отрезок / -— [ — 1, l-j-l] (рис. 55). Так как функ-
функция f(x), будучи непрерывной на (— со, со), равномерно непре-
непрерывна на /, то существует o = 8fyj^>0 (8<^1) такое, что для
370 почти периодические функции [доп.
любых точек хи х2(^1, для которых \xi — х.2|<С§, справедливо
неравенство
Пусть теперь х и у — произвольная пара точек из (— оо, оо),
удовлетворяющая условию:
Для точки х найдется -^-конгруэнтная точка х' = х-\г т?[0, /].
Тогда, так как &<[1, то для у имеется ~-конгруэнтная точка
у
Рис. 55.
Учитывая неравенство B.1), имеем
Следовательно, f(x) равномерно непрерывна на (— оо, оо).
Следствие 1. Дпя каждого е^>0 множество в-почти пери-
периодов почти периодической функции f (x) содержит относительно
плотное множество отрезков фиксированной длины
tj = tj(s), т. е. существует число L = L(s) такое, что на любом
отрезке [a, a-\-L] имеется подотрезок [%, a-j- tj], все точки которого
? G Vх, aJrTi\ являются г-почти периодами функции f (х).
Действительно, пусть ij = b(y|, где 8 определяется из сеои-
ства равномерной непрерывности функции / (х). Положим
где / у —число из определения п. п. функции (§ 1).
Рассмотрим произвольный отрезок [a, a -f- L]. Из определения п. п.
следует, что существует -^-почти период T(Ha-|--|,a-|-L — -у].
Тогда т —у, т-f-y c:[a, a-\-L\ (рис. 56). Отсюда при любом
§ 31 АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ 371
i (Z L _ -1, z _|_ Aj, учитывая неравенство 11 — т |< 8 (J-j, no- ¦
лучим
Таким образом, отрезок [я, a-f т,1, где я = т — |-, целиком со-
состоит из г-почти периодов функции / (х).
а а+Т
Рис: 56.
Следствие 2. Для почти периодической функции f{x) для
каждого в > 0 существует относительно плотное множество г-почти
периодов 1, являющихся целыми кратными числа -г) = т)(е).
§ 3. Арифметические действия
с почти периодическими функциями
Лемма 1. Для двух почти периодических функций при лю-
любом е>0 существует относительно плотное множество их об-
ших в-почти периодов.
Доказательство. Пусть /(*) и g(x)-n. п. функции и
g „8 (L.) 8,=8 (—) — числа, характеризующие их равномерную
непрерывность (§ 2).
Положим
В силу следствия 2 (§ 2) существуют числа /1 = /Д-^) и Ц —
= / (-?-) такие, что каждый из отрезков [а, а + Л] и [а, а + ^1
будет содержать соответствующие --почти периоды т/ и т?, крат-
кратные числу т). Если положить / = тах(/ь /,), то на каждом от-
отрезке [а, а-\-1] найдется пара ~-почти периодов zf = n'i\ и rg =
= п"т, где п' и /г" — целые числа и , т, — tg j sg /.
Так как т, ~ т. - (п' - п") т) = щ, где п - целое число, при-
причем !лт)|^/, то п может принимать лишь конечное число
372 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
значений; пусть это будут величины п^, п.^, ..., прт], и пусть
«представителями» их являются пары —-почти периодов №\ z_l>),
т. е.
Положим
max | zf | = T.
s
Покажем, что каждый отрезок длины L = l-\-2T содержит по
меньшей мере один общий е-почти период z = zf (е) = zg (е) функ-
функций f(x) и g(x).
Действительно, пусть [а, а-\-1-\-2Т\ есть произвольный от-
отрезок длины L. Возьмем на отрезке [a -f- T, ,a-\-l -\- T] длины /
два у-почти периода¦ zf = п'-ц и zg = n"i\, и пусть zf — zg = nsti =
T(s) ~\s)
/ ? ¦
Отсюда получаем
C.1)
Так как ^ ^ [c-f- T, a-)- /-J- Г] и | т^?> | sg T, то z ^ [а, а + ' + 2Т].
Нетрудно видеть, что число т является общим е-почти периодом
функций f (х) и g(x).
В самом деле, на основании формулы C.1) имеем
+ \g(X - tW) ~g((x- zf) + тИ) |< | + | = E,
Лемма доказана.
Замечание. Лемма 1 легко распространяется на конечное
число функций.
Теорема 1. Сумма двух почти периодических функций есть
функция также почти периодическая.
Доказательство. Пусть f(х) и g(x) — п. п. функции и,
следовательно, f(x), g(x) (= C( — со, со). Отсюда f(x)-{-g(x)?
^ С ( — со, со). Согласно лемме 1 для функций f (х) и g (x) при
§ 3] АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ 373
каждом s ^> 0 существует относительно плотное множество их общих
почти периодов i = zf(^-\ = zgl~). Отсюда имеем
т. е. z = zf+g(s), что и доказывает почти периодичность суммы
f() + ()
f() + g)
Следствие 1. Сумма конечного числа почти периодических
функций (или периодических функций с любыми периодами) есть
функция почти периодическая.
Следствие 2. Линейная комбинация
п
f (х) —- ^ ckfk (х) (ск — постоянные)
почти периодических функций fk{x) (k=\, ..., п) есть функция
почти периодическая.
В частности, каждый тригонометрический полином
(ХА, действительны) является п. п. функцией.
Замечание. Существуют п. п. функции, не являющиеся
периодическими.
Например, f (x) = sin x + sin (*]/~2~) есть п- п- функция, не
сводящаяся к периодической.
Теорема 2. Произведение двух почти периодических функций
есть функция почти периодическая.
Доказательство. Пусть f(х) и g(x) — n. п. функции и
{т} — относительно плотное множество их общих г-почти периодов:
z = zf (г) = zg (s).
Замечая, что f(x)g(x)^C(—оо, оо) и полагая (§ 2)
M = sup5/(;t)| и N = sup\g(x)\,
X X
будем иметь
Так как число (М -\- N)e может быть произвольно малым, то
отсюда вытекает почти периодичность произведения f(x)g(x).
374 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
Следствие 1. Произведение конечного числа почти периоди-
периодических функций есть функция почти периодическая.
Следствие 2. Целая положительная степень почти периоди-
периодической функции есть функция почти периодическая.
Лемма 2. Если f (х) — почти периодическая функция и
in! |/(д)|=й>0,
<Слг<Ссо
риодическая функция
Действительно, если i = xf(zh1), то имеем
то ji— также почти периодическая функция.
Д
f(x)
|
fix)
Теорема 3. Частное ~j-r двух почти периодических функций
f(x) и g{x), где
есть функция почти периодическая.
Доказательство непосредственно следует из формулы
f(x),
g(x) /w g(x) '
теоремы 2 и следствия 2.
§ 4. Равномерно сходящаяся последовательность почти
периодических функций
Теорема 1. Если последовательность почти периодических
функций /i (x), fi(x), ..., fn(x),... равномерно сходится на всей
числовой оси —оо<^х<[«з, то предельная функция
f(x) = \\mfn(x)
п —> оэ
является почти периодической.
Доказательство. Пусть &^>0 произвольно мало. В силу
равномерной сходимости
существует число N = N (&) такое, что
l/W-/jvWKf D.1)
причем f (х) ^ С (— оо, со).
§ 4] РАВНОМЕРНО СХОДЯЩАЯСЯ ПОСЛЕДОВАТЕЛЬНОСТЬ 375
/ E
Пусть z — zj l-g-j — почти период функции fN(x) с точностью
до ~. Используя неравенство D.1), имеем
+ "О -
J + \fN(x)-f(x)
Отсюда, учитывая относительную плотность множества чисел т,
заключаем, что предельная функция f (x) почти периодическая.
Следствие 1. Каждая функция
f(x) = lim Pn(x),
ге->со
допускающая равномерную аппроксимацию конечными тригоно-
тригонометрическими полиномами:
(я—1, 2, ...), является почти периодической.
Замечание. Справедлива также обратная теорема, т. е.
каждая п. п. функция является равномерным пределом некоторой
последовательности тригонометрических полиномов (см. § 16).
Следствие 2. Сумма равномерно сходящегося на (— оо, со)
ряда почти периодических функций есть функция почти периоди-
периодическая.
Теорема 2. Если почти периодическая функция f (х) имеет
равномерно непрерывную на действительной оси — со <^ х <^ оо
производную f (x), то эта производная также почти периодиче-
периодическая.
Доказательство. Пусть
ft —О
Полагая h = — (п = 1, 2, ...), очевидно, имеем
Функции
376 ПОЧТИ ПЕРИОДИЧР.СКИЕ ФУНКЦИИ [ДОП.
(/2=1, 2, ...), представляющие линейные комбинации п. п. функ-
функций, очевидно, почти периодические. Имеем
1 1
Г (х) - /„ (х) = п [f /' (х) dt - \ f (х +1) dt\ =
о о
= n\ir{x)-r(x + t)]dt. D.2)
и
Так как функция f (х) равномерно непрерывна на (—с», со),
то существует 5 = 8 (е) ~> 0 такое, что
Поэтому из формулы D.2) при п> Л^ =-^-— имеем
j 1
fn(x)Zf'(x).
х
Отсюда в силу теоремы 1 функция [ (х) п. п.
§ 5. Интеграл почти периодической функции
Теорема. Интеграл
F(x) = \ f(t)dt
почти периодической функции f (x) является функцией почти пе-
периодической тогда и только тогда, если он ограничен, т. е. если
sup \F(x) | <^оо.
— оэ<л:<со
Замечание. Эта теорема была доказана рижским матема-
математиком Болем (см. [68]) дл^ более узкого класса почти периоди-
периодических функций с конечным базисом частот (так называемых
квазипериодических функций) и обобщена Бором (см. [66]) на
обший случай п. п. функций.
Доказательство. Так как п. п. функция ограничена (§ 2),
то необходимость условия теоремы тривиальна.
Докажем достаточность условия теоремы, причем, оче-
очевидно, можно предполагать, что функции / (х) и F (х) вещественны.
§ 5] ИНТЕГРАЛ ПОЧТИ ПЕРИОДИЧЕСКОЙ ФУНКЦИИ 377
1) Очевидно, F (х) ^ С(— со, -j-co). Пусть F(х) ограничена и
m = MF{x), M = supF(x),
X Л"
причем можно допустить, что т<^М.
Покажем, что для F (х) на оси (—со, -]- со) существует отно-
относительно плотное множество пар точек \х\, х.г\, реализующих
колебание функции
osc F (х) = М — т
— со <С х <Z -'г оо
с точностью до s. Действительно, по свойству нижней и верхней
Рис. 57.
граней функции существует пара точек (гь г2) (Z (—°°, со) та-
такая, что
F(z!)<im-{-^ . F(г^~^>М—~, E.1)
где ?^>0 произвольно (рис. 57), и пусть
Рассмотрим пару сдвинутых точек
E.2)
где
и |дг, —
= rf. В силу почти периодичности
функции f(x), точки т, а следовательно и точки jc = г -f- т, обра-
образуют относительно плотное множество, и, следовательно, сущест-
существует число / = If [-~\ такое, что всякий отрезок [а, а -(- /] будет
содержать точку х, конгруэнтную г. Поэтому на любом отрезке
[о, a -j- L] длины L = I -\- d будет содержаться пара точек \xit x.>}
378 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
и, таким образом, эти пары точек образуют относительно
плотное множество.
Далее, имеем
F(xl)-F(x1) =
= [F(zt)+ \ f(t)dt]~ [/=•(*,) + \ f(t)dt} =
= F (г.2) - F (г,) -f 'f [/(* + *)- f @1Л-
Отсюда
т. e.
[M-Ffe)] + [fW-ffl]<f E-3)
Так как числа М — F (xq) и F(Xx) — m неотрицательны, то из не-
неравенства E.3) получаем
лг<у, E.4)
т. е. пара точек {хи х%\ реализует колебание функции osc/(x) =
X
= М — тс точностью до г, причем на каждом отрезке [a, a-\-L]
длины L, зависящей только от s, найдется по меньшей мере одна
такая пара точек.
2) Пусть теперь т-г= zf 1^-) • Оценим снизу и сверху разность
F(x + x)-F(x).
Для оценки снизу выберем на отрезке \х—g", x -\- у точку
Xi, для которой выполнено второе из неравенств E.4):
fW<m + |,
причем, очевидно, \х — Xi \ ^ -к- ¦ Тогда получим
F{x + x)-F(x) =
\ f(f)dt]-[F(Xl)+\ f(t)dt] =
l U (< + *)-f(*)ldt>
^\^..^==_e. E.5)
§ 6] ТЕОРЕМА О СРЕДНЕМ ЗНАЧЕНИИ 379
Аналогично для оценки сверху выберем на отрезке х — у, х -f- -у
точку хг, для которой выполнено первое из неравенств E.4):
/?(*,)>Л*-у,
где \х — Л'21 s^ у. Имеем
J f(t)dt]-lF(Xi)
.-^ = e. E.6)
Из односторонних оценок E.5) и E.6) находим
для любого х ? (— со, со).
Таким образом, х = х/г(е) и функция F (х) п. п.
Теорема доказана.
Следствие. Если f(х) — почти периодическая функция и
где а — постоянная, <f(t) — ограниченная функция, то y(t) — поч-
почти периодическая функция.
§ 6. Теорема о среднем значении
почти периодической функции
Теорема 1. Для каждой почти периодической функции f (x)
существует конечное среднее значение
т
Af {/}= lim y[ f(x)dx.
Доказательство (см. [66]). 1) Выведем сначала оценку для
смещенного интеграла
а+7
\ f(x)dx.
380 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
Пусть е^>0 произвольно и l = lA--\ — длина, соответствующая
числу ~. Пусть, далее, z = xf i~\ (= [а, а-\-1] почти период
с
О
a-t
'а* Г
Рис. 58.
функции / (х) с точностью до -т- (рис. 58). Имеем
а + Т Т
^ f (x)dx— \ f (x)dx =
а О
х+Т Т а+Т т
= [ J f(x)dx-\f(x)dx]-\- $ f{x)dx+\f(x)dx= .
i 0 х+Т а
Т х+Т х
= \U(* + *)-fW}dx- $ f(x)dx+lf(x)dx.
0 а+ Т а
Отсюда, учитывая, что
получаем
а+ 1
\ f(x)dx~
где Г = sup |f (x)\.
X
2) Покажем, что последовательность
, F.1)
— \ f(x)dx (n = 1, 2,. ...)
имеет предел при п ->¦ со.
§ fi]
ТЕОРЕМА О СРЕДНЕМ ЗНАЧЕНИИ
381
Для этого применим критерий Коши. А именно, для любых
натуральных чисел пит имеем
ilj f(x)dx
о
l
о
т
\—Л f(x)dx — -\f(x)dx) «s-1- m{f(x)dx— [f(x)dx 4-
0
о
т
~n\f(x)
О
(k-\)n
n km
f(x)dx- ^f(x)dx
k — \'(k — \)m 0
Отсюда, используя формулы F.1), получим
nm \4 ' ) ' nm \4 ' 2
Выбирая теперь N столь большим, чтобы
re ' m
при п, тп^> N будем иметь
Следовательно, критерий Коши выполнен и, таким образом,
существует
п
lim M / (х) d*.
F.2)
3) Теперь нетрудно доказать, что
М{/}= Hm-J
382 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
Действительно, полагая
[ДОП.
где п — натуральное число и 0^q<^l, и учитывая ограничен-
п
ность выражения — \ / (х) dx, при Т -> сх> будем иметь
о
Т п п Т
0
6'
Отсюда непосредственно вытекает равенство F.2).
Теорема о среднем доказана.
Теорема 2 (усиленная теорема 6 среднем).
всякой почти периодической функции f{x) равномерно по
метру а? (— оо, оо) имеет место предельное соотношение
т
lim-=
Г-оо '
Для
пара-
параF.3)
Доказательство. Из формулы F.1) при любом а имеем
а (- Г
где i = if[ — ] и Г = sup | / (х) |.
\ 4 / х
Отсюда, в частности, получаем
vf Г
F-4)
(v - 1O"
= l, 2, ...).
Следовательно, для среднего арифметического
п чТ Т пТ
v=t (v-\)T
также будем иметь
--y. \f{x)dx
S 6]
ТЕОРЕМА О СРЕДНЕМ ЗНАЧЕНИИ
383
Переходя к пределу в последнем неравенстве при п -»• оо, в силу
существования среднего значения М {f{x)) находим
МШ*)}— ±
Из неравенств F.4) и F.5) выводим
а-\-1
если только
т .'
F.5)
F.6)
А это и значит, что
1
{/(*)} при 7->со.
Следствие I. При любом а = а(Т) имеем
а(Т)+Т
lim [
Г-»оо
F.7)
а (Г)
Действительно, из формулы F.6) находим
а{Т\+ Т
8/Г
а\Т)
при Г^> —. А это, очевидно, эквивалентно формуле F.6).
Следствие 2. Полагая а(Т) — — Т в формуле F.7), по-
лучим
М {/ (*)} = lim Af. \ f (х) dx = lim ~ \ / (х) dx.
Среднее значение п п. функции /(х) обладает следующими
очевидными свойствами:
1) если /(je) = c = const, то М{с}=с;
2) М {/ (х)} ^0 при / (л-) 5з О, М {/"W} = М]Щ};
3) М{Дх +а)} = {/(*)}
(а — произвольное действительное число);
4) М{/(ах4-^Н=М {/(*)}
(а Ф 0 и 6 — произвольные действительные числа);
384 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
5) М {а/ (л-) + U (*)} = *М {/ (Л')} + ЗМ {g (А')},
в частности,
(/(л) и g{x)— п. п. функции, у. и р — произвольные комплекс-
комплексные числа);
6) |M{
X
7) если fn(x) (n=l, 2, ...) — п. п. функции и
fn(x)^tf(x) на (— со, со),
х
ТО
limM{M*)}=M {/(*)}. F-8)
п —> со
Действительно, при п^> N (s.) имеем
1М*)-/(*I<е.
Поэтому
и, значит, справедлива формула F.8).
В частности, для равномерно сходящегося на (—со, со) ряда
^ сря (х) п. п. функций сря (х) имеем
Если f (x) — п. п. функция, то \f(x)\ является также п. п.
функцией (см. § 1). Следовательно, существует
М
7U» ' 0
Очевидно, М {j / (x) j} Ss 0, причем М {0} = 0. Докажем, что
М{|/(*)|} = 0 тогда и только тогда, когда /(я) = 0. С этой целью
докажем следующее предложение.
Теорема 3. Если почти периодическая функция ((х)фО, то
Доказательство. Пусть
В силу известного свойства п. п. функции (§ 1, замечание) суще-
существует число /^>0 такое, что каждый отрезок [(k—1)/, kl]
§ 6]
ТЕОРЕМА О СРЕДНЕМ ЗР1ЛЧЕНИИ
385
(k—l, 2, ...) длины / содержит точку !л
— -конгруэнтна точке х0, т. е.
/ а \
г,у I, которая
(k = l, 2, ...). Отсюда
1/E*) |=|/(*и)-{/(*.)-/М
На основании свойства равномерной непрерывности п. п. функ-
функции f (х) (§ 2, теорема 2) существует § = 8(-^!^>0 \Ъ<^-^) такое,
что
] х' — х" | < 8.
Поэтому на каждом отрезке [(/г—1)/, /г/] найдется правый или
левый подотрезок Ik = [\kt \k -\- А] С l(k — 1) /, ^], где A=dtS
X
Kl
Рис. 59.
(рис. 59), для любой точки которого
неравенство
[ik,
х
справедливо
Следовательно,
l/toli
при х f [lk, :ikJr
l/(y-/W 1>т~т=т
, 2, ...). Таким образом,
п kl
13 Б. П. Демидович
386 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
Переходя в этом неравенстве к пределу при п-*-со, будем иметь
что и требовалось доказать.
Следствие. Для каждой почти периодической функции /(*)=? О
выполнено неравенство
{
Замечание. Отметим еще одно свойство среднего значения,
которое нам понадобится в дальнейшем. А именно, если /„ (х)
(п=1, 2, ...) — п. п. функции и
}n(x)zX,f(x) при л-* со, F.9)
} = М{|/(*)|8}. F.10)
га—>со
Действительно, из условия F.9) получаем, что / (х) — п. п.
функция (§ 4) и
х
ТО
1Ы*)-/.«1О при n>N
Отсюда находим
l/»(*)KI/WI + e^sup|f(*)| + l=r1 при
Следовательно, при n^>NB имеем
Таким образом,
А так как |/ге(х)|г и |/(х)|2—-п. п. функции, то на основании
свойства 7) справедливо соотношение F.10).
Полезно отметить, что если f (х) и g(x) — п. п. функции, то
среднее значение их произведения удовлетворяет обобщенному
неравенству Коши — Буняковского:
Действительно, при любом Т^>0 имеем
г г т
Отсюда, переходя к пределу при Т-*¦ ос, получим неравенство F.11).
§ 7] ПРОСТРАНСТВО ПОЧТИ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ 387
§ 7. Пространство почти периодических функций
Определение 1. Совокупность П всех п. п. функций f(x),
где х?(—со, со), будем называть пространством п. п. функций.
Если /(*), g(x)?TL и а, [3—любые комплексные числа, то
а/ (х) -f- |3g (x) ? П. Поэтому пространство П линейное.
Если f(x), g (x) d П, то сопряженная функция g(x)? П и
f(x)g(x)? П (§ 2). Следовательно, существует среднее значение
г
М { / (х)^Щ] = lim \ f (*)?"(*) dx.
Определение 2. Под скалярным произведением функции
П понимается число
}• G.1)
Из формулы G.1) следует, что для скалярного произведения
(/, g) выполнены обычные свойства:
1) (/, /) = М {| f (х) \-} ^0, причем (/, /) = 0 тогда и только
тогда, когда /(я) = 0;
2) (g, /) = (/T7);
3) (a/, g) = a(/, g), (/, ag) = a(/, g) (« — комплексное число);
(f/. &€П, /=1Г2)." §
Определение 3. Под нормой функции /(*)?П понимается
неотрицательное число
/11 =V(/, /) = [М{|/(х)|2}]2. G.2)
Введенная норма (определение 3) обладает всеми обычными
свойствами нормы:
1) для V / (х) 6 П имеем || / (л:) || =г 0, причем || f (x) || = О
тогда и только тогда, когда /(*) = 0 (в силу теоремы 3 из § 6);
2) || я/ W || =| * I || / (*) || , в частности, || -/ (х) || = || / (х) || ;
3) для V / W> g(x) € П справедливо неравенство
^II/WII + llgWll. G.3)
Действительно, при любом Т имеем
г т
О
7 Г 7
= т J I f(x) Г2 ^ + 7 \ I ff (*)Г d* + 7 S Re
7 S
О
13»
388 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
Так как
I Re [/ (x)g(x)] | <; | / (x)g(x) \ < | f(x) I \g(x) |,
то в силу неравенства Коши — Буняковского (см. [51.1) находим
7 Т 1
{$ Re [/ (дс) g (х)] dxY ^\\!{х)\Ых\\ё (х)\* dx.
О О U
Следовательно,
т
Переходя к пределу при Г -> со в последнем неравенстве, оче-
очевидно, получим неравенство G.3).
Если f(x), g(x)?II, то, как обычно, вводим расстояние
Р (/. g), полагая
Р(/. g) = \\f(x)-g(x)\\=Vh{\f(x)-g(x)\*}.
Из свойств нормы следует, что если f(x), g(x), h(x)^U, то
1) Р(/. g)^0> причем р(/, g) = 0 тогда и только тогда, когда
f{x)=g{x);
2) р(/, g) = P(g, /") (симметрия);
3) р(/, g)!^p(f, h)-\-p(h, g) (неравенство треугольника).
Следовательно, пространство п. п. функций П представляет
собой линейное метрическое пространство (см. гл. V, § 5).
Определение 4. Две функции / (х), g (x) С И называются
ортогональными, если
Функция f(x)? П называется нормированной, если || f(x) \\ =1,
т. е.
Рассмотрим континуальную систему чистых колебаний e\ — eilx,
где X — произвольное действительное число (—оо<]Х<^со). Оче-
Очевидно,
| eilx | = | cos Хд: -}- i sin \x \ = 1,
причем при X уб 0 функция еах имеет период
Тх=щ-
НЕРАВЕНСТВО БЕССЕЛЯ
389
Лемма. Совокупность чистых колебаний \еПх) образует ор-
ортогональную и нормированную систему, короче, ортонормирован-
ную систему, в пространстве почти периодических функций
П, т. е.
1>А) = 8ы. G-4)
где 8^ — символ Кронекера:
О,
Доказательство. Имеем
г
(et\xt ещх) = м {ег'-хе'&х\ = Jim -~ \ е[ Л - &х их.
Л О. - id 7
G.5)
Так как
С ,(!,_ttU ,„ ~1 , есЛИ X ф а;
11 I Т , если Х = [л,
то из формулы G.5) вытекает соотношение G.4).
§ 8. Неравенство Бесселя
Пусть / (х) С П и {егХл} — совокупность чистых колебаний
(X действительно). Тогда произведение / {х)е~1КХ ? П. Следовательно,
для каждой п. п. функции f(x) существует
спектральная функция
а (X) = (/ (х), еах) = М [f (х) е~^\. (8.1)
В случае векторного пространства под
проекцией (числовой) вектора л: на орт е
понимается число
пр<,л; = (л;, е).
Поэтому если п. п. функции рассматри-
рассматривать как рад и усы-векторы функциональ-
функционального пространства П, то а (X) представляет
собой числовую «проекцию» функции / (х) на орт
При этом векторная ортогональная проекция функции f (х) на
орт еА, очевидно, есть а(^)е"'х.
Лемма. Если функция f (х) почти периодическая, то для
любого конечного набора Хь X., Хдг различных действительных
чисел справедливо неравенство Бесселя:
\
а (Я)
Рис. 60.
= е°~х
= е°~х (рис. 60).
f ()
(8.2)
390 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
Доказательство. Полагая для краткости а„ = аA„),
еп = еа"х, рассмотрим выражение
ДЛ' = Р- (/ (х), 2 ап1п) = (/ (х) ~ 2 апеп, / « - 2 amem) =
N N
n=l m=l
JV JV
n=\ m—\
В силу формулы (8.1) имеем
= (f(x), е„) = ап,
(fix), em) = am;
кроме того, так как чистые колебания \elU) образуют ортонор-
мированную систему в пространстве П, то
где Ъпт — символ Кронекера. Поэтому из формулы (8.-3) получаем
-21а»1'>°- (8-4)
л=1
Следовательно,
(8.5)
л=1
Следствие. Неравенство Бесселя остается верным для
счетной совокупности действительных чисел Х,, Х2, ...
В самом деле, из формулы (8.5) получаем, что для любой
последовательности действительных чисел Хь X.i( ... , Хя> ... ряд
со оо
2 1м*=21а(х»I*
л=1 л=1"
сходится, причем при TV -> со имеем
2 а^^М {;/(*),¦}.
S 9)
ПОНЯТИЕ О РЯДЕ ФУРЬЕ ПОЧТИ ПЕРИОДИЧЕСКОЙ ФУНКЦИИ
391
§ 9. Понятие о ряде Фурье почти периодической
функции
Лемма. Для каждой почти периодической функции f (x) ее
спектральная функция
a(k) = M.{f(x)e~iXx} (9.1)
отлична от нуля лить для конечного или счетного множества
значений аргумента X.
Доказательство. Пусть Л = {Х: а(Х)^0}. Очевидно,
Рассмотрим те значения X, для которых
(k= 1, 2, ...). В силу неравенства Бесселя (§ 8), если это мно-
множество не пусто, то оно содержит лишь конечное число элемен-
элементов. А именно, если \a(hs)\^-r
E=1, ..., /V), ТО
Отсюда
N
О
\а(А)\
! КЛЛ
Рис. 61.
w{i/(*m<co.
Таким образом, Л является
объединением счетного множества
конечных множеств и, следовательно, мощность его не более чем
счетна.
Итак,
за исключением, быть может, конечной или счетной последова-
последовательности значений Хь )ч, ... (рис. 61).
Определение 1. Те значения \, для которых а(л)т^0,
представляющие собой конечную или счетную последовательность
действительных чисел X,, Х.2 называются показателями Фурье
соответствующей п. п. функции f(x), а числа
392 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
— ее коэффициентами Фурье. На основании формулы (9.1) имеем
Лп =^^ Л\ IJ \х) е п' |. (У.^)
Совокупность всех показателей Фурье п. п. функции будем назы-
называть ее спектром.
Определение 2. Рядом Фурье п. п. функции /(х) назы-
называется конечный или бесконечный тригонометрический ряд
)'(х)сл^]АпеГАпХ, (9.3)
п
где {Х„}— спектр функции /(х) и Ап, определяемые формулой (9.2)
(/1=1, 2, ...), —коэффициенты Фурье. Порядок членов ряда
Фурье п. п. функции, вообще говоря, произволен и зависит от
упорядочения ее спектра {).п\. Заметим, что для п. п. функции
/(х) = 0 (и только для такой, как будет показано ниже (§ 14))
спектр функции представляет собой пустое множество и ее ряд
Фурье формально не определен. Обобщая понятие ряда Фурье
п. п. функции, разрешим дополнять сумму (9.3) любым количе-
количеством нулевых членов вида 0-е"'х и тогда будем считать, что
п. п. функции /(х) = 0, с пустым спектром, соответствует нулевой
ряд Фурье
О с/э 2 0 ¦ еПпХ,
о
где счетная совокупность Хь Х3, ... произвольна.
Ряд Фурье п. п. функции / (х) иногда выгодно записывать
в виде континуальной суммы:
/ (х) то 2 а (X) еах (—оо<Х<оо), (9.4)
х
без явного выделения показателей Фурье Х„, где а (X) опреде-
определяется формулой (9.1). Здесь подразумевается, что а(Х) = 0 для
X, не равного показателю Фурье функции, f (х); с этой, более
общей точки зрения числа а (к) будем также называть коэффи-
коэффициентами Фурье п. п. функции f{x). Свободный член ряда
Фурье представляет собой среднее значение функции, т. е.
а @) = М {/(*)}.
Заметим, что члены ряда Фурье (9.4) являются векторными
ортогональными проекциями п. п. функции f (х) на соответствую-
соответствующие орты е'Хх.
Замечание. Для непрерывной чисто периодической функ-
функции f (х) периода Т ряд Фурье (9.3) совпадает с ее обычным
рядом Фурье:
л—со
2n-xi
§ 9] ПОНЯТИЕ О РЯДЕ ФУРЬЕ ПОЧТИ ПЕРИОДИЧЕСКОЙ ФУНКЦИИ 393
где
Т ->n-xi
1 /»
7 dx
6
(n = 0, rtl, ±2, ...), если, конечно, не учитывать порядок чле-
членов ряда и пропуск членов ряда с нулевыми коэффициентами.
Действительно, для любого целого m имеем
ml
v = l (v-'l) T
m
= ' У e~D- (v-4 T \ f (x) e-ax dx =
C°T i
Отсюда, если Х = ^ (л — целое), то
m ^
v=l
и поэтому
яГ Г
\f(x)edx = \
о 6
Если же \ф^-, то е~1кТФ 1. Следовательно,
-»й"-чг= 1~е ""''1--»о
при m^-оо, и таким образом,
Теорема 1. Для каждой почти периодической функции f(x)
сумма квадратов модулей ее коэффициентов Фурье А,г образует
сходящийся ряд, причем справедливо неравенство Бесселя:
Vi^f^MflfWr). (9.5)
394 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
Теорема непосредственно вытекает из доказанного раньше
неравенства Бесселя (§ 10).
Следствие. Коэффициенты Ап ряда Фурье почти периодиче-
периодической функции f (х) стремятся к нулю при я-»-со, т. е.
НтЛп=ИгпМ{/(*)е-'х«*}==0.
Замечание. Как будет доказано выше, в формуле (9.5)
всегда имеет место знак равенства.
Теорема 2. Равномерно сходящийся на оси — со<^х<^со
тригонометрический ряд
(9.6)
п=\
является рядом Фурье своей суммы f (х).
Доказательство. Отметим, прежде всего, что сумма f(x)
равномерно сходящегося ряда есть п. п. функция-(§ 4, теорема 1).
Далее, так как для равномерно сходящегося ряда п. п. функций
знак среднего и знак суммирования перестановочны, то
M {/ (х) е~ах} = М {? спё "'„-м ^} =
л=1
0,
Следовательно, числа \ъ \г, ... образуют спектр функции f(x), a
сл(я=1. 2, ...) являются ее соответствующими коэффициентами
Фурье. Таким образом, ряд (9.6) есть ряд Фурье функции
Следствие 1. Если
л=1
то тригонометрический ряд
л=1
есть ряд Фг/рьё своей суммы.
Следствие 2. Существуют почти периодические функции
с произвольным счетным спектром.
gldl ФОРМАЛЬНЫЕ ОПЕРАЦИИ НАД РЯДАМИ ФУРЬЕ 395
Действительно, пусть Хь д.2, ... — произвольное счетное мно-
множество вещественных чисел. Тогда сумма равномерно сходящегося
ряда
со
где ^ |с„|<^оо, будет представлять собой п. п. функцию с дан-
п = 1
ным спектром {Хп}.
Заметим, что структура спектра Л = {Х„} п. п. функции может
быть весьма сложной. Например, могут существовать конечные
точки сгущения спектра, спектр может быть всюду плотным на
действительной оси и т. п. Этим объясняется трудность изучения
ряда Фурье п. п. функции по сравнению с чисто периодической
функцией F (х) данного периода Т — 21, имеющей ряд Фурье:
п — — оо
спектр которого представляет арифметическую прогрессию
К = ™ (п = 0, ±1, ±2, ...).
§ 10. Формальные операции над рядами Фурье почти
периодических функций
Пусть f(x) и g{x) — n. п. функции, т. е. f (x), g (х) ?~П.. Рас-
Рассмотрим их ряды Фурье:
Тогда справедливы следующие соотношения:
1) я/ (х) + Pg (х) то ^ [м: (*) + Рй (^)l e'u
х
(а, р — произвольные комплексные числа);
2) /(дс4-Л)сл>2>МеДАе"*
Л
(/г — произвольное действительное число);
((а — произвольное действительное число);
Л
396 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ (ДОП.
Соотношения 1) — 4) легко вытекают из общих свойств сред-
среднего значения п. п. функции (§ 6).
Пусть f(x), /'(лОЕ-П (см. § 4). Для производной f (х) построим
ее ряд Фурье:
Интегрируя по частям, будем иметь
а, (Х) = М {/'(*) e"fU} ==
= lim ["'
где я (а) — коэффициент Фурье функции f{x).
Следовательно,
f (х) оо ^ О-а (к) еах A0.1)
>,
и, таким образом, ряд Фурье производной п. п. функции в случае
ее почти периодичности получается формальным почленным диф-
дифференцированием ряда Фурье самой функции:
f(x)zo^a(l)e*x. A0.2)
Л
В частности, спектр производной f (х) совпадает со спектром
функции f(x), за исключением точки л = 0.
Пусть / (х) — п. п. функция и
т. е. функция F (х) является ограниченной (§ 7). Положим
FWot^c W eilx.
Так как F' (x) = f(x), то на основании формул A0.1) и A0.2)
имеем
Не (X) = а ().).
Отсюда необходимо должно быть
а@) = 0
и
с(к) = Ц^ при л^О.
§ И] СВЕРТКА ПОЧТИ ПЕРИОДИЧЕСКОЙ ФУНКЦИИ 397
Следовательно,
где с(О) = гА\ \ f (t)dt\.
о
Таким образом, если для п. п. функции f (x) ее среднее зна-
значение
и интеграл F (х) ограничен (§ 7), то ряд Фурье интеграла этой
функции получается путем формального почленного интегрирова-
интегрирования ряда Фурье самой функции. В частности, спектр интеграла F (х)
совпадает со спектром функции / (х) (не считая X — 0).
Замечание. Условие
необходимо для почти периодичности интеграла F (х). Однако,
как показывает приведенный ниже пример, оно не является до-
достаточным для почти периодичности этого интеграла.
Пример. Функция
0
почти периодическая, причем так как свободный член ее равен
нулю, то M{/(x)} = 0. Однако ее интеграл
F{x) = \f(t)dt
о
не является п. п. функцией.
Действительно, если бы интеграл F(x)^II, то для его ряда
Фурье мы бы имели
1
что невозможно, так как коэффициенты Ап = -т- этого ряда не
стремятся к нулю при я->оо (см. §9, теорема 1, следствие).
§ 11. Свертка почти периодической функции
Пусть / (х) (^ П, тогда при любом фиксированном х (^ (— со, со)
функция
398 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
где f (t) — функция, сопряженная f(t), является почти периоди-
периодической. Следовательно, существует
F (*) = М {<р, (/)} = М {/ (х + О Щ},
t 1
т. е.
F(x) = lim *\f(x + t)W)dt. A1.1)
Функция F (х) называется сверткой функции / (л:).
Рассмотрим «неполную свертку».
т
\f(x-}-t)W)dt (Г>0). A1.2)
о
Лемма 1. Для каждого Г^>0 неполная свертка FT(x) почти
периодической функции f (х) почти периодична по х, причем
FT(x)^.F(x) при Г->со, A1.3)
х
где
/=•(*) = м {/(* +о Ш}.
t
Доказательство. 1) Докажем сначала, что FT (x) равно-
равномерно непрерывна по х на (— со, со). Действительно, пусть
и S = 8 (е) ]> 0 таково, что
!/(х')-/(*"IО при |/-х
Тогда при \h\<^b на основании формулы A1.2) имеем
т
ij<tt = sl\ A1.4)
и
что и доказывает равномерную непрерывность функции FT (x).
Из неравенства A1.4) вытекает, что каждый у"почти период
функции / (х) является е-почти периодом функции FT (x). Следо-
Следовательно, FT (x) — почти периодическая функция.
2) Для каждого х?(—со, оо) имеем
§ 11] СВЕРТКА ПОЧТИ ПЕРИОДИЧЕСКОЙ ФУНКЦИИ 399
Пусть т — любой .^р-почти период функции / (х). Тогда
\ 2Г ^ 2Г
Таким образом, каждый почти период т==тЛктг) функции / (л-)
является s-почти периодом функции r-?x(t). Следовательно, для
почти периодического семейства {'-px(t)} существует положительное
число /(е) такое, что любой отрезок [а, а-\-1(г)] длины 1(г) со-
содержит по меньшей мере один s-почти период для каждой
функции ср* @ (—оо<]х<^оо). На основании усиленной теоремы
о среднем (§ 6, неравенство F.6)) для каждой п. п. функции <?x(t)
будем иметь
при
^¦^ 8/(?)Г
1 > I .
что равносильно соотношению A1.3).
Лемма 2. Если f (x) почти периодична, то для почти перио-
периодической функции
средние по х и по t перестановочны, т. е.
/ X
Доказательство. Прежде всего, свертка
F(х) = ГЛ {f {х-\-t)]Jf)}
t
как равномерный предел п. п. функций FT (x) есть функция почти
периодическая. Следовательно, существует
X t
Далее, на основании усиленной теоремы о среднем (§ 8), имеем
400 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
Поэтому М {f(x -f- 0/@} почти периодична по / и существует
Докажем теперь, что выполнено равенство A1.5). Так как
функция f(x-\~f)f(t) непрерывна по совокупности переменных х
и t, то при любых конечных Г^>0 и Х^>0 имеем
х т т х
i § dx-~ § f(x + f)W)dt = Y \ dt± \ f(x + t)JJT)dx. A1.6)
Но
X X+t
\
при Х-»-со. Следовательно, в левой части равенства A1.6) можно
совершить предельный переход при X ->¦ со под знаком инте-
интеграла, и мы получим
хт т х
lim -L *i dx-l= \ f(x + t)Ylt)dt = ~ [ dt- lim -^ [ f(x + t)JJt)dt
0 0 0 0
ИЛИ
7 7
' ' " — /. (Ц.7)
Так как в силу леммы 1
г
при
х I
то, переходя к пределу при Г-»-оо в соотношении A1.7), на
основании свойства 7) среднего значения (§ 8) окончательно будем
иметь
* t t х
что и требовалось доказать.
§ 111 СВЕРТКА ПОЧТИ ПЕРИОДИЧЕСКОЙ ФУНКЦИИ 401
Теорема. Для всякой почти периодической функции / (х) ее
свертка F (х) есть функция почти периодическая, причем
. A1.8)
Доказательство (см. [66]). То, что свертка
есть функция почти периодическая, следует из того (как уже
было упомянуто в лемме 2), что свертка является равномерным
пределом п. п. неполных сверток FT (x) (лемма 1). Впрочем, почти
периодичность свертки легко доказать также непосредственно.
Далее, используя перестановочность средних М и М (лемма 2)
X t
и усиленную теорему о среднем (§ 8), имеем
{
X t
=м {7@ м {/(*+он=м{Пом{/(*)}} =
t X t X
Следствие. Если для почти периодической функции f(x) ряд
Фурье есть
то ее свертка F(x) имеет следующий ряд Фурье:
F (*) сл> ^ | а (X) | Vх* A1.9)
х
Действительно, так как
то
М {F (х) е'ах} = М {М {/ (х + О ПО еах}} =
X X t
= М {f @ е1™ М {/ (х + 0 <гХ(*+'>Н = М {f @ еш ¦ М {/ (х) е~ах}\
t X t X
402 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
Замечание. Аналогично доказывается, что если / (х) и g (x) —
п. п. функции, то их свертка
есть функция почти периодическая.
§ 12. Теорема единственности
Как известно, две непрерывные периодические функции, имею-
имеющие одинаковые ряды Фурье, совпадают между собой, т. е. такие
функции однозначно определяются своими коэффициентами Фурье.
Докажем, что эта теорема единственности верна также
для почти периодических функций. Так как для разности п. п.
функций их коэффициенты Фурье равны разностям соответствую-
соответствующих коэффициентов Фурье данных функций, то теорему един-
единственности можно сформулировать в следующем виде: не суще-
существует отличной от тождественного нуля почти периодической
функции, все коэффициенты Фурье которой равны нулю.
Теорема единственности нетривиальна, и доказательство ее
довольно сложно. Мы приведем здесь незначительно видоизменен-
видоизмененное доказательство Бора — де ла Валле-Пуссена (см. [69]). Пред-
Предварительно понадобится несколько лемм.
Пусть / (х) — п. п. функция и
т
aQ) = M{f(x)e-lx*}= lim ~ [ f{x)e~axdx A2.1)
— ее коэффициенты Фурье. Положим
г
axdx @<Г<оо), A2.2)
6
где ао0{\) = а{\).
Лемма 1. Функция ат {к) равномерно мала при ^^
| X j -> оо, т. е. для всяких е j> 0 и То ^> 0 существует А = А (е, Г0
такое, что
A2.3)
при Г0<Г^сю и |Х|>А.
Доказательство. Выполняя ,замену переменной
% 121 ТЕОРЕМА ЕДИНСТВЕННОСТИ
в интеграле A2.2), будем иметь
f
м -'Ч-+-9
т-г
Г
Складывая равенства A2.2) и A2.4), находим (рис. 62)
т (X) = - -f
+ Т
Пусть
Г
403
A2.4)
и 8 = 8 (е) ]> 0 — число, характеризующее равномерную непрерыв-
I I
Рис. 62.
ность функции f(x). Тогда из равенства A2.5) при
и Г>Г0 имеем
если |Х|>тах х> -— ==Л.
2Гя
404 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ 1ДОП.
Следствие. Из A2.6) при Т-*¦ оо получаем
\aa(\)\ = \a(\)\^t при |Х|>Л.
Лемма 2. Пусть все коэффициенты Фурье почти периодичес-
периодической функции f (х) равны нулю, т. е.
при — оо <^ X <^ оо. Тогда для всякого
— То (е) ^> 0 такое, что
т
существует То =
A2.7)
при Т^Ть и Х?( — оо, со).
Доказательство. В силу леммы 1 для заданного
можно выбрать число Л так, чтобы
|аг(Х)|<в при
и |Х|>Л.
A2-8)
Поэтому для больших | X | неравенство A2.7) выполнено.
Пусть теперь | X | sg Л. Так как
г
а(\)= Um aT(k)= lim -^\f(x)e-tXxdx — 0,
Г-»оо Г-.оо ' J
то на основании усиленной теоремы о среднем (§ 6) для всякого
фиксированного Х? [ — Л, Л] существует 7\(X)S=1 такое, что
при
где а ? (— оо, оо) произвольно. Для точки X рассмотрим ее ок-
окрестность
где r = sup|/(jf)|.
X
Заметим, что для любых действительных аир имеем
I
ТЕОРЕМА ЕДИНСТВЕННОСТИ
405
Поэтому, если У ? 1Ъ то для каждого Н? [Те(к), 2Тг(Щ по-
получаем
Н+а
f(x)e-x'xdx
-н ) пх>
и
Н+а
Н+а
так как
Н
¦ н
Т. (к)
2.
A2.9)
Пусть теперь T~^>TeQ.) и & 5=0—целое число, удовлетво-
удовлетворяющее условию:
2*M
Тогда, полагая Н = -—, где n = 2fe, будем иметь
Отсюда, представляя аг(^') в виде среднего арифметического, в
силу неравенства A2.9) получим
1
Ш
пН
е'а'х dx
v=l (v-l)H
л vH
v=l
406 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
если только Х?1\. Таким образом, для каждого Xg [—Л, Л]
существует окрестность /х, для любой точки которой У ? /^ при
T^>Tt(k) выполнено неравенство A2.10). Система \1Х} покрывает
отрезок f—Л, Л]. В силу леммы.Гейне — Бореля можно выбрать
конечную систему /хр Г^, ¦ ¦ ¦, 1\ , также покрывающую отрезок
[— Л, Л]. Полагая
Г0(е)= max Г. (**) 3*1, A2.11)
*=1 TV
находим, что для любой точки Х?[—Л, Л] выполнено нера-
неравенство
т
\ат(Ц\= 4" \ f(x)eaxdx <s A2.12)
при ТУТ,(г).
Отсюда с учетом неравенства A2.8) получаем полное докэ
зательство леммы.
Теорема единственности. Если все коэффициенты Фурье
почти периодической функции f(x) равны нулю, то эта функция
тождественно равна нулю, т. е. из условия
a(\) = M{f(x)e-ax} = 0 A2.13)
(— оо<^Х<^оо)
следует, что
f(x) = O при — оо<^х<^-{-оо.
Иными словами, п. п. функция f(x), ортогональная ко всем
чистым колебаниям ех = еа"(— оо<Х<^оо), тождественно равна
нулю.
Доказательство. Предположим противное, что /(х)=?0,
sup|/(jc)| =
х
Рассмотрим свертку (§11)
Г— oo L '
которая также является п. п. функцией.
Имеем
A2.14)
§ 121 ТЕОРЕМА ЕДИНСТВЕННОСТИ 407
так как если а = 0, то (§ 9, лемма 1) F(x)=0 и, значит,
отсюда /(.*:) = 0, что противоречит предположению.
Из формулы A2.14) получаем
т
J \Р(х)\Ых^~ при
Так как (§11, лемма 1)
т
Fr(x) = ± \ f(
при Т -»¦ оо и F (х) ограничена, то
при Г^оо,
X
и, следовательно, число То можно выбрать столь большим, чтобы
при Т^>То имело место неравенство
т
4-
Рассмотрим функцию
где
fT(x) = f(x) при 0<л:<2Г
= fr(x) (рис. 63).
Н
Легко видеть, что функция Фт(х) непрерывна и 2Г-перио-
дична. Полагая
408 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
для 2Г-периодической функции Фг(л'), получим ее обычный ряд
Фурье:
Вводя обозначения
6
27
5
и используя 2Г-периодичность функции Фт(х), для ее коэффи-
коэффициентов Фурье cf(ja) получим следующие выражения:
27
6 о
Т IT
27» S WJ*dt
о
2Г+С
[
о t
7 2Г
27»
Для непрерывной периодической функции Фг(х) имеет место
известное равенство Парсеваля:
27
2T J
о и- м-
Так как согласно условию теоремы функция / (х) почти пе-
периодическая с нулевыми коэффициентами Фурье, то в силу лем-
леммы 2 при достаточно большом Т равномерно по ja справедлива
оценка:
С* (Т>Т0),
121
ТЕОРЕМА ЕДИНСТВЕННОСТИ
409
где ?^>0 произвольно мало. Далее, так как Рг(^) представляет
собой коэффициенты Фурье ограниченной кусочно-непрерывной
2Т-периодической функции fr (х), то выполнено неравенство
Бесселя:
Поэтому
2Г \
и, значит,
Отсюда и подавно
2Г
С другой стороны, при
\2T и, следовательно,
г
при Г>Г0.
A2.16)
имеем
Отсюда на основании неравенства A2.15) получаем
т т
±r
A2.17)
Неравенства A2.16) и A2.17) противоречивы, если выбрать
е достаточно малым. Таким образом, теорема единственности
доказана.
Следствие. Две почти периодические функции, имеющие
одинаковые ряды Фурье, совпадают между собой.
Замечание. Если f(х) не п. п. функция, то функциональ-
функциональное уравнение
M{f(x)eiU} = 0 (-oo<X<-foo)
может допускать нетривиальные решения. Например, если / (х)
абсолютно интегрируема на [0, со), т. е.
410 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
то для всякого действительного X, очевидно, имеем
7
M{f(x)e-iXx} = lim -^ [ f (x) e~ax dx = 0.
Отметим один важный вывод из теоремы единственности.
Теорема. Если для почти периодической функции f (x) ее ряд
Фурье
!{х)ю^Апеап* A2.18)
п
сходится равномерно, то сумма его равна данной функции, т. е.
^Апе*п*. A2.19)
Доказательство. Как известно (§ 9, теорема 2), равно-
равномерно сходящийся тригонометрический ряд A2.18) является ря-
рядом Фурье своей суммы 5 (л:), т. е.
5 (х) сл> 2 К etx"x-
п
Таким образом, функции f(x) и S(x) имеют одинаковые ряды
Фурье и, следовательно, в силу теоремы единственности они
совпадают. Отсюда вытекает формула A2.19).
Следствие. Если для почти периодической функции f(x)
ее ряд Фурье
a
сходится абсолютно, т. е.
У I А
п
то справедливо разложение
п
§ 13. Равенство Парсеваля
Теорема 1. Для всякой почти периодической функции f (x)
с рядом Фурье
п
имеет место равенство Парсеваля:
\. A3.1)
13] РАВЕНСТВО ПАРСЕВАЛЯ 411
Доказательство. Рассмотрим свертку (§11)
Так как на основании неравенства Бесселя (§ 8) им—
то ряд Фурье свертки F {х) сходится равномерно и, следовательно,
имеет место равенство
Полагая здесьл: = 0, очевидно, получим равенство Парсеваля A3.1).
Замечание. Если модули коэффициентов Фурье а (к)
рассматривать как величины проекций п. п. функции / (л:) на орты
е\ = ё1х, то равенство Парсеваля представляет теорему Пифа-
Пифагора в пространстве п. п. функций П.
Определение. Говорят, что последовательность п. п. функ-
функций ft (x), ft(x),..., fn(x),... сходится в среднем к предельной
п. п. функции f(x), если
М { | /„ (х) — f'(x) |3 } -v 0 при п -*¦ оо.
Аналогично ряд
п=1
сходится в среднем к F (х), если последовательность частных сумм
сходится в среднем к F {х).
Теорема 2. Для всякой почти периодической функции f (x) ее
ряд Фурье сходится в среднем к f (x) (при любом порядке слагаемых).
Доказательство. Для отрезка ряда Фурье
согласно (8.4) и A3.1) имеем
м{|/(*)-2л,^*|»}
V=l ¦
если n^>N(t). А это и значит, что ряд Фурье-функции f(x)
сходится в среднем к f (х).
412 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
§ 14. Теорема аппроксимации
Как было доказано выше (§ 2), предел равномерно сходящейся
последовательности тригонометрических полиномов есть функция
почти периодическая. Справедливо и обратное положение, что
всякую п. п. функцию f (х) можно рассматривать как предел
равномерно сходящейся последовательности тригонометрических
полиномов, т. е. п. п. функции допускают равномерную аппрокси-
аппроксимацию тригонометрическими полиномами с любой степенью точ-
точности. Оригинальное доказательство этой теоремы аппроксимации
Бора, опирающееся лишь на определение п. п. функции, было
дано Н. Н. Боголюбовым (см. [70]). Мы здесь приведем доказа-
доказательство Н. Винера (см. [71], [67]), основанное на применении
равенства Парсеваля (§ 13).
Теорема аппроксимации. Если f(x) — почти перио-
периодическая функция, то для всякого е>0 существует конечный
тригонометрический полином
удовлетворяющий неравенству
sup|/(*) —Р.(*I*?е,
X
где в качестве \п могут быть взяты показатели Фурье функции
f(x).
Доказательство. Пусть
Функция g (л:) — почти периодическая.
В самом деле, учитывая, что
| sup cp (t) — sup <]> (t) | ==? sup | cp (t) — <[> (t) |,
/ i t
при любом действительном h имеем .
A4.1)
14]
ТЕОРЕМА АППРОКСИМАЦИИ
413
Отсюда, так как функция f(x) ограничена и равномерно не-
непрерывна на (— оо, оо), то g (h) -*¦g @) = 0 при ft->-0 и, следо-
следовательно, g (x) также ограничена и равномерно непрерывна на
(—оо, оо). Кроме того, из неравенства A4.1) вытекает, что всякий
е-почти период функции / (х) является е-почти периодом функции
g(x) и, таким образом, эта функция
почти периодическая.
Пусть sj>0 произвольно. Рассмот-
Рассмотрим функцию
1 —
при
при г/>т
Рис. 64.
(рис. 64).
Так как функция <?(у) равномерно
непрерывна на [0, оо), то сложная
функция y(g(x)) является почти периодической (см. § 1). Функция
<?(g(x)) неотрицательна, и так как у (g @)) = у @) = 1, то
<? (g Iх)) Ф 0- Поэтому ее среднее значение
Положим
тогда, очевидно, ф(*) — п. п. функция и
A4.2)
Рассмотрим функцию
Используя равенство A4.2), имеем
^(x-t)}. A4.3)
Но согласно определению функция ф (лс —1) = — <?(g(x — ^))
ова, что если ф (л: — /) ^ 0, то ^
* —9 = sup |/(*—
414 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
Отсюда при и = 0 будем иметь
\f(x)-f(t)\<~.
Таким образом, из неравенства A4.3) получаем
1/(*)-М*I<1М{ф(х-0} = |. A4.4)
Для п.. п. функции / (*) рассмотрим ее ряд Фурье
Обозначая через у\ произвольно малое положительное число, на
основании неравенства Бесселя (§ 8) выберем N = N (i]) так,
чтобы
Пусть
И
Так как
f; Aneinx,
то, используя равенство Парсеваля, получим
М{|/?ЛГ(*)П= S И»Г<Ч- 04.5)
Положим
Рг (х) = М { SN (t) ф (х - t) ) =2 ^„М { ф @ е~д«' } • e'x^.
' л=1 '
Очевидно, Р, @ есть тригонометрический полином, причем Х„ —
показатели Фурье функции f(x).
Имеем
§151 ТЕОРЕМА КОМПАКТНОСТИ БОХНЕРА 415
Отсюда, применяя известное неравенство Коши—Буняковского
(§ 8) и используя неравенство A4.5), получаем
[у, A4.6)
если выбрать
1 ^- 4 М { ф2 (t) }'
t
Из неравенств A4.4) и (Н.6) находим
|/(л:)— Ре(х)\<^? при — oo<^*<-)-oo.
Теорема аппроксимации доказана.
§ 15. Теорема компактности Бохнера
Определение. Функция f(x)?C(— оо, оо) называется
нормальной, если из каждой бесконечной последовательности ее
сдвигов { / (х -j- hn)} (hn(^(— оо, оо)) можно выделить равномерно
сходящуюся на всей действительной оси подпоследовательность.
Иными словами, функция f(x) нормальная, если семейство функции
{ f(x-\-h)} (— oo<^ft<^oo) компактно в смысле равномерной схо-
сходимости.
Всякая нормальная функция f(x), очевидно, ограничена. Дейст-
Действительно, если существует последовательность |л:„} такая, что
| / (хп) | -*¦ оо, то из последовательности { / (х -f- xn)} нельзя вы-
выбрать сходящуюся при x = 0, а следовательно и на (—-оо, оо),
подпоследовательность.
Пользуясь понятием нормальности, Бохнер (см. [72]) дал другое
определение п. п. функции, полезное для приложений.
Теорема Бохнера. Непрерывная функция является почти
периодической тогда и только тогда, когда она нормальная.
Доказательство (см. [67]). 1) Докажем сначала необхо-
необходимость этого условия., т. е. мы предположим, что функция
f(x) почти периодическая, и докажем, что она нормальная.
Рассмотрим произвольную последовательность
гдеЛ„(/г=1, 2,...) — действительные числа. Так как функция
/ (л:) ограничена (§ 7), то эта последовательность также ограни-
ограничена. На числовой оси — оо <[ х <^ оо возьмем счетное всюду
416 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
плотное множество точек xlt х.г>... (например, множество рацио-
рациональных чисел). Из ограниченной числовой последовательности
),..., f(x14rhny,...
выберем сходящуюся подпоследовательность
Далее, из ограниченной числовой последовательности
выберем сходящуюся подпоследовательность
Ам), / (*а + А,,),. •., / (хъ -f
Этот процесс продолжаем неограниченно. Тогда диагональ-
диагональная функциональная последовательность
/(* + А„), /(JC + A,,),..., /(* + Авя),... A5.1)
будет сходиться в каждой точке хт (т = 1, 2,...) нашего всюду
плотного множества.
Действительно, согласно построению члены последовательности
/(*» + Лн), /(ДСт + Ам),-.-, /(Jfm + A,.),... A5.2)
при п^т входят в состав сходящейся последовательности
/(*m +Ami), /(*m + Am«), •••, / (-«m + Amn),- • •
и, значит, последовательность A5.2) сходится.
Докажем, что диагональная последовательность A5,. 1) сходится
равномерно на всей действительной оси (—оо, оо). Пусть е^>0
произвольно. Согласно определению п. п. функции существует
число 1 = 1 [^Л такое, что каждый отрезок [а, а 4-1] длины /
\ ° I
содержит хотя бы один почти-период •с = -с/(^|. Далее, пусть
8 = 8 — —положительное число, определяемое на основе равно-
равномерной непрерывности функции f (х). На отрезке [0, /] из точек
всюду плотного множества {хт} построим конечную 8-сеть:
'•\==Хт1, ^2 == Xm%t • • •> 4s — Xms,
ГД6 (/=1, 2,..., s-l; «,
§ 15] ТЕОРЕМА КОМПАКТНОСТИ БОХНЕРА 417
Так как диагональная последовательность A5.1) сходится
в точках сь Ss, ..., ^ и число их конечно, то равномерно для
совокупности этих точек выполнен критерий Коши, т. е. сущест-
существует N = N Dн такое, что
+ h№) - f (?,- + hqq) |<-i- (/=1,2,..., s),
если только р, q^>N.
Пусть теперь х — любая точка-из (—оо, оо) и х'(^[0, I] есть
-^-конгруэнтная ей точка (§ 1), т. е. x' = x-\-t 4-)'. Обозначая
через \k (k(^[l, s]) ближайшую к х' точку S-сети, при р,
будем иметь
Так как число Л^ не зависит от е, то отсюда следует, что по-
последовательность { f(x-\-hnn) } равномерно сходится на (—оо, оо)
и, таким образом, f(x) есть нормальная функция.
Заметим, что предельная функция
<f(x) = limf(x-{-hnH),
очевидно (§ 4), является почти периодической.
2) Докажем теперь достаточность условий теоремы, т. е.
предположим, что f(x)?C(—oo, оо) и является нормальной;
требуется доказать, что / (л:) — п. п. функция.
Предположим противное. Пусть / (х) не есть п. п. функция.
Тогда существует ?0]>0, для которого нельзя подобрать соответ-
соответствующую длину /(е0), т. е. для любого /^>0 найдется отрезок
[h — /, h-\-l] длины 2/ такой, что для каждой точки ?? [к — /,
h-\-l] имеем
sup |/(дс+ ?)-/(*) l^e,. A5.3)
Для краткости такие отрезки будем называть «особыми». Построим
последовательность особых отрезков [hn — /„, hn -j- ln] (п. = 1, 2,...)
таких, что
14 Б, П. Демидович
418 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
(п = 2, 3,...), где li произвольно. Так как при т<^п имеем
то
если т<^п.
Рассмотрим функциональную последовательность
где Аь hi, ..-, hn,... — центры наших особых отрезков. Для любой
ее подпоследовательности
/(х + hPl), f (x + hP2),...,f(x + hPn), ...
при pm<_pn имеем
= sup I / (x + hPn — hpj — f (x) | Ss ee,
так как АРп — hPm принадлежит особому отрезку
\Kn-lPn,hPn + lPn].
Следовательно, подпоследовательность { / (х -j- hPn) } несходится
равномерно на (—оо, оо) и, значит, функция f(x), вопреки пред-
предположению, не является нормальной функцией. Полученное про-
противоречие и доказывает достаточность условия теоремы.
Замечание. Так как нормальность функции является не-
необходимым и достаточным услозием почти периодичности ее, то
это свойство можно принять за определение п. п. функции.
Пользуясь свойством нормальности, получаем простое доказа-
доказательство почти периодичности суммы или произведения конечного
числа п. п. функций.
§ 16. Почти периодические матрицы
Определение 1. Матрица
) (-cx>O<TO) A6.1)
называется почти периодической, если все элементы ее fjk (x)
являются п. п. функциями.
Используя норму матрицы (гл. I, § 4), можно дать другое
определение п. п. матрицы.
Лемма. Матрица F (х) является почти периодической тогда
и только тогда, когда для любого г ^> 0 существует относительно
§ 16] ПОЧТИ ПЕРИОДИЧЕСКИЕ МАТРИЦЫ 419
плотное множество чисел -с (г-почти периоды матрицы) таких, что
||F(* + t)-F(*)||<s A6.2)
при — oo<*<oo (где под нормой понимается I, II или III
норма матрицы, гл. I, § 4).
Доказательство. 1) Докажем сначала необходимость
условия A6.2), причем доказательство будем проводить для III
нормы матрицы:
la- A6.3)
/. ft
Доказательства для остальных норм аналогичны.
Пусть матрица ^(л:) типа пХт и s^>0 произвольно. Для
конечной совокупности п. п. функций fjk(х) существует отно-
относительно плотное множество {т } общих е -почти периодов (§ 3,
у пт
лемма 1), т. е.
для у/, k и —
Отсюда
)
;, к
Таким образом, неравенство A6.2) выполнено.
2) Докажем достаточность условия. Предположим, что
для некоторого относительно плотного множества {х}, завися-
зависящего от произвольного числа s^>0, имеет место неравенство A6.2).
Тогда
для любых / и k. Следовательно,, все функции fJk (x) почти
периодические и, значит, матрица ^(л:) также почти периодическая.
Лемма доказана.
Из определения 1 легко следует, что если матрицы F (х) и
G (х) почти периодические, то матрицы AF (x), F (х) А (А — по-
постоянная матрица), F(x)-\-G{x), F(x)G(x), Fr(x), F* (x) \\F(x)\\ —
также почти периодические.
Естественно также для п. п. матрицы F(x) устанавливается
понятие ряда Фурье
где
14'
420 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
Для непрерывной матрицы легко обобщается понятие нормаль-
нормальности.
Определение 2. Матрица F(х) ? С(— 6о, оо) называется
нормальной, если из любой последовательности F (х -j- hy),
+ h)F h)
(Л*€(-То. оо); k = l, 2,
можно выбрать подпоследовательность
равномерно сходящуюся на всей действительной оси, т. е. суще-
существует матрица Ф(х) такая, что
при k^> N (в) и —оо<^л:<^оо, причем, очевидно, Ф (х) ?
?С(-сю, со).
Обобщенная теорема Бохнера (см. [73]). Для почти
периодичности непрерывной матрицы F (х) необходимо и доста-
достаточно, чтобы она была нормальной.
Доказательство. 1) Пусть (п X /п)-матрица
почти периодическая и
{F (х + hp)} = {{fjk (x + hp))} (p = 1, 2, ...)
— произвольная последовательность ее сдвигов вдоль действитель-
действительной оси. Так как все функции fjk (x) почти периодические, то
в силу теоремы Бохнера (§ 17) из последовательности {fn(x-\-hp)}
можно выделить равномерно сходящуюся последовательность
{/»(* +Аи.*)}-
Далее, из последовательности {fn(xJrnii,p)} выделяем равно-
равномерно сходящуюся подпоследовательность {fi*(x-\- hiip)}, причем,
очевидно, подпоследовательность {/n (x-\-hn p)} также равномерно
сходится. Так как число функций fjk(x) конечно, то, продолжая
этот процесс, мы в конце концов получим подпоследовательность
hp = hnmp (/7=1, 2, ...), для которой все подпоследовательности
{/,*(* +А?)} (/=1 л; Л = 1 т; р=\, 2, ...)
равномерно сходятся на оси (— со, оо).
Следовательно, существует (п X /п)-матрица Ф (х) такая, что
) при р-+оо,
причем предельная матрица Ф (х) почти периодическая,
§ 171 ЛИНЕЙНАЯ СИСТЕМА С ПОСТОЯННОЙ МАТРИЦЕЙ 421
2) Пусть теперь матрица F(x) = \fjk(x)] нормальная. Тогда
из теоремы Бохнера непосредственно вытекает, что все функции
fjk (х) почти периодические. Отсюда на основании определения 1
получаем, что матрица F (х) также почти периодическая.
В дальнейшем нам придется иметь дело с семейством почти
периодических по х матриц F (х, у), зависящих от параметра у.
Определение 3. Матрица F(x, у) называется почти пе-
периодической по х равномерно относительно параметра y?Y,
если для каждого е^>0 существует относительно плотное множе-
множество общих, не зависящих от у, s-почти периодов •с = т/г(е) се-
семейства {F (х, у)}, т.е. при всех х E (—оо, оо) илюбом y(^Y
имеем
\\F(x + *, y)-F(x, y)\\<*.
§ 17. Линейная система с постоянной матрицей
и свободным почти периодическим членом
Рассмотрим систему
ft=Ay+f(t), A7.1)
где у — («X 1)-вектор, А = [aJk] — постоянная (п X «)-матрица и
f(t) — почти периодический (лХ 1)-вектор.
Мы будем изучать свойства решений n\(t), ограниченных на
всей действительной оси, т. е. таких, что
sup || ц@ ||=М<со. A7.2)
t
Лемма. Если скалярное уравнение
% = 4 + f(t), A7.3)
где X = [A-|-tv — комплексное число и f{t) — п. п. функция, имеет
ограниченное решение
то это решение почти периодическое.
Доказательство (см. [73]). Общее решение уравнения
A7.3) имеет вид
] A7.4)
где с — произвольная постоянная,
422 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
1) Пусть <x=ReA>0. Тогда || ех'|| =еа/-»оо при t-+oo. Из
формулы A7.4) вытекает, что для того, чтобы y{t) было ограни-
ограниченным, необходимо, чтобы
lim [с + \ (Г* f (s) ds] = с + \ e'ls f (s) ds = 0.
/-»OO Q Q
Отсюда
oo
c = — \e-Xsf(s)ds, A7.5)
0
причем, так как
где
r = sup|/(s)|,
то интеграл A7.5) сходится. Поэтому ограниченное решение су-
существует и имеет вид
причем
со оо
h @ ! *S \ I ^{t-s) I ! / (s) I ds ^ Г \ e*V-s) ds = J.
i 6
Если x = %f(&) есть е-почти период функции f{t), то имеем
tj (t + х) = — \ e^'+w>/ (s) ds = — ] e'V-v f (s + x) ds;
t+i 0
отсюда
Следовательно, функция tj(/) почти периодическая.
§ 17] ЛИНЕЙНАЯ СИСТЕМА С ПОСТОЯННОЙ МАТРИЦЕЙ 423
2) Пусть a = ReX<0. Тогда |еи \ = е°* ->оо при t-+ — со.
Аналогично случаю 1) получаем, что ограниченное решение имеет
вид
t
= \ eH's)f(s)ds
и является почти периодическим.
3) Пусть a—Re Х = 0, X = iv и существует ограниченное ре-
решение
Тогда
t
\е-ыf (s) ds
о
о
ограничен и, следовательно, представляет собой п. п. функцию
(§ 7). Таким образом, в этом случае все решения
у(t) = еы \с + (е~"° f (s)ds] (|с|<оо)
о
ограничены и почти периодические.
Замечание. Если однородное уравнение
A7.6)
не имеет нетривиальных ограниченных на (— оо, оо) решений,
т. е. ReAy^O, то неоднородное уравнение A7.3) допускает един-
единственное ограниченное и почти периодическое решение.
Если же однородное уравнение A7.6) имеет нетривиальные
ограниченные решения, т. е. ReX = 0, то неоднородное уравне-
уравнение A7.3) или не имеет ограниченных на (—оо, оо) решений,
или существует бесконечное множество ограниченных и
почти периодических решений.
Обобщенная теорема Бора — Нейгебауэра. Всякое
ограниченное решение линейной дифференциальной системы A7.1)
с постоянной матрицей и почти периодическим свободным членом
является почти периодическим1).
!) Эта теорема обобщает аналогичный результат Бора и Нейгебауэра
[74], полученный ими для линейного дифференциального уравнения с,по-
с,постоянными коэффициентами и почти периодическим свободным членом.
424
ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
[ДОП.
Доказательство. Приведем доказательство Кордуняну [73].
С помощью неособенного преобразования
(det S Ф 0) систему A7.1) можно перевести в систему с постоян-
постоянной нижней треугольной матрицей
о
Имеем
A7.7)
dz
-ZjT = bniZi + bntfi + • • • + KZn + gn
dt
где
ff(/) = colon
— очевидно, п. п. вектор-функция.
Пусть
п(9=
(9
— ограниченное решение системы A7.1), тогда
*Г (9
.401 (9J
будет являться ограниченным решением треугольной системы
A7.7). Так как
то в силу леммы имеем, что функция zi01 (9 почти периодическая.
Далее, так как
§ 181 КВАЗИЛИНЕЙНАЯ ПОЧТИ ПЕРИОДИЧЕСКАЯ СИСТЕМА 425
то на основании леммы функция 4°' (t) также почти периодиче-
периодическая. Продолжая это рассуждение, находим, что все функции
z'k' @ (k — l, ..., п) являются почти периодическими, а следова-
следовательно, решения zM (t) и ц (t) также почти периодические.
Теорема доказана.
Следствие. Если корни щ, jig [а„ характеристического
уравнения
dt(A
не имеют нулевых вещественных частей:
Rety^O (/ = 1 п),
то система A7.1) допускает единственное почти периодическое
решение (см. гл. IV, § 10).
В этом случае, предполагая, что
х
нетрудно построить ряд Фурье ограниченного п. п. решения
Формально подставляя (§ 10) эти ряды в систему A7.1), будем
иметь
? ike (k) ёи = %Ас (X) еш + ^Ь(к) еш.
XXX
Отсюда
с (X) = — (А — iAE)-1 Ь (л) (det (А — i\E) ф 0)
и, следовательно,
ц (t) w 2 (А? — А)'1 Ь (к) еш.
§ 18. Квазилинейная почти периодическая система
Рассмотрим квазилинейную систему
% = Ay+f(t) + w(t, у), A8.1)
где у = (уи..., уп); А = [а]к] — постоянная (п X я)-матрица;
/ @ е С (It) и q> (*, у) ? С (/< X s^P - (я X 1 )-векторы; ^ - ма-
малый скалярный параметр, причем выполнено условие Липшица
||q>(*. «)-<?(/, У) || <iV || г-у || A8.2)
СУ G sffiy z G ^y ^ ~ постоянная).
426 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
Теорема Бирюк [75]. Если
1) ReХу (Л) 9*0;'
2) / (t) — почти периодична по t;
3) <р ft у) — почти периодична по t равномерно по у на каждом
компакте Y,
то при |р|<^0, где [i0 достаточно мало, система A8.1) допу-
допускает почти периодическое решение ц = ц ft p.).
Доказательство. В силу теоремы Боля (гл. V, § 10) си-
система A8.1) при | A1 ^ [А, имеет равномерно ограниченное на оси It
решение т] = т1(/, (i), удовлетворяющее интегральному уравнению
Ч(/, 1*)= S С(<-^)[/й) + ^ф(<ь ч(^„ 1*))]ЛЬ A8.3)
— со
где матрица G@ такова, что
||G@||<ce"e|" A8.4)
(с и а — положительные постоянные).
Пусть
II П(*. 1*)||<Ь<оо ПРИ *ЕЛ и ||*Ki*,.
Покажем, что при достаточно малом | [а | вектор-функция tj (f, [a)
почти периодична по i. Пусть t = if (s) — общий почти период
вектор-функции f(t) и семейства q>(/, у) (|| у \\ ^ Ь). Из формулы
A8.3) при |(i l^jij имеем
j») = f G(t + т - /,) [/ft) + цф ft, r, ft,
Отсюда с учетом A8.2) и A8.4) получим
{sup || /(^ 4- т) —/ @1| +1 [x I [sup
t t.y
G(t)\\dt<
§ 18] КВАЗИЛИНЕЙНАЯ ПОЧТИ ПЕРИОДИЧЕСКАЯ СИСТЕМА 427
где
— оо
Поэтому
^ t, p)-n(t, v)\\
и, следовательно,
если только
Таким образом, при достаточно малом | [а | решение -ц (t, [i) почти
периодическое.
Замечание. Почти периодическое решение ц(t, ji) системы
A8.1) может быть найдено- методом последовательных
приближений:
r\(t, (i)= limr\p(t, ji),
p->oo
где
— единственное почти периодическое решение системы
(р = 0, 1, 2, ...).
Так как
(t )fit v) при 1
то решение ц (t, jx) непрерывно по jj. в окрестности точки |» = 0 и
lim i\(t, |x)=j;o(O.
ц-»0
428 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
§ 19. AZ-класс почти периодической системы
Рассмотрим нелинейную дифференциальную систему
&=/«, х) (St),
где х = (хи ..., хп) ? <fflnx — искомый действительный (п X 1)-век-
тор, t?It = {—co, 00} и f(t, х)— данный (я X 1)-вектор.
Предположим, что
1)/С ) ?C(IA)
0
•
•
/
/
/ /
¦ {
ч
*-~
-—.—•
о,
1
\ 1
1 i
где y4.v — область действительного евклидова пространства <М%,
причем /(/, X) равномерно непрерывна по л: на каждом_ замкну-
замкнутом подмножестве It X Вх, где
BX(^ZAX — компакт (т. е. ограничен-
ограниченное замкнутое множество) (рис. 65);
2) f(t, x) почти периодична по /
равномерно по х на любом BX(ZAX.
В этом случае в силу теоремы
существования [11] для любых на-
начальных данных ^о G h и хо G Ах
будет существовать решение x = x(t)
системы St такое, что x(to) = x<,
(вообще говоря, не единственное).
Рис. 65. Из условия 1) и 2) вытекает,
что f(t, x) ограничена на каждом
множестве Ity^Bx. Действительно, пусть s^>0 фиксировано и
8 = 8 (е) — соответствующее положительное число, определяемое
на основе равномерной непрерывности по х вектор-функции f(t, x)
на 1(ХВХ- Для каждой точки Х^ВХ построим сферу Sb(x).
Из бесконечного покрытия \J Ss(x)^)Bx выберем конечное под-
х?Вх
покрытие
USe(**)DS*.
ft =1
Так как вектор-функции f(t, xk) (k=l N) почти перио-
периодические по t, то они ограничены (§ 2), и пусть
Г, = тах||/(/, х„)\\.
k
Для любой точки х^Вх найдется сфера S^(xk)~Z)^C- Поэтому
\\f(t, x)\\^\\f(t,xk)\\ + \\f(t, x)-f(t, **)
т. е. f(t, х) ограничена на It X Вх.
Пусть {hp} — произвольная последовательность действительных
чисел. Так как вектор-функция f(t, x) почти периодична по t,
§ 19] tf-КЛАСС ПОЧТИ ПЕРИОДИЧЕСКОЙ СИСТЕМЫ 429
то в силу обобщенной теоремы Бохнера (§ 16) для каждого х ? Ах
существует подпоследовательность \hq} (q = q (/?)) такая, что по-
последовательность {f\t-{-hq, x)} сходится равномерно по t на оси
— оо<^<^оо. В силу условий 1) и 2) на множестве С =/, ХВХ
число 8 = 8 (е) ^> 0 для равномерной непрерывности по t вектор-
функции f(t, x) можно выбрать не зависящим от точки (/, х),
а длина / = /(е)^>0 для почти периодической вектор-функции
f(t, х0) (Хо ? Вх) может быть взята не зависящей от точки хй.
Поэтому, выбирая на множестве С всюду плотное множество
точек (tr, xr) (/" —1, 2, ...), по аналогии с доказательством обоб-
обобщенной теоремы Бохнера (§ 16) легко доказать, что существует по-
последовательность {hr}, для которой последовательность {f(t-\-hr, x))
сходится при г->оо равномерно по совокупности переменных
(t, X) на C = It У(ВХ, где Вх— данный компакт.
Более того, полагая
где Вх] — компакты, и используя диагональный процесс, можно
построить последовательность {f(t-\-hs, x)} (s=l, 2, ...), кото-
которая будет сходиться равномерно на любом замкнутом мно-
множестве It X Вх, где Вх — компакт. В этом случае предельная
функция
g{X, t) = \i
будет равномерно непрерывна по X на каждом множестве 1(У(ВХ
и почти периодична по t равномерно по х на этом множестве
и, следовательно, непрерывна по совокупности переменных (t, x)
на ItXAx.
Пусть
№ + нр- *) (Р=1. 2, ...), (SMp)
где
t, x) при
В таком случае будем говорить, что система St+h при р-+оо
сходится к системе
где h обозначает последовательность {hu 1ц, ...), что условно
записывается следующим образом:
SM=\\mSM A9.1)
р-юа Р
430 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ 'ТОП.
Близость систем (St+h ) и (St+h) в точке (t, х) будем оценивать
абсолютной величиной р
\St+h-St+hp\ = \\g(t, X)-f(t + hp, x)\\,
обладающей обычными свойствами. Заметим, что в силу преды-
предыдущих рассуждений сходимость
SMp-*Stih при р->оо-
можно предполагать равномерной по совокупности переменных (t, x)
на каждом множестве It X Вх, где В* — компакт.
Для краткости будем называть системы (St+h) присоединенными
к системе (St). Заметим, что каждая присоединенная система,
очевидно, является почти периодической и для нее справедливы
условия 1") и 2).
Определение (см. [76], [73]). Совокупность всех присо-
присоединенных систем St+h, соответствующих всем последовательно-
последовательностям {hp}, для которых существуют равномерные пределы A9.1),
будем называть Н-классом почти периодической системы St, т. е.
а всякую систему St+h ? Я (St) будем называть представителем
Я-класса.
Таким образом, Я-класс системы St является замыканием
всех смещенных систем St+h .
Заметим, что в Я-класс системы St входят все системы вида
g=/(* + a, у) (а = const),
так как в качестве последовательности {hp} можно выбрать схо-
сходящуюся последовательность а, а, ...
Отметим основное свойство Я-класса почти периодической
системы St.
Лемма. Н-класс почти периодической системы St определяется
любым своим представителем St+h, т. е.
Доказательство. Пусть
S/ = St+h = lim
р-»оо
т. е.
SM — lim St+k
§20] ОГРАНИЧЕННЫЕ РЕШЕНИЯ ПОЧТИ ПЕРИОДИЧЕСКИХ СИСТЕМ 431
Имеем
l^-S^K-1 A9.2)
при p>iVb (t, x)?ItXBx и
\SM-St+hp\<^ A9.3)
при p>N,, (t, x)QItXBx.
Заменяя в неравенстве A9.2) t на t-\-kp, будем иметь
|Ц-^ЛК{ A9.4)
при p>Nu (t,
Из неравенств A9.3) и A9.4) при р^>тах(Л/ь iV2), (t, x) ?
ItXBx получаем
т. е.
p-*co
и, значит,
Таким образом,
Аналогично показывается, что
H(St)(ZH(St+h).
Следовательно,
§ 20. Ограниченные решения почти периодических систем
Рассмотрим почти периодическую систему St со свойствами
1) И 2).
Пусть | = ?(/) — ограниченное решение системы St, опреде-
определенное в максимальном интервале а <^ t <^ р и для всех / ^ (а, р),
принадлежащее некоторому компакту КХС1АХ. Тогда из извест-
известной теоремы существования решений системы дифференциальных
уравнений вытекает, что решение | (t) бесконечно продолжаемо
432
ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
[ДОП.
влево и вправо, т. е. существует в бесконечном интервале
(— оо, оо), причем
sup||i(OH = c<oo.
t
Определение. Следуя Америо [76], ограниченное решение
КО G &х (t G It) почти периодической системы_S, называется раз-
разделенным (separated) в данной области I, X Вх, если или оно
единственно в Вх, или для всякого другого ограниченного реше-
решения т] (t) ? Вх при t ? It вы-
выполнено неравенство
О
B0.1)
где р — положительная по-
постоянная, зависящая только
от | @ (рис. 66). В дальнейшем
t мы будем придерживаться
изложения Кордуняну [73].
Рис. 66. Л е м м а 1. Если все огра-
ограниченные решения \(t) (^ Вх
почти периодической системы St_ разделены в It X Вх, где
Вх — компакт, то в области 11 X Вх существует лишь конечное
число ограниченных решений.
Доказательство. Пусть {|@} — множество всех огра-
ограниченных решений в It X Вх. Так как Вх — компакт, то мно-
множество функций {|@} равномерно ограничено, т. е.
sup.
Кроме того, имеем
l(t)=f(t, КО),
где f(t, х) ограничена в 1(У(БХ (§ 19), и, значит,
pi
Отсюда
у ко-ко и=И/а ut))dt\\^\\\f{t,
Следовательно, множество функций {|@} равностепенно непре-
непрерывно.
§20] ОГРАНИЧЕННЫЕ РЕШЕНИЯ ПОЧТИ ПЕРИОДИЧЕСКИХ СИСТЕМ 433
Если множество {§(?)} бесконечно, то в силу теоремы Арцеля
(гл. V, § 2) существует последовательность ограниченных реше-
решений lp(t)?ItXBx (p=\, 2, ...) такая, что
S,<0l?S*(9 при р^аэ
равномерно на каждом ограниченном интервале а <^<С?> причем
предельная вектор-функция |* (t) на основании непрерывной за-
зависимости решений от параметра есть ограниченное решение си-
системы St в It X Вх-
Так как
infill* (9-1,@11 = 0,
*.р
то решение |* (t) не является разделенным в It X Вх.
Лемма доказана.
Лемма 2. Если почти периодическая система_St допускает
ограниченное решение § (t) ? Вл при ^ ^ lt, где Вх — компакт,
то любая присоединенная система Si+h также имеет ограничен-
ограниченные решения ц (t) (^ Вх при t ^ It.
Доказательство. Пусть правая часть системы St+h есть
g(t, x) = limf(t + hp, x),
р-»со
где
f(t-\-h X)l?g(t, X) при Р-+СО
t, X
и (t, x) ? It X 5д.. Рассмотрим последовательность вектор-функций
t|p@ = S(' + Ap) (P = l, 2, ...),
где, очевидно,
4pWG5, при /?/„
причем
Чя@=/(' + Ар. V (р=1, 2, ...).
Эта последовательность равномерно ограничена и равностепенно
непрерывна. Следовательно, существует предел некоторой ее под-
подпоследовательности
t|@ = Hmt| (9-
Очевидно,^ ц (t) является ограниченным решением системы S/+h
и r\(t)?Bx при t?It.
Лемма 3. Если почти периодическая система St допускает
положительно ограниченное решение | (t) ^ Вх при 15= ^о. где
Вх — некоторый компакт, то каждая присоединенная система St+h
имеет ограниченное решение r\ (t) ^ Вх при t ^ It.
434 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
Доказательство. Рассмотрим множество вектор-функций
Ip(t) = l(t + P) (/> = 1, 2, ...)•
Очевидно, tp(t) есть решение системы
P,lp) (p=l, 2, ...),
определенное в промежутке [to — p, оо), причем %p(t)^Bx при
t^t0 — р. Поэтому для любого промежутка [Т, оо) существует
подпоследовательность {hp\, для которой последовательности
{1лр@} и {/(^+^Р. •*)} являются сходящимися при р->-оо рав-
равномерно по tvi х в каждой области [Г, Г'] Х^* (Т'^>Т). Пола-
Полагая Т = — 1, — 2, .. •, диагональным процессом построим после-
последовательность {|ft (t)} такую, что на всей оси —оо <^ t <^ со имеем
ft
равномерно на каждом ограниченном интервале (а, !3) ? /^ причем
f(t-\-hp, X)l?f(t, X) при р^оо
и (/, *)?/,ХЯ«._
Отсюда 1 (^) ^ Бд. при / ^ // и I (/) является ограниченным
решением системы
входящей в Н-класс системы S,. А так как^(§ 19, лемма) Я-класс
системы St совпадает с Я-классом системы St, то в силу леммы 2
всякая присоединенная система St+h также будет иметь ограни-
ограниченное решение ц (t) ? Вх при t?It.
Лемма 4. Если почти периодическая система St имеет огра-
ограниченное решение % (t) ?ВХ при t ? It и все ограниченные реше-
решения ц (t) ^ Вх при t^ 1( присоединенных систем St+h ^ H (St)
являются разделенными в Ity^Bx (Вх — компакт), то они рав-
норазделенные в Ity..Bx, т. е. существует число р^>0, общее для
всего класса Н (St) и такое, что_ для любых двух различных огра-
ограниченных решений i\'(t) ?IfXBx и ц"(t)?ItXBx произвольной
системы S1+h выполнено неравенство
!l
Доказательство. В силу леммы 1 система St имеет ко-
конечное число ограниченных решений ?,i(t) Ijv(O> содержа-
содержащихся при t (^ It в компакте Вх, причем
§ 201 ОГРАНИЧЕННЫЕ РЕШЕНИЯ ПОЧТИ ПЕРИОДИЧЕСКИХ СИСТЕМ 435
Рассмотрим ограниченные решения {f\(t)\ произвольной си-
системы S/+A такие, что т] (/) ? 11 X Вх. В силу леммы 2 эти реше-
решения существуют, а так как они по условию леммы являются
разделенными, то число их А^ конечно. Так как Se+h ? Н (St),
то для некоторой последовательности {hp} существуют пределы
(q = \ N) B0.2)
равномерно на каждом конечном интервале а<^<^р. Вектор-
функции r\q(t) (q=l, ..., N) являются ограниченными решениями
присоединенной системы St+h, содержащимися при t^_It в ком-
компакте Вх. Очевидно, при г Ф s имеем
inf || 1, (/ + hp) -Ъ,(* + К) II = ^ IIЬ @ - Is (О II ^ Р > О
и, следовательно,
inf|K@-4,@||=P>0. B0.3)
t, гфв
Таким образом, ограниченные решения цд (t) (q = 1, ..., JV)
попарно различны и, значит, NV^N. Так как (§ 19) S,?H (St+h),
то аналогично имеем N^Ni\ отсюда Ni = N, т. е. число огра-
ограниченных решений ц (t), целиков содержащихся в компакте Вх,
для всех присоединенных систем S/+ft одно и то, же, причем все
эти решения могут быть получены по формуле B0.2). Отсюда на
основании неравенства B0.3) вытекает справедливость леммы.
Замечание. Если ограниченные решения почти периодиче-
периодической системы St разделены в области It X Вх, то отсюда еще не
следует, что в этой области являются разделенными и ограни-
ограниченные решения всех присоединенных систем St+h.
Пример (см. [77], [67]). Рассмотрим скалярное уравнение
fif)x, B0.4)
где
Так как ряд B0.5) равномерно сходится на всей действительной
оси — оо <[ t <[ оо, то / @ — почти периодическая функция (§ 4),
Интегрируя уравнение B0.4), будем иметь
B0.6)
436 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
где
2sin2iB0 7)
Пусть n — произвольное натуральное число и
г„=1 -3... Bм+1)т.
Так как все члены ряда B0.7) неотрицательны, то, учитывая,
что sini7rFjjrLrT. = l при k = Q, 1, ..., п, имеем
Z (Zrt -у- 1 )
2/e+i °
А=0 о
Следовательно, функция Z7 (^) положительна и неограничена на
оси —оо<^/<^оо. Отсюда на основании формулы B0.6) уравне-
уравнение B0.4) имеет единственное ограниченное решение
х = 0,
соответствующее с = 0. Таким образом, решение является раз-
разделенным в любой области It X Вх.
С другой стороны, для последовательности функций \f(t-\-tn)},
принимая во внимание, что " ==irBr -f- 1), где г — целое чис-
число при 0 sg k s^ n, имеем
п со
. t-\-tn , у 1 . t-\-tn
Sln 2k+ \ + Zi BA+ IK Sln W+T~
k=n+l
со
. t . VI 1 . t-\-tn
mt Zi !2kSm
k=n+\
причем е„ (^) =^ 0 при п -»- oo. Отсюда
n
VI 1
~~ L Bk+
ft0
§ 2Ц ТЕОРЕМЫ АМЕРИО И ФАВЛРА 437
и поэтому уравнение
ft = -f(t)y B0.8)
является присоединенным к B0.4). Общее решение уравнения
B0.8) имеет вид
причем
inf[y(t)\ = Q.
t
Таким образом, все решения уравнения B0.8) ограничены, но,
очевидно, не являются разделенными.
§ 21. Теоремы Америо и Фавара
Теорема Америо (см. [76]). Если, почти, периодическая
система
имеет ограниченное решение | (/), содержащееся в некотором ком-
компакте Вх при t ? It, причем ограниченные решения из Вх всех при-
присоединенных систем S!+h разделены в It~X Вх (§ 20), то все эти
ограниченные решения почти периодические.
Доказательство [73]. Пусть ! = §(/) — ограниченное
решение системы St такое, что t(<N Bx при t?lt. Чтобы убе-
убедиться в почти периодичности этого решения, достаточно дока-
доказать, что вектор-функция | (/) нормальная, т. е. из любой после-
последовательности ее сдвигов {% (t-\-hp)} можно выделить подпосле-
подпоследовательность {\{t-\-ha. )}, равномерно сходящуюся на всей дей-
действительной оси — оо <^ t <^ -\- со.
Предположим противное. Пусть существует последователь-
последовательность {^(t-\-hp)}, сходящаяся равномерно па каждом конечном
промежутке а<^/<^р (этого всегда можно добиться в силу тео-
теоремы Арцеля), причем любая ее подпоследовательность ||(/-[-?р)}
не сходится равномерно на бесконечной оси —со<^<^схэ. Так
как f(t, x) почти периодическая, то на основании теоремы Бох-
нера можно предполагать, что последовательность {f(t-\-kp, x))
сходится равномерно на lt X ~ВХ.
Пусть р -- пОоТОжительное число, характеризующее равнораз-
деленность ограниченных решений систем {St+Jl} в lty^Bx
438 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
(лемма 4 из § 20). Если ограниченное решение |(?) единственно,
то число р>0 можно взять произвольным.
Положим
<РИ(О=1М (* + *„)-?(* + *,) || {Р<Я)
Так как последовательность {%,(t-\-kp)} сходится в каждой точке
/ ? 11, то при достаточно больших ряд множество If- ® не пусто,
причем
Р<4
Очевидно, урд {t) непрерывна на It.
Пусть
8р? = sup <ри(О<-у-
Если
lim Sw = 0, B1.1)
p,q-*co
то последовательность {|(^-|-^р)} сходится равномерно на оси It.
Действительно, при условии B1.1) для любого е^>0, где
0 <^ е <^ ~, имеем
8р?<е ПРИ
Отсюда срр9(t)<е<\, если t?l?'9\ причем срр?(О>-у. если
t?lf'4\ Но функция <рм@ непрерывна на It\ поэтому l\p'q) = It
при р, q^N,, и, следовательно, ||(^ + ^р)} сходится равномерно
на (— со, -)- оо). В этом случае теорема доказана.
Предположим противное, т. е. что соотношение B1.1) не имеет
места. Тогда
Пт 8р? = 2т>0 B1.2)
р, 4->со
и, следовательно, найдутся последовательности {рг} и {17,.} такие,
что
W>T (г=1. 2,...).
Отсюда в силу определения функции &pq вытекает, что существует
последовательность {tr} ? l\pr' qr\ для которой
tpr9r Vr) ^ У
§ 21] ТЕОРЕМЫ АМКРИО И ФАВАРА 439
и, значит,
¦}^n(tr-\-kPr)-t(tr + kgr)\\^-t (r = l,2,...). B1.3)
Так как §(/) ограничена, то из последовательностей {%(tr-{-kp)}
и \%(^r-7~kq)) можно выбрать одновременно сходящиеся подпо-
подпоследовательности:
s-»oo
где t's — tr, ls = kp w \is — kq . Переходя к пределу в неравен-
неравенстве B1.3) по последовательности rs(s~\, 2, ...), будем иметь
-J^||«-w||^|. B1.4)
Рассмотрим последовательности {%(t -\- t's-\- Xs)} и {|(/ -)- t's-\- \i.s)\.
Так как эти последовательности равномерно ограничены и равно-
равностепенно непрерывны, то по теореме Арцеля (гл. V, § 2) из них
можно выделить подпоследовательности, сходящиеся равномерно
на каждом конечном интервале а <^ t <^ р. Чтобы не усложнять
обозначений, мы будем предполагать, что сами эти последова-
последовательности сходятся, т. е. существуют
Ъ @ = lim g(* + /; + (i,).
S-KO
Вектор-функции tj, (t) и щ (t) являются, соответственно, решениями
присоединенных систем
где
gi(t, y) = \imf(t-\-t's-\-\5, у) B1.5)
И
g.2(t, y) — ]\mf(t-{-t's-\-}}.s, у), B1.6)
440 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
причем опять предполагается, что в случае надобности выбрана
равномерно сходящаяся на lt X Вх подпоследовательность.
Покажем, что пределы B1.5) и B1.6) совпадают. Действи-
Действительно, так как согласно нашему выбору последовательность
\f(t-\-kp, х)} сходится равномерно на ItX~Bx и {).s\, {[xs\ суть
подпоследовательности последовательности {kD\, то
= g(t, у)
\?-s> У)\\<*
при s^N (s) и (t, у) ? // X бх. Отсюда
II gi V, у) - gi (t, у) || =с || gi (t, у) -
s, У) II +
если s^iV(s) и (t, y)?ItXBx.
Следовательно,
t (t, у) = gi (t, у) при (t, y)tItX B~x.
Таким образом, % (t) и % @ являются ограниченными реше-
решениями одной и той же присоединенной системы St+h в области
ItX~Bx. Так как
причем на основании неравенства B1.4) имеем
y^Ni@)-%@)||<|, B1.7)
то эти решения различны. Поэтому в силу выбора числа р должно
быть выполнено неравенство
inf || m (*)-%(') II s*P>0.
t
Однако это противоречит неравенству. B1.7).
Теорема доказана.
§ 211 ТЕОРЕМЫ АМЕРИО И ФАВЛРЛ 441
Следствие. Еслл почти периодическая система St имеет
единственное ограниченное решение g (t) и все системы ее Н-класса
{St+h\ также обладают единственными ограниченными решениями,
то все эти ограниченные решения почти периодические.
Рассмотрим линейную однородную систему
где Р (t) — почти периодическая матрица, и пусть
dt
где
— ее Я-класс.
Теорема Фавара (см. [77], [67]). Если каждая присоеди-
присоединенная система y,t+h не имеет ограниченных нетривиальных реше-
решений, то для любой неоднородной системы
%t = P(f)y+f(t), (St)
где f (t) — почти периодическая вектор-функция, ее ограниченное
решение, если оно существует, является почти периодическим.
Доказательство. Я-класс системы St имеет вид
где
Так как разность двух решений неоднородной системы St+h пред-
представляет собой решение однородной системы 2^+/7, то в силу
услозий теоремы любая система Sf+!l имеет единственное
ограниченное решение. Отсюда на основании следствия к теореме
Америо получаем, что ограниченное решение системы St, если
оно существует, является почти периодическим.
Замечание. В условиях теоремы единственные ограничен-
ограниченные решения присоединенных систем Sl+h также будут почти
периодическими.
442 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
Упражнения
1. Исследовать на почти периодичность функции: sin (sin х V2), sin i -*r |,
sin л:2, cosy^x, In B + cos л:-j-cos x ]/2), sgn (sin x).
2. Доказать, что если f (x) —действительная п. п. функция, то
О , /(x)<0
О , /(*)ssO,
также п. п. функции.
3. Доказать, что если f (х) — действительная п. п. функция и
то существует относительно плотное множество точек {i}^/x таких, что
4. Показать, что если/(лг) — непрерывная «-периодическая функция на
(—со, +°°). то
о
5. Пусть f (х) — п. п. функция и
М {/(*)} =0.
Доказать, что функция /(х) имеет относительно плотное множество
нулей.
6. Показать, что для функции
при у^€(—оэ> +°°) имеем
М{/(лг)е-д*}=0.
7. Пусть f(x, у) почти периодична по х при ^^ К, где К—компакт, и
равномерно непрерывна по у на множестве /Л х К.
Доказать, что /(лг, у) почти периодична по х равномерно относительно
параметра _у? У.
8. Пусть х — скаляр и
= o(t
где a(t) и Ь (t) — действительные почти периодические функции, причем
a (t) Э= а > 0,
где а — положительная постоянная.
Доказать, что уравнение (*) имеет единственное почти периодическое
решение (см. [78]).
9. Пусть в скалярном уравнении первого порядка
/
УПРАЖНЕНИЯ 443
f(x) — монотонно возрастающая функция такая, что
/' (х) :> k > О
(k — постоянная), и g (t) — почти периодическая функция.
Доказать, что существует единственное почти периодическое решение
уравнения (**) (см. [79]).
10, Пусть
— неавтономная система, где f(t, х) ? Cf^ kh X е$х) и f(t, x) «-перио-
«-периодична по t.
Если система (***) допускает ограниченные на It решения, которые
являются разделенными в некоторой области It х.Ъх(Вх— компакт), то все
эти решения «-периодичны.
И. Пусть
|=Ас+/(д;) + «((), (****)
где A = [ajk] — постоянная (п X и)-матрица, f (х) ^ С У{<МХ), g (t) — п. п.
вектор-функция и у. — скалярный параметр, причем
Re А; (А) ф 0 и/@)=/@) = 0.
Доказать, что при малых | jj. | уравнение (****) имеет единственное п. п.
решение (см. [28]).
12. Пусть
ft = Ay+f(t), (I)
где A — \ajk] — постоянная (п X и)-матрица и f(t) — конечный тригономе-
тригонометрический полином:
N
/"@=2 (аР cos lpt + bp sin у)-
Доказать (см. [80]), что система (I) имеет почти периодическое решение
тогда и только тогда, когда выполнены условия ортогональности:
где г|з5 (<) (s = l, ... , q) — полная совокупность линейно независимых п. п.
решений сопряженной системы
%—А'х. (II)
13. Модулем называется числовое множество оМ = {а} такое, что если
а, ?(^Л то а — Р?а//Л
Пусть линейная система
444 ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ [ДОП.
с постоянной матрицей Лис почти периодическим свободным членом f(t)
допускает единственное почти периодическое решение r\ = i)(t),
причем почти периодическая вектор-функция / (t) имеет множество показа-
показателей Фурье, принадлежащее модулю <М. Доказать, что показатели Фурье
решения r\ (t) принадлежат этому же модулю.
14. Пусть
dx
автономная система, где f (х) ? С1
Доказать, что: а) для каждого ограниченного измеримого множества
^ его объем
инвариантен относительно данной системы (см. [12], [35]);
б) всякое ограниченное решение Z (t) системы, двусторонне устойчивое
по Ляпунову при t-->±co, является почти периодическим (см. [81]).
ПРИЛОЖЕНИЕ
ЖОРДАНОВА ФОРМА МАТРИЦЫ
1°. Прямая сумма линейных подпространств.
Пусть ?л — я-мерное векторное пространство (гл. I, § 5), эле-
элементами которого являются комплексные п-векторы:
где хи ... , 'хп— координаты вектора х в некотором базисе.
Определение!. Подмножество ЧЖС%" называется подпро-
подпространством линейного пространства 2", если оно само является
линейным пространством относительно введенных в 8" основных
операций умножения на число и сложения, т. е. из условия
х> У ?Е -1-1' следует, что ах-\- $у ?j Ш, где а и р — произвольные ком-
комплексные числа.
Заметим, что любое подпространство 9Я содержит нулевой
элемент 0, так как если | ? Ш, то
О = 0ЮШ.
П р и м е р. Совокупность векторов
у = Ах,
где А — (их «)-матрица, очевидно, представляет собой подпространство Ш
в 1'л.
В частности, при А —О и Л=? будем иметь так называемые несоб-
несобственные подпространства Ш = 0 и Ш = $.'л.
Отметим, что сумма подпространств
где л; ^ "В?! и. у ?j 9)ц, а также их пересечение
Mi П a)f«
суть также подпространства в ?Л.
Пусть л;A), ... , х{к) — максимальное число линейно
независимых векторов, содержащихся в линейном подпростран-
подпространстве Ш. В таком случае
446 ПРИЛОЖЕНИЕ
где аи ... , ak — произвольные комплексные числа, т. е. jcA), ...
... , xik) является базисом для Ш. Число k называется размер-
размерностью подпространства Ш, т. е.
dim аи = А,
где 0 =sS k s=s n.
Обратно, множество
натянутое на векторы х{1\ ... , x(h) E4 , ak — ком-
комплексные числа), является линейным подпространством, причем
если данные векторы линейно независимы, то размерность под-
подпространства Щ равна k.
Определение 2. Линейное пространство Ш называется пря-
прямой суммой (см. [5]) линейных подпространств Ш;- (/ = 1, 2 s),
если каждый вектор х ? Ш допускает единственное пред-
представление
где ха)?Щ (/=1, 2, ... , s).
Из определения 2 вытекает, что соотношение A) выполнено
тогда и только тогда, когда нулевой вектор 0 не допускает не-
нетривиального разложения
где |l;) (^ Ttj (/= 1, 2, ... , s), причем не все векторы I'-" нулевые.
Очевидно, из A) следует, что
Wj Г) S»t = 0 при / ^ k. B)
Обратно, если для слагаемых суммы A) попарно выполнены
условия B), то сумма A) прямая.
Теорема 1. Если линейное пространство 1(" представляет
прямую сумму подпространств 5JJ/ (/ = 1, ... , s):
$?"=ан,© ... ®т„
то объединение любых базисов этих подпространств является
базисом пространства ?л.
Обратно, если объединение некоторых базисов подпространств
Э)?у- (/=1, ... , s) есть базис пространства 2п, то 8Л представ-
представляет собой прямую сумму этих подпространств.
ЖОРДАНОВА ФОРМА МАТРИЦЫ 447
Доказательство. 1) Докажем сначала первую часть тео-
теоремы, причем доказательство будем проводить для прямой суммы
двух подпространств
in ~ W © Шя C)
размерностей р и q. Переход к общему случаю, очевидно, не пред-
представляет затруднений.
.Пусть у{[) у(р) и гп), ... , г{д)—некоторые базисы,
соответственно, подпространств Шр и Шд. Из формулы C) сле-
следует, что для любого вектора х (^ !*" справедливо представление
x=y-\z, D)
где у ? Шр и г ? W. Отсюда
t t M(/), E)
где аь ... , а„ и Рь ... , Р9 — координаты векторов у п z в соот-
соответствующих базисах. Так как представление E) единственно,
то векторы уA\ ... , у{р), г{1), ... , z{q) линейно независимы и
образуют базис пространства 8".
2) Докажем теперь вторую часть теоремы. Пусть для под-
подпространств Шр и Шя существуют базисы _у(". ... , у{р) и
гA), ... , ?(<?), объединение которых есть базис пространства S".
Тогда для каждого х ^ l справедливо разложение - E), и это
разложение единственно. Но в таком случае имеет место един-
единственное представление D) и, следовательно, 1!" есть прямая
сумма подпространств Шр и Ш9.
Следствие. Сумма подпространств
является прямой тогда и только тогда, когда
dim Ш = 2 dim Wij.
Определение 3. Пусть
Ш Ц) Ш.
— вложенные'подпространства линейного пространства 8".
Векторы |A), ... , |(р) из Ш будем называть линейно незави-
независимыми относительно подпространства 91 (см. [10]), если 1) они
линейно независимы и 2) подпространство, натянутое на эти век-
векторы, имеет с 9i лишь нулевое пересечение, т. е.
р
У=1
448 ПРИЛОЖЕНИЕ
тогда и только тогда, когда
оц = а., =.., = %р = 0.
Заметим, что векторы I'1' |*-0), линейно независимые от-
относительно 91 = 0, являются линейно независимыми в обычном
смысле.
Теорема 2. Пусть
s»=щт э тт .о.о a»i э я?о=о F)
— цепочка вложенных друг в друга различных подпространств и
If, ... , Щ (Р = 1. ••• . т' kp^\) G)
— максимальная система векторов из Шр, линейно независимых
относительно Шр i. Тогда объединение всех систем G) пред-
представляет базис пространства 8я.
Доказательство. Прежде всего, заметим, что полная со-
совокупность векторов G) является набором линейно независимых
векторов пространства Й". Действительно, пусть
2 2
= 0, (8)
где a(?) = 0 при q^>p и a<f) =? 0 для некоторого г^[1Др]. Тогда
*р
2 af.;I|l.p) в силу соотношения (8) представляет ненулевой эле-
мент из подпространства, натянутого на векторы Цр\ ... , Цр\
принадлежащий подпространству Шр^, что невозможно.
Докажем теперь, что векторы G) образуют базис простран-
пространства 1'л. Доказательство будем проводить методом математиче-
математической индукции по числу т элементов цепочки (исключая Шй).
Если т=\, т. е.
то векторы G) представляют собой максимальную систему линейно
независимых векторов в I'" и, следовательно, образуют его базис.
Предположим теперь, что теорема верна для любой цепочки
вложенных подпространств
содержащей т — 1 элементов (т^>1), отличных от нуля. Иными
словами, мы предполагаем, что базис подпространства Шт^ может
ЖОРДАНОВА ФОРМА МАТРИЦЫ 449
быть построен указанным выше способом. Пусть х ? Шт. Можно
предполагать, что векторы
1(.т) l{km\ X (9)
т
линейно независимы, ибо в противном случае вектор х являлся
бы линейной комбинацией векторов Цт^ I*™1 и, следова-
следовательно, теорема была бы доказана. Подпространство
натянутое на векторы (9), в силу свойства максимальности си-
системы G) имеет с подпространством Шт_\ ненулевое пересечение
где, очевидно, b Ф 0. Но на основании индукционного предполо-
предположения для подпространства Шт_\ теорема верна, т. е. z пред-
представляет собой линейную комбинацию векторов %(т~1), ...
• •• . 1а""'. •¦• » l^1'. ••• . Щ]- Таким образом, из A0) получаем,
что произвольный вектор х ?j Шт может быть выражен в виде
линейной комбинации векторов %(р (р = \, ..., т; /= 1, ..., kp).
Отсюда вытекает, что система векторов G) есть базис про-
пространства Йл, что и требовалось доказать.
Следствие. Для каждого подпространства Шр (d im Шр — р)
линейного пространства 8" существует дополнительное подпро-
подпространство S)i?(dim9)i* = <7) такое, что
Действительно, имеем
?ч D Жр D 0.
В пространстве ?ге выберем максимальную совокупность векто-
векторов т]A), ... , ц{9), линейно независимую относительно W, и
пусть |A), ... , |(р) — максимальная совокупность векторов, ли-
линейно независимых относительно 0, т. е. линейно независимых
в обычном смысле. Объединение
?A) ?(/>) «A) п(Я)
в силу теоремы 2 представляет базис пространства 8Л, поэтому
Отсюда
где Шя — подпространство, натянутое на векторы т]A), ...,
15 Б, П. Демидович
450 ПРИЛОЖЕНИЕ
2° Инвариантные подпространства. Пусть в век-
торном пространстве 8" задано линейное преобразова-
преобразование Л (гл. I, § 5), переводящее 2" в самое себя или в свою
правильную часть, т. е.
Определение 4. Подпространство Ш?2$.п называется ин-
инвариантным относительно преобразования А, если каждый век-
вектор х С Ш преобразованием А переводится в вектор у = Ах ? Ш,
т. е.
Am с ш.
Очевидно, нулевое подпространство и само пространство 8"
инвариантны относительно любого линейного преобразования в 8Л.
Кроме того, сумма и пересечение подпространств простран-
пространства 8Л, инвариантных относительно линейного преобразования А,
суть также ^подпространства, инвариантные относительно преоб-
преобразования А.
Если в пространстве 2п выбран базис ё! гп и
...-\-аппгп,
то преобразованию А соответствует матрица (матрица преобра-
преобразования в данном базисе, гл. I, § 5)
А =
ап ... а1п
A2)
Матрица А, очевидно, является транспонированной относительно
матрицы системы A1). Отметим, что если A = [aJk], то а;-к пред-
представляет собой /-ю координату й-го преобразованного базисного
вектора.
Отсюда для любого вектора
имеем
ЖОРДАНОВА ФОРМА МАТРИЦЫ
451
Таким образом, вектор у = Ах в данном базисе будет иметь
представление
где А — матрица преобразования.
Теорема 3. Если линейное пространство распадается в пря~
мую сумму нескольких подпространств:
инвариантных относительно данного линейного преобразования
А в ?", то в надлежащем базисе матрица А этого преобразо-
преобразования имеет квазидиагональный вид
As), A3)
где Aj — квадратные матрицы, соответственно, порядков П) =
= dimsDJ/ (/=1 s) и «! + ••• + ns = n.
Доказательство (см. [5]). Выберем в подпространствах
Шь Wit ..., Wls соответственно базисы: г^\ ..., е^; е^\ ...
..., ей; ...; е^\ ..., 8^>. Тогда в силу теоремы 2 их объединение
будет базисом пространства 2п. Так как
при p^q (p=l, ..., s), то
Отсюда, полагая
будем иметь формулу A3).
Замечания. Матрицу Лр(р=1, ... , s) можно рассматри-
рассматривать как матрицу преобразования Ар, индуцируемого данным
15*
452 ПРИЛОЖЕНИЕ
преобразованием А на инвариантном подпространстве Шр; иными
словами, преобразование Ар есть преобразование А, рассматри-
рассматриваемое лишь на подпространстве Шр.
3° Алгебра преобразований. Пусть А и В — преоб-
преобразования, действующие из ?" в ?". Для х (^ 8" естественно
определяются комбинированные преобразования (см. гл. I, § 5):
а) произведение преобразования А на скаляр а:
(в частном случае, если а = 0, имеем нулевое преобразование
0л: = 0);
b) сумма преобразований А и В:
(А + Ё)х=Ах-\-8х;
c) произведение преобразований А и В:
(АВ)х=А(Вх)
и
(ВА)х = В(Ах).
В общем случае
АВфВА.
Вводя единичное преобразование
можно определить обратное преобразование Л как преобразова-
преобразование (если оно существует), удовлетворяющее условию:
Если А~х и В'1 существует, то легко проверить, что
Обычным способом определяются целые степени преобразо-
преобразований:
причем
Л° = ?.
Очевидно, при любых целых р и q имеем
ЖОРДАНОВА ФОРМА МАТРИЦЫ 453
Используя понятие степени преобразования для заданного по-
полинома
?B)==а0г ~т" alz ~Т---~Гат
с числовыми коэффициентами а0, аи ..., ат, можно найти соот-
соответствующее преобразование
где А ° = Ё .
Покажем, что если преобразованиеА А линейное (гл. I, § 5),
то полиномиальное преобразование <?(Л) также линейное. Дейст-
Действительно, для любых х, _у G ^" и произвольных чисел аир
имеем
к- (ад: -;- р_у) = А (лАх
Лт (ад; + р_у) = Л
Отсюда, умножая эти равенства на коэффициенты а0, аь а.,, ... ,ап
и почленно складывая, получим
т. е. преобразование <р (Л) линейное.
Отметим, что если преобразования А п В линейные, то ал-
алгебраическим операциям над этими преобразованиями соответст-
соответствуют такие же алгебраические операции над их матрицами (в од-
одном и том же базисе).
4° Первая теорема приведения. Пусть Л — линейное
преобразование, действующее из 2Л в 2", и Л — («X я)-матрица
этого преобразования в некотором базисе.
Многочлен
b(\) = det(\E — A) A4)
называется характеристическим полиномом преобразования А
(или матрицы Л), а его корни — характеристическими числами
(или собственными значениями) преобразования Л (а также мат-
матрицы Л).
Как известно, характеристический полином, а следовательно,
и характеристические корни преобразования Л не зависят от вы-
выбора базиса.
Согласно теореме Кейли (гл. I, § 10) матрица Л является кор-
корнем своего характеристического полинома, т. е. полином Д (Л)
аннулирует матрицу А:
Д(Л) = 0.
454 ПРИЛОЖЕНИЕ
Так как алгебра линейных преобразований вполне аналогична
алгебре матриц, то преобразование А также является корнем своего
характеристического полинома, т. е.
Д(Л) = б. A5)
Поэтому полином Д(г) может быть назван полиномом, аннули-
аннулирующим преобразование А.
Ненулевой вектор х, удовлетворяющий условию
А х = 1х,
где X — некоторое число, называется собственным вектором пре-
преобразования А, отвечающим его собственному значению X (ср.
гл. I, § 5).
Если А есть матрица данного преобразования А в некотором
базисе, то собственные векторы преобразования А в этом базисе
могут быть определены как нетривиальные решения однородной
линейной системы (А — ХЕ) х = 0. Поэтому все собственные значе-
значения X преобразования Л являются корнями векового уравнения
det(X? — Л) = 0,
причем для каждого корня Х = Ху существует один или несколько
линейно независимых соответствующих собственных векторов пре-
преобразования А.
Пусть Хи ..., Хт (т^п) — различные собственные значения
преобразования А и ри ..., рт — их кратности (р;-^1, /=1,...
.... т; />! + ••• + Рт = п). Тогда, очевидно, имеем
и, следовательно,
Определение 5. Совокупность всех векторов х ? i", удов-
удовлетворяющих условию:
{А-1]Ё)р)х = Ъ (/=1, ..., т), A7)
где pj — кратность характеристического корня Kj, будем называть
корневым подпространством преобразования А, принадлежащим
его собственному значению Ху1).
1) Обычно (см., например, [5]) под корневым пространством преобра-
преобразования А, принадлежащим его собственному значению 1j, понимается со-
совокупность всех векторов х? I, для которых хотя бы при одном нату-
натуральном k = k[x] выполнено соотношение
(A — l/E^x — O.
Так как впоследствии доказывается, что при построении корневого подпро-
ЖОРДАНОВА ФОРМА МАТРИЦЫ 455
Замечание. Для любого собственного значения Ху преоб-
преобразования А принадлежащее ему корневое подпространство 9W,
содержит собственные векторы этого преобразования, отвечающие
Ху, и, следовательно, не сводится к нулевому вектору.
Действительно, если
то имеем
(Л — ljE)Pix = {A — ijEfr х (А — XjE)x = 0
и, следовательно, х ? Ш;-.
Заметим, что корневое пространство Tlj не содержит собст-
собственных векторов преобразования А, отвечающих его собствен-
собственным значениям кк, отличным от Xj. В самом деле, если
Ау = Ку (У^О),
где Aft ^6 Ay, то
(Л — \jE)pjy = (Л — \jE)pi~ ' (Л —
и, следовательно, _у G -^'/-
Таким образом, преобразование Л на каждом его корневом
подпространстве Wtj (/ = 1, •-., т) имеет единственное соб-
. ственное значение X,-.
Лемма 1. Для всякого линейного преобразования А в %п его
любое корневое подпространство 2)?у является подпространством
пространства S", инвариантным относительно данного преобра-
преобразования А.
Доказательство. Пусть Ш;- (/ = 1, ... , т) — корневое
пространство линейного преобразования, принадлежащее его соб-
собственному значению Ху, т. е. множество всех векторов х (^ ?",
удовлетворяющих условию A7). Для любых х^Ш] и у E Ш]
и произвольных чисел а и C имеем (см. 3°)
(А — \]Ё)р1{гХ -f Рз») = а (Л — Xy?)p/jc + р (Л — Ху?)р/>> =
Следовательно, ajf-j-^S 3)^> т- е. Я)?у есть подпространство
пространства Sn.
странства можно ограничиться показателями k^pj, где pj—кратность ха-
характеристического корня ).j, то определение 5, введенное ради краткости
изложения, эквивалентно обычному.
456 ПРИЛОЖЕНИИ ¦
Подпространство Wj инвариантно относительно преобразова-
преобразования А, так как, учитывая перестановочность преобразований
(А — ~kjE)pi и А, при х ? Ш] получаем
(А — ijEfi Ах=А [(А — ijEfix] = АО = О,
т. е. Ах^Шу.
Теорема 4 (первая теорема разложения). Комп-
Комплексное векторное пространство ?га представляет собой прямую
сумму инвариантных корневых подпространств любого своего ли-
линейного преобразования А, принадлежащих всем его различным
собственным значениям Хь..., Xm(m=^n).
Доказательство (см. [5]). Пусть Д (X) из A4) — характери-
характеристический полином преобразования А. Разлагая дробь 1/Д(Х) на
простейшие, будем иметь
Д(Х) A) {mfm
где A{J< (/=rl,..., ш; /г = 1,..., ру-) — некоторые постоянные.
Отсюда находим
1 = Pi(M i , Pm (X)
где Ру (X) (/ = 1 , ¦ • •, /л) — целые полиномы, причем дроби
Р;. (Х)/(Х — \j)"j — несократимые, т. е. Ру (Ху-) ^ 0.
Таким образом, получаем тождество
1=Р,(Х)Д1(Х) + ...+ Рт(Х)Дт(Х), A8)
где
М*) = -^- (/=1.-,«) 09)
— также целые полиномы.
Для любого вектора х ? 2" положим
XlJ) = P,(A)bj(A)x (/ = 1,..., т). B0)
Так как на основании формулы A8) имеем
Ё= р, (Л) д, (А) +... -j- Pm (Л) дт {А),
то л л
д;=Р1(/1)Д1(Л)х + ... + Рт(Л)Дт(Л)д: B1)
и, следовательно, справедливо разложение
x = xw+ ...-{-х{т). B2)
ЖОРЯАНОВА ФОРМА МАТРИЦЫ 457
Пусть Ж/ — корневое подпространство преобразования А,
отвечающее его собственному значению л, (/ = 1,..., т), т. е.
tEflj = \х ? 8" : (А — )чЁ)р1х = Щ.
Покажем, что хи) ? Ш;. Действительно, используя формулы A9)
и B0), на основании теоремы Кейли получаем
(А — ljE)p]x{1) — Pj (А) А (А) х = 0,
т. е. xU) ? Wlj.
Докажем, что разложение B2) на компоненты х (/) ? ЭД,-
(/ = 1,..., /п) единственно. Действительно, пусть, кроме B2),
имеем
где у{>] ^ ЭДу (/= 1,..., т). Учитывая, что при k Ф j и г
справедливо соотношение
А, (Л> = (Л - a,?)p' ... (Л - X,-.
... (Л _ \mEfmZ = ]"[ (л - Х,?)р* . (Л - \jE)% = 0,
s ^4 ;,
sr? к
и используя формулы B1) и B0), будем иметь
Уи) = t Pk (A) \ (A)yU) = Pj (Л) \j {А)уа) =
= Ру (А) А;. (Л) д; = x{J) (j = 1,..., т).
Таким образом, всякий вектор X (^ ?" единственным
образом может быть представлен в виде суммы B2), где xlj) (^
^ Sty (/=1,..., ш), и, следовательно, пространство ?" является
прямой суммой корневых подпространств:
8" = а»10...еа)?т, B3)
где
Следствие 1. ?слы линейное преобразование А в 8™ имеет
единственное собственное значение Хь то пространство S'! явля-
ется корневым для А, принадлеокащим Хь /п. е.
8я = {jc G 8" : (Л — А.^)".» = 0}.
458 ПРИЛОЖЕНИЕ
Следствие 2. Размерности корневых подпространств 9R/
(у = 1,..., т) совпадают с кратностями соответствующих собст-
собственных значений Ху, т. е.
dim®ij = Pj (/=1 т). B4)
Доказательство будем проводить методом индукции относи-
относительно числа т собственных значений преобразования А.
Если преобразование А допускает единственное собственное
значение ii(m^=l), то его характеристический полином имеет
вид-
Отсюда кратность корня Xj есть рх = п, и эта кратность совпа-
совпадает с размерностью единственного корневого подпространства
Пусть теперьл наше утверждение верно для в.сех линейных
преобразований В любого линейного пространства $k, допуска-
допускающих т — 1 различных собственных значений (т 5= 2).
В пространстве ?л рассмотрим линейное преобразование А,
имеющее т различных собственных значений \и..., лт с крат-
кратностями, соответственно, pi,--., pm, где
Р1 + -- + Рт = П. B5)
Пусть W\j (j = 1,..., т) — корневое подпространство преобразо-
преобразования А, принадлежащее собственному значению Ху. Прямая
сумма
представляет собой некоторое линейное подпространство 8*, на
котором^ на основании приведенного выше замечания преобразо-
преобразование А имеет лишь т — 1 различных собственных значений
Хь ..., Хт_,. В таком случае в силу индукционного предположения
получим
dim 3Rs = ps (s= 1,..., tn— 1).
Кроме того, как было доказано, имеем
8"=a»1e...-ea)fm_1©g»m;
поэтому
т — \ т — 1
п = dim «" = 2 dim 2Й4 + dim Шт ^=^]ps + dim Ша.
ЖОРДАНОВА ФОРМА МАТРИЦЫ 459
Отсюда, учитывая формулу B5), получаем
и, таким образом, наше утверждение доказано.
Следствие 3. Если линейное преобразование А рассматри-
рассматривать на его корневом подпространстве Ш/ (/ = 1,..., п), при-
принадлежащем собственному значению Ху, то характеристический
полином этого преобразования имеет вид
Dj{z) = {z~lJ)p>, B6)
где р/ — кратность корня Ху-.
Формула B6) вытекает из того обстоятельства, что на кор-
корневом подпространстве Ш;- преобразование А имеет единствен-
единственное собственное значение А;-, причем размерность )SRj равна pj.
На основании первой теоремы разложения (теорема 4) и тео-
теоремы 3 получаем первую теорему приведения:
Теорема 4'. Всякую (п X п)-матрицу А, имеющую различ-
различные собственные значения Х1( ..., \т (mscn) с соответствующими
т
кратноапями р , рт, где^р^ = п, путем преобразования по-
добия с некоторой неособенной матрицей S можно привести к
квазидиагональному виду:
S AS'* = diag[ At ()ч),..., Ат(\т)],
где Aj(kj) (/=1,..., т) — квадратная матрица 'порядка pJt
допускающая единственное собственное значение X/, т. е. такая,
что ее характеристический полином имеет вид
Dj (I) = det [Е(рЛ - А, (А,)] = (X - \,)К
Таким образом, остается изучить структуру квадратных мат-
матриц, обладающих единственным собственным значением.
5° Вторая теорема приведения. Для изучения струк-
структуры корневых подпространств линейного преобразования введем
понятие циклического пространства.
Определение 6. Линейное пространство ?п называется
циклическим относительно его линейного преобразования А, если
некоторая цепочка векторов
образует базис этого пространства (циклический базис).
Это определение дословно переносится на инвариантное под-
подпространство.
460
ПРИЛОЖЕНИЕ
Лемма 2. Если А — линейное преобразование в 2п с единст-
единственным собственным значением X и пространство 8" — цикли-
циклическое относительно преобразования
то матрица А преобразования А в циклическом базисе
Ц1 > ЦЭ ^—~ -Owl * • • C« —— ?3 Ц1
представляет собой клетку Жордана
~Х 1 ... О О"
О X ... О О
B7)
J(X) =
О О ... X 1
^о о ... о U
B8)
соответствующую числу X.
Доказательство. Так как пространство,, ?ге является
корневым подпространством для преобразования А, принадлежа-
принадлежащим собственному значению X, то
(см. следствие 1 теоремы 4).
Из соотношений B7), полагая |п+1 = 0, имеем
=l, ..., п),
поэтому
Следовательно, матрица преобразования А в базисе B7) пред-
представляет клетку Жордана B8).
Теорема5(втораятеоремаразложения). Пусть Ш;—
корневое подпространство линейного преобразования А в 8", при-
принадлежащее его собственному значению Xj. Тогда sMj разлагается
в прямую сумму инвариантных подпространств
циклических относительно
B9)
ЖОРДАНОВА ФОРМА МАТРИЦЫ 461
Доказательство. Пусть dim 9йу = Ру A<;/>у<;/г). По-
Положим
где Б;- определяется формулой B9).
Очевидно, имеем
ру ру-1 Э ¦ • • Э ©1D @о = О,
причем <?;,(& = О, 1, ..., pj) — подпространства в 2)iy, инвариант-
инвариантные относительно преобразования By.
Пусть
И*» S(?*> (k=l, ..., Pj) C0)
— все векторы из @ь линейно независимые относительно @fe^i
(определение 3), т. е. векторы C0) линейно независимы и под-
подпространство, натянутое на них, имеет с <2fc_i нулевое пересече-
пересечение, причем число их максимально.
Положим
!?-'>=?;¦ $> (А=1 qh\l<k). C1)
Тогда векторы |^~'' ^®*_г и линейно независимы относительно
@/г 1Л при
Действительно, имеем
?*-<!<*-/> = ?*$?> = 0,
т. е.
Далее, векторы %^~1) линейно независимы, так как, если
ТО
Отсюда, учитывая, что векторы C0) линейно независимы относи-
относительно @й_ь находим
т. е.
462 ПРИЛОЖЕНИЕ
и, таким образом, векторы C1) линейно независимы. Наконец,
пусть
Тогда
и, следовательно,
ft
Но векторы |/f' линейно независимы относительно <Sk-u поэтому
at = a2 =... = a?fe = О,
т. е. # = 0, и, таким образом, векторы §{н~1) линейно независи-
независимы относительно S*_/_i.
Пусть ®r (I s=cr==^pj) — подпространство в 93?/ наивысшей раз-
размерности, содержащее ненулевые векторы, линейно независимые
относительно @г_]. Такое подпространство существует, так как
преобразование Л на инвариантном подпространстве 9)?у имеет по
меньшей мере один собственный вектор | ^ 0, соответствующий
собственному значению Ху-, т. е.
который, очевидно, входит в Si и является линейно независимым
относительно So = 0.
В подпространстве &г построим максимальную систему век-
векторов
линейно независимых относительно подпространства S/-_i. Как
было показано выше, векторы
^"'^ВДГ (А=1, .... «/.)
принадлежат подпространству <Sr_i и линейно независимы отно-
относительно 'Зг__2- Дополним эту систему, если это необходимо, до
максимальной системы векторов
линейно независимых относительно Sr_a-
Продолжая этот процесс дальше, мы в каждом подпростран-
подпространстве @? A sg&==^r) будем иметь максимальную систему векторов
life>, .... &*' (k = r, г-l, .... 1; qu.tSsq,,), C2)
ЖОРДАНОВА ФОРМА МАТРИЦЫ
463
линейно независимых относительно
отношения
причем справедливы со-
сог).
(зз)
Согласно теореме 2 объединение всех векторов C2) представ-
представляет собой базис подпространства ЗЛ/. Каждый из этих базис-
базисных векторов |а E<Sft такои> что By-|ft + ' =? |д , порождает пол-
полную цепочку (серию векторов)
§А . OygA , ..., tij ёд (O;§A = (J), (.34)
которая является циклическим базисом подпространства 9J раз-
размерности &, натянутого на векторы цепочки,лпричем 9?, очевидно,
инвариантно относительно преобразования Bj.
Нумеруя эти циклические подпространства 9?i, ..., 9^s (s = qi)
и учитывая, что объединение их базисов является базисом под-
подпространства Ш;, на основании теоремы 1 получаем, что 2)iy- пред-
представляет собой прямую сумму:
mj=%@ ... е>%, C5)
что и требовалось доказать.
Замечание. Из данной конструкции построения базиса под-
подпространства 2)(у вытекает, что в сумме C5) имеется ровно
Чи — Чк+\ слагаемых 9?г, для которых
dim9?; = ^ (k = r, r—1 1; qr+1 = 0),
причем максимальная размерность подпространства 91/ равна г и
¦• +(<?* —<7а)-2+ (<7i—<7jH =
Теорема 5' (вторая теорема приведения). Пусть
(п X п)-матрица А имеет единственное собственное значение X.
Тогда эту матрицу с помощью преобразования подобия с неосо-
неособенной матрицей S можно привести к квазидиагональному виду
где
X 1 ... О О
О X ... О О
О 0 ... X 1
_О О ... О X
— клетки Жордана различных порядков ek{ex-\- ... -j-es = n).
Формула C6) непосредственно вытекает из разложения C5),
теоремы 3 и леммы 2.
464 ПРИЛОЖЕНИЕ
Объединяя первую и вторую теоремы приведения (теоремы
4' и 5'), получаем следующий результат.
Теорема 6. Всякая (п X п)-матрица А = [aJk]' подобна не-
некоторой матрице
имеющей жорданову форму
y = diag[J1(X1), ..., Jm(K)] (m<n), C7)
где Хь ..., Xm— различные собственные значения матрицы А,
Jk (\„) = diag [Jkl (Xk) Jh/k (XA)]
hh (h) = hEie"b + /'**' (A = 1, • ¦ • , lk\ k = 1, ... , m)
— клетка Жордана с собственным значением Хь причем каждому
собственному значению Xfc кратности матрицы А соответствует
одна или несколько клеток Жордана порядка ekh, где
ekx-\- ... -\-eKlk = pk (k—\ т)
Pl+ ••• +Рт = П.
Число lk клеток Жордана, отвечающих собственному значе-
значению Хь совпадает с максимальным числом линейно независимых
собственных векторов матрицы А, соответствующих значению Xft.
Замечание. Если матрица А действительная, то базис,
в котором она имеет жорданову форму C7), можно выбрать так,
что составляющие циклические базисы, соответствующие действи-
действительным собственным значениям, будут действительны, а ком-
комплексно-сопряженным — комплексно-сопряженные.
Укажем один из способов нахождения элементарных делите-
делителей данной квадратной матрицы A = [ajk] порядка п. Рассмотрим
Х-матрицу
Пусть г — ранг матрицы F (X) A<г<п)иО;- (X) (/ = 0, 1,..., г) —
наибольший общий делитель ее миноров /-го порядка, где поло-
положено ?>о(Х) = 1. Функция
являющаяся целым полиномом, называется j-м инвариантным
множителем матрицы А (см. [82]).
Если X,, ..., Xm (ms^n) — различные характеристические корни
матрицы А, то можно доказать справедливость разложения
где множители (X — ХА)"*/ (ekJ-^l), не сводящиеся к постоянным
величинам, являются элементарными делителями мат-
матрицы А. Последнее разложение дает возможность эффективно
вычислять элементарные делители данной матрицы.
ЖОРДЛНОВА ФОРМА МАТРИЦЫ
465
Упражнение. Пусть А = [о_,*1 — действительная (и х га)-матрица,
}p = ap±i)p (]р^Ь0) (/i=i, 2, ...) — ее комплексные собственные значения,
a ¦fg(q—\l 2, ...) — ее действительные собственные значения. Доказать, что
тогда матрицу А с помощью действительной неособенной матрицы Т можно
представить в виде
А=Т~1ВТ,
где
причем
и
fi = diag
(см. [17])
[К, (X,)
Кр (Хр)
I /
Jq К
¦ , i
-Sj,
0»
0,
.0,
k
-
E
s
С
с
V
= 1
~iq
0
0
0
B t
p
o
1
V?
0
0
... 02
... 0,
... Sp
... 0,
r
, P),
... 0
... 0
• ¦ ¦ ~(q
... 0
1
0
0
0
1
¦ ,
o.2 -
0,
?'»¦
sp r
0"|
l]
-
JQ (TfQ)],
= ! О]-
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
[1] Булгаков Б. В., Колебания, Гостехиздат, 1954.
[21 К у р о ш А. Г., Курс высшей алгебры, «Наука», 1965.
[3] Д ё м и д о в и ч Б. П., Марон И. А., Основы вычислительной мате-
математики, «Наука», 1966.
[4] Г е л ь ф а н д И. М., Лекции по линейной алгебре, Гостехиздат,
1861.
[5] Мальцев А. И., Основы линейной алгебры, «Наука», 1967.
[6] Б е л л м а н Р., Теория устойчивости решений дифференциальных
уравнений, ИЛ, 1954.
[7] ФихтенгольцГ. М., Курс дифференциального и интегрального
исчисления, т. I, «Наука», 1966; т. II, Физматгиз, 1962.
[8] Смирнов В. И., Курс высшей математики, т. III, ч. 1, «Наука»,
1967.
[9] Петровский И. Г., Лекции по теории обыкновенных дифферен-
дифференциальных уравнений, «Наука», 1964.
[10] Понтрягин Л. С, Обыкновенные дифференциальные уравнения,
«Наука», 1965.
[11J Степанов В. В., Курс дифференциальных уравнений, Физматгиз,
1959.
[12] Н е м ы ц к и й В. В. и Степанов В. В., Качественная теория диф-
дифференциальных уравнений, Гостехиздат, 1949.
[13] Ляпунов А. М., Общая задача об устойчивости движения, Гос-
Гостехиздат, 1950.
[14] Малкин И. Г., Теория устойчивости движения, «Наука», 1966.
[15
[16
Ч е т а е в Н. Г., Устойчивость движения, Гостехиздат, 1955.
Красовский Н. Н., Некоторые задачи теории устойчивости
движения, Физматгиз, 1959.
[17] Г а н т м а х е р Ф. Р., Теория матриц, «Наука», 1967.
[18] В i h a r i J., A gcnralization of a lemma of Bellman and its applica-
application to uniqueness problems of differential equations, Ada math. Acad. Scient.
Hung. VII, 1 A956), 81—94.
[19] Ландау Э., Введение в дифференциальное и интегральное исчис-
исчисление, ИЛ, 1948. "
[20] Еругин Н. П., Приводимые системы, Труды Матем. ин-та АН
СССР ХШ A946).
[21] Л е ф ш е ц С, Геометрическая теория дифференциальных уравне-
уравнений, ИЛ, 1961.
[22] Wazewski, Sul la limitation des integrates des systems d'equations
differentielles lineaires ordinaires, Studia Math. 10 A948), 48—59.
[23] L e v i n s о n N., The asymptotic behavior of system of linear differen-
differential equations, Amer. J. Math. 68 A946), 1—6.
[24] В r a u e r, Nonlinear differential equations with forcing terms, Proc.
Amer. Math. Soc. 15, 5 A964), 758—765.
[25] Perron O., Die Ordnungszahlen der Differentialgleichungssysteme,
Math. Zeitschr. 31 A930), 748—766.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА 467
[26] Perron О., Ober eine Matrixtransformation, Math. Zeitschr. 32
A930), 465—473.
[27) Виноград Р. Э., Новое доказательство теоремы Перрона и не-
некоторые свойства правильных систем, УМН, 9:2 F0) A954), 129—136.
|28] Коддингтон Э. А. и ЛевинсонН., Теория обыкновенных
дифференциальных уравнений, ИЛ, 1958.
[291 Н а 1 а п а у "A., Theoria calitativa a ecua^iilor different,iale, Ed. Acad.
RPR, 1963.
[30] Фрезер Р., Дункан В. и К о л л а р А., Теория матриц и ее
приложения, ИЛ, 1950.
[31] Стокер Дж., Нелинейные колебания в механических и электри-
электрических системах, ИЛ, 1952.
[32] Гантмахер Ф. Р., Лекции по аналитической механике, Физмат-
гиз, 1960.
[33| Уиттекер Е. Т., Аналитическая динамика, ОНТИ, 1937.
[34] Г е л ь ф а н д И. М. и Л и д с к и й В. Б., О структуре областей
устойчивости линейных канонических систем дифференциальных уравнений
с периодическими коэффициентами, УМН 10:1 F3) A955), 3—40.
[35] Гурса Э., Курс математического анализа, т. II, ч. 2; т. III, ч. 1,
Гостехиздат, 1933.
[36] Зубов В. И., Колебания в нелинейных и управляемых системах,
Судпромгиз, 1962.
[37] Ч е з а р и Л., Асимптотическое поведение и устойчивость решений
обыкновенных дифференциальных уравнений, «Мир», 1964.
[38] Conti R., Sulla stabilita dei sistemi di equazioni differenziali lineari,
Rlv. mat. Univ., Parma 6 A955), 3—35.
[39] Borg G., Ober die Stabilitat gewissen Klassen von linearen Differen-
tialgleichungen, Ark. Math. Astr. Fys., set. 31A, 1 A944), 460—482.
[40] Kolodner Ignace I., Power dissipated in linear systems with pe-
periodic coejficients, J. Math, and Mech. 12, 5 A963), 675-682.
[41[ Йосидзава Т., Функция Ляпунова и ограниченность решений.
Сб. переводов «Математика», «Мир», 9:5 A955), 95—127.
[42] Барбашин Е. А. и Красовский Н. Н., О существовании
функции Ляпунова в случае асимптотической устойчивости в целом, ПММ,
К, вып. 3 A954), 345—350.
[43] П е р с и д с к и й К. П., Об устойчивости решений дифференциаль-
дифференциальных уравнений, ИАН Казахской ССР 97, вып. 4 A950).
[44] М а с с е р а X. Л., К теории устойчивости. Сб. переводов «Мате-
«Математика», ИЛ, 1:4 A957), 81 — 101.
[45] Лефшец С, Л а-С а л л ь Ж., Исследование устойчивости прямым
методом Ляп) нова, «Мир», 1964.
[46] Liang Zhong-chao, The bondedness of solutions of certain non-
nonlinear differential equations, Chinese Math. 3, 2 A963), 169—183.
47 П л и с с В. А., Нелокальные проблемы теории колебаний, «Наука», 1964.
48 Д е м и д о в и ч Б. П., О диссипативности некоторой нелинейной
системы дифференциальных уравнений, I, Вестн. МГУ, 6 A961), 19—27; II,
1 A962), 3—8.
[49] Лузин Н. Н., О качественном исследовании уравнения движения
поезда, Матем. сб. 39 C) A932), 6—26.
[50] L e v i n s о n N., Transformation theory of non-linear differential equa-
equations of the second order, Ann math. 45, 4 A944), 723—737.
[51 ] Колмогоров А. Н. и Фомин С. В., Элементы теории функций
и функционального анализа, изд. МГУ, вып. 1 A954), вып. 2 A960).
[52] V е j v о d а О., On the existence and stability of the periodic solution
of the second kind of a certain mechanical system, Чехословацкий математи-
математический журнал 9 (84) A959), 390—415.
468 ЦИТИРОВАННАЯ ЛИТЕРАТУРА
[52а| Андронов А. и В и т т А., Сб устойчивости по Ляпунову,
ЖЭТФ 3, вып. 3 A933).
[53] Wintrier A., An Abelian lemma concerning asymptotic equalibria,
Amer. Journ. of Math. 68 A946), 451—454.
[54J Antosiewicz H. A., On non-linear differential equations of the
second order with integrable forcing term, J. London Math. Soc. 30 A955),
64—67.
[551 Красносельский А\. А. и К р е й н С. Г., О принципе усред-
усреднения в нелинейной механике, УМН 10:3 F5) A955), 147—152.
[56] Б о г о л ю б о в Н. Н., О некоторых статистических методах в мате-
математической физике, И АН УССР, 1945.
[571 Spath H., Uber das asymptotische Verhalten der Losungen linearer
Diiferentialgleichungen,..Afa^. Zeitschr. 30 A929), 487—513.
[58] Perron O., Uber lineare Differentialgleichungen, bei dencn die unab-
hangig Variable reel ist, Journ. f. relne und angew. Math. 143 A913),
25—50.
[59] Lev in son N., The asymptotic nature of solutions of linear systems
of differential equations, Duke Math. Journ. 15 A948), 111—126.
[60] Рапопорт И. М., О некоторых асимптотических методах в теории
дифференциальных уравнений, ИАН УССР, 1954.
[61] Дснидович Б. П., Об ограниченных решениях некоторой нели-
нелинейной системы обыкновенных дифференциальных уравнений, Матем. сб.
40 (82), 1 A956), 73—94.
[62] Боль П., О некоторых дифференциальных уравнениях общего ха-
характера, применяемых в механике, Юрьев, 1900.
[63] Д е м и д о в и ч Б. П., О некоторых свойствах характеристических
показателей системы обыкновенных линейных дифференциальных уравнений
с периодическими коэффициентами, Учен. зап. МГУ, 163; Математика 6
A952), 123—132.
[64] Е р у г и н Н. П., Линейные системы обыкновенных дифференциаль-
дифференциальных уравнений, ИАН БССР, 1963.
[65] Кучер Д. Л., О некоторых критериях ограниченности решений
системы дифференциальных уравнений, ДАН СССР 69, 5 A949), 603—606.
[66] Бор Г., Почти периодические функции, Гостехиздат, 1934.
[67] Левитан Б. М., Почти периодические функции, Гостехиздат, 1953.
[68] Bohl P., Uber eine Differentialgleichungen der Stdrungstheorie,
Crelles Journ. 131 A906), 268—321.
[69] Vail ее Poussin C. J., Sur les ionctions presque-periodiques de
H. Bohr. Ann. Soc. scien. Bruxelles 47 A927), 141—158.
[70] Боголюбов Н. Н. и Крылов Н. М., Новые методы нелинейной
механики, рНТИ, 1934.
[71] Winer N., Generalised harmonic analysis, Ada math. 55 A930),
117—258.
[72] В о с h n e r S., Beitrage zur Theorie der fastperiodische Funktioncn,
1 Teil: Funktionen einer Variablen, Math. Ann. 96 A927), 119—147; II Teil:
Funktionen mehrerer Variablen, там же, 383—409.
[73] Corduneanu С, Functii aproape-periodice, Ed. Acad. RPR,. 1961.
[74] Bohr H. und Neugebauer O., Ober lineare Differentialgleichun-
Differentialgleichungen mit konstanten Koeffizienten und fastperiodischer rechter Seite, Gott. Nachr.
A926), 8^22.
[75] Бирюк Г. И., Об одной теореме существования почти периоди-
периодических решений некоторых систем нелинейных дифференциальных уравне-
уравнений с малым параметром, ДАН СССР 96, 1 A954), 5—7.
[76] Amer io L., Soluzioni quasiperiodiche, о limital, di sistemi differen-
ziali non lineari quasi-periodici, о limitati, Annali Mat. pura ed. appl. 39A955),
97—119.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА 469
[77] Favard J., Sur lcs equations differentielles a coefficients presque-
periodiques, Act a math. 51 A927), 31—81.
[78] Б о р у x о в Л. Е., О периодических и почти периодических реше-
решениях уравнений v' + q (x)y*=f(x), Научи, ежегодник Саратовского ун-та
за 1954 г., 656-657.
[79] Д е м и д о в и ч Б. П., Об одном случае почти периодичности реше-
решения обыкновенного дифференциального уравнения первого порядка, УМН
8:6 E8) A953), 103—106.
[80] Малкин И. Г.,-Некоторые задачи теории нелинейных колебаний,
Физматгиз, 1956.
|81] Helms L. L., Putnam С. R., Stability in incompressible systems,
Jour'n. Math, and Mech. 7, 6 A958), 901-903.
[82] Бохнер М., Введение в высшую алгебру, ГТТИ, 1933.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Америо теорема 437
Андронова — Витта теорема 312
теоремы аналог 305
Арцеля теорема 325
Асимптотическая фаза решения 298
Базис векторного пространства 25
— нормированный 25
ортогональный 25
Барбашина—Красовского теорема248
Бесселя неравенство 389
Билинейная форма 32
Бирюк теорема 426
Бихари лемма 110
Боголюбова теорема 332
Боля теорема 361
Бора — Нейгебауэра теорема обоб-
обобщенная 423
Бохнера теорема 415
обобщенная 420
Важевского неравенство 149
Вектор, длина (модуль) 23
— я-мерный 22
Вектор-столбец (-строка) 11
Векторы, линейно независимые отно-
относительно подпространства 447
Вронского определитель 73
Гамильтонова система дифферен-
дифференциальных уравнений 203
Гронуолла—Беллмана лемма 108
Гурвица полином 91
— теорема 97
Движение невозмущенное 234
Диссипативные системы (D-системы)
289
Дифференциальная линейная система
правильная 165
приводимая 154
— система 64
, спектр 137
Дифференциальная система, спектр
полный 145
Дифференциальные системы асимпто-
асимптотически эквивалентные 159
Единичный косой ряд 14
Еругина теорема 154
Жордана клетки 36
Интеграл матрицы 52
Интегральная непрерывность реше-
решений 66
функции 328
Иосидзавы теорема 290
Квадратичная форма действительная
положительно определенная <34
— — эрмитова 33
Кейли тождество 48
Конгруэнтные точки 368
Коши неравенство 24
Коши — Буняковского неравенство
386
Красносельского и Крейна теорема
329
Кронекера символ 13
Кронекера — Капелли теорема 26
Ла-Салля теорема 276
Лашю — Данилевского условие 117
Линейная зависимость векторов 24
— независимость векторов 24
Ляпунова интегральный признак
устойчивости 202
— константа 201
— критерий устойчивости по пер-
первому приближению 267
— матрица 153
— неравенство 151
ПРЕДМЕТНЫЙ УКАЗАТКТЬ
471
Ляпунова преобразование 154
— теорема об устойчивости 238, 239
— асимптотической 240
периодического реше-
решения 294
— — — условной 314
_ квазилинейной системы
257
о неустойчивости 244
• нормальности фундаменталь-
фундаментальной системы 142
построении нормальной фун-
фундаментальной системы решений 145
— правильности треугольной
линейной системы 174
— приводимости периодиче-
периодической линейной системы 188
•— характеристических пока-
показателях решений линейной си-
системы 135
Ляпунова — Пуанкаре теорема 213
Массера теорема об асимптотической
устойчивости 271
¦ о существовании периодиче-
периодического решения 221
Матрица 11
¦— единичная 13
—, жорданова форма 36
— квазидиагональная 20
— клеточная 19
•— комплексно-сопряженная 15
— , логарифм 59
— неособенная (несингулярная) 16
— нулевая 11
— обратная 16
— ортогональная 17
— особенная (сингулярная) }6
•— перехода 29
— почти периодическая 418
•— нормальная 420
— преобразования 28
в данном базисе 450
•— противоположная 12
— равномерно почти периодическая
421
— симметрическая 15
— сопряженная 16
— транспонированная 15
— унитарная 18
— фундаментальная 70
— — нормированная 72
—, характеристическое уравнение
35
— , элементарные делители 37
Матрицант 74
Матрицы подобные 30
Матричный ряд, сходимость 42
, — абсолютная 42
, — разномерная 43
степенной 44—48
Мера неправильности системы 271
Михайлова критерий 106
Множество числовое относительно
плотное 367
Модуль матрицы 22
Мультипликаторы 185
Непрерывность семейства функции
равностепенная 325
Норма матрицы 20
— функции 387
Область притяжения решения 68
Ограниченность семейства функций
равномерная 325
Оператор 337
— линейный 337
— непрерывный 337
Остроградского — Лиувилля формула
73
Отображение сжатое 337, 338
Парсеваля равенство 410
Перрона теорема 170
о триангуляции линейной си-
системы 180
Персидского теорема 254
Подпространство инвариантное 450
— линейного пространства 445
— преобразования корневое 454
Полином возвратный 211
Полутраектория отрицательная 296
— положительная 296
Почти период функции 367
— периодическая функция 367
— периодические системы, разделен-
разделенное решение 432
, /У-класс 430
Предел последовательности 336
— функции верхний 123
— — нижний 124
Преобразование единичное 27
— линейное 28
— нулевое 27
— обратное 27, 452
•— самосопряженное (эрмитово) 31
Принцип сжатых отображений 338
Произведение матриц 13
— матрицы на число 12
— преобразований 452
— функций скалярное 387
472
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Производная матрицы 50
— по времени в силу системы 238
Пространство векторное я-мерное
23
— евклидово 24
комплексное 24
— линейное 24 , 337
— метрическое 335
— полное 336
— почти периодических функций
387
—¦ циклическое 459
Прямая сумма 446
Пуанкаре признак 313
Размерность подпространства 26
Ранг матрицы 26
Решение неустойчивое 67
Решения предельно ограниченные
289
Свертка функции 397, 398
Сильвестра формула 49
Симплектическая единица 209
Система квазилинейная 257
— порождающая 222
— приведенная 235
— с конвергенцией 281
— сопряженная 168
Системы взаимно сопряженные 169
Скалярное произведение векторов 23
След матрицы 18, 58
Сложение векторов 23
Собственный вектор преобразования
31, 454
Степень матрицы 18
Сумма матриц 12
— матричного ряда 42
— преобразований 452
Сходимость в среднем последователь-
последовательности 411
ряда 411
— семейства функций равномерная
324
Теорема аппроксимации 412
— единственности для почти перио-
периодических функций 406
— о среднем для почти периодичес-
периодических функций 379
усиленная 382
— разложения векторного простран-
пространства (вторая) 460
(первая) 456
Траектория решения 295
Умножение вектора на число 23
Уравнение возвратное 211
Уравнения в вариациях 294
Устойчивость по Лагранжу 278
— решения 66
— ¦— асимптотическая 68
• в целом 68, 248
при постоянно действующих
возмущениях 69
равномерная 67
условная 314
экспоненциальная 251
орбитальная 296
асимптотическая 297
— состояния равновесия 260—261
Фавара теорема 441
Флоке теорема 183
Фундаментальная последовательность
336
— система (матрица) нормальная 139
Функции ортогональные 388
Функция, бесконечно большой низ-
низший предел 248
—, — малый высший предел ?37
— , сильный 248
— знакоопределенная 236
— знакопостоянная 235
— нормальная 415
— нормированная 388
— отрицательно определенная 236
— положительно определенная 235
Фурье коэффициенты 391, 392
— показатели 391
— ряд 392
Характеристический показатель ин-
интеграла 131
линейной периодической си-
системы' 184
— •— Ляпунова 125
матрицы 132
строгий 130
— полином преобразования 453
Характеристические числа (характе-
(характеристические корни, собственные
значения) матрицы (преобразова-
(преобразования) 31, 35, 453
Четаева теорема 246
Экспоненциал матрицы 54