А. Д. МЫШКИС
МАТЕМАТИКА
для втузов
СПЕЦИАЛЬНЫЕ КУРСЫ
Допущено Министерством
высшего и среднего специального образования СССР
е качестее учебного пособия Ьлп студентов
еыеших технических учебных заведений
ИЗДАТЕЛЬСТВО «НАУКА»
-ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
' МОСКВА' 1 97Г

617
MS6
УДК 510 @22)
АННОТАЦИЯ
Книга представляет собой пособие по специаль-
специальным главам математики для втузов и является естест-
естественным продолжением общего курса математики этого
же автора. Книга содержит следующие главы: тео-
теория поля, теория аналитических функций, опера-
операционное исчисление, линейная алгебра, тензоры, ва-
вариационное исчисление, интегральные уравнения,
обыкновенные дифференциальные уравнения. Изложе-
Изложение проводитси с позиций современной прикладной ма-
математики с максимальным использованием интуиции и
аналогий, со специальным вниманием к качествен-
качественному и количественному описанию фактов.
Книга рассчитана на студентов втузов, преподава-
преподавателей, инженеров и научных работников в области
технических наук.
НЕ БОЛЕЕ »И КНИГИ В (
ОДНИ РУКИ И 2ХВД8Е )
Анатолий Дмитриевич Мышкис
МАТЕМАТИКА ДЛЯ ВТУЗОВ
Специальные курсы
М., 1971 г.. 632 стр. с илл.
Редакторы Н. А. Карпова, Н. Д. Копачевский
Техн. редактор В. Н. Кондакова
Корректоры Л. Н. Боровика, О. А. Сигал
Сдано в набор 11/ХП 1970 г. Подписано к печати 3/V 1971 г. Бумага
60X90/,». Физ. печ. л. 39.5. Условн. печ. л. 39.5. Уч.-изд. л. 44,44.
Тираж 100 000 экз. Т-06253. Цеиа книги 1 р. 66 к. Заказ 1637.
Издательство «Наука»
Главная редакция физико-математической литературы
Москва, В-71, Ленинский проспект, 15.
Ордена Трудового Красного Знамени
Первая Образцовая типография имени А. А. Жданова
Главполиграфпрома Комитета по печати при Совете Министров СССР
Москва, М-54, Валовая, 28

ОГЛАВЛЕНИЕ
Предисловие . 7
Глава 1. Теория поля 9
§ 1. Оператор Гамильтона 9
1. Операции первого порядка A0). 2. Правила действий A1). 3. Инте-
Интегральные формулы A2). 4. Операции второго порядка A3). б. Разрывные
поля A4).
§ 2. Специальные типы полей 16
1. Потенциальные поля A6). 2. Безвихревое поле в мпогосвязной области
A7). 3. Соленоидальные поля A9). 4. Примеры B1). 5. Ньютонов потен-
потенциал B3). 6. Построение векторного поля по заданным ротору и диверген-
дивергенции B5).
Глава П. Теория аналитических функций . 27
§ 1. Дифференцирование и отображения 27
1. Производная B7). 2. Условия Коши—Римаиа B8). 3. Сопряженные rap.
моннческие функции B9). 4. Геометрический смысл производной C0).
5. Конформные отображения C1). 6. Линейные отображения C2). 7. Рас-
Расширенная комплексная плоскость C3). 8. Дробно-лпленное отображение
C4). 9. Степенные отображения C7). 10. Многозначные функции н точки
разветвления C9). 11. Отображение и)=-д-( z-j ) D2). 12. Показатель-
ное и связанные с ним отображения D5). 13. Поверхность Римана D7).
14. Приложение к теории плоских полей D8). 15. Примеры E0).
16. Краевые задачи и конформные отображения E2). 17. Общие замеча-
замечания о конформных отображениях E6). 18. Применение метода малого пара-
параметра E8).
§ 2. Интегрирование и степенные ряды . С1
1. Интеграл F1). 2. Интеграл от аналитической функции F2). 3. Ряды
Лораиа F3). 4. Разложение аналитической функции в ряд Лорана F5).
5. Рид Тейлора F7). 6. Аналитические отображения н принципы максимума
G0). 7. Аналитическое продолженке G2). 8. Варианты G4).
§ 3. Особые точки и нули 78
I. Изолированные особые точки G8). 2. Полюс G9). 3. Теорема Коши
о вычетах (81). 4. Применение к несобственным интегралам (83). 5. Ин-
Интегральные формулы Пуассона (91). 6. Поведение функции иа бесконеч-
бесконечности (94). 7. Логарифмические вычеты (95). 8. Теорема Руше (96).
9. Зависимость нулей от параметра (98). 10. Нули многочленов A00).
II. Результант двух многочленов A04). 12. Мероморфные функции A06).
13. Формула Кристоффеля—Шварца A08). 14. Понятие об эллиптических
функциях (III).
§ 4. Асимптотические разложения .* 114
1. Введение A14). 2. Свойства A16). 3. Интеграл типа Фурье A18).
4. Интеграл с параметром в вещественном показателе A22). 5. Метод пере-
перевала A25).

4 ОГЛАВЛЕНИЕ
Глава III. Операционное исчисление 129
§ I. Общая теория 129
1. Преобразование Лапласа A29). 2. Образы простых функций A30),
3. Основные свойства преобразовавши Лапласа A33). 4. Обратное преобразо-
преобразование Лапласа A36). 5. Разложение прообраза в сумму A39). 6. Численное
определение прообраза A42).
§ 2. Приложения 144
1. Основная идея A44) 2. Обыкновенные дифференциальные уравнения
A45) 3 Разностные и дифференциально-разностные уравнения A49).
4. Интсмральиые и иитегро-дифференциальиые уравнения A50). 5. Уравнения
с частными производными A51).
§ 3. Варианты 155
1. Дискретное преобразование Лапласа A55). 2. Преобразование Фурье рас-
растущих функций A57). 3. Другие интегральные преобразования иа бесконеч-
бесконечном интервале A58). 4. Интегральные преобразования иа конечной
интервале A62).
Глава IV. Лииейиая алгебра 164
§ 1. Сопряженные отображения 165
¦' 1. Прямая сумма A65) 2. Инвариантные подпространства A66). 3. Сопря-
Сопряженные отображения A67). 4 Разложение, связанное с сопряженными отоб-
отображениями A68). 5. Отображение пространства в себя A69). 6. Самосопряжен-
Самосопряженное отображение A70) 7. Экстремальное свойство собственных значений A71).
§ 2. Квадратичные формы ¦ 174
I. Введение A74). 2. Закон инерции квадратичных форм A75). 3. Метод
Якбби и теорема Сильвестра A76). 4. Одновременное приведение двух квадра-
квадратичных форм к диагональному виду A78)
§ 3. Структура .линейного отображения 179
1. Отображение с единственным собственным вектором A79). 2. Отображение
с единственным собственным значением A82). 3. Общий случай A83). 4. Отоб-
Отображение вещественного пространства A86). 5. Применение к вычислению
функций от матриц A88). 6. Другое представление отображения вещественного
пространства A90). 7. Структура перестановочных отображений A91).
§ 4. Некоторые численные методы 192
1. Метод Гаусса A92). 2. Норма матрицы и обусловленность системы A94).
3. Метод улучшения иевязки A96). 4. Спектр симметрической матрицы A97).
б. Метод Якоби A98). 6. Вычисление старшего собственного значения путем
итераций A99). 7. Вычисление последующих собственных значений B01).
8. Матрицы с неотрицательными элементами B02). 9. Метод А. Н. Крылова
B03). 10. Метод малого параметра B04). 11. Метод непрерывного продолже-
продолжения B05).
§ 5. Задачи линейного программирования 207
1. Основная задача B07). 2. Примеры B08). 3. Геометрические замечания
B10). 4 Геометрический смысл основной задачи B12). 5. Стандартный вид
основной задачи B14). 6. Метод последовательного улучшения решения B15).
7". Приложение к матричным играм B19). 8. Варианты B25).
Глава V. Тензоры . . . . , 228
§ 1. Тензорнаи алгебра 229
1. Примеры B29). 2. Евклидовы тензоры, общее определение B31). 3. Действия
над тензорами B32). 4. Тензоры 2-го ранга B34). 5 Примеры из механики
(?,35). 6. Общие аффинные тензоры B37). 7. Аффинные тензоры в евклидовом
пространстве B39). 8. Индефинитные метрические формы B40). 9. Замеча-
Замечание о размерностях B43).
§ 2. Тензорные поля . ' 244
I. Поле евклидова тензора B44). 2. Поступательный перенос вектора в криво-'
линейных координатах B45). 3. Ковариантное дифференцирование B48).
4. Доле на многообразии евклидова пространств* B51). 5. Внутренняя;
геометрия и римаковы пространства B53). ' '

. ОГЛАВЛЕНИЕ 5
Глава VI. Вариационное исчисление 257
§ 1. Первая вариация и необходимые условия экстремума 267
I. Примеры задач вариационного исчисления B57). 2. Функционал B59).
3. Функциональные Пространства B61). 4. Вариация функцио-
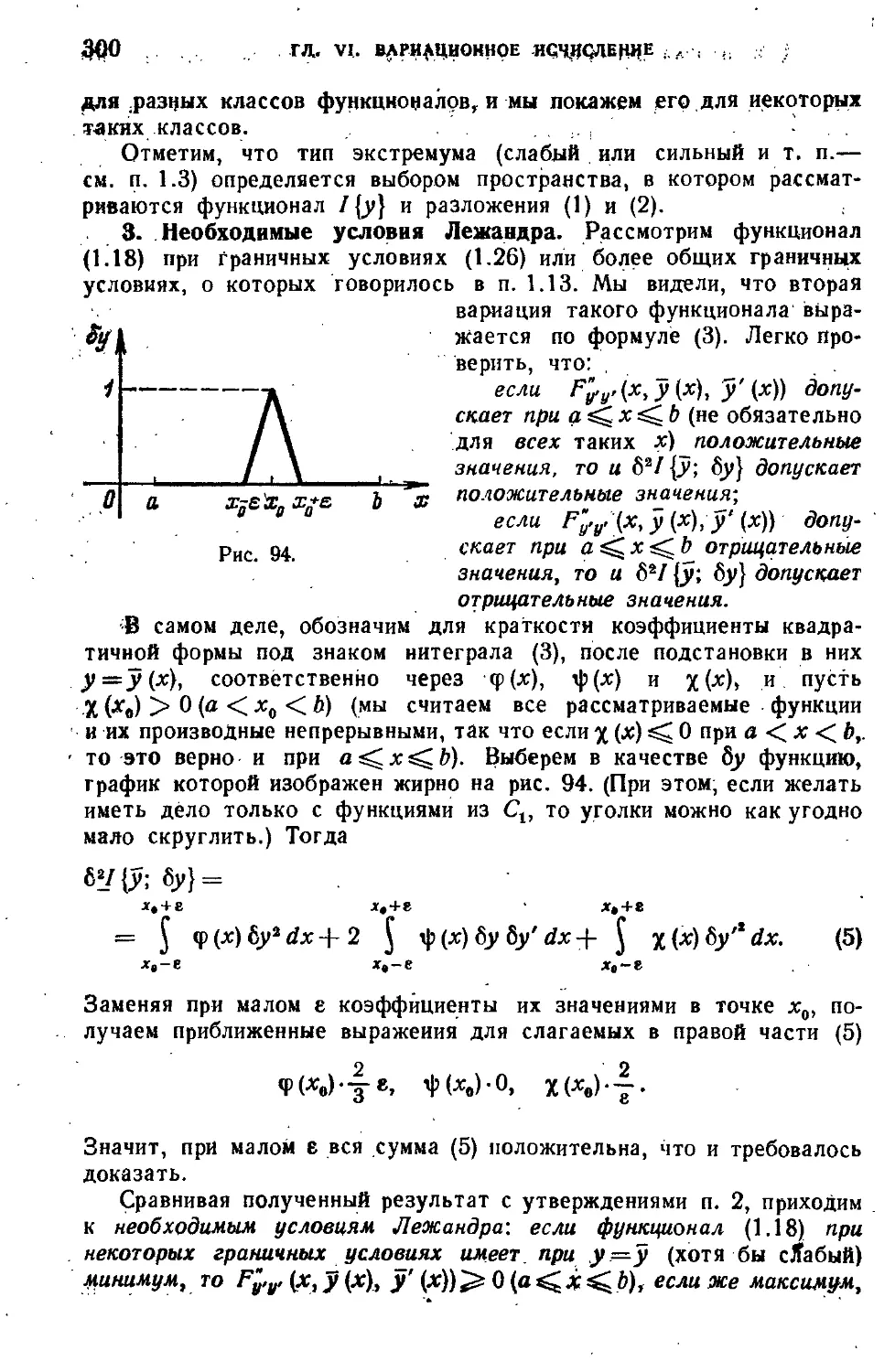
функционала B64). 5. Уточнение B67). 6. Необходимое условие вкстремума B69).
7. Уравнение Эйлера B70). 8. Примеры B73). 9. Функционалы с производ-
производными высшего порядка B75). 10. Функционалы от нескольких функций B75).
II. Функционалы от функций нескольких переменных B 77). 12. Условные
экстремум с интегральными связями B79). 13. Условный экстремум с конеч-
конечными или дифференциальными связями B82). 14. Задачи, сводящиеся к задач*
Лагранжа B85). 15 Задачи с подвижными концами на плоскости B86).
16. Условия трансверсальности B88), 17. Задачи с подвижными концами
В пространстве B90). 18. Трансверсальность для функций, нескольких пе-
переменных B92). 19. Высвобождающие связи B93). 20. Разрывные задачи B95).
§ 2. Вторая вариация и достаточные условия экстремума 297
1. Вариации высших порядков B97). 2. Условия экстремума в терминах вто-
второй вариации B99). 3. Необходимые условия Лежаидра C00). 4. Квадратич-
Квадратичный функционал C01). 5. Условия Якоби C04). 6. Геодезические линии
C07). 7. Условия сильного экстремума C09). 8. Вариационная теория
собственных значений C11). 9. О существовании минимума C16). 10. Основ-
Основное условие минимума C17). 11. Зависимость собственных значений от функ-
функционала C20).
§ 3. Канонические уравнения и вариационные принципы 323
X. Канонические уравнения C22).—77 Первые интегралы C23). 3. Канониче-
Канонические преобразования C24). 4. Контактные преобразования C26). 5. Теорема
Нётер C28). 6. Случай функций нескольких переменных C30). 7. Уравнение
Гамильтона — Якоби C32). 8. Плоскость Лобачевского C34). 9. Вариацион-
Вариационные принципы C36). 10. Принцип Гамильтона в простейшем случае C38).
П. Принцип Гамильтона для систем с конечным числом степеней свободы
C40). 12. Принцип Гамильтона для сплошных сред. Струна C43). 13. Стер-
Стержень и пластинка C4S). .14. Общая схема вариационного подхода к фивиче-
сним полям C48). 15. Уравнения движения упругой среди! C51). 16. Дисен-
патнвиые системы C52). 17. Принцип минимума потенциальной виергии C64).
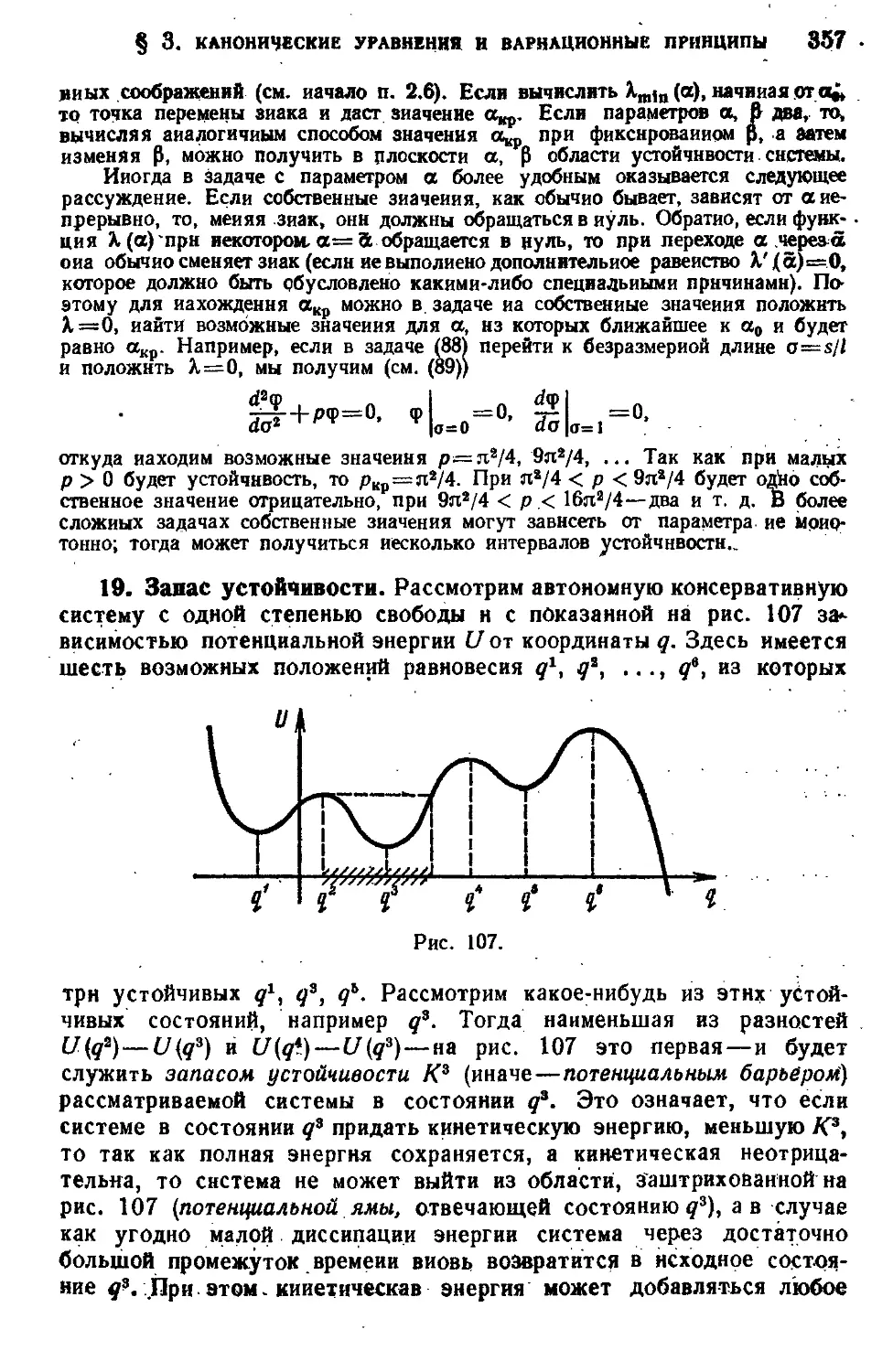
18. Примеры C55). 19. Запас устойчнвостк C57). 20. Вариационные принципы
в конформных отображениях C59).
§ 4. Прямые методы
1. Метод Ритца для квадратичного функционала C61). 2. Применение к реше-
решению краевых задач C66). 3. Метод счетного множества переменных C67).
4. Метод Ритца для функционалов от функций нескольких переменных C69).
5. Метод Трефтца C73). 6. Метод Ритца для собственных значений C74).
7. Метод Ритца для иеквадратичиых фуикцисчалов C76). 8. Метод наимень-
наименьших квадратов C79). 9. Метод Канторовича C80). 10. Метод Эйлера C82).
Глава VII. Интегральные уравнения 384
$ 1. Введение . . 384
1. Примеры C84). 2. Основные классы интегральных уравнений C86). 3. Еще
'••" о пространстве Гильберта C87).
§ 2. Теория Фредгольма 389
1. Уравнения с вырожденными ядрами C89). 2. Общий случай C94). 3. Приг
менеиие бесконечных систем алгебраических уравнении C98). 4. Применение
численного интегрирования D01). 5. Уравнения с малыми ядрами D04).
6. Принцип сжимающих отображений D07). 7. Воамущеине ядра D09).
8. Характер решений D11). 9. Уравнения Вольтерра 2-го рода D13). 10. Урав-'
; веиия со слабой особенностью D14). 11. Уравнения с вполне непрерывными
операторами D16). 12. Уравнении с положительными ядрами D17).
. | 8. Уравнеивя с симметричными ядрами 418
1. Аналогия с конечномерными уравнениями D18). 2. Разложение ядра по
Собственным функциям D19). 3. Следствия D21). 4. Переход от иесимметрич-
вого ядра к симметричному D25). 5. Экстремальное свойство характеристнче-
. Сних чисел D27). б. Уравнения с самосопряженными операторами D30).
§ 4. Некоторые специальные классы уравнений , . . 433
1.('Урав8«П1Я BwrbTepjia 1-городЗ D33"). 2. Уравнения Фредголъма 1-го род*
• симметричным ядром D35). 3. Приятие р некорректных вадачах D37).

G ОГЛАВЛЕНИЕ
4. Уравнения Фредгольма 1-го рода, общий случай D37). 5. Применение про-
производящих функций D39). 6. Уравнение Вольтерра с разностным ядром D43).
7. Уравнение Фредгольма с разностным ядром на осн D45). 8. Уравнение
Фредгольма с разностным ядром на полуоси D50).
§ 5. Сингулярные интегральные уравнения 454
1. Сингулярные интегралы D66). 2. Формулы обращения D68). 3. Непосред-
Непосредственное применение формул обращения D59). 4. Переход к краевой задаче,
простой пример D61)- 5. Общий замкнутый контур D63). 6. Незамкнутый
контур D67). 7. Приведение к бесконечной системе алгебраических уравнений
D69).
§ 6. Нелинейные интегральные уравнения 471
1. Переход к конечным уравнениям D71). 2 Мечод итераций D73). 3. Метод
малого параметра D75). 4. Применение теории симметричных ядер D76).
5. Применение теории неподвижных точек D78). 6. Вариационные методы
D80). 7. Уравнения с параметром D81). 8. Разветвление решений D82).
Глава VIII. Обыкновенные дифференциальные уравнения 487
§ 1. Линейные уравнения и системы 487
h Общие свойства D87). 2. Периодические системы D91). 3. Уравнение
Хилла D94). 4. Параметрический резонанс D98). 5. Гамильтоновы системы
D99). 6. Неоднородные системы E01). 7. Почти-периоднческие функции F03).
8. Асимптотическое разложение решений прн t ¦* ю E05). 9. Еще об асимпто-
асимптотическом поведении решений E08). 10. Осцилляция решений уравнений второго
порядка <Б11) 11 Системы, зависящие от параметра E14). 12. Точки пово-
поворота E18).
§ 2. Автономные системы 520
1. Общие понятия E20). 2. Предельное поведение траекторий F22). 3. Точки
покоя на плоскости, линейные системы E23). 4. Общий случай E27). Б. Циклы
иа плоскости F30). 6. Вращение векторного поля E33). 7 Точки покоя •
в пространстве E36). 8. Циклы в пространстве F39). 9. Структурно устой-
устойчивые системы E41). 10. Разрывные системы E42). 11. Системы иа м ного-
образнях E45). 12. Системы с интегральным инвариантом E47). 13. Эргодич-
Эргодичность E49).
§ 3. Устойчивость решений 553
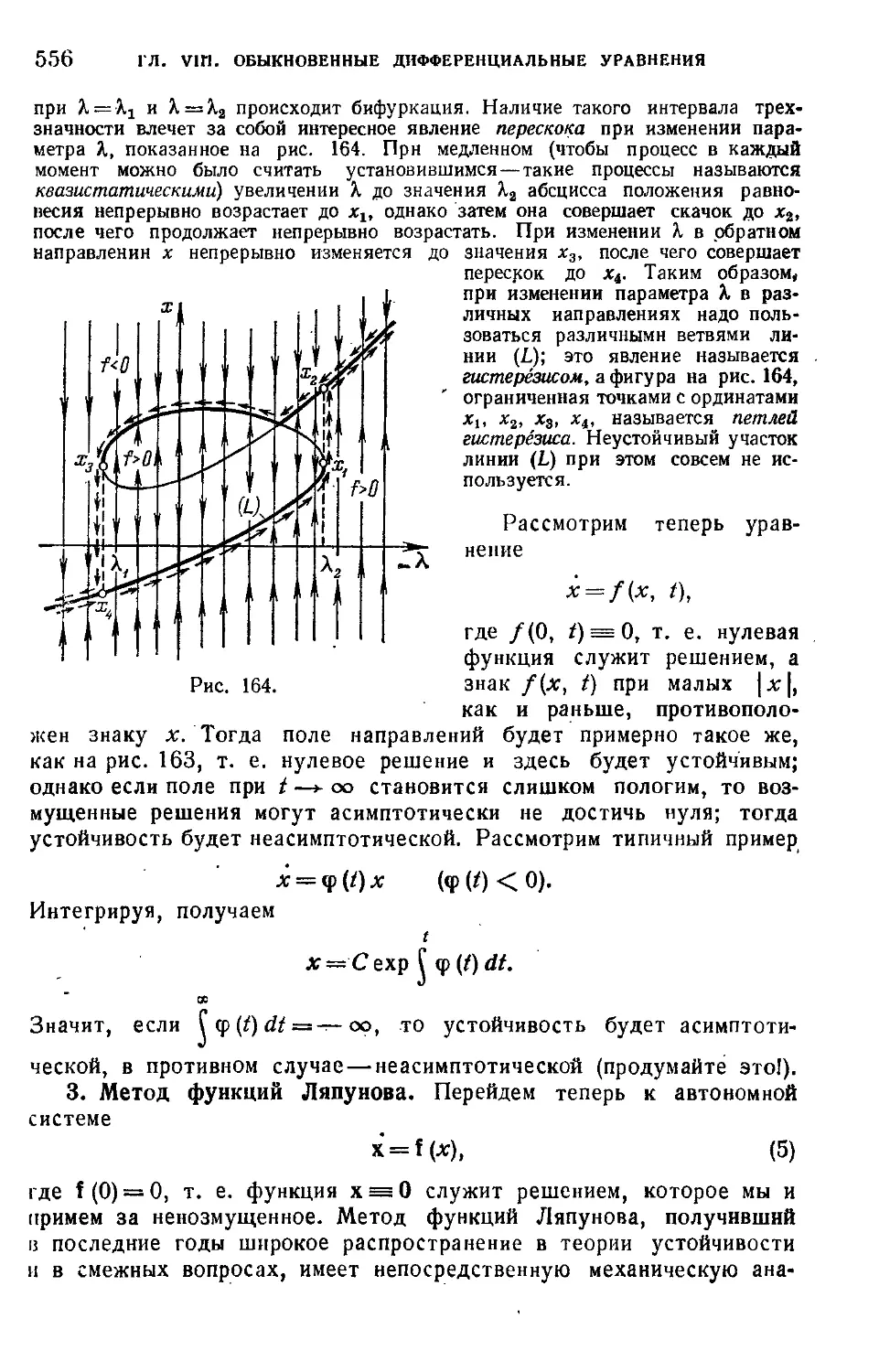
1. Введение F53). 2. уравнения первого порядка F65). 3. Метод функций
Ляпунова E56). 4. Устойчивость по первому приближению F60). Б. Особые
случаи E64). 6. Специальные классч механических систем E69). 7. Системы
автоматического регулирования E76). 8, Техническая устойчивость E80)
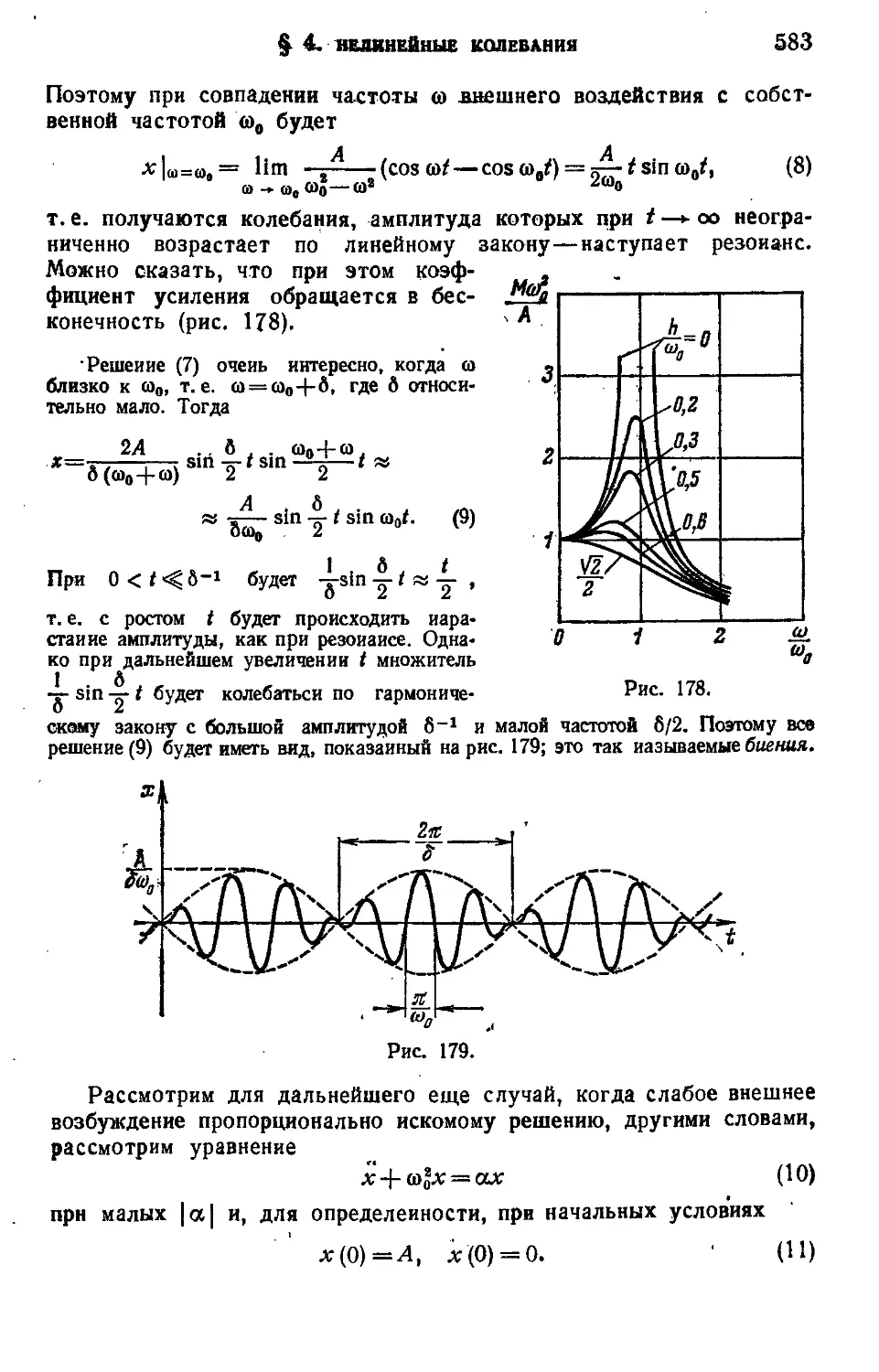
§ 4. Нелинейные колебания 581
1. Введение (Б81). 2 Свободные колебании автономной консервативной системы
с одной степенью свсбоды F87). 3. Вынужденные колебания системы с малой
нелинейностью, основной случай F92). 4. Особые случаи E94). Б. Субгармо-
Субгармонические колебания E99). 6. Еще о вынужденных колебаниях F00). 7. Авто-
Автоколебания F02). 8. Релаксационные колебания F06). 9 Пограничный слой
F07). 10. Непериодические колебания F10) 11. Асимптотические разложения
по Н. М. Крылову — Н. Н. Боголюбову F15). 12 Системы с дискретным
временем F17).
Литература 621
Алфавитный указатель 626

ПРЕДИСЛОВИЕ
Эта книга представляет собой пособие по специальным гла-
главам курса математики для инженерно-технических специальностей
высших учебных заведений, написанное с единых позиций совре-
современной прикладной математики, какими их понимает автор. Книга
предназначается в основном для студентов старших курсов вту-
втузов и инженеров различных специальностей, но она может быть
полезной также физикам и другим специалистам, имеющим дело
с прикладной математикой. Книга основана на курсах лекций, про-
прочитанных автором в разные годы, и рассчитана как на аудиторное
обучение, так и на самообразование.
По стилю изложения книга близка к «Лекциям по высшей мате-
математике» (третье издание, издательство «Наука», 1969 г.; в даль-
дальнейшем будет именоваться «ЛВМ») того же автора и может
рассматриваться как их продолжение, хотя и чиЛется независимо.
Она опирается на общий втузовский курс математики (этим объяс-
объясняется ее название) и имеет целью развить и укрепить отвечающие
современной прикладной математике взгляды на основные математи-
математические понятия и факты, а также облегчить применение матема-
математики к специальным дисциплинам. Значительное внимание обращается
на развитие правильной интуиции и возможно больший показ работа-
работающего аппарата, тогда как формальная полнота формулировок и
доказательств не является самоцелью. (Поэтому хочется специально
подчеркнуть, что эта книга не может обучить доказательству тео-
теорем на уровне «чистой» математики, она имеет совсем другое наз-
назначение.)
По каждому из освещаемых разделов систематически излагается
некоторый необходимый минимум—основные понятия и идеи, представ-
представление об области приложений и т. п. За дальнейшими сведениями и дета-
деталями читатель отсылается к дополнительной литературе, список
которой приведен в конце книги; ссылки на этот список обозна-
обозначаются номерами в квадратных скобках. При выборе этих разделов,
в значительной мере условном, автор в некоторой степени ориенти-
ориентировался на официальную программу 1969 г. спецкурсов математики
для втузов.
Отдельные главы, а в некоторых случаях и более мелкие разделы
книги можно читать более или менее независимо, в соответствии

3 ПРЕДИСЛОВИЕ
с потребностью. Примеры, а также материал, который при первом
чтении можно опустить, напечатаны петитом. Для облегчения чтения
материал, уже освещенный в ЛВМ, в необходимых случаях весьма
кратко напоминается. Этой же, цели должен служить подробный
алфавитный указатель, помещенный в конце книги; с его помощью
легко разыскать разъяснение встретившегося непонятного термина.
В целом стоит отметить, что данная книга написана более сжато,
чем ЛВМ, и не рассчитана на быстрое чтение.
В каждой главе параграфы, в каждом параграфе пункты и фор-
формулы нумеруются подряд, начиная с первого номера. При ссылках
номера текущих главы и параграфа не упоминаются: например, в тек-
тексте § 3 гл. IV выражение «формула B)» означает «формула B)
§ 3 гл. IV», выражение «формула A.2)» означает «формула B)
§ 1 гл. IV», а «формула (Ш.4.2)» означает «формула B) § 4 гл. III».
Содержание i4iinrn ясно из подробного оглавления. Из-за недо-
недостатка места за ее пределами остался ряд важнейших в современ-
современной прикладной математике разделов, таких, как математическая
физика, элементы функционального анализа с приложением к тео-
теории численных методов, дополнительные вопросы теории обыкновен-
обыкновенных дифференциальных уравнений, теории вероятностей (в частности,
теория случайных процессов) и математической статистики и т. д.
Конечно, хорошо бы написать продолжение, содержащее указанные
разделы, но трудно сказать, удастся ли это осуществить...
Первоначальный текст рукописи был переработан на основе заме-
замечаний Р. С. Гутера, Н. Д. Копачевского, М. А. Красносельского,
А. Д. Тюпцова, а также коллектива преподавателей кафедры выс-
высшей математики МИХМ, в частности Г. Л. Лунца и А. Г. Младова;
Всем этим моим товарищам я рад выразить свою глубокую при-
признательность. '---
А. Д. Мышкис
1 октября 1969 г.

Глава I
ТЕОРИЯ ПОЛЯ
Основные понятия теории скалярных и векторных полей (произ-
(производная по направлению и градиент, векторные линии и поток, ди-
дивергенция, циркуляция и ротор) входят в общий курс математики, и
мы будем предполагать, что читатель знает эти понятия. В частно-
частности, достаточно просмотреть ЛВМ, пп. IX.9, XII.1, 2, 4, XVI.21—27;
там же "приведены примеры физических. полей, встречающихся в
реальных исследованиях. Здесь мы продолжим изложение этой тео-
теории. Дальнейшие сведения см., например, в книгах [15, 53].
§ 1. Оператор Гамильтона
Напомним, что со скалярным полем и связывается векторное поле
его градиента
i+j + rzk, A)
где х, у, z—декартовы координаты. Впрочем, градиент- может быть
определен и независимо от выбора системы координат, на основе
понятия производной по направлению; поэтому градиент, как и даль-
дальнейшие рассматриваемые здесь «производные поля», связан с задан*
ным полем инвариантно. С векторным полем А связываются
ное поле его дивергенции -
и векторное поле его ротора
дивергенция также допускает инвариантное определение на основе
понятия потока, а ротор—на основе понятия циркуляции. Диверген-
Дивергенция входит в одну из основных формул векторного анализа—формулу
Остроградского для потока вектора (точнее, векторного поля)через
замкнутую поверхность (а):
§ ^ф ) = l div AdQ; D)
(а) (а) (Q)

10
ГЛ. 1. ТЕОРИЯ ПОЛЯ
Бдесь (ь2)—область, ограниченная поверхностью (о), а п — направле-
направление внешней нормали к (а), т. е. нормали, идущей нз (Q). Ротор
входит в другую основную формулу—формулу Стокса для цирку-
циркуляции вектора по ваыкнутой ориентированной линии (/,):
§ А • йт ( -* § Л, dL)
rot A. dS;
вдссь r-^.vi-f-j/j+rk—радиус-вектор, т—направление касательной
к (L) в сторону обхода контура, (S) — поверхность^ ограниченная
линией (L) и ориентированная в соответствии с ориентацией (/.)
(см., например, ЛЗМ, п. VII.11).
Для плоских полей все формулы естественно упрощаются.
С векторным полем связываются также векторные линии, запол-
заполняющие всю область, занятую полем, и идущие в каждой своей
точке но направлению поля.
1. Операции первого порядка. Гамильтон заметил, что опера-
операции A)—C) можно более просто записать, если ввести символ
называемый пйбла (от греческого vap"Xa — арфа, форма которой
напоминает значок V). Сам по себе этот символ представляет собой
знак действия над полем, т. е. оператор (по поводу понятия опе-
оператора см., например, ЛВМ, пп. XIV.26 и XV.20). Этот оператор
Гамильтона векторно-дифференциальный и при своем действии обла-
обладает как свойствами вектора, так и свойствами оператора диффе-
дифференцирования.
«Умножение», т. е. действие оператора Гамильтона на скаляр
(точнее, на скалярное поле) и и на вектор А, производится по сле-
следующим естественным правилам:
. д . , д , , д \ . ди , ,ди , . ди
дАх dAv дА,
i j k
дх ду дг
В формулах, содержащих V, этот оператор действует как диф-
дифференциальный только на расположенный за ним множитель; резуль-
результат такого действия дальнейшие множители уже не дифференцирует.
Поэтому следует избегать записи вида yuv, которую более естест-

§ 1, ОПЕРАТОР ГАМИЛЬТОНА 11
венно понимать как (Vh) © = (grad «)¦» = ¦» grad н, но иногда ее пони-
понимают как V (uv) = grad(Hi>), а это, конечно, не одно и то же.
¦Если же в каком-либо выражении за наблой нет множителей, то
оно представляет собой оператор; например,
; + }±
— это скалярный днффенциальный оператор, который может дей-
действовать на скалярное или векторное поле. На основании формулы
для производной по направлению этот оператор можно записать
также в виде А тт-, где /д—направление вектора А. В частности,
для скорости изменения скалярного или векторного поля вдоль
траектории (ЛВМ, п. ХИЛ) получаем выражение
d г, , д
2. Правила действий. При действиях с оператором V надо поль-
пользоваться правилами векторной алгебры и правилами дифференциро-
дифференцирования. Например,
(X = const), (8)
так как умножение на скаляр и дифференцирование обладают этим
свойством линейности. В то же время в формуле (8) нельзя было
бы считать % зависящим от точки пространства, т. е. скалярным
полем, так как тогда получилось бы, что мы вынесли переменную
величину за знак производной. Чтобы охватить этот случай, заме-
заметим, что в обычной формуле для производной произведения
(uv)' = u'v + uv' (9)
первое слагаемое получается, если в процессе дифференцирования
считать v постоянным, а второе—если в этом процессе считать и
постоянным (продумайте этот подход, исходя из правила дифферен-
дифференцирования сложной функции). Поэтому дифференцирование (9) можно
выполнить так:
(uv)' = (ucv)' + (uvc)' = ucv' -f- u'vc = uv' 4- u'v,
где индекс с указывает, что при дифференцировании к данной вели-
величине надо относиться как к постоянной; конечно, если величина
стоит вне знака дифференцирования, то индекс с у нее можно снять.
Таким образом,'
grad {uv) ¦= V (uv) = V (ucv) + V (uvc) =
= uyv + vV« = и grad v 4- v grad u.

12 ГЛ. 1. ТЕОРИЯ ПОЛЯ
.Покажем еще несколько примеров действия с наблой:
div (иА) = V • (иА\ = V • (»СА) + V • (иА^ =
; A0)
(здесь надо воспользоваться формулой для векторно-векторного про-
произведения (ЛВМ, п. VII. 16), однако расположить множители в таком
порядка, чтобы набла действовала на тот множитель, который счи-
считается переменным)
= A(V-B)—(A-V)B + (B-V)A—B(V-A) =
= AdivB —BdivA + (B-V)A —(A-V)B;
(здесь надо воспользоваться свойствами векторно-скалярного произ-
произведения (ЛВМ, п. VII. 15) н переставить сомножители в нужном
порядке)
VXA) = B-rotA — A-rotB.
Продумайте эти вычисления!
3. Интегральные формулы. Из формулы Остроградского D)
можно получить две другие полезные формулы преобразования по-
поверхностного интеграла в объемный. Для этого положим сначала
в D) A = ai; тогда получим
<р и cos (n, i) do = l
Помножив обе части на I, а затем" проделав то же с полями A =
и А = ик и сложив результаты, получим (проверьте!)
(ст)
= ф gradudQ. A1)
Q) *
Эта формула имеет простой физический смысл. Пусть объем (Q) заполнен
покоящейся жидкостью и под действием поля внешних сил с объемиой плот-;
ностью f в ней образовалось поле давлений и. Тогда grad и = f (докажите это,
рассмотрев силы, действующие на малый кубик со сторонами, параллельными
осям координат), а потому правая часть A1) равна сумме всех объемных сил,
действующих на (Q). В то же время левая часть A1) равна с противополож-
противоположным знаком сумме сил, действующих на поверхность (о). Поэтому равенство
A1)—это необходимое условие равновесия: сумма всех объемных сил должна
быть противоположна сумме всех поверхностных сил, т. е. общая сумма всех
сил равна нулю.
Для вывода другой формулы подставим вместо А в формулу D)
^J—Лук. Так как dlv(i4J—Аук) = ^ —
a (AXl)-«lo=(cl<TXA)-i = (d<TXA)J(.( то формула D) даёт
(J^J
(а) , . (О)

§ 1. ОПЕРАТОР ГАМИЛЬТОНА 13
Помножив обе части на 1, а затем прибавив аналогичный выражения
для двух других координат, получим, что
$$ A2)
(a) (Q)
Если обе части каждой из формул D), A1) и A2) разделить
на й, а затем перейти к пределу, когда (Й) стягивается в точку,
мы получим инвариантные, ие связанные с выбором системы коорди-
координат определения величин divA, grad и, rot А соответственно. Срав-
Сравнение получающихся формул с формулами F), E) и (?) приводит
к символической формуле для оператора Гамильтона
(a) {da)
4. Операции второго порядка. После применения дифференциаль-
дифференциальной операции к полю получается новое поле, к которому можно
вновь применять эти операции; повторное применение двух операций
первого порядка, описанных в п. 1, называется дифференциальной
операцией второго порядка. Конечно, не всякие комбинации имеют
смысл; например, не имеет смысла комбинация divdivA, так как.
dlv А образует скалярное поле, от которого уже нельзя брать ди:
вёргёнцию. Мы предоставим читателю убедиться в том, что с по-
помощью комбинации операций grad, div и rot можно получить ровно
пять осмысленных дифференциальных операций второго порядка:
div grad и, rot grad ы, grad div A, div rot A, rot rot A. A3)
Начнем со второй комбинации; ее можно записать в виде V ХG")-
Но для «обычного» вектора а и «обычного» скаляра и всегда
аХ(аи)=О A4)
(почему?). Значит, если вместо а в левую часть подставить его
разложение по декартовым осям и произвести вычисления по фор-
формальным правилам векторной алгебры, то мы получим нуль. Но
вычисление комбинации V X (V") производится по тем же формаль-
формальным правилам, что и A4), только вместо ах, а , а надо взять
д д д о
ч-, j-, ^-. Значит, и здесь получится нуль, т. е. всегда
rot grad и — 0. A5)
Аналогично получаем (проверьте!), что всегда
div rot A = 0. A6)
Это простое свойство, имеет важное следствие. Именно, для любого
поля А можно наряду с векторными линиями рассматривать вихревые
линии, т. е. векторные линии поля rot А. Однако дивергенция любого
векторного поля равна плотности источников векторных линий этого
поля (ЛВМ, п. XVI.23). Поэтому формула A6) говорит, что вихревые ,

14 ГЛ. I. ТЕОРИЯ ПОЛЯ
линий не могут иметь ни источников, ни стоков, т. е. они не
могут ни начинаться, ни кончаться.
Первую комбинацию A3) можно записать в виде V- V« = (v- V)« ==
= Уаи, где Va—скалярный дифференциальный оператор второго
порядка
+k
который называется оператором Лапласа {лапласианом) и иногда
обозначается символом Д. Итак,
Рассмотрим, наконец, последнюю комбинацию A3). Пользуясь
формулой для векторно-векторного произведения (ЛВМ, п. VII. 16)
и располагая множители так, чтобы наблы действовали на поле,
получим
rot rot А = V X (V X А) = V (V • А) — (V ¦ V) А = grad div A — V2A. A8)
5. Разрывные поля. Если поле имеет разрывы, то применение
дифференциальных операций к нему требует особого внимания, так
как в результате таких действий могут появиться дельта-функция
н другие обобщенные функции (см. первоначальные сведения о них
в ЛВМ, пп. XIV.25 и 27, XVI. 19). Мы рассмотрим здесь только не-
некоторые виды разрывов, наиболее распространенные в физических
приложениях; систематически подобные вопросы рассмотрены в
книге [30].
Напомним, что если функция f(x) имеет конечный скачок при
х = а, который мы обозначим через [/(а)] = /(a-f-0)—/(а — 0), то
при ее дифференцировании получится
N(x-a), A9)
где q> (x) = f (х) (х Ф а)—обычная, необобщенная функция.
Пусть теперь рассматривается скалярное поле и с конечным
скачком на плоскости х = 0:
О (х < 0),
I, г) (х > 0).
Вычисляя по формуле A) градиент и пользуясь правилом A9),
получим
| 0 (лг < 0),
где <P=jgrad^ (Лг>о)
Обращаем внимание читателя на то, что дельта-слагаемое появ-
появляется только у г-, но не у т- и т-. Грубо говоря, дело в том,

§ 1. ОПЕРАТОР ГАМИЛЬТОНА 15
что если находиться на склоне крутого оврага, но двигаться вдоль
оврага, то... (продумайте, что будет).
Если поле и имеет конечный скачок [к] при переходе с внутрен-
внутренней стороны некоторой ориентированной поверхности (S) на внешнюю
сторону, то, пользуясь независимостью градиента от выбора осей
координат) получим, что
[u]6(s)n°, B0)
где <p = grad/ ((л:;у; z)~? {S)), s—длина дуги, отсчитываемая от (S)
в направлении внешней нормали, а п° — единичный вектор этого
направления, своего в каждой точке (S). (Напомним, что «?» озна-
означает «принадлежит», а «~?» — «не принадлежит».) Если в простран-
пространстве введена криволинейная ортогональная система координат Я, [»,
v и E) имеет уравнение к = к0, то вместо 6(s)n° в формуле B0)
надо написать у- б (к—А.0)еъ где /х—коэффициент Ламе (ЛВМ,
п. XVI. 15), а ех—единичный вектор, касательный к координатной
линии L
Аналогичное рассмотрение векторного поля А, имеющего конеч-
конечный скачок [А] на поверхности (S), которое мы предоставляем
читателю, приводит к формуле
uivA = y(x,y,z) + [An]6(s), B1)
где ip = divA ((лг; _у; z)~? E))—обычная (не обобщенная) функция. Так
как выражение вида об (s) можно истолковать как объемную плот-
плотность массы, распределенной по E) с поверхностной плотностью <г,
то из B1) вытекает, что на {S) распределен источник векторных
линий с обильностью [Ап] на единицу площади. (Получите этот
результат непосредственно, рассмотрев поток вектора А через по-
поверхность соответственно выбранного малого цилиндра.) Подобным
образом, rot А = % {х, у, z) + п X [А] б (s).
Рассмотрим теперь поля с точечной особенностью, для опреде-
определенности, в начале координат. Как разъяснялось в ЛВМ, п. XIV.27,
функция, заданная своими значениями в точках пространства и имею-
имеющая интегрируемые особенности, еще не является обобщенной, но
при дифференцировании такой функции может получиться обобщенная
функция. (Там рассматривались функции одного переменного, но тот
же результат справедлив для функций любого числа переменных.)
«Водораздел» между интегрируемыми и неинтегрируемыми функциями
с точечной особенностью проходит по степенным порядкам особен-
особенностей; более точно, если/(лг, у, z) при г —»-0 (г = |г| = |/лга + _у2 + г2)
имеет порядок г~р, то при р < 3 функция / интегрируемая, а при
/>^3—неинтегрируемая (ср. ЛВМ, п. XVI.17). С другой стороны,
легко проверить на простых примерах, что при дифференцировании
порядок степенной особенности повышается на единицу (например,.
(#-5)'=—5х~* и т. п.). Поэтому при применении дифференциальных

16 ГЛ. I. ТЕОРИЯ ПОЛЯ
Операций первого порядка к полю, имеющему степенную изолиро-
изолированную особенность ниже второго порядка, получается особенность
ниже третьего порядка, т. е. такое применение не требует привле-
привлечения обобщенных функций. *
Значительный интерес представляют изолированные степенные
особенности второго порядка; они играют для изолированных осо-
особенностей в пространстве ту же роль, что конечные скачки для
функций одного переменного. Если в формулах D), A1) и A2) за
(а) принять малую сферу с центром в начале координат, то так как
о = 4яг2, при г—*0 левые части имеют конечные пределы, а потому
подынтегральные функции в правых частях имеют дельта-слагаемые.
Например, если поле А имеет в начале координат изолированную
степенную особенность второго порядка, то div А имеет слагаемое
k Ъ(г) = kЬ {х)Ь (у)б (z), где k = lim -?—|- i^ A¦ йо; другими словами,
'-• Ш (а)
у такого поля в начале координат начинается, k векторных линий
(см. п. 4).
1 Для пространственных полей с особенностью вдоль ¦ некоторой
линии, а также для плоских полей аналогичную роль играют сте-
степенные особенности первого порядка.
\ § 2. Специальные типы полей
1. Потенциальные поля. Векторное поле А называется, потен-
циальным, если оно является градиентом некоторого скалярного
поля, т. е. если
A = gradq>; A)
при этом поле <р называется потенциалом (точнее, скалярным по-
потенциалом) поля А. .
Обращаем внимание читателя на то, что часто потенциал опре-
определяется формулой А = —grad<p(= grad(— <p)). Так введенный по-
потенциал отличается множителем (—1) от того, который мы будем
рассматривать. Иногда для различения этих двух подходов приме-
применяются термины «потенциал» и «потенциальная функция», однако
такая терминология не общепринята. Поэтому при чтении работы,
в которой применяются потенциалы, надо уточнять, в каком из этих
двух смыслов употребляется это понятие.
Так как градиент постоянного скалярного поля и только такого
поля равен, нулю (почему?), то потенциал любого поля, если он
имеется, определен с точностью до произвольного .^постоянного сла-
слагаемого. Подбирая это слагаемое, можно пронормировать потенциал
(т. е. избавиться от этого произвола), например, сделав это значе-
значение равным нулю в некоторой заданной точке. Чаще всего потен-
потенциал нормируют условием равенства нулю иа бесконечности—если
там потенциал- имеет вполне определенное конечное значение.

§ 2. СПЕЦИАЛЬНЫЕ ТИПЫ ПОЛЕЙ
17
¦ Далеко не всякое поле является потенциальным. Именно, из A)
и общей формулы A.15) сразу следует, что ,
rotA = 0, B)
т. е. всякое потенциальное поле является безвихревым. С другой
стороны, в ЛВМ, пп, XVI.27 и XIV.24 было показано, что если поле
А задано в односвязной области (G), то условие B) равносильно
независимости интеграла \ А • dr от контура интегрирования, или,
что то же, условию
Adr =
C)
для любого замкнутого контура (L), расположенного в (О). Таким
образом, безвихревое поле, заданное в односвязной области, явля-
является бесциркуляционным. Там же было показано, что нз C) следует,
что выражение А ¦ dr = Axdx + Aydy + Azdz является полным диффе-
дифференциалом. Но равенство Adr = rf<p равносильно A) (почему?), т. е.
всякое бесциркуляционное поле является потенциальным; обратно»
тоже, верно,, что мы предлагаем доказать желающим.
Если А—поле сил, то интеграл \ A-dr равен работе, производимой по-
полем, когда частица, на которую оно действует, проходит линию (L). Поэтому
для такого поля условие C) наиболее наглядно—поле потенциально тогда и
только тогда, когда его работа по любому замкнутому контуру равна нулю.
Итак, в односвязной области условия A), B) и C) равносильны,
т. е. условия потенциальности, отсутствия вихря и отсутствия цир-
циркуляции векторного поля эквива-
эквивалентны.
2. Безвихревое поле в мно-
многосвязной области. Рассмотрим
безвихревое поле А в мно-
госвязиой области (О). В Этом
случае циркуляция вектора А "по
замкнутому контуру- уже не обя-
обязана равняться нулю; из доказа-
доказательства формулы C) вытекает
только, что циркуляция заведомо
равна нулю, если контур внутри
области (G) можно стянуть в
точку. Например, на рис. 1, где
область получается, если из про-
пространства изъять два бесконечных цилиндра (такая область навы-
вается трехсвязной), заведомо равна нулю циркуляция вектора А по
контуру (?).
• - Что касается ' замкнутых контуров, которые нельзя стянуть
в точку, то о- них можно утверждать лишь, что если два контура
Рис. 1.

10 ГЛ. I. ТЕОРИЯ ПОЛЯ
(Lt) и (L[) можно путем непрерывной деформации перевести один
в другой, не выходя за пределы области (О), то циркуляции вектора А
по этим контурам одинаковы. Действительно, если соединить эти
контуры линией AD (см. рис. 1) и рассмотреть изображенный пунк-
пунктиром составной контур ABCADEFDA, то его уже можно стянуть
в точку (почему?), откуда
ADE
f f J J J
ABCADEFDA ABCA AD DEFD DA
= ф A-dr + j[ kdr $ ^
(L[) AD <?.,) DA
Но интегралы по соединительной линии взаимно уничтожаются (по-
(почему?) и мы, таким образом, получаем
& А • dr — ф А ¦ dt = 0, т.е. & А • dr = ф А • dr.
(Ч') (il) (Ч') <L«>
В то же время циркуляция по контуру (Z,2) (рис. 1), вообще
говоря, совершенно независима от циркуляции по.(?х). Легко прове-
проверить, что для случая трехсвязной области, изображенной на рис. 1,
циркуляции по контурам (Lt) и (?2) (эти циркуляции мы обозначим
буквами 1\ и Гг) образуют полную систему независимых циркуляции
в том смысле, что циркуляцию по любому другому замкнутому кон-
контуру легко выразить через 1\ и Гг. Например, циркуляция по кои-
туру (Z.s) равна I^ + Tg (для доказательства этого надо деформи-
деформировать A3) так, как это показано пунктиром); циркуляция по (Z.4)
равна Г2—21\ и т. д. Для (&+ 1)-связной области (говорят также —
области порядка связности Л.+ l) число независимых циркуляции
равно k. В самом простом случае, для двухсвязной области (такими
являются пространство, из которого изъят бесконечный круговой
цилиндр, внешность или внутренность тора и т. п.) имеется лишь
одна независимая циркуляция.
Теперь легко понять, что будет, если для безвихревого поля
в миогосвязной области строить потенциал по той же формуле
Ф (М) = J d(p = J А ¦ dr
~М„М "МцМ
("М0М—любая дуга, соединяющая фиксированную точку Мв с те-
текущей точкой М по области), что и в односвязном случае. Соот-
Соотношение A) будет выполнено, однако в данном случае функция
ф (М) (т. е. потенциал) будет, вообще говоря, многозначной. Напри-
Например, если непрерывно продолжать значение функции ф (М) вдоль
линии (Z.j) на рис. 1 и совершить при этом полиый обход этой линии,
то потенциал получит приращение \ A-dr = I\. Тот же результат

§ 2. СПЕЦИАЛЬНЫЕ ТИПЫ ПОЛЕЙ 19
получится при обходе контура (L[), а при обходе контура (?г) по-
потенциал получит приращение Г2. По этой причине константы Г1 и Гг
называются также периодами потенциала.
Итак, потенциал безвихревого поля в многосвязной области явля-
является, вообще говоря, многозначной функцией; такое поле с много-
многозначным потенциалом не считается потенциальным. Только в том
частном случае, когда все периоды потенциала равны нулю—дру-
нулю—другими словами, когда поле бесциркуляционное,—потенциал является
однозначным, т. е. поле —потенциальным.
3. Солеиоидальиые поля. Векторное поле А называется солено-
идальным, если оно является ротором некоторого векторного поля,
т. е. если
А = rotO»; D)
при этом поле Ф называется векторным потенциалом поля А.
Векторный потенциал соленоидального поля определен с точностью
до градиента произвольного поля. В самом деле, если Ф1 = Ф ~f- grad i|),
то в силу A.15)
rot Bt = rot В + rot grad \|з = A + 0 = A}
легко проверить и обратное. Пользуясь этим свойством и подбирая
функцию \|> соответствующим образом, можно производить ту или
иную нормировку векторного потенциала. '
Поле, соленоидальнре в некоторой области, не имеет внутри нее
источников векторных линий, так как из D) и общей формулы A.16)
следует, что
div А = 0. E)
Этим и объясняется название «соленоидальное поле», так как ти-
типичным векторным полем, не имеющим источников, является любое
магнитное поле, в частности, поле, возникающее при прохождении
тока через катушку (соленоид).
Проверим теперь, что поле, заданное во всем пространстве и не
имеющее источников векторных линий, соленоидальное. Для этого
будем искать векторный потенциал в специальном виде Ф = Р (х, у, z) i-j-
4~Q(X) У> 2)j, тогда подстановка в D) и приравнивание проекций
дают
— ESL-A ?--А W--EL-A 1&)
дг ~Л*' дг ~ЛЯ дх ду ~А*' (й>
Из первого равенства можно определить Q с точностью до произ-
произвольной функции f(x, у); например, можно положить
Q(x, у, z) = QQ(x, у, z)+f(x, у), где Q0(x, у, *) —
У, 0*С G)

20 ГЛ. I. ТЕОРИЯ ПОЛЯ
Аивяогйчно из второго равенства F) получим Р(х, у, z) вЯ0 (х,у,х)'+
"f /i(x, у), где fx произвольна. Подставим выражения для Q пР
в третье равенство F), положив /±^0 (нам надо найти какой-
нибудь векторный потенциал, а произвола в выборе / будет доста-
достаточно). Мы получим для нахождения / уравнение
дх ' дх ду *' дх г дх
Однако последняя правая часть не зависит от г, так как
дА дА,__
L(a dQ» дР9\_дА, д (dQ9\ д /дРл\
дг\ * дх Т ду ) дг дх \ дг ) ^ду \ дг )
в 'силу выполнения условия E). Поэтому, обозначив правую часть
х
(8)/через F(x, у), найдем f(x, y) = )F(%, ^)d|, т. е. потенциал Ф
о
полностью построен.
Если поле рассматривается не во всем пространстве, а в некоторой об-
лайтй (G), то возникают трудности с применением формулы G). Более деталь-
детальное исследование этого вопроса, которым мы здесь не будем заниматься, пока-
показывает, что для соленоидальностн всякого векторного поля в (G) без
дивергенции необходимо и достаточно, чтобы любую расположенную в (G)
замкнутую поверхность типа сферы можно было путем непрерывной деформацин
стянуть в точку; не выходя за пределы (G). (Здесь выражение «типа сферы»
означает поверхность, полученную из сферы путем непрерывной деформации;
например, поверхность тора не имеет типа сферы.) Это свойство области назы-
называется ацикличностью в размерности 2, в отлнчие от односвязности, которая
иначе называется ацикличностью в размерности 1. (Примеры: выпуклые области
ацикличны в размерностях 1 н 2; тор (тело)—в размерности 2, но не 1; про-
пространство с изъятым шаром—в размерности 1, но не 2; пространство с изъятым
тором — ни в размерности 1, нн в 2). Можно доказать, что область в трехмерг
ном пространстве ациклична в размерности 1 тогда н только тогда, когда она
ограничена н имеет связную (состоящую из одного куска) границу нлн когда
она не ограничена и все компоненты связности (кускн) ее границы также
йростираются в бесконечность.
Поток соленоидального поля через любую заМкнутую поверхность (о)
равен нулю. Если поле задано всюду внутри (а), то это вытекает
из формулы Остроградского A.4). Чтобы проверить утверждение
в общем случае, разобьем (а) на малые площадки (do) и ориенти-
ориентируем их контуры в соответствии с ориентацией (а). Тогда сумма
циркуляции df вектора Ф по всем этим контурам равна нулю
(почему?). Однако dT = rotn Ф do =» Anda, откуда ф Ando = <р dT = 0,
«п
что и требовалось доказать.
Обратно, если
'.t ' .; FX^10 = 0 для любой замкнутей поверхности (tf) (9)

§ 2. СПЕЦИАЛЬНЫЕ ТИПЫ ПОЛЕЙ 21*
в некоторой области (О), то поле А в этой области соленоидальнов.
Из (9) и инвариантного 'определения дивергенции вытекает E^
откуда- с помощью доказанного в следующем за E) абзаце получа-
получается наше утверждение, если (G) совпадает со всем пространством.
Доказательство справедливости утверждения для любой области (О)
более сложное, и мы не будем его проводить.
Теперь понятна роль требования ацикличности в размер ноств 2. Если это
требование выполнено н, кроме того, divA=0 в @), то для любой замкнутой
поверхности (а) в (G) поле А оказывается заданным всюду внутри (а), и потому
к (а) можно првменнть формулу Остроградского, нз которой и вытекает (9).
Однако пусть (G) не ациклична, например (G) получается изъятием нз про^
странства двух шаров, (K,i) и (/Сг), а каждая из замкнутых поверхностей @{)
(i=l, 2) содержит внутрв себя шар (/С,-) и ие содержит точек другого шара.
Тогда нз E), вообще говоря, не вытекают равенства
(о,) (а,)
однако из E) и A0) уже вытекает (9), т. е. поле А будет соленондальным.
В заключение отметим, что поле А может быть одновременно
потенциальным и соленоидальным, т. е. в рассматриваемой области
не иметь нн вихрей, нн источников векторных линий. Тогда А = grad <pj
но так как div A = 0, то должно быть
divgrad<p = O, т. е. (см. п. 1.4) Va<p = O. A1)
Это уравнение называется уравнением Лапласа, а его решения назы-
называются гармоническими функциями (не путать с гармонической, т.«,
синусоидальной зависимостью!). Итак, для того чтобы потенциальное
поле было также и соленоидальным, необходимо, а для поля, задан-
заданного во всем пространстве (или— более общий случай—в области,
ацикличной в размерности 2), и достаточно, чтобы потенциал был
гармоническим.
Уравнение Лапласа встречалось еще в работах Л. Эйлера, ио
название свое получило по имени П. Лапласа, рассмотревшего это
уравнение в своих работах по теории тяготения в 1782 г.
4. Примеры. Рассмотрим центрально-симметричное поле в про-
пространстве, определенное формулой
) A2)
Из определения дивергенции легко получить (ЛВМ, n.XVI.23), что
divA = —|-т(г'/(г)). В частности, центрально-симметричное поле
без источников вне начала координат характеризуется тем, что
/•»/(/•)= const, откуда /(/•) = §-, А-?г. A3)
Это так называемый закон Кулона, названный по имени видного
французского физика Ш. Кулона A736—1806), который впервые

22
ГЛ. I. ТЕОРИЯ ПОЛЯ
обнаружил применение этого закона в теории электрических и маг-
магнитных взаимодействий. Поток такого поля через любую сферу с
С
центром в начале координат равен -^ - 4ял2 = 4яС, т. е. не зависит
от г; другими словами, в самом начале координат в данном случае
начинается АпС векторных линий, уходящих на бесконечность. Мы
предоставляем читателю подумать, где начинаются и где заканчи-
заканчиваются (или куда уходят) векторные линии, если /(г) при г —¦¦ О
возрастает медленнее или быстрее, чем г".
Однако точечный источник обильности Q = 4nC имеет плотность
Q6 (г) = Q8 (х) б (у) б (г), т. е. мы приходим к важной формуле
Аналогичное рассмотрение плоского центрально-симметричного
поля вида A2) с r = *i-f-j/j дает, что если вне начала координат
нет источников, то /(г) =—, Q = 2nC,
dlv
= Q6 (х) б (у)).
Получающуюся при этом картину можно истолковать как точечный
источник векторных линий обильности Q на плоскости, либо как
источник, распределенный в пространстве
вдоль оси z с обильностью Q на единицу
длины.
Диполь получается при наложении
источника и стока равной обильности,
расположенных в бесконечной близости
друг от друга. Однако если при этом
обильности источника и стока остаются
конечными, то их поля просто взаимно
уничтожаются. Поэтому указанные обиль-
обильности должны быть бесконечно больши-
большими, причем такими, чтобы произведение
обильности источника на расстояние меж-
между источником и стоком (это произведе-
произведение называется моментом диполя) оставалось конечным. Наряду
с моментом диполь имеет ось, проходящую через источник и сток
в направлении от последнего к первому.
Векторное поле для случая диполя можно получить из рассмот-
рассмотрения рис. 2, где / — ось диполя. При достаточно малом h в любой
точке М будет
Чяг?
Рис. 2.

§ 2. СПЕЦИАЛЬНЫЕ ТИПЫ ПОЛЕЙ
23
где т — момент диполя. (Этот прием, посредством которого мы
нашли поле A4), годится не только для поля A3), но для любого
исходного поля.) Упрощая правую часть A4), получим (проверьте!)
т
1 dr 3r dr
т
Аналогичное рассмотрение диполя для плоского поля дает результат
Если для простоты считать ось / совпадающей с осью х, то поле
в декартовых координатах приобретает вид
m
" 2я (jfi
Интегрирование уравнения -г- — -т~
Лх Ау
линий дает
для векторных
(проверьте!) хг -\-уг — Су. Векторные линии для плоского диполя
изображены на рис. 3.
5. Ньютонов потенциал. Легко
проверить, что поле A2) имеет потен-
потенциал <р(г)= \ f(r)dr. В частности, ку-
лоново поле A3) имеет потенциал
С Q
= -.—, где Q—обильность
г 4пг ' ^
источника векторных линий, располо-
расположенного в точке г = 0. Пусть теперь
источник векторных линий безвихре-
безвихревого поля А распределен в простран-
пространстве с объемной плотностью /(г) =
—f(x,y, z). Такой источник можно полу-
получить в результате наложения беско-
бесконечно малых источников, каждый из
которых расположен в некоторой точке
(х<>\Уо', го) и имеет обильность f(r0)dQ0 (dQ9 = dxod,yodzo), и потому
потенциал в точке с радиусом-вектором г равен
Рис. 3.
Суммируя эти потенциалы, получаем потенциал поля А
/ (хп, у<» г0)
dx0dyodz0, A5)

24 "" гл. ». теория ноля
где интеграл распространен по всему пространству или, что равно-
равносильно, по объему, занятому источником, т. е. где /ФО. Выражение
A5) называется ньютоновым потенциалом с плотностью /.
Приведенный вывод формулы A5)—это стандартный пример применения
функции влияния (ЛВМ, пп. XIV.26 и XVI. 19): переход от плотности
источников безвихревого векториого поля к его потенциалу является линейным
оператором с функцией влияния—-.—j г, где г0 и г—радиусы-векторы
4Я|Г — Го |
точек воздействий и наблюдения.
Полученный результат имеет простой физический смысл. Точечный заряд q,
помещенный в начале координат, порождает в вакууме электрическое поле
E=ft-jTe, где коэффициент k определяется выбором системы единиц. Это поле
имеет в начале координат источник векторных линий обильности Q=4jift?
и потенциал — k —. Таким образом, A5) представляет собой потенциал электри-
электрического поля, порожденного зарядами, распределенными в пространстве
с объемной плотностью j-г / (г). Аналогичный результат, но с противополож-
противоположным знаком, получается для гравитационного поля, порожденного распреде-
распределенными в пространстве массами.
Если функция / принимает конечные значения и фииитиа (т. е. вне
некоторой конечной области тождественно равна нулю), как мы будем
для простоты считать, то интеграл A5) имеет единственную особен-
особенность при г„ = г; однако после перехода к сферическим координатам
с центром в точке (х; у; г) и эта особенность пропадает. (Если же
какое-либо нз этих двух условий не выполнено, то надо еще забо-
заботиться о сходимости интеграла; например, для сходимости интеграла
на бесконечности достаточно, чтобы \/(х, у, z)\ при г—¦• со убывала
быстрее г~г (почему?).)
Полученный результат допускает также следующую трактовку.
Так как /(r) = div А (г) = div grad ф (г) = V2<p(n- 1- 4), то ньютонов
потенциал A5) представляет собой решение трехмерного уравнения
Пуассона (выведенного С. Пуассоном в 1813 г.)
v2q>=/(*, у, г), A6)
которое является неоднородным вариантом уравнения Лапласа A1).'
В предположениях предыдущего абзаца легко проверить, что ф(г)—<-0
при г—>-оо; можно показать (но мы здесь иа этом не будем оста-
останавливаться), что при таком условии на бесконечности уравнение A6)
имеет лишь одни решение-, т. е. то, которое дается интегралом A5).
Существенность условия на бесконечности видна уже в случае /гзО, так
как если этого условии не ставить, то наряду с «основным» решением фаз О
появляются не только решения ф = const, не играющие роли в теории потен-
потенциала, ио также и «нетривиальные* решения вида <р = ах-\-Ьу-\-сг—потенциалы
диполей, расположенных на бесконечности,— и решения с. еще большей
РОСТЬЮ роста. ..:••.•:•;''•.-. у ¦¦;

§ 2. СПЕЦИЛЛЬНЫВ ТИПЫ ПОЛКИ 25
Аналогичное рассмотрение плоских полей приводит взамен A5)
к логарифмическому потенциалу *
= Ш V<*<>¦ Уд1п У(х-хо)Л + (Уг-Уо
который удовлетворяет двумерному уравнений Пуассона. Если функ-
функция / фнннтна и принимает конечные значения, то при г—>¦ оо этот
потенциал обращается, вообще говоря, в бесконечность; однако
производные от него стремятся к нулю. Йтим условием решение
уравнения Пуассона определяется с точностью до произвольного-
постоянного слагаемого.
6. Построение векторного поля по заданным ротору и дивер-
дивергенции. При исследовании общих векторных (полей возникает задача
(см. конец этого пункта) о построении векторнрго поля Ф, если заданы
rotO=A(r), divO = a(f). A7).
Мы будем рассматривать поля, заданные во всем пространстве,,
и считать поля А и а финитными или достаточно быстро стремя-
стремящимися к нулю при г—*ою; кроме того, должно выполняться необ-
необходимое условие divA = 0 (п. 3). Оказывается, что эта задача при
дополнительном естественном требовании
Ф(г) — 0 A8)
г -* <*>
имеет одно и только одно решение.
. Для построения решения возьмем ротор от обеих частей первого
уравнения A7) и воспользуемся формулой A.18), получим
72<I> = graddivO—rot rot Ф = grad a—rotA. A9)
Так как правая часть задана, то получаем уравнение Пуассона
вида A6), но уже для векторного поля; однако так как можно пе-
рейтн к проекциям этого поля, то решение Ф(г) уравнения A9) все
равно получится в виде ньютонова потенциала (продумайте!) и будет
удовлетворять требованию A8).
Чтобы проверить, что поле Ф, найденное из уравнения A9)»
удовлетворяет уравнениям A7), перепишем A9) в виде
grad(dn^—a) == rot (rot Ф— А). B0)
Взяв дивергенцию от обеих частей, получим, что У2^гуФ—а) = 0,
откуда из условия стремления к нулю при г —»¦ с» получаем, что
<11уф—а=0, т. е. второе уравнение A7). Если же взять ротор от
обеих частей B0), воспользоваться формулой AД8) и учесть,:что
div{rot4D—А) = 0—divA = 0, то аналогично получим выполнение1
первого уравнения A7).

26 ГЛ. I. ТЕОРИЯ ПОЛЯ
Построенное решение единственно. В самом деле, разность двух
полей, удовлетворяющих уравнениям B0), удовлетворяет аналогичным
однородным уравнениям (т. е. с А = 0, а^О), и наше утверждение
вытекает из A9) (почему?).
Из доказанного, в частности, следует возможность представления
любого финитного (или достаточно быстро исчезающего на беско-
бесконечности) поля А в виде суммы потенциального и соленоидального
полей:
B1)
при дополнительных условиях div<D = 0, <р |«, = 0, Ф|„ = 0 такое
представление однозначко.
В самом деле, взяв дивергенцию от обеих частей B1), получим
Y2<p = divA, откуда при условии ф^^О находим ф единственным
способом. После этого, записав условия для Ф в виде
rotO = А—gradф, div® = 0, Ф|„о = 0,
мы можем применить доказанный выше результат, т. е. и Ф опреде-
определяется единственным образом. Отметим, что в силу A9) уравнение
для Ф имеет вид
^»ф = grad 0—rot (A—grad ф) = —rot A,
т. е. Ф, как и ф, получается в виде ньютонова потенциала.

Глава II
ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
В этой главе мы будем систематически исследовать комплексные
функции от комплексного переменного. При этом будут предпола-
предполагаться известными основные свойства комплексных чисел, включая
простейшие алгебраические и трансцендентные действия над ними,
а также понятие о степенных рядах с комплексными членами (см.,
например, ЛВМ, § VIII. 1, пп. VIII.8 и 11, XVII. 14). Сейчас теория
аналитических функций представляет собой значительно разработан-
разработанную дисциплину, имеющую большое количество приложений. Неко-
Некоторые разделы этой теории, например теория конформных отображе-
отображений, непосредственно применяются к изучению плоских полей. Еще
обширнее применения теории аналитических функций к исследованию
сложных интегралов, рядов, уравнений и т. д., появляющихся в раз-
разнообразных приложениях аналитических методов математики.
Мы сможем здесь осветить лишь некоторые общие положения
и отдельные специальные важные для приложений вопросы; система-
систематическое изложение теории и приложений аналитических функций
можно найти, в частности, в книгах [66, 74, 83, 92, 102, 104, 107,
120, 121].
§ 1. Дифференцирование и отображения
1. Производная. Пусть на всей плоскости комплексного пере-
переменного z илн на некоторой ее области задана (однозначная) функция
w=f(z), принимающая комплексные значения. Мы уже упоминали
в ЛВМ, п. VIII.11, что производная от такой функции определяется
по обычной формуле
§=/'(*)= Нш ?= «ш
"z Дг -> о Аг Дг -+ о Аг
где предел должен быть вполне определенным при произвольном
стремлении Az к нулю. При этом остаются в силе все основные
свойства производной и формулы дифференцирования, выведенные
для функций от вещественного переменного.
Функция, непрерывная в некоторой области и имеющая в каждой
ее точке конечную производную, называется аналитической в этой
области. Грубо говоря, требование аналитичности функции f(z) озна-
означает не только то, что она не должна иметь точек и линий разрыва,

28 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
но также и то, что при вычислении значений /{г) над z должны
производиться действия (алгебраические, образование суммы ряда
и другие предельные операции) как над комплексным агрегатом, без
расчленения z на вещественную и мнимую части. Такой является,
например, функция w = zz, хотя ее и можно, обозначив z = x + iy,
представить в виде w = x%-\-i2xy—у2. В отличие от этого, такие
величины,, как, например, s — x2—iy% или t — z*=x—iy, являются
функциями от z, так как, зная значение z, можно найти соответ-
соответствующие значения х = Re z, у = Im z, а с их помощью найти s nt;
однако эти функции не аналитические, так как выражения 5 {х, у)
и t (x, у) нельзя «свернуть» в алгебраические или аналитические
выражения вида s{z) и t(z).
Отметим, что с точки зрения приведенного определения такую
функцию, как, например, \/z, нельзя считать аналитической на всей
плоскости г. Эта функция аналитическая в области, полученной
выбрасыванием из плоскости z точки 7 = 0, в которой непрерывность,
а потому и аналитичность нарушаются. Такая точка называется
особой точкой аналитической функции. Иногда употребляется другая
терминология: функция \fz называется аналитической во всей пло-
плоскости z, регулярной при z=?Q и имеющей особенность (особую
точку) при 7=0.
2. Условия Кош и — Римана. Пусть задана функция
•=/(*). B)
Обозначим
т. e. z=x-\-iy, w =
Тогда, если заданы х и у, то получается и z, откуда в силу B)
определяется w, а потому и и v; таким образом,
и = н(лг, у), v = v(x, у). C)
Обратно, задание функций C) полиостью определяет функцию B),
Итак, задание комплексной функции B) от комплексного аргумента•
равносильно заданию двух вещественных функций C) от двух ве-
вещественных аргументов каждая. Проверьте, например, что равенство
w = e' равносильно системе из двух равенств
« = e*cos_y, v**e*smy. D)
Если требовать, чтобы функция B) была аналитической, то функ-
функции C) будут удовлетворять определенным соотношениям, которые
мы сейчас выведем. Заметим, что в силу C)
Аи d (а + iv) _ (и + iv)x dx+ (u + tv)'y dy ._.
dz ^dlx+iy) dx + idy ' yf
Так как dz — dx+idy произвольно, то между dx и dy может быть
произвольное отношение /. Разделив числитель и знаменатель правой

§ 1. ДИФФЕРЕНЦИРОВАНИЕ И ОТОБРАЖЕНИЯ 29
части E) u&'dy и поделив затем числитель иа знаменатель, получим
., (u + i
>)x-\
_ __
Для существования единой производной A) необходимо н достаточно,
чтобы полученное выражение не зависело от t, т. е. чтобы {u-\-iv)'y —
— i(u -\-lv)'x = 0 или, что равносильно, и'у -f- ivy — iu'x—v'x. Прирав-
Приравнивая вещественные и мнимые части, получаем условия Коши—Римана
ди ди ди ди ,?.
Fx = dy' дх==~ду' ()
необходимые и достаточные для аналитичности функции B). (Про-
(Проверьте выполнение этих равенств для функций D).)
Равенствам F) можно придать более компактный вид. Пусть из
некоторой точки плоскости х, у выходят направления пит, причем л
получается из т поворотом на 90° против часовой стрелки. Тогда,
вычисляя производную по направлению (ЛВМ, п. XII. 1) и пользуясь
равенствами F), получим (проверьте!)
|- cos [(«?*) + 90°] + g cos [яСх) =
л ди ._.
G)
= Fx cos (ю, лг) + ц sin (m, x) =
ди , л . , ди , л . ди
cos(/»>r)+cos(wy)
Обратно, равенства F) легко получить из G) (как?).
3. Сопряженные гармонические функции. Из уравнений F) можно
исключить функцию v. Для этого продифференцируем первое ра-
равенство по х, а второе—по у; тогда средние члены окажутся
равными (почему?) и, приравнивая крайние члены, получим
д*и
"ду~*
Таким образом (ср. п. 1.2.3), функция и (х, у) гармоническая. Мы
предоставляем читателю проверить, исключая из уравнений F) функ-
функцию н, что и функция v(x, у) гармоническая. Две гармонические
функции, удовлетворяющие уравнениям Коши — Римана, называются
сопряженными. Итак, вещественная и мнимая части аналитической
функции являются сопряженными гармоническими функциями.
Из двух сопряженных гармонических функций приходится различать
Первую и вторую. Проверьте, что если поменять нумерацию этих функций,
то для сохранения сопряженности одну из иих надо помножить иа —1.
' Для ^любой заданной гармонической функции можно-построить
сопряженную гармоническую функцию. Пусть, например, задана

30 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
ническая функция v(x, у); тогда уравнения F), из которых надо
найти функцию и(х, у), можно совместно записать в виде
ди . ди . до до ,л*
du = rj- dx 4- •*- dy = -к- dx—з-dy. (8)
дх ' ду у ду дх J s '
Получилась задача о построении функции по ее полному дифферен-
дифференциалу, которая была рассмотрена в ЛВМ, п. XIV.24. Условие ее
разрешимости для правой части (8) равносильно требованию гармо-
гармоничности функции v (проверьте!), так что задача действительно
разрешима; решение определяется формулой
(*; у) <*; у)
и(х'У)~ \ du-\- const = \ ( 5- dx—-^-dy) 4- const
J J \oy ox * j
<*.; 2/0) <*<,; y<,)
и определено с точностью до произвольного постоянного слагаемого.
Если область, в которой осуществляется построение, многосвязная,
то построенная функция и может получиться многозначной; тогда
при обходе вокруг «пустот» области она будет получать постоянные
приращения (ср. п. 1.2.2).
4. Геометрический смысл производной. Мы уже упоминали в
ЛВМ, п. VIII.11, что функция B) определяет отображение плоско-
плоскости г (или некоторой ее области, если значения z берутся только
из этой области) в плоскость w, это отображение можно записать
и в вещественном виде C). Если функция B) однозначная (а мы
позже увидим, что в теории аналитических функций приходится
рассматривать и многозначные функции, ио это всегда будет огова-
оговариваться), то и отображение будет однозначным, т. е. каждой точке г
будет отвечать единственная точка w. Если для разных г не может
получиться одно и то же w, другими словами, если функция, обрат-
обратная к B), однозначная, то отображение B) называется однолистным',
это значит, что при отображении B) плоскость z покрывает плос-
плоскость w только один раз. (В противном случае отображение называется
многолистным — оно может быть двулистным, трехлистным и т. д.,
даже бесконечнолистным.) Однозначное однолистное отображение
иначе называется взаимно однозначным (ср. ЛВМ, п. XI. 13). Такие
отображения наиболее наглядны, так как каждому z отвечает ровно
одно w, а каждому w—ровно одно z. При этом все время имеются
в виду либо полные плоскости г и w, либо некоторые области
в этих плоскостях.
Если функция B) аналитическая, то и соответствующее отображе-
отображение называется аналитическим. Рассмотрим вид этого отображения
в малой окрестности некоторой фиксированной точки z0, предполагая
дополнительно, что
(9)

§ 1. ДИФФЕРЕНЦИРОВАНИЕ И ОТОБРАЖЕНИЯ 31
Обозначив
z—zo = AZj wo=f{zo), w—wo = Aw, \/'(zo)\ = ko, arg/'Be) = a0,
получим с точностью до малых высшего порядка
dw=f (za) Лг, т. е. | Ли;| = ko\ h.z j, Arg Ли; = Arg Лг + аи.
Значит, если представить себе плоскости z и w совмещенными, то
каждый малый вектор Ля с вершиной в точке z0 при отображении
будет перенесен вершиной в w0, растянут в k0 раз и повернут на.
угол <х0. Поэтому и вся малая окрестность точки z0 при рассматри-
рассматриваемом отображении испытает, с ¦ точностью до малых высшего
порядка, поступательный перенос, всестороннее рас-
растяжение и поворот, причем значения модуля и аргумента
производной в точке z0 служат соответственно коэффициентом рас-
растяжения и углом поворота.
Итак, если в некоторой области (G) плоскости z будет f {г)фО,
то образ каждой малой фигуры, расположенной в (G), будет, с точ-
точностью до малых высшего порядка, геометрически подобен прооб-
прообразу; в частности, мы видим, что при аналитическом отображении
малый круг переходит снова в круг (а не в эллипс, как для общих
отображений (ЛВМ, п. XI.14)), а углы между пересекающимися
линиями сохраняются. Из доказанного вытекает также, что при
аналитическом отображении ориентация плоскости сохраняется, т. е.
если обходить малый замкнутый контур плоскости z в некотором
направлении, то и образ будет обходиться в том же направлении.
Можно доказать, что и обратно, если некоторое отображение плос-
плоскости сохраняет подобие бесконечно малых фигур (или даже только
углы между пересекающимися линиями) и ориентацию плоскости,
то это отображение аналитическое.
Из свойства сохранения углов вытекает, в частности, что линии
и (х, у) = Сг и v (х, у) = С2 плоскости х, у образуют два взаимно орто-
ортогональных семейства линий (почему?). Это дает возможность, зада-
задаваясь различными аналитическими функциями f(z), получать разно-
разнообразные ортогональные системы координат на плоскости (примеры
см. ниже). Выведите эту ортогональность также из равенства G).
В отдельных точках, в которых условие (9) нарушается, вид
отображения B) будет иной, мы его рассмотрим в п. 2.6. Однако
если f[z) =? const, то наличие таких отдельных особых точек не
нарушает наших общих выводов о характере аналитического отобра-
отображения.
5. Конформные отображения. Взаимно однозначное отоб-
отображение некоторой плоской области, при котором сохраняются подо-
подобие бесконечно малых фигур и ориентация плоскости, называется
конформным; если подобие сохраняется, но ориентация меняется на
противоположную, то отображение называется антиконформным (гово-
(говорят также о конформных отображениях 1-го и соответственно 2-го

32 ГЛ. II. ТЕОРИЯ, АНАЛИТИЧЕСКИХ ФУНКЦИЙ
рода). Из п. 4 вытекает, что для конформности отображения,
осуществляемого функцией B), необходимо и достаточно, чтобы эта
функция и обратная к ней в рассматриваемой области были одно-
„ dz f dw\-1
значными и аналитическими. Так как -г-~ ("jr )» т0 условие ана-
аналитичности обратной функции равносильно условию f(z) Ф 0.
При конформном отображении сохраняется подобие лишь бес-
бесконечно малых фигур, тогда как форма конечных фигур может
существенно измениться. Например, квадрат
ABCD плоскости z, разбитый на 16 квадрати-
квадратиков, может отобразиться на показанную на
рис. 4 криволинейную фигуру A'B'C'D' с пря-
прямыми углами на плоскости w. Дело в том, что
хотя каждый малый участок плоскости z при
отображении испытывает всестороннее растяже-
растяжение и поворот, но для разных участков коэф-
коэффициенты растяжения и углы поворота раз-
различны, что и приводит к такому искажению.
Теперь легко разобраться в формуле анти-
антиконформного отображения плоскости z в пло-
плоскость w. Если совершить дополнительно зер-
Рис. 4. кальное отображение w1—w*1 то получим кон-
конформное отображение (почему?), т. е. w1=f(z).
Отсюда получаем, что w = \f(z)]*, где f(z) — аналитическая функция.
Конформные отображения широко применяются в теории плоских
полей. Ниже мы приведем ряд примеров таких отображений.
6. Линейные отображения. Линейные отображения определяются
формулой
A0)
где а и Ъ — заданные комплексные числа. Это самый простой класс
отображений. Так как -т— = а = const, то все малые участки плос-
плоскости испытывают одинаковое растяжение в \а\ раз и одинаковый
поворот на угол arg а. Значит, и вся плоскость z испытает равномер-
равномерное всестороннее растяжение в \а\ раз и поворот на угол arg а.
Если считать плоскости z и w совмещенными и Ъ = 0, то при отоб»
ражении точка z = 0 остается на" месте; если же Ь^О, то непод-
неподвижная точка определяется из уравнения nz-\- b = z.
Таким образом, линейное конформное отображение является линей-
линейным и в смысле общей теории отображений (ЛВМ, п. XI.6). Отметим
тут же, что общее линейное отображение плоскости не обязано быть
конформным: так, растяжение вдоль одной оси и сдвиг меняют углы
и потому не конформные. ¦ . ,
Частные случаи: если а = «'а, где а вещественное, то отобра-
отображение A0) представляет собой поворот плоскости на угол а; напри-

§ 1. ДИФФЕРЕНЦИРОВАНИЕ И ОТОБРАЖЕНИЯ
33
мёр,, если a = i = e ~^—это поворот на 90° в положительном на-
направлении. Если а—вещественное, а> 0, то отображение A0)—это
всестороннее растяжение, в а раз. Если е = 1, т. е. w*=z-\-b, то
отображение сводится к поступательному переносу плоскости на
вектор Ь.
7. Расширенная комплексная плоскость. Перед рассмотрением
дальнейших примеров сделаем несколько общих замечаний. В тео-
теории аналитических функций принято считать, что кроме обычных,
конечных точек комплексной плоскости z имеется еще одна несоб-
несобственная, иначе, бесконечно уда-
удаленная точка z—oc, служащая
пределом . любой последователь-
последовательности конечных точек zlt zit
za, ... , для которой \zn\ -т- оо.
Комплексная плоскость с добав-
добавленной к'ней бесконечно удален-
удаленной точкой называется расши-
расширенной комплексной плоскостью.
Чтобы понять, на что похожа
расширенная* комплексная пло-
плоскость, допустим, что комплексной
плоскости касается некоторая
сфера {S) и все точки этой плоскости проектнруются на сферу с по-
помощью лучей, проведенных через точку Р? (S), противоположную точке
касания О (рис. 5). Этим проектированием определяется взаимно одно-
однозначное отображение комплексной плоскости на сферу E) с выброшен-
выброшенной точкой Р, которой не соответствует никакая конечная точка плоско-
плоскости. Однако если последовательность А, В, С,... точек плоскости
произвольным образом уходит в бесконечность, то последовательность
А', В', С,... соответствующих точек [S) стремится к Р (почему?).
Поэтому естественно к плоскости добавить бесконечно удаленную
точку; считая, что она при этом соответствии отвечает самой точке Р.
Расширенная плоскость взаимно однозначно отображается на полную
сферу, причем видно, что как само отображение, так и обратное
к нему являются непрерывными (отображение / называется непре-
непрерывным, если изх—>¦ х0 всегда вытекает, что f (х)—>¦ f (х0)). Заметим,
что бесконечно удаленная точка, подобно нулевой точке, не имеет
определенного аргумента. Окрестностью точки z = oo естественно
считать часть плоскости z, внешнюю по отношению к какой-либо
замкнутой линии (продумайте это!).
Если между двумя множествами возможно установить взаимно однознач-
однозначное непрерыввое в обе сторовы соответствие, то эти мвожества называются
гомгомбрфными, или топологически эквивалентными. Дело в том, что имеется
специальный отдел математики—топология (от греческого «топос»—место, «ло-
«логос»—слово, наука),—изучающий наиболее глубокие геометрические свойства
2 А. Д. Мышквс
I НЕ БОЛЕЕ 1Й КНИГИ В

$4 ГЛ. Н. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
множеств, многообразий, пространств, именно, свойства, сохраняющиеся при
гомеоморфизмах (взаимно однозначных непрерывных а обе стороны отображе-
отображениях). Поэтому с точки зрения топологии гомеоморфные множества являются
эквивалентными: все топологические свойства, которые имеют место в одном
из них, имеют место и в другом. Например, с точки зрения топологии окруж-
окружность, эллипс или многоугольник эквивалентны между собой, но не эквива-
эквивалентны отрезку или кругу. Вывод, сделанный в предыдущем абзаце, можно
сформулировать так: расширенная комплексная плоскость топологически экви-
эквивалентна сфере.
Таким образом, символ оо имеет два различных смысла: «веще-
«вещественная» и «комплексная» бесконечности. Обычно из контекста
бывает ясно, какой из них имеется в виду, однако в сомнительных
случаях не мешает делать объяснения по этому поводу.
8. Дробно-линейное отображение. Оно определяется формулой
где а, Ь, с, d — заданные комплексные числа. Рассмотрим сначала
частный случай:
где k > 0. Переходя к модулю и аргументу, получим
\®>\-=-щ, Argw=—Argz. A3)
Допустим сначала для простоты, что аргумент не менялся бы,
т. е.. рассмотрим отображение s = s(z), для которого.
Если считать плоскости z и s совмещенными, то из второго равенства
вытекает, что каждый луч с вершиной в начале координат преобра-
преобразуется в себя (почему?). Но как? Из первого равенства A4) мы
видим, что при |z| = A будет и \s =k; при |г|< Сбудет |s|>As,
причем, во сколько раз меньше г\, во столько раз больше \s\,
так что при | z | —>¦ 0 будет 151 —* оо; при | z \ > k картина аналогичная.
На рис. 6 показаны образы нескольких точек, причем соответствующие
друг Другу точки снабжены одинаковыми индексами. Полезно обратить
внимание на то, что из |s|=-j—р вытекает |z|=-j—р, другими сло-
словами, прообраз переходит в образ, а образ—в прообраз. (Иначе говоря,
рассматриваемое отображение плоскости в себя само себе обратно;
такие отображения называются инволюциями.) Все точки окружности
|.г| = ? отображаются в себя, т. е. остаются на месте; концентриче-
концентрические окружности радиуса < k переходят в окружности радиуса > k
и обратно (рис. 6). Точки 0 и оо переходят друг в друга.
Отображение A4) называется инверсией или зеркальным отра-
отражением плоскости г относительно окружности [х\ = к, а точки, пере-

§ 1. ДИФФЕРЕНЦИРОВАНИЕ И ОТОБРАЖЕНИЯ
35
ходящие друг в друга при инверсии, называются симметричными
относительно этой окружности. Последнее название объясняется', в
частности, тем, что в малой окрестности любой точки инвариантной
окружности это отображение, с точностью до малых высшего по-
порядка, представляет собой обычное зер-
зеркальное отражение. (Можно проверить,
что если на рис. 5 считать, что точка О —
это начало координат, а сфера (S) имеет
радиус As/2, то отображение A4), пере-
перенесенное на эту сферу, индуцирует зер-
зеркальное отражение сферы (S) относи-
относительно плоскости, проходящей через центр
этой сферы параллельно плоскости z.)
Докажем следующее важное круговое
свойство инверсии: при инверсии все окру-
окружности, а также прямые преобразуются
в окружности или в прямые (причем окруж-
окружность, равно как и прямая, может преоб-
разоваться либо в окружность, либо в
прямую). Для этого заметим, что уравнения всех окружностей и пря-
прямых плоскости лг, у можно представить в единой форме
а(х*+у*) + $х + уу + 6 = 0, A5)
так как при а=^=0 получаются окружности (почему?), а при а = 0 —
прямые. Если обозначить z = x-{-iy, s=p-\-iq, то отображение A4)
определяет формулы (выведите их!)
рис
„ .
У
Подставляя эти формулы в A5), получим после преобразований
уравнение линии-образа (проверьте!)
Так как k = const, то это уравнение снова имеет внд A5), только с
другими коэффициентами. Значит, получается окружность или прямая.
(Докажите, что прямая получится тогда и только тогда, когда ис-
исходная окружность или прямая проходили через начало координат.)
Отображение A3) получается из A4) с помощью добавочного
отображения |w| = |s|, Argis» = —Args, т. е. w — s*. Значит, отобра-
отображение A3) представляет собой комбинацию инверсии и зеркального
отражения плоскости относительно вещественной оси. Так как
функция A2) аналитична всюду, кроме точки z = 0, то она осуще-
осуществляет конформное отображение плоскости z с выброшенной этой
точкой на себя. Впрочем, его же можно рассматривать как конформное
отображение расширенной плоскости на себя. Что касается инверсии,
то она представляет собой антиконформное отображение (п. 5).
2*

36 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
Перейдем теперь к общему дробио-лйиейному отображению A1).
Преобразовав правую часть по формуле
мы видим, что w можно получить из z с помощью последовательных
преобразований:
C ' r '
Если изображать все переменные z, s, t, да на одной плоскости, то
получается, что рассматриваемое отображение представляет собой
последовательную комбинацию поступательного переноса, инверсии
с зеркальным отражением н линейного отображения (п. 6). Так как
все эти отображения обладают круговым свойством, то этим свойством
обладает и общее дробно-линейное отображение. Отсюда же видно,
что такое отображение переводит точки, симметричные относительно
окружности или прямой, в точки, симметричные относительно образа
этой линии.
Выражая из A1) z через да, проверяем, что отображение, обратное
к дробно-линейному, ' само является дробно-линейным, хотя у>ке,
в отличие от A2), .вообще говоря, не совпадает с прямым отображе-
отображением, т. е. не является инволюцией. Аналогично можно проверить,
что результат последовательного выполнения дробно-линейных отобра-
отображений снова является дробно-лииейцым отображением.
В правой части A1) имеется четыре комплексных параметра; но
так как при умножении их на общий множитель функция A1) не ме-
меняется, то прн выборе этой функции, имеется не четыре, а только
три комплексных степени свободы (илн шесть вещественных, так
как одна комплексная степень свободы равносильна двум вещественным;
по поводу степеней свободы см. ЛВМ, п. Х.2). Поэтому при таком
выборе надо поставить три комплексных условия; например, можно
выбрать какие-либо три значения z и задать соответствующие им
(различные!) значения да; тогда можно проверить, что отображение A1)
определится однозначно.
Потребуем, например, чтобы при отображении A1) точки г=0, 1, да пере-
перешли соотиетствеино в точки и>= — I, —i, 1. Подставляя эти значения в A1),
получим, что должны иметь место равенства
Ь_ а+Ь а .. „
c+d с
Выражая все параметры через какой-нибудь один и подставляя в A1), находим
требуемое отображение ,
ш=-?^- ¦¦'¦¦ A6)

§ 1. ДИФФЕРЕНЦИРОВАНИЕ И ОТОБРАЖЕНИЯ
37
(проверьте!). В силу кругового свойства при этом отображении окружность,
проходящая черев три. заданные точки г, т.е.. вещественная ось, переходи»
в окружность, проходящую через соответствующие точки ш, т. е, единичную
окружность |о)| = 1. А в силу сохранения ориентации верхняя полуплоскость
Rez>0 отображается на единичный круг \ш\ < 1. (Продумайте! А на что
отображается нижняя прлуплоскость? См. рис. 7.)
Рис. 7.
Отображение A6) не едииствеиное конформное отображение верхней полу-
полуплоскости на единичный круг, так как в качестве образов тех же точек г=0,
), оо можно было задать три любые точки единичной окружности, следующие
друг за другом при ее обходе в положительном направлении. Поэтому совокуп-
совокупность таких отображений имеет три вещественных илн, что то же, полторы
комплексных степени свободы. Можно показать, что общий вид такого отображе-
отображения ш=е1а ¦
— п*'
где а—любое вещественное, а р—любое комплексное числа.
причем Im p > 0. • .
9. Степенные отображения. Они определяются формулой
w = z\ A7)
где k—-заданное вещественное число. Рассмотрим сначала частный
случай
• = *». A8)
Переходя к модулю и аргументу, получим
Допустим сначала для простоты, что модуль не менялся бы, т. е.
рассмотрим отображение s — s(z), для которого
Каждая точка при отображении поворачивается вокруг начала ко-
координат (почему?), причем точки, имевшие до отображения одина-
одинаковый аргумент, т. е. лежащие на одном луче с вершиной в начале
координат, перейдут в точки, также имеющие одинаковый аргумент,
причем в два раза больший (рис. 8). Таким образом, любой такой

88
ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
¦¦ . . : . ¦ . i ¦¦ '¦-:¦:.¦¦ ,.л ' '¦
Рис. 8.
луч при отображении поворачивается вокруг своей вершины, как
твердый стержень. Если теперь рассматривать всевозможные такие
лучи, то получается такая картина, как будто приоткрытый веер
из стержней, соединенных в начале координат шарниром, при отображе-
отображении равномерно раскрывается в два раза
шире. Чтобы при этом веер не перекрыл
сам себя, нужно, чтобы он в исходном со-
состоянии— т. е. прообраз — занимал угол,
не больший 180°.
Вернемся к отображению A9). По срав-
сравнению с отображением B0) здесь допол-
дополнительно происходит следующее: точки,
для которых |.г|<1, приближаются к
началу координат, так как для них
\w\ = |z|2 < \s\ = \г\; тонки :же, для ко-
которых \z\ > 1, удаляются от него. Таким
образом, при отображении точки сколь-
скользят вдоль поворачивающихся лучей. Одна-
Однако на общую картину это не влияет, и
мы получаем, таким образом^ что функ-
функция A8) осуществляет конформное отоб-
ражение угла размера а<я;с вершиной
в начале координат на угол размера 2 а. КонформностЬ/Нарушается
в самбм начале координат, где -т- = 2.г|г=о = О (ср. п. 5); впрочем,
это ясно и из того, что угол с вершиной в точке z = 0 при
отображении увеличивается в два раза.
Если в предыдущем абзаце положить а = л, то требуется неко-
некоторое уточнение: именно, отображаемую область нужно считать
открытой, т. е. ее границу к ней не причислять. Тогда и область-
образ будет открытой, и мы получаем отображение, показанное
на рис. 9, где область-прообраз и область-образ заштрихованы;
не причисленная к ним граница показана пунктиром, изображены
еще некоторые линии до и после отображения. Мы виднм, что
функция A8) осуществляет конформное отображение открытой пра-
правой полуплоскости z (т. е. полуплоскости Re z > 0) на плоскость w
с изъятой полуосью г> = 0, —оо<и^0, или, как говорят иначе,
на плоскость с разрезом вдоль указанной полуоси. Если бы мы
рассматривали отображение замкнутой полуплоскости, то на границе
после отображення произошло бы перекрытие (почему?), т. е. отобра-
отображение потеряло бы однолистность (п. 4).
Угол размера п в плоскости г не обязательно выбирать в поло-
положении, показанном на рис. 9. Проверьте, например, что та же функция
A8) осуществляет конформное отображение открытой верхней (а также
нижней) полуплоскости z на плоскость w с разрезом вдоль вещест-
вещественной положительной полуоси.

§ 1. ДИФФЕРЕНЦИРОВАНИЕ И ОТОБРАЖЕНИЯ
39
Если рассматривать функцию A8) на всей плоскости г,- то
плоскость та» окажется покрытой дважды (почему?). Значит, это
отображение однозначное, но двулистное (п. 4). Из рис. 9 видно,
что если точка г совершит полный оборот вокруг точки z = 0,
то соответствующая точка та» совершит два полных оборота вокруг
точки да = 0. .
Аналогичный характер имеет функция A7) при любом ?>1.
Она осуществляет конформное отображение открытого угла раз-
размера 2 л/k с вершиной в начале координат на плоскость w с разрезом
Рис. 9.
вдоль некоторого луча с вершиной в начале координат. Отметим,
что если k не целое, то это утверждение нуждается в уточнении,
так как тогда функция A7) неоднозначна (почему?). Это делается
так: для какого-нибудь конкретного z выбирают одно из значений zh
(чаще всего при z — \ принимают та»=1), а для прочих z эти
значения продолжаются по непрерывности (ср. п. 10). Если k целое,
а функцию A7) рассматривать на всей плоскости z, то соответ-
соответствующее отображение будет А-листным.
Если 0<?<1, то функция A7) осуществляет конформное
отображение плоскости z с разрезом вдоль луча с вершиной в на-
начале координат на открытый угол размера 2nk с вершиной в начале
координат плоскости та». Случай k < 0 мы предоставляем разобрать
читателю.
10. Многозначные функции и точки разветвления. Рассмотрим
подробнее функцию A7) при k — \j2, т. е. w — \^z. Это функция
двузначная. (Отметим распространенную ошибку: по аналогии с ве-
вещественными радикалами записывают эти два значения в виде
wt = -\-yz и w2 = —Vz, забывая, что нет никакого «арифметиче-
«арифметического» значения корня из комплексного числа, и потому все равно

40
ГЛ. 11. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
надо уточнять, что такое V^z; подобным образом, без специального
уточнения значений корней нельзя писать У—z = i]fz и т. п.) Так,
при 2 = 1 она принимает два значения: и> = 1 и —1. Остановимся
на' каком-то одном, например w = 1, и будем, меняя z, непрерывно
продолжать значение |/г. Пусть, например, точка z проходит еди-
единичную окружность в положительном направлении, принимая положения
zv z2,
(рис. 10). Так как
= -g- Argz, то соответст-
соответствующая точка w пойдет в два раза медленнее^ и когда точка z
Рнс. 10.
совершит полный оборот вокруг начала координат, придя в поло-
положение г4 = га = \, точка w совершит только полоборота и придет
в положение wi = — 1. Таким образом, исходя из одного значения
Vz |z=i = 1 и непрерывно его продолжая, мы по необходимости при-
приходим к другому значению Vz\z=i=t— 1. Если теперь точка z
совершит еще один обход вокруг начала координат, показанный на
рис. 10 пунктиром, то соответствующая точка w пройдет еще пол-
полоборота н придет к исходному значению та>8 —доо = 1.
Ясно, что аналогичная картина будет прн любом обходе вокруг
начала координат плоскости г, не обязательно по окружности.
Разобранный пример, который является типичным, указывает на
принципиальное различие многозначных функций комплексного пере-
переменного и вещественного переменного. Для многозначной функции
вещественного переменного можно естественно ввести ее однозначные
ветви (см., например, ЛВМ, п. I. 20): так, под Yx всегда понимается
«арифметическая ветвь» двузначной функции dbVx. В отличие от это-
этого, значения многозначной функции комплексного переменного, как
правило, настолько неразрывно связаны друг с Другом, что непре-
непрерывно переходят одно в другое, когда независимая переменная
совершает оборот вокруг определённых точек, называемых точками,

§ 1'.' ДИФФЕРЕНЦИРОВАНИЕ И ОТОБРАЖЕНИЯ 4Н
разветвления {ветвления) заданной функции. Для двузначной функции
w=tfz такой точкой в силу предыдущего является z — О. Впрочем,
точку z — oo также принято считать точкой разветвления этой
функции, так как «совершить оборот вокруг бесконечности»—это
значит обойти окружность большого радиуса с центром в конечной
точке (рис. 5), а при этом, как и выше, значения Ух. непрерывно
перейдут одно в другое.
Поэтому, для того чтобы можно было говорить о непрерывных
однозначных ветвях многозначной функции f{z) порознь, нужно
каким-то способом воспрепятствовать тому, чтобы точка Z могла
совершать обороты вокруг точек разветвления этой функции. Для
этого обычно в плоскости г проводят разрезы (ср. п. 9), соединяющие
точки разветвления, причем так, что если точке z запрещено пере-
пересекать эти разрезы, то Значения f(z) не могут переходить одно
в другое. Например, если на рис. 9 поменять наименования плоскостей,
то иа плоскости z (на рис. 9 правой) будет как раз разрез, соеди-
соединяющий точки разветвления z = 0 н г = оо. В плоскости с таким
разрезом можно определить однозначную ветвь функции w — У z,
принимающую при г = \ значение w—\; эта ветвь осуществляет
показанное на рис. 9 коиформное отображение этой плоскости с раз-
разрезом на правую полуплоскость w. Другая ветвь, для которой
w[zmi — —1, осуществляет отображение плоскости z с тем же
разрезом на левую полуплоскость w. Каждая из этих ветвей имеет
разрез линией своего разрыва, так как на разных берегах этого
разреза ветвь принимает разные предельные значения, т. е. имеет
конечный скачок. Так, из рис. 9 видно, что на разных берегах разреза
в точке г=—1 изображенная там ветвь принимает предельные
значения w= —/ (на нижнем) и I (на верхнем берегу).
Аналогичным образом функция w=yz, где я — 2, 3, 4, ...,
является л-значнрй и имеет точки разветвления z = 0 и z — oo, при
обходе вокруг которых значения функции сменяют друг друга. После
я-Кратного обхода вокруг точки разветвления все значения функции
приходят к своим исходным; такая точка называется точкой разветв-
разветвления порядка я. Функция w=zmln, где я = 2, 3, 4, ..., a m —
целое число, не имеющее общих делителей с я, также имеет две
точки разветвления 2 = 0 и 2 = оо порядка я. Таким образом, чем
больше знаменатель, тем больше значений у функции и тем Выше
порядок точки разветвления. Функция w = zk = ek tnг, где k ирра-
иррациональное, является бесконечнозначной, и при обходе вокруг
точек разветвления 2 = 0 или z = oo эти значения сменяют друг
друга, никогда не возвращаясь к исходному. Такие точки разветв-
разветвления называются логарифмическими, иначе точками разветвления
бесконечного порядка.
:Наличие точек разветвления является характерным свойством
многозначной аналитической функции* Конечно, такая функция, как,

42 ' гл. п. тЬо^ия аналитических функций
например, w = ]fz2 — ± г, не имеет точек разветвления, но ее ветви
•w — z и w=—z не переходят друг в друга при своем продолже-
продолжении, т. е. она является не единой многозначной функцией, а скорее, '
в каком-то смысле объединением двух однозначных. Подобным обра-
образом, если, скажем, функция w = \^z рассматривается в малой окрест-
окрестности точки z0^=0, оо, то две ее ветви не сменяют одна другую
и тоже не составляют единой многозначной функции. Однако можно
доказать, что если многозначная функция задана в односвязной.
области (в частности, быть может, на всей плоскости) и ее значения
могут сменять друг друга при непрерывном продолжении по замкну-
замкнутому контуру, то такая функция обязательно имеет в этой области
хотя бы одну точку разветвления. (Подумайте, какова здесь роль
требования односвязности области.)
Для функций, заданных простыми формулами, точки разветвления обычно
распознаются по обращению в нуль или в бесконечность выражений, стоящих
под знаком раднкала (точки конечного порядка) или логарифма (логарифмиче-
(логарифмические точки). Рассмотрим, например, функцию
ш = >^гг=4: B1)
Это двузначная функция с точками разветвления, определяемыми из уравнения
г2 — 4=0, откуда г12=± 2. Так как ее можно записать в виде u>=J^z—2x
xVz+2, то если г обойдет по маленькой окружности вокруг точки ,.2i=2,
а потому z—2—вокруг нуля, первый множитель перейдет к новому значению,
а второй останется, каким был, т. е. вся функция B1) сменит значение. После
вторичного обхода оба множители, а потому и вся функцвя, вернутся к исход-
исходному значению; таким образом, точка zt и аналогично точка г2 являются для
функции B1) точками разветвления второго порядка. Точка z=oo, хотя и обра-
обращает подкоренное выражение в бесконечность, не является для функции B1)
точкой разветвления. В самом деле, эту функцию можно представить в виде
Если г обходит большую окружность, то оба множителя, а потому и вся функ-
функция возвращаются к своим исходным значениям (почему?). Значит, в окрест-
окрестности бесконечности здесь имеются две не связанные друг с другом ветви.
Мы предоставляем читателю проверить, что функция Уг-\- у/г—1 шести-
шестизначная и имеет точки разветвления г=0 второго перядка, 2=1 третьего
порядка и г=ос шестого порядка.
П. Отображение «>==—( z-\-—). Отображение ¦ ..
к> = 4(г + -М (с>°) " B2)
применяется в гидро- и аэродинамике и часто связывается с именем Н. Е. Жу-
Жуковского, который периым стал широко пользриаться методами теории анали-
аналитических функций в этих дисциплинах.

§ 1. днФФЕРЕнцироалние и отображения 43
Введем в плоскости z=x-\-iy полярные координаты, так что *=pcos<p,
p^p'sirt fcp, т. е'. 2=pe/?. Тогда 'в силу B2) # ¦ . •
потому
cos
B3)
При p=const > 1 и <p, меняющемся от 0 до 2л, мы получаем параметрические
уравнения эллипса (см., например, ЛВМ, (П.26)) с полуосями
-
Таким образом, окружность р = const > 1 плоскости г функцией B2) взаимно
'МЖУ///,Ш.
Рис. П.
однозначно отображается на эллипс B3) плоскости w (рис.11) Половина рас-
расстояния между его фокусами по известной формуле из аналити еской reof етрия
(ЛВМ, п. НЛО) равна
-тУ ('•+•+?)-('¦-•+?)-'
Таким образом, параметр отображения B2) получает геометрическое истолкование.
Если теперь рассматривать всевозможные р > 1, то в плоскости w полу-
получится семейство эллипсов (рис. 11), причем так как с ие зависит от р, то все
эти эллипсы имеют одинаковые фокусы. При р—>• оо будет и а—»¦ оо, Ь—»- оо
(причем а—Ь—>-0), а при р—*-1+0 будет а—>-е+0, Ь—>+(). Мы видим
(рис. 11^, что функция B2) осуществляет конформное отображение внешней по
отношению к единичной окружности части плоскости г на плоскость w с раз-
разрезов Вдоль отрезка :— С, с вещественной оси-. Сама единичная окружность

44
ГЛ, И. ТЕОРИЯ АНАЛИТИЧЕСКИХ. ФУНКЦИЙ
явулиетно отображается иа разрез, причем в точках г==±1» где-г-=-
0, конформность отображения нарушается (впрочем, это ясно и из
A—~з )
11) М
С
X
рис. 11). Мы предоставляем читателю проверить, что открытый единичный круг
плоскости z функцией B2) отображается на плоскость, да,с тем. же разрезом
(причем О —j- оо). Поэтому функция B2), рассматриваемая на всей плоскости г,
осуществляет двулистное отображение ее на плоскость, ад обратное отображение
двузначное с точками разветвления второго порядка'й;='^ с.'"' '"'
Рис. 12.
Рис. 13.
Рис. 14.
Комбинация простых конформных отображений дает возможность значи-
значительно расширить класс отображаемых областей. Рассмотрим в качестве" примера
задачу об отображении области, показанной иа рис. 12, на полуплоскость
Rew>0. Обращая отображение B2) При с=1 и изменяя обозначения, полу-
получаем, что функция
отображает заданную область.на область, показанную на рис. 13, при этом мы
пользуемся однозначной ветвью кория, положительной при вещественных г > 1.
Нетрудно проверить, далее, что дробно-линейное отображение
преобразует область рис.
вершить отображение w-
что функция
13 на угол Re q > 0, Im q < 0; теперь остается cb-
= iq*. Комбинируя полученные формулы, получаем,
B4)
дает решение поставленной задачи.
Полученный результат можно применить для приближенного отображения
области, показанной на рис. 14, на полуплоскость; эта область представляет
собой полуплоскость Re г > 0 с некоторым числом разрезов, примыкающих
к оси у не слишком близко друг к другу и ие слишком уклоняющихся от от-
отрезков у — const. Для этого, заменим приближенно, один из разрезов иа отрезок
0=6, 0 < х < а (рис.. 14), и совершим отображение гх=Ф (—: (г — ib) J , где

§ 1. ДИФФЕРЕНЦИРОВАНИЕ И ОТОБРАЖЕНИЯ
45'
Ф(г)—функция B4). Тогда из заданной области мы получим полуплоскость
Re ij > 0 с разрезами того же типа, что раньше, но число их будет уже на
одни меньше. Затем заменяем приближенно один из полученных разрезов) на
отрезок Ух=Ь1у 0 < xt < alt совершаем отображение 22=ф(— (гх—ibj) J
и т. д., пока все разрезы не распрямятся.
12. Показательное н связанные с ним отображении. Рассмотрим
функцию
w = e*.
Положив z = x-\-iy, получим
w = e*e'y, т.е. \w\ = e*, Aigw=y + 2kn. B5)
Если у — const, —со < х < со, то Argw = const, 0<|да|<со;
таким образом, прямая у — const взаимно однозначно отображается
ШШ'ЯЖШ
77/////
ycon$
V/V/Ш.У.
Рис. 15.
на луч с вершиной в начале координат плоскости w (рис. 15). Если
рассматривать такие прямые при различных у, получится семейство
лучей с общей вершиной. Для заполнения такими лучами всей пло-
плоскости w нужно, чтобы определяющий их полярный угол изменился
на 2я, например, чтобы —я<_у<я, как на рис. 15. Таким обра-
образом, функция B5) осуществляет конформное отображение открытой
полосы ширины 2я, параллельной вещественной оси, на плоскость w
с разрезом вдоль луча с вершиной в начале координат (на рис. 15 —
вдоль вещественной отрицательной полуоси).
При этом отображении прямые х = const переходят в окружности
| w\¦ = е* = const, т. е. декартова координатная сетка плоскости z
переходит в полярную сетку плоскости да. При х^ — со будет
w—»-р, так что левый «конец» полосы переходит в общее начало

46
ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ 4>УНКЦИЙ
лучей — начало координат, тогда как правый «конец» — в бесконечно
удаленную точку плоскости w.
Если рассматривать отображение B5) иа всей плоскости z, то'
каждая горизонтальная полоса ширины 2я отобразится на всю пло-
плоскость w, так что в результате эта плоскость будет покрыта бес-
бесконечное •шсло раз, т. е. отображение B5) является бесконечно-
листным. Соответственно обратное отображение z = Lnw является
бесконечнозначным и имеет точки разветвления а/ = 0 и w — oo бес-
бесконечного порядка: если w описывает обороты в положительном
направлении вокруг начала координат, то Ln«> вновь и вновь полу-
получает приращения по 2ш, никогда не возвращаясь к исходному зна-
значению. Если на плоскости w провести разрез, соединяющий точки
Рис. 16.
разветвления, то можно говорить об однозначных ветвях логарнфми-.
ческой функции; так, на рис. 15 показано конформное отображение
плоскости w с разрезом вдоль вещественной отрицательной полуоси
на полосу —оо<л;<оо, —я<_у<я, осуществляемое главной
ветвью логарифма, z = lna/ = ln \w\-\-iargw. (Напомним, что под
arg понимается главное значение аргумента, —it <
С показательным отображением непосредственно связаны некоторые другие.
Так, отображение
tt>=chz=
можно получить с помощью двух отображений
Первое отображает (см. рис. 15) полуполосу 0 < х < оо, —я < у <,я иа об-
область | s | > 1, разрезанную вдоль интервала s"=0, — оо < s' < — 1 (s—s'-^is").
Второе отображаег эту область на плоскость ш, разрезанную вдоль интервала
—1, 1 вещественной оси (рис. 11); а так как при этом интервал s"=»0,
— оо < s' < — 1 переходит в интервал о=0, — оо<и< — 1, то в итоге пло-
плоскость w получается с разрезом вдоль интервала 0=0, —to < и < 1. Итоговое
конформное отображение показано на рис. 16, причем соответствующие друг

§ 1, ди<КФерандиРОВАниЕ и отображения 47
другу гранкчные точки отображаемых областей имеют одинаковые индексы.
Мы предоставляем читателю исследовать характер отображения a>=chz иа
всей плоскости w.
Аналогичными свойствами обладают отображения
a>=cosz = chit, a>=sln z— cos (-*—z
. 1 . . , . . ( , ni\
tt)==shz=-r-Slll IZ= — I СП I Z+-g- I .
На этом мы заканчиваем рассмотрение простейших конформных
отображений; один важный общий класс отображений будет рассмот-
рассмотрен в п. ЗЛЗ. Дальнейшие сведения об этих, а также о других
элементарных конформных отображениях см. в книгах, указанных
на стр.'27. Специально конформным отображениям посвящена книга
[51], содержащая, в частности, каталог таких отображений.
13. Поверхность Римана. Понятие поверхности Римана оказывается полез-
полезным при.рассмотрении многозначных аналитических функций. Вернемся к рас-
рассмотрению двузначной функции ш="|Лг (п, 10) и представим себе два нало-
наложенных Друг на друга экземпляра пло--
скости г с разрезом вдоль полуося
у=0, — оо<х<0. Будем считать,
что точка г может произвольно пере^
мещаться по любому из этих экзем-
экземпляров плоскости (листов) и может так-
также пресекать разрез, однако при каждом
таком пересечении она переходит с одного
листа на другой. Другими словами,
листы следует представить себе как бы
склеенными так, что верхний берег пер-
первого листа приклеивается к -нижнему бе-
берегу второго, а нижний берег первого — Р 17
к верхнему второго. Это склеивание
условно показано на рис. 17; условность
состоит в том, что при попытке изготовления такой конструкции, например,
из бумаги возникнет линия самопересечения, показанная на ркс. 17 бледно.
Однако мы уже имели много случаев убедиться в том, что в математике
поверхность (как и любое многообразие) вовсе не обязательно представлять себе
изготовленной из бумаги и вложенной в трехмерное физическое пространство.
Поэтому ничто нам не мешает считать, что вдоль бывшего разреза верхний
берег первого листа смыкается с нижним берегом только второго, но не
¦ первого листа, а верхний берег второго листа—с нижним берегом только
первого, но не второго листа; тогда никакой линии самопересечения, конечно,
не будет. Полученная при этом поверхность (S) и называется поверхностью Ри-
Римана (или римановой поверхностью), отвечающей функции w=yrz.
Рассмотрим теперь функцию, равную одной из ветвей У г, о которых
говорилось в п. 10, на одном листе построенной поверхности и дру-
другой из ветвей Yz на другом листе. Эта функции будет однозначной и непре-
непрерывной на (S), так как в п. 10 при переходе через разрез ветви непрерывно
сменяли одна другую, а теперь эта смена обеспечивается тем, что при пере-
переходе через бывший разрез точка одновременно переходит с одного бывшего
листа (S) на другой (продумайте это!). На рис. 17 хорошо видно, что если
точка г'обходит вокруг начала координат О, то функция y^z .приходит к ис-
исходному значению лишь после двух, таких обходов. Отображение w=zY~z,

.48 ГЛ. II; , ТЕОРИЯ АНАЛИТИЧЕСКИХ •УНКЦЯЙ
. а потому и z—w1 является взаимно однозначным отображением, рнмановой
поверхности (S) переменкой г иа плоскость ш. .. . ..,'...
Аналогично трехзначная функция у/г является однозначной и непрерыв-
непрерывной? на сиоей римаиовой поверхности, которая конструируется из трех экземп-
экземпляров плоскости z с такими же разрезами, как выше, если их приклеить в
циклическом порядке, т. е. верхний берег первого листа подклеить к нижнему
второго, верхний второго—к ниянщму третьего и, наконец, верхний третьего —
к нижнему первого. Бескоиечнозначная функция Lnr требует для этой же
цели бесконечного числа таких же экземпляров плоскости z, которые подклеи-
подклеиваются друг к другу s виде последовательности, бесконечной в обе стороны."
Подобная конструкция возможна для любой многозначной функции f (х).
Чтобы построить римаиову поверхность, отвечающую этой функции., надо
взять столько экземпляров плоскости г, сколько значений принимает функция
при каждом г (это число одно и то же для всех г, за исключением точек
разветвления); затем надо пронести разрезы, дающие возможность выделить
все однозначные ветви этой функции, после чего вдоль разрезон подклеить
один листы к другим в соответствии с тем, как сменяют друг друга ветви при
п«реходе через эти разрезы. На своей римаиовой поверхности функция / (г)
является однозначной, и при переходе через бывшие разрезы, теперь заклеен-
заклеенные, она уже не испытывает скачка, как ее однозначные ветви.
Если функция w—g (г) однозначная и аналитическая во всей плоскости г
(за исключением, быть может, отдельных точек разрыва)) ио миоголистная, то
она осуществляет взаимно однозиачиое отображение плоскости г на риманову
поверхность, отвечающую обратной функции g~ (w) к g (z). Это отображение
будет конформным, за исключением точек разрыва функции g(z) и точек раз-
разрыва и точек разветвления функции g~ (ш). Если функция g{z) миогрзначвая
и многолистиая, то. она осуществляет взаимно однозначное отображение своей
римановой поверхности иа римаиову поверхность обратной функции.
В п. 7 мы уже говорили о том, что комплексная плоскость, дополненная
бесконечно удаленной точкой, топологически эквивалентна сфере. Можно дока-
доказать, что аналогичным .образом расширеивая римаиова поверхность, отвечаю-
отвечающая конечнозиачной функции, топологически эквивалентна сфере, либо сфере
с ручкой (что топологически то .же—тору), либо сфере с двумя ручками (т. е.
поверхности кренделя) и т. д. По числу этих ручек можно классифицировать
римаиовы поверхности. Строение римановых поверхностей, отвечающих беско-
нечиозначиым функциям, может быть значительно более сложным. (Но ие
обязательно! Например, из п. 12 следует, что римаиова поверхность, отве-
отвечающая функции Lnz, гомеоморфиа плоскости.)
14. Приложение к теории плоских полей. Пусть в некоторой
плоской области (G) плоскости х, у задано векторное поле А, не
имеющее ни вихрей, ни источников векторных линий, т. е. для ко-
которого
rot А = 0, divA = O. B6)
Такое поле может иметь различный физический смысл, однако для
простоты и единообразия его можно трактовать как поле скоростей
плоскопараллельного потока идеальной (т. е. без вязкости, и которая
всегда порождает вихри) несжимаемой жидкости,,
В п. 1.2.3 мы видели, что поле, обладающее свойствами B6),
является градиентом гармонической функции ц>(х, у). Согласно п. 3
для этой функции можно построить сопряженную гармоническую
функцию ty(x, у), называемую функцией тока; при этом величина

•§ 1. ДИФФЕРЕНЦИРОВАНИЕ И ОТОБРАЖЕНИЯ
49
и> = ф-|-/ф, называемая Комплексным потенциалом поля А, является
аналитической функцией переменной z = x-\-ly. . ':
Выясним смысл производной -т- . Так как в силу п. 2 ее можно
вычислять, приняв dz = dx, то
dw
rfF~ Ш Ш~1ду~л* 1Лу
(во втором переходе мы использовали второе из равенств Коши—
Римана F), а в третьем—определение градиента). Поэтому, если в
какой-либо точке z изобразить комплексное значение (-?•) / не -^1J
вектором, мы как раз получим вектор поля А в этой точке (почему?).
Из этого, в частности, следует, что даже если аналитическая
dw
функция w получится многозначной, то ее производная -т- должна
быть однозначной, так что любые две однозначные ветви функции
w(z) отличаются друг от друга на
постоянное слагаемое. Обратно, любая
аналитическая функция да (z) = <р + Zip
с однозначной производной ~ служит
комплексным потенциалом плоского по-
поля А, удовлетворяющего условиям B6).
Таким образом, рассмотрение плоских
полей, удовлетворяющих условиям B6),
сводится к рассмотрению различных
аналитических- функций, что, конечно,
гораздо проще.
. Рассмотрим линию, уровня функции
тока, т.е. линию ty(x,y) — const. Так
как в любой точке М эта линия в си-
силу п. А ортогональна проходящей через М линии <р = const, а вектор
А = grad ф также ортогонален этой линии (ЛВМ, п. XII.4), то вектор А
.в точке М касается линии гр = const (рис. 18). Но так как М—любая
точка, то линии ijj = const—это как раз векторные линии поля А;
в частности, для поля скоростей:—это линии тока, чем и объяс-
объясняется название «функция тока».
Из формулы G) вытекает еще следующее. Соединим какие-либо
точки М, и Mt любой линией (/) (рис. 18). Тогда
к
Рнс. 18.
С)
т. е. приращение функции тока вдоль любой линии (I) равно потоку
поля через (/) слева направо по направлению движения вдоль (/).

50
ГД. U. ТЕОРИЯ . АНАЛИТИЧЕСКИХ ФУНКЦИЙ
Теперь легко понять смысл возможной многозначности функции
w (г), которая может представиться, только если область (О) неод-
носвязна (ср. п. 1.2.2). Пусть точка z обходит в положительном
направлении замкнутый контур (L), внутри которого расположена
«полость» (D) области (О) (рис. 19); эта
полость может, в частности, состоять из
единственной точки.. Тогда приращение
Д?ф = TD функции <р равно (п. 1.2.2) цир-
циркуляции поля А по (?); а в силу преды-
предыдущего абзаца приращение ALty = QD
. функции гр равно потоку поля А через
(L) в направлении изнутри.наружу; прира-
приращение же ALw = А^ + /Ajr_4jj = TD -f- iQjy,
Итак, многозначность функции w сви-
свидетельствует о наличии в полостях обла-
¦-•' Рис. 19. сти (О) источников циркуляции или ис-
;.''-•¦•¦-¦¦¦•'• точников векторных линий поля А. (За-
(Заметим, что внутри (О) таких* источников в силу условий B6) не
может быть.)
Пусть область (G) конечносвязна, например, А-связна B^ k <oo);
это значит, что у нее имеется k— 1 полостей (Z>x), :(D8), ... , (?>fc-1).
Выберем в (^замкнутый контур (S), охватывающий, всё эти поло-
полости, и будем проходить его в отрицательном направлении.
Тогда в приращений AsW — FaB-j-iQa, величину Г» естественно
трактовать как циркуляцию поля, порождаемую на бесконечности,
a Q»—как обильность источника векторных линий на бесконечности.
Легко проверить (продумайте это!), что :
rOl+TDl+..'
Если область (G) конечная, то роль бесконечности играет внеш-
внешняя компонента связности (т. е. связный кусок) границы (О). Если
область (О) бесконечная и имеет некоторые из компонент связности
границы бесконечными (например, граница полосы, из которой вырезан
круг, имеет две бесконечные и одну конечную компоненты связности),
то при рассмотрении Г„ и QM такие компоненты причисляются к
бесконечно удаленной точке.
Подчеркнем в заключение, что. функция w(z) аналитична виутри
(О) (или, что то же, в открытой области (О)). В отдельных точках
границы (О) аналитичность может нарушаться.
15. Примеры. Рассмотрим комплексный потенциал
B7)

§ 1. ДИФФЕРЕНЦИРОВАНИЙ И ОТОБРАЖЕНИЯ
51
где Г — вещественное число. Приравнивая ч|? = Im тю постоянной,
получим линии тока 1п|г| = const, т. е. окружности )"л?j = const
(рис. 20). Функция B7) аналитична в двусвязной области z =й= О
и при обходе вокруг точки z = 0 J^w = -^- -2я = Г. Таким образом,
в этой точке порождается циркуляция Г (на рнс. 20 показан слу-
случай Г > О). Точка z = 0 для потенциала B7) называется вихревой
точкой, а соответствующее поле А называется элементарным вихрем;
так как
dw _ Г 1 _ Г 1 _ Г — у—ix
dz ~2ni г ~2ш x+iy ~~ 2п хг-\-у* *
то в силу п. 14
Любопытно, что поле элементарного вихря при z=j*=O является без-
безвихревым; если трактовать А как поле скоростей плоскопараллель-
плоскопараллельного потока жидкости (тогда естественно говорить о вихревой оси
Рис 20.
Рис. 21.
х—у = 0), то малые объемы жидкости испытывают поступательный
перенос и деформационные движения (подробнее об этом см. в п. V.I.5.),
тогда как угловые скорости равны нулю.
Если рассматривать поле во всей плоскости х, у, включая точку г=0,
то рассуждая аналогично п. 1.2.4, получим, что
divA=0, rotA=rd(*N(i/)k,
так что первое из условий B6) не выполняется. Значит, для применения рас-
рассмотрений п. 14 точку х=у—0 необходимо исключить.
Аналогичное рассмотрение комплексного потенциала
1 w — ~Lnz (Q вещественное)
'2я
B9)
приводит к точечному источнику, показанному на рис.21 при<?>0
и уж€ рассмотренному в п. 1.2.4.

52
ГЛ. И. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
Из потенциалов B7) и B9) можно получить другие распростра-
распространенные поля. Так, диполь (п. 1.2.4), расположенный в точке я = 0
с осью х и моментом М имеет комплексный потенциал
—M/h
-«¦•¦г. C0)
Если источник поля распределен вдоль некоторой линии (L) с Ли-
Линейной плотностью 9— ?(?)> гДе ?€(?)> то соответствующее поле
называется простым слоем и имеет потенциал
()
где |rf?| равно элементу длины дуги (I). Результат аналогичных
распределений вихря B7) вдоль линии называется вихревой линией,
а диполя C0) с осью по нормали к линии — двойным слоем. Мы пре-
предоставляем читателю вывести формулы
для соответствующих комплексных по-
потенциалов
Рис. 22.
2п J *-t "*•
. ¦ . (t) .
Рассмотрим еще простой пример потен-
потенциала
ш=*гя=*я—уг+i2xy.
C1)
Линии тока имеют вид гипербол jcy=const (рис. 22); векторные линии обра-
образуют седло (ЛВМ, п. XV.7). Чтобы иайти ваправление поля вдоль этих ли-
линий, достаточно построить вектор поля в какой-либо одной неособой точке,
Тогда в остальных точках это направление можно продолжить по непрерыв-
непрерывности (в близких точках и направления поля близкя). Так как, например.
(S)'L-«•!«-*
то направления будут такими, как показано иа рис. 22 (проверьте!).
Любое поле можно рассматривать не на всей плоскости г, а на некоторой
ее области. Если рассматривать поле с потенциалом C1) лишь в квадранте
*S=0, у^О, то.таким, в частности, будет поле скоростей идеальной жидкости,
обтекающей изнутри прямой угол.
16. Краевые задачи и конформные отображения. В п. 14 мы видели, что
пря построении в заданной плоской области (G) поля А, удовлетворяющего усло-
условиям B6), имеется высокая степень произвола: это поле может иметь в. каче-
качестве комплексного потенциала любую (вообще говоря, многозначную) анали-
аналитическую в (G) функцию си (г) с однозначной производной. Поэтому если из
таких полей надо выбрать какое-либо одно, вполне определенное, то должны
быть указаны дополнительные условяя, обеспечивающие разрешимость задачи

§ 1. ДИФФЕРЕНЦИРОВАНИЕ И ОТОБРАЖЕНИЯ 63
и единственность решения. Обычно эти условия имеют вид некоторого скаляр-
скалярного краевого условия, т, е. равенства, связывающего проекции искомого поля
(н, быть может, нх производные) вкаждой точке границы (S) области (б).
(Поэтому краевое условие имеет здесь вид функционального равенства, т. е.
равенства, связывающего функции, а не числового, как в ЛВМ, п. XV.16.)
В такую краевую задачу (т. е. задачу о построении поля при заданных кра-
краевых условиях) может входить также несколько числовых равенств.
Пусть, например, область (G) конечна (тогда краевая задача называется
внутренней), и. односвязна, а поле. А истолковывается как поле скоростей
идеальной жидкости. Тогда из физических соображений естественно, что это
поле однозначно определяется, если в каждой точке M?(S) задать интенсив-
интенсивность потока, протекающего через (S) в этой точке, т. е. задать функцию -•
Ап\м^В(М) (A*€(S)), . C2)
где в качестве п для определенности берется направление внешней нормали.
При этом должно выполняться условие
^Q C3)
(S)
(почему?). Можно доказать н математически, без всякой ссылки на физику,
что задача о построении поля А, удовлетворяющего уравнениям B6) н краевому
условию C2), прн необходимом соотношении C3) имеет ровно одно решение.
Если область (G) конечна, но 6-связна (*3г2), то вокруг ее полостей
могут возникнуть циркуляционные движения (см. п. 14); поэтому должны
быть дополнительно заданы значения
fxdL=Tj (/==1, 2, .... ft-1)
(Lj)
для замкнутых контуров (L{), (L2), ... , (L^-i), каждый из которых содержит
внутри себя только одну из полостей области (G). Если область (G) получает-
получается выбрасыванием из плоскости одной или нескольких конечных областей
(тогда краеиая задача называется внешней), то опять-таки из физических
соображений следует, что дополнительно надо задать значение А» поля на беско-
бесконечности («скорость набегающего потока жидкости»). Это условие также можно
оправдать математически. Отметим, что при математическом уточнении надо
потребовать, чтобы поле не имело на (S) особенностей типа диполей (п. 15)
или более высокого порядка.
Имеется н много других типов ираевых условий. Подробно различные
краевые задачи исследуются в теории уравнений математической фнзнкн, здесь
мы приведем только некоторые простые соображения, непосредственно примы-
примыкающие к материалу этой главы.
Остановимся для определенности на внешней краевой задаче о построение
плоского поля А, удовлетворяющего вне некоторого замкнутого контура (S)
условиям B6), а также краевому и добавочным условиям
А„\($>=*=0, А» задано, ш A^dL = T (задано). C4)
(t)
Решение можно истолковать как поле скоростей идеальной жидкости, набега-
набегающей со скоростью Аоо на непроницаемый контур (S), которое имеет заданную
циркуляцию Г по некоторому контуру (/,), охватывающему (S) (рнс. 23).
Будем искать комплексный потенциал а) (г) поля А (п. 14); тогда условия C4)
можно переписать в виде

54
ГЛ. Н. ТЕОРИЯ. АНАЛИТИЧЕСКИХ ФУНКЦИЙ
(продувайте!).. Первое из этих условий—функциональное—можно записать в
так: ^ зэ 0, т. е. Ira w tm const, вся (S) принадлежит одной нз линий
тока, что очевидно и из физических соображений.
Основная-идея метод» решения поставленной краевой задачи, основанного
на применении конформных отображений, состоит в следующем. Пусть, нам
удалось осуществить конформное
отображение ?=/ (z) области (G),
внешней по отношению к (S), на об-
область (Я) плоскости ?, внешнюю
по отношению и некоторой замкну-
замкнутой линии (Т). При этом отображе-
отображении точки линии (S) отвечают точ^
кам линии (Т), а точка z=oo отве-
отвечает точке ?=оо. Пусть линия (Т)
оказалась настолько простой, что
в области (Я) мы можем решить
аналогичную краевую задачу о по-
построении аналитической-функции
о) (?), удовлетворяющей условиям
Im <в I = const,
Рнс. 23.
=Ь,
C6)
постоянной Ъ будет вскоре уточнено, а под (Л) понимается какой-
(ff), охватывающий (Т). «внесем» з (Я)
где значение постоя
либо контур в (Н), охватывающий (Т). «Снесем» значения' ш с точек (Я) в соот-
соответствующие точки @),т. е. положим О) (г)=to (Hz)). Тогда нетрудно проверить
(проделайте это!), что эта функция аналитичная внутри (G) и удовлетворяет
первому и третьему из условий C5). Кроме того, . >.
.,...¦ dz
значит, и второе из условий C5) будет удовлетворено, если в C6) положить
Рассмотрим пример. Пусть (S)—это окружность |z| = i?j а вещественно;
С f Z /? \
Г=0. В силу п. 11 функция %,=-к\-пЛ ) осуществляет конформное от-
-. \ ^ ^ J
ображение области (G), внешней по отношению к (S), на область (Я), внешней
по отношению к отрезку (Г) с концами ? = —с а ?=с. Для такой области крае-
2aR 2aR
вая задача C6) с 6=
j7"
= имеет простое решение <в= С (проверь-
с , с
/ () ,
Ttt). Снося эти значения в (G), получим решение в плоскости z
— потенциал бесциркуляционного обтекання окружности. Отсюда легко найти
и потенциал циркуляционного обтекания окружности
Г
г )
(проверьте!). Снося этот потенциал в различные области, можно получить ре-
решение задачи C5) для различных контуров (S).
К внутренним краевым задачам конформное отображение применяется со-
совершенно аналогично.

§ !. ДИФФЕРЕНЦИРОВАНИЕ И ОТОБРАЖЕНИЯ
55
• Конформные отображения применяются также к интересному н пока' не-
недостаточно изученному классу краевых задач, в которых граница области (С)
заранее полностью или частично не задана; такие краевые задачи иногда на-
называют обратными. Покажем для примера схему решения одной из таких за-
задач, именно плоской задачи о свободном истечении струи невесомой идеальной
жидкости. Пусть истечение происходит, как на рис. 24, причем твердые стеики,
показанные жирно, заданы; а свободная поверхность ае струи заранее неиз-
неизвестна. Точки Ь, с, d, e находятся на бесконечности; таким образом, точка
z=oo янляется двойной точкой границы (G): в далеких точках сосуда имеется
источник, а в далеких точках струи—сток жидкости.
На не заданном заранее участке границы должно-быть поставлено доба-
добавочное граничное условие. В рассматриваемой задаче условием, добавочным
к А„ = 0 (А— вектор скорости), является равенство 4=const, которое легко
Л
Рис. 24.
Рис. 25.
вытекает из закона сохранения энергии. Для построения линии ее и комплекс-
комплексного потенциала w (г) поля А рассмотрим отображение области (G) в плоскость ?,
определяемое формулой ?=oi' (г). Вспомнив смысл этой производной (п. 14), а
также граничные условия для поля А, получим, что при этом отображении
образом области (G) служит четверть-круга, т. е. область (Я) с известной
границей (см. рис. 25, где указаны также точки, отвечающие обозначенным
точкам контура (G)). Действительно, при таком отображении отрезок cd пере-
переходит н отрезок вещественной оси c'd', включая нулевую точку (почему?), так
как на cd будет Ах > О,
А =0.
а отрезок Ьа—в отрезок мнимой оси Ь'а'
в силу граничных условий 'ЛЛ=0, Ау < 0.
Задача о построении поля B6) в (Я), удовлетворяющего граничному усло-
условию /4„=0 и имеющего источник обильности Q в с' и сток в d', легко решается
с помощью конформного отображения (Я) иа область более простого иида, иа
чем мы не будем здесь останавливаться. Оказывается, что соответствующий
20 / С R \
комплексный потенциал ш(?) равен Ln (-^ р-J ; снося его в ^.по-
^.получим потенциал oi=(o(? (г)) исходной задачи. Но ?=-г-, т. е. мы прнходим
к равенству hi=<d (-з-) . представляющему собой дифференциальиое уравнение
относительно функции w (г), так что еще надо решить это уравнение (в Этом
и проявилась специфика обратной задачи), и только после этого мы получим
искомый потенциал. Зиая его, уже легко получить линию ае как линию юна,
. проходящую через заданную точку о. Вычисления, которые мы предоставляем
желающим, приводят к уравнению линии ее:

56 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
где А,—ширина струи иа выходе, а параметр t меняется отОдо я/2. Переход
20
к пределу при t —* л/2 дает значение km~ho—-^k ширины струи на беско-
бесконечности. Нр A«R==Q (почему?), откуда #=тр (l+-r-J, Параметры Ло aQ
остаются произвольными. ¦ .
17. Общие замечания о конформных отображениях. Здесь мы
приведем без доказательства некоторые общие сведения о конформ-
конформных отображениях. Доказательства этих фактов, которые полезно
иметь в виду, порой довольно сложны; их можно найти в литературе,
указанной в начале главы. .
Прежде всего возникает вопрос о принципиальной возможности т-
иезависимо от технического осуществления—конформного отобра-
отображения произвольной области (О) на любую другую область (Н). Бу^
дем впредь считать эти области открытыми и не содержащими беско-
бесконечно удаленной точки. Б. Рнман в 1851 г. доказал, что если каж-
каждая из областей (G), (Н) одноевязна и не совпадает со всей плоскостью,
то такое отображение всегда возможно. При выборе этого отображения
имеется три вещественные степени свободы. В частно-
частности, если задать образ в (Я) одной из точек (О) (это два вещест-
вещественных условия) и угол поворота малой окрестности этой точки (еще
одно условие), то отображение определено однозначно. Для этой
же цели можно задать образы одной внутренней и одной граничной
точек (G), нлн трех граничных точек (О) (в последнем случае образы
на границе (Я) должны располагаться в том же порядке, что про-
прообразы на границе (G)).
Для многосвязных областей дело обстоит сложнее. Прежде всего,
области различного порядка связности (п. 1.2.2) конформно (и даже
вообще гомеоморфно—см. п. 7) отобразить друг на друга невоз-
невозможно; в частности, одиосвязиую область (О) никогда нельзя кон-
конформно отобразить на неодносвязную область (Я). Впрочем, последнее
легко понять: если отображение возможно и (S)—замнутый контур
в (Я), окружающий какую-либо из полостей (Я), a (Z.)—соответст-
(Z.)—соответствующий E) контур в (G), то, стягивая (?) в точку и следя за со-
соответствующим изменением E), мы приходим к противоречию (про-
(продумайте это!).
Но и области одинакового порядка связности далеко не всегда
можно конформно отобразить одна на другую. Например, можно до-
доказать, что каждую двухсвязную область, отличную от плоскости
с выколотой точкой, можно конформно отобразить на кольцо /?0 <
<|г|<1, где 0<1#0<1 и число/?0 определено однозначно, т.е.
кольца с разными Ro друг на друга конформно отобразить нельзя.
Для областей высшего порядка связности картина еще сложнее, и
мы не будем ее здесь рассматривать.
При конформном отображении открытой области (О)на открытую
область (Я) граничные, точки 9тих областей также находятся во

§ IV
и
57"
взаимно однозначном соответствии. (Это выражают также словами:
конформное отображение (б) на (//) можно продолжить до гомеоморф
физма соответствующих замкнутых областей.) При этом надо иметь
в виду, что граничная точка, к которой имеются существенно раз:
личные пути подхода из области (точнее—пути, не деформируемые
один в другой в пределах области в достаточно малой окрестности
этой точки), Называется кратной точкой границы, т. ё. считается за
несколько точек в зависимости от числа таких путей. Например, дли
односвязной области, показанной на рис. 26 и имеющей вид беско-"
неЧной полосы с крестообразным разрезом, граничные точки полосы,
за исключением точек z = oo и z = a, имеют кратность I, т. е. яв-
являются простыми; точка г = 6о и все точки разреза, за исключением
центра креста, имеют кратность 2; центр креста имеет кратность 4.
На рис. 26 пунктиром показано, в ка-
каком порядке ;граничные точки этой
области отображаются на точки окруж-
окружности, если сама область конформно
отображается на круг; в частности,
центру креста отвечают четыре раз-
различные точки окружности.
Отображение сохраняет - конформ-
конформность и на границе областей, за исклю-
исключением Отдельных точек. Именно, пусть
а—некоторая точка границы (G), а
а' — соответствующая точка границы (Я); будем считать обе точки
конечными. Тогда, если в а и а' граница без излома и имеет конеч-
конечную кривизну (последнее требование можно существенно ослабить),
то отображение в этнх точках конформно. Если же область (О) обра-
образует вблизи точки а угол а, а область (Я) вблизи а'—угол а\ то
конформное отображение (О)—-*(Я) имеет вблизи а с точностью до
малых высшего порядка вид ^=a' + C(z—а)а'/а (ср. п. 9; заме-
заметим, что второе слагаемое в некоторых случаях имеет добавочный
множитель типа [Ln(z—а)Р), так что при аФа' конформность
отображения в точке а наверняка нарушается.
Иногда применяется следующее простое правило симметрии при
конформном отображении. Допустим, что граница области (О) содер-
содержит прямолинейный участок ab и что вся область (О) расположена
по одну сторону от прямой (/), служащей продолжением этого уча-
участка; область (Я) обладает теми же свойствами для участка а'Ь' и
прямой (/'). Пусть при конформном отображении ?=/(z) области (G)
на область (Я) указанные участки соответствуют один другому.
Произведем «удвоение» области (О), присоединив к ней ее зеркаль-
зеркальный образ относительно (/), а также интервал ab (см; рис. 27, на
котором исходная область (G) заштрихована). Обозначи» лолучениую
«двойную»1 область через (б) и осуществим аналогичное' удвоение
Рис, 26.

58 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
области (Я) до (#). Теперь легко расширить (продолжить) отображе-
отображение / до конформного отображения (б) на (И): для этого надо, если z
находится в (G) или иа границе (О), считать f(z) таким же, как до
удвоения, а если zx и z2 симметричны относительно (/) (рис. 27),
считать, что /BХ) и /(г2) симметричны относительно (/'). Мы пре-
предоставляем читателю проверить, что так
определенное отображение конформно в
зеркальном образе (О), а потому н во
всем (G).
Подобное продолжение конформного.
отображения на основе симметрии можно
осуществлять и через дугу окружности
(п. 8). Оказывается, что аналогичное
продолжение можно производить через
дугу без особых точек любой линии,
рнс 27. если предварительно с помощью добавоч-
добавочного конформного отображения «распря-
«распрямить» эту дугу; однако в общем случае указать более широкие
области, на которые продолжается отображение, бывает , весьма
трудно (а продолжение нелинейного отображения на всю плоскость
заведомо невозможно).
Ряд результатов получен различными авторами в проблеме изучения за-
зависимости конформного отображения от изменения границы отображаемой об-
области. Эти результаты в некоторых случаях дают возможность получить раз-
различные характеристики отображения области со сложной границей, заключив
последнюю между двумя простыми границами, для которых отображение легко
выписывается. Мы ограничимся для примера лишь формулировкой принципа
Линделёфа, относящегося к изменению конформного отображения области на
круг при ее уменьшении (см. ниже), отослав интересующихся за доказатель-
доказательствами, дальнейшими результатами н их приложениями к книге [66].
Итак, допустим, что одиосвязная область (G) с границей (S) целиком со-
содержится в конечной одиосвязиой области (Н) Ф (G) с границей. (Т), и пусть
функция X (z) отображает конформно (G) на единичный круг, а г|> (г)—область (Я)
на тот же круг, причем 0?(G), % @) = ob @) = 0. Тогда оказывается, что при
любом г, 0</-<1, замкнутый контур \%(г)\=г расположен строго внутри
(без соприкосновений!) замкнутого контура | ф (г) \ = г; | X' @) | > | ф' @) |; если
(S) и (Т) имеют до крайней мере одну общую точку г„, то | X' (г0) I < | ф' (г„) |;
если (S) и (Т) имеют полярные уравнения соответственно р = а(ф) и р = Р(ф)
с однозначными правыми частями, причем Р (фо)—а(<ро)=тах !Р(<Р)—а(фI.
то а (ф0) | х' (а (<Ро) Л) IS* Р (Фо) IФ' (Р (<Ро) *'?-) |-
Полезно иметь в виду также, что влияние изменения границы отображае-
отображаемой области на небольшом участке при удалении от этого участка быстро за-
затухает.
18. Применение метода малого параметра. Так как в реальных
вычислениях точно отобразить конформно друг на друга удается лишь
области сравнительно простого вида, то разработан п,елый ряд ме-
методов приближенного конформного отображения, пригодных, для более
широких классов областей. Эти методы описаны в книгах [66] и осо-

§ 1. ДИФФЕРЕНЦИРОВАНИЕ И ОТОБРАЖЕНИЯ 59
бенно [44, 51, 84, 116]. Здесь мы рассмотрим только применение
метода малого параметра (ЛВМ, п. V.5) для конформного отобра-
отображения на круг области, близкой к кругу. Полученный результат
можно применить к более общей задаче о конформном отображении
мало измененной области (О) на область (Я), если (G) и (Н) имеют
сравнительно простой вид. В самом деле, пусть функцииg(z) и h(z)
осуществляют конформное отображение областей (G) и (Н) соответ-
соответственно на единичный круг, а область (GJ получена из (О) малым
изменением контура. Тогда область g(Gt) близка к единичному кругу
(почему?). Если функция fl осуществляет отображение этой области
на единичный круг, то функция h~ (ft {g(z))), где черточкой обозна-
обозначена обратная функция, осуществляет конформное отображение (Gx)
на (Н):
Нам потребуется простая лемма.
Лемма. Для того чтобы функция, разложенная в комплексный ряд Фурье
(ЛВМ, п. XVII.26)
•¦' • /<*>=»¦ 2 с*еМ' <37>
п = — а> . '
имела постоянный модуль, необходимо и достаточно, чтобы
2 сЬп+Р=0 (Р=1. 2, 3, ...); C8)
л= — «
при выполнении этого условия
2 \с„\з. C9)
Для доказательства нужно помножить равенство C7) на сопряженное
п т
1/@1а=
2
п. т т, р
2m+ 2 (St
щ РФО \ т
откуда вытекают условия C8) при р Ф 0 я равенство C9). Однако
2сяся-р=('2с'»сп+;Л* (проверьте!), так что у с ловя я C8) достаточно потре-
потребовать лишь при р > 0. Лемма доказана.
Перейдем теперь к применению метода малого параметра. Пусть область (G)
ограничена замкнутым контуром с уравнением
г=е"-г-а Jj dnM, D0)
n=-«
где ос—вещественный, малый параметр, а множятелем при нем стоит произ-
произвольная перяодяческая функция с периодом 2л, что требуется для замкнутости
контура. Пря а=0 область (GJ Представляет собой единичный круг, так что

60 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
можно исходить из тождественного отображения ?=z. Следуя методу малого
параметра, примем, что'приа Ф 0искомое отображение области (<?а) иа круг(Я) .
имеет вид " ' ' ¦'¦'•
4-e^Ti «+'... D1)
Для нормировки отображения примем, что, как и при о=0,
Здесь четыре вещественных равенства (почему?), тогда как конформное отобра-
жевие в силу п. 17 нормируется тремя. Поэтому введем дополнительную«тепень
свободы, не фиксируя заранее радиус R круга (Я): |?| < #.' ¦ • ¦
Будем искать все функции g/(г) в виде сумм степенных рядов. Тогда из
формул D1) и D2) вытекает, что у этих рядов свободные н ^инейные члены
должны отсутствовать, т. е. получаем : ¦ ' ч
Задача состоит в том, чтобы найтн все коэффициенты ад.
Так иак граница области (G) должна перейти в окружность |И=/?;\то
функция от t, получающаяся в результате подстановки выражения D0) в пра»
вую часть D3), т. е. •
2 2
ft=2 L n=-» J ' ¦¦-¦
должна иметь постоянный модуль R. Значит, можно воспользоваться доказан-
доказанной выше леммой, имея в виду, что все коэффициенты с„, которые можно
получить с помощью перегруппировки членов в выражении D4), представляют
собой ряды по степеням а; поэтому каждое из равенств C8) порождает целую
серию соотношений-, полученных приравниванием нулю коэффициентов при
каждой степени а. Выпишем начальные члены разложений коэффициентов с„:
cn=adn4-..-(n<0); c1 = l+arf1-(-...; cn=a(dn+aln)+...(/i^2). D5)
Подставляя эти разложения в C8) и выписывая коэффициенты при а, получим
(проверьте!) {dp+l-\-alt p+i)+dt-p=Q, откуда
«i*=-<**-<?-* (А=2, 3, 4, ...). D6)
Для получения коэффициентов ац, надо было бы продолжить разложения D5)
до членов с а1, а в разложениях C8) выписать коэффициент при аа, что мы
предоставляем читателю, Заметим также, что нз C8) н D5) вытекает начало
разложения для R*:
#»= 1+2 Re <*!«-(¦¦... D7)
Если бы мы хотели получить отображение области (Ga) на круг единичного
радиуса, то следовало бы функцию D3) разделить на найденное значение R,
Линейную часть полученного результата можно представить также,в ин-
интегральной форме, которая иногда оказывается предпочтительнее. Для этого
построим соответствующую функцию влияния (ЛВМ, п. XIV.26); но так как
задача о построении конформного отображения нелинейна, то надо воспользо-
воспользоваться замечанием, сделанным в конце указанного пункта, т. е. иайти про-
пронормированный результат малого влияния. Поэтому допустим сначала, что

§ 2. ИНТЕГРИРОВАНИЕ И СТЕПЕННЫЕ РЯДЫ
61
полярное , уравнение .контура области (йр) имеет вид р==1-f Р6 (ф—ф,)
@<ф<2я), где | Р'I <^ 1, а 6—дельта-функция. Это же уравнение можно
записать в виде z=elf-{-P& (ф—щ) е1?, откуда, сравнивая с D0), полагаем
<=ф, а=Р, dn=r^— ea~n)ifo (проверьте!). Будем считать, что .(//)-^единич-
.(//)-^единичный круг, для чего функцию D3) разделим на значение R из D7); учитывая
формулу D6), получаем функцию влияния для возмущения отображающей
функции
G{z; ф„)^г lim w(\~z)~ I™ тИ U-^S (dk+dt-k)zk+ ... X
V L *=2 - J
(»ро*ерьте!). Отсюда по общей методике применения функции влияния, если
контур отображаемой области имеет полярное уравнение р=1+р(<р), где
| р (<р) | <^ 1, то отображение, с точностью до малых высшего порядка, имеет вид
2л 2л . ,„_/„_
Г» ¦ 1С.'
ш=г+\ 0(г; ф0) р (^й j
Г»
\
0
'¦/-. По поводу дальнейших результатов в этом направлении (в частности, для
областей иного вида), а также их приложений см. [66].
§ 2. Интегрирование и степенные ряды
1; Интеграл. Пусть в комплексной плоскости г задана ориенти-
ориентированная линия (L), а в ее точках заданы значения некоторой функ-
функции /(г). Тогда определение интеграла
A)
дается совершенно аналогично тому, как
для криволинейного интеграла по коор-
координате (ЛВМ, п. XIV.23), причем смысл
обозначений показан на рис. 28. Если
линия (I) имеет конечную длину, а функ- Рнс зд
цня /(г) в точках z?{L) принимает ко-
конечные значения, то и интеграл A) имеет определенное конечное
комплексное значение. Если же хотя бы одно из этих условий не
выполняется, то интеграл J f(z)dz несобственный, и вопрос о его
(t)
сходимости решается аналогично тому, как это делается для веще-
вещественных интегралов.

62 ГЛ. П. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
Интеграл A) легко сводится к вещественным криволинейным ин-
интегралам. Для этого обозначим f{z) = u(z)-\- iv{z), z — x-\-iy; тогда
B)
Поэтому интеграл A) обладает теми же простыми общими свойствами,
что и криволинейные интегралы по координатам. Отметим, в част-
частности, что прн перемене ориентации линии (?) интеграл A) умно-
умножается на —1.
Если для функции f{z) удается найти первообразную F{z), то
для вычисления интеграла A) можно воспользоваться формулой
Ньют он а—Лейбница
где символ в правой части означает приращение функции F(z),
когда точка z проходит линию (?) в соответствии с ее ориентацией.
Если прн этом функция F(z) получится многозначной (а функция
f(z) подразумевается однозначной), то надо начать от какого-либо
одного ее значения, а затем следить за его непрерывным изменением.
Учитывая, что модуль суммы не превосходит суммы модулей,
a \dz\ = dL (элементу длины), получим оценки интеграла
, C)
где под ?, как обычно, понимается длина линии (?).
2. Интеграл от аналитической функции. Пусть функция f(z)
однозначная и аналитическая во всех точках некоторой открытой
области (О). Тогда для интегралов в правой части B) выполнено
необходимое условие независимости интеграла от контура интегри-
интегрирования. В самом деле, для интеграла \ (Pdx-\-Qdy) это условие
имеет внд rr-==-r-^ (ЛВМ, п. XIV.24); оно же означает, что поле
А = Pi + Qi безвихревое. Если это условие применить к интегралам
в правой части B), то получатся как раз соотношения Коши—Ри-
мана A.6) (проверьте!), которые для аналитической функции выпол-
выполняются.
Применяя к интегралам B) результаты пп. 1.2.1,2, непосредственно
получаем следующие утверждения.
Если область (О) односеязная, то интеграл
г
D)
'**
при фиксированной zt зависит только от z, но не зависит от кон-
\f{z)dz

§ 2. ИНТЕГРИРОВАНИЕ И СТЕПЕННЫЕ РЯДЫ 63
тура интегрирования, расположенного в (G); этот интеграл представ-
представляет собой первообразную к f(z). Имеет место равенство
)dz = Q E)
для любого замкнутого контура (L) в (G).
Если область (О) не односвязная, то интеграл D) представляет
собой, вообще говоря, бесконечнозначную функцию z, различные ветвн
которой отличаются друг от друга на постоянное влагаемое и Слу-
Служат первообразными к f{z). Равенство E) гарантируется для зам-
замкнутых контурдв, внутренность которых целиком принадлежа (G).
Для 'остальных Замкнутых контуров (?) можно утверждать только,
что интеграл (pf(z)dz остается неизменным, если контур (L) не-
прерывно деформировать, не выводя его в процессе деформации
за пределы, (Q). (Это верно н для разомкнутых контуров, если
в .процессе деформации контура не менять его концы.). . , .:
В. частности, мы вндим, что если функция f(z) однозначная и
аналитическая, всюду внутри замкнутого контура (L) и на нем, то
имеет Mecjo формула E). Это важное предложение называют теоре-
теоремой Коми.
Отметим, что под словами «аналитичность на контуре» обычно понимается,
«аналитичность в некоторой полоске, содержащей этот коитур». В теореме
Коши и в других аналогичных предложениях достаточно требовать аналитич-
аналитичность функции строго внутри контура, а на самом контуре требовать только,
чтобы функция сохраняла непрерывность.
Подчеркнём еще раз, что здесь н всюду в дальнейшем мы рас-
рассматриваем интегралы только от однозначных функций, о чем мы
не будем впредь постоянно упоминать. Если подынтегральная функ-
функция по первоначальному определению многозначная, то мы будем
пользоваться ее определенной ветвью н считать, что контур инте-
интегрирования не пересекает разрезы. В более сложных вычислениях
иногда приходится от этого условия отказываться; тогда нужно
тщательно указывать, какие именно значения подынтегральной функ-
функции имеются в виду,, а возможность применения интегральных теорем
требует каждый раз специального исследования.
,3. Ряды Лораиа. Ряды Лорана, названные по имени французского
математика П. Лор&на A813—1854), широко применяются в теории
аналитических функций. Эти ряды являются обобщением степенных
и имеют общий вид
Таким образом, по сравнению с обычными степенными рядами здесь
допускаются также степени с целыми отрицательными показателями.

64 ГЛ. 11. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
Поэтому ряд Лорана, вообще говоря, бесконечен в обе стороны,
хотя в частных случаях он может быть конечным в одну или даже
в обе стороны. Ряды '
co + clZ + c2z»+... и ?=3 + ^« + ?^+-... G)
называются соответственно регулярной (иначе правильной) и сингу-
сингулярной (главной) частями ряда F).
Первый ряд G)—это обычный степенной ряд, а потому он схо-.
дится в некотором круге ]z|</?a (ЛВМ, п. XVII.14). Второй ряд
G)—это степенной ряд относительно —, а потому он сходится'
в некоторой области —
< р, т. e. | z | > — = /?j. Чтобы сходились
оба ряда G), должно быть Rt < | z\ < /?a. В случае R1<.Ri, а только
он и представляет интерес, это условие опре-
определяет в плоскости z кольцо (К) (рис. 29),.,в
точках которого и сходится ряд F). Он может
сходиться также в некоторых точках окружно-
окружностей | z | = R1 и | z | = /?2, тогда как при | г \ .< Rx
и |z{>/?2 ряд F) расходится. Рис. 29 отно-
относится к случаю, когда /?j > 0, Rt < oo; поду-
подумайте, что будет, если одно нли оба из этих
условий нарушаются.
В силу предыдущего абзаца на ряды вида
Рис. 29. F) естественно распространяются свойства
обычных степенных рядов (ЛВМ, п. XVII. 11).
В частности, если обозначить сумму ряда F) в (Л') через /(г), то
формулу
/(*)-= 2 V*. *€(*), (8)
, *=«
глтхно почленно дифференцировать любое число раз, а потому сум-
сумма ряда Лорана представляет собой в кольце его сходимости анали-
аналитическую функцию. При почленном интегрировании ряда F) возникает
осложнение, так как при с_1^0 получается сумма
(9)
ряда Лорана и многозначной логарифмической функции. Поэтому,
если проинтегрировать формулу (8) по замкнутому контуру [L), обхо-
обходящему по (К) внутреннюю окружность один раз в положительном на-
направлении .(рис!. 29), и воспользоваться формулой Ньютона—Лейбница,
мы получим
§f{z)dz^Fi<z)\(L) = 0-\-c_i.2ni. A0)

§ 2. ИНТЕГРИРОВАНИЕ И СТЕПЕННЫЕ РЯДЫ 65
Все члены в правой части (9), кроме последнего, представляют со-
собой однозначные функции и потому при обходе замкнутого контура
не получают приращения.
Ряд Лорана может иметь также вид
00
2 cft(z—ze)*;
тогда он будет сходиться в некотором кольце с центром в точке Яо.
Такие ряды встречались уже в работах Л. Эйлера 1748 г.
4. Разложение аналитической функции в ряд Лорана. В п. 3
мы показали, что сумма ряда Лорана представляет собой аналити-
аналитическую функцию в кольце его сходимости. Сейчас мы проверим,
что и, обратно, функция f(z), однозначная и аналитическая в неко-
некотором кольце (К), разлагается в нем в ряд Лорана
оо
где zt—центр кольца; эта важная теорема была доказана П. Лора-
Лораном в 1843 г.
При доказательстве для простоты записи будем считать, что центр кольца
находится в точке z=0, т. е. кольцо определено неравенствами Rt < \г\ <Rit
где 0<Ri<Ri<ao. Положим z=pelv, где р постоянно, Ri < р < R%.
Тогда величина / (peh) будет функцией от ср, периодической с периодом 2л
(почему?). Разложим ее в комплексный ряд Фурье (ЛВМ, п. XVII.26)
Ч A2)
коэффициенты которого, зависящие от зафиксированного р, onpv-деляютси фор-
формулой
Л 2л
Чтобы уточнить эту зависимость, продифференцируем обе части по р, учиты-
учитывая, что р входит под знак интеграла как параметр (ЛВМ, п. XIV.20):
2я 2я
! [ ] l
о о
Проинтегрируем теперь полученный интеграл по частям, положив e~l/if=u,
откуда du——e~lk4kd<f, o = — f (pety (проверьте!).
Это дает
2я
3 А. Д. Мышкно

66
ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
Внеинтегральный член равен нулю (почему?), и, сравнивая результат с A3),
приходим к дифференциальному уравнению
rfCft k „ dCk .dp „ . .
~д§~~ск, откуда -^=ft-f. cft(P)=cftpft
(проверьте!). Подставляя этот результат в A2) и A3), получаем разложение
00 00 00
справедливое для всех z <; (К). Итак, утверждение предыдущего
абзаца доказано.
Чтобы получить формулу для коэффициентов ck, поменяем в пра-
правой части A1) обозначение индекса суммирования к на / и затем
поделим обе части иа {г—zo)k+1; это даст
f{z)(z-zo)-"-l= 2 ci {z-za)l-*-\ A4)
/ = — оо
Теперь проинтегрируем обе части по какому-либо замкнутому кон-
контуру (L), обходящему по (К) точку zt один раз в положительном
направлении. При этом надо воспользоваться тем, что для любого
целого т Ф—1 будет ф (z—zo)mdz=O, тогда как ф (z—zu)~xdz—2ni
(почему?). Поэтому после интегрирования правой части A4) останется
только член с l = k, и мы получим d)f(z)(z—zu)~k~1dz = ck-2ni,
откуда
(*-о.
Формула (И) может оказаться справедливой и за пределами
кольца (К). Пусть, например, это кольцо иа рис. 30 заштриховано,
а функция f(z) аналитична на всей пло-
плоскости z, за исключением точек и линии
разрыва, отмеченных на рис. 30 звездоч-
звездочками. Тогда в концентрическом с (К)
кольце между окружностями (SJ и (S2)
(рис. 30) все предыдущие рассуждения
пригодны, и потому формула A4) и здесь
справедлива. Как будет показано в п. 5,
еще далее расширять кольцо сходимости
нельзя, т. е. внутри (SJ и снаружи от'
(S2) ряд A4) расходится. Таким образом,
окружности, ограничивающие область
справедливости разложения аналитиче-
аналитической функции в ряд Лорана, должны «сидеть» на точках или линиях
разрыва этой функции. Подчеркнем, что в ряд Лорана можно разлагать
только однозначную функцию. Конечно, можно проводить разложение
Рис. 30.

§ 2. ИНТЕГРИРОВАНИЕ И СТЕПЕННЫЕ РЯДЫ 67
в такой ряд и однозначной ветви многозначной функции; тогда на
граничную окружность могут попасть и точки разветвления, через
которые проходят линии разрыва разлагаемой ветви.
Ряд Лорана для заданной функции существенно зависит от выбора коль-
кольца, в котором производвтся разложение. Например, функция /(«)=——т +
1 '
+ -—„ аналитична на всей плоскости г, за исключением точек г=— 1 и
z—/
г=2. Пользуясь формулой A— а)-1=1 + а+а2 + .. .(\ а\ < 1), легко полу-
получить три разложения:
Z*
(проверьте!).
б. Ряд Тейлора. Пусть дано, что функция f(z) однозначная и
аналитическая в круге \z — zo|</?, за исключением, быть может,
его центра z — z0, вблизи которого она ограничена. Тогда в «кольце»
О < \z—zQ | < R справедливо разложение A1) с коэффициентами A5).
Примем за (L) окружность \z—zo| = p—>-0 и воспользуемся оценкой
C), получим
i , ^- 1
Мы видим, что для k < О при р—>-0 правая часть стремится к нулю;
но левая часть не зависит от р, а потому она просто равна нулю.
Итак, в приведенных предположениях ряд Лорана не содержит син-
сингулярной части, а потому превращается в обычный степенной ряд
Тейлора. (Напомним, что всякий степенной ряд есть ряд Тейлора
для своей суммы, см. ЛВМ, п. XVII. 13.)
Из сказанного вытекает, в частности, что однозначная аналити-
аналитическая функция в некоторой окрестности любой своей обыкновенной
(т. е. ие особой) точки разлагается в ряд Тейлора. Этот на первый
взгляд мало интересный результат влечет за собой целый ряд след-
следствий. Так, мы видели в ЛВМ, п. XVII. 14, что сумма степенного
ряда имеет непрерывные производные всех порядков. Поэтому (п е р-
вое следствие) и функция, аналитическая в некоторой области,
имеет в ней непрерывные производные всех порядков — факт довольно
удивительный, так как при определении аналитичности в п. 1.1 мы
требовали наличие производной только первого порядка.
Вот второе следствие. Пусть функция f(z) аналитична
в некоторой области (О) и f(z)^0 в некоторой области (Н), содер-
содержащейся в (G); тогда и /(z)s=0 всюду в (G). В самом деле, пусть
3*

68 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
8JQ не так и некоторая линия (L) ограничивает область, в которой
f(z) 5= 0 (рис. 31). Тогда в этой области и все производные /*"> (z)^0,
а в силу их непрерывности оии равны нулю и на (L). Но тогда,
взяв любую точку a?(L) и разлагая /(.г) по степеням z—а, мы
получим, что/(/) = 0 и всюду в некоторой окрестности точки а,
вопреки предположению, т. е. следствие доказано.
Третье следствие. Пусть функция f(z) ф 0 аналитична и
/(с) = 0; тогда говорят, что точка z = с является нулем функции f(z).
Разложение этой функции по степеням z—с
не может иметь все коэффициенты нулевыми
(почему?), т. е. оно начинается с некото-
некоторого члена cn(z — с)". Показатель п назы-
называется кратностью (порядком) рассматривае-
рассматриваемого нуля (это то же, что кратность корня
z =о с уравнения f(z) =¦ 0, см. ЛВМ, п. VIII.8);
в частности, если п—\, то нуль называется
р „ простым, в противном случае — кратным.
Таким образом, мы. видим, что однозначная
аналитическая функция /(г)фО имеет все
нули конечного и притом целого порядка. Нули нецелого или беско-
бесконечного порядков могут появиться только' в точках разветвления
многозначной функции (например, z3/a, г1/г).
Полезно обратить внимание на то, что для вещественных фуикцяй вещест-
вещественного переменного, обладающих производными (даже любого порядка),
ин одно из перечисленных свойств, вообще говоря, ие имеет места. (Проду-
(Продумайте это!)
Можно проверить также утверждение, сделанное в предпоследнем
абзаце п. 4 о кольце сходимости. Для этого надо применить только
что доказанное второе следствие к разности между левой и правой
частями формулы A1). Так как эта разность равна нулю в области,
заштрихованной на рис. 30, то она равна нулю и всюду, где ряд
A1) сходится, а функция f(z) аналитична (почему?). Если бы ряд
сходился в более широком кольце, чем показано на рис. 30, то так
как сумма этого ряда в своем кольце сходимости" не имеет особых
точек, и функция f(z) ие имела бы там особых точек, вопреки пред-
предположению. Значит, утверждение доказано.
Из этого утверждения вытекает, в частности, важный вывод о
радиусе сходимости ряда Тейлора прн разложении однозначной ана-
аналитической функции f(z) по степеням z — с, где с—любая обыкно1
венная точка этой функции: этот радиус равен расстоянию от с до
ближайшей особой точки функции f(z). (Напомним, что если прово-
проводится разложение однозначной ветви многозначной функции, то к
числу особых точек надо отнести и точки разветвлении.) В част-
частности, если функция f{z) при конечных z не имеет особых точек—
такая аналитическая функция называется целой,— то радиус сходи-

§ 2. ИНТЕГРИРОВАНИЕ И СТЕПЕННЫЕ РЯДЫ
69
мостн равен бесконечности. Этот вывод дает возможность находить
раднус сходимости ряда Тейлора, не исследуя остаточного члена
этого ряда.
Вычислим, например, радиус сходимости разложения функции
th ?h_E.
¦ ~~chz ~
A6)
по степеням z. Так как числитель и знаменатель—целые функции, то частное
будет однозначной аналитической функцией для всех г, за исключением тех,
прн которых знаменатель равен нулю. Значит, функция A6) имеет особые точки
при
z=-yt+Jbrt (ft=0, ±1, ±2, ...)
(проверьте!). Ближайшими к точке г=0 являются ± -=- i, значит, радиус схо-
я
димости рассматриваемого разложения равен -к-.
Рис. 32.
Рис. 33.
Интересно, что если считать независимую переменную вещественной, т. е.
рассматривать разложение функции th x по степеням х, то коэффициенты ряда,
а потому и радиус сходимости будут такими же, как и для комплексного слу-
случая, т. е. интервалом сходимости будет —
-^-. Это может показатьсн
я
странным, так как точки х=±-д- ие являются особыми для функции th*,
и потому непонятно, что препятствует ряду сходиться на большем интервале.
Положение разъясняется при переходе к комплексному переменному: мнимые
особые точки z=± -^-i определили круг сходимости, а указанный интервал
получилси в результате пересечения этого круга с осью х (рис. 32). Так мни-
мнимые особые точки повлияли иа чисто вещественное явление.
Из доказанного выше первого следствия вытекает иногда применяемое об-
обращение теоремы Коши из п. 2, называемое теоремой Морерй: если функция
{(г) непрерывна в открытой области (G) и для любого контура (L) в (G) имеегА
место формула E), то эта функция аполитична в (G). В самом деле, тогда
интеграл D) не зависит от контура интегрирования, а при зафиксированном г0
г
зависит только от г, т. е. \ / (г) йг=Ф (г). Но тогда Ф' (z) = / (г), т. е. Ф (г) —

70 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
аналитическая функция. Так как оиа имеет производные верх порядков, то в
/(г)=Ф'(г) имеет производную, т. е. аиалитична.
Из теореыы Морера вытекает, в частности, что если область (G) разделена
линией (&) на части (G{) и (G2) (рис. 33) и иа (Gx) задана аналитическая
функция fx (г), а на (Ga) — аналитическая функция /2(z), причем эти функции
имеют иа (S) одинаковые и притом непрерывные предельные значения, то
«составная» функция
hi') <«€(Gi)).
будет аналитической в (G). В самом деле, эта функция, очевидно, непрерыв-
непрерывная, а формула D) для контуров вида abed (рис. 33) вытекает из равенства
J f(z)dz = J f(z)dz+ J /(г)<1г« j /a(z)rfz+ J f^dz.
abeda abepa apeda abepa apeda
Таким образом, аналитическая функция может иметь линию разрыва, ио
ие «линию излома», вдоль которой сама функция была бы непрерывна, но ее
производная претерпевала бы разрыв. Другими словами, непрерывных кусоч-
кусочно-аналитических функций не бывает.
Предоставляем читателю доказать другое следствие из теоремы Морера:
если последовательность функций, аналитических в открытой области (G),
равномерно сходится (определение этого дается, как в ЛВМ, п. XVI 1.8), той
предельная функция аналитична в (G).
6. Аналитические отображении и принципы максимума.
Пусть функция w=f{z) аналитична в некоторой открытой области (G).
Мы уже говорили в п. 1.4, что тогда отображение z—> w называется
аналитическим, и если в некоторой точке zt g (G) будет /' (zo)^=O,
то отображение малой окрестности точки z0, с точностью до малых
высшего порядка, сводится к поступательному переносу, всесторон-
всестороннему растяжению и повороту. Но что будет, если /' (zt) = 0, однако
f(z) ф. const? Тогда в ряде Тейлора по степеням z — z0 линейный
член отсутствует, и потому этот ряд имеет внд
f(z) = f(zo) + cn(z—zo)n + высшие степени (л>2), A7)
где в правой части выписан первый после постоянного член ряда с
коэффициентом, отличным от нуля. Значит, с точностью до малых
высшего порядка, w—wo = cn{z—zo)n, т. е. малая окрестность
точки zu испытывает л-листное отображение (п раз покрывает ок-
окрестность точки w0), описанное в п. 1.9; умножение на сп добавляет
всестороннее растяжение и поворот этой окрестности, от чего кар-
картина отображения принципиально не меняется. Ясно, что при этом
отображение z—*-w не может быть взаимно однозначным.
Из сказанного вытекают различные полезные следствия. Так, из
формулы A7), справедливой и при п = \ (т. е. при /' (z0) Ф 0), видно,
что в малой окрестности точки zt значение wo='f(zo) принимается
только при z = z0, а в остальных точках этой окрестности будет

§ 2. ИНТЕГРИРОВАНИЕ И СТЕПЕННЫЕ РЯДЫ
71
Отсюда, в свою очередь, получается следующее. Пусть функция /()^
аналнтнчна в некоторой конечной замкнутой области (Л'); это, по определению,
означает, что она аналитична в некоторой открытой области (G), содержащей (К).
Тогда f(z) может иметь е (К) лишь конечное число нулей. В самом деле, в
противном случав можно воспользоваться доказываемой в университетских
курсах математического анализа и наглядно очевидной теоремой Больцано —
Вейерштрасса, согласно которой из всякого бесконечного ограниченного множе-
множества точек евклидова пространства можно выделить сходящуюся последова-
последовательность точек. Но предел последовательности нулей функции будет нулем
той же функции, и мы приходим к противоречию с утверждением предыдущего
абзаца (продумайте это!).
Если функция f (г) аиалнтнчна на всей плоскости г, то она может иметь
бесконечное число нулей: например, такой будет f (г)=sin z. Но так как в
каждом конечном круге она имеет лишь конечное число нулей, то, выбирая
расширяющуюся последовательность кругов, в пределе исчерпывающую плос-
плоскость, мы получим, что все нули такой функции f (г) можно расположить в
последовательность гх, г2, гз, ¦¦•> уходящую на бесконечность.
Применяя доказанное к- разности двух функций, получаем, например,
такое усиление второго следствия из п. 5: если две функции аполитичны в
некоторой области (G) и совпадают в ней на дуге какой-либо линии, то они
совпадают в (G) тождественно. Между прочим, отсюда вытекает простое дока-
доказательство возможности перехода от. вещественных тождеств к комплексным,
о которой мы упоминали в ЛВМ, п. VIII.4. Как доказать, например, что
sin2 г== 1 — cos2 г? Левая и правая части представляют собой аналитические
функции г, совпадающие при вещественных г, т. е. на прямой Im г=0. Значит,
они совпадают и при всех г.
Пусть функция f(z) ф. const аналнтична в некоторой окрестности
точки za. Тогда маленький круг (Kz) с центром z0 отображается
Рис. 34.
функцией f(z) на маленький круг (Kw) с центром в f{z0) (с поправ-
поправками высшего порядка малости) (рис. 34). Выберем в (Kw) вблизи
и»0|
(Kz).
Эта точка w бу-
буТаким образом,
|[
то0 какую-либо точку то, для которой |то|>
дет служить образом некоторой точки z z
в любой близости от zt можно найти точку г, для которой
>|/(го)|, и потому |/B)| не может иметь г0 точкой максимума
(продумайте это!).
Отсюда получаем такое следствие. Пусть функция f{z) ана-
аналитична в некоторой конечной замкнутой области (К). Тогда |/(г)[,
как вещественная непрерывная функция, принимает на (К)

72 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
наибольшее значение (ЛВМ, п. IX.4). Из доказанного выте-
вытекает, что это значение достигается обязательно на границе (К).
Аналогично проверяется, что и Re/(г) не может иметь г„ точкой экстре-
экстремума (продумайте!). Отсюда легко вывести, что функция, непрерывная в конеч-
конечной замкнутой области и гармоническая во всех ее внутренних точках, дости-
достигает наибольшего и наименьшего значений на границе этой области.
Утверждения, подобные тем, которые были доказаны в двух по-
последних абзацах, носят название принципов максимума.
7. Аналитическое продолжение. Пусть функция f (г) аналитична в области
(G), a g(z)— в области (D), причем (G) и (D) имеют общую область (Н)
(рис. 35), в которой f (z) = gB). Тогда «составная» функция
будет, очевидно, аналитической в «составной» области (Gx), состоящей из всех
точек (G) и (D). (В силу п. 5 для этого достаточно даже, чтобы (G) и (D)
примыкали друг к другу по линии, на которой обе функции имеют одинако-
одинаковые и притом непрерывные предельные значения.)
Эта функция fi (г) называется аналитическим
продолжением каждой из функций f (г) и g(z).
Такое продолжение получается обычно, если
имеются две формулы, задающие аналитические
функции и пригодные для различных областей г,
которые имеют общую часть, где обе формулы
дают одинаковый результат.
Функция ^ (г) в свою очередь может быть
аналитически продолжена на еще более широкую
р «с область и т. д. Теоретически говоря, после всевоз-
можных таких продолжений мы приходим к пол-
полной, т. е. уже далее не продолжаемой аналити-
аналитической функции F (г). Эта функция F (г) определяется функцией f (г)
однозначно, так как из п. 6 легко следует, что если вдоль какого-либо кон-
контура (L) плоскости г, начинающегося в (G), функцию / (г) возможно аналити-
аналитически продолжить, то только одним способом. Однако если такой контур (Z.)
при своем продолжении вновь попадет в (О) (рис. 35), то совсем не обяза-
обязательно, чтобы мы вернулись к значениям f (г). Другими словами, даже если
исходная функция была однозначной, то результат ее аналитического продол-
продолжения может оказаться многозначной (даже бесконечнозначной) функцией.
Так как аналитическое продолжение осуществляется всегда через некото-
некоторую дугу на границе области определения функции, то непродолжаемость
аналитической функции обычно распознается по тому, что эта функция опре-
определена на всей комплексной плоскости, без разрезов, хотя и может иметь на
ней особые точки, в частности точки разветвления.
Приведем примеры. Сумма ряда
сходящегося при |г| < 1, представляет собой функцию, аналитическую в этом
круге. Но там эта сумма равна
4
а последнее выражение представляет функцию, аналитическую во всей пло-
плоскости г, за исключением точки 2=1. Значит, аналитическим продолжением

§ 2. ИНТЕГРИРОВАНИЕ И СТЕПЕННЫЕ РЯДЫ 73
функции S (г) служит полная аналитическая функция F (г). Говорят также,
что F (г) является расширением функции S (г), a S (г)—сужением функщи. F (г).
Подобным образом бесконечнозиачная функция Ln A +«) представляет
Z* Z3
собой полное аналитическое продолжение суммы ряда г—д" + "о—•••> С1Годя-
? О
щегося в том же круге | г | < 1.
Интеграл, определяющий гамма-функцню (ЛВМ, п. XIV. 17)
Г (р) » С е-*х*-1 dx= С exp [~х+(р— 1) In x] Jx, A8)
о о -
как нетрудно проверить, сходится не только для вещественных, но и для мни-
мнимых р, если Rep>0. Так как правила дифференцирования интеграла по
параметру (ЛВМ, § XIV.5) непосредственно распространяются и на комплекс-
комплексные значения параметра, то интеграл A8) имеет производную по р и потому
представляет аналитическую функцию от р в полуплоскости Re p > 0. Как и
для вещественных р, легко проверяется, что в этой полуплоскости Г(|1)
= рГ(р). Поэтому функция
определенная и аналитическая в полуплоскости Rep > —1 (почему?), за исклю-
исключением особой точки при р=0, в первой полуплоскости совпадает с Г(р);
таким образом, Гг (р) представляет собой аналитическое продолжение фу акции
Г (р) с первой полуплоскости на вторую. Аналогичным образом фуйЯция
Г3 (р) = г *"~*~ представляет собой аналитическое продолжение функции
1\(р) на еще более широкую полуплоскость Rep >—2. Продолжая таким
образом, мы получаем полную гамма-функцию, которая также обозначается
через Г (р) и представляет собой однозначную аналитическую функцию на всей
плоскости р, за исключением особых точек р=0, —1, —2, ... Тождество
' Г (р+1) — рГ (р) выполняется на всей плоскости р.
Один из общих способов аналитического продолжения основан на правиле
симметрии (п.1.16). Из этого правила следует, например, что если граница
области определения аналитической функции / (г) содержит отрезок вещест-
вещественной оси и на этом отрезке функция / (г) принимает вещественные значения,
то формула f(z*) = [f (г)]* осуществляет аналитическое продолжение функции
f (г) через этот отрезок.
Для аналитического продолжения функции, заданной разложением в сте-
степенной ряд, может оказаться полезным следующее преобразование Эйлера.
Допустим, что требуется продолжить функцию
причем функция g(z), разложение которой вокруг точки г=0 имеет вид
.| B0)
известна на всей плоскости г (т.е. g(z) уже продолжена на всю плоскость г).
Чтобы выразить / (г) через g (г), умьожим обе части B0) на у0 и вычтем из
A9), получим
f-Yog=(Yi-Yo)CiZ + (Ya-Yo)C2Za + (Y>-Yo)C3Z3 + --. B1)
Теперь продифференцируем обе части B0), умножим результат на (Vi—Yo) z=
= Ayjjz и вычтем из B1), получим
/ - Yog - AYo*g'=(Ya - 2yt + Yo) c>za + (Ys - 3Yi + 2Yo) V3 +... B2)

74 ГЛ. П. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
Теперь продифференцируем B0) еще раз, умножим результат иа -^(Уг —
+Y0)za= —Д2у0га и вычтем из B2) н т.д. Можно показать, что подмеченная
закономерность будет проявляться и дальше, н в пределе мы приходим к раз-
разложению
f(z)=yog(z)+-^zg'(z)+^zy'(z) + ..., B3)
справедливому 0 некоторой окрестности точки г=0, если коэффициенты у„
не растут при п —>¦ со по абсолютной величине слишком быстро (допускается
рост ие выше экспоненциального). Однако правая часть B3) может оказаться
аналитической далеко за пределами круга сходимости ряда A9) н, таким
образом, дать аналитическое продолжение функции f (г).
Так, допустим, что уп представляет собой многочлен от п некоторой сте-
степени ft. Тогда Ду„ есть многочлен от п степени k—1 (почему?) и т. Д., а
потому ряд и правой части B3) обрывается, и мы получаем конечное пред-
представление суммы ряда A9) через функцию g (г), т. е. функция / (г) оказывается
продолженной на всю плоскость г.
Другой полезный частный случай получится, если положить
Тогда со=1, сх=—yy > с»~ о\ и Т'Д1> и из №) и $3) получим фор-
формулу
(проверьте!). Результат особенно прост, если взять р = \.
Возьмем, например, р=1; у„=—XT' ^огда с помоЩью последователь-
ного вычисления разностей легко проверить, чтоД*у„=т— —'
и (— 1)к
откуда получаем AgVo = \,t > т- е-
Ряд в левой части сходится при | г \ < 1 (это разложение функции
по степеням г). Ряд в правой части сходится при
z
< 1, т. е.
\x+iy\*< \х-{-{у-{-\ |а нлн х>—-к-. Значит, формула B4) осуществляет
аналитическое продолжение ряда, стоящего н левой части, иа полуплоскость
Re*> —j.
8. Варианты. Аналитические функции вещественного переменного. Если
у функции и>=/ (х) незаннсимая деремеиная х по своему смыслу вещественна,

§ 2. ИНТЕГРИРОВАНИЕ И СТЕПЕННЫЕ РЯДЫ
75
X
Рис. 36.
то принятое в п. 1.1 определение аналитичности неприемлемо. В этом случае,
исходя из результатов п. 5, говорят, что функция аполитична на интервале
а < х < Ь, если для любого х0 из этого интервала она разлагается в ряд Тей-
Тейлора по степеням х—х0, сходящийся в некоторой окрестности х0. Чтобы
установить связь этого определения с определением п. 1.1, подставим мысленно
в тейлоровское разложение функции f(x) вместо вещественного х комплексное
г; тогда получится функция f (г), аналитическая в некотором круге с центром
х0 и принимающая заданные' значения при г=х. Если проделать это для раз-
разных х0, мы получим функцию /(г), аналитическую в смысле п. 1.1 в некоторой
области (плоскости г), содержащей интервал а, Ь вещественной оси (рис. 36)
н совпадающей при z=* с исходной функцией f (х). "(Подумайте, почему прн
определении f (г) при разных
х0 мы не можем получить tj
противоречие.) Итак, поль-
пользуясь терминологией п. 7,
можно сказать, что анали-
аналитическая функция веществен-
вещественного переменного допускает
расширение (аналитическое
продолжение) до аналитиче-
аналитической функции комплексного
переменного и, обратно,
первая является сужением
второй.
Аналитические функции
нескольких переменных. Бу-
Будем говорить для простоты записи о функциях двух переменных. Функция
f (zi> га) двух комплексных переменных г1( г2, определенная в некоторой откры-
открытой области (G) двумерного комплексного числового пространства Z2 (ЛВМ, п
VII. 20), называется аналитической в этой области, если в некоторой окре-
окрестности любой точки (z10; г20) 6 (б) эта функция разлагается в двойной ряд
Тейлора (ЛВМ, п. XVII.17) по степеням (zt—г10), (гг—z20). Подобным обра-
образом определяетси и понятие аналитической функции двух вещественных пе-
переменных.
(Обращаем внимание читателя на недоразумения, которые иногда возни-
возникают нз-за неточной терминологии. Например, рассмотрим функцию w=y—х*
для вещественных х, у. Это аналитическая функция, равная нулю на
линии у=*а, но не тождественно равная нулю. Может показаться, что это
противоречит свойствам аналитических функций, доказанным в п. 6. Но на
самом деле ничего страшного нет: дело в том, что рассматриваемая функция
аиалитична как функция вещественных (или даже комплексных!) переменных
х, у, но не аиалитична как функция переменного z~x-\-iy.)
Если f (xlt *2)—аналитическая функция вещественных переменных хх, х%,
то она аналитична и по каждому из этих переменных в отдельности, т.е. при
зафиксированном другом. (Впрочем, обратное тоже верно, за исключением
специально построенных примеров, не имеющих практического значения.)
Более того, если имеется любая аналитическая линия (L)\ x1 = <f1(t), x3 = y2(t)
(это значит, что функции q>t и ф2 аиалитнчны), проходящая по области, где
функции / аиалитична, то и сложная функция /((pt (t), <p2 (t)) аналитическая.
Из этого свойства, которое выводится нз возможности подстановки ряда в ряд
(ЛВМ, п. XVII.12), вытекает, например, что если малая дуга линии (L) содер-
содержится в каком-либо множестве уровня функции /, то и вся линия (L) содер-
содержится в этом множестве (почему?).
Иногда приходится рассматривать неявные аналитические функции. Пусть,
например, рассматривается уравнение
B5)

76 ГЛ. II, ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
причем функция f аналитичиа и выполняются условия
f(cv C2)=0, ftt(ct, с2)ф0 B6)
(второе известно как условие существования неявной функции, ср. ЛВМ,
п. IX. 13). Тогда можно доказать, что в достаточной близости от точки (сг\ са)
уравнение B5) может быть (и притом однозначно) разрешено относительно z2;
кроме того, получающаяся функция za (zt) также является аналитической, т. е.
разлагается в ряд Тейлора по степеням г1—сг. Это разложение можно найти
либо с помощью последовательного дифференцирования равенства B5), в koto-
kotoром считается га = гг(г1), и вычисления производных
либо с по-
1
мощью непосредственного применения метода неопределенных коэффициентов.
Отсюда, в частности, видно, что если аналитическая функция I является веще-
вещественной, т. е. принимает при вещественных значениях аргументов сама веще-
вещественные значения, а также числа с1; с2 вещественные, то и аналитическая
функция za (zt) вещественна.
Если не предполагать второго условия B6), то положение осложняется,
но в случае двух независимых переменных может быть без труда разобрано
до конца. Будем для простоты предполагать, что Cj—са = 0 (в противном слу-
случае надо предварительно ввести новые переменные гк-=^гк—с/,), и рассмотрим
разложение функции / по степеням г1г г2, перенумеровав в каком-либо порядке
все его фактически присутствующие, т. е. с не равными нулю коэффициентами
члены:
B7)
где все dj Ф 0, все т./, и пк—целые Гэ=О. Уже самые простые примеры, как
f=z1-\-z\— za и т.п., показывают, что в общем случае решения уравнения
B5) в виде ряда по целым степеням г1 может и не существовать. Однако те
же примеры подсказывают, что можно пытаться построить решение в виде
суммы ряда более общего вида
оо оо „
га= 2 oksk, где sq'= ги т.е. za= "У, akZig' B8)
k=\ ft=1
(q' целое > 0), называемого рядом Пюизд. Можно доказать (иа чем мы здесь
ие будем останавливаться), что это и есть решение уравнения B5) в самом
общем случае.
Особенно просто—и часто вполне достаточно—найти главный, т.е. первый
фактически присутствующий член в разложении B8). В самом деле, если
z2 = AsP-\-... (многоточием обозначены члены высшего порядка малости), где
Zi — sV, то из B7) получаем
¦'.., B9)
Так как сумма этих степеней должна равняться нулю (почему?), то все члены
должны взаимно уничтожиться; в частности, в выражении B9) должно быть
по крайней мере два главных члена (с наименьшими степенями s), так как
главные члены не могут «погаситься» членами высшего порядка малости. Но
dkA"k Ф 0, н потому мы приходим к выводу: целые числа рЗэ 1, q^ 1 должны
быть такими, чтобы среди сумм pn^-j-qm/, (k—l, 2, 3, .. .) было по крайней
мере две одинаковых, тогда как исе остальные были бы большими. Если таквв
р, q найдены, то коэффициент пр должеи удовлетворять алгебраическому урав-
уравнению при естественном смысле обозначений
п). C0)

§ 2. ИНТЕГРИРОВАНИЕ И СТЕПЕННЫЕ РЯДЫ
77
В конкретных примерах можно действовать следующим образом. Отметим
на плоскости с координатами т, п все наборы показателей, фигурирующие
в разложении B7); так, на рис. 37 показана картина, отвечающая функции
(проверьте!). Из первого условия B6) вытекает, что начало координат не отме-
отмечено (другими словами, в. разложении B7) отсутствует свободный член){
кроме того, всегда можно предпола-
предполагать, что на каждой из осей т, п п
имеется по крайней мере одна отме-
отмеченная точка, так как в противном
случае уравнение B5) можно сокра- й-
тить иа степень гх или га. Если теперь
некоторая прямая проходит по край- J
ней мере через две отмеченные точки Ч'
и отделиет остальные от начала ко- с
ординат, то, записав ее уравнение в
виде pn-\-qm — const, мы получим
как раз искомые р, q (их следует
брать минимально возможными, т. е.
без общих делителей), после чего из
уравнении C0) можно найти соответ-
соответствующий коэффициент А"к. (Отрез- .
ки таких прямых образуют ломаную, " \а \ j "Чс т
называемую диаграммой Ньютона; на
рис. 37 она показана сплошными ли- Рнс. 37.
ниями.) Так, мы предоставим чита-
читателю проверить с помощью рис. 37, что для уравнения B5) с функцией C1)
возможные главные члены решений имеют вид
\
VS,
\
\
\
к
)
22!,
za=—tt=-
za = —-7—-
), где s» = zt (для прямой аа);
(ДЛЯ ПриМОЙ ЬЬ)\
где sa=z1 (для прямой ее).
Первые три формулы в случае комплексного zt образуют единую трехзначную
функцию z2= j/ —г-i, аналогично две последние можно записать в виде za=
-л/А.
У 2
_?к.. Такое кажущееся увеличение числа решений возникает всегда при
q>\, так как из п. 5 легко вытекает, что если одна ветвь многозначной функ-
функции удовлетворяет уравнению вида B5), то и все остальные ветви—тоже.
Впрочем, если, как это часто бывает, считать гх вещественным, то под s надо
понимать какую-либо определенную ветвь многозначной функции; тогда все
найденные семь решений следует считать различными.
Прн построении дальнейших членов разложения B8) надо иметь в виду,
что значение q' в формуле B8) может либо равняться найденному для глав-
главного члена значению q, либо же иметь добавочный неизвестный заранее цело-
целочисленный множитель. Поэтому в уравнении B5) надо сделать замену z1 = s4,
Zi=sP (А+г3) и перейти к уравнению для zs(s). Если для преобразованного
уравнения выполнено условие существования неявной функции, т. е. в соот-
соответствующей диаграмме Ньютона точка @; 1) будет отмеченной, то г3 будет
получено в виде ряда по целым степеням s, откуда, в частности, q' = q. Если
же это условие не выполнено, то надо вновь искать возможные главные члены
разложения z8 (s), т.е. положить z3=/l1sjt+..., s=sj', после чего совершить

78 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
эамену переменных s=s**, zs=s^» (А1-)-г4) и т. д. В реальных примерах после
одной-двух таких замен мы приходим к случаю, когда выполнено второе усло-
условие B6), и потому можно далее применить хотя бы метод неопределенных
коэффициентов. В более полных курсах (см., например, [19, 58, 131[) показы-
показывается, что общее число решений уравнения B5) с одним и тем же главным
членом АьР равно кратности А как корня уравнения C0). Отсюда, в частности,
вытекает, что общее число решений za (гх) уравнения B5) вблизи начала коор-
координат равно наименьшему из показателей степени в разложении /'@, га). Если
для всех главных членов этих решений уравнения C0) имеют только простые
корни, как в примере C1), то после первой же из описанных замен условие
существования неявной функции начинает удовлетворяться.
В приложениях часто бывает, что все участвующие величины должны быть
вещественными. Тогда общее число решений уравнения B5) может оказаться
меньшим, чем указано в предыдущем абзаце, так как вещественное уравнение
может иметь несколько пар мнимых сопряженных решений (ЛВМ, п. VIII.8),
которые теперь приходится отбросить. Так, в примере C!) получается пять
решений при гх>0 и три—при гу<0. (Легко понять, что если в случае про-
простых корней уравнения C0) старший коэффициент получится вещественным, то
и дальнейшие, а с ними и все решение также будут вещественными.) Если
уравнение B5) содержит некоторый параметр, то при переходе его через
некоторые значения число вещественных решений может скачком измениться;
такие значения часто играют в прикладных задачах важную роль.
§ 3. Особые точки и нули
1. Изолированные особые точки. В этом параграфе мы будем
рассматривать только изолированные особые точки однозначных ана-
аналитических функций; при этом особая точка называется изолирован-
изолированной, если в некоторой ее окрестности аналитичность функции нару-
нарушается только в одной этой точке. Из первого абзаца п. 2.5 выте-
вытекает, что в такой точке функция обязательно становится неогра-
неограниченной (хотя и не всегда обращается в бесконечность, см. п. 2).
Отметим сразу, что иногда говорят об устранимых особых точках,
которые пропадают после правильного определения значений функции
в этих точках (ср. ЛВМ, п. III..13): например, функция не опре-
определена при z — О, т. е. формально имеет там как бы особую точку;
= 1(так как lim -—= 1 ), то особой
г=0 V г-0 г' J
точки не остается. Впредь мы будем считать такие неопределенности
устраненными, т. е. не будем считать их за особые точки.
Итак, пусть однозначная аналитическая функция f(z) имеет при
z = а изолированную особую точку. Тогда из п. 2.4 вытекает, что в
некоторой окрестности точки а эту функцию можно представить
в виде суммы ряда Лорана
се
-i-c1{z — a)+ct{z—a)* + ;.; A)
sin г
но если положить

§ 8. ОСОБЫЕ ТОЧКИ И НУЛИ 79
Этот ряд сходится во всей окрестности, за исключением, конечно,
самой точки а. Наружной границей области сходимости ряда служит
окружность с центром в а, проходящая через ближайшую к а дру-
другую особую точку функции f{z) (к которым причисляются и точки
разветвления, если f(z) представляет собой однозначную ветвь мно-
многозначной функции). Если особых точек, кроме а, нет, то ряд A)
сходится на всей плоскости z при гфа.
Чаще всего оказывается, что в сингулярной части разложения
A) содержится лишь конечное число чл-енов, т.е. это раз-
разложение имеет первый член (хотя может не иметь последнего). Такая
особая точка называется полюсом. Если же в разложении A) при-
присутствует бесконечное число членов с отрицательными
показателями, то z = а называется существенно особой точкой функ-
функции /(г).
Коэффициент c_t разложения A) называется вычетом функции
f(z) в ее особой точке z = a я обозначается Выч/(г), или по-фран-
г=а
цузски Resf(z). Важность этого коэффициента при вычислении
г-а
интегралов ясна из п. 2.3.
Разложение многозначной аналитической функции / (г) в окрестности своей
точки разветвления г=а имеет более сложный вид. Так, если это точка раз-
разветвления конечного порядка п, то, обозначив г—а=?п, получим, что если ?
| опишет маленькую окружность с центром ? = 0, то г обойдет п раз вокруг
точки а, и потому f (г) вернется к исходному значению. Значит, /(г) представ-
представляет собой однозначную аналитическую функцию ? и потому разлагается
в ряд Лорана
/(«)= 2 с*С*= 2 ck(z-afn. B)
к=-» к=-«
Последний ряд B) по целым степеням величины (г—а)х/п иногда называют
рядом Лорана—Пюизб; все п значений функции получатся, если придавать в нем
этой величине ее п возможных значений.
2. Полюс. Разложение функции в ряд Лорана в окрестности ее
полюса имеет вид
B-
если при этом с_„^0, то говорят, что этот полюс имеет порядок
(кратность) п. Таким образом, полюс может быть простой (если п — 1)
или кратный (порядка 2, 3 и т. д.). Для полюса порядка п в разло-
разложении C) член CZ."\n ПРИ г -"*¦а является главным (в каком смыс-
смысле?), т. е. при z —*- а величина f(z) бесконечно большая, эквивалентная
•.—^г—; если принять за эталон, то это величина порядка л
(ср. ЛВМ, п. III.11). Мы видим, в частности, что в своем полюсе
функция обязательно обращается в бесконечность,

80 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
Довольно часто лолюсы появляются при рассмотрении отношения
двух аналитических функций, для которых точка а является обыкно-
обыкновенной (не особой), однако h(a) = 0. Если при этом g(a)^Q, то f{z)
имеет при z — а полюс, причем такого тюрядка, каков порядок
нуля у h (г) (п. 2.5). Если же и g(a) = 0, причем g(z) имеет
при z=?a нуль порядка р, a h(z) — нуль порядка q>p, то f(z)
имеет при z = а полюс порядка д—р (что будет при ^7
Все эти утверждения легко получаются, если разложить q (г) и h (г)
в ряды по степеням г—а, затем вынести из числителя и знаменателя наиболь-
наибольшие возможные степени и поделить ряд иа ряд, как это описано в ЛВМ,
п. XVII.12.
Легко проверить, что если какая-либо однозначная аналитическая функция
(ие обязательно первоначально заданная в виде D)) имеет при z —>¦ а рост
не выше конечного порядка по сравнению с ———, т. е. если /(z) =
= ol- — j, то функция ?(г) = (г—a)" f (г) уже не имеет при г=а осо-
особенности, и потому особая точка г = а для f (г) может быть только полюсом.
Этим и объясняется распространенность полюсов.
Вычет функции особенно просто вычислить в полюсе периого
порядка. В самом деле, если
то (z — a)/B) = c_1 + c0B— a)+c,{z — аJ+ ..., и потому
Выч f{z) = с_х = Mm [{z — a)f(z)].
г=а г-+а
В частности, для функции D), если g(a)=?bQ, Л(а) = 0, Н'(а)ф0
(последнее как раз и означает, что в знаменателе стоит нуль
первого порядка), получаем v
Выч
Здесь мы применили правило Лопиталя (ЛВМ, п' IV. 13), которое,
как можно убедиться, имеет место и для аналитических функций
комплексного переменного. (Вывод этого иа основе формулы Тей-
Тейлора мы предоставляем желающим.)
Для общего случая полюса порядка п из C) получаем
Если продифференцировать обе части п—1 раз, получим
[{z — a)"f(z)Yn~1)=:(n— l)!c_!+ члены, содержащие положительные
степени z — а (проверьте!). Отсюда, переходя к пределу при z—*a,

§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ 81
выводим требуемую формулу
= с_1 = ?--ЦяИт [(z-a)»f{z)y»-». F)
?Ц
При ее применении порядок я полюса должен, быть предварительно
найден, как это было описано выше. Формула F) справедлива н в
случае, когда порядок полюса меньше я (но не больше я), так как
в предыдущем рассуждении с_„ могло равняться нулю.
Поведение функции f(z) в окрестности своей существенно особой точки
г=а значительно сложнее. Мы видели, что значения f(z) при г —»¦ а не огра-
ивчены степенной функцией ни с каким показателем; тем не менее оказывается,
что они не являются и бесконечно большими! В самом деле, задав любое
комплексное число k, легко доказать, что функция —j-г—j— не может быть
/(г)—к
ограничеииой в окрестности точки а (в противном случае надо воспользоваться
разложением этой функции в ряд Тейлора; продумайте это!). Но это значит,
что функция /(г) вблизи а принимает значения, как угодно близкие к k, при-
причем для любого к. Эту любопытную теорему доказал в 1868 г. русский матема-
математик Ю. В. Сохоцкий A842—1929). Из нее вытекает, что существенно особую
точку никак нельзя считать просто полюсом бесконечного порядка!
Примером существенно особой точки может служить точка г=0 для
функции
Подумайте о характере изменения этой функции при различных способах
приближения г к нулю.
Формулы типа F) для существенно особых точек уже непригодны. Впрочем,
если удалось получить разложение в окрестности этой точки в ряд Лорана,
то вычет сразу получается; так, из формулы
G) следует, что Выче'/г^К
(LI
. 3. Теорема Коши о вычетах. Вычеты
имеют важное применение к вычислению
интегралов по замкнутому контуру вида
)f(z)dz.
Пусть функция f(z) однозначная и ана-
аналитическая всюду на (L) и всюду внутри Рис. 38.
(?), за исключением конечного числа~точек
zv Zz,...,zN, расположенных внутри (L); контур (L) ориентирован в
положительном направлении. Разобьем область, ограниченную этим
контуром извне, на ./V частей так, чтобы внутри каждой из них
имелась лишь одна особая точка (см. рис. 38, где принято N= 3),
и ориентируем контур (Lk) каждой из этих частей в положитель-
положительном направлении. Тогда
§ Y*§z> I8)

82 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
так как в правой части интегралы по пунктирным линиям взаимно
уничтожаются (почему?). Теперь продеформируем каждый контур
(Lk) в маленькую окружность с центром в гк (на рис. 38 это пока-
показано для k = \); как указано в п. 2.2, при этой деформации инте-
интегралы не меняются. Для маленькой окружности действует разложе-
разложение f(z) вокруг zk в ряд Лорана, и потому в силу B.10)
= 2nt-C-l (для этого ряда) = 2я/-Выч/(,г).
z=zk
Подставляя в (8), получаем теорему Коши о вычетах
N
f{z)dz =2я1 ^ ВичДг). (9)
Подчеркнем, что в правой части суммирование распространяется
на все особые точки функции f(z), расположенные внутри (L).
Если таких точек нет, то интеграл равен нулю, так как сумма без
слагаемых равна нулю; таким образом, теорема Коши из п. 2.2
представляет собой частный случай общей теоремы (9).
Бывает, что мы заранее не знаем, является ли некоторая точка
особой; например, там может оказаться устранимая особенность.
Тогда, применяя формулу (9), надо эту точку включить в число
точек zk, имея в виду, конечно, что вычет функции в неособой
конечной точке всегда полагается равным нулю. При этом формулы
E) и F) остаются в силе.
Теорема Коши о вычетах дает возможность получать точные
значения рассматриваемых интегралов, минуя вычисление соответст-
соответствующих неопределенных интегралов, которые могут оказаться гро-
громоздкими или вовсе не берущимися в конечном виде. Поэтому при-
применение этой теоремы часто оказывается весьма полезным в анали-
аналитических исследованиях. Отметим, что она может применяться и к
вычислению вещественных интегралов с помощью их искусственного
сведения к комплексным.
Приведем простой пример. Пусть надо вычислить интеграл
2Я
/
J a
о
J +b cos t+c sin t ' A0)
о
при условии 62+с2 < а2, равносильном требованию, чтобы знаменатель - ие
обращался в нуль. Переходя с помощью формул Эйлера от тригонометрических
функций к показательным и выполняя подстановку elt=z, получим (проверьте!)
i=c9 (bi+c)z*+2iaz + (bi-c) dz-
где (L)—единичная окружность, ориентированная в положительном направле-
направлении. Подынтегральная функция имеет два простых полюса, из которых вну-

§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ 83
три (L) находится только одни:
а— Уа2—Fа+с2)
~ ЩГ
Отсюда по формулам (9) и E) получаем окончательно
2я
/=
Yd?— (
Здесь существенным было то, что интеграл A0) взят по периоду подынте-
подынтегральной функции: в других пределах контур (L) мог получиться незамкнутым,
и тогда формулу (9) применить было бы нельзя.
Из теоремы Коши о вычетах вытекает, в частности, интеграль-
интегральная формула Коши, дающая представление аналитической функции
внутри замкнутого контура через ее значения иа этом контуре.
Для вывода этой формулы рассмотрим интеграл
а-.
где функция /(z) однозначная и аналитическая всюду внутри кон-
контура (Z.) и на нем, а точка z0 находится внутри (L). Тогда подынте-
подынтегральная функция, т. е. ¦, имеет внутри (L) ровно одну особую
точку — простой полюс z = za с вычетом /(z0) (почему?). Значит,
по теореме Коши интеграл A1) равен 2nif(z0), откуда и получается
интегральная формула Коши
(Чему равна правая часть, если точка z0 находится вне
¦ Если продифференцировать обе части A2) по параметру га, получаются
формулы
§10Ь f^b
которые иногда применяются для оценки производных.
4. Применение к несобственным интегралам. Теорема Коши
о вычетах широко применяется при вычислении несобственных инте-
интегралов, причем при таких применениях довольно часто приходится
проявлять высокое аналитическое искусство. Мы здесь укажем лишь
простые результаты в этом направлении; дальнейшие сведения можно
найти в указанных выше общих курсах (см., в частности, [66])
и в специальной литературе.
Рассмотрим сходящийся несобственный интеграл общего вида
00
/= 5

84
ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
(U
предполагая, что функция / определена не только для вещественных,
но и для мнимых значений аргумента так, что f(z) является одно-
однозначной аналитической функцией в полуплоскости imz^O, за исклю-
исключением конечного числа особых то-
точек гг, г2, ..., zN, причем все
Im.zft>0. Непосредственно приме-
применить теорему о вычетах к интегралу
A3) нельзя, так как нет замкнуто-
замкнутого контура; поэтому производится
искусственное «замыкание» контура
с помощью некоторой последова-
последовательности дуг (Z-j), (Z.2), (L3), ...
(рнс. 39). Тогда каждая дуга (Ln)
вместе с отрезком ап, Ьп оси х,
на который она опирается, образует
замкнутый контур (?„)'. Пусть для данной функции f(z) дуги (/.„)
удалось подобрать так, что
1°. ап —*¦ —со, Ьп—*¦ со при Л —»¦ со;
2°. Для достаточно больших-л все особые точки zlt z2, ..., zpj
расположены внутри (?„)';
3°. J f(z) dz—+0 при л —*¦ со.
Тогда интеграл A3) легко вычислить. В самом деле, для достаточно
больших п в силу теоремы о- вычетах н условия 2°
Рис 39
\Ax)dx+
Выч/(г); A4)
Если теперь п—t-co, то первое слагаемое в средней части по усло-
условию 1° стремится к /, а второе по условию 3°—к нулю, так что
в пределе получаем
Выч/(г).
A5)
Для некоторых классов интегралов A3). последовательность
дуг (Z.J с требуемыми свойствами оказывается нетрудно подобрать.
Так будет, в частности, если f(z) в верхней полуплоскости при
z —»¦ со стремится к нулю быстрее, чем l]z, т. е.
со, Imz>0)
A6)
(по поводу этого обозначения см. ЛВМ, п. III. 11). В самом деле,
тогда в качестве (?„) можно взять просто полуокружность радиуса л
с центром в точке 2 = 0; тогда условие 3° (первые два условия
очевидны) сразу следует из оценки B.3).

§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ
Пример. Вычислим для вещественных ш^О, р>0 интеграл
1
-j- eiuiX dx
, р > 0),
85
A7)
встречающийся в физике. (Интересно, что соответствующий неопределенный
интеграл не выражается через элементарные функции.) Здесь при z = x-\-iy,
У 2s 0,
1
1
й-«>У\
1
-Of '
(г ->¦ oo),
т. е. условие A6) выполнено. Значит, по формуле A5),
~ 2pi ~~ p '
' = 2ni Выч
Если функция / (г) имеет также некоторое число вещественных изолиро-
изолированных особых точек хъ xit ..., хм, то интеграл A3) является сингулярным
(ЛВМ, п. XIV.19). Однако легко проверить, что если сингулярные части
лорановскях разложений функции /(г) вокруг этнх точек содержат лишь нечет-
нечетные степени, то интеграл A3) обладает главным значением, причем взамен
формулы A5) получается
• N м
v. р. V f(x)dx = 2ni 2 Выч / (г) + то" 2 Выч / (г).
A8)
2
*=1 2 =
В самом деле, пусть для простоты М=1; выберем вместо контуров, показан-
показанных на рнс. 39, контуры с добавочной полуокружностью (уп) радиуса е„, произ-
произвольно стремящегося к нулю при п -»• оо
(рис. 40). Тогда в средней частя A4) ^
вместо первого слагаемого будет стоять
С f(x)dx+ С/(г) dz+ С f(x)dx.
ал (V») xi+en
Однако средний интеграл в приведенных
предположениях при п -* оо стремится
к —я* Выч /(г) (почему?). Отсюда и вы-
2 = Ж,
текает формула A8), из которой видно,
что особые точки, расположенные на
оси интегрирования, дают в интеграл половинный вклад. (Проверьте, что если
*! —полюс и в сингулярной части его лорановского разложения имеется
по крайней мере одна четная степень, то интеграл A3) главным значением не
обладает.)
Оказывается, что для интегралов, обобщающих A7),
Рис. 40.
С / (х) е'шХ dx (ш > 0)
A9)
условие A6), поставленное для применимости описанного метода, можно сущест-

86 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
венно ослабить, заменив его на следующее:
/ (г) ->- 0 (г -+ оо, Im г> 0). B0)
(В частности, в качестве / (х) можно взять любую правильную рациональную
дробь, не имеющую вещественных полюсов; в этом случае при вычислении
интеграла A9) единственная возможная трудность состоит в вычислении нулей
знаменателя.) И в этом случае соответствующий интеграл по «верхней» полу-
полуокружности
радиуса R с центром в точке z=0 стремится к нулю при R ~»-оо, Для дока-
доказательства надо положить z = Rel9 и применить первую оценку B.3):
я
|/# I < \ If (Re'f)\ | ехр (ta>R cos ф—со/? sin ф) |
о
я
= R \ 11 (Relf) I ехР (—<°^ s'n ф) ^ф ^
о
я
<max |f (z)|-/?\ exp (—со/? sin ф) cfcp.
Так как первый множитель в правой части в силу условия B0) стремится к
нулю при R —I- оэ, то достаточно проверить, что второй при этом остается огра-
ограниченным. Однако
R\
в
Я
exp (—
= 2# \ ехр (—a>R — ф)
о ф
2
ехр (—со/?— ф) Лр( B1)
О
в последнем переходе использовано неравенство
которое легко вытекает из рассмотрения графика синуса. Но правая часть B1)
меньше, чем
00
ехр .— со/? — ф ) d<f=—=const,
о ^ п ' w
откуда и вытекает наше утверждение 1ц —»- 0 при условии B0); этоутвержде-
ние называется леммой Жордана. (Так же называется легко выводимое из
доказанного утверждение
О «о>0) {22)

§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ 87
при условии f(z)-*O (z~»-oo, Rez<0), где (Af/j)—«левая» полуокружность
радиуса R с центром в точке z=0.)
Отметим, что сходимость (вообще говоря, неабсолютная!) интеграла A9)
при условии B0) доказывается так же, как это было сделано в ЛВМ,
00
S1
— sin х dx.
X
Если функция / (г) имеет при Im z > 0 бесконечную последовательность
особых точек, уходящую на бесконечность, то при применении описанного
метода R не может произвольно возрастать, а должно пробегать некоторую
последовательность Rlt Rit R3,...—t-oo. Как видно из проведенного доказа-
доказательства, и выполнение условия B0) можно было требовать лишь на полуок-
полуокружностях (Lr), т. е. сформулировать его так:
max | / (Rneh)\ -+ 0,
0<ф<Я п-юо
тогда как поведение (Ьц) между этими полуокружностями несущественно.
После применения теоремы о вычетах и перехода к пределу при л-»-оо,
интеграл A9) получится равным сумме бесконечного ряда; аналогичное заме-
замечание относится и к формуле A5).
Иногда контур интегрирования для интеграла, содержащего параметр,
приходится замыкать для различных значений этого параметра по-разному.
Так, в физике встречаются интегралы вида
/=$/(«) «*»**. B3) о
где функция f (г) однозначная и аналитиче- ' j[ /?\ /^\
екая на всей плоскости г, за исключением
конечного числа особых точек, среди кото- О
рых могут быть и вещественные (на рис. 41
особые точки отмечены), причем f (г) —>¦ 0;
контур (L) идет вдоль вещественной' оси, ИС-
но обходит расположенные на ней особые
точки сверху или снизу; ш ф 0 вещественное. Для вычисления интеграла B3)
при ш > 0 надо замкнуть (L) большой верхней полуокружностью, что в силу
леммы Жордана даст
/ = 2я» 2 Выч U (z) e'wZ\ (ш > 0),
верх 2==2»
где сумма распространена на все особые точки г$ функции /(г), расположен-
расположенные выше (L) (в том числе лежащие на оси х и обходимые снизу). При ш < О
надо замкнуть (L) большой нижней полуокружностью и учесть, что тогда
замкнутый контур будет проходиться в отрицательном направлении; это даст
/= —2га 5] Выч U (г)е'ш*] (ш < 0).
Особенного внимания требуют манипуляции с многозначными функциями,
которые иногда появляются после аналитического продолжения подынтеграль-
подынтегральной функции. Рассмотрим в качестве примера вещественный интеграл
00
J / (х) х"-1 dx @<a< 1), B4)
0

88
ГЛ. И. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
где функция f(x) допускает продолжение на всю плоскость z=x-\-iy до функ-
функции / (г), однозначной и аналитической всюду, за исключением точек zlt z2,...,z,y,
не лежащих на полуоси 0<х < оо. Для вычисления этого интеграла рассмот-
рассмотрим вспомогательный комплексный интеграл
= J
B5)
где замкнутый контур (SRr), показанный на рис. 42, состоит из двух окруж-
окружностей радиусов R и г и отрезка /•<*<#, проходимого дважды в проти-
противоположных направлениях и изображенного для наглядности на рис. 42 дваж-
дважды. Так как подынтегральная функция в B5) многозначна, то надо еще
уточнить, какой ветвью мы пользуемся.
Поэтому проведем разрез вдоль полуоси
О < х < оо (он контуром (S#r) не пере-
пересекается, что очень важно!) и условимся
Рис. 42.
пользоваться ветвью функции га~1, равной ха~х на его верхнем берегу.
Тогда на нижнем берегу эта ветвь равна e2*'«»-i> Xе (почему?), так что
два интеграла по отрезку г<д:<У? не уничтожаются взаимно, как это было
бы для однозначной подынтегральной функции; это и дает возможность
вычислить интеграл B4). При достаточно малом г и достаточно большом R имеем
(Cr)
-|-A
B6)
J
(CT)
Однако \ / (г) г"-1 dz —> 0 (почему?); значит, если
(C)
[ Дг)гв-»& ->¦ 0,
«4,
то, переходя в B6) к пределу при г -+• О, R -* оо, получаем, что интеграл B4)
сходится и равен правой части B6), деленной на 1— e2*/<e-i>.
Если дополнительно дано, что функция f (x) четная или нечетная, т. е.
^(—jt)s=e/(x), Где 8=1 либо 8= — 1, то можно воспользоваться контуром,
показанным на рис. 43. Это привело бы к аналогичному результату с дели-
делителем ^

§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ 89
, Применяя полученный результат, находим, в частности, при 0 < а < 1
(проверьте!)
J 1+ДГ 1 е2м (а-1)г__1 \1-|-г/ 1 eW(a-l) sin JM '
Однако в силу формул J1BM,-(XIV.73) и (XIV.70) этот же интеграл равен
В (а, 1—а)=Г(а)ГA—а). Приравнивая результаты, а затем пользуясь тео-
теоремой п. 2.6 о совпадении двух аналитических функций, приходим к инте-
интересному тождеству для гамма-функции
Г(г)ГA— г) = ——, B7)
' ' sm яг v '
справедливому для любого комплексного г. Из него, в частности, следует,
tyro функция Г (г) совсем не имеет нулей, а при г = —п (л=0, 1, 2,...) имеет
(—1)"
простой полюс с вычетом -—~— (почему?).
Подобно B4) рассматриваются интегралы вида
-1
где функция f (г) однозначная аналитическая на всей плоскости г, за исклю-
исключением конечного числа точек, не лежащих на интервале интегрирования, а
на бесконечности удовлетворяет условию A6). (Для этого нужно выбрать в
качестве контура интегрирования совокупность двух эллипсов с эксцентри-
эксцентриситетом е-* О и е-*• 1 и полюсами г=±1.) Докажите, что этот интеграл
равен
_^1__ V Выч Г (±=±Y f (г)] , B8)
где сумма распространяется на все особые точки функции / (г), а в качестве
степени берется ее однозначная вне интервала интегрирования ветвь, равная
единице при г=оо. (Если условие A6) не выполняется, то в правой части B8)
в сумму должен войти также вычет при г=оо; см. по этому поводу п. 6.)
Для других типов интегралов применяются другие способы «замы-
«замыкания» контура интегрирования; именно в выборе такого «замыка-
«замыкания» и состоит главная хитрость этой теории.
С вычислением несобственных интегралов непосредственно свя-
связано вычисление сумм рядов вида
s= 2 /(*>•
где функция f(z)— однозначная аналитическая на всей плоскости г,
за исключением изолированных особых точек z^^O, ±1, ±2,...;
прочие предположения будут указаны далее. Для этого рассмотрим
вспомогательный интеграл
/„= S ctg(ju)/(z)rfz, B9)

90
ГЛ. И. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
распространенный по контуру, показанному на рио, 44, Допустим,
что на (Ln) нет особых точек функции f(z) й
<Ln)
Тогда и fn —> 0, так как на совокупности контуров функция ctgJts
ограничена. Однако по теореме Коши о вычетах этот интеграл равен
[л "I
У , —/(w)+Zj Выч c\g(Az)f(z) ,
*—« П I z=zi J
где вторая сумма взята по всем особым точкам функции f(z), попав-
фуц f(),
шим внутрь (Z.J. Переходя к
пределу при п—*оо, полу-
получаем отсюда, что
со
*=-»
-il-I
), C0)
Рис. 44.
где сумма в правой части
распространена по всем особым
точкам функции f(z) в пло-
плоскости z. При этом требуется
дополнительно, чтобы, если таких точек бесконечное число, ряд в
правой чаСти был сходящимся.
Если среди особых точек функции /(г) были целые вещественные точки,
то из этого же рассуждения следует, что формула C0) остается справедливой,
если из суммы в левой части исключить все такие точки.
Пример.
1
2
1 У —
(* Ф 0)
" вы
-т К [(i-T
Рассматривая взамен B9) интеграл J sin (яг)<h> Л6ГК° В ТСХ Ж6
(i)
(in)
положениях доказать еще формулу
ft=- о»
ы,4йЦ
=2j sin (яг)

§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ 91
б. Интегральные формулы Пуассона. Это формулы, дающие
выражения для гармонической функции б полуплоскости или б круге
через значения этой функции на границе области. Для вывода первой
формулы рассмотрим интеграл
/W [^+щ-г^щ] d*
где функция f(z) аналитическая в полуплоскости
|/B)| = о(|2|) (z^oo, Imz >0).
Тогда для всей подынтегральной функции выполнено условие A6)
(почему?). Вычисляя интеграл C1), как описано в п. 4, получаем
2nz/(? + rn). Отсюда, производя сложение б квадратной скобке,
приходим к формуле
Отделяя вещественную часть, получаем формулу Пуассона
которая дает представление гармонической функции в верхней полу-
полуплоскости через граничные значения этой функции.
Взяв в квадратных скобках в C1) сумму дробей вместо их раз-
разности, мы аналогичным образом получаем формулы (проверьте!)
(Л>0), C2)
L Г (*-ё)«(*,0)
посредством которых каждая из двух сопряженных гармонических
функций выражается через граничные значения другой. Для справед-
справедливости этих формул достаточно, чтобы
|/@)| = оA) (т. е. /(г)-*0) (г-юо, Imz>0).
Впрочем, из леммы Жордана следует, что если f{z)=fl{z)eiu>z
(со > 0), то достаточно, чтобы \f1(z)\ = o( \z\) (а для справедли-
справедливости C1)—чтобы \/г(г)\ = о(\г\2)).

92 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
Г / (х)
Рассматривая сингулярный интеграл \ I dS,, как указано в п. 4, мы,
J % 5
аналогично C2), приходим к формулам
C3)
CO OD
Иногда атнм формулам придают другой вид: заметив, что v. р. \ г=0> п0-
J x S
лучаем
C4)
и (х, 0)-ц (I, 0) .
Эти интегралы при л: = | регулярны, а при х— ± оо сингулярны (почему?).
Выбирая различные конкретные функции f (г), можно получить с помощью
формул C3) и C4) значения многих интересных интегралов. Например, поло-
положив [(г) = е1г, | = 0, из первой формулы C3) получаем значение интеграла
f sin*
— со
Аналогичные формулы рассматриваются при интегрировании по
окружности. Для этого надо взамен C1) исходить из интеграла
dz' C5)
взятого по окружности z — ae^ @^ф^2я), где ? = ге'* (г < а),
а функция f(z) предполагается аналитической всюду при |z|^a;
.точки Z и а2/?* симметричны относительно окружности |г| = а
(п. 1.8). Так как интеграл C5) равен 2л//(?), то, воспользовавшись
простым преобразованием
у [a2 —2ar cos (у —
получаем
(проверьте все эти вычисления!). Здесь также можно отделить веще-
вещественную часть и получить формулу, дающую представление гармо-
гармонической функции в круге через ее значения на окружности.

§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ
Положив в C6) г = 0, получаем интересную формулу
2Я
93
C7)
т. е. значение аналитической (а потому и гармонической) функции
в центре круга равно ее среднему значению на окружности.
Взяв в C5) сумму дробей вместо разности и воспользовавшись
формулой C7), получаем формулу
из которой легко получить формулы, аналогичные C2).
Мы предоставляем читателю, исходя яз интеграла ф {. d\
формулы C7), доказать, что
2Я
/ («и») = f @)-± v. p. J / («'*) ctg 5LZ^ (bp,
а отсюда вывести формулы
(r = а) и
о
2Я
м(а,0)=м@)+— v. p. J о (а, <р) ctg
9L_-
о
2Я
)=о@) —— v. p.
C8)
г 2Я 2Я-в \
( Отметим, что при 0=0 здесь надо считать, что v. р. \ = lim \ . ]
V 0J е^ + ° 8 /
Например, положив /(г) = гп (л=1, 2, 3, ...), т. е. M = p"cosnd,
w=p"sinnO, и положив о=1, мы получаем полезные формулы
2Я
— v. р. \ si
i-^—^ф =
о
2Я
-д— v. р. \ соз/гф-ctg 2-^—?^ф=—sin nb.
о
_ , ф—О з!пф + в1пО „
Воспользовавшись тождеством ctg ?—?—= ¦!—' -г-, перейдя к интег-
2 cos ф—cos v
рированию от —я до я и применяя правило интегрирования четных и нечет-
нечетных функций, мы можем переписать предыдущие соотношения в виде
я я
sin/гО (' sin пир sin у ,
v \ — з-аф=—ncos
J фф cos О
о о
(я= 1,2,3, ...)¦
я я
С cos лф , sin/гО (' sin пир s
v. р. \ —тг^ф = я—:—г-, v. р. \ —
F J cos ф—cos О у sin О v J cos ф —c

94 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
Положив при выводе л.=0, мы получаем, что первая группа формул верна
и при я = 0. Эти формулы нам понадобятся в п. VI 1.5.7.
6. Поведение функции на бесконечности. Пусть функция f(z)
однозначная и аналитическая в окрестности точки z = oo, т. е. для
всех достаточно больших \г\. Тогда из п. 2.4 вытекает, что она
допускает в этой окрестности разложение в ряд Лорана B.8)!
«=-00
(Впрочем, можно применять и более общее разложение B.11).) Нали-
Наличие особой точки при z= оо и ее тнп, по определению, распознаются
так: надо сделать замену z = y, после чего посмотреть, что будет
у полученной функции при ? = 0. Поэтому полюс при z*=oo будет,
если в соответствующем разложении B8) присутствует конечное
число (причем не менее одной) степеней с положительными
показателями, а существенно особая точка будет, если таких степе-
степеней бесконечное число. Если же f(z) ограничена на бесконечности,
то из первого абзаца п. 2.5 (примененного после перехода от z к ?)
вытекает, что в разложении B.8) нет положительных показателей,
откуда, в частности, вытекает, что /(оо) имеет определенное конеч-
конечное значение; тогда говорят, что функция f(z) аналитична в точке
z= оо.
Из последнего утверждения вытекает, в частности, теорема Коши—Лиу-
вилля: если функция f (z) однозначна, аналитична и ограничена на всей пло-
плоскости г, то она постоянная. В самом деле, в силу принципа максимума
модуля из п. 2.6 для любого R>Q
max |/(«)-/(«) | = max |/(«)-/(со) |;
если теперь R—> оо, то правая, а потому и левая части стремятся к нулю,
откуда и получается теорема.
Из нее в свою очередь следует, что если /(г) однозначна и аналитична.на
всей плоскости г, за исключением особых точек, которые при конечных г и при
г=оо могут быть только полюсами, то /(г)—рациональная функция (обратное
утверждение мы предоставляем читателю). В самом деле, прежде всего, из
сформулированных требований вытекает, что особых точек может быть только
конечное число: в противном случае из теоремы Больцано—Вейерштрасса
(п. 2.6) следовало бы наличие неизолированной особой точки при конечном г
или при г=оо. Установив это, выпишем разложение /(г) около каждой из ее
особых точек в ряд Лорана и составим сумму g(z) всех сингулярных частей
этих рядов (отметим, что в разложении вокруг точки г=оо сингулярной
является сумма степеней с положительными показателями степени).
Если особые точки могут быть только полюсами, то Есе эти сингулярные
части состоят из конечного числа членов, и потому функция g(z) рациональ-
рациональная. С другой стороны, нетрудно проверить, что разность f\z)—g(z) ограни-
ограничена на всей плоскости г (продумайте это!), и потому по теореме Лиувилля
есть константа; отсюда и вытекает утверждение, сделанное в начале этого
абзаца.

§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ 95
В частности, однозначная аналитическая функция, не имеющая конечных
особых точек и с полюсом на бесконечности, есть целая рациональная функция
(полином). Можно проверить, что алгебраические иррациональные функции
всегда обладают точками разветвления. Таким образом, среди однозначных
аналитических функций, обладающих конечным числом особых точек на всей
плоскости г, существенными особыми точками (конечными или бесконечно
удаленной) обладают трансцендентные функции и только оии,
Вычетом функции f(z) в точке z = oo называется число —с_и
составленное для разложения B.8) в окрестности этой точки.
(Обратите внимание на то, что этот вычет может быть отличен от
нуля и для функции, аналитической в точке z = oo!) Докажем теперь,
что сумма всех вычетов однозначной аналитической функции, имею-
имеющей на всей плоскости z конечное число особых точек, равна нулю.
В самом деле, пусть окружность |z| = /?, ориентированная в поло-
положительном направлении, содержит внутри себя все конечные особые
точки zv <г2, ...,% функции f(z). Тогда по теореме о вычетах
z = 2niS\ Вич/(г).
С другой стороны, написав разложение B.8) в окрестности точки
г = оо, получим, что тот же интеграл равен 2л1с_1= — 2ш'Выч/(,г).
Приравнивая результаты и сокращая на 2я/, получаем сформулиро-
сформулированное выше утверждение, которое иногда немного сокращает труд
по вычислению вычетов.
7. Логарифмические вычеты. Пусть функция f(z) однозначная
и аналитическая в окрестности некоторой (конечной) точки z0, за
исключением, быть может, самой этой точки, в которой f(z) имеет
либо нуль, либо полюс. Тогда функция -т^Т имеет ПРИ z — zu кэ°-
лированную особенность и ее вычет
^Tlt <39)
по определению называется логарифмическим вычетом функции f(z)
в точке z0 (название объясняется тем, что -j- = (Ln/)'j.
Если f(z) имеет в точке z0 нуль (полюс) порядка п, то лога-
логарифмический вычет C9) равен п (соответственно —л). В самом деле,
в обоих случаях можно написать
= (z-z0Y g(z),
где v = /z в случае нуля и v= —п в случае полюса, а функция g(z)
аналитинна в точке z0, причем g(zo)^O (продумайте это!). Отсюда
Г (г) =
, f(z)

96
ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
и, подсчитывая вычет этой функции по формуле E), получаем
Rum Г (Z). Vg(Zo) + (Zo-Zo)g'(Zo)
z=l /W ~ g(zo) + (zo-zo)g'(zo) V)
что и требовалось доказать.
Из теоремы Коши о вычетах (9), примененной к /'//, и доказан-
доказанного сейчас предложения вытекает теорема о логарифмиче-
логарифмических вычетах. Пусть функция /(г)—однозначная, аналитическая
и отличная от нуля всюду на замкнутом положительно ориентирован'
ном контуре (L) и всюду внутри него, за исключением, быть может,
конечного числа нулей и полюсов, расположенных внутри (L). Тогда
имеет место формула
§!^ P), D0)
где N и Р—общее число нулей, соответственно полюсов, располо-
расположенных внутри (L), причем каждый нуль и каждый полюс учитыва-
учитываются со своей кратностью (простой нуль или простой полюс счи-
считаются за один, двойной — за два и т. д.).
Так как левая часть формулы D0) равна
(буквами Аа, обозначено приращение, когда точка х проходит кон-
контур (L)), то из D0) получаем
В правой части здесь стоит число оборотов, которые совершает
точка f(z) в положительном направлении
вокруг начала координат, когда точка z
проходит контур (L). Форма D1) теоремы о
логарифмических вычетах называется прин-
принципом аргумента.
Заметим, что в формулировке этого принци-
принципа требование аналитичности функции / (г) на
самом контуре (L) (другими словами, в некото-
некоторой полоске, содержащей этот контур) можно
Рис. 45. ослабить: достаточно требовать, чтобы функция/(г)
оставалась на йем непрерывной и была отлична
от нуля. Для доказательства можно, например, применить формулу D1) к
контуру (?'), аппроксимирующему (L) изнутри (рис. 45), после чего перейти н
пределу при (V) —h (L).
8. Теорема Руше. Пусть функции f(z) и g(z)—однозначные
и аналитические всюду внутри замкнутого контура (L) и на нем, при-
причем на (L) имеет место строгое неравенство \ g(z)\ < |/(г)| Тд

§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ 97
внутри (L) функции f(z) и f{z) + g(z) имеют одно и то же число
нулей (здесь и далее каждый нуль считается со своей кратностью).
Для доказательства этой теоремы Рушё применим принцип аргумента
к функции /a(z) = /{z) + ag(z), где а—вещественный параметр,
O^a^l. Если точка г проходит (L) в положительном направлении,
то точка fa(z) описывает ориентирован-
ориентированный замкнутый контур (Ма), обходящий
Na раз вокруг начала координат (см.
рис. 46, на котором Ма==3). В силу фор-
формулы D1), где в данном случае Р=Ь,
Na 'как раз равно числу нулей функции
/a(z) внутри (L). Если а изменится мало,
то и контур (Ма) изменится мало, а i Ч_Ч>4_—-^?M )
потому число оборотов Nt останется *¦ ^~г7 «J
неизменным (продумайте это!). Опасным
мог бы быть только случай, если бы
контур (Ма) при некотором а прошел ис'
„через начало координат, т. е. для некоторого z?(L) было бы
/,(z)~=/(z)+ «?•(*) = 0;
/но тогда |/(z)| = a|?-(z)|<;|g-(z)|, вопреки условию теоремы, т. е.
.'Описанный случай невозможен. Значит, Na остается постоянным
во всем диапазоне изменения а, откуда, в частности, получаем
JVO = NX, т. е. утверждение теоремы.
В этом доказательстве, которое мы советуем тщательно продумать, при-
применены сразу два метода, распространенных в современных теоретических
исследованиях по прикладной математике. Прежде всего, это метод искусствен-
искусственного введения параметра (ведь в исходной формулировке не было никакого
параметра), который применяется для непрерывного перехода от одного из двух
заданных объектов к другому. Во-вторых, это метод непрерывного продолжения
по параметру: для доказательства справедливости какого-либо свойства (в дан-
данном примере—равенства Na=NB) в конечном интервале изменения пара-
параметра убеждаются, что оно выполняется в некоторой точке интервала и что
в малой окрестности каждой точки интервала оно либо всюду выполнено,
либо всюду не выполнено. Это простое рассуждение позволяет переходить
от утверждений локального (по параметру) характера к соответствующим утверж-
утверждениям тотального характера.
Среди следствий из теоремы Руше отметим «основную теорему
алгебры», упомянутую уже в ЛВМ, п. VIII.8, которую мы докажем
здесь в усиленной формулировке: всякий многочлен степени п
имеет ровно п комплексных нулей. Для доказательства нужно при-
принять f{z) = aoz", g(z) = alzn~1-{-a2z"~2Jr ... +ап, обозначить че-
через (L) окружность |z| = /? с любым достаточно большим R и непо-
непосредственно применить теорему Руше, что мы предоставим сделать
читателю.
4 А. Л. Мышкиа

98 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
9. Зависимость нулей от параметра. Пусть/a(z)=/(z; a)—це-
a)—целая функция переменного z, т. е. однозначная аналитическая функция
на всей плоскости z, зависящая также от некоторого параметра а.
(Аналогично можно рассмотреть функцию с любой областью анали-
аналитичности, даже зависящей от а.) Пусть в любой конечной части
плоскости эта функция зависит от а непрерывно в смысле равномер-
равномерного уклонения, т. е. при выбранном а и малом Да равномерное
уклонение /а+ла (z) от Д(г) будет малым. Тогда оказывается, что
нули функции fa(z), т. е. корни уравнения
/а(*) = 0 D2)
зависят от а непрерывно; доказательство и подробное описание этого
свойства сейчас последуют.
Допустим сначала, что z—простой, т. е. не кратный корень уравнения D2)
при некотором значении а, причем /-(z)^0, a (L)—любая фиксированная
достаточво малая окружность с центром в г. Тогда из утнерждения второго
абзаца п. 2.6 следует, что f~ (г) Ф 0 на (L), а потому и min | f~(z) |= h > 0.
a 1 *
Если теперь Да достаточно мало, то в силу условия теоремы разность
¦ - (г)—/-(г) будет на (L) по модулю меньше фиксированного числа h.
Но тогда из теоремы Руше, в которой указанную разность надо принять
за g(z), вытекает, что функция f- (г) имеет, как и f~(z), внутри (I) ровво
один простой нуль, т. е. при малом изменении а корень г уравнения D2)
изменился как угодно мало.
Если теперь г—корень кратности k, то аналогичное рассуждение показы-
показывает, что при малом изменении а из z возникает какое-то количество корней
уравнения D2), расположенных вблизи г, сумма кратностей которых равна k.
Таким образом, может либо сохраниться один корень кратности k, либо вза-
взамен г появиться k простых корней, либо же получиться какой-нибудь промежу-
промежуточный случай. Этим еще раз подтверждается, что корень кратности k есте-
естественно считать за k совпавших друг с другом корней, которые при изменении
параметра могут полностью или частично разойтись.
Не следует думать, что доказанное сейчас утверждение является
чем-то само собой разумеющимся. Если пользоваться только веще-
вещественными числами, то оно, вообще говори, оказывается несправед-
несправедливым. Например, если в уравнении х* + а = 0 вещественный пара-
параметр а, возрастая, проходит через нуль и становится положительным,
то тогда пришлось бы сказать, что два корня ± У —а совпали,
после чего исчезли. Лишь привлечение совокупвости комплексных
чисел, достаточно полной для решения уравнений, позволяет полу-
получить доказанное выше утверждение, которое можно трактовать как
устойчивость корней уравнения относительно изменения самого этого
уравнения.
Если параметр а вещественный, то в силу доказанного корни
уравнения D2) будут при непрерывном изменении а описывать неко-

сс>0
§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ 99
торые непрерывные линии в плоскости г. (При этом мы впредь остав-
оставляем в стороне более сложный случай, когда при некоторых из
рассматриваемых значений а будет /Л(г)е^0.) Отметим некоторую
специфику, возникающую при продолжении этих линий: если, напри-
например, два простых корня z1 (а) и гг(а) при некотором значении а = а0
сольются в одни двойной корень, а затем вновь разойдутся, то, как
правило, в принципе невозможно распознать, какой именно корень
пошел по одному пути, а какой — по другому; так что нумерацию
корней после а0 приходится осуществлять заново. Так, поведение
корней в примере предыдущего абзаца
показано на рис. 47. Корни в момент их
слияния 'при а = 0 теряют индивидуаль-
индивидуальность, и сказать, какой именно из них
после этого пошел вверх, а какой вниз, ±л z=z=Q
невозможно. —<^—».'
При продолжении корней уравнения
D2) может оказаться, что при каком-либо
конечном а = ос0 один или несколько из сс>0
корней уйдут на бесконечность и таким
образом пропадут, так как мы здесь рас-
рассматриваем только конечные корни; при рвс 47.
переходе а через а0 эти корни вернутся
из бесконечности. За счет этого общее число корней на плоскости
при отдельных значениях параметра может понижаться, что не про-
противоречит доказанной выше устойчивости этих корней.
Из всего сказанного вытекает следующее правило для подсчета
числа корней уравнения D2) в заданной области (О) плоскости г.
Допустим сначала, что эта область конечная и при некотором зна-
значении а0 известно число N этих корней в (О). Тогда если при
любом а из рассматриваемого диапазона на границе (Г) корней нет,
то при каждом таком а число корней в (G) равно N (почему?).
Если при каком-то а на (Г) имеются один или несколько корней,
то, установив, входят ли эти корни при изменении а внутрь (О)
или, наоборот, выходят из (О), мы определяем, насколько изменится
число корней при переходе а через а. Если область (О) бесконеч-
бесконечная, то при этом исследовании надо иметь в виду также возмож-
возможность ухода корней, расположенных внутри (G), на бесконечность
и прихода из нее; здесь иногда помогает рассмотрение асимптоти-
асимптотического выражения для' функции / при z —*• оо.
Важным частным случаем является тот, когда аналитическая
функция f{z) является вещественной, т. е. принимает при вещест-
вещественных z вещественные значения. Тейлоровское разложение ее по степе-
степеням z—z0 должно иметь при вещественных ^вещественные коэффи-
коэффициенты, а потому при мнимых сопряженных z функция принимает
сопряженные значения, т. е. /(г*) = [/(г)]* (продумайте это, исходя из
4*

100 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
свойств сопряженных чисел, ЛВМ, п. VIII.3). Отсюда следует, что
если /(с) = 0, то /(с*) = 0, если /'(с) = 0, то и /'(с*) = 0 (так как
производная от вещественной аналитической функции будет снова
вещественной), и т. д. Итак, вещественная аналитическая функция
вместе с мнимым нулем всегда обладает соприженным нулем, причем
той же кратности. (Ср. аналогичное рассуждение для многочленов
в ЛВМ, п. VIII.8.)
Отсюда, в частности, вытекает, что если левая часть уравнения
D2) — вещественная аналитическая функция, то его простые веще-
вещественные корни не могут при изменении параметра «самостоятельно»
сойти с вещественной оси, они обязаны в момент схода слиться
в кратный корень (см. рис. 47).
Численное построение линий г^ (а) можно осуществить по способу непре-
непрерывного продолжения, который будет описан во второй половине и. IV.4.11,
перейдя предварительно от комплексного уравнения D2) к системе двух веще-
вещественных уравнений относительно Re г и Im z. В момент слияния корней
соответствующая свстема дифференциальных уравнений вырождается; поэтому
непосредственно после такого слияния лучше воспользоваться разложением
корней по степеням приращения параметра (п. 2.8), а уже продолжать эти
разложения, решая дифференциальные уравнения. По расположению поля
направлений можно выяснить и характер указанного выше пересечения траек-
траекториями корней контура (Г).
10. Нули многочленов. Применим соображения п. 9 к исследо-
исследованию-зависимости от вещественного параметра а нулей многочлена
P. (z) = а„ (а) z" + a1(a)zn-1 + ...+ а„ (а), D3)
коэффициенты которого непрерывно зависят от а. Как было пока-
показано в конце п. 8, при ао(а)=^=О имеется ровно п таких нулей,
zx (a), zt (а),... ,zn (а), среди которых, впрочем, могут быть и сов-
совпадающие. При изменении а эти нули опишут п траекторий (с ого-
оговоркой п. 9 о произволе в нумерации этих траекторий после их
встречи).
Если при каком-то значении а = а степень многочлена D3) по-
понижается на k^l, т. е. если ав (а) = а^а) = ... = ак^1 (а) = 0,
ак(а)-ф0, то в этот момент остается лишь п—k нулей; это означает,
что при данном значении параметра а ровно k траекторий ушло на
бесконечность. Если при переходе через а станет вновь а„ (а) Ф 0,
то это значит, что траектории возвратились из бесконечности.
Допустим, что аь(а)Ф0 при всех рассматриваемых значениях а-
и что нас интересует чнсло^(а) нулей многочлена D3) в правой
полуплоскости, т. е. в области Re2>0, причем для некоторого
значения а = а0 это значение NB известно. (Такая задача естест-
естественно возникает в вопросах устойчивости, см. ЛВМ, п. XV.22.) Для
простоты будем считать коэффициенты многочлена D3) веществен-
вещественными, хотя аналогично рассматривается и случай комплексных коэф-
коэффициентов.

§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ 101
Так как нули меняются непрерывно и не могут уйти на беско-
бесконечность или прийти оттуда, то N(a) может измениться лишь при
значении а = а, для которого по крайней мере один нуль z попа-
попадет на границу области, т. е. будет Re2 = 0. Обозначим z = iy
(у вещественное); тогда, подставляя в D3) и отделяя веществен-
вещественную часть от мнимой, получим два равенства
«о(«) У" — а*Й У"-* + а^ («) }-*—.... =0
и . D4)
«i(«) У"-1—а3(а)у"-3 + аъ(а) у"-* — ...=0,
которые оба должны выполняться. Исключая из них у, мы прихо-
приходим к соотношению между коэффициентами; оно и определяет зна-
значения а, при которых число N(a) может измениться. При этом,
если найдены значения а, у, удовлетворяющие обоим равенствам D4),
то при переходе возрастающего а через а значение N(a) увели-
увеличится или уменьшится на единицу за счет прохода нуля через iy
в зависимости от того, будет ли
жч" eta ~ ^ dPJdz
положительным или отрицательным.
a=a, z=iy
D5)
Если поляном содержит несколько вещественных параметров, например
<хх, <х2, ..., ад, то аналогичным образом можно выделить в А-мерном простран-
пространстве параметров области, которым отвечает то или иное зиачение N (alt a8,..., ад);
такое разбиение пространства параметров называется D-разбиением, оно наи-
наиболее наглядно при k=l или 2. Области D-разбиения отделены друг от друга
(ft — 1)-мерными поверхностями, уравнения которых получаются из требования
наличия у полинома чисто мнимого нуля. (Напомним, что число 0 мы относим к
чисто мнимым числам.) Аналогично определяется D-разбиение для любой целой
функции, содержащей параметры, однако при этом в пространстве параметров
могут добавиться поверхности, для которых нули с Rez > 0 уходят в бесконеч-
бесконечность. В последние годы появился ряд работ, в которых осуществляется
?)-разбиеиие для различных классов полиномов и квазиполиномов, т. е. функ-
функций вида
m
2а*г"*Л* (все nftSs0 целые). D6)
Особенно важен случай, когда все нули полинома имеют отри-
отрицательную вещественную часть, т. е. находятся в левой полуплос-
полуплоскости. Такой полином называется устойчивым (почему?) или гурви-
цевым по имени немецкого математика А. Гурвица A859—1919),
доказавшего в 1895 г. следующую теорему, которую мы здесь при-
приведем без доказательства (см., например, [133]). Для устойчивости
полинома
/>(*) = aQz» + a1z»-l+...+an_1z + an (a0 > 0) D7)

102 ГЛ. П. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
с вещественными коэффициентами необходимо и достаточно, чтобы
при всех k=\, 2,. .., п было
-1 "l  ••• ft-3
a_fc ai-k a6-ft ••• a2ft-fc
где все коэффициенты ayC_/<0 или у> л надо положить равными
нулю. Этот критерий Гурвица очень удобен для полиномов невысо-
невысоких степеней.
Полезно иметь в виду также следующее простое необходимое
условие: у устойчивого полинома D7) с вещественными коэффициентами
все они {коэффициенты) положительные. Это сразу вытекает из воз-
возможности разложить вещественный полином на вещественные линей-
линейные и квадратичные множители (ЛВМ, п. VIII.8); если же исходный
полином устойчивый, то эти множители будут иметь положительные
коэффициенты (почему?) и, раскрывая скобки, приходим к сформу-
сформулированному необходимому условию. Подчеркнем, что оно является
достаточным лишь при л=1 и я = 2 (проверьте!). Однако можно
доказать, что если оно выполнено и Ап_1 > О, Д„_3 > 0 и т. д.
(через один), то многочлен D7) устойчивый; это несколько облег-
облегчает проверку условий Гурвица.
Общая проблема определения числа нулей с положительной веще-
вещественной частью у заданной целой функции называется проблемой
Рйуса — Гурвица. Если для полинома D7) все определители Дх,
Д2, ..., Д„ отличны от нуля, то, как показал Гурвиц, искомое
число нулей равно числу перемен знака в ряду чисел 1, Д1(
Аа Аз А„
Дх' Д2' •••' AB_X-
Рассмотрим, например, полином г3+Згг + Зг+а с вещественным пара-
параметром а. Применение уравнений D4) приводит к значениям (проверьте!)
а=0 и 9, которые и осуществляют D-разбиение оси а иа три части. Про-
Проверка знака выражения D5), которую мы предоставляем читателю, показывает,
что при переходе через <х=0 число N нулей с положительной вещественной
частью убывает на единицу, а при переходе через а=9—возрастает на два.
Так как при а=1,таких нулей нет (почему?), то получаем, что N=\ при
— oo<a<0, JV = O при 0 < а < 9 (это интервал устойчивости рассматри-
рассматриваемого полинома) и JV = 2 при 9<а<оо. (Получите этот же результат из
признака Гурвица.)
Другой способ решения проблемы Рауса — Гурвица основан на
непосредственном применении принципа аргумента п. 7. Мы опишем
этот способ применительно к многочленам
хотя он распространяется и на многие другие классы функций.
Допустим, что многочлен P(z) не имеет нулей на мнимой оси и

§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ
103
имеет неизвестное нам число N нулей в правой полуплоскости.
Тогда в силу принципа аргумента при достаточно большом R образом
замкнутой линии {LR), показанной на рнс. 48, а, служит замкнутая ли-
линия (?'?), схематически показанная на рнс. 48, б и N раз обходящая
вокруг начала координат; другими словами, ^- Аа) ArgP(z) = N.
Однако в силу асимптотического выражения Р (z) ~ aBzn, пригодного
для больших | z |, соответ-
соответствующее приращение вдоль
полуокружности таково:
Д Arg P(z) ж шт. Поэтому,
если обозначить
-«<</<¦» ArgP(iy),
D8)
то получаем, что
D9)
-R
(Подумайте, откуда здесь а)
V
Рис. 48.
знак минус; проверьте, что
на рис. 48, б принято N= 4,
3 \
п = 5, (х = — ~2'1 Ф°РмУла D9) и дает решение проблемы, причем
значение \i из D8) можно подсчитать с помощью ЭЦЕМ (для больших \у |
удобно заменить у на т) = —, чтобы т)—s-О), либо путем ориен-
ориентировочного построения от рукн лннни (М') (рнс. 48, б) по точкам
после вычисления необходимых значений P(iy).
В частности, полагая Af—О, мы получаем [i = /z/2—необходимое
и достаточное условие устойчивости многочлена, которое иногда
называется критерием А. В. Михайлова.
Если полином P(z) устойчивый и у пробегает вещественные
значения от —оо до оо, то ArgP(iy) монотонно (почему?) возрастает
на ял. Поэтому точка P(iy) пересекает вещественную, а также
мнимую оси по п раз каждую (быть может, один раз в пределе,
при .у—*-±оо). Но это означает, что если разложить
P(iy) = Q(y) + iR(y), E0)
где Q, R—вещественные многочлены, то нули этих многочленов
будут вещественными, простыми и перемежающимися (между двумя
соседними нулями одного многочлена лежит ровно один нуль другого).
Обратно, если после разложения E0) нули многочленов Q, R обла-
обладают указанными свойствами (а их нетрудно проверить с помощью
вычисления на ЭЦВМ), то нули многочлена Р(г) находятся либо

104 ГЛ. II. ТЕОРИЯ. АНАЛИТИЧЕСКИХ ФУНКЦИЙ
все в левой полуплоскости, либо все в правой, а в какой именно —
легко узнать, выяснив с помощью вычисления, в какую сторону
закручивается точка P(iy). (Докажите это обратное утверждение,
разобрав на основании сведений о нулях, как ведет себя точка P(iy)
при возрастании у от —оо до оо.)
11. Результант двух многочленов. В связи с материалом п. 10 остановимся
на вопросе, который встречается в различных разделах математики. Допустим,
что заданы два многочлена Р (г) и Q (г). Как исключить г из системы двух
уравнений
Р(г) = 0, Q(z) = O, E1)
другими словами, каково условие на коэффициенты этих многочленов, необхо-
необходимое и достаточное для наличия у уравнений E1) по крайней мере одного
общего решения? (Продумайте равносильность этих двух формулировок.)
Для простоты изложения мы примем, что многочлен Р(г) имеет третью, а
Q (г) — вторую степени, т. е. уравнения E1) имеют вид
авг3+а1г2+а2г+а3=0, Ьогг+М+г>2 = 0; E2)
впрочем, из результата будет ясен ответ и для любых степеней. Допустим,
что уравнения E2) имеют общее решение г=г0 и умножим результат под-
подстановки г0 в первое уравнение на г0, а результат подстановки г0 во второе
уравнение—на г* и г0. Получатся равенства
=0,-
0
bo
0
0
«1
b,
bo
0
=0. E3)
= 0,
= 0;
их можно рассматривать как систему из пяти алгебраических однородных
уравнений первой степени относительно пяти величин: г*, г», ..., 1. Посколь-
Поскольку эти величины не все равны нулю, то определитель системы должен равняться
нулю (ЛВМ, п. VI.6):
и, о, О
ау аг а3
6а О О
6, Ь, О
ь0 ьх ьг
Этот определитель, который аналогичным образом составляется и для много-
многочленов Я (г) и Q (г) других степеней (его порядок равен сумме степеней
многочленов Р и Q), называется результйнтом этих многочленов. Мы сейчас
проверили, что равенство E3) необходимо для наличия у уравнений E2)
общего конечного кория. Если имеется общий бесконечный корень, т. е. если
ao = bo = Q (см. п. 10), то ясно, что E3) все равно выполняется. Можно про-,
верить, что равенство результанта нулю является не только необходимым, но
и достаточным для наличия у двух многочленов общего конечного или бесконеч-
бесконечного нуля.(см., например, [62]).
Результант многочленов Р (г) и Р' (г) называется дискриминантом много-
многочлена Я (г). Равенство дискриминанта нулю необходимо и достаточно для
наличия у Р (г) кратного или бесконечного нуля (почему?). (Составьте дискри-
дискриминант многочлена аг*-\-Ьг-\-с; в чем отличие от дискриминанта, известного
из школьного курса?)

§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ 105
С помощью составления результанта возможно, во всяком случае в прин-
принципе, перейти от системы уравнений
где Р и Q—многочлены, к алгебраическому уравнению D(Z!)=0 с одним
неизвестным; впрочем, в конкретных примерах это может привести к непрео-
непреодолимо громоздким выкладкам. Аналогично применяется результант к построе-
построению решения системы уравнений
Р(ги г», г3)=0, Q (гь га, г3)=0
в окрестности точки г1 = г2 = г3 = 0 с помощью диаграммы Ньютона (п. 2.8)
для получающегося уравнения D(zI,z2) = 0.
12. Мероморфные функции. Однозначная аналитическая функция, задан-
заданная на всей плоскости г и имеющая при конечных z из особых точек только
полюсы, называется меромбрфной функцией. Так как в каждой конечной части
плоскости такая функция может иметь лишь конечное число полюсов (почему?),
то если всех полюсов бесконечное число, они накапливаются к бесконечно удален-
удаленной точке, которая будет в этом случае неизолированной особой
точкой. Типичным примером мероморфной функции служит tgz с полюса-
полюсами при г = ——\-кп (fe = 0, ±1, ±2, ...) и неизолированной особой точкой
при z = oo.
Если мероморфная функция / (г) имеет лишь конечное число полюсов, то,
составив сумму s (z) сингулярных частей соответствующих лорановских разло-
разложений во всех полюсах, мы получаем представление / (z)=s (z)-\-[f (г)—s(z)|
функции / (z) в виде суммы рациональной и целой функций. Оказывается, что
аналогичное представление возможно для широкого класса мероморфиых функ-
функций с бесконечным числом полюсов, однако при этом is (z) будет, естественно,
суммой бесконечного ряда из рациональных функций. Мы приведем здесь
лишь самую простую теорему в этом направлении.
Пусть для мероморфной функции f (г) с бесконечным числом полюсов воз-
возможно подобрать последовательность замкнутых контуров (Lx), (Ц), ...
,.. , (Ln), ..., каждый из которых содержится внутри следующего, причем
1°. min \г\ —»¦ оо, т. е. контуры уходят на бесконечность.
z6(Ln) п ->• «о
2°. Ltt = O (min | г |), т. е. длина контура имеет не более высокий поря-
док, чем минимальное его расстояние от начала координат, и
3°. sup max | / (г) \ < оо (под sup понимается верхняя граница, см. ЛВМ,
п i€(Ln)
п. IV. 19), т. е. функции f (г) на совокупности всех контуров ограничена.
Тогда имеет место представление
f (?) = 2 is« (z)-s« (г«I+f (z°)- E4>
л = 1
где sa{z)—сумма сингулярных частей лорановских разложений функции f (г)
у всех ее полюсов, расположенных между (in_x) и (Ln) (при п—\ расположенных
внутри (Lj)), а г0—любая неособая точка функции /(г). При этом ряд E4)
сходится равномерно в каждой конечной части плоскости г.
Для доказательства зафиксируем неособые точки г0, г и рассмотрим вспо-
вспомогательную функцию от ?:
Она имеет полюсы ? = г с вычетом / (г), ? = г0 с вычетом —/ (z0) (почему?) и,

106
ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
кроме того, все те же полюсы Е, = гъ г2, га, ..., что и функция /(?). Приме-
л
нение формулы F) к каждому сингулярному слагаемому вида
ложении / (?) показывает (проверьте!), что
(Ъ-чУ
в раз-
раз?=**
>.
J
где ff. (г)—сингулярная часть разложения функции в точке г=г^. Поэтому
в силу теоремы Коши о вычетах
Г \ N
(Ly) \ ° « = 1
Если теперь N-*», то из формулы E5), оценки B.3) и условия теоремы
следует, что левая часть стремится к нулю, причем для переменного г равно-
равномерно в каждой конечной части плоскости г.
:ч Отсюда и вытекает утверждение теоремы.
^ Применим доказанную теорему к функции
/(z) = tgz, приняв го=О и выбрав за (Lj), (L2),...
квадраты, один из которых изображен на рис. 49.
Так как
ит.
-/да
тс
|tg(x±mn)| =
tg х ± i th nn
i th ля tg*
Рис. 49.
- V+WnnWx -* l + th*ntg-;c < C°nSt
(проверьте!), то условие 3° теоремы выполнено,
прочие же условия очевидны. Но функция \gz имеет полюсы при г = -^.+ ^п
с сингулярной частью— г—[-^-+йя ] (проверьте!); поэтому формула
E4) дает
OD
— 1 1 1
-Е Ы
*=-«>
E6)
Если здесь объединить члены с &=0 и с k= — \, члены с k=\ и с ?ь=— 2
и т. д. (строго говоря, так и надо было делать по формуле E4)), то получим
tgz= —2г
1
=о
Если в формуле E6) произвести суммирование сначала от ?=—п до k = n,
а затем перейти к пределу при я-*- оо, то легко проверить, что сумма вторых
слагаемых стремится к нулю, т. е.
tgz=v. р.
Лж
к--»
E7)

§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ 107
со я
где по определению V. р. У] =lim У] (ср. ЛВМ, п. XIV.19). Ряд E7)
расходящийся, и сумма его берется в смысле главного значения.
Интегрирование формулы E7) от 0 до г и потенцирование полученного
результата приводит к еще одной интересной формуле
C0S2 = V. p. I]
fc = — со
CO
где бесконечное произведение JJ и его главное значение определяются ана-
аналогично тому, как это делается для бесконечного ряда.
Для некоторых других целых функций / (г) разложение в бесконечное
произведение удается получить, проводя аналогичные манипуляции с разло-
Г (г)
жеиием мероморфиои функции ' в ряд. Так, можно проверить (мы ие ста-
Г" (г)
нем здесь этого доказывать), что мероморфная функция _, ' удовлетворяет
приведенным выше условиям теоремы о разложении E4), и потому, приняв
го=1, получаем (проверьте!)
Г|
Этот результат обычно преобразуют к следующему виду, обозначив
со ел
Г'(г)
=—Э:
СО
Г(г> - -,
л=1
Интегрирование от 1 до г дает
00
2(^у). E9)
л = 1
Полагая г=2, получаем
п
N
л=1
lim [ У,——lnJV—1
N N
lim fY-L-lnJv)- lim ln^±^= lim

108 ГЛ. 11. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
т. е. это та самая постоянная Эйлера, которая была введена в ЛВМ, п. XVII.1.
Подставляя в E9) выражение
ft — I
(проверьте!) и потенцируя, получаем требуемое разложение
Г" (г)
Логарифмическая производная fo (г) = _ , определенная формулой E8),
а также ее производные
СО 00
/1 = 0 /2 = 0
применяются при вычислении сумм числовых рядои вида
со
Р(п)
где Р и Q — многочлены, причем знаменатель имеет все нули вещественные
и его степень по крайней мере на 2 превышает степень числителя. Для этого
Р (г)
надо отношение _ ' разложить на простейшие рациональные дроби (ЛВМ,
п. VIП. 10), после чего воспользоваться формулами F0) и E8). Отметим простую
формулу . .
(докажите ее!), которая дает возможность ограничиться таблицами значений
typ (х) только на интервале длины 1.
13. Формула Кристоффеля — Шварца. Сначала отметим важное применение
принципа аргумента п. 7 к конформным отображениям. Пусть в некоторой
открытой односвязной конечной области (G) задана аналитическая функция
w—f(z), непрерывная вплоть до границы (Г) этой области. Пусть при этом
образом (Г) служит граница (?>) открытой конечной области (Н) плоскости w,
причем если точка w совершает один обход (Г) в положительном направлении,
то соответствующая точка w совершает один обход (D) в положительном
направлении (взаимная однозначность заранее не предполагается). Тогда функ-
функция f (г) осуществляет конформное отображение области (G) на (//). Для
доказательстиа применим формулу D1) к функции f (г)—ш0, где w0—любая
точка (Н); из этой формулы получаем, что иа w0 отображается ровно одна
точка z (? (G). Аналогично, если ы*0 находится во внешней области к (D), то
иа мH ие отображается ни одни точка (G). Отсюда с помощью результатов
первого абзаца п. 2.6 и вытекает высказанное утверждение о конформности.
Доказанное утверждение позволяет при проверке конформности отображе-
отображения ограничиться рассмотрением его свойств только на границе области. Это
утверждение легко распространяется и иа неограниченные области (с помощью
аппроксимации их конечными), если под положительным направлением обхода
контура такой области понимать 'raitoe направление, при котором эта область
остается слева.

§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ
109
Рассмотрим теперь в верхней полуплоскости 1тг > 0 функцию
Z
F1)
где С Ф О, С-1 — произвольные комплексные постоянные, Im г0 > 0, все аь, щ —
произвольные вещественные постоянные, причем ах< аг< ... <ап, все
|afe| < I, 2aft=2. Подынтегральную функцию можно считать в верхней
к
полуплоскости однозначной, если положить (?—aft)"* =ехр [(ак— 1) In (?—aft)|
(п. 1.12). Поэтому функция F1) осуществляет аналитическое отображение
верхней полуплоскости (G) плоскости г на некоторую область (Н) плоскости ш;
вид этой области сейчас будет выяснен.
Так как
dw _ _a ,_a \-Оп
dz "
то при изменении г вдоль вещественной оси—границы области (G)—аргумент
dw
— остается постоянным, т. е. до изменяется вдоль прямолинейного отрезка
Рис. 50.
(п.1.4), пока г не переходит через одну из точек ад. При таком переходе
dw
Arg(z—ад) возрастает иа —я, а потому Arg-j на а^я, т. е. точка w иачи-
нает следовать вдоль нового направления, составляющего угол а^я с преды-
предыдущим (рис. 50). Таким образом, ось * отображается на я-угольиик.с вер-
вершинами а'и аь, ..., а'„. (Точка г=оо, 1тг^0, как мы предоставим дока-
доказать читателю на основе равенства 2 щ=2, отображается иа одну из точек
отрезка a'na'i.) Если этот я-угольник получится без «внутренних» самопере-
самопересечений (рис. 51), то из теоремы, доказанной в начале этого пункта, вытекает, что
функция F1) осуществляет конформное отображение верхней полуплоскости г
на внутренность указанного п-угольника. Проверьте, что таких самопересечений
наверняка не будет, если все а* > 0 или если п < 4. Формула F1) назы-
называется формулой Кристоффеля—Шеарца.
Справедливо и обратное утверждение, которое мы здесь ие будем доказы?
вать: если в плоскости w задан n-угольиик, то параметры в формуле F1)
всегда можно подобрать так, чтобы получить отображение именно на этот

по
ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
я-угольиик; однако иа практике этот подбор может оказаться далеко ие прос-
простым. Впрочем, читатель может легко проверить (хотя это служит только под-
подтверждением, но не доказательством сформулированного обратного утвержде-
утверждения), что число таких существенных действительных параметров как раз на 3
превосходит число параметров при задании п-угольиика, в соответствии с тремя
степенями свободы при отображении полуплоскости на себя (п. 1.16). Эта сво-
свобода дает возможность, в частности, произвольно задать три из значений а^,
МОЖНО
МОЖНО
Рис. 51.
НЕЛЬЗЯ
а разыскивать лишь остальные. Особенно часто полагают а„ = оо; для этого
надо в формуле F1) вместо С написать С (—а„)ап, а затем совершить переход
к пределу при ап—>¦ оо, откуда видно, что при а„ = оо последний множитель
в подынтегральной функции надо просто устранить.
Рис. 52.
Рис. 53.
Если какое-либо из ак в формуле F1) будет Э= 1 (но обязательно <3),
то интеграл при г=ак расходится, т. е. соответствующая вершина «много-
«многоугольника» уйдет на бесконечность. Поворот направления обхода контура
в этой вершине, как и ранее, равен а^я. Проверьте, например, что «четырех-
«четырехугольнику» рис. 52 отвечают значения щ=.—, а^=—^-, &a=-w > а4=—<г'
Пусть, например, требуется конформно отобразить верхнюю полупло-
полуплоскость г на «четырехугольник» (Я), показанный иа рис. 53. Здесь 0^=03=1,

§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ I I I
—-а > а4=—у! примем а! = —1, а2=0, а4=оо, тогда формула F1) дает
2С /Г ds- С ds
F2)
(При вычислении последнего интеграла мы воспользовались логарифмом, более
удобным при действиях с комплексными величинами, чем арктангенс.) При
дальнейших преобразованиях требуется добавочное внимание в связи с приме-
применением многозначных функций. Так как г меняетси в верхней полуплоскости,
то в качестве области изменения s можно принять первый либо третий квад-
квадрант; примем впредь для определенности первый. Чтобы уточнить ветви лога-
логарифма, воспользуемся условием / (о2)=а2, т. е. f@)=0:
2С / 1 1
I _Ln(-l)- I Ln(-1
Выражая отсюда Сх и подставляя в F2), получим
1 L У^^^^Л F3)
причем то же условие а>@)=0 показывает, что надо выбрать ветви логарифма,
удовлетворяющие условию Lnl=0. Легко проверить, что если s изменяется
в первом квадранте, то дроби, стоящие под знаком логарифма в F3), описы-
описывают нижнюю и соответственно верхнюю половины единичного круга; поэтому
при Imz > 0 надо пользоватьси главной ветвью логарифма (продумайте это!).
Далее, чтобы область (Я) получилась правильно повернутой, необходимо,
чтобы -г- при вещественном г > 0 было вещественным; отсюда в силу первого
равенства F2) вытекает, что и С вещественно. Наконец, остается условие
оу (оо)=1 +1. Подставляя s=oo в F3) и учитывая сделанное выше замечание
об областях изменения дробей, стоящих под знаком Ln, получаем
fl1
Подставляя эти значения в F3), получаем окончательно
1тг>0.
1—S 1—S
¦ Советуем читателю внимательно продумать приведенные рассуждения.
Беспечное обращение с многозначными функциями может привести к прямым
ошибкам в ответе.
14. Понятие об эллиптических функциях. Интеграл F1), как правило, не
выражается через элементарные функции. В частности, при отображении
полуплоскости на внутренность прямоугольника получается эллиптический
интеграл; напомним (ЛВМ, п. XIII.11), что в общем случае эллиптическими
называются интегралы вида
J R (х, /P(F)) dx, F4)

112 ГЛ. П. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
где R — рациональная функция от своих двух аргументов, а Р (х) — многочлен
третьей или четвертой степени. Хотя при выполнении определенных равенств,
связывающих коэффициенты, интеграл F4) выражается через элементарные
функции (тогда он называется псевдоэллиптическим), но, как правило, рас-
рассчитывать на это не приходится. Можно показать (см., например, [6]), что
интеграл F4) с помощью элементарных преобразований всегда можно предста-
представить в виде комбинации элементарных функций и интегралов вида
Г , dt С /l-W^ С
J VA-I«)A-*V)' J У I-'1 ' J
dt
где k и / — постоянные; это нормальные эллиптические интегралы Лежандра
соответственно 1-го, 2-го и 3-го рода. Однако не следует слишком надеяться
на эти преобразования: как правило, они громоздки, а интегралы 3-го рода
весьма неудобны в обращении и даже не затабулированы. Поэтому на прак-
практике, если интеграл F4) не сводится как-то просто к интегралам Ьго или
2-го рода, то лучше воспользоваться приближенным или численным интегрк-
рованием.
Совершим в первых двух интегралах F5) подстановку f=sin q> и перей-
перейдем, чтобы избавиться от произвольных постоянных, к определенным интегра-
интегралам с нулевым нижним и переменным верхним пределамн. Мы получим функции,
имеющие специальные обозначения:
Величины ф н k называются соответственно' амплитудой н модулем эткх
эллиптических интегралов; в большинстве приложений эти величины вещест-
венны. Такие интегралы прн 0<Ф<-5- , 0<:/t<l подробно затабулированы;
для других значений (р надо воспользоваться четностью н периодичностью
подынтегральной функции, а случай k > 1 сводится к k < 1 с помощью под-
подстановки fesinij)=sjnijI (проверьте, считая интегралы вещественными!).
Особенно часто применяются полные эллиптические интегралы
К (k)=F (-?.*). Е »)=Е (?, ft) »
Например, мы предоставляем читателю вывести, исходя из канонического
уравнения эллипса и общей формулы длины дуги, что длина эллипса с боль-
большой полуосью а и эксцентриситетом е равна АаЕ (е); отсюда И происходит
название «эллиптический интеграл»,
Вернемся к первому интегралу F5), причем будем теперь считать незави-
независимую переменную комплексной. Сравнивая с формулой F1), получаем, что
функция
$ (О < А < 1) F6)
(в которой однозначная иетвь подынтегральной функции выбрана так, что она
равна единице прн ?=0) осуществляет конформное отображение верхней полу-
полуплоскости z на внутренность прямоугольника плоскости w; прн этом в вер-
вершины прямоугольника переходят точки г=±1 и г=±тг~- При г=±1

§ 3. ОСОБЫЕ ТОЧКИ И НУЛИ
получаем w=± К (к), а при z=± 1/fe будет
ИЗ
i = ± *(*)+'
1-***»)]
= ±
1
J [(i-T2)(i-
= ±
(проверьте!). Это н есть вершины упомянутого прямоугольника.
Поэтому обратная к F6) функция, которая обозначается г=впш (подроб- •
нее, sn (ю, k)) и называется эллиптическим синусом, осуществляет конформное
отображенне внутренностн указанного прямоугольника на верхнюю полупло-
полуплоскость г. Пользуясь правилом симметрии (п. 1.16), несложно показать (см.,
Рис. 54.
например, [66])> что функцию sn w можно продолжить с этого прямоугольника
на всю плоскость w, после чего получится однозначная мероморфная функция
с простыми полюсами в точках w=iK (k')-\-2mK (k)-\-2inK (k1), где т и л —
любые пелые числа. Она обладает интересным свойством
sn{w+4mK(k) + 2inK(k'))^snw (т, я = 0, ±1, ±2, ...),
т. е. имеет два независимых периода 4К {k) и 2iK (k'). Функции комплексного
переменного, обладающие таким свойством, называются двоякопериодическими.
Эллиптический синус называется также синусом амплитуды. (Это назва-
название объясняется тем, что если в интеграле F6) совершить, как выше, подста-
подстановку z = sin<p, то ф—верхний предел полученного интеграла—принято назы-
называть его амплитудой, т. е. амплитудой для w.) Аналогично вводятся функции
косинус амплитуды en w=yi—sn2 ai и дельта амплитуды dn и>= У1—k'2sin*w,
нормированные условием равенства единице при «i = 0. Можно показать, что
эти функции также мероморфные и двоякэпериодические. Между функциями
sn w, сп ю и dn w, введенными Якоби, имеются многочисленные соотношения.
Отметим, что для вещественных w эти функции принимают вещественные зна-
значения, причем периодичны; нх графики при некотором k показаны на рнс. 54
В частности, sn х = sin <p (х), где <р(х)—функция, обратная к возрастающей
функции x(y) = F(y, k).
Имеется ряд других эллиптических функций, тесно связанных с описан-
описанными здесь. Свойства этих функций можно иайти в [6] и в различных курсах
специальных функций.

114 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
§ 4. Асимптотические разложения
Мы уже упоминали об асимптотических разложениях в ЛВМ,
п. XVII.19. Сейчас они широко применяются в прикладной матема-
математике в качестве эффективного аппарата как для вывода приближен-
приближенных формул в «околопредельных» ситуациях, так и для вычислений.
Теория асимптотических разложений непосредственно связана с теорией
аналитических функций (хотя многие результаты первой имеют чисто
вещественный характер) и иногда, даже при анализе прикладных за-
задач, требует проведения сложных и тонких математических рассуж-
рассуждений. Здесь мы приведем лишь некоторые общие сведения об асимпто-
асимптотических разложениях, отослав читателя за дальнейшими сведениями
к книгам [52, 139, 16].
1. Введение. Как уже говорилось, функция f(x), по определению,
допускает при х ~* оо асимптотическое разложение
если для любого /2 = 0, 1, 2, ... имеет место представление
«. + -?+...+-jg- + o(^) (при лг^оо). B)
( Если сравнить эту формулу с формулой следующего приближения,
то видно, что остаточный член можно записать также в виде
О (-^+1) ¦ ) При этом вовсе не требуется обязательно, чтобы ряд,
стоящий в правой части A), сходился в обычном смысле к Дх)
и даже чтобы он вообще сходился к какой-либо функции; так, в ЛВМ,
п. XVII.19, получено разложение
1
X
1 1! , 2! 3! , . . ...
+ _r___+...(*_>oo), C)
хотя ряд, стоящий в правой части, расходится при любом х. Так,
частные суммы ряда последовательно равны:
при х = 2 . .
0,50; 0,25; 0,50; 0,125; 0,875; ...|
при х = 5
0,200; 0,160; 0,176; 0,166; 0,174; 0,166; 0,176; 0,163; 0,183; .. :i
при лг= 10
0,10 000; 0,09000? 0,09200; 0,09140; 0,09164; 0,09152; 0,09159;
0,09154; 0,09158; 0,09155; 0,09158; 0,09154; 0,09159;...
Интересно, что из вывода формулы C) легко понять (продумайте это!),
что при любом фиксированном х > 0 остаточный член при переходе

§ 4. АСИМПТОТИЧЕСКИЕ РАЗЛОЖЕНИЯ 115
от каждого п к следующему меняет знак. В этом случае, самом
удобном для вычислений, точное значение разлагаемой величины заклю-
заключено между любыми двумя последовательными частными суммами ряда,
что дает возможность получить двустороннюю оценку этого значения.
Так, в разобранном примере
0,25 </B) < 0,50; 0,166</E) < 0,174;
0,09155 < /A0) < 0,09158,
т. е. можно принять /B) = 0,4; /E) = 0,170; /A0) = 0,09156. Мы
видим, что с ростом х точность результата повышается.
Если двустороннюю оценку получить не удается, то иногда, имея
выражение для остаточного члена в виде интеграла и т. п., оказы-
оказывается возможным получить его оценку и тем самым получить пред-
представление о точности результата. Но и если точная оценка остаточ-
остаточного члена неизвестна, то, вычисляя последовательные частные суммы,
удается получить приближенное значение разлагаемой величины
и правдоподобную оценку ошибки, так как обычно, когда частные
суммы ряда отчетливо сближаются (а значение х не слишком мало),
они оказываются приближенно равными этой величине, а ошибка — по
порядку равной первому из отброшенных членов.
Применяются также разложения вида
+ + г+ • • • ) >
D)
f(x)~g(x) («0 +1Г + • • • + -рг+ • • •
и т. п. Смысл этих формул аналогичен смыслу формулы A).
При рассмотрении асимптотического разложения однозначной ана-
аналитической функции
f{z)~a9+± + %+. .. + %+... E)
должно быть указано, какие способы удаления z на бесконечность
допускаются. Если формула E) справедлива при произвольном способе
z-+oo, то нетрудно показать (попробуйте!), что в правой части E)
ctqht разложение в ряд Лорана функции f(z) на бесконечности
(п. 3.6) и равенство E) является не асимптотическим, а точным.
Более содержательная теория получается, если требовать, чтобы
равенство E) имело место, только когда г—»-оо, оставаясь внутри
некоторого заданного угла, другими словами, если аргумент г удо-
удовлетворяет некоторому заданному неравенству вида a^Arg^^p.
(В частности, если a = j3 = 0, мы получаем разложение A).) Довольно
типичной является следующая картина: задается неравенство
a<Arg2<C, а формула

116 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
имеет место при г -*¦ оо в любом «строго внутреннем» угле
a'^Argz^P', т. е. а < а'<!{}'< р. Интересно, что тогда в раз-
разных углах, не имеющих общих лучей, одна и та же функция f{z)
может иметь различные асимптотические разложения; это явление
называется явлением Стокса.
2. Свойства. Мы будем для простоты говорить о разложениях
вида A) при лг-э-оо; аналогичные свойства имеют место и для раз-
f (х\
ложеиий D); первое, кстати, можно переписать в виде . ,' ~ а0 -{-
+—+..., т. е. свести к A); второе сводится к A) подстановкой
хР—у.
Прежде всего заметим, что далеко не каждая функция, даже
конечная при х-+ оо, допускает разложение A); например, такое раз-
разложение невозможно для f(x) = s\nx, х~р (р > О не целое), пх
и т. п. С другой стороны, легко доказать, что если разложение
все же возможно, то его коэффициенты определены однозначно,
т. е. у одной и той же функции не может быть двух различных
разложений вида A). В самом деле, если кроме A) имеет место фор-
формула f{x)~a'0-\—--{- ... и л^О—наименьший номер, для которого
а„фа'п, то наряду с B) можно написать, что
и, вычитая, мы приходим к противоречию (продумайте!). Этим свой-
свойством, в частности, объясняется оговорка об общих лучах, сделан-
сделанная в последней фразе п. 1.
В то же время две различные функции могут иметь одинаковое
разложение A). В самом деле, функция, стремящаяся к нулю при
х -*¦ оо быстрее любой степени х (например, е~х), имеет тождественно
нулевое разложение (почему?). Значит, добавление такой функции
к левой части A) не меняет правой части. Таким образом, по задан-
заданному разложению разлагаемая функция определяется лишь с точ-
точностью до слагаемого указанного типа; однако в конкретных за-
задачах эта небольшая неопределенность обычно оказывается несуще;
ственной. ч
Переходим к действиям над разложениями A). Исходя из форму-
формулы B), легко проверить, что такие разложения можно почленно скла-
складывать, умножать на число (при умножении на функцию надо перейти
к первому разложению D)). Аналогично проверяется, что разложения A)
можно перемножать по правилу умножения многочленов, а также
делить столбиком или по методу неопределенных коэффициентов

§ 4. АСИМПТОТИЧЕСКИЕ РАЗЛОЖЕНИЯ 117
(ЛВМ, п. XVII.12), если у знаменателя коэффициент а0ф0. Возмож-
Возможно асимптотическое разложение функции F(/(x)) с помощью подста-
подстановки ряда в ряд, если F(y) разлагается в ряд Тейлора по степеням
у — а0; аналогично для Ftf^x), /2(x) /*(¦*))•
Асимптотическое равенство A) можно почленно интегрировать,
что дает
^a1\nx~b,—af—g,—gf- •••» F)
где b0 — некоторая постоянная, зависящая от х0^.оо. Для доказа-
доказательства перенесем в формуле B) первые два слагаемых правой
части в левую и проинтегрируем результат от х до оо , заметив, что
ю
эт0
00
Поменяв с обеих сторон знаки и добавив I \f(s)—а0 ds=
00 »
= fO(-j-)ds = const, получаем F) (проверьте!).
Из доказанного нетрудно вывести, что равенство A) можно и по-
почленно дифференцировать, т. е.
ги~-3»?-?-.... о
если известно, что функция /' (х) допускает асимптотическое разло-
разложение. (Попробуйте доказать это, исходя из разложения функции f (x)
и проверив с помощью интегрирования, что оно обязательно имеет
вид G).)
Если отказаться от последнего условия, то возможно построить искусственные
примеры, в которых дифференцирование асимптотического равенства оказы-
оказывается незаконным. Однако в примерах, представляющих практический интерес,
такая ситуация не возникает. Отчасти это объясняется тем, что для разложе-
разложений E), сходящихся внутри угла а < Argz < Р (в смысле, указанном в конце
п. 1), возможно доказать, что почленное дифференцирование законно всегда,
причем получающаяся формула асимптотич-на в том же смысле, что исходная.
А в реальных примерах асимптотическая формула, справедливая при х ->¦ оо,
обычно справедлива и в некотором угле | Arg г \ < е.
Отметим, что в более сложных задачах иногда удается получить не полное
разложение вида A), а только формулу тИпа B) при' фиксированном я. Даже

118 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
и такие формулы, хотя бы при п=0, а тем более при больших п, могут ока-
оказаться очень полезными.
При рассмотрении асимптотических разложений функций от нескольких
аргументов надо иметь в виду, что такие разложения могут оказаться различ-
различными для различных соотношений между аргументами. Пусть, например,
дана функция
Х ' -'- 1 ' * - *-, (8)
/v ' *' у ' х+у
причем х ->¦ оо, у-+¦ оо. Тогда если х и у одного порядка, y=kx, то разложе-
разложение имеет вид
Г(х, их)—— ,
где k=y/x заключено между положительными постоянными и, в частности,
может быть само постоянным. Если у второго порядка по сравнению с х,
т. е. y=kx2, то
В (8) возможно положить i/=oo, что даст
f(*> со)==Т*~Ш<>+5Тхп~--' >
с другой стороны, положить х=оо в (8) невозможно.
Из-за того, что соотношение между аргументами недостаточно уточнялось,
не раз возникали недоразумения.
3. Интеграл типа Фурье. Рассмотрим интеграл
ъ
'(v) = $/(*)«'»*<**, (9)
а
предполагая, что функция 'fix) имеет непрерывные производные всех
порядков на конечном интервале a^jc^b; такие интегралы часто
появляются в теории интегрального преобразования Фурье (ЛВМ,
§ XVII. 5). Легко получить полное асимптотическое разложение
интеграла (9) при вещественном v -> ±оо. Для этого произведем
интегрирование по частям несколько раз, например, два раза,
дифференцируя функцию f(x):
ь
1
(MX ehx \\ь i
/мтг-/' &w) L+Ы
Видно прежде всего, что /(v)->-0 при v -*¦ ± оо; а так как послед-
последний интеграл в A0) того же типа, что (9), т. е. и он стремится

§ 4. АСИМПТОТИЧЕСКИЕ РАЗЛОЖЕНИЯ 119
к нулю прн v-*-±oo, то, проводя дальнейшее интегрирование по
частям, получаем при естественном смысле обозначений
?/<»-» (в)-в''ь??/("'1>(&) (И)
л=1 л=1
(проверьте!).
Эта же формула верна н если а=—оо (тогда первая сумма
обращается в нуль), либо если Ь=оо (тогда вторая сумма обра-
обращается в нуль), если интеграл (9) абсолютно сходится.
В самом деле, для «хороших» функций ц>(х) из сходимости интеграла
со <ю
V \<p(x)\dx вытекает, что <р(оо)=0 и что \ |<р' (д:) | djc <оо, а последнее дает
а а
возможность перейти и к дальнейшим производным. Последнее неравенство
гарантируется, например, если <р (х) имеет конечное число интервалов монотон-
Р
ности, так как на каждом таком интервале \ |<р' (х) \ йх=\ <р ф)— ф (а) |.
а
Однако в общем случае утверждения первой фразы этого абзаца допускают
построение искусственных противоречащих примеров: первому утверждению
. / , 2+sin х \
противоречит функция вида дгехр \ехт——^ с очень тонкими «столби-
Ч d /
ками», уходящими на бесконечность, а второму—функции с бесконечно учаща-
учащающимися колебаниями, например —|- sin х2 (продумайте эти примеры!).
Мы не будем здесь принимать во внимание эти искусственные примеры и потому
не будем делать соответствующие оговорки; более полные формулировки со
всеми оговорками интересующийся читатель может найти в указанной лите-
литературе.
Отсюда, в частности, получается нывод об асимптотическом
поведении фурье-образа заданной абсолютно интегрируемой при
— оо <.* < оо функции /(х). Допустим, что для некоторого целого
/м^О все ее производные порядка <^т непрерывны, тогда как
/ш{х) имеет по крайней мере один разрыв, причем 1-го рода. Тогда,
разбивая интеграл
на части, отвечающие участкам непрерывности /(Я1) (х), н проводя
интегрирование по частям т-\-\ раз, как было описано выше, полу-
получаем, что / (k) -*¦ 0 при k -*- ±°о со скоростью \k\~lm+1). (Ср. при-
пример, разобранный в конце п. XVII.32 ЛВМ.) Если же у f(x) непре-
непрерывны производные всех порядков при —оо<лг<оо, то / (k) ->¦ О
при k-^-±oo быстрее любой отрицательной степени.
Рассмотрим еще случай, когда в интеграле (8) пределы интегри-.
рования конечны, но подынтегральная функция на одном из этих'

120 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
пределов обращается в бесконечность. Пусть, например, интеграл
имеет вид
ь
{x—a)'-1f(x)ei*xdx, A2)
а
где 0<а< 1 (это нужно для сходимости интеграла), а /(х) такая
же, как в интеграле (9), причем /(а)фО (в противном случае надо
сначала несколько раз произвести интегрирование по частям). Мы огра-
ограничимся выводом лишь главного члена асимптотического разложения
интеграла A2) при v -*¦ оо. Для этого представим сначала /(v) в виде
ь . ь
/(v)= ^ (х—а)"-1 f {a) ehxdx + Ux—a)"f (x)~f ^ ehxdx.
a a
Так как во втором интеграле подынтегральная функция уже непре-
непрерывна, то с помощью интегрирования по частям легко доказать,
что он равен О( —) . В первом же интеграле замена х = а~\— дает
vF — a) vF —о)
/(а) С if«-1v1-«e'<Ive'i^ = /(a)e'e»v-'1 Г t"'1 elt dt.
о о
CD
Последний интеграл при v—юо стремится к интегралу \i*~1etidt,
о
который, как можно показать, равен е'1»/* Г(а).
Для доказательства надо рассмотреть ин-
интеграл
д
ехр[/г + (а—I) In z\dz
.)
по замкнутому контуру, показанному на рнс. 55,
в комплексной плоскости z = t-\-is. По теореме
\ р
Коши п. 2.2 У=0. Прн р—»-0 * R —>оо со-
рнс gg ответствующне интегралы по дугам окружно-
окружностей стремятся к нулю в силу оценки B.3)
я леммы Жордана п. 3.4. Поэтому в пределе получаем
00 О
С expl« + («— \)lnt]dt = — ^ exp[i-is+(a— l)lnis]ids =
о •
= i J e~s е' <я-1)я/« s«-i ds = e'ia/a r (a)_
6
Подводя итог, получаем окончательно
(v—> оо) A3)

§ 4. АСИМПТОТИЧЕСКИЕ РАЗЛОЖЕНИЯ 121
(продумайте!) Нетрудно показать, что вместо o(v~") здесь можно
написать O(v-1). По поводу дальнейших членов разложения см. [52].
Полученные результаты можно применить к более общему инте-
интегралу
ь
с непрерывными функциями /, ф и ф'. Если ф' (х) > 0 (
то можно сделать замену ф(лг)=_у> в СИЛУ которбй
Ф(Ь)
S (>')^^, A4)
Ф(
= S
где под ф~ понимается функция, обратная к ф (т. е. д: = ф~ (у)).
Получился интеграл типа (9), для которого можно пользоваться раз-
разложением A1). Ограничиваясь первым членом, получим при v—>¦ ± оо
[*'"/(q>- (у)) ф
(проверьте!).
Та же формула получается, если ф' (х) < 0 (а ^ х ^ Ь). Если
же q> (jc) имеет при а ^ х ^ й по крайней мере одну стационарную
точку, то формула принципиально меняется; мы сейчас покажем,
что старший член асимптотического разложения Ix (v) определяется по-
поведением функций/и ф именно в этих точках. Для этого заметим прежде
всего, что с помощью разбиения интервала интегрировавия на части
можно перейти к случаю, когда на таком интервале (концы которого
мы опять обозначим через а, Ь) имеется лишь одна стационарная
точка функции ф(лг), причем в конце интервала. Мы предположим
для определенности, что ф'(а) = 0, ф' (х) > 0 (а <*<;&), ф"(а)>0;
прочие случаи разбираются аналогично. Тогда замена у = ф (х) вблизи
точки х = а, с точностью до малых высшего порядка, имеет вид
с—а)%, откуда
i—
Поэтому интеграл A4) имеет тип A2), и формула A3) дает
1Х М =
И здесь вместо о (-т=\ на самом деле можно поставить О( —|.

122 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
4. Интеграл с параметром в вещественном показателе. Перей-
Перейдем теперь к интегралам вида
ь
(v-*oo) A5)
с вещественными непрерывными функциями / и ср. Естественно, что
при большом v наиболее существенными оказываются те х, при
которых ф(д:) достигает наибольшего на интервале а^.х^.Ь зна-
значения (продумайте это!). Как и в конце п. 3, можно считать, что
такое значение х только одно и притом в конце интервала интегри-
интегрирования. Пусть для определенности ф(а)>ф(л;) (а < x^ib), причем
(f(x) — ср(а)~— k(x — a)« (k,a>0,x->-a + 0) A6)
и /{а)фО. Заменяя, подобно п. 2, в интеграле A5) f(x) на /(а),
а ф(д;) на его выражение из A6), получим при v->-oo
= \kv(x—a)a =
Законность указанных замен вытекает из того, что при любом е > О
ь ь
\ f(x)e^x)dx\s^\,\f(x)\dx-ex.p[v max ф(*)],
a+e a a+e«*<(>
т. е. получается выражение значительно меньшее, чем правая часть A7),
a+e
а потому основной вклад в интеграл A5) дает \ . Эту законность
а
можно обосновать и с помощью более тщательного математического
анализа, проведенного в специальной литературе. Если <р (х) дости-
достигает наибольшего значения при х = Ь, причем <р (х) — фF)^
~ — k{b—xf'ix-^-b—0), то в правой части A7) надо заменить а на Ь.
Если наибольшее значение достигается во внутренней точке с интер-
интервала интегрирования, причем ф(*) — ф(с)~ — k\x—с|а(х-*¦ с), то
с помощью разбиения интеграла на два получаем, что в правой
части A7), где вместо а надо поставить с, появится добавочный
множитель 2.

§ 4. АСИМПТОТИЧЕСКИЕ РАЗЛОЖЕНИЯ 123
В качестве примера рассмотрим асимптотическое поведение гамма-
функции
Т(р) = ]е-ххР-Чх=^ехр{р [—~+?ly-\nx] ) dx
при р -*¦ оо. Так как квадратная скобка принимает максимальное зна-
значение при х=р — 1 (почему?), то сделаем предварительную замену
переменной х = (р— 1)/, чтобы зафиксировать аочку максимума.
Получится
о
Обозначив (f(t)=— t+lnt, получим, что ф'A) = 0, ф" A) =—1,
т. е. ф(^) — фA)~—s- (t — IJ (/-»-1), а потому по соответственно
измененной формуле A7) получаем
(Обратите внимание, что (р — 1)^ при р -*¦ оо эквивалентно не рР,
как это может сначала показаться, а р"'*.) Эту важную формулу
иногда записывают также в виде
— лч-JL
~|/2ял 2 е~п (л-»-оо) A8)
н называют формулой Стирлинга по имени шотландского матема-
математика Д. Стирлинга A692—1770), получившего в 1730 г. асимпто-
асимптотическое разложение для In (я!) (это был первый случай применения
асимптотически сходящегося ряда), из которого сразу следует фор-
формула A8). В 1812 г. Лаплас получил более полную формулу
из которой, в частности, видно, что формула A8) имеет относитель-
относительную погрешность я* т^-, тогда как добавление в правой части мно-
1,1 1
жителя 1 -f тд- понижает эту погрешность до
В некоторых случаях удается применить описанный метод .к интегралам
более общего вида, чем A5), у которых функции / и ф зависят, кроме х, также

124 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
от v. Покажем это иа примере интеграла
00
Кч(а)=-? \ exp(vx—achx)dx @<a=const, v-* 00),
— OS
играющего важную роль в теории функций Бесселя. Так как показатель дости-
достигает максимума при значении x=arsh—, зависящем от v, то для нормировки
v
совершим замену x=arsh \-t, что даст (проверьте!)
С
J
ехР
Получился интеграл типа A5), у которого, однако, функция / зависит также
от V. Но характер этой функции при большом v (продумайте его!) дает воз-
возможность применить описанную методику и к интегралу A9), что дает при v-*oo
2rV2/ \2
Покажем еще, как находить дальнейшие члены асимптотического разло-
разложения A7), считая для простоты а=0, ф(а)=0, а=1, k=\ (этих условий
легко добиться с помощью простых замен). Пусть вблизи л:=0 имеют место
разложения
00
ft=l
ФМ=-дс+2**«Э* A < Pi < Ра < Рз <-..
Сделав в интеграле A5) замену vx—s, получим
/ (V)= С v-(a'+1)sa' e~* fax + У. aft
0J L * = 2
Если разложить экспоненту в ряд Маклорена, раскрыть скобки (в том числе
квадратные скобки в B0)) и привести подобные члены, мы получим выражен
ние вида
/(v)=fv-(a' + I)sa'e-s(a1+|]Cftv-V*s«*)ds> . B1)
о Ч *=2 '
где

§ 4. АСИМПТОТИЧЕСКИЕ РАЗЛОЖЕНИЯ 125
(Чтобы фактически получить разложение B1), можно задаться показателем
степени v, до которого будет производиться асимптотическое разложение,
и все появляющиеся при вычислениях члены с высшими степенями отбра-
отбрасывать; см. примеры в ЛВМ, п. XVI 1.12. Можно также, совершив в пре-
преобразуемом произведении квадратной скобки и экспоненты в B0), равном
/ (—j ( — | 1ехр<ф1—\ -\ >, замену s — tk, после которой все показа-
показатели при t станут целыми, применить разложение по t в ряд Маклореиа.)
Интеграл B1) надо разбить нк сумму, в каждом слагаемом заменить верхний
предел иа оо, что не влияет на асимптотическое разложение (почему?); это
даст окончательно
»
ft = 2
б. Метод перевала. Функция f(x) в пп. 3 и 4 могла принимать
и комплексные значения; это не сказывается на полученных там
асимптотических формулах. Однако если q>(x) принимает комплекс-
комплексные значения, то положение существенно осложняется, так как точка
хл, в которой | eVI?U) j, т. е. ev Re<p(*>, принимает наибольшее значение,
не обязана быть стационарной для 1тф(*), т. е. вблизи х0 значе-
значения evtPU) могут сильно осциллировать и потому взаимно уничто-
уничтожаться, не давая главный вклад
в асимптотическое выражение для
интеграла. Поэтому при вычислении
асимптотического выражения для /А—ifflS-gfet'C^ У„ "*
комплексного интеграла
[ B2)
нельзя просто записать контур (I) Рис. 56.
в параметрическом виде z = z(t),
перейти к переменной интегрирования t и затем автоматически при-
применить результаты пп. 3 и 4. Однако если / и <р—однозначные
аналитические функции, то можно предварительно воспользоваться
вытекающей из п. 2.2 возможностью деформировать контур (L) без
изменения значения интеграла B2).
Допустим, что контур (L) удалось подобрать таким, чтобы он
прошел через точку z0, в которой ф'(гг0) = 0, причем |е?1г>| дости-
достигает в z0 наибольшего на (L) значения. Схема окрестности точки z0
при условии <р" {гд)фО показана на рис. 56, где заштрихована область
| е«>(г> | > | е«><го> j, т. е. Re ф (z) > Re ф (zt), и пунктиром показана
линия lm ф (г) = Im ф (г0). При построении этой области надо пред-
представить ф(г) вблизи z0 в виде ф(г) = ф (г0)-f-ф i!* (г—го)*-\-...,
а затем записать: z = x-\-iy, ф" (г0) = о -j- ib; тогда последнее нера-
неравенстве, с точностью до членов высшего порядка, можно пере-
переписать в виде Re {(a -f ib) [{x—xt) -f / (y —уо)]г) > 0, т. e. a (x—x0J—
2Ь()( ) ( )*0 (Продумайте эту схему и

126 ГЛ. II. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
постройте аналогичную схему для случая ср" (zo) = 0.) Мы будем пред-
предполагать, что контур (L), проходя через «перевал» г0, переходит
в окрестности этой точки из «ложбины» /, т. е. одной из областей,
где Re ср (г) < Re ср (г0), в другую «ложбину» //; поэтому метод полу-
получения асимптотической формулы на основе деформации исходного
контура интегрирования в контур, обладающий описанным свойством,
называется методом перевала.
Деформируем малый участок контура (L), показанного на рис. 56
жирно, так, чтобы после деформации часть контура прошла через
перевал по линии Im ф (г)=1тф (z0). (В силу п. 1.4 эта линия
в каждой своей точке направлена, если идти от z0, по вектору
— grad Re ф (z), а потому и по вектору — grad | e<?U) |; поэтому упо-
упомянутое сейчас деформирование называется методом наибыстрейшего
спуска.) Если дугу z1zozt (рис. 56) представить в параметрическом
виде z — z{t) {a^.t^.b), то соответствующую часть интеграла B2)
можно представить в виде
\f(z(t)) Z' (t) eV[Req><z<O) + t lmq>(z<O)I<ft = e*vlmq><zo) ^ д (t)ev<tiWdt, B3)
a a
где обозначено /x@ = f(z (t)) z' (t), ц>1^) = Яец> (z(t)). К последнему
интегралу можно при вещественном v -*¦ оо применить методику
п. 4, а в ряде случаев получить и его полное асимптотическое раз-
разложение. Оно и будет служить разложением интеграла B2), так как
аналогично п. 4 можно доказать, что интеграл по (L) с выброшен-
выброшенной дугой zxzuz^ при v -*¦ оо будет значительно меньше каждого
члена этого разложения.
Ограничимся случаем ф"(гй)=?0, /(го)^=О и найдем первый член
разложения интеграла B2) при v -*¦ оо. Так как в окрестности z0
будет ф(г) = ф(го) + У—^{г—го)г-\-..., а вдоль дуги z^zuz% меняется
только Re ф (z) и притом убывает от .?„, то параметр t можно ввести
по формуле ф (z) = (f(zo) — t\ откуда z = zo+ у ф-^*+>--> где
для корня берется то из двух значений, при котором точка z пере-
переходит из ложбины / в ложбину //, когда /, возрастая, переходит
через нуль. Применяя к правой части B3) соответственно изменен-
измененную формулу A7), получим
. 2 Ш Г ф <v*<0)( _?|a v )-'/2 =

§ 4. АСИМПТОТИЧЕСКИЕ РАЗЛОЖЕНИЯ
127
Можно доказать, что это асимптотическое равенство допускает следую-
следующее уточнение:
в котором указан порядок ошибки. Эта формула справедлива и в случае
/(»о)=О.
В качестве примера рассмотрим выражение
B5)
где (L)—какой-либо замкнутый контур, обходящий вокруг точки z—ц в поло-
положительном направлении; можно показать, что Рп —это те самые многочлены
Лежандра, о которых говорилось в ЛВМ,
п. XVI 1.20.. Будем считать, что ц — по-
постоянное вещественное число, причем
||i| < 1, так что можно обозначить ц=
=cos 0; где 0 < 0 < я.
Если контур (L) выбрать симметрич-
симметричным относительно оси х и обозначить
интеграл в B4) по Верхней половине
через A-\-iB, то интеграл по нижней
половине будет равен —(А — iB) =
=—A-\-iB (почему?),а весь интеграл будет
равен 2/В; значит, при интегрировании
можно ограничиться верхней половиной
контура, а от результата взять мнимую
часть. Представим интеграл в виде B2), _
1 , . т 2^—1 Рис. 57.
где /(z) = , v=n, ф(г)=Ьп ,
причем надо взять какую-либо однозначную ветвь этой функции, имеющей
точки разветвления при г=1, — 1, [г. Так как
то |e'fBr>| имеет точки перевала (т. е. точки, где ф'(г)=0) при г=ц ±
± ур*—1 =cosO± ]/cos2e— 1 =е±|9. Легко проверить, что линия
Re cp (z) = Re ф (ей) состоит из двух окружностей с центрами в точках ± 1, про-
проходящих через точку перевала гй=е!'1 (рис. 57). Так как ф" (го) = (('е" sin 0)~'
(проверьте!), то формула B4) дает асимптотическое представление при п -> оо
i
e«-cosO
-SL 1«й sin о
е2И-' VI.
e^-cosQ J ]
Так как выписанный радикал должен иметь отрицательную вещественную
часть (почему?), то он равен 1/ — sin в е'(Зя/4+б/г). уПрОщая, получим
окончательно при п -*¦ оо
/?^е'Cл/4+9/2>

128
ГЛ. 11. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
Из доказательства видно, что это асимптотическое равенство расшифро-
расшифровывается как
а не I/ :—rT sin I яй+тг + т" I I l+o I — J ) (продумайте разницу!).
Подобное уточнение относится и к другим случаям, когда главный член асимп-
асимптотического выражения имеет нули.'
Рассмотрим еще пример:
„ix sin г — ivz
dz,
B6)
(L)
где х > 0 и v—вещественные параметры, a (L) — про-'
извольный контур, «идущий от оо i в ft — оо I»
(рис. 58), т. е, имеющий асимптоты лс—О и х—п.
Нетрудно проверить, что интеграл B6) сходящийся
(причем с весьма большой скоростью) и не зависит от
конкретного выбора линии (L). Функция Я^( (х) на-
называется функцией Хйнкеля 1-го рода; можно пока-
показать, что она равна Jv(x)-\-iYv(x), где J и У— функ-
функции Бесселя (ЛВМ, п. XV.26).
Рассмотрим поведение функции B6) при постоянном v и х -* оо. Для этого
в формуле B6) надо заменить v на х, после чего обозначить / (г)=е~'*г,
<р(г) = 1 sin г. Точкой перевала служит г=—, и применение формулы B4),
которое мы предоставляем читателю, дает
Рис. 58.
Отсюда, в частности, получаются и асимптотические формулы для функций
Бесселя при х -*¦ оо
B8)
(см. графики в ЛВМ, рнс. 299).

Г л а в а Ш
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Операционное исчисление, созданное в конце прошлого века анг-
английским физиком О. Хевисайдом A850 —1925) без достаточного обо-
обоснования, было позже обосновано на базе теории аналитических функ-
функций. Оно непосредственно связано с теорией преобразования Фурье,
краткие сведения о которой приведены в ЛВМ, § XVIF.5; его поэто-
поэтому полезно (но ие обязательно!) читателю просмотреть. Сейчас опера-
. ционное исчисление широко применяется в прикладной математике, в
технической физике и в инженерных дисциплинах, по нему имеется
целый ряд руководств; укажем, в частности, книги [34, 36, 47, 50,
54, 75], а также соответствующие главы книг [3, 66, 102] и других.
§ 1. Общая теория
1. Преобразование Лапласа. Операционное исчисление основа-
основано на так называемом преобразовании Лапласа. Пусть задана (вообще
говоря, комплексная) функция f(t) вещественного аргумента t,
0^*<оо. Ее лаплас-образом называется функция
f(p) =
от комплексного переменного р. Формула A) и определяет преоб-
преобразование Лапласа, т. е. оператор (ЛВМ, п. XIV.26) специального
вида, для которого функция f(t) является прообразом (оригиналом),
а функция F(p)—образом (изображением). Эту связь между прооб-
прообразом и образом мы будем в этой главе записывать так: f(t)—*-F(p),
имея в виду всегда преобразование Лапласа; применяются также
йапиеи f(t)==F(p) и другие.
2\, Так как интеграл A) несобственный (ЛВМ, § XIV.4), то для его
^сходимости нужно принять некоторые меры предосторожности. Мы
.Сбудем считать, что функция f(t) конечна при конечных t (доста-
(достаточно Требовать абсолютную интегрируемость), а при t—*oo либо
остается конечной, либо, если растет по модулю, то не быстрее экспо-
экспоненты.' В общем случае можно написать
B)
5 А. Д. Мышкпе

t30: ГЛ. III. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
где Мг и,.se — иекрторые постоянные. Функции, растущие при i-*¦, оо
быстрее экспоненты, конечно, имеются, например ' е*'г однако, прак-.
тнческое значение их пока весьма невелико; таким образом, огра-
ограничение B) не является обременительным.
Если предстазить p — s-\-ir, то легко проверить, что при усло-
условии B) и при s > s0 интеграл A) абсолютно сходится, в самом деле,
тогда
:':...'.: \,е-р' fit)| = \*-«e-Mf[t)| = е—1/@1 <Me- (*-•.>.',. C).,
я интеграл от затухающей экспоненты сходится. Таким образом,
функция F(p) определена, во всяком случае, в полуплоскости
Rep>s0. В этом состоит существенное отличие преобразования
Лапласа от преобразования Фурье: там требовалось, чтобы преоб-
преобразуемая функция обращалась в нуль ¦ на бесконечности, а здесь
добавление гасящего множителя e~st позволяет преобразовывать функ-
функции, экспоненциально растущие на бесконечности.
,Для разных прообразов значения $в, вообще говоря, различны.
Поэтому если в рассмотрении участвует несколько прообразов, то
можно просто считать, что значение Rep достаточно велико, не
уточняя, насколько именно, если этого ие требуется.
Можно проверить, что при Rep > s9 интеграл A), зависящий отр
как от параметра, имеет производную по р, которая вычисляется
по"',известному правилу Лейбница (ЛВМ, § XIV.5; то, что теперь
параметр комплексный, не играет при этом никакой роли). .",",
Для этого достаточно заметить, что если р меняется в малой окрестности
какрго-.либо значения, то для всех таких р можно провести единую оценку
вида C), подставив вместо s наименьшее значение из этой окрестности; зна-
значит, интеграл A), а также и интеграл, полученный после дифференцирования
по р, сходятся в этой окрестности правильно (ЛВМ, п. XIV. 21), чем и обо-
обосновывается'законность дифференцировании. '
Итак, F(p) в полуплоскости Rep > s0 является однозначной ана- •
литической функцией.
Из формулы A) видно, что если складываются прообразы, то
складываются и образы; если прообраз умножить на константу, то
и образ умножится на ту же константу. Другими словами, преоб-
преобразование Лапласа представляет собой линейный оператор. Как было
указано в ЛВМ, п. XVII.33, отсюда вытекает, что если прообраз,
а потому и образ зависят от некоторого параметра X, то производ-
производная' Ш параметру от прообраза Преобразуется в производную по .
параметру от образа. '
2. Образы простых функций. 1. Образ экспоненты вычисляем
непосредственно:
eat Т ~* .. ., ««-'+** I" 1 I
— р + а I — р + а р — а'

§ 1. ОБЩАЯ ТЕОРИЯ iSi
н? верхнем пределе получается нуль, так как в п. 1 мы видели, что
Rep можно считать достаточно большой, а «-« = 0. "¦
В частности, полагая а = 0, видим, что
¦1-.-L ' ¦ ¦¦ ¦¦ ¦ ¦
,¦ ¦ . р'
2. В левую и правую части D) а входит как параметр; произ-
производя дифференцирование по параметру (см. конец п. 1), получим
В частности,
Эта формула легко обобщается на любые вещественные л >• — 1
(это неравенство нужно для интегрируемости прообраза при t = 0):
(см. ЛВМ, п. XIV. 17). При замене переменной ннтегрирования можно было
считать р > 0 вещественным; однако образ, являющийся аналитической функ-
функцией и равный правой части F) при вещественных р, должен равняться ей
и _ при мнимых р (позему?).
3. Если в формуле D) считать а = а-f ф комплексным, то получали
Отсюда легко вывести, что образом Рг (р) первого слагаемого
в леиой части служит первое слагаемое Фх(р) в праиой части,1
аналогично со вторыми слагаемыми F2(p) и Ф2(/>). >
, В самом деле, в силу линейности преобразования Лапласа образом левой
части служит F1(py+iF,{p), так что F1(p)+iFi(p)^Q>l(p)-Jt-iOi(p). Но
все выписанные функции принимают при вещественных р вещественные
значения (почему?), так что при вещественных р получаем -Рг{р)=Ф\{рУ^
/7а:(р)=фа (р);/ однако аналитические функции, совпадающие при вещест-
вещественных р, совпадают тождественно (ем. п. 11.2.6), что и требовалось до-
доказать.
•"Итак, получаем ¦-..-'¦
6 COS р^ > -?-.... —
(d^~" ОС J^ —I— D^
e«'sin
-H—
(р—

132
ГЛ. III. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
4. Пусть /(/) периодична с периодом Т > 0; тогда ее oi5pa3
можнб вычислить по формуле (проверьте!) '
(U+-I) Т
J
2
n=0
«=о
*"*/(*) Л Ч «7 + * = '1
= \ e~i*f(x)dx
л=0
5. Образ дельта-функции 8(t) (ЛВМ, п. XIV.25). Так как Инте-
Интегрирование в A) начинается от значения t=О, где сосредоточена
вся особенность дельта-функции, то требуется уточнить, какая часть
этой особенности интегрируется. Будем считать, ,что особенность
интегрируется лолностыо, т. е. в условной записи, нижним пределом
интегрирования служит — 0 (или, что то же, вместо S (t) берется
b(t—0)). Тогда получим
+ 0 »
С e-Pf8{t)dt+ С <?-/¦'6
-o +o
+o
=¦1. (8)
—0
Соберем полученные формулы перехода, которые в приложениях
встречаются наще. всего, в маленькую таблицу:
1
tn
gat
(aeat
««' COS P<
««' sin p/
6@
1
p—a
p—tt
P

1
КОЛОХЗА '¦ .
О<ЖОР*СА 1 § l* опция теория 133
В каждом курсе операционного исчисления имеются таблицы,
: по которым можно найти образы, а также прообразы разнообразных
функций. Наиболее полные таблицы имеются в книгах [35, 37].
3. Основные свойства преобразования Лаиласа. 1. Пусть
f(t)—*-F(p). Тогда при постоянном ft>0
» -»4-
(проверьте выкладки!).
2. Пусть /(О—«-^(/О- Тогда при постоянном т
о . . »
-х о
о
e-r*f(t) dt.
—г
Полученный результат имеет особенно простой вид, если г > 0 и
/(*)== О при t <0: тогда получаем
В такой форме этот результат называется теоремой запаздывания,
так как независимая переменная t в операционном исчислении обычно
трактуется как время, а тогда f(t—x) означает тот же закон во
времени, что f(t), но включенный на т позже.
3. Пусть f(t)—>F(p). Тогда при любом постоянном комплексном с
ect f(t) —* $ e-f* ectf{t) dt=^ <?-«*-<•> *f{t) dt = F{p—c).
: 0 0
Этот результат называется теоремой смещения.
4. Пусть'/@—*F(p). Тогда при помощи интегрирования по ча-
частям получаем
о
I ОС-
— f/(/)e~"(— P)dt*=pF{p)-?-f\,-\-b). (9)
<5=0 О Г
J
КОЛОХ2А

134 гл. ш. операционное исчисление
Результат подстановки верхнего предела равен нулю, так как /(/).
если и растет, то не быстрее экспоненты, а в п. 1 мы видели, что
вещественную часть р можно считать как угодно большой. В правой
части мы написали /( + 0), так как функция /(/), вообще говоря,
мОжет при t = 0 иметь скачок.
Повторяя дифференцирования, получим
Г W**[f V)]'-+p\pFW-f{ + 0)]-f ¦{+<>)= ¦
=р*р (р) —рД+о) -/ (+о).
вообще
Особенно простой вид приобретает формула (9), если /(-)-0)±=@,;
тогда f'(t)—>-pF(p); аналогичное замечание относится к формулам
для последующих производных.
Возможна следующая трактовка формулы (9), полезная для выяснения
сути дела. Будем считать, что преобразуемые функця и /(/)" определены на
всей оси t (ие только при <SsO) и /(f)sO при t < 0; кроме того, пусть в
основной формуле A) нижним пределом служит—оо или, что равносильно,
—0. Тогда формула (9) всегда имеет вид /' (t) —>• pF (р). Однако если
/(+0).^0 (и; конечно), то /'(<)' имеет б-слагаемое /( + 0N@ (ЛВМ,
п. XIV. 25). Если на минуту обозначить через [/' (<)] функцию /' (t) с отбро-
отброшенным этим слагаемым, то :
PF (р) — /' @ = W @1+/ (+ 0) S @-
Отсюда в силу примера 5 п. 2 (где теперь ие нужно уточнять, какая часть
особенности дельта-функции янтегрируется) получаем, что образом функции
V С)] — а это по существу и есть функция, рассмотренная в формуле (9),—
служит pF (р) — /(+0). При рассмотрении /"(/) появится функция б'(<)
(ЛВМ, п. XIV. 27) и т. д. Если не бояться этих функций, то картина в целом
упрощаете и, хотя некоторые из излагаемых в дальнейшем фактов приходится
продумать заново.
Впрочем, мы далее ие будем пользоваться такой трактовкой.
Мы предоставляем читателю доказать, что если f(t)—*-F{p),re
. A0)
5. Дифференцируя обе части формулы A) по р, получаем (про-
(проверьте!)
Отсюда, если функция -^- конечна или хотя бы абсолютно инте-
интегрируема при ? —0 и если на минуту обозначить ее образ через Ф{р),
*^-*-Ф'и»), т. е.
Ф'(Р)=— F(P), и потому Ф(р)=— ^F(p)dp.

§ 1. ОБЩАЯ ТЕОРИЯ
Но так как из A) видно, что образ любой функции при веществен-
вещественном р = -f со обращается в нуль, то получаем окончательно
¦
6. Сверткой двух функций /х (t), /a (t), заданных при 0 ^ t < оо*
называется новая функция от t, определенная формулой
t .
@<*<оо). .A2)
(Следует иметь в виду, что значение этой функции при любом i > О
зависит от значений свертываемых функций на всем интервале 0 ^ т.^/,
так что точнее было бы писать не /i(tf)*/2@> a (Л*/а)@; однако
это практически не очень удобно.)
Если в правой части A2) совершить замену переменной x=t — Tlt
то получим (проверьте!), что '..'
Можно было бы проверить, что и прочие обычные свойства умно-
умножения выполняются и для свертывания; впрочем, это будет вскоре
ясно из других соображений.
В качестве примера свернем t2 с t:
о -
Пусть теперь Д \t) -+F1(p), /a (t) -± F^ip); тогда
)
/ f
Л @#/. (О — J *-* ( J/i (T)/a(^-
О V)
=5S
о о
Переставляя порядок интегрирования (см. ЛВМ, п. XVI.9), получим
>.••<
d)d^=^ о») ^ о»)-

136 ГЛ. 111. ОПЕРАЦИОННОЕ «СЧИСЛЕНИЕ
' Таким образом, при свертывании прообразов образы перемножаются.
Этим свойства умножения распространяются на свертывание, например
формула A3) после перехода к образам означает обычную переста-
перестановочность умножения. Из этой же связи между свертыванием и
умножением и из формулы (8) видно, что дельта-функция прн сверты-
свертывании играет ту же роль, что тождественная единица при умножении,
т. е. свертывание с дельта-функцией оставляет любую функцию
неизменной; впрочем, это легко проверить непосредственно.
Исходя из формул п. 2 и применяя доказанные здесь свойства,
можно получить большое число формул перехода от прообразов к
образам, однако мы не будем здесь этим заниматься.
4. Обратное преобразование Лапласа^ Напомним формулы для
прямого и обратного преобразований Фурье (ЛВМ, (XVII.138) и
(XVIU41)):
ю
— и
справедливые для любой абсолютно интегрируемой функции ф(/).
Чтобы их применить к преобразованию A), обозначим p =
" \ 0 (t < 0),
где s фиксировано и достаточно велико (должно быть «> s0, где
st входит в оценку B)). Тогда
о » .
= — С ф (/) e~lrtdt-f — Сф (/) e~lrtdt =
-oo О
00
-i r2n/@e~s'e-'v'd/= {e~<s+irUf(t)dt = F(s + ir). A6)
(Теперь видно, что обозначение A5) понадобилось, чтобы записать
интеграл A) в виде первого интеграла A4).) Поэтому из второй
формулы A4) вытекает, что
Из первой строки A7) получаем, что при / > О
со - ¦
= г J t»*l»F(8 + lr)dr. ; A8)
Когда г меняется от —-ор.до оо, значение psss^f.ir проходит в
комплексной плоскости прямую, параллельную мнимой оси; мы будем

. § 1. ОБЩАЯ ТЕОРИЯ 137.
условно писать, что р меняется от «— too до s-\-Loo. Принтом
dp = ldr, так что из A8) получаем .
4 ePtF(p)dp ^>0)-
Это и есть формула обращения для преобразования Лапласа.
Обратите внимание на то, что в правой части s—произвольное
постоянное достаточно большое число. Проведенное доказательство
показывает, что результат интегрирования не зависит от конкрет-
конкретного выбора такого s. (Докажите это независимо с помощью теоремы
Коши п. II.2.2, выведя сначала из B) оценку
\F(s + ir)\<-~ (s>s0).)
ft
Из второй формулы A7) видно, что при t <0 правая часть A9)
равна нулю. Отсюда на основе аналогичного свойства для преобра-
преобразования Фурье (см. ЛВМ, конец п. XV11.32) заключаем, что при
^ = 0 правая часть A9) равна х\х /( + 0). Из доказанного вытекает
также важный вывод, что не только образ по прообразу, иол про-
прообраз по образу восстанавливаются однозначно, т. е. оператор,
определенный формулой A), является взаимно однозначным.
Отметим, что интеграл A9) может получиться расходящимся при
p=s ±,/00. Специальное исследование показывает, что тогда его надо понимать:
в -смысле главного значения (ЛВМ, п. XIV. 19). :
Как известно, для преобразования Фурье имеет место равенство Парсе-
валя (ЛВМ, конец п. XVII.33). Для рассмотренных функций <р и <р оно
приобретает вид (проверьте!) . ¦
ев до
2я J | / @1« е~™* dt =* J \F (s+ir) |t dr (s 3s «,)
0 ' -o>
и в такой форме иногда применяется.
Иногда приходится исходить из образа, т. е. из F (р), и находить соответ-
соответствующую фунхцию /.(<)• ПРИ этом возникает вопрос, кахие функции F (р) могут
служить образами. Мы видели, что функция F (р) должна быть, аналитической ,
в каждой полуплоскости Rep^s (s > s0). Кроме того, из A) и B) можно
без особого труда вывести, что если f (t)—обычная (не обобщенная, т. е. ие
типа б (t)) функция, то * этой полуплоскости F (р) -»-0 при | р \ -* оо. Оказы-
ваетси, что этих условий в основном и достаточно, чтобы функция F (р) могла
служить образом при преобразовании Лапласа. В самом деле, предположим
ов
дополнительно, что V \F (s-\-ir)\ dr < <п (это условие можно значительно
— to
ослабить), и определим фуихцию / (t) при t > 0 формулой A9). Однако при
t < 0 интеграл A9) равен нулю. (Дли доказательства этого надо обозначить
< = —(о, p=s—z, перейти, хак это делалось в п. П.3.4, от интегрирования
по прямой к : иитегрированпЬ) по левой' полуокружности плоскости г и вЪс-
пользоватьея леммой Жордана (II.3.22).) Значит, можно перейти к формула»

гл. in. Операционное исчисление
<17), а оттуда с помощью A5) и A4)—к последнему равенству (Щ, которое
и означает, что F (р)-^-это лаплас-образ функции /.(/). , ,,
Рассмотрим в качестве примера фуикцию
нормированную условием V~p\p=i==l- Из A9) получаем прообраз
s + tao _ ¦¦ "¦¦¦•¦!
B0)
B1)
Для вычисления этого интеграла применим теорию интегрирования аналити-
аналитических функций (it. П.3.4). Если плоскость р раз-
разрезать вдоль иещестиеииой отрицательной полуоси,
то подынтегральную, фуикцию можно считать одно-
однозначной (почему?). Пусть интеграл берется сначала
по контуру, показанному на рис. 59, где кривыми
линиями служат окружности радиусов R -* оо и
р-*-0. Тогда интеграл по участку I в силу B1)
стремится к 2я( f(t). Интегралы по участкам II н VI
в силу леммы Жордана (И.3.22) (и которой надо
положить w=f, г=р—s и заметить, что в ией и
качестве (М#) можно было взять лишь часть указан-
указанной там полуокружности)- стремятся к нулю. Интег-
Интеграл по участку IV' стремится к—2ж" (докажите
это, разложив экспоненты под знаком интеграла в
ряды). На участках/// и V, где p==™i»j_& <ё< оо,
будет соответственно y'^Wi ^% и У*/» ±='— Y^
(продумайте!), сумма соответствующих интегралов стремится к
Рис. 59.
Но интеграл по всему контуру равен нулю; поэтому, переходя к пределу,,
получаем, сокращая иа 2i:
B2)
Чтобы вычислить интеграл / (t) в левой части, продифференцируем его по
параметру t: •
dl
dt
= - Г е-«Ып
4=1
VI
xdx?

,,....§ 1. ОБЩАЯ ТЕОРИЯ 139
Если раскрыть квадратные скобки и разбить интеграл на два, то первый
берется и равен нулю (проверьте), тогда как второй равен *
B3)
(I \2
ж— — j в показателе к интегралу B3) осу-
осуществляется, как в конце стр. 600 ЛВМ, либо с помощью применения тео-
теоремы Коши п. П.2.2.) Но так'как /(оо)=0, то
Поэтому из B2) получаем
1/2 VT
Г
(см. это обозначение в, ЛВМ, п. XIV.12). Это и есть прообраз функции B0).
Пользуясь свойством 4 из п. 3, получаем также
Мы предоставляем читателю доказать в качестве упражнения, что
5. Разложение прообраза в сумму. В п. 1 мы видели, что
функция F{p) однозначнаи и аналитическая в полуплоскости Rep > se.
Во многих случаях (см., например, п. 2) эта функция и во всей плос-
плоскости рявлиется однозначной аналитической, за исключением отдель-
отдельных изолированных особых точек. Конечно, это, вообще говоря, не
обязательно, так как функция F(p) прн своем продолжении на* всю
плоскость р может иметь и точки разветвления (п. II.1.10), как
в примере B0). Однако мы сейчас предположим, что функция F(p)
однозначна во всей плоскости р.
Допустим дополнительно, что F(p) имеет конечное число
особых точек р„ pt, ..., р„ и стремится к нулю при произволь-
произвольном (а.не только для Rep^s, как раньше) стремлении р-* оо.
Тогда интеграл A9) можно вычислить на основе теории вычетов,
как это описано в п. И.3.4, с помощью леммы Жордаиа A1.3.22).

ГЛ. III. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Это дает (проверьте!)
f(t) = -2^- 2я/ 2 Выч [e*F(p)] = 2 Выч К F(p)}. B6)
В частности, все указанные требования на функцию ^(jp) выпол-
выполнены, если она представляет собой правильную рациональную дробь
(почему?). Особенно простой получается формула, если
t(P)~ Q(P)' -
где многочлен Q(p) имеет все нули р,, ра,...,р„ простые и его
степень п выше степени многочлена Р(р). Тогда для вычисления
вычетов можно пользоваться формулой (II.3.5), н мы получаем
Если F (р) имеет бесконечное количество изолированных особых точек
Pi, р2 то из теоремы Больцано—Вейерштрасса (п. П.2.6) легко вывести,
что Pk t—*• °°- Тогда, конечно,- условие F (р) —> 0 не может выполняться
я -* оо р -* оо
(почему?), однако бывают случаи, когда оно выполняется на некоторой после-
последовательности левых полуокружностей с центром в точке p=s, радиусы
которых неограниченно возрастают. В таких случаях, рассуждая, как в п. II.3.4,
получаем представление f (t) в виде суммы бесконечного ряда, аналогичного B6).
Имеется еще один важный случай, когда прообраз функции
F(p) оказывается возможным разложить в ряд простого вида: так
Гудет, если она оказывается аналитической в точке р = оо (п. Н.З.'б).
В самом деле, тогда в окрестности этой точки имеет место раз-
разложение
%)=2^», B7)
*=»
причем так как F(oo)=0 (почему?), то с„ = 0, т. е. суммирование на
самом деле производится от А=1. В силу E) отдельный член
ряда B7) имеет прообраз с_ь7г—-ттт, а так как прообраз суммы ра-
вен сумме прообразов, то получаем
B8)
(Здесь мы воспользовались законом линейности для бесконечного
числа слагаемых, что требует обоснования; однако более подробное
исследование, которого мы не будем проводить, показывает, что
тут все в порядке.)

§ 1,. общая творяя 141
Приведем пример. Пусть • . , ¦ . : ' "•
где радикал считается' положительным для вещественных р > 0. Эта функция
при продолжении иа всю плоскость р становится двузначной, но если
ограничиться только окрестностью точки р=оо, то рассматриваемая ветвь
функции F (р) однозначна и имеет разложеиие по формуле бинома Ньютона
Р
Раскрыв скобки и воспользовавшись формулой B8), получим прообраз
. 1 <2 , 1-3 t* 1-3-5 <•
1 + +
1-2-3-4
Произведя сокращение, получим после простых преобразований
+
Но это как раз разложеиие функции Бесселя J»(t) (ЛВМ, (XV.173)), которая,
таким образом, и служит прообразом функции B9).
Отметим, что лаплас-образ, т. е. функция вида A), далеко не всегда
имеет разложеиие вида B7); однако оиа, как правило, имеет асимптотическое
разложеиие (п. II.4.1) аналогичного вида, действующее' при Rep^*s>s0,
\р\—>-оо. Это доказывается, как в п. Н.4.3; -например, если f(t) допускает
при малых t разложеиие в ряд Тейлора
Т, 001
*=0
то с помощью последовательного интегрирования по частям интеграла A)
легко получить разложеиие (проделайте это!)
¦Д Я*> @)
ПР) - 2 -рИТГ • C0
4=0
Обратно, по этому разложению легко восстановить ряд C0) (т. е, значении
f(t) при малых /),_ ио никак не всю функцию f(t), так как произвольное
изменение ее значений при конечных и больших t инкак не сказывается иа
разложении C1).
В частности, из C1) мы видим, что
р -*¦ m .; ¦
Легк» < доказать и обратную формулу при $0 < 0:
C2)

142 ГЛ. 111. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
В сзмом деле, •
и
(В W
«/. @) + $ «""/' @ * г* Н0)+\ /' (/) Я=/ (*)•
с, " ° j
Отметим интересное приложение формулы C2). Применим сначала свойстио
A0) к формуле A1), это даст
О р
отсюда в силу C2) получаем, изменяя обозначения т иа /, q на р:
\Up.diJF{p)dp.
0 0
Эта формула дает возможность легко вычислить миогие интегралы, для .кото-
.которых неопределенные не выражаются через элементарные функции. Например,
из второй формулы G) при а=—\<0 получаем
Имеются методы более детального изучения поведения /(/) при /—>- а>.
Приведем без доказательства, в ¦частности, такой результат. Пусть функция
F (р) при своем продолжении в полуплоскость Rep<s0 имеет одну особую
точку ро с наибольшей вещестиениой частью (т. е. F(p)—однозначная анали-
аналитическая функция в полуплоскости Rep>Reр0, за исключением точки р0);
Лусть в окрестности р0 функция F(p) имеет разложение
2
где все %ь иещестиенны- и Хй<1к1< ...—> оо. Пусть в формуле обраще-
обращения A9) от интегрирования по прямой оказывается возможным перейти
к интегрироианию по пути, показанному на рис. 60. Тогда при / —>¦ оо имеет
место асимптотическое разложение
*=о
понимаемое в естественном смысле (п. II.4.1). Если наибольшую веществен-
вещественную часть имеет несколько особых точек функции F (р), то. соответствующие
разложения C3) надо сложить.
в. Численное определение ирообраза. Формулу обращения A9) или равно-
равносильную ей формулу A8) можно использовать для численного определения

. § 1. ОЭЩДЯ ТЕ9РИЯ . ,
¦1.43
прообраза / (t) по заданному образу F (р), применяя численное интегрирова-
интегрирование (ЛВМ, п. XIV.13), в результате которого f (t) окажется приближенно
представленной в виде произведения e5i на сумму ряда Фурье. Однако из-
известно (ЛВМ, п. XVI 1.25), что такой ряд сходится тем быстрее, чем разла-
разлагаемая функция «глаже», т. е. имеет больше непрерывных производных. Раз-
Разрывы у функции f (t) и у ее производных легко выявляются по виду F (р):
например, если /(/0+0)—/(/0—0)=А ?^ 0 (t0 > 0), то
легко проверить, что F (р) содержит слагаемое вида V
е~'оР i , X
я ¦, аналогично выявляются разрывы f'(t) и т. д. >
p,, ...
Поэтому 'за счет' выделения из F(p) таких слагаемых
возможно добиться того, что прообраз оставшейся
функции уже достаточно гладок. Потеря гладкости на
всей оси t может произойти. также из-за того, что инте-
интеграл A8), как мы видели, вообще говоря, имеет скачок
при /=0. Здесь также можно улучшить картину за счет
выделения из F (р) «опасных» слагаемых с известными
прообразами: так, если /(+0) конечно и1 не равно нулю,
то F (р) при р —»• оо (Re p велико) имеет главный член
вида—(с=/(+0))ит. д. в соответствии с F). Кроме
того, если f (+0)=0 (т. е. (pF (р)) ^ _ „=0), a f (+0) Рис. 60.
конечно (т. е. (paf (р))\ р_и конечно), то можно продол-
продолжить интеграл A8) с вынесенным множителем est нечетным образом с полуоси
• - ¦ Л на полуось / < 0, т. е. рассмотреть функцию
Т{t) =
e'rtF (s¦•+ir) dr ~ J e"Mp (s+l>)dr
J
00
=— est \ si
sin rt-F(s+ir) dr.
Тогда f (t) и / (t) не имеют разрывов при t=0.
Депустим, что такое продолжение осуществлено, и воспользуемся фор-
формулой трапеций с узлами л = —я, где Т > 0—некоторое фиксированное число,
а п=0, ±1, ±2, ... Мы получим приближенное представление7@. а потому
и / @, при t > 0 в виде произведения экспоненты на сумму ряда Фурье
(проверьте!):
Конечно, при этом Т должно быть выбрано заметно-большим тех значений f,
для которых нам требуется зиать f (t).
Приведем еще одии способ числениого построения прообраза, основанный
иа использовании .значений F (р) при вещественных р. Будем считать, что
s, < 0 (этого всегда можно добиться с помощью применения теоремы смеще-
смещения) и что /(-fOj=O 1см. выше). Пусть при некотором вещественном q >9
известны значение
: {«'=0, 1, ...).

144 ГЛ.- Ill, .ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Совершим в интеграле A) замеиу переменной «-*'=cos. О и обозначим
при этом / @)=7( Y )=0. Эта замена дает (проверьте!)
я/2
qbn= С (cos G)s" sin */(*)<**•
о
Ясно, что задачи о построении функций /(*) и /D) равносильны.
Будем считать функцию / (ft) продолженной нечетным образом че
точку,д=0 и четным—через точку d=— f т. е. J[-r—Ф)™7 ("о"!
Тогда эта функции будет 2л-периодичиой, и ее можно разложить в ряд Фурье:
7(*)=2cnsinBn+l)d C5)
(продумайте!); в частности, эта формула справедлива при (XfleS-jj-. Под-
Подставив C5) в C4), после несложных выкладок получим для коэффициентов с„'
треугольную систему уравнений
42
=^— qblt
4*
+ 5са + с,=— qbit
вз которой и находим коэффициенты с„, дающие возможность получить зна-
значения функции /"(#) по формуле C5).
Заодно мы получили утверждение, представляющее теоретический интерес:
функция f (t), а потому и F (р), полностью определяется значениями F,(p,J
для последовательности вещественных значений рп —<¦ со, образующих арифме-
арифметическую прогрессию.
§ 2. Приложения
1; Осиовнаи идея.. Допустим, что некоторый процесс описы-
описывается функциями времени х (t), у (t), ..., которые и являются
искомыми. На математическом изыке это обычно означает, что
между этими, а также некоторыми заданными функциями составля-
составляются уравнения, которые требуется решить. Однако часто оказы-
ваетси, что уравнения, связывающие образы искомых функций, зна-
значительно проще и нх значительно легче решить, чем уравнения
для исходных функций-прообразои. (Например, в п.1.3 мы видели,'

§2. приложения 145
что если неизвестная функция дифференцируется, то ее образ мно-
множится на р, а если она интегрируется, то ее образ делится на р,
так что действия над образами значительно проще, чем над прооб-
прообразами.) Тогда от уравнений для прообразов мы переходим к урав-
уравнениям для образов, решая, находим образы искомых функций,
а затем уже возвращаемся к прообразам.
Конечно, далеко не любые уравнений удается решить таким
способом. Прежде всего, требуется, чтобы уравнения были линей-
линейными или могли быть легко преобразованы в линейные. Жела-
Желательно, чтобы коэффициенты были постоянными, в противном случае
положение, как правило, существенно осложняется. Однако если
эти условия выполнены, то операционный метод, т. е. переход от
прообразов к образам, часто значительно облегчает отыскание .тре-
.требуемых функций .времени. Такой метод опирается на разработанную
систему правил и формул перехода, которые и составляют опера-
операционное исчисление; преобразование Лапласа обычно используется
лишь для установления этих правил и основных формул, но'для их
приложения оно уже не требуется.
Может получиться, что в сложном исследовании участвует целав
цепочка подобных рассуждений, так что найденные функции времени
используются для отыскания еще каких-то функций и т. д. В таких
случаях оказывается полезным проводить все исследование в обра-
образах и лишь на самом последнем этапе перейти к прообразам функ-
функций, которые в конечном счете и требуются.
Приведем несколько примеров такого приложения.
' 2. Обыкновенные дифференциальные уравнения. Линейные диф-
дифференциальные уравнения с постоянными коэффициентами, а также
системы таких уравнений (ЛВМ, пп. XV. 17, 18, 21) составляют
наиболее обширную область приложения операционного исчисления.
Пусть, например, требуется решить уравнение
при начальном условии
*@) = а, *'@) = р. B)
Совершая над обеими частями уравнения A) преобразование Лапласа
и пользуясь свойством линейности (сумма переходит в сумму, см.
п. 1.1) и свойством 4 нз п. 1.3, получаем
а{р*Х—ар — р) + Ь(рХ—а) + сХ=F(p) (Х
где под Х(р) понимается лаплас-образ искомой функции x(i), а под
F(p)—образ заданной функции f(t). Мы видим, что относительно
X получилось алгебраическое уравнение первой степени. Решая его,
.получаем
p (8)

146
ГЛ. Ш. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
т, е.
ар^+Ьр+с
D)
f(t)
система
x(t)
(Обратите внимание, что в знаменателе получился характеристиче-
характеристический многочлен уравнения A), см. ЛВМ, п. XV. 17; так будет всегда,)
Если x(t)—гне окончательная искомая функция, а предназначается
для использования, скажем, в качестве правой части некоторого
другого уравнения вида A), то можно
считать, что задача уже решена: ведь
в формуле вида D) используется не
сама правая часть, а именно ее образ.
Если же x(t)—окончательная искомая
функция, то надо еще от формулы D)
перейти к прообразу по методам
пп. 1.4, 1.5; при этом вычеты в формуле A.28) будут браться по
нулям характеристического многочлена (почему?), а также но осо-
особым точкам функции F(p).
Таким образом, при решении дифференциального уравнения
операционным методом начальные условия учитываются с самого
начала процесса решения, что очень удобно. Вычисления приоб-
приобретают наиболее простой вид, если начальные условия B) нулевые:
тгогда просто
Рис. 61.
где D{p)—характеристический многочлен, a Z(p) = ^j- называется
передаточной функцией. Как известно (см., например, ЛВМ, конец
Рис. 62.
п. XV. 18), во многих случаях f[t) в уравнении A) можно тракто-
трактовать как внешнее воздействие на какую-либо физическую систему,
которая определяется коэффициентами в левой части, a x(t)—как
отклик системы на это воздействие (иначе, f(t)—входная, a x(t)~—
выходная функция; см. рис. 61). Таким образом, в случае нулевых
начальных условий образ отклика получается из образа воздействия
простым умножением на передаточную функцию. Это делает особенно
удобным рассмотрение в- лаплас-образах' агрегатов, в которых вы-
выходная функция для некоторой системы служит входной функцией
для следующей и т. д. (рис. 62).

¦ § 2. Приложений 147
Если начальные условия не - нулевые, то формулу D) можно
записать в виде '
т. е. к отклику добавляется слагаемое, определяемое свойствами
системы и начальными данными, ио не зависящее от внешнего воз-
воздействия. , .-¦.-. >¦
Нетрудно понять, каков смысл прообраза г @ передаточной фувкции.
Так как Z(p) в E) получается из X (р) при F (р)=з1, то из примера 5 и. 1.2
вытекает, что г (/) представляет собой отклик системы на внешнее воздейст-
воздействие b(t), т. е. на единичный импульс, подействовавший на нее в начальвый
момент времени, если система перед этим покоилась. Это можно понять и из
других соображений: непосредственно после импульса внешнее воздействие
прекращается, т. е. как бы /(/)ssO, йо система приобретает начальные усло-
условия х(+0)=0; х' (+0)=— (см. аналогичные рассуждении в ЛВМ, конец
п. XV.16); но тогда из D) получается, что X (p)=Z{p). -'¦ ' ¦
На основе свойства 6 из п. 1.3 формула E) в прообразах имеет вид
...
F)
В такой форме решение можно получить из общих соображений, связанных
с построением функции влияния (ЛВМ, п. XIV.26), Функция влиянии здесь
имеет вид г (t—т), а не z(t, т) (как в общем случае), так как рассматри-
рассматриваемая система ие только линейная, ио и автономная (не меняет своих свойств
С течением времени), так что при сдвиге-воздейстиия во времени соответст-
соответствующий отклик сдвигается на столько же, не меняя своей формы.
< .Саму передаточную функцию Z (р) ¦ можно еще трактоиать следующим
образом. Допустим, что при фиксированном комплексном р внешнее воздей-
воздействие имеет вид / (/)=е^*. Тогда уравнение A) имеет в качестве одного из
своих частных .решений *(f)=j—— eP<=Z (p)ePf (если только D(p) ф 0, т. е.
если отсутствует резонаиё). В частности, если p = iw чисто мнимое, то речь
идет о коэффициенте усиления гармонического внешнего воздействия; тогда
Z (ш) называется частотной характеристикой рассматриваемой физической
системы. .При этом, если система устойчивая, т. е. если свободные колебании
в ней затухают (это значит, что Z (р) имеет полюсы только при Re p < 0),
то при внешнем воздействии eiwt и при любых начальных условиях соответ-
соответствующее решение (т. е. отклик) е ростом t приближается к Z (ш) elat с 9кс-
поиеициальиой скоростью. > , .
, Иногда предпочитают рассматривать, результат z1(t) воздействия 8а си-
систему ие импульсной, а единичной функции /(/)=!. Тогда, при нулевых
начальных услбвиих из E) получаем
Z1(p)=Z(p)-~, т. е. Z(p).=i/»Zi(p), .
откуда при любой функции /(/) из. E) следует, что . . . .. ,....,.

143 гл. ш. операционное исчисление
Возвращаясь к прообразам, получаем тогда
Of
Эту формулу легко получить и из F), заметив, .что г(/)=?i@-
Операционный метод можно применить ие только к начальной, но и к
краевым задачам (ЛВМ, п. XV. 16), хотя для них вычисления получаются
более громоздкими. Пусть, например, требуется решить уравнение A) для
0</<а,при краевых условиях *@)=а, х(Т)=у. Будем считать решение
продолженным с этого отрезка иа всю полуось-0<<< оо и обозначим через
р неизвестное значение «'(О). Тогда, совершая над A) преобразование
Лапласа, мы можем перейти к формуле D), в которой E—пока неизвестный
параметр. Переходи к прообразам, получаем для решения выражение вида
х=фA; Р), после чего E находим из второго краевого условия <р(Т; Р)=у.
Приведем еще пример решения дифференциального уравнения с перемен-
переменными коэффициентами
t"+' + t0. G)
Обозначим х' @)=а, х @) = р. Переходя к лаплас-образам и используя свойства
4 в 5 из п. 1.3, получим уравиение
т. е.
Таким образом, для Х(р) получилось обыкновенное дифференциальное урав-
уравнение 1-го порядка. Решая его, находим
*(/>)=
откуда
x(t)=CJ0(t)
(см. A.29)). Уравнение G)—это частный случай уравнения Бесселя (см. ЛВМ
(XV. 167) при р=0>). Получилось только одно решение, так как другое при
<=0 бесконечно, а потому к нему нельзя применить свойство 4 из п. 1.3.
Если рассматривается не одиночное уравнение вида A), а система
линейных дифференциальных уравнений с постоянными коэффициен-
коэффициентами, то после перехода к лаплас-образам получаем матричное урав-
уравнение вида (по поводу подобных уравнений см. ЛВМ, п. XI.3)
D(p)X(p) = F(p), (8)
где D(p)—характеристическая Матрица, Х(р)—столбец из образов
искомых функций, F{p)—столбец из образов заданных функций
(для нулевых начальных данных это столбец из образов неоднородных
члейов системы, а для ненулевых- начальных данных надо внести
поправку иа эти данные, как в уравнении C)). Решая уравиение (8),
получаем
где Z(p) = [D(p)]~l—передаточная матрица. По правилу построения
обратной матрицы (ЛВМ, п. Х1.3) ее элементы- будут иметь в зна-

- § 2. приложения . 149
менателе характеристический многочлен detD(p), поэтому при пере-
переходе к прообразам придется брать вычеты по нулям этого много-
многочлена, т. е. по корням характеристического уравнения.
3. Разностные и дифференциально-разностные уравнения.
О разностных уравнениях для функций мы упоминали в ЛВМ (конец
п. XVII.16). Пусть, например, рассматривается уравнение
, ax(t) + bx(t—h) + cx(t—k)=f(t) @</<oo); (9)
где 0 < А < А. В качестве начального условия" можно задать x{t)
при —А^* < 0. Тогда в принципе возможно применить следующий
метод шагов: пока t меняется от 0 до А, второе и третье слагаемые
в левой части (9) заданы (почему?), т. е. можно иайти решение
x{t) при 0^Г< А; затем считаем, что t меняется от А до 2А; тогда
x(t—h) и x(t—k) уже найдены (почему?), и из (9) можно иайти
x(t) при А^^<2А и т. д. Этот метод удобен как численный даже
для нелинейных и неавтономных случаев, но для исследования решения
он не очень хорош.
Для линейных автономных систем возможно применить операцион-
операционный метод.-Для этого применим к обеим частям (9) преобразование
Лапласа, воспользовавшись свойством 2 из п. 1.3; получим
ч~РкХ+
о
-fee"'* \е~Р*x(t)dt — F{p), A0)
-*
откуда Легко иайти Х(/>) (заметим, что в интегральных членах зна-
значения x\t) берутся при t < 0, т. е. эти значения, заданы в силу
начального условия). Как и в п. 1, наиболее прост случай нулевого
начального условия: тогда из A0) получаем опять формулу вида E),
где 'передаточная функция имеет вид
Полюсы этой функции, по которым будут браться вычеты, срав-
сравнительно просто определить, если А и k соизмеримы (имеют рацио-
рациональное отношение), т. е. А = дат, А—йт, где т и л—целые; тогда
для нахождения нулей знаменателя надо решить алгебраическое
уравнение
после чего положить р = -г- — Ln и. В несоизмеримом случае приходится
численно решать трансцендентное характеристическое уравнение.

150 ГЛ. III. ОПЕРАЦИОННОЕ «СЧИСЛЕНИЕ
Диалогично исследуются дифференциально-разностные уравнения,; напри-
например, вида - .
«'@+te@+«'('-*i)+«M/-A,)=/@ ' @<<<оо), A2)
где Л4 > 0, Аа > 0. В качестве начального условия можно задать х (t) при
— А<< < 0, где h—большее из. чисел hlt Ла; кроме того, задается значение
х(-\-0), которое не обязано совпадать с х(—0). И здесь можно применить
метод шагов, причем размер каждого шага равен меньшему из чисел Aj, h.2.
Мы предоставляем читателю получить лаплас-образ решения и передаточную
функцию
Z (р) = (ар+Ь + ере - Ър+de - h*P) -».
Нахождение ее полюсов сводится к вычислению нулей квазиполинома
(см. (I I.3.46)).
. Обращаем внимание читателя на то, что при решении начальной задачи
для уравнения вида A2) в этом уравнении обязательно должен присутствовать
член со старшей Производной при наибольшем зиаченнн аргумента: например,
в уравнение A2) нельзя было бы добавить членя" {t —h{). В нротивном случае
можно доказать, что характеристический квазиполином обязательно будет
иметь нули с как угодно большой вещественной частью, что не дает возмож-
возможности построить решение операционным методом (почему?).
4. Интегральные и пптегро-дифференцнальные ураввеипя. Опера-
Операционный метод можно применить и ко многим интегральным уравне-
уравнениям, а также интегро-дифференциальным уравнениям (в которые
искомая функция входит как под знак интеграла, так и под знак
производной). Здесь мы не будем излагать теорию таких уравнений,
а прйнедем два простых примера.
1. Рассмотрим интегральное уравнение
где / и g—заданные функции, а х—искомая. Применяя свойство
6 из п. 1.3, получим X(p)G{p)=zF(p), т. е.
Впрочем, здесь еще надо проверить, что правая часть может служить
лаплас-образом (п. 1.4), а это далеко не при любых функциях / и в будет
так, ибо правая часть может не стремиться к нулю прн Rep^s, |pf—»-oo.
Интересно, что операционным методом могут быть, в виде исклю-
исключения, решены даже некоторые нелинейные интегральные урав-
уравнения специального вида. Например, уравнение
О . '
после перехода к образам принимает нид X*{p) — F(p), откуда
УЛ т.. д. • : ".,.'' .. ..

§ 2. ПРИЛОЖЕНИЯ 151
2. Рассмотрим интегро-дифференцнальное уравнение
x'{t)+lx(x)g(t~x)dx=/(t) @</<оо),
о
где дополнительно задано Jc( + 0) = a. Переход к образам дает
p '
откуда легко найти
В данном случае условие стремления правой части к нулю выполнено
(почему?), так что мы действительно получили лаплас-образ решения.
5. Уравнения с частными производными. Уравнения с частными
произиодными уже встречались в ЛВМ, пп. XVII.31 и 34. Теория
таких уравнений весьма обширна, и мы также не будем ее здесь
касаться^ а только приведем пример применения операционного
исчисления к решению так называемого уравнения теплопроводности
ди д2ы
a
В курсах уравнений математической физики доказывается, что этому
уравнению удовлетворяет температура u = u(t, x) в момент времени
t в точке х прямолинейного стержня, если тепло подается или отво-
отводится только через его концы. Коэффициент температуропроводности
а определяется только материалом стержня.
Рассмотрим сначала случай, когда стержень бесконечен, т. е.
— оо<дг<оо, причем будем считать заданным распределение темпе-
температур в нем в начальный момент времени:
в 11=0 = ф (*) (заданоI. A5)
Таким образом, математическая задача состоит в решении уравне-
уравнения A4) при заданном начальном условии A5). Для решения этой
задачи совершим преобразование Лапласа над обеими частями урав-
уравнения A4), считая х параметром, т. е. u(t, x)~>¦ ?/(/>, x). Применяя
правило дифференцирования по параметру (см. конец п. 1.1) и фор-
формулу A.9), получим ¦" ¦•.:.-....:•
А это уравнение при любом фиксированном р представляет собой
обыкновенное дифференциальное уравнение, которое можно
переписать в виде
gp?/=-<p(*). , A6)
В этом и состоит идея применения преобразования Лаплас!а:
оно превращает одну из независимых переменных (по которой

152 . ГЛ. III. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
производится преобразование) в параметр, понижая тем самым число
этих переменных на единицу. Естественно, что чем меньше незави-
независимых переменных, тем, вообще говоря, уравнение проще; в част-
частности, если их было две, то после перехода к лаплас-образам остается
одна независимая переменная, т. е. получается обыкновенное диффе-
дифференциальное уравнение, что и произошло в рассматриваемом примере.
Вернемся к решению уравнения A6), причем сначала будем счи-
считать, что ф(х) = б (х) (дельта-функции). Тогда прилг^ОуравнениеA6)
.является однородным и потому имеет решение
при этом величины Ct н С, при х < О и х > 0, вообще говоря,
различны и, кроме того, могут зависеть от р (они постоянны только
по х). Условимся при больших Rep под 1/ — понимать ветвь, ко-
которая при вещественных р > 0 принимает положительные значения.
Тогда из условия обращения Ui(p, х) в нуль при р —>¦ оо (как лю-
любого лаплас-образа), получаем, что . .¦¦.-'
^ A7)
Однако, интегрируя (.16) при <$(х) = Ь{х) от —0 до -}-0 два раза,
приходим к равенствам
т
Отсюда получаем, что в A7) Cl-=Ci = —у=- (проверьте!), т. е.
2 у ар •
'*' (х^О), A8)
Однако правая часть A8) получается нз правой части табличной
формулы A.25) заменой р на — р с последующим умножением на
^kj-. Поэтому из формулы A.25) и свойства 1 п. 1.3 вытекает, что
прообразом функции A8) служит (проверьте!)
*УЩ.
J
»¦, ,
A9)

§ 2. ПРИЛОЖЕНИЯ - .¦;
Если теперь ф(л:) = 6 (*—?), то в'силу инвариантности уравне*
ния A4) относительно сдвигов по х и соответствующее решение
аолучнтся из A9) заменой х на х—\. Отсюда, если ф(дг) произ-
произвольна, то, применяя принцип суперпозиции (ЛВМ, п. XIV.26),
получим окончательное решение задачи :
полученное впервые Пуассоном иным методом.
Рассмотрим еще одну задачу для уравнения A4), именно задачу
о разогреве полубесконечного стержня с конца, лричем допустим,
что закон изменения температуры на этом конце известен, а в на-
начальный момент времени стержень не разогрет. Задача математи-
математически сводится к решению уравнения A4) для O^t < ос*, 0-^х < оо
при начальном условии
. «Ь=. = 0 ,@<*<оо)
и граничном условии
и|*=в = ф(') (задано). B0)
Совершая преобразование Лапласа по t над уравнением A4) и усло-
условием B0), получим
Решение этой задачи дает, подобно A7), . ¦ :
U(p, х)=*Ф(р)е-ум'ах. B1)
Так как прообразом функции е~^^ах, согласно A.24), служит
2УпЧ V 2У5г*
то в силу свойства 6 п. 1.3 прообразом функции B1) служит.
И ((, X) =—^=г Г (t — Т)-»/а в~*'/4О (<-т) ф (Т) dx
о
Это и есть решение поставленной задачи. •
Как видим, при применении операционного метода приходитея
пользоваться не только основными свойствами преобразования Лап-
Лапласа, но также разнообразнымн формулами перехода от конкретных
прообразов к образам и обратно. • .
Приведем еще пример решения, приводящего к сумме бесконеч-
бесконечного ряда. Именно, рассмотрим задачу о разогреве конечного стержня.

154 ГЛ. III. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Будем решать уравнение A4) при 0 <*<;/, 0 <;/<«» мри началь-
ном условии "'' '"; ;
(стержень не был разогрет) и граничных условиях
оо) B2)
(на левом конце поддерживается постоянная температура иа, a ira
правом—нулевая температура). Совершая преобразование Лапласа
над уравнением A4) и условиями B2), получаем ; ........
U\ =&, U\ =0.
Решение этой краевой задачи при любом значении параметра р,
которое мы предоставляем читателю, имеет вид .,
^shV ?(l-*)
~F
shV a
При фиксированном х эта функция однозначная (почему?) и анали-
аналитическая на всей плоскости/?, за исключением точкиpt = 6.» течек,
определяемых нз уравнения
Г T' =
^./ = 0, откуда еГ T' = i, 2 y^Z I = 2Ая/,
ак*я* .. л п .
Рк=> рГ. (ft==1' 2, ...)•:
В этих точках функция U имеет полюсы первого порядка. Поль-
Пользуясь формулой A.26) (но для бесконечного числа членов) и фор-
формулой (II.3.5), получаем
u{t, *) = «„
oft» я8'
*=i
ft=i
Интересно отметить, что будет после установления процесса,
т. е. при t—»-оо. Из предельной формулы A.32) вытекает, ч.то
и(оо, х)=ш[Ри(р, х))= нш а/
р-в р-»« ,
Впрочем, этот же результат вытекает и из формулы B3), описы-
описывающей переходный процесс.

.. .§3. варианты 155
В.,заключение отметим, что операционное, исчисление имеет и
разнообразные интересные математические приложения к вычисле-
вычислению определенных интегралов, установлению различных формул,
связывающих специальные функции, и т. д.; см., например, [3, 37].
•., , § 3. Варианты
. Помимо интегральных преобразований Фурье н Лапласа, имеется целый
ряд других аналогичных преобразований, приспособленных для решения раз-
различных классов задач. Это приложение проводится по схеме § 2: поставлен-
поставленная задача формулируется в терминах образов искомых функций, и если она.
окажется достаточно простой, то решается, после чего выполняется обратное
преобразование. Здесь мы кратко укажем иа некоторые из этих преобразова-
преобразований, отослав интересующегося читателя к дальнейшей литературе.
1. Дискретное преобразование- Лапласа. В теории импульсных систем
широко' применяется дискретное преобразование Лапласа, которое ставит в со-
соответствие последовательности чисел хв, хи х2, ...—ее мы будем сокращенно
обозначать {х„\—функцию X (р) от комплексного переменного p=s-j-i/-по
формуле
п=о
Если х„ при я—>- оо остается ограниченным или растет по модулю ие быст-
быстрее экспоненты', то функция X (р) аиалитична при достаточно больших s и
2я-тгериодична по г. Легка Доказать формулы преобразовании
{1, 0, 0, ...}-* 1; {I, 1, 1, ...)
„_. . B)
Iе ' еР—еа'
(k=@, 1, 2, ...) я т. д. Свойства этого преобразования напоминают свойства
из я, 1.3; они подробно изложены в книгах [130, 34]. Отметим, например,
такое: .:•,¦¦;'¦¦¦ • ¦
C)
Дискретное преобразование Лапласа можно првменить, в частности, к ре-
решению линейных разностных числовых уравнений с постоянными коэффициен-
коэффициентами (ЛВМ, п. XVH.16). Пусть, например, надо решить уравнение (ЛВМ,
(XVII.68))
.. = ..-,.- «** + P"*«+i + Y*»+i>=0 (n=0, 1, 2, ...), D)
если ха и xv заданы. Совершая дискретное преобразование Лапласа над всеми
членами уравнения D) и применяя линейность и свойство C), получаем
аХ
откуда

156 ГЛ. Ш. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Теперь надо либо разложить эту рациональную относительно е? функцию иа
сумму простейших (ЛВМ, и. VIU.10) и воспользоваться формулами B) (запи-
(записав их в, виде
JFL_.t_e-«{e«}_{e-«I о,б, ...'}¦
и т. п. для кратных знаменателей), либо воспользоваться формулой обра-
обращения. .. . . . ,
Формула обращения преобразования A), записанного в виде
где. считается, что ж„=0 при п < О, сразу вытекает из формулы для коэф-.
фициеитов комплексного ряда Фурье (ЛВМ, п. XVH26); . "
откуда
•+/Я
• - Х»=Ш 1 X<,P)e"PdP (я^О.1,2,...), F)
где sг— любое достаточно большое число.. Из доказательства видно также, что
при л =—1, —2, ... интеграл F) равен нулю.
Иногда пользуются несколько более простым г-преобразованием, кото-
которое получается из преобразования A) простой заменой еР=г. Обозиачвм
г-образ последовательности {«„} через X (г); тогда
*M«=XW=JV4 G)
Так как Rep должно быть.велико, a Imp произвольно, то ряд G) сходится
для любых г с достаточно большим \г\, т. е. представляет собой разложение
в ряд Лорана па бесконечности функции Х(г), аналитической в точке г—«о
(п. И.3.6). Соответственно просто изменятся формулы B) (иапрвмер, {*"} —*¦
-г* ——-г . и т. п. | и свойства. Формулу обращепия F). можно переписать
в виде
Ф -idz (n=0,. 1, ...),
где R достаточно велико, а окружность \z\=R ориентирована в положитель-
положительном направлении. К вычислению этого интеграла можно нримевить теорию
вычетов (продумайте'это для првмера E)). ¦ . . ... .
В заключение отметим, что дискретное преобразрваиве Лапласа последо-
последовательности {*„} —это ве что иное, как обычное преобразование Лапласа uw
пульсной функции -, ' .-....- .....'-¦'.! ¦ '
(проверьте!).

§ 3. ВАРИАЙТЫ 1ST
S. Преобразование Фурье растущих функций. Применение преобразования
Фурье бывает затруднено тем, что преобразуемая функция должна быть абсолютно
интегрируемой и потому должна иа бесконечности обращаться в нуль. Рас-
Рассмотрение фурье-образа как аналитической функции позволяет устранить это
затруднение. Пусть сначала
.. .. ¦.,/(*) и? О(-op <*<*„), \ Цх) К Me** (х„<х<<х>); (8)
будем в формуле преобразовании Фурье Ч
'«-i I
f(x)e-lk*dx ' (9)
считать' ft- комплексным. Тогда легко, проверить, что f(k) будет, аналитической
функцией k, во всяком случае, при 1mA <—а. Обозначив Ш=р, f(k)=F(p);
мы (при дсо5=О) приходим к преобразованию Лапласа A.1), так что все рас-
рассмотренные выше свойства преобразования Лапласа легко переформулировать
и на преобразование (9). В частности, формула обращения имеет вид
да+is
f(x)*= J J(k)e'»xdk (Im* = s<—a).
-x+ls
Если функция f(x) растет и при х—*¦ — оо, то можно применить следую-
следующий прием. Пусть
- |f(*)|<Sf»e«+* @<*<оо),
Положим . ...-.-
0 (-«><*<<)), . . . f f(x) (-»<*<0),
@ <*<«), 'w\
Тогда нх фурье-образы f+ (k) и /_ (k) будут аналитическими функциями ft,
первая при lm k <—а+, а вторая—при Imfe>—а_. Формула обращения
имеет вид N
J 1-(k)e?**dk, A0)
где s+ <—a+, s_ >—a_.
Легко проверить, что если в оценке Щ М заменить на функцию М (х)
со сходящимся интегралом, то при Imft<—а интеграл (9) будет правильно
сходящимся (ЛВМ, n.'XlV.2l), а потому функция f(k) непрерывна в замкнутой
полуплоскости 1тА<—а, включая граничную прямую. Аналогично формули-
формулируются свойства непрерывности функций f+ и ?_. В частности, если функ-
функция f(x) абсолютно интегрируема, то можно принять a+=a_=0, и полу-
получается такая картина: функции f+ (k) аналитична в нижней полуплоскости
fe я непрерывна на граничной вещественной оси (ио может в точках этой оси
потерять аналитичность-); функция f_ (k) аиалятичиа в верхней полуплоскости
и также непрерывна на вещественной оси, ио уже «с другой стороны», а на
санбй Ьси f+ (А)-ь7- <*)==/(*)• (Последнее видно, если в равенстве A0) пе-
перейти к пределу лри s+-^ 0, s_—»-0.)
Покажем применение введенных понятий к выводу формулы Пуассона для
суммы ряда
5= 2 '*"> <Р>°>-

t'58 гл. ш. операцнйнн'Ье исчисление
где f (jt) (—00 < х < оо Wнепрерывная суммируемая фушшвя. Для этого будем
исходить из формулы A0), в которой s+ н s_ —любые положительные числа.
Подставим х—рп и произведем суммирование по п от —ао до ею. Но первый
интеграл, равный /+ (х), обращается в нуль при л < 0,. так что суммировать
достаточно по п^О; аналогичным свойством обладает второй внтеграл,-а, по-
потому ¦
до » +/s+ -оо «o + fs_
/_(fe)(l — е^*)-МА. A1)
. . i .-.....¦
_
Примем для простоты, что функция¦( (х) прн х—>¦ ±<х> стремится к нулю
с экспоненциальной скоростью. (На самом деле оказывается, что это предпо-
предположение можно сиять.) Тогда можно принять s+ > 0, s_ < 0 и контур пер-
первого интеграла в правой части A1) замкнуть большой полуокружностью снизу,
а второго интеграла—сверху. Интегралы по полуокружностям стремятся к
нулю и, применяя теорему Коши о вычетах, находим
Полученная формула
применяется в теоретических исследованиях и в вычислениях. [ Доиажите ее
•также е помощью формулы' \ fg* dx=2n \]g*dk, вытекающей вз равенства
Парсеваля, ЛВМ, п. XVII.33, подобрав соответствующую функцию g(x) в вос-
воспользовавшись формулой
3. Другие интегральные преобразования на бесконечном интервале. .Каж-
.Каждое интегральное преобразование определяется (с точностью до обозначений)
формулой вида
b
¦ - " ¦ ' <12)
где К(р, t)—ядро, которое и определяет преобразование: так, для преобра-
преобразования Фурье
для преобразовании Лапласа
а=0, 6=оо, /((р, <)=е~",

...... §3., варианты 1S9
длд косинус- и,синустпреобразоваиий Фурье (ЛВМ, п. XVII.32) а==0, Ь=оо,
а К (р, t) соответственно равно — cos pt и — sin pt.
Остальные'интегральные преобразования так или иначе связаны с преоб-
преобразованием' Фурье. Так, рассмотрим преобразование Меллина
03)
о
где р=s-\-ir—комплексная переменная. Замена переменной по формуле
<=е~* показывает (проверьте!), что при фиксированном s функция F(s-\-ir)
служит фурье-образом функции 2ne~Sxf(e~x). Отсюда по формуле обращения
для преобразования Фурье
¦ : ¦ . . . во
2яе -**/ (е - *) = [ F (s -f- ir) е"~х dr,
— OB
откуда получаем формулу обращения для преобразования A3)
s + leo
Мы предоставляем читателю продумать, какой должна быть функция f (t), чтобы
ее преобразование A3) имело смысл в некоторой области плоскости р, и каким
должно быть s в формуле A4). Различные свойства и приложения преобра- '
зования Меллииа, как и других интегральных преобразований, содержатся
в книгах [36, 113].
Преобразование Гильберта широко применяется в теории- сингулярных
интегральных уравнений (§ VI 1.5). Допустим, что функция /(/) вещественна
и абсолютно интегрируема на всей оси t; f(a)—ее фурье-образ; функции.
7(ю) и' F (if)'Определены формулами . ' ' ' '
"> 2'- F @=-2 Im ! «*¦>'Да>) d». A5)
> < О), . J
Заметив, что вещественность функции f (t) равносильна свойству ее фурье-
образа
(докажите это!), получаем, что
2Re J е><»*?((й) da>= J eMf (ш
*) <te>=±f(t).

160 ГЛ. Ш. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Мы получили, что фурье-прообразом функции /(со) служит
А 00
-f Иго|=-j[/(t)-iF(t)),
j
-w 0 0
т. е.
"Поэтому при ю > 0
21m ? e'm< ? (a>) du>=2 lm С «/"* tf (a>
Из второй формулы A5), переставляя порядок интегрирования, получаем
00 * 00
=—2Im
О — оо
ш N
1 ,
-»oo
J
8
Л ЛГ-»<в J t —<
Разбивая последний иитеграл иа три:
* . A7)
где б>0—малое фиксированное число, получаем, что при N—> со из-за
частой осцилляции косинуса 1-й и 3-й Интегралы стремятся соответственно и
t-e
1GU и [Ж*
т— < J т—f
/+8
(формально это можно доказать с помощью замены N (т—t)=s). Что касается
среднего интеграла A7^, .то разлагая / (т) в ряд по степеням t—t, получаем,
что он стремится к нулю ири г—>-0. Вспомнив определение главного значе-
значения (v. р.) сингулярного интеграла (ЛВМ. п. XIV. 19), получаем окончательно

§ 3. ВАРИАНТЫ 161
Подобным образом, из формулы A6) приходим к формуле
Эти дне формулы, справедливые в силу их линейности и для комплексных
функций от вещественного аргумента, и определяют преобразование Гильберта
и обратное к нему. (Докажите, что при этом преобразовании sin t —> cos t;
см. но этому новоду также формулы A1.3.33).)
Некоторые из интегральных преобразований выводятся вз формул крат-
кратного преобразования Фурье для функций нескольких неременных. Приведем,
вапример, формулы для двойного преобразования Фурье:
(*. y)dxdy, A8)
1
<2я]
OD
GO
f
— OD
GO
GO
С
— GO
A9)
Эти формулы получаются просто с помощью последовательного выполнения
преобразования Фурье по каждой из независимых переменных. Аналогично
выглядят формулы для любого числа независимых неремеиных.
Допустим теперь, что функция / (х, у) после перехода к полярным координа-
координатам р, ф оказывается ие зависящей от <р, т. е. /=/ (р). Тогда, переходя к поляр-
полярным координатам a, if в плоскости ?, г|, нерепишем правую часть A8) в виде
се 2Л
—LjfpdpC e~f (осоа*.рсоаф+а sin *
О О
В силу периодичности косинуса внутренний интеграл равен
(см. ЛВМ, п. XVII.24). Мы видим, что функция A8) также оказывается ра-
диальио-симметричной, т. е. F=F(o), где
B0)
Аналогичным образом формула A9) дает
се
/ (р)=2я jj Jo (op) F (с) с do, B1)
о
Формулы B0) и B1) определяют преобразование Ханкеля и его обращение.
Обычно они пишутся без коэффициентов перед интегралами, так как 2nF (a)
6 А. Д. Мышквс

162 ГЛ. III. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
можно вновь обозначить через F(a). Преобразованием Ханкеля называется
также преобразование, которое получится, если для любого фиксированного
п—0, 1, 2, ... принять f=f(p)ela4. Проверьте, что тогда F=F(о)е/|И|, где
f (р) и F (о) связаны формулами ¦ <
F (or) = ¦—¦ J Jn (orp) f(f>)pdo, f (р)=2л*« J /„ (op) F (a)
о о
Свойства преобразования Ханкеля и формулы преобразования конкретных
функций можно получать либо непосредственно, либо возвращаясь к преобра-
преобразованию Фурье A8), A9), так как
/(р)=/ (yV2-f-(/2), F(p)=F (W+*l2)*
ч . .
4. Интегральные преобразования на' конечном интервале. Применяются
также интегральные преобразования на конечном интервале—обычно с теми
же ядрами, что были указаны выше, но с конечными а и Ь в формуле A2)
Свойства н приложения таких преобразований указаны в гл. VI книги [113].
Мы остановимся здесь для примера на конечном синус-преобразованин Фурье
B2)
будем эту связь между функциями f(f) я F (р) обозначать, как и раньше,
знаком / @ —> F (р). Верхний предел интегрирования может быть и другим:
проверьте, что если
I
Ф (р) = $ sin pt-f (t) dt,
о
то
Если функция f (t) в формуле B2) абсолютно интегрируема при 0</<я,
то функция F (р) аналитична на всей плоскости р, т. е. является целой функ-
функцией. Формулу для разложения / (I) в ряд Фурье по синусам
/(o=26*sinW'
k=i
где
можно записать в виде
B3)
и трактовать как формулу обращения преобразования B2).

§ S. ВАРИАНТЫ 163
¦Обозначим образ функции f"(t) через FA(p); тогда
я я .•¦¦..-.
Fa(p)= J sinpt.r(i)dt=sinpt-r (Q |"=0 -Р J cos pi. f'(t)dt =
О О
п
= sin яр/' {л)-р cos pt-f (t) |я=о -p* J sinp/-/ @ dt=»
0
=_ p*F (p)+sIn яр-/' (я)-р cos яр-/ (n)+4>t @); B4)
при этом /' (л) понимается как f (я—0) и т. п.
Другие свойства преобразования B2) можно либо доказать непосред-
непосредственно, либо же заметив, что F (р) в формуле B2) представляет собой обыч-
обычное синус-преобразование Фурье функции
:«); ;¦
этот подход возможен н к другим интегральным преобразованиям на конеч-
конечном интервале.
Свойства преобразований можно, как и в § 2, применить к решению раз-
различных уравнений. Пусть, например, требуется решить уравнение B.14) для
0< / < оо, 0<x<:rc, если задано начальное условие B.15) (для <)<.*< я)
и граничные условии
«U=o=t(O. «lx=j=X(O (заданы, 0</< оо).
Совершим над и (t, х) ' преобразование типа B2) по х, т. е. обозначим
u(t, х)—»• U (/, р), считая / параметром. Тогда в силу формул B4) и B.14)
получим
BU ди
-тг=—ар2и-\-ain лр-v- —pcos np-XtO + P^v)» B5)
ot Ox x=n
тогда как начальное условие даст
я
<26)
Имея в ниду применение формулы обращения B3), положим в B5) р раниым
любому целому k=\, 2, 3, ... Тогда второй член в правой части B5) выпа-
выпадет, и мы получим обыкновенное линейное дифференциальное уравнение пер-
первого порядка, которое при начальном условии B6) имеет решение
(проверьте!). Теперь искомое решение u(t, x) получается с помощью формулы
обращения типа B3):
00
u(t,x) = —2^V(t, tysinfe*.
6*

Г л а в а IV
ЛИНЕЙНАЯ АЛГЕБРА
Язык, «психология» и методы линейной алгебры все более ши-
широко применяются в современной прикладной математике. Линейная
алгебра предоставляет естественный аппарат для единообразного
изучения различных линейных физических и математических процес-
процессов, часто подсказывает само направление исследования. С помощью
методов линейной алгебры изучаются и нелинейные задачи на основе
линеаризации; многие нелинейные методы испытываются на линейных
моделях. По этой причине элементы линейной алгебры в последние
годы введены в общий курс математики для втузов. Мы будем
предполагать знание этих элементов в том или ином объеме (опре-
(определители и системы линейных алгебраических уравнений, ма-
матрицы и квадратичные формы, линейные пространства и линейные
отображения); в частности, достаточно просмотреть ЛВМ, §§ VI. 1,2,
VII.1—3,6, XI.1—3, включая мелкий шрифт.
Однако более сложные приложения требуют более глубокого
изучения линейных отображений, квадратичных форм и других объек-
объектов линейной алгебры. Поэтому здесь будут изложены дополнительные
сведения из линейной алгебры, как углубляющие указанные эле-
элементы, так и принципиально новые. Дальнейший материал можно
найти, например, в книгах [28, 118, 134].
Напомним, что линейным пространством называется совокупность (R)
некоторых объектов, над которыми можно выполнять линейные
действия — сложение нх друг с другом и умножение их на числа,—
причем эти действия должны удовлетворять некоторым естественным
требованиям, аксиомам линейного пространства. В зависимости от
того, допускается умножение только на вещественные или на любые
комплексные числа, (/?) называется линейным пространством над
полем вещественных или над полем комплексных чисел или, короче,
вещественным или комплексным линейным пространством. Мы будем
рассматривать только конечномерные пространства; в я-мерном про-
пространстве (/?) любая совокупность из л линейно независимых векторов .
(элементов) называется базисом и каждый элемент X (Е (Щ (€ — знак
принадлежности) однозначно разлагается по базисным векторам.
Линейное пространство называется евклидовым, если в нем вве-
введено понятие скалярного произведения, удовлетворяющее определен-
определенным естественным аксиомам; евклидово пространство также может
быть вещественным или комплексным. Основной пример л-мерного

§ 1. СОПРЯЖЕННЫЕ ОТОБРАЖЕНИЯ 165
евклидова пространства—это совокупность всех «-мерных числовых
векторов, т. е. столбцевых матриц высоты п, причем скалярное про-
произведение определено по правилу:
(х, y) = xiyl+...+xnyn
(в вещественном случае),
I*
(в комплексном случае),
где звездочкой обозначается комплексно сопряжейное число. (Мы бу-
будем в этой главе обозначать числовые векторы прямым полужирным
шрифтом, в отличие от элементов произвольного линейного простран-
пространства, для которых будет применяться полужирный курсив.) В обоих
случаях годится формула х-у=(х, у)=у*х, где звездочкой обозначается
переход к сопряженной матрице, получающейся из исходной матри-
матрицы с помощью ее транспонирования и для матриц с комплексными
элементами замены этих элементов на комплексно сопряженные.
Другие л-мерные линейные или евклидовы пространства в опре-
определенном смысле равносильны (изоморфны) этому. В евклидовом
пространстве можно говорить об ортогональности (перпендикулярно-
(перпендикулярности) векторов, о норме (длине) вектора и о евклидовых базисах,
составленных из попарно ортогональных нормированных векторов.
Одним из центральных является понятие линейного отображения
у = Ах (х ? (R), У € (S)) линейного пространства (/?) в линейное про-
пространство (S); при этом х пробегает все (/?) и требуется, чтобы
A(.xr + x2)~ AjCj + AjCj, a (Xjc) = % Ах. Совокупность A (R) всех
образов, на которую отображается (/?), не обязана совпадать с (S),
а представляет собой, вообще говоря, некоторое (линейное) под-
подпространство (S). (Обратите внимание иа различие терминов *ото-
бражение в» и «.отображение на», т. е. заведомо на все.) Если
в (/?) и в (S) выбраны базисы, то каждый вектор x?(R) (соответ-
(соответственно у(Е (S)) полностью характеризуется набором х (соответст-
(соответственно у) своих координат, и имеет место соотношение у = Ах, где
А—матрица отображения А в выбранных базисах.
§ 1. Сопряженные отображения
1. Прямая сумма. Пусть у пространства (R) указаны какие-то
его подпространства (/?j), (/?г), ..., (Rm), причем размерность подпро-
подпространства (Rk) равна лл^0. Тогда говорят, что (R) разложено в
прямую сумму этих подпространств, если каждый вектор х € (R)
можно представить и притом единственным способом в виде
х=xt + х2+... + хт, где х1 € (/?!>, х2 € (#*), • - •, *„ € (RJ. A)
Например, в трехмерном пространстве применяется как разложевие век-
вектора по трем осям (это значит, что /п=3, п1=п2=п3 = 1), так и разложение
по оси и не параллельной ей плоскости (этозначит, что/п=2, «!=!, па=2).

ТЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
Легко проверить свойства разложения в "прямую сумму:
1. Любая совокупность ненулевых векторов ak € (/?*) (k = 1, 2,..., m)
линейно независима. В самом деле, если, например, а1 = ааа+...
- • • + Vе»,. т0> обозначив хх = av хг = — сса2,..., хт = — уат, полу-
получим, 'ЧТО
=0 = 0+0+... +0,
а это противоречит (так как жх =5*= 0) единственности представления
вектвра О в виде A).
2. лх+й8 + ... +ят = л. В самом деле, если в каждом прост-
пространстве (Rk) выбрать базис из nk векторов, то совокупность веек
этих векторов при всех k = \, 2, ..., т образует базис (R) (про-
(продумайте, почему).
Ми предоставляем читателю проверить, что и обратно, если
у Щ) даны подпространства (/?х), (/?г), ..., (Rm) и выполнено первое
свойство, то совокупность (R) векторов х вида A) представляет
содой подпространство пространства (R) и разлагается в прямую
сумму своих подпространств (/?х), (R2), ...,(/?„). Если к тому же
выполнено второе свойство, то (/?) = (/?).
2. Инвариантные подпространства. Пусть задано отображение А
пространства (R) в себя. Подпространство (Rt) пространства (R) на-
называется инвариантным (относительно отображения А), если это
отображение переводит (/?х) в себя, т. е. если для всех х € (RJ
будет Ax^(Rl). При этом мы будем впредь исключать тривиальный
случай, когда (/?х) нульмерно, т. е. состоит только из нуль-вектора.
Пусть, например, рассматривается вращение трехмерного пространства
вокруг «екоторой оси. Тогда совокупность векторов, параллельных этой оси,
образует одномерное инвариантное подпространство; совокупность векторов,
перпендикулярных этой осн, образует двумерное инвариантное подпростран-
подпространство; совокупность всех векторов образует трехмерное инвариантное подпростран-
подпространство (так как каждое пространство можно считать подпространством самого
себя). Другой пример: совокупность собственных векторов, отвечающих задан-
заданному собственному значению отображения А, представляет собой инвариант-
инвариантное подпространство (почему?).
Пусть пространство (/?) разлагается в прямую сумму инвари-
инвариантных подпространств (Rk) размерности пк (й=1, 2, ...,/»).
Выберем в (R) базис /х, /а, ...,/„ так, чтобы первые пх его век-
векторов содержались в (/?х), следующие пг — в (/?а) и т. д. В таком
базисе матрица А отображения А имеет характерную структуру.
В самом деле, вспомните, что /-й столбец матрицы А — это столбец
из координат вектора А/у в выбранном базисе. Значит, при/= 1, 2, ...
..., пг только первые пх элементов у этих столбцов могут быть
отличными от нуля (почему?); при /=п1-{-\, лх + 2, ..., nt-\-nt
могут быть отличными от нуля только элементы с такими же номе-
номерами и т. д. Мы получаем (продумайте это1), что матрица А имеет

§ 1. СОПРЯЖЕННЫЕ ОТОБРАЖЕНИЯ 1167
следующий вид (в условной записи):
А-1 •. 1; B)
\ А»/
по диагонали разместились квадратные матрицы Ах, Аг, ..., Ат
соответственно порядков nv n2, ..., пт) а все прочие элементы
равны нулю. Матрица вида B) называется квазидиагональной с на-
набором порядков (лх, п2, ..., пт). Например, матрицы
квазидиагоиальные, с наборами порядков A, 1, 1), A, 2), C) соот-
соответственно (впрочем, первой матрице можно также приписать набор
порядков A, 2), B, 1) или C)).
Обратно, если в некотором базисе матрица отображения А имеет
вид B), то подпространство (/?х), натянутое на первые пх базисных
векторов (т. е. составленное из всех линейных комбинаций этих век-
векторов), подпространство (/?2), натянутое на следующие п2 базисных
векторов, и т. д.—все инвариантны. Из A) получаем
A* =.Ajcx + Адсг + • ¦ • + Ажга.
Таким образом, если выяснить, как действует отображение А в каж-
каждом подпространстве (Rk) (т. е. какова структура матриц Ак), то мы
получим и структуру всего отображения А: оно сводится к незави-
независимому действию над компонентами вектора в инвариантных прямы*
слагаемых (/?х), (R2), ..., (Rm).
3. Сопряженные отображения. Пусть даны евклидовы комп-
комплексные пространства (R), (S) (для вещественных пространств все
рассмотрения совершенно аналогичны) и дано линейное отображение А
пространства (/?) в (S); коротко это записывают так: (R)—»•(.$) или
А:(/?)—>(S) (не путать с переходом к пределу!). Тогда линейное
отображение В:E)—>-(/?) называется сопряженным к А, если
(Ах, y)(S) ¦= (х, By)iR) для всех * € {R), У € (S)', ¦ C)
здесь индекс указывает, в каком нроетранетве берется скалярное
произведение. Севряженное к А отображение обозначается буквой А?.
Подчерняем, еще раз, что если А ото&ражает (R) » (S), то А* ого-
бражает fS) #(/?). ..:¦-.,
Выберем в (/?) евклидов базис рх, р2, ...,рп, а в E)—евклидов,
базис qv q2, ..., Щт. Пусть в этих базисах А будет иметь матрицу

168 ГЛ. IV. ЛИНЕЙНАЯ. АЛГЕБРА
А, а В—матрицу В. Тогда легко проверить, что для справедливости
соотношения C) необходимо и достаточно, чтобы В=А*; другими
словами, в евклидовых базисах сопряженные отображения имеют со-
сопряженные матрицы, и обратно. В самом деле, в силу правила пост-
построения матрицы отображения в заданных базисах (см., например, ЛВМ,
п. XI.6), элементами матрицы А служат числа aJk = (Apk, qj) (/=1,
2, ..., п; k=\, 2, ..., /я), а элементами матрицы В—числа (Bqk,
Pj). Отсюда в силу C) получаем b/k = (Bqk, pf) = (Ap/t qk)* = a*kl, т. е.
n m
B = A*. Обратно, если B=A*, JC = 2 arPr> 3'=2Pj9j' t0 левая
r=\ s=T
часть (З) равна 2arP*afr> a правая часть равна 2arPJ^s =
г. s г, s
-2ХР*^.
Г, S
Из доказанного вытекает, что для всякого отображения имеется
сопряженное и притом только одно (именно, .отображение с сопря-
сопряженной матрицей); сопряженное к сопряженному отображению есть
исходное отображение, т. е. А** = А, отображения А* и А взаимно
сопряженные.
Если (?) = (/?) и А* = А, то отображение А называется самосо-
самосопряженным. В евклидовом базисе ему отвечает матрица А = А*, т. е.
aik==atfi такая матрица называется самосопряженной или эрмитовой
по имени французского математика Ш. Эрмита A822—1901). Для ве-
вещественных матриц самосопряженность равносильна симметричности.
Геометрические примеры сопряженных отображений легко получить с по-
помощью транспонирования соответствующей матрицы. Пусть, например, мы
рассматриваем отображения вещественной плоскости в себя; тогда растяжение
вдоль оси, всестороннее растяжение, зеркальное отражение, проектирование
на прямую—это самосопряженные отображения. Поворот ва угол асопряжен
с поворотом на угол—а, а сдвиг вдоль некоторой осн сопряжен с аналогичным
сдвигом вдоль перпендикулярной оси.
4. Разложение, связанное с сопряженными отображениями.
Прямое разложение (п. 1) евклидова пространства называется ортого-
ортогональным, если векторы из различных прямых слагаемых обязательно
ортогональны друг другу. Например, трехмерное пространство можно
представить в виде ортогональной прямой суммы плоскости и пер-
перпендикулярной ей прямой. Для любого подпространства (Rt) прост-
пространства (/?) можно указать и притом единственным способом орто-
ортогональное дополнение, т. е. подпространство (R2), образующее вме-
вместе с (/?х) ортогональное прямое разложение (/?): для этого нужно*
взять совокупность всех векторов из (/?), каждый из которых орто-
ортогонален (/?j), т. е. всем векторам из (/?j). Отметим, в частности,
что О и (/?) служат ортогональными дополнениями друг друга.
Пусть дано линейное отображение А пространства (/?) в прост-
пространство (S). Совокупность всех векторов x?(R), для которых Ах —О,
называется ядром этого отображеиия, это ядро обозначается А~1(О);

§ 1. СОПРЯЖЕННЫЕ ОТОБРАЖЕНИЯ 169
совокупность всех векторов вида А* (х ? (/?)) называется образом
при отображении А; он обозначается А (/?). Мы предоставим чита-
читателю проверить, что А(О) представляет собой линейное подпро-
подпространство {/?), a A (R)—линейное подпространство {S), причем раз-
размерность А (/?) равна рангу матрицы отображения А при произвольно
выбранных базисах в (/?) и (S).
Пусть теперь пространства (/?) и (S) евклидовы. Тогда (R) раз-
разлагается в ортогональную прямую сумму своих подпространств А (О)
и A* (S).
В самом деле, легко проверить ортогональность этих подпространств: если
Х\?А-1(О), Х2?А* (S),to по определению Ах1=О, х%—А*у(у?(8)) и всилу
формулы C) (хи x2)iR)—(x1, A*y)iR) = (Ax1,y)iSy={0, y)iS)=0. Остается про-
проверить, что каждый вектор x?(R) можно представить в виде суммы .«,-{-х2,
где Хх^А*1 (О), jc2?A*(S). Обозначим через ха проекцию вектора х на под-
подпространство A*(S); тогда (х—хг, х')<#)=0 для любого вектора x'?A*(S).
Другими словами, (х—xit А*у)^=0 для любого,у?E). В силу C) получаем,
что (А{х—хг), y)tSi=Q, а так как у произвольно, то А (ж—д;г)=0. Значит,
х—x\=X\?h~x @), т. е. справедливость ортогонального разложения доказана.
Так как отображения А и А* взаимно сопряженные, то, применяя
доказанное утверждение к А*, мы получим, что и (S) разлагается
в ортогональную прямую сумму своих подпространств А* @) и
A (R). Другими словами, уравнение Ах = Ь при заданном Ь ? {S) имеет
по крайней мере одно решение х € {R) тогда и только тогда, когда Ь
ортогонально А* (О), т. е. ортогонально всем линейно независимым
решениям уравнения А*у = О {у ? {$))¦ Оказывается, что это свойство
имеет место и для целого ряда классов линейных уравнений в бес-
бесконечномерных пространствах.
Из доказанного ортогонального разложения вытекает, в частно-
частности, что
dim А  @) + dim A* (S) = dim (/?), dim A*  @) -f dim A (#) = dim (S),
где буквами dim обозначается размерность, от французского
dimension. Кроме того, если ввести в (R) н (S) евклидовы базисы,
то видно, что всегда dim А (/?) = dim A* (S) (у сопряженных матриц
ранги одинаковы!). Отсюда вытекает, что dim А (О)—dim A* @)=
= dim(/?)—dim {S). В частности, если (R) — (S), т. е. рассматри-
рассматривается отображение пространства в себя, то dim A @) = dim A*~x{0),
т. е. число линейно независимых решений уравнения кх = 0 равно
аналогичному числу для уравнения к*у = 0.
б. Отображение пространства в себя. Если (/?) = (S), то можно
говорить о собственных значениях и собственных векторах отобра-
отображения А, а также А*. Легко доказать, что если Я служит собст-
собственным значением отображения А, то К* служит собственным зна-
значением отображения А*, причем той же кратности. В самом деле,
после выбора в (/?) евклидова базиса соответствующие характери-
характеристические уравнения det(A—XI) = 0 и det(A*—Я1) = 0 получаются

170 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
одно из другого заменой всех коэффициентов на их сопряженные
значения, и потому наше утверждение вытекает из свойств сопря-
сопряженных комплексных чисел (ЛВМ, пп. VIII.3 и 8).
Докажем следующее свойство ортогональности: если р и Я—соб-
Я—собственный вектор и соответствующее собственное значение для ото-
отображения A, a q и \i — для отображения А*, причем Я=^=ц*, то
{р, Я) = 0. Это вытекает из сравнения правого и левого членов
в цепочке равенств
Ь{Р, Я) = &Р, Я) = {Ьр, Я) = (Р, A*q) = (p, \iq) = \i*(p, q).
Отсюда вытекает такое следствие. Пусть все собственные зна-
значения klf Яг, ..., Я„ отображения А простые (различные) и plt pt,.
..., р„ — соответствующие ненулевые собственные векторы; как из-
известно, они обязательно линейно независимы (ЛВМ, п. XI.4) и по-
потому могут быть приняты за базис в (/?). Мы видели, что Я? , Х%,, ...
..., К%—собственные значения отображения А*; пусть qlt q2, ...
... ,qn—соответствующие ненулевые собственные векторы. Тогда эти
два базиса (R) биортогональны друг другу, т. е.
D)
При j азложении любого вектора по заданному базису знание биор-
тогонального базиса позволяет просто вычислить коэффициенты раз-
разложения: в самом деле, умножив равенство
скалярно на qk и воспользовавшись формулой D), получим
(*. **) = «*(/»*. Ян), т- е- а* = ^^) (* = 1' 2' ••" ")•
Ортогональный базис—это базис, биортогональный сам с собой.
Для каждого базиса ръ р2, ..., р„, независимо от его происхождения,
можно построить биортогональный базис qlt q2< •••.flm который определяется
однозначно с точностью до скалярных множителей. В самом деле, qx надо
взять,ортогональным к (п—1)-мерному подпространству, натянутому на р3,...
.... р„, и т. п.; проверьте, что такие векторы <7/будут линейно независимыми,
т. е. будут на самом деле образовывать базис. В /г-нериом евклидовом прост-
пространстве нетрудно ввести понятие векторного произведения [хг,х2, ..... хп-^,
обладающего свойствами, аналогичными свойствам обычного векторного про-
произведения двух векторов в трехмерном пространстве. Тогда можно просто по-
положить q1 =\р2, р3, ..., р„] и т. п.
6. Самосопряженное отображение. Пусть А—самосопряженное
отображение пространства (/?) в себя; это значит, что А* = А, т. е.
(А*, у) = {х, Ау) для всех х, у €(#). E)
Напомним, что для этого необходимо и достаточно, чтобы матрица А
отображения А в любом евклидовом базисе была эрмитово^, т. е.
чтобы А* = А.

§ 1. СОПРЯЖЕННЫЕ ОТОБРАЖЕНИЯ 171
Все собственные значения самосопряженного отображения веще-
вещественны: В самом деле, если кх^ = \хх (х1=^О), то, подставляя
в E) х=у = хг, получим после сокращения на (хг, ху) = | ж, |2 Ф О,
что Х = Х*, откуда н следует наше утверждение.
Ортогональное дополнение к инвариантному подпространству для
отображения А также является инвариантным. В самом деле, пусть
(/^—инвариантное подпространство (/?), a (R2)— ортогональное до-
дополнение к (/?j). Возьмем любой вектор х € (R2); надо доказать, что
и kx?(R2), т. е. кх ортогонален любому вектору J>€(/?i). Однако
это вытекает из E), так как ky g {Rt).
Отсюда вытекает важное следствие: в (R) можно выбрать евкли-
евклидов базис из собственных векторов заданного самосопряженного ото-
отображения А. В самом деле, выберем сначала какой-нибудь собст-
собственный вектор /j, притом единичной длины. Тогда в силу доказан-
доказанного (я — 1)-мерное подпространство E) всех векторов, ортогональ-
ортогональных /1( будет инвариантным. Значит, можно рассматривать А только
на (S), Это будет самосопряженное отображение E) в себя; выберем
какой-нибудь собственный вектор 1г этого отображения, затем рас-
рассмотрим (л—2)-мерное подпространство всех векторов из (S), орто-
ортогональных /2, и т. д. Продолжая таким образом, мы построим иско-
искомый базис.
Это следствие можно сформулировать на чисто матричном языке.
Как известно, при переходе от одного декартова базиса к другому
матрица отображения преобразуется по формуле А' = Н~ХАН, где
матрица перехода Н удовлетворяет соотношениям
= НН*=1, т.е. H* = H-»;
такие матрицы Н называются унитарными (вещественные унитарные
матрицы называются ортогональными). Таким образом, мы получаем,
что для каждой эрмитовой матрицы А можно подобрать такую уни-
унитарную матрицу Н, что матрица Н-1АН будет диагональной с соб-
собственными' значениями, матрицы А на главной диагонали.
На основании доказанной вещественности собственных значений
получаем, что следствия, приведенные в последних двух абзацах,
справедливы и для самосопряженного отображения вещественного
евклидова пространства в себя, а также для вещественных симмет-
симметричных матриц.
7. Экстремальное свойство собственных значений. Пусть А —
самосопряженное отображение вещественного пространства (R) в себя.
Поставим каждому вектору X в соответствие значение (кх, X), полу-
получим числовую функцию, заданную на (/?). Рассмотрим значения этой
функции на единичной сфере этого пространства, т.е. на (л—1)-мер-
ном многообразии (S) векторов, удовлетворяющих соотношению
|х|=. Тогда собственные векторы отображения А — это векторы,
в которых функция {кх, X) принимает стационарные значения на (S),
а сами эти значения равны соответствующим собственным значениям.

172 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕВРА
В частности, наибольшее и наименьшее собственные значения равны
соответственно наибольшему и наименьшему значениям функции
(Ах, X) на (S), тогда как на собственных векторах, которым отве-
отвечают промежуточные собственные значения, эта функция имеет ми-
нимакс.
Для доказательства введем в (/?) евклидов базис из собственных
векторов 1г, /2, ..., /„ отображения А, тогда каждый вектор x?(R)
можно разложить по этому базису: X = хх1х -(- хг1% -f-... -f xata. Рас-
Рассматриваемая функция запишется в виде
(A*, x) = k1xl + kixl + ...+knx*n==f(xi, *„.._.., *„),
где Kv К2, ..., Кп—собственные значения отображения А, а урав-
уравнение сферы (S) примет вид
Таким образом, мы пришли к обычной задаче иа условный экстремум
(ЛВМ, п. ХИЛО). Для отыскания условных стационарных значений
пользуемся методом Лагранжа:
^L(f-M)^2Xkxk-2lixk = 0 (*=1, 2, .... я), F)
где буквой ц обозначен множитель Лагранжа. Так как все хк не могут
равняться нулю, то из F) получаем, что какая-нибудь из разностей
Хь — \л равна нулю, например, при k = j. Но тогда из F) видим, что
все координаты xk, для которых kk=?kj, должны равняться нулю;
а этим условием и определяются собственные векторы, которым
отвечает собственное значение Ау (почему?).
Утверждение о максимальном (и аналогично о минимальном)
собственном значении сразу получается, если считать все Лл зану-
занумерованными в порядке Я.Х^Я.2^.. ,^Я„ и представить
(А*, Х) = К1 (*? + *?+ . • • +*»—
(продумайте это!). Отметим, что если собственное значение %t
является «/-кратным, где </^2, то максимум функции (Ах, X) в /,
является нестрогим, так как она принимает постоянное значение Ях
на всем (й—1)-мерном пересечении (S) с подпространством, натя-
натянутым на векторы /х, /2, ..., 1Л.
На рис. 63 показана возможная картина линий уровня функции
(Ajr, x) на единичной сфере в трехмерном пространстве с отмечен-
отмеченными направлениями убывания функции. При этом рнс. 63, а иллю-
иллюстрирует случай Я,1>Я.2>Я.,, а рис. 63, б—случай А,1 = Я.а>Я,8
(продумайте эти рисунки!).
Доказанные свойства справедливы и для самосопряженного отображения
комплексного евклидова пространства (R) в себя. Прн этом полезно иметь
в виду следующее свойство: отображение А такого пространства (R) в себя

§ 1. СОПРЯЖЕННЫЕ ОТОБРАЖЕНИЯ
173
является самосопряженным тогда и только тогда, когда функция (Ад-, х) при-
принимает в (R) только вещественные значения. В самом деле, для самосопря-
самосопряженного А имеем (Аде, *)• = (*, Адс)=(Алс, х), т.е. (Аде, *) вещественно; при
этом в базисе из собственных векторов будет (Ах, х) = Х1\х1 |2+А.2|дс2|2-|-..-
...+%п\хП\\ \x\t=\x1\*+\xt\t+...+\xn\* (проверьте!), откуда и выте-
вытекают упомянутые свойства. Обратно, легко проверить, что любое отображение
А можно представить в виде Ax + tA,, где А1=—-^—, А2=—^. само
сопряженные отображения; поэтому если значения (Ах, x) = (&iX, х) + ((А2ж, *)
вещественны, то (А2ле, *)=^0, откуда А2лезз0 (почему?), т.е. А=АЬ А=А*.
а)
Рнс. 63.
Иногда взамен функции (Ал:, X) (X 6 (•?)) рассматривают функцию
cp(jr) = l—'—f на всем пространстве (R) (кроме вектора х=0, в кото-
\Х, X) ¦ '
ром функция ф имеет разрыв). Так как функция ср постоянна иа
каждой прямой, проходящей через начало координат, то доказанные
выше стационарные и экстремальные свойства собственных значений
можно сформулировать и в терминах функции qp.
Эти экстремальные свойства применяются для оценок и прибли-
приближенного вычисления наибольшего и наименьшего собственных зна-
значений и приближенного вычисления соответствующих собственных
векторов для заданного самосопряженного отображения или для
заданной симметрической матрицы с помощью численного решения
задачи на экстремум функции нескольких переменных. Этот метод
предложил выдающийся английский физик Дж. Рэлей A842—1919).
Для вычисления второго по величине собственного значения К2
и соответствующего собственного вектора /, можно воспользоваться
тем, что, как видно из предыдущего, Х2 равно максимуму функции
ф (х) на подпространстве векторов, удовлетворяющих условию
(д;, /1)'= 0. Для вычисления Я,8 надо воспользоваться двумя условиями
(X,Л) = 0> (Х,.1,) = 0"н т.д.

174 ГЛ. IV.'ЛИНЕЙНАЯ АЛГЕБРА
При вычнслевнн н особенно нсследовавнн собствевных зваченнй иногда
пользуются также следующей теоремой Р. Куранта, которая дает выражение
для каждого собствевного значевня, не связавное с построевнем предшест-
предшествующих ему собственвых векторов:
л*= min f max (Ад:, х)~\ (*=! л). G)
Г max (А*, *)"| (*=1 л).
1х, а,) = ...=<*, <п_,)=0
L 1*1=1 J
Здесь максимум при выбравных векторах аъ ..., «д_! берется по совокуп-
востн ортогональвых им всем векторов еднвнчвой длины, а затем берется
наимевьшее значение этого максимума, зависящего от выбора совокупвостн
векторов at a*-i. для всевозможных таких совокупвостей.
В самом деле, прн заданвых аь ..., a^~i среди векторов вида -х =
=ei'i+-••+«*'* обязательво найдется по крайней мере одвн, удовлетво-
удовлетворяющий условиям (л:, ai)=.. .=(jc, o*-i)=0, |л:| = 1 (почему?); во для вего
(Ajc, *)=X1a»+...4-^fta|^A.ft; значит, и вся правая часть G) ве меньше Х^.
Но еслв выбрать ax=/i e*-i = '*-i> TO выражение в квадратвых скоб-
скобках G) равво Хк (проверьте!), а потому н вся п'равая часть G) равва Хд.
§ 2. Квадратичные формы
1. Введение. Формой от нескольких переменных в алгебре назы-
называют однородный многочлен от этих переменных; в соответствии со
степенью этого многочлена форма может быть линейной, квадратич-
квадратичной, третьей степени и т. д. Здесь мы будем рассматривать квадра-
квадратичные формы с вещестненными коэффициентами от нещественных
переменных. Как известно из вводного курса линейной алгебры,
квадратичную форму F от переменных х1г х2, ..., х„ можно запи-
записать в виде F=x*Ax, где х—столбец из этих переменных, а А—
симметрнческан матрица задавной формы. При линейной замене пере-
переменных по формуле х = Нх' форма преобразуется по формуле
/=-=х'*А'х', где А' = Н*АН (ЛВМ, п. XI.11).
Из результатов п. 1.6 вытекает, что всегда можно подобрать
такую ортогональную матрицу Н, что матрица А' будет диагональ-
диагональной, т. е. в новых переменных квадратичная форма будет иметь вид
F=
где Kv К2, ..., %п—собственные значения всходной матрицы А.
Такая квадратичнан форма, без попарных произведений переменных,
также называется диагональной.
Если все собственные значения матрицы А положительны, форма
F называется положительно определенной, если все Xk < О,— отри-
отрицательно определенной; те н другие формы называются дёфинйт-'
ными; для них характерно то, что они равны нулю только при
х1 = хг= ... =хп = 0 {почему?). Если имеются кк = 0, форма F
называется вырожденной; для этого необходимо и достаточно, чтобы
detA = O. Из A) видно, что вырожденная форма после соответст-
соответствующей линейной замены становится функцией менее чем п пере-
переменных.

§ 2. КВАДРАТИЧНЫЕ ФОРМЫ 175
Описанное приведение квадратичной формы к диагональному
виду A) имеет простой геометрический смысл. Уравнение F(xt, х2, . ..
..., хп) = 1 определяет в вещественном числовом пространстве- Ен
многообразие {Щ размерности л—1, которое естественно называть
поверхностью второго порядка; при этом, так как F{—хг, —х2, . ..
..., —xn)=E=F(xx, x2, ..., хп), то (М) имеет центр симметрии
в начале координат О. Замена переменных по формуле х = Нх'
с ортогональной матрицей Н означает поворот осе.й координат вокруг
О (ЛВМ, п. XI.9); значит, производится такой поворот осей, после
которого уравнение поверхности (М) примет вид
X1x? + Xlx'* + ...+Xnx? = h B)
называемый каноническим (вспомните канонические уравнения линий
и поверхностей второго порядка). Из уравнения B) видно, что
оси х[, х'г, ..., х'п служат осями симметрии поверхности (S), они
называются ее главными осями; поэтому и описанное преобразо-
преобразование квадратичной формы называется приведением ее к главным
осям.
Если форма F была невырожденной, то может получиться л-f-l
тип поверхностей, в зависимости от числа положительных и отри-
отрицательных из чисел Xk. В частности, если все Xk > 0, получается
эллипсоид с полуосями ¦ г—' (почему?), если все Кк < 0, получается
мнимая поверхность; в остальных случаях получаются гиперболоиды
различных типов. (Что будет, если форма F вырожденная?)
В заключение скажем об эрмитовых квадратичных формах вида
F= z*Az с эрмитовой (п. 1.3) матрицей А и комплексным столбцом г.
Так как F* = F (почему?), то такая форма принимает только веще-
вещественные значения. После соответствующего унитарного преобразо-
преобразования z = Hz' (п. 1.6) получаем
2. Закон инерции квадратичных форм. Вернемся к веществен-
вещественным квадратичным формам F=x*Ax. Такую форму можно привести
к диагональному виду многими различными способами, не требуя
ортогональности приводящей матрицы Н (см., например, п. 3). При
этом коэффициенты при квадратах неизвестных в диагональном виде
отнюдь не являются инвариантами. Однако количества положитель-
положительных, нулевых и отрицательных этих коэффициентов не зависят от
способа приведения квадратичной формы к диагональному виду; этот
факт называется эаконом инерции квадратичных форм. Набор этих
количеств называется сигнатурой заданной формы, только сигнатура
и является инвариантом формы при ее произвольных преобразованиях.
Для доказательства закона инерции допустим, что форма F при-
приведена к диагональному виду двумя способами: х = Н'х' и х = Н"х",

176 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
Приравнивая результаты, получим
К*?+№? + ...+№**К*?+ №?+ •••+*>&• C)
Мы докажем только, что количества положительных коэффициентов
слева и справа одинаковы; тогда, поменяв знаки, получим как след-
следствие, что и количества отрицательных коэффициентов одинаковы,
а из этих двух фактов вытекает, что и количества нулевых коэф-
коэффициентов одинаковы.
Допустим, что в левой части формулы C) положительны коэф-
коэффициенты Х[, Х'г, ..,, Х'к, а в правой—коэффициенты X"lt XI, ...,. А,*»,
причем, для определенности, k" > k'. Приравняем
xi = 0, xt = 0, ..., х'ь> = 0, х"ь»+1 = 0, д:^«+2 = 0, ..., х"п — 0.
Если сюда подставить выражения всех х) и х) через хъ хг, ..., ха,
то мы получим относительно последних систему линейных однород-
однородных уравнений, причем уравнений будет k'-\-(n—k") < n, а неиз-
неизвестных п. Такая система обязательно имеет по крайней мере одно
ненулевое решение (почему?). Найдя соответствующие значения всех
х) и x"j и подставив их в C), получим, что левая часть ^0, а пра-
правая > 0 (продумайте это!). Полученное противоречие и доказывает
Закон инерции.
3. Метод Якббн и теорема Сильвестра. Здесь мы опишем пред-
предложенный К. Якбби метод приведения вещественной квадратичной
формы /?==х*Ах к диагональному виду, ие требующий решения
алгебраических уравнений. При этом предполагается, что главные
миноры матрицы А, т. е. мииоры, примыкающие к ее левому верхнему
углу,
"а ан ••• ат
¦a-* Une • • • «п„
все отличны от нуля.
Предлагаемое преобразование имеет треугольный вид
'г + «18*8 + • • • + ащХ'п,
и должно привести к тождеству
2 auxixJ^p1x'11+p2x'i1+...+р^. E)
Неизвестные коэффициенты ctJy- и р,- можно иайти по этапам. Положим

§ 2. КВАДРАТИЧНЫЕ ФОРМЫ 177
сначала в формулах D) и E) х'2 = х'л= ...—х*„ = 0, получим
откуда р1 = а11 = А1. Положим затем в D) и E) х'3¦= х\ = ...
... — х'п = 0, получим
= x~haX Х Х
Подставив первые две формулы.в третью и приравняв коэффициент
при x[x't нулю, получим уравнение для нахождения а1г
откуда можно получить а12, так как по условию а1х ф 0. Применяя
к соотношениям F) формулу А' = Н*АН и заметив, что в данном
случае detH = detH*= 1, получим после перехода к определителям
li
= Д2, откуда р2 = -4.
Полагая далее х\ = х'ъ = ... = х'„ = 0 и приравнивая коэффициенты
при х[х'3 и х'2х'3 нулю, получим систему из двух уравнений первой
степени для нахождения а13 и с^з, так как а1а уже найдено. Можно
показать, что определитель этой системы равен Д2, и так как по
условию Д2 Ф 0, то возможно найти а18, а23. Из формулы преобра-
преобразования "матрицы квадратичной формы получаем, что
/У>Л = Д3, откуда Р* = -ц-
Продолжая далее таким же образом, мы получим требуемое преоб-
преобразование, приводящее исходную форму к диагональному виду
Следствие. Если все Дйф0, то форма х*Ах имеет сигна-
сигнатуру (п — s, 0, s), где s — число перемен знака в последовательности
1, Лх> Д2, ..., А„. В самом деле, это число как раз равно числу
отрицательных коэффициентов в формуле G). А так как нулевые
коэффициенты по условию отсутствуют, то остальные п — s коэф-
коэффициентов положительные.
Теорема Сильвестра (Д. Сильвестр, 1814—1897, англий-
английский математик). Для положительной определенности формы х*Ах
необходимо и достаточно, чтобы все главные миноры матрицы А
были положительны. В самом деле, если все &кф0, то утвержде-
утверждение вытекает из предыдущего абзаца. Пусть теперь некоторый ми-
иор ДА = 0; это значит, что сумма 2 aijXtXj как квадратичная

178 ГЛ: IV. ЛИНЕЙНАЯ АЛГЕБРА
форма от д:1> xt, ..., xk является вырожденной, а потому навер-
наверняка можно подобрать ненулевую (нетривиальную) комбннацию значе-
значений x1 = b1, xt = bt, ..., xk = bk, обращающую эту форму в нуль.
Но тогда исходная форма прн ненулевой комбинации значений
xl = b1, ..., xk = bk, хк+1 = 0, ..., хп = 0 обращается в нуль
и потому не может быть дефинитной. Теорема доказана. Отметим,
что она оказывается справедливой и для эрмитовых квадратичных
форм (п. 1).
4. Одиовремеииое приведение двух квадратичиых форм к диа-
диагональному виду. Пусть заданы две вещественные квадратичные
формы /г=х*Ах и G=x*Bx, из которых первая положительно опре-
определенная. Тогда существует единое вещественное преобразование
х = Нх', приводящее первую форму к сумме квадратов, а вторую—
к диагональному виду.
В самом деле, осуществим сначала преобразование х —Ку, при-
приводящее форму F к диагональному виду ргу\ +р*у| + • • • +РпУп-
Тогда все рк > 0, и потому можно осуществить преобразование
р/У)-у): т- е- л=у^Уь л=у%у* •••'•Уя=Yt; у'ю Ko"
ротко y = Ly', приводящее F к виду
В реаультате обоих этих преобразований из G получается форма
O=y'*L*K*BKLy' = y'*B'y', где B'=-L*K*BKL (B'* = B'). Осущест-
Осуществим теперь приведение формы у'*В'уг к диагональному виду с по-
помощью ортогонального преобразования у' = Н'х'. Получим
окончательно
x = KLH'x' = Hx', где H = KLH';
форма О станет диагональной по выбору Н', а форма F перейдет
в х'*х' = дг'х2 -f- х'гг ¦+¦... + *в* (почему?). Утверждение доказано.
Нетрудно установить, какие получатся коэффициенты у формы О.
В самом деле, нз равенств Н*АН = 1, H*BH = diag (gv g2, ..., gn)
вытекает, что
(почему?). Значит, диагональные коэффициенты gj—это корни урав-
уравнения det(^A—В) = 0 или, так как *.А — В = — A(A-1B— Kl), это
собственные значения матрицы А-1В. Заодно мы видим, что при
сделанных предположениях матрица A-1B, хотя, вообще говоря, не
симметрическая, должна иметь все собственные значения вещест-
вещественные.
Это утверждение имеет важное применение в теории колебаний.
Пусть некоторая автономная (т. е. не меняющая своих параметров
со временем) система с конечным числом степеней свободы и обоб-
обобщенными координатами qlt qt, ..., qn обладает потенциальной энер-

§ 3. СТРУКТУРА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ 179
гией U=U{q1,q2, ...,qn) и находится вблизи состояния равновесия
qx = 0, q\ = 0, ..., qn = 0. Тогда можно показать, что, с точностью
до малых выше второго порядка, кинетическая и потенциальная
энергии системы имеют вид квадратичных форм
причем первая форма будет положительно определенной. Если со-
совершить линейную замену обобщенных координат по формуле
q = Hq', то q = Hq\ т. е. форма Т преобразуется так же, как если
бы точек над координатами не было. Пользуясь доказанным утверж-
утверждением, мы получаем, что можно перейти к обобщенным координа-
координатам q[, <7s> • • •. q'm B которых кинетическая и потенциальная энер-
энергии имеют вид
1
(9)
Эти координаты называются нормальными координатами системы.
Из выражения (9) можно вывести, что если все |ift > 0 (т. е. форма U
в (8) была положительно определенной), то рассматриваемое поло-
положение равновесия устойчивое, если же имеется \ik < 0, то это по-
положение неустойчивое.
§ 3. Структура линейного отображения
Рассмотрим линейное отображение А комплексного линейного
л-мерного пространства (/?) в себя. В элементах линейной алгебры
(ЛВМ, пп. XI.4,8) доказывается, что если это отображение имеет л
различных собственных значений, то каждому из этих значений Kh
отвечает один линейно независимый собственный вектор lk. В базисе
из собственных векторов матрица отображения имеет диагональный
вид diag^j, л-,, ..., Я„), т. е. координаты векторов преобразуются
по формулам
Ух = ^1#ц У г — ^a*2> • • • 1 У а—
где штрихом обозначены координаты в указанном базисе. Таким об-
образом, отображение А сводится к комбинации растяжения в Xt раз
в направлении lv растяжения в Х2 раз в направлении /2 и т.д.
Однако если характеристическое уравнение для собственных
значений имеет кратные корни, то отображение А имеет, вообще
говоря, более сложную структуру. Цель этого параграфа состоит
в описании этой структуры.
1. Отображение с единственным собственным вектором. За-
Заметим прежде всего, что отображение А имеет в силу основной
теоремы алгебры по крайней мере одно собственное значение, которому

180 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
отвечает d-мерное (d^l) подпространство собственных векто-
векторов. В этом пункте мы будем считать, что собственное значение
только одно и </=1, т. е. собственный вектор определен с точ-
точностью до скалярного множителя однозначно. Будем считать сна-
сначала, что к = 0, т. е. собственные векторы определяются равен-
равенством Ajr = 0.
Нам понадобится следующая простая лемма: если отображе-
отображение А имеет только нулевое собственное значение и для некоторых
x?{R) и k = 0, 1, 2, ... элементы х, кх, А2*, ..., АкХ линейно
зависимы, то ккХ — 0.
Доказательство. Пусть х Ф О, и пусть, присоединяя к х последо-
последовательно векторы Аде, Аалг мы обнаружим, что векторы х, Ах,' А2ж, ...
..., к1~хх еще линейно независимы, а векторы х, Ах, А*х А1~1х, А1х
уже линейно зависимы (/<?). Тогда А1х линейно выражается через преды-
предыдущие векторы (почему?), т. е. выполняется соотношение вида
Atx+a1At-*x+... +at.1Ax+alx=0, A)
где alt .... в/_1, at— некоторые скаляры. Как известно из алгебры, мно-
многочлен
можно разложить на линейные множители
Р(г)=B-г1)(г-2а)...B-г/) B)
(см. ЛВМ, п. VIII.8). Поэтому в силу A) получим
(A-21I)(A-22I)...(A-2/I)jc=0, C)
где I—тождественное отображение. Обозначим (А—гг1).. .(А—гг1) х через у,
тогда у ф-0 (почему?). Из C) получим
(А—г11)у=О, т. е. Aj»=2j>.
Значит, гх—собственное значение, т. е., по предположению 2i=0. Но так как
в разложении B) сомножители можно переставлять, то и г2—... =г(=0,
т. е. Я(г) = г', откуда а,= ... =za[^1=a[=Q, и из A) получаем, что А1х=0,
но тогда и А*ж=А*-'АОс=0. Лемма доказана.
Будем теперь для простоты считать, что л = 3, т. е. что ос-
основное пространство (R), в котором действует отображение А,
трехмерно. По предположению, подпространство {St) собственных
векторов одномерно. Выберем такой вектор xo€Ej) (? — знак
непринадлежности); могут представиться два случая.
1. Пусть кгХоф0. Обозначим тогда 11 = Х9,1г = кхЛ, 1ъ — к^ха.
В силу доказанной леммы эти векторы линейно независимы и по-
потому образуют базис в (/?). Так как At1 = li, AB=(8. А(8 = 0
(последнее вытекает из той же леммы, так как А/, = А3лгв), то мат-
матрица отображения в выбранном базисе имеет вид

§ 3. СТРУКТУРА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ 181
Вектор /8 собственный, т. е. натянутое на него подпространство
совпадает с (S^. Легко проверить (проделайте это!), что двумер-
двумерное подпространство (?2), натянутое на векторы /а н /8, опреде-
определяется соотношением А2х = 0.
2. Пусть А2х0 = 0. Обозначим через у0 Ф 0 какой-либо собствен-
собственный вектор и выберем любой вектор хг € (/?) вне двумерного под-
подпространства, натянутого на х0 и у0. Тогда АгхгФО, так как
в противном случае можно написать (проверьте!):.
А (А*о) = 0, Ах0 = оув (а Ф 0); А (А хх) = О,
А фх0—ах1) = $ау0 - сфу0 = О, $Х0 - ахг = уу0, jr, - ? х0 - ?
и мы-пришли бы к противоречию. Итак, если обозначить lt = xu
1г = Ах1г /3 = A2jt1, то мы возвращаемся к случаю 1.
Мы предполагали, что собственное значение X равно нулю.
Чтобы рассмотреть общий случай, достаточно воспользоваться про-
простым свойством: х является собственным вектором отображения А,
отвечающим собственному, значению X, в том и только том слу-
случае, если он является собственным вектором отображения А—eel,
отвечающим собственному значению X—а. В самом деле, равенства
Ах = Хх и (А—al)x — (X—<х)х равносильны.
Поэтому если отображение А имеет собственное значение X, то
отображение At = A —M имеет нулевое собственное значение, и мы
приходим к исследованному случаю. Выберем для отображения Ах
векторы /j, lt, 1Я, как описано выше. Тогда в терминах отображе-
отображения А получим (А — %1I1 = 1г и т. д., т. е.
Af; «Mj + Z,. AJ2 = M2-M3, А/8 = Х/3, D)
а потому матрица отображения А в таком базисе имеет вид
/Я. 0 0\
А'-М*.О1 E)
До 1 X)
Такая матрица называется жордановой клеткой по имени француз-
французского математика К. Жордйна A838—1922); для других л она
имеет вид:
д.
Векторы* lv /2, связанные соотношениями D) (и аналогичными соот-
соотношениями при других л) называются присоединенными к собствен-
собственному вектору /,. Подпространства (SJ, (St) и (St) = (/?), натянутые

182 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
соответственно на векторы /3; /2 и /s; llt la и 13, определяются
соотношениями (A—kl)x = O; (A — XlJx = O; (A — UKx = 0.
2. Отображение с единственным собственным значением. Будем
опять для простоты считать, что л = 3, а собственное значение
равно нулю. Случай, когда подпространство (S) собственных векторов
одномерно, был разобран в п. 1. Пусть теперь (S) двумерно; выбе-
выберем произвольно /, € (S) (h € (#)) и обозначим /2 == А1г. Тогда /2 ? (S)
(в противном случае кЧг^0и в силу леммы п. 1 векторы /„ /2
н А/2 можно принять за базис с теми же свойствами, что в п. 1,
а это противоречит двумерности (S)); выберем произвольно 13 ? (S),
h$h- Тогда векторы llt /2, 1Ъ составляют базис (/?), причем
Для произвольного собственного значения мы получаем в этом
случае аналогично п. 1
Таким образом, векторы /2 и 13 собственные, а вектор /t присоеди-
присоединен к 1а; в выбранном базисе отображение имеет матрицу
Д О 0
А' = ( 1 К О
V0 0
Получилась квазидиагональная матрица (п. 1.2), составленнаи из
жордановых клеток второго и первого порядков. Соотношения
(А — %\)х = 0 и (А — %\ух = О определяют соответственно (S) и (R).
Наконец, в случае, когда (S) трехмерно, т. е. (S) — (/?), можно
выбрать базис llt /2, /3 произвольно, и матрица будет иметь вид
Л О О
А' = @ Я. О
\0 0
Получается диагональная матрица, т. е. квазидиагональная матрица
из трех жордановых клеток первого порядка. Все векторы (/?) удо-
удовлетворяют соотношению (А — К1)х = 0.
Оказывается, что аналогичный результат имеет место при любой
размерности р пространства (/?), если отображение А имеет един-
единственное собственное значение к. Именно, после соответствующего
выбора базиса lv /2, ..., 1р матрица А' этого отображения при-
приобретает квазидиагональный вид, составленный нз жордановых клеток
некоторых порядков рг, рг, ..., pd, где рх +рг +•••+/><*=/>> причем
в каждой клетке на диагонали стоит К. Таким образом, векторы
/х, 12, ...,/„_, будут присоединенными к собственному вектору 1р>,
векторы lpilx, lpi+,, .... tPl+p,-t—K собственному вектору lpi+"pt
и т. д. При этом d-мерное подпространство (Sx), натянутое на век-

§ 3. СТРУКТУРА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ 183
торы lpi, lPi+p,, ..., lpt+Pt+...+pd — lp,—это как раз подпро-
подпространство собственных векторов, т. е. решений уравнения (А—Щх=О.
Подпространство («У2), натянутое на все собственные векторы и на
присоединенные векторы, непосредственно предшествующие собствен-
собственным,— это подпространство решений уравнения (А — АЛJ х — Ои т. д.
Обозначим через dk размерность подпространства (Sk) (d1 = d).
Прн переходе от (St) к (S2) размерность увеличилась на d2—йг.
Но она должна увеличиться на количество добавленных присоеди-
присоединенных векторов, т. е. на количество жордановьГх клеток, порядок
которых больше единицы (почему?). Значит, количество клеток, по-
порядок которых равен единице, равно йх — (di — d1) = 2d1 — d2. Анало-
Аналогично получаем, что количество клеток, порядок которых равен двум,
равно (d2—dt) — (d3—di) — 2di — dt—dg и т. д. (Проверьте, что
сумма полученных выражений равна числу dt всех клеток.)
3. Общий случай. Пусть задано произвольное линейное отобра-
отображение А линейного комплексного л-мерного пространства (/?) в .себя.
Вектор x?(R) называется корневым вектором этого отображения,
отвечающим значению X, если (А — %\)hx = 0 для некоторого А = 1,
2, 3, ... Легко проверить следующие свойства.
1. Совокупность (/?') всех корневых векторов, отвечающих задан-
заданному значению X, образует инвариантное подпространство (/?). В самом
деле, если хг и лс2—два таких вектора, т. е. (А — Х1)*>х1 = 0,
(А — M)*J лс2 = 0, а х = ах1 + рлс2 и, для определенности,
№к 0
M)J лс2 = 0, а х = ах1 + рлс2 , x^v
то (А — №)кхх — 0 (почему?), т. е. и х такой вектор. Значит, (/?')
есть подпространство (/?). Его инвариантность вытекает из равенства
(A — M)*(Ajt) = A[(A—M)*jc] (продумайте это!).
2. (/?') имеет ненулевую размерность тогда и только тогда, когда
X есть собственное значение отображения А. В самом деле, если
К—собственное значение, то (/?'), во всяком случае, содержит соот-
соответствующее подпространство собственных векторов (для них
(А — М)х = О). Обратно, пусть (/?') имеет ненулевую размерность,
т. е. для заданного Я- имеется по крайней мере один корневой век-
вектор хф-О. Пусть k — наименьший показатель, для которого
(А—АЛ)*лс = О. Обозначив (А—XI)* х — у, получим, что уфО,
(А—%1)у==0, т. е. Я-—собственное значение отображения А.
В соответствии с этим свойством будем рассматривать только
корневые векторы, отвечающие собственным значениям отображения А.
Обозначим- все различные собственные значения через Ки
Я-2, ..., "Кт, а соответствующие подпространства корневых векто-
ров-через (/?J, (/?,), ..., (/?„).
3. (R) разлагается в прямую сумму подпространств корневых
векторов (RJ, (R2), ..., (Rm).
Доказательство этого громоздко и будет проведено по этапам.
Докажем сначала теорему Гамильтона — Кэли: пусть Р(Я-) =
— det (А — XI) — характеристический многочлен какой-либо матрицы А;
тогда Р (А) = 0. Другими словами, каждая квадратная матрица

184 ' ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
удовлетворяет своему характеристическому уравнению. Для доказатель-
доказательства обозначим через Q (X) транспонированную матрицу из алгебраи-
алгебраических дополнении к А—XI; обе они—полиномиальные матрицы,
т. е. их элементами служат многочлены от X. Тогда
(A-XI)Q(X) = P(X)I F)
(почему?). С другой стороны, легко проверить, что любой многочлен
вида Р(и)—P(v) делится нацело на и—v, т. е. Р (и)—Р(г>) =
^э(а—1>)Ф (и, v), где Ф—некоторый многочлен от двух переменных.
Отсюда и из F) получаем (продумайте эти вычисления с матрицами!)
Р (А) - Р (Я.1) + (А—ЯЛ) Ф (А, XI) =
.-Р(ХI + (А—XI) Ф (А, XI) = (A—XI)[Q(X)+<p(A, XI)] =
= А[О(Х) + Ф(А, XI)]—Х[О(Х) + Ф(А, XI)].
Но последняя квадратная скобка должна тождественно (по X) рав-
равняться нулю, так как в противном случае ее элемент, содержащий
X в наивысшей степени, остался бы с X и во всей правой части
(почему?), а в левую часть X не входит. Эти и доказывает теорему
Гамильтона—Кэли.
При доказательстве свойства 3 для простоты будем считать, что отобра-
отображение А имеет лишь, два различных собствениых зиачения А^, Я^, и обозначим
через Р(М характеристический многочлен этого отображения (т. е. матрицы А
в любом оазисе, так как известно, что этот многочлен не зависит от выбора
базиса). Тогда Р (X.) == (X.j—X.)»i (X.g—Х.)п>. Будем временно под (/?/) понимать
подпространство векторов, для которых (А—\jl)ni х=О.
Разложив для дальнейшего рациональную функцию 1/Р (к) на простейшие
рациональные дрсбя 1-го типа (ЛВМ, п. VIII.10), а затем умножив обе части
разложения иа Р (X), мы придем к тождеству вида
1 a Dt (X) (JL-aJ-. + D, (X) (Х-X,)».,
где Dj(%)—некоторые многочлены; отсюда
I^D1(A)(A-X1I)«. + Di(A)(A-XiI)«.. G)
В силу G) для любого вектора х можно написать
х=D2 (А) (А—X-jjI)". х + Dt (A) (A— ^I)"! x. (8)
Однако из теоремы Гамильтона—Кэли следует, что первое слагаемое в правой
части принадлежит {Rj), а второе—{R2) (почему?). Значит, разложение по
этим подпространствам возможно. Чтобы доказать его единственность, допус-
допустим, что
Применяя к обеим частям отображение Dx (А) (А—Xjl)"! и пользуясь тожде-
тождеством G) и определением пространств (Rj), получим
O=D1 (А) (А-М)л. хг=х2-О2 (А) (А-Х,1)»» *,=*!;
аналогично х^=0. Итак, разложение (R) в прямую сумму (Rt) и (R2) доказано.
Осталось проверить, что временное определение (Rj) равносильно исход-
исходному, т. е. если (А—Х.11)*ж=0 при каком-нибудь к, то и (А—X^I)"! x=O.

§ 3. СТРУКТУРА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ 185
Но, применив достаточное число раз левую часть G) к левоф части (8), а пра-
правую—к правой и пользуясь теоремой Гамильтона—Кэли, получим в таком
случае x=[Ds(A)]r(A—Л21)а*г х, откуда и следует наше утверждение. Итак,
свойство 3 полностью доказано.
В силу свойств 1—3 и п. 2 вопрос о строении отображения А
в (R) сводится к аналогичному вопросу для каждого из подпро-
подпространств {Rj). А этот последний решается на основе свойства
4. Отображение А имеет в подпространстве (RJ) единственное
собственное значение Ау. В самом деле, нустн x?{Rj), хфО,
Ax = AJC. По определению {Rj) будет (А — Ayl)*jc=0. Если в левой
части раскрыть скобки и воспользоваться тем, что Ajc=ajc, A*JC =
= A (Ajc) = А (кх) = ААж, A3jc = a3jc и т. д., то получим (проверьте!)
(А—к/)кХ—О, откуда А = Ау.
Теперь из результатов пп. 1.2 и 2 вытекает, что после выбора
в каждом из подпространств (Rj) соответствующего базиса из соб-
собственных и присоединенных векторов матрица отображения А примет,
квазидиагональный вид, составленный из жордановых клеток. Матрица
такой формы называется нормальной или жордановой. При этом у
каждой клетки иа главной диагонали стоит одно из собственных
значений отображения А, а каждому собственному значению отвечает
столько клеток, сколько ему отвечает линейно независимых собст-
собственных векторов. Порядки (размеры) клеток определяются, как опи-
описано в конце п. 2, т. е. по размерностям подпространств векторов,
удовлетворяющих при данном у соотношениям (А—"kj\)x = O,
(А—%jl)ax = O и т. д. Порядок, в котором жордаиовы клетки сле-
следуют друг за другом, несуществен, так как, если изменить порядок
нумерации инвариантных подпространств, то и «маленькие» матрицы,
из которых составлена квазндиагоиальная матрица, соответственно
переставляются.
Полученный результат можно сформулировать на чисто матричном
языке. Рассмотрим любую комплексную квадратную матрицу А по-
порядка я. Ее дтожно истолковать как матрицу некоторого отображе-
отображения А комплексного л-мерного линейного пространства с как-то
выбранным базисом. При переходе к новому базису матрица отобра-
отображения преобразуется по формуле А' = Н~1АН (ЛВМ, п. XI.7), где
Н г—невырожденная матрица перехода. Таким образом, мы получаем,
что для каждой матрицы А можно подобрать такую невырожденную
матрицу Н, чю матрица А' = Н~1АН будет иметь нормальную (жор-
данову) форму. Прн этом на главной диагонали каждой жордановой
клетки, из которых составлена А', стоит одно из собственных
значений матрицы А. Размеры клеток определяются, как описано
выше, причем в конкретных примерах можно исходить из того, что
размерность подпространства векторов, удовлетворяющих соотноше-
соотношению (A—Kjl)kx = O, равна л — rang (A—Kjl)k (ЛВМ, пп. XI.5,6), так
что и размеры клеток выражаются через характеристики исходной
матрицы А.

186 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
В книгах [28, 118, 134] описан другой способ выяснения порядков жор-
дановых клеток, который мы не будем здесь рассматривать. В нем матрице А
по определенному довольно громоздкому правилу сопоставляется серия много-
многочленов вида (к—Х.у)*, называемых элементарными делителями матрицы А.
После приведения матрицы А к жордановой форме А" каждому нз этих дели-
делителей отвечает в А' жорданова клетка порядка k с числом Xj на главной
диагонали.
4. Отображение вещественного пространства. Пусть теперь
А — линейное отображение вещественного пространства (/?)
в себя. Тогда, если характеристическое уравнение для отыскания
собственных значений имеет только вещественные корни, то все
предыдущие рассмотрения остаются в силе, т. е. в соответственно
подобранном базисе матрица отображения А имеет жорданову форму.
Другими словами, (R) разлагается в прямую сумму инвариантных
подпространств (Rj), в каждом из которых матрица отображения А
в соответствующем базисе имеет вид жордановой клетки с собствен-
собственным значением Kj на главной диагонали. (Здесь мы применяем более
«мелкое» разложение (/?), чем в п. 3, так что теперь различным j
могут отвечать одинаковые Я-,-.) Если какое-либо из (Rj) одномерно,
то отображение А на нем сводится к растяжению в А,у- раз; так
будет, в частности, если Я-у—простое собственное значение или
в более общем случае, если количество линейно независимых соб-
собственных векторов, отвечающих Kj, равно его кратности как, корня
характеристического уравнения. (Из п. 3 следует, что указанное
количество всегда меньше либо равно этой кратности.) Если (Rj)
двумерно,, то в соответствующих осях на (R') отображение приоб-
приобретает вид
где (лх; хг)—координаты вектора-прообраза, а (yt; уг)— координаты
вектора-образа. При ^фО это комбинация всестороннего растяжения
в Xj раз и сдвига вдоль оси хг (что будет при А-у = О?). Мы пред-
предлагаем читателю разобрать геометрический смысл отображения,
отвечающего жордановой клетке третьего- порядка.
Пусть теперь характеристическое уравнеиие может иметь мнимые
(т. е. невещественные) корни. Такой корень k = [A-)-rv (\и н \фО
вещественные) не является собственным значением отображения А
в (/?). Поэтому расширим (R) до комплексного линейного простран-
пространства (S) комплексной размерности п так, чтобы базис xlt хг, ..., х„
пространства (/?) одновременно служил базисом (S); для этого до^
статочно рассмотреть совокупность формальных выражений вида
а1х1 + а2х2-}-... -$-апх„ с любыми комплексными ak и естественными
правилами сложения и умножения на число. Отображение А также
можно продолжить до линейного отображения (S) в себя, так как,
если даны образы базисных векторов, то линейное отображение
полностью определяется. Матрица продолженного отображения в ба-

§ 3. СТРУКТУРА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ
187
зисе Xi," JC2, ..., х„ та же, что матрица исходного отображения,
поэтому корень % = \i-\-iv будет собственным значением продол-
продолженного отображения. ;
Из алгебры известно, что алгебраическое уравнение с веществен-
вещественными коэффициентами вместе с мнимым корнем всегда обладает
сопряженным мнимым корнем, причем той же кратности (ЛВМ,
п. VIII.8). Поэтому 'k* = \i — iv также будет собственным значением
продолженного отображения А. Записывая соотношения вида D) в
координатах относительно базиса хи хг, , хп и переходя к со-
сопряженным числам, мы получим, что если/lt l2, 1а—присоединенные
и собственный вектор для собственного значения Я, то векторы /J,
II, Ч с сопряженными координатами являются присоединенными и
собственным вектором для собственного значения к*. Эти векторы не
принадлежат (/?), так как их координаты мнимые. Отделяя у этих
координат вещественные части от мнимых, мы получим принадле-
принадлежащие (/?) векторы l'k, Гк (*=1, 2, 3), для которых
4 = l'k-Ui (* = 1, 2, 3).
После подстановки этих векторов в D), получим (проверьте!)
(A = l, 2),
Соотношения между сопряженными векторами 1% не дадут ничего
нового. Поэтому, если в общем базисе заменить шесть векторов
lk, l% (k=l, 2, 3) на шесть векторов 1'к, Гк {k=l, 2, 3), то в ин-
инвариантном подпространстве (/?), натянутом на последние векторы,
отображение А будет иметь матрицу
(9)
(X
V
1
0
0
V
H*
0
1
0
0
0
—V
1
0
0
V
0
о
0
0
0
о
0
0
0
V
0 0 0 1 —v (xj
Так можно поступить со всеми мнимыми собственными значениями.
В результате мы получим базис (/?), в котором матрица отображения А
имеет квазидиагональный вид, составленный из вещественных матриц
типа E) (любого порядка) и вещественных матриц типа (9) (любого
четного порядка). Аналогично формулируется теорема о приведении
матрицы к вещественному нормальному виду, причем матрица пере-
перехода Н здесь также будет вещественной.
Матрица (9) в простейшем случае имеет вид
Если представить n = /Wcosa, —v = Msm<x GW>0) и считать

188
ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
/j, l"x декартовым базисом на плоскости, то легко проверить, что
соответствующее преобразование состоит в комбинации всестороинего
растяжения в М раз и поворота на угол а. Для недекартова базиса
получается «аффинно преобразованный поворот» плоскости.
5. Применение к вычислению функций от матриц. Пусть ска-
скалярная (обычная) функция f(x) допускает разложение в ряд
f{x) = ae + alX + a2x*+ ... +а„х»+ ....
а А — квадратная матрица. Тогда по определению
2A2+ ... +а„А»+ ... A0)
В соответствии с п. 3 представим А = НА'Н~1, где А' — жордаиова
матрица; тогда А* = НА'Н-1НА'Н-1 = НА'*Н-1> А3 = НА'3Н и т. д.,
и мы получаем
/(А) = Нао1Н-1 + На1А'Н-1 + На2А'2Н-1+ ... =Н/(А')Н.
Для вычисления /(А') воспользуемся простым непосредственно
проверяемым свойством: при умножении двух кеазидиагональных
матриц с одинаковыми наборами порядков получается квазидиаго-
квазидиагональная матрица с таким же набором порядков по следующему
правилу:
'А,
о
о
в,
о
о
в„
0
0
т. е. одинаково расположенные матрицы, стоящие на диагонали, пе-
перемножаются независимо от остальных матриц. Из этого свойства
вытекает, в частности, что для квазидиагональной матрицы
А2 О
о
/(А,)
о
о
/(AJ,
(почему?). Значит надо вычислить /(Aft), где \к—жорданова клетка.
Рассмотрим для определенности клетку E); ее последовательные
степени равны (проверьте!)
и т. д.,

§ 3. СТРУКТУРА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ
189
причем коэффициенты вычисляются по тому же правилу, что при
последовательном раскрытии скобок в выражениях (A,-f-1)*, (Х-4-1)8,
(Х + 1L н т. д. Значит, вообще
(Д." О О
(•)х-х. о
(?) >•¦- (i)х"~' *¦•/
где ( п j = " *"~ ' V. *"~ биномиальный коэффициент. Под-
Подставляя в A0) и учитывая, что
ав+at К + аг X* + ай I3 + ... =/(*.),
получим окончательно
(И)
Аналогичный результат получается для жордановых клеток любого
порядка, чем и завершается вычисление /(А).
В качестве примера рассмотрим вопрос о логарифмировании матри-
матрицы А, т. е. о подборе матрицы В, для которой ев = А. Оказывается,
что такой логарифм всегда существует, если матрица А не имеет
нулевых собственных1 значений. Для доказательства, как и выше,
достаточно рассмотреть логарифмирование жордановой клетки E)
при \ф0. Однако
= 1п
= LnX.-I-Hn
A2)
где Ln X — общее значение логарифма. (Отметим, что при преобра-
преобразовании логарифма произведения в сумму логарифмов, которое для
матриц возможио не всегда, мы пользовались равенством еА+в = Ав

190 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
справедливым для перестановочных матриц А и В, см. ЛВМ, п. XVH.18.)
Последний логарифм в правой части A2) можно вычислить с помощью.
разложения In (I -J-a;) = — __)_.,. t правая часть которого в дан-
данном случае содержит лишь конечное число слагаемых (почему?).
По поводу решения более сложных матричных уравнений и даль-
дальнейших свойств матриц см. [23].
Иногда применяются функции вида /(/А), где /—параметр. Тогда
взамен A1) надо пользоваться формулой
О О
/(Л) О
t
проверить которую мы предоставляем читателю. Например,
/АО 0\ /#А ° °Х /10Ч>
expj t t% О ] =
6. Другое представление отображения вещественного прост-
пространства. Пусть А — линейное отображение вещественного евклидова
пространства (R) в себя. В п. 1.6 было показано, что е?ли это
отображение самосопряженное, то оно просто представляет собой
комбинацию равномерных растяжений вдоль взаимно перпендикулярных
направлений собственных векторов, причем коэффициентами растя-
растяжения служат соответствующие собственные значения. Мы сейчас
покажем, что общее отображение А представляет собой комбинацию
самосопряженного отображения и ортогонального отображения (вра-
(вращения (R) вокруг начала координат); при этом квадратами коэф-
коэффициентов растяжения служат собственные значения самосопряжен-
самосопряженного отображения А А*.
Это утверждение,можно сформулировать и на матричном языке.
Будем рассматривать заданную вещественную квадратную матрицу А
как матрицу отображения в некотором евклидовом базисе. Тогда
после перехода к базису из собственных векторов упомянутого самосо-
самосопряженного множителя получим
H-JAH = UA, откуда A = HUAH-1 = KAL, A4)
где А—вещественная диагональная матрица, а Н и U, а потому
и КиЬ—ортогональные матрицы; при этом у А8 на диагонали стоят
собственные значения матрицы АА*. (Проверьте, что последняя мат-
матрица симметрическая и все ее србствениые значения неотрицательные.)
Обратно, если имеет место представление A4), то, переписав его

§ 3. СТРУКТУРА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ 191
в виде A = (KL)(L~1AL) = (KL) (L*AL), получаем утверждение пре-
предыдущего абзаца о строении отображения А.
Для доказательства формулы A4) приведем симметрическую мат-
матрицу АА* к диагональному виду, а так как у полученной диагональной
матрицы на диагонали будут стоять неотрицательные числа, то ее
можно представить в виде квадрата другой вещественной диагональ-
диагональной матрицы:
^AA* К = Аа A5)
(К — ортогональная, а А — диагональная матрицы). Так как диаго-
диагональные элементы \х}- матрицы А можно считать занумерованными
в порядке (xt^ (х2^ ... ^ (х„ (ц„^0), то будем считать, что пер-
первые k (О ^ k ^ п) из этих элементов положительные, а остальные
равны нулю. Построим теперь числовые векторы vy = —Wy (/=1,
2, ..., k), где wy-—/-й столбец матрицы А*К; так как из A5) следует,
что эти векторы ортогональные н нормированные, то их можно до-
дополнить векторами vA+1 vn до ортогональной матрицы V; пра-
практически это можно сделать с помощью процесса ортогонализации
(ЛВМ, п. VII. 21). Из построения матрицы V следует, что
A*K = VA, откуда A = KAV* = KAL,
где обозначено L = V*. Возможность представления A4) доказана.
7. Структура перестановочных отображений. Лемма. Пусть
А и В — квадратные матрицы порядка п, причем А диагональная
и имеет первые пг элементов главной диагонали равными Кг, следую-
следующие nt элементов равными %г и т. д., а все числа Кк попарно различны.
Тогда для равенства АВ = ВА необходимо и достаточно, чтобы мат-
матрица В была квазидиагональной с набором порядков (л1, я2, ...).
В самом деле, легко проверить общие равенства
«Ai «At • • • aAn
Для совпадения правых частей необходимо и достаточно, чтобы
для всех у, k имели место равенства a.jbjk = akbjk, т. е. чтобы
при cty^a* было Ь/к = 0. Отсюда и вытекает утверждение
леммы.

192 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
Пусть теперь дана произвольная совокупность А, В, С, ...
линейных отображений комплексного пространства (R) в себя, при-
причем каждое из этих отображений имеет жордановы клетки только
первого порядка, т. е. имеет в некотором базисе диагональную мат-
матрицу. Тогда для попарной перестановочности всех этих отображе-
отображений, т. е. для справедливости равенств АВ = ВА, АС = СА,
ВС = СВ, ..., необходимо и достаточно, чтобы в некотором общем для
всех отображений базисе каждое из них имело диагональную матрицу.
Достаточность сразу следует из того, что диагональные матрицы
всегда перестановочны. Для доказательства необходимости допус-
допустим, что все заданные отображения попарно перестановочны, и выбе-
рем базис в (R) так, чтобы матрица отображения А имела вид, опи-
описанный в лемме. Тогда из этой леммы будет следовать, что
подпространство (Rt), натянутое на первые /г, базисных векторов
(оно же—подпространство собственных векторов отображения А,
отвечающих собственному значению Хг), подпространство (Я2), натя-
натянутое на следующие пг базисных векторов, и т. д.—все они инва-
инвариантны для каждого из заданных отображений. Поэтому можно
рассмотреть отображение В на каждом из подпространств (Rj)
и выбрать в нем базис так, чтобы матрица отображения В (лу-го
порядка!) приобрела вид, описанный в лемме. Такое изменение базиса
внутри каждого из подпространств (Rj) не изменит вида матрицы
отображения А (почему?) и приведет к разложению каждого (Щ)
в прямую сумму подпространств (Rj^), инвариантных для каждого
из отображений. Далее выбираем в каждом (Rj^) базис, руковод-
руководствуясь отображением С, и т. д. Так как такое последовательное
разложение в прямую сумму не может производиться более чем п—1
раз (почему?), то через конечное число шагов (даже если задано
бесконечное количество отображений!) мы придем к базису, в кото-
котором матрицы всех заданных отображений имеют диагональный вид.
§ 4. Некоторые численные методы
Имеется весьма большое количество методов численного решения
различных классов задач линейной алгебры, эти методы описаны в боль-
большинстве курсов численных методов (укажем, например, на книги
[10, 33, 67]). Наиболее полной в этом отношении является книга [115].
Здесь мы рассмотрим лишь несколько таких методов. Естественно,
что при вычислениях взамен общих пространств и отображений поль-
пользуются числовыми векторами и матрицами.
Вычислительные методы линейной алгебры группируются вокруг
задач о решении системы линейных уравнений и вычислении (полном
или частичном) спектра, т. е. совокупности собственных значений
матрицы.
1. Метод Гаусса. Основным методом численного решения систем
линейных уравнений является метод Гаусса, указанный в ЛВМ, п. VI.5.

iv- § 4. НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ ' 193
>. Для системы литейных уравнений общего вида
или, коротко,
Ах = Ь, B)
этот метод в своем простейшем варианте имеет следующий вид.
Первое из уравнений A) делится на alit что дает равенство вида
= *;- C)
Затем это равенство множится независимо на —asl, ¦—flSn- • •»—*nt
и прибавляется- соответственно ко второму, третьему, ... ,л-му урав-
уравнениям системы A), что приводит к уравнениям вида
а'ггх2 + ...+ ainxn =
Таким образом, xt исключен. Затем делим первое уравнение системы D)
на a'ti, что дает
х% + а'пХя + ...+ а'^х„ = Ь"п
п,
и исключаем хг и т. д., пока не приходим к одному уравнению
с одним неизвестным х„. Из последнего уравнения находим ха, затем,
зная хю из предыдущего уравнения находим xtt_i и т. д., наконец,
из уравнения C), зная хп,...,ха, находим лг,, на чем решение
и заканчивается.
Для возможности выполнения первого шага в описанном варианте
должно быть ап *?= 0. В системе D)
«и = а»» — «si a'i* = а*г — а21~ = -jj •
! где Aft—А-й главный минор матрицы А (п. 2.3); значит, для воз-
I; можности выполнения второго шага в методе Гаусса должно быть
»Лг=^0. Можно проверить, что последующие коэффициенты, на кото-
Ррые придется производить деление, равны А3/^г> А4/А3 и т- *•> так
Цмто для возможности Доведения вычислений по описанной схеме до
Оконца необходимо и достаточно, чтобы все главные миноры матрицы А
Цбыли отличны от нуля. Более того, если даже это условие выпол-
Ц'нено, но какой-либо из главных миноров окажется" слишком близким,
f'K нулю, то точность вычислений может существенно понизиться.
: В этом случае, который обнаруживается в процессе вычислений,
можно производить деление на какой-либо из других, не малых
коэффициентов, что равносильно перенумерации неизвестных и урав-
уравнений (даже если эта перенумерация фактически не выписывается).
7 А. Д. Мышкио

194
ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
Нетрудно проверить, что с матричной точки зрения метод Гаусса
равносилен представлению матрицы А в уравнении B) в виде
А = НВ, E)
где Н — нижняя треугольная матрица, т. е. матрица, имеющая все
элементы выше главной диагонали равными нулю, а В — верхняя тре-
треугольная матрица. При этом строками матрицы В служат коэффициенты
уравнений C), D) и т. д., т. е. все элементы ее главной диагонали
равны единице. Это вытекает из формул (проверьте их!)
k 0 ... 0\ /ank~i- a^k-1 .. . alak-*\
О I ... О \ аа агг ... аг
из которых видно, что каждый переход в методе Гаусса равносилен
выделению из матрицы коэффициентов в качестве левого сомножи-
сомножителя некоторой нижней треугольной матрицы. А так как произведение
нижних треугольных матриц будет снова нижней треугольной матрицей
(почему?), то после выполнения всех переходов мы и приходим
к разложению E).
После того как система B) переписана в виде НВх = Ь, ее очень
просто решить, обозначив Вх = у и перейдя, таким образом, к по-
последовательности двух треугольных систем Ну = Ь, Вх = у. Впрочем,
если в методе Гаусса производить действия не только над левыми
частями системы B), но и над правыми, то мы прямо переходим
к треугольной системе Вх = Н~1Ь с известной правой частью.
Полезные соображения по поводу метода Гаусса см. в книге [117].
2. Норма матрицы и обусловленность системы. Пусть линейное
отображение А вещественного евклидова пространства (/?) в себя
имеет в некотором декартовом базисе (квадратную) матрицу А. Тогда
нормой || А || этого отображения, а также нормой ||А|| матрицы А назы-
называется наибольший коэффициент удлинения векторов при рассматри-
рассматриваемом отображении, т. е.
Легко доказываются следующие свойства нормы (докажите их!):
1. ||0||=0, норма прочих матриц положительна.
2. | Ах | ^ || А|| | х'|; при этом имеются векторы х Ф 0, для которых
это неравенство обращается в равенство.

§ 4. НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ 195
3.
4. ||
5. ||АВЦ ^ ||А|| • HBllj отсюда следует, в частности, что
A^^Il
Ml^l^lll^,
6. Норма ортогональной матрицы равна 1,
7. Норма симметрической матрицы равна наибольшей из абсолют-
абсолютных величии ее собственных значений.
8. Квадрат нормы любой матрицы А равен наибольшему из соб-
собственных значений матрицы АА\
(При доказательстве свойств 7 и 8 вспомните результаты п. 3.6.)
Эти свойства немедленно распространяются на отображения, и также
на комплексные матрицы и отображения.
Вычисление нормы по свойству 8 требует определенных усилий.
Можно пользоваться простой оценкой, которая вытекает из
определения F) и неравенства Коши—Буняковского—Шварца
(ЛВМ, (VII.26))!
откуда
"АН
Оценку нормы снизу можно получить из следствия из свойства 5.
Норма матрицы применяется, в частности, при изучении важного
в вычислительном отношении понятия обусловленности линейной
системы B). Допустим, что в правой части допущена некоторая
погрешность ДЬ; тогда и решение будет иметь погрешность Дх,
причем так как А (х + Дх) = b + ДЬ (коэффициенты системы считаем
для простоты абсолютно точными), то АДх=ДЬ. Отсюда и из B)
получаем
откуда
lAvl I AK I
(8)
при этом для некоторых ненулевых b и АЬ оба неравенства G), а
потому и неравенство (8), обращаются в равенства,
Таким образом, произведение ||А|| || А. * ||, называемое мерой
обусловленности системы B) (или матрицы А), равно наибольшему
возможному коэффициенту увеличения относительной погрешности
решения по сравнению с относительной погрешностью столбца правых
частей. Если эта мера, которая не может быть меньше единицы,
будет близка к единице, то система B) называется хорошо обусловь
ленной; относительная погрешность решения такой системы будет
близка к относительной погрешности известных параметров этой
системы. Если мера обусловленности велика, то система B) назы-
называется плохо обусловленной и при ее решении относительная
7*

ГЛ. 1У. ЛИНЕЙНАЯ АЛГЕБРА
погрешность может существенно возрасти; такие системы неудобны
для численного решения.
Нетрудно проверить (продумайте это!), что мера обусловленности
матрицы А равна отношению наибольшей к наименьшей из полуосей
эллипсоидов, которые служат образами сфер при отображении А.
Квадрат этой меры равен отношению наибольшего собственного
значения матрицы АА* к ее наименьшему собственному значению.
Таким образом, при решении линейных систем опасность состоит
не просто в малости определителя, как мы для краткости писали
в ЛВМ, п. VI.6: если бы это было так, то за счет простого умно-
умножения всех уравнений системы на одно и то же большое число можно
было бы любую плохую систему сделать хорошей. На самом деле
опасна плохая обусловленность системы, а мера обусловленности
при таком умножении не меняется.
'При простых преобразованиях системы, например при умножении всех
членов какого-либо из уравнений системы на одно и то же число ит. п.,
мера обусловленности, вообще говори, меняется. Проверьте, например, что
мера обусловленности системы
равна Eй*+2+У*25/г4+1Бй* + 4)/2|й|, хотя решение, конечно, не зависит
от fe; найдите, при каком k эта мера принимает самое малое значение и объ-
объясните, почему она стремится к бесконечности при k—>-0 и при k—> ±00.
Отметим в заключение, что применяются и другие определения
нормы матрицы и меры обусловленности.
3. Метод улучшения невязки. Даже при применении «точного»
метода Гаусса к уравнению B) из-за ошибок округления может по-
получиться приближенное решение х1( точность которого нас не устраи-
устраивает. Если тогда обозначить x = x1-f-z, то для г получается уравнение
Az = A(x—Xj) = b—Ах„ т. е. Az = r,, (9)
где через rt обозначена невязка Ь—Ах, приближенного решения х,.
Так как обычно |г,|<^|Ь|, то уравнение (9) удается решить с го-
гораздо более высокой абсолютной точностью, чем B), что дает
возможность повысить относительную точность исходного при-
приближенного решения (продумайте это!).
Если заметить, что решение уравнения B) равносильно отысканию
минимума квадрата невязки, т. е. минимума функции
F(xt,xt *„) = |Ах—Ь|« A0)
(йвадрат берется для удобства вычислений), то к рассматриваемой
задаче оказывается возможным применить прямые методы отыскания
минимума. Отметим, в частности, метод наискорейшего спуска
(ЛВМ, п. XII.10). Так как grad (х, а) = а, и потому
grad|Ax-b|* = 2grad(Ax—b, (Ах—b)const) =
= 2 grad (x, A*(Ax-b)const) = 2A*(Ax-b),

§ 4. НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ Г97
то последующее приближение в данном методе выражается через
предыдущее по формуле
**+1 = **—2'А* (Ах*- Ь) = xk + 2/AV* ' . .
где t — tk подбирается из условия минимизации функции A0). При-
Применение необходимого условия минимума по t, которое мы предостав-
предоставляем читателю, приводит к формуле
по которой и можно производить итерации, начиная с какого угодно
нулевого приближения.
В частном случае, когда матрица А симметрическая и форма
(Ах, х) положительно определенная, решение уравнения B) служит
единственным минимумом фуикции (Ах—2Ь, х). Докажите это и по-
постройте на этой основе более удобный нтерационный способ решения
уравнения B) в рассматриваемом случае
Такие матрицы возникают, в частности, в задачах вариационного
исчисления (см. п. VI.4.1).
4. Спектр симметрической матрицы. Перейдем теперь к задаче
о вычислении спектра (совокупности собственных значений) матрицы А
и начнем со случая, когда А — вещественная симметрическая матрица.
Ее наибольшее и наименьшее собственные значения (а во многих
задачах,, связанных со спектром, именно эти значения играют наи-
наибольшую роль) можно находить численно на основе экстремаль-
экстремального свойства из п. 1.7. Покажем, как это сделать с помощью
метода наискорейшего спуска. Для этого будем исходить из любого
вектора х0 единичной длины. Годограф векторной функции
xo-f-grad(Ax, x)lXCXo< х„4-2Ахо<
Х~ |ж,+вг««1(Ах,х)|жяж#/|
представляет собой дугу большого круга на единичной сфере, на-
направленную при t = 0 в сторону наибыстрейшего возрастания фуикции
(Ах, х) на зтой сфере. Подберем t таким, чтобы величина
,. (А(х„4-2Ахо<), хо+2Ах„О ._.
1АХ)Х) (X.+2AV, Х.+2АЖ,/) 1"'
принимала для этого t наибольшее или наименьшее значения, т. е.
найдем относительные экстремумы функции (Ах, х) на рассматриваемой
дуге. Применение необходимого условия экстремума по t к.функг
цни A2), которое мы предоставляем читателю, приводит к уравнению
- 4KYo-PJ)'i + 2(oA--P.Yo)-' + (PA-'Vl)-0. -03)
в котором обозначено
, х0), ро = (А2хо>хо), у, = (Ахв, Хо), бо = (хо,х0).

1&8 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
Положительный и отрицательный корни уравнения A3), подставленные
в правую часть A1), и дают точки относительного максимума и
минимума соответственно. Затем над полученными векторами надо
повторить описанную процедуру (продвигаясь, конечно, только
в нужном направлении изменения величины (Ах, х)) и т. д. После
необходимого количества итераций мы получаем не только наибольшее
и наименьшее собственные значения матрицы А, но также и соот-
соответствующие собственные векторы.
Если иас интересуют и промежуточные собственные значения
н соответствующие • собственные векторы, то надо два найденных
Собственных вектора 11( 12 дополнить до евклидова базиса lt, 12, . . .
и выразить квадратичную форму (Ах, х) в новых координатах:
(Ах, х) = (А'у, у); затем в силу ортогональности собственных векторов
надо положить ^=^ = 0, т. е. перейти к форме от п — 2 координат
и проделать над ней описанные действия, и т. д.
Бывают задачи, в которых надо иайти наименьшую из абсолютных величин
собственных значений матрицы А. Тогда надо найти наименьшее собственное
значение матрицы А2 и нз него извлечь квадратный корень (почему?). Эта за-
задача возникает, в частности, при рассмотрении отстройки, от резонанса
системы х = Вх+ее-*с, где надо положить А = В—(J-I (продумайте термин
«отстройка от резонанса»).
Полезные качественные и вычислительные соображения, связанные
с определением спектра матриц, содержатся в книге [58].
5. Метод Якоби. Этот метод вычисления собственных значений
и собственных векторов для вещественной симметрической матрицы А
был предложен К. Якоби в 1846 г. и принадлежит к числу итера-
итерационных методов. Геометрический смысл его состоит в следующем.
Мы уже знаем (п. 2.1), что уравнение х*Ах=1 задает в Еп поверх-
поверхность (М) второго порядка—для определенности, эллипсоид — и задача
состоит в отыскании главных осей этого эллипсоида. Выберем какие-
либо два из исходных базисных векторов 1{, Ь (у lt г'-я координата
равна единице, остальные равны нулю, аналогично для \р 1ф]\,
тогда плоскость, натянутая на векторы 1(-, 1у, пересечет (М) по
некоторому эллипсу (М)ц. Перейдем к новому базису в Ет направив
векторы \\, \'j по главным осям эллипса (М)у и оставив базисные
векторы с другими номерами без изменения. Затем среди базисных
векторов 1[, \'г, ...,1„ опять выберем какие-либо два и повернем их
в их плоскости, чтобы они пошли по главным осям эллипса, полу-
получающегося в пересечении этой плоскости с (/И), и т. д.
Этот процесс будет, вообще говоря, бесконечным. В самом деле,
пусть, например, в = 3и векторы 1^, \'г получены из llt 12 поворотом
вокруг 1„, так что 1з = 18- Пусть, далее, 1"г, 1, получены из V2, lg по-
поворотом вокруг 1[, так что li = U. Но после этого lj, \\ уже не будут
направлены по главным осям эллипса, получающегося в плоскости
этих векторов, так что требуется новый поворот и т. д. Главные
оси эллипсоида получаются только в пределе.

§ 4. НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ 199
Аналитическое оформление метода имеет следующий вид. Выби-
Выбирается один из элементов а^фОAф]) матрицы А (предпочтительно
из числа ббльших по абсолютной величине). Если приравнять нулю
все координаты, кроме xt и Хр то форма х*Ах примет вид
Как известно из аналитической геометрии (ЛВМ, п. 11.13), для при-
приведения этой формы к диагональному виду надо повернуть оси коор-
координат на угол фх, определяемый из равенства tg2(pt=—-——• При
этом координаты меняются по формулам х{ = х\ cos cpt—x}sin(pit
Xj — x'i sin cpj + x'i cos ф1; xs = x's (s Ф I, j). В новых координатах мат-
матрица квадратичной формы будет иметь вид A' = HJAH1; где элементы
матрицы Нг определяются так: /*,-,• = hjj = cos (pit прочие диагональные
элементы равны единице; йу = —siiKpj, AyY = sin91, прочие недиаго-
недиагональные элементы равны нулю. У матрицы А' выбираем какой-либо
элемент a'rk ф О (г ф k), находим поворот плоскости х'г, х'к на угол ф2,
определяемый из равенства tg 2фа = , a'k, , в результате чего
arr—akk
матрица преобразуется по формуле А" = НгА'На, где матрица Ня
определяется аналогично Ht, и т. д. Процесс продолжается до тех
пор, пока внедиагональные члены матрицы Alm) не станут по абсо-
абсолютной величине достаточно малыми; тогда его можно прекратить
и принять диагональные элементы матрицы А<я" за собственные зна-
значения матрицы А. Кроме того, так как A<m) = H*AH, где Н =
= HiHj .. . Hm, то окончательная связь между координатами имеет
вид х = Hxlm); отсюда соответствующими собственными векторами
матрицы А служат столбцы матрицы Н (почему?).
6. Вычисление старшего собственного значения путем ите-
итераций. Перейдем теперь к общим квадратным матрицам с, вообще
говоря, комплексными элементами. Пусть задана матрица А, все
собственные значения %t, Яа,...,Яп (заранее неизвестные) простые,
причем значение 1%^ строго больше остальных |ЯА|. Обозначим
соответствующие собственные векторы, также заранее неизвестные,
хг, х2, .,., х„, выберем произвольный вектор у^О и будем строить
последовательность векторов ут по формулам yj = Ay0, Уа = Ауи ...
Так как у0 допускает разложение у0 = а^ + ааха + ••• -\-апхп> то
У1 = Ау0 = ахАх! + а2Ах2 + ... + а„Ахп =
У» = АУ! = a^fx, + ааЯ1ха + ... + апЯ*
и т. д., вообще
ут = а№ х, + а^?ха + • • • + OLnK х„ =
+ ... +*„

300 ' ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
По предположению о | A,t |, при больших т будет ут
Значит, если обозначить через у%* Ar-й элемент столбца ут, то
Я,, = lira
m -» » »m"
если только о^л:'** =^ 0. За собственный вектор хх можно принять
Лга (ц„ ут), где fim—нормировочные множители (ця=тг—i или
m •* » Ч I Уя» I
йГи т" "¦)•
Рассмотрение присоединенных векторов показывает, что для
осуществимости данного метода существенно только предположе-
предположение о I Я,ж j и о простоте собственного значения Хг (более точно,
А., не должны отвечать жордаиовы клетки выше первого порядка),
тогда как прочие собственные значения могут быть кратными. Выпол-
Выполнение же этих существенных предположений выясняется в процессе
вычислений из самого существования предела A4), который не дол-
должен зависеть ни от k (кроме особых случаев, когда #<*> = (), они
распознаются по более медленному возрастанию у?}), ни от у0
(кроме весьма специальных случаев, когда ах = 0; если брать эле-
элементы у0 наугад, можно ручаться, что этого не будет).
Если имеются два простых старших по модулю собственных зна-
значения Xlt Х,г, причем Х,г = — %lt то для больших т получится
У я ~ ЭД1 [aixi + (—l)maA]> T- е- существует два различных предела
вида A4) для четных и для нечетных т; так этот случай и распо-
распознается. Здесь можно положить
„(ft>
"к\ — lira -~fp .
т -* « Ущ
До сих пор мы считали матрицу А, вообще говоря, комплексной,
хотя, конечно, для вещественных матриц вычисления существенно
проще. Если матрица А вещественная, то имеется еще один важный
случай, когда она имеет два старших мнимых сопряженных простых
собственных значения, т. е. Яг = A,*=j?^i- Тогда и соответственные
элементы собственных векторов сопряженные, т. е. для веществен-
вещественного у„ для больших т будет
cc*jcife>* = 2Arm cos (та + Ь), A5)
где обозначено a1x^] = Aeib, k1=reia. С ростом т знак у%} будет
меняться сложным образом, чем и распознается данный случай. Если
обозначить через
О • A6)
квадратное уравнение с вещественными коэффициентами, которому
удовлетвормют Xlt XJ, то из равенств A5), в которых ~ заменено

§ 4. НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ 201
на =, легко получить (проделайте это!), что • , ¦
Придавая в этом соотношении k какие-нибудь два значения, мы по-
получим значения р, д, которые должны стабилизироваться (стремиться
к пределам) с ростом ж и не зависеть от выбора k; после этого
из A6) находим Klt A,J. Соответствующий собственный век-
вектор Я^оуц находим нз A5), выбрав для т два- последовательных
больших значения.
7. Вычисление последующих собственных значений. Если у
матрицы А порядка п известен собственный вектор х1( отвечающий
собственному значению Xlt то задачу о разыскании остальных соб-
собственных векторов и значений можно свести к аналогичной задаче
для некоторой матрицы At порядка п—1. К последней задаче можно
применить метод п. 6, после чего опять понизить порядок на еди-
единицу и т. д.
Для перехода к матрице At обозначим первую строку матрицы А
буквой г и условимся нормировать собственные векторы хк матри-
матрицы А (определенные с точностью до скалярного множителя) так,
чтобы их первая координата равнялась единице. Обозначим
В = А — х,г; тогда из последнего условия вытекает, что первая строка
матрицы В состоит из одних нулей (почему?). Далее, мы предостав-
предоставляем читателю доказать равенство тхк = Кк. Из этого соотношения
и нз равенства
Axft = Xkxk
следует, что
B(xft—xt) = Axk—Xjrxft — AXj + x1rx1 =
В(жк-х1) = Я,к(ж»-ж1). A7)
Обозначим через yft столбец высоты п — 1, голучающийся из xk—xt
отбрасыванием верхнего, нулевого элемента; через А, обозначим
матрицу порядка п—1, получающуюся нз В зачеркиванием первой
строки и первого столбца. Тогда из A7) следует, что К^к = 'ккУь
(почему?), т.е. yft(ft = 2, 3, ..., п)—собственный вектор матрицы
Alt отвечающий собственному значению Хк; вектор yt нулевой и
потому неинтересен. Найдя вектор ук, надо к нему сверху приписать
нуль, после чего к полученному вектору прибавить х,, тогда мм
получим хк; при этом yft нормируется так, чтобы rxk=Xk, тогда нз
A7) легко получить, что Axk=A,ftxft.
Может оказаться, что указанная в последней фразе нормировка невозможна,
тогда при любом выборе нормировочного множителя при уйбудетг(х/;—х1)=0,
т.е. гхд=%г|. В этом случае легко проверить, что собственному значению кк
отвечает собственный вектор xft—xlt верхний элемент которого равен нулю и
потому не поддается нормировке на единицу.' Если же верхний элемент у хх

202
ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
равнялся нулю, то взамен верхнего можно нспользовать любой другой элемент.
Поэтому описанный метод применим во всех случаях, когда собственные зна-
значения матрицы А простые. Если матрица А вещественная н найдена пара мни-
мнимых сопряженных собственных значений, а также пара соответствующих соб-
собственных векторов х12=хг ± ix2, то можно показать, что задачу о разыскании
прочих собственных значений н соответствующих векторов можно за один шаг
свести к аналогичной задаче для вещественной матрицы А2 (п — 2)-го порядка.
Для этого векторы х1г нормируются условием аф2 — Ь1а2 = 1, где a/, bj—
первые два элемента вектора Ху (/ = 1, 2). Тогда матрица С = А—(b2xi—&ixa)r+
-HaaXi—a"{x2)s имеет первые две строки нулевые, где г н s—первые две
строки матрицы А. Вычеркнув из С эти строки, а также первые два столбца,
получим А2. Если A2Z? = Ji?Z?, то, приписав к z# сверху два нуля и прибавив
вектор (иЬг—ча2) х1-\-{хш1—ubx) xs, получим собственный вектор хд матрицы А,
отвечающий собственному значению "к^, при
этом скаляры и, v подбираются так, чтобы
rXft=«X,j, sxft=wX.ft. Все это мы предоставляем
доказать желающим.
8. Матрицы с неотрицательными эле-
элементами. Матрицы с вещественными неотри-
неотрицательными элементами встречаются в ряде
прикладных задач. Для таких матриц раз-
развита теория, позволяющая, в частности,
эффективно оценивать их наибольшее соб-
собственное значение (см., например, [23, 56]).
Итак, пусть матрица А удовлетворяет
условию
ajk^Q (/, k=\, 2 л). A8)
Мы будем писать в этом пункте х ]^= у (чи-
(читается: вектор х следует за вектором у или
совпадает с ним), если х1^у1, х^^уъ ...
..., х„^ву„; заметим, что если х ^ у, то
Ах^Ау. Докажем сначала, что при условии A8) матрица А имеет по
крайней мере один собственный вектор х ]^= 0; собственное значение, отве-
отвечающее этому вектору, должно быть вещественным неотрнцательным (почему?).
Для доказательства допустим для наглядности, что л=3, н будем рас-
рассматривать А как матрицу отображения некоторого вещественного евклидова
пространства в себя (рис. 64). Тогда из условия A8) вытекает, что каждый луч
(/) с вершиной в начале координат 0, расположенный в первом октанте, пре-
преобразуется в луч (/'), расположенный там же, если только не переходит весь
в начало координат (почему?). В последнем варианте векторы, параллельные
(/), являются собственными (нм отвечает собственное значение А, = 0), так что
наше утверждение доказано; поэтому впредь мы будем этот вариант считать
исключенным.
Нам нужно доказать, что по крайней мере один луч из первого октанта
отображается на себя. Для этого рассмотрим треугольник (Т), определенный
условиями
x1-\-x2+xs=l,
Рис. 64.
Так как между его точками н лучами первого октанта имеется естественное
взаимно однозначное соответствие, то отображение лучей на лучн индуцирует
отображение треугольника (Т) в себя (рнс. 64), которое будет непрерывным.
Однако латвийский математик П. Боль A865—1921) в 1904 г. и независимо
голландский математик Л. Брауэр A882—1966) в 1911—1913 гг. доказали заме-
замечательную теорему о том, что при любом непрерывном отображении замкнутого
ограниченного выпуклого конечномерного тела в себя по крайней мере одна точка

§ 4. НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ 203
остается неподвижной, т. е. переходит в себя (впрочем, это вытекает из резуль-
результатов п. VIII.2.6). Отсюда и следует наше утверждение о луче, а потому и о
собственном векторе.
Предположим дополнительно, что неравенства A8) строгие (впрочем, для
дальнейшего достаточно, чтобы выполнялось A8) и все элементы какой-нибудь
нз матриц А2, А3, ... были отличны от нуля). Тогда все элементы построен-
построенного в предыдущем абзаце собственного вектора х0 строго положительны и
соответствующее собственное значение Л > 0 (почему?). Докажем, что если
некоторый вектор xlt у которого по крайней мере один элемент положитель-
положительный, удовлетворяет неравенству Axt ]^= ахь то Л ^ а. В самом деле, пусть
k—наибольшее возможное значение, для которого х0 ^ kx{. Тогда Ах0 ^ A(&xj),
т. е. Лх0 ^ ka\u х0 ^ I — k J xlf и неравенство а > Л противоречило бы опре-
определению k. Аналогично доказывается, что если вектор х2 имеет все элементы
положительными и удовлетворяет неравенству Рх2 )р= Ах2, то р й= Л.
Из первого утверждения сразу следует, что вещественные собственные
значения матрицы А не могут превосходить Л, а из второго—что любой соб-
собственный вектор х ^ 0 отвечает собственному значению Л. Оказывается, что
справедливы более сильные утверждения, на доказательстве которых мы здесь
не будем останавливаться: собственное значение Л простое, а все остальные
собственные значения матрицы А (в том числе мнимые, если такие имеются)
по модулю меньше Л. Поэтому при Л < 1 уравнение х=Ах+6 имеет ровно
одно решение, причем если 6^0, тоих^О (это следует из метода итераций,
см. ЛВМ, п. XVII.18).
Из доказанных выше неравенств ЛЭ=а и Л<р можно получить простые
двусторонние оценки для Л. Так, полагая х1 = х2 = A, 1, ..., 1)* и подбирая
соответствующие ос и р, мы получаем оценку
п п
min Уа,-?<Л< max V а.-ц
^1 «</<4<gJl
(докажите эту оценку, а также, выбирая по-другому вектор хъ оценку
Л3= max а,,).
</<
Более специальный класс, чем матрицы с неотрицательными элементами,
составляют осцилляциониые матрицы: именно, матрица А называемся осцилля-
ционной, если все ее миноры неотрицательны, а у некоторой степени А, А2,
А3, ... все миноры положительны (впрочем, второе требование можно заменить
на такое, равносильное: det А > 0, все а/,/+1 > 0, fl/+i,y > 0). Это, казалось
бы, трудно проверяемое свойство на самом деле может вытекать из теорети-
теоретических соображений, в результате чего осцилляционные матрицы появляются
в некоторых задачах теории колебаний. У осцилляционных матриц все собст-
собственные значения положительные и простые, а отвечающие им собственные
векторы имеют все увеличивающееся число перемен знака у элементов, напо-
напоминая последовательность функций sin kx @ <д;<;я, ft=l, 2 п). Свой-
Свойства и приложения осцилляциониых матриц описаны в книгах [23, 24].
9. Метод А. Н. Крылова. Прн раскрытии характеристического
многочлена det (А—XI) оказынается удобным следующий метод,
предложенный А. Н. Крыловым. Если матрица А имеет порядок л, то
det(A—Я1)за( —1)«Я» + в1а»-1 + в1Я»-1+...+в,,,
н задача состоит в том, чтобы найти коэффициенты alt аг ап.
В силу теоремы Гамильтона — Кэли (п. 3.3) имеем

204 - . ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
Помножив обе части справа на произвольный столбец х0 высоты л
и перенеся первое слагаемое в правую часть, получим
Если записать это векторное равенство по координатам, то получим
систему из л уравнений первой степеии с л неизвестными ех, еа, ...
..., а„, откуда и находим этн неизвестные. Отметим, что при этом
степени матрицы А вычислять не нужно, а надо последовательно
вычислять Ах0, А8х„ = А(Ах0), А3х„ —A(Asx0) и т.д.
Метод А. Н. Крылова имеет варианты, более удобные для вычи-
вычислений; на этих вариантах мы здесь не будем останавливаться.
10. Метод малого параметра. Рассмотрим лишь один из вари-
вариантов применения метода малого параметра. Пусть у матрицы А
все собственные значения %1У kit ..., А,„ и соответствующие соб-
собственные векторы хх, xs, ..., х„ известны, а требуется опре-
определить собственные значения и собственные векторы матрицы A-f-eB,
где е—малый параметр. Мы предположим для простоты, что все
значения кк различные; чтобы избежать произвольных скалярных
множителей в собственных векторах, будем считать эти векторы
единичной длины.
Разложим k-e собственное значение кк и соответствующий соб-
собственный вектор хк матрицы A-f-eB, зависящие от е, в ряды по
степеням е:
** = *¦* + "!**+•••, xft = x/k + eyft+...; A9)
при этом мы учли, что для е = 0 должны получиться заданные
результаты Хк, хк. По определению собственных векторов имеем
Раскрывая скобки и приравнивая коэффициенты при е, получим
Ау* + Вхл = %кук + ркхк, т. е. (А — Ьк1) ук = - Вхк + цЛ. B0)
Пели рассматривать последнее равенство как уравнение для нахож-
нахождения ук, то, как известно из п. 1.4, для существования решения
необходимо и достаточно выполнение условия ортогональности
»ft, гк) ж—z?Bxft + ]хкг*кхк = 0,
где гк—единственный, с точностью до скалярного множителя, соб-
собственный вектор матрицы А*—A.JI. Отсюда находим цк — Zktx*- .
При таком выборе fift уравнение B0) для ук имеет однопараметри-
ческое семейство решений ук = укй -\- Схк, где С—произвольная по-
постоянная. Параметр С находим из условия нормировки вектора xft,
так как из этого условия вытекает, что yJxft = O (почему?).

§ 4. НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ 205
Более простой результат получится, если матрица А эрмитова
(п. 1.3). Умножив первое равенство B0) слева на xj(j^k) и вос-
воспользовавшись ортогональностью собственных векторов, а также
равенством х)Аук = (у1А%у)*=(ук'Х/%/^Х/%*1ук, получим, что \*,ук=
В
=«¦'__Г , откуда окончательно (проверьте!)
5^
Аналогично можно найтн дальнейшие члены разложений A9).
Случай кратных собственных значений затронут в книге [28].
11. Метод непрерывного продолжения. С методом малого пара-
параметра непосредственно связан метод продолжения решения по пара-
параметру, также один из наиболее универсальных методов. Пусть фор-
формулировка задачи включает некоторый параметр X, который меняется
существенно, не мало, и решение задачи известно при некотором
значении Х = ХЛ. Метод состоит в построении дифференциального
уравнения с независимым переменным X относительно искомого
решения. Численное решение дифференциального уравнения с началь-
начальным условием при Х — Хо, обычно не представляющее существенных
трудностей (ЛВМ, пп. XV.32—34), и дает требуемый результат.
Покажем этот метод на примере построения обратной матрицы.
Пусть элементы квадратной матрицы А зависят от X, А = А(Я,), и
при А, = А,0 известна (например, вычислена по методу Гаусса) обрат-
обратная матрица А^1. Дифференцируя равенство А (X) А~1(к) = 1 по X,
легко получим (проверьте!)
._а-.?а-. о.)
Обозначив А = (а,.у), A~1 — {btj) и приравнивая выражения для эле-
элементов матрицы в обеих частях B1), получим систему из я* диф-
дифференциальных уравнений относительно функций by (к). Решая эту
систему численно при заданном начальном условии, мы и получим
А-»(*).
Если интервал изменения X достаточно велик, то следует время
от времени проводить коррекцию построенного решения. Это можно
делать следующим образом. Пусть при некотором Х = ХХ мы полу-
получили для А^) приближенное значение Вх; обозначим А* (А,х)—
— Вх = ДВХ, это и есть поправка, которую надо найтн. Обозначив да-
далее А (Я,х) = Ах (это известная матрица), получим А (Я,х) Ах = I, т. е.
(ВХ + ДВХ)АХ = 1, АВ1-А1 = 1—BjA»
= A-ВхАх)Вх + A—ВХАХ)ДВХ.
Итерируя последнюю формулу, получим (проверьте!)
ВхАхKВх+... B2)

206 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
Так как Вх«Af1, то В^ «I, и мы получаем в правой части
хорошо сходящийся ряд.
Метод непрерывного продолжения по параметру можно применить
и для решения нелинейных уравнений. Допустим, что задана систе-
система уравнений
,/1{Х1, Х2, ..., Хп\ А,) = 0,
/¦ («1, *1, •••, хп; Я,) = 0, ..., /n(xv Х2, -.., хп] Х) = 0 B3)
п для некоторого Я,=-Я,о известно какое-либо (не обязательно един-
единственное) из решений х\, х%, ..., х°п. Если теперь менять Я,, то и
решение будет изменяться, т.е. xi = xi(%) (/=1, 2, ..., п). Диф-
Дифференцируя равенства B3) по Я,, получим
откуда
л ,
/= 1
где fy/= ?,y (*n x2, ..., xn; X) — элементы матрицы, обратной к
А = (М-) . Эти элементы удовлетворяют системе из п2 уравнений,
полученных из равенства B1). Эта система не может быть решена
независимо, так как элементы матрицы А зависят от заранее неиз-
неизвестных величин *,-; однако если присоединить к этой системе урав-
уравнения B4), мы получим замкнутую систему дифференциальных урав-
уравнений относительно п2-\- п функций х((Х) и Ь^(Х), которую можно
численно решить для заданных при Я, = Я,0 начальных условий.
Для корректировки решения можно по мере его продолжения
при отдельных значениях X применять к системе B3) метод Ньюто-
Ньютона (см., например, ЛВМ, п. XII.12), выбрав результат продолжения
в качестве нулевого приближения. Так как естественно ожидать,
что это приближение будет в достаточной близости от точного ре-
решения, то метод будет быстро сходиться, даже если при его при-
применении пользоваться после линеаризации найденными приближен-
приближенными значениями btj. После уточнения значений xt можно уточнить
и значения &,-у- по формуле, аналогичной B2), а затем, приняв уточ-
уточненные значения за начальные данные, вновь решать дифферен-
дифференциальные уравнения.
Продолжение решения прекращается, если при конечном Я, по
крайней мере одно из.*,- обратится в бесконечность (это возможно,
так как решаемая система дифференциальных уравнений нелинейна,
ср. ЛВМ, гл. XV, пп.15 и 31), либо если прн конечных х: получится
det f^-J=O, так как тогда правые части B4) обратятся в беско-
бесконечность (почему?). В последнем случае нарушается условие суще-

§ 5. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 207
ствования неявных функций (ср. ЛВМ, пп. IX.13 и XII.3), и реше-
решение может разветвиться на несколько или стать мнимым; мы не
будем здесь исследовать этот вопрос.
Этот метод настолько эффективен, что если исходная система
уравнений
* 1 \*i» xz> • • • 1 хп) = "> 'г \хи хг> • • • i хп) == "> • • •
..., /=•„(*!, *„ ..., хп) = 0 B5)
не содержала параметров, то для ее решения иногда применяется
метод искусственного введения параметра. Он состоит в построении
системы B3) с параметром (обычна в том или ином смысле родст-
родственной B5)), изменяющимся, .скажем, в пределах О^Я,^ 1, притом
такой, чтобы при А, = 0 система B3) легко решалась, а при к=\
она становилась равносильной B5). Тогда, исходя из решения си-
системы B3) и продолжая его по параметру, если это окажется воз-
возможным, мы при Я, = 1 придем к решению системы B5). При этом
важно правильно угадать вид системы B3), чтобы и при всех про-
промежуточных значениях А. продолжаемое решение находилось на ветви,
приводящей при % — 1 к интересующему нас решению системы B5).
§ 5. Задачи линейного программирования
1. Основная задача. Основной задачей линейного программиро-
программирования является отыскание экстремума линейной функции в области,
заданной системой линейных равенств и линейных неравенств. Таким
образом, если обозначить число независимых переменных через п,
то речь идет об отыскании экстремума функции цели (критерия
качества)
z = c1x1 + cixt+...+cnxn A)
при условиях
anxi + aaxt + •••+«/А = b( A=1, 2, ..., k), B)
dnxt + dJixi+...+ dJnxn > ej (j = 1, 2, ..., m). C)
Неравенства вида dtxt + d2xt + .. ¦ + dnxn <I e можно отдельно не
рассматривать, так как они приводятся к неравенствам вида C)
после умножения обеих сторон на —1.
Естественно требовать, чтобы уравнения B) были непротиворе-
непротиворечивыми и независимыми, а А<я (почему?). Тогда k из независимых
переменных можно выразить через остальные п—k; подставив эти
выражения в правую часть A) и в левую часть C), мы получим анало-
аналогичную задачу, но все условия, наложенные на независимые пере-
переменные, будут иметь вид неравенств. Таким образом, с принципиальной
точки зрения поставленная задача представляет собой частный слу-
случай задачи на экстремум с ограничениями (см. ЛВМ, п. XII. 11). Однако
применение общей методики в данном случае мало что дает. Вскоре мы
увидим, что заданные ограничения определяют в пространстве незавк-

208 ГЛ. IV.' ЛИНЕЙНАЯ АЛГЕБРА '
сймых переменных'многогранник, а функция цели достигает экстремума
в каких-либо из его вершин. Поэтому в принципе было бы достаточно
сравнить значения z во всех вершинах и выбрать из этих значений
крайние. Но если число ограничений велико, то и число вершин велико,
все их надо находить, и потому такой «слепой» способ оказывается не-
непомерно громоздким. Методы линейного программирования дают воз-
возможность организовать целенаправленный перебор вершин, при ко-
котором объем вычислений значительно сокращается.
Появление линейного программирования связано с применением
математики в вопросах планово-экономического характера. Впервые
подобные задачи систематически изучали советский математик
Л. В. Канторович (р. в 1912 г.) и его сотрудники, начиная с 1939 г.;
с 1948 г. задачи такого рода независимо начинают интенсивно
исследовать математики США, которые и ввели сам термин «линей-
«линейное программирование» (не совсем удачный, так как он может быть
спутан с программированием для вычислительных машин). Сейчас
этот раздел математики значительно разработан и продолжает интен-
интенсивно развиваться, как и примыкающие к нему разделы. Здесь мы
сможем дать лишь представление о подходе к задачам линейного
программирования, отослав читателя, желающего ближе познако-
познакомиться с этим предметом, к книгам, специально ему посвященным
(см., например, [26, 42, 46, 100, 101, 140]).
2. Примеры. Укажем несколько примеров, приводящих к зада-
задачам линейного программирования. Каждый из них имеет варианты,
из которых мы приведем только один.
1. Задача о смесях. Пусть имеются продукты Ях, /72, ..., Пт,
каждый из которых содержит компоненты Klt Kit ..., Кп (например,
продуктами могут служить удобрения, а компонентами — химические
элементы, из которых они состоят; продуктами могут служить про-
продукты питания, а компонентами—жиры, белки, углеводы и вита-
витамины, и т. п.). Пусть каждый килограмм продукта Я,- стоит с{ руб-
рублей и содержит а(/- кг компоненты Kj (/=1, 2, ..., л). Пусть из
заданных продуктов составляется смесь, которая должна содержать
f>, кг компоненты /(„ Ьг кг компоненты Кг, ..., Ьп кг компоненты Кп.
Это, вообще говоря, можно сделать многими способами. Задача
состоит в том, чтобы общая цена необходимых для смеси продук-
продуктов была минимальной.
Для математической формулировки задачи обозначим через х(
количество килограммов продукта /7,- в смеси. Тогда функцией цели A)
служит цена смеси Ц — J^ сгх(, и задача состоит в ее мииими-
зации при условиях
т
xt>0 (i = \, .... т); Y*aijxi"=bj (/=1, •••, л).

§ 5. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 209
. Если количество каких-либо продуктов .ограничено, то добавятся
еще неравенства вида jc(.^e,-, т.е. —х{^—е{..
2. Транспортная задача. Пусть заводы Зх, 32, ..., Зт произво-
производят некоторую продукцию, . причем.каждый завод 3,- производит ее-
в количестве at тонн в год. Эта продукция доставляется потреби-
потребителям Пи Пг, ..., Пп, причем каждому потребителю /7у в количе-
количестве Ь, тонн в год. Предполагается, что выполнено условие баланса
т я
У *(Ж2 */• т- е- общее производство равно общему потреблению.
Пусть расстояние от завода 3, до потребителя П} по дороге равно
а,у км. Задача состоит в таком распределении продукции (прикреп-
(прикреплении потребителей к заводам), при котором общий объем перевозок
был бы минимальным.
Для математической формулировки задачи обозначим через Хц
количество тонн продукции, доставляемой в год с завода 3,- потре-
потребителю Пу. Тогда функцией цели служит общий объем перевозок
т п
z — 2j 2j at/xih
измеряемый в тонно-километрах, и задача состоит в ее минимизации
при условиях
%>0 (i=l, .... т; у=1, ..., л), ^%=a,- (/= 1, .. .,/я),
т
2*,7 = ^ (/=1, .... л)
(продумайте их!).
Наличие двух индексов у неизвестных не имеет принципиаль-
принципиального значения, так как неизвестные можно расположить н в едивом
порядке, например, обозначив yt =#u, Уг — Хц, ¦¦-, yn = xw
Уп+1=Х*1> Уп+*=Х2*, .-••, J\. = *i«, ^„ + 1 = ^31 н Т.Д. ВПЛОТЬ ДО
Ум=хтп (N—mn). Тогда получится частный случай общей задачи
п. 1. На практике такого изменения обозначений можно и не делать.
Задачу можно осложнить наличием различных видов транспорта,
введением стоимости перевозки, ограничением пропускной способно-
способности дорог и т. п. Все это будут задачи того же типа.
Аналогичный характер имеет задача об организации производ-
производства, когда определенное количество ресурсов (сырья, рабочей силы
и т. д.) отпущено на производство нескольких видов продукции и
требуется так распределить эти ресурсы, чтобы по какому-либо
выбранному критерию получить наибольшую выгоду, а также многие
другие задачи математической экономики. Важнейшую роль в этих
задачах играет правильный выбор функции цели,- от которого может
существенно зависеть искомое оптимальное решение, т. е. решение,
придающее этой функции экстремальное (в нужную сторону) значе-
значение при заданных условиях. Так, если максимизируется выгода

210 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕВРА
в задаче об организации производства и при этом может потребо-
потребоваться перестройка уже налаженного производственного процесса,
то функция цели должна учитывать затраты на эту перестройку
(т. е. «игра может не стоить свеч») и т. п.
Подчеркнем, что в правильно поставленной задаче функция цели
должна быть только одна. Поэтому распространенные выражения
вида «получить максимальную выгоду при минимальных затратах»
неправильны; надо говорить: «получить максимальную выгоду при задан-
заданных затратах» (функцией цели служит выгода) или «получить заданную
выгоду при минимальных затратах» (функцией цели служат затраты).
3. Геометрические замечания. Как известно из аналитической
геометрии, уравнение ах-\-Ьу = с на плоскости определяет прямую,
ограничивающую две полуплоскости, в одной из которых будет вы-
выполняться неравенство ах-\-Ьу~^ с, а в другой — неравенство ах +
+ by <! с. (Мы считаем полуплоскости замкнутыми, т. е. причисляем
к ним граничную прямую.) Уравнение ax-\-by-\-cz — d в простран-
пространстве определяет плоскость, ограничивающую два полупространства:
ax-\-by -\-cz^d и a-x-\-by -\-cz^.d. Аналогично уравнение
и
2J djX~b определяет в я-мерном вещественном числовом прост-
пространстве (я—1)-мерную плоскость (S) (иногда говорят «гиперпло-
«гиперплоскость»), ограничивающую два полупространства: (П+)(/(х)^Ь)
и (П~)(/(х)^Ь), где, по определению, х = (х1; хг; ...; xn), f(x) =
п
2
a.jXj. Плоскость (S) разделяет эти полупространства, так как,
если следовать вдоль любого непрерывного пути из любой точки
р?(П+) в любую точку q ?(П~), то значение f(x) вдоль этого пути
непрерывно переходит от f(p)~^b до f(q)^b и потому по дороге
должно хотя бы один раз равняться Ь, а тогда x?(S).
Если заданы две точки р{рх; рг; ...; pn), q(q1; q2; ...; qn)
в Еп, то координаты точки х, расположенной на отрезке pq и де-
делящей его в отношении — = Х, находятся, как в аналитической гео-
геометрии на плоскости или в пространстве, по формулам
_ Pi + kqj ... 2 ,
Xj — j . ^ \t 1 , -i, . . . , П).
1 X
Если обозначить т^Гх = а, ттл—$> т0 можно также записать
' = !> 2, .... л), где 0<а, р<1, а + р = 1. D)
Множество (М) точек Еп называется выпуклым, если оно вместе
с любыми двумя своими точками содержит и весь отрезок, соеди-
соединяющий эти точки. Так, плоскость любого числа измерений, полу-
полуплоскость или полупространство, отрезок, круг, угол (как часть
плоскости), меньший 180°,—все это выпуклые множества. В отли-

§ 5. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 211
чие от этого, угол, больший 180°, совокупность из конечного числа
А^2 точек (как и вообще любое несвязное множество), окруж-
окружность (как и любая кривая линия), любая неплоская поверхность—
это невыпуклые множества. В связи с последними примерами отме-
отметим, что термин «выпуклость» может иметь различный смысл:
выпуклые линии и поверхности в наглядно-геометрическом смысле,
если их рассматривать как множества точек, не являются выпук-
выпуклыми множествами.
(Аналогично вводится понятие выпуклости множества (М) век-
векторов в линейном пространстве: здесь вместе с любыми двумя век-
векторами р, д множество (М) должно содержать
каждый вектор а/> + Р<7> где 0<1а, E<11,
Пересечение (т. е. общая часть) любого коли-
количества выпуклых множеств в одном пространстве
всегда является выпуклым множеством. В самом
деле, любые две точки р, q пересечения принадле-
принадлежат каждому из пересекающихся множеств; в силу
их выпуклости и отрезок pq принадлежит каж-
каждому из этих множеств, а потому и пересечению.
Пусть теперь дано произвольное, вообще
говоря, невыпуклое множество (М) точек. Обоз- Рис' 65>
начнм через (Мх) пересечение всех выпуклых
множеств, содержащих (М) (такие есть, например все простран-
пространство). Тогда множество (Afx) выпуклое, содержит (М) и содер-
содержится во всяком выпуклом множестве, содержащем (М) (почему?);
другими словами, (Mj) — минимальное выпуклое множество, содер-
содержащее (М), оно называется выпуклой оболочкой множества (М).
На рис. 65 показан пример выпуклой оболочки плоского множе-
множества, состоящего из двух компонент связности, причем (М) за-
заштриховано густо, a (Mj) — редко. Если (М) состоит из конеч-
конечного числа точек р±, рг, ,,,? рк, то (Мх) представляет собой вы-
выпуклый многогранник, размерность которого равна наибольшему
числу линейно независимых векторов из PjP2, PtP3, . i., P-J>n, а вер-
вершинами которого служат некоторые (не обязательно все!) из то-
точек (М). Обратно, всякий выпуклый многогранник представляет
собой выпуклую оболочку совокупности своих вершин. Если (М)
представляет собой совокупность всех точек некоторого количества
лучей с общей вершиной О, то (Жх) есть выпуклый конус (так го-
говорят, хотя точнее было бы говорить «полуконус») с вершиной О,
натянутый на (М); в частности, (Жх) может совпасть со всем про-
пространством Еп. (Какой вид имеет (Мх), если (М) состоит из конеч-
конечного числа лучей с общей вершиной?)
Пусть (М) состоит из трех точек р, q, r; тогда (Мг) представ-
представляет собой треугольник, который, впрочем, может выродиться

212> ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
в. отрезок, если эти точки, лежат на одной прямой. Этот треуголь-
треугольник уожно получить, соединив г отрезками со всеми точками от-
отрезка pq. Поэтому в силу D) любая точка (Mt) имеет координаты
х{ *= a'rt, + 8' (apt + $q;) = alPi-Jr a^t + a3r( (/ = 1, 2, ..., я),
где все а,->0 и <х1 + а1 + <х, = Р'а + р'р + а' = Р'(а+В) + а'«=.
р' ' 1
р
Аналогично можно проверить, что если (М) состоит из k точек
р, q, ..., 5, то координаты всех точек (Mt) (и только их) можно
представить в виде
*,-= «!/>, +«,?,+ -..+<V?, (/=1, 2, .:., л), E)
где все
l. F)
Если же допускать для а;- и отрицательные значения, но сохранить
второе условие F), то совокупность всех точек с координатами E)
заполнит плоскость (S) минимальной размерности l^.k — 1(/^я),
содержащую все точки р, q, ..., s. В частности, если / = ?-— 1
(т. е. две точки не совпадают, три точки не лежат на одной пря-
прямой и т. п.), то величины alt аг ак определяются точкой
х ? (S) однозначно, они называются барицентрическими координатами
точки х; их k, но так как их сумма равна единице, то имеется
k—1=/ степеней свободы, как и должно быть. Название объ-
объясняется тем, что если в точках р, q, ..., s поместить соответст-
соответственно массы а„ а4, ,.., ак, то центр тяжести получениой системы
точек окажется как раз в х. Когда / = А—1, множество (М^ на-
называется /-мерным симплексом: нульмерный симплекс—это точка,
одномерный—это отрезок, двумерный—треугольник, трехмерный —
тетраэдр и т. д.
. Аналогично решается задача о построении выпуклой оболочки
для множества, состоящего из конечного числа лучей с общей
вершиной О. Если эти лучи параллельны векторам р, q, ..., s
соответственно и одинаково направлены с ними, то требуемая обо-
оболочка получится, если из О отложить все векторы вида <хгр -f- <x2q -\- ...
...-\-aks, где все О/^О.
4. Геометрический смысл основной задачи. Допустим сначала
для простоты, что п — 2 и условия вида B) отсутствуют. Тогда
каждое из условий C) определяет некоторую полуплоскость, и об-
область (G), в которой сравниваются значения функции цели, полу-
получается в результате пересечения этих полуплоскостей. На рис. 66
показан случай пересечения пяти полуплоскостей, каждая из кото-
которых заштрихована вблизи ограничивающей ее прямой. Мы видим,
что в данном примере область (О) представляет собой выпуклый
четырехугольник ABCD. Возможны и принципиально иные случаи:
например, если полуплоскость, примыкающую к (/4), заменить на
другую полуплоскость, примыкающую к (lt), то область (G) будет.

§ 5. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
213
Рис. 66.
неограниченной; если вместо этого проделать то же с (/,), то (О)"
станет пустым множеством, т. е. не будет содержать ии одной
точки, система неравенств C) окажется противоречивой.
Аналогичным образом при любом л совокупность неравенств (8)
определяет либо выпуклый многогранник, либо выпуклое многогран-
многогранное тело, простирающееся в бе-
бесконечность, либо, наконец, пу-
пустое множество. При этом мно-
многогранник и многогранное тело,
вообще говоря, будут л-мерными,
однако возможны специальные
случаи, когда размерность полу-
получится меньшей: например, если -
на рис. 66 поступательно пере-
перенести прямую (/,) так, чтобы она
прошла через точку В, то си-
система неравенств C) определит
единственную эту точку, т. е.
«нульмерныймногогранник». Сход-
Сходные выводы получаются и в случае, когда имеются также условия
вида B), так как эти условия, если не противоречат друг другу,
определяют в Еп некоторую плоскость (размерности л—rang(fl,,)),
на которой и надо рассматривать ограничения C).
Вернемся опять к рис. 66 и изобразим на той же плоскости
линии уровня функции цели A) (рис. 67). Так как это линейная
функция, то линии уровня будут параллель-
параллельными прямыми. Если эта функция убывает в
направлении, указанном на рис. 67 черточ-
черточками, то очевидно, что оиа принимает наи-
наибольшее в области (G) значение в вершине
В и наименьшее—в вершине D. Впрочем,
если линии уровня параллельны одной из
сторон четырехугольника ABCD, то экстре-
экстремальное значение будет достигаться во
всех точках этой стороны.
Аналогичным образом при любом л по-
поверхности уровня функции цели представляют
собой параллельные друг другу (л—^-мер-
(л—^-мерные плоскости. Если (G)—многогранник, то функция цели принимает
наибольшее и наименьшее значения, вообще говоря, в двух верши-
вершинах, крайних в определенном смысле (в каком?). При специальных
направлениях поверхностей уровня эти значения могут достигаться
на гранях (G) размерности 2^1. Если (G)—неограниченное много-
многогранное тело, то может получиться, что функция цели на (G) будет
неограниченной сверху или снизу (или и сверху н снизу); тогда соот-
соответствующая задача на экстремум решения не имеет.
Рис. 67.

214 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
б. Стандартный вид основной задачи. Перед решением задачи
A) — C) ее приводят к тому или иному стандартному виду в зави-
зависимости от применяемого метода. Мы будем рассматривать метод,
в котором стандартным видом ограничений, взамен B), C), является
2, .... к), G)
(8)
Можно показать, что от ограничений любого вида B), C) можно
перейти к этому стандартному виду. Неравенства (8) чаще всего
присутствуют в постановке задачи (см. примеры п. 2); если же это
не так, то нужно выбрать какие-либо нз п линейно независимых
левых частей B), C), обозначить через yt, уг, ...,уп разности
между этими левыми частями и соответствующими правыми частями,
после чего всюду перейти от величин X к величинам у. Если нера-
неравенства (8) уже присутствуют и, кроме того, имеется ограничение
вида C): d1x1 + й^сг + • • • + Л^с„ ^ е, то надо обозначить d1xl -f
+ ?МГ2+ • • • ~\-dnxn — e — xn + v в результате чего число независимых
переменных увеличится на единицу, а указанное ограничение заме-
заменится на условия
d1x1 + йгхг + ... + dnxn—хп+1 = е, хп+1 > О,
из которых первое присоединится к G), а второе—к (8). Если
имеется еще одно ограничение вида C), то надо ввести xn+i и т. д.
Наконец, если в равенстве вида B) будет Ь{ < 0, то надо с обеих
сторон поменять знаки. Так мы приходим к стандартному виду
ограничений G), (8).
Мы будем рассматривать задачу о наименьшем значении функции
A) при условиях G), (8). Задачу о наибольшем значении можно
рассмотреть аналогично, а можно воспользоваться простым равенстюм
max (c,x, + с2л;2 + ... + спхп) = — min ( — сгхг—сгх2 —... — спхп).
Поставленная задача допускает еще одно геометрическое истол-
истолкование, отличное от приведенного в п. 4. Для этого введем А-мер-
ные числовые векторы а1, а2, .,., ап — столбцы матрицы коэффици-
коэффициентов а(у; ^-мерный столбец b из правых частей Ь(; (k-\- 1)-мерные
столбцы а/(/=1, 2, ,.,, л), полученные присоединением к а, снизу
коэффициента Cj функции A). Условия G) можно записать в виде
векторного равенства
Если произвольно менять все лг^^О, то левая часть опишет
конус (ср. п. 3), который мы будем называть натянутым на векторы
Лц а2, . . ., ап и обозначать через /С; этот конус представляет собой
совокупность векторов, но его можно, отложив все векторы от
начала координат, рассматривать и как совокупность точек Ек, коор-

§ 5. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 215
динаты которых мы будем обозначать %и Н2, ,,., %к. Система G),
(8) непротиворечива тогда и только тогда, когда b g К (почему?).
С другой стороны, совокупность всевозможных векторов вида
' 'п, где все х} > 0, (9)
образует конус К' в пространстве Ek+1 с координатами %lt |2,,,., %k, z,
который при проектировании на Ek отображается на К. При этом,
если какой-либо из векторов (9) проектируется на- Ь, то выполняются
соотношения G), (8), и потому соответствующее значение г = х1с1 +
-\-хгсг -f-... -f- xncn—одно из значений A), подлежащих сравнению.
Так как из этих значений нужно выбрать наименьшее, то задача
сводится к отысканию координаты z
самой низкой (считая «верхом» поло-
положительное направление оси г) точки
пересечения прямой \х — Ьи §2 = &2, ...
..-, !» = *„ с конусом К'.
6. Метод последовательного улуч-
улучшения решения. Этот метод решения
задачи линейного программирования,
записанной в стандартной форме, назы-
называется также симплексным методом и
имеет простой геометрический смысл,
который мы покажем для случая k — 2.
Допустим, что векторы ау и b в пло- Рис. 68.
скости ?2 расположены, как на рис.68;
на каждый вектор а,- проектируется вектор а}, не показанный на
рисунке. Пусть из векторов а,- указаны какие-либо два, например
а3 и а8, причем такие, что если принять их за базис в Е2, то век-
вектор b будет иметь положительные координаты: Ъ = а1л3-{-$1ль;
at > 0, рх > 0. Тогда значения x1=xt = xi = xt = x4 = 0, x3 = av
хь = pt удовлетворяют всем условиям G), (8), и потому соответ-
соответствующее значение A) получается в результате пересечения пло-
плоскости (Hi), проведенной через векторы а3 и aj, с прямой (/), про-
проведенной через конец вектора b параллельно оси z. (Напомним, что
мы считаем все векторы отложенными из начала координат.) Если
среди векторов л] нет ни одного, лежащего ниже (HJ, то и весь
конус К' расположен выше (Ilj, и лишь имеет грани в (Пх), так
что полученное значение г = а1с3-(-р1с6 и будет искомым наимень-
наименьшим значением z. Но пусть какой-нибудь из векторов а)- расположен
ниже (Ili), например это а\; тогда мы заменяем в базисе а5 на а1.
(Замена а3 на at при изображенном на рис. 68 положении векторов
привела бы к отрицательному коэффициенту разложения вектора b
по новому базису at, a5.) После этого проводим через а^ и а3 пло-
плоскость (П2) н повторяем то же рассуждение, что выше с (IIj). Если,
например, вектор а^ расположен ниже (П2), то мы переходим к базису
at, а4 в Ег и т. д. Так как после каждого шага соответствующее

216 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
значение A) уменьшается, а всех вариантов (способов выбора базиса
из заданных векторов AJ) имеется лишь конечное число, то через
конечное число шагов мы придем к неулучшаемому варианту, т. е.
к решению задачи.
Если задача поставлена неправильно, то возможен также следу-
следующий случай: пусть, например, вектор я!ч (рис. 68) окажется ниже
плоскости, проведенной через а.[ и а'4. Тогда нельзя перейти ии
к базису alt а,, ни к базису а4, а7, ие нарушив требования
положительности координат вектора Ь. Но в этом случае прямая (/)
углубляется в конус К' как угодно далеко вниз (почему?), т. е.
поставленная задача иа наименьшее значение решения ие имеет.
В случае любого k процедура аналогичная. Мы исходим из не-
некоторого базиса в Ек, выбранного из заданных векторов ау, причем
такого, в котором все координаты вектора b положительны;
эти координаты служат значениями Xj с соответствующими но-
номерами, тогда как остальные Xj равны нулю. Затем мы заменяем
один из вектороа в базисе на одни из оставшихся ау, затем
еще один и т. д., все время следя за тем, чтобы все коор-
координаты вектора b были положительными, а соответствующие значе-
значения A) убывали. Тогда, если задача поставлена правильно, то через
конечное число шагов мы приходим к неулучшаемому варианту, т. е.
к решению задачи.
Теперь перейдем к формальному описанию процедуры, так как
пользоваться только геометрическими соображениями при вычисле-
вычислениях затруднительно. Мы предположим (условие невырожденности),
что заданный вектор b ие разлагается ни по каким k—1 из задан-
заданных векторов а1( а2, ..., а„. Естественно считать также, что k < п
(почему?).
Мы исходим из какого-либо базнса а;,, а;,, ..., a,-t, выбранного
среди векторов а1, а2, ..., а„ так, чтобы в разложении
b = a,a<t -f a2a(, -f • • • + «V^ A0)
были все <Ху > 0 (о выборе этого базиса см. ниже). Затем надо
найти коэффициенты разложений всех векторов а,- по этому базису:
(' = 1.2 п); A1)
это делается при каждом / с помощью решения системы из k
уравнений 1-й степени с к неизвестными. Если мысленно предста-
представить себе плоскость (ПД проведенную через векторы а/„ а,!„ .. .
. .., &'ik, то перемещению на вектор а,^ в плоскости Ek отвечает
перемещение точки в (Е^) на c(j вдоль оси z (почему?). Вычислим
выражения, смысл которых показан на рнс. 69, • •
<*«— Ci=PilCil+Piicit+...+pikclk — с, (/ = 1,2, ..'., я). (Т2)
Если все они <10, то в силу предыдущего мы получаем решение
поставленной задачи: Xil=al, xit = at, ..., xik—o.k, прочие х{—0;

§ 5. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
этому решению отвечает значение
217
Пусть теперь какая-либо из разностей A2) положительна, напри-
например при / = г (на рис. 69 г='2); если положительны несколько раз-
разностей, то из иих естественно выбрать наибольшую. Тогда из A0)
и A1) при /=г вытекает, что при любом 9>0
b = («j -QPrl) а,, + (a,-ВРгг) а,, + ... + (ак-QPrk) а,-4 + 8аг. A3)
При этом могут быть два случая. Если/>гГ <; 0, р?г^0, .,., ргк^.0,
то при как угодно большом 6 все коэффициенты в разложении A3)
будут положительны, и такому разложе-
разложению будет отвечать значение г—>— оо.
Значит, поставленная задача решения
не имеет.
Если же имеются рг/ > 0, то в
можно увеличивать только до значе-
значения
! = —— = min
Prs
<"г/>
— A4)
Рис. 69.
(почему?). При таком 9 в правой ча-
части A3) член с а;, пропадет, тог-
тогда как остальные коэффициенты будут положительными. Заменим в
базисе а*,, а,-а, ..., Яцк вектор а^ на аг и перенумеруем полученные
k векторов заново так: а,-' , а,-' , ..., а,-'. Тогда из равенства A1)
при i = r легко выразить вектор а;, через эти к векторов;
отсюда, в частности, следует, что и векторы а,-^, а,', ..., a,'ft.
образуют базис в Ек. Подставляя полученное выражение для а*5
в A0) И A1), мы получим разложения вида
b =
a,- =*ptlii't +P't2% + ... +p'uWk V= 1.2 я).
( ¦'
Теперь все подготовлено к следующему шагу. Вновь составляем
выражения вида A2), проверяем их знаки и т. д. Совершая так шаг
за шагом, мы за конечное число тагов (обычно от к до 2k) при-
приходим к окончательному, т. е. не улучшаемому, решению, либо до-
доказываем неразрешимость задачи.
Условие невырожденности, сформулированное выше, не требует
специальной проверки. Вырожденность обнаружится сама, если
в разложении A5) или в каком-либо из дальнейших аналогичных
разложений некоторые из коэффициентов окажутся равными нулю.
Тогда можно наугад и притом достаточно мало изменить заданный
вектор Ь. После этого задача станет невырожденной и ее решение
можно будет довести до конца; а построенный окончательный базис

218 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
в измененной задаче, если изменения достаточно малы, будет давать
решение и исходной задачи.
Нам остается сказать о выборе исходного базиса ait, а,-2, ..., а,к.
В некоторых случаях его удается подобрать просто, рассматривая
заданные векторы а1, а2, ..., ап, Ь, либо из реального смысла по-
поставленной задачи, исходя из какого-либо решения, подлежащего
улучшению. '
Если это не удается сделать, то можно применить следующий
искусственный метод. Введем в задачу новые независимые перемен-
переменные хп+1, хп+2, ..., хп+к, записав функцию цели и условия в виде
z = ctxt + сгх2 + ... + спхп + солг„+1 + солг„+2 + ... -f ах„+к,
xn + xn + i = bi (/ = 1, 2, ..., k), } A6)
Здесь со— весьма большое число, которое можно не уточнять
оставляя его при вычислениях в виде буквы и считая, что
aco-f-#> cco + d(a, b, с, d—обычные числа) всякий раз, если а > с
либо если а = с и b > d; нелинейные выражения от со в процессе
вычислений появиться не могут. При таком условии решить старую
задачу A), G), (8) — все равно, что решить новую задачу A6) и
обнаружить после этого, что хп + 1 = лгп + 2 = ... = хп+к — 0 (почему?).
Однако совокупность векторов ап+1, ап+2, ..., an+fc—это как,
раз основной базис в Ек; если все Ь( > 0 (это условие невырож-
невырожденности), его можно принять в задаче A6) за исходный базис,
который для первоначальной задачи называется искусственным.
Затем по описанному выше способу мы осуществляем последова-
последовательную замену векторов в базисе, пока не придем к окончательному
решению новой задачи. Если при этом все векторы искусственного
базиса окажутся замененными, то это решение будет одновременно
решением исходной задачи. Если же в окончательном базисе оста-
останется хотя бы один искусственно введенный вектор, то это значит,
что условиям G), (8) не удовлетворяет ни один набор значений
хи лг2, ..., лг„, т. е. эти условия противоречивы.
Используя некоторые из векторов а1; а2, ..., а„, иногда оказы-
оказывается возможным организовать аналогичным образом исходный
базис, введя менее чем k искусственных векторов.
В заключение отметим, что из-за основной ориентировки на
приложения к экономике в линейном программировании применяется
следующая терминология: всякий набор значений х1г хг, ..., хп,
удовлетворяющий условиям G), (8), называется планом; если у плана
п — k из значений x-t равны нулю, то план называется опорным,
каждый такой план определяет (во всяком случае, если задача не-
невырожденная) базис в Ek; план, доставляющий минимальное значе-
значение функции цели, называется оптимальным. Как мы видели, опти-
оптимальный план — это один из опорных планов.

§ 5. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 219
Универсальный симплексный метод пригоден для любых задач
линейного программирования. Однако для отдельных классов задач—
таких, например, как транспортная (п. 2), — разработаны более
удобные специальные методы, которые можно найти в литературе,
указанной в п. 1.
Еще раз подчеркнем, что при небольшом числе неизвестных и
неравенств задачу линейного программирования нетрудно решить
простым перебором. Однако когда число переменных, как в реаль-
реальных задачах, достигает десятков и сотен, количественные трудно-
трудности перерастают в качественные, простой перебор становится не-
невозможным и задача требует принципиально иного подхода, и
породившего новую область математики—линейное программирование.
7. Приложение к матричным играм. Теория игр—это недавно
возникшая область математики, изучающая задачи о выработке
оптимальной стратегии (наивыгоднейшей линии поведения) в той или
иной конфликтной ситуации, т. е. ситуации, в которой «враждующие
стороны» преследуют противоположные цели и результат каждого
мероприятия одной из сторон зависит от того, какой образ действий
выберет «противник». Рассматриваемые в этой теории математические
схемы охватывают как собственно игры, так и различные ситуации,
возникающие из многих практических вопросов: рациональные про-
производственные и экономические решения, вопросы военной тактики, во-
вопросы выбора системы экспериментов («игра человека с природой»)
и т. д.
Впервые систематически задачи теории игр рассмотрел в 1909 г.
немецкий математик Э. Цермёло A871 —1953), основополагающие
результаты получил в 1928 г. Дж. Нейман; значительное внимание
к этим задачам было привлечено в годы второй мировой войны и
непосредственно после нее. Сейчас имеется целый ряд курсов по
теории игр, из которых мы укажем на [11, 22, 77, 78].
Здесь мы рассмотрим только одни вид игр, именно матричную
игру с двумя участниками, имеющую следующую схему. Пусть каж-
каждый из противников А и В, независимо один от другого, называет
номер, А — от 1 до л, а В—от 1 до /и. При этом, если А назвал
номер i, а В — номер j, то игрок В выплачивает игроку А выиг-
выигрыш а,у (конечно, если a{j- < 0, то на самом деле выигрывает В);
здесь (а,у) — платежная матрица, известная обоим игрокам. Такая
игра может многократно повторяться.
Специфику игры можно понять уже на самом простом примере
т. е. когда каждый из игроков независимо от другого называет одну
из цифр, 1 или 2, и если цифры совпадут, то выигрывает А, а если
не совпадут, то В, причем размер выигрыша во всех случаях оди-
одинаков. Ясно, что если игра совершается лишь один раз, то ни один

220 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
из игроков не имеет преимуществ перед другим, и дать никакие
указаний по выбору хода нельзя. Однако если игра повторяется и
после каждой «партии» оба игрока узнают о ходе противника, то
возникает борьба стратегий, в которой каждый стремится разгадать
стратегию противника. Например, если А будет все время называть одну
и ту же цифру, или называть 1 и 2 попеременно, или, скажем, называть
ту цифру, которую в предыдущей партии назвал В, и т. п., то В, разгадав
эту стратегию, может все время выигрывать; но, с другой стороны, н А
может разгадать стратегию В. Если В существенно сильнее А (например,
если А — человек, а В—ЭЦВМ с хорошо составленной программой),
то даже очень сложная чистая стратегия А, т. е. такая, в которой
каждый следующий ход А по какому-то продуманному заранее пра-
правилу однозначно определяется результатами предыдущих встреч,
рано или поздно разгадывается В. Более того, если А, желая сбить
с толку В, начинает называть цифры, по собственному мнению,
наугад, то и в этих ходах игрок В может подметить какую-то за-
закономерность (хотя не такую жесткую, как в чистой стратегии) и
в результате выигрывать чаще, чем А.
Однако имеется простой способ избежать проигрыша даже са-
самому сильному противнику. Для этого надо, чтобы выбор каждого
хода игроком А был совершенно случайным, с вероятностью 0,5
для обоих исходов: например, А может перед каждым ходом под-
подбрасывать монету и называть 1, если выпадет цифра, и 2, если
выпадет герб. Такая стратегия, в которой каждый ход является
случайным, но заранее устанавливается его вероятность, называется
смешанной.
Вернемся к случаю общей платежной матрицы (а,у) и допустим,
что оба игрока избрали смешанную стратегию, так что игрок А
называет номер i с вероятностью pt, а игрок В называет номер j
с вероятностью ду, при этом, конечно,
m
=i, 2?/=15 все />i
При таких стратегиях среднее значение выигрыша игрока А за одну
игру, подсчитанное по простым правилам теории вероятностей (см.,
например, ЛВМ, пп. XVIII.4 и 13), равно
п m
v*=v(p, ?)= 2 2
i=l/=1
где для краткости обозначено р = {pv pit ..., рп), q = (qv qt,..., qm).
Допустим, что А старается увеличить это значение за счет под-
подбора стратегии, а В этому сопротивляется, причем для простоты
будем считать, что стратегии обоих друг другу известны. Тогда
при любой стратегии р игрок В изберет стратегию q, для Которой
v = m\nv(p, q), и потому самый большой средний выигрыш игрока Л

§ 5. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
221
будет равен
v' = max (min ¦»(/>, q)).
р. ч
A8)
Обратно, если В старается минимизировать свой средний проигрыш,
а А этому сопротивляется, то получаем значение
v"^=min(maxv(p, q)). A9)
ч р
Основная теорема Дж. Неймана состоит в том, что эти значе-
значения равны, v' — v"; это общее значение называется ценой игры.
При этом существует пара стратегий (не обязательно единственная),
р=р и q — q, для которой
) — maxv(p,
P
) = minv(p, q).
Q
Отсюда вытекает (продумайте!), что при применении смешанных
стратегий эти стратегии р, q являются оптимальными (наиболее
выгодными) сразу для обеих сторон:
если А изберет стратегию, отличную
от р, то В сможет, вообще говоря,
уменьшить свой проигрыш (во всяком
случае, не увеличить его); а если В
изберет стратегию, отличную от q, то
на этом А может лишь выгадать. В
случае л = /я = 2, когда имеются лишь
две независимые переменные plt qlt
возможная картина линий уровня сред-
среднего выигрыша показана на рис. 70;
Впрочем, точка (pl7 q±) может по-
попасть на границу квадрата и не быть
стационарной точкой функции v(pv qt).
В частности, для примера A7) будет р
(проверьте!).
= 1/2, v' = 0
Не следует думать, что равенство выражений A8) и A9) вытекает просто
из возможности перестановки порядка действий max и min. На самом деле
такая перестановка, вообще говоря, невозможна. Проверьте, например,
max I min (x+y—1J|=0, min
max (х+у—1)*]=!..
< 4
Еще более простой пример: если ( и / меняются от 1 до п и д(у =
j дР" |^Ч' то max(mind;/)=0, min (max A;/) =1.'На самом деле дока-
доказательство теоремы Неймана совсем не простое, и мы его здесь не приводим.

222 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
Чтобы отыскать цену игры и оптимальные стратегии, предполо-
предположим, что все Я;у> 0. Этого всегда можно достичь, добавляя ко всем
исходным а(у одно и то же достаточно большое число а. Тогда
просто ко всем выигрышам добавится а, т. е. от полученной цены
придется а вычесть; а на оптимальных стратегиях такое добавление
не скажется. Заметим далее, что для любых чисел а1г а2, ..., а„
равен наименьшему из чисел о^, а2, ..., ат (почему?). Значит, при
заданных ри р2, ..., рп
т [ п
min v (p, q) = min 2 2 aipl
я я у=1 \« = 1
п
равен наименьшему из чисел У\а^-Р{ для у=1, 2, ,.., т. Если
обозначить этот минимум через vp, то ясно, что vp > 0 и
2 atjPi>vp (/=1, 2, .... /и), B0)
причем по крайней мере для одного j это неравенство должно об-
обратиться в равенство. Обозначив pi / vp = xit получим, что
*,>0 (г = 1, 2, ..., п), . B1)
2 "//*/>! (У=1. 2, ..., /и), B2)
f=i
тогда как
Так как г>-=г>' (почему?), то для значений xl^xi=pj/v' удов-
удовлетворяются условия B1), B2), а левая часть B3) равна \/v'fi С
другой стороны, пусть x'i — решение задачи о минимуме суммы B3)
при условиях B1), B2). Вычислим соответствующее значение v'p
по формуле B3) и положим р\ — х'{о'р. Тогда 2^p'i=\, и так как
по крайней мере одно из неравенств B2) при лг; == a:J должно обра-
обратиться в равенство (почему?), то из B2) и B0) получаем, что фор-
формально введенное v'p как раз равно vp и потому меньше или равно
11
v', откуда —;^ —. Значит, по смыслу задачи на минимум, v' =»fp,
Vp V
т. е, цена игры получается с помощью сформулированной задачи
на минимум, которая является одной из задач линейного програм-
программирования (п. 1); вероятности р{ для оптимальной стратегии пропор-
пропорциональны компонентам xt оптимального плана. Оптимальную стра-
стратегию q можно найти аналогичным образом.

§ 5. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 223
Рассмотрим численный пример. Пусть платежная матрица (а,у) имеет вид
(-2 3 ~!) (т- е- n=2> m==3)-
Добавив ко всем элементам число 3, мы приходим к задаче на минимум суммы
*i+*a при условиях
лт^О, х225 0, 4x1+x23sl, 3*!+ 6х2 5=1, 2x1 + 4x2 S& 1.
Переходя к стандартному виду (п. б), введем переменные xs, xit хъ:
2—xx=\, 2
Согласно методу последовательного улучшения решения (п. 6) положим
-(I )•-(! )• -П )• —Н )¦ -(-?)¦'"(:)
Не будем искать опорный базис, а введем искусственный базис, как в п. 6:
заменив функцию цели на г = Х1 + х2+0>л:в+0)д::7+0)л:8- Составим разложения
вида A0), A1), а также выражения A2):
Ь=ав+а,+а8;
— 1 =9со— 1 > 0;
—l = llco—1 > 0;
а3=— ав> d3—c3=— со < 0;
а4=—а7, d4—ct=—со < 0;
а5=—а8) ds—с5 = — со < 0.
Наибольшее значение для d/-~c/ получается при » = 2, поэтому введем в опор-
опорный базис вектор а2; так как наименьшее значение A4) достигается при i'=7
1 1 2
(почему?)., то из базиса исключаем aj. Так как а,=— а2—ё~ав—5*а8, то
о о о
получаем
.1 ,5 ,1
а3 = — ав> d'3—c3=— со;
Л 4-— 4-— d'— — —i-4- —
а5=—а8, d'6— c5=— со;
112 „ 1 11
Теперь надо ввести в базис а^ а исключить а„ (проверьте!).

22„4 ГЛ. IV. ЛИНЕЙНАЯ АЛГЕБРА
2 1 ¦ •
Так как а« = -уа1—=-а2, то
а3=—yai+ya2, rf—ca= — — ;
i 4 2 „ 12
a4 = 2-rai-2Ta2+Ta8> d't-ci^-T + -<u;
аь = —а8> dTb—сь=— о;
2 1 1
¦»=yai—j*z< <\—c» = -j—<u\
2 15
-,Ta8, d7-c7=y-T о.
Теперь надо ввести а4 и исключить а„; так как искусственные векторы все.
исключены, то можно ими больше не заниматься. Имеем а8 = — тт
,2 ,3
4-у-а2 + уа4, откуда
аэ = — уа!+уа2, d3 —са = — — \
1' 2 3 J#// 1
a5=T4ai-Taa—2 а«' d» -c» — У
Так как разности A2) получились отрицательными, то мы пришли к опти-
3 1 1
мальному плану дг1=—, дг2=-=- , дгэ = О, хь=^-х > ^ь = 0. По формуле B3) по-
подучаем, вычитая добавленное число 3, цену игры
1 о 1 - 3 - 2
и==^+73-3=--5; при 8ТОМ ">= "
Мы предоставляем читателю проверить, что оптимальная стратегия второго
- 2 - - 3
игрока имеет вид 0i = — q^ — 0, </э=тг • ^т0 можно сделать либо с по-
о о
мощью независимого решения задачи на максимизацию суммы |/1 + у2+!/8 ПРИ
условиях
У!>0, Уг^О, Уа^О, 4у1 + Зу2 + 2Уз<,1, ух + 6у2 + 4j/3< 1, B4)
либо же просто, положив «/i+j/2 + j/3= ( 3—г-) =-т-т и приняв во внима-
V & / 14
иие, что для оптимального решения по крайней мере одно из неравенств B4)
должно обратиться в равенство. Первый способ более громоздкий, но в нем
заодно проверяется найденная цена игры.
Итак, приведенная игра невыгодна для первого игрока. Если второй иг-
игрок положит два белых и три черных шарика в урну и будет перед каждым
ходом наугад вытягивать их, называя номер 1 при вытягивании белого ша-
шарика и номер 3 при вытягивании черного, то никакой игрок не сможет бо>
роться с такой стратегией.

§ 5. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 225
8. Варианты. Имеются различные классы задач, близкие по своей
постановке к основной задаче линейного программирования (п. 1), но
не сводящиеся к ней. Решение таких задач, хотя часто и значительно
более сложное, чем разобранное выше, все же в большинстве случаев
удается довести до практически приемлемого результата. Не имея
возможности осветить здесь разработанные методы решения этих
задач, мм приведем для ориентировки читателя применяемую тер-
терминологию, отослав по поводу методов к специальной литературе
(см., в частности, [42, 63, 126]).
Иногда по смыслу поставленной задачи все или некоторые из
искомых величин X] могут принимать значения лишь из заранее за-
заданного дискретного набора, например принимать лишь целые зна-
значения; тогда говорят о целочисленном (линейном) программировании.
Если ожидаемые отличные от нуля значения искомых величин до-
достаточно велики, то часто поступают так: сначала решают задачу,
не обращая внимания на требование целочисленности, а затем
округляют значения параметров в полученном решении до ближа*.
ших целых чисел, удовлетворяющих ограничениям задачи. Однако
если значения невелики, то этот метод может оказаться неприем-
неприемлемым. В указанной литературе приведены алгоритмы для решения
задачи целочисленного линейного программирования, однако эти ал-
алгоритмы пока еще недостаточно эффективны.
Если параметры, входящие в постановку задачи (коэффициенты,
входящие в функцию цели и в условия), могут изменяться и тре-
требуется изучить влияние этого изменения на оптимальное решение
задачи, то говорят о параметрическом программировании. Пусть, на-
например, меняются только коэффициенты функции цели. Тогда из гео-
геометрического смысла основной задачи (см., в частности, рис. 67)
вытекает, что решение остается неизменным до некоторого момента,
после чего оно скачком заменяется на другое решение, отвечающее
соседней вершине многогранника, в котором рассматривается функция
цели; после этого решение опять остается неизменным до некоторого
момента, когда оно меняется скачком, н т. д.
Иногда—особенно, если рассматривается управление некоторым
процессом, развивающимся во времени — требуется принятие целой
серии последовательных решений, причем решение, принятое на лю-
любом этапе, существенно влияет иа формулировку задачи на последую-
последующих этапах. Тогда говорят о многоэтапном или динамическом програм-
программировании.
Если число неизвестных величин и условий весьма велико, то
общий метод построения оптимального решения может оказаться чрез-
чрезмерно громоздким и даже недоступным мощности современных вычи-
вычислительных машин. Тогда стараются разбить искомые величины иа
группы и приблизиться к оптимальному решению для всей системы
с помощью решения аналогичных задач для отдельных групп с по-
последующим внесением поправок на взаимное влияние этих групп друг
8 Д. Д. Мышкио

226 гл. rv.; Линейная алгебра
на друга. Такое направление в решении «больших» задач с помощью
решения «малых» называется блочным программированием.
Основную идею блочного решения задач можно понять на сле-
следующем простом примере. Пусть требуется решить систему уравнений
B5)
в которой коэффициенты щ и Р; сравнительно малы. Тогда можно
в качестве нулевого приближения положить их равными нулю и ре-
решить две полученные системы уравнений, каждая из которых имеет
лишь две неизвестных; это, конечно, проще, чем решать полную
систему B5). Для внесения поправок можно подставить найденные
значения неизвестных в члены с а(, |5; и вновь решить полученные
две системы, а если надо, провести итерацию этого процесса; конечно,
перед проведением итераций надо обратить матрицы { * ь1) и
чтобы не делать Этого каждый раз заново.
( ' h 1 >
Таким образом, матрица коэффициентов системы B5) оказалась
разбитой на четыре квадратные матрицы второго порядка, роль кото-
которых в описанном процессе различна. В общем случае матрица, раз-
разбитая на какое-то число (вообще говоря, прямоугольных) матриц мень-
меньшего размера, называется блочной..
Если выбор плана осуществляется в условиях неполной информа-
информации, то параметры, входящие в формулировку задачи, являются
случайными величинами; тогда говорят о стохастическом програм-
программировании.
Обширный класс составляют задачи нелинейного программирова-
программирования, в которых функция цели или функции, задающие ограничения,
или и те и другие нелинейны. В самом общем виде эта задача необоз-
необозрима по сложности. Однако при различных существенных предполо-
предположениях о классе рассматриваемых функций известны алгоритмы для
решения соответствующих задач, хотя в целом эти алгоритмы су-
существенно сложнее, чем в линейном случае.
В частности, сравнительно более разработаны задачи выпуклого
программирования, в которых функция цели и область, в которой
ее значения сравниваются, предполагаются выпуклыми. При этом
функция f(x), где x = (xt; xt; ... ; х„), называется выпуклой, если
при любых а^О, Р^О, а + Р = 1 и для любых точек х = а, Ь
f(oux + Щ < а/ (а) + р/ (*). B6)
Нетрудно проверить, что это условие равносильно следующему:
пересечение поверхности z=f(x) в (я-f 1)-мерном пространстве z, x

§ 5. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 227
с любой 2-мерной плоскостью, параллельной оси z, представляет
собой линию, выпуклую книзу (считая «верхом» положительное на-
направление оси z).
Из B6) следует, что если /(а) ^ с, f(b)^.c, то и/(аа + |5?)г^с;
таким образом, при любом с множество всех точек, в которых
f(x)^c, является выпуклым. Поэтому основная задача выпуклого
программирования ставится так: найти минимум функции f(x) при
условиях ер,- (х) ^ с{ (i = 1, 2, ,.. , k), где все функции / и ер,- выпу-
выпуклые. Отметим, что любая линейная функция выпукла (почему?),
так что линейное программирование — частный случай выпуклого.
В число функций ц>{ обычно входят функции —х{, причем соот-
соответствующие с{=0; тогда в число ограничений оказываются вклю-
включенными неравенства х^О (« = 1, 2, ... , л).
Из B6) нетрудно вывести также, что если в некоторой точке х¦= а
выпуклой области (G) функция / имеет локальный минимум—внут-
минимум—внутренний или краевой, то во всех точках лг^(О) будет /(дг)^/(в),
т. е. указанный минимум обязательно является также и тотальный
(продумайте это!). Это свойство существенно облегчает построение
оптимального решения.
Частным случаем выпуклой функции является квадратичная
функция
если симметрическая матрица (а,у) имеет все собственные значе-
значения ^ 0. Если при этом все ограничения линейные, то говорят о
квадратичном программировании. Такие задачи после линейных разра-
разработаны в наибольшей степени.

Глава V
ТЕНЗОРЫ
Понятие тензора (от латинского tendo—напрягаю, растягиваю)
принадлежит к числу основных, фундаментальных математических
понятий и широко применяется сейчас в механике, электродинамике,
теории относительности и т. д. Первоначально возникшее в рабо-
работах XIX века по теории упругости, оно было систематически иссле-
исследовано в 1886 —1901 гг. итальянским геометром Г. Рйччи-Курбйстро
A853 —1925)и итальянским математиком и механиком Т. Лёви-Чивй-
та A873—1942). Внимание к новому аппарату существенно возросло
после создания в 1915—1916 гг. великим
ученым, физиком А. Эйнштейном A879 —
1955). общей теории относительности, мате-
математическая часть которой целиком основана
па тензорном исчислении.
Физические величины, которые нам встре-
встречались до сих пор, были либо скалярными,
либо векторными. Однако существуют физн-
/ ^ ческие величины более сложной природы.
fa Например, однородное напряженное состоя-
состояние упругого тела характеризуется плотно-
Рис. 71. стыо р силы, с которой одна часть тела
действует на другую через мысленно вы-
выделенную плоскость ((?) (рис. 71); однако при этом р для различных
направлений плоскости (Q) будет различным. Таким образом, вели-
величина, характеризующая напряженное состояние, уже не является
вектором, она представляет собой тензор 2-го ранга (определение
см. в п. 2). Оказывается, что и многие другие важные величины,
характеризующие состояние сплошных сред, также являются тен-
тензорами.
К настоящему времени тензорная алгебра, а также тензорный
анализ (т. е. теория тензорных полей, связанная с применением диф-
дифференцирования и интегрирования) представляют собой значительно
разработанные дисциплины. В этой главе мы осветим лишь самые
простые вопросы. Специально тензорному нечислению посвящен ряд
книг, из которых мы укажем на [15, 53, 79, 99, ПО]; главы, содер-
содержащие основы тензорного исчисления, имеются также в [39, 98, 103]
и в других книгах.

§ 1. ТЕНЗОРНАЯ АЛГЕБРА 229
§ 1. Тензорная алгебра
1. Примеры. К понятию тензора можно прийти уже размышляя иад
описанием векторов в обычном пространстве с помощью чисел. Как
известно из векторной алгебры, все действия над векторами удобно
осуществлять, выбрав евклидов базис i, j, k, после чего можьо любой
вектор а разложить по этому базису
я = ах1 + ау] + ажк _ A)
и взамен действий над векторами осуществлять действия над их про-
проекциями, т. е. над числами — коэффициентами разложений. Более
того, даже задавать конкретные векторы обычно бывает удобнее
с помощью разложения A), чем каким-то геометрическим способом.
Однако задумаемся теперь, что это за векторы i, j, k. В некото-
некоторых случаях, когда в задаче имеется естественная система отсчета
направлений (например, во многих задачах статики), эти векторы
можно описать вполне точно, «привязав» их к данным задачи. Но.во
многих случаях привлечение такой «абсолютной» системы отсчета
является весьма искусственным либо вообще невозможно. Тогда по-
получается на первый взгляд парадокс: мы пользуемся проекциями
вполне определенного вектора, которые зависят от выбора баэиса,
но не уточняем, как этот базис выбирается...
Эта трудность будет преодолена, если с самого начала отка-
отказаться от выбора какого-то одного базиса, а считать, что все ба-
базисы равноправны и каждому выбору баэиса i, j, k отвечает на-
набор значений ах, ау, а2 в соответствии с формулой A). Подобный
набор величин, приобретающих определенные значения лишь после
выбора базиса и преобразующихся по определенному правилу при за-
замене базиса (см. ниже), и называется тензором (или тензорной вели-
величиной), а сами эти величины, составляющие в определенном порядке
тензор, называются его компонентами. (Отметим некоторое несо-
несоответствие: в векторной алгебре принято компонентами вектора а
называть векторы аж\, ау\, azk. Однако в этой главе мы будем
компонентами называть величины ах, ау, az.)
Оказывается, удобнее писать ex, ег, е3 и а„ а2, а, вместо
I, j, k и ах, ау, аг, так что
а = я^е, + агег + а3е3 = 2 afit-
'=1
В тензорном исчислении принято не писать знак суммы по повто-
повторяющемуся индексу, а при повторении индекса всегда осуществлять
такое суммирование, т. е. писать последнюю формулу в виде
а= a fit (= «/»,= aktk =...). B)
Здесь индекс суммирования является немым и может быть обозна-
обозначен любой буквой, а пределы суммирования определяются размер-
размерностью пространства, в котором рассматривается тензор.

230 ГЛ. V. ТЕНЗОРЫ
Выведем закон преобразования проекций вектора при замене
базиса, впрочем, известный из теории линейных отображений (ЛВМ,
п. XI.7). Переход от евклидова базиса е^ е2, еэ (коротко е,)
к другому евклидову базису е\ осуществляется по формулам
з
е; = 2 а,-/е/' коротко е,' = auef, C)
где индекс /, в отличие от немого индекса /, называется свобод-
свободным. Записав формулу B) в новом базисе и подставив в нее C),
получим
а = а'{е1 = а[аиег
Но так как результат должен равняться B), т. е. а^-, то
т. е. al = a}ia'l. • D)
Tcjc как матрица (а^) перехода от одного евклидова базиса к дру-
другому, ортогональная, а потому обратна к своей транспонированной,
то, разрешая равенства D) относительно величин а'(, получим
а\ — aifaf E)
(продумайте эти переходы). Это и есть требуемый закон.
•Применение тензорной записи сокращает вычисления (в част-
частности, делает их независимыми от размерности пространства), но
требует некоторых навыков в действиях со свободными и немыми
индексами. Покажем пример. Пусть мы хотим подставить выраже-
выражение E) для штрихованных координат в правую часть D). Тогда
надо в E) заменить обозначение свободного индекса на j, а для
этого надо предварительно заменить немой индекс любой другой
буквой (но не /, так как i занято в D)!). Таким образом, a\=^ajkak,
откуда получаем
ai = ajiajkak- F)
Немецкий математик Л. Крбнекер A823—1891) в 1866 г. ввел
полезное сокращенное обозначение, символ Кронекера:
С помощью этого символа можно написать at — bikak (почему?),
откуда в силу F) получаем
Эта формула равносильна требованию ортогональности матрицы (щ^
В качестве другого важного примера тензора укажем на сово-
совокупность девяти элементов матрицы (а^) заданного линейного
отображения А линейного пространства в себя. Эти элементы при-
приобретают определенные значения лишь после выбора базиса ef,

§ 1. ТЕНЗОРНАЯ АЛГЕБРА 231
причем, если у = Ах, то координаты векторов х, у связаны соотно-
соотношением У{ = o.i/Xf (в тензорной записи). После замены ej = г ~
евклидова базиса в силу второй формулы D) получаем
Заметим, что переход от первой формулы D) к E) осуществляется
простой перестановкой коэффициента из одной части равенства
в другую. Поэтому из G) получаем y'k — akia(jasjx's, откуда
В последией формуле индексы /, у свободные, а индексы k, s иемые,
по иим осуществляется двойное суммирование.
2. Евклидовы тензоры, общее определение. Обобщая примеры
п. 1, мы приходим к следующему определению. Пусть в п-мериом
вещественном евклидовом пространстве (R) каждому евклидову
базису е,- отвечает набор из п? вещественных величии ву...4 (здесь р
индексов, каждый из которых может принимать значения 1,2, ..., л).
Пусть при переходе к новому евклидову базису e.\ = ai^j эти вели-
величины преобразуются по формуле
a'ti... s = aitfljjt • • • Vw • • - *i» (8)
где в правой части подразумевается р-кратиое суммирование по
иемым индексам *х, Jv ... , st. Тогда мы говорим, что в (R) задан
евклидов тензор размерности п и ранга (валентности) р с компо-
компонентами uij^s. Здесь слово «евклидов» указывает иа то, что мы
пользуемся только евклидовыми базисами; общие базисы и соот-
соответственно общие тензоры будут рассмотрены в п. 6.
Таким образем, в силу п. 1 проекции вектора образуют теиаор
(мы будем опускать слово «евклидов») ранга 1, а элементы матрицы
отображения—тензор ранга 2. Теизор ранга 0 имеет лишь одну
компоненту, не зависящую от выбора базиса; такой теизор, есте-
естественно, называется скаляром.
Чтобы задать конкретный теизор, достаточно задать значения
всех его компонент при каком-то одном выборе базиса (причем это
можно сделать совершенно произвольно), так как их значения при
любом другом выборе базиса получаются из формулы (8).
К понятию тензора возможен и иной подход, которым мы будем
широко пользоваться. Вспомним о том, что вектор мы рассматриваем
обычно не как тройку чисел, а как выражение B), даже если мы
не думаем о его геометрическом смысле. Поэтому введем формаль-
формальную сумму
..е„ (9)
коэффициенты которой образуют теизор в описанном выше смысле,
т. е. приобретают определенные значения после конкретного выбора
базиса, а при замене базиса преобразуются по формуле (8). Если

232 - гл.:<у. тензоры.
на минуту забыть эту формулу, а просто подставить в правую
часть выражения е,- = 0,-,,-eJ,, 6j=a)t/i'lx, ... , затем по обычным
формальным правилам раскрыть скобки (не переставляя векторов-
сомножителей!) и привести подобные члены, мы получим
или, после изменения обозначения немых индексов и применения
формулы (8),
т = К/, • • • #,««,«//, • • • ass) eft ¦ • • *'s = а'ц ... ,e,'e} ... e; = Г, .
если под Т' понимать выражение (9) в новом базисе.
Поэтому впредь мы, как правило, под тензором будем понимать
сумму (9), остающуюся инвариантной при любой замене базиса.
Другими словами, мы будемN не исходить из формулы (8), а при
переходе от одного базиса к другому просто подставлять выраже-
выражения старых базисных векторов через новые, тогда коэффициенты
сами собой преобразуются нужным образом. При этом в принципе
не важно, вадан ли тензор Т своим выражением во всех базисах
(конечно, если эти выражения в описанном смысле согласованы,
т. е. получаются одно из другого) или сначала только в одном
каком-нибудь, так как из этого одного выражения легко получить
с помощью подстановки и выражение в любом другом базисе.
Например, пусть двумерный геизор 2-го ранга в некотором фиксироваи-
2 q J ; тогда и этом базисе его, можно
записать и ииде
2е,е1 + 5е1е2-3е2е1. A0)
Упрощения здесь невозможны; обращаем, и частности, внимание, что тензор-
тензорное выражение вида е^з ие имеет ничего общего со скалярным произведе-
произведением e!tea = O.
3. Действия над тензорами. Будем считать пространство (/?),
а потому и размерность рассматриваемых тензоров фиксированными.
Мы будем для простоты показывать действия над тензорами невы-
невысоких рангов, хотя те же правила остаются в силе для любых
рангов.
1. Линейные действия над тензорами одинаковых рангов осу-
осуществляются по естественным правилам:
т. е. складываются соответственные компоненты;
При этом выполняются аксиомы линейных действий, т. е. сово-
совокупность всех тензоров заданного ранга р образует линейное про-
пространство размерности пр.

§ 1. ТЕНЗОРНАЯ АЛГЕБРА 233
2. Тензорное умножение тензоров осуществляется по правилу
(a/7eie/) (bt/k*P/4) = (ei/eie/) (*«*е Ае*) = (по определению) =
Таким образом, при умножении тензоров рангов р и q получается
тензор ранга p-\-q, компоненты которого находятся с помощью
умножения каждой компоненты первого тензора на каждую компо-
компоненту второго; при этом обозначении индексов у- первого и второго
тензоров должны различаться, в противном случае эти обозначения
надо предварительно изменить, как в примере A1). Легко проверить
(мы не будем этого делать), что правая часть A1) действительно
представляет собой тензор.
В частности, при тензорном произведении векторов получается
тензор 2-го ранга
(bfi,)='afijefi/, A2)
который называется диада. Каждое из трех слагаемых в A0) — это
частный пример днады.
3. Свертывание (сокращение) тензора состоит в отождествлении
двух индексов у его компонент. Прн этом отождествленный индекс
оказывается дважды повторенным, т. е. он становится немым (по
нему производится суммирование), и потому ранг тензора умень-
уменьшается на 2. Например, после свертывания тензора 3-го ранга
с компонентами ai]k по первому и третьему индексам получается
тензор 1-го ранга с компонентами bj=-aifi. Проверим, что это
действительно тензор. Пусть произведена замена C); тогда новые
значения компонент будут равны (проверьте!)
b'i = «</»"= ntiPiiPibfiijjb. = (a««.a«ft,) а//А,л*. -
= вМ,аУ/,в«./* = aJhaUhh = aJ/Pj\>
что и требовалось доказать.
В частности, при свертывании тензора 2-го ранга с компонен-
компонентами а,у получается скаляр аи. Таким образом, мы видим, что сумма
диагональных элементов матрицы линейного отображения (такая
сумма называется следом матрицы) в евклидовом базнсе не зависит
от выбора этого базиса. Впрочем, это вытекает и из того, что
такая сумма равна сумме всех корней соответствующего характе-
характеристического уравнения (почему?).
Если два вектора а,ег и bfii перемножить тензорно, а затем
свернуть полученную диаду A2), то мы приходим к скалярному
произведению вД- исходных векторов. Аналогично можно определить
скалярное произведение любых тензоров рангов р~^\ и q~^\\ при
этом получится тензор ранга p-\-q—2. В частности, скалярное
произведение тензора 2-го ранга на вектор вычисляется так:

234 гл. v. тензоры
Получается образ вектора х при отображении, отвечающем тен-
тензору auefif.
4. Перестановка индексов. Например, нз тензора a/yfte/eyeft с по-
помощью перестановки индексов можно получить тензор akjiefijek
и еще четыре других тензора (каких?). Вообще говоря, все эти
тензоры различные. Тензор называется симметрическим по всем или
некоторым индексам, если при перестановке любых двух из этих
индексов он не меняется; тензор называется кососимметрическим
по указанным индексам, если при любой такой перестановке он
множится на —1. Легко проверить, что для симметричности (косо-
(кососимметричности) тензора достаточно, чтобы он обладал этим свой-
свойством при каком-то одном выборе базиса.
4. Тензоры 2-го ранга. Как было сказано выше, такой тензор
можно истолковать как набор элементов матрицы заданного линей-
линейного отображения при произвольном выборе евклидова базиса.
Поэтому теория тензоров 2-го ранга непосредственно связана с тео-
теорией матриц. (Обратите внимание, в частности, что умножению
матриц отвечает не тензорное, а скалярное умножение соответ-
соответствующих тензоров!)
Каждый тензор 2-го ранга можно представить и притом единст-
единственным способом в виде суммы симметрического и кососимметри-
ческого тензоров. Это осуществляется по формуле •
aa+a ™e в (в+в) а ^ааУ
прн этом переход от тензора Т = а(/е,еу к a^^efij называется сим-
симметрированием, а к altjfifij—альтернированием тензора Т. Дока-
Доказательство единственности указанного представления мы предо-
предоставляем читателю. Нетрудно определить аналогичные действия
и для тензоров любого ранга.
Для симметрического тензора а^ер^ всегда можно выбрать ¦
базис так, что все внедиагональные компоненты, т. е. aif при 1ф/,
окажутся равными нулю; при этом диагенальные элементы будут
равняться собственным значениям матрицы {atj). Все это хорошо
известно из теории "симметрических матриц (п. IV. 1.6). Выбор такого
базиса называется приведением тензора к главным осям, так как
этот базис будет направлен по главным осям поверхности второго
порядка aijXjXj=\ (п. IV.2.1), кстати, не зависящей от выбора
базиса (попробуйте это доказать!).
Для кососимметршеского тензора Т в трехмерном пространстве
всегда можно подобрать такой вектор Ь, что для любого вектора х
будет Ти = ЬХх. В самом деле, достаточно указать вектор b при
каком-то одном выборе базиса, так как ни левая, ни правая части
не зависят от этого выбора. Но при выборе базиса тензору Т
отвечает вполне определенная кососимметрическая матрица, общий

§ 1. ТЕНЗОРНАЯ АЛГЕБРА 235
О вр\
вид которой [ —а О у I. Отсюда
<—Р — у О/
Т • х = {ах2 + Р*3) ei + (—axl + ух3) ег + (— fa — ухг) е3.
Однако тот же результат получится при векторном умножении
вектора Ь = — Vei + Pe2—ае3 на х (проверьте!).
5. Примеры из механики. Мы будем рассматривать точки и
векторы в обычном пространстве, но пользоваться тензорными
обозначениями.
1. Если зафиксировать начало координат, то координаты дт(-
любой заданной точки, равные проекциям ее радиуса-вектора на
оси координат, образуют тензор 1-го ранга. Перемножив его тен-
зорно на себя, получим диаду с компонентами xtXj.
Пусть теперь задано материальное (вообще говоря, неоднород-
неоднородное) тело (Q) с плотностью р. Тогда набор величин
xix/pdQ = С XiXjdm (dm = pdu) A3)
W (й)
образует теизор 2-го ранга, так как после перехода к интегральной
сумме мы получаем линейную комбинацию диад (XiXf)Mefij для раз-
разных точек M?(Q). Свернув этот тензор, умножив полученный
скаляр на единичный тензор с компонентами 8[f (п. 1) и производя
вычитание, получим симметрический тензор инерции тела (Q) отно-
относительно выбранного начала координат
/ S
(В)
Его диагональные элементы Уи = \ (xl -f- xl) dm, аналогично JM, J33,
называются моментами инерции тела (Q) относительно соответ-
соответствующих осей координат; внедиагональные элементы, взятые
с обратным знаком, т. е. выражения A3) при 1ф], называются
произведениями инерции или центробежными моментами инерции.
Главные оси тензора инерции, в которых центробежные моменты
отсутствуют, называются главными осями инерции. Так как моменты
инерции положительны, то квадратичная форма J^x^j положительно
определенная (почему?), и потому уравнение Ji,xiXf=l определяет
эллипсоид инерции, введенный Коши в 1827 г. Чтобы получить У11,
надо положить в этом уравнении хг=х3 = 0, тогда Jn=Xi*, и так
как ось #! можно выбрать произвольно, то мы получаем, что момент
инерции тела (Q) относительно любой оси, проходящей через начало
координат, равен обратному квадрату расстояния от начала коорди-
координат до точки пересечения этой оси с эллипсоидом инерции.
Введенные величины широко применяются при изучении враща-
вращательного движения твердого тела. В частности, можно показать,

236 ГЛ. V. ТЕНЗОРЫ
что главные оси инерции имеют непосредственный физический
смысл: если тело (Q) закреплено в начале координат н приведено
во вращение вокруг одной из этих осей, то при отсутствии внеш-
внешних сил это тело продолжает вращаться вокруг этой оси как
вокруг неподвижной. Моменты инерции служат мерой инерции тела
в отношении вращательного движения, а через произведения инерции
выражаются реакции, возникающие в закрепленных точках оси
вращения.
2. Пусть в пространстве зафиксировано начало координат
и задано некоторое линейное однородное векторное поле А, т. е.
поле, представляющее собой линейную однородную функцию коор-
координат. (Другими словами, если рассматривать А как функцию
радиуса-вектора г, то должно быть А (г1 + гг) = A (rt) -f- А (г2).)
Тогда Ai — aijXy {atj—некоторый заданный тензор 2-го ранга).
В силу п. 4 его можно представить в виде суммы симметрического
н кососимметрического тензоров, откуда
A = e,(y)rye( + bXf A4)
для соответственно подобранного вектора Ь.
В частности, если A = v представляет собой поле скоростей
точек сплошной среды, то второе слагаемое в A4) означает вра-
вращение всего пространства как абсолютно твердого тела с угловой
скоростью Ь вокруг оси, параллельной Ь. Смысл первого слагаемого
становится ясным, если выбрать в качестве осей координат главные
оси тензора aClj)Qfij. В таких осях оно примет вид "KjXfii% т. е.
означает сумму трех так называемых деформационных движений
в направлении этих осей.
Если поле А нелинейное, то в малой окрестности любой точки Мо
по формуле Тейлора можно представить
где нулевым индексом обозначено значение в Мо, а многоточием
обозначены члены высшего порядка малости. В этом случае раз-
разложение A4) можно применить к группе членов первого порядка
малости, т. е. оно справедливо с точностью до малых высшего
порядка. В частности, для A = v мы получаем утверждение о пове-
поведении малых объемов среды в процессе движения, причем дефор-
I dv; \
мационные движения и вращение определяются тензором ! —±-1 е,е,
и к ним добавляется еще поступательное перемещение со скоро-
скоростью v0. Об этом поведении мы сообщали без доказательства
в ЛВМ, п. XVI.26.
Если A = u—поле перемещений точек среды, то после приме-
применения формулы Тейлора и разложения, аналогичного A4), мы полу-
получим, что второе слагаемое, с точностью до малых высшего порядка,

§ 1. ТЕНЗОРНАЯ АЛГЕВРА 237
определяет простой поворот окрестности точки Мл (почему?).
Поэтому в вопросах, связанных с изменением формы этой
окрестности, основную роль играет тензор с компонентами
1 (дщ ди.Л
Т\—f-д—), отвечающий первому слагаемому. Он называется
тензором деформации.
В связи с рассмотрением формулы Тейлора отметим тензор
k-то ранга
d*f
где значения производных функции /(х1г хг, ..., хк) взяты в фик-
фиксированной точке. Этот тензор при подстановке dx{ вместо
е;(/ = 1, 2, ... , п) превращается в dkf.
6. Общие аффинные тензоры. До сих пор при рассмотрении
тензоров мы пользовались только евклидовыми базисами. Однако
имеется ряд вопросов, в которых приходится пользоваться общими
базисами, т. е. общими аффинными координатами в пространстве.
Тогда теория тензоров приобретает новые черты. В этом пункте
мы рассмотрим тензоры в общем л-мерном линейном пространстве,
т. е. когда отсутствуют понятия евклидова базиса, ортогонального
отображения и т. п.
Упомянутые новые черты проявляются уже при л=1. Тогда
базис состоит из одного вектора е; выбрать его—это все равно,
что указать на прямой единицу масштаба и направление отсчета.
Пусть мы увеличили единицу масштаба в два раза, т. е. е' = 2е.
Тогда ясно, что координата любой точки уменьшится в два раза,
т. е. х' = -^х. Такая величина, меняющаяся «противоположным спо-
способом», по отношению к базисным векторам (точное определение
см. ниже) называется контравариантной. С другой стороны, рассмот-
рассмотрим иа той же прямой линейную функцию у = ах. После указанной
замены ее выражение будет у = 2ах', т. е. можно написать у = а'х',
где а' — 2а. Таким образом, коэффициент у линейной функции ме-
меняется по тому же закону, что и базисный вектор; такие величины
называются ковариантными. Именно различие между ко- и контра-
вариантиостыо и является характерным для общих аффинных тен-
тензоров.
Переходим к общему определению аффинного тензора. Рассмот-
Рассмотрим для определенности тензор 3-го ранга. Он, как и в п. 2, за-
задается системой л3 компонент, занумерованных тремя индексами и
приобретающих конкретные значения только при конкретном выборе
базиса в пространстве. Однако теперь обязательно должно быть
указано, какие из этих индексов являются ковариантными, а какие —
коитравариантными; первые пишутся снизу, а вторые — сверху (их,
конечно, не следует путать с показателями степени, которые здесь

238 гл. v. тензоры
не будут встречаться). Пусть, например, первый и третий индексы
ковариантные, а второй—контравариантный (здесь возможны любые
сочетания); тогда компоненты записываются в виде a\[k, где точка
означает пропущенный индекс. Такой тензор называется смешанным:
«два раза ковариантным и один раз контравариантным». Если все
индексы ковариантные (соответственно контравариантные), то и тензор
называется ковариантным (контравариантным).
Тензорное правило суммирования (п. 1) применяется теперь
только для индекса, встречающегося один раз сверху, а другой —
снизу, например:
ai!kbl= alkb1 +a'ikb* + ...+ aj.kb";
результат можно обозначить, например, через с?* или с*'.
Закон преобразования компонент при замене базиса имеет сле-
следующий вид. Пусть мы от базиса е? переходим к базису е* = а} в/.
Тогда старый базис через новый выражается по формулам е^— Р?,е|-,
где каждая из матриц (ai1) и (р.'/) обратна к транспонированной
другой (продумайте это!); это соотношение между матрицами можно
записать в виде
«,•'„»,-«,%-8',=
Если тензор в базисе е(- имел компоненты a'lik, то в базисе в/ он
должен иметь компоненты
(a№ = aihplh*t*at[\. A6)
Другими словами, на ковариантные индексы действует матрица (а/),
а на контравариантные—матрица ф1^). Формула A6) (и анало-
аналогичная ей для тензоров любых рангов) и служит определением аф-
аффинного тензора.
Аффинный тензор можно записать в виде, аналогичном (9). Для
этого надо выбрать в пространстве взаимный базис е' к е,-, который
при переходе к в; = а^е^ преобразовывался бы по формуле (е')' =
= Р!,е/. (Это можно сделать так: при некотором фиксированном
базисе е,- выбрать е' произвольно, а при изменении первого базиса
менять второй по указанному закону.) Тогда тензор с компонентами
a'/k можно записать в виде
Т = аЛе'е/е*. A7)
Легко проверить, что при замене всех компонент и базисных векто-
векторов на штрихованные будет Т' = Т. (Проделайте это, опираясь на
равенства A6) и A5).)
Нетрудно показать, подобно п. 1, что координаты вектора обра-
образуют контравариантный тензор 1-го ранга, т.е. вектор надо
записывать в виде х = х'е{. В самом деле, если ej = af'e,, то

§ 1. ТЕНЗОРНАЯ АЛГЕБРА 239
Jt'e,.= (*')'e; = (*')Vey= (*/)'а/е,., откуда х< = а/ (л:/)' и (*/)' = р/?*',
(*')' = P-V*^> что и означает контравариантность. В отличие от этого,
коэффициенты линейной формы образуют ковариантный тензор 1-го
ранга, т. е. такую форму надо записывать в виде у — а^'. В част-
частности, для заданной функции и(х') значения производных -s-j в за-
заданной точке, как коэффициенты в du, образуют такой тензор; он
обозначается — .Коэффициенты квадратичной формы образуют дважды
ковариантный симметрический тензор 2-го ранга, а элементы матрицы
заданного отображения у' = а'/х^—смешанный тензор 2-го ранга.
ЗА1
Смешанный тензор образует также набор производных — для за-
дх>
данного векторного поля А, этот тензор обозначается ^-. Все это
мы предоставляем доказать желающим.
Отметим, что если матрица (а}1) ортогональная, то ф'/) = (а/)
(почему?). Этим и объясняется то, что в п. 2, когда мы пользова-
пользовались только заменами базиса с помощью ортогональных матриц,
различие между ко- и контравариантными индексами не проявля/шь.
Действия над аффинными тензорами аналогичны действнямчрад
евклидовыми тензорами. Естественно, что складывать можно только
тензоры, у компонент которых одинаковые по номеру индексы рас-
расположены одинаково, т. е. оба вверху илн оба внизу. Свертывание
возможно только по индексам, один из которых ковариантен, а другой
контравариантен. Перестановка возможна только ковариантных индек-
индексов между собой, либо контравариантных индексов между собой.
7. Аффинные тензоры в евклидовом пространстве. Общими
аффинными базисами можно пользоваться и в евклидовом простран-
пространстве. Здесь взаимный базис (п. 6) легко построить явно. Именно,
достаточно для любого базиса е, выбрать базис е1 так, чтобы
е;-е> = 6?/. A8)
Это делается так: каждый вектор е? располагается перпендикулярно
(л—1)-мерной плоскости, натянутой на векторы е? (i=ji=j), а длина
его выбирается такой, чтобы е^-еу=1; ясно, что этими условиями
вектор е/ однозначно определяется (ср. п. IV. 1.5). Из соотношений A8)
легко вывести (проделайте это!), что базис е' действительно
является взаимным к базису е? б смысле п. 6; кроме того, в силу
симметрии формул A8) и базис в; взаимен к базису еЛ При описанном
построении евклидов базис можно определить .как базис, взаимный
сам себе. (Почему?) Поэтому для евклидовых базисов сумма A7)
переходит в выражение вида (9).
В евклидовом пространстве существенную роль играют ко- и
контравариантный метрические тензоры, компоненты которых опреде-
определяются формулами
&/ = егеу, #'/=e'V. A9)

240- гл. v. тензоры
Это симметрические тензоры 2-го ранга, удовлетворяющие соотно-
соотношению
gijgJk = ®t> B0)
В' самом деле, левая часть представляет собой смешанный тензор
2-го ранга. Если выбрать в качестве е,- евклидов базис, то формула
B0) легко проверяется. Но величины б* сами образуют смешанный
тензор 2-го ранга (почему?), и потому совпадение левой ча-
части с правой в каком-то одном базисе влечет их
совпадение в любом базисе.
Из B0) следует, что при любом фиксированном выборе базиса
симметрические матрицы (gtj) и (glt) обратны друг другу. Легко
проверить, что отвечающие им квадратичные формы являются поло-
положительно определенными. (Докажите это!) Мы предоставляем чита-
читателю также проверить формулы
gi^ = 4 ff"e, = e'. B1)
Мы ввели ковариантный метрический тензор по формуле gy =
= Jfce^, исходя из заданного в пространстве скалярного произведе-
произведения. Однако иногда приходится делать обратное. Именно, если в
линейном пространстве (R) задан симметрический ковариантный тензор
2-го ранга с компонентами gtj, причем квадратичная форма g;jX'x}
положительно определенная, то можно по определению поло-
положить
и тогда (R) превратится в евклидово пространство, для которого
исходный тензор будет ковариантным метрическим тензором.
С помощью метрических тензоров A9) осуществляется поднима-
поднимание или опускание индексов у произвольных тензоров: так, если дан
тензор Т = с'е,- (вектор), то, пользуясь формулами B1), получаем,
что Т = a'g1jef=(aJgji)et = afii1 где по определению ai = gi/af. Ана-
Аналогично
a' = gffa/, a'i* = gihgkk*aiHkl и т. п. ¦-
С помощью такого поднимания или опускания индексов можно пере-
переходить от одних тензорных соотношений к другим, равносильным,
которые иногда оказываются удобнее.
8. Индефинитные метрические формы. Требование положительной опреде-
определенности метрвческой формы g,yx'V раввосильно тому, что хх > 0 (х у? 0), а
последнее неравеиство служит одной из аксиом скалярного произведения. В по-
следвие годы широко применяются псевдоевклидовы пространства, т. е. веще-
вещественные линейные пространства с псевдоскалярным произведением; для такого
произведения последе я я аксиома уже ие требуется, тогда как все остальвые
аксиомы предполагаются выполненвыми: Другвми словами, от метрической
формы gjjX'xi уже ве требуется положительной определенвостн, она может быть

§ 1. ТЕНЗОРНАЯ АЛГЕБРА 241:
индефинитной (т. е. не дефинитной, см. этот термин в п. IV.2.1; мы говорим
сб индефинитности, так как легко проверить, что отрицательно определенные
метрические формы не дают ничего существенно нового.)
Выбрав соответствующий базнс, можно привести метрическую форму к диа-
диагональному виду, после чего, изменяя длины базисных векторов, сделать те
диагональные коэффициенты, которые отличны от нуля, равными ± 1 (ср. начало
п. VI.2.4). В таком базисе псевдоскалярное произведение равно
+ • • • +К*"У", B2)
где коэффициенты %i могут принимать только три значения: ± 1 и 0. Отсюда
следует, что псевдоевклидовы пространства (R) и (S), метрические формы ко-
которых имеют одинаковую сигнатуру (п IV.2.2), изоморфны между собой; это
значит, что между элементами (R) и E) можно установить взаимно однозначное
соответствие, сохраняющее линейные действия и псевдоскалярное произведение.
Для этого надо в обоих пространствах выбрать базисы так, чтобы формулы B2)
получились одинаковыми, после чего сопоставить друг другу векторы с одина-
одинаковыми наборами коэффициентов разложения по этим базисам (ср. ЛВМ, пп. VI 1.19
и VII.21). С другой стороны, с помощью закона инерции квадратичных форм'
(п. IV.2.2) легко доказать, что пространства с метрическими формами различ-
различной сигнатуры не могут быть изоморфными.
Для пространств с индефинитной метрической формой характерно наличие
векторов х Ф 0, для которых х-х=0, т. е. ненулевых векторов, ортогональных
самим себе или, что то же, имеющих нулевую псевдодлину, по определению
равную fxx. Если некоторые из собственных значений матрицы (g,y) отрица-
отрицательные, то существуют векторы х, для которых х-х < 0, т. е. имеющие мнимую
псевдодлину. Все это требует при рассмотрении псевдоевклидовых пространств
некоторой перестройки интуиции, воспитанной на евклидовых пространствах.
Основной пример псевдоевклидова пространства заданной сигнатуры—это
совокупность векторов в числовом вещественном га-мериом пространстве Еп, где
псевдоскалярное произведение двух векторов с координатами х' и у' по опреде-
определению полагается равным B2), при наборе коэффициентов X; в соответствии
с заданной сигнатурой.
С точки зрения введенной терминологии, евклидовы пространства—это
псевдоевклидовы пространства с сигнатурой (я; 0; 0). В теории относительнее™
большую роль играют псевдоевклидовы пространства с сигнатурой (п—1; 0; 1);
такое пространство называется пространством Лоренца по имени выдающегося
голландского физика, создателя электронной теории Г. Лоренца A853—1928), а
лниейиое отображение пространства Лоренца в себя, сохраняющее псевдодлину
(точнее, ее квадрат), называется преобразованием Лоренца. (Из формулы х-у =
= -г- [(х + у)г—(х—уJ) вытекает, что из сохранения псевдодлин вытекает со-
сохранение скалярных произведений; обратное очевидно.) Преобразования Лореица
играют для пространства Лореица ту же роль, что движения — для евклидова
пространства.
Рассмотрим более подробно случай лоренцевой плоскости, т. е. случай л=2.
Точки такой плоскости удобно представлять себе как точки обычной плоскости
с координатами х, t и псевдоскалярным произведением, вычисляемым
по формуле
где i, j, как обычно,—это векторы, идущие из начала координат в точки
A; 0) и @; 1) соответственно. Отсюда квадрат псевдодлины вычисляется по
формуле
Координата к в физике истолковывается как пространственная координата, а
координата t — как время. Векторы вида а (рис. 72), параллельные одной из

242
гл.1 v: тензоры
прямых t=±x, имеют нулевую псевдодлину. Более пологие векторы вида Ь,
с, i имеют положительную псевдодлину; такие векторы иазываются простран-
ственноподобными. Более крутые векторы вида d, j имеют мнимую псевдо-
псевдодлину, они иазываются времениподобными. Если записать преобразование Ло-.
ренца в виде x1=ooc-{-pt, /1 = ly.*+6<, то из^основного условия х\-
при дополнительных требованиях 6 > 0, ™
ческих соображений) легко вывести формулы
х1 == (ch ф) х— (sh ф) (, х--
> 0 (они естественны из физи-
физичто. мы предоставим читателю. Здесь ф—параметр, определяющий преобразова-
преобразование, аналогичный углу поворота при вращении; последовательное выполнение
\
S
S
V
¦/
•*
1
/
а
/
/V
X
Рис. 72.
Рис. 73.
двух преобразований с параметрами qplt <р2 равносильно выполнению одного
преобразования с параметром «Pi + Фа (проверьте это с помощью умножения
матриц!). Если истолковывать это преобразование как отображение плоскости
х, t при зафиксированном начале координат на себя, то оно называется гипер-
гиперболическим поворотом плоскости относительно прямых лс=± t, переходящих
при этом повороте в себя. Название объясняется тем, что при таком отображе-
отображении гиперболы хг—t2=C также переходят в себя. На рис. 73 показаны образы
нескольких точек при таком повороте. Подбирая ф, можно перевести ось х
в любое из пространственноподобных положений, которые, таким образом,
в этой теории все равноправны. (Подобно тому как на евклидовой плоскости
вообще все направления оси х равноправны.) Соответственно меняется ось t;
в свизи с этим следует заметить,- что изображение осей х и t на рис. 72 и 73
взаимно перпендикулярными никакой роли не играет, оси хг и ti на рис. 73
ничуть не «хуже» осей х и t.
В теории относительности каждая точка плоскости х, t истолковывается
как событие, состоящее в указании «где» и «когда», причем мир для простоты
считается одномерным. Оси х, t и xlf t\ на рис. 73—это собственные оси про-
пространства и времени дли двух наблюдателей, движущихся равномерно друг
относительно друга, второй относительно первого со скоростью th ф (почему?).
Так как | th ф| < 1, то эта скорость всегда меньше единицы. (В физике вели-
величины х, t размерны и метрическая форма имеет вид х*—сЧг, где постоянная
с—предельная скорость распространения сигналов — равна скорости света; тогда
и относительная скорость движения наблюдателей меньше с.) Из формулы

§ 1. ТЕНЗОРНАЯ АЛГЕБРА 243
th <Pi + th ф»
—;—тг-^—пг^— получаем правило сложении относвтельных ско-
l-|-th«pi Шф2
ростей. Из рис. 73 видна относительность понятия одиовремеиности событий;
так, события А, В, С, одновременные с точки зрении первого из наблюдателей,
не одновременны с точки зрения второго. (Которое с его точки зрения произо-
произошло раньше?)
В пространстве Лоренца при я > 2 совокупность пространствеииоподобиых
радиусов-векторов отделена от совокупности времениподобных векторов световым
конусом векторов нулевой псевдодлины. Первая совокупность связна, т. е. все
простраиствеииоподобиые направлении равноправны. Вторая-совокупиость состоит
из двух компонент связности (кусков); вто означает, что ии в какой системе
отсчета нельзя, увы, начать двигатьси назад во времени.
9. Замечание о размерностях. В предыдущем изложении мы, как
обычно в математических рассмотрениях, считали все участвующие
величины безразмерными. Тогда теория получается более простой;
поэтому при действиях с размерными величинами часто в самом
начале исследования с помощью выбора характерных единиц пере-
переходят к безразмерным величинам, чтобы в дальнейшем только с ними
иметь дело. Однако это не всегда удобно.
При действиях с размерными тензорными величинами применяются
два различных подхода; об этом иногда забывают, что приводит
к недоразумениям уже в линейной алгебре. Именно, в разложении
x = Jt'e,- размерного вектора (и аналогично тензора любого ранга)
можно считать либо
1) скалярные (в смысле векторной алгебры) величины jc' имеющими
ту же размерность, что х, а векторы е,- безразмерными, либо
2) величины х! безразмерными, а векторы е,- имеющими ту же
размерность, что х.
Векторная алгебра, тензорная алгебра допускают любой из этих
подходов; однако всегда надо отчетливо представлять, какой именно
подход применяется.
Более универсальным является первый подход, он позволяет поль-
пользоваться в одном рассмотрении тензорами (в частности, векторами)
самых разнообразных размерностей. Здесь размерность каждого вновь
вводимого тензора может быть произвольной, одинаковой для исех
компонент, называемых при таком подходе физическими составляю-
составляющими тензора; размерность суммы и произведения тензоров полу-
получается по обычным правилам. В этом подходе приходится пользоваться
не вполне наглядным пространством безразмерных векторов, в кото-
котором и выбираются базисы: например, говорить о векторе, имеющем
заданное направление и модуль, равный 5 (не 5 единиц длины!).
(Однако небольшое размышление показывает, что такой вектор не
намного абстрактнее, чем просто безразмерное число 5.) Метрический
тензор здесь безразмерен, так что при поднимании и опускании ин-
индексов (п. 6) размерность тензора не меняется; поэтому суммы вида
а^а^а" бессмысленны.
Второй подход более нагляден, он не требует какого-либо иного
пространства, кроме пространства векторов х, но он, естественно,

244 гл. у. тензоры
имеет более узкую область применения. Здесь возможны те же дей-
действия, что и с безразмерными величинами; впрочем, пользоваться
метрическим тензором не совсем удобно. Векторы взаимного базиса
имеют размерность, обратную размерности х. Здесь уже нельзя
считать тензор простым набором компонент, а надо пользоваться
выражением вида A7), которое и определяет размерность тензора:
в общем случае она равна размерности х в степени, показатель ко-
которой равен разности между числом контравариаитных и ковариант-
ных индексов у компонент.
§ 2. Тензорные поля
1. Поле евклидова тензора. Ограничимся для определенности
полями в трехмерном пространстве, хотя аналогичное рассмотрение
можно провести для любого числа измерений. Пусть в каждой точ-
точке М. пространства или некоторой его области задан евклидов
тензор (п. 1.2)
е,...е, A)
(одинакового ранга для всех М), тогда мы говорим, что задано по-
поле евклидова тензора Т; далее в этом пункте мы будем слово «евкли-
«евклидова» опускать. Скалярное и векторное поля — это частные случаи
тензорных полей, если ранг равен соответственно нулю и единице.
Поля ранга 2 широко применяются и имеют непосредственный физи-
физический смысл в механике сплошной среды: например, такими полями
описывается состояние упругого тела (ср. конец п. 1.5). При дей-
действиях над этими полями получаются поля и более высокого ранга.
Над тензорными полями можно производить те же алгебраические
действия, что над одиночными тензорами (п. 1.3), а также действии
тензорного анализа, основанные иа дифференцировании и интегриро-
интегрировании. Так, производная от поля A) вычисляется по естественной
формуле
Легко проверить (проделайте это!), что при замене евклидова базиса
величины _LL—_?t которые иначе обозначаются aif #st, преобра-^
зуются по тензорному правилу (п. 1.2), т. е. выражение B) есть тензор,
причем на единицу высшего ранга, чем A). Производная B) от суммы
в произведения полей вычисляется по обычным формулам дифферен-
дифференциального исчисления. Через производную выражается и диффе-
дифференциал
ЯТ
играющий обычную роль.

§ 2. ТЕНЗОРНЫЕ ПОЛЯ 245
Через производную, так определенную, выражаются, в частности,
основные операции векторного анализа: именно,
(a,.V)a = s,-a, ,•; (
Чтобы получить ротор, надо ввести псевдотензор (отличающийся от обыч-
обычного тензора тем, что при изменении «смысла» тройки базисных векторов
компоненты получают добавочный множитель —1) третьего ранга е с компо-
компонентами в любой правой системе координат e123=8312=823i= I, ei32—82i3 =
= 8321= — 1, прочие е,уА=0. Тогда легко проверить, что rot а= —e//ft ajt &е,-.
По аналогии с дивергенцией векторного поля вводится дивер-
дивергенция тензорного ноля: например, для полей ранга 2
div, (а{/е,еу) = atJ, ,еу, divu (a,7e;ey) = aiu у-е„
т. е. получается поле на единицу меньшего ранга. Для несимметри-
несимметрических тензоров надо указывать, по которому индексу берется ди-
дивергенция.
Естественно вводятся понятия интеграла от тензорного поля
по линии, поверхности и объему. Это тензор того же ранга, что
интегрируемый (почему?). При вычислении потока \T-do (и анало-
аналогично циркуляции) тензора он скалярно множится иа вектор, т. е. по-
получается тензор (одиночный, не поле!) на единицу меньшего ранга;
если тензор Т не симметрический, то при этом надо указывать,
по которому его индексу берется скалярное произведение, а потому
и поток.
На тензорные поля легко распространить формулу Остроград-
Остроградского A.1.4). Рассмотрим, например, поле тензора второго ранга
Т = а,уе,еу. Зафиксируем базис в пространстве и применим к вектор-
векторному полю ujj&i формулу A.1.4); мы получим
? aijni da = С aijt t dQ.
(о) Q
Помножив обе части на ву и просуммировав по /', мы придем к тре-
требуемой формуле
(a) Q
в которой поток и дивергенция взяты по одному и тому же индексу.
Окончательная формула не связана с конкретным выбором базиса,
т. е. имеет тензорный смысл. Оиа справедлива для тензоров любого
ранга и дает возможность истолковать дивергенцию как отношение
потока поля через бесконечно малую замкнутую поверхность к объе-
объему, ограниченному этой поверхностью.
2. Поступательный перенос вектора в криволииейиых коорди-
координатах. В дальнейшем мы будем рассматривать тензорные (в частности,
векторные) поля, заданные с помощью криволинейных координат

246 ГЛ. V. ТЕНЗОРЫ
в линейном или евклидовом пространстве любой размерности я. (Пер-
(Первоначальный материал по криволинейным координатам см. в ЛВМ,
пп. XVI.14, 15.) Для простоты можно представлять себе, что л = 2
илн 3, так как рассмотрения одинаковы при всех л.
Пусть в некоторой области (О) линейного пространства (R) введе-
введены общие криволинейные координаты х1, хг, ...., х". Тогда в каж-
каждой точке M?(G) векторы е, = (—,) , вообще говоря, можно при-
\дх'/м
нять за базис; однако этот базис будет свой в каждой точке М,
т. е. получается поле базисов. (В этом случае вместо «базис»
говорят также репер, что по-французски означает «метка», «значок»,
т. е. получается поле реперов.) При переходе к другой, также общей
системе координат х1', х2', ... , х"' базис преобразуется по формуле
е,_ дг = дг дх/ _ дх!
(Заметим, что, как легко проверить, в производной —- индекс /' ко-
дх!
д дг дх!
вариантен, а в коитравариантен; поэтому в выражении —-—-
подразумевается суммирование по /) Поэтому в силу п. 1.6 коорди-
координаты любого вектора а = а'е, при такой замене преобразуются
А о дх'' .
по формуле а1 ——у а'.
Рассмотрим теперь задачу, важную для дальнейшего. Пусть
вектор а поступательно, т. е. без изменения длины и направления,
переносится в пространстве и в каждый момент этого переноса рас-
раскладывается по базису, отвечающему положению начала этого век-
вектора. Если базис в каждой точке свой, то ясно, что координаты
вектора будут по мере его переноса меняться. По какому закону?
Так как вектор а = о'е,- постоянен, то
. . C)
Однако по формуле полного дифференциала
D)
где через Г/j обозначены коэффициенты разложения вектора
—1- = —^—. по базису е,, е„, ... , е„. Эти важные коэффициенты
дх! дх1дх1
были введены в 1869 г. немецким математиком Э. Кристбффелем
A829—1900) и называются символами. Кристоффеля 2-го рода или
коэффициентами связности, так как с их помощью связываются
одинаковые векторы в разных точках пространства; они обозначаются
также {i//}. Расположение индексов в этих символах выбрано таким,

§ 2. тензорныЕ поля 247
чтобы применять тензорное правило суммирования (п. 1.6), хотя сим-
символы Кристоффеля не являются тензорами; в каждой точке про-
пространства онн зависят не только от базиса в этой точке, но н от
характера изменения базнса при отходе от нее. Поэтому при замене
системы координат символы Кристоффеля преобразуются не по тен-
тензорному, а по некоторому более сложному закону, на котором мы
не будем останавливаться. Отметим, что Г*/ s= Tfe н что для любой
аффинной системы координат все Г^у = 0 (почему?).
Подставив D) в C) и приравняв коэффициенты при базисных век-
векторах, получим соотношения
dak + a'Yfjdxf = О (k = 1, 2, ... , п), E)
которые в совокупности равносильны условию da = 0, т. е, дают
решение поставленной задачи.
Если (R) не только линейное, но евклидово пространство, то воз-
возможно выразить символы Кристоффеля через коэффициенты метри-
метрического тензора (п. 1.7). Для этого помножим равенство -jp-=r*ye/k
скалярно на ег, это даст (см. A.19))
Л F)
Это выражение называется символом Кристоффеля 1-го рода и обо-
обозначается Гг1 ij, [ij, I] нли [у]. Таким образом,
Гг,,7 = <?Л Т^^"Т1г1/; G)
второе вытекает из взаимной обратности матриц (gtk\ и (glk) (п. 1.7).
Продифференцируем теперь равенство e,-eft = ^ft no xm; с уче-
учетом F) и D) получим
г I r dgik .„.
1 к, 1т~Г L I, km — ~дхш' \°)
Произведя здесь два раза циклическую перестановку индексов и учи-
учитывая, что всегда Tust—TTtts, получим вместе с (8) систему из
трех уравнений с тремя неизвестными, решив которую, придем к фор-
формуле (проверьте!)
1 / d dglm dgk
'-+^ dxi
Отсюда с помощью G) находим
Вычислим в качестве примера выражения для коэффициентов связности
в полярной 'системе координат р, ф на плоскости. Так как
r=pcos q>i + psin ф j,
то, применяя индексы р, ф вместо 1, 2, получим
], е?=г^=— р sin ф i+p cos ф j. A0)

248 гл. »v. тензоры
(Обращаем внимание читателя иа то, что в ЛВМ, п. XVI .28, аналогичное
обозначение применялось для векторов того же направления, но дополнительно
нормированных длиной на единицу.) Отсюда
^0, -^2- = —!L=— slnqpl + cosqpj.
де
Xz~~ Р cos Ф '— р sin ф j.
сер
Разлагая »ти векторы по базису A0), найдем искомые коэффициенты Г?р =
=С=Г2ф=Гфф=°- Грф=71 Гфф=-Р (прочьте!).
Если система координат Х[ ортогональная, то в базисе е; компоненты ко-
варнантного метрического тензора gjj=lf , g//=0(/ Ф j), где /,•—коэффициенты
Ламе. Поэтому с помощью формулы (9) и символы Tf, выражаются через ко-
коэффициенты Ламе. (Вычислите таким способом коэффициенты связности для
полярных координат.)
Выведем еще формулы для дифференцирования взаимного базиса
(пп. 1.6,7), считая для простоты (R) евклидовым; тот же результат
справедлив для общего линейного пространства. Продифференцируем
равенство A.18) по хк и подставим разложение производной базисного
вектора по своему базису:
где Mjks — какие-то коэффициенты. Применяя равенства A.18), по-
получим Tfk + Mjki = 0, т. е. Mjki = — Y{k- Изменив обозначения ин-
индексов, получаем окончательно
—i. = Тъьи, —. — — Гке*. A1)
dxi ' дх!
8. Ковариантное дифференцирование. Пусть в евклидовом
пространстве задана криволинейная система координат х' и векторное
поле а = о'е/. Тогда в силу п.. 2 получим (проверьте!)
da = (da' + а^Т)к dxk) e,- = f~k + TljkaAeiek-dxses. A2)
Так как вектор dxses = dr произволен и, как и da, не зависит от
выбора системы координат, в частности, от базиса е,-, то и выражение
. va=(S+rK>e'-efc A3)
— ковариантная производная вектора а—является тензором (сме-
(смешанным тензором 2-го ранга), причем этот тензор не зависит
от конкретного выбора системы координат. Для его компонент при-
принято обозначение

§ 2. тензорные поля 249
Аналогично определяется производная от тензора любого ранга.
Проверьте, например, опираясь на формулы A1), что
(при этом для приведения подобных членов мы изменяли обозначение
немых индексов а^Г^е* = а^ЛГ|,е' и т. п.). Отсюда
a}'ktl = ^-Г&оД-г- IV;8*- П,о}/,. A4)
Итак, получается теизор на единицу высшего ранга, чем исходный,
с одной добавочной ковариантностью. (Продумайте закон, по кото-
которому составлена правая часть A4).)
В частности, ковариантная производная скалярного поля
_ ди , ,, ди
есть градиент этого поля. Дивергенция векторного поля получается
с помощью свертывания поля A3), т. е.
Va = diva = af, = ^-j-I>A A5)
Этому выражению можно придать более компактный вид, если
воспользоваться определителем g= det [gif) и заметить, что произ-
производная от определителя по любому его элементу всегда равна ал-
алгебраическому дополнению этого элемента (почему?). Но эти допол-
дополнения связаны с элементами обратной матрицы (как?), откуда
dg dg dg/k dg/k
= l_=:ora/* = CM. (8) =
dx> dgJk дх1 ёё dxf ' '
|
ft/)= |см.
Отсюда правую часть A5) можно переписать в виде
дх1 2gdx? Vg дх'
Можно доказать, что ротор векторного поля в трехмерном пространстве
равен

250 гл. у. тензоры
где ai=gijaf (см. п. 1.7). Для этого иадо проверить — иа чем мы не будем оста-
останавливаться— что правая часть A6) действительно является вектором, т. е.
остается иивариантиой при любой замене системы координат; после этого из
справедливости A6) в декартовой системе координат вытекает, что эта формула
верна и в любой системе.
Из формулы A2) и аналогичной формулы для тензоров любого
ранга вытекает, что
dT = VT-dr = (V,T)^', A7)
где в скалярном произведении осуществляется свертывание (п. 1.3)
по ковариантному индексу дифференцирования и контравариантному
индексу у dxf; под V;T понимаются тензорные компоненты тензора VT,
определенные формулой VT = (V/T)e'. Из A7), в частности, вытекает
формула
dt dxl
для скорости изменения тензорного поля вдоль траектории (ср. п. 1.1.1).
Для скалярного и векторного полей получаем
Обычные правила для производной суммы н произведения спра-
справедливы и для ковариантной производной. Это вытекает из того, что
последняя определена через дифференциал, для которого эти пра-
правила справедливы.
Ковариантная производная метрического тензора g — gye'V равна
нулю. В самом деле, в декартовых координатах g = e1e1-f ... +е„еи,
т. е. этот тензор постоянен во всем пространстве; значит, dg = O,
и потому Vg = 0 (продумайте!). Аналогично и V(^'-'eie;) = O. Другими
словами, g./tl=*gf{ = Q.
Над полем можно совершать несколько последовательных опе-
операций дифференцирования. В частности, важную роль играет опера-
оператор Лапласа—Бельтрами (Е. Бельтрйми A835—1900)—итальянский
геометр), обозначаемый Д2м:
Так как это выражение не зависит от выбора системы координат,
а в декартовых координатах превращается в лапласиан A.1.17), то
A8) можно рассматривать как запись лапласиана в произвольной
системе координат.
Подобным образом можно переписать в произвольной системе
координат любое дифференциальное выражение, примененное к за-
заданному полю. Для этого достаточно результат на основе правил

§ 2. ТЕНЗОРНЫЕ ПОЛЯ 251
тензорного исчисления переписать в тензорно-инвариантной форме,
т. е. так, чтобы этот результат не зависел от выбора системы ко-
координат и в какой-нибудь определенной системе имел заданный вид.
Тензорно-инвариантная запись основных уравнений широко применяется
в теоретической физике, механике сплошной среды и т. д.
4. Поле на многообразии евклидова пространства. Мы начнем
с рассмотрения обычной двумерной поверхности (S) в обычном трех-
трехмерном пространстве. Если на (S) задана система координат х1, хг,
то для любой точки M?(S) векторы ех —-j-j, e2 = ^-j расположены
Рис. 74.
в касательной плоскости (Рм) к (S) в М (рис. 74). При замене сис-
системы координат эти векторы преобразуются по тому же правилу,
что было указано в начале п. 2; это дает возможность задавать
скалярные, векторные и, в общем случае, тензорные поля на (S) в
точности так же, как в евклидовом пространстве.
При малом изменении координат будет
а квадрат длины этого вектора равен
ds2 = dr ¦ dr = (djc'e,) • {dx^j) = (e, • e;) dx' dx> = gtJdx' dx>. A9)
Это выражение, коэффициенты которого составляют коварнантный
метрический тензор, называется первой основной квадратичной фор-
формой поверхности (S); она была введена К. Гауссом в 1828 г. Если
эта форма известна, то можно найти угол между линиями на (S)
в точке их пересечения по формуле
cos (dr, Tr)
ds ds у/ glJ dxi dx/ у/ giJ dxt dxj
длину любой линии (L), расположенной на (S),

252 гл.^. тензоры
площадь любой фигуры (сг)
S У
()
(о) «j)
dx* (g= det (fty)) B0)
(продумайте эти формулы!).
Формулы вида A1) теперь придется видоизменить, так как век-
бе-
тор <—^, вообще говоря, не параллелен плоскости (Рм) (почему?).
Поэтому ограничимся разложением проекции этого вектора иа пло-
плоскость (Рм):
ПР<Я)Э=1>*; B1)
мы не пишем индекс М, так как это разложение можно осуществить
в любой точке (S). Тогда формула F) все равно верна, а с ней и
формула (9) для коэффициентов связности (проверьте!). Вторая фор-
формула A1), как и первая, верна после проектирования обеих ее ча-
частей на касательную плоскость.
ческие
Рассмотрим в качестве примера сферу радиуса R и введем иа ней сфери-
сфериие координаты #, ф (ЛВМ, п. Х.1). Здесь
г= /? (sin & cos ф 1 +sin d sin ф J + cos & k),
ej=^r = /? (cos© cos ф i + cos ©sin ф j—sin ©k),
e?=/?(—sin ©sin ф1 + вт ©cos ф J),
откуда
и применение формулы (9) дает
(Получите эти формулы также с помощью разложения B1).)
Соответственно изменяются рассуждения, приведенные в начале
п. 3, так как вектор da, вообще говоря, имеет добавочную компо-
компоненту, направленную по нормали к (S). Однако ковариантная произ-
производная по определению получается после проектирования на (Р),
т. е. после отбрасывания этой компоненты, так что формула A3)
все равно справедлива, причем тензор Va не зависит от выбора
системы координат на (S).
С помощью аналогичного проектирования вводятся коэффициенты
связности для любого л-мерного многообразия в /»-мерном простран-

§ 2. тензорные поля 253
етве и понятие ковариантной производной тензорного поля любого
ранга на этом многообразии. Основные формулы пп. 2, 3, связанные
с этими понятиями, остаются в силе, однако члены с полными диф-
дифференциалами могут содержать добавочные нормальные слагаемые.
Замечательно, что утверждение Vg = O также остается справедливым,
хотя приведенное в п. 3 доказательство, конечно, уже не годится.
Однако это утверждение можно было доказать и формально, вычи-
числив g(jt j по формулам, аналогичным A4), и подставив выраже-
выражения (9) для коэффициентов связности; а так как эти формулы и эти
выражения справедливы и для многообразия, то справедливо н вы-
вытекающее из ннх равенство ?//,/ —О-
5. Внутренняя геометрия и римановы пространства. Вернемси к началу
п. 4 н допустим, что поверхность (S) подвергнута изгибанию без растяжений
или сжатяй, т. е. как лист бумаги, вместе с координатной сеткой Hi ней. При
этом все длины линий на (S) не изменятся, а потому в квадратичная форма A9)
останется инвариантной, все ее коэффициенты не изменятся (хотя зависимость
гг=г(л!, xt) станет уже иной). Обратно, если на поверхностих (S) и (S) как-то
введены координаты х1 и х1 и в соответствующих точках (для которых х'=х1)
квадратичные формы A9) одинаковы (т. е. gc]=gij), то эти поверхности можно
наложить друг на друга без растяжений и сжатий. Дли этого достаточно каж-
каждой точке (S) сопоставить соответствующую точку (S) н заметить, что при
этом отображении длины, углы, н площади, которые в силу п. 4 выражаются
через коэффициенты gjj, сохраняются. Такие две поверхности (S) и (S) назы-
называются изометричными.
Все геометрические свойства, одинаковые для нзометричиых поверхностей,
относятся к внутренней геометрии этих поверхностей. Например, малые куски
плоскости, цилиндрических и конических поверхностей имеют одинаковую вну-
внутреннюю геометрию, так как каждый из этих кусков можно развернуть на
другой. К внутренней геометрии относятся все величины, выражающиеси через
коэффициенты gjj—не только длины, углы и площади, но и коэффициенты
связности, а также выражающийся через инх результат абсолютного дифферен-
дифференцирования поля, заданного на поверхности. С другой стороны, кривизна линии,
расположенной на поверхности, или расстояние между двумя точками поверх-
поверхности (равное длине отрезка прямой в пространстве) не относятся к внутренней
геометрии, так как при изгибании поверхности эти величины мениютси. Не от-
относится к внутренней геометрии н полный дифференциал 6л поля касательных
векторов а, определенного на поверхности, так как при ее изгибании нормаль-
нормальная составляющая da измениетси (ср. п. 4).
Аналогично определиется внутренний геометрия любого я-мериого много-
многообразия. В ней несущественно, как именно вложено это многообразие в содер-
содержащее его евклидово пространство высшей размерности, а важен только метри-
метрический тензор gij этого многообразии в зависимости от координат на ием.
Чтобы перейти к общему понятию риманова пространства, остается сделать
еще одни шаг—полиостью отказаться от рассмотрения объемлющего евклидова
пространства, оставив ,только многообразие с метрическим тензором на нем.
Этот шаг, сделанный Б. Рйманом в 1854 г., важен потому, что многообразие
как совокупность каких-то объектов с п степенями свободы может появиться
вне всякой свизи с евклидовыми пространствами (ЛВМ, п. Х.2).
Итак, риманово пространство (R)—это n-мерное многообразие, в каждой
точке которого задан метрический тензор и,-ц. Это симметрический дважды ко-
вариантиыи тензор; другими словами, коэффициенты gjj принимают в каждой
точке (/?) определенные значения после выбора в окрестности этой точки

254 гл. v. тензоры
системы координат х', а прн переходе к новой системе координат хA они ме-
меняются по тензорному правилу
i dxli dxh
81/ш=а*' дхТ8ixJl'
С помощью метрического тензора в (/?) вводится понятие элемента длины:
по определению
d^d'dJ B2)
Чтобы этот элемент получился положительным, требуют, чтобы квадратичная
форма B2) была положительно определенной.
Знание элемента длины дает возможность, как в п. 4, находить длину
любой лиинн в (/?) н угол между линиями в точке нх пересечения. Взамен
формулы B0) получится формула \ Y^dx1 dx2...dxn — o дли я-мерного объема
любой области (а), так как можно доказать, что именно по такой формуле
вычисляется я-мерный объем области я-мерного многообразия в евклидовом
пространстве. Мы предоставляем читателю продумать, как надо вычислять
fe-мерный B<Д<я — 1) объем области ^-мерного многообразия, расположен-
расположенного в (/?), основываясь на том, что такое многообразие само является рнма-
новым пространством. Умение вычислять объемы дает возможность обьМным
образом ввести интеграл от функции, заданной на области в (/?) или на обла-
области многообразия меньшей размерности, расположенного в (/?).
Некоторая трудность возникает при рассмотрении векторов в (/?), так как
(R) не является линейным пространством; это то же, что рассматривать век-
векторы на кривой поверхности, не пользуясь объемлющим эту поверхность
пространством. Однако эта трудность не очень существенна, так как на самом
деле в теории поля достаточно пользоваться только бесконечно малыми векто-
векторами, тогда как конечные векторы получаются в результате их той или иной
нормировки, которую можно указывать с помощью скалярного множителя,
а не геометрически. Например, вектор скорости v=-jt не обязательно изобра-
изображать в виде вектора конечной длины, его можно изобразить в виде бесконечно
малого вектора dt, при котором стоит множитель 1/<#, или даже, что фор-
формально проще, в виде малого вектора неопределенной длины в направлении
dt, при котором указан модуль, т. е. v. Подобно этому, векторное поле а на
(R) можно задать, указав в каждой точке M?(R) направление поля с по-
помощью бесконечно малого вектора и при нем значение модуля а. Этих данных
вполне достаточно для того, чтобы производить любые действия над такими
векторами, как бы начинающимися в точке М, фактически нх никуда не
откладывая. В частности, если на (R) задана система координат х1, то в каж-
каждой точке М вектор е^ аналогично е2, ..., е„, задается направлением век-
вектора dxv (причем вектор г сам по себе не рассматривается), и модулем, рав-
равным 0-j = YSu- Это дает возможность записывать векторные н тензорные
поля в обычном виде а=а'е,-, g=ftye'e/ н т. п. и производить над инмн
алгебраические действия, если они сводятся к действиям над векторами или
тензорами, заданными в одной н той же точке.
Более серьезен вопрос об установлении связности в (/?), т. е. правила
параллельного иереноса векторов в (/?), без чего невозможны действия над
векторами, заданными в различных точках (/?), в частности, бессмысленно
выражение da (почему?). Связность устанавливается с таким расчетом, чтобы
для многообразия, расположенного в евклидовом пространстве, мы получили
процедуру, формулируемую в терминах внутренней геометрии. Однако мы уже
упоминали, что для такого многообразия да состоит из двух слагаемых: каса-

§ 2. тензорные поля 25S
тельного ya-dr, He меняющегося при изгибании многообразия, и нормального,
зависящего от этого изгибания Поэтому естественно по определению
нояожить
da=vadr, B3)
где dr—вектор бесконечно малого перемещения, а уа, как и раньше, вычис-
вычисляется по формуле A3), в которой коэффициенты связности Г/fc определяются
формулами (9) через коэффициенты заданного на (/?) метрического тензора.
Аналогично B3) определяется дифференциал для тензорного поля любого ранга.
Дифференциал и ковариантная производная полей в римановом простран-
пространстве обладают свойствами, аналогичными тем, которые были описаны в пп. 2,3
для полей, заданных в евклидовом пространстве. Однако здесь имеются и
новые черты, которые проявляются при поступательном переносе вектора а
началом вдоль некоторой линии; при этом должно быть da=O, т. е. как и в
п. 2, должны выполняться соотношения E). Оказывается, что в любой, даже
малой, ио конечной окрестности исходной точки направление, вектора после
этого переноса, вообще говоря, зависит от пути переноса. Поэтому ни в ка-
какой области риманова пространства, вообще говоря, не существует поля па-
параллельных векторов.
Этот факт легко понять на примере двумерной сферы, рассматриваемой
как рлманово двумерное пространство, т. е. во внутренней геометрии. Векторы
этого пространства можно изображать в виде
векторов, касательных к сфере, а поступатель-
поступательность переноса такого вектора в смысле гео-
геометрии риманова пространства означает, что
при бесконечно малом перемещении начала век-
вектора его проекция на касательную плоскость
должна измениться на малую высшего порядка.
Если это начало обходит коитур АВСА,
показанный иа рнс. 75 и составленный из дуг
экватора и днух меридианов, а вектор а в
начальный момент занимал положение а„, то в
процессе поступательного переноса вектор
будет принимать положения, изображенные на
рис. 75, что вытекает даже из простых сооб-
соображений симметрии. Мы видим, что в конце р ™.
поступательного переноса вектор а займет
положение alt отличное от а0.
Если поступательно переносить сразу два вектора, то нх скалярное про-
произведение остается неизменным, так как d(a-b) = da-b + a-db=O. (Отметим,
что из условия da=O не вытекает, что а = const, так как в римановом
пространстве последнее равенство бессмысленно.) Отсюда, в частности, следует,
что и модуль вектора, равно как и угол между двумя векторами, в процессе
поступательного переноса не меняются (почему?).
Пусть в двумерном римановом пространстве (R) выбрана область (а)
с контуром (L); обозначим через ам угол, на который повернется произволь-
произвольный вектор а, если его поступательно перенести началом вдоль (L). Угол
будем считать положительным, если, как на рис. 75, вектор поворачивается
в направлении обхода контура. Из предыдущего абзаца следует, что угол а(з)
не зависит от конкретного выбора вектора а; легко проверить также, что он
, не зависит и от выбора на (L) места старта. (Строго говоря, приведенное
определение годится лишь для достаточно малых областей (а), чего нам будет
достаточно; к большим областям (а) обычно можно перейти с помощью непре-
непрерывного деформирования малых.)
Легко проверить также (продумайте!), что для угла a((rt справедлив закон
сложения: если (а) разбита на два куска (о^) и (ст2), то а(а)=аC ) + а(сг).
Это дает возможность стандартным способом (см., например, ЛВМ, п. XVI.7)

256 ГЛ. V. ТЕНЗОРЫ
ввести плотность величины а
эта величина называется кривизной пространства (/?) н точке М; обратно,
величина а равна интегралу от своей плотности!
aw=\Kdo.
(о)
Так, для сферы радиуса R средняя кривизна области АВСА на рис. 75
равна "о"- g ~"в5" (проверьте!). Но так как сфера во всех своих точках
одкиакова, то и ее кривизна одинакова во всех точках и потому равна 1/R2.
Можно доказать, что во внутренней геометрии двумерной поверхности, распо-
расположенной в трехмерном пространстве, введенная сейчас кривизна—«то как раз
полная кривизна, рассмотренная в ЛВМ, п. XII.9.
В римаиовом пространстве (R) размерности >3 предел B4) зависит не
только от точки М, но и от направления площадки (о), поэтому криви»н* (R)
в М уже не является скаляром. Можно показать, что.эта кривизна полиостью
характеризуется некоторым тензором кривизны, который имеет ранг 4 и вы--
ражается через коэффициенты связности.
В заключение отметим, что в последнее время широко применяются мно-
многообразия с заданным на них метрическим тензором, для которого квадратич-
квадратичная форма B2) уже не является положительно определенной; такие много-
многообразия называются псевдоримановыми пространствами. Согласно общей теории
относительности четырехмерное физическое «пространство-время» является
именно таким пространством. Его трехмерное «пространственное» сеЧвиие,
характеризующее состояние физического пространства в некоторый момент
времени, является римановым пространством и имеет в каждой точке опреде-
определенный тензор кривизны. Из этого при некоторых дополнительных физиче-
физических предположениях можно вывести, что вселенная имеет конечный объем
(т. е. замкнута, наподобие сферы), и получить оценку этого объема. Подчерк-
Подчеркнем, что вопрос «В какую сторону искривлена вселенная?», который первым
приходит в голову и мучил меня в детстве, на самом деле бессмысленный;
так как ответ на него можно дать только с позиций ннутренней геометрии,
а с этих позиций, риманово пространство не может быть искривленным ни
в какую сторону.
Теория рнмановых пространств подробно изложена в книгах [99] (где
изложены также математические основы теории относительности) и [136].

Глеев VI
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Вариационное исчисление, основанное в XVIII в. Л. Эйлером и
Ж. Лагранжем, было значительно развито в XIX в. в трудах ряда
математиков и в настоящее время превратилось в один из важней-
важнейших разделов теоретической и прикладной математики. Вариацион-
Вариационные принципы, имеющие глубокое идейное значение, дают пути к
единообразной трактовке различных физических и прикладных задач
и общие подходы к их исследованию; вариационные методы решения
задач оказываются одними из наиболее эффективных в качествен-
качественном и количественном отношениях.
Вариационное исчисление непосредственно примыкает к элемен-
элементарной теории экттрумумпч (ЛВМ, §§ IV.6 и XII.2), которую мы
советуем сейчас просмотреть. По нему имеется целый ряд курсов;
см., например, [5, 12, 29, 64, 65, 105, 106, 129, 137, 138].
§ 1. Первая вариация и необходимые условия экстремума
1. Примеры задач вариационного исчисления. Исторически
первой задачей, известной в глубокой древности и отнесенной впо-
впоследствии к задачам вариационного исчисления, явилась так назы-
называемая задача Дидб. Легенда говорит, что Дидо—царица одного
из государств Древней Греции, преследуемая царем соседнего госу-
государства, бежала в Северную Африку и попросила у местного насе-
населения участок земли, который можно охватить шкурой вола. Получив
согласие на столь ничтожную просьбу, она на глазах у изумленных
зрителей разрезала шкуру на тонкие ремешки и, связав их друг с
другом, охватила полученной нитью изрядный по тем временам уча-
участок; развернув иа нем строительство, оиа основала иа этом участке
знаменитый в древности город Карфаген.
Уже античные ученые заинтересовались математической стороной
этой легенды: допустим, что нить уже связана; как тогда надо
расположить ее, чтобы охваченный ею участок имел наибольшую
площадь?
Эта задача имеет ряд вариантов. Рассмотрим, например, такой:
пусть концы нити расположены в заданных точках А и В (рис. 76)
на берегу моря. Если тогда выбрать осн координат, как на рис. 76,
9 А. Д. Мышквс

ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ .
то задача сводится к максимизации площади, т. е. интеграла
ь ¦¦;¦¦¦¦
A)
(у=у(х)—уравнение сухопутной границы участка), при заданном
значении длины нити, т. е. интеграла
B)
и заданных краевых значениях
C)
Уже в древности было обнаружено, что искомой формой нити
служит дуга окружности. В п. 11 мы вернемся к этой задаче.
Ц0;Н)
В(Ъ;в)
Рис. 76.
Рис. 77.
Другая знаменитая задача, которая привела к зарождению мето-
методов вариационного исчисления, была предложена в 1696 г. И. Бер-
нулли н решена различными способами Я. Бернуллн, Г. Лейбницем,
Г. Лопнталем н И. Ньютоном. Она состоит в следующем. Допустим,
что под влиянием тяготения материальная точка М скатывается по
некоторой линии у—у(х) без начальной скорости н без трения из
заданной точки А в заданную точку В (рис. 77) за некоторое
время Т. Спрашивается, как выбрать путь скатывания у=у(х) (ска-
(скажем, как построить ледяную горку, по которой скатываются са-
саночки), чтобы Т было минимально возможным. И здесь легко перейти
к чисто математической задаче. Будем сначала считать, что линия
скатывания у=у(х) задана. Тогда в силу закона сохранения энергии
т. е. v =

§ 1. ПЕРВАЯ ВАРИАЦИЯ И НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА. 259'
ОТКУДА' ¦ • :..;:.. . ¦ ... .... .,.,,....,
—y) .. -ш/ 1 + у'2 .
и потому
—-—
йх
ах.
D)
Однако вспомним теперь, что на самом деле линия у=у(х) не за-
задана, а ищется. Таким образом, речь идет о подборе функции у (х),
минимизирующей значение интеграла D); при этом функция у (х)
должна дополнительно удовлетворять гра-
граничным условиям
y@)^h, у(Ь) = О. E)
Рассмотрим; наконец, задачу о форме
равновесия мыльной пленки, натянутой на
два колечка, насаженных на общую ось
(рис. 78), причем для простоты будем
считать колечки равными. Если прене-
пренебречь весом пленки, то из теории поверх-
поверхностного натяжения будет следовать, что
пленка расположится так, чтобы иметь
минимально возможную площадь. Исходя
из наглядных соображений, примем ги-
гипотезу, что пленка примет форму поверхности вращения, уравне-
уравнение сечения которой обозначим через у=у(х). Тогда математически
задача сведется к минимизации интеграла
ь
5 = 2я [yV\+y'2dx, F)
Рис. 78.
равного площади поверхности вращения, при граничных условиях
у (-&) = /?, y{b) = R. G)
2. Функционал. Нетрудно уяснить общие черты приведенных
задач. Прежде всего, все они являются задачами на экстремум —
максимум или минимум. Мы уже сталкивались с задачами на экстре-
экстремум, которые решалась средствами дифференциального исчисления.
Если задача сводилась к рассмотрению экстремума функции f(x)
одного переменного (ЛВМ, § IV.6), то искомым было значение х —
это задача с одной степенью свободы. Если надо было найти
экстремум функции f(xv xt, ..., х„) от п переменных (ЛВМ, § ХН.З),
то искомым был набор значений xlt xit ..., хп—это задача с п
степенями свободы. В задачах же п. 1 искомой является линия, ели,

260 • : гл. vi. влрилциошое «счислений
на аналитическом языке, функция, от которой требуется только,
чтобы она удовлетворяла заданным граничным условиям. Но при
произвольном выборе такой функции имеется бесконечное число
степеней свободы (почему?); таким: образом, можно сказать, что
вариационное исчисление изучает экстремумы в задачах с бесконеч-
бесконечным числом степеней свободы,
К сказанному возможен еще такой подход. Рассмотрим, напри-
например, интеграл F); если в него вместо у (х) подставить любую функ-
функцию у(х), заданную при—b^.x^.b и удовлетворяющую граничным
условиям G), то он примет определенное численное значение. Такой
закон, по которому каждой функции из некоторого класса функций
ставится в соответствие определенное число, называется функциона-
функционалом. (Мы уже упоминали это понятие в ЛВМ, п. XIV.4: Кроме того,
здесь для простоты считаем все величины безразмерными; в общем
случае вместо «число» надо было бы говорить «скалярная величина».)
Задача состоит в подборе функции у(х), для которой интеграл F)
принимает минимальное значение. Таким образом, вариационное
исчисление изучает экстремумы функционалов. ¦
Приведем несколько конкретных примеров функционалов. Пусть
Этот функционал определен для всех функций у(х), заданных при
0 ^#^2 и принимающих там конечные значения (или даже беско-
бесконечные, если интеграл (8) получится сходящимся). Например,
2
для функции у = х2 @^jc^2) получится /=] х* dx — 6,4;
о
) » /1119;
» » y = sinx @<jc<2) » /=1
» » « = __!_ @<jc<2) » /=2/2 = 2,83 и т. д.
Vх
Обратите внимание на то, что 1\у\ — это отнюдь не то, что
раньше понималось под сложной функцией, скажем, F{y(x)) = [y(x)]*
и т. п. Такая функция при подстановке каждой у(х) дает новую
функцию, значение которой при каждом лг = лг0, т.е. F(y{xtt)), пол-
полностью определяется значением у (х0). В отличие от этого, функцнот
нал J\у) при каждой конкретной функции у(х) есть число, которое
определяется, вообще говоря, не каким-то одним ее значением,
а всей зависимостью у(х). Можно сказать, что функционал—это
функция, у которой значениями независимой переменной у (х) служат
обычные функции, а значениями зависимой переменной / служат
числа (продумайте вто!). . ......

§ 1. ПЕРВАЯ ВАРИАЦИЯ И НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА 261
Формула .
2 .
определяет другой функционал, причем линейный, т. е.
J{Cy} = CJ{y) (C=const), J\y1+y2}^J{yi\ + J{yth (9)
Формула
определяет еще один функционал, отличный от (8), так как К {у}
задан на другом классе функций у (х), именно, определенны^ при
'.3. В то же время функционал ¦ •
2
Hz\=[z*dx
совпадает с (8), т. е. можно написать l{y\^\L$\, и т. д.
3. Функциональные пространства. При рассмотрении функцио-
функционалов и их экстремумов бывает полезно уточнить область опреде-
определения функционала, т. е. совокупность функций, для которых он
рассматривается. Обычно эта совокупность представляет собой не-
некоторое линейное пространство (общее понятие линейного простран-
пространства см. в ЛВМ, § VH.6)—или его часть,—состоящее из функций,
над которыми линейные действия выполняются по простейшим пра-
правилам. Такие пространства называются функциональными простран-
пространствами, они чаще всего бесконечномерные. . ;
Функциональные пространства обычно являются нормированными,
т. е.- в них имеется понятие нормы, характеризующей уклонение
функции от тождественного нуля. Норма функции / обозначается
через ||/||, она представляет собой конечное действительное число
и должна удовлетворять следующим требованиям (аксиомы нормы):
1. ||/||^0, причем ||/|| = 0 только для тождественно нулевой
функции /.
z' I Л/|| — I Л I I/
(А, = const).
В ЛВМ, п. XVII.7 мы отмечали, что понятие уклонения функций
может быть введено по-разному. Соответственно этому рассматри-
рассматривают различные функциональные пространства, состоящие из функ-
функций, заданных на каком-либо интервале а^С*^?>. (Отметим, что
все функции, составляющие линейное функциональное пространство,
должны быть заданы на одном и том же интервале, так как в про-
противном случае их нельзй было бы складывать друг с другом.)'Эти
пространства подробно изучаются в курсах функционального

262 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
анализа; наиболее употребительны следующие пространства. (Мыбудем
для простоты в этой главе считать все участвующие величины
вещественными, а все области определения функций конечными.)
1. Пространство С [а, Ь] функций, заданных и непрерывных на
конечном интервале а^.х^.Ь, с нормой
= max
Эта норма отвечает равномерному уклонению функций друг от друга.
2. Пространство С1 [а, Ь] функций, заданных и непрерывных при
вместе со своей производной, с нормой
||/||= max |/(*)|+ max \f'(x)\. A0)
< < Ь < < Ь
(В качестве нормы в С1 можно взять также не сумму, а наибольшее
из слагаемых, стоящих в правой части; это различие оказывается
несущественным.)
Аналогично вводится пространство Сп[а, Ь] при л = 2, 3, 4, ...
3. Пространство Гильберта I2 [a, b] функций, заданных при
а ^.х^Ь н не обязательно непрерывных, для которых норма
= К $[/(*
принимает конечное значение. При конечных a, b это означает, что
функция f(x) должна быть либо конечной, либо, во всяком случае,
квадратично суммируемой (термин суммируемая функция всегда озна-
означает абсолютно интегрируемая). Эта норма отвечает среднеквадра-
среднеквадратичному уклонению двух функций друг от друга.
Можно проверить (мы предоставляем это желающим), что каждая
из указанных здесь норм удовлетворяет необходимым аксиомам 1—3.
Еели из текста не ясно, какая именно норма имеется в виду, то
надо писать более подробно: ||/||cto,w и т- п- Подчеркнем, что
в нормированном пространстве норма каждого элемента конечна.
Проверьте, например, что
II 1-2 II — __!__ II
II Л II U ГО, 1] — у-= > "
стало быть, функция у — х3 входит в пространство Z.g [0, 1] (является
его элементом, обобщенным вектором), а функция у = — не
входит.
В нормированном пространстве вводится понятие расстояния р
между любыми элементами /, g по формуле
р(/, *)=||/-«1|;
для функциональных пространств такое расстояние есть как раз
уклонение функций fug друг от друга.

§ 1. ПЕРВАЯ ВАРИАЦИЯ И НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА 263
¦ В курсах функционального, анализа доказывается, что указанные здесь
пространства обладают важным свойством полноты; это означает, что любая
последовательность fy /2, /3> ••¦ элементов пространства, для которой
|| /„—/от [I —»¦ 0, имеет в этом пространстве предел. Грубо говоря, полнота
п'-+ оо
Ш-* 00
пространства означает, что никакая последовательность его элементов не может
в смысле выбранной нормы сходиться к элементу, не принадлежащему простран-
пространству. (При этом сходимость /„ —> / означает, естественно, что || /„—/ || —>¦ 0.)
Например, если норму A1) ввести в совокупность всех"непрерывных функций
на конечном интервале а<*<&, то хоть все аксиомы линейного пространства
и нормы выполнены, но такое пространство не будет полным, так как предел
в смысле среднего квадратичного уклонения последовательности непрерывных
функций может быть разрывной функцией (ЛВМ, п. XVII.9). И лишь после
пополнения этой совокупности по выбранной норме, т. е. после присоединения
всех среднеквадратичных пределов последовательностей непрерывных функцвч
мы получаем все пространство L2 [а, Ь\, которое уже является полным.
Линейное нормированное полное пространство коротко называется Ьсшйхо-
вым пространством по имени одного из крупнейших польских математиков
С. Банаха A892—1945), который впервые и притом глубоко исследовал свойства
таких пространств. : :
Подчеркнем, что всякая функция из Ct [а, Ь] принадлежит С [а, Ь],
а всякая функция из С [а, Ь] принадлежит Z.2 [a, b]. Тем не менее
Cj [a, b] нельзя считать подпространством С[а,Ь], так как эти
пространства рассматриваются неразрывно
от своих норм, а нормы в С и в С, раз-
различные.
Отчетливое представление о функци-
функциональных пространствах полезно при рас-
рассмотрении экстремумов функционалов. В
самом деле, пусть функционал / {у} имеет
при у — у{х) локальный максимум. Это
знвчит, что для всех функций у(х), не ° а 6 а
тождественно равных у(х) и достаточно рис. 79.
близких к у (х), будет / {у} </ {.у}. Но что
ознвчает выражение «достаточно близкие функции», например, можно
ли считать на рис. 79 функцию ^(лг) близкой к у(хO Так как сущест-
существуют различные виды уклонений функций, то ответ на этот вопрос
зависит от того, какой иид уклонения, т. е. какое функциональное
пространство, принять за основу. Так, на рис. 79 у (х) близка ку{х),
если их рассматривать в С [а, Ь], но далека в Ct[a, b] (проду-
мвйте это!).
Соответственно этому рассматриваются различные типы экстре-
экстремумов функционалов. В дальнейшем мы будем исследовать, как пра-
правило, функционалы, которые естественно рассматривать либо в Cv
либо в С. Тогда, если / {у} < / {у} для всех у, близких к у в смысле С,
то говорят, что на функции у(х) достигается сильный максимум
функционале 1{у}; если же 1{у\<1{у) Для всех у, близких: к у

264
ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
в смысле Cv то говорят о слабом максимуме. При этом сильный
экстремум всегда будет также и слабым (почему?), но'обратное не
обязательно.
¦ Это видно из следующего простого примера. Пусть точка может двигаться
по плоскости со скоростью, зависящей от направления движения по закону,
изображенному на рис. 80, где а—угол, который составляет вектор скорости v
точки с направлением фиксированной оси (/). (Подобная картина может воз-
возникнуть при движении парусно-весельной лодки, если выбрать ось (/) в на-
направлении, противоположном ветру.) Пусть требуется пройти нз точки А в точку В
за минимальное время, причем отрезок АВ параллелен оси (/) (рнс. 81). Каждой
линии (S), соединяющей Л с В, т. е. каждой возможной трассе отвечает опре-
определенное время Т ее прохождения, т. е. пвлучается задача на минимум функ-
функционала Т \(S)). Нетрудно видеть, что прямолинейная трасса (АВ) осущест-
осуществляет слабый минимум h/v0 времени, так как для близких по направлению
(I)
Л
V V
< л
Рис. 81.
путей вида (/1S)X будет длина больше, а скорость меньше (см. рнс. 80 и 81).
В то же время, если рост углово-скоростиой характеристики при а, близком
к ¦ J; л/2, достаточно крутой, то пилообразная трасса ввда (ЛВJ с весьма малыми
участками поворота может дать время, меньшее h/v0. (Продумайте это!) При
этом такая трасса может пройти в любой близости от {АВ), т. е. слабый минимум
здесь, ие будет сильным, (Эта задача еще более эффектна, если скорость, завися
от аг уменьшается при удалении от отрезка АВ, например, если вдоль этого
отрезка течение наиболее сильно. Тогда, чем мельче зубчики пилообразной
трассы, тем меньше время ее прохождения. Конечно, реально картина полу-
получится несколько иной, так как направление движения нельзя изменить как
угодно быстро, что в данной задаче не учитывалось.)
В заключение отметим, что при применении описанных и других функцио-
функциональных пространств надо проявлять определенную гибкость, не цепляясь
догматически за раз навсегда выбранное пространство. Например, если задача
была первоначально поставлена в Cj, но решения там не оказалось, надо по-
подумать, нет ли .решения в С или в еще более широком пространстве, а если
такое решение найдется, то каков его физический смысл и т. д, В процессе
этого исследования могут обнаружиться такие стороны изучаемой задачи, ко-
которые первоначально было бы трудно предвидеть.
4. Вариация функционала. Вариация—одно нз центральных
понятий при изучении нелинейных функционалов, оно играет ту же
роль, что понятие дифференциала при изучений нелинейных функций.
Дифференциал нелинейной функции равен главной линейной части её'
приращения, замена приращения на дифференциал означает лннеари-

§ 1. ПЕРВАЯ ВАРИАЦИЯ И НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА 265
зацию функции, при малом изменении аргумента (ЛВМ, пп. .IV.8 и
IX. 11); вариация нелинейного функционала равна главной линейной
части его приращения, замена приращения на вариацию означает
линеаризацию функционала при переходе от одной функции (от ко-
которой зависит значение функционала) к другой, близкой функции.
Рассмотрим, например, функционал (8). Пусть функция у(х), от
которой зависит его значение, сначала сов-
совпадала с некоторой у(х), а затем мы пе- Ц
решли к некоторой другой, близкой функ-
функции у (х) 4- Ьу (лг). Здесь бу (х) (символ
бу надо понимать как единый) — это ва-
вариация функции у (х), т. е. произвольная
функция, мало уклоняющаяся от нуля и
добавляемая к исходной функции у(х) для
получения новой, проварьированной функ-
функции у(х)-{-ду(х) (рис. 82). (При этом """"^
малое уклонение от нуля понимается в j
смысле той нормы, которая, согласно п. 3,
принята за основу; например,: на рис, 82
малость понимается в смысле Cv)
При переходе от у(х) к у(х)-\-8у(х) функционал (8) получит
приращение
2 2
A2)
hjf)
-**цщй
Рис. 82.
2
= 2 [у (х)-Ъу [x)dx + J [бу (х)]* dx.
Пусть теперь функция у(х) зафиксирована, а функцию бу (л?) можно
выбирать произвольно. Мы видим, что тогда Д/ состоит нз двух
частей, каждая из которых представляет собой функционал отно-
относительно 6jy= .у—у. Первая часть
2
2\y{x)by{x)dx
A3)
обладает свойством линейности, т. е. это линейный функционал
(п. 2), тогда как вторая часть
2
при малых 6jy имеет высший порядок малости. Таким образом, A3)
представляет собой главную (т. е. с точностью до члена высшего
порядка малости) линейную часть приращения A2) функционала (8)

1266 " ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
при переходе от у(х) к у(х) + Ьу(х): Выражение A3) и называется
(первой) вариацией 67 функционала (8); можно написать
2 2
б/= б J f dx = 2 J.у (*) 6> (ж) *r.
о о :
(В силу произвольности функции у (х) мы заменили ее обозначение
на у{х).)
Разобранный пример является типичным. Если задан произвольный
функционал I {у} и мы переходим от функции у(х) к функции
у (х) + Ьу (х), то, как правило, приращение функционала
можно представить в виде суммы двух слагаемых
д/=/1{.у;6>}+я1{з';6>}, (И)
первое из которых при фиксированной функции у(х) представляет
собой линейный функционал относительно 8у (х), а второе имеет
относительно 8у (х) высший порядок малости. Тогда первое слагаемое
в правой части A4) и называется вариацией функционала /, т. е.
В случаях, когда слагаемым высшего порядка малости можно пре-
пренебречь, можно сказать просто, что.вариация функционала — это его
бесконечно малое изменение, т. е. изменение, полученное за счет
бесконечно малой вариации функции, от которой зависит этот функ-
функционал. Замена приращения функционала на его вариацию означает
линеаризацию этого функционала. Все эти рассуждения совершенно
аналогичны рассуждениям, проводимым при введении понятия диф-
дифференциала функции (ЛВМ, пп. IV.7,8).
В конкретных примерах вариация функционалов вычисляется
с помощью формулы Тейлора (ЛВМ, пп. IV. 15 и XII.6). Пусть,
например, рассматривается функционал вида
A5)
где в процессе интегрирования^ считается зависящим от х, у=у(х).
Тогда
ь
А/ = J [F(x, y + 8y) dx—F(x, у)] dx. A6)
а
Но так как
= F(x, y)-\-F'y(x, _y) 6y-f-члены высшего порядка малости,

§ 1. ПЕРВАЯ ВАРИАЦИЯ И НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА 267
то, подставляя в A6) и отбрасывая эти члены, получим . ¦¦
ь ь ...
б/= б J F(х, у) dx = J Fy (х, у) 6у dx. A7)
а а
Для функционала
ь
= \F{x,y,y')dx _ A8)
а
аналогично получаем (проверьте!)
ь .
б/= \ [F; (х, у, у') бу+F'f (х, у, /) 6/] dx, A9)
а
где бу' можно понимать и как 8(у') и как (Ьу)', так как произвол-,
ная от разности двух функций равна разности их производных.
б. Уточнение. Чтобы уточнить смысл разложения A4), нужно указать
функциональное пространство (п. 3), в котором—или на части которого —
рассматривается выбранный функционал. Например, функционал A5) естест-
естественно рассматривать в С [а, Ь], функционал A8)—в Ci\a, b] и т. д.; в некото-
некоторых случаях это пространство подсказывается физическими соображениями,
о чем в дальнейшем будет сказано, в других—удобством, законченностью
результатов, традициями и т. п. Пусть пространство, а потому и вид нормы
ll/fl выбраны. Тогда второе слагаемое в A4) при выбранной функции у (х)
должно удовлетворять оценке
I Ri {У, М 1=о(П by ||) (при || by || — 0); (Щ
это и означает, что оно имеет высший порядок малости относительно by. При
этом фактически обычно удовлетворяется более сильная оценка
\Rx\y\ Ъу}\ = О(\\Ъу\\*) (при || ft» И —0),
т. е. /?! относительно by имеет не менее чем второй порядок малости.
Первое, линейное относительно by слагаемое в A4) должно прн выбранной
у (к) удовлетворять оценке
\li{y. by}\<K\\by\\. B1)
Прн этом все равно, требовать ли ее выполнения для всех вообще djr или
для всех by с достаточно малой нормой, так как в силу первого свойства
линейности (9) при умножении бу на константу С обе части умножатся на |С|.
Линейный функционал, удовлетворяющий оценке вида B1), называется
ограниченным, а наименьшее возможное значение постоянной К, прн которой
выполняется оценка B1), называется нормой этого линейного функционала.
Эта норма представляет собой положительное число, лишь для нулевого функ-
функционала (все значения которого равны нулю), она равна нулю. Например,
можно было бы проверить, что если первое слагаемое в правой части A2) при
фиксированной у(х) рассматривать в зависимостн от 8(/?С[0, 2], то оно будет
представлять собой ограниченный линейный функционал с нормой
2
(попробуйте это доказать!).
2$ \y(.x)\dx
о

26§ ГЛ. VI, ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Приведем еще пример. Пусть линейный относительно у (х) функционал
I. - ¦
ll{y}=Zy'{Q)+\xy(x)dx B2)
о
рассматривается в пространстве С1 [О, 1]. Тогда этот функционал ограничен,
так как
I
I А Ы 1<3 тах I «/'(*) 1+ тах \у(х)\ \xdx<Z\\y\\ с [0 ц
О
(см. (Ю)). Но если то же выражение B2) рассматривать в пространстве С [0. 1],
то оно будет представлять собой лииейиый неограниченный функционал. В са?>;ом
деле, для последовательности функций #„(*) = —sin nx (л=1, 2, 3, ...) будет
I
Л Ы=3+ С — sin я* d* -+ 3, || у„ ||с [0> ,з —> 0,
о
а такого для ограниченного функционала не может быть (почему?). Более
того, Для функции y=Vх, принадлежащей С [0, 1] (но ие принадлежащей
Ct [0, 1] !), функционал B2) ие имеет конечного значения.
Разобранный пример является типичным. В курсах функционального ана-
анализа доказывается, что если линейный функционал определен на всем банаховом
пространстве (R) (т. е. в каждой точке (R) принимает определенное конечное
значение), то он ограничен в (R).
Скажем еще о возможности линеаризации функционала. Хорошо известно,
что наряду с функциями /(^/дифференцируемыми при всех х, имеются—и
применяются—также функций, даже непрерывные, ио теряющие дифферен-
цируемость при отдельных значениях х; типичными примерами служат функции
у=3/я, у=^/х2, у—\х\, непрерывные, но не дифференцируемые, т. е. не
допускающие линеаризации, при я=0 (вспомните их графики!). Аналогичным
образом и "функционал / {{/}, даже непрерывный (т. е. мало меняющий свое
значение при малой относительно выбранной нормы вариации функции у(х)),
может в некоторых точках функционального пространства, т. е. для некоторых
функций у{х), быть нелинёаризуемым.
Рассмотрим например, функционал :
/~ydx B3)
в пространстве С [0, 1]. Он непрерывен, однако вблизи «точки», т. е. функции
^ (#) = 0 @ «< * < 1.) не допускает линеаризации (продумайте это!). Функцио-
Функционал B3) иелииеаризуем также в окрестности любой функции, имеющей целый
интервал нулей, но не равной нулю тождественно. Можно было бы проверить,
что линеаризация функционала B3) теряется в окрестности любой функции у (х),
имеющей по крайней мере один нуль порядка ЗгЗ/2, тогда как нули порядка
< 3/2 для линеаризации опасности ие представляют.
Для более общего функционала A5) в С[а,Ь] с непрерывной функцией
F(x, у), как видно из формулы A7), для линеаризации представляют опас-
опасность точки и линии (конечно, если они имеются), в которых FH (x, у) терпит
разрыв. Если у=у(х)—такая особая линия, то линеаризация невозможна
для любой функции у (х), совпадающей с q> (x) во всех точках, какого-либо
интервала. Если Fu (х, у) при .у—<р(*)—•¦ 0 обращаетси в бесконечность по-

§ 1. ПЕРВАЯ ВАРИАЦИЯ И НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА 269
рядка р, то Линеаризация невозможна для любой функции у (X), у которой
у(х)— ф (jc) имеет по крайней мере один нуль порядка ^ 1/р.
В заключение отметим еще одни возможный подход к понятию вариации.
Допустим, что в функционал, например, вида A5) мы подставляем функцию у (х)
какого-либо специального вида у=у(х; X), содержащую скалярный параметр %,
который мы можем произвольно менять, в результате чего зависимость у(х)
будет меняться. Тогда и значение функционала / станет функцией X, 1 = 1 (X).
Производя линеаризацию, получим
by=d,<?=d^d%, 6/=d,/=^X. - B4)
Отсюда легко получить формулу A7) (как?). При таком подходе надо иметь
в виду, что если мы хотим, чтобы вариации Ьу были произвольными, то и одио-
параметрнческое семейство q> (x; X) надо считать произвольным, а не каким-то
одним, фиксированным. Аналогичный подход возможен н в случае, когда
зависимость у (х) включает более одного параметра.
6. Необходимое условие экстремума. Это условие совершенно
аналогично необходимому условию экстремума функции одной или
нескольких переменных. Допустим, что некоторая функция у (х)
реализует локальный максимум нлн минимум функционала f{y} в выб-
выбранном функциональном пространстве (/?), причем этот функционал
имеет вариацию 6/{_у; 8у}, т. е. допускает вблизи у—у(х) линеа-
линеаризацию. Кроме того, будем считать, что рассматривается внутрен-
внутренний (не граничный) экстремум (ср. ЛВМ, пп. IV.19 и ХН.П), т. е.
функционал I {у} определен для всех у, достаточно близких к у
в смысле выбранной нормы; это будет предполагаться всюду далее,
если не оговорено противоположное.
Тогда для любой 8y?(R) должно быть
61 {у; 8у} = 0. B5)
В самом деле, пусть для определенности при у—у(х) функционал /
имеет минимум и 6/{jr, 8y] >0 для некоторой 8у. Подставим в A4)
kby вместо Ьу, где k—скаляр; получим
$ у; kby) =
Однако при малых | k \ левая часть должна быть положительной,
а правая имеет знак k (докажите это, учитывая оценку члена /?Д
т. е. может быть как больше нуля, так и меньше нуля. Получен-
Полученное противоречие и доказывает необходимость условия B5).
Условие B5) вытекает также из второй формулы B4). В самом деле, если
у(х) — <р(х; к), то функция I (К) имеет при Х,= Х, экстремум, откуда
-гг-
иК
_=0, и мы получаем B5).
Как видно из п. 1, в конкретных задачах часто рассматривается
экстремум функционала не среди всех функций, составляющих

270 ГЛ. VI. ВАРИАЦИОННОЕ' ИСЧИСЛЕНИЕ
определенное функциональное пространство, а только среди функ-
функций, удовлетворяющих некоторым добавочным линейным неоднород-
неоднородным условиям, например
у{а)=Уа> УФ)=Уь (заданы). B6)
В этом случае условие B5) должно выполняться для любой вариа-
вариации Ду, удовлетворяющей соответствующим однородным условиям,
т. е. для условий B6)
6у(а) = 0, 6^) = 0. B7)
В самом деле, для таких бу функция y-^kby также удовлетворяет
условиям B6) (почему?), а потому можно повторить то же доказа-
доказательство, что было приведено выше для B5).
Линейные неоднородные условия определяют в пространстве (R) Гипер-
Гиперплоскость (ср. ЛВМ, п. VII.19, но теперь речь идет о гиперплоскостях в бее-
' конечномерном функциональном пространстве). Если ставится задача об
экстремуме функционала / {(/} на некотором криволинейном многообразии (S)
пространства (/?), то, проводя линеаризацию в точке экстремума y?(S), полу-
получаем, что условие B5) должно выполняться для любой Ьу, принадлежащей
касательной гиперплоскости к (S), проведенной в у. ¦,•¦.¦
7. Уравнение Эйлера. Во многих задачах удается, пользуясь
необходимым условием экстремума, найти искомое решение у (х).
Однако форма B5) этого условия не совсем удобна, так как она
включает в себя произвольную функцию бу. Поэтому необходимое
условие преобразуют к другой, равносильной форме, содержащей
только искомое решение. Такое преобразование различно для раз-
разных классов функционалов, и дальнейшее содержание § 1 в основ-
основном посвящено рассмотрению этих классов; читатель может судить
о них по заголовкам пунктов и знакомиться с этими пунктами по
мере потребности. Необходимое условие, получающееся для реше-
решения, обычно состоит из двух частей: из уравнения Эйлера (обычно
дифференциального), которому решение должно удовлетворять
внутри области своего определения, и из добавочных граничных
условий, которые могут быть частично заданы заранее, а частично —
выведены из условия B5).
Начнем с простых частных случаев.
Необходимое условие B5) экстремума для функционала
l B8)
а
в силу формулы A7) имеет вид
ь
~ B9)

§ 1. ПЕРВАЯ ВАРИАЦИЯ И НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА 27.1
Если, для определенности, задача рассматривается для всех непре-
непрерывных у(х), т. е: в С [a, ft], то условие B9) должно выполняться
для любой непрерывной функции 8у (х). Но отсюда легко сле-
следует, что
Fy(x,y(x))~0. C0)
В самом деле, обозначив на минуту левую часть через ф (лг) и по-
положив просто Ьу = у(х), получим в силу B9)
= 0, C1)
откуда и следует, что ф (лг) = 0 (почему?), т. в. C0). Таким обра-
образом, уравнение Эйлера для функционала B8) имеет вид
^ (*.*)-=<>. C2)
Это условие можно получить также, заменив приближенно интеграл B8)
иа интегральную сумму
Так как функция "у (х) произвольна, то мы можем менять значение "yk, зафик-
сирэвав все остальные. Если при_этом сумма C3) имеет экстремальное значе-
значение, то производная от нее по щ, должна раввяться нулю, и мы приходим
к C2).
Часто встречается функционал
ь
,/)dx, A8)
вначения Которого мы будем сравнивать для всех непрерывно диф-
дифференцируемых функций у (х) (т. е. для у ? С\ [в, Ь]), удовлетворяю-
удовлетворяющих заданным граничным условиям
У(")=Уа, У(Ь)=Уь- B6)
На основании формул B5) и A9) получаем, что должно быть
ь
I [Р'у (х, У (х), у' (х)) бу + F'y. (х, у (х), / (х)) бу'] dx = 0 C4)
а
для любой функции бу g Q [а, Ь], удовлетворяющей условиям B7).

272 . ГЛ. VI. ВАРИАЦИОННОЕ. ИСЧИСЛЕНИЕ ;
Чтобы выяснить . отсюда, какому уравнению должна удовлетво-
удовлетворять функция у(Х), проинтегрируем второй член C4) по частям:
ь
\Fy,(x,y(x),y'(x))8ydx =
о .«»
Ь
== [F'y(*. У (х), У (х)) «yj$=0 — 5 [F'y, (х, ~у (х), "у (х))]' бу dx =
о
Ь
= ~[[F-,(xJ(x),P(x))\6ydx, C5)
а
так как в силу условий B7) проинтегрированный член равен нулю.
Подставляя C5) в C4), получаем
^ {F'y{x, у(х), у' (х)) — [^'(-У, у(х), у' (х))]} бу^лг=О.
а
Но отсюда следует, что выражение в фигурных скобках тождест:
вемно равно нулю при а^дг^й, т. е. в сокращенной записи
d
где под -г- понимается полная производная, составленная с учетом
зависимости у и у от х. Для доказательства этого обозначим на
минуту выражение в фигурных скобках через ф (х). Если ф (а) =
= ф(?)) = 0, то можно просто положить 6у~ц>(х) и рассуждать,
как при выводе C0). В общем случае можно положить, что Ьу = у(х)
на интервале а-^г^х^Ь—е, где е>0 весьма мало, а к точ-
точкам х=а и х — Ъ значение ф(дг) спадает до нуля. Устремляя 8
к нулю, мы опять приходим к C1), а оттуда к C6). ;
Таким образом, для функционала A8) при условиях B6) уравне-
уравнением Эйлера служит C6). Если раскрыть выражение полной произ-
производной по формуле производной сложной функции (и писать у
вместо у), мы получим
Fy(x,y, у')-F-;y,(x, у, у')-
- Flv. (х, у, у') у - />„, (х, у, у') у" = 0 C7)
(проверьте!). Мы виднм, что это обыкновенное дифференциальное
уравнение второго порядка. (Исключением является случай, когда
F"y,y, ==0, т. е. когда функция F линейно зависит от у'. Мы не
будем здесь рассматривать этот вырожденный случай.) Всякое ре-
решение уравнения Эйлера C7) называется экстремалью функцио-
функционала.A8), оно придает этому функционалу стационарное значение
в. следующем хмысле: если у(х).—любое такое решение, взятое иа

§ 1. ПЕРВАЯ ВАРИАЦИЯ И НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА 273
некотором интервале ак^х^Ь± ¦¦(а^.а1 <b^^b; в частности,
может быть al = a, bx = b) и если произвольно проварьировать у(х)
на этом интервале, не меняя значения _y(ei) и у(Ь,), то
^*' у, y')dx^0.
Это доказывается с помощью тех же преобразований, которые
были проделаны в предыдущем абзаце (проверьте!). Экстремалями
называются также графики решений, т. е. интегральные линии урав-
уравнения C7).
Совокупность экстремалей, как общее решение обыкновенного
дифференциального уравнения второго порядка, образует двухпара-
метрическое семейство функций. Двух граничных условий B6) в прин-
принципе как раз достаточно для отыскания требуемых частных реше-
решений. Правда, уравнение Эйлера редко интегрируется в квадратурах,
и потому приходится пользоваться численным интегрированием
краевых задач, по поводу которого мы отсылаем читателя к соот-
соответствующим руководствам.
Отмегим, что из возможности двух равносильных определений экстрема-
экстремалей—как интегральных линий уравнения Эйлера и как линий, придающих
функционалу стационарные значения,— вытекает, в частности, следующее свой-
свойство инвариантности уравнения Эйлера. Допустим, что мы в функционале A8)
перешли от переменных х, у к новым переменным Х = Х(х, у), Y = Y (x, у) и
составили уравнение Эйлера для нового функционала. Так как при этом отобра-
отображении линии стационарности одного функционала переходят в линии стацио-
стационарности другого функционала, то и одно уравнение Эйлера после указанной
замены переходит в другое.
8. Примеры. Имеется важный частный случай, когда уравнение
Эйлера C6) допускает первый интеграл (ЛВМ, п. XV.13), т. е. пе-
переход к дифференциальному уравнению первого порядка: это слу-
случай, когда функция F в функционале A8) ие зависит от х. В самом
деле, тогда в уравнении C7) отсутствует второй член, и после
умножения обеих частей на у' это уравнение можно записать так
(проверьте!):
Интегрируя, получаем упомянутый первый интеграл
У')-У'Ру'{У' /)=С1, <38)
где Cj — произвольная постоянная.
Случай, когда F— Р(х, у'), мы предоставляем разобрать читателю.
Рассмотрим второй пример п. 1, в котором требовалось миними-
минимизировать функционал D) при граничных условиях E). Это как раз
¦пример функционала вида A8) с F>=F(y, у'). Применение первого

274
ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
интеграла C8) дает (проверьте!)
1
C9)
Полученное уравненне можно преобразовать к форме у' = /(у), после
чего совершить разделение переменных; однако быстрее совершить
искусственную подстановку
1— cost /, sin / ,,\ ,.л.
{ddt} D0)
Вычисления, которые мы предоставляем читателю, дают в силу C9)
dx = ±J-(\-casi)dt, *^-L(*_sin*) + C2 D1)
(± можно не писать, так как t можно заменить на —t). Уравне-
Уравнения D0) и D1) совместно определяют циклоиду (ЛВМ, A1.12)), полу-
полученную при качении круга радиуса R ——- по прямой y = h. Так
2d
Рис. 83.
как линия должна пройти через точку @; К), то там должна быть
точка возврата циклоиды, т. е. можно принять С2 = 0. Семейство
таких циклоид показано на рис. 83. Значение R, которое остается
пока произвольным, выбирается так, чтобы удовлетворить второму
граничному условию, т. е. так, чтобы циклоида прошла через
точку (?>; 0). Подставляя эти координаты в D0) и D1) и исклю-
исключая t, легко составить трансцендентное уравненне для R. Имея
изображение одной из арок циклоиды, с каким-либо R, легко найти
требуемое R из соображений подобия (продумайте это!). Интересен
случай, когда Ь > nh: тогда искомая линия частично проходит ниже
точки финиша, чего можно было заранее и не предвидеть. Но дело
в том, что если трасса достаточно длинна, то выгодно сначала
заглубить ее, чтобы точка набрала достаточную скорость, быстро
прошла трассу, а у финиша уже поднялась на требуемую высоту.

§ 1. ПЕРВАЯ ВАРИАЦИЯ И НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА 27§
Аналогичное применение интеграла C8) к третьему примеру п. 1
приводит к уравнению
(проверьте!). Интегрирование этого уравнения, которое мы предо-
предоставляем читателю, дает
y=Clch^, . ' D2)
причем из соображений симметрии следует, что Cs = 0. Эта линия
получается из графика у — с\\х подобным преобразованием ,с коэф-
коэффициентом подобия Cj, который находится из граничного условия;
она называется цепной линией, а соответствующая поверхность
вращения—катеноидом.
9. Функционалы с производными высшего порядка. Рассмот-
Рассмотрим функционал вида
ь
i{y\ = lF(*,y, /, /) ах D3)
о
с граничными условиями
У{а)=Уш, у'(а)=у'а, У(Ь)=уь, /ф)=у'ь (заданы). D4)
Вариация функционала D3) имеет вид :
б ¦
б/= ^(P'^y + P^y' + F'^y^dx. , ; <45)
Применяя необходимое условие экстремума B5) и рассуждая, как
в п. 7 (причем последнее слагаемое в D5) придется интегрировать
по частям два раза), приходим к соответствующему уравнению
Эйлера
F»~IxFy'~lr'dx*P»"~(i'
Это обыкновенное дифференциальное уравнение четвертого порядка;
четырех граничных условий D4) в принципе как раз достаточно,
чтобы получить искомое частное решение у(х), реализующее экст-
экстремум.
Функционалы с производными порядка до k > 2 включительно
рассматриваются аналогично; уравнение Эйлера для такого функ-
функционала имеет порядок 2k.
10. Функционалы от нескольких функций. Функционал может
зависеть не от одной, а от нескольких функций одного перемен-
переменного. Так будет, в частности, в таких задачах на экстремум, где
искомой является не плоская, а пространственная линия (почему?);
впрочем, такие задачи возникают и независимо от их геометриче-
геометрического истолкования.

276 '¦ ! Г Я: VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Рассмбтрим функционал
6
I (Л. У*)=\р (*. Ун /и Л. /•) dx, D6)
зависящий от двух функций у^х), yt-(x), заданных при а
причем никакой связи между этими функциями не предполагается —
одну из них можно зафиксировать, а другую произвольно варьиро-
варьировать. Фиксируя yt (х) и варьируя уг (л:), мы получаем частную вариа-
вариацию 6yJ, аналогичную частному дифференциалу (ЛВМ, п. IX.10),
«i ЬУг + F' вуЛ Л*. D7)
Аналогично выражается частная вариация по yt
ь
ь*Лу» у*, «л*- $ (^вл+^.в
Если ставится задача об экстремуме функционала D6) при про-
простейших граничных условиях
Л(в) = Ла. Л(*)=Ль- Л(в)=Л«. Л(*)=Л» (заданы), D9)
то для функций yt(x), Уъ(х), реализующих экстремум, обе частные
вариации необходимо должны равняться нулю. Рассуждая, как
в п. 7, мы приходим к системе уравнений Эйлера
f'v—t-F' =°. Fl—4-F' =0. E0)
Общее решение этой системы двух обыкновенных дифференциаль-
дифференциальных уравнений второго порядка содержит четыре произвольных по-
постоянных, которые определяются из четырех граничных условий.
Аналогично рассматриваются функционалы, зависящие от боль-
большего числа функций, а также функционалы, зависящие от несколь-
нескольких функций и выражающиеся через производные более высокого
порядка.
Если ввести векторную функцию скалярного аргумента
'«-US)
(ЛВМ, пп. VII.23, XI.I), то функционал D6) можно считать зависящим от
•той функции
_•••'¦ "*
F(x, у, y')dx. E1)

§ 1. ПЕРВАЯ ВАРИАЦИЯ Ц НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА 277
Естественно говорить о полной вариации этого функционала, равной сумме
частных вариаций D7) и D8), т. е.( после простых преобразований;
ь
'*'{у; М= S (F'y-*y+F's
а
где под Fy понимаетси вектор типа градиента (ЛВМ, п. ХИЛ)
- E2)
а точка означает скалярное произведение. Граничные условия D9) и систему
уравиений Эйлера E0) можно также записать в векториом виде
Как видим, получаются в точности те же формулы, что в скалярном случае.
Такая векторная запись удобна тем, что она одинакова при любом числе'
фуикций, от которых зависит функционал. Кроме того, в ряде задач именно
векторная функция является первичной, тогда как скалярные функции—ее
проекции — появляются лишь после введения в пространстве у декартового ба-
базиса. В таких задачах векторная запись особенно предпочтительна своей инва-
инвариантностью, т. е. независимостью от выбора базиса.
С функционалами от нескольких фуикций иепосредствеиио связаны функ-
функционалы, заданные в параметрической форме. Пусть первоначально был задан
функционал вида A8) или более общего вида
/((/.))= J Р{х, у, y')dx, E3)
(L) . "
где (Z,)—произвольная ориентированная линия. Такую лйиию часто бывает
удобно записать в параметрической форме x=x(t), y=(/(i), что даст
КОН ф КОН
/((/.)) = I р(х,у,±)х'<И = J Fib, у, x,i)dt, E4)
нач нач . "
т. е. мы получаем функционал вида D6). Характерные свойства полученной
функции Ft таковы: она не включает новую независимую переменную t-и яв-
является однородной функцией измерения 1 относительно х, у (ЛВМ, п. IX.12).
(Легко проверить, что и обратно, если эти свойства выполнены, то из E4)
можно получить E3).) Система уравнений Эйлера оказывается зависимой (про-
(проверьте это, продифференцировав тождество Эйлера Fx'x х-\- р\-у у=F). Поэтому
в общем решении остается произвольная функция, отвечающая различным
способам параметризации линии (L). Задавшись таким способом, мы эту функ-
функцию исключаем: например, добавочное равенство х — 1 означает, что за пара-
параметр взята координатах; равенство х2 + {/2=1 — что за параметр взята длина
дуги, и т. д.
Случай функционалов, зависящих от линий в пространстве .высшей размер-
размерности, рассматривается аналогично. ' . <; .
11. Функционалы от функций нескольких переменных. Функ-
Функционал может зависеть также от функции нескольких переменных;
будем для определенности рассматривать функции z(x, у) двух

278
ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЯ
независимых переменных, заданных в некоторой области (G) пло-
плоскости х, у, т. е. при {х; у) ? (О). Тогда функционал, аналогич-
аналогичный A8), имеет вид
О, E5)
5
(О
а его вариация равна
(О
sl) dO,
где /? и ^—стандартные сокращенные обозначения для -д— и
E6)
дг
а 6д- = -4—-. Граничное условие, аналогичное B6), состоит в том,
что значение функции z (х, у) задано на
контуре (Г) области (О), т. е.
(задано; М—(х;у)). E7)
Рис. 84.
Геометрически это означает (рис. 84), что
сравниваются между собой всевозможные
поверхности, имеющие уравнение вида
z = z{x, у) и «натянутые» на один и
тот же контур (показанный на рис. 84
жирно) с уравнением E7).
Для получения необходимого усло-
условия экстремума функционала E5) при
условии E7) надо воспользоваться общим
условием B5), а затем, как в п. 7, про-
извести интегрирование по частям по схеме
где вертикальная черта означает двойную подстановку граничных
для х значений. Но аналогично п. 7 из условия E7) получаем, что
(бг)|(Г) = 0, а потому результат этой подстановки равен нулю, т. е.
правая часть E8) равна — I ~-8zdG. Преобразуя подобным же
(С)
образом последний член в E6), приходим к уравнению Эйлера для
функционала E5)
*".-г^-зИ=0: E9)
оно было получено впервые М. В. Остроградскнм в 1834 г. и потому
называется также уравнением Остроградского. Обращаем внимание

§ 1. ПЕРВАЯ ВАРИАЦИЯ И НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА
...... д д
на своеобразие производных j- и ^- в этом уравнении: например,
производная ч- берется при зафиксированном у, но с учетом того, что
в Fp в качестве г, ч- и -к- подставлены их выражения через х, у.
Поэтому развернутая форма уравнения E9) такова (проверьте!):
F" —4-9F" Л^-А- Р" &2г Л-F" — -LF" ^4-Я" -4- F" —F' — О
РР дх2 ~*~ ""дхду + «ф"+ г" а*~Г г<?di/"*"^"^ У» г~ '
—4-9F Л^-
дх2 ~*~ ""дхду
Это уравнение с частными производными второго порядка, так что
вариационная задача сводится к решению этого уравнения при гра-
граничном условии E7). Общую теорию таких граничных задач мы
в этой книге не будем рассматривать.
Случай более чем двух независимых переменных хи xt, ..., х„
рассматривается аналогично; в этом случае принято обозначение
дг
Р
Подобным образом разбирается случай, когда функционал имеет.вид
_ Г
- j
дг дг д^г дЧ д*г
, у, г, ^, щ, Wi
(G)
при граничном условии
дп
где под п понимается направление внутренней нормалв к (Г). Мы предостав-
предоставляем читателю проверить, что уравнение Эйлера будет вметь вид
/V-J- Fp-1- Fa + ^x Fr + ^- Fs + ^2Ft=Q,
дх р ду ч дх2 ^ дхду ду2 .
дЧ д2г д*г п
где под г, s, t понимаются соответственно ^-j, ^—-т-, ^-j . При доказатель-
доказательстве этого следует обратвть внимание на то, что из равенств (бг),г, =0,
гг—бг ) =0 следуют равенства [-^-Ьг ) =(^-6z) =0.
дп )(Г) АУ v \дх )(Т) \ду Дг)
Если, подобно п. 10, г в E5) представляет собой й-мерный вектор, то
соответствующее уравнение Эйлера имеет вид E9), где г, р и q—векторы,
а дифференцирование по вектору понвмается аналогично E2). Это система из k
уравнений с частными производными второго порядка.
12. Условный экстремум с интегральными связями. Вернемся
к функционалу A8) и предположим, что функция у(х) берется не
произвольной, а должна, кроме граничных условий B6), удовлетво-
удовлетворять дополнительному условию вида
ь
O(x, у, y')dx = g (задано). F0)

280 v ГЛ. VI, ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ,, .,-.,..,. ;
Тогда и вариация Ьу должна удовлетворять дополнительному усло-
условию, полученному линеаризацией F0):
67 {у; 6у} = $ (О'уЬ + G'yty) <** = 0.
а
Пусть функция у{х) реализует экстремум (или просто стацио-.
парное значение) функционала A8) при граничных условиях B6) и
связи F0). Тогда можно рассуждать следующим образом. Разобьем
отрезок a^Lx^.b на большое число п равных частей длины
к = , обозначим xk = a-\-kh, ук=у(хк). Заменяя интеграл на
интегральную сумму, а производную на разделенную разность (не
стремясь к особой точности аппроксимации, так как мы рассматри-
рассматриваем только принципиальную картину), получаем, что требуется
найти экстремум величины
( **)h
при заданных ул =уа, уп =уь и при условии
= g. F2)
Так как теперь мы имеем дело с функциями конечного числа
независимых переменных ylt уг, ..., у„_г, то можно применить
теорию условного экстремума для функций нескольких переменных
(ЛВМ, п. ХИЛО). Согласно этой теории при отыскании .такого
экстремума следует написать условия безусловного экстремума для
функции
( ^)( ук, м±^Ь.)h. F3)
Возвращаясь к интегралам, получаем, что для отыскания функции
>> (л;), реализующей условный экстремум, следует написать уравнение
Эйлера для функции
F*(x, у, у'; X) = F(x, у, у')—кО(х, у, у'). F4)
(К этому выводу можно было бы прийти и без перехода к интег-
интегральным суммам, непосредственно рассматривая задачу A8), F0).)
Общее решение этого уравнения содержит две произвольные посто-
постоянные и параметр X, которые находятся нз двух граничных условий
B6) н уравнения связи F0). Параметр к (множитель Лагранжа),
как показано в ЛВМ (там же), равен —т^--

§ 1. ПЕРВАЯ ВАРИАЦИЯ И НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА 28?
Если- имеется несколько условий вида F0)
ь . - .
\Gi(x,y,y')dx = gl (/ = 1, 2, ...,
а
то взамен F4) надо воспользоваться функцией
F5)
Теперь мы можем вернуться к первому примеру п. 1, где
требовалось максимизировать функ-
функционал A) при граничных условиях
C) и связи интегрального вида B).
(Отметим, что по аналогии с этим при-
примером вариационные задачи с интег-
интегральными связями вида F5) или дру-
другого подобного вида часто называют
изо периметрическими.) Согласно дока-
доказанному нужно решить уравнение Эйле-
Эйлера для функции
F*(x, у, у'; X) ^у-ХуТТТ1- F6)
Так как в нее не входит х, можно воспользоваться первым ин-
интегралом C8), что даст
у
Разрешая это уравнение относительно у!, получим
dy Y
РИС'
dx
I
У—Ci
откуда, разделяя переменные и интегрируя, приходим к уравнению
окружности
Постоянные С,, Сг, X определяются граничными условиями - C) и
связью B). Другими словами, из всех дуг окружностей, изображен-
изображенных на рис. 85, надо выбрать ту, которая имеет заданную длину L.
Некоторое сомнение могут вызвать дуги вида аАВСЬ, вдоль которых у.не
является однозначной функцией х, а ведь этой однозначностью мы пользовались
при выводах. Но здесь, как н во многих других аналогичных случаях, можно
прибегнуть к следующему рассуждению. Пусть линия типа аАВСЬ, которую
мы еще не знаем, реализует искомый экстремум. Возьмем любую ее малую ,
дугу АВ и выберем новые оси координат |, г| так, чтобы, эту дугу можно было
записать в виде г| = т|(?) с однозначной т| (|) (рис. 85). Но если зафиксировать
точки А и В и менять дугу АВ, сохраняя ее длину, то мы.не сможем увеличить
площадь участка (почему?). Другими словами, дуга линии, решающи задачу

282 tn. vi. вариационное исчисление ; ' '
на экстремум', сама решает аналогичную задачу на экстремум. (Конечно, то
же остается в силе, если речь идет ие об экстремуме, а о стационарном зна-
значении функционала.) Но дуга АВ в силу однозначности т) (?) представляет собой
дугу окружности. А если всякая малая дуга линии (L) есть дуга окружности,
то и вся (L)—дуга окружности, что и требовалось доказать.
Можно сослаться также на инвариантность уравнения Эйлера, о которой
Говорилось в конце п. 7. В самом деле, всегда можно выбрать криволинейные
координаты и, V, в которых вся рассматриваемая линия получит однозначное
представление и=и (и). Но тогда оиа должна в новых координатах удовлетворять
уравнению Эйлера, а в силу указанной инвариантности—и в старых тоже.
Дуга окружности является одновременно решением задачи на условный
экстремум, двойственной исходной: найти линию наименьшей длины, ограни-
ограничивающей заданную площадь. Это можно доказать с помощью рассуждения,
также имеющего довольно общий характер. Пусть заданная площадь равна 5
и соответствующая линия (L) имеет минимально возможную длину L, ио не
является дугой окружности. Тогда в силу исходной задачи (L) можно изменить,
перейдя к близкой линии (U) с длиной L'==L и площадью S' > S. Теперь
можно деформировать (/,') в (L"), уменьшив одновременно и длину и площадь
(например, с помощью равномерного сжатия к оси х), доведя площадь до 5*=5,
ио тогда U < U, т. е. L" < L, и мы приходим в противоречие с определением
линии (L).
Двойственность задач на условный экстремум становится еще более ясной,
если говорить ие об экстремальном, а о стационарном значении функционала
A8) при связи F0) или F0) при связи A8). В самом деле, первая задача сво-
дитси к решению уравнения Эйлера для F—kfi, а вторая—к решению для
G—V. Но
и после сокращения мы получаем_то же уравнение, что в периой задаче. Исклю-
Исключением служат случаи ta =—^=0 или к,==—^-=0, имеющие характер
dl(y) dJ{y)
вырождения. Отметим, что аналогичная двойственность имеет место'и для задач
на экстремум с конечным числом степеней свободы.
Вариационные задачи на экстремум с интегральными связями
сейчас широко распространены. Во многих случаях возникает ситуа-
ситуация, в которой требуется распорядиться определенными ресурсами,
чтобы получить максимальную выгоду. Если при этом возможная
линия поведения определяется произвольной функцией, то для ее
отыскания получается вариационная задача, в которой задание ре-
ресурсов определяет интегральные связи.
13. Условный экстремум с конечными или дифференциальными
связями. Рассмотрим для определенности задачу на экстремум функ-
функционала
ь
НУ»У» У») = 1?(*, У'« У» Л. У2, Уз, y'3)dx F7)
а
с тремя искомыми функциями yt (x), у2 (х), у3 {х). Пусть на них
наложена конечная (иначе голономная) связь
Щх, у1г уiy y») = h(x) (задано). F8)

§ 1. ПЕРВАЯ ВАРИАЦИЯ И НЕОБХОДИМА УСЛОВИЯ ЭКСТРЕМУМА 283
Тогда вариации этих функций должны быть связаны очевидным
соотношением • • ;
Пусть ставится задача об экстремуме (или просто о стационарном
значении) функционала F7) при конечной связи F8) и граничнык
условиях
укЬ (А = 1, 2, 3),
удовлетворяющих уравнению связи, т. е.
¦ Н(а, yla, у2а, y3a) = h(a), H(b, ylb, y2b, y3b)=h(b).
(Это условия согласования граничных условий со связью.)
Если удастся более или менее просто выразить из F8) одну из
искомых функций через остальные, например представить ,у,=
= ф (х, ух, у2), то это выражение можно подставить в FJ) и перейти
тем самым к задаче на безусловный экстремум с двумя искомыми
функциями yt (x), уг(х) (п. 10). В общем случае можно рассуждать,
как в п. 12, но тогда взамен F2) появятся соотношения
"(**, Ун,, У* Л») = *(**) (A = l, 2, .... я-1). F9)
В силу правила отыскания условного экстремума надо для каждой
левой части F9) взять свой множитель Лагранжа, т. е. искать без-
безусловный экстремум для функции
Я~1 — — Я-1
F[xk, У*, 1 , • • • ) h— 2- V(**. J'ift' J'i*. Уг>к)-
k=о к=1
Возвращаясь к интегралам, получаем, что для отыскания функций
У\ (х)< У г (х)> Уз (х)> реализующих условный экстремум, следует на-
написать систему уравнений Эйлера для функции
р(*> У» J'i. Уг> Уг> Уз> Уз)—г(х)Н(х, yv yt, у3) G0)
с фиксированной (т. е. не варьируемой), но неизвестной заранее
функцией г (х) (функциональным множителем Лагранжа). Уравнения
Эйлера вместе с уравнением связи F8) образуют систему из четырех
уравнений с четырьмя искомыми функциями уг(х), уг (х), у3 (х), г(х);
произвольные постоянные, которые появятся при ее интегрировании,
определяются граничными условиями.
Подобным образом, если на функции ylt y%, у3 наложены две
независимые конечные связи (а более двух таких связей, в отличие
от интегральных, на три функции не может быть наложено)
#1 (X, Л, У». Уз) = К (X), Нг (X, ух, уг, ys) = К (X),
то взамен функции G0) надо пользоваться функцией
F-r1(x)H1-ri(x)f13.

284 .... ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
-Если, кроме этого, имеются интегральные связи F5), то к правой
части надо добавить—2^^
Аналогичным образом рассматриваются дифференциальные (иначе
неголономные) связи вида
Н(х, ylt y'v у„ у'г, у„ y'3) = ft(x);
и здесь к функции F надо добавить—г(х)Н. Отличие будет в том,
что в систему уравнений Эйлера теперь войдет не только г (х), но
и г' (х) (почему?). Задача на экстремум функционала с конечными
или дифференциальными связями называется также задачей Лагранжа.
Рассмотрим в качестве примера задачу С. А. Чаплыгина об облете макси-
максимальной площади самолетом за заданное время Т при постоянном ветре. Обо-
Обозначим через v скорость ветра и выберем ось у в направлении этой скорости;
через V обозначим скорость самолета относительно воздуха. Тогда должно
выполняться соотношение (продумайте его!)
*a+(fif—»J=V2, G1)
где точкой обозначена производная по времени. Вспомнив выражение (ЛВМ
(XIV.31))
'-y*)<ll G2)
для площади, ограниченной замкнутым контуром (хф)—х(Т)=х0, (/@) =
= у G*) = !/„), получаем задачу о максимизации интеграла G2) при дифферен-
дифференциальной связи G1). Согласно доказанному нужно составить систему уравнений
Эйлера для функции
Эта система имеет вид (проверьте!)
Интегрирование по t дает ..
)i = Cu -x+2r(t)(i-v) = Ct. G3)
С помощью параллельного переноса осей координат всегда можно добиться
того, чтобы С1=С2=0 (почему?), как мы и будем впредь для простоты счи-
считать. Исключая г (t) из G3), получим
— У х л, х dx 4- у йи
—-==-. , откуда dt— L-2—2.
х y—v Щ
Подставляя это выражение в G1), получим дифференциальное уравнение, свя-
связывающее только величины хну:
¦..-•¦¦ &(х*+уа)<1х* = У*(хйх+у<1уK. ¦ G4)
Это уравнение, однородное относительно х и у (ЛВМ, п. XV.4, класс 2); однако
его проще решить с помощью перехода к полярным координатам р, <р. Под-

§ 1. ПЕРВАЯ ВАРИАЦИЯ И НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА 285
ставляя в G4) je=pcos<p, у=р5Шф и извлекая корень, получим (проверьте!)
rip^ ? оsinq> ± бэшф (г=—\
. р V ± v eos ф ¦ 1 ± е cos ф \ V/
Интегрируя и потенцируя, находим полярное уравнение искомого семейства
линий
_ С
Р 1 ± ecos ф '
где С—гпроизвольная постоянная. Так как по смыслу задачи е < 1, то, срав-
сравнивая с уравнением ЛВМ A1.29), видим, что получилось семейство всех эллип-
эллипсов с одинаковым эксцентриситетом e,-=v/V, большая ось которых перпендику-
перпендикулярна направлению ветра.
Для функционалов от функций нескольких переменных, помимо конечных
(или дифференциальных) и интегральных связей, встречаются связи промежу-
промежуточного типа. Пусть, например, иа функцию г (*, у) в функционале E5) нало-
наложена связь вида
где интегрирование проводятся по у (т. е. интеграл однократный) в пределах
области (G). Тогда рассуждение, аналогичное проведенному в начале этого
пункта, показывает, что уравнение Эйлера надо составить для функции F—г {х) G,
в результате чего получится уравнение с двумя неизвестными функциями
г(х, у) н г (х), к которому для решения надо присоединить интегро-диффереи-
циальиое уравнение связи G5).
14. Задачи, сводящиеся к задаче Лаграижа. К задаче Лагранжа сводятся
многочисленные другие классы задач вариационного исчисления иа условный
экстремум. Укажем примеры таких задач, по образцу которых можно и в дру-
других случаях осуществлять аналогичное сведение.
Так, разобранная в п. 12 задача об экстремуме функционала A8) при
интегральной связи F0) сводится к задаче Лаграижа, если ввести новую иско-
искомую функцию
X
(s. У (s), у' (s)) ds.
Тогда получается задача об экстремуме функционала A8) при дифференциаль-
дифференциальной связи z' = G(x, у, у') и граничных условиях
У(а) = Уа, УФ)=УЬ, г(а)=0, z(b)=g.
Пусть требуется найти две функции у1 (х), (/а (х), связанные между собой
уравнением '
/(*, Ух. Уи Vi, У*) = 0 G6)
и удовлетворяющие граничным условиям
УгЬ. G7)
для которых Ух ф) принимает экстремальное (по сравнению с другими функ-
функциями, удовлетворяющими тем же соотношениям) значение. Эта задача Майера
сводится к задаче Лаграижа с помощью введения новой искомой функции
: \h=y'v. • G8)

286 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Тогда задача сводится к экстремизации функционала
" ь
при дифференциальных связях G6) и G8) и граничных условиях G7), т. е.
к задаче Лаграижа. (Может показаться, что в ней слишком мало граничных
условий; однако в пп. 15, 16 мы увидим, как исследовать задачи, в которых
граничных условий меньше, чем было в подробно разобранных ранее случаях.)
Диалогично рассматривается задача Майера с любым числом п искомых
функций, связанных между собой системой из т дифференциальных уравнений,
конечно, если т < п (зачем это требование?).
Подобный характер имеет также задача, которую мы предоставим рассмо-
рассмотреть читателю, об экстремуме значения у ф) для решения дифференциального
ураииения y'=f(x, у, ф (*)), включающего произвольную функцию (скажем,
некоторый коэффициент) <р (х), удовлетворяющую соотношению вида
ь
\ G (х, у, <p)dx=g, при заданном начальном условии у(а)=уа.
а
В задаче Больца требуется экстремизировать функционал
.... ь
J F (х, у, у', К) dx+ Ф (у (а), у F), Ц G9)
о
с параметром К (этих параметров, как и искомых функций, может быть любое
число, могут быть добавлены конечные, дифференциальные и интегральные
евязи). Она сводится к задаче Лагранжа об экстремуме функционала
ь
[F(x, у и у
а
при дифференциальных связях
1/2 = 0, у'3=0
и добавочном граничном условии
(Ь-а) у3 (а)—Ф ^ (а), У1 (Ь), уг (а)) = 0 (80)
(проверьте!). В связи с (80) отметим, что граничное условие может связывать
значения искомых функций на обоих концах интервала, где они строятся.
Задача об экстремуме функционала, аналогичного G9) в двумерном и трех-
трехмерном случаях, равного сумме интегралов по области и по ее границе, рас-
рассмотрена в [106].
15. Задачи с подвижными концами на плоскости. Вернемся
опять к функционалу вида A8). До сих пор мы рассматривали для
него только граничные условия вида B6), другими словами, считали
концы линии у=у(х) фиксированными. Однако бывают задачи с гра-
граничными условиями другого вида.
Пусть значения функционала A8) сравниваются для функций
^1[а, Ь], удовлетворяющих граничным условиям
/itV(«). /(*)) = 0, Л (УФ), У'№ = 0 (81)

§ 1. ПЕРВАЯ ВАРИАЦИЯ Н НЕО&ХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА 287
более общего, чем B6), вида. Другими словами, задается не орди-
ордината концевой точки, а соотношение между ординатой и наклоном
линии в ней. Пусть функция у=у(х) реализует экстремальное зна-
значение функционала. Тогда этот экстремум достигается и среди более
узкого множества функций с граничными значениями
у(а)=у(а), y'(a)=J'(a), y(b)=y(b), y'{b)=?(b)y
так как для этих функций условия (81) все равно выполняются.
Поэтому, произвольно варьируя у(х) внутри интервала а^х^Ь и
рассуждая, как в п. 6, мы получим, что функция у(х) удовлетво-
удовлетворяет уравнению Эйлера C6). Однако теперь две произвольные по-
постоянные, входящие в общее решение этого уравнения, надо опре-
определять из двух граничных условий (81).
Ясно, что это рассуждение имеет общий характер^ т. е. при
любых граничных условиях функция, реализующая экстремум функ-
функционала, будет решением уравнения Эйлера. -
Рассмотрим теперь естественную вариационную задачу, в которой
граничные условия полностью сняты, т. е. значения функционала A8)
сравниваются для всех функций у (х) ? С1 [а, Ь]. Тогда, прежде всего,
рассуждая как выше, получаем, что функция у(х), реализующая
в этом случае экстремум, удовлетворяет уравнению Эйлера. При
произвольной ее вариации получим с помощью интегрирования rid
частям
ь
Однако последняя скобка равна нулю, т. е. :
Ы{у~; by} = F'y,(b, y(b), 7mby(b)-F'y,{a, у (с), у'(а))Ьу(а). .
В силу необходимого условия B5) и произвольности 8у(а), бу(Ь),
получаем отсюда, что искомая функция у(х) должна удовлетворять
граничным условиям
F'yr (а, у (а), у' (а)) = 0, F'y. (Ь, у (Ь), у' (Ь)) = О, (82)
называемым естественными. Конечно, если условие (81) снято только
на одном конце, то и естественное условие ставится только на этом
конце.

288
ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Мы предоставляем читателю доказать, что естественные граничные условия
для несколько более общего функционала
Ь
F (х, у, у') dx + ъ (у)^=о+ъ (у)\у=ь (83)
а
имеют вид
16. Условия трансверсальности. Рассмотрим теперь более общую естествен-
естественную вариационную задачу для функционала вида A8), в которой значения а,
Ь не зафиксированы заранее, но требуется, чтобы концевые точки (а; у (а)) и
(Ь\ у(Ь)) лежали иа заданных линиях с уравнением соответственно
/и(*. </) = 0 (К)
У >
h(x, </)=0 и /„(*. </) = 0
(рис. 86). Отметим, что теперь сравниваемые фуикт
ции у (х) уже не образуют линейного пространства
(почему?). Однако подход к понятию вариации
функционала, указанный в конце п. 5, полностью
сохраняет силу, хотя формулы для вариации из-
изменятся, так как надо учитывать возможность
изменения пределов интегрирования. Линеаризуя,
получаем
ь ь
о $ F (*, у, у')dx=^ (F'y Ьу+F'y by')dx+
рис gg +F(x, у, y')\x=bbb-F(x, у, у')\КтаЬа
Рассуждая, как в начале п. 15, получаем, что
функция у (х), реализующая экстремум функционала, удовлетворяет уравне-
уравнению Эйлера. Поэтому, пользуясь необходимым условием B5) и проводя инте-
интегрирование по частям, получаем
С другой стороны, уравнения (85) дают
(86)
i\x
(87)
Однако Ьу \х-ь и б [у (Ь)] не одно и то же!
малых высшего порядка видно, что
Из рис. 87 после отбрасывания"
=fA (88)
и аналогично для 6 [у (а)]. Подставляя эти выражения в (87), находя после
этого Ьу \х=а и &у \х-ь и подставляя в (86), а затем пользуясь произволом 6а,
6Ь, приходим к соотношениям
( }
(проверьте!), которые и служат естественными граничными условиями в рас-
рассмотренной задаче. Если известно направление линии I (или II) в некоторой
ее leetee М (рис. 86), то известно и соответствующее значение fx:f'y и потому
условия (89) определяют направления, которые в этой точке может- иметь

ПЕРВАЯ ВАСИАЦИЯ И НЕОБХОДИМНЕ УСЛОВИЯ ЭКСТРЕМУМА 289
^Экстремальная линия. Эти последние направления называются трансеерсйль-
ными первому, а условия (89) называются условиями трансверсальности. ¦
Обратите внимание иа то, что условия (82) представляют собой частный
случай условен (89) (почему?). ¦
Таким образом, в каждой точке плоскости х, у каждому направлению
с угловым коэффициентом k отвечает некоторая совокупность трансверсальных
направлений, угловой-коэффициент / которых определяется из уравнения
(*-/>?>(*, у, l)+F(x, у, 0=0. (90)
Рассмотрим, например, вариант задачи Дидо (п. 1). .в котором концы А и
В нити находятся на берегу с произвольны» уравнением у=<р (х) (рис. 88) и
у
1
А
ь
ь /
b+ib Ух
Рис. 87.
Рис. 88.
заранее не фиксируются. Тогда формула для площади взамен-A) принимает
в*Д'< ¦¦¦••¦¦'•.•'
ь
Соответственно надо изменить и функцию F6), что скажется только на усло-
условиях трансверсальности, которые принимают вид (проверьте!)
а так как они ставятся иа линии У=Ч>(х), то получаем
''¦— {k-l)U—Я,A + Р)=0, т.е. */ + 1=0, 1=-~.
Это хорошо известное условие перпендикулярности двух направлений (ЛВМ,
п. П.9, задача 5). Итак, если положение ковцов иитн заранее не задано, то
нить в своих концах должна быть направлена, нормально к берегу.
Заметим, что мы вывели условия трансверсальности (90) для задачи иа
безусловный экстремум, а применяли ее к задаче иа экстремум с интегральной
связью. Однако можно показать, что необходимые условия в задачах со сво-
свободными концами и в других подобных задачах вариационного исчисления без
изменения распространяются на задачи с интегральными, конечными и диффе-
дифференциальными связями, если эти условия применять к соответственно изменен-
измененному посредством множителей Лаграижа функционалу. .
Отметим в заключение, что в процессе вывода условий трансверсальности
мы, по существу, получили Выражение для вариации функционала A8) при
10 д. Д. Мышкис

л ..-ч; ..- гд, VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ! ..; i .;
произвольных вариациях функции у (л:) и пределов интегрирования:,;
* ь ......
{
»ЙЬ- F'y |,= аб [y(a)]-(F -y'F'y) \x=a6a. (91)
Оно дает, в частности, возможность рассмотреть также задачу, в которой на
конце линии сняты вообще какие бы то ни было условия, т. е. этот конец
может произвольно варьироваться. Тогда из (91) получаем, что на таком конце
должны выполняться равенства
F=0, F'y=0.
Эти два равенства (равно как уравнение связи и условие трансверсальности
в разобранном выше случае) вместе с выражениями для у и у' из общего ре-
решения уравнения Эйлера дают одно соотношение между двумя произвольными
постоянными в этом решении, отвечающее рассматриваемому концу линии.
17. Задачи с подвижными концами в пространстве. Рассмотрим функцио-
функционал D6), который можно трактовать как функционал от линии в пространстве
*• Vi> У%- В п. 10 концы этой линии были закреплены (на каждом конце за-
задано х, ух, у2). Подобно п. 10 рассматривается случай, когда на каждом из
концов задано по три независимых уравнения, связывающих х, уъ у\, у2, </2.
Однако бывают и задачи, в которых таких уравнений задается два или
одно. (Хоть одно обычно задается.) Мы рассмотрим здесь только случай конеч-
иых саязей, т. е. связей, наложенных на координаты. Так как оба конца
исследуются аналогично, то будем для простоты варьировать только конец
лс=6. Заметим, что из п. 15 следует, что функции (/i(*), й (д:), реализующие
экстремум функционала, удовлетворяют системе уравнений Эйлера.
Пусть сначала конец х=Ь имеет две степени свободы, т. е. на него нало-
наложена одна связь вида
. " /(*. Ух. </2) = 0. (92)
Аналогично (86) и (87) получаем, что равенство
должно выполняться всякий раз, как
Отсюда заключаем, что при jc=ft выполняются равенства
'ui _ ht _ fx+fyiyi + fy,y2 .„..
' — ' — р • laV
' F ' F •
гУх rVi
которые и служат в данной задаче условиями трансверсальности, заменяя два
недостающих граничных условия. В каждой точке пространства (х, уъ у2)
в зависимости от направления касательной плоскости к (92) (оно определяет
значения f, (.., /'. с точностью до коэффициента пропорциональности), из
¦* ¦ Ух У%
двух уравнений (94) можно определить два неизвестных у{, у'ъ, вообще говоря,
получается одно или несколько, т. е. дискретное множество (одномерных) на-
направлений, траисверсальных этой касательной плоскости.

§ 1. ПЕРВАЯ ВАРИАЦИЯ И НЕОБХОДИМЫЕ. УСЛОВИЯ ЭКСТРЕМУМА 291
Рассмотрим частный случай. Пусть дай функционал от линий на плоско-
плоскости х, у в параметрической форме E4), имеющий специальный вид
'к
'кон
|}= J Ф(ж, y)Vx*+y*dt. <95)
'нач
Если на одни из концов линии наложена связь
/(*. 0=0, . (96)
то из (94) получаем условие трансверсальности
.' Фх ' Фу
t- =ft: L
Но это означает ортогональность экстремали x=x(t), y=y(t) и (96) (почему?).
Итак, для интеграла (95) условие трансверсальности превращается в условие
ортогональности. Можно было бы доказать, что (95)-представляет собой самый
общий вид функционала, для которого в каждой точке плоскости х, у транс-
трансверсальность превращается в ортогональность. Аналогичный результат спра-
справедлив и для функционалов, заданных на линиях в евклидовом пространстве
любого числа измерений.
Полученное утверждение имеет наглядное оптическое истолкование. Пусть
свет распространяется в изотропной но, вообще говоря, неоднородной среде,
так что его скорость в каждой точке равна с{х, у) (мы рассмотрим для про-
простоты плоскую задачу). Тогда функционал (95) с Ф=—есть время, за которое
свет может пройти линию (L) (почему?). Однако из волновой теории света
вытекает, что световыми лучами служат линии, для которых это время прини-
принимает стационарное значение, т. е. экстремали. Если из некоторой точки исходят
во все стороны световые лучи, то линия (в пространстве—поверхность), кото-
которой они достигнут за одно и то же время, называется фронтом волны. Так как..
для точек этой линии рассматриваемый функционал принимает стационарное
(даже постоянное на экстремалях) значение, то доказанное утверждение о транс-
трансверсальности означает просто, что световые лучи в каждой точке ортогональны
фронту волны.
Пусть теперь на конец х=Ь наложено две связи:
h (*. Уъ Уг)=О, /2 (х, уи уа)=0. (97)
Тогда равенство (93) должно выполняться всякий раз, как
Отсюда легко вытекает (как?) соотношение
F,,' F./ F
t\yt fly, fut+Z'ijr А+ /1^2
ftVt fty, fix + fiVl У1 + f 2Й У 2
=0, (98)
которое и служит соотношением трансверсальности. В каждой точке М прост-
пространства в зависимости от направления / линии (97) в ней соотношение (98)
определяет, вообще говоря, одну или несколько конических поверхностей
с вершиной М, составленных из направлений, траисверсальных к / в Af.
Функционалы, зависищие от любого числа п искомых функций,.рассмат-
функций,.рассматриваются аналогично. Если одни из концов искомой линии n-fl-мерного
10*

j JVh VI. ВАРИАЦИОННОЕ
пространства х, (/i,, </»,..., ул может свободно скользить по fe-мерному много-
многообразию (S),, то и каждой точке М пространства в зависимости от расположе-
расположения 6-мерной касательной гиперплоскости (Р) к E) определяется,: вообще го-
говоря, одна или несколько (п+1—*)-мерных конических гиперповерхностей
с вершиной М, составленных из направлений, траисверсальных к \Р) в М.
Подобным образом разбираются н функционалы вида D3), зависящие от
производных выше нервого порядка. Впрочем, с помощью обозначения у'=г
задачу можно преобразовать в задачу на экстремум функционала
'- ' ¦ '¦¦* '¦ ' .
. ' - " [ F (х, у, г, г') dx
с дифференциальной связью у*—г=0. В силу п. 12 дело сводится к усло-
условиям трансверсальности типа (94) нли (98) для функции F {х, у, г, г') —
-г.г (х) (у'—г). Мы предоставляем читателю получить таким способом, напри-
например, концевые условии
iV=0, fyF
если на соответствующий конец наложена связь вида f(x, y)=0.
18. Трансверсальность для функций нескольких переменных. Рассмотрим
еще задачу с подвижной границей на экстремум функционала от функции не-
нескольких, неременных. Пусть рассматривается функционал' вида E5), но
область (О) заранее не фиксирована, она своя для каждой из сравниваемых
поверхностей г—г(х, у)((х; y)?(G)), от которых требуется только, чтобы их
контуры (х; у; г{х, у))({х; </)? (Г))
располагались на заданной поверх-
поверхности (S) с уравнением
f{x, у, г)=0. . (99)
Как и н п. 15, получаем, что для
поверхности г=г(ж, у), реализующей
экстремум, удовлетворяется уравнение
Эйлера E9). Варьируя функционал
E5), с учетом ^возможного изменения
области (G), интегрируя по частям
по образцу E8) и учитывая уравне-
уравнение Эйлера, получаем
б/{г;6г} =
= J F6s dT + ?bz (F'pdy—Fqdx), A00)
(Г) (Г)
причем во втором интеграле контур
проходится в положительном направ-
направлении; в первом интеграле, получен-
полученном'от вариации области (G), 6s означает ширину (вообще говоря, непостоян-
непостоянную и любого знака!) колечка, добавленного к (G) при этой вариации (рис. 89).
Бели обозначить через п орт внешней нормали к контуру (Г) в любой
его точке, то при переходе от точки (Г) по нормали к точке проварьнрован-
ного контура получаем
6x=nv6s> 6y=riybs, .
откуда в силу (99) ....
. / л, л, \
=0.
Рис. 89.

§ 1. ПЕРВАЯ ВАРИАЦИЯ Я НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА
Выразим отсюда Ьг и подставим во второй интеграл A00), а затем йреобрз-
зуем его в криволинейный интеграл по длине дуги с помощью' формул
dx=—riydr, dy—nxdY; получим (проверьте!)
дг
(Г)
7,
~nv dsdl\
Пользуясь необходимым условием экстремума B5) и произвольностью 6s', по-
получаем, что выражение в квадратных скобках, стоящее под знаком интеграла,
должно равняться нулю в каждой точке (Г). Это и есть условие трансверсаль-
трансверсальности в рассматриваемой задаче. Оно в каждой точке М пространства связы-
дг дг
вает значения -^и ¦=-, причем эта связь зависит, от расположения касатель-
касательной
дх
ПЛОСКОСТИ К (S) В М.
Если рассматривается
функции двух переменных
экстремум функционала, аналогичного (83), для
(О)
дг
*• У< г< л: • а7.
f
(Г)
(х, у, г)йТ
с фиксированной областью (G), то, подставляя в последнем интеграле A00)
di/=cos (п, x)dT, dx=—cos (п, y)dT и пользуясь произволом бг|(Г), прихо-
приходим -к естественному граничному
условию
f'p cos (n, x) + F'q cos(n,
A01)
Этот результат аналогичным образом
распространяется на функции от лю-
любого числа независимых переменных.
19. Высвобождающие связи. Вер-
Вернемся к функционалу A8) н допу-
допустим, что- на переменные х, у наложена
высвобождающая конечная связь вида
ft.
0
V
V
i
1
i
а
(й)
Е
ж
к
ж
1\в
т
1
Ъ х
Рис. 90.
/(*, y>SsO.
Другими словами, графики сравни-
сравниваемых функций у(х) должны быть расположены в заданной замкнутой (т. е.
с присоединенной границей) области (G) плоскости х, у. Типичным приме-
примером . является задача о кратчайшем пути, соединяющем по заданной области
(G) две .заданные точки (рис. 90, где область (G)—незаштриховаиная часть пло-
плоскости); здесь речь идет о минимизации функционала
Ь
VT^ A02)
График функции у (дс), реализующей экстремум, состоит из участков, рас-
расположённых строго внутри (G) (на рис. 90 это AD, EK и LB), и участков,
расположенных на границе (G) {DE и KL). Рассуждение, аналогичное прове-
проведенному в п. 13, показывает, что первые участки являются экстремалями,
т. е. вдоль них удовлетворяется уравнение Эйлера. Конечно, участки второго
типа- экстремалями не являются, так что и в целом значение I {у}, вообще
говор'я, не будет стационарным, а имеет характер краевого экстремума (ЛВМ,

294
ГЛ. VI. ВАРИАЦИОННОЕ НСШСЛЕЖШ
пп. IV. 19, XII.11). Необходимое условие иа этих участках зависит от типа
экстремума и от направления, в котором происходит высвобождение от связи.
Пус,ть, например, идет речь о минимуме, а высвобождение иа некотором
участке происходит, как на рис. 90, в сторону увеличения у. Варьируя
у иа этом участке и .'.выполняя интегрирование по частям, получаем обычное
выражение для вариации if Fu — -г- Fy J by Ах. Но теперь уже требуется,
чтобы в/ ё= 0 при любой
участке должно быть
теперь уже
отсюда заключаем, что иа рассматриваемом
о c+Sc х
A03)
(продумайте это!). Это и есть требуемое необходимое условие. При одиократ-
} ной перемене типа экстремума или
направления высвобождения это нера-
неравенство надо заменить на противопо-
противоположное.
Например, для функционала A02)
неравенство A03) равносильно тому, что
у" < 0 (проверьте!), т. е. мы получаем
наглядно очевидный' факт, что экстре-
экстремальная линия на- рис. 90 может огибать
заштрихованную зону лишь иа участках,
выпуклых наружу от зоны (почему?).
Чтобы выяснить условие в точке
выхода графика функции у (х) иа граии-
цу области (G), рассмотрим значение
6/ при произвольной вариации Ьу вбли-
вблизи этой точки (рис. 91). Аналогично формуле (91), ио с учетом отбрасывае-
отбрасываемого интеграла по DD' получаем
б/ =/v \x=ckbc+(F-y'Fy) \x=c бс-F (с, у (с), k) be,
где под k понимается угловой коэффициент границы области в точке D выхода.
Так как Ьс может быть любого знака, то получаем необходимое условие
в толке выхода на границу:
' ¦ F'y {с,у(с), y'(c))[k-y' (c)] + F(c~y(c),~y~'(c))-F(c,~y'(c), k)=0. A04)
Это условие_ наверняка выполняется, если у'(c)=k, т. е. если в точке
выхода график у (х) не претерпевает излома. Имеется простой случай, когда
такое отсутствие излома необходимо. В самом деле, левая часть A04) равна
k г
"с, у (с), q)dq-
Рис. 91.
(проверьте!). Значит, если Fyy в точке D при всех у' не меняет знака и не
тождественно равна нулю, то обязательно у'(c)=k. В частности, достаточно,
чтобы функция Fyy (x, у, у") была непрерывна и не имела нулей.
В связи со сказанным отметим, что вообще возможность обращения
Fyy (x, у, у') при некоторых значениях х, у, у' в нуль вызывает значитель-
значительные осложнения в задачах на экстремум функционала A8) в областях, где
такие значения могут появиться (поэтому любой набор таких значений назы-
называется особым элементом функционала A8)). В самом деле, пря таких значе-
значениях уравнение Эйлера C7) вырождается, понижай свой порядок, а уже иа
простых примерах в ЛВМ мы видели, что в случае подобного вырождения

§ 1. ПЕРВАЯ ВАРИАЦИЯ И НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА 2&5
начальные условия могут определять более одного решения или вообще ии
одного решения и т. п. Проиерьте, что для функционала вида D6) е любым
числом я функций уь аналогичную роль играет обращение в нуль определи-
определителя я-го порядка det/'f"» Л.
V VkVi)
Задача с высвобождающей связью для линий в трехмерном пространстве
рассмотрена в [65], § 79.
20. Разрывные задачи. Во многих задачах вариационного исчи-
исчисления экстремум достигается не на гладких, а на кусочно-гладких
линиях, т. е. на линиях с изломами (угловыми точками). Такие за-
задачи называются разрывными, причем обычно имеется в виду разрыв
не у самой искомой функции, а у ее производной, входящей в
выражение для функционала.
Рассмотрим сначала случаи, когда разрыв предусмотрен самой
постановкой задачи. Разберем задачу об
отражении экстремали, в которой ищется
экстремум функционала
$ Ft{x, уг, y'2)dx,
где функции yx (х), _у2 (х) удовлетворяют
граничным условиям (рис. 92)
0
X
Рис. 92.
У ЛЬ)-У ЛЬ)- A05)
Рассуждение, аналогичное проведенному в п. 13, показывает, что
для пары функций уг(х), уг{х), реализующих экстремум, yt будет
решением уравнений Эйлера для Ft, а _у2—Для F* (в частности,
если Ft s= Ft, получаем кусочно-гладкую экстремаль для единого
уравнения Эйлера). Как и в п. 13, получаем
\y\ ,„; (Ь, У, Ф), у', (Ь)) буа (Ь).
Поэтому из общего необходимого условия экстремума и равенства
A05) получаем необходимое условие на линии отражения
Р\у'г Ф, У г Ф), Уг W) + ^„; V, уг ф), У', (Ь)) = 0.
Если at > Ъ, то лучше говорить о преломлении экстремали.
Если линия отражения расположена произвольно, то, рассуждая, как пря
выводе формулы (90), получаем более общее условие отражения
{k-li)Fw(x, у,
, у, /,) +
У, /|) = 0, A06)

296
ГЯ. W. ВЛРИАШйУЙНбЕ ЙбЧЙСЛЙНИЕ
где k, (i, ,/а-^.это соответственно угловые коэффициенты линии, отражении, па-
падающей экстремали и отраженной экстремали в точке отражения.
Рассмотрим теперь случай, когда излом экстремали постановкой задачи
. не подразумевался. Именно, пусть функционал A8) при граничных усло-
вяях B6) рассматривается не только иа функциях нз Ci[a, Ь], т. е. на глад-
гладких функциях, но и на кусочно-гладких функциях у (х). Тогда, как и в п. 13,
получаем, что.если кусочно-гладкая функция у(х) реализует хотя бы слабый
экстремум этого функционала (нетрудно уточнить, что это означает), то в про-
промежутках между точками излома она удовлетворяет уравнению Эйлера. Если
же точка М излома имеет некоторую абсциссу х, то, записав функционал A8)
в виде
—F)dx
и проведи через М произвольную линию, мы можем принять ее за линию
преломлении и применить условие A06), которое, таким образом, должно быть
по к тождеством. Полагая FX=F, Рг=—F
и приравнивая коэффициенты при к я сво-
свободные члены в A06) нулю, получаем (про-
(проверьте!), что при переходе через точку из-
излома значения
F'y(x, у, у') и F(x, у, y')-y'F'y.(x, у, у')
должны изменяться непрерывно, хотя у' при
этом переходе испытывает скачок. Другими,
словами,, каждое из выражений по обе сто-
стороны от точки излома должно иметь одина-
одинаковое значение. . Эти условия называются
условиями Вейерштрасса—Эрдмана. Из
первого вытекает, что излом может быть
только . в точках (х; у), в которых
F"yy (*. У, У') может обращаться в нуль (в
противном случае функция F'y (x, у, I) была
бы монотонна по I, и потому из равенства
Ру (*. У, 'i)=/v(*> У> 'г) вытекало бы,
что li — lt, т. е. излома нет). Из второго,
условия A07) можно вывести, что в точке
(х; у) излома выражение F'yy (x, у, у') при изменении у' должно обратиться
в нуль по крайней мере два раза,
Для функционала от нескольких функций, например вида D6), условие
Вейерштрасса—Эрдмана, как легко проверить, состоит в непрерывности выра-
выражений F'. , F" > и F—y\F".—уг? > при переходе через точку излома.
Ух Vi Hi Уг
Интересный случай решения с изломами может получиться в третьей за-
задаче п. 1. В п. 8 мы показали, что для получения сечения искомой поверх-
поверхности вращения нужно подобно растянуть график y=ch* от начала коорди-
координат так, чтобы ои прошел через след колечка на плоскости х, у; так, иа рис. 93
жирно локазаио сечение, если следом служит точка Mv Все такие подобно
преобразованные кривые заполняют в первом квадранте некоторый угол
— ^zk=\ga (получите трансцендентное уравнение для k и найдите из него
численно ?=1,51). Но как быть, если след колечка попадет подобно М2 в угол
У,
0
¦ lit
/l
¦у !
и
-;
г
N 'х
Рис. 93.

§ 2. ВТОРАЯ ВАРИАЦИЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА 297 ;.,¦
М- < k1 Другими словами, что произойдет С пленкой, если колечки раздвинуть
достаточно далеко? Тогда плёнке «выгодно» по возможности сжать свой'
перешеек, и она расцепится на два кружка, натянутых на колечки. Если
условно принять, что эти кружки соединены по оси вращения цилиндром иу-
леаой ширины (это не изменит значения площади), то получается, что сече-
сечением поверхности в первом кваиДраите служит ломаная ONM%. Условие
Вейерштрасса—Эрдмана выполняются во всех точках оси х, так как там все
сравниваемые выражения тождественно равны нулю. (Строго говоря, наши
рассмотрения, связанные с условиями Вейерштрасса—Эрдмана, неприменимы
к участку NM2, где у не является функцией х. Однако задачу можно преоб-
преобразовать к равносильной параметрической форме п. 10 с функционалом вида
\ F (х, у, х, y)dt, а для такого функционала нетрудно проверить, что условия
Вейерштрасса—Эрдмана состоят в непрерывности F'^ . и F¦ , откуда мы вновь
придем к особой роли точек оси х, которая, впрочем, ясна и из самой поста-
постановки задачи.)
Если для следа М2 колечка пользоваться только гладкими решениями, :
то мы сможем как угодно приблизиться к минимальной площади с помощью
линий вида, показанного на рис. 93 пунктиром, однако сама минимальная плс*
щадь при этом достигнута не будет. Таким образом, данная задача,иа мини-
минимум, первоначально поставленная в пространстве Съ оказыиается не имеющей
в этом пространстве решения и, чтобы получить решение, потребовалось соот-;
ветствующим образом расширить пространство. В такях случаях обычно топо*
рят, что мы получили обобщенное - решение первоначальной задачи.
§2. Вторая вариация и достаточные условия экстремума -
Вспоминая о глубокой аналогии между дифференциальным и
вариационным исчислениями (пп. 1.4 и 5), естественно ожидать, что;
при переходе к достаточным условиям экстремума функционалов
будат введено понятие, играющее в этом вопросе ту же роль, что
дифференциал второго порядка при исследовании экстремума функ-
функций (ЛВМ, пп. IV.18 и XII.7). Этим понятием является вторая ва-
вариация.
1. Вариация высших порядков. Замена приращения функцио-
функционала на его вариацию (п. 1.4), как и замена приращения функции
на ее дифференциал, может быть уточнена с помощью добавления
членов высшего порядка малости. Это приводит к разложению
в ряд • .
= 6/(у; ву} + 1б«/{у; 8у} + 1б»/{у; 8у}+...,-- A)
совершенно аналогичный ряду Тейлора для функций (ЛВМ, (IV.62)).
Здесь -б2/, б2/, ... —вариации соответственно второго, третьего
и т. д. порядков (коротко—вторая, третья и т. д. вариации) функ*
ционала L Каждая из них получается с помощью варьирования пре-
предыдущей (т.е. б2/ = о(б/) и т.д.), в процессе которого бу счи-
считается не зависящим от у, т. е- не варьируется. Каждая из этих

' ГЛ. Vl. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
вариаций обладает относнтельно 6у свойством однородности с соот-
соответствующим показателем:
6й/{у; Сбу} = С"Ьп1 {у; 6>} (С= const);
это означает, что члены в правой части A) имеют последователь-
последовательно первый, второй, третий и т. д. порядки малости относнтельно.
8у (точнее говоря, относительно ||бу||, см. п. 1.3, где норма берется
в том пространстве, в котором рассматривается функционал), если
только не обращаются в нуль.
В § 1 мы пользовались только первым членом ряда A). В этом
параграфе мы будем пользоваться также и вторым членом, т. е.
более точной формулой
/ {у + ву} -/ {у} = 8/ {у; ву} +1' ЬЧ {у; by} + О (|| 6> ||3). B)
В конкретных примерах разложение A), а потому и B) полу-
получаются с помощью обычного ряда Тейлора. Например, для функ-
функционала A.18) получаем
ь ь
1 \У + Д.У} = 5 F (*• У + 8У> У' + б/> dx=l\F+ (F'8y + F'y,by') +
а а L
где в F, F'y и т. д. должны быть подставлены значения х, у, у'.
Отсюда получаем для первой вариации выражение A.19), а для
второй—
ь
ЬЧ {у; 6>} = J (F"yy8y* + 2Р"уу>Ъу by' + F"y,y.8y'2) dx; C)
a
отметим, что здесь, конечно, бд>2 = (бу)г, by' =^(бу'J.
S2/ {у; Ьу) при фиксированной функции у(х) представляет собой квадра-
квадратичный функционал относительно Ьу. В общем случае понятие квадратичного
функционала / (у) в любом линейном пространстве (/?) вводят так. Сначала
определяется понятие билинейного функционала <р (у1у у2), определенного яри
всех yi?(R), У2^(Ю и линейного по каждому из этих элементов в отдельности;
затем полагают по определению
f(y)=<p(y, у)-
Если пространство (R) нормированное, то квадратичный функционал / (у) в нем
называют ограниченным, если он удовлетворяет оценке
при этом наименьшее возможное значение К называется нормой этого функцио-
функционала. В задачах вариационного исчисления пространство (/?), в которой рас-
рассматривается функционал, обычно подбирается так, чтобы он был ограниченным.
Аналогично вводятся понятия полилинейного функционала q> (ylt y2, ..., у„)
и отвечающего ему функционала f (y)=q>(y, у у), В правой части A) сла-
слагаемые имеют относительно by именно такой характер.

§ 2. ВТОРАЯ ВАРИАЦИЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА $99
Формулу A) можно получить в точности так же, как в. ЛВД1, п. XII.6,
была из формулы Тейлора для функций одного переменного получена анало-
аналогичная формула для функций нескольких переменных. Именно, при зафик-
зафиксированных у и by надо рассмотреть числовую функцию / {у -{-. к dyj числового
переменного к и разложить ее в обычный ряд Тейлора по степеням X:
Выражения в квадратных скобках и представляют собой вариации соответ-
соответствующих порядков. Полагая в D) А,= 1, получаем A).
Другой способ вывода формулы A) аналогичен примененному в п. 1.11
при получении функции F4). Заменив приближенно функцию у (х) набором
конечного числа ее значений, мы заменяем тем самым функционал / {у} на
функцию / (^0, t)i, ...,уп) от конечного числа числовых переменных. Разложив
приращение
,. Уп-\гЪуп) — ЦУа, 01 Уп)
по степеням приращений этих переменных и вернувшись обратно к функцио-
функционалам, мы н получаем разложение A). Из этого рассуждения роль второй
вариации в теории экстремумов становится совершенно очевидной.
2. Условия экстремума в терминах второй вариации. Пусть
функционал I{у} принимает для у =у~ стационарное значение, т. е.
б/ {у; бу}=0; другими словами, пусть выполнено основное необхо-
необходимое условие A.25) для экстремума. Тогда при у =у в правой
части B) первый член отсутствует, и потому главным становится
второй. Поэтому, рассуждая, как в ЛВМ, п. XII.7, при рассмотрении
экстремума функции нескольких переменных приходим е следующим
выводам:
если 62/>0 для любой 8у (конечно, кроме вариации бу = О,
когда б2/=0), то при у—у функционал I{у} имеет минимум;
если б2/< О для любой Ьу, то при у=у функционал I {у} имеет
максимум; ' ¦
если Ь21 может принимать значения обоих знаков, то при у=у
функционал 1(у) имеет минимакс и экстремума не будет.
Единственный случай, когда по б2/ нельзя судить о наличии
экстремума, тот, когда б2/ знака менять не может, но может обра-
обращаться в.нуль (в частности, если она тождественно по бу равна
нулю). Мы не будем разбирать этот сложный случай.
Более тщательный анализ показывает, что достаточное условие минимума
в общем случае имеет вид б2/ {у; бу}э=С||6у||2 (C=const > 0). Это условие
для функциональных пространств более сильное, чем просто б2/ > 0. Однако
для обычных задач вариационного исчисления это уточнение несущественно.
Эти формулировки, как и условие A.25), желательно преобразо-
преобразовать к равносильному виду требования, наложенного непосредственно
на искомую функцию у ($). Это преобразование проводится различно

ГЛ.. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ ,, .,. ;
для .разных классов функционалов, и мы покажем его для некоторых
таких классов. ..:.,' •
Отметим, что тип экстремума (слабый или сильный и т. п.—
см. п. 1.3) определяется выбором пространства, в котором рассмат-
рассматриваются функционал I {у} и разложения A) и B). :
3. Необходимые условия Лежандра. Рассмотрим функционал
AЛ8) при граничных условиях A.26) или более общих граничных
условиях, о которых говорилось в п.1.13. Мы видели, что вторая
вариация такого функционала выра-
Stfl жается по формуле C). Легко про-
проверить, что: .
если Ftfy,{x,y(x), у'(х)) допу-
допускает при а^.х^.Ь (не обязательно
для всех таких х) положительные
значения, то и б2/ {р; бу} допускает
А
а x-elr х+& Ь X положительные значения;
' ' " если F"y,y.(x,y(x),y'(x)) допу-
рис 94. екает при а ^ х ^ Ь отрицательные
значения, то и б2/ {у; бу} допускает
отрицательные значения.
:В самом деле, обозначим для краткости коэффициенты квадра-
квадратичной формы под знаком интеграла C), после подстановки в них
у=у(х), соответственно через <р(х), т!р(х) и хМ» и пусть
X (х„) > 0 (о < х0 < Ь) (мы считаем все рассматриваемые функции
и их производные непрерывными, так что если % (*) ^ О ПРИ а < х < ^»-
то это верно- и при a^CIjc^fr). Выберем в качестве Ьу функцию,
график которой изображен жирно на рис. 94. (При этом, если желать
иметь дело только с функциями из Си то уголки можно как угодно
мало скруглить.) Тогда
J x(x)by'*dx. E)
Заменяя при малом е коэффициенты их значениями в точке jc0, по-
получаем приближенные выражения для слагаемых в правой части E)
Значит, при малом е вся сумма E) положительна, что и требовалось
доказать.
Сравнивая полученный результат с утверждениями п. 2, приходим
к необходимым условиям Лежандра: если функционал A.18) при
некоторых граничных условиях имеет при у=у (хотя бы слабый)
тнимум, то F"vv (х, у (х), у' (х)) ^ 0 (а < # <; 6), если же максимум,

§ 2. ВТОРАЯ ВАРИАЦИЯ И ДОЙТАТОЧЙЙК УСЛОВИЯ ЭКСТРЕМУМА
то F"y,y\x,y(x), /(*))<0 (a<*<fr). Заодно мы получаем доста-
тачное условие для минимакса: если для экстремали у (х) функция
Fy.y(x, у (х), у' (х)) принимает при а ^.х^.Ь значения обоих знаков,
то при у=у функционал A.18) имеет минимакс. (Продумайте все
эти утверждения!) . !
Необходимые условия Лежандра не являются достаточными;
см. по этому, поводу п. 5.
Аналогично рассматриваются функционалы от нескольких функций, напри-
например от двух функций, вида-A,46). Здесь разложения A) и B) также имерт
место, но у и Ьу уже являются векторными функциями. Вторая вариация,
взамен C), приобретает вид ;
64 {у; oyj = J (Щ F"m byt ЬУ/+? ?щ^ Ьуг Ьу) +
где индексы I, j принимают независимо один от другого для фуикциошла
A.46) значения 1, 2, а в случае л искомых функций—все л значений. Рассуж-
Рассуждая, как выше, приходим к необходимым условиям Лежаидра и в этом случае:
если функция у=у (х) доставляет рассматриваемому функционалу при некоторых
граничных условиях минимум, то квадратичная форма
. F)
при любом *(а<лг<Ь) не должна принимать отрицательные значения, т. е,
должна быть неотрицательной (все собственные значения ее матрицы должны
быть ЗгО); если для у=у будет максимум, то форма F) должна быть всюду
на отрезке а<*<Ь неположительной. Если же для экстремали у-(х) матрица
(F ¦ ) имеет, хотя бы при различных х, собственные значения обоих знаковую
при у=у функционал A.46) имеет минимакс. ¦ ¦
4. Квадратичный функционал. Рассмотрим функционал
ь
l{y] = \[P{x)y'* + Q{x)f]dx G)
а
при граничных условиях
у(а) = 0, у{Ь) = О (8)
с непрерывными (достаточно—конечными) коэффициентами Р(х), Q(x),
причем впредь всегда будет требоваться, чтобы
Р(лг)>0 (а<*<&). (9)
Уравнение Эйлера для квадратичного функционала G) имеет вид
(P(x)y')'—Q(x)y = 0, . . A.0)
т. е. является линейным однородным дифференциальным уравнением
второго порядка. Ему, а также условиям (8), удовлетворяет, в част-
частности, функция у =2 0; таким образом, она придает рассматриваемому
функционалу стационарное значение, что, впрочем, очевидно и ие-

302 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
посредственно (почему?). Но будет ли это значение экстремальным?
Ответ на этот вопрос дают следующие утверждения.
Рассмотрим решение y=Y(x) уравнения A0) при начальном
условии
' . A1)
Если Y (х) при a<dx^.b не имеет нулей, то значение /{0}=0
является 'минимальным. Если Y(x) имеет при а<л;<& no крайней
мере один нуль, то значение /{0} = 0 минимаксное.
Отметим, что при перемене значения С начальные условия A1)
изменяются пропорционально, а потому и функция Y(x) умножается
на константу, т. е". ее нули не
зависят от С, можно было счи-
считать, например, С—\. Первый
нуль а функции У(х) при х > а
называется точкой, сопряженной
с точкой Х—а (относительно
уравнения A0) или относительно
функционала G)); если таких ну-
нулей нет, а уравнение A0) опре-
Рис. 95. делено при а ^х < оо, то можно
условно принять 5 = со. Таким
образом, утверждения предыдущего абзаца можно сформулировать
так: если а > Ь, то функционал I \у] имеет при у==0 минимум,
а если а < Ь,— то минимакс. (Можно проверить, что если а — Ь, то
при у == 0 будет нестрогий минимум.)
Докажем сначала первое утверждение. Пусть 2 > 6; тогда, прежде всего,
нз непрерывной зависимости решения н его производной от начальных данных ¦
(ЛВМ, п. XV.28) следует, что решение Yt (x) уравнения A0) при начальных
условиях у (а—е)=0, у' (а—е)=С будет для достаточно малых в > 0 отлично
от нуля на всем интервале a«?x<i (рис. 95). Прибавим к правой части G)
слагаемое
" ь
= 0
а
(в силу (8)), где функцию v (x) подберем так, чтобы новая подынтегральная
функция
представляла собой полный квадрат. Для этого должно быть—
PY'
и легко непосредственно убедиться, что функция v= г^ удовлетворяет
этому уравнению (проверьте!). Но отсюда получаем, что при у^0 будет
/ \у\ > 0, что и требовалось доказать. (Продумайте это искусственное доказа-
доказательство; где было использовано условие а > bf)

§ 2. ВТОРАЯ ВАРИАЦИЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА 3Q3
Докажем теперь второе утверждение,. Пусть й < Ь; тогда положим, , , ..
Это кусочно-гладкая экстремаль (п. 1.20). Но так как в точке х=а излома
условия Вейерштрасса—Эрдмана не выполняются (проверьте!), то значение
/ {iw}=0 не экстремально,"и потому имеются функции W1(x), wz(x), для кото-
которых / {к/,} > 0, / {oj2} < 0. Но тогда и / {Ая^} > 0, / {Хдаг} < 0 при любом
к=const Ф 0, т. е. при у = 0 будет мииимакс. Оба утверждения доказаны.
Рассмотрим частный случай, когда коэффициенты Р> 0 и Q посто-
постоянны. Ясно, что если Q^O, то значение /{0} минимальное. Пусть
теперь Q <0; тогда уравнение A0) при начальном условии (И) имеет
решение у —Cl/ TQ-;sin l/ ^-^-(x—а) (проверьте!), которое для
значений х > а обращается в нуль при х = й = а-\-лу ^пТ • Значит,
если в рассматриваемом случае разность b—с будет меньше чем
п/'.
г-qj , то значение b — а минимальное, а если больше,— то
минимаксное.
Квадратичный функционал общего вида
ь
2 + Q(x)y*]dx A2)
при граничных условиях (8) приводится к виду G) с помощью инте-
интегрирования среднего члена по частям: ~
ь
[t ()] A3)
при этом уравнения Эйлера для функционалов A2) и A3) совпадают
(проверьте все это!). Значит, полученные нами выводы о характере
значения /{0} автоматически распространяются на функционалы
вида A2).
Рассмотрим теперь функционал, аналогичный G), зависящий от любого
числа функций
ь ¦
1 М= J [У'*Р М У' + У*О (*) У] dx, A4)
а
где у—столбец (числовой вектор, зависящий от х), Р (jc), Q (дс)—квадратные
симметрические матрицы, непрерывно зависящие от х, звездочка означает тран-
транспонирование. Если граничные условия имеют вид
у(а) = 0, у(&)=0,
то более общий квадратичный функционал с добавочным членом y'*R (x) у под
знаком интеграла в случае симметрической матрицы R (х) приводится к виду

304 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ .'
A4) (как?). Система уравнений Эйлера, для функционала A4) в матричной
записи такова: . . - . ¦ ¦
Проверьте, перейдя к скалярной записи функционала и применив равенство
Пусть квадратичная форма ?*Р(дг)$— положительно определенная . при
каждом рассматриваемом значении х. Обозначим через Y* (дг) (?=1, 2, ..., п)
решение системы A5) при начальных условиях у (а) == О, у'(а)=С*, где векторы
С* произвольны, лишь бы определитель матрицы (С1, С2,,.., С") был Ф 0. Тогда
сопряженной с а точкой а называется первое значение х > а, для которого
det (Y1 (x), Y2 (дг), ..., У"(х))=0. (Можно показать, что а не зависит от вы-
выбора векторов С*.) Рассуждая таким же образом, как в скалярном случае, можно
доказать те же утверждения о характере значения У {0} = 0, что были приве-
приведены в третьем абзаце этого пункта.
5. Условий Якоби. Полученные в № 4 результаты можно при-
применить к квадратичному относительно 6у, функционалу C). Пусть
для некоторой функции .у (х) удовлетворяются уравнение Эйлера A.36)
и граничные условия A.26), т. е. "Ъна придает функционалу A.18)
при таких условиях стационарнде значение. Обозначим для краткости
Fyy=rFyy(x,y (x),yr (х)} и т. д. Тогда, прежде всего, в силу п. 3, если
Fy-y- меняет знак на интервале а^.х^.Ь, то значение / {у} мини-
минимаксное. Кроме того, мы уже упоминали в п. 1.15, что наличие нулей у
Fy>y> всегда вызывает существенные осложнения. Поэтому мы будем
предполагать, что /у^ сохраняет знак, для определенности
yy (<<)
Обозначим на минуту Sy==z в функционале C), куда подставлено
у = у {х); тогда уравнением Эйлера для него будет
= 0- : 06)
Оно называется уравнением Якоби для исходного функционала A.18).
Обозначим через а точку, сопряженную с а относительно этого
уравнения; обратите внимание, что, в отличие от квадратичного
исходного функционала, для общего функционала A.18) такая сопря-
сопряженная точка зависит не только от функционала, но и от выбора"
экстремали у (х). Тогда, если о > ft, то в силу п. 4 функционал C)
имеет при Sy = O минимум, а, потому согласно п. 2 функционал 1\у\
имеет при у=у~(х) слабый минимум; если же а < Ь, то функционал
/{у} имеет при у=у(х) слабый минимакс. Ясно, что если
Ffy- < 0 (о^дг^й), то вместо минимума надо говорить о макси-
максимуме. Эти условия экстремума, выраженные в терминах сопряженных
точек, называются условиями Якоби.

§ 2. ВТОРАЯ ВАРИАЦИИ fo ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА '305
... Условия Якоби имеют простой геометрический смысл: Рассмотрим одно-
параметрнческое семейство экстремалей, удовлетворяющих первому из гранич-
граничных условий A.26), т. е. проходящих через заданную точку А {а; уд). Такое
семейство называется центральным, полем экстремалей (продумайте это назва-
название); типичный вид такого поля показан на рис. 96, Зафиксируем одну из этих
экстремалей у(х); подставляя у=у(х)-{-6у в уравнение Эйлера A.37) р от-
отбрасывая члены выше первого относительно 6у порядка малостя (т. е. варьируя
уравнение A.37), что мы предоставим читателю), мы получаем как раз уравнение
A6). Таким образом, A6) —это линеаризованное уравнение для экстремалей,
близких к у(х). В частности, мы видим, что а—это абсцисса первой после А
точки пересечения экстремали у^=у(х) с бесконечно близкой экстремалью
п.,
На
0
—i
i
а
l
п
У |\
i
i
'у *
7?
> |\АХ
1 х
J, X
. Рис. 96. • . '
центрального поля, т. е. абсцисса первой точки С касания экстремали y==~y(x)
с огибающей семейства (рис. 96). Если F^, > 0 ¦» конечная точка В, экстре-
' Мали находится до С, то функционал 1 принимает на экстремали АВг слабо
минимальное значение (по сравнению с близкими линиями с теми же концами).
Однако если конечная точка экстремали В2 расположена после С, то, '«срезая»
эту экстремаль (т. е. переходя к кусочно-ломаной экстремали ADBt и т. д.,
вплоть до «нижней» дуги АВ2), мы уменьшаем значение функционала, откуда
и получается минимакс.
В качестве примера рассмотрим задачу о минимальной поверхности вра-
вращения (пп. 1.1 и 1.7). Здесь F=2nyV\ -{-у", т. е. F"yy > 0 при у > 0, и по-
потому максимальных значений у функционала нет. Выбра в конкретную экстремаль
X
rri (см. A.42)), получим уравнение Якоби (проверьте!)
2'\ +-Г--
ch*
-=0.
A7)
Гак как это линейное однородное уравнение имеет одним из частных решений
/ X ' ~ X
z=sh-r-, то оно допускает понижение порядка по формуле z = wsh —
(J1BM, п. XV. 14, свойство 4), что приводит к общему решению (проделайте
вычисления!) уравнения A7)

зов
ГЛ. Vi. ВАРИАЦИОННОЕ ИСЧЯСЛЕНИВ
При а = — Ь < О начальное условие г (а) = 0, г' (а) Ф О удовлетворяется при
= 1, откуда после преобразований получаем
<
Ь
8hT
sh
Z:==:"
sh
х+6
sh -г- sh -г
к k
Таким образом, сопряженная с —Ь точка —Ъ представляет собой первый
нуль этой функции при х >—Ь. Так как при —6<х<0 эта функция
положительна, а с помощью дифференцирования легко убедиться, что при
О < х < оо последняя круглая скобка моно-
монотонно убывает от оо до —оо, то неравенства
—Ь>Ь и —Ъ<Ь равносильны неравенствам
shT 26. 6 Л ' , Ь Ь . Ь
* ^^ ^~ 3*1 "J~" ^ \Jt 1 > С V-H , ¦ ^~^ |~" 3*1 |~ s* \Jt
t О К К К К К
*"
или соответственно < 0. А эти неравенства
равносильны тому, что точка (Ь; k ch -^
лежит на цепной линии
— kch— до ее со-
J "д прикосновения с огибающей семейства этих
линий (рис. 93) или после. Значит, из двух
Рис. 97. цепных линий, проходящих через след М ко-
колечка (рис. 97), первая порождает геликоид
с минимальной площадью, а вторая—с минимаксной площадью.
Можно показать (мы не будем здесь этим заниматься), что первая поверх-
поверхность имеет минимальную площадь и среди всех не обязательно осесимме-
тричных поверхностей, удовлетворяющих заданным граничным условиям. Тем
самым высказанная в п. 1.1 гипотеза об осесимметричной форме равновесия
мыльной пленки оправдывается. Это не является чем-то само собой разумею-
разумеющимся, так как задача с симметричными (в данном примере осесимметричными)
условиями может, вообще говоря, иметь несимметричное решение.
Аналогично выводятся условия Якоби для функционала
*, У, y')dx, y(o) =
A8)
зависящего от векторной функции у (х), другими словами, от нескольких
скалярных функций. Здесь выражение для второй вариации, взамен C),
имеет вид
ь
у; 6у }. J [dy* (F*m.) 6у+26у*
"т) 6у' + бу'* (F"y, y.) оу'] &х. A9)
Если матрица^/7 ,) симметрическая, то для выяснения знака этого квадра-

§ 2. ВТОРАЯ ВАРИАЦИЯ-И ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА 3f07
тичиого функционала можно воспользоваться результатами, приведенными
в конце п. 4.
6. Геодезические линии. Из услоннй Якоби вытекает, в частно-
частности, такое следствие. Пусть вдоль некоторой экстремали у =у (х)
(а^.х^.Ь) будет Fyy< > 0, а коэффициенты уравнения A6) огра-
ограничены. Тогда любой достаточно малый кусок этой экстремали
ь,
(а2 <;*<;#!) реализует минимум функционала' J F (х, у, y')dx
а»
(У (ai) =У (ai)> У (*i) ~У (*i))- Аналогичное утверждение справедли-
справедливо и для функционалов от нескольких функций, например вида
A.46), если матрица (F • Л имеет в каждой точке экстремали все
собственные значения положительные.
Для доказательства последнего утвержденяя можно оценять каждый член
в средней квадратячной форме под знаком янтеграла A9) по формуле (дока-
(докажите ее!) ¦
Atyt by) Ss —^ ФУ if - И I у ФУ!J' B0)
где е > 0—любое положятельное чясло. После этой оценки объединим первые
слагаемые в правой частя B0) с первой квадратичной формой в A9), а вто-
вторые—с третьей. Тогда пря фяксяроваином достаточно малом е третья квадра-
квадратичная форма останется положятельно определенной, так как свойство формы
быть положятельно определенной устойчиво относительно язменения коэффи-
коэффициентов (почему?). Значит, в сялу приведенных утверждеяяй о функционале
A4) пря достаточно малом Ь—а функционал, полученный после оценки B0).
будет принимать только положительные значения, а значит, и исходный
функционал также.
Отметим еще аналогичное свойство дли функционалов \ F (х, у, у'х) dQ
(О)
от функций нескольких переменных. Здесь для реализации минимума необхо-
необходимо, чтобы матрица (Fpp.) была неотрицательно определенной, и достаточно,
чтобы она была положительно определенной, а область (О)—достаточно малой.
Эта локальная гарантнрованность экстремума особенно наглядна
при рассмотрении геодезических линий на заданной поверхности (S),
т. е. линий, длина которых
имеет между любыми двумя их
точками стационарное значе-
значение. Другими словами, если
мало изменить по отклонению . рис gg
и по направлению (т. е. в
смысле Cj) любую дугу {1АВ) такой линии, не меняя концов А, В этой
дуги и не вылезая из {S), то длина изменится на малую высшего
порядка. Так как отклонение на большом участке АВ можно полу-
получить в результате наложения отклонений на малых участках (AFt,
AtB2 и А2В на рис. 98), то достаточно требовать, чтобы длина

308 у-''¦'¦'¦' ' ¦' ' ГЛ. VI, ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ - ¦•'
малых участков геодезической линий имела стационарное значение.
=(Это рассуждение имеет общий характер, оно применимо и к другим
вариационным задачам.) Но на малом участке всегда можно, выбрав
соответственно декартовы координаты, представить поверхность
уравнением z = q>(x, у), а линию иа ней—уравнением у=*у(х), z =
**у\х, у (х)) (почему?). Значит, речь идет о стационарном значении
функционала
¦¦/.;:{:У dx* + dy* + dz* = • J У 1 +/« + 1Ф; (х, у) + <р'у (х, у)у'}* dx B1)
lip)».заданных значениях' у {а), уф). Так как соответствующее
уравнение ЭйлераA.36) второго порядка, то мы приходим к выводу,
^ * через' каждую точку (S) в каждом направлении проходит ровно
геодезическая линия. Так как /у^ > 0 (проверьте!), то.любан
дуга геодезической линии реализует не только стационарное,
но .даже минимальное значение длины (причем, как будет показано
6. п. 7, не только слабый, но даже сильный минимум).
В to же время большие, участки геодезических линий могут,
придавать длине не минимальное, а минимаксное значение. Это хо-
хорошо видно, если в качестве (S) взять сферу, на которой геодези-
геодезическими служат дуги больших кругов, т. е. сечений сферы плоско-
плоскостями, проходящими через ее центр. Если такай дуга меньше полу-
полуокружности, то ее длина минимальна пб сравнению с длинами дуг
с теми же концами; вообразите, например, что между этими концами
натянута нить, которая при таком натяжении для любой поверхиости
(S) должна пойти по геодезической (почему?). Но если дуга боль-
большого круга больше полуокружности, то ее длина имеет минимаксное
значение, так как с помощью как угодно малой деформации этой
дуги, без смещения ее концов, можно ее длину как увеличить, так
и.уменьшить (как это сделать?).
Если поверхность (S) произвольная, то чтобы выяснить, до
каких пор геодезическая линия (/), выходящая из некоторой точки А,
реализует минимум длины,, нужно в силу условий Якоби взять пер-
первую точку А пересечения (/) с другой геодезической, выходящей
из А по бесконечно близкому с (/) направлению. Точка А, сопря-
сопряженная с А вдоль (/), и отделяет дуги минимальной длины, с на-
началом в А, от дуг минимаксной длины. Если указанного пересечения
нет, то асе дуги (/) с началом в А реализуют минимальную длину.
. На геодезических линиях видна еще одна особенность многих
задач вариационного исчисления. Рассмотрим две точки А, В на
поверхности прямого кругового цилиндра (рис. 99). Так как при развер-
развертывании цилиндра на плоскость (как и при любом изгибании поверхности
без изменения длин на ней)геодезические переходят в геодезические
(почему?), а на плоскости геодезическими служат прямые, -то на
прямом круговом цилиндре геодезическими являются винтовые ли-

§ 2. ВТОРАЯ ВАРИАЦИЯ. И ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА ^809
нии с любым шагом h и их предельные формы—окружности (когда
h = Q) и прямые (й = оо). Однако точки А, В можно соединить
бесконечным числом дуг винтовых линий (три из них показаны на
рис. 99), для каждой из которых длина имеет минимальное значе-
значение. Таким образом, задача .о минимальной длине дуги, соединяю-
соединяющей две точки, имеет в данном случае бесконечное число решений,
из которых одно реализует тотальный минимум (на рис. 99 9to
дуга /), а все остальные — только локальные.
Такая многозначность решения встречается в"
ряде задач вариационного исчисления, хотя,
конечно, она далеко не обязательна, напри-
например в задачах п. 1 ее не было.
Геодезические линии на поверхности (S) имеют
интересную механическую интерпретацию, для полу-
получения которой запишем функционал B1) в парамет-
параметрической форме
с конечной связью Н (х, у, г) = 0— уравнением по- рис. 99-
верхиости (S). В силу п. 1.13 для получения геодези-
геодезических надо написать систему уравнений Эйлера для вспомогательной функции
x, у, г).
Это даст
= 0 и т. д.
Помножив эти уравнения на орты осей и сложив результаты, получим
g Я=0,
где т—единичный вектор касательной к искомой линии (L). Но так как вектор
-ту направлен по главной нормали к (L), а вектор gradtf—по нормали к (S)
(ЛВМ, пп. VII.24 и XII.2), то мы получаем, что главная нормаль к геодези-
геодезической должна в каждой ее точке совпадать с нормалью к поверхности. Но
у точки, движущейся без тангенциального ускорения по некоторой линии,"
вектор ускорения, а потому и силы направлены по главной нормали к линии.
Поэтому траекториями материальных точек, движущихся по поверхности'«по
инерции», т. е. без внешних сил и без треиии, служат геодезические линии
На этой поверхности. (Продумайте это!)
Понятие геодезических линий вводится аналогичным образом в многообра-
многообразиях евклидовых пространств любого числа измерений, а также в общих-
римановых пространствах (пп. V.2.4, 5). Эти геодезические, свойства которых
те же,'что и для линий на поверхности, играют в теории этих многообразий
и пространств центральную роль, ту же, что прямые линии для евклидовых
пространств. Мы еще остаиовимси иа этом и § 4.
7. Условия сильного экстремума. Рассмотрим теперь условия
сильного экстремума (п. 1.3) для функционала A.18) при граничном

зм>,-
ГЛ. VI. ВАРИАЦИОННО^ ИСЧИСЛЕНИЕ
условии A.26). Пусть у(х) (а^х^.Ь)—экстремаль, удовлетворя-
удовлетворяющая граничным условиям и описанным в п. 5 условиям Якоби,
достаточным для слабого минимума. Так как эти условия «почти
необходимые» (сомнительным является только «тонкий» случай, ко-
когда строгие неравенства в условиях Якоби могут обратиться в ра-
равенства), а в п. 1.3 мы видели, что возможны «грубые» примеры,
когда слабый, минимум не является сильным, то ясно, что условия
Якоби существенно недостаточны для сильного минимума. Добавоч-
Добавочное условие, достаточное вместе с условиями Якоби для сильного
минимума (и «почти необходимое» в том же смысле), получил
К. Вейерштрасс.
Введем функцию Вейерштрасса
Е(х, у, р, q) = F(x,y, q)—F(x, у, p) — (q—p) F'p (x, у, р).
(Обозначив q=p-\-h, легко увидеть, что это есть нелинейная часть
разложения функции F(x, у, p-\-h) по степеням h.) Тогда упомяну-
упомянутое добавочное условие имеет вид
Е (х, у {х), у' (х), q) > 0 (а < х < Ь) B2)
для всех q Фу' (х) (ясно, что Е (х, у, р, р) == 0). Если же
Е(х, у(х), у'(х), «7)<0 B3)
хотя бы для одного набора значений х, q, то сильного минимума
при у=У не будет.
Из простой формулы
ds
ф (q)—ф (Р) — (Я—Р) ф' (Р) = S dr
р р
(проверьте ее!) вытекает, что условие B3) выполняется, в частно-
стиЛ если F'pp(x, у, р) > 0 для _у =
=у(х)нвсех значений/). (Отсюда,
между прочим, вытекает упомянутое
в п. 6 утверждение о том, что ма-
малые куски геодезических реализуют
сильный минимум длины.)
Доказательство приведенных утвер-
утверждений, связанных с функцией Вейер-
штрасса, можно найти в курсах вариа-
х ционного исчисления. Мы здесь приве-
приведем только грубые соображения по это-
Рис 100. МУ П0В°ДУ- Допустим, что дуга BD
экстремали заменена на «зубец» BCD
(рис. 100^_ с наклоном q участка CD,
существенно .отличающимся от наклона Р = у'(Ь{) экстремали в точке D.
Тогда линия ABCDE будет близка к экстремали АЕ в смысле С [а, Ь], но не
в смысле Сх [а, Ь\. Обозначив для краткости XQ—Xc=*h и пользуясь на ин-

§ 2. ВТОРАЯ ВАРИАЦИЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА 311
тервале оь bt формулой A.91), получим выражение для Ы при такой замене:
-pF'y'(h, Уъ P)](-h) + F (h, ylt q)h = E(b1, yih^y'ib^qih.
Значит, если для каких-либо х, q выполняется условие B3), то, приняв это
х за blt можно описанным способом уменьшить значение I \у\,т. е. сильного
минимума при у=у не будет. Если же для любых х, q выполнено неравен-
неравенство B2), то любая описанная деформация приводит, к увеличению / { у },
а комбинируя такие деформации, можно прийти к более или менее любой
линии, близкой к исходной экстремали в смысле С, но не Cv Если же бли-
близость будет и в смысле Clt то действуют условияЯкоби.
Для функционала A8) условия сильного минимума совершенно аналогич-
аналогичные, причем функции Вейерштрасса имеет вид
?{*. У, Р, q} = F{*, У, q}-F{x, у, р }-(q*-p*)F'p(x, у, р).
Максимум для /{</} служит минимумом для —/{</}. Поэтому в
дальнейшем мы будем обычно говорить именно о минимуме функцио-
функционалов.
8. Вариационная теория собственных значений. К исследова-
исследованию квадратичного функционала G) при условии (9) имеется еще
один, весьма полезный подход, совершенно аналогичный исследова-
исследованию квадратичных форм и самосопряженных отображений на основе
экстремального свойства собственных значений (пп. IV.1.6,7). Мы
будем рассматривать функционал G) при граничных условиях (8).
Исходя из упомянутой аналогии с теорией квадратичных форм,
рассмотрим значения функционала G) при интегральной связи
гйх=\. B4,)
Эти значения ограничены снизу, так как при условиях (9) и B4)
ь ь
у2dx = m\nQ(x).
Возьмем функцию yt (x), для которой это значение является наи-
наименьшим. (Существование такой функции требует доказательства,
так как, например, в п. 1.20 мы видели, что в других задачах
бывают случаи, когда значения функционала ограничены снизу, ио
наименьшее значение не достигается, во всяком случае, если не
вводят обобщенных решений. См. по этому поводу п. 9.) Согласно
правилу п. 1.12 функция уг (х) удовлетворяет уравнению
-kiy1] = 0. B5)
Если обозначить для краткости
B6)

312 : '¦¦ гл. vi. вариационное исчисление
то уравнение B5) можно переписать так:- .
B7)
Если трактовать выражение L [у] как линейный оператор в про-
пространстве функций, то формула B7) показывает, что ух является
собственным вектором (говорят также—собственной функцией) этого,
оператора, отвечающим собственному значению Я,х.
Для дальнейшего полезна формула,, справедливая для любых
функций и (х), v(x), удовлетворяющих граничным условиям (8):
ь ь
{) (Lu) v dx = {) uLv dx; B8)
a a
мы предоставляем читателю доказать ее с помощью интегрирования
по частям.
Конечно, при этом подразумевается, что функции берутся только такие,
у которых рассматриваемые здесь производные конечны или, во всяком случае,
таковы, что встречающиеся тут интегралы абсолютно сходятся; мы не будем
впредь это оговаривать. Наглядно рассматривать такие функции как элементы
гильбертова пространства Ща, Ь] (ЛВМ, п. XVII.28); в частности, тогда
формула B8) означает-, что оператор L, рассматриваемый на подпространстве
функций, удовлетворяющих условиям (8), является самосопряженным (п.IV. 1.6).
Построив функцию ух {х), мы ищем минимум функционала G)
при тех же граничных условиях и двух интегральных связях
ь ь
ly*dx=l, \yi(x)ydx = 0. B9)
а а
Функция у2 {х), реализующая этот минимум, в силу п. 1.11 должна
удовлетворять уравнению L [у2] = к%у2 + fi^y, (проверьте!). Однако
если умножить обе части на у1 и проинтегрировать от а до Ь,
а затем воспользоваться .формулами B8), B7) и B9) (проделайте
это!), та мы получаем, чтоц2 = 0, т. е. у2 (х) является собственной
функцией оператора L, отвечающей собственному значению К2.
Третья собственная функция у3(х), отвечающая собственному
значению Х3, реализует минимум функционала G) при граничных
условиях (8) и интегральных связях
н т. д. Таким путем мы получаем бесконечную последовательность
Ух (х), У2 {х), уг (х), ... C0)
собственных функций оператора L Для граничных условий (8). Все
эти функции в силу наложенных при их построении связей Ортого-

§ 2. ВТОРАЯ ВАРИАЦИЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА 313
нальны друг другу и нормированы; последнее означает здесь, что:
они удовлетворяют условию B4).
Ясно, что I{у±} ^1{Уъ} ^1{Уз} ^г- • •> так как при наложении
дополнительных связей множество сравниваемых функций сужается,
и потому наименьшее значение функционала на этом множестве
может измениться только в сторону увеличения. (Продумайте это
общее соображение!) Можно Доказать (на этом мы не будем здесь-
останавливаться), что последовательность 1{у„} стремится к бе с ко --
нечности. Наконец, с помощью интегрирования по частям первого
члена в интеграле G) легко доказать формулу
ь
ba, C1)
из которой с помощью равенств L[yn] = Xnyn и B4) получаем, что
ь
Ку«У«** = К- C2)
Нэбор значений %„ называется спектром оператора L при усло-
условиях (8) (этот термин был уже применен в ЛВМ, п. XV. 16). . .
Важнейшим свойством последовательности C0) является то, что
она не только ортогональная, но и полная, т. е. в ряд по ней
может быть разложена любая функция (ЛВМ, п. XVII.21). Исчер-
Исчерпывающее доказательство этой полноты содержится в курсах инте-
интегральных уравнений и спектральной теории дифференцнальных опе-
операторов. Однако причину полноты нетрудно понять: в самом
деле, если подобно п. 1.12 заменить каждую функцию у (х) набо-
набором ее значений у0, уг, ..., уп (а еще лучше говорить о величинах
У hyk, где h — шаг по х)^ то функционал G) превратится в квад-
квадратичную форму от этих значений; тогда описанная процедура пре-
превращается в точности в описанную в п. IV. 1.7 процедуру отыскания
собственных векторов квадратичной формы, а эта совокупность,
как было показано, обладает свойством полноты.
Рассмотрим, например, функционал
I
l{y} = \«'idx C3)
о
при граничных условиях (8), т. е.
0@) =y(Q = O. . C4)
Уравнение для собственных функций прнобретает вид—у"=Ку, у@)=уA)=0.
Решение этого уравнения, которое мы предоставляем читателю, приводит
к последовательности собственных функций и соответствующих собственных
значений
•¦/Г kn
= у f»mT
*=1.. 2>3- •••>• <35>

314 ГЛ. VI. ВАРЙАЦЖММЮЕ ИСЧИСЛЕНИЕ
Эти значения были уже найдены в ЛВМ, п. XV. 16 (коэффициент перед сину-
синусами нужен для нормировки собственных функций). Ряд по найденным собст-
собственным функциям—это хорошо известный ряд Фурье по синусам (ЛВМ
(XVII. 107)).
Отметим, что при рассмотрении полноты в последнем перед петитом абзаце
аппроксимирующую квадратичную форму надо рассматривать ие во всем
(п+1)-мериом пространстве ув, ух у„, а в его (п—1)-мериом подпростран-
подпространстве, определяемом равенствами уо=0, уп=0. Поэтому и разложением по
собственным функциям чаще всего пользуются для функций, удовлетворяющих
условиям (8). И действительно, в ЛВМ, п. XVII.25, мы видели, что для рав-
равномерной сходимости ряда по найденным в предыдущем абзаце синусам нужны
ие только непрерывность разлагаемой функ-
функции }(х), но и равенства /@) = /(/)=0. Для
^^—~ общего функционала G) и граничных условий
а^/ \ - (8) ситуации аналогичная. (Если же мы хотим,
I \^^Jft чтобы и после почленного дифференцирования
¦ >w"^ ' ряд сходился равномерно, то / (х) должна
иметь непрерывную производную и т. д.) Но
если рассматривать более свободную сходимость
разложения в среднем квадратичном, т. е. в
смысле L2 [a, b], то функции / (х), как и для
*? рядов Фурье, может ие только ие удовлетворять
условиям (8), ной не быть непрерыв-
Рис. 101. . ной, а только квадратично сумми-
суммируемой.
Оператор L и его собственные значения часто рассматриваются при гра-
граничных услоииях, отличных от (8). Здесь также возможен вариационный под-
подход. Так, можно осуществить описанное выше построение, еслн на одном вли
на обоих концах граничное значение дли функционала G) снято (т. е. ие ста-
ставится). Тогда в силу п. 1.15 собственные фуикцнн будут на этом конце удов-
удовлетворять естественному граничному условию A.82), которое для функционала
G) превращается просто в у"—0. Все приведенные рассуждения и свойства
остаются справедливыми я для этого случая.
Если взамен G) рассматривается более общий функционал
[Р (х) у'* + Q (*)V] dx+ <Цу (а)]* + $[у F)]», C6)
причем граничные условия ие ставятся, то в силу п. 1.13 естестнеииые гра-
вичиые условия (см. A.84)) будут иметь вид
(Р(х)у'-ау)х=а=0, (Р(х)у'+$у)х=ь=0. C7)
Схема построения собственных значений н собственных функций остается без
изменения, однако минимизируется, конечно, уже функционал C6), а не G).
Интересно, что при этом формула B8) дли функций, удовлетворяющих усло-
условиям C7), остается в силе, равно как и окончательнаи формула C2), в кото-
которой / вычислиется в силу C6). (Проверьте это с помощью интегрирования по
частям.)
Могло бы показаться, что тот же результат можно получить, минимизи-
минимизируя функционал G) при условии B4) иа совокупности функций, удовлетво-
удовлетворяющих граничным условиям C7), затем добавить условие ортогональности
и т. д. Однако существенно заметить, что это не так. Дело в том, что любую
функцию—скажем, из С1—можно как угодно мало изменить вместе с значе-
значением функционала G), поеле чего она будет удовлетворять условиям C7), Для
этого надо, зная концевые, значения у, подсчитать из C7) концевые значения
у', после чего соответствеиио изогнуть кончики графика у(х), как на рис. 101.

§ 2. ВТОРАЯ ВАРИАЦИЯ И Д0СТ.АТ,ОЧЦЦЕ УСЛОВИЯ ЭКСТРЕМУМА 315
Поэтому .в. принципе, нет разницы, ищется ли наименьшее значение функцио-
функционала G) на функциях, удовлетворяющих условиям C7), или вообще на всех
функциях. Но так как функция уо{х), реализующая минимум функционала
G) (при условии B4)) на совокупности всех функций, удовлетворяет условиям
у'(а)^=у' (&)=0, то мы получаем, что на функциях, удовлетворяющих C7),
функционал G) наименьшего значения не достигает, а при приближении к его
нижней грани (см. это различие ЛВМ, п. IV. 19) мы в пределе получаем
функцию уа(х), которая условиям C7) ие удовлетворяет. (Подумайте, почему
в" случае граничных условий (8) аналогичное рассуждение не проходит.)
Совершенно аналогично строится теория собственных значений для опера-
операторов от функций нескольких переменных. Например, минимизация квадра-
квадратичного функционала
(О)
прн связи " ' •
Jz2dG = l C9)
(О
и граничном условии
г1(Г)=° D0)
приводит к первой собственной функции гг (х, у) и наименьшему собственному
значению К-^ оператора
Ш--^-д^+а(х,у)г D1)
при условии D0). Добавочная связь KzzxdG^O приводит ко второй собст-
(G)
венной функции, отвечающей следующему по величине собствениому значению
и т. д. (Впрочем, можно показать, что для задач с двумя независимыми пере-
переменными более естественно снабжать собственные значения и собственные функ-
функции двумя индексами.) При этом оказывается, что все основные утверждения,
приведенные выше для функционала G), остаются н здесь в силе.
Если снять граничное условие D0) со всего контура или с какой-либо
его части, то на этой части собственные функции будут удовлетворять естест-
естественному граничному условию (см. A.101))
дг , ^\. дг , ^. дг
^cos(n, *)+^cos (n, jf)=O, т. е. ^=0.
Аналогично, если вместо C8) рассматривается функционал
(О) . (Г)
при снятых граничных условиях, то описанная конструкция приводит к еоб-
ственным функциям оператора для естественных граничных условий
0. О существовании минимума. Остановимся еще иа вопросе о существо-
существовании функции, реализующей наименьшее значение функционала; этот вопрос

316 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ • ч ¦,
проявляется и во многих других аналогичных задачах. Пусть; например, -
рассматривается функционал ' - . : *
G)
о
с Р (х) > 0 при граничных условиях
у(а)=0, у(Ь)=О • (8)
и интегральной связи
*
' B4)
Мы уже упоминали о том, что значении этого функционала ограничены снизу.
Поэтому, если наименьшее его значение и не достигается, то, во всяком слу-
случае, можно построить последовательность функций Yn (дг), удовлетворяющих
условиям (8) и B4), для которой lim / {Ya\ принимает наименьшее возможное
значение; любая из таких последовательностей называется минимизирующей
функционал /. (Подобно тому как среди положительных чисел нет наимень-
наименьшего, но последовательность 1, 1/г> ¦ • •, '/и> • • • имеет наименьший возмож-
возможный предел_нуль, она будет одной из минимизирующих, как и последователь-
последовательность {l/~2ln2}, н т. п.)
Если бы последовательность функций Yn(x) или какая-либо ее подпоследо-
подпоследовательность сходилась—скажем, равномерно—к некоторой предельной функции
Y (х), то Y (дг) как раз реализует требуемое наименьшее значение функционала.
В самом деле,
ь ь
С K2(jt)dx=lim \ Y%(x)dx=l,
a a
b b
\ Q (x) K* (x) dr=lim f Q (x) Y* (x)dx,
тогда как '
P (x) Y'* (x) dx < lim J P (x) Y2 dx
(Последнее соотношение кажется сначала странным, так как может показаться,
что правая часть обязательно равна левой. Но на самом деле она может ока-
оказаться и больше левой; обе эти возможности проиллюстрированы на рис. 102.)
Поэтому
l{Y\<limI{Yn},
но так как последовательность Yn минимизирующая, то /{К} и есть наимень-
наименьшее значение функционала / при заданных условиях. (Продумайте это.рас-
это.рассуждение!).
При установлении существования такой сходящейся последовательности
важнейшую роль играет понятие компактности. Именно, некоторое множество
(М) точек нормированного или более общего метрического пространства (J?1
называется компактным в (R), если у всякой последовательности точек (М)

§ 2. ВТОРАЯ ВАРИАЦИЯ ; И ДОСТАТОЧНЫ» УСЛОВИЯ ЭКСТРЕМУМА 317
имеется по крайней мере одна сходящаяся подпоследовательность; В этих терминах
теорему Больцано—Вейерштрасса (стр.71) можно сформулировать так: если
(/?)—конечномерное евклидово пространство, то всякое ограниченное множество
его точек (М) компактно в нем. Легко видеть, с другой стороны, что неогра-
неограниченное множество всегда некомпактно,. для этого достаточно взять в нем
любую последовательность точек, уходящую на бесконечность. Таким образом,
для конечномерного евклидова пространства (R) компактность множества (М)
в (R) равносильна ограниченности (М). ' '
Однако характерной чертой бесконечномерных пространств, значительно
усложняющей их исследование, является то, что в них ограниченные множе-
множества не обязаны быть компактными! Характерным примером служит после-
последовательность функций sin х, sin 2x, sin3x; ..., ограниченная, но не компакт-
компактная в пространстве С [а, Ь] при любых фиксированных а, Ь: конечные перепады
«высот» на отрезках, длина которых стремится к нулю, не дают возможности
Ъ х
перейти к равномерному пределу. (Продумайте этот пример!) Тем не менее
можно' вполне строго доказать, что упомянутая выше минимизирующая после-
последовательность Y'„ не только ограничена, но и компактна в С [а, Ь], так как
подобные перепады высот привели бы к безграничному увеличению интеграла
ь ••'¦"¦
\ У,}dx, а с иим к /{К,,}. Эт.им'и обеспечивается наличие у последователь-
а
ностн У„ равномерно сходящейся подпоследовательности, для предела кото-
которой рассматриваемый функционал принимает, как мы видели, наименьшее
значение.
Конечно, приведенные рассуждения имеют лишь наводящий характер и
при математическом анализе нуждаются в уточнении во многих пунктах (см.,
например, [86]). Тем ие менее общая схема этих рассуждений—проверка огра-
ограниченности функционала снизу, выбор минимизирующей последовательности
н доказательство ее компактности в соответственно подобранном простран-
пространстве—лежит в основе многих теоретических работ, посвященных обоснованию
разрешимости задач ни экстремум функционала. Правда, такие рассуждения
часто бывают недостаточно конструктивны, т. е. не дают указаний на то, как
же искомое решение построить хотя бы Приближенно. Однако такое обоснова-
обоснование служит подтверждением правильности постановки математической задачи
и тем самым вдохновляет на поиски эффективных методов приближенного и чис-
численного нахождения решения и установления его свойств.
\й. Основное условие минимума. В терминах собственных зна-
значений можно сформулировать основное условие минимума квадратич-
квадратичного функционала, имеющее весьма универсальный характер. Будем
считать, что в каждом вз граничных условий C7) для функционала
G) один .вз коэффициентов равен нулю, в потому в силу C1) для

318 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
функций у (л:), удоилетиоряющих этим условиям, имеет место фор-
формула
I{y\=\L\y\ydy. D2)
а
Воспользовавшись полнотой системы C0) собственных функций
оператора L при условиях C7), разложим у (х) в ряд по этой си-
системе:
у (х) = 11у1 (х) + 12у2 (*)+...= S \пУп (х), D3)
где коэффициенты %; находятся по обычным формулам для ряда по
ортогональным функциям
ъ
а
Ь
(см, ЛВМ, (XVII.100); в данном случае знаменатель \y\dx отсут-
а
ствует из-за нормировки собственных функций). Подставив разло-
разложение D3) в D2), производя перемножение и пользуясь ортогональ-
ортогональностью и нормировкой собственных функций, получим
. = 2 Ъ„Ът\КУпУтйх=:%%нЦ. D4)
я, m—i а п — х
Так как коэффициенты \п могут быть произвольными, то мы
приходим к следующим основным выводам: если все собственные
значения %п положительны, то функция у = 0 реализует тотальный
минимум функционала D2) при условиях C7); если имеется по
крайней мере одно отрицательное собственное значение, то при у = 0
будет минимакс. ^Эти же выводы мОжно сформулировать в терминах
наименьшего собственного значения Ят!п (такое обязательно имеется,
так как Я„—>оо, в рассматриваемом сейчас случае просто ЯГП1П = Я1):
если Япнп > 0, то -будет минимум, если Ят!п < 0, то минимакс.
(Видно также, что если Ят1П = 0, то при _у = 0 будет нестрогий
минимум.)
Приведенное доказательство имеет совершенно общий характер, поэтому
полученные выводы справедливы и для многих других классов квадратичных
функционалов; это особенно ясно, если с самого начала исходить из записи
такого функционала в виде правой части D2). Существенно только, чтобы опе-
оператор L при выбранных граничных условиях был самосопряженным, т, е. для
него выполнялась формула вида B8) (этим обеспечивается вещественность соб-

§ 2. ВТОРАЯ ВАРИАЦИЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА ЗДЭ
ственных значений), я чтобы * соответствующая система собственных функции
была полной. В частности, эти выводы Справедливы для функционалов от
функций нескольких переменных, когда условия Якоби уже неприменимы. ¦
Для функционалов / более общего вида, не обязательно квадратичных,
полученные выводы можно, как и в п. б, применить к б2/ и получить доста-
достаточные, а также необходимые условия локального слабого минимума в терми-
терминах собственных значений оператора, отвечающего линеаризованному уравнению
Эйлера. (Единственным отличием является то, что в случае Х,р,,п=0 уже не
обязан быть нестрогий минимум, так как тогда начинают влиять члены выше
второго порядка малости.)
Реальная задача на экстремум функционала обычно содержит параметры,
от которых непрерывно зависят собственные значения соответствующего опера-
оператора; впрочем, эта зависимость может иметь и разрывы, если при достижении
некоторых соотношений между параметрами сама задача претерпевает разрыв
или в каком-то смысле вырождается. Более прост случай, когда этот параметр
а одни. Тогда, найдя (обычно численно) зависимость X,mjn of а и подсчитав
ее нули и точки разрыва, если они имеются, мы получаем возможные крити-
критические значения для • а, при которых Х,т,„ сменяет знак, и потому минимум
сменяется на минимакс или обратно. Если параметров два, мы получаем ана-
аналогичным образом критические линии в плоскости параметров. Если парамет-
параметров более двух, то ситуация, конечно, сложнее, однако и тогда можно пред-
предпринять попытку получить с помощью интерполяции приближенную формулу
для критической гиперповерхности.
Формула D4) совершенно аналогична формуле приведения квадратичной
к главным осям (п. IV.2.1), она приводит квадратичный функционал
\у} к диагональной форме после перехода в пространстве Ц \а, Ъ] к евкли-
евклидову базису, состоящему из соответствующих собственных функций CD). Однако,
в отличие от конечномерного случая, это приведение действует не во всем про-
пространстве, а только в подпространстве функций у, для которых ряд в правой
частя D4) сходится. Это объясняется тем, что функционал / {(/}, как видно из
C2), неограничен (см. п. 1).
Рассмотрим, например, функционал C3) при граничных условиях C4), для
которого собственные значения и собственные функции имеют вид C5). Тогда
прежде всего для сходимости ряда D4) требуется, чтобы функция у{х)
была непрерывной и удовлетворяла тем же условиям C4), так как в про-
противном случае из ЛВМ, п. XVII.25 следует, что ?„ имеет порядок 1/я,
и потому ^nln не стремится к нулю при п—>¦ со. Кроме того, для конеч-
конечности значения I \у\ функция у(х) должна иметь квадратично суммируемую
производную. Совокупность функций у (х), удовлетворяющих этим требованиям,
и составляет подпространство, в котором действует формула D4).
Между прочим, обращаем внимание читателя на кажущийся парадокс, воз-
возникающий для разобранного примера функционала: для функции у=1 левгя
часть D4) равна нулю, тогда как правая — бесконечности. Объяснение в том,
что при применении разложений D3) при граничных условиях C4) надо рас-
рассматривать не у^ 1, а функцию
а тогда у' имеет дельта-слагаемые, которые квадратично не суммируемы; таким
образом, обе части равенства D4) на самом деле равны бесконечности.
Для более общих квадратичных функционалов, рассмотренных в этом
пункте, подпространство, в котором происходит приведение к главным осям,
также состоит из функций с квадратично суммируемой производной, причем
граничные условия определяются постановкой исходной задачи .на .минимум
функционала. ¦ • . . .

.; 32Q ... , . ГЛ. VL ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ ¦¦<¦'¦
п. , ,11. Зависимость собственных значений от функционала. Рас-
Рассмотрим функционал G) страничными условиями (8). Как мы видели,
: соответствующий оператор B6) имеет при этих условиях последо-
последовательность собственных функций C0) и соответствующих собст-
собственных значений C2). Как изменятся эти собственные значения,
если заменить коэффициенты Р{х), Q{x) или пределы интегрирова-
;:ния о, Ь илн вид граничных условий? В некоторых случаях удается
ответить на этот вопрос.
:. Если увеличить коэффициенты Р, Q, то все собственные значе-
значения увеличатся; точнее, если
Р(х)^Р{х), Q(x)^Q(x) (а <*<&), D5)
то %п > Я„ (я=1, 2, 3, ...; Ка—новые собственные значения),
за исключением тривиального случая^ когда оба неравенства D5)
обращаются в равенства.
Доказательство для первого собственного значения сразу выте-
вытекает из его построения по методу п. 8:
(Продумайте каждый из этих переходов!)
Утверждение для п-ro собственного значения вытекает, аналогичным обра-
образом из следующей теоремы Р. Куранта: Хп есть наибольшее из чисел
X (pj, р2 Pn-i) при всевозможном выборе функций pt (jc) Pn-i(*).'
;.(a,<x<fr), где Я.(р1( р„, .... p^-j) есть, минимум функционала G) на функ-
функциях, удовлетворяющих условиям (8) и B4) и ортогональных каждой из функ-
функций р/(лс) (ср. конец п. IV. 1.7).
При добавлении к Q(x) константы ко всем собственный значениям,
добавляется та же константа. В самом деле, в силу всегда присут-
присутствующей в п. 8 связи B4)
ь ¦'. 6
J [P(x)y'x + (Q W + Q?] dx - J [P{x)y* + Q(x)?]dx + C,
а а
так что ко всем значениям функционала G) попросту прибавляется С.
Из доказанных двух свойств сразу вытекает самая грубая оценка собствев-
иых значений:
) (я=1, 2, 3, ...)• D6)
В самом деле, при оценке \п, например, сверху можно на основании первого
¦ свойства заменить коэффициенты Р (х) и Q (х) их наибольшими значениями,
затем на основании второго свойства совсем устранить член- суа и воспользо-
воспользоваться результатом C5) для функционала C3). (Продумайте это!)
Для получения более точной оценки собственных значений совершим за-
замену переменных ¦

§ 2. ВТОРАЯ ВАРИАЦИЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА 321
причем такую, чтобы уравнение связи B4), а также условия ортогональности
типа B9) в новых переменных сохранили бы свой вид, а функционал G) пе-
перешел бы в интеграл вида
Из первого требования получаем, что <p2t|) = l, а из второго—что P<p2/t|)
(проверьте!). Отсюда
Ф(*)=[Я(*)Г1/4, Ъ(*)
Т. е.
кроме того, s—2r's==T^>"—Тк^^'2"!"^ (проверьте!). Заметив, что при
рассматриваемой замене собственные значения остаются неизменными, получаем,
применив формулу D6), и доказанные свойства об изменении собственных зна-
значений: _
+ min (±Р'—^р-»Р
6
+max ^i.p-—ip-ip'»+Q) (n = l, 2, 3, ...).
a /
В отличие от оценки D6), здесь разность между левой н правой частями огра-
ограничена при п—»¦ ов.
При увеличении а или уменьшении Ь все собственные значения увеличи-
увеличиваются.
В самом деле, пусть, например, а^=а, Ь > Ь; продолжим функцию yi(x)
иа интервал b <:*<:? тождественным нулем и обозначим продолженную функ-
функцию через г (дс). Тогда
M*/(W«7C>7&)=«*i.
Неравенства для дальнейших собственных значений получаются аналогично
из теоремы Кураита.
Если иа одном или обоих концах интервала а, Ь граничное условие для
функционала G) снято, то, как уже было сказано, собственные функции будут
на этом конце удовлетворять граничному условию у'=0. Все приведенные
-выше утверждения о собственных значениях сохраняют силу и для таких гра-
иичиых условий, причем доказательства почти ие изменяются К этим утверж-
утверждениям можно добавить еще такое: при замене на каком-либо из концов интер-
интервала а, Ь условия у=0 на условие i/'=0 все совете, нные значения уменьшаются.
В самом деле, в силу только что сказанного такая замена означает просто,
что иа соответствующем конце граничное условие совсем снимается; ио тогда
совокупность сравниваемых значений функционала G) расширяется, и наимень-
наименьшее значение в ней уменьшается,
Аналогичными свойствами обладают собственные значения в ряде других
задач, в которых для построения этих значений возможно применить вариа-
вариационные методы. Например, из рассмотрения функционала C8) вытекает такой
результат: при сужении области (G) все собственные значения оператора D1}
при. граничном условии D0) увеличиваются и т. д. :
11-А. Д. Мишине

822 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
§ 3. Канонические уравнения и вариационные принципы
1. Канонические уравнения. Во многих исследованиях общего
характера оказывается удобным преобразовать уравнения Эйлера
к канонической форме, позволяющей более единообразно трактовать
различные классы вариационных задач. Это особенно полезно в ряде
задач физики и механики, где вводимые при таком преобразовании
переменные имеют непосредственный физический смысл.
Мы будем рассматривать задачу о стационарном, в частности
экстремальном, значении функционала
ь
р(х, yv yt, ..., уя, у[, y't, ...,y'Jdx, A)
при каких-то граничных условиях. В силу п. 1.10 система уравнений
Эйлера для этого функционала имеет вид
pyt-hF'y'i =0 (/=1-2- •••-п); * B)
она представляет собой систему из п обыкновенных дифференциаль-
дифференциальных уравнений второго порядка с п искомыми функциями
У Ах), У Ах) У„{х). C)
Введем величины
Р/ = /7»; (¦*, Уи Л» • • •> Уп, /i. y't, ••-, Уя) (*' = !. 2- • ¦ •. л). W
которые вместе с переменными _у,- называются каноническими пере-
переменными для функционала A), причем величины y-t и р; называются
сопряженными друг другу; для любых выбранных функций C) вели-
величины D) также представляют собой некоторые функции х. Введем,
кроме того, функцию Гамильтона, отвечающую функционалу A):
н(х, Уг Уп, Р\ Рп) =
П
У1, ••-,Уп,Уи • • ¦. Уп) + ^y'tPi' E)
при этом в правой части величины _у,- считаются выраженными через
х, yt, ..., уп, pv ..., рп в силу соотношений D), которые можно
рассматривать как систему из п конечных уравнений с п не-
неизвестными^, ...,у'п.
Как известно из теории неявных функций (ЛВМ, пп. IX.13 и XII.3),
решение такой системы является принципиально возможным, во всяком случае
локально, если соответствующий якобиан отличен от нуля. Этот якобиан есть
det (F"y".y'), и на существенность его отличия от нуля мы уже обращали вни-
внимание в п. 1.19.
В качестве примера предлагаем читателю проверить, что функция Гамиль-
Гамильтона для функционала A.102) имеет вид

§ 3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 323
Дифференцируя формулу E) и пользуясь равенствами D), по-
получаем
rftf = -F'xdi-^Fy. dy{-2Fyl d(y'i) + 2d(y'i)Pi +
Значит, если считать канонические переменные и х независимыми,
то
Если теперь функции C) удовлетворяют уравнениям Эйлера B),
то из второго и третьего равенств F) получаем
dp; дН dy; дН .. 1 q \ i7\
Ас %,- \ dx др{ v ' ' ' ' v '
Это и есть каноническая форма уравнений Эйлера или прости ка-
каноническая система уравнений, отвечающая функционалу A); она
представляет собой систему из In обыкновенных дифференциальных
уравнений первого порядка с 2л искомыми функциями )»,-(#), Pi(x).
Интересно отметить, что р,- и Н—это те самые величины, которые в силу
условий Вейерштрасса—Эрдмана (п. 1.20) должны были вместе с х и у; оста-
оставаться непрерывными при переходе через точку излома кусочио-гладкой экстре-
экстремали. Это становится более ясным, если переписать выражение для произволь-
произвольной вариации функционала A), наподобие A.91) в векторной записи
ь ь
b\F{x, у, у') dx= С (V' -4/у) -bydx+ip-d \у(х)]-НЬх) I* (8)
а а
и вспомнить вывод условий Вейерштрасса—Эрдмана.
2. Первые интегралы. Пусть задана некоторая функция
Ф(*> 'Уи У2> • • •> Ую Pv Рг> • • •> Рп)- Если ее рассматривать вдоль
решения системы уравнений G), т. е. подставить вместо независи-
независимых переменных yh pt решение этой системы, то мы получим слож-
сложную функцию х, для которой
дФ dp;
dp; dx
п
дФ , V' ( дФ дН дФ дН
Выражение
\dyidPi dptd
называется скобкой Пуассона функций Ф н Н н обозначается.
1 11*

324 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ ;
[Ф, Н]. Таким образом, формулу (9) можно записать так:
Отметим простые свойства скобок Пуассона (докажите!)
[Ф, ?] = -[?, Ф]; [Ф, <D]s=sO; [Ф,+Фг, ?] =
= [ФХ) Щ + [Ф„ П
[СФ, V] = С \Ф, W] (С = const); [ФХФ2, W] =± Ф, [Ф2, Y] + Ф2 [Фи V].
Из A0) мы видим, в частности, что соотношение
g + [<D, Я]^0 A1)
необходимо н достаточна для того, чтобы вдоль любого решения
системы G) было
Ф(х, уъ ...,уп,рл pn) = const;
таким образом, мы получаем первый интеграл (ЛВМ, п. XV.13)
системы G). Как известно, знание k независимых первых интегралов
позволяет понизить число уравнений в системе на k (ЛВМ, п. XV.13).
Пусть, в частности, функция Н не зависит от х. Положив
тогда Ф = #, видим, что соотношение A1) выполняется. Итак,
в рассматриваемом случае функция Н постоянна вдоль любого ре-
решения системы G), т. е. вдоль любой экстремали. [Докажите это
же, вычислив -г- в- силу уравнений G). J Прн д=1 мы получаем
как раз первый интеграл A.38).
Другим простым случаем, когда можно найти первый интеграл,
является тот, когда функция Н не зависит от какой-либо из пере-
переменных у[ илн pi, тогда можно положить Ф=р,или соответственно
ф=^(. (проверьте!).
3. Канонические преобразования. При изучении и применении
¦канонических уравнений G) не обязательно вое время помнить
о первоначальном происхождении величин р{; эти уравнения можно
рассматривать в Bй-(-1 )-мерном пространстве х, у, р (а если Н не
зависит от х, то и в 2л-мерном пространстве у, р) как обычные
дифференциальные уравнения, независимо от первоначальной связи
между рассматриваемыми величинами. При этом Н рассматривается
как некоторая заданная функция 2л+1 переменных х, у, р, опре-
определяющая правые части системы G). Естественность такого подхода
основана, в частности, на замечательной симметрии, с которой пе-
переменные у и р входят в систему G).
: Конечно, не любая система обыкновенных дифференциальных
уравнений в пространстве х,- у, р имеет канонический вид. Именно,

§ 3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 325
если задана система
Й = Ф,-(*. Л. ...,*», Рь .-..A,), g^,^...) (/=1 л),
то она является канонической тогда и только тогда, когда
Зр/ dpi dyj ду{ ' ^7 dPi .
(почему?). Поэтому если и канонической системе G) совершить
замену переменных
** = #(*. Л Уп-Л Рп), Л-*|(-..) (/-!,..., л), A2)
то полученная и переменных ж, Y, Р система уравнений уже не
обязана быть канонической. Если все же такая каноничность сохра-
сохраняется, то преобразование A2) называется каноническим (для исход-
исходной системы G), так как преобразование по тем же формулам A2)
другой канонической системы может нарушить каноничность).
Мы укажем здесь важный класс канонических преобразований,
заметив для этого, что систему G) можно рассматривать как систему
уравнений Эйлера для функционала
ь
$'x A3)
(проверьте!). Но мы уже упоминали в п. 1.7, что если в системе
уравнений Эйлера совершить замену переменных, то получится та-
такой же результат, как если заменить переменные в функционале,
после чего составить уравнения Эйлера для измененного таким
образом функционала. Значит, если после замены A2) функционал
A3) примет вид
\PiY'l—H(x, Y, P)\dx + const
И?'
(мы сокращенно пишем Y вместо Ylt K2, .-.., Ya), то преобразова-
преобразование A2) каноническое. Так будет, если преобразование A2) удов-,
летаоряет тождеству вида
2>;4у,—Н(х, у, p)dx-=
= %Р{<1У;—Н(х, У, P)dx + dQ>ix, у, Y), A4)
где функция Ф{х, у, Y) называется производящей функцией канони-
канонического преобразования A2). (Заметим, что \</Ф»=Ф , а так как
при построении экстремалей можно искомые функции считать иа
концах интервала заданными, то последний.член в A4) доставляет
рассматриваемому функционалу лишь несущественное постоянное
слагаемое.) Знание производящей функции позволяет восстановить

326 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
все преобразование рассматриваемого класса, так как из A4) выт.е-
кабт, что если принять х,- у, Y за независимые переменные, то
имеют место формулы
*.• = !' Я,. = -^ (/ = 1,2, ...,«), Н = Н+%. A5)
Обратно, ясно, что из A5) вытекает A4). Таким образом, для полу-
получения канонического преобразования можно задаться (вообще говоря,
произвольной) функцией Ф(х, у, Y), затем написать формулы A5);
из первых п формул выразить, если это окажется возможным, Y
через х, у, р, после чего подставить результат в следующие п
уравнений A5), что и приведет к каноническому преобразованию A2).
Иногда оказывается более удобным выбирать производящую функцию Ф
как функцию переменных х, у, Р. Если тогда, взамен A5), положить
то вместо A4) получится тождество
Pl dVi-
(проверьте!). Поэтому и здесь преобразование у, р —>¦ Y, Р оказывается кано-
каноническим.
Рассмотрения канонических преобразований упрощаются, если
функция- Гамильтона Н не зависит от х; тогда естественно принять,
что и функции gj, hj в A2), а также Ф в A4) не зависят от х. Из
A5) мы видим, что тогда Н=Н, т. е. функция Гамильтона при
рассматриваемых канонических преобразованиях остается инвариант-
инвариантной, а из A4) — что разность
: SPidytSPtdY,
должна быть полным дифференциалом функции Ф(.у. Y). Можно
доказать (мы пропустим доказательство), что для этого необходимо
и достаточно, чтобы
[Yt, Yj] = 0, [/>,, Ру] = 0, [Р{, Г,.] = 0 (i^j), [/>,, К,] = 1,
где квадратными скобками обозначены скобки Пуассона (п. 2). Если
ато условие выполнено, то для любых функций Wlt W2 скобка
Пуассона [W{, W2], вычисленная в переменных у, р, принимает то
же значение, что и в переменных Y, Р, т. е. она является инва-
инвариантной относительно таких канонических преобразований.
4. Контактные преобразования. Первые 2л формул A5) допускают замеча-
замечательное геометрическое истолкование. Рассмотрим два л-мерных пространства:
у и К; при этом значение х будет считаться произвольным, но зафиксирован-
зафиксированным, так что зависимость от х мы указывать не будем. Поставим каждой точке
0—i&i, У-г уп) первого пространства (я—1)-мерную поверхность второго

§ 3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫ* ПРИНЦИПЫ 327
пространства с уравнением
Ф(у, Y)=C, A6)
где С—некоторая зафиксированная постоянная. Пусть теперь у может сдви-
сдвигаться на произвольный бесконечно малый вектор dy, перпендикулярный неко-
некоторому выбранному направлению а° (нулнк означает единичный вектор соот-
соответствующего направления). Тогда в пространстве Y получается «бесконечно
узкое» (л—1)-параметрическое семейство поверхностей, пересекающихся в не-
некоторой точке Y (их может быть и несколько), зависящей не только от
выбора точки у, но и от выбора "направления а0. Направление общего перпен-
перпендикуляра к этим поверхностям в Y обозначим через" А0, оно также зависит от
у н о0. Таким образом, здесь преобра уется не точка в точку, а линейный
элемент {у; а0) (т. е. точка с элементом (л—1)-мерной касательной плоскости
в ней, так как направление плоскости задается перпендикуляром к ней) в ли-
линейный элемент (Y; А0). Такое преобразование называется контактным, или
преобразованием прикосновения, а функция Ф (строго говоря, Ф—С), которая
его порождает, называется производящей функцией для этого преобразования.
Если в пространстве у дана (л—1)-мерная поверхность («), то в каждой ее
точке имеется касательная плоскость, т. е. э.-ой точке отвечает точка простран-
пространства Y, н мы нолучаем (л—1)-мерную поверхность (S), соответствующую (s).
(При этом особым точкам (s), например коническим, отвечают целые много-
многообразия на (S).) Если поверхности (st) и (s2) касались в некоторой точке у, то
и соответствующие поверхности (St) и (S2) касаются в соответствующей точке Y;
но если (st) и (s2) пересекались в у под ненулевым углом, то в пространстве Y
точке у будут отвечать две различные точки V^g^) н Fag(S2).
В качестве простого наглядного примера разберите при л=3 контактное
преобразование с производящей функцией
причем пространства у и Y здесь удобно считать совмещенными.
Построение контактного преобразования непосредственно связано с теорией
огибающих, упомянутой при л = 2 в ЛВМ, п. XII.5. Рассмотрим прн любой л
fc-параметрическое семейство (л—1)-мерных поверхностей A<?<л—1) с
уравнением
FQb. К2> ..., Yn; Clt C2, .... CA)=const. A7)
Тогда аналогично случаю л=2 легко проверить, что огибающая этого семей-
семейства, вообще говоря (за исключением различных особых случаев), представляет
собой (л—1)-мерную поверхность, уравнение которой получается исключением
параметров из уравнения A7) семейства и уравнений
F'Cl(Ylt Y2 Yn; Clt С, CA) = 0 (i=l, .... k). A8)
При этом каждая из поверхностей A7) прилегает к огибающей по (л—1—k)-
мерному многообразию, получающемуся в результате пересечения этой поверх-
поверхности со всеми бесконечно близкими поверхностями семейства; впрочем, доста-
достаточно ограничиться пересечением с k поверхностями, каждая нз которых полу-
получается бесконечно малой вариацией одного из параметров семейства. (Случаи
л=3, ft=l и л=3, ft=2 показаны на рис. 103; вторая картинка одновременно
иллюстрирует контактное преобразование линейного элемента прн л=3).
В частности, если k=n—1, каждая из поверхностей семейства нрилегает
к огибающей поверхности, вообще говоря, не по многообразию, а по одной или
нескольким дискретным точкам.
Так как уравнения A8) можно короче записать в виде 3С/7=О, где
С=(СЪ С2 Ck), dcF=F'Ci dCx +F'Ci dC2 + ... +FCn dCn, то, возвращаясь
к A6), видим, что контактное преобразование получается добавлением к A6)

828
ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
условия
или, что равносильно,
дуФ(у, У) = 0 для всех dyj_o°
Y)\\a»,
A9)
где под gradj, понимается градиент в пространстве у при зафиксированном Y.
При этом направление нормали к поверхности определяется уравнением
grady<I>G/, К) || А» B0)
(ЛВМ, п. XII.2). При заданных у и а0 соотношения A6) и A9) образуют
систему нз л уравнений с л неизвестными Yu Yit ..,, Yn, найдя которые, мы
можем из B0) найти А0. Интересно отметить, что в силу полной симметрии
полученных соотношений относительно обоих пространств рассмотренное нами
"отображение является одновременно контактным преобразованием нз простран-
пространства Y в пространство у с той же производящей функцией A6).
Рис. 103.
Применяя полученные результаты к каноническому преобразованию A5),
мы видим, что его производящая функция Ф определяет такое контактное
преобразование из пространства у в пространство Y, при котором линейный
элемент (у; р°) преобразуется в линейный элемент (Y; Р<>).
5. Теорема Нётер. Эта теорема дает возможность для функционалов, обла-
обладающих определенной инвариантностью, получать первые интегралы для
системы уравнений Эйлера, что во многих задачах может иметь принципиаль-
принципиальное н практическое значение.
Сначала введем общее понятие непрерывной группы преобразований (ото-
(отображений) пространства ?„ (или области в ием) в себя, причем для краткости
записи будем вместо точки (дсх; >г2; ...; хп) рассматривать ее радиус-вектор х.
Тогда формулы отображения
Х1 = Ф,-(Хи Хг,
можио коротко записывать так:
*„)
х=Ф(х).
2,
B1)
B2)
(Конечно, это не означает, что прямолинейные отрезки при-отображении оста-
остаются примолинейнымн! Формула B2) говорит только об отображении
концов радиусов-векторов по закону B1).) ' : '.
Пусть задано однопараметрическоё семейство взаимно однозначных отоб-
отображений _
к=Ф(х;/), B3)

§ 8. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 329
где t—вещественный скалярный параметр. Такое семейство называется непре-
непрерывной группой преобразований, если результат последовательного выполне-
выполнения отображений с параметрами t-^ и t2 равносилен отображению того же
семейства с параметром /t + /2 (это групповое свойство). Отсюда, в частности,
вытекает, что отображение с параметром <=0—тождественное, т. е. Ф(х; 0) = х,
а также, что отображении Ф (х; t) и Ф (х; —/) взаимно обратные (почему?).
Например, отображение Ф(х, t) может состоять в поступательном переносе
пространства на t вдоль некоторой фиксированной оси; при л=3—в повороте
на t вокруг фиксированной оси; могут быть, конечно, и нелинейные отображе-
отображения. Параметр / удобно истолковывать как время, а семейство отображений
B3) —как поток в Е„\ тогда групповое свойство просто означает, что этот
поток стационарный. Векторное поле.
- Ф„(х) = Ф;(х; 0) B4)
— это соответствующее поле скоростей, так что при малом Si
Дх=Ф(х; t + \t)—Ф(х; /) =
= Ф (х; ДО—х= Фо (х) М+о (М); B5)
поэтому вспомогательное отображение х=Ф0 (х), уже ие зависящее от пара-
параметра, называется не совсем удачно бесконечно малым производящим отобра-
отображением для группы B3). Обратно, из B5) следует, что семейство отображе-
отображений B3) получается нз своего производящего отображения при помощи решения
системы дифференциальных уравнений в векторной записи
-JL=®0 (x); x|t=0 = x.
Вернемся д функционалу A) и допустим, что в (л+1)-мерном простран-
пространстве х, у задана однопара метрическая группа отображений
*=Ф(*, у; t), у=Ф(*, у; t), B6)
оставляющая этот функционал инвариантным. (Запись B6) по существу
равноценна B3), но приходится писать более громоздко, так как в функцио-
функционале A) роль координаты х отличается от уъ ..., у„). Это означает, что если
трактовать A) как функционал от линии у=у (>г) (о<аг<6), то он должен
принимать одинаковые значения на всех' линиях, полученных друг из друга
с помощью отображения B6).
Обозначим в соответствии с B4)
) = Ф<(*. У. 0), Ф„(>г, у) = ф',(*, у, 0)
и сравним значении функционала на некоторой дуге экстремали и на линии,
полученной из этой дуги отображением B6) с бесконечно малым t. Тогда
левая часть формулы (8) равна нулю в силу инвариантности функционала,
а в правой части интеграл^ пропадает, и в силу B5) мы получаем
т. е.
(р.ф„—Я<р„)
у=у(б)
Последнее равенство справедливо для любых двух точек выбранной экстремали.
Таким образом,. вдоль каждой экстремали будет
Р-Фо(*. У)-Я(а:, у, р)Ф,(х. y)=const, B7)

330 v ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
т, е. мы получили первый интеграл системы уравнений Эйлера. В этом и
состоит теорема немецкого математика Э. Нётер A883—1935) для функциона-'
лов Вида A).
Пусть, например, функция F в этом функционале не зависит от х. Это
значит, что функционал инвариантен относительно группы преобразований
х=х-\-а, у—у; но тогда Фо=0, 90 = 1> и потому мы получаем нз B7) пер-
первый интеграл //=const, уже отмеченный в п. 2.
Группа преобразований, оставляющих функционал инвариантным, может
содержать более одного параметра. Например, при л=3 можно рассматри-
рассматривать двухпараметрическую группу всех винтовых движений вдоль некоторой
оси или трехпараметрическую (почему?) группу" всех вращений вокруг неко-
некоторой точки и т. д. (Отметим, что последняя группа некоммутативна, т. е.
результат последовательного выполнения двух отображений здесь, вообще
гоноря, зависит от порядка, в котором они выполняются.) Если имеется k
параметров, то формула для отображений, взамен B3), имеет внд
х=Ф(х; tlt tt, .... h). B8)
При этом семейство B8) должно содержать тождественное отображение, вместе
с каждым отображением—обратное к нему и вместе с любыми двумя отобра-
отображениями— результат их последовательного выполнения. Тогда с помощью
вычисления частных производных по каждому из параметров возможно соста-
составить k независимых первых интегралов типа B7) для системы уравнений
Эйлера и тем самым понизить на k число уравнений в этой системе.
Теория непрерывных групп преобразований, называемых также группами
Ли (С. Ли A842—1899)—норвежский математик), к настоящему времени зна-
значительно разработана и имеет многочисленные применения.
Бывают случаи, когда функционал остается инвариантным для группы
преобразований, зависящей от некоторого числа k произвольных функций.
(Например, прн рассмотрении параметрической формы A.54) функционала он
оказывается инвариантным относительно любой замены вида t~ t (t) переменной
интегрирования, так как такая замена означает введение новой параметризации
вдоль линии (L), а значение функционала не зависит от выбора параметриза-
параметризаций; таким образом, в данном случае k=l.) Тогда вторая теорема Нётер
говорит о том, что в системе уравнений Эйлера имеется k независимых соот-
соотношений, т. е. k уравнений из системы можно отбросить.'
в. Случай функций нескольких перемеиных. Докажем теперь теорему Нётер
для функционалов от функций нескольких переменных, например внда A.55), одна-
однако вместо х, у будем писать xlt xit так как получаемые формулы справедливы
для любого числа m независимых перемеиных. Прежде всего по аналогии с
вычислением A.58) получаем взамен A.91) сбщую формулу для вариации функ-
функционала прн изменении как функции, так и границы области интегрирования:
F
(G)
= J (F'z-divF'pNzdG+ J (F'p)n6z dr+ J F Fr)n <JT; B9)
(G) (Г) (Г)
здесь, как обычно, Fp—вектор с проекциями Fp., а г=2*/е/ — радиус-век-
радиус-вектор. Кроме того, аналогично A.88) получаем
йг | (Г) = й [г (х)]—grad z-fir.
(Кстати, если принять, что точки (Г) варьируются по нормали к (Г), то
с помощью формулы B9) легко вывести условия Вейерштрасса для кусочно-

§ 3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 331
гладких экстремальных поверхностен, что мы предоставляем читателю (см.
A.107)): при переходе через линию излома выражения (Fp)n и F—(F')„ г'п
должны изменяться непрерывно.
Если вариация границы области получилась в результате вариации всех
точек областв, то бг задано во всей области (G), и потому к контурным инте-
интегралам в B9) можно применить формулу Остроградского С А„ dT= f div AdG
(Г) (G)
и формулу для бг | ^Г), что даст
J()
(G) (G)
+ div(f'p.F[2(x)] — gradz-6r) + For]dG. C0)
Пусть теперь задана однопараметрическая группа отображений
х=Ф(х, г; t), 7=Ф(х, г; t), C1)
оставляющая рассматриваемый функцвонал инвариантным в том же смысле,'
что было описано выше. Отправляясь от формулы C0) и рассуждая как при
выводе равенства B7), получаем, что для любой экстремали г=г(х) и любой
области (G) будет
J divJFp(O0-gradz-cp0)+/?4>0]dG=0.
(О)
Отсюда в силу произвола области (G) заключаем, что
div [Fp (<D0-grad z.q>0) + Fq>0]=0. C2)
Это соотношение, справедливое вдоль любой экстремали г (х), и заменяет пер-
первый интеграл B7) для функционала вида A.55);отметим, что в соотношении C2)
р означает, в отличие от B7), вектор с проекциями г'х.
Та же формула C2) получается для семейства отображений более общего
чем C1) вида
х=ф(х, г, z'x; f), 7=Ф(х, г, г'х; 0.
оставляющих функционал вида A.55) инваряантным. Эти формулы при зафяк-
сированном / и любой выбранной функции г (х) дают функцию г (х) в пара-
параметрическом виде (почему?) и тем самым, как и C1), преобразуют поверхности
в поверхности. (При этом требуется, чтобы
<р (х, г, гх; 0) = х, Ф (х, г, г'х; 0) = г.)
Формула C2) утверждает отсутствие источников векторных линий в про-
пространстве х у векторного поля
/=-р(Ф0—grad2-<po) + f<po
(рассмотрения ЛВМ, пп. XVI.23, 24 по поводу дивергенции и источников век-
векторных линий проводятся одинаково для любого числа измерений) для каж-
каждого решения г (х) уравнения Эйлера; тем самым она выражает некоторый
закон сохранения, физический смысл которого различен для разных конкрет-
конкретных функционалов.
Формула, аналогичная C2), справедлива и для функционалов вида
I f (х, 2, -?-\dG от любого числа п функций от пг переменных. При.этом

332 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЯ
под Fp надо понимать матрицу (fa*(/d*i) размера т X п, а под grad г — мат-
матрицу ( ф- J размера п X т.
7. Уравнение Гамильтона — Якоби. Рассмотрим функционал A).
Так как общее решение соответствующей системы уравнений Эйлера
содержит In произвольных постоянных, то при задании двух точеИ А
и В в пространстве х, у1У у2, ..., у„, через которые должна пройти
экстремаль, для определения этих постоянных получается как раз
2л конечных уравнений; таким образом, вообще говоря,-имеется
некоторая дискретная совокупность (одна или больше, а иногда и
ни одной) экстремалей, соединяющих эти две точки. Обозначим
через 1АВ значение функционала для каждой из таких экстремалей,
считая А ее началом и В—концом.
Будем считать точку А зафиксированной, а точку В(х; у{, уг;. ..
...; у„) текущей и обозначим
S(x,yltyt, ...,уп) = 1Ав- ¦ C3)
Это, вообще говоря, многозначная функция, определенная для тех
точек, которые можно соединить с А экстремалью. Рассмотрим
какую-либо однозначную ветвь этой функции. Если точка В меняет
свое положение, то из (8) получаем
(продумайте обозначения!). Другими словами,
Отсюда получаем, что функция C3) удовлетворяет уравнеиию с част-
частными производными первого порядка
dS , и ( dS dS dS \ п /й..
~- + Н[х,У1,у yn>Wi, ж, .....ajJ-O, C4)
называемому уравнением Гамильтона — Якоби.
Легко проверить, что для любого однопараметрического семей-
семейства решений S=S(x, y^, у2, ..., уп; а) уравнения C4) каждая
экстремаль должна удовлетворять соотношению
$а (х, yt, у*, ..., уп; а) = р. C6)
В сакгом деле, применяя уравнения G), получим
dx ^ dx +*f dy; dx = dx da
Однмсо правая часть представляет собой результат дифференциро-
дифференцирования по а левой части C4), куда подставлено 5 = 5, и потону

§ 3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 333
равна нулю; отсюда и вытекает C5). Соотношение C5) позволяет
исключить в системе уравнений Эйлера B) одну из неизвестных
функций и тем самым понизить порядок системы на два, т. е. до.
2л— 2 (в расчете на эквивалентное уравнение высшего порядка).
Аналогичным образом знание Л-параметрнческого семейства ре-
решений уравнения C4) позволяет с помощью соотношений
S'ai(*> Уг, --.,Ун1-«г> •••. а*) = Р/ (' = 1. 2. •••» *) <36)
понизить порядок системы B) на 2k. При k = n соотношения C6)
дают общее решение системы уравнений Эйлера B).
Если функция Гамильтона Н не зависит от х, то при решении уравнения
C4) можно ограничиться функциями вида
S=—hx+W{ylt у2 у„) (ft=const);
тогда это уравнение можно переписать так:
¦ dW dW • dW\_
*• y"'dy~i' ду~» Wn) ¦
Допустим, что возможно иайти функцию W (у, Р) (j/—(ft, .... у„), i*=>
= (Pi, ..., Р„)), содержащую п параметров Р и обращающую левую часть
в постоянную h=h(P). Примем W за производящую функцию каиовического
преобразования (п. 3), т. е. положим
ят яш ~
* Y "
Таким образом, каноническая система уравнений в новых переменных приоб»
ретает вид
Ах ' dx дР[
и потому имеет общее решение
Pl=C(, Yi=h'Pf(Cu С Cn)x+D; (t = l, 2 n),
где С,-, D,-—произвольные постоянные.
Величине Jab, ° которой говорилось в первом абзаце этого пункта, можно
дать замечательное геометрическое истолкование. При этом удобно рассматри-
рассматривать координаты как равноправные и потому перейти к параметрической форме
типа A.54) для функционала. Для л координат хг, xt, ..., х„ эта форма
такова:
'кон - .
Fi(*i, *2 *п> *ь **. .•••. xn)dt, C7)
ч
где функция Fi однородная измерения 1 относительно xt, хг, .... х„; примем,
что всегда tBa4 < ^и-
Допустим, -что Ft > 0 (конечно, кроме значений *t =.*2 =... =*п=0, для
которых.в силу однородности Fj=0) и что для любых точек А, В функционал
C7) достигает на семействе линий, соединяющих Ас В, наименьшее значение,
которое мы обозначим через. р (А, В). Легко проверить (продумайте это!), ..что
велнчяна р обладает следующими свойствами:
В) > 0 (А ф В), р(А, А)—0-,. 1
КОЛОХ2А

334 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
2. р(Д В)=р(В, А);
3: (неравенство треугольника) р(Л, С)<р(Л, В) + р(В, С).
Эти трн свойства называются аксиомами метрики, и всякий раз, как они
выполняются, величину р(Л, В) можно принять за обобщенное расстояние
между точками А и В. Пространство с таким обобщенным расстоянием (мет-
(метрикой) между точками называется метрическим пространством. Теперь значе-
значение функционала C7) естественно трактовать как (обобщенную) длину линии
(L), отвечающую выбранной метрике, экстремали—как геодезические линии
(п. 2.6) в этой метрике, а /^в—как длину этих геодезических, соединяющих
А с В. Элемент длины, как видно нз C7), равен
<*/ = М*1. *2 х„, dxlt dx , dxn), C8)
откуда во многих примерах можно перейти к обычной форме метрического тен-
тензора в римановом пространстве (п. V.2.5).
Пространство, в котором все это происходило, могло быть не евклидовым,
а любым многообразием с обобщенными координатами хъ хг, ..., х„. Функ-
Функционал C7), заданный в этом пространстве и удовлетворяющий указанным тре-
требованиям, превращает это многообразие в метрическое пространство, а если
квадрат правой части C8) представляет собой квадратичную форму относи-
относительно дифференциалов, — то н в риманово пространство.
Если указанные требования не выполнены, то представляют интерес,
в частности, случаи, когда некоторые пары точек вообще нельзя соединить
линиями, на которых функционал принимал бы вещественное значение: напри-
например, так будет для фукцнонала jj Vdx\—dx\, если | х^в —xlA \ < \ xiR—xiA I
(почему?). Понятие обобщенного расстояния между такими точками теряет смысл.
8. Плоскость Лобачевского. Приведем одни замечательный пример. Пусть
в полуплоскости —со <>г<оо, 0 < у < оо рассматривается функционал
(?)
В силу п. 1.17 экстремали этого функционала можно трактовать как лучи
света, распространяющегося в указанной полуплоскости и имеющего в каждой
точке (>г; у) скорость, пропорциональную у. В метрике, отвечающей этому
функционалу, квадрат элемента длины
1
й!г=—{йх2-\-йу2). C9)
Интегрирование соответствующих уравнений Эйлера, которое мы предоставляем
читателю, показывает, что экстремалями, т. е. геодезическими линиями в но-
новой метрике, служат всевозможные верхние полуокружности с центрами на
осн х, а также их предельные положения—полупрямые лг=const, у > 0. Если
условиться называть эти экстремали «прямыми», указанную полуплоскость —
«плоскостью», а точки понимать в обычном смысле, то можно проверить, что
будут выполняться все аксиомы евклидовой геометрии на плоскости, за исклю-
исключением аксиомы о параллельных. (Убедитесь, например, в том, что через каж-
каждые две точки проходит ровно одна «прямая».) В то же время через точку А,
лежащую вне «прямой» (/) (рис. 104), можно провести целый пучок прямых,
которые при своем безграничном продолжении не пересекают (/). (Обратите
внимание, что в силу формулы C9) подходу по «прямой» к оси х отвечает
удаление по новой метрике в бесконечность.) Этот пучок ограничен двумя
«¦прямыми», одна из которых асимптотически приближается (конечно, имеется
в виду по новой метрике) к (/) в одну сторону, а другая—в другую.
Такая геометрия, в которой выполнены все евклидовы аксиомы, за исклю-
исключением аксиомы о параллельных, называется геометрией Лобачевского; ее от-

§ 3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 335
крыли в начале XIX века независимо друг от друга выдающийся венгерский
математик Я. Ббйаи A802—1860), К. Гаусс и Н. И. Лобачевский, причем
последний разработал ее наиболее далеко и первым опубликовал сообщение
о этом открытии.
0
at
Рис. 104.
Многие результаты планиметрии Лобачевского можно получить, исходя из
ее указанной здесь реализации. Так, из изотропности правой части C9) выте-
вытекает, что угол между двумя линиями в точке их пересечения по Лобачевско-
Лобачевскому—это обычный угол между этими линиями в плоскости х, у. Отсюда выте-
вытекает, что «движениями» плоскости Лобачевского следует считать конформные
отображения верхней полуплоскости в себя (п. II.1.8), которые п» необходи-
необходимости являются дробно-линейиыми
и потому не только сохраняют
углы, но в силу кругового свой-
свойства сохраняют «прямолинейность».
Из C9) вытекает формула для
«площади» фигуры (S):
У
откуда, выполнив интегрирование
по у, получаем также, что
S=(f —dx, D0)
Рис. 105.
где контур (L) фигуры (S) проходится в положительном направлении.
Отсюда получается весьма интересная формула для площади треуголь-
треугольника ABC с углами а, Р, у (рис. 105). Так как вдоль дуги АВ можно перейти к
параметрическому представлению х=а-\- R cos ф, j/ = #sin(p, то вклад этой
дуги в интеграл D0) равен
I
1
R sin ф
d(a+R cos <р) =
?, е. углу, под которым дуга АВ видна из своего центра. Аналогично находим
вклады двух других сторон, т. е.
D1)
Н» так как при обходе замкнутого контура ABC касательная совершает пово-
поворот на угол — Флв+(я—Р)—Фвс+(п—7) + флс + (п—<*)• который должен

336 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
равняться 2я, то из D1) получаем окончательно
Мы видим, что в геометрии Лобачевского сумма углов треугольника всегда
меньше я, а площадь треугольника зависит только от суммы его углов: чем
меньше площадь, тем эта сумма ближе к я. Кроме того, получается, что в
геометрии Лобачевского нет понятия подобия: из равенства соответственных
углов двух треугольников вытекает равенство самих треугольников (дока-
(докажите это!).
Аналогичную конструкцию (продумайте ее!) можно осуществить в полу-
полупространстве г > О пространства х, у, г для интерпретации стереометрии Лоба-
Лобачевского. ¦ '
9. Вариационные принципы. Каждый вариационный принцип утверж-
утверждает, что для некоторого класса задач, если заданы условия задачи,
то из всех мыслимых состояний, процессов и т. п., в определенном
смысле совместимых с этими условиями, на самом деле реализуются
такое состояние, такой процесс, которые придают некоторому харак-
характерному для этого принципа функционалу стационарное значение.
Иногда говорят не о стационарном, а об экстремальном значении,
что имеет близкий, но не всегда равноценный смысл. Таким обра-
образом, вариационный принцип характеризуется указанием класса
задач, понятием совместимости сравниваемых процессов (будем для
определенности говорить о процессах) с условиями задачи и опреде-
определенного на этих процессах функционала, который должен принимать
стационарное или экстремальное значение.
Мы уже упоминали во введении к этой главе о значении вариа-
вариационных принципов и основанных на них вариационных методах ре-
решения задач. Этн принципы естественно излагаются в специальных
дисциплинах, вне курса математики, так как каждый из таких прин-
принципов обычно действует внутри одной дисциплины. Тем не менее
мы упомянем о нескольких из них либо из-за их универсального зна-
значения, выходящего за рамки одной дисциплины, либо из-за необхо-
необходимости на них ссылаться в курсе математики, либо же просто для
примера. Некоторые принципы (впрочем, мы таких здесь не будем
рассматривать) представляют помимо специального также общемате-
матнческнй интерес.
Имеются две основные группы вариационных принципов. К одной
из них, восходящей еще к Ферма и имеющей дело с задачами «чис-
«чистой» и прикладной физики и ряда других дисциплин, в наибольшей
степени применимо определение, данное в начале этого пункта.
Здесь идет речь об изучении объективно существующих процессов.
Такой принцип, независимо от его исторического происхождения,
обычно может быть выведен из локальной теории процесса (напри-
(например, из его дифференциального уравнения, которое оказывается
уравнением Эйлера для функционала, характеризующего принцип).
В этом случае в принципе обычно говорится о стационарном зна-
значении функционала, так как для локальных свойств экстремальность

§ 3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 337
этого значения несущественна. (Тем не менее бывают классы за-
задач, в которых и экстремальность несет дополнительную информа-
информацию, например говорит об устойчивости процесса.) Отметим, что
даже если вариационный принцип оказывается эквивалентным диф-
дифференциальному уравнению, этот принцип все равно часто приносит
большую пользу из-за его более универсального по сравнению с
уравнениями вида, облегчающего возможность аналогий и обобще-
обобщений, а также из-за удобства применения численных методов. '
Другая основная группа вариационных принципов развилась лишь
в последние десятилетия и имеет дело с задачами теории регули-
регулирования, математической экономики и ряда других дисциплин. Здесь
идет речь о выработке в заданных условиях определенной страте-
стратегии, линии поведения, которая обеспечивала бы в этих условиях
максимальную пользу. Значение этой - пользы, функции цели
(п. IV.5.1) и служит функционалом, определенным на совокупности
стратегий, причем в данных задачах, конечно, требуется максими-
максимизировать этот функционал. Задачи этой второй группы обычно на-
называют задачами оптимального управления, оптимального регулиро-
регулирования и т. п. Здесь мы не будем их касаться. Отметим только,
что для многих из этих задач характерно наличие высвобождающих
связей (п. 1.19), так что решение задачи на экстремум может и не
придавать функционалу стационарного значения. Поэтому для построе-
построения таких ' решений приходится вырабатывать свои специфические
методы, отличные от методов классического вариационного исчис-
исчисления, основанных главным образом на использовании стационарности.
.Одним из самых простых и наглядных вариационных принципов
первой группы является лринцип Ферма в геометрической оптике, уже
упомянутый в ЛВМ, п. IV.19. В первоначальной формулировке этот
принцип говорил, что из всех возможных путей, идущих из одной
заданной точки в другую, луч света выбирает такой, который он
проходит за минимальное время. Здесь сравниваются между собой
всевозможные пути, совместимые с геометрией оптического устрой-
устройства, а минимизируемым функционалом служит время прохождения
светом этих путей. Из принципа Ферма вытекают законы распрост-
распространения света в однородной и неоднородной средах, законы отра-
отражения и преломления. Однако приведенная формулировка принципа
представляется несколько загадочной: как может свет, «сравнить»
все пути и «выбрать» из них оптимальный? Разгадка основам на
том, что можно указать случаи, когда время прохождения светом
реального пути имеет не минимальное, а минимаксное значение
([41], § XII.10). Таким образом, в принципе Ферма существенно не
минимальное, а стационарное время прохождения светом пути; а
в такой локальной форме этот принцип можно вывести из вол-
волновой теории света (на путях, не обеспечивающих указанной ста-
стационарности, происходит интерференция). Минимальность же вре-
времени прохождения в простейших случаях вытекает из структуры:

338 гл- VI. . ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
функционала, который должен принять стационарное значение. (Дока-
(Докажите, например, перейдя к интегрированию по х, что на каждой
достаточно малой дуге экстремали функционал A.95) принимает
сильное и даже тотальное минимальное значение для всех линий,
соединяющих две заданные точки.)
10. Принцип Гамильтона в простейшем случае. Вариационный
принцип Гамильтона, являющийся одним из наиболее универсальных
принципов современного естествознания, мы рассмотрим сначала на
простом примере. Пусть материальная точка массы т может дви-
двигаться по оси х, причем в процессе движения на эту точку дейст-
действует направленная по оси х сила f(x, t), зависимость которой от
координаты х и времени t предполагается заранее заданной. Тогда
закон x(t) движения точки должен удовлетворять хорошо извест-
известному-дифференциальному уравнению Ньютона
«* = /(*, /). D2)
Обозначим первообразную по х для функции —/(х, t) через U(x,t),
например можно положить
это потенциал рассматриваемого силового поля (п. 1.2.1); кроме
того» обозначим
это кинетическая энергия движущейся точки. В таких обозначениях
уравнение D2) можно переписать в виде
-?/;-^Г;=0. D3)
Если же заметить, что U не зависит от х, а Г —от х, и обозначить
L(t, х, *) = ?—U
(это функция Лагранжа для рассматриваемой механической системы),
то уравнение D3) можно записать так:
^*—J^i=0- D4)
Но это как раз уравнение Эйлера для функционала
U
J L (t, х, х) dt, D5)
имеющего несколько странное название действие. Так как в силу
предыдущего условие его стационарности при зафиксированных

§ 3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 339
значениях
полностью равносильно уравнению D2), то мы видим, что диффе-
дифференциальный закон движения Ньютона можно сформулировать так:
если заданы начальное и конечное состояния системы (т. е* моменты
времени и положения точки в эти моменты), то из всех возможных
законов движения на самом деле реализуется талой, для которого
действие принимает стационарное значение. В этом состоит вариа-
вариационный принцип Гамильтона.
Из структуры подынтегральной функции D5) легко вывести (см.
начало п. 2.6.), что для любого реального закона движения точки
на любом достаточно малом интервале времени действие принимает
не просто стационарное, а минимальное значение; поэтому принцип
Гамильтона иногда называют также принципом минимального дейст-
действия. Однако такое название не совсем удачное, так как уже на
самых простых примерах легко проверить, что для больших проме-
промежутков времени действие будет иметь не минимальное, а минимакс-
минимаксное значение. Поэтому лучше говорить о принципе не минимального,
а стационарного действия.
Рассмотрим, например, линейный осциллятор. Здесь /==— kx, где k—по-'
kx2
стоянный коэффициент упругости, откуда 1/=-—,
и D5) превращается в квадратичный функционал с постоянными коэффициен-
коэффициентами. Этот случай был в других обозиачеинях рассмотрен в п. 2.4, где было
показано, что при tt—t0 < пУm/k значение функционала получается мини-
минимальным, а при t1—10 > пУт/k—минимаксным. Отметим, что пУт/к=
= л/а>0—это полупериод свободных колебаний осциллятора, т. е. промежуток
времени между соседними моментами прохождения осциллятором положения
равновесия *=0.
Как видим, -вывод вариационного принципа свелся в данном случае к ис-
искусственной подгоике уравнения движення D2) к внду уравнения Эйлера D4).
Тем не менее этот переход оказывается полезным не только ввиду дальнейших
обобщений; в § 4 мы увнднм, что целый ряд задач и для одномерного случая
значительно удобнее решать после такого перехода.
В связи с подобными переходами возникает следующий общий вопрос:
можно ли заданное дифференциальное уравнение представить в виде уравнения
Эйлера для некоторого функционала? Ограничимся функционалами A.18); тогда
из A.37) ясно, что речь идет о дифференциальных уравнениях вида
V(*. У, уГ)уГ+У{х, у, iO = 0. D6)
Из равенств
. V(x, у, *) = F'g(x, у, 2)-Га(х, у; г)-Гуг(х, у, г)г ] <4''
легко вывести необходимое условие для возможностн подбора F:
. . D8)

940 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Можно проверить, что оно является и достаточным, причем F подбирается так:
сначала из первого равенства D7) находим F с точностью до слагаемого, линей-
линейного относительно г, а это слагаемое находим, подставляя полученное выраже-
выражение для F во второе равенство D7). Условие D8) теоретически всегда можно
обеспечить, умножив обе части исходного уравнения _{46) на соответственно
подобранный множитель R (*, у, у'), хотя на практике это может оказаться
затруднительным. Если условие D8) уже выполнено, то функция F опреде-
определяется с точностью до слагаемого, которое получится,' если в равенствах D7)
положить UssVssO (почему?). Но тогда яз первого равенства D7) получаем,
что
F=a(x, у)г+Ь(х, у).
Подставляя это выражение во второе равенство D7), видим, что
а'
X
>Ь'у, т. е. а=<р' (*, у), *=q>;(*, у).
Таким образом, неопределенное слагаемое в F имеет вид
х,у)=^Ч>(х, у).
Это можно было предвидеть, так как добавление такого члена к F, например
при граничных условиях A.26), приводит просто к добавлению к I {у) постоян-
постоянного слагаемого.
Результаты последнего абзаца иепосредственио переносятся на функционалы
вида D5) от векторных функций у(х), а также на функционалы от функций
нескольких переменных. Например, уравнение Эйлера—Остроградского A.59)
остается неизменным при добавлении к функции F любого выражения дивергент-
дивергентного типа
faA(x, у, г)+щВ(х, у, г)
(проверьте!).
П. Принцип Гамильтона для систем с конечным числом сте-
вевей свободы. Рассмотрим теперь систему дифференциальных
уравнений, обобщающих уравнение D2):
01*1 = /| (*1> **» • • • . xNy *) (l = \,-2, ... , N).
Этими . уравнениями описывается, например, система из г точек
в пространстве, на которые не наложено никаких связей и действуют
силы, зависящие от координат всех точек и от времени. (При этом
•*и х3, х3 — декартовы координаты первой точки массы mt = tni = mi\
х4, хь, ха — координаты второй точки массы /»4 = /и5 = дав и т. д.;
N=3r—число степеней свободы такой системы.) Пусть силовое
поле имеет потенциал U(xA, x2l ... , xN, t), т. е.
// = -¦?¦¦ С = Ь 2 N). D9)
Такой потенциал (потенциальная энергия системы), в отличне от п. 10,
имеется не всегда, а только для потенциальных полей, признаком
которых служат равенства
9h df,
-Г-^~- (i, y=l, 2, .... АО
dxj dxi v ' J ' • '¦' :

§ 8. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 341
(ср. п. 1.2.1). Рассуждая, как в п. 1.2.1, легко показать, что U равно
работе, которую совершает силовое поле в фиксированный момент
времени при переводе системы из любого текущего состояния
(xv х2, ... , xN) в некоторое заданное (х10, х20, ... , Xjvo)J ПРИ этом
такая работа не должна зависеть от способа перевода, что и
является критерием потенциальности. Произвол в выборе конечного
состояния равносилен добавлению к U произвольной функции вре-
времени, что несущественно для дальнейшего.
Обозначив далее
~2
и проведя рассуждения по образцу п. 10, мы приходим к тому же
выводу о стационарном значении действия, т. е. интеграла
U
j L (t, xv х3, ... , Xjy, xlt x3, ... , Xjy) at
и
для реального закона движения.
В курсах механики несложно доказывается, что принцип Гамиль-
Гамильтона остается справедливым и в случае, когда на рассматриваемую
систему точек наложены голономные связи
хг, ... , xN, 0 = 0 (г = 1, 2, ... , v; v < N). F0)
Тогда в формулировке принципа Гамильтона сравнению подлежат
только законы движения, совместимые с этими связями, т. е. удо-
удовлетворяющие уравнениям E0); другими словами, речь идет об условно
стационарном значении (п. 1.13). Чтобы избавиться от этоЯ услов-
условности, которая не всегда удобна, обычно выбирают обобщенные
координаты qv q3, ... , qn (где n — N—v есть число степеней сво-
свободы в системе), характеризующие положение системы. Через них
выражаются координаты точек системы
xi = xi(ql,qt,...,qn,t) A = 1, 2, ... , N) E1)
(это, по существу, общее решение системы уравнений E0) в пара*
метрической форме), а потому и потенциал U(qvqt,..., qn, t),
кинетическая энергия T(t, qv qt, ... , qn, qv q3, ... , qn) и функ-
функция Лаграижа L=T—U. Так как уравнения связей учтены теперь
самим выбором координат qt, то мы переходим к аадаче на безу-
безусловно стационарное значение функционала
J Z. {t, qv qt, ..., qn, qlt qt, ... , qH) dt F2)
при заданных начальном н конечном состояниях системы.

342 : ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Заметим, что Т, а потому и L представляют собой многочлены второй
степени относительно qlt q2, ... , qa с коэффициентами, зависящими от qlt
?з. ¦••. <7л. U причем квадратичная форма, составленная из членов второй
степени, положительно определенная (почему?); в остальном функция L со-
совершенно произвольная. Поэтому методы и результаты исследования механи-
механических систем с конечным числом степеней свободы можно применить к любому
функционалу A), у которого подынтегральная функция имеет описанную
структуру. Из этого, в частности, в силу начала п. 2.6 вытекает, что реальный
закон движения, т. е. экстремаль функционала E2) на каждом достаточно
малом временном интервале придает этому функционалу сильно минимальное
значение.
Если система автономная, т. е. в потенциал и в уравнения
связей E0) не входит /, то t не входит и в правые части E1),
а потому Т представляет собой квадратичную форму относительно
Чи Qv • • • i Яп- Тогда функция Гамильтона (см. E)) имеет особенно
простой смысл:
= T+U
(мы воспользовались теоремой Эйлера об однородных функциях,
см. ЛбМ, п. IX.12), т. е. Н есть полная энергия системы. Так как
В автономном случае функция L под знаком интеграла E2) не за-
зависит от /, то в силу п. 2 мы получаем первый интеграл: //=const
для любого реального закона движения системы. Таким образом,
в автояомном случае полная энергия в процессе движения остается
постоянной. Это свойство системы называется ее консервативностью.
Канонические переменные /з,-=Т^. называются обобщенными им-
импульсами; для декартовой системы координат это обычные
импульсы
. В некоторых случаях для получения первых интегралов удается применить
теорему Нётер п.  (см. примеры в [29]). Докажите, например, с помощью
этой теоремы, а также непосредственно с помощью уравнений Эйлера, что если
функция L не зависит от одной из координат qi, то имеет место первый
интеграл р,= const (закон сохранения импульса).
Для автономных систем принцип стационарного действия имеет интересное
геометрическое истолкование. Мы видели, что в этом случае имеет место
первый интеграл
T(q, q)+U(q) = h (= const) C3)
(для краткости вместо qt, q%, ... , qn пишем просто q). Поэтому ограничимся
сравнением законов движения, удовлетворяющих дифференциальной связи E3),
с заданным значением А. Но так как
то принцип стационарного действия можно переписать в форме
б [ Т (.<?, q)dt=O. E4)
Однако
Т = У о,у (Я) qi'q/, откуда dt = -^ V^fli/ (q) dq,dq/.

§ 3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 343
Подставляя в E4) и учитывая, что T=h—U, получаем
6 j V[h-U(t))]^lau(q)dgidqJ = 0. E5)
Таким образом, время t полностью исключено и связь E3) можно не учиты-
учитывать: при заданной траектории движения системы в пространстве q из этой
связи можно определить dt и тем самым получить закон движения системы
по этой траектории.
Введем теперь в пространстве q—состояний системы—метрику по формуле
А»-[А-1/(?)| 2 au(q)dqidqj. E6)
Тогда основное уравнение E5) можно переписать в виде 6 V ds = 0, т. е, мы
получаем (п. 2.6), что траекториями реальных движений q (t) системы будут
служить геодезические линии в этой метрике. Различным потенциальным
силовым полям и различным значениям полной энергии h отвечают различные
способы введения метрики E6) в пространство состояний системы.
12. Принцип Гамильтона для сплошных сред. Струна. Рас-
Рассмотренный в п. 10 принцип Гамильтона обладает той замечательной
особенностью, что он формулируется не в терминах координат,
а в терминах кинетической и потенциальной энергий системы. Это
дает возможность с помощью предельного перехода распространить
принцип на сплошные среды, а также на физические поля, для
которых имеется естественная замена этих видов энергии, например
на электромагнитные и т. п. Принцип Гамильтона сохраняет свое
действие и при переходе к релятивистской механике.
Рассмотрим несколько примеров. Выведем сначала уравнение плоских
паперечных малых колебаний струны, натянутой с силой Р между точками
х = 0 и х = 1 оси х, если на струну действует поперечная сила с плотностью
/ (х, t). При этом струной считаетси одномерная среда, работающая только
на растяжение, но не на изгиб, т. е. не сопротивляющаяся изгибу.
Будем считать, что сила натяжения Р в процессе колебания не меняется
(это оправдано, если колебания малы по амплитуде) н что каждая точка х
струды в процессе колебаний смещается перпендикулярно оси х; обозначим
ординату этой точки в момент t через и (х, t). Функция и (х, t) и определяет
закон колебания, ее график в фиксированный момент времени представляет
форму струны в этот момент.
Если перевести струну в некоторый момент t из состояния и(х, t) в не-
нагруженное состояние равновесия и == 0, то будет произведена работа
t)udx
продумайте это выражение!), которую и надо принять за потенциальную
энергию U рассматриваемой системы. Разлагая радикал в ряд и отбрасывая
в предположении малости | и | члены с и'х*, получим
</-=$ [т«*2-/(*. i)u]
dx;

844 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
при этом члены в квадратных скобках считаем одного порядка малости.
Кинетическая анергия струны равна
I
о
где р—линейная плотность струны. Поэтому функция- Лагранжа такова
I
L=T— U= Г -§- и? я- и'х + f (х, t) и 1 dx. E7)
о
(Более точно называть это выражение не функцней, а оператором, преобразую-
преобразующим'функцию и (х, t) в некоторую функцию от t.) Действие выразится двой-
двойным интегралом
х, t)u\dx. E8)
6 " ,
Так как действие должно иметь стационарное значение, то должно
удовлетворяться соответствующее уравнение Эйлера A.59)
f (х, Q-j-ipu't) - -^ (- Ри'х ) = 0. . E9)
Будем считать р постоянным (т. е. струну однородной) и обозначим
Тогда из E9) получим окончательное уравнение колебаний струны
;*, 0. F0)
которое в случае свободных колебаний (/=0) уже встречалось в ЛВМ,
(XVII.131).
Из E7) видно, что функция Лаграижа имеет плотность
Если вепомнить о возможности приближенной замены, по образцу п. 1.12,
струны на систему материальных точек с конечным числом степеней свободы,
то ясно, что для струны можно говорить о плотности импульса
П = —7-=ры<>
out
а также о плотности функции Гамильтона
т, *._ Л+И; П =.?. и? + L.u'*-f (х, 0 и,
из которой сама функция Гамильтона получается интегрированием: .
I
И$ п. 11 следует, что в автономном случае, когда f не зависит от /, функ-
функция л постоянна вдоль каждого решения (закон сохранения полной энергии).

§ 3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 345
фго мокло вывести и непосредственно из уравнения F0), так как, дифферен-
дифференцируя интеграл F1) по параметру t и пользуясь граничными условиями
и|ЛяО = и|К!,г=*О, получаем
I
-^ mua + Puttbt^hu-futdx-
i
С Г ' / Р - f \ • • г' . -Л j
i i
[Р (uiux)'x—ft и] <** = — \ ft u-dx,
б ¦ . о
откуда и вытекает наше утверждение.
Интересно отметить, что, в отличие от п. 10, значение действия E8)
является минимаксным для как угодно малого интервала времени. В самом
деле, пусть для простоты / = 0; положим при некотором k = l, 2, 3, .».
{. kn . akn .
°
При (,с0в как угодно малом фиксированном tt > 0 всегда можно выбрать
k так, чтобы —г < tv Легко проверить непосредственно, что / { ио}=»0 я что
на линии излома < = -т условия Вейерштрасса—Эрдмана (п. 1.20) не выпол-
выполняются. Отсюда и вытекает наше утверждение о минимаксности (продумайте,
почему!). '
Мы предлагаем читателю вывести уравнение малых поперечных колебаний
мембраны . '
ии = а*{ихх+иУу) + f1(x,.y, t), ' F2)
натянутой с силой Р иа едвницу длины. Мембрана, как и струна, работает
только на растяжение; смысл букв в F2) аналогичен их смыслу в F0).
• Важным обобщением уравнений F0) и F2), а также аналогичного, уравне-
уравнения в трехмерном пространстве является уравнение Клейна—Гордона.. Оно
получается, если допустить, что на струну или мембрану наложена равномерно
раснределеинаи линейная упругая связь, стремящаяся возвратить нх в поло-
положение и = 0. Докажите, что это сводится к добавлению в правой части F0)
или F2) добавочного члена — ku (к > 0).
13. Стержень и пластинка. Рассмотрим теперь продольные колебания
прямолинейного стержня, расположенного вдоль ося х, в неиагруженном со-
состоянии равновесия от * = 0 до х = 1. Пусть и (х, t)—отклонение точки х
стержня в момент t вдоль оси х. Будем считать для общности, что на
стержень действует продольная внешняя сяла с плотностью f (x, t) и что
концы стержня упруго заделаны с коэффициентами упругости а„ и а, соот-
соответственно. Так как при относительном удлинении j- элемента dx стержня
в этом элементе по закону Гука возникает сяла упругости

346 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
где F—площадь поперечного сечения, а Е—модуль упругости, определяю-'
щийся материалом стержня, то работа, необходимая для такого удлинения
из состояния и =5 0, равна
(Откуда взялся коэффициент 1/2?) Поэтому потенциальная энергия стержня
в произвольно растянутом состоянии равна
-J [±-FEu?-f(X, П
J [
±-
Кинетическая энергия стержня равна
1 ¦ i
где р—объемная плотность материала стержня. Считая стержень однородным
и применяя принцип Гамильтона, получаем дифференциальное уравнение
продольных колебаний стержня
/~Ё~ f
—, /i = — • Естественные
граничные условия в силу п. 1.15 (см. A.84)) имеют вид
(F?«;-aou);(.=o = O, (F?«;+a/u);(.=j=0; F4)
они называются (однородными) граничными условиями 3-го рода. (Получите
их непосредственно из формулы F3) и продумайте смысл знака перед а.)
Если какой-либо из концов, например правый, свободен, то с^ = 0, и соответ-
соответствующее граничное условие принимает вид
это граничное условие 1-го рода. Наконец, абсолютно жесткой заделке отвечает
«/==»; поделив второе условие F4) на аг и устремив а^ к оо, получаем
граничное условие 1-го рода
В качестве следующего примера рассмотрим поперечные колебания такого
же стержня; при этом примем, что при таких колебаниях стержень работает
только иа изгиб. При изгибе в каждом элементе стержня возникает восстанав-
восстанавливающий момент М, который мы будем считать пропорциональным кривизне
—- (ЛВМ, п. VII.25) с постоянным коэффициентом пропорциональности ц
(зависящим от материала стержня и момента инерции поперечного сечения
стержня). Работа, необходимая для такого изгиба из прямолинейного состоя-
состояния, равна -х-М | dqp j =-^-(ifeiWs. Примем для общности, что на стержень
действует поперечная внешняя сила, распределенная с плотностью /. Если
вспомнить, что

§ 8. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 347
и произвести линеаризацию, мы получим выражение для действия
ри;8_±ци2 +f(x, 0 «]
t, о
Соответствующее уравнение Эйлера имеет вид
* iv
—l"W
Вид граничных условий определяется режимом, поддерживаемым на кон-
концах стержня. Если какой-либо из концов абсолютно жестко неподвижно
заделан, то на этом конце граничное условие имеет вид
и=0, ы* = 0. F5)
(В случае абсолютно жесткой заделки возможно также принудительное движе-
движение, когда правые частк в граничном условии представляют собой заданные
функции времени.) Если конец свободно оперт, то соответствующее граничное
условие имеет вид •
u=0, и^=0; F6)
последнее равенство вытекает из формулы M = \ik, но может быть получено
и как естественное граничное условие, что мы предоставляем читателю. Рас-
Рассмотрим еще случай, когда на концы наложены линейные упругие связи,
сопротивляющиеся поперечному перемещению и повороту этих концов. Тогда
к выражению для потенциальной энергии надо добавить члены
и рассматривать естественные граничные условия, имеющие в данном случае
инд (проверьте!)
F7>
г—Ро««)х=о=0,
Граничные условия F5) и F6) получаются из этих как предельные случаи.
Если на концах приложены еще внешняя сила и внешний момент, произво-
производящие работу при перемещении н повороте концов, то получатся неоднородные
условия вида F7). (Разберите этот случай!)
В рассмотренной задаче о поперечных колебаниях стержня, прямолиней-
прямолинейного в ненагруженном состоянии равновесия, часто вместо термина стержень
употребляется термин балка. В двумерном случае в аналогичной задаче говорят
о пластинке; здесь требуется, чтобы она в ненагруженном состоянии равно-
равновесия была плоской.
Чтобы получить выражение для потенциальной энергии элемента пластинки
в точке Мо, выберем декартовы координаты с началом Мо так, чтобы пло-
плоскость х, у касалась элемента. Тогда уравнение пластинки вблизи Мо имеет вид
[(z^2+2(z^A{ + (z^s] + i высшего порядка малости. F8)
2
Примем по аналогии с одномерной задачей, что в случае малых деформаций
потенциальная энергия элемента пластинки является квадратичной фор-
формой относительно производных второго порядка. Так как эта энергия не
может зависеть от выбора осей координат, то, приводя квадратичную форму
в F8) к главным осям, получим

348 ГЛ. VI- ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
где *! и Аа—соответствующие собственные значения, равные по абсолютной
величине (ЛВМ, п. XII.9) кривизнам главных нормальных сечений в Afe,
a dS—площадь рассматриваемого элемента. Примем пластинку изотропной;
тогда j4=C, обозначим это общее значение через ц/2. Применяя соотношения
между собственными значениями, т. е. корнями характеристического уравнения
и коэффициентами этого уравнения, получим (проверьте!)
=Т (*'хх + г"ууУ +(В~М(г"ххг"уу~ г"ху);
Поэтому потенциальная энергия изогнутой пластинки равна
-uZ)\ dS-
(При этом мы перешли от проектирования элементов пластинки иа касательные
плоскости к проектированию их на единую плоскость н=0 ненагруженного
равновесного -состояния пластинки; однако при малых колебаниях поправочные
члены имеют высший порядок малости н при линеаризации должны быть от-
отброшены.) Составляя интеграл действия, получаем соответствующее уравнение
Эйлера
Р««=—И- WLc+bQuu + tfyn)- (m)
Оператор, действующий на и в круглых скобках полученного выражения,
называется биеармоническим: .
пользуясь значком Д для оператора Лапласа, можно уравнение F9) записать
в виде
ри«= — цД2и.
Рассмотрение соответствующего неоднородного уравнения, а также граничных
условий, мы предоставляем читателю.
14. Общая схема вариационного подхода к физическим полям. Мы уже
упоминали и п. 12, что принцип Гамильтона в соответственном видоизменении
можно применять к весьма широкому классу физических полей. В частности,
большое число примеров такого применения содержится в гл. 3 книги [92],
к которой мы и отсылаем читателя (см. также [29]). Здесь мы сделаем только
весколько общих замечаний по этому поводу и разберем один тип полей.
. В основе принципа Гамильтона всегда лежит функция Лагранжа, а для
полей — плотность функции Лагранжа. Составление этой функции далекр ие
всегда так просто, как в задачах механики, так как для других типов полей
часто бывает трудно отчетливо отделить кинетическую энергию от потенциаль-
потенциальной; например, энергия заряда, движущегося в магнитном поле, имеет черты
как кинетической энергии (зависит от скорости движения), так и потенциальной
(заиисит от поля). -Поэтому иногда приходится, как мы это делали в п. 10,
исходить в простейших задачах из уравнений движении, «подгонять» их под
вид. уравнений Эйлера, а затем, .сравнивая несколько подобных задач, поста-
постараться разумно определить функцию Лагранжа, которую можно было бы
распространить и на более сложные задачи. Помогает при этом выявление
скалярных инвариантов рассматриваемой физической задачи, так как функция
Лагранжа и ее плотность должвы выражаться через эти инварианты.
Пусть плотность L функции Лагранжа выбрана; обычно оиа выражается
через некоторые скалярные полевые переменные $/=$/'(Ei> ?г> !з> li) (l"li

§ 3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 349
2, ... , л), т. е. величины, значения которых характеризуют состояние поля
в дайной точке пространства (?х; |а; ?3) в данный момент времени <=?4. и
через их производные 4)ift=^i • (Некоторые из полевых переыеииых могут слу-
служить компонентами вектора или тензора.) Кроме того, в случае неоднородного
поля или иеаффинных координат L может зависеть также от |,, |а, ?з> а в
неавтономном—от ?4. Тогда полный лааранжев интеграл, который служит
обобщением интеграла действия, имеет/вид
& " G1)
и должен быть инвариантом относительно преобразований, допустимых в рас-
рассматриваемой теории (скажем, преобразований Лореица в релятивистской
теории и т. п.). Требоваине стационарности интеграла G1) при заданных
граничных условиях приводит в силу п. 1.11 к системе уравнений Эйлера
^ «-..о A = 1.2 «), G2)
которые в механике, как известно, называются уравнениями Лаграижа.
Отметим, что при включении в рассмотрение точечных, линейных и по-
поверхностных масс, зарядов и т. п. к интегралу G1) могут добавиться интегралы
низшей размерности. С помощью дельта-функции их всегда можно объединить
с интегралом G1) (ср. ЛВМ,- п. XIV.25), хотя на практике это может оказаться
и нецелесообразным.
Как мы упоминали в п. 10 для более специального случая, при добавле-
добавлении к L выражения дивергентного типа
4
^ Ж" Ак & ^4> ^ V»)
К интегралу G1) добавится слагаемое, определяемое граничными условиями, а
система уравнений Лаграижа—Эйлера G2) не изменится. Этим иногда Поль-
Пользуются для упрощения вида плотности функции Лагранжа.
Величина
(' » 2«) (га)
называется плотностью канонического импульса, в задачах механики это плот-
плотность обобщенного импульса. Переписав уравнение G2) в виде, подобном
закону Ньютона,
з
dt fr
мы получаем в правой части аналог плотности обобщенной силы; при этом
первый член часто бывает связан с наличием виешник сил, действующих на
поле, а второй—с воздействием поля йа величину ф,-.
Квадратная матрица W четвертого порядка с элементами

350 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ '
называется матрицей напряжения-энергии. В частности,
L G5)
есть плотность энергии поля. Если L, а также пространственная область (G),
занятая полем, и значения всех величин ib,- иа границе (G) не зависят от t,
л С С
то и интеграл \ \ \ Н d|, d|a di3 не зависит от < (проверьте!).
(С)
Выразив, если это окажется возможным, из равенств G3) величины %4
через все остальное и подставив результат в G5), получим выражение Н через
координаты, полевые переменные, их пространственные производные и канони-
канонические импульсы. Если переписать интеграл G1) в виде
и записать соответствующую систему уравнений Эйлера (ср. п. 4), то получим
каноническую форму
з
Щ*^' 1Г=ф7 (а==1'2 я) G6)
системы G2). (Докажите, что уравнения G2) и G6) равносильны, и выведите
вид правых частей G6) с помощью конечномерной аппроксимации поли по
примеру п. 1.11.)
Исходя нз выражений G4) и пользуясь уравнениями G2), легко проверить
непосредственно (проделайте это!), что
-ЩГ=—W ('=1.2.8,4); G7)
здесь в левой части стоят полные производные, составленные с учетом зависи-
зависимости Wy от всех 1|>г и if>rs, тогда как в правой части производная берется.
лишь по I;, явно входящему в L.
Будем для простоты считать координаты 1и |а> ?з декартовыми (Цх—х,
it —У» 6з = г) и обозначим
Тогдд, если L не зависит от t, то из G7) при 1 = 4 получаем
Следовательно, вектор S представляет плотность потока энергии поля; поэтому
он называется вектором интенсивности, поля. Вектор
2
(проверьте!) называетси плотностью импульса поля. Из G7) мы видим, что
если L не зависит от |lf ?Sl |3. то
'./=1

§ 3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 35.1
Остановимся еще на следствии из теоремы Нётер (п. 6) для рассматривае-
рассматриваемых полей, причем для простоты мы будем считать поле заданным во- всем
пространстве |1( |а, |3 и быстро убывающим на бесконечности. Пусть полный
лагранжев интеграл G1) инвариантен относительно одиопараметрического се-
семейства отображений, в векторной записи
¦g» a)> G8)
где a—скалярный параметр. (Эта инвариантность означает, что если для лю-
любого поля if (|) при любом а вычислить поле *|>(l) в.силу формул G8), то
\ L(|, if, ifg)di=\ L(|, tf, if^)d|). Тогда в силу п. 6 векторное поле
л ЙФ
где ф0=:
да
а=0
не имеет в четырехмерном пространстве | источников векторных линий. Но
тогда поток этого поля через любые две гиперплоскости /( = ?4) =const одинаков
(почему?), т. е. мы приходим к закону сохранения во времени интеграла
I И { (
где значок < означает временную проекцию вектора.
. Пусть, например, плотность L функции Лагранжа не^ зависит от одной из
координат I/. Тогда можно положить |у=|у+<х, прочие 1/^=1/;, if=ij), откуда
Фо-= tj, Ф„=0, и мы приходим к независимости от времени интеграла
V \ \ Wy4 dSx di2 d?3 (проверьте!). Итак, если плотность функции Лагранжа
ие зависит от пространственных координат, то имеет место закон сохранения
импульса, а если не зависит от времени,—то закон сохранения полной энергии
(последнее уже 'было показано выше).
По поводу закона сохранения момента" количества движения см. [29].
15. Уравиевия движевия упругой среды. В качестве примера рассмотрим
вывод основных уравнений движения упругой среды в однородном изотропном
случае. Пусть хг, х2, х3—декартовы координаты и и = и(хг, х2, х3, t)—поле
перемещений точек упругой среды. Мы уже упоминали в п. V.1.5 о тензоре
деформаций с компонентами
1 / fa. diij
''~+~~) G9>
Наряду с ним в теории упругости рассматривается евклидов тензор напря-
напряжений с компонентами О;/, каждая из которых равна /-И проекции силы
^отнесенной к единице площади), с которой среда действует на малую площадку
с внешней нормалью по i-й оси. Это симметрические тензоры, связанные в
случае изотропной среды при малых деформациях (при линейнрм законе
упругости) соотношением
где приняты обычные тензорные обозначения (п. V.1.1), а постоянные А. и \i
определены упругими свойствами среды. Отметим, что они связаны с другими
упругими характеристиками. Так, в случае простого растяжения, т. е. когда
O//=Q6n6J1, будет

352 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
(проверьте!); Поэтому и(ЗА.+2ц)/(А.4-ц)—этв и есть модуль упругости, фигу-
фигурирующий в формуле F3). Отношение ^,/2(A.+|i) поперечного сжатия к про-
продольному растяжению называется коэффициентом Пуассона. В случае всесто-
всестороннего сжатия, т. е. когда а,-/=—Qd/y (изотропное давление), получаем
е,у = — Qd,y/CA.-f-2|i). Но так какхумма е,-,- равна относительному увеличению
элементарного объема, то константа (ЗА. + 2(г)/3 является модулем всестороннего
сжатия изотропной упругой среды.
Мысленно выделив элементарный кубик с ребрами, параллельными осям
координат, и проследив за его деформацией при возрастании напряжений от
нуля, получаем (продумайте это!), что при этой деформации накапливается
потенциальная энергия с плотностью
~2 aUEi/ = 
В силу G9) отсюда получаем
Плотность кинетической энергии равна
где р—плотность среды. Отсюда легко написать выражение для плотности
функции Лаграижа L=-T—U. Полевыми переменными ф,- будут служить три
проекции н,- вектора перемещения. Уравнения Лагранжа—Эйлера G2) прини-
принимают вид (проверьте!)
Умножая на орты ссей и складывая, приходим к уравнению свободных коле-
колебаний упругой однородной изотропной среды
ри« = (Я. + ц) grad div u + ц\2u,
играющему центральную роль в теории упругости. Предлагаем читателю про-
проверить, что плотность полной энергии поля Н равна T-\-U; вектор интенсив-
интенсивности, поля S=—<ru/, где <г=(а,у)—матрица тензора напряжений; плотность
импульса поля P = p(Vu)-u/, где в круглых скобках стоит тензорное произве-.
дение векторов (п. V.1.3); пространственная часть W матрицы W вычисляется,
по тензорной формуле W'= — (Vu)-ff—LI.4
16. Диссипативиые системы. Ограничимся автономными систе-
системами. Мы уже отмечали в п. \\, что такая система, если к ней-
можио применить принцип Гамильтона, должнаЧ5ыть консервативной.
Тем не менее оказывается, что в линейном случае можно с помощью
искусственного приема распространить действие принципа Гамильтона,
и на неконсерватнвиые системы, в частности на системы с дисси-
диссипацией, т. е. рассеянием энергии (например, с трением). Для этого'
к исходной системе мысленно присоединяется «зеркально отраженная»
система, поглощающая ту энергию, которую первая выделяет.

fj 3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 353
(Вторая система должна быть с отрицательным трением!) Тогда
полная система, состоящая из реальной н присоединенной к иея.,
консервативна и допускает применение принципа Гамильтона.
Будем рассматривать набор координат qt, q2, ... , qa, определяю-
определяющих положение системы, как числовой вектор q н допустим, что
дифференциальные уравнения движения системы в матричной форме
имеют вид
Mq + Rq -f Kq =" 0, (80)
где М, R, К—--постоянные квадратные матрицы порядка л; в про-
простейшей задаче о системе упруго связанных осцилляторов матрица
М диагональная, однако для дальнейшего это несущественно. Тогда
«зеркально отраженная» система имеет уравнение
M*s—R*s + K*s = O, (81)
где звездочка означает транспонирование матрицы. Перемена знака
перед средним членом имеет физический смысл замены поло-
положительного трения иа отрицательное.
Легко непосредственно проверить (проделайте это!), что урав-
уравнения (80) и (81) в совокупности представляют собой уравнения
Эйлера для функционала
s*Mq -Ь -J s*Rq—- s*Rq—s*Kq ) dt.
(При доказательстве этого полезно иметь в виду, что если под —
понимать числовой вектор с элементами —- , то
Таким образом, можно принять за функцию Лагранжа
L = s*Mq + - s*Rq — 1 s* Rq—s*Kq;
правда, она теперь имеет линейные члены относительно производ-
производных, чего не могло быть раньше в автономном случае, но это
несущественно для дальнейшего. Вычисляя импульсы р,- по пере-
переменным q( и Г{ п.о переменным sit а затем функцию Гамильтона,
получим (проверьте!):
1 f ¦ ¦
P = JW S g-К 8, Г =
-1 (
г—Y
В силу п. 2 эта функция принимает постоянное значение вдоль
любой пары решений уравнений (80) и (81).
12 А.- Д. Мышкио

854
ГЛ. VI. ВАРИАЦИОННОЕ, ИСЧИСЛЕНИЕ
17. Принцип минимума потенциальной энергии. Будем рассма-
рассматривать только автономные консервативные системы, причем сначала
с конечным числом п степеней свободы и обобщенными координата-
координатами 9i» 9а» • • • > Яп- Пусть система находится в состоянии равновесия
в положении q° = (q\, 9§i ¦¦•> Яп)- Так как такое состояние можно
считать частным случаем движения, то к нему можно применить
Принцип Гамильтона (п. 8) и вытекающие из него уравнения Эйлера,
которые для этого случая приобретают простой вид
U'qt(& q\ gi) = 0 [i=\, 2 л).
Таким образом, возможные положения равновесия—это точки ста-
стационарности потенциальной энергии.
Однако теперь, в отличие от предыдущих пунктов этого пара-
параграфа, существенную роль будет играть характер рассматриваемой
стационарной точки (минимум, макси-
максимум, минимакс). В самом деле, пусть
в точке q° функция U(q) имеет изо-
изолированный локальный минимум (см.
рис. 106, где принято л = 2). Тогда
нетрудно проверить, что положение
равновесия в такой точке будет устой-
устойчивым, по Ляпунову (ЛВМ, п. XV.22):
если в начальный момент времени бес-
бесконечно мало изменить координаты q{
и придать системе произвольные беско-
бесконечно малые скорости qb то система
будет продолжать оставаться в беско-
бесконечной близости от q" на протяжении
всего дальнейшего времени. В самом
деле, заключим q" в произвольно малую фиксированную окрестность
(О) с границей (Г) (рис. 106). Наименьшее значение ?/(Г) функции
U на (Г) будет превосходить значения Ug=U(q°) (почему?). Но
тогда при произвольном достаточно малом изменении начальных
данных, о котором говорилось выше, полная энергия Н системы
будет меньше ?/(г>. А так как полная энергия не зависит от вре-
времени (п. 8), то эта система никогда не сможет достичь какой-либо
из точек (Г) (почему?), т. е. должна все время оставаться в окрест-
окрестности (Q), что и требовалось доказать.
Отметим, что приведенное доказательство пригодно не только
для консервативных, но и для диссипатнвных систем (п. 11).
С другой стороны, можно показать, что если функция U(q) имеет
при q = q° максимум или минимакс, то состояние q = q" равновесия
системы будет неустойчивым. Это наглядно ясно, если учесть, что
потенциальную энергию с графиком, показанным на рис. 106, имеет
материальная точка массы т, свободно движущаяся на изображенной

§ 3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 355
поверхности в поле тяготения g= —, направленного вертикально
вниз. Промежуточный случай составляет неизолированный минимум.
(Например, функция U(qlt q2) = q'i имеет линию минимума qt = Q.)
Наглядный подход, который подтверждается более точными рассуж-
рассуждениями, показывает, что и в этом случае консервативная система
(но не днссипатнвная!) неустойчива, поскольку как угодно малые
начальные скорости могут увести систему за достаточно большое
время на конечное удаление от исходного положения; однако при
этом скорости не будут нарастать до конечных значений, как в слу-
случаях максимума или минимакса.
Итак, задача о нахождении положений равновесия и об опреде-
определении их устойчивости для систем с конечным числом п степеней
свободы приводит к нахождению и исследованию стационарных точек
функции от п аргументов. Поэтому аналогичная задача для сплош-
сплошных сред, для которых л = оо, решается методами вариационного
исчисления, причем, как виднм, для выявления устойчивости состоя-
состояния равновесия, если она не ясна нз самой постановки задачи (на-
(например, из физических соображений), приходится применять доста-
достаточные признаки минимума функционала.
18. Примеры. Рассмотрим в качестве примера задачу о форме равновесия
однородной ннти, подвешенной в однородном поле тяжести интенсивности—gj.
Будем считать, что нить имеет линейную плотность р, не растяжима и не со-
сопротивляется изгибу, а концы ее для простоты имеют координаты (—Ь; 0) и
{Ь\ 0). Тогда в силу сказанного выше задача сводится к минимизации функцио-
функционала
ь
\ ygdm=gp \ у V 1 +у'* dx
при интегральной связи
Ь .
[ V l + y"dx=L (задано, L > Щ (82)
-Ь
и граничных условиях
<,(-&)=0, у(Ь)=О. (83)
Стандартное првмеиение метода п. 1.12, которое мы предоставляем читателю,
приводит к общему решению соответствующего уравнения Эйлера
которое и служит обоснованием названия «цепная линия», введенного в п. 1.8.
Применение граничных условий (83) и уравнения сиязи (82) дает искомое част-
частное
р у () ур
решение у=Сх \ с\\——cb —), где
ClSh^=L. (84)
12»

356 ГЛ.' VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Так как левая часть (84) при изменении Cj от 0 до оо монотонно убывает от оо
до Ь (проверьте!), то мы получаем ровно одно состояние равновесия. Вопрос
о его устойчивости в данной задаче не возникает, хотя желающие могут прй-
верить эту устойчивость, т. е. условную минимальность значения функционала,
с помощью метода п. 2.5.
Рассмотрим еще задачу о потере устойчивости сжатой балкой (п. 13). Пусть
конец s==0 балки жестко заделан, распределенные внешние силы отсутствуют,
но к свободному концу s=/ приложена сосредоточенная сжимающая внешняя
сила Р, параллельная оси х. Обозначив через ф угол наклона элемента стержня
к оси х, получим в силу п. 13 выражение для потенциальной энергии изогнутого
стержня
Мы видим, что достаточно ограничиться рассмотрением функции q> (s), не пере-
переходя к декартовым координатам. Функционал (85) рассматривается при гранич-
граничных условиях
<: 4>Uo=°. «fcUi=0. (86)
Уравнение Эйлера имеет вид
— Was—Psinq>=0 (87)
и, между прочим, решается в эллиптических функциях (п. II.3.14), на чем мы
здесь не будем останавливаться, так как иам надо только выяснить, будет ли
придавать экстремаль ф = 0 минимальное значение функционалу (85) при усло-
условиях (86). В силу п. 2.10 дело сводится к установлению знака наименьшего
собственного значения Хт\п линеаризованного уравнении (87), т. е. значения X,
при котором краевая задача
-|хф"-Р(р=Х,ф, ф|,=о=О, ф'Ь=1=0 (88)
имеет нетривиальное решение. Непосредственное интегрирование, которое мы
предоставляем читателю, показывает, что
¦ ¦ 1 —п* .. Р
Л1шп — 4J* ~
Таким образом, критическим значением сжимающей силы служит
Ч~ 4/» ,
Если Р < Ркр, то прямолинейное положение равновесия устойчиво, если
Р > Ркр—неустойчиво.
Обычно бывает удобнее пользоваться безразмерными комбинациями физи-
физических параметров, так как указание одной лишь сжимающей силы Р еще не
говорит о том, устойчива ли балка, насколько она близка к потере устойчи-
устойчивости и т. п. В рассмотренной задаче такой комбинацией служит «безразмерная
сила»
"—рг- <89>
Она пропорциональна «физической» силе, но включает и менее подвижные па-
параметры /, A. Критическим значением дли нее служит число -г-= 2,467.
В более сложных задачах приходится .применять приближенное вычисле-
вычисление \т;а. Если в задачу входит параметр а, то часто бывает, что при некото-
некоторых его значениях а—аф устойчивость ясна из физических или каких-либо

§ 3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 357
иных соображений (см. начало п. 2.6). Если вычислить Хт\п (а), начиная от о?
то точка перемены знака и даст значение а^. Если параметров а, В два, то,
вычисляя аналогичным способом значения о^, при фиксированном р, а затем
изменяя Р, можно получить в плоскости а, Р области устойчивости системы.
Иногда в задаче с параметром а более удобным оказывается следующее
рассуждение. Если собственные значения, как обычио бывает, зависят от а не-
непрерывно, то, меняя знак, онн должны обращаться в нуль. Обратно, если функ-.
ция Я,(а)прн некотором. а= 5 обращается в нуль, то при переходе а.через а
оиа обычио сменяет зиак (еслн иевыполиенодополнительиое равенство A,'j(a)=0,
которое должно быть обусловлено какими-либо специальными прнчинамн). По-
Поэтому для нахождения акр можно в задаче иа собственные значения положить
Х=0, иайти возможные значения для а, нз которых ближайшее к а0 и будет
равно <хкр. Например, если в задаче (88) перейти к безразмерной длине a=sjl
и положить Х=0, мы получим (см. (89))
&+>—¦
Ф =0,
о=0
ф| =
da <j=l
откуда находим возможные значения р~лг/4, 9л2/4, ... Так как при малых
р > 0 будет устойчивость, то ркр—п*/4. При я*/4 < р < 9я*/4 будет oijio соб-
собственное значение отрицательно, при 9л2/4 < р .< 16п2/4—два и т. д. В более
сложных задачах собственные значения могут зависеть от параметра ие моно-
монотонно; тогда может получиться иесколько интервалов устойчивости..
19. Запас устойчивости. Рассмотрим автономную консервативную
систему с одной степенью свободы н с показанной на рис. 107 за»-
висимостью потенциальной энергии С/от координаты q. Здесь имеется
шесть возможных положений равновесия q1, дг, ..., д", из которых
1
U
\
\
h
г'
j\ 1
! Т*^
/Tv.
Г 1 1
i !
¦ ¦
/ i \
У I \
• i Л
4 i
«
\
v 1
Рис. 107.
трн устойчивых q1, q3, qb. Рассмотрим какое-нибудь из этих устой-
устойчивых состояний, например ^3. Тогда наименьшая из разностей
U{q2)—U(q3) и U(q*)—U(q3)—на рис. 107 это первая—и будет
служить запасом устойчивости К3 (иначе—потенциальным барьером)
рассматриваемой системы в состоянии q3. Это означает, что если
системе в состоянии ^3 придать кинетическую энергию, меньшую К3,
то так как полная энергия сохраняется, а кинетическая неотрица-
неотрицательна, то система не может выйти из области, заштрихованной на
рис. 107 (потенциальной ямы, отвечающей состоянию q3), а в случае
как угодно малой диссипации энергии система через достаточно
большой промежуток времени вновь возвратится в исходное состоя-
состояние <?3. При этом, кииетическав энергия может добавляться любое

358 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
чнеяо раз, лишь бы в сумме эта добавка была меньше запаса устой-
устойчивости. Аналогично определяется запас устойчивости и потенциаль-
потенциальная яма для других устойчивых состояний равновесия. Своеобразной
потенциальной ямой служит также область состояний q^> q*, выходя из
которых без начальной скорости, система уходит на бесконечность.
Для систем с конечным числом п степеней свободы наряду с точками ми-
минимума потенциальной энергии U(q) (q—(q,> q2, .... </„)) возможны «много-
«многообразия минимума», на которых значение и постоянно, т. е. вдоль которых
система может безразлично перемещаться; такие многообразия обычно бывают
у систем, обладающих той или иной симметрией. Компактные (п. 2.9) многооб-
многообразия минимума рассматриваются в точности так же, как точки минимума, по-
поэтому, говоря в дальнейшем «точки минимума» мы будем иметь в виду «точки
или многообразия минимума». Если q°—одна из точек минимума, то для по-
получения запаса устойчивости в </° нужно соединить </° всевозможными линиями (/)
со всеми другими точками минимума, а также с бесконечностью; на каждой из
этих линий взять наибольшее («самое трудное» для системы) значение UU), после
чего взять линию (/), для которой значение UU) является наименьшим (т. е.
линию, по которой системе «легче всего» пройти из qu в другое устойчивое со-
состояние равновесии или иа бесконечность; продумайте все это на рис. 107).
Разность
/C°=mfnmax U (M)—U (q°) (90)
@ М(/>
я будет служить запасом устойчивости системы в положении q°.
Задача о нахождении величины (90) есть задача вариационного исчисления,
так как {/(n =max U есть функционал, и потому речь идет о минимуме функ-
функционала на линиях определенного класса. Однако классический подход, осно-
основанный на приравнивании вариации функционала нулю, здесь приводит только
к заранее очевидному результату: для линии, реализующей минимум (90), точка,
в которой U принимает наибольшее значение, является безусловно стационар-
стационарной точкой для U (как правило, точкой минимакса нли точкой многообразия
минимакса; возможен особый случай, когда это точка (я—: 1)-мерного многообразия
максимума, если изучаемой точкой был центр вулканического кратера). Но вне
этой наивысшей точки линия, реализующая минимум, обладает весьма высокой
степенью произвола, так что ни о каком дифференциальном уравнении для нее
типа уравнения Эйлера говорить не приходится. Подобные некласснческие за-
задачи на минимакс широко распространились в последние годы (см., в частности,
п. IV.5.7), хотя встречались и ранее.
Потенциальная яма, отвечающая точке </.°, получится, если взять содержа-
содержащую <7° компоненту связности (в пространстве положений системы) совокупности
всех положений, для которых U (q) < U (<70)—Ь /С0. При я=2 можно наглядно
представить себе, что в точке ( q\\ <&; U ( q\, q%)) открылся источник, наполня-
наполняющий впадину над поверхностью U — U (qu q3) водой; тогда в момент, когда
вода впервые прольется наружу, глубина озера будет равна К°, а его зеркало
образует потенциальную ям.у (ср. рис. 107).
На улавливании минимакса на границе потенциальной ямы может быть
основан численный метод определения запаса устойчивости. Пусть л=2 (это
несущественно) и линии уровня имеют вид, как на рис. 108; конечно, эти ли-
линии в реальной задаче нам неизвестны. Пусть ориентировочно известен способ (/),
по которому система должна выйти из ямы. Если тогда из последователь-
последовательны* точек (/) идти по лнниям наибыстрейшего спуска, решая уравнение
д= — grad U (q), то вблизи </° эти линии приведут обратно в <Д а вдалеке —
в другую точку минимума или' на бесконечность. Поэтому расхождение двух
соседних линий наибыстрейшего спуска указывает на наличие вблизи минимакса.

§ 3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ 1359
который в дальнейшем можно уточнить по методу Ньютона (ЛВМ, п. XI 1.12),
решая систему уравнений i/?i==0. (Отметим, что миинмаксы могут иметься и
внутри потенциальной ямы, поэтому существенно, чтобы линии наибыстрейшего
спуска не только расходились, но и вели к разным минимумам.) Если имеются
конкурирующие способы выхода из имы (как (т)
на рис. 108), то запас устойчивости даст наимеиь-
шаи из высот перевалов. Если способы экономного
выхода из ямы ориентировочно неизвестны, то
можно наугад испытать несколько способов и вы-
выбрать для иих самый низкий перевал.
Прн анализе запаса устойчивости систем с
бесконечным числом степеней свободы (сплошных
сред) можно пользоватьси конечномерными аппрок-
симациими.
20. Вариационные принципы в конформных
отображениях. Здесь мы приведем вариационный
принцип совсем иного рода, чем предыдущие, в
нем конкурирующими будут аналитические функ-
функции комплексного переменного. Этот способ можно
применить для приближенного осуществления кон-
конформного отображения (§ ИЛ) одной заданной
области на другую.
Рассмотрим сначала отображение
f(«)=«+«*¦+*«•+... (91)
круга >(/Cj?)=|z| < R на некоторую область (Н).
Так как элемент площади dK испытывает при этом равномерное растяжение а
|/' (г) I4 Раз (п- II.1.4), то площадь области (//) равна
(если отображение многолистное, то получается площадь с учетом кратности
покрытия). Подставив в последний интеграл разложение (91), раскрыв скобки
и интегрируя сначала по <р, а затем по р, получим (проверьте!)
Я=яЯ* A +21 с8 |*Я*+3 | с3 |*/?*+ ...).
Отсюда мы видим, что отображение (91) всегда увеличивает площадь круга (Kg),
за исключением тривиального случая тождественного отображения, когда пло-
площадь сохраняется.
Пусть теперь ставится задача о построении конформного отображения
w=<fo(z) заданной односвязной области F)^0 на круг \w\ < R (радиус ко-
торого заранее не задай) при дополнительных условиях нормировки
Фо(О)=О, ф'0@)=1; (92)
возможность такого отображении вытекает из теоремы Римаиа (п. II. 1.16; от-
отметим, что здесь задан ие только угол поворота, но и коэффициент растяжения
малой окрестности точки г=0, но это компенсируется тем, что радиус круга-
образа заранее не задай). Тогда легко проверить, что площадь указанного круга
меньше площади любой другой области, на которую может быть отображена (G)
с помощью аналитической функции, удовлетворяющей условиям (92), и, таким
образом, функция фф(г) является решением задачи иа тотальный минимум ин-
интеграла
$ ф' (г) (ф' (г))* dG (z=x + iy, dG=dxdy) (93)

360 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
среди всех аналитических на (О) функций, удовлетворяющих условиям (92). Для
доказательства этого достаточно применить утверждение предыдущего абзаца
к функции ш (ф<Г(о>)), где функция фо обратнаяк ф0 (продумайте это рассуждение!).
В гл. V книги [44] указана методика применения этого принципа для при-
приближенного конформного отображения заданной области на круг. Это вариант
метода Рнтца (п. 4.1): функция ф' (г) приближенно строится в виде
с какнми-лнбо аналитическими g/, (г) (например, gk (z)=z*-1, причем константы ск
подбираются из требования минимизации интеграла (93) при условии Д, c^gfe @)= 1-.-
Там указан также еще один принцип, который может быть использован для
этой цели: среди всех аналитических на (G) функций, удовлетворяющих усло-
условиям (92), функции фо (г) придает тотально минимальное значение интегралу
\f'(z)\dL
(где (L)—.контур области (G)), равному длине образа (L).
§ 4. Прямые методы
Классический метод решения вариационных задач, основанный на
сведении их к дифференциальным уравнениям Эйлера, зачастую ока-
оказывается недостаточно эффективным, несмотря на большое теоре-
теоретическое значение этого метода. Хотя мы видели ряд примеров, когда
уравнение Эйлера оказывалось возможным решить в квадратурах и
даже в элементарных функциях, но для сколько-нибудь более слож-
сложных задач, особенно для функций нескольких переменных, такого
решения не существует, и мы приходим к необходимости численно
решать линейную или нелинейную краевую задачу для дифферен-
дифференциального уравнения, что возможно, но отнюдь не просто и в этой .
книге рассматриваться не будет. Поэтому естественно, что были
разработаны методы численного решения вариационной задачи в ее
исходной постановке, без перехода к уравнению Эйлера; они полу-
получили название прямых методов вариационного исчисления.
Некоторые сведения о прямых методах, а также примеры их при-
применения, содержатся в литературе, указанной на стр. 257. Широкое
теоретическое исследование этих методов и большое число приме-
примеров содержатся в гл. IV книги [44] и в книгах [90, 91].
В различных разделах математического анализа имеется, грубо
говоря, два основных класса методов' приближенного отыскания не-
неизвестных функций: методы сужения числа степеней свободы и ме-
методы дискретизации. (Конечно, имеются и методы смешанного типа,
а также не укладывающиеся в эти два класса.) В методах первого
класса независимые переменные в принципе остаются непрерывными,
но функция ищется в том или ином специальном виде, включающем
несколько параметров, которые затем подбираются и» требования
наилучшим образом удовлетворить условиям задачи; типичными

§ 4. ПРЯМЫЕ МЕТОДЫ * 361
представителями здесь являются метод интерполяции или метод на-
наименьших квадратов. В более сложных задачах эти методы предо-
предоставляют обширное поле приложения физической интуиции и аналИ'
тического искусства, так как, если удается правильно предвидеть
форму искомого решения, применив лишь небольшое число пара-
параметров, и удачно выбрать критерий качества приближения, то метод
может оказаться чрезвычайно эффективным (в частности, если сама-
исходная задача содержит параметры). В методах.второго класса —
они называются также сеточными—мы с самого начала заменяем
искомую функцию набором ее значений в узлах некоторой сетки;
здесь типичными являются методы численного интегрирования обык-
обыкновенных дифференциальных уравнений. Сеточные методы обычно
бывают менее специфичны (более универсальны) и более алгорит-
мичны, чем методы предыдущего класса; поэтому они широко при-
применяются при работе на ЭЦВМ.
1. Метод Ритца для квадратичного функционала. Метод Ритца,.
предложенный в 1908 г. немецким физиком и математиком В. Ритцем
(р. в 1880 г.)—также один нз типичных методов сужения числа
степеней свободы. Изложим его сначала на самом простом примере
отыскания экстремали функционала A.18) при граничных условиях
A.26), предположив, что функционал квадратичный:
y)dx. (I)
(Отметим, что мы здесь рассматриваем более общий — неоднородный —
вид квадратичного функционала, чем в п. П.4. Включение членов
с уу' н у' не приводит к расширению общности, так как их можно
устранить интегрированием по частям, что, впрочем, в конкретных
примерах делать не обязательно.)
Метод Рнтца состоит в том, что приближенное выражение для
искомой экстремали строится в виде
я -
y = ge(x)+^,ckgft{x), B)
k= l
где go(x), gt(x), ..., gn(x) — некоторые выбранные функции, тогда
как параметры ск будут подбираться из условия стационарности
значения функционала A). Функция ge(x) обычно выбирается удрв-
летворяющей условиям A.26), причем желательно, чтобы она по
возможности лучше изображала искомое решение, если о последнем
что-либо известно. (После ее выбора иногда делают замену
y = go(x)-{-z, чтобы перейти к однородным граничным условиям
z(a) = z(b) — 0.) Базисные (иначе координатные) функции gk{x)(k=*
= 1,2, ...,л) выбираются удовлетворяющими однородным усло-
условиям A.26), т. е. gjt{o)=gk(b) = 0; тогда при любых значениях с4

362 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
сумма B) будет удовлетворять условиям A.26) и, таким образом,
о них можно не беспокоиться.
В теоретических исследованиях функции glt ..., gn составляют
часть бесконечной системы функций
gi(x), Sit*). •••> &W, ?n+i(x), •••. C)
линейно независимой и полной в пространстве функций /^С1[а, Щ,
удовлетворяющих условиям f(a)—/(t) = O. При этом линейная неза-
независимость означает, что ни одна из этих функций не является линей-
линейной комбинацией конечного числа остальных, а полнота (см. п. 1.3) — ¦
что любую такую функцию f(x) можно как угодно хорошо прибли-
приблизить (в смысле Cj) линейной комбинацией конечного числа функций C).
(Чаще всего, если не учитывается конкретный вид функционала (Г),
берутся системы
gk(x) = x>'-1(x-a) (х—Ь) D=1,2,3,...) D)
или
^^ (A = l,2, 3, ...); E)
можно проверить, что каждая из этих систем линейно независимая
и полная в Сг) Можно доказать, что если Р(х) > 0 и исход-
исходная задача имеет единственное решение, то приближенные решения,
построенные по методу Ритца, при п—>оо сходятся к точному.
Условие о единственности выполнено, например, если Q(x)~^0.
В конкретных приложениях теоремы о сходимости использовать
затруднительно, они скорее имеют утешительный характер. Более
реальны теоремы с двусторонними оценками отличия точного решения
от приближенного; такие теоремы для метода Ритца впервые получил
в 1918 г. советский математик Н. М. Крылов A879 —1955). Однако
такие оценки, удобные для практического использования, получены
лишь для весьма узкого класса задач, так что их на практике обычно
не применяют.
При практическом применении метода стремятся к его практи-
практической сходимости, т. е. к тому, чтобы при небольшом числе базисных
функций он дал решение с хорошей точностью. Здесь также можно
использовать первые члены систем D) и E) или каких-либо иных
систем. Если удается использовать конкретный вид функционала A),
то обычно скорость сходимости метода улучшается. Например, если
а = — Ь и по смыслу задачи решение должно быть четной функцией,
то ясно, что при применении системы D) нужно пользоваться только
нечетными k; но если четность решения заранее неясна, то нельзя
пользоваться только четными функциями gk(x), так как при этом мы
навязываем решению свойство четности, которым оно могло не обла-.
дать. Если интуиция подсказывает, что точное решение будет где-то
иметь «горбик», то желательно одну из первых функций gk (x) взять

§ 4. ПРЯМЫЕ МЕТОДЫ 363
с таким горбиком и т. п. Некоторые дальнейшие соображения по
этому поводу будут высказаны ниже.
Вариационные задачи бывают двух типов: можно искать функцию,
реализующую экстремальное или стационарное значение функционала,
а можно искать и само это значение функционала. Ясно, что искать
стационарное значение выгоднее, чем реализующую его функцию,
так как ошибка в отыскании такой функции даст в соответствующем
стационарном значении ошибку высшего порядка-малости (сравните
с задачей о нахождении стационарного значения функции одной
переменной). Поэтому желательно, когда это возможно, сводить более
сложные задачи к задачам на отыскание стационарных значений
(мы об этом уже говорили в ЛВМ, п. IV.18).
Вернемся к приближенному решению B). Подставив его в правую
часть A), раскрыв скобки и произведя интегрирование, мы получим,
многочлен второй степени относительно пока еще произвольных
параметров
Hci. ct, .... сп). F)
Ясно, что если, например, исходная задача была задачей о минимуме,
то желательно подобрать параметры ck так, чтобы и выражение F)
приняло минимально возможное значение. Это же относится и к любому
стационарному значению функционала A), так как в зоне медленного
изменения функционала и выражение F) должно медленно меняться
при изменении параметров. Поэтому мы приходим к системе уравнений
V0\(c,, с„ .... с„)-0 D=1, 2, .... я), G)
из которой и надо найти параметры ck.
Введем рабочее обозначение
(Л g): = S [p(*)f WS' (x) + Q(x)/(x) g(x)] dx.
a
Тогда квадратичная часть функции F) имеет вид
п
2 (Еь> gt)i ckci (8)
к. 1=1
(проверьте!). Поэтому G) представляет собой систему линейных
алгебраических уравнений относительно с,, с2, ...,
ческой матрицей
2 ((?»,&)/) (*. /=1. 2, .... л).
и потому при небольшом п легко решается. Отметим, что если
Р(х) > 0, (?(лг)^О и функции gv g2, ..., gn линейно независимы,
то нетрудно доказать (попробуйте!), что квадратичная форма (8)
положительно определенная, что облегчает решение системы G)

964с- ГЛ. VI., ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
{см. конец л. IV.4.3). Подставив найденное решение в правую
часть B), мы и получаем приближенное решение по методу 'Ритца.
Реальную опасность составляет возможность того, что матрица ((g/ц gi)j).
получится «почти вырожденной», точнее говоря, плохо обусловленной (п.,IV.4.2).
Так как эта матрица симметрическая и не имеет отрицательных собственных
значений, то мера обусловленности системы G) равна отношению наибольшего
собственного значения матрицы коэффициентов к наименьшему; такая мера
обращается в бесконечность, когда система вырождается. Если система плохо
обусловлена, то в процессе ее решения существенное влияние оказывают ошибки
округления и неточности в исходных данных. Поэтому результат получается
мало достоверным, и может оказаться даже, что с увеличением числа базисных
функций в методе Ритца точность приближенного решения не растет, а убывает.
С точки зрения обусловленности лучше всего, если
Ifeft. ?/)/1=6*1. (9)
так как тогда указанная мера обусловленности равна единице. Если исходная
система базисных функций не обладала этим свойством, то его можно «органи-
«организовать» с помощью метода, совершенно аналогично известному процессу орто-
гоиализации (ЛВМ, п. VII.21). Отметим, что свойством (9) обладают,'в част-
частности, функции
где А,* и уь (х)—собственные значения и собственные функции соответствующего
оператора B.26), построенные в п. 2.8 (докажите!). Если же эти собственные
функции затруднительно найти хотя бы приближенно, то иногда пользуются
собственными функциями оператора с измененным младшим коэффициентом Q (х),
. так как можно показать, что они асимптотически удовлетворяют соотношениям (9).
Если и это не получается, то приходится изменить и старший коэффициент,
хотя при атом возможность получить плохо обусловленную систему значительно
повышается. В частности, при Ps I, Q=0 получается система E) с точностью
до постоянных множителей. (Почему?)
.Эти соображения по подбору базисных функций применяются и для
функционалов от функций нескольких переменных. .
; Для выяснения точности приближенного решений, полученного по методу
Ритца, на практике обычно пользуются сравнением результатов вычислений,
полученных при выбранном базисе и при расширенном (пополненном другими
функциями) или совсем замененном базисе, так как маловероятно, чтобы хорошее
совпадение результатов оказалось случайным. (Отметим, что при расширении
базиса существеиио сравнить не коэффициенты при одинаковых базисных функ-
функциях, а решения в целом; дело и том, что для плохо обусловленной матрицы (8)
значительное расхождение указанных коэффициентов еще не говорит о значи-
значительном расхождении решений.) Если производится целая серия однотипных
вычислений, то такой контроль производят для одного или нескольких типичных
примеров.
Приведем пример. Пусть ищется экстремаль функционала
I
dx A0)
о ¦ .
при граничных условиях
Здесь легко иапйсать точное решение
sh* \ A2)

§ 4. Прямыв методы 363
с которым мы будем сравнивать приближенные. Положим в B) g0(x)—x, а в
качестве базисных функций будем брать первые функции системы D). Пусть
сначала п = 1; это означает, что мы ищем приближенное решение в виде
1—х).
Подстановка в A0) дает после интегрироваиия (проверьте!)
5
Приравнивание производной нулю дает значение с=—^ , т. е. мы получаем
приближенное решение задачи
Vi прябл=*-^*A-л;)=0>7736л;+0,2264л;». A3)
Возьмем теперь п=2, т. е. приближенное решение в виде
После подстановки в A0) получаем (проверьте!)
Приравнивание частных производных нулю приводит к системе уравнений
69 7
решая которую находим с1==——=— 0,1459, с8=—j^=—0,1628, и потому
»ц Ир«б,=*-0,1459*A-*)-0,1628 *»A-*)=
1 =0,8541*—0,0169ж2 + 0,1628х*. A4)
Вычисление значений точного решения и построенных приближенных
решений дает следующие результаты:
х 0,0 0,2 0,4 0,6 0,8 1,0
очн 0,0000 0,1713 0,3495 0,5417 0,7557 1.0000
првбя 0,0000 0,1638 0,3457 0,5457 0,7638 1.0000
' , Уп прибл 0,0000 0,1714 0,3494 0,5415 0,7558 1,0000
Сравнивая их, мы видим, что уже приближение A3), полученное с весьма малой
затратой труда, имеет точность, достаточную для многих практических целей,
тогда как приближение A4) является практически точным. Еще более эффек-
эффективно сравнить соответствующие значения фуикциоиала /:
/ {0то,в} = §-}= 1.313, / {Н „Р„б,}=^= 1.314,
так что погрешность составляет всего лишь 0,1%; а чтобы уловить погрешность
/ {УцорвблЬ потребовались бы вычисления со зиачительио большей точностью.
Отметим, что функция A2) реализовала тотальный минимум функционала A0)
при граничных,условиях A1) (почему?), поэтому естественно, что его значения
на приближенных решения/ оказались больше, чем на точном.
В разобранном примере точное решение выражалось через элементарные
функции. (Впрочем, и здесь приближенное решение A3) может представлять
интерес, так как оно выражается через более простые функции.) Однако не

366 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
сложнее рассматривается, скажем, функционал
1
$ @'я
экстремали которого уже ие иыражаются через элементарные функции. Так как
это «пример однотипный с A0), то и точность приближенных решений должна
получиться примерно такой же.
Если на одном или обоих концах интервала граничное условие имеет вид
#' = 0 или более общий вид B.37), то хотя в принципе при построении приб-
приближенного решения соответствующее условие на конце можно просто снять,.как
естественное, но для ускорения сходимости лучше пользоваться базисными
функциями, удовлетворяющими однородным граничным условиям того вида,
который должен получиться для точного решения. Например, для граничных
условий (/@)=б, у'(/) = 0 можно воспользоваться функциями
хг
gi (*)=*—2] . gk(x)=xk-1 A-х)* (*=2, 3, 4, ...).
(Подумайте, зачем нужна первая функция.)
Впрочем, при любых граничных условиях иногда поступают так: при вы-
выборе системы базисных функций ие обращают внимаиия иа граничные условен
(например, берут просто систему степеней 1, х, хг, ...), которые затем учвты-
п
вают в виде связей на коэффициенты в разложении у ='2 c^g^ix).
Для функционалов с производными высшего порядка, функционалов
от нескольких функций и для задач на условно стационарное значе-
значение применение метода Ритца в принципе не отличается от рассмот-
рассмотренного и также достаточно эффективно.
2. Првмеиение к решению краевых задач. Эффективность приближенного
метода Рвтца породвла следующий способ приближенного решения краевой
задаче для дифференциального уравнения: подбирается функционал, для которого
уравнение Эйлера было бы равносильно заданному, после чего к этому функ-
функционалу применяется метод Ритца. Так, чтобы подобрать такой функционал
инда A) для уравнения
a(x)y"+b(x)y'+c(x)y=f(x),
надо это уравнение помножить на некоторый множитель \i(x), после чего
должно быть
—2Р=а(г, —2Р'=6|г, 2Q=c(i, —R=f\i. A5)
Из первых двух равенств находим
X
Р=ехр \ —dx, ii= Р,
J а а
после чего вз последних равенств A5) находим Q и R.
Пронерьте, например, что уравнение Бесселн (ЛВМ, п. XV.26)
ху+Ху'+(х*-р*)у=0
равносильно уравнению Эйлера дли функционала

§ 4. ПРЯМЫЕ МЕТОДЫ 367
Для интервала 1 < х < 2 применение метода Рнтца уже с одной базисной
функцией вида D) или E) приводит к очень хорошей точности.
Интересно, что для применения описанного метода минимизируемый функ-
функционал можно фактически не выписывать. Чтобы разобраться в этом, вспомним
вывод уравнения Эйлера в п. 1.7, и, обобщая, допустим, что вариацию функ-
функционала / {</}, который мы хотим минимизировать по методу Ритца, удалось
представить в виде
61 {у; 6«/}=(L{«/}, 6у), A6)
где L—некоторый оператор. (Например, в п. 1.7 было Lr{y} = Fy(x, у, у') —
— -r-F^(x, у, (/').) Тогда уравнение Эйлера приобретает вид L{y) =0 и легко
проверить, что
Таким образом, приравнивание нулю этих производных, необходимое для ми-
минимизации, дает такой же результат, как построение приближенного решения
уравнения Эйлера с помощью формулы B) по методу моментов (ЛВМ, п, XV.29),
взятых относительно функций gx, g2 gn.
Остается сделать еще одни шаг и при заданной краевой задаче для. урав-
уравнении L{(/}=0, не связывая эту задачу ни с какими функционалами,. просто
искать приближенное решение в виде B) (учитывая краевое условие выбором
функций gi), а коэффициенты с,- находить из условия равенства , нулю мо-
моментов
(Ч2о+2С*Ы. S/)= '
г ( \
= \ Ц go (х) + 2 ckSk (*) g/ (*) dx (/=1,2 n).
a \ *=« /
Этот метод называется методом Галеркина (или Бубнова—Галеркина), так как
он был впервые применен в 1913 г. при решении задач теории упругости рус-
русским механиком И. Г. Бубновым A872—1919), а в более общей форме —
в 1915 г. русским советским механиком Б. Г. Галеркииым A871—1945). Этот
метод для уравнений Эйлера вариационного исчисления совпадает с методом
Ритца, ио приводит к цели и для многих дифференциальных уравнений —
обыкновенных и с частными производными,— которые не являются уравнениями
Эйлера, а возникают вне связи с вариационными задачами. Метод Галеркииа
является одним из наиболее универсальных методов решения краевых задач
для указанных уравнений. Применяется также следующий вариант этого ме-
метода, предложенный в 1940 г. советским механиком Г. И. Петровым (р. в 1912 г.):
решение задачи ищется в том же виде B), ио моменты, которые приравниваются
нулю, берутся относительно какой-либо иной системы функций hx (x), А2 (х), ...
.... hn(x). См. по этому поводу книги [90, 91].
3. Метод счетного множества переменных. Иногда, если очень
повезет, удается найти общую формулу для коэффициентов ck
в разложении B) и затем, перейдя к пределу при п—(-оо, получить
искомое решение в виде суммы ряда. При этом можно с самого
начала искать решение в виде сумиы ряда с неизвестными коэффи-
коэффициентами, откуда и происходит название—метод счетного множе-
множества (т. е. бесконечной последовательности) переменных.

368 ГЛ. VI. НАРИАЦЙОИНОЕ ИСЧИСЛЕНИЕ
Рассмотрим, например, задачу о минимизации интеграла
. 1 Г ( Г ds\
/{(/}= ^ I \ у ($) ¦ j y(x)dx A7)
при условии
J{y}= J y(x)dx=S (задано) A8)
и граничных условиях
у(—1) = уA) = О; A9).
при этом внутренний интеграл в A7) является сингулярным и понимается
в смысле главного значения (ЛВМ, п. XIV. 19). Эта задача встречается в тео-
теоретической аэродинамике, где у(х) имеет смысл зависимости циркуляции по-
потока, обтекающего крыло, от координаты, отсчитываемой вдоль крыла; 2/—раз-
2/—размах крыла; / \у\ пропорционален сопротивлению крыла (без учета сжимаемости
потока и трения); J {«/} пропорционален подъемной силе; таким образом, речь
идет о таком распределении циркуляции вдоль крыла, при котором для дайной
подъемной силы получилось бы наименьшее лобовое сопротивление.
Для решения задачи совершим замену независимой переменной х = — /cos 0;
тогда концам интервала отвечают значения 0 = 0, л. Исходя из граничных
условий A9) будем искать решение в виде
B0)
Подстановка B0) в A8) дает
я
С (/4j sin Ф + А% sin 2ff+...) / sin в db=S,
о
. откуда легко получаем (проверьте!), что
А = —
Подстановка B0) в A7) дает
AjA*k^
/= 1 *= 1 о .
Внутренний интеграл равен (см. предпоследнюю формулу в п. .11.3.5)
¦ . Подстановка этого результата в B1) и применение свойства ортого-
S1F1 v
вадьности синусов дает
Но так как А1 уже найдено, а остальные коэффициенты Аь пока произвольны,
то ясно, что I \у\ примет наименьшее возможное значение, если At = Az=
,= Л4=...=0, т. е.
Это и есть решение задачи.

§4. ПРЯМЫЕ МЕТОДЫ 469
4. Метод Ритца для функционалов от функций нескольких
переменных. Этот метод в принципе тот же, что и для функций
одной переменной. Затруднения могут возникнуть при подборе ба-
базисных функций, удовлетворяющих заданным граничным условиям,
особенно для областей сложной формы. Рассмотрим, например, слу-
случай двух независимых переменных. Если решение строится в неко-
некоторой области (О) с границей (Г) н граничное условие имеет вид
ulr=0,
то стараются подобрать непрерывную функцию <о (х, у), положи-
положительную всюду в (О) и равную нулю всюду на (Г); если это удается,
то можно выбрать в качестве базисной
двухиндексную систему функций
xty*<s>Jfi, у) (j, * = 0, 1, 2, ...). B2)
В частности, если сама область
(О) определена каким-то неравенством
F{*i У) > 0. т0 можно просто положить
@=/\ Комбинируя такие функции для
ПРОСТЫХ Областей, ВОЗМОЖНО наЙТН ИХ И рнс |Qg
для областей более сложного вида. Так,
если построены функции «>, (лг, у) - для области (О,) и «>,(>;, у) для
области (G2) (рис. 109), то для пересечения (общей части, дважды
заштрихованной иа рис. 109) этих областей можно положить
<» = «>,(*, У)®х(х, У),
тогда как для их объединения (т. е. части, заштрихованной на рис.
по крайней мере один раз) можно положить
j «>, (л;, у) в (Ог) вне (О2),
«> = < «г(дг, у) в (О2) вне (G,),
( а>1{х, у) + (х>2(х, у) в пересечении @^ с (О2)
(проверьте непрерывность этой функции!). Такие пересечения, и объ-
объединения можно производить любое число раз.
Если область (G) в некоторой разумной криволинейной системе
координат и, v определяется неравенствами а^и^р y
то в качестве базисной обычно берут систему функций вида
gj(u)hk{v) (J, k=\, 2, 3, ...),
где функции gj(u) являются базисными на интервале а^«<;р и
обращаются в нуль на его концах, a hk (v)—то же для интервала
¦у^да^б (см. аналогичную конструкцию в ЛВМ, п. XVII.30).
В частности, на каждом из этих интервалов можно взять ту или
иную, систему собственных функций.

370
ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Для областей, составленных из двух или более областей про-
простого вида (рис. ПО), можно применить также следующий прием:
на общей граничной линии (/) задаемся приближенной формулой для
решения, включающей несколько парамет-
параметров сг, с , ст, и строим по методу
Ритца решение на каждой из составляю-
составляющих областей порознь, требуя стационар-
стационарности значения функционала по всем уча-
участвующим параметрам, включая с„ ...,ст.
Рассмотрим в качестве примера задачу о при-
придании стационарного значения функционалу
а Ь
A)
Рис. ПО.
в области (<?):
й ф
-ъ
•]
Я- +2Аи\ dy B3)
—&<#<;& с заданными нулевыми значениями
(Г) Э й
искомой функции на контуре (Г). Эта задача равносильна краевой задаче
(A — const)
V*« = А (в (О)), и|(Г)=0. B4)
Пользуясь системой функций B2), надо положить <о=(а2—хг) (б2—уг) и брать
только четные /и к. (Из последнего принципа максимума п. II.2.6 следует,
что решение задачи B4) единственно; но задача инвариантна относительно
отображений х -*¦—х и у -»—у, поэтому решение обязано быть четным отно-
относительно х и относительно у—продумайте это рассуждение!) Воспользуемся
самым простым вариантом метода Ритца, с одним сла-
слагаемым, т. е. будем искать приближенное решение в
виде
и^=с1(а2—хг) (Ьг — у2).
Подстановка в B3) дает (проиерьте!)
"9
откуда из условия стационарности
5А
т. е.
получаем сх=
0
Рис. 111.
" 8(а2+Ь2I
Сравнение с более точным решением, которого мы
здесь не приводим, показывает, что при а=Ь погрешность этого решения для
•разных точек (G) не превышает 6%, а в среднем равна 1%.
Другой пример. Пусть требуется придать стационарное значение фуик-
цноиалу
Где (О)—треугольник, изображенный на рис. 111, при граничном условии
(Интеграл B5) для любого числа независимых переменных называется инте-
интегралом Дирихле по имени немецкого математика Л. Дирихле A805—1859)
и встречается в различных разделах математики; уравнением Эйлера для него

§ 4. ПРЯМЫЕ МЕТОДЫ 371
служит уравнение Лапласа.) Таким образом, катеты треугольника (С) свободны
от граничного условия. Чтобы перейти к однородному граничному условию,
сделаем замену
которая иреобразует функционал B5) в
V , fteV , . дг
(О)
а граничное условие—в
В качестве базисной можно выбрать систему функций
т. е. искать приближенное решение в виде ,
К B6)
Однако учет конкретных обстоятельств позволяет при выбранном л понизить
число свободных параметров ац, и тем самым уменьшить объем вычислений,
а при выбранном числе свободных параметров повысить п, т. е. "повысить
точность аппроксимации. Для этого заметим, что задача инвариантна относи-
относительно преобразования (х, у)->-(у, х), поэтому ajk=akj. Кроме того, так как
трчное решение удовлетворяет иа катетах естественному граничному условию
ди п .
з-=0, т. е. -
дп
дх
=0, |?| =0, B7)
х=о ду\у=о 1 '
то подчиним и решение B6) этому условию, причем дли простоты заменим/:
иа оо. Так как •
дх \х=
i,k=0
2 S
4=0 4=0
/?=0
то из B7) получаем
%=% alk=aok+fli,*_i (ft=l, 2, 3, ...)• B8)
Диалогично из второго условия B7) .получается
Ooi=«eo. в*1=ЯАо+я*-1,1 (*=1, 2, 3, ...); B9)
это и есть требуемые соотношении между коэффициентами. Между прочим, при
конечном, л раиеиства B8) и B9) обеспечивают ие точное, а лишь приближен-
приближенное иыполиеиие условий B7) (почему?); но это все же лучше, чем соьсем не
учитывать этих условий.

ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Итак, если положить, например, я==1, то мы получаем вместо четырех
свободных параметров всего лишь один: '
а при п = 2 вместо девяти—три (проверьте!).
Остановимся еще на функционале
а Ь
/"{«}= J dx J [(V2«)a-2/(*, y)u]d9,
-а -Ь
уравнением Эйлера для которого служит неоднородное бигармоническое урав-
уравнение (см. 3.70))
при граинчиых условиях
u =0, jr
(Г)
дп
(Г)
=0.
Здесь в качестве базнсных можно пользоваться функциями
(хг—а*)*(у*—&*)*xJyk (/, ft=0, 1, 2, ...).
Можно воспользоваться также функциями
где ф/(х)—собственные функции соответствующей одномерной задачи
C0)
C1)
а функции t|)ft((/) определяются аналогично. Легко проверить, что обизательно
X > 0 (для этого надо обе части уравнения умножить иа о и проинтегрировать
М I М,"
у».
Рис. 112.
от:—а до а, а затем левую, часть проинтегрировать по частям два раза). Поэто-
Поэтому общее решение уравнения для собственных функции имеет вид
p=Cxch \/Tx+Ctsh J
Применение граничных условий, которое мы предоставляем читателю, приводит

§ Ч. ПРЯМЫЕ МЕТОДЫ 878
! -двум типам собственных функций: - '
cos у ка . 4/— 4/— ¦ „ 4/~ . 4/т-
р= fy=—ch у кх—cos у кх, где tb у ка=—tg у ка,
sini/Яа , 4/— . 4/г ., 4/— 4/т
v= * sh |/ Хх —sin |/ Хх, где th |/Xa=tg у ла
sh у Ка
(эти функции определены с точностью до постоянного множителя, который
выбран так, чтобы при больших X они оставались порядка 1). Обозначив
|/Ла=ц, т. е. Я, = Ц*/а4. мы вндим, что собстненные значения X находятся
нз уравнения th|x=±tg|x, графический смысл которого показан на рис. 112.
Значит, имеется бесконечная последовательность собственных функций, кото-
которые нетрудно нычнслить с хорошей точностью.
Вычисления прн /ее const, a=ft показывают, что применение системы )
с одним свободным параметром дает погрешность в решении, меньшую
а системы C1)—меньшую l-n-%-
5. Метод Трефтца. Если уравнение Эйлера является линейным,
однородным и достаточно простым, а область имеет сложный кои-
тур, то эффективным оказывается следующий метод Трефтца: в ка-
качестве базисных функций выбираются решения уравнения Эйлера,
а коэффициенты в их линейной комбинации определяются граничньтн
условиями. Покажем этот метод на примере задачи о стационарном
значении интеграла Дирихле B5) при граничном условии
(г>=/ (задано). Щ
Обозначим через ио(х, у) неизвестное иам решение втой задачи
и будем искать прнближеиное решение в виде
«пр = 2 ЧЧ (х, у), C3)
*=1 ¦ i
где и/,—гармонические функции (т. е. удовлетворяющие уравнению
Эйлера для функционала B5)). Примем на минуту, что функция и0
известна, и подберем коэффициенты ск так, чтобы функция ияр ми-
минимизировала интеграл
j
(С)
«*«по du0V /d«no duov"l
Ы*-ж) +(-w-w) da <34>
Точное решение этой задачи, без учета формулы C3), привело бы,
очевидно, к функции и0 с точностью до произвольного постоян-
постоянного слагаемого. (Проверьте, что интеграл C4) как раз равен
/{ипр} — /{й„}> если считать и произвольной функцией,
удовлетворяющей условию C2).) Приравнивание нулю- частных

374 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
производных по Су приводит к уравнениям
я
: V4 f* /duy-du/c диу дик\ Г /диу ди„ диу диЛ
f^. j \ дх дх ' ду ду J * J \дх ~дх~ "•" ~ду ~ду) ' '
(О (О
(проверьте!). Однако легко проверить, что для любой гармонической
функции v и любой функции и справедлива формула
С gradH-gradfrfG= Г u-^dT.
(С) (Г)
(Для доказательства достаточно применить формулу Остроградского
к полю uyv и воспользоваться формулой A.1.10).) Поэтому уравне-
уравнения C5), учитывая C2), можно переписать в виде
?(У1ж c/-i. а *)- C6)
4=1 МП / (Г)
В,эти уравнения от и0 входят только ее заданные граничные
значения /, поэтому мы можем теперь отказаться от предположения,
что «о нам известна; однако если мы решим систему уравнений (86)
относительно ск и полученные значения подставим в C3), то резуль-
результат, как мы видим, получается в точности такой же, как если бы
мы минимизировали интеграл C4).
Вычисления показывают высокую эффективность метода Трефтца,
особенно если угадать, какими гармоническими функциями можно
хорошо аппроксимировать искомое решение и0. Отметим, что метод
применим и в случае, когда граничное условие взамен C2) имеет
вид ~1 =/; тогда надо правую часть C5) преобразовать в интег-
интеграл \ U
«г» .
6. Метод Ритца для собственных значений. Задача на собст-
собственные значения, например, вида
равносильна задаче о придании стационарного значения функционалу
ь
функцией у ^ 0 при тех же граничных условиях. Совершив, согласно
методу Ритца, подстановку B) с ?0==0, мы получаем квадратичную
форму с параметром вида
кс/сь (а/*=а*/. Ь/к = Ьк])

§ 4. ПРЯМЫЕ МЕТОДЫ 373
с известными коэффициентами. Условия ее стационарности имеют
вид
2 (/=1. 2,..., в). C7)
Так как нас интересует нетривиальное (т. е. ненулевое) решение,
то определитель системы должен равняться нулю:
dei((aJk)-X(bJk)) = O. (»8)>
Значения %, найденные из этого алгебраического уравнения, служат
приближениями для собственных. значений задачи; подставив их в
C7) и найдя cft, мы с помощью B) получаем приближенные выра-
выражения для соответствующих собственных функций.
Решения уравнения C8) лучше всего аппроксимируют меньшие по
абсолютной величине собственные значения, тогда как ббльшие
итогут аппроксимироваться плохо. Для их получения нужно увели-
увеличивать п; при таком увеличении становится одновременно видна
достигнутая точность. При большом п, особенно для задач на
собственные значения с несколькими независимыми переменными,
вычисление значений определителя C8), нужное для улавливания его
нулей, может оказаться громоздким делом. В таких случаях может
©казаться выгоднее вычислять эти значения со сравнительно большим
шагом по к, а затем проводить обратную интерполяцию (ЛВМ,
п. V.8).
Рассмотрим в качестве примера задачу на собственные значения
-»'=**. </1*=-1=</1*=1 = 0. . C9)
Сначала проверим, что собственные функции этой задачи могут быть либо
четными, либо нечетными (это рассуждение не использует конкретного вида
уравнения, а только симметрию интервала и четность коэффициентои Р (х) и
Q (х)). В самом деле, при преобразоианни х ¦—>¦—х задача переходит и себя; но
при заданном А, собственная функция определена с точностью до постоянного
множителя, поэтому i/(—x) = ky{x). Заменив и этом тождестве х на — х,
получаем у (x) — ky (—х)=кгу (х), откуда k=± 1, что и требовалось доказать.
Собственные значения в данной задаче легко найти точно, они равны
(см. B.35))
А,1=^=2,46740, Х, = п«=9,8696, Ха=^-=22,21 и т. д.
Функционал, отвечающий задаче C9), имеет вид
1
$ <V't-V)<k- D0)
-1
Воспользуемся сначала одной лишь первой функцией системы D), т. е. положим
у=<ц{\—х2). Подстановка и D0) дает
III 8 < 16. о
-- Я Ifi
уравнение C8) —ураинение первой степени ——угХ=0—имеет решение Х1пр«=
= 2,5, которое аппроксимирует А,х с точностью до 1,3°/о-

87ft ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Если ограничиться четными собственными функциями, то в качестве еле;
дующего .приближения надо взять ; . • •>
Уравнение C8) здесь уже будет второй степени. Вычисления, которые мы пре-
предоставляем читателю, дают
Х1П?=2,46744, Х3пр = 25,6.
(Напомним, что Xg отвечает нечетной собственной функции.) Как видим, погреш-
погрешность в Хх получилась 0,002°/0, а в Х3—13°/0. Если взять следующее прибли-
приближение дли четных собственных функций, то погрешность в Хх будет 3-10~70/0,
в К,—0,5%, зато в Х6—30°/„. Хорошо видна неравномерность аппроксимации,
о чем.говорилось выше. Погрешности в значениях собственных функций немного
выше и имеют ту_ же тенденцию.
В разобранном примере приближенные собственные значения получились
большими точных. Можно доказать, что это не случайно. Например, Х1 можно
получить как решение некоторой задачи иа минимум в классе всех функций,
удовлетвориющнх условию нормировки и граничным условиям (п. 2.8); A,1Jtp.
получается как решение той же задачи в более узком классе функций специ-
специального вида (линейных комбинаций базисных функций), поэтому всегда
^inp^Xj. (Когда здесь будет знак равенства?)
Сделаем еще одно, замечание, которое полезно иметь в виду. Пусть при
(Среднем» л (скажем, 3 или 4) мы намерены раскрыть определитель C8) и Чис-
леино решать получающееся алгебраическое уравнение каким-либо итерационным
методом. Как известно, для этого желательно иметь хорошее нулевое прибли-
приближение. Это приближение для Хх можно получить, приравняв нулю один из
главных миноров (п. IV.2.3) матрицы (а/к)— Mty*). Хотя бы первый, так как
легко проверить, что при этом получится приближенное уравнение для X, по
методу Ритца с соответственно уменьшенным числом базисных функций. При-
Приближенное выражение для X» можно получить, приравняв нулю второй глав-
главный минор и воспользовавшись формулой для суммы корней алгебраического
уравнении, и т. д.
7. Метод Ритца для неквадратичных функционалов. Схема приме-
применения метода Ритца для функционалов общего вида такая же, как
и в п.- 1, однако система уравнений для параметров получается
нелинейной* со всеми вытекающими отсюда осложнениями. Здесь
не обязательно при построении приближенного решения требовать,
чтобы параметры в него входили линейно, т. е. можно это решение
строить в виде
у = у(х; cit c2, .... с„)
(аналогично для функций нескольких переменных). Так как решение
нелинейной системы существенно усложняется с ростом числа неиз-
неизвестных, и, кроме того, желательно отправляться от значений, близ-
близких к точному решению, то особенно возрастает роль интуиции,
котораи иногда дает возможность, используя небольшое число пара-
параметров, хорошо аппроксимировать возможные формы искомого реше-
решения. Если интуиция ничего не подсказывает, то можно использовать
приближенные решения вида B), так как тогда будет хоть уверен-
уверенность в достаточной «гибкости» (приблизительной полноте) таких
решений. Как и раньше, близость решений, полученных для разных
л (причем решение, полученное для меньшего л, можно взять в

§ 4. Прямые методы 37?
качестве отправной точки для построения решения при большем л)
или для разных систем базисных функций позволяет сделать вывод
о точности приближенного решения рассматриваемой, а с ней и
сходных задач.
Пусть исходная вариационная задача была задачей на минимум. Тогда
после подстановки D1) получается задача на минимум функции конечного
числа л независимых переменных clt c2,..., с„. Подобные задачи на минимум
функции л переменных могут возникать и вне вариационного исчисления,
например в нелинейном программировании (п. IV.5.8). Сейчас разработай ряд
методов решения таких задач; мы опишем один из них, метод градиентного
спуска, довольно эффективный в простых случаях. При этом мы будем незави-
независимые переменные обозначать буквами хг, х2,..., х„.
Допустим сначала, что требуется найти безусловный минимум функции
f(xi> х?> •••. хп)- Тогда можно воспользоваться тем, что в любой точке *==
*=(xv *»; •••; хп) вектор —grad/(;c) направлен в сторону наибыстрейшего
убывания функции"^. Поэтому система дифференциальных уравнений
i . _ f' /*• г г \ (i —19 п\ (А9\
определяет в пространстве х траекторию, вдоль которой значения / (х) непре-
непрерывно убывают, причем—во всяком случае, локально—наиболее быстрым спо-
способом. Если функция f остается конечиой при конечных х, то такая траектория
может либо уходить на бесконечность, либо входить в точку локального мини-
минимума. (Теоретически возможен также случай, когда траектория входит в точку
мииимакса, однако как угодно малым изменением начальных условий для тра-
траектории этого случая можно избежать; можно ручаться, что этот случай не
представится, если начальные условия брать наугад.) Таким образом, если
обнаружится, что траектории приближается к некоторой точке, то это и будет,
точка минимума. При этом, если локальный минимум совпадает с тотальным
(см. .по этому поводу конец п. IV.5.8), то мы получаем наименьшее значение
функции /; если же это заранее неизвестно, а нас интересует тотальный .мини-
.минимум, то можно попытаться улучшить результат, строя траектории при различ-
различных, выбираемых наугад начальных данных. - - :
Некоторое затруднение возникает в связи с тем, что при приближении
к точке минимума движение по траектории, определенное системой D2), замед-
замедляется, так что эта точка достигается лишь в пределе, при t —> оо. Так,
в типичном примере, при. л=1, f(x)=x\ уравнение D2) имеет вид -п-=?
=—2*! я решениех{=х\е~2**~*^—>¦ 0. Чтобы избавиться от этого-затруднения,1
можно в правые части D2) ввести общий множитель, например
который,, не изменяя траектории, компенсировал бы это замедление (как?).
Можно поступить и иначе: когда движение достаточно замедлится, перейти к
решению системы уравнений fx.=0 (» = 1, 2,..., л) по методу Ньютона.
Пусть теперь ищется условный минимум функции f(xt, хг,..., х„) при
k < п независимых соотношениях вида ¦
?.> *»)=0' (*=1. 2 k). 'D3)
Поэтому элементарные перемещения в пространстве х должны быть связаны
соотношениями
.
?*•<*-* «-I.*,....'"* D4)

378 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Элементарное перемещение, по которому функция f убывает быстрее всего,
получается в результате проектирования вектора —grad/ на (я—й)-мернуга
плоскость, определенную уравнениями D4). Эту проекцию b можно найти,
например, так: ввести числовые векторы
¦¦? %)' .»-.*•».* т
(звездочка означает ^транспонирование), перпендикулярные плоскостям D4), и
положить
b=-gradf + X1a1 + Xaa2+...+Mft. (Щ
подобров коэффициенты 'Х,- так, чтобы вектор b оказался перпендикулярным
всем векторам а,- (продумайте это!). Приравнивая нулю скалярные произведения
выражения D6) на все векторы а,-, получим систему уравнений первой степени
для X/, определитель которой D=det (а,а/) называется определителем Грима
для векторов а,-. Так как это определитель матрицы квадратичной формы
(*1а1+*А+ •• • +**айJ> а потому равен произведению собственных значений
этой матрицы, то он положителен, если векторы а/ линейно независимы, и
равен нулю в противном случае (продумайте это!). Поэтому условие D Ф- 0 для
незавясимых соотношенвй D3), вообще говоря, выполняется (ЛВМ, п.XI.15).
Итак, локально наибыстрейшее перемещение к условному минимуму функ-
функции / определяется из системы уравнений
¦^=*М*1. * *») 0 = 1.2 я), " D7)
где bj—проекции вектора D6). При этом коэффициенты X,- для небольших k
можно иайти непосредственно из системы уравнзднй Ь-ау=О (/=1, 2,..., к),
тогда как при больших к можно, как в п. IV.4.6 присоединить к D7) систему
из к" уравнений для элементов матрицы (а^а/). Для корректировки можно
при некоторых t, выбрав какие-либо я—к из найденных значений X;, пересчи-
пересчитать остальные из уравнений D3) по методу Ньютона, после чего уточнить
матрицу (а,--ау)~' по методу п. IV.4.6. Бороться с замедлением сходимости при
подходе к точке минимума можно так же, как в случае безусловного минимума.
Заметим, что при применении метода Ньютона к отысканию условного экстре-
экстремума надо проводить линеаризацию как по основным неизвестным *,-, так и по
множителим Лаграижа X,- (см., например, ЛВМ, п. XII.10). При этом за
уточняемые значения этих величин можно нзять значения, полученные при
решении дифференциальных уравнений, так как из формул D6) и D5) видно,
что в точке минимума при Ь = 0 найденные величины X,- как раз служат мно-
множителями Лагранжа.
Если занедомо известно, что при рассматриваемых значениях X; какие-либо
к из этих переменных, например последние, представляют собой дифференци-
?>(ф,, ф,,. .., фь)
руемые функции остальных, т. е. если -=п ——— — г 5е О, то
и\хп-к + Ъ Xn-k + i хп)
можно не пользоваться множителями Лаграижа, а строить траекторию наибы-
наибыстрейшего спуска н пространстве xlt xit..., ж„_д. При приближении этого
якобиана к нулю можно «переключиться» на другой набор из я—k перемен-
переменных Х(.
Если исходная задача была не на минимум, а просто на стационарное
значение функции f, то метод градиентного спуска можно применить к функции
Ф =2 /*'• Одиа*о надо иметь в виду, что функция ф может иметь точки
минимума не только н стационарных точках функции f (продумайте, например,
случай я—1), поэтому для решения задачи может оказаться полезным по-
повторный градиентный спуск из различных, выбираемых наугад начальных точек.
В заключение отметим, что метод градиентного спуска можно в принципе
осуществить непосредственно для функционала, без его конечномерной аппрок-

§ 4. ПРЯМЫЕ МЕТОДЫ 379
симации. Для этого допустим, что для некоторого функционала / {у} нам уда-
удалось представить его вариацию в виде A6).' Тогда оператор L играет роль гра-
градиента функционала / \у\, а уравнение спуска по градиенту приобретает вид
dt~ '*'¦
Так как теперь надо считать уже, что у = у(х; t), то это получается уравнение
с частными производными, которое надо решать при каком-то выбранном началь-
начальном условии у \t=o = !/o (*) и ПРИ граничных условиях, наложенных на функ-
функционал /. Это практически возможно, хотя не совсем просто и приведет опять-
таки к необходимости той или иной конечномерной аппроксимации. В этой книге
методы решения уравнений с частными производными мы не рассматриваем.
8. Метод наименьших квадратов. Мы уже упоминали в п. 1,
что на эффективности метода Ритца основан способ приближенного
решения дифференциальных уравнений, состоящий в приведений
исходной краевой задачи к вариационной, которая и решается затем
методом Ритца. Наиболее просто (хотя и не всегда наиболее эффек-
эффективно) такой переход можно осуществить, минимизируя средний
квадрат невязки — быть может, с некоторым весом. Этот метод
наименьших квадратов, который уже упоминался в ЛВМ, п. XV.29,
можно применять не только к дифференциальным, но и к любым
другим уравнениям, в которых искомой является функция или
несколько функций.
Рассмотрим, например,' задачу об интегрировании уравнения
У'=/(х,У), а<х^Ь D8)
при начальном условии
У(а)=Ув (задано). D9)
Эта задача, очевидно, равносильна задаче о минимизации функционала
*)]¦<**. E0)
а
если при х — а поставлено условие D9), а при х — Ь условие снято.
К ней и можно применить метод Ритца.
"Интересно, что уравнение Эйлера для функционала E0)
2 [/-/(*, У)][-Г,,(х, у)]-| 2 [/-/(*, у)\=о, E1)
т. е.
f =fx (*, у) +/(х, у)/'у (х, у), E2)
имеет второй порядок и получается в результате дифференцирования
исходного уравнения D8). Уравнение E2) имеет двухпараметрическое
семейство решений, тогда как исходное уравнение D8) — только
однопараметрическое. И лишь привлечение естественного граничного
условия при х = Ъ, имеющего вид [у'—f(x, У)]х*=ь — О, позволяет
перейти от E2) к D8). (Проделайте это, используя форму E1)
уравнения E2).)

ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
В этом повышении порядка производных состоит некоторый
недостаток метода наименьших квадратов, несмотря на его универ-
универсальность. Поэтому, если заданное дифференциальное уравнение
2/г-го порядка удается переписать в форме уравнения Эйлера для
функционала J с производными А-ro порядка, то лучше применять
метод Ритца к У, а не пользоваться методом наименьших квадратов,
где придется привлекать функционал с производными 2А-го порядка.
Ведь чем выше порядок производных в функционале, тем, вообще
говоря, выше погрешность метода Ритца.
Взамен функционала E0) можно было минимизировать функционал
ь
\W-ti*. У)\**х+\у(а)-уа]*,
а
сияв условие D9). Это простое замечание дает возможность предложить сле-
следующий вариант метода наименьших квадратов в случае любого числа незави-
независимых переменных, любой области, любого уравнения и любых граничных
условий. Пусть в области (G) с границей (Г) требуется решить уравнение ивда
М [и}=0 (после переноса всех членов в левую часть) при граничных условиях
=0 (/=!.. 2 k). . ;
Тогда искомое решение доставляет минимум функцноналу
.: в„ J (M [«])MG.+ 2 «/ J
(О) / = » (Г)
где е0, аъ ..., а^—любой набор положительных постоянных, который может
оказаться полезным, чтобы в каком-то смысле уравнять влияние уравнения и
всех граничных условий. (Впрочем, можно положить для простоты все а/=1.)
К- функционалу E3) можно применить метод Ритца с любой системой базис-
базисных функций, например целых рациональных одночленов, так как граничные
условия теперь сняты. Возможен частный случай, когда "уравнение М [и)=0
столь просто (например, уравнение Лапласа), что не представляет труда ука-
указать семейство его решений, содержащее параметры н достаточно гибкое для
аппроксимации' искомого решения. Тогда можно в методе Ритца воспользо-
воспользоваться этим семейством и, таким образом, в минимизируемом функционале E3)
останутся только интегралы по (Г).
. Метод очевидным образом распространяется н на системы уравнений
с несколькими искомыми функцними.
1>. Метод Канторовича. Этот метод, предложенный Л. В. Канто-
Канторовичем в 1933 г., представляет собой развитие метода Ритца для
функционалов от функций нескольких переменных. Ои состоит в том,
что в качестве коэффициентов при базисных функциях берутся: не
неизвестные константы, а неизвестные функции от некоторой одной
переменной. Тогда после подстановки и функционал и применения
условий стационарности (уже вариационных!) мы получаем краевую
задачу для системы обыкновенных дифференциальных уравнений
относительно этих неизвестных функций. Решая эту задачу точно

§ 4. прямые Методы
381
иди ¦численно (что—по крайней мере в линейном случае, т. е. дли
квадратичного функционала,— вполне доступно современным вычис-
вычислительным средствам), мы и получаем приближенное решение ис-
исходной вариационной задачи. Так как функции более гибки, чем
константы, то с помощью их оптимального подбора (оптимальность
обеспечивается самой структурой метода) удается значительно лучше
приблизиться к точному решению, чем в методе Ритца.
Рассмотрим в качестве примера задачу о придании стационарного значения
функционалу %
/ {«!•= \ l—1+l — i —2и\ dG E4)
J L\dx/ \dyj I
(С)
при граничном условии
«|(Г>=°> ¦ С55)
где область (G) показана на рис. 113. Для этого воспользуемся базисной функ-
функцией gi(x, у) — у(х—у), равной нулю при у=х и у=0, и по методу Канто-
Канторовича будем искать приближенное решение за-
задачи в виде у
u=a(x)gl{x, y)=a(x)y(x—y), E6)
где функция а (х) будет удовлетворять гранич-
граничным условиям
аA)=0, аB)=0.
E7)
Тем самым произведение E6) будет удовлет- ¦
вор ять граничному условию E5). В методе
Ритца мы задавались видом функции а (х) =
= с(х—1) (х—2), оставляя свободным только
коэффициент пропорциональности с; в отличие
от этого, в методе Канторовича подбор функ-
функции определяется самой постановкой задачи, она будет придавать функциона-
функционалу E4) стационарное значение в классе функций вида E6).
Подстановка E6) в E4) дает после вычислений
Рис. 113.
'М-Дзо*1" +6
(проверьте!). Уравнением Эйлера для этого функционала будет г
xV + Sxa'— 10a=— 5;
оно решается в элементарных функциях (ЛВМ, п. XV. 19), общее решение
имеет вид
f
Подбор произвольных постоянных из условий E7) приводит к решению
2V 2^
2^"-5
= i. (l _ 0,2951л;1'»»—6,7049*-V«).

382 ГЛ. VI. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Эту функцию и надо подставить в E6) для получения приближенного ре-
решения.
Для получения решения с большей точностью можно вместо E6) восполь-
воспользоваться суммой
и=а(х)у(х—у) + Ь{х)у*(х-у) E8)
и после подстановки в E4) получить систему из двух линейных дифферен-
дифференциальных уравнений относительно функций а и Ь. Можно также воспользо-
воспользоваться более простым, ио более грубым методом коллокации (ЛВМ, п. XV-.29)
на части у=0 контура (Г). (Этот прием также был предложен Канторовичем.)
Это делается так: уравнением Эйлера для функционала E4) служит
дац &и _
дх* + ду* """
Вспомнив о том, что точное решение задачи должно ему удовлетворять, потре-
потребуем, чтобы приближенное решение E8) удовлетворяло ему хотя бы при у=0.
Это даст '.
\а" (х) у (х—у)+2а1 (х) у-2а (х) + Ы (х) у2 (х-у) +
у
откуда Ь=^-Bа—1). Подставляя это выражение в E8), мы видим, что при-
приближенное решение надо искать в виде
и=—Ц-(х—у) +? (*г-у2) а(х). E9)
Подставляя в E4), получаем из условия стационарности дифференциальное
уравнение для а (х) и т.'д. Естественно ожидать, что решение вида E9). полу-
получится более точным, чем вида E6), так как новая формула имитирует все те
же свойства точного решения, что и предыдущая, и, кроме них, еще одно. *
Если областью интегрирования служит прямоугольник, то приближенное
решение можно искать также в виде и=а (х)Ь{у), где обе функции а(х), Ь(у)
неизвестные. Написав для них систему уравнений Эйлера, что мы предостав-
предоставляем читателю, можно решать ее методом итераций.
Большое число примеров на метод Канторовича содержится
в книге [44], где он назван методом приведения к обыкновенным
дифференциальным уравнениям.
10. Метод Эйлера. Этот типичный метод дискретизации (см.
введение к этому параграфу), по существу описанный в п. 1.12
в связи с вопросами теории, может быть применен и как численный
метод. Как мы видели, метод состоит в приближенной замене функ-
функционала A.18) на сумму A.61), зависящую от конечного числа
дискретных значений ук искомой функции. Из условий стационар-
стационарности этой суммы можно иайти величины ук, которые естественно
считать приближенными значениями искомого решения в узловых
точках. Если требуются значения решения в других точках, их
можно найти по узловым с помощью интерполяции. Точность метода
легко повысить, применяя более совершенные, чем в A.61), формулы
численного дифференцирования и численного интегрирования.

§ 4. ПРЯМЫЕ МЕТОДЫ
383
Рассмотрим пример, заимствованный из книги [129]. Пусть требуется
минимизировать функционал
при граничных условиях у() у(
приняв п=5; мы получим выражение
/6=о,2
Условия стационарности дают:
= уA)=0. Воспользуемся формулой A.61),
Эта-система линейных алгебраических уравнений, хоть и не диагональная,
легко решается следующим методом прогонки, широко применяемым в настоя-
настоящее время. Из первых двух уравнений исключаем yt; затем из полученного
уравнения и третьего исключаем уг\ наконец, из полученного уравнения и
четвертого исключаем у3 (это этап прямой прогонки). Из оставшегося уравне-
уравнения с одним неизвестным находим yt. Пользуясь .им, из последнего уравнения
заданной системы находим у3; зная yt и у3, нз второго от конца уравнения
системы находим у2; наконец, из третьего от конца уравнения системы находим
ух (это этап обратной прогонки). В общем случае метод прогоикн применяется
для линейных алгебраических систем как угодно высокого порядка, у которых
матрица коэффициентов (а,-/) содержит отличные от нуля элементы лишь на
главной диагонали и недалеко от нее при \i—/|<} (как в разобранном при-
примере) или при |t—/|<2 и т. п.
Приведем результат решения системы F0), а также точные значения иско-
искомой функции (в данном примере уравнение Эйлера легко решается),
X
—104уприбл
—104Угочн
0,0
0
0
0,2
286
287
0,4.
503
505
0,6
580
583
0,8
. 442
444
1,0
0
0
Как видим, результат неплох. Однако отметим, что приведенные рассужде-
рассуждения имеют скорее методическое значение, так как в вычислительном отношении
процедура получается в точности такая же, как если от вариационной задачи
перейти к уравнению. Эйлера, а затем решать для этого уравнения краевую
задачу с помощью обычного разностного метода.

Г л а в а VII
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Теория интегральных уравнений, т. е. уравнений, в которых
искомая функция находится под знаком интеграла, - составляет сей-
сейчас значительный отдел математического анализа и имеет большое
теоретическое и прикладное значение. Хотя отдельные интеграль-
интегральные уравнения встречались уже в первой половине XIX в., но си-
Стематиче'ская их теория была заложена на рубеже XIX и XX вв.
в работах итальянского математика В. Вольтёрра A860—1940),
шведского математика И. Фредгбльма A866—1927), Д. Гильберта
и других математиков.
Из общих курсов интегральных уравнений укажем на [40, 73,
87, 88, 96, 105, 114, 129].
§ 1. Введение
1. Примеры. Мы уже упоминали в ЛВМ, п. XIV.26, что если
внешнее воздействие на какую-либо линейную систему описывается
функцией /(х) {а^.х^.Ь), то результат этого воздействия описы-
описывается функцией . ,
ь
/(*)=>$ О(*; &/(&)«$, A)
а
где С(х\ ?)—функция влияния, определяемая рассматриваемой си-
системой. Например, /(х) может означать плотность нагрузки, рас-
распределенной вдоль балки, а /(х) — соответствующий прогиб и т. п.
Допустим, что вид воздействия нам неизвестен, но известен
отклик системы на это воздействие и требуется по этому отклику
восстановить воздействие. Тогда в соотношении A) функция f (х)
(как и О(х; %)) будет заданной, а /(х)—искомой, т. е. мы прихо-
приходим к интегральному уравнению.
Бывают случаи, когда известной оказывается некоторая линей-
линейная комбинация <р (дс) = ос/ (х) + $/(х) функций, описывающих внешнее
воздействие и соответствующий отклик. Тогда для восстановления
внешнего воздействия потребуется решить интегральное уравнение
ъ
а/(х)+$ I G(х; I)/&)<%=<д(х}. B)

§ 1. ВВЕДЕНИЕ 385
Приведем еще одну задачу, сводящуюся* к уравнению вида B).
рассмотрим уравнение вынужденных поперечных колебаний струны,
закрепленной,при х — 0 и х=*1 (см. (VI.3.59)):
* - P»"u = Pu'xx+f{x, t). C)
"'; Если внешнее воздействие является гармоническим,
~п нас интересует вынужденное колебание, происходящее с той же
частотой о, т, е.
в {х, t) = v (x) cos <о/,
то после подстановки в C) мы приходим к краевой задаче
При <в==0 получилась бы задача на стационарное отклонение струны
под действием внешней нагрузки; эта задача в других обозначениях
и без физического истолкования была рассмотрена в ЛВМ, конец
п. XV. 16. Там было получено решение
е где функция влияния в данной задаче равна
Г
?•• Однако при ш^О к внешней нагрузке ц> (х) добавляется инер-
дионный член pa>*v(x), зависящий от искомого решения. Если
на минуту считать его известным и воспользоваться решением D),
то мы придем к соотношению -
i i
Но так как v(x) на самом деле неизвестна, то это соотношение
представляет собой интегральное уравнение, принем того же типа,
что и B).
Появление интегральных уравнений при исследовании краевых
задач является естественным, так как такие уравнения связывают
¦ежду собой значения известных и неизвестных функций на конеч-
конечном интервале, а не на бесконечно малом, как дифференциальные
авнения. .
;13 А. Д. Мышнве

386 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
2. Основные классы интегральных уравнений. Интегральное
уравнение
ь
\К(х, ?)в(?)<?«=/(*) (<*<*<&) E)
а
с искомой функцией и (л:) называется уравнением Фредгольма 1-го
рода, функция К(х, |) называется ядром этого уравнения. Уравнение
ь
и{х)=1к(х, l)u(l)dl+f(x) F)
а
называется уравнением Фредгольма 2-го рода. Это, очевидно, линей*
ныс неоднородные уравнения; если /=0, получаются соответ-
соответствующие однородные уравнения.
Если в E) или F) интеграл распространен от а до х, то гово-
говорят об уравнениях Вольтерра 1-го или 2-го рода. Впрочем, если
для уравнения Вольтерра формально положить К (х, ?) = 0 при | > х,
то его можно считать частным случаем уравнения Фредгольма (про-
(продумайте это!). Другой важный подкласс уравнений Фредгольма со-
составляют уравнения с симметричным (иначе симметрическим) ядром,
для которого К(х, ?) — К(^,, х) в вещественном случае и К(х, ?)—
= [/С(|, х)]* в комплексном; в комплексном случае такие ядра назы-
называются также эрмитовыми, как и матрицы (п. IV.1.3). Рассматри-
Рассматриваются также уравнения с ядрами вида К(х, |)=7(х—Ъ), завися-
зависящими от разности аргументов, н т. д.
Наиболее прост случай, когда а и b конечны, а ядро К(х, |) —
непрерывная функция. Основные свойства решений, которые мы
будем рассматривать ниже, оказывается возможным без большого
труда распространить также на квадратично суммируемые ядра,
зля которых выполнение указанных условий не требуется, но
ь ь
l\\K{xtl)\tdxd^<0oi G)
а а
поэтому многие авторы говорят о фредгольмовых или вольтерровых
уравнениях, если только выполнено это условие.
Если ядро обращается в бесконечность, то обычно это проис-
происходит при x = Z- Поэтому специально рассматривается класс урав-
уравнений со_ слабой особенностью, для которых при конечных а и b
^У @«х<1). (8)
Если при этом 0<ос<у, то выполняется условие G) (почему?),
т. е. уравнение является фредгольмовым. Если ос=1, то интеграль-
интегральные уравнения E) и F) называются сингулярными, тогда интеграл
надо понимать в смысле главного значения (ЛВМ, и. XIV.19).

§ 1. ВВЕДЕНИЕ 387
Нелинейные уравнения изучены и расклассифицированы гораздо
менее полно, чем линейные. Некоторые виды нелинейных уравнений
мы рассмотрим в § 6.
' Приведенные определения естественно распространяются на си-
системы т интегральных уравнений с т искомыми функциями, а также
на уравнения с искомыми функциями от л независимых переменных.
В последнем случае аналог уравнения F) имеет вид
и (М) = J К (М, N) и (N) dNG+f(M), (9)
(О)
где М и N—точки некоторой л-мерной области (или даже л-мер-
ного многообразия) (О), а значок N при дифференциале указывает,
по какой точке происходит интегрирование; впрочем, уравнение (9)
можно записать и в координатной форме с л-кратным интегралом.
Определение ядра со слабой особенностью, взамен (8), имеет вид
где р (М, N)— расстояние между точками М и N.
Рассматриваются также нагруженные интегральные уравнения, в который
вместо обычных интегралов (интегралов Лебега) применяются интегралы по
мере (интегралы Стилтьеса, см. ЛВМ, п. XVI. 19):
н(М)=2 J K/(M> N)u{N)dN]4+f(M). A0)
1@)
Например, если кроме меры Лебега рассматривается мера, сосредоточенная
в точке M0?(G), то получается нагруженное уравнение вида
и(М)= \ К(М, N)u(N)dflG+L(M)u(M0)+f(M) , ,.
(О)
(продумайте это!) и т. п.
3. Еще о пространстве Гильберта. В п. VI.1.3 мы уже упоми-
упоминали о пространстве Гильберта Ьг [а, Ь] (а и Ъ не обязательно
считать конечными) квадратично суммируемых функций с нормой
(VI.1.11). При этом мы будем для определенности рассматривать
вещественное пространство, т. е. будем считать, что функции при-
принимают вещественные значения; комплексное пространство Гильберта
вводится совершенно аналогично, в нем норма определяется фор-
формулой
/~~ь
\f(x)\*dx.
Здесь под f понимается функция /(*), рассмотренная как элемент
(обобщенный вектор) линейного, пространства.
В ЛВМ, п. XVII.28 мы уже упоминали, что пространство' Гиль-
Гильберта—- это бесконечномерное евклидово пространство :со
13*

388 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
скалярным произведением
ь
_(*,«)=] f(x)g(x)dx (t, g ?L2[a,b]).
a
Из указанных там свойств отметим неравенство
/6 \ 2 6 Ь
{\f(x)g(x)dx)^\p(x)dx\g*{x)dx, (И)
\а / а а
которое можно переписать более наглядно так:
¦ • i(t.g>i<imiii*ii.
Покажем, что если ядро К(х, у) удовлетворяет условию G) и
ц [х) € Lt [a, b], то и ,
ь
\к(х,1)и(Ъ)й\<Цг[а,Ъ}. A2)
а
В самом деле, применяя неравенство A1), получаем
Ь /Ь \2 6/6 6
6 6 6
A3)
Таким образом, если обозначить левую часть A2) через А и (х), то А пред-
представляет собой линейный оператор, отображающий пространство L2 [a, ft] в себя.
Если извлечь квадратный корень из обеих частей неравенства A3), то это не-
неравенство можно переписать в виде
A4)
где обозначено
Линейный оператор, удовлетворяющий оценке A4), называется ограниченным,
а наименьшее значение постоянной М, для которого выполняется оценка A4),
называется его нормой (ср. аналогичные определения для функционалов
в п. VI.1.5). Таким образом, интегральный оператор А с ядром, удовлетворяю-
удовлетворяющим условию G),— это линейный ограниченный оператор в Ц [a, ft]. В терми-
терминах этого оператора уравнение F) можно переписать в виде u = Au4-f- Это.по-
Это.позволяет включить теорию интегральных уравнений Фредголы^а в более общую
стройную теорию операторных уравнений. Мы упомянем об этом в п. 2.11.
Аналогичными свойствами обладает пространство Гильберта на области мно-
многообразия любого числа измерений, для функций, принимающих векторные
значения, а также при использовании любой неотрицательной меры и (т. е.
р^О)

: §2. ТЕОРИЯ ФРЕДГОЛЬМА 389
§ 2. Теория Фредгольма
В §§ 2 и 3 всюду, где не оговорено противное, будет считаться,
что ядро удовлетворяет условию G), а неоднородные члены уравне-
уравнений и решения берутся в L2[a, b]; впрочем, почти всюду читатель
может для простоты считать все функции непрерывными. Мы будем
рассматривать уравнения Фредгольма 2-го рода, теория которых
значительно проще, чем уравнений 1-го рода, причем более подробно
будем разбирать одномерный случай. Рассматриваемые в этом пара-
параграфе функции, вообще говоря, могут принимать комплексные зна-
значения.
1. Уравнения с вырожденными ядрами. Ящ>оК(х, ?) называется
вырожденным, если его можно представить в виде суммы
произведений функций, зависящих только от л; и только от |.
Например, если ядро представляет собой многочлен от х, |, то оно,
очевидно, вырожденное.
Без. ограничения общности можно считать, что система функ-
функций Фу (я), равно как и Wjfe), линейно независима. В самом деле,
если, например, Ф, (х) линейно выражается через остальные Фу (х),
то, подставив это выражение в A) и сгруппировав члены с одина-
одинаковыми Фу, мы просто получим представление ядра с помощью
меньшего числа слагаемых (продумайте это рассуждение!).
Мы будем рассматривать уравнение A.6) с добавочным множи-
множителем (параметром) Я, при ядре, который окажется полезным во
многих вопросах, т. е. уравнение
Ь V . . .
и (*)» A, J К(х,1)« ft) <% +/(х) =
в
ь р
5'^
Оказывается, что оно немедленно сводится к системе р линейных
алгебраических уравнений с р неизвестными.
В самом деле, допустим, что решение и (х) уравнения (Щ- при
заданном Я, существует, и обозначим
ъ , ъ v
uJ=[v/Wu(x)dx[ = lvj®u$,)db) (/=1,2 р). C)
а \ а / ........
Тогда из B) получаем
¦ 𠦕
а (*)== Я Д«уФу (*)+/(*). * D)

3<Э0 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Изменив обозначение индекса суммирования на k (зачем?) и подста-
подставив в C), получаем
и,-*. Jj а/как=/, (/=1,2,..., р), E)
где обозначено
ь ь
aJh = \ Wf(x)Ok(x)dx, /у = S Wj(x)f(x)dx (/, й- 1, 2, ..., p).
a a
Обратно, легко проверить (проделайте это!), что, подставив
любое решение системы E) в правую часть D), мы получим реше-
решение уравнения B), причем удовлетворяются равенства C). Таким
образом, формулы C) и, как мы видим, обратная к ним формула D)
устанавливают взаимно однозначное соответствие между
решениями интегрального уравнения B) и решениями системы линей-
линейных алгебраических уравнений E).
Как известно, разрешимость системы E) зависит от ее опре-
определителя
/ ь ч
D (к) = det ф/к—kaJk) = det f bJk—к \ 4f (x) Фк (x) dx):
\ a /
если D (к) Ф 0 (основной случай), то система имеет ровно одно ре-
решение, если же ,
= 0 F)
(особый случай), то она либо не имеет ни одного, либо же имеет
бесконечное количество решений. В силу предыдущего абзаца этим
же свойством обладает уравнение B). Для этого уравнения D(X)
называется определителем Фредгальма, а его нули, т. е. корни урав-
уравнения F), называются характеристическими числами. 1ак как D (к) —
многочлен степени ^р, то мы получаем, что уравнение B) имеет
не более р характеристических чисел.
Из доказанного вытекает также, что если значение X не является
характеристическим, то уравнение B) имеет ровно одно решение
при любой функции f(x). Это первая теорема Фредгальма. Иногда
ее формулируют так: для того чтобы уравнение B) имело ровно
одно решение при любой функции f(x), необходимо и достаточно,
чтобы -соответствующее однородное уравнение (т. е. уравнение B),
в котором положено /(л;) = 0) имело только тривиальное решение
и(х)=вО.
Если решать систему E) по формулам Крамера (ЛВМ, п. VI.4),
а затем определители, стоящие в числителях, разлагать по элемен-

§ 2. ТЕОРИЯ ФРЕДГОЛЬМА 391
там столбца свободных членов, то получатся выражения вида
= 1,.2, ...,
где Djk(%) — некоторые многочлены степени не выше р—1 (почему?).
Подставляя эти формулы в D), получим
т. е.
в (*) = *.$ Г (*, 6; *)/F) <?+/(*), G)
а
где обозначено
I). . (8)
/=ik=i
Это так называемая резольвента уравнения B) (от латинского
resolvo—решаю, так как через нее по явной формуле G) выражается
искомое решение). При фиксированных х, | она представляет собой
дробную рациональную функцию комплексного переменного Я. Под-
Подставив G) в B) (для чего надо в первом интеграле B) поменять
обозначение переменной интегрирования) и воспользовавшись произ-
произволом функции f{x), получим уравнение, которому должна удовле-
удовлетворять резольвента (проверьте!):
ь
Г (*, I; к) = I J К(х, ц) Г (ть I; к) dx\ + K(x, I); (9)
а .
в нем не только к, но и ? служат параметрами.
Рассмотрим однородное сопряженное (иначе, союзное) с B) урав-
уравнение
? "
таким образом, сопряженное ядро получается из исходного с помощью
перестановки независимых переменных и перехода к комплексно
сопряженным значениям (вспомните определение сопряженных матриц).
Обозначив через Ь,к и Е (ц.) новые значения коэффициентов ujk и

392 ГЛ. VIC. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
определителя Фредгольма, легко получим
- $ Ф/
*= [det F/ft—(A&/ft)]*=det (в4у-|1%) = det {Ь„-
Отсюда сразу следует, что если Я, служит характеристическим числом
уравнения B), то "К* служит характеристическим числом сопряжен-
ного уравнения A0) (конечно, и обратно, так как уравнения B) и
A0) взаимно сопряженные). Кроме того, из (8) легко вывести (по-
(попробуйте!), что резольвентой уравнения A0) при ц = ^,* служит
(Г (?, х; Я,))*; написав уравнение вида (9) для этой резольвенты и
перейдя к сопряженным величинам, а затем поменяв обозначения
х и ?, получим еще одно уравнение для резольвенты -*•
Г(дг, Б; Ь) = Ь$К(ть |)Г(х, itk)di\J-K(x, I) A1)
а
(проверьте!).
Пусть теперь К—характеристическое число уравнения B). Тогда
все решения однородного уравнения, отвечающего B), называются
собственными функциями уравнения B). Они образуют линейное
пространство, размерность которого (т. е. число линейно независи-
независимых собственных функций, отвечающих 'выбранному характеристи-
характеристическому числу) равна размерности пространства, решений однородной
системы уравнений, отвечающей E) (почему?). Но эта размерность
равна р—rangFyft—kajk) (ЛВМ, п. XI.5), а потому размерность ана-
аналогичного пространства для уравнения A0) при (»=Д* равна
р—rang (b/k—X*bJk) =p—rang (bkJ—Ьа/к)*=р—rang (bJH—Ka/k),
так как у сопряженных матриц ранги одинаковые. Итак, размерности
пространств собственных функций уравнения B) для характеристи-
характеристического числа X и сопряженного уравнения A0) для |л = Л,* конечные
и одинаковые. Это вторая теорема Фредгольма.
Запишем уравнение B), как в конце п. 1.3, в форме u=A,Au+f. Если
X,— характеристическое чясло, то ураиненяе и=Я,Аи, т. е. Au=-r-u, имеет
А ¦ ~ .
нетривиальное решение; таким образом, -т- (а не Я,) является собственным зна-
значением оператора А, а соответствующие собственные функции оператора—это
как раз собственные функции интегрального уравнении. Очевидно, и величина,
обратная любому ненулевому собственному значению оператора А, является
карактеристическим числом уравнения B).
Отметим еще, что в силу § IV.3 размерность пространства собственных
функции, отвечающих выбранному характеристическому числу X, может либо
равняться кратности корня К уравнения F), либо быть меньше этой кратности
(так как, кроме собственных векторов, бывают еще присоединенные!). '

§ 2. ТЕОРИЯ фРЕДГОЛЬМА 393
Рассмотрим, наконец, неоднородное уравнение B) в случае, когда
к—-характеристическое число. Тогда для существования по крайней
мере одиогв решения у уравнения B), т. е. у системы E), функция /
должна удовлетворять некоторым дополнительным условиям. Как было
показано в п. IV. 1.4, для существования по крайней мере одного
решения у системы линейных алгебраических уравнений необходимо
и достаточно, чтобы столбец свободных членов был ортогонален
любому решению сопряженной однородной системы уравнений. В при-
применении к системе E) это означает, что должны выполняться ра-
равенства
р
?//»/= О A2)
Для любого решения Vj системы уравнений
/Ля0 (/=1, 2, ...,/>).
Равенства A2) можно переписать так:
Е (l%(x)f(x)dx^(jo)(x)v(x)dxSJ =0, A3)
где v(x) — соответствующее решение уравнения A0) при |а = А,*.
Заменяя во втором интеграле обозначение переменной интегрирова-
интегрирования на ? и объединяя оба интеграла, перепишем A3) в виде
ь ь р
S
а 1=1
Отсюда, применяя соотношение A0) и сокращая на X, получим
окончательно
ь
Q. A4)
Итак, если К—характеристическое число, то для существования
у уравнения B) по крайней мере одного решения необходимо и до-
достаточно, чтобы функция / была ортогональна всем решениям
однородного сопряженного уравнения A0) с |а = ЛЛ Это третья
теорема Фредгольма. Если это условие ортогональности выполнено,
то общее решение уравнения B), как у любого линейного неодно-
неоднородного уравнения, равно сумме какого-либо его частного решения
и общего решения соответствующего однородного уравнения.
В формулировке третьей теоремы Фредгольма можно убрать тре-
требование характеристичности X.; тогда она вместе со второй теоре-
теоремой будет содержать первую как частный. случай (продумайте это!).

394 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Выведем формулу для представления решения уравнения B) через резоль-
резольвенту в случае, «основном среди особых», когда звачение Я = А0 служит про-
простым нулем определителя D (к). Тогда в силу (8)
Ь Ц, - A5)
где функция 1\ аналитична при к—к0. Подстановка в (9) показывает, что
откуда видно, что Г0(д:, ?) при фиксированном ? должна быть пропорциональ-
пропорциональна единственной собственной функции ио(х) ядра К, отвечающей собственному
значению А,о. Привлекая еще аналогичное рассуждение для A1), получаем, что
Т0(х, ?)=Соио(х)[»„(?)]*, где vo(x)—единственная собственная функция со-
сопряженного ядра при Я. = А.0-
Подставляя разложение A5) в G), получаем
Пусть теперь К —»• А,о. Мы вновь видим, что функция 4 М должна быть орто-
ортогональна собственной функции оо (х); если же это условие выполнено, то мы
.юлучаем при Я=л.„
ъ
и(х)=К J Г,(ж, I; K)ta)dl+f(x)+Cu0(x),
а
где С—произвольная постоянная. Это и есть требуемое представление. Если
>ч—собственное значение произвольной кратности, то представление имеет
тот же вид, причем 1\ — регулярная часть разложения резольвенты в ряд Ло-
раиа около точки Ко.
Отметим, что мы нигде не пользовались упомянутой в начале
пункта линейной независимостью систем Фу и W/, однако уменьше-
уменьшение р, возможное в случае линейной зависимости, очевидно, выгодно
при вычислениях.
2. Общий случай. Рассмотрим теперь общее уравнение Фред-
гольма 2-го рода
ь
A6)
с параметром—множителем при ядре. Ядро К можно с любой сте-
степенью точности аппроксимировать вырожденными ядрами. Такую
аппроксимацию можно осуществить многими способами: с помощью
разложения в двойной ряд Фурье (ЛВМ, п. XVII. 30) или восполь-
воспользовавшись какой-либо иной ортогональной полной системой функ-
функций, с помощью аппроксимации многочленом от х, ? и т. д.' Если
ядро непрерывно и пределы a, b конечны, то аппроксимацию можно

§ 2. ТЕОРИЯ ФРЕДГОЛЬМА 395
осуществлять в смысле пространства С (т. е. в смысле равномер-
равномерного уклонения); если разрывно — то в смысле Lt; см. по этому
поводу [58].
Заменив ядро на вырожденное, можно к полученному уравнению
применить все результаты п. 1. Тем самым все теоремы Фредголыла
оказываются справедливыми и для общего уравнения A6) с ядром,
удовлетворяющим условию A.7). (В более полных курсах интеграль-
интегральных уравнений, указанных выше, законность такого перехода дока-
доказывается со всей строгостью.) Единственным существенным отли-
отличием от п. 1 является то, что в общем случае определитель
Фредгольма D(К) уже не является многочленом. При все более точ-
ной; аппроксимации ядра вырожденными количество слагаемых, т. е.
р, приходится увеличивать, н в пределе D(k) становится «много-
«многочленом бесконечной степени»—^целой аналитической функцией.
Поэтому и характеристических чисел у уравнения A6) может быть
бесконечное количество (впрочем, их может быть и конечное коли-
количество и даже, как мы увидим, ии одного). Не так как D@)=l,
то D(X)j?0, и потому по одной из теорем теории аналитических
функций (п. II.2.6), если характеристических чисел бесконечное ко-
количество, то их можно расположить в последовательность Xv ha,
^,j, '..., уходящую на бесконечность. Это четвертая теорема Фред-
Фредгольма.
Соответственно и резольвента Г (х, 5; К) в общем случае равна отношению
двух целых функций и потому представляет собой уже^ не рациональную, а
мероморфную функцию (п. II.3.12).
Однородное сопряженное уравнение взамен A0) в общем случае
имеет вид
ь - ,
v (х) = |i J L (х, I) v (I) dl, где ' L (х, I) = [К (Б, *)]*. A7)
а
(Можно обозначить сопряженное ядро через К*, но тогда придется
писать К* (х, |) = [/((?, ¦*)]*» чт0 требует известной бдительности.)
Сопряженное ядро связано с исходным ядром простым соотноше-
соотношением: для любых функций ф (лс) и г|з (дг)
ЬГ Ь  Ь Г Ь ~\*
J J К{х, I) ф (I) dl г|>* (x)dx= $ Ф (х) К Цх, I) ф (Б) dl dx A8)
о l_a J a \_a J
о
(проверьте!).
Если исходное уравнение, как A.6), не содержит параметров, то
для применения первых трех теорем Фредгольма надо положить
Л, = |д, == 1. При этом взамен «если 1 не является характеристиче-
характеристическим числом» можно говорить «если однородное уравнение, соответ-
соответствующее данному, имеет только тривиальное решение». Тогда го-
говорят также, что имеет место первый (иначе основной) случай

396 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
альтернативы, Фредгольма (альтернатива — необходимость выбора
между двумя, как в данном случае, или несколькими исключающими
друг друга возможностями), если это не так—то второй (особый)
случай альтернативы.
Описанный теоретический подход является одновременно методом
численного решения уравнения A6) при конкретных Я, а также ме-
методом численного отыскания характеристических чисел и собствен-
собственных функций этого уравнения.
Рассмотрим в качестве примера уравиенве
причем будем искать его характеристические числа, а также решение при
Я. = -д-. Воспользуемся разложением синуса в ряд Маклорена
Взяв сначала одни член ряда» получим уравнение
и (x)=X
о
Согласно п. 1 надо обозначить
1 '¦''.¦
«i=$6«tt)d8, B0)
о
что даст
— а (*)=*«,*+1.
Подстановка этого выражения в B0) даст
Отсюда характеристический определитель
D"» (А,) = 1 — -— = 1 — О.ЗЗЗЗХ..
единственное характеристическое число- А.<1>=3, а решение ири Х=ту
««>(*) = 1+0,3* @<*<1).
Взяв два члена ряда A9), получим (проверьте!)
1

§ 2. ТЕОРИЯ ФРЕДГОЛЬМА
S97
i-i
B1)
i+-
+ 42
=1—^Х —
*^!—0.3095X—0.0013Х*.
^'=3,16,
> = —247,
, - ;««• (*) = 1+0,297*—0,025x* @<;*<;l).
Отчетливо в в дна сходвмость првближенных выражеввй для D (К), %1 и и (х)
при увелвчеиви pel до 2. Мы предлагаем желающем положить />=3, т. е.
взять трв члена ряда A9) в посмотреть, какие получатся следующее првблв-
жевня. Отметвм, что прв решение евстем ввда B1) с относительно малым Я,
можно пользоваться методом втерацвй (ЛВМ, п. VI.5), а при решевви алгеб-
ранческвх уравненвй с корнямв, значвтельно разлвчающвмвея по абсолютвой
велнчвне, удобно вспользовать соотвошеивя между корнямв (ЛВМ, (VIII.33)).
Например, уравненве Dw (к)=0 можно было решать так: свачала перепвсав
его в виде Ji=(l— 0,00Ш2)/0,3095 в вачав с ^"'=3, найтв втерацвямв Ji{2),
после чего воспользоваться формулой для суммы корней квадратного ураввенвя.
Укажем еще одвн метод численного решеивя уравненвя A6), освованвый
на првмеиенвв формулы A8) в нэпом внающвй метод моментов (ЛВМ,
п. XV.29). Еслв в формуле A8) вместо ф(лг) взять вскомое решенве и (х) урав-
уравнения A6), мы получим равенство
6 г Ь -\* Ь
г
b(x)U(x)-X*
J
которое должно выполняться для любой функцвн ip (х). Подставвм вместо ij) (x)
какне-лнбо фуикцив i|>i (ж), tyi(x), .... 1|)л(ж), обычво это первые п членов
некоторой полной евстемы фувкцвй. Тогда получвтея
Ь Ь
J и (х) gf (х) dx= J / (х) tf (x) dx (/=1.2 я), B2)
а а
где обозначено
• 6
8/ (*) = % (*)-^* J L(x, 8)ty®*
.••:.•¦¦.¦• а ¦ ¦ '
Таким образом, вскомая .фуикцвя и(х) должва удовлетворять п лввейным
соотвошевиям, в потому ее естествевно искать в ввде лнвейиой комбвнации
B3)
какой-либо системы функций hk (х) с п произвольными коэффицвентамн. Под-
Подстановка B3) в B2) првводит к евстеме нз п алгебранческвх лннейвых урав-
уравнений, из которой можно найти эти коэффициенты, а потому и приближенное

398 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
решение B3) уравнения A6). В качестве h^ (х) обычно берутся первые
члены какой-либо полной системы функций. В частности, если А, не является
характеристическим числом, то можно положить Л^ (*)=gft (х), так как в этом
случае нетрудно проверить, что н система функций g* полна. (Докажите это,
исходя из следующего, равносильного определения полноты: система функций
полна в Lt \a, b], если ненулевая функция не может быть ортогональна всем функ-
функциям из этой системы.) Можно предварительно ортогоиализовать функции gf,
тогда система уравнений для нахождения С/, будет диагональной.
Все' приведенные общие результаты непосредственно распрост-
распространяются на уравнения вида A.9) с искомыми функциями от не-
нескольких переменных, на нагруженные уравнения A.10), а также на
системы т уравнений с т искомыми функциями. Такие системы
можно записывать в том же виде A6) или A.9), но К считать мат-
матрицей /ихт, а и и /—векторами. Конечно, тогда условие ортого-
ортогональности, аналогичное A4), имеет вид ^f*vdG=0.
3. Применение бескоиечных систем алгебраических уравнений. В примере
п. 2 можно было воспользоваться и полвым рядом A9); и в некоторых дру-
других примерах бывает возможно разложить ядро в ряд по вырожденным ядрам
вида
Тогда возможно— во всяком случае, в теории—точное построение решения По
методу п. 1, но с заменой верхнего предела суммирования р иа оо, т. е. в
виде суммы бесконечного ряда. Правда, вместо E) получится система
со
M/-Ji2a/ft"ft=// (/=1,2,3,...) B4)
k=\
из бесконечного числа уравнений с бесконечным числом неизвестных, которую
на практике обычно приходится решать методом усечения, т. е. путем пере-
перехода при некотором выбранном р к снстеме E), так что получается то же самое,
как если с самого начала приближенно заменить ядро К иа вырожденное.
Однако бывают случаи, когда удается решить точно полную систему B4) или
извлечь из нее какие-либо полезные следствия.
Например, такое точное решение возможно, если системы функций Фу (х)
и 4Fj (х) биортогональны, т. е.
В самом деле, тогда внедиагональные члены системы B4) обратятся в нуль и
ее точное решение будет иметь вид
= (!-*$*/(*) Ф/ (х) dx ) fj (/=1, 2, 3,...).

§ 2. ТЕОРИЯ ФРЕДГОЛЬМА 399
Характеристическими числами будут служить тогда
/Ь
» = 1, 2,
(если апп Ф 0), а соответствующими собственными функциями—функции Ф„ (л;).
Другой важный частный случай—если бесконечная матрица (ад) треу-
треугольная, т. е. если все а/ь=0 при / > k (верхняя треугольная матрица), либо
все fl/ft —0 при / < k (нижняя треугольная матрица). В обоих случаях, при-
приравнивая нулю, определитель, находим характеристические числа А,„=а~в'
(л = 1, 2, 3,...). Для верхней треугольной матрицы легко найти соответству-
соответствующие собственные функции, так как, положив в однородной системе B4)
"n + i=un + 2= • • • =0, мы приходим к однородной системе п уравнений с л
неизвестными и нулевым определителем. Поэтому собственные функции будут
иметь вид конечных линейных комбинаций функций Ф/(*>- (Докажите, пап-
'{¦:
ример, что числу ^ отвечает собственная функция Фх (х); числу Я,8—собствен-
Я,8—собственная функция Ф2 (х) ——Ф1 (•*) и т д.; конечно,' предполагается, что
аХ1—а22
встречающиеся при этом знаменатели отличны от нуля.)_
Особенно прост случай, когда а/й=0 при всех / > k и всех / < k—1.
Тогда однородная система B4) имеет вид
A — Kajj) и, — Jw/./+i и/+1=0 (/== 1, 2, 3,...),
откуда
вообще
Jjllf±!i) («=1.2,3,...)
(при т=1 получается произведение без сомножителей, оно полагается равным
единице). Отсюда при к — <*~,} получается опять, что и„+1 = и„+2=.<. =0, и
мы приходим к явным выражениям для иъ и2 ип. Можно показать, что
прочие значения % приводит, вообще говоря, к расходящимся рядам для
и (х), т. е. собственных функций не дают.
Для иижией треугольной матрицы (ад) легко найти решение неоднородион
системы B4) (как?). Однако вид собственных функций получается более сложным,
чем для верхних треугольных матриц. Например, подставив h=h1=a-f в од-
однородную систему B4), получим последовательно
___Дз1ц1+Д3аИ2_ Г Дз1 i а21вза "Г
ац—а33 Laii—азз (аи—а2г) (fln—a3s)J l
3
и т. д. Подставляя в формулу D) (с р=оо, /^0), получим выражение первой
собственной функции в виде суммы ряда. При вычислении собственной функ-
функции, отвечающей числу Х=^%п=а-^, надо положить и1=и2= ... =и„_1==0,
а затем с помощью аналогичной процедуры выразить остальные коэффициенты
м/ через ип.
Бесконечные системы уравнений вида B4) встречаются в различных разделах
прикладной математики, однако здесь мы не будем излагать общие свойства
таких систем (см., например, § 1.2 книги [44]). На практике эти системы часто

\
400 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
переписывают в виде • ¦ • • . ¦
¦ «/=*• 2 «/*«*+// (/=1,2,3,,..), B5)
после чего применяют естественный метод итераций, который приводит к цели,
если все коэффициенты 1лjk достаточно малы. Если коэффициенты с малыми /, k
ие малы, то можно несколько, скажем, «, первых уравнений B5) разрешить отвоси-
тельно и,, «J, .... и„, после чего нрнписать к нолучеииым формулам прочие
уравнения B5) н проводить итерации.
Имеется еще один интересный класс систем B4), также встречающийся в
приложениях, для которого a/*=0 при | /—к] > 1. Рассмотрим здесь только
однородные системы, т. е. системы вида
A-
[— %a22) иг — %а23и3=О,
—ba32u2+(l—},ag3)u3—'ka3iUt=Q,
Обозначив —?±i=l/ft, =Pft, —=Qk' *' к+1—гк* получаем (нро-
верьте!) ' "
-1t/*=0 (fe=2, 3,4, ...).
Отсюда
При fe=2 это даст
Подставляя fe=3 в B7), а затем результат в B8), получим :
1/,= 1- . B9)
Затем: подставляем *=4 в B7), а результат в B9) и т. д. Мы приходим, н
бесконечной цепной (иначе непрерывной) дроби, которая условно записывается
так:
Ul== ptb-i-q2- psl-i- qt- PiX-i-qt- ••• <30>
Цепные дроби имеют интересные свойства и разнообразные применения, на
которых мы здесь ие будем останавливаться. При вычислении таких дробей
для коэффициентов общего вида нх на практике просто обрывают, т. е. нере-
ходят к конечной цепной дроби; это равносильно тому, чтобы в рекуррентном
соотношении B6) положить какое-либо 1?п=0, а затем последовательно найти
Из C0) и.первой формулы B6) получается уравнение для характеристи-
характеристических чисел Я,. Если его удастся решить каким-либо приближенным методом,
то из B6) легко последовательно найти Uu Ua, U3, .... т. е. и соответствую'
щую собственную функцию.
Отметим в заключение, что у системы B4) может оказатьсн лишь конеч-
конечное число отличных от нуля коэффициентов ajk; этот случай, конечно, теоре-
теоретически-наиболее прост. ¦ ¦ •:.

§2. ТЕОРИЯ ФРЕДГОЛЬМЛ • 401
4. Применение числениого интегрирования. К теорема» Фред-
гольма можно прийти также другим способом, который тоже может
служить основой для численного метода. Для этого применим к ин-
интегралу A6) какую-либо из формул численного интегрирования
(ЛВМ, п. XIV. 13). Каждая из таких формул имеет вид
ft=i
где xk—некоторые узловые точки, а Нк—коэффициенты. После
такого применения подставим вместо х любое из узловых значений
и заменим знаки я* на =. Получится
«/ = * 2#** (*/> *k) »k+fj U= 1,2,..., л), C2)
ft=i
где обозначено
«/ = «(*/), //=/(*/)•
Возьмем, например, одну из довольно грубых формул:
-4, ЯЛ = А, где А=Ь^; C3)
тогда равенства C2) примут внд
«, = ХН 2 К (хр xk) uk+fj (У= 1, 2, ..., /i). C4)
Другими словами, мы воспользовались тем, что интеграл—это • по
существу, сумма большого числа малых слагаемых. Таким образом,
мы непосредственно пришли к системе из л линейных алгебраиче-
алгебраических уравнений с п неизвестными. Так как для таких систем тео-
теоремы Фредгольма представляют собой переформулировки их условий
разрешимости, то этим теоремы в пределе при л—»-оо распростра-
распространяются и иа уравнения A6).
Этот метод также возможно полностью математически обосно-
обосновать. Тем не менее я предпочел начать с вырожденных ядер не
только из-за того, что в простых задачах их применение наиболее
эффективно, но также из-за того, что уравнения с вырожденными
ядрами—это уже интегральные уравнения, тогда как уравнения C2)
в принципе требуют предельного перехода.
На практике, конечно, стараются подобрать формулу типа C1),
которая при одном и том же объеме вычислений давала бы наилуч-
наилучшую точность. Разнообразные методы численного интегрирования
содержатся в курсах приближенных вычислений; специально этим
методам посвящена книга [61]. Здесь мы в дополнение к материалу
ЛВМ остановимся лишь на методе Гаусса, одном из наиболее эф-
эффективных.

4Q2 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Прежде всего с помощью линейной замены переменной интегри-
интегрирования х— а + (Ь—а)-*у— перейдем от интегрирования a, b к
стандартному интервалу (—1, 1). Будем впредь считать, что эта
замена уже осуществлена. Постараемся при выбранном п подобрать
так коэффициенты Hk и узлы хк, чтобы формула
4=1
оказалось -совершенно точной для всех многочленов степени
где р по возможности велико. Достаточно, чтобы она была точной
для функций ф(дг)=1, х, хг, ..... хР (почему?). Подставляя их в
C5), мы получим р+1 уравнений
2ВД (s = 0,l,2 р), C6)
1 *=1
которым надо удовлетворить. Но при произвольном подборе коэф-
коэффициентов и узлов у нас имеется 2л степеней свободы, так что в
самом лучшем варианте можно надеяться, что будет р = 2п — 1.
Формула Гаусса и является реализацией этой надежды.
Вспомним о полиномах Лежандра (ЛВМ, п. XVII.20). Можно по-
показать (на этом мы здесь не будем останавливаться, а для первых
полиномов это легко проверить непосредственно), что все нули
полинома Рп(х) вещественные, простые и расположены на интервале
—1 <дг<1. Они и берутся в качестве узлов хь (вскоре будет
яс,но, что это дает). Выбрав узлы, положим в равенствах C6)s = 0,
1, ..., п — 1. Тогда относительно коэффициентов Нк получится
система из Л уравнений с п неизвестными, из которой и находятся
коэффициенты Нк.
Проверим, что для так выбранных узлов и коэффициентов ра-
равенства C6) при s = 0, I, ..., 2л — 1 выполняются. В самом деле,
для O^s^/z—1 это так по построению коэффициентов; значит,
равенство C5) является точным для всех многочленов степени
<л—1. Пусть теперь n-^.s-^.2n—1. Разделив Xs на Рп{х), мы
получим в частном многочлен Qs_n{x) степени s—п и в остатке
многочлен R<n(x) степени < п. Таким образом, xs = Qs_n(x) Pn(x) -f-
+ R<n(x) и равенство C6), которое нужно доказать, приобретает
вид
Qs-n (х)Р„ (х) йх + J R<n(x)dx=
-1
я п
k=l k=l

§ 2. ТЕОТРИЯ ФРЕДГОЛЬМА 403
Но так как s—п<п, то многочлен Qs_n {x) можно представить в
виде линейной комбинации полиномов Лежандра степеии < л (почему?)
и, значит, в силу основного свойства ортогональности полиномов
Лежандра первый интеграл в C7) равен нулю—этой есть причина,
почему в основу метода были положены полиномы Лежандра. В пра-
правой части C7) первая сумма равна нулю по построению узлов хк.
Отбросив в C7) нулевые члены, приходим к тому, что надо дока-
доказать равенство вида C5) для полинома степени- <л. А это уже
показано во второй фразе этого абзаца.
Значения узлов xk и коэффициентов Нк можно найти в справоч-
справочниках, а при вычислениях на ЭЦВМ они заложены в стандартную
подпрограмму численного интегрирования по методу Гаусса. Приведем
для примера их значения для небольших п:
л = 2: хиг= ±0,57735, ЯЬ1=1;
л=3: хЬ1 = ±0,77460, ха=0; #lf , = ¦§-. //,-¦§¦;
п = 4: Xl 4= ±0,86114, х2г , = ±0,33998;
Я1( 4 = 0,34785, Я2> з = 0,652-15;
п = 5: хх Б = ±0,90618, х2< 4= ±0,53847; х3 = 0;
Я1>6= 0,23693, Я2>4 = 0,47863, Я3 = 0,56889.
К методу Гаусса близки методы численного интегрирования Ньютона —
Кбтеса и Чебышева. В первом методе узлы х%=—1 + 2 г F=1, 2 п)
задаются, а коэффициенты Я/, подбираются так, чтобы формула C5) была точ-
точной для всех многочленов степени < п—1. Во втором методе все иоэффици-
енты Hk считаются равными, а узлы х^ подбираются так, чтобы формула C5)
была точной для всех многочленов степени < п. Соответствующие значения
коэффициентов и узлов можно найти в справочниках. Интересно, что в методе
Чебышева возможны только значения я<7 и я=9.
Отметим, что при решении системы уравнений C6) относительно коэффи-
коэффициентов Нк определителем системы служит
1 1 ... 1
.. хп
D=
х%
%
х»1»*-1»... ж»-'
C8)
Этот определитель (при произвольных значениях чисел х^) встречается в раз-
разных вопросах математики и называется определителем Вандермбнда. Для него
имеет место интересная формула
D=(xi—xJ(xa-x1)...(xa—x1)(xa—Xi)...(xn-x,)...(xn—xn-d. C9)
В самом деле, будем считать хь дс2, .... х„ независимыми переменными.
Тогда D будет представлять ссбой форму (т. е. однородный многочлен) степени
1 + 2 + ... + (л — 1) =i=-— . Если вычесть из i;ro столбца определителя C8)
j-ft столбец, то все элементы полученного столбца будут делиться иа xj—xj (по-
(почему?). Значит, D делится на каждую из скобок, стоящих в правой части C9),
а так как эти скобки без общих множителей, то D делится и на произ-
произведение этих скобок. Но так как это произведение имеет ту же степень, что

404 ГЛ. VH. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
tf D (почему?), то оно может отличаться от D только числовым ' множителем.
Однако произведение элементов, стоящих иа главной диагонали определителя,
всегда входит в полное разложение этого определителя со знаком плюс (проду-
(продумайте это)); но это как раз произведение первых элементов всех скобок правой
части C9). Значит, упомянутый числовой множитель может равняться только
единице, т. е. формула C9) доказана.
Из нее, в частности, следует, что если все числа отличны друг от друга,
¦ то определитель Ваидермоида ие равен нулю. Это замечание существенно и
для возможности определений коэффициентов Н/,.
Скажем еще об уравнениях F) со слабой особенностью (п. 1.2) На диа*
гонали, т. е. при дс=|. Быстрое и нерегулярное изменение ядра около диаго-
диагонали, даже если разрыв испытывает ие само ядро, а его производная, служит
дополнительным источником ошибок в приближенном решении. Если же ядро
иа диагонали обращается в бесконечность, то Требуется принятие особых мер
предосторожности, чтобы диагональные члены в формуле численного иитегри-
решения не приобрели чрезмерно большой роли, которой оии на самом деле
в силу сходимости интегралов не должны обладать.
Здесь возможны разные выходы, все оии применяются в вычислительной
практике. Так, если К (Хк, **)=?«>, можно вместо АС (ж*, Хь) пользоваться
значением \K(xk, Xb+h) + K (xk, хк—А)]/2, где А имеет порядок шага Кхк.
Можно предварительно преобразовать уравнение A6) к виду
(*),
ь -16
1-Х J К (х, |) d? \u (x)=X J К (х, |) [и (?)-«
a J а
после чего уже применять формулы численного интегрирования, заменяй диаго-
диагональное значение подынтегральной функции в правой части на нуль (почему?).
Можно воспользоваться также следующим методом, предложенным в 1929 г.
советскими математиками Н. М. Крыловым и Н. Н. Боголюбовым (р. в 1909 г.):
используются дискретные значения искомой функции и.о с р едие и и ые зна-
значения ядра. Пусть, например мы применяем узлы и коэффициенты' C3). Тогда
можно приближенно заменить '' '
Ь „ Г a-ffth "I
«(E)d|« 2 ) \
Так как при вычислении коэффициентов ядро проинтегрировано, то оии уже
не обращаются в бесконечность. (Кстати, этот прием можно применить и для
сингулярных ядер, п. 1.2.) Для ядер простого вида можно получить явные
точные значения коэффициентов, а в более сложных случаях применить численное
интегрирование с выделением особенности (ЛВМ, п. XIV. 16).
5. Уравнения с малыми ядрами. Как известно (ЛВМ, пп. VI.5
и XVII.18), для систем линейных алгебраических, уравнений вида
*)=S «/*** + */ (/=1.2, .... п)
с достаточно малыми коэффициентами ajk решение можно получить
с помощью простейщега, метода итераций: нулевое приближение
подставляется в правые части, получается первое приближение; оно
опять подставляется в правые части и т. д., причем метод сходится,
т. е. в пределе (а практически после определенного-числа итераций)
мы получаем точное решение. Приближенная запись уравнения A6)

§ 2. ТЕОРИЯ ФРЕДГОЛЬМЛ 405
в форме линейной алгебраической системы C2) говорит, что и для.
уравнения A6) при достаточно малом |Я| метод итераций сходится,
т.. е. в пределе дает то.чное решение. '
Опишем процесс итераций подробнее. Мы будем исходить нз
нулевого приближения
в0 (*)=/(*)
(как будто в A6) положено А, = 0), хотя теоретически можно исхо-
исходить из любого в0 (х), а практически для ускорения сходимости
желательно выбрать в„ (х) по возможности ближе к точному решенню,
если о нем что-лнбо известно. Подставив в„(дг) в правую часть A6),
получим первое приближение
ь. ¦ '
D0)
(иам будет удобнее записывать уравнение, начиная с неоднородного
члена). Для получения и2 {х) нам понадобится и, (?), поэтому в D0)
поменяем обозначение переменной интегрирования:
* Г Ь 1
в, (х) =/ (х) + Х J K(x, I) f (I) + X J К(Ъ, л)/(л) dr\ № =
a L a J
•' ь ь ь ^
^f(x) + xlK(x,l)/(l)dl + ^\K(x,l)dllK(l,r])f(r])ari. D1)
в ¦ . а а
. В последнем интеграле поменяем порядок интегрирования, а затем
обозначения переменных интегрирования; это даст
Ь _ Ь Ь j Ь \ ^
J /(т,) йц J К (х, I) К {I, л) dl = 5 ( J К (х, х)) К (л, Б) А|)/(!) й\ =
а в а >л /
где обозначено
/Сг(ДГ,|) =
итерированное ядро. Подстановка в D1) дает
ь ь
ur(x) =f(x) + K J K(x, l)f(l) di+k* J Kt (x,
a a
Повторение этого процесса приводит к выражению
, &)/<?)<*?, ¦ D2)

406 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
где Kt (x, %) = К{х, ?), а последовательные итерированные ядра
составляются по формуле
ь
$ D3)
такое действие называется свертыванием ядра Kk {x, ?) с ядром
К {х, I). Это действие совершенно аналогично умножению матриц
(ЛВМ, п. XI.2) и превращается в такое умножение, если при вычис-
вычислении интеграла D3) пользоваться формулой численного интегриро-
интегрирования C1) с узлами и коэффициентами C3), а каждое ядро L {х, 6)
заменить набором значений hL {xj, xk) (проверьте!). Поэтому свертыва-
свертывание ядер обладает свойствами умножения матриц; оно употребляется
чаще, чем, например, обычное умножение ядер.
Из D3) видно (и можно доказать более строго), что последова-
последовательность ядер Kk возрастает со скоростью геометрической прогрессии.
Значит, если | А. | меньше, чем обратная величина знаменателя этой
прогрессии, то при увеличении п ряд в правой части D2), а с ним
и весь метод, получится сходящимся, и в пределе мы получим
точное решение уравнения A6)
и (х) =/(*) + 2 W 5 Kk (*
D4)
а
Ь
а
где обозначено
Г<*. &;*.)= 2 а-* ЯП*.»- D5)
Это ряд Неймана, дающий представление резольвенты (см. G)) урав-
уравнения A6) при достаточно малых |Я,|. Как это следует из теории
аналитических функций (п. II.2.5), его радиус сходимости равен
наименьшему из модулей особых точек функции Г (рассматриваемой
как аналитическая функция от Я,), или, как можно показать, наи-
наименьшему из модулей характеристических чисел уравнения A6). Для
больших \Х\ резольвента представляет собой аналитическое продол-
продолжение суммы ряда Неймана.
Тот же результат D4) получится, если исходить из любого
другого нулевого приближения, так как различие при повторении
итераций в пределе сойдет на нет.
Метод итераций может быть использован и на практике для чис-
численного построения решений с помощью нескольких итераций, либо
для исправления приближенного решения, построенного каким-либо
другим методом. Однако такое построение или исправление возможно
только в пределах сходимости ряда D5), что практически распоз-

§ 2. ТЕОРИЯ ФРЕДГОЛЬМА 407
нается по сближению итераций. За этими пределами «поправки»
только уводят приближенное решение от точного!
в. Принцип сжимающих отображений. Сходимость метода итераций для
уравнения A6) с малым | X \ является хорошей иллюстрацией общего принципа
сжимающих отображений, который широко применяется в последние годы при
проверке сходимости этого метода дли самого разнообразного класса задач. Было
замечено, что такай проверка проходит во многих случаях в главных чертах
одинаково, что и дало основание для формулировки общего принципа этой про-
проверки в наиболее общем виде.
Естественной областью действия этого принципа является метрическое про-
пространство. Напомним (п. VI.3.7), что метрическим пространством называется
некоторая совокупность (R) объектов (элементов, точек), в которой имеется
понятие расстояния р(а, р) между любыми двумя его точками а, ??(/?), при-
причем это расстояние должно удовлетворять трем аксиомам метрики, указанным
в п. VI.3.7. Евклидовы пространства любого числа измерений, нормированные
(в частности, функциональные нормированные) пространства (п. VI. 1.3) и любые
совокупности точек в них—это всё примеры метрических пространств. Но в по-
понятие метрического пространства не заложено никакой линейности, так что,
скажем, римаиовы пространства (п. V.2.5) также являются метрическими, и т. д.
В метрическом пространстве естественно вводится понятие сходимости'
последовательности точек (а„ —»- а означает, что р (а„, а) —»- 0) и многие
П-КО П-* 05
понятия, связанные со.сходимостью, иа которых мы здесь не будем останавли-
останавливаться. Любое множество (/?г) точек пространства (/?), если в (R^) пользоваться
той же метрикой, что и в (R), само образует метрическое пространство (почему?),
которое называется подпространством пространства (/?).
Многие (ио далеко не все!) метрические простоаиства обладают важным
свойством полноты, уже упомянутом в п. VI. 1.3. (Отметим, что это свойство
не имеет ничего общего с полнотой системы базисных функций, о которой гово-
говорилось в п. VI.4.1.) Полнота метрического пространства допускает различные
определения, которые, как можно доказать, являются равносильными, например:
1) любая последовательность о^, <х2, а3, ... точек (R), для которой
Р (ап. ат) »¦ 0. сходится к некоторой точке (/?);
т, л-»»
т
2) то же, ио при условии У] р (аА, а*+1) < оо;
• А=1 - '
3) последовательность точек (R) не может сходиться к не принадлежащей
(R) точке какого-либо пространства, содержащего (/?) в качестве подпространства.
Перечислим некоторые полные пространства; доказательства их полноты
можно найти в курсах функционального анализа. Так, полны все конечномерные
евклидовы пространства. Полны пространство С [а, Ь] и вообще любое простран-
пространство С (/С) всех вещественных или вгех комплексных (скалярных или векторных)
непрерывных функций иа каком-либо замкнутом множестве (К) коиечиомериого
евклидова пространства, если за расстояние между двумя функциями прини-
принимается их равномерное уклонение. (При этом замкнутость множества означает,
что оно содержит пределы всех сходящихся последовательностей его точек.)
Между прочим, для пространств С второе определение полноты есть просто
признак Вейерштрасса равномерной * сходимости (ЛВМ, п. XVII.8; продумайте
это!). Полны пространство L2 \a, Ь] и вообще аналогично определяемое про-
пространство Гильберта L2 (М) для произвольного множества (М) с неотрицательной
мерой, в частности,, для многообразия (М) в конечномерном евклидовом про-
пространстве с обычной мерой Лебега. Полны и многие другие пространства, которых
мы здесь не рассматриваем, а также любые замкнутые в только что указанном
смысле подпространства полных метрических пространств (докажите!). В то же
время незамкнутые подпространства всегда неполны; например, неполны

408* ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
совокупности всех непрерывных функций в Ц[а, Ь] или всех непрерывно диф-'
ференцнруемых функций в С [а, Ь] (почему?).
Пусть теперь задано отображенне В полного метрического пространства (R)
в себя; другими словами, каждой точке <*?(/?) поставлена в соответствие не-
котораи точка Bag(/?). Это отображенне называется сжимающим, если суще-
существует такое положительное число к < 1, что для любых а, "?(/?)
(
р(Ва,Вр-)«;*р(а, р). D6)
Допустим, fe=-s- • тогда условие D6) означает, что все расстояния в (R) при
отображении уменьшаются по крайней мере в два раза.) Сжимающее отобра-
отображение всегда является непрерывным, т. е. из ап —¦ Ъ, вытекает, что Ва„ —> Ва
(почему?); сбратиое, конечно, не обязательно: например, отображение у=х\ (
т. е. х—»¦ хг вещественной числовой оси непрерывное, но не сжимающее.
f Хотя при ^-^ <х<^ оно сжимающее, ) Отметим, что условие D6) для
вещественной числовой оси—это неравенство ЛВМ, (V.14), введенное именно
в свизи с исследованием сходимости метода итераций.
Пусть рассматривается «уравнение» ¦
а=Во; D7)
* *
другими словамв, ищется точка а, которая 'при отображении В переходит
в себя, она называется неподвижной точкой этого отображения. Эту точку
естественно искать по методу итераций: как-то выбрать нулевое приближение а„,
а последующие приближения строить по формулам о^сгВао, а2^=Ва1, вообще
а„+1==Вап. D8)
Принцип сжимающих отображений состоит в следующем: если простран-
пространство (/?) полное и его отображение В в себя сжимающее, то последовательность
приближений ап, построенных по формуле D8), сходится к неподвижной точке
отображения В. Эта неподвижная точка единственная. (Подчеркнем, что этот
принцип дает только достаточные условия сходимости итераций.)
Доказательство принципа очень простое. Последовательно примения нёра-^
венство D6), получим ' '
Р («1. а*)=Р (Bo* Box) < ftp (а«, а,),
р (а*, аа)=р (Bet!, Во») < ftp (otj, а») < ftap («Ко. «i) и т. д.
Так как рид из правых частей сходится, то в силу второго определении полноты
последовательность сц, аь а2, ... сходится к некоторой точке а. Переходя
в равенстве D§) к пределу при я —>¦ оо, получаем, что а удовлетвориет урав--
нению D7), т. е. это неподвижная точка. Если была бы еще одна неподвижная
точка о Ф а, то
р (а, а)=р (Ва. Ва)<ftp (а, а),
н мы приходим к противоречию. Все утверждении доказаны. Кстати, это хороший
пример того, что общее рассмотрение может оказаться проще, чем частное, так
как в общем выделено «в чистом виде» существенное, а в частном это сущест-
существенное может быть так заслонено спецификой, что «за деревьями не увидишь леса».
Чтобы применить принцип к уравнению специального вида, надо записать
это уравнение в форме D7), уточнить, в каком пространстве действует отобра-
отображение В, и проверить полноту пространства и сжвмающий характер отобра-
отображения. Применим¦ этот принцип к уравнению A6), рассматривая его в. полном

§ 2. теория фредгольма •'¦ 409
пространстве ?j [a; b]. Тогда надо обозначить
ь
Ви (*)=*,'$/С (*,&
а ' ¦ :
В силу п. 1.3, если ядро удовлетворяет условию A.7), a fgLgfa, b], то
и Bug/,j [a, 6J, т. е. получается отображение пространства Ц[а, Ь] в себя.
При этом
6
1р (Ви, BvI» = ||Bii—Bv||*^= J I Ви (к).—Во (*) 1» dx=*
а
ft ft
=| Х|« J | 5 К (х. I) [и G)-v
a a
Применяй неравенство A.11), получим, что правам часть не превосходит
ft ft
a e.
Таким образом, если
fb б . N
"''. D9)
то условия принципа выполнены и последовательные приближения, «построен-
«построенные в п. 5„ сходятся к единственному решению уравнения A6). Заодно мы
получаем оценку наименьшего из модулей характеристических чисел уравне-
уравнения D7): этот модуль не меньше правой части D9) (почему?). .
Еще раз подчеркнем, что оценка D9) является лишь достаточной не только
для разрешимости уравнения A6), но и для сходимости метода итераций. На
самом деле сходимость имеет место сбычно в более широком круге плоскости А,,
радиус которого равен наименьшему из модулей характеристических чисел
ядра К. Применяя различные нормы в функциональных пространствах, рас-
рассматривая проитерированное уравнение, возможно получить различные*условия
сходимости, которые часто оказываются лучшими, чем D9).
7. Возмущение ядра. Если для какого-либо ядра мы знаем одно
нз характеристических чисел и отвечающие ему собственные функ-
функции, то, применяя метод малого параметра, мы можем получить
соответствующие характеристические числа и собственные функции
для близких «возмущенных» ядер.
Рассмотрим уравнение
ь •
, I; й) «<?><*&, • E0)
где fi—-малый вещественный параметр,, и допустим, что нам известно
некоторое характеристическое значение Я,„: ядра К0{х, %)=-К(х, |; 0),

410 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
причем этому значению 'отвечает лишь одна линейно независимая
собственная функция и„ (х). Чтобы найти соответствующие харак-
характеристическое число Я, и собственную функцию и (х) рри ц Ф О,
проведем разложение
К (ж, I; A) = Ко (х, 1) + |хАГх (ж, |) + ^К% (х, I) + ...,
X = Ka + ]iXi + li42 + ...1 в (ж) = «,.(*) +1114 (ж)+ |Л», (*) + ••-E1)
Подстановка в E0) и приравнивание коэффициентов при одинаковых
степенях ц приводит к равенствам
ь
E2)
ь ь
К, (х, 1) «„ (|) ^ + Х,5 Кв (х, I) и„ A) <& E3)
6
и т. д. Первое из них выполняется по определению К„ и ий\х).
Из равенства E3) в силу третьей теоремы Фредгольма мы видим,
что сумма членов с и„ должна быть ортогональна собственной
функции v0 (x) сопряженного с E2) уравнения
ь ь • ч
I, $ /Сг (х, 1) и; (I) d| + К J /Со (ж, I) и, (|) d|, ¦?„ (ж)) = О,
а а /
откуда, пользуясь равенством E2), получим
ь ь ь
лх = — л0 \ \ /Ci (•?, |) иа (§) f J (jc) eg dx \ uB (x) vJ (л;) djc.
a a ¦ a
Найдя %1 и удовлетворив тем самым условию ортогональности,
мы получаем общее решение уравнения E3) в виде и1(х) = у1(х)+
-\-С1и„(х), где Cj—произвольная постоянная. Этот произвол несу-
несуществен, он связан с возможностью умножения и (х) на люббе раз-
разложение 1 + Схц -f- С2ц2 4- • • • Поэтому Q подбираем из какого-либо
условия нормировки решения или просто полагаем равным нулю.
Затем обращаемся к уравнению E4), из которого на основании
условия ортогональности неоднородного члена к функции va нахо-
находим А,2, после чего из уравнения находим и2 (х), и т. д.

§ 2. ТЕОРИЯ ФРЕДГОЛЬМА 4J 1
Если характеристическое значение Хв ядра Ка является кратным, то
при ц^О ему может отвечать несколько характеристических чисел
ядра К. В этом случае разложение E1) надо проводить по дробным
степеням параметра ц, и выкладки усложняются; мы не будем здесь
ими заниматься.
Аналогично рассматривается возмущение ядра для многомерных уравнений.
Представляет интерес также рассмотрение возмущенных уравнений вида
К{М, N; \i)u(N)dN~G,
у которых ие только ядро, ио и область зависят от параметра. Здесь иногда
делают замену переменных ЛГ = ф(М; ц), отображающую область (G^) взаимно
однозначно на некоторую область (G'), не зависящую от ц; тем самым
мы переходим к уже разобранной задаче. Можно этого и ие делать, если не
бояться дифференцировать интеграл по параметру, определяющему область
интегрирования. Тогда, например, в правую часть E3), переписанную для
многомерного случая, в силу ЛВМ, п. XVI. 18, добавится член
(So)
где (So)—граница области (Go), а область (GJ задается неравенством
8. Характер решений. Хотя мы ищем решение уравнения A6)
в пространстве Li[a, b], элементы которого не обязаны быть не-
непрерывными, но часто бывают случаи, когда решение все же полу-
получается непрерывным и даже имеет непрерывную производную и т. д.
-Пусть,, например, а и b конечны, а ядро К(х, 5) и неоднородный
член f(x) — непрерывные функции своих аргументов. Тогда легко
доказать, что и решение н(;е) обязано быть непрерывным. В самом
деле, применяя неравенства A.11) и \a-\-b|2^21 а|2 + 2|&|2, полу-
получаем
ь
- К (х, D] и (I) й\ + [/(х + Ах) -/ (х)) |»
откуда и видна непрерывность функции и (х). (А если при том же
ядре от f(x) уже не требовать непрерывности, то аналогично легко
проверить, что будет непрерывной разность и(х)—f(x), т. е. ре-
решение имеет такие же разрывы, как и неоднородный член.)
Пусть теперь ядро К (х, ?) может иметь точки или линии раз-
разрыва, а функция f(x) непрерывна. Тогда у решения и(х) могут

412
ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
оказаться разрывы только при тех х = хл, для которых прямая х**х0
имеет отрезки линий разрыва ядра. Так, на рнс. 114 жирно изобра-
изображены линии и точки разрыва ядра. Так как интегрирование в A6)
проводится по вертикальным отрезкам, то при переходе от х=^х1<^х^
к близкому значению х = х2> х0
интеграл может получить .конечное
приращение, а это и означает разрыв
решения.
В частности, если линии разрыва
ядра не содержат отрезков, парал-
параллельных оси ?, а функция /(х) неп-
непрерывна, то и решение и (х) непре-
непрерывно.
Рассмотрим довольно распростра-
распространенный случай, когда ядро имеет раз-
разрыв или излом (разрыв в производ-
производных) при х = \, а для хф\ является
«хорошим». Тогда обычно ядро имеет
при 1 < х и при !>•* различные аналитические выражения, и
поэтому удобно обозначить
хотя К± и Kt составляют единую функцию. Уравнение A6) можно
переписать в виде
х ь
и (х) = X J Кг (х, 1) и A) d| + k J К, (х, 1) и
• о * ..
Отсюда еще раз видно, что если функции
непрерывны, то и решение н {х) непрерывно. Если дополнительно
дано, что К±, К8 и / имеют непрерывные производные по х, то,
вычисляя производную от интеграла по параметру (ЛВМ, п. XIV.20),
получим ~
т. е. и решение имеет непрерывную производную по х. Легко указать
дальнейшие требования на Kv Kt и /, при которых и* непрерыв-
непрерывна, и т. д. Таким образом, сведения о степени гладкости решения
можно извлечь, опираясь на сведения о ядре и неоднородном члене.

§ 2. ТЕОРИЯ "ФРЕДГОЛЬМА 413
Полуденные результаты распространяются и на л-мерные урав-
уравнения вида A.9). В частности, получается, что* если ядро K{M,N)
имеет разрыв только при M-=N, то интеграл в A.9) зависит от
точки М непрерывно; а поэтому, если и неоднородный член непре-
непрерывен, то и решение и (М) обязательно . непрерывно. Интегралы
такого типа применяются в математической физике и называются
интегралами типа потенциала, так как нх частными случаями явля-
являются ньютонов и логарифмический потенциалы (п. 1.2.5). В матема-
математической физике изучаются также условия их дифференцируемое™,
однако мы здесь этим не будем заниматься.
9. Уравнения Вольтерра 2-го рода. Рассмотрим теперь линейное
интегральное уравнение Вольтерра 2-го рода (п. 1.2)
|. . . ч " : E5)
причем а будем считать конечным. Можно доказать, что это урав-
уравнение не имеет характеристических чисел, т. е. при каждом К урав-
уравнение E5) обладает ровно одним решением (имеет место первый
случай альтернативы Фредгольма, п. 2).
В самом деле, в противном случае соответствующее однородное
уравнение
• ' ¦¦ • u(x) = ^K(x,l)u(l)dl E6)
, о
в силу первой теоремы Фредгольма имело бы нетривиальное реше-
решение. Если принять сначала, что х изменяется от а до некоторого
а + А> а, и условиться считать
К (х, I) =з 0 при | > х, E7)
то из A.13) получим
. , a+h ¦ a+ha+h o+h'
• а а " о а
Если А настолько малб, что произведение первых двух множителей
аг правой части меньше единицы, то отсюда следует, что u{x)ssO
(а <^ х<! a -f А) (почему?). А если бы решение и (х) стало отличным
от нуля после некоторого at > а, то, заменив в E6) ннжиий пре-
предел на а1 и рассуждая таким же образом, мы пришли бы к про-
противоречию. Тем самым утверждение предыдущего абзаца доказано.
При построении итерированных ядер в методе итераций из E7)
следует, что
-:•'¦' 6 ' х ь х
*2 (х, |) = 5 К(х,. т]) /С(ть I) dr\ + ] + $ - J K(x, Ti) К (%
а 6*6

414 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
отсюда видно также, что и ядро Кг удовлетворяет условию E7).
Рассматривая затем К3 и т. д., получаем, что все итерированные
ядра удовлетворяют условию E7), а в формуле D3) интеграл можно
брать от ? до х. Поэтому и формулу D4) для решения можно за-
записать в виде
х
в (*)=/(*) + Я J Г {х, I; А) /A) й\. E8)
а
Кроме того, резольвента как функция А, для: уравнения Вольтерра
не имеет особых точек, а потому ряд D5), а с ним и метод итера-
итераций, сходится при всех конечных значениях А.
Будем обозначать незавнсвмую переменную буквой t и истолковывать ее
как время. Тогда оператор Вольтерра
t
Аи (t) = С К (t, х) и (т) dx (t Э* f0).
'о
в отличие от общего оператора Фредгольма,. характеризуется тем, что значение
функции Аи в любой момевт t определяется значениями фувкции и только
при значениях т<Л Операторы (в том числе нелинейные), обладающие этим
свойством, называются операторами типа Вольтерра н широко применяются
при изучении процессов с последействием (подумайте, почему!). Естественно,
что н решение E8) оказалось в каждый момент времени определяемым вели-
величиной внешнего воздействия / только в предшествующие моменты.
Для уравнения Вольтерра 2-го рода E5) характерна возможность продол-
продолжения решения: скажем, можно построить решение сначала на некотором ин-
интервале а<,х<,аи затем при х^ах переписать уравнение в виде
) = Х$ К(х,
ot
Го, -1
X $ * (*, 8иF)«? + /(*)
L a J
и решать его дальше, так как сумма в квадратных скобках уже определена
и т. д. Для общего уравнения Фредгольма A6) невозможно построить решение
только на частв интервала а, Ь, так как по смыслу уравнения все значения
искомой функции на этом интервале завязаны друг с другом.
Имеются различные варианты переноса понятия уравнения Вольтерра на
функции нескольких переменных. Например, такой:
где (Н) — некоторая область в пространстве х2, ..., хп. Такое уравнение также
не имеет характеристических чисел.
10. Уравнения со слабой особенностью. Теоремы Фредгольма можно рас-
распространить на уравнение A6) с ядром, удовлетворяющим оценке A.8), и ko-n
нечнымн а, Ь. Покажем вкратце, как это делается. Прежде всего проверим,
что еслни(*) ? Ща, Ь], то справедливо утверждение A.12), хотя доказатель-
доказательство A.13) придется изменить (почему?). Однако теперь можно рассуждать так

§ 2. ТЕОРИЯ ФРЕДГОЛЬМА 415
(проверьте!)!
откуда и вытекает A.12). Таким образом, и для ядра со слабой особенностью
оператор А, введенный в п. 1.3, будет ограниченным.
Центральным пунктом в теории ядер со слабой особенностью является то,
что итерированные ядра (п. 5) обладают все более слабыми особенностями,
а начиная с некоторого номера и вовсе теряют особенность. Это и дает воз-
возможность перейти от исходного уравнения к уравнению, для которого спра-
справедливость теорем Фредгольма уже установлена.
Проверим утверждение об ослаблении особенности. Для этого допустим,
что ядро К (х, ?) удовлетворяет оценке A.8), а некоторое ядро Цж, ?) — ана-
аналогичной оценке с показателем р. Тогда ядро, полученное в результате сверты-
свертывания К с L, удовлетворяет оценке
ь ь
\\К(х,
При s=0 и s=l этот интеграл сходится, а при \s\—>-оо подынтегральная
функция эквивалентна |s|-(a+P', и потому весь интеграл не превосходит
Сг+С2|*—g|«+p-i (почему?). Подставляя эту оценку в E9), получаем, что
(Случай а+Р = 1 можно не рассматривать, так как в оценке A.8) всегда можно
немножко увеличить а.)
Из доказанного следует, что ядро Я2 имеет особенность порядка a—A—а),
если это число положительно; /С3 имеет особенность порядка a—2A—а) а
т. д., пока мы не дойдем до отрицательного числа a—т A—а), а тогда ядро
К уже будет ограничено.
(Отметим, что для я-мерных интегралов справедлив аналогичный результат,
однако в оценках F0) вместо а+Р — 1 тогда надо поставить а+[$—п.)
Допустим для простоты, что а—A—а) < у, т. е. ядро Я2 удовлетворяет
оценке A.7). Запишем уравнение A6) в краткой форме
(I—XA)n=f, F1)
где I—единичный оператор (оставляющий все функции без изменения), и при-
применим к обеим частям оператор I + ХА. Получим уравнение
т.е. u = \2A2u + (I + \A)f, F2)

416 ГЛ. VII. ИНТЕГРАЛЬНЫЕ, УРАВНЕНИЯ
где (I+XA)f—заданная функция, а А»-—интегральный оператор с ядром Kt,
для которого выполнены теоремы Фредгольма. Прн этом. нз доказательства
видно, что каждое решение уравнения F1) удовлетворяет н уравнению F2).
В частности, положив /аО, видим, что если и—собственная функция урав-
уравнения F1), отвечающаи характеристическому числу X, то она будет также
собственной функцией уравнения F2), отвечающей собственному числу Хг.
Отсюда сразу получается, что поскольку для уравнения F2) имеет место 4-я
теорема Фредгольма (п. 2), то она имеет место и для уравнения F1); отсюда '
же вытекает, что для каждого характеристического числа уравнения F1) про-
пространство соответствующих собственных функций конечномерно (почему?).
Будем считать в дальнейшем, что X зафиксировано, причем так, что —X
не являетси характеристическим числом уравнения F1). (В более полных курсах
интегральных уравнений с помощью итераций высшего порядка показывается,.
что это предположение для справедлнвости окончательных утверждений несу-
несущественно.) Тогда легко доказать, что любое решение ураинення F2) удовлет-
удовлетворяет и уравнению F1), т е. уравнения F1) н F2) полностью равносильны. Это
получается, если переписать уравнение F2) в виде
[(I — ХА) и—f]=(—X) А [A— Хк)и—f]
(почему?).
Уравнение, сопряженное с F1) при конкретном X, а потому с подставленным:
сопряженным значением параметра, имеет вид
(I—X*k*)v=0. F3)
Аналогично предыдущему абзацу показывается, что оно равносильно уравнению
v = X**A*4 F4)
причем легко непосредственно проверить, что уравнение F4) будет сопряженным
к F2), так как итерированное сопряженное ядро будет сопряженным к итери-
итерированному основному ядру (продумайте это!). Применяй третью теорему"
Фредгольма к уравнению F2), получаем, что для его разрешимости, а потому
н разрешимости уравнения F1) необходимо и достаточно выполнение условия
ортогональности
((I + *A)f, v)=0 F5).
для любого решения уравнения F4), т. е. F3). Однако легко непосредственно
провервть (проделайте это!), что (Af, v)={f, A*v), а потому условие F5) можно
переписать в виде
. . 0=(f, уН-(Ш, v)=(f, v) + (f, A,*A*v)=2(f, v), ,
т. е. мы приходим к третьей теореме Фредгольма для уравнения F1). Первая
теорема Фредгольма, как было указано в п. 1, вытекает нз третьей н второй.
Итак, для уравнения со слабой особенностью справедливы все четыре
теоремы Фредгольма.'
11. Уравиення с вполие непрерывными оиераторами. Подробный анализ
теорем Фредгольма, проводимый в курсах интегральных уравненнй и функцио-
функционального анализа, показывает, что эти теоремы имеют место в значительно.
более обшей /ситуации, чем описано выше. Общие формулировки, которые мы
здесь приведем без доказательства, делают эти теоремы более обозримыми
(ср. п. 6). .. ... ,-
• .Пусть задано некоторое гильбертово пространство (Я); это может быть
какое-либо пространство функций, е которых мы говорили в п. 1.3, но может
быть и просто некоторое бесконечномерное еиклидово пространство, природа
элементов которого для нас в данном вопросе несущественна. Пусть дан линей-
линейный оператор А, отображающий (Я) в себя. Такой оператор называется -
конечномерным, если он отображает (Я) на его конечномерное подпространство.

If
§2. ТЕОРИЯ ¦РЕДГОЛЬМЛ 417
Это обобщение понятия интегрального' оператора с вырожденным ядром,- так
как оператор
6 р
отображает все L% [a, b] на подпространство линейных комбинаций функций
Ф, (х), Ф2 (х) Ф^ (*) (почему?). Конечномерные операторы всегда огра-
ограниченные (см. определение ограниченности и нормы оператора в п. 1.3).
Линейный оператор А называется вполне непрерывным, если он может
быть с любой точностью аппроксимирован конечномерным, т. е. если он может
быть представлен в виде суммы конечномерного оператора н оператора с как
угодно малой нормой. Так, вполне непрерывными являются фредгольмовы
интегральные операторы и, по существу, именно об этом говорилось в начале
п. 2. Можно доказать, что н интегральные операторы со слабой особенностью
вполне непрерывны.
Часто пользуются другим, равносильным определением: оператор А назы-
называется вполне непрерывным, если он всякое ограниченное множество преобразует
в множество, компактное в (Я). (Определение компактности было приведено
в п. VI.2.9, где было показано также, что в бесконечномерном пространстве
ограниченное множество не обязано быть компактным; более того, возможно
доказать, что только в конечномерных пространствах . каждое ограниченное
множество компактно.) Отсюда видно, что всякий вполне непрерывный оператор
ограничен, но обратное не обязательно: например, единичный оператор в любом
бесконечномерном пространстве ограничен, но не вполне непрерывен.
Для каждого линейного оператора А возможно построить сопряженный
линейный оператор А*, также отображающий (Я) в (Я) н связанный с А соот-
соотношением
(Ах, у) = (х, А* у) для всех х, у g Я F6)
(см. аналогичное определение в п. IV.1.3). Для интегральных операторов это
просто оператор, отвечающий сопряженному ядру (см. формулу A8)). Если А
вполне непрерывный, то и А* вполне непрерывный.
Венгерский математик Ф. Рнс A880—1956) распространил теорию Фред-
Фредгольма на операторные уравнения
F7)
где t—заданный, и—искомый элементы- гильбертова пространства (Я), а А —
вполне непрерывный линейный оператор, отображающий (Я) в себя. Оказалось,
что для такого уравнения справедливы все четыре теоремы Фредгольма в точ-
точности том виде, как они были приведены в п. 1 (конечно, вместо собственных
функций теперь надо говорить о собственных элементах). При этом роль
сопряженного уравнения к F7), естественно, играет уравнение
v=(iA*v.
Her смысла повторять здесь формулировки этих теорем
Таким образом, для возможности применения теорем Фредгольма достаточно
убедиться в полной непрерывности соответствующего оператора. Проверка этого
иногда требует навыков в «чистой» математике, поэтому если возникают сомне-
сомнения, следует обратиться к курсам функционального анализа или просто к
математикам.
.. 12. Уравнен в и с иоложительиыми ядрами. Во многих прикладных задачах
ядро уравнения A6) неотрицательно:
К(х, 1K*0 (о<х, \<.Ь). F8)
Уравнения с такими ядрами в одномерном и многомерном случаях, а также
нелинейные аналоги этих уравнений обладают рядом интересных свойств,
подробно рассмотренных в книгах [40, 56].
14 А. Д. Мышкио

€16 ГЛ. V». ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Именно, оказывается, что все утверждения, приведенные, в п. 1У.4.8для
матриц с положительными элементами, остаются справедливыми для уравнении
A6) с непрерывным положительным ядром (т. е. неравенство F8) должно быть
строгим); при этом вместо вектора с неотрицательными проекциями надо говорить
о функции, принимающей неотрицательные значения, а вместо наибольшего
по модулю собственного значения—о наименьшем по модулю характеристиче-
характеристическом числе. Утверждения оказываются справедливыми также для многомерных
уравнений, разрывных ядер и нестрогого неравенства F8). Правда, в последнем
случае ядро должно удовлетворять некоторым дополнительным предположениям,
приведенным в указанных книгах; из реально встречающихся уравнений этим
предположениям не удовлетворяют лишь уравнения Вольтерра, которые, как
известно (п. 9), не имеют характеристических чисел'/ На интегральные уравне-
уравнении 'распространяется также теория осцилляцнонных матриц, упомянутая
en.IV.48. . . .
Абстрактным аналогом теории уравнений с положительными ядрами служит
теория операторных уравнений и пространствах с конусом: понятие конуса
обобщает понятие совокупности неотрицательных функций или совокупности
векторов; с неотрицательными проекциями. Более точно, конусом в гильбертовом
ияи банаховом пространстве (Я), называется любая замкнутая совокупность (К)
точек; обладающая следующими свойствами:
1)" если, х g (К), у € К, аЗаО^р1 >0, то ах+р"у € (К);
. 2), если ».? (К), х ф О, то — х ? (К).
(Подумайте, что это означает для двумерного илн трехмерного евклидовых
пространств.) Например, в любом функциональном пространстве совокупность
всех неотрицательных функций образует конус (почему?). Аналогом интеграль-
интегрального оператора с неотрицательным ядром служит любой линейный вполне
иепрерывный (п, 11) оператор, отображающий конус (К) в себя. Для уравнения
F7), в котором оператор А обладает этим свойством, оказывается возможным
при соответствующих предположениях получить нее утверждения, приведённые
в и. 'IVA.-8- для конечномерного случая.
Теория пространств с.конусом основана советским математиком М. Г. Крей-
ном (р. в 1907 г.). .
§ 3. Уравнения ч: симметричными ядрами
1. Аналогия с конечномерными уравнениями. Вернемся к урав-
уравнению B.16), причем ядро К(х, |) будем считать вещественным к
симметричным, т. е. удовлетворяющим' условию
К{х,.Ъ)^К{Ъ, х). A)
Как известно, теория симметрических матриц обладает рядом харак-
характерный черт (п. IV.1.6; ЛВМ, п. XI.10), которые распространяются
и на уравнения с симметричными ядрами. При установлении соот-
соответствующих свойств мы пойдем по упрощенному пути, считая
законной приближенную замену интегрального уравнения B.16) на
систему линейных алгебраических уравнений B.34), а желающих
ознакомиться с более математически строгими доказательствами мы
отошлем к курсам интегральных уравнений.
Так как для симметричного ядра К и матрица коэффициентов
системы B.34) будет симметрической, то из свойств таких матриц
получаем, что все характеристические числа уравнения с вещественным
симметричным, ядром вещественные. Это свойство дает возможность

§ 3. УРАВНЕНИЯ С СИММЕТРИЧНЫМИ ЯДРАМИ 419
впредь в этом параграфе рассматривать только вещественные функции,
если не оговорено противное, о чем мы больше не будем упоминать.
Если обозначить элементы собственных векторов уравнения
B.34), отвечающих двум различным собственным значениям, через
«у} и и%\ то, как известно из теории симметрических матриц, вы-
выполняется соотношение ортогональности
Умножив обе части на А и считая h достаточно малым, получаем,
что собственные функции уравнения с симметричным ядром, отве-
отвечающие различным характеристическим числам, ортогональны друг
другу.
Симметричное ненулевое (т. е. не тождественно равное нулю) ядро
имеет по крайней мере одно характеристическое число. В самом деле,
в конечномерном приближении это означает, что симметрическая
матрица, не все элементы которой равны нулю, имеет по крайней
мере одно ненулевое собственное значение. (Для несимметрических
матриц э1о, вообще говоря, неверно—отсюда и получается отсут-
отсутствие характеристических чисел у уравнения Вольтерра!) Ведь, сим:
метрическую матрицу всегда можно привести к диагональному виду,
причем на диагонали будут стоять собственные значения; если в<се
они равны нулю, то после приведения получится нулевая матрица,
¦ai', тогда она и до приведения должна быть нулевой (почему?),.. ..
2. Разложение ядра по собственным функциям. Расположим
все характеристические числа заданного симметричного ядра К(х, Ъ)
в конечную или бесконечную последовательность ' '•"
™1г > • • • » "ft» • • • 1 B)
причем каждое число будем повторять столько раз, какова размер-
размерное» отвечающего ему пространства собственных функций. В силу
4-й теоремы Фредгольма, если последовательность B) бесконечная,
то kk—>оо.
Выберем теперь для каждого характеристического числа отве-
отвечающую ему собственную функцию; при этом, если некоторому
числу отвечает несколько линейно независимых собственных функ-
функций, то мы. их выберем ортогональными друг другу, что всегда
возможно (почему?). Кроме того, после умножения этих функций
на соответствующие константы всегда можно считать, что норма
каждой из этих функций равна единице. Мы получаем последова-
последовательность нормированных собственных функций
<Pi(*), ф,(*), .... ф*(ж), •.. , , C)
каждые два члена которой ортогональны друг другу: функции, от-
отвечающие разным характеристическим числам, — в силу п. 1> а
отвечающие одинаковым числам — по построению, , .¦..*•¦
14*

420 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Допустим сначала,,что у ядра имеется лишь одно характеристи-
характеристическое число и что ему отвечает лишь одна линейно независимая
собственная функция. Тогда легко доказать, что
? MS). (¦)
В самом деле, докажем, что у симметричного ядра
Кй (х, I) = К (х, Б) -? Ф, (*) <Pi (I) E)
нет ни одного характеристического числа, а тогда /@ = 0 в силу
п. 1. Но пусть ф (х) ^0 — собственная функция ядра E), т. е.
Ь
к J К (х, I) ф (|) d\ - А
а о
Умножим обе части на q>l (х) и проинтегрируем от а до Ь, восполь-
воспользовавшись тем, что в силу симметрии ядра К
а а
Поэтому нз F) получится, что
^ G)
Но тогда та же формула F) показывает, что ф (дг) должна быть
собственной функцией ядра К, а значит, она пропорциональна ф^.»),
н мы приходим к противоречию с G). Формула D) доказана.
В общем случае, когда ядро К, имеет любое число собственных
функций, аналогичным образом доказывается, что система характе-
характеристических чисел и собственных функций ядра E) получится, если
у каждой из последовательностей B) н C) вычеркнуть первый
член. (При доказательстве этого нужно проверить также, что каждая
функция (pj(x) при /> 1 является собственной функцией ядра Ко,
отвечающей характеристическому числу %/, это мы предоставим
читателю.) Затем можно проделать аналогичное преобразование
с ядром E) н т. д. Мы получаем, в частности, следствие: если
симметричное ядро имеет лишь конечное число характеристических
чисел, то это ядро вырожденное.

§ 3. УРАВНЕНИЯ G СИММЕТРИЧНЫМИ ЯДРАМИ 421
Если же ядро К невырожденное, мы приходим к ряду
Можно показать (на чем мы здесь не будем останавливаться), что
если выполнено условие A.7), то этот ряд обязательно сходится
в среднем. А так как рассуждение, аналогичное проведенному в связи
с ядром E), показывает, что у ядра
нет ни одного характеристического числа, то мы приходим к фор-
формуле разложения симметричного ядра по его собственным функциям:
Мы здесь не пишем пределы суммирования, так как они могут быть
либо конечными в случае вырожденного ядра, либо бесконечными
в случае невырожденного.
3. Следствия. Из разложения (8) вытекают многочисленные
полезные формулы. Так, возведем обе части равенства (8) в квадрат
и проинтегрируем результат по х и по ? от а до Ь. Тогда в силу
ортогональности собственных функций попарные произведения про-
пропадут и, вспоминая о нормированное™ собственных функций, полу-
получим формулу
№**•
±. (9)
/ Ч
Если же в (8) положить \ = х и проинтегрировать результат, мы
получим фо'рмулу для следа непрерывного ядра К
A0)
Формула для итерированного ядра (п. 2.5) дает
ь ¦
к{х, г\)К{г\,
Yj Ь W Ф/ <Ч) Е х;

422 - гл. vii. интегральные уравнения
Диалогично получаем (проверьте!)
Кп{х, 1) = Етт
Так как "к,
A2)
оо, то с увеличением п ряды в правой части схо-
Я1ТСЯ- все лучше и лучше. Из A2) аналогично предыдущему абзацу
получаем - '
ьь • ь ....
a a j ' а 7
Последнюю формулу можно применить для приближенного вычисления
первых собственных значений. В самом деле, допустим, что \XV\ <\Хг\ <...
Тогда с ростом п в каждой из правых частей A3) становится преобладающим
первое слагаемое. Отбрасывая остальные слагаемые, получаем приближенную
фярмулу
-.. _ .. . _1/я
"*
I-'/.»
J
а зиаж %i совпадает со знаком второго интеграла при нечетных п. Можно
пользоваться также отношениями следов
ь Ь
/Crt+1 (x, x) dx
а а
Я Т. П.
Дли вычисления Х2 можно воспользоваться тем, что в разложение вели-
ь
J К„ (х,
[Ь 11 Н
J Кп (х, *)<**-$$ [к„ (х, §]2 dx d%
a J aa
членом будет
(почему?), откуда
\вп\ •
На итерациях основан также следующий метод Кёллога для приближен-
с Х В ф f ()
р у
наго вычисления Х^ Возьмем произвольную функцию
Г ft ft
ft (*)= 5 AT (ж, ?) f a) dk. h (*)= $ * (*.
о а
я т. д. Отсюда легко получить (проверьте!), что
и положим
(E) <

§ 3. УРАВНЕНИЯ С СИММЕТРИЧНЫМИ ЯДРАМИ ' 423
Если f1 Ф О, то при больших п в /„ (х) преобладает первое слагаемое. Поэтому
можно воспользоваться приближенными формулами
™w~ Hf.II
Для уверенности в неравенстве /х ф 0 можно проверить результат, начав
с другой функции / (ж). (Подумайте, как- распознать н как исследовать случав,
когда Я2 = ± А,!-)
Формула для резольвенты (см. B.45)) такова
г х я_у^-1у _L
я= 1 j '
Переставляя порядок суммирования и пользуясь тем, что
получим
М ФУ
j
Эта формула получена пока для малых |Х|. Но так как обе. части
этого равенства являются аналитическими функциями %. во всей
плоскости К, за исключением точек X = %j, то, совпадая при малых
\К\, они совпадают и тождественно (п. II.2.5). Значит, формула A4)
дает представление резольвенты для всех К; мы видим, в частности,
что резольвента симметричного ядра может иметь полюсы только
первого порядка.
При выводе формулы (8) мы исходили из заданного ядра К (х, |). Бывают
случаи, когда задан ряд
где ф1, <Ра,.--—какан-то система поп-арио ортогональных нормированных
функций, a l/Xj—какне-то коэффициенты, ряд из квадратов которых сходится
(см. (9)). Тогда ряд A5) сходится в среднем квадратичном (докажите это, опи-
опираясь иа сведения из первой половины п. 2.6) к некоторой функцнв К (х, 5),
удовлетворяющей условию A.7). При этом <р^ (лс)—собственные функции ндра К,
отвечающие характеристическим числам Ху, и других линейно независимых
собственных функции ядро К не имеет (почему?).
Отсюда получаем, н частности, такое следствие из формул A2) н A4):
ядро К.п (х> ?) и резольнента Г (х, |; X) имеют тот же набор C) собственных
функций, что исходное ндро К (х, |), причем эти функции отвечают характе-
характеристическим числам Xnj и X/—X соответственно.

424 ' ГЯ. V». ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Подставляя A4) в B.44), получаем формулу для решения
и (х) =/(*) + ?^/$/A) ф/ (|) dl).b(x), A6)
! \ J
справедливую для всех нехарактеристических значений К. Если же X
характеристическое, то мы видим, что для существования решения
необходимо, чтобы f(x) била ортогональна всем'собственным функ-
функциям, отвечающим этому значению К; впрочем, это вытекает и из
третьей теоремы Фредгольма (почему?). В этом случае коэффициенты
при указанных собственных функциях в формуле A6) надо заменить
на произвольные постоянные, оставив прочие коэффициенты без
изменения.
Пусть теперь дана какая-либо функция F(x), которую возможно
представить в виде'
ь
Р (х) =\ К {х,1)/&)<%,, " A7)
a
где /6 ?а [а, Ь\; такие функции F(x) называются представимыми
через ядро. Подставляя в правую часть разложение (8), получаем
Значит, функцию, представимую через ядро, возможно разложить по
собственным функциям этого ядра; это теорема Гильберта—Шмидта.
Эта теорема допускает следующее истолкование. Рассмотрим, как и раньше,
интегральный оператор Аи (ж) = \ К {х, |)«(i)d(?). Областью его определения
служит Ща, Ь], а множеством значений—подпространство функций, преДста-
вимых через ядро. Теорема Гильберта —Шмидта говорит, что последователь-
последовательность функций C) образует евклидов базис в этом подпространстве. Если
элементами этого подпространства можно с любой точностью аппроксимировать
любую функцию из Ц [а, Ь] (а такие случаи возможны), то тем самым полу-
получится, что система функций C) полна в L2 [а, Ь]. Зтэ наиболее распростра-
распространенный способ проверки полноты.
Все приведенные функциональные ряды сходятся, во всяком-
случае, в смысле ?8, т. е. в среднем квадратичном. В курсах интег-
интегральных уравнений указаны дополнительные условия, при которых
эти ряды сходятся равномерно. *
Результаты пн. 1—3 без существенных изменений распростра-
распространяются на другие виды уравнений Фредгольма 2-го рода, упомянутые
в п. 1.2, с вещественным симметричным ядром (в том числе на
нагруженные уравнения). Правда, для уравнений с искомой функ^
цией от п независимых переменных более естественно нумеровать
характеристические числа и собственные функции с помощью л

§ 3. УРАВНЕНИЯ С СИММЕТРИЧНЫМИ ЯДРАМИ 425
индексов, но это не имеет принципиального значения. Если рассмат-
рассматривается система уравнений, то ядро К представляет собой квад-
квадратную матрицу-функцию, а условие симметрии A) заменяется на
где звездочка означает транспонирование, а в случае комплексных
функций, для которых приведенные результаты также справедливы,—
еще и переход к комплексно сопряженным значениям. В этом случае
разложение (8) приобретает вид
К(х, 6) = ?-^-Ф/(«)[ф>(Б)]*,
соответственно видоизменятся и другие приведенные здесь формулы.
4. Переход от несимметричного ядра к симметричному. Бывают случаи,
когда в исходном уравнении ядро не является симметричным, однако возможно
с помощью тех нли иных преобразований перейти к уравнению с симметрич-
симметричным ядром, после чего воспользоваться теорией уравнений с симметричными
ядрами. Рассмотрим, например, уравнение
ь
и (х) = I \ К {х, Б)'(х)8(Б>и(Б)<? + /(х), A8)
а
где /С {х, ?) =/С (|, х), а г и s—произвольные положительные функции, так
что в целом ядро К. (х, ?)/• (ж) s (?) уравнения A8) несимметрично. Однако
совершив замену искомой функции
ч/'Т*)"
м= 1/ о.
Г я(ж) '
мы придем к равносильному уравнению
&
о (x) = 3i I* /С (х, I) Vr (х) s (х) /• (|) s (I) о (I) <i|+ ]/^| / (*)
уже с симметричным ядром.
Важным классом ядер, приводимых к симметричным, точнее говоря, к эр-
эрмитовым ядрам, являются антисимметричные, а в комплексном случае анти-
эрмитовы ядра, определяемые соотношением
/С (Б. х) = -
ядро — К (х,
B.16) в виде
Однако тогда ядро — К (х, I) эрмитово (почему?) и, переписав уравнение
мы можем полностью перенести на него результаты теории уравнений с эрми-
эрмитовыми ядрами. Отметим, в частности, что при построении характеристических
чисел значении Xi получатся вещественными, а потому значения К—чисто
мнимыми.

426 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Иногда может оказаться полезным односторонний переход от несимметрич-
несимметричного ядра к симметричному. Рассмотрим общее уравнение B.16) с вещественным
несимметричным ядром. Поменяв обозначение х на s, умножив после этого обе
части на К (s, х), проинтегрировав по s и изменив обозначения s на i в одно-
однократных интегралах, получим (проверьте!)
ь ь
J [К (I, х)-Ыа (х, %)] и (|) a\= J К а, х) f ©<fc A9)
а а
где обозначено
Ь
'*«(*. 6)=$К-(«. х)К(8. l)ds
а
— левое итерированное ядро. Из A9) и B.16) получаем, что и(х) удовлетворяет
уравнению
B0)
и (*)=Х J [К (х, |)+ К (L х)-ЬКж (х
с симметричным ядром, правда, зависящим от Я. Аналогично проверяется,
что решения сопряженного к B.16) уравнения B.17) удовлетноряют также
уравнению с симметричным ядре»!
Ь
где К „—правое итерированное ядро:
Ь
Мы предоставляем читателю проверить, что все характеристические числа
ядер К3 и Кп положительны и что формулы
B1)
а л
устанавливают взаимно однозначное соответствие между собственными функ-
функциями этих ядер, причем
Ь Ь
\ ф/ (х) <Ps (х) dx= J ijy (дг) 4>ft (дг) dx=6jk.
a a
С помощью этих собственных функций возможно представление исходного ядра
в виде суммы ряда
К (х, .©=V -т= Ь(хLр; ©, B2)
ГУ *
где Ху—характеристические числа ядра Лл (нли, что то же, /fB).

§ 3. УРАВНЕНИЯ С СИММЕТРИЧНЫМИ ЯДРАМИ 427
В самом деле, пользуясь формулами B1), получаем
frft
ftfr
l\ •¦'
а правая часть равна нулю в силу формулы A0), примененной к /Сл.
Из формулы B2) можно получить следствия, аналогичные приведенным
в п. 3, даже если само ядро К не имеет (как, например, ядро Вольтерра) ни
одного характеристического числа. Приведем, например, аналог теоремы
Гильберта—Шмидта.ч Для этого предположим, что функцию F (х) можно пред-
представить через ядро К с помощью формулы A7). Тогда, подставляя в правую
часть разложение B2), получаем
. /ft \
F (х) = У-7= К / (?) <Р/ (?) € ) %¦ {х),
/V h V J У
т. е. эту функцию можно разложить по собственным функциям ядра Ка.
Аналогично фуикцяю F (к), представимую через ядра К с помощью формулы
ft
(этого различия не было для симметричных ядер), можно разложить по- соб-
собственным функциям ядра Кя-
5. Экстремальное свойство характеристических чисел. Ха-
Характеристические числа уравнений Фредгольма с симметричным
ядром обладают экстремальными свойствами, совершенно аналогич-
аналогичными свойствам собственных значений самосопряженного отображе-
отображения конечномерного евклидова пространства в себя (п. IV. 1.7; см.
также п. VI.2.8). Мы ограничимся дли простоты одномерными
скалярными вещественными уравнениями, хотя те же свойства имеют
место в общем случае.
Рассмотрим значения квадратичного функционала
6ft-
1 {У } = I i * (*• '&>У МУ ® ** dl B3)
а а
при интегральной связи
ь
*(x)dx=\. B4)
Нетрудно усмотреть прямую аналогию с п. IV.1.7, если переписать
функционал B3) в виде )[) К(х, Ъ,)у (|) й\-у (x)j dx и заметить,
что условие B4) определяет единичную сферу в пространстве

428 , ГЛ. V!!. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
.i.j,[a, ft]. Новым моментом, кроме бесконечномерности, является то,
что система собственных функций ядра К. уже, вообще говоря,
не является полной в L% [a, b] (например, для вырожденного ядра
она наверняка не полна, но она может быть неполной н для ядер,
не являющихся вырожденными). Однако это в данном вопросе
оказывается несущественным.
Подставив в B3) разложение (8), мы получим после простых
преобразований
Чу)=1*тЛ 125)
i '
где обозначено
В силу нормированности функций фу это коэффициенты разложения
функции у (х) по ортогональной системе функций C) (ср. ЛВМ,
и. XVII.21). Если бы система C) была полной, то у (х) = y^
в общем же случае можно ручаться только, что
*(*>=2*/М*>+*м. B6)
где ув(х) ортогональна всем функциям C) (проверьте!),. Подста-
Подстановка этого разложения в B4) дает
ь
S.V?+$.yJ(*>*f=U B7)
i a
Допустим сначала, что все Ку > 0, причем kt ^
как из B5) и B7) вытекает, что
ТО МЫ ВИДИМ, ЧТО
причем знак равенства достигается, только если ^в(лт)==О и V.— 0
при Ау > Я1} другими словами, только для нормированных собствен-
собственных функций, отвечающих kt (см. B6)). Если такая функция
известна, то, приняв ее за <ft{x) и поставив дополнительную связь
y(x)^{x)dx = 0, B8)
а
аналогично получим, что /{.Н^у» причем равенство достигается
А2

§ 3. УРАВНЕНИЯ С СИММЕТРИЧНЫМИ ЯДРАМИ . 429
только на собственных функциях,, отвечающих Я,2 (и ортогональных
()) затем ставим две дополнительные связи
И Т. Д.
В силу B5) необходимым и достаточным условием положитель-
положительности всех характеристических чисел является, неравенство
/{^}>0 для всех у (х)? Z.2 [e, Ь].
Функционал B3) и ядро К, обладающие этим свойством, называются
неотрицательно определенными. Если это неравенство является
строгим для всех функций у(х)^0, функционал и ядро называются
положительно определенными. Из B5) и B6) вытекает, что для
положительной определенности функционала B3) необходимо и до-
достаточно, чтобы выполнялись два условия: все Kj > 0, а система C)
полна (почему?). (Отметим, в частности, что в силу формулы A1)
ядро Кг всегда неотрицательно определенное.)
Если все "Kj < 0, то картина аналогичная, но -т— ^ / {у } ^ О,
где Kt—наименьшее по абсолютному значению характеристическое
число. Если же имеются Xj обоих знаков, то 1{у) заключено между
обратными величинами наименьшего по абсолютному, значению из
Xj < О и наименьшего из Xj > 0, причем эти крайние значения
I {у} достигаются для соответствующих собственных функций.
Если такая функция ф, (х) известна, то, добавив условие ортого-
ортогональности B8), мы соответственно суживаем интервал изменения
/ {у$, и т. д. Взамен условия B8) можно в силу п. 2 перейти
к ядру E) и рассматривать задачу на экстремум отвечающего ему
квадратичного функционала при единственной связи B4).
Пели искать средствами вариационного исчисления функции, придающие
функционалу B3) стационарное значение при связи B.4) (п. VI. 1.12), то мы
приходим к собственным функциям ядра К. Для несимметричного ядра К
та же задача приводит к собственным функциям симметризованиого ядра
~[К(х, 1) + КA, х)\ (прозерьте!).
Описанное экстремальное свойство может служить основой для
применения общего метода Рнтца (п. VI.4.1) к приближенному вы-
вычислению характеристических чисел и собственных функций сим-
симметричного ядра, что сводится этим методом к аналогичной задаче
для квадратичной формы конечного числа переменных. При этом
нет надобности заранее знать, каконы знаки у всех Xf. если в про-
процессе вычислений окажется, что 1{у}>0 хотя бы для одной
функции у(х), то среди Ау имеются положительные, т. е. имеет
смысл задача на максимум функционала 1{у}; аналогично посту-
поступаем, если обнаружится, что 1{у) может быть меньше нуля.

430 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
В уравнении B0) встретилось ядро, зависящее от X. Такие ядра, не обя-
обязательно симметричные, встречаются и' в других вопросах, поэтому скажем
здесь несколько слов о них. Пусть ядро К (х, |; X) является аналитической
функцией X в некоторой области (G) комплексной плоскости. Так как в урав-
уравнении B.16) X можно считать постоянным, то первые три теоремы Фредгольма
остаются справедливыми и для таких ядер. Аналогия с вырожденными ядрами,
котораи может быть обоснована строго, показывает что определитель Фред-
Фредгольма D(X) (пп. 2.1, 2), нули которого дают характеристические числа ядра К,
представляют собой аналитическую функцию X в (G). Значит, если D (X) ф. 0,
то эти нули образуют либо конечное множество, либо последовательность,
уходящую к границе (G), к которой причисляется и точка Я,= оо; так будет,
в частности, если 0? (G), так как значение Х—0 не может быть характери-
характеристическим. Однако возможен также случай D {X) = 0, тогда все значения
Х? (G) будут характеристическими. (Проверьте, например, что для ядра
К (х, !)=-пГ+*?. —К*. ?<1. все значения X Ф 0 характеристические,
причем каждому, из этих значений отвечает собствеиная функция <рх (дс)=г-^= ,
3 / 3~
а значению Х=-^-—еще и собственная функция ^(х) = 1/ — х.
6. Уравнения с самосопряженными операторами. Свойства интегральных
уравнений с симметричными ядрами распространяются на общие уравнения
B.67) с iвполне непрерывным самосопряженным оператором А. При этом линей-
линейный оператор А, отображающий вещественное гильбертово 'Пространство (Щ
в себя, называется самосопряженным, если он совладает со своим сопряжен-
сопряженным,'другими словами (ср. B.66)), если
¦ (Ах, у) = (х, Ау) для всех х, у€ (#)• B9)
Мы перечислим эти свойства в терминах собственных значений оператора А;
при этом ладо иметь в виду, что собственные аиачения обратны по величине
характеристическим числам, и поэтому нулевому собственному значению- не
отвечают характеристические числа. (А характеристическое число равняться
нулю не может.)
Прежде всего доказывается, что если оператор А не нулевой, т. е. если
А (Н) Ф 0, то А обладает по крайней мере одним ненулевым собственным зна-
значением. Обозначим это собственное значение через Ху, а отвечающий ему
собственный вектор, который мы возьмем нормированным—через q>x. Оператор
Ai=A.1<-, «Pi)q>i (это означает, что А1х=Х1(х, <Pi) <J>,) самосопряженный
и имеет единственное ненулевое собственное аиачение ль которому отвечает
единственный собственный вектор q>j (проверьте!). Рассуждая, как в п. 2, не-
несложно доказать, что если собственному значению Хх оператора А отвечает
лишь один собственный вектор q>t, то оператор
А—Х1(-, ф^ф!
имеет те же собственные значения и ¦собственные векторы, что и А, за исклю-
исключением Х^ и ф!. Продолжая таким образом, мы приходим к представлевию
оператора А в виде суммы
^М /)Ф/ C0)
взятой по всем ненулевым собственным значениям оператора А и соответствую-
соответствующим им собственным лекторам. При этом, если какому-либо собственному
значению отвечает k линейно независимых собственных векторов, то соответ-
соответствующее собственное значение повторяется к раз, а собственные векторы
берутся ортогональными друг другу и нормированными. Собственные же

§ 3. УРАВНЕНИЯ С СИММЕТРИЧНЫМИ ЯДРАМИ 431
векторы, отвечающие различным собственным значениям, всегда ортогональны
друг другу.
Из формулы C0) вытекают те же следствия, что в п. 3 для интегрального
оператора. Так, из вычисления
= Щк/Хк(х, ФйМф*. Фу) фу = 2 *¦?(*. 47) ФУ
(проверьте!) получаем, что
А2=Ух/(-, фу) фу;
вообще
2 =1. 2, 3, ...).
Умножив эти равенства на любые коэффициенты н просуммировав по п, по-
получим, что
где F (к)—любая однозначная, аналитическая функция, для которой F. @)=0
и значения Я ие являются особыми точками. Из формулы C0) нетрудно вывести
также, что норма оператора А (см. п. 1.3) равна max | Яу| (в силу 4-й теоремы
Фредгольма» если собственных значений бесконечное количество, то они обра-
образуют последовательность, сходящуюся к нулю).
Обратно, для любой ограниченной последовательности kj н любой ортого-
ортогональной системы нормированных векторов фу формула C0) определяет линей-
линейный ограниченный самосопряженный оператор с собственными значениями kj
и соответствующими собственными векторами фу (о нулевом собственном значении
будет сказана позже). Этот оператор будет вполне непрерывным тогда и только
тогда, когда Ху —»- 0. Если зафиксировать векторы фу н произвольно менять
/-* »
значения Лу, мы получим семейство операторов с заданными собственными век-
векторами; эти операторы попарно коммутируют, так как
М- Ф/>Фу) BМ§>
(В отличие от этого, если векторы ф и if линейно независимы и ие ортого-
ортогональны, то операторы (•, ф) ф- и (•, ф) ф не коммутируют—докажите!) Теперь
можно лучше понять смысл левой части формулы C1): если в указанном
семействе норма А достаточно мала (меньше радиуса сходииости ряда для F (к)),
то F (А) определяется суммой ряда Маклорена; если же норма А не мала, то
правая часть C1) дает аналитическое продолжение этой суммы по всем Ху.
Из C1) получается, в частности, разложение резольвентного оператора
Г (к), по определению равного
r(X)=A(I-U)-» = ^rz^(-, Ф/)Фу.
Легко непосредственно убедиться в том, что
A + кТ{к))A-кА) = 1
(проверьте)). Поэтому, записав уравнение B.67) в виде (I—XA)u=f я умножив

432 ГЛ. V!!. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
обе части иа I + КГ (X), получаем
Это, конечно, не что иное, как формула B.7) (оиа же B.44)).
Как видим, более общее изложение делает картину более простой и позво-
позволяет глубже разобраться в основных связях,
Из п. IV 1.4 вытекает, что (Я) разлагается в ортогональную прямую сумму
'своих подпространств А (Я) и А @) (правда, там рассматривались конечно-
конечномерные пространства, ио при доказательстве разложения конечномерность ие
использовалась). В силу формулы C0) первое подпространство состоит из эле-
элементов, которые можно разложить по векторам <р/. Второе же подпространство,
если оио ие нулевое, состоит из всех собственных векторов, отвечающих нуле-
нулевому собственному значению (почему?). Таким образом, мы получаем, что
система ортогональных векторов q>, является полной в (Я) тогда и только
тогда, когда оператор А не имеет нулевого собственного значения. Для урав-
уравнения B.16) с симметричным ядром это означает, что однородное уравнение
К (х, |) и (|) а% = 0 (а<х<Ь)
не должно иметь нетривиального решения.
Все указанные свойства справедливы и для комплексного гильбертова
пространства (Я); в этом случае оператор, удовлетворяющий условию B9), на-
называется эрмитовым (ср. п. 1.2). К перечисленным свойствам можно еще до-
добавить, что все собственные значения эрмитова оператора вещественны. (Дли
самосопряженного оператора это тоже так, ио о мнимом собственном значении
оператора А, действующего в вещественном пространстве (Я), можно говорить
только после комплексного расширения этого пространства, т. е. после перехо-
перехода к совокупности элементов вида x + iy, где
x2)— i(xit у2) + (Уь у2),
)=Ax+iAy;
а после такого перехода самосопряженный оператор становится эрмитовым —
проверьте!)
Подобно п. 4 вводится понятие антиэрмитова оператора, для которого
А* = —А, т. е. (Ах, у) =—(х, Ау); все его свойства те же, что у эрмитовых
операторов, однако все собственные значения чисто мнимые. Любой линейный
оператор можно представить в виде суммы эрмитова и аитиэрмитова опера-
операторов по формуле
, А-А*
Разделив и помножив второе слагаемое иа i, получаем другое представление
произвольного оператора в виде
где Ai и А2—эрмитовы операторы; при этом A*=Ai—i'A2 (почему?).
Из C0) вытекает, что
(Ах, х)=
С другой стороны, ломиожив скалярио иа себя оба члена равенства

§ 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ КЛАССЫ УРАВНЕНИЙ 433
в котором хе ортогонален всем «ру, получим, что
i
КОЛОХ2А
(это неравенство Бесселя, ср. ЛВМ, п. XVII.27); при этом неравенство обра-
обращается в равенство, если хо=О, т. е. если х разлагается по векторам фу. От-
Отсюда легко вывести вариационный принцип для нахождения собственных зна-
значений Ху, аналогичный описанному в п. 5, что мы предоставляем читателю.
§ 4. Некоторые специальные классы уравнений
1. Уравнения Вольтерра 1-го рода. Рассмотрим уравнение
О)
Ясно, что для его разрешимости необходимо условие
/И = 0. B)
Допустим, • что ядро К(х, ?), в котором считается а^^^дг, непре-
непрерывно на диагонали ? = Ат, и продифференцируем обе части A) пох
Это приведет к уравнению
X
К (AT, X) U (AT) + $ К (AT, I) U (I) (Ц = /' (AT), C)
а
которое при условии B) равносильно A). Если К (х, х) Ф 0, то, раз-
разделив обе части C) на К (х, х), мы приходим к уравнению Вольтерра
2-го рода. Если К(х, аг) = О, то можно проделать описанную про-
процедуру еще раз.
Рассмотрим теперь типичный случай уравнения, у которого ядро
обращается в бесконечность на диагонали:
где 0<<*<1, а функция И(х, ?) конечна на. диагонали. Поменяем
обозначение х на *, умножим обе части на _ „_а, проинтегри-
проинтегрируем по s от а до х и в левой части переставим порядок интегри-
интегрирования; получим (проверьте!)
Можно перейти и от E) к D) и показать, тем самым, что эти урав-
уравнения равносильны; мы не будем здесь это делать, г
КОЛОХЗА
ПГ.ЮТ PIT A

434 ГЛ. V!!. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Заменив в ядре уравнения E), стоящем в квадратных скобках,
переменную интегрирования по формуле s = g-f-(.*r—g) t, получаем,
что это ядро равно
f Я E+(*-?)<.?) ..
о
и потому на диагонали, т. е. при | = лг, принимает конечное
значение
(см. ЛВМ, п. XIV.18 и формулу (II.3.27) этой книги). Поэтому
к уравнению E) возможно применить описанный выше метод ^
ференцирования...-.
Пусть, например, Н (х, |) = 1, т. е. уравнение D) имеет вид
Тогда ядро уравнения E) равно —. и, дифференцируя обе части, получаем
решение
' X
и(х)= -т- \-.—-±г-.— ds=\x—s=p—a\=
v ' я dx J (*—s)'-.«
a
д:
sin na d f* /(a+x—p)
~~T~dx) (p-a)>-« dp =
¦ e
slnnaf
Эту формулу можно рассматривать как формулу обращения для интегрального
преобразования F).
Покажем применение полученного результата к решению следующей задачи:
в однородном пояс тяжести материальная точка М скользит без треиия вдоль
линии (L) (рис. 115); какой должна быть эта линия, чтобы период колебаний
не зависел от амплитуды? Для решения допустим, что М„—наивысшее,
а @; о)—наинизшее положения колеблющейся точки; тогда & силу формулы
(VI. 1.4) период колебаний Т равен
4 Г 1 Vl
Обозначив иа минуту V l-{-r\'2jx\'=u(r\), мы можем совершить обращение по

§ 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ КЛАССЫ УРАВНЕНИЙ 435
формуле G) с а= 1/2, что даст . ; .
Vl+y"r ITf^ I
У' п 4 уГу'
Получилось диффереициальиое уравнение для у(х). Его удобно решить с по-
помощью искусственной подстановки
где /?=
Вычисления, которые мы предоставляем чи-
читателю, показывают, что
!пф).
О
а х
Получилась циклоида с вершиной в начале рис Ц5
координат (проверьте!). Уравнение F) при
сС=1/2 рассматривал Н.Абель.
Применяются также многомерные аналоги ураввения Абеля. Так; совершая
над уравнением
I(if-i|)i-(*-9ir1/1 и a, tD 4 drj=/ (х, у),
где (aXi у)—треугольник 0<т|<у, \х— ||<У—ц, преобразование, аналогич-
аналогичное приведенному выше, можно прийти к равенству
а отсюда с помощью дифференцирования—к формуле обращения
См. 188], § 1.6.
2. Уравнения Фредгольма 1-го рода с симметричным ядром.
Рассмотрим уравнение
(8)
с вещественным симметричным (или комплексным эрмитовым) ядром
и с системой характеристических чисел C.2) и собственных функ-
функций C.3). Тогда в силу теоремы Гильберта—Шмидта (п. 3.3) для
существования решения необходимо прежде всего, чтобы функция
f(x) разлагалась по собственным функциям C):
Если это условие выполнено, то можно искать решение в виде
A0)

436 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Подстановка в (8) и сравнение с (9) дают
jjr = (/, Фу), откуда U — Xjif, ф/).
Поэтому, если мы хотим, чтобы решение, как обычно, принадлежало Ща, Ь],
то надо потребовать, чтобы функция f удовлетворяла дополнительно требованию
2^/|(/. Фу) I* < °°- Эт° вытекает из теоремы Фишера—Риса A907), согласно
которой при любой ортогональной системе нормированных функций фу (х) ряд
A0) сходится в среднем квадратичном тогда н только тогда, когда Х|"у|* < со-
(«Тогда» вытекает нз первого определения полноты для Ц [аг Ь], см. п. 2.6;
«только тогда»—из того, что остаток последнего ряда равен квадрату среднего
квадратичного уклонения частной суммы рнда A0) от его полной суммы—про-
суммы—продумайте это!)
Как всегда, для получения общего решения уравнения (8) надо
к его частному решению A0) прибавить общее решение соответст-
соответствующего однородного уравнения, другими словами, как было пока-
показано в п. 3.5,— любую функцию, ортогональную всем функциям
C.1$). Значит, если система C.3) полна, то решение уравнения (8)
единственно, в противном случае — не единственно и даже может
содержать ¦> бесконечное число произвольных постоянных; например,
так будет для любого вырожденного ядра (почему?).
Если, все А.у > 0 и f (х) такова, что уравнение (8) разрешимо (но функции
• фу(х) не заданы!), то решение A0) можно получить по методу итераций, как"
предел последовательности функций ип (ж)," построенных по формуле
6
] (n=i,2.3, ...). (ID
а
где «0 (х) произвольна, а А. > 0 достаточно мало. В самом деле, если обозна-
обозначить и„ (х) =2 «л> уфу (х), f (*) = Х/уФу(х) (ортогональная ядру компонента
в Ub(x) исчезает после первой же итераинн н потому несущественна), то из
(II) получаем
b (fy г
Отсюда при увеличении п
а потому процесс сходится, еслв 1—т-\ < 1, т. е. если 0 < X. < 2Х.1, где
| К] | . .
V,—наименьшее из характеристических чисел. (Реально мы "Кх обычно ие знаем,
так что значение X можно подобрать эмпирически, задаваясь различными зна-
значениями и прослеживая, какая при этом получится скорость сходимости.) Пе-
Переходя в A1) к пределу при п—*¦ оо, видим, что предельная функция удов-•
летворяет уравнению (8), т. е. является искомым решением.
Впрочем, картина на самом деле сложнее, чем это может показаться из
предыдущего абзаца. Хорошо сходятся лвшь коэффициенты при первых собст-

§ 4. НЕКОТОРЫЕ. СПЕЦИАЛЬНЫЕ КЛАССЫ УРАВНЕНИЙ 437
венных' функциях, тогда как дальнейшие сходятся плохо из-за близости коэф-
коэффициента сходимости 1 — т- к единице. Это делает процесс в целом плохо схо-
дящимся, если ио(х) существенно отличается от-искомого решения в высших
компонентах. Здесь можно применить итерации, начиная от различных нуле-
нулевых приближений мв (ж): если после нескольких итерации, результаты получатся
близкими, то естественно ожидать, что тем самым решение получено с хорошей
точностью.
3. Понятие о некорректных задачах. Еще более существенно, что если
функции C.3) не образуют полную систему в Ц [а, 6],.то ортогональное ядру
слагаемое в и„ (х), возникшее из-за неточности в задании функции / и погреш-
погрешностей вычисления (округления, неточность формул численного интегрирова-
интегрирования) с ростом п увеличивается. Подобные задачи, решение которых может
существенно измениться и даже перестать существовать при малом изменении
исходных данных, называются некорректными; естественно, что на решении
этих задач существенно сказываются и погрешности вычисления. Впервые на
некорректные задачи обратил внимание выдающийся французский математик
Ж- Адамар A865—1963), но систематическое их изучение началось с работ
советского математика и геофизика А. Н. Тихонова (р. в 1906 г.). Многие
задачи, как классические (например, задача численного дифференцирования или .
рассмотренная выше задача о решении уравнения Фредгольма 1-го рода), так
и новые, являются некорректными, н для их решения предложен ряд методов.
регуляризации (корректизации), дающих возможность аппроксимировать некор-
некорректную задачу корректными.
Мы не имеем здесь возможности останавляваться на этих методах; укажем
в качестве примера на метод перехода к уравнению 2-го рода с помощью добав-
добавления к одной из частей уравнения (8) члена аи (х). При этом коэффициент а
должен быть выбран не слишком большим (иначе существенно изменится реше-
решение) и не слишком малым (иначе добавленный член практически не скажется).
Подходящее значение а можно подобрать эмпирически, .с помощью анализа
модельных задач с известными решениями.
Более точно это означает следующее. В реальных задачах характер реше-
решения обычно бывает известен. Выберем функцию и (х) того же характера, что и
искомое решение и (х) (прн расшифровке неопределенного термина «того же
характера» существенная роль принадлежит опыту и интуиции, которые должны
подсказать, какие из особенностей решения являются наиболее важными), и
вычислим
$*(*, 6) и F) «=/(*).
Теперь можно рассматривать это равенство как интегральное уравнение с задан-
заданной функцией J (х) и искомой и (х). Применив к нему численный метод, кото-
который мы хотим испытать, мы можем сравнить полученное приближенное реше-
решение с точным, т. е. с и (х); если результат получится удовлетворительным, то
можно с известным, основанием считать, что и для исходного уравнения (8)
метод будет пригоден. Если характер решения известен недостаточно, то можно
испытать метод на нескольких функциях и (х).
Ясно, что эти общие соображения значительно выходят за рамки инте-
интегральных уравнений.
4. Уравнения Фредгольма 1-го рода, общий случай. Рассмот-
Рассмотрим теперь уравнение (8), не предполагая ядро симметричным. Будем
считать, что решение этого уравнения существует.

438Ч РЛ. V». ИНТЕГРАЛЬНЫЕ УРАВНЕНИЙ
Теоретические условия существования и единственности решения нетрудно
сформулировать аналогично п. 2, исходя из разложения C.22). При этом функ-
функция f (х) должна разлагаться по системе ty/, а решение и (х) надо разлагать по
системе q>/.
Будем искать решение уравнения (8) в виде
«(*)=• 2 «/«)(*)*(*), A2)
где gu g2, g3, ...—некоторая полная на интервале (а, Ь) система
функций, а \{х) — некоторая «весовая функция», которую жела-
желательно выбрать ближе к искомому решению, чем будет улучшена
сходимость ряда A2); если о решении мало что известно, то можно
положить \(х)=\. Подстановка A2) в (8) дает
где обозначено
^ A4)
Таким образом, надо найти коэффициенты и} разложения A3).
Бывают случаи, когда разложение A3) совсем просто, например,
если kf(x) — CjXJ (/=0, 1, 2, ...) или если функции hf йопарио
ортогональны. Если это не так, то можно с помощью- процесса
ортогоналнзацни (ЛВМ, nn.VII.21 н XVII.20) получить ортогональ-
ортогональную систему функций
v _ь у -Lf, (**> Xi) ч v _A (fh, Хг) (К Ш)
затем разложить / по системе X/ н подставить в это разложение
выражение функций %/ через hk (A = l, 2, ..., у), которое вытекает
из A5). Можно разложить функции / и hj по какой угодно полной
системе функций:
*«*W G=1,2,3,...),
затем, если это удастся сделать эффективно, обратить второе раз-
разложение (т. е. обратить матрицу (hjk)) и подставить в первое.
Если разложение функции А/(ж) в степенной ряд начинается с члена
с х> (/=0, 1, 2, ...), то можно воспользоваться равенствами, вытекающими
из A3).
/ @)=«Л @). V @)=ил @M-«i*I @).
г (О)=; ;
и т. д.

§ 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ КЛАССЫ УРАВНЕНИЙ 439
Рассмотрим, например, уравнение
я
J «farms „©<?=/(*),
о
встречающееся в теории распространения волн. Будем искать решение в виде
со
U (X) = 2 ил cos "*•
/1 = 0
Тогда в силу формулы A4)
я
Кп (х) = jj e'*C0l>& cos n? d? = я»"У„ (*)
о
(см. ЛВМ, (XVII. 113)). Разложение A3) приобретает вид
(см. ЛВМ, (XV. 170)). Отсюда
f f(P)—ув,—Je, и т.
(проверьте!), что дает возможность последовательно вычислить иоэффициенты ип.
Если ядро уравнения (8) имеет при ж=| конечный скачок ф (g), то от
этого уравнения можно с помощью дифференцирования, аналогично п. 1, пе-
перейти к уравнению Фредгольма 2"-го рода. В самом деле, тогда
где L есть производная от К по ж без учета дельта-слагаемого. После диффе-
дифференцирования обеих частей (8) по х получаем
ь
[<р (?) б (х —1)+L (х, |)] и (|) dg= f (х),
а .
т. е. " .
ь
и(х)=— V —тЧ^ и (|) d^ -\ г—г
а
— уравнение 2-го рода. Если ядро уравнения (8) непрерывно на диагонали,
но его производные 1-го порядка испытывают скачок, то надо произвести диф-
дифференцирование еще раз, и т. д. Таиая ситуация возникает, в частности, если
ядром уравнения (8) служит функция Грина (п. 1).
5. Применение производящих функций. Функция Ф (t, x) называется про-
производящей для системы функции
8о(х), gi(x), g2(x), ..., A6)
если .
00

440 ГЛ; VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
где а„ Ф 0—некоторые постоянные, другими словами, если функции A6) полу-
получаются в результате разложения Ф (t, х) в ряд по степеням t. Многие важные
системы функции удается просто исследовать, рассматривая свойства их произ-
производящих функции. Отметим, что из-за произвольности коэффициентов а„ одна
и та же система функций A6) может иметь различные производящие функции.
Приведем без доказательства некоторые производящие функции. Так, в раз-
разложении
каждая из функций Т% (х) оказывается полиномом степени п; они называются
полиномами Гегенбауера и при зафиксированном р" образуют на отрезке
—1<«О ортогональную с весом A-х2)? (ЛВМ, п. XVII.29) полную
сястему функций. В частности, Т"п (х)=Рп (х) (полиномы Лежандра),
Уя/2 пТ~У'(х)=Тп(х) (полиномы Чебышева, ЛВМ, п. XVI1.29). В разложении
функции Lti(x)—также полиномы степени л; они называются полиномами Ла-
Лагерра а при зафиксированном а образуют на интервале 0<х < оо ортогональ-
ортогональную с весом хае~х полную систему функций. (При этом имеетси в виду пол-
полнота в пространстве L2[0, оо) с весом хРе'*; это гильбертово пространство со
скалярным произведением (/, g)= \ f (x)g(x) xae~xdx.) Наконец, в разложении
о .
00
±Hn(x).t" A8)
п=о
функции Нп(х)—вновь полиномы степени п; они называются полиномами Эр-
мита и образуют иа интервале —оо < х < оо ортогональную с весом е~**
полную систему функций. Все эти полиномы обладают многими полезными
свойствами, которых мы здесь ие будем касаться.
Допустим, что для некоторой производящей функции A7) система функций
A6) оказалась вещественной и ортогональной с весом р (х) 5г 0 на некотором
интервале а, Ь. Рассмотрим уравнение
и &)a% = f{x), A.9)
где функция f (х) аналитична в окрестности точки х=0. Его решение можно
искать в виде
2 B0)
Подстановка A7) и B0) в A9) дает в силу соотношений ортогональности
2 «„«„llg«F *"=/(*).

§ 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ КЛАССЫ УРАВНЕНИЙ 441
где положено к
Отсюда получаем
fin) (П\
ь
*=$[gn Ml2 p (*)**.
а
Подстановка этих значений в. B0) дает искомое решение, которое в случае
полноты системы A6) является единственным.
Например, исходя из производящей функции A8), мы получаем возмож-
возможность решить уравнение
GO
$ / B1)
встречающееся в теории распространения тепла, с помощью ряда по полиномам
Эрмита. При вычислении коэффициентов следует иметь в виду формулу || Нп ||2=
¦= 2"я! Уп, которую мы также не будем здесь доказывать.
Заметим теперь, что, исходя из какого-либо ядра К (х, ?), для которого мы
можем решить уравнение (8), возможно построить много других ядер, обла-
обладающих тем же свойством, с помощью следующего общего приема. Рассмотрим
уравнение
ь
LXK (х, 6)и(В d?=M*). B2)
где Lx—некоторый линейный (например, дифференциальный) оператор, дей-
действующий по переменной х (т. е. при его действии | считается параметром).
Допустим, что мы можем найти сбщее решение уравнения
Тогда, подставив это решение в правую часть (8), мы тем самым сводим урав-
уравнение B2) к (8); значит, и для уравнения B2) возможно построить решение.
Например, из разложения A8), которое можно переписать в виде
вытекает, что
dxk \\_dxk J*=o/t)=i-*
= {*-ч' Hk (п)}ч=8_, =(-1)* е-»-»1», (x-l);
последний переход сделан на основании того, что
л н"(-x)t" =--|te-|i
т. е. Я„ (—дс) = (—\)пНп(х). (Это пример того, как с помощью производящей
функции выводятси свойства произведенных ею функций.) Поэтому мы получаем
возможность решить любое уравнение вида
• N
V e-(*-E)I2e*w*(*-6)"F)'«=/i(*) (все aft=const), B3)

442 ' ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
решив сначала простое уравнение
а затем уравнение B1). (Впрочем, уравнение B3) можно решать непосредственно,
воспользовавшись формулой
л=0
и подставив вместо и (!) ряд по полиномам Эрмита с неопределенными коэффи-
коэффициентами.) Можно положить и N=oo.
Другой способ решения уравнения B2) возможен, если ядро, как это иногда
бывает, удовлетворяет уравнению вида
LxK{x, 1)=М^К(х, 1), , ... B4)
где линейный оператор М% действует по переменной |„ Подставив B4) в B2) и
перебросив, если это удастся (например, с помощью интегрирования по частям),
оператор с К на и, мы приходим к уравнению вида
г J #г (*. © м» и ©<«=/¦ м-' '"':.
решив которое, еще придетси вернуться от М^и (?) к и (?).
К рассматриваемым вопросам близка проблема моментов, которая состоит
в построении функции и (х) по ее заданным моментам ¦
ь . . . . . .
^u(x)x"p(x)dx=Mn (л=0, 1, 2, ...), B5)
а
где p(xKsO—заданная весовая функция. Отметим сразу же, что ее можно
менять, нереписав равенства B5) в виде . .
v
где
Этим можно пользоваться, чтобы, используй имеющуюся информацию о и (ж),
получить v (х) по возможности более удобной структуры (нзяример, близкую
к константе). В качестве интервала (а, Ь) можно взять одни из интервалов
(—1, 1), @, оо) и (— оо, оо), так каи остальные приводятся к этим с помощью
линейной замены переменной интегрирования, что сводится к пересчету момен-
моментов (продумайте это!).
Один из методов решения проблемы состоит в построении, с номощью орто-
гоналнзации последовательности степеней, системы полиномов
/=о
ортогональной на интервале (а, Ь) с весом р (х). Если искать решение в виде
«W=S^QnD B6)
я=0 " '

§ 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ КЛАССЫ УРАВНЕНИЙ 443
ы иметь
то коэффициенты должны иметь вид
с"=
(л=0' !-2' "+
Конечно, при этом ряд B6) должен получиться сходящимся. Этот метод при-
пригоден и в случае, если моменты берутся не относительно системы степеней, а
относительно какой-либо иной системы функций.
Другой метод состоит в переходе к интегральному уравнению 1-го рода.
Разложи» какое-либо подходящее ядро К (ж, %)'по степеням ?;
{ 2
мы получим нз B5) уравнение
к которому .можно применить какой-либо из рассмотренных выше способов
решении.
в. Уравнение Вольтерра с разностным ядром. Уравнение
(a = const) B7)
(при а=?^0 получается уравнение 2-го рода, при а = 0—1-го рода)
можно решить с помощью преобразования Лапласа, как это описано
в п. III.2.4. Обозначая большими буквами лаплас-образы рассматри-
рассматриваемых функций, из B7) получим
г B8)
откуда
и остается лишь воспользоваться формулой обращения (III.1.19).
Так как функции F{p) и К(р) аналитичны в некоторой полуплоско-
полуплоскости Re/> > const и стремятся там к нулю при р.—<-оо, то прн а=^=0
и U(p) удовлетворяет этому условию обратимости. Если же а = 0,
т. е. рассматривается уравнение 1-го рода, то стремление правой
части B9) к нулю при р—>-оо, Re/> > const приходится дополни-
дополнительно потребовать.
Если уравнение B7) решается лишь на конечном интервале
б^л^х,, то можно функции k(x) и f(x) вне этого интервала про-
продолжить произвольным образом, например положить их равными нулю,
после чего уже проводить преобразование Лапласа.

444 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Нетрудно проверить, что итерированные ядра (п. 2.9) также явля-
являются разностными: например, второе итерированное ядро равно
$|ц—S = e|= J k((x-l)-s)k(s)ds.
6 о
Поэтому и резольвента уравнения
X
и (х) = к 5 k (х—s) и (s) ds +f{x)
о
зависит от х—?; обозначим ее через у (х—\; X). Из B.9) вытекает,
что она удовлетворяет уравнению
у(х—1; Я,) «*,$*(*—ц)у(г\
i
Полагая 5 = 0, получаем подобно B9) лаплас-образ резольвенты
r<W*> = r=$W C0)
Рассмотрим, например, уравнение
X
и (*)=* J (х-ЪГ и (Е) ? + .' (ж) (а > -1).
о
В силу формулы (III.1.6)
. /С (*»)=Г(а+1)/>-
откуда
Т(р. U- Г(«+1)
(обратите внимание иа различный смысл буквы Г в этой формуле!). Заменяя
дробь суммой бесконечной геометрической прогрессии и пользуясь формулой
(II 1.1.6) в обратном направлении, получим выражеиие резольвенты в виде суммы
ряда (проверьте!)
г
л= 1 ¦
При а=0, 1, 2. ... этот ряд свертывается в конечную сумму по методу, опи-
описанному в ЛВМ для ряда (XVII.52).
Если ядро уравнения B7) удовлетворяет по х линейному однородному диф-
дифференциальному уравнению с постоянными коэффициентами, то можно применить
также следующий прием. Пусть, например,
kT+qk'+rk=O. C1)
- Продифференцировав уравнение B7) два раза, получаем
х
аи' (x)+k(())u(x)+\k> (х-1)иа)<Щ.=Г (х), C2)
о
х
' @) и (х) 4- \ ft" (х—I) и (|) d?—f* (x). C3)
о

§ 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ КЛАССЫ УРАВНЕНИЙ ' 445
Умножив уравнение B7) на г, C2)—на q и сложив с C3), получаем в силу C1)
ош"+[к @) +aq) u'+lk' (O) + qk @)+«r] «=/" (x)+qf (x)+rf(x).
Решив это простое дифференциальное уравнение (откуда взять начальные усло-
условия?), находим и(х). Метод пришдеи и при а=0.
Еще более простой вид имеет этот йетод перехода к дифференциальному
уравнению для уравнений Фредгольма 2-го рода, если ядро, даже вида К (х, ?),
удовлетворяет по х линейному однородному дифференциальному уравнению,
коэффициенты которого могут зависеть от х. (Впрочем, в последнем случае
могут возникнуть трудности с решением этого дифференциального уравнения.)
Отметим, что такие ядра по необходимости являются вырожденными, так что
здесь можно применить и методы п. 2.1.
По поводу описанного метода см. [92].
7. Уравнение Фредгольма с разностным ядром яа оси. К урав-
уравнению
и (х) = к I г (х—1) и (I) dl+f(x) C4)
-« ^
теория Фредгольма заведомо неприменима, так как интеграл A.7)
всегда равен бесконечности (почему?). Здесь обычно применяется
преобразование Фурье (ЛВМ, § XVII.5)
C5)
Напомним, что его можно применить к любой функции, абсолютно
интегрируемой на всей оси, причем формула обращения имеет вид
GO
/(*)= [f{k)e**dk C6)
(ЛВМ, п. XVII.32). Нам понадобится, кроме линейности, еще сле-
следующее свойство свертывания, которое доказывается так же, как
аналогичное свойство преобразования Лапласа (п. III. 1.3): фурье-обра-
зом функции J Л (ж—S)/, (?)<*? служит 2n/l(k)/i{k).
— an ' ¦
Применим эти свойства к решению уравнения C4), предполагая
все участвующие функции абсолютно интегрируемыми на всей оси.
Подобно B9) и C0) мы получаем образы решения и резольвенты
u(k)=—f(kK , y(k; K) = Г-Щ,— C7)
(легко проверить, что и здесь резольвента имеет вид у(х—?¦; X)),
если полученный знаменатель не имеет нулей на оси k. Теперь нужно
еще воспользоваться формулой обращения C6) и затем преобразо-
преобразовать, если это удастся, полученный интеграл к более удобному виду

446 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
по методу п. Ш.1.5. Если 1—2nXr(k) имеет нули при веществен:
ных k, то уравнение C4), вообще говоря, не имеет абсолютно ин-
интегрируемого на всей оси х решения.
Описанный метод можно применить и к уравнению 1-го рода
ч
]r{x-t)u(l)<fi-=f{x);
однако при этом надо дополнительно требовать, чтобы отношение
f(k)/r(k) допускало, обратное преобразование Фурье, т. е. чтобы оно
было абсолютно интегрируемо на всей оси k.
Для я-мерного ураинения, аналогичного C4), скажем, при я = 2,
и(х, у) = к I $г(*—I, у-ц)иA, n)did4+f(x, у)
—а, —а>
с тем же успехом можно применить кратное преобразование Фурье
(п. Ш.3.3).
' ¦' Единртвеиность решения уравнения C4) гарантируется лишь и классе абсо- s
лютно интегрируемых иа всей оси х функций. Вие итого классе' однородное
уравнение C4) может вметь нетривиальные решения вида и(х)=еаж; подста-
подстановка в C4) показывает после замены %—*х—?, что для этого необходимо и
достаточно, чтобы
00 ¦ .:,..:*¦
=1 • C8)
(если этот интеграл сходящийся). Подобно ЛВМ, п. XV. 17, можно показать,
что если а является m-кратным корнем уравнения C8), то однородному урав-
уравнению C4) удоилетворяют функции еах, хе°х, ... , хт~1еах.
Требования абсолютной интегрируемости всех участвующее функций, а
также необращения в нуль знаменателя в {37) являются чрезмерно жесткими и
могут быть и значительной акре преодолены, если считать к комплексным, как
это описано в п- Ш.3.2. При этом нам «кажется полезной следующая простая
Лемма. Пусть . .......
причем Р+ < а_, а+ < р"_. Тогда свертка \ /<х—g)(p(g)dg определена и
удовлетворяет оценке
0D
-% (-oo<jc<0),
+*. <0<x<oo),

§ 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ КЛАССЫ УРАВНЕНИЙ 447
где у-—наименьшее из чисел «_, р._; у+— наибольшее из чисел л+, р+; Р_,
Р+—некоторые постоянные (в случае совпадения соответствующих показателей
эти показатели' надо заменить на линейные функции х).
Для доказательства леммы допустим, например, что хЭгО, <х+ Ф Р+; рас-
рассмотрение остальных случаев мы предоставим читателю. Тогда
Ох »
| J J
-о» \-оо О X
О-
•• ¦ -С
-со-
откуда и следует утверждение леммы.
Допуствм теперь, что в уравнении C4) функции /(х), г (х) и и (х) . удов-
удовлетворяют оценкам вида C9) с показателями соответственно а±, Р± и у±,
причем . ,
Р+<р^, «+<Р_, Y+<P- P+<«-. P+<V- DQ)
Представив f(x)=f+ (x) + f_ (ж), и(х)=и+(x)+u_ (х) (п. 1П.3.2), получим
из C4)
u+ W-k J r (Jf-I)»+ ©*-Л+ (*>=
¦- ¦ ¦ 'се ¦ ¦
Х 5|/-(*). D1)
Обозначим общее значение левой в правой частей через <р (х). Применяя при
х < 0 доказанную лемму к левой части D1), а при х> 0—к правой, получаем,
что <р(х) удовлетворяет оценке C9) с показателями р±, а потому в силу
п.III.3.2 фувиция <p(fe), как и г (k), аналвтична в полосе
— Р_ < Imfe<— P^; D2)
обе эти функции стремятся в этой полосе к нулю при ft—>¦ оо.
Переходя в равенстве D1) к фурье-образам, получаем
и+ (*)-2яХ? (kfu+ (k)-f+ (ft)= - «_ (*)+2лХг>)«-
откуда
l-2n\r(k) 1 —

448 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Пользуясь формулой обращения (III.3.10), получим
00 + /S +
W J 1-2ккг(к)
— oo+is +
^ J \-2ius(k)
где s+ <—Т+, s_ >—V-! ПРИ этом в СИЛУ произвольного выбора s+ и s_
'можно считать, что на контурах интегрирования нет нулей функции 1—2nXr (k)
(этого произвола не было, пока мы считали k вещественным).
Если в D3) считать дополнительно, что s+ <—а+, —{5_ < s+ < — |5+,
аналогично для s_ (здесь используются условия D0)), то каждый из интег-
интегралов в D3) можно разбить на два. Объединив интегралы с ф (к), к ним можно
применить теорему Коши о вычетах, что в силу произвольности ф (k) даст
оо + is +
Г
и(х)
= Г U
J l-2
2nlr(k)
где Aj—произвольные постоянные, а сумма распространена на все нули функ-
функции 1—2яАг (к) (при выбранном X), попавшие в полосу D2). В случае т-крат-
ного нуля kj вычисление вычета по формуле (II.3.6) показывает, что к "послед-
"последней сумме в D4) надо добавить члены с *»«*>*, ..., хт~хе^)х (почему?). Это
Находится в полном соответствии с первым абзацем петита (где a=ik), так как
последняя сумма в D4) представляет собой решение уравнения C4) при / (х) ез 0.
ЭгуТумму можно трактовать "как собственную функцию уравнения C4); тогда
получится, что характеристические значения к уже не будут 'дискретными, как
в фредгольмовом случае, а будут заполнять область — сбраз полосы D2) пря
отображении \=Bлг (к))-' (почему?).
Рассмотрим в качестве примера уравнение
и(х)=Х J e-lx-i]u<t)d? + f(x). D5)
Здесь Р+ = —1, Р_ = 1; значит, в силу D0), неоднородный член f(x) и соот-
соответственно решение и (х) могут при х—»¦ ± оо экспоненциально расти по модулю,
однако не быстрее ес'*', где с < I, т. е. а+ = 1, а_=— 1. Так как
О
_i_

§ 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ КЛАССЫ УРАВНЕНИЙ 449
(проверьте!), то прообразом функции
для первого интеграла D4) служат
+
^ <46>
— OO+IS +
Подынтегральная функцня имеет полюсы в точках ftj>2=± i Vl—2Х. Пусть X
(вообще говоря, комплексное) таково, что | Im fe^ s I < 1, причем klt 8 # 0; рас-
рассмотрение остальных случаев мы предоставим читателю. При х > 0 коитур
интегрирования в D6) можно замкнуть сверху большой полуокружностью,
и тогда в силу выбора s+ < — а+ оба полюса попадут ннутрь замкнутого кон-
контура. По теореме Коши о вычетах мы получаем, что интеграл в D6) равен
Аналогично при х < 0, замыкая контур интегрировании в D6) большой полу-
полуокружностью снизу, получаем, что интеграл равен нулю.
Первый интеграл в D4), как прообраз произведения, получается с помощью
свертывания прообразов сомножителей, т. е. равен
GO CC
f Ы*-6Jя6 (g) dE-f/+(*-{
Аналогичное вычисление второго интеграла в D4) дает тот же результат, но
с f _ вместо /+ (проверьте!). Поэтому из D4) получаем решение уравнения D5)
при указанных условиях на X:
в(*)=/(*)-
где Лг, i42—произвольные постоянные.
Отметим, что уравнение D5) можно свести к дифференциальному: для этого
надо его переписать в виде
обозначить эти интегралы через v(x) и w(x), продифференцировать их и т. д.
(Проделайте это до конца, а также подумайте, почему при | Im fe1( s | > 1 в ре-
решение интегрального уравнении не войдут произвольные постоянные, тогда как
в решение дифференциального уравнения войдут.)
15 А. д. Мышкио

450 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Иногда для решения ураинеиия C4) применяют не преобразование Фурье
C5), а двустороннее преобразование Лапласа
F{p)= J e-P*f(x)dx
(ср. (III.1.1)). Это и принципе то же самое, так как
=±-F (ik), т. е. J(k)=~F(p), где p=ift.
Некоторые уравнения приводятся к виду C4) с помощью соответственно
выбранной подстановки. Например, уравнение
СО
и (х)=К J" г (-|) и © j + Дх) @ < х < оо), D7)
о
првводвтся к виду C4) с помощью подстановки
*=е*., i=eSi, «(e*.)=«i(*i). г(в*.)=г1 (*i), f(e*i)=/1 (дсх)
(проверьте!). Так как это та самая подстановка, которая переводит преобразо-
вавве Меллина (п. Ш.3.3) в преобразование Фурье, то к уравнению D7) можно
непосредственно применить преобразование Меллина, которое переведет его
в уравнение вида B8). Мы не будем здесь этим заниматься.
Чтобы решить уравнение
к (*)=*, J r (х+1) и (|) dg+f (x), D8)
заменим | на —| и введем обозначения и(—x)=v(x), г(—х)=р(х). Тогда
из D8) мы получим свстему уравнеивй (проверьте!)
и{х)=\ J г (*-& о
ивда C4). К этой системе можно применить преобразование Фурье как для
абсолютно интегрируемых, так и для растущих функций, что мы предоставляем
сделать читателю.
8. Уравнение Фредгольма с разностным ядром ва полуоси. Рассмотрим
уравнение
и (х)=Х 5 г (*—& ы © ^ (°<* < «)• D9)
о
Оказывается, что для его решения можно также применить преобразование
Фурье, однако привлекая некоторые новые соображения, вменно так называемый
метод Винера—Хопфа.
Заметим прежде всего, что хотя функция г (х) должна быть задана на всей
оси х, ио решение и (х) по смыслу задачи ищется лишь при х^О. Однако
если,'- найдя это решение, положить и (х) при х < 0 равным правой части D9),

§ 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ КЛАССЫ УРАВНЕНИЙ
451
то мы получим функцию, удовлетворяющую.уравнению D9) на всей оси х;
так мы и будем впредь считать. Применяя обозначения п. 7, можем написать
E0)
Будем, как в п. 7, считать, что функция т (х) удовлетворяет оценке вида
C9) с показателями $±, причем 0+ < 0_, а решение и (л:)—оценке |и(х)|<
<Л«?Т+* @<* < оо), причем Р+ < Y+ < Р-- Тогда в силу леммы п. 7 будет
| и (х) | < Ве^~х (—оо < х < 0). Переходя в уравнении к фурье-образам, получим
)) u+ (fe)=— и_ (fe). E1)
и+
«- (*)=2яХ? (к) и+ (к), т. е. A—
Области гарантированной аналитичности участвующих здесь функций показаны
на рис. 116. При этом каждая из функций и+ (k), u-{k) стремится к нулю
при к -*¦ оо в своей области аналитичности (почему?).
1тк
Т <
Рис. 116.
Основная идея метода Винера—Хопфа состоит в факторизации, т. е.
в разложении на множители с заранее предписанными свойствами коэффициента
в уравнении E1). Если такая факторизация окажется осуществимой, то из
этого одного уравнения будет возможно иайтн две неизвестные функции
и+ и «_. Именно, допустим, что возможно представить
!) = _1 ,.v (—В_ < Imfe <—Y+),
где функция <Pi(fe) аналнтнчна в полуплоскости lm k <—у+, а ф2(й)—и полу-
плоскости Imfe >—Р_, причем обе эти функции имеют иа бесконечности поря-
порядок роста ие выше k*{m = \. 2, 3, ...)• Переписав уравнение E1) и виде
«Pi (*)«+(*)< <Pi (*) в- (*).
E2)
мы получаем, что обе части этого равенства служат аналитическими продол-
продолжениями одна другой (п. 11.2.7) и потому образуют на всей плоскости k единую
"аналитическую функцию Р (к). Эта функция имеет на бесконечности порядок
ниже km, т. е. представляет собой многочлен степени < m (п. II.3.6). Из E2),
15*

455! ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
пользуясь формулой обращения, получаем решение уравнения D9)
со + is
«М= f ?тй«'*** @<*<ю; s<-Y+).
— 00 +(S
Факторизация наиболее проста, если функция 1—2ккг (k) рациональна.
Тогда можно, разложив ее числитель н знаменатель на множители вида я—а,
отнести к фх все скобки числителя с \та >—р*_ и все скобки знаменателя
с 1та^г— v+; это нужно, чтобы по возможности уменьшить т и тем самым
количество неопределенных параметров в ответе. Впрочем, в этом случае урав-
уравнение D9) можно, подобно п. 7, привести к обыкновенному линейному диффе-
дифференциальному уравнению с постоянными коэффициентами.
В общем случае факторизацию можно осуществить следующим образом.
Прежде всего, если функция 1—2nXr (я) не имеет при
— Р_<1тк< —у+ E3)
нулей, то ее надо записать в виде v(k)—ewik) (w(k) = \n (I — 2пАг (k)), после
чего нужно представить до (я) в виде разности функций, аналитических
в соответствующих полуплоскостях. Для этого можно воспользоваться интег-
интегральной формулой Коши (П.3.12), взяв контур интегрирования, изображенный
на рис. 116 пунктиром. Если увести боковые стороны на бесконечность (про-
(проверьте, что интеграл по ним стремится к нулю!), то в пределе мы получим
co + iSx as + ist
w 2nl J я — x 2ro J k—v. v
Это н есть требуемое разложение. Если же функция 1—2яХг (к) имеет в по-
полосе E3) нули clj кратности пу, то эту функцию нужно представить в виде
B/J. v (k), где Q (k) ¦— JJ (k—а/)"-*, а R (k) —любой многочлен, эквивалентный
К (в) ¦
Q (я) при k -+¦ оо и не имеющий нулей в полосе E3). Затем нужно записать
v (k) = ew (ft' и т. д., а с отношением Q(k)/R(k) поступить, как в предыдущем
абзаце.
При рассмотрении неоднородного уравнения D9) после произвольного про-
продолжении функции / (х) на полуось — оо < х < 0 мы приходим аналогичным
образом взамен E2) к уравнению
ф1(«)«+ (к)-ф2(*)?+ (k) = [-u_ (*) + ?_ (ft)] <p2(?). E5)
Теперь нужно с помощью процедуры, описанной в предыдущем абзаце, пред-
представить вычитаемое в виде разности
где функция i|)i(fe) аналнтична при Imft<— у+, а г|J(я)—при (,
причем обе эти функции имеют на бесконечности порядок роста не выше сте-
степенного. Тогда из E5) получаем
ф1 (к) ~и+ (*)-ih (*) = [-«_ (*) + ?_ (*)] ф2 (*)-ih (ft)
н дальше рассуждаем, как для уравнения E2).
Метод Винера—Хопфа можно применить также для решения интегральных
уравнений 1-го-рода аналогичной структуры.

§ 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ КЛАССЫ УРАВНЕНИЙ 453
Рассмотрим в качестве примера уравнение Милна (Э. Милн A896—1950) —
английсквй астрофизик)
В курсах физики доказывается, что этому уравнению удовлетворяет интенсив-
интенсивность излучения, проходящего через полупространство -О^дс < оо, —оо < у,
г < оо, заполненное однородной средой, ие поглощающей, но изотропно рас-
рассеивающей это излучение; при этом х—безразмерная длина, взятая в расчете
ва так называемую среднюю длину свободного пробега.
Вычисление дает (проверьте!)
r(k) =
о
о
4я J s J J 4я J Vl-j.
\+ik
0 \-^CD 0
Поэтому требуется профакторнзовать функцию
1п (б7)
в полосе
— 1 < Imfe < 1. E8)
Переходя в E7) к разности логарифмов и пользуясь рядом Тейлора, прове-
проверяем, что при ft=0 получается нуль второго порядка; можно доказать также,
что других нулей функция E7) в полосе E8) не имеет. Поэтому нз E7) выде-
fe2
лнм множитель
fe2
^ * , откуда получаем
В формуле E4) можно положить s1=0, что даст
cp1(fe) = -—гехрк—: \ -г In —-з
Так как при k -»¦—ioo эта функция эквивалентна fe, а и+ (ft) -> 0, то в этом
процессе будет Р (ft)=o (k), а потому многочлен Я (k) равен постоянной. Отсюда
" /« ^ ft—' — I С 1 ¦ Гн2+1Л arctgxNT , ., , „.
и+ (ft)=C-rr- exp-^r—г \ г In —^-[ 1 2—) dn (Imft < 0).
+ w ft2 r 2яг J ft —x L и V и / J

454
ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Метод Винера—Хопфа можно применить- и к некоторым другим уравне-
уравнениям, родственным D9). Рассмотрим, например, парные уравнения
в(*) =
J. тх (х-1) ««)«+/(*) (-<»<*< 0),
Обозначив
»(*) =
«М- ? ''а (ж—I) в (!)
(- со < * < 0),
— со
мы мажем, их переписать в виде системы уравнений
и (*) = J тг (*-© а E) <?+к+ (x)+f- (х) =
= ] rt
09)
(проверьте!). Прн соответствующих оценках порядков роста участвующих функ-
функций—указать этн оценки мы предлагаем желающим—можно перейти к фурье-
образам, что даст
*>. E9>
Исключая отсюда и (k), получим в некоторой полосе
f^[
l—2ar1(k)
Теперь надо профакторнзовать коэффициент (частное), а для неоднородной сис-
системы—еще написать представления типа E6); после этого рассуждения, анало-
аналогичные проведенным для уравнения E2), дают возможность найти* v+ (k),
а в силу E9) — ни (к).
§ 5. Сингулярные интегральные уравнения
Теория сингулярных интегральных уравнений, в которых искомая-
функция входит под знак сингулярного интеграла, существенно
сложнее теории фредгольмовых уравнений, однако и она имеет ряд
важных приложений. Мы приведем лишь краткие сведения о сингу-
сингулярных уравнениях, ограничиваясь скалярным одномерным случаем-.
Дальнейшие сведения о таких уравнениях можно найти в книгах

§ 5. СИНГУЛЯРНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ *55
[40, 87, 105, 114]. Специально теорнн сингулярных интегральных
уравнений посвящены кннгн [21, 89, 93].
1. Сингулярные интегралы. Мы будем здесь рассматривать
интегралы вида
№*¦
а также сходных видов. Будем с.нтать сначала е и b конечными.
В ЛВМ, § XIV.4, мы упоминали, что интеграл A) прн %, = х, вообще
говоря, расходится. Его главное значение, есля а < х < Ь, опреде-
определяется формулой
a
Исходя из формулы
ь
Ь—х
а—х\
а
(докажите ее!) и преобразуя интеграл A):
а
получаем, что
О)
Последний интеграл для непрерывной, дифференцируемой при \ = х
функции ф(?) является собственным (почему?), а значит, принимает
определенное конечное значение. Впрочем, можно проверить, что и
для непрерывных неднфференцируемых функций этот интеграл
является если и несобственным, то сходящимся (за исключением
искусственных примеров, не имеющих практического значения), н
непрерывно зависит от х. Если же функция ф(?) разрывна при % = х,
то на простых примерах легко убедиться в том, что интеграл C)
при %=*х может обратиться в бесконечность, даже если функция
ф(?) конечна. Аналогично первый член в правой части C) показы-
показывает, что левая часть обращается в бесконечность с логарифмиче-
логарифмической скоростью при х = а-\-0, если ф(а)^0, ± оо; аналогично при
х = Ь—0.
Проследите этн свойства на примере

456 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
тогда
v. p. I JL^Ldl^lnl—Z (_ КЖ1).
Полезно обратить внимание также на формулу
(Выведите ее из формулы (II.3.28) с учетом сделанного в п. II.3.4 замечания
о том, что для особых точек, лежащих на контуре интегрирования, а их здесь
будет две из-за возможности подхода к точке z=* сверху нли снизу, вычеты
берутся с коэффициентом 1/2.) Из формулы D) легко выводится, что если функ-
функция ф (|) при подходе к ?=а (аналогично к %=Ь) имеет порядок (|—а)~*
(О < а < 1), то и интеграл A) как функция х имеет тот же порядок.
Аналогичными свойствами обладает часто применяемый интеграл
¦dl, E)
Г ф (S) ctg:
где ф(?)—2я-периодическая функция, а интеграл взят по какому-
е х 2
либо отрезку длины 2л: в самом деле, разность ctg^—
остается при | = JC конечной.
Если а = — со или Ь = оо, причем интеграл A) на бесконечном
конце абсолютно сходится, то, выделив из интервала интегрирова-
интегрирования конечную часть, содержащую X, получаем, что оставшаяся ре-
регулярная часть не может изменить указанных свойств сингулярной
части.
Мы будем применять также комплексные интегралы, аналогич-
аналогичные A),
%, . F)
где (L)—конечный ориентированный замкнутый или разомкнутый
контур в комплексной плоскости, а ф (?) — функция, заданная вдоль
этого контура. Если г 6 (Ц, то интеграл F) имеет те же свойства, что
A), правда, может дополнительно обращаться в бесконечность в
точках излома контура, если такие имеются (разберите это на
простейших примерах!). Если же z?(L), а функция <р непрерывна
или хотя бы абсолютно интегрируема, то интеграл F) становится
регулярным. Так как возможно произвести дифференцирование ин-
интеграла F) по параметру г, то мы видим, что его значение Ф(г)
представляет собой (однозначную) аналитическую функцию г всюду,
кроме линии (L), которая служит, как мы сейчас покажем, линией
разрыва для этой функции.

§ 5. СИНГУЛЯРНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
457
В самом деле, пусть точка г, g (L) находится вблизи точки
z0 6 (?)• Выберем некоторое е > 0 и обозначим через (Le) дугу,
показанную на рис. 117, а через (Le) — остальную часть линии
(L). Тогда
Первое слагаемое для всех 2, достаточно близких к z0, можно
считать приближенно равным —- v. p. \ У dt,. k(Q
<,L)
Во втором слагаемом положим приближенно
ф (?) = ф (,г0); тогда это значение вынесется, и
оставшийся интеграл будет равен приращению
величины In (^—г), когда ? проходит (LE) от 2_B
до гг. Но это приращение приближенно равно ш',
если г находится, как на рис. 117, слева от z0
(если глядеть вдоль (L) в соответствии с ори-
ориентацией), и —ni, если г находится справа от
г„. Обозначая через Фд(?0) и Ф" (гл) предельные
значения Ф (z), когда г ? (L) приближается к
Рис. 117.
при е
соответственно слева или справа,
>-0, получаем
и переходя к пределу
Это и означает, что (L) служит для Ф(г) линией разрыва.
При манипуляциях с сингулярными интегралами приходится соблюдать
некоторую осторожность. Например, если требуется продифференцировать ин-
интеграл A) по х, то это нельзя сделать по обычному правилу Лейбница, так
как тогда получится интеграл, у которого главное значение отсутствует. Поэтому
сначала, пользуясь переходом B), производят интегрирование по частям,
ь
а затем уже производят дифференцирование и получают ответ: V. р. \ е [-
Ф (Ь) Ф (я) „ . °
-{- .— . Другой пример: можно проверить, что допустима перестановка
порядка интегрирования сингулярного интеграла с обычным; однако формула
для перестановки двух сингулярных интегрирований (которой мы, впрочем,
не будем пользоваться) имеет вид
(L)
г—с (С—г
d*\-n*F(c,c)
(с6

458 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
2. Формулы обращения. Один из основных методов изучения
сингулярных интегральных уравнений опирается на применение формул
обращения сингулярных интегральных преобразований. Напоминаем
формулы, которые были выведены в пп. П.3.5 и III.3.3.
Преобразование с ядром Коши (|—х)~г: если
то
~±'-> i в*
Преобразование с ядром Гильберта: если
|==-^-v.p. f/<|)ctg^=
то
(при выводе последней формулы надо, кроме (И.3.38), принять во
внимание (II.3.37)). В этих преобразованиях функции / и F 2я-пе-
риодические, а интеграл взят по периоду. Впрочем, можно преобразо-
преобразование выполнять н на каком-либо фиксированном отрезке длины 2я.
Выведем еще формулы обращения для интеграла F) в случае
замкнутого контура (/.), когда
(9)
Для этого обозначим
Будем считать (Z.) ориентированным против часовой стрелки (для
окончательного вывода это несущественно), а г± произвольно меняю-
меняющимся внутри (L). Мы видели, что ф и Ф—аналитические функции,
принимающие при z?'(L) предельные значения
<р» (z) =±v.p. (f ¦^-zdZ+f(z) = F(z)+f(z), A1)
Ф» (*) = зп v.р.
Выражая из A1) F(z) и подставляя в A0), получаем
A)

§ 5. СИНГУЛЯРНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 459
Однако в> силу интегральной формулы Коши (Н.3.12) интеграл в
правой части равен 2nf(zl}.. Значит, Ф (г^ з=з ф (zt), Фл (z) — фл (z),
и из A1) и A2) мы получаем
J Ш A3)
Это и есть формула обращения преобразования (9). Значит, это
преобразование само себе обратно (теорема Пуанкаре—Бертра-
Пуанкаре—Бертрана; Ж. Бертрйи A822 —1900)—французский математик).
Более точный анализ показывает, что если преобразуемая функ-
функция квадратично суммируема,, т. е. из ?а, то и преобразованная
также из ?2.
Приведем без доказательства еще одну формулу обращения: если
(-1<*<1), (И)
где С—постоянная (см. п. 6). Проверим только, что последний член при любом
ении С обращает правую- часть A4) в нуль:
то
Это можно сделать с помощью формулы B), так как неопределенный интеграл
легко берется, однако проще сделать подстановку ?=cos<p, x=cosfl', после
чета воспользоваться формулами, выведенными в конце п. 1Г.3.5. (Отметим, что
а интегралах вида A) замена переменных осуществляется по обычным фор-
формулам.)
Если рассматривать формулу (9) как определение сингулярного интеграль-
интегрального оператора F=Sf в La (Г), то можно доказать его ограниченность. В то
же время из формулы обращения S2 = I вытекает, что этот оператор уже не
является вполне непрерывным (п. 2.11). В самом деле, произведение вполие
непрерывных операторов всегда вполие иепрерывно (почему?), а тождественный
оператор в бесконечномерном пространстве ие может быть вполне непрерывным.
В этом и состоит глубокая причина отличия сингулярных операторов от фред-
гольмоиых,- которая приводит, как мы увидим в дальнейшем, к существенно
новым моментам в формулировках теорем о разрешимости сингулярных
интегральных уравнений.
3. Непосредственное применение формул обращении. Рассмот-
Рассмотрим уравнение
Д$ «gA6)

460 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
где а, р — постоянные, причем аа^Ра. Применение преобразования
(9) к обеим частям дает, с учетом формулы обращения A3),
f ? A7)
Исключение из A6) и A7) интеграла дает решение
где F(z) определено формулой (9). Как видим, здесь опасен вовсе
не случай <х=0 (уравнение 1-го рода), а случай а=±р.
Продела" то же преобразование над более общим уравнением
= Д*. Р. § ¦^rdl+fK(z, l)u{l)dl+f{z) A9)
m
с фредгольмовым ядром К, мы получим формулу вида A8), в которой
вместо / надо подставить сумму двух последних членов уравнения
A9) и соответственно изменить F. Меняя порядок интегрирования
в двойном интеграле, получим в итоге соотношение
1 Г ""' ' ""'"' ' &Kx(z, C)ii(Qd?l, B0)
где
Кг% l) = aK{z, Q + JLy.p.ffKgiSldw B1)
(проверьте, пользуясь возможностью перестановки сингулярного и
простого интегралов, см. п. 1). Можно доказать, что ядро B1)
фредгольмово; тем. самым мы свели исходное сингулярное урав-
уравнение A9) к фредгольмову уравнению B0), как говорят, произвели
регуляризацию уравнения B0). Так как к уравнению B0) применимы
все результаты § 2, то мы получаем, в частности, что для реше-
решений уравнения A9) справедливы три теоремы Фредгольма.
В связи с этими теоремами обращаем внимание, что сопряженным к ядру
К (г, ?) будет [К (?, г)]* г-т—- Jt . Докажите это, исходя из определения
B.66) сопряженного оператора и определения скалярного произведения в La (L)
= J
U)
U.)
Уравнение
00 ф
J fzr^+ J /C(*. l)u(t)dl+f(x)

§ 5. СИНГУЛЯРНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 461
рассматривается аналогично. При применении преобразования A5)
к уравнению
iJ^ J(Jf, Б)«(Б)
(все участвующие функции 2я-периодичны) из первого члена в пра-
вой части появится добавочное слагаемое—-~ \ и (?)dg, которое на-
надо отнести к преобразованному ядру К^
Для решения уравнения
i i
ae(*)=-|v.p. ^f~^+^K(x, S)effi)dg + fW B2)
-i -I
надо изменить обозначения | на s, д; на |, затем умножить обе части на
1 /"i м
— 1/ т ^
обращения A5) получаем
и проинтегрировать от —1 до 1. Тогда в силу формулы
Затем представляем левую часть в виде суммы сингулярного и регулярного
членов
(проверьте, что второй интеграл регулярный!) и из полученного и исходного
уравнений исключаем сингулярный интеграл. Таким образом, н для уравне-
уравнения B2) возможна регуляризация.
4. Переход к краевой задаче, простой пример. Рассмотрим
уравнение
a(z)«(z) = ii?U. p. f-?%</?+ /(z) B3)
с непрерывными коэффициентами a(z) и р (z), обобщающее A6),
для замкнутого или разомкнутого конечного контура (L). Один
из основных методов его исследования, а во многих случаях и
решения, состоит в переходе к равносильной краевой задаче теории
аналитических функций; этот метод детально изучен в книге [27].

462 гл. vii. интегральные уравнения
Пусть u(z) (z? Щ)—искомое решение. Введем функцию
В п. 1 мы показали, что это однозначная аналитическая функция
на всей плоскости zlt кроме линии (L); ясно также, что U(oo) = 0.
В точках линии (L) удовлетворяются соотношения (см. G))
iL)
Исключая из этих двух равенств и из уравнения B3) u{z) и интег-
интеграл, приходим к равенству (проверьте!)
<25>
Таким образом, мы пришли к следующей краевой задаче: найти
функцию U(zt), однозначную и аналитическую на всей плоскости гг
за исключением линии разрыва (L), равную нулю при z1= oo и удо-
удовлетворяющую иа (L) краевому условию B5). Это задача Римана —
Гильберта. Можно доказать, что и, обратно, имея ее решение
U(z}), мы получим по формуле U(z) = Ua{z) — Un{z) (см. B4)) ре-
решение уравнения B3); таким образом, это уравнение полностью
равносильно краевой задаче Римана — Гильберта.
Допустим сначала, что (L) — замкнутый, ориентированный в по-
положительном направлении контур. Тогда функцию U{z1) более есте-
естественно рассматривать как две: одну Ua (zt), определенную внутри
(L), и другую U" (zx), определенную вне (L), а на (L) эти функции
должны быть связаны соотношением B5). Специфику задачи Рима-
Римана— Гильберта можно понять на простом примере, когда (L) пред-
представляет собой окружность |г| = 1, а условие B5) имеет вид
U3I{z) = zmUa(z)+f1(z) (|*|=1; л»—целое). B6)
Функцию ил(г1), аналитическую в круге |я, |<1, можно разложить
в ряд Тейлора, а функцию Ua {zx), аналитическую при |г, |>1,
разложить в ряд Лорана, где в силу условия ?/п(оо) = 0 будут
только отрицательные показатели. Кроме того, разложим /\ (е'ч) в
комплексный ряд Фурье. Мы получим
S*{, A)t,
k=0 k=l
2

§ 5. СИНГУЛЯРНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 463
где коэффициенты ск заданные, а ак и Ък—искомые. Условие B6)
дает
2v2v 2 v
Отсюда получаем различные случаи в зависимости от значения
т, которое называется индексом поставленной задачи:
Если /я=0, то задача имеет ровно одно решение:
Оо=с0, o* = cft, &* = — с_к (*=1, 2, 3, ...)•
Если m > О, то задача имеет m-параметрическое семейство реше-
решений. В самом деле, из B7) получаем
Из второй строки мы видим, что, например, а0, at, ..., am_l можно
задавать произвольно, а тогда bt, Ьг, ...,bm определяются. В част-
частности, соответствующая однородная задача (Д(,г) = 0) имеет п
линейно независимых решений
U*[z1) = zklt Ua(zx) = z\-m [k = 0, 1, ..., да—I).
Если m<CQ, то в левой части B7) будут отсутствовать члены
е~'*, ..., e~imf, а потому для разрешимости задачи необходимо и
доетаточно, чтобы с_1 = с_2= ... = с_т = 0, т. е. чтобы функция
/j (г) удовлетворяла \ m \ соотношениям ортогональности
аи
$/(e*f)^*-Pdcp = O (ft=I, 2, ..., |л»|).
о
Если эти соотношения выполнены, то задача имеет ровно одно ре-
решение
«о = сО) ak = ck, bk = —cm_k (ft=l, 2, 3, ...).
S. Общий замкнутый контур. Вернемся к общей задаче B5)
с произвольным замкнутым контуром (L). Оказывается, что ее ре-
решение обладает теми же свойствами, которые были отмечены для
задачи B6); при этом индекс m равен числу оборотов, которые со-
совершает точка — iftr \ ВОКРУГ начала координат, когда z прохо-
проходит контур (/.).
При построении решения будем для простоты считать, что точка
х = 0 расположена внутри (L) (как этого добиться?). Положим
B8)
где значения логарифмической функции, произвольно выбранные для
некоторой точки г € (Ц, затем непрерывно продолжаются вдоль (L).

464 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
При полном обходе (L) уменьшаемое и вычитаемое в B8) получают
приращение 2nim (почему?), а значит, функция \а (г) вернется к своему
исходному значению, т. е. будет на (L) непрерывной и однозначной.
Введем затем однозначные аналитические на всей плоскости zv за
исключением линии (?,), функции
§0^
Тогда, исходя из равенств
можно преобразовать условие B5) к виду (проверьте!)
V (z) = z«Va (z) -f/, (г) (z 6 (?)), B9)
где обозначено
Таким образом, для функции V мы получили условие вида B6),
хотя и на произвольном контуре. Естественно, что характер раз-
разрешимости задачи будет существенно зависеть от ее индекса т.
Пусть т = 0. Тогда задача B9) имеет решение
b^k* C0)
(проверьте!). Это решение единственно: в самом деле, разность
W(zt) двух таких решений должна на (L) удовлетворять условию
W (Zj) — W (г^), а значит, эта функция будет аналитической во
всей плоскости zlt включая (L) (п. II.2.5); но, равная нулю при
Z1 = oo, она должна равняться нулю тождественно (почему?). Таким
образом, в случае /я=0 и задача B5), а потому и уравнение B3),
имеют единственное решение. Учитывая равенства
(L) '
можно получить выражение решения u(z) непосредственно через
функции а, {$, /; мы предоставим это читателю.

§ 5. СИНГУЛЯРНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 465
Пусть т > 0. Обозначим тогда
Fiz)=l
К " \ z?V(zt) (z1 снаружи (?)).
Эта функция, аналитическая всюду, кроме точек (Z.), на (Z.) удов-
удовлетворяет условию
/"(*) = ft*)+/,(*) (г €(?)).
Значит, ^(г) можно найти по формуле C0). Но если к этому инте-
интегралу прибавить произвольный многочлен степени ^.т — 1, то функ-
функция V(zt), определяемая из равенств C1), все равно будет равна
нулю на бесконечности (почему?). Таким образом,
(Ц
V" (Zl) = ^fL)Z=t dl +# + #T+ * * * +~1f '
где Со, Cv ..., Cm_x — произвольные постоянные. Аналогично пре-
предыдущему абзацу можно показать, что других решений нет. Зна-
Значит, и исходное уравнение B3) имеет /и-параметрическое семейство
решений.
Пусть, наконец, т < 0. Введя опять обозначение C1), получим
при больших [ Zj | разложение в ряд Лорана
V \Z-t ) = Z\ Г (^,1=21 ^—:
k=0 (L)
Но так как должно быть Vn(oo) = 0, то мы приходим к равенствам
= 0 (А = 0, 1, .... ||Я| —1), C2)
§ Л
необходимым и достаточным для разрешимости задачи. Если оии
выполнены, то уравнение B3) имеет ровно одно решение, если хоть
одно из них нарушено, решение отсутствует.
Если ввести, как указано в п. 3, понятие сопряженного уравнения к B3),
то легко проверить, что его индекс равен —т. Значит, при т. < 0 однородное
сопряженное уравнение имеет | т. | линейно независимых решений и оказывается,
что условия C2)—это как раз условия ортогональности функции / (г) *пш
решениям.

466 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Для более общего уравнения
(г, Q а (?) dg+
+ f W (г € (Ц, а? (г) - р« (г) ^ 0), C3)
где ядро К фредгольмово (или со слабой особенностью), можно интеграл с этим
ядром объединить с /, после чего применить полученные выше формулы. При
этом, как и в переходе от A9) к B0), мы получим для и (г) уравнение Фред-
гольма 2-го рода. Однако если уравнение C3) имеег индекс т > 0 (ои вычи-
вычисляется по тому же правилу, что и для уравнения B3)), то неоднородный член
полученного фредгольмова уравнения будет содержать т произвольных постоян-
постоянных. Если же т < 0, то иа комбинацию ф Kudt,-{-f будет наложено | т | усло-
условий ортогональности, которые в конечном счете, поскольку и линейно выра-
выражается через f, представляют собой условия ортогональности на f.
Если таким способом регуляризовать сопряженные уравнения C3), то можно
проследить, что и полученные фредгольмовы уравнения получатся сопряженными,
а потому в силу п. 2.2 соответствующие однородные фредгольмовы уравнения
имеют одно и то же число, скажем, feS=0, линейно независимых решений (если
k=0—только тривиальное решение). Подробный анализ, которого мы здесь
не будем проводить, показывает, что тогда при m3*0 однородное уравнение рЗ)
имеет т-\-1 линейно независимых решений, гдеО</<? (типичный случаи —
/=0), а однородное, соприжеииое к C3), имеет / решений; если же т < 0, то
числа решений соответственно равны I и \m\-\-l. Таким образом, во всех
случаях разность между числом линейно независимых решений однородного
уравнения C3) и соответствующим числом для сопряженного уравнения равна
индексу уравнения C3), который не зависит от вполне непрерывного члена
\Kudt, в уравнении. Кроме того, можно доказать, что для существования
у неоднородного уравнения C3) по крайней мере одного решения необходимо
и достаточно, как и для уравнений Фредгольма, чтобы неоднородный член f (x)
был ортогонален всем решениям однородного сопряженного уравнения. (Необхо-
(Необходимость этого условия доказывается весьма легко по общей схеме: если Au=f,
A*v=0, то (f, v)=(Au, v) = (u, A*v)=(u, 0)=0; серьезным является доказа-
доказательство достаточности.)
Для разомкнутого контура, для систем сингулярных уравнений вида C3),
для аналогичных уравнений с любым числом независимых переменных оказы-
оказываются справедливыми оба последних утверждения, выделенных курсивом
(теоремы Нётера). (Дли системы вида C3), где а и Р—квадратные матрицы,
индекс равен деленному на 2я приращению аргумента величины det [а (г) -}-
+ р (z)]/det [а (г)—1$ (г)], когда г проходит (L).) Таким образом, наличие
индекса является характерным для невырожденных сингулярных интегральных
уравнений: для уравнений Фредгольма он всегда равен нулю, а для сингуляр-
сингулярных уравнений—не всегда. Если конечномерным аналогом уравнений Фред-
Фредгольма служат системы линейных алгебраических уравнений, в которых число
уравнений равно числу неизвестных, то аналогом сингулярных интегральных
уравнений служат такие системы, в которых это равенство уже не требуется.
При этом роль индекса для таких систем играет разность между числом неиз-
неизвестных и числом уравнений в системе (продумайте это, исходя из п. IV. 1.4.
и ЛВМ, п. XI. 5).
Невырожденность для уравнения C3) означает, что а2 (г)—рг (г) s*0. Если
эта разность имеет нули, ситуация осложняется. Допустим, например, что
a (z).+ ft (г) = 0, д(г)—Р (г) Ф 0. Но тогда из условия B5) легко вывести,. что
функция / (г) должна удовлетворять бесконечному числу условий ортогональ-
ортогональности (продумайте это для случая, когда (L)—окружность). Если же эти условия

§ 5. СИНГУЛЯРНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 467
выполнены, то в силу произвольности Ua общее решение уравнения B3) будет
содержать бесконечное число произвольных постоянных.)
Если в правую часть C3) добавить сингулярный член более общего вида
v- p\r f-lz " (?)*%» где ЯДР° ^(*. О непрерывно при ?=z, то это не будет
О.)
существенным обобщением. В самом деле, если представить
и объединить первый из полученных интегралов с первым членом в правой
части C3), а второй—со вторым, то мы вновь приходим к уравнению вида C3).
Сингулярное уравнение с ядром Гильберта (п. 2)
приводится к уравнению C3) с помощью подстановки z=e/*, C=«^,* причем
контуром (L) будет служить окружность |г|=1 (проверьте!).
6. Незамкнутый контур. Рассмотрим теперь уравнение B3) для
незамкнутого контура (L) с началом а и концом Ь. Обозначим через
g{z) какое-либо определенное значение функции Ln"; ,,., не-
a (z) — р (г;
прерывно занисящее от г^ (L), и после перехода к краевой задаче
введем функцию
by ехр И J. Д§
V(Zl) = U(zt) Ъ—af (zt-by ехр И J. Д§ dg ], C4)
L ' J
где ц, v—целые числа, которые будут подобраны позже. Это одно-
однозначная аналитическая функция на всей плоскости ги за исключением
линии (?), где она удовлетворяет условию
V*(z) = Vn(z)+f1(z)
Л B) =
(проверьте и сравните с B9)).
Теперь надо было бы пользоваться формулой
<36>
однако функция /г(г) может оказаться слишком быстро растущей
при z —> аи г-+й потому неинтегрируемой. Именно для этого
в формулу C4) были введены степени. Так как квадратная скобка
в C5) имеет при z—+ а порядок x--g(a)ln(z—а), т.е.экспонента—

468 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
—а\ ^2я/ /
порядок \z—а\ ^2я/ / (почему?), то в качестве ц надо взять
целое число, удовлетворяющее неравенству
С другой стороны, из C4) и требования интегрируемости U(z) вблизи
z — a легко вывести, что эта же сумма должна быть <1 (а если
мы хотим, чтобы U{z) оставалась конечной, то сумма должна быть
меньше или равна нулю). Аналогично в качестве v надо взять целое
число, удовлетворяющее неравенству
Теперь применяем формулу C6). При этом, если m =
то к правой части можно прибавить еще произвольный многочлен
степени ^.т—1, так как из C4) видно, что UizJ все равно оста-
останется решением поставленной краевой задачи. Таким образом, при
т > 0 уравнение B3) имеет m-параметрическое семейство решений.
При /и = 0 решение ровно одно. Наконец, при т<0 функция V{гг)
должна при zi —> оо иметь порядок о {z™); как и в п. 5, выводим,
что для этого функция /(г) должна удовлетворять \т\ условиям
ортогональности, получаемым из разложения интеграла C6) в ряд.
Если эти условия выполнены, то решение ровно одно.
Аналогично результаты п. 5 распространяются и на уравнения вида C3)
с незамкнутым контуром (L), а также на случай, когда (L) состоит из несколь-
нескольких незамкнутых дуг.
В качестве примера выведем формулу обращения A5). Для этого рассмотрим
уравнение
lz ж=0, -1
)
Таким образом, здесь
В качестве ц можно взять —1 (если мы хотим, чтобы решение оставалось
конечным при г=—1) или 0 (если этого ие требовать, ио стремиться к повы-
повышению индекса); аналогично, за v можно взять 0 или 1. Примем jx=0, v=l;
тогда (проверьте!)
[-^ v.p. J ^dS-4 ml =
(корень арифметический);

§ 5. СИНГУЛЯРНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 469
и (х) = U (x+ iO) — U (х— iO) =
-_!_ (г l/EI ГУ „
~2ш'(х—1I У 14-х р'
w. [ i
..p.
Это формула A5). Мы предоставляем читателю проверить, что если принять
i = v = 0, т. е. искать решение, конечное при х=1, то получится
Полезно рассмотреть также случай }i=—1, v=0, в нем появится условие
-i
7. Приведение к бесконечной системе алгебраических уравнений. Как
и уравнения Фредгольма (п. 2.3), некоторые сингулярные интегральные уравне-
уравнения удается численно решить, сведя их непосредственно (без регуляризации)
к бесконечной системе линейных алгебраических уравнений. Рассмотрим, напри-
например, уравнение
^^^ . C7)
Сделав замену переменных
*=cos*. g=cosq), и (х)=«(#), /(x)=F(«), K(x, l) = L(b, ф),
перепишем C7) в виде
в (Ф) sin Ф dff + F (Ь) @<д<я). C8)
Теперь надо разложить «@) в ряд по какой-либо полной системе функций
и после подстановки в C8) получить систему линейных алгебраических уравнений
относительно коэффициентов разложения. Воспользуемся, например, такими
разложениями:
ОС 00
v @)=2 vicos ft' ^ (*)= 2 fj cos ft'
C9)
.... I
COS ,

ГЛ. VII. ИНТЕГРАЛЬНЕЕ УРАВНЕНИЯ
Так как
2 2 S ^№s cos /* sin fe(P cos s<p=
,= 0 * = 1 s=0
да oo ов
v (f )=
2
/=o ft=i s=o
то в силу формул, приведенных в конце п. II. 3.5,
я
v.p
J
о
я
v.p. f L (г<>' ф) ' v (ф) sin ф <f<p=*
J COS ф—COS# Т/ Т Т
о
1 = 0 fc=
s=0
где штрих означает, что надо пропустить член с k=s. Преобразуя D0) далее,
удобно все суммирования проводить от —оо до оо, считая, что все коэффициенты
с индексами, не указанными в C9), равны нулю. Получим
I к
(fc-f s-
[cos (k-s
Разбив это выражение на четыре суммы, перейдем в первой к суммированию
по Ar, s и r=A+s-f-/, в» второй—по h, s и /r=&+s—/ и т. д. Объедавяж
результаты, получим
i-r, ft)
r*.
Меняя обозначение индекса л на / и подставляя результат в C8), получим после
приравнивания коэффицяентов при косинусах
ото=—— (
av/= - т I
s=0
s=0
*. k + Lk

-s.k) K
J
(/=1, 2, 3, ...),
причем здесь коэффициенты LPt к при р < 0 следует считать равными нулю.
Эту систему иногда удается решить с помощью методов, указанных в п. 2.3;
однако надо иметь в впду, что, в отличие от п. 2.3, здесь коэффициенты при
неизвестных иа главной диагонали, а также на параллельных ей линиях, имеют

§ 6. НЕЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 471
отлвчиые от нуля пределы. Если члены на главной диагонали все же домини-
доминируют, то можно их перенести в левую часть и применить итерации; если ври-
хватить и члены с ближайших параллельных линий, то можно применить ком-
комбинацию цепных дробей с итерациями, и т. д.
§ 6. Нелинейные интегральные уравнения
Теория нелинейных интегральных уравнений значительно менее
стройна и едина, чем теория линейных уравнений. Для различных
классов нелинейных уравнений получено большое число теорем
о разрешимости и о свойствах решений; см., в частности, [19, 20,
56, 57, 58]. Численное решение нелинейных интегральных уравнений
часто оказывается затруднительным, хотя и здесь известен ряд
подходов. Мы по необходимости коснемся лишь небольшого числа
из них.
1. Переход к конечным уравнениям. Имеется специальный класс
интегральных уравнений, аналогичных уравнениям с вырожденными
ядрами (п. 2.1), непосредственно сводящихся к конечным уравнениям.
Рассмотрим, например, уравнение
Обозначив
b
a
получаем
n
e(*)= 2 C/D,(*)+/(*)•
Подставив в B), приходим к системе нелинейных конечных уравнений
_ . M)+f(l) )dS=cy (;=i,2 л), C)
полностью равносильной уравнению A). К системе C) могут быть
применены любые методы численного решения систем конечных
уравнений, а в простых случаях она допускает точное решение.
Уже на самых простых примерах можно увидеть специфику не-
нелинейных уравнений.
Рассмотрим уравнение с параметром к
i
J % (t,

472
ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
прячем будеи интересоваться только вещественными решениями. В силу ска-
сказанного выше положим
==C. откуда
ХС
После подстановки получаем соотношение между С и Я
=0.
E)
Линия с уравнением E) на плоскости X, С показана жирио иа рис. 118. Мы
видим, что при —оо < X <—2 и при 0<Х < оо уравнение D) имеет только
нулевое решение, а при —2 < к < 0—также два ненуле-
ненулевых. Поэтому, если по аналогии с линейным случаем
считать характеристическим значение X, при котором
уравнение D) имеет по крайней мере одно ненулевое ре-
решение, то здесь получается целый интервал характери-
характеристических чисел; однако каждому такому числу отвечает
иа бесконечное, как в линейном случае, а конечное ко-
количество решений (в данном примере три). Особый интерес
представляет значение Х=— 1. В самом деле, допустим,
что параметр возрастает, начиная от больших отрица-
отрицательных значений, а решение должно зависеть от пара-
параметра непрерывно. Тогда до значения Х~— 1 решение
должно быть нулевым, тогда как при Х=— 1 проис-
происходит ветвление (бифуркация) решений, так что реше-
решение может либо остаться нулевым, либо пойти по другой
ветви и уйти при Х=—0 в бесконечность. При об-
обратном изменении параметра решение после X—— 1
также может либо остаться нулевым, либо пойти по
другой ветви, чтобы пропасть (стать мнимым) %ри
Х = -2—0.
Подчеркнем, что наличие при некотором X у нелинейного уравнения
D) только нулевого решения вовсе не означает, что соответствующее неоднород-
неоднородное уравнение (с +/(*) в правой части) имеет ровно одно решение. Здесь не
действует ни одна из теорем Фредгольма.
Непосредственный переход к конечным уравненням возможен и для интег-
интегральных уравнений более общего чем A) вида
Рис. 118.
и (х)=Р ( х, J Ф, (х) 4>t (I, и
\ а
0,
и т. п. Нетрудно уяснить сбщую структуру таких уравнений.
Если точный переход к конечным уравнениям возможен лишь
в весьма специальных случаях, то приближенный переход
возможен всегда и является одним из основных способов чис-
численного решения и исследования нелинейных уравнений. Рассмотрим,
например, уравнение Урысона (П. С. Урысби A898—1924) — совет-
советский математик)
*
F)
(возможен также многомерный аналог этого уравнения). Будем искать

§ 6. НЕЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 473
приближенное решение в виде u=c<f>(x; С1( C2, ...,С„) относительно
которого, как всегда, требуется, чтобы при небольшом числе пара-
параметров это выражение могло хорошо аппроксимировать точное реше-
решение. После подстановки в уравнение F) мы получаем невязку
ь
<р(дг; Сх, Cg, .... С„) — $/(*, I, <р(?; Q, С2, .... Q)dg
которую можно затем улучшать теми же методами (метод моментов,
метод наименьших квадратов, метод коллокации), которые были ука-
указаны в ЛВМ, п. XV.29, в связи с решением дифференциальных
уравнений.
2. Метод итераций. Метод итераций, описанный в п. 2.5, при-
пригоден и для некоторых классов нелинейных уравнений. Это, прежде
всего, уравнения Вольтерра 2-го рода
X
и(х) = \/(х, I, «(?))<*? + !
а
( г
u(x) = F[x, \ К (х, I) и (I) i
\ а
(*. Б, i\)ufc)
а также иных видов, которые объединяет то, что уравнение разре-
разрешено относительно и (х), а в правой части и стоит под знаком
интеграла с верхним пределом х. Возможность решения уравнений G)
маленькими шагами по х, о которой говорилось в п. 2.9, а также
возможность линеаризации на каждом таком шаге приводят к тому,
что обычно каждое из этих уравнений обладает единственным реше-
решением, которое можно получить с помощью стандартного метода ите-
итераций, начиная от любого нулевого приближения.
В связи с рассмотрением уравнений Вольтерра отметим, что если для спе-
ь х
циальных типов уравнений, рассмотренных в п. 1, заменить С на С , то Легко
а а
перейти к начальной задаче для обыкновенных дифференциальных уравнений,
которую можно решить с помощью численного интегрирования. Например, если
для уравнения
«(*)=$ 2 Ф/W V/ F. и E)) <?+/ (х) (8)
а /=1 . . .. ¦

474 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
обозначить
а
то мы получим систему дифференциальных уравнений
(ж, 2 ф/ W y/+/ W )
\ /= i /
=V/ (ж, 2 ф/ W y/+/ W ) 0 = 1.2 я),
которая при начальных условиях
V/(a) = 0 (/=1, 2 л)
полностью равносильна исходному уравнению (8).
Метод итераций можно применить также к уравнениям с малыми
нелинейными ядрами, скажем, вида
ь
и (х) = ц J / (х, I, и (I)) dt + y (х), (9)
а
где | ц | достаточно мало. Последовательные приближения, естест-
естественно, определяются формулой
$ (л = 0, 1, 2, ...),
а
и из равенства
«„-и
= I* J [Я*. 6, «.(Е))—
видно, что при малом | ц \ эти приближения сходятся со скоростью
геометрической прогрессии. На практике эта малость обычно рас-
распознается с помощью сравнения последовательных приближений
друг с другом.
Явные, хотя практически редко применяемые условия сходимости метода
итераций можно получить с помощью принципа сжимающих отображений
(п. 2.6). Для этого будем рассматривать итерации в пространстве С [а, Ь] и
допустим, что имеет место оценка
\fu(x, fc «0|<*(«,$) A1)
для всех значений и или, во всяком случае, для значений, используемых
в процессе итераций. Обозначая через р (и, v) равномерное уклонение функций
и (х) и v {х) друг от друга, т. е. расстояние в рассматриваемом пространстве,
из A0) с помощью формулы конечных приращений (ЛВМ, п. V.4) получим

§ 6. НЕЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 475
откуда
» ь
Р («п+г. «»)< 1 М-1 max \ К (х, I) d?-p (а„, «„_,).
а
Отсюда, иа основании принципа сжимающих отображений, метод итераций
сходится, если
ь
I/max С/((*,?)<? A2)
(В частности, отсюда. следует, что при таких |i уравнение (9) имеет по крайней
мере одно решение; однако если неравенство A1) выполняется лишь в указан-
указанном диапазоне изменения и, то решение ие обязательно единственно.) Условие
A2) является только достаточным для сходимости, иа самом деле сходимость
будет в более широком интервале ц, в частности всегда, если | |х | меньше наи-
наименьшего характервстического значения ядра К- Более детальный анализ пока-
показывает, что сходимость при достаточно малых | \i | будет и в случае, если
ь
max \ К (х, fe) ag= oo.
х
3. Метод малого параметра. К уравнению (9) в случае малого ц
можно применить также обычный метод малого параметра (ЛВМ, п. V.5).
Это можно сделать н для любого линейного уравнения, возмущен-
возмущенного малой нелинейностью. Покажем метод на примере уравнения
Ляпунова—Лихтенштейна
ь ь ь
u(x)=f(x) + X J К, (х, I) и (t) dfi + |i J $ *,(*, Е, |i) в (Б) uD)<%dr\ A3)
а а а
(могут быть также добавлены аналогичные члены с К3, К, и т. д.),
если % не является характеристическим числом ядра Kt (фредголь-
мова или со слабой особенностью), a \i—малый параметр. Разложение
и (х) = и0 (х) + цН1 (х) + р*иг (*) + ... (И)
после подстановки в A3) и приравнивания коэффициентов при одина-
одинаковых степенях ц приводит к равенствам
ь
«о (*) =/(x) + l\ Kt (x, I) и0 (Е) dl, A5)
а
Ь Ь Ь
ut{x) = 'k\Kt(x, I)Bl(E)dE + J S^(x, E, r\)«о(Б)«о(ЦL<*Ч> A6)
a a a
Ь
b b
. + S S *• (*• S. Л) К (t) «i D) + «! (D «о (Ч)] dg ^П A7)

476 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
и т. д. Мы видим, что построение каждого коэффициента в разло-
разложении A4) сводится к решению линейного уравнения с одним
й тем же ядром Кх и свободным членом, определяемым предыдущими
коэффициентами. В силу предположения о Я это построение воз-
возможно; оно особенно просто, если известна резольвента ядра Кх.
Пусть теперь Я—характеристическое число ядра Kt и ему отве-
отвечает г линейно независимых собственных функций. Тогда в силу A5)
функция /(х) должна удовлетворять k условиям ортогональности
собственным функциям сопряженного уравнения; если эти условия
выполнены, то решение ий(х) уравнения A5) будет содержать про-
произвольные постоянные Clt Сг, ..., Ск. Подставляя это решение в.
A6) и пользуясь условиями ортогональности неоднородного члена
собственным функциям сопряженного уравнения, получаем систему
из k квадратичных уравнений относительно Сх, С2, ..., Ск, из ко-
которых и приходится находить эти постоянные (для других исходных
интегральных уравнений может получиться система из к конечных
уравнений более общей структуры). Удовлетворив этим условиям,
получаем общее решение уравнения A6) с произвольными постоян-
постоянными C'v С'г, ..,, С'ь. Подставив это решение в неоднородный член
уравнения A7), найдем эти постоянные из условий ортогональности
(при этом уравнения для нахождения С[, С2, ..., С'к будут линей-
линейными, т. е. эти постоянные уже найти легко, как и для дальнейших
членов разложения A4)) и т. д. Продолжая таким образом, мы
можем построить любое число членов разложения A4).
Функции /, Kv Кг и даже пределы интегрирования в уравнении
A3) могут дополнительно зависеть от \i; тогда после разложения
всех этих величин по степеням \i метод применяется аналогично.
4. Применение теории симметричных ядер. Рассмотрим уравнение Гаммер-
штёйна
ь
а
с симметричным ядром К.
Нам потребуется простая оценка для норм в L2 ia> b]f.
" I! 1
K(x,l)v(l)dl \\<TrT\\v(x)\\, A9)
u
где Xj — наименьшее по абсолютному значению характеристическое число ядра/(#
В самом деле, в силу C.8)
(проверьте!).

§ 6. НЕЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 477
Теперь легко доказать, что если в уравнении A8)
ФиA, и)<а<|^|. B0)
то это уравнение имеет ровно одно решение, которое можно найти методом ите-
итераций. В самом деле, правая часть A8) определяет отображение Ви простран-
пространства L2 [a, b] в себя (предполагается, что f?L2). Так как
W) I
то наше утверждение вытекает из принципа сжимающих отображений (п. 2.6).
Покажем применение полученного результата к теории колебаний точечного
маятника. Дифференциальное уравнение плоских вынужденных колебаний без
учета трения легко выводится, оно имеет вид
q> + ^-elnq>=jiF(O. B1)
где ф—отклонение маятника от вертикали, g—ускорение земного тяготения,
/—длина невесомой нити, т—масса маятника, F (t)—вынуждающая сила, дей
ствующая по касательной. Будем считать как заданную вынуждающую силу, так
и искомое движение <р (t) нечетными и периодическими во времени с заданным
Т
периодом Т. Тогда достаточно построить решение на интервале 0<<<; — при
граничных условиях
<Р@)=0, <p(-J")=°. B2)
чтобы после нечетного периодического продолжения получить решение для
всех t.
Решение уравнения y = f(t) при граничных условиях B2) было указано
в ЛВМ, п. XV. 16; оно имеет вид
Г/2
Ф@= J Q(t, x)f{x)dx,
о
где симметричное ядро G определено формулами
-(г-2тН/Г @<<<т<772),
-(Г-2<) т/Т @<т<г<Г/2).
Применяя этот результат к B1), мы видим, что это уравнение при граничных
условиях B2) равносильно интегральному уравнению
Г/2 Г/2
Ф @ = f- J G (t, х) sin Ф (т) dt + -L j G (t, x) F (т) dr. B3)
о о
Характеристические числа ядра G сбратны по знаку точкам спектра урап-
нения ф + Яф=0 при граничных условиях B2) (почему?); эти точки были ука-
f2y
, . , f2ny
заны там же, из иих наименьшее по абсолютной величине Aj—— I -=- I

478 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Применяя общее условие B0), мы видим, что если выполнено неравенство
вр < 4л», B4)
то поставленная задача имеет ровно одно решение, которое можно найти мето-
методом итераций.
5. Применение теории неподвижных точек. Мы уже отмечали в п. 2.6 и
показали еще раз в п. 4, что отыскание решения многих уравнений можно
свести к отысканию неподвижной точки у соответственно подобранного отобра-
отображения некоторого множества точек в себя. Принцип сжатых отображений —
один из основных принципов, гарантирующих наличие такой неподвижной
точки. Другой метод отыскании неподвижной точки в конечномерном случае
основан на применении теоремы Боля—Брауэра (п. IV.4.8). Иногда пользуются
таким следствием из этой теоремы: если шар (Р) конечномерного евклидова
пространства (?) непрерывно отображен в (?) и при этом ни одна из точек
границы (Р) не перешла вдоль по радиусу в направлении от центра, то это
отображение имеет по крайней мере одну неподвижную точку. (Подумайте,
как можно было бы вывести это из теоремы Боля — Брауэра.) Имеются и более
сильные теоремы в этом направлении.
Подобные теоремы имеют топологический характер, так как они справедливы
для топологически эквивалентных тел (см. петит в конце п. 11.1.7). Например, тео-
теорема Боля—Брауэра справедлива для тела подковообразного вида, но не справед-
справедлива для кольца (почему?). Поэтому методы, с помощью которых существова-
существование решения задачи устанавливается иа основе применения теорем о неподвиж-
неподвижной точке нли других аналогичных теорем, называются топологическими; по
поводу этих методов см., в частности, книгу [57]. Топологические методы часто
оказываются применимыми в условиях, когда все другие методы отказывают.
К сожалению, топологические методы обычно решают задачу как бы наполовииу:
гарантируя, что по крайней мере одно решение существует (что само по себе
очень важно!), они не говорят о том, сколько таких решений н как их по-
построить; для этого приходится привлекать другие методы. (Отметим, что прин-
принцип сжимающих отображений не топологический, а метрический, так как поня-
понятие сжимающего отображения не топологическое.)
В бесконечномерном банаховом пространстве обычно взамен теоремы Боля —¦
Брауэра пользуются теоремой Шаудера, которая формулируется в точности,
как первая, но от отображения х-* Ах требуется не только непрерывность, ио
полная непрерывность (п. 2.11), т. е. образ рассматриваемого тела должен быть
компактным. (Доказательство теоремы Шаудера основано иа аппроксимации
заданного отображения последовательностью конечномерных отображений, при-
применении к этим отображениям теоремы Боля — Брауэра и использовании ком-
компактности полученной последовательности аппроксимирующих неподвижных
точек.) К отображению х -¦¦ Ах можно применить также утверждение, набран-
набранное выше курсивом, которое, действует и в данных условиях. Имеется и ряд
других подобных и более сильных утверждений.
Покажем применение теории неподвижных точек к уравнению A8). Для
этого допустим сначала, что функция Ф (?, и) непрерывна н ограничена при
всех g, и (atS*b,tS*b, —оо < и < со), скажем, |Ф(|, «)|<ФФ. Обозначим пра-
правую часть A8) через Аи; тогда из п. 2.11 легко вывести, что это вполне непре-
непрерывный оператор. Кроме того, из оценки A9) следует, что для всех u?L2[a, b]
будет
||Аа||<^Ф,УТ=5+||1||. B5)
Значит, если в качестве тела (Р) взять шар в L2 [а, Ь] с центром
в начале координат и радиусом, равным правой части B5), то выпол-
выполняются все условия теоремы Шаудера. Таким образом, уравнение A8) для
любой ограниченной непрерывной функции Ф имеет по крайней мере одно

§ 6. НЕЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 479
решение. В частности, это относится и к уравнению B3), т. е. задача, рас-
рассмотренная в конце п. 4, имеет по крайней мере одно (уже не обязательно
единственное) решение и в случае, если неравенство B4) не выполняется Между
прочим, на этом примере мы видим, что в нелинейной колебательной система
отсутствует явление резонанса.
Аналогичный результат получится, если функция Ф (§, и) удовлетворяет
менее жесткому ограничению
©, где k<~ Ф0(|)€Ыа, Ь] B6)
I Л|
(докажите!).
Предположим дополнительно, что ядро К положительно определенное'
(п. 3.5), а /(х)==0. Тогда можно доказать еще более сильное утверждение,
рассмотрев отображение и-» Аи в шаре || и [| s? R, где R достаточно велико.
и применив бесконечномерный аналог следствия из теоремы Боля—Брауэра,
приведенного в начале этого пункта. Мы будем считать, что функция Ф E, и)
непрерывна и удовлетворяет оценке
|ФF,и)|<;С|и|+Фв(|), где Ф,©€Ма. Ч W)
с какой-то постоянной С; отсюда можно вывести, что отображение А вполне
непрерывно. Если какая-нибудь из точек сферы ]| u || = R перешла вдоль по
радиусу в направлении от центра, это означает, что для некоторой функции
и(х) будет
ь
и || = Д. $К(*,&)Ф(Е, и<?))<16=A +а)и(х) (о>0). B8)
а
Обозначим
* ь
J U (X) фу (*) dx = U/, J Ф (X, U (X)) фу (ДС) dx = Vj (/=1, 2, 3,. . .),
а а
где <plt <p2> ••• — система собственных функций ядра К. Тогда из B7) легко
следует, что
Vj—(\ +a) \fUf, откуда и/о/ = A +а) fya? Ss (I +a) XjU?.
Суммируя обе части по /, получим (проверьте!)
ь ъ
A + a) A.J \ и2 (х) dx < \ и (х) Ф (х, и (х)) dx.
а а
Чтобы применить указанное выше следствие, нам надо предотвратить воз-
возможность такого соотношения при достаточно больших |[ и ||. Но для этого
достаточно потребовать, чтобы неравенство B6) выполнялось, когда Ф (|, и)
одного знака с и (почему?). Другими словами, достаточно одностороннего огра-
ограничения
' U
Таким образом,. если выполнены неравенства B7) и B9), то уравнение A8)
с положительно определенным ядром /Си / = 0 имеет по крайней мере одно
решение.
Нетрудно доказать справедливость полученного результата и для неотрица-
неотрицательно определенного ядра К, аппроксимируя его положительно определен-
определенными ядрами.

480. ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Подчеркнем, что мы здесь не имели в виду показать наиболее далекие
результаты, а хотели только продемонстрировать применение теорем о неподвиж-
неподвижных точках. Продвижение в этом направлении требует более серьезных мате-
математических знаний и навыков и изучения специальной литературы.
в. Вариационные методы. Для численного решения интегральных уравне-
уравнений, линейных или нелинейных, применяются также вариационные методы.
(Эти методы применяются и для исследования общих вопросов разрешимости
нелинейных уравнений; см. по этому поводу книги [19, 57].)
Иногда удается записать заданное уравнение в форме уравнения Эйлера
для подходяще подобранного функционала, чтобы применить затем метод Рнтца.
Так, легко проверить, что уравнение B.16) с симметричным ядром представ-
представляет собой уравнение Эйлера для функционала
ь ь ь ь
/{«}== J и» (х) dx-K J J К (х, I) и (х) и (I) dx dl-2 j / (х) и (х) dx.
а а а а
Во всех случаях можно попытаться применить метод наименьших квадра-
квадратов (п. VI.4.7).
Иногда приведение к форме уравнения Эйлера получается более сложно.
Рассмотрим, например, уравнение Гаммерштейна
ь
аи (*)=$*(*,?)/ (?, и &)) 4 (а=const) C0)
а
с симметричным неотрицательно определенным ядром К, собственные значе-
значения Xj и собственные функции фу (х) которого известны. Введем ядро L (х, |) =
/ первая итерация которого дает К, а также функцию
и
F (|, «)= \ / (|, s) ds. Тогда уравнение Эйлера для функционала
b b
\ Fix, \ L (x, ?) v (t) d\ ) dx
a a a
имеет внд (проверьте!)
О
av (*)= J L (x,t) f (l. J L (I, t]) v ft) dr\\ dl
a a
Отсюда, обозначив
ь
$ C2)
легко получить C0). Значит, придав функционалу C1) приближенно стацио-
стационарное значение, мы после перехода C2) получим приближенное решение урав-
уравнения C0).
Возможно также применение метода счетного множества переменных
(п. VI.4.3). Рассмотрим вновь уравнение C0), не требуя уже- определен-
определенности ядра К. Так как функция и (х) при а Ф 0 представлена через ядро
(п. 3.3), то возможно разложение

§ 6. НЕЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ' 481
(при «=0 надо требовать полноту ядра К). После подстановки в C0) и; ска-
скалярного умножения на ф/ получаем систему конечных уравнении
равносильную C0). Но это система условий стационарности функции
ь
Ф («х> и,; а„ .. .)=«2V?-2 S f E. 2 "
I
(проверьте!). Приблизиться к стационарной точке можно методом усечения,
т. е. путем приближенного перехода к конечному числу переменных. Если
стационарная точка есть точка минимума, то можно применить методы градиент-
градиентного спуска или наискорейшего спуска.
7. Уравнения с параметром. Часто бывает, что в заданное
интегральное уравнение входит один или несколько параметров н
требуется проследить за изменением решения этого уравнения прн
изменении параметров. Мы изложим простые результаты в этом на-
направлении на примере уравнения'
ь
и(х)=\/(х, %,и(Ъ); y)dl C3)
а
с одним параметром у, хотя эти результаты немедленно переносятся
и иа уравнения иного вида с любым числом параметров. Как н рань-
раньше, все величины будут считаться вещественными.
Допустим, что при некотором значении параметра Y = Yo нам
известно одно из решений йУо (х) уравнения C3) (это уравнение
может при у—Yo иметь и другие решения). Если у немного изме-
изменится, то и решение и=и^(х), вообще говоря, немного изменится,
кроме особых случаев, о которых будет сказано позже. Продиф-
Продифференцировав обе части равенства C3) по у, получим
ь
-Г/Ж g, «т. (Е>;
V=Vo
b
Мы видим, что производная -^
ду
определяется из линейного
у Y=Vo
уравнения Фредгольма 2-го рода с ядром
¦'..!....•'. . /Ж?,%.(?); y.)
В силу п.'2.2 эта производная определяется однозначно, если для
ядра C4) (без дополнительного параметра К) имеет место первый
16 А. Д. Мышкио

482 гл. va. интегральные уравнения
случай альтернативы Фредгольма, т. е. если для этого ядра значе-
значение К =1 не является характеристическим. Подобно теореме о неяв-
неявных функциях (ЛВМ, пп. IX.13 и XII.3) можно подробно показать,
что это условие является и достаточным для того, чтобы уравне-
уравнение C3) при малых ]у—Yol имело однозначно определенное ре-
решение и7 (я), непрерывно зависящее от у и равное «v, (х) при у =» у9.
Если в обе части C3) подставить разложение
то легко проверить, что ф0 (д;) = вУо {х), фх (¦*) =
диЛх)
-|—
_
а для
определения каждого из последующих коэффициентов ц>к{х) полу-
получается линейное интегральное уравнение Фредгольма 2-го рода с тем
же ядром C4) и со свободным членом, выраженным через уже опре-
определенные коэффициенты <р„(х), Ц>г{х), ..., ц>к_1{х). Поэтому в прин-
принципе эти коэффициенты можно находить один за другим, сколько
потребуется, хотя практически, если резольвента ядра C4) неиз-
неизвестна, то это довольно громоздко.
Для приближенного решевия уравневия C3) при малых \у—Yol можно
также переписать его в виде
ь ь
« W- J /'„ (*. Б. «Vo AУ. Yo)« <&) <?= J [/ (х, I, и (I); v)-
после чего примевить метод последовательных приближений, начивая от и (х).
Так как вариация правой части при v=Yo> «="т (•*) равна вулю (проверьте!),
то она будет мала и при близких у, и; это и обеспечивает сходимость ите-
итераций (ср. ЛВМ, п. V.3).
Продолжение решения по параметру возможно, если только оио
при конечном у не уйдет в бесконечность,4 либо не дойдет до ко-
конечных значений, при которых функция / разрывна (если такне раз-
разрывы имеются), нли, наконец, до значений, при которых ядро C4)
имеет характеристическое число Я, = 1.
8. Разветвление решений. Допустим теперь, что значение К = 1
является характеристическим дли ядра C4). Мы рассмотрим только
основной случай, когда этому значению отвечает лишь одна соб-
собственная функция иг (х) (с точностью до скалярного множителя),
а стало быть, сопряженному уравнению—одна собственная функ-
функция г^ (х); мы будем считать эти функции известными (теоретически —
точно, на практике обычно—приближенно). Рассмотрим вспомога-
вспомогательное уравнение
ь
и(*)=\ [/(х, I, и(I); у) + в, (|)v,{х)иЩ dl-sv,(x), C5)

§ 6. НЕЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 483
где s—добавочный параметр. Если принять дополнительно
ь
Hl(i)W(i)dE, C6)
а
то уравнение C5) будет полностью равносильно C3). Однако это
искусственное преобразование приводит к тому, что для уравнения
ь
C5) при Y = Vo. s = so = ^u1(l)uu(l)dl, и = и^{х) выполнено усло-
а
вие п. 7 продолжимости решений (по двум параметрам у, s).
В самом деле, пусть для уравнений C5) линеаризованное ядро
(аналогичное C4)) имеет к = 1 характеристическим'числом.Это озна-
означает, что уравнение
ь
и (х) = J [/„' (х, I, иТл (I); Yo) + Щ. (Е) f 1 (*)] «(Е) dl C7)
имеет нетривиальное решение U(x). Переписав уравнение C7) при
u = U(x) в виде
ь ь
«(*)=$ /и (х, I, иТо (I); Yo)" (Е) ^5+.J «х (Е) ^(Е) dE-t»x (Jt), C8)
а а
мы видим в силу третьей теоремы Фредгольма, что такое возможно,
только если функции u^nU ортогональны. А тогда из C8) получается,
что U должна быть пропорциональна иг, и потому их ортогональ-
ортогональность невозможна.
Полученное противоречие показывает возможность продолжения
по параметрам y> * решения
и = Мр(х; у, s), C9)
где ty(x; Yo. s«) = »IoW, при малых |?—Vol. l* — *ol:- более того,
по методу п. 7 это решение можно разложить в ряд по степеням
(Y—Yo)> (s—so)- Подставив решение C9) в правую часть C6), мы
получаем уравнение разветвления
ь
s— $ их (Е) г|> (?; y, s)dl = 0, коротко F{s, y) = Q, D0)
а
связывающее s н у. Найдя отсюда s(y) и подставив результат в C9),
получим решение уравнения C3).
Однако дифференцируя уравнение C5) по 5 или по у в рассуж-
рассуждая, как с уравнением C8), легко доказать (проделайте это!), что
/*.>„. То)-0,
ь ь ь
Ру («о. То) * -И Л (*' *. "то (Е); То) "i (х) dx dlj\ v\ (x) их. D1)
а а . а
16*

484
ГЛ.. Y". ИНТЕГРАЛЬНЫЕ.
Значит, уравнение D0) разрешить однозначно относительно s, вообще
говоря, невозможно. Если двойной интеграл в D1) отличен от нуля,,
то уравнение D0) можно разрешить относительно у, и тогда связь
между shy будет такой, как показано на рис. 119. В первом,
основном случае получается, что при изменении у два решения при
<у=--7о сливаются- и в дальнейшем становятся мнимыми, т. е. про-
пропадают.
Если двойной интеграл в D1) равен нулю, то надо действовать,
как было описано в п. II.2.8 в связи с уравнением (II.2.25). Здесь
особенно важен случай, когда нам при всех значениях у известна
или реже
7о У
Го
Рис. 119.
одна из ветвей ит (х) решения уравнения C3) и нас интересует, не
может ли при некотором значении у от нее отщепиться другая ветвь
решения. Как было отмечено в п. 1, такое отщепление называется
бифуркацией, а потому соответствующие значения параметра у на-
называются бифуркационными. Мы будем без ограничения общности
считать, что и^(х) = 0. (К этому случаю можно всегда прийти с
помощью замены и—u^(x) = v.) Тогда из уравнений C3) мы видим,
что должно быть
ь
\f(x, I, 0; y)dl =
а потому
t, I, 0;
Значит* двойной интеграл вD1) равен нулю, и потому в разложении
функции F(s, у) по степеням s(s0 —р), у—ув линейные члены от-
отсутствуют. Так как квадратичные члены обычно, присутствуют, а в
силу C6) известная ветвь s(y) будет s==0, то типичное располо-
расположение линии D0) около точки (yq; 0) получается, как на рис. 120
(почему?). Это означает, что при переходе у через у0 как в одну
сторону, так и в другую происходит бифуркация, т. е. решение
можно продолжать двумя способами.
Расположение может оказаться и иным, однако можно показать,,
что всегда, если значение к — 1 является простым нулем определи-

§ 6. НЕЛИНЕЙНЫЕ 'ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
485
теля Фредгольма ядра f'u(k,\, 0; yQ), то при у = уя обязательно
будет бифуркация хотя бы в одну сторону от у^. То же будет для
нулей нечетной кратности: при этом в общем случае надо
иметь в виду, что может отщепиться и более одной ненулевой ветви.
Для нулей четной кратности бифуркации
может не произойти, так как отщепившиеся
ветви могут оказаться мнимыми но обе
стороны от у0. В некоторых случаях уда-
удается показать, что эта кратность несуще-
несущественна, например для уравнения A8) с "* о ^'Уц
симметричным положительно определенным
ядром К, если Ф(?, 0) = 0. **
Рассмотрим, например, уравнение D), имеющее, "ИС- .
в частности, нулевое решение при всех значениях
параметра %. Так как в данном случае ядро fu (х, ?, 0; Х)= —2Кх имеет харак-
характеристическое значение 1 при Ко= — 1, причем и1(х)=х, jI(jc)=l (проверь-
(проверьте!), то уравнение C5) имеет вид
a(Jt)
=J{—5-дс[и»
0
D2)
Здесь удобио обозначить Л» —|— 1 = |х, так что|х0=0. Подставляя в D2) разложение
и (х)=а (x)s+b (х) |х+с (jc) s*+d (х) S|x+e (х) ц» + .„,
легко найдем (проверьте!), что
fl(jc) = 3jc, Ь(х)=0, с(*) = -у*—j, d(*)=-f§
9
откуда уравнение разветвления D0) примет вид -r-s2
3
—к Щ + члены• не1 нвже
3-й степеии=0. Значит, при ц=0 происходит бифуркацвя по закону s =
2 . - „ .-.:::.!.. | ¦.
= -г- |i + • • •, т. е. и(х)—2х (>i, + l) +члены не ниже 2-й степени относительно
о
^+1. Эта бифуркация была отмечена и в п. 1, а главный член разложения
нетрудно вывести из E).
Если характеристическому значению л-=1 ядра C4) отбечает k > J соб-
собственных функций, то рассуждать можно так же, как при k=\. Вводятся
вспомогательные уравнения, аналогичные C5) и C6), с k добавочными пара-
параметрами Sj, s2, . .., sk, после чего составляется система взй уравнений
разветвления, связывающих параметры s1; s2, ..., sft, %.. Вообще говоря, ис-
исследование таких систем существенно сложнее, чем одного уравнениях двумя
Параметрами. Тем не менее бывают случаи, когда в результате последс)ватель-
вых исключений оказывается возможным перейти к одидКгу* уравнению в'тем
самым довести задачу до концаt ' , > ¦¦> • tt1; , i--.---i> ¦ ¦¦'..
К уравнению C3) в рассматриваемом особом случае можно и непосред-
непосредственно применить метод неопределенных коэффициентов (м$тод, раэаруца,—
Некрйсовй). Как было показано в п. II.2Д в условиях, когда теорема о не-
неявной функции неприменима, одну из двух величин', 'входящих в'конечное
уравнение, можно получить р виде суммы ряда Пюизо по-дробным степеням
другой. Поэтому естествеидо решение s (у) уравнения! радвешвления |<и> анало-
аналогично системы уравнений разветвления), а с ним и решение и (х) уравнения

486 ГЛ. VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
C3) для малых |у—Vol искать в виде суммы рйда
и(х)—и (*)+»! (х)д+юа(х)д*-Ь.., где &Р=у—у0,
однако целое число р S* 1 заранее неизвестно и уточняется в процессе построе-
построения решения. Подстановка в C3) дает
W
Задавшись значением р, разложим правую часть по степеням 6. Приравнивая
коэффициенты при одинаковых степених, получим уравнения ввда
ь
WJW =\f'u(*. 5. «ТоО; Yo)«у©<?+Ф/ (*) D3)
(/=1,2,3,...),
где <Pi (х)—вполне определенная функция, а каждая из дальнейших функции
Ф/(х) выражается через функции шх (х), ша (х) w/_i(*)-
Так как для уравнения D3) имеет место второй случай альтернативы
Фредгольма, то функция «pt (x) должна удовлетворять k условиям ортогональ-
ортогональности; если они ие удовлетворяются, то р выбрано неверно. Если же они удовле-
удовлетворяются, то уравнение D3) при /=1 определяет a>i(x) с k произвольными
постоянными. Значит, и функция <ра (х) содержит k произвольных постоянных;
ио для возможности определения w2(x) из уравнений D3) прн /=2 функция
Фа (х) должна удовлетворять k условиям ортогональности, откуда эти постоян-
постоянные и определяются. Тогда щ (х) будет определена с точностью до k новых
произвольных постоянных, которые войдут в ф3 (х) н потому определятся из k
условий ортогональностя и т. д. Можно показать, что, начиная с .некоторого
шага, уравнения для нахождения произвольных постоянных становятся линей-
линейными (алгебраическими) с неизменной невырожденной матрицей, т. е. больше
никакого произвол* не остается. Если мы дошли до этого шага, то препят-
препятствий (несовместных систем) больше не может встретиться и возможно, во
всяком случае " принципе, построить любое число членов разложения иско-
искомого решения. . - ¦

Глава VIII
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
¦ Общий курс математики содержит главу, посвященную тео-
теории обыкновенных дифференциальных уравнений (ЛВМ, гл. XV), и
мы будем предполагать известными основные сведения, содержа-
содержащиеся в этой главе. Уже из общего курса становится ясна выдаю-
выдающаяся роль этой области математики для приложений. Однако сейчас
широко применяются многие разделы этой теории, значительно вы-
выходящие за рамки указанной главы. Здесь мы .коротко осветим
некоторые из этих отделов, причем отдельные параграфы могут
читаться в значительной мере независимо один от другого.
§ 1. Линейные уравнения и системы
1. Общие свойства. Напомним некоторые факты, известные из
общего курса математики. Мы будем рассматривать линейные си-
системы вида
*i = «и С) *i + *1. (*) *. + • • •'+«1» W xn +A (t),
К = e»i@*i + an2 (<)*,+ ... +.в™, (t)*„+/„(
при этом независимая переменная обозначается буквой t, так как
она обычно может быть истолкована как время, а во многих задачах
и в самом деле является временем. Если не оговорено противное,
то независимая переменная будет, считаться вещественной, а коэф-
коэффициенты и искомые функции — вообще говоря, комплексными. Введя
числовые вектор-функции и матрицу коэффициентов
¦А"
х = [ •¦ I, f = | f" I, А = |
мы можем систему A) переписать в векторно-матричном виде
k = A(t)x + i(t), B)
которым мы обычно и будем пользоваться.

488 ГЛ. VIH. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ/УРАВНЕНИЯ
Как показывается в общем курсе, линейные уравнения и системы
линейных уравнений любого порядка можно с помощью введения
добавочных искомых функций свести к системам первого порядка,
т. е. системам вида B).
Коэффициенты ajk(t) и неоднородные (свободные) члены fj(t)
будут считаться заданными на некотором бесконечном или конечном
открытом или замкнутом интервале а, р и принимающими конечные
значения (впрочем, допускается обращение в бесконечность, но с
сохранением абсолютной интегрируемости). Тогда система B) при
любом начальном условии
х(д=х0 C)
имеет ровно одно решение, определенное на всем интервале а, р.
Рассмотрим однородную систему (векторно-матричное уравнение)
У = А(*)У, D)
соответствующую системе B). Совокупность ее решений образует
л-мерное линейное пространство. Любой базис в нем, т. е. любая
совокупность из п линейно независимых решений
YiW, У,(<), -.., У„С) E)
системы D), называется ее фундаментальной системой решений.
Легко проверить, что после подстановки в E) любого фиксирован-
фиксированного значения t — t0 получится система линейно независимых векто-
векторов: в самом деле, если, например, у1 (t0) = С2у2 (t0) + ... + Спу„ (t0),
то два решения yt (t) и С2уг (t)+ ... + Спуп(t), совпадая при t = /0»
должны совпадать тождественно (почему?), а это противоречит фун-
фундаментальности системы решений E).
Полезным оказывается понятие сопряженной с D) системы
z = — A*(t)z. F)
Легко проверить, что для любого решения у (t) системы D) и любого
решения z(t) системы F) будет i ; :
(у, гM= г*у == const. ... . .
В самом деле, . . . . . , ,. .
(у, z)- = (y, z) + (y, z) = (Ay, z) + (y, —A*z)=0.
(Получите это же, дифференцируя z*y.) Если А (/)==—А*(/), т. е.
матрица А антиэрмитова, то система D) самосопряженная.
Наряду с D) часто рассматривают матричное уравнение
Y-AWY, G)
где ? = Y(/)—искомая квадратная матрица порядка л. Если зани-

§ I. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ
489
сать это уравнение в скалярной форме, то для элементов каждого
из столбцов матрицы Y получится та же система, которая коротко
записана в виде D) (проверьте это для первого столбца!). Поэтому
общее решение уравнения G) получается так: надо взять какие
угодно п вектор-функций, являющихся решениями уравнения D), и
составить из них матрицу. Так как при любом постоянном векторе с
столбец Y(at)c равен линейной комбинации столбцов матрицы. Y (х)
(почему?), то У(лг)с представляет собой решение уравнения D); это
легко проверить непосредственно:
(Yc)- = Yc = A it) Yc = A (t) (Yc)
(где использовано постоянство вектора с?).
Для определителя матрицы Y(^)—он называется также опреде-
определителем Вронского (по имени польского математика и философа
Ю. Вронского A778—1853), который ввел такие определители
в 1812 г.) для набора решений E) системы уравнений D)—имеется
простая формула. Мы будем исходить из формулы дифференциро-
дифференцирования функциональных определителей
Уи У1
2 • •
Ут Уп2 • •
¦4-
Уи
У'шг
У 31
Уш
¦ Ут
¦Угп
• Упп
Ун. ••
Ум ••
Уз2 • •
Ут ¦¦
=
У и
Уп
Ут
• Ут
Г У2,
• У.ШП
• У/
гп
1
Н
Ун
У 22 •••
У«2 •••
" • • • "Т*
Ут
Угп
Упп
Уи
Уп
Ун-ч
Ут
Уи
У22
V V J
, 1 Уп — Л
Уп.2
."¦• У1П,
.' •: Угп
,' i Уп— 1, п
'¦ • ¦ Упп
(8)
для доказательства которой нужно раскрыть , определитель в левой
части, произвести почленное дифференцирование, а затем вновь
сгруппировать слагаемые и свернуть их в определители. (Проду-
(Продумайте, это доказательство для л=2 или 3.) Если каждый столбец
в левой части удовлетворяет системе D), то вместо первого сла-
слагаемого в правой части можно написать, приняв для простоты л—3,
Умножив вторую строку иа —ala, a третью иа —а19 и добавив
их к первой, получим- a^detY(t). Аналогично преобразуются

490 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
остальные слагаемые в правой части (8), и мы получаем
[det Y (<)]' = сл.А (f) det Y(f),
откуда
det Y (t) = det Y (t0) exp J сл.А (т) dx, <9)
U
где под сл.А (применяется также обозначение SpA от немецкого
Spur — след) понимается след матрицы А:
Формула (9) была получена в 1827г. Абелем для уравнений
второго порядка н в 1838 г. Лиувиллем и М. В. Остроградским
в общем случае.
Если для решения У(^) уравнения G) будет detY(^)=^=O, то
Y (t) называется фундаментальной матрицей системы D). Это будет
тогда и только тогда, когда столбцы этой матрицы образуют фун-
фундаментальную систему решений уравнения D). Особенно удобно
пользоваться матрщйнтом системы D), т. е. фундаментальной мат-
матрицей, удовлетворяющей начальному условию .
Эту матрицу мы будем обозначать буквами Y"(/, tQ); через нее ре-
решение системы D) с начальным условием у(^0) = у0 выражается так:
y(t) = Y{t,tt)y0 A0)
(почему?). Эта матрица удовлетворяет соотношению
в самом деле, обе стороны этого равенства удовлетворяют уравне-
уравнению G) и совпадают при 7 = ^ (продумайте это!). Положив t = ta,
мы получаем также, что
Так как Y (t, t0) с при произвольном векторе с представляет со-
собой общее решение системы D), то, согласно методу вариации
произвольной постоянной (ЛВМ, п. XV.21), решение системы B)
можно искать в виде x = Y(/, t0) q> (t). Подстановка в B) дает
(УфI = Уф + Yq> = А Уф + Y<p =
t
откуда <р = у-^, ЧР(/)=$1У(т, *,)]-Ч (т)</т + с, т. е. в силу A1)
/0)c A2)

§ I. линейные Уравнения и системы - 491
Так как при t — t0 правая часть равна с, то для начального усло-
условия C) надо в A2) просто заменить с на х0.
Нетрудно написать матрицу Y {t, t0) в виде суммы ряда. Для
этого, проинтегрировав обе части G) от t0 до некоторого t, перей-
перейдем к интегральному уравнению
t
Y(O = H-jA(x)Y(T)dT.
to
Проводя итерации, придем к формуле (проверьте!)
t t т, . ¦
Y (*,/.) = I + S A (Tl) d4 + J A (Tl) dx, J A (t.) dx2 +
$(t,)rfT, + ... A3)
Проверьте, что матрицаит системы F) равен
Z(/, to) = [Y(fo. 01*. (Н)
Полученные результаты особенно просты, если матрица А коэф-
коэффициентов постоянная. Тогда Y(t, to)=± е<'-'»' А (см. ЛВМ, п. XVII.18),
и формула A2) приобретает вид
t
х = $ e«-fl Af (т) dx + е<'-'«)А с
(проверьте ее непосредственно). Из вида фундаментальной матрицы
и правила вычисления функций от матриц (п. IV.3.5) легко следует,
в частности: для того чтобы все решения уравнения у=Ау стрв'
молись к нулю при t—»-оо; необходимо и достаточно, чтобы все
собственные значения" "kj матрицы А имели отрицательную вещест-
вещественную часть. Для того чтобы все эти решения были ограниченными
при t—юо, необходимо и достаточно, чтобы все Re^y^O, а соб-
собственным значениям с ReAy = O отвечали жордановы клетки только
" первого порядка (см. формулу (IV.3.13)).
2. Периодические системы. Допустим, что все коэффициенты
системы D) периодичны с одним и тем же периодом Г> 0, т. е.
Тогда
Y(t+T,to + T)~Y(t,to), A5)
так как если начальное условие сдвинуть во времени на период,
те и решение сдвинется во времени на период. Докажем, что можно
подобрать такую постоянную матрицу М, что матрица-функция
Y(tf, 0)е~ш будет Г-периодичиа; обозначив это произведение

492 ГЛ. VU1. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
через R (t), мы видим, что имеет Metro представление
Y(*,0) = R(/)e'M, A6)
где функция R (t) периодична с периодом Т (это теорема Флокё).
В самом деле, в силу свойств A1) и A5), требуемое условие
Т-периодичности можно записать так:
Г, 0) е~
Г, T)Y(T,
- т. е.
где логарифм матрицы берется по правилу п. IV.3.5. Теорема до-
доказана.
Формула A6) показывает, что для того чтобы все решения
Т-периодической системы D) стремились к нулю при t—»• ос, необхо-
необходимо и достаточно, чтобы все собственные значения матрицы М
имели отрицательную вещественную часть, т. е. чтобы все собст-
собственные значения матрицы Y (Т, 0) были по модулю меньше единицы;
аналогично концу п. 1 формулируются и условия того, чтобы все
решения были ограничены при t—><х>. Собственные значения мат-
матрицы Y (Г, 0) называются мультипликйторами Т-периодической си-
системы D), а сама эта матрица Y(T,0)— ее матрицей монодромии.
Так как
V{Т+ /., *„) = Y (Т+Л. Т)Y (T, 0)Y@, tt) =
T, O).[Y(*§iQ)]-S
то собственные значения и собственные векторы матрицы монодро-
монодромии не зависят от выбора начального момента времени (почему?).
Каждому мультипликатору р и соответствующему собственному
вектору d отвечает решение у = Y (t, 0) d, обладающее следующим
свойством: . . -...¦:• . .
py(t). A7)
Этим и объясняется название «мультипликатор». Для каждой кон-
конкретной периодической системы их нетрудно подсчитать с помощью
численного интегрирования этой системы, а для коэффициентов,
близких к постоянным,— с помощью метода малого параметра
(попробуйте разобрать его для системы у = (А4;«В(*))У, где |а|
мало).
Так как произведение всех собственных значений матрицы равно
ее определителю (почему?), то из (9) получаем, что произведение
всех мультипликаторов (в котором каждый мультипликатор берется

..... .... . § 1. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ 493
столько раз, какова его кратность) равно
Пр/ = ехр \cn.A(t)dt. A8)
. ¦ т .
Поэтому если Re J ел.A (t) dt > 0, то среди ру должен найтись по
о
крайней мере один, по модулю больший чем единица, а тогда соот-
соответствующее решение A7) будет неограниченным при t—> оо.
(А можно проверить, что если неограничено хоть одно решение, то
неограничены и все решения, за исключением некоторой их сово-
совокупности с менее чем п степенями свободы; продумайте это свойство,
исходя' из вида общего решения линейной системы.) Аналогично,
если Re \сл.А (t)dt < 0, то система D) имеет решения, неогра-
0
ничейные при t—>—оо. Отсюда вытекает, в частности, что для
того, чтобы все решения Т-периодической системы D) были огра-
ограничены на всей оси t, необходимо (но не достаточно!), чтобы
т
Re
Последнему условию удовлетворяет, в частности, система
</i=«/s. k=-PV)yi (т. e.^-fp@«/i=0), p(t + T)^p(t), A9)
исследованию которой посвящено большое число работ; эта система имеет два
мультипликатора, произведение которых в силу A8) равно единице. Анализи-
руя ряд A3) для матрицы А(<) = ( ), Ляпунов доказал, что если
\—Р (О О/
функция р (t) S= 0 вещественная и
т
то у характеристического уравнения для матрицы монодромии
Р*-{Уп(Т,0) + Уп(Т, 0))р+1=0 B0)
дискриминант. отрицательный, а потому |pl| = |p2| = l, pt ф р2, т. е. каждое
решение системы A9) ограничено на всей оси t.
Если для периодической системы D) произвести замену y = R(/).z,
в обозначениях начала этого пункта, то получится система z = Mz
(проверьте!). Вообще, если для какой-либо системы D) возможна,
линейная замена у = Н (t) г с ограниченными на всей оси матрич-
матричными функциями Н (/) и [H(rf)]", после выполнения которой D)
переходят в систему с постоянными коэффициентами, то S'a си-
система D) называется приводимой. Для приводимой системы все .вы-
.выводы об ограниченности или стремлении к нулю решений можно

494 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
сделать из аналогичных утверждений длят преобразованной системы,
имеющей постоянные коэффициенты. Мы видим, что всякая перио-
периодическая система является приводимой.
В ряде работ детально изучен вопрос о приводимости периодических
и даже почти-периодических (п. 7) систем, коэффициенты которых близки
к постоянным. Здесь приводящая матрица Н(/) получается в виде суммы
асимптотически сходящегося (п. П.4.1) ряда по степеням малого параметра
и само приведение понимается в соответствующем асимптотическом смысле.
По поводу приводимых систем см. книги [38, 135].
8. Уравнение Хилла. Так называется уравнение
J •]</=<>. B1)
в котором все функции fj(t) периодичны с одним периодом; для простоты мы
будем считать, что все fj(t-\-n)ss=fj(t), так как к этому случаю всегда можно
перейти с помощью замены t -*¦ kt\ все величины будем считать вещественными.
Важный частный случай, когда в квадратных скобках стоит %-\- ц cos 2г, назы-
называется уравнением Матьё. Мы рассмотрим вопрос об ограниченности решений
уравнения B1) на всей оси t в зависимости от значений параметров Лиц.
Обозначим через ф (г; К, ц) и ¦ф (t; %, ц) решения уравнения B1) при на-
начальных условиях j/@) = l, j/@)=0 и j/@)=0, у@)=1 соответственно; в обо-
обозначениях, п. 1 это уп (г, 0) и уц (t, 0). Кроме того, обозначим
. А = А(Х, |1)=у-[ф(я; К rt+*(«! *. V)]- B2)
Тогда из характеристического уравнения B0) видно, что при | А \ < 1 будет
| рх {=| р2 | = 1, pi ф р2> т. е. каждое решение уравнения B1) будет ограни-
ограничено иа всей оси t; если же А > 1 (А < — 1), то 0 < рх < 1 < р2 (соответст-
(соответственно ра < — 1 < рг < 0), т. е. каждое ненулевое решение уравнения B1) неог-
раиичено; но как дать ответ в терминах заданных функций /у (t) и парамет-
параметров X, (х?
Считая | ц | малым, разложим функцию <р по степеням fi:
Ф(*; К, ц)=<ро(г; X) + Vl(f; Я)^ + ф2(<; К)р+...
Подстановка в уравнение B1) и в начальное условие дает после приравнивания
коэффициеитов при одииаковых степеиях ]t:
Фо+Я,фо=0, Фо1*=о=1. Фо1<=о=О.
фз|(=о=0, '
Отсюда можно последовательно найти ф0==со8 У~М, фь ф8 и т. д. Аналогично.
разлагая функцию t|), получаем i^,=—-p=-sin V"Arf, тогда как рекуррентные
уравнения для дальнейших ф/ те же, что для фу. Отсюда в силу B2) получаем
A=cosVbn+jl<(i(n; Х) + 4»1(я; X)j|i + ... B3)
Так как области на плоскости К, [i, которым отвечают ограниченные реше-
решения уравнения B1), отделяются от областей, которым отвечают неограничеияые
решения, критической линией [А (\, ц)]2= 1, то из B3) получается, что эта

§ 1. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ
495
линия пересекает ось X в точках \—пг (п=0, 1, 2, ...), причем промежутки
оси между этими точками принадлежат областям ограннченности. Можно пока-
показать (на чем мы здесь не будем останавливаться), что эти точки при п > О
служат точками самопересечения указанной линии, так что картина выглядит
примерно, как на рнс. 121, где области неограниченности, заштрихованы.
Для построения этях областей можно
применить следующий прием. Заметим,
что ветвям критической лннин, проходя-
проходящим через точки %=пг с четным п, отве-
отвечает значение Л=1, а потому мультипли-
мультипликаторы р1# 2= 1. Значит, для каждой точки
этих ветвей возможно построить я-пе-
риодическое решение уравнения B1)
y(t\ ц) (зависимости от А, нет, так как
вдоль таких ветвей к является функцней ц,).
Воспользуемся методом неопределенных
коэффициентов и подставим в B1) прн
некотором выбранном я=0, 2, 4, ...
разложения
У=
B4)
Риг 121
так что рассматриваемая ветвь критиче-
¦ской линии проходит через точку (п2; 0).
Подставив эти разложения в B1) и пряравняв коэффициенты при одинаковых
степенях ц, получим уравнения
B5)
B6)
8/1 + ««ft=- fat+h &П У о (*).
У г + n*yt=- fa+/i @] Vi (t) -
Из первого уравнения
(/о = A cos nt+В sin nt.
Так как правая часть B5) периодична с периодом л, то ее можно разложить
в ряд Фурье по функциям cos 2kt, sin 2kt. Но так как и функция ух (t) должна
бить л-периодична, то для отсутствия резонанса в этом разложении члены с
cos nt, sin nt должны отсутствовать, что дает
B7)
B8)
[ai+/i @1 (A cos nt+B sin nt) 3Jirf*«=0.
Пусть л=2, 4, 6, ... Тогда из B7) получаем
(а.+а1)А + $В=0, $А + (у+а1)В=О,
где обозначено -
2 f 2 Г
a=— \ f J (t) cos3 л* df, р =— \ f t @ cos nf sin я/ dt,
Y=-r
sin3 nf (if.

496 ГЛ. VHi. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Если система B8) имеет ненулевое решение, то необходимо
"Г1 Y-fUH- «>
откуда находим два вещественных (почему?) значения а1( отвечающие двум на-
направлениям пересечения критической линией оси X при Х=пг. Каждому из
этих значений отвечают в силу B8) значения А, В, определенные с точностью
до коэффициента пропорциональности. Но так как и все решение у (t; fi) опре-
определено с точностью до скалярного множителя, то у можно пронормировать,
например, условием у @; ц)=1, т. е..
уо@)=1, М0)=0, г/г@)=О, ... C0)
Первым из этих равенств коэффициенты А, В определяются однозначно.
Удовлетворив условиям B7), мы можем найти сбщее решение уравнения
B5) в виде
tcos nf + Bi sin nt.
где Yx (t) — некоторая п-пернодическая функция, а Ах, Вх—произвольные по-
постоянные. Этн произвольные постоянные, а также коэффициент а2, находим из
требования отсутствия резонанса для уравнения B6) и из второго равенства C0)
и т. д. Продолжая таким образом, можно найти любое число членов разложе-
разложений B4). (Отметим, что бывают случаи, например для рассматриваемого ниже
уравнения Матье при п |S= 2, когда корни уравнения B9) совпадают, а различие
ветвей критической линии, пересекающих ось X, обнаруживается в членах с
высшими степенями ц,.) При этом мы, вообще говоря, получаем лишь одно
периодическое решение уравнения B1), другое обычно имеет вид ty (t, ц) +
-\-yit, (х) (</(r-f-2n, p) = y(t, [!)), т. е. неограничено.
Для комбинаций значений X, ц, которым отвечают неограниченные реше-
решения, т. е. для заштрихованной на рнс. 121 зоны, нетрудно получить асимпто-
асимптотические разложения мультипликаторов по степеням ft. Такие решения в силу
п. 2 должны иметь вид
y=e±s>R(t) (e±Krt=pli2; R{t + n) = R (t)), C1)
где s вещественное (почему?). Так как
sln=o=°> R Щ» = п = A cos nt +В smnt,
то при подстановке C1) в B1) положим X,=n2-f-Xl(x+X2(x2-(-...,
s=sln-J-s»H*+"-.; R (t) = A cos nt +В s\nnt + /fx @1*+/?a @ (** + C2)
Приравнявая после подстановки коэффициенты при р., получим
j?1-fn27?1 = — [h+h @1 (Л cos nt + B sin nt)^2nSx (A sinnt + B cos nt),
откуда нз условия отсутствия резонанса находим (проверьте!)
(X,+aL+(T2nsI-fp)B=0, (±2bs1 + Р) А + (К + У) В=*0, {33)
где обозначения а, {$, у имеют тот же смысл, что в B8). Из C3) получаем
±2nS!-f-B
т. e. . . ¦
Отсюда

.§: Ь ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ 497
а для вещественности.¦ правой части Xj должно содержаться в интервале
Теперь из C3) можно найтн А:В. Аналсгично можно получить дальнейшие
члены разложений C2). Эти разложения приведены в книге [124].
1 ....... ... я
При /t=0 будет </0 = 1 и взамен B7) получаем равенство \
°.
=0, откуда получаем только одно значение
Дальнейшие выкладки подобны проведенным выше.
Аналогично, если п нечетное,-то A = — l, Pii2=~l. и решение уравнения
B1) будет удовлетворять соотношению у (t-\- л) =— у (t), откуда у (t-\-2n) = #(<)•
Значит, можно написать разложение B4) и проводить выкладки,' как выше, Ко
счятая" все участвующие функции не л-, а 2л-периодическями.
Рассмотрим, например, критическую линию для уравнения Матье в окрест*
ностн значения Х=12. Мы получаем
...)=0. C5)
Отсюда, как выше,
Уо+Уо—Q, т.е. уо = А cos t + Bsiut.
Далее,
^+ (/t — — (at-|-cos20(>4cos< + Bsin/). C6)
Из условия отсутствия резонанса получаем, (проверьте!)
откуда ах = ±-^-. Заметим, что уравнение Матье переходит в себя при подста-
подстановке (х —». — (х, t —> -jp +1; поэтому достаточно рассмотреть одну ветвь кри-
критической линии, вторая получится заменой (х—»¦ — (х. Положим ^ = — 1/2,
тогда 6=0, а в силу C0) А = \ (если выбрать ^=1/2, то у надо нормировать
вначе, например, приняв уф, fi) = l). Из C6) получаем
c3/ + ^ c°s t + Bi sin t.
Но из C5), приравнивая коэффициенты при |i3, получаем
Vt+Vi=— (a,+cos 20 (/! @^-02«/o @=
= —f — у + совгг Д ygCosSf + ^cosf + B! sin Л—a2cos <.
Из условия отсутствия резонанса получаем a2=—50, Bl=Q (проверьте!), а из
второго равенства C0) ^i = ~T5- Ограничившись этими вычислениями, нахо-
находим уравнение критической линии Jli=l— -jrfi—5S(x2-f-...

498 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Каждой из ветвей критической линии для уравнения Матье, проходящей
через точку Х=па, ц=0, отвечает одно (с точностью до постоянного множи-
множителя) четное или нечетное периодическое решение, которое прв |*=0 обращается
соответственно в cos nt или в sin nt. При определенной нормировке эти реше-
вня называются функциями Матье и обозначаются соответственно через
се„ (t; q) и sen (t; q), где q= 16ц, (условие нормировки: в ряд Фурье для
cea(t; q) член с cos nt входит с коэффициентом 1; аналогично для sen (t; q)).
Теории и приложениим функций Матье посвящена книга [80].
4. Параметрический резонанс. Обращаем внимание на то, что хотя при
малых |ц| коэффициент Л-f-ц/^ (f) + • • • уравнения B1) как угодно близок к
постоянному, а все решения при замороженном коэффициенте ограничены, тем
не менее оказывается возможным выбрать параметры так, что из-за специаль-
специального характера периодического изменения коэффициента решение получится
экспоненциально раскачивающимся при t—»-оо. Это явление называется пара-
параметрическим резонансом. Как видно из п. 3, параметрический резонанс будет
наблюдаться, в частности, для уравнения (/ + A +f*cos It) y=0.
Явление параметрического резонанса легко наблюдать на примере маятника,
точка подвеса которого совершает принудительные колебания по заданному
закону y=f(t). Уравнение колебаний такого маятника, которое мы предлагаем
вывести читателю, имеет вид ¦&+[(?/0 + (Г@/0) sin ¦&=0, где ¦&—угол от-
отклонения от вертикали, g—ускорение земного тяготения и /—длина маятника.
Полагая
у—ю*, f(t)—Mcosa>t, ш<=2<!
и ограничиваясь линейным приближением, получаем уравнение
(проверьте1). Мы видим, что при 2<йо/ш=1, т. е. когда частота колебаний
. точки подвеса в два раза превышает собственную частоту колебаний, наступает
параметрический резонанс, т. е. амплитуда колебаний маятника начинает раз-
разрастаться. (Аналогичная ситуация используется прн раскачиваиии на качелях,
которые можно схематизировать как маятник переменной длины. Мы видим,
что для такого раскачивания нужно на протяжении каждого полного цикла
качаний дважды приседать и дважды подыматься; это эмпирически известно
всем детям.) Еще более' эффектно рассмотрение обратного маятника, располо-
расположенного вертикально вверх от точки подвеса; конечно, такой маятник должен
быть подвешен не на иити, а на стержне пренебрежимо малого веса. Уравнение ко-
колебаний получается заменой g на —g, т. е. в C7) нужно перед ( —- V поме-
поменять знак. Из рис. 121 видно, что если при заданных Mai выбрать ш0 / са
достаточно малым, т. е. заставить точку подвеса вибрировать достаточно часто,
то вертикальное положение обратного маятника окажется устойчивым!
К понятию параметрического' резонанса можно прийти также из следующих
более грубых, но полезных соображений. Будем считать К > 0 конечным
(порядка 1), а р. малым. Легко проверить, что при A=0 выражение
/(
пропорциональное полной энергии системы, остается инвариантным, т. е. не
зависит от /. Если же р Ф 0, то
| -Ы. C8)

§ 1. ЛИНЕЙНЫЕ- УРАВНЕНИЯ И СИСТЕМЫ 499
При малых (J. решения уравнения B1) должны быть «почти гармоническими»,,
т. е. иметь внд у=М sin A^ \t-\-qi), где M=M(t), ф=ф(/)—медленно ме-
меняющиеся функции, т. е. функции, скорость изменения которых обращается
в нуль вместе с р.. Из C8) получаем тогда, что с точностью до величин высшего
порядка малости
sin B -^1<+2(р) ,@# .. C9)
Так как фурье-компоненты функции / (t) имеют частоты 2, 4, 6, ..., то если
У~Х не является целым числом, то среднее значение правой части за большой
промежуток времени близко к нулю, т. е. средняя скорость изменения / имеет
порядок малости выше (х. Если же Я,= 12, 22, , то среднее значение правой
части C9) может быть отлично от нуля, т. е. / будет изменятьси со скоростью
порядка (х. Например, если f(t)=cos2t и Х—1, то среднее значение скорости
У
иМ2Ук
изменения / равно — -—¦?¦—sin ф, т*пе. / будет расти или убывать в зави-
зависимости от значения начальной фазы ф. И этот факт хорошо известен детям:
если приседать на спуске и вставать на подъеме, то качания будут усиливаться,
а если поступать наоборот,— то затухать.
б. Гамильтоиовы системы. Пусть в канонической системе урав-
уравнений (VI.3.7) функция Гамильтона Н представлиет собой квадра-
квадратичную форму
Hit, У, Р) = уУ*Р@У + Р*О@У + 1" P*R@P, P* = P, R* = R D0)
с вещественными коэффициентами. Тогда эта система приобретает
вид
j?=Q(*)'y + R(OP. Р = — Р@у—0*(*)р, D1)
т. е. является линейной. Иногда эту систему записывают в виде одного
векторно-матричного уравнения
p/ VQW.
где под J понимается квадратная матрица 2л-го порядка
— I О
(Докажите эквивалентность формул D1) и D2), опираись на сле-
следующее простое полезное правило умножения блочных матриц: это
умножение проводится по обычным формулам, если размеры блоков
согласованы так, что выполняемые действия имеют смысл: например,
AQ-f BSN
^R
если сомножители имеют размеры (k -J- /) X (Ш -f- n) и {m-\-n)x(u-{-v)
прн естественном смысле этого сокращенного обозначения.)

500 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Нетрудно проверить, что для любых двух решений („) и (У)
уравнения D2) будет.
Для доказательства ;этого достаточно продифференцировать левую
часть no t и воспользоваться уравнением D2), а также равенствами'
J2=-4oi>-J*J
(проделайте это!). Аналогичным свойством обладает Bл X к) матрич-
матричное (k любое) решение уравнения
Рассмотрим теперь каноническую систему D2) с Т-периодическими
коэффициентами и докажем для иее теорему Ляпунова—Пуанкаре:
характеристическое уравнение для матрицы монодромии этой системы
является возвратным. При этом уравнение вида
*, = 0 D4)
называется возвратным, если ао = а2п, al = ain_i, ..., другими сло-
словами, если р2п/A/р)=/(р).
Для доказательства будем считать матрицу-функцию U (t) в урав-
уравнении D3) квадратной и удовлетворяющей начальному условию
U @) = 1ага (т. е. единичной матрице порядка 2л); тогда U( T) и будет
матрицей монодромии. В силу доказанного будет U* (t) 3U (t) = const,
и потому из начального условия следует, что
Кроме того, так как след матрицы коэффициентов в правой части D3)
равен нулю, то в силу (9) будет det U (t) = const, а потому из на-
начального условия следует, что
Поэтому для характеристического полинома/(р) матрицы U (Г) будет
(проверьте вычисления!)
/(?)==det [U(T)^71*"]=det [J"'(U*
= det [(UG))l2n]
=^ [detU*(T)]"Met [U*(T)-pI2n] =^
что и требовалось доказать.

§ 1. ЛИНЕЙНЫЕ УРАВНЕНИЯ Н СИСТЕМЫ 501
Возвратное уравнение D4) вместе с любым корнем р имеет также
корень 1/р. Поэтому гамильтонова периодическая система не может
иметь все решения стремящимися к нулю при t—>-оо. Для ограни-
ограниченности всех решений необходимо, чтобы все мультипликаторы по
модулю равнялись единице.
В книге [82] приведены некоторые результаты М. Г. Крейна, относящиеся
к параметрическому резонансу (п. 4) для гамнльтоновых систем с более чем
одной степенью свободы. Рассматривается система "вида
где все Hj—квадратичные формы переменных уъ ..., уп, pt р„ с я-пе-
рноднческнмн по t коэффициентами, причем форма Но имеет постоянные коэф-
коэффициенты и положительно определенная. Пусть при Х=1, ц,=0 система имеет
корни характеристического уравнения все различные и чисто мнимые, равные
± ('о>1, ± to>2, ..., ± ю„, т. е. все решения этой системы ограничены
при —оо < t < оо. Тогда, как и в п. 3, в плоскости X, р, могут быть областя
параметрического резонанса. Не останавливаясь здесь на вопросе о нахождении
границ этих областей, отметим только, что эти области могут примыкать к оси \
2N
лишь в точках — , где N=\, 2, 3, ... (Сопоставьте это утверждение
с результатами п. 3 и рассмотрите вопрос о частотах параметрнчёского возбуж- '
дения заданной линейной автономной гамильтоновой системы.)
6. Неоднородные системы. Некоторые утверждения о поведении
решений системы B) непосредственно иытекают из.формулы A2).
1. Пусть ||Y(f, T)||<const(/,<T<f<oo), 5 ||f(tf) || <tf<oo. То-
Тогда все решения системы B) ограничены при t—+6o.
2. Пусть \\Y(t, 1)||<Се-«-»(*0<т<*<оо; о > 0), ||! (/) ||<
< const. Тогда все решения системы B) ограничены при t—*¦«>.
' , 3. Пусть ]| Y (t, t) || < Се-««*-«'(/0 ^ т</ < оо; а > 0), Ц/(/) || -^ О
при t—»• об. Тогда и все решения системы B) стремятся к нулю при
*—юо. . ' ¦¦¦¦¦¦¦¦'
Для доказательства последнего факта (остальные доказательства
мы предоставляем читателю) заметим, что в приведенных предполо-
предположениях . '., . ..
4 \
rU+ta)/2 t -j
L 'o « + <.)/2J
max ||«(x)t|e-w.-w/a+ max
откуда и вытекает наше утверждение (почему?).
В приведенных теоремах утверждалось, что все решения систе-
системы B) обладают тем или иным свойством. Имеется большое число

502
ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
теорем, в которых утверждается, что система B) обладает по край-
крайней мере одним решением с заданным свойством (ограниченностью,
стремлением к нулю, периодичностью и т. п.). Здесь мы остановимси
только на вопросе о существовании периодического решения. Рас-
Рассмотрим сначала систему с постоянными коэффициентами
D6)
Разложим функцию f {t) и искомое решение х (t) в ряды Фурье:
Подстановка в D6) и приравнивание коэффициентов дают
(А—1Ш)хк = — ik (* = 0, ±1, ±2, ...).
Таким образом, поставленная задача имеет ровно одно решение,
если ни одно из чисел ikca не является собственным значением ма-
матрицы А. Если при каком-либо» k0 это условие нарушено, то век-
вектор ffto должен удовлетворять соответствующим условиям ортого-
ортогональности, в противном случае наступает резонанс, и периодическое
решение отсутствует. Если же эти условия ортогональности выпол-
выполнены, то решение определено с точностью до слагаемого ¦eik"oi \ка,
где хА —любой собственный вектор матрицы А, отвечающий собст-
собственному значению ika. (Продумайте все эти утверждения; об орто-
ортогональности ч е м у здесь говорится?)
Рассмотрим теперь неоднородную периодическую систему
x.= Atf)x + f(*), А(< + ГMзА(<), t(< + T) = t«). D7)
Эта система остается инвариантной при замене t—+ t-\-T\ поэтому
• для любого ее решения х (t) функция х (t -f- Т) также будет реше-
решением этой системы. Но отсюда следует, что если какое-либо реше-
решение системы D7) удовлетворяет условию
х@) = х(Т), D8)
то х (t) = х {t + Т): в самом деле, обе части этого равенства удов-
удовлетворяют системе D7) и совпадают при t = 0, a значит, тождест-
тождественно совпадают (почему?).
В силу формулы A2) условие периодичности D8) можно перепи-
сатБ"в виде
т
х @) = J Y (Г, т) f (т) dx+Y (Г, 0) х @). D9)
Таким образом, если значение 1 не является собственным для ма-
матрицы монодромии Y(T, 0), то уравнение D9) однозначно разрешимо
относительно х@), т. е. система D7) имеет ровно одно Т-периоди-
ческое решение при любой Т-периодической функции f(rf). Если же

§ 1. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ '503
значение 1 ивляется собственным, то средний член в D9), а тем
самым и функция f(t) должны удовлетворять условиям ортогональ-
ортогональности, при выполнении которых значение х@) определено с точно-
точностью до произвольного собственного вектора матрицы Y(T, 0), от-
отвечающего собственному значению 1.-Наличие собственного значения 1
у матрицы монодромии означает, что соответствующая D7) одно-
однородная система имеет ненулевые Т-периодические.решения. Можно
доказать (попробуйте!), что если в этом случае все решения одно-
однородной системы ограничены при t—к», а указанные условия орто-
ортогональности не выполнены, то решение системы D7) при t—»-оо
становится неограниченным со скоростью степенной функции, т. е.
наступает резонанс.
Для свстем D7), а также D6) иногда пользуются следующим крите-
рием," доказать который мы предоставляем желающим: для существования по
крайней мере одного Т-периодического решения необходимо и достаточно, чтобы
т
\ (z (/), l(t))dt = O для всякого 7'-периодического решения соответствующей
о
сопряженной системы F).
Разновидностью неоднородных систем служат системы с импульсными воз-
воздействиями; решение х (t) такой системы в заданные моменты времени tj (где
/0 < tl < <2 < ... —>- оо) испытывает конечные скачки Д/х, которые в простей-
простейшем варианте заданы (а вообще могут зависеть от искомого решения), а в про-
промежутках между импульсами удовлетворяет уравнению B). Такую систему можно
с помощью дельта-функции (ЛВМ, п. XIV.25) записать в виде
х = А(Ох + 1 @+
Поэтому для решенвя можно воспользоваться той же формулой A2), но с видо-
видоизмененной функцией f (t). Применив основное свойство интеграла, содержащего
дельта-функцию (ЛВМ, (XIV. 102)), получим
t
х @= J [Y (t, т)] f (т) dt+Y (t, t0) xo + Д; t Y (/, tj) Ayx.
С помощью этой формулы, которую легко вывести также из принципа суперпо-
суперпозиции (как?), и можно проводить исследование системы.
7. Почтя-периодические функции. Важное расширение класса периодических
функций составляют почти-периодические функции, которые получаются в ре-
результате наложения колебаний с, вообще говоря, несоизмеримыми периодами.
Дело в том, что если мы имеем две периодические функции /х (t) и /2 (tj, пе-
периоды Тг и 7'2 которых соизмеримы, т, е. находятся в рациональном отноше-
отношении, Тх = т{Г, Т2 = т2Т (mx, m2—целые), то сумма этих фувкций, а также их
произведение и т. п. представляют собой периодические функции с периодом
т^т^Т. Однако если периоды Г, и Га несоизмеримы, то сумма /i(<)+/a@ уже
не будет периодической: например, функция sin t-j- sin }^2t ие периодична,
она првнадлежит к более широкому классу функций, называемых почти-перио-
почти-периодическими.
Почти-периодическими являются по определению все функции,, которые
можно равномерно аппроксимировать на всей оси / с любой степенью точности

504 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
конечными суммами вида - '¦¦¦[¦¦¦:¦ ~. - . ... . ¦¦¦¦¦-,.¦
'" ' ' Н0=2е/е'мЛ ¦•¦.¦¦ E0)
где ©у—любые вещественные числа, a Cj—любые комплексные коэффициенты.
В частности, такими будут всевозможные суммы бесконечных рядов вида E0),
для которых
Si с/К». (si)
что обеспечивает примененве к ряду E0) признака Вейерштрасса равномерной
сходимости на всей оси t (ЛВМ, п. XVII.8). (Впрочем, пользуясь другими ви-
видами уклонения функций, можно ослабить требование E1), а также рассматри-
рассматривать разрывные почти-периодические функции.) Различные классы таких функ-
функций и их свойства рассмотрены в книге датского математика Г. Бора A887—1951)
[14], положившего начало этой теории в 1923 г., а также в [69].
Отметим без доказательства некоторые свойства непрерывных почти-перио-
почти-периодических функций. Сумма, произведение, частное (если знаменатель не может
как угодно приближаться' к нулю) двух таких функций, предел равномерно
сходящейся на всей оси t последовательности этих функций будут снова почти-
периодическими функциями. Для почти-пер иодичности непрерывной функции / (/)
необходимо и достаточно, чтобы из любой последовательности «сдвижек» /(/ + т„)
можно было выделить равномерно сходящуюся подпоследовательность Из по-
последнего вытекает, в частности, что если /(/)=? const, то она не может стре-
митьси к постоянной при /—>оо. Подчеркнем, что всякая периодическая функ-
функция в- то же времи ивляетси почти-периодической, тогда как обратное отнюдь
ие обязательно.
Всякая почти-периодическая функция ограничена иа всей оси t и обладает
средним значением •
а + Т
Щ= lim JL f fit)dt,
а-Т
не зависящим от значения а. Так как ,
0 (со ф 0), ' ¦' ; '• ¦
1 (со=0) ' ' : :
(проверьте!),.то из представления E0) вытекает, что ...;. .
f{t)e-iwt = f ch *й.н » Равно одному из щ,
\ 0 дли всех остальных и.
Таким образом, спектр (т. е. набор частот coy) заданной каким угодно способом
почти-периодической функции / (<), а также соответствующие амплитуды Cf, можно
установить с помощью вычисления средних значений/(/) в~'™*1 Из E0) следует
также формула ' ^_
\fit)\1=fit)lfit)]*=,
погорая для периодических функций превращается в равенство Парсеваля
(ЛВМ, п. XVII.27). . ... ... ,. >;. „ . . ;
Отметим характерную особенность вещественных почти-периодических функ-
функций, которая легко следует из E2): в спектр этой функции вместе с любой
частотой ©у входит и частота ©_/=—©у, причем c_y=c/v
ч

..,:. ; .§ 1. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ,: ,. 505
Рассмотрим теперь систему дифференциальных уравнений с постоянными
.коэффициентами и почти-периодическим неоднородным членом:
V E3)
Если искать решение в виде почти-периодической функции с тем же спектром,
т. е. x(t)=^j e ю) ху, то мы получим, что должно быть '
Если ни одно из значений to/ не является собственным для матрицы А, то
искомое решение должно иметь вид
И/- E4)
Так и будет на самом деле, если матрица А не имеет чисто мнимых собст-
собственных значений: тогда система E3) имеет ровно одно почти-периодическое
решение, которое определяется формулой E4). Однако если имеется собствен-
. ное значение to, даже если и и не входит в спектр, то среди чисел йу могут
найтись как угодно близкие к и, а тогда норма ||(А—t coy I)—* Ц будет как
угодно велика (почему?) и ряд E4) может разойтись, если это возрастание не
будет нейтрализовано убыванием коэффициентов fy. . .
В приложениях чаще всего встречаются почти;периоди,ческие функции,
спектр которых получается в результате наложения конечного числа несоизме-
несоизмеримых частот, другими словами, состоит из частот вида cp=m.lcoi+macoa-|-...
• \-т.р(Ор, где величины a>lt со2, ..... со» заданы, a 'mlt п%2, ,..., тр—про-
тр—произвольные целые числа. Такие функции называют квазипериодищскими. Их
впервые начал изучать П. Г. Боль в 1893 г.; он, в, частности, заметил, что
каждую такую функцию можно записать в виде f (со^, ы%(, ..... (s>pt), >где
f (slt s2, .... sp) — некоторая функция, 2я-периодическая по каждому аргу-
аргументу (обратное очевидно, если разложить функцию / в р-кратный ряд Фурье).
8. Асимптотическое разложение решений при t—+oo. Имеется
большое число математических работ, в которых изучается асимп-
асимптотическое поведение решений системы D) при t—*оо в общем и
специальных случаих. Мы приведем лишь несколько результатов
в этом направлении, отослав интересующихся к дальнейшей лите-
литературе [2, 9, 18, 49, 132].
Рассмотрим сначала вопрос об асимптотическом разложении реше-
решений при t—>¦ оо. Чтобы знать, чего здесь можно ожидать, примем
сначала л=1 и рассмотрим скалярное уравнение <
где k^0 — некоторое целое число. Разделение переменных, интег-
интегрирование и последующее потенцирование дают '
Разложение при больших t второй экспоненты в ряд и приведение
подобных членов приводит к формуле вида . - ' ' •¦
4

506 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
В случае k=-—=1 формула получается аналогичная, но без пер->
вой экспоненты. Наконец, для k < — 1 получается формула вида
\ bl I bi I
(проверьте!).
Оказывается, что .и для любого я разложения решений имеют
вид, аналогичный приведенному, однако в случае k ^ 0 полу-
получающиеся ряды сходятся, вообще говоря, лишь асимптотически
(пп. Н.4.1,2). Рассмотрим систему
у = А(^*У, где *=0,1, 2, ...; A(t) = Ао + ^- + ^+... E5)
(последнее равенство может пониматься в асимптотическом смысле).
Тогда можно доказать, что каждому собственному значению Kj мат-
матрицы Ао отвечает решение E5), имеющее вид
^^) E6)
где ряд в последних круглых скобках сходится к своей сумме,
вообще говоря, лишь асимптотически. Постоянные сц, ..., ak, P,
Ьо, bx, b2, ... можно подобрать по методу неопределенных коэф-
коэффициентов, подставив E6) в E5), что после сокращения даст
E7)
и приравняв после раскрытия скобок коэффициенты при одинаковых
степенях, t.
Пусть для определенности fe=l и собственное значение Xj простое. Тогда
такое приравнивание приводит к равевствам
E8)
А0Ь0—Х/ЬО=О; АОЬХ—X/bi=a1be—Aib0; \
ob2-¦XJb1=a1b1—Aibii + pbo-A2bo; \
|Ь»—A.yb3=aib4—A1b2-)-Pb1—А2Ьх—Ь1—А3Ь0;... J
Из первого мы видим, что Ьо—это собственный вектор матрицы Ао, отвечаю-
отвечающий собственному значению Ху. Зафиксировав этот вектор, мы можем найти at
из условия ортогональности правой части второго равенства вектору d Ф О,
для которого Ajd=A,*d (вспомните условие разрешимости уравнения Ах=Ь),
т. е.
«1 (bo, d)-(A!b0, d)=0 E9)
(несложно показать, что для простого собственного значения (b0, d) Ф 0). Если
это условие выполнено, то из второго равенства E8) вектор bj получается
с одной степенью свободы: b1 = bi + C1b0. Условие ортогональности для третьего

§ 1.' ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ 507
равенства E8) в силу E9) можно переписать в вида
ttl (hi, d)-(A!b;, d) + p (b0, d)-(A2b0. d)=0, F0)
и потому из него определяется р, после чего получаем bj=bi+C2b0. Записав
затем условие ортогональности для четвертого равенства E8), мы с помощью
условий E9) и. F0) получаем однозначно Сг (проверьте!), после чего Ь3 =
= Ь3 + С3Ь0. Затем из следующего равенства получаем Сг и т. д.
Таким путем можно получить асимптотическое разложение всех решений
системы E5), если все собственные значения матрицы _А0 простые или, что
немного шире, если матрица Ао имеет жордановы клетки только первого по-
порядка (п. IV.3.3). Форму разложения решения в случае клеток выше первого,
порядка, а также доказательство того, что построено не просто какое-то разло-
разложение, формально удовлетворяющее системе E5), а асимптотическое разложе-
разложение некоторого решения этого уравнения, можно иайти в указанных выше книгах.
Рассмотрим в качестве примера уравнение Бесселя (ЛВМ, п. XV.26)
хУ+*У' + (*2—Рг)У=0 @ <*<оо). F1)
Обозначив y=yv у' = Уг, перейдем от уравнения F1) к системе
У\=У\, Л
^ (g)—^. j F=)
Мы получили систему вида E5) с fe=0 и матрицей
собственные значения которой Я,12=± I. Выбрав Хъ получаем на основании
E6), что асимптотическое разложение решения "надо искать в виде
Непосредственная подстановка и F1), что равносильно подстановке ух и у2
в F2), и приравнивание коэффициентов при одинаковых степенях х приводят
к равенствам (проверьте!)
из которых находим последовательно
Отсюда получаем асимптотическое разложение решения
Сравнение с формулой (II.4.26) показывает, что если принять 60 =
= у — ехр —i' ( ^- + х ) > то мы получим функцию Яр1' (х). Отделяя
вещественную часть от мнимой, можно получить асимптотические разложении
функций Jp(x) и Yp(x).
Если k = —1, то решение, взамен E6), ищется в форме
F3)

i
508 ГЛ. VIM. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Для нахождения коэффициентов вместо E7) получается соотношение
_
—
(проверьте!). Раскрыв скобки, мы приходим к равенствам
(A0-pI)b0 = O, [A0-(P-l)I]bl = ~A1b0,
[А0-(Р-2) I] b, = -A,b0- A.b,,...
Из первого йы получаем, что р должно быть одним из собственных
значений матрицы А"о, а Ьо—одним из соответствующих собствен-
собственных векторов. Выбрав р н Ьо, мы из второго равенства, если р—'1
не является собственным значением для Ао, находим bt, затем из
третьего, если р — 2 не является собственным значением, находим
Ь2 и т. д. Таким образом, появляется еще один особый случай,
который мы здесь не будем рассматривать,— когда р — т для
некоторого целого т > 0 будет собственным значением матрицы
Ао. Если это не так и если ряд E5) для A (t) сходился в обычном
смысле, то в упомянутых выше книгах показывается, что и полу-
получающийся ряд в F3) при достаточно больших t сходится в обычном
смысле, так что мы получаем обычное (не ¦ асимптотическое) разло-
разложение искомого решения.
Если А^ — 2, то решение надо искать в виде. ,
где вектор Ьо произволен. (Разберите, как найти коэффициенты
Ьц Ь2, ...) Здесь ряд для решения также получается сходящимся
в обычном смысле. ' ¦•••¦¦
9. Еще об асимптотическом поведении решений. Асимптотическое
разложение, дающее весьма точную информацию об асимптотиче-
асимптотическом поведении решения, к сожалению, не всегда возможно — на-
например, если коэффициенты системы D) имеют периодические ком-
компоненты. В таких случаях приходится пользоваться формулиров-
формулировками, имеющими качественный характер, из которых мы для при-
примера приведем две. Нам потребуется'
Лемма об интегральном неравенстве. Пусть имеет
место неравенство '
t '
F4)
t
где р (t) ^ 0. Тогда и (t) < Сexp f р (т) dx (t0 < t < tx).

,..§. 1. ЛИНЕЙНЫЕ УРАВНЕНИЯ И, СИСТЕМЫ , , 5Q9
В сдмом.деле, из. того что р ^Q,: следует ....... . ...
а потому в силу F4)
t х
¦«@ < 5 Р (т) [J P (Tf) и (Tt) dTl + С] dx+ С.
Другими словами, неравенство F4) можно итерировать. Проводя
дальнейшие итерацнн н переходя к пределу, мы получим в правой
части, как известно из п. VII.2.9, решение интегрального уравнения
t .
v(t)=\p(x)v(x)dx-{-C
(продумайте это!). Но с помощью дифференцирования легко пока-
i . •
зать, что это решение равно Сехр С р (т) dt, откуда и вытекает
утверждение леммы.
Теоремы, которые мы сейчас приведем, позволяют по известному
асимптотическому поведению решений системы D) (например, с по-
постоянными илн периодическими коэффициентами) сделать заключе-
заключение об асимптотическом поведении решений системы
i = [А (/) + В (*)]*, F5)
где матрица-функция В (t) в том или ином смысле мала при t—юо.
Ряд результатов в этом направлении приведен в книге [9].
1. Пусть .
\\Y(t, т)||< const (if0<T<*<oo), ^\\B(t)\\dt <oo F6)
(под нормой матрицы здесь можно для простоты, в отличие ат
п.,IV.4.2, понимать сумму модулей ее элементов). Тогда все реше-
решения системы F5) ограничены при t-r+oo. . . .
Для доказательства раскроем в правой части F5) квадратные
скобки и, считая на минуту B(<)z известной функцией t, с помо-
помощью формулы A2) получим
' ¦ t '¦' '.•¦¦¦
г (t) = J Y (t, х) В (т) г (т) dx + Y (t, t0) z0. F7)
'• ...'¦..¦
Однако нетрудно неаосредственно проверить, что введенная норма

510 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
. обладает свойствами
IIA + BIKHAH + IIBII, ||АВ|К||А||-||В||,
HAxlKHAll lixll, || Jx(/)««||<$ Их (*)«<«,
где под нормой числового вектора мы здесь аонимаем сумму модулей
его элементов. Поэтому из F7) и из условий теоремы получаем
t
II* С)II <ci S И8 (Т)Н • »z МИ dx + Ct lizo|| (/„ < t < оо), F8)
t
где С1; С2 — некоторые постоянные. Пользуясь леммой об интеграль-
интегральном неравенстве, выводим отсюда, что
Г г„В(т)||Л]
Lх г." т" TJ
II*(ОН <c2llzo" ехР ci ) »в (Т)И dr\ (to<t< оо),
откуда и вытекает утверждение теоремы.
Отметим, что первое условие F6) выполнено, в частности, для
систем с постоянными или Т-периодическими коэффициентами и всеми
ограниченными решениями,. кроме того, оно не зависит от выбора t0
(докажите!).
2. Пусть
\\Y(t, т)||<Се-«('-^) (*„<-*<' <оо),
HB(Oll<e<-J (*.<*<«>), F9)
где С, а, е—положительные постоянные. Тогда все решения системы
F5) стремятся к нулю при t —+ оо. . \
В самом деле, из F7) аналогично F8) получаем
t
||z (ОН < Се J e-«('-t) ||Z (Т)ц dx + Ce-a«-''> ||zo||,
t,
откуда
t
||z (Oil eat < Ce
Применяя лемму об интегральном неравенстве, выводим, что
llz (ОН еа* < Се<*''\\го\\ вСв«-«.) (*„<*< оо),
откуда и вытекает утверждение теоремы.
Первое условие F9) выполнено, в частности, для систем с посто-
постоянными или. Т-периодическими коэффициентами и всеми решениями,
стремящимися к нулю при / —»оо. Выполнение второго условия

§ 1. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ 511
F9) можно требовать лишь при достаточно больших i\ достаточно
поэтому потребовать просто, чтобы В (t) —>- 0.
i ->¦ а>
В то же время обращаем внимание читателя, что из ограничен-
ограниченности решений системы D) и условия В (t) —> 0, вообще говоря,
не вытекает ограниченность решений системы F5). Простейший при-
пример: решения скалярного уравнения у = Оу ограничены, а уравнения
z=(o+-^"\ г—нет.
Приведем еще простую оценку решений системы D); эта оценка иногда
может быть полезной:
t t
IУ Со) I exp J 1т1п (т) dx < | у @ | < | у (t0) | ехр ^ Ягаах (т) dr.
to - h
где kmjn и Я,шах—наименьшее и наибольшее собственные значения эрмитовой
матрицы -s-[A (f) + А* (/)]. Для доказательства заметим, что
(IУ 1а)-=(У*У)" =у*у+у*у=у*А*у+у*Ау = у* (А+А*) у,
откуда в силу экстремального свойства собственных значений
*т1п(9<(Ы1O2|!М1<Ьш„@ И Т. Д.
10. Осцилляция решений уравнений второго порядка. Линейные
дифференциальные уравнения второго порядка
у' + а(х)у' + Ь(х)у = 0 G0)
(здесь мы будем, как в ЛВМ, обозначать независимую переменную
буквой х) встречаются в различных разделах теоретической и прик-
прикладной математики. Свойства этих уравнений изучены особенно
глубоко.
Рассмотрим сначала вопрос об упрощении уравнения G0) с по^
мощью линейной замены
¦У = а($г, G1)
где функция а (х) Ф 0 будет подобрана. Подстановка G1) в G0)
дает уравнение для z
z' +-^[2a' +a(x)a]z' +±-[a' + a(x)a' + b (x)a]z = 0. G2)
Мы можем, в частности, устранить член с z'; для этого нужно,
( 1 С \
чтобы 2а' -\-а(х)а = 0, откуда а = ехр(—-^\ а (?) d? ). Подста-
\ % /
новка такого а в G2) приводит к уравнению
гГ + [ь (х) ~ а' (х) — 1 о» (x)J z = 0 G3)
(проверьте!^.

512 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Имеется также другой способ,устранения члена с производной
первого порядка, основанный на замене независимой переменной
6 = ф(*), . G4)
где функция ф(лг) будет подобрана. (Аналогичная G4) замена искомой
функции v\ = ty(y) привела бы к нелинейному уравнению для ц.) Под-
Подстановка G4) в G0) дает уравнение для у (|):
W (*)]*-0 + [ф" (*) + а (*) <р' (*)] | + Ъ (х)у = О G5)
(проверьте!), куда надо еще подставить выражение JC(E), определенное
из G4). Приравнивание нулю коэффициента прн -^ дает (р(х) =
= Jexp(— ja(s)dsjd?, откуда уравнение G5) приобретает вид
[
Исходя из сказанного, мы впредь в этом пункте будем рассматри-
рассматривать специальный вид
0_ G6)
уравнения G0). Коэффициент р (х) и искомое решение у (х) будем
считать вещественными.
Рассмотрим сначала простейшее уравнение
У+ЯУ-0 G7)
с постоянным коэффициентом. Поведение решений этого уравнения
принципиально различается для р>0 и для р < 0. Если р > 0, то
общее решение имеет вид
у = С^ cos V^px -\- Сг sin V^px = M sin (Урх -f- a).
Любое решение этого уравнения бесконечное число раз меняет знак
(осциллирует), причем расстояние между соседними нулями равно
-^=, т. е. тем меньше, чем больше р. При каждом р нули двух.
V.P
непропорциональных решений перемежаются, т. е. между любыми
двумя соседними нулями одного решения содержится ровно один
нуль другого.
Совсем иначе выглядят решения уравнения G7) в случае р < 0.
Здесь ни одно решение ие может менять знак более одного раза
(почему?); такие решения называются неосциллирующиш.
. . Оказывается, что аналогичными свойствами обладают решения
более общего уравнения G6), хотя мы здесь не располагаем явной.

§ 1. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ
513
аналитической формой решения. Это утверждение основано на сле-
следующей теореме, доказанной в 1836 г. французским математиком
Ш. Штурмом A803—1855): пусть наряду с G6) рассматривается
уравнение
)z = 0, ¦ G8)
причем р (x)~^q(x). Тогда между любыми двумя нулями любого
(ненулевого) решения уравнения G8) содержится но крайней мере
один нуль любого решения уравнения G6).
Теорема доказывается от противного. Допустим, что а и Ъ—два
соседних нуля некоторого решения z (х), а какое-то решение у (х)
не имеет между а и b нулей. Допустим для определенности, что оба
решения между а и Ъ положительны (рис. 122), ведь любое решение
допускает умножение на—1. Проинте-
Проинтегрировав равенство y>z
(yz'—y'z)'=yz"—y"z =
\р()
от а до Ь, получим
y(b)z'(b)—y(a)z'(a) =
= \[p(x)-q(x)]y(x)z(x)dx. G9)
х
Рис. 122.
Однако сравнение знаков всех членов
этого равенства приводит к противоречию (продумайте это!), что
и доказывает теорему.
Теорема Штурма охватывает также случай, когда р (х) s= q (x),
т. е. когда рассматриваются два решения одного и того же урав-
уравнения. (Тогда при анализе равенства G9) полезно заметить, что если
z(a) = 0, то z' (а) ф 0, так как в противном случае в силу единствен-
единственности решения уравнения. G8) с начальными данными при х = а
было бы z (х) = 0.) Другими словами, нули двух любых непропорцио-
непропорциональных решений уравнения G6) перемежаются. Обратите внимание
на то, что если два решения уравнения G6) имеют общий нуль, то
они пропорциональны (почему?).
Сравнивая на основе теоремы Штурма уравнение G6) с уравне-
уравнением G7), получаем следствия (продумайте их!):
1. Если р {х) ^ 0, то никакое решение уравнения G6) не может
менять знак более одного раза, т. е. не осциллирует.
2. Если р (х) ~^рх > 0, то никакое решение уравнения G6) не
может сохранять знак на интервале длины > -^т=.
У Pi
3. Если р"{х)^р2, где рг > 0, то расстояние между нулями лю-
любого (ненулевого) решения уравнения G6) должно быть ~^-j=..
V Рг
17 А. Д. Мышкис

514 ГЛ. VIII. -ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
4. Если р (х) —*р > 0, то любое (ненулевое) решение уравнения
Х-*- 00
G6) при х—> со бесконечно осциллирует, причем расстояние между
соседними нулями стремится к —^.
VP .
Рассмотрим в качестве примера уравнение F1). Замена G1), которая в данном
примере имеет вид y=z/}^x, приводит к уравнению G3)-
В силу следствия 4 получаем, что функцни Бесселя любого порядка при х—> оо
бесконечно осциллируют, причем расстояние между соседними нулями стремится
к я. К этому же результату можно прийти из асимптотических выражений
(И.4.28).
Можио получить более точный признак осциллирования решений уравнения
G6) на полуоси х0 < х < оо, сравнив его с уравнением
г"+^-г = 0 @ <х < оо).
Непосредственное интегрирование этого уравнения, которое мы предоставляем
читателю (см. ЛВМ, п. XV. 19), показывает, что для k > 1/4 все решения
бесконечно осциллируют при х—>-оо, а для ft < 1/4 каждое решение имеет не
более одного нуля. Поэтому на основе теоремы Штурма получаем, что если
Jim х2р (х) > 1/4, то все решения уравнения G6) при х—> оо бесконечно осцил-
х-* »
лируют, тогда как, если litn х2р (х) < — , каждое ненулевое решение уравнения
х-+ m 4
G6) может иметь лишь конечное число нулей.
Отметим в заключение, что если для общего уравнения G0)
обозначить у' = г, мы получим систему первого поридка
y' = z, z' = —b(x)y—a(x)z.
В силу п. 1 определителем Вронского для такой системы служит
W(x) =
где индексы означают номера решений. Формула (9) приобретает вид
Н/Ч-
В частности, для уравнения G6) W (х) = const.
11. Системы, зависящие от параметра. Рассмотрим систему
У = А(/;о)у (80)
с параметром а. Ее решение, удовлетворяющее, например, фиксиро-
фиксированным начальным условиям, также будет зависеть от а: у = у(/; а).
Если коэффициенты зависят от а непрерывно, то и решение будет

'-> § 1. ЛИНЕЙНЫЕ-УРАВНЕНИЯ И СИСТЕМЫ 513
зависеть от а непрерывно; это ясно из смысла решения дифферен-
дифференциального уравнения и может быть доказано строго на основании
леммы п. 9 об интегральном неравенстве (продумайте это!). Но что
будет, если зависимость коэффициентов от а становится разрывной,
например, имеет полюс (п. И.3.2)?
Допустим, что это полюс первого порядка и его расположение
а0 не зависит от t (т. е. система не имеет коэффициентов, скажем,
вида (t—а)); после замены а—>-ав + а всегда можно считать,
что ав = 0, как мы и .будем делать. Тогда, умножив обе части
системы (80) на а, мы приходим к системе, вида
ау = А(*;а)у, (81)
коэффициенты которой в правой части уже зависят от а при малых
{ об | непрерывно и даже допускают разложение в ряд Тейлора
A (t; а) = S А. (*) а*. (82)
*=о . •
Нас будет интересовать структура фундаментальной матрицы
системы (81) при малых |а|. Эту структуру легко понять на частном
случае п=\, т. е. для скалярного уравнения вида (81), которое
легко интегрируется:
* a *=о
t ев oo t t
l У Ak (i) dta*-1 = Сехр У \ Ak+1(t)dtak-exp Y-^-dt.
Первую экспоненту можно разложить по целым неотрицательным
степеням а, и мы окончательно получаем
(83)
Здесь С—произвольная постоянная, а коэффициенты Bh{t) можно
найти по методу неопределенных коэффициентов, подставив выра-
выражение (83) в (81) и приравняв коэффициенты при одинаковых степенях
а. (Найдите Во (t), B1 (t); некоторая неопределенность, получающаяся
при этом, объясняется тем, что вместо С в формуле (83) можно
поставить любой ряд С (а), что повлияет иа коэффициенты В^. Чтобы
избежать этой неопределенности, можно задать значения этих коэф-
коэффициентов при некотором t = tu, например положить B0(te) = l,
. Оказывается, что и для общих систем (81) структура общего
решения аналогична (83). Приведем здесь только окончательный
17*

516 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
результат, отослав читателя за подробностями к книге [18], в которой
рассмотрены разнообразные вопросы, связанные с асимптотическими
разложениями по независимой переменной и по параметру решений
начальной и краевых задач для линейных и нелинейных дифферен-
дифференциальных уравнений.
Итак, допустим, что в некоторой окрестности точки t = t0 матрица
коэффициентов допускает разложение (82), причем ряд в правой
части может сходиться «по-настоящему» или лишь асимптотически
при а—>-0 (п. 11.4.1). Пусть все собственные значения матрицы А„ (/„)
различны. Обозначим через |it (t), ц2 (/),..., цп (t) собственные зна-
значения матрицы Ао (t) для t, близких к t0. Тогда система (81) имеет п
линейно независимых решений вида
У/(*) = Z В*У W a* exP [lti^-dt (/= 1, 2, .... л), (84)
ft=o i «
причем коэффициенты Вй (/) можно найти по методу неопределенных
коэффициентов. Для этого подставим (84) в (81), получим равенства
(проверьте!)
Из первого получаем, что Bo/(t) — q>o/{t)aj (t), где a^t)—произ-
a^t)—произвольно нормированный собственный вектор матрицы А„ {(), а ска-
скалярная функция <po/(tj пока произвольна. Подставим полученное
выражение для Во/ во второе равенство (85):
j (t) + Фо/ it) a} @ + Фо/ (t) A, (t) ay (/). (86)
Для разрешимости этого уравнения относительно Вгу необходимо
и достаточно (п. IV. 1.4), чтобы его правая часть была ортогональна
собственному вектору bj(t) матрицы AJ (t), отвечающему собствен-
собственному значению ji/(/). Из условия этой ортогональности получаем
линейное дифференциальное уравнение первого порядка для фо/(/),
решив которое, находим эту функцию с точностью.до несуществен-
несущественного постоянного множителя. Теперь в силу (86) получаем
В1у- (t) = В1;г (t) -f- ф,у (t) Я/(t), где Bv (t) — вполне определенная вектор-
функция, а скалярная функция 4>t/(t) пока произвольная. Выписывая
условие разрешимости третьего уравнения (85), получаем диффе-
дифференциальное уравнение для ф1у- и т. д.
При этом ряд в (84) оказывается сходящимся, вообще говоря,
лишь асимптотически, однако это не имеет существенного значе-
значения, так как практически все равно обычно пользуются лишь
небольшим числом членов этого ряда. Получающееся разложение
действует на любом конечном замкнутом интервале оси t, содер-

§ 1. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ 517
жащем t0, на котором все собственные значения матрицы Ач(/)
различные. В то же время по а данная конструкция является
существенно локальной и диапазон значений а, для каких ее можно
применять, обычно распознается с помощью численного интегриро-
интегрирования контрольных примеров. Если зависимость коэффициентов от а
имеет несколько полюсов, то установить связь между решениями,
построенными в окрестности различных полюсов, бывает не очень
просто; впрочем, это иногда удается сделать с помощью численного
интегрирования или из каких-либо теоретических соображений,
например из представлений, пригодных одновременно для различных
полюсов.
Рассмотрим н качестве примера уранненне
o»»+[Q (<)]•» = 0, (87)
которое после нведення обозначений у = Ух, аг/=(/2 можно переписать н ннде
Записав решение (84) при / = 0 и заменив сумму н правой части иа
го
ехр 2 С к @ а* (возможность этого будет ясна нз последующих нычисленнй),
мы получаем решение ураннения (87) н ннде
(88)
Чтобы иайти коэффициенты Cj (t), подстаним (88) н (87). После сокращения
на экспоненту и прнравнннання коэффициентов при одинаковых степенях а
получим систему раненстн (проверьте!)
± iQ ± 2iQC0 = 0, Co± 2iQCx+Со = О,...
Отсюда
dt, ...
Подстанляя в (88), получим решение ураннення (87) с точностью до членов
порядка а включительно:
т ехР
Еще чаще пользуются предыдущим приближением
(89)
' ехр ±i-^Q(x)dx \. (90)

518
ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Метод асимптотического построения решения уравнения (87), приводящий
к формулам (90) и (89), был развит в 1926 г. независимо физиками Г. Вент-
целем, X. Крамерсом и Л. Бриллюэном в связи с задачами квантовой меха-
механики; в честь этих авторов метод часто называют методом ВКБ или методом
фазовых интегралов. Ему посвящены книги [119, 125], где особое внимание
уделено важному случаю перехода Q (t) через нулевое значение (п. 12), для
чего полезно изучать уравнение (87) при комплексном значении t.
Если точка а = 0 представляет собой полюс порядка /и^1 для
коэффициентов системы (80), т. е. взамен (81) надо написать
ату = A (t; а) у, то конструкция решения аналогична, однако в фор-
С Р/ @
\ -—
муле (84) взамен
dt надо взять
где коэффициенты Qkj{t) находятся по методу неопределенных
коэффициентов, вместе с Bkf(t).
12. Точки поворота. Точка t = t0 называется точкой поворота (точкой
перехода) для системы (81), если матрица Ао (t0) имеет кратные собственные
значения. Наиболее простой пример
уравнения с точкой поворота—это
уравнение
ay—ху=0 (91)
(мы здесь будем обозначать независи-
независимую переменную буквой х, а производ-
производную по ией—штрихом), которое при
обозначениях y—yt, ay' = yi преоб-
преобразуется в систему
1 = Уз,
Рнс. 123.
с матрицей Ао (х) = f °, q) . Так
как
ее собственные значения р,1( j= ± У х , то значение х = 0 будет точкой поворота.
Замена независимой переменной по формуле х = а!ч переводит (91) в урав-
уравнение §йри
-JL—sy=0. (92)
Из п. 10 видно, что характер решений этого уравнения совершенно различный
при s > 0 и прн s < 0 (рис. 123): при s > 0 решения не осциллируют, а для
s < 0 осцилляции становятся при s —>-— оо все более частыми.
Решение уравнения (92) можно получить по методу контурного интегри-
интегрирования, аналогичному методу применения преобразования Лапласа (§ Ш.2).
Здесь решение строится в виде интеграла в комплексной плоскости
y(s)=
(93)
(Г)

§ 1. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ 519
причем как контур (Г), так и функция о (г) должны быть подобраны. Под-
Подстановка (93) в (92) ц интегрирование второго члена по частям приводят, если
Внеинтегральная подстановке е"&(г)[(Г) обращается в нуль, к уравнению
z»«(z)+y'(z) = 0
с очевидным решением о = ехр(—za/3). Таким образом,
exp(sz—z3/3)d2 (94)
(Г)
(в общем случае метод контурного интегрирования можно применять к линей-
линейным дифференциальным уравнениям с коэффициентами—полиномами не выше
1-Й степени—см. последний пример п. III.2.2).
Теперь видно, что в качестве (Г) можно взять любой контур, уходящий
обоими концами на бесконечность по каким-либо направлениям, для которых
Re (z8) > 0, т. е.
я я я 5 5 я ....
— -g- < argz < •?-, y <argz < -g-я или — -g- я< argz <—-^-; (95)
при этом значение интеграла (94) зависит не от выбора конкретного контура,
а только от того, из какого сектора (95) в какой ведет этот контур. В част -
иости, если контур интегрирования ведет из третьего сектора во второй, то
интеграл (94), деленный на 2л/, обозначается через Ai (s) и называется функ-
функцией Эйри 1-го рода. Эта функция прн вещественных s принимает веществен-
вещественные значения и стремится к нулю при s —»¦ оо (почему?). С помощью метода
перевала (п. П.4.5) нетрудно получить (попробуйте!) асимптотическое пред-
представление
Деформируя контур интегрирования (94) в мнимую ось, можно также получить
формулу
аи
Ai (S) =-i f cos f-j P+sAdt.
0
Другое линейно независимое решение Bi (s) уравнении (92) стремится
к бесконечности при s—>оо, как на рнс. 123.
Интеграл (94) имеет смысл не только для вещественных, но и для мни-
мнимых s, и представляет собой целую аналитическую функцию комплексного
переменного s. Разлагая подынтегральную функцию в ряд по степеням s, можно
установить выражение функции Эйрн через функции Бесселя
в котором все участвующие величины выбираются вещественными при s = —1,
а затем однозначцо продолжаются на всю плоскость s.
Возвращаясь к уравнению (91), мы получаем его общее решение.
у=*С1АЦа-2'*х) + С,ВЦа-*'3х). > (96)
Мы видим, что поведение решения для конечных х > 0 и х < 0 при а—>¦ оо
существенно различное.
Рассмотрим теперь общее уравнение (81) при л = 2 с точкой поворота
/=0; это означает, что матрица А@; 0) имеет двойное собственное значение.

520 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Так как замена у—>-еа у приводит к уменьшению его на р, то без ограни-
ограничения общности можно считать, что это собственное значение равно нулю.
Тогда det А (^; 0) имеет при t = 0 нуль, и мы предположим, что этот нуль
простой. Оказывается (см. [18]), что прн этом предположении возможно со-
совершить замену искомых функций н независимой переменной
= exp(^-J сл.А(т; O)dtJP(Ou, < = <p(s), . (97)
о
с соответственно подобранными Р (t) и <р (s), после выполнения которой си-
система (81) преобразуется в систему аналогичного вида
au = B(s; a)u, у которой В (s; 0) = (° qV. (98)
Затем возможно выполнить еще одну замену
и=2 <Ы*)«Ч (99)
ft=o
которая преобразует систему (98) в
«v= (J J) v. A00)
Коэффициенты замены (99), как и функции Р (t), <p (s) в (97), могут быть
найдены по методу неопределенных коэффнциентов.
Так как система A00) равносильна уравнению (91), а все упомянутые
замены были невырожденными вблизи значений t — 0, a=0, то мы получаем,
таким образом, что и в общем случае решение в окрестности точки поворота
выражается через функции Эйрн (см. (96)), т. е. имеет тот же характер осо-
особенности, что и в разобранной примере (91).
§ 2. Автономные системы
Мы уже упоминали в ЛВМ, п. XV. 12, что автономной системой
дифференциальных уравнений называется система вида
0)
I
'„=/„(
правые части которой не содержат независимой переменной t.
Геометрические представления, на которых основано рассмотрение
таких систем, сейчас широко применяются, и мы осветим здесь их
коротко. Дальнейшие результаты можно найти, в частности,
в книгах [4, 71].
Все участвующие величины будем считать вещественными.
1. Общие понятия. Решения системы A) удобно рассматривать
в пространстве xlt х2, . . . , х„, называемом фазовым пространст-
пространством. Его точки будем обозначать одной буквой, например

§ 2. АВТОНОМНЫЕ СИСТЕМЫ 521
Х=(хг; хг; ...; хп); более того, так как координаты по отдель-
отдельности мы здесь почти не будем использовать,, то индекс при обо-
обозначении точки будет обычно означать ее номер, а не координату.
Радиус-вектор точки х будем обозначать через х. (Таким образом,
л: не является модулем вектора х!)
Умножая каждое из уравнений A) на орт соответствующей оси
координат и складывая почленно результаты, получим более короткую
. запись той же системы
k = f(x). B)
Таким образом, в фазовом пространстве оказывается заданным поле
скоростей, которое можно наглядно истолковать как стационарный
поток, тогда как каждое решение x = x(t) описывает закон дви-
движения частицы в этом потоке.
Мы предположим, что правые части системы B) удовлетворяют
условиям, обеспечивающим существование и единственность реше-
решения задачи Коши Jt(O) = Jto для этой системы (см. по этому поводу
ЛВМ, п. XV.12); обозначим это решение через x = x(t; x0). Это
непрерывная функция, удовлетворяющая условиям
л:@; *„) = *„, x(t; x(t^, xu)) = x{t + tl; x0). C)
(Продумайте второе равенство, которое является условием стацио-
стационарности потока.)
Сейчас часто говорят о потоке, заданном в некотором пространстве, если
задано однопараметрическое семейство x = x(t; x0) (параметр t истолковывается
как время) отображений этого пространства в себя, удовлетворяющее усло-
условиям C), независимо от его происхождения, т. е. без обязательного «привязы-
«привязывания» потока к дифференциальным уравнениям.
Если x(t)—решение системы B), то ориентированная линия,
описываемая точкой x = x(t) при возрастании t, называется траекто-
траекторией (иначе характеристикой) этой системы. Функция x(t —10) при
любом t0 также будет решением, ей соответствует та же траекто-
траектория, но проходимая с запаздыванием t0 во времени.
Мы будем для простоты считать, что система B) задана во всем
пространстве Еп, а каждое решение определено при — оо < t < оо.
Бывают случаи, когда система задана лишь в некоторой области в
Еп, а также когда некоторые решения уходят в бесконечность прн
конечном t; однако эти случаи не вносят принципиальных изме-
изменений.
Возможны траектории, состоящие всего лишь из одной точки;
это точки покоя. Для того чтобы точка х0 была точкой покоя,
необходимо н достаточно, чтобы
*(*„) = <> №
(почему?).
Из стационарности потока сразу следует, что если траектория
дважды проходит через одну и ту же точку, то это замкнутая

522 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
линия (она называется циклом), а соответствующее решение x(t)
будет периодическим. Таким образом, имеется три типа траекторий:
незамкнутые, замкнутые (циклы) и точки покоя. Каждая точка
фазового пространства принадлежит ровно одной траектории.
2. Предельное поведение траекторий. Для характеристики по-
поведения незамкнутых траекторий применяется понятие предельного
множества. Пусть x(t) — одно из решений системы B), которому
отвечает траектория (/); тогда совокупность пределов всевозможных
сходящихся последовательностей вида x(t{), где ti—*-oo, называется
омега-предельным множеством этой траектории, а если tl—+ — оо,
— ее альфа-предельным множеством (название объясняется тем, что
альфа и омега — соответственно первая и последняя буквы грече-
греческого алфавита). Например, на рнс. 124
показана траектория, у которой лльфа-
предельное множество состоит из един-
единственной точки а, а омега-предельное
множество представляет собой цикл
(/.); показано, как последовательность
точек ж A), ж (8), ж A6),... сходится к
некоторой точке р? (L), но ясно, что и
для любой другой точки (L) можно по-
построить подобную последовательность.
Рис. 124. • Перечислим некоторые свойства
предельных множеств, доказываемые
в математических курсах теории автономных систем, впрочем, доволь-
довольно наглядные. Для определенности будем говорить об омега-предель^
иом множестве. (Отметим, что прн обращении времени омега- н альфа-
предельные множества меняются ролями.)
1. Если омега-предельное множество пусто, т.е. не содержит
ни одной точки, то траектория при t—»-оо уходит на бесконечность,
т. е. |х(/)|—*-оо. (Если дополнить Еп единственной бесконечно уда-
/ -> 03
ленной точкой, как это было сделано в п. II. 1.7 для комплексной
плоскости, то можно сказать, что омега-предельное множество
СОСТОИТ-ИЗ ОДНОЙ ЭТОЙ ТОЧКИ.) •
2. Если омега-предельное множество состоит из единственной
точки а, то а—точка покоя и траектория при t—*-оо входит в эту
точку, т.е. |х(/)—а|—>-0. (Вспоминая о возможности обращения
/ -> 03
времени, получаем, таким образом, что на рис. 124 точка а есть точ-
точка покоя.) Подчеркнем, что траектория не может входить в точку по-
покоя в конечный момент времени, это противоречило бы тому, что
две различные траектории не могут иметь общих точек. Когда тра-
траектория (/) входит в точку а при t—»¦ оо, то сама эта точка к (/)
не причисляется.
3. Омега-предельное множество является замкнутым (как множе-
множество, т. е. оно содержит все свои предельные точки).

§ 2. АВТОНОМНЫЕ СИСТЕМЫ
523
4. Омега-предельное множество (й(г>) состоит из целых траекто-
траекторий: если p€(S(/))i то и вся траектория, проходящая через р, при-
принадлежит (й</)).
5. Если омега-предельное множество ограничено, то оно связно.
(Если оно не ограничено, то становится связным после добавления
к нему бесконечно удаленной точки пространства; см., например,
рис. 125, где омега-предельное множество состоит из двух прямых.)
Часто в фазовом пространстве оказывается возможным выделить
области, заполненные траекториями с одинаковым асимптотическим
поведением, т. е. имеющими одно и то же омега-предельное множе-
множество, (я—1)-мерные поверхности, разделяющие эти области, назы-
называются сепаратрисами (от латинского separo — отделяю), на них
предельиое поведение траекторий обыч-
обычно отличается от поведения траекторий о
как с одной стороны сепаратрисы, так
ис другой. На рис. 126 показана воз-
возможная картина с тремя точками по-
покоя и с сепаратрисой (/).
(I)'
Рис. 125.
Рис. 128.
3. Точки покоя на плоскости, линейные системы. Будем коор-
координаты на плоскости обозначать через х, у и запишем систему B)
в скалярной форме
х = Р(х,у), p = Q(x, yj. E)
Из E) следует, что дифференциальное уравнение траекторий имеет
вид
Q(x,y)dx-P(x,y)dy = O, ' F)
а потому эти траектории можно приближенно построить при помощи
изоклин, как это описано в ЛВМ, п. XV.3. Для этого построения
полезно изобразить также вид семейства траекторий в окрестности
особых точек уравнения F), которыми служат точки покоя системы E)
(почему?).
Разлагая правые части E) в окрестности точки покоя (х$ у0) по
степеням х—х0, у—у0 и пользуясь условием D), получим
yo) + ..., G)
где многоточием обозначены члены выше первого порядка малости, а
а = Р'х(х9, у0), b = P'u(x0, ye), c = Q'Ax9, у0), d = Q'y(x9, у„). (8)

524
T.i. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Примем, что точкой покоя служит начало координат, т. е. что
лго=_уо = О; этого всегда можно добиться с помощью замены
х —>¦ ха-{-х, у—*уй-\-у- При малых \х\, \у\ естественно отбросить
члены высшего порядка малости, т.е. рассмотреть взамен G) уко-
укороченную систему
x = ax + by, y'=cx+dy, (9)
или, в векторно-матричной записи,
г = Аг,
где обозначено
A0)
Будем считать, что матрица А невырожденная, другими словами,
что начало координат для системы (9) служит изолированной точкой
покоя (подумайте, почему это одно и то же!).
Для упрощения системы A0) совершим аффинное преобразование
плоскости по формуле г = Тг' (ср. ЛВМ, п. Х1.6); подстановка в A0)
дает уравнение траекторий после пре-
преобразования
Т (г')' = АТг', т. е. (г')' = Т^АТг'. A1)
Дальнейшее исследование идет по-раз-
по-разному в зависимости от корней харак-
характеристического уравнения матрицы А
Л с d-x)-v> T-e; A2)
l—bc = O.
det
1. Пусть корни Ях, Я2 уравнения
A2) вещественны и противоположного
знака. Как известно из теории мат-
матриц (ЛВМ, п. XI.8), всегда можно так
подобрать матрицу Т, что Т~1АТ =
= diag(A1, Я2). Тогда система A1) при-
с'< (у')' = Ку'> откуда х' = С^', у' = С2ек>', т. е.
у' = С\х'\к^*. A3)
Получается семейство линий, напоминающих гиперболы и имеющих
асимптотами оси х' и у', которые также являются траекториями.
В исходной плоскости х, у получается аффинно преобразованная
картина (рис. 127). Как известно из ЛВМ, рис. 290, такая особая
точка называется седлом.
Направления, по которым интегральные линии проходят через
особую точку, можно найти непосредственно. В самом деле, если
Рис. 127.
обретает вид (дг')- = ;

§ 2. АВТОНОМНЫЕ СИСТЕМЫ
525
эта линия имеет уравнение y = kx, то из (9) получаем
c + dk
k=-
¦bk
A4)
(проверьте!), откуда легко найти оба значения k. Чтобы ориентиро-
ориентировать траектории, т. е. выяснить, по какому направлению происходит
по ним движение, достаточно, взяв какую угодно одну точку,
построить в ней вектор скорости (9), а затем пр'одолжить по непре-
непрерывности направление на со-
соседние траектории, с них на
дальнейшие и т. д.
2. Пусть Kit K2 веществен-
вещественны, одного знака и различны.
Тогда, как и в случае 1, при-
приходим к равеиству A3), однако
картина получается иной (рис.
128): все траектории входят
в точку покоя, как на рис. 128',
или все выходят из нее (если
обернуть стрелки), причем каж-
каждая с определенного направ-
направления. Такая особая точка
называется узлом. Более под-
подробно, здесь получается узел
с двумя направлениями входа:
все траектории входят с одного направления (если не различать
противоположных направлений, имеющих одинаковый угловой коэф-
коэффициент), а пара (АО и ВО на рис. 128) — с другого.
3. Пусть корни мнимые, но не чисто мнимые, hi> 2 = (Л ± iv.
Тогда к диагональному виду привести матрицу А нельзя, если мы
хотим, чтобы приводящая матрица Т была вещественной. Однако в
п. IV.3.4 было доказано, что А можно привести к виду ( ¦* 1 ;
тогда система A1) будет иметь вид
(X'y^iix' + vy1, (/)• = —v^ + ii/.
Переходя в плоскости х', у' к полярным координатам, получим
уравнение (проверьте!)
р =
= — v, откуда р = Се -
Это логарифмические спирали, а в плоскости х, у получатся аффинно
преобразованные логарифмические спирали (рис. 129). Особая точка
называется фокусом.
4. Пусть корни чисто мнимые. Тогда аналогично получим р = С,
т. е. в плоскости х, у получается семейство подобных эллипсов

526
ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
с общими осями симметрии. Особая точка называется центром
(рис. 130).
5. Пусть корень Я двойной. Тогда в силу п. IV.3.3 матрицу А
можно привести либо к виду (. . J, либо к виду L . ;
У)
нетрудно
Рис. 129.
Рис. 130.
проверить (попробуйте!), что второй подслучай будет, только если
a = d, 6 = с = 0.
В первом подслучае система A1) примет вид
(*')• = Я*', (/)•
и интегрирование даст (проверьте!)
Xy'=x'(\n\x'
Получается узел с одним направлением входа (рнс. 131).
Во втором подслучае получаем
у I у = Сх, т.е. интегральными лини-
линиями служат все прямые, прохо-
проходящие через начало координат.
Это звездообразный узел.
Если коэффициенты а, Ь, с,
d в системе (9) выбирать про-
произвольно, то основными являются
первые три случая, так как они
обеспечиваются неравенствами
между коэффициентами (напри-
(например, для 1-го случая должно
быть ad—be Ф 0, (a-f-fif)8—
—4 (ad—be) > 0, ad—be < 0,
т. е. здесь остается четыре сте-
степени свободы, тогда как в 4-м
и 5-м случаях имеется толькогри степени свободы (почему?)).
х

§2. АВТОНОМНЫЕ СИСТЕМЫ
527
узы
седла
Рис. 132.
Кроме того, так как неравенства строгие, то при малом измене-
изменении коэффициентов они сохраняются, т. е. и типы первых трех
точек покоя сохраняются, тогда как точки двух последних
типов могут при таком изменении превратиться в точки других
типов (каких?). Коротко говоря, первые три случая являются гру-
грубыми, а последние два — тонкими
(см. ЛВМ, п. Х.2).
Узел и фокус могут быть как
устойчивыми, так и неустойчивыми,
в соответствии с тем, будет ли
движение по траекториям направлено нецатйчиЗый^- "*
к точке покоя или от нее. Исходя из узел
основного признака устойчивости по -
Ляпунову (ЛВМ, п. XV.22) и из
уравнений A2), докажите, что для
устойчивости узла или фокуса необхо-
необходимо и достаточно, чтобы a-\-d<CQ-
Обозначив коэффициенты характеристического уравнения A2)
через р= —(a-f-d), q — ad—be, мы получаем (рис. 132) на плоскости
р, q части, которым отвечают различные типы точек покоя. Линия,
отделяющая узлы от фокусов, имеет уравнение q—p2/4, ей отвечают
узлы, описанные в случае 5.
4. Общий случай. Вернемся к системе G). Более полное иссле-
исследование, проводимое в математических курсах, показывает, что точка
покоя (дг0; ^0) для нее имеет тот же
тип, что и точка @; 0) для системы (9).
Конечно, рис. 127—131 будут де-
деформированы, притом тем сильней, чем
дальше от начала координат, однако
не только общий вид малой окрестности
начала, но и направления входа в него
траекторий останутся неизменными. Так
как наименования типов точек покоя от-
относятся именно к их малым окрестностям,
то н получается, что при добавлении
членов высшего порядка малости тип
точки остается неизменным.
Единственным исключением является
центр, так как добавлением членов как
угодно высокого порядка малости центр можно превратить в фокус
(рис. 133). В реальных нелинейных примерах, если нет .специальных
причин, порождающих центр (п.4.2), этот тип ие встречается.
Полезно обратить внимание на то, что хотя для отыскания точки,
покоя в конкретных системах E) надо решать систему конечных
нелинейных уравнений P=Q=0, но для выявления характера этой
точки в грубых случаях (п. 3) не требуется знать ее координаты
Рис. 133.

528
ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
слишком уж точно. В самом деле, 'ее тип определяется строгими
неравенствами между коэффициентами линеаризованной системы,
равными производным от правых частей (см. (8)), а неравенства
между производными, выполненные в одной точке, выполняются и в
ее окрестности. Корни уравнения A4), определяющие направления
входа траекторий в точку покоя, также устойчивы относительно
малого изменения этих производных.
Если среди точек покоя рассматриваемой конкретной системы имеются седла,
то для правильного представления о расположении семейства траекторий на
плоскости полезио изобразить соответствующие сепаратрисы. Это можно сделать
с помощью численного интегрирования
следующим образом. Направление выхода
сепаратрисы из точки покоя определяется
с помощью уравнения A4), примененного
к линеаризованной системе. Отойдя по
этому направлению иа некоторое расстоя-
расстояние (рис. 134), надо выбрать ось в попе-
поперечном направлении и, принимая ее точки
за начальные, проводить численное интег-
интегрирование вперед или назад (на рис. 134
назад) во времени. По какую сторону
сепаратрисы находится начальная точка,
определится тем, куда отнесет траекторию
после того как она пройдет вблизи точки
покоя. Нащупав таким образом точку
сепаратрисы, можно продолжить эту се-
сепаратрису с помощью численного интег-
интегрирования.
Не следует думать, что перечисленными типами точек покоя они все исчер-
исчерпываются. В случае, если матрица А вырожденная—в особенности, если она
нулевая,— линейное приближение неприменимо, и приходится пользоваться
более сложными методами исследования, которые обнаруживают огромное раз-
разнообразие типов точек покоя «высшего порядка».
Часто в типе такой точки удается разобраться с помощью перехода к поляр-
полярным координатам, д;=рсонф, «/=рвшф. Подстановка в E) приводит к урав-
уравнениям (проверьте!)
р=Р(рсоэф, рsin ф)cos ф+Q ( )вшф, рф=ф( )созф—Р( )зшф,
откуда
dp _ Р (р cos ф, р sin ф) cos ф + Q ( ) sin ф
dq> ^ Q( ) cos ф — Р( ) sin ф
Допустим, что разложение функций Р, Q по степеням х, у начинается с членов
степени т^ 1, так что
Р(х, у) = Рт'(х, у) + .--, Q(x, y)=Qm(x, г/) + ...,
где Рт, Qm—однородные многочлены степени т (один из них может быть
нулевым), а многоточием обозначены члены высшего порядка малости. Подстав-
Подставляя в A5) и проводя сокращение, получим
Рис. 134.
A5)
A6)
где обозначено для краткости
q
— Рт{
)sin i

§ 2. автономные системы
а многоточия состоят из членов, содержащих р. Отметим, что
529
Будем истолковывать ф, р как декартовы координаты на некоторой вспо-
вспомогательной плоскости и рассматривать A6) как обычное дифференциальное
уравнение на этой плоскости; при этом надо иметь в виду, что правая часть A6)
2ах-периодична по ф и что нас ин-
интересуют лишь малые значения р.
Мы сразу видим, что если
В (ф) Ф 0 @ < ф < я), то так как
уравнение A6) обладает частным
решением р (<р) = 0, семейство ин-
интегральных линий имеет примерный
вид, показанный на рис. 135. Если
вернуться к плоскости х, у, то это
значит, что начало координат в
данном случае будет фокусом, а в
некоторых специальных случаях—
центром; например, для рис. 135
получатся спирали, накручиваю-
накручивающиеся иа особую точку в положи-
положительном направлении (почему?).
Пусть теперь В (ф) имеет нули,
ио ^ 0. Тогда на оси <р уравнение
Рис. 135.
A6) имеет в этих нулях особые
точки. Допустим для простоты, что В(фо)=0, В' (фо) Ф 0, А (фо) Ф 0. Тогда,
согласно предыдущему, можно перейти к уравнению A6) с укороченной пра-
правой частью, т. е.
dP ___k P
dy (p— <р„'
где k=
Л(<Ро)
В' (Фо)
Мы получаем узел, если k > 0, и седло, если k < 0 (проверьте!). Так можно
проверить каждый нуль функции В (ф) в отдельности. (Отметим, что уравне-
уравнение В(<р) = О есть алгебраическое
уравнение (т+1)-й степени отно-
относительно tg ф.) Если указанные
условия простоты не выполнены,
то можно перейти к полярным коор-
координатам новой плоскости с полюсом
в особых точках.
Разобравшись в картине в пло-
плоскости <р, р, можно вернуться к
плоскости х, у. Пусть, например,
иа оси ф рядом оказались, как иа
рис. 136, узел при <p=(pi и седло
при ф=фг. Тогда в некотором сек-
секторе с вершиной в начале координат
в плоскости х, у картина семейства
ь
Рис. 136.
X траекторий будет, как на рис. 137:
по направлению <рх к началу коор-
координат примыкает целый пучок траек-
траекторий, тогда как по направлению
ф2—тольро одна. Так можно построить картину в полной окрестности точки
покоя высшего порядка.
Если Л(ф)эеО или В(ф)з=0, то в A5) надо продолжить разложение
числителя, соответственно знаменателя.

530
ГЛ.
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Чтобы получить представление о расположении траекторий на фазовой
плоскости, полезно разобраться также с их поведением на бесконечности. Для
этого можно произвести, например, преобразование инверсии (п. II.1.8); можно
также, считая у/х ограниченным, совершить преобразование |=1/де, т)==<//х
(продумайте erol), а затем, считая х/у ограниченным, совершить преобразование
f = l/y, т) =х/у; полученные при этом
сведения надо переформулировать в
координатах х, у. Аналогично рас-
/ сматривается бесконечность для фа-
/ зового пространства любой размер-
размерности.
б. Циклы на плоскости. Изо-
Изолированные циклы (в достаточной
близости которых нет других
циклов) на плоскости могут быть
устойчивыми, неустойчивыми и —
гораздо реже—полуустойчивыми
(рис. 138), в-соответствии с по-
поведением траекторий в его узкой
окрестности: например, для устой-,,
чивого цикла все эти траектории
при своем продолжении бесконеч-
бесконечно наматываются на него снаружи
и изнутри, безгранично к «ему приближаясь, т. е. имеют этот цикл
омега-предельным множеством (п. 2). Вообще цикл называется пре-
'дельным, если он служит омега- или альфа-предельиым множеством
х
Рис. 137.
цикл-
цикл, ус/лойчаНьй изнутри
и шщапашибый. снаруот
Рис. 138.
для некоторой незамкнутой траектории; таким образом, изолирован-
изолированные циклы на плоскости являются предельными. Возможен также
случай, когда некотораи область на плоскости- целиком заполнена
циклами, как в случае центра; такие циклы будут, неизолированными.
Движение, описываемое устойчивым предельным циклом, назы-
называется автоколебанием. Для него характерно, что при любых доста-

2. АВТОНОМНЫЕ СИСТЕМЫ 531
точпю малых возмущениях:—точнее, не выводящих из области
жения этого цикла,—движение асимптотически (а реально—после
переходного режима) выходят вновь на этот цикл.
При отыскании предельных циклов полезной оказывается следую-
следующая теорема, которую мы здесь не будем доказывать; впрочем, она
довольно наглядна: если некоторая траектория при f^t0 целиком
содержится в конечной области, внутри и на границе которой нет
точек покоя, то эта траектория либо замкнутая, ~ либо при t —-»¦ оо
. безгранично приближается к замкнутой, на-
накручиваясь на нее. Применяется эта теорема
обычно так: допустим, что нам удалось по-
построить кольцевую область (рис. 139), граница
которой пересекается траекториями внутрь обла-
области (это легко проверить, построив на границе
поле скоростей), причем в этой области и на
ее границе отсутствуют точки.покоя, которые
находятся непосредственно из условия D). Тог-
Тогда, начав с любой точки внутри области или
на ее границе и продолжая с помощью чи-
численного интегрирования системы E) траекто-
траекторию вперед по времени, мы выйдем в пределе —
а практически при большом t — на цикл. Если Рис* 139*
граница области пересекается траекториями
изнутри области наружу, то надо то же построение осуществить
назад по времени. На практике можно никакого кольца не
строить, а просто проводить численное интегрирование, начиная с
различных точек области, в которой ожидается цикл, и строя полу-
полученную траекторию на миллиметровке; при этом довольно часто
удается нащупать цикл. Для этой же цели можно применить графи-
графическое интегрирование с помощью достаточно густой сети изоклин
(ЛВМ, п. XV.3) или более специальных построений, описанных в
курсах теории колебаний.
Может оказаться, полезным следующий отрицательный ре-
результат: если в некоторой односвязной области (G) сумма Px-\-QyHe
меняет знака и фО, то в (Q) не может целиком содержаться цикл.
В самом деле, если (/) — такой цикл, ограничивающий фигуру (S),
то по формуле Остроградского
§ (« + Ql)n dl = J (P'x + Q'y) dS.
@ (S)
Однако левая часть равна нулю, а правая нет (почему?); это про-
противоречие и доказывает наше утверждение. (Аналогично, если
в А-связной области (О) сумма P'x-\-Q'y не меняет знака и ^0, то
число циклов в (О) менее k.)
При исследовании циклов, а также в некоторых других вопро-
вопросах, оказывается полезной следующая конструкция. Выберем

532
ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
произвольно две дуги (t), (/') без контакта, т. е. нигде не касающиеся
поля скоростей, причем так, чтобы траектории, начинающиеся в точ-
точках (/), достигали (/') (рис. 140). Тогда эти траектории осущест-
осуществляют отображение (/) на (/'), которое называется точечным отобра-
отображением. Если ввести координату а вдоль (/) и координату а'
'(I)
Рис. 141.
вдоль (I'), то точечное отображение будет описываться функцией
последования а! (а), монотонной и непрерывной.
В частности, если (/') — (/), то функция последования а' (а) будет
возрастающей (рис. 141), а равенство а'(ао) = ао необходимой доста-
достаточно для того, чтобы точка а0 определяла цикл: другими словами,
*e <* /'
щтошп&ыи.
Рис. 142.
эта точка при точечном отображении должна быть неподвижной. На
рис. 142 показан вид функции последования для различных типов
предельных циклов; впрочем, надо иметь в виду, что поскольку
сама функция последования строится с помощью численного интегри-
интегрирования системы E), то привлечение функции последоваиия в дан-
данной ситуации нужно скорее для осмысливания этой ситуации.

§ 2. АВТОНОМНЫЕ СИСТЕМЫ
533
Например, становится хорошо видеи тонкий характер полуустойчивого
цикла, который при как угодно малом изменении системы E) может либо
совсем пропасть (если график функции последования поднимется кверху),
либо превратиться в пару близко расположенных циклов противоположного х"а-
рактера (если он опустится книзу). Пожалуй, единственное реальное значение
полуустойчивых циклов состоит в том, что если система E) включает в себя
параметр и при его изменении в некоторый момент два
цикла сливаются, то в этот момент возникает полуустой-
полуустойчивый цикл.
В заключение отметим, что не следует думать,* будто -
ограниченная при t -*¦ оо незамкнутая траектория на
плоскости должна либо входить в точку покоя, либо
накручиваться на цикл. Может еще быть случай, когда
омега-предельное множество такой траектории состоит из
нескольких незамкнутых траекторий и точек покоя; см.,
например, рис. 143.
Рис. 143.
6. Вращение векторного поля. При рассмот-
рассмотрении плоского векторного поля, в частности
поля скоростей, полезным оказывается понятие вращения этого
поля; оно подробно разобрано в книге [59].
Пусть дано плоское векторное поле
A(x,y) = P(x,y)lm+Q(x,y)}
и Выбрана какая-нибудь замкнутая линия (/„) (не обязательно траек-
траектория!), не проходящая через особые точки поля А, к которым
ВрЛ0
Рис. 144.
ВрА=~2
причисляются точки, где оно обращается в нуль или терпит раз-
разрыв. Тогда вращением Вр А поля А вдоль линии (L) называется
а.)
число полных оборотов в положительном направлении, которые описы-
описывает вектор А (М), когда точка М проходит линию (L) один раз
в положительном направлении (см. рис. 144). Вращение обладает
следующими простыми свойствами,
1. Вр А — целое число.

534, ГЛ. VIM. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
• 2. Если непрерывно деформировать контур (L) или поле А, при-
причем так, чтобы в процессе деформации на контур не попадали осо-
особые точки поля, то вращение Вр А будет оставаться постоянным.
<?)
В самом деле, при малом изменении контура или поля полный пово-
поворот вектора поля вдоль контура если изменится, то мало. Но,
будучи целочисленной величиной, он не может мало измениться, не
оставаясь постоянным. (Продумайте это рассуждение!)
Из этого свойства, в частности, следует, что если внутри (L)'
поле не имеет особых точек, то Вр А = 0 (почему?).
.(М-
3. Если внутренняя по отношению к (L) часть плоскости разбита
на части с контурами (Z.,), (L2) (Lk), то
Вр А = Вр А + Вр А + ... + Вр А
(докажите это1).
В конкретных примерах вращение можно определить либо на-
наглядно, как на рис. 144, либо с помощью формулы
Пусть теперь Мя—изолированная особая точка поля А, Выберем
контур (L) так, чтобы внутри него содержалась точка Мо и ие было
других особых точек поля. Это можно сделать различными спосо^
бами, однако в силу свойства 2 значение Вр А для всех таких кон-
<?>
туров-одинаковое; оно называется индексом Инд А особой точки Ме
м0
поля А. Например, из рис. 127—131 видно, что при рассмотрении
поля скоростей индекс седла равен минус единице,- а узла, фокуса
или центра равен единице. (Проверьте!)
Допустим теперь, что внутри контура (L) содержатся особые
точки Mv Ж2, ...,Mk. Разобьем внутреннюю по отношению к (L)
часть плоскости на части так, чтобы внутри каждой содержалось
по одной особой точке. Применяя свойство 3, получаем формулы
рА У]дА, A8)
<?) Т М)
где сумма распространена на все особые точки поля, попавшие
внутрь (L). Эта формула напоминает теорему Коши о вычетах
(II.3.9), и это сходство не просто внешнее: например, из фор-
формулы A8) нетрудно вывести принцип аргумента (п. II.3.7) теории
аналитических функций (попробуйте!), она объясняет геометриче-
геометрический смысл этого принципа.
Все сказанное имеет непосредственное отношение к теории авто-
автономных систем, так как каждая такая система задается векторным
полем скоростей. Даже если оно не имеет разрывов, оно будет

НЕ БОЛЕЕ 1И КНИГИ В I
ОДНИ РУКИ И 2Х В ДВЕ ]
§ 2. АВТОНОМНЫЕ СИСТЕМЫ
S35
иметь особые точки в точках покоя системы. Заметим, что враще-
вращение поля вдоль любого цикла равно единице (почему?). Поэтому
в силу следствия, из свойства 2 получаем, что внутри любого
цикла (L) имеется по крайней мере одна точка покоя. Более точно,
из формулы A8) получается, что сумма индексов этих точек равна
единице; поэтому, например, если эти точки могут быть только
типов, описанных в п. 3, то число седел должно быть иа единицу
меньше общего.числа точек остальных типов.
Отметим в заключение, что для сложных точек покоя (п. 4)
индекс может равняться любому целому числу (продумайте это!).
Понятие вращения векторного поля имеет смысл для евклидова простран-
пространства любого числа измерений; будем для определенности говорить о трехмерном
пространстве. Пусть дано векторное поле А (г, у, г) и выбрана какая-нибудь
замкнутая поверхность (S), не проходящая через особые точки поля. Любой
Рис. 145.
точке M?{S) сопоставим точку
(So), где (So)—фиксированная
сфера радиуса 1 с центром О, по следующему правилу: ОМ' = А (М)/| А (М) |
(рис. 145). Вращение ВрА показывает, сколько раз при этом отображении (S)
(S)
в (So) эта сфера окажется покрытой, причем покрытые участки засчитываются
со знаком плюс или минус в зависимости от того, сохраняется ли ориентация
при отображении на эти участки или нет. (При этом поверхности (S) и (So)
считаются ориентированными естественным образом, т. е. наружной стороной
в бесконечность. В л-мерном случае это означает, что ориентация каждой из
этих (л—1)-мерных поверхностей порождается естественной ориентацией огра-
ограниченного ею конечного л-мерного тела, см. ЛВМ, пп. XVI.20 и 29, а естест-
естественная ориентация ?„ определяется последовательностью точек A; 0; ...; 0),
@; 1; ...; 0), .... @; 0; ...; 1), @; 0; ...; 0); продумайте это для л=2 и 3.)
Так определенное вращение поля обладает всеми-свойствами, указанными
выше для плоского поля. Можно получить и формулу, аналогичную A7): если
где еу—орт оси xj, то
ВрЛ_ 1 Г у
(S) «fc-i^jL
! вивлисуг1^'* I
КОЯОХЗА ¦
1 ЛЛ1//\Г.1^ А 1
А=2^(^'
a«i "• аху_1
uti " * их •
дг2, ..., дги) еу,
^«t
а да"
" dxJ+l '"
дхп
дап
дха
cos(n,«/)
д ' ' dS.
ИНВ № 33 1
НЕ БОЛЕЕ Ю КНИГИ В |
ОДНИ РУКИ И 2Х В ДВЕ ]

536 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
где п—орт внешней нормали к (S), a wn_x — (п—1)-мерная мера (So),
которую можно вычислить по рекуррентной формуле
я/2
ш„_,=2 ^-у \ sin«(pd(pwn_2(/i = 2, 3, ...; шо = 2);
о
п — \ /1—3 1 п
-й"-й=2 - Т (" НеЧеТНОе)-
Аналогично плоскому случаю вводится и индекс особой точки поля.
7. Точки покоя в пространстве. Исследование малой окрестно-
окрестности точки покоя в пространстве любого числа п измерений в гру-
грубых случаях просто. Ограничимся случаем трехмерного простран-
пространства xiy xiy x3, так как рассмотрение пространства высшего числа
измерений проходит аналогично.
Примем, как и. в п. 3, за точку покоя начало координат и про-
проведем линеаризацию. Тогда мы вновь получим систему вида A0),
где обозначено
г= лг, , А =
С помощью преобразования г = Тг' мы переходим к системе A1),
так что опять встает вопрос о приведении матрицы А к по возмож-
возможности более простому виду с вещественной преобразующей матри-
матрицей Т.
Ответ зависит от корней Xit Хг, К3 характеристического урав-
уравнения
det(A —М) = 0. A9)
Если все корни вещественные и различные, то матрицу можно
привести к диагональному виду, тогда система A1) будет иметь
вид Xj="KjXj и общее решение —
Х/ = С/еЧ' (У= 1,2,3). B0)
Если, например, Ях < К2 < К3 < 0, то легко проверить, что при
t ¦—>- оо. любая интегральная линия входит в точку покоя, причем
для Сьф0 — с направления оси х3, для С3 — 0, Сгф0 — с направле-
направления оси лг2 и для С3==С2 = 0, СгФ0 — с направления оси xv По-
Получается устойчивый узел с тремя направлениями входа. Если все
"Kj > 0, получается неустойчивый узел. Если корни кратные, то все
равно получается узел, но число направлений входа может быть

§ 2. АВТОНОМНЫЕ СИСТЕМЫ
537
иным. Узел получается и при п > 3, если все корни одного знака.
Если корни вещественные и различные, но не одного знака, то
получается та же формула B0), но геометрический смысл будет
иной: так, на рис. 146 для случая К3 < 0 < Хг < К2 показаны
проекции траекторий на координатные плоскости (эти проекции сами
служат траекториями), а также—жирно — одна из существенно про-
пространственных траекторий. Это седло. (Седло получится и в случае
Рис. 146.
Рис. 147.
кратных корней различного знака.) В точку покоя здесь попадают
только траектории при t—>•— оо с плоскости х[, х'г, которая слу-
служит сепаратрисой (п. 2), и при /-+оо с оси x's; все прочие траек-
траектории минуют точку покоя. Седло всегда неустойчиво.
Если уравнение A9) имеет пару мнимых сопряженных корней, то
в силу п. IV.3.4 систему (И) можно привести к виду
vx't
х\ = — \х\
откуда после перехода к полярным координатам в плоскости х[,
и интегрирования получаем
Если |х н Х3 одного знака, получается картина, имеющая черты
как узла, так и фокуса; такой узло-фокус может быть как устойчивым
(рис. 147), так и неустойчивым. Если |х н К3 различного знака,
получается седло-фокус (рис. 148), который всегда неустойчив.
Если ц = 0, то получается картина, как на рис. 149.
При добавлении членов высшего порядка малости картина в це-
целом сохраняется, за исключением рис. 149, который может при

638
ГЛ. VIII- ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
этой перейти как в узло-фокус, так и в седло-фоку«, Кроме того,
огромное разнообразие доставляет случай вырожденной (в частности,
нулевой) матрицы А.
При п > 3 получаются сходные случаи; новым будет лишь то,
что если матрица А имеет несколько пар мнимых собстненных зна-
значений, то получится наложение нескольких вращений, а в чисто
мнимом случае — квазипериодичность (п. 1.7).
Рис. 148.
Рис. 149.
Так как формула г—>-Аг при det А Ф 0 определяет аффинное отображение
пространства на себя, сохраняющее ориентацию, если det A > 0, и меняющее
ее в противном случае, то из определения индекса (п. 6) следует, что если в
точке покоя будет det ["вгЛ > 0 (< 0), то ее индекс равен единице (соответ-
(соответственно — 1). Если det ( ~ j =0, то индекс может принимать и другие значения.
Аналогом теоремы п. 6 о точке покоя внутри замкнутой траектории является
следующее утверждение, Пусть в я-мериом пространстве, где задана автоном-
автономная система B), дано тело (Т), гомеоморфное я-мериому шару, с поверх-
поверхностью (S), которая может быть гладкой или кусочно-гладкой (точнее, иметь
особенности размерности <я—2). Пусть поле скоростей в каждой точке (S)
отлично от нуля и направлено внутрь (Т) или, в крайнем случае, по каса-
касательной к (S), так что при хо?(Т) и *ЭгО будет х (t; xo)?(T). Тогда внутри (Г)
имеется по крайней мере одна точка покоя. В самом деле, из условий вытекает,
что вращение, поля скоростей на (S) равно единице (продумайте это!).
Интересно, что при я = 3 заменить в этом утверждении шар на тор нельзя,
так как тогда при выполнении прочих условий точки покоя может и не быть.
Однако в качестве (Т) можно взять шар с двумя или ббльшим числом «ручек».
(Тор гомеоморфен шару с одной «ручкой».) В курсах алгебраической топологии
указывается общее условие на тело (Т) любой размерности, достаточное для нали-
наличия по крайней мере одной точки покоя у автономной системы, заданной на (Т),
траектории которой не могут покидать. (Г) с возрастанием времени. Этим
условием служит отличие от нуля эйлеровой характеристики э. х.(Г) тела (Г).
Мы здесь не будем давать общее определение этой характеристики; отметим

§ 2. АВТОНОМНЫЕ СИСТЕМЫ * 539
только, что это целое число, инвариантное относительно гомеоморфизмов тела (Т).
Для n-мерного шараэ. х. = 1, а для (я—1)-мерной сферы э х. = 1—(—1)".
Для трехмерного шара с k ручками э. х»=1—k, а для поверхности этого
тела э. х. =2—Ik.
,\
8. Циклы в пространстве. Цикл для системы B) определяется
некоторым ее периодическим решением xo(t); пусть Т—период.
Чтобы исследовать поведение решений в узкой окрестности этого
цикла, совершим подстановку х^=хо(^) + |, разложим правую часть
по степеням проекций g и отбросим при малом ||| члены выше
первого порядка малости. Получим линейную систему
!=*«(*. (О )S Bi)
с Т-периодической матрицей коэффициентов. (Напомним, что по
определению ^х = (^0-) В силу п. 1.2 поведение решений систе-
системы {21) при t—>¦ сю определяется ее мультипликаторами р^, которые
в конкретных примерах можно вычислить, построив с помощью чис-
численного интегрирования матрицу монодромии и подсчитав ее собст-
собственные значения..Как и при исследовании точек покоя, поведение
решений полной системы при малых 11 ] в основных случаях такое
.же, как для укороченной системы \2\). Однако надо иметь в виду,
что так как система B) наряду с х0 (t) имеет однопараметрическое
^семейство решений xB(t + 'K) = xB{t) + 'kxB(t)-f..., то система B1)
имеет одним из своих частных решений х0 (t), которому отвечает
мультипликатор р = 1. Поэтому классификация циклов проводится
по значениям остальных мультипликаторов, и мы приходим к сле-
следующим выводам.
Если все указанные мультипликаторы системы B1) по модулю
меньше единицы, то цикл xo(t) притягивающий, т. е. все траекто-
траектории, начинающиеся от него достаточно близко, асимптотически
к нему стремятся при t—юо, бесконечно на него накручиваясь.
(Более того, Ляпунов доказал, что для каждой такой траектории
x(t) имеется значение т (сдвиг во времени), для которого расстоя-
расстояние между точками x(t-}-x) и xo(t) стремится к нулю при t—юо;
это значение т, свое для каждого решения x(t), называется асимп-
асимптотической фазой.) Если все эти мультипликаторы по модулю больше
единицы, то цикл хв (t) отталкивающий. Если же среди мультипли-
мультипликаторов имеются как большие, так и меньшие единицы по модулю,
то цикл х0 (t) неустойчив, ио имеет седловой характер, так как
к нему при t—»-оо стремятся траектории, заполняющие многообра-
многообразие размерности < п. Случай, когда система имеет мультипликаторы,
по модулю равные единице (кроме тривиального, упомянутого в конце
предыдущего абзаца), а прочие все больше единицы или все меньше
единицы, является сложным, и мы не будем его рассматривать.

540 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Отсюда вытекает совсем простой признак устойчивости цикла для автоном-
автономной системы E) иа плоскости. Пусть этот цикл имеет уравнения x=<p(t),
y—ty (t) и период Т. Тогда линеаризованная система имеет вид
Воспользуемся формулой A.18). Из нее, в силу равенства одного из мультипли-
мультипликаторов единице, вытекает, что если
( < 0, B2)
то рассматриваемый предельный цикл устойчив; если же этот интеграл поло-
положителен, то цикл неустойчив. Этот признак получил Пуанкаре.
К исследованию циклов можно применить также метод точечных
отображений (п. 5), который, кстати, исключает тривиальный муль-
мультипликатор р = 1; поясним этот метод для трехмерного простран-
пространства. Для этого допустим, что выбрана некоторая поверхность (S)
без контакта (рис. 150) с уравнением F(x) — 0
и на ней выбрана система координат а = (ах; а2),
так что х = ф(а). Допустим, что траектория,
начинающаяся в точке ф (а), вновь пересека-
пересекает (S) в точке х' — (p(a')-x(t'; ф(а)), которую
можно найти из уравнения F(x(t; у(а)))— 0.
Тогда а' (а) и есть точечное отображение,
определяющее после перехода к координа-
координатам ctj, ct2 функцию последования, Цикл
определяется условием а„ = а0 (рис. 150),
рис 150 а характер этого цикла определяется свойст-
свойствами отображения а'(а) вблизи а0. В ча-
частности, можно показать, что собственные значения матрицы
(-J—) как раз равны мультипликаторам системы B1), за исклю-
исключением тривиального р=1, который при этом выпадает; отсюда
можно вновь получить выводы, указанные в предыдущем абзаце.
Метод точечных отображений можно применить также для оты-
отыскания заранее не заданного цикла, если примерно известно, где он
должен находиться. Значение а'=ф(а) при любом конкретном а
можно найти с помощью численного интегрирования системы B) и
проверки знака F(x) вдоль траектории. Поэтому притягивающие
циклы можно найти с помощью простой итерации ач+1==ф(ап),
а отталкивающие — аналогичным образом, интегрируя назад во вре-
времени. Циклы других типов можно найти, решая уравнение а==ф(а)
численно но методу Ньютона (ЛВМ, п. XII.12); необходимые для
этого значения производных ¦=—можно находить с помощью уравне-
уравнений в вариациях (ЛВМ, п. XV.28) либо применяя формулы числен-
численного дифференцирования.

§ 2. АВТОНОМНЫЕ" СИСТЕМЫ 541
При построении циклов следует иметь в виду, что незамкнутая
траектория в я-мерном пространстве, ограниченная при t—> оо и не
содержащая в своем омега-предельном множестве точек покоя, в слу-
случае л^З не обязана, как это было при л = 2, накручиваться на
цикл, ее асимптотическое поведение может быть более сложным.
Для построения и исследования циклов можно применить также следую-
следующий прием, принадлежащий Пуанкаре. Пусть рассматривается система вида B)
с одним нли несколькими параметрами
x=f(x, (г) (\i = (H, Pi I*»)). B3)
общее решение которой в силу ее автономности имеет вид
x=F(t-t0; С, (г) (C=(Clt C2, .... С,,.!)).
Пусть при некотором значении jx=(х0 известно периодическое решение
F(t—10; Со, ц0) системы B3), периода То. Имеются ли периодические решения
при ц, близких к ц0?
Если обозначить через Т (неизвестный заранее!) период такого решения,
то опять-таки из автономности системы условие периодичности решения можно
записать в виде
F(T; С, n)=f@; С, (г), т.е. F (Т; С, \i)-F(O; С, ц)=0. B4)
По условию последния система уравнений при Т = Т0, С — Сй, ц. = щ УДовле-
творяетси. Значит, по теореме о неявных функциях (ЛВМ, п. IX. 13), если при
этих значениях будет
d(F(T;C, (iJ-FffiC, (г))
д(Т,С) *° B5)
(в левой части стоит якобиан /г-ro порядка!), то при малом | ц — \i0 | система
B4) может быть однозначно разрешена относительно Т, С, т. е. система B3)
имеет ровно один цикл, близкий к заданному.
Так как условие B5) ставится на заданном цикле, то в этом условии за F
можно принять решение системы B3), линеаризованной на этом цикле при
(А=ц0. Конечно, и для линеаризованной системы решение удается найти лишь
в специальных случаях, однако такая линеаризация может оказаться полезной
для численной проверки условия B5) и, что еще более важно, для численного
построения зависимостей Т (\i), С (\i) для искомого цикла при малых | ц,—\io\
с последующим продолжением этих зависимостей по общему методу п. IV.4.11.
Мы не будем касаться здесь обширных исследований случаи, когда уела
вне B5) нарушено. Так будет, если при (х=[х0 система имеет кратный цикл,
готовый расщепиться на несколько или пропасть, или если она имеет целое
многообразие циклов. Эти исследования изложены в книге [81].
9. Структурно устойчивые системы. В разных Местах курса мы уже гово-
говорили о значении структурно устойчивых (иначе грубых) объектов, сохраняю-
сохраняющих свои основные свойства при достаточно малом изменении параметров, от
которых рассматриваемый объект зависит. Это значение можно мотивировать
тем, что если эти параметры имеют реальный смысл, то можно говорить только
о достаточно узком диапазоне их значений (ЛВМ, п. 1.6), а потому структурно
неустойчивые (тонкие) свойства не могут точно реализоваться.
Конечно, это не означает, что негрубые случаи не нужно исследовать.
Пусть, например, в формулировку некоторой задачи входит непрерывный пара-
параметр К. Тогда условие Х,=0 (как и X, равно любому заранее заданному конкрет-
конкретному значению) является негрубым. Однако именно это условие может входить
в математическую схематизацию задачи (например, X,—это коэффициент треиия,
а мы схематизируем процесс как происходящий без диссипации энергии и т. п.)
Далее, исследование случая К=0 может на основании метода малого параметра

542 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
или какого-либо иного метода продолжения по параметру служить базой для
рассмотрения случая К ^ О, уже грубого. Если рассматривается серия задач,
в которых X непрерывно меняется, переходя от отрицательных значений к по-
положительным, то исследование случая Х,=0 может оказаться необходимым.
Но даже если X берется произвольным, то | X | с определенной вероятностью
может оказаться весьма малым, а тогда замена Я на значение 0 может ока-
оказаться в каких-либо отнршениях приемлемой и в то же время существенно
упрощающей исследование. Сказанное, впрочем, отнюдь не умаляет и роли
грубых случаев.
Приведенное определение структурной устойчивости допускает разнообраз-
разнообразные трактовки в соответствии с тем, какие объекты рассматриваются, какие
возмущения параметров допускаются и какие свойства должны быть при этих
возмущениях инвариантными. Советские ученые—- специалист в области теории
колебаний А. А. Андронов A901—1952) и математик Л. С. Понтрягии
- (р. в 1908 г.) в 1937 г. ввели и исследовали понятие cfpyKTyproft устойчивости
для автономных систем иа плоскости, расширенной как в теории аналитических
функций (п. II.1.7). При этом они называли систему грубой, если при любом
достаточно малом изменении правых частей и их производных вся картина
расположения траекторий в целом не меняется, точнее, если все траектории
возмущенной системы переходят в траектории исходной при некотором взаимно
однозначном дифференцируемом в обе сторовы отображении плоскости на себя.
Они обнаружили, что для такой грубости необходимо и достаточно, чтобы:
1) точек покоя было конечное число и каждая из них принадлежала в ли-
линейном приближении одному из первых трех типов п. 3;
2) циклов было конечное число и каждый из иих имел один из мульти-
мультипликаторов отличным от единицы;
3) ие было сепаратрис, идущих из седла в седло (продумайте эти условия!).
При достаточно малом изменении грубой системы вновь получается грубая
•система. В то же время негрубую систему с помощью как угодно малого изме-
изменения можно превратить в грубую. (Это можно сравнить со следующим: непо-
непостоянная функция при достаточно малой вариации остается непостоянной, тогда
как постоянную функцию можно с помощью как угодно малой вариации пре-
превратить в непостоянную.)
Каждая устойчивая точка покоя и каждый устойчивый предельный цикл
определяют на плоскости некоторую область притяжения, т. е. часть плоскости,
покрытую траекториями, имеющими эту точку или этот цикл своим омега-пре-
омега-предельным множеством. Плоскость, иа которой задана грубая автономная система,
разбивается на конечное число таких областей притяжения, отделенных друг от
друга сепаратрисами, идущими в седла.
Для автономных систем в /i-мерном пространстве при п ^ 3 легко указать
необходимые условия структурной устойчивости, аналогичные указанным выше
условиям 1—3, однако эти условия в совокупности ие будут достаточными.
Необходимые и достаточные условия пока неизвестны. Недавно было обнару-
обнаружено, что не всякую структурно неустойчивую систему можно при помощи как
угодно малой вариации превратить в-структурно устойчивую.
10. Разрывные системы. В приложениях встречаются случаи, ког-
когда система B) определена с обеих сторон от некоторой (л—^-мер-
(л—^-мерной поверхности (S), однако при переходе -через (S) правая часть
испытывает конечный скачок. При этом возникают новые обстоя-
обстоятельства, которые мы поясним, положив для наглядности л = 3.
Будем представлять ситуацию так, как будто в окрестности \S)
заданы дие азтономные системы, однако с одной стороны (S) надо
пользоваться одной из них, а с другой стороны—другой. Наиболее
прост случай, когда на (S) траектории обеих систем направлены

§ 2. АВТОНОМНЫЕ СИСТЕМЫ
543
в одну и ту же сторону от E) (рис. 151). Тогда при переходе
через (S) траектории разрывной системы, вообще говоря, испытывают
излом, однако каких-либо осложнений в связи с этим обычно не
возникает. При построении траекторий проводится припассовывание
решений одной системы к решениям другой, т. е. конечные условия
для одного решения служат начальными для другого.
Рис. 151.
Рис. 152.
Случай, когда на (S) траектории обеих систем направлены от {S)
(рис. 152), вызывает осложнения, если начальная точка траектории
находится на (S), так как такую траекторию можно стоить в лю-
любую сторону от (S). Таким образом, этим начальным точкам отве-
отвечает по две траектории. Однако при дальнейшем продолжении тра-
траектория не может пересечь поверхность с
таким характером разрыва поля скоростей
(почему?), так что других осложнений
здесь не будет.
Наиболее интересен случай, когда на
{S) траектории обеих систем направлены к
(S) (рис. 153). Здесь траектория, дойдя
до (S), не может сойти с (S) ни в одну,
ни в другую сторону.. Но предельные
значения вектора скорости направлены
под углом к (S); поэтому, казалось бы,
мы приходим к противоречию, т. е. траектории, дойдя до {S),
должны прекратиться.
Чтобы'иметь в последнем случае возможность разумного продол-
продолжения траектории, вводится следующее понятие обобщенного решения
системы B). Отложим от любой точки а ? (S) предельные значения
vx и v2 вектора скорости с обеих сторон (S) (рис. 153) и иа отрезке,
соединяющем концы этих векторов, выберем точку а' так, чтобы
вектор \ = аа' касался (S). Тем самым на (S) получится поле каса-
касательных векторов; траектории этого поля (это так называемый сколь-
скользящий режим) естественно считать продолжениями траекторий, по-
попавших на (S). При таком продолжении траектория может либо
Рис. 153.

544
ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
навсегда остаться на (S), либо же, выйдя из зоны скользящего
режима, «сорваться» с (S).
Если на рис. 153 векторы vx н v2 направлены противоположно
друг другу, то v = 0, т. е. а служит точкой покоя для скользя-
скользящего режима. Бывают случаи, когда на (S) имеется целая область,
состоящая из таких точек; это зона нечувствительности.
Приведем несколько примеров, пользуясь простейшей разрывной функцией
сигнум (signum по-латынв—знак):
( -1 (-оо <*<0),
= < О (*=0),
\ 1 @ < X < оо),
щпх
связанной с единичной функцией е (х) (ЛВМ, п. XIV.25) формулой 2е (X) =
= sgn;e+l. Такие функции обычно появляются в системах с переключениями.
Рис. 154.
Рис. 155.
дифференциальный закон развития которых меняется скачком при достижении
системой определенного состояния.
Уравнение x-\-asgnx=Q равносильно системе
Непосредственное интегрирование при х > 0 и х < 0 приводит при а > 0 к кар-
картине траекторий («фазовый портрет»), показанной на рис. 154 (проверьте!). На
линии разрыва х^О ситуация, как иа рис. 151. Случай а < 0 мы предостав-
предоставляем читателю.
Система с переключением
х=хг, хг=—с
! — a sgn x2
имеет при а > 0 фазовый портрет, показанный на рис. 155 (проверьте!). Интер-
Интервал —a <*!*?? а оси xt образует зону нечувствительности, в любой его точке
возможно положение равновесия. При любых начальных условиях система
после конечного числа колебаний "за конечное время приходит в эту зону
и там останавливается. Интересно, что если после такой остановки беспоря-

§ 2. АВТОНОМНЫЕ СИСТЕМЫ
545
дочно «встряхивать» систему, то она будет иметь тенденцию перейти в состоя-
состояние, отвечающее значениям хг=х2—0 (почему?).
В последнем примере, который мы приведем, разрывны не сами правые
части системы, а нх производные. Это осциллятор с люфтом, простейшая схема
которого показана на рис. 156. Уравнение движения такого осциллятора имеег
вид т'х+у (х) = 0, где
k(x+a) (—*> <х<— а),
О ( — а < х < а),
k(x—a) (а< х < оо).
Соответствующая система имеет вид
1
и фазовый портрет, показанный на рис. 157. Интервал — a<LXi<La оси xt
состоит из точек покоя, т. е. образует зону нечувствительности; однако эта
нечувствительность иного типа, чем на рис. 155, поскольку как угодно малое
«встряхивание» приводит здесь к воз-
возникновению медленных колебаний конеч-
конечной амплитуды. (Какой нх физичеекнй
смысл?)
Большое количество подобных и
более сложных примеров подробно разо-
бране в книге [4].
Рис. 156.
Рис. 157.
В заключение отметим, что физическая система с переключениями может,
задаваться и несколькими автономными системами B), заданными в одной и
той же области и сменяющими друг друга по определенному закону. Траек-
Траектория точки, изображающей решение такой системы с переключениями в фа-
фазовом пространстве, может иметь самопересечения.
11. Системы иа многообразиях. До сих пор мы считали, что
система B) задана на всем пространстве Еп или на некоторой об-
области в этом пространстве. Однако эта система может быть задана
и на некотором л-мерном многообразии с обобщенными координатами
Пусть, например, рассматривается система с одной степенью
свободы, причем определяющая координата ф имеет смысл угла,
а значениям ф и ф + 2я отвечает одно и то же положение системы.
Тогда для описания положений системы достаточно ограничиться
интервалом 0^ф^2л, причем концам интервала отвечает одно и
то же положение. Поэтому многообразие положений такой системы
представляет собой окружность (более точно, гомеоморфно окруж-
окружности— продумайте это!).
18 А. Д. Мышкио

546
ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Если упомянутая система описывается уравнением ф=/(ф, ф),
то функция / должна быть 2я-периодическоЙ по ф. Фазовым про-
пространством здесь служит пространство (ф, ф); каждой точке этого
пространства отвечает определенное состояние системы, "т. е. ее
положение и скорость. Так как совокупность положений образует
в данном случае окружность, а совокупность скоростей—бесконеч-
скоростей—бесконечную прямую, то фазовое пространство представляет собой круговой
цилиндр, который служит топологическим произведением окружности
на прямую. Таким образом, в данном случае векторное поле скоро-
скоростей, траектории, точки покоя и т. п. следует представлять на цилинд-
цилиндре. Эту систему можно изображать и на обычной плоскости (рис. 158),
однако при этом надо помнить, что все полосы ширины 2л по ф
должны быть отождествлены, т. е. как бы этой плоскостью нужно
обмотать цилиндр с длиной окружности 2rt. (Проверьте, например,
что на рис. 158 изображена одна точка покоя, две замкнутых и одна
незамкнутая траектории.)
Аналогичным образом, если все правые части системы A) перио-
периодичны по каждой из переменных х} с периодом a}(j=\, 2, ...,п),
то фазовым многообразием этой системы служит топологическое
произведение я окружностей. В частности, при п — 2 получается
поверхность тора, так как между точками на ней и парами угловых
координат имеется естественное взаимно однозначное соответствие
(какое?). Впрочем, обычно слово «поверхность» опускают, а говорят
просто об автономной системе, заданной на торе (а при любом
л—на л-мерном торе). Такую систему можно изображать также на
обычной плоскости xlt x2, разбитой на прямоугольники ширины аг
и высоты а2, причем все эти прямоугольники должны быть ото-
отождествлены.
-Автономная система может быть задана на сфере любого числа
измерений и т. д. Возможны и более сложные фазовые многообразия:

§2. АВТОНОМНЫЕ СИСТЕМЫ 547
например, при рассмотрении движения твердого тела вокруг непод-
неподвижной точки многообразием состояний будет служить трехмерное
многообразие ортогональных матриц третьего порядка с определи-
определителем 1 (почему?). Все эти многообразия подробно изучаются в кур-
курсах алгебраической (раньше говорили «комбинаторной») топологии.
Торы, сферы—это примеры компактных многообразий, цилиндры—
некомпактных. В компактном многообразии омега- и альфа-предельные
множества любой траектории обязательно содержат по крайней мере
одну точку (почему?), замкнуты, состоят из целых -траекторий и
связны (п. 2).
Теория автономных систем на многообразиях обладает , рядом
новых черт по сравнению с теорией систем в Е^ поясним, это для
случая л = 2. Прежде всего, замкнутая линия на двумерном много-
многообразии не обязана делить его на конечную и бесконечную части:
она может делить его на две конечные части (любая замкнутая
.линия на сфере) или на две бесконечные части (верхний цикл на
рис. 158), или вообще не делить на части (меридиан или параллель
на торе). Поэтому на торе или на цилиндре из наличия цикла от-
отнюдь не всегда вытекает наличие точки покоя. С другой стороны,
из результатов, приведенных в конце п. 7, вытекает, что автономная
система, заданная на сфере, всегда имеет по крайней мере одну
точку покоя независимо от наличия циклов, тогда как на торе это,
конечно, не так. Таким образом, хотя локальные свойства систем
на двумерных многообразиях (строение поля вблизи точек покоя
и Т. п.) те же, что на плоскости, но свойства в целом (тотальные
свойства) существенно зависят от топологической структуры мно-
многообразия.
12. Системы с интегральным инвариантом. Рассмотрим для
определенности систему B), заданную на Е„, хотя все сказанное
будет относиться и к системам, заданным на многообразии. Пусть
(V)—некоторая область в Еп; тогдапод (V)t будем понимать ре-
результат сдвига (V) по траекториям системы B) на временной интер-
интервал t, другими словами, совокупность всех точек x(t; лг0) (xo?(V))
при данном t. Функцию р (х), заданную на Еп, будем называть
плотностью интегрального инварианта для системы B), если для
любой конечной области (V) интеграл
B6)
не зависит от t; он называется интегральным инвариантом. Геомет-
Геометрический смысл этого условия При л = 2 показан на рис. 159: объем
цилиндрического Тела, построенного на «окрашенной» области плос-
плоского потока, должен оставаться неизменным.
.' Чтобы вывести уравнение для плотности интегрального инва--
рианта, заметим, что для инвариантности интеграла B6) необходима
18»

548
ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
и достаточна инвариантность каждого его элемента, т. е.
D(p{x)dV) = 0,
B7)
где под D понимается дифференциал, полученный в результате
сдвига по траекториям на время dt. Однако
D(р dV) = DpdV+ pD{dV) = grad p-xdt dV+ pdivxdVdt
(см. смысл дивергенции вектора скорости в ЛВМ, п. XVI.23). Поэтому
в силу B) и B7) получаем урав-
уравнение
div(Pf(Ar)) =
= grad p • f (x) + р div f (х) = 0, B8)
выражающее необходимое и доста-
достаточное условие того, чтобы функ-
функция р (лг) была плотностью интег-
интегрального инварианта системы B).
Если р == const служит такой
плотностью, то при сдвиге по
траекториям сохраняется л-мерный
объем каждой области. Из B8)
видно, что для этого необходимо
и достаточно, чтобы divf(A;) = O. Этим свойством обладают, в
частности, канонические системы
Рис. 159.
дН
дИ
(i == 1, 2, ..., л; Я = Я (*!, ..., х„, pv ..., />„))
(п.' VI.3.1), рассмотренные в'2л-мерном фазовом пространстве х, р
(проверьте!); поэтому 2л-мерный объем в этом пространстве при сдвиге
по траекториям сохраняется (теорема Лиувилля).
Если для любой плотности р (лг) интегрального инварианта ввести
меру (ЛВМ, п. XVI. 19) по формуле
(V)
то мы получим меру, инвариантную относительно сдвига по траек-
траекториям. Наибольший интерес представляет случай, когда р (лг) > 0.
Будем впредь считать, что .плотность. р(х) непрерывна и
0<р(лг)<оо. Нетрудно показать, что любая система B) в окрест-
окрестности любой своей точки, не являющейся точкой покоя, обладает
интегральным инвариантом. Однако из этого утверждения мало что
можно извлечь, основной интерес представляют системы с интег-
интегральным инвариантом во всем фазовом пространстве.
Существенно подчеркнуть, что далеко не всякая автономная система

§ 2. АВТОНОМНЫЕ СИСТЕМЫ
549
обладает интегральным инвариантом; в реальных задачах наличие
такого инварианта примерно равносильно отсутствию в рассматри-
рассматриваемой физической системе диссипации или подкачки
энергии.
Пусть в системе с интегральным инвариантом имеется точка
покоя х„. Тогда, полагая в B8) х — хв, мы видим, что divf (;со) = О.
Но левая часть равна сумме корней характеристического уравнения
системы B), линеаризованной в х0 (почему?). Значит, если имеются
корни с положительной вещественной частью, то должны иметься
и корни с отрицательной вещественной частью, и обратно. Тем са-
самым исключаются грубые притягивающие и отталкивающие точки
покоя; например, из точек, перечисленных в п. 3, для систем с ин-
интегральным инвариантом возможны
только седла и центры. Устойчивые
узлы и фокусы характерны для си-
систем с диссипацией, а неустойчи-
неустойчивые— с подкачкой энергии (проду-
(продумайте это!).
К этим же выводам можно прий-
прийти из наглядных соображений. Рас-
Рассмотрим, например, устойчивый узел
(рис. 160) и в его окрестности не-
некоторую область (V). Тогда при
t —>¦ оо она будет вырождаться в
точку, а это противоречит инвари-
инвариантности интеграла B6) (почему?).
То же рассуждение показывает, что в системе с интегральным
инвариантом невозможны притягивающие или отталкивающие предель-
предельные циклы, а также вообще притягивающие или отталкивающие
•многообразия размерности ниже, чем размерность фазового про-
пространства.
13. Эргодичность. Пусть на компактном многообразии (М) задана
автономная система с-интегральным инвариантом (такие системы
иногда называются динамическими). Как мы знаем, такая система
определяет на (М), во-первых, поток, т. е. преобразование х—>xt
(п. 1), а во-вторых, меру [X, инвариантную относительно этого потока.
Пусть теперь на (М) задана любая конечная функция f(x); рассмот-
рассмотрим ее среднее значение вдоль траектории, начинающейся в неко-
некоторой точке аг, другими словами,
г
/(*) = Hm ±r\f(xt)dt. B9)
о
Американский математик Г. Бйркгоф A884—1947) доказал, что это
среднее значение имеется для всех х, за исключением, быть может,
множества меры нуль, как говорят иначе, для почти всех значений х.
Рис. 160.

550 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
(Немного раньше Дж. Нейман доказал несколько более слабый вариант
г
1 С
этой эргодйческой теоремы, именно, что -=-\/(.*rf) d/ при Т-
- oo
сходится к f(x) в среднем квадратичном, т. е. в смысле Ьг (М).)
Функция f(x) сохраняет постоянное значение вдоль каждой
траектории (почему?), т. е. инвариантна относительно
сдвига по траекториям. Кроме того, легко проверить, что
J (*)d[i= J f(x)d\x. C0)
Ш) . Ш) :
В самом деле, разбивая (М) на кусочки и пользуясь инвариантностью
меры, получим
\
Ш
v Ь Ъ *)
Ш) R " Ш)
(продумайте этн вычисления!), откуда в пределе получаем
J /{Xt)dfL= J f(X\d]X: C1)
Ш) (М)
Но тогда и
[г
о
[
о J "о (A() (M)
и в пределе прн Т—>-оо приходим к C0). *
Смысл функции f(x) особенно нагляден в следующем случае.
Пусть (Л) — некоторое множество точек {М) и функция/(/1) (дг) опре-
определена так:
это—характеристическая функция множества (А). Тогда в силу B9)
Ал) (х) есть среднее время пребывания в множестве (А) траектории,
начинающейся в точке х, другими словами, вероятность попадания
в (А) точки, движущейся вдоль этой траектории.
Динамическая система называется эргодйческой, если инвариант-
инвариантными функциями в ней являются только константы (более точно,
если любая инвариантная функция почти всюду равна константе).
Для такой системы f(x) =/= const, а потому из C0) следует, чтр
т. е. / равно среднему значению функции f(x) по инвариантной

§ 2. АВТОНОМНЫЕ СИСТЕМЫ 551
мере \i. Формула B9) приобретает вид
о Ш)
другими словами, для почтм всех х временное среднее значение
функции равно ее фазовому (т. е. пространственному) среднему.
Это утверждение имеет весьма большое значение в физике (в осо-.
беннбсти в статистической механике), так как дает возможность
подсчитать плотность вероятности (ЛВМ, п. XVIIL8) пребывания
системы в определенном состоянии с помощью фазового осреднения.
Эргодические системы обладают следующим важным свойством
перемешивания, имеющим наглядное истолкование. Будем истолко-
истолковывать заданный поток как поток жидкости в фазовом пространстве
и допустим, что в момент времени t ¦= О жидкость в некоторой обла-
области (V) окрашена. Как распределится окрашенная порция жидкости
П?и t—»-оо; другими словами, если (А) — произвольное множество,
то как ведет себя |i((V)tnH)) при t—>оо (П—Знак общей части,
т. е. пересечения множеств, так что (V)tf\(A)— это порция окра-
окрашенной жидкости, попавшей в момент t в мысленно выделенный
объем (А))? Так как
о
то, умножая обе части на /(V) (x) и интегрируя по х, получим
т
? Ш /<л, (*t) Лv, W ^1 dt -— Ш ц (V). C2)
О L(Af) . J
Интеграл в квадратных скобках в силу формулы C1) равен
Jw>(*)/<v> (*-*)*!*• C3)
Ш)
Однако /(v) (x-t) есть характеристическая функция множества
(V)t, а потому интеграл C3) равен \i ((V)t П (А)) (продумайте это!).
Подставляя в C2), получаем окончательно
1 ГрЦУ
Г J у,
о
df 1Ш_
у, (А) "' г-» ц(Л1)-
о
Таким образом, среднее значение доли окрашенной жидкости в (А)
при большом Т приближенно равно ее доле в (М). При дополни-
дополнительных предположениях оказывается возможным доказать «переме-
шиваемость в сильном смысле», т. е. более сильное утверждение
ц [А)

552
ГЛ. VIII. ОБЫКНОВЕННЫЕ'ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Но как узнать, что заданная динамическая система эргодична?
К сожалению, простые достаточно широкие признаки этого пока
отсутствуют. Поэтому во многих физических исследованиях прихо-
приходится принимать это важное свойство лишь на основании отдален-
отдаленных аналогий, без достаточного обоснования.
¦ Разницу между эргоднческнмн н неэргодическими динамическими системами
легко понять на следующем простом примере. Рассмотрим автономную систему
ф1 = <а1, -ф2 = «>2, C4)
где щ и со2—постоянные, а координаты фх, ф2 имеют характер углов, так
что добавление к иим любых целых чисел не меняет точки многообразия, на
котором рассматривается поток; другими словами, система C4) рассматривается
Рис. 162.
на торе (п. 11), но ее можно изображать и на полной плоскости, считая отож-
отождествленными все квадраты 1X1 с целочисленными координатами вершин.
Очевидное интегрирование показывает, что траекториями на этой плоскости
служат прямые линии (рис. 161) и что площадь при сдвиге по траекториям
сохраняется, т. е. мы имеем динамическую систему. Имеется принципиальная
разница между случаями рационального н иррационального отношения <Bi/a>2.
В первом случае все траектории замкнутые и нетрудно построить инвариантную
функцию, отличную от константы: например, для <в1/<в2 = 3/2 можно взять
характеристическую функцию множества, заштрихованного на рис. 162 (про-
(проверьте!). Таким образом, этот случай не эргоднческий.
В отличие от этого, если ю1/ю2 иррационально, то все траектории незамкну-
незамкнутые. Можно доказать, что каждая такая траектория при своем безграничном
продолжении заполняет тор всюду плотно, т, е. проходит в любой близости
от любой его точки (но, конечно, не исчерпывает его, подобно тому как сово-
совокупность рациональных чисел на отрезке заполняет его всюду плотно, но не
исчерпывает его). Кстати, отсюда следует, что как омега-, так и альфа-пре-
дельиыми множествами любой траектории служит полный тор. Мы видим, что
любая кусочно-непрерывная инвариантная функция должна быть константой
(почему?). Это оказывается верным и для функций без требования кусочной
непрерывности, так что мы имеем эрг-одическую систему. (Проверьте, что пере-
мешиваемости в сильном смысле здесь ие будет.)
Легко проверить, что совокупность рациональных чисел на прямой имеет
меру нуль и, таким образом, иррациональные числа в определенном смысле
ивляются более типичными, чем рациональные. Поэтому и эргодический слу-
случай в рассматриваемом примере более типичен, чем неэргодический.

§ 3. УСТОЙЧИВОСТЬ РЕШЕНИЙ 553
В заключение отметим, что в приложениях к каноническим кон-
консервативным системам (п. VI.3.11) фазовое пространство обычно
бывает некомпактно; однако тогда все построения можно осущест-
осуществлять на компактном многообразии фазового пространства,
отвечающем заданному уровню полной энергии.
Математическое изложение эргодической теории можно найти
в книгах [122, 128].
§ 3. Устойчивость решений
В ЛВМ, п. XV.22, мы уже упоминали об одном из весьма важ-
важных понятий прикладной математики—устойчивости по Ляпунову.
Здесь мы рассмотрим это понятие, а также некоторые смежные
вопросы более подробно. Глубокое исследование различных вопро-
вопросов, связанных с устойчивостью решения дифференциальных урав-
уравнений, можно найти в ряде книг, в частности в [8, 60, 68, 82, 133J.
1. Введение. Рассмотрим систему уравнений
JV=/r/O'i. у* уа: 0 (/=1. 2. •••• «).
определенную на бесконечном интервале времени *0^/<оо. Как
и в § 2, мы будем пользоваться сокращенной записью
у = f cv. ty ' " (.и
Пусть начальным условиям t = t9, y—ya отвечает решение y=y(f)
(^0^^<оо), которое мы будем называть невозмущенным. Решения
y(t) той же системы A) при любых других начальных условиях
i = te, y—yB будем называть возмущенными. В классической поста-
постановке Ляпунова невозмущенное решение у (t) называется устойчивым,
если при бесконечно малом изменении начальных данных возмущен-
возмущенное решение остается в бесконечной близости от невозмущенного на
протяжении всего дальнейшего времени. Другими словами, это
означает, что
шах |у @—у @1 — 0 при |Уо_уо|-+О. B)
(Продумайте это определение; отметим, что здесь более точно пи-
писать sup, а ие max, так как наибольшее значение может дости-
достигаться только в пределе, на бесконечности). Если условие B) не
выполнено, то невозмущенное решение у (t) называется неустойчи-
неустойчивым по Ляпунову.
Уже сам Ляпунов отметил одио из видоизменений понятия устой-
устойчивости: он назвал решение у (t) асимптотически устойчивым, если
кроме B) дополнительно дано, что при достаточно малых | у0—уо|
будет обязательно у (t) — у (t)—>-0. Сейчас рассмотрен целый ряд
t

554* ГЛ. VI!!. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
других подобных видоизменений. Отметим, например, определение,
в котором возмущается не только начальное условие, но и сама си-
система уравнений, так что у (t) удовлетворяет системе уравнений вида
При этом y(t) называется устойчивым при постоянно действующих
возмущениях, если
max |у @ — у @1-*-0 при |у0 — уо| -> 0 и max] <p [у, t)\ ->-0.
tt < t < оо у, t
В реальных задачах возмущению системы A) может отвечать нало-
наложение да физическую систему неучитываемых малых внешних сил
на протяжении всего процесса движения. _ „,
Впрочем, можно показать, что во многих случаях нз асимптотической
устойчивости решения вытекает его устойчивость при постоянно действующих
возмущениях. Так будет, например, если функция F, а также решение не за-
зависят от / или периодичны по t с одинаковым периодом.
Обычно исследование устойчивости движения сводят к исследо-
исследованию устойчивости равновесия с помощью переноса начала коор-
координат в движущуюся точку, т. е. с помощью замены у =
После этой замены система A) перейдет в
i = y—y(O = F(* + y(O. О—У@,
или, короче, в
x = f(*, t), C)
а иевозмущеиное решение—в тождественно*нулевое. Обращаем
внимание на то, что даже если исходная система A) была авто-
автономной, т. е. правая часть не содержала t, то система C) все равно
будет неавтономной, за исключением того случая, когда изучается
устойчивость состояния равновесия (т. е. у (t) = const) автономной
системы. Полезно заметить также, что если невозмущенное решение
у (t) было ю-периодическим, а система A) автономная или ю-перио-
дическая, то и система C) будет ш-периодической.
Впредь мы будем рассматривать систему C) с нулевым невоз-
невозмущенным решением.
Бывают случаи, когда нас интересует не малость всех компонент возму-
возмущенного решения, а малость некоторых из них или некоторых их комбинаций,
или, в общем случае, некоторых функционалов от решения. Например,убывает
полезно знать, что скорость системы остается малой, хотя координаты могут и
возрастать, или что мал интеграл от квадрата отклонения координат, и т. п.
В этом случае говорят об устойчивости относительно выбранных комбинаций
или функционалов.
Иногда рассматриваются не произвольные возмущення начальных условий,
а только связанные определенными соотношениями; в этом случае говорят об
устойчивости относительно выбранного класса возмущений.

§-3. УСТОЙЧИВОСТЬ РЕШЕНИЙ
555
2. Уравнения первого порядка. Вопрос об устойчивости реше-
няя уравнения первого порядка обычно решается до конца без
привлечения общей теории. Рассмотрим сначала уравнение
*='/<*)
D)
и допустим, что оно имеет тождественно нулевое решение; это
знаяит, что /@) = 0. Устойчивость этого решения зависит от знака
f(x) при х, близких к нулю.
Допустим, что когда х, возрастая, переходит через нуль, функ-
функция f(x) меняет свой знак с + на —. Так как изоклинами урав-
уравнения D) служат прямые х = const, то получается картина распо-
расположения интегральных кривых, как на рис. 163. Ясно, что решение
х
¦ '////// //// IT/
Рис. 163.
является асимптотически устойчивым. Скорость стремления
)*0 легко определить, так как уравнение D) просто интегри-
/ -*¦ 00
руется, она зависит от скорости стремления /(*) —>-0. (Проверьте,
что в основном случае, когда f(x)~kx, k < 0, решение x(t)
стремится к нулю со скоростью экспоненты, а при |/(лг) | ~ |kx\m,
да>1— только со степенной скоростью.)
При любой другой комбинации знаков f(x) при малых |лг| ре-
решение хнэ 0 будет неустойчивым (почему?).
Применим полученный результат к уравнению, содержащему параметр
считая для простоты функцию / непрерывной. Пусть, например, линия (L):
/ = 0 в плоскости к, х и распределение знаков / такое, как показано на рис. 164.
Тогда при каждом фиксированном А, направление изменения х показано на
рис. 164 стрелками. Отсюда легко указать участки (L), которым отвечают
устойчивые положения равновесия; на рис. 164 эти участки показаны более
жирно. Мы видим, что при к < X,! и при % > Х2 имеется одно устойчивое по-
положение равновесия, а при ^ < к < Х2—два устойчивых и одно неустойчивое;

556
ГЛ. V1I1. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
при Х = 1к1 и Х=Х2 происходит бифуркация. Наличие такого интервала трех-
значности влечет за собой интересное явление перескока при изменении пара-
параметра Я, показанное на рис. 164. Прн медленном (чтобы процесс в каждый
момент можно было считать установившимся—такие процессы называются
квазистатическими) увеличении X до значения Х2 абсцисса положения равно-
месия непрерывно возрастает до xlf однако затем она совершает скачок до хг,
после чего продолжает непрерывно возрастать. При изменении X в обратном
направлении х непрерывно изменяется до значения х3, после чего совершает
перескок до xt. Таким образом,
при изменении параметра X в раз-
различных направлениях надо поль-
пользоваться различными ветвями ли-
линии (L); это явление называется
гистерезисом, а фигура на рис. 164,
ограниченная точками с ординатами
хи х2, xs, xt, называется петлей
гистерезиса. Неустойчивый участок
линии (L) при этом совсем не ис-
используется.
Рассмотрим теперь урав-
уравнение
* = /(*, О,
где /(О, *) = 0, т. е. нулевая
функция служит решением, а
Рис. 164. знак /(х, t) при малых \х\,
как и раньше, противополо-
противоположен знаку х. Тогда поле направлений будет примерно такое же,
как на рис. 163, т. е. нулевое решение и здесь будет устойчивым;
однако если поле при t —»- оо становится слишком пологим, то воз-
возмущенные решения могут асимптотически не достичь нуля; тогда
устойчивость будет неасимптотической. Рассмотрим типичный пример
Интегрируя, получаем
Значит, если С ф (t) dt — — оо, то устойчивость будет асимптоти-
асимптотической, в противном случае—неасимптотической (продумайте это!).
3. Метод функций Ляпунова. Перейдем теперь к автономной
системе
x = f(*), E)
где f @) = 0, т. е. функция х==0 служит решением, которое мы и
примем за ненозмущенное. Метод функций Ляпунова, получивший
и последние годы широкое распространение в теории устойчивости
и в смежных вопросах, имеет непосредственную механическую ана-

§ 3. УСТОЙЧИВОСТЬ РЕШЕНИЙ
557
логию, которую мы поясним на примере колебаний линейного осцил-
осциллятора с одной степенью свободы. Уравнение этих колебаний
(ЛВМ, (XV.115)) после перехода к фазовой плоскости приобретает
вид системы
хх — хг, х2 = — (&1х1—2кхг. F)
Легко проверить, что полная энергия осциллятора, с точностью ядо
коэффициента пропорциональности, равна (ЛВМ, (XV.72))
G)
и потому имеет в состоянии равновесия х±=х2 = 0 минимальное
значение; линии Е= const на фазовой плоскости показаны на рис. 165.
Однако при наличии трения, т. е.
при h > О, полная энергия в про-
процессе колебаний должна убывать; это
нетрудно доказать и формально:
X,
¦21 ,
Ё =
^ + 2х2х2 —
— 2hx2) =
= — Ahx\ < 0. (8)
2х2 ( —о
рис
Таким образом, линии равной
полной энергии на фазовой плоско-
плоскости пересекаются траекториями сна-
снаружи внутрь, откуда видно, что
рассматриваемое состояние равновесия будет асимптотически устой-
устойчивым. Если й = 0, т. е. когда трение отсутствует, будет Е — const.
Движение в фазовой плоскости будет происходить по эллипсам
рис. 165, т. е. получится неасимптотическая устойчивость. Наконец,
если А < 0 (такое отрицательное трение • возможно для систем с
подкачкой энергии), то Ё > 0, эллипсы будут пересекаться изнутри
наружу, т. е. будет неустойчивость.
В этих рассуждениях не так уж было важно, что Б пропорцио-
пропорционально полной энергии, существенны только поведение функции
Е(х1У х2) в окрестности положения равновесия (минимум), а также
характер изменения этой функции вдоль траекторий (убывает, воз-
возрастает). Поэтому, обобщая проведенные рассуждения и возвращаясь
к системе E), мы приходим к следующей осиовной теореме Ляпунова
об устойчивости. Пусть в некоторой окрестности точки х = О суще-
существует непрерывная функция V (х), для которой V @) =0, V (х) > О
{х^1=0) (такие функции по аналогии с квадратичными формами будем
называть положительно определенными) и
Тогда невозмущенное решение лг='О является устойчивым.

558 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Для доказательства этого наглядного утверждения допустим, что
нам задано какое-либо малое число е > 0. Тогда функция V (х),
непрерывная и положительная на сфере E), с центром х = 0 ра-
радиуса е, имеет там (строго) положительное наименьшее значение /и,.
Выберем теперь столь малую сферу E)г, чтобы внутри нее было
V(x)<.mt. Тогда если |xo|<fi, т. е. траектория начинается Внутри
{S)i, то в силу условия (9) она навсегда останется внутри E),
(почему); а это н означает устойчивость.
Конечно, в теореме об устойчивости можно было бы поменять
знак у V, т.' е. считать, что V(x)<Z.O, V(x)^Q. Это замечание от-
относится и к дальнейшим теоремам.
Небольшое изменение этого рассуждения, которое мы здесь не
будем проводить, показывает, что если условие (9) заменить на более
сильное требование отрицательной определенности функции V(x), то
решение х = 0 будет асимптотически устойчивым. Условие (9) не
гарантирует асимптотической устойчивости, так как оно не исклю-
исключает того, что вдоль некоторых траекторий будет У==0, т. е.
V= const, а такие траектории не могут входить в точку х = 0.
Однако если в дополнение к (9) потребовать, чтобы многообразие,
на котором V=0, при х^=0 не содержало целых дуг траекторий,
то такое -явление исключено, и решение л: = 0 будет асимптотически
устойчивым. Это небольшое полезное замечание применимо, в част-
частности, к примеру F)—(8) при h > D, так как в этом примере Е не
является отрицательно определенной, однако она обращается в нуль
только на прямой х2 — 0, rfe содержащей целых дуг траекторий
(почему?).
Если функция Ляпунова V (х) строится нелокально, то оиа может выявить
большую или меньшую часть зоны притяжения устойчивого решеиия. Допустим,
например, что эта фуикция задана во всем пространстве х (аналогичио рассмат-
рассматривается случай функции, заданной в области конечных, не малых размеров)
и множество, на котором V=0, не содержит при f (*) ф 0 целых траекторий.
Тогда, если V (х) имеет при *=0 минимум, то отвечающая ему яма (п. VI.3.13)
целиком принадлежит зоне притяжения решения jcs=0, хотя, вообще говоря,
не исчерпывает ее. Если же дополнительно даио, что х=0 служит единственной
точкой покоя системы E) н У (оо) = оо, то все ее траектории при t —*- оо входят
а точку *=0; тогда решение joO называется асимптотически устойчивым
в целом.
Для неустойчивости решения лг=О достаточно существование
в окрестности точки х — 0 функции V(x), принимающей положитель-
положительные значения в любой близости от х = 0, причем функция V (х) поло-
положительна всюду, где V (х) > 0. В самом деле, пусть функция V
положительна в области, заштрихованной на рис. 166, где E) —
окружность фиксированного малого радиуса. Тогда для любой как
угодно близкой к нулю начальной точки х0 в этой области значе-
значение V (х) вдоль траектории, начинающейся в х0, будет возрастать*

§ 3. УСТОЙЧИВОСТЬ РЕШЕНИЙ
559
Поэтому такая траектория не может слишком близко подойти к
границе заштрихованной области, где V= 0; но тогда вдоль этой
траектории min F> 0, а потому она в конечное время обязана выйти
на E), что н означает неустойчивость (продумайте это рассуждение!).
Приведенная теорема, обобщающая аналогичные результаты Ляпу-
Ляпунова, указана в 1934 г. советским механиком Н. Г. Четаевым
A902—1959).
Как и раньше, здесь можно допустить, чтобы V=0 где-нибудь
при V > 0, если многообразие таких точек не содержит целых дуг
траекторий. Отметим, что это
полезное добавление, как и мно-
многие другие обобщения и обраще-
обращения теорем Ляпунова, принадле-
принадлежит советскому математику и
механику Н. Н. Красовскому (р.
в 1924 г.) [60].
При рассмотрении неавтоном-
неавтономных систем C), а также функций
Ляпунова вида V(x, t) приведен-
приведенные теоремы и их доказательства
остаются справедливыми, если
сделать к ним необходимые уточ-
уточнения. Так, в теореме об устой- рис J66.
чнвости надо пользоваться по-
положительно определенной функцией V(x, t), понимая под этим, что
V(x, t)^ V1(x), где функция Vt {x) положительно определенная.
(Таким образом, например, функция |х| A -^-г'а)~1 положительная, но
не положительно определенная.) Конечно, V вычисляется теперь по
формуле V(x, t) = V't + grad V (x, t)-f(x, t). В теореме об асимпто-
асимптотической устойчивости надо добавить условие
4 maxV(.*:, t) —>¦ 0
t x-+0
(этим исключается, например, функция ^|л:|). В теореме о неустой-
неустойчивости надо дополнительно потребовать, чтобы в каждой области,
где V превосходит какую-либо положительную постоянную, функ-
функция V также превосходила некоторую положительную постоянную.
При зависимости участвующих функций от t может оказаться, что и усло-
условия теорем Ляпунова выполняются только при t^tlt где tt > tt. Тогда надо
иметь в виду, что такие локальные (по х) свойства, как устойчивость, неустой-
неустойчивость, асимптотическая устойчивость, не зависят от значения t, при котором
задаются начальные условия, так как при малом |х(Л>)| будет мало и |x(fj)|
(и обратно). Нелокальные свойства, такие, как асимптотическая устойчи-
устойчивость в целом, могут зависеть от выбора начального значения t (продумай-
(продумайте это!). ' • ¦

560 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Некоторые авторы, следуя Ляпунову, называют метод выяснения
устойчивости и неустойчивости на основе применения функций Ля-
Ляпунова вторым методом, в отличие от первого метода, основанного
иа непосредственном построении решения) обычно в виде сумм тех
или иных рядов. Теперь обычно методы изучения свойств решений,
обходящиеся без точного построения этих решений, называют ка-
качественными.
Примеры на применение теорем Ляпунова будут даны позже.
В последние годы в ряде работ были исследованы системы урав-
уравнений, обладающие свойствами устойчивости в целом, т. е. для
всех решений. Приведем простейший результат в этом направлении.
Пусть правая часть 'системы C) для всех значений аргументов
удовлетворяет неравенству
¦- (f(*. t) — t(y, *))•(» —УК О
Тогда для любых двух ее различных решений х(^) и у (t)
(|x-y|2)- = [(x-y).(x-y)]'==2(f(A;, t)-f(y, /))•(»—у)< О,
т. е. любые два таких решения с ростом t сближаются друг с'дру-
гом. См. по этому поводу книгу [55].
4. Устойчивость по первому приближению. Так как при иссле-
исследовании устойчивости нулевого решения системы C) рассматриваются
лишь малые х, то естественно произвести разложение правой части
в ряд по степеням Xj, что даст
, t) (а(/)=(|)х=0), A0)
где ф объединяет члены выше первого порядка малости по х, а
затем перейти к системе первого приближения
х = А(/)х. - A1)
Мы будем для простоты предполагать, что в уравнении A0)
<f(x, t) = o(\x\), т. е. ф имеет порядок малости выше первого рав-
иомерио по /. (Тем самым не допускаются члены вида trf, коэффи-
коэффициенты при которых безгранично нарастают во времени.) Если для
любых таких добавок ф нулевое решение системы A0) будет устой-
устойчивым, то решение xs=0 системы C) называется устойчивым по
первому приближению; аналогично для неустойчивости.
Система A1) линейная; поэтому из формулы A.10) вытекает, что
для устойчивости ее нулевого решения необходимо и достаточно, чтобы
все ее решения были ограниченными при /¦—> <»; для асимптотической
устойчивости необходимо и достаточно, чтобы все решения стремились
к нулю при t —*¦ оо (докажите!). Отметим, что для лииейиых систем,
в отличие от нелинейных, из устойчивости одного решения вытекает
устойчивость любого другого, поэтому можно просто говорить об

§ 3. УСТОЙЧИВОСТЬ РЕШЕНИЙ 561
устойчивой системе уравнений; аналогично для асимптотической
устойчивости и неустойчивости.
Более прост случай, ког*да матрица A — A(t) постоянная. Тогда
в силу конца п. 1.1 для асимптотической устойчивости системы A1)
необходимо и достаточно, чтобы все корни характеристического
уравнения
det(A—XI) = О - A2)
имели отрицательную вещественную часть. (При этом скорость стрем-
стремления общего решения к нулю при t—>¦ оо, т. е. степень устойчиво-
устойчивости, определяется наибольшей из этих вещественных частей). Можно
показать, что в этом случае и решение х = 0 системы A0) асимп-
асимптотически устойчиво.
Мы не будем проводить доказательство в полном объеме, а ограничимся
случаем, когда все корнн уравнения A2) вещественные и различные. Так как
после подстановки х=Ну система х = Ах преобразуется в Ну=АНу, т. е.
у=Н~1АНу, то всегда можно выполнить подстановку так, что у полученной
системы матрица коэффициентов будет диагональной, равной diag (Aj, Яг А„).
Допустим, что такая замена уже произведена, так что система A1) диагоиаль-
иая, и положим
2iM /
(Напомним, что все "kj < 0.) Это функция положительно определенная. В то же
время, вычисляя полную производную в силу системы A0), получим (про-
(проверьте!)
У=— 2 (Ах, х)=—2(А2х, х)+о(|х|2)=
2
Тем самым выполняются условия теоремы Липунова об асимптотической устой-
устойчивости, откуда и вытекает наше утверждение.
В случае мнимых корней характеристического уравнения часто применяются
линейные преобразования, приводящие к комплексным искомым функциям.
Например, система уравнений
*i = № + v*2. *а—— v*i + !x*2) x3=Xxa + (f(x1) A3)
после замены
Z1=X1 + iXt, 22=*! — 1Х2, Z3=X3,
т. е.
переходит в систему (проверьте!)
где функции Zy (t) уже принимают комплексные значения. К системе вида A5)
возможен двоякий подход. Иногда удобно считать г,- произвольными комплекс-
комплексными величинами. Тогда функция Ляпунова V (г) должна принимать вещест-
вещественные значения' для всех комплексных г, например она может иметь вид
эрмитовой формы

562 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
откуда
Ясно, что если будет доказана устойчивость или асимптотическая устойчивость
нулевого решения системы A5), то это же верно и для системы A3); неустой-
неустойчивость для системы A5) требует при переходе к A3) некоторого рассуждения,
так как «уходящим» от точки г=0 решениям второй системы не обязаны отве-
отвечать вещественные решения первой. Возможен и иной подход, когда
рассматриваются только такие значения z, которым отвечают вещественные х;
для формул A4) это означает, что гх н г2 должны быть сопряженными, а г3
вещественным. Такой подход, в частности, необходим, если функция ф по
своему смыслу определена лишь для вещественных значений аргумента. При
втором подходе функция Ляпунова должна быть вещественной только для
указанных значений г, ее можно даже считать определенной только для
этих г, а понятия устойчивости и неустойчивости для исходной н преобразо-
преобразованной систем совпадают. Полезно иметь при этом в виду, что если начальным
значениям г отвечают вещественные х, то и все решение г (t) системы A5)
обладает этим свойством (почему?)
Описанное выше построение функции Ляпунова неудобно на практике,
так как приведение матрицы к диагональному виду требует решения уравне-
уравнения A2). Можно применить следующий прием: зададим произвольную симмет-
симметрическую матрицу С и покажем, что с помощью решения системы линейных
уравнений- можно подобрать симметрнческую матрицу U, для которой
(Ux, х)' ее (Сх, х) ' A6)
(производная берется в силу системы х=Ах, которая предполагается асимпто-
асимптотически устойчивой). В самом деле, равенство A6) можно переписать в виде
2 (UAx, x)»(Сх, х). A7)
Если это равенство переписать в скалярной форме и приравнять коэффициенты
при одинаковых членах XjX^, то мы получим систему из N=n (п-{-1)/2 урав-
уравнений 1-й степени с N неизвестными элементами матрицы U (что за число Л'?).
Для разрешимости такой системы необходимо и достаточно, чтобы соответст-
соответствующая однородная система имела только тривиальное решение. Но если бы
при С=0 существовало решение U Ф О, то из A6) следовало бы, что для лю-
любого решения x(t) будет (Ux, x)=const, а это противоречит асимптотической
устойчивости (почему?).
Итак, возможность (кстати, и единственность) подбора матрицы U доказана.
В частности, если выбрать форму (Сх, х) положительно определенной, то из
асимптотической устойчивости системы х=Ах вытекает, что форма (Ux, x)
будет отрицательно определенной. В самом деле, в силу теоремы п.З о неустой-
неустойчивости функция V {*)=(Ux, x) не может принимать положительных значений.
Но тогда н значение V (х)=0 (х ф 0) невозможно, так как V (х) > 0. Значит,
функцию V (х) можно принять за функцию Ляпунова.
Отметим попутно, что так как (UAx, x)=(A*Ux, x) (почему?), то равен-
равенство A7) можно переписать в виде ((UA+A*U)x, x) = (Cx, х), а так как мат-
матрица UA+A*U симметрическая,—то и в виде
UA + A*U=C. ' A8)
Таким образом, доказана однозначная симметрическая разрешимость матрич-
матричного уравнения A8) для любой матрицы А с устойчивым характеристическим
полиномом и любой симметрической, матрицы С; при этом, если матрица С по-
положительно определенная, то U—отрицательно определенная н обратно.
Доказанная возможность построения формы (Ux, x) является частным слу-
случаем 'значительно более общей теоремы Ляпунова о том, что уравнение
lUm(x)']—Cm(x), где Ст{х)—заданная форма m-й степени, а 11т(х) — нско-

§ 3. УСТОЙЧИВОСТЬ РЕШЕНИЙ 563
мая форма той же степени, однозначно разрешимо тогда и только тогда, когда
никакая сумма из т собственных значений (быть может, повторяющихся) мат-
матрицы А не равна нулю.
" Описанное построение матрицы U применяется, в частности, при выводе
достаточных услоний асимптотической устойчивости и целом линейных систем,
возмущенных малыми нелинейными добавками. Пусть рассматрннается
система
x=Ax+t|j(*)x, A9)
причем система х=Ах асимптотически устойчива. Зададимся отрицательно
определённой формой (Сх, х) и построим положительно определенную форму
(Ux, x), производная которой в силу последней системы равна (Сх, х). Тогда
произнодная в силу A9) равна
. (Ux, X)' = (Сх, х) + 2 (Ux, f (x) x).
Если праная часть при любом «замороженном» значении if представляет собой
отрицательно определенную квадратичную форму (это можно проверить по
признаку Снльнестра), то нуленое решение системы A9) будет .асимптотически
устойчнным н целом.
Аналогично локазынается, что если хотя бы один корень уран-
нения A2) имеет положительную вещестненную часть, то решение
х==0 системы A0) неустойчиво. Случаи, когда уранненне A2) не
'имеет корней с положительной вещестненной частью, но имеет по
крайней мере одни корень с нулевой вещестненной частью, янляют-
ся особыми {критическими); для линейной системы необходимое и
достаточное условие устойчиности формулируется в терминах жор-
дановых клеток (п. 1.1), а на устойчивость для полной системы A0)
может оказать существенное влияние вид функции ф (п. 5).
Проверка знаков иещественных частей корней ураинения A2)
осуществляется по методам п. Н.3.10.
Аналогично рассматривается случай периодической матрицы
A{t): именно, если модули всех мультипликаторов системы A1)
меньше единицы, то решение х = 0 системы A0) асимптотически
устойчиво по первому приближению, если же хоть одни из этих
модулей больше единицы,—оно неустойчиво. Этот факт немедленно
вытекает из показанной в п. 1.2. возможности приведения линейной
периодической системы к системе с постоянными коэффициентами.
Для распознавания асимптотической устойчивости можно применить
методы п. Н.3.10 к логарифму матрицы монодромии (п. i.2). Но
' так как эта матрица находится, вообще говоря, с помощью числен-
численного интегриронаиия, то в конкретных числовых примерах факт
устойчивости-или неустойчивости периодической системы A1) можно
выяснить без всякой «науки», с помощью численного интегрирова-
интегрирования системы на протяжении нескольких периодов при случайно вы-
выбранных начальных данных. Рост или убывание полученного реше-
решения по модулю будут определяться наибольшим нз модулей муль-
мультипликаторов, для уверенности можно перепробовать несколько
вариантов начальных данных.

564
ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
X.
Для матричных коэффициентов A (t), отличных от рассмотренных здесь, а
также в пп. 1.8, 9, эффективные аналитические критерии устойчивости отсут-
отсутствуют. В конкретных примерах можно применить вычислительный экспери-
эксперимент, проводя численное интегрирование системы при случайно выбираемых
начальных данных на отрезке, длину которого можно считать достаточной для
выявления устойчивости или неустойчивости. (Так как решение скалярного
.уравнения х~ах меняется в 10 раз на отрезке Д<==1п 10/ | а | = 2,3/| а |, то и в
общем случае длину интервала интегрирования нужно взять по крайней мере
в несколько раз больше обратной величины наибольшей нз абсолютных вели-
величин коэффициентов системы.) За поведением решения на шкале экспонент можно
проследить, вычисляя значение — In ] x (t) | по ходу численного интегрирования.
Если решения системы A1) будут экспоненциально затухающими (возрастаю-
(возрастающими), то решение х = 0 системы A0) будет асимптотически устойчивым (соот-
(соответственно неустойчивым).
Следует предостеречь против бездумного применения метода заморажива-
замораживания, который состоит в заключении о поведении решений системы A1) на осно-
основании поведении решений систем, с замороженными коэффициентами вида
х=А(т)х при любом зафиксированном значении т: асимптотическая
устойчивость замороженных систем в общем
случае ни необходима, ни достаточна для
асимптотической устойчивости системы A1).
Чтобы понять это, допустим,. что п = 2 и
при каждом т замороженная система имеет
при ж=0 устойчивый фокус (рис. 167), одна-
однако с изменением т изображенная картина
поворачиваетси вокруг точки х=0. Хотя
малый участок решения x(t) системы A1)
при f=T следует участку замороженной
системы, но в следующий момент надо поль-
пользоваться повернутой замороженной системой
и т. д.; при' этом х (t) может, как на рис.
167, все дальше и дальше отходить от на-
начала координат, т. е. получится неустойчи-
неустойчивость. Для возможности- перехода от за-
замороженных систем к размороженной тре-
требуются дополнительные условия, которые
мы здесь не будем рассматривать.
б. Особые случаи. Мы уже упомянули в п. 4 об особых случаях, когда
выиснение устойчивости нулевого решения системы A0) по анализу системы
первого приближения A1) с постоянной или периодической матрицей А (/) ста-
становится невозможным. Уже Ляпунов подробно исследовал случай одного нуле-
нулевого или двух чисто мнимых сопряженных корней характеристического уравне-
уравнения; с тех пор исследованы и некоторые другие случаи. Эти исследования
довольно громоздки, и здесь мы для примера рассмотрим только простейший
случай одного нулевого корня при и = 2.
Рассмотрим систему уравнений
Рис. 167.
, у), y=
, у),
B0)
где разложения q> и ф содержат только члены выше первого порядка малости;
допустим, что характеристическое уравнение для системы первого приближения
имеет один нулевой и один отрицательный корни. Тогда, как в начале петита
п. 4, можно перейти к системе
B1)

§ 3. УСТОЙЧИВОСТЬ РЕШЕНИЙ ¦ 565
Нам понадобится еще одна замена. Так как для уравнения
tyi~btyi(xi>yi)—Q B2)
удовлетворяется условие существования неявной функции (II.2.26), то из него
можно найти yi=/(JCi) в виде суммы ряда, причем без линейных членов (по-
(почему?). После обозначения
из B1) получаем систему
|=Ф(|, г)), т)=Хт) + ЧГ(?, ц) ' B4)
(проверьте!), где обозначено
ЧГ (I, 4) = *, (I, г) + / (Б))-*! E, / (|))-/' (|) ф1 (?, г, + / О). B5)
Разложим
тогда из B5) видно, что разложение ЧГ»(?)=ЧГ(|, 0) начинается с более высо-
высоких членов, чем у Фв (|); для этого и понадобилась замена B3). Оказывается,
что характер устойчивости нулевого решения системы B4), а потому и B0)
определяется видом первого члена разложения функции Фв(|).
Допустим сначала, что
Фо (|) = а|2 + члены высшего порядка (а ф 0),
и выберем функцию Ляпунова в виде
V& r))=i+*ir) + /if, B7)
где коэффициенты />, / подберем позже. Так как в силу B6)
"Ф(|, t]) = а|2 + Pit) +-ут)8 + члены высшего порядка,
то из B7) и B4) получаем
1/=ое|2 + Р?т|-|-уп2 + ^'ПЧХ/т)г + члены высшего порядка.
Значит, если положить ft= — р/А,, /=(а—y)J2K то мы получим, что
1/=а(|г + тJ). Но тогда можно применить теорему п. 3 о неустойчивости
(с точностью до знака функции V), т. е. нулевое решение системы B0) в рас-
рассматриваемом варианте неустойчивое.
Тот же результат с помощью немного более громоздкой конструкции по-
получится н в общем случае, если разложение функции Фо (|) 4 начинается
с четной степени ?•
Допустим теперь, что разложение функции Фо (Q начинается с третьей
степени ?; тогда можно написать:
Выберем функцию Ляпунова в виде
^ : B8)
При вычислении V будем выписывать только члены порядка малости, ие выс-
высшего чем |4 нлн т)г. Получим (проверьте!)

56»
гл. viii. Обыкновенные дифференциальные уравнения
Значит, если положить кг=—РД, fts = — (Y+ftie)A> 1 = л/2\, то получим
Значит, если а < 0, то в силу п. 3 нулевое решение системы B0) будет асимп-
асимптотически устойчивым; если же а > 0, то оно будет неустойчивым. Тот же
результат получается, если разложение функции Фо (?) начинается с любой
нечетной степени |.
Пусть, наконец, ФО(?) = О; тогда и Wt(%)^0, и система B4) приобре-
приобретает вид
? = Ф1 (?) Ц + Фа(?I2+'"' 'П:==^Т1 + ЧГ1© T) + ?S ($) ТJ + ... ^gg»
(Ф1(О)=чг1(о)=о). l ;
Эта система удовлетворяется, если положить ?=const, т) = 0; таким образом,
в плоскости |; т| получается целая прямая положений равновесия. Из C0) при
г) ф 0 получаем уравнение
йц
6=1D).
C1)
для которого начало координат служит обыкновенной (ие особой) точкой. Значит,
траектории системы C0) идут по интегральным кривым уравнения C1). Но из
второго уравнения C0) видно, что направле-
направление движения по траекториям такое, как
показано на рис. 168. Поэтому нулевое ре-
решение является в данном случае неасимпто-
неасимптотически устойчивым; ось %, т. е. линия B2),
образует зону нечувствительности (п. 2.10).
\" у ^^Ji^s / Исследование особых случаев имеет
>^ jf / / важное применение к выяснению опасных и
'—^^* '**^—* *—*- безопасных участков границы области устой-
устойчивости системы, зависящей от параметров.
Пусть, например, рассматривается система
вида B0) с одним параметром, т. е.
x=a(s)x+b(s)y-\-<p(x, у; s),
у=с (s) x+d (s) у+$ (х, у; s)
Рис. 168. (случай любого числа переменных и пара-
параметров рассматривается аналогично), и пусть
при переходе s через некоторое значение se один из двух отрицательных
корней характеристического уравнения становится положительным, так что
область устойчивости (на оси параметра) расположена только при s < se. Если
коэффициенты зависят от параметра иепрерывно, то и корни изменяются непре-
непрерывно, так что при *s=s0 мы имеем как раз случай одного нулевого корня,
разобранный выше.
Допустим, что при s—s0 нулевое решение является асимптотически устой-
устойчивым; мы видели (на примере Фо (|) ~ а|3), что тогда можно построить поло-
положительно определенную функцию Ляпунова B8), полная производная которой
B9) отрицательно определенная, чем и гарантируется асимптотическая устойчи-
устойчивость. Но что произойдет, если мы будем пользоваться той же функцией
Ляпунова, когда s немного превзойдет s0? Ясно, что функция V E, *)) проварь-
ируется мало, а потому она может стать положительной только в малой окрест-
окрестности начала координат. Поэтому картина пересечения траекториями линий
уровня функции V получается примерно такой, как иа рис. 169, т. е. только
самые близкие к началу линии уровня могут пересекаться траекториями изнутри
наружу. Это означает, что хоть нулевое решение теперь будет неустойчивым,
но решение, «сбившееся» с него, будет содержаться в его непосредственной

§ 3. УСТОЙЧИВОСТЬ РЕШЕНИЙ
567
близости. Типичная картина расположения траекторий после такой потери
устойчивости показана на рис. 170: бывший устойчивый узел превратился
в седло, в непосредственной близости которого образовалось два новых устой-
устойчивых ума. В аналогичном случае, при наличии иа границе устойчивости пары
чисто мнимых корней характеристического уравнения, типичная картина траек-
траекторий сразу-после перехода этой границы будет, как иа рис. 171: устойчивый
Рис. 169.
Рис 170.
фокус превратился в неустойчивый и из него выделился маленький устойчивый
предельный цикл, на который и накручиваются траектории, пришедшие издалека.
В разобранных случаях граница s0 области устойчивости называется без-
опасной, так как небольшой переход через нее не уводит далеко систему от
состояния равновесия, а только чуть-чуть «сваливает иа бок» или вызывает
колебания малой амплитуды. Так, на рис. 172 показано осевое сечеиие чашки
Рис. 171.
Рис.
со стержнем, поставленной на дно. Если высота' стержня s стаиовитси больше
высоты чашкн Н, вертикальное положение становится неустойчивым, однако
устойчивое (с точностью до поворотов) косое положение мало отличается от
вертикального. Впрочем, если параметр значительно перейдет даже через безо-
безопасную границу устойчивости, от этой устойчивости может ие остаться даже
следов. ..
Аналогично исследуется случай, когда при s=s0 нулевое решение оудет
неустойчивым. В этомслучае для s, немного меньших s0, нулевое решение будет

568
ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
формально устойчивым, но «запас устойчивости» будет весьма мал, так что
сколько-нибудь существенное возмущение начальных условий уводит решение
яалеко от нуля. Типичный фазовый портрет такого «слабо устойчивого» решения
в случае одного нулевого корня характеристического уравнения при s=su
показан на рис. 173; случай двух чисто мнимых корней получается из рис. 171,
если поменять направления стрелок на противоположные. Здесь граница s0
области устойчивости называется опасной. Пример устойчивого положения
вблизи опасной границы устойчивости
показан на рис. 174. При удалении
s от so(s<so) запас устойчивости,
вообще говоря, будет увеличиваться,
w т. е. система будет «укрепляться».
Рис. 173.
Рис. 174.
В конкретных примерах для выяснения характера устойчивости системы
на границе области устойчивости и тем самым для выявления опасных и без-
безопасных участков этой границы можно применить вычислительный эксперимент,
подобный описанному в п. 4.
Из особых случаев для периодических систем рассмотрим только наиболее
простое скалярное уравнение
(А-= 2, 3, 4, ...),
C2)
где все aj (t) — Г-периодические функции. Если
т
то все ясно: надо в уравнении C2) отбросить члены высшего порядка малости,
что даст
1 ' -*(*-!)/,
т. е.
Отсюда видно, что при четном k всегда будет неустойчивость, а при нечётном k
для / > 0 будет неустойчивость, а для / < 0—устойчивость. Если же /=0,
то начинают влиять члены высшего порядка малости. Чтобы разобрать и этот
случай, можно с помощью подстановки у=х-\-^^ (t) **+tyfc+1 (t)xk+1-\- ...
с периодическими коэффициентами привести уравнение C2) к виду i/=6fti/* +
+ ^*1+«" c постоянными IJii, bk+lt ... (При этом последовательно на-

§ 3. УСТОЙЧИВОСТЬ РЕШЕНИЙ 569
ходятся bk, ^ft(/), bk+1, iJ)A+1 (t), ,..; мы предоставляем желающим подробно
разобрать эту процедуру.) После такого преобразования устойчивость иулевого
решения определяется первым фактически присутствующим членом в правой
части.
К исследованию устойчивости нулевого решения уравнении вида C2)
сводится упомянутая в п. 2.4 проблема исследования точки покои на плоскости
в случае чисто мнимых корней характеристического уравнения. Как мы видели,
тогда система после аффинного преобразования плоскости приобретает вид
х'=ку' + М (*', у'), y' = -Xx' + N(x\ У),
функц
к по
•7f=
где разложения функций М и N содержат только члены выше первого порядка.
После перехода к полярным координатам р, ср на плоскости х', у' получаем
f (Pc°sq>,
§¦=- Я+ ^ [N (...) cos ф-М (...) sin q>],
откуда, деля первое уравнение на второе, мы получим относительно р (ф)
уравнение вида C2). (Разберите, что отсюда следует.)
По поводу дальнейших особых случаев см. [82].
6. Специальные классы механических систем. Рассмотрим
автономную потенциальную систему с конечным числом степеней
свободы и обобщенными координатами qlt дг, ..., qn вблизи поло-
положения равновесия, за которое мы примем начало координат. Кине-
Кинетическая энергия T(q, q) представляет собой положительно опреде-
определенную квадратичную форму относительно qlt q2,..., qn, тогда как
потенциальная энергия U{q) имеет при q= 0 стационарную точку.
Канонические уравнения движения (§ VI. 3) имеют вид
dpj дН dq,- дН
~df=~'dq~j> ~Ж = ~др}'
где
dJ^B = f. C3)
d
Имеет место закон сохранения энергии: вдоль любого решения
Н = const.
Из сказанного сразу вытекает теорема Лагранжа: если U(q) имеет
при q = 0 минимум (изолированный, т. е. строгий), то состояние
равновесия q =р = 0 будет устойчивым. В самом деле, в этом случае
можно принять Н(р, q) за функцию Ляпунова и применить теорему
об устойчивости п. 3. Если же минимум U{q) не изолированный
и достигается на некотором многообразии (М), то легко проверить,
что состояние равновесия будет устойчивым лишь относительно
импульсов, тогда как конечные перемещения вдоль М могут быть
вызваны как угодно малыми возмущениями начальных данных.

570 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Для дальнейшего запишем главные части кинетической и потен-
потенциальной энергий в окрестности положения равновесия 0 = 0:
T(q, q) = у 2 А/н (Я) kflk =уЕ Wjik + ° 0) 1<*11
(а/к = А/к@)),
Если совершить линейную замену координат q = Hrj, то q = Hrj,
т. е. обе квадратичные формы преобразуются одной и той же мат-
матрицей Н. Но так как первая форма положительно определенная,
то в силу п. IV.2.4 матрицу Н всегда можно подобрать так, что
в новых координатах главные части энергий примут вид
причем сигнатура последней квадратичной формы такая же, как
формы (Bq, q), a jx,- представляют собой собственные значения
матрицы А-1В. Эти новые координаты называются нормальными.
В нормальных координатах уравнения движения C3) после линеа-
линеаризации имеют весьма простой вид
йЪ dri i
Tt = ~ № Ж = Ь (у = 1, 2, .... л) C4)
(в данном случае обобщенный импульс |у- с точностью до малых
высшего порядка совпадает с т];). Чтобы раскрыть характеристиче-
характеристический определитель, удобно искомые функции перенумеровать в по-
порядке |1( т]„ |21 г\2, ... Корни характеристического уравнения ока-
оказываются равными ±V—цх, ±У—ц2, ..., ± V—Цп (проверьте!).
Применяя вывод, сделанный во втором абзаце этого пункта, а также
результаты п. 4, получаем:
если все \ij > 0, то рассматриваемое состояние равновесия устой-
устойчивое; если хотя бы одно \ij < 0, то это -состояние неустойчивое.
(Можно доказать, что вообще, если U(q) не имеет при ^ = 0
минимума, хотя бы нестрогого, то положение # = 0 неустойчивое.)
Так как положительность всех \ij равносильна положительной оп-
определенности, то к выяснению этого факта можно применить кри-
критерий Сильвестра (п. IV.2.3).
Если какое-либо }xf > 0, то решение системы C4)
r\i=:M sin (Yy-it+4>)> прочие т)у = О (/ ф 0)
определяет нормальное колебание рассматриваемой линеаризованной системы.
В исходных координатах нормальное колебание описывается формулами
(/=1.2, ...,п),
т. е. это одночастотное, иначе, собственное колебание. (Если несколько собст-
собственных частот совпадают, то выбор соответствующих нормальных координат ие

§ 3. УСТОЙЧИВОСТЬ РЕШЕНИЙ
571
определен однозначно, а когда такой выбор сделай, класс собственных колебаний
оказывается формально шире класса нормальных колебаний. Почему?) Подстав-
Подставляя в уравнения движения
/ = 1.2,...,/»),
или короче,
дол-
долвыражение q = Mh/sin (}^ц^ + ф) для решения, получаем, что вектор
жен удовлетворять соотношению
< (fija—b)hj=O, т. е. (а~хЬ) h/=fxzh/.
Из определения нормальных координат, в силу которого
H*aH = I, H*bH = diag(ni, ц ц„),
легко вывести (как?), что
(ah;, hk) = 6/k, (bh/r hft)=0 []ФЩ, (bh/( Ъ,)=рр ' C5)
(Отсюда, между прочим, по образцу п. IV. 1.7 можно развить экстремальную
теорию собственных частот: так, [ilt наибольшее из цу, равно max ((bh, h)/(ah, h)),
h
для отыскания следующего надо добавить условие (ah, h1)=0 и т. д.) Общее
колебание в рассматриваемой системе есть сумма нормальных колебаний:
л
q =? 2 4/@. где Ч/ @ = Mfhj sin (У~\С/ < + фу),
/=•
а все Mj, ф/ произвольны. Отсюда в силу C5) следует, что
^^у2
Таким образом, кинетическая и потенциальная энергии колебания в каждый
момент складываются из соответствующих энергий нормальных компонент.
х-2
Количество х величин [Ху < 0 называется степенью неустойчиво-
неустойчивости рассматриваемого положения равновесия # = 0. (На рис. 175
показана возможная степень неустойчивости материальной точки,

672
ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
движущейся без трения по поверхности под действием силы тяже-
тяжести.) Случай и = л называется полной неустойчивостью.
Довольно ясно, -что всякое наложение связи на координаты в по-
положении равновесия может либо оставить степень неустойчивости
без изменения, либо понизить ее на единицу. (Это хорошо видно на
среднем рис. 175, если проводить через ось U различные плоскости
и каждый раз требовать, чтобы движущаяся точка оставалась в этой
плоскости.) Поэтому, если степень неустойчивости и < л и нет зна-
значений цу = 0, то после на-
наложения y. связей можно
получить устойчивую си-
систему. Вполне неустойчивая
система при наложении свя-
связей остается вполне ие-
Лц. \/v- А-Л/4 /* Устойчнвой-
\ \ . Утверждение первой фразы
I I предыдущего абзаца можно
доказать строго следующим об-
рис j^g , разом. Прежде всего заметим,
что в силу C4) ?,=—ц.Д^, и
потому значения Цуможно найти, если разыскать нетривиальные решения лине-
линеаризованной системы (в любых, не обязательно нормальных координатах) в виде
т] = еш*с, а затем положить ц.=— to2. Пусть теперь задана связь вида ? Aft\j—O.
Мы приходим к задаче на стационарное значение интеграла \ (Т—U) dt при
одной конечной связи; такая задача в силу п. VI. 1.12 приводит к системе
уравнений Эйлера
(/=1,2,
п).
Если искать решение в виде f\)=-Cj e', то из этих уравнений и уравнения связи
получим (проверьте!)
C6)
Пусть для простоты все Aj ф О и все ц,у различны (исключенные случаи можно
получить с помощью перехода к пределу). Тогда график левой части C6) по-
получается таким, как на рис. 176 (почему?). Значит, все п— I корней уравнения C6)
вещественны, различны и перемежаются со значениями ц,у. Отсюда и вытекает
доказываемое утверждение.
Если рассматриваемая система зависит от параметров а±, ...,ак,
то возникает задача о нахождении в пространстве параметров об-
областей, которым отвечают устойчивые состояния равновесия. Если
система имеет потенциальную энергию U{qu ..., дп; aL ak),
то состояния равновесия определяются из уравнений
U' =0, U'a =0, ...., Ug =0, C7)

§ 3. УСТОЙЧИВОСТЬ РЕШЕНИЙ
573
которым, вообще говоря, удовлетворяют точки некоторой совокуп-
совокупности ^-мерных поверхностей в (л + &)-мерном пространстве q, a.
Каждому значению а = (а1, ..., ak) отвечает какое-то количество
значений q (быть может, ни одного), удовлетворяющих уравнениям
C7), причем степень неустойчивости соответствующего положения
равновесия равна числу отрицательных корней уравнения
д&ци'Ч1Я)—%&ц) = 0 _ C8)
(почему?). Если считать все рассматриваемые функции и производные
непрерывными, то изменение степени неустойчивости может произойти
только там, где
Это как раз точки, в которых нарушается условие существования
неявной функции q (а). Таким образом, наряду с исследованием раз-
разветвления этой функции здесь приходит-
приходится следить за знаками корней уравнения
C8). Впрочем, в некоторых практически
важных случаях оказывается достаточ-
достаточным следить только за знаком А =
=det(l/w): например, там, где А<0,
заведомо будет неустойчивость (почему?).
Наиболее прост случай л = й=1.
Тогда взамен C7) получится уравнение
Wq (?> а) —0) определяющее линию равно-
равновесия на плоскости a, q; вдоль этой линии
надо следить за знаком U'q'q. (Проверьте,
например, что если знак U'q таков, как
изображено на рис. 177, то устойчивыми будут участки линии равно-
равновесия, показанные на этом рисунке жирно.)
При й=1 иногда к этому простому случаю удается перейти и для п > 1.
Пусть, например, из последних п—1 уравнений C7) оказывается возможным
определить цг qn через glt а; обозначим результат подстановки получен-
вых выражений в U' через / (qv а). Тогда на плоскости a, qt получается ли-
линия равновесия f=0. Можно проверить прямым вычислением, что
Рис. 177.
Это дает возможность получить заведомо неустойчивые участки линии равновесия
(Д < 0), чего может оказаться достаточно.
Рассмотрим еще вопрос о наложении непотенциальных сил на систему. Для
этого перепишем канонические уравнения C3) в виде
J
dt
dU_ _ll_?2_.
dqj' dt dp/
тогда видно, что эти налагаемые силы надо добавлять к первой правой части.
Ограничиваясь нормальными координатами и линеаризованными уравнениями,

574 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
рассмотрим сначала диссипативные силы вида
п
Qj=— 2 cikh (с/к=еф
где квадратичная форма ^Lc^i/ik неотрицательно определенная; если же оиа
положительно определенная, то говорят о полной диссипации. Легко проверить,
что при таких силах
J
Поэтому если положение равновесия было устойчивым, т. е. функция U (т\) имела
при к]=0 минимум, то в силу теоремы п. 3 об устойчивости это же положе-
положение для системы с добавленными диссипативными силами также будет устой-
устойчивым. Если же диссипация является полной, то в силу теоремы того же пункта
об асимптотической устойчивости с добавлением о целых траекториях положение
т)=0 будет асимптотически устойчивым. Можно показать,' что изолированное
неустойчивое состояние равновесия," а также неизолированное состояние равно-
равновесия с положительной степенью неустойчивости при наложении диссипативных
сил остаются неустойчивыми.
Другой важный класс составляют гироскопические силы
п
Q/= 2?/*?*• где S/k^—gk/'
k=i
для них характерно, что их работа при любом перемещении системы
При одновременном действии гироскопических и диссипативиых сил
отсюда, как и выше, получаем, что устойчивое состояние равновесия при нало-
наложении таких сил остается устойчивым, а в случае полной диссипации—асимп-
диссипации—асимптотически устойчивым. Можно показать, что изолированное неустойчивое состои-
иие равновесия при одиовремеииом наложении гироскопических и вполне дис-
диссипативиых сил остается неустойчивым. При наложении оке одних только
гироскопических сил неустойчивость сохраняется, если степень неустойчивости
к была нечетной, но может перейти в неасимптотическую устойчивость,
если к было четнымХ Пусть, например, п=2,
тогда для временного множителя ekt получаем уравнеиие (проверьте!)
При g > 2 У а все корни этого уравнения будут чисто мнимыми, откуда и
вытекает устойчивость. Большая сила, ортогочальиая направлению движения,
заставляет систему совершать квазипериодические колебания вокруг положения
равновесия. Впрочем, наличие как угодно малой, но постоянной диссипации
приводит в конце концов к нарушению такой временной устойчивости. (Про-
(Продумайте все эти рассуждения на примере вращающегося волчка.)
Важным способом создания новых механических систем является объеди-
объединение нескольких исходных систем (их называют парциальными) в одну путем
установлении между ними жестких или упругих связей: например, два маят-

§ 3. устойчивость решений 575
кика ыожно связать стержнем (жесткая связь) или пружиной (упругая связь).
Допустим, что две автономные линейные консервативные системы с обобщен-
обобщенными координатами q' = (q'i, q'%, .'.., q'n>) и q"=(q[, qt, .'..., q^>) и кинетиче-
кинетической н потенциальной энергиями (a'q', q'), (b'q\ q') для первой и (a"q*, q"),
(b*q",. q") для второй объединены линейными упругими связями. Тогда полу-
получится система с п'+п" степенями свободы и обобщенными координатами
q=(q', q"). Если новые связи безынерционны (нх масса пренебрежимо мала),
то кинетическую и потенциальную энергии составной системы можно записать
в виде (aq, q) н (bq, q), где
О \ L (Ъ' г
где г—матрица связи между парциальными системами размера п'Хп". При
этом должно быть
. Ч")
(почему?) или, что равносильно,
(rq", q')S=0.
Отсюда следует, что если парциальные системы были устойчивыми, то и состав-
составная система будет устойчивой; можно показать, что частоты собственных коле-
колебаний составной системы содержатся между наименьшей и набольшей из всех
парциальных частот, т. е. собственных частот парциальных систем. Если объ-
объединяющие связи слабы, т. е. элементы матрицы г относительно малы, то для
нахождения частот составной системы удобно применить метод возмущений
(п. IV.4.10), взяв систему парциальных частот за нулевое приближение.
7. Системы автоматического .регулирования. В последнее время
широкому изучению подверглись уравнения систем автоматического
регулирования; это нелинейные автономные уравнения, которые со-
сохраняют некоторые черты линейных, что дает возможность далеко
продвинуть их исследование. Впервые систематически исследовал
такие уравнения советский механик А. И; Лурье (р. в 1901 г); сей-
сейчас на эту тему имеется уже несколько книг [1, 70, 72, 76].
Примем, что объект регулирования является линейным и описы-
ваетси системой уравнений х = Ах, х = (д;1; х2; ...; хп); это пред-
предположение оправдывается тем, что при нормальной работе объекта
отклонение от состояния равновесия не должно быть нелнко. Регу-
Регулирование осуществляется с помощью управляющего воздействия ?,
которое мы для простоты предположим скалярным; таким обра-
образом, управляемый объект описывается уравнением х==Ах—?Ь, где
Ь—некоторый заданный вектор. Это воздействие формируется сигна-
сигналом обратной связи а, который мы также предположим скалярным,
по формулам ? = ф(а) в случае прямого регулирования и | = <р(ст)
для непрямого регулирования; здесь q> (ст)—заданная характерис-
характеристика управляющего устройства. Сигнал обратной связи определяется
состоянием регулируемого объекта и управляющего воздействия,
так что а = с*х—'р|, где с—заданный вектор, а р — заданный
скаляр.

576 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Таким образом, полная система уравнений в случае, например,
непрямого регулирования имеет вид
х = Ах—$Ь, 5 = ф@), а = с*х—р$ C9)
н имеет лишь одну нелинейность <р(а). Допущение нелинейных
характеристик естественно, так как в реальных системах управляю-
управляющее устройство может работать в существенно нелинейном режиме,
например характеристика может иметь вид <р (а) = k sgn а (k > 0).
Впредь мы будем без специальной оговорки предполагать, что выби-
выбираемые характеристики обладают свойствами
ф
sgn ф (о) — sgn a, f ф (а) rfa = оо, Сф(а)<*а =— оо.
Одним из наиболее изученных является вопрос, поставленный
А. И. Лурье: найти, какой должна быть матрица А и коэффициенты
Ь, с, р, чтобы нулевое решение системы C9) было асимптотически
устойчивым в целом (п. 3) при любом выборе характеристики ф (а).
Если это свойство выполнено, то система C9) называется абсо-
абсолютно устойчивой. При этом, так как регулирование может быть
как угодно слабым, естественно предполагать и исходную систему
х = Ах асимптотически устойчивой.
Для исследования этого вопроса перейдем от искомых функций
х, ? к искомым функциям у, а по формулам
у = Ах—?Ь, а = с*х—р?. D0)
Тогда система примет вид (проверьте!)
у = Ау—Ф(о)Ь, <х = с*у—рф (а).1 D1)
При, этом преобразование должно быть невырожденным, т. е.
Однако для определителей имеет место следующая общая формула,
которую мы здесь приведем без доказательства: если А, В, С, D —
матрицы соответственно размеров пхп, nXtn, mxn, mxm w
detA^O, то
det A =detA-det(D—CA~XB). D3)
Поэтому неравенство D2) можно переписав в виде условия
*А-Ч>, D4)
которое мы будем впредь предполагать выполненным. Из него выте-
вытекает, в частности, что система D1) имеет единственное состояние
равновесия у = 0, а — О (почему?).

§ 3. устойчивость решений 577
Для установления достаточных условий абсолютной устойчивости
системы D1) зададимся видом функции Ляпунова
V (у, а) = у*Ву + J ф (в,) dalt D5)
о
где положительно определенная симметрическая матрица В будет
подобрана позже. Это непрерывная положительно определенная функ-
функция, для которой У(оо) = оо. Непосредственное вычисление дает
(проверьте!)
имеет
*y, D6)
где
С = —(А*В + ВА), d = Bb—i-c. D7)
Чтобы можно было применить теорему п. 3 об асимптотической
устойчивости в целом, правая часть D6), представляющая собой
квадратичную форму относительно уи ..., уп, <р (а) (вот где прояви-
проявились «линейные черты» рассматриваемой нелинейной системы!),
должна быть положительно определенной. Но так как эта форма
д* й), то в силу критерия Сильвестра и формулы
D3) для этого необходимо н достаточно, чтобы матрица С была
положительно определенной н
р > й*С~Ч ( = (b*B—i-c* ) С (ВЬ— у с)) . D8)
Однако в п. 4 было показано, что для любой симметрической
положительно определенной матрицы С можно иайтн ровно одну
симметрическую матрицу В, удовлетворяющую первому равенству
D7), причем В будет положительно определенной, так что В==В(С).
Таким образом, для того чтобы для функции Ляпунова заданного
вида D5) выполнялись условия теоремы об асимптотической устой'
чивости в целом, необходимо и достаточна (а тем самым для абсо-
абсолютной устойчивости системы C9) достаточно) существование сим-
метрической положительно определенной матрицы С, удовлетворяю-
удовлетворяющей неравенству D8).
Можно доказать, что дня асимптотически устойчивой матрицы А и симмет-
симметрической положительно определенной матрицы С построенный вектор d удов-
удовлетворяет неравенству d*C-»d > c*A~lb. Это, делает излишней проверку усло-
условия D4).
Рассмотрим частный случай, когда A=diag(X,x, .... Х„), где все X/—ве-
X/—вещественные отрицательные числа. Выберем матрицу С а специальной форме
99 А. Д. Мышкис

678 ГЛ.* VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
C=diag(ai, ..., ап), где все о/ > 0. Тогда
.Выберем коэффициенты а/ так, чтобы сделать правую часть по возможности
.меньше; нетрудно проверить (проделайте это!), что это наименьшее значение
Е' bJcJ
—-, где сумма распространена лишь на положительные слагаемые.
/
На основании D8) мы приходим к достаточному условню абсолютной устойчи-
вости рассматриваемой системы: р >
В 1961 г. румынский математик В. Попов, применяя преобразование Фурье,
получил более сильное и более просто проверяемое условие абсолютной устой-
устойчивости, которые мы приведем здесь без доказательства, применительно к сис-
системе D1) при добавочном условии р т= с*Ь. Он рассматривал функции Ляпу-
а
нова более общего вида, чем D5), равные сумме Р \ Ф (ffj da^ и квадратичной
о
формы относительно уг уп, ст. Им- показано, что для возможности удов-
удовлетворения такой функцией условий теоремы об асимптотической устойчивости
в целом необходимо и достаточно существование числа q^O, для которого
Re[(l + icD?)c*A-4(«l —А)Ь] + ?(р—с»Ъ)>0 <49)
при всех вещественных и. Это условие, как и D8), является лишь достаточным
для абсолютной устойчивости; но так как функции Ляпунова берутся из более
широкого класса, чем ранее, то новое условие ближе к необходимому (почему?).
В то же время условию D9) можно дать непосредственное геометрическое ис-
истолкование. В самом деле, построим на плоскости линию (L) с параметриче-
параметрическими уравнениями
х—а Im [c*A-! (i'cdI—А) Ь] — p+e*J>,
(—оо < ш < оо). Тогда условие D9) можно записать в виде: «для некоторого
qSsO должно быть (/(со)—qx(m)^0». А это равносильно тому, что линия
(L) должна целиком вмещаться в некоторую полуплоскость y^qx.
Для неустойчивых объектов регулирования мы ограничимся тем, что пока-
покажем возможность стабилизации с помощью линейного векторного управляю-
управляющего воздействия. По аналогии с переходом от системы х=Ах к системе D1),
наше утверждение означает, что для любой (пхп)-матрицы А (все величины
считаются вещественными) всегда можно подобрать такие матрицы В, С, D,
размера nxtn, тХп.п тхт соответственно (т тоже подбирается), что матрица
(с* I) «
будет иметь все собственные значения с отрицательной вещественной частью.
Такой переход от А к E0) называется окаймлением матрицы А; таким обра-
образом, любую матрицу можно с помощью окаймления сделать асимптотически
устойчивой.

§ S. УСТОЙЧИВОСТЬ РЕШЕНИЙ 579
Допустим для простоты, что матрица А имеет все жордаиовы клетки пер-
первого порядка, в общем случае конструкция аналогичная. Тогда в силу п. IV.3.4
можно подобрать матрицу Н так, что А'—Н-^АН будем иметь квазнднаго-
иальный вид, составленный из матриц первого порядка (kj и матриц второго
порядка I _JV J \ . Если %j ^k 0, то (kj) можно окаймить так:
и v)'
нетрудно проверить (проделайте это!)^ что за счет подбора и, ti можно сделать
коэффициенты, а потому и корни характеристического уравнения любыми напе-
наперед заданными числами. Подобным образом матрицы второго порядка с Цу ^ О
можно окаймлять гак:
/ У/ °\
и v w/
(проверьте!). После такого «персонального» окаймления жордановых клеток
можно с помощью одновременной перестановки строк и одноименных столбцов,
ве меняющей собственных значений (почему?), перейти к асимптотически устой-
устойчивому окаймлению матрицы А'; затем надо воспользоваться формулой
'Н 0 \ (А' В\ /Н 0 \ -1_ (А НВ\
1«Дс оДо \J -\ch-i d ;•
которая и даст требуемое окаймление матрицы А. (Из доказательства видно,
что с помощью окаймления заданной матрицы можно получить матрицу доста-
достаточно высокого порядка с любыми наперед заданными собственными значениями.)
Конечно, описанная процедура не была нацелена на экономию значения т.
Различные нопросы стабилизации см. в [8], гл. II.
В заключение упомянем о проблеме М. А. Айзермана, близкой
к проблеме замораживания (п.4). Пусть в некоторой системе диффе-
дифференциальных уравнений, содержащей лишь одну нелинейную функцию
одного переменного, скажем вида D1), эта нелинейность имеет вид
Ф (о) = i|) (а) а, причем a^i|)(o")^p и дано, что прн [подстановке
вместо ф(о") любой линейной функции i|j0o" (a ^ i|>0 ^ ($) система
будет асимптотически устойчивой в целом. Будет ли тогда асимп-
асимптотически устойчивой в целом и исходная система с нелинейной
функцией ф (а)? Ясно, что если это так, то мы получаем простой
признак устойчивости.
Исследованию этой проблемы посвящен ряд работ; си., в част-
частности, книгу [97]. Оказалось, что в общем случае приведенное
утверждение несправедливо. Тем не менее имеются различные классы
систем, для которых оно верно.
Рассмотрим, например, систему
x=ity (x)x-\-ay, y=zbx-\-cy. E1)
Условие асимптотической устойчивости такой системы с замороженным коэффи-
циевтом $ (х) имеет' вид (проверьте!)
19*

580 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Рассмотрим положительно определенную функцию
(cx-ay)>, E3)
о
равную оо на бесконечности. Ее полная производнаи по времени равна
V=№ (х) с-аЬ] х [i|> (х) х+ау] + (сх-ау) {с [i|> (х) х+ау]-а (Ьх+су)} .
)
Из условий E2), которым удовлетвориет и размороженный коэффициент, выте-
вытекает, что F<0, причем V=0 только на оси у, ие содержащей при а Ф 0 целых
траекторий; этим в силу п. 3 доказывается асимптотическая устойчивость
в целом при а Ф 0. Для а = 0 тот '¦» результат получится, если 'взамен E3)
взять функцию Ч=Ахг-\-уг, где А достаточно велико (проверьте!). Таким
образом, для систем E1) проблема Айзермаиа решается положительно.
8. Техническая устойчивость. Вернемся к общей системе C). Пусть задана
оценка или система оценок возмущения начальных данных; например может
быть дано, что ша.х | х/ (t0) | < h, —это оценка, или что | х/ (t0) | < А/ (/— I,
2, ..., я)—это система оценок. Кроме того, если возмущается и праваи часть
C), то должна быть задана оценка или система оценок этого возмущении иа
заданном интервале времени (t0, Т), где Т может быть конечным либо беско-
бесконечным. Наконец, пусть задана оценка или система оцеиок, которым должно
удовлетворять возмущение решении. Тогда некоторые авторы говорит,. что
невозмущениое решение «технически устойчиво» относительно всех этих оцеиок,
если при любых удовлетворяющих заданным оценкам возмущениях начальных
данных и правых частей возмущение решения удовлетворяет заданным дли него
оценкам на заданном интервале времени.
Название «техническая устойчивость» неудачное, а приводимая иногда
мотивировка, что инженера интересует ие бесконечное время и бесконечио малые
возмущения, а конечное время и конечные возмущения, основана иа недоразу-
недоразумении (ЛВМ, п. XV.22). Оценки, нацеленные иа наихудший вариант и полу-
полученные с помощью последовательно усиливающихся неравенств, редко оказы-
оказываются практически приемлемыми, чаще более эффективным оказывается вычи-
вычислительный эксперимент.
Тем ие менее возможны случаи, когда подобные гарантиронаииые оценки
возмущений решения небесполезны. Если возмущаются только начальные данные,
то речь идет попросту об оценке решения Заданного дифференциального урав-
уравнения при заданной оценке начальных данных. Такую оценку можно получить
из точного решения, если оно возможно, нз первых интегралов (ЛВМ, п. XV.13),
из численного интегрирования при нескольких вариантах выбираемых наугад
начальных данных.
Иногда удается применить метод функций Ляпунова. Именно, если удастся
подобрать функцию V (х, t), для которой
ПО, 0=0. V(х, t) > 0 (х ф 0),
то для любого решении ;
V(f, x)<V(te, x0) (/0«<Г), E4)
откуда можно получить оценку \(t) при заданной оценке х«. Например, если
V{x. Q «
где А(/) при каждом t—симметрическая положительно определенная матрица,
«о из неравенства E4) следует, что
х @ | < | х01 K*.mlK<>e)Aml,,@ exp \k (to-t)l2\,

§ 4. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ 581
где под Хтах и Хт[а понимаются наибольшее и наименьшее собственные значе-
значения матрицы А (докажите!)'.
Если возмущаются также правые части системы, то неравенство У<0 может
оказаться справедливым лишь вне некоторой окрестности начала координат
пространства х, размер которой зависит от заданной оценки возмущений правых
частей. Тогда и оценка E4) гарантируется лишь до тех пор, пока решение
не попадет в эту окрестность. Для линейной системы C) можно воспользоваться
формулой A.12), приняв, что возмущающая функция f (t) удовлетворяет задан-
заданной оценке.
Вопросы «технической устойчивости» рассмотрены в книге 145].
§ 4. Нелинейные колебания
1. Введедие. Напомним сначала некоторые простые факты из
теории колебаний линейных автономных систем с одной степенью
свободы (ЛВМ, пп. XV.15, 17, 18). Уравнение свободных колебаний
такой системы имеет вид
где А^О и <оо > О—параметры системы. (Для случаи простейших
механических систем 2h=fm~1, a»% = km~1, где /—коэффициент
трения, т—масса осциллятора и k—коэффициент упругости.) Общее
решение уравнения A) легко находится по методу Эйлера; это реше-
решение имеет вид
y = e-flt{C1 cos ю^ + С, sin щ t) (а>! = К©}—А1), B)
если А < ю0 (это при А > 0 случай затухающих колебаний), и
у = С, ехр [—(Л—]/"A^=F«) t] + С8 ехр [ — (A + j/>—<o«) t] ,
если А >• <оо (это апериодическое затухание, соответствующее дви-
движение назынается также лимитационным). Исходя из нида B) реше-
решения, А называют коэффициентом затухания, а-А—постоянной вре-
времени; это время, за которое амплитуда колебаний затухает в е раз.
(Более точно здесь говорить о затухании экспоненциального множи-
множителя при синусоиде, так как понятие амплитуды, строго говоря,
относится лишь к периодической функции, каковой B) не является,
однако эта небольшая неточность в терминологии несущественна.)
Безразмерная величина 2лАа>?~1 называется декрементом, она равна
логарифму отношении амплитуд за время условного периода, т. е.
периода гармонического сомножителя.
Если затухание отсутствуем т.е. А = 0, то решение B) имеет
совсем простой вид
у = Сх cos ю0* + Ct sin ю0* == М sin (ю^ -f- ф»),
где Ct, С% илн М, ф0—произвольные постоянные. Существенно
заметить, что здесь частота колебаний ю0 не зависит от их ампли-
амплитуды М; эта изохрднность, как мы увидим в п. 2, не имеет места
дли нелинейных автономных систем.

582 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Уравнение вынужденных колебаний для гармонического внешнего
воздействия имеет вид
где А и ©—амплитуда и частота внешнего воздействия. Уравнение
C) имеет общее решение (проверьте!)
х= — [ — (юа — ©*) cos С9< + 2Аюsin ©<]+
ina1t), D)
представляющее собой результат наложения гармонического коле-
колебания, происходящего с частотой внешнего воздействия и однозначно
им определяемого, и общего свободного колебания, зависящего от
начальных условий. При наличии в системе диссипации, т. е. при
А > 0, второе слагаемое при возрастании / затухает, так что при
большом i практически остается лишь первое, гармоническое коле-
колебание, происходящее с амплитудой
М = А [(©2 — ю|5
Безразмерный коэффициент усиления Ма>%/А, равный
Mml А=\[{ — — 1 ) + 4 — ) — , E)
представляет собой функцию двух безразмерных параметров: безраз-
безразмерной вынуждающей частоты ©/©„ и безразмерного коэффициента
диссипации А/ю„. Зависимость этого коэффициента от первого пара-
параметра при постоянных значениях второго показана на рис. 178. Эти
графики называются амплитудно-частотными характеристиками.
Коэффициент E) дри заданной диссипации г = А/ю0^]/ 2/2 при-
принимает наибольшее значение Br ]/l—г2I при ©/©0 = j/l —2г2
(проверьте; а что будет при г > ]/2/2?). При А/ю0—>0, ю/ю0 -* 1
коэффициент усиления неограниченно возрастает (продумайте физи-
физическую причину этого!).
Если диссипация отсутствует, то формула D) приобретает более
простой вид
Д
х = —z cos at + Ct cos ©„^ + Сг sin ©0^, F)
<в0 — <в2
т. е. решение получается квазипериодическим (п.1.7), а для соизме-
соизмеримых ю, ю0 — периодическим. В частности, при начальных условиях
д;@)==0, л:@.) = 0
из F) получаем
д
х = —Z (cos Ш—cos ю J). G)

§ 4. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
583
Поэтому при совпадении чахтоты <о внешнего воздействия с собст-
собственной частотой ю„ будет
А А
¦Я|ш=ю,— lint —г (cos at—cos u>ot) = n—tsinaj, (8)
«в - ио<Во—w8 °
т. е. получаются колебания, амплитуда которых при t —*¦ оо неогра-
неограниченно возрастает по линейному закону—наступает резонанс.
Можно сказать, что при этом коэф-
коэффициент усиления обращается в бес-
бесконечность (рис. 178).
•Решение G) очень интересно, когда ш
близко к <а0, т.е. ш = шо+в, где в относи-
относительно мало. Тогда
Х=
2Л .. в . .
-г-; ; г Sin-„-/ SHI
6(шо+<в) 2
-г— sin -? t sin atat.
i
(9)
При 0</<б-1 будет i-sln-i < да-^ ,
т. е. с ростом / будет происходить иара-
стаиие амплитуды, как при резонансе. Одна-
ко при дальнейшем увеличении t множитель
-т-sin-^-/ будет колебатьси по гармониче-
2
%
О
2 OL
(О,
Рис- 178.
скому закону с большой амплитудой 8-1 и малой частотой 8/2. Поэтому все
решение (9) будет иметь вид, показанный на рис. 179; это так называемые биения.
Рис. 179.
Рассмотрим для дальнейшего еще случай, когда слабое внешнее
возбуждение пропорционально искомому решению, другими словами,
рассмотрим уравнение
ax (Ю)
прн малых |а| и, для определенности, при начальных условиях
(И)

584 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Задачу легко решить точно (проверьте!):
x = AcosVu>f—at, A2)
т. е. описанное возбуждение влечет изменение частоты колебаний,
что очевидно и непосредственно, так как это возбуждение равно-
равносильно изменению коэффициента упругости.
Однако допустим, что мы хотим применить к задаче A0), A1)
стандартный метод малого параметра. Тогда
t)a*+... .A3)
Подстановка в A0), A1) дает
хв + ®*ахо = 0> хл@) = А, *0@) = 0, откуда xa(t) =Л cos a>at;
это очевидное невозмущенное решение. Далее,
) = 0t лг1(О) = О,
откуда jfj (t) дается формулой (8). Остановившись пока на этом, мы
получаем решение с поправкой первого порядка малости, учитываю-
учитывающей возбуждение:
^slnm,*; A4)
Этот же результат получится после первой итерации, если приме*
нить к задаче A0), A1) метод последовательных приближений.
Но пусть нас интересует поведение решения x(t) на бесконеч-
бесконечном интервале времени, например при t—»-оо. Тогда ясно, что
«приближенное» решение A4) совершенно неправильно передает это
поведение, хуже даже, чем невозмущенное решение х0 (t). В самом
деле, второй член в правой части A4), даже при малом |ос|=?О,
при t—> оо будет неограниченно возрастать по амплитуде и потому
подавит первый член. (Такне члены с амплитудой, возрастающей по
степеннбму закону, называются секулярными— по-русски вековыми,—
так как в задачах о движении планет, где вперзые обратили вни-
внимание на этн члены, онн сказываются лишь после большого числа
оборотов планеты вокруг центрального тела.) Получается, как будто
в рассматриваемой системе имеет место резонанс, тогда как точное
решение A2) показывает, что на самом деле резонанса нет. Вычи-
Вычисление дальнейших членов разложения A3) еще более искажает
А ' А
картину, например xu(t) — —g-j ^* cos ©/-f-jr-jtf sin atf (проверьте!)
при t—>» возрастает еще быстрее, чем xt(t) (хотя на конечном
интервале / точность становится все лучше!).
То же разложение A3) можно получить, непосредственно рас-
раскладывая точное решение A2) по степеням а. Для этого обозначим

§ 4. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ 585
а>1—об = ю0—р, откуда
Кроме того,
x{t) = A cos(a>0—$)t —
Если в правую часть вместо {5 подставить разложение A5) и
объединить члены с одинаковыми степенями а, мы и получим A3).
Отсюда ясно происхождение вековых членов, создающих иллюзию
резонанса: частичные суммы рядов Маклорена для coss и sins хо-
хорошо изображают разлагаемые функции на конечном интервале s,
но совершенно непригодны при s—»-оо (продумайте это!).
В более сложных примерах точное решение нельзя выписать
в конечном виде, и потому иллюзорность резонанса, полученного за
счет вековых членов, обнаружить труднее. Такие члены обычно по-
появляются при исследовании колебаний автономных систем по тому
или иному варианту метода возмущений, если в качестве нулевого
приближения взято колебание с неправильно определенной частотой.
(Как бы ии было мало |е|>0, разность cos(юв-|-е)?—cos<D0i при
t—»-оо не является малой.)
Колебательные свойства линейных автономных систем с конеч-
конечным числом степеней свободы вытекают из рассмотрений пп. 3.6 и
1.6, 7. Остановимся здесь только на понятии амплитудно-частотной
характеристики такой системы. Если уравнение вынужденных коле-
колебаний системы при гармоническом внешнем воздействии с частотой
ю имеет вид
de''«°f A6)
(а, Ь, с—квадратные матрицы, \(t)—искомый вектор, d—задан-
d—заданный постоянный вектор), то решение, имеющее вид гармоники
с той же частотой, равно
| = (—©"а + /сое -f- b)-x Аеш.
На эту гармонику накладывается общее свободное колебание си-
системы, зависящее от начальных условий, которое при наличии пол-
полной диссипации (по всем координатам) затухает. Таким образом,
роль амплитудно-частотной характеристики здесь играет матрица
Z (©) = (—tfa + iatc + b)-1. A7)
Если уравнения A6)—это уравнеиия Лагранжа для рассматриваемой
системы, то каждый элемент zJk матрицы Z = (zJk) представляет со-
собой комплексный коэффициент усиления отклика /-й координаты на
гармоническое воздействие частоты ю, поданное на к-ю координату.
19*А. Д. Мышкио

686
ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Часто можно говорить просто об отклике /-го элемента системы на
гармоническое возбуждение ее А-го элемента; таким образом, мат-
матрица A7) характеризует взаимосвязь между элементами системы
относительно гармонических воздействий.
Вместо полной характеристики A7) можно пользоваться упрощен-
упрощенной амплитудно-частотной характеристикой ||Z(a>)||, взяв в качестве
нормы матрицы сумму модулей
. всех ее элементов. Это веще-
вещественная скалярная функция ве-
вещественного аргумента ю, по-
поэтому ее можно изобразить на
графике (рис. 180). Ясно, что
если норма матрицы Z (со) мала,
то при данном ю все коэффи-
) циенты усиления малы, т. е. си-
система данной частотой слабо
возбуждается; если же норма ве-
велика (на рис. 180 при <?> — <?>t,
ю2, ©s), то система возбуждается сильно (точнее говоря, внешнее
воздействие можно так приложить, что по крайней мере один
элемент системы возбудится сильно). На собственной частоте ю0
системы без диссипации наступает резонанс, т. е. || Z (ю0) || = со.
Например, для уравнений
*,+<b!iXi = >¦(.*„—«О, хл+(о*о4Слт=г(Х1— хг) (г>0),
описывающих колебания системы из двух упруго связанных осцилляторов
(п. 3.6), получаем (проверьте!)
Z(<b)=[<b«—(<nS§ §
Рис. 180.
В частности,
\ г _
значит, если возбуждать первый из осцилляторов на его парцяальной частоте,
то второй будет возбуждаться тем сильнее, чем ближе парциальные частоты.
Нелинейные колебания, к систематическому рассмотрению кото-
которых мы теперь переходим, обладают рядом специфических особен-
особенностей, проявляющихся уже для систем с одной степенью свободы.
Невозможность суперпозиции решений, в частности умножения ре-
решения на константу, влечет за собой неизохронность свободных
колебаний автономной консервативной системы, т. е. зависимость
частоты таких колебаний от их амплитуды. Так как у системы нет
собственной частоты, то в случае вынужденных колебаний нелиней-
нелинейной системы отсутствует явление резонанса. С другой стороны, мы
увидим, что в такой системе возможно принципиально новое явле-
явление— вынужденные колебания, период которых кратен периоду воз-

§ 4. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ 587
буждающего воздействия (это субгармонические колебания). Для
автономных неконсервативных систем принципиально новой в нели-
нелинейном случае является возможность автоколебаний, о которых мы
упоминали в п. 2.5. Параметрические колебания неавтономной нели-
нелинейной системы, вызванные периодическим изменением ее парамет-
параметров, из-за отсутствия суперпозиции также происходят на определен-
определенных амплитудах; если эта амплитуда бесконечная, в системе будет
параметрический резонанс (п. 1.4). Для систем с несколькими сте-
степенями свободы нелинейный случай осложнен невозможностью пере-
перехода к независимым колебаниям нормальных координат.
По колебаниям вообще и нелинейным колебаниям в частности
имеется обширная литература; см., например, [4, 7, 13, 17, 25,31,
43, 48, 81, 85, 94, 95, 108, 109, 111, 112, 123, 124].
2. Свободные колебания автономной консервативной системы
с одной степенью свободы. Речь идет о решениях уравнения
*+/(*) = О, A8)
где функция f(x) имеет тот же знак, что х. Из наличия первого
интеграла
X
V{x, x)^±x*+§f&)dl= const A9)
(проверьте!) вытекает, что уравнение A8) интегрируется в квадра-
квадратурах.
Так как левая часть A9) имеет при х~х = 0 минимум, то (ср.
п. 3.6) при достаточно малых начальных значениях х и х решения
будут периодическими. Для несимметричной функции f(x) амплиту-
амплитуды налево Ал и направо Аа будут, вообще говоря, различными, и
так как в момент достижения этих амплитуд будет х = 0, то из A9)
следует, что связь между Ая и Аа такова:
о
- J f(x)dx=
— Ая
Если функция f(x) нечетная, то АлшзАа.
Найдем связь между амплитудой и периодом колебаний. Для
этого положим хо — Ап, х„ = 0 при t = 0\ тогда из A9) получим
откуда
19**

588 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
т. е. координата х дойдет до значения дг = О за время
Лц / Лц \-1/а
dx.
Ли f Ли \ -
И2 $/©<?)
о \ * /
Проделав то же вычисление для х < 0, получаем период коле-
колебания
О / * 4-1/2 Ап , А„ ч -1/2
П f U \
О / * 4-1/2 Ап , А„ ч -1/2
Г=2 П-2 f/(?)^j dx+2 U2 \f(l)dl) dx. B0)
-Ax ^ -Лл ' 0 ^ x '
Например, при f(x)=<x\x|*sgn* (a>0, —1 <ft<oo) получаем Аа
¦Ал=А и
A , А ч -1/2
f (
0 ^
0 ^ x
(ЛВМ, пп. XIV. 17, 18). Мы видим, что за исключением линейного случая (й=1)
перЕод колебаний зависит от амплитуды. При к > 1 с ростом амплитуды период
убывает. Этот факт не связан с конкретным степенным видом функции / (х),
а может быть выведен из того, что эта функция при х > 0 выпукла книзу,
а при х < 0—кверху, так как тогда с ростом амплитуды роль упругих сил по
сравнению с инерционными повышается (продумайте это). Восстанавливающая
сила с таким характером выпуклости называется жесткой. Аналогично при
k < 1 получается мягкая восстанавливающая сила, имеющая противоположный
характер выпуклости, и период колебаний с ростом амплитуды растет.
Для прикидочных расчетов периода колебаний часто оказывается возмож-
возможным из каких-либо соображений заменить восстанавливающую характеристику
f (х) иа линейную, после чего подсчитать период уже легко. Оказывается, что
для нечетной f (x) одной из наиболее точных является замена / (х) на kx, где
k подбирается из условия минимизации интеграла
А
о
При этом получается формула для периода колебаний (проверьте!)
5 Г \~V'
значительно более простая, чем B0).
Решения уравнения A8) наглядно изображаются на фазовой
плоскости (пп, 2.3—5), для чего надо перейти к эквивалентной

§ 4. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
589
системе уравнений первого порядка
х=у, y =—f(x). B1)
Так как система B1) каноническая (для какой функции Гамиль-
Гамильтона?), то в силу п. 2.12 при сдвиге по траекториям площади со-
сохраняются, а потому притягивающие и отталкивающие точки покоя
(т. е. узлы и фокусы) нлн циклы невозмож-
невозможны. При построении фазового портрета си-
системы B1) полезно обратить внимание на
то, что все траектории в верхней полупло-
полуплоскости (у > 0) идут направо, а в нижней —
налево; ось х пересекается траекториями
ортогонально, за исключением точек покоя,
которые могут располагаться только на
этой оси (этими свойствами обладает фазо-
фазовый портрет и для более общего урав-
уравнения x-\-f(x, х) = 0).
~ Рис. 181.
т9,
Рассмотрим в качестве примера уравнение
колебанвй математического маятника, т. е. мате-
материальной точки, подвешенной на идеально жестком
невесомом нерастяжимом стержне в однородном поле тиготения (рис. 181),
В обозначениях рис. 181 имеем
откуда
ml2x=—mg&mx-l,
х + j- sin x=0
(проверьте размерности1). Соответствующая система первого поридка имеет вид
*=У. У= — у sin*
и фазовый портрет, показанный иа рис. 182 (проверьте его правильность!). Так
как х—это угол, то картина повторяется с периодом 2я по х, т. е. фазовым
пространством здесь служит цилиндр (п. 2.11). Точками покои здесь служат
центры, четно кратные я и отвечающие устойчивому состоинию равновесия,
и седла, нечетно кратные я, отвечающие неустойчивому состоинию равновесия
маятника. Уравнения траекторий на основании интеграла A9) нмеют уравнение
в частности, уравнение сепаратрисы, проходящей через седла (при х=я
должно быть у=0, откуда С=2 у-\ , имеет вид
У=±
= ±2 у fcos~-.
Сепаратриса делит полосу —я<:х<я (рис. 182) на три части. Средняя за-
заполнена циклами, которым отвечают либрацийнные движения, т. е. покачивания
вокруг положения устойчивого равновесия. Верхняя заполнена траекториями,

590
ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
замкнутыми на фазовом цилиндре (но незамкнутыми на фазовой плоскости!),
которым отвечают ротацибнные движения, т. е. вращения маятника вокруг
точки подвеса с неограниченным возрастанием фазового угла. Нижняя область
фазовой плоскости также отвечает ротационным движениям, но с противопо-
противоположным направлением вращения. (Какому движению отвечает сама сепаратриса?)
Связь B0) между периодом и амплитудой при либрации легко выразить через
эллиптический интеграл (п. Н.3.14), что мы предоставляем читателю.
Рис. 182.
Интересно отметить, что каждое либрационное движение в рассматриваемом
случае неустойчиво по Ляпунову. В самом деле, так как период колебаний
зависит от амплитуды, то для как угодно малого сдвига начальной точки на
другую траекторию при безграничном увеличении t изображающие точки ра-
разойдутся на конечное расстояние (затем опять сблнзятси и т. д.). Но так как
изображающая точка возмущенной траектории при этом все время будет дви-
двигаться вблизи невозмущенной траектории, то описанная ситуация называется
орбитальной устойчивостью.
В физике при рассмотрении либрациониых и ротационных движений при-
применяется также специальная система переменных, отличная от х, х. Покажем
ее для автономной консервативной системы с одной степенью свободы и функ-
функцией Гамильтона
где параметр т > 0 может зависеть от q. В силу п. VI.3.7 уравнение Гамиль-
Гамильтона— Якобн приобретает внд
откуда
W « ^ /2m [Л— U (q)] dq + consf.
B2)
Если в последний интеграл подставить какое-либо выражение А=А(Р), то
получится функция W (q, P), которую можно принять за производящую

§ 4. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ 651
функцию канонического преобразования
и закон движения приобретает вид (п. VI.3.7):
Р=const, Q=h' (P) t+const.
Из B3) и B2) видно, что h ергь полная энергия системы.
Упомянутая специальная система перемениых для /габрационных движений
вблизи устойчнвого положении равновесия получится, если в качестве Р вы-
выбрать переменную действия
равную, с точностью до коэффициента 1/2я, площади, ограниченной замкнутой
траекторией в фазовой плоскости q, p. (Проверьте, что приращение действия
аа один цикл периода То равно 2л/—ht0, чем и объясняется наименование J.)
Так как / растет вместе с А, то имеет смысл говорить и об обратной зависи-
зависимости h (/), которая и порождает описаиное выше каноническое преобразование.
dW
Канонически сопряженная с / величина $—-тт называется угловой перемен-
переменной. Ее приращение за один цикл равно
Закон движения в новых переменных имеет вид
A=ft'(./)f+A0=|2-f+*0, /=consi.
Проверьте, например, что при /л=const и линейной восстанавливающей
силе, т. е. при ^=у <Л будет
/=1/ -?-й, A=arcsin
g — 4 ,—
Для ротационного движения интеграл B4) берется по периоду функции
p(q), т. е. по циклу ротации, в остальном преобразования те же, что при
либрации.
При наличии диссипации циклы невозможны, а точки покоя, отвечающие
устойчивым состояниям равновесия, превращаются в фокусы для малой дисси-
диссипации в в узлы—для большой (почему?); конечно, тогда система становится
уже неконсервативной. Соответствующая фазовая картина для математического
маятника с малой диссипацией показана на рис. 183. (Изобразите картину для
большой диссипации!) При как угодно большой начальной скорости маятник
после конечного числа ротаций переходит иа затухающие либрации. (Какова
роль сепаратрис?)
В свизи со сказанным упомянем еще об одном полезном понятии, которое
активно изучается в последние годы. Для системы общего вида
i=t(x, t) B5)
некоторое ft-мерное (К ft <n) многообразие (S) (я+1)-мерного пространства

592
ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
х, t называется интегральным, если E) составлено из целых графиков реше-
решений (интегральных линий), т. е. если из (х0, to)?(S) вытекает, что н
(x{t; tt, х0), t)?S для всех t, где x(t; t0, x0)—решение системы B5) при на-
начальном условии x\t=t =x0. Любая интегральная линия образует одномерное
интегральное многообразие. Если система B5) автономная, то из-за возмож-
возможности произвольного сдвига любого ее решения во времени каждая траектория
в пространстве х определяет двумерное цилиндрическое интегральное многооб-
многообразие, направляющей которого служит эта траектория, а образующие парал-
параллельны оси t. Исследование интегральных многообразий иногда дает возмож-
возможность, отвлекаясь от каждого индивидуального решения, получить те или иные
н.
Рис. 183.
основные свойства совокупности решений в целом. (См. по этому поводу поня-
понятие первого интеграла в ЛВМ, п. XV. 13; ясно, что каждый первый интеграл
определяет расслоение пространства #» t на /г-мерные интегральные многооб-
многообразия.) Различные авторы рассматривали также иопросы о зависимости интег-
интегрального многообразия от параметра, входящего в систему B5), об устойчи-
устойчивости по Ляпунову сечения интегрального многообразия плоскостью t=const
(в приведенных выше примерах это обычная устойчивость по Ляпунову и
орбитальная устойчивость) и т. д.
3. Вынужденные колебания системы с малой нелинейностью,
основной случаи. Рассмотрим уравнение
х -f-2Ajj + ю*лг=A cos at+fL (х, х, t}a+/2(x, x, t)a*+ .. .,B6)
где а—малый параметр, а все функции fj периодичны по / с пе-
периодом Г = 2л/о) и разлагаются в ряды Тейлора по степеням х, х.
Это уравнение C), возмущенное малой нелинейностью. Будем считать,
что АфО, а если А = 0, то w =,?©„; этим исключаются особые
случаи, которые будут рассмотрены в п. 4.
В уравнении C) можно было возмутить и коэффициенты А, <о§
и А, например, вместо h написать h-\-hla-\-hiai-{-...; это не
является существенным обобщением, так как члены с hj можно
отнести к fj. Однако еелн была возмущена частота возбуждения,

§4. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ 593
т. е. вместо ю всюду поставлено ^щ
дует проводить разложение косинуса и функций /у по степеням а,
что привело бы к появлению вековых членов (п. 1), а лучше просто
обозначить & + ta1a + &ta* + ... через новое ш.
Согласно методу малого параметра будем искать решение урав-
уравнения B6) в виде
x=xjt)+x1{t)a+x2{t)a*+... _ B7)
Подстановка в B6) и приравнивание коэффициентов дают
'x0 + 2hx0 + alxB = Aco&(i)t, B8)
*, + 2hxx + сфгг =/г (х0, х0, t), B9)
Я + 2hxt + <*г, = \jsh (*о + ах1г х\ + ах„ /)] в=0 +
и т. д. B8)—это как раз уравнение C), так что xo(t) имеет выра-
выражение D). Будем искать только Т-периодическое решение, представ-
представляющее наибольший интерес; тогда
[-("'-"о) cos mf+ 2Лю»з1па»<]. C1)
Подставив это выражение в правую часть B9), мы получим Г-перио-
дическую функцию, которую можно разложить в ряд Фурье по
функциям cos mat, sianat; после этого аналогично C1) получаем x1(t)
в виде суммы ряда по этим же функциям, т. е. в виде Т-периоди-
ческой функции. Затем обращаемся к уравнению C0) и т. д.
Рассмотрим, например, уравнение Дуффинга
& — Acoswt+ax3 (ш Ф соо). C2)
Здесь
поэтому уравнение B9) принимает вид
откуда .
^4^W] C3)
(проверьте!). *г(/) будет уже линейной комбинацией функций cos at, cos 3cof
и cos5urf, и т. д. Таким образом, в решении уравнения C2) на основную гар-
моиику с частотой ш окажутся наложенными верхние гармовнки с частотами
За, So и т. д. и с амплитудами все более высокого порядка малости.

594 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Отметим, что в правой части B6) вместо A cos &t могла стоять
произвольная 7*-периодическая функция f(t); тогда после разложе-
разложения правой части B8) в ряд Фурье построение решения не отли-
отличается от проведенного. Если f(t)~O (т. е. А = 0), то можно
сделать замену х==ау н после сокращения B6) на а разложить все
/у (ay, ay, t) по степеням а; если /х @, 0, t) == 0,- то это преобра-
преобразование можно повторить. Отметим также, что из формулы C3) н
аналогичных формул для нелинейности более общего вида ясно, что
особыми являются не только случай а> = <а0, но и случай в> = ©,/2,
юв/3 и т. д.
Рассмотрение систем с ббльшим числом степеней свободы в ос-
основном случае, т. е. когда прн а = 0 ни одна нз собственных частот
не является целой кратной частоты возбуждения, проводится совер-
совершенно аналогично.
На практике нам часто приходится иметь дело с конкретными
числовыми примерами, в которых, как подсказывает интуиция, нели-
нелинейность не является слишком большой. В таких случаях можно
какой-нибудь нз сравнительно малых числовых коэффициентов, по-
порождающих нелинейность, объявить малым параметром, т. е. написать
вместо этого коэффициента а и т. п. (ср. ЛВМ, п. XV.27). Можно
также перед всей группой нелинейных членов поставить искусствен-
искусственный множитель а, который после проведения вычислений полагается
равным единице. Ограничиваясь небольшим числом членов разложе-
разложения, можно получить представление о точности результата, проводя
численное интегрирование на ЭЦВМ или на моделирующих ВМ конт-
контрольных примеров с типичными или экстремальными значениями
параметров. Это замечание, конечно, относится ко всем вариантам
применения метода малого параметра.
4. Особые случаи. Рассмотрим теперь случай, когда система
с одной степенью свободы возбуждается на частоте, близкой к соб-
собственной, т. е. когда в уравнении B6) й = 0, ю = (йв. Мы будем
опять искать Т-периодическое решение, остающееся конечным при
а = 0; тогда в уравнении B6) должно быть А = 0, т. е. будет рас-
рассматриваться уравнение
х+<й*х=/1 {х, х, t)a + Д(х, x,t)a*+..., C4)
где все функции /у Г0-периодичны по t (Гв = 2л/аH).
Будем пользоваться тем же разложением B7). Тогда х0 + (й%х0 = О,
т. е.
х0 (t) = a cos &ot + b sin co01, C5)
где постоянные а, Ь пока неизвестны. Далее (см. B9))
x=f1 (a cos ю0/+ ^ sin ю0/, —аю0 sin (aot + b(a0cos(a0t, t). C6)
Если мы хотим, чтобы функция хх [t) была периодической, то в раз-
разложении правой части C6) в ряд Фурье должны отсутствовать

§ 4. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ 595
члены с costugt и sin(aat (почему?), т. е. должно быть
Д (a cos (ntt -\- b sin aot, —аю„ sin ю^ -f b<ut cos ©e/, t) X
X cos o)o/ dt — 0,
гл/с>>о
Д (a cos mot + ft sin aat, —aca0 sin caat -f- ?ю0 cos aot, t) x
X sin oaot dt = O.
C7)
Это— система определяющих уравнений, из которой находятся воз-
возможные значения для а, Ь; так как она нелинейная, то таких зна-
значений, вообще говоря, получится несколько (а быть может; и ни
одного).
Удовлетворив уравнениям C7), мы получаем общее, решение
уравнения C6) р виде
хх (t) = cpt (t) + ах cos ш0/ + #i sin a>J, C8)
где (f1 (t)—вполне определенная Тв-периодическая функция, а alt
bt — произвольные постоянные. Теперь надо обратиться к уравне-
уравнению C0) для дг2 (t). Подставив в его правую часть выражения для хв (t)
и x±(t) и пользуясь условиями отсутствия резонанса, получаем си-
систему из двух уравнений первой степени относительно аг, blt из
которой находим эти постоянные, затем пишем общее решение
уравнения C0) и т. д. ¦¦
* Подчеркнем, что в рассмотренном случае малое внешнее воз-
воздействие порождает колебание с конечной, не малой амплитудой.
Это не удивительно, так как система оказывается в состоянии,
близком к резонансу. В то же время наличие в системе малой дис-
диссипации (за счет х в правой части) или малой нелинейности, меняю-
меняющей собственную частоту при изменении амплитуды, не дает воз-
возможности вынужденному колебанию разрастаться неограниченно.
(Разберите самое простое уравнение этого вида х-\-<й\х = —ahx -f-
-f- <zA cos (nj.)
Случай, когда в правой части C4) добавлена Г0-пернодическая функ-
функция fo(t), фурье-разложение которой не содержит cos a>ot и sin coo/, сводится
к разобранному с помощью замены x=y + ty(t), где функция г|з (t) представ-
представляет собой какое-либо решение уравнения x + a>lx=f0 (/)•
Рассмотрим в качестве примера вариант уравнения Дуффинга с малым за-
затуханием
x+ah'x + alx=a.A cos Ы+akx3 (h > 0, a >.O),
где
сй=<в0 4-co1a4-u>2as +... C9)
Согласно началу п. 3 перед разложением по степеням а проводим замену
а>1 = [а — (a^a -|- cea2 -J-)]2 = ю»—гш^с*+(wf—2юв>2У а2

596 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
это дает . •
cos
Подставляя x=x0 @+*i @ a+..., получим
—й*0 + A cos cof+fee?+2СИ»!*,, D0)
и т. д. Из первого уравнения получаем C5) с w вместо <в0. Подставляя C5)
в правую часть D0) и выписывая условия отсутствия резонанса, получаем
после вычислений определяющие уравиения (проверьте!)
3
Для исследования этой системы уравнений удобно ввести величину т=Уа*-\-Ь2,
разную предельной амплитуде колебаний при а->-0. Из D1) получаем
Bww, +±j-knfi J a—/icd&=—А, [2шш1+— fern2) fr-fftu>a=0r
возводя эти соотношения в квадрат и складывая, приходим к сравнительно
простому уравнению
--kmA* т* + Н*а>*т*=*А* . D2)
для этой амплитуды. Чтобы сделать это уравнение еще более обозримым,
в частности уменьшить в нем число параметров, введем безразмерные прираще-
нне частоты и амплитуду
, <й. т . *
где безразмерные коэффициенты г, s мы используем для уменьшения числа
параметров (проследите за этим общим приемом!). Тогда взамен D2) мы полу-
получим уравнение
(проверяйте вычисления!). Значит, если положить
и обозначить 9=A2<»~as~2=A2 (т*^2) та> мы ПРИДЯ1 к УРавиеиию
»!. т.е.
Графическое решеиие этого уравиения при заданных I, q показано на рис. 184-
Так как относительно р,2 уравнение третьей степени, то здесь могут быть либо
три вещественных кория, либо один. На рис. 185 показано соотношение между i
и (А при различных фиксированных значениях q^O. Несложное исследование,
которое мы предоставляем читателю, показывает, что при <?ЗзЗ/4 функция р (V|
однозначная, тогда как при 0 < q < 3/4 оиа имеет интервал трехзиачности; из
смысла q вытекает, что последнее будет при относительно малой диссипации

§ 4. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
597
или большом возбуждающем воздействии. (Условие q < 3/4 можно выразить
непосредственно в терминах относительного коэффициента диссипации аи и т. п.,
что даёт возможность в численных примерах проверять его непосредственно.)
I
-А
Рнс. 184.
Рис. 185.
Наличие такого интервала трехзначности влечет за собой явление перескока
амплитуды вынужденных колебаний прн изменении возбуждающей частоты,
т е К показанное на рнс. 186 и совершенно аналогичное явлению перескока,
описанному в п. 3.2. Можно показать, что участок амплитудно-частотной харак-
характеристики между точками с ординатами
Hi и Цз отвечает неустойчивым вынуж-
вынужденным колебаниям.
Отметим, что если правая часть
C4) имеет вид
где все функции Fj(t) Тв-перио-
дичны, то в силу п. 2 можно гоио-
рить о собственных частотах си-
системы (если отбросить все члены
с Fj), заиисящих от амплитуды ко- ^
лебаний; при этом значение а0 ~
может при а^=0 и не входить в интервал этих частот. Но мы
'Рис. 186.
может при а^0 и не вд р
строили решение периода Тв, значит, это решение описывает вынуж-
вынужденное колебание, происходящее с частотой внешнего возбуждения.
Эта частота может не совпадать с собственной частотой исходной
невозмущен-ной системы (вопреки тому, как это может показаться
из проведенного общего рассмотрения), а только должна быть
близка к ней, так как уравнение C4) могло быть, как в разобран-
разобранном примере, получено после растяжении времени; ведь в уравне-
уравнении C9) &Ф ю„ (продумайте это!).
Аналогично рассматривается случай, когда для некоторого опре-
определенного m = 2,3,4, ... все функции /у в C4) имеют по t период «Т.;

598
ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
особенность этого случая была отмечена в кевде п. 3. Здесь надо
пользоваться теми же формулами B7) и C5). Правая часть C6)
имеет период тТ0, и потому в ее фурье-разложенин могут, вообще
говоря, оказаться гармоники с частотами соо=/»Bя//»7о), приводящие
к резонансу. Поэтому надо воспользоваться условиями C7) отсут-
отсутствия таких гармоник, затем найти а и Ь, перейти к формуле C8)
с л*Г0-периодической функцией <рх (t) и т. д. Полученное решение будет
иметь период /»Г0, однако в нем будет основное слагаемое C5)
периода Го (см. рис. 187, где/и = 3). Соответствующие колебания
называются ультрагармоническими, для них основная компонента
Рис. 187.
имеет частоту, кратную частоте внешнего воздействия (и близкую
к собственной частоте колебаний невозмущенной системы). Так как
и сейчас малое воздействие порождает конечное колебание, то излу-
излучается как бы резонанс нз периоде, кратном собственному. Это не
удивительно, так как в нелинейных системах гармоники редко фигу-
фигурируют в «чистом» виде, они сразу «обрастают» фурье-разложени-
ямн, т. е. гармониками с кратными частотами, иначе, дробными
периодами. В частности, /я^-периодическая гармоника индуцирует
Т0-периодическую, которая и порождает резонанс.
Исследование особого случая для систем с более чем одной
степенью свободы в принципе проходит так же, как и для одной
степени свободы. Формула C5) будет векторной, причем постоян-
постоянные векторы а, Ь будут включать 2k произвольных параметров, где
k—число собственных частот невозмущенной системы, равных сов.
Но и условие отсутствия резонанса в данном случае состоит, из
2k скалярных равенств (почему?), так что система определяющих
уравнений будет состоять из 2k уравнений относительно 2k упомя-
упомянутых параметров. При k=\ вычисления получаются не намного
сложнее, чем для случая одной степени свободы.

¦§ 4. ЯЕЯПКЙИЫЕ «ОЯЕВАИИЯ
599
6. Субгармонические колебания. Своеобразное положение зани-
занимает случай, когда частота ю внешнего воздействия близка к
«i-кратной собственной частоте. С одной стороны, это основной слу-
случай (п. 3), т. е. малому возбуждению отвечает и малое колебание.
С другой стороны, мы сейчас увидим, что, кроме малого колебания,
может быть также и конечное, частоты со//» (как мы упоминали
в п. 1, эти колебания называются субгармоническими порядка 1/т),
так что и здесь получается как бы резонанс, причем -на частоте,
кратяой собственной. Происхождение таких колебаний" можво понять
следующим образом. Для линейного уравнения x-\-alx=A cos ma>at
Рис. 18в.
общее решение имеет вид суммы частного, периода TJm, и свобод-
свободного колебания периода То, причем последнее зависит от начальных
условий; таким образом, и здесь получается колебание на частоте
соо =/»соо//я = ш//». Однако при наличии в системе как угодно малой
диссипации свободное колебание в силу возможности суперпозиции
с течением времени устраняется. В нелинейной же системе все гар-
гармоники взаимосвязаны, так что ни одна из них не может меняться,
не влияя на остальные; поэтому возбуждение гармоники частоты
лиоо может порождать гармонику частоты ш0, а потому и резонанс.
Формально рассуждение проходит следующим образом. Допустим,
что в правой части C4) все функции /у имеют по t период TJm.
Тогда они имеют и период То, и потому мы можем перейти к фор-
формуле C5) и определяющим уравнениям C7). В рассматриваемом
случае значения а = Ь = 0 обязательно удовлетворяют этим уравне-
уравнениям; эти значения приводят к решению, построенному в п. 3.
Однако уравнения C7) могут иметь и ненулевые решения, которые
и породят субгармонические колебания; возможный вид таких коле-
баний показан иа рис. 188, где принято /»=3.
Рассмотрим, например, еще один вариант уравнения Дуффинга
l (x + A cos 3w0fK.

600 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Определяющие уравнения C7) после выполнения интегрирований, которое мы
предоставляем желающим, принимают вид
^?а-ЬМ=0, Ь (^ |- +
Отсюда, кроме тривиального решения а=Ь=0, получаем решения
6=0, * + Ла+2Л»+?%=0, т.е. а=-± ± ^-Ia^-^
Эти решения пригодны лишь при комбинациях значений параметров, для кото-
которых корни не будут мнимыми.
6. Еще о вынужденных колебаниях. Сделаем еще несколько
замечаний.
1. При изучении вынужденных колебаний широко применяется
также следующий метод гармонического баланса, который в принципе
не требует наличия малого параметра. Пусть, например, левая часть
уравнения .
/(х, X, х, /) = 0 D3)
периодична по t с периодом Т и нас интересует решение этого
уравнения, имеющее тот же период. (Если периоды уравнения и
искомого решения не совпадают, но соизмеримы, то общую меру
можно принять за общий период.) Это решение можно разложить
в ряд Фурье
» = 2я/Т), D4)
с неизвестными коэффициентами. Условие же того, что эта сумма
удовлетворяет уравнению D3), можно написать в виде
г
en+2 (a/cos/co^ + ft-sin/citf), со 2 /(—a,sin jat + b, cos Ш).
\
— со* 2 f (e/ c°s Р* + bj sin pt), t J cospt dt = 0 (J= 0, 1, 2,...),
т
f(...)siaptdt = O (/=1,2,3,...). D5)
о - ¦
Таким образом, относительно коэффициентов разложения D4) полу-
получается система из бесконечного числа нелинейных уравнений с бес-
бесконечным числом неизвестных. Для ее приближенного решения можно
применить метод.усечения, т. е. как суммирование D4), так н соот-
соотношения <45) применять только до некоторого /,; это означает, что
невязка уравнения D3) должна быть сбалансирована так, чтобы ее

§ 4. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ 601
фурье-разложение не содержало компонент, -по которым ищется
разложение решения»
Таким образом, при У0 = 0 получается уравнение
т
$/(а„ 0, 0, i)dt = O
о •
с одним неизвестным, при уо= 1 —система из трех уравнений с тремя
неизвестными и т. д. Последовательно переходя от у0 к /У+Ь
можно для решения получающихся систем применять какой-либо
'итерационный метод, выбирая нулевое приближение с помощью ре-
решения, построенного на предыдущем шаге. Если о решении х(()
известны дополнительные сведения, например, что оно является
четной или нечетной -функцией или что в его разложении преобла-
преобладают какие-либо компоненты, то приближенное решение и условия
баланса строятся с -учетом этих сведений, что при том же объеме
вычислений позволяет значительно повысить точность приближенного
решения.
2. Если вычисления показали, что при заданных значениях пара-
параметров системы и возбуждения возможно несколько стационар-
стационарных колебаний (т. е. периодических решений), то возникает вопрос,
какое из них реализуется на самом деле. Естественно, что реали-
реализуются именно устойчивые решения; вопрос об устойчивости может
быть решен на основе исследования линеаризованного уравнения
(п. 3.4), которое представляет собой линейное уравнение с периоди-
периодическими коэффициентами. В частности, для систем с одной сте-
степенью свободы, т. е. для скалярных уравнений второго порядка,
после применения преобразований, указанных в п. 1,10, получаем
уравнение Хилла (п. 1.3). Если имеется несколько устойчивых стацио-
стационарных режимов колебаний, то каждый из них имеет свою область
притяжения начальных данных; кроме того, при «встряске» возмо-
возможен перескок с одного режима на другой. Общих аналитических
мето^й^йолучения этих областей нет, ио можно «нащупывать» их
с помощью численного интегрирования на ЭЦВМ или моделирующих
машинах при различном выборе начальных данных.
3. Рассмотрим еще случай полигармонического (т. е. квазиперио-
квазипериодического, см. п. 1.7) возбуждения нелинейной системы иа нескольких,
вообще говоря, несоизмеримых частотах; пусть для определенности
идет речь об уравнении
00 ¦ -
'х + со 1х = а 2 atxi+Aicosait + Ai cos att, D6)
причем для каждой из частот colf cog имеет место основной случай
(п. 3). Аналогично предыдущему можно принять
Х„ = 2 г 2 COS СОц* -f „ * „ COS tOj/,
*0 А. Д. Мышкио

662 ГЛ. VIII. ОБЫКИОВЯЙНЫ* ДЙФФЕГЕИЦИАЛЫЩЕ УРАВНЕНИЯ
пбсле чего для Xx(f) получится уравнение
х% + со**, = V а (-А-*cos »i' + ~Г~2cos <v
*-¦ / \Сй0—°>i шо—ша
/ = о
Для решения этого уравнения нужно в правой части раскрыть скобки
и преобразовать каждое из полученных слагаемых в сумму косину-
косинусов. Нетрудно видеть, что при этом получатся члены вида
A cos (/WjCuj -f- /»асоа) t с произвольными целыми щ, тх любого знака.
Поэтому в выражении для xt появятся члены вида
COS (/»,©( + /
Однако для несоизмеримых со4, ©2, т. е. для иррационального а^а^
выражение соо—[ml(ai + «jCOj) = e>a {(toe/©a)—[% (aj/aj)-f /»a]} при
любом заданном со может быть сделано за счет подбора щ, т2 как
угодно малым. (Это сразу вытекает из утверждения о всюду плот-
плотности траекторий на торе, приведенного в петите п. 2.13.) Эта
трудность малых делителей, замеченная Пуанкаре, существенно за-
затрудняет доказательство сходимости метода малого параметра. Если
в правой части D6) вместо бесконечного ряда стоит конечная сумма,
то и каждое Xj получится в виде конечной суммы, однако та же
трудность возникает пря J—*¦ оо. В реальных вычислениях она прео-
преодолевается уменьшением, в случае необходимости, применяемых зна-
значений а.
7. Автоколебания. Рассмотрим автономную систему с одной
степенью свободы, описываемую уравнением
x+e>lx = afl(x, х)+а%(х, х) + ... D7)
с малым параметром- а. В п. 2.5 мы говорили, что такая система
может иметь предельные циклы, т. е. автоколебания; покажем, как
их найти.
Существенным отличием автоколебаний от вынужденных колебаний
является, в частности, то, что частота со автоколебаний заранее
не задается, но может быть.найдена в процессе вычислений. Поэтому
напишем разложение
4а2 +... D8)
с неизвестными (кроме соо) коэффициентами и совершим замену не-
независимой переменной по формуле со/ = Ф. Обозначая и производ-
производные по О точками, перепишем D7) в виде
(соо -f toxa -f ayx* +•••
...).*)+ ... D9)

§ 4» нелинейные иолевлияя . 603
Решение, как и раньше, будем искать разложенным по степеням: <?
* = *о (<>)+ *t (*)<*+*»(*) <*2+ .-. F0)
Тогда из D9) получим
Особенностью автономных колебаний является также возмож-
возможность произвольного выбора начальной фазы, т. е. произвольного
выбора точки на цикле, отвечающей моменту / = 0 (этого не было
для вынужденных колебаний). В частности, можно положить х @)=0,
откуда
*о(О) = <>. *1«Ч = 0, *а@) = 0, ... F2)
Теперь можно приступить к решениям уравнений E1). Из пер-
первого с помощью E2) получаем
E3)
где амплитуда b пока неизвестна. Подставляя E3) в правую часть
второго уравнения E1) н пользуясь условием отсутствия резонанса,
получаем равенства
2л
[2co0@i& sin ft -f/i {b sin d, ©0?> cos Щ cos § d* = 0,
2Я
0
которые можно переписать в виде
2я
со1=—
Первое равенство E4) является определяющим уравнением для на-
нахождения амплитуды Ь; найдя Ь, мы из второго равенства E4)
непосредственно получаем ©ц. Затем нз второго уравнения E1)
получаем xt = <pj (О) -f bl sin d (<рц @) = 0), из отсутствия резонанса
для следующего уравнения находим bt и ©а и т. д. (Проведите
аналогичное исследование с помощью замены в D7) соо=со—сОцСС—..м
как в п. 4, и объясните получающееся различие.)
Чтобы выяснить устойчивость построенного цикла, надо записать D7)
в виде системы первого порядка, после чего применвть общее условве B.22).
20»

604 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Вычисления, которые мы предоставляем читателю, показывают, что если
a С f'k (b sin d, coofc cos d) db < 0, E5)
о
то построенный цикл устойчив, если же левая часть положительна—то не-
неустойчив.
Рассмотрим в качестве примера уравнение ван дер Поля .
a(x—kx*) -(fe = const> 0). E6)
При а > 0 и малых скоростях здесь получается как бы осциллятор с отри-
отрицательным коэффициентом трения (почему?), т. е. на фазовой плоскости в начале
координат будет неустойчивый фокус. Для больших скоростей член kx* будет
преобладать над х, т. е. решение будет быстро затухающим. Поэтому естественно
ожидать появления устойчивого предельного цикла на «средних» скоростях.
Определяющее уравнение в данном примере имеет вид (проверьте!)
жо„&— -т-nftco?63 = 0, откуда
4 . соо У 3fe
из-за инвариантности уравненвя E6) относительно замены х—у—х решение
Ь=—2(<в0 у^З/г) не дает ничего нового. Отсюда с помощью признака E5) сразу
получается, что при а > 0 построенный цикл устойчив; это, впрочем, ясно и
из рассуждения, приведенного в начале абзаца. Из второго уравнения E4)
получаем cuj = O, т. е. для выяснения характера изменения частоты разложение
придется продолжить. (Равенство со^О можно было предвидеть, заметив, что
уравнение E6) переходит в себя при замене а—»•—a, t—»¦—t, a потому со
должно быть четной функцией а—продумайте это!) Вычисления дают
х1 = - 2 (cosd— c
3<в0 у 3k
_• coa sin «4 %=¦ (—sin 0 + 3sin Щ +
3ft 3a>/3*
d —r—7=^(—sind + 3sin3d)+fc!COsO [
L 3ft>oy 3fe J
Применяя условии отсутствия резонанса, получаем (проверьте!) ^ = 0,
cog=l/2(Bo.
Проверьте, что применение к уравнению E6) метода п. 4 привело бы
к нулевому решению.
В заключение отметим, что автоколебания реально чаще всего
возникают, когда рассматриваемая автономная система поглощает
энергию из внешнего постоянного источника, который и поддер?
живает колебания, тогда как наличие в системе диссипации не дает
им разрастаться слишком сильно. Такие системы называются актив-
активными, в отличие от пассивных, у которых нет источников энергии,
т. е, энергия которых может либо сохраняться, либо диссипировать.
Широко известные примеры таких самоподдерживающихся колеба;
ний-г-колебания скрипичной струны, возбуждаемой смычком, скрип
дверных петель, ветровые колебания телеграфных проводов, слыщ-

§ 4.'нелинейный колония•¦•-<
605
ные, если приложив' ухо к телеграфному сТ6лбу','!<<*шум Шря> в
раковине, флаттер крыльев самолета н т. д. -.'
Аналогично исследуется задача о частоте малых колебаний сильно
нелинейной консервативной системы, описываемой уравнением x+(olx—f(x)
(где /@) = 0); в этой задаче малым параметром служит амйлитуда"Колебаййй:
например, можно доложить *@)«>а, дг(О) = О. Здесь надо воспользоваться
разложением D8) н заменой a>t = Q, но взамен E0) написать дг=д;1(д)а4-
i0
+ ..., где *i@)=l, JCa(O)=...=O, ic10)=x2(O) = ...=O. Мы
предоставляем читателю проследить за вычислениями. . .
, 8. Релаксационные колебания. Рассмотрим теперь поведение
решений уравнения более специального, чем D7), вида
с большим параметром а, т.е. при а—» со. Если ввести новые
переменные по формулам х—у, * = а|, t — at, а~* — е, получим
систему уравнений (проверьте!)
W = * e^=-»S.+/0'). E7)
где е мало.
Система E7) представляет собой частный случай систем вида
*-Р(х v
Q(x, У, «)
F8)
с малым параметром 8 > 0. Если разделить второе уравнение на в,
то иидно, что прн малых е поведение траекторий в той или иной
области плоскости х, у в значи-
значительной мере определяется знаком
функции Q(x, у, 0) в этой обла-
области: например, если этот знак
плюс, то при малых 8 вертикальная
соста вляющая скорости потока весь-
весьма велика, а горизонтальная ко-
конечна, т.е. поток направлен почти
вертикально вверх.
Линия (L) с уравнением Qo {x,y)^
^Q(x, у, 0)^=0 разделяет пло-
плоскость х, у на части, в которых
поток направлен почти вертикаль-
вертикально' вверх или почти вертикально
вниз фис. 189). Вблизи точек самой '
линии (L) скорость потока остается конечной, так что' точки
могут двигаться в непосредственной близасти (L) вдоль (I); направ-
направление атого движения определяется знаком функции Р (х, у,Щ
на (I). Надо различать устойчивые (АВ и CD на ' рис' 189) и
неустойчивые (ВС) дуги (L). (Возможны также полуустойчивые дуги;
Рис. 189.

гл. vni. OBbriftioeiteHbre'ди**еРенцилльйые уравнения
котдрые мы здесь не будем рассматривать.) К устойчивым дугам
траектории «притискиваются», так что, попав на такую дугу, тра-
траектория вынуждена следовать вдоль «ее, пока дуга не перейдет
в неустойчивую (на рис. 189 вблизи точки В). В отличие от этого,
траектории, следующие вдоль неустойчивой дуги (Z-K очень легко
сталкиваются с нее, так что иа деле не реализуются.
Распределение знаков функции Р (х, у, 0) вдоль (L) может быть
таким, что траектория будет периодически проходить одну и ту же
трассу, приближаясь к предельному циклу,
кото'рый при 8—»¦ 0 будет состоять из не-
нескольких устойчивых дуг (L), проходимых с
конечной скоростью, и нескольких верти-
вертикальных отрезков, проходимых с беско-
бесконечно большой скоростью. (Конечно, имеет-
имеется в виду скорость движения изображающей
точки на фазовой плоскости, в расчете иа
единицу т.) Поэтому при конечном, ио
малом е колебание будет состоять из мед-
медленных и быстрых этапов—обычно это этапы
медленного накопления энергии и быстрой
ее разрядки. Такие колебания называются
релаксационными.
Вернемся к системе E7) и допустим, что график (L) функции
? = —у/СУ) таков, как показано иа рис. 190. Тогда в пределе при
щ
8—*0 у системы будет цикл (С), показанный иа рис. 190 сплошной
линией. Нетрудно подсчитать соответствующий период колебаний:
&.
так как ат = —, то •
*****
1
H
a
\
у
с
b
1
1 '1
Рис. 190.
аЬ
(Этот же прием легко распространить на общую систему E8).)
2
В частности, для уравнения E6) /{у) =у—ky\ и потому уа = -
уь = —-7=- (проверьте!), откуда период по т равен
ЧУзк
'JVM
Если а велико, но конечно, то предельный цикл будет близок
к изображенному на рис. 190, а полученное выражение после умно-
умножения на а (чтобы вернуться к «настоящему» времени /) даст
главный член асимптотического выражения для периода колебаний.

§ 4. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
,607
.Советский механик А. А. Дородницын • (р. в 1910 г.) в 1947 г.
подучил дальнейшие члены этого выражения (см. [13]):
,0087^
Скачки рассматриваемого типа на фазовой плоскости проявляются уже при
рассмотрении свободных колебаний линейного осциллятора с весьма малой
инерционностью, описываемого уравнением
mx+fx+kx—Q
E9)
с постоянными коэффициентами и весьма малым т. В пределе при т —*¦ 0
получаем уравнение первого порядка fx-{-kx~O, поэтому здесь говорят о си-
системе с 1/2 степенями свободы. На фазо-
фазовой плоскости из E9) получаем систему
уравнений
х=у, my=—ty—kx;
соответствующий фазовый портрет при
исчезающе малом т показан на рис. 191.
При любом начальном состоянии скорость
осциллятора мгновенно перестраивается,
т. е. точка на фазовой плоскости совер-
совершает мгновенный перескок на прямую
&*+/#=0 (это возможно в силу безынер-
ционностн), после чего осциллятор с ко-
конечной скоростью по экспоненциальному
закону сползает в положение равновесия.
Конечно, при просто (не нсчезающе) малом
т траектория на фазовой плоскости будет такой, как показано на рис. 191
пунктиром.
9. Пограничный слой. В связи с материалом предыдущего пункта остано-
остановимся более подробно иа системах диффереицнальиых уравнений, содержащих
малый параметр а > 0 и полностью или частично вырождающихся при а=0.
Пусть рассматривается система вида
Рис. 191.
х=»(/, х, у; a) ay=g(f, x, у, а),
F0)
где искомые векторы х (t) и у (t) имеют размерность пит соответственно.
При а=0 вторая группа уравнений F0) вырождается, переходя в систему
конечных уравнений
Z(t, х. у; 0)=0, F1)
которая определяет в (п+/п+1)-мерном пространстве f, x, g некоторую
(п+1)-мерную поверхность (S).
При малом а любая интегральная линия х (t), у (t) системы F0) подобно
п. 8 может иметь участки двух типов: расположенные иа конечном расстоянии
от (S) и проходящие в непосредственной близости (S). Для участков 1-го типа
можно с точностью до малых порядка а считать величины t, x постоянными,
а величину у удовлетворяющей системе уравнений
¦?=*(*> *• У' °)
Гт=——быстрое время).
F2)

608 ГЛ. VIII. ОБЫКНОВЕННЫЙ ;ДИ«1*ё№НЦ,ЙЛЛЬНЫЕ УРАВНЕНИЯ
Для участков 2-го типа приближенно -выполняется система ¦
§ = *('. х, У. Q). ,'
y=(t ) F1)
Пу
где y=%(t, x) определено из системы F1).
Пусть задано начальное условие
<=0, х=х0, y=y0,
определяющее в Еп+т+1 точку Afo, которая, вообще говоря, не лежит на E).
Тогда соответствующая интегральная линия начинается с участка 1-го типа, опре-
определенного автономной системой F2), написанной для t=0, х=х0. Мы огра-
ограничимся рассмотрением случая, когда точка </0 принадлежит области притяжения
некоторой асимптотически устойчивой точки покоя ув этой системы; поэтому мы
будем считать, что @, х0, yo)€(S) и все собственные значения матрицы
dg(O, х0, у, О)/ду|^_^ имеют отрицательные вещественные части. Из послед-
последнего вытекает, в частности, что det(dg/dy) |0 х^ Ф 0, и потому вблизи
точки Мв @; х0; у0) уравнение поверхности (S) можно представить в виде
y=%(t, x), после чего перейти на (S) к уравнению F3).
Итак, прн малом а рассматриваемая интегральная лнния состоит из участка
быстрого перехода от Мо в непосредственную близость точки М„ и дальнейшего
участка следования вблизи (S) в соответствии с вырожденным уравнением F3).
Интервал независимой переменной t, отвечающий первому участку, называется
пограничным слоем, он нужен решению для перехода от произвольно заданных
начальных значений @; х0; у0) к значениям @; х0; у0), согласованным с вы-
вырожденной системой F1). Ширина пограничного слоя условна, но при любом
таком условии она оказывается, с точностью до малых высшего порядка, обратно
пропорциональной крутизне поля F0), т. е. прямо пропорциональной а (ср.
ЛВМ, п. XV.28).
Отметим еще, что интегральная ляння, следующая вдоль (S), может «сор-
«сорваться» с (S), только когда указанное выше условие аснмптотической устойчи-
устойчивости окажется нарушенным.
Чтобы получить более точное асимптотическое представление рассматривае-
рассматриваемого решения, заметим, что в силу описанного выше характера этого решения
в его разложении должны присутствовать как функции от т, главные втгогранич-
ном слое, так и функции от t, главные при t^>a. Поэтому напишем
„
Конечно, такое представление решения неоднозначно: например, положить
(j>0 (f) ее f, Фх(т)^0 все равно, что <po(<)s=O, Фх(т)е=т; однако для даль-
дальнейшего это несущественно.
Подставим разложения F4) в F0) и преобразуем после этого правые части
по следующей схеме:
Фо (ат) + «фх (ат) + ... + Ф„ (tj + аФх (т) +... , $0 (ат) +
...; a)-f(ат, фо(ат) +
л..., ifo(at)+at|I(at)+...; a)],
н аналогично второе уравнение F0). Затем разложим правые части по степеням
а и приравняем члены при одинаковых степенях а отдельно для функций от
t н для функций от х. Это даст прежде всего ф'0(х)^0, откуаа и Ф0(т)е=0,

.:¦¦¦¦::! § 4. НЕЛИНЕЙНЫ^ КОЛЕВ\ИИЯ ; ., .4,609
так как постоянной слагаемое можно передать от Фо к,ф4. .Далее получаем
V;(/)=f(<, tft{t), ^„(t); 0), 0=g(*. Фо(/). ^0@; 0), F5)
Vo W=g @, q>0 @), to @)+ 4% (t); 0)-g @, ф0 (О), to @)! 0); F6)
кроме того, должны выполняться начальные условия
0)=х„, *в@)+Ч'о(О)=уо. F7)
Иа F6) и F7) видим, что функции х=ф0 @. У~%(() удовлетворяют предель-
предельной (при а=0) системе F0) при начальных условиях фв@)=х0, ^аЩ=Уо-
Поэтому начальную задачу для главного члена Уо (х) пограничного слоя можно
в силу F6) переписать в виде
4ro(T)=g(O. фо@), 4>0@) + »F0(T); 0), У0@)=у0-у0.
Таким образом, функция у^Уо+^о (*) удовлетворяет системе F2) при t—0,
х=х„. Кроме того, из предположения о собственных значениях матрицы dg/dy
вытекает, что Ч^ (х) > 0 со скоростью экспоненты.
Приравнивание следующих членов разложения приводит к уравнениям
= «r,C Фо(О. to(O: 0)Vl@+f;(...)*i@+4(-->). F8)
=вхС »d@. toCO: 0)»i@+e'y(...)ti@+ee(-;-). F9)
=f(O, Фо@), t»@)+*o(*); 0)-f@, ф„@), to(O); P), G0)
y @) }
- {й< (О, фо @), ^o @); 0) t+g; (...) [Ф; (О) т+ ф1 @)] +
+gy(•••)[*'„ @)T+ti@)l+g«(...)]} G1)
и начальным условиям '
Ф1@) + Ф1@) = 0, tiW+^iW)-». G2)
Из уравнения G0) и условия Ф1(оо)=0 получаем
, фо@), to@); 0)—f(о, Фв@),
откуда, в частности, определяется Фх @), а потому в силу G2) и фх(О). Выра-
Выражая из F9) неизвестную функцию ti@ через фх (<) и подставляя результат.
в F8), получим систему первого порядка относительно фх, из, которой, зиая
ф! @), находим ф1@. а потому и ti @- Затем из' G2) можно найти ^(О), а
из G1)—функцию ^ift). При этом нетрудно показать (попробуйте!), что
Фх (т) »¦ 0 и Чг1 (t) »- 0 со скоростью экспоненты.
Аналогично находятся дальнейшие члены разложения F4). Более подробное
исследование показывает, что получающиеся ряды асимптотически (при а—>-0)
сходятся к рассматриваемому решению начальной задачи иа любом интервале
0*?*<Г, на котором решение предельной (вырожденной) задачи проходит по
той области поверхности (S), где выполняется указанное выше условие асимп-
асимптотической устойчивости. : , ,:•,•¦¦..:,. .. • •.

610 ГЛ. VUI. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
10. Непериодические колебания. Методы, описанные выше, при-
пригодны в основном для построения и исследования периодических.—
вынужденных или свободных—колебаний. Для изучения'переходных
процессов в колебательных системах, почти-периодических и других
непериодических колебаний более приспособлен метод, предложенный
ван дер Полем в 1927 г. и значительно развитый А. А. Андроно-
Андроновым A930), Н. М. Крыловым и Н. Н. Боголюбовым A937), Ю. А. Мит-
ропольским и другими авторами (см. [13, 81, 85]).
Метод, описанный в п. 3, <3ыл пригоден для построения не только
периодических, но и переходных процессов. Поэтому мы рассмотрим
особый случай уравнения C4) с Т0-периодичными G0 = 2я/(ов) по t
функциями fft как было указано в п. 3, к этому уравнению приво-
приводится и исследование возбуждения системы с малой нелинейностью
на частоте, близкой к резонансной.
Введем наряду с «обычным» временем t медленное время т = а/.
Основная идея метода состоит в построении решения в виде
- .1
*=2 akV> *)<** G3>
ft=0
(впрочем, этот ряд может при а—>-0 сходиться лишь асимптотиче-
асимптотически, см. п. II.4.1). Конечно, такое представление неоднозначно, что
видно уже нз равенства т + 0а = 0 + ta. Это дает возможность на-
наложить на коэффициенты ak те или иные дополнительные требова-
требования. Мы будем здесь требовать, чтобы они при каждом фиксированном
т были Т0-периодичны по t. В самом деле, при а = 0 решения,
очевидно, Гд-периодичны. Поэтому естественно ожидать, что и при
малом а решения будут напоминать Т0-периодичесюге функции с
медленно меняющимися амплитудой "и начальной фазой; а эти изме-
изменения можно будет учесть зависимостью решения от т. Впрочем,
правильность поставленных дополнительных требований на коэффи-
коэффициенты будет выявлена в процессе последующих вычислений, так
как при неправильных требованиях удовлетворить уравнению не
удастся.
Из формулы G3) получаем
2 f
ft=0
Подставим эти выражения в C4) и потребуем, чтобы полученное
уравнение удовлетворялось тождественно по а при любых зафик-
зафиксированных t, т. (Конечно, это требование избыточное: например,
для верного равенства t-j-Oa = 0-j-ta оно не выполняется; однако
если нам удастся удовлетворить этому требованию, то и уравне-

§ 4. НЕЛИНЕЙНЫЕ КОЛЕВЛВКЖ 611
ние C4) удовлетворится, а победителей ведь.не судят!) Приравни-
Приравнивав коэффициенты при одинаковых степенях а, получим
(«.)« + «;ао = О,
(aju + ©Ц = — 2(ао)"н +Л(в., (aa\t, t), ... G4)
Из первого равенства находим
at(t, т) = Л0(т)созю0/ + В0(т)8тй>0г'. G5)
Подставим это выражение в правую часть G4); тогда получится
функция, которая при каждом фиксированном т Т0-периодична по t.
Но так как и решение at должно быть То-пернодичным по t, то
должны выполняться условия отсутствия резонанса, которые после
простых преобразований приобретают вид (проверьте!)
г.
А'°W = ~ к U1 {А°(т) cos Шо/+s°(T) sin <v>
о
—<в0 Ло (т) sin caot + <Во?о (т) cos caot, f) sin aot dt,
, If G6>
К W = 2^ J Л <Ло (T> C0S Ш»# + S« (T> Sln C0^'
0
—ш0 'Л „ (т) sin ш0/ -f ЮцВд (т) cos (aot, t) cos ca^^ dt.
Таким образом, получилась система из двух обыкновенных диффе-
дифференциальных уравнений относительно двух неизвестных функций
/40(т), Вл(х), из которой и можно найти эти функции. Удовлетво-
Удовлетворив условиям отсутствия резонанса, мы можем в силу G4) написать
at (t, t) = <pt (t, x) + At (t) cos ©0/+В, (т) sin a>at,
где «ft—вполне определенная функция, Т0-периодическая по t при
любом фиксированном т, а функции Л1 (т), В± (t) пока неизвестны.
Написав уравнение для аг, следующее за G4), и воспользовавшись
условиями отсутствия резонанса, получим систему из двух обыкно-
обыкновенных дифференциальных уравнений относительно А1 (т), Вл (т)
и т. д. Этот процесс можно в принципе продолжить как угодно
далеко.
Систему уравнений G6) можно получать также с помощью следующего
рассуждения. Запишем уравнение C4) в виде системы
*=<ВДГ, у'=— <0e*+T-/i(*. «>о0. *)+••• С77)
Так как при а=0 соответствующий поток на фазовой плоскости*, у совпадает
с ее равномерным вращением в отрицательном направлении с угловой ско-
скоростью <а0, то естественно и при малом а Ф 0 решение системы G7) рассматри-
рассматривать в подвижной, равномерно вращающейся с угловой скоростью щ системе
коордиват. Это означает, что надо совершить замену искомых функций по

612 ГЛ. VIII. ОбЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
формулам
¦' . G8)
где х, у не постоянны, как при а=0, а изменяются (естественно, что медленно
прн малом |а|) с изменением /. Подстановка G8) в G7) дает (проверьте!)
—.^ _ — f1(Xcos <?>ot -\-y sin(V. —©оде sin a>0/ +
+ а>оу cos wef, <) + ... sin e^t G9)
и аналогичное выражение для -^г.. Прн малом |а| правая часть близка к пе-
периодической, так как х, у почти постоянны, а общее направление изменения х
определяется постоянным слагаемым ее фурье-раэложення (прочие компоненты
дают малые Г „-покачивания вокруг этого направления). Чтобы получить это
главное слагаемое, надо произвести осреднение правой части (ЛВМ, п. XVII. 23),
что после отбрасывания членов высшего порядка малости и приводит к урав-
уравнениям G6) (проверьте!). По этой причине описываемый метод называется
также методом осреднения (усреднения). В такой форме метод можно приме-
применять и к уравнениям, не содержащим малого параметра (в случае вынужден-
вынужденных колебаний под а>0 в G8) надо понимать частоту внешнего воздействия),
ие забывая о необходимости контроля.
Мы предоставляем читателю проверить, что тот же результат получится,
если в C4) подставить решение х=х co&(ott-\-ysin<oat, отбросив при этой
d2x d*y
подстановке члены с -р-, •—¦, после чего приравнять с обеих сторон фурье-
компоненты с cosoV и sino>of.
Если нас интересуют только Г0-периодические решения х{{), то
коэффициенты uj не должны зависеть от т, а потому коэффициенты
Aj, Bj должны быть постоянными. Тогда уравнения G6) превраща-
превращаются в определяющие уравнения C7), и мы возвращаемся к методу,
описанному в п. 4. Однако можно рассматривать и непостоянные
решения системы G6). Заметим, что G6)—автономная система и
ее- можно рассматривать на плоскости Ао, Вв с помощью методов,
описанных в пп. 2.3—6. Точкам покоя на этой плоскости отвечают
периодические решения уравнения C4), причем соответствующие
колебания происходят с частотой внешнего воздействия; тогда
говорят о синхронизации или о захвате частоты. Циклам отвечают
квазипериодическне решения, получающиеся в результате наложения
частоты <оо и частоты цикла (соответствующие колебания называ-
называются комбинационными, а так как первая частота существенно больше
второй, то появляются биении). Траекториям, входящим в точку
покоя, отвечают переходные процессы установления периодических
колебаний и т. п.
Наиболее прост случай, когда функция ft не зависит от t. Тогда можно
перейти на плоскости Аа, Во к полярным координатам по формулам Аа = р cos ф.

§ 4. НЕЛИЛЕЙНЫЕ КОЛЕБАНИЯ 613
B0=psln(pp что даст
="«СГ \fi (p c°s (gH* — Ф). —«oP sin (a)of — ф)) sin (aot—ф) Л =
2я
=-2^-J/i(pcosi|), — шор siri>) sin
0
т. е. получилось уравнение первого порядка с одной неизвестной функцией,
которое решается методом разделения переменных. Найдя р (т), можно получить
q> (x) из равенства
2я
d<?—-/Л "' п л'4 -1-- ? •, (pcosi|), — соорsin г|з)ее
Можно было рассмотреть несколько более общее, чем C4),
уравнение, допуская зависимость функций fj также от т; тогда
система G6) будет неавтономной, но в ряде примеров она оказы-
оказывается более простой, чем исходное уравнение C4). Отметим кстати,
что система уравнений для нахождения 'Av Blt вообще говоря, со-
содержит А9 (т), Ва (х) и потому также не является автономной, если
только не рассматривать систему для Ао, Ва, Аь В% совместно
в четырехмерном пространстве.
Если рассматривается устойчивое колебание, то систему G6)
можно применить для приближенного нахождения с помощью чи-
численного интегрирования значений Ао (оо), Во (оо), которые опреде-
определяют амплитуду и фазу колебания в нулевом приближении. Впрочем,
можно с помощью численного интегрирования только подойти к этим
значениям, после чего применить к системе определяющих уравне-
уравнений метод типа Ньютона.
Рассмотрим в качестве примера вынужденные колебания в системе с само*
.возбуждением E6):
x-\-aU = a(x—kxa)-\-aMcosat, где w=o)o + Wi<*- (80)
Как в п. 4, проводим замену шо=ш—о^а, что даст
'x'-\-(x>*x=Bw>1x~\-x—kxa-t-Mcosat)a—(x>ixa*. . (81)
Согласно G3) пишем
x=aB(t, x)+at(t, x)a+..., x=at.
i
Отсюда, как в общем случае,
(82)

614 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Приравнивая в (81) коэффициенты при а, получим
= 2 «iCO (Ло cos at + 50 sin to/) -J- 2а> (Л'„ sin <о/ — Во cos а><)—
—о» (Ал ein <о/—Во cos <о/)+fe<o* (Д, sin <el—Ва cos ©<)* + A* cos at.
Из условия отсутствия резонанса получаем систему уравнений (проверьте!)
|-0 + ) )
8 1 (83)
Это и есть автономная система, траектории которой определяют формы вы-
вынужденных колебаний в нулевом приближении в силу равенства (82), которое
можно переписать в виде
at= Ao(oU) cos Ы-\-Ва (at) sin a>t.
Подробное исследование, результаты которого приведены в [108], показывает,
что при малых a>i траектории системы (83) входят в точки покоя, т. е. реше-
решения уравнения (80) асимптотически (при t —*¦ оо) периодичны; если же %
велико, то система (83) имеет устойчивый предельный цикл, т. е.- появляются
комбинационные колебания.
Как и в п. 5, если функции /у имеют по t период Т0/т (т = 2, 3, ...),
то описанное построение приводит к субгармоническим колебаниям порядка
1/т; см. по этому поводу [124].
Метод усреднения можно применить и для систем с более чем одной сте-
степенью свободы. Например, обобщая уравнение G9), можно рассмотреть систему
вида
x=of(*. /, a), (84)
правая часть которой периодична или даже почти-периодична (п. 1.7) по t.
Обозначим осредненную по t функцию f при а=0 через
. t, Q)dt (85)
и совершим замену переменных по формуле
J i (86)
(обращаем внимание, что как в (85), так и в (86) х и у под знаком интеграла
рассматриваются как параметры). Учитывай, что у=0(а), получим после аа-
мены (проверьте!)
еменных по формуле
y+J J f {у, tlt a) d^-ifiy)
У—а jffo, <i, <«)<«!-/?"(»
, t, а)-(т0(а!) )
Отбрасывая члены высшего порядка малости, получаем осреднеиную систему (84)
i (87)

§ 4. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ 615
. Система (87) автономная, и, конечно, проще, чем (84); некоторые вопросы
для нее—такие, например, как тип и устойчивость точек покои,—в ряде при-
примеров могут быть разрешены. Можно показать, что каждой точке покоя сис-
системы (87) отвечает периодическое или соответственно почти-периодическое реше-
решение системы (84), расположенное от этой точки на расстоинии порядка а, при-.
чем если точка покоя устойчива, то и соответствующее решение системы (84)
устойчиво. По поводу построения методом усреднения приближений высшего
поридка см. [81].
Метод усреднения применяется также к более общим, чем (84), системам
вида
x=af (х, Q, t, а), А=(Х,1, Х,а Л^'+аф^х, #, t, a), (88)
где 0=(dt, 0а, ..., Ьр)—набор угловых переменных, от которых все функции
/у и ф/ зависят периодически. Здесь осредненная система имеет вид
г
y=a lim 7тГ \ f (у, tk, t, 0) At,
! (у, Л, /. 0) it, .
так что переменные у отделяются. Решения осредненной системы и здесь ап-
-проксимируют решения полной системы с точностью до членов высшего порядка
малости.
К системам (88) приводятся, в частностн, системы с быстро вращаю-
вращающейся фазой
x=f (х, в, t), Ь=М (Хх, Л* ^р)* + Ф (*. *. О» (Щ
где М—>-оо—большой параметр. В самом деле, после введения быстрого вре-
времени s=Mt и малого параметра a=Af-1 из (89) получаем систему (проверьте!)
¦g=af (х,0, as), ^=(^i. *,,.... V+«? (*. *. as)
типа (88).
11. Асимптотические разложения по Н. М. Крылову — Н. Н. Боголюбову.
В 1937 г. Н. М. Крылов и Н. Н. Боголюбов предложили новый, один из наи-
наиболее гибких методов асимптотического разложения решения по степеням малого
параметра, входящего в уравнение. Покажем этот метод на примере автоном-
автономного уравнения D7). Здесь решение ищется в виде
х=асоз^+х1(а, $)а+хг(а, <ф)аа + --- (а=а(/, a), i])=i|>(f, a)), (90)
где все функции Xj (a, ty) 2л-пернодичны по ф; цри этом функции а, тр должны
удовлетворять уравнениям
а=Лг (а)«+Л»(а) «*+•••. $=:щ+В1(а)а, + В2(а)аР+..., (91)
коэффициенты которых строятся в процессе построения решения. (Проверьте
правильность выбранной формы для решения при а=0.) Для построения
функций Xi, Aj, Bj требуется, чтобы после вычисления х (a, i|r) и х (а, ф) из
(90) и (91) по формальным правилам и подстановки полученных выражений
в D7) это уравнение удовлетворялось при фиксированных a, tf тождественно
по о; этого, конечно, достаточно, хоть и иё необходимо, так как а и г|) сймн
зависят от а. Кроме того, для нормировки требуетси, чтобы фурье-разложения
функций Xj не содержали членов С cos ф и sin ф: в самом деле, такие члены
можно выделить и объединить с первым членом в правой части (90).

616 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Покажем, как получить приближение первого порядка. Имеем
— a sin \р
= АХ (a)cosij>*a—
*"=—2co0i41 (a) sin f a — acosf <& — 2Bi (a) acao cosijva + &h a>l
при вычислениях мы отбрасывали члены с а2. Подставляя в D7) и приравни-
приравнивая члены с а, приходим к равенству
= /, (acosif, — a«»0sin ф) + 2щА^ (a)sinф + гаю.^(a) cos$.
(92)
Из условвя отсутствия резонанса получаем
я
Аг (а)=— -g^- J /t (a cos г|з, —a«0 sin г|з) sin г|з dip,
-я
jr
(a cos г|з, — am0 sin г|з) cos г|> rff.
Разложив при выполнении этих равенств правую часть (92) в ряд Фурье
СО
So (а) + 2 \Sj (a) cos /tf + hj (a) sin /ф],
мы получаем в силу указанного в предыдущем абзаце условия нормировки
СО
Е Ц ^ (fl>cos ^+Л^ ^ sin
4^
Таким, образом, построенная функция
где аи\|1 определяются из уравнений
а=А1(а)а, ф=w0 + S, (а) а, (94)
будет удовлетворять уравнению D7) с точностью до членов порядка а2. Отсюда
можно вывести, что построенное приближенное решение отличается от точного
при одинаковых начальных условиях (им можно удовлетворить за счет появле-
появления при интегрировании уравнений (94), которое выполняется весьма просто,
произвольных постоянных) на величину порядка аН. Аналогично, хотя и более
громоздко, строятся приближении более высоких порядков.
Если приближенное решение рассматривается на времеиибм интервале
порядка I/a, безгранично возрастающем при.a—>-0, то ошибка приближенного
решения (93) будет иметь порядок а (почему?), т. е. в формуле (93) нет смысла
удерживать второе слагаемое, и приближенное решение можно записать просто
в виде й cos tf, где а и т|) определены из ураииений (94). При этом получится
в точности тот же результат, что и в первом приближении по методу п. 10,
если предварительно преобразовать время, как в п. 7 (проверьте!).

§ 4. НЕЛИНЕЙНЫЕ- КОЛЕБАНИЯ i : : 617
Если рассматривается-система с медленно меняющимися параметрами, т. е.
в уравнении D7) правая часть и коэффициент а>§ зависит от медленного вре-
времени т=а< (п. 10), то все строящиеся функции X/, Ар В/ надо считать.зави-
считать.зависящими также и от т. (Проследите, как изменятся формулы для приближения
первого порядка, я покажите, что дли уравнения (m(x)x)'+k(x)x=t (x, х)а
в первом приближении x=acosty будет a=const [т (х) k (x)]~tf*, а для урав-
* С /~k (х)
нения (т(x)x)'+k(x) *=/(*, х) а будет т|>=\ 1/ —y^dt; подумайте, почему
получились такие простые формулы.)
Для уравнения вынужденных колебаний C4); в котором все функции ff
Т-периодичны по /, причем Т несоизмеримо с Т1о = 2я/<Оо (т. е. в нерезонанс-
нерезонансном случае), решение можно построить в виде
a, г|>, t)a+x2 (a, ij>, 1)а* + ...,
где все функции х/ 2я-периодичны по ф, Т-периоднчны по t, а амплитуда и
фаза удовлетворяют уравнениям {91). Построение функций xj осуществляется
совершенно аналогично тому, как в автономном случае, однако прн этом надо
пользоваться разложением в двойные ряды Фурье (ЛВМ, п. XVII.30), по ф
н t. Предоставляем читателю получить формулы для приближения 1-го"
порядка.
В резонансном случае, т. е. когда Т = —Тв, где р, q—натуральные чис-
числа, решеняе оказывается, более удобно строить в виде
где все х/ <7^'"пеРН0Днчны по '. а величины а, О удовлетворяют уравнениям
а=А1(а, Ща + Аг(а, й)аг+..., 4=В,(а, &)а + В2(а, й)а2 + ...,
правые части которых, подобно (91), строятся в процессе построения решения.
По поводу деталей этого довольно громоздкого построения см. [13]. Отметим
только, что ряды по степеням малого параметра а, получающиеся здесь, ока-
оказываются сходящимися, вообще говоря, лишь асимптотически (п. II.4.1). Од-
Однако это не имеет практического значения, так как реально пользуются Лишь
приближениями невысокого порядка—чаще всего первого. Практически суще-
существенно только знать, начиная с каких а можно пользоватьси получающимися
асимптотическими формулами; а это можно выясннть с помощью контрольного
численного интегрирования модельных примерев.
В [13] содержится также применение описанного метода к исследованию
одночастотиых колебаний в системах с более чем одной степенью свободы.
Здесь взамен (90) получаетси'разложенне
(а, г|>)а+х2(а, г|>)а*+...,
где ф—соответствующий собственный вектор при а=0, а величины a, if Удов-
Удовлетворяют скалярным ураниеииям (91). Правда, при этом получается представ-
представление лишь двупараметрического семейства частных решеннй, ио в ряде прак-
практически важных случаев решении этого семейства представляют наибольший ин-
интерес, так как они притягнвают к себе все другие достаточно близкие решения.
12. Системы с дискретным временем. В теории нелинейных колебаний, как
н в ряде других вопросов, оказывается полезным понятие системы с дискрет-
дискретным временем. Такая система задается двусторонней последовательностью
гомеоморфизмов (т. е. взаимно однозначных взаимно непрерывных отображений)
*'=»**(*) (*=*...* -2, г-1, 0, 1, 2, ...) (95)
n-мериого пространства x={xv *a. •• •» ха) на себя. При этом номер k играет

618
ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
роль, момента времени, а формула (95) определяет закон перескока, происходя-'
щего в этот момент, тогда как в промежутках времени между перескоками
точка .покоятся.
Чтобы получить закон движения отдельной точки, надо задать ее положение
ж=х0 непосредственно перед перескоком с некоторым номером k0. Тогда после
этого перехода до следующего точка будет находиться в положении ф^, (хф); непо-
непосредственно перед перескоком ko-\-2—в положении фй„+1 0|э*„ (*)) и т. д. Можно
вдтн и в обратном направлении: точка х„ получается в результате перескока
к,— 1 из точки ty? 1(х0) (гДе верхний минус означает обратное отображение)
и т. д. Таким образом, мы получаем закон движении—двустороннюю последо-
последовательность
x=x(k; К, х») (*=..:, -2, -1, 0, 1, 2, ...), (96)
определяемую свойствами
ypk(x(k; k0, xo))=x(k+l; k0, хо), x(k0; ka, xa)~xa. (97)
Более прост случай, когда отображения (95) не зависят от k; такие дис-
жретиые системы аналогичны автономным системам дифференциальных урав- _
нений первого порядка. Тогда положение скачущей точки зависят только от
начального положения и количества перескоков, т. е. взамен (96) и (97) надо
написать
x=x(k— k0; х0), ip(*(*; xa))^=x(k+l; х0), хф; хо)—хо.
Подобно п. 2.1, получается нечто вроде дискретного потока в Еп, однако роль
траекторий играют двусторонние последовательности точек. Как и в п. 2.1,
можно различать три типа траекторий: незамкнутые (здесь—состоящие из бес-
бесконечного числа точек), замкнутые (состоящие яз конечного чясла точек,
повторяющихся в циклическом порядке) и точки.покоя, определяемые уравне-
уравнением if> (*)=*. (Для большей аналогии с дифференциальными уравнениями '
можно было бы задавать основное отображение формулой x'=x+f (jc); тогда
течки покоя определялись бы из уравнения f(x)—0.) Подобно п. 2.2, можно
говорить о предельных множествах траекторий, причем и для дискретных тра-
траекторий выполняются все перечисленные там свойства, конечно, за исключением
свойства 5.
При исследовании окрестности точки покоя, за которую мы примем начало
координат, основную роль играет поведение траекторий линеаризованной системы
х'=Ах, (98)
где А—матрица л-го порядка. Для такой системы закон движения весьма прост:
x(k; хо)=А*хо.
Отсюда сразу видно, что дли асимптотической устойчивости нулевого (а потому
и любого) решения сястемы (98) необходимо и достаточно, чтобы все собствен-
собственные значения матрицы А были по модулю меньше единицы, а если хоть одян
из этих модулей больше единицы, то нулевое решение неустойчиво. Для более
детального исследования можно ввести в Е„ новую аффинную систему коордя-
ват, связанную со старой равенством х=Ту; в новой системе координат урав-
уравнение отображения вместо (98) прямет вяд у'=Т~1АТу, н можно подобрать'
патрицу Т так, чтобы новая матрица T-1AT отображения приняла по возмож-
возможности более простой (например, жорданов, см. п. IV.3.4) вид. Мы предоставляем
желающим провести полную классификацию изолированных точек покоя линей-
линейной автономной системы с дискретным временем на плоскости по образцу п. 2.3.
Как и в п. 2.4, тип точки покоя при переходе от линеаризованной системы
к полной сохраняется, за исключением точки типа центр, т. ё. когда матрица А
имеет собственные значения, по модулю равные едяняце. После соответствую-
игго аффинного преобразования плоскости ее отображение (98) сводится в случае
«еитра к повороту вокруг начала координат на некоторый угол ns (где е* *"' —•

. § 4. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ 619
собственные значения матрицы А). Поэтому для рационального * все траекто-
рии.-кроме самой точки покоя, представляют собой циклы (какого порядка?),
а для иррационального s все эти траектории всюду плотно заполняют эллипсы.
Из других вопросов теории систем с дискретным временем остановимся еще
иа линейных неоднородных системах с постоянными коэффициентами
к'=Ах+а*. (99)
Легко проверить, что если начальное условие задается при k = 0, то решение
. при k > 0 имеет внд
и т. д.,
вообще
(Напишите решение при k < 0.)
Пусть, в частности, последовательность а^ периодична с периодом т, т. е.
*й+я^**- Тогда, для того чтобы начальная точка х0 определяла периодическое
решение с тем же периодом, необходимо и достаточно, чтобы хст=х0> т. е. чтобы
(Ая—I) хо=— Ат-Ча—кт-Чг —... —ая_!.
""Для однозначной разрешимости этого уравнения необходимо и достаточно, чтобы
det(A<»—1)^0, A00)
т. е. чтобы нн одно нз значений у 1 не было собственным для матрицы А.
Если это условие выполнено, то для отыскания периодического решения удобно
воспользоваться представлением
т-\
ак= ^ «р (~-pft) ср (*=0, ±1, ±2, ...), A01)
аналогичным ряду Фурье и возможным для любой m-пернодической последо-
последовательности а*; коэффициенты в этом представлении находятся по формуле
ср=-}- ? ехр (-—/*)¦* (р=0, 1, .... /л-1). A02)
(Проверьте вто, иепосредственио подставив A02) в A01). Как можно доказать
единственность представления A01)?) Если искать m-периодическое решение х
системы (99) также в виде A01) с неопределенными коэффициентами Ар вме-
вместо ср, то несложные вычисления, которые мы предоставляем читателю, при-
приводят к формуле
Таким образом, если выполнено условие A00), то для любой т-периоди-
ческой последовательности як система (99) обладает т-периодичеашм реше-
нием\ можно показать, что такое решение единственно. Если же для некото-
некоторого р=Ро число ехр [—ро\ будет собственным значением матрицы А, то
при с^ 5* 0 в системе, вообще говоря, наступает резонанс, т. е. периодическое
решение отсутствует.
Системы (95) .и (99) аналогичны системам дифференциальных уравнений
первого порядка. Нетрудно написать аналоги дифференциальных уравнения

620 ГЛ. VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
и систем высшего порядка. Так как систему (99) можно записать в виде
**+i=A*ft4-*ft. то аналогом скалярного уравнения второго порядка будет
**+i+«*+i+***=-e» A03)
и т. п., т. е. мы приходим к разностным уравнениям, упомянутым в п. III.2.3
и ЛВМ, п. XVI 1.16. От разностных уравнений и систем любого порядка
всегда можно перейти к системе первого порядка: например, если для уравне-
уравнения A03) обозначить xk+l=yk, мы получим систему из двух уравнений
первого порядка
*ft+i = 0ft. 0ft+i=— Ьхк—ayk+ak. A04)
Поэтому на уравнения A03) распространяются, в частности, приведенные выше
утверждения о периодических решениях, что, впрочем, легко показать непо-
непосредственно, без перехода к системе A04); при этом взамен A00) надо потре-
потребовать, чтобы ни одно из значений у 1 не было корнем характеристического
уравнения
Кроме случая Ь — —1 Та, когда один из корней равен ±1, для вещественных
коэффициентов возможно уравнение A03)
хк+1+хк-ак A05)
f , 2т \
i± — ро1;
с корнями характеристического уравнения f-it2 — expi± — ро1; уравнение
A05) является аналогом уравнения *+<»о*=7(О-
Такая далекая аналогия между системами с дискретным и с непрерывным
временем позволяет, в частности, распространить на первые большинство
методов, описанных в этой главе. Мы предоставляем продумать это желающим.
Скажем еще о возможном пряменении систем с дискретным временем
к исследованию (вообще говоря, нелинейных) периодических систем с непре-
непрерывным временем, например вида
K=f(*, t) A06)
с Го-периодической по t правой частью. Произвольно выбрав и зафиксировав
некоторое значение t = t0, поставим в соответствие каждой точке хо?Еп зна-
значение 1|>(*о) при t = to-\-To решения x(t; t0, х0) сястемы A06), удовлетво-
удовлетворяющего начальному условию x\t-to^=x0. В силу периодичности системы
A06) переходы от ta-{-TB к <о+27\>7 от to+2TB к to+^Ta и т. д. определяют
то же отображение tj>, которое иногда называется оператором сдвига по
траекториям системы A06) ва период. (Правда, оно зависит от выбора /№,
но легко проверить, что эта зависимость не влияет на дальнейшее.) Таким
образом, обозначая x(tQ~\-kT0; tQ, *„)=*>, мы приходим к автономной
системе с дискретным временем хк+1 = ^(хк), к которой, в отличие от A06),
можно применять обычные методы анализа автономных систем, в частности,
с помощью привлечения фазового пространства. Такой метод исследования
Г0-перйодической системы A06) называется стробоскопическим, так как полу-
получается такая картина, как будто совокупность решений системы A06) осве-
освещается мгновенными вспышками в моменты времени /0-(-?Г0. При этом точке
покоя полученной дискретной системы отвечает Го-периодическое решение си-
системы A06), циклам дискретной системы отвечают субгармоникя системы A06)
и т. д. Правда, применение метода осложнено тем, что явный переход от A06)
к соответствующей дискретной системе затруднителен, но применение разло-
разложений по малому параметру, численного интегрирования и иногда припассо-
вывания дают возможность расширить область применения этого прозрачного
в теоретическом отношении метода.

ЛИТЕРАТУРА
l) Айзерман М. А., Гантмахер Ф. Р., Абсолютная устойчивость
регуЭшруемых систем, «Наука», 1965.
2. Айис Е., Обыкновенные дифференциальные уравнения, Харьков,
1939.
3. Аи го А., Математика для электро- и радиоинженеров, изд. 2-е,
«Наука», 1967. :
4. Андронов А. А., Витт А. А., X айки н С. Э., Теория колеЙаиий,
изд. 2-е, Физматгиз, 1959.
5. Ахиезер Н. И., Лекции по вариационному исчислению, Гостех-
издат, 1955. *
6. Ахиезер Н. И., Элементы теории эллиптических функций, изд. 2-е,
«Наука», 1970.
7. Бабаков И. М., Теория колебаний, изд. 2-е, «Наука», 1968.
8. Барбашин Е. А., Введение в теорию устойчивости, «Наука»,
1967.
9. Б е л л-м а и Р., Теория устойчивости решений дифференциальных Урав-
Уравнений,-ИЛ, 1954.
10. Берез и и И. С, Жидков Н. П., Методы вычислений, т. I,
изд. 3-е, «Наука», 1966.
11. Блекуэлл Д., ГнршикМ., Теория игр и статистических реше-
решений, ИЛ, 1958.
12. Б лисе Г., Лекции по вариационному исчислению,, ИЛ, 1950.
13. Боголюбов Н. Н., Митропольскнй Ю. А., Асимптоткческие
методы в теории нелинейных колебаний, изд. 3-е, Физматгиз, 1963.
14. Бор Г., Почти-перноднческне функции, Гостехнздат, 1934.
15. Борисенко А. И., Тарапов И. Е., Векторный анализ и начала
тензорного исчисления, изд. 3-е, «Высшая школа», 1966.
16. де Б рей и Н. Г., Асимптотические методы в, анализе, ИЛ, 1961.
17. Булгаков Б. В., Колебания, Гостехнздат, 1954.. . ,
18. В а зо в В., Асимптотические разложения решений обыкновенных
дифференциальных уравнений, «Мнр», 1968. ....',
19. Вайнберг М. М., Вариационные методы исследования нелинейных
операторов, Гостехиздат, 1956.
20. Вайнберг М. М., Т ре йог и и В. А., Теория ветвления решений
нелинейных уравнений, «Наука», 1969. ,
21. Веку а Н. П., Системы сингулярных интегральных уравнений и неко-
некоторые граничные задачи, Гостехнздат, 1950. .
22. Веитцель Е. С, Элементы теории игр, изд. 2-е, Физматгиз,
1961.
23. Гантмахер Ф. Р., Теория матриц, изд. 2-е, «Наука», 1966. .
24. Гантмахер Ф. Р., К рей и М. Г., Осцилляционные матрицы Я
ядра и малые колебания механических систем, Гостехиздат, 1950. .,:,..¦-
25. дёи Гартог Дж., Механические колебания, Физматгиз, 1960.
26. Г ас с С., Линейное программирование, Физматгиз, 1961.

622 ЛИТЕРАТУРА
. 27. Г ахов Ф. Д., Краевые задачи, изд. 2-е, Физматгиз, 1963.
28. Гельфанд И. М., Лекцяи по линейной алгебре, изд. 3-е,
«Наука», 1966. ,
29. Гельфанд И. М., Фомин С. В., Вариационное исчисление,
Физматгиз, 1961.
30. Гельфанд И. М., Шилов Г. Е., Обобщенные функции и действия
над ними, Физматгиз, 1958.
31. Горелик Г. С, Колебания и волны, Физматгиз, 1959.
32. Давенпорт В., Рут В., Введение в теорию случайных сигналов
и шумов, ИЛ, 1960.
33. Демидович Б. П., Марон И. А., Основы вычислительной мате-
математики, изд. 3-е, «Наука», 1966.
34. Дёч Г., Руководство к практическому применению преобразования'
Лапласа, «Наука», 1965.
35. Д нтк и и В. А., Кузнецов П. И., Справочник по операционному
исчислению, Гостехиздат, 1951.
36. Диткии В. А., Прудников А. П., Интегральные преобразова-
преобразования и операционное исчисление, Физматгиз, 1961.
37. Диткин В. А., Прудников А. П., Справочник по операционному
исчислению, «Высшая'школа», 1965.
38. Е р у г и н Н. П., Системы лииейиых дифференциальных уравнений,
Минск, 1963.
39. Жермеи П., Механика сплошных сред, «Мир», 1965.
40. За брей ко П. П. и др., Интегральные уравнения, справочник,
«Наука», 1968.
41. Зельдович Я. Б., Мышкис А. Д., Элементы прикладной мате-
математики, нзд. 2-е, «Наука», 1967.
42. Зуховицкяй С. И., Авдеева Л. И., Линейное и выпуклое
программирование, изд. 2-е, «Наука», 1967.
43. Каннингхэм В., Введение в теорию нелинейных систем, Энерго-
издат, 1962.
44. Канторович Л. В., Крылов В. И., Приближенные методы выс-
высшего анализа, изд. 5-е, Физматгиз, 1962.
45. Карачаров К. А., Пилютик А. Г., Введение в техническую
теорию устойчивости движения, Физматгиз, 1962.
46. Карпе^левич Ф. И., Садовский Л. Е., Элементы линейной
алгебры и линейного программирования, изд. 3-е, «Наука», 1967.
47. Карслоу X., Егер Д., Операционные методы в прикладной мате-
математике, ИЛ, 1948.
- 48. Ка у дер ер Г., Нелинейная механика, ИЛ, 1961.
49. Коддингтон Е., Левинсои Н., Теория обыкновенных диффе-
дифференциальных уравнений, ИЛ, 1958.
. 50. Конто рович М. И., Операционное исчисление и нестационарные
явления в электрических цепях, Гостехиздат, 1953.
51. Коппенфельс В., Штальман Ф., "Практика конформных ото-
отображений, ИЛ, 1963.
52. Копсои Э., Асимптотические разложения, «Мир», 1966.
53. Кочин Н. Е., Векторное исчисление и начала тензорного исчисле-
исчисления, изд. 8-е, Изд. АН СССР, 1961.
54. Краснов М. Л., Макаренко Г. И., Операционное исчисление.
Устойчивость движения (Задачи и упражнения), «Наука», 1964.
55. Красносельский М. А., Оператор сдвига по траекториям диф-
дифференциальных уравнений, «Наука», 1966. -
56. Красносельский М. А., Положительные решения операторных
уравнений, Физматгиз, 1962.
57. Красносельский М. А., Топологические методы в теории нели-
нелинейных интегральных уравнений, Физматгиз, 1962.

ЛИТЕРАТУРА
68. Красносельский М. А. и др., Приближенное, решение операторных
уравнений, «Наука», 1969. " '¦ " ¦ ¦' '
59. Красносельский М. А. и др., Векторные полйнаплоскостн, Физ-
натгаз, 1963.
60. Красовский Н. Н., Некоторые задачи теории устойчивости движе-
движении, Физматгиз, 1959.
61. Крылов В. И., Приближенное вычисление интегралов, изд. 2-е,
«Наука», 1967.
62. Курош А. Г., Курс высшей алгебры, нзд. 9-е, «Наука», 1968.
63. Кюнци Г., Крелле В., Нелинейное программирование, «Советское
радио», 1965.
64. Л ав рентьев М. А., Люстерник.Л. А., Курс вариационного
исчисления, Гостехнздат, 1950.
65. Лаврентьев М. А., Люстерник Л. А., Основы вариационного
исчисления, т. I, ч. II, ОНТИ, 1935.
66. Лаврентьев М. А., Шабат Б. В., 'Методы теории функций ком-
комплексного переменного, изд. 3-е, «Наука», 1965.
67. Л а не Дж., Численные методы для быстродействующих вычислитель-
вычислительных машин, ИЛ, 1962.
68. Ла-Салль Дж., Лефшец С, Исследование устойчивости прямым
методом Ляпунова, «Мир», 1964.
6JL Л е в и т а н Б. М., Почти периодические функции, Гостехиздат, 1953.
yi е т о в А. М., Устойчивость нелинейных регулируемых систем,
; Фнзматгиз, 1962.
71. Лефшец С, Геометрическая теория дифференциальных уравнений,
Д961.
2gj Лефшец С, Устойчивость нелинейных систем автоматического управ-
управления, «Мир», 1967.
73. Ловитт У., Линейные интегральные уравнения, Гостехнздат, 1957.
74. Лунц Г. Л., Эл ьсгол ьц Л. Э., Функции комплексного перемен-
переменного с элементами операционного исчисления, Фнзматгнз, 1958.
75. Лурье А. И., Операционное исчисление и его приложении к задачам
мехарики, Гостехнздат, 1950.
-—*"СТ6/)Л у р ь е А. И., Некоторые нелинейные задачи теории автоматического
регулирования, Гостехнздат, 1951.
77. Ль юс Р., Райфа X., Игры и решения, ИЛ, 1961.
78. Мак-Кинси Д., Введение в теорию игр, Физматгиз, 1960.
79. Мак- Ко ни ел А., Введение в тензорный анализ с приложениями
к геометрии, механике и физике, Фнзматгиз, 1963.
80. Мак-Лахлан Н., Теория и приложения функций Матье, ИЛ, 1953.
81. Мал к ин И. Г., Некоторые задачи теории нелинейных колебаний,
Гостехиздат, 1956.
82. М а л к и н И. Г., Теория устойчивости движения, изд. 2-е, «Наука», 1966.
83. Маркушевич А. И., Краткий курс теории аналитических фуннцнй,
изд. 3-е, «Наука», 1966.
84. Мелентьев П. В., Приближенные вычисления, Физматгиз, 1962.
85. Митропольский Ю. А., Нестационарные процессы в нелинейных
колебательных системах, Изд-во АН УССР, 1955.
86. М и х л и н С. Г., Вариационные методы в математической физике,
изд. 2-е, «Наука», 1970.
87. М и х л и н С. Г., Интегральные уравнения и их приложения к неко-
некоторым проблемам механики, математической физики и техники, изд. 2-е, Гостех-
Гостехиздат, 1949.
88. М их л ии С. Г., Лекции по линейным интегральным уравнениям,
Фнзматгиз, 1959.
89. М их лин С. Г., Многомерные сингулярные интегралы н интеграль-
интегральные уравнения, Физматгнз, 1962.

. 624 . ЛИТЕРАТУРА
¦ 90. Ми х л ян С. Г., Проблема' минимума квадратичного функционала,
Гостехяздат, 1952. ¦:-.-.¦ .-..,..
91. Михлия С. Г., Чясленяая реалязацяя вариационных методой,
«Наука», 1966. ., ,
92. М о р с Ф., Феш б а х Г., Методы теоретической физякя, т. I, ИЛ,
93. Мусхел яшв и л я Н. И., Сянгулярные янтегральные уравненяя,
изд. 3-е, «Наука», 1968.
94. Пановко Я. Г., Основы прикладной теорнн упругих колебаний,
язд. 2-е, Машгиз, 1967.
¦ 95. Пановко Я Г., Губанова И. И., Устойчивость и колебания
упругях систем, «Наука», 1967.
96'' Петров с к н й И. Г., Лекции по теорнн интегральных уравнений,
язя. 3-е, «Наука», 1965. ,,
97. Плнсс В. А., Некоторые проблемы теорнн устойчивости двяження
в целом, нзд-во ЛГУ, 1958.
98. П р а г е р В. Введение в механику сплошных сред, ИЛ, 1963.
99. Рашевскнй П. К., Рнманова геометрия . н тензорный анализ,
«Наука», 1967.
100. Рейнфельд Н., Фогель У., Математическое программярованне
ИЛ, 1960.
101. Ромакин М. И., Элементы линейной алгебры я лянейного програм-
няровання, «Высшая школа», 1963. .
102. Свешников А. Г., Тяхонов А. Н., Теория функций комплекс-
комплексной переменной, «Наука», 1967.
103. Седов Л. И.,~ Введение в механику сплошной среды, Фнзматгнз,
1962.
104. Смирнов В. И., Курс высшей математики, т. Ш, ч. 2, нзд, 8-е
«Наука», 1969. . х '
105. Смирнов В. И., Курс высшей математики, т. IV, Физматгнз, 1958.
106. Смирнов В. И., Крылов В. И., К а нтор ов и ч Л. В., Вариа-
Вариационное исчисление, КУБУЧ, 1933.
107. Сто и лов С., Теория функций комплексного переменного, тт. 1, 2,
ИЛ, 1962.
108. Стокер Д., Нелинейные колебания в механических и электряческях
сястемах, нзд. 2-е, ИЛ, 1953.
109. Стрелков С. П., Введеняе в теорию колебаний, нзд. 2-е, Фязмат- .
гяз, 1964.
110. Схоутен Я-, Тензорный аналяз для физиков, «Наука», 1965.
111. Теодор чик К. Ф., Автоколебательные системы, Гостехяздат,
1952.
112. Тимошенко С. П., Теория колебаний в инженерном деле, Физмат-
гиз, 1959.
113. Т ранте р К-, Интегральные преобразования в математяческой фя-
зяке, Гостехнздат, 1956.
114. Трнкомн Ф., Интегральные уравнения, ИЛ, 1960.
115. Фаддеев Д. К., Фаддеева В. Н., Вычислительные методы ляней-
ной алгебры, нзд. 2-е, Фнзматгнз, 1963.
116. Ф и л ь ч а ко в П. Ф., Приближенные методы конформных отображе-
няй, «Наукова думка», Киев, 1964.
117. Форсайт Дж., Мол ер К., Чясленное решен яе систем лянейных
уравненяй, «Мяр», 1969.
118. Фрезер Р., Дункан В., Ко л л ар А., Теоряя матряц я ее пря-
ложеняя к дифференциальным уравненяям я дянамнке, ИЛ, 1950.
119. Ф рема я Н., Фрёман П., ВКБ-приблнженяе, «Мир», 1967.
120. Фукс Б. А., Левин В. И., Функция комплексного переменного
и их приложеняя, Гостехнздат, 1951.

ЛИТЕРАТУРА '¦ 625
121. Фукс Б. А.,Шабат Б. В., Функции комплексйого переменного
и некоторые их приложения, изд. 3-е, «Наука», 1964. "¦¦*'¦• .< -«..чи-. = -
122. Халмош П., Лекций по эргодической теории, ИЛ, 4939. ''
123. X а р к е в и ч А. А., Нелинейные и параметрические явления Ъ радио-
радиотехнике, Гостехиздат, 1956. •¦¦¦•. .. , , . ...
124. X а я с и Т., Нелинейные колебания в физических системах, «Мир»; 1968.
125. Хединг Д., Введение в метод фазовых интегралов (Метод ВКБ),
«Мир», 1965." :- : •'¦<•.¦ '.•¦-¦
126. Хедли Д., Нелинейное и динамическое программирование,1 «Мир»,
1967.
127. Хейл Д., Колебания в нелинейных системах, «Мир», 1966.
128. X и н ч и и А. Я., Математические основания статистической механики,
Гостехиздат, 1943. . : ¦•¦
129. Цлаф Л. Я., Вариационное исчисление и интегральные уравнения,
Физматгиз, 1966. :
•130. Цып к ии Я. 3., Теория линейных импульсных систем, Физматгнз,
1963.
131. Чеботарев Н. Г., Теория алгебраических функций, Гостехяз-
дат, 1948.
132. Чеаари Л., Асимптотическое поведение и устойчивость решений
обыкновенных дифференциальных уравнений, «Мир», 1964.
133. Чета ей Н. Г., Устойчивость движения, изд. 3-е, «Наука», 1965.
134. Шилон Г. Е., Введение в теорию линейных пространств, изд. 2-е,
Гостехнздат, 1952.
135. Штока л о И. 3., Линейные дифференциальные уравнения с пере-
переменными коэффициентами, Изд-во АН УССР, I960. :
136. Эйэеихарт Л., Римаиова геометрия, ИЛ, 1948.
137. Эльсгольц Л. Э., Вариацяонное исчисление, Гостехнздат, 1952.
138. Эльсгольц Л. Э., Дифференциальные уравнения и вариационное
¦ исчисление, изд. 2-е, «Наука», 1969.
139. Э рдей и А., Асимптотические разложения, Физматгиз, 1962.
140. Юдин Д. Б., Гольштейн Е. Г., Линейное программирование,
Фнзматгнз, 1963.

АЛФАВИТНЫЙ УКАЗАТЕЛЬ*)
Абель Н. 435, 490
Абсолютная устойчивость 576
Автоколебания 530—531, 602—605
Автономная система 178, 342, 520—553
Адамар Ж. 437
Аксиомы метрики 334
Активная система 604
Альтернатива Фредгольма 395—396
Альтернирование тензора 234
Альфа-предельное множество 522
Амплитуда эллиптического интеграла 112
Амплитудно-частотная характеристика 582,
585-586
Аналитическая линия 75
— функции 27—28
— — вещественного переменного 74—75
нескольких переменных 75
Аналитическое отображение 30
— продолжение 72
Андронов А. А. 542, 610
Антиконформное отображение 31
Антисимметричное ядро 425
Антиэрмитов оператор 432
Антнэрмитово ядро 425
Апериодическое затухание 581
Асимптотическая устойчивость 553
в целом 558
— фаза 539
Асимптотическое разложение 114—118,
505-508, 514-517, 615-617
Аффинный тензор 237—240
Ацикличность 20
Базис 164
Базисные функции 361
Балка 347
Банах С. 263
Банахово пространство 263
Барицентрические координаты 212
Безвихревое поле 17—19
Безопасность границы области устойчи-
устойчивости 566—567
Бельтрамн Е. 250
Берег 41
Бернулли И. 258
Бернулли Я. 258
Бертраи Ж. 459
Бесконечно малое производящее отобра-
отображение 329
— удаленная точка 33, 94—95
Бесконечное произведение 107
Бигармонический оператор 348
Биения 583
Билинейный функционал 298
Биортогональность 170
Биркгоф Г. 549
Бифуркация 472, 482—485
Блочная матрица 226
Блочное программирование 226
Боголюбов Н. Н. 404, 610, 615
Бойяи Я- 335
Боль П. Г. 202, 505
Большой круг 308
Бор Г. 504
Брауэр Л. 202
Бриллюэи Л. 518
Бубнов И. Г. 367
Быстрое время 607, 615
В («отображение в») 165
Валентность тензора 231
Ван дер Поль 610
Вариационное исчисление 260
Вариационный принцип 336—338
Бариацня функции 265
— функционала 264—269
Вековые члены 584
Вектор интенсивности поля 350 ,
Векторно-дифференциальиый оператор 10
Векторный потенциал 19
Бентцель Г. 518
Верхняя полуплоскость 37
— треугольная матрица 194
Ветвление решений 472, 482—485
Ветвь многозначной функции 41
Вещественная аналитическая функция 76,
99—100
Вещественное линейное пространство 164
Вещественный нормальный вид матрицы
187
Взаимный базнс 238—239
Вихревая линия 13, 52
— ось 51
— точка 51
Внешняя краевая задача 53
Внутренний экстремум 269
Внутренняя геометрия 253
— краевая задача 53
Возвратное уравнение 500
Возмущенные решения 553
Вольтерра В. 384
Восстанавливающая характеристика 588
Вполне непрерывный оператор 417
Вращение векторного поля 533—535
Времениподобность 242
Временная устойчивость 574
Бронский Ю. 489
Всестороннее сжатие 352
Всюду плотность 552
Второй метод Ляпунова 560
Выпуклая оболочка 211
— функция 226
*) Термины, содержащиеся • указателе к ЛВМ, как правило, не повторяются.

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
627
Выпуклое множество 216—4Stt
— программирование 226—377 '
Выпуклый конус 211
— многогранник 21I
Вырожденная квадратичная форма 174
Вырожденное ядро 389—394
Высвобождающая связь 293
Вычет 79—82, 95
Вычисление несобственных интегралов
83-89
Галеркяи В. Г. 387
Гаиальтои У. 10
Гаыильтоиова система 499
-Гамма-функция 73, 89
Гармоническая функция 21, 29
Гаусс К- 251, 335
Геодезическая линия 307—309
Геометрия Лобачевского 334—336
Гильберт Д. 384
Гиперболический поворот 242
Гиперплоскость 210
Гироскопические силы 574
Гистерезис 556
Главная ветвь логарифма 46
— ось инерции 235
— — поверхности второго порядка I7S
— часть ряда Лорана 64
Главный мииор 176
Голономиая связь 282
Гомеоморфизм 33—34
Градиент 9, 249
Граничный экстремум 269
Группа Ли 330
Групповое свойство 329
Гурвиц Л. 101
Гурвяцев полином 101
Двойной слой 52
Двойственная задача 282
Двоякопериодическая функция 113
Двустороннее преобразование Лапласа
450
Действие 838
Декремент 581
Дельта амплитуды 113
Дефяинтиая форма 174
Диаграмма Ньютона 77
Дяада 233
Дявергенция 9. 249
динамическая система 549
Динамическое программирование 225
диполь 22
дирихле Л. 370
дискретное преобразование Лапласа
А155-156
Дискриминант 104
Днссипативнаи система 352—353
Диссипатнвные силы 574
дифференциальная связь 284
дифференциально-разностное уравнение
150
Дородницын А. А. 607
дробио-линейиое отображение 34—36
О-раэбиеиие 101
Евклидов базис 165 * .
— тензор 231—234
Евклидово пространство 164
Единичная окружность 37
— сфера 171
Единичный круг 37
— тензор 235
Естественней зариациониая задача 287
Естественные граничные условии 287—288.
293
Жесткая восстанавливающая сила 588
Жордан К. 181
Жордаиова клетка 181, 186—187
— форма матрицы 185
Жуковский Н. Е. 42
Задача Больца 286
— Дидо 257
— Лаграижа 284
— Манера 285
— о смесях 208
— Рямаиа — Гильберта 462
— Чаплыгина 284
Задачи на мииимакс 221, 358
Закон инерции квадратичной формы 17S
— сохранения импульса 342
Замкнутость множества 407
Замыкание контура 84—89
Запас устойчивости 357
Затухающие колебания'581
Захват частоты 612
Звездообразный узел Б26
Зеркальное отражеияе относительно окр уж-
иости 34
Зона иечувствительиостя 544
2-преобразоваиие 156
Идеальная жядкость 48
Изображение 129
Изолированная особая точка 78
— точка покоя 524
Иаолироваииый цикл 530
Иэометричиые поверхностя 253
Изопериметрическая задача 281
Изохронность 581
Импульс 342
Импульсное воздействие 503
Инвариантная мера 548
Инвариантное подпространство 166
Инверсия 34—35
Ииволюцня 34
Индекс интегрального уравнения 463
— особой точки 534, 538
Иидефииитиость 241
Интеграл Дярихле 370
— типа потенциала 413
Интегральная связь 279, 285
— формула Кош и 83
Интегральное многообразие 591—592
— неравенство 508
— уравнение 150, 384—387
Интегральный аивариант 547—548
Иитегрально-даффереяцяальиое уравнена*
150—151
Искусственный базис 218
Истечение 55 . - • •
Итерированное ядро 405, 421—422
Каноническая система уравнений 323, 569
Канонические переменные 322
Каноническое преобразование 325
Канторович Л. В. 208, 380
Катеноид 275
Качественные методы 560
Квадратично суммируемая функция 262
Квадратичное программирование 227
Квадратичный функционал 298
Квазидиагональиая матрица 167
Квазипериодическая функция 50S
Квазиполином 101
Квазистатическнй процесс 556
Козариантная производная 248
Ковариантность 237—238
Комбинационные колебании 612
Компактность 316—317
Комплексное линейное пространство 114
Комплексный потенциал 49

efcaf
АЛФАВИТНОЙ УКАЗАТЕЛЬ
Компонента связности 50.
— тензора 229 .
Конечная связь 282
Конечномерный оператор 416
Консервативность 342
Контакт S32
Контактное преобразование 327
Контравариантность 237—238
Конус 418
Конфликтная ситуация 219
Конформное отображение 31—32
Координатные функции 361
Корневой вектор 183
Косинус амплитуды 113
Кососнмметрнческий тензор 234
Кошн О. 235
Коэффнцнеи- затухания 581
Коэффнцие и./ Ламе 24S
— Пуассона а62
— связности 246
— температуропроводности 151
— усиления 582
Краевая задача 53, 366—367
Краевое условие 53
Крамере X. 518
Краеовскнй Н. Н. 559
Кратное преобразование Фурье 161
Кратность нуля 68
— полюса 79—80
— точни границы 57
Крейи М. Г. 418, 501
Кривизна 256
Кристоффель Л. 246
Критерий Гурвица 102
— качества 207
— Михайлова 103
Кронекер Л. 230
Круговое свойство 35
Крылов А. Н. 203
Крылов Н. М. 404, 610, 615
Кулон Ш. 21
Лагранж Ж. 257
Лаплас П. 21
Лапласиан 14
Лаплас-образ 129
Леви-Чнвита Т. 228
Левое итерированное ядро 426
Лейбниц Г. 258
Лемма Жордана 86
Лн С. 330
Лнбрацнонное движение 589
Лнмитацнонное движение 581
Линеаризация функционала 266, 268
'Линейное отображение 32, 165
— программирование 207
— пространство 164
Линейные действия 164, 232
— колебания 581—586
Линейный функционал 261
— элемент 327
Лист 47
Лнувилль Ж. 490
Лобачевский Н. И. 335
Логарифм матрицы 189
Логарифмическая точка разветвления 41
Логарифмический вычет 95—96
— потенциал 25
Лопйталь Г. 258
Лоран П. 83, 65
Лереиц Г. 241
Лурье А. И. 575/576
Люфт 545
Ляпунов А. М. 493, 553, 560, 5в4
Малые делители 602
Математический маятник 589
Матрица монодромни 403/ . , '
— напряжения-энергии Д4Й—ЗВО ', '.','.
— отображения 1б5>- . . . ' . ,
— связи 575 , " ".' .'"','" к
Матрицант 490 .., .','.
Матричная игра 2I&—52?;) :
Медленно меняющиеся функции 499
Медленное время 610
Мембрана 345 '
Мера обусловленности 195. '
Мероморфная функция 105—Ю'б
Метод А.Н. Крылова. 203.
— Бубнова-гГалерклна 367
— ван дер Поля 610—615 '
— Винера —Хопфа 450—452
— В KB 518
— Галеркина 367
— Галеркина —Петрова 367
— гармонического баланса 600
— Гаусса 192-193, 401-403
— градиентного спуска 377—379
— замораживания 563, 564
— искусственного введения параметра 97,
207
— Канторовича 360—381
— Келлога 422 ¦ • = •
— контурного интегрирования 618
— Крылова — Боголюбова 404
— малого параметра 58—60, '204—205.
409-410, 475-476
— Назарова —Некрасова 485—486
— наибыстрейшего спуска 126
— наименьших квадратов 379—380
— непрерывного продолжения по парамет-
ру 97, 205-207
— Ньютона —Котеса 403
— осреднения 612
— перевала 125—126
— последовательного улучшения решейня
215-218
— приведения к обыкновенным дифферен-
дифференциальным уравнениям 382
— Рнтца 361—367, 374—377
— Рэлея 173
— счетного множества переменных 367
— Трефтца 373—374
— улучшения невязки 196
— усечения 398 "
— усреднения 612
— фазовых интегралов 518
— Чебышева 403
— шагов 149—150
— Эйлера 382
— Якоби 176, 198 .
Метрика 334
Метрический тензор 239, 253
Метрическое пространство 334, 407
Мнлн Э. 453
Минимизирующая Последовательность 31В
Мнтропольскнй Ю. А. 610 ,
Многогранное тело 213 :
Многозначная функция 39—42
Миоголистное отображение 30
Многоэтапное программирование 225
Модуль всестороннего сжатия 352
— эллиптического интеграла 112
Момент диполя 22
— инерции 235 ' . '.
— функции 442
Мультипликатор 492 ,
Мягкая восстанавливающая' сила 588
На («отображение на») 165
Набла 10 . ' . .
Нагруженное интегральное уравнение 387,
398

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
629
Натягивание конуса 211, 214
- пространства 167 '
Невоанущённое решение 653
Неголононная связь 284
Нейман Дж. 219. 650
Некорректная задача 437
Нелинейное программирование 226
Нелинейные колебания 586—617
Немой индекс 229
Необходимые условия Лежандра 300—301
Неосцнллирующее решение 512
Неотрицательно определённое ядро 429 : .
Неподвижная точки 202—203, 408
Непрерывная группа.преобразований 328—
329 ' '
-г д>бь 400
Непрерывное отображение 33
Непрямое регулирование 575
Неравенство Бесселя 433
Несобственная точка 33
Нестрогий максимум 172
Нётер Э. 330
Неустойчивое по Ляпунову решение 553
Неустойчивый цикл 530
Неявная аналитическая функция 75—76
Нижняя треугольная матрица 194
Норма 261
— вектора 165
— линейного оператора 388
— матрицы 194
— отображения 194
— функционала 267, 298
Нормальная форма матрицы 185
Нормальное колебание 570
Нормальные координаты 179, 570
Нормальный эллиптический интеграл Ле-
Лежандра 112
Нормированное пространство 261
Нормировка 313
Нуль многочлена 100—104
— функции 68, 98—104
Ньютон И. 258 '
Ньютонов потенциал 23—24
Область определения функционала 261
— притяжении 531, 542
Обобщенное решение 297
Обобщенные импульсы 342
— координаты 341
Обратная краевая аадача 55
— связь 575
Обратный маятник 498
Обтекание 54
Объединение 369
Ограниченный линейный оператор 388
— функционал 267, 298
Однолистное отображение 30
Окаймление 578—579
Омега-предельное множество 522
Опасность границы области устойчивости
666-668
Оператор Гамильтона 10—16
— Лапласа 14'
— Лапласа —Бельтрамн 250
—типа Вольтерра 414
Операторное уравнение 388, 416—417,
430-433
Операционный метод 145
Опорный план 218
Определитель Вандермонда 403
— Вронского 489
— Грама 378
— Фредгольна 390, 395
Определяющие уравнении 595
Оптимальная стратегия 219 '
Оптимальное регулирование 337
— решение 209
Оптимальное управление 337
Оптимальный план 218 ' : ...
Опускание индекса 240
Орбитальная устойчивость 690 '' '. ;
Оригинал 129 ' ¦•¦ • ¦¦. = •••¦•
Ортогональное дополнение 168
— разложение 168
Ортогональность 16&- - •
Основная теорема алгебры 97 '-
Особая точка 28, 633
Особенность 28 '
Особый элемент функционала 294: '
Остроградский М. В. 278, 4$0
Осцнлляционная матрица 203 ¦
Осцилляция 512 . - •". ¦
Ось диполя 2 2 '
Относительная устойчивость 564 '
Отражение экстремали 295' ¦ ',
Отталкивающий цикл 539
Параметрические колебания 587'
Параметрический резонанс 498
Параметрическое программирование 225
Парные уравнения 454
Парциальная система 574 '
— частота 575 "
Пассивная система-604
Первая основная квадратичная фордо 251
Первый метод Ляпунова 560
Передаточная матрица 1.48
— функция 146 . .
Переменная действия 591
Перемешивание 551
Пересечение множеств 211, 369
Перескок 556, 597 '
Перестановочные отображения 191—192
Период потенциала 19
Петля гистерезиса 556 •
Петров Г. И. 367
План 218
Пластинка 347
Платежная матрица 219
Плоское поле 48—62
Плотность импульса поля 350 .
— интегрального инварианта 547
— канонического импульса 349
Плохо обусловленная система 195
Поверхность Рима на 47—48
Пограничный слой 608—609 :
Поднимание индекса 240
Подпространство 407
Показательное отображение 45—46
Поле базисов 246 "\
— евклидова тензора 244—245
Полевая переменная 348—349 '
Полнгармоиическое возбуждение 601
Полилинейный функционал 298
Полином Гегенбауера 440
— Лагер'ра 440
— Эрмита 440
Полиномиальная матрица 184
Полная аналитическая функция 72
— диссипация 574
— неустойчивость 572 ч
Полнота пространства 263, 407
— системы функций 362
Полный лагранжев интеграл 349 " '
— эллиптический интеграл 112 .
Положительно определенная функция 557,
559
— определенное ядро 429
— определенный функционал 429
Полуустойчнвый цикл 630
Полюс 79-81 •
Понтрягнн Л. С. 542
Поперечные колебания стержня 34в
Попов В. 678 ' :'.

630
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Пополнение 263 ¦
Порядок вариация 297
— нуля 68
— полюса 79
— связности 18
— точки разветвления 41
Постоянная времени 581
Потенциал 16, 19
Потенциальная энергия 340
— яма 357
Потенциальное поле 16—17. 19
Потенциальный барьер 357
Потеря устойчивости ЗБ6—357
Поток 52 Г
<Почтв все» 549
Почти-периодическая функция 503
Правило симметрии 57—58
Правильная часть рида Лорава 64
Правое итерированное ядро 426
Предельный цикл 530
Представимость через ядро 424
Преломление экстремали 295
Преобразование Гильберта 159—161
— Лапласа 129—138
— Лоренца 241
— Меллина 159
— прикосновения 327
— Хаикеля 161—162
— Эйлера 73
Приближенное конформное отображение 58
Приведение квадратичной формы к глав-
главным осям 175
— тензора к главным осям 234
Приводимая система 493
Принцип аргумента 96, 102—103
— Гамильтона 339—343, 348—351
. — Линделефа 58
— максимума 72
— минимального действия 339
— минимума потенциальной энергии 354
— сжимающих отображений 408
Припассовыванне 543
Присоединенный вектор 181
Притягивающий цикл 539
Проблема Айзермана 579—580
— моментов 442—443
— Рауса- Гурвнца 102
Прогонка 383
Продолжение решения 414
Произведение инерции 235
Производная аналитической функции
27—28, 30—31
— в силу системы 561
Производящая функция для системы функ-
функции 439—440
канонического преобразовании 325
Простое растяжение 351
Простой нуль 68
— полюс 79
— слой 52
Простраистваиноподобность 242
Пространство Гяльберта 262, 387—888
с весом 440
— Лоренца 241
Прямая сумма 165—166
Прямое регулирование 575
— слагаемое 167
Прямые методы вариационного исчислении
360
Псевдодлина 241
Псевдоевклидово пространство 240
. Псевдорнманово пространство 256
Псевдоскалярное произведение 240
Псевдотензор 245
Псевдоэллиптический интеграл 112
Пуассон С. 24 ¦
Пустое множество 213
Разветвление решений 482—486 ,
Разложение ядра по собственным фунт
цням 421
Разностное уравнение 149
Разрез 38 , ,
Разрывная вариационная-задача 295
— система 542—544
Разрывное векторное поле 14—16
Ранг тензора 231
Расширение функции 73
Расширенная комплексная плоскость 33
Регуляризация 437, 460
Регулярная функция 28 ¦ *
— часть ряда Лорана 64
Резольвента 391, 395, 423
Результант 104
Релаксационные колебания 603
Репер 246
Раман Б. 56, 253
Рима нова поверхность 47—48
Риманово пространство 253
Рнс Ф. 417
Ритц В. 361
Рнччн-Курбастро Г. 228
Род граничного условия 346
— конформного отображения 31—32
— эллиптического интеграла 112
Ротационное движение 590
Ротор 9, 249
Рэлей Дж. 173
Ряд Лорана 63—65
— Лорана — Пюнзо 79
— Неймана 406
— Пюнзо 76
— Тейлора «7
Самосопряженная матрица 168
Самосопряженное отображение 168,
172-173
Самосопряженный оператор 430
Свертка функций 135
Свертывание тензора 233
— ядер 406
Световой конус 243
Свободный индекс 230
Связность в римановом пространстве 254
Сдвиг по траекториям 620—621
Седло 524, 537
Седло-фокус 537
Секулярные члены 584
Сепаратриса 523
Сжимающее отображение 408
Сигнатура 175
Сигнум 544
Сильвестр Д. 177
Сильный экстремум 263—264
Символ Крнстоффеля 246—24 7
— Кроиекера 230
Симметрирование тензора 234
Симметрический теиэор 234
Симметричное ядро 386, 418
Симметрия относительно окружности
34—35
Симплекс 212
Симплексный метод 215—218
Сингулярная часть ряда Лораиа 64
Сингулярное интегральное уравнение 386.
Сингулярный интеграл 455—458
Сниус амплитуды 113
Сннхроннаацня 612
Система автоматического регулирования
575-58Q
— первого приближения 560
— с быстро вращающейся фа»ой 615
— с дискретным временем 617—620
— в переключениями 544

алфавитный
Скаляр 2J1
Скалярное произведение тенаеров 233
Скалярный потенциал (в
Скобка Пуассона 323—324
-Скользящий режим 543
Слабея особенность 386, 387, 414—416
Слабый экстремум 264
След матрицы 233, 490
— ядра 421
Смешанная стратегия 220
Смешанный тензор 238
Собственная функция 312, 392
Собственное колебание 570
Событие 242
Сокращение тензора 233
' Солеиондальиое поле 19—21
Сопряженная матрица 165
— система 488
— точка 304
Сопряженное интегральное уравнение 391
— отображение 167—168
— ядро 391
Сопряженные величины 322
. — гармонические функции 29
Состояние системы 546
Сохоцкий Ю. В. 81
Союзное уравнение 391
Спектр оператора 313
Стационарное значение функционала 272
Степенное отображение 37—39
Степень неустойчивости 571
— устойчивости 561
Стержень 345—346
Стирлннг Д. 123
Стохастическое программирование 226
Стробоскопический метод 621
.Структурно устойчивая система 541—542
•.Струна 343
Субгармонические колебании 587, 599
Сужение функции 73
Суммируемая функция 262
Существенно особая точка 79
Тензор 228-239
— деформации 237
;— ииерцни 235
— кривианы 256
— напряжений 351
Тензорное умножение 233
Тензорно-ннварнантная форма 25Г
Тензорный аиалив 22В, 2.44
Теорема Больцано— Вейерштрасса 71
— Боли—Брауэра 202. 478
— Гамильтона—Кэлн 183—184
. — Гильберта—Шмндта 424
— Гурввца 101 — 102
— Дж. Неймана 221
— запаадывання 133
— Кошн 63
— Коти—Лнувнлля 94
— Кошн о вычетах 81—82
— Куранта 174, 320
— Лаграижа 569
— Лиувилля 548
— Ляпунова—Пуаккаре 500
— Морера 69
— Нетер 329—330
— о логарифмических вычетах 96
— Попова 578
— Пуанкаре—Бертрана 459
— Римана 56
— Рулю 96—97
— Сильвастра 177
— смащюия 133
— Сохоцкого 81
— Фишера—Риса 436
— Флоке 492
Теорема Четаева 559'
— Шаудера 478
— Штурма 513
Теоремы Ляпунова 557, 562
— Нетера 466 '
— Фредгольма 390, 392—893, 393
Теория игр 219 .
Техническая устойчивость 580—581
Тихонов А. Н. 437
Топологическая эквивалентность 33"
Топологическое произведение 546
Топология 33
Тор 646. 552
Точечное отображение 532
Точечный источник 22, ¦SI
Точка перехода 518
— поворота 518—520
4 — покоя 521
— разветвления 41
Траектория 521
Трансверсальность 289—293
Транспортная задача 209
Угловая переменная 591, 615
Узел 525, 526, 536
Узло-фокус 537
Ультрагармоинческие колебания 598
Унитарная матрица 171
Управляемый объект 575'
Управляющее воздействие 575
Уравнение Абеля 434—435
— вая дер Поля 604
— Вольтерра 386, 413—414. 433—434,
443—446. 473
—• Гамильтона—Якобн 332
— Гаммерштейна 476
— Дуффиига 593, 599—600
— Клейна—Гордона 345
— Лапласа 21
— Ляпунова—Лихтенштейна 475
— Матье 494
— Милна 453
— Остроградского 278
— Пуассона 24—25
— разветвления 483
— с симметричным ядром 386, 418—429
— теплопроводности 151—164-
— Урысона 472
— Фредгольма 1-го рода 386, 435—442
2-го рода 386, 389—418, 445—452
— Хилла 494
— Эйлера 270—273
— Эйри 618
— Якобн 304
Урысои П. С. 472
Условие вевырождеиности 2F
Условия Бейерштрасса—Эрдмана 296
— Коши—Римаиа 29
— согласовании 283
— Якоби 304
Условнмй период 581
— МШтрвмум функцноиала 279—284
Уотойчнвость относительно класса возму-
щеяи.й 554
— — выбранных комбинаций или функци-
функционалов 554
— по Ляпунову 553—675
— — первому приближению 560
— при постоянно действующих возмуще-
возмущениях 554
Устойчивый полниом 101
— цикл 530
Устранимая особая точка 78
Фазовое пространство 520
Фазовый портрет 544
Факторизация 451—452

632
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
.Физическая составляющая 243
Форме (в алгебре) 174
Формула Крнстоффеля—Шварца 109—110
— обращения 137, 458—466 .
— Пуассона 91—83, 157— 1Б8
— Сткрлинга 123
Фредгольм И. 384
Фундаментальная матрица 490
— система решений 488
Функционал 260
Функциональное пространство 261
Функция Вейерштрасса 310—311
— Гамильтона 322
— Лаграижа 338
— Ляпунова 557—658
— Мзтье 498
— от матрицы 188—190
— последования 532
— тока 48—49
— Ханкеля 1-го рода 128
— цели 207
— ЭЯри 619
Характеристика (траектория) 521
— управляющего устройства 576
Характеристическая матркца 148
— функция 550
Характеристическое число 390
Хевисайд О. 129
Хорошо обусловленная система 1SS, 364
Целая функцкя 68—69
Целочисленное программирование 226
Цена игры.221
Центр 626
Центральное поле экстремалей 305
Центробежный момент ннерцнн 235
Цепная дробь 400
— линия 278, 3S8
Цермело Э. 219
Цикл 521—522, 530—633, 639— 641
Частная варкзция 276
Частотная характеристика 147
Четаев Н. Г. 559
Числовой вектор 165
Чистзн стратегия 220
Штурм Ш. 513'
Эйлер Л. 21. 66, 257
Эйлерова характеристика 538—639
Эйнштейн А. 228
Экстремаль 272
Элементарный вкхрь 61
— делитель 186
Эллипсоид инерцнн 235
Эллиптический интеграл 111 — 112
— синус 113
Вргоднческзя скстема 560
— теорема 54 9—550
Эрмнт Ш. 168
Эрмитов оператор 432
Эрмитова кввдратнчкая форма 176
— матркца 168
Эрмитово ядро 386
Явление Стокса 116
Ядро 158, 386
— Гильберта .458 -
— Кошн 458
— отображения 168
Якоби К- ИЗ, 176, 198
УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
. Зиакн векторного н тензорного акалнза V 10: д 1*5 "/:& 238I Stj
246; Г,, lj, Щ. Ц. V I П 247; ajft 248.
Знакк теории аналитических фуккций Выч / (г), Res / (г) 79.
г=а г=а-
•Зиаки теории специальных функций tj>p(z) 108; F(<p, ft), Б <0>,
112; sn(o>. ft), cn(u>, ft), un{w. k) 113; Kv(a) 124; #</>(*) 128; 7J %
Ня(х) 440; се„</; в), sen (<; g) 498; Al (s), Bl (s) 519. .
Знаки линейкой алгебры x 164; x 165; A* 167; A~> @) 168; dim 169; ел. A, SpA 490.
Знаки теорки функциональных пространств к варнацноккого исчисления ||/|) 261;
С [о, Ч, Сп1а, Ч. L, [а. Ч 262". Р {f. й) 262; 6у 265; Ы 266.
Некоторые другие знаки ~ 129; h*f, 135; Бр А 633; sgnx 644.
238; г?/' {'»'}
ft) 112; К (k), Я (ft)
440j L%(x) 440f
УбЪцителыш просьба
Hn cctul- члйющинъ и рамматривага
щииь книги, эстампы ф«лграф|и и т д.
1) Н
oTrt-ЬтСкъ не д*п
j при n
юдь
нт!. раскраш
ь;
J пСре
ь иедп^кно И аккуратно,
чтабь неч^ЯИло углы «граница И пакле-
енныхъ рясуннов ь пе Загнуть пне смять,
а т&кже проклавку ц?ъ qiannpD^Hoh bywa-
ги лешду рAсункапи не испортить,
4> при ра5^матривал1и scTafflrOBbj фо-
Тограф!й и рисунчовьвъннигахъиеиури^ь
h табачнымъ дымол-ь ихъ не оСяавать,-
5) лерелт! начиломъ рэгсмаг^Ёап№ и
чтент pyi№ тщательно мьлъ: ротными
вунами такие огчюдь не брать:
6] къ Серому рисунку fia эстэ^ла
таграфю^ъ и т- Д. П^±.цамн не прикасать
7J ОСгожку иги лереглет* книги
ред-ь irehieF* о?ерть!эать въ Ojiriary:
В) листы ННКГИ Una лалнти неза
Э^ въ кэрманахъ ннигЪ п« носи
же употребляв при атомъ особою предосто-
ромнисть^ чтобы лниги не испачкались И
НЕ БОЛЕЕ Ш КНИГИ В I
ОДНИ РУКИ И 2Х В ДВЕ }
КОЯОХЗА