Автор: Бамберг П. Стернберг Ш.
Теги: математика физика математическая физика переводная литература издательство москва
ISBN: 5-7036-0110-Х
Год: 2006
Текст
Иломо СТЕРНЕ
4и курс лекций
профессоров
университета
I1J ернберга
1ьшои полу-
пи физиков и
1ЮЩИХ для
ИМ14М освоить
основные элементы
ооцм'моннои м.нематики.
I опционных
одержит
। юлогии и
готический
Максвелла,
•........ 11И зсимп
J тласа и
динамики,
этих
разд* п>л|.м тики и
|фии,
IHO для
,.н •<* и И .1 жрпнтов
ИТ тов
лм тро
ип тщие
эния
и мате
|фи)ике
Я. Г. Синай
на ступенях МГУ
(фоте
/ Г ( инаи
ли1 РАН
и В. И. Арнольд
в сентябре 1963 года
J. Moser)
История преподавания
математического анализа,
начиная с его изобретения
Ньютоном, изобиловала крутыми
поворотами. К середине XX века
традиционные изложения стали
отличать полное исключение
всех геометрических понятий и
представлений, с одной стороны,
и полный отрыв от физики и всех
приложений, с другой.
Предлагаемая книга знаменует
возвращение преподавания
математики к естественнонауч-
ному подходу, для которого
характерны явная геометрич-
ность и прямое представление
математики как части физики,
непосредственно пригодной для
многочисленных приложений
как в естествознании, так и
в инженерном деле.
Это возвращение математики
в русло естественных наук
происходит сейчас и на уровне
новых научных исследований, а
его проявление в преподавании
давно стало абсолютно
необходимым.
В. И. Арнольд
академик РАН
Пол БАМБЕРГ
Шломо СТЕРНБЕРГ
КУРС МАТЕМАТИКИ
для
СТУДЕНТОВ-ФИЗИКОВ
Том II
Главы 12-22
ПЕРЕВОД С АНГЛИЙСКОГО
к.ф.-м.н., доц. Л. П. Котовой (МФТИ)
ПОД РЕДАКЦИЕЙ
к.ф.-м.н., доц. А.Н.Якивчика (МГУ)
+
МОСКВА
2006
УДК 51
Издание осуществлено при поддержке
Центрального аэрогидродинамического
института имени Н. Е. Жуковского,
директор В. Г. Дмитриев
и
Фонда « КНИГА-НАУ К А-КУЛЬТУ РА»,
директор В. Б. Филиппов
Бамберг П., Стернберг Ш.
Курс математики для студентов-физиков. Том II, главы 12-22.
Перев. с англ. Л. П. Котовой под ред. А. Н. Якивчика.
- М.: ФАЗИС, 2006. 664 с. (xix-xxxvi, 575-1220)
ISBN 5-7036-0110-Х
Paul Bamberg & Shlomo Sternberg
A Course in Mathematics for Students of Physics
© Cambridge University Press 1990 (Vol. 2)
Издательство ФАЗИС
123557 Москва, Пресненский вал, 42-44
e-mail: publisher@phasis.ru http://www.phasis.ru
Типография «Наука» Академиздатцентра РАН
121099 Москва Г-99, Шубинский пер., 6
Заказ №3639
ISBN 5-7036-0110-Х
© ФАЗИС, 2006
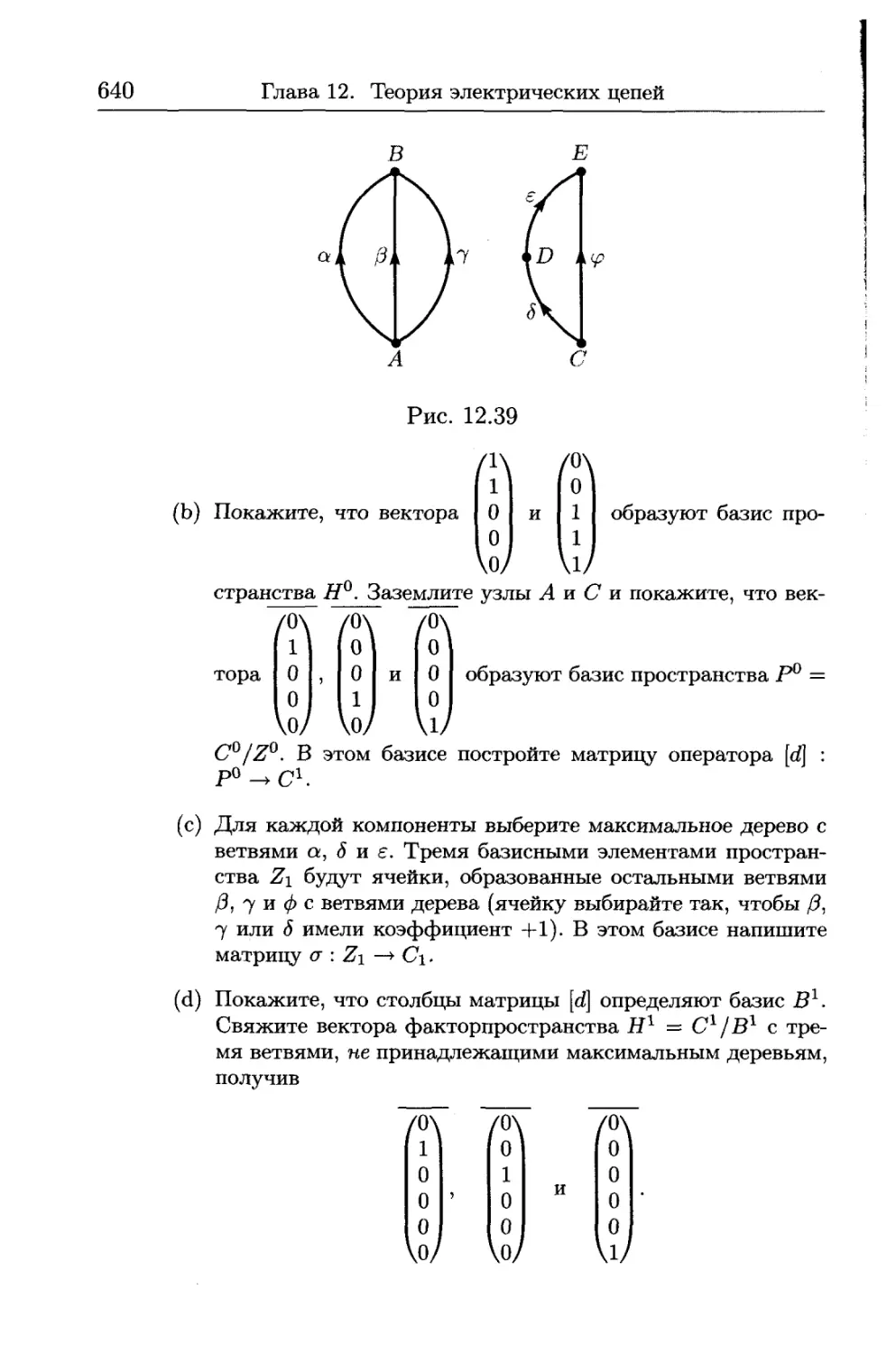
Оглавление тома II
Предисловие...................................................XXV
От издателя русского перевода................................XXXV
Глава 12. Теория электрических цепей......................... 575
Введение................................................... 575
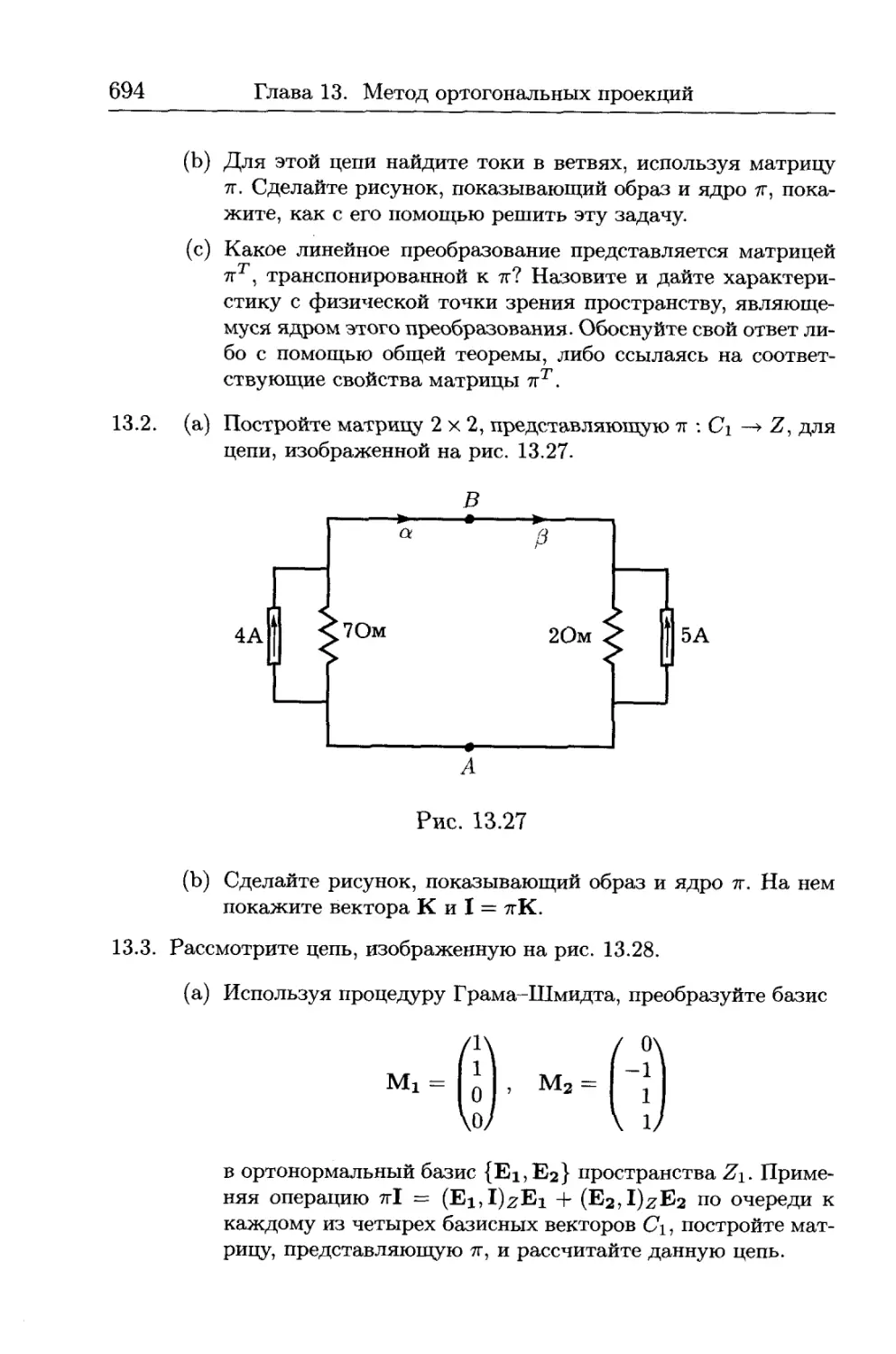
12.1. Линейные цепи с резисторами............................ 580
12.2. Топология одномерных комплексов........................ 590
12.3. Коцепи и d-оператор.................................... 604
12.4. Базисы и дуальные базисы............................... 607
12.5. Методы Максвелла....................................... 610
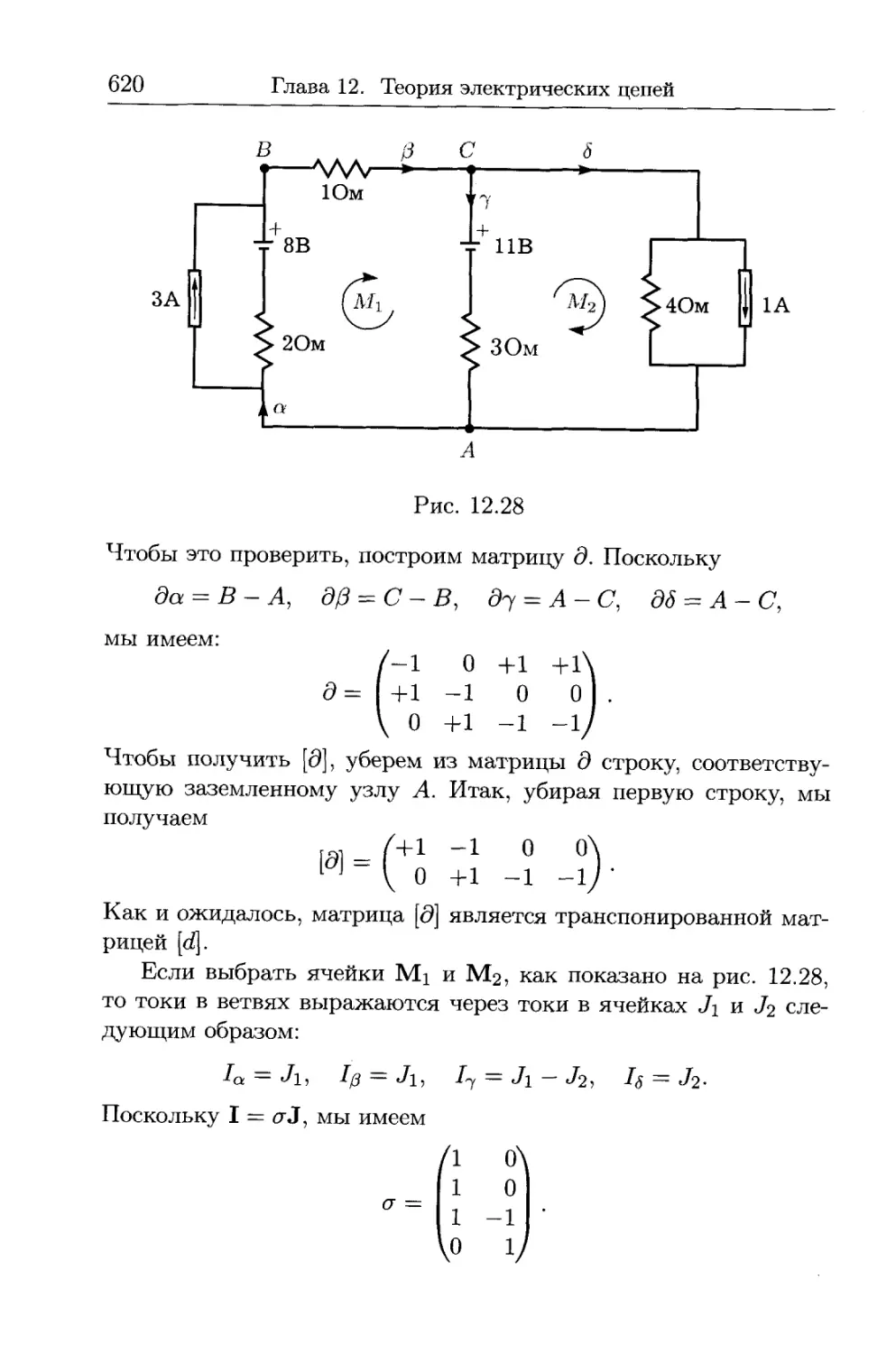
12.6. Матричные выражения для операторов..................... 614
12.7. Теорема Кирхгофа..................................... 626
12.8. Цепи переменного тока в стационарном режиме и фильтры... 630
Резюме....................................................... 636
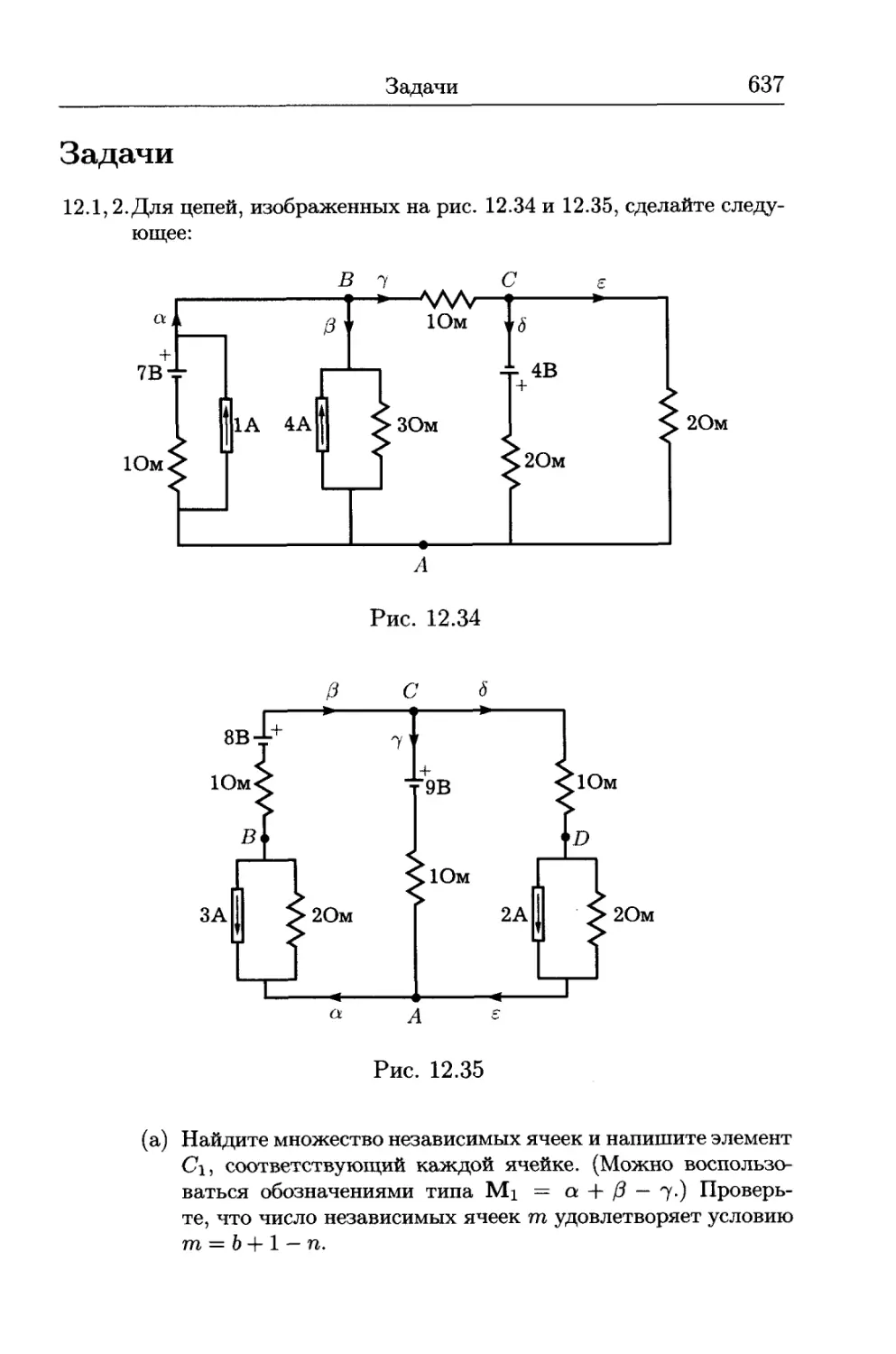
Задачи....................................................... 637
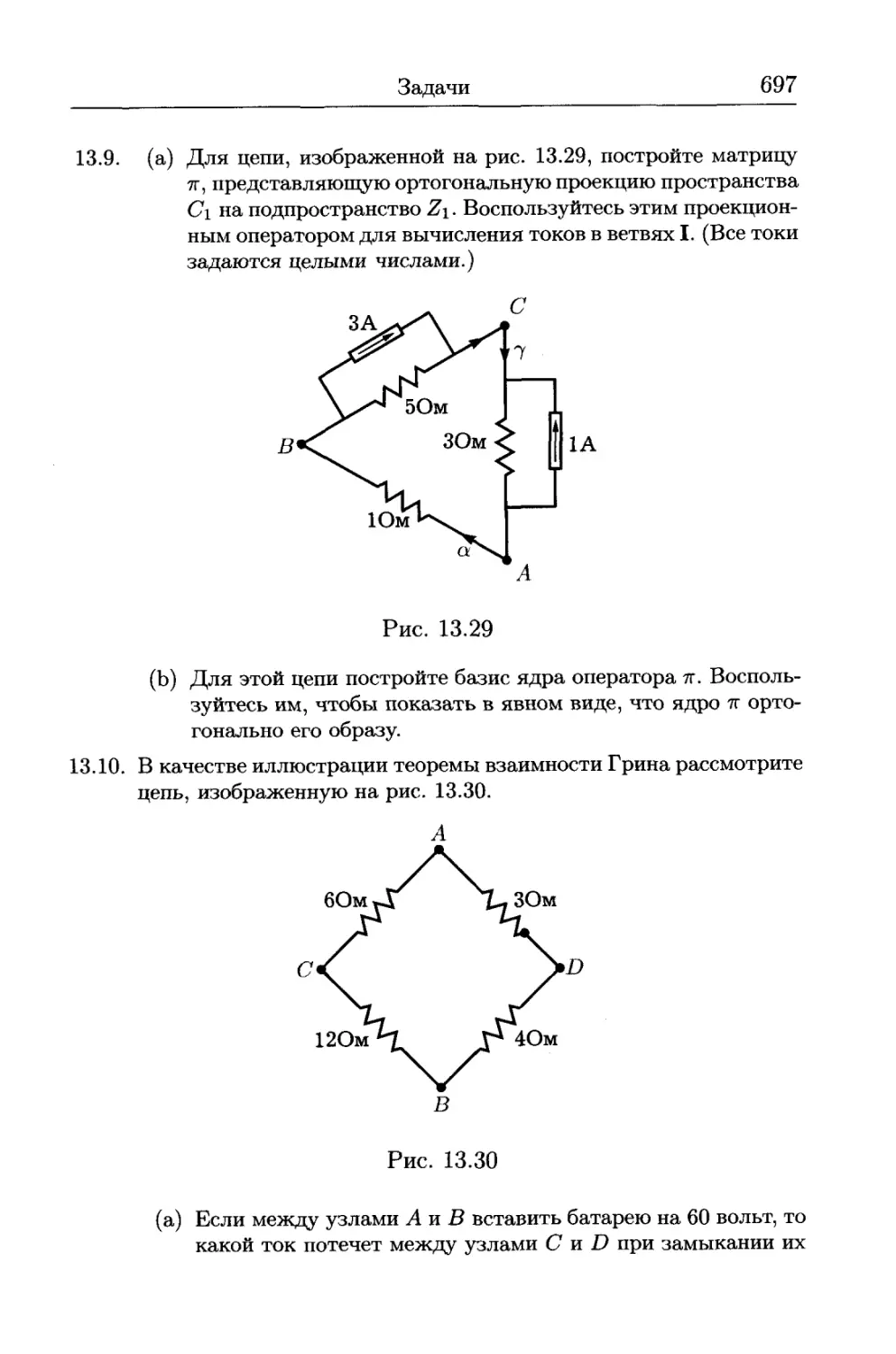
Глава 13. Метод ортогональных проекций....................... 645
13.1. Метод ортогональных проекций Вейля..................... 645
13.2. Метод Кирхгофа......................................... 650
13.3. Теорема взаимности Грина............................... 656
13.4. Цепи с конденсаторами.................................. 661
13.5. Краевые задачи......................................... 667
13.6. Решение краевых задач методом ортогональных проекций
Вейля........................................................ 671
13.7. Функции Грина.......................................... 678
13.8. Ядро Пуассона и случайное блуждание.................... 683
13.9. Теорема взаимности Грина в электростатике.............. 686
Резюме....................................................... 692
Задачи....................................................... 693
Глава 14. Комплексы высших размерностей...................... 705
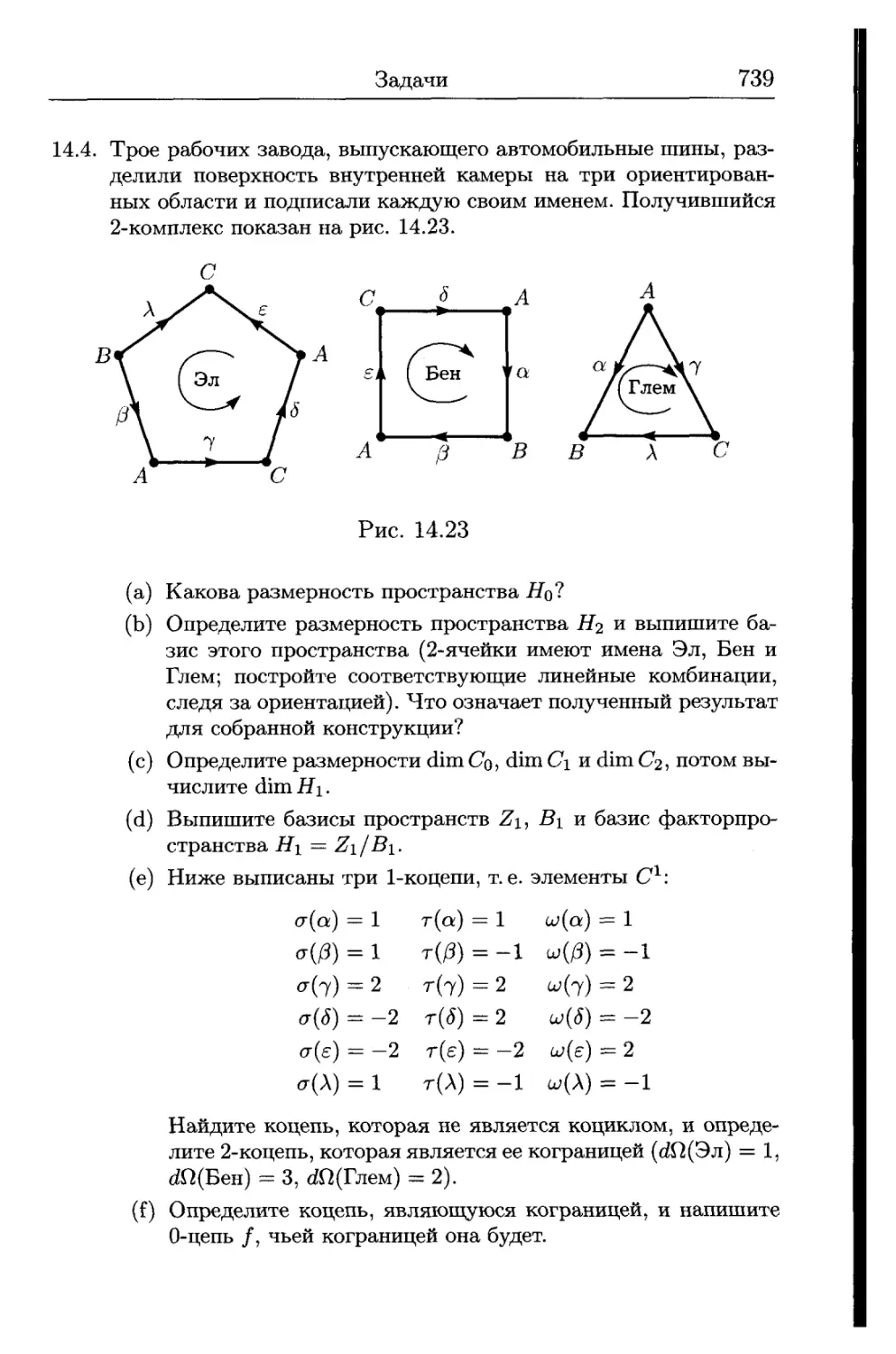
14.1. Комплексы и гомологии.................................. 705
14.2. Дуальные пространства и когомологии.................... 728
XXII
Оглавление тома II
Резюме....................................................... 737
Задачи....................................................... 737
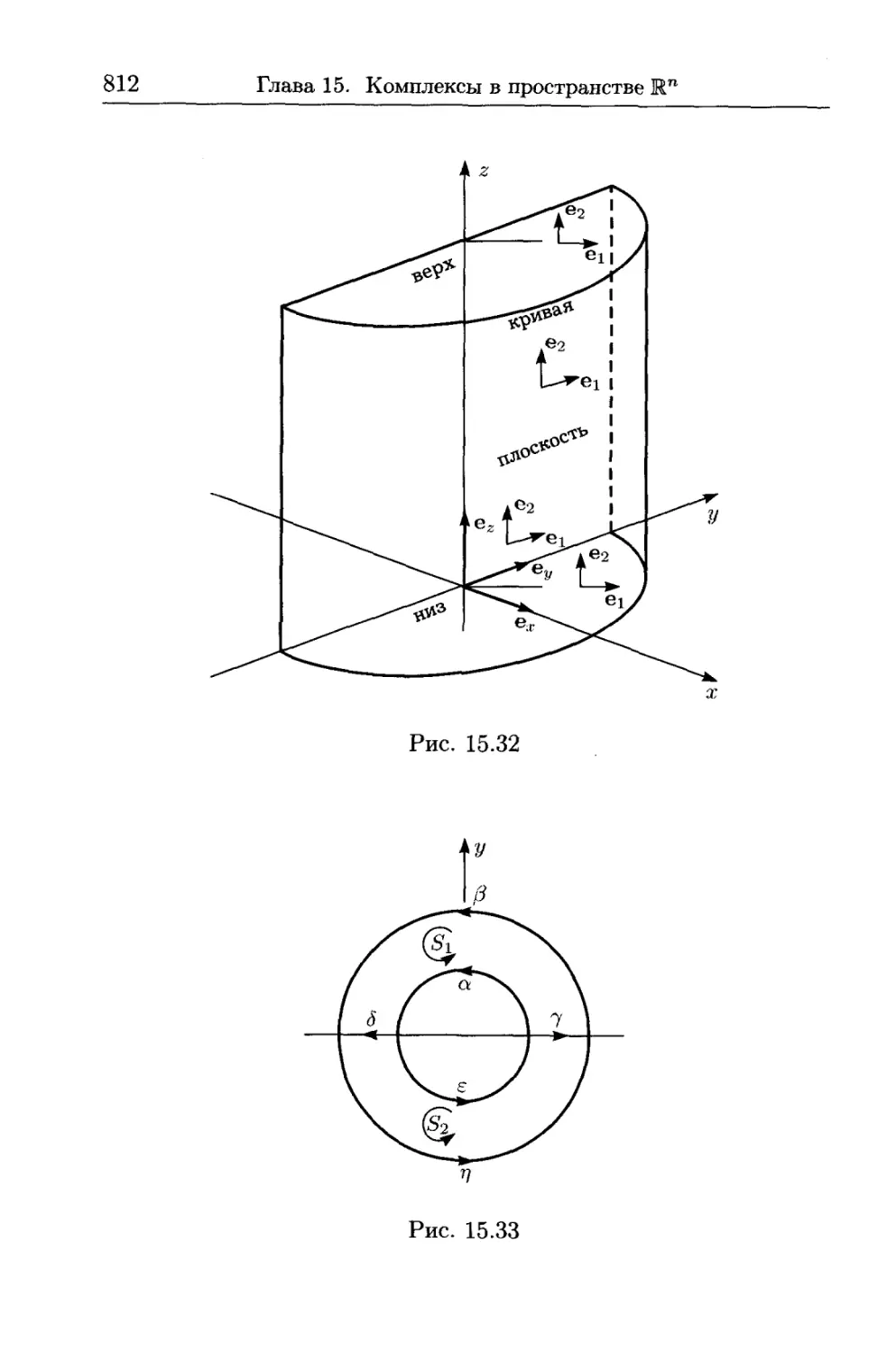
Глава 15. Комплексы в пространстве ]Rn....................... 745
Введение..................................................... 745
15.1. Внешняя алгебра........................................ 749
15.2. й-формы и оператор d................................... 757
15.3. Интегрирование Аг-форм................................. 760
15.4. Теорема Стокса........................................ 777
15.5. Дифференциальные формы и когомологии................... 792
Резюме....................................................... 805
Задачи....................................................... 806
Глава 16. Электростатика в пространстве К3.................. 817
16.1. От дискретности к непрерывности........................ 817
16.2. Граничный оператор..................................... 820
16.3. Телесный угол.......................................... 822
16.4. Напряженность электрического поля и электрическое смещение 824
16.5. Диэлектрическая проницаемость.......................... 836
16.6. Звездный оператор в трехмерном евклидовом пространстве.. 837
16.7. Формулы Грина.......................................... 842
16.8. Гармонические функции.................................. 844
16.9. Метод ортогональной проекции........................... 848
16.10. Функции Грина......................................... 850
16.11. Интегральная формула Пуассона......................... 853
Резюме....................................................... 859
Задачи....................................................... 859
Глава 17. Токи, потоки и магнитостатика...................... 863
17.1. Токи................................................... 863
17.2. Потоки и векторные поля................................ 865
17.3. Внутреннее произведение................................ 871
17.4. Производные Ли......................................... 879
17.5. Магнетизм.............................................. 883
Приложение: альтернативное доказательство фундаментальной
формулы дифференциального исчисления......................... 890
Резюме....................................................... 893
Задачи....................................................... 893
Глава 18. Звездный оператор.................................. 897
18.1. Скалярные произведения и внешняя алгебра............... 897
18.2. Звездный оператор...................................... 901
18.3. Интеграл Дирихле и лапласиан.......................... 909
18.4. Оператор □ в четырехмерном пространстве-времени........ 916
18.5. Алгебра Клиффорда...................................... 920
18.6. Звездный оператор и геометрия.......................... 931
18.7. Звездный оператор и векторный анализ................... 933
Приложение: тензорные произведения........................... 936
Оглавление тома II
XXIII
Резюме....................................................... 953
Задачи........................................................ 953
Глава 19. Уравнения Максвелла................................. 969
19.1. Уравнения............................................... 969
19.2. Одномерное однородное волновое уравнение................ 974
19.3. Однородное волновое уравнение в пространстве R3 ........ 977
19.4. Неоднородное волновое уравнение в пространстве R3 ...... 981
19.5. Лагранжиан электромагнитного поля и тензор
энергии-импульса.............................................. 983
19.6. Волновые фронты и принцип Гюйгенса...................... 988
Резюме........................................................ 994
Задачи........................................................ 994
Глава 20. Комплексный анализ.................................. 997
Введение...................................................... 997
20.1. Комплекснозначные функции............................. 999
20.2. Комплекснозначные дифференциальные формы............... 1001
20.3. Голоморфные функции...................................1004
20.4. Вычисление вычетов....................................1010
20.5. Приложения и следствия............................. 1021
20.6. Локальное отображение.................................1031
20.7. Контурные интегралы...................................1040
20.8. Пределы и ряды........................................1047
Добавление: связь между голоморфными и гармоническими
функциями...................................................1052
Резюме........................................................1055
Задачи........................................................1056
Глава 21. Асимптотическое вычисление интегралов...............1065
Введение..................................................... 1065
21.1. Метод Лапласа.........................................1066
21.2. Метод стационарной фазы...............................1072
21.3. Гауссовы интегралы................................... 1076
21.4. Групповая скорость....................................1080
21.5. Формула обратного преобразования Фурье................1082
21.6. Асимптотическая оценка формулы Гельмгольца............1084
Резюме....................................................... 1086
Задачи........................................................1087
Глава 22. Термодинамика.....................................1089
22.1. Теорема Каратеодори...................................1090
22.2. Классическая термодинамика по Борну и Каратеодори.... 1100
22.3. Энтропия и абсолютная температура ................... 1108
22.4. Системы с одной конфигурационной переменной...........1115
22.5. Условия равновесия....................................1131
22.6. Системы и состояния в статистической механике.........1137
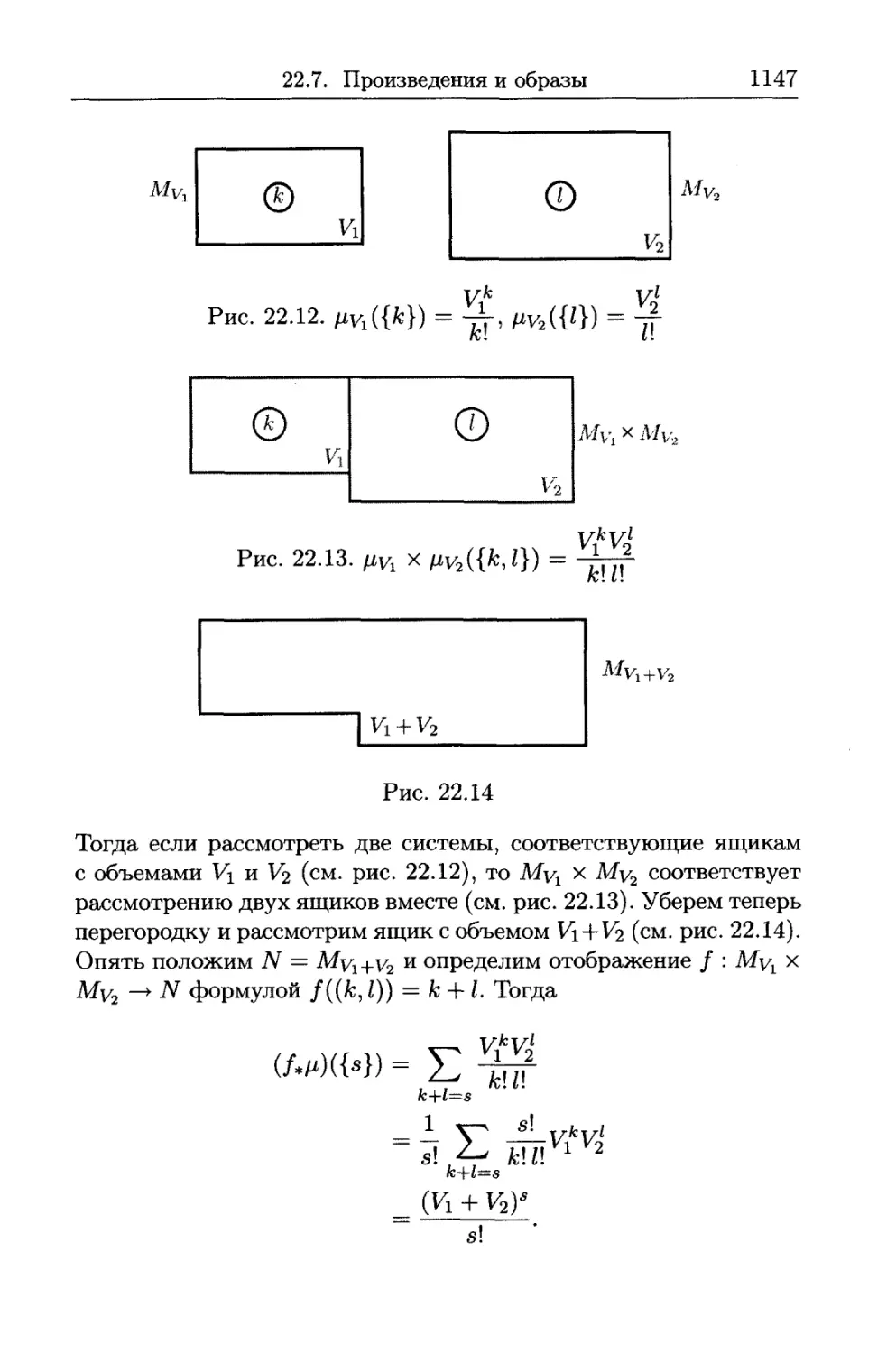
22.7. Произведения и образы................................ 1144
XXIV
Оглавление тома II
22.8. Наблюдаемые, ожидаемые значения и внутренняя энергия...1149
22.9. Энтропия...............................................1158
22.10. Равновесие в статистических системах..................1161
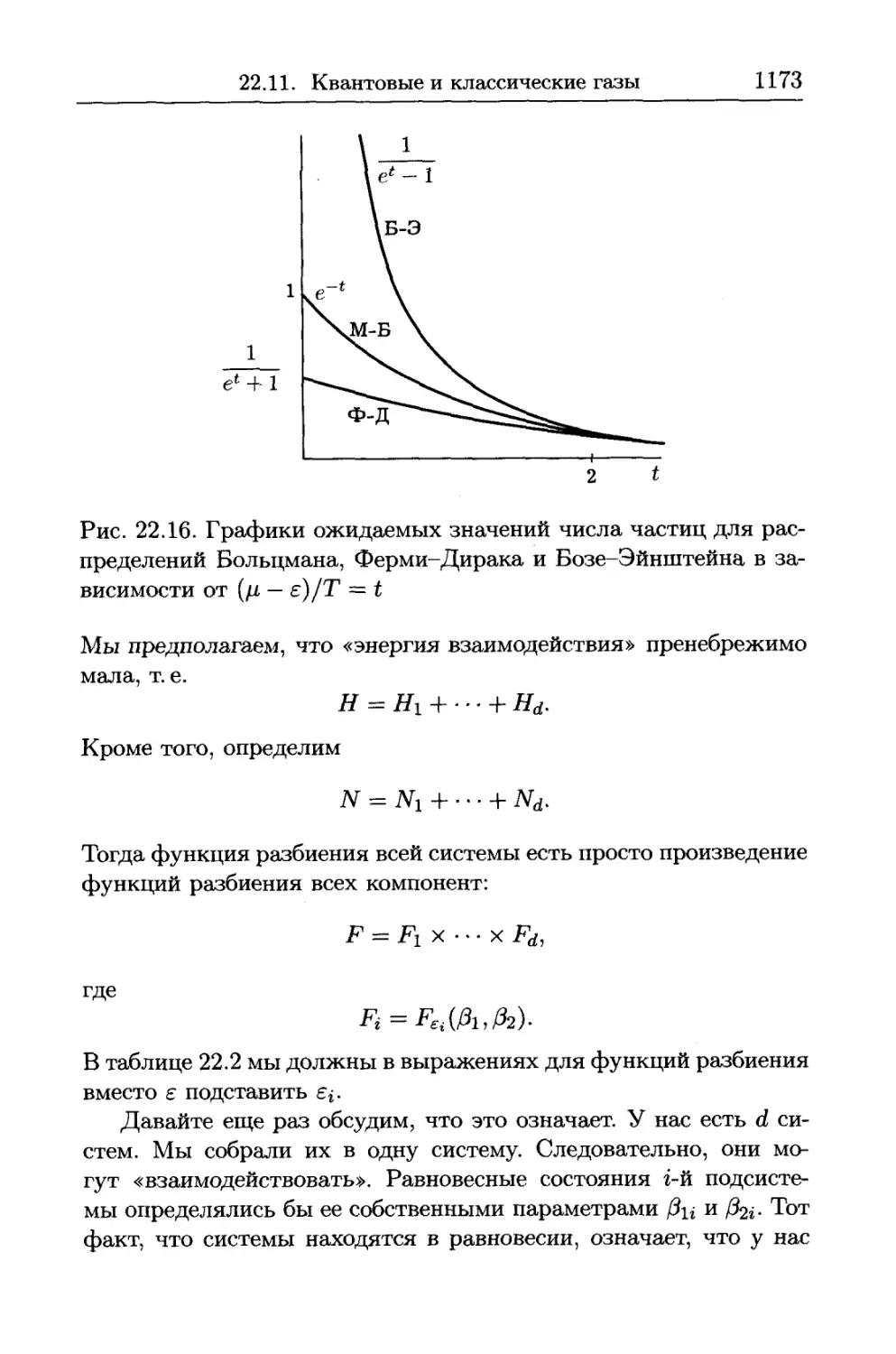
22.11. Квантовые и классические газы.........................1171
22.12. Определители и следы..................................1175
22.13. Квантовые состояния и квантовая логика............... 1182
Резюме.......................................................1188
Задачи.......................................................1189
Приложение: доказательство теоремы о нормальной форме........1192
Рекомендуемая литература.....................................1201
Предметный указатель.........................................1207
Предисловие
В этой книге излагается курс математики, который мы пре-
подавали в Гарварде в течение восьми лет. Курс предназначен
для студентов, интересующихся физикой и имеющих хорошую
подготовку по математическому анализу функций одной пере-
менной. Полезно некоторое знакомство с линейной алгеброй, но
это не обязательно. Большинство наших студентов одновремен-
но с этим курсом изучают сложные курсы по физике, так что
они могут соединить излагаемые здесь сведения со своими фи-
зическими знаниями. Такое совмещение полезно, но не обяза-
тельно. Основное содержание нашего курса — теория и физиче-
ские приложения линейной алгебры и математического анализа
функций нескольких переменных, включая внешнее исчисление.
Наш педагогический метод — изложение по «спирали», т. е. мы
рассматриваем одну и ту же тему несколько раз, возвращаясь к
ней на все более высоком уровне, одновременно расширяя облас-
ти ее применения. Такое построение мы предпочитаем «прямо-
линейному» строгому логическому порядку. Надеемся, что при
этом мы избежим логических ошибок типа «порочного круга»,
но часто будем начинать с простого случая того или иного по-
нятия, а затем возвращаться к нему для обобщений, делая это
только после ознакомления с родственными понятиями и, как
следствие, приобретения более широкого взгляда на предмет.
Такой подход требует от студентов определенного доверия и тер-
пения. Но мы надеемся, что, в конце концов, они будут возна-
граждены более глубоким интуитивным пониманием предмета
в целом.
XXVI
Предисловие
Теперь расскажем о содержании книги более детально. Цель
первых четырех глав — познакомить читателя с алгеброй и ана-
лизом квадратных матриц. Таким образом, изучив эти главы,
студент должен научиться думать о матрицах как о самостоя-
тельных объектах, а не просто как о наборе чисел, выстроенных
по квадрату. В этих главах мы рассматриваем почти исключи-
тельно матрицы 2x2, когда самые сложные вычисления сводятся
к решению квадратных уравнений. Но каждый раз мы формули-
руем результаты, имея в виду матрицы более высокого порядка.
Глава 1 начинается с объяснения связи закона умножения
матриц 2 х 2 и геометрии прямых линий на плоскости. Далее
излагается алгебра матриц 2x2, обсуждается детерминант и его
отношение к плоскости и ориентации. Мы вводим определение
абстрактного векторного пространства в общем случае, объясня-
ем понятие базиса и замены базиса в одномерном и двумерном
векторном пространстве.
В главе 2 мы обсуждаем конформную линейную геометрию
на плоскости, т.е. геометрию линий и углов и их связь с опре-
деленного вида матрицами 2x2. Кроме того, вводятся понятия
собственных значений и собственных векторов, столь важные в
квантовой механике. Мы пользуемся этими понятиями, чтобы по-
строить алгоритм вычисления степеней матрицы. В качестве при-
мера, где это применяется, обсуждаются основные свойства цепей
Маркова.
Основная задача главы 3 — показать, что система однород-
ных линейных дифференциальных уравнений с постоянными ко-
эффициентами может быть записана в виде du/dt — Au, где А
— матрица, а и — вектор, и что решение этой системы имеет вид
еЛ*ио, где ио задается начальными условиями. При этом, конеч-
но, требуется объяснить, что означает экспонента, в показателе
которой стоит матрица. Кроме того, описывается качественное
поведение решений в неоднородном случае, в том числе обсуж-
дается явление резонанса.
Глава 4 посвящена изучению скалярных произведений и квад-
ратичных форм. В ней имеется много физических приложений, в
том числе обсуждение нормальных форм и детальное изложение
специальной теории относительности.
Предисловие
XXVII
В главах 5 и 6 изложены основные положения дифференци-
ального исчисления.
В главе 5 определяется дифференциал отображения одно-
го векторного пространства на другое, обсуждаются его основ-
ные свойства, в частности, правило дифференцирования компо-
зиции. В качестве физических приложений рассматриваются за-
дача Кеплера и приближение Борна. Мы даем определения част-
ной производной и производной по направлению, определяем ли-
нейные дифференциальные формы.
В главе б продолжается изложение дифференциального ис-
числения. Мы представляем в векторной форме теорему о сред-
нем значении, формулу Тейлора и теорему об обратном отобра-
жении. Обсуждаем поведение критических точек и множители
Лагранжа.
Главы 7 и 8 знакомят читателя с интегральным исчислением.
Глава 7 посвящена изучению линейных дифференциальных
форм и их интегралов. Особое внимание уделено замене перемен-
ных. Кроме того, обсуждаются и другие одномерные интегралы,
например, длина дуги.
Глава 8 посвящена изучению внешних форм второй степени
и соответствующих им двумерных интегралов. Вводится понятие
внешней производной и подчеркивается инвариантность относи-
тельно замены переменных. Доказывается двумерный вариант
теоремы Стокса, т. е. теорема Грина. Рассматриваются поверх-
ностные интегралы в трехмерном пространстве.
В главе 9 результаты первых восьми глав используются при
построении физической теории — оптики. Вся глава посвящена
приложениям, и ее можно опустить без ущерба для понимания
последующего материала.
В главе 10 мы возвращаемся назад и доказываем основные
свойства конечномерных векторных пространств и их линейных
преобразований. Обычно это непосредственное обобщение резуль-
татов, полученных в первых четырех главах в двумерном случае.
Но при этом дан новый алгоритм редукции матрицы по строкам.
Вводятся два новых понятия — дуальное пространство и фак-
торпространство (в начале курса их было трудно определить).
В дальнейшем эти понятия окажутся чрезвычайно важными.
XXVIII
Предисловие
Глава 11 посвящена свойствам детерминантов матриц п х п.
Тема рассмотрена аксиоматически, показаны основные вычисли-
тельные алгоритмы.
Главы 12-14 знакомят читателя с математикой формы, т. е. с
алгебраической топологией.
В главе 12 мы начинаем изучение электрических цепей. При
этом рассматриваются два аспекта. Во-первых, изучаются «про-
вода» цепи, т. е. как соединяются между собой различные ветви.
На математическом языке это называется топологией одномер-
ных комплексов. Во-вторых, мы изучаем реакцию цепи в целом,
если нам известно поведение отдельных ветвей, в частности из-
менение мощности и энергии. Мы приводим несколько примеров
цепей, интересных с физической точки зрения.
В главе 13 мы продолжаем изучение цепей. Исследуем крае-
вые задачи, связанные с емкостными цепями, и применяем изло-
женные методы для решения ряда классических задач электро-
статики, включающих проводники.
В главе 14 мы кратко показываем, как результаты, получен-
ные в главах 12 и 13 в одномерном случае, обобщаются на случай
большего числа измерений.
Главы 15-18 посвящены разработке внешнего дифференци-
ального исчисления, рассматриваемого как непрерывная версия
дискретной теории комплексов.
В главе 15 излагаются основные сведения о внешнем исчис-
лении: внешняя алгебра, &-формы, замена переменных, внешняя
производная и теорема Стокса.
Глава 16 посвящена электростатике. Мы рассматриваем ди-
электрические свойства вакуума как непрерывный аналог емко-
сти цепи, причем эти диэлектрические свойства определяют ев-
клидову геометрию в трехмерном случае. Излагаем основные по-
ложения теории потенциалов.
В главе 17 мы продолжаем изучение внешнего дифференци-
ального исчисления. Основные темы: векторные поля и потоки,
внутренние произведения и производные Ли. Полученные резуль-
таты применены для решения задач магнитостатики.
Глава 18 заканчивает изучение внешнего исчисления углуб-
ленным обсуждением общего случая звездного оператора.
Предисловие
XXIX
Главу 19 можно считать кульминацией всего курса. В ней ре-
зультаты, полученные в предыдущих главах, применяются для
исследования уравнений Максвелла и связанных с ними волно-
вых уравнений.
Главы 20 и 21 никак не связаны с главами 9-19, и их можно
читать независимо. Обычно они не включаются в наш годовой
курс. А вот главы 1-9, 20 и 21 могут составить самостоятельный
краткий курс математики.
Материал главы 20 представляет собой относительно стан-
дартное изложение теории функций комплексного переменного,
которое вполне доступно для студентов, подготовленных к чте-
нию этой книги.
В главе 21 обсуждаются простейшие аспекты асимптотик.
В главе 22 показано, как, следуя идеям Бора и Каратеодори,
внешнее исчисление можно использовать в классической термо-
динамике.
Большинство математиков и все физики, результаты которых
представлены в этой книге, работали в первом десятилетии два-
дцатого века. Это значит, что изложенному материалу уже по
крайней мере 90 лет. И, тем не менее, он еще не вошел в наши
элементарные курсы математики, хотя большая его часть (за ис-
ключением, может быть, теории цепей) должна изучаться совре-
менными физиками, что они и делают на определенном этапе сво-
ей карьеры. Причины этого, в значительной мере, исторические.
У. Гамильтону (1805-1865) было очевидно, что вещественных и
комплексных чисел недостаточно для глубого изучения геомет-
рического анализа, что в декартовой геометрии дву- и трехмер-
ного пространства возникает желание рассматривать числа па-
рами и тройками, как самостоятельные объекты с собственны-
ми алгебраическими свойствами. Для этого он разработал ал-
гебру кватернионов, которая была очень популярна в Англии в
середине девятнадцатого века. Однако, теория имела ряд изъ-
янов: кватернионы более естественны в пространстве четырех,
а не трех измерений. Геометрия трех измерений возникала как
часть более общей конструкции, а не как самостоятельная теория.
Кроме того, кватернионы имели слишком сложную алгебраиче-
скую структуру. Например, очень громоздкой была связь между
XXX
Предисловие
умножением кватернионов и геометрическими построениями в
трехмерном пространстве. (Конечно, первый недостаток сегодня
считался бы не очень серьезным, но вместо него возникло бы
другое возражение: теория ограничена четырьмя измерениями.)
В конце концов, векторная алгебра в трехмерном пространстве
с ее скалярным и векторным произведениями была очищена от
теории кватернионов. Ее объединили с необходимыми дифферен-
циальными операциями, в результате чего появился векторный
анализ, окончательно разработанный Дж. Гиббсом (1839-1903) и
обнародованный им в своей знаменитой книге «Элементы вектор-
ного анализа», оказавшей сильное влияние на дальнейшее разви-
тие науки.
Итак, векторный анализ с его операциями grad, div, curl и т. д.
стал стандартным языком изложения геометрических законов
физики. Однако, несмотря на то, что векторный анализ прекрас-
но описывает геометрию трехмерного пространства, он тоже име-
ет ряд существенных недостатков. Первый — и наименее серьез-
ный — состоит в том, что в нем не просматривается очень важное
единство: например, не ясно, что фундаментальная теорема ис-
числения одна — сейчас ее называют общей теоремой Стокса, а
теоремы Грина, Гаусса и классическая теорема Стокса являются
ее частными случаями. В рамках векторного анализа мы не мо-
жем это увидеть. Более серьезный недостаток состоит в том, что
фундаментальные операторы (например, grad, div) предполага-
ют евклидову структуру пространства, т. е. подразумевают трех-
мерное пространство и ориентацию (например, curl). Это значит,
что теория работает только в трехмерном ориентированном ев-
клидовом пространстве. При этом возникает еще одна пробле-
ма — при произвольном изменении координат операторы ведут
себя неприятно, их выражения в неортогональных координатах
очень громоздкие. Уже А. Пуанкаре (1854-1912) в своих фун-
даментальных научных и философских работах, предшествовав-
ших теории относительности, подчеркивал необходимость делать
различие между «топологическими» законами геометрии и физи-
ки, т. е. законами, которые зависят только от дифференциальной
структуры пространства и поэтому инвариантны относительно
гладких преобразований, и законами, зависящими от геометри-
Предисловие
XXXI
ческой структуры, например, от понятия расстояния. Теория от-
носительности оказала огромное влияние на развитие математи-
ки главным образом потому, что она поощряла изучение теории
многомерных пространств, которая уже существовала в матема-
тической литературе, но не считалась важной для изучения гео-
метрии. Кроме того, необходимо было исследовать произвольные
изменения координат. Векторный анализ не мог решить эти две
задачи и поэтому позднее его дополнили тензорным анализом.
Но и тензорный анализ с его обилием индексов тоже имеет много
серьезных недостатков. Главный изъян состоит в том, что неве-
роятно трудно сказать, какие операции имеют общее геометриче-
ское значение, а какие связаны только с данной системой коорди-
нат. Таким образом, тензорный анализ очень хорош для вычис-
лений, но трудно сказать, что именно вычисляется. Вся работа,
начатая еще Гамильтоном и направленная на создание матема-
тического аппарата, в котором объекты имеют геометрический
смысл, оказалась напрасной. Для того, чтобы заставить теорию
работать, необходимо было ввести аффинную связь — доволь-
но изощренную геометрическую конструкцию. Но даже с такой
конструкцией геометрическое значение операций не стало про-
зрачным. По существу интуитивно ясный векторный анализ так
и не был вытеснен тензорным анализом из программ начального
университетского обучения.
Математики в основном уже согласились, а физики постепен-
но привыкают к тому, что самым удобным аппаратом для гео-
метрического анализа является внешнее дифференциальное ис-
числение Грассмана и Картана. Его преимущество состоит в том,
что наряду с простыми и четкими правилами вычисления все
объекты имеют прозрачный геометрический смысл. Внешнее ис-
числение работает при любом числе измерений, хорошо себя ве-
дет при отображениях и изменениях системы координат, облада-
ет существенным единством основных теорем и четко различает
«топологические» и «метрические» свойства. В рамках внешне-
го анализа геометрические законы физики принимают простую и
элегантную форму. Чтобы это продемонстрировать, полезно при-
вести таблицу, взятую из книги «Курс математической физики»,
написанную Тиррингом.
XXXII
Предисловие
Таблица 1. История записи уравнений Максвелла.
Константы с, /щ, и со положены равными 1.
Однородное уравнение Неоднородное уравнение
Самая ранняя форма
^ + ^ + ^ = о дх 1 dv ' dz дЕг дёх _ ~dlz — fa дх - uEy дЕх дх ду — , дЕу дЕг _ л дх ду ' dz Р ду dz &х дЁ^_дВ3__ х . £ fa дх ~ Jy^ ^У ЭВ. _ + Ё дх ду ~ +
Конец XIX века
V-B = 0 V х Е = -В V Е = р V х В = j + Ё
Начало XX века
*F^>,a=0 = JP
Середина XX века
dF = 0 6F = J
В 1844 году Г. Грассман (1809 1877) опубликовал книгу «Aus-
dehnungslehre». Математическое сообщество не оценило эту ра-
боту и ведущие немецкие математики того времени проигно-
рировали ее. Фактически, Грассман так никогда и не получил
место в университете; всю свою жизнь он преподавал матема-
тику в школе. Однако, похоже, что он прожил счастливую и
плодотворную жизнь. У Грассмана была большая семья и он
считался признанным экспертом по санскритской литературе.
В конце жизни он попробовал еще раз выпустить новое изда-
ние «Ausdehnungslehre», но оно также не имело успеха. Толь-
Предисловие
хххш
ко немногие из математиков того времени оценили его работу.
Среди них был К. Мебиус (1825-1908). Тем не менее, в книге
«Ausdehnungslehre» впервые появились ключевые в современной
математике понятия и большинство алгебраических структур,
используемых в этой книге. В ней были определены: векторное
пространство, внешняя алгебра, внешнее и внутреннее произве-
дение, теорема Стокса в обобщенной форме.
В настоящее время общепризнано, что Э.Картан (1869-1951)
является крупнейшим специалистом по геометрии в XX веке. Его
ранние работы, относящиеся к группам Ли и дифференциальным
уравнениям в частных производных, имеющие огромное значение
для современной математики, тоже сначала не были поняты. Но
в 1920 году они стали известны широкому кругу ученых. К это-
му времени теория групп Ли начала играть ключевую роль в
математике и физике, и Г. Вейль заново представил их в своих
статьях. В настоящее время работы Картана по основным уз-
лам и связям (известные под общим названием «калибровочные
теории») являются основой теории элементарных частиц. В 1922
году Картан опубликовал книгу «Лекции по интегральным инва-
риантам», где показал, что изобретенное им внешнее дифферен-
циальное исчисление является гибким инструментом не только
для геометрии, но и для вариационного исчисления с широким
кругом физических приложений. Как уже было сказано, призна-
ние пришло не сразу, но сегодня и физики, и математики счита-
ют, что внешнее исчисление позволяет наилучшим образом фор-
мулировать геометрические законы физики. И нам кажется, что
пришла пора заменить им векторное исчисление в программах
начального университетского обучения.
Необходимо пояснить, почему в книге так много внимания
уделено теории электрических цепей, хотя обычно эта тема не
входит в учебные программы по математике. Прежде всего, это
оправдано с педагогической точки зрения. Данная тема все-
гда нравится студентам. Она позволяет на очень приземленном
уровне ввести понятия дуального пространства и факторпро-
странства. Иначе эти понятия кажутся студентам слишком аб-
страктными и поэтому трудно воспринимаются ими. Кроме того,
в дискретном, алгебраическом подходе к теории цепей теорема
XXXIV
Предисловие
Стокса появляется, по существу, как естественное определение,
что позволяет понять роль оператора d и теоремы Стокса при
формулировке внешнего исчисления. Конечно, есть более глу-
бокие, философские причины, почему мы приняли решение по-
дробно рассказать о теории цепей. Уже почти сто лет, как люди
думают, что силы, удерживающие макроскопические тела, име-
ют электрическую природу. Таким образом, понятие твердого
тела и отсюда евклидова геометрия вытекают из электростати-
ки (конечно, в нерелятивистском приближении, когда понятия
твердого тела и геометрия Евклида имеют смысл). Физические
исследования как предельно малых объектов (элементарных ча-
стиц), так и предельно больших (космология) заново ставят фун-
даментальные вопросы о геометрии пространства и времени. Мы
полагаем, что разумно уже в самом начале изучения математики
дать студентам представления о связи геометрии и физики. Без
сомнения, сторонники компьютеров и ряда современных теорий
в физике зададут вопросы о дискретности, противопоставляе-
мой непрерывному характеру пространства и времени (пробле-
ма, поднятая Риманом в его диссертации об основах геометрии).
Надеемся, что наше обсуждение может быть полезно тем, кто в
будущем станет решать эту проблему.
Наш курс математики читается в течение одного года, и по-
этому мы вынуждены были опустить некоторые важные темы.
Мы не обсуждаем бесконечномерные векторные пространства,
в частности, гильбертовы пространства; не даем определения и
не изучаем абстрактные дифференцируемые многообразия и их
свойства. Наш опыт показал, что эти темы слишком сложны для
студентов, и усилия, которые необходимо затратить на их объ-
яснение, лучше использовать по-другому. Конечно, в книге есть
места, где нам приходится компенсировать отсутствие этих по-
нятий. Однако, более серьезно то, что в книге нет подробного
обсуждения гармонического анализа Фурье, классической меха-
ники и теории вероятностей. Мы только слегка касаемся этих
тем, не давая подробного изложения. Нас может извинить только
то, что каждая из этих тем потребовала бы семестрового курса,
а их подробное изложение на современном уровне легко найти.
В конце книги приводится список рекомендуемой литературы.
От издателя и редактора русского перевода
XXXV
Нам приятно поблагодарить профессора Даниэла Гороффа,
тщательно прочитавшего рукопись, за многочисленные исправ-
ления и полезные предложения. Мы искренне благодарим Джин
Моррис за отличное качество набора, за то, что она внимательно
сопровождала производство книги на протяжении восьми лет —
с самого начала проекта до его завершения.
От издателя и редактора
русского перевода
Данный курс является примером глубокого синтеза матема-
тических и физических знаний и методов. По нашему мнению,
хотя он называется «Курс математики для студентов-физиков»,
с тем же успехом его можно рассматривать как «Курс физики
для студентов-математиков».
Первый том содержал изложение основополагающих матема-
тических понятий и теорий, таких как дифференциальное и ин-
тегральное исчисление, векторные пространства и линейные пре-
образования, линейные дифференциальные уравнения. На этом
этапе в качестве области применения изучались теория колеба-
ний, специальная теория относительности и гауссова оптика.
Во втором томе математический аппарат не только замет-
но развивается, но и находит важные физические приложения.
Прежде всего это электромагнитные явления — от теории элек-
трических цепей (глава 12) до уравнений Максвелла (глава 19).
Термодинамике и статистической механике посвящена глава 22.
То обстоятельство, что курс рассчитан всего на один год, но
при этом затрагивает самые разные разделы математики, кото-
рые на математических специальностях российских университе-
тов преподаются на протяжении большей части срока обучения,
XXXVI
От издателя и редактора русского перевода
вынуждает авторов использовать местами весьма конспективный
стиль изложения. Это выражается в том, что опускаются детали
строгих математических доказательств важных результатов (на
которые, впрочем, обычно дается ссылка). А некоторые области,
как теория вероятностей или алгебраическая топология, вообще
представлены только начальными сведениями. Построение курса
также не в полной мере соответствует российской университет-
ской программе. Так, ряды Фурье (без которых трудно предста-
вить решение многих современных задач физики и других есте-
ственных наук) вводятся только в конце главы 20, посвященной
комплексному анализу. (Учитывая важную роль гармонических
функций в физике, в частности, как потенциалов силовых полей,
редактор сделал к той же 20-й главе небольшое добавление о вза-
имосвязи между гармоническими функциями двух переменных и
аналитическими функциями комплексного переменного.)
При переводе и редактировании были исправлены многочис-
ленные ошибки и неточности оригинала. Редакторы (первого и
второго томов) добавили к тексту довольно много примечаний.
Обновлены и уточнены списки рекомендуемой литературы, даны
ссылки на имеющиеся русские переводы. Заново составлен пред-
метный указатель; во втором томе он охватывает материал всей
книги.
Мы надеемся, что этот современный курс, весьма отличаю-
щийся от отечественных образовательных традиций, будет инте-
ресен не только студентам, но и преподавателям.
Надеемся также, что издание будет полезно широкому кругу
научных работников разнообразных физических, технических и
математических специальностей.
Мы будем благодарны читателям за любые замечания по кни-
ге; просим направлять их нам по адресу publisher@phasis.ru.
Москва, май 2006
Глава 12
Теория электрических цепей
Главы 12-14 можно считать введением в математи-
ку формы, т. е. в алгебраическую топологию. В гла-
ве 12 мы начинаем изучение электрических цепей.
Здесь имеются два аспекта. Во-первых, изучается си-
стема проводов цепи с точки зрения связи между со-
бой различных участков. На математическом языке
это называется топологией одномерных комплексов.
Во-вторых, предполагая, что мы знаем поведение от-
дельных участков, изучается реакция цепи в целом,
в частности, рассматриваются мощность и энергия.
Приводятся примеры цепей, интересные с физической
точки зрения.
Введение
Теория электрических цепей является приближением к электро-
магнитной теории, когда предполагается, что все интересные яв-
ления происходят в проводах и других элементах этих цепей. При
этом также предполагается, что цепь может быть разложена на
различные компоненты с определенным характером поведения,
и задача состоит в том, чтобы предсказать поведение всей цепи,
если ее компоненты соединяются различными способами.
Основные переменные теории цепей хорошо известны по
бытовым приборам: это ток, напряжение и мощность. Фунда-
ментальной единицей электромагнитной теории является заряд
576
Глава 12. Теория электрических цепей
электрона. К моменту написания этой книги (до обнаружения
кварков) частица, заряд которой был бы долей заряда электро-
на, неизвестна. На практике единицей заряда считается кулон,
который противоположен заряду 6.24 х 1018 электронов. В 1819
году Эрстед заметил, что поток электрического заряда создает
силу, действующую на магнитную иголку, причем эта сила про-
порциональна скорости потока заряда. Этот эффект измерять
гораздо легче, чем электростатические силы, которые требуются
для измерения заряда. Поэтому именно ток, а не заряд, счита-
ется основной переменной теории цепей. Единицей тока является
ампер, причем 1 ампер = 1 кулон/секунду. Ток будем обозначать
буквой I, Итак,
j —
dt ’
где I - ток, измеряемый в амперах, Q — заряд, измеряемый в
кулонах, a t — время, измеряемое в секундах. Вообще говоря, мы
могли бы ожидать, что ток, протекающий по цепи, зависит от
точки наблюдения. В теории цепей предполагается, что ток при-
нимает определенное значение на каждом линейном участке (вет-
ви) цепи (но может и меняться со временем). Пусть а обозначает
некую ветвь в цепи, тогда Ia(t) обозначает ток, протекающий че-
рез а в момент t.
Проходя вдоль участка цепи, элемент заряда приобретает
энергию или теряет ее. Изменение энергии (измеряемой в джо-
улях) на единицу заряда (измеряемого в кулонах) называется
напряжением. Это значит, что 1 вольт — 1 джоуль/кулон. На-
пряжение будем обозначать буквой V, Напряжение (разность
потенциалов) между двумя концами ветви а в момент I обозна-
чается Va(f). Произведение тока на напряжение имеет размер-
ность энергии/время и называется мощностью, измеряемой в
соответственно ваттах, т. е.
1ватт = 1 вольт х ампер = 1 джоуль/секунду.
В теории цепей предполагается, что существует три типа ветвей:
индукторы, конденсаторы и сопротивления. Для каждого типа
имеется определенное соотношение между напряжением и током.
В индукторе напряжение пропорционально скорости изменения
Введение
577
тока, т. е. если а обозначает индуктор, то
dla _ а
La dt ~ V ’
где постоянная La называется индуктивностью. Соответствую-
щая единица индуктивности называется генри, т. е.
1 генри = 1 вольт/(ампер/секунду) = 1 вольт х секунду/ампер.
В конденсаторе ток пропорционален скорости изменения напря-
жения. Если а — конденсатор, то
где постоянная Са называется его емкостью и измеряется в фа-
радах, т. е.
1 фарад — 1 кулон/вольт.
Для сопротивлений (резисторов) существует функциональное со-
отношение, связывающее ток и напряжение (но не их производ-
ные) . В классической теории линейных пассивных цепей оно име-
ет вид V ~ RI, где постоянная /?, измеряемая в омах, называется
сопротивлением ветви. График1 этого соотношения на плоско-
сти /, V изображен на рис. 12.1. Это прямая линия, проходящая
Рис. 12.1. Простой резистор Рис. 12.2. Реальная батарея
через начало координат. Любой прибор, описываемый (неодно-
родным) линейным уравнением по I и V, мы будем считать ли-
нейным сопротивлением. Например, реальная батарея (рис. 12.2)
Называемый вольт-амперной характеристикой. — Прим. ред.
578
Глава 12. Теория электрических цепей
с внутренним сопротивлением Ra может быть описана урав-
нением Va — Wa + RaIa, где постоянная Wa называется ЭДС
(электродвижущей силой) батареи. Идеальная батарея, создаю-
щая напряжение Wa при любом токе, описывается уравнением
Va — Wa. На рис. 12.3 изображена горизонтальная линия. Иде-
альный источник тока, создающий ток Ка независимо от напря-
жения на его полюсах, описывается уравнением 1а — Ка, т. е.
графиком будет вертикальная линия.
J kV
7
Рис. 12.3. Идеальная батарея
Анализируя цепи, в которых напряжение и токи зависят от
времени, мы должны рассматривать источники напряжения и
тока, тоже зависящие от времени. В этом случае линейное со-
противление в общем виде описывается уравнением
где и Ka(t) — заданные функции времени.
В более общем случае рассматриваются нелинейные сопро-
тивления, индукторы и конденсаторы. Например, диод или тер-
мистор могут считаться нелинейными сопротивлениями, описы-
ваемыми нелинейной функцией Ia = f(Va) типа изображенной
на рис. 12.4.
Любое обобщенное сопротивление характеризуется функцио-
нальным соотношением 7?(/, V,t) ~ 0 с единственным ограниче-
нием: в него не входят производные I и V.
Обобщая понятие индуктора, можно предположить, что ин-
дуктивность зависит от тока I, и записать
V = L(/)^.
at
Введение
579
Такое, например, может реализоваться в индукторе с желез-
ным сердечником, используемом для больших токов. Аналогично
можно рассмотреть нелинейный конденсатор
/ = с(г)^,
который получается, если использовать диэлектрик с нелиней-
9
ным ОТКЛИКОМ .
Мы еще будем говорить о нелинейных устройствах. Однако
важно осознать, что последующая теория, в основном, будет ка-
саться получения уравнений для электрических цепей, а не их
решения. Причем эти уравнения будут одинаково применимы как
к линейным элементам, так и к нелинейным.
А сейчас предположим, что наша электрическая цепь состоит
из b ветвей трех типов, о которых говорилось выше. Все вет-
ви как-то соединены друг с другом. Мы хотели бы определить
токи и напряжения в каждой ветви, т. е. найти 26 неизвестных
величин. Для каждой ветви у нас есть только одно уравнение
(либо дифференциальное уравнение, либо функциональное соот-
ношение между током и напряжением). Нам надо иметь еще Ъ
уравнений. Эти уравнения известны как законы Кирхгофа.
Кирхгоф, будучи студентом на семинаре Нейманна, впервые
исследовал проблемы цепей. Его результаты были опубликованы
в период с 1845 по 1847 год. Он доказал существование решения
проблемы цепей для случая, когда есть только пассивные линей-
ные сопротивления. Занимаясь этой задачей, Кирхгоф первым
стал изучать алгебраические свойства формы. Почти пятьдесят
лет спустя Пуанкаре создал абстрактную теорию формы, как ма-
тематическую дисциплину, которую назвал analysis situs. Сейчас
это называется алгебраической топологией. Природа методов ал-
гебраической топологии наиболее очевидна в случае цепей, состо-
ящих из пассивных линейных сопротивлений. Поэтому сначала
2 Имеется в виду (нетривиальная) зависимость диэлектрической проница-
емости материала между пластинами конденсатора от напряженности элек-
тростатического поля. Строго говоря, при достаточно больших значениях на-
пряженности это явление имеется у всякого диэлектрика, так как наступает
его пробой (резкий рост диэлектрической проницаемости, а затем переход в
состояние проводника). — Прим. ред.
580
Глава 12. Теория электрических цепей
мы очень подробно изучим именно эти цепи, прежде чем перей-
дем к общему случаю. Исследуя такие цепи, мы будем следовать
статье Г. Вейля (1923 год), в которой результаты Кирхгофа пред-
ставлены в форме, прямо показывающей связь с алгебраической
топологией.
Законы Кирхгофа, переоткрытые Максвеллом, формулиру-
ются очень просто. Первый закон вытекает из закона сохранения
заряда и состоит в том, что алгебраическая сумма токов, сходя-
щихся в точке разветвления проводников, равна нулю. Второй
закон утверждает, что существует такая функция Ф, называемая
электростатическим потенциалом, что напряжение в каждой вет-
ви определяется разностью значений Ф на ее концах. Максвелл
придумал два метода решения проблемы цепей с сопротивления-
ми, известные сейчас как метод круговых токов и метод узловых
потенциалов. Мы начнем работать с примерами, иллюстриру-
ющими методы Максвелла, и по ходу дела сформулируем язык
алгебраической топологии.
12.1. Линейные цепи с резисторами
Резисторы соединяются проводами с пренебрежимо малым со-
противлением. Соединение, изображенное на рис. 12.5, называ-
ется параллельным. Предположим, что к батарее, создающей по-
стоянное напряжение V, присоединены несколько резисторов,
причем г-й резистор имеет сопротивление Вг. Введем величи-
ну Gi = называемую проводимостью3 г-го резистора. Мы
хотим вычислить полный ток, поставляемый батареей, а после
того, как процесс установится, — ток в каждой ветви. Соеди-
нение верхних входов резисторов обеспечивает на них одинако-
вый потенциал в стационарном состоянии. Аналогично имеются
одинаковые потенциалы на нижних входах резисторов. Следова-
тельно, на каждом резисторе мы имеем одно и то же напряжение,
равное напряжению V, создаваемому батареей. С точки зрения
теории цепей мы можем считать, что все верхние и нижние про-
вода стягиваются в точки. Поэтому рис. 12.5 можно заменить на
3Единица проводимости, обратная единице сопротивления ом, носит на-
звание сименс. — Прим. ред.
12.1. Линейные цепи с резисторами
581
Рис. 12.5 Рис. 12.6
рис. 12.6, где две вершины А и В (вверху и внизу) соединяют
п + 1 ветвей, на одной из которых находится батарея.
Поскольку ко всем резисторам приложено одно и то же напря-
жение V, то из уравнения V = RI или I — GV следует, что то-
ки, протекающие через соответствующие резисторы, равны G]V.
GqY^ ..., GnV. Согласно первому закону Кирхгофа, ток, проте-
кающий через ветвь с батареей, должен быть равен по величине
и противоположен по знаку алгебраической сумме токов в ветвях
с резисторами, т. е.
— (Gi + G2 + • • • + Gn)V.
(На рис. 12.6 стрелками обозначены направления токов, причем
токи, текущие сверху вниз, считаем положительными, а токи,
текущие в обратном направлении, — отрицательными.) Таким
образом, мы решили задачу для этой простейшей цепи, т. е. знаем
напряжение и ток в каждой ветви. Из полученного результата
следует, что полный ток, подаваемый батареей в этом случае,
равен току от батареи, если бы в цепи был только один резистор
с проводимостью G — Gi +G2 Ч----FGn и сопротивлением Н, где
£ _ 1 1 1
R ~ Rj. + R2 +"' + R”
Итак, если несколько резисторов соединены параллельно, то
они эквивалентны одному резистору, обратное сопротивление
582
Глава 12. Теория электрических цепей
которого равно сумме обратных сопротивлений всех отдельных
резисторов. Это хорошо известный результат, который препода-
ется в элементарных курсах.
Рис. 12.7
На рис. 12.7 изображена группа резисторов, соединенных про-
водами последовательно. Пусть в цепи имеется батарея, созда-
ющая напряжение У, в результате чего возникает постоянный
ток I. (По первому закону Кирхгофа тот же самый ток I протека-
ет через каждую ветвь, поскольку в каждом узле алгебраическая
сумма токов должна быть равна нулю.) Пусть сопротивления ре-
зисторов равны 7?i, > Rn соответственно. Поскольку через
г-й резистор протекает ток 7, то напряжение на нем равно R4I.
Из второго закона Кирхгофа следует, что напряжение на батарее
должно быть равно сумме напряжений на всех резисторах, т. е.
V = + R2 + • • • + Rn)I.
Поскольку мы знаем У, то из этого уравнения получаем ток I. Та-
ким образом, задача полностью решена - мы знаем ток и напря-
жение в каждой ветви. Итак, если несколько резисторов соеди-
нены последовательно, то они эквивалентны одному резистору,
сопротивление которого равно сумме сопротивлений отдельных
резисторов. Опять хорошо известный результат.
А теперь давайте рассмотрим более сложную цепь, состоящую
из батареи с напряжением У, соединенной с тремя резисторами,
обладающими сопротивлениями fli, Я2 и Яз, так, как это пока-
зано на рис. 12.8. Точка, из которой выходят два или более про-
водов, ведущих к различным элементам, называется узлом или
вершиной. Точка А является узлом, к которому подходят два про-
вода: от батареи и от резистора. К точке В подходят провода от
12.1. Линейные цепи с резисторами
583
трех резисторов. К точке С подходят два провода от резисторов и
один от батареи. Нижний правый угол схемы не считается узлом,
потому что он соединяется с точкой С проводом с нулевым со-
противлением и, следовательно, совпадает с узлом С. Итак, цепь
имеет три узла А, В и С и четыре ветви: ветвь с батареей, со-
единяющая узлы А и С; резистор, соединяющий узлы АиВ; два
резистора, соединяющие узлы В и С. Длина и форма проводов,
соединяющих все эти точки, не имеют никакого значения. Важ-
ны только ветви и узлы, и то, как они соединены друг с другом.
Таким образом, на рис. 12.8 и рис. 12.9 изображена одна и та же
цепь, в которой есть параллельные и последовательные соедине-
ния.
Рис. 12.9
Рис. 12.8
Сопротивления R% и R% соединены параллельно и, следова-
тельно, с точки зрения всей цепи, эквивалентны одному рези-
стору, обратное сопротивление которого равно + R^1, т. е.
имеющему сопротивление
Д2Д3
R1 + R3
Этот эквивалентный резистор соединен последовательно с сопро-
тивлением . Это значит, что для батареи есть один резистор с
сопротивлением
R — +
R2R3
т?2 + Ri
584
Глава 12. Теория электрических цепей
Ток, вытекающий из батареи, равен
I - V/R.
Такой же ток протекает через резистор 7?i, т. е. Д — V/R. Тогда
падение напряжения на резисторе Д1 равняется У1 = ДД1. Ток
I делится между резисторами и R$ в пропорции, обратной их
сопротивлениям, как мы уже видели из обсуждения резисторов,
соединенных параллельно. Таким образом, токи, протекающие по
резисторам /?2 и /?з, равны
т _ ЛЗ/ т __ R2I
2“ Л2 + Д3 И 3“ Я2 + ЙЗ'
Отсюда мы видим, что падение напряжения, одинаковое для ре-
зисторов /?2 иЯз? равно
Д2Д3 j
R2 + Дз
Итак, мы полностью рассчитали цепь, состоящую из резистора
Д1, соединенного последовательно с резисторами R^ и Д3, кото-
рые соединены параллельно. Такая процедура4 очень удобна для
расчетов простых цепей. Для сложных цепей необходимо разра-
ботать более систематический метод. На примере этой простой
цепи мы продемонстрируем оба метода Максвелла.
Прежде чем перейти к этому, нарисуем цепь еще раз, изобра-
жая ветви (с их ориентацией), узлы и способ их соединения меж-
ду собой, но не показывая природу отдельных ветвей (рис. 12.10).
Итак, у нас есть три узла А, В, С и четыре ветви ск, /3, 7 и 5. Ветвь
а идет от точки А к точке В. Запишем это символически
да = В — А.
Символ д называется граничным оператором. Выписанное со-
отношение интерпретируется следующим образом: ветвь си имеет
две граничные точки В и А; ветвь выходит из точки А, поэтому
4 Вышеописанный анализ параллельных и последовательных соединений
называют также методом эквивалентных сопротивлений. — Прим. ред.
12.1. Линейные цепи с резисторами
585
Рис. 12.10
мы пишем ее со знаком минус; ветвь приходит в точку В, поэто-
му мы пишем ее со знаком плюс. Граничные соотношения для
других ветвей записываются аналогично:
д$ = С-В, д^ = С-В и д8 = А — С.
Под траекторией мы будем подразумевать последовательность
ветвей, проходимых в их собственном или в обратном направ-
лении так, что конечная точка одного отрезка пути становится
началом следующего отрезка. Например, траектория а + /3 идет
из А в В и потом из В в С. Граничное соотношение для этого
пути д(а + /3) — В — А + С — В — С — А. Траектория /3 — 7 идет из
В в С вдоль /3, потом из С в В вдоль ветви 7. Граничное соотно-
шение для этого пути <Э(/3 ~ 7) = С — В — (В — С) = 0. Траектория
представляется как последовательность: узел, ветвь, узел, ветвь,
..., ветвь, узел, в которой каждая ветвь ограничена двумя узла-
ми. Траектория последовательно соединяет первую и последнюю
точки. Траектория называется замкнутой, если первая и послед-
няя точки совпадают. В общем случае мы не предполагаем, что
все ветви вдоль траектории разные; мы можем проходить через
один и тот же узел или вдоль одной и той же ветви несколько
раз. Если все элементы траектории различны (кроме первой и
последней точек для замкнутой траектории), то она называется
простой. Простая замкнутая траектория называется ячейкой^.
5 С точки зрения русского читателя естественнее назвать такую траек-
торию не ячейкой (mesh), а контуром. Термин «ячейка», а чаще «клетка»
(cell), более подходит для математической теории комплексов, обсуждаемой
в последующих главах. -- Прим. ред.
586
Глава 12. Теория электрических цепей
Таким образом, Mi = а 4- /3 + 8 является ячейкой, так же, как
и М2 ~ 7 — /3 (рис. 12.11). В ячейке не важно, что является на-
чальной точкой, т. е. ячейка /3 + 5 + а совпадает с Mi — а + /3 + 6.
Однако направление имеет значение: —7 + (3 ~ —М2 не то же
самое, что М2.
Рис. 12.11
Рассмотрим третью ячейку М3 — ее+7 + 5. В каком-то смысле
эта ячейка не является независимой от других: если мы формаль-
но сложим Mi и М2, то при выполнении коммутативного закона
для сложения получим
Mi + М2 — а + /3 + 5 + 7~/3 — а + 7 + 5 = М3.
В следующем параграфе мы подробнее займемся математиче-
ским обоснованием таких манипуляций. В рамках метода кру-
говых токов Максвелла выберем набор независимых ячеек (точ-
ное определение в следующем параграфе), например, Mi и М2.
Введем неизвестные токи Ji и протекающие по этим ячейкам
(рис. 12.12). Ток Ji течет по резисторам 7?i, R3 и батарее; ток J2
течет вниз через резистор Т?2 и вверх через резистор 7?3. Если мы
знаем значения токов R и J2, то сразу же можем вычислить зна-
чения токов во всех ветвях. Действительно, поскольку резистор
7?1 есть только в ячейке Mi, то ток через Mi равен Л. Такой же
ток протекает по батарее. Поскольку резистор R2 принадлежит
только ячейке М2, то ток J2? проходящий через эту ячейку, ра-
вен току через резистор /?2- Ветвь, содержащая резистор /?3, де-
лает положительный вклад в ячейку Mi и отрицательный вклад
в ячейку М2. Таким образом, ток, протекающий через резистор
7?з, равен J\ — +2-
12.1. Линейные цепи с резисторами
587
Согласно второму закону Кирхгофа, при обходе любой ячей-
ки изменение потенциала должно быть равно нулю. Например,
в случае ячейки Mi мы имеем падение напряжения RiJi вдоль
ветви а, падение напряжения R3(Ji — J2) вдоль ветви /3 и рост
напряжения V вдоль ветви 5, содержащей батарею. Откуда сле-
дует
RxJi + R3(Ji-J2)~V = 0.
Аналогично для ячейки М2 получаем
R2J2 + R3{J^ — Л) = 0.
Итак, у нас есть два уравнения для двух неизвестных Ji и J2-
Очевидно, решив эти уравнения, мы получим предыдущий ре-
зультат.
Таким образом, идея метода круговых токов состоит в выбо-
ре независимого набора ячеек, по которым протекают неизвест-
ные токи. Тогда токи в каждой ветви выражаются через токи
в ячейках. Затем для каждой ячейки применяется второй закон
Кирхгофа, утверждающий, что изменение потенциала при обхо-
де вокруг нее равно нулю. Так получаются уравнения для каж-
дой ячейки, т. е. мы получаем столько уравнений, сколько у нас
имеется неизвестных. В каком-то смысле идея метода сводится
к следующему: неизвестные токи вводятся таким образом, что-
бы автоматически выполнялся первый закон Кирхгофа, а потом
используется второй закон. В следующих параграфах мы дадим
точное определение «независимых» ячеек и докажем, что этот
метод работает, т. е. докажем единственность решения для цепей
с резисторами.
588
Глава 12. Теория электрических цепей
А теперь попробуем объяснить суть второго метода Максвел-
ла — метода узловых потенциалов. Поскольку функция электри-
ческого потенциала определена с точностью до аддитивной посто-
янной, выберем потенциал равным нулю в одном из узлов. (Если
один из узлов соединен с землей, то удобно именно в нем счи-
тать потенциал равным нулю.) Рассмотрим тот же пример, см.
рис. 12.13. Пусть потенциал равен нулю в точке С. Потенциал в
точке Л, создаваемый батареей, равен V. Мы не знаем потенциал
только в точке В. Обозначим этот неизвестный потенциал бук-
вой х. Применим первый закон Кирхгофа к узлам с неизвестным
потенциалом, т. е. в нашем случае к точке В. Токи, протекаю-
щие через узел В, запишем через сопротивления каждой ветви,
входящей в него, и через разность потенциалов соответствующих
узлов. Итак, ток, приходящий в точку В через резистор Ri, равен
(V — x)/R\] ток, приходящий в точку В через резистор R<2. равен
(О — ток, приходящий в точку В через резистор /?з, равен
(О — х)/Вз- Согласно первому закону Кирхгофа, алгебраическая
сумма токов в каждом узле равна нулю, т. е.
(У — x)/Ri — x/R? — x/R% ~ 0.
Мы можем решить это уравнение и получить напряжение и токи
во всех ветвях. В следующем параграфе мы приведем обоснова-
ние этого метода в общем случае.
^0
С
Рис. 12.13
Заметим, что в нашем примере второй метод работает лучше
первого, потому что надо найти только одну неизвестную величи-
ну, а не две. Но преимущества этого метода по сравнению с анали-
зом последовательных и параллельных соединений не очевидны.
12.1. Линейные цепи с резисторами
589
Поэтому, рассчитывая цепь в общем случае, мы советуем сна-
чала проверить, насколько легко ее можно представить в виде
параллельных и последовательных соединений. Если это трудно,
то, вероятно, не имеет смысла заниматься таким разложением.
Тогда посмотрите, сколько получается независимых ячеек и соот-
ветственно сколько неизвестных токов. Аналогично, определите,
сколько неизвестных узловых потенциалов. Выбирайте тот ме-
тод расчета цепи, для которого получается меньше неизвестных.
(Число неизвестных часто могут сократить соображения симмет-
рии.) Несмотря на то, что мы рекомендуем делать выбор между
двумя методами Максвелла только после тщательного рассмотре-
ния, существует и общее правило: если в цепи мало ячеек и много
узлов, то лучше работает первый метод (контурных токов), а ес-
ли в цепи мало узлов и много ячеек, то лучше воспользоваться
вторым методом (узловых потенциалов). Другим важным факто-
ром является тип источников питания. Если ток в цепь подается
источником с заданным напряжением, то это уменьшает число
узлов с неизвестными потенциалами, что говорит в пользу мето-
да узловых потенциалов. Если же заранее известны токи, то это
говорит в пользу метода круговых токов. Чтобы учесть все ука-
занные соображения, обычно хорошо нарисовать две диаграммы
цепи, на которых отметить число неизвестных в одном методе и
число неизвестных в другом. И только после этого сделать ра-
зумный выбор между ними.
До сих пор мы рассматривали цепи, содержащие только ре-
зисторы. Оба метода Максвелла применяются также для изуче-
ния стационарного (осциллирующего) поведения линейных це-
пей с индукторами и конденсаторами. (Линейность означает, что
все индуктивности и емкости предполагаются постоянными.) Ес-
ли все генераторы производят ток с одинаковой частотой а?/2тг,
т. е. все источники напряжения имеют вид Ve1^, а все источни-
ки тока — Ielcv*, то, как хорошо известно (тривиальное следствие
определений)6, для индуктора с индуктивностью L имеем фор-
мулу V = iuL/, а для конденсатора с емкостью С — формулу
6Предлагается рассматривать вывод нижеследующих формул для импе-
дансов индуктора и конденсатора из определений на с. 577 как несложное
упражнение. — Прим, ред.
590
Глава 12. Теория электрических цепей
V — (l/iCcu)I. Теперь можно воспользоваться теми же прави-
лами, что и раньше, но с комплексными сопротивлениями или
импедансами. Однако в этом случае решения существуют не все-
гда из-за явления резонанса. Например, пусть индуктор с L = 1
соединен с конденсатором, имеющим С = 1. Если мы к ним при-
соединим генератор тока с частотой ш = 1, то правило сложения
сопротивлений дает R = i+1/i — 0, т. е. короткое замыкание с бес-
конечным током. В следующем параграфе мы обсудим некоторые
условия, позволяющие избежать такой нереальной ситуации.
12.2. Топология одномерных комплексов
Два термина — ориентированный граф и одномерный комплекс
— являются синонимами. Они оба относятся к математической
структуре, выражающей соединение различных ветвей в электри-
ческую цепь при условии, что мы не интересуемся природой этих
ветвей. Такая структура дает нам возможность изучать законы
Кирхгофа в абстрактной форме и видеть, как свойства отдель-
ных ветвей влияют на решение всей задачи.
Одномерным комплексом мы называем структуру, состоящую
из двух множеств: из множества объектов нулевой размерности,
или узлов, обозначаемого {А, В,... } — So, и множества одномер-
ных объектов, или ветвей, обозначаемых {си,/3,...} — Si. При
этом существует правило, согласно которому каждой ветви со-
ответствуют два различных узла: начальная и конечная точка
ветви. Итак, нам дано отображение из Si в So х Sq.7 В дальней-
шем будем считать, что множества So и Si конечны.
Определим термины траектория, ячейка и т. д., введенные
в предыдущем параграфе. Траектория определяет целое число
для каждой ветви, т. е. сколько раз проходится данная ветвь для
данной траектории с учетом ориентации. Если ветвь проходится
от начальной точки к конечной, то ее вклад равен +1, а если в
обратном направлении, то —1. Таким образом, каждая траекто-
рия определяет вектор р = . )Т с целыми координатами,
имеющими индексы, соответствующие ветвям. Например, ра —
7So х So обозначает декартово произведение множества So на себя, т. е.
So х So является набором упорядоченных пар узлов.
12.2. Топология одномерных комплексов
591
это целое число, которое обозначает, сколько раз ветвь а прохо-
дится в положительном направлении, минус сколько раз она про-
ходится в отрицательном направлении. Можно сказать, что рас-
пределение тока в цепи определяется вектором I = (Za, ... )г,
координаты которого имеют индексы, соответствующие ветвям.
Например 1а ~ это вещественное число, определяющее ток (в ам-
перах), проходящий по ветви а (если наш одномерный комплекс
представляет собой ветви электрической цепи). Это значит, что
для любого комплекса можно ввести векторное пространство, со-
стоящее из векторов К = (Ка, ... )т, компоненты которого
имеют индексы, соответствующие ветвям. (Если это специально
не оговаривается, то полагаем, что все компоненты являются ве-
щественными числами, так что мы имеем вещественное вектор-
ное пространство.) Обозначим это пространство Ci и назовем его
1-цепью. Каждую ветвь k задаем вектором, у которого k-я ком-
понента равна 1, а остальные равны нулю, т. е. а = (1,0,0,... )г,
/3 — (0,1,0,... )т и т. д.8
Аналогично построим вещественное векторное пространство
Со, состоящее из векторов, компоненты которого имеют индек-
сы, соответствующие узлам, и назовем его 0-цепью. Узлу А соот-
ветствует вектор, A-я компонента которого равна 1, а остальные
равны нулю, так что теперь узел становится элементом вектор-
ного пространства Cq. В частности, А — В тоже является эле-
ментом векторного пространства Cq. Заметим, что размерность
пространства Ci равна числу ветвей, а размерность пространства
Cq — ЧИСЛУ УЗЛОВ.
Определим теперь линейное отображение д из Ci в Со, на-
зываемое граничным отображением. Чтобы это сделать, доста-
точно задать его значения для каждой ветви, поскольку вет-
ви образуют базис в пространстве С\. Каждая ветвь имеет на-
чальную и конечную точки, поэтому по определению д(ветви) =
(конечный узел) — (начальный узел). Например если а — ветвь,
идущая из точки А в точку В, то да — В — А.
8 В этом абзаце и в дальнейшем вектор в пространстве Rn обозначается
/ а\
(а, 6,... )Т вместо I & I, чтобы занимать меньше места.
592
Глава 12. Теория электрических цепей
Давайте разберемся, что означает оператор д. Предположим,
что К = (Ка, Кр, Ку,...)т к дК = L, где L = (La,Lp, Ly,... )г.
Вычисляя, например, мы получим сумму определенных ко-
эффициентов К, т. е.
la = {KS1 + • • • + KSl) - (к£1 + • • • + K£k),
где 5i,..., — ветви, входящие в узел А, а ед,..., ~~ ветви,
выходящие из него. Таким образом, для узла, изображенного на
рис. 12.14, мы имеем
La = Кр — К-q — Ка.
Рис. 12.14
Отсюда видно, что первый закон Кирхгофа имеет очень про-
стую формулировку.
Первый закон Кирхгофа: Если I является 1-цепью, задающей
распределение электрического тока, то
51-0.
Напомним, что простая замкнутая траектория называется
ячейкой. На рис. 12.15, например, траектория а + (3 4- 5 явля-
ется ячейкой, которой соответствует вектор pi = (1,1,0,1)т;
траектория — /3 + 7 — тоже ячейка, и ей соответствует вектор
Р2 — (0, — 1,1,0)г. Сумма этих двух векторов Рз = Pi + Р2 —
(1,0,1,1)т соответствует ячейке а + 7 + 5. Очевидно, что каждая
из этих ячеек не имеет границ, т. е. 5pi — 5р2 = 5рз = 0.
Для любого одномерного комплекса подпространство Ci, со-
стоящее из 1-цепей К, удовлетворяющих условию 5К — 0, будем
12.2. Топология одномерных комплексов
593
Рис. 12.15
обозначать Z\. Запишем это символически: Zi — кегЭ С Ci. Эле-
менты подпространства Z\ назовем циклами. Каждая ячейка яв-
ляется циклом, но не каждый цикл является ячейкой. Например,
вектор
/3/2 \
1
1/2
\3/2/
удовлетворяет условию di i — 0, но он не описывает ячейку, по-
тому что его элементы не все равны 1, —1 или 0. Этот вектор
представляет на самом деле набор токов, удовлетворяющий пер-
вому закону Кирхгофа. По существу, легче всего убедиться, что
11 является циклом, написав у каждой ветви соответствующий
ток и проверив, что алгебраическая сумма токов в каждом узле
равна нулю (см. рис. 12.16).
Или, по-другому, запишем вектор в виде Ii = |pi + |р2*
Поскольку pi и Р2 являются элементами пространства Zi, то и
11 принадлежит этому же пространству. В этой простой цепи две
ячейки pi и р2 образуют базис пространства Z±.
Определив подпространство Zi С Ci как ядро граничного
отображения 9, рассмотрим теперь образ д. Пусть Bq — подпро-
странство Со, являющееся образом д. Символически это можно
записать как
Во = ЭС1 С Со*
Подпространство Bq будем называть пространством границ.
594
Глава 12. Теория электрических цепей
Смысл пространства Во может стать яснее, если посмотреть
на рис. 12.17. Граница ветви а, равная А — В — (1, — 1,0)г, при-
надлежит пространству Со и лежит в подпространстве Bq. Ана-
логично граница (3 равна В — С — (0,1, — 1/. Сумма этих двух
векторов А — С = (1,0, — 1/ тоже является элементом простран-
ства Cq и границей траектории а + /3.
Однако, не каждый элемент подпространства Во реализуется
как граница траектории. Например, (2, — 1,— 1)т является эле-
ментом Во, но не соответствует никакой траектории.
Если мы рассмотрим те элементы пространства Со, которые
не лежат в подпространстве Во, то увидим, что они не образуют
подпространства. Рассмотрим цепь, изображенную на рис. 12.17.
Вектора А = (1,0,0/ и В = (0,1,0/ не являются элемента-
ми пространства Во, но их разность А — В — (1,-1,0/ ле-
жит в этом подпространстве. Мы можем образовать факторпро-
странство Но — Со/Bq, элементы которого суть классы эквива-
лентности элементов Со, разность которых лежит в Bq. Векто-
ры А = (1,0,0)т и В — (0,1,0/ в пространстве Со соответ-
ствуют тому же вектору в Но, потому что их разность равна
вектору (1,—1,0/, лежащему в Bq. Обозначим этот класс эк-
вивалентности А или (1,0,0) . Аналогично векторы (2,0,0/ и
(0,1,1/ принадлежат одному и тому же классу эквивалентнос-
ти (2,0,0) , потому что их разность (2, —1, — 1/ лежит в Bq. Для
цепи, изображенной на рис. 12.17, каждый вектор из простран-
ства Со лежит в том же классе эквивалентности, что и вектор
типа (А, 0,0/, где А — вещественное число. Поэтому фактор-
пространство Но = Cq/Bq является одномерным векторным про-
странством, изоморфным пространству вещественных чисел.
Рис. 12.17
Рис. 12.18
12.2. Топология одномерных комплексов
595
На рис. 12.18 изображен пример комплекса, для которого фак-
торпространство Но является двумерным. Векторы (1,0,0,0)т и
(0,0,1,0)г не принадлежат одному классу эквивалентности, по-
тому что из разность (1,0, —1,0)т не является границей никако-
го элемента Ci. В этом случае класс эквивалентности вектора
(1,0,0,0)т и класс эквивалентности вектора (0, 0,1,0)т образу-
ют базис двумерного векторного пространства Но- Заметим, что
если бы к комплексу добавить ветвь 7, соединяющую Л и С, то
(1,0, — 1,0)т стал бы элементом пространства Bq, а факторпро-
странство Но стало бы одномерным.
Смысл Но и Zi
Первая задача, стоящая перед нами — дать геометрическую ин-
терпретацию пространств Но и Zi, что поможет лучше понять
метод круговых токов. Мы хотим доказать следующие два фак-
та (точные формулировки дадим в процессе обсуждения):
(i) dim Но равна числу связных компонент комплекса;
(ii) можно найти базис Zi, состоящий из ячеек.
Начнем с (i). Что такое связные компоненты? Мы говорим,
что траектория соединяет узел А с узлом D, если А является
начальной точкой первого отрезка пути, a D — конечная точка
последнего отрезка. Если Р — 1-цепь с целыми коэффициентами,
соответствующая этой траектории, то очевидно, что дР — D — A,
потому что значение дР можно вычислить, складывая границы
отдельных ветвей. При этом исчезают все промежуточные узлы.
Комплекс называется связным, если все его точки могут быть
соединены друг с другом. В этом случае произвольную 0-цепь9
L= 22 LnN = (La,Lb,..3
N=A,B,C,...
можно записать в виде
L = ^LN{(A + (N - A)} = ^LNA + 2 Ln(N — А),
N^A
9Напомним, что под N здесь в выражении LnN понимается вектор -
набор чисел, занумерованный узлами, у которого N-я компонента равна 1, а
остальные 0. — Прим. ред.
596
Глава 12. Теория электрических цепей
или, что то же самое,
L = (La + LB + ..., 0,0,... )т + £в(-1,1,0,0,... )т
+ Lc(-1,0,1,0,... )т + • • • .
Для связного комплекса N ~ А является границей для всех N
(/ Л) и
L- А = 22 Ln(N-A)
\ N / N^A
является элементом Bq. Таким образом каждая 0-цепь L содер-
жится в классе эквивалентности некоторого кратного А, а каж-
дый элемент факторпространства Но = Cq/Bq является кратным
А - - класса эквивалентности А. С другой стороны, само А не яв-
ляется границей, поэтому А 0. Итак, мы доказали, что для
любого связанного комплекса размерность Но равна 1.
Пусть А — узел произвольного комплекса. Рассмотрим все
ветви, для которых А является граничной точкой, начальной или
конечной. Точку А свяжем со всеми узлами, находящимися на
другом конце ветвей. Теперь добавим все остальные ветви, ис-
ходящие из этих узлов, и все новые точки на концах этих вет-
вей. Продолжаем эту процедуру до тех пор, пока не останется
ни узлов, ни ветвей, которые можно было бы еще присоединить.
В результате получим набор узлов So (И) и набор ветвей Si (А).
Причем граничные точки любой ветви из Si (А) принадлежат на-
бору Sq(A). Таким образом, (So(A), Si (А)) образует подкомплекс
начального комплекса. Если он не совпадает со всем комплек-
сом, то можно выбрать узел В, не лежащий в So(A), и повто-
рить всю процедуру. Действуя таким образом, мы получим се-
мейства непересекающихся множеств: узлов Sq(A), Sq(B) и т. д.
и ветвей Si (A), Si (В) и т. д. При этом связные подкомплексы
So (A), Si(A), So(B), Si(B) и т. д. не соединены друг с другом. Мы
получим соответствующие векторные пространства Со (А) и т.д.
и разложения в прямую сумму10 Со = Со (А) ф Со (В) ф • • • и Ci =
10Прямая сумма Vi ©Vi двух векторных пространств VI и Vi есть декартово
произведение Vi х Vi, превращенное в векторное пространство по естествен-
ным правилам: (111,112) + (1111,1112) = (hi + u>i, 112 + 1112) и г(111,112) = (mi, m2).
12.2. Топология одномерных комплексов
597
Ci(A) ф Ci(B) Ф • • •, причем ЭСЦА) с С0(А), дС^В) с С0(В)
и т. д. Отсюда мы видим, что Bq — Hq(A) ф Hq(B) ф • • *, поэто-
му размерность Hq равняется числу слагаемых и числу связных
компонент.
Теперь рассмотрим (й). Ячейка — это простой замкнутый
путь. Следовательно, каждая ячейка определяет элемент М в
Ci с координатами, равными либо +1, либо —1, либо 0, а это зна-
чит, что ЭМ = 0. Мы говорим, что множество ячеек независимо,
если линейно независимы соответствующие элементы CV (Это
и есть строгая формулировка понятия независимости, которое
мы использовали в предыдущем параграфе.) А сейчас мы хотим
показать, что можно найти такое семейство ячеек, что соответ-
ствующие элементы Mi,..., М2 образуют базис в пространстве
Z\. В процессе доказательства будет показана процедура нахож-
дения такого семейства ячеек. Заметим, что в силу сказанного
при обсуждении пункта (i) достаточно работать со связным ком-
плексом. Если комплекс не связен, то процедура применяется для
каждой связной компоненты отдельно. Поскольку компоненты не
зависят друг от друга, то мы получим результат для всего ком-
плекса.
Связный комплекс, не содержащий ячеек, называется дере-
вом. В дереве имеется по крайней мере один узел, который явля-
ется граничной точкой только для одной ветви. (Мы исключаем
тривиальный случай, когда в комплексе есть только один узел и
нет ветвей.) Чтобы доказать этот факт, начнем с любого узла. Ес-
ли к узлу подходит несколько ветвей, то выберем одну и двинемся
вдоль нее к противоположному концу. Если этот новый узел не
обладает требуемым свойством, то двинемся вдоль другой ветви
(не той, вдоль которой пришли) к следующему узлу. Продолжим
эту процедуру. Поскольку в комплексе нет ячеек, мы никогда не
Если U и W являются подпространствами векторного пространства V таки-
ми, что каждый элемент v G V может быть записан единственным образом
в виде v = и + w, где и е V, v б Ж, то v (u, w) дает изоморфизм V
с прямой суммой U и W. В этом случае мы пишем V — U Ф W, причем
dimV — dim U -FdimlV. [Обычно говорят, что V является внутренней пря-
мой суммой подпространств U и W, в отличие от описанной вначале внешней
суммы независимых векторных пространств, а также используют для внут-
ренней прямой суммы другое обозначение операции, например, V = U -j- W.
- Ред]
598
Глава 12. Теория электрических цепей
вернемся в исходный узел. Так как в комплексе конечное чис-
ло узлов, то в конце концов мы придем в узел, который будет
границей только одной ветви.
Предположим, что у нас есть дерево и мы начали с узла, кото-
рый является концом только одной ветви. Начиная с этого узла,
мы построим все дерево, добавляя по одной ветви (рис. 12.19).
Поскольку нет ячеек, то каждый раз, добавляя ветвь, мы до-
бавляем узел. Таким образом, у дерева число узлов на единицу
больше числа ветвей: если b обозначает число ветвей, ап - число
узлов, то
п ~ b + 1.
Мы уже доказали, что dim Но = 1 для любого связного ком-
плекса. Ввиду Но = Со/Во имеем dim Но = dim Со — dim Во, от-
куда следует, что dim Во — dim Со — dim Но — п — 1 = Ь, Поэтому
Во, являясь образом отображения д, имеет ту же самую размер-
ность, что и пространство Ci, где действует д. Мы знаем, что для
любого линейного отображения Т : V —> W выполняется условие
dim(ImT) + dim(KerT) — dim У. Применяя его к отображению
в, мы получаем, что dim(Ker9) = dimCi — dim Во = b — b — О,
следовательно, Kerd — {0}, т. е. Z\ — {0}. Таким образом, мы
доказали (ii) для случая дерева: если нет ячеек, то нет нетриви-
альных циклов.
Предположим, что у нас есть связный комплекс, построенный,
как только что было показано, начиная с одного произвольного
узла. Каждый раз добавляя ветвь, мы можем добавить или не
добавить новый узел. В конце концов, поскольку комплекс связен,
12.2. Топология одномерных комплексов
599
когда мы включим все ветви, мы добавим и все узлы. Итак, в
общем случае для связного комплекса мы имеем
п < b + 1.
Поскольку для связного комплекса dim7?o = 1, a dim Со —
dim Bq = dim Bq, находим п — dim Bq = 1 и dim Во — п — 1.
Поскольку Во является образом д и Z\ является ядром 3, то
dim Во + dim Zi — dim С\ -- b, или (n — 1) + dim Z± — b. Поэтому
для любого связного комплекса
dim Zi — b + 1 — n.
Чтобы доказать (ii), мы должны найти b+ 1 — п независимых
ячеек, которые образуют базис в пространстве Zi. Для этого сна-
чала разделим множество всех ветвей Si на максимальное дерево
Г, которое содержит все узлы нашего комплекса11, и множество
ветвей Т, которые не принадлежат дереву. Делать будем следую-
щим образом: выберем любую ветвь, являющуюся частью ячей-
ки, пусть она будет элементом подмножества Т. Все оставшиеся
ветви по-прежнему соединяют все узлы. Повторим эту процеду-
ру, пока не останется ни одной ячейки. Тогда ветви, не помещен-
ные в подмножество Г, образуют максимальное дерево Г. Такая
процедура не обеспечивает единственность максимального дере-
ва12. На рис. 12.20 изображены два различных способа, которы-
ми данный комплекс может быть сведен к максимальному дереву
(сплошные линии) путем удаления ветвей (пунктирные линии),
являющихся частями ячеек. Поскольку Т образует дерево, свя-
зывающее п узлов, то оно содержит п — 1 ветвь. Подмножество Т
содержит b~ (п — 1) = Ь +1 — п ветвей. Концы каждой ветви из Т
соединены ветвями из множества Г, поскольку Т соединяет все
11Дерево максимально в том смысле, что при добавлении к нему любой
новой ветви первоначального комплекса подкомплекс перестает быть дере-
вом. Кстати, как легко видеть, дерево будет максимальным как раз в том и
только том случае, если оно соединяет все узлы данного комплекса, что дает
альтернативный способ построения такого дерева: не выбрасывать по ветви
(как описано ниже), а добавлять по узлу. — Прим. ред.
12Максимальное дерево единственно только при отсутствии в комплек-
се ячеек, за исключением ветвей с совпадающими началом и концом. —
Прим. ред.
600
Глава 12. Теория электрических цепей
Рис. 12.20. Два различных максимальных дерева
для одного комплекса
узлы. Более того, поскольку Т не содержит ячеек, то связываю-
щая траектория единственна. Каждая ветвь из Т в комбинации с
этой единственной траекторией в Г, соединяющей ее концы, об-
разует ячейку. Поскольку число ветвей в Т равно b + 1 — п, что
совпадает с размерностью Zi, нам остается только доказать, что
построенные нами ячейки линейно независимы.
Для доказательства линейной независимости i-ю ветвь в Т
обозначим аг. Пусть М$ обозначает ячейку, содержащую ветвь
&i. Рассмотрим линейную комбинацию ячеек ^CiMi. Поскольку
ветвь присутствует только в ячейке Mi с коэффициентом
+1, то коэффициент при в сумме должен быть с^. Поэтому
^сгМг = 0 выполняется только если все ci = 0. Отсюда следует,
что ячейки линейно независимы.
Деревья и проекции
Заметим, что выбор максимального дерева Т определяет проек-
цию рт пространства Ci на подпространство по правилу:
если ai Е Г, то — 0;
если Е Т, то рт(ог) — Mi.
Например, для максимального дерева, состоящего из а и /3 (см.
рис. 12.21), проекционный оператор рт есть рт(о) = 0, рт(/3) = 0,
12.2. Топология одномерных комплексов
601
Рис. 12.21
Рг(т) — а + Z? + 7> Рт{$) = ~а + (Заметим, что каждая ячейка
М* включает в себя ветвь 6 Тс коэффициентом +1, а не — 1.)
Проекция рт может быть записана в виде матрицы
(0 О 1 —1\
0 0 1 о
0 0 1 о
0 0 0 1/
Если мы имеем дело с несвязным комплексом, то (ii) доказы-
вается выбором максимального дерева для каждой связной ком-
поненты и построением проекции рт.
Метод круговых токов
Теперь становятся понятной важность метода круговых токов,
разработанного Максвеллом. Выбирая семейство независимых
ячеек и приписывая каждой ячейке круговой ток Ji, мы образу-
ем элемент -|------+ JmMm пространства Z\. Таким образом
можно получить наиболее общее выражение для токов, удовле-
творяющих первому закону Кирхгофа, т. е. наиболее общий вид
элемента пространства Z\.
Ранее мы уже пользовались уравнением
1 — dim Z\ — п — b (12.1)
для связных комплексов. Применяя его к каждой компоненте
произвольного комплекса и складывая, получаем
dim//о — dimZi — dim Со — dimCi. (12.2)
602
Глава 12. Теория электрических цепей
Поскольку dim Hq = dim Со — dim Bq и dim Bq = dim Ci — dim Zi,
уравнение (12.2) есть прямое следствие определений различных
пространств, связанных с д.
В рамках этого метода Максвелла мы считаем, что круговой
ток определяет токи в каждой ветви. Это можно сформулиро-
вать математически строго: рассмотрим пространство круговых
токов как еще одну копию пространства Zi; назовем его Hi. Это
пространство круговых токов, будучи копией Zi, рассматривает-
ся как абстрактное векторное пространство, не являющееся под-
пространством С\. А теперь рассмотрим процедуру нахождения
токов в ветвях, определяемых круговыми токами, как линейное
отображение ст : Н\ Ci, которое идентифицирует Hi с подпро-
странством Zi пространства Ci. Например, в цепи, изображенной
на рис. 12.21, пространство Н\ двумерно. Отображение а припи-
сывает ячейке Mi токи в ветвях а+/3+7, так что можно написать
<т(М1) — а + /3 + у
и аналогично
<т(М2) = 7-/3.
Итак, если мы используем Mi и М2 в качестве базиса абстракт-
ного пространства Hi (пространства токов), а а, /3, 7, 6 — в ка-
честве базиса пространства Ci, то матрица о, связывающая эти
базисы, имеет вид
/1 0\
1 -1
0 1 *
V 0/
Таким образом, мы видим, что метод круговых токов сводит
задачу обращения линейного отображения из пространства Hi
в его дуальное пространство, обозначаемое Н1.
Возвращаясь к уравнению (12.2), можно теперь написать
(12-3)
dim Hq — dim Hi — dim Cq — dim Ci.
Второй закон Кирхгофа утверждает, что напряжение в каж-
дой ветви может быть получено как разность потенциалов от
12.2. Топология одномерных комплексов
603
потенциальной функции, определенной на узлах. Поскольку име-
ет смысл только разность потенциалов, мы можем положить
потенциал на одном узле каждой связной компоненты равным
нулю. Тогда потенциалы всех остальных узлов определят напря-
жение на ветвях. Например, рассмотрим цепь, изображенную на
рис. 12.22. Если положить потенциалы ФА — Ф° — 0, то напря-
жения ветвей будут равны: Va = Фс, V& = Фв, Vs = Фс — Фв,
Vy = ФЕ. Поскольку число узлов равно dim Со, а число связных
компонент равно dim Но, существует только dim Со—dim Но неза-
висимых способов определения напряжений в ветвях, совмести-
мых со вторым законом Кирхгофа. Это значит, что, грубо говоря,
число условий, налагаемых вторым законом Кирхгофа, равно
dimCi — (dim Со — dim Но) — dim Hi.
E
A D
Рис. 12.22
Поскольку число независимых распределений токов в ветвях,
совместимых с первым законом Кирхгофа, равно dim Hi (чис-
лу линейно независимых ячеек), то первый закон Кирхгофа на-
лагает dimCi — dim Hi условий. Оба закона вместе налагают
dimCi = Ь условий. (Законы независимы, потому что один от-
носится к токам, а второй к напряжениям.) Связь между током
и напряжением в каждой ветви дает еще Ь уравнений. Таким об-
разом мы имеем 2Ь уравнений для 2Ь неизвестных токов и на-
пряжений. Теорема Кирхгофа для линейной цепи с резисторами
утверждает, что эти уравнения могут быть разрешены. Чтобы
доказать эту теорему, мы должны обратиться ко второму закону
Кирхгофа.
604
Глава 12. Теория электрических цепей
12.3. Коцепи и d-оператор
Прежде всего отметим, что напряжение в каком-то смысле двой-
ственно току. Произведение напряжения V7 на ток /7, который
течет по ветви у, дает мощность, выделенную в этой ветви. По-
этому если мы введем вектор напряжений V — (Уа, 03,...), то
он должен лежать в пространстве, дуальном пространству С±.
Тогда введем это дуальное пространство и назовем его простран-
ством 1 -коцепей. Обозначим его С1. Таким образом, С1 — это
пространство линейных функций в Ci. Аналогично введем про-
странство С° линейных функций на Со, и назовем его простран-
ством 0-коцепей. А теперь давайте введем несколько обозначений,
которые на первый взгляд могут показаться странными, но по-
том окажутся весьма продуктивными в смысле обобщения. Пусть
даны вектора К - (Ка, е С и W - (Wa, W& ...) € С1.
Значение линейной функции W на векторе К будем обозначать
/к w Тогда
[ w = WaKa + + • • .
Jk
Аналогично значение 0-коцепи f — ( fA, fB,... )т 6 С° на 0-цепи
с = (са, св, • • )Г будем обозначать fc f. Тогда
У f = fACA + fBCB + • • •
Следующее обозначение связано с отображением д. Граничное
отображение д является линейным отображением из С± в Со. Его
сопряженное будет линейным отображением из С° в С1. Это со-
пряженное отображение будем обозначать d и назовем его когра-
ничным оператором. Итак, если f есть 0-коцепь и К есть 1-цепь,
то значение df на К равно /, вычисленному на ЭК. В терминах
уже введенных обозначений, мы можем написать
[ df= [ f. (12.4)
Jk J эк
12.3. Коцепи и d-оператор
605
(Наши обозначения выбраны таким образом, чтобы это урав-
нение было похоже на фундаментальную теорему дифференци-
ального исчисления. Конечно, в уравнении нет никаких инте-
гралов; это вычисление линейных функций от векторов в век-
торном пространстве, т. е. конечных сумм. Однако, если пред-
ставить, что f ~ дифференцируемая функция на прямой, df —
как f'(x)dx, а К — как интервал А < х < В, то левая часть
уравнения (12.4) может быть интерпретирована как интеграл
(х) dx — f(B) — /(А), а правую часть этого уравне-
ния именно так и надо понимать. А теперь мы просим читателя
на время забыть эту аналогию. Мы вернемся к ней в параграфе
15.2.)
Если си обозначает ветвь и да = В — А, то уравнение (12.4)
принимает вид fa df — f(B) — f(A). Второй закон Кирхгофа
утверждает, что для узлов существует такая функция Ф, т. е.
0-коцепь, что Va = Ф(А) — Ф(В) для любой ветви а такой, что
да = В — А. Тогда этот закон Кирхгофа можно записать в виде
V = -d$.
(Заметим, что если уравнение JK V = — J^K Ф справедливо для
всех ветвей, то оно справедливо для всех 1-цепей, поскольку ветви
образуют базис пространства 1-цепей. Тогда V и —йФ принимают
одно и то же значение на всех 1-цепях, т. е. V = — с£Ф.)
Из двух законов Кирхгофа следует теорема Теллегена. Пред-
положим, что для данной электрической цепи I G С\ обозначает
распределение токов по ветвям, которое удовлетворяет первому
закону Кирхгофа 91 = 0. Предположим также, что для той же
цепи распределение напряжений V удовлетворяет второму зако-
ну Кирхгофа V — —d$. Тогда полная мощность, выделенная во
всех ветвях, равна
Однако, по определению оператора d,
Ji Jdi
606
Глава 12. Теория электрических цепей
поскольку д! = 0. Этот результат показывает, что в электриче-
ской цепи сохраняется энергия — батареи и генераторы подают
ровно столько энергии, сколько рассеивается в резисторах. Важ-
но отметить, что никакие предположения о природе элементов
цепи не делаются.
Для рассмотрения токов оказалось полезным ввести два под-
пространства — ядро и образ граничного отображения д: под-
пространство циклов Zi = Кег д С С± и подпространство границ
Во = Imд С Со- Давайте сделаем то же самое для кограничного
оператора d.
Пусть Z° С С° обозначает ядро оператора d. Тогда Z0 яв-
ляется подпространством потенциальных функций на узлах, об-
ладающих тем свойством, что все напряжения на ветвях равны
нулю. Для связного комплекса все напряжения будут равны ну-
лю тогда и только тогда, когда потенциал во всех узлах одинаков.
В общем случае Z0 есть подпространство потенциалов, постоян-
ных на каждой связной компоненте. Сложение элемента из Z0 с
элементом из С° не имеет физического смысла — при этом изме-
няется только произвольный уровень, от которого отсчитывается
каждый потенциал.
Пусть Ф является элементом пространства Z0, так что d& = 0.
Пусть ЭК обозначает произвольный элемент пространства гра-
ниц Bq. Тогда
[ Ф = / dФ = 0.
J9K JK
Другими словами, элемент из Z0, действуя на элемент из Bq, дает
нуль. И обратно, предположим, что Ф = 0 для всех К. Тогда
d$ = 0 для всех К. Следовательно, </Ф = 0, т. е. это нулевая
функция в пространстве С1 и Ф 6 Z0. Именно поэтому говорят,
что Z0 есть пространство, аннулирующее Bq.
Рассмотрим факторпространство Hq — Cq/Bq, элементы ко-
торого являются классами эквивалентности элементов простран-
ства Со, разность которых лежит в Bq. Пусть с± и С2 являются
элементами пространства Со, разность которых с\ — с% лежит в
Bq. Тогда для любого Ф 6 Z0 имеем
[ Ф _ [ ф = f Ф = 0.
J Cl J С2 J Cl— С2
12.4. Базисы и дуальные базисы
607
Следовательно, /С1 Ф — fC2&, если ci = (mod Во). Итак, эле-
мент Z0 принимает одно и то же значение на любом представите-
ле данного класса эквивалентности. Поэтому Z0 может рассмат-
риваться как пространство линейных функций на Bq.
Связь пространства Z° с Со, Bq и Во является примером
общего принципа, с которым мы встретились: ядро отображе-
ния, сопряженного к линейному преобразованию, является анну-
лирующим подпространством образа этого преобразования. Оно
является также дуальным пространством факторпространства
по образу преобразования. В нашем случае мы имеем преобра-
зование д, действующее на Ci; сопряженное преобразование d,
действующее в С°, и ядро сопряжения Z0, являющееся аннули-
рующим пространством Bq = Im д и дуальным к пространству
Во = Со/Во.
А теперь рассмотрим факторпространство Р° = (7°/Z0. По-
скольку Z0 состоит из функций, постоянных на каждой связной
компоненте, элементы пространства Р° являются классом экви-
валентности функций, отличающихся на каждой связной компо-
ненте только постоянной. Итак, если мы к вектору из простран-
ства (7° добавим физически несущественную постоянную, воз-
можно, разную для каждой связной компоненты, то результиру-
ющий вектор остается тем же элементом пространства Р°. Когда
мы прибавляем произвольную аддитивную константу к каждой
связной компоненте, то именно Р° соответствует пространству
потенциалов. Для данного вектора напряжений V, удовлетворя-
ющего второму закону Кирхгофа, соответствующий потенциал
Ф, удовлетворяющий условию V — — с/Ф, определен с точностью
до элемента пространства Р°, которое определяет Ф.
12.4. Базисы и дуальные базисы
Чтобы выбрать базис для Р°, удобно в каждой связной компо-
ненте заземлить один узел. После этого выбрать dim (7° ~ dim Z°
базисных векторов, для которых потенциал равен единице в од-
ном незаземленном узле и нулю во всех остальных узлах. Напри-
мер, в цепи, изображенной на рис. 12.23, узлы А и D заземлены,
а вектор (ФВ,ФС,ФВ) представляет произвольный элемент Р°.
608
Глава 12. Теория электрических цепей
A D
Рис. 12.23
Отображение d : С° —> С1 индуцирует отображение [d] : Р° —>
С1, которое будем называть ограниченным кограничным отобра-
жением. Матричное представление [d] получается из матричного
представления d, если убрать столбцы, соответствующие зазем-
ленным узлам. Так, для цепи, изображенной на рис. 12.23, мы
убираем первый столбец (А) и четвертый (D), т. е.
/-1 1 0 0 0\
0-1 10 0
1 0-10 0
\ 0 0 0 1 -1/
/ 1
a [d] = J
\ о
о 0\
1 о
-1 о
0 -1/
Поскольку Z0 — аннулирующее пространство для Во, любые
два элемента С°, отличающиеся на элемент Z0, дают одинаковый
результат при действии на элемент Bq. Так факторпространство
Р° = C®/ZQ может быть идентифицировано с дуальным про-
странством Bq. Сопряженным к отображению [с/] : Р° —> С1 яв-
ляется ограниченный граничный оператор [<Э] : Ci —> Bq. Для Bq
удобно пользоваться базисом, дуальным к базису, выбранному
для Р°. Тогда матричное представление [9] есть просто транспо-
нированное матричное представление [d]. По отношению к этому
базису вектор в пространстве Во есть вектор в пространстве Со,
из которого убраны компоненты, соответствующие заземленным
узлам. Например, для цепи, изображенной на рис. 12.23, где за-
землены узлы А и В, мы имеем
да ~ В — А.
12.4. Базисы и дуальные базисы
609
В векторных обозначениях это выглядит так:
/1\
Л 0
0
W
кроме того,
1 °\
0 0
-1 0
0 1
0 -1/
/1 -1 о
но [<Э] — I 0 1 — 1
\о о о
Пусть В1 обозначает подпространство С1, являющееся обра-
зом d. С физической точки зрения В1 — это пространство век-
торов напряжений на ветвях, подчиняющихся второму закону
Кирхгофа. Более того, согласно теореме Теллегена, доказанной
нами ранее, В1 является аннулирующим пространством для Zy.
любое распределение напряжений, удовлетворяющее второму за-
кону Кирхгофа, при применении к любому распределению токов,
подчиняющихся первому закону Кирхгофа, дает нуль. Если мы
образуем факторпространство В1 = С'1/В1, то его можно иден-
тифицировать с дуальным пространством Hi (известным также
как Zi). Доказательство этого утверждения очень простое. Пусть
Vi и V2 — вектора в пространстве С1, а разность между ними
лежит в пространстве В1, так что Vi — V2 = —с/Ф для некото-
рой функции Ф. Тогда для произвольного вектора тока I Е Zi,
удовлетворяющего условию 91 — 0, имеем
откуда следует, что = Ji УД Таким образом, V\ и V2, ко-
торые соответствуют одному и тому же элементу В1, совпадают
как элементы дуального пространства Hi.
Теперь подведем итог соотношениям между пространствами
С°, С1, Z1, В1 и Zi.
610
Глава 12. Теория электрических цепей
о Преобразование d действует в пространстве С° и отобража-
ет С° С1.
о Его сопряжение д действует в пространстве С\, отображая
G -»Со.
о Ядро д есть Zi, его аннулятором является В1 = Imd, а его
дуальное пространство есть Н1 = С1 /В1.
12.5. Методы Максвелла
Мы рассмотрели процедуру построения базиса ячеек в простран-
стве Zi путем выбора максимального дерева. Пусть ст обозначает
отображение, которое определяет каждый вектор в Zi = Н± как
элемент пространства С±. Теперь выберем базис для Л1, кото-
рый будет дуален базису, выбранному для Н±. Пусть з обозначает
проекцию пространства С1 на факторпространство Н1 = С1/В1.
Тогда з и ст — взаимно сопряженные преобразования, и матричное
представление одного будет транспонированным представлением
другого.
Матрицы а и з построить очень просто. Рассмотрим цепь,
изображенную на рис. 12.24, с максимальным деревом, состоя-
щим из а и 7. Тогда базис пространства Zi имеет вид
Mi — а + /3 + 7 —
/А
1
1
w
Мг = -7 + 8 =
Следовательно, матрица преобразования а есть
1
\о
Заметим, что
(7
/ л \
л
Jl — J2
\ J2 /
12.5. Методы Максвелла
611
т. е. а определяет правило, по которому токи в ветвях вычисля-
ются через круговые токи.
Матрица преобразования s — транспонированная матрица а:
/11 1 0\
V0 0 -1 1/
Заметим, что
// va \\
V1
va + v^3 + Г7
-Г7 +
откуда следует, что компоненты вектора <$V равны напряжениям
на ветвях, просуммированным по всем ячейкам, выбранным в
качестве базиса Ну.
Полученные соотношения сводятся к следующему:
Р° с1 Д я1,
Г> & гт
<— Cl*— Til.
Векторные пространства, расположенные одно над другим, ду-
альны друг к другу: С1 и Су; Р° и Bq; Н1 и Ну. Более того, [d] и
[5] сопряжены, так же, как s и а. Оба отображения [d\ и а инъ-
ективны (имеют нулевое ядро), в то время как [9] и s сюръектив-
ны (все векторное пространство является их образом). Наконец,
612
Глава 12. Теория электрических цепей
Im (у — Кет [Э] и Im[d] = Kers. Учитывая это, законы Кирхгофа
можно записать в симметричной форме.
Первый закон Кирхгофа: I = crj, J 6 Hi;
Второй закон Кирхгофа: V = — [й]Ф, Ф е Р°.
Теперь мы можем обсудить теорему Кирхгофа для цепей с
резисторами. Предположим, что наша электрическая цепь состо-
ит из резисторов, вольт-амперная характеристика которых для
каждой ветви а является прямой линией на плоскости (Ia, Vе*).
Сделаем реалистичное (и упрощающее) предположение, что эта
прямая не параллельна ни одной из осей. Это значит, что любой
источник напряжения соединен с некоторым резистором после-
довательно, а любой источник тока соединен с сопротивлением
параллельно, т. е. нет источников, подающих постоянное напря-
жение при любом токе, и нет источников тока, создающих посто-
янный ток независимо от напряжения. Таким образом, мы пред-
полагаем, что любая ветвь а с да — В — А имеет вид, изображен-
ный на рис. 12.25.13
Напряжение на резисторе равно Vе* — ГИа, а ток, протекающий
по нему равен 1а — Ка. Тогда вольт-амперная характеристика
системы определяется формулой
(V“ - W“) = za(Ia - Ко).
Здесь при za ф 0 заданы значения Wa и Ка (причем любое из них
может быть равно нулю14). Если в цепи есть только резисторы,
13Показано широко используемое в элементарных курсах физики разложе-
ние реального источника питания на простой резистор и идеальный источ-
ник напряжения (с нулевым внутренним сопротивлением) или тока (с «бес-
конечно большими» сопротивлением Ra и напряжением Г ° — R(yK(y). ~~~
Прим. ред.
14Авторы, вероятно, имеют в виду, что для создания вышеописанной ли-
нейной вольт-амперной характеристики вида Vе* = za{Ia — 7Са) = zaIa — Wa
достаточно добавить к резистору источник только одного (любого) из этих
двух типов. Принято называть Wa напряжением холостого хода реального
источника, а Ка - его током короткого замыкания. Отметим, что ветвь с
двумя источниками, удовлетворяющими соотношению Wa = zaKa (при со-
блюдении указанной полярности), ведет себя с точки зрения остальной цепи
как простой резистор. — Прим. ред.
12.5. Методы Максвелла
613
Рис. 12.25
то — положительное вещественное число. Мы можем также
рассмотреть стационарное состояние линейной цепи, содержащей
конденсаторы и индукторы. В этом случае za — комплексное чис-
ло, зависящее от частоты. Величины 1а и Va неизвестны. Пусть
Z : С1 С1 — линейное преобразование, матрица которого в
базисе, состоящем из всех ветвей, диагональна, и на диагонали
стоят соответствующие za. Тогда предыдущее уравнение можно
переписать в форме
V —W —Z(I —К).
Комбинируя это соотношение с законами Кирхгофа, получаем
уравнения
V-W - Z(I-K), I — oJ, V = ~[d]$
для неизвестных J 6 Я1 и Ф Е Р°, при заданных W, К и Z. Эти
уравнения мы будем пытаться решать одним из двух методов
Максвелла, описанных ниже.
Метод круговых токов
(i) Запишем I = crj, чтобы удовлетворялся первый закон Кирх-
гофа. После этого применим s к уранению V — W — Z(aJ — К).
Поскольку из второго закона Кирхгофа sV = s(—[Я]Ф) = 0, мы
614
Глава 12. Теория электрических цепей
получаем — sW = sZaJ — sZK или (sZcr)J — s(ZK —W). Правая
часть этого равенства известна, как и линейное преобразование
sZa. Если преобразование sZa обратимо, то
J = (sZa)~1s(ZK — W), (12.5)
из которого могут быть получены все токи и напряжения, так
как I = crJ, V = W + Z(I — К). В этом состоит метод круговых
токов. Он зависит от обратимости преобразования sZa.
Метод узловых потенциалов
(ii) Запишем V — — [<2]Ф, чтобы обеспечить выполнение второ-
го закона Кирхгофа. После этого обратим преобразование Z,
которое задается диагональной матрицей, и получим I — К =
Z-1(—[с£]Ф — W). К обеим частям этого равенства применим [5].
Поскольку, в силу первого закона Кирхгофа, [5]1 = 0, мы полу-
чаем
-[5]К = -[djz-1 [</)Ф - [a]^-1W
или
([d]Z~1 [<фФ = [d](K - Z^W).
Если преобразование [d]Z~1 [d] обратимо, мы получаем
Ф = ([д^ИГЧдКК - Z-'L'W), (12.6)
после чего все токи и напряжения находятся из уравнения
У = -ИФ, I = K + Z-1(V- W). (12.7)
В этом состоит метод узловых потенциалов. Он зависит от обра-
тимости преобразования
12.6. Матричные выражения для операторов
Уравнения (12.5)-(12.7) дают нам суть методов Максвелла. Что-
бы можно было с ними работать, надо получить матричные вы-
ражения для операторов. Поэтому необходимо выбрать соответ-
ствующие базисы и базисы, дуальные к ним. В этом параграфе
мы еще раз посмотрим, как это делается и приведем несколько
12.6. Матричные выражения для операторов
615
примеров. Доказательство того, что эти методы всегда работают
в случае цепей с резисторами, мы дадим в начале параграфа 12.7.
Базис для пространств Bq, Hq, Z® и Р° определяется выбором
заземленного узла в каждой связной компоненте цепи. Например,
на рис. 12.26 можно сделать заземление в узле А для одной связ-
ной компоненты и в узле Е для другой. Тогда базис пространства
Bq состоит из границ траекторий, соединяющих заземленные уз-
лы с другими узлами той же компоненты. В этом случае базисные
векторы имеют вид
Чтобы построить базис факторпространства Hq — Cq/Bq, надо
базис пространства Bq расширить до базиса пространства Со,
введя базисные вектора, у которых на месте какого-либо одно-
го заземленного узла стоит 1, а все остальные элементы равны
нулю. После этого для каждого из этих векторов берется класс
эквивалентности. В нашем примере это дает
Рис. 12.26
616
Глава 12. Теория электрических цепей
В пространстве Z0, являющимся ядром d и дуальным к Ко? ба-
зисными элементами будут потенциалы с постоянным значением
1 поочередно на каждой связной компоненте. В нашем примере
мы имеем
которые, очевидно, дуальны hi и 112, приведенным выше. Чтобы
выбрать базис факторпространства F0 — С° /Z0, мы просто по-
ложим последовательно потенциалы на каждом незаземленном
узле равными 1 и для каждого возьмем класс эквивалентности.
В нашем примере мы получим
Очевидно, что эти классы эквивалентности дуальны постро-
енному выше базису {bi,b2,Ьз,b4} в пространстве Bq. Поэтому
матричное представление [d] : Р° —> С° является транспониро-
ванным к матричному представлению [5] : Cq —» Bq. Столбцы [d]
и строки [5] отвечают незаземленным узлам, которые соответ-
ствуют базисным векторам.
Теперь рассмотрим пространства Zi, В1 и К1, которые свя-
заны с ядром д и образом d. Для полноты картины рассмотрим
также факторпространство Gi = Ci/Zi, дуальное к простран-
ству В1. Во всех этих пространствах выбор базиса определяется
выбором максимального дерева. На рис. 12.27 изображено такое
дерево с ветвями а, /3 и е.
Как мы уже видели, базисные элементы пространства Zi —
это ячейки, связанные с ветвями, не принадлежащими макси-
12.6. Матричные выражения для операторов
617
Рис. 12.27
мальному дереву. В нашем примере это будут
ТП1 =
и m2 —
о
о
1
V/
связанные соответственно с ветвями у и 8. Для факторпростран-
ства Gi = Ci/Zi, которое представляет нарушение первого зако-
на Кирхгофа, мы можем образовать классы эквивалентности век-
торов, имеющих 1 на месте соответствующей ветви максимально-
го дерева и нули в остальных местах. В нашем случае мы имеем
Поскольку эти вектора имеют 0 на месте каждой ветви, не при-
надлежащей дереву, то ни одна линейная комбинация из них не
может быть ячейкой. Это значит, что они являются независимы-
ми элементами пространства Gi.
Для подпространства В1, образованного кограницами — на-
пряжениями ветвей, подчиняющимися второму закону Кирхго-
фа, мы можем построить базис, приписывая напряжение, равное
1 одной из ветвей максимального дерева, и нулю всем осталь-
ным его ветвям. Такая процедура приписывает потенциал каж-
дому узлу (с точностью до константы), и эти потенциалы можно
618
Глава 12. Теория электрических цепей
использовать для определения напряжений на ветвях, не при-
надлежащих дереву. Или, другими словами, поскольку каждая
ветвь, не принадлежащая максимальному дереву, связана с един-
ственной ячейкой, содержащей эту ветвь и другие ветви, которые
принадлежат дереву, то каждую такую ячейку можно использо-
вать для определения напряжений на таких ветвях. Например на
рис. 12.27 эта процедура приводит к базисным векторам, связан-
ным соответственно с ветвями о, /3 и е:
Ь1 = (1 0 1-1 0),
Ь2 = (О 1 - 1 0 0),
Ь3 = (0 0 0 -1 1).
Эти вектора, аннулирующие ячейки mi и m2, дуальны базису gi,
g2, ёз пространства G}. Они не совпадают со столбцами [d], но
они задают то же самое подпространство пространства С1.
Итак, базисные вектора пространства В1 могут ассоцииро-
ваться с ветвями, принадлежащими максимальному дереву. Точ-
но так же базисные вектора Н1 = С1 /В1 ассоциируются с вет-
вями, не принадлежащими дереву. Они являются классами эк-
вивалентности векторов напряжений, которые имеют 1 на месте
одной ветви, не принадлежащей дереву, и нули на всех осталь-
ных местах. Таким образом, в нашем примере базисные вектора
пространства 7?i имеют вид
Они соответствуют единичным нарушениям второго закона
Кирхгофа в ячейках 1 и 2 соответственно. Очевидно, что h1 и h2
дуальны ячейкам mi и m2. Вследствие этого матрица преобразо-
вания s : С1 Н1 является транспонированным по отношению
к матрице а : Z\ —> С\.
Иногда удобнее пользоваться другим методом выбора базис-
ных векторов в пространстве В1 (напряжений, подчиняющихся
12.6. Матричные выражения для операторов
619
второму закону Кирхгофа). В этом случае потенциал выбирается
равным 1 последовательно в каждом незаземленном узле и нулю
во всех остальных узлах. На получившиеся потенциалы действу-
ем оператором d. (Или, что то же самое, можно взять потенциалы
равными —1 последовательно в каждом незаземленном узле и за-
писать напряжения на ветвях). В нашем примере заземлен узел
А. Базисные вектора, связанные с узлами В, С и D соответствен-
но, имеют вид:
а1 = (0 -1 1 0 0),
а2 = (1 10-1 0),
а3 = (0 0 0 1 - 1).
В качестве дуального базиса в пространстве Gi — C\)Z\ мы
должны выбрать распределения токов, для которых единичный
ток протекает из заземленного узла вдоль дерева поочередно к
каждому незаземленному узлу. В нашем примере мы получаем
базисные вектора
соответствующие единичным нарушениям первого закона Кирх-
гофа в незаземленных узлах В, С и D соответственно.
Давайте применим оба метода Максвелла к цепи, изображен-
ной на рис. 12.28. Ее топология уже знакома нам по рис. 12.24.
Сначала мы произвольно выбираем заземленный узел, пусть это
будет узел А. Тогда Фл = 0. Напряжения в ветвях выражаются
через потенциалы в других узлах следующим образом:
уа — -Фв, — Фв - Фс, V7 = Фс, V5 — Фс.
Поэтому для того, чтобы получить V = — [й]Ф, мы находим
и =
-1
о
\ 0
0\
+1
-1
-V
620
Глава 12. Теория электрических цепей
Рис. 12.28
Чтобы это проверить, построим матрицу д. Поскольку
да = В - А, дд = С- В, ду = А - С, дб = А- С,
мы имеем:
/-1 0 +1 +1\
д= I +1 -1 0 0 .
\ 0 +1 -1 -1/
Чтобы получить [3], уберем из матрицы д строку, соответству-
ющую заземленному узлу А. Итак, убирая первую строку, мы
получаем
(+1 -1 0 0\
"1-1 0 +1 -1 -1/
Как и ожидалось, матрица [5] является транспонированной мат-
рицей [d].
Если выбрать ячейки Mi и М2, как показано на рис. 12.28,
то токи в ветвях выражаются через токи в ячейках Ji и J2 сле-
дующим образом:
— Ji, 1(3 — <Л, Л — Л — Л, 1$ = J2-
Поскольку I — crj, мы имеем
/1 0\
1 0
°- 1-1 •
\0 1/
12.6. Матричные выражения для операторов
621
Для проверки построим матрицу з, выражая падение напряже-
ния £ в каждой ячейке через напряжения на ветвях.
В ячейке 1: £х = Va + V0 + V7.
В ячейке 2: £2 = -V7 + Vs.
Поскольку £ = «V, мы имеем:
= Л 1 1 0\
5 До 0 -1 1J '
Как и ожидалось, матрица з является транстпонированной к мат-
рице а.
Далее мы должны записать вектора W и К, которые пред-
ставляют источники напряжения и тока в четырех ветвях. До-
говариваемся считать напряжение батареи W положительным,
если направление убывания потенциала (от положительного по-
люса к отрицательному, противоположное направлению ЭДС)
совпадает с направлением прохода ветви, указанным стрелкой,
в противном случае — отрицательным. Для цепи, изображенной
на рис. 12.28, мы имеем:
wa = -8, W'3 = О, IV7 = +11, Ws - 0.
Аналогично, источник тока дает положительный вклад, если его
направление совпадает с направлением прохода ветви по стрелке,
и отрицательным, если наоборот. Следовательно,
Ка - +3, К$ -0, Ку = 0, Ks = +1.
Теперь мы можем ввести вектора для описания источников в
цепи:
/-8\ /3\
W п и К 0 .
\ 0/ \1)
Наконец, запишем матрицу Z, описывающую резисторы. По-
скольку
R& = 2, Rp - 1, Ry = 3, Rd = 4,
622
Глава 12. Теория электрических цепей
мы имеем:
/2 0 0 0\
„ 0 1 О О
Z 0 0 3 0’
\0 0 0 4/
Чтобы применить метод круговых токов, запишем уравнение
J = (sZa)-1s(ZK - W).
Перемножение матриц дает
„ _ /1 1
sZ° ~ (о о
1
-1
/2
о
о
\0
о
1
о
о
о
о
3
о
0\
о
о
1
1
1
о
°\
о
-1
6 -3\
-3 7/ ’
следовательно,
(sZar‘ = 5з (з
ОО \ О
0
1
3
б
Кроме того, получаем
ZK-W =
/2
О
о
\0
о
1
о
о
о
о
3
о
0\
о
о
4/
/з\
о
о
V/
о
11
О
-11
откуда
1
1
О -1
о
1
о
-11
\ 4/
3\
15/
И, наконец,
Т = — f7 3W = (2\
J 33 \3 6/ \15/ 33 \99/ \3/’
откуда получаем J\ = 2 и = 3. Итак,
I = <7 J =
/1
1
1
\0
0\
V
( 2\
2
-1
V 3/
12.6. Матричные выражения для операторов
623
Если внимательно проследить за процедурой вычисления, то
можно убедиться, что для любой цепи справедливы следующие
утверждения.
1. В матрице sZa каждый диагональный элемент равен сумме
сопротивлений ветвей, образующих ячейку. В нашем случае
ячейка Mi, состоящая из ветвей а, и 7, имеет полное
сопротивление, равное 6 омам — левый верхний элемент
матрицы.
2. В матрице sZa каждый недиагональный элемент равен со-
противлению в ветви, общей для двух ячеек (с точностью
до знака ±). В рассматриваемой цепи ячейки 1 и 2 имеют
общее сопротивление, равное 3 омам, а знак — возникает
из-за того, что ветвь 7 в ячейках Mi и М2 проходится в
разных направлениях.
3. Элементы матрицы (sZa)J равны падению напряжения, ко-
торое возникло бы при обходе каждой ячейки при отсут-
ствии источников15. Например, если Ji = 2 и J3 — 3, то при
обходе ячейки 1 возникает падение напряжения в 3 вольта.
4. Элементы матрицы ZK — W равны скачкам напряжения16
в ветвях, если бы все токи в ячейках были равны нулю. На-
пример, если Ji = 0, то в ветви о будет ток в 3 ампера, про-
текающий через резистор с сопротивлением в 2 ома. Тогда
скачок напряжения в этой ветви будет равен (2 • 3 + 8) = 14
вольтам.
5. Элементы матрицы s(ZK — W) являются скачками напря-
жения при обходе различных ячеек, если бы все токи в вет-
вях были равны нулю. Например, если J\ = J2 = 0, то при
обходе ячейки 1 полный скачок напряжения будет равен 3
вольтам.
15и тех же токах. Это падение напряжения в замкнутом контуре (корот-
кое замыкание) можно интерпретировать как (катастрофический) результат
мгновенного отключения ЭДС источника. — Прим. ред.
16Этим (не слишком корректно звучащим) термином обозначается возрас-
тание потенциала (voltage rise) вдоль участка цепи, в отличие от убывания
(voltage drop), называемого падением напряжения. — Прим. ред.
624
Глава 12. Теория электрических цепей
6. Поэтому уравнение (sZa)J = s(ZK — W) означает, что для
каждой ячейки суммарное падение напряжения в ячейках,
создаваемое токами, протекающими через резисторы, рав-
но сумме скачков напряжения, которые получились бы при
условии, что все токи в ячейках равны нулю. Тогда полное
падение напряжения при обходе каждой ячейки при име-
ющихся токах в ячейках и источниках равно нулю, что и
требуется вторым законом Кирхгофа.
Чтобы воспользоваться методом узловых потенциалов, рас-
смотрим уравнение
Ф = ([djZ-1 [d])-1 [d](K - Z^W).
Перемножение матриц дает
/1/2 О О
/1-1 0 0\ 0 1 0
~ \0 1 -1 -1) 0 0 1/3
\ о о о
= /3/2 -1\
\-1 19/12/'
0\ / 1
0 -1
1/4/ \ 0
°\
1
-1
-1/
Откуда
(Иг-'Н)-1 = Ц /9/19 Л .
ОО \ 1 О/
Кроме того, получаем
/ 7 \
0
-11/3
\ 1 /
следовательно,
[5](K-z-1w) = L
-1 о 0\
1 -1 -1/
/ 7 \
0
-11/3
\ 1 /
' 7
8/3/
12.6. Матричные выражения для операторов
625
Тогда
24 /19/12 1\ / 7 X 24 /165/12Х = /10\
33 V 1 3/2/ \8/3j “ 33 \ И ) V8/ ’
откуда получаем неизвестные потенциалы на узлах Фв = 10,
Фс = 8.
Здесь также, внимательно проследив процедуру вычисления,
можно увидеть, что для любой цепи справедливы следующие
утверждения.
1. Диагональные элементы матрицы [9]Z"1[d] равны сумме
обратных сопротивлений (проводимостей) всех резисторов,
подходящих к узлу. В нашем примере к узлу В подсоеди-
нены два резистора с сопротивлениями 1 и 2 ома. Поэтому
левый верхний элемент равен 1 + 1/2 = 3/2.
2. Недиагональные элементы матрицы [5]Z-1[<i] равны (с точ-
ностью до знака ±)17 обратному сопротивлению в ветви,
соединяющей два соответствующих узла. Поскольку у нас
узлы В и С соединены резистором с сопротивлением в 1 ом,
то недиагональный элемент матрицы равен —1.
3. Компоненты вектора [Э]^-1[б/]Ф представляют суммарный
ток, который вытекал бы из каждого узла, если убрать из
цепи источники. Так, в вышеуказанном примере, если нет
источников, Ф"4 = 0 и Фв — 8, то ток в 5 ампер будет течь
от узла В к узлу А через резистор с сопротивлением в 2
ома, и ток в 2 ампера будет течь от узла В к узлу С через
резистор с сопротивлением 1 ом, создавая полный ток в 7
ампер. Можно проверить, что первая компонента вектора
[с£]Ф равна 7.
4. Компонентами вектора К — Z“1W являются токи в ветвях,
которые возникли бы при условии, что все узловые потен-
циалы обратились в нуль. В нашем случае, если ФЛ и Фв
17Выбор знака, как и в методе круговых токов (пункт 2 на с. 623), зависит
от направления прохода ветви. Точную формулировку оставим читателю в
качестве упражнения. - Прим. ред.
626
Глава 12. Теория электрических цепей
приравнять нулю, то в ветви а через резистор с сопротив-
лением в 2 ома протекал бы ток в 4 ампера, а полный ток
был бы равен 4 + 3 = 7 амперам. Первая компонента тока
К — Z“XW действительно равна 7.
5. Компонентами вектора [Э](К—Z-1W) являются токи, кото-
рые втекали бы в каждый узел при условии, что все узловые
потенциалы равны нулю. Итак, если Ф"4 = Фв — Фс = О,
то в узел В будет втекать ток в 7 ампер по ветви а. Не бу-
дет никакого тока в ветви /3, текущего к узлу С. Поэтому
суммарный ток в узле В будет равен 7 амперам.
6. Уравнение [5]^“г[с/]Ф = [5](К — Z-1W) показывает, что
сумма токов, вытекающих из каждого узла по ветвям че-
рез резисторы в силу имеющейся разности потенциалов на
узлах, равна сумме токов, втекающих в этот узел, если бы
все узловые потенциалы были равны нулю. Поэтому полный
ток, втекающий в каждый узел в силу имеющихся разности
потенциалов и источников, равен нулю, что соответствует
первому закону Кирхгофа.
Если теперь сравнить шесть утверждений, касающихся мето-
да узловых потенциалов, с шестью утверждениями относительно
метода круговых токов, то можно увидеть их двойственность.
Замените термин узел на ячейку, ток на напряжение и сопро-
тивление на проводимость - и факты замечательно совпадут.
В рассмотренном примере есть одна особенность, которая не
выполняется в общем случае: размер матрицы, которую надо об-
ращать, был одинаковым для двух методов, поскольку там было
две независимых ячейки и два незаземленных узла. Однако число
независимых ячеек не всегда равно числу незаземленных узлов,
поэтому матрицы могут быть разного размера.
12.7. Теорема Кирхгофа
Возникает вопрос: будет ли метод круговых токов работать для
любой цепи? Эта проблема сводится к обратимости отображения
sZa. Поскольку sZcr является отображением из пространства Н\
12.7. Теорема Кирхгофа
627
(пространство круговых токов) на пространство Н1, дуальное к
нему (пространство напряжений при обходе ячеек), то оба эти
пространства имеют одинаковую размерность. Поэтому нам на-
до только проверить, что sZa — инъективное отображение, т. е.
что его ядро равно нулю. Рассмотрим произвольный ненулевой
элемент J в пространстве Н^. Его образ (sZcr)J является эле-
ментом дуального пространства Н1. Нам надо показать, что этот
элемент не равен нулю. Сделаем это, просто вычислив его значе-
ние на элементе J. Поскольку s является сопряжением <7, то мы
имеем [(sZa)J](J) = [ZcrJ](crJ). Однако crj есть просто вектор
тока I в ветви, a ZaJ = ZI. Следовательно,
[(sZa)J]J = (ZI)I = f ZI = 52
Ji 7
где сумма берется по всем ветвям. Если у матрицы Z все диа-
гональные элементы положительны, то ZI > О, кроме случая,
когда 1 — 0. Поскольку ст инъективно, то условие I — crJ = 0
означает, что J — 0, т. е. все токи в ветвях равны нулю, только
если равны нулю все токи в ячейках. Таким образом, для нену-
левого J мы имеем [(sZa) J] J > 0. Отсюда можно заключить, что
(sZa)J не может быть нулевым элементом пространства Н1, ес-
ли J 0. Поэтому sZa, имея нулевое ядро, является обратимым
отображением. Следовательно, мы доказали, что метод круговых
токов работает для любых цепей, содержащих только резисторы.
Аналогичные аргументы показывают, что в этом случае [5]Z-1[d]
также обратимо. А это значит, что работает и метод узловых по-
тенциалов.
В более общем случае, когда в цепи имеются резисторы, кон-
денсаторы и индукторы, изложенная процедура также дает инте-
ресную информацию. Если в цепи b ветвей, то Z задается диаго-
нальной матрицей b х Ь, с матричными элементами (импедансами
ветвей), зависящими от частоты о>/2тг. Если каждая ветвь содер-
жит только один конденсатор или один индуктор, то импеданс
будет равен либо icuL, либо — i/шС. Если в цепи есть т независи-
мых ячеек, то sZcr будет матрицей т х т с матричными элемен-
тами, зависящими от Определитель этой матрицы приводится
628
Глава 12. Теория электрических цепей
к полиному степени не выше тп. Оператор sZa не будет об-
ратимым при условии — 0. Это значит, что существует не
более т значений о;2, для которых sZa необратим. Такие частоты
си/2тт называются резонансными частотами системы. Для каждой
из этих резонансных частот уравнение (sZcr)J — 0 имеет ненуле-
вое решение, несмотря на нулевую правую часть, указывающую
на отсутствие источников, т. е. токи могут течь по системе даже
без источников напряжения или тока. Решения этого уравнения
определяют нормальные моды системы. Аналогичные соображе-
ния, примененные к матрице размера (Ъ — т) х (Ь — т),
показывают, что может быть не более Ь — т резонансных частот.
Поэтому для нахождения резонансных частот цепи мы строим
матрицу оператора sZa или \d\Z~1 [d] (у которой меньше размер)
и вычисляем частоты (о;2), для которых определитель матрицы
равен нулю.
В качестве примера рассмотрим цепь, изображенную на
рис. 12.29. Эта цепь имеет ту же топологию, что и цепь на
рис. 12.28. Поэтому
Л о\
/1 1 1 о\ 10
5 ~ \р О -1 1/ ’ ° ~ 1 -1
\о 1/
В этом случае матрица Z содержит импедансы различных ком-
понент:
za — 2\wL, гр ~ — icu£, z$ — —i/2wC.
12.7. Теорема Кирхгофа
629
Тогда
/2о>£ 0 0 ° \
0 -(wC)-1 о о
Z-1 0 О шЬ о
\ 0 0 0 —(2сиС)-1у
Перемножая матрицы, получаем
_ . /3wL - (wC)-1 -wL \
sZa ~ 1 \ -шЬ шЬ - (2cuC)-1J
Определитель этой матрицы равен
Det(sZcr) = -(3wL - - (2wC)-1) + ш2Ь2,
ИЛИ
Det(sZa) = -2u2L2 + 5L/2C - 1/2ш2С2.
Полагая Det(sZcr) = 0, получаем уравнение, квадратичное по ш2:
Р(а?) = 2L2^4 - 5Lu2/2C + (2С'2)-1 = 0.
Оно легко разлагается на множители:
(Ьш2 - С^(2Ьш2 - (2С)-1) = 0.
Таким образом, резонансные частоты этой цепи равны
w2 = 1/LC и ш2 = 1/4LC.
Чтобы найти соответствующие нормальные моды, для каждой
резонансной частоты решим уравнение (sZcr)J — 0. Например,
для ш — у/1/LC
sZa = i
2vT7c -vT7c\
-yjLjC \JlJC)'
Решением уравнения (sZcr)J = 0 является • Это значит, что
ток в ячейке 2 в два раза больше тока в ячейке 1. Аналогично
для as — y/l/4LC имеем
sZa i
-IvTTC -^^L/C\
-Wl/c -WlJc)'
630
Глава 12. Теория электрических цепей
так что уравнение (sZa)J = 0 имеет решение . Это значит,
что в нормальной моде с частотой и>/2тг токи по ячейкам и J%
имеют одинаковую амплитуду, но противоположные фазы.
12.8. Цепи переменного тока в стационарном
режиме и фильтры
Понятие импеданса, использовавшееся в предыдущем параграфе
для определения резонансных частот цепей, содержащих индук-
торы и конденсаторы, может быть использовано для анализа це-
пей переменного тока в установившемся режиме. Предположим,
что все источники тока и напряжения имеют одинаковую частоту
Со>/2тг, так что токи в ветвях образуют вектор
а напряжения на ветвях образуют вектор
Здесь компоненты /а, 7^,... и . являются комплексны-
ми величинами; вещественная часть каждой компоненты пред-
ставляет истинный ток или напряжение. (Вспомним, что —
coscetf 4- isinutf.) Источники напряжения и тока представляются
соответственно векторами
Wa\
W = I еы и К =
Для каждой ветви по-прежнему выполняется соотношение
Va - Wa = za(Ia - Ка),
12.8. Цепи в стационарном режиме и фильтры
631
где za является диагональной матрицей, элементы которой —
комплексные импедансы в различных ветвях. Формализм, раз-
работанный нами для цепей постоянного тока, переносится прак-
тически без изменения на цепи переменного тока в стационарном
режиме. Необходимо сделать только несколько изменений.
1. Физические напряжения и токи в ветвях определяются
вещественной частью соответствующей компоненты ком-
плексных векторов или
2. Амплитудные значения напряжений и токов в ветвях опре-
деляются модулем комплексной величины, которая пред-
ставляет напряжение или ток, т. е. если в ветви а ток пред-
ставляется /а, то его амплитудное значение равно
|Л>| = V(Re/Q)2 + (Im /а)2.
3. Средняя мощность, выделенная в ветви а, определяется
средним значением произведения вещественных частей
комплексных величин Va и т. е. средняя мощность Р
выражается формулой
Ра — Среднее от [Re(Vaelu?t) Re(/aelu?t)]
= 1 Среднее от [(Vaeiu,t + V“*+ /*6"^)]
= 1 Среднее от (V“lae2icjt + VaPa + Va*Ia + у«*/*е-2^
где знак * обозначает комплексное сопряжение.
Поскольку члены, содержащие е21и?г и при усреднении
по времени обращаются в нуль, мы имеем
Ра = | (Уа*1а + VaI*a) = 1 Re(VaI*a).
В случае, когда ветвь а состоит только из резистора, т. е. Va —
RIa, это выражение упрощается, и мы получаем
Ра = ^Ш2а.
632
Глава 12. Теория электрических цепей
Если ветвь состоит только из конденсатора или индуктора, то ее
импеданс za чисто мнимый, поэтому средняя выделенная мощ-
ность в этой ветви равна нулю.
В качестве простого примера цепи в стационарном режиме
рассмотрим так называемый низкочастотный фильтр, изобра-
женный на рис. 12.30. Будем считать, что в цепи есть две вет-
ви. Базисом для Z\ является ячейка а + /3, так что ст = ,
(7? 0 \
0 i/шС ) ’ Т° сРазУ же полУчаем
sZa = (1
= R - i/шС.
Рис. 12.30
Напряжение на ветви а равно Wa = —£е1Ш* (полярность ука-
зана на рисунке). Тогда ток в ячейке равен
Амплитудное значение этого тока равно модулю этого выраже-
ния, т. е.
£
R - i/cdC
£
y/R2 + (с^С2)-1 ’
И =
а амплитудное значение напряжения в ветви /3 равно
И = \zpl0\ =
-\SjwC _ £
R - i/шС ~ y/(uRC)2 + l
12.8. Цепи в стационарном режиме и фильтры
633
Это значение уменьшается от 8 для си — 0 до нуля при си —> оо.
Отсюда и происходит название низкочастотный фильтр18.
Эту цепь можно слегка усложнить, присоединив последова-
тельно к конденсатору индуктор. В этом случае импеданс ветви
(3 равняется zl = i(wL — а ток в ячейке равен19
J = £/(R + i(wL- (wC)-1)).
Легко видеть, что этот ток достигает максимальной амплитуды
при L = 1/си2(7 или cu = y/\/LC. Эта частота называется резо-
нансной частотой цепи, изображенной на рис. 12.31.
На рис. 12.32 изображен более сложный пример цепи. Теперь
базис Z состоит из двух ячеек Mi ~ а+/3 и М2 = —/З+7, поэтому
Поскольку
О
icoL
О
0\
М *
а =
18 Описанное поведение снимаемого с ветви /3 напряжения - убывание с
ростом частоты — дает возможность отделить низкую частоту сигнала (на-
пример, звука) от модулированной им высокой частоты электромагнитных
волн. Данный принцип лежит в основе работы всей радиосвязи. — Прим. ред.
19 Здесь и далее для упрощения записи опускается фазовый множитель
е1иЛ. — Прим. ред.
634
Глава 12. Теория электрических цепей
мы имеем
Рис. 12.32
R wL 0 \ _*Л
О — iwL ~i/wCj I Q 11
(R + 'wL —iwL
—iwL icoL — i/wC,
Нетрудно получить обратную матрицу
1
/ у \-1 _ 1 fiivL — i/wC шЬ \
” R(icvL - i/cvC) + LC-1 \ iuL R + icjLJ ’
Чтобы определить токи в ячейках, запишем вектор
W —
и вычислим
J = (^-Ч-sW) = R^L_^ + LC^ (^^С)
Интересным является решение для резонансной частоты о>/2тг,
8 ( ° \
L/C \ioJ7’
где ojL — 1/ыС и J =
В этом случае в ячейке М
1
нет тока, и в резисторе не выделяется мощность.
Наша техника позволяет анализировать цепи переменного то-
ка произвольной сложности так же легко, как и цепи постоянного
тока той же топологии. В качестве примера рассмотрим двухсту-
пенчатый фильтр (рис. 12.33).
12.8. Цепи в стационарном режиме и фильтры
635
Рис. 12.33
Поскольку эта цепь имеет три ячейки и только два незазем-
ленных узла, то проще воспользоваться методом узловых потен-
циалов. Пусть узел А заземлен. Тогда
В этом случае
№"’И = (J
(—ifijjL 0\
о о\ 'шС 0
_i _i) VuL -i/“L
' 0 iwC
\ О -X/R)
\шС — 2i/wL i/wL
- (i/wL) + 1/Я
Чтобы обратить эту матрицу, воспользуемся формулой
и определим потенциалы узлов В и С. Ограничимся решением
задачи для резонансной частоты, когда шС = l/u)L. В этом слу-
чае обращаемая матрица имеет вид
= (д“ос
iwC\
1/Я/ ’
636
Глава 12. Теория электрических цепей
Заметим, что для этой частоты
[d]Z-TW = f
i£wC
О
Тогда
(фв\ = 1 ( 1/R -iwC\ ('wC\
\ФС) (~iuC/R)-u2C2\-wC -iGjCJ \Q )
ИЛИ
(фв\ = £ (iu>C/R\
\фс) ~ (—шС/R) - ш2С2 \ ш2С2 ) ’
Резюме
А. 1-комплексы
Для заданной схемы, представляющей 1-комплекс, Вы должны
знать, как построить максимальное дерево и связанные с ним
базисные ячейки пространства Z± и как написать матрицы для
a, s, д и d.
Вы должны знать определения подпространств Во, Но?
Н°, Р° и В1 и уметь строить для них базисы.
В. Цепи с резисторами
Вы должны уметь писать соотношение между V и I для ветви,
содержащей батарею, источник тока и резистор.
Для расчета электрических цепей Вы должны знать и уметь
пользоваться методами Максвелла: методом круговых токов и
методом узловых потенциалов.
С. Цепи переменного тока
Вы должны уметь пользоваться методами Максвелла для нахож-
дения стационарных решений и нормальных мод сетей, содержа-
щих индукторы, конденсаторы, синусоидальные источники тока
и напряжений.
Задачи
637
Задачи
12.1,2. Для цепей, изображенных на рис. 12.34 и 12.35, сделайте следу-
ющее:
Рис. 12.35
(а) Найдите множество независимых ячеек и напишите элемент
Ci, соответствующий каждой ячейке. (Можно воспользо-
ваться обозначениями типа Mi = о + /3 — 7.) Проверь-
те, что число независимых ячеек т удовлетворяет условию
т = b + 1 — п.
638
Глава 12. Теория электрических цепей
(Ь) Выразите ток в каждой ветви через токи в ячейках и най-
дите напряжения на ветвях.
(с) Применяя второй закон Кирхгофа к каждой ячейке, по-
стройте систему уравнений для токов в ячейках. Решите
эту систему.
(d) Пусть узел А заземлен. Выразите напряжения и токи че-
рез остающиеся неизвестные узловые потенциалы. Приме-
няя первый закон Кирхгофа к каждому узлу, получите си-
стему уравнений для узловых потенциалов и решите ее.
12.3,4. Для комплексов, изображенных на рис. 12.36 и 12.37, сделайте
следующее:
Рис. 12.36
(а) Определите размерность пространств Ci, Zi, Со и Hq. Про-
верьте, что dim Hq — dim Zi = dim Со — dim Ci.
(b) Для каждой связной компоненты найдите дерево Г, которое
соединяет все узлы. После этого постройте базис простран-
ства Zi и запишите явно проекцию рт в виде
= О,
Рт(/3) = /3 + 7“^ ит.д.
(с) Определите, сколько необходимо иметь уравнений для то-
ков в ячейках и для узловых потенциалов, чтобы рассчитать
цепь с данной топологией.
12.5. Для каждой из трех ветвей, изображенных на рис. 12.38, найдите
соотношение между V и I, В каждом случае постройте ветвь с
тем же соотношением, содержащую только подходящие батарею
и резистор (но не источник тока), а потом — источник тока и
резистор (но без батареи).
Задачи
639
Рис. 12.38
12.6. Рассмотрите комплекс, изображенный на рис. 12.39.
(а) Напишите матрицы д и d, соответствующие порядку ветвей
а, Д 7, <5, 6, ф.
640
Глава 12. Теория электрических цепей
Рис. 12.39
(Ь) Покажите, что вектора
о
1
1
\1/
образуют базис про-
странства HQ. Заземлите узлы Л и С и покажите, что век-
/0\
о
о
о
\1/
тора
образуют базис пространства Р° =
С® /Z®. В этом базисе постройте матрицу оператора [с/] :
Р° — С1.
(с) Для каждой компоненты выберите максимальное дерево с
ветвями о, 6 и е. Тремя базисными элементами простран-
ства Zi будут ячейки, образованные остальными ветвями
/3, 7 и ф с ветвями дерева (ячейку выбирайте так, чтобы /3,
7 или 6 имели коэффициент +1). В этом базисе напишите
матрицу о : Zi —> Ci.
(d) Покажите, что столбцы матрицы [d] определяют базис В1.
Свяжите вектора факторпространства В1 = С1 /В1 с тре-
мя ветвями, не принадлежащими максимальным деревьям,
получив
Задачи
641
Покажите, что эти три вектора образуют базис простран-
ства Я1, дуальный к базису, выбранному для Z\.
(е) В этом базисе постройте матрицу з : С1 —> Н1. Убедитесь,
что матрица з есть транспонированная матрица к а.
(f) Покажите, что границы траекторий, соединяющих зазем-
ленные узлы с незаземленными, образуют базис простран-
ства Во, дуальный к базису пространства Р°.
(g) Покажите, что классы эквивалентности заземленных узлов
образуют базис пространства Но = С°/В0, дуальный к ба-
зису пространства Z0.
12.7. Для цепи, изображенной на рис. 12.34 (задача 12.1), постройте
И, [а], о-, з, z,Khw. Составьте уравнения для токов в ячейках
и уравнения для узловых потенциалов, используя эти матрицы и
вектора. Проверьте, что получатся в итоге те же уравнения. При-
мите, что узел А заземлен, а ветви (3 и 6 образуют максимальное
дерево.
12.8. Сделайте то же самое для цепи, изображенной на рис. 12.35 (за-
дача 12.2), считая, что узел А заземлен, а ветви о, (3 и б образуют
максимальное дерево.
12.9. Воспользуйтесь методом круговых токов и найдите токи в вет-
вях 1У для цепи, изображенной на рис. 12.40. Используйте
ячейки, определенные выбором /3 в качестве максимального де-
рева.
12.10. Рассмотрите цепь на рис. 12.41. Пусть матрица преобразования
з имеет вид
_ /-1 +1 0 +1\
s \ 0 О +1 -1J
Найдите в явном виде базис пространства Zi, который опреде-
ляется этой матрицей s. Какое максимальное дерево приведет к
этому базису? Пусть базис в пространстве Р° выбран так:
/0\ /о\
р1 = I 1 I, р2 = I о 1.
\0/ V/
642
Глава 12. Теория электрических цепей
Рис. 12.40
Рис. 12.41
(2 \
1 I через базисные вектора р1 и р2. Напишите
4/
матрицы, представляющие [9] и [d]. Для данной цепи воспользуй-
тесь методом узловых потенциалов и вычислите Фв и Ф°.
12.11. Рассмотрите цепь, изображенную на рис. 12.42. Для этой цепи
напишите матрицы д и d. Пусть ветви а и 7 образуют макси-
мальное дерево. Напишите базис пространства соответству-
ющий этому максимальному дереву, и в этом базисе постройте
матрицу а. Воспользуйтесь методом круговых токов и получите
токи в ветвях этой цепи.
Задачи
643
Рис. 12.42
12.12. (а) Используя метод круговых токов, определите частоты нор-
мальных мод для цепи, изображенной на рис. 12.43, т. е.
определите значения а?/2тг, для которых матрица sZa вы-
рождена. Для этих частот найдите решения уравнения
(sZa)J = 0.
Рис. 12.43
(Ь) Рассчитайте эту цепь методом узловых потенциалов. Если
узел А заземлен, то все равно придется обращать матрицу
3x3. Почему существуют только две нормальные моды?
(с) Соединив последовательно ветви ас^ибсеи убрав узлы
С и D, преобразуйте эту цепь в цепь, содержащую только
644
Глава 12. Теория электрических цепей
два узла. Рассчитайте цепь методом узловых потенциалов.
На этот раз остается работать с матрицей 1x1!
12.13. (а) Используя метод круговых токов, определите частоты нор-
мальных мод для цепи, изображенной на рис. 12.44. Для
каждой моды выразите частоту а>/2тг через величину о>о =
1 /д/L о Со и получите отношение токов в ячейках /J\.
Рис. 12.44
(Ь) Для той же цепи методом узловых потенциалов определите
частоты нормальных мод.
12.14. (а) Для цепи, изображенной на рис. 12.45, постройте комплекс-
ную матрицу sZa.
Рис. 12.45
(Ь) Предположим, что генератор в ветви а подает напряже-
ние, равное вещественной части £оегиЛ- Получите выраже-
ния для стационарных напряжений V& и Vs.
12.15. Вернемся к упражнению 12.13 и предположим, что последова-
тельно с конденсатором между узлами Ли В соединен источник,
создающий ток К = Re(Ko^Iu;oi)5 еде cj0 = I/v^ZqCo- Получите
выражения для токов в ячейках Ji и J2.
Глава 13
Метод ортогональных проекций
В этой главе мы продолжаем изучать электрические
цепи. Исследуем краевые задачи, возникающие в це-
пях с конденсаторами, и используем изложенные ме-
тоды для решения ряда классических задач в электро-
статике при наличии проводников.
13.1. Метод ортогональных проекций Вейля
Рассмотрим еще два метода, используемых для расчета электри-
ческих цепей: метод ортогональных проекций Вейля и ориги-
нальный метод Кирхгофа. Оба метода интересны и их стоит изу-
чить, хоть они и ограничены только цепями с сопротивлениями,
т. е. случаем, когда все импедансы za — положительные числа,
~ ^*Ot > б*
Начнем с метода Вейля. Уравнение, связывающее векторы
напряжений на ветвях V и токов в ветвях I, имеет вид
V-W-Z(I-K).
Перепишем его в виде
V = W + 7(1 - К)
или
V = Z(Z-1W +1 — К).
Матрицу Z используем для определения положительно опре-
деленного скалярного произведения в пространстве С± токов,
646
Глава 13. Метод ортогональных проекций
протекающих по ветвям:
(I, I')z = fz*' = тМ* + + • • • .
Предположим, что у нас есть произвольное распределение токов
по ветвям I', удовлетворяющее первому закону Кирхгофа дТ = О,
и произвольное распределение напряжений V, удовлетворяющее
второму закону Кирхгофа V — —</Ф. Нам известно, что V — 0.
Поскольку V = Z(Z"1W + I — К), можно написать
Z(Z“XW + I - К) = 0.
Если это соотношение выразить через скалярное произведение,
введенное выше, то его можно переписать в виде
(Г, Z^W +1 - K)z = 0.
Это значит, что вектор (К —Z-1W)~ I ортогонален всем циклам.
Теперь мы можем задачу о цепи с сопротивлениями сформу-
лировать по-другому. Нам дано пространство Ci, образованное
токами в ветвях. Внутри него лежит подпространство циклов Z\.
Для сети с заданными векторами источников W и К можно по-
строить вектор К — Z-1W, который описывает токи в ветвях,
существующие при условии, что все узловые потенциалы равны
нулю. В общем случае этот вектор не является элементом под-
пространства Zi. Теперь мы хотели бы получить такой вектор
I 6 Zi, чтобы вектор (К — Z“1W) — I был ортогонален всем
циклам. Итак, мы свели расчет цепи с резисторами к геометри-
ческой задаче, изображенной на рис. 13.1. Для данного вектора
К — Z-1W в пространстве Ci надо вычислить его ортогональ-
ную проекцию на подпространство Z\ относительно скалярного
произведения, определенного матрицей Z.
Тогда вектор К — Z-1W записывается в форме
К - Z~ 1W = I + (К - Z"XW - I),
где I принадлежит пространству Zi, а К — Z-1W — I = — Z-1V
ортогонален Zi. Пусть тг обозначает линейное преобразование,
13.1. Метод ортогональных проекций Вейля
647
Рис. 13.1
которое проектирует Ci ортогонально на Z\. В этом случае ре-
шением задачи о цепи является
I = тг(К - Z-1W),
V = Z(7T - 1)(К - Z-1W).
Геометрически очевидно, что существует единственный проекци-
онный оператор яг, а следовательно, существует единственное ре-
шение задачи для данной цепи.
Одним из способов получения ортогональной проекции из
Ci в Zi основан на выборе ортонормированного базиса. Пусть
{ei,e2,... , em} — ортонормированный базис пространства Z±.
Тогда если и — элемент пространства Ci, то его проекция на
подпространство Z\ дается формулой
7ги = (ei, u)ei + (е2, u)e2 +-Ь (em, u)em.
Процедура вычисления матрицы тг довольно утомительна.
Сначала мы должны выбрать базис подпространства Zi, напри-
мер, семейство независимых ячеек. После этого применяем проце-
дуру Грама-Шмидта, чтобы этот базис преобразовать в ортонор-
мированный относительно скалярного произведения, определен-
ного матрицей Z. Наконец, мы должны брать по очереди каждый
базисный вектор пространства Ci и вычислять его проекцию на
пространство Zi, беря сумму проекций на векторы ортонормиро-
ванного базиса Zi. Каждая такая проекция определяет столбец
матрицы тг.
648
Глава 13. Метод ортогональных проекций
В качестве иллюстрации метода Вейля рассмотрим цепь,
изображенную на рис. 13.2. Для этой цепи пространство Су дву-
мерно. В ней есть только одна ячейка а + /3, поэтому подпро-
Zi одномерно и натянуто на вектор (| )• Матрица Z
странство
имеет вид
1 0 ]
О ЗГ
Чтобы вычислить проекционную матрицу тг, мы должны по
очереди спроектировать два базисных вектора
на
подпространство Zi. Сначала отнормируем базисный элемент Z\:
длина вектора
равна
— 4, поэтому мы
делим вектор
2, в результате получая вектор
длина которого равна 1. Проекция вектора
равна
'1\ А 0\ Л/2\\ Л/2\ Л/4\
Р/’\0 3) V/2/J V/2J ~ V/4/ ’
13.1. Метод ортогональных проекций Вейля
649
©
а проекция вектора
равна
/1 0\ Л/2\\ Л/2\ _ /3/4\
W ’ ко У \УУ) \УУ ~ \УУ
п /1/4 3/4\ л .
Отсюда матрица 7г = 11/4 3/4/ ^ля и,епи? из°браженной на
рис. 13.2, получаются вектора К = I 1 и W =
1). Поэтому
к - z~xw =
. Применяя матрицу тг к этому
вектору, получаем
Z’1
1/4 3/4'
1/4 3/4
Тогда решение имеет вид 1а = — 2. Заметим, что вектор
г7— 1ЛХ7 Т (^\ f^\ ( т
К — Z W —1= I I — I I = I J 1 ортогонален I, как и должно
быть. Расчет этой цепи графически изображен на рис. 13.3. По-
скольку введенное скалярное произведение не является обычным
евклидовым, то подпространство Z\ и его ортогональное допол-
нение представляются не перпендикулярными прямыми.
Понятно, как найти явное выражение проекционного операто-
ра Вейля тг, используя решение методом круговых токов. Вспом-
ним, что в этом методе I = aJ, где J = (sZa)~1s(ZK — W).
650
Глава 13. Метод ортогональных проекций
Тогда I — a(sZa) 1sZ(K — Z XW). Сравнивая этот результат с
формулой Вейля I = тг(К — Z-1W), получаем, что
тг = a(sZcr)“1sZ.
Легко проверить, что %2 — тг, как и должно быть для любого
проекционного оператора1.
13.2. Метод Кирхгофа
Рассмотрим метод, разработанный самим Кирхгофом. И хотя он
был придуман за много десятилетий до метода Вейля, мы обра-
щаемся к нему сейчас, потому что он дает явную формулу для
проекционного оператора тг через деревья в цепях.
Предположим, что у нас есть связный комплекс и пусть Т
обозначает максимальное дерево. Вспомним, что для каждого
такого дерева мы определили проекционный оператор рт'
z х ГО, если а е Г,
] л/г еспи о d Т
где Ма есть цикл, соответствующий единственной ячейке, содер-
жащей ветвь о, а все остальные ветви принадлежат Г. (Цикл сле-
дует выбирать так, чтобы он содержал +а, а не -а.) Например,
на рис. 13.4 одна ветвь /3 образует максимальное дерево. Тогда
рт{а) = а-/3, рт(/3) = 0, ртЬ) = 7 + 0.
Поэтому матрица, представляющая эту проекцию рт, имеет вид
/ 1 ° 0\
I —1 0 11. Заметим, что все диагональные элементы рт равны
\ 0 0 1/
либо +1, либо 0.
Любой такой оператор рт является проекционным операто-
ром на пространство Z±: его образ есть Z\ и рт(М) = М для
1 Математическое название этого свойства проекции — идемпотентность.
Каждый идемпотентный оператор тг в конечномерном векторном простран-
стве может быть геометрически охарактеризован как проекция на образ Im тг
вдоль ядра Кегтг. — Прим. ред.
13.2. Метод Кирхгофа
651
Рис. 13.4
М 6 Zi. Однако он не является ортогональным проекционным
оператором, потому что его ядро не ортогонально подпростран-
ству Zi (по отношению к скалярному произведению, определен-
ному матрицей Z). Другими словами, рт — не самосопряженный
оператор, потому что в общем случае для двух ветвей а и (3
Итак, рт для отдельно взятого максимального дерева Т -
не самосопряженный оператор, но в комплексе есть много раз-
личных максимальных деревьев. Открытие Кирхгофа состояло
в нахождении процедуры получения самосопряженного операто-
ра: различные проекционные операторы усредняются с опреде-
ленным весом. Предположим, что для каждого максимального
дерева Т мы имеем вещественное число Ат, причем 0 < < 1 и
52т — 1, где сумма берется по всем деревьям. Тогда оператор
Рх = У2 ^тРт
т
тоже является проекцией на пространство Z\\ его образ есть Zi,
и он отображает любой вектор в пространстве Zi в самого себя.
Вообще говоря, р\ - не ортогональная проекция, но существует
такой набор Ат, что ортогональность имеет место. Рецепт Кирх-
гофа состоит в том, что для каждого максимального дерева Т
определяем
Qt = В Г/з,
Мт
652
Глава 13. Метод ортогональных проекций
т. е. произведение сопротивлений тех ветвей, которые не принад-
лежат Т. Весовые множители X? выбираются пропорциональны-
ми Qt так, чтобы их сумма равнялась единице, т. е.
Хт = Qt/R, где R — У2 Qt-
т
Таким образом, мы получили явный вид проекционного операто-
ра Вейля 7г, а именно
7Г = Я
т
Теперь мы должны показать, что этот оператор самосопря-
женный; другими словами, что самосопряжен оператор Дтг =
Поскольку ветви образуют базис в пространстве Ci,
то достаточно показать, что для любой пары ветвей а и /3 мы
имеем
т т
Для фиксированных а и /3 мы суммируем по всем максималь-
ным деревьям. Имеются три случая, изображенных на рис. 13.5.
Случай 1 Случай 2 Случай 3
Рис. 13.5
Случай 1. Ветви а и /3 принадлежат дереву. В этом случае
Рт(се) = 0 и рт($) = 0. Поэтому от дерева нет никакого вклада в
обе части уравнения.
Случай 2. Ветви а и (3 не принадлежат дереву. В этом слу-
чае рт(а) является ячейкой, которая не содержит /3, поэтому
= 0- Аналогично (а,рт(/3))я ~ 0, поэтому опять от
дерева нет никакого вклада.
13.2. Метод Кирхгофа
653
Случай 3. Ветвь а не принадлежит дереву, а /3 принадлежит.
В этом случае если /3 входит в ячейку Ма, образованную а и дру-
гими ветвями дерева (иначе ситуация такая же, как в случае 2),
то мы имеем
где берется знак +, если а и /3 входят в Ма с одинаковыми зна-
ками, и знак —, если эти ветви входят в ячейку в противопо-
ложными знаками. Например на рис. 13.6(a) мы имеем рт(<^) ~
а —— (3 + 6 к (рт(а), ff)z — Всегда существует единственное
максимальное дерево Г', образованное заменой ветви /3 на а в де-
реве Т, для которого рт!{(3) = +рт{ос), так что (q, рт'(/3))и —
Такое дерево Tf показано на рис. 13.6(6).
а) Дерево Т б) Дерево Т
Рис. 13.6
Если из дерева Т убрать ветвь /3, то останутся те же ветви,
что и при удалении из Tf ветви а. Значит, для этих двух деревьев
справедливо равенство и оба выражения и
Qxra являются произведениями сопротивлений остающихся вет-
вей. Соотношения между Т и Т' симметричны относительно пе-
рестановки ветвей а и 13. Тогда
Qt(pt<+0)z ~ QTf(<+pTf(3)z-
Каждому дереву Т, для которого левая часть равенства не рав-
на нулю, соответствует дерево Г', удовлетворяющее этому равен-
ству, и наоборот. Таким образом, если просуммировать по всем
Т, то получим желаемый результат
^2<Эт(рта,/3)^ — У^<Эт(о£,рт^)7,
т т
654
Глава 13. Метод ортогональных проекций
где добавлены некоторые нулевые слагаемые. Итак, доказана
формула Кирхгофа
тг = Я”1 QtPt?
т
где
Qt = К rQ, R = Qt,
а$Т Т
и суммирование ведется по всем максимальным деревьям.
В качестве иллюстрации метода Кирхгофа рассмотрим цепь,
изображенную на рис. 13.7 и имеющую ту же топологию, что и
цепь на рис. 13.4. В цепи есть три максимальных дерева: ветвь а
(дерево Ti), ветвь fl (дерево Тг) и ветвь 7 (дерево Т3).
Для дерева Ti
/О -1 1\
РТг = I 0 1 О I и QT1 = 2 • 3 = 6.
\° 0 V
Для дерева Тг
/ i ° 0\
рт2 = I —1 0 1 I и Qt2 = 1-3 = 3.
\ ° ° 1/
13.2. Метод Кирхгофа
655
Для дерева 7з
/1 0 0\
рТз = I 0 1 О I и QT3 - 1 • 2 = 2.
V 1 °/
Тогда
R — Qti + Qt? Qt3 = 6 + 3 + 2 = 11.
Следовательно,
тг = [6рТ1 + Зрт2 + 2рт3],
или
, / 5 -б б\
тг = — 1-3 8 3 .
11 \ 2 2 9/
Эта матрица проецирует на подпространство Zi, натянутое на
/ 1\ /0\
векторы ячеек I — 1 I и ( 1 J. Можно проверить, что
\ °/ V/
Матрица 1 — тг равна
х / 6 б —б\
1 - тг = — 3 3 -3 .
11 \-2 —2 2/
Она проецирует на ортогональное дополнение к Zi. Ее образ, яв-
ляющийся ядром тг, есть одномерное пространство, определяемое
/ б\ / 1\
вектором I 3 1. Этот вектор ортогонален обеим ячейкам I — 1 ]
\—2/ \ О/
/0\
и I 1 I. Заметим, что
\1/
/ б\
Z 3
\-2/
1 0 0\ / б\ / б\
О 2 0)( 3= 6.
О 0 3/ \-2/ \-б/
656
Глава 13. Метод ортогональных проекций
/ 6\
Как и следовало ожидать, вектор ( 6 I задает напряжения в
\—6/
ветвях, что соответствует второму закону Кирхгофа.
13.3. Теорема взаимности Грина
Изучение цепей с резисторами мы закончим мощным результа-
том, называемым теоремой взаимности Грина. С этой теоремой
мы встретимся еще раз при изучении цепей, содержащих емко-
сти, и в электростатике. Чтобы доказать эту теорему, представим
себе цепь, в которой все ветви, кроме двух, содержат только ре-
зисторы без источников тока и напряжения, а в двух ветвях си и
(3, кроме резисторов, могут быть такие источники тока или на-
пряжения. При определенном выборе источников в ветвях а и (3
мы получим решение с токами I, удовлетворяющими первому за-
кону Кирхгофа, и напряжениями V, удовлетворяющими второму
закону Кирхгофа. Выбрав другие источники, мы получим другое
решение, для которого токи I и напряжения V также удовлетво-
ряют двум законам Кирхгофа. (Типичная ситуация, к которой
применима теорема Грина, показана на рис. 13.8.) Поскольку оба
вектора токов I и I удовлетворяют первому закону Кирхгофа, то
они лежат в пространстве Z\. Аналогично, поскольку оба векто-
ра напряжений V и V удовлетворяют второму закону Кирхгофа,
Рис. 13.8
13.3. Теорема взаимности Грина
657
они лежат в пространстве В1. Мы знаем, что любой элемент про-
странства В1, действуя на любой элемент пространства Zi, дает
нуль. Отсюда можно сделать вывод, что
Тогда, если записать сумму по ветвям, мы получим
Е vyiy = Е
по всем ветвям по всем ветвям
Из сумм выделим слагаемые, соответствующие ветвям а и /3:
22 vuy = vaia+v%+ 22 W7.
по остальным по остальным
ветвям ветвям
Мы предположили, что все ветви, кроме а и /3, имеют только
резисторы. Поэтому V7 = и У7 = гТогда
Е^’Е^М^Е^А-
и мы можем сократить суммы по другим ветвям в обеих частях
уравнения. В результате получаем
Уа1а + У01(3 = vaia + у%,
что и называется теоремой взаимности Грина.
С помощью теоремы взаимности можно получить ряд удиви-
тельных свойств пассивных цепей, содержащих резисторы, т. е.
цепей, в которых нет никаких источников. Взяв такую цепь, мы
можем добавлять к ней новую ветвь двумя способами, как это
показано на рис. 13.9. Начав с цепи, содержащей только резисто-
ры (рис. 13.9(a)), мы можем присоединить новую ветвь а между
двумя узлами (рис. 13.9(6)). Такая «спайка» не создает новых
узлов. Эта новая ветвь может быть как коротким замыканием,
так и содержать источники тока, источники напряжения или ре-
зистор. Новую ветвь можно подключить и так, как показано на
рис. 13.9(b), т. е. мы можем «перекусить» провод и вставить в
разрыв новую ветвь, создав новый узел.
658
Глава 13. Метод ортогональных проекций
Рис. 13.9. (а) Исходная цепь, (б) Новая ветвь без создания новых
узлов (спайка), (в) Новая ветвь с новым узлом (вставка)
Предположим, что у нас есть линейная цепь, показанная на
рис. 13.10, и к ней присоединены две новые ветви: ветвь а между
узлами А и В, а ветвь 3 между узлами С и D. Несущественно,
как мы это сделали: припаяв новый провод или вставив в старый.
Из теоремы взаимности можно сделать следующие выводы.
Рис. 13.10
Рис. 13.11
Случай 1. Вставим батарею, создающую напряжение £ в
ветвь си, и измерим ток I в ветви /3. После этого ту же батарею
вставим в ветвь /3 и измерим ток в ветви а (см. рис. 13.11).
Поскольку = 0 и Va = 0 (обе ветви соединены накоротко),
13.3. Теорема взаимности Грина
659
из теоремы взаимности следует, что
V% = VaIa.
Мы использовали одну и ту же батарею, так что V& = Va = 8.
Поэтому 8 Ip ~ 81а и 1р = 1а. Этот результат интересен тем,
что хотя сама цепь не обязана обладать свойствами симметрии,
соотношение между приложенным напряжением и возникающим
током симметрично.
Случай 2. Вставим источник тока j в ветвь а и измерим
получившееся напряжение на ветви /3 в разомкнутом состоянии.
Потом тот же источник вставим в ветвь /3 и измерим ток в ветви
о (см. рис. 13.12). Поскольку = 0 и 1а = 0 (разомкнутые цепи),
то теорема взаимности говорит, что в этом случае
vaia = v%.
Но
Л* = 1(3 =
следовательно,
= v?j,
и мы получаем
уа У@,
Рис. 13.12
В общем случае мы можем рассмотреть резисторный п-порт,
из которого выходят п пар проводов. Если к различным портам
присоединены источники тока /а, , то возникающие напря-
жения ... будут зависеть от токов согласно формуле
V = Д1,
660
Глава 13. Метод ортогональных проекций
где R — матрица п х п. Приведенные соображения показывают,
что матрица R должна быть симметричной, потому что для
любых портов Лиц зависимость УЛ от 1^ точно такая же, как
зависимость от /д.
Теорему взаимности Грина можно также вывести как след-
ствие решения, полученного методом круговых токов. В случае,
если нет источников тока, т. е. К — 0, то мы имеем
J = (sZar^-W).
Следовательно,
I = = —<t(sZct)_1sW.
Матрица Z симметрична, а матрица s — транспонированная мат-
рица а. Поэтому матрица
G =
симметрична. Тогда можно написать
I = GW,
где матрица G, выражающая токи в ветвях через приложенное
напряжение батареи, симметрична. Аналогично можно начать с
решения, полученного методом узловых потенциалов:
Ф = - Z-1W).
Если нет источников напряжения, т. е. W = 0, то
¥ = -ИФ = -И([а]2-1иг1да.
На этот раз матрица [d] — транспонированная матрица [<Э]. Тогда
матрица
выражающая напряжения на ветвях через приложенные токи,
симметрична.
В связи с этим стоит заметить, что зависимость V от W или
I от К в общем случае не дается симметричной матрицей.
13.4. Цепи с конденсаторами
661
13.4. Цепи с конденсаторами
Немного изменим задачу -- вместо цепей с резисторами рассмот-
рим цепи с конденсаторами. Теперь каждая ветвь может иметь
батарею и конденсатор, соединенные последовательно. Когда
подсоединена батарея2, на пластинах конденсатора накаплива-
ется заряд и со временем устанавливается стационарное состо-
яние. Поскольку заряды не могут пересечь расстояние между
пластинами конденсатора, то в цепи не будет никакого тока. Нам
нужно узнать величину заряда Qa на конденсаторе в ветви а и
напряжение Va на этой ветви.
г А
Vа = фЛ-фв
В
Рис. 13.13
Типичный пример такой цепи изображен на рис. 13.13. На
ветви о обозначены знаки зарядов на пластинах конденсаторов.
Заметим, что так же, как и раньше, положительные значения
Va и Wa относятся к падениям напряжения, когда ветвь прохо-
дится в направлении, указанном стрелкой. Положительный знак
Qa означает, что сначала проходится положительно заряженная
пластина конденсатора. Договорившись об этом, обозначим С&
емкость ветви и напишем уравнение
Са
Постоянного тока. — Прим. ред.
662
Глава 13. Метод ортогональных проекций
Мы можем рассматривать вектор Q = (Qa,Q/3-> • • •) как
1-цепь, а вектор V = (Va,V^,...)T — как 1-коцепь. Однако,
теперь связь между напряжением и зарядом дает энергию, а не
мощность3. В векторных обозначениях мы можем написать
V-W = CXQ,
где С — диагональная матрица с матричными элементами Са.
Если заменить Z на С~г и мощность на энергию, то ситуация
формально совпадает с той, что возникает в цепях с резисторами.
Напряжение V по-прежнему получается из потенциала V = — ЙФ.
Поскольку ток не может течь через конденсаторы, то полный
заряд на конденсаторах, соединенных с любым узлом, не может
изменяться. Если вначале конденсаторы не были заряжены, то
полный заряд на каждом узле будет равен нулю и 5Q — 0, точно
так же, как мы имели д! ~ 0 для цепей с резисторами.
Изолированные цепи конденсаторов, которые вначале не бы-
ли заряжены и для которых справедливо условие 5Q = О, можно
рассматривать так же, как мы рассматривали цепи с резисто-
рами. В предыдущих результатах надо только заменить I на Q
и Z на С-1. Батареи, как и раньше, представляются вектором
W, и нет ничего, что играло бы роль источника тока. Тогда по
аналогии с методом круговых токов можно ввести заряды ячеек,
описываемые вектором Р Е Zi. В этом случае любое распределе-
ние зарядов, удовлетворяющее условию 9Q — 0, можно записать
в форме Q ~ сгР. Тогда
Р = (sC-1cr)-1(—sW).
Аналогично, мы можем заменить Z~l на С в методе узловых
потенциалов и получить
Ф = _ ([5]C[d])-1[5]CW.
3 Следует напомнить, что в отличие от выделяемой в резисторном участке
цепи с сопротивлением R при напряжении U и токе I мощности Р = UI =
IR2 — U2R~\ потенциальная энергия конденсатора емкости С при заряде
пластин ±<Э и напряжении U составляет Е = \UQ = \CU2 = |Q2C-1; так
что аналогия «мощность-энергия» здесь имеет место лишь с точностью до
множителя — Прим. ред.
13.4. Цепи с конденсаторами
663
В общем случае, если конденсаторы вначале были заряже-
ны, на пластинах, присоединенных к узлу А, может быть фик-
сированный полный заряд ра- Вектор р ~ рв,- ••) может
рассматриваться как 0-цепь. Поскольку мы договорились, что с
конечным узлом ветви соединена отрицательная пластина кон-
денсатора, то в общем случае можно написать 9Q = —р. (Посмот-
рите на рис. 13.14 и убедитесь в правильности знака —.) Сумма
зарядов на двух пластинах каждого конденсатора равна нулю,
следовательно,
52 РА = °-
по всем узлам
ХМ — Q& Qg + Q-
Рис. 13.14
Уравнение 9Q = — р называется законом Гаусса. Закон по-
казывает связь между зарядами узлов и зарядами на пласти-
нах конденсатора в ветвях. В главе 16 мы будем изучать элек-
тростатику и там увидим, что аналогом узловых зарядов будет
плотность заряда р, а аналогом Q — диэлектрическое смещение
D. Мы объясним, что D можно рассматривать как 2-форму в
трехмерном пространстве и опишем, как надо ставить физиче-
ский эксперимент, чтобы измерить значение D. Окажется, что за-
кон Гаусса -- это просто трехмерный вариант теоремы Стокса. В
большинстве книг электростатика излагается в рамках векторно-
го анализа, где диэлектическое смещение D считается векторным
полем. Закон Гаусса становится теоремой о дивергенции. Однако,
в рамках нашего исследования цепей с конденсаторами уравне-
ние 9Q — —р означает, что каждому узлу мы приписываем сумму
664
Глава 13. Метод ортогональных проекций
зарядов на пластинах конденсатора, присоединенного к нему. До
конца этой главы мы будем изучать цепи без источников напря-
жения, т. е. с W = 0, где конденсаторы имеют первоначальный
заряд. Тогда наши уравнения принимают вид
Q = CV, V = и 9Q - -р.
Эти три уравнения можно собрать вместе и получить
-dCd<S> = -р.
Это уравнение называется уравнением Пуассона, Оно связывает
функцию потенциала с зарядами узлов. Оператор —dCd, стоя-
щий в левой части уравнения Пуассона, называется лапласианом
и обозначается Д. Тогда уравнение Пуассона можно переписать
в форме
ДФ = -р.
Теперь оператор d отображает С° —> С1, С отображает С1 С\
и д отображает Ci —> Со- Поэтому лапласиан Д отображает
С° —> Со- Как и следовало ожидать, потенциал Ф, стоящий в
левой части уравнения Пуассона, принадлежит С°, а р из правой
части этого уравнения принадлежит Cq.
Полезно написать явную форму лапласиана. Пусть и — эле-
мент пространства С°, а А — узел. Если ветвь а имеет А в каче-
стве одного из концов, то
du(a) — ±(ц(А) — и(ВУ), если да = ±(Л — В),
Поэтому С du имеет коэффициент
±Ca(tz(A) — для ветви а.
Подействуем теперь оператором д и найдем коэффициент в узле
А (суммируя по всем а с условием да = ±(А — В) для узла В):
(Ди)(А)= £ Са(и(В) — и(А)).
а: да=±(В—А)
В частности, и удовлетворяет уравнению Лапласа
Аи = О,
13.4. Цепи с конденсаторами
665
тогда и только тогда, когда
где сумма берется по всем узлам В, являющимся концами ветвей,
выходящих из узла А, как это показано на рис. 13.15. Другими
словами, уравнение Лапласа говорит, что значение и на узле А
есть среднее от всех значений на ближайших соседних узлах,
причем весами являются емкости соответствующих ветвей.
Рис. 13.15
Эту интепретацию следует сравнить с уравнением в частных
производных
д2и д2и
Аи = дх* + dyi ~
введенным в главе 6. Это уравнение говорит, что значение и в точ-
ке Р есть среднее от и по малым окружностям с центром в точке
А. Там, чтобы определить понятие окружности, мы должны были
иметь евклидову геометрию на плоскости. Здесь, чтобы опреде-
лить усреднение по ближайшим соседям, нам требуется матрица
емкостей С. Существует аналогия между выбором матрицы С
и выбором евклидовой геометрии на плоскости. Мы рассмотрим
это подробнее в главе 16.
А пока вернемся к изучению уравнения Пуассона. Заметим,
666
Глава 13. Метод ортогональных проекций
что потенциал Ф в левой части уравнения определен с точно-
стью до функции, которая постоянна для всех связных компо-
нент цепи. Действительно, любая такая функция принадлежит
ядру d и, следовательно, ядру Д = —dCd. Величина р в пра- <
вой части уравнения лежит в подпространстве Bq пространства
Со, поскольку, по определению, узловые заряды получаются в ре-
зультате действия д на заряды ветвей. Вспомним, что мы ввели
факторпространство Р° = С®]Z\ ограниченный кограничный
оператор [d] : Р° —> С1 и ограниченный граничный оператор
[5] : Ci —> Bq. Ситуацию в целом можно изобразить на схеме
отображений
С° C1" C1 c<>-
A
Это значит, что можно ввести ограниченный лапласиан [Д] —
— и рассмотреть ограниченное уравнение Пуассона
[Д]Ф = -р
для Ф € Р°. (Другими словами, Ф является потенциалом, опреде-
ленным с точностью до аддитивной постоянной на каждой связ-
ной компоненте цепи.) Далее, поскольку оператор С дается по-
ложительной диагональной матрицей в стандартном базисе С1 и
Ci, из теоремы Кирхгофа (с формулировкой для узловых потен-
циалов), мы знаем, что матрица [<Э]С[й] обратима и, следователь-
но, решение ограниченного уравнения Пуассона имеет вид
ф = (деиг1?.
Пример. Задача, где применяется простое уравнение Пуас-
сона, изображена на рис. 13.16. На узле В заряд равен 4, на узле
С он равен 1. Мы хотим найти потенциалы на всех узлах. (Для
конкретности заряд будем определять в микрокулонах, емкость
в микрофарадах, а потенциал в вольтах.)
Пусть узел А заземлен. Тогда ограниченный граничный опе-
ратор
rm А -1
'' (<1 1 -0
13.5. Краевые задачи
667
(напоминаем, что убрана строка, соответствующая узлу А). Мат-
рица оператора [d] является транспонированной к матрице [<Э],
т. е.
и
1
-1
о
/1 о 0\
Матрица С равна I 0 2 0 1, поэтому
\0 0 3/
Л -1 о\ । 0
l«= i ; о 2
' \о о
0\ / 1
° I 1-1
3/ \ о
о\
11
1/
/ 3 -2\
\-2 5/ ‘
Решение уравнения Пуассона имеет вид
/raw^-i 1 /5 2\ т 1/5 2\ /4\
(ИСИ) - n (2 3) > Ф- 11 (2 3/(1)
2\
1J ‘
13.5. Краевые задачи
Задача для уравнения Пуассона, которую мы только что ре-
шили, аналогична электростатической задаче, когда вычисляет-
ся потенциал Ф(г), создаваемый распределением заряда р(г) в
668
Глава 13. Метод ортогональных проекций
вакууме, когда не заданы граничные условия. В электростати-
ке возникают более интересные задачи, когда конкретизируются
граничные условия для нулевого потенциала на определенных
проводниках, или когда фиксируется потенциал на границе об-
ласти. Здесь мы рассмотрим несколько таких примеров.
На рис. 13.17 изображена система конденсаторов, причем ни
в одной ветви нет батерей. Узлы этой цепи разделим на два клас-
са: граничные узлы и внутренние узлы. Граничные узлы А и В
соединяются с внешними источниками, которые поддерживают
на них определенные значения потенциалов. Поскольку заряды
могут свободно перетекать по проводам, соединяющим эти узлы
с внешними источниками, то нет смысла задавать на граничных
узлах значение полного заряда. Внутренние узлы С н D соеди-
нены только с другими узлами цепи, и не подходят к внешним
источникам. Полный заряд на таких узлах постоянен и может
быть задан. При этом нет смысла задавать потенциал на внут-
ренних узлах.
Для расчета такой цепи в общем случае мы будем задавать
потенциал на граничных узлах и полный заряд на внутренних уз-
лах. Задача в том, чтобы найти потенциалы на внутренних узлах
и полные заряды на граничных. По существу эта задача может
быть представлена как суперпозиция двух более ограниченных
проблем.
1. Задача Дирихле. Полный заряд на каждом внутреннем узле
полагается равным нулю, а потенциал на каждом гранич-
13.5. Краевые задачи
669
ном узле имеет определенное значение (в общем случае не
равное нулю).
2. Задача для уравнения Пуассона. Потенциал на каждом гра-
ничном узле полагается равным нулю, а полный заряд р
на каждом внутреннем узле имеет определенное значение.
Задача именно такого типа изображена на рис. 13.15, где
узел А является граничным.
Решение общей задачи всегда может быть представлено как
суперпозиция решений задачи Дирихле с соответствующими гра-
ничными условиями и задачи Пуассона с соответствующими зна-
чениями зарядов на внутренних узлах.
Разделив узлы на два класса, мы получили два векторных
пространства: Со (узловые заряды) и С° (узловые потенциалы).
Пространство Со есть прямая сумма
Со-СогранфСовнутр,
где СфРан состоит из 0-цепей, имеющих ненулевые коэффициенты
только на граничных узлах, и СдНутр состоит из 0-цепей, имею-
щих ненулевые коэффициенты только на внутренних узлах. Ана-
логично мы имеем
С° — С° гтч ро
^гран ^внутр?
где Со₽ан состоит из тех линейных функций, которые обращаются
в нуль в СдНутр, а С° тр состоит из функций, обращающихся в
нуль в согран.
Потенциал Ф может быть разложен единственным способом в
сумму элементов из пространства Срран и Санутр, т. е.
Ф — Фгран “И Фвнутр-
Для цепи, изображенной на рис. 13.17 с граничными узлами А,
В и внутренними узлами С, D, такое разложение имеет вид
/ФЛ\
Ф^ |
I
/Фл\ / 0 \
Фв I О
о
\ 0 / \Ф°/
670
Глава 13. Метод ортогональных проекций
Аналогично разлагается вектор, представляющий заряды узлов
р = + рвнутр.
Тогда в цепи, изображенной на рис. 13.17, мы имеем
<Ра\
РВ
PC
\Pd)
/ о \
0
Рс
\pd)
Теперь задачи могут быть сформулированы в терминах раз-
ложений этих векторных пространств.
1. Задача Дирихле. Поскольку потенциал задается на каж-
дом граничном узле, вектор Фгран известен. Более того, поскольку
на внутренних узлах нет зарядов, вектор рвнутр = 0. Мы долж-
ны найти такой вектор ФВНуТр? чтобы на всех внутренних узлах
выполнялось условие
Д(Фвнутр Фгран) — 0-
На граничных узлах мы имеем уравнение
Д(Фвнутр + Фгран) -~ргран.
Решив эти уравнения, мы узнаем потенциалы и заряды на всех
узлах.
2. Задача Пуассона. На каждом внутреннем узле задает-
ся заряд. Следовательно, вектор рвнутр известен. Поскольку по-
тенциал равен нулю на каждом граничном узле, Фгран — 0. Мы
должны найти такой вектор ФВНутр? чтобы на всех внутренних
узлах выполнялось условие
Д(Фгран +Фвнутр) = -рВНуТР-
Раз потенциал известен, распределение зарядов на граничных
узлах определяется уравнением
рП>ан = _Д(Фгран + фвнутр).
13.6. Решение краевых задач методом Вейля 671
13.6. Решение краевых задач методом
ортогональных проекций Вейля
Сначала мы рассмотрим связную цепь, имеющую Пг внутренних
узлов и щ граничных узлов. Обе задачи могут быть решены ме-
тодом ортогональных проекций Вейля. Для определения скаляр-
ного произведения напряжений на ветвях в пространстве С1 вос-
пользуемся емкостной матрицей С : С1 —> Ci и напишем формулу
(V,V)c= [ у= у cavava.
Jcrv
* по всем ветвям
Это скалярное произведение положительно определено, потому
что С — диагональная матрица, у которой все матричные эле-
менты положительны. Не удивительно, что это выражение мо-
жет быть интерпретировано через энергию. Действительно, для
любого значения V формула
|<v,v)c = £5Co(v")2
представляет полную энергию, накопленную в конденсаторах.
Относительно этого скалярного произведения пространство
С1 разлагается в ортогональную прямую сумму
С1 =d(C'°)®C'-1Zi.
Действительно, мы знаем, что с?(С°) является аннулирующим
пространством подпространства Z± пространства С\. Вычисле-
ние скалярного произведения элемента V из С\ на элемент типа
С~г1 равносильно вычислению скалярного произведения V на Г.
(V,C-1/)c = Jv.
Разложим далее пространство d(C°). Поскольку dC®uyTp является
подпространством С°, то его ортогональное дополнение внутри
dC° есть подпространство dC°, которое обозначим D1. Тогда мы
имеем разложение в виде прямой суммы
dc° = D1^dc^!rTp.
672
Глава 13. Метод ортогональных проекций
Следовательно,
является разложением пространства С1 на три попарно орто-
тональных подпространства. Заметим, что всякий элемент про-
странства D1 имеет вид t/Ф, потому что D1 С dCQ. Кроме того,
если V е Р1, то V ± и тогда
О — (К с/ФВНутр)с “ / </ФБнутр — / Фвнутр-
JCV J9CV
Для любого внутреннего узла мы можем найти такую функцию
Фвнутр, которая не равна нулю на этом узле и обращается в нуль
на всех других узлах. Тогда dCV должна иметь нулевые компо-
ненты для всех внутренних узлов, т. е. dCV Е Сдран. Но V ~ — с/Ф.
следовательно,
ДФ — 0 для всех внутренних узлов.
Другими словами, D1 состоит из йФ, где Ф есть решение зада-
чи Дирихле. Тем самым dimC'-1Zi = dimZj = т. Если есть по
крайней мере один граничный узел, то d : Свнутр —> С1 инъектив-
но, поэтому dimdCgHyTp — Кроме того, dim С1 = п + т — 1 =
пъ — 1 + щ + т. Тогда из уравнения (13.1) следует, что
dimP1 = пь — 1.
Если исключить заземленный узел, то останется пъ~ 1 граничных
узлов, на которых мы можем задать произвольные значения Ф.
Таким образом, задача Дирихле имеет решение всегда.
В качестве примера разложения (13.1) рассмотрим цепь, изоб-
раженную на рис. 13.18. Здесь А, В и С — граничные узлы, а
D — внутренний узел. Поскольку в цепи есть четыре ветви, то
dim С1 — 4. Тогда получаются следующие ортогональные про-
странства.
1. Одномерное подпространство с базисным вектором
13.6. Решение краевых задач методом Вейля
673
1\
Этот вектор соответствует распределению заря-
\ о/
дов С
, для которого р — 0 во всех узлах.
Конечно, при этом нарушается второй закон Кирхгофа, по-
этому эти заряды нельзя получить из потенциала.
2. Одномерное подпространство </CgHyTp с базисным векто-
ром
-1
О
. Этот вектор описывает напряжения на ветвях,
возникающие от потенциала
фА фВ = фС Q, фГ> = 1
3. Двумерное подпространство D1 с базисными векторами
/2/3\
1/3
1
\ о/
( 1/3\
-i/б
i/б ’
\ 2/3/
674
Глава 13. Метод ортогональных проекций
Эти вектора описывают напряжения на ветвях, возникшие
из
фл — фс — О, Фв = 1 и Фл = Фв = О, Фс = 1
соответственно. Причем в обоих случаях р& = 0. (В общем
случае совсем не просто сразу написать базис для D1.)
Решение уравнения Пуассона
Сейчас мы уже можем решить уравнение Пуассона методом ор-
тогональных проекций Вейля. Предположим, что на всех внут-
ренних узлах заданы значения зарядов р. Мы построим любое
распределение напряжений V, для которого — дСУ = р имеет
данные значения на всех внутренних узлах. (При этом V может
даже нарушить второй закон Кирхгофа.) Тогда существует един-
ственное разложение
V-V +W,
где V является элементом и W ортогонален dC®HyTp. Бу-
дучи элементом dC^HyTpi распределение напряжений V может
быть получено из потенциала при условии, что на граничных уз-
лах Ф = 0. Поскольку вектор W ортогонален V, то он лежит
в D1 ® C~XZ\ и поэтому удовлетворяет условию 5CW — 0 для
всех внутренних узлов. Тогда для внутренних узлов — дСУ =
—dCV ~ р, и V является решением задачи. Если тг обознача-
ет ортогональную проекцию С1 на dCgHyTp, то решение можно
записать в форме
V-7TV.
Решение задачи Дирихле
Задача Дирихле тоже может быть решена методом ортогональ-
ных проекций. Пусть Ф обозначает потенциал, который принима-
ет определенные значения на граничных узлах и который равен
нулю на всех внутренних узлах. Пусть V = —t/Ф. Тогда
V = ttV + (1 - 7Г)V.
13.6. Решение краевых задач методом Вейля
675
Поскольку ttV е dC2KyTp, мы можем написать 7rV = —d/ф, где
ф = 0 на граничных узлах. Если записать
(1 - тг)У = ~ЛФ,
то поскольку (1 — tf)V G D1, на всех внутренних узлах удовле-
творяется уравнение ДФ = 0. Более того, поскольку
—</Ф = —d/ф — б?Ф
и — 0 для всех граничных узлов, то на границе Ф — Ф. Тогда
Ф и есть желаемое решение задачи Дирихле.
Примеры
Оба подхода к решению задачи могут быть продемонстрированы
на примере цепи, изображенной на рис. 13.19.
Для этой цепи базисом в пространстве dCgHyTp является век-
тор
/ Л
676
Глава 13. Метод ортогональных проекций
квадрат длины которого (в соответствии с определением скаляр-
ного произведения через матрицу С) равен 1 + 2 + 1 — 4. Тогда
для любого вектора V е С1 мы имеем
ttV = i(V,U)cU.
Действуя оператором
тг на базисные вектора
получим матрицы
/1\
о
о
\°/
/о\
1
о
\°/
-1
О
—2
2
О
2
О
О
О
О
и (! - тг) = J
/3
1
О
2
2
О
—2
О
О
4
О
А
-1
О
3/
Предположим,
для pd = 1. Заряд, равный единице на узле D, может
ЧТО
мы хотели бы решить уравнение Пуассона
быть в
случае Qa ~ Q@ — Qy = 0 и = — 1, так что V =
. Тогда
7TV= 1
4
-1
О
дает нам решение задачи.
1
П ~ 4
1
О
О
О
.., мы
закону
Заметим, что V не обязан удовлетворять второму
Кирхгофа. Кроме того, pjj = 1 и при другом распределении
1 Л 1 Л Л 1
зарядов: Qa = Qp = = 1, Qt = Тогда
О О о
/ 1/3\
-1/6
2
Это распределение напряжений не удовлетворяет второму закону
Кирхгофа, потому что сумма падений напряжения при обходе
13.6. Решение краевых задач методом Вейля
677
ячейки /? + а — 7 не равна нулю. И тем не менее
7TV = 7
4
/ 1
-1
О
V-1
-2 О
2 О
О О
2 О
-1\
1
О
/ 1/3\
-1/6
2
/ 1\
-1
О
\-1/
1
4
что является правильным решением задачи.
Чтобы построить V, проще всего (когда это возможно) при-
писать заряд на каждом внутреннем узле одной ветви, которая
связывает эту ветвь с граничным узлом. В сложных цепях, где
некоторые внутренние узлы связаны только с внутренними уз-
лами, лучше всего начинать именно с таких узлов и двигаться
изнутри наружу. Например, на рис. 13.20 граничные узлы — это
А и Е. Лучше всего начинать с узла С. Если рв = 1, рс — 2,
PD = 3, то выберем Qy = 2. Тогда Q$ = 5, Q& = “1? так что
V 5/
/-Л
о
6
\20/
1/zF „ 2/zF j nF \nF
—£_||—_g-||—U-||—_t-||------•
Л —1+1 В 11 c +2'L2 D +5—5 E
Рис. 13.20
Возвращаясь к рис. 13.19, давайте решим задачу Дирихле для
Фл — 0, Фв — 5 и — 6. Положим Ф = Ф на границе и Фр = 0,
/0\
так что V = — d$ =
. Тогда
W
/16\
1 4
4 20
\8/
/4\
1
5
\2/
678
Глава 13. Метод ортогональных проекций
дает правильное решение при Ф^ = 4. То же самое решение
можно было бы получить для любого произвольно выбранного
значения Ф^.
13.7. Функции Грина
Отображение, приписывающее распределению зарядов р соответ-
ствующий потенциал и, с которым решается уравнение Пуассо-
на, называется оператором Грина. Матричные элементы этого
оператора G в базисе Со, состоящем из узлов, будем обозначать
G(A, В), где А и В — соответствующие узлы. Мы используем обо-
значение G(A,B) вместо привычного Сдв, потому что позднее,
когда будут рассматриваться непрерывные распределения заря-
дов, они удобнее для соответствующих формул. Таким образом,
G(A, В) = потенциалу в узле В
благодаря решению уравнения Пуассона
с единичным зарядом в узле А.
Функция G, приписывающая узлам Л и В матричный элемент
G(A, В), называется функцией Грина. Она зависит от двух пере-
менных. Если фиксировать первую переменную и рассматривать
зависимость от второй переменной, то получается элемент про-
странства G^HyTp. Пусть Д2 обозначает оператор Д, примененный
к элементу G(A, •) пространства CgHyTp. Тогда
-ДС(Д.) = ^
G(A, В) — 0 для узла В на границе.
Повторим эту операцию:
д . W) х^внутр
* ^внутр > ^0
Оператор, обратный к —Д, есть G, поэтому
—Ли — р, если Gp — и.
13.7. Функции Грина
679
Оператор А симметричен, следовательно, симметричен и опера-
тор G. Если взять базис, заданный узлами, то
и(В) — ^2р(А)С(Д В) для всех В,
где суммирование ведется по всем внутренним узлам А.
Функцию Грина можно использовать для решения задачи Ди-
рихле. Для этого удобна формула для суммирования, известная
как формула Грина. Заметим, что если и и v — произвольные
элементы С°, то
22 «(А)Дг?(А) = 22 u(A)dCdv(A)
по всем А по всем А
I и = / du — (du, du),
JdCdv JCdv
где символ (•,•) обозначает симметричное скалярное произведе-
ние в С1. Тогда
22 «(a)av(a) = 22
по всем А по всем А
Если мы разделим всю сумму на слагаемое по граничным узлам
и слагаемое по внутренним узлам, то получим формулу Грина:
(u(A)Av(A) — Au(A)v(A))
по внутр. А
= - 52 («(B)Av(B) - Ди(В)и(В)). (13.2)
по гран. В
Давайте возьмем две внутренних точки и Аг, и в формуле
Грина положим и = G(Ai,-) и v = G(A2,-)- Правая часть (13.2)
обращается в нуль, потому что на границе G(Ai,-) и G(A2,-)
равны нулю. Во внутренних точках и(А) = 0, если А / Ai и
u(Ai) — 1. Аналогично для v и А2. Тогда обращение в нуль левой
части (13.2) значит, что
G(A1,A2) = G(A2,Ai).
680
Глава 13. Метод ортогональных проекций
Если мы напишем и = Ф, Ди = —р и v — Ф, Ди = —Д то
уравнение (13.2) преобразуется в
22 (рсФс-ЭсФс)= 22 (АвФв-рвФв). (13.3)
внутр. С гран. В
Итак, мы видим, что формула Грина есть теорема взаимности
Грина для цепей, содержащих емкости.
Теперь предположим, что Ф является решением задачи Дири-
хле для заданных значений на границе, так что р — 0 внутри. В
формуле (13.3) возьмем Ф = G(A, •). Тогда мы получим
22 (-АС(А, С)Фс - pcG(A, С))
внутр. С
= 22 (pbG(A,B) + ДС(А,В)Фв).
гран. В
Вспомним, что —AG(A, С) = 1, если С = А и нулю во всех
остальных случаях, потому что G(A, С) есть решение уравне-
ния Пуассона с единичным зарядом в узле А и нулевыми заряда-
ми на других внутренних узлах. Кроме того, мы предположили,
что рс — 0 на внутренних узлах. Поэтому в левой части уравне-
ния выживает только один член ФЛ В правой части мы имеем
G(A, В) = 0. Следовательно,
фл= 22 дс(дв)фв.
гран. В
Таким образом, значение потенциала Ф"4 на внутреннем узле А
равно среднему значению потенциалов Фв на граничных узлах с
весовым множителем AG(A,B), который является значением от-
рицательного заряда, индуцированного на граничном узле В, ес-
ли в узле А помещен единичный положительный заряд, а потен-
циал на всех границах равен нулю. Матрица (AG(A, В)), пред-
ставляющая линейное преобразование от GppaH к Санутр, называ-
ется ядром Пуассона.
Давайте применим функцию Грина к расчету цепи, изобра-
женной на рис. 13.18. Поскольку в цепи есть только один внут-
ренний узел В, нам необходимо решить уравнение Пуассона для
13.7. Функции Грина
681
случая рв = 1. Мы уже это сделали и получили вектор напряже-
ний
Поэтому, если узлы А, В и С заземлены, то потенциал на узле
D равен G(D,D) ~ Для этой цепи заряды на граничных
1 1 1 ™
узлах равны: рд = —рв = —рс — — Тогда мы имеем
11 1
AG(P,A) - AG(P,B) - - и SG(D,C) - С помощью
функции Грина мы легко решаем задачу Дирихле для этой цепи.
Если рв — 0, то является усредненным значением граничных
потенциалов с весовыми множителями ДО:
Фв = ДСЩ Л)ФЛ + AG(£>, В)Фв 4- ДС(Г>, С)Фс
= ±фЛ + -фв + -фс
4 2 4 ‘
Существует другой вариант формулы Грина (называемый
второй формулой Грина), который иногда бывает полезен. Возь-
мем граничный узел А. В формуле
Ди(А) = 52 Са(и(А)-и(В))
±да^(В~А)
сумму справа разделим на две части: ветвь а соединяет две гра-
ничные точки или ветвь соединяет граничную точку с внутрен-
ней. Тогда получим
Ди(А)= 52 Ca(u(A)-n(B))
±да==(В—А)
В — внутр, узел
+ 52 Са(и(А) — и(В)).
±да=$В-А)
В — гран, узел
682
Глава 13. Метод ортогональных проекций
Вторую сумму обозначим Дграии(Л). Ветвь, соединяющую две
граничные точки, будем считать отдельной цепью. Тогда Дгран
будет оператором Лапласа для этой подцепи, определяемым ем-
костями ветвей, соединяющих граничные узлы. Следовательно,
52 (и(А)ДгРани(А) - Дгран«(А)у(А)) = О
гран. А
и поэтому
52 (u(A)Av(A) - Ди(А)г(А))
гран. А
= 52 (u(A)Ca(v(A) - v(B)) - Ca(u(A) - u(B))v(A)).
гран. A
da=±(B-A)
внутр. В
Члены, содержащие и(А) г?(А) справа, сокращаются, правая
часть равенства упрощается и принимает вид
52 Ca(u(B>(A)-tz(A)>(B)).
гран. А
внутр. В
Подставляя это в формулу Грина, мы получаем еторую формулу
Грина:
52 (и(А)Д«(А) - Au(A)v(A))
внутр. А
= 52 Ca(u(A)v(B)-u(B)v(A)).
гран. А
да=±(В~А)
внутр. В
13.8. Ядро Пуассона и случайное блуждание
683
13.8. Ядро Пуассона и случайное блуждание
Продолжим изучение задачи Дирихле. Пусть Q = AG — ядро
Пуассона. Тогда если ф G Срран определяет конкретный гранич-
ный потенциал, то 1/, определяемое формулой
т/(А)= £ <2<АВ)ф(в),
гран. В
дает решение задачи Дирихле с краевым условием ф. В преды-
дущем параграфе мы видели, как найти G и, следовательно, Q,
используя метод ортогональных проекций. В этом параграфе мы
дадим вероятностное построение Q. И хотя этот метод обычно
не применяется в конкретных расчетах, он дает нам как новый
взгляд на проблему, так и итерационную процедуру вычисления
матрицы Q.
Сначала вспомним еще раз, в чем состоит задача Дирихле.
Пусть А — любой внутренний узел. Пусть В — ближайший со-
сед узла А, т. е. узел В является началом или концом некоторой
ветви Д соединяющей его с узлом А. (Узел В может быть как
внутренним, так и граничным.) Пусть
(\ -1
Е с°) •
да=±(В-А) /
Тогда условие
(Ди) (Л) = О
совпадает с условием
= ^2и(в)рВ,А,
где сумма берется по всем ближайшим соседям. Заметим, что по
построению
Ра,в>0, =
В
Положим
Ра,A = 1, РА,,А = 0, А' Ф А
684
Глава 13. Метод ортогональных проекций
для всех граничных узлов. Тогда пусть Р обозначает матрицу
п х п с матричными элементами Ра,в* Чтобы определиться с
обозначениями, будем сначала писать граничные узлы, так чтобы
верхний левый угол матрицы Р был единичной матрицей к х Д
где к есть число граничных узлов. Столбец, соответствующий
внутреннему узлу, будет иметь элемент Рв,А на узле В, если В
- ближайший сосед узла А, и нулю во всех остальных случаях.
Условие
Aw — 0 на внутреннем узле А
превращается в
и = иР,
если рассматривать и — (w(Bi), w(B2),...) как вектор-строку.
Если первые к компонент вектора и задаются ф, то таковы же
будут и для первые к компонент wF, поскольку первые к столбцов
Р имеют 1 на fc-м месте и 0 на остальных. Итак, задача Дирихле
может быть сформулирована следующим образом:
иР — w, и первые к элементов и определяются ф.
С другой стороны, матрица Р имеет структуру матрицы веро-
ятностей перехода. Действительно, предположим, что у нас есть
частица, находящаяся в каком-то узле цепи в каждый дискрет-
ный момент времени t — 1,2,... Допустим, что она двигается
согласно следующему правилу. Если в какой-то момент времени
t она находится в граничном узле, то она там и остается. А ес-
ли она находится на внутреннем узле, то должна перескочить на
какой-либо соседний узел, при этом вероятность ее перехода на
узел В равна Рв,А-
Матрица PN представляет вероятность перехода после N ша-
гов. Очевидно, что предельное поведение матрицы PN имеет ве-
роятностную интерпретацию. Начав с любого внутреннего узла,
после достаточно большого числа шагов получится ненулевая ве-
роятность частице оказаться на граничном узле, и с вероятно-
стью меньше единицы она останется во внутренней части це-
пи. Последняя вероятность при некотором N допускает единую
оценку сверху для всех начальных внутренних узлов, поэтому с
дальнейшим ростом числа шагов вероятность частице остаться
13.8. Ядро Пуассона и случайное блуждание
685
на внутренних узлах стремится к нулю. Таким образом, предель-
ное выражение матрицы PN принимает вид
где I — единичная матрица к х /с, a Q — матрица, у которой к
строк и п — к столбцов, причем п — к есть число внутренних узлов.
Матричный элемент Q(A, В) представляет вероятность того, что
частица, начав двигаться из точки А, в конце концов придет в
граничную точку В. (Путь частицы рано или поздно закончится
в некой граничной точке.) Тогда PN Н и, следовательно,
pN+i __ pNp откуда HP — Н. Поэтому если v — какой-то
потенциал, то для vH выполняется условие
(vH)P - vH
и, следовательно,
u vH
является решением задачи Дирихле, когда краевыми условиями
будут первые к компонент вектора v. Если первые к компонент
задаются </>, т. е. если v выбирается в виде
v = (ф, w), w — любой из п — к векторов-строк,
то vH является решением задачи Дирихле. Из вида матрицы
Н очевидно, что для любого внутреннего узла А выполняется
условие
и(А) = (уЯ)(Л) = £ 0(A)Q(A,B).
гран. В
Следовательно, Q действительно является ядром Пуассона.
Матрице Р, т. е. предельному виду матрицы PN, можно дать
интересную геометрическую интерпретацию. Матричный эле-
мент P7V(A2,Ai) определяет вероятность перехода из А-± в А^
после N шагов. Эта вероятность равна сумме вероятностей всех
TV-шаговых траекторий, ведущих из А^ в А2. (Если А^ — гранич-
ный узел, то некоторые из этих траекторий фактически имеют
меньшую длину, т. е. в течение последних т шагов частица стоит
686
Глава 13. Метод ортогональных проекций
в точке А2-) Вероятность любой траектории равна произведению
Рв,А по всем ветвям а, проходимым вдоль траектории. Если А
— внутренний узел, а В —- внешний, то очевидно, что с ростом
N при вычислении P7V(B,A) мы добавляем все более длинные
пути. Тогда
Q(b,a) = (вероятность пути).
по всем путям,
соединяющим
А с В
13.9. Теорема взаимности Грина
в электростатике
В качестве небольшого обобщения цепей с емкостями можно рас-
смотреть систему заряженных проводников, каждый из кото-
рых имеет определенный заряд р и определенный потенциал ф
(рис. 13.21). Чтобы описать аналог ветви для системы такого ти-
па, требуется введение поля диэлектрического смещения и по-
этому должно быть отложено до главы 16, в которой мы будем
изучать электростатику. Однако, описание цепи через заряды и
потенциалы имеет много общего с описанием емкостных цепей.
Полный заряд на каждом проводнике может описываться век-
Рв I в пространстве, обозначаемом Со; потенциал
же образует вектор ф = (фА, фв,...) в его дуальном пространст-
ве С°. Для цепей с емкостями скалярное произведение элемента
пространства С° на элемент пространства Со дает электроста-
тическую энергию системы проводников, т. е. энергию, равную
/рФ = Т^РлФА> (В главе 16 мы увидим, что это выражение
равно интегралу
J\(1ф, с1ф) dx dy dz
по пространству между проводниками, где ф обозначает электро-
статический потенциал. А сейчас мы просто ограничиваемся
описанием того, что происходит в проводниках.)
13.9. Теорема взаимности Грина в электростатике
687
Рис. 13.21
Полный заряд проводника р может быть выражен через по-
тенциал ф с помощью оператора Лапласа Д, т. е.
р = —Дф.
Оператор Д зависит от формы различных проводников, от их
распределения в пространстве и физических констант электро-
статики. Кроме ряда частных случаев, когда в системе есть па-
раллельные плоскости, концентрические сферы или цилиндры,
вычисление Д очень трудно. Однако, как мы узнаем в главе 16,
для системы проводников выполняется теорема взаимности Гри-
на, точно так же, как она выполняется для цепей с емкостями.
Говоря точнее, если риф обозначают возможное распределение
полного заряда и напряжений в системе проводников, a pf и ф'
обозначают другое распределение, то теорема взаимности Грина
утверждает, что
[ ф= [ф'.
Jpf Jp
Отсюда немедленно следует, что оператор Д самосопряжен
и представляется симметричной матрицей. Чтобы это увидеть,
положим
р = —£±ф, pf — —кф'.
Тогда
/ Ф = f Ф^
J—j—&ф
т. е.
(Аф'.ф) = (ф',Дф),
688
Глава 13. Метод ортогональных проекций
откуда следует, что Д самосопряжен. В физической литературе
оператор Д обычно называют матрицей емкостных коэффици-
ентов.
Матрица, обратная к — Д, называется матрицей потенциаль-
ных коэффициентов. Мы напишем эту матрицу для ряда простых
частных случаев через хорошо известные формулы элементарной
электростатики. Например, рассмотрим систему двух концентри-
ческих сфер (рис. 13.22) с радиусами г а и г в- Для сферы с ради-
усом го, обладающей единичным положительным зарядом, элек-
трический потенциал, выраженный в гауссовых единицах, имеет
вид
Ф(г>=(;/г” ’°’’
4 7 [ 1/т (г > Го).
(См., например книгу Purcell «Электричество и магнетизм», па-
раграф 1.11.) Позднее в параграфах 16.1 и 16.2 мы выведем этот
результат альтернативным путем из первых принципов.
Рис. 13.22
Если pa — 1, рв = 0, то потенциалы фА = 1/гд, фв = l/r^.
Однако если рА — 0, рв = 1, то оба потенциала равны фА — фв —
1/гв- Отсюда следует, что
д-1 = (у;*
V/rB
1/гв\
Утв) '
Эта матрица позволяет нам вычислить потенциал двух сфер для
произвольного распределения зарядов. Обратная матрица дает
13.9. Теорема взаимности Грина в электростатике
689
оператор Лапласа
_________V1 f 1/гв -1/гвА
\гВГА Т2В) \-^-/гв ^/та)
или
_Д ГАТВ /1 -1 А = ГВ / ГА -Га\
ГВ ~ ГА к-”1 Гв/га) Гв ~ ГА \~ГА ГВ) *
Эта матрица определяет заряды на двух сферах при заданных
потенциалах. В случае Фа — 1, Фв — 0 мы имеем
(рд\ = глгв / 1\
\Рв) г в “ ГА \“1/ ’
т. е. на двух сферах есть два заряда с противоположными знака-
ми, равные гагв/(гв — гд). Эта величина гагв/(гв — га) назы-
вается емкостью двух сфер.
Матрицу -Д'1 одинаково легко написать для любого числа
концентрических сфер. Например, для трех сфер, изображенных
на рис. 13.23, она равна
(1/гд 1/гв 1/гс
1/гв 1/гв 1/гс
1/гс 1/гс 1/гс
Рис. 13.23
690
Глава 13. Метод ортогональных проекций
А сейчас представим себе цепь с емкостями и пусть некото-
рые проводники будут граничными проводниками, потенциалы
которых определяются подсоединенными батареями, а на других
проводниках, называемых внутренними, задается заряд. В за-
даче Пуассона мы имеем потенциалы ф' ~ 0 на всех граничных
проводниках и заряды р* на всех внутренних. Требуется найти ф'
для всех внутренних проводников и р' для всех граничных. А в
задаче Дирихле нам дано, что р — 0 на внутренних проводниках
и ф на всех граничных. И мы должны найти ф для внутренних
проводников и р для граничных.
Эти две задачи связаны между собой теоремой взаимности
Грина. В общем случае
Р1аФА + У? РвФВ = У? РаФ'А + У? РвФ?В•
гран. А внутр. В гран. А внутр. В
Нам дано, что ф' — 0 на граничных проводниках (задача Пуассо-
на) и р — 0 на внутренних (задача Дирихле). Тогда получаем
22 р'вФв = 52 р'^А-
внутр. В гран. А
Допустим, что в задаче Пуассона Q(C, А) обозначает заряд
Рд на граничном проводнике А, имеется единичный заряд на
внутреннем проводнике С, а заряды всех остальных внутренних
проводников равны нулю. Тогда слева выживает только один
член, и мы имеем
фс = -£<Э(С,А)фА, где Q(C,A) = -£G(C,A).
Эта функция Грина является решением задачи Дирихле.
На практике довольно часто для системы проводников мож-
но легко решить задачу Дирихле, а затем с помощью теоремы
взаимности решить уравнение Пуассона. Рассмотрим, например,
систему из трех больших параллельных проводящих плоскостей,
показанную на рис. 13.24. На этой схеме А и С - граничные
проводники, а В — внутренний. В этой геометрии потенциал яв-
ляется линейной функцией положения между плоскостями. Сле-
довательно,
фв = ФА+ -АФС - ФА)
о
13.9. Теорема взаимности Грина в электростатике
691
АВ С
Рис. 13.24
или
Фв = \фА+\фс-
о о
Это и есть решение задачи Дирихле.
А теперь рассмотрим уравнение Пуассона с зарядом pfB на
внутренней плоскости. При этом ф'А — ф(С — 0. Из теоремы
взаимности следует, что
РвФВ = -р'аФА - РсФС-
Однако для произвольной задачи Дирихле фв — ^фА + ^ФС
следовательно,
Рв ’ + Рв ’ ^ФС — ~~РаФА “ РсФС•
о о
Отсюда следует, что
/ 2 ' г! - 1 л'
Ра —-^Рв, Рс — ~~^Рв^
т. е. мы выяснили, как индуцированный заряд распределяется
между двумя граничными плоскостями.
В общем случае теорема взаимности Грина может применять-
ся в задачах, где имеются как проводники, так и распределе-
ния зарядов в области, ограниченной этими проводниками. На-
пример, если заряд помещен вблизи бесконечной заряженной
692
Глава 13. Метод ортогональных проекций
Рис. 13.25
плоскости (рис. 13.25), то электрический потенциал везде на той
же стороне плоскости, где находится заряд, может быть опреде-
лен методом изображений, т. е.
<КР) = --11
г г
(см. параграф 16.1). Для этой потенциальной функции можно по-
лучить распределение отрицательного заряда вдоль проводящей
плоскости. А это, в свою очередь, дает возможность решить за-
дачу Дирихле, когда везде на плоскости задан потенциал и тре-
буется найти распределение потенциала во всем пространстве.
Аналогичным способом строится функция Грина для решения
уравнения Пуассона, когда точечный заряд находится внутри за-
земленной проводящей сферы. Потом эта функция используется
для решения задачи Дирихле, когда на поверхности сферы задан
потенциал и требуется найти потенциал в области, ограниченной
сферой и свободной от зарядов.
Резюме
А. Ортогональные проекции
Вы должны знать свойства самосопряженного проекционного
оператора тг для цепей с резисторами и использовать его для
расчета таких цепей.
Вы должны уметь строить оператор тг, пользуясь процедурой
Грама-Шмидта или методом Кирхгофа.
Задачи
693
В. Цепи с емкостями
Вы должны уметь рассчитывать цепи с емкостями с помощью
методов Максвелла или обращения оператора Лапласа.
Для расчета цепей с емкостями Вы должны уметь решать
уравнение Пуассона или задачу Дирихле с помощью ортогональ-
ных проекций; должны описывать связанное с этим разложение
С1 на ортогональные подпространства.
С. Функции Грина
Вы должны уметь строить функцию Грина для цепи с емкостями
и использовать ее для решения уравнения Пуассона и задачи
Дирихле.
Задачи
13.1. Рассмотрите цепь, изображенную на рис. 13.26.
(а) Напишите базис пространства Zi. Объясните смысл утвер-
ждения «оператор тг представляет проекцию Су на подпро-
странство Zi». Выполнив соответствующие вычисления, до-
кажите, что матрица
1 /5 2 2\
тг = - 4 3 —4 I
7 \1 -1 6/
представляет проекцию С\ на Z\.
694
Глава 13. Метод ортогональных проекций
(Ь) Для этой цепи найдите токи в ветвях, используя матрицу
7г. Сделайте рисунок, показывающий образ и ядро тг, пока-
жите, как с его помощью решить эту задачу.
(с) Какое линейное преобразование представляется матрицей
тгг, транспонированной к тг? Назовите и дайте характери-
стику с физической точки зрения пространству, являюще-
муся ядром этого преобразования. Обоснуйте свой ответ ли-
бо с помощью общей теоремы, либо ссылаясь на соответ-
ствующие свойства матрицы тгт.
13.2. (а) Постройте матрицу 2x2, представляющую тг *. С± Z, для
цепи, изображенной на рис. 13.27.
(Ь) Сделайте рисунок, показывающий образ и ядро тг. На нем
покажите вектора К и I = тгК.
13.3. Рассмотрите цепь, изображенную на рис. 13.28.
(а) Используя процедуру Грама -Шмидта, преобразуйте базис
Mi =
/ц
1
о
\о/
в ортонормальный базис {Ei,E2} пространства Z±. Приме-
няя операцию тг! — (Ei,I)^Ei 4- (Е2,1)^Ез по очереди к
каждому из четырех базисных векторов С±, постройте мат-
рицу, представляющую тг, и рассчитайте данную цепь.
Задачи
695
4А
Рис. 13.28
(b) Для этой цепи докажите формулу тг = (t(sZct) xsZ.
(с) Постройте матрицу Z(1 — тг) и покажите, что ее образ есть
пространство В1.
Ответ:
1
50
28 24 4\
36 -12 —2 I
-8 36 6 I
-8 36 6/
13.4. (а) Для цепи, изображенной на рис. 13.28, постройте матрицу,
представляющую
т t С1
которая проектирует пространство С1 на В1, причем про-
ектирует ортогонально по отношению к скалярному произ-
ведению, определенному преобразованием Z-1, т. е.
(V,V')z-x = [ V.
Jz~rv'
Чтобы построить базис для пространства В1, положите по-
тенциал равным нулю в узле А (заземлите его) и — 1 в узлах
В и С.
(Ь) Покажите, что V = t(W — ZK) и используйте эту формулу
для расчета цепи, изображенной на рис. 13.28.
13.5. (а) Найдите явное выражение для матрицы т из предыдущего
упражнения через [d], Z~l и [5]. С помощью этой матрицы
696
Глава 13. Метод ортогональных проекций
покажите, что т2 = г, что образ т есть В1, что т — самосо-
пряженная матрица по отношению к скалярному произве-
дению, определенному Z-1.
(Ь) Покажите, что для любой цепи матрица
+ <t(sZ<t)~1sZ,
представляющая линейное преобразование из С\ в Ci, яв-
ляется единичной матрицей.
13.6. Для цепи, изображенной на рис. 13.28, с помощью метода Кирх-
гофа сделайте следующее.
(а) В цепи есть пять различных максимальных деревьев. Для
каждого дерева получите матрицу р? (4x4). Заметим, что
каждая пара ветвей, кроме {а, /?}, образует дерево. (Следи-
те за знаками — все диагональные элементы матрицы рт
должны быть >0.)
(Ь) Для каждого дерева вычислите Qr и найдите R = ^,Qt-
(Получится R = 50, что совпадает с Det(sZcr). Будет ли это
так в общем случае?)
(с) Воспользуйтесь формулой Кирхгофа
т
чтобы получить проекционный оператор тг методом Вейля.
13.7. Придумайте изменение в методе Кирхгофа, чтобы построить са-
мосопряженный проекционный оператор т : С1 —> С1, облада-
ющий таким же свойством V = t(W — ZK), что и усредненное
значение проекций С1 на Z1, взятых с определенными весами, и
не являющееся самосопряженным оператором. Один из способов
сделать это — начать с метода Кирхгофа в пространстве С\ и
потом обе части умножить на Z.
13.8. Докажите формулу для проекционного оператора Вейля тг =
cr(sZa)~1sZ, проверив, что тг обладает требуемыми свойствами:
(а) тг является проекцией: тг2 = тг;
(Ь) образом тг является Zj;
(с) тг — самосопряженный оператор относительно (•, -)z, т. е.
(ttI,I')z = (I,7tI')z.
Задачи
697
13.9. (а) Для цепи, изображенной на рис. 13.29, постройте матрицу
тг, представляющую ортогональную проекцию пространства
Ci на подпространство Zi. Воспользуйтесь этим проекцион-
ным оператором для вычисления токов в ветвях I. (Все токи
задаются целыми числами.)
(Ь) Для этой цепи постройте базис ядра оператора я. Восполь-
зуйтесь им, чтобы показать в явном виде, что ядро тг орто-
гонально его образу.
13.10. В качестве иллюстрации теоремы взаимности Грина рассмотрите
цепь, изображенную на рис. 13.30.
Рис. 13.30
(а) Если между узлами АиВ вставить батарею на 60 вольт, то
какой ток потечет между узлами С и D при замыкании их
698
Глава 13. Метод ортогональных проекций
накоротко? Если, наоборот, батарею вставить между узлами
С и D и устроить короткое замыкание А с В, то какой ток
потечет через АВ?
(Ь) Если источник тока на 25 ампер вставить между узлами А
и В, то какое напряжение возникнет в CD (узлы разомкну-
ты)? Если, в свою очередь, тот же источник тока вставить
между узлами С и D, то какое напряжение возникнет в АВ?
13.11. (а) Для цепи, изображенной на рис. 13.31, постройте симмет-
ричную матрицу Ztt, Используйте ее для определения на-
пряжения на ветвях V, если в ветвь а вставлен источник
тока, дающий 8 ампер. Найдите V также в случае, когда
тот же источник вставлен в ветвь 7.
(Ь) Для той же цепи постройте симметричную матрицу ttZ”1.
Воспользуйтесь ей для определения токов в ветвях I, если
в ветвь а вставлена батарея, дающая напряжение 16 вольт?
Какой будет ток, если ту же батарею вставить в ветвь 7?
Рис. 13.31
Рис. 13.32
13.12. Определите заряд на каждом конденсаторе цепи, изображенной
на рис. 13.32, используя метод круговых токов и метод узловых
потенциалов. Предположим, что [5]Q = 0, т. е. что до подклю-
чения батарей все конденсаторы не были заряжены. (Если нуж-
но, определим единицы: напряжение V измеряется в вольтах, ем-
кость С — в микрофарадах, а заряд Q — в микрокулонах.)
13.13. В цепи, изображенной на рис. 13.33, рв ~ 13 и рс = —1, поэтому
рА = —12. Решите уравнение Пуассона ДФ = ~р для этой цепи и
определите Фв и Фс. Вычислите заряды на ветвях Q и проверьте,
/~12\
что 5Q = - I 13 I.
\ -1/
Задачи
699
Рис. 13.33
Рис. 13.34
13.14. Для цепи, изображенной на рис. 13.34, напишите матрицы d и д.
Для рв = Ю и рс = —2 решите уравнение Пуассона и найдите
потенциалы узлов Фв и Фс.
13.15. Рассмотрите цепь конденсаторов, изображенную на рис. 13.35.
Узлы А и В — граничные, а узел С — внутренний.
Рис. 13.35
(а) Постройте матрицу 2x2 оператора тг, который является
ортогональной проекцией (относительно скалярного произ-
ведения, определенного С) С! на ^С^нутр.
(Ь) Вектор W = соответствует ситуации, когда на узле
С находится заряд 4. Воспользуйтесь оператором тг для на-
хождения распределения зарядов в случае, если узлы А и
В заземлены.
(с) Предположим, что потенциал узла А равен Фл = 0, потен-
циал узла В равен Фв = 4 и заряд узла С равен нулю.
700
Глава 13. Метод ортогональных проекций
Воспользуйтесь оператором тг и определите напряжения в
ветвях Va и V&.
13.16. Рассмотрите систему конденсаторов, показанную на рис. 13.36.
В этой цепи узлы А и D граничные, а узлы В и С внутренние.
(а) Для этой цепи напишите матрицы д и d.
(b) Пусть =
/°\
1 и ф2 =
\о/
— векторы в пространстве
С°. Вычислите d0i и d02- Покажите, что они ортогональны
по отношению к скалярному произведению, определенному
матрицей емкостей С.
(с) Пусть тг представляет ортогональную проекцию из С1 на
подпространство, заданное векторами d$i и dfa- Вычислите
(1\
0 J.
°/
(d) Пусть на узле В находится единичный заряд, на узле С
заряд равен нулю, а узлы А и D заземлены. Воспользуйтесь
ортогональной проекцией и вычислите потенциалы узлов В
и (7. Найдите заряды на узлах А и D.
Рис. 13.37
Рис. 13.36
Задачи
701
(е) Пусть Фл = 5, = 0, на узлах В и С нет зарядов. Вос-
пользуйтесь методом ортогональных проекций и определи-
те напряжения на ветвях V.
(f) Для задачи, поставленной в пункте (е), покажите, как найти
Фв, используя функцию Грина из пункта (d).
13.17. Рассмотрите цепь конденсаторов, показанную на рис. 13.37. Узлы
А и В — граничные, а узлы С и D — внутренние.
(а) Вектора
являются элементами пространства С°. Назовите, какое
пространство они задают, и дайте ему физическую характе-
ристику. Определите и ^2» Покажите, что они образу-
ют ортогональный базис подпространства С1 относительно
скалярного произведения, определенного С.
(Ь) Пусть тг обозначает ортогональную проекцию пространства
С1 на подпространство, для которого только что получен
базис. С физической точки зрения дайте характеристику
векторам, которые принадлежат ядру оператора тг. Вычис-
'0'
0
лите тг
(с) Пусть на узле D находится единичный положительный за-
ряд, на узле С заряда нет, а узлы А и В заземлены. Ис-
пользуя результат пункта (Ь), найдите заряды и напряже-
ния всех ветвей.
(d) Пусть на узле D находится заряд 2, на узле С заряда нет,
ФА = 4и Фв = 1. Используя только что полученную функ-
цию Грина, определите потенциал узла D. (Указание: эта
задача является суперпозицией задачи Дирихле и задачи
Пуассона.)
13.18. Рассмотрите цепь, изображенную на рис. 13.38. Узлы А, В иС
— граничные, а узлы D и Е — внутренние.
702
Глава 13. Метод ортогональных проекций
(а) Получите базис подпространства С С° и dC®HyTp С
С1. Проверьте, что матрица
8 1 8 2 3\
2 5 2 10 —4
8 18 2 3
2 5 2 10 -4
6—4 6—8 7/
проектирует С1 на это подпространство.
(Ь) Постройте матрицу 1 — тг и проверьте, что ее образ ортого-
нален образу тг.
(с) Проверьте, что Н1 (образ Zi при действии С"1) является
ядром тг.
(d) Постройте матрицу (1 — тг)й, представляющую преобразова-
ние из С° в С1. Проверьте в явном виде, что если Ф — произ-
вольный базисный вектор в CJ? , то V = — (1 — тг)</Ф описы-
вает множество напряжений ветвей, для которых дС\ = 0
на внутренних узлах D и Е.
13.19. Для цепи, изображенной на рис. 13.38, используйте матрицу
(1 — ?r)d и решите задачу Дирихле для потенциалов ФА = 3,
Фв = —5, Фс = 0 при pD — Ре — 0- Получите Ф^*, Ф^, рд, рв
и рс.
13.20. В предыдущем упражнении решите уравнение Пуассона для слу-
чая, когда
РЕ = 1, PD - 0, ФА = Фв - Фс = 0.
(а) Выберите любое значение Q, удовлетворяющее условиям
PD = 0, рв = 1. Постройте вектор напряжений в ветвях
V = C^Q.
Задачи
703
(b) Вычислите V = ttV и определите такой потенциал, чтобы
на границе Ф = 0 и — t/Ф = V.
(с) Повторите пункты (а) и (Ь) с другими значениями Q. Вы
должны получить тот же самый ответ.
(d) Решите уравнение Пуассона для случая р& = 1, рЕ = 0. Для
этой цепи уже построена функция Грина. Воспользуйтесь
ей и решите уравнение Пуассона для рр = Ю и рЕ = 7.
(е) Используя функцию Грина, постройте ядро Пуассона
ДС(Л, В). Это будет матрица с тремя столбцами и двумя
строками, которая представляет отображение
Транспонированная к ней матрица отображает
(f) Проверьте, что ядро Пуассона дает правильное решение за-
дачи Дирихле, поставленной в упражнении 13.18(c).
13.21. Конденсатор состоит из трех длинных коаксиальных цилиндров
с длиной I и радиусами г а = а, г в ~ 2а, г с ~ 8а.
(а) Решите задачу Дирихле, когда цилиндр В не заряжен, а
разница потенциалов между цилиндрами А и С равна Ф°.
(Ь) Используя теорему взаимности Грина, решите уравнение
Пуассона, если цилиндры А и С заземлены, а заряд Q на-
ходится на цилиндре В.
13.22. Три концентрических проводящих сферы имеют радиусы га ~ 2,
г в = 3, гс ~ 4 соответственно.
(а) Для этой системы напишите матрицу — Д-1, обратите ее и
постройте оператор Лапласа — Д.
(Ь) Пусть потенциалы равны фА = 0, фв = 1, фс ~ 0. Опреде-
лите заряд на каждой сфере.
13.23. Четыре больших проводящих плоскости (площади Ло каждая)
находятся на расстоянии I друг от друга (рис. 13.39).
704
Глава 13. Метод ортогональных проекций
Рис. 13.39
(а) Решите задачу Дирихле, когда заданы потенциалы фА. ф®,
а плоскости В и С не заряжены.
(Ь) Используя теорему взаимности Грина, решите уравнение
Пуассона для задачи, когда плоскости А и D заземлены,
а на внутренних плоскостях находятся заряды Qb и Qc>
Определите потенциалы фв, фс и заряды Qa, Qp.
Глава 14
Комплексы высших
размерностей
В этой главе мы закончим введение в алгебраическую
топологию. Вкратце опишем, как одномерные резуль-
таты, полученные в главах 12 и 13, обобщаются на
случай большего числа измерений.
14.1. Комплексы и гомологии
В этой главе мы прервем изучение электрических цепей и рас-
смотрим ряд обобщений тех математических методов, которыми
мы занимались в предыдущих главах. Мы определили одномер-
ный комплекс как систему, состоящую из объектов нулевой раз-
мерности, названных узлами, и одномерных объектов, названных
ветвями. Ветви соединяются между собой в узлах. Такие ком-
плексы представляют особый интерес с точки зрения связности,
что нашло свое отражение в пространстве Но. Важным также
является число независимых ячеек, которое равно размерности
пространства Hi. В этой главе мы будем рассматривать ком-
плексы с большим числом измерений, т. е. содержащие двумер-
ные, трехмерные и т. д. элементы. В двумерном комплексе или
2-комплексе, помимо узлов и ветвей, имеются двумерные элемен-
ты (куски поверхности), которые мы будем называть 2-ячейками
или гранями. На рис. 14.1 показано, что эти грани соприкасаются
друг с другом вдоль ветвей. Граница грани состоит из несколь-
ких ветвей, причем каждая входит со знаком плюс или минус.
706
Глава 14. Комплексы высших размерностей
Трехмерный комплекс содержит трехмерные элементы (объем-
ные куски), называемые 3-ячейками, которые касаются друг дру-
га вдоль граней. Граница 3-ячейки состоит из нескольких граней,
причем каждая входит со знаком плюс или минус.
В общем случае п-комплекс состоит из конечного множества
п + 1 элементов So, Si, S2, • •., Sny связанных между собой рядом
условий, которые мы опишем позже, после введения обозначе-
ний. Множество So состоит из элементов нулевой размерности,
т. е. из узлов. Множество Si состоит из одномерных элементов,
т. е. из ветвей. Множество S2 состоит из двумерных элементов,
т. е. из граней и т. д. Поскольку у нас нет достаточного числа
подходящих алфавитов для обозначения объектов различной раз-
мерности, то элементы So обозначаем О1,О2,Оз,..., элементы Si
обозначаем li, I2,I3, * • •, элементы S2 обозначаем 21,2г, 2з ... и
так далее. В последующих примерах для обозначения элементов
So будем пользоваться латинскими буквами, элементы Si будем
обозначать греческими буквами, элементы S2 будем обозначать
словами (например, цветами Красный, Синий и т. д.).
Для каждого множества S& введем векторное пространство
fc-цепей Cfc, состоящее из векторов, компоненты которых индек-
сированы элементами S^. Из изучения электрических цепей нам
известны пространства Со и Сь В общем случае размерность про-
странства Ск равна числу элементов S&. Как и раньше, элемент
множества Sk будем идентифицировать с вектором, у которого
одна компонента, соответствующая этому элементу, равна еди-
14.1. Комплексы и гомологии
707
нице, а остальные компоненты равны нулю. Например, для ком-
плекса, изображенного на рис. 14.1, мы имеем вектора в прост-
ранстве Со : 01 = А = (1,0,0,... )т, О2 — В = (0,1,0,... )т, и т. д.;
в пространстве Ci : li = а = (1,0,0,... )т\ 21 = (3 = (0,1,0,... )г
и т. д.; в пространстве : 21 = Красный = (1,0)т, 22 = Синий =
(0,1/.
Чтобы закончить описание комплекса, мы должны опреде-
лить граничный оператор, в действительности последователь-
ность граничных операторов, которую будем обозначать тем же
символом д : > Cfc-i для любого к. Оператор д приписы-
вает каждому элементу определенную комбинацию элементов
множества Sk-i (с соответствующим знаком), которая и образует
границу этого элемента. Оператор д определен для каждого ба-
зисного элемента Ck и, следовательно, определяет линейное отоб-
ражение Ck на Cfc-i. (Для к = 0 мы выбираем 5 = 0, поскольку
не существует элементов отрицательной размерности.)
Для 2-комплекса, показанного на рис. 14.1, мы имеем
да = В — А, д/3 = С — А, и т. д.
Эти соотношения определяют граничное отображение из (Д в Со,
которое представляется матрицей 8x6. Чтобы написать этот опе-
ратор в явном виде, необходимо на рисунке изобразить стрелками
ориентацию каждой ветви. Аналогично, чтобы написать гранич-
ный оператор из в Ci, мы должны задать ориентацию каждой
грани (по часовой стрелке или против). Границей грани являет-
ся замкнутый путь вдоль ее периметра, проходимый в направле-
нии, совпадающим с ориентацией грани. Например, на рис. 14.1
^(Красный) = а + 7 — /3, а Э(Синий) — 7 + — s — 5. В качестве
отображения из С2 в Ci граничный оператор задается матрицей
/ 1 0\
-1 о
1 1
о о
о о
\ 0 V
708
Глава 14. Комплексы высших размерностей
в базисах {Красный, Синий} пространства С2 и {а,/?, 7,е, А,
пространства Ci.
При изучении одномерных комплексов мы обнаружили, что
полезно рассматривать подпространства ядра и образа операто-
ра д. Обобщим эту идею, определив пространство k-циклов Z^,
которое будет подпространством С&, состоящим из элементов с
нулевой границей, т. е. ядро д : Например, на рис. 14.1
• Z2 является нулевым подпространством, потому что нет
такой нетривиальной линейной комбинации Красный и
Синий, которая имеет нулевую границу;
• Zj является трехмерным подпространством, порожденным
ячейками
Mi = а + 7 — /3, М2 = 7 + ^ — 6 — 5, М3 = А — ц —
• Zo есть все пространство Со, поскольку по определению
дс — 0 для любой 0-цепи с.
Аналогично определим В& — пространство fc-границ, которое бу-
дет подпространством С^, состоящим из элементов, являющими-
ся границами элементов пространства C^+i, т. е. образ д : С&+1 —*
Cfc. Для комплекса, изображенного на рис. 14.1,
• В2 является нулевым подпространством, потому что не
существует трехмерных элементов в двумерном комплек-
се (точно так же, как в одномерных комплексах, которые
мы рассматривали, В± всегда было нулевым подпростран-
ством) ;
• Bi является двумерным пространством, базис которого об-
разуют ^(Красный) — а + 7 — /3 и З(Синий) = 7 + 2/ — 6 — 5;
• Во является пятимерным подпространством; так же, как
если бы комплекс был одномерным, а не двумерным.
В этом примере каждое пространство В^ является подпро-
странством соответствующего Z^, т. е. каждая граница являет-
ся циклом. Немного подумав, можно убедиться, что это свой-
ство должно выполняться для любого двумерного комплекса,
14.1. Комплексы и гомологии
709
схема которого подобна рис. 14.1. Поскольку нулевое, оче-
видно, что оно является подпространством Z^ Поскольку грани-
ца любого многоугольника — замкнутая траектория, то Bi есть
подпространство Zi. И наконец, поскольку Zq — это все про-
странство Со, очевидно, что Bq есть подпространство Zq. Усло-
вие Вк С Zk можно вывести и по-другому. Поскольку Вк есть
образ д : C&+i —> С& и Z& есть ядро д : Ск Ck-i, то усло-
вие Вк С Zk означает, что композиция д о д : Cfc+i —> Ck-i равна
нулю. Другими словами: граница границы есть нуль. Из последу-
ющих примеров станет ясно, почему это справедливо для любого
комплекса.
Гомологии
Поскольку В к является подпространством Z&, то можно образо-
вать факторпространство Нк = Zk/Bk, которое называется про-
странством к-мерных гомологий комплекса. Оказывается, что
оно имеет более фундаментальное значение, чем Zk и В к по от-
дельности. Пространства Zk и В к связаны со свойствами данного
комплекса, a Н^ как мы скоро увидим, связано со свойствами
пространства, построенного из элементов комплекса.
При изучении электрических цепей мы уже встречались с про-
странствами Hq и Я1. Вспомним, что размерность Но равна чис-
лу связных компонент, а его дуальное пространство Я0 интер-
претируется как пространство потенциалов, которые постоянны
на каждой связной компоненте. Поскольку пространство границ
Bi нулевое для 1-комплекса (в нем нет двумерных элементов), то
Hi — Zi/Bi — Z±. Таким образом, для любого один-комплекса
Hi есть пространство циклов Zi, которое играет столь важную
роль в методе круговых токов Максвелла.
Давайте рассмотрим пространство Нк для 2-комплекса, изоб-
раженного на рис. 14.1. Поскольку у этого комплекса нет 2-цик-
лов, пространство Z2 есть {0}, аналогично пространство Н^ тоже
пулевое. Поскольку Z\ — трехмерное пространство, a Bi — дву-
мерное, то факторпространство Hi ~ Zi/Bi одномерно. Если по-
смотреть на рисунок, то видно, почему: путь А — р — у не является
границей никакого элемента пространства С*2- Если треугольник
CEF добавить к комплексу в качестве третьего элемента С2, то
710
Глава 14. Комплексы высших размерностей
путь А — — и стал бы границей и размерность пространства
Hi была бы равна нулю. И наконец, поскольку комплекс связен,
пространство Hq одномерно.
В качестве примера трехмерного комплекса рассмотрим тет-
раэдр со всеми его гранями, ребрами (ветвями) и вершинами (уз-
лами), показанный на рис. 14.2(a). Развернутая поверхность тет-
раэдра изображена на рис. 14.2(6). В комплексе имеется четыре
вершины: А, В, С, В; шесть ребер: а, /3, 7, 6, е, 77; четыре грани:
Красный, Жёлтый, Зелёный, Синий. Ориентация каждой грани
выбирается так, чтобы стрелка, показанная на рисунке, враща-
лась против часовой стрелки, если смотреть на тетраэдр снаружи
(см. Зелёный и Жёлтый на рис. 14.2(a)), и по часовой стрелке,
если смотреть на него изнутри (см. рис. 14.2(6)).
Из рисунка легко увидеть, что граничный оператор из С% в
Ci определяется формулами
^(Красный) — —а — /3 — 7,
^(Зелёный) = а + е — 5.
Поскольку граница каждой грани является циклом, то каждая
такая граница имеет нулевую границу, т. е.
5[5(3елёный)] = д(а + г - 5) - (В - А) + (В - В) - (В - А) — 0.
14.1. Комплексы и гомологии
711
В этом комплексе имеется один трехмерный элемент — сам
тетраэдр. Чтобы написать граничный оператор из Сз в С2, на-
до приписать этому элементу ориентацию. (Хотя совсем не про-
сто изобразить эту ориентацию на рисунке.) Мы должны сделать
это в абстрактной форме. Выберем так называемую правосторон-
нею ориентацию. Это значит, что когда мы смотрим на элемент
снаружи, то все грани, составляющие его границу, должны быть
ориентированы против часовой стрелки. Ориентация называет-
ся правосторонней, потому что если положить правую руку на
поверхность тетраэдра так, чтобы большой палец смотрел нару-
жу, то пальцы правой руки будут поворачиваться так, что грань
войдет в границу со знаком плюс. Конечно, это утверждение вы-
глядит короче, если записать его алгебраически через граничный
оператор из Сз в С2'.
^(Тетраэдр) = Красный + Жёлтый + Зелёный + Синий.
Если для тетраэдра выбирается левосторонняя ориентация, то
все четыре грани войдут в выражение для границы со знаком
минус. Таким образом, изменение ориентации любой грани ведет
к изменению ее знака в выражении для границы.
Очевидно, что граница тетраэдра — замкнутая поверхность,
имеющая нулевую границу. Это легко показать алгебраически,
используя выражения для граничных операторов их Сз в С2 и из
С2 bCi:
<Э[5(Тетраэдр)] = ^[Красный + Жёлтый + Зелёный + Синий]
= (-о - - 7) + (/? + ц - г) + (а 4- в - 5) + (7 + 6 - ту) = 0.
Этот результат никак не зависит от выбора ориентации самого
тетраэдра, его граней или ребер. (Попробуйте измените ориента-
цию какой-нибудь грани и пары ребер и убедитесь в этом.)
Итак, наши комплексы первоначально были изображены ри-
сунками, потом мы преобразовали рисунки в алгебраические вы-
ражения для граничного оператора д. Очевидно, что граничный
оператор, как и рисунок, определяет комплекс полностью. Поэто-
му очень хочется уметь задавать комплекс, не рисуя его, а про-
сто выписывая его элементы и граничный оператор. Когда мы
так сделаем, то покажем, что для любого элемента с комплекса
выполняется условие д(дс) = 0.
710
Глава 14. Комплексы высших размерностей
путь А — /1 — г/ стал бы границей и размерность пространства
Hi была бы равна нулю. И наконец, поскольку комплекс связен,
пространство Hq одномерно.
В качестве примера трехмерного комплекса рассмотрим тет-
раэдр со всеми его гранями, ребрами (ветвями) и вершинами (уз-
лами), показанный на рис. 14.2(a). Развернутая поверхность тет-
раэдра изображена на рис. 14.2(6). В комплексе имеется четыре
вершины: А, В, (7, В; шесть ребер: а, /3, 7, 5, 6, ту; четыре грани:
Красный, Жёлтый, Зелёный, Синий. Ориентация каждой грани
выбирается так, чтобы стрелка, показанная на рисунке, враща-
лась против часовой стрелки, если смотреть на тетраэдр снаружи
(см. Зелёный и Жёлтый на рис. 14.2(a)), и по часовой стрелке,
если смотреть на него изнутри (см. рис. 14.2(6)).
Из рисунка легко увидеть, что граничный оператор из С% в
Ci определяется формулами
^(Красный) — —а — /? — 7,
Э(Зелёный) = а + е — 5.
Поскольку граница каждой грани является циклом, то каждая
такая граница имеет' нулевую границу, т. е.
<Э[Э(Зелёный)] - д(а + г - 6) = (В - А) + (В - В) - (В - А) - 0.
14.1. Комплексы и гомологии
711
В этом комплексе имеется один трехмерный элемент — сам
тетраэдр. Чтобы написать граничный оператор из Сз в С2, на-
до приписать этому элементу ориентацию. (Хотя совсем не про-
сто изобразить эту ориентацию на рисунке.) Мы должны сделать
это в абстрактной форме. Выберем так называемую правосторон-
нею ориентацию. Это значит, что когда мы смотрим на элемент
снаружи, то все грани, составляющие его границу, должны быть
ориентированы против часовой стрелки. Ориентация называет-
ся правосторонней, потому что если положить правую руку на
поверхность тетраэдра так, чтобы большой палец смотрел нару-
жу, то пальцы правой руки будут поворачиваться так, что грань
войдет в границу со знаком плюс. Конечно, это утверждение вы-
глядит короче, если записать его алгебраически через граничный
оператор из Сз в
Э(Тетраэдр) = Красный + Жёлтый + Зелёный + Синий.
Если для тетраэдра выбирается левосторонняя ориентация, то
все четыре грани войдут в выражение для границы со знаком
минус. Таким образом, изменение ориентации любой грани ведет
к изменению ее знака в выражении для границы.
Очевидно, что граница тетраэдра — замкнутая поверхность,
имеющая нулевую границу. Это легко показать алгебраически,
используя выражения для граничных операторов их Сз в Съ и из
С2 bCi:
<Э[<Э(Тетраэдр)] = ^[Красный + Жёлтый + Зелёный + Синий]
= (-а - 3 - 7) + ((3 + ц - е) + (а + е - 5) + (7 + 6 ~ р) = 0.
Этот результат никак не зависит от выбора ориентации самого
тетраэдра, его граней или ребер. (Попробуйте измените ориента-
цию какой-нибудь грани и пары ребер и убедитесь в этом.)
Итак, наши комплексы первоначально были изображены ри-
сунками, потом мы преобразовали рисунки в алгебраические вы-
ражения для граничного оператора д. Очевидно, что граничный
оператор, как и рисунок, определяет комплекс полностью. Поэто-
му очень хочется уметь задавать комплекс, не рисуя его, а про-
сто выписывая его элементы и граничный оператор. Когда мы
так сделаем, то покажем, что для любого элемента с комплекса
выполняется условие д(дс) = 0.
712
Глава 14. Комплексы высших размерностей
Давайте разберемся, почему условие д(дс) — 0 разумно для
любого комплекса, даже, например, для поверхности, которую
нельзя построить в трехмерном пространстве, или для комплек-
сов, элементы которых включают четырехмерное пространство-
время. Чтобы доказать, что условие д(дс) = 0 выполняется для
всех элементов с, достаточно проверить, что оно выполняется
для генераторов, т. е. для элементов пространства S&. Для лю-
бого такого элемента мы можем построить подкомплекс, состоя-
щий из этого элемента, всех элементов пространства S^-i, кото-
рые входят в выражение для его границ нетривиальным образом,
всех границ и так далее. Граничные соотношения между этими
элементами определяются свойствами того элемента, с которого
мы начали. Несмотря на то, что взаимосвязи между различны-
ми строительными блоками могут быть достаточно сложными,
мы ожидаем, что отдельные элементы, из которых построен наш
комплекс, будут вполне знакомыми геометрическими объектами.
Например, предположим, что каждый элемент пространства S3
является выпуклым многогранником в трехмерном пространстве
(по крайней мере, если нам интересны его соотношения с гра-
ницами, мы допускаем любые непрерывные искажения реальной
геометрической формы объекта — так же, как раньше мы не ин-
тересовались формой проводов при изучении электрических це-
пей). Граница такого многогранника будет состоять из конечного
числа многоугольных граней, каждая из которых ориентирована
против часовой стрелки, если смотреть на многогранник снаружи
(рис. 14.3). Когда мы вычислим сумму границ этих многоуголь-
ных граней, каждое ребро будет входить дважды от каждой гра-
ни с противоположными знаками. Поэтому сумма всех границ
будет равна нулю. В этом случае граница каждого элемента S3
является циклом. Аналогично, мы могли бы предположить, что
каждый элемент S2 является выпуклым плоским многоугольни-
ком. Очевидно, что граница каждого элемента S2 будет циклом
(по существу это соответствует ячейке).
Давайте исследуем пространства гомологий комплекса, явля-
ющегося тетраэдром. Если нас интересует 7/q, то мы можем про-
игнорировать С2 и Сз и рассмотреть 1-комплекс, заданный вер-
шинами и ребрами. Это связный 1-комплекс с dimTTo = 1.
14.1. Комплексы и гомологии
713
Рис. 14.3
Чтобы определить Н^ рассмотрим 2-комплекс, заданный вер-
шинами, ребрами и гранями. Пространство Zi проанализируем с
помощью метода, которым мы пользовались при изучении элек-
трических цепей. Рассмотрим рис. 14.2. На нем ветви £, s и ту
образуют максимальное дерево. Каждая из остальных ветвей а,
(3, у определяет независимый цикл. Следовательно, dimZi — 3.
Каждый из этих циклов является границей грани, следовательно,
сПшВз = 3. Отсюда следует, что dim Hi = dimZi — dimBi — О,
т.е. Я1 - {0}.
Теперь рассмотрим Н2. Сначала возьмем пространство 2-цик-
лов — ядро оператора Э, действующего на С2. Мы уже ви-
дели, что образ 5, т.е. пространство Bi С С2, трехмерен. По-
скольку С2 ~ четырехмерное пространство, ядро д одномерно.
Базисом пространства Z2 является элемент Красный+Жёлтый+
Зелёный + Синий, т. е. поверхность тетраэдра, которая имеет ну-
левую границу. Конечно, этот элемент принадлежит и простран-
ству В2, поскольку он является границей тетраэдра. Следова-
тельно, dimB2 = 1, dimZ2 = 1 и dimH2 “ 0.
Наконец, рассмотрим Н3. Заметим, что в нем нет 3-циклов,
так что dim Z3 — 0 и dim Н3 = 0.
Теорема Эйлера
Изучая электрические цепи, мы доказали, что
dim Hq — dim Hi — dim Со — dim Ci.
714
Глава 14. Комплексы высших размерностей
Теорема Эйлера обобщает этот результат на п-комплексы:
dim Но — dim Н± + dim Н% — • • • ± dim Нп
= dim Со — dim Ci + dim С2 — • • • ± dim Сп.
Стоящее в обеих частях этого равенства число называется эй-
леровой характеристикой комплекса. Мы скоро докажем этот
результат в общем случае, но сначала проверим его для случая
тетраэдра. Поскольку dim Но = 1, а пространства Hi, Н% и Н$
тривиальны (равны {0}), имеем
dim Но — dim Hi + dim Н2 — dim H3 = 1.
С другой стороны,
dim Со — dim Ci + dim C2 — dim C3 = 4 — 6 + 4 — 1 = 1.
Предположим, что вместо тетраэдра (с внутренностью) мы
рассматриваем 2-комплекс, состоящий из поверхности тетраэдра.
Единственное отличие в том, что теперь в комплексе нет трех-
мерного элемента. Как и раньше, dim Но = 1 и dim Hi = 0. По-
прежнему dimZ2 — 1, поскольку поверхность тетраэдра имеет
нулевую границу. Однако теперь dim В2 = 0, поскольку нет трех-
мерного элемента, границей которого был бы какой-нибудь дву-
мерный элемент. Поэтому имеем dimH2 = dimZ2 — dimB2 — 1.
Тогда для этого комплекса dimHo—dimHi+dimH2 = 1—0+1 = 2,
a dim Со ~ dim Ci + dim С2 = 4 — 6 + 4 = 2
Давайте проделаем то же самое для сплошного (трехмерного)
куба. Он изображен в перспективе на рис. 14.4(a), а его разверну-
тая поверхность изображена на рис. 14.4(b). Как и в предыдущем
случае, dim Но = 1, потому что комплекс связен, и dim Из = 0,
потому что нет 3-циклов.
Чтобы найти разверность Zi, рассмотрим максимальное дере-
во, состоящее из семи ветвей, показанное на рис. 14.4 жирными
линиями. Каждая из оставшихся пяти ветвей определяет цикл.
Следовательно, dimZi = 5, но dim Bi = 5, поэтому dim Hi = 0.
Теперь займемся пространством Н2. Поскольку dimC2 = 6 и
dim В2 = 5, мы делаем вывод, что dimZ2 — 1. Базисом Z2 явля-
ется вся поверхность куба. Но эта поверхность является границей
куба, поэтому dim В2 = 1 и dim Н2 = dim Z2 — dim В2 = 0.
14.1. Комплексы и гомологии
715
б)
Рис. 14.4
Оказывается, что пространства гомологий куба и тетраэдра
одни и те же. Для куба мы получаем dim Hq — dim Н\ + dim Н% —
dimT/з = 1. Нетрудно также проверить, что
dim Cq — dim Ci + dim С% — dim C3 = 8 — 12 + 6 — 1 — 1.
Инвариантность гомологий
С точки зрения топологии есть фундаментальная причина, поче-
му комплекс куба и комплекс тетраэдра имеют одни и те же про-
странства гомологий. Пространство, заполняющее куб, — это то
же самое пространство, которое заполняет тетраэдр, и, в свою
очередь, совпадает с пространством, заполняющим шар. Все эти
пространства могут быть непрерывным образом преобразованы
друг в друга1. Аналогично, поверхности куба, тетраэдра и шара
представляют одно и то же пространство. Рис. 14.5(a) показы-
вает, как поверхность сферы может перейти при разбиении на
1Точнее, говорят, что такие пространства гомеоморфны, или топологичес-
ки эквивалентны — каждое из них допускает взаимно-однозначное непре-
рывное в обе стороны отображение (гомеоморфизм) на другое. — Прим. ред.
716
Глава 14. Комплексы высших размерностей
Рис. 14.5
грани в поверхность тетраэдра, а рис. 14.5(6) показывает, как
эта же поверхность преобразуется в поверхность куба. Конечно,
комплекс тетраэдра и комплекс куба отличаются, но они пред-
ставляют собой различные способы разбиения одного и того же
пространства.
В топологии имеется теорема, которая, грубо говоря, утвер-
ждает следующее. Предположим, что мы строим пространство
X, соединяя различные ячейки друг с другом вдоль гранич-
ных ячеек, размерность которых на единицу меньше. Например,
построим поверхность сферы, соединяя вместе четыре 2-ячейки
вдоль их ребер, как это показано на рис. 14.5(a), или соединяя
вместе шесть 2-ячеек, как это показано на рис. 14.5(6). Други-
ми словами, мы можем построить трехмерный ансамбль много-
гранников, соединяя ячейки вдоль их граней, подобно скоплению
мыльных пузырей. Тогда теорема говорит, что пространства го-
мологий результирующего комплекса зависят только от про-
странства X и не зависят от способа соединения. Если про-
странство X разложить на ячейки каким-то другим способом,
то мы получим другой комплекс. Пространства для разных
комплексов будут изоморфны при каждом к.
На рис. 14.6 показано, как сфера может быть разложена в
комплекс еще проще, чем преобразование в куб или тетраэдр.
Поверхность сферы разбивается на два треугольника, соответ-
14.1. Комплексы и гомологии
717
Рис. 14.6
ствующие северной и южной полусферам, соединяющимся вдоль
экватора.
У этого 2-комплекса существует только одна ячейка <т + /? + 7,
которая является границей обеих полусферических поверхностей.
Следовательно, dimZi = dimBi — 1 и опять dim Hi — 0. Сумма
этих двух граней имеет нулевую границу, поскольку
5(Север) = се + /3 + 7, а д(Юг) — —се — (3 — 7.
Поэтому так же, как и для поверхности куба или тетраэдра,
имеем dimH2 = dimZ2 — 1. И опять замечаем, что для 2-ком-
плекса
dim Со — dim Ci + dim С2 = 3 — 3 + 2 — 2
= dim Но — dim Hi + dim H2.
К сожалению, мы не готовы доказать упомянутую выше тео-
рему и даже дать ее точную формулировку. Чтобы это сделать,
надо иметь точные определения понятий пространство, дефор-
мация, соединение и т. д. Когда эти понятия строго определены,
то совсем не сложно сформулировать и доказать теорему, но раз-
витие необходимой для этого базы уведет нас слишком далеко.
Тем не менее, мы будем пользоваться этой теоремой, не заботясь
о том, насколько точно она сформулирована. С ее помощью мы
проделаем ряд вычислений, чтобы получше познакомиться с про-
странствами Hfc.
718
Глава 14. Комплексы высших размерностей
Тор
Рассмотрим пример 2-комплекса, имеющего пространства гомо-
логий, отличные от тех, которые мы уже рассматривали. Для это-
го получим разложение двумерного тора, т. е. поверхности бубли-
ка. (Вместо того, чтобы разрезать мячик, мы разрежем камеру
колеса.) Рис. 14.7(a) показывает, как тор разбивается на две об-
ласти; рис. 14.7(6) показывает, как эти области делаются плоски-
ми; рис. 14.7(b) показывает, как эти области разделяются. Можно
считать, что рис. 14.7(b) показывает элементы тора, и попытать-
ся понять, в чем принципиальное отличие этого набора элементов
от набора элементов сферы, который получился бы, если бы мы
разделили на элементы рис. 14.5(a).
Посчитав вершины, ребра и грани, мы находим dim Со = 4,
dim Ci = 8 и dim С2 = 4. Откуда получаем, что dim Со — dim Ci +
dimC2 ~ 4 — 8 + 4 = 0. (Вспомним, что для 2-комплекса, образо-
ванного из поверхности сферы, эта величина всегда равна 2.)
Рассмотрим пространства гомологий для комплекса тора.
Так как этот комплекс связный, то пространство Hq одномер-
но. Поскольку вся поверхность тора имеет нулевую границу, то
dim^2 = 1. (Проверьте самостоятельно, что для указанных ори-
ентаций ^(Красный + Жёлтый + Зелёный + Синий) =0.) Мы
рассматриваем 2-комплекс, поэтому в пространстве С2 не может
быть элементов, являющихся границами. Значит, dimB2 = 0 и
dim #2 = dim^2 — dimB2 = 1. (В общем случае очевидно, что по
тем же причинам для любого 2-комплекса, полученного делени-
ем гладкой связной поверхности, являющейся границей области
в пространстве R3, имеет место dim #2 = 1-)
Наконец, рассмотрим пространство Рис. 14.8 показывает
максимальное дерево, состоящее только из трех ребер. Самосто-
ятельно проверьте, что если к этому максимальному дереву до-
бавить любое из оставшихся пяти ребер, то получается цикл! На-
пример, а + (3 является циклом, так же, как е + А и р + ц. Поэтому
для этого комплекса dimZi = 5. С другой стороны, dimC2 = 4.
Ядро оператора д, действующего на — пространство Z2 —
является одномерным, а образ д в пространстве В\ имеет раз-
мерность 3. Поэтому
dim Н\ = dim Zi — dim By = 5 — 3 = 2.
14.1. Комплексы и гомологии
719
Полезно далее построить базисы для пространств Bi и Нь
Проще всего в качестве базисных элементов в В\ взять ячейки,
которые являются границами четырех граней, например,
Э(Жёлтый) = г] — /3 + е + 5,
д(Зелёный) = а — А — 7 — ^z,
д(Синий) = А + /3 + ^ — 6.
720
Глава 14. Комплексы высших размерностей
А в D А А
------» -----------►------•
*) к 7
С
Т) <8
Рис. 14.8
Элементами факторпространства Н\ = Z\/B\ являются клас-
сы эквивалентности по модулю В\. Поэтому мы должны найти
два цикла, которые не являются границами и, более того, любая
их линейная комбинация тоже не граница. Если посмотреть на
рис. 14.7(a), то там сразу видно два таких цикла: цикл а + /3,
идущий вокруг тора в одном направлении, и цикл е + А, иду-
щий вокруг тора в другом независимом направлении. Поэтому
базис пространства Hi состоит из классов эквивалентности а + /3
и е + А. Конечно, есть много других циклов, не являющихся гра-
ницами, но все они попадают в класс эквивалентности некоторой
линейной комбинации а + /3 и е + А. Например, цикл 7 + 5 лежит
в классе эквивалентности а + /3, потому что
7 + 5 — а + /3 + ^(Красный) + ^(Жёлтый).
Цикл а + е + 5 — ц может быть представлен в виде
(а + /3) + (е + А) — З(Синий).
Поэтому он лежит в том же классе эквивалентности, что и
а + /3 + е + А.
Смысл пространства Hi
Сейчас мы уже можем в общем случае понять смысл dim Hi. Гру-
бо говоря, это число независимых замкнутых кривых, которые
не ограничивают никакой области. На сфере любая замкнутая
14.1. Комплексы и гомологии
721
кривая обязательно ограничивает какую-то область и поэтому
dim Hi — 0. С другой стороны, на торе существует два различ-
ных типа замкнутых кривых, которые не являются границами
подобластей, как это показано на рис. 14.9. Поэтому для тора
dim7?i = 2. Заметим, что для комплекса, который мы постро-
или для тора, выполняется условие dim Со — dimCi -F dimC2 =
4 — 8 + 4 = dim Но — dim Hi + dim Ho- Посмотрим, как изменится
пространство Hi, если мы приделаем к тору ручку (рис. 14.10).
Это значит, что на его поверхности вырезаются два диска и на
их место вставляется (искривленный) цилиндр, открытый с обо-
их концов: верхнюю часть цилиндра мы прикрепляем к границе
одного диска, а нижнюю — к границе второго диска. Выберем
такое разбиение исходной поверхности, чтобы каждый диск был
ячейкой этого разбиения. Пусть это будет квадрат, а цилиндр
мы представим, как будто он склеен из четырех граней. Присо-
единяя цилиндр таким образом, мы не создаем новых узлов, но
добавляем четыре новых ветви (ребра «квадратного» цилиндра).
Теперь удалим из два элемента (внутренние части дисков) и
добавим четыре новых (грани цилиндра), см. рис. 14.11. Для по-
лучившейся в результате поверхности по-прежнему пространства
Но и Hi одномерны. Вычисляя Zi для нового комплекса, мы мо-
жем выбрать максимальное дерево, которое не содержит ни одну
из новых ветвей (поскольку каждая новая ветвь лежит на ячейке
— вспомним процедуру построения максимального дерева, кото-
рая была сформулирована при изучении электрических цепей).
Итак, мы построили максимальное дерево, целиком состоящее из
ветвей первоначального комплекса. Каждая ветвь цилиндра те-
перь дает новую независимую ячейку, что приводит к увеличе-
Рис. 14.9
Рис. 14.10
722
Глава 14. Комплексы высших размерностей
нию размерности В\ на 4. С другой стороны, размерность С% и,
следовательно, В± увеличилась на 2. Но тогда и размерность Н±
тоже увеличилась на 2. Итак, мы показали, что добавляя ручку,
мы увеличиваем размерность Hi на 2. Если к сфере прикрепить
к ручек, то dimHo = 1, dim#1 — 2к и dim#2 ~ I-2 Например,
тор можно представить себе как сферу, к которой прикрепили
одну ручку (рис. 14.12). Это дает нам еще одно доказательство
результатов, полученных для тора.
Можно исследовать результат вырезания отверстия в поверх-
ности. В качестве примера рассмотрим комплекс, который (вмес-
те с внутренностью) образует на плоскости квадрат. Очевидно,
что для такого комплекса dimHo = 1? dim Hi — 0 и dim #2 — 0.
Предположим, что из внутреннего квадрата мы вырезали отвер-
стие (рис. 14.13). Если бы у нас было разбиение исходного квадра-
та, для которого вырезанное отверстие было одним из элементов
52, то мы бы увидели, что удаление отверстия не изменяет Zi, но
уменьшает размерность С% и, следовательно, В± на 1. Но тогда
размерность Hi увеличивается на 1. Итак, если на плоскости име-
ется область, из которой вырезаны к отверстий, то dim Hi = fc,
dim По = 1 и dimH2 = 0. Аналогичные рассуждения в трехмер-
ном пространстве показывают, что если из трехмерной области
вырезать к (трехмерных) отверстий, то dim Но = 1, dim Hi = 0,
dim Н2 — к и dim Н3 — 0.
2 Известно, что всякая замкнутая (не имеющая края) компактная связная
ориентируемая двумерная поверхность топологически эквивалентна сфере с
добавлением определенного количества ручек, которое называется родом по-
верхности и обозначается g (genus). Таким образом, род равен половине раз-
мерности пространства Hi одномерных гомологий поверхности. — Прим. ред.
14.1. Комплексы и гомологии
723
Бутылка Клейна
При изучении электрических цепей Вы, должно быть догадались,
что существуют цепи, подобные изображенной на рис. 14.14, ко-
торые не могут быть уложены на плоскости так, чтобы не пере-
секались отдельные провода. Однако, такие цепи всегда можно
собрать в трехмерном пространстве. Точно так же существуют
2-комплексы, которые нельзя собрать в трехмерном простран-
стве. Хорошо известным примером является бутылка Клейна,
из поверхности которой получается комплекс, изображенный
на рис. 14.15(a). Несмотря на близкое сходство с тором3 (см.
рис. 14.7(6)), эту поверхность в трехмерном пространстве по-
строить нельзя. Этот (развернутый) комплекс можно собрать в
цилиндр, изображенный на рис. 14.15(6). Но при этом оказыва-
ется невозможно соединить вместе ребра е и А с соблюдением
их ориентации. Для комплекса, представляющего бутылку Клей-
на, гомологические пространства отличаются от гомологических
пространств тора. Конечно, dim Но = 1? потому что комплекс
связный. Однако dim Н% — 0, потому что в пространстве С% нет
3Бутылка Клейна, в отличие от сферы и тора, относится к неориенти-
руемым (односторонним) поверхностям. Неориентируемая поверхность мо-
жет быть получена из ориентируемой заменой на лист Мёбиуса (односторон-
нюю поверхность с краем-окружностью) одного или нескольких дисков. —
Прим. ред.
724
Глава 14. Комплексы высших размерностей
элемента с нулевой границей. (Границей всего распрямленного
комплекса (см. рис. 14.15(a)) является 2е + 2Л. Проверьте са-
мостоятельно, что при изменении знака одной или нескольких
2-ячеек в пространстве С2 не появится элемент с нулевой грани-
цей.) Для комплекса, изображенного на рис. 14.7, dimZi = 5, а
для комплекса бутылки Клейна dimBi = 4 и dim ГД = 5 — 4 — 1.
Это значит, что существует только один независимый цикл, ко-
торый не является границей. Цикл а + /3 не является границей ни
на рис. 14.7(6), ни на рис. 14.15(a). А вот цикл е + Л, который не
является элементом пространства В\ в случае тора, в случае бу-
тылки Клейна становится элементом В\. Это половина границы
всего комплекса, изображенного на рис. 14.15(a).
Рис. 14.15
И для тора, и для бутылки Клейна мы имеем dim Со = 4,
dimCi = 8 и dimC2 = 4, так что
dim Со — dim Ci + dim С2 — 4 — 8 + 4 = 0.
Полезно заметить, что для бутылки Клейна мы также имеем
dim Hq ~ dim Hi + dim H2 — 1 — 1 + 0.
14.1. Комплексы и гомологии
725
Доказательство теоремы Эйлера
В общем случае докажем формулу
dim Но — dim Hi + dim Н% — • • • ± dim Нп
~ dim Со — dim Ci Ч-± dim Сп,
которую мы уже проверили в нескольких частных случаях. До-
казательство состоит из очень простых шагов.
(1) Поскольку Нк — Zk/Bk, то dim/Д — dimZ^ — dimB^.
(2) Если теорему о ранге и дефекте применить к д : Ск-у —> С&,
то dimCfc+i = dimZfc+i + dimB^.
(3) Для n-комплекса dim Вп — 0, потому что не существует
объектов размерности п + 1.
(4) dim Zq = dim Со, потому что граница любой ячейки нулевой
размерности по определению равна нулю, а в комплексе нет
объектов отрицательной размерности.
Собирая вместе (1) и (2), получаем
dim Нк = dim Zk — dim Ck+i + dim Zk+i
для 1 < к < n. Для к = 0 в силу (4) мы имеем
dim Hq — dim Со — dim Су + dim Zy,
а в силу (3) для к ~ п имеем
dimBn = dimZn.
Таким образом,
dim Но — dim Ну + dim Н2 + • • • ± dim Нп
— (dim Со — dim Су + dim Zy) — (dim Zy — dim C2 + dim Z2)
+ (dim Z2 — dim C3 + dim Z3) — • • • ± dim Zn
— dim Co “ dim Cy + dim C2 — • • •± dim Cn.
726
Глава 14. Комплексы высших размерностей
В качестве применения этого результата рассмотрим выпук-
лый многогранник, который будем рассматривать как комплекс,
образованный в результате разрезания поверхности сферы на от-
дельные ячейки. Если мы считаем, что согласно теореме, упо-
мянутой раньше, размерности пространств 77о, Н\ и Н<2 такие
же, как у любого комплекса, образованного разбиением данной
поверхности, то можно сделать вывод, что dim Но ~ dim Hi +
dimHg = 1 — 0 + 1 = 2. Этот результат мы уже получили рань-
ше для куба и тетраэдра. Таким образом, для любого выпуклого
многогранника
dim Со — dim Ci + dim С2 — 2
или «(число вершин) — (число ребер) + (число граней) = 2».
Ориентация и оператор д
Как уже было сказано, мы не дали строгого определения понятия
пространства, лежащего в основе комплекса. Здесь мы попытаем-
ся изложить, как следует понимать данную ситуацию. Каждая к-
ячейка, т.е. каждый элемент пространства S&, следует понимать
как связный выпуклый многогранник в пространстве с опре-
деленной ориентацией. (Напоминаем, что в пространстве и,
следовательно, в любом его открытом подмножестве мы можем
выбирать одну из двух ориентаций, фиксировав некоторый упо-
рядоченный базис.) Теперь границей этого выпуклого многогран-
ника будет объединение конечного множества выпуклых много-
гранников размерности к — 1, лежащих в некотором аффинном
подпространстве размерности к — 1. Выбрав начало координат
и базис, мы можем отождествить каждое такое подпространство
с Предположим, что в итоге таких идентификаций в на-
шем комплексе каждый (к — 1)-мерный многогранник соответ-
ствует (к — 1)-ячейке, т.е. элементу пространства Sfc-i. Но эти
элементы пространства Sk-i имеют определенную ориентацию.
Поэтому мы должны увидеть, как ориентация fc-ячейки связана
с ориентацией (к — 1)-ячейки на ее границе. Такая информация
закладывается в оператор д.
Пусть vi,..., vjt является базисом пространства так что
V2, — .,Vjfe касателен к выбранной (к — 1)-мерной грани нашей
14.1. Комплексы и гомологии
727
А:-ячейки С, Кроме того, вектор Vi направлен из fc-ячейки на-
ружу. Предположим, что ориентация пространства опреде-
ленная векторами Vi,..., v&, совпадает с ориентацией С. Тогда
V2,..., Vfc определяют ориентацию конкретной (к—1)-мерной гра-
ни, соответствующей, скажем, F С Sk-i- Эта ориентация может
как совпадать, так и не совпадать с ориентацией F. Если ориен-
тации совпадают, то мы приписываем подпространству F знак +,
в противном случае — знак —. Тогда
дС = 22 ±F,
где сумма берется по тем F, которые соответствуют граничным
(к — 1)-граням С. Конечно, если базис vi,...,v^ соответствует
противоположной ориентации С, то знак меняется на противопо-
ложный.
Если к > 2, то вектор можно заменить на —Vfc, если нам
требуется получить «хороший» базис. При к — 1 пространство
есть нулевое векторное пространство. Здесь «ориентация»
означает выбор знака + или —. Согласно нашим правилам, мы
выбираем знак +, если вектор Vi, показывающий ориентацию,
показывает наружу, и знак — в противном случае:
vi +
Конечно, каждая (к — 1)-ячейка может появиться в границах
нескольких fc-ячеек. Но поскольку fc-ячейки образуют базис С,
то, как мы показывали раньше, каждая /с-ячейка определяет ли-
нейное отображение д : —> Ск-1-
Чтобы проверить равенство дд = 0, достаточно проверить,
что для каждой /с-ячейки выполнено д(дС} = 0. Теперь каждая
(к — 2)-ячейка F, которая может появиться в выражении д(дС),
действительно там появляется, потому что это граница для двух
(к — 1)-мерных граней ячейки С, скажем, для Fi и F^. Читате-
лю рекомендуется самому убедиться в справедливости равенства
д{дС) — 0, проверив свое понимание понятия ориентации и опре-
деления оператора д.
728
Глава 14. Комплексы высших размерностей
Рассматривая каждый элемент S& как выпуклый многогран-
ник, мы можем определить гладкое отображение комплекса в це-
лом в пространство R^. Это сводится к правилу, согласно которо-
му / приписывает каждой точке fc-ячейки точку в пространстве
R7^ Если отождествить тем или иным образов /с-ячейку С с вы-
пуклым многогранником в пространстве R^, то отображение /,
ограниченное на С, можно рассматривать как отображение из
выпуклого многогранника в Rfc в пространство R-^. Мы хотим,
чтобы это отображение было гладким. По существу мы хотим
работать с отображением д. определенном в большей области,
где оно гладко (так, чтобы включить внутрь области С и все его
границы). Мы подробно займемся этим в главе 15.
14.2. Дуальные пространства и когомологии
А теперь займемся семейством дуальных пространств к про-
странствам Cfc. Эти пространства будем обозначать Ск. Элемент
такого пространства Ск, называемый коцепью, является линей-
ной функцией элементов пространства Ck, которые мы называем
fc-цепями. Если а является fc-коцепью и с — й-цепь, то значение
коцепи а на цепи с будем обозначать точно также, как мы
делали в случаях к — 0 и к — 1 при рассмотрении электрических
цепей.
Рассмотрим транспонированное преобразование d к гранич-
ному оператору d : Cfc+i —> С&, которое мы будем называть по-
граничным оператором. Итак, d : Ск Ск+1 определяется фор-
мулой
da = ст, где а е Ск и се С&+1.
J с Jдс
Из того факта, что граница границы равняется нулю, следует,
что dod = 0. (Конечно, имеется в виду композиция d : Ск Ск+1
с d : (7fc+1 —> Ск+2.) В только что введенных обозначениях можно
написать
/ d(da) — da — а = 0, поскольку д(дс) = 0.
Jc Jdc J д(дс)
14.2. Дуальные пространства и когомологии
729
Для того, чтобы почувствовать смысл коцепи и важность ко-
граничного оператора d, рассмотрим 2-комплекс, изображенный
на рис. 14.16. Элемент С°, т.е. 0-коцепь Ф, полностью определя-
ется заданием значений в каждом узле. Например,
Фл = ! фВ = 3 фс = 2) фО = 5
Потенциальные функции, которые играют огромную роль в
теории электрических цепей, являются примерами 0-коцепей.
Действие кограничного оператора d на 0-коцепь дает 1-коцепь
б/Ф. Чтобы вычислить значение с/Ф на ветви, мы воспользуемся
тем, что d сопряжен к д. Например, поскольку да — В — А,
то f d$ = }^аФ = Фв — Ф"4* Как нам уже известно, оператор
d : > С1 преобразует потенциальную функцию, являющуюся
0-коцепью или линейной функцией, заданной в узлах, в функцию
скачка напряжения, т. е. в 1-коцепь, определенную для ветви как
линейная функция.
Продолжим исследовать смысл оператора d : С1 —> С2, При-
мером 1-коцепи может служить линейная функция W, принима-
ющая следующие значения:
Wa = 1, W0 - 2, Ж7 = 1 W6 = 2, We = -3 Wv = 2.
Напряжения на батареях в одном из примеров электрической
цепи определяли такую 1-коцепь.
Действие оператора d на 1-коцепь W должно давать 2-коцепь
dW, которая является линейной функцией 2-цепей. Мы можем
730
Глава 14. Комплексы высших размерностей
вычислить значение dW на 2-ячейке Красный, используя опре-
деление
f [ W.
J Красный «/^(Красный)
Поскольку Э(Красный) — а + /3 — 7, мы имеем
( dw = Wa + Wd - W7 = 1 + 2 - 1 = 2.
J Красный
Аналогично
f dW = W6-W£ + WT, = 2 + 3 + 2 = 7.
J Синий
Теперь известны значения dW в базисе пространства Но тог-
да из линейности могут быть получены ее значения на любом
элементе пространства С2.
В качестве последнего примера, рассмотрим 3-комплекс тет-
раэдра, показанный на рис. 14.17. Пусть 7?, У, G и В обозначают
четыре грани тетраэдра, причем все они ориентированы против
часовой стрелки, если смотреть на них снаружи.
Рис. 14.17
Тогда 2-коцепь Т определяется ее значениями на гранях, т. е.
TR = 1, TY — 2, TG = 4, Тв — —1. Действие оператора d : С2 —->
С3 на 2-коцепь Т дает 3-коцепь dT, определенную на элементах
пространства С3. Нам надо только вычислить значение dT для
сплошного тетраэдра. Если тетраэдр имеет правостороннюю ори-
ентацию, так что
д(Тетраэдр) = R + Y + В + G,
14.2. Дуальные пространства и когомологии
731
то
f dT - TR + TY + TG + Тв = 1 + 2 + 4 - 1 = 6.
J Тетраэдр
Читатель, знакомый с электромагнитной теорией, возмож-
но, уже заметил сходство между кограничным оператором и
некоторыми операциями физического происхождения. Напри-
мер, 2-коцепь Т может рассматриваться как поток электриче-
ского поля через грани тетраэдра. В этом случае 3-коцепь с/Т по
закону Гаусса будет пропорциональна полному электрическому
заряду внутри тетраэдра. В предыдущем примере, если 1-коцепь
W представляет напряжения, индуцированные изменением маг-
нитного поля, то 2-коцепь dW по закону Фарадея будет пропор-
циональна скорости изменения магнитного потока через соот-
ветствующие 2-ячейки. Действительно, кограничный оператор d
преобразуется в дифференциальный оператор, который позволя-
ет дать точные формулировки всех уравнений Максвелла.
Чтобы выделить подпространства пространств рассмот-
рим образ и ядро кограничного оператора. Говоря конкретнее,
образ d : —> Ск называется подпространством кограниц и
обозначается Вк, а ядро d : Ск —* Ск+г называется подпростран-
ством коциклов и обозначается Zk. Поскольку d о d = 0, любая
кограница обязательно является коциклом, и тем самым Вк явля-
ется подпространством Zk. Кроме того, мы образуем факторпро-
странство Нк = Zk/Bk^ называемое пространством к-мерных
когомологий комплекса.
Многие аспекты этих пространств уже проявлялись при изу-
чении электрических цепей. Например, в случае к = 0 простран-
ство Z0 (пространство 0-коциклов) было пространством физи-
чески осмысленных потенциалов, которые были постоянны на
каждой связной компоненте цепи. Пространство В0 было ну-
левым, поскольку 0-коцепь никоим образом не могла принад-
лежать образу d. В результате получалось факторпространство
Н° ~ ZQ/В® — Z0. (Раньше при обсуждении этого пространства
мы использовали только обозначение В0.)
Для 1-комплекса пространство Z1 совпадает со всем про-
странством С1. Причина этого очень проста и состоит в том,
что при отсутствии 2-коцепей каждая 1-коцепь должна лежать
732
Глава 14. Комплексы высших размерностей
в ядре d. Пространство кограниц В1 содержит те распределения
напряжений, которые получаются из потенциала. В этом слу-
чае факторпространство Н1 = Z1 /В1 совпадает с пространством
С1 /В1. Вспомните, что пространство Н1 дуально пространству
Hi (в случае 1-комплекса оно совпадает с Zi).
Простейшим примером ситуации, когда Zk, Вк и Нк не три-
виальны, является случай к ~ 1 для 2-комплекса. Рассмотрим
комплекс, изображенный на рис. 14.18. Пространство С1 шести-
мерно, потому что в комплексе шесть ветвей. Чтобы определить
размерность пространства Z1, мы должны посмотреть на образ
и ядро оператора d : С1 —> С2.
Сначала рассмотрим образ d : С1 —> С2, т. е. пространство
В2, Поскольку пространство С2 двумерно, то В2 не может иметь
размерность больше, чем 2. Чтобы показать, что его размерность
равна 2, достаточно найти базис С2, который лежит в образе d.
1-коцепь V, которая приписывает значение 1 ветви а и 0 другим
ветвям, обладает свойством:
сГУ(Красный) = 1, йУ(Синий) = 0.
Аналогично, 1-коцепь W, которая приписывает 1 ветви (3 и 0
другим ветвям, обладает свойством:
сГ\¥(Красный) — 0, <Л¥(Синий) = 1,
14.2. Дуальные пространства и когомологии
733
Поэтому В2, т. е. образ d, заданный векторами dV и dW, имеет
размерность 2. В силу теоремы о ранге и дефекте, ядро d, т. е.
пространство Z1, удовлетворяет условию
dim Z1 = dim С1 ~ dim В2 — 6 — 2 — 4.
Обратим теперь внимание на пространство В1 и рассмотрим
d : С° —> С1. Ядро этого оператора, т. е. пространство Z0 (кото-
рое совпадает с В0), имеет размерность 1, потому что комплекс
связен. Следовательно,
dimB1 = dimC0 - dimZ0 = 4 - 1 = 3.
Значит, существуют три независимых 1-коцепи, которые вы-
водятся из потенциалов.
Мы видим, что пространство Z1, состоящее из 1-коциклов,
имеет размерность 4, а пространство В1, состоящее из 1-кограниц,
имеет размерность 3. Поэтому dimB1 = dimZ1 — dimB1 =
4 — 3 = 1. Это значит, что существуют «интересные» коцик-
лы, которые лежат в ядре d, хотя они и не могут быть вы-
ведены из потенциала. Класс эквивалентности одного такого
коцикла дает базис одномерного факторпространства Z1. Да-
вайте, например, выберем коцикл V, для которого Va =
= |, У7 = V5 — |, Vе = О, У77 = 0. Очевидно, что
этот коцикл не может быть выведен из потенциала, потому
что сумма падений напряжений при обходе цикла а + /? или
7 + 6 не равна нулю. С другой стороны, V принадлежит ядру
d : С1 —> С2, потому что сТУ(Красный) = Va — V5 — | — | = 0 и
сГУ(Синий) = У^ - У7 = i - | = 0.
Из этого анализа очевидно, что существование «интересных»
коциклов тесно связано с наличием дырок в комплексе. Если до-
бавить к комплексу диск с ветвями 7 и 6 (назовем его Жёлтый),
то кограницами будут только коциклы. Например, коцепь V, рас-
смотренная выше, будет удовлетворять условию сТУ(Жёлтый) =
1 и не будет коциклом. Именно таким образом пространства ко-
гомологий комплекса показывают наличие дырки, точно так же,
как анализ пространств гомологий.
В этом примере сразу же видно, что пространство В1 ду-
ально Hi в том смысле, что базисный элемент V приписывает
734
Глава 14. Комплексы высших размерностей
1 любому циклу, который обходит дырку против часовой стрел-
ки. Рассмотрим, например, цикл I = а + е — д + р. Мы видим, что
Ji V — + Vе — V5 + V77 = | = 0. Однако, все циклы, обхо-
дящие дырку один раз против часовой стрелки, образуют класс
эквивалентности, который может быть базисом Hi. Кроме того,
конкретный выбор элемента V в качестве представителя этого
класса эквивалентности не имеет значения. Предположим, что
мы выбрали W — V + с£Ф. Тогда для любого цикла М выполня-
ется условие
[w=[v+[d$=[v+[ Ф= [ V,
JM Jm Jm УМ JdM JM
поскольку <ЭМ = 0, если М — цикл. В этом смысле класс эквива-
лентности V (базис для Н1) определяет линейную функцию от
класса эквивалентности I (базис для Hi). Для вычисления этой
функции находим Jj V, взяв любой элемент класса эквивалент-
ности.
Попробуем доказать в общем случае, что Нк — это дуальное
пространство Н^. Сначала установим, что dim77fc = dimT/^, по-
том покажем, что любой элемент Нк определяет линейную функ-
цию в пространстве Н^
Результат получается из того, что мы уже знаем. Ядро сопря-
женного оператора аннулирует образ; образ сопряженного опера-
тора аннулирует ядро. Рассмотрим следующую диаграмму:
1 (~ik+l
Л* Г'* &
Cfc-l «— Cfc+1
Сначала посмотрим на д : Ck+i —> С к и его сопряженный опера-
тор d : Ск —> Ск+Х. Ядро сопряженного оператора d является про-
странством коциклов оно аннулирует образ д, которое являет-
ся пространством границ Вк- А теперь рассмотрим д : С к Ck-i
и его сопряженный d : Ск~г Ск. Образ сопряженного операто-
ра есть пространство кограниц Вк\ он аннулирует ядро д, которое
является пространством циклов Z^.
Однако, мы знаем, что для любого подпространства простран-
ства С*, сумма размерности подпространства и размерности его
14.2. Дуальные пространства и когомологии
735
аннулирующего пространства должна быть равна размерности
Ck- Следовательно,
dim Bk + dim Zk = dim Ck = dim Zk + dim Bk.
Отсюда следует, что
dim Zk — dim Bk — dim Zk — dim B&,
t. e.
dimB^ = dim/ffc,
поскольку
Hk = Zk/Bk и Hk = Zk/Bk.
Типичным элементом пространства Hk является класс экви-
валентности V, состоящий из коциклов вида V + </Ф. Если V не
является нулевым элементом, то V — не кограница. Аналогич-
но, типичным элементом пространства Hk является класс экви-
валентности I, состоящий из циклов вида I + дт. Если I ~~ не
нулевой элемент, то I — не граница. Мы определяем значение V,
действующего на I, т. е. V, давая возможность любому элемен-
ту класса V действовать на любой элемент класса I. Тогда
/v + [d$+ [ v + [ d$
Ji Ji Jdr Jdr
V + t/Ф
Однако, di = 0, потому что I — цикл; dV = 0, потому что V —
коцикл и, конечно, = 0. Следовательно,
Wv-
Другими словами, не имеет значения, какой элемент класса эк-
вивалентности мы выбираем. Мы имеем корректное определение
элементов Нк как линейных функций в пространстве Hk- Таким
образом, мы произвели отождествление пространства Нк с ду-
альным пространством Hk-
736
Глава 14. Комплексы высших размерностей
Ранее говорилось, что пространства гомологий Нк, относя-
щиеся к комплексу, зависят только от пространства, лежащего
в основе комплекса, и не зависят от того, как комплекс был об-
разован. Теперь понятно, что то же самое справедливо для про-
странств когомологий Hk. Поскольку коцепи, из которых полу-
чаются Нк, тесно связаны с физическими величинами, то эти
пространства открывают связь топологии и теории электромаг-
нетизма.
Прежде чем закончить рассмотрение комплексов, имеет смысл
подвести итоги того, что мы изучили, на диаграмме, изображен-
ной на рис. 14.19. Диаграмма нарисована для 3-комплекса, на ней
показаны все связи между пространствами, которые мы изучили.
Z1 аннулирует В\
В1 аннулирует Zi
Я1 = Z1/B1 дуально Я1 = Zi/Bx
Яз нулевое
В3 аннулирует Z3
Я3 — С3/В3 дуально Я3 = Z3
Z0 аннулирует Во
BQ нулевое
Я0 = Z0 дуально Но = Со/Во
Z2 аннулирует В2
В2 аннулирует Z2
Н2 = Z2/B2 дуально Н2 = Z2/B2
Рис. 14.19
Задачи
737
Резюме
А. Комплексы высших размерностей
Вы должны знать определения пространств Zfc, В к и для п-
комплексов и уметь строить базисы этих пространств.
Для заданной диаграммы, представляющей ячейки 2-ком-
плекса, надо уметь определить, что это за комплекс: сфера, тор
или что-то еще.
В. Когомологии и оператор d
Для n-комплекса Вы должны уметь определить оператор d и
пространства Zfe, Вк, Нк; должны уметь строить базисы этих
пространств.
Вы должны понимать, как доказать и применять дуальность
пространств Нк и Н^.
Задачи
14.1. Пять 2-комплексов, изображенных на рис. 14.20, представляют в
каком-то порядке следующие фигуры:
(а) искривленная поверхность цилиндра;
(Ь) лист Мёбиуса («перекрученный» цилиндр);
(с) сфера;
(d) тор;
(е) бутылка Клейна.
Опознайте эти фигуры и вычислите для каждой из них dim Hi и
dimH2. В каждом случае найдите базисы пространств Zi, Bi и
Hi. Проверьте, что
dim Со — dim Ci + dim С2 = dim Hq — dim Hi 4- dim H2.
14.2. Для каждого комплекса из предыдущего упражнения постройте
базисы пространств Z1, Н1 и Н1.
14.3. Резиновая надувная игрушка разделена на три части, окрашен-
ные в разные цвета. На рис. 14.21 показаны две из этих областей.
(а) Определите <Э(Красный) и <Э(Синий).
(Ь) Определите размерности пространств Z2, Н2 и Но-
738
Глава 14. Комплексы высших размерностей
Рис. 14.21
(с) Найдите базисы пространств Zi, Bi и Hi.
(d) На рис. 14.22 показана третья область. Каковы будут раз-
мерности пространств Со, Ci, С2, Hi, Н2 после того, как
вся игрушка собрана? Получится ли мячик (dim Но = 1,
dimHi = 0, dimH2 = 1), плавательный круг (dim Но = 1,
dimHi = 2, dimH2 = 1) или что-то другое?
Рис. 14.22
Задачи
739
14.4. Трое рабочих завода, выпускающего автомобильные шины, раз-
делили поверхность внутренней камеры на три ориентирован-
ных области и подписали каждую своим именем. Получившийся
2-комплекс показан на рис. 14.23.
Рис. 14.23
(а) Какова размерность пространства Hq?
(b) Определите размерность пространства Н% и выпишите ба-
зис этого пространства (2-ячейки имеют имена Эл, Бен и
Глем; постройте соответствующие линейные комбинации,
следя за ориентацией). Что означает полученный результат
для собранной конструкции?
(с) Определите размерности dim Со, dim Ci и dim С2, потом вы-
числите dim Hi.
(d) Выпишите базисы пространств Zi, Bi и базис факторпро-
странства Hi = Z1/B1.
(е) Ниже выписаны три 1-коцепи, т. е. элементы С1:
<т(а) = 1
<т(^) = 1
ст(7) = 2
ст(<5) = —2
<т(г) = —2
а(А) = 1
т(а) = 1
т(/3) = -1
т(7) = 2
т(5) = 2
т(е) = -2
т(А) = -1
w(a) = 1
w(/3) = -1
ш(7) = 2
w(5) = —2
tu(e) = 2
ш(Л) = -1
Найдите коцепь, которая не является коциклом, и опреде-
лите 2-коцепь, которая является ее кограницей (йП(Эл) = 1,
йП(Бен) = 3, сШ(Глем) = 2).
(f) Определите коцепь, являющуюся кограницей, и напишите
0-цепь /, чьей кограницей она будет.
740
Глава 14. Комплексы высших размерностей
(g) Покажите, что оставшаяся коцепь является коциклом, но
не будет кограницей. Вычислите ее для двух базисных эле-
ментов пространства Н±.
(h) Постройте второй коцикл, который не является кограницей,
но будет вторым базисным элементом пространства Н1.
(i) Напишите базисы пространств В1 и Z1.
14.5. Возрожденная Римская империя послала уполномоченного пред-
ставителя Гая Юлия Цезаря обследовать ситуацию на междуна-
родной космической станции «Новая Галлия». В его отчете, начи-
навшемся словами: «Вся Новая Галлия разделена на три части»,
были три карты, изображенные на рис. 14.24. Карты показывают
территории, контролируемые аквитанцами (Aqu), белгами (Bel)
и кельтами (Cel) соответственно. Эти враждующие племена не
смогли договориться о единой (непротиворечивой) ориентации
всей поверхности этой станции. Дайте ответы на следующие во-
просы относительно комплекса «Новой Галлии».
(а) Вычислите границу каждого региона: Q(Aqu) и т. д.
Рис. 14.24
Задачи
741
(b) Найдите максимальное дерево. С помощью этого дерева вы-
числите dimZi, dimBi и dimHi. Постройте базис Вр В
этом базисе выразите а — 7 + # — туи /3 + 7.
(с) Если ш есть 1-кограница (элемент В1), удовлетворяющая
условиям = 2 и (л)8 = 1, то каковы значения си7 и о/7?
(d) Если т есть 1-коцепь, значения которой для каждой ветви
равны 1, то чему равны dr(Aqu) и dr (Bel)?
(е) Вычислите dimZ1. Если а есть 1-коцикл (элемент Zi), удо-
влетворяющий условиям сга =3, =1, а5 = 2, = 4, то
каковы значения <т7 и <те?
(f) Постройте базис В1, дуальный к базису Hi из пункта (Ь).
В этом базисе выразите класс эквивалентности а.
(g) Может ли поверхность «Новой Галлии» быть сферой? ци-
линдром? тором?
14.6. На небольшой планете живет колония, разделенная на две про-
винции, Красный и Зелёный, как показано на рис. 14.25.
Рис. 14.25
(а) Вычислите «Э(Красный) и Э(Зелёный). С помощью результа-
та определите размерность В2 для этого 2-комплекса. Объ-
ясните полученный результат и скажите: занимает ли коло-
ния всю поверхность планеты или нет?
(Ь) Максимальное дерево для этого комплекса состоит из вет-
вей о, /3 и J. Найдите базисы пространств Zi, В\ и Hi. Дайте
742
Глава 14. Комплексы высших размерностей
географическое объяснение базисному элементу простран-
ства Hi.
(с) Определите пространство В1. Какое пространство оно будет
аннулировать? Докажите свой ответ. Рассмотрите 1-коцепь
W, для которой Wa = 2, — —1, W6 = 1.
(d) Найдите такие значения ТУ7, W£, ТУ77, чтобы W было ко-
границей.
(е) Пусть ТУ7 = 3, We = 2, W77 = 1. Вычислите dW.
(f) Найдите такие значения ТУ7, ТУ£, ТУ17, чтобы W было ко-
циклом, но не кограницей. Вычислите эту коцепь в базисе
пространства Hi.
14.7. (а) Найдите размерности пространств: Ci, Сг, Я1, Bi и Hi для
комплекса, изображенного на рис. 14.26(a).
(Ь) Найдите размерности пространств Hq и Н^\ докажите, что
dim Со—dim Ci+dim С2 = dim Hq — dim Hi + dim H2. (14.1)
(с) Пусть к комплексу добавили новую ветвь а и новый узел
С, как показано на рис. 14.26(6). В явном виде напишите
матрицы операторов д : Ci —> Со и д : С2 —> Ci и вычислите
матрицу д о д ; С2 —> Со-
Рис. 14.26
Задачи
743
(d) Вдоль ветви <т сделан разрез, разделивший ее на tri (на сто-
роне Зелёный) и <72 (на стороне Синий), рис. 14.26(b). На-
пишите д : Ci —► Cq. Построив базис, найдите размерность
Но. Что это говорит о данной цепи? Постройте базис про-
странства Hi и проверьте уравнение (14.1).
(е) Пусть 1-коцепь т имеет значение 1 на всех ветвях между
различными точками и значение 0 во всех остальных слу-
чаях. Чему равны dr (Зелёный) и dr (Синий)?
14.8. На рис. 14.27 изображен 2-комплекс, состоящий из двух частей.
Рис. 14.27
(а) Вычислите ^(Красный) и ^(Зелёный), отсюда определите
dimZg.
(b) Для этого комплекса найдите максимальное дерево. Ис-
пользуйте его для нахождения dimZi, dim Bi и dim Hi.
(с) Найдите базис пространства Hi, ив этом базисе выразите
7 и а + 6 + (3.
(d) Пусть си — это 1-кограница, удовлетворяющая условию
— 2. Вычислите ш(Х.
(е) Пусть 1-коцепь т принимает на каждой ветви значение 1.
Вычислите dr.
(f) Определите dim В2 для этого комплекса.
Глава 15
Комплексы в пространстве Rn
В главах 15-18 внешнее дифференциальное исчисле-
ние излагается как непрерывная версия дискретной
теории комплексов. В главе 15 сформулированы ос-
новные положения внешнего исчисления: внешняя ал-
гебра, /с-формы, операция переноса (pullback), внеш-
няя производная и теорема Стокса.
Введение
До сих пор, рассматривая различные комплексы, мы не интересо-
вались тем, как комплекс может быть расположен в пространстве
Rn. Изучая электрические цепи, мы пренебрегали формой прово-
дов и даже не ставили вопрос, может ли данная цепь быть реали-
зована на плоскости. Сейчас мы начнем изучать частный случай
комплекса, помещенного в пространство Rn, чтобы увидеть, как
естественным образом из геометрических или физических сооб-
ражений возникают коцепи.
Сначала обсудим 1-комплекс в пространстве R3 типа изобра-
женного на рис. 15.1. В этом пространстве узлы являются точ-
ками, а ветви — дифференцируемыми кривыми. Поскольку ко-
цепь однозначно определена своими значениями в каждом уз-
ле комплекса, мы можем рассматривать ее как функцию узлов.
Один из очевидных путей получения такой функции — это задать
функцию, определенную в R3. Каждая такая функция
746
Глава 15. Комплексы в пространстве Rn
определяет 0-коцепь Ф согласно правилу Фл — Ф(хЛ, уЛу £Л), где
хл, ул, zA являются координатами узла А.
Функция ф может рассматриваться как зародыш 0-коцепи в
том смысле, что она определяет 0-коцепь для любого комплекса,
расположенного в этом пространстве.
Чтобы таким же способом получить 1-коцепь, нам надо иметь
правило, по которому любой ветви комплекса приписывается чис-
ло. Такое правило получается, например, из дифференциальной
1-формы си, определенной в пространстве R3. Тогда если каж-
дая ветвь комплекса является дифференцируемой дугой, то, ин-
тегрируя си вдоль каждой ветви, мы можем построить 1-коцепь.
Например, если ветвь а описывается параметризованной кривой
a(i), то 1-коцепь, определенная си, будет принимать на ветви а
значение faco. Таким образом, 1-форма си может рассматривать-
ся как зародыш 1-коцепи. Она определяет 1-коцепь для любого
комплекса, расположенного в R3.
Предположим, что ф — непрерывно дифференцируемая функ-
ция, и мы образуем ее дифференциал, т. е. 1-форму ш = дф. Пред-
положим, что для ветви а выполняется условие да = В — А, так
/ж(^\
что а описывается кривой I y(t) с условиями:
v(<)/
(х(0)\ /хА\
3/(0) = УА
г(0)/ \zAJ
(х(1)\ /жв\
у(1) I = [ Ув I •
г(1)/ \zBJ
Введение
747
Тогда
f tv — f <1ф = [ а* (1ф = f d(a* ф)
J a Jot Jo Jo
= а*ф(1) - а*0(О) - ф(В) - ф(А).
Функция ф определяет 0-коцепь Ф с условиями ФЛ = ф(А) и
Фв = ф(В). Из этой 0-коцепи мы можем образовать 1-коцепь с1Ф,
значение которой на ветви а равно
[аФ= [ ф = фв - фа = ф(в) - ф(А).
J a J dot
Мы используем одно и то же обозначение d для двух различ-
ных ситуаций: во-первых, как линейный оператор, действующий
на 0-коцепь Ф и образующий 1-коцепь dФ: во-вторых, как диф-
ференциальный оператор, который действует на функцию ф и
образует дифференциальную форму dф. Сейчас становится оче-
видным, что такое использование d корректно в том смысле, что
если из функции ф получается 0-коцепь Ф, то из 1-формы dф по-
лучается 1-коцепь dФ, В пространстве R3 рассмотрим простран-
ство гладких функций Q°(R3) и пространство гладких 1-форм
Q1(R3). Тогда можно построить диаграмму, отражающую непро-
тиворечивость определения d:
CQ
Эта диаграмма коммутативна в том смысле, что от функции
ф к 1-коцепи можно перейти как через (7°, так и через Q1.
Теперь мы должны проделать нечто похожее для 2-коцепей
и 3-коцепей. В следующем параграфе мы введем объекты, на-
зываемые дифференциальными 2-формами и 3-формами, из ко-
торых в результате соответствующего интегрирования получатся
2-коцепи и 3-коцепи соответственно. Надо будет определить такой
дифференциальный оператор d, который преобразует 1-формы
748
Глава 15. Комплексы в пространстве
в 2-формы и 2-формы в 3-формы. Причем это преобразование
должно быть совместимым с действием оператора d на соответ-
ствующие коцепи.
В частном случае 2-комплекса, расположенного на плоско-
сти, мы можем увидеть, как будет работать эта программа. Заро-
дыш 2-цепи должен будет приписывать число каждой ориентиро-
ванной области на плоскости; значения, приписываемые каждой
ячейке Q этого комплекса, будут определять 2-коцепь. Сейчас мы
можем перейти от 1-формы (зародыша 1-коцепи) и к 2-форме Т
двумя различными способами, как это показано на рис. 15.2. Рас-
смотрим, например, путь а + /3 + 7, являющийся границей ячейки
Q. Один способ состоит в том, чтобы образовать 1-коцепь W из
си, вычисляя интеграл по пути вдоль каждой ветви комплекса. А
уже потом подействовать оператором d : С1 —> С2. Это дает
[ Т = [ dW = [ w = Wa + WP + VH = [ ш + [ ш + [ ш.
Jq Jq JdQ Ja Jy
Рис. 15.2
Другой способ состоит в том, что действуя дифференциаль-
ным оператором d на oj, есть надежда получить 2-форму г, кото-
рую можно проинтегрировать по области Q и получить значение
2-коцепи Т на ячейке Q,
В этом случае теорема Грина на плоскости говорит нам, ка-
кую форму должен иметь оператор d. Вспомним, что согласно
15.1. Внешняя алгебра
749
этой теореме, если ориентированная область Q на плоскости име-
ет границу dQ, то интеграл по траектории1
Г л , [ (дВ дА\ ' ,
/ Adx + Bdy = —---— ] dx A dy.
JdQ Jq \ dx dy J
В этом частном случае кажется целесообразным ввести 2-формы
вида т — /(z, у) dxA dy. В результате повторного интегрирования
из 2-формы получается 2-коцепь, и 2-форма может быть получе-
на из 1-формы согласно правилу
,/4 7 „ , \ (дВ дА\ л
d(A dx + В dy) — ------dx A dy.
\дх ду J
15.1. Внешняя алгебра
В случае 0-коцепей и 1-коцепей мы уже имеем дифференциаль-
ный оператор, прекрасно согласующийся с кограничным опера-
тором. Зародышем 0-коцепи является дифференцируемая функ-
ция ф, которая каждой точке приписывает вещественное число.
Зародышем 1-цепи является 1-форма си, приписывающая каждой
точке элемент пространства V*, дуального к используемому нами
основному пространству V. Функция ф принадлежит простран-
ству Q°(V), а 1-форма си принадлежит пространству QX(V). Мы
определили оператор d : Q°(V) —> Q1(V), согласованный с когра-
ничным оператором.
Сейчас мы будем строить последующие пространства Q2(V),
Q3(V), ..., Qk(V), которые позволят обобщить дифференци-
альный оператор d. Элемент си, принадлежащий пространству
Qfc(V), называется дифференциальной к-формой. Каждой точке
области си он будет приписывать элемент пространства A.k(V*).
Обычно это называют «&-я внешняя степень пространства V*»,
для нас это — обобщение дуального пространства V*. Чтобы
определить fe-коцепь, мы будем интегрировать /с-форму. По-
сле этого мы сможем определить дифференциальный оператор
1 Напомним, что в русской математической литературе он называется кри-
волинейным интегралом второго рода. — Прим. ред.
750
Глава 15. Комплексы в пространстве Rn
d : > Qfc+1(y), который будет согласован с преобразова-
нием комплексов d : Ск —> Cfc+1. В качестве первого шага в этом
направлении введем пространство Afc(y*).
Пусть V — некое векторное пространство размерности п< а У*
— его дуальное пространство. Дуальное пространство V* являет-
ся пространством линейных функций из V в R, т. е. £(V; R). Сна-
чала рассмотрим B(V, У;К) — пространство билинейных функ-
ций из V х V в R. Мы говорим, что функция t(vi,V2) били-
нейна, если для фиксированного значения V2 функция t(vi,V2)
линейно зависит от первого аргумента, т.е. r(avi + /?wi,V2) =
or(vi, V2) + /3r(wi,V2) и, аналогично, для фиксированного зна-
чения vi функция т линейно зависит от второго аргумента. Про-
странство Б(У, У;К) является векторным пространством, где вы-
полняются обычные правила сложения функций и умножения
функции на число.
Внутри пространства функций Б(У, У;К) есть подпростран-
ство, обозначаемое Л2(У*). Это пространство кососимметричных
билинейных функций, удовлетворяющих условию r(vi,V2) =
—t(v2,vi). Из любой билинейной функции cr(vi,V2) мы можем
построить кососимметричную функцию
r(vi,v2) = cr(vi,v2) - cr(v2, Vi).
Из элементов пространства У* не сложно построить элементы
Л2(У*). Для заданных элементов сиг,6 У* введем функцию
сиг Л cuJ согласно определению
Л o/(vi, V2) = o/(vi)o?(V2) — CV*(V2)O?(V1).
Поскольку функции и со3 линейны, то а>1 Л ссР билинейна. Более
того,
Ao?(v2, Vi) = cu4(v2)cuj(vi) — o/(vi)o?(v2) = — сиг AcuJ(vi, v2),
следовательно, функция а)г Л — кососимметричная.
Из определения внешнего произведения следует, что оно дис-
трибутивно по сложению:
(си1 + си2) Л си3.= си1 Л си3 + си2 Л си3.
15.1. Внешняя алгебра
751
Чтобы доказать это утверждение, рассмотрим произвольные век-
тора vi и V2- Тогда
[(й? +а>2) Aa?](v1? v2)
= [(cu1 + iu2)(vi)]oj3(v2) “ [(a;1 +o>2)(v2)]a?(vi)
= kAvi) +u;2(vi)]cu3(v2) - [o?(v2) + cv2(v2)]<v3(vi)
= a? Acj3(vi, v2) +oj2 Acj3(vi, v2).
Предположим, что мы выбрали дуальные базисы: базис ei,
е2, ..., еп пространства V и базис 51, s2, ..., бп пространства V*;
таким образом,
г/ \ fl, если i — j.
£ 4е?) = 1 П • /
v [0, если г д.
Если выразить а;1 и а?2 через базис V*, то
о;1 л cu2 = (aie1 + a2s2 Ч-) Л (bis1 + Ь2г2 Ч-)
будет суммой членов вида е1 Л е7. Однако, s7 Л ег = —е1 Л е-7. По-
этому каждый элемент вида си1 Л и2 может быть выражен через
элементы вида бг Л е-7, где i < j, В общем случае, пусть т являет-
ся элементом пространства Л2(У*). Вследствие билинейности и
кососимметричности т оказывается, что т определяется значени-
ями т(е^,е7-) для i < j. Введем новое обозначение r(ei,ej) = Ьгз.
Величина ^2 А принимает те же значения, что и т, на всех
ед., е/. Следовательно, т — ^Ъ^еъ А б-7. Значит, элементы Л е7
порождают пространство A2(V*). С другой стороны, легко про-
верить, что все они линейно независимы. Тогда из п базисных
элементов пространства V* мы можем построить ^п(п — 1) ли-
нейно независимых элементов пространства A2(V*), потому что
элементы Л е*7 при i < j образуют базис пространства Л2(У*).
В случае, когда пространством V является R3, в качестве
базисных элементов V* удобно взять dx, dy и dz. Тогда базис
A2(R3*) состоит из трех элементов dx /\dy. dx /\dz и dy /\dz.
Взяв два элемента пространства V*, мы можем, воспользо-
вавшись внешним произведением и правилом о;-7 Л иЧ _ —о? Л о?-7,
умножить и упростить, например, (dx Ч- dy) Л (dx Ч- 2dy — 3dz) =
2dx /\dy — 3dx /\dz + dy /\dx — 3dy hdz — dx /\dy — 3dx /\dz-3dy f\dz.
752
Глава 15. Комплексы в пространстве Rn
Действие элемента пространства Л2(У*) удобно выразить че-
рез определитель, т. е.
1*2/ \ <x/(v2)\
0) Acc/(vi,v2) = Det 2s X 2/ \ •
v (vi) ar(v2)y
Мы воспользуемся этой формулой для обобщения внешнего про-
изведения на случай, когда множителей больше двух.
Функция /, зависящая от трех векторов в пространстве У,
называется трилинейной, если /(vi,v2,v3) зависит линейно от
Vj (г = 1,2,3), когда два других вектора фиксированы. Трили-
нейная функция f называется кососимметричной, если
/(v2,vi,v3) = -/(vi,v2,v3) и /(vi,v3,v2) = -/(vi,v2,v3).
Из этих соотношений следует, в частности, равенство
/(v3,v2,vi) = -/(vi,v2,v3).
Например, определитель матрицы 3x3 является трилинейной
кососимметричной функцией столбцов.
А теперь давайте построим пространство Л3(У*), т. е. про-
странство кососимметричных трилинейных функций из У в R.
Элементы этого пространства можно построить, воспользовав-
шись обозначениями внешнего произведения и обобщив опреде-
ление на языке определителей следующим образом:
/V(vi) o/(v2) cul(v3)\
о? Ло? Awfe(vi, V2,v3) = Det I oP(vi) cuJ(v2) оР(уз) I .
\wfe(vi) wa(v2) wfc(v3)/
Функции Л ш3' /\шк обладают рядом свойств, являющихся след-
ствием линейности o/(v) и элементарных свойств определителя.
(а) Для фиксированных векторов v2 и v3 функция сиг Л си-7 Л
линейно зависит от vi, потому что элементы первого столб-
ца определителя линейны по vi, а определитель является
линейной функцией элементов первого столбца.
(Ь) Функция сиг Л си-7 Л cufe линейна также по v2 и v3, т. е. она
трилинейна.
15.1. Внешняя алгебра
753
(с) Функция а? Л и-7 Л шк изменяет знак при перестановке двух
соседних аргументов (т.е. vi и V2 или V2 и V3) меняются
местами, потому что определитель меняет знак при пере-
становке соседних столбцов.
(d) Функция Л Л шк меняется знак на противоположную
при перестановке двух соседних «множителей» в ней (т.е.,
например, Л ег Л ек = так как определитель
меняет знак при перестановке соседних строк.
(е) о/ До/ Ли/ = 0, потому что определитель с двумя одинако-
выми строками равен нулю.
(f) Тройное внешнее произведение дистрибутивно относитель-
но сложения по каждому множителю, потому что опреде-
литель дистрибутивен по каждой строке.
(g) Если vi, V2 и V3 линейно зависимы, то
(V1 * AcUfe(vi,V2, V3) — О,
потому что определитель равен нулю, если линейно зависи-
мы его столбцы.
(h) Если о/, си-7 и шк — линейно зависимые элементы простран-
ства V*, то и/ ЛаР Ли/ — 0, потому что определитель равен
нулю, если линейно зависимы его строки.
Как и раньше, несложно доказать, что элементы е1 Л е7 Л ек при
i < j < к образуют базис пространства Л3(У*), если £г, ек
являются базисными элементами пространства V*. Существует
п возможностей выбрать г, затем п — 1 возможность выбора j и
п — 2 возможности выбора fc, потому что если любые два индекса
равны, то £1 Л €7 Л / — 0. Но комбинация из трех индексов
допускает 3-2-1 = 6 перестановок, соответствующих только
одному элементу с i < j < к. Следовательно,
1 ti I
dimA3(V*) = -n(n - l)(n - 2) = '
О О! О)
754
Глава 15. Комплексы в пространстве Rn
Теперь мы можем дать определение пространства A.k(V*) при
произвольном к. Это подпространство пространства2 полилиней-
ных функций £(V, V,..., V;R), которые кососимметричны в том
смысле, что функция изменяет знак при перестановке любых
двух соседних элементов. Элемент пространства Л* (У*), называ-
емый ^-формой, может быть построен из к элементов простран-
ства V* согласно правилу:
й/1 Л О?2 Л * • • Л o/fc(vi, V2, - • • , Vfc)
~ Det
o/2(vi)
V^fc(vi)
^г1^2)
u/2 (v2)
cSk (v2)
wl2(vfc)
шгк(ук))
Размерность пространства Afc(V*) равна n\/(k\(n — fc)!),3 а его
базис состоит из всех элементов Л ё12 Л • • • Л егк при условии
й < г2 < • * * < з&.4 * * Заметим, что пространство An(V*) одномерно,
и его единственный базисный элемент равен е1 Л s2 Л • • • Л еп, ав
случае к > п пространство Afc(V*) — {0}.
Для нас будет важна еще одна алгебраическая операция —
«внешнее» умножение элемента пространства AP(V*) на эле-
мент пространства АДУ*), в результате чего получается элемент
Лр+<?(У*). Если пользоваться базисными элементами, то внешнее
умножение определяется формулой
(ви Л5г2Л- ♦ •Аегр)л(е-71 Ле-72 Л* • -Ле-79) = s21 Л - • -Аг^Ле71 Л - • - Ле7*.
Это определение может быть продолжено на линейные комбина-
ции базисных элементов так, чтобы сохранялась линейность по
2обычно называемого пространством тензоров типа (fc,0), или к раз ко-
вариантных. Таким образом, Afc(V*) есть пространство кососимметрических
тензоров типа (&, 0). — Прим. ред.
3Это выражение представляет собой биномиальный коэффициент
(другой вариант обозначения — (£)), а именно, коэффициент при хк в разло-
жении многочлена (Ц-х)п, равный числу способов выбора неупорядоченного
набора к элементов из n-элементного множества. — Прим. ред.
4Как и прежде, имеется в виду, что е1, е2, ..., Еп — некоторый базис про-
странства V*. Доказательство линейной независимости указанных элементов
и порождения ими всего Afc(V*) оставляем читателю в качестве упражнения.
— Прим. ред.
15.1. Внешняя алгебра
755
каждому множителю отдельно, т. е. должен выполняться дистри-
бутивный закон умножения. Например, если
w — 5s1 Л s7 + 3s2 As4 и а = 6s1 Л s5 + 2s3 As5 — 9s3 Л s6
являются элементами пространства A2(V*), то элемент си/\а про-
странства A4(V*) вычисляется следующим образом:
си Л а = 5(s1 Л s7) Л ст + 3(s2 Л s4) Л а
— 30s1 Л s7 Л г1 Л s5 + 10s1 Л s7 Л s3 Л г5 — 45s1 As7 As3 Аг6
+ 18s2 Л s4 Л s1 Л s5 + 6s2 As4 А? A? - 27s2 As4 As3 A s6.
Первое слагаемое в правой части равно нулю, потому что в него
элемент s1 входит два раза. Остальные слагаемые надо преоб-
разовать, чтобы превратить их в базисные элементы; при этом
возможны изменения знаков. Например,
s1 Л s7 Л s3 Л s5 — s1 Л s3 Л s5 Л s7,
потому что s7 надо переставлять на два места назад, а
S2 As4 As3 As6 = -s2 As3 Л s4 A s6.
Итак,
си Л о — 10s1 Л s3 Л s5 Л s7 — 45s1 Л s3 Л е6 A s7
+ 18s1 Л s2 Л s4 A s5 - 6s2 Л s3 A s4 Л s5 4- 27s2 Л s3 A s4 Л s6.
Мы настоятельно рекомендуем читателю сделать побольше
примеров внешнего умножения, чтобы почувствовать, как устро-
ена эта операция. До конца книги внешнее умножение будет
одним из основных вычислительных методов. Поэтому усилия,
вложенные в приобретение подобных вычислительных навыков,
окупятся сторицей в дальнейшем. Читатель должен убедиться в
справедливости следующих правил:
Ассоциативный закон: (си Л а) Л т — ш Л (ст Л т).
Дистрибутивный закон: w Л (а + т) = си А сг + си Л г.
756 Глава 15. Комплексы в пространстве
Антикоммутативность (сегодня это часто называют суперкомму-
тативностью) значит следующее5 *:
(V Л г = (—1)рдт Л о;, если ш Е AP(V*) и т Е A9(V*).
Эти правила ускоряют процедуру вычисления внешнего произве-
дения.
С логической точки зрения наше определение не совсем удо-
влетворительно, потому что кажется, что есть зависимость от
выбора базиса. Строго говоря, мы должны доказать, что если
выбрать другой базис в пространстве V, соответственно получив
другой базис пространства AP(V*), то результат умножения эле-
ментов не изменится. Это можно показать непосредственным вы-
числением, что довольно утомительно. Гораздо лучше дать более
абстрактное определение умножения, которое будет автоматиче-
ски удовлетворять всем правилам, так что формула для умно-
жения станет следствием этого определения. Мы сделаем это в
приложении к главе 18, но если читателю это очень интересно,
пусть прочитает это приложение прямо сейчас — оно независи-
мо от остального материала. Гораздо важнее приобрести навык
вычисления внешнего произведения.
В качестве примера рассмотрим четырехмерное пространство
V. Имея в виду очевидную интерпретацию как пространства-
времени, обозначим базисные элементы пространства V* как dt,
dx, dy и dz. В этом случае получим полный набор пространств
Afc(V*):
• пространство A°(V*) одномерно; единственный базисный
элемент назовем 1;
• пространство AX(V*) четырехмерно; это пространство V*,
его базисные элементы: {dt,dx,dy,dz};
• пространство A2(V*) шестимерно; базисные элементы: dt Л
dx, dt Л dy, dt Л dz, dx A dy, dx A dz, dy A dz;
• пространство Л3(У*) четырехмерно; базисные элементы:
dt /\dx Л dy, dt f\dx A dz, dt /\dy A dz, dx /\dy A dz;
5 Аккуратное доказательство этого свойства также является хорошим
упражнением. — Прим. ред.
15.2. fc-формы и оператор d
757
• пространство Л4(У*) одномерно; базисный элемент dtf\dxf\
dy Л dz.
15.2. A-формы и оператор d
Чтобы перейти от пространства Afc(V*) к пространству Qfc(V),
мы сделаем такое же расширение, как мы делали, переходя от
дуального пространства V* (обозначаемого также Л1(У*)) к про-
странству Q1(V). Элементом пространства Qfc(V) является функ-
ция, которая каждой точке приписывает элемент пространства
Л* (У*), т. е. коэффициентами базисных элементов Afc(V*) стано-
вятся функции, принимающие вещественные значения. Напри-
мер, общий вид элемента пространства Q2(R3) — это
а(ж, т/, z)dx f\dy + b(x, г/, z)dx /\dz + c(x, г/, z)dy A dz,
где a,b,c — вещественнозначные функции. Что касается алгебра-
ических операций, в том числе сложения и внешнего умножения,
то элементы пространства Qfc(V) ведут себя так же, как элемен-
ты пространства Л^(У*). Элементы пространства Qfe(y), назы-
ваемые дифференциальными k-формами или просто к-формами,
будут выступать как зародыши fc-коцепей. Мы должны научить-
ся дифференцировать и интегрировать их. Рассмотрим простран-
ство V = и пусть dx1,... ,dxn образуют базис пространства
У*. (Мы используем также обозначения dx, dy и т. д.)
Мы уже знакомы с дифференциальным оператором d, припи-
сывающим 1-форму 0-форме. Если f(x,y,z) — дифференцируе-
мая функция (0-форма), то
df^/dx + ^Ldy + ej_dz.
дх оу dz
В конечном счете мы хотим построить fc-форму как объект,
который мы будем интегрировать по «fc-мерной гиперповерхно-
сти». Кроме того, мы хотим доказать теорему Стокса, которая
говорит, что
758
Глава 15. Комплексы в пространстве Rn
где S — это «fc-мерная гиперповерхность» и dS — ее граница. В
главе 8 мы видели, что это уравнение, примененное к инфините-
зимальным параллелограммам, давало определение оператора с?,
действующего на 1-формы. Тогда мы получили, что
d(f dg) =df Л dg.
Поскольку любая 1-форма является суммой таких выражений,
то это давало нам определение d для 1-форм. Может быть, сей-
час полезно вернуться назад и еще раз посмотреть на основные
формулы главы 8, выписанные на с. 425.
Давайте в качестве примера проделаем алгебраические вы-
кладки для 1-формы. Мы хотели бы получить
d(J dg Л dh Л • • •) = df Л dg Л dh Л • • • . (*)
Это заставляет нас определить действие оператора d на &-форму
в следующем виде:
если т = f dx4 Л • • • Л dxik + д dx?1 Л • • • Л dx3k Н-,
то dr — df Л dx4 Л • • • Л dx4 + dg Л dx31 Л • • * Л dx3k. (15.1)
После действия оператора d бывает необходимо перегруппи-
ровать члены, чтобы собрать коэффициенты при каждом базис-
ном элементе.
Рассмотрим пример действия d на 2-форму в пространст-
ве R3. Пусть т = Bxdy Л dz — Bydx Л dz + Bzdx Л dy. где Вх.
Ву. Bz — дифференцируемые функции х. у. z. которые мож-
но рассматривать как компоненты векторного поля. Тогда dr —
dBx Л dy Л dz — dBy Л dx f\dz + dBz /\dx /\dy. Подставляя диффе-
ренциалы и используя тот факт, что внешнее произведение равно
нулю, если совпадают любые два множителя, мы получаем
, f dBx dBy дВЛ
dr — ( I dx Л dy Л dz.
\ дх оу dz J
Те, кто знаком с векторным анализом, могут заметить сходство
между d : fl2(R3) —> Q3(R3) и операцией div.
Оператор d обладает рядом полезных свойств, которые следу-
ет отметить. Каждое свойство достаточно проверить для случая
15.2. /с-формы и оператор d
759
fc-формы вида Q — f dx Л dy Л • • •. Общий случай становится по-
нятным в силу линейности оператора d.
Первое свойство связано с результатом действия оператора
d на произведение функции и &-формы. Пусть f и д — диф-
ференцируемые функции и Q = gdx Л dy Л • • •. Тогда d(/Q) =
d(fgdx Л dy Л • • •) = d(fg) Л dx Л dy Л • • •. Но для дифферен-
циалов существует правило d(fg) = f dg + gdf. Отсюда следу-
ет, что d(/J2) — f dg Л dx A dy Л • • • + gdf A dx Л dy Л • • • или
d(/Q) = f d(g dx A dy A • • •) + df A (g dx A dy A • • •). Тогда мы
получаем
d(fty = fdtl + df Afi.
Второе свойство относится к действию опрератора на произ-
ведение р-формы ш и g-формы Q. Пусть ш = f dx1 Л • • • A dxp и
Q = gdy1 А • • • Л dyq. где f и д — дифференцируемые функции.
Имеем d(u Л П) = d(fgdx1 Л • • • Л dxp Л dy1 Л * • • Л dygf Поэтому
d(w Л Q) = f(dg Л dx1 Л • • • Л dxp A dy1 Л • • • Л dyq) +gdf A dx1 А • • • А
dxp Ady1 А- • • Adyg. В первом члене переставляем dg и множитель
dx1 Л • • • Л dxp, в результате чего получается знак (—1)р. Тогда
d(cu Л Q) = dx1 Л • • • A dxp) Л (dg Л dy1 Л • • • Л dyp)
+ (df Л dx1 А • • • A dxp) Л (д dy1 Л • • • Л dyp).
Поскольку каждая р-форма есть сумма членов вида f dx1 Л • • • Л
dxp и каждая g-форма есть сумма членов вида gdy1 Л • • • Л dyp,
мы имеем
d(u АО) = (~1)р^ Л dQ + dcj Л П. (15.2)
Третье свойство касается двукратного действия оператора d.
Сначала рассмотрим d(df), где f(x,y,...) — дважды дифферен-
цируемая функция. В этом случае
fdf df \ d2f d2f
d(df) = d -^-dx + ~z~dy + • • • = -^dy/\dx+--~-dx/\dy+- • • .
dy ) dydx dxdy
Из равенства смешанных частных производных и соотношения
dy/\dx = —dxf\dy следует, что d(df) — 0. Теперь рассмотрим более
общий случай fc-формы и — f dx Л dy Л • • •. В этом случае dcj —
df A(dx/\dy/\ - • •) и d(du?) = df /\d(dx/\dy/\ - • • )+d(d/)AdxAdpA- * •.
760
Глава 15. Комплексы в пространстве Rn
Однако d{dx /\ dy Л • • *) — 0 и d(df) — 0. Отсюда следует, что в
общем случае
d(dw) = 0. (15.3)
Это согласуется со свойством кограничного оператора:
d о — 0.
Конечно, уравнение (*) теперь следует из (15.2) и (15.3).
Если мы считаем, что dx — это результат действия оператора
d на координатную функцию х, то определение (15.1) становится
следствием (15.2) и (15.3). Поэтому, когда Вы убедились в су-
ществовании оператора с/, остается только запомнить следующие
его свойства:
(1) df — (df /dx)dx + (df /dy)dyA-, где z, у,... координатные
функции;
(2) d аддитивен, т. е. d(iv + ст) = div + dcr;
(3) как оператор d действует на произведение, т.е. (15.2);
(4) dod = 0.
С помощью этих четырех правил можно вычислить действие
d на любую форму.
15.3. Интегрирование А>форм
Чтобы закончить идентификацию fc-форм в качестве зародышей
к-коцепей, мы должны объяснить, как й-форма Q приписыва-
ет fc-коцепь каждому комплексу с дифференцируемыми ячейка-
ми, находящемуся в n-мерном пространстве. Сначала рассмотрим
случай к — 1. Пусть в пространстве Rn имеется гладкая кривая,
соединяющая точки А и В, и мы хотим вычислить интеграл от 1-
формы oj на этой кривой. Для этого выберем произвольную глад-
кую параметризацию кривой, т. е. произвольное гладкое отобра-
жение а : R —► Rn, которое отображает отрезок [0,1] в желаемую
кривую с условиями а(0) — А и а(1) — В, как это показано на
15.3. Интегрирование А>форм
761
рис. 15.3. Затем произведем перенос (pullback) 1-формы си и по-
лучим выражение типа g(t) dt. Определим интеграл по тра-
ектории от формы со вдоль кривой а формулой fa(V — Jq((T*Cj).
Это определение полезно тем, что результат не зависит от спосо-
ба параметризации кривой а. В этом случае интеграл по кривой
сводится к интегрированию по отрезку [0,1]. Ключевым пунк-
том построения является процедура переноса для 1-формы: если
cj — f dx + gdy -I-, то a*w — (a*f) d(a*x) + (a*g) d(a*y) + • • *.
Очень важно доказать (с помощью цепного правила), что резуль-
тат не зависит от параметризации.
В этом определении и в соответствующей теории двумерного
интегрирования, которую мы обсуждали в главе 8, перенос иг-
рает чрезвычайно важную роль. Поэтому в первую очередь мы
должны обобщить эту процедуру. Пусть ф : Rfc —> Rn — диффе-
ренцируемое отображение. Мы хотим определить операцию </>*,
называемую переносом, которая любой дифференциальной фор-
ме cj (любой степени) в пространстве приписывает дифферен-
циальную форму ф*ш (той же степени) в пространстве При
этом нужно, чтобы ф* сохраняла операции сложения и умноже-
ния, т.е. выполнялись равенства
ф*(^1 + ^2) = Ф*(1^.4)
и
ф*(а?1 Л ufy) ~ Ф*^1 Л (15.5)
762
Глава 15. Комплексы в пространстве Rn
Кроме того, мы хотим, чтобы ф* оставалось нашей прежней опе-
рацией переноса, когда она действует на 0-формы (т. е. на функ-
ции) и на линейные дифференциальные формы. Это значит, что
если f 6 Q°(Rn) — функция, то должны выполняться равенства
Ф*/ = /°Ф,
(15.6)
И
фЧ/ = (15.7)
Условия (15.4)—(15.7) полностью детерминируют построение. На-
пример, рассмотрим отображение ф : R3 —> R3, определяемое
следующим образом:
х = г sin# cos Vs
где у = г sin в sin V>,
z — г cos в.
Тогда, как следует из (15.6),
ф*х = г sin в cos Vs
и так далее. Предположим, что нам надо вычислить ф(<1х Л dy Л
dz). Мы имеем
Л dy Л dz)
= $*dx Л ^^dy Л ^^dz из (15.5)
— (^1ф*х) Л (с1ф*у) Л faj)*z) из (15.7)
— [d(r sin# cos VO] [d(r sin # sin VO] A [c?(rcos#)] из (15.6).
Внутри каждого множителя этого тройного произведения мы
пользуемся обычными правилами вычисления дифференциала от
функции, так что d(r sin в cos ф) — sin # cos ф dr — г sin 0 sin фdф +
г cos 0 cos фd0 и т. д. Затем мы пользуемся правилами внешнего
умножения, чтобы выразить тройное произведение через dr /\d0Л
dф. В результате получаем
ф*(с1х /\dy Л dz) = г2 sin 0dr /\d0 Л dф.
15.3. Интегрирование £-форм
763
(Обычно эту формулу называют евклидовым объемом в сфери-
ческих координатах6.)
В общем случае следствием условий (15.4)-(15.7) является
определение
- (/o</>)d(?1o</>)A...Ad(^feo</>), (15.8)
где хг (г = 1,2, ...,п) — координаты в пространстве Rn. В си-
лу условия (15.4) наиболее общий вид ф* является суммой таких
выражений. Если взять (15.8) и его обобщение на суммы в каче-
стве определения процедуры переноса, то мы должны вернуться
назад и проверить, что условия (15.4)-(15.7) выполняются. Это
простое вычисление, и мы оставляем его читателю как упражне-
ние. Из определения оператора d и свойств процедуры переноса
следует, что
ф*[</(/dx1 Л dxj Л • • •)] — Л dx1 Л • • • ]
= d^f)\d$*xiN---
= d[(^f'^*xl К—]
-4ф*(/^Л-..)].
Проделав такие вычисления с суммами выражений такого вида,
мы получаем основную формулу
$*dw = (15.9)
Этот результат чрезвычайно важен. Он показывает, что если сна-
чала подействовать оператором d и потом применить перенос, то
получится то же самое, что и если сначала сделать перенос, а
потом подействовать оператором d.
Есть еще одна важная формула для процедуры переноса, ко-
торую следует отметить. Пусть ф : Rp так что мы можем
рассмотреть композицию ф о ф : Rp Rn. Тогда мы знаем, что
для любой функции f справедливо равенство
(</> О 1p)*f = f о (</> о V>) = (/ оф) оф = ф*ф*ф.
6 он же — определитель матрицы Якоби отображения координатного про-
странства в координатное пространство х,у, г; смысл определителя в
двумерной ситуации обсуждался в разделе 8.5 (с. 407). — Прим. ред.
764
Глава 15. Комплексы в пространстве IRn
Но тогда из полученных правил следует, что
(фоф)*и = 0//М (15.10)
справедливо для любой дифференциальной формы
Давайте соберем вместе различные правила внешнего диффе-
ренциального исчисления.
Алгебраические операции - сложение и умножение дифференци-
альных форм:
• При сложении и умножении на скаляр дифференциальные
формы (любой заданной степени) образуют векторное про-
странство.
• Произведение формы степени р на форму степени q образу-
ет форму степени р + q.
• Дистрибутивный закон: (од + о^) А <т — cui Л а + ^2 А сг.
• Ассоциативный закон: (оц Л о^) A шз = оц Л (о>2 А о?з).
• Антикоммутативность: ацЛсиг = (—1)pqcu2 Auji? если степень
tui равна р и степень равна q.
Оператор d:
• Если ш является формой степени р, то dw будет формой
степени р + 1, где df — (df /dx)dx + (df /dy)dy H-в коор-
динатах (x, p,...).
Кроме того,
d(to\ + ^2) = du?i + dw^y
d(a) A cr) = dw A a + (—l)pcu A dcr, если степень w равна p,
и
d(daf) ~ 0.
15.3. Интегрирование fc-форм
765
Перенос:
<f>*f = f °ф для функции /,
Ф*(и>1 + = Ф*ш1 + Ф*Ш2,
ф*(ш /\а) — ф*ш Л ф*сг,
Ф*а = аф*
и
(ф О 0)* = Ф* О ф*.
Во всех рассуждениях предполагалось, что отображения ф, ф
и т. д. и формы си, ст и т. д. определены во всем пространстве. Ко-
нечно, это не обязательно. Мы можем определить различные опе-
рации над формами, отображениями и так далее, когда они опре-
делены на различных открытых множествах. Надо только быть
уверенным, что области определения соответствуют друг другу.
Так, если ф определено на некотором открытом множестве С7, то
достаточно, чтобы си было определено на открытом множестве
О, которое содержит ф(и). Тогда мы сможем определить перенос
ф*ш. Если ф определено только на открытом множестве О, то мы
должны предположить, что ф(Р) С J7, если хотим определить
ф оф.
Определение интегрирования по областям в пространст-
ве Сейчас мы хотим определить интеграл от fc-формы по
ориентированной области U в пространстве т. е. мы рассмат-
риваем ситуацию, когда степень формы равна размерности про-
странства. Предположим, что U — ограниченная область, и она
«хорошая» в следующем смысле. Пусть на пространство на-
ложена сетка с ячейками г, так что оказывается составлен-
ным из неперекрывающихся кубиков с ребром е. Пусть 1ппе((7)
обозначает полный объем всех тех кубиков, что целиком лежат
в области U, a Out£(l/) — полный объем всех кубиков, которые
хотя бы частично лежат в данной области (см. рис. 15.4). Тогда
можно составить разность
Oute(C7) - 1пп£(П)
766
Глава 15. Комплексы в пространстве Rn
Рис. 15.4
и сделать ее достаточно малой, выбрав соответствующее малое
значение е. Это значит, что, вычисляя аппроксимирующие рима-
новы суммы, мы не должны беспокоиться о кубиках вдоль грани-
цы. Например, очевидно, что любой ограниченный многогранник
в этом смысле «хороший». Кроме того, если U — хорошая область
и гр — дифференцируемое отображение, определенное в облас-
ти немного большей, чем С7, то из теоремы о среднем значении
следует, что 'ipfJJ) тоже хорошее. (Вы можете доказать это само-
стоятельно или прочитайте главу 8 книги Loomis and Sternberg,
Advanced Calculus^ где подробно объясняются основные факты
об интегралах Римана в n-мерном пространстве.) Предположим
также, что ориентация U стандартная (задаваемая стандартным
базисом и соответствующими координатами ж1,... ^хк\
Пусть Q обозначает fc-форму в пространстве Тогда можно
написать
Q — fdx1 Л • • • Л dxk,
где f — дифференцируемая функция. Для любой ячейки е можно
составить аппроксимирующую риманову сумму
J2/(pi)Vol(Di)=efc22/(pi),
где и пробегает по всем кубикам сетки в области
U (или хотя бы частично попадающим в нее). Непрерывность
(равномерная) f гарантирует, что эта сумма стремится к пределу
при е 0, не зависящему от выбора как рг в кубиках, так и от
самой сетки. Этот предел будем обозначать
[ П.
Ju
15.3. Интегрирование fc-форм
767
Важно помнить, что в этом определении область U имеет стан-
дартную ориентацию пространства lRfe. Приведем очевидные
свойства этого интеграла. Предположим, что U = U • • • U (7Р яв-
ляется конечным объединением хороших подобластей, имеющих
стандартную ориентацию. Тогда
Игнорирование множеств меньшей размерности. Будем
говорить, что множество S имеет нулевую меру7, если для любо-
го положительного числа 6 мы имеем Oute(s) < 6 при достаточно
малом выбранном значении г. (Другими словами, S имеет нуле-
вую меру, если полный объем кубиков в сетке, которая пересекает
S, может быть сделан сколь угодно малым, выбирая размер ячеек
сетки достаточно малым.) Например, если S лежит в линейном
подпространстве размерности < /с, то очевидно, что S имеет ну-
левую меру. Множества нулевой меры не дают никакого вклада
в интеграл, т. е. если U — Uf U S, где S имеет нулевую меру,
то Q. Отсюда, например, следует, что если мы раз-
делим многогранник на подмногогранники (рис. 15.5), то можно
при вычислении интегралов не беспокоиться о гранях меньшей
размерности. Кроме того,
если U — единичный куб {0 < Xi < 1, i — 1,..., к}, то
/ Q = fc-кратному интегралу от f = / • • • / f dx± • • • dxk.
Ju Jo Jo
Доказательство точно такое же, как и для случая двух измерений
(см. с. 389 в главе 8). Конечно, так же как и в случае двух изме-
рений, вместо куба можно взять любую область, приводящую к
кратному интегралу.
7 Подразумевается определение меры в смысле Жордана, которая отли-
чается от «стандартной» меры Лебега более узким классом измеримых мно-
жеств. Ограниченное множество в евклидовом пространстве измеримо по
Жордану (или квадрируемо), если существует интеграл Римана (по объем-
лющей области) от его характеристической функции, при этом мера мно-
жества равна значению интеграла. — Прим. ред.
768
Глава 15. Комплексы в пространстве Rn
Рис. 15.5
Формула замены переменных. Предположим, что ф : —>
— взаимно однозначное, дифференцируемое, сохраняющее
ориентацию отображение, для которого существует дифферен-
цируемое обратное. Тогда для любой fc-формы си, определенной
в пространстве образов, и для любой хорошей области U в про-
странстве прообразов мы имеем
[ [ ф*ш.
J$(U) Ju
(Как всегда, ф должна быть определена в области, немного боль-
шей, чем J7, а си должна быть определена в области немного боль-
шей, чем ф(и).)
Доказательство формулы замены переменных.
(i) Пусть А : —> Rfc — линейное отображение. Тогда для
любой связной хорошей области Vol(AU)/Vol(l7) = |Det А|.
Начнем с доказательства того, что левая часть этого равен-
ства не зависит от U. Это делается так же, как и для двумерного
пространства (см. параграф 1.9). Давайте обозначим левую часть
равенства Vol(A). Тем самым Vol(A) показывает, во сколько раз
отображение А изменяет объем. Из определения следует, что
Vol(AB) = Vol(A) • Vol(B).
Из главы 11 мы знаем, что
Det(AB) = Det А • Det В.
15.3. Интегрирование /с-форм
769
Мы хотим доказать, что
Vol(A) = | Det (*)
для всех кхк матриц. Из предыдущих двух равенств можно сде-
лать заключение, что если (*) справедливо для А и В, то оно
верно и для АВ. Если А — диагональная матрица, то легко уви-
деть, что (*) выполняется. Если у матрицы А все элементы под
диагональю равны нулю, на диагонали стоят 1 и над диагона-
лью только один элемент не равен нулю, то Vol(A) = 1 (это по
сути двумерное утверждение относительно преобразования сдви-
га) . Из этого следует, что если А = U — верхне-треугольная мат-
рицы с 1 на диагонали (под диагональю стоят только нули), то
Vol ((7) — Det U = 1. Аналогично для нижне-треугольных мат-
риц. Итак, можно сделать вывод, что (*) верно для всех матриц
А, что можно записать как
А = LDU,
где L — нижне-треугольная, D — диагональная и U — верхне-
треугольная. Когда можно разложить матрицу А таким образом?
Внимательное изучение процедуры редукции по строкам в пара-
графе 10.8 показывает, что такое разложение возможно тогда и
только тогда, когда в редукции по строкам матрицы А не требу-
ется делать транспонирование. А это происходит тогда и только
тогда, когда ни один из главных миноров не обращается в нуль,
(главные миноры — это определители квадратных матриц, возни-
кающие на пересечении первых г строк и столбцов матрицы А.)
Итак, должны выполняться условия:
«и 7^ 0, («и«22 ~ &2i«i2) 7^ 0, ..., Det А ± 0.
Однако, для любой матрицы А все эти неравенства можно обес-
печить, делая сколь угодно малые изменения матричных элемен-
тов. Поскольку Vol(A) и Det А — непрерывные функции А, то
равенство (*) выполняется для всех матриц.
Теперь приведем другое доказательство формулы (*), осно-
ванное на другом способе разложения несингулярных матриц в
770
Глава 15. Комплексы в пространстве Rn
произведения. Для любой матрицы А матрица Л* А — самосопря-
женная, поскольку
(А* А)* = А*А** - А*А.
Более того, если А несингулярна, то все собственные значения
матрицы А*А положительны, так как (А*Ах,х) = (Ах, Ах} > О
для любого ненулевого вектора ж. Поэтому А*А имеет положи-
тельно определенный квадратный корень, т. е. матрицу S, ко-
торая симметрична, положительно определена и удовлетворяет
условию S2 = А*А. (Действительно, мы можем написать, что
А*А = OLO*, где L — диагональная матрица с положительны-
ми диагональными элементами и О — ортогональная матрица.
Тогда S — ОМО\ где М — диагональная матрица, элементы
которой равны квадратным корням из соответствующих элемен-
тов матрицы L.) Утверждается, что матрица А5-1 ортогональна.
Действительно,
(AS^x.AS^y) = (S~xx,A*AS~1y) = (S~lx, S2S~1y) = (x,y),
поскольку S~r — самосопряженная матрица. Тогда можно напи-
сать
A — SK,
где К — AS-1 ортогональна. Однако S — ОМО*. Поэтому
А = ОМО*К,
где О (и О* = О”1) и К ортогональны, а М — диагональ-
ная матрица с положительными элементами. Для М мы имеем
Vol(M) = DetM. Ортогональные матрицы сохраняют длину и
поэтому сохраняют объем, т.е. Vol(O) = Vol(i<) = 1. С другой
стороны, Det О = ±1 (потому что Det О • Det О* = DetOO* = 1
и Det О ~ Det О*). В этом и состоит другое доказательство фор-
мулы (*).
(и) Пусть ф — А : — линейное отображение. Тогда
^(dx1 Л • • • Л dxk) = (Det A)dx* Л • Л dxk. (**)
15.3. Интегрирование &-форм
771
Из определения процедуры переноса и внешнего произведения
следует, что ф*хх = ацх1 + ai2^2 + • * • + и т. д. Поскольку
aij постоянны, получаем
ф* dx1 — a^dx1 + • • • + a^kdxk,
ф*dxk = akidx1 Ч----h akkdxk.
Теперь ф*dxl Л • • • Л ф*dxk будет кратно dx1 Л • • • Л dxk. Соответ-
ствующий множитель обозначим /(А). Это некоторая числовая
функция А, которая удовлетворяет всем аксиомам определителя.
В силу единственности такой функции, доказанной в главе 11, мы
считаем, что формула (**) справедлива.
(iii) Пункты (i) и (ii) дают формулу замены переменных для
случая, когда ф — линейное отображение, т. е. для ф — А при
условии, что Det А > 0. Докажем это. Запишем ш = gdx1 Л * • • Л
dxk, где д — функция. В силу (ii)
ф*ш — Л Det Adx1 Л • • • Л dxk, где h(x) — #(Ах).
Покроем область U сеткой с малыми ячейками, как это показа-
но на рис. 15.6. Это значит, что область ф(1Г) делится на малые
параллелепипеды, причем объем каждого параллелепипеда отли-
чается от объема соответствующего кубика множителем Det А.
ИЯШИННИИНШ;
niflsissfssssiissssi
Рис. 15.6
^ЖЖЖЖЖЖЖЖЖЖЖЖЖМЖЖЖ’
|^1ЖЖЖЖЖЖЖЖЖЖЖЖЖЖЖ^
772
Глава 15. Комплексы в пространстве Rn
Возьмем произвольное значение е > 0. Мы можем сделать
размер ячейки достаточно малым, чтобы в каждом параллелепи-
педе функция д менялась бы не больше, чем на е:
1я(р) -p(q)l < £
при условии, что р и q лежат в одном и том же параллелепипеде.
Это значит, что если □ обозначает один из внутренних кубиков,
а </>(□) обозначает соответствующий параллелепипед, то
( - p(p)Vol(0(n))
0(D)
(***)
где р - произвольная точка из <£(□)• Однако в силу (i)
Уо1(<ХП)) = DetA-Уо1(П).
Поэтому
[ 5(р) Det А • Vol(Q)
6.
Пусть Uf обозначает объединение всех внутренних кубиков сет-
ки. Суммируя неравенства (****) по всем внутренним кубикам,
получаем
^(□)
-J25(4r) Det A- Vol(D)
<
где г — любая точка в кубике □. Суммирование ведется по всем
внутренним кубикам. Когда сетка измельчается, в пределе куби-
ками вдоль границы можно пренебречь, и тогда
а
£2$(Ar)DetA- Vol(D) -»• J ф*ш.
(iv) Давайте посмотрим, что надо изменить в предыдущих
рассуждениях, если ф уже не предполагается линейным. Прежде
15.3. Интегрирование fc-форм 773
всего, ф*со = hDetf^/dxjdx1 Л ••• Л dxk. Поэтому постоянная
Det А заменяется функцией Ъе1(дф/дх), где (дф/дх) обозначает
матричную функцию
/«-./я ч ( дф^/дх1 дфх/дхк \
{дф/дх) \^дфк/дх1 ... дфк/дхк )'
В этом случае аппроксимирующая риманова сумма становится
равной
У2 <?(^г) Det (дф/дх) Vol (□).
Неравенство (***) все еще выполняется, если сетка достаточно
мелкая. Но </>(□) Уже не будет параллелепипедом, и у нас уже не
будет точного равенства
Уо1(</>(П)) - Det(5<£/ar)(r)Vol(Q).
Но нам достаточно знать, что это равенство выполняется при-
близительно, т. е. что
|Уо1(</>(П)) - Det(^/^)(r)Vol(Q)| < sVol(Q).
Это неравенство следует из теоремы о среднем значении. Дета-
ли доказательства достаточно просты. Их можно найти в книге
Loomis and Sternberg, Advanced Calculus, глава 8, с. 343 344. Мы
еще раз отсылаем читателя к этой главе для последовательно-
го изучения теории интегрирования в пространстве Rfe. Этим мы
завершаем обсуждение формулы замены переменных.
Интегрирование А;-форм по fc-цепям комплекса. Предполо-
жим, что а; — fc-форма в пространстве Rn. Пусть ф : Rfc —> Rn —
гладкое отображение, a U обозначает область в пространстве Rfc.
Рассмотрим интеграл
/ ф*ш.
Ju
Пусть К — комплекс, а ф — отображение этого комплекса в про-
странство Rn. Напомним: это значит, что ф отображает каждую
ячейку комплекса С в пространство Rn, причем ограничение ф
на С — дифференцируемое отображение.
774
Глава 15. Комплексы в пространстве Rn
Это имеет смысл, потому что каждая ячейка С является вы-
пуклым многогранником в некотором евклидовом пространстве.
По существу, мы требуем, чтобы отображение ф удовлетворя-
ло более сильному (с технической точки зрения) условию: для
каждой Ат-ячейки С комплекса существует область U (окрест-
ность С) в пространстве и такое дифференцируемое отобра-
жение ф : U Rn, что ограничения ф и ф на С совпадают.
Каждая Ат-ячейка С комплекса ориентирована. Поэтому можно
рассмотреть интеграл
[ Ф*"
JC
по ячейке С. Пусть с — некоторая Ат-цепь. Тогда с является ли-
нейной комбинацией Ат-ячеек:
с =
где Cj — Ат-ячейки, а гу — вещественные числа. Тогда интеграл
от ф*ш по цепи с дается формулой
У Jc Ф*ш-
Очевидно, что это выражение линейно зависит от с. Таким обра-
зом, Ат-форма и вместе с отображением ф определяет Ат-коцепь на
комплексе К.
Например, предположим, что наш комплекс К содержит гра-
ни, ребра и вершины тетраэдра. Для простоты пусть все грани
ориентированы «согласованно». Под этим подразумевается, что
если с = Ci + С2 + Сз + С4, то дс — 0.
Представим себе, что центр тетраэдра находится в начале коор-
динат пространства R3.
Независимость от деления на ячейки. Рассмотрим проекцию
(рис. 15.7) из центра тетраэдра на поверхность единичной сферы
S и назовем ее отображением ф. Легко видеть, что ф — гладкое
отображение тетраэдра в пространство R3. Каждая грань тетра-
эдра отображается в часть сферы, а ф будем рассматривать как
15.3. Интегрирование £-форм
775
бором ориентации). Если ш — 2-форма в R3. то fc ф*и — интеграл
от по сфере (также с выбором ориентации), что записывается
в виде
Это обозначение неявно содержит ряд правомерных допущений.
Прежде всего, предполагается, что граничные кривые треуголь-
ных областей, на которые мы разделили сферу, можно игнориро-
вать. Связано это с тем, что при вычислении двумерного инте-
грала определение через римановы суммы означает, что гладкие
кривые не вносят вклада. Более важное предположение состоит
в том, что конкретный выбор разбиения на треугольные области
(комплекса К и отображения ф) не имеет значения. Вследствие
теоремы о замене переменных нас интересует только поверхность
сферы (покрываемая один раз) с определенной ориентацией. Да-
вайте объясним это. Допустим, что мы рассматриваем другой
комплекс £, состоящий из граней, ребер и вершин куба, с цен-
тром в начале координат. Обозначим /1 отображение комплекса
L на поверхность сферы, задаваемое проекцией куба из центра
(рис. 15.8). Предположим также, что грани комплекса L ориен-
тированы согласованно, так что
е — Fi + F2 + F3 + F4 + F5 + Fq удовлетворяет условию де = О,
776
Глава 15. Комплексы в пространстве Rn
где Fi (г — 1,2,..., 6) — грани куба. Утверждается, что
(15.11)
со знаком +, если ориентации е и с «совпадают». (В процессе
доказательства мы объясним, что это значит.)
Действительно, рассмотрим кривые на сфере, являющиеся об-
разами ребер комплекса К (при отображении ф) и комплекса L
(при отображении //). Эти кривые делят поверхность сферы на
много подобластей (рис. 15.9).
Каждая треугольная область на сфере состоит из нескольких
таких подобластей, и точно так же каждая «квадратная область»,
происходящая от куба. Пусть W обозначает одну из таких под-
областей. Тогда мы можем написать
w =
где U — подобласть одной из граней К
и
W — где V — подобласть одной из граней L.
Рассмотрим отображение ф : U V, заданное ф = рГ1 о ф. Тогда
<£ = М °
откуда
ф*ш = ф*(р*и) и У = ф(1Р).
(Легко проверить, что ф — дифференцируемое отображение.)
15.4. Теорема Стокса
777
Из формулы замены переменных имеем
[ = ± [ ф*и
Jv Ju
где знак + берется тогда и только тогда, когда сохраняет ориен-
тацию. Легко видеть, что отображение которое мы построили
для подобласти РИ, будет сохранять ориентацию тогда и только
тогда, когда соответствующие отображения для всех других под-
областей тоже сохраняют ориентацию. Если это происходит, то
мы говорим, что сие создают одинаковую ориентацию на сфере.
Суммирование по всем подобластям доказывает (15.11) и объяс-
няет введенное обозначение. Мы уже кратко набросали доказа-
тельство справедливости нашего обозначения для случая сферы.
Конечно, оно работает и в гораздо более общем случае. Для лю-
бой ориентированной поверхности в трехмерном пространстве (в
общем случае для любого ориентированного подмногообразия М
в пространстве Rn) интеграл fM а? имеет смысл и не зависит от
того, как мы «нарезали М на куски», чтобы записать его как
объединение образов ячеек.
(Итак, мы определили интеграл от 2-формы по ориентирован-
ной 2-сфере, «разрезав ее на куски» и потом показав, что резуль-
тат не зависит от способа разрезания. Существует другое (эк-
вивалентное) определение, которое состоит в «покрытии сферы
заплатками», а не в разрезании ее на куски. В конце следующего
параграфа мы коротко расскажем об этом.)
15.4. Теорема Стокса
Теорема Стокса, которую мы докажем в этом параграфе в общем
случае, говорит следующее. Пусть К — некоторый комплекс, а ф
— гладкое отображение К в пространство Rn. Пусть, далее, ш —
(к — 1)-форма вГ, ас - fc-цепь. Тогда
[ ф*<1ы = [ ф*и. (15.12)
J с Jdc
Если фиксированы </> и то обе части этого равенства — линей-
ные функции с. Поскольку любая цепь является линейной ком-
бинацией ячеек, то равенство (15.12) достаточно доказать для
778
Глава 15. Комплексы в пространстве IRn
случая, когда с — ячейка. Доказывать будем так же, как это де-
лалось в двумерном случае в главе 8, и только в самом конце
будет небольшое отклонение.
В качестве первого шага рассмотрим случай, когда ячейка С
является кубом. Можно предположить, что это единичный куб
в пространстве Пусть — координаты в Тогда
можно написать
ф*ш = di du2 Л • • • Л duk + а>2 du1 Л du3 Л * • • Л duk Ч-
+ а>к du1 Л • • • Л duk~\ (15.13)
так что левая часть равенства (15.12) принимает вид
[ ф*(к> = [ d$*u
Jc Jc
Jc си2, дик J
Напомним правило выбора знаков для оператора д, действую-
щего на ячейку комплекса. Вспоминаем, что ориентация ячейки
С определяет, «правильно» или «неправильно» упорядочены ба-
зисные вектора. «Неправильное» множество базисных векторов
преобразуется в «правильное» либо перестановкой двух векторов
с соседними номерами, либо изменением знака одного вектора.
Правильные и неправильные множества для к = 1, 2,3 показаны
на рис. 15.10.
Граница ориентированной fc-ячейки состоит из суммы ориен-
тированных (fc—1)-ячеек. Общее правило определения знака каж-
дой ячейки на границе: в точке на границе ячейки С строим мно-
жество векторов, в котором первый вектор направлен из ячейки
С, а остальные к — 1 векторов образуют правильно ориентирован-
ный базис граничной ячейки. Если получившееся множество к
векторов является правильно ориентированным множеством для
ячейки С, то граничная ячейка входит в дС со знаком плюс; в
противномом случае она входит со знаком минус.
На рис. 15.11 показано применение этого правила в случае
к — 1. Вектор Vi направлен наружу, а других векторов нет. В
15.4. Теорема Стокса
779
неверно
Рис. 15.10
неверно
Рис. 15.11
точке В вектор vi имеет правильную ориентацию относительно
ветви а, а в точке А - - неправильную. Следовательно, да = В—А.
На рис. 15.12 показан случай к = 2 для треугольной ячейки
С, ориентированной против часовой стрелки.
Вектор V2 выбран так, что он касателен к ветви, а его направ-
ление определяет ориентацию ветви. Вектор vi всегда направлен
из ячейки (7. Для ветвей а и /? эта пара векторов правильно
780
Глава 15. Комплексы в пространстве Rn
ориентирована (в соответствии с ориентацией ячейки С про-
тив часовой стрелки), а вот для ветви 7 вектора ориентированы
неправильно. Следовательно, дС = а + /3 — 7.
Вернемся к рассмотрению случая, когда ячейка С = Ik явля-
ется кубом, ориентированным посредством стандартного базиса
vi, V2, . • •, Vjt (его векторы параллельны ребрам куба). Рассмот-
рим отдельные члены, получающиеся в результате подстановки
(15.13) в Рассмотрим различные грани дС. Начнем с
двух граней, для которых и1 — const. На грани Bi, где и1 — 1,
вектор vi направлен наружу и остальные вектора V2,..., ори-
ентированы правильно. На грани Л1, где и1 — 0, вектор vi на-
правлен внутрь и поэтому V2,..., Vfc ориентированы неправиль-
но. Эта ситуация в случаях к = 2 и к = 3 показана на рис. 15.13.
Когда мы вычисляем </>*и на этих двух гранях с уравнения-
ми и1 = const, все члены в т, содержащие множитель du1, дают
нуль. Остается только ai(tt1, и2,... ,ик) du2Л - • -/\duk, Вычисление
этого члена на грани Bi, где V2,..., v& упорядочены правильно,
15.4. Теорема Стокса
781
дает f/k-i «1(1, «2,... уик) du2 ... duk. А вычисление его на гра-
ни А1, где вектора V2,...,Vfc упорядочены неправильно, дает
— f/k~i «1(0, и2,..., ик) du2 ... duk. Все вместе дает интеграл
[ [«1(1, «2,... ,ик) — «1(0, и2,... ,«^)] du2 ... duk.
Из фундаментальной теоремы дифференциального исчисле-
ния имеем
«1(1, «2,..., ик) — «1(0, «2,..., ик) = [ ^^(iz1, и2,... ,ик) du1.
Jo
Поэтому общий вклад от двух граней с и\ — const равен
f 9«1 1 L,
J/к OUL
где теперь интеграл вычисляется по единичному кубу в прост-
ранстве
Выполнив такую же процедуру для граней с и2 = const,
заметим, что множество векторов V2, Vi, V3,..., упорядочено
неправильно. На грани, где и2 = 1, вектор V2 направлен на-
ружу и поэтому остальные вектора vi, V3,..., упорядочены
неправильно. На грани, где и2 = 0, вектор V2 направлен внутрь,
а остальные вектора Vi, V3,..., упорядочены правильно. При
вычислении т вклад дает только член «2(«х, и2,..., ик) du1 Л du3 Л
• • • Л duk. Поэтому мы получаем
f [—«2(«S 1, * • •, ик) + «2(tz1,0,... du1 du3 ... duk
= - [ du2 ... duk.
Jfk duz
Аналогичные соображения показывают, что вклад от граней, где
u*7 = const, равен ± /1к(да3/дид) du1... duk\ причем берется знак
+ для нечетных j, и знак — для четных. Если просуммировать
вклады от всех 2к граней в д1к, то получится (15.12).
Итак, мы доказали теорему Стокса для куба. Теперь надо
рассмотреть ячейки более общего вида. Как мы показали в гла-
ве 8, на плоскости любой многоугольник может быть разложен
782
Глава 15. Комплексы в пространстве Rn
на треугольники. Действительно, любой многоугольник можно
разложить на выпуклые многоугольники, которые, в свою оче-
редь, разлагаются на треугольники, если выбрать точку внутри
и соединить ее со всеми вершинами.
Аналогично в трехмерном пространстве любой многогран-
ник может быть разложен на тетраэдры. Действительно, сделаем
предварительное разложение и предположим, что С — выпуклый
многогранник. Предположим, что все его грани уже разложены
на треугольники. Опять выбираем точку р внутри С. Тогда этот
многогранник разлагается на тетраэдры, основанием каждого из
которых является треугольник из разложения грани, а вершина
находится в точке р. Таким образом, в случае 2-форм теорему
Стокса достаточно доказать для тетраэдра.
С помощью индукции мы можем проделать эту процедуру и
в пространстве к измерений. Пусть S € будет множеством,
определенным формулой
S = | Xi > 0 для всех i и
/с-симплекс — это подмножество пространства являющееся
образом S при обратимом аффинном отображении. Таким обра-
зом 1-симплекс — это отрезок, 2-симплекс — это треугольник и
3-симплекс — это тетраэдр.
Предположим, что мы разложили С на симплексы [Дф Утвер-
ждается, что если мы знаем теорему Стокса для всех симплексов,
то мы знаем ее для С, Действительно, рассмотрим комплекс, ко-
торый разлагается на ячейки — симплексы. Тогда комплекс С
можно идентифицировать с цепью в нем, т. е. можно написать
с = ^дь дс = ^д^-
Поэтому
/ “ = ш
JdC Jd&i
= J dw (в силу теоремы Стокса для
= [ dw.
Jc
15.4. Теорема Стокса
783
Итак, теорему Стокса достаточно доказать для симплекса.
Воспользуемся инвариантностью интеграла относительно про-
цедуры переноса и сведем доказательство к случаю куба. Здесь
мы рассмотрим доказательство для треугольника.
Чтобы доказать теорему Стокса для треугольника, достаточ-
но доказать ее для равностороннего треугольника Л, поскольку
для любого треугольника можно найти аффинное преобразова-
ние, которое преобразует его в равносторонний. Предположим,
что длина стороны треугольника равна 1. Пусть линейная диф-
ференциальная форма г тождественно равна нулю за пределами
круга, центр которого находится в одной из вершин и который
не достигает противоположной стороны (рис. 15.14).
Рис. 15.14
Тогда dr также тождественно равняется нулю за пределами
круга. В силу теоремы Стокса в этой ситуации вклад в интеграл
возникает только от внутренней части круга, так что мы можем
без ущерба нарастить «внешнюю» часть треугольника, достроив
его до параллелограмма (рис. 15.15).
Таким образом, если □ обозначает параллелограмм, а Д обо-
значает треугольник, то поскольку т и dr равны нулю за преде-
лами круга, мы имеем
[ т — [ т и [ dr= [ dr.
Jan JdA jq Ja
Однако, с точностью до замены переменных параллелограмм —
это просто квадрат. Следовательно, JqqT — J\jdr и поэтому
fdAr = f&dr-
Теорема Стокса будет доказана для Д, если мы установим
следующее. Каждая гладкая дифференциальная форма (опреде-
ленная в окрестности Д) может быть записана в виде суммы трех
784
Глава 15. Комплексы в пространстве Rn
членов
Т = Г} + Т2 + Т3,
где каждый член тождественно равен нулю вне круга Di. При-
чем центр круга находится в вершине треугольника, а радиус R
изменяется8 в пределах 2/3 < R < 3/4 (так что три круга покры-
вают весь треугольник, но ни один круг не достигает противопо-
ложной стороны треугольника, см. рис 15.16).
Чтобы это доказать, потребуется свойство функции одной пе-
ременной.
Лемма. Функция
( и>0,
[О, и < О
бесконечно дифференцируема во всех точках.
Доказательство. Очевидно, что для и ф 0 функция / имеет
производные всех порядков и /^(и) = 0 для и < 0. Поэтому мы
должны доказать, что f(k\u)/u —> 0 при и —> 0 для любого к.
Мы имеем /^(и) — РД1/и)е~1/и, где — некоторый полином9,
8Более последовательный подход — зафиксировать радиус R = 1/д/2.
Причина объясняется в сноске на с. 786. — Прим. ред.
9Полезное упражнение — вычислить его в явном виде индукцией по к. —
Прим. ред.
15.4. Теорема Стокса
785
и поэтому
lim(l/iz) /^(и) = lim sPk(s)e~s — О,
и—>0 s—*оо
потому что es стремится к бесконечности быстрее любого поли-
нома.
Заметим, что / тождественно равна нулю для и < 0 и строго
положительна для и > 0.
Пусть Г{ обозначает расстояние от г-й вершины. Определим
функцию gi формулой
_ (-Л = f f(R ~ Гг(х)), гДх) < R,
9г{ ’ [ 0, п(ж) > R.
Тогда Qi бесконечно дифференцируема и
, . ( >0, Гг(яг) < R,
t = о, г.М > 0.
Пусть
9 = 91 + 92 + S3-
Поскольку каждая точка в А - внутренняя для по крайней мере
одного из кругов т. е. поскольку г^х) < R хотя бы для одного
из i = 1,2,3, то
д(х) > о
для каждого х 6 А. Поэтому мы можем разделить на д и опре-
делить
Фг = -, L = 1,2,3.
д
Тогда
, ( л ( >0, гДх) < R,
t = 0, г,(х) > 0
и
</>i(x) + + Фз(х) = 1 для всех х £ А.10
Умножая последнее уравнение на т, получаем
т = 0iT + Ф2Т + Ф$Т.
10Построенный набор функций фг принято называть разбиением единицы,
подчиненным данному покрытию многообразия (треугольника) множества-
ми Di (тремя кругами). Это понятие играет важную роль в анализе на мно-
гообразиях. Подробнее см. в конце этого раздела на с. 791. — Прим. ред.
786
Глава 15. Комплексы в пространстве Rn
Если мы положим Ti = фгт. то получим желаемое разложение
т = тг + т2 + Т3.
Очевидно, что это доказательство можно провести и в случае
п измерений. Только вместо 3 будет соответственно п+1 (по числу
вершин симплекса) шаров функций ^ит.д., а радиус шаров
можно выбрать R = 1/у/2.п Итак, теорема Стокса доказана.
На самом деле мы не должны быть настолько педантичны-
ми. Надо просто покрыть симплекс конечным числом шаров
так чтобы пересечение Di с симплексом имело вид части куба,
разбить на куски и свести к случаю куба.
Пример
В качестве применения теоремы Стокса и вычисления форм на
ячейках рассмотрим 2-форму т — (х2+у2 + z2) dx/\dy в простран-
стве R3 и ячейку С, являющуюся сплошным полушарием радиуса
Д, обладающую правосторонней ориентацией и изображенную на
рис. 15.17. В явном виде мы вычислим и f^dr.
Сплошное полушарие ограничено двумя ячейками: полусфе-
рической поверхностью А и диском В в экваториальной плоско-
сти. Пусть эти ячейки ориентированы против часовой стрелки,
если смотреть на них снаружи, тогда дС = А + В.
11 Происхождение данной величины, вероятно, следует пояснить, учитывая
небрежность авторов в этом месте оригинала. Если симплекс правильный
(как n-мерный многогранник) и длина его ребра равна 1, то его высота
а расстояние от вершины до центра симплекса
j _ п h - I ™
п + 1 у 2(n + 1)
То, что шары радиуса R = с центрами в вершинах симплекса покрыва-
ют симплекс и не достигают противолежащих граней, вытекает из очевидных
неравенств dn < 1 / \/2 < hn, причем обе последовательности сходятся к 1/ д/2
при п —> оо. Геометрически это выглядит так: с ростом п прямоугольный
треугольник «вершина симплекса-центр противоположной грани - вершина
грани» с гипотенузой 1 и катетами hn и dn-i стремится к равнобедренному.
— Прим. ред.
15.4. Теорема Стокса
787
Рис. 15.17
В качестве параметров для описания полусферической по-
верхности воспользуемся сферическими координатами в и ф. Дву-
мерное параметрическое пространство изображено на рис. 15.18.
В принципе можно ввести параметры и — 20/тг и v = ф/2тг, так
что областью интегрирования будет единичный квадрат, но пря-
моугольник не менее удобен для вычисления.
Рис. 15.18
Перенос х, у z при указанной параметризации а имеет вид:
— 7?sin0cos</>, а*у — 7?sin0sin</>, = Bcos0. Тогда
a*dx = R cos 0 cos ф d0 — R sin 0 sin ф dф^
a*dy = R cos 0 sin ф d0 + R sin 0 cos ф dф.
788
Глава 15. Комплексы в пространстве Rn
Следовательно,
а*т = а*(х2 + у2 + z2y)(ot*dx) Л
= R?(R? sin 0 cos 0 cos2 ф$0 /^ф — R2 sin 0 cos 0 sin2 d0)
— 7?4 sin 0 cos 0d0 A d</>.
Чтобы проверить, что а сохраняет ориентацию, посмотрим на
образы упорядоченного множества векторов ei и Образы vi
и V2 соответствуют ориентации полусферы А, что показано на
рис. 15.18.
Для вычисления 2-формы т на полусфере А мы просто вычис-
лим двойной интеграл f а*т = /qJq f^0 s^n ® cos 0d0 d(f> = kR^.
Для диска В удрбко выбрать параметры г2 — х2 + у2 и угол ф.
Чтобы диск В имел правильную ориентацию, выбираем порядок
ф, г. Соответствующее параметрическое пространство изображе-
но на рис. 15.19. Тогда образы ei и правильно упорядочены
для ориентации В против часовой стрелки, если смотреть на диск
снизу, и по часовой стрелке, если смотреть на него сверху.
Для параметризации /3 перенос имеет вид: /3*х ~ г cos ф, (3*у —
Г8тф, (3* z ~ 0, следовательно, (3*т = г2 (cos ф dr — rsY^lфdф) Л
(sin ф dr + rcos0d</>) = г3 dr Л dф = —г^ф/^г. Таким образом,
значение т для ориентированного диска В равно
R /*2тг
—r^dфdr = —-тг/?4.
Zi
г=0 70=0
15.4. Теорема Стокса
789
Собрав вместе результаты для двух ячеек на границе, мы полу-
чаем
[ = [ т + [ t = kR4- ^тгЯ4 = Itt/Z4.
JdC J a Jb 2 2
Теперь вычислим fcdr. Поскольку т = (х2 + у2 + z2) dx Л dy,
dr = 2zdz A dx A dy — 2zdx A dy A dz. Мы параметризуем
ячейку С, используя сферические координаты г, в, ф. Перенос,
соответствующий данной параметризации: ф*х — г sin 0 cos ф,
ф*у — г sin 0 sin ф, ф* z = rcos0. После вычислений мы получаем
0*(dr) — 2r3sin0 х cos в dr Л dd Л dф. Для нахождения значе-
ния dr на С интегрируем по прямоугольному параллелепипеду в
параметрическом пространстве:
/» /*тг/2 /*2тг j
dr — / / / 2r3 sin 0 cos 0 dr d0 с1ф = -tvR4.
J C Jr=QJ9=0 2
Давайте покажем кратко, как можно использовать доказа-
тельство теоремы Стокса, приведенное выше, чтобы дать аль-
тернативное определение интегрирования fc-формы по /г-мерному
подмногообразию. Это альтернативное определение будет совпа-
дать с определением интегрирования по fc-цепи, которое мы дали
в случае, когда подмножество является образом /с-цепи. Потом
более детально покажем, как доказать, что интеграл по Ахцепи
не зависит от способа разложения на ячейки. Сделаем это так
же, как уже сделали в конце предыдущего параграфа для сферы.
При первом чтении материал с этого места и до конца параграфа
можно опустить.
Заплатки
Доказывая теорему Стокса, мы использовали набор функций
{01,..., фп}, причем каждая из этих функций непрерывно диф-
ференцируема, неотрицательна и
01 + • • • + 0n = 1 в рассматриваемой области (симплексе).
Кроме того, каждая функция ф^ за пределами шара Di обраща-
ется в нуль. Шар Di выбран так, чтобы выполнялись желаемые
790
Глава 15. Комплексы в пространстве Rn
свойства. (При доказательстве теоремы Стокса мы хотели, что-
бы с помощью дифференцируемого отображения пересечение Di
с симплексом могло быть преобразовано в подмножество куба.)
А теперь вспомним определение подмногообразия М в про-
странстве Rn. Подмножество М в пространстве Rn называлось
подмногообразием размерности fc, если вокруг каждой точки р
подмногообразия М мы можем найти шар D и его диффеомор-
физм f на открытое подмножество U в пространстве Rn, так
что f(D А М) = U где идентифицируется с fc-мерным
подпространством пространства Rn, заданным условием, что по-
следние п — к координат равны нулю. Предположим, что мы мо-
жем покрыть подмногообразие М конечным числом таких ша-
ров Di,... ,Dr. (Это всегда можно сделать в случае, если М —
компактное, т. е. замкнутое и ограниченное подмножество в про-
странстве Rn.) На каждом Di определен свой диффеоморфизм А
и
= £7* ПК*.
Это подмножество обозначим Wi. Тогда
Wi = Ui П Rfc
будет открытым подмножеством пространства Rfc. Для любого
перекрытия DiC\Dj мы можем рассмотреть ограничение либо А,
либо fj. Поэтому fi(Di A Dj) есть открытое подмножество Ui и
fj(Di A Dj) — открытое подмножество Uj. Тогда
Л0//1 отображает fj(DiQDj) в Л(ААДу)
и переводит
Wj A/j(AnDj) в А/ДД APj).
Итак, наша ситуация выглядит следующим образом: мы покрыли
М множествами Oi — Di А М. Пусть обозначает ограничение
fi на Oi. Тогда gi будет взаимно-однозначным отображением Oi
на открытое подмножество Wi в пространстве Rfc.12
12 Описанный набор областей Oi С М, покрывающий многообразие М,
вместе с диффеоморфизмами дг : Ог Wi С принято называть атласом
карт данного (гладкого) многообразия. — Прим. ред.
15.4. Теорема Стокса
791
Далее, отображение
9ij = 9i 0 9j 1 из Wj r]gj(Pi П Oj) в Wi П дг(.Ог П Oj)
дифференцируемо и имеет дифференцируемое обратное, опреде-
ленное формулой gji = gj о д~\ См. рис. 15.20.
Мы можем вообразить, что многообразие М покрыто «заплат-
ками». Отображения д^1 говорят, как Wi покрывают многообра-
зие, а отображения gij говорят, как Wi и Wj сшиваются вместе.
Каждое отображение g2j может либо сохранять ориентацию, либо
менять ее на обратную. Допустим, что в нашем случае все отоб-
ражения д^ сохраняют ориентацию13. (Это определяет «ориен-
тацию» на М. Интуитивно ясно, что если М связно, то на нем
существуют только две ориентации.) Пусть теперь набор функ-
ций ., фг обладает свойствами:
0 < < 1, фг ~ 0 вне Di и ф± + • • + фг = 1 на М.
Теперь для каждой й-формы ш мы можем написать
и) — ф]_ш + * • • Т фгш.
13 Следовательно, многообразие М ориентируемо. Возможность выбора ат-
ласа, для которого все отображения склейки сохраняют ориентацию, и
есть критерий ориентируемости многообразия. — Прим. ред.
792
Глава 15. Комплексы в пространстве Rn
Все слагаемые справа обращаются в нуль вне шара Di. Тогда
можно было бы определить
[ “ = Е [
Jm JWi
Другими словами, вместо разрезания М на отдельные куски, мы
можем записывать любую форму в виде суммы небольших кус-
ков, каждый из которых помещается внутрь одной-единственной
координатной заплатки на М. Эту форму можно интегрировать
посредством переноса на подмножество пространства Повтор-
ное применение формулы замены переменных показывает, что
это определение интеграла не зависит от выбора функций
или от заплаток (т.е. от выбора Oi и gj, но зависит от выбора
ориентации М. Для детального изучения этого определения мы
опять отсылаем читателя к книге Loomis and Sternberg, Advanced
Calculus, главы 9-12.
15.5. Дифференциальные формы
и когомологии*
Для произвольного комплекса, расположенного в простран-
стве Rn, fc-формы, которые мы определили, будут зародышами
fc-коцепей, а дифференциальный оператор d совместим с погра-
ничным оператором d. Аналогично подпространствам, которые
мы определили через образ и ядро пограничного оператора, сей-
час мы можем построить подпространства (бесконечномерных)
пространств QW(Rn) с помощью дифференциального операто-
ра d.
Если fc-форма ш удовлетворяет условию dev = 0, она называет-
ся замкнутой. Такая fc-форма после интегрирования по ячейкам
становится fc-коцепью W, удовлетворяющей условию dW = 0, и
поэтому она принадлежит пространству fc-коциклов Zk. Другими
словами, замкнутая й-форма является зародышем й-коцикла.
Если fc-форма ш может быть записана в виде и = dr, то она
называется точной. В этом случае после интегрирования г по
*При первом чтении этот параграф можно опустить.
15.5. Дифференциальные формы и когомологии
793
ячейкам комплекса получается (к — 1)-коцепь Г, а а> порождает
fc-коцепь ТУ, так что W — dT. Поэтому коцепь W лежит в под-
пространстве fc-кограниц Вк. Другими словами, любая точная
&-форма является зародышем кограницы.
Мы знаем, что для любого комплекса пространство Вк яв-
ляется подпространством Zk. Соответствующее утверждение от-
носительно /с-форм состоит в том, что любая точная fc-форма
(зародыш элемента пространства Вк) также замкнута (зародыш
элемента пространства Zk). Доказательство очень простое: если
tv точная, то и — dr и поэтому dui = d(dr) = 0. Следовательно,
замкнута.
Для любого комплекса факторпространства (пространства
когомологий) Нк — Zk/Вк зависят лишь от основного простран-
ства и не зависят способа его разрезания в комплекс. Поэто-
му разумно ожидать, что пространства Нк можно получить,
рассматривая дифференциальные формы: от бесконечномерного
пространства замкнутых форм (dw = 0) мы переходим к фактор-
пространству по пространству точных форм (cu = dr). Образо-
вавшиеся пространства определяют так называемые когомологии
де Рама основного пространства, на котором определены диф-
ференциальные формы.
Для построения базиса пространств Нк вспомним, что для
любого комплекса пространство Нк дуально гомологическому
пространству Н^. Поэтому разумно ожидать, что базисный эле-
мент для пространства Нк будет определяться его значениями на
fc-цепях, которые образуют базис Нк в любом удобном комплексе
пространства.
Давайте рассмотрим несколько совсем простых примеров для
иллюстрации этих абстрактных рассуждений.
Пример 1А. Пусть основное пространство — отрезок прямой
(рис. 15.21). В этом пространстве построим 0-формы, которые
будут дифференцируемыми функциями /(£), и 1-формы, имею-
щие вид cu — g(t) dt.
a b t
Рис. 15.21
794
Глава 15. Комплексы в пространстве Rn
В этом случае замкнутые 0-формы — это постоянные функ-
ции, определяющие одномерное подпространство. Точных 0-форм
не бывает, поэтому факторпространство HQ замкнутых 0-форм
по точным одномерно. Так отражается тот факт, что комплекс,
полученный из отрезка, всегда связен и имеет dimHo — 1-
При рассмотрении 1-форм мы обнаруживаем, что каждая
1-форма точная: для заданной oj = g(t) dt мы образуем перво-
образную функцию G(t) = f g{t) dt такую, что си = dG. Следо-
вательно, в этом случае пространство Н1 имеет нулевую размер-
ность.
Пример 1В. Пусть основное пространство состоит из двух непе-
ресекающихся отрезков прямой (рис. 15.22). В этом случае про-
странство Н° = И0 двумерное: оно состоит из функций, которые
имеет одно постоянное значение на отрезке [а, 6] и другое, мо-
жет быть отличное от первого, постоянное значение на отрезке
[с, d]. Это отражает тот факт, что комплекс, построенный на этом
пространстве, будет иметь две связных компоненты.
—I-------1-----1-------1—
а Ъ с d
Рис. 15.22
В общем случае при любой размерности основного простран-
ства замкнутые 0-формы будут функциями, принимающими по-
стоянное значение на каждой связной компоненте. Они будут об-
разовывать пространство HQ = Z® с размерностью, равной числу
связных компонент в основном пространстве. С этого момента и
дальше мы будем рассматривать только связные пространства, и
нам не нужно будет возвращаться к пространству Н®.
Пример 2А. Основное пространство прямоугольник на плос-
кости (рис. 15.23). Это пространство связно, поэтому Я0 одномер-
но. Изучая 1-формы заметим, что любая 1-форма си точная. Мы
доказали это, рассматривая криволинейные интегралы. Поэтому
пространство Н1 имеет нулевую размерность.
Рассмотрев теперь 2-формы, замечаем, что каждая 2-форма
точная. Общий вид 2-формы — это т — f(x, у) dx Л dy. Образуем
15.5. Дифференциальные формы и когомологии
795
У
Рис. 15.23
функцию
F(x,y)= [ f(t,y)dt
Jo
такую, что
dF // а
Тогда
d(Fdy) — /(х, у) dx f\dy — т.
Отсюда следует, что Н2 имеет нулевую размерность.
Пример 2В. Пусть опять основное пространство будет прямо-
угольником на плоскости, но с одной выкинутой точкой — нача-
лом координат (рис. 15.24). И на этот раз пространство Н® одно-
мерно, потому что основное пространство связно. А пространство
Н2 имеет нулевую размерность, потому что каждая 2-форма точ-
ная. Однако, если мы рассмотрим 1-формы, то появится новое яв-
ление: теперь существуют замкнутые 1-формы, которые не будут
точными. Так что в этом случае пространство Н1 нетривиально.
Рис. 15.24
Чтобы получить базис пространства 7?1, сначала рассмотрим
пространство гомологий Ну для 2-комплекса, построенного на
этом пространстве (см. рис. 15.25). Поскольку начало коорди-
нат не принадлежит пространству, то в комплексе не может быть
796
Глава 15. Комплексы в пространстве Rn
ячейки, включающей начало. В результате цикл типа а + (3 + 7,
окружающий начало координат, не может быть границей. Класс
эквивалентности такого цикла (по модулю пространства границ
Bi) образует базис одномерного пространства Н\. Для того же
комплекса пространство когомологий Н1 дуально Hi. Его базис-
ный элемент будет классом эквивалентности 1-коцикла W, кото-
рый не является кограницей. Поскольку Н1 дуально УД, мы ожи-
даем, что W принимает фиксированное ненулевое значение для
любого цикла типа а + (3 + 7, обходящего начало один раз против
часовой стрелки. Чтобы получить базис для пространства кого-
мологий де Рама Нг, мы должны найти зародыш коцикла для W:
замкнутую 1-форму cuq с фиксированным ненулевым значением
для любой кривой, окружающей начало один раз. Такую 1-форму
можно получить, рассмотрев функцию в = arctan(z//a;), которая
определена везде, кроме начала координат, и которая может быть
сделана непрерывной везде, кроме одной прямой, выходящей из
начала координат (обычно это ось х в отрицательном направле-
нии, так что —к < 0 < тг). Тогда напишем дифференциал
а?о — d0 =
xdy — у dx
х2 + у2
Эта 1-форма определена и непрерывна везде, кроме начала ко-
ординат. Кроме того, она замкнутая: duiQ = 0, что можно про-
верить прямым вычислением. С другой стороны, она не точная:
нет такой непрерывной функции f(x,y), чтобы = df. Для лю-
бой кривой се, обходящей начало координат п раз против часовой
стрелки, мы имеем
/ с^о = 2тгп.
J а
Поэтому базисом пространства Н1 является класс эквивалент-
ности
__ xdy — у dx
cuo —--2“——2--1" dg,
xz + ул
где g(x,y) — любая дифференцируемая функция.
Пример ЗА. Пусть основное пространство — прямоугольный па-
раллелепипед в пространстве R3 (рис. 15.26). Без доказательства
15.5. Дифференциальные формы и когомологии
797
утверждаем, что
HQ одномерно (связная область);
Н1 = {0} (каждая замкнутая 1-форма точна);
Я2 = {0} (каждая замкнутая 2-форма точна);
//3 — {0} (каждая 3-форма точна).
Эти результаты для пространств Н\ Н2, Н3 являются след-
ствиями общей теоремы, известной как лемма Пуанкаре. Грубо
говоря, лемма утверждает, что на любом пространстве, которое
можно непрерывно стянуть в точку, все замкнутые дифференци-
альные формы точные. Интересные случаи возникают, если про-
странство имеет «дырки» и поэтому его нельзя стянуть в точку.
Конечно, в этих случаях существуют циклы, не являющиеся гра-
ницами, и поэтому дуальные пространства Hi, H%,... ненулевые.
Пример ЗВ. Пусть основное пространство опять будет прямо-
угольным параллелепипедом в пространстве R3, но на этот раз
выкинуто начало координат. Результаты для 77°, Н1 и Я3 не ме-
няются. Однако теперь пространство Н2 одномерно. Дифферен-
циальная форма
х dy Л dz + у dz Л dx + z dx Л dy
То= (ж2 + у2 + г2)3/2
798
Глава 15. Комплексы в пространстве Rn
определена везде, кроме начала координат. Она замкнута, что
можно проверить, проделав громоздкие вычисления. Однако,
— 4тг для любой замкнутой поверхности S, окружающей
начало координат. Конечно, такая поверхность является циклом,
но не границей. Не удивительно, что она принадлежит классу
эквивалентности, который дуален 7/2.
Пример ЗС. Пусть основное пространство будет прямоугольным
параллелепипедом в пространстве R3, из которого выкинута ось
г. В этом случае Н1 одномерно, и его базис
__ х dy - у dx
—2П—2~ + d9-
х2 + у2
При этом пространство Н2 имеет нулевую размерность.
Пример 3D. Пусть основное пространство - поверхность тора,
расположенного в пространстве R3 (см. рис. 15.27). В этом случае
Н1 двумерно. Один из его базисных элементов имеет вид
__ xdy ~ у dx .
= —о~—2-----h
х2 + у2
и определяет, сколько раз замкнутая кривая обходит ось z. Дру-
гой базисный элемент
— (77 1) dz z dR j п э , оТ
“1= +d9' +9)-
Значение этой формы на любой замкнутой кривой определяет
сколько раз кривая пройдет по окружности единичного радиу-
са в плоскости ху. Таким образом, базисные элементы ц и
дуальны двум типам циклов для любого комплекса на торе.
Рис. 15.27
15.5. Дифференциальные формы и когомологии
799
А сейчас мы докажем лемму Пуанкаре, чтобы обосновать
утверждения, сделанные в этих примерах. Мы получим точный
рецепт, как строить (k — 1)-форму 0, обладающую свойством
дф ~ где iv — заданная замкнутая fc-форма. Лемма будет до-
казана для случая, когда tv определена на открытом множестве в
пространстве Rn, обладающим тем свойством, что каждая точка
множества может быть соединена с началом координат отрезком
прямой, целиком принадлежащим множеству. Такое множество
называется звездным. Позднее мы обобщим доказательство на
случай множества, которое с помощью гладкого отображения
может быть взаимно-однозначно преобразовано к звездному. На
рис. 15.28 показаны примеры таких множеств.
Для данной звездной области Q с координатами ж1,..., хп мы
можем построить отрезок прямой, соединяющий начало коорди-
нат с произвольной точкой р. Поскольку Q звездна, то этот отре-
зок целиком лежит в области Q. Определим функцию (3, которая
для каждой точки р отображает [0,1] в этот отрезок. Таким обра-
зом, если точка р имеет координаты х1,..., хп, то прямолинейный
отрезок задается параметрически формулой
Если воспользоваться терминологией переноса, то мы имеем
Рис. 15.28. а) Звездность относительно точки О (но не точки р).
б) Внутри области дырка, поэтому нет звездности относительно
какой-либо точки, в) Область на поверхности сферы не звезд-
на, но это образ звездной области, г) Поверхность всего тора не
является образом никакой звездной области
800
Глава 15. Комплексы в пространстве Rn
Любая функция д, определенная в области Q, с помощью пе-
реноса может быть преобразована к области Q х [0,1]. Напри-
мер, функция д(и\ ..., ип) в результате переноса преобразуется
в функцию (3*д = g(tx\ ... ^хп). По существу, это значит, что
/3*д является функцией р — (ж1,... ,хп) и t; при изменении t от
0 до 1 она пробегает значения д вдоль отрезка, соединяющего
р с началом координат. Конечно, если р меняется, то значения
д берутся вдоль другого прямолинейного отрезка. Внимательно
посмотрите на рис. 15.29, чтобы осознать смысл
Согласно обычным правилам, мы можем проделать перенос с
любой базисной 1-формой любой /с-формы:
/?*du1 = d(txl) — хг dt + tdx\
Произвольная fc-форма о>, определенная на Q, может быть запи-
сана в координатах и1,..., ип:
ш • • • ’иП) Л • • • Л du%k.
Проделав перенос с такой формой, получим
/3*^= ^2 > • • • ,txn)
х (t dx11 4- ж*1 dt) A • • • A (t dxtk + xtk dt).
15.5. Дифференциальные формы и когомологии
801
Эта fc-форма /3*и> является суммой членов вида
ri(t) = A(t, ж1,..., хп) dx4 Л • • Л dx4
или
72(f) = B(t,x\ ... ,хп) dt Л dx4 Л • • • Л dx4-1.
Определим линейный оператор L, действующий на эти формы
следующим образом:
Zti = 0,
Lt2 = B(t, х1,... ,хп) dt^ dx4 Л • • • Л dx4-1.
Этот оператор обладает замечательными свойствами:
dLri + Ldri = Ti(l) - 7i(0)?
dLr2 + Ldr2 = 0.
Они доказываются прямым вычислением.
Начнем с т±. Конечно, dLri = 0. Кроме того,
дА
dri = —— dt Л dx4 Л • • • Л dx4 + члены без dt.
dt
Поэтому
Z*1 /дА \
Ldn - / HF dx4 Л-- Л dx4 I dt
Jo \dt J
= (А(1,жх,... ,xn) — А(0,х*,... ,xn)) dx11 - A dx*k.
Для Т2 мы имеем выражение
Lt2 — B(t,x\ ... ,xn) dt^ dx4 A • • Л dx4-\
которое не зависит от t. Вычисляя dZ/T2, мы дифференцируем под
знаком интеграла и получаем
dLri = dtj dx^ Л dx11 Л • • • Л dx111-1.
802
Глава 15. Комплексы в пространстве Rn
С другой стороны,
п о
dT2 = У^ dx* /\dt Л dx11 Л.--- Л dxtk~l
дхз
J=1
или
dr2 = — У^ тг—г dt Л dx3 Л dx4 Л • • • Л dx4*-1,
дх>
3=1
так что
гс. / /*1 Я/? \
LdT2 = — dtj Л dx11 Л • • • Л dx1*-1,
откуда следует, что dLr% + Ldrz — 0.
Итак, если мы рассмотрим dL(j3*w) + Ld(/3*cj), то можно иг-
норировать все члены вида Т2, содержащие множитель dt. Для
всех к > 0 мы имеем тДО) = 0, поскольку множитель t стоит при
каждом dx1. Положив 4 = 1, мы получаем
dL((3*w) + Ld(3*w = а11..лк , • • • dx4 Л • * • Л dxtk = си.
Однако нам известно, что d/3*cu = /3*dcu, поэтому
dL(3*v + L(5*dw = ш.
Таким образом, оператор S — L/З* удовлетворяет тождеству
dScv + Sdw — ш.
Если си замкнута, т. е. dw = 0, то
dSu) — и.
Итак, мы доказали, что си точная.
До сих пор мы предполагали, что ш определена в звездной
области Q. Сейчас давайте распространим наше доказательство
на случай, когда ш определена в области Ф(<2), которая являет-
ся образом звездной области при гладком взаимно-однозначном
15.5. Дифференциальные формы и когомологии
803
отображении Ф. Если ш замкнута, то Ф*си тоже замкнута, потому
что с£Ф*си = Ф*<йи — 0. Поэтому можно написать Ф*и — й(5Ф*о;).
Поскольку Ф обратимая, то можно применить обратный перенос
(Ф*)”1 и получить
ш = (Ф*)</(£Ф*а>) или ш = (Ф*)-15Ф*ал
Итак, для формы а/, определенной в области D, мы имеем се-
мейство неопределенных интегралов (Ф*)~15Ф*о;, соответствую-
щих различным способам выражения D в качестве образа звезд-
ной области: D = Ф(ф). Есть и другой взгляд на эту ситуацию.
В области D мы можем ввести различные системы координат,
так чтобы область в координатном пространстве, отображаемая
в D, была звездной. Тогда оператор (Ф*)-15Ф* соответствует ин-
тегрированию вдоль прямых линий в координатном пространст-
ве. Если, например, D — поверхность Мексиканского залива, то
мы получаем S, интегрируя вдоль прямых линий, соединяющих
точки области D с центром Земли (или с другим началом ко-
ординат). Введя сферические координаты, мы построим другой
неопределенный интеграл (Ф*)-15Ф*, когда каждая точка залива
соединяется с началом координат линией, представляемой пря-
мой на карте с проекцией Меркатора.
Давайте сформулируем процедуру получения неопределенно-
го интеграла от дифференциальной формы
LU = , xn)dx4 Л • • • Л dx4.
Шаг 1. Построим перенос /3*си? сделав замену хг —> tx1 в аргумен-
тах всех функций так, чтобы
а(х\ ... ,хп) —► a^tx1,... ,tan),
и заменив
dx1 —> хг dt + tdx\
Шаг 2. Выбросим все члены, в которые не входит dt. Во всех
остающихся членах dt сдвигаем влево, внимательно следя за зна-
ками.
804
Глава 15. Комплексы в пространстве Rn
Шаг 3, Обращаемся с dt как в обычном интеграле и интегрируем
по t от 0 до 1. Эта процедура в явном виде показана на следующих
примерах.
Пример 1. си = у2 dx + 2xydy (замкнутая 1-форма).
Шаг 1. /3*а> — t2y2{xdt + tdx) + 2t2xy{y dt + tdy).
Шаг 2. = {t2xy2 + 2t2xy2) dt + другие члены.
Шаг 3. Sw = xy2 3t2dt = xy2.
Проверка. d{xy2) = y2 dx + 2xy dy.
Пример 2. w — sin xdx A dy.
Шаг 1. = sin(£x)(xdt + tdx) A {y dt + tdy).
Шаг 2. /3*ш = xt sin tx dt Ady — yt sin tx dt A dx + члены, не содер-
жащие dt.
Шаг 3.
S(jj = {xdy ~ ydx) I tsmtxdt
Jo
f x (sin# — xcosx\
= {xdy - ydx) I -----%----- I
(sinx — xcosx\ _ /sinx — xcosx\ ,
------------] dy - у I ------5----- dx
x J \ x2 J
или
(xcosx —sinx\ _ sinx ,
--------5---- dx 4-----dy.
xz / x
Ответ отличается от «очевидной» первообразной — cos х dy на
точную 1-форму
/ у . \ х cos х — sin х , sin х ,
d I — sin x =-----z-----у dx H----dy.
\x / xz x
Пример 3, /3*cu = {y2 — x2)z dx Ady + (x2 — z2)y dz A dx + {z2 —
y2)xdy A dz.
Шаг 1.
= t3{y2 — x2)z{x dt + t dx) A {y dt + t dy)
+ t3(x2 — z2)y{z dt + t dz) A (x dt + t dx)
+ t3{z2 — y2)x{y dt + t dy) A {z dt + t dz).
Резюме
805
Шаг 2.
[3*о) = t\—(y2 — x2)zy + (ж2 — z2)yz) dt A dx
+ ((у2 - x2)zx — (z2 - y2)xz) dt Л dy
+ (—(x2 — z2)yx + (z2 — y2)xy) dt Л dz
+ члены, не содержащие dt.
Шаг 3.
f1
So) = i4 dt(2x2yz — y3z — yz3) dx
Jo
+ (2y2zx — x3z — xz33) dy + (2z2xy — xy3 — x3y) dz
или
2
So) — ~(x2yzdx + y2zxdy + z2xy dz).
5
Мы только что показали, что ядро S : является
подпространством образа S : На самом деле это
весь образ. Предположим, например, что fc-форма удовлетворяет
условию So) = 0. Тогда, поскольку о) = Sdo) + dSo), мы знаем, что
о) — Sdo), т. е. что о) является образом S. Итак, Seo = 0 тогда и
только тогда, когда о) ~ Зф для некоторого ф.
Резюме
А. Внешняя алгебра и дифференциальное исчисление
Вы должны уметь определять пространства A.k(V*) для произ-
вольного n-мерного пространства V и записывать базис для каж-
дого из них.
Необходимо знать и уметь применять свойства оператора d
для дифференциальных форм произвольной степени, включая
процедуру переноса.
В. Интегрирование дифференциальных форм
Вы должны уметь вычислять интеграл от fe-формы по ^-ячейке,
представленной в виде образа единичного /с-куба.
806
Глава 15. Комплексы в пространстве Rn
Вы должны знать, уметь доказывать и применять теорему
Стокса.
С. Дифференциальные формы и когомологии
Вы должны знать, как строить коцепи посредством интегриро-
вания дифференциальных форм; должны уметь находить фор-
мы, определяющие базисные элементы пространства Нк для
2-комплекса и 3-комплекса.
Для данной дифференциальной А>формы ф, удовлетворяю-
щей условию с1ф — 0 и определенной в звездной области, надо
уметь строить (к — 1)-формы 8ф, обладающие свойством (13ф ~ ф.
Задачи
15.1. (а) Пусть r(vi, V2, V3) — кососимметричная трилинейная функ-
ция (т.е. 3-форма). Не обращаясь к свойствам определите-
лей, докажите, что если vi, v2 и V3 линейно зависимы, то
t(vi, v2, v3) = 0.
(b) Пусть о;1, u;2, cf3 — три элемента пространства V*. Не ис-
« « 12
пользуя свойства определителей, докажите, что если cf , и ,
си3 линейно зависимы, то о;1 Л и)2 Л си3 = 0.
15.2. Пусть в четырехмерном пространстве-времени дана 2-форма Е —
dt Л (Ех dx + Eydy + Ez dz). Пусть В = Bz dx A dy — By dx A dz +
dy /\dz. Вычислите E A B.
15.3. Предположим, что детерминант линейного преобразования А :
Rn Rn имеет вид
Det А = dx1 Л dx2 Л • • • Л dxn [Aei, Ае2,..., Аеп],
где {dx1, dx2,..., dxn} дуальны {ei,е2,...,en}.
(а) Докажите, что если А — единичная матрица, то Det А = 1.
(Ь) Докажите, что если А* обозначает матрицу, сопряженную
к А, то
Det А = A* dx1 Л A* dx2 Л • • - Л A* dxn(ei,e2,... , еп).
15.4. Вычислите следующие определители, используя результаты пре-
дыдущего упражнения:
Задачи
807
(2 —1 з\ Г / 2\ /-1\ / з\
—1 3 2 I = dx/\dy/\dz I — 1 ), I 3 |, I 2 j
3 2 -1/ |Д 3/ \ 2/ X-1/
(Ь)
-ь о 0\
а —Ь О
b а —Ъ
О b а/
/а
b
О
Det
15.5. Пусть A3(V) обозначает пространство всех кососимметричных
трилинейных функций из V х V х V в R. Допустим, что V —
четырехмерное пространство и пусть е1, е2, г3, е4 образуют базис
дуального пространства V*. Используя обозначения Л, напишите
базис Л3(И) и напишите формулу, как базисный элемент действу-
ет на тройку векторов (vi,v2,vs).
15.6. Пусть (л) = f dx + dy ъ г = gdx + dz, где f и g — дифференци-
руемые функции х, у и z. Вычислите d(w Л т), записав ответ как
множитель при dx /\dy Adz.
15.7. Пусть /3 обозначает дифференцируемое отображение из аффин-
ного пространства А (размерности т) в пространство В (размер-
ности п). Пусть r(q, w) - -- 1-форма в пространстве В, где q явля-
ется точкой в этом пространстве, w — вектор, направленный из
этой точки. Тогда dr можно определить как
dr(q,wi, w2) = наилучшее линейное приближение к
t(q + Wi, w2) - т(д, w2) - r(q + w2, wi) + t(q, Wi).
Перенос 1-формы определяется следующим образом:
(/?*r)(g,v) = r(^g,d/3(v)),
а для 2-формы а:
(/?*cr)(q,vi,v2) = CT(/3g,d/3(vi),d/3(v2)).
(а) Воспользовавшись этими определениями (и при необходи-
мости цепным правилом), докажите, что
d/3*r = 0*(dr).
808
Глава 15. Комплексы в пространстве Rn
(b) В пространстве А введите аффинные координаты и1, ...,
ит, а в пространстве В — координаты ж1, .хп. Тогда
/3 можно задать с помощью дифференцируемых функций
переноса
(З'х1 = F1^1,... ,um),
^x2^F2(u\.,.,uTn\
^xn^Fn(u\.,,.um\
а
T = ^GJ(a;1,...,xn)^,
где G-7 — дифференцируемые функции. Вычислите явно
d(3*r и (3*(dr) и покажите, что они равны.
(с) Пусть т и А — 1-формы. Покажите, что если Q = т Л А, то
/3*П = (/3*т)Л(/3*А).
15.8. Сферические координаты г, 0, ф связаны с декартовыми коорди-
натами z, у и z формулами
= г sin0cos</>, а*у = г sin# sin(/>, a^z~rcosOy
где а ~ отображение, переводящее точку I 0 I в пространстве
V/
(x\
у I с координатами r, 0 и ф,
z /
Вычислите переносы следующих дифференциальных форм (т. е.
выразите их в сферических координатах):
(Ъ)
(a) a*(xdy — ydx)-,
*х dx + у dy 4- z dz
a (x2 +y2 4- г2)3
a* x dy A dz 4- у dz A dx 4- z dx A dy
(d)
(z2 4- y2 4- z2)3/2
a* dx /\dy A dz.
Задачи
809
15.9. (а) Пусть f —дифференцируемая функция в пространстве R3.
Пусть А обозначает 2-форму
А = ~ dy Л dz + dz Л dx + dx Л dy.
dx оу dz
Покажите, что dA = Af dx Л dy Л dz, где А обозначает
лапласиан д2/дх2 + d2/dy2 + д2/dz2.
(b) Пусть Fx, Fy, Fz —- дифференцируемые функции в прост-
ранстве R3, удовлетворяющие условию
dFx dFy dFz
Определим
В =
dFz dFy\. JdFx
------— J dx+ (
dy dz J \ dz
9FA
dx J
dFy dFx
dx dy
Покажите, что dB = AFX dy/\dz + AF^ dz A dx + AFZ dx/\dy.
15.10. Тело вращения вокруг оси z ограничено: снизу — диском х2 +
У2 < 1? £ = 0; сбоку — поверхностью цилиндра х2 + у2 = 1,
0 < z < 2; сверху — параболоидом z = 1 -j- х2 + у2, задаваемым
параметрически в виде
/3*т = г cos 0, (3*у = г sin#, /3*z = 1 + г2.
Если смотреть снаружи, то все поверхности ориентированы про-
тив часовой стрелки, как это показано на рис. 15.30.
(а) Вычислите интеграл от 2-формы т = xdy Ndz — у dx f\dz по
поверхности верхнего параболоида.
(Ь) Вычислите интеграл от т по поверхности цилиндра.
(с) С помощью теоремы Стокса выразите объем этого твердого
тела через только что полученные интегралы.
15.11. Пусть Я = xdy Л dz.
(а) Вычислите J Q по диску х2 + у2 < R2, z — 0.
(b) Рассмотрите полусферу t2+t/2 + z2 = В?, z >0, которую па-
раметризуем сферическими координатами (см. рис. 15.31):
z — RcosQ, х — Rsin0 cosф, у = F sin# sin ф.
Выразите Q через R, в и ф. Потом вычислите J Q по этой
полусфере.
810
Глава 15. Комплексы в пространстве Rn
Рис. 15.30 Рис. 15.31
(с) Воспользуйтесь теоремой Стокса и запишите интеграл от
3-формы, который равняется разности двух поверхностных
интегралов, вычисленных в пунктах (Ь) и (а). Выясните
геометрический смысл этого интеграла и вычислите его.
15.12. (а) Рассмотрите твердое тело с однородной плотностью р, кото-
рое занимает область Q в пространстве R3. Покажите, что
интеграл от 2-формы
т = (х3 dy /\dz — у3 dx Л dz)
о
по границе Q дает момент инерции Izz этого твердого тела.
(Ь) Придумайте 2-форму интеграл от которой по dQ дает
момент инерции 1ху. Почему ответ в этой задаче не един-
ственный?
(с) Используйте результат пункта (а) для вычисления момента
инерции сферы радиуса а относительно ее диаметра. Вос-
пользуйтесь сферическими координатами.
15.13. (а) Пусть W обозначает область в пространстве R3, занятую
твердым телом с однородной плотностью р. Покажите, что
координата z центра масс этого тела z может быть опре-
делена как частное от двух поверхностных интегралов, вы-
численных по границе тела т. е.
z = [ ^pr2 dx /\dy / I zdx A dy,
Jaw / Jaw
где r2 — x2 4- y2 + z2.
Задачи
811
(b) Переход сферическим координатам дается формулами:
а* х = г sin0cos</>, а*у = rsin0sin(/>, о* 2 = г cos0.
Вычислите a*(dx Л dy).
(с) Используя результат пункта (Ь), вычислите
[ 1 2j
/ —г dxЛ dy
hwl
для случая, когда W является внутренностью полусферы
радиуса а с правосторонней ориентацией.
15.14. Пусть С обозначает половину цилиндра, ограниченного плоско-
стями z = 0 «низ», z — 1 «верх», плоскостью х = 0 «плоскость»
и боковой поверхностью х2 4- у2 = а2 «кривая». С имеет право-
стороннюю ориентацию, так что вектора еж, е^, ez образуют пра-
вильно упорядоченный базис, как это показано на рис. 15.32. Для
каждой грани С имеется упорядоченный базис, который опреде-
ляет ее ориентацию.
(а) Напишите выражение для <ЭС, следя за знаками.
(Ь) Имеется 2-форма т = х2 dy Л dz — 2xz dx Л dy. Вычислите
перенос т при отображении, заданном следующим образом:
/3*& = a cos а, /3*у = asinw, /3*2 = v. Вычислите интеграл от
т по боковой поверхности «кривая».
(с) Пусть задано отображение: а*х = rcos#, а* у = г sin#,
а*2 = 1. Вычислите интеграл от т по поверхности «верх».
(d) Чему равен интеграл от т по другим двум поверхностям?
Объясните.
(е) Вычислите dr. Используя теорему Стокса, объясните, с по-
мощью этого результата проверить ответы в пунктах (Ь),
(с) и (d).
15.15. Рассмотрите 2-комплекс, изображенный на рис. 15.33.
(а) Пусть W 1-коцепь. Выразите 2-коцепь dW через W, т. е.
выразите fSi dW и fs^ dW через Wa и др.
(b) Рассмотрите 1-форму и — ydx + xdy = d(xy). Вычислите
1-коцепь ТУ, определенную интегрированием ш по ветвям.
Проверьте, что dW = 0.
812
Глава 15. Комплексы в пространстве Rn
Рис. 15.32
Рис. 15.33
Задачи
813
(с) Сделайте то же самое для 1-формы w = (xdy — ydx)/r2.
Покажите, что она определяет коцепь W, которая является
коциклом, но не кограницей. Будет ли W коциклом, если
S3, внутренний круг, ограниченный а и е, тоже включить в
комплекс?
15.16. Единичный куб, изображенный на рис.
15.34, определяет 3-ком-
плекс с шестью гранями:
Si: х = О,
S? •* х = 1,
S3 : У = О,
О < у, z < 1
О < у, z < 1
О < х, z < 1
S4: у = 1,
S5 : z = О,
S6: z = 1,
О < У, z < 1:
О < х, у < 1
О < я, у < 1
Каждая грань ориентирована против часовой стрелки, если смот-
реть на нее снаружи. Внутренняя область куба R имеет границу
OR - Si + S2 + S3 + S4 + S5 + S6.
(а) Пусть T - произвольная 2-коцепь. Получите выражение
для dT.
(b) Имеется 2-форма т — х2 dy Л dz + ху dz Л dx + xz dx Л dy.
Постройте соответствующую 2-коцепь Г, интегрируя т по
каждой грани. Вычислите dr и постройте соответствующую
3-коцепь. Проверьте, что она равна dT.
(с) Имеется 1-форма ш ~ x2ydz. Вычислите dw. Получите
1-коцепь W, соответствующую си на ветвях о, /3, 7, 5, е,
г]. Получите 2-коцепь Г, соответствующую dw на гранях S2
Рис. 15.34
814
Глава 15. Комплексы в пространстве Rn
и S3. Проверьте, что Т, полученная для S2 + S3, равна W,
полученной для границы S2 + S3.
15.17. (а) В пространстве R3 имеется 2-форма т ~ adx /\ dy + bdx /\
dz + cdy /\dz, где а, 5, с — дифференцируемые функции ж,
у, z. Пусть ф будет отображением из R2 (координаты u, v)
в R3 (координаты х, у, z). Оно задано формулами
ф*х = F(u, v), ф*у = G(u, v), ф* = Н(и, v).
Проделав вычисления в явном виде, проверьте, что ф* (dr) ~
dffir). Конечно, придется использовать цепное правило.
(Ь) Пусть vi и V2 вектора в пространстве R2. Тогда перенос ф*т
определяется в виде
^T(vbv2) = r[d0(vi),d^(v2)]
(имейте ввиду, что в каждой точке dф представляется мат-
рицей Якоби 3x2). Используя это определение и цепное
правило, докажите, что — d(</>*r).
15.18. Используя оператор S, описанный в параграфе 15.4, сделайте
следующее.
(а) Найдите такую функцию /(х, у, г), чтобы
df = yeyz dx + (я + xyz)eyz dy + xy2eyz dz.
(b) Найдите такую l-форму cu, чтобы
dw = x dy A dz + у dx Л dz.
(с) Найдите такую 2-форму г, чтобы
dr — xy2z3 dx /\dy A dz.
15.19. Пусть В = z2 dx A dy + уz dx A dz — xz dy A dz.
(а) Пусть W — любая область в пространстве R3. Покажите,
что
[ В = 0.
Jdw
(b) Найдите такую 1-форму Л, чтобы dA = В.
Задачи
815
15.20. Рассмотрите 2-комплекс, изображенный на рис. 15.35. Он имеет
четыре узла, пять ветвей и одну 2-ячейку 5, заштрихованную на
рисунке. Пусть
xdy-ydx
v = d0 = -*
х* + ул
Определите 1-цепь W, которая соответствует со. Вычислите Wa,
W7, W6, We. Покажите, что W является коциклом, но не
кограницей.
Рис. 15.35
15.21. Пусть R1,3 обозначает четырехмерное пространство-время с упо-
рядоченными аффинными координатами х, у, z.
(а) Напишите базис для Л2(R1,3).
(Ь) Рассмотрите 2-форму
W = А(х, г/, t) dt f\dx + В(х, у, t) dt f\dy + C(x, ?/, t) dx A dy.
Если dW = 0, то какие отношения между частными произ-
водными Л, В, С должны выполняться?
Глава 16
Электростатика в пространстве
R3
Глава 16 посвящена электростатике. Мы считаем, что
диэлектрические свойства вакуума дают непрерыв-
ный аналог цепей с емкостями и что именно эти ди-
электрические свойства определяют евклидову гео-
метрию в трехмерном пространстве. В этой главе
представлены основные положения теории потенци-
алов.
16.1. От дискретности к непрерывности
Пусть А0 = Q°(R3) обозначает пространство гладких функций
в R3 (мы их считаем формами нулевой степени). Пусть, далее,
А1 — QX(R3) обозначает пространство гладких линейных диф-
ференциальных форм, А2 — пространство гладких форм второй
степени, а А3 — пространство гладких форм третьей степени. Мы
будем рассматривать Аг как зародыш коцепи степени г, т. е. если
в пространстве R3 у нас есть комплекс, то каждая форма сте-
пени г в результате интегрирования определяет коцепь степени
г. Таким образом г-формы определяют правила, приписывающие
цепям соответствующие числа. На эту картину можно взглянуть
и с другой стороны. Если мы фиксируем определенную цепь с
степени г, то считаем, что с определяет линейную функцию на
пространстве Аг: каждой форме ш степени i мы приписываем
818
Глава 16. Электростатика в пространстве R3
число fcas. Если есть две формы оц, cu2 степени г, а а и b — веще-
ственные числа, то из свойств операции интегрирования следует,
что
У (ао>1 + t*cu2) = а + b Jо?2;
другими словами, интеграл Jcu является линейной функцией
формы ш.
В качестве простейшей иллюстрации рассмотрим 0-цепь с.
Пусть эта 0-цепь состоит из единственной точки Р Е R3 с ори-
ентацией +. В этом случае интегрирование сводится к простому
вычислению: цепь с порождает линейную функцию на простран-
стве А0, которая каждой функции f Е А0 приписывает значение
f(P). Можно полагать, что f(P) является энергией, соответству-
ющей такому распределению зарядов, когда в точке Р находится
единичный заряд и создается потенциал /. Такая «обращенная»
точка зрения, когда Р считается линейной функцией /, имеет
определенные преимущества. Допустим, что мы хотим дискрет-
ное распределение зарядов, сконцентрированное в точке Р, за-
менить на «размазанное», или непрерывное распределение заря-
дов с плотностью р. Предполагается, что плотность р — гладкая
функция с компактным носителем. (Последнее означает, что р
обращается в нуль за пределами некоторого ограниченного мно-
жества.) Мы можем поступить следующим образом. Рассмотрим
3-форму (с компактным носителем) pdx/\dyf\dz. Каждую функ-
цию f Е А0 мы умножаем на р dx Л dy Л dz и получаем 3-форму
fpdx/\dyf\dz, которая является 3-формой с компактным но-
сителем в пространстве R3. Имея фиксированную ориентацию в
R3, интегрируем эту 3-форму и получаем число. Таким образом,
форма pdx Л dy Л dz определяет линейную функцию в прост-
ранстве А0. Эта линейная функция каждой f Е А0 приписывает
число JR3 fpdx/\dy/\dz. (Заметим, что если полный интеграл от
функции р равен 1 и если р становится все более сконцентриро-
ванной вокруг точки Р -- другими словами, если мы устремим
непрерывное распределение зарядов к точечному вокруг Р, — то
значение интеграла будет стремиться к f(P). Пусть Аз обознача-
ет пространство 3-форм с компактным носителем в пространстве
R3. Мы уже показали, что каждая pdx /\dy /\dz Е Аз определяет
16.1. От дискретности к непрерывности
819
линейную функцию на пространстве А0. Тогда элемент простран-
ства A3 оказывается размазанной 0-цепью.
На самом деле электрические заряды, как известно, дискрет-
ны. Но сейчас мы наметим, как можно аппроксимировать дис-
кретное распределение непрерывным. Предположим, что есть
плотно упакованное распределение небольших зарядов c(PJ. Тог-
да получаем линейную функцию
'• • . Рис. 16.1
• •
от функций. Эта линейная функция может быть хорошо аппрок-
симирована (для широкого класса функций /) размазанным рас-
пределением зарядов pdx Л dy Adz в том смысле, что
У fpdx Ady Л dz Рис. 16.2
близко к
Введем непрерывные аппроксимации для 1-цепей, 2-цепей и т. д.
Пусть обозначает пространство гладких 2-форм с компакт-
ным носителем. Утверждается, что элемент Q пространства А2
можно рассматривать как своего рода размазанную 1-цепь, т. е.
что Q определяет линейную функцию на пространстве А1. Чтобы
это увидеть, рассмотрим си (элемент пространства А1) и образуем
luAQ. Это 3-форма с компактным носителем, которую можно ин-
тегрировать по пространству R3 и получить число. Другими сло-
вами, П 6 Аз определяет линейную функцию на пространстве А1,
которая каждой си приписывает число j^3 cuAQ. Аналогично, если
Ai обозначает пространство гладких 1-форм с компактным носи-
телем, то каждый элемент пространства Ai определяет линейную
функцию в пространстве А2 и может рассматриваться как раз-
мазанная 2-цепь. Если Ао обозначает пространство 0-форм (т. е.
гладких функций) с компактным носителем, то каждый элемент
Ао определяет линейную функцию в пространстве А3 и может
820
Глава 16. Электростатика в пространстве R3
рассматриваться как размазанная 3-цепь. Итак суммируем полу-
ченные результаты:
А0 спаривается с А,
А1 спаривается с А,
А2 спаривается с А,
А3 спаривается с Аъ
в том смысле, что если си Е Аг и Q 6 то мы получаем число
/кз <u Л Q. Для фиксированной Q это линейная функция си, а для
фиксированной си это линейная функция Q. Кроме того, это спа-
ривание инвариантно относительно любого сохраняющего ориен-
тацию взаимно-однозначного отображения ф пространства R3 на
себя, имеющего дифференцируемое обратное. Если ф — именно
такое отображение, то для любой 3-формы т с компактным но-
сителем из формулы замены переменных в интеграле получаем
JR3 ф*т = т. С другой стороны, ф*(сиЛП) = ф*сиЛ</>*П. Поэтому
У ф*ш Л ф*а = У w Л Q.
Другими словами, спаривание инвариантно относительно сохра-
няющей ориентацию замены координат.
16.2. Граничный оператор
Поскольку у нас есть отображение d : Аг Аг+1, то мы име-
ем также сопряженное отображение д, которое каждой линейной
функции с на пространстве приписывает линейную функ-
цию дс на пространстве Аг по формуле (дс) (cu) = c(dcu). Это
означает, что мы должны уметь найти такое отображение д из
в Д, чтобы для любого (7 Е Aj+i и любого CU Е Аг было
справедливо равенство
/ си Л 9сг — / dcuAcr.
Чтобы найти такой оператор 5, заметим, что
d(cu Л а) = dw Л а + (—l)\u Л da
16.2. Граничный оператор
821
и по теореме Стокса (благодаря тому, что си Л ст имеет компактный
носитель, так что интегрирование по R3 можно заменить инте-
грированием по некоторой конечной области, на границе которой
форма си Л а обращается в нуль) интеграл JR3 d(w Л ст) становится
равным нулю. Тогда
(—1)г+1 I ш Л da = I dat/\a.
Отсюда мы видим, что
д= (-iy+1d.
Другими словами,
д — —d В пространстве Д),
д = d в пространстве Л1,
д =—d в пространстве А-2,
d = d = Q в пространстве ^3-
Таким образом, мы получили последовательность отображений
А0 4 А1 4 А2 4 А3,
Аз 4- А2 4- Ai 4- Ао,
где д — (—1)г+1с/ в пространстве A+i.
Иногда оператор д называют формальным транспонировани-
ем d. Причина для появления слова «формальный» состоит в
том, что оператор д может быть выражен через ф и формула
ш /\да ~ j dw Л а
справедлива только тогда, когда интегрирование ведется по об-
ласти, где границы не вносят вклада. Мы обеспечили это, проин-
тегрировав по всему пространству при условии, что а имеет ком-
пактный носитель. Эта формула выполняется также, если tu име-
ет компактный носитель, т. е. мы считаем, что d является отоб-
ражением из Ai в Ai+i, а д — отображением из Аг в Лг+1. Таким
образом, мы можем рассматривать формы с компактным носите-
лем как фундаментальные объекты и считать, что отображение
д определено на пространстве линейных функций Аг.
822
Глава 16. Электростатика в пространстве R3
16.3. Телесный угол
В качестве иллюстрации вышеуказанной обращенной точки зре-
ния, давайте проделаем ряд вычислений. Пусть дана точка Р в
пространстве R3 с координатами тр, ур, zp. Пусть тр обозна-
чает телесный угол, наблюдаемый из точки Р, определяемый
2-формой
__ (х — хр) dy /\dz — (у — ур) dx /\dz + (г ~ zp) dx Л dy
Здесь гр обозначает расстояние до точки Р. Форма тр определе-
на не на всем пространстве R3, а только в пространстве R3 — {Р},
т. е. в трехмерном пространстве, из которого удалена точка Р. И
тем не менее форма тр определяет линейную функцию в прост-
ранстве Ai. Действительно, пусть — adx + bdy+cdz обозначает
линейную дифференциальную форму с гладкими коэффициента-
ми и компактным носителем. Тогда
Л тр — Гр3[а(х — хр) + b(y — ур) + c(z — zp)] dx /\dy Л dz.
Коэффициент dx/\dy/\dz не определен в точке Р, но особенность
в Р порядка Гр2 (поскольку в точке Р выражение в квадратных
скобках имеет нуль первого порядка). Следовательно, при вы-
числении интеграла точка Р не создает проблем. Поскольку ш
имеет компактный носитель, то интеграл по всему пространству
определен корректно. Чтобы вычислить этот интеграл, удобно
перейти к сферическим координатам с центром в точке Р. Если
гр, в, ф - такие координаты, то
тр — sin OdO Л dф.
(Таким образом, тр дает нам телесный угол, заметаемый поверх-
ностью, по которой мы интегрируем, рис. 16.3.) Предположим,
что в этих сферических координатах си = F drp + G dO + H dф.
Тогда
(jj Л тр = F sin 0 drp Ad# Л dф.
Итак,
f /*27Г /*7Г { /»ОО >
I а>/\тр = / sin#< / F(rp,0,<j>) drp \dOd(^>.
Jr3 Jo Jo I Jo j
16.3. Телесный угол
823
Рис. 16.3
Давайте рассмотрим случай, когда w = du для некоторой глад-
кой функции и с компактным носителем. Тогда в предыдущей
формуле в сферических координатах F = ди/дтр, и внутрен-
ний интеграл в правой части сводится к постоянному значению
—и(Р\ так что интегрирование по в и ф сводится к умножению
на площадь поверхности единичной сферы 4тг. Таким образом,
мы доказали базисную формулу
du Л тр = —4ли(Р). (16.1)
Пусть 5р обозначает 0-цепь, которая каждой функции и припи-
сывает значение и(Р), т. е. 8р представляет единичный заряд, со-
средоточенный в точке Р.1 Тогда правая часть уравнения (16.1)
есть значение 0-цепи на функции и, равное — 4тг<5р. А левая часть
уравнения есть значение тр, вычисленное для du. Тогда уравне-
ние (16.1) можно записать в виде
дтр = —4тг5р. (16.2)
(Заметим, что в предыдущем уравнении д нельзя приравнивать
к d. Форма тр не определена в точке р, поэтому drp там тоже не
определена. Во всех точках, где тр определена, мы имеем drp — 0.
И тем не менее уравнение (16.2) справедливо как равенство fl-
цепей, т. е. линейных функции от функций.)
Предположим, что у нас есть конечное число точек Pj, Р2,
Р3 и т.д. Заряд ci помещаем в Pi, с<2 в Р^ и т.д. Значит, мы
1 Принято называть др делъта-функцией Дирака, сосредоточенной в точке
Р. Она относится к так называемым обобщенным функциям, которые игра-
ют фундаментальную роль во многих задачах анализа и математической
физики. — Прим. ред.
824
Глава 16. Электростатика в пространстве IR3
рассматриваем 0-цепь
Q = C]/pi + С2<5р2 Н-.
Пусть
D = -(ciTP1 + с2тр2 + •••).
Тогда D корректно определяет линейную функцию в простран-
стве Л1, и мы имеем формулу
dD = -4ttQ.
Если вместо дискретного распределения конечного числа заря-
дов, нам дано распределение зарядов с гладкой функцией плотно-
сти р, имеющей компактный носитель, то предыдущее определе-
ние D через сумму заменяется на соответствующий интеграл, т. е.
мы теперь пишем D — f р(Р)тр dP и Q = pdx/\dy Л dz, при этом
выполняется предыдущее уравнение. В этом случае непрерыв-
ного распределения несложно показать (мы это сделаем очень
скоро), что D — гладкая 2-форма, определенная во всем прост-
ранстве.
16.4. Напряженность электрического поля
и электрическое смещение
Сейчас мы уже можем дать определения фундаментальных по-
нятий теории электростатики. Напряженность электрического
поля Е является линейной дифференциальной формой, проинте-
грировав которую по любой трактории, мы получаем падение на-
пряжения на ней. Величина Е имеет физическую размерность на-
пряжение/длину. (Поскольку размерностью напряжения являет-
ся энергия/заряд, а размерностью силы является энергия/длину,
то можно также считать, что Е измеряет силу/заряд.) Основное
уравнение, которому удовлетворяет Е, имеет вид
dE — 0.
Это уравнение локально эквивалентно существованию потенциа-
ла и, т. е. условию
Е = ~du.
(16.3)
16.4. Напряженность поля и электрическое смещение 825
Мы будем пользоваться этим уравнением для большинства рас-
сматриваемых областей.
Будем рассматривать Е как зародыш 1-цепи, а и — как заро-
дыш 0-цепи. Кроме того нам понадобится объект, представляю-
щий размазанную 1-цепь. Это будет 2-форма D, называемая элек-
трическим смещением. Она должна представлять размазанный
вариант 1-цепи, дающей заряды ветвей. Мы также хотим иметь
размазанный вариант 0-цепи, представляющей заряды узлов. Это
будет 3-форма pdx Ady Adz. В нашей модели емкостной цепи мы
имели
^(заряды вервей) = —заряды узлов.
Поэтому мы ожидаем, что
dD — —pdx Л dy Л dz.
Стандартное определение единиц измерения D и р (в системе
СГС) таково, что это соотношение верно с точностью до множи-
теля 4тг:
QD — -4тгр(&г Ad?/ Л dz. (16.4)
Это называется законом Гаусса. Вследствие теоремы Стокса и
того, что для 2-форм выполняется условие д — —d, мы можем
написать
/ D = 4% / pdx Ady Adz,
Jdw Jw
что связывает интеграл от D по поверхности, ограничивающей
область И7, с полным зарядом внутри нее.
Конечно, уравнение dD — —kjrpdx Л dy Adz не определяет D
однозначно. Прибавление к D любой замкнутой формы не влия-
ет на уравнение. Частично 2-форма D дает нам информацию об
электростатической системе. В принципе она может быть изме-
рена следующим образом. Напишем
D = Dx dy Л dz + Dy dz A dx + Dz dx A dy.
Чтобы измерить Dz, поместим в исследуемую среду две
небольшие параллельные плоскости ху металлические пластины
826
Глава 16. Электростатика в пространстве R3
(рис. 16.4). Соединим пластины вместе, а потом вновь разделим
их. Пластины приобретут заряды ±Q. Тогда
л .. заряд верхней пластины (со стороны +z)
Dz = 4тг lim ------------------------------------------
площадь—>0 площадь пластин
(4тг появляется за счет системы СГС.) Этот метод работает в лю-
бом диэлектрике, даже если мы не знаем его диэлектрическую
проницаемость s, и при этом нигде не упоминается электриче-
ское поле.
По существу это определение D можно обобщить и дать опре-
деление Р, не связанное с системой координат. Для любой па-
ры векторов Vi и V2 образуем плоскопараллельный конденсатор
(рис. 16.5), пластинами которого являются параллелограммы, по-
строенные на векторах hv\ и /iv2. Тогда
х Л заряд на верхней пластине
T>(vi, v2) = 4тг hm---------г-----------.
h^O ПГ
Рис. 16.5
16.4. Напряженность поля и электрическое смещение 827
Какую пластину считать верхней, зависит от ориентации2, по-
скольку ориентация изменяется при перестановке Vi и V2:
-O(V2, V1) = -Z>(vi,v2).
Поскольку заряд аддитивен, то D — билинейная функция vi и
V2. Поэтому, по определению, D является 2-формой.
Итак, мы обобщили топологические уравнения для сетей с
емкостями на случай электростатики.
V — —заменяется Е = ~du;
dQ — — р заменяется dD = — kxpdx Ady Л dz.
Если D — гладкая 2-форма, то dD — +4.'xpdx Ady A dz.
Сейчас мы должны вспомнить, что Е может рассматриваться
(при выборе, например, стандартной ориентации) как линейная
функция от Р, которая приписывает D число
[ EAD.
Jr3
В этой формуле мы все еще считаем, что либо Р, либо Е имеет
компактный носитель. Но по существу этот интеграл может быть
определен для другой пары Е и Р, у которой произведение Е Л
Р достаточно быстро стремится к нулю на оо. Например, если
произведение стремится к нулю как г~4 или быстрее, то интеграл
сходится. Мы не должны забывать об этой возможности.
Теперь у нас есть непрерывные размазанные версии тополо-
гической части нашей теории цепей с емкостями. Но нам еще
надо иметь вариант матрицы С, удовлетворяющей соотношению
Q — CV. Поэтому мы хотим иметь отображение
Р = С(Р),
определяющее электрическое смещение по напряженности поля.
В следующем параграфе мы будем подробно изучать такое отоб-
ражение С. Здесь мы получим ряд следствий из описанных ниже
предположений относительно С.
2Очевидно, имеется в виду, что векторы vi, V2, w образуют положительно
ориентированный базис R3, если w направлен от нижней пластины к верхней.
- Прим. ред.
828
Глава 16. Электростатика в пространстве R3
Вспомним, что в теории цепей отображение С было диаго-
нальной матрицей относительно напряжений ветвей. В частнос-
ти, если на какой-то ветви напряжение равно нулю, то обращает-
ся в нуль и заряд этой ветви. В качестве слабой аналогии с этим
условием предположим, что
(а) отображение С локально в том смысле, что если Е тожде-
ственно равно нулю внутри какой-то области, то D = С(Е)
тоже там тождественно равно нулю.
По аналогии с теорией цепей предположим, что
(Ь) отображение С симметрично, т. е. если есть два электриче-
ских поля £i и то
У Л С(Е2) = У Е2 Л С(Ех).
В следующем параграфе мы опишем отображение С с пози-
ций его реальной физической интерпретации. Мы увидим, что
существует тесная связь между отображением С для вакуума и
геометрией Евклида. Во всех средах выполняются условия (а) и
(Ь). А сейчас мы получим некоторые следствия из них.
По определению, проводящий материал не оказывает сопро-
тивления при движении электрического заряда. Другими слова-
ми, в проводнике форма Е, которая измеряет работу, выполнен-
ную при движении электрического заряда, должна обращаться в
нуль. Тогда, используя свойство (а), мы видим, что
Внутри любого проводника формы Е и D должны об-
ращаться в нуль. Следовательно, функция и долж-
на быть постоянна на каждой системе соединенных
проводящих тел.
Так как внутри проводника D — 0, то и р = 0. Поэтому внутри
проводников не может быть электрических зарядов (в рамках
электростатики). Или, говоря словами Фарадея,
все заряды проводника располагаются на его поверх-
ности.
16.4. Напряженность поля и электрическое смещение 829
Конечно, плотность этого поверхностного заряда определяется
формой D. Полный заряд pi отдельного проводника получается
интегрированием D по его поверхности.
Давайте предположим, что заряды есть только на проводни-
ках. Мы считаем, что вне проводников dD = 0. Тогда для двух
потенциалов и и й с соответствующими D и D мы имеем
d(uD) = du Л D + и dD
= —E/\D
вне проводников, так как там dD — 0. Тогда по теореме Стокса
(Е, Ё) I Е Л Ь = I uD.
I по области вне / по поверхностям
проводников всех проводников
На поверхности г-го проводника и принимает постоянное значе-
ние Ф^. Тогда и можно вынести из поверхностного интеграла и
получить
(Е,Е)= J2 фР-
проводникам
Это теорема взаимности Грина, рассмотренная в параграфе 13.8.
Третье свойство отображения С состоит в том, что скалярное
произведение (•, •) положительно определено. Таким образом, ес-
ли в предыдущем уравнении взять Е — Е, то получим
(Е,Е)= 22
проводникам
Если заряды всех проводников равны нулю, то правая часть это-
го уравнения равна нулю. Вследствие положительной определен-
ности это значит, что Е = 0 и следовательно все потенциалы
Ф равны. Если мы рассматриваем один проводник (скажем, во-
ображаемый проводник на бесконечности) как заземленный, то
заряды р определяют потенциал Ф единственным образом. Ана-
логично, потенциалы однозначно определяют заряды. Тогда мы
имели бы отображение из пространства потенциалов всех провод-
ников Ф на простанство зарядов всех проводников р, и это дало
бы нам возможность использовать результаты главы 13.
830
Глава 16. Электростатика в пространстве R3
При этом предполагается, что для любого заданного распре-
деления потенциалов Ф по различным проводникам мы можем
получить соответствующие Е и D (единственным образом). В
этом вопросе взгляды математика и физика расходятся.
С точки зрения математика поставлена интересная и нетри-
виальная задача Дирихле. Это вопрос теоремы существования в
теории уравнений с частными производными. Решение ее потре-
бовало огромных усилий многих талантливых математиков по-
следней трети девятнадцатого века. В конце концов она была
решена положительно с помощью различных методов, каждый
из которых вызвал к жизни интересное математическое разви-
тие, часто с важными следствиями в физике. Соответствующая
проблема для более общих уравнений с частными производными
более общего вида все еще активно исследуется. В следующих па-
раграфах мы еще поговорим об этой математической проблеме,
но ее подробное обсуждение не входит в задачу этой книги.
С точки зрения физика вопрос о существовании не столь ва-
жен и относится к логической последовательности математичес-
кой идеализации физической модели. Физик знает, что гипотеза
о распределении статического заряда является лишь приближе-
нием к реальности. Если модель работает, т. е. если идеализация
распределения статического заряда на поверхности проводника
при постоянных потенциалах и соответствующих электрических
полях дает разумное описание ситуации, то, конечно, теорема су-
ществования должна выполняться, потому что каждый провод-
ник мы можем снабдить любым зарядом, каким захотим. Если
же теорема существования нарушается, то либо потому, что ма-
тематики придумали немыслимые проводники, которые нельзя
построить на практике (или другие «физически бессмысленные»
условия), либо потому, что есть фундаментальная ошибка в тео-
рии. Гораздо проще вывести логические следствия из предпола-
гаемого существования решения и проверить на опыте, выпол-
няются ли физические предсказания. Если они выполняются, то
нарушения теоремы существования, вероятно, представляют что-
то экзотическое и не имеет большого физического значения.
В дальнейшем этот параграф излагается с физической точки
зрения. Мы предполагаем существование решений для данного
16.4. Напряженность поля и электрическое смещение 831
распределения зарядов или напряжений на проводнике. Предпо-
ложим также, что решения зависят от заданных граничных усло-
вий непрерывно.
А теперь получим несколько важных заключений.
Принцип электрической экранировки. Допустим, что неко-
торые из проводников, скажем, с первого по седьмой, полностью
окружены другим — восьмым — проводником (рис. 16.6). Допу-
стим, что на окруженных проводниках нет зарядов. Рассмотрим
произвольное распределение зарядов на остальных проводниках.
Тогда возникнет электрическое поле Е — —due соответствующим
электрическим смещением D и потенциалами, индуцированными
на всех проводниках. В результате действия зарядов восьмой про-
водник приобретет постоянный потенциал Ф§.
Рис. 16.6
Априори мы не знаем, каковы индуцированные заряды и по-
тенциалы на внутренних проводниках. Предположим, что мы
рассматриваем новую функцию и' = и вне и uf = Ф§ внутри
полости восьмого проводника. Это является решением нашей за-
дачи, причем внутри полости Е = D = 0, и на всех внутренних
проводниках заряды нулевые. В силу единственности оно сов-
падает с исходным решением, потому что ни один заряд не попал
на внутренние проводники, и то же самое было бы и при измене-
нии потенциалов внешних проводников. Короче, внутренняя по-
лость восьмого проводника экранирована от всей электростатиче-
ской системы вне этого проводника. Этот принцип используется
832
Глава 16. Электростатика в пространстве R3
при создании электростатических измерительных инструментов,
чтобы внешние электрические помехи не влияли на наблюдае-
мый эффект. (Если мы хотим иметь возможность видеть внут-
ренность полости, то можно оставить маленькое отверстие или
заменить часть проводника проволочной сеткой, которая экрани-
рует почти так же хорошо, как и сплошной проводник.) Помимо
практической важности, принцип электрического экранирования
очень полезен при вычислениях, когда он применяется вместе со
следующим принципом.
Замена эквипотенциальной поверхности проводящим
слоем. Предположим, что для некоторой системы зарядов или
потенциалов у нас есть решение Е — —du, D = СЕ. Пусть 5 обо-
значает поверхность, на которой потенциал и постоянен и равен
Ф. (Тогда S называется эквипотенциальной поверхностью.) До-
пустим, что поверхность S заменили тонким проводящим слоем,
на котором поддерживается потенциал Ф. Природа отображе-
ния С такова, что оно фактически не изменяется вставкой этого
проводника. Поэтому вставка проводника практически не про-
изводит эффекта. Внутри этого тонкого проводящего слоя Е
и D обращаются в нуль, заряды аккумулируются на его двух
поверхностях, но все остальное остается без изменения.
Например, рассмотрим среду, инвариантную относительно
вращений. Тогда потенциал заряда Q, помещенного в начало
координат, должен иметь вид
и = Af(r).
(В следующем параграфе мы увидим, что если система инвари-
антна относительно всех евклидовых движений, то
где с — некоторая постоянная.) Теперь вставим тонкий проводя-
щий сферический слой радиуса а. Поля внутри и вне этой сферы
не изменятся, a D внутри обратится в нуль. Если внутри прово-
дящего слоя сферы нарисовать еще одну сферу, то полный заряд
внутри нее должен быть равен нулю. Таким образом, на внут-
ренней поверхности проводящей сферы аккумулируется полный
16.4. Напряженность поля и электрическое смещение 833
заряд — Q (а на внешней — полный заряд Q). Мы можем теперь
разрядить внутреннюю поверхность (с помощью провода, соеди-
няющего заряд в начале координат и внутренней поверхности
проводящей сферы). В силу принципа электрического экрани-
рования, вне сферы ничего не произойдет, но потенциал внутри
сферы станет постоянным. Таким образом, потенциал поля, со-
здаваемого заряженной сферой, имеет вид:
Qf(r), г>а,
где /(г) обозначает потенциал единичного заряда, находящегося
в начале координат. Этот метод позволяет нам вычислять поле и
емкость сферического конденсатора, пластинами которого явля-
ются два концентрических заряженных проводника (рис. 16.7).
Рис. 16.7
Давайте опять поместим заряд Q в начало координат, а затем
окружим его двумя сферическими проводниками. Заряды собе-
рутся на внутренних и внешних поверхностях проводящих сфер.
Разрядим внутреннюю поверхность внутренней сферы, соединив
ее проводом с началом координат. А внешнюю поверхность внеш-
ней сферы разрядим, заземлив ее. Поля внутри и вне обеих сфер
обратятся в нуль. Функция и между двумя сферами остается без
изменения, при этом остается заряд Q на внешней поверхности
внутренней сферы и заряд — Q на внутренней поверхности внеш-
ней сферы.
834
Глава 16. Электростатика в пространстве R3
Рассмотрим еще один пример. Предположим, что заряд Q
/-Л /1\
помещен в точку О I на оси т, а заряд — Q в точку О I. Тогда
\ °/ \°/
получится потенциал
Q(/(r+) -/(г_)),
где Г- и г+ обозначают расстояния до этих двух точек. При
условии инвариантности относительно евклидовых преобразова-
ний /(г) — с/г. Эквипотенциальные поверхности в этой ситуации
изображены на рис. 16.8.
Вдоль одной из эквипотенциальных поверхностей вставим
проводящий слой. Поле с одной стороны этого проводника убира-
ем, соединив его с зарядом —Q. Тогда мы получаем поле, созда-
ваемое точечным зарядом Q и оставшейся заряженной поверх-
ностью вставленного проводника (рис. 16.9). Например, если в
качестве проводящей поверхности мы возьмем плоскость х = 0 с
нулевым потенциалом (рис. 16.10), то получим решение для за-
дачи с точечным зарядом в присутствии заземленного плоского
проводника. На поверхности проводника, обращенной к заряду
Q, индуцируется заряд —Q. Поле с другой стороны проводника
обращается в нуль, а поле со стороны заряда будет таким же, как
если бы на другой стороне проводника (в симметричной точке)
16.4. Напряженность поля и электрическое смещение 835
находился заряд — Q. Это один из примеров применения метода
образов.
И наконец, еще один пример, который мы используем позд-
нее. Рассмотрим сферу радиуса R. Заряд Q поместим в точку
(х\
О I. Пусть х' таково, что xxf = 7?2. Из подобных треугольников
°/
(рис. 16.11) следует, что для любой точки на поверхности сферы
х1 R 17?
— — — или — — —.
Г/ Т* Т* / /у»*
X 1 X ' X 1 X
836
Глава 16. Электростатика в пространстве R3
/х'\
Поместив заряд —Q(R/x) в точку I 0 ], мы получаем, что
\°/
потенциал на сфере равен нулю. Это позволяет вычислить потен-
циал для точечного заряда, находящегося в любой точке внутри
заземленной проводящей сферы.
16.5. Диэлектрическая проницаемость
Рассмотрим задачу нахождения электростатического аналога
отображения из (71 в Ci, определяемого матрицей емкостей, т. е.
отображения Q = CV.
Вспоминаем, что матрица С диагональна, если в качестве ба-
зиса взяты ветви. Другими словами, вклад распределения заря-
дов в распределение напряжений в любой ветви локализован на
этой ветви. Примем аналогичную гипотезу в электростатике: мы
хотим получить такое линейное отображение Е £), чтобы в
любой точке значение D зависело от значения Е в этой же точке.
Другими словами, если
Е = Exdx + Eydy + Ez dz
и
D = Dx dy A dz + Dy dz A dx + Dz dx A dy
(где коэффициенты Ex,.. ->DZ являются функциями), то соотно-
шение между Е и D определяется матрицей из функций
е = (е0).
Тогда
Dx — ецЕх + е^Еу +
Dy — £21Ex + £22Еу + €2з£Д
Dz = £31Ex + £32Еу + еззЕг-
Каждый матричный элемент Sij является функцией, и матрица
е = feij) определяет диэлектрическую проницаемость среды.
Связь между D и Е можно записать в форме
D = еЕ.
16.5. Звездный оператор в трехмерном пространстве 837
Теперь электростатические уравнения принимают вид
Е = —du, dD = —47rpdx Л dy Adz
и
D = eE.
Можно собрать эти уравнения вместе, введя оператор Лапласа
(Ди) dz A dy Adz = —де du
и получить уравнение Пуассона
Аи — —4тгр.
Чтобы продвинуться дальше, надо иметь больше информации
относительно е.
Для произвольной среды мы знаем только, что е — симмет-
ричная матрица. Причины те же, что и для матрицы С. Больше
ничего сказать нельзя. Существуют, например, кристаллы под
давлением, для которых е — переменная симметричная матрица.
Среда называется однородной, если е инвариантна относи-
тельно трансляций, и в этом случае она постоянна. Среда назы-
вается изотропной, если соотношение между Е и D инвариант-
но относительно вращений. Далее мы рассмотрим однородные и
изотропные среды и посмотрим, как выглядит е в этих случаях.
16.6. Звездный оператор в трехмерном
евклидовом пространстве
Начнем с линейного отображения
* : Л1^3*) —► Л2(К*3),
которое инвариантно относительно вращений. По определению
*dx = dy A dz,
*dy = dz A dx,
*dz — dx A dy.
838
Глава 16. Электростатика в пространстве R3
Далее нужно продолжить оператор по линейности, т. е. опреде-
лить * : AX(R3*) —» A2(R*3) правилом
★ (a dx + b dy + с dz) = a dy Л dz + b dz Л dx + cdx Л dy.
Пусть
ш — a dx + b dy + с dz
и
ст = Adx + В dy Сdz.
Заметим, что
Л а = (аЛ + ЬВ + сС) dx Ady Л dz.
Последнее уравнение запишем по-другому. Скалярное произведе-
ние в евклидовом пространстве R3 определяет скалярное произ-
ведение в R3* (в пространстве 1-форм) согласно формуле
(си, ст) = аА + ЬВ + сС.
Скалярное произведение с учетом ориентации выделяет кон-
кретную форму объема dx Л dy Л dz. Тогда последнее уравнение
принимает вид
Л ст — (си,ст) dx Ady Л dz. (16.5)
Если немного подумать, то становится понятным, что это уравне-
ние определяет отображение * единственным образом. Однако,
справа в уравнении содержится только скалярное произведение
и учитывается ориентация (как функция си и а). Любое вращение
сохраняет и то, и другое. Следовательно,
Оператор ★ инвариантен относительно вращений.
Утверждается, что с точностью до скалярного множителя *
является единственным отображением ★ : AX(R3*) —> A2(R*3), ин-
вариантным относительно вращений. Таким образом, мы утвер-
ждаем, что если г : A1(R3*) —> A2(R*3) — другое отображение,
инвариантное относительно вращений, то г = а* для некоторо-
го скаляра а. Сначала отметим, что либо г = 0, либо г имеет
16.6. Звездный оператор в трехмерном пространстве 839
нулевое ядро. Действительно, ядро г является подпространством
R3. Если г инвариантно относительно вращений, то это подпро-
странство тоже должно быть инвариантно относительно враще-
ний. Но в пространстве R3 нет подпространств, инвариантных
относительно вращений, кроме тривиальных подпространств {0}
и R3. Таким образом, или г = 0, или г является изоморфизмом.
Если г = 0, то доказывать нечего. Если же г — изоморфизм, то
рассмотрим отображение
I = г"1*, I : R3* R3*.
Согласно предположению, I инвариантно относительно враще-
ний, т. е.
l(Rev) = Rl(ev)
для любого вращения R. Запишем
lev — aev Т Lev,
где Lev перпендикулярно ev. Другими словами, разложим lev на
компоненты вдоль и перпендикулярно cv. В силу вращательной
инвариантности коэффициент а определяется формулой
(lev,ev) =
и не зависит от ev. Утверждается, что Lev = 0. Действительно, для
любого вращения R мы должны иметь LRev — RLev. Выберем по-
ворот R, который оставляет на месте ev, но является нетривиаль-
ным вращением в перпендикулярной ev плоскости. Тогда Rev = ev,
но RLev ф Lev, если Lev / 0. Значит, Lev — 0. Тогда
lev — aev, или rev — a*ev,
что и требовалось доказать.
Таким образом, с точностью до скалярного множителя ★ —
это единственное отображение из AX(R3*) в A2(R3*), инвариант-
ное относительно вращений.
(Стоит отметить и обратное утверждение. Оператор * одно-
значно определяет скалярное произведение (*,•), стоящее в пра-
вой части уравнения (16.5), следовательно, оператор * в прост-
ранстве R3* определяет скалярное произведение и ориентацию.)
840
Глава 16. Электростатика в пространстве R3
Пусть
cu = a dx + b dy + с dz
— дифференциальная форма, т.е. мы считаем, что ^дис-
функции. Как и раньше, определим оператор ★ формулой
★cu — a dy Л dz + b dz Л dx + с dx Л dy.
Опять
★си Л г = (си, т) dx Л dy Л dz,
где си и т — дифференциальные формы.
Мы предположили, что работаем в однородной и изотропной
среде. Это значит, что
£ = £★,
где е — константа, называемая диэлектрической постоянной сре-
ды. Например, в вакууме е ~ где £о ~ константа. И обратно,
поскольку оператор * из AX(R3) в A2(R3) детерминирует скаляр-
ное произведение, мы можем сказать, что диэлектрические свой-
ства вакуума определяют евклидову геометрию пространства.
В дальнейшем мы предполагаем, что единицы измерения Е,
D и е таковы, что s поглощается оператором ★ . Тогда уравнения
электростатики принимают вид
Е = —du, D — *Е, dD — 47vpdx /\dy Л dz,
откуда
Au = “4тгр,
где непосредственное вычисление показывает, что
д2и д2и д2и
U дх2 ду2 + dz2 ’
Важно заметить, что оператор * не инвариантен относитель-
но дифференцируемых отображений. Поэтому, вообще говоря,
мы не имеем равенства
= ★<£*(си).
16.6. Звездный оператор в трехмерном пространстве
841
Равенство будет только в случае, если ф является сохраняющим
ориентацию евклидовым преобразованием. Тем не менее, мы мо-
жем вычислять оператор * в более общей системе координат, ис-
пользуя его определение. Например, мы хотим вычислить опера-
тор * в сферических координатах, определяемых формулами
г = у/х2 + у2 + г2, 0 = arctan (д/х2 + у2/z), ф = arctan (у/ж).
Вычислим дифференциалы от этих функций и запишем их в
базисе dx, dy, dz, а координаты для удобства выразим через г, 0
и ф. Тогда получим
dr = sin в cos фdx + sin 0 sin фdy + cos в dz,
d0 = - (cos в cos фdx + cos в sin фdy — sin в dz),
r
.— (— sinфс1х + cos фdy),
rsmtf
Прямое вычисление с использованием ортонормированности dx,
dy, dz показывает, что в каждой точке (г, 0, ф) пространства R3*
dr, d0 и dф являются ортогональными элементами, и что
(dr,dr) = 1, (d0,d0) — Дт, (d</>,dф) — 9
г2 г2 snr О
Чтобы подвести итоги этих вычислений, заметим, что dr,
rdO, г sin 0dф образуют ортонормированный базис пространства
A1(R3), следовательно, эти три дифференциала можно вычис-
лять так же, как мы это делали с dx, dy и dz. В результате полу-
чаем
★ dr = г2 sin в dO Л dф,
★ (г d0) = ~r sin 0 dr Л dф,
★ (г sin 0 dф) = г dr Л d0.
Воспользовавшись линейностью, мы можем затем вычислить *d0
или ★ dф.
842
Глава 16. Электростатика в пространстве R3
16.7. Формулы Грина
В этом параграфе мы распространим формулы Грина, выведен-
ные в главе 13, на непрерывный случай. Пусть U обозначает огра-
ниченную область в пространстве R3 с границей dU, и две линей-
ные дифференциальные формы
Е ~ Exdx + Eydy + Ezdz и F = Fx dx + Fy dy + Fz dz
определены в U. Их скалярное произведение (Е, F)u вычисляется
по формуле
(E,F)u = [ EMF= f (ExFx+EyFy+EzFz)dxdydz = (F,E)u.
Ju Ju
Соответствующая электростатическая энергия равна
где 2
||Я||а = (Е, Е)и = JjE2 + E2y + Е2) dx dy dz.
Предположим, что
Е — —du и F — —dv,
где и и v — гладкие функции. Тогда
d(u*dv) — du Л * dv + ud*dv
— du A *dv + wA v dx A dy A dz
или
du A — d(u*dv) — (uAt?) dx /\dy A dz.
Соответственно
(du, dv)y = / du/\*dv~ / d(u*dv) — / vAv dx A dy A dz
Ju Ju Ju
и тогда
(16.6)
16.7. Формулы Грина
843
Это первая формула Грина. Поскольку (E,F)u = (F,E)u, в пер-
вой формуле Грина и и v можно переставить, а потом из одной
формулы вычесть другую. Тогда получим
(16-7)
Это вторая формула Грина. Пусть точка Р лежит в области 77, и
дан маленький шарик В£ с радиусом е и с центром в Р, который
целиком находится в области U (рис. 16.12). Применим вторую
формулу Грина к области 17, из которой вынут шарик В£. Грани-
ца этой области будет состоять из dU и дВ£. с противоположной
ориентацией. Возьмем
v — Гр\
тогда
dr
dv = —*dv = —тр
г2р
и
Av = 0 для U — В£.
На поверхности дВ£ функция v принимает постоянное значение
е"1. Тогда мы получаем
*du
игр Н----
Гр
I игр + 8 1 /
дВе JdB(
Г Aw _ _ _
/ ---dx f\dy Л dz.
и—ве rP
844
Глава 16. Электростатика в пространстве R3
Согласно теореме Стокса,
так что этот интеграл порядка е3. Следовательно, третий член
слева стремится к нулю как О(е2). Предполагается, что функция
и дифференцируема, и поэтому и(х) = iz(P) + О(е) на границе
дВ£. Тогда мы можем заменить
игр
с погрешностью порядка О(е). Однако
I тр = 4%,
JdB£
т. е. равен площади сферы единичного радиуса. Устремив е —> О,
мы получаем
/1->\ 1 f / *du\ 1 f Аи . , , /.z.
и(Р) = — ( игр 4---) - — / ------dxdydz. (16.8)
4?г JdU V гр / 4тг Jv гр
16.8. Гармонические функции
Функция и называется гармонической, если Д?х = 0. Для гармо-
нических функций последний член в уравнении (16.8) обращается
в нуль и мы имеем
(16.9)
Это показывает, что гармоническая функция и внутри области
определяется ее значением и значениями ее производных на гра-
нице. На самом деле мы докажем, что функция и определяется
только своими значениями на границе dU. Давайте применим по-
лученную формулу к шарику W с центром в точке Р (лежащим
внутри U, см. рис. 16.13):
/1 f f ★du
= итр+ —.
47Г JdW JdW rP
16.8. Гармонические функции
845
Величина гр постоянна на 9W, и по теореме Стокса
/ *du = / d*du ~ 0, поскольку Aiz = 0.
JdW Jw
Тогда
u(P) = [ игр. (16.10)
47г JdW
Выражение справа — это просто среднее значение и по сфере dW.
Итак, мы доказали следующее.
Если и — гармоническая функция в некоторой облас-
ти, то значение и в любой точке равно ее среднему
значению по любой сфере с центром в этой точке,
внутренняя область которой целиком находится внут-
ри области.
Отсюда можно получить несколько интересных следствий.
Предположим, что вокруг точки Xq имеется окрестность Z, та-
кая, что
u(x) < и(х0) во всех точках внутри Z.
Пусть Sa — сфера с радиусом а, целиком лежащая в области
Z и имеющая центр в точке xq. Тогда ц(х) < 'и(хо) во всех
точках Sa- А среднее значение и по сфере Sa меньше или равно
и(хо). Предположим теперь, что есть некоторая точка у из Sa,
где и(у) < 'u(xo). Тогда u(x) < и(хо) во всех точках х вблизи у,
и поэтому среднее от и по сфере Sa будет строго меньше и(хо).
Но это невозможно. Тогда
и(у) = 'u(xq) во всех точках сферы Sa-
846
Глава 16. Электростатика в пространстве R3
Теперь предположим, что W — открытое и связное множест-
во, т. е. допустим, что любые две точки области W могут быть
соединены непрерывной кривой, целиком лежащей в W. Допу-
стим также, что функция и достигает своего максимума в неко-
торой точке хо G W. Пусть у — любая другая точка W и пусть
С — кривая, соединяющая точки хо и у. Вокруг каждой точки х
на кривой мы можем построить достаточно малый шарик с цен-
тром в точке х, целиком лежащий в ИЛ В силу компактности С
мы можем выбрать конечное число таких шариков, покрываю-
щих С. Теперь можно утверждать следующее. Имеется конечное
число сфер Sai,..., Sak таких, что внутренняя часть всех сфер
лежит целиком в W. Сфера Sai имеет центр в точке хо, центр хг
сферы Sai+1 лежит в§йрау Е 8ак (см. рис. 16.14). Но это значит,
что ti(xo) — u(xi) = ••• = u(xfc) = 'u(y). Другими словами, мы
установили следующее.
Пусть и — гармоническая функция в открытом связ-
ном множестве W. Предположим, что она достигает
максимума в некоторой точке xq G W. Тогда и посто-
янна на множестве ИЛ
Отсюда непосредственно следует вывод3.
Называемый (в том числе далее в этой главе) принципом максимума
для гармонических функций. Вышедоказанная теорема о среднем и соответ-
ственно принцип максимума справедливы для гармонических функций не
только в R3, но и в пространстве Rn любой размерности п > 2. — Прим. ред.
16.8. Гармонические функции
847
Пусть U — открытое связное множество и пусть U обо-
значает его замыкание, так что U = U U dU, где dU
обозначает границу U. Предположим, что U ограни-
чено. Тогда если и — функция, гармоническая в U и
непрерывная на J7, то либо
u(x) < maxy€0[7u(y) для любого х Е Г,
либо и постоянна.
Доказательство. Поскольку U замкнуто и ограничено, то оно
компактно. Функция и непрерывна на U. Теорема из веществен-
ного анализа говорит, что и должна достигать своего максимума
в некоторой точке хо множества U. Если одной из таких точек
будет Xq Е U, то из наших предыдущих результатов следует, что
и постоянна. Если же и не постоянна, то хо 6 dU, и мы доказали
наше предположение.
Отсюда можно получить еще один результат.
Пусть U открытое связное множество, а его замы-
кание U компактно. Пусть и и и - функции, непре-
рывные на U и гармонические в U. Допустим, что
u(y) = v(y) для всех у Е dU.
Тогда
w(x) — v(x) для всех х Е U.
Доказательство. Функция и — v гармоническая и обращает-
ся в нуль на границе dU. В силу предыдущего принципа и(х) —
г(х) < 0 для х Е U. Аналогично, v(x) — u(x) < 0, что и требова-
лось доказать.
Другая формулировка последнего предложения: в области U
гармоническая функция полностью определяется своими значе-
ниями на границе. В этом состоит теорема единственности:
существует только одна гармоническая функция, определяемая
своими граничными значениями. При этом возникает проблема:
верна ли соответствующая теорема существования? Эта пробле-
ма известна как задача Дирихле.
848 Глава 16. Электростатика в пространстве R3
16.9. Метод ортогональной проекции
Давайте рассмотрим другое доказательство единственности ре-
шения задачи Дирихле для ограниченной области U. Воспользу-
емся первой формулой Грина (16.6)
(du,dv)y — / u*dv — / u^vdx Л dy Л dz.
JdV Ju
Пусть C° обозначает пространство всех дифференцируемых
функций на 17, а — его подпространство, состоящее из
функций, тождественно равных нулю на границе dU. Пусть Н
обозначает пространство гармонических функций v в области U,
которые непрерывны на U и удовлетворяют уравнению Дг = 0 в
области 17. Тогда, если и € С^нутр, то поскольку и — 0 на границе
dU, мы имеем
I u*dv = 0 для любой гладкой функции и.
JdU
Если v е Н, то пДг = 0 для любой функции и. Тогда если и Е
С^нутр и v е Н, то (du, dv)u = 0. Другими словами, пространства
^внутр и dH ортогональны относительно (•,•)[/. В частности,
предположим, что и — гармоническая функция, обращающаяся
в нуль на границе. Тогда
(du, du)u = 0.
Однако
(du, du) и
dx /\dy Л dz.
Это выражение обращается в нуль только при условии, что все
частные производные и равны нулю в области U. Но тогда и
должна быть постоянной, и поскольку и = 0 на границе dU, то
и = 0. Таким образом, гармоническая функция, которая равна
нулю на границе dU, дрлжна быть равна нулю везде. Как и рань-
ше, это доказывает единственность решения задачи Дирихле.
16.9. Метод ортогональной проекции
849
Пространства dC°, dH и так далее являются бесконечно-
мерными векторными пространствами. В этой книге мы не зани-
мались такими пространствами или проекционными операторами
тг в таких пространствах. Эта теория может быть разработана и,
следуя Герману Вейлю, может быть доказан следующий принцип.
Пространство dH является ортогональным дополне-
нием dCgHyTp к dCQ.
Или другими словами, если Е — dv и (£J, du) = 0 для всех
и е С°ну1,р, то = 0 в области U. Поэтому, взяв любую функцию
мы можем разложить в сумму
dip = du + dv, где и € С^нутр и v € Н.
Другими словами, du = тг d'lp, где тг обозначает проекцию на
компоненту dCgHyTp, и dv = (1 — ir)dip. Теперь можно решить
задачу Дирихле’, для данной гладкой функции ф, определенной
на dU, найти такую функцию v, чтобы выполнялось уравнение
Av — 0 и v — ф на границе dU.
Решение. Выберем произвольную функцию ф, которая совпа-
дает с ф на границе dU и определена во всей области U. Разложим
дф на слагаемые, как это показано выше. Тогда поскольку и об-
ращается в нуль на границе dU, мы знаем, что v совпадает с ф
на границе dU и, следовательно, является искомым решением.
Заметим, что поскольку (du,dv)u = 0, то
\№\\и = + IHltn
откуда следует, что
№\\Ь > \\dv\\b.
Таким образом, среди всех функций, значения которых совпа-
дают с ф на границе, решение задачи Дирихле v может харак-
теризоваться как функция с наименьшим значением ||dv||^. Это
так называемый принцип Дирихле. Если считать, что —
энергия электрического поля, то принцип Дирихле говорит, что
решением задачи Дирихле является такая функция V, у которой
dv дает минимальную энергию, при условии, что на границе dU
выполняется равенство v = ф.
850
Глава 16. Электростатика в пространстве R3
Мы не доказываем здесь, что решение задачи Дирихле су-
ществует для произвольных областей (доказательство можно
найти в главе 12 книги Loomis and Sternberg). Тем не менее,
мы покажем, как решается эта задача для областей определен-
ного типа. Кроме того, мы выведем некоторые общие принципы
электростатики.
16.10. Функции Грина
Предположим, что в области U задача Дирихле может быть ре-
шена. Здесь мы получим для этой области U аналог той функции
Грина, которая обсуждалась в главе 13 в дискретном случае.
Для любой точки х в пространстве R3 положим
К(х,у) = 4тг ||х — у|| ’
Рассматривая К как функцию у (при фиксированном х), мы
имеем
★dK(x, •) = —тх.
47Г
Формулу (16.8) из параграфа 16.7 мы можем переписать через К
в виде
н(х) — f + K(x.,-)*du) — f K(x,')/±udV.
Jdu Ju
Теперь для заданного x G U функция K(x, у) является диффе-
ренцируемой функцией у, когда у изменяется вдоль границы dU.
По предположению мы можем найти такую функцию Л(х, •), гар-
моническую в области U и непрерывную на J7, чтобы выполня-
лось условие
/г(х, у) = — К(х,у) для всех у G dU.
Далее, для фиксированного значения у функция Л(х, у) является
непрерывной функцией х. В соответствии с принципом максиму-
ма гармоническая функция /i(xi,y) — Л(х2,у) достигает своего
максимального значения на границе dU. Следовательно,
|fr(xi,y) - Л(х2,у)| < max |K(xi,z) - jK(x2,z)|.
zedU
16.10. Функции Грина
851
Также очевидно, что К(х, z) равномерно непрерывна по х для
всех z € dU, пока х находится на ограниченном снизу расстоянии
от dU. Итак, мы построили такую функцию hu, для которой
выполняются следующие условия:
(i) функция hu(x., у) непрерывна по х и у для х, у е U и
дифференцируема по у в области 17;
(ii) для каждого фиксированного значения х выполняется урав-
нение Ду/гсг = 0, т. е. Д/г{/(х, •) — 0;
(iii) G(/(x,y) = /С(х,у) + fy/(x,y) = 0 для у € dU.
Функция Gu называется функцией Грина области U. Пред-
положим, что Gu существует, и давайте выясним ее свойства. В
дальнейшем мы будем писать G вместо Gu, если ясно, о какой
области U идет речь. Сначала покажем, что для х € U и у € U
выполняется условие
G(x,y) = G(y,x).
Пусть BXj£ и Ву?е обозначают маленькие шарики вокруг точек
х и у. Применим вторую формулу Грина к функциям и — G(x, •)
и v = G(y, •), заменив область U на U — Вх>£ — Ву£. Поскольку
обе функции гармонические в рассматриваемой области и обра-
щаются в нуль на границе dU, мы получаем
[ G(x, -)*dG(y, •) + [ G(x, -)*dG(y, •)
*7 OBjQ,e *
= [ G(y, •)*dG(x, ) + [ G(y,-)*dG(x, •).
*7dBxte *7 dB-y^e
Теперь покажем, что при е —> 0 левая часть равенства стре-
мится к G(x,y), а правая — к G(y,x). В силу симметрии доста-
точно установить это для левой части.
Запишем
[ G(x,-)*dG(y, ) = [ G(x,-)*d7<(y, •)+ [ G(-x.,-)*dh.
JdByi£ JdByi£ JdBy>£
852
Глава 16. Электростатика в пространстве R3
Первый член справа стремится к G(x, у), как и в параграфе 16.6,
поскольку 4тг*сУ< — это телесный угол из точки у. Второй член
стремится к нулю, потому что G(x, •) и h — гладкие функции в
области Ву,£. С другой стороны,
/ G(x,.)*dG(y,.)
J дВх>£
= f К(х,-)*dG(y, •) + f h(x,-)*dG(y,-).
J дВх,£ J
Так же, как и выше, второй член стремится к нулю. Первый член
можно переписать в виде
Т/ *dG(y,-) = ±l d*dG(y,-)=0,
47Г JdBx>£ 47Г
поскольку G(y, •) — гармоническая функция в области Вх,£. Итак,
мы доказали, что G(x,y) = G(y,x).
Пусть и обозначает любую гладкую функцию в области U.
Применим вторую формулу Грина к и и v = G(x, •) в области
U — В^ £. Поскольку G(x, •) = 0 на границе 5/7, мы получим
/ u*dG(x, •) — / u*dG(x, •) + / G(x, -)*du
JdU JdBX£ JdB^e
= [ G(x, ^Audx1 Л • • • /\dxn.
Ju
Третий интеграл слева можно записать в виде
/ К(х, -)*du + / Л(х, -)*du
JdBXj£ JdBXi£
— ~Г— [ *du+ [ Л(х, -)*du — G(s2) + O(s2).
4теЛвх,е JdBx,£
Следовательно, он стремится к нулю. Тогда мы получим
'u(x) = / G(x, ^Audx1 Л • • • Л dxn + / ?/*dG(x, •).
Ju JdU
16.11. Интегральная формула Пуассона
853
Это уравнение показывает, что если мы знаем, что сущест-
вует решение задачи Пуассона AF — / с условием F = 0 на
границе, то оно имеет вид
Г(х) = J G(x,y)f(y)dy.
(16.11)
Аналогично, если мы знаем, что существует гладкое решение
задачи Дирихле
Ди = 0, и(х) = /(х) для х G dU,
то оно имеет вид
(16.12)
16.11. Интегральная формула Пуассона
Важно отметить, что эти формулы являются следствием суще-
ствования функции Грина для U, т.е. они справедливы во всех
случаях, когда мы можем найти такую функцию h, что (ii) и
(iii) выполняются. В качестве примера мы можем в явном виде
построить функцию Грина для шара В/? с радиусом R. Для про-
стоты предположим, что начало координат находится в центре
шара.
Пусть для х 0 точка х' обозначает ее образ при инверсии
по отношению к сфере радиуса R, т. е.
х' = т—ппХ (см. рис. 16.11).
Определим функцию Gr формулой
4тгСд(х,у) = <
R
INI ||у - х'||’
1|У|| Я’
если х О,
если х = 0.
854
Глава 16. Электростатика в пространстве R3
Если х 6 В#, то xz 6 Br и поэтому вторые слагаемые в правой
части формулы являются непрерывными и гармоническими в
Вд. Нам надо просто проверить выполнение свойства (iii). Для
||у|| — R из подобных треугольников (или прямым вычислением)
мы имеем
Д .. Цу-х'||
М ||у- х||’
следовательно,
GR(x,y) = 0 для ||у|| = R.
А это и есть свойство (iii). Итак мы проверили, что Сд является
функцией Грина для шара с радиусом R.
Чтобы применить нашу формулу к решению задачи Дирихле
с помощью функции Грина, мы должны вычислить *(1Gr на
сфере радиуса R. Имеем
R
4ir*dGR(x, •) = тх - jj—-тх/
НХН
yi-xi
Цу-х||3
R уг — хг ,
йлГн„ „/из*<*У •
Но
INI ||у _Х'||3 Д2||у-Х||3’
Итак, мы видим, что для ||у|| — R
если ||у || = R.
4тг*</б!я = -——jig V ( уг
Пу — ХП3 \
Д2 — ||х||2
||у - х||37?2
_ R2 - ||х||2
Ву-хряг*г*-
- х'
1Х1|2 г Д2 Л j 1
~ мН ”iy
Если мы подставим в наше решение задачи Дирихле
u(x)= f
JdU
u{y)-kdG(x,y),
R
Л
16.11. Интегральная формула Пуассона
855
то получим
4™(x) = ZBF^F&“(y)*r‘,r'
Однако на сфере радиуса R форма *rdr просто равна RcISr, где
(ISr — элемент площади сферы радиуса R, Подставив это в по-
следнюю формулу, получаем интегральную формулу Пуассона:
R2 - ||х||2 Г и(у)
и(х) =——-— / 7:----------(16.13)
4тгЯ JSr ||у - х||3
При выводе формулы (16.13) мы воспользовались предполо-
жением, что функция и дифференцируема в некоторой окрест-
ности шара Br, и что она гармоническая для ||х]| < R. На самом
деле нам было достаточно предположить, что и ~ дифферен-
цируемая и гармоническая при ||х|| < R и что она непрерывна
на замкнутом шаре ||х|| < Д. По существу, формула (16.13) для
любого ||х|| < R останется верной, если заменить R на Да, где
х < R& < Д. Если затем Да устремить к Д, то формула (16.13)
восстанавливается в первоначальном виде в силу предположения
о непрерывности функции и.
Формула (16.13) дает решение задачи Дирихле для шара при
условии, что мы знаем, что такое решение существует, т. е. ес-
ли и — произвольная гармоническая функция на открытом шаре
и непрерывная на замкнутом, то она удовлетворяет уравнению
(16.13). А сейчас покажем, что (16.13) действительно является
решением задачи Дирихле для заданных граничных значений.
Предположим, что нам дана непрерывная функция и, опреде-
ленная на сфере Sr. Тогда нам дана и(у) для всех у е Sr. Пусть
уравнение (16.13) определяет ц(х) для ||х|| < Д. Мы должны по-
казать, что
(а) и гармоническая в области ||х|| < Д,
(Ь) и(х) и(у0), если х —> у0 и ||у||0 = Д.
Чтобы доказать (а), заметим, что G/?(x, у) — дифференциру-
емая функция х и у в области ||х|| < Д1 < Д, Д1 < ||у|| < Д2/Д1.
856
Глава 16. Электростатика в пространстве R3
Кроме того, по построению она — гармоническая функция от у.
Для ||х|| < R и ||у|| < R мы знаем, что
G/?(x,y) = Gj?(y,x).
Тогда для фиксированного у, при условии ||у|| < Д, функция
С?н(-,у) гармоническая в области Br — {у}. Устремив ||у|| —>
В, мы видим, что Gr(x, у) — гармоническая функция х для
||х|| < Д1 < R и любого фиксированного у е Sr. Таким об-
разом, <9G#(x, у)/5уг — гармоническая функция х для любого
у € Sr. Другими словами, все коэффициенты *</Ст?(-,у) явля-
ются гармоническими функциями х для каждого у 6 Sr. Это же
можно сказать и о всех коэффициентах 7/(y)*dG/?(-,y). Следо-
вательно, функция 'u(x) = fs u*cIGr(x., •) является гармониче-
ской функцией х, поскольку интеграл сходится равномерно при
||х|| < Ri < R (так же, как и все интегралы от различных произ-
водных по х). Это доказывает (а).
Для доказательства (Ь) сначала отметим, что тождественная
единица является гармонической функцией везде, поэтому к ней
применимо уравнение (16.13). Тогда получаем
R л [ и ^„3 = 1 для любого ||х|| < R. (16.14)
47T-R JsR Ну - х||3
Пусть уо обозначает точку на сфере Sr и пусть и — непрерывная
функция на этой сфере. Для любого е > О мы можем найти такое
6 > 0, что
|«(у) - «(уо)| < Е при ||у-уо|| < 2<5, yeSR.
Пусть
Z1 = {у G Sr : ||у-уо|| > 2<5} и Z2 = {у G Sr : ||у-уо|| < 2<5}.
Тогда в силу (16.13) и (16.14) для ||х|| < R мы имеем
.lM 1 R2 ~ 11ХИ2 [ ~ и(уо>> НЯ
»(Х) - «(Уо) = JSr ||у_х||з МЯ.
Поэтому
|и(х) - и(уо)| < J1 +12,
16.11. Интегральная формула Пуассона
857
где R2 - ||х||2 Г |ц(у) -ц(уо)| ,q 11 = Л.-Лу-хЦЗ dS“
и R2 - ||х||2 г Му) -м(Уо)| 12 = 4х/г /га -||у-х||з
Если ||уо — х|| < 6, то для всех у € Zi мы имеем ||у — х|| >
Ну — Уо|| - IIх - Уо1Ь так что ||у - х|| > 6. Итак, для всех х,
удовлетворяющих условию ||х—уо|| < интеграл в Д равномерно
ограничен. Поскольку ||х|| —> R при х —* уо, мы приходим к
выводу, что 11 —> 0 при х —> уо*
Займемся теперь I2- Мы знаем, что |и(у) — и(уо)| < в для всех
у G Z2, так что
Д2 - ||Х||2 Г edSR = Д2 - ||х||2 Г dSR
**R Jz2 Ну - х||3 £ JSr ||у - х||3
в силу (16.14). Таким образом, мы доказали (Ь).
Итак, доказана
Теорема. Пусть и — непрерывная функция, определенная на
сфере Sr. Существует единственная непрерывная на ограни-
ченном ею шаре ||х|| < R функция, которая совпадает с дан-
ной функцией на сфере Sr и является гармонической в области
||х|| < R и. Эта функция определяется для всех ||х|| < R урав-
нением (16.13).
Мы затратили изрядное количество усилий на подробное до-
казательство существования решения задачи Дирихле в простом
случае сферы. Детали доказательств для более сложных обла-
стей мы приводить не будем. Дадим только идею одного метода,
подробности которого при желании можно восстановить.
Давайте аппроксимируем евклидово пространство сетью. В
конце каждого вектора v, координаты которого являются дво-
ичными дробями со знаменателем 2N, поместим узел. Вектора v
имеют вид
где k,l,m — целые числа.
858
Глава 16. Электростатика в пространстве R3
Здесь 7V — фиксированное большое целое число. Каждый узел
соединим с шестью ближайшими соседями (рис. 16.15); тогда все
пространство разделится на кубические ячейки. Каждой ветви
присвоим емкость 2N, а через Д^у обозначим оператор Лапласа
для этой сети. Легко видеть, что для любой дважды дифферен-
цируемой функции и
—> Atz при N оо.
Если нам дана ограниченная область U с границей dU, то
можно рассмотреть конечную подсеть, состоящую из всех узлов
в области U и всех ветвей, соединяющих эти узлы. Узлы, распо-
ложенные ближе всего к границе, назовем граничными узлами.
Используя наши результаты для конечных цепей, мы можем ре-
шить задачу Дирихле для такого конечного приближения. Зада-
дим непрерывную функцию ф на границе dU. Можно приписать
значения фм на граничных узлах нашего конечного приближе-
ния, взяв (/>дг(п) = </>(х), где х — это ближайшая к узлу п точка на
границе. (Если таких ближайших точек несколько, то выбираем
одну из них.) Таким образом, непрерывную задачу Дирихле мы
аппроксимировали дискретной конечной задачей, которую умеем
решать. При N оо мы ожидаем, что последовательность ре-
шений Un будет сходиться к функции и (определенной для всех
двоично-рациоанльных векторов и продолженной по непрерыв-
ности), которая дает решение исходной задачи Дирихле. Этот
метод доказательства работает, если форма границы не слишком
«дикая». Само доказательство требует аккуратных оценок, что
находится за рамками этой книги.
Резюме
859
Резюме
А. Электростатика и дифференциальные формы
Вы должны уметь формулировать законы электростатики в тер-
минах дифференциальных форм D и Е.
Вы должны знать формулы Грина, уметь их доказывать и
применять в задачах электростатики в пространстве R3.
В. Звездный оператор в пространстве R3
Для данной дифференциальной формы w в пространстве R3, за-
писанной в координатах, дифференциалы которых взаимно ор-
тогональны, надо уметь строить ортогональный базис и с его по-
мощью строить
Вы должны уметь понимать связь между электростатикой в
пространстве R3 и теорией цепей с емкостями, а также уметь объ-
яснить, как звездный оператор играет ту же роль, что и матрица
емкостей.
Задачи
16.1 . Пусть D = то = (х dy Л dz 4- у dz Л dx 4- z dx Л dy)/r\ где г2 =
я2 4- у2 + z2. Эта формула дает электрическое смещение в слу-
чае единичного положительного заряда, находящегося в начале
координат.
(а) Вычислите D, где Ri —• диск z = zo, х2 4- у2 < а2.
(Ь) Вычислите , где R? — боковая поверхность цилиндра
2 2 2
-zq < z < zq, х* + у = а .
(с) Используя результаты (а) и (Ь), проверьте, что /Яз D =
4тг, где R% — цилиндр с боковой поверхностью R? и двумя
дисками Ri снизу и сверху.
16.2 . Дана 1-форма А = Ах dx 4- Ау dy 4- Az dz. Величины Ах, Ау и Az
являются функциями т, у, z. Используя линейный оператор ★,
удовлетворяющий условиям
* dx = dy Л dz,
*dy Adz — dx,
*1 = dx Ady Adz,
*dy — dz A dx,
*dz A dx — dy,
*dx A dy A dz = 1,
*dz = dx A dy,
*dx Ady = dz,
вычислите следующее:
860
Глава 16. Электростатика в пространстве R3
(a) *dA\
(b) 'kd'k А;
(с) 'kd'kdA\
(d) *d*df, где f(x, г/, г) — скалярное поле;
(е) *(А Л В), где А и В — 1-формы;
(f) *(А Л *В), где А и В — 1-формы.
16.3 . Сферические координаты г, 0 и ф определены формулами
х = г sin0cosф, у = 1$т0$тф, z — rcos0.
(а) Выразите dx, dy, dz, dy Л dz, dz A dx, dx A dy dx /\dy A dz
в сферических координатах (т. e. используя формулы заме-
ны координат, сделайте перенос этих дифференциальных
форм).
(Ь) Звездный оператор, определенный в упражнении 16.2, яв-
ляется линейным преобразованием, которое задано его дей-
ствием в базисе dx, dy, dz, dy /\dz, ... Вычислите этот опе-
ратор в сферических координатах, т. е. выразите *dr, *d0 и
★ dф через d0 А dф, dф A dr и dr Л d0. Выразите *(d0 А dф),
*(Иф Л dr) и *(dr A d0) через dr, d0, Нф.
(с) Выразите через сферические координаты 2-форму то из
упражнения 16.1 и покажите, что она равна *d(l/r).
16.4 . Если и обозначает электрический потенциал в пространстве R3,
то его лапласиан Ли можно записать в виде
Au dx f\dy /\dx — d*du.
(а) Считая, что u является функцией х, у и z, проверьте, что
д2и д2и д2и
Ли = + di? + дИ ’
(Ъ) Считая, что и является функцией г, 0 и ф, получите фор-
мулу для Aw через частные производные и по г, 0 и ф.
16.5 . Рассмотрите 2-форму D, которая в сферических координатах
имеет вид D = r3(l — г) sin0d0 Л dф (г < 1), D = 0 (г > 1).
(а) Проверьте, что если Е = r(l — r)dr для г < 1, то D =
(Заметим, что dr A *dr = dx A dy A dz.)
Задачи
861
(b) Найдите такую потенциальную функцию и. для которой
Е = —du. Вычислите dD (которая равна —dD). Проверьте,
что fD Е = — и, как это утверждается теоремой Стокса.
(Вспомните, что fDE = fR3 Е Л D.)
16.6 . Дифференциальная форма, представляющая D для единичного
положительного заряда, может быть выражена в сферических
координатах в виде т = sin OdO Л d(j).
(а) Вычислите fs т, где S — сфера х2 + у2 + z2 = 1.
(b) Покажите, что dr = 0.
(с) Используя теорему Стокса, объясните, почему не может
существовать 1-форма tu, определенная во всем простран-
стве R3, за исключением, может быть, начала координат,
для которой dw = т.
(d) Найдите 1-форму си, определенную первом октанте про-
странства R3 (где х > 0, у > 0, z > 0), для которой т = dw.
При этом для нахождения соответствующей си можно поль-
зоваться сферическими координатами, но потом выразите
си в декартовых координатах т, у, z.
16.7 . Пусть w(r, 0) — гладкая функция в пространстве R2 с компакт-
ным носителем. Вычислите
[ dubu, г№
JR2 X2 + У2
(Поскольку си не определена в начале координат, сначала надо
интегрировать по области вне диска с радиусом е и центром в
начале координат, а потом взять предел при £ —> 0.)
16.8 . Пусть ф обозначает поворот в пространстве R3, так что ф пред-
ставляется матрицей Л, для которой АЛ* = It и Det А = +1. Дана
1-форма cu = Fx dx + Fy dy + Fz dz. Докажите, что в этом случае
*(<£*cu) = 0*(*cu).
16.9 . Рассмотрите пять функций
V1 = г2, V2 = г2 cos2 0(= z2), V3 = г4, V4 = г4 cos2 0(— r2z2),
г»5 = г4 cos4 0(j= z4).
Они определяют пятимерное векторное пространство, которое
обозначим С°.
862
Глава 16. Электростатика в пространстве R3
(а) Для каждой из этих пяти функций вычислите dv, *dv и Ди.
(Ь) Вычислите все скалярные произведения типа (ctoi, dv2)u>
считая, что U — единичный шар г < 1.
(с) Найдите базис двумерного пространства Н подпростран-
ства С°, которое состоит из функций, удовлетворяющих
условию Дг = 0.
(d) Постройте матрицу I — тг, которая является ортогональной
проекцией dCQ на dH. Выпишите также матрицу тг.
(е) Используя матрицу Л — тг, найдите функцию и, удовлетво-
ряющую условию Дгх = 0 и равную cos4 0 + cos2 0 на сфере
т = 1. (Задача Дирихле.)
(f) С помощью тг найдите функцию ф, которая удовлетворяет
уравнению Д</> = 5г2 — 4г2 cos2 0 + 1 и обращается на еди-
ничной сфере в нуль. (Решение уравнения Пуассона.)
Глава 17
Токи, потоки и магнитостатика
В этой главе мы продолжаем изучение внешнего диф-
ференциального исчисления. Здесь рассматриваются
потоки и векторные поля, внутренние произведения и
производные Ли. Все это прилагается к задачам маг-
нитостатики.
17.1. Токи
На первый взгляд кажется, что можно сразу же дать непрерыв-
ный вариант описания цепей с сопротивлениями. Все, что на-
до сделать, — это лишь немного изменить то, что уже обсужда-
лось в предыдущей главе. Мы сохраняем форму Е и уравнение
Е — — du, но энергию заменяем мощностью. Электростатическую
2-форму D заменяем на 2-форму J, которая должна представ-
лять размазанный вариант токов, текущих по ветвям. У нас есть
спаривание между током J и электрическим полем Е:
У Е/\ J,
что измеряется в единицах мощности. Согласно первому закону
Кирхгофа, д! = 0. Поэтому соответствующий размазанный ва-
риант имеет вид
5J-0
или, поскольку д = —d,
dJ -0.
864
Глава 17. Токи, потоки и магнитостатика
Вместо соотношения D = е*Е для изотропной электростатиче-
ской среды мы имеем
J = &*Е,
где а называется проводимостью. Если мы теперь введем вели-
чину г = 1/<т, называемую удельным электрическим сопротив-
лением, то предыдущее уравнение принимает вид
Е = r^J,
что является размазанным вариантом закона Ома
V = RI.
Теперь надо остановиться и понять, что же представляет со-
бой форма J. Рассмотрим некоторую поверхность S. Что означа-
ет fs Л Пусть мы имеем конечную цепь, и поверхность пересе-
кает ветви а, /3 и 7, ориентация которых показана на рис. 17.1.
Тогда, принимая во внимание эти ориентации, можно считать,
что S определяет коцепь, приписывающую каждому току I чис-
ло 1а — 1/з +В общем случае S определяет коцепь, приписыва-
ющую каждому току I полный ток, протекающий через поверх-
ность S с учетом соответствующей ориентации. Таким образом,
в размазанном варианте можно считать, что J представляет
собой ток, протекающий через поверхность S.
Если мы представляем ток как движущиеся заряды, то js J
оказывается скоростью переноса зарядов через поверхность S.
Рис. 17.1
17.2. Потоки и векторные поля
865
Если S — замкнутая поверхность, т. е. S = dU, то мы имеем
[ J = [ dJ = Q.
Js Ju
Это значит, что полная скорость переноса заряда через поверх-
ность S равна нулю, и заряд внутри нее не накапливается, что
полностью согласуется с первым законом Кирхгофа, который мы
обсуждали раньше. Значит, все прекрасно работает.
Существует, однако, геометрическая интерпретация, которая
требует дополнительного объяснения. Мы знаем, что на самом де-
ле ток создается движущимися электронами. Каждый электрон,
будучи точечной частицей, движется вдоль некоторой кривой.
Тогда форма J, проинтегрированная1 * по поверхности S, на са-
мом деле считает число электронов, пересекающих поверхность
S (в любом направлении) в единицу времени. У нас должен быть
геометрический объект, непосредственно связанный с семейством
траекторий отдельных электронов, который описывает их движе-
ние и из которого мы можем восстановить 2-форму J. В дальней-
шем мы увидим, что таким объектом является векторное поле.
17.2. Потоки и векторные поля
В этом параграфе, чтобы избежать нагромождения индексов, мы
в основном будем работать в пространстве R3. Однако, тот факт,
что это пространство имеет три измерения, нам нигде не потре-
буется. Поэтому все выводы и формулы будут справедливы для
пространств любого числа измерений.
Пусть U обозначает открытую область в пространстве Rfe и
пусть I — некоторый интервал в R, содержащий начало коор-
динат. Кроме того, пусть ф : I х U —> Rfc — дифференцируемое
отображение. Момент времени будем обозначать t 6 I. Тогда мы
можем рассматривать ф двумя способами. Выберем точку р е U.
Тогда отображение
</>(•, р) : t -> </>(t,P)
1 Здесь имеется в виду абсолютный, или неориентированный, интеграл
(первого рода). Его значение неотрицательно. — Прим. ред.
866
Глава 17. Токи, потоки и магнитостатика
определяет кривую в Конечно, каждой точке р соответ-
ствует своя кривая. Рассмотрим касательный вектор ^(t, р) =
(d/cft)</>(f, р). С другой стороны, для каждого момента времени
t мы можем рассмотреть отображение фг : U —> заданное
формулой
= ф(ф,р).
Предположим, что
Фо = id,
т. е. что
</>(0,р) = Р
для всех точек р. Тогда для каждой точки р касательная </>z(0, р)
к кривой ф(-,р) является касательным вектором в этой точке р.
Итак, мы получили правило, согласно которому каждой точке
р в области U ставится в соответствие касательный вектор в
этой точке. Это правило называется векторным полем в области
U (рис. 17.2). Векторное поле будем обозначать £. Итак, £(р)
является касательным вектором в точке р.
Рис. 17.2
Для произвольной точки р предположение фо — id означа-
ет, что (1фо — id, т. е. d(0«)p несингулярна для достаточно ма-
лых значений t. По теореме о неявной функции оказывается
взаимно-однозначной функцией с дифференцируемой обратной в
некоторой окрестности точки р. Чтобы избежать нагромождения
обозначений, предположим, что фг : U —> имеет дифференци-
руемое обратное во всей области U. Выберем момент времени
17.2. Потоки и векторные поля
867
stl. Тогда определим
tl>t = Ф1 ° Ф71-
Тогда фч обладает всеми свойствами фг и при этом
Фэ = id.
Итак, для каждого момента времени s G I мы получаем вектор-
ное поле £s. Значит, мы показали, что при данном ф : I xU —>
получается однопараметрическое семейство векторных полей £s.
Для каждой точки р е U существует некоторая окрестность W
вокруг р и некоторая окрестность К вокруг 0, так что явля-
ется векторным полем, определенным в W,
Пример, (а) Зададим вектор w. Пусть </>(£, р) = р + tw. Тогда
<//(0,р) = w для всех р. Кроме того,
Ф^ФтЧр) = ^t(p-«w)
= р + (t - s)w
=
следовательно,
£s(p) = w для всех v и s.
(b) Пусть задана матрица А. Определим ф(фр) — etAp. Тогда
<Д0,р) = Ар.
Кроме того,
‘М'АгЧр) = ем(е"мр)
= е^~^Ар
= фц-8(р)
и, следовательно,
€8(р) = для всех s.
868
Глава 17. Токи, потоки и магнитостатика
В этом случае векторное поле каждой точке р ставит в соответ-
ствие вектор Ар.
Заметим, что в обоих примерах векторное поле не зависит
от s. Это является следствием тождества
&0 Ф71 = Ф^*
или, заменив s на —з, тождества
Ф1+з ~ Фъ ° Фз*
Отображение </>, удовлетворяющее этому тождеству всюду, где
определены обе части, называется (стационарным) потоком. В
случае ф^и) — U и I = R мы говорим об однопараметрической
группе преобразований области U.
Итак, для потоков мы получили фиксированное векторное
поле £ — для всех з.
Давайте сначала рассмотрим линейное векторное поле
£(р) = Ар,
где А ~~ заданная матрица. Тогда, опираясь на результаты гла-
вы 3, мы знаем, что можно построить etA и потом определить ф
по формуле
Ф(Ф, Р) = etAp.
Итак, мы получили теорему существования для обычных диф-
ференциальных уравнений. Начав с £, мы получили ф. Соответ-
ствующая теорема справедлива и в общем случае.
Пусть векторное поле £s зависит гладко от s е I и р G
U. Тогда для каждой точки р существует окрестность W Э
р в пространстве Rfc и окрестность К нуля в R такие, что
отображение ф : К х W —> Rfe, фо — id гладкое, а зависящие
от з векторные поля, определяемые ф, точно совпадают с £s.
Если же = £ (т. е. не зависит от з), то ф удовлетворяет
тождеству
фз+k = Фз ° </>£
всюду, где определены обе части.
17.2. Потоки и векторные поля
869
Доказать эту теорему несложно. Это делается методом после-
довательных приближений. Здесь мы не будем приводить это до-
казательство. Оно стандартно, и его можно найти в любом учеб-
нике по теории обыкновенных дифференциальных уравнений, в
частности, в главе 6 книги Loomis and Sternberg.
Предположим, что имеются векторное поле £ и дифферен-
цируемая функция /. В каждой точке р мы можем построить
производную по направлению: Тогда получается новая
функция, которая каждой точке р приписывает значение
Например, предположим, что в пространстве R3 имеется вектор-
ное поле
А(р)\
€(р) = ь(р) ,
\с(р)/
где а, b и с — функции. Тогда
£><(₽)/ = а(р)^(р) + ь(р)^(р) + c(pwp)-
Или, в сокращенном виде,
ох ду oz
Поэтому в дальнейшем мы будем писать
. д д д
< = а— + Ь— +с—.
дх ду dz
В этих обозначениях, например, символ д/дх обозначает посто-
янное векторное поле
(1\
0 I *
°/
Однако,
Dd/dxf =
870
Глава 17. Токи, потоки и магнитостатика
так что данное векторное поле действует как частная производ-
ная. Аналогично, векторное поле
/а\
е= н
\с/
можно записать в виде
> 9,9 д
( = adi + bB-y+cai-
Оно действует на функции по формуле
дх ду dz
Можно изложить это по-другому: дифференциал
d!°Ld:cfLdy+vdz
дх ду dz
можно рассматривать как функцию, которая каждой точке при-
писывает вектор-строку
( df , ч df , . df , A
/ P ’ТГ P >7F P *
\dx dy dz J
Тогда в каждой точке мы можем вычислить произведение этого
/а\
вектора-строки на вектор-столбец 6 I и получить выражение
\с/
а/ df df\
дх' ду' dzJ
дх ду dz ’
Итак,
Dtf^&df).
Очень полезно интерпретировать величину D^f еще одним спо-
собом. Пусть имеется такое же отображение ф : I х и -+ Rfc и
17.3. Внутреннее произведение
871
соответствующие векторные поля £s. В каждый момент времени
t мы можем рассмотреть функцию ф^/. Вспомним, что
= /w>t(p)) = р)).
Так что
|ш-/)
— по-прежнему хорошая функция. Вычислив ее в некоторой точ-
ке v и устремив t —> 0, мы увидим, что
- /)(р) = lim |[/W>(t,p) - Лр))1
= Dswf-
Откуда получаем
Теперь мы видим, что естественным геометрическим объек-
том, связанным с потоком, является векторное поле. В предыду-
щем параграфе мы увидели, что электрический ток (который по
существу является потоком электронов) определяется 2-формой.
Поэтому нам требуется математическая операция, которая поз-
волит перейти от векторного поля, описывающего поток электро-
нов, к 2-форме, определяющей ток. Эта 2-форма будет зависеть
от плотности электронов. Очевидно, что более высокая плотность
электронов, двигающихся вдоль тех же линий потока, будет со-
здавать больший ток. Поэтому нам нужна такая математическая
операция, которая даст возможность переходить от векторных
нолей £ и 3-форм pdx Л dy Л dz к 2-формам. Эту операцию мы
опишем в следующем параграфе.
17.3. Внутреннее произведение
Пусть V ~ векторное пространство, а tv обозначает элемент
Afc(V*). Вспомним, что iv является функцией (полилинейной и
872
Глава 17. Токи, потоки и магнитостатика
кососимметричной) к векторов в пространстве V. Для каждого
набора vi,..., Vfc мы получаем число
w(vi,v2,...,vfc).
Пусть v обозначает вектор в V. Определим функцию к — 1 век-
торов в пространстве V, подставляя v на первую позицию в си.
Таким образом, мы рассматриваем функцию Wi,..., w^-i, зада-
ваемую
w(v,Wl,. . . ,Wfc_i).
Эта функция векторов w также оказывается полилинейной
и кососимметричной. Следовательно, она является элементом
Назовем эту функцию внутренним произведением v
и w и будем обозначать ее
i(v)cu.
Итак,
i(v)w(wi,..., Wfc_i) = w(v, wb..., Wfc-i).
Давайте посмотрим, как выглядит внутреннее произведение в
различных случаях. Допустим, что в пространстве R3 у нас есть
базис
д
дх
д
ду
д
dz
и элемент дуального базиса
и элемент дуального базиса
и элемент дуального базиса
dx = (1,0,0),
dy = (0,1,0),
dz = (0,0,1).
Тогда если к = 1, т. е. ш является 1-формой, то z(v)lj равняется
w(v), т. е. есть число. Таким образом,
/ Q \ / Q \ \
i I — I dx — 1, z ( — I dy — 0, г ( — ) dz = 0
\ дх ) \дх ) \дх )
и так далее.
17.3. Внутреннее произведение
873
Если к = 2, то
д '
дх^
г
— dx
= ch/(w),
поскольку dy(d/dx) = 0. Значит,
/д\,
г — dx Л dy = dy.
\дх J
Аналогично
.( 9\ .
г тг- ] dx Л dz = dz
\дх J
и
I d \
i I 7Г- 1 dy A dz = 0.
\ox j
Кроме того,
г
— dx
— —dx(yv).
Отсюда
. f 9 \ _ . . . f 9 \ n . / 9 \ .
г — ) dx f\dy = —dx, г — dx A dz = 0, г — ] dy A dz
\9y J \9yJ \dyj
dz.
Аналогично
/д\, 7 Л .
г — dx/\dy = 0, г
\dz /
—dx, i
dy.
874
Глава 17. Токи, потоки и магнитостатика
Кроме того,
г ( — ) (dx Ady Л dz)(wi, w2) = (dx Ady Л dz) I y,Wi,W2
\ (JJb 1 \ C/37
- Det I dar(wi) \dx(w2) / 1 = Det 1 cfc(wi) \dar(w2) = Detfdy(wi) VZ/(w2) Ш) Mi) dy(wi) dz(wi) dy(w2) cte(w2) 0 0 \ dy(wi) dz(wi) dj/(w2) dz(vi2)J dz(yvi)\ dz(w2)J '
Следовательно,
\
— I (dx Ady A dz) = dy A dz.
ox J
Аналогично
(d \
— ) (dx Ady A dz) = —dx A dz
dyj
И
/ Q \
г I — ) (dx Ady A dz) = dx A dy.
\oz J
Теперь ясно, что i(v)cu билинейна no v и w. Поэтому если
л Одд
t = aei + ba-v + cai
И
ш — pdx Ady Л dz,
то
— pddy Adz — pb dx Adz + pc dx A dy.
Итак, мы определили внутреннее произведение i(£)u векто-
ра £ и элемента си пространства Однако, используя это
17.3. Внутреннее произведение
875
определение в каждой точке, мы можем также определить внут-
реннее произведение г(£)о>, где £ ~~ векторное поле, а — диффе-
ренциальная форма степени к. И тогда все полученные формулы
выполняются в пространстве R3.
В частности, если мы рассмотрим векторное поле £, пред-
ставляющее стационарный поток электронов, и 3-форму ш =
pdx/\dy/\dz, дающую плотность электронов (точнее, размазанное
приближение к ней), то получим 2-форму
J = Ц&и,
определяющую ток. Явный вид формулы в декартовых коорди-
натах дается предыдущим выражением. Чтобы понять, почему
J представляет ток, можно воспользоваться исходным опреде-
лением внутреннего произведения. Возьмем точку р и построим
небольшой параллелограмм на векторах wi и W2, выходящих из
точки р. Вектор v = h£(p) представляет линейное приближе-
ние движения частицы, помещенной в точку р, на протяжении
небольшого временного интервала h. Другими словами, парал-
лелепипед, построенный на векторах v, wi и W2 (рис. 17.3), да-
ет (приблизительно) область, проходимую параллелограммом за
время h. Полный заряд этого параллелограмма дается выраже-
нием
u>(v,Wi,W2) = [z(v)a>](wi, W2)
= /i[i(£(p)H(wi,w2)
= /iJ(p)(wi, w2).
Итак, J(p)(wi,w2) действительно представляет скорость потока
заряда через параллелограмм, построенный на векторах wi и w2.
Рис. 17.3
876
Глава 17. Токи, потоки и магнитостатика
Поэтому, если J проинтегрировать по поверхности, то получится
скорость потока заряда через эту поверхность.
В заключение этого параграфа давайте докажем очень важ-
ную формулу для внутреннего произведения:
г(£)[^1 Л о>2] = (XC)W1) Л + (—l)degW1u>i Л г($)о>2. (17.1)
(Проверка показывает, что в пространстве R3 формула (17.1)
справедлива для всех случаев, которые мы рассмотрели.) В фор-
муле (17.1) £ обозначает векторное поле, a o>i и о>2 дифферен-
циальные формы. Поскольку (17.1) — чисто алгебраическое вы-
ражение, то достаточно доказать его для каждой точки, т. е. в
случае, когда £ = v является вектором в пространстве V, оц —
элементом Afc(V*), а о?2 ~ элементом Лг(У*). Обе части выраже-
ния линейны по и С1>2, когда два других аргумента фиксиро-
ваны. Мы можем написать £ = ajyi Ч-----1-anvn, где {vi,..., vn}
является базисом. В силу линейности по £, достаточно проверить
формулу для £ = т. е. для базисного элемента. Без потери общ-
ности предположим
£ = vi.
Сначала докажем формулу в случае, когда иц является 1-фор-
мой. В силу линейности можно считать, что
Ш1 = V*, i — 1,...,п,
т. е. является элементом дуального базиса. Кроме того, предпо-
ложим, что 1^2 является базисным элементом вида
= v*x Л • • • Л V* .
Рассмотрим теперь разные возможности.
(а) Пусть i = 1, ji > 1. Тогда vj(vi) = 0 для всех j = д,... ,ji,
и в определителе выражения для
(о>1 Ao>2)(vi, wi,..., w/)
17.3. Внутреннее произведение
877
все элементы, кроме левого верхнего, обращаются в нуль. Напри-
мер, если о?2 = v2 Л V3 Л V4, то
(wi Л w2)(v, Wi, w2, W3) = Det
- Det
= Det
/vl(vl) v2(vl) v3(vi) V4(V1)\
Vl(wi) v2(wi) v3(wi) V^(Wi)
v*(w2) v2(w2) v3(w2) V4(w2)
\vl(w3) v2(w3) v3(w3) V4(w3)/
/ 1 0 0 0 \
Vl(wi) V2(Wi) v3(wi) v^(wi)
vj(w2) v2(w2) v3(w2) vj(w2)
\yi(w3) v2(w3) v3(w3) V4(w3)/
/V2(wl) v3(wx) V^(W1)\
1 v^(w2) v^(w2) V^(w2) |
\V2(w3) v£(w3) V4(w3y
= (V2 Л V3 A v^)(wi,w2,w3).
Итак, выражения для (a>i A tu2)(v, wi,..., w/) и cu2(wi,..., w/)
чрез определители совпадают. Следовательно,
i(v)(cui Л о>2) = CU2 = [^(v)cui]a>2 — cji A z(v)cu2,
поскольку в этом случае i(v)o>i = 1 и i(v)oj2 — 0.
(b) Пусть i ~ 1, ji = 1. Тогда cui A cu2 = 0. В этом случае
z(vi)cji — 1 и тогда
(i(vi)oji) Л cj2 = w2.
В то же время
z(vi)a;2 — Vj2 Л • • • Л
Тогда
Ш1 A i(vi)oj2 — V1 Л v*2 Л • • • Л VjL = cu2.
Таким образом,
i(vi)o?i Л cu2 — oji Л i(vi)cu2 — u>2 — о?2 — 0.
(с) Пусть i > 1, ji — 1. В этом случае можно написать о;2 =
V} Ло,3. Тогда левая часть формулы (17.1) переписывается в виде
i(v)[o>i Л v| Л о>3] = — i(v)[vj Л (u?i Л си3)] (переставляя vi с о>1)
= — cji Л си3,
878
Глава 17. Токи, потоки и магнитостатика
согласно случаю (а). Первый член в правой части формулы (17.1)
обращается в нуль, а второй член равен — u>i Л шз (еще раз при-
меняем случая (а)).
(d) Пусть г > 1, ji > 1. Тогда
t(vi)(wi Л w2) = °,
t(vi)a?i = О
и
i(vi)o>2 = 0.
Поэтому обе части формулы (17.1) обращаются в нуль. Итак, мы
доказали формулу (17.1) для случая, когда degu>i = 1. Но тогда
ассоциативный закон внешнего умножения дает нам возможность
доказать эту формулу в общем случае. Например, предположим,
что — tri Л <72, где deg <71 = deg<72 = 1. Тогда
a(v)(<7i Л <72 Л w2)
= i(v)<Ti Л (<72 Л Ш2) — <71 Л z(v)(<72 Л О>2)
= z(v)<7i Л (<72 Л О>2) — <71 Л z(v)<72 Л Ш2 + <71 Л <72 Л i(v)<J2
= [i(v)<7i Л <72 — <71 Л z(v)<72] Л W2 + Л <72 Л t(v)<jJ2
= z(v)(<71 Л <72) Л О>2 + (<71 Л <72) Л z(v)<V2.
Итак, мы доказали формулу, когда од = oiA<72, и тем самым, в си-
лу линейности, для всех случаев, когда degcui = 2. Дальше дока-
зательство продолжаем по индукции. Например, если degai = 1
и deg<72 = 2, то
i(v)(<71 Л<72 Ло>2)
= z(v)<71 Л (<72 Л U>2) — <71 Л z(v)(<72 Л О?2)
= «(v)<71 Л <72 Л <J2 — <71 Л z(v)<72 Л W2 — <71 Л <72 Л z(v)w2
= i(v)(<7i Л <т2) Л о>2 — <71 Л ст2 Л i(v)u>2.
Поэтому
z(v)u>i Aw2 = z(v)o>i Л о>2 — a>i Л z(v)o>2,
если deg a>i — 3, и так далее.
17.4. Производные Ли
879
17.4. Производные Ли
Так же, как в параграфе 17.2, пусть ф : I х U —> Rfe. Тогда для
каждого t Е I мы имеем отображение
Ф^и-^, <Мр) = Жр),
причем предполагается, что
Фо = id.
Пусть £ = £0 обозначает векторное поле, связанное с </>* в момент
t = 0.
Пусть ы — дифференциальная форма степени к. Рассмотрим
форму ф%ш и соответственно форму
при t ф 0. Утверждается, что это выражение имеет предел при
t = 0. Действительно, если ш = f — функция, то такой предел
при t — 0 существует и, как мы уже видели, он записывается в
виде
Если си = d/, то
ФМ = <1фу
и поэтому
L L
Мы имеем право переставить пределы в частных производных,
определяющих d и D$. Тогда получим
hm|(0*d/-d/) = dP^.
Наиболее общий вид линейной дифференциальной формы явля-
ется суммой выражений вида f dg. Тогда
^*(/d5) - fdg = Ш)Ф№ — f dg
= ФУ ф*уд - f фУд + fffidg) - f dg.
880
Глава 17. Токи, потоки и магнитостатика
Следовательно,
| (<# fdg-fdg) = (D(f) dg + f d(D^g).
Итак, Ит4_+о(1Л)(Ф*^—cu) существует для любой 1-формы. Более
того, этот предел можно выразить через £ и Этот предел будем
обозначать Далее, если
СО = UJ1 Л CU2,
где u>i и о>2 — 1-формы, то мы имеем
Л CU2) — CU1 Л CU2 — CU1 Л Ф1^2 — Л CU2
— (</>£lUi — СЩ) Л </>*CU2 + О>1 Л (^CU2 - <U2).
Разделив это выражение на t и вычисляя предел, получим, что
Ит -(</>£(а>1 Л CU2) — CU1 Л CU2)
t—>0 t
существует и равен
D^CUi Л CU2 + CU1 Л 1)^2'
Так как любая 2-форма может быть представлена как сумма
членов вида cui Л cu2, то
lim ^-(ф*со — си)
t—о tv 7
существует для любой 2-формы си. Этот предел мы будем обозна-
чать Dgv, потому что он зависит только от £ и си. Действуя таким
образом, мы убедимся, что этот предел существует для форм си
любой степени и зависит только от £ и си. Мы его обозначим D^cu
и назовем производной Ли от си по £. Для любых форм cui и си2,
как и выше, можно доказать формулу
D$(cui Л cu2) = A cu2 + cui Л Z?£cu2-
Определение и равенство дф* = ф*й, показывают, что
dD^co — D$dw.
17.4. Производные Ли
881
Существует формула, связывающая внутреннее произведение
г(£), внешнюю производную d и производную Ли D$. Прежде чем
получить эту формулу, вспомним, что d отображает /-формы в
(/ + 1)-формы и удовлетворяет равенству
d(o?i A о^) = dw± А о?2 + A dwz,
если степень равна к. Кроме того, г(£) отображает /-формы в
(/ — 1)-формы и удовлетворяет равенству
А о>2) = А о>2 + (-l)feu>i А г($)си2.
Поэтому с/ог(£) отображает /-формы в /-формы и удовлетворяет
равенству
[с/ о i«)](o;i A CU2) = d(i(£)cJi А о?2 + (“1)^1 Л г(€)^г)
= di(g)cui Л о>2 + Л da>2
+ (~l)kdwr Л i(£)w2 + (“l)2fc^i Л di(g)W2‘
Заметим, что (—l)2fc = 1. Кроме того, имеется аналогичная фор-
мула
[г(£) о d](u?i A lo2) ~ i(£)dwi Л о>2 + (-~l)fc+1c/^i А г($)о>2)
+ (-l)fcz(£)cui Л dab + Л г(^)с/о?2.
Если мы сложим эти два выражения, то средние члены сокра-
тятся, и мы получим правило Лейбница
[г(£) о d + d о г(£)] (tc>i Л и>2)
= [i(£)d + di(g)]coi Л ш2 + wi А [г(£)с/ + сй(£)]си2.
А сейчас докажем фундаментальную формулу дифференциаль-
ного исчисления
(17.2)
Доказательство. Обе части этого уравнения являются опера-
торами, которые, действуя на произведения, удовлетворяют тож-
деству Лейбница. Каждая форма является суммой произведений
D£ = i(&d + di(&.
882
Глава 17. Токи, потоки и магнитостатика
функций f и дифференциалов dg. Поэтому нам достаточно про-
верить тождество
D$w — i(£)dw + dz(£)cu
для cu = f и для w = dg. В случае w = f по условию мы имеем
г(£)/ = 0 (не существует (—1)-форм). Тогда формула упрощается
D^f = i(&df = df(&,
что мы уже получили в параграфе 17.2. В случае cu = dg мы
имеем
D^dg = dD$g
= d(i{£)dg)
= («(£)<* + di(£))dg,
поскольку d? = 0. Итак, формула верна в общем случае. В при-
ложении к этой главе мы дадим другое доказательство этой фор-
мулы в более общем виде.
Например, предположим, что
cu = р dx Л dy Л dz
в пространстве R3. Тогда dw = 0, поскольку в трехмерном прост-
ранстве не существует ненулевых 4-форм. Тогда
D^w — di(£)w.
Если мы положим
J —
то условие
dJ = O
эквивалентно
D$w — 0.
Это — инфенитезимальный способ выражения того, что — w
для всех t. Тем самым, первый закон Кирхгофа можно перефор-
мулировать так: поток сохраняет плотность заряда си, так что
Dgw — 0.
17.5. Магнетизм
883
17.5. Магнетизм
Электрические и магнитные явления в очень примитивной форме
были известны еще с древних времен. Исследования этих загадоч-
ных явлений учеными семнадцатого и восемнадцатого веков при-
вели в девятнадцатом веке к пониманию фундаментальной роли
электромагнитных сил в природе и к революционным изменени-
ям в обществе, возникшим в результате открытия электрических
технологий.
В древности было известно, что если потереть янтарь (окаме-
невшую древесную смолу) тканью, то небольшие кусочки легкого
материала поднимутся в воздух и приклеются к нему. Янтарь по-
гречески называется «электрон». В книге «О магнетизме», опуб-
ликованной в Лондоне в 1600 году, У. Гилберт ввел термин «элек-
тричество» для обозначения притяжения, свойственного янтарю.
Он посвятил янтарю целую большую главу, «чтобы показать при-
роду притяжения тел к нему и подчеркнуть огромную разницу
между этим свойством и магнитными действиями» и отличить
«простую симпатию, связывающую железо и магниты, от нераз-
борчивого поведения янтаря». Древние рассматривали притяже-
ния янтаря и магнитов как одинаковые явления, давая им одина-
ковые объяснения. Кардано (1550) осознал ряд различий между
электрическими и магнитными притяжениями. Однако, только
Гилберт обнаружил, что электростатическое свойство притяже-
ния янтаря может быть и у многих других твердых веществ. Ко-
нечно, электростатическое притяжение заряженного тела к лег-
кому нейтральному телу за счет индуцированной поляризации и
более сильное притяжение к телу с зарядом противоположного
знака — очень сложные явления как для точного теоретическо-
го расчета, так и для эксперимента. Легкие кусочки бумаги ле-
тят к янтарю хаотически и приклеиваются к нему. Затем через
некоторое время они падают. Поэтому, конечно, поведение янтаря
по сравнению с постоянным притяжением железа к магниту или
магнита к магниту можно считать «неразборчивым». По суще-
ству прошло еще почти два века, пока люди осознали, что фунда-
ментальное притяжение и отталкивание в рамках электростатики
действует между заряженными телами, и пока был открыт пра-
вильный закон взаимодействия между ними. Это было сделано
884
Глава 17. Токи, потоки и магнитостатика
Кулоном в 1789 году в тщательно поставленном эксперименте с
помощью изобретенных им крутильных весов.
В древнегреческих источниках имеются сведения о камнях,
которые могут притягивать железо. Сообщалось, что один такой
большой камень в окрестности города Магнезия в Малой Азии
вытягивает кусочки железа из амуниции пастухов и гвозди из
их ботинок. По имени этого города мы и получили термин «маг-
нит». Было обнаружено, что этот камень может передавать свой-
ство притягивать железной игле, причем у последней оно будет
зависеть от направления. В том же эксперименте с крутильными
весами Кулон обнаружил и измерил силы притяжения и отталки-
вания между магнитными полюсами. (Он еще раз открыл закон
обратного квадрата.) Однако, современное понимание природы
магнитных сил пришло после работ Ампера. Оказалось, что ис-
тинным объектом изучения было не притяжение железа к маг-
ниту или притяжение между магнитами, а сила, которую магнит
оказывает на движущийся заряд (или, еще точнее, сила, с кото-
рой один движущийся заряд действует на другой).
Весной 1820 года, читая лекцию об электрических токах,
Эрстед заметил, что стрелка компаса, случайно оказавшегося
рядом, отклоняется током. Объявление об этом результате — что
электрический ток действует на магнит — всколыхнуло научный
мир. Электричество и магнетизм, разделенные в течение почти
двух веков, вновь оказались связанными между собой. Ампер
осознал, что если ток отклоняет магнитную стрелку, то магнит
должен действовать на ток и два тока должны действовать друг
на друга. В течение нескольких недель с 18 сентября по 9 октяб-
ря 1820 года, Ампер без устали провел серию блестящих экспе-
риментов и геометрических исследований. В некотором смысле
понятие дифференциальных форм возникло из математическо-
го анализа, проделанного Ампером, который открыл основные
законы магнитостатики.
Магнитное поле создает силу, действующую на ток, а ток
представляется нам как система движущихся зарядов. Значит,
магнитное поле действует на заряды. В то же время сила зави-
сит от скорости движения заряда. Магнитная индукция является
17.5. Магнетизм
885
2-формой В в пространстве R3. Предположим, что заряд е дви-
жется через точку р со скоростью v. Тогда возникает сила
ei(y)Bp.
В этом выражении В является 2-формой, поэтому Вр равно зна-
чению В в точке р, т. е. является элементом Л2(К3). Таким обра-
зом i(v)Bp — линейная функция касательных векторов в точке
р, т. е. то, что мы называли силовым полем (ср. том 1, с. 348).
Итак, если частица с зарядом е движется вдоль кривой 7, то
в момент t на нее действует сила
ег(У(*))^7(*)-
Тогда из определения внутреннего произведения немедленно сле-
дует, что
i(v)i(w)cu — — i(w)i(v)cj
для любых v, w и В частности,
i(v)i(v)cu = О,
или, если ш е Л2(У*), то
[i(v)w](v) = 0.
Это значит, что составляющая силы вдоль направления дви-
жения отсутствует. Тогда сила, действующая на линейный про-
водник с током, будет перпендикулярна этому проводнику. (Это
было проверено Ампером в остроумном эксперименте, когда ток
протекал по подвижному проводу, соединяющему два сосуда со
ртутью.)
В каждой точке форма В 0 будет определять направление
в пространстве — прямую, задаваемую уравнением
z(w)B — 0.
(Читателю следует убедиться, что это два линейно независимых
уравнения для w.) Железные опилки, помещенные в магнитное
поле (способные вращаться, но не двигаться поступательно) по-
вернутся вдоль этого направления, создавая магнитные силовые
886
Глава 17. Токи, потоки и магнитостатика
линии. (На токи вдоль именно этих направлений не действует
сила.)
Ампер не только открыл силу, с которой магнитное поле дей-
ствует на ток. Он также вывел количественную формулу зако-
на (впервые обнаруженного Эрстедом), согласно которому ток
создает магнитное поле. Для этого полезно ввести 1-форму Н,
которую вслед за Зоммерфельдом будем называть магнитным
возбуждением или магнитным полем. Второй закон Ампера го-
ворит, что если произвольная поверхность S ограничена кривой
7 = 3S, то
Другими словами, интеграл от магнитного поля по замкнутой
кривой, ограничивающей некоторую поверхность, равен потоку
тока через эту поверхность.
По теореме Стокса это то же самое, что
dH = 4% J.
В отличие от электростатики, мы можем сформулировать еще
один закон магнитостатики в виде
I В = 0 для любой замкнутой поверхности S.
Js
(Согласно Герцу, это значит, что «не существует магнитных за-
рядов».) И, наконец, нам надо получить закон, связывающий В
и Я. В неферромагнитных материалах он имеет вид
В =
где р называется магнитной восприимчивостью. А сейчас да-
вайте выпишем все законы магнитостатики.
(i) Сила, действующая на элемент тока I = ev в точке р,
равна г(1)Вр.
(ii) Js В = 0 для любой замкнутой поверхности S. Следова-
тельно,
dB^O.
17.5. Магнетизм
887
(in) fas ff = 47r fsJ’
dH = 4тгJ (закон Ампера).
(iv) В — [i*H.
Предположим, что мы находимся в области С7, где H2(U} = 0.
Тогда условие dB = 0 означает, что
B = dA
для некоторой 1-формы А. Конечно,
А = Ах dx + Ау dy + Az dz
не определяется однозначно уравнением В — dA, поскольку
функция Л + где — произвольная функция, удовлетво-
ряет тому же уравнению. Давайте возьмем такую функцию
чтобы
д2/ф д2/ф д2еф _ / дАх дАу 5АА
дх2 + ду2 dz2 \ дх + ду dz )
Как только мы выбрали А, задача сводится к решению уравнения
Пуассона.2 Тогда, заменив А на А + мы получим
дАх дАу дА^
дх ду dz
Теперь
Н =
м м
и
dH = J.
Предположим, что в рассматриваемой области ц — постоянная.
Тогда
d*~rdA — /j,J.
2Последующие вычисления станут яснее после того, как мы введем общую
форму оператора *. См. следующую главу.
888
Глава 17. Токи, потоки и магнитостатика
В этом случае
JZ . , х дАх , , дАх ,
d(Ax dx) — —-— dx Л dy Н—dz Л dx.
ду dz
поэтому
, ч ЭАХ , дАх ,
★ rd(Ax dx) = —— dz + dy
И
,, -1,V4 92 Ах ,1 лЛ 92 J AJ
(a* d)(Ax dx) = — „ dx /\dz---dy Л dz
дхду ду2
д2Ах , J д2Ах , J
+ д-д- dx /\dy---—dy Л dz.
dzdx dzz
Проделав те же вычисления для Ау dy и Azdz и сложив все вмес-
те, получаем
(d*-1d)А = —(ДАХ dy Л dz + АА.У dz /\dx + ДА2 dx Л dy),
где
_ д2 д2 д2
дх2 ду2 dz2
— обычный оператор Лапласа. Тогда если написать
J ~ Jxdy /\dz + Jydz /\dx + Jz dx Л dy,
то уравнения
dA = B,
В = /л*Н,
dH = 47г J
сводятся к решению трех уравнений Пуассона:
= 4тг<7х,
ДАу — —47г7у,
ДДг = ~ 4%Л.
Например, мы хотим получить В и Н вне длинного тонкого
прямолинейного провода, по которому течет постоянный ток L
17.5. Магнетизм
889
Предположим, что радиус провода равен а, и расположен он
вдоль оси z. В этом случае Jx = Jy = 0 и
{О вне провода,
I
—х внутри провода.
7Г0Г
Тогда Ах = Ау = 0. Решая уравнение для получаем
Az — —2fil log \/ж2 + т/2
для точек вне провода. Тогда
dAz дАг
В = аА = —-— dx f\dz-------— ау Л dz
дх ду
(х у \
-zdx/\dz + -^dy/\dz]
2ц1 ,
=----dr A dz
r
в цилиндрических координатах
x = rcos0, у = г sin0, z — z,
г = y/x^+ у2.
Силовыми линиями являются круги с центром в середине про-
вода, и Н — пропорционально d&. Если бы мы заранее
знали, что
H = fde,
то из соображений симметрии мы могли бы заключить, что f =
f(r). Тогда из соотношения
f Н = 4тг1
А
мы получили бы
х 21
/(г) =
Поскольку d0/г = dr Л dz, мы бы тогда имели
В = р,-кН - 2уТ dr Л dz.
890
Глава 17. Токи, потоки и магнитостатика
В общем случае решение уравнения Пуассона показывает, что
А определяется объемным интегралом
Аналогичные формулы получаются для Ау и Az.
Приложение: альтернативное доказательство
фундаментальной формулы
дифференциального исчисления
Здесь мы дадим альтернативное доказательство основной фор-
мулы (17.2). По существу, мы докажем ее в более общем случае.
Пусть W С Rm и Z С Rn — открыты! множества. Предположим,
что нам дано дифференцируемое отображение ф : W х I —* Z,
где I — некоторый интервал в R, содержащий начало коорди-
нат. Для каждой фиксированной точки w G W мы получим кри-
вую </>(w, t), зависящую от t. Пусть £t(w) обозначает касательный
вектор к кривой 0(w, i). Это касательный вектор в пространст-
ве образов Rn, но зависящий от t и w G W. Кроме того, пусть
отображение ф* : W —> Z определено как
Мы считаем, что </>t образуют однопараметрическое семейство
отображений из W в Z.
Пусть а — дифференциальная (к + 1)-форма в пространстве
Z. Для каждого t определим й-форму </£г(^)(т в W согласно
формуле
№i£t)cr]('nv ,‘Пк) = • -^Фепк),
где 771, • • •> Лк ~~ касательные вектора в точке w. Все к + 1 век-
торов, возникающие внутри а в правой части этого соотноше-
ния, являются касательными векторами к кривым </>*(w). Поэто-
му правая часть имеет смысл. Примем это как определение левой
части данной формулы. Для обобщения формулы (17.2) мы хо-
тим доказать следующее.
Приложение
891
Пусть at обозначает гладкое однопараметрическое се-
мейство форм в Z. Тогда ф^сгъ является гладким се-
мейством форм в IV, и основная формула дифферен-
циального исчисления форм принимает вид:
4^*^ = »(&>(. (17.3)
at at
Сначала докажем формулу для частного случая, когда W =
Z = М х Z, где М является открытым подмножеством простран-
ства Rm, a (/>t является отображением : М х I —> М х I, опре-
деленным формулой
V>t(x,s) = (х, s + t).
Наиболее общий вид дифференциальной формы в М х I можно
записать в виде
ds Л а + Ь,
где а и b являются формами в М, которые могут зависеть от
t и s. (В терминах локальных координат s, х\ ..., хп эти формы
оказываются суммами членов вида где с является
функцией, зависящей от t, s и х.) Чтобы показать зависимость
от х и s, мы перепишем наше выражение в виде
at = ds Л а(х, s, t) dx + 6(х, s, t) dx.
В этих обозначениях очевидно, что
— ds Л а(х, s + t, t) dx + b(x, s + t, t) dx
и поэтому
d'llrfot , да, x _ db , . ,
—t— — ds a — (x, s + t, t) dx + t^(x, s + t,t) dx
dt ds ds
.da, . . db
+ ds A — (x, s + t, t) dx + — (x, s + t, t) dx.
dt dt
Следовательно,
d^ot ( d(yt\ , da, . , db , 4
—7-----V’t I ~r I — ds/\ — (x, s+i, i) dx+ — (x, s+t, i) dx. (17.4)
dt \ dt J dsy 7 dsv v 7
892
Глава 17. Токи, потоки и магнитостатика
В этом случае также очевидно, что вектор, касательный к кривой
^(х, s), равен d/ds, вычисленной в точке (х, s +1).
Тогда d/ds оказывается векторным полем и
.(д\ л
г — a* — а ах.
Yds /
Следовательно,
G (^"0 ^0 = 5 + М) dx
и поэтому
✓ ( д \ \ да
d^t — 7r-(x,54-i, t) dshdx+dxa(x.,s+t,t) dx. (17.5)
у yas J J os
Здесь dx обозначает внешнюю производную формы a(x, s+i, t) dx
в M при фиксированном значении s. Аналогично
дЬ
da. = —ds Л dxa dx + — ds Л dx + dxb dx.
as
Тогда
. / 0 \ , db ,
г — dat = —dxa dx + — dx
\ds) as
и
V»*? ( ^-) dot — —dxa(x, s +t, t) dx 4- ^-(x, s +1, t) dx. (17.6)
\ US J
В результате сложения соотношений (17.4)-(17.6) мы получаем
доказательство формулы (17.3) для
Пусть теперь ф : W х I —* Z имеет вид 0(w,s) = <£s(w).
В результате действия ф прямые, параллельные I и проходящие
через w в Wxl, переходят в кривые <^s(w) в Z. Другими словами,
(о \
тг ) = €t(w)-
08 / (w,t)
Если мы рассмотрим отображение I : W W х I, заданное
правилом Z(w) — (w, 0), то отображение можно записать как
Резюме
893
фоф^о],. Тогда = 1*ф1ф*сг1, Поскольку I и ф не зависят от t,
мы имеем
^ф^ = 1*^(ф*ъ)-
В точке w, t пространства W х I можно написать
* Ф*Ъ = | (г (^Ф^) ст‘) } =
и тогда
G (^) ф*а^=1*ф*ф*№^=ф^ш.
Подстановка в формулу для (d/dt)^^*^] дает (17.3).
Резюме
А. Дифференциальные формы, векторные поля
и магнетизм
Для данного векторного поля £ и дифференциальной формы ш
надр знать, как определить и вычислить производную Ли Dgw.
Вы должны знать определение внутреннего произведения век-
тора и дифференциальной формы, уметь вычислять его и исполь-
зовать для формулировки закона о магнитной силе.
Вы должны знать формулировки законов магнитостатики и
технику вычисления В для данного тока J с помощью диффе-
ренциальных форм.
Задачи
17.1. Пусть вектора {е1? ©2, ез} образуют базис в пространстве R3, так
что
dx[ei] = d?/[e2] = dz[e3] = 1.
Пусть £ = х&2 — уе^. Это векторное поле £ описывает скорость,
связанную с равномерным вращением вокруг оси z. Мы можем
переписать это выражение в виде £ = х(д/ду) — у(д/дх).
894
Глава 17. Токи, потоки и магнитостатика
(а) Имеется постоянная плотность заряда, описываемая фор-
мой о; = p$dx /\dy Л dz. Используя соотношение J =
определите ток, связанный с вращением этого однородного
распределения заряда.
(Ь) Пусть w = zdx Л dy. В явном виде проверьте выполнение
тождеств .Ogee = i(£)dw + di(£)w и dD^tv = D^dcv, где £ =
х(д/ду) - у{д/дх).
17.2. Пусть I обозначает ток на единицу длины, который распростра-
няется аксиально симметрично относительно оси z таким обра-
зом, что, проходя через поверхность цилиндра радиуса г, ось ко-
торого является осью г, не зависит от г. В этом случае скорость
носителей заряда определяется формулой
:ei + уе2 1 ( д д\
х2+у2 ИЛИ х2 + у2 \ дх +Уду) ‘
Вычислите 2-форму J, используя равенство J = i(£)dx f\dy Л dz
и убедитесь, что dJ = 0.
17.3. Предположим, что В = B^dz. где Во — константа. Найдите
функцию Л, удовлетворяющую условиям
В ~ dA и
дАх дАу dAz
дх ду dz
17.4. Предположим, что по проводу с радиусом а движется аксиально
симметричный ток J, величина которого пропорциональна г2. В
этом случае очевидно, что Jx = Jy = 0 и
0
Jz =
21(х2 + у2)
7га4
вне провода,
внутри провода.
(а) Найдите функцию Az, зависящую только от г = у/х2 -{-у2,
для которой
= -4тгЛ.
(Ь) Вычислите В и Н в цилиндрических и декартовых коорди-
натах. Проверьте, что dH = 4?rJ.
17.5. Очень длинный цилиндр с радиусом а и осью вдоль z имеет од-
нородную плотность заряда р$. Вне цилиндра зарядов нет. Ци-
линдр вращается вокруг своей оси с угловой скоростью си, так
что J = curpo Для г < а.
Задачи
895
(а) Выразите J в цилиндрических и декартовых координатах
(см. задачу 17.1).
(Ь) В силу симметрии форма В имеет вид В = f(r) dx Л dy
dz. Получите такое Н, чтобы выполнялось
условие dH = 4тг J.
(с) Найдите функцию Л внутри и вне вращающегося цилиндра.
В цилиндрических координатах А будет иметь вид g(r) dO.
Глава 18
Звездный оператор
В этой главе мы даем общее обсуждение звездного опе-
ратора. Это позволит нам сформулировать в следую-
щей главе уравнения Максвелла и понять связь между
ними и геометрией пространства-времени. Кроме то-
го, мы объясним различные операторы и тождества
векторного анализа.
18.1. Скалярные произведения и внешняя
алгебра
Пусть V обозначает конечномерное векторное пространство с
невырожденным скалярным произведением. Мы не предполага-
ем, что это скалярное произведение (•, •) положительно определе-
но. Однако, полезно иметь в виду положительно определенный
случай, чтобы интуитивно чувствовать, что происходит. В этом
параграфе мы хотим объяснить, как (•,•) индуцирует скалярное
произведение в каждом из пространств Afe(V*). Идея состоит в
том, что за понятием длины следуют площадь параллелограмма,
объем параллелепипеда и так далее.
Сначала отметим, что скалярное произведение в простран-
стве V индуцирует скалярное произведение в пространстве V*.
Действительно, любое скалярное произведение в V индуцирует
отображение L : V —> У*, задаваемое формулой
L(v)(w) = (v,w), v,wEV.
898
Глава 18. Звездный оператор
В этом уравнении L(v) является элементом V*, т. е. функцией
в пространстве V, и поэтому ее можно вычислить для любого
w е V. Отображение L определено так, что вычисление приводит
к (v,w). Если (•, •) невырождено, то из того, что (v,w) — О
для всех w, следует, что v = 0. Следовательно, соотношение
L(v)(w) = 0 для всех w означает v = 0, т. е. из L(v) = 0 следует,
что v — 0. Поскольку DimV* = DimV, можно сделать вывод,
что (•,•) не сингулярно тогда и только тогда, когда L является
изоморфизмом. Мы предположили, что (•,•) невырождено, но
тогда на самом деле L оказывается изоморфизмом. Теперь можно
определить скалярное произведение в пространстве V*
(а, /3)у* = (Ь-1а, а, /? € V*.
Например, предположим, что V = Rn состоит из векторов-
столбцов. Тогда V* = Rn* состоит из векторов-строк. В общем
случае скалярное произведение в пространстве Rn дается сим-
метричной матрицей S. Допустим, что S диагональна. Тогда
(v,w)y = ^SiXiyi,
если V В этом случае Итак, если то = 1:1 и w = I : I . \Яп / \?/n J Lv = (sisi,... ,snxn). а = (ai,... ,ап), /«i/sA /ЛАЛ V^n/^n/ \0п/8nJ
18.1. Скалярные произведения и внешняя алгебра
899
Следовательно,
Si
Заметим, что Si стоит в знаменателе. Поэтому мы должны пред-
положить, что все Si ф 0. А это и есть предположение о невы-
рожденности (•,•).
Если (•, •) положительно определено и {ei,...,en} является
ортонормированным базисом в пространстве V, то {вр...,е*}
будет дуальным базисом. Исследование определения L показы-
вает, что
Z(eJ = е*
и, следовательно, {е^,..., е* } образует ортонормированный базис
в пространстве V*. В более общем случае, если не предполагать
положительной определенности (•,•) (но при этом предполагать
невырожденность), то можно взять в качестве {ei,...,en} ор-
тогональный базис с условием (е«,е«) = ±1. Тогда {е*,...,е*}
оказывается ортогональным базисом в V* и
(е*,е*)у. = (e^ejy.
Теперь можно дать определение (•, •) для двух любых линейных
дифференциальных форм. Например, в евклидовом пространст-
ве Rn базис 1-форм dx1,..., dxn ортонормирован и
(dx\ dx1) = +1.
Пусть в пространстве R3 есть две формы ш = Axdx-\-Ay dy+Az dz
и т = Bxdx + Bydy + Bz dz. Тогда (cu, r) ~ AXBX 4- AyBy 4- AZBZ.
Заметим, что (cu,r) является функцией.
Давайте рассмотрим пространство Afe(V*). Каждый элемент
этого пространства является суммой вида
а = а1 Л • • • Л ак + /З1 Л • • • Л (Зк 4-.
Утверждается, что существует единственное скалярное произве-
дение, определенное в пространстве Л^(У*) и удовлетворяющее
условию
(а1 Л • * • Л ак, 71 Л • • • Л ук) — Det((a\7J)).
900
Глава 18. Звездный оператор
Очевидно, что если такое скалярное произведение существует,
то этим уравнением оно определено единственным образом, по-
скольку в силу билинейности (•, •) можно продолжить на все а и
7, которые представляют собой суммы разложимых элементов,
т. е. выражений вида а1 Л • • • Л ак и 71 Л • • • Л 7^). Задача состоит
в том, чтобы доказать согласованность такого определения, т.е.
показать, что если а и/или 7 записываются в виде сумм разло-
жимых элементов двумя различными способами, то мы получим
одно и то же значение (се, 7). Такое доказательство становится
простым, если мы воспользуемся более абстрактным определени-
ем пространства Afe(y*), чем то, чем пользовались до сих пор.
Это определение и доказательство приводятся в приложении к
этой главе, поэтому здесь мы не будем отвлекаться.
Сейчас получим скалярное произведение (значения которого
суть функции) в пространстве fc-форм. Например, для 2-форм
(й? Л и;2, т1 Л г2) — (иД т1)^2, г2) - (оД r2)(w2, г1).
В пространстве R3 для евклидова скалярного произведения
(dx Л dy, dx Л dy) = +1.
В четырехмерном пространстве-времени для скалярного произ-
ведения Лоренца мы имеем
(dt Л dx, dt Л dx) = —1,
но
(dx Л dy, dx Л dy) = +1.
В качестве иллюстрации, как делать такие вычисления в более
общей системе координат, рассмотрим сферические координаты
в пространстве R3, которые определяются формулами
г — у/х2 + у2 + г2, в = arctan (Д(х2 + y2)/z), Ф = arctan(y/x).
18.2. Звездный оператор
901
Если мы вычислим дифференциалы этих функций и выразим
результаты через базис {dx, dy, dz} с коэффициентами, записан-
ными для удобства в координатах г, 0 и ф, то получим
dr = sm0cc^dx + sin0sin^dy + cos0dz,
d0 = -(cos0cos0dx + cos0sin0ds/ — sinfltte),
r
dф = —:—- (— sin ф dx + cos ф dy).
r sint/
Используя ортонормированность dx, dy и dz, прямое вычисление
показывает, что dr, d0 и d$> являются ортогональными элемента-
ми пространства V* в каждой точке (г, 0,ф). При этом
(dr,dr) = 1, (d0,d0) = -l = 1 2 .
г2 г2 sm 0
Отсюда немедленно следует, что dr Л d0, dr Л dф и dO Л dф обра-
зуют ортогональный базис в пространстве A2(R3), а скалярные
произведения
(dr Л d0, dr Л d0) — и т. д.
Наконец, мы можем вычислить скалярное произведение базисно-
го элемента dr /\d0 Л dф на себя:
(dr Л df) Л dф, dr /\ dO Л dф) ~ .
г4 sinz 0
Чтобы подвести итог полученным результатам, лучше всего от-
метить, что
dr, rd0, г sin 0dф
образуют ортонормированный базис Л1(Ж3*) в каждой точке. По-
этому мы можем работать с этими тремя дифференциалами так
же, как с dx, dy и dz.
18.2. Звездный оператор
Рассмотрим конечномерное векторное пространство V. В гла-
ве 8 мы обсуждали понятие ориентации векторного простран-
ства V. Вспомним это определение. Любые два базиса {ei,..., еп}
902
Глава 18. Звездный оператор
и связаны между собой матрицей замены базиса В.
Два базиса называюься эквивалентными или определяют оди-
наковую ориентацию, если Det В > 0. В противном случае они
определяют противоположные ориентации. Множество всех ба-
зисов разбивается на два класса эквивалентности, и каждый
класс эквивалентности называется ориентацией. С помощью
пространства ЛП(У) мы можем сформулировать это иначе. Базис
{ei,...,en} определяет ненулевой вектор в одномерном прост-
ранстве An(V), а именно
ех Л ••• Леп.
Второй базис {fi,..., fn} определяет элемент fi Л • • Л fn. Эти
два элемента отличаются скалярным множителем Det В. Таким
образом, выбор ориентации пространства V равносилен выбору
одного из двух классов эквивалентности ненулевых элементов
An(V). Эти два элемента считаются эквивалентными, если они
отличаются друг от друга положительным множителем.
Предположим, что в пространстве V есть невырожденное ска-
лярное произведение. Пусть {ei,...,en} будет ортогональным
базисом в V, с условием (е^,е^) = ±1. Два таких базиса от-
личаются друг от друга матрицей замены базиса В, для кото-
рой Det В = ±1. Таким образом, выбор ориентации V вместе
со скалярным произведением определяет единственный элемент
ei Л • • Л еп пространства An(V). Поэтому у нас есть также един-
ственный дуальный элемент из пространства An(V*), который
будем обозначать а.
Предположим, что мы рассматриваем дифференциальные
формы. Тогда в каждой точке пространства V мы получаем
единственный элемент ЛП(У*), другими словами, мы получаем
n-форму. Чтобы избежать громоздких обозначений (но рискуя
возможной путаницей), эту n-форму тоже будем обозначать а.
Итак, если V — Rn — n-мерное евклидово пространство, то
cf = dx1 Л dx2 Л • • • Л dxn.
Рассматривая пространство-время, договоримся время считать
первой координатой. Тогда для четырехмерного пространства
а = dt /\dx /\dy Л dz.
18.2. Звездный оператор
903
(Заметим, что в этом случае (ст, сг) = —1.)
Сейчас мы уже можем определить линейное отображение из
Л.к(У*) ъ Л.п-к(У*}, называемое звездным оператором. Для этого
будем идентифицировать и Afc(V*) и An~fe(V*) с пространством
линейных функций на An'fc(V*). Потом отождествим элементы
Afc(V*) и An-fe(V*), которые соответствуют одной и той же ли-
нейной функции. Такая идентификация Afc(V*) и An fc(V*) будет
называться звездным оператором.
Сначала покажем, как внешнее произведение вместе с выбо-
ром а е An(V*) приписывает каждому элементу А е Afc(V*) ли-
нейную функцию на пространстве An“fe(V*). Действительно, ес-
ли о» € An“fc(V*), то А Л си является элементом An(V*). Следова-
тельно, эта функция должна быть пропорциональна некоторому
множителю сг. Другими словами, мы можем написать
А Л си = /(си) ст.
Итак, каждый элемент А определяет линейную функцию
Ш /(ш).
При этом существует единственный элемент пространства
An“fc(V*), обозначаемый в дальнейшем *А, который определяет
ту же самую функцию /(си) из An-fc(V*) в К через скалярное
произведение
(*А,си) = /(си).
Таким образом, задав любой элемент A G Afc(V*), мы можем
определить *А € An~fe(y*) условием
А Л cu = (*А,си)сг
для всех cu е An-fc(V*). Заметим, что это определение звездного
оператора зависит от выбора ориентации. Изменение ориентации
меняет знак сг и, следовательно, знак *А.
Чтобы вычислить *А, в общем случае мы должны применить
это определение, используя в качестве си по очереди каждый ба-
зисный элемент An~fc(V*). Однако, если А является базисным эле-
ментом Afc(V*) вида dx4 Л • • • Л dxlk^ то нам достаточно рассмот-
реть только один базисный элемент An“^(V*), а именно тот си,
904
Глава 18. Звездный оператор
который содержит п — к множителей, не входящих в Л. В этом
случае Л Л си оказывается внешним произведением всех диффе-
ренциалов от dx1 до dxn в каком-то порядке, т. е. оно равно ±ст.
Тогда *А = ±си. Осталась единственная трудность — правильно
определить знак.
Общее определение
А Л cu — (*A,cu)cr
следует дополнить соглашениями для случаев к = п и к = 0.
Базисный элемент пространства Л°(КП) обозначим 1. При этом
скалярное произведение (1,1) = 1 и тривиальное внешнее про-
изведение 1 Л си = си Л 1 = си. Тогда если А = а, то нам надо
рассмотреть только базисный элемент cu — 1 и
ст Л 1 = (*А, 1)ст,
так что ★ст — 1. С другой стороны, если А — 1, то рассматриваем
ш = а и получаем
1 Л а — (*А, ст)ст.
В этом случае *1 = (ст, сг)сг. Это значит, что если мы работаем с
евклидовым скалярным произведением, для которого (ст, ст) = 1,
то мы имеем ★ст = 1 и ★! = а. Однако, в важном случае двумер-
ного или четырехмерного пространства-времени, со скалярным
произведением Лоренца, (ст, ст) = —1, следовательно,
★ст = +1, но *1 — —ст.
Вычисление звездного оператора лучше всего иллюстрирует-
ся на примерах.
Пример 1. В пространстве R2 имеется евклидово скалярное про-
изведение. Базис пространства ЛХ(У*) образован dx и dy с усло-
виями (dx, dx) = 1, (с?2/, dy) — 1 и ст ~ dx Л dy.
★ (dx Л dy) — 1 (верно всегда);
dx /\dy = (*dx, dy) dx A dy, поэтому *dx = dy;
dy A dx = (★dy, dx) dx A dy, поэтому *dy = —dx;
★ 1 = dx A dy, потому что (ст, ст) = +1.
18.2. Звездный оператор
905
Пример 2. Дано двумерное пространство-время, где определе-
но скалярное произведение Лоренца. В пространстве A1(V) име-
ется базис {dt,dx}, удовлетворяющий условиям (dt,dt) — +1,
(dx, dx) = — 1 и а = dt A dx.
*dt A dx = 1;
dt f\dx = (★dt, dx) dt A dx, поэтому *dt = —dx;
dx /\dt = (★ dx, dt) dt A dx, поэтому ★dx = —dt;
★ 1 = —dt A dx, потому что (ст, a) = —1.
Пример 3. В пространстве R3 определено евклидово скалярное
произведение. Базисом пространства A1(V) является {dx,dy,dz}.
При этом выполняются условия (dx, dx) — (dy, dy) = (dz, dz) ~ 1
и a — dx A dy A dz.
*(dx /\dy A dz) = 1
(dx A dy) f\dz = (*(dx A dy), dz)a, тогда ★ (dx A dy) = dz;
(dx A dz) /\dy = (*(dx A dz),dy)cr, тогда ★ (dx A dz) = —dy;
(dy A dz) t\dx — (*(dy A dz), dx)a, тогда *(dy A dz) = dx;
dx A (dy A dz) = (*dx, dy A dz)a, тогда *dx — dy A dz;
dy A (dx A dz) = (*dz, dx A dy)a, тогда *dy = —dx A dz;
dz A (dx A dy) = (*dz, dx A dy)a, тогда *dz — dx A dy;
★ 1 = dx A dy A dz.
Пример 4. Рассмотрим четырехмерное пространство-время, где
определено скалярное произведение Лоренца. Базисом простран-
ства A^V) является {dt,dx,dy,dz} с условиями (dt,dt) = 1,
(dx,dx) = (dy,dy) = (dz,dz) ~ — 1 и а = dt A dx A dy A dz.
Тогда
★ (dt A dx /\dy A dz) — 1.
Далее,
(dt A dx A dy) /\dz = (*(dt Ndx A dy), dz)a,
поэтому
★ (dt A dx A dy) — —dz.
906
Глава 18. Звездный оператор
Аналогично
* (dt /\dx Л dz) = +dy,
* (dt /\dy A dz) — — dx.
Кроме того,
(dx /\dy A dz) /\dt = (*(dx /\dy A dz), dt)a,
поэтому
* (dx /\dy A dz) = —dt.
Рассмотрим 2-формы:
(dt A dx) A (dy A dz) = (*(dt A dx), (dy A dz))a,
тогда
★ (dt A dx) — dy A dz.
Аналогично
★ (dt A dy) = —dx A dz,
* (dt A dz) = dx A dy.
Далее,
(dx A dy) A (dt A dz) — (*(dx A dy),dt A dz)a.
Тогда
★ (dx A dy) — —dt A dz.
Аналогично
★ (dx A dz) = dt A dy,
* (dy A dz) = —dt A dx.
Теперь рассмотрим 1-формы:
dt A (dx /\dy A dz) = (*dt, dx /\dy A dz)a.
18.2. Звездный оператор
907
Таким образом,
★dt = —dx /\dy Л dz.
Кроме того,
dx Л (dt /\dy Л dz) ~ (*dx, dt /\dy A dz)a,
так что
★dx = —dt /\dy A dz.
Аналогично
*dy — dt /\dx A dz,
*dz — —dt /\dx A dy.
И наконец,
★ 1 = —dt /\dx f\dy A dz.
Очевидно, что в приведенных примерах ★(★А) — ±А. Что-
бы сформулировать общее правило, в пространстве V выберем
ортогональный базис ei,...,en, при условии, что (е^,е$) = ±1.
Рассмотрим случай, когда А Е Afc(V*) является произведением
к векторов е*, и и является произведением оставшихся (п — к)
векторов е* с некоторым знаком ±. Допустим, что А и си таковы,
что А Л си — а (например, А = dx, cu — dy Л dz в пространстве R3).
Тогда *А = ±си и *си — ±А. Чтобы определить знаки, положим
★А — cicu и *cu — С2А. Тогда
а — А Л си = (★ А, си)<7.
Откуда
(★A,cu) — ci(cu,cu) = 1.
Кроме того, согласно правилу перестановки множителей во внеш-
нем произведении,
(4)*<nA = WAA = (*M<7>
откуда
(*w, А) = с2(А, А) = (—l)fe(n-/c).
908
Глава 18. Звездный оператор
Поскольку А и си являются базисными элементами, мы имеем
(A, А)(а>,а>) = (А Л А Л iu) = (а, ст).
Откуда
С!С2(а,а) = (-1)^4
Поскольку (ст, а) — ±1, мы можем перенести этот множитель в
другую часть уравнения. Тогда получим
★ (★А) == ci ★cu = С1С2А,
где
с1с2 = (-1^п-к\<7,а).
В силу линейности оператора ★, если все выписанные урав-
нения выполняются для каждого базисного элемента Afe(V*), то
они должны выполняться и для всех элементов Afc(V*). Итак, мы
доказали, что
= на Afc(V*).
Если п — нечетное число и (ст, ст) = +1, что справедливо
для пространства R3 с евклидовым скалярным произведением,
то *(*А) — А. Однако, в общем случае это не выполняется.
Используя только что полученный результат, т. е. что
мы можем вывести полезную формулу для скалярного произ-
ведения двух любых fc-форм. Сначала заметим, что поскольку
★★си = ±си, то четыре последовательных применения звездного
оператора приводят к тождеству, т. е.
★ = CU.
По определению звездного оператора
(★★★★A, cu)cr — ★★(★А Л о/) ~ (—сг)*А Л и
18.3. Интеграл Дирихле и лапласиан
909
выполняется для двух любых fc-форм Лио;. Следовательно,
(A,w)<t = (-l)fe<n-fe\a,a)*AAw
— cu Л *А(сг, сг).
Однако,
★★★сг = **(1) — (сг, сг)1.
Действуя оператором ★★★ на обе части уравнения, получаем
(А,си)(сг, сг)1 — Л *А)(сг, сг)1
или
(А, си) — ★★★(си Л *А) — ★★★(А Л ★си).
Еще один полезный результат получается из
(★А, ★си)сг — А Л ★CU.
Действуем оператором ★ на это уравнение и получаем
(★А, ★си) = ★(А Л ★си) — ★(си Л ★А).
С помощью полученных здесь формул скалярные произведения
могут быть записаны через звездный оператор.
18.3. Интеграл Дирихле и лапласиан
Пусть си обозначает /с-форму, а А - (fc - 1)-форму. Тогда
с/(А Л ★cu) = dX Л *cu + (—l)fc-1A Л d(*cu).
Поэтому для любой (ограниченной) области U мы имеем
f dX Л *си + (—l)fc-1 f AAd(*cu) = f d(AA*cu).
Ju Ju Ju
Предположим, что А или cu обращаются в нуль на границе dU (в
том числе если U неограничена и если А или си имеет компактный
910
Глава 18. Звездный оператор
носитель внутри U или если они стремятся к нулю на бесконеч-
ности достаточно быстро). Тогда по теореме Стокса имеем
I dX Л ★и + [ (—1)^ Л = 0.
Ju Ju
Действуя ★ на формулу (р,т) = ***(р Л *т), мы видим, что
dX Л = (dA, со)* 1.
С другой стороны, си является fc-формой, поэтому *си является
(п—&)-формой и, следовательно, d*co является (п—&+1)-формой.
Тогда
Л Л d*w = Л А
= (-i)(fc-i)(n-fc+i)(A5
Далее, *d*cu является формой степени п — (п — к + 1) — к — 1.
Тогда поскольку = id, получаем
*~^*ш — **(*d*co) = (—l)(fc-1)(n_fe+1)((7, &)*d*co
и
сг = (ст, сг)*1.
Таким образом,
А Л d*tO = (A, ***d*co)*l.
Итак, мы можем написать
dX Л *со + (—1)^ 1А Л ditto = [(dA,cu) + (—1)^ ^(А,* ^d*cu)]*l.
Значит, если А или to обращаются в нуль на границе dU (если
область U ограничена) или имеют компактный носитель (или
убывают достаточно быстро на бесконечности), то
I (dA, си) = I (А, (~l)k***d*ti?)(T.
Ju Ju
18.3. Интеграл Дирихле и лапласиан
911
Определим оператор d* согласно формуле
d*u> = (—1)^— (—1)^* 1d^cu.
Таким образом, d* отображает /с-формы в (к — 1)-формы. Для
произвольных fc-форм Лит давайте напишем
(Х,т)и = Du(X,t)(t = [ (А,т)ст.
Ju
В этом случае получим
Z)/7(dA,u) = Dt/(A,d*cj)
для А или си, равных нулю на границе dU (или достаточно быстро
убывающих на бесконечности).
Заметим, что
d*d* = О,
поскольку
dd ~ 0.
Давайте определим оператор Лапласа □, отображающий
fc-формы в fc-формы, формулой1
□ = dd* + d*T
Утверждается, что
□ d = dd,
□ d* =d*d,
= TtQ.
Чтобы установить равенство Dd = dd, заметим, что
□ d — (dd* + d*d)d — dd*d
и
dd — d(dd* + d*d) = dd*d,
хЭтот оператор □ отличается от лапласиана, определенного в предыду-
щих главах, знаком минус.
912
Глава 18. Звездный оператор
поскольку dd ~ 0. Аналогичное вычисление показывает, что
□ d* = d*CL
Доказательство равенства чуть сложнее, потому что
необходимо следить за знаками. Начнем с равенства
= (—r)k***d*w для А:-формы cu.
Заменив fc-форму cu на (п — &)-форму *си, мы имеем
d*CU = ( —1)П ^★★★d^'A'LU.
Поскольку d(**cu) является (fc + 1)-формой,
**d(**w) =
А поскольку си является А>формой,
**w = (a, <r)w.
Собирая вместе эти результаты и учитывая, что (<т,а)2 = 1, мы
получаем
d**u = (-l)’l-fc(-l)(fc+1)(n-fc-1)(-l)fc(”-fc)*dw
или
С этим результатом и формулой = (—доказатель-
ство становится совсем простым:
*rOu> =
★ □w = (-l)kd*du + (-l)fc+1d*dw.
В то же время
□ *cu = dd* -кш = d*d*w,
□ *w = (—l)fc+1d*do) + (-l)fc</*d*u>.
18.3. Интеграл Дирихле и лапласиан
913
Следовательно,
★П —
Оператор □ в пространстве R3. Вычислим явный вид лапла-
сиана в пространстве R3. Для функции / имеем
□/ = dd*f + d*df.
Однако, */ является 3-формой и dfl = 0 для любой 3-формы
в R3. Поэтому □/ = d*df. Далее,
df = —dx + —dy + — dz
dx dy dz
и
df , df , л ,
*— dx — — dy A dz.
dx dx
Отсюда
, df , d2f ,
d* — dx ~ —5- dx Ady A dz
dx dxz
и
„ (df j \ -ь df J d2f
\dx J dx dxz
Проделав аналогичные вычисления для остальных двух членов,
получаем
\dx2 dy2 dz2)'
Давайте вычислим лапласиан для 1-форм. В этом случае до-
статочно вычислить Пси для (j = adx. Оператор □ определяет-
ся только скалярным произведением и ориентацией. Поэтому он
коммутирует со всеми вращениями, и оси можно переставлять.
Тогда, если мы получим формулу для □(adx), то аналогичная
формула получится для □(bth/) и □(cdz). В силу линейности мы
будем иметь формулу и для adx + bdy + cdz. Итак,
7 \ 7 7 da 1 , da . .
d(a dx) = da Adx = — dy Adx + — dz A dx.
dy dz
Поэтому
/ 7/ j w da - da ,
*(d(adx)) — —— dz + — dy.
dy dz
914
Глава 18. Звездный оператор
Итак,
j j/ j \ j j ^2q> j j ®2(l j j d2(l j j
d*d(adx) = — — dxhdz— —~ dy/\dz~\--^—~- dx/\dy+ —dz/\dy.
dxdy dy2 dxdz dz2
Следовательно, используя свойство * — *-1 для 2-форм в прост-
ранстве R3, получаем
d2a d2a d2a d2a
d d(a dx) = *d*d(a dx) — ~ — dy — 7—5- dx + dz — —7 dx.
dxdy dy2 dxdz dz2
Далее,
d*(adx) = —*d*(adx) = —*d(adyf\dz)
/ da _ _ , \
= тг- dx A dy A dz I
\dx )
dx
Итак,
d2a d2a d2a
Отсюда следует, что
D(adx) — (JJa)dx
_ / d2a d2a d2a\
\<9x2 dy2 dz2) X
Таким образом, если or = a dx+b dy+c dz, то мы можем вычислить
□ cj, подействовав оператором □ на каждый член.
Произвольная 2-форма в пространстве R3 может быть запи-
сана как *0;, где (V является 1-формой. Поскольку мы
видим, что для 2-формы
Q = A dx Л dy + В dz Л dx + С dy Л dz
получается тот же результат
□ Q = (□ Л) dx Л dy + (□ В) dz /\dx + (□ С) dy A dz.
18.3. Интеграл Дирихле и лапласиан
915
Аналогично для 3-формы
□(р dx Л dy Л dz) = (Пр) dx /\dy Л dz.
Итак, в обычных прямоугольных координатах в пространстве R3
мы можем вычислить □ для любой формы, действуя оператором
□ на каждый коэффициент.
А теперь давайте повторим рассуждения из последнего пара-
графа главы 17 — сведение уравнений магнитостатики к уравне-
нию Пуассона. Предположим, что выбраны такие единицы, для
которых р — 1. Тогда положим
j =
Теперь уравнения можно записать в виде
dB = 0,
d*B = 4ttj.
Выберем такое А', чтобы
dA' = В.
(Это возможно, так как мы предположили, что Н1 = 0.) Решаем
уравнение Пуассона
□ V> = d*A'.
Заменяем А* на
А - А' - d^
и получаем
dA = B.
Поскольку 'ф является функцией, то
□ ^ = d*d^ = d*A'.
Следовательно,
d*A = d*Af - d*d^ = 0.
Итак наше второе уравнение принимает вид
d*dA =
916
Глава 18. Звездный оператор
или, поскольку d*A = О,
□А = 4%).
Кажется, будто в этом доказательстве мы использовали тот
факт, что В является 2-формой, А — 1-формой, а ф — функцией.
На самом деле это верно в общем случае. Пусть В является к-
формой в n-мерном пространстве. Мы хотим решить уравнения
dB = 0,
d*B = 4ttj.
Предположим, что рассматриваемая область такова, что В = dAf
для некоторой А'. Тогда решаем уравнение Пуассона
D^ = d*A'.
Напишем
А - А' - d^.
Тогда
d*A = dd*^.
Следовательно,
dd*A = О
и
□ A = (dd*+d*d)A-47rj.
Таким образом, мы опять свели задачу к решению уравнения
Пуассона.
18.4. Оператор □ в четырехмерном
пространстве-времени
Рассмотрим четырехмерное пространство-время с координатами
£, z, 1/, z и скалярным произведением, для которого выполняются
18.4. Оператор □ в четырехмерном пространстве-времени 917
условия (dt,dt) ~ 1, (dx,dx) = (dy^dy) = (dz.dz) — —1. Подей-
ствуем оператором □ на функцию
□/ = d*df
= -*“Ч* (^-dt + ^dx + ^-dy + ^-dz\
\ dt дх ду dz J
(д f df
— dx Л dy Л dz — dt Л dy Л dz
dt dx
+ dt /\dx /\dz - ^J~dt /\dx A dy |
dy dz J
( d2f d2 f Q^f d2f\
= "*”1 \ dt2 + d^ + Ж? + ^)^AdxAdyAdz.
Откуда
dt2 dx2 dy2 dz2
В качестве 1-формы сначала рассмотрим a dt. Получим
,, , , да , ,, да , , да , „
d(a dt) = — dx Л dt + — dy A dt + — dz A dt,
dx dy dz
тогда
,, , . да , , да , , да , ,
*d(a dt) = — — dy Adz + 7— dx A dz — — dx Л dy
dx dy dz
и
d2a
d*d(a dt) = . dt Ady A dz
dtdx
^2° j. j d2a
+ 7 dt /\dx /\dz — 7—7 dx Ady A dz
dydt dy2
52a d2a ,
— „ 7 dt Adx Ady — 777? dx Ady A dz.
dzdt dz2
Следовательно,
d*d(adt) — * ^d+dtadt)
/ d2a d2a d2a\ d2a d2a d2a
= + d^ + d^)dt+ dxdt dx + dydt dy + tedt dZ‘
918
Глава 18. Звездный оператор
С другой стороны.
d*(adt) — — * 1d*(ad£)
= *~xd(adx f\dy A dz)
~ida 1
— * — dt Л dx Л dy Л dz
dt y
_ да
dt
Откуда
d2 01 At d2 a A d2 a r! 92 a Л
M(a<U} = -^,U-—dx-—dv--^dz.
Итак, получаем
O(adt) — (Da)dt —
d2a d2a d2a d2a\
dt2 dx2 dy2 dz2 )
Аналогичное вычисление (или использование вращательной ин-
вариантности2) показывает, что
D(bdx) = (Db)dx,
D(cdy) = (Oc)dy,
и так далее.
То же самое выполняется и для 2-форм. Например, рассмот-
рим a dt /\dx. Получим
d*(adt Л dx) — 'k^d+iadt Л dx)
— 'k~1d(ady Л dz)
_i (да . , , \ 1 (да ,
— ★ — dt Л dy Л dz + ★ — dx Л dy Л dz
\dt J \дх
да , да _
= — — dx — — dt.
dt дх
2 Здесь под вращениями следует понимать собственные преобразования
Лоренца, сохраняющие лоренцево скалярное произведение и ориентацию
пространства-времени. — Прим. ред.
18.4. Оператор □ в четырехмерном пространстве-времени 919
Откуда
d2a d2a\ д2а д2а
хтт + ТГ?. ] dt Л dx- —- dy Л dx- dz Л dx
dt2 дх2 J dtdy dtdz
d2a d2a
- dt/\dy — dt A dz.
dxdy dxdz
С другой стороны,
da da
d(a dt A dx) = — dy /\dt /\dx + — dz /\dt A dx,
dy dz
поэтому
, x da 1 da 1
*d(adt A dx) = —— dz + — dy
dy dz
и
, , ч (d2a d2a\ d2a
d*d(a dt A dx) — - + 7—7 I dy A dz — - — dx A dz
\dy2 dz2 ) dydx
d2a _ _ d2a d2a
- dt/\dz+ ^-7- dt A dy + dx A dy.
dydt dzdt dxdz
Тогда
d*d(adt A dx) — — *~ld*d(adt A dx)
и
□(a dt A dx) = (□ a) dt/\dx ~
d2a d2a d2a 52a\
dt2 dx2 + dy2 + dz2 J
dtAdx.
Мы предоставляем читателю самостоятельно проверить, что
D(bdx A dz) = (□ b) dx Л dz.
Итак, мы получили, что для любой 2-формы, записанной через
di, dx, dy, dz, действие оператора □ равносильно действию это-
го оператора на коэффициенты. Справедливость аналогичного
утверждения для 3- и 4-форм вытекает теперь из рассмотренных
случаев 0-, 1- и 2-форм и равенства *□ —
920
Глава 18. Звездный оператор
18.5. Алгебра Клиффорда
Теперь читатель уже, должно быть, догадался, что в пространст-
ве мы можем вычислить действие оператора □, записанного
в евклидовых координатах, на произвольную А;-форму как дей-
ствие этого оператора на каждый коэффициент. Кроме того, уже
понятно, что если мы попробуем доказать этот результат теми
же методами, которые использовались в последних двух пара-
графах, то просто запутаемся. Цель этого параграфа — ввести
алгебраический формализм, который позволит нам доказать все
очень просто. В этой книге нам больше не понадобятся резуль-
таты данного параграфа — ведь мы уже доказали результаты в
важных случаях трех и четырех измерений. Однако, излагаемые
здесь идеи оказались очень важными в современной физике.
Наше доказательство будет основано на следующем свойстве
т) = сГт) + граничные члены.
Это свойство можно перефразировать, говоря, что d* является
формальным сопряжением d. Слово «формальный» означает «по
модулю граничных членов». У нас есть равенство
Du(dcj,r) = Du(co,d*r),
только когда делаются различные предположения, которые га-
рантируют отсутствие вклада от границы. Давайте рассмотрим
эту ситуацию в более общем случае.
Пусть Е и F обозначают векторные пространства, в каждом
из которых имеется свое скалярное произведение. Тогда мы мо-
жем идентифицировать Е с Е* и F с F*. В частности, если
А : Е F - линейное отображение, то мы можем рассмат-
ривать А* : F* —> Е* как линейное отображение А* : F —> Е.
определенное условием
(e,A*/h = (Ae,f)K,
где (-5-)в и обозначают скалярные произведения в про-
странствах Е и F соответственно. Теперь предположим, что
18.5. Алгебра Клиффорда
921
в векторном пространстве V мы выбрали систему координат
Х1,... ^хп. Тогда соответствующая форма объема имеет вид
(j = dx± Л • • • Л dxn.
Рассмотрим пространство гладких функций из V в Е1 обозначае-
мое F(V, Е). Если иг и U2 — такие функции, a U — ограниченная
область, то можно определить
Du(ui,u2) = / (t4i,iz2)Ecr.
JU
(Если область U не ограничена, то все равно мы можем опре-
делить Du для тех пар функций, которые достаточно быстро
убывают на бесконечности.) Можно рассмотреть операторы L из
Е) в F). Тогда каждой функции и Е Е) ставится в
соответствие элемент Lu пространства F). Оператор L назы-
вается линейным дифференциальным оператором первого поряд-
ка^ если существуют такие линейные отображения А± : Е —► F,
Д : В —> F, ..., Ап : Е —> F и В : Е —> F, что
_ А 9и А ди
Lu = Ai —----!-••• + Апъ---1" ^и.
ОХ± иХп
В общем случае отображения Ai,..., Ап и В могут зависеть от
точки в пространстве V, т. е. Ai и В — это функции в простран-
стве V, значения которых являются линейными отображениями.
Тогда предыдущее уравнение можно записать в форме
ди
(Lu)(x) = А1(ж) —(ж) Н-----1- Ап(ж)-—(ж) + В(ж)и(ж).
UX OX/ji
Если AiH В постоянны, то мы говорим, что L является линейным
дифференциальным оператором первого порядка с постоянными
коэффициентами.
Теперь пусть и Е F(V, В) и v Е F(V, Е). Тогда
д ( ч (dAi \ ( ди \ ( dv\
— (AiU,v)F = ,v + Atu, —
uXi \ dxi J p \ dxt J p \ dxi J p
( . du \ ( f дАЛ* \ / л*ди\
= Ai —+ lu, I 7—) и + «,А;—-
\ dxi J p \ \ dxi J J p \ oxi J p
922
Глава 18. Звездный оператор
Поэтому
л* А
С7Хг / £
Итак, если мы определяем
то
о
(Lu,v)f = (u,L*v)e + 52
Последний член справа сводится к умножению граничного
члена на а и интегрированию. Действительно, если мы напишем
д
т = -— (Aju, v)f dx2 Л • • • Л dxn
dxi
д
— —— (А2и, v)р dx\ Л dxs Л • • • Л dxn + • • • ,
0x2
то
dr
iU, v)р dxi Л • • • Л dxn
Тогда
Таким образом, оператор L* является формально сопряженным
оператора L.
Строго говоря, fc-форма cv не является функцией из простран-
ства V в фиксированное векторное пространство. (Потому что
а>(х) является элементом пространства кососимметричных поли-
линейных fc-функций на касательном пространстве в точке х, а
касательное пространство изменяется от точки к точке.) Однако,
как только мы выбрали систему координат, fc-форму cv можно
рассматривать как функцию из V в Afc(V*). Таким образом, мы
18.5. Алгебра Клиффорда
923
можем считать, что Е = Afe(V*). Если мы хотим в качестве диф-
ференциального оператора L взять d, то полагаем F = Afc+1(V*).
Тогда можно написать
J д д
d — £1 д--h • • • + 5
(7X1 (7X^2
где обозначает линейное отображение Afe(V*) —> Afc+1(V*),
состоящее из внешнего умножения на dx&, т. е.
= dxk Л ал
Теперь для вычисления d* нам нужна формула для Утвер-
ждается, что
= ±г > причем знак соответствует (dx^,dxfc) = ±1.
Чтобы это доказать, предположим, что к = 1 (это просто
вопрос обозначений) и исследуем, что происходит с базисными
элементами
oj — dxi± Л • • • Л dxik
пространства Л*(У) и базисом A/c+1(V*). Существует две возмож-
ности.
(а) «1 = 1. Тогда Siiv = 0. С другой стороны, для
т = dxj± Л • • • Л dxjn
мы имеем
(д 'Х
—— ) т = 0 (если Ji > 1)
<7X1 /
и
(д \
—— I т — dxj2 Л • • • Л dxjn (если Ji = 1).
(7Х 1 /
В любом случае мы имеем
(f д \ \
I т;— I т I — 0.
\<7Х1/ /
924
Глава 18. Звездный оператор
(b) > 1. Тогда
Sio; = dx\ Л dxir Л • • • Л dxik
и
д \ ГО,
-— ) т =
uxi J dxj2 Л • • • Л dxjk+1
если Ji > 1,
если ji — 1.
В этом случае
если ji > 1.
Если же ji = 1, то мы по-прежнему имеем
кроме случаев, когда j2 = ii, = i% и так далее. Если j*2 — й,
j3 = г2 и т.д., то
(sicu,r) = (dxi,dxi)(cu,cu),
а
Это доказывает, что
ej = (dxi,dxi)i
В общем случае доказательство показывает следующее. Пусть
L : V —> V* обозначает линейное отображение, определенное ска-
лярным произведением в пространстве V. Пусть 0 — произволь-
ная 1-форма и е(0) — внешнее умножение на 0. Тогда
Определим
Lp — ±г
— £
18.5. Алгебра Клиффорда
925
Мы показали, что
Из антикоммутативности внешнего произведения следует, что
epeq + eqep = 0 для всех р и q.
Следовательно (или непосредственно из свойств внутреннего про-
изведения),
ьрьд + bqbp = O для всех р и q.
Если р ф д, то внешнее умножение на dxp и внутреннее умноже-
ние на г(3/3хд) удовлетворяют равенству
i
e(dxp) + e(dxp)i
Действительно, достаточно проверить это равенство для р — 1,
q — 2. Это простое вычисление мы оставляем читателю. С другой
стороны, для базисных элементов ш мы имеем
i ( -— 1 e(dxi)cu = <
\9xiJ I cu,
/ , ( д \ cu,
£(dxi)z —- cu = <
\dxxj О,
если cu = dxi Л • • ,
если cu = dx2 Л • • • ,
если cu = dxi Л • • • ,
если cu = dx2 Л • • • .
Таким образом,
. ( д \ . , ч , , х. ( д \
г ~— €(dxi) + б(с(Х1)г -— = id.
\&Г1/ \dxij
Естественно обобщая со случая х± на случай хр1 можно сделать
вывод, что
tpSp + £pLp ~ ±id, где ± соответствует знаку (dxp, dxp).
926
Глава 18. Звездный оператор
И наконец, поскольку операторы tp и eq постоянны (в нашей
системе координат), то мы имеем
Итак, мы доказали формулу для □ в евклидовых координатах.
В случае положительно определенного скалярного произведе-
ния операторы ер и bq имеют очень важное значение в квантовой
физике, где они известны как операторы рождения и уничто-
жения фермионов. Равенства
£p£q + £q£p — 0, ^p^Q ^Q^P —
_ Jo, p q,
£pbq ~h Lq£p — \
(i, p = q
называются антикоммутационными соотношениями для этих
операторов.
Алгебра, порожденная этими операторами, т.е. множество
всех сумм и произведений ei и является частным случаем се-
мейства алгебр, построенного Клиффордом в девятнадцатом ве-
ке. Эти алгебры, т. е. множества объектов, для которых опреде-
лены операции сложения и умножения, были разработаны Клиф-
фордом как обобщение систем комплексных чисел и кватернио-
нов Гамильтона. Они играют очень важную роль в современной
физике, поэтому мы и расскажем здесь о них.
Начнем с переформулировки предыдущего примера антиком-
мутационных соотношений между операторами рождения и уни-
чтожения фермионов. Пусть V — векторное пространство, а V*
— его дуальное пространство. Рассмотрим пространство прямой
суммы W = V ф У*. Тогда вектором пространства W является
18.5. Алгебра Клиффорда
927
w = (V ), где v G V и a EV*. Определим скалярное произведе-
ние в пространстве W формулой
(w,w') = |(a(v') + a'(v)),
где
Пусть vj,..., vn образуют базис пространства V, а а1,..., ап —
дуальный базис пространства V*. Тогда вектора
образуют базис пространства W. Обозначим эти вектора ер и ig,
т.е. положим
. _ ( ° \
19 _ U9/
В этом случае
(вр, вд) 0, (ip, 1g) О,
О, если р ф q
Теперь мы можем записать антикоммутационные соотношения
для Si и Li в краткой форме. Будем считать, что ер соответствует
ер, a Lq соответствует iQ, т.е. рассмотрим линейное отображение
7, определенное формулами
7(ер) = £р,
'У(ч) = ч-
Тогда для
w = viei Ч------F- vnen + cJii Ч---1- ап\п
928
Глава 18. Звездный оператор
получаем, что
7(w) = viei 4----1- vnen + а1^ 4--1- anin
является элементом нашей алгебры и
7(w)?(w/) + 7(w/)7(w) ” 2(w,w')id.
Это можно обобщить на любое векторное пространство W, име-
ющее скалярное произведение (•,•) (возможно, вырожденное).
Итак, каждому векторному пространству W со скалярным про-
изведением (•, •) соответствует ассоциативная алгебра3 С(1У), на-
зываемая алгеброй Клиффорда для W и (•,•). Должно существо-
вать такое линейное отображение 7 : W —> С (ТУ), что
(i) каждый элемент C(W) может быть записан в виде суммы
произведений элементов 7(ТУ) (и кратных К);
(ii) 7(w)7(w9 +7(w')7(w) — 2(w,w')I.
(Когда мы говорим «алгебра Клиффорда для ...», то подразу-
мевается теорема — для данного пространства W со скалярным
произведением (•, •) существует алгебра С(Ж), удовлетворяющая
условиям (i) и (ii). При этом С(ТУ) единственна с точностью до
изоморфизма. В приложении к этой главе мы дадим краткое до-
казательство этой теоремы.)
Давайте рассмотрим несколько примеров.
(а) Пусть одномерное пространство W имеет отрицательно
определенное скалярное произведение. Это значит, что сущест-
вует вектор е, для которого
(е,е) = -1
и каждый элемент пространства V кратен е. Согласно (ii),
7(e)2 = -1,
3Под ассоциативной алгеброй А мы подразумеваем, что А является век-
торным пространством с билинейным отображением А х А А, называемым
умножением. Предполагается, что это умножение удовлетворяет ассоциатив-
ному закону и что для него существует нейтральный элемент I.
18.5. Алгебра Клиффорда
929
а условие (i) говорит нам, что каждый элемент C(W) можно
записать в форме
al + 67(e).
Если положить 7(e) = i, то сразу видно, что C(VK) оказывается
алгеброй комплексных чисел.
(Ь) Пусть V = R2, причем скалярное произведение противо-
положно обычному. Тем самым
(v, v) = ~х2 - у2,
Пусть
Условие (й) говорит, что
i2 - -I,
j2 = -I
и
ij + ji = 0.
Тогда условие (i) означает, что каждый элемент C(IV) можно
записать в форме
al + Ы + cj + dk,
где мы положили
k = ij.
Тогда
k2 = ijij = —iijj = -I,
так что
i2 = j2 = k2 = -I.
Кроме того,
ij = k,
jk = jij = — ijj = i,
ki = iji = iij = j,
930
Глава 18. Звездный оператор
а
kj = ijj = —i
И
ik = iij = -j.
Подведем итоги:
i2 =j2 =k2 = -I,
ij = k, jk = i, ki = j,
ij = - ji, jk = -kj, ik = -ki.
Эта алгебра называется алгеброй кватернионов. Впервые она бы-
ла найдена Гамильтоном.
В общем случае для проверки условия (ii) достаточно пока-
зать, что
7(w)2 = (w,w)I.
Действительно,
y(w + w')2 = [?(w) + 7(w')]2
= 7(w)2 + 7(w)7(w') + 7(w')7(w) + 7(w')2
и
7(w + w')2 = (w + w', w + wz)ll
= (w, w)H + 2(w, w')H + (wz, w)I,
т. e. условие (ii) доказано.
Приняв это во внимание, возьмем W = R1’3, т.е. пусть W
будет пространством-временем с лоренцевой метрикой. Положим
W А\ х 1 У 1 V/ и 7(w) = ( 0 0 t — z \-ж + iy 0 0 -x - iy t + z t + z x — iy 0 0 x + iy t — z 0 0
Тогда
/1 o 0 0\
7(w)2 = (t2 - x2 - у2 - 2, 0 1 Z } 0 0 0 0 1 0
\0 0 0 V
18.6. Звездный оператор и геометрия
931
Итак, если единичную матрицу 4x4 обозначить I, то условие (ii)
будет выполнено. По существу мы можем рассматривать C(W)
как определенную подалгебру алгебры комплексных матриц 4x4.
Эта алгебра C'(VK) называется алгеброй Дирака. Она была разра-
ботана Дираком, когда он исследовал электрон. Сейчас она иг-
рает важную роль в теории элементарных частиц.
(с) Пусть W — произвольное векторное пространство, а ска-
лярное произведение (•, •) тождественно равно нулю. Тогда усло-
вие (ii) говорит, что
7(w)7(w') = - 7(w')7(w)
для любых w и w'. В этом случае C'(iy) оказывается в точности
внешней алгеброй A(VK).
18.6. Звездный оператор и геометрия
В главе 16 мы видели, что звездный оператор, действующий из
AT(R3) в A2(R3), определяет евклидово скалярное произведение
в пространстве R3. Это не что иное, как математическое выра-
жение того факта, что диэлектрические свойства вакуума опре-
деляют евклидову геометрию пространства.
Сейчас мы можем поставить следующий вопрос. Пусть V
обозначает векторное пространство с заданной ориентацией, и
пусть (•,•) и (•,•)' — два невырожденных скалярных произведе-
ния в пространстве V. Предположим, что при некотором fc, где
1 < k < п = dim V, они дают один и тот же звездный оператор
из Afc(V*) в An“fc(V*). Значит ли это, что (-,-) — (•,-)/? Ответ
почти утвердительный. Рассмотрим несколько примеров.
Возьмем V = R2 с обычным скалярным произведением. Тогда
мы можем AX(R2*) идентифицировать с R2. Как мы уже видели,
звездный оператор ★ : AX(R2*) —> AX(R2*) в этом случае является
просто поворотом на девяносто градусов. Всякое другое скаляр-
ное произведение в пространстве R2 (или в R2*) определяется
формулой
(u, v)' = (Au, v),
932
Глава 18. Звездный оператор
где А — симметричная матрица. Если (•,•)' определяет тот же
самый оператор, то мы должны иметь равенство
(★u, *v)' — (u, v).
Откуда
R~rAR = А.
Однако, если RAR1 = А для некоторого нетривиального вра-
щения R (не на 0 или 180 градусов), то А должна быть пропор-
циональна единичной матрице.4 Тогда
(u, v)' = А(и, v),
где А — число, отличное от нуля.
Мы сейчас покажем, что (•,•)' при А > 0 определяет тот же
самый оператор ★. Таким образом, на плоскости оператор ★ не
определяет геометрию Евклида, но определяет конформную гео-
метрию. Этот факт является основой теории функций комплекс-
ного переменного. Введение в эту тему мы изложим в главе 20.
Давайте посмотрим, как в общем случае масштабное преоб-
разование (замена v на cv, где число с отлично от нуля) действует
на оператор ★. При умножении длины на с площадь умножается
на с2, объем умножается на с3 и так далее. Поэтому в простран-
стве A.k(V*) мы умножаем на ck. Тогда, чтобы масштабный мно-
житель с не оказывал никакого эффекта, должно выполняться
равенство
( „к X _ Jc \ л /с, .
(с Л,с си)с сг = с ЛЛс CU.
Чтобы получить ту же линейную функцию си, мы должны иметь
с2к~п = 1.
Итак, при k — п/2 масштабное преобразование не влияет на
★ : Afc(V*) —> Afc(V*). Несложно доказать, подобно тому как
мы делали это в главе 16 для ★ : A1(R3*) —> A2(R3*), что во
всех остальных случаях звездный оператор определяет скалярное
произведение однозначно.
Аналогичное утверждение справедливо в евклидовом пространстве лю-
бой размерности; доказательство оставляем в качестве упражнения. —
Прим. ред.
18.7. Звездный оператор и векторный анализ
933
Вернемся к очень важному вопросу, который мы здесь толь-
ко слегка затронем. Вспомним, что обсуждая диэлектрическую
постоянную, мы допускали возможность, что £ может быть пере-
менной симметричной матрицей
£хх &ху &xz
£ух ёуу £yz
&ZX £zy &zz
все элементы которой являются функциями в пространстве R3.
Но тогда возникает мысль, что само понятие длины должно ме-
няться от точки к точке, т. е. что скалярное произведение двух
касательных векторов £ = (x,v) и г] = (z,w) в точке х дается
формулой
где и — координаты векторов v и w. Идея, что скалярное
произведение может меняться от точки к точке, впервые была
высказана Риманом и с тех пор является одной из основ геомет-
рии. В частности, именно отсюда пошла теория относительности
Эйнштейна. Теория звездного оператора без проблем распростра-
няется на риманову геометрию.
18.7. Звездный оператор и векторный анализ
Как обычно, существование скалярного произведения устанавли-
вает соответствие между пространством V и его дуальным про-
странством У* — ЛХ(У), которое можно использовать для иден-
тификации дифференциальной формы с векторным полем. Для
удобства обозначений векторное поле, связанное с дифференци-
альной формой, будем помечать тем же символом со стрелкой
над ним, т. е. если А — 1-форма, то А обозначает векторное поле,
связанное с ней формулой
cu[A] = (A, cu) для всех 1-форм си.
Итак, если имеется векторное поле
А = Aiei + А%е2 + • • • ,
934
Глава 18. Звездный оператор
то связанная с ним 1-форма
А — ±Ai dx1 ± А% dx2 Ч---,
где знак каждого члена выбирается в соответствии со знаком
(е^е^) = ±1. В частности, в пространстве R3 с евклидовым ска-
лярным произведением, если
А ~ AXGX “h AyGy J-
то
A = Ax dx + Ay dy + Az dz.
Для четырехмерного пространства-времени с лоренцевым ска-
лярным произведением, если
А — A^Gt + Axgx + AyGy + Azgz,
то
A — At dt — Ax dx — Ay dy — Az dz.
Теперь в пространстве R3 мы можем записывать операции
векторного анализа через звездный оператор и оператор d. Тогда
скалярное произведение5 можно записать в виде
АВ = *(А Л *В) = *(В Л ★>!),
а векторное произведение в виде
А х В = *(А Л В).
Дифференциальные векторные операторы принимают вид
grad / = df,
rot А = *dA,
div A = *d*A.
5 Читателю следует отличать скалярное произведение из векторного ана-
лиза (dot product), имеющее физико-геометрическую природу, от соответ-
ствующего термина линейной алгебры (scalar product) с его формальным
определением. Это объясняет различие в английских названиях и в обозна-
чениях. — Прим. ред.
18.7. Звездный оператор и векторный анализ
935
В системах координат, отличных от декартовой, связь между
векторным полем А и дифференциальной формой А устанавлива-
ется, если сначала построить ортонормированный базис 1-форм
в каждой точке. Например, в цилиндрических координатах dr,
г dd и dz являются ортонормированными 1-формами, дуальными
к (единичным) базисным векторам ёг, ё# и ёг. Тогда
A — Aj'G^ + Аеее ~Н Azgz
соответствует 1-форме
А — Ar dr + A#(r dO) + Az dz.
Аналогично в сферических координатах dr, rdf), г sin 0 d<fr — ор-
тонормированные 1-формы, дуальные к базисным векторам ёг,
ее, ёф. Тогда
А = Агёг + Аеёе + Афёф
соответствует
А = Аг dr + Aer dO + АфГ sin 0 d<£.
Теперь очень просто вычислять div, grad, rot в цилиндриче-
ских или сферических координатах. Правило применения опе-
ратора d одинаково во всех системах координат. Звездный опе-
ратор действует на ортонормированный базис {dr,r d0,dz} или
{dr, г d0, г sin 0d</>} точно так же, как и на базис {dx,dy,dz}. На-
пример, мы хотим вычислить rot А в цилиндрических координа-
тах, используя rot А = *dA:
А = Агёг + Аеёе + Агёг,
А = Ardr + Aer dO + Az dz,
. . (9AZ д(гАе)\ 1 , ,Л , x (dAr 9AZ\
dA = ( —---------- I -{rdO A dz) + I —-— ) {dz A dr)
\ dO dz J r \ dz dr J
(d{rAe) dAr\ , д .
Л
.. (dAz d{rAe)\l.(dAr dAz\
\ dO dz J r \ dz dr J
{ d{rAe) dAr \ 1
+ ----------- dz-
\ dr dO J r
936
Глава 18. Звездный оператор
Теперь заменяем dr на ёг, rdf) на ё# и dz на ez и получаем
rot А =
ЭАД Л
д(гАо) <ЭАГ\ 1.
дг дО ) rGz'
Аналогично вычисляется дивергенция радиального вектора в
сферических координатах, используя div А = *d*A:
А = Агёг,
А = Ar dr,
-kA = Ar(r dO Л r sin в dtp) = г2Ar sin 0 dd Л dp,
dkA = sjn 0dr /\d0 f\dp
dr
1 c)(r2 Д.) .
= —-—- dr Л r d0 /\ r smddp,
r£ or
1 d(r2Ar) -
*d* A = —-—- = div A.
H or
Итак, секрет состоит в том, что сначала надо выразить все диф-
ференциальные формы через ортонормированные 1-формы и
только потом действовать звездным оператором.
Приложение: тензорные произведения
Для того, что мы делаем в этой книге, очень важно понятие
тензорного произведения двух или более векторных пространств.
Это одно из основополагающих понятий в теории векторных про-
странств. Мы должны здесь дать его краткое изложение, потому
что оно отсутствует во многих учебниках по элементарной линей-
ной алгебре.6
6 Этим недостатком не обладают большинство учебников линейной алгеб-
ры на русском языке. С другой стороны, необходимо отметить, что в этой
книге авторы так и не приводят явного определения тензора — столь же
фундаментального понятия линейной алгебры (и не только), включающего
в себя большинство изучаемых ею объектов и давшего название изучаемой в
этом приложении операции над векторными пространствами. — Прим. ред.
Приложение: тензорные произведения
937
Пусть у нас есть векторные пространства V, W и U. Отобра-
жение f : V х W —* U называется билинейным, если
/(vi + v2, w) = /(vi, w) + /(v2, w),
/(v, wx + w2) = /(v, Wl) + /(v, w2)
и
/(av,w) = a/(v, w) — /(v,aw) для скаляра a.
Другими словами, отображение f называется билинейным, если
оно линейно по v при фиксированном w и линейно по w при
фиксированном V.
Известным примером, когда V = W — U, является векторное
произведение в обычном трехмерном пространстве.
Взяв пространства V и IV, мы хотим построить векторное
пространство Z и билинейное отображение b : V х W —> Z, ко-
торое будет универсальным в следующем смысле. Предположим,
что f : Vx W —> U - произвольное билинейное отображение. Тог-
да существует единственное линейное отображение If : Z —> U
такое, что
f = lfob.
На диаграмме это можно изобразить так:
Таким образом, для любого f существует единственное линейное
отображение I/, для которого If о Ь = /, т. е. диаграмма коммута-
тивна.
Заметим, что если b и Z существуют, то они единственны с
точностью до изоморфизма. Действительно, предположим, что
Ь' и Z' — другое универсальное билинейное отображение. Тогда,
положив U — Z1 и f ~ У а нашей диаграмме, мы получим
V х W-------^Z
938
Глава 18. Звездный оператор
Таким образом, имеем отображение Zy : Z —> Z' с
У = I# о Ь.
Аналогично получаем линейное отображение Z& : Z' —► Z с
b = 1Ь о У.
Но тогда
b = (/(>oZb/)ob.
В то же время
Значит, I = id и I = 1Ь о Zy удовлетворяют уравнению
b — lb.
В силу единственности мы приходим к выводу, что
1ъ ° h' — id
и аналогично
Zy О lb = id.
Таким образом, Zy дает изоморфизм Z с Z' и У — Zy о Ь. Поэтому
с точностью до изоморфизма b и Z определены однозначно.
Наша задача состоит в том, чтобы показать существование
такой пары (Ь, Z). Мы здесь приведем два построения, которые
на первый взгляд выглядят различными. Однако в силу единст-
венности они должны давать одинаковый результат.
Пусть Y обозначает пространство всех скалярных билиней-
ных функций, определенных в пространстве V х W. Тогда а € У
является билинейным отображением V х W —> R. Очевидно, что
множество всех билинейных функций а образуют векторное про-
странство Y. Возьмем
Z-У*.
Приложение: тензорные произведения
939
Тогда вектор в пространстве Z является линейной функцией на
пространстве У. Отображение b : V х W —* Z определим форму-
лой
[b(v,w)](a) = q(v,w).
Это значит, что b(v, w) является такой линейной функцией, ко-
торая каждой билинейной функции а приписывает значение
a(v, w). Очевидно, что b(v,w) зависит линейно от а и билинейно
от v и w. Утверждается, что b и Z дают решение нашей общей
задачи.
Действительно, пусть f : V х W —> U — билинейное отобра-
жение. Здесь U обозначает векторное пространство. Для каждого
v е U* мы получаем билинейную функцию
у о f е У.
Итак, мы определили линейное отображение /* : U* —> У:
/*(р) = г/о/.
Отсюда получаем его сопряженное Г* : Z — У* —> {/**. По
определению
Z**(b(v, w))(i/) = b(v, w)(Z*(i/))
= (/»)(v,w)
= (^°/)(v,w)
= ^(/(v,w)).
Другими словами, Z**(b(v,w)) оказывается той линейной функ-
цией в пространстве U*, которая каждому у приписывает чис-
ло ^(/(v,w)). А сейчас вспомним, что существует канонический
изоморфизм7
U Л J7**,
где каждый элемент u G U идентифицируется с линейной функ-
цией i(u) на пространстве [/*, согласно формуле
i(u)(p) = i/(u), ие (7, у G U*.
7Напомним, что он называется отображением вычисления. В дальнейшем
для значения элемента a G U* на векторе и € У также используется «сим-
метричное» обозначение (о, и) = (и, а) = г(и)(а) = а(и). — Прим, ред.
940
Глава 18. Звездный оператор
Тогда мы можем написать
Z**(i>(v,w)) = i(/(v,w)).
Используя эту идентификацию г, можно написать Z** = г о /, где
I является отображением Z —> (7. Итак, мы нашли отображение
I : Z —► Z7, удовлетворяющее условию
l°b = f.
Предположим, что существует два таких отображения. Тогда для
их разности т следует, что
(т о b)(v, w) = 0 для всех v, w € V.
Значит,
m*(p)(b(v, w)) = 0 для всех v е U*.
Итак, е Y является такой билинейной функцией на про-
странстве V х W, которая приписывает 0 всем парам (v,w), т. е.
т*(р) является нулевой билинейной функцией. Поскольку т* пе-
реводит все элементы пространства U* в нуль, это нулевое линей-
ное отображение. Отсюда следует, что т — 0. Таким образом, мы
доказали единственность I.
Пространство Z называется тензорным произведением про-
странств V и W и обозначается V ® W. Кроме того, мы будем
пользоваться обозначением
Z>(v, w) = v ® w.
Предположим, что пространства V и W конечномерны. Пусть
{ei,..., em} — базис пространства V, a {fi..., fn} — базис про-
странства W. Тогда билинейная функция (3 на пространстве
V 0 W полностью определена своими значениями /?(е$, fj). Мы
можем записать
где Eij — билинейная функция, определенная формулами:
Eij(v,w) = ViWj, если v = vjei Н------bvmem,
W = Wifi H----h Wnfn.
Приложение: тензорные произведения
941
Очевидно, что элементы eij линейно независимы и порождают
пространство Y, являясь его базисом. Дуальным базисом про-
странства Z = Y* является b(ei, fj) — ег ® fj. Тогда
если является базисом пространства V,
a {fi,... , fn} является базисом пространства W, то
{е^ ® оказывается базисом простран-
ства V ® W. Кроме того,
dim(V ® W) = (dimV) х (dimW).
Опишем другой способ построения пространства V ® W. Он
более прямой и абстрактный, но имеет один недостаток — ис-
пользуются бесконечномерные пространства. Для произвольно-
го множества М обозначим F(M) векторное пространство всех
линейных комбинаций элементов этого множества8. Тогда F(M)
будет состоять из конечных сумм вида
+ * ’ ' +
где mi — элементы М, a — скалярные коэффициенты. Такие
выражения складываются путем приведения подобных членов.
Если М — конечное множество, то F(M) будет пространством
всех функций на этом множестве, причем функция f соответ-
ствует формальной сумме
22 Лт)ш-
тЕМ
Если же М бесконечно, то можно считать, что F(M) является
пространством всех функций на множестве 7И, которые равны
нулю везде, кроме конечного числа точек. (Здесь мы отождеств-
ляем т 6 М с функцией обладающей свойствами: 6т(п) — О,
если п 7^ т, и 6т(т) — 1. Тогда общий вид элемента F(M) — это
конечная линейная комбинация 6т. Отображение М —> F(M),
переводящее т —» Sm, дает возможность рассматривать М как
подпространство F(M).)
8 О но называется свободным векторным пространством над данным мно-
жеством. — Прим. ред.
942
Глава 18. Звездный оператор
Пространство F(M) универсально по отношению к отображе-
ниям М на векторные пространства: для данного отображения
ф : М U, где U — векторное пространство, существует един-
ственное линейное отображение Ьф : F(M) —> U такое, что
Ьфо5т ~ ф(т).
Действительно, эта формула связывает Ьф с элементами
и, следовательно, в силу линейности Ьф распространяется на все
элементы F(M).
Теперь вернемся к нашей задаче. Возьмем М = V х И7. Если
ф — отображение множества V х W —> U, то существует Ьф :
F(V х W) —> £7, которое линейно и удовлетворяет уравнению
Ьф о 6т = ф(т) для всех т е V х W. Если f : V х W —> U
билинейно, то Lf должно обращаться в нуль на всех элементах
^(V1+V2,W) “ ^(Vi,w) “ ^(V2,w)? ^(v,Wl+W2) “ ^(v,Wl) “ fyv,W2)?
^(rv,w) ^(v,w) ? ^(v,rw) ^(v,w) *
Итак, Lf должно обращаться в нуль в подпространстве В, по-
рожденном этими элементами. Тогда можно определить V ® W
как факторпространство
V0W = F(VxW)/B
и отображение JkVxW7—формулой
6(v,w) = [<5(v,w)],
где [•] обозначает класс эквивалентности mod В. Теперь должно
быть ясно, что это определение b и V ® W удовлетворяет сфор-
мулированным свойствам универсальности.
Давайте получим ряд следствий из этой универсальности.
Пусть Vf и W* обозначают два других векторных пространства.
Пусть А : V —> Vf и В : W ~> Wf — линейные преобразова-
ния. Рассмотрим отображение, переводящее (v,w) в Av ® Bw.
Очевидно, что оно билинейно. Следовательно, существует един-
ственное линейное отображение V ® W —> Vf ® Wf, обозначаемое
А® В, для которого справедлива формула
(А ® B)(v ® w) = Av ® Bw.
Приложение: тензорные произведения
943
Предположим, что Af : V1 —> V,f и Bf : Wf W" — еще одна
пара векторных пространств и линейных преобразований. Тогда
отображение, переводящее (v, w) в Af Av ® BfBw, обозначается
А'А ® В'В : V 8 W V" ® W".
Кроме того, у нас есть отображения
A®B:V®W->Vf®W'
и
А ® В* : Vf®Wf^ V" ® W".
Поэтому мы получаем
(А ® В') о (А 0 В) : V ® W -» V" ® W".
По построению (А' ® Bf)(Av ® Bw) — AAv ® BB'w. Следова-
тельно, в силу единственности мы имеем
(А' 0 Bf) о (А 0 В) = А А ® В’В.
Приведем еще одно следствие свойств тензорного произведе-
ния. Предположим, что в пространствах V и W имеются скаляр-
ные произведения (-,-)у и Рассмотрим скалярную функ-
цию /, определенную на пространстве (V х ТУ) х (У х ТУ) фор-
мулой
/((v,w),(v',w')) = (v,v')y(w,w')iv.
Для заданных vf и w' функция f билинейна по v и w, т. е. опре-
деляет линейную функцию /(v/jWq на пространстве V ® ТУ, удо-
влетворяющую условию
J(v',w')(v®w) “ (v,v')y(w,w')w.
Для заданных v и w это выражение билинейно по v' и w'. По-
скольку каждый элемент а Е V ® ТУ является конечной суммой
элементов вида v 0 w, заключаем, что
^(v/,w/)(^)
944
Глава 18. Звездный оператор
билинейна по v' и w' для любого заданного а в пространстве
V 0 W. Итак, существует линейная функция 1а в пространстве
V 0 W, для которой
/"(v'ow') = Z(v,;W,)(a).
Тогда линейна по о и по /3. Легко проверить, что
(«Жж = т
определяет скалярное произведение в пространстве 1/0W. Под-
ведем итоги.
Существует и однозначно определено скалярное про-
изведение (•, в пространстве V0 W, которое об-
ладает свойством
(v 0 w, v' 0 w')v0iv = (v, v')v(w, w')vv.
Тензорные произведения и пространства линейных отоб-
ражений. Здесь мы приведем еще одно полезное определение,
связанное с тензорными произведениями. Пусть есть два век-
торных пространства V и W. Определим векторное простран-
ство Нот (И7, V) как пространство всех линейных преобразова-
ний из W в V. Это векторное пространство имеет размерность
(dimly)(dimV). Для каждого v 6 V и ц Е W* рассмотрим ли-
нейное преобразование Ту : W V ранга 1, определенное фор-
мулой
7^(w) = </z,w)v.
Здесь (/z, w) — это значение линейной функции ц Е ТУ* на век-
торе w Е 1У. Очевидно, что отображение линейно зависит
от v для фиксированного ц и линейно зависит от для фикси-
рованного V. Таким образом, мы имеем единственное линейное
отображение
i : V 0 W* Нош(1У, У),
определенное формулой
i(y 0 m)w — (м, w)v.
Приложение: тензорные произведения
945
Легко проверить, что отображение i инъективное. Оно отобра-
жает V ® И* на подпространство Hom(W, V), состоящее из ли-
нейных преобразований конечного ранга. Если хотя бы одно из
пространств W или V конечомерно, то это подпространство сов-
падает с Нот (И7, V). Если же оба пространства V и W бесконеч-
номерны, то оно — собственное подпространство.
Тензорные произведения более высокого порядка. Су-
ществуют несколько обобщений и модификаций понятия тен-
зорного произведения, на которых мы здесь кратко остановим-
ся. Предположим, что вместо двух векторных пространств V и
W мы имеем к векторных пространств Vi,...,14- Тогда мож-
но определить &-линейное (или полилинейное) отображение f :
Vi х •' • х Vk —> (7, которое должно быть линейным по каждой из
переменных, когда все остальные фиксированы. В этом случае
существует универсальное пространство Vi®- • -®V4 и полилиней-
ное отображение т : Vi х • • • х Vk —> Vi® - • - ®14, которое обладает
теми же свойствами, что и в случае двух сомножителей. Из свой-
ства универсальности следует, что существует изоморфизм
(V1 ® • • • ® Vk) ® (Vfc+1 ® ® Vk+i)
с
Vi ® • - • ®
поскольку они оба удовлетворяют свойству универсальности для
(fc + /)-линейных отображений.
Как и в случае к — 2, если нам даны линейные отображения
Ai : Vi Wi, А2 : V2 W% и так далее, то мы получаем линейное
отображение
Ai ® • • • ® Ак : Vi ® • • • ® Vk Wi ® • • • ® Wk-
Также получается обобщение правила вычисления композиции.
Кроме того, при идентификации (Vi ® • • • ® Vk) ® (14-м ® * • • ® 14+/)
с Vi ® • • • ® Vk^i мы получаем идентификацию (Ai ® • • • ® Ак) ®
(Afc+i ® • • • ® Ak+i) с Ai ® • • • ® Ak+i.
Предположим, что Vi = V2 = • • • = Vk — одно и то же вектор-
ное пространство. Мы говорим, что полилинейное отображение f
946
Глава 18. Звездный оператор
пространства V х • • • х V (к раз) в (другое) векторное простран-
ство W кососимметрично, если
для всех i = 1,2, Другими словами, перестановка двух
любых соседних индексов изменяет знак /. Отсюда следует, что
для любой перестановки тг индексов (1,..., к) можно написать
/(vw(i),...,vw(fc)) = (sign7r)/(vi,...,vfc).
Теперь можно искать универсальное пространство и кососиммет-
ричное полилинейное отображение, т. е. мы ищем векторное про-
странство Afc(y) и такое кососимметричное полилинейное отоб-
ражение mk : V х * • • х V (к раз) —* Afe(V), чтобы для любого косо-
симметричного полилинейного отображения / : V х • • • х V —> U
существовало единственное линейное отображение If : Afe(V) —►
17, для которого I о mk ~ /. Изобразим это на диаграмме:
к раз
V х 7. X ?-----—------* Afe(V)
и
Таким образом, для данного отображения f должно существо-
вать единственное отображение If.
Отсюда немедленно следует, что если mk и Afc(V) существуют,
то они единственны с точностью до изоморфизма. Кроме того,
любое из приведенных нами доказательств существования тен-
зорных произведений приводит, с небольшими изменениями, к
доказательству существования Afe(V) и В частности, первое
доказательство показывает следующее.
Пусть V* — дуальное пространство к V. Тогда Afc(V*)
можно идентифицировать с пространством всех к-ли-
нейных кососимметричных функций на пространстве
V х ••• х V.
Приложение: тензорные произведения
947
Внешняя алгебра. Рассмотрим отображение m.k^t простран-
ства V х • • • х V (к + I раз) в пространство A.k+l(V). Оно по-
лилинейно и кососимметрично по первым к переменным, с одной
стороны, и по остальным I переменным — с другой. Следователь-
но, оно определяет отображение
Afc(V)®Az(V) -+Afc+'(V),
известное как внешнее умножение и обозначаемое символом Л.
С помощью свойства универсальности легко проверить, что Л
ассоциативно, т.е.
(си Л а) Л т — си Л (<7 Л т),
где обе части отображают пространство Afc(V) ®AZ(V) ®AP(V)
на пространство Afe+/+p(V), си € Afc(V), ст 6 Л*(У) и т G АР(У).
Кроме того, вычисляя значения на базисных элементах, можно
проверить, что
creAz(V).
Наконец, предположим, что V имеет скалярное произведение.
Тогда функция в пространстве (У х • • • х V) х (V х • • • х V) (каждый
множитель входит к раз), заданная формулой
/(V1, • • •, Vfe; Wi,..., wfe) = Det((vi; wj)y),
полилинейна и кососимметрична no vi,..., и полилинейна и
кососимметрична по wi,..., w^. Тогда, как мы уже обсуждали
для индуцированного скалярного произведения в пространстве
V ® ТУ, из универсальности следует, что / индуцирует скалярное
произведение в пространстве Afc(V). Другими словами, мы полу-
чаем единственное скалярное произведение (-,-)Afe(V)> Для кото~
рого справедливо равенство
(vi Л • • • Л vfc, wi Л • • Л wjb)Afc(y) = Det((vb Wj)y).
Теперь идею «универсального объекта» можно использовать
для построения алгебр, которые мы изучали в этой главе, т. е.
для внешней алгебры и для алгебры Клиффорда.
948
Глава 18. Звездный оператор
Приведем некоторые детали. Векторное пространство А на-
зывается алгеброй, если задано отображение т
т : А 0 А А,
называемое умножением. Образ т(а ® Ь) будем обозначать а • b
или просто ab. Алгебра называется ассоциативной, если
а(Ьс) = (ab)c
для всех а, b и с. Говорят, что она является алгеброй с единицей,
если существует элемент, обозначаемый 1д (или просто 1, если
нет риска путаницы), для которого выполняется равенство
1да = а
для всех элементов А. Если это специально не оговаривается, то
все алгебры ассоциативны и имеют единицу.
Тензорная алгебра. Пусть V обозначает векторное простран-
ство. Рассмотрим следующую универсальную задачу: надо най-
ти такую алгебру U и линейное отображение г : V —> (7, чтобы
для произвольной алгебры А и любого линейного отображения
f : V А, существовал единственный гомоморфизм ф : U А,
для которого справедливо равенство
0(1(7 ) = 1а
и
0(zv) — /(v) для всех v G V.
V-^U
А
(Здесь слово гомоморфизм означает, что ф - линейное отобра-
жение, удовлетворяющее условию ф(аЬ) = 0(а)0(6).) Если U и i
существуют, то пара (17, г) единственна с точностью до взаимно-
однозначного гомоморфизма в силу тех же аргументов, которые
Приложение: тензорные произведения
949
применялись для всех универсальных построений. (Они действи-
тельно являются аргументами, принадлежащими теории катего-
рий.) Как всегда, наша задача — построить одну такую алгебру.
Рассмотрим (бесконечную) прямую сумму
Т( V) = R®F®(W)®(W®V)®---.
Превратим ее в алгебру, определив отображение
р раз q раз p+q раз
m = mpq : (V ® ® V) 0 (V 0 — 0 V*) —> V 0 • • • 0 V,
которое должно быть единственным и удовлетворять формуле
m[(vi 0 • • • 0 vp) 0 (wi 0 • • * 0 wg)] = vi 0 • • 0 vp 0 wi 0 • * • 0 wQ
(где просто убраны скобки). Полилинейность гарантирует, что
это отображение корректно определено. Поэтому мы знаем, как
умножать ар на bq, где
р раз
ар G Тр(У)
bq е r9(V).
(Для г Е R мы полагаем г • а ~ га.) Поскольку каждый элемент
оо
T(V) = ®Tr(V)
г—О
является конечной суммой а = ао + а± + • • • + аг. где элемент
ар Е Тр(У), то дистрибутивный закон (билинейность) определяет
умножение в Т(У). Возьмем U — T(V) и пусть i : V T(V)
— отображение, которое идентифицирует V как кусок прямой
суммы Т(У) для г = 1, обозначаемый ТДУ).
Возьмем линейное отображение f : V —> А. Тогда
/(vi)/(v2)
950
Глава 18. Звездный оператор
(умножение в А) билинейно по vi и V2. Следовательно, оно опре-
деляет отображение
02 : V ® V А.
Аналогично
фг : Tr(V) А
однозначно определяется формулой
<MV1 ® ® Vr) = /(Vi) • • /(Vr).
Наконец, положим
0(gq + • • • + ат) = 0о(&о) + • • • 4- фт(аг),
где 0о(^о) = ао * 1д- Легко проверить, что ф является гомомор-
физмом, причем единственным, и удовлетворяющим условию
0(zv) = /(v) для всех v е V.
Таким образом, (T(V),i) является «универсальной» алгеброй над
пространством V.
Пусть А является алгеброй. Тогда подпространство I С А
называется (двусторонним) идеалом, если
а е A, b G I означает, что ab е I и ba е I.
Теперь мы можем определить умножение в факторпространстве
В = А/1
формулой
[а/1] • [a’/I] = [аа’/1],
где мы класс эквивалентности a mod I обозначаем [а//]* Оказы-
вается, что это умножение корректно определено, т. е. оно не за-
висит от частного выбора а или a! mod I.
Алгебра Клиффорда. Теперь мы можем воспользоваться этим
определением факторалгебры, чтобы решить другие вопросы об
Приложение: тензорные произведения
951
универсальных объектах. Например, давайте рассмотрим алгеб-
ры Клиффорда. Пусть V обозначает векторное пространство, где
имеется квадратичная форма Q и связанное с ней скалярное про-
изведение (-,*). Пусть А обозначает соответствующую алгебру
с единицей 1д. Отображение Клиффорда ~ это такое линейное
отображение
/ : V - А,
для которого
7(v)2 = Q(v)lx для всех v е V.
Это уравнение можно переписать в форме
/(u)/(v) +/(v)/(u) = 2(u,v)1a.
Алгеброй Клиффорда над пространством V называется алгеб-
ра C(V, Q) вместе с отображением Клиффорда j : V —* C(V,Q),
которая является универсальной в обычном смысле: для любо-
го заданного отображения Клиффорда / : V —► А существует
единственный гомоморфизм ф : C(V,Q) —> А, удовлетворяющий
условию f = фо j.
V---* <Ж Q)
А
Как обычно, если алгебра С (У, Q) существует, то она должна
быть единственной с точностью до изоморфизма. Наша задача
построить такую алгебру. Построение диктуется свойствами тен-
зорной алгебры. Если существует такое отображение j простран-
ства V в алгебру C(V, Q), то мы должны иметь единственный
гомоморфизм ф : T(V) —* С(У, Q), для которого
j = фог.
у г .
C(V,Q)
952
Глава 18. Звездный оператор
По-прежнему предполагая, что C(V,Q) и j существуют, обозна-
чим через J С T(V) множество всех b в Т(У), для которых
V>(b) = 0.
Тогда J является идеалом, и мы должны получить изоморфизм
алгебр
индуцированный ф:
ф[а//] = ф(а) (независимо от выбора а в [a/J]).
Тогда элементы
V ® V - Q(v)lT(V)
обязаны лежать в J в силу определения отображений Клиффор-
да. Следовательно, J должно содержать все суммы правых и ле-
вых кратных этих элементов. Поэтому давайте начнем сначала.
Итак, пусть I является идеалом в T(V), порожденным элемен-
тами v ® v — Q(v)l^(y), т. е. I состоит из всех (конечных) сумм
выражений вида
а • (v ® v - Q(v)lT(V))b,
где а и b принадлежат T(V), a v — пространству V. В этом случае
I является идеалом. Определим
C(V,Q) = T(V)//
И
j : V С(У, Q), j(v) = [*(v)/I] = [v//].
По построению j является отображением Клиффорда. Читателю
рекомендуется проверить, что все свойства универсальности вы-
полняются. В частном случае, когда Q = 0, условие Клиффорда
принимает вид
/(u)/(v) = -/(v)/(u).
Тогда читателю рекомендуется проверить, что алгебра Клиф-
форда оказывается внешней алгеброй Л(У). Подробный анализ
структуры алгебры Клиффорда приводится в этой главе после
задач.
Резюме
953
Резюме
А. Скалярные произведения и звездный оператор
Для данного ортонормированного базиса в пространстве AX(V*)
надо уметь вычислять скалярные произведения в пространстве
Л*(У*).
Для данного векторного пространства со скалярным произ-
ведением (не обязательно положительно определенным) и ориен-
тацией с помощью определения звездного оператора надо уметь
вычислять *А для произвольной базисной fe-формы А.
Вы должны уметь определять оператор Лапласа и выражать
его через частные производные в декартовых координатах.
В. Векторный анализ
Вы должны уметь определять div, grad и rot через d и * и исполь-
зовать эти определения для доказательства тождеств векторного
анализа и для записи дифференциальных операторов в ортого-
нальных системах координат.
Задачи
18.1. В двумерном пространстве-времени имеются аффинные коорди-
наты I, х и скалярное произведение (е^е*) = +1, (ех,еж) = —1,
(et,ex) = 0. Базисная 2-форма имеет вид dt /\dx.
(а) Используя определение звездного оператора
А Л и; — (*А, cj)a,
вычислите ★!, *dx и Л dx),
(b) В этом пространстве вводится другая пара аффинных ко-
ординатных функций
и = t — х, v = t + х.
Вычислите du, dv, * du, ★ dv.
(с) Пусть f — дважды дифференцируемая функция в двумер-
ном пространстве-времени. Вычислите ее лапласиан
□/ = -d*df
через частные производные f по t и х.
954
Глава 18. Звездный оператор
(d) Вычислите □/ через частные производные f по и и v.
18.2. На плоскости вводятся полярные координаты. Вектора ег и
образуют ортонормированный базис во всех точках плоскости,
кроме начала координат, где угол в не определен. Пусть 1-формы
dr и г dO дуальны этим базисным векторам.
(а) Используя определение звездного оператора
Ш /\ X — (*Ш, Л)<7,
вычислите *dr и *d0.
(b) Пусть / — дважды дифференцируемая функция на плоско-
сти. Вычислите ее лапласиан
□/ = ~d*df
через частные производные f по г и 0.
18.3. Перепишите следующие тождества в обозначениях векторного
анализа (/ обозначает функцию, А — 1-форму, но ответы должны
содержать вектор А).
(a) d(df) = 0.
(b) d(dA) = 0. (В пространстве R3 оператор ★* является тож-
дественным.)
(с) d(JA) — df Л А 4- fdA. (Примените * к обеим частям.)
(d) d(AAB) = dA/\B ~ A/\dB. (Посмотрите на (*d*)*(AAB).)
(е) d(f*A) = df А *А + fd*A. (Примените ★ к обеим частям.)
18.4. Пусть f (t, х, у, z) — дважды дифференцируемая функция в четы-
рехмерном пространстве-времени. Вычислите лапласиан □/ че-
рез частные производные /.
18.5. Векторное поле задано в сферических координатах В = Вгег +
Во&о 4- Вф&$. Вычисляя *d*B, где В — соответствующая 1-
форма, получите выражение для div В.
18.6. (а) Пусть А = Ахех + Ауеу 4- Azez. Вычисляя (dd* 4- d*d)A,
где А — соответствующая 1-форма, получите формулу для
векторного лапласиана от А через частные производные
Ах, Ау, Az.
(b) Проделайте то же самое в цилиндрических координатах,
когда А = Агег 4- Афеф 4- Azez. Будьте внимательны: ко-
эффициент при dO будет г А#!
Задачи
955
18.7. Получите выражение для rot А в сферических координатах, т. е.
начните с
А — Агег + Age# +
где соответствующая 1-форма имеет вид
А = Ar dr + A$r dd + АфГ sin 0 d<j>.
Вычислите * dА и представьте результат в виде вектора.
Цель последующего обсуждения — описать все (конечномер-
ные) алгебры Клиффорда над вещественными числами. Вспом-
ним, что алгебра Клиффорда С (V, 1У) полностью определена век-
торным пространством V и квадратичной формой Q. Отсюда и
из свойства универсальности алгебры Клиффорда следует вывод.
Пусть имеется линейное отображение f : V —* Vх, которое
«сохраняет длину», т. е. удовлетворяет условию
Qz(/(v)) = Q(v) для всех v е V.
Тогда f индуцирует единственный гомоморфизм ф/ : C(V, Q) —>
C(VX,QX), для которого
Ф;(v) = /(v) для v е V,
если мы считаем, что V является подпространством C(V, Q). В
частности, если f — изометрия, то есть f также является ли-
нейным изоморфизмом V с Vх, то ф/ является изоморфизмом
C(V,Q) с C(VX, Q). Таким образом, классификация алгебр Клиф-
форда совпадает с классификацией векторных пространств, снаб-
женных квадратичными формами. Ответ на эту задачу класси-
фикации мы знаем: квадратичная форма полностью классифици-
рована ее сигнатурой (р, q). Более точно, пусть V1 С V обозна-
чает подпространство V, состоящее из всех векторов и, которые
удовлетворяют условию: (u, v)q = 0 для всех v е V. Тогда Q ин-
дуцирует невырожденное скалярное произведение в факторпро-
странстве V/V^. Из процедуры Грама-Шмидта мы знаем, что
это индуцированное скалярное произведение определено с точ-
ностью до изоморфизма числами р и q знаков + или — в своей
записи в ортонормированном базисе. Если мы выберем векторное
пространство W, дополнительное к в V, так что V =
956
Глава 18. Звездный оператор
то W будет изометрично V/V^. Если dimV = п, то V изометрич-
но Rn, где стандартный базис 51,... ,6п ортогонален и выполня-
ются равенства:
<Э№) = 1, 1 < г < р,
Q($i) = -1, р+ 1 < i < q,
Q№) — 0, р + q < i < п.
Итак, алгебра Клиффорда полностью задана целыми числа-
ми (п,р, <?), удовлетворяющими условию р + q < п. Нам хоте-
лось бы увидеть, что собой представляет каждая из этих алгебр.
Начнем с элементарного, но очень важного свойства. Изометрия
f : V —* Vх индуцирует изоморфизм ф$ соответствующей алгеб-
ры Клиффорда. Рассмотрим отображение пространства V в себя,
определенное формулой
/(v) = -V.
Это, очевидно, изометрия и /2 = id. Поэтому оно индуцирует
изоморфизм алгебры Клиффорда С — C(V,Q) на себя. Этот
изоморфизм будем обозначать и. Тогда
ш
Из общих принципов следует, что если f : V —> Vf и д : Vf —> Vtf
— изометрии, то
Фд°/ = Фд ° Ф/-
Возьмем V = Vf — Vn и д = /. Тогда получим
фр — и?2.
Но /2 = id. В силу единственности фу ф\& должно быть тождест-
венным изоморфизмом С, Тогда
cu2 — id.
Мы говорим, что является инволюцией С.
Хз-градуировка. Пусть Со является подпространством С, со-
стоящим из всех с, которые удовлетворяют условию
си (с) — с,
Задачи
957
и пусть С\ является подпространством, состоящим из с, которые
удовлетворяют условию
сс(с) — —с.
Тогда любое с можно записать в виде
с = со + сх, где со =T(c + w(c)), сх = ^(с - о>(с)),
Z Zi
при этом
со G Со и ci € Ci.
Итак,
С = Со © Ci
как векторное пространство. Кроме того, если
<v(c) = (-iyc и w(c') = (-!/</,
то
w(cc') = (-l)i+i'cc'.
Поэтому
CqCq € Cq, если со € Со и Со G Со,
cqc^ е Ci, если Со G Со и c'l G С1,
С1Со £ если ci € Ci и Cq G Со,
cic{ е Со, если Cl G Cl и с; g Ci.
Мы можем подвести итог:
Со • Со С Со,
Со Ci С Ci,
Ci • Со С Ci
Ci • Ci С Со.
958
Глава 18. Звездный оператор
Мы говорим, что С является Z2-градуированной алгеброй. Теперь
V С Ci и 1 6 Со, а каждый элемент С может быть записан (воз-
можно, несколькими способами) как суммы произведений (еди-
ницы и) элементов пространства V. Таким образом, Со состоит
из тех элементов, которые можно записать в виде сумм произ-
ведений элементов V, имеющих четное число множителей, a С\
состоит из сумм произведений нечетного числа множителей.
Скрученные тензорные произведения. Возьмем две ^-гра-
дуированных алгебры: А = А0ФА1 и В — Bq©Bi. Определим их
скрученное тензорное произведение, обозначаемое A0B, следую-
щим образом. Как векторное пространство А 0 В - это обычное
тензорное произведение А 0 В для А и В, т. е. в данном случае
А 0 В = (Ао Ф АД 0 (Во Ф В1)
= А ® Во Ф Ai ® Во Ф Ао 0 Вх ф Ai ® Bi.
Умножение определяется правилами:
(ао 0 f>o) * (az ® bf) = aaf 0 b$b,
(а 0 b) • (ао 0 У) = аа$ 0 ЬУ,
(а 0 bi) • (ai 0 У) = -аа\ 0 bib',
где нижний индекс обозначает, четный или нечетный элемент.
Отсутствие нижнего индекса означает, что уравнение выполня-
ется независимо от четности данного элемента. Запишем эти пра-
вила в сжатой форме:
(а 0 У)(а'- 0 У) — (-l)^aa'- 0 УУ.
Другими словами, при перестановке а' и У надо умножать на
(— l)v. Полезность понятия скрученного тензорного произведе-
ния состоит в следующем. Пусть у нас есть два векторных про-
странства V и W, где имеются квадратичные формы Qy и Qw
соответственно. На прямой сумме пространств V ф W возьмем
прямую сумму Qv©Hz этих форм. Это значит, что квадратичная
форма Qy@w совпадает с Qy на пространстве Гис Qw на про-
странстве W, а V и W относительно нее ортогональны. Тогда мы
имеем изоморфизм
С(у ф W, Qv®w) * C(V, Qy) 0 C(W, Qw).
Задачи
959
Опишем это подробнее. Отображения f : V —> V ф ИЛ где /(v) —
v®0, >Уф W, где #(w) = Оф w, «сохраняют длину» и
поэтому индуцируют гомоморфизмы
0/ : C(V, Qv) -» C(V ф W, Qv®w)
и
Фд : C(W, Qw) -+ С(у ф W, Qv®w)-
Отображение
Ф : C(V, Qv) ® C(W, Qw) C(V Ф W, Qv®w)
определим формулой
Ф(а ® b) = ф/(а) • фд(Ъ).
Мы утверждаем, что ф является изоморфизмом. Сначала мы
должны показать, что ф — гомоморфизм, т. е. что
ф((а 0 5) • (а' 0 Ь')) = Ф(а ® &) * <Ка' ®
Это достаточно проверить для
b = wi... Wi
и
а! = vi... vj.
Далее, для v е V и w € W мы имеем (v,w) — 0 в пространстве
V ф W. (Мы пишем v вместо /(v) = v ф 0 и аналогично для w.)
Поэтому для алгебры Клиффорда C(V ф И7, Qv®w/) мы имеем
v • w + w • v = О
и, следовательно,
ba' =
Это как раз и доказывает, что ф является гомоморфизмом. Чтобы
показать, что ф является изоморфизмом, рассмотрим отображе-
ние h : V ф W C(Vy Qy) 0 C(W, Qw\ заданное формулой
h(y ®w) = ly0w + v0 lw<
960
Глава 18. Звездный оператор
где 1у — единица из С(У, Qy), a lw — единица из C(W, Qw)- Из
определения ® немедленно следует, что
A(v ф 0)Л(0 ® w) + h(0 ф w)Zi(v ф 0) = 0,
в то время как h(y ф О)2 — Q(v)ly и Л(0 Ф w)2 — Q(w)ly/. Та-
ким образом, в силу свойства универсальности C(V ф W,
отображение h индуцирует гомоморфизм
Фь : С(у ф W, Qvew) С(К Qv) ® СЖ Qw)
и
Ф 0 Фк(ч ® w) = </>(v 0 Ipy + ly ® W
= ф/(у 0 Ivy) + Фд(1\У <t> w)
— v + w.
Итак, ф о фь — id в пространстве V ф W. Следовательно, в силу
единственности
ф о фь z= id на V 0 И7,
т. е. фь является правым обратным к ф. Аналогичные соображе-
ния показывают, что фн о ф = id, а это значит, что ф — изомор-
физм.
Например, если U — векторное пространство с квадратичной
формой Q = 0, то его алгебра Клиффорда есть просто Л(С7) (это
следует из определений). Пусть V — произвольное векторное про-
странство с квадратичной формой Q. Вспомним, что мы можем
написать
V = V1 ф W,
где ограничение Qw формы Q на подпространство W невы-
рождено. Тогда ф устанавливает изоморфизм между (7(У, Q) и
A(V-L) ® C(W, Qw)- Следовательно, с точностью до включения в
скрученное тензорное произведение внешней алгебры, мы можем
ограничиться только невырожденными квадратичными форма-
ми. Введем обозначение
C(p,q) = C(Rn,Qp>q),
Задачи
961
где QPyq обозначает стандартную квадратичную форму в прост-
ранстве Rn (р + q — п), в которой р плюсов и q минусов. Нам
хотелось бы понять структуру С(р, q).
Расщепленный случай. В качестве примера рассмотрим р = q.
В этом случае моделью для С(р,<?) может быть U + С7*, где U —
р-мерное векторное пространство, в котором возьмем (и, и') = О,
(и*, и'*) — 0 для и,и' е 17, и*, и'* е U* и
(и*, и) = (и*, и) (отображение вычисления).
Как уже обсуждалось ранее в основном тексте, у нас есть описа-
ние соответствующей алгебры Клиффорда через операторы рож-
дения и уничтожения в Л(С7). Дальнейшее изучение покажет, что
алгебра Клиффорда идентифицируется с алгебрами всех линей-
ных преобразований на Л(С7). Поскольку размерность Л({7) рав-
на 2Р, то алгебру Клиффорда С(р,р) можно идентифицировать
с R(2P), где R(n) обозначает алгебру всех вещественных матриц
п х п.
В случае р q замечаем, что Rn можно записать как пря-
мую сумму Rp с положительно определенной формой и R9 с от-
рицательно определенной формой. Следовательно, по теореме о
прямой сумме мы имеем
C(p,g) = C'(p,0)®C(0,Q).
Если ввести обозначения С(р) = С(р, 0) и C(~q) = C(0,q), то это
уравнение переписывается в виде
С(р,д) = С(р) ® С(-д).
Теперь надо понять структуру С(р) и С(—q).
Невырожденный случай. Однако сначала мы рассмотрим
произвольное векторное пространство V с невырожденной квад-
ратичной формой Q, Положим
C = C(V,Q).
Пусть {ei,...,en} будет ортонормированным базисом V (при
этом Q(ei) = • • • = Q(ep) — 1 и Q(eJ = -1 для i — р + 1,..., п).
Рассмотрим элемент
7 = е1 * * * еп в С.
962
Глава 18. Звездный оператор
Если
п
~ 1, . . . , 71,
j=l
— произвольные элементы пространства У, то из ортогонально-
сти ej следует, что
• • • хп = Det(aij) ei • • • en = Det(aij) 7.
В частности, если {fi,... ,fn} — другой ортогональный базис, то
fi * * * fn = iei • • * en.
Итак, с точностью до знака элемент 7 не зависит от выбора бази-
са. (В алгебре Дирака С(1,3) элемент 7 в физической литературе
обычно обозначается 75. Индекс 5 соответствует тому факту, что
в четырехмерном случае 7 является произведением четырех эле-
ментов.) Заметим, что
у? —
Число п(п — 1)/2 возникает из-за перестановок ei после е2 • • • еп,
ег после ез • • • еп и так далее. Число q появилось потому, что
ер+1 = • • • = = -1, где п - р = q.
Наконец, заметим, что для любого г (1 < г < п) справедливы
равенства
7е* = ei • • • ene; = (-l)n“lei • • • е<ед+1 • • • en
и
e^7 — ‘ ( 1) ‘
Тогда
?ег = (- 1)п-1ег7-
Поскольку ei образуют базис пространства V, мы имеем
7V = (—l)n~1V7 для всех v € V.
Следовательно,
7а = (х;(а)п“1а7 для всех а 6 С.
Задачи
963
Примеры пространств малой размерности. Рассмотрим два
важных примера. Пусть V = R2. Мы утверждаем, что
С(2) = Л/(2) = алгебре всех матриц 2x2,
где символ = обозначает изоморфизм. Чтобы это доказать, возь-
мем отображение
ф : R2 ->• М(2),
заданное формулой
ф
О = (х
V -х) '
Тогда
х2 4- у2 О
О х2 + у2
Откуда получаем
<£(u)2 = Q(v) Q
и, таким образом, М(2) обладает всеми свойствами алгебры
Клиффорда С(2). Если взять ортогональный базис
то соответствующие элементы алгебры Клиффорда Af(2) имеют
ВИД
/1 0\ /0 1\
е* V) -1/ и е2 (10/’
так что
у = eie2 =
Заметим, что 72 — — 1, как и требуется. Четная часть Со алгеб-
ры С состоит из всех матриц 2x2, которые коммутируют с 7.
Это — множество конформных матриц. Нечетная часть Су алгеб-
ры С в этом частном случае состоит из самого подпространства
R2, представленного пространством симметричных матриц, име-
ющих нулевой след.
964
Глава 18. Звездный оператор
Мы уже рассмотрели случай (7(—2) и показали, что эта ал-
гебра изоморфна кватернионам. Давайте еще раз посмотрим на
эту конструкцию. Пусть элементом i в С(—2) будет вектор ,
а элементом j — вектор . Тогда
i2 = -1, j2 = -1, ij + ji = О
в силу свойств алгебры Клиффорда. Далее, положим
к = 7 = 4-
Тогда
к2 = -1
и
ki + ik = 0 = kj + jk.
Таким образом, С (—2) задается 1, г, j и /с, а приведенные выше
соотношения определяют свойства кватернионов. Такая алгебра
часто обозначается Н.
Пусть А и В — алгебры. Определим их тензорное произведе-
ние А 0 В как алгебру, которая является векторным простран-
ством А® В, а закон умножения в ней имеет вид
(а 0 Ь) (а' 0 6') = аа! 0 bbf.
(Заметим, что в отличие от скрученного тензорного произведения
здесь не меняется знак.)
Периодичность. Мы хотим доказать следующие основные фор-
мулы:
С(р,«)0С(2) = С(д + 2,р),
С(рЛ)0С(1,1)^С(р+1,д + 1),
C(p,q)0C(-2)^C(q,p + 2),
где = обозначает изоморфизм.
Задачи
965
Сначала давайте докажем первую формулу. Пусть V (р + q)-
мерное векторное пространство (скажем, Жп), снабженное квад-
ратичной формой типа (р, q). Далее пусть W = Ж2 с положитель-
но определенным скалярным произведением. Обозначим 7 = eie2
для C(VK) = 0(2). Рассмотрим отображение
V©W-^C(p,g)0C(2),
заданное формулами
V>(v) = v 0 7, v е V
и
V’(w) = 1 ® W.
Далее,
(v 0 7)(1 ® w) + (1 0 w)(v 0 7) — v 0 (7W + W7) = О,
откуда
+ ^(w)^(v) — 0.
Кроме того,
^(w)2 — 10 w2 — ||w||2l
И
i/)(v)2 = (v 0 7)(v 0 7) = v2 0 72
= v2 0 (-1)
— -Q(v)l 0 1.
Итак, меняем Q на — Q в пространстве V и берем прямую сумму
—Q на V и || • ||2 на W. Для этой квадратичной формы в прост-
ранстве V ф W отображение ф удовлетворяет тождествам Клиф-
форда. Эта квадратичная форма имеет q + 2 плюсов и р минусов.
Таким образом, отображение продолжается до гомоморфизма
: C(q + 2,р) = C(V ф VP) —> С(р, q) 0 С(2).
В качестве упражнения читателю рекомендуем построить обрат-
ное отображение и проверить, что является изоморфизмом. Те
966
Глава 18. Звездный оператор
же самые аргументы (только теперь ||w||2 отрицательно) дают
изоморфизмы
С(р, g) ® С(1,1) С(р + 1, q + 1)
C(p,q)®C(-2)*C(q,p + 2).
Приведем ряд приложений этих изоморфизмов.
И ® Н = О(—2) О О(—2)
= 0(0,2) ® О(—2)
— 0(2,2)
SR(22)=1(4),
следовательно,
И® И = R(4).
Далее,
0(1) = R ф R
для изоморфизма, переводящего
х1 + уе —> (х - у, х + у),
что можно легко проверить (упражнение). Таким образом,
О(-3) ~ 0(1) ® О(—2) “ (R ф R) ® Н
*н®и.
Мы уже проверили, что О(—1) = С. Следовательно,
0(3) “ О(-1) ® 0(2) = С ® R(2).
Это алгебра комплексных матриц 2x2, обозначаемая С(2). Ана-
логично
С ® И = С(-1) ® С(-2) “ С(0,1) ® 0(0,2)
“0(1,2)
“0(0,1)® 0(1,1)
“C®R(2) =С(2).
Откуда С ® Н ~ С(2).
Задачи
967
Эти изоморфизмы мы можем использовать для заполнения
таблицы всех элементов С(р, q):
Например, чтобы найти (7(1,2), мы элемент С = (7(0,1) тен-
зорно умножаем на R(2) = (7(1,1) и показываем, что (7(1,2) =
С(2). Аналогично, чтобы найти (7(3,1), мы элемент R(2) = (7(2,0)
тензорно умножаем на R(2) и находим, что (7(3,1) = R(2) 0R(2).
Однако, по определению матричной алгебры R(r) 0R(Z) = R(r/).
Поэтому R(2) 0 R(2) = R(4). Аналогично
(7(1,3) *И®К(2) =H(2),
т. е. алгебра всех матриц 2 х 2 с кватернионными элементами.
(Заметим, что (7(1,3) и (7(3,1) не изоморфны.) Аналогично,
С(4,0) (7(0,2) 0 (7(2,0) — И 0 R(2) Н(2)
и
С(0,4) ~ (7(2,0) 0 (7(0,2) ~ Н(2).
Продолжая таким образом, мы получаем следующую таблицу:
968
Глава 18. Звездный оператор
Остальные элементы таблицы могут быть получены, двигаясь
вдоль диагонали и на каждом шагу тензорно умножая на R(2).
Эта таблица 8x8 определяет все алгебры Клиффорда, так как
С(п + 8,0) О(п, 0) ® R(16) и 0(0, п + 8) 0(0, п) ® R(16),
что следует из четырехкратного применения базисных изомор-
физмов. Например, чтобы вычислить 0(9), мы начнем с 0(1),
последовательно проводя тензорное умножение на О(—2), 0(2),
О(—2), 0(2). Это то же самое, что и
0(2) ® О(-2) ® 0(2) ® О(—2) О(—4) ® 0(2) ® О(-2)
^О(6)®О(-2)
= 0(8) = О(—8) = R(16).
Такие же соображения показывают, что
O(fc + 8) = 0(fc) ® R(16)
и
О(—fc — 8) = O(—fc) ® R(16).
Таким образом,
С (8г + к) = С (к) ® R(16r) (периодичность Ботта)
и
О(—8г - к) O(-fc) ® R(16r).
Это полностью определяет структуру всех конечномерных алгебр
Клиффорда.
Глава 19
Уравнения Максвелла
Главу 19 можно считать кульминацией курса. Резуль-
таты предыдущих глав применяются к изучению урав-
нений Максвелла и соответствующих волновых урав-
нений.
19.1. Уравнения
Электростатика и магнитостатика являются всего лишь прибли-
женными теориями. Для полей, зависящих от времени, их надо
заменить теорией Максвелла. Начнем с закона индукции Фара-
дея, согласно которому для любой поверхности S', натянутой на
кривую 7, производная по времени от поля В связана с Е равен-
ством
Перепишем это выражение в форме, удобной для пространства
четырех измерений. Рассмотрим временной отрезок [а, Ь] и трех-
мерный цилиндр S х [а, Ь], границей которого является боко-
вая поверхность — двумерный цилиндр 7 х [а, Ь] и торцевые по-
верхности — нижняя S х {а} и верхняя S х {Ь} (см. рис. 19.1).
Проинтегрировав закон Фарадея по времени t от а до 6, получаем
уравнение
[ В - [ В + I Е Л = 0.
JSx{b} JSx{a} Jyx[a,b]
970
Глава 19. Уравнения Максвелла
Пусть
F = В -|- Е Л dt,
так что F — это 2-форма в четырехмерном пространстве. И пусть
С обозначает трехмерный цилиндр С — S х [а, 6], у которого
дС = S х {Ь} - S х {а} + 7 х [а,Ь\.
Здесь В — 2-форма, содержащая только пространственные про-
изводные и потому обращающаяся в нуль на боковой поверхности
цилиндра 7 х [а, Ь], а дифференциал dt и, следовательно, Е Л dt,
обращается в нуль на обоих торцах нашего цилиндра. Таким об-
разом, закон индукции Фарадея можно записать в виде
[ F = Q.
Jac
Кроме того, мы можем рассмотреть трехмерную область С,
содержащую только пространственные координаты при фикси-
рованном времени. В этом случае дС будет поверхностью, на ко-
торой dt = 0, так что
/ F = j в
JdC Jdc
и, в силу отсутствия истинного магнетизма1, поверхностный ин-
теграл должен быть равен нулю. Таким образом, J$c F — 0 для
хт. е. отсутствия «магнитных зарядов». — Прим. ред.
19.1. Уравнения
971
всех трехмерных кубов, ребра которых параллельны любым трем
из четырех координатных осей. Этого достаточно, чтобы выпол-
нялось равенство dF = 0, где, конечно, d обозначает внешнюю
производную в четырехмерном пространстве. Поскольку
F — Вх dy Л dz — Ву dx Л dz + Bz dx Л dy
+ Exdx /\dt + Ey dy /\dt + Ez dz Л dt,
уравнение dF = 0 эквивалентно четырем уравнениям
дВх дВу dBz дх ду dz = 0, дВу dt dEz дх 4. дЕх dz = 0,
дВх дЕу дЕг dt dz + ду = 0, dBz dt ду дЕу дх = 0.
Мы воспользуемся законом Фарадея для определения единицы
измерения В
напряжение • время энергия • время
площадь заряд • (длина)2
Закон Ампера связывает ток с магнетизмом — поток электри-
ческого тока через поверхность S, имеющую границу 7, равняется
циркуляции магнитного поля по контуру 7. Согласно великому
открытию Максвелла, мы должны писать поток электрического
тока в виде двух слагаемых dD/dt + 4ttJ, где D - электриче-
ское смещение, a J — плотность тока движущихся зарядов. (Для
медленно меняющихся полей первый член пренебрежимо мал по
сравнению со вторым, и поэтому его нет в первоначальной фор-
мулировке закона Ампера.) Циркуляция магнитного поля полу-
чается интегрированием линейной дифференциальной формы Н,
называемой напряженностью магнитного поля, по 7. Тогда мо-
дифицированный Максвеллом закон Ампера имеет вид
Рассмотрим трехмерный цилиндр С = S х [а, Ь] и положим
G = D - Н Л dt.
972
Глава 19. Уравнения Максвелла
Проинтегрируем закон Ампера по t от а до Ь. Тогда получаем
[ [ J Kdt.
JdC Jc
Если мы рассмотрим трехмерную область R при постоянном вре-
мени, то dt обращается в нуль на границе dR и интеграл от
G по dR точно такой же, как интеграл от D, что равняется
4тгх (полный заряд внутри области R) = 4тг f pdx/\dy/\dz. Таким
образом, для областей при постоянном времени мы имеем
I G — 4тг / pdx Л dy Л dz.
JdR Jr
Положим
j = р dx Л dy Л dz — J A dt,
тогда мы видим, что
[ G = 4тг [ j
JdC Jc
для любого трехмерного куба, ребра которого параллельны осям
координат. Тогда
dG = 4irj,
откуда следует, что dj = 0.
Итак, подведем итоги:
Положим тогда из уравнений Максвелла имеем
F = В + Е Л dt, dF = 0,
G~D-H/\dt dG = kxj.
Заметим, что уравнения Максвелла инвариантны относитель-
но гладкой замены координат.
Воспользуемся законом Ампера для определения Н. Элек-
трическое смещение D измеряется в единицах заряд/площадь,
так что dD/dt измеряется в единицах заряд/(площадь • время), а
плотность тока J — в единицах ток/площадь = заряд/(площадь •
время). Таким образом, Н измеряется в единицах заряд/(время •
длина). В вакууме мы имеем конститутивные соотношения
D = во*Е и В =
19.1. Уравнения
973
где £о измеряется в единицах
заряд длина (заряд)2
площадь напряжение энергия • длина’
a До — в единицах
энергия • время время • длина __ энергия • (время)2
заряд • (длина)2 заряд (заряд)2 • длина
При этом величина 1/ео/^о имеет размерность
(длина)2/(время)2 = (скорость)2.
Таким образом, в теорию электромагнетизма принципиально
встроена фундаментальная скорость. Великое открытие Макс-
велла состоит в том, что эта скорость является не чем иным, как
скоростью света с! Поэтому вместо dt введем cdt. Тогда четырех-
мерный оператор ★ принимает вид
* (dx Л dy) = —cdt A dz,
* (dx Л dz) = cdt A dy,
* (dy A dz) — —cdt A dx,
★ (dx A cdt) — — dy A dz,
*(dy A cdt) = dx A dz,
*(dz A cdt) — —dx A dy.
В этом случае
★F — c(Bz dz A dt + By dy A dt + Bz dx A dt)
— (l/c)(Ex dy Adz - Ey dx Adz + Ez dx A dy).
Тогда конститутивные соотношения можно записать в виде
G = -—*F.
Ро
Наконец, в вакууме, где величина во/До постоянна, можно пере-
определить j, включив в него все константы, и записать уравне-
ния Максвелла в виде
dF — 0 и d*F = 4tfj.
974
Глава 19. Уравнения Максвелла
Из последней главы мы знаем процедуру решения такой системы
уравнений: предположив соответствующее топологическое усло-
вие, мы ищем 1-форму А, удовлетворяющую условиям
dA — F, d^A — О
и
—□Л — 4% *j.
Таким образом, решения уравнений Максвелла тесно связаны с
изучением волнового оператора
З2 д2 д2 д2
dt2 дх2 ду2 dz2 ’
если используется система координат, в которой с = 1.
19.2. Одномерное однородное волновое
уравнение
В этом параграфе в качестве подготовки к изучению уравне-
ний Максвелла рассмотрим уравнение, представляющее самосто-
„ 2
ятельныи интерес :
д2и д2и __
dt2 дх2
Если мы сделаем замену переменных р = х + q = х — i, то
уравнение перепишется в виде
-О,
решениями которого являются функции
и = ui(p) + u2(q)
или
и(х, t) = ui(x +t) + и2(х — t). (19.1)
2 Оно известно также под названием уравнения колебаний струны и имен-
но в этой интерпретации обычно изучается одним из первых в курсах урав-
нений с частными производными. — Прим. ред.
19.2. Одномерное однородное волновое уравнение
975
Очевидно, что любая функция такого вида будет решением.
Функция U2^x — t) может рассматриваться динамически. В каж-
дый момент времени t график функции и%(х — t) является гра-
фиком uz^x), смещенным вправо на величину t. Мы говорим, что
функция uz^x—t) описывает волну, движущуюся вправо без иска-
жений. Таким образом, общее решение одномерного однородного
волнового уравнения является суммой двух волн, распространя-
ющихся вправо и влево без искажений.
Как правило, представляет интерес описание волнового дви-
жения, соответствующего некоторому начальному возмущению,
скажем в момент t — 0. Поскольку мы имеем дело с уравнением
второго порядка, то можно задать начальные значения ио и vq,
где
/ _ ди , .
ио = и{х,0) и Vo = — (х,0).
(У L
Действительно, пусть A(x,t) обозначает операцию усреднения по
интервалу длины 2t (или радиуса t) с центром в точке х. Тогда,
по определению, для любой функции w
j rx+i
A(x,t)w = - I w(s)ds.
2 Jx—t
Утверждается, что
д
v(x, t) — A(x, t)vo + [А(ж, t)uo]
является единственным решением волнового уравнения с задан-
ными начальными условиями. Действительно, записав и(х, t) =
+ t) + uz(x — t), мы видим, что
u(#,0) — Ui(x) + Uz(x)
и
ди
— (ж,0) =ui(x) -и'2(ж).
Подставим vq = du/dt в последнее уравнение и проинтегрируем.
В результате получаем
[х
и\{х) — uz(x) — I vo(s)d$ + c,
Jo
976
Глава 19. Уравнения Максвелла
где с — некоторая константа. Складывая и вычитая уравнение
uq — щ(х) + из(х), видим, что
2ui(x) — uo(x) + / i?o(s)ds + c,
Jo
2uz(x) = uo(x) — / uo($) ds — c.
Jo
Поэтому из формулы (19.1) имеем
1 /
u(x,t) = - I Uo(x + t) + Uq(x — t) + / Vo(s)ds
2 \ Jx—t
Это еще один способ записи решения.
Заметим, что мы доказали теорему существования и единст-
венности для нашей задачи с начальными условиями. Из явной
формулы также видно, что малые изменения начальных значе-
ний приводят к небольшим изменениям в решении. В этом случае
мы говорим, что задача корректна. Кроме того, значения функ-
ции и в точке (хо,^о) зависят не от всех значений и и du/dt при
t = 0, а только от значений в интервале [то — £о, хо + ^о] (рис. 19.2).
С другой стороны, решение в точке (ж,0) влияет только на
те точки пространства-времени, которые лежат внутри конуса
||ж0|| — Poll (рис. 19.3). Это —- известный принцип причинности.
Рис. 19.2. Область зависимости
Рис. 19.3. Область влияния
19.3. Однородное волновое уравнение в пространстве R3 977
19.3. Однородное волновое уравнение
в пространстве R3
Мы хотим найти решение уравнения
д2и д2и д2и д2и _
dt2 дх2 ду2 dz2
с начальными условиями
u(x,0) = it0(x),
г)?/,
— (х,0) = и0(х).
ot
Пусть A(t,x) обозначает усреднение по сфере радиуса |t| с цен-
тром в точке х. Тогда
= [ f(x + t-)r.
Js
Здесь /(х, t-) обозначает функцию на сфере S единичного ра-
диуса, значение которой на любом векторе v с ||v|| = 1 равно
/(х + tv) ит — элемент телесного угла, умноженный на 1/4тг.
Утверждается, что функция и, заданная формулой
zz(x,Z) = tA(t,x)v0 + x)u0],
является единственным решением нашей задачи.
Прежде всего, покажем, что эта функция является решением.
Для этого проверим, что она удовлетворяет начальным условиям.
Для малых значений t можно написать
iz(x, t) — A(t, x)uq + O(t).
Очевидно, что предел A(t, х) при усреднении по сферам с цен-
тром в точке х, радиус которых стремится к нулю, равен uq(x).
Таким образом,
tz(x,0) = -uo(x).
Кроме того,
— (х,0) = lim
dt t—о
дА
A(/,x)v0 + — (i,x)tz0
978
Глава 19. Уравнения Максвелла
поскольку все остальные члены суть O(i). Однако,
(0, х)и„ = = °-
поскольку среднее значение нечетной функции (такой, как коор-
дината Xi) по единичной сфере должно обращаться в нуль.
Чтобы доказать, что и удовлетворяет волновому уравнению,
достаточно доказать, для любой функции о/, зависящей от х,
функция
1У(х, t) = М(£,х)о>
удовлетворяет волновому уравнению. Действительно, наше вы-
ражение для и является суммой двух членов: один вида W, а
другой вида dW/dt. Если W является решением волнового урав-
нения, то и dW/dt также является его решением.
Для любой дважды дифференцируемой функции ш мы имеем
/ \^2+^2+W2]dxdydz^ / d^
= / *dw,
где S^t обозначает сферу с радиусом |t| и центром в точке х.
На поверхности сферы с радиусом г мы можем написать
/ , ч , дш , . ,
\*dw) /\аг = — dx /\dy Л dz
or
и
dx A dy A dz = т A dr.
Тогда
1 f , д л/ ч
Таким образом,
^(‘'Х)Ш=4^/у-х|ф,(Д“)(У)''У
19.3. Однородное волновое уравнение в пространстве R3 979
Дифференцируя это выражение по t, получаем
^=-^l‘dp д“)(у) ds+Дш(у) ds-
Теперь положим Ж(х,<) — tA(t, х)а;. В этом случае
+ / Aa;(y)dS.
dt* dt dt* 4Trt J|y-X|=|t]
Ho
A1V = _L [ Axcu(x + fv) dS = —[ Acv(y) dS,
4?r J|v|=1 47™ J|y-x|=|t|
следовательно, W — решение волнового уравнения.
Можно выстроить эти рассуждения по-другому и доказать
единственность нашего решения, сведя трехмерное однородное
волновое уравнение к одномерному. Мы доказали интегральную
формулу
[ Att(y)dy —г2 [ “-u(x + vr) dcu.
J|y-x|^r J|v|=l иг
Поэтому для функции u(x5t) мы имеем
Л(г, x)tz.
Если и удовлетворяет уравнению
а? = д“-
то это можно подставить в предыдущее уравнение и получить
4тгг2Л(г,х)и = f |^?(у,£)^У= / dP [ ^(X^dS-
*/|у—х|^Г «/О </|у—x|=r ut
Дифференцирование по г показывает, что функция
Z(r,t) = г A(r, х)и(х, г)
4 2д
— 4тгг —
дг
980
Глава 19. Уравнения Максвелла
dZ dZ п ,,
= 2w (г + t),
dr dt
удовлетворяет одномерному волновому уравнению
d2Z _ d2Z
dr2 dt2
Таким образом,
Z(г, t) — Г А(т, x)u(x, v) = Wi(r + t) + W2(r — t).
Поскольку Z(0,t) = 0, мы имеем
Wl(£) = _W2(_f).
Написав w вместо wi, получаем
Z(r, t) = w(r +1) — w(t — r).
Дифференцируем это выражение по г и переходим к пределу
г —> 0. В результате получаем
'ц(хД) — Л(0,х)гг(хД) =
Кроме того,
следовательно,
гл(х, г) = 2w'(r) — lira 2w'(r +1) — lim ——h lim -7—.
v 7 v 7 v 7 t—>0 dr t^o dt
Подстановка выражения для Z в эту формулу дает
1/(х, г)
= 4~(т~[ и(х + r~f, Q) dS + [ ^(x + r7,0)ds) .
dr у4тг J|7|=1 4тг J|7|=1 dt J
Но
u(x + Г7,0) = uq(x + Г7)
и
du . . , .
— (x + Г7) = v0(x + Г7).
Если в этом соотношении положить г = t, то получим наше
исходное решение, что доказывает его единственность.
19.4. Неоднородное волновое уравнение в пространстве R3 981
19.4. Неоднородное волновое уравнение
в пространстве R3
Мы можем решать уравнения Максвелла, решая последователь-
ность уравнений вида
г-1 Г г-1 д2 Л
□и = /, □ = ^2 - Д.
Давайте сначала покажем, как решить это уравнение с началь-
ными условиями
и(х,0) = 0, ^(х,0)=0.
Ub
Неоднородное волновое уравнение можно решить, сводя его к ре-
шению однородного волнового уравнения с последовательностью
начальных условий следующим образом. Пусть г>(х,/,т) — реше-
ние задачи с начальными условиями
dv
□v = 0, v(x,r,r)=0, —(х,т,т)=/(х,т).
Положим
= — I v^t^r^dr.
Jo
Тогда очевидно, что u(x, 0) — 0 и
ди, х ч /** dv . ч ,
Но v(x,J,t) — 0 в силу начальных условий для v. Поэтому
= ^’Т}ЛТ
и, следовательно,
ди. Л.
Л(х’0>=0-
Кроме того, дифференцирование уравнения для du/dt дает
д'2 и. dv f d2v.
-а^(х’‘)= a(x’f't) + /„
982
Глава 19. Уравнения Максвелла
a t
Au = - / u(x,
Jo
так что
/ д2 Л\ /
\dt2 A)u~f-
Теперь функция v определяется выражением
v(x,t,r) = (t-r)A(x,t-r)/=-Г(«-т) [ /(x+(f-r)7,r)d-7,
47Г J|7|=l
следовательно,
u(x,t) = -2- f (t-т) [ f(x + (t-r)'y,T)d'TfdT
47Г Jq J|-y|=l
If* f
- — / r' f (x + Tz7, t - t’) drf drf.
4% Jo </|7-i
В этом выражении положим у — х + т'7, тогда последний инте-
грал принимает вид
/Ч [ f(y,t-T')dSdT'
47Г Jo т J\y-x|=|t|
= _JL [ /(у^~ 11у-х||)
4тг /|у_х|=|т'| ||у - х||
Итак, мы получили формулу для запаздывающих потенциалов:
u(x,()=4
Она похожа на формулу Пуассона для потенциала, но вклад от
сферы с радиусом а и центром в точке х задается величиной 1/а,
умноженной на значение f в момент времени, равный а единиц.
Раз мы получили решение неоднородного уравнения с нуле-
выми начальными условиями, то теперь решение неоднородного
уравнения с произвольными начальными условиями можно све-
сти к решению однородного уравнения путем вычитания уже по-
лученного решения.
19.4. Лагранжиан и тензор энергии-импульса
983
Воспользуемся последней формулой, чтобы решить неодно-
родное волновое уравнение для каждой компоненты ^-потенци-
ала А в уравнениях Максвелла. Получим
А(х) = - / - 'V Х''-' dx.
J |х -х'|
Это решение называется потенциалом Льенара Вихерта для за-
данного распределения плотности тока j. Общее решение урав-
нений Максвелла получается прибавлением к А потенциала,
компоненты которого удовлетворяют однородному волновому
уравнению.
19.5. Лагранжиан электромагнитного поля
и тензор энергии-импульса
Пусть А — 1-форма и j - 3-форма в пространстве Минковского
R1,3. Рассмотрим 4-форму
£ — £(A,j) — — | dA A - 4%A A
Проинтегрируем £ по любой ограниченной четырехмерной облас-
ти N и получим функцию
- [ £.
Jn
Здесь мы считаем, что N и j 'заданы и фиксированы, так что
L является только функцией А. Мы говорим, что А является
экстремалью L, если
для любого дифференцируемого семейства 1-форм As, удовле-
творяющих условиям Ао = А и А5 — А на границе dN. Пусть
^1 = В. Тогда
-j-(As,j)\s=o = A *dA + dA A *dB) — 4тгВ A j.
ds 2
984
Глава 19. Уравнения Максвелла
Теперь
d(B Л *dA) — dB Л *dA + В Л d*dA
и
dB Л — dA Л *dB,
следовательно,
— В Л [d*dA — 4;rJ] = d(B Л ★dA).
s=0
Интеграл f^N В Л *dA обращается в нуль, потому что на границе
В — 0. Таким образом,
dLp/j (As)
ds
s=0
В Л [d'kdA — 4тгД.
Если это выражение равно нулю для всех В, обращающихся в
нуль на границе, то мы должны иметь
d*dA = 4тг/.
Однако, в области, где Н2 — 0, это эквивалентно уравнению
Максвелла F — dA. Чтобы эти уравнения можно было решить,
необходимо выполнение условия
dj = 0.
Таким образом, мы вывели уравнения Максвелла из вариаци-
онного принципа', уравнения Максвелла в точности совпадают с
уравнениями для критических 1-форм А лагранжиана L. Форму-
лировка в терминах лагранжиана обладает рядом преимуществ.
Одно из них состоит в том, что изменяя лагранжиан L, мы по-
лучаем процедуру модификации уравнений для его экстремалей
и, таким образом, можем открывать различные законы природы.
Другое преимущество в том, что с помощью лагранжева форма-
лизма мы получаем процедуру перехода от классической механи-
ки к квантовой. Функция L играет ключевую роль в квантовой
электродинамике. Третье преимущество — в рамках лагранже-
ва формализма каждая однопараметрическая группа симметрий
19.5. Лагранжиан и тензор энергии-импульса
985
лагранжиана L дает нам закон сохранения с помощью метода, из-
вестного как теорема Нётер. Этот метод мы объясним в частном
случае электромагнетизма.
Пусть £ — векторное поле в пространстве R1,3, обладающее
свойством
для всех 2-форм и.
Как мы уже видели, любое конформное преобразование про-
странства-времени сохраняет действие звездного оператора на
2-формы. Поэтому £ может быть векторным полем, связанным
с любой однопараметрической группой конформных преобразо-
ваний. В частности, £ может быть любым постоянным векторным
полем, что соответствует трансляциям, или любым инфинитези-
мальным преобразованием Лоренца.
Итак,
D^C = — - dD^A Л *dA — ^dA D$*dA — D$A A Anj — A A
Z Zi
Поскольку
T)gkdA — kD^dA = kdDgA
и
dD^A A kdA = dA/\ *dD$A,
первый и второй члены равны, поэтому они складываются в
—dD$A A kdA = —d(D^A A kdA) + D$A A dkdA.
Таким образом,
D$£ = ~d(D$A A kdA) + D$A A (dkdA — 47rj) — А А 4тгD$j.
В силу уравнений Максвелла dkdA = Arj. Поэтому
D%£ = — d(D$A A -kdA) — A A AxD^j
= -d((i(g)dA + di(g)A) A kdA) - A A 47rZ>€j
= — d[i(g)F A *F] — di(g)A A dkdA — A A AivD^j
= — d[i(£)F A *F] — di(£)A A 4ttj — A A
986
Глава 19. Уравнения Максвелла
где мы использовали dA = F и d*dA = j. С другой стороны
D$A = i(£)dA + dA + di(£)A
= i(g)F + di(g)A,
a
= -fyp A *F) = D((A Л 4тг»
= \di(g){F N *F) - (i(£)F + di(£)A) A]-Ab D^j,
поскольку d(F A *F) = 0, потому что F A *F — 4-форма. При-
равнивая эти два выражения для Z)g£, получаем
— d[i(£)F Л *F] — di(£)A Л 4ttj — А Л D^j
— -|^(£)FA*F+FAi(£)*F]-i(£)FAj-di(£)AA4^j-^A47rP£7
Z
или
d|[F Л i(^)*F - i^)F Л *F] = -t($)F Л 4лj.
Если нет токов, т.е. если j = 0, оказывается, что 3-форма
C(e) = |[FAi(e)*F-i(€)FA*F]
замкнута. Этот факт интерпретируется как закон сохранения:
интегралы от С(£) по двум трехмерным областям, ограничиваю-
щим некую четырехмерную область, равны.
Если при стремлении к бесконечности в пространственных на-
правлениях F достаточно быстро убывает, то два интеграла от
С(£) по любым трехмерным пространственноподобным поверх-
ностям равны.
Например, в некоторой системе координат возьмем трех-
мерные поверхности, заданные уравнениями t — t± и t = t%
(рис. 19.4). Полное значение величины С(£) в момент t = ti
равно полному значению (7($) в момент t = £2- Это значит, что
полное значение величины С(£) сохраняется во времени. Поэтому
уравнение dC(£) — 0 называется законом сохранения.
19.5. Лагранжиан и тензор энергии-импульса
987
Например, давайте возьмем £ — d/dt, что соответствует ин-
финитезимальной трансляции во времени (в смысле некоторого
расщепления на пространство и время). Прямое, но весьма по-
учительное вычисление, которое мы оставляем читателю, пока-
зывает, что
С(С = |(||Е||2 + ||В||2)^ f\dy Kdz
Z
Л- P\dy /\dz f\ dt — P2 dx f\dz f\dt + P3 dx /\dy A dt,
где
Pi = EyBz — ByEz,
P2 = EXBZ — BXEZ,
P3 = ExBy — BxEy,
или, более кратко,
P = Ё x В.
(Трехмерный вектор Р называется вектором Пойнтинга.) Таким
образом, на поверхности t — const интеграл от С(£) дает пол-
ную энергию электрического и магнитного полей, т. е. наш за-
кон сохранения становится законом сохранения энергии. Осталь-
ные компоненты С (С) в этом случае описывают поток (локальной
плотности энергии) через любую поверхность.
988
Глава 19. Уравнения Максвелла
Точно так же, как энергия связана с временной трансляцией,
х-компонента импульса связана с бесконечно малым смещением
в направлении х. Это общий принцип механики (см., например,
Loomis and Sternberg, глава 13, или более сложное изложение в
книге Guillemin and Sternberg, глава 2). Таким образом, С(д/дх)
будет замкнутой 3-формой, интеграл от которой по простран-
ственноподобной трехмерной поверхности t = const дает полный
импульс электромагнитного поля в направлении х. Интегрирова-
ние по поверхностям вида [а, Ь] х S, где S — поверхность в про-
странстве R3, а [а, Ь\ - временной интервал, величины С(д/дх)
дает поток х-компоненты импульса через поверхность S в тече-
ние времени [а, Ь].
Для любого постоянного вектора £ величина С(£) являет-
ся 3-формой, а *С(£) — 1-формой. Таким образом, равенство
Т($,77) = *С(е(г7) имеет смысл для некоторого другого посто-
янного вектора тр Функция Т = Т(£,7у) называется тензором
энергии-импулъсщ потому что в ней закодированы все компонен-
ты плотности и потока энергии и импульса.
При наличии тока j формы С(£) уже не будут замкнутыми,
но они удовлетворяют условию
dC(^)-^)FA47Tj.
Это называется силой Лоренца и представляет передачу энергии-
импульса от электромагнитного поля току зарядов.
19.6. Волновые фронты и принцип Гюйгенса
Решение волнового уравнения
вида
u(x,t) = /(x)g(h(x) ±4)
называется распространяющейся волной. Выражение Л(х±£) на-
зывается фазой волны, а поверхности уровня h — const — волно-
выми фронтами.
19.6. Волновые фронты и принцип Гюйгенса
989
Мы уже видели, что в одномерном пространстве, взяв f = 1,
h(x) = х и произвольную функцию 5, получаем решение, кото-
рое в общем случае может быть записано как сумма двух таких
выражений, одно со знаком +, а другое со знаком —.
В трехмерном пространстве в качестве h возьмем функцию,
линейную по х
/г(х) = к • х,
f = 1 и произвольную функцию д. Чтобы решить уравнение,
накладывается единственное условие ||k|| = 1. (По существу мы
свели задачу к одномерному случаю: с помощью вращений мож-
но сделать так, что k = (1,0,0). Поэтому решение зависит только
от х и t, что равносильно решению волнового уравнения в про-
странстве одного измерения.)
В частности, если мы возьмем д(0) — е16>, то получим функции
e^k’x-t\ ||k|| = 1.
Важность этих решений с синусоидальными волнами объясня-
ется следующим: это теорема, согласно которой каждая гладкая
функция в пространстве R1,3 (или в общем случае в простран-
стве Rn), которая на бесконечности достаточно быстро убывает,
может быть записана в виде суперпозиции функций вида е1к х,
т. е. любую такую функцию можно записать в форме
/(х) = 77^ / №е**а*’
(27r)d/2 J
где f — подходящая функция. В главе 21 мы дадим очень крат-
кое доказательство этого факта. Оказывается, что эта формула
обратного преобразования Фуръе верна и в более общем случае.
В нашем же случае общее решение волнового уравнения может
быть записано как суперпозиция функций е1(к х~*); где ||к|| = 1.
В качестве второго примера рассмотрим сферически симмет-
ричные решения волнового уравнения (определенного вне прямой
г = 0). Запишем лапласиан в сферических координатах:
__ 1 д 2ди 1 д . ди 1 д2и
U г2 дгГ дг г2 sin0 д0 8Ш д0 г2 sin2 0 дф2 ’
990
Глава 19. Уравнения Максвелла
так что для сферически симметричной функции и = и(г, t) вол-
новое уравнение принимает вид
д2и 1 д 1 д2и
dt2 г2 дг дг г дг дг2
1 д2
= 'гв^'
Таким образом, функция v ~ ги удовлетворяет одномерному
волновому уравнению
(д2 д2\
(dt2 dr2JV~ °'
Общее решение этого уравнения дается формулой
^(r, t) = /О'* +1) + g(r - t),
так что общее решение сферически симметричного волнового
уравнения имеет вид
U\r,t) ~--------1--------•
Г г
Здесь первый член представляет падающую волну, а второй —
испускаемую. В частности, возьмем f = 0 и g(s) = elks. Тогда
eik(r-t)
Wk(t,r) =-------
г
представляет испускаемую (синусоидальную) волну с частотой
к. Действительно, легко проверить, что с точностью до нормиро-
вочной постоянной
pifcr
^(г) =
г
является «фундаментальным решением» приведенного волново-
го оператора Д + А:2, т. е.
(А + к2)Ек = 0
при г 7^ 0, и
У Efc(4 + A:2)4>dx = <X0)
19.6. Волновые фронты и принцип Гюйгенса
991
для любой гладкой функции ф. В главе 15 мы доказали этот ре-
зультат в случае к = 0 из формулы Грина. Аналогичное доказа-
тельство сработает и здесь.
Далее, если D — любая ограниченная область в R3 и и
удовлетворяет приведенному волновому уравнению (уравнению
Гельмгольца)
Аи + к2и = О,
то из формулы Грина можно видеть, что верна следующая фор-
мула Гельмгольца:
"gifcrp / е1ктр
----*du—u*dI ----
Гр \ Гр
ti(P), если Р е D
О, если Р D,
где гр обозначает расстояние от Р.
Во многих приложениях нам интересна ситуация, когда вмес-
то ограниченности области D она является внешней для некото-
рой поверхности S. Сначала воспользуемся полученной форму-
лой для ограниченной области Dp, содержащей пересечение D с
шаром радиуса R и центром в точке Р. Если R выбирается доста-
точно большим (рис. 19.5), то интеграл становится суммой двух
интегралов по поверхностям, и мы получаем формулу
если Р 6 D,
если Р £ D.
Рис. 19.5
992
Глава 19. Уравнения Максвелла
Здесь — сфера радиуса R. Тогда
/ pifcr
d —
\ г
eikr
Ч Я Я
ifc------dr
г
и *dr — R2dw на поверхности где dw — элемент телесного
угла на этой поверхности. Таким образом, второй интеграл при-
нимает вид
Эи \
—---iku ) + и
dr /
i dw.
- r=R
При R оо интеграл по сфере стремится к нулю, если
УУ* |u| dw = о(1) и
— iku dw = o(R !).
г
Здесь интегралы вычисляются при г = R. Эти условия называ-
ются условиями излучения Зоммерфельда. Их значимость опре-
деляется тем, что они представляют ситуацию, когда решение
и содержит только испускаемые волны, а падающих волн нет .
Предположим, что это условие выполнено. Тогда значение и вне
некоторой поверхности S задается формулой
U(P) = i /
47Г Js
eikr ( \
----*du — u* d (--- I
т---\ г /
(19-2)
3 Строгое математическое объяснение условий излучения Зоммерфельда
можно найти в книге Lax and Phillips, с. 120-128. Идея доказательства состо-
ит в следующем. Пусть f = {/i,/?} — данные Коши для волнового уравне-
ния. Мы ищем решение волнового уравнения
d2w
— Aw = 0
dt2
с начальными условиями w(x,0) — f± и (dw/dt)(x,ty = /2- Мы говорим, что
/ описывает расходящуюся волну, если существует некоторая константа с,
такая что w = 0 для |х| < t — с. Если мы ищем решение с фиксированной
частотой, то соответствующие начальные условия Коши имеют вид {w, ikw}.
Предположим, что w -- решение приведенного волнового уравнения вне неко-
торой ограниченной области. Тогда условие {w, ikw} обеспечивает расходя-
щееся решение тогда и только тогда, когда выполняются условия излучения
Зоммерфельда.
19.6. Волновые фронты и принцип Гюйгенса
993
Таким образом, решение за пределами области S описывается
расходящимися сферическими волнами, излученными поверхно-
стью S. Именно Гюйгенсу принадлежит идея, что распростра-
нение возмущений в волновой теории представляется суперпо-
зицией вторичных возмущений от промежуточной поверхности,
скажем от S. Однако, он не дал адекватного объяснения, почему
не существует обратной волны (падающей волны), т. е. почему
волны распространяются только от поверхности. Идея, что об-
ратные волны могут уничтожать друг друга в силу разности их
фаз, принадлежит Френелю. Френель думал, что если все ис-
точники находятся внутри поверхности S, то вторичное излуче-
ние (т. е. подинтегральное выражение в формуле Гельмгольца)
в силу интерференции для каждого элемента поверхности будет
создавать нулевой эффект в каждой внутренней точке. Приве-
денные соображения, принадлежащие по существу Гельмгольцу,
были первым строго математическим подходом к проблеме. Они
показывают, что волны уничтожаются внутри области благодаря
суммарному эффекту от границы. И тем не менее, как мы уви-
дим в главе 21, Френель был прав с точностью до членов порядка
1/fc. Это будет сделано с помощью асимптотической оценки ин-
тегралов в формуле Гельмгольца.
До сих пор мы работали с монохроматическим излучением
щ соответствующим зависящей от времени функции г (ж, у, z, t) —
u(x,i/,z)e"lfct. Для фиксированной точки Р введем функцию
vp(x, у, z, t) = v(x, y,z,t- г),
где г — расстояние от Р до (x,£/,z). Подстановка в формулу
Гельмгольца дает
1 f f ,/1\ 1 ди , 1 \
v(P, Т) = — / I vP*d ( - ~ *dr - - *dvP .
47rZsA \rj г dtp г J
Это формула Кирхгофа. Поскольку она линейна по v не содержит
в явном виде частоту, то она верна для любой суперпозиции моно-
хроматических волн с различными частотами, а следовательно,
для произвольного решения волнового уравнения. В этой форме
связь с принципом Гюйгенса очевидна.
994
Глава 19. Уравнения Максвелла
Резюме
А. Уравнения Максвелла
Вы должны знать законы Фарадея и Ампера в интегральной и
дифференциальной форме и уметь доказывать, что 2-формы
F — В + Е /\dt и G = D - Н Л dt
удовлетворяют условию G — *F в вакууме.
Вы должны уметь приводить уравнения Максвелла к виду
□А — 47rj и описывать решения этого волнового уравнения.
Вы должны знать, как формулируется закон сохранения энер-
гии-импульса для электромагнитного поля через дифференци-
альные формы.
Задачи
19.1. В четырехмерном пространстве-времени (используются едини-
цы, когда с = 1) (dt, dt) ~ 1, (dx, dx) ~ (dy,dy) = (dz,dz) — — 1 и
a = dt A dx Л dy Л dz. 2-форма F, представляющая электромаг-
нитное поле, может быть выражена через координаты х, у, z,t в
виде F = Bz(x,y,t) dx /\dy — Ex(x,y,t) dt /\dx — Ey(x,y,t)dt /\dy.
Все другие члены равны нулю.
(а) Какое соотношение должно выполняться для частных про-
изводных Bz, Ех и Еу, чтобы выполнялось равенство dF =
О?
(Ь) Выразите *d*F через частные производные Bz, Ех и Еу.
19.2. Преобразование Лоренца о, соответствующее скорости v вдоль
оси х можно записать в терминах переноса (для удобства мы
положили с — 1) следующим образом:
a*tf = ^(t — vx),
a*xf = y(x — vt),
a*yf = y,
a z — z,
где 7 = 1/V1 — v2. Если x, y, z,t — координаты системы отсчета
наблюдателя, стоящего на платформе, ат', у', z', tf — коорди-
наты системы отсчета наблюдателя, сидящего в поезде, который
Задачи
995
движется со скоростью v вдоль оси х, то о* преобразует коорди-
наты события я/, у', 2', tf, наблюдаемое в поезде, в координаты
того же события в системе отсчета наблюдателя на платформе.
(а) Покажите явно, что а* сохраняет звездный оператор, т. е.
что Используя звездный оператор для ко-
ординат х, у, z, £, т. е. *dt — dx Л dy Adz и т.д., проверьте
следующее:
dx' Л dy' Л dz' — *a*(dx' Л dy' Л dz'),
a**dt' Л dy' Л dz' ~ Л dy' Л dz'),
a**dt' Л dx' = *a*(dt' A dx'),
a**dx' A dy' = *a*(dx' A dy').
(b) Потенциал А может быть записан через координаты пасса-
жира поезда в форме
А = A' dt' + A' dx' + A' dy' + A' dz',
Вычислите о* А и приравняйте полученный результат
At dt 4- Axdx + Ау dy 4- Az dz,
откуда получите выражения для At, Ах, ... через A't, А'х,
19.3. Выполните упражнение 19.2 для 2-формы
F = В' + Е' К dt',
F ~ B'xdyf Adz' + - - + E'z dz' A dt'.
Вычислите и сравните результат с
F = Вх dy Л dz 4- • • • 4- Ez dz A dt.
Получите выражения для компонент поля Вх, Ву, Bz, Ех, Еу, Ez
через В'х, В' B'z, Е'х, Е' E'z.
19.4. Точечный заряд покоится в начале координат в системе отсчета
поезда. Для этого заряда, как известно,
_ if dx' + У' dy' + dz' . .
F = В А Е Adt = A dt'.
(x/z 4- у 2 4- zfZ)s/2
Вычислите a*F и опишите поля заряда, совершающего равно-
мерное движение вдоль оси х.
996
Глава 19. Уравнения Максвелла
19.5. Из 2-формы F можно построить две различные 0-формы:
/1=*(ГЛГ), /2 = i(FA*F).
Выразите эти величины, инвариантные относительно преобразо-
ваний Лоренца, через компоненты F, т. е. через Ву, ..., Ez.
Глава 20
Комплексный анализ
В этой главе приводится достаточно стандартное из-
ложение теории функций комплексного переменного.
Введение
Настоящая глава посвящена изучению теории функций ком-
плексного переменного. Эта теория, в ее различных модификаци-
ях, является главным достижением математики XIX века. Здесь
мы кратко рассмотрим только ключевые результаты. Вспомним
основные положения теории функций нескольких переменных, в
частности, двух переменных (главы 7-8). Пусть х и у — коорди-
наты в пространстве IR2. Основные объекты дифференциального
исчисления — функции, линейные дифференциальные формы и
формы второй степени. Каждый из них может быть определен
только на открытом подмножестве пространства R2. Функция f
приписывает число f(x,y) точке (х,у). Если специально не ого-
ворено, то все функции предполагаются дифференцируемыми.
Линейная дифференциальная форма имеет вид
tv — adx + bdy,
где а и b — функции. Если 7 — ориентированная кривая (кусочно-
дифференцируемая и лежащая в области определения си), то
можно вычислить криволинейный интеграл Если имеется
суперпозиция (объединение) 7 — 71... 7П, где 7$ — дифференци-
руемые кривые, параметризованные Xj(t), yt(t) при at С t /%,
998
Глава 20. Комплексный анализ
то
где
/*
J7i J ai
Заданная функция / имеет дифференциал d/, являющийся ли-
нейной дифференциальной формой вида
df =*^-dx + ^~ dy.
ох ду
Теорема Стокса для функций (фундаментальная теорема диффе-
ренциального исчисления) говорит, что если 7 — любая кривая,
соединяющая точки р и д, то Д df = f(q) — f(p)-
2-форма имеет вид
Q = cdx Л dy,
где с — функция. Если D — ограниченная область на плоскости
(содержащаяся в области определения Q), то можно сформиро-
вать интеграл fD Q. Если при этом D имеет стандартную ориен-
тацию, то fD Q — двойной интеграл
I w = / с(х, у) dx dy.
JD JD
(Если D имеет противоположную ориентацию, то необходимо из-
менить знак.) Предполагается, что все области имеют кусочно-
дифференцируемую границу, которая обладает индуцированной
ориентацией. Эта граница (с ориентацией) обозначается dD. Если
cu — adx + bdy, то dcu является 2-формой вида
(да 0Ъ\
dw — I ---— I dx /\dy,
уду дх J
и теорема Стокса (для 1-форм) гласит
[ ш = [ Ош.
JdD JD
20.1. Комплекснозначные функции
999
Мы предполагаем, что читатель знаком с основными свой-
ствами комплексных чисел. Каждое комплексное число с можно
записать в форме с — г + is, где г и s — вещественные числа,
i2 = — 1. При этом т называется вещественной частью и s — мни-
мой частью комплексного числа с. Число с — г — is называется
комплексно-сопряженным от с, и сс = |с|2 = г2 + s2. Для ком-
плексных чисел выполняются все законы алгебры, в частности,
коммутативный и ассоциативный законы для операций сложения
и умножения и дистрибутивный закон.
20.1. Комплекснозначные функции
Теперь мы рассматриваем функции и дифференциальные фор-
мы, которые могут иметь комплексные значения, т.е. комплекс-
нозначная функция f приписывает комплексное число f(x,y) —
u(x, у) + iv(x, у) каждой точке на плоскости, где и и v — веще-
ственнозначные функции. Другими словами, задание комплекс-
нозначной функции означает задание пары вещественнозначных
функций, т. е. то же самое, что задание отображения (открытого
подмножества) R2 в R2. Мы говорим, что f дифференцируема,
если дифференцируемо это отображение, т. е. дифференцируемы
функции и и v. Таким образом, формулы df /дх = ди/дх+\ди/дх
и df /ду — ди/ду + \дь/ду задают частные производные функ-
ции /. Можно рассматривать различные линейные комбинации
этих частных производных с вещественными или комплексными
коэффициентами. Например, рассмотрим выражение
W W
2дх 2ду
Можно считать, что это результат действия дифференциального
оператора ^(д/дх + \д/ду) на функцию f. В последующем изло-
жении этот оператор чрезвычайно важен для нас, поэтому введем
для него специальное обозначение d/dz. Таким образом,
д
dz
1 (д~ \
2 удх + ду)
(20.1)
1000
Глава 20. Комплексный анализ
Аналогично определим
_5__ 1
dz 2 \dx 1ду)
(20.2)
Несколько позже станет понятна причина для введения этих обо-
значений. Заметим, что если f = и + iv, то
df _ du ,dv
dz dz ldz
_ 1 / du . du \ i / dv . dv \
2 1 dy/ 2 ydx Xdy) 1
так что, собирая вместе вещественную и мнимую части, мы по-
лучим
df_ = l(9u_ 9v\ , 1 f Г20 оч
dz 2 \dx dy) 2 \dy dx) ' k '
Заметим, что для любой пары дифференцируемых функций f и
g мы имеем
= (20'4>
и аналогичное равенство справедливо для d/dz.
Рассмотрим комплекснозначную функцию z(x,y) = х + iy.
Запишем это в виде
z = х + iy (20.5)
и аналогично
z = х — iy.
Тогда функция z2 задается формулой
z2 — (х2 — у2) + i2xy, a z2 — (х2 — у2) — 212ху
и
ZZ = \z\2 — х2 + у2.
Аналогично можно сформировать полином от г, например, 17г3 —
5г2 + 2z — 3, полином от г, или смешанный полином, например,
20.2. Комплекснозначные дифференциальные формы 1001
Зг2г — 2гг3 + г2 — 5г + 1 и т. д. Все это — примеры комплексно-
значных функций. Если в формулу (20.3) вместо f подставить г,
где и(хуу) ~ х и v(x,y) = у, то получим
dz
-.0 (20.6)
и аналогично
dz
Из формулы (20.4) и линейности d]dz мы заключаем, что если
Р — P(z) — произвольный полином только от г, то
Если Р(г) = ао Ч- a^z Ч-----h апгп, то
dP Л п-1
— ai + 2a%z Ч----Н nanz
dz
Это полином Pf(z) — обычная производная полинома Р. Таким
образом,
dz dz
20.2. Комплекснозначные
дифференциальные формы
Рассмотрим дифференциальные формы, имеющие комплексные
значения. Линейная дифференциальная форма имеет вид
adx + bdy у
где а и b - комплекснозначные функции. Сохраняются опреде-
ление криволинейного интеграла и одномерный вариант теоре-
мы Стокса, только теперь значениями будут комплексные числа.
Определим линейные дифференциальные формы dz и dz
dz — dx 4- i dy, и dz — dx — i dy.
1002
Глава 20. Комплексный анализ
Отметим, что эти дифференциальные формы линейно независи-
мы в каждой точке и, кроме того,
dx — l:(dz + dz), dy = -^(dz — dz).
Z ZI
Таким образом, произвольная линейная дифференциальная фор-
ма может быть записана в виде
a dx + b dy = A dz + В dz,
где
А = “(а — ib) и В = -I- it>).
z z
В частности, для любой дифференцируемой комплекснозначной
функции f мы имеем
df = —dx + — dy
дх ду
= 1
2 \ дх 1 ду J
df .df\
дх ду)
Используя определения (20.1) и (20.2), мы можем это переписать
в виде
df = У- dz + dz. (20.7)
dz dz
Давайте рассмотрим несколько примеров. Если взять f = z, то из
(*20.5) и (20.6) имеем d(z) — dz. Таким образом, наши обозначения
логичны (именно поэтому мы ввели символы д/dz и dfdz). Если
f — Р — полином ОТ Z, то
dP = P' dz.
В этом выражении отсутствует член с dz. Возьмем f = |z|2 = zz,
тогда получим
d\z\2 = zdz + zdz.
Определим комплексную экспоненциальную функцию ez фор-
мулой
ez — ex(cosy + i sin у).
20.2. Комплекснозначные дифференциальные формы 1003
Тогда
dez — ex(cosy + isiny) dx + ex(— sin у + icosy) dy
= ex (cos у + i sin у) (dx + idy),
и, следовательно,
dez — ez dz.
Из этого выражения получаем
Комплекснозначная 2-форма имеет вид
cdx Л dy,
где с — комплекснозначная функция. Из двух линейных ком-
плекснозначных дифференциальных форм o>i и о>2 мы можем об-
разовать внешнее произведение cui Л ^2- Тогда, например,
dz Adz = (dx + i dy) Л (dx — i dy)
= —2idx Л dy
или
dx A dy = - dz A dz.
В частности,
dA
d(Adz) = 0, если и только если -— = 0.
dz
Теорема Стокса сохраняется без изменения, только теперь си —
линейная комплекснозначная дифференциальная форма. Напри-
мер, если Adz = 0 удовлетворяет равенству d(Adz) = 0, то тео-
рема Стокса говорит, что для любой области D, содержащейся в
области определения А, мы имеем
0.
9D
Этот важный результат называется теоремой Коши.
1004
Глава 20. Комплексный анализ
20.3. Голоморфные функции
Дифференцируемая функция /, определенная в некоторой облас-
ти D пространства R2, называется голоморфной1, если она удов-
летворяет тождеству
% = 0. (20.8)
dz
Так как это определение является основным для всей темы, то
этот параграф посвящен обсуждению эквивалентных формули-
ровок и простейшим следствиям понятия голоморфности. По-
скольку d/dz — дифференциальный оператор, то мы имеем урав-
нения
д . . df dg д . j. \ 9f „dg
dz dz dz dz dz dz
9 (f\ 1 (df dg\
a~z{g) = 72[ai9~fdi)’ 9*0'
Из этих соотношений мы видим, что сумма, произведение и част-
ное двух голоморфных функций тоже голоморфны (в случае
частного знаменатель нигде не должен обращаться в нуль). В
предыдущем параграфе мы уже пользовались этим замечанием,
чтобы получить тождество (d/dz)P(z) = 0, т. е. что любой поли-
ном (только от г) — голоморфная функция. Аналогично, любая
рациональная функция, т. е. отношение двух полиномов Р/Q, —
голоморфная функция в области D при условии, что Q нигде не
обращается в нуль в этой области.
С учетом (20.7), функция f голоморфна, если и только если
df = hdz, (20.9)
т. е. если и только если df не имеет членов с dz. Здесь, конечно,
h = df /dz. Это условие можно записать в эквивалентной форме
d(fdz) -0. (20.10)
1а также аналитической. При этом предполагается непрерывность част-
ных производных первого порядка, что иногда в дальнейшем не уточняется,
но используется. — Прим. ред.
20.3. Голоморфные функции
1005
Пусть f = u+iv, где вещественнозначные функции ими являют-
ся вещественной и мнимой частью /. Теперь, полагая веществен-
ную и мнимую части df /dz равными нулю и используя (20.3),
мы видим, что
du = dv_ ди = _ду_
дх ду" ду дх'
Это система дифференциальных уравнений в частных производ-
ных первого порядка, называемых уравнениями Коши-Римана.
Таким образом, функция / голоморфна, если и только если вы-
полняются уравнения Коши-Римана.
Существует другой способ записи уравнений Коши-Римана.
Рассмотрим дифференциальную форму
и dx + v dy.
Тогда в евклидовой метрике на плоскости
★(tz dx + v dy) = —v dx + и dy.
Тем самым уравнения Коши-Римана эквивалентны равенствам
d(u dx + v dy) = 0 и d*(udx + vdy) = 0.
Заметим, что они аналогичны уравнениям Максвелла в простран-
стве R1,3. В уравнениях Максвелла мы имели дело с 2-формами в
четырехмерном пространстве. Уравнения Коши-Римана написа-
ны для 1-формы в двумерном пространстве. Как уже было отме-
чено в главе 18, звездный оператор ★ : Лп/2 —> Лп/2 (п — четное
число) зависит только от конформной структуры.
Будем полагать, что / — отображение (подпространства) R2
в R2, переводящее (х,у) в (и(ж,у),г;(ж,2/)). Матрица Якоби этого
отбражения равна
/ди/дх ди/ду\
\dv/dx ди/ду)'
Из формул (20.11) следует, что эта матрица имеет вид [ j.
\ о а I
В пространстве R2 матрица имеет такой вид, где а2 + Ь2 0, если
1006
Глава 20. Комплексный анализ
и только если она конформна (т. е. сохраняет углы) и сохраняет
ориентацию. Тогда (20.11) можно переписать так:
/ди/дх ди/ду\ или равна нулю, или конформна2 ,
ydv/dx dv/dyj и сохраняет ориентацию. ' ’ '
Пусть f = u + iv и g — г + is - комплексные функции. Будем
рассматривать fag как отображения (подпространства) R2 вК2.
Если образ g лежит в области определения /, то можно постро-
ить композицию f о д. В силу цепного правила, матрица Якоби
f о д (рассматриваемая как отображение R2 в R2), вычисленная
в (т,у), является произведением матрицы Якоби функции /, вы-
численной в точке (г(х,2/), з(т,у)), на матрицу Якоби функции
д, вычисленной в точке (х,у). Произведение двух конформных
сохраняющих ориентацию матриц тоже конформно и сохраня-
ет ориентацию. Кроме того, произведение нулевой матрицы на
любую матрицу равно нулю. Из (20.12) следует, что композиция
двух голоморфных функций тоже голоморфна. Для композиции
двух голоморфных функций мы используем стандартное выра-
жение: если, например, /(г) = ez и g(z) = Зг2 —2, то fog = е3^2-2.
Поскольку dfdz — линейная комбинация операторов d/dx и д/ду
(с постоянными коэффициентами), из цепного правила следует
(20.13)
dz ydz ) dz
Поэтому для примера, приведенного выше, мы имеем
^-е322'2 = бге322-2.
dz
Другими словами, для голоморфных функций действие операто-
ра dfdz можно вычислять как обычную производную функции
одной переменной. Причина вскоре станет ясна.
Условие (20.12) не слишком удобно, потому что в нем есть
два разных случая: матрица Якоби равна нулю или не равна
нулю. Давайте запишем условие (20.12) несколько по-другому.
Рассмотрим матрицу
2По этой причине голоморфная функция, для которой df /dz 0 всюду
в рассматриваемой области, задает конформное отображение. — Прим. ред.
20.3. Голоморфные функции
1007
Матрица
коммутирует с J, т. е. выполняется равенство
A J = JA,
если и только если а — dn с = —Ь, как легко увидеть, перемножая
матрицы. Таким образом, AJ = JA, если и только если матрица
А имеет вид
л (а —Ь\
А - ,
у о a J
где а и Ь могут быть равны нулю. Тогда условие (20.12) можно
записать в виде
/ди/дх ди/ду
\dv/dx dv/dy
с комплексным чис-
ди/дх ди/ду\
dv/dx dv/dyJ
(20.14)
Мы можем дать интересную интерпретацию равенству A J = JA
и тем самым условию (20.14). Матрица А имеет размер 2x2.
Она задает линейное преобразование вещественного двумерно-
го векторного пространства R2 в себя. Пространство IR2 можно
идентифицировать с одномерным комплексным векторным про-
странством С, идентифицируя вектор
лом x+iy. Умножение этого числа на i переводит его в — y+ix. Но
(—т / х\
I = J (1.
Таким образом, J — матрица умножения на i с вещественной точ-
ки зрения3. Произвольное линейное преобразование одномерного
комплексного векторного пространства С - это линейное преоб-
разование пространства R2. Но не каждое линейное преобразо-
вание А пространства R2 над вещественными числами соответ-
ствует линейному преобразованию пространства С над комплекс-
ными числами. Комплексное линейное преобразование должно
3В обычной евклидовой метрике R2 это поворот на угол 90° (в направле-
нии от к еу). Умножение на число с = а 4- ib представляет собой компо-
зицию гомотетии с коэффициентом г = |с| — у/а2 + Ь2 и поворота на угол 0
(аргумент с), удовлетворяющий условию с — r(cos0+isin0), т. е. конформное
линейное преобразование. — Прим. ред.
1008
Глава 20. Комплексный анализ
коммутировать с умножением на комплексные числа, в частнос-
ти, на i. Таким образом, чтобы матрица А соответствовала ком-
плексному линейному преобразованию, должно выполняться ра-
венство AJ — JA. Если А удовлетворяет этому условию, т. е.
л fa —Ь\ .
I, то легко проверить, что А соответствует у mho-
ci /
b
жению на комплексное число а + ib, т. е. А соответствует
(а + ib)(x + iy), Очевидно, что умножение на комплексное чис-
ло в пространстве С комплексно линейно. Таким образом, (20.14)
можно переписать в форме
рт f ди/дх ди/ду
Преобразование
комплексно линейно.
(20.15)
Ни одна из приведенных эквивалентных формулировок, за ис-
ключением уравнений Коши-Римана (20.11), не была известна
математикам XIX века. А теперь дадим классическую формули-
ровку, наиболее близкую к (20.15). Пусть f — дифференцируемая
функция, не обязательно голоморфная, а [ ) — точка из облас-
ти определения /. Кроме того, пусть J — малый вектор. Тогда
из определения дифференцируемости мы имеем
4СЛ0)-/О^^1,+о((||‘2+,2||)1/2)'
Здесь частные производные вычисляются в точке
Пусть z = x+iynh= k+il. Будем писать f(z) вместо f
Тогда предыдущее уравнение можно переписать в форме
f(z + h)~ f(z) = ^k+%-I+<,(№-
ох оу
Используем (20.7) и перепишем еще раз:
/(г + Л)-Лг) = ^Л+^Л + о(|Л|).
20.3. Голоморфные функции
1009
Это уравнение содержит комплексные числа. Поэтому если h Ф 0,
то обе части делим на h и получаем
/(2 + л)-/(г) a/.a/j.
------h-----=& + aih+<,(1)'
Заметим, что левая часть этого равенства выглядит как обыч-
ное разностное отношение, но только здесь комплексные числа.
Предположим, что \h\ —> 0. Величина h/h может быть любым
комплексным числом, модуль которого равен единице. (Напри-
мер, если h — вещественное число, то h/h = 1, а если h — is,
т.е. чисто мнимое, то h/h = —1.) Поэтому предельное выраже-
ние справа может зависеть от угла, при котором h —> 0. Если мы
хотим, чтобы этот предел существовал, т. е. не зависел от угла,
надо потребовать, чтобы df /dz = 0 в точке . Таким образом,
если / — голоморфная функция, то предел левой части равенства
существует во всех точках области определения /, и этот предел
равен df /dz и является непрерывной функцией. Обратно, пред-
положим, что в каждой точке существует предел
№ + >.)-№) = ,
h J v 7
(независимо от того, как h стремится к нулю) и является непре-
рывной функцией. Выбирая h вещественным числом, можно по-
казать, что df /dx существует и непрерывна, а выбирая h чисто
мнимым, можно показать, что df /dy существует и непрерывна.
Тогда f — непрерывно дифференцируемая функция. Предыду-
щее рассуждение показывает, что df /dz = 0 и f(z) = df /dz.
Итак, мы доказали, что f голоморфна, если и только если су-
ществует предел
/(г + Л)
h—>0 П
независимо от того, как h стремится к нулю, и этот предел —
непрерывная функция. Короче условие (20.16) можно сформу-
лировать так: функция f непрерывно дифференцируема с ком-
плексной точки зрения. Именно так рассуждали математики в
1010
Глава 20. Комплексный анализ
XIX веке. Такой подход довольно обманчив, потому что условие
комплексной дифференцируемости имеет гораздо больше ограни-
чений, чем обычное условие дифференцируемости. Тем не менее,
мы принимаем обозначение как более удобное, чем df /dz.
Как уже было отмечено, из теоремы Стокса и (20.10) следует
[ f(z)dz = 0, (20.17)
JdD
что является интегральной теоремой Коши для любой области
D, лежащей в области определения голоморфной функции /. И
обратно, если f — произвольная функция, то
[ f(z)dz = [ d(fdz).
JdD Jd
Этот интеграл обращается в нуль для всех Р, если подынтеграль-
ное выражение тождественно равно нулю, т. е. если f — голо-
морфная функция.
Таким образом, мы показали, что все условия (20.8)-(20.17)
эквивалентны. Функция, удовлетворяющая любому из них (а тог-
да и всем им), голоморфна.
20.4. Вычисление вычетов
Начнем с вычисления контурного интеграла Д zn dz, где 7 —
окружность с центром в начале координат. Если п 0, то функ-
ция zn голоморфна на всей плоскости, тогда из теоремы Коши
следует, что этот интеграл равен нулю. Для отрицательных зна-
чений п функция zn не голоморфна (и не определена) в начале ко-
ординат, и следовательно, мы должны вычислять интеграл пря-
мым способом. Если окружность 7 имеет радиус г, то в полярных
координатах можно написать z = re10. Тогда вдоль окружности
7 имеем dz — ire10 df). Итак,
zndz = irn+1ei(-n+1^de
И
f zndz = irn+1 / * ei(n+i)e M
20.4. Вычисление вычетов
1011
Этот последний интеграл равен нулю всегда, кроме случая
п — — 1, когда он равен 2тг. В этом случае rn+1 = 1 и поэтому
[ „ , 10, если п ф -1,
/ zn dz = <
J у I 2тг1, если п = — 1.
Пусть D — некоторая область, содержащая начало координат
(рис. 20.1), и пусть f — функция, голоморфная в области D — {0}.
Далее предположим, что вблизи начала координат можно напи-
сать
/ = a_nz~n + a-n+iz~n+1 Н----1- a-iz-1 + д,
где д — голоморфная функция вблизи начала координат.
Давайте вычислим f(z) dz. Нарисуем окружность 7 не-
большого радиуса с центром в начале координат, целиком ле-
жащую в D и в области, где работает выписанное разложение
(рис. 20.2). Тогда f голоморфна в той части D, которая явля-
ется внешней по отношению к 7. Поэтому, в силу интегральной
теоремы Коши,
[ fdz= [ f dz.
J dD J 7
Если сюда подставить разложение f и проинтегрировать каждый
член, то все отрицательные степени дадут нуль, кроме a^iz-1.
При этом fygdz = 0, поскольку д — голоморфная функция.
Тогда
/ jf(z) dz = 2тгкг_1.
JdD
1012
Глава 20. Комплексный анализ
Поскольку начало координат было выбрано произвольно, то его
можно заменить любой другой точкой или конечным числом то-
чек в области D. Говорят, что функция f имеет полюс4 в точке
о, если она голоморфна в области U — {а}, где U — некоторая
окрестность точки а, и если в ее окрестности функция f имеет
разложение
f(z) = a_n(z - а)~п Ч----h a-i(z - а)-1 + д,
где д — голоморфная функция вблизи а. Число а_1 называется
вычетом функции f в точке о и обозначается resa(/). Из преды-
дущих рассуждений следует, что интеграл от f(z)dz по малой
окружности вокруг а равен 2тг1а_1 — 27riresa(/). Функция, го-
ломорфная в области D, за исключением полюсов, называется
мероморфной.
Предположим, что f мероморфна в области D и имеет в ней
конечное число полюсов (рис. 20.3). Тогда вокруг каждого полю-
са можно нарисовать маленькую окружность (рис. 20.4) и, при-
менив интегральную теорему Коши, написать
/ (z) dz = 2-zri ^2 resa(/)-
по полюсам а
Эта формула называется теоремой Коши о вычетах. Она очень
полезна при вычислении определенных интегралов. Например,
4В предположении, что старший коэффициент разложения а_п / 0, число
п называется порядком полюса. ~ Прим. ред.
20.4. Вычисление вычетов
1013
мы хотим вычислить определенный интеграл
ае
а + cos 0'
где а > 1. Запишем его в форме
1 г2эт ае
2 Jo ° + cos 0
Теперь положим z = е1в, тогда на единичной окружности dzj'xz =
dO. Кроме того, 2 cos 0 = е16> + е-10 = z + г-1. Тогда наш интеграл
принимает вид
1 Г dz
2 iz(a + |(z -I- г-1))
1 Г dz
i J7 (г2 + 2az + 1) ’
где 7 — единичная окружность. В то же время
z2 + 2az + 1 = (z — oti)(z — аг)»
где
ai = — а + \/а2 — 1 и аг = —а — х/а2 — 1,
откуда мы получаем
1 _ 1 / 1 _ 1 \
z2 + 2az + 1 ai — аг — ai 2 ~ а2 )
Поскольку а > 1, имеем аг < —1, и поэтому аг лежит вне еди-
ничной окружности. А так как aiaz = 1, то ai лежит внутри еди-
ничной окружности. Кроме того, Функция l/(z —аг) голоморфна
внутри этой окружности, поэтому наша формула показывает, что
вычет равен
1 _ 1
«1 — «2 2-Ja2 - 1
Таким образом, согласно теореме Коши о вычетах, получаем
ответ
/>7Г dB _ 1 f dz _ %
Jo а + cose 2i У7 z2 + 2az + 1 Va2 - 1
1014
Глава 20. Комплексный анализ
Мы вскоре увидим, что любая рациональная функция вида
R(z) = P(z)/Q(z) мероморфна и имеет полюса в точках, где Q
обращается в нуль. (Это следует немедленно из разложения раци-
ональной функции на дроби. Но здесь мы это не предполагаем.)
Кроме того, мы получим эффективный способ вычисления вы-
четов. Тогда это позволит нам вычислять, например, интегралы
вида 7?(cos0, sin#) d0, сделав подстановку z = и учтя, что
cos0 = (l/2)(z 4- г-1) и sin# = (1/21)(г — г-1), после чего проде-
лывая процедуру, описанную выше.
Начнем с леммы. Предположим, что д голоморфна в области
D 5, кроме конечного числа точек oi,..., Предположим, что
в каждой из этих точек функция д удовлетворяет условию
lim \z — а| |5(г)1 = 0.
2—
Тогда
/ gdz — 0.
JdD
Для доказательства этого утверждения нарисуем маленькие
окружности 7г вокруг каждой точки ai. Тогда, как и раньше,
gdz = ^fy.g dz. При этом
I g{z)dz
7г
2ттг7Иг,
где г — радиус окружности 7г, и Мг ~ максимум |g| на 7г. В силу
предположения гМг —► 0 при г —> 0. Таким образом, устремляя к
нулю радиусы окружностей, мы получим fdDgdz = 0.
А теперь пусть f голоморфна в области D и а — точка в
области D. Применим доказанную лемму к функции
9(г)=
5D — замыкание области D: она содержит все точки области D плюс точ-
ки на границе. [Голоморфность функции на замкнутом множестве подразу-
мевает выполнение соответствующих условий в некоторой открытой окрест-
ности этого множества. — Ред.]
20.4. Вычисление вычетов
1015
Функция д голоморфна в D везде, кроме точки а. Более того,
(г — a)g(z) = f(z) — /(а) и это выражение стремится к нулю при
z а. Тогда
[ M-Mdz=0.
JdD - а
Но /(а) — постоянная и
— 27ri.
Откуда получаем
f(a) dz
z — а
= 27ri/(a),
и теперь можно написать
/(a) = J_ Г dz.
2tti JdD z-a
Для удобства заменим а на z и z на £ и напишем интегральную
формулу Коши
= <% (20-18)
JdD S ~ z
Эта формула является краеугольным камнем, на котором стро-
ится вся теория комплексного анализа.
Сформулируем следующую лемму. Пусть ф — комплексно-
значная функция, определенная и непрерывная на границе dD
некоторой области D. Тогда функция
голоморфна в области D и обладает свойством
= nFn+1(z).
Докажем эту лемму по индукции. Прежде всего докажем, что
F1 непрерывна в D. Пусть zq — некоторая точка в области D.
Выберем а настолько малым, что окрестности \zff — го| < 2а и
1016
Глава 20. Комплексный анализ
\zf — го| < а целиком находятся в области D. Таким образом,
расстояние от г' до всех точек границы dD не меньше а и, сле-
довательно, при £ е 8D неравенство
1 1 1
IC - z'\ 1£ - 2о| 2а2 < а2
выполняется для всех таких z. Теперь убираем штрих и приме-
няем равенство
1 1 1 ( х
k-z (мтг Zoj’
так что
JdD ~ “ zo)
^|z-20|4 / 10(01
° J9D
Это означает, что Fi — непрерывная функция. Более того,
^(г)-^(г0) Г
- ^0 JdD (С “ *)(£ “ ^0)’
Если фиксировать значение го, то функция <№)/(£ — го) непре-
рывна на границе dD. Следовательно, правая часть этого равен-
ства — непрерывная функция от г, и оно выполняется для всех
z ф zq. Устремляя z —> го, мы видим, что Fi — дифференцируе-
мая функция в комплексном смысле и
Кроме того,
1(z - Zq) = 1
(е - 0(е - ^о) (е - w - *о) (е - о2 ’
поэтому
F2(z) -F2(z0)
= г г ф(№ .х f 0m
J (е-^-го) J ^-^2±{г ZQ)J (e-z)2(e-zo)’
20.4. Вычисление вычетов
1017
что показывает (с учетом предыдущих соображений) непрерыв-
ность функции F2 и голоморфность функции Fi. Далее,
*2(г) - F2(z0) _ R^-R^zo) ! Г </>(£)<%
Z-ZQ Z-Zq J (f - z)2(£ - ZoY
где
1( ’ /({-«-«I’
Поскольку функция 0(C)/(C —го) непрерывна на границе сЮ, бла-
годаря предыдущему результату мы приходим к выводу, что Ri
дифференцируема и jRj (го) = f (Ф(£)/(С—го)3) Переходя к пре-
делу в нашем уравнении, получаем, что F2 — дифференцируемая
функция в комплексном смысле и
F£ - 2F3.
Теперь процедура индукции уже очевидна. Предположим, что
мы доказали свойство F/l_1 = (п — l)Fn для всех непрерывных
функций ф. Используя тождество
1 г — го _ 1
(С - 2)П-1(С ~ Хо) + (С - Х)п(£ ~ ZQ) (С ~ Х0)п'
мы видим, что
Fn(z) - Fn(zo)
= [ f f
J (е-ад(е-^о) J (ад0)п 1 0)J (адиадо)
= Rn-i(z) - Яп-Лэд) + (*-*))/
где функции
»м = [ *
связаны с непрерывной функцией <^>(С)/(С ” го)- Итак, мы дока-
зали, что Fn непрерывна.
В силу предположения индукции Bn-i(zo) = (п — 1)7?п(го) =
(n — l)Fn+i(^o), поэтому разделим уравнение для Fn(z) — Fn^o)
1018
Глава 20. Комплексный анализ
, = п!_ [
2mJaD(i-zr+l-
на г - го и перейдем к пределу z —> zq. В результате получим
Ffn — nFn+i, что и требовалось доказать.
Применим этот результат к интегральной формуле Коши
(20.18). Поскольку функция f непрерывна, мы приходим к уди-
вительному заключению: если функция f голоморфна в области
Р, то она в ней бесконечно дифференцируема, причем каждая
производная (комплексная) голоморфна и удовлетворяет усло-
вию
(20.19)
Из формул (20.18) и (20.19) можно получить много важных
следствий, что мы и сделаем в следующих параграфах. Начнем
с принципа устранимых особенностей. Предположим, что функ-
ция f определена и голоморфна в области D — {а}, где а 6 Р,
т. е. во всей области Р, кроме одной точки а. Необходимым и
достаточным условием того, что существует голоморфная функ-
ция, определенная в области Р, которая совпадает с / в области
Р — {а}, является Нт2^а(г — a)/(z) = 0. Такая продолженная
функция (если она существует) определена однозначно.
Доказательство. Пусть f(a) обозначает значение продолжен-
ной функции в точке а. Поскольку продолженная функция голо-
морфна, она непрерывна в точке а и limz_>a f(z) = Поэтому
— a)/(z) — Итг^а(г — а)/(а) — 0, что доказывает необ-
ходимость. Чтобы доказать достаточность, нарисуем небольшую
окружность 7 с центром в точке а, целиком лежащую в области
Р. Рассмотрим функцию
1
2%i J z
Это функция голоморфна внутри 7. Нарисуем другую окруж-
ность 71 вокруг а, лежащую внутри 7. Тогда во всех точках коль-
ца между 71 и 7, согласно интегральной формуле Коши (20.18),
Согласно нашему предположению, если фиксировать z и радиус
окружности 71 устремить к нулю, то второй интеграл обратится
20.4. Вычисление вычетов
1019
в нуль. Поэтому
для всех z а внутри 7. Это означает, что справа стоит голо-
морфная функция, определенная внутри 7, причем она совпадает
с / при z ф а. Очевидно, что такая продолженная функция един-
ственна, потому что для нее должна выполняться интегральная
формула Коши. В дальнейшем мы будем обозначать эту продол-
женную функцию также буквой /.
Пусть f голоморфна в области D, и пусть а — точка в этой
области. Применим принцип устранимых особенностей к выра-
жению
Очевидно, что функция Д определена и голоморфна в области
D — {а} и обладает свойством Пт^_,а(г — а)Д(г) — 0. Следова-
тельно, ее можно продолжить до голоморфной функции, опреде-
ленной во всей области £>, и написать
f м 1 f /«)- Л°)
При этом
1 , _ ______L_
(e-a)(e-z) z) e-*
откуда
/(С - /(g) 1 [ /(£) - /(а)
е - а С 2т Д е - z
= /(а)-Ж).6
6 В этой и следующей формуле учитывается, что
f=0,
и этот интеграл прибавляется к выражению для fi(z) с коэффициентом
/(а)/2тп. — Прим, ред.
1020
Глава 20. Комплексный анализ
Таким образом,
Ж = /(а) + (г~о)Л(Д где Ш =
Конечно,
Л(а) = /'(а).
Ту же процедуру можно применить к Д и определить Д из вы-
ражения Д(г) — Д(а) + (г — а)Д(г). Таким образом можно про-
делать п шагов
/(*) = /(а) + (z - a)f!(z),
fi(z) = Л(а) + (z- a)f2(z),
fn-1 = + (z~ a)fn(z),
так что
f(z) = /(a) + (z- a)fi(a) H------I- (z - a)n 1fn-i(a) + (z - a)nfn(z).
Дифференцируя это формулу к п раз, получим Д(а) =
(l/fe!)/(fc)(а). В результате получается ряд Тейлора с остатком
f(z) = f(a) + (z - a)/'(a) + (a) + • • • + (z - a)”/„(4
(20.20)
где, как и раньше,
(20.21)
для всех z внутри 7.7
Из формулы (20.21) можно получить полезную оценку остат-
ка. Предположим, что 7 — окружность с радиусом R и центром
7Доказательство формулы (20.21) индукцией по п оставляем читателю в
качестве упражнения. — Прим. ред.
20.5. Приложения и следствия
1021
в точке а, а М обозначает максимальное значение |/(£)| для £ на
окружности 7. Подстановка в формулу (20.21) дает
1/nWI
м
Rn-\R- |z-s|)’
(20.22)
Поскольку /п(а) = (1/п!)/<п)(а), с помощью формул (20.21) и
(20.22) мы получаем
|/^(а)| < Mn\R~n.
(20.23)
и
(20.24)
(Здесь 7 — окружность с радиусом 7?, центром в точке а, М —
максимум функции f на этой окружности.)
Обратите внимание на замечательное логическое развитие
ситуации. Мы начали с предположения, что функция f имеет
непрерывную производную первого порядка, которая удовлетво-
ряет уравнениям Коши-Римана в частных производных. Из этих
уравнений следует, что / имеет производные всех порядков, и что
n-я производная функции f (в комплексном смысле) существу-
ет и определяется простым выражением (20.23) через значения
самой функции /.
В следующем параграфе мы получим ряд следствий из этого
факта.
20.5. Приложения и следствия
В качестве первого примера применения формулы (20.24) дока-
жем теорему Лиувилля.
Голоморфная и ограниченная на всей плоскости функ-
ция должна быть постоянной.
Доказательство. Пусть |/(z)| С М для всех z. В формуле
(20.24) положим п = 1. Значение R можно выбрать сколь угодно
большим, а это значит, что /'(а) = 0 для всех а. Таким образом,
1022
Глава 20. Комплексный анализ
обе частные производные f тождественно равны нулю, т. е. f
постоянна.
Следствием теоремы Лиувилля является основная теорема
алгебры, согласно которой
любой полином положительной степени имеет по край-
ней мере один корень.
Доказательство. Напишем Р(г) = anzn + Ч----|- ао,
где п > 0 и ап / 0. Тогда
|Р(г)| S (Ы - | И’1 + + |аа| |гГ")]|г!"
Для достаточно больших |z| выражение в квадратных скобках
> ||ап|. Таким образом, |Р(г)| —> оо при |z| —> сю, и, следова-
тельно, функция 1/Р голоморфна и ограничена вне некоторой
окружности большого радиуса. Если бы P(z) нигде не обраща-
лась в нуль, то функция 1/Р была бы голоморфна и ограничена
на всей плоскости, т. е. была бы постоянной. Но поскольку Р — не
постоянная функция, то это невозможно. Таким образом, должен
быть, по крайней мере, один нуль функции Р, что и требовалось
доказать.
Если Р(а) ~ 0, то (z — a)[P(z)/(z — а)] —> 0, и мы можем
воспользоваться принципом устранимых особенностей и утвер-
ждать, что P(z)/(z—а) — голоморфная функция. Далее, посколь-
ку z^-ai = (z — a)(zJ-1H---HaJ-1), то P(z) —Р(а) можно разде-
лить на z — а. А поскольку Р(а) = 0, то P(z)/(z — а) — полином
степени п — 1. Если п > 1, то опять можно применить основную
теорему алгебры и утверждать, что
полином степени п имеет ровно п корней, считая с
кратностями.
Следующий пример. Покажем, что голоморфная функция,
определенная в некоторой связной области D, не может обра-
щаться в нуль вместе со всеми производными в любой точке а
внутри области D, если только она не равна нулю тождествен-
но. Действительно, предположим, что /(а) — 0 и /(п\а) — 0 для
всех п. Выберем R так, чтобы диск радиуса R с центром в точке
20.5. Приложения и следствия
1023
Рис. 20.5
а целиком лежал в области D (рис. 20.5). Сначала покажем, что
f тождественно равна нулю на этом диске. Из формул (20.20) и
(20.22) мы знаем, что (20.22)
/(2) = (г - a)n+1/n+i, где |/n+l(z)| < ,
rtyrt — |,
откуда
М \z — а
(R-\z-a\) ’
Поскольку \z — а| < R и п может быть сколь угодно большим,
это неравенство означает, что /(г) = 0. А теперь возьмем произ-
вольную точку внутри диска в качестве нового центра, увеличив,
таким образом, область, где мы знаем, что /(г) = 0 (рис. 20.6).
Если b — любая другая точка в области 7?, то точки а и b можно
соединить кривой, которая вся лежит в области D и, следова-
тельно, на конечном расстоянии от границы. Можно нарисовать
конечное число дисков (рис. 20.7), начав с диска, имеющего центр
в точке а и закончив диском с центром в точке 5, получив, таким
образом, /(5) = 0. Итак, мы доказали следующее.
Предположим, что f голоморфна в некоторой связной
области D и равна нулю вместе со всеми производны-
ми в точке а, лежащей внутри области D. Тогда f
тождественно равна нулю.
1024
Глава 20. Комплексный анализ
Рис. 20.6
Предположим, что ап — последовательность точек в облас-
ти Z), причем ап —> а, где а тоже лежит внутри D. Предпо-
ложим, что f(an) — 0 для всех п. Тогда /(а) = lim/(an) — 0
и /'(а) = lim(/(a) — f(an))/(a — ап) — 0. Утверждается, что
в этом случае все производные f(k\a) — 0 и, следовательно,
f = 0. Действительно, предположим, что k — первое положитель-
ное целое число, для которого f^(a) 0. Тогда, в силу (20.20),
f(z) = (z - a)kfk(z), где / 0, и, следовательно, fk(z) / 0
для z в окрестности а. Но поскольку z — а ф 0 для z Ф а, можно
утверждать, что /(г) ± 0 для всех г, достаточно близких, но не
равных а. Но это противоречит исходному предположению, что
f(an) — 0, где ап —> а. Только что доказанную теорему формули-
руют так: нули (нетривиальной) голоморфной функции должны
быть изолированными. Если / и д — две голоморфные функ-
ции, то предыдущий результат можно применить к голоморфной
функции f — д. Тогда утверждается следующее.
Если / и д — голоморфные функции в связной области
D и если f(an) — д(ап) для последовательности точек
ап, имеющих предел а = liman, лежащий внутри D,
то f = д во всей области D.
Этот результат показывает, насколько сильно отличается тео-
рия голоморфных функций от теории бесконечно дифференци-
20.5. Приложения и следствия
1025
руемых функций (класса С°°) вещественного переменного. Функ-
ция /, заданная формулой
// \ для х > 0,
f&) = ) n п
0 для х 0,
является С°°-функцией в пространстве R. Она тождественно рав-
на нулю для всех отрицательных х. Таким образом, поведение
С 00-функции в одной части области ее определения не оказывает
никакого влияния на ее поведение в другой части, расположенной
на конечной расстоянии. Ситуация с голоморфными функциями
совсем другая. Если нам задано поведение голоморфной функции
в какой-то части области определения, то она полностью опреде-
лена во всей области.8
Мы уже видели, что голоморфная функция д не может быть
равна нулю вместе со всеми производными в любой точке внутри
области определения. Поэтому, если д(а) = 0 в некоторой точке
а, то существует наименьшее число /с, для которого д^к\а) 0.
С ледовате льно,
g(z) = (z — a)kgk(z) / 0 для z вблизи a, z ± а,
где дь — голоморфная функция. Предположим, что / тоже голо-
морфна в той же области. Давайте рассмотрим функцию h = f /д,
которая определена для z вблизи си, но z ф се. Напишем разложе-
ние (20.20) функции / в окрестности а
f(z) = /(a)+(z-a)/'(a)+-..+(z-a)(fc-1)=^^+(z-a)fc/fe(2).
Тогда
, , . .. . , , . /(а) 1 f'(a) 1
h(z) = f(z) g(z) = ---пг—-т-r + 7-----U-1 ( . Ч--
(z-a)kgk(z) (z - а)к 1 gk(z)
f<k~1l(a) 1 fk(z)
+ (z- a)(k - 1)! gk(z) + gk(z) '
8Под частью области определения имеется в виду ее открытое подмно-
жество. Процедура восстановления голоморфной функции по ее ростку,
определенному на такой части, во всю область называется аналитическим
продолжением. — Прим. ред.
1026
Глава 20. Комплексный анализ
Поскольку 1/gk голоморфна вблизи а, то ее также можно разло-
жить в окрестности а:
l/fffcfc) = bo + 61 (z - а) + • • • + (z - a)kbk(z),
где
bo = 1/Ыа) = Kl/g(k\a) ит.д.
Если это разложение подставить в формулу для Ь, то получим
/i(z) = a_k(z-a)~k+a_fe+1(z-ce)(_fc+1)4---Fa_i(z-a)-1+/io(z),
где
а-к = /(a)60 = /(a)/gfe(a),
a-k+1 = fiotjbi + J'(a)6o,
и т. д., a /io голоморфна вблизи а. Итак, мы доказали следующее.
Частное двух голоморфных функций — мероморфная
функция.
Предыдущие формулы упрощаются, если д имеет простой нуль в
точке аг, т. е. если к = 1. В этом случае утверждается следующее.
Если д(а) = 0 и gf(ot) 0, то частное //р имеет
простой полюс в точке аг. Вычет в этой точке равен
/ (аг)/У (аг), т.е. /(z)/#(z) = а_1(г-а)“1 + /iq(z) вблизи (20.25)
аг, где a_i — /(а)/</(а?) и h§(z) — голоморфная функ-
ция вблизи а.
Число к, которое мы использовали сейчас, называется поряд-
ком нуля. Таким образом, голоморфная функция д имеет нуль
первого порядка в точке аг, если д(а) = 0 и ^'(аг) / 0. Она имеет
нуль порядка к в точке аг, если д(а) = • * * = д^-^а) ~ 0, но при
этом д^(аг) 0 9
Предположим, что функция f голоморфна в ограниченной
области D и имеет конечное число нулей в этой области, т.е.
мы предполагаем, что есть конечное число различных точек
ai,..., аг, где функция f равна нулю. И пусть kj — порядок нуля
9Эквивалентное условие состоит в том, что функция 1/д имеет в точке а
полюс порядка к. — Прим. ред.
20.5. Приложения и следствия
1027
функции f в точке &j. Тогда /(г) = (г — ai)fcl#(£), где функция
д обращается в нуль только в точках и имеет тот же
порядок нулей в этих точках, что и функция /. Далее можно
написать g(z) = (z — &2)k2h(z), где функция h обращается в нуль
в точках аз,..., аг. Продолжая таким образом, мы получим
f(z) = (z - ai)fcl (z - а2)*2 • ••(z - ar)^F(z),
где F — голоморфная функция в области D, которая не равна
нулю ни в одной точке этой области. Продифференцировав это
выражение и разделив его на /, получаем
Г(^) fei . . fcr F'(z)
f(z) z - «1 z - ar F(z) ’
где Ff/F — голоморфная функция в области D. В частности,
если д — другая голоморфная в области D функция, то gf'/f
имеет только простые полюса в точках вычеты в которых
равны kjg(&j). Используя формулу Коши, получаем следующий
результат.
Предположим, что f и д — голоморфные функции в
ограниченной области Е, причем f имеет в области
D конечное число нулей в точках оц,..., аг, порядок
которых равен fci,..., кг соответственно. Пусть, кроме
того, f 0 на границе dD.
А / 9{^y§rd£, = kig(ai) + --- + krg(ar). (20.26)
27Г1 JqD f(£)
В частности, если взять д = 1, то имеем
+ • • • + кг
числу нулей функции f
с учетом их кратности.
Заметим, что если f — голоморфная функция в большей области
Е, такой, что D содержится в Е, тогда f может иметь только ко-
нечное число нулей в области D. В противном случае f была бы
— [
2" JaD /К)
1028
Глава 20. Комплексный анализ
равна нулю в последовательности точек, сходящейся к пределу,
расположенному в области Е.10 А это означало бы, что / тож-
дественно равна нулю. Таким образом, можно утверждать, что в
этом случае предположения для (20.26) и (20.27) справедливы.
Теорема Руше утверждает следующее.
Если J и h — голоморфные функции в ограниченной
области D и непрерывны в D == D U dD. и если всюду , .
на D |/(z) — Л(з)| < \ f (г)|, то / и h имеют одинаковое ' ’ '
число нулей (с учетом их кратности) в этой области.
Из посылок теоремы следует, что / не равна нулю на границе
dD, и, следовательно, не равна нулю в полосе вблизи этой гра-
ницы. Поэтому У имеет конечное число нулей в области D. То
же самое можно сказать и о функции h. На самом деле можно
утверждать, что для любого 0 t 1 функция заданная
формулой
ht{z) = /(z) + - /(z)),
голоморфна в области D, не равна нулю на границе dD и имеет
конечное число нулей в D, которые можно сосчитать по формуле
(20.27). Формула (20.26) непрерывно зависит от t и дает в резуль-
тате целое число. Следовательно, это число является константой.
При этом Ло = У и Лх — Л, так что f и h должны иметь одинако-
вое число нулей, что и требовалось доказать.
Предположим, что функция f голоморфна во всех точках z ±
(3 в окрестности /3, но |/(z)| —► оо при г —> /3. Тогда функция f ф 0
для z достаточно близких к /3 и поэтому 1/У(г) — голоморфная
для z достаточно близких к /3, кроме z — /3, и 1/У (г) —» 0 при z —>
/3. Это означает, что 1/ f имеет устранимую особенность в точке
/3. Таким образом, она становится голоморфной не только вблизи
/3, но и в самой этой точке, если мы положим ее там равной нулю.
Поскольку теперь 1/f голоморфна в точке /3 и в ее окрестности,
и она — не тождественный нуль, то она должна иметь в точке
/3 нуль конечного порядка, т.е. l/f(z) = (z — /3)Jgj(z)y где gj
голоморфна вблизи /3 и gj(J3) ф 0. Но тогда
У(г) = (z — /3)~J/z(z), где h = 1/gj голоморфна вблизи (3.
10 Точнее, на границе сЮ, которая в силу ограниченности D является ком-
пактным множеством. — Прим, ред.
20.5. Приложения и следствия
1029
Если для функции h использовать разложение Тейлора в точке
/3, то увидим, что / имеет полюс порядка j в этой точке. Итак,
мы доказали, что
если f голоморфна всюду при z /3 в окрестности
(3 и |/(z)| —> оо, когда z —> /3, то она имеет полюс
конечного порядка в точке /3.
Предположим, что f мероморфна в ограниченной области Z),
непрерывна на границе dD и не обращается нигде на ней в нуль.
Тогда эта функция может иметь лишь конечное число нулей и
полюсов в области D. Проделав вышеописанную процедуру с
каждым нулем и с каждым полюсом, получим
, (г - ai)fcl • • • (z -
/(г)=
где F голоморфна и не имеет нулей в области D. (Здесь ai —
нули порядка и Д — полюса порядка ji.) Дальше мы можем
рассуждать так же, как и при доказательстве (20.25) и (20.26). В
результате получаем следующее.
Предположим, что f — голоморфная функция в огра-
ниченной области 2?, непрерывна в D и вблизи гра-
ницы dD. Далее предположим, что д — голоморфная
функция в области D и непрерывна на ней. Тогда
йТГ! JdD Л?)
= + • • + М(«г) - Н---+ Зр9^р)\
Здесь «1,..., аг — нули функции f порядка , кг
соответственно, и Д,..., (Зр — полюса этой функции /
порядка Д,..., jp. Пусть д = 1, тогда
7—: / “F77T = числу нулей функции f
2тг1 J^n f (с)
ои J — число ее полюсов
(с учетом их кратности).
1030
Глава 20. Комплексный анализ
Предположим, что f голоморфна для z ф 7 в окрестности
точки 7. И пусть 7 — не устранимая особенность функции, и не
является ее полюсом (так что у нас нет условия |/(z)| —* 00 при
z —> 7). В этом случае 7 называется существенной особенностью
f. Некоторое представление о сложном поведении функции вбли-
зи существенной особенности дает следующий результат.
Допустим, что / голоморфна вблизи 7, но не в са-
мой точке, где эта функция имеет существенную осо-
бенность. Тогда для любого заданного комплексного (20.29)
числа с можно найти такую последовательность точек
а. ъ что /(а-) _> а
Докажем от противного. Предположим, что это утверждение
не выполняется для некоторого числа с. Это значит, есть такая
окрестность U точки 7, что /(г) отличается от с на конечное
значение при всех z внутри области [7, z у. Скажем, пусть
|/(г) — с| > 1/М для некоторого числа М. Определим функцию
g(z) — l/(f(z) — с). Она голоморфна в области U везде, кроме
точки 7, и |^(z)| < Af. Поэтому функция д в точке 7 имеет устра-
нимую особенность. Но тогда f — 1/д + с мероморфна в точке
7 (в худшем случае имеет там полюс), что противоречит наше-
му предположению. Примером функции, имеющей существенную
особенность в точке 0, является е1/*. Покажем в явном виде, что
для этой функции справедливо условие (20.29). Мы должны по-
казать, что значение функции е1^ можно сделать сколь угодно
близким к любому комплексному числу, если z —> 0. Сделаем за-
мену переменной w = 1/z. Тогда мы хотим показать, что значение
ew можно сделать сколь угодно близким к любому комплексно-
му числу с при условии |w\ > R для произвольного значения R.
Напишем с — ге10 и w — и + w. Тогда условие |w| > R выпол-
няется, если выбрать v > R. Теперь ew = еи • ew. Поэтому, если
г > 0, то можно взять и — log г и v = в + 2тгп, где п — доста-
точно большое целое число, чтобы выполнялось условие v >
Мы нашли точное решение уравнения ew = с при сколь угодно
большом п, так что z = 1/w приближается к нулю. Есть только
одно значение комплексного числа с, в которое мы не можем по-
пасть - - это с = 0. Но можно взять последовательность —> 0,
Ск 0 и соответствующую последовательность w&, где \wk\ —> 00
20.6. Локальное отображение
1031
и ewk ~ Ск Тогда ~ искомая последовательность точек,
стремящихся к нулю, когда eZk —> 0.
Такое поведение функции типично для голоморфных
функций вблизи существенной особенности, т. е. мы можем ре-
шить точно уравнение /(г) = с в любой окрестности z = 7 для
всех комплексных чисел с, кроме одного. (Для функции e1/Z" это
было с = 0.) Это факт весьма глубокий, и доказательства его мы
здесь не приводим.
20.6. Локальное отображение
В этом параграфе мы исследуем более подробно локальные свой-
ства голоморфных функций. Первый результат — это очевидное
следствие теоремы Руше:
Предположим, что f голоморфна и не постоянна в
окрестности точки а, причем /(а) = Ь. Тогда сущест-
вует такое е > 0, что для всех w, удовлетворяющих (20.30)
условию |w — b| < s, найдется такое z вблизи а, что
/С*) = W.
Доказательство. Пусть g(z) — /(2) — b. Тогда д имеет нуль
конечного порядка в точке а. Мы можем найти достаточно малое
г, для которого g(z) 0, если \z — а| С г, кроме самой точки
а. Пусть область D — это диск радиуса г с центром в точке а.
Выберем такое е > 0, что |p(z)| > в для z G dD. Предположим,
что |w — Ь\ < е, и определим gw условием
9w(z~) = /(г) - w = g(z) + (Ь - w).
В силу теоремы Руше (20.28), функция gw имеет такое же число
нулей (с учетом их кратности), в области D, что и функция д.
Поскольку д имеет, по крайней мере один нуль, то и gw имеет,
по крайней мере, один нуль, поэтому можно найти, по крайней
мере, одно значение z в области D, где /(г) — w.
Утверждение (20.30) иногда формулируется по-другому: го-
ломорфная функция определяет открытое отображение, т. е. ес-
ли точка принадлежит образу, то в нем целиком содержится и
некоторая окрестность этой точки.
1032
Глава 20. Комплексный анализ
Утверждение (20.30) демонстрирует еще одно поразительное
отличие теории голоморфных функций комплексной переменной
от теории гладких функций вещественной переменной. Рассмот-
рим отображение R —► R, преобразующее х в и ~ х2. Тогда значе-
ния и могут быть только неотрицательными (рис. 20.8). Поэтому
0 принадлежит образу этого отображения, но никакая окрест-
ность 0 в нем не лежит. Мы можем легко изменить этот пример,
рассмотрев отображение плоскости в плоскость, т. е. пусть (т, у)
преобразуется в (u, v), где и — х2 и v = у. При таком отображе-
нии плоскость складывается вдоль оси у, так что в образе нет
точек (и, v) с отрицательными и (рис. 20.9).
Утверждение (20.30) говорит, что такого не бывает в случае
отображений, соответствующих голоморфным функциям. На-
пример, если взять /(г) = г2, то для w — ге1в ф 0 можно найти
два значения г, а именно z = тх12ё®12 и z — r1/2e1(7r+0/2), для
которых г2 — w. Поэтому вместо отсутствия решений уравнения
z2 = w в некоторой области w мы имеем два решения.
Это также типичное свойство функции f(z) ~ z2. Предпо-
ложим, что f — голоморфная функция в окрестности а, где
/(а) — 6. Вернемся к доказательству (20.30). Функция у, введен-
ная при доказательстве, имеет нуль конечного порядка в точке
а. Пусть к — порядок этого нуля. Если к > 1, то д'(а) = 0. Мож-
но выбрать такое г (возможно, меньшее, чем при доказательстве
(20.30)), так что не только у, но и gf не имеет нулей в области D.
20.6. Локальное отображение
1033
Таким образом, в обоих случаях к — 1 и к > 1 функция д вообще
не имеет нулей в области D, за исключением точки а, а функ-
ция gf не имеет нулей в D, кроме, возможно, точки а. Заметим,
что функция gw, введенная при доказательстве (20.30), отлича-
ется от д на константу. Таким образам, gfw — д' и, следовательно,
g'w(z) 7^ 0 в области D при z а. Однако, для w b функция gw
не имеет нуля в точке а. Это означает, что каждый из нулей gw
должен быть простым и, следовательно, у этой функции должно
быть к различных нулей. Итак, мы доказали следующее.
Пусть f - голоморфная функция в окрестности точ-
ки а и /(а) — Ь. Предположим, что д, определенная
формулой g(z) = f(z) — b, имеет нуль порядка к в точ-
ке а. Тогда можно найти г > 0 и г > 0 такие, что (20.31)
для любого w 0 b из окрестности | w — Ь| < е сущест-
вует к различных значений z: Zi,..., z&, для которых
\zi - а| < г и f(zi) = w.
Утверждение (20.31) демонстрирует истинный смысл нуля по-
рядка к. Это ситуация, при которой к различных корней совпа-
дают.
Рассмотрим частный случай к = 1 утверждения (20.31), ко-
торый весьма важен для нас.
Пусть f — голоморфная функция в окрестности точ-
ки а, где /(а) = b и ff(a) 0. Тогда можно найти
такие г > 0 и е > 0, что для всех w, удовлетворяющих
условию |w — b\ < s, существует единственное значе- , .
ние г, для которого \z — а| < г и /(z) = w. Другими ' * '
словами, существует единственная функция д, опре-
деленная при |w — Ь| < 6, удовлетворяющая условиям
|$(w) - b| < г и /(p(w)) = W.
При этом мы утверждаем, что
функция д, определенная в (20.32), голоморфна и
p'(w) = 1//W))- ( J
В утверждении (20.32) мы можем выбрать г так, чтобы
f(z) ф 0 для |z — а| < г. Поэтому, чтобы доказать (20.33), доста-
точно доказать, что функция д дифференцируема в комплекс-
ном смысле в точке b и gf(b) — Аналогичные аргументы
1034
Глава 20. Комплексный анализ
потом приведем для произвольной точки z — g(w), и формула
для gf покажет, что она непрерывна. Итак, предположим, что
f(a) — с 7^ 0. Пусть г] < ^|с|. Из определения производной функ-
ции f можно найти такое 6 > 0, что
z — а
для \z — а| < 8.
(20.34)
Выбирая 8 в качестве нового г (если это необходимо) в (20.32),
мы видим, что для всех w, достаточно близких к Ь, имеем
где z = g(w) или
w — Ь
-----с
z — а
поэтому
|w-b| > Mz-a)\,
&
z — а
(w — b)c
2
И2'
Если теперь умножить обе части равенства (20.34) на соответ-
ствующие части предыдущего неравенства, то получим
1 _ g(w) - а
f'(a) w — Ь
<2|с| V
Мы можем сделать т] сколь угодно малым, выбирая 8 и, следо-
вательно, е достаточно малыми. Это и доказывает, что д диф-
ференцируема в комплексном смысле в точке Ь и д'(Ь) ~ 1//'(а),
тем самым доказано утверждение (20.33). Утверждения (20.32) и
(20.33) составляют теорему о неявной (обратной) функции для
случая голоморфных функций. Следует, однако, подчеркнуть,
что эта теорема локальная. Давайте еще раз вернемся к функ-
ции /(г) = г2. Известно, что для любого значения w 0 есть
два корня уравнения /(z) = w. Предположим, что мы выбра-
ли квадратный корень положительного числа положительным.
Например, для /(а) = 1 возьмем а = 1. Утверждение (20.32)
означает, что для w в окрестности единицы, мы будем выбирать
единственный квадратный корень — тот, который близок к еди-
нице, а утверждение (20.33) означает, что функция g(w) — w1/2
будет голоморфной в окрестности w = 1. Действительно, легко
20.6. Локальное отображение
1035
видеть, что в (20.33) можно взять в качестве е любое число, мень-
шее единицы. Конечно, мы можно взять любую точку w внутри
диска радиуса г с центром в w = 1 в качестве нового значения
Ь, a g(w) в качестве нового значения а, и еще раз применить тео-
рему о неявной функции. Предположим, что мы взяли последо-
вательность таких точек с условием |w| = 1, как это показано
на рис. 20.10. Когда, пройдя таким образом по всему кругу, мы
вернемся на положительную ось w, то получим отрицательное
(противоположное) значение квадратного корня, что не удиви-
тельно. Итак, хотя (20.32) гарантирует существование локальной
функции, обратной к /, последовательное применение (20.32) мо-
жет привести к глобальной несогласованности. В случае функции
/(z) = z2 не существует глобально определенной функции w1/2
на плоскости w.
Существует два способа работать с этой проблемой неопре-
деленности, и каждый из них мы продемонстрируем на примере
квадратного корня. Один способ — просто жить с этой неопреде-
ленностью. Плоскость z рассматривается как двулистное накры-
тие плоскости w с точкой ветвления в нуле, где значению w со-
ответствует только одно значение z. Любую заданную функцию
типа cos(w3/2 + l) мы рассматриваем не как функцию, определен-
ную в плоскости w, а как функцию от z, т. е. cos(z3 + l). Плоскость
z — это риманова поверхность^ связанная со всеми функциями
1036
Глава 20. Комплексный анализ
гу1/2 в том смысле, что все они определены как функции от z.
Такой точки зрения придерживался сам Риман. Подробное ис-
следование структуры римановых поверхностей различных голо-
морфных функций способствовало развитию геометрии, тополо-
гии и алгебры вплоть до настоящего времени. Однако, здесь мы
не будем останавливаться на этом.
Другой, более приземленный подход к проблеме определения
w1/2 состоит в задании некоторой кривой, выходящей из начала
координат и идущей на бесконечность вдоль пути, где мы счи-
таем, что w1/2 не определен, чтобы сделать определение корня
единственным везде. Например, предположим, что мы разрезали
плоскость w вдоль отрицательной оси w. Таким образом, каж-
дое значение w вне этого разреза может быть записано в виде
w = те13, где —тг < 0 < тг. Тогда, выбирая w1^2 — г1/2 для 0 = 0
(т. е. положительный квадратный корень для положительных w),
и двигаясь далее (через первый и четвертый квадрант) ко всем
значениям 0 указанного интервала, имеем
wi/2 _ для — тг < 0 < тг.
Поэтому, например, при таком выборе квадратного корня
i1/2 = е17Г/4 и (—i)1/2 = е~17Г/4 (рис. 20.11).
Вопрос, где провести разрез, решается каждый раз в зависимости
от задачи. Вышеуказанный выбор разреза применяется довольно
часто, и иногда его называют главной ветвью квадратного корня.
Рис. 20.11
20.6. Локальное отображение
1037
Покажем, как выбор разреза применяется для вычисления
некоторых интегралов, которые потом будут очень важны для
нас. Рассмотрим интеграл
е-лх2/2 dx_
Когда Re А > 0, функция е~Хх2/2 быстро стремится к нулю на
±оо, и интеграл сходится абсолютно. Когда же Re Л < 0, функ-
ция e-Aj?2/2 стремится к бесконечности, и этот интеграл не имеет
смысла. Когда ReX = 0, абсолютное значение функции е“Лж
равно единице для всех х, поэтому заведомо ясно, что интеграл
не сходится абсолютно. И тем не менее, утверждается, что инте-
грал сходится. По существу, утверждается следующее.
Интеграл /2^ е-Аж2/2 сходится равномерно, когда
для А выполняются условия Re А О, |А| 1, и по-
этому он является непрерывной функцией А в этой
области.
Чтобы доказать равномерную сходимость, надо показать, что
для любого 8 > О можно найти Re (зависящее от 8, но не от А)
такое, что
е Xx2/2dx
~Хх2/2 dx
< 8
для всех S > R > Re. Далее,
Ае-Ах2/2 = _Ххе->^2/\
ах
поэтому интегрирование по частям дает
[ e~Xx2/2dx = - [ \-j~e Xx2/2dx
Jr Jr As dx
- 1 г~АД2/2 _ J_ -XS2/2 _ £ [S -Xx2/2
XR XS XJR x?
1038
Глава 20. Комплексный анализ
Поскольку |е Лх2/2| 1 для всех х и рассматриваемых значе-
ний А, интеграл справа можно оценить как х~2 dx, и, таким
образом, (поскольку S > R) получаем оценку
е Xx2/2dx
4
|Х|Я’
что меньше е, если R > 4|А| х. Точно так же оценивается и
f~R Поскольку |А| 1, то можно взять R£ = 4/е. (Заметим,
что вместо условия |А| 1 можно взять |А| с, где стоит лю-
бое фиксированное с > 0, и получить равномерную сходимость.)
Поскольку функция е“Лх2/2 непрерывно зависит от А и ж, равно-
мерная сходимость интеграла обеспечивает то, что интеграл яв-
ляется непрерывной функцией А. Вычислим этот интеграл для
Re А > 0, где он сходится абсолютно. При этом поступим весьма
хитро. А именно, вычислим квадрат этого интеграла, перейдя к
полярным координатам:
: Лж2/2 • е Xy2^2dxdy
^2+V2)/^dxdy
е Xr2/2rdrd@
= 2%
е Хг2/2т dr = 2тг/А.
Таким образом,
е Xx2^2dx = (27Г/А)1/2.
(20.35)
Какой корень взять? Когда А — вещественное положительное
число, подынтегральная функция е~Хх2/2 — тоже положитель-
ная, поэтому интеграл должен быть положительным. Следова-
тельно, для вещественных и положительных А мы должны вы-
брать положительный квадратный корень. Поскольку интеграл
— непрерывная функция А, мы должны взять главную ветвь
квадратного корня. Это типичная иллюстрация того, как сама
задача говорит нам, как определять квадратный корень.
20.6. Локальное отображение
1039
В силу непрерывности, формула (20.35) справедлива для всех
Re А 0. В частности, положив А = —it и А = ii, получаем
важные формулы
/оо „ /»оо
eitx /2 dx = е^\2тг/^2, / e~itx >2 dx = e^^Tr/t)1/2,
-оо J—оо
справедливые для всех вещественных t > 0, где подразумевает-
ся положительный квадратный корень. Эти интегралы, чрезвы-
чайно важные для оптики, называются интегралами Френеля.
Позднее мы к ним вернемся.11
Все, что здесь говорилось о квадратном корне, справедливо
и для корня степени п (с небольшими изменениями), где п —
любое положительное число. Это же на самом деле относится к
экспоненциальной функции. Функция ez отображает плоскость z
на плоскость w бесконечное число раз. Каждая полоса ширины
2тг, параллельная оси ж, отображается на всю12 плоскость w. Ло-
гарифмическая функция log w не однозначна. Она определена с
точностью до произвольного кратного 2тп. И на этот раз есть два
подхода к неопределенности. Один подход: полагаем, что плос-
кость z является бесконечнолистным накрытием всей плоско-
сти w. Любая функция, содержащая logw, рассматривается как
функция z. Другой подход: разрезаем плоскость w, например,
вдоль отрицательной вещественной оси. Тогда можно написать
w — те10, —тг < 0 < тг.
Главная ветвь логарифмической функции определяется при
этом условием
log w — log г + i0.
В силу (20.32) и (20.33), мы знаем, что logw — голоморфная
функция, производная которой равна 1/w. Определив логарифм,
11 Не менее важен и случай вещественного Л > 0. Подынтегральное выра-
жение е~Хх /2, деленное на значение интеграла ^/2тг/Л, представляет собой
плотность нормального, или гауссовского распределения случайной величи-
ны, которое играет основополагающую роль в теории вероятностей и стати-
стике. — Прим. ред.
12Исключая значение w ~ 0, см. выше. — Прим. ред.
1040 Глава 20. Комплексный анализ
можно определить степень комплексного числа w с произволь-
ным комплексным показателем с, а именно
wc = ecI°sw.
Как уже упоминалось выше, есть две возможные интерпретации
этого выражения. Согласно первой интерпретации, рассматрива-
ем wc как многозначную функцию w, т.е. рассматриваем ее не
как функцию w, а как функцию z. Согласно второй интерпрета-
ции, надо выбрать ветвь, например, главную ветвь logw. Тогда
wc становится определенной для всех точек, за исключением w,
лежащих на отрицательной вещественной оси.
20.7. Контурные интегралы
Теорема Коши о вычетах применяется для вычисления опреде-
ленных интегралов. Типичные применения мы показали в пара-
графе 20.4. В параграфе 20.5 изложен удобный прием вычисления
вычетов, в частности, формула (20.25). В этом параграфе мы да-
дим еще несколько показательных примеров, причем некоторые
их них мы используем позднее. Во всех случаях требуется опреде-
ленная изобретательность при выборе контура интегрирования.
Итак, мы должны вычислить определенный интеграл. Обычно
это значит, что надо вычислить интеграл вдоль кривой в ком-
плексной плоскости. К этой кривой добавляются другие, чтобы
образовать границу некой области. А затем применяется теоре-
ма Коши о вычетах. Куски контура выбираются так, чтобы их
вклад в интеграл был известен, пропорционален искомому инте-
гралу, или же бесконечно мал при переходе к соответствующему
пределу.
(а) Пусть R(x) ~ P(x)/Q(x) — рациональная функция, т.е. Р
и Q — полиномы. Предположим, что Q не имеет вещественных
нулей. Если степень Q больше степени Р по крайней мере на два,
то интеграл R(x) dx сходится и равен пределу f^r R(x) dx
при г —► оо. Мы считаем, что берется интеграл от комплекс-
ной функции R(z) вдоль отрезка прямой от точки —г до точ-
ки г, расположенных на вещественной оси. Соединим эти точки
20.7. Контурные интегралы
1041
полуокружностью радиуса г, лежащей в верхней полуплоскости
(рис. 20.12).
Теперь у нас имеется замкнутая траектория, ограничиваю-
щая полукруг в верхней полуплоскости, и можно применить тео-
рему Коши. С другой стороны, для точек z на полуокружности
|Д(г)| < Кг-2, где К — некоторая константа. Поскольку полу-
окружность имеет длину тгг, то интеграл по ней стремится к ну-
лю, когда г —> оо. Таким образом, получаем
РОО
/ R(x)dx = 2%i resfl(z),
Imz>0
где сумма берется по всем полюсам в верхней полуплоскости.
(Ь) Рассмотрим интеграл f^elxR(x) dx, где R — P/Q — ра-
циональная функция, не имеющая полюсов на вещественной оси.
Если degQ degP + 2, то можно действовать, как и в преды-
дущем случае. Если degQ degP + 1, то нам известно толь-
ко, что R(x) ведет себя на бесконечности как 1/х. Однако в
этом случае еще можно доказать, что интеграл сходится. Как
и в параграфе 20.6, можно интегрировать по частям. Поскольку
е1Х — —\(d/dx)eix, мы имеем
f elxR(x) dx — “ielsД(з) + ieirP(r) + /* elxRf(x) dx,
Jr Jr
причем функция Rf ведет себя на бесконечности как I/#2. Чтобы
вычислить этот интеграл, мы опять возьмем предел интеграла
от —г до г, соединив эти точки полуокружностью в верхней по-
луплоскости. Но здесь, оценивая интеграл по полуокружности,
надо быть более осторожными. Если z = re1# = г (cos в + isin0),
то
__ ёгг cos0£—г sin#
1042
Глава 20. Комплексный анализ
и получается оценка интеграла по полуокружности
I f eizR(z) dz\ = I Г eircosee~rsineR(reie)r d&\
* J по дуге । ' J 0 *
Гe~rsiaer\R(reie)\d6.
Jo
Теперь функция |r/?(re^)| ограничена константой, скажем, К.
Поэтому нам надо оценить интеграл
/»7Г /*7Г/2
/ e-rsined0 = 2 / e~rs™ede.
Jo Jo
Здесь мы воспользуемся неравенством sin# 20/тг для 0 < 0
тг/2. (Действительно, обе части равны в конечных точках, и их
разность имеет один максимум внутри.) Поэтому
ртг/2 Г^/2
/ e-rsinedO^ / e-2re/'KdO = (7г/2г)(1 - е~г) 0.
Jo Jo
Таким образом, интеграл по полуокружности стремится к нулю,
и мы получаем
f exxR{x)dx~2m res7?(^),
00 Imz>0
где сумма берется по всем полюсам в верхней полуплоскости. Ес-
ли Q имеет нуль на вещественной оси, то рассмотренный выше
интеграл, в принципе, не имеет смысла. Но тем не менее, иногда
он может иметь смысл, если рассматривать его как предел осо-
бого рода, называемый главным значением Коши. Покажем это
на примере. Предположим, что функция R имеет простой полюс
при z ~ 0 с вычетом А, так что 71(a) ~ А/z + Rq(z), где функция
Rq голоморфна в окрестности нуля. Рассмотрим тот же интеграл,
что и раньше, но теперь в контур вставим полуокружность ради-
уса е в нижней полуплоскости, чтобы обойти начало координат
(рис. 20.13). Теперь охватываемая область содержит все полюса
в верхней полуплоскости плюс полюс в начале координат. Ин-
теграл от A/z по малой полуокружности равен тпА, сокращая
20.7. Контурные интегралы
1043
половину вычета от точки 2 = 0. Тогда
e™R{x)dx
= ИА + 2-7ri res(e,zR(z)).
1шл:>0
Здесь Р(-) означает главное значение Коши. Например, пусть
7?(ж) = 1/ж, тогда
— dx ) — ?ri
х /
Возьмем вещественную часть этого равенства и получим, что
F(J^(cosx/x)dx) = 0. Результат очевиден, поскольку cosx/x
— нечетная функция. Если взять мнимую часть равенства, то
получаем P(J^o(sinx/x) dx) = тг. Функция sinx/x не имеет осо-
бенности в начале координат, поэтому нет нужды брать главное
значение этого интеграла. Функция sinx/x четная, поэтому
sin х , тг
Jo х 2
Мы еще используем этот интеграл в теории рядов Фурье.
(с) Рассмотрим интегралы вида /0°° хаР(х) dx, где а — веще-
ственное число, причем 0 < а < 1, R — рациональная функция,
которая на бесконечности убывает как 1/х2 и в худшем случае
имеет полюс первого порядка в нуле. Трюк состоит в том, что де-
лается замена переменной: х = i2, так что теперь интеграл имеет
вид 2 Jo°° i2a+1P(i2) dt. Для его вычисления удобно выбрать ветвь
функции г2а, которая получается, если плоскость z разрезать
1044
Глава 20. Комплексный анализ
вдоль отрицательной мнимой оси. Тогда можно написать z — те10,
где -7г/2 < 0 < Зтг/2, a z2a = г2ле12а^ где -тга < 2а0 < Зтга. Те-
перь мы должны выбрать контур так, чтобы он не проходил через
отрицательную мнимую ось. Пусть контур состоит из двух отрез-
ков прямой вдоль отрицательной и положительной вещественной
оси, а также большой и малой полуокружностей, лежащих в верх-
ней полуплоскости (рис. 20.14). Мы считаем, что интегралы по
полуокружностям стремятся к нулю, когда радиус большой дуги
стремится к бесконечности, а радиус малой — к нулю. Тогда
ZOO Л ОС
z2ol+xR{z2} dz ~ I (z2a+1 + (-г)2а+1)Я(г2) dz.
-оо Jo
Мы выбрали ветвь Z2ot так, ЧТО ( — z)2a == е2тпаг2а дЛЯ положи_
тельных значений z. Поэтому последний интеграл имеет вид
ЛОО
(1 — е2я1“) / t2a+1R(t2)dt.
Jo
Поскольку 1 — е27Г1а 0, на этот коэффициент можно разделить и
получить значение нашего интеграла. Слева мы должны просум-
мировать вычеты функции z2a+1R(z2) в верхней полуплоскости.
Они совпадают с вычетами функции zaR(z) во всей плоскости,
разрезанной вдоль положительной вещественной оси. Поэтому
другой способ решить нашу задачу состоит в том, что не надо
делать замену х = t2, а просто разрезать плоскость z вдоль поло-
жительной вещественной оси и использовать ветвь функции
определенную условием z = re10, где 0 < 0 < 2%. Заметим, что
Рис. 20.14
Рис. 20.15
20.7. Контурные интегралы
1045
мы разрезали плоскость точно вдоль пути исходного интеграла!
Поэтому мы не можем получить наш интеграл как часть интегра-
ла по замкнутому контуру. Вместо этого мы интегрируем вдоль
пути, параллельного положительной вещественной оси, но слег-
ка сдвинутого в верхнюю полуплоскость, имея в виду переход
к пределу для получения нашего интеграла. Итак, рассмотрим
замкнутый контур, состоящий из двух прямолинейных отрезков,
один чуть выше положительной вещественной оси, а другой —
чуть ниже, а также из большой и малой окружностей, взятых
почти целиком (рис. 20.15). Вклад обеих окружностей в пределе
обращается в нуль. Вклады от двух прямолинейных отрезков не
сокращают друг друга, потому что определение функции za вы-
ше и ниже вещественной положительной оси отличаются на мно-
житель е27ГШ. Таким образом, именно неопределенность функции
za в нуле позволяет нам вычислить интеграл.
(d) Интегрирование по контуру можно использовать для вы-
числения сумм бесконечных рядов. Идея состоит в том, чтобы
применять теорему Коши о вычетах ко все увеличивающимся об-
ластям, чтобы интегралы по границе области стремились к ну-
лю. Тогда останется (бесконечная) сумма вычетов, которая то-
же должна давать нуль. Перенеся одно из слагаемых в другую
часть уравнения, получим сумму бесконечного ряда. Проиллю-
стрируем этот метод на примере сумм, полезных при изучении
тригонометрических функций. С этой целью сначала определим
тригонометрические функции комплексной переменной:
cos г = ^(е1* + e~lz), sin г = — ^(е12 — е-12).
Очевидно, что эти функции голоморфны во всей комплексной
плоскости и для вещественных z совпадают с тригонометрически-
ми функциями вещественной переменной. Заметим, что sin z — 0,
если и только если e21z = 1. Это выполняется только для вещест-
венных значений 2 — птг. Аналогично, комплексные нули cos г —
только в вещественных точках (п + 1/2)тг. Определим
sin z cos z
tan г —----, cot z = ——.
cos z sin z
1046
Глава 20. Комплексный анализ
Эти функции мероморфны и имеют полюса, расположенные в
нулях их знаменателей. Можно воспользоваться (20.25) и вычис-
лить вычеты в этих полюсах, потому что все нули простые. На-
пример, cot z имеет полюса в точках птг, и все вычеты в них рав-
ны 1. Заметим, что функция
+ e-iz
cot z — i—----—
exz - e~xz
будет ограничена по абсолютному значению до тех пор, пока
z находится на конечном расстоянии от точек П7Г. В частности
| cot z\ будет равномерно ограничен на всех окружностях радиуса
(п + ^)тг с центром в начале координат. Рассмотрим интеграл по
этим окружностям
г cote
Jci2-^ '
где z ф тг — фиксированное комплексное число. Если радиус
окружности устремить к бесконечности, то интеграл будет стре-
миться к нулю, потому что | cot £| ограничен, а в знаменателе
стоит полином второй степени по £. Полюса подынтегрального
выражения находятся в точках ±z и птг. Вычеты в точках ±z
равны | cot z/z, а в точках тг они составляют (п27Г2 — z2)-1. По-
этому
оо
£2Н + £(п27Г2_г2)-1 = 0.
z 1
Первый член перенесем вправо, умножим это равенство на z и из
суммы выделим член с п = 0. В результате получим формулу
1 °° 1
cot г = - + 2г ^2 2 _ п2п2 (20.36)
Ряд справа сходится, причем сходится равномерно при всех z, на-
ходящихся на конечном расстоянии от всех полюсов. Если /(z) =
sinz, то /'(z)//(z) — cotz. Можно также написать /'(z)//(z) =
(d/dz)(log/(z)). После этого (20.36) переписываем в форме
d f sinz\ / 2 2 2\
20.8. Пределы и ряды
1047
Функция sin г/г не равна нулю в пределе при г = 0. Проинте-
грируем это уравнение по контуру, соединяющему 0 с точкой z и
проходящему на конечном расстоянии от всех точек птг. Получим
уравнение
сю
1о§(8шг/г) — log 1 = ^2(log(^2 — тг2тг2) — log(—п2тг2)).
1
Это уравнение содержит неоднозначности, потому что значения
логарифма, определенные правилом, что log<? равняется инте-
гралу от д'/д, зависит от выбранного контура интегрирования.
Однако если вычислить экспоненту обеих частей, то все неопре-
деленности исчезают, и мы получаем известную формулу
sin г = z
г2
П2ТГ2
представляющую sin z как бесконечное произведение.
20.8. Пределы и ряды
Начнем с применения интегральной формулы Коши.
Пусть fn — последовательность функций, голоморф-
ных в области D. Предположим, что fn —> /(г) равно-
мерно в D. Тогда f — голоморфная функция в области
D, и /п(г) сходится к ff(z) равномерно на любом под- ' * '
множестве D1 расположенном на конечном расстоянии
от границы dD.
Доказательство. Для любой точки z € D выберем окруж-
ность С, диск которой лежит внутри D (а точка z внутри С).
Тогда
f ( X __ 1 f fn(£)
Переход к пределу дает
2тГ1 Jc q z
1048
Глава 20. Комплексный анализ
Из обсуждения, следующего после (20.18), мы знаем, что это
означает голоморфность функции /. Из формулы (20.19) имеем
/ \ _ 1 f fn(£) if
Ш 2?П Jc (£ - z)2
которое, очевидно, равномерно сходится к
Часто возникает желание применить утверждение (20.37) в слу-
чае, когда область D является ограниченной подобластью неко-
торой большей области, где последовательность fn определена
и сходится, т.е. функции fn определены и голоморфны в боль-
шой области Е и равномерно сходятся на каждой из подобластей
Dk С Е, образующих последовательность с U Dk — Е. Применяя
утверждение (20.37) к каждой области приходим к выводу,
что f голоморфна во всей области Е.
Применим утверждение (20.37) к частичным суммам и рядам.
Если ряд из голоморфных слагаемых /(г) ~ fi(z) +
/2(^)4--равномерно сходится в области Е, то сумма
f — голоморфная функция, и ряд можно дифферен- ' ’ 7
цировать почленно.
Наиболее важный ряд, связанный с голоморфными функци-
ями, - ряд Тейлора. Предположим, что f голоморфна в области
I?, и диск радиуса R с центром в точке а целиком лежит в облас-
ти D. Пусть z — точка внутри этого диска, причем \z — а| < R.
Тогда можно воспользоваться (20.22) и оценить последний член
в формуле (20.20). Его абсолютное значение не превышает
М\z — а| \z — а|п-1
R — \z — а| Лп-1
и равномерно стремится к нулю на любом диске меньшего радиу-
са. Таким образом, из утверждения (20.38) получаем следующее.
20.8. Пределы и ряды
1049
Если / голоморфна в области D и а — произвольная
точка в Д то ряд
/W+/'(a)(z-a)+£^(z-<.)2+. • •+ - (20 39)
сходится к f(z) на самом большом открытом диске с
центром в точке а, целиком лежащем в области D.
Этот ряд называется рядом Тейлора функции f в окрестности
точки а. Многие операции с голоморфными функциями соответ-
ствуют простым операциям с их рядом Тейлора. Для упрощения
записи положим а ~ 0. Тогда если
/(г) = а0 + «1^ + 4----
и
g(z) ~ b0 + brz + b2z2 Ч-,
то получаем
/'(г) = ai + 2a2z + 3«зг2 Ч-,
/(г) Ч- g(z) = (а0 + Ьо) + («1 + b±)z + (а2 + b2)z2 Ч-
f(z)g(z) = ао6о + (ai&o + + («2^0 + «1^1 + aob2)z2 Ч-.
Если «о = Ьо — 0, то
/(s(^)) = ai(brz + b2z2 + •••) + a2(biz 4- b2z2 + • • • )2 Ч- • •
— aibiz + (aib2 4- a2b2)z2 4- (ftii>3 4- 202^1^2 4- a$bf)z^ + • • • .
Если мы знаем степенной ряд функции /, тоиз этого последнего
уравнения можно рекурсивно определить степенной ряд функ-
ции, обратной к /. Пусть мы знаем значения и хотим найти
такие Ь{, чтобы /(<j(z)) — 2. (Чтобы обратить функцию, необхо-
димо предположить, что f'(0) 0.) Тогда
~ 1, Ь\ = 1,
«1&2 + «2^12 = 0, b2 — -ai-1(a2bi2),
ai&3 4- 2a2bib2 Ч- &з&13 ~ 0, 63 = —ai~^(2a2b\b2 4- азЬ13)
1050
Глава 20. Комплексный анализ
и т. д. Вообще коэффициенты при zn будут выражениями типа
^1ЬП+ (члены, содержащие bi порядка, меньше, чем п). Поэтому
можно последовательно находить каждое Ьп.
Известен элементарный факт, что любой степенной ряд име-
ет радиус сходимости R (возможно, и 0); при этом ряд сходится
для \z\ < R и не сходится для |z| > R. Из (20.38) следует, что
ряд представляет голоморфную функцию внутри радиуса сходи-
мости. И обратно, из (20.39) следует, что ряд Тейлора для голо-
морфной функции в качестве радиуса сходимости имеет радиус
самого большого диска, содержащегося в истинной области опре-
деления13 функции у.
Ряд вида ао 4- a^iz^1 + а_2^-2 Н-можно рассматривать как
степенной ряд по переменной 1/г. Поэтому он будет сходиться
вне окружности радиуса R (возможно, что R — оо). Говорят, что
ряд вида 52^°ооа^П сходится, если и только если сходятся его
положительные и отрицательные части. Положительная часть
будет сходиться при |г| < /?2 Для некоторого и отрицательная
часть будет сходиться при |z| > для некоторого R^. Поэтому
для двойного ряда будет непустая область сходимости тогда и
только тогда, когда Ri < R^. В этом случае, в силу (20.38),
он будет представлять голоморфную функцию в кольце R\ <
\z\ < i?2- И обратно, предположим, что / голоморфна в таком
кольце. Покажем, что в этом случае функция f представима
в виде двойного ряда. Для доказательства мы должны только
показать, что можно разложить / в сумму / = /1 + Уг, где
У1 голоморфна при \z\ < Я2 и /2 голоморфна при |Д > R±.
Причем Уг(1 /г) должна иметь устранимую особенность в нуле,
так что /2(1/^) голоморфна для |l/z| < 1/Ri. Чтобы это сделать,
определим
где интеграл берется по любой окружности радиуса го с условием
|Д < T2 < R2] И
13т. е. области, за пределы которой функцию невозможно продолжить из-за
полюсов или существенных особенностей на границе. — Прим. ред.
20.8. Пределы и ряды
1051
где интеграл берется по любой окружности радиуса и, причем
R1 < П < \z\- Очевидно, что Д голоморфна при \z\ < R% и
/2 голоморфна при |z| > Др Из интегральной формулы Коши
следует, что Л (г) + Д(^) — /(^). Если положить zf = \/z и
подставить £' = 1/£ в интеграл для /2, то получим
/(1/СТ г'
|£'|=1/п
Это показывает, что /2(1/2') голоморфна по z' для |z'| < 1/Д1.
Функцию /1 можно разложить в степенной ряд
ОО
о
1 / АС
где ап = — / —гт «С,
2?п J|ei=r Cn+1
а функцию /2(1/2') — в ряд
ОО
1
где
Л 1 [
здесь г — любое значение между Ri и /?2- Полагая а_п = Ьп
получаем искомое разложение, называемое рядом Лорана
оо
/(*) = ^2anZn,
—ОО
где an = f d£.
27Г1 j|C1=r e+1
(20.40)
В дальнейшем нам понадобится явный вид этой формулы в слу-
чае Ri < 1 < /?2- Итак, мы предполагаем, что функция f опреде-
лена и голоморфна в некоторой окрестности единичного круга,
т. е. \z\ = 1. Пусть F(0) — и в формуле (20.40) г = 1. Тогда
получаем
i /*2тг
/(z) = Van2n, где an = — F(eyne№. (20.41)
2тг Jo
1052
Глава 20. Комплексный анализ
В частности, взяв z = е10 (на единичной окружности) и подставив
это в ряд Лорана для /, имеем
оо
F(0) =
— ОО
(20.42)
где коэффициенты ап определены формулой (20.41). Ряд (20.42)
называется рядом Фурье функции F. Если f голоморфна в об-
ласти R < |z| < 1/Л, где R — некоторое число, причем R < 1, то,
поскольку ап — коэффициенты сходящегося степенного ряда, из
критерия сходимости степенных рядов получаем, что
|an| сг~1п1 для любых г > R
и соответствующей константы с = сг.
Добавление: связь между голоморфными
и гармоническими функциями
Пусть f = tz+w — функция, голоморфная в области D. Тогда, как
доказано в параграфе 20.4, она бесконечно дифференцируема,
т. е. имеет в D производные любого порядка. Для первых частных
производных выполняются уравнения Коши-Римана
ди dv ди dv . .
~ * (20.11)
дх ду ду дх
Продифференцируем первое уравнение по ж, второе по у и сло-
жим. В правой части смешанные частные производные второго
порядка от v сокращаются, и мы имеем
д2и д2и __
дх2 + ду2
Итак, функция и удовлетворяет двумерному уравнению Лапласа
Э2 д2
Ли-0’ д “ +
Добавление
1053
и является гармонической. Аналогично, гармонической функци-
ей является мнимая часть и (чтобы убедиться в этом, можно сно-
ва продифференцировать уравнения Коши-Римана или заменить
функцию f на — i/).
Таким образом,
вещественная и мнимая часть всякой голоморфной
функции, рассматриваемые как функции двух вещест-
венных переменных, являются гармоническими.
И обратно, каждая гармоническая функция и в односвязной
(не имеющей «дырок») плоской области может быть реализована
как вещественная часть голоморфной функции, причем послед-
няя определена однозначно с точностью до аддитивной (чисто
мнимой) постоянной. Иначе говоря, существует единственная по
модулю константы функция г?, которая связана с и уравнениями
Коши-Римана. Функция и — также гармоническая и называется
сопряженной к и.
Доказательство. Применим звездный оператор ★ к диффе-
ренциалу функции и(х,у):
, ди 1 ди , , ди . ди 1
du= — ах + — dy, *du — —— ах + — ау.
ох ду ду дх
Полученная 1-форма *du является замкнутой, так как
, _ i ( ди ди , \ / д2и д2и\
d*du = а dx + — dy ] = ] dx Л dy = 0
\ ду дх J \дх2 ду2 J
в силу гармоничности и. Но тогда, как показано в параграфе 7.3,
эта форма является точной, если рассматривать ее в звездной
области. На самом деле область достаточно предполагать одно-
связной. Следовательно, форма *du является дифференциалом
некоторой функции и:
, j ди * ди _
= du — — dx + -z-dy.
dx dy
При этом функция и определена однозначно с точностью до ад-
дитивной константы. Равенства коэффициентов при dx и dy в
1054
Глава 20. Комплексный анализ
выражениях для *du суть уравнения Коши-Римана. Тем самым
f = и + ir является искомой голоморфной функцией.
Отсюда легко вывести, что: 1) если и ~ гармоническая функ-
ция в области Р, а функция д голоморфно отображает область
G в область Р, то и о д является гармонической функцией в G;
2) всякая гармоническая функция является бесконечно диффе-
ренцируемой.
Кстати, последнее утверждение справедливо для функций
любого числа переменных. Всякая гармоническая функция име-
ет внутри области определения частные производные всех поряд-
ков, которые, в свою очередь, также являются гармоническими
функциями.
Отметим, что предположение об односвязности области су-
щественно. Гармоническая функция и = log г — |log(x2 + у2)
определена на всей плоскости, за исключением начала коорди-
нат 0. Она является вещественной частью комплексной логариф-
мической функции log,?, которую можно определить однозначно
только в односвязной подобласти области определения.
Вывод теоремы о среднем. Пусть функция / голоморфна в
круге D радиуса R с центром в точке z — с и непрерывна на D.
Согласно интегральной формуле Коши, имеем
/(C) = _L f
Ц ’ 2niJSD(-c'
Замена переменной £ = с + Re10 на окружности dD дает
----— idf) — ds,
£~с R
где ds — элемент длины дуги. Таким образом,
Итак, значение / в центре круга совпадает со средним значением
по окружности. Переходя к вещественной части, имеем двумер-
ную теорему о среднем для гармонических функций.
Резюме
1055
Решение задачи Дирихле для круга. Пусть D — круг ради-
уса R с центром в точке с, и а = a{z) — непрерывная функция на
окружности dD, Тогда решение задачи Дирихле
Ди = 0 внутри D, и = а на dD
существует и дается интегральной формулой Пуассона
/ \ 1 f a(^)(J?2-r2)
u(z) = 'rn 1~~2—w-----То—лл d6' где z = с + ге'
2тг J$D R2 + г2 — 2ягсов(0 - ф)
Мы только кратко опишем идею вывода формулы в предпо-
ложении существования решения. Чтобы вычислить u(zq):! где
zq — с + ге1*^ г < Я, применим дробно-линейное преобразование
w = g(z) =
R(z - £р)
R2 ~ (?0 “ c)(z - c)’
которое голоморфно и взаимно-однозначно отображает круг D на
единичный круг Dy ~ {|w| < 1}, причем точка zq переходит в 0.
Далее, пусть v — решение задачи Дирихле на единичном круге:
&v(w) = 0 при |w| < 1, v(w) = при |w| ~ 1.
Легко видеть, что u(z) = является решением исходной
задачи Дирихле. При этом u(zq) = v(g(zo\) = г;(0) вычисляется
как среднее значение по окружности dD\ = {|w| = 1}.
Детали доказательства оставляем читателю.
Описанный метод решения задачи Дирихле переносится на
достаточно широкий класс областей, являющихся конформными
образами круга.
Резюме
А. Голоморфные функции
Вы должны знать определение голоморфной функции через
2-формы и уметь показывать, что ее матрица Якоби представля-
ет конформное преобразование.
Вы должны уметь выводить интегральную теорему Коши и
формулу для вычетов из теоремы Стокса.
1056
Глава 20. Комплексный анализ
Вы должны уметь вычислять вычет функции в простом или
в кратном полюсе.
В. Интегрирование по контуру
Вы должны уметь вычислять интегралы с помощью теоремы
о вычетах для выбранного контура. Для некоторых типичных
интегралов нужно уметь находить соответствующий контур.
С. Степенные ряды
Вы должны уметь раскладывать голоморфную функцию в ряд
Тейлора или Лорана и уметь вычислять радиус сходимости этих
рядов.
Задачи
20.1. (а) Предположим, что f(z) — голоморфная функция. Пусть
z = х + iy, f(z) = и+ iv. Покажите, что семейства кривых
и(х, у) = const и v(x,y) = const ортогональны, т.е. что они
пересекаются под прямым углом.14
(Ь) Проверьте это свойство для функции /(г) = z2. Нарисуй-
те несколько кривых. Сделайте то же самое для функции
/(z) = 1/z. Что в этом случае происходит в нуле?
20.2. (а) Предположим, что /(z) — голоморфная функция, веще-
ственная часть которой равна Зх2?/ — у3. Получите мнимую
часть f(z).
(b) Может ли функция быть голоморфной, если ее веществен-
ная часть равна ху27 Если да, то получите ее, а если нет, то
объясните, почему.
20.3. Голоморфные функции cosz и sinz можно определить тожде-
ствами
cosz = |(е13 + е“1г), sinz = ^(е1г — e~12)?
используя определение комплексной экспоненциальной функции.
14Это означает, что ортогональны векторы касательных (и нормалей) к
кривым и = const и v = const в каждой точке (то, г/о)- Если об этом помнить,
то доказательство данного пункта не составит труда. — Прим. ред.
Задачи
1057
(а) Выразите cos z и sin z через тригонометрические и гипербо-
лические функции х и у. Используя эти выражения, вычис-
лите d(cosz) и d(sinz).
(b) Докажите, что формулы сложения эт(г + w) = sin z cos w +
cos z sin w и cos(z + w) = cos z cos w — sin z sin w выполняются
для комплексных z и w.
(с) Используя формулы сложения, покажите явно, что функ-
ции sin z и cos z непрерывно дифференцируемы в комплекс-
ном смысле. Получите производные этих функций, вычис-
ляя соответствующие пределы.
20.4. С помощью метода, изложенного в параграфе 20.7, получите зна-
чения определенных интегралов:
(а) [ smG0d6
Jo 1®
cos в dO __ тга 2
1 — 2а cos 0 + а2 1 — а2 ’ <
20.5. С помощью метода, изложенного в параграфе 20.7, пункт (а),
проверьте формулы для определенных интегралов:
/ х /°° dx тг
(а) / т---—= —, а > 0;
J-OO (х + Ь)2 + а2 а
ГМ Г dx я
Jo (х4 + 4а4) 8а3' а
Г°° х2 dx _ тг
с) JQ F+T = б‘
20.6. (а) Предположим, что f(z) голоморфна в некоторой области
за исключением точки z = а, где она имеет полюс второ-
го порядка. Докажите, что вычет в этом полюсе задается
формулой
res = lim -—((z - a)2f(z)).
dz
(b) С помощью этой формулы вычислите интеграл
J00 dx
J-оо (х2 + а2)2
1058
Глава 20. Комплексный анализ
(с) Обобщив этот метод, вычислите интеграл
Г°° dx
J-oo (ж2 + a2)fc
для произвольного целого положительного числа к.
20.7. (а) Здесь излагается метод, альтернативный методу, изложен-
ному в параграфе 20.7, пункт (Ь). Пусть R(z) = P(z)/Q(z),
где Р и Q — полиномы, степени которых связаны условием
deg Q deg Р + 1, так что
для некоторой константы А и достаточно больших \z\.
Предположим, что Q не имеет вещественных нулей. Сле-
дуя изложенному ниже плану, докажите, что интеграл
JX R(x)elx dx сходится, т. е. предел
lim / R(x)elx dx
Xi—>оо
существует, и выполняется равенство
2тп У2 гев(Л(г)е1г)1
где сумма берется по всем полюсам, лежащим в верхней
полуплоскости.
Шаг 1. Выберем достаточно большие Xi, Х2 и У, такие, что-
бы прямоугольник, изображенный на рис. 20.16, содержал
все полюса в верхней полуплоскости.
X2 + iK
IV
III
мН
I Х2
Рис. 20.16
Шаг 2. Покажите, что
;lz dz
Jn Jo и
для достаточно больших Х2 •
€ dy^T2
Задачи
1059
Шаг 2'. Покажите, что
R(z)elz dz
Шаг 3. Покажите, что
R(z)exz dz
Ae~Y(Xi + Х2)/У.
Шаг 4. Пусть Y —► оо. Докажите, что
[ R(x)elx dx — 2?ri res(7?(z)e12:)
и завершите доказательство.
(b) Вычислите интеграл
/*°° cos х ,
' х2 + a2 dx'
q х а
20.8. Предположим, что Q(0) = 0, a Qz(0) / 0, так что функция R(z)elz
имеет простой полюс в 0. Пусть В — вычет этой функции в 0.
Рассмотрите тот же прямоугольный контур, но с обходом начала
координат в нижней полуплоскости по малой полуокружности
радиуса 6 (рис. 20.17).
Х2-НУ
-X.i +iK
Х2
Рис. 20.17
(а) Покажите, что предел интеграла по полуокружности при
<5 —> 0 равен я1В.
(Ь) Докажите, что главное значение Коши определяется фор-
мулой
R(x)elx dx ] — 2тг1 ге8(Я(г)е1*) 4-
/ г^О
1060
Глава 20. Комплексный анализ
(с) Покажите, что
sm х _ тг
---ах = —
х 2
20.9. Пусть /(г) = (ЛДг)) — матричная функция. Мы говорим, что
f голоморфна в области D, если каждый матричный элемент fij
является голоморфной функцией в области D. Пусть 7 — про-
извольная кривая. Интеграл J fij(z) dz должен быть матрицей,
ij-й элемент которой равен f fij(z) dz. Заметим, что если В и С
— постоянные матрицы и f ~ голоморфная матричная функ-
ция, то BfC — тоже голоморфная матричная функция, и для
произвольной кривой 7 мы имеем
Рис. 20.18
/1
(а) Пусть А = I 0
\0
0 0\
2 0 I и /(z) = (zi — А)"1, где
0 3/
/1 о 0\
1= 0 1 о .
\0 0 1/
Покажите, что f голоморфна везде, кроме точек z = 1,
z = 2 и z = 3. Пусть Р7. = (1/2тп) J f(z)dz (контуры 7^
показаны на рис. 20.18). Вычислите Р7г для i = 0,1,2,3.
Задачи
1061
(b) Пусть D — матрица 3 х 3 с собственными значениями 1, 2
и 3. Пусть g(z) = (гЛ — D)”1. Покажите, что д голоморфна
везде, кроме точек z — 1,2,3. Пусть
Опишите Im Q71 и Ker Q71. Что такое Q^L 7 Опишите Im Q72
и KerQ72. Что такое Q72?
(с) Сформулируйте общую теорему. Пусть А ~ матрица п х п
с различными собственными значениями Ai,..., Хп. Пусть
/(г) = (г! — Л)-1. Где голоморфна функция /? Пусть 7
— кривая, которая не проходит через какие-либо собствен-
ные значения и ограничивает область, содержащую точки
Ai ..., Afc и не содержащую ни одно из остальных собствен-
ных значений. Положим
Л = 2й//(г)<'2 = й1/<2|1'ЛГ'‘/2'
Что такое ImP7? Что такое КегР7? Что такое Р^?
20.10. (а) Пусть f(z) обозначает ветвь функции z1/4, определенную
везде, кроме положительной вещественной оси, и обладаю-
щую свойством
lim f(x + is) = |тр/4 (вещественное число).
Вычислите /(—х) и предел lime—о — is) для веществен-
ных х.
(Ь) Используя контур, изображенный на рис. 20.19, вычислите
определенный интеграл
/.оо ti/4dt
Jo (t + аУ
Обсудите вклад от каждой окружности.
20.11. Используя метод, изложенный в параграфе 20.7, пункт (с), вы-
числите интегралы по контуру, изображенному на рис. 20.14.
/*°° тг
(а) / dx=-~—. 0 < а < 1,
Jo X 4- 1 sin О7Г
1062
Глава 20. Комплексный анализ
20.12.
/>_\ Г 1 j (1—а)тг Л
(Ь) / ——— dx = —;-----------, 0 < а < 2.
Jq х + I)2 sinct7F
(а) Вычислите f f(z)\ogzdz по контуру, изображенному на
рис. 20.15. Используя ветвь log г, определенную условием
log z = log г + i0, 0 < в < 2тг,
докажите формулу
Jo
которая верна всегда, когда f(z) стремится к нулю при |г| —►
оо достаточно быстро, чтобы интеграл по большому кругу
стремился к нулю.
(Ь) Покажите, что
/•ОО
тга + 2Mog(fe/a)
- ' 2Ь(а2 + Ь2) ’ а'Ь>°'
(с) Рассмотрев интеграл f f (^)(logz)2 dz, придумайте способ
вычисления интеграла
Jo
С его помощью докажите формулу
Г00 log х , я log а
/ S3 ~ —Л-
Jo х2 + а2 2а
Задачи
1063
20.13. (а) Получите ряд Лорана для функции
z1 — 5г/2 4-1
с помощью интегрирования по единичной окружности. Где
сходится этот ряд?
(Ь) Этот же ряд получите с помощью разложения функции
/(г) на простые дроби. Затем разложите каждый член по
степеням z или 1/z так, чтобы ряд сходился при |г| — 1.
(с) Получите ряд Фурье для функции
F(0) = (5/2 +2 cos Я)”1.
20.14. Получите ряд Фурье для функции
F(0) = 0, -тг < 0 < тг.
Можно ли это получить как разложение голоморфной функции
в ряд Лорана?
Глава 21
Асимптотическое вычисление
интегралов
Введение
Асимптотическое поведение интегралов позволяет понять многие
физические законы. В этой главе мы дадим элементарные при-
меры математических приемов, используемых в настоящее время
во многих приложениях физики и математики.
Асимптотическая формула Стирлинга — одна из первых и
до сих пор важнейших:
п! ~ (2тг)1//2пп~1~1//2е~п,
Она получена Джеймсом Стирлингом в первой трети XVIII века.
Знак ~ следует понимать в том смысле, что отношение обеих
частей формулы (они обе стремятся к ос с ростом п) стремится
к 1 при п —> оо. Мы приведем и докажем здесь более точную
версию этой формулы вместе с оценкой погрешности.
Хотя формула Стирлинга должна применяться только при
больших значениях п, она дает удивительно точное приближе-
ние (в смысле относительной погрешности) даже при малых п.
Так, для п = 1 мы имеем n! = 1, а правая часть формулы Стир-
линга дает 0.92. Для п — 10 мы имеем п! — 3628800, а правая
сторона дает 3 598600, т. е. ошибка меньше одного процента. Это
систематическое явление. В этой главе мы дадим оценки, спра-
ведливые для больших значений параметра, но оказывается, что
эта формула хорошо работает и при малых значениях.
1066 Глава 21. Асимптотическое вычисление интегралов
21.1. Метод Лапласа
Мы применим этот метод для получения более точной версии
формулы Стирлинга. Интегрирование по частям показывает, что
гамма-функция, определенная формулой
Г(х) = i dt, х > 0,
Jo
удовлетворяет условию
Г(х + 1)-хГ(х), Г(1) = 1,
так что
Г(п + 1) — п!.
Таким образом, можно переписать формулу Стирлинга в виде
Г(ж) ~ е~ххх
На самом деле мы докажем более точный результат. Покажем,
что
Г(х) - е'ххх
1
288х2
Асимптотический ряд в этой формуле означает, например, что
1 \
288х2 J
и т. д., где Ci — константы. Другими словами, обрывая ряд в лю-
бом месте, можно оценить погрешность через следующую, более
21.1. Метод Лапласа
1067
высокую степень ж"1. Начнем с формулы Г(х) = Г(ж + 1)/ж и
получим
1 Г°°
Г(ж) = — / e~ltx dt
я, Jo
= е~ххх Р e-*[w-iog(i+w)] dw
1*00
= е~ххх J е~хрМ dw,
где t = (1 + w)x, так что dt = xdw и t = 0 О w — —1, t — оо
w — оо, где функция
p(w) = w — log(l + w) = ~w2 — ~w3 + • •
Z о
раскладывается указанным образом в ряд Тейлора в нуле. За-
метим, что pf(w) — 0 только при w = 0, и р имеет абсолютный
минимум в нуле. Множитель е~ххх присутствует в правой части
формулы Стирлинга. Поэтому нам надо исследовать асимптоти-
ческое поведение интеграла
[°°e~xp^dw.
J-1
Прежде всего отметим, что для больших х единственный боль-
шой вклад в интеграл получается от w в окрестности нуля —
минимума функции р. Например, если е — любое фиксированное
положительное число, то
[ ' e~xp{w)dw< [ £e~x w^2dw< [ £ e~xw2/2 dw.
J—1 J—1 J—oo
Можно получить грубую оценку последнего интеграла, написав
—xw2/2 —xw2/4 . — xw2/4 —е2ж/4 —xw2/4
для —oo < w < —e. Поэтому
f \-™2lidw^C(x)e-£2xl\
J—oo
/*0 2
где C{x) = / e~xw /4dw — сходящийся интеграл
J—oo
1068 Глава 21. Асимптотическое вычисление интегралов
и, более того, С(х) —> 0 при х —» оо. Следовательно, интеграл
экспоненциально убывает с ростом х. Аналогично, при w > 0
функция p(w) строго возрастает, так что
f °° е~хр^ dw < е~р^х/2 [°° е~хр^12 dw.
Je Jе
Этот второй интеграл сходится абсолютно и равномерно в облас-
ти х > 0 (причем все быстрее, когда х —> оо). Таким образом,
мы можем контролировать оба интеграла и и заняться
интегралом е dw для г > 0. Теперь р(0) = 0, р'(0) = 0 и
p,z(0) = 1. Поэтому можно сделать замену переменной w —
в окрестности нуля, так чтобы р приняла вид $2/2, т.е.
p(w(s)) = s2/2.
Напомним читателю, как это делается. Поскольку р(0) — 0, мы
имеем
rw 1*1
p(w) = I p(r)dr~w I pf(wu}du,
Jo Jo
где мы положили г — wu при переходе от первого интеграла ко
второму. Аналогично,
p\w) — w I pH(wu) du
Jo
так что
p(w) = -w2q(w),
z
где *
#(w) = 2 I I upft(uvw)dudv.
Jo Jo
Заметим, что q — дифференцируемая функция от w и <?(0) — 1.
Значит, q(w) > 0 для достаточно малых w. Теперь можно сделать
замену переменных ____
s = w\/q(w)
и
p(w(s)) = |s2.
z
21.1. Метод Лапласа
1069
Выберем г > 0 настолько малым, чтобы такая замена переменной
была допустима при — е < w < г q(w) (т. е. чтобы функция
была положительна в этом интервале). Теперь сделаем замену
переменной в интеграле e~xP(w) dw и получим
Г e-xp(w) dw = Г2 e-xs2/2 <ds
J—e J-ex \dsj
где в2 = и ”ei ~ (см. график на рис. 21.1).
Рис. 21.1
При оценке интеграла играет роль только область в окрест-
ности s = 0. Например, предположим, что у нас есть бесконечно
дифференцируемая функция р такая, что р = 1 при |$| < т/ и
р = 0 при s > 2т], где —£i < ~2т] и 2т] < е (рис. 21.2). Тогда
обозначим
6(s) = p(s)^, т.е. 6(s) = ^(s) для |s| < 7J.
Напишем
f е xs2/2w\s}ds~ f е xs2^2b(s) ds + погрешность,
-61
1070 Глава 21. Асимптотическое вычисление интегралов
где погрешность экспоненциально стремится к нулю с ростом ж,
в частности, быстрее по порядку величины, чем е~г/ х. (Это яв-
ляется следствием того, что погрешность дается интегралами ви-
да f2£1 e-xs2/2(b(s) — w'(s)) ds и Ц2 e~xs2/2(b(s) — w'(s)) ds. Тогда
подынтегральное выражение стремится к нулю быстрее, чем кон-
станта на е-7? х.)
Интеграл f^21 e~xs /2b(s) ds можно заменить интегралом
Г e-xs2/2b(s)ds
J—оо
поскольку Ь = 0 для s < si и $ > Е2- Таким образом, мы все свели
к оценке этого последнего интеграла.
Воспользуемся формулой Тейлора с остатком и напишем
Ь($) = i>o + + b2s2 Ч---h + Ьдг(«)«^,
где bx(s) - гладкая ограниченная функция. Тогда
РОО /*0О гоо
/ e~xs /2b(s} ds = b0 / e~xs /2 ds + bU e~xs 12 s ds
J—oo J— oo J— oo
+ b2 e~xs/2s2ds + --- + RN(s),
J—CO
где
RN(s) = [°° e~xs2/2bN(s)sN ds.
J—oo
Следовательно,
f00
|«at(s)| DN / e~xs2/2\s\Nds,
J—oo
где
Dn = sup|&jv(s)|.
В силу симметрии
roo 2
I e~xs /z$k _ q, если к нечетно.
—oo
21.1. Метод Лапласа
1071
Для четного числа к сделаем замену переменной
1/2 j &У
х ' s = y, так что as = -777 •
Тогда имеем
г°°
e~xs /2sk ds = х~^2~к I ё~у /2yfc dy
J —00
= Ckx-1^2,
где
/*°° о
ck= e~y/2ук dy
J—oo
не зависит от x (причем Co = л/2тг). Заметим, что
Г е~у2!2ук dy = 2 [°° е~и(2и/к-1^2 du = 2<*+1>/Т (^±2),
J-oo Jo \ 2 /
откуда
ск = 2(fc+1)/2r (^-±2) .
V 2 J
Аналогично, остаточный член можно оценить произведением
x-i/2-N/2 на константу. Возьмем N = 2п, тогда
[ e-xs2/2^s)rfs = (ao+aiZ^H------Fan_ix“n+1+sn(x)),
J-oo \4
где £n(%) = o(x~n). Здесь ao = bo, ai = Ьг, «2 = ^/а/Зтг и т.д.
Функции Ьи dw/ds имеют одинаковое разложение в ряд Тейлора
в 0. Подстановка разложения Тейлора функции p(w) = w—log(l+
w) дает более точное приближение Стирлинга.
Предположим, что нам дана гладкая положительная функ-
ция р с единственным абсолютным минимумом в точке to внут-
ри области определения этой функции (рис. 21.3), и при этом
pff(to) > 0- Предположим, что a(t) — другая гладкая функция.
Рассмотрим интеграл
a(t)e-kp^dt.
1072 Глава 21. Асимптотическое вычисление интегралов
to
Рис. 21.3
Это можно переписать в виде
e-fcP(to) / a(^e-fc(P(t)-p(t0))
где функция p(t)— p(t0) имеет минимальное значение 0 при t = to-
Изложенный выше метод позволяет доказать принцип Лапласа
(открыт в 1820 году):
a(t)e~kp^ dt
е fcp(to) /2тг\ / ai а2
(“" + Т + ^ +
где ao = a(to), a последующие коэффициенты выражаются через
функции а и р и их производные в точке to-
21.2. Метод стационарной фазы
Давайте разберемся, что произойдет с методом Лапласа, если в
экспоненте —кр заменить на ikp. Окажется, что справедлива ана-
логичная формула, но в этом случае в ней учитываются все кри-
тические точки функции р, а не только абсолютный минимум. В
методе Лапласа множитель е~р^ в подынтегральном выраже-
нии экспоненциально убывает по сравнению со значением вблизи
минимума р. Поэтому вся информация об асимптотике функции
была локализована в этом минимуме. Когда мы рассматриваем
интеграл
J eikp^a(y)dy,
множитель е1кр<-у> уже не стремится к нулю при к —> оо. Вмес-
то этого он быстро осциллирует как функция от у везде, где
pz(p) / 0. Быстрые осцилляции приводят ко взаимным сокраще-
ниям, поэтому существенный вклад в интеграл вносят области в
21.2. Метод стационарной фазы
1073
окрестности критических точек. Чтобы это увидеть, давайте рас-
смотрим случай, когда не обращается в нуль во всей области,
где а(у) 0 0. Точнее, предположим, что функция а(у) имеет про-
изводные всех порядков и компактный носитель, т. е. равна нулю
вне конечного интервала. Кроме того, предположим, что
|р'(у)| > С > 0 для всех у, где а(у) / 0.
Тогда можно утверждать, что для любого числа N существует
постоянная Сдг такая, что
J eikp(y> dy
CN
kN'
Другими словами, мы утверждаем, что интеграл стремится к ну-
лю быстрее, чем любая отрицательная степень к. Действительно,
рассмотрим дифференциальный оператор
Рг(.У)ду''
который (в силу наших допущений) имеет смысл в области, где
а(у) 0, и
DeikpW> = ike'kp^
или
gifcp(y) = _l(£)eifcP(j/)).
Тогда
[ elkp^a(y)dy= [ ^(DeikpM)a(y)dy
J J
где
/ a(y) \
i dy \pt(y) J '
1074 Глава 21. Асимптотическое вычисление интегралов
Здесь мы проинтегрировали по частям и воспользовались тем,
что функция а вместе со своими производными равна нулю на
границах области интегрирования. Функция с обладает теми же
свойствами, что и а, поэтому эту процедуру можно повторить и
получить
J b(y)eikp^ dy = J cN(yyk^dy
для соответствующей функции Если теперь обозначить
cn = / cN(y)elkp^ dy
то наше утверждение доказано.
Рассмотрим теперь общий случай. По-прежнему считаем, что
а ~~ гладкая функция с компактным носителем. Но теперь мы
не исключаем, что р'(у) имеет нули. Однако предполагаем, что
функция р имеет конечное число критических точек у\,..., ут
(в которых р*(у) — 0), и что р/х(у) 0 в каждой из них. Тогда
утверждается, что
а(у)е^р(2/) dy ~
/2% \1/2 A e±7ri/4eifcp^) / aij
\ к ) + к + ”
где ао^ = ft(yj) ~ aj, а остальные коэффициенты выражаются
через а, р и их производные в точке yj. Знак + в функции е±7П/4
берется в точке минимума, где pff(yj\ > 0, а знак — в точке мак-
симума, где p”(yj) < 0. В этой формуле функция р принимает
вещественные значения, а функция а может быть комплексной
функцией у. Это называется формулой стационарной фазы. До-
кажем ее. В окрестности каждой критической точки уг можно
найти такую координату s, для которой
Р(У(«)) = ±*2/2
(знак выбирается в зависимости от знака р"(уД). Сделаем замену
переменной и получим
dy = 1
ds а/1р"(у^)1
в точке yj.
21.2. Метод стационарной фазы
1075
Рис. 21.4
<Р1 ^2 <рЗ
Рис. 21.5
Этим объясняется множитель 1/у/1р"(у?)1 в формуле стационар-
ной фазы.
В окрестности каждой точки yj определим такую функцию
фу, что ф3 = 1 вблизи yj и фу = 0 вне малой окрестности, где опре-
делена процедура замены переменной (рис. 21.4); причем окрест-
ности различных точек не пересекаются (рис. 21.5). Тогда функ-
ция
Ь ~ а — (<ъф1 + а%ф2 + * • • + агфг)
имеет компактный носитель и р'(у) ф 0 везде, где 6(у) 0. Таким
образом, можно применить предыдущий результат к b и получить
j eikpady = ^ f eikp(aj<l>j)dy + O(k~N)
для любого значения N. Каждый член суммы можно рассмот-
реть отдельно, сделав в нем соответствующую замену перемен-
ной. Для j-ro слагаемого получаем
/e±ifcs2/2 ds-
Определим функцию ф равенством
dy
Тогда функция ф имеет компактный носитель, и мы свели задачу
к вычислению интеграла
/•оо
J —а
e±iks2/2^s)ds.
Чтобы это сделать, сначала рассмотрим гауссовы интегралы. Мы
уже слегка коснулись этого вопроса в предыдущей главе.
1076 Глава 21. Асимптотическое вычисление интегралов
21.3. Гауссовы интегралы
Материал, излагаемый в этом параграфе, основывается на равен-
стве
]= Г e-2/2dx = l.
Его можно доказать, взяв квадрат от левой части
Функция
1 [ e-^/^dx
\/27Г J-oo
сходится равномерно для всех комплексных значений т] в про-
извольной компактной области. Следовательно, этот интеграл
определяет аналитическую функцию, которую можно вычислить
для вещественных т] и потом аналитически продолжить. Для ве-
щественного числа ту показатель экспоненты дополняем до пол-
ного квадрата и делаем замену переменной
Г° e~x2/2~xridx = Г e-^+^+^dx
2тг J—оо %/2тг J—оо
1 Г00
= 12 dx
л/2тг J —оо
- е^2/2.
Эта формула верна для всех комплексных т/. Если взять т] = i£,
то получим
1 /*°°
1 / e~^/^dx = e~e/2r
х/2тг J—оо
Другими словами, преобразованием Фурье функции е~х2?2 явля-
ется е"^ /2. Теперь положим х — у/Х и, где у/Х > 0 - положитель-
ное вещественное число. Тогда dx ~ y/Xdu. Положив £ = л/АС,
21.3. Гауссовы интегралы
1077
получаем
f e-Xu2/2e-i^u du= -^=е~^/2.
л/2тг J д/2тг
Этот интеграл сходится для всех А при условии, что Re А > 0 и
А 0. Действительно, для S > R > 0 имеем
[S e-Ax2/2e-i^ dx=fS J A(e-Ax2/2)e-i^ dx
Jr Jr dx
e~XR2/2e~i£R e-XS2/2e~i^S rS ^2^ d / e^x A
XR XS + Jr e dx\Xx)
В последнем интеграле можно написать
е-Ах2/2 _ 1 _£е-Лх2/2
Хх dx
и еще раз проинтегрировать по частям. Тогда получим
rS 1 / 1 \
/ e-^2/2 -i£r dr = О I — I
\Jr I
Отсюда видно, что функция
_L_e~Xx2/2
\/2тГ
равномерно (но не абсолютно) сходится по А в произвольной об-
ласти вида
Re А > 0, | А| > при любом 5 > 0.
Сделаем аналитическое продолжение. Значения функции зада-
ются той же формулой, что и при вещественных положитель-
ных А, но теперь квадратный корень должен быть аналитическим
продолжением положительного квадратного корня. В частности,
если взять А = —ir, г > 0, то
Д1/2 = |Л|1/2е--/4
И
_£= / eirx2/2e-i^ dx = em/4r-l/2e-i42/2r
\/2% J
1078 Глава 21. Асимптотическое вычисление интегралов
Если взять А — ir, то аналогично
1 f g-irx2/2e-i^ dx = e-7ri/4r-l/2ei7?2/2r
у/Ъг J
Теперь можно закончить доказательство формулы стационар-
ной фазы. Для этого нам надо получить асимптотическую оценку
интеграла вида
f e±ifcs2/2^) fa
J—ос
где -0 — функция с компактным носителем, которая имеет вид
^(з) ~ ^(0) + зх(з).
Умножим это равенство на функцию р, которая тождественно
равна 1 там, где / 0 и равна нулю для больших значений |з|.
Тогда
V>(s) = 'фо(з) + зр(з)х(з),
где
^о($) = p(s)^(0) = V>(0) вблизи з — О.
Таким образом,
У ^o(s)e±lks^2 ds = + погрешность,
где погрешность убывает быстрее любой степени к. Однако,
[ з[р(з)я(з)]е1Ь2/2с/з — -Д- /[р(з)х(з)]-^- e±lfcs2/2 ds
J ±ik J ds
1 Л/ J (Хо
и (с//с/з)[р(з)х(з)] равняется нулю для больших |з|. Эту процедуру
можно повторять, пока не получим асимптотический ряд, что и
завершает доказательство нашей формулы.
Давайте получим n-мерную версию гауссова интеграла. Пусть
яА /±П 0
: — векторная переменная и Q —
Хп/ \ о ±гп/
21.3. Гауссовы интегралы
1079
является матрицей п х п для всех > 0 и sgnQ равняется
числу плюсов минус число минусов. Тогда |п| • • • |гп| = | Det(Q)|.
Умножая формулы для одномерных интегралов, получаем
1
(27Г)П/2
ехр(—• х) dx = |Det(Q)| 1//2
— exp
7П _
jSgnQ
xexp(-^Q Ч
\ £
где теперь £ — тоже вектор, a Q”1 — обратная матрица. Итак, мы
доказали формулу для диагональной матрицы Q. Однако, для
любой несингулярной симметричной матрицы Q можно найти
ортогональную матрицу О такую, чтобы матрица OQO~X была
диагональной. Это значит, что полученная выше формула верна
для всех таких матриц Q.
Мы можем использовать n-мерную версию гауссова интегра-
ла, чтобы получить n-мерную версию формулы стационарной фа-
зы. Пусть р — функция с конечным числом критических точек.
Предположим, что все критические точки функции р невырож-
дены. Тогда гессиан
является невырожденной матрицей во всех критических точках
yj. Пусть а — обозначает сигнатуру j-й критической точки.
Тогда
е7"^4 ( / ч ai(z/j)
V|Det(^(yj))| \<yj) к
где сумма берется по всем критическим точкам. Здесь величи-
ны ai(yj), «2(Pj) и т. д. выражаются через функции а и р и их
производные различных порядков в точках pj.
1080 Глава 21. Асимптотическое вычисление интегралов
21.4. Групповая скорость
В качестве применения метода стационарной фазы в одномерном
пространстве рассмотрим следующую ситуацию. Пусть у нас есть
семейство бегущих волн
e-(i/h)(E(p)t~px)
где h — малое число, так что 1/h играет роль нашего большого
параметра к. Волновое число для пространственной вариации
равно p/h в каждый момент времени t. Мы полагаем, что Е за-
висит от р, т. е. каждая волна имеет свою скорость. Предполо-
жим, что мы сложили семейство бегущих волн, что выражается
интегралом вида
J а(р)е-0/л)(Е(р)*-рх) dp
Далее, предположим, что функция а(р) сосредоточена вокруг
некоторого фиксированного значения ро- Другими словами, мы
предполагаем, что функция а отлична от нуля только для зна-
чений р в небольшой окрестности ро* Согласно методу стацио-
нарной фазы, существенный вклад в интеграл возникает только
от тех значений р, где производная по р показателя экспоненты
равняется нулю, т. е. только при условии, что
Ef(p)t - х = 0.
Поскольку Др) равняется нулю, если р не лежит в малой окрест-
ности ро, то это уравнение дает нам связь между х и t. Из уравне-
ния следует, что интеграл практически равен нулю везде, кроме
тех значений х и t, для которых равенство
х = E'(po)t
выполняется приближенно. Другими словами, интеграл выгля-
дит как небольшой сгусток, если рассматривать его как функ-
цию х, причем этот сгусток движется со временем со скоростью
Е'(р). (Этот сгусток называется волновым пакетом, а его ско-
рость Е*(р) называется групповой скоростью.)
21.4. Групповая скорость
1081
Давайте исследуем, какой должна быть функциональная за-
висимость Е от р, если потребовать, чтобы выражение Е -t — p-x
было инвариантно относительно преобразований Лоренца. Со-
гласно преобразованию Лоренца, точка (i,x) может перейти в
точку (£', xz) при условии, что выполняется равенство
2x2 2 2х/2 /2
С Г — X — С t — X .
Тогда (Е,р) преобразуется в (Е\р'), причем
Е2-С2р2 = Е'2-<?р'2.
Таким образом, единственная инвариантная связь между Е и р
имеет вид
Е2 — с2р2 — const.
Обозначим эту константу т2с4, так что
Е2 — с2р2 = т2с4
или
Е(р) = ((ре)2 + m2c4)lyZ2.
Тогда
где
Е(р) = Мс2 и М — (т2 + (рс)2 )1у/2,
так что, если р/с мало по сравнению с т, то М = т). Если
считать, что М — это масса, то связь между групповой скоростью
Е'(р) и р — это в точности соотношение между скоростью и
импульсом. Таким образом, мы связали волновое число к = p/h
с импульсом р, а соответствующая длина волны
1 h , _ _ v
А — -г = — (формула де Бройля),
fc р
Если считать, что Е — энергия, то связь между энергией и ча-
стотой у временной вариации дается формулой
Е = hv (формула Эйнштейна).
1082 Глава 21. Асимптотическое вычисление интегралов
В этих формулах стоит малый параметр h, который мы устремля-
ли к нулю. Великое открытие квантовой механики состоит в том,
что параметр h не должен стремиться к нулю. Это фундамен-
тальная константа природы, известная как постоянная Планка.
В формуле Эйнштейна она возникает как множитель, связыва-
ющий энергию и обратное время, следовательно, ее размерность
энергия х время. Значение постоянной Планка равно
h = 6.626 х 10-34Дж с.
21.5. Формула обратного преобразования
Фурье
Давайте рассмотрим очень важное применение формулы стацио-
нарной фазы. Пусть п ~ 2, координаты обозначим х и £. Возьмем
функцию
Р(®Л) =Рп(ж,С) =ж(С-7?),
где т] — фиксированное число. Эта функция имеет только одну
(невырожденную) критическую точку, а именно
х — 0, £ = г]
с сигнатурой а = 0.
Тогда
± f £) dxd^ = 1 (о(0, + • • •) .
2% J к \ к /
Эта формула была доказана для а(х,£) с компактным носите-
лем. Дальнейшее обобщение доказательства показывает, что она
годится для функций, обращающихся на бесконечности в нуль
вместе со своими производными любого порядка. Причем они
стремятся к нулю быстрее, чем любая отрицательная степень к.
В частности, допустим, что
а(ж,С) =
21.5. Формула обратного преобразования Фурье
1083
где f и д — гладкие функции одной переменной, быстро стремя-
щиеся к нулю на бесконечности вместе со своими производными.
Тогда можно написать
/I f^g^e~ikx^ dxd£ = ±f(O)g(?i) + О (1) .
В этом интеграле сделаем замену переменной и = кх. Тогда
i/IOsto) + О (±) = -L // g)
Пусть д — Фуръе-образ функции д, определенный формулой
Ж) = 4= f 9№~iuidt.
у2тг J
Подставим это выражение в предыдущую формулу и получим
|4= [ f (j) gt^du = i/(0)s(4) + О (Г).
к у2тг J к/ к \kz J
Предположим, что функция f удовлетворяет условию /(0) = 1.
Тогда
4= [ f(l)g(u)^du=-^= [ g(u)^du + o(^.
х/2тг J \к/ v2tt J \к;
Переходя к пределу к —> оо, получаем
9(п) = [ g(u)e~MTI du.
у2тг J
Эта формула называется формулой обратного преобразования
Фуръе. Она показывает, как восстановить функцию по ее Фурье-
образу.
Аналогично доказывается формула для пространства п изме-
рений
д(д) — 7—f £(u)e~1W? du.
(2тг)п/2 J
1084 Глава 21. Асимптотическое вычисление интегралов
21.6. Асимптотическая оценка формулы
Гельмгольца
Пусть и является решением приведенного волнового уравнения
(А + к^и = 0 в трехмерном пространстве. В параграфе 19.6 мы
показали, что если и удовлетворяет этому уравнению, то для то-
чек Р вне некоторой замкнутой поверхности 5, работает формула
Гельмгольца
—О-
При этом для точек Р внутри S тот же интеграл равен нулю. Там
мы упоминали, что Гельмгольц таким образом объяснил прин-
цип Гюйгенса — отсутствие обратных волн. Однако, обращение
интеграла в нуль внутри S зависит от вкладов со всей поверх-
ности. Френель полагал, что если бы внутри S были все волны,
то интеграл от каждого малого элемента поверхности давал бы
нулевой эффект внутри за счет интерференции. Используя ме-
тод стационарной фазы, мы сейчас покажем, что Френель был
прав с точностью до членов порядка 1/к. Когда мы применяем
метод стационарной фазы, функция и в правой части формулы
осциллирует. Прежде, чем двигаться дальше, необходимо сделать
ряд предположений относительно нее. Предположим, что вбли-
зи поверхности S эта функция имеет вид и — ае1к^^ где а и ф -
гладкие функции. Кроме того, пусть || grad </>|| = 1. Такая функ-
ция будет, например, описывать излучение от точки Q, лежащей
внутри поверхности S, где ф(у) = у — Q.
Далее, предположим, что мы находимся достаточно далеко от
поверхности S, так что 1/г2 пренебрежимо мало по сравнению
с fc, и что а п da тоже малы по сравнению с fc. Подставим все
в формулу Гельмгольца и получим, что член самого высокого
порядка (относительно степеней к) имеет вид
— [[ (a/r)elfc^+r\*d</> — *dr).
J Js
Здесь точками стационарной фазы являются точки у на поверх-
ности S, где ф(у) + gradr(y) перпендикулярен S. При этом воз-
никают две возможных ситуации (рис. 21.6).
21.6. Асимптотическая оценка формулы Гельмгольца 1085
Рис. 21.6. Два типа: a) grad^(y) = - gradr(y), *(1ф(у) = —*dr(y),
Р = У + г grad ф(уУ, б) grad</>(j/) = 2(grad ф(у), ri)n - gradг(у),
^ф(у) = *dr(y), Р = у- r(2(grad</>(y),n)n - gradr(?/))
Сначала предположим, что у — невырожденная критическая
точка типа (б). Член самого высокого порядка в формуле стацио-
нарной фазы равен нулю, и полный вклад в формулу Гельмголь-
ца от такой точки у будет порядка 1/к. (Заметим, что если бы
поверхность S была выпуклой и grad</> был направлен наружу,
то для любой точки Р внутри поверхности S все критические
точки были бы типа (б). В некотором смысле это оправдывает
точку зрения Френеля, что есть локальное сокращение обратных
волн.) Для невырожденной критической точки типа (а), посколь-
ку *d(j>(y) = —*dr(y), при вычислении вклада самого высоко-
го порядка в формулу стационарной фазы мы можем заменить
прежний интеграл интегралом вида
(a/r)eife^+r) d*r.
Это показывает, что (с точностью до порядка 1/fc) индуцирован-
ное вторичное излучение от поверхности S обладает следующи-
ми свойствами:
(i) его амплитуда равна значению А, умноженному на ампли-
туду первичной волны, где А = 2тг/& — длина волны;
(ii) его фаза на одну четверть периода опережает фазу первич-
ной волны. (Этим объясняется множитель i.)
1086 Глава 21. Асимптотическое вычисление интегралов
Именно эти два свойства Френель постулировал в своей фор-
мулировке принципа Гюйгенса, и поэтому многие рассматривали
его теорию как случайную. Мы здесь показали, что эти пред-
положения являются следствием метода стационарной фазы и
формулы Гельмгольца.
Теперь необходимо обсудить ситуацию, когда критические
точки не вырождены. Исследуем точки типа (а). (Точки типа
(б) рассматриваются аналогично.) Мы воспользуемся здесь теми
же аргументами, что и при исследовании излучения. Определим
экспоненциальное отображение Е : S х R —> R3 формулой
E(y,r) = у + г grad ф(у~).
Тогда критические точки на поверхности S, связанные с точкой
Р, — это как раз те точки у, для которых E(y^r) = Р, где
г = ||у — Р||. Если grad(/>(y) не касателен к поверхности S, то
Е является диффеоморфизмом в окрестности (у,0).
Нетрудно показать, что у — вырожденная критическая точка
для Р = Р(у,г), если и только если (у, г) — точка, в которой
отображение Е сингулярно. В этом случае назовем точку Р фо-
кальной точкой отображения Е в у. Если же Р не фокальная
точка, то индекс гессиана ф + г в точке у — это число фокальных
точек (с учетом их кратности) в сегменте от у до Р. Доказать это
мы оставляем читателю.
Резюме
А. Асимптотическое разложение интегралов
Для данной функции, определенной интегралом вида
j е~хР^(1ш,
надо уметь находить область значений дающую основной
вклад в интеграл для больших т, и получать первые два чле-
на асимптотического разложения интеграла.
В. Стационарная фаза
Для интеграла вида
a(y)eikp^ dy
Задачи
1087
надо уметь получать формулу для первых двух членов асимпто-
тического разложения при больших к.
Методом стационарной фазы надо уметь получать формулу
для обратного преобразования Фурье.
Задачи
21.1. Модифицированная функция Бесселя третьего рода определяет-
ся интегралом
fc0(x) = i / e-xcoshtdt.
2 J — ос
Получите первые два члена асимптотического разложения функ-
ции fco(x).
21.2. Функция Бесселя Jo(^) определяется интегралом
1 /*27Г - •
J0(x) = — / e™mtdi.
Jq
Методом стационарной фазы получите первые два члена асимп-
тотического разложения Jo(x).
21.3. Бета-функция В(я + 1,х + 1) представляется интегралом
1 = [1[t(l~t)]xdt= [
JO JO
(а) Где набирается основной вклад в интеграл для очень боль-
ших х?
(Ь) Получите главные члены асимптотического разложения
В(х + 1, х + 1).
(с) Опишите возможно подробнее, как получить следующие
члены асимптотического разложения. Вычислите еще один
член.
21.4. (а) Опишите процедуру получения асимптотического разложе-
ния интеграла вида
Г #2
1= e-'ixp^q(e)d0.
Jet
Предположите, что р(0) имеет единственную критическую
точку 0 = а на отрезке [#i, О2] *
1088 Глава 21. Асимптотическое вычисление интегралов
(Ь) Примените эту процедуру для получения главного члена
асимптотического разложения функции Бесселя
Jn(x) = - fRe Г е^Ое-^ав
К \ Jo
где п — целое число.
Глава 22
Термодинамика
В этой главе показано, как внешнее дифференциаль-
ное исчисление используется в классической термоди-
намике, следуя идеям Борна и Каратеодори.
Тема этой главы — равновесная термодинамика, имеющая
несколько ветвей. Первая из них — «классическая термодина-
мика» — имеет дело с понятиями тепла и работы, из которых
следуют понятия энтропии, температуры и знаменитое «второе
начало термодинамики». В классической термодинамике обсуж-
даются общие принципы, но не делается попыток описать пове-
дение вещества или вычислять измеряемые величины в рамках
микроскопической модели. Вторая ветвь — «равновесная стати-
стическая механика» в классическом или квантовом варианте —
дает явные формулы для всех «макроскопически наблюдаемых
величин» равновесного состояния в рамках модели атомных или
молекулярных взаимодействий. Эти формулы имеют общую при-
роду, т. е. все они имеют общую форму и связаны с именами Макс-
велла, Больцмана и особенно Гиббса. Третья ветвь занимается
объяснением, почему эти формулы работают, изучает проблемы с
точки зрения теории вероятностей или динамики, или того и дру-
гого, занимается проблемами установления равновесия. В этой
главе мы совсем немного будем говорить об этой третьей ветви.
В первых двух параграфах рассматривается классическая термо-
динамика. Но при этом мы начнем с чисто математической теоре-
мы Каратеодори, которая геометрически вполне наглядна, хотя
ее доказательство во всех деталях мы завершим в приложении
1090
Глава 22* Термодинамика
к этой главе. Эта теорема является математическим инструмен-
том, согласно которому в рамках подхода Борна и Каратеодори
к термодинамике функция энтропии существует. После этого мы
получим ряд физических следствий теории, а конец главы посвя-
тим равновесной статистической механике.
22.1. Теорема Каратеодори
Пусть а = Ai dx1 + • • • + Ап dxn — линейная дифференциальная
форма в пространстве Rn, где все Ai — вещественные функции
на этом пространстве. Возьмем некоторую фиксированную точ-
ку Р и будем рассматривать значение а в точке Р как вектор-
строку (Ai(P),..., АП(Р)). Если этот вектор не равен нулю, то
его нулевое пространство — это (п — 1)-мерное пространство всех
/ХЛ
X = I : I таких, что
\%П/
Ai(P)X1 + --- + АП(Р)ХП =0.
Пусть 7 = x(t) — кусочно-дифференцируемая кривая. Тогда
J а = -I---h An(x(t))xn(t)] dt.
В частности, если для каждого t касательный вектор x(t) =
: I лежит в нулевом пространстве (Ai(#(t)),..., An(rr(t))),
то интеграл f а — 0. Кривая 7 называется нулевой кривой си, ес-
ли 7 непрерывна и кусочно-дифференцируема и если при каждом
i, для которого определена x(i), эта x(t) лежит в нулевом про-
странстве (Ai(x(i)),..., An(z(i))). Сейчас мы хотим рассмотреть
геометрическую задачу.
Предположим, что мы начали с некоторой точки Р. Где нахо-
дятся те точки Q, которые соединяются нулевыми кривыми с Р?
22.1. Теорема Каратеодори
1091
Например, предположим, что для некоторой функции / выпол-
няется равенство
а = df.
Тогда если 7 — нулевая кривая, соединяющая Р и Q, мы имеем
0= [ a = /(Q)-/(P).
А
Тогда /(Q) = /(Р). Если df 0, то уравнение / — /(Р) — const
задает (п—1)-мерную поверхность1 (рис. 22.1), проходящую через
точку Р, и Q должна быть на этой поверхности.
Рис. 22.1
При этом существуют точки, сколь угодно близкие к Р, кото-
рые не могут быть соединены с Р посредством нулевых кривых.
То же самое верно и в случае, когда а = gdf, где д — неко-
торая ненулевая функция, и df 0. В самом деле, 7 — нулевая
кривая для а, если и только если она является нулевой кривой
для g~la = df. И условия, чтобы быть нулевой кривой, те же.
Поэтому, чтобы можно было соединить точки Q и Р нулевой кри-
вой, Q должна лежать на (п — 1)-мерной поверхности / = /(Р).
Заметим, что если а = gdf, то da — dg /\df и поэтому
а Л da ~ д df Л dg Л df = 0.
*В приложениях, где форма а = df интерпретируется как силовое поле, а
функция / — как его потенциал, такая поверхность называется эквипотен-
циальной. — Прим. ред.
1092
Глава 22. Термодинамика
А теперь рассмотрим форму
а — dz + xdy,
определенную в пространстве R3. В этом случае da = dx Л dy и
а Л da = dx Л dy Л dz
нигде не обращается в нуль. Покажем, что любые две точки мож-
но соединить нулевой кривой для dz + xdy. Для этого достаточно
показать, что можно соединить начало координат 0 с любой дру-
гой точкой Q. Напишем
Q =
Сначала предположим, что b ф 0. Теперь видно, что ось х явля-
ется нулевой кривой для а, потому что dz и dy равны нулю вдоль
прямой z = у ~ 0. В силу этих же причин, любая прямая, парал-
лельная оси х, является нулевой кривой для а. Теперь пусть за
время 0 t 1 мы сдвигаемся вдоль оси х от начала 0 до точки,
х-я координата которой равна —с/Ь. Далее двигаемся из точки
вдоль
/-с/Ь\ / 0 \
x(t) = I 0 ) + I (t — 1)6 ] , 1 t 2.
\ 0 / \(£-1)с/
Поскольку
0\
6 1 и (А1(х(£)),А2(х(<)),Лз(х(г))) = (о, —^,1) ,
с/
мы видим, что это тоже нулевая кривая. Наконец, перейдем из
точки
в точку
22.1. Теорема Каратеодори
1093
вдоль
(—с/Ь\ /(t - 2) (а - с/Ь}
b j + I 0
с I \ 0
2 < t 3.
Поскольку эта прямая параллельна оси х, она тоже являет-
ся нулевой кривой. Итак, мы перешли из точки О в точку Q
вдоль непрерывной траектории — ломаной, состоящей из трех
прямолинейных отрезков. Эта траектория является кусочно-
дифференцируемой нулевой кривой.
Если 6 = 0 и с О, то сделаем немного по-другому. Сначала
(1\
с j. Сначала идем в
°/
/0\ /1\
I с I вдоль х = z = 0, а затем в I с ] вдоль у — с, z = 0
\°/ \°/
(параллельно оси х). Наконец, перейдем из точки
в точку
вдоль
/1\ / ° \
x(i) = I с j + | ~(t — 3)с | ,
\0/ \ (t — 3) /
2 < t < 3.
Поскольку вдоль этой кривой dz — с dt, dy = — cdt и х = 1, мы
видим, что sz + х dy тождественно равно нулю на этой кривой,
поэтому она — нулевая кривая. Теперь можно перейти в точку
Q вдоль прямой, параллельной оси х, т.е. координаты у и z
фиксированы, а координата х меняется от 1 до а.
Конечно, если b = с = 0, можно сразу попасть их 0 в точку
Q вдоль оси х. Итак, мы доказали, что любые две точки в про-
странстве R3 можно соединить нулевой кривой формы dz + х dy.
1094
Глава 22. Термодинамика
В пространстве R3 можно рассмотреть три типа 1-форм.
Тип
Пример
(i) а, где а 0 0, но da = 0 а = dz
(ii) а, где da / 0, но а Л da 0 а = xdy
(iii ) а, где а Л da / 0 а ~ dz + xdy
В случае (i) мы знаем, что если da ~ 0, то локально можно най-
ти такую функцию f, что а = df. (Это можно сделать в любой
звездной области, содержащейся в области определения а.) Если
а? не обращается в нуль в некоторой точке Р, то из теоремы о
неявной функции следует, что можно сделать такую замену пе-
ременной, что функция / станет одной из координат, скажем, z.
Другими словами, с точностью до замены переменной пример из
первой строки представляет ее общий случай. Математическая
теорема, которую мы здесь приведем, говорит, что это справед-
ливо и в двух других случаях, т.е. любая форма типа (ii) или
(iii) сводится к соответствующему примеру. Позднее в этом па-
раграфе мы дадим формулировку теоремы и наметим вкратце,
как ее доказать, а все детали доказательства дадим в приложе-
нии. Теорема и ее доказательство верны не только в трехмерном
пространстве, но и в пространстве п измерений. Мы уже видели,
что в случае (iii) можно соединить любую точку с любой близ-
лежащей с помощью нулевой кривой формы а. Следовательно,
если форма а такова, что для любой точки Р существуют точки
Q, сколь угодно близкие к ней, которые нельзя соединить с Р
посредством нулевой кривой формы а, то имеет место случай (i)
или (ii). Это утверждение, точнее его п-мерное обобщение, и есть
содержание теоремы Каратеодори.
Теорема Каратеодори. Пусть о — линейная дифференци-
альная форма, обладающая тем свойством, что для любой точки
Р существуют сколь угодно близкие к ней точки Q, которые не
могут быть соединены с Р с помощью нулевой кривой формы о.
Тогда (локально) существуют такие функции f и #, что
а = fdg.
22.1. Теорема Каратеодори
1095
Это выражение для а не единственное. Действительно, если
Н дифференцируемая функция одной переменной, производ-
ная которой нигде не равна нулю, и
G = Hog,
то, согласно цепному правилу, dG — Hf(g)dg. Поэтому можно
писать
а = FdG, где G = Н о д, F - f/H'(g).
Прежде чем продолжать чисто математическое обсуждение
теоремы Каратеодори, давайте кратко опишем, как она исполь-
зуется в термодинамике. Детальное обсуждение с точными опре-
делениями читатель найдет в следующем параграфе.
Можно измерять количество тепла, выделенное в химической
реакции, которая проводилась в известных условиях, например,
при постоянном объеме или при постоянном давлении. (Это мож-
но сделать, например, в умном приборе, называемом ледяным
калориметром. Он использует тот факт, что объем льда при тая-
нии сокращается. При этом в обычных условиях, чтобы растаяло
данное количество льда, требуется определенное количество теп-
ла.) Количество тепла, необходимое для небольшого изменения
какой-нибудь величины (например, повысить температуру одно-
го грамма воды на один градус или увеличить его объем), когда
эксперимент выполняется каким-то заданным способом, (прибли-
зительно) линейно связано с этими малыми изменениями. Поэто-
му «количество тепла, сообщенное» системе в равновесном со-
стоянии, является линейной дифференциальной формой о. В те-
чение довольно долгого времени было принято считать, что эта
форма точная, т. е. что существует такая функция С (называе-
мая калорической), представляющая «полное количество тепла
в системе», для которой a = dC. Другими словами, мы считаем,
что «калорическая функция» в системе изменяется на величи-
ну сообщенного тепла. Только постепенно ученые осознали, что
форма а не замкнута и поэтому не может описывать бесконечно
малое изменение какой-либо функции.
С другой стороны, довольно рано стало понятно, что работа,
совершенная над системой, тоже задается линейной дифферен-
циальной формой (V, которая не замкнута. Действительно, пусть
1096
Глава 22. Термодинамика
в цилиндре находится газ, тогда при сжатии его поршнем совер-
шается работа тем большая, чем больше давление газа и соответ-
ственно выше его температура. Вдавим поршень в цилиндр при
высокой температуре, сокращая объем, и потом охладим систему
в этом положении (поршень неподвижен, и работа не совершает-
ся) , при низкой температуре вернем поршень в исходное положе-
ние и нагреем газ до той же температуры, что и вначале. Таким
образом, мы завершили «цикл», т. е. мы прошли вдоль замкнутой
кривой, вдоль которой интеграл от си не равен нулю. (Конечно,
эффективный способ проверить, замкнута форма или нет, — это
проинтегрировать вдоль замкнутой кривой. Вот почему «циклы»
играют такую важную роль при изучении задач термодинамики.)
Согласно первому закону термодинамики2, несмотря на то,
что формы а и си не замкнуты, их сумма замкнута, т. е. d(a+cu) =
0. Другими словами, первый закон термодинамики говорит, что
(локально)
а + cu = dU,
где 17 — функция системы (определена с точностью до аддитив-
ной постоянной). Эта функция называется внутренней энергией
системы. Существование функции U — это один из вариантов
закона сохранения энергии.
Второй закон термодинамики следует из поведения системы,
к которой не подводится тепла извне. Если мы поместим систему
в оболочку (называемую адиабатической оболочкой), через ко-
торую невозможно обмениваться теплом, то состояние системы
сможет изменяться только по нулевым кривым формы а. В при-
роде замечено, что в этих условиях для любого состояния систе-
мы существуют близкие состояния, в которые невозможно перей-
ти. Согласно теореме Каратеодори, это значит, что существуют
такие функции f и д, для которых
а = fdg.
2К двум основным принципам термодинамики в русскоязычной литера-
туре часто применяется название «начало» вместо «закон». — Прим. ред.
22.1. Теорема Каратеодори
1097
Конечно, это условие не определяет f и д полностью, о чем
мы уже говорили выше. Однако, анализ обмена между система-
ми, находящимися в тепловом контакте, показывает, что в каче-
стве функции f можно взять универсальную функцию Т для всех
систем, называемую абсолютной температурой, которая опреде-
лятся с точностью до постоянного коэффициента (масштабного
множителя). Это значит, что при фиксированном масштабе абсо-
лютной температуры для каждой системы функция д определя-
ется с точностью до аддитивной постоянной. Обычно эту функ-
цию обозначают буквой S и называют энтропией системы. Итак,
согласно второму закону термодинамики, существует универ-
сальная температура Т (называемая абсолютной температурой
и определенная с точностью до постоянного множителя), и для
каждой системы существует функция S (называемая энтропией
и определенная с точностью до аддитивной постоянной при фик-
сированном масштабе температур), для которых
а— Т dS.
Температурную функцию выбирают так, чтобы она всегда бы-
ла положительной. При этом условии изменение энтропии всегда
имеет тот же знак, что и количество тепла, сообщенное системе
вдоль любого касательного вектора системы (т. е. бесконечно ма-
лое изменение). Поскольку изменение S вдоль любой замкнутой
траектории должно быть равно нулю, это означает, что для лю-
бого цикла, если где-то добавляется тепло, в другом месте оно
должно изыматься. Кельвин дал известную формулировку вто-
рого закона термодинамики: «не существует циклических про-
цессов, в которых взятое у системы тепло полностью переходит
в работу». Работа может производиться только с помощью теп-
ловой машины, переводящей определенное количество тепла в
холодный резервуар.
В следующем параграфе мы сюда вернемся и дадим точные
формулировки всех этих законов. А сейчас обсудим чисто мате-
матически теорему Каратеодори. Давайте рассмотрим форму
а = dz + х dy
в шестимерном пространстве R6 с координатами х, у, z, и, v,
w. Очевидно, что любая кривая, вдоль которой постоянны у и
1098
Глава 22. Термодинамика
г, является нулевой кривой формы а. Поэтому мы можем дви-
гаться из 0 в любую точку Q пространства R6 вдоль нулевой
кривой формы а, сначала двигаясь в трехмерном пространстве
и ~ v = w = 0 до точки, у которой первые три координаты сов-
падают с соответствующими координатам точки Q, а затем уже
вдоль прямой линии до точки Q. (Вдоль этой прямой х, у и z
постоянные.) А теперь рассмотрим форму
ос — dz + х dy + и dv.
Как и раньше, в пространстве, где и — v = w = 0, мы
двигаемся из начала координат до точки, первые три координаты
которой совпадают с соответствующими координатами точки Q.
Затем, сохраняя значения х и у, мы можем изменить нужным
образом координаты и и потому что вдоль любой кривой у =
const форма а принимает те же значения, что и форма dz+u dv, и
мы, таким образом, сводим к случаю трехмерного пространства.
Наконец, можно изменить координату w, фиксируя остальные
пять координат.
Далее рассмотрим форму
а — w dz + х dy + и dv.
Предположим, что у точки Q координата w не равна нулю, т. е.
w(Q) — г Ф 0. Сначала двигаемся от точки О вдоль прямой
х~у — z = u~ v — 0 до точки, у которой координата w
равна г. Теперь мы остаемся в гиперплоскости w = г. Но для
любой кривой в этой гиперплоскости форма а принимает те же
значения, что и форма
а1 — г dzf + х dy + и dv.
Если мы сделаем замену переменной / = rz, то
af — dzf + х dy + и dv.
Теперь, как и раньше, можно придать нужные значения осталь-
ным пяти переменным, используя трехмерный случай. Аналогич-
но, если координата х или и точки Q не равна нулю, то исполь-
зуются те же соображения, просто изменяется роль различных
координат.
22.1. Теорема Каратеодори
1099
С другой стороны, если точка Q находится в трехмерном под-
пространстве, заданным условием х = и — w — 0, то любая кри-
вая в этом подпространстве является нулевой кривой. Поэтому
можно соединить начало координат с точкой Q. Итак, в прост-
ранстве R6 можно рассмотреть шесть типов 1-форм.
Тип Пример
(i) а / 0, но da = 0 dz
(ii) da / 0, но а Л da = 0 xdy
(iii) а Л da 0, но da Л da = 0 dz + xdy
(iv) da Л da Ф 0, но а Л da Л da = 0 xdy + и dv
(v) а Л da Л da 0, но da Л da Л da = 0 dz + xdy + и dv
(vi) da Л da Л da 7^ 0 wdz + xdy + и dv
Наши рассуждения показывают, что в случае формы типов
(iii)—(vi) можно двигаться между двумя любыми точками вдоль
нулевой кривой. Имеется математическая теорема о нормальной
форме, согласно которой для любой из форм одного из типов,
стоящих слева, можно сделать локальную замену координат, так
что в новых координатах форма а принимает соответствующий
вид, указанный справа. (Набросок доказательства этой теоремы
дается в приложении.) С учетом этого факта мы можем доказать
теорему Каратеодори в шестимерном пространстве следующим
образом.
Сначала покажем, что
da Л da Л da = 0.
Предположим противное — выражение da Л da Л da не равно
нулю тождественно. Тогда в некоторой точке Р (и поэтому в
окрестности Р) мы имеем дело со случаем (vi). Следовательно, в
окрестности точки Р можно сделать замену координат, так чтобы
форма а имела вид, стоящий справа. Но тогда точку Р можно
соединить с любой точкой с помощью нулевой кривой формы
а. Но ведь мы предположили, что каждая точка имеет в своей
окрестности точки, в которые нельзя попасть с помощью нулевых
кривых. Противоречие! Поэтому da Л da Л da = 0. Но эти же
рассуждения показывают, что
а Л da Л da ~ 0,
1100
Глава 22. Термодинамика
поскольку иначе мы будем иметь дело со случаем (v) вблизи неко-
торой точки и так далее. Таким образом, мы можем двигаться
дальше и доказать, что а Л da = 0, а это значит, что теорема Ка-
ратеодори доказана. Аналогичные соображения работают в про-
странстве п измерений.
22.2. Классическая термодинамика по Борну
и Каратеодори
В этом параграфе мы изложим основные положения термодина-
мики с точки зрения Борна и Каратеодори. Преимущество это-
го подхода состоит в том, что можно избежать довольно слож-
ных соображений относительно цикла Карно и невозможности
построить вечный двигатель. Этот подход основывается на аб-
страктных идеях, далеких от повседневного опыта, и ряде фи-
зических законов, которые просто формулировать. Здесь тепло
— производное понятие. Теория формулируется в стандартных
терминах элементарной механики. Однако, несмотря на то, что
в теории содержатся понятия механики, ее законы должны быть
модифицированы. Именно модификация этих законов приводит
к понятиям температуры и тепла. После этого два простых фи-
зических закона вместе с теоремой Каратеодори приводят к по-
нятиям абсолютной температуры и энтропии.
Основное предположение, общее для почти всех физических
теорий, состоит в том, что мы можем выделить интересующую
нас часть из остальной Вселенной. Эту часть Вселенной мы назы-
ваем системой. Система может существовать в различных состо-
яниях. Описание всех состояний системы может быть невероятно
сложной задачей. Например, если наша система — газ в некото-
ром объеме, то этот газ может совершать турбулентное движение.
В этом случае для описания состояния газа мы должны будем
определять локальную скорость каждой малой порции. Таким об-
разом, следовало бы ожидать, что множество всех состояний газа
может быть бесконечномерным в соответствующем смысле. В лю-
бом случае в нашей теории мы будем работать с неопределенны-
ми терминами — с «системой» и «состоянием». Позднее, когда мы
22.2. Классическая термодинамика
1101
разработаем «модель» термодинамики, будут даны математиче-
ские определения. Другой термин, также понятный интуитивно,
но пока не определенный, — взаимодействие. Предполагается,
что можно конкретизировать различные взаимодействия нашей
системы с другими системами или со Вселенной.
Следующее фундаментальное предположение — среди всех
возможных состояний системы существует выделенный класс со-
стояний, называемых равновесными. Если все взаимодействия
системы со Вселенной фиксированы, то система будет перехо-
дить из одного состояния в другое, стремясь при этом к опре-
деленному равновесному состоянию (оно определяется началь-
ным состоянием системы в момент, когда были фиксированы все
взаимодействия). Хотя произвольные состояния системы очень
сложны, класс равновесных состояний относительно просто опи-
сывать, он может быть параметризован конечным числом пере-
менных. Итак, множество равновесных состояний имеет структу-
ру подмногообразия3 конечномерного векторного пространства.
Это многообразие равновесных состояний является подмноже-
ством множества всех состояний системы.
Следующее предположение выделяет определенные типы вза-
имодействий. Существует особая форма взаимодействия между
двумя системами, называемая диатермальным контактом. При
взаимодействии такого типа не происходит наблюдаемого макро-
скопического движения и обмена веществом. Возникающие изме-
нения можно описать следующим образом. Объединим две сис-
темы в одну новую систему (рис. 22.2). Эта составная система
является прямым произведением двух первоначальных систем в
том смысле, что состояния новой системы — это пара состояний
(pi,P2)> гДе Р1 ” состояния первой системы, а р2 - состояния
второй. При диатермальном контакте равновесные состояния
объединенной системы — это подмножество множества пар рав-
новесных состояний исходных систем (рис. 22.3). Другими сло-
вами, если pi — равновесное состояние первой системы, а р% —
равновесное состояние второй системы, и обе системы находятся
в диатермальном контакте, то не обязательно, что объединенная
система будет в равновесном состоянии, но она будет стремиться
3См. обсуждение подмногообразия в параграфе 10.9.
1102
Глава 22. Термодинамика
Система 1 Система 2
Комбинированная система
Рис. 22.2
Рис. 22.3
к определенному равновесному состоянию (qi, #2), где q± — новое
равновесное состояние первой системы, а 42 — новое равновесное
состояние второй системы. Тогда мы говорим, что первая систе-
ма в состоянии qi находится в тепловом равновесии со второй
системой в состоянии <72 •
22.2. Классическая термодинамика
1103
Этот наблюдаемый закон природы иногда называется нуле-
вым законом термодинамики. Согласно ему, тепловое равнове-
сие является отношением эквивалентности. Это означает сле-
дующее. Пусть мы имеем три системы, причем pi, Р2 и рз — рав-
новесные состояния этих систем. Предположим, что первые две
системы в этих состояниях (pi и Р2), будучи приведены в диатер-
мальный контакт, оказываются в тепловом равновесии, и то же
самое справедливо для второй и третьей систем (в состояниях Р2
и рз). Тогда первая и третья системы (pi и рз) при диатермальном
контакте также будут в тепловом равновесии.
Класс эквивалентности всех систем, находящихся в тепловом
равновесии, называется абстрактной температурой. Предполо-
жим, что мы фиксируем одну определенную систему и некото-
рую численную функцию равновесных состояний этой системы,
которая принимает различные значения в состояниях, принадле-
жащих различным абстрактным температурам4. Таким образом,
у нас есть численная функция 0, определенная для всех равно-
весных состояний всех систем, называемая эмпирической темпе-
ратурой. Выбранная система вместе с ее функцией называется
термометром.
Кроме того, мы полагаем, что для любой системы 0 — диф-
ференцируемая функция на множестве равновесных состояний.
(Возможность выбрать дифференцируемую 0 — тоже часть «ну-
левого закона термодинамики».) Более того, можно найти неко-
торую систему и для нее выбрать такую функцию 0, что d0 Ф 0 на
всем множестве равновесных состояний этой системы. Только та-
кие функции 0 мы будем использовать в качестве эмпирических
температур. Конечно, если & — другая эмпирическая температу-
ра, то она — строго монотонная дифференцируемая функция 0.
И обратно, взяв любую строго монотонную дифференцируемую
функцию и применив ее к 0, получим новую эмпирическую тем-
пературу О'. В любом случае два состояния имеют одинаковую
абстрактную температуру, если и только если они имеют оди-
наковое значение функции 0 при любом выборе эмпирической
температуры.
4Иначе говоря, множество абстрактных температур превращается в одно-
параметрическое семейство. Достаточность одного численного параметра —
это еще одно нетривиальное допущение. — Прим. ред.
1104
Глава 22. Термодинамика
Существует ряд функций, которые играют важную роль при
описании любой системы. Так например, если у нас есть газ, за-
ключенный в некоторый сосуд, то такой функцией будет объ-
ем, а также массы различных химических составляющих газа.
Эти функции называются конфигурационными переменными. Та-
ким образом, каждая система имеет п функций, определенных на
множестве ее состояний и называемых конфигурационными пе-
ременными. Число конфигурационных переменных п зависит от
системы, но всегда п 1. Если рассматривать только равновес-
ные состояния, то конфигурационные переменные являются диф-
ференцируемыми функциями. Конфигурационные переменные и
функция 0 образуют систему локальных координат на множе-
стве (п + 1)-мерных равновесных состояний. Конфигурационные
переменные обозначим xi, Х2, • • • , хп. Тогда 0, Xi, Х2, ..., хп —
локальная система координат на множестве равновесных состоя-
ний. Во многих случаях одной из конфигурационных переменных
является объем V. Обычно берут Xi — V, так что 0, V, Х2, . *.,
хп — локальные координаты, где Х2, ..., хп — остальные конфи-
гурационные переменные.
Поскольку dO нигде не обращается в нуль, то в силу теоре-
мы о неявной функции множества 0 = const образуют п-мерные
подмногообразия. Подмногообразия 0 — const называются изо-
термами. Конфигурационные переменные можно использовать
как локальные координаты для изотерм.
Существует другой важный класс взаимодействий системы
с остальной Вселенной, которые называются адиабатическими
взаимодействиями. таких взаимодействий равновесие нару-
шается только при изменении конфигурационных переменных.
Если все взаимодействия системы в наблюдаемый период адиаба-
тические, то такую систему называют адиабатически замкнутой.
Примером адиабатически замкнутой системы (приблизительно)
является термос.
Кривая 7, соединяющая состояния р и р1 адиабатически за-
мкнутой системы, называется адиабатической кривой, или адиа-
батой. Обобщение экспериментального опыта — первый закон
термодинамики — говорит нам, что адиабатически замкнутая
система переходит из одного состояния р в другое pf за счет со-
вершения внешней работы, величина которой не зависит от спо-
22.2. Классическая термодинамика
1105
соба ее приложения. Поэтому на пространстве состояний этой
системы существует функция (7, называемая внутренней энерги-
ей. Она обладает тем свойством, что количество работы, совер-
шенной над системой при переходе из состояния р в состояние р!
вдоль любой адиабатической кривой, равно W = U(p') — U(p).
Если система не является адиабатически замкнутой и за счет
взаимодействия она переходит из одного состояния р в другое р'
вдоль некоторой кривой, то количество внешней работы уже не
равняется U(p) — U(pf). Разность U(p) — U(pf) — W — Q назы-
вается теплом, сообщенным системе в данном процессе. В этом
случае количество совершенной работы и тепла, сообщенного си-
стеме, зависят от процесса, а не только от начального и конечного
состояний р и pf.
Это — формулировка первого закона термодинамики в рам-
ках подхода Борна-Каратеодори. Обратите внимание, что при
таком подходе тепло определяется как разность между измене-
нием внутренней энергии и работой, совершенной над системой.
Идея рассматривать тепло не как фундаментальную, а как про-
изводную величину, является одновременно и сильной, и слабой
стороной подхода Борна-Каратеодори. Сила заключается в том,
что здесь отражается фундаментальный взгляд в физике, суще-
ствующий более века, — основным объектом является энергия,
которая сохраняется с учетом всех ее форм. А слабость — в том,
что этот подход не отражает экспериментальные и исторические
реалии. Обычно тепло, подводимое к системе, легче всего изме-
рять. Джоуль провел в 1840 году основополагающие эксперимен-
ты с целью получить механический эквивалент тепла. Если си-
стема переходит в некоторое другое состояние за счет определен-
ного количества тепла, подведенного к ней, то такое же изменение
системы может произойти, если над ней совершить определенную
работу. Но полное количество совершенной работы не зависит от
того, как эта работа была выполнена. Поэтому в реальных экспе-
риментах измеряется именно подведенное количество тепла и со-
вершается разного рода работа. Из существования единственного
механического эквивалента тепла мы делаем вывод, что полная
работа для перевода системы из одного состояния в другое не за-
висит от способа выполнения этой работы, при условии, что она
выполняется адиабатически.
1106
Глава 22. Термодинамика
Следующее фундаментальное понятие теории — обратимая
кривая. Кривая у называется (почти) обратимой, если в каждый
момент времени t состояние у(£) равновесное (достаточно близко
к равновесному).
Интуитивно понятие обратимости состоит в том, что все вза-
имодействия в системе происходят очень медленно по сравнению
со «временем релаксации» системы, т. е. со временем, необходи-
мым для восстановления равновесия в системе5. Например, пред-
положим, что в цилиндре с поршнем находится газ. Взаимодей-
ствие — это движение поршня, изменяющее объем газа. Если газ
находился в равновесии, и мы внезапно сдвинули поршень, то но-
вое состояние газа уже не будет равновесным. В нем будут разно-
го рода ударные волны и вихри. Конечно, если поршень оставить
в этом положении, то в цилиндре установится со временем новое
равновесие. Можно полагать, что скорость возвращения в равно-
весное состояние достаточно велика, так что если поршень дви-
гать достаточно медленно, то состояния системы будут все время
(приблизительно) равновесными. Такая кривая состояний назы-
вается обратимой. В случае изменения объема из опыта известно,
что существует функция р, называемая давлением, такая, что ра-
бота, совершенная над системой вдоль любой обратимой кривой
у, задается выражением — f^pdV.
Заметим, что до сих пор мы измеряли работу через изменение,
внешнее по отношению к системе. Давление — функция равновес-
ных состояний, позволяющая нам вычислить совершенную рабо-
ту посредством обратимого изменения объема. Замечено, что су-
ществуют аналогичные функции, соответствующие другим кон-
фигурационным переменным, т. е. в пространстве равновесных
состояний существуют такие функции z^,..., vn, что работа, со-
вершенная над системой вдоль любой (почти) обратимой кривой
7, равна (приблизительно) интегралу вдоль 7 от линейной диф-
ференциальной формы
dxi 4---4- уп dxni
5Такой процесс изменения состояния системы называют квазистатиче-
ским. — Прим. ред.
22.2. Классическая термодинамика
1107
так что
Ж(7) - /* ал
А
Поэтому тепло, подведенное к системе вдоль пути 7, задается
интегралом
Q(7) =f а,
А
где а — линейная дифференциальная форма а — dU — cu. В слу-
чае, когда xi = V — объем, принято называть р — —Pi давлением.
Следовательно,
ш = — р dV + V2 dx2 Ч-+ vn dxn
и
а — dU — = dU + р dV — V2 dx2 — • • • — dxn.
В частности, по определению, адиабатическая обратимая кри-
вая — это кривая на множестве равновесных состояний, которая
является нулевой кривой для линейной дифференциальной фор-
мы а.
Итак, мы подошли к знаменитому «второму закону термоди-
намики». Каждодневный опыт говорит, что определенные типы
работы, выполняемые над системой, не могут быть возвращены.
Точнее, для адиабатически замкнутой системы существуют опре-
деленные типы работ, совершаемые над системой, такие как силь-
ное встряхивание или размешивание, когда нельзя получить эту
работу обратно вдоль какой-либо адиабатической кривой. Утвер-
ждается, что это может происходить вблизи любого равновесного
состояния. Итак, формулировка второго закона термодинамики
такова.
В окрестности любого равновесного состояния р сис-
темы существуют сколь угодно близкие равновесные
состояния, которые нельзя соединить с р с помощью
обратимых адиабатических кривых.
Как мы увидим в дальнейшем, это простое утверждение имеет
далеко идущие следствия. Закон говорит, что в окрестности лю-
бой точки множества равновесных состояний существуют произ-
вольно близкие точки, в которые нельзя попасть вдоль нулевых
1108
Глава 22. Термодинамика
кривых формы а. Из теоремы Каратеодори следует, что для лю-
бой системы существуют такие функции Л и ф на множестве рав-
новесных состояний, что а = Абф.
Конечно, для любой заданной системы ни функция Л, ни
функция ф не определяются полностью равенством а — A d</>. Од-
нако, если выбрать функцию А, то ф определяется с точностью
до аддитивной константы. Мы покажем в следующем парагра-
фе, что из рассмотрения поведения формы а при объединении
систем можно сделать вывод, что существует предпочтительный
выбор температурной функции Т (определенной с точностью до
постоянного множителя), при этом для всех систем можно по-
ложить А — Т. Эта функция Т называется абсолютной темпе-
ратурой. В терминах некоторой выбранной эмпирической тем-
пературы в утверждается, что существует такая универсальная
функция Т — Т(0), что для всех систем можно выбрать А — Т(0).
Если мы решили использовать для нашей температурной
шкалы абсолютную температуру, то для любой системы мож-
но написать
a~TdS
где функция S определена с точностью до аддитивной константы.
Эта функция S называется энтропией.
22.3. Энтропия и абсолютная температура
Предположим, что две системы находятся в диатермальном кон-
такте. Можно также считать, что энергия, необходимая для объ-
единения этих систем, пренебрежимо мала. Между системами
нет сдвигаемых перегородок и нет прямого обмена веществом.
Тогда полная внутренняя энергия U объединенной системы рав-
на сумме энергий состояний отдельных систем
U{pi,p2) = t^i(pi) 4- /72(^2)
для любого состояния объединенной системы (р1,/>г)- Здесь U
обозначает функцию внутренней энергии объединенной системы,
Ui — внутреннюю энергию первой системы, a U2 — внутреннюю
энергию второй системы.
22.3. Энтропия и абсолютная температура
1109
Дифференциальная форма, описывающая работу, тоже адди-
тивна:
U = СсД + иД>.
Здесь ид — линейная дифференциальная форма, определенная
на множестве равновесных состояний первой системы. Она может
рассматриваться как линейная дифференциальная форма, опре-
деленная на произведении пространств, состоящем из всех пар
равновесных состояний. При этом на од не влияют равновесные
состояния второй системы. Аналогично на множестве таких пар
равновесных состояний определена форма о>2, которая не зависит
от состояния первой системы. Следовательно, форма ид+и>2 опре-
делена на множестве всех пар равновесных состояний. Простран-
ство равновесных состояний объединенной системы, находящейся
в тепловом контакте, есть подмногообразие множества всех пар
(определяемое условием 01 ~ 02, см. рис. 22.4). Это значит, что
и является ограничением формы од + и>2 на это подмножество.
Отсюда следует, что (в том же смысле)
а — ад 4- 02-
получаем
Написав
ot = A <1ф, ад = Ai , ai2 — А2 d02 ?
Состояния равновесия комбинированной
системы задаваемой уравнением
01 - 02
Рис. 22.4
1110
Глава 22. Термодинамика
Для любой системы температуру можно изменять адиаба-
тически (например, изменяя V при постоянном давлении). Это
означает, что для первой системы формы oi и d0x линейно неза-
висимы; и аналогично для второй системы. Условие «i = Ai d$i
означает, что дифференциальные формы d(f>i и d0x линейно неза-
висимы. В силу теоремы о неявной функции, это значит, что
можно сделать замену переменных, так что 0х и фх станут первы-
ми координатами, т. е. (#i, </>i, j/i,...) — локальные координаты на
множестве равновесных состояний первой системы. Аналогично
для второй системы. Поэтому в качестве локальных координат
на множестве пар равновесных состояний можно взять
(01> 02, Ф1, Ф2', У1, • • • ;^2, . • • )•
Равновесные состояния объединенной системы (в тепловом кон-
такте) задаются условием 0х = 02- Поэтому можно взять пере-
менные
(Оь</>2; —
в качестве координат на множестве равновесных состояний объ-
единенной системы. Уравнение (*) показывает, что в этих ко-
ординатах dф является линейной комбинацией d</>± и dф2J т. е.
ф = F(0i, </>2). Другими словами, функция ф объединенной систе-
мы зависит только от значений функций фх и Ф2 и не зависит от
остальных координат. К любой системе в любом состоянии мож-
но подвести тепло, поэтому форма а и, следовательно, X нигде
не обращается в нуль. Поэтому уравнение (*) можно разделить
на Л и написать
dф = (Ai/A)J^>i + (А2/А)б?</>2- (**)
Это значит, что
Al/А = фг), где А = дР/дфъ
зависит только от фх и и аналогично
Аг/А = /2(^1, Фэ), где /2 = дР/дф2.
Первое из этих уравнений можно разделить на второе, поскольку
ни одна из функций Ai, А2 и А не обращается в нуль. Получаем
А1/А2 — fl//2
22.3. Энтропия и абсолютная температура
1111
или
log Al - logA2 = log(/i//2),
где правая часть зависит только от фг и (fa. В частности, если
вычислить частную производную этого равенства по 0, то правая
часть обратится в нуль, и мы получим
dlogAi _ d log Аз
до ’ “ де '
Слева стоит функция от переменных, описывающих первую
систему, т. е. от (0, фг, уг,...), а справа стоит функция от перемен-
ных (0, </>2, ^2,...). Единственная возможность совпадения этих
функций — это когда обе части этого равенства зависят толь-
ко от 0, причем являются одной и той же функцией 0. Другими
словами, существует некоторая универсальная функция д, для
которой
5(IogA)/^ = ^)
для всех систем. Исследование конкретных систем показывает,
что функция g нигде не обращается в нуль.
Теперь предположим, что делается замена переменной в эмпи-
рической температуре, т. е. заменим 0 на Т(0). Тогда будем иметь
координаты (71, </>,...) и равенство
d(iogA)/#r = [a(iog Х)/дв](дв/ат) = [a(iogA)/a0](ar/56>)-1.
Если выбрать Т так, что
dT/de = Tg(0^ (***)
то
d(log А)/ЭТ - 1/Т - d(\ogT)/dT.
Уравнение (***) определяет Т с точностью до постоянного мно-
жителя. Действительно, Г(0) — ceG^e\ где G — неопределенный
интеграл от <?, а с — константа. Такой выбор функции Т назы-
вается абсолютной температурой. Давайте вернемся к началу
этого параграфа, но вместо 0 будем использовать абсолютную
температуру Т. Тогда для каждой системы мы имеем
log Аг = logT + logG;,
1112
Глава 22. Термодинамика
где Gi не зависит от Т. Тогда
Ai = TGi, A2-TG2, X = TG,
где функции Gi, G2 и G не зависят от Т. Кроме того, мы знаем,
что Ai/A2 зависит только от ф± и 02. Но Ai — функция первой
системы, следовательно, она не зависит от </>2, и аналогично, А2
не зависит от ф±. Следовательно, для любой системы каждая Gi
зависит только от ф^.
Давайте опустим индексы. Итак, мы показали, что для любой
системы выполняется равенство
а = TG(</>) (1ф,
где функция G нигде не обращается в нуль и зависит только от
переменных системы. Но тогда можно решить уравнение
dS = Gd<£,
которое определяет S с точностью до аддитивной константы.
Другими словами, функция S есть неопределенный интеграл от
G. Тогда мы имеем а = Т dS, Итак, мы доказали следующее.
Существует универсальная шкала абсолютной тем-
пературы Т, определенная с точностью до постоянно-
го множителя. Фиксируя этот множитель и таким об-
разом выбирая функцию Г, мы определяем функцию
S на множестве равновесных состояний любой систе-
мы. Эта функция S определена с точностью до ад-
дитивной константы (одной для каждой системы) и
называется энтропией. Дифференциальная форма а
для тепла имеет вид
a = TdS,
Как мы уже отмечали, из существования функции S и уравне-
ния а = Т dS следует кельвиновская формулировка второго зако-
на термодинамики: для любой замкнутой кривой (циклического
процесса) мы должны иметь f dS = 0, функция Т имеет посто-
янный знак (который обычно выбирается положительным). Если
22.3. Энтропия и абсолютная температура
1113
вдоль одной части цикла к системе подводится тепло, то в другой
части этого цикла тепло должно быть извлечено. Следователь-
но, невозможен цикл, в котором тепло полностью преобразуется
в работу. Таким образом, «вечный двигатель второго рода» су-
ществовать не может.
Рассмотрим простой цикл С (рис. 22.5). Это кривая, состоя-
щая из четырех частей, две из которых, скажем, Сз и находят-
ся на поверхностях, где функция S постоянна (и поэтому тепло
не передается); вдоль одной из них, скажем, Ci система находит-
ся в тепловом контакте с большой системой (называемой тепло-
вым резервуаром) при высокой температуре Т\. Вдоль четвертого
участка Сч система находится в тепловом контакте с холодным
резервуаром при низкой температуре Т2. Пусть Qi — а —
полное количество тепла, поглощенного системой на участке Ci,
a Q2 = - /с2 а ~ полное количество тепла, излученного ею на
участке С2. Тогда Qi = fc TdS = Т\ fCi dS и Q2 — — T2 fC2 dS.
Ho
0= [ dS= [ dS+ [ dS,
Jc Jci Jc2
поэтому
Qi __ Ti
Q2 T2
Рис. 22.5
1114
Глава 22. Термодинамика
Тогда можно написать
О = / dU — I cu 4- let = I tu + Qi —
Jc Jc Jc Jc
Итак, если W — работа, совершенная самой системой, так что
W = — то
W = Q1(1-T2/T1).
Это известная формула, которую можно найти в любом учеб-
нике. Она определяет работу, совершенную в цикле Карно, меж-
ду резервуарами с температурами Т2 и Тр На самом деле Карно
утверждал, что это наиболее эффективный способ получить ра-
боту за счет этих температур, т. е. эта формула дает максималь-
ное значение работы для любой машины, получающей тепло Qi
при температуре Т\ и выделяющей тепло при температуре Т^.
В основе этого факта лежит изменение функции S при необра-
тимых адиабатических процессах. Давайте сформулируем общее
утверждение, а определение эффективности работы6 оставим чи-
тателю (его можно найти в стандартных учебниках).
Если два равновесных состояния си и можно соединить об-
ратимой адиабатической кривой, то (как мы уже знаем) они ле-
жат на одной поверхности S = const, т. е. S(cri) = 5(сг2). Предпо-
ложим, что сначала система находится в равновесном состоянии
сг1. Рассмотрим адиабатический процесс, не обязательно обрати-
мый, который переводит систему в равновесное состояние сг2- В
этом случае кривая, соединяющая состояния од и <72, может и
не лежать в подмножестве равновесных состояний, хотя конеч-
ные точки находятся именно там (рис. 22.6). Например, у нас
имеется жидкость в термосе, и мы размешиваем ее миксером.
Когда размешивание заканчивается, жидкость в термосе пере-
ходит в равновесное состояние с другим значением энтропии 5.
Опыт показывает, что мы не можем вернуться в исходное состо-
яние, если не отвести тепло из такой системы. Тогда (если мы
выбрали постоянный множитель такой, что температура Т по-
ложительна) для такой необратимой адиабатической кривой мы
6Другое (не менее распространенное) название — коэффициент полезного
действия (КПД). — Прим. ред.
22.4. Системы с одной конфигурационной переменной 1115
Рис. 22.6
имеем S(oi) < S(02). Дадим теперь более строгую формулировку
второго закона термодинамики.
Если равновесные состояния 0*1 и 02 могут быть соеди-
нены адиабатической кривой (т. е. если в данном про-
цессе замкнутая адиабатическая система может пере-
вести систему из состояния в сг2), то
Sfr) < S(a2),
причем 5(0’1) = 5(02), если и только если состояния ai
и <72 соединяются обратимой адиабатической кривой.
22.4. Системы с одной конфигурационной
переменной
В этом параграфе мы рассмотрим важный частный случай, когда
система имеет только одну конфигурационную переменную и,
следовательно, множество равновесных состояний такой системы
двумерно. Будем полагать, что такой переменной будет объем.
Соответствующая функция, входящая в выражение формы для
работы, — это давление, а работа, совершенная над системой,
имеет вид
cu — — р dV.
Тем не менее соображения этого параграфа применимы и ко мно-
гим другим физическим системам. Надо только заменить объем
соответствующей конфигурационной переменной, а давление —
1116
Глава 22. Термодинамика
Таблица 22.1. Системы с одной конфигурационной переменной
Система Конфигура- ционная переменная Обобщенная сила Форма для работы си в Дж = Н • м
Газ Объем V в м3 Давление р в Н/м2 <jj = —pdV
Струна Длина L в м Натяжение Т в Н cv — Т dL
Мембрана Площадь А в м2 Поверхностное натяжение S в Н/м ui = SdA
Электричес- кая цепь Заряд Q в Кл Напряжение Е в В (jj — E dZ
Магнитный материал Полный магнитный момент М в А/м Магнитное поле Н в А/м2 w = pqH dM
соответствующей «обобщенной силой». В таблице 22.1 приводят-
ся некоторые из важных физических систем. В этом параграфе
мы не будем больше говорить о них.
Прежде чем начать обсуждение, следует сделать несколь-
ко замечаний об истории вопроса и соответствующей литерату-
ре. Многие из основных математических понятий, которыми мы
пользуемся здесь, такие как «множество», «функция», «много-
образие», «координаты», «линейная дифференциальная форма»,
были введены (в их современной форме) или стали общеприня-
тыми уже после фундаментальных открытий в термодинамике.
Более того, большинство героев этой истории (за исключением
Кельвина и Гельмгольца) не имели математического образова-
ния, или (как Карно) предпочитали не пользоваться математи-
ческим языком. В результате вплоть до наших дней в большин-
стве книг материал излагается языком первоначальных пред-
ставлений, довольно туманным с математической точки зрения,
в котором, однако, используются соотношения между частны-
ми производными. Приведем пример. Понятие линейной диффе-
22.4. Системы с одной конфигурационной переменной 1117
ренциальной формы, криволинейный интеграл от нее и вариант
теоремы Стокса (на плоскости) были введены Ампером в начале
1920-х годов в серии оригинальных статей, где сочетались но-
вый важный математический аппарат и остроумные физические
эксперименты. Более общая версия теоремы Стокса для кри-
волинейного интеграла от 1-формы в трехмерном пространстве
впервые появилась в письме, которое Кельвин написал Стоксу в
1850 году. (Через несколько лет Стокс опубликовал эту версию в
качестве экзаменационного вопроса.) Тем не менее, в своих ста-
тьях по термодинамике Кельвин никогда не использовал теорему
Стокса, хотя это значительно упростило бы его доказательства.
Итак, мы записали тепло, подведенное к системе, в виде ли-
нейной дифференциальной формы а, определенной на многооб-
разии равновесных состояний. Функции Т и V имеют независи-
мые дифференциалы. Поэтому, если указанное многообразие дву-
мерное, можно использовать Т и V как локальные координаты и
написать
a = AydV + CydT\ (22.1)
где А у и Су — функции на многообразии равновесных состояний.
Аналогично, независимы функции р и Г, и поэтому они тоже
могут быть локальными координатами. Тогда
a — Apdp + CpdT (22.2)
где Ар и Ср — две другие функции. (Строго говоря, с историче-
ской точки зрения мы должны использовать эмпирическую тем-
пературу 0 вместо Г, поскольку мы обсуждаем ситуацию, сло-
жившуюся до открытия второго закона термодинамики. Но тог-
да, вернувшись к современной трактовке, мы должны были бы
переписать все формулы через Т. Поэтому мы решили предо-
ставить читателю самому сделать все эти замены.) Конечно, все
четыре функции связаны между собой формулой замены пере-
менных, связанной с переходом от координат V, Т к координа-
там р, Т. Скоро мы вернемся к этому вопросу. Соответствующие
физические законы, выраженные двумя предыдущими утвержде-
ниями, были сформулированы как «доктрина скрытого и явно-
го тепла». Функция Ау была известна как «скрытая теплота по
отношению к объему», а функция Су — как «теплоемкость при
1118
Глава 22. Термодинамика
постоянном объеме». Аналогично, функция Лр была известна как
«скрытая теплота по отношению к давлению», а функция Ср —
как «теплоемкость при постоянном давлении». Поясним смысл
термина «скрытый». На протяжении длительного времени бы-
ла путаница между понятиями теплоты и температуры. Ученые
думали, что температура тела отражает «полное количество теп-
ла, содержащегося в нем». Это, конечно, бессмыслица, поскольку
мы знаем, что форма а не замкнута. Если мы подводим тепло,
то температура тела повышается. Но, если тепло подводится при
увеличении объема или давления, то оно становится «скрытым»
или «латентным». Конечно, уравнения (22.1) и (22.2) дают чет-
кую математическую формулировку этой загадочной физической
«доктрине».
В пространстве двух измерений многие вычисления сильно
упрощаются, потому что если Qi и _ 2-форма и Q2 Ф О,
то Qi — /^2? где / — некоторая функция. Другими словами,
можно взять «отношение» двух 2-форм и получить функцию,
при условии, что знаменатель не равен нулю. Тогда мы пишем
/ = Qi/Q2.
В качестве примера рассмотрим функцию
а Л dp _
aKdV =J'
Что это такое? Для любой точки х пусть £ — вектор, касатель-
ный к адиабатической кривой, проходящей через точку х, так
что а(£) ~ 0, а т} — некоторый вектор, независимый от £, так что
а(ту) / 0. Тогда, вычислив формы а Л dp и а Л dV на параллел-
лограмме, построенном на векторах £ и ту, получаем
/(х) =
<Ш)
dV^Y
Это уравнение можно переписать как
/ — (dp/dV^адиабат. ?
где правая часть обозначает отношение линейных дифференци-
альных форм dp и dV, вычисленных на векторах, касательных к
22.4. Системы с одной конфигурационной переменной 1119
адиабатам. Аналогично, напишем
dT Л dp _
dT Л dV ~ \аР/аУ ^изотерм.-
Если взять внешнее произведение уравнения (22.2) на dp. то по-
лучим
а Л dp = Ср dT Л dp.
а если взять внешнее произведение (22.1) на dV. то получим
а /\ dV - Су dT Л dV.
Разделим первое уравнение на второе и получим важный резуль-
тат
(dp/dV) адиабат. — 0^ (^Р/^О изотерм, э где Ср/Су. (22.3)
Если ввести плотность р = m/V. то уравнение (22.3) можно
записать в виде
(dp/dp)адиабат. ~ изотерм., У ~ CpfCy. (22.4)
Приведем физические и исторические причины важности этого
результата. Один из известных выводов, сделанных Ньютоном из
его законов, определяет скорость звука в газе с формулой
(? —dp/dp. (22.5)
где Ньютон предположил, что р и р связаны соотношением
р = N р. где N — const, (22.6)
т.е. что
pV — const. (22.7)
Давление, плотность и скорость звука (например, в воздухе) мо-
гут быть измерены независимо. И утверждение Ньютона, что
с2 — р/р. противоречило экспериментам на протяжении почти ста
лет. Было обнаружено, что скорость звука превышала предска-
занное формулой Ньютона в 1.4 раза. С другой стороны, экспе-
рименты Гей-Люссака и других показывали, что при постоянной
1120
Глава 22. Термодинамика
температуре формула (22.7) верна, но константа в правой части
зависит от температуры. Итак, если мы пользуемся независимы-
ми функциями р и V в качестве координат на многообразии рав-
новесных состояний, уравнения (22.7) для различных значений
постоянной справа являются уравнениями изотерм, и формулу
Ньютона можно написать в виде
С — (dp/dp)изотерм. •
В 1816 году Лаплас высказал идею, что формулу Ньютона сле-
дует заменить выражением
С — (dp/dp)адиабат. — 7(^Р/dp)изотерм. *
(22.8)
Его аргументы были чисто физическими: скорость распростране-
ния возмущения гораздо больше скорости переноса тепла. Про-
цитируем самого Лапласа: «Истинная скорость звука равна про-
изведению скорости, полученной из формулы Ньютона, на квад-
ратный корень из отношения удельной теплоемкости воздуха при
постоянном давлении и различных температурах к удельной теп-
лоемкости при постоянном объеме». Кроме того, Лаплас подчер-
кивает, что мы можем использовать наблюдаемую скорость звука
для экспериментального определения 7. Конечно, если мы знаем
7 и уравнения изотерм, то уравнение (22.3) можно рассматривать
как дифференциальное уравнение для адиабатических кривых.
Например, для многих газов при низком давлении величина 7
почти постоянна. (Водород является исключением из этого пра-
вила.) Кроме того, уравнение (22.7) верно при постоянных тем-
пературах. Если предположить, что (22.7) является уравнением
изотерм и 7 постоянна, то из уравнения (22.3) следует, что адиа-
батические кривые задаются формулой
pF7 — const.
(22.9)
Заметим, что в этом параграфе мы до сих пор не пользовались ни
первым, ни вторым законами термодинамики. Мы пользовались
только предположением, что множество равновесных состояний
двумерно, и что тепло определяется линейной дифференциаль-
ной формой, — т.е. «доктриной скрытого и явного тепла».
22.4. Системы с одной конфигурационной переменной 1121
Теперь введем оба закона: первый закон — dU = а — р dV и
второй закон — а = Т dS. Соберем их вместе и получим
dU ~TdS-pdV. (22.10)
Возьмем внешнюю производную от этого уравнения и получим
dT KdS = dp/\dV. (22.11)
Как определить функции Г, S и U из эксперимента, скажем в
координатах р и V? Чтобы проиллюстрировать метод, предполо-
жим, что наблюдаемые изотермы и адиабаты задаются уравне-
ниями (22.7) и (22.9) соответственно. Введем функции
*(?, V) = pV (22.12)
и a(p,V)=pV\ (22.13)
Тогда изотермы — линии уровня t (22.14)
и адиабаты — линии уровня а. (22.15)
Поскольку t и Т имеют одни и те же линии уровня и поскольку
их дифференциалы нигде не обращаются в нуль, то функция
Т может быть выражена как функция t, т. е. что Т = T(t) и
Tf(t) нигде не обращается в нуль. Точно так же заключаем, что
S = S(a). Наша задача — определить T(t) и S(a). Далее, из
уравнения (22.11) имеем
dT/\dS = T\t)S\a) dt/\da — dp/\ dV,
Мы должны использовать явные выражения для t и а как функ-
ций от р и V, чтобы выразить dt Л da через dp Л dV. Тогда мы
получим, что отношение
dp Л dV
dt Л da
1122
Глава 22. Термодинамика
является произведением функции от t и функции от а, и таким
образом найдем Tf и Sf. Итак,
dthda = (pdV + Vdp) Л (ypV^dV + У7dp)
= (7 — l)pV7 dp Л dV = (7 — 1)а dp Л dV,
откуда
dp/\dV f, -i
di7^=[h-1)oi '
Это значит, что
r(t)5/(a) = [(7-l)a]-1.
В этом уравнении умножим Tf на любую константу к, a Sf умно-
жим на к-1. Это отражает тот факт, что абсолютная температу-
ра определена с точностью до постоянного множителя. Поэтому
без потери общности можно предположить, что Т' = 1 и тогда
Sf(a) = [(7 — 1)а]-1. Следовательно,
T = t + T0, S = (7 — l)-1 log а + So,
где To и Sq — константы. Вспомним, что функция S определена
именно с точностью до аддитивной константы. Но нам еще надо
определить То и U. С этой целью подставим их значения в (22.10)
и после простых вычислений получим
dU = (7 - I)-1 [То d log а + dt].
Вспомним еще один эксперимент — Джоуля-Томпсона, — кото-
рый показывает, что если газ расширяется адиабатически в ваку-
ум, то его температура при этом практически не изменяется. При
таком расширении не совершается работа, и система не получает
дополнительное тепло, поэтому внутренняя энергия U не изменя-
ется. Но при этом расширение является необратимым процессом
и поэтому увеличивается энтропия S. Это может произойти толь-
ко при условии, что То = 0. Тогда
и = (7 - (22.16)
Конечно, количество внутренней энергии пропорционально пол-
ному количеству газа. Это значит, что существует константа, свя-
зывающая t с выбором универсальной шкалы температур. Поэто-
му можно написать
t = nRT,
(22.17)
22.4. Системы с одной конфигурационной переменной 1123
где п — количество молей газа, и Т — универсальная температу-
ра, измеряемая в кельвинах. (При таком выборе шкалы разность
между температурой замерзания и кипения воды равна 100°. Точ-
ного соглашения относительно этой шкалы мы не приводим.) Тог-
да R — постоянный множитель, преобразующий единицы темпе-
ратуры в единицы энергии, называемый газовой постоянной7. Из
(22.10) следует, что
dU Л dV - а Л dV - Су dT Л dV.
Тогда из (22.16) и (22.17) получаем, что
Су = (7 — 1)-1п7?
является константой. Теперь Ср тоже должна быть постоянной и
Ср — Су — nR.
Все перечисленные свойства получены на основании трех пред-
положений, которые определяют идеальный газ:
(i) законы Гей-Люссака и Бойля (уравнение (22.7)):
pV — nRT]
(ii) внутренняя энергия U зависит только от Т (эксперимент
Джоуля);
(iii) 7 — постоянная величина.
Давайте теперь соберем вместе наши результаты, но писать их
будем для одного моля. Итак, считаем, что п = 1, и дальше
пишем v вместо И, ср вместо Ср и т. д. Тогда получаем
Законы идеального газа.
• Изотермы pv — RT;
• адиабаты - pv7 = const;
7Численное значение R ~ 8.31 Дж/К. — Прим. ред.
1124
Глава 22. Термодинамика
• u = (7 - l)~l RT-,
• cv = (7 - 1)-1Я;
• Ср = [7/(7 - 1)] R, откуда Ср - cv = R;
• s = (7 - l)-1Klogpv7 + So = 7?logv + Cv logT + Sq.
Для реальных газов можно измерять величины р, v, Г, с^, Ср
и 7. Чтобы измерить с^, газ помещают в стальной сосуд с тон-
кими стенками, вокруг которого намотана нагревательная спи-
раль. Тепло, подводимое к газу, определяется по известному току,
протекающему по обмотке, и измеряется изменение температу-
ры газа. Чтобы измерить Ср, газ пропускают через аналогичный
нагревательный элемент при постоянном давлении; измеряется
температура втекающего и вытекающего газа. Ниже приводятся
результаты этих экспериментов при низком давлении, когда газ
ведет себя почти как идеальный.
Для всех газов и Ср зависят только от Т, и
Ср Cd — R.
Для одноатомных газов, таких как Не, Ne, Аг, и паров боль-
шинства металлов cv постоянна в широкой области температур
Т и очень близка к ЗЛ/2. Поэтому Ср очень близка к 57?/2. Ве-
личина 7 постоянна в широкой области температур Т и близка
к 5/3.
Для двухатомных газов, таких как О2, N2, NO, СО и воз-
дух8, при обычных температурах cv постоянна и примерно рав-
на 5R/2, Поэтому Ср примерно равна 7R/2, а 7 тоже постоянна
при обычных температурах и примерно равна 7/5. Эта константа
уменьшается с ростом температуры.
Именно это значение 7 = 7/5 участвует в рассуждениях Ла-
пласа относительно скорости звука в вохдухе. Истинное значение
дробей 3/2, 5/2 и т. д. становится очевидным только в рамках ста-
тистической механики.
8который на 98% состоит из двухатомных компонент — азота N2 (75%) и
кислорода О2 (23%). — Прим. ред.
22.4. Системы с одной конфигурационной переменной 1125
Для реальных газов можно привести такие же рассуждения,
начав с уравнения (22.14). Теперь мы уже не предполагаем, что
изотермы и адиабаты задаются уравнениями (22.12) и (22.13),
или что у — постоянная величина. Но экспериментально можно
определить изотермы и значение у, следовательно, решить урав-
нение (22.3) (возможно, только численно) и получить адиабаты.
После этого можно найти T'(t) и S'(а), что даст возможность по-
лучить S, а затем U с помощью уравнения (22.10). Эта информа-
ция собиралась на протяжении 150 лет для различных веществ,
и теперь она собрана в виде специальных диаграмм. Кроме это-
го, введены новые функции в дополнение к уже рассмотренным,
весьма полезные для определенных задач. Например, энтальпия
Н, определяемая уравнением
Я- U + pV.
Объясним, почему эта функция важна для нас. Из уравнения
(22.10) следует, что тепло, подведенное к системе при постоян-
ном объеме, равно изменению внутренней энергии U. Но в хими-
ческих лабораториях гораздо удобнее проводить опыты при по-
стоянном давлении (скажем, при атмосферном давлении) и при
этом изменять объем. Дифференцируя определение энтальпии,
получаем
dH ~ а + V dp.
Поэтому изменение Н определяет количество тепла, подведенно-
го к системе при постоянном давлении. Тогда теплота химической
реакции задается изменением энтальпии.
Среди различных эмпирических диаграмм особенно полезны-
ми являются диаграммы Моллье, на которых р и Н — координат-
ные оси, и в этой системе координат изображаются линии уровня
S, V и Г. На следующей странице в качестве примера приводится
диаграмма Моллье для кислорода.
Существуют другие комбинации (7, р, V и S, из которых полу-
чаются функции, полезные при решении определенных задач. Их
обозначения меняются, поэтому здесь мы не будем их описывать.
Однако, есть функция, очень полезная для практических целей и
имеющая важное теоретическое значение. В последующих пара-
графах мы будем неоднократно обращаться к ней. То, что будет
РМЯЯЛКЕ » АТМОвгаПВ
Диаграмма Моллье для кислорода. Если заданы значения любых двух из пяти
функций р, V, Н, Т, S, то можно найти точку, в которой достигаются эти значения,
как пересечение соответствующих линий уровня. Тогда можно определить значения
остальных трех функций диаграммы и функции U из равенства U = Н — pV.
22.4. Системы с одной конфигурационной переменной 1127
сделано здесь, на первый взгляд, может показаться весьма стран-
ным, но в рамках статистической механики это будет вполне убе-
дительным. Рассмотрим функцию Планка У, определенную ра-
венством
Y = S - (RT)~lU - (ЯТ)-1рИ
Чтобы записать эту формулу в более удобной форме, введем
ХЗ = (/?Г)-х, и = 0р. (22.18)
Заметим (например, из уравнений (22.16) и (22.17)), что R —
множитель, связывающий энергию и температуру, поэтому раз-
мерностью (3 является обратная энергия, скажем, в единицах
(Дж)"1, а размерностью v — обратный объем, так что (3dU и
v dV — безразмерные величины. Предположим, что с самого на-
чала мы включили R в определение температуры Г, чтобы изме-
рять температуру в единицах энергии. Тогда газовая постоянная
исчезает. Поскольку размерностью а ~-Т dS является энергия, и
мы измеряем температуру Т тоже в единицах энергии, то в та-
кой температурной шкале энтропия S становится безразмерной.
Тогда S и функция Планка
Y = S-/3U-vV (22.19)
безразмерные. Комбинируя первый и второй законы термодина-
мики, уравнение (22.10) можно записать в виде
dS = (3dU + vdV. (22.20)
Тогда из формулы (22.19) следует, что
dY ^-Udfi-Vdv. (22.21)
Уравнения типа (22.20) и (22.21) будем интерпретировать сле-
дующим образом. Рассмотрим четырехмерное пространство R4 с
координатами (/3, н, С/, V). В этом пространстве введем внешнюю
2-форму
Q - d/З Л dU + du Л dV. (22.22)
Во всем пространстве R4 мы имеем
Q = d(/3dU + иdV) и Q = d(~Ud/3-Vdu).
1128
Глава 22. Термодинамика
Двумерное подмногообразие £ пространства R4 называется ла-
гранжевым^ если 2-форма Q, ограниченная на £, тождествен-
но обращается в нуль. Для любого двумерного подмногообразия
пространства R4 величины (Зыу можно рассматривать как функ-
ции. Если их дифференциалы линейно независимы при ограниче-
нии на подмногообразие, то функции (3 и у можно использовать
в качестве локальных координат. Аналогично, функции U и V
можно рассматривать в качестве локальных координат, если их
дифференциалы линейно независимы. См. рис. 22.7.
Рис. 22.7. Подмногообразие £ лагранжево. Проекция на плос-
кость /3, у взаимно-однозначна, поэтому можно рассматривать
/3, и как локальные координаты на £. По той же причине можно
в качестве локальных координат на £ взять (7, V
Если подмногообразие £ является лагранжевым, то при огра-
ничении на это подмногообразие имеем
d(J3dU + ydV) — О,
и, следовательно, (локально) существует функция S, определен-
ная на £ так, что выполняется уравнение (22.20). Аналогично,
поскольку при ограничении на подмногообразие £ мы имеем
d(-Ud/3- V dy) -0,
то можно сделать вывод, что (локально) существует такая функ-
ция У, что выполняется уравнение (22.21). Таким образом, можно
дать общую формулировку для первого и второго законов:
22.4. Системы с одной конфигурационной переменной 1129
многообразие равновесных состояний является лагран-
жевым подмногообразием в пространстве с координа-
тами (/3, /у, {7, V).
Продолжим наше математическое рассуждение. Предполо-
жим, что мы ввели функции U и V в качестве локальных ко-
ординат (см. рис. 22.7), и предположим, что мы знаем функцию
S. Это означает, что нам задана функция S, явно зависящая от
U и V. Если сопоставить равенство
ds = (dS/dU) dU + (dS/dV) dV
с равенством (22.20), то получим выражения для f3 и у через U
и V, а именно
fi = 8S/dU и y^dS/dV. (22.23)
Это, конечно, определяет подмногообразие £. Другими словами,
если у нас есть диаграмма Моллье в координатах U и V с ли-
ниями уровней и значениями только функции S, то можно вос-
становить С и, следовательно, по крайней мере в принципе, все
необходимые термодинамические функции. Вся информация от-
носительно С закодирована в S, если S является функцией U и
V. Мы называем S производящей функцией лагранжева подмно-
гообразия £.
Аналогично, если в качестве локальных координат взять /3 и
у и задать Y как функцию /3 и у, то из равенства (22.21) можно
восстановить функции U и V в зависимости от /3 и у с помощью
равенств
U = —дУ/д/З и V = -ЭУ/ду.
Таким образом, У — производящая функция £. (Заметим, что
это дает обратное отображение, выражая /3 и у как функции от
/7 и V.)
Мы можем проделать то же самое, выбрав в качестве локаль-
ных координат другие переменные. Например, можно написать,
что на всем пространстве R4
Q-d(-C/d/3 + pdV)
и соответственно на С
dZ = —Ud/3 + ydV,
изо
Глава 22. Термодинамика
где функция Массье Z определятся выражением
z - S - (3U. (22.24)
Таким образом функция Массье — производящая функция для
£ в координатах [3 и V. В уравнении (22.24) закодированы пер-
вый и второй законы термодинамики вместе с полным описанием
равновесных состояний нашей системы!
Когда мы перейдем к изучению равновесной статистической
механики, то увидим, что функции S и Z являются базисными.
Будет дана интерпретация функции S на языке теории вероятно-
стей, из чего станет ясно, что ее значение распространяется да-
леко за пределы термодинамики. Будет показано, что функция
Z обеспечивает связь между микроскопической теорией и наблю-
даемыми макроскопическими явлениями, т. е. из общей конструк-
ции станет понятно, как модель энергии на атомном или молеку-
лярном уровне приводит к определенному выражению для Z как
функции от {3 и V. (Многие технические аспекты станут чисто ма-
тематической задачей — как вычислять или оценивать это выра-
жение.) И, конечно, мы разовьем теорию так, чтобы она работала
для систем с несколькими конфигурационными переменными.
Прежде чем переходить к статистической механике, следу-
ет еще обсудить ряд идей относительно равновесия. Это будет
сделано в следующем параграфе. Но в заключение этого пара-
графа обратимся к замечанию, сделанному в самом начале. Мы
говорили, что многие физически измеряемые величины задают-
ся отношением 2-форм на поверхности равновесных состояний, и
показали это на примере двух типов «теплоемкостей». Приведем
еще два примера.
Коэффициент теплового расширения при постоянном давлении dV Л dp VdT Kdp
Коэффициент сжимаемости при постоянной температуре dV Л dT VdT Kdp
Другие примеры величин и способов обращения с ними мы
дадим в задачах к этой главе.
22.5. Условия равновесия
1131
22.5. Условия равновесия
Рассмотрим системы с произвольным числом конфигурационных
переменных. До сих пор мы определяли функцию S только на
многообразии равновесных состояний. Важно отметить, что неко-
торые функции, например, температура или давление, определя-
ются только на многообразии равновесных состояний. Нет смыс-
ла говорить о температуре газа (как целого), если он не находит-
ся в равновесии. В свое время было сделано великое открытие —
энтропия является функцией, определенной на множестве всех
состояний, т. е. существует функция Ent такая, что
Ent(p) = $(р),
если р — равновесное состояние. Здесь мы не будем давать опре-
деление Ent, поскольку это потребует описания произвольных со-
стояний системы. Такое определение будет дано, когда мы будем
заниматься статистической механикой. Тогда мы напишем явную
формулу для Ent, фактически полученную Больцманом. Однако,
многие идеи, излагаемые в этом параграфе, принадлежат Клау-
зиусу и другим, кто работал до открытия статистической интер-
претации.
Мы воспользуемся свойством аддитивности энтропии для
двух систем, находящихся в контакте. (Сейчас это свойство бу-
дем рассматривать как аксиому, но потом оно будет доказано в
рамках статистической механики.) Итак, под двумя системами,
находящимися в контакте, мы подразумеваем большую систему,
построенную из двух меньших, так что состояние большой систе-
мы р является парой состояний р — (ръръ) отдельных компонент
системы, и внутренняя энергия
С/(р) = J7i(pi) + ^2(^2)*
Другими словами, «энергия взаимодействия» пренебрежимо ма-
ла по сравнению с суммой индивидуальных энергий. Мы не пред-
полагаем, что контакт только тепловой (рис. 22.8). Например,
возможно движение поршня между резервуарами, так что воз-
можен «обмен объемами». Или имеется проницаемая перегород-
ка между системами, так что возможен обмен молекулами газа
1132
Глава 22. Термодинамика
Рис. 22.8. Две системы, находящиеся в контакте трех видов. Они
могут обмениваться теплом (сверху), веществом (в середине) и
объемом (внизу)
и т. д. Энтропия составной системы является суммой энтропий
составляющих систем, т. е.
Ent(p) = Ent(pi) + Ent(p2)> если р ~ (pi,p2).
Далее мы будем использовать это важное свойство. Если мы
функция энтропии определена на множестве всех состояний, то
разумно дать более сильную формулировку второго закона тер-
модинамики.
Если система адиабатически замкнута, то энтропия
любого состояния не может убывать со временем. Бо-
лее того, энтропия всегда возрастает, если только си-
стема уже не находится в равновесном состоянии.
Поскольку энергия сохраняется, это приводит к важной характе-
ристике равновесных состояний, наиболее важной в статистиче-
ской механике.
Принцип максимальной энтропии: среди всех состояний
с данной внутренней энергией равновесное состояние обладает
максимальной энтропией.
Принцип минимальной энергии Гиббса: если р — равновес-
ное состояние, а сг — другое состояние с той же энтропией, что и
р, т.е. Ent(cr) = Ent(p), то U(p) U(a).
22.5. Условия равновесия
1133
Чтобы получить правило Гиббса из принципа максимальной
энтропии, воспользуемся физическим опытом. Мы всегда можем
подводить тепло к системе и поэтому непрерывно увеличивать
энергию и энтропию системы, причем это можно делать, не из-
меняя конфигурационных переменных. Предположим, что р —
равновесное состояние, и предположим, что (вопреки опыту) есть
другое состояние а в окрестности р, причем Ent (ст) = Ent(p) и
U(а) < U(p). Подводя тепло к системе, мы можем непрерыв-
но увеличивать энергию и энтропию, пока не достигнем нового
состояния с той же внутренней энергией, что и /?, но большей
энтропией, что противоречит принципу максимальной энтропии.
Это доказывает принцип Гиббса.
Прежде чем пользоваться принципом Гиббса, сделаем ряд
предварительных замечаний. Предположим, что Д,... ,fk -
функции от конфигурационных переменных системы. Фиксируя
значения этих функций, можно получить новую систему. Напри-
мер, предположим, что две системы, изображенные на рис. 22.8,
сначала были разделены, и каждая имела свой поршень. До объ-
единения мы имели систему, которая была просто прямым про-
изведением двух подсистем. Поэтому у нас было четыре конфи-
гурационные переменные: объемы подсистем — Vi и V2, полная
масса газа в каждой подсистеме - Mi и ЛД. (Для упрощения
обсуждения предположим, что в подсистемах был одинаковый
газ.) Приводя подсистемы в контакт, как показано на рис. 22.8,
мы имеем фиксированные полный объем и полную массу. Дру-
гими словами, мы наложили ограничения на формы / = const и
д — const, где
f ~ Vi + V2 и д = Mi + ЛД,
сократив число независимых переменных с четырех до двух.
Возьмем некоторую систему и перейдем к новой системе, на-
ложив некоторые ограничения на конфигурационные перемен-
ные. Такая система будет иметь собственные равновесные состо-
яния, которые характеризуются максимумом энтропии и миниму-
мом внутренней энергии, но, конечно, по отношению к более огра-
ниченному классу состояний, т. е. тех, что удовлетворяют ограни-
чениям. Предположим, что нам задано подмножество М состоя-
ний исходной системы (без ограничений), которое содержит все ее
1134
Глава 22. Термодинамика
равновесные состояния, и предположим, что М — многообразие.
Кроме того, предположим, что функция Ent и ограничивающие
функции Л,... ,fk дифференцируемы на Л4. Пусть р — равно-
весное состояние системы с ограничениями, в которой функции
fs постоянные. Согласно принципу Гиббса, функция U должна
иметь локальный минимум в состоянии р при условии, что
Ent — const, /i = const, ..., fk = const.
Воспользуемся методом множителей Лагранжа. Существуют
функции Ao, Ai,..., А&, для которых
dU — Aq d Ent + Ai df i + • • • + A& df(22.25)
Например, в случае системы, изображенной на рис. 22.8, многооб-
разие М должно быть парой равновесных состояний отдельных
систем, когда они не контактируют друг с другом. Каждая под-
система в отдельности имеет конфигурационные переменные V и
М. Тогда для двух подсистем имеем
dUi = Ti dSi — pi dVi + p-i dM\ и dU2 = T2dS2 —Р2^^2 + p2 dM2.
Коэффициент p при dM называется «химическим потенциалом».
Многообразие М шестимерное, поскольку множество равновес-
ных состояний каждой подсистемы трехмерное. Мы предполага-
ем, что
U = l/i + и2.
Свойство аддитивности энтропии означает, что
Ent = Si + S2.
Тогда
dU = Ti dSi + T2 dS2 — pi dVi — p2 dV2 + pi dMi + p2 dM2.
Из условия (22.25) следует, что
dU - A0(dSi + dS2) + Ai(dVi + dV2) + A2(dMi + dM2),
поскольку Vi + V2 и Mi + M2 — ограничивающие функции.
22.5. Условия равновесия
1135
Дифференциалы, стоящие в правой части этих двух равенств,
независимы на многообразии Л1, поэтому мы имеем
Pl = Р2, Ml — М2-
Таким образом, давление, температура и химические потенциалы
должны быть равны. Очевидно, что это утверждение обобщает-
ся на случай нескольких систем, находящихся в контакте, когда
каждая подсистема может содержать смесь разного количества
разных веществ. Поэтому, если выражение для внутренней энер-
гии на множестве равновесных состояний каждой отдельной сис-
темы имеет вид
dUi = TidSi-pidVi + + uldMf + ,
то получаем условия равновесия объединенной системы
Т1 = Т2 = - - • ,
Pl = Р2 = * * ' ,
Ml = М2 = • • • ? (22.26)
М| — М2 — • • • ,
И Т.д.
Эти равенства являются общими условиями равновесия. Они да-
ют нам возможность почувствовать, что такое «интенсивные пе-
ременные»: Г, р, // и т.д.
В качестве примера рассмотрим газ, состоящий только из од-
ного вещества. Каждый участок такого газа можно рассматри-
вать как подсистему. Если каждая такая подсистема, взятая в
отдельности, находится в состоянии равновесия, то мы имеем для
нее определенные значения Т^ри р. Другими словами, мы счита-
ем, что Т.ри м являются функциями в трехмерном пространстве,
которые каждой точке приписывают значения температуры, дав-
ления и химического потенциала в небольшой окрестности этой
точки. Условие того, что газ как целое находится в состоянии
равновесия, состоит в том, что эти функции должны быть по-
стоянными по всему объему газа. Тогда газ как целое, скажем,
1136
Глава 22. Термодинамика
с постоянной полной массой имеет только одну конфигурацион-
ную степень свободы V. Мы можем использовать р и Т в каче-
стве координат двумерного пространства равновесных состояний
газа как целого. Это означает, что величина р выражается как
функция координат р и Т. Тогда для газа, состоящего из одного
вещества, находящегося в состоянии равновесия, химический по-
тенциал р это некоторая определенная функция от р и Г, т. е.
ц = №газ{р,Т). Предположим, что это вещество может находить-
ся и в жидкой фазе. Для жидкости в состоянии равновесия мы
получим другую функцию р — Мжидк.(р, Г). А теперь рассмот-
рим комбинированную систему, состоящую из газа и жидкости
одного вещества. По отдельности газ и жидкость находятся в со-
стоянии равновесия. Предположим, что эта система, как целое,
тоже находится в равновесии. Тогда из условий (22.26) следует,
что
Ржидк. — Ргаз? ДкидК. — Тгаз, р-жидк. ~ Ргаз-
Если р и Т обозначают общие значения для первых двух условий,
то третье условие принимает вид
Ржидк. (Р,Т) = Мгаз(р5Г).
Поскольку, как правило, ДЖИдк. и цгаз — независимые функции
от р и Г, то последнее равенство определяет кривую на плоско-
сти р, Т. Другими словами, жидкая и газообразная фаза одного
и того же вещества могут находиться в равновесии только при
определенном соотношении между температурой и давлением.
Если имеются три фазы одного вещества, скажем, газ, жидкость
и твердая фаза, то условия равновесия в такой системе имеют
вид
Р тверд. (Р, -^) = Ржидк. (Р?^) — Ргаз(р?^)-
Тогда решением этих уравнений будет так называемая тройная
точка с определенным значением температуры и давления. И на-
конец, четыре фазы одного вещества не могут находиться в рав-
новесии. Именно так Гиббс получил свое знаменитое правило фаз.
Оно (как и его обобщения) содержится в условиях (22.26), кото-
рые являются прямым следствием равенства (22.25) — принципа
минимальной энергии Гиббса.
22.6. Системы и состояния в статистической механике 1137
22.6. Системы и состояния в статистической
механике
В этом параграфе мы займемся микроскопическими теориями,
которые могут послужить моделью для термодинамики. Нач-
нем с классической статистической механики, в рамках которой
«состояние» определяется как «мера вероятности» определенно-
го рода, и энтропией состояния будет «количеством беспорядка
этого состояния». Математические основы теории вероятностей
были заложены в первой трети XX века, главным образом, Боре-
лем, Лебегом и Колмогоровым. Это произошло гораздо позднее
появления фундаментальных идей статистической механики, вы-
двинутых Больцманом и Гиббсом. Таким образом, и здесь возник
коммуникационный барьер. Языком теории вероятностей являет-
ся теория меры. Мы будем пользоваться этим языком, не вдава-
ясь глубоко в саму теорию. Для любого серьезного результата
теории вероятностей, связанного с бесконечным числом возмож-
ностей, существенно использование всего аппарата теории меры.
Поскольку мы будем рассматривать наиболее простые факты, то
пользоваться будем только самыми простыми понятиями, смысл
которых станет ясным на конкретных примерах.
Измеримое пространство — это множество М вместе с семей-
ством А подмножеств этого множества. Мера р задает правило,
согласно которому каждому множеству А семейства А ставится
в соответствие неотрицательное число (или +оо) р(А). Для се-
мейства А и меры р существует ряд аксиом, на которые мы не
будем здесь отвлекаться. (Для нас существенно, что А ~ замкну-
тое семейство относительно счетного объединения, пересечения и
дополнения9, и что /z(|J Д) — ^2ц(А) Для любого счетного объ-
единения непересекающихся множеств Д.) Мы не рассматриваем
набор всех подмножеств М, чтобы избежать противоречий, воз-
никающих при рассмотрении сильно патологических множеств.
В большинстве случаев мы здесь рассматриваем очень про-
стые множества М. Например, пусть М — конечное множество,
и пусть семейство А будет семейством всех подмножеств М. Тог-
да множества, состоящие из одной точки М, тоже будут входить
9Такое семейство множеств принято называть а-алгеброй. — Прим. ред.
1138
Глава 22. Термодинамика
в наше семейство, и каждому такому множеству {т} приписы-
вается неотрицательное число м({™})- Зная эти числа, можно
восстановить меру ц, поскольку
м(^) = 52 м({™})-
теА
Если f — произвольная (вещественная или векторная) функция
на М, то можно определить «интеграл по мере ц» в виде
/ = 52 Лт)м({™})-
тем
(Это такая же договоренность, которая была сделана в теории
электрических цепей.)
В качестве М можно было бы взять Z — множество всех це-
лых чисел, или N — множество всех неотрицательных целых чи-
сел. А в качестве А можно было бы взять семейство, состоящее
из всех подмножеств. Определение меры означает задание неот-
рицательного числа для каждого целого числа (в случае Z) или
для каждого неотрицательного целого числа (в случае N). Тогда
мы получили бы такое же выражение для ц(А), как и раньше,
но сумма справа в этом случае будет бесконечной, которая мо-
жет сходиться, а может и нет. Если она сходится, то ц(А) равно
пределу суммы; если же она расходится, то ц(А) = +оо.10 То же
самое происходит и для функции /, для которой мы определяем
интеграл f fp в виде суммы. Сумма теперь становится бесконеч-
ным рядом. Мы говорим, что функция / интегрируема, если ряд
сходится абсолютно, и тогда f fp определяется как сумма этого
ряда. В противном случае J fp не имеет смысла.
В качестве М можно взять вещественную прямую R. Тогда
семейство А должно содержать все отрезки [а, Ь] = {х | а
х Ь}. Обычная мера (Лебега) каждому отрезку приписывает
его длину
ц([а, b]) ~ b — а.
10Легко видеть, что если 52п^({п}) — сходящийся ряд (для п € Z или
п е N), то мера всякого множества конечна и не превосходит суммы ряда. —
Прим. ред.
22.6. Системы и состояния в статистической механике 1139
Если f — произвольная кусочно-непрерывная функция, доста-
точно быстро стремящаяся к нулю на бесконечности, то мы зна-
ем, как вычислять интеграл11
[ /м = [ f(x) dx.
J J — OQ
Аппарат теории меры предназначен для построения достаточно
богатого класса семейств Д, на которых определена мера /г, и до-
статочно широкого класса функций, интегралы от которых опре-
делены. Мы будем рассматривать достаточно простые множества
функций, и поэтому нам не придется вдаваться в детали теории
меры. Как мы уже говорили, необходимо задействовать весь ап-
парат теории меры, если заниматься глубокими проблемами.
Вероятностная мера приписывает значение 1 самому мно-
жеству М, т. е. = 1. Это соответствует принятому в теории
условию, что «вероятности» принимают значения от 0 до 1.
Фундаментальное понятое «системы» в статистической меха-
нике — это пространство с мерой. Множество М, семейство А и
мера // заданы нам физикой или геометрией задачи. В общем слу-
чае мера р не будет вероятностной мерой. Она играет роль «апри-
орного состояния знания» системы. Покажем это на нескольких
примерах.
А. Пространство конечной выборки с равной априорной веро-
ятностью. Это простейший пример. М — конечное множество,
А — семейство всех подмножеств М. В этом случае = 1
11 в смысле Римана. Интеграл Лебега численно с ним совпадает, но опре-
делен для значительно более широкого класса функций (в том числе таких
всюду разрывных, как функция Дирихле, равная 1 в рациональных точках и
О в иррациональных), и процедура его вычисления существенно отличается
от римановых сумм, поскольку разбивается не область определения функ-
ции, а область значений. Для вещественной функции f интеграл f fp по
мере Лебега р = dx (или другой мере р) равен пределу при h 0 сумм вида
52 У‘^({Х I Vi < У*+1})>
где {уДгея — такое разбиение области значений /, что 0 < ?/i+i — yi < h. —
Прим. ред.
1140
Глава 22. Термодинамика
для каждого т G М. Так описывается ситуация, когда есть ко-
нечное число возможностей, и у нас нет оснований предпочесть
одну возможность другой.
В. М ~~ вещественная прямая R со стандартным семей-
ством измеримых множеств и мерой Лебега р. Тогда =
Ь—а для любого отрезка [а, Ь]. Мера р показывает «априорную ве-
роятность» отрезка, пропорциональную его длине. Конечно, р не
является вероятностной мерой, потому что /х(К) = оо. Заметим,
что если р — произвольная интегрируемая функция, для которой
/оо
р(х) dx — 1,
-оо
то р определяет вероятностную меру pdx на множестве R, где
Р([а, £>])= f p(x)dx.
J—оо
Таким образом, мера р{= dx) определяет выделенный класс ве-
роятностных мер на множестве R. (На языке теории меры это
класс тех вероятностных мер, которые абсолютно непрерывны по
dx. Не все вероятностные меры на R обладают этим свойством.
Например, рассмотрим вероятностную меру F, которая припи-
сывает значения Р({0}) — 1/2, Р({1}) = 1/2 и Р(А) = 0, если
{0,1} П А — 0. Тогда Р обозначает вероятность в случае, когда
достигаются точки либо 0, либо 1, причем их шансы одинаковы.
При этом очевидно, что Р не представляется12 мерой вида pdx.)
Для любой меры р на измеримом пространстве и для любой
интегрируемой неотрицательной функции р мы получаем новую
меру, которую обозначаем рр, положив
рд(А) = / рр.
JA
Здесь следует ввести общее
Определение: пусть (М, Л, р) — пространство с мерой. Состоя-
ние (статистическое) (М, Д, р) — это вероятностная мера в прост-
ранстве М вида рр, где р 0 — интегрируемая функция. Други-
ми словами, состояние соответствует такой интегрируемой функ-
ции р, для которой f рр — 1.
12если не рассматривать обобщенных функций. — Прим. ред.
22.6. Системы и состояния в статистической механике 1141
С. Пусть М = R и у — где Н(х) = 0 при х О
и Н(х) = 1 при х > О.13 Это соответствует ситуации, когда мы
уверены, что данное вещественное число положительное, причем
все положительные числа равновероятны. Конечно, можно с тем
же успехом взять М = — {х | х > 0}, поскольку здесь
сконцентрирована мера ц.
D. Число заполнения для классических частиц. В этом слу-
чае М — N — {0,1,2,3,... } и p({k}) = 1/к\. Мера ц приписывает
вес 1/fc! вероятности к частицам находиться в ящике. Объясним,
почему это подходящая мера. Предположим, что у нас есть неко-
торое количество ящиков п и несколько частиц N. Число спосо-
бов размещения частиц по ящикам, так чтобы к± частиц попали
в первый ящик, &2 — во второй и т. д. равно
7V!
(Конечно, здесь частицы предполагаются «различимыми»: обмен
парой частиц между разными ящиками изменяет способ разме-
щения частиц. Существует 7V! различных перестановок частиц,
но мы должны разделить это число на к±1... кД потому что пе-
рестановка частиц внутри каждого ящика не дает новый способ
их размещения.) Если нам не известны числа N и п, то лучшее,
что мы можем сказать, — это что число способов размещения
частиц так, чтобы в первом ящике было к\ частиц, пропорцио-
нально 1/fci!.14 Это и есть наше априорное знание относительных
вероятностей.
Е. Число заполнения для частиц Ферми-Дирака. В этом слу-
чае в каждый ящик можно поместить только одну частицу. Тог-
да М — {0,1} и /х({0}) = ц({1}) ” 1- Это, конечно, част-
ный случай примера А. Мы также могли бы взять М = N —
неотрицательным целым числам, причем да({0}) = /z({1}) — 1 и
13Указанная функция Н называется функцией Хевисайда. Она является
первообразной для обобщенной дельта-функции Дирака (сосредоточенной в
нуле). — Прим. ред.
14Данное утверждение справедливо лишь при N < п, в противном случае
самым вероятным числом частиц в ящике будет ближайшее целое к N/n. —
Прим. ред.
1142
Глава 22. Термодинамика
= 0 для всех к > 1. В этой схеме заполнения отражен
«принцип запрета». В одном ящике не может быть больше одной
частицы. Наличие частицы в ящике или ее отсутствие априор-
но рассматриваются как равновероятные события15. Конечно, в
реальной интерпретации ящик может быть достаточно абстракт-
ным. Например, это может быть квантовое состояние одной ча-
стицы для частиц, подчиняющихся принципу запрета Паули.
F. Число заполнения для частиц Бозе-Эйнштейна. Здесь
М = N = {0,1, 2,3,... } и ц({к}) = 1. Любое число частиц в ящи-
ке может быть обнаружено с одинаковой вероятностью. Если,
например, частица - это возмущение среды (пятно на экране) и
две частицы представляют возмущение двойной интенсивости, то
при распределении N «единиц возмущения» по п «ящикам» на-
до учесть, что «частицы» «не различимы» в том смысле, что все
их распределения равновероятны. Таким образом априори мера,
приписываемая наличию к± частиц в первом ящике, равна 1.
В квантовой механике все частицы делятся на два класса:
частицы Ферми-Дирака и частицы Бозе-Эйнштейна. Частицы
Ферми-Дирака (электроны, протоны, нейтроны и т. д.) называ-
ются фермионами, а частицы Бозе-Эйнштейна (фотоны, пионы
и т. д.) назывются бозонами.
G. Биномиальная мера. Предположим, что у нас есть боль-
шое число N частиц, каждая из которых может быть в двух по-
ложениях — «вверх» или «вниз». Причем состояние их совокуп-
ности описывается только полным числом частиц в положении
«вверх» минус полное число частиц в положении «вниз». Тогда
М — {—7V, —N + 2,..., N — 2, N}. Для простоты предположим,
что N — четное число. Тогда число частиц в положении «вверх»
минус число частиц в положении «вниз» равняется 2m, когда
(7V/2) + т частиц находятся в положении «вверх», a (7V/2) — т
частиц — в положении вниз. Число способов сделать это равно
N \ N!
7V/2 + mJ “ (7V/2 + m)!(7V/2-m)!’
15при условии, что мы не знаем отношение числа частиц к числу ящиков.
То же относится и к следующему примеру. — Прим. ред.
22.6. Системы и состояния в статистической механике 1143
Если нам интересно знать относительную частоту появления
2т, надо разделить на самый большой биномиальный коэффи-
ЛУ \
циент I уу/2 ) и тогда
М2тП=(Я }(N 'U________________________________
\N/2 + m)\N/2) (JV/2 + m)!(2V/2-m)!'
Использование формулы Стирлинга TV! — \S2ttN • NNe~N пока-
зывает, что для больших чисел 7V последнее выражение очень
хорошо аппроксимируется функцией e-2m . На этом основан
следующий пример.
Н. Дискретная гауссова мера. Пусть М = Z — множество
всех целых чисел и
д({т}) = e~2m2lN.
Заметим, что когда т ~ y/N/2, значение /Д{т}) равняется к
Предположим, что мы хотим знать величину m/N,
т.е. что каждое состояние «вверх» или «вниз» дает вклад ±1/N
в измеряемую величину. Тогда функция m/N имеет очень острый
пик в окрестности 0 для больших чисел 7V. Например, если N ~
1024, то /Д{т}) уменьшается в е раз, когда m/N сдвигается от О
на величину 10~12.
Чтобы «увидеть» распределение, мы должны изменить мас-
штаб множителем 7V1/2, и не N. Если взять = 2А;/У1//2, то
ь
м({а хк Ь}) = У2е~^/2-
а
Сумма справа растет приблизительно как У1/2. Действитель-
но, если разделить это выражение на (2тгУ)~1//2, то правая часть
стремится к
[be-^dx.
Тем самым мы подошли к следующему примеру.
L М = R и р — (нормированная) непрерывная гауссова мера
М(М]) = -^== / e~x2/2dx.
1144
Глава 22. Термодинамика
J. В качестве последнего примера рассмотрим классическую
механику. В этом случае пространство М — фазовое простран-
ство механической системы. Фазовое пространство имеет выде-
ленные координаты (канонические координаты) д, р и выделен-
ную меру (мера Лиувилля)
р ~ dpdq.
Например, точечная классическая частица движется в про-
странстве R3. Координаты gi, g2, дз описывают ее положение, а
координаты pi, Р2? Рз задают ее импульс. Тогда М = R6 и
dp dq — dpi dp2 dp3 dqi dq2 dq%.
т. e. пространство R6 с обычной мерой.
22.7. Произведения и образы
В этом параграфе мы обсудим различные способы построения си-
стем. Сначала обсудим понятие произведения. Предположим, что
у нас есть две системы (M^Aupi) и (М2, А2^р2). Можно образо-
вать их произведение (Mi х М2, Ai х Аъ, Pi х Р2)- Например, пусть
(М1,А1,Ц1) и (М2,Л2,М2) — системы, описанные в примере Е
предыдущего параграфа, т. е. они представляют возможное чис-
ло частиц в ящике (см. рис. 22.9). Тогда (Mi х М2, Ai х Д2? Pi х р2}
представляет систему, состоящую из двух ящиков, соединенных
вместе (см. рис. 22.10).
Мера pi х р2 характеризуется выражением
(pi х //2X^1 х А2) = pi(Ai)p2(A2)
для произведений множеств А — Ai х А2, где Ai G i = 1, 2.16
Конечно, состояние р системы-произведения не обязано иметь
16 Семейство измеримых подмножеств Ai х Аъ произведения измеримых
пространств и (М2, Аг) состоит из счетных объединений «прямо-
угольных» множеств вида Ai х Аг, где Аг е Ai, т.е. является пополнением
семейства {Ai х А2} до ст-алгебры. Произведение мер х р2 определяется
предыдущим равенством и свойством аддитивности. — Прим. ред.
22.7. Произведения и образы
1145
Mr
Рис. 22.9. д({&}) = //({/}) = ±
Рис. 22.10. (/Xi х д2)(М) = тгут
вид pi х р2. Если же это состояние типа р = pi х р2, то соот-
ветствующая вероятностная мера (pi х Р2)(/^1 х М2) — М1М1 х М2М2
на множестве Mi х М2 тоже является произведением мер. Это
означает, что событиям в пространствах М\ и М2 приписывают-
ся независимые вероятности.
Можно построить произведение любого17 количества систем
где i пробегает произвольное множество индексов I.
Другой способ построения системы использует отображение.
Пусть (М, Л, /х) — одна система, и (N, Б) — измеримое простран-
ство, т. е. N — множество с выделенным классом подмножеств.
Пусть f : М N — отображение. Предположим, что для каж-
дого В G В подмножество /~1(В) множества М принадлежит
семейству Д.18 Тогда можно определить правило f*p,. согласно
которому каждому В £ В приписывается значение
Лм(В) = мСГМ
17В принципе число сомножителей может быть бесконечным, но к опре-
делению измеримых множеств произведения в этом случае необходим более
осторожный подход. — Прим. ред.
18Тогда отображение f называется измеримым. В частности, измеримы
относительно обычной меры все кусочно-непрерывные отображения евкли-
довых пространств. — Прим. ред.
1146
Глава 22. Термодинамика
0
Mi х М2
Рис. 22.11
Если функция на множествах из В является мерой, то она
называется переносом19 меры р при отображении /. Тогда мы
имеем новую систему (NyB, f*p\ называемую образом системы
(Л/, Л, р). Например, начнем с произведения М = Mi х М2 двух
систем из того же примера Е. Пусть N — это большой ящик, из
которого удалили перегородку (см. рис. 22.11). Тогда отображе-
ние f задается формулой
f^l^ = k + l.
Таким образом, при отображении f игнорируется то, что в
ящике слева находится к частиц, а в ящике справа — I частиц.
Оно оставляет только информацию, что в большом ящике на-
ходятся к + I частиц. Тогда для любого положительного целого
числа s можно написать
(/*м)({«}) 52 fciji= 52 дТ/г
fc+Z=s k+l=s
Откуда
2s
СМ({*}) = 7 •
Оба способа построения — с помощью произведения или с по-
мощью отображения — в данном случае становятся интуитив-
но более понятными, если немного изменить пример Е. Давайте
определим систему, соответствующую ящику с объемом V, поло-
жив
Vk
Mv = 7V, ру({к}) = —.
К1
19В оригинале pushforward, т.е. движение вперед. Действительно, в отли-
чие от переноса дифференциальной формы (pullback, см. примечание на с. 291
в томе I), при этой операции область определения меры перемещается в том
же направлении, что и точки при отображении. — Прим. ред.
22.7. Произведения и образы
1147
7VfV1
Рис. 22.12. gvi({fc}) = MV2({/}) =
MVl x A-/v2
ykyl
Рис. 22.13. nVl x /zy2({fc,Z}) =
fc! ll
My1+y2
Vi+V2
Рис. 22.14
Тогда если рассмотреть две системы, соответствующие ящикам
с объемами V± и V% (см. рис. 22.12), то Му± х Му2 соответствует
рассмотрению двух ящиков вместе (см. рис. 22.13). Уберем теперь
перегородку и рассмотрим ящик с объемом V1+V2 (см. рис. 22.14).
Опять положим N = Му1+у2 и определим отображение f : Му± х
Му2 N формулой /((fc, Z)) = к + I. Тогда
(/./*)({»})
52
fc+Z—s
УМ
к\1\
_ 1 V s! vkvl
- s\^ kWV1V2
= + v^s
s!
1148
Глава 22. Термодинамика
Вернемся к рассмотрению общего случая. Пусть (М, Д, /х) —
система, и отображение F : М —> N дает нам образ системы
f*p)- Если а — произвольное состояние из (TV, Z3,/*ц), то
функция /*сг = его f определяет состояние из (М, A, р). Действи-
тельно, /*сг 0, тогда из определения интеграла следует, что
У = У сг(А^) = 1.
Таким образом, состояния, определенные на множестве 7V, за-
дают состояния, определенные на множестве М. Состояние р
на множестве М также определяет состояние на множестве
7V, но это определение лежит значительно глубже. Давайте сна-
чала рассмотрим пример. Рассмотрим пространство Mi = R2
со стандартными семейством измеримых множеств А и мерой
р(= dxdy). Пусть отображение f : R2 —» задано формулой
f(x,y) — (х2 + у2}1!2. Тогда = 2тггdr. Пусть р(х,у) — произ-
вольная непрерывная функция на плоскости, удовлетворяющая
условию f рdxdy = 1. Тогда р является состоянием. Определим
состояние условием
1 Г27Г
f*p(r) = — / p(r cos#, г sin#) dO.
Jo
Таким образом, f*p(r) — состояние, «усредненное» по окружнос-
ти с радиусом г, т. е. среднее от р по /-1(г). Тогда
[ (Up)p = [ U*p)(r)2irrdr
Jr+ Jo
/•оо г2тг
= I I p(r cos 0, г sin 0) dr dO
Jo Jo
/ОО /’OO
/ p(x,y)dxdy = 1.
-oo J — oo
Отсюда следует, что f*p~ состояние, определенное на множестве
N. Заметим, что f*f*cr = сг, но, вообще говоря, f*f*p не обязано
быть равным р. В общем случае, когда р — состояние, опреде-
ленное на множестве М, рр является вероятностной мерой на М.
22.7. Наблюдаемые, ожидания и внутренняя энергия 1149
Поэтому f*(pp) — вероятностная мера на множестве N. Кроме
того, если В 6 В любое множество, удовлетворяющее условию
(Ад)(В) = о, то »(ГЧВ)) = П,
и, следовательно,
(А(рд))(В) = (рм)(/-1(В)) = [ рр = 0.
JB
Итак, равенство (/*//) (В) = 0 означает, что f*(pp,)(B) = 0. Тео-
рема из теории меры, называемая теоремой Радона-Никодима,
утверждает, что если У\ и у^ ~ две меры такие, что для всех В
из Уъ^В} — 0 следует, что ^i(B) = 0, то существует такая функция
а, для которой r'i(B) = сгуъ- Если взять у± = f*(pp) и у% ~
то мы приходим к заключению, что существует неотрицательная
интегрируемая функция а, определенная на множестве ЛГ, для
которой справедливо равенство
(/*(рм))(в)= [ р(М
JB
для любых В. Из того, что f*(pp) — вероятностная мера, следует
[ = 1-
Jb
Тогда а — состояние, определенное на множестве f*p), и
мы получаем
f*P =
22.8. Наблюдаемые, ожидаемые значения
и внутренняя энергия
Частным случаем отображений является обычная функция с чис-
ленными значениями f : М —► R. Такое отображение называется
наблюдаемым для данной системы. Грубо говоря, наблюдаемая
величина какой-то системы — это просто численное свойство
1150
Глава 22. Термодинамика
системы, которое можно измерить. Обсуждая чисто теоретиче-
ские вопросы, будем обозначать наблюдаемое буквой J. Кон-
кретные наблюдаемые, когда они будут появляться, обозначают-
ся буквами, отражающими их физический смысл. Конечно, как
часть нашего определения наблюдаемого, мы предполагаем, что
J“1([a,6]) принадлежит семейству А для каждого отрезка [а, Ь]
на вещественной прямой, т. е. предполагается измеримость отоб-
ражения J.
Пусть J — наблюдаемое и р — состояние. Для каждого отрезка
[а, Ь] можно рассмотреть подмножество 7-1([а,Ь]) множества М,
и тогда интеграл
/ рр
есть как раз размер множества 7~г([а, 6]) по отношению к веро-
ятностной мере рр. Другими словами, это есть вероятность того,
что точка множества М лежит в J”1 ([а, 6]), когда мы приписы-
ваем вероятности в соответствии с вероятностной мерой рр. То
же самое можно сказать по-другому: это есть вероятность того,
что наблюдаемое J принимает значения на отрезке [а, Ь], когда
мы приписываем вероятности на множестве М согласно вероят-
ностной мере рр. Запишем это утверждение в следующем виде.
Prob(J е [а, Ь], когда система находится в состоянии
Р) =
или короче
Prob(J € [а,Ь];р) — [ рр. (22.27)
Таким образом, наблюдаемое и состояние вместе приписывают
значение вероятности на вещественной прямой. Вероятность,
приписанная любому отрезку, есть вероятность измерения на-
блюдаемой J на этом отрезке, когда система находится в состоя-
нии р; она задается предыдущей формулой.
В теории вероятностей существует язык, который мы будем
здесь использовать. Интеграл
/ Jpp
Jm
22.8. Наблюдаемые, ожидания и внутренняя энергия 1151
называется математическим ожиданием или ожидаемым зна-
чением функции J по отношению к вероятностной мере рд. Это
есть среднее значение J, когда вес подмножеств множества М бе-
рется в соответствии с вероятностной мерой рр. Таким образом,
ожидаемое значение J в состоянии р определяется интегралом
E(J;p) = [ Jpp. (22.28)
Jm
Приведем пример. Пусть М — фазовое пространство классичес-
кой частицы, так что М = R6 с координатами gi, g2, дз, Pi,
р2, Рз и стандартной мерой. Пусть J ~~ это функция энергии,
равная сумме кинетической и потенциальной энергий, так что
J = H = K + V, т.е.
H(qi,q2,q3,Pl,P2,Ps) = |(р? + Р2 + Рз) + ^1, 92,9з),
£
где К — кинетическая энергия
К = |(Р1 +Р2 +Рз)
и У - потенциальная энергия. В этом случае состояние — это
неотрицательная функция р, определенная на пространстве R6,
интеграл от которой по всему пространству равен 1. По опреде-
лению
Е(Н\р)^= [ Hpdqidqidqzdpidpzdpz. (22.29)
JR6
Предположим, что мы хотим рассмотреть энергию «свободной
частицы, помещенной в ящик В с объемом V». Это можно
сделать, предположив соответствующую форму потенциала V.
Пусть V равняется 0, когда точка (gi, дг, Яз) лежит внутри ящика
В, и У становится чрезвычайно большим за пределами ящика.
Таким образом, предполагается, что частица должна преодолеть
очень высокий барьер, чтобы вылететь из ящика. Выбранный
потенциал внесем в выражение для Н в формуле (22.29). Пред-
положим теперь, что состояние р таково, что оно приписыва-
ет пренебрежимо малую вероятность очень большим значениям
1152
Глава 22. Термодинамика
энергии, т.е. предположим, что Prob(# > Е; р) практически рав-
на нулю для очень больших Е. Чтобы быть совсем точными,
давайте предположим, что приписываемое значение вероятности
настолько мало, что при вычислении интеграла (22.29) можно
пренебречь вкладом от точек (<7i, </2? <7з)> лежащих за пределами
ящика. Внутри ящика V — 0, и интеграл принимает вид
I i(Pi + Р2 + РзЫ<11 Л2,?з>Р1,Р2,Рз) dqx dq2 dq3 dpi dp2 dp3.
JBxTR3 &
(22.30)
Чтобы двигаться дальше, необходимо иметь больше информации
о состоянии р. Например, предположим, что когда частица на-
ходится в ящике, то она с одинаковой вероятностью находится
в любой его точке, т. е. р не зависит от координат положения
(91?92?9з)? а зависит только от (Р1,Р2?Рз)- Тогда интеграл (22.30)
принимает вид
v f ^Pi+P2 + P3)p(Pi’P2,P3)dpidp2dp3. (22.31)
JR3 2
Далее предположим, что в состоянии р распределение скоростей
частицы задается так называемым распределением Максвелла с
параметром /?, т. е. что
р(Р1,Р2,Рз) = Fp exp[-0{pl +Р2 +Рз)/2],
где Fp — нормировочная константа, зависящая от j3. Мы должны
теперь выбрать Fp так, чтобы полный интеграл JM рр = Т т.е.
мы должны взять Fp = /мРР, что составляет
F/з = У(2тг/3)-3/2.
Тогда формула (22.31) принимает вид
(Х?/2тг)3/2 У |(р? + ?! + Рз) ехр[-/Э(р? + р22 + Рз)/2] dpi dp2 dp3.
Это гауссов интеграл, значением которого является (3/2)/5'~1.
Тогда, с учетом всех сделанных предположений, мы имеем
Е(Н-р) = (3/2)(3~\
22.8. Наблюдаемые, ожидания и внутренняя энергия 1153
Как это следует понимать? С точки зрения математики, форму-
лы (22.29)--(22.31) представляют чисто интегральные выражения.
Это стандартные процедуры математической теории вероятно-
стей. С точки зрения кинетической теории газов, рассматривает-
ся огромное количество молекул газа, заключенных в ящик и не
взаимодействующих друг с другом20. Тогда p(qi, <12,43,Р1?Р2,Рз)
определяет относительную частоту появления молекул газа в
окрестности точки (91?^2?9з?Р1?Р2?Рз) фазового пространства. В
такой интерпретации процедура усреднения, входящая в опреде-
ление Е(Н\ р), есть усреднение по молекулам газа, и тогда можно
сказать, что Е(Н',р) — средняя энергия, приходящаяся на одну
молекулу газа.
Понадобился гений Гиббса, чтобы осознать, что не следует
связывать себя такой интерпретацией. Мы вполне можем ис-
следовать систему, состоящую из одной молекулы в ящике. Тео-
рия вероятностей применима и в этом случае, вся математика
остается без изменения. Выбрав некоторое состояние р, мы рас-
сматриваем вероятность энергии принимать определенные значе-
ния в любом интервале или вероятность нахождения частицы в
определенной области фазового пространства. Конечно, если мы
захотим исследовать более глубокие проблемы, то нам придется
изучить общий смысл термина «вероятность» на более высоком
уровне. К сожалению, несмотря на то, что математическое обос-
нование теории вероятностей было сделано более пятидесяти лет
назад, нельзя сказать то же самое о ее философской интерпре-
тации. Когда пишется эта книга (1987 год), все еще существуют
серьезные разногласия относительно «истинного» смысла вероят-
ности. Сторонники одной крайности — «частотники» — ограни-
чивают область применения вероятности только ситуациями, ког-
да «одно и то же» явление повторяется много раз, так что веро-
ятность имеет смысл частоты. С другой стороны, есть «последо-
ватели Байеса», которые рассматривают вероятность как способ
мышления ~ теория вероятностей выражает, как должен думать
каждый здравомыслящий «рациональный» гражданин. Экстре-
мисты из каждой школы рассматривают членов другой школы
20 Это одно из постулируемых свойств идеального газа, которое довольно
хорошо выполняется в обычных условиях. — Прим. ред.
1154
Глава 22. Термодинамика
как людей, у которых в голове «каша» и т.д. Эти философские
споры приводят к ощутимым последствиям в реальной статисти-
ческой практике. Различные взгляды приводят к разным стати-
стическим процедурам, особенно если рассматривается неболь-
шое число объектов. К счастью, эти споры не имеют отношения
к статистической механике, поскольку число рассматриваемых в
ней объектов чрезвычайно велико. Важна только математическая
сторона этой задачи, т.е. вычисления с данными определениями.
Однако, Гиббс работал около ста лет назад, когда математиче-
ская теория еще не была разработана. Поэтому ему приходилось
заниматься и философией тоже. Кажется, что он скорее разделял
точку зрения «частотников». Поэтому, описывая вероятностную
меру типа р/х, он говорил об «ансамбле», подтверждая интерпре-
тацию «частотников». К сожалению, эта терминология и слово
«ансамбль» как синоним вероятностной меры прочно засели в
стандартных учебниках.
Но, независимо от интерпретации, мы уже готовы переки-
нуть первый мостик между понятиями статистической механики
и термодинамики. Если в качестве наблюдаемого рассматривать
энергию 7/, то
внутренняя энергия состояния р определяется как
Е(Н-р).
Другими словами, внутренняя энергия есть ожидаемое значе-
ние энергии в данном состоянии. Конечно, функция энергии Н —
фиксированная функция на множестве М. Существуют различ-
ные состояния р, дающие значения энергии Е(Н; р). Запишем это
определение в форме
С7(р)-Е(7?;р), (22.32)
так что внутренняя энергия - это функция на пространстве со-
стояний.
Мы уже сказали, что Н — фиксированная функция на мно-
жестве М. Но в общем случае мы позволим функции Н зависеть
от некоторых дополнительных параметров. Например, еще раз
рассмотрим газ, находящийся в ящике. Но теперь пусть в ящике
имеются различные поршни (рис. 22.15), так что его форма изме-
няется соответственно значениям Qi, Q2? • • •, Qd, определяющим
22.8. Наблюдаемые, ожидания и внутренняя энергия 1155
Рис. 22.15. Зависимость У от параметров
положение поршней. Тогда потенциальная энергия У (предпола-
гается, что она равна 0 внутри ящика и «+оо» за его пределами)
зависит от формы ящика и, следовательно, от параметров Qi,
Qs? • • • > Qd-
Таким образом, энергия U также зависит от этих параметров:
С/ = .
Итак, у нас имеются понятия состояния и внутренней энергии.
Что такое равновесные состояния? Мы можем определить их с
помощью принципа максимальной энтропии. В общем случае мы
сделаем это в параграфе 22.11. А сейчас вернемся к примеру газа,
заключенного в ящик.
Для каждого положительного значения /3 рассмотрим функ-
цию е~~@н в пространстве R6. (Здесь /3 — параметр, имеющий
размерность обратной энергии, так что /ЗН — безразмерная чис-
ловая функция. Очень скоро /3 станет играть роль, о которой
говорилось в параграфе 22.4.) Поскольку У и, следовательно, Н
обращается в +оо, когда точка (qx, 92> Уз) находится за пределами
ящика, функция там равна нулю, и она везде неотрицатель-
на. Поэтому в качестве состояния можно использовать F^1e~^H,
где постоянная F выбирается так, чтобы интеграл от этой функ-
ции по всему пространству был равен 1, т. е.
F— [ dqidqzdqzdpxdpzdps. (22.33)
Jr6
1156
Глава 22. Термодинамика
Мы уже вычисляли этот интеграл. Интегрирование по простран-
ственным переменным (Qi, Q2, <7з) проводится только внутри ящи-
ка, где функция Н от них не зависит. Поэтому это интегрирова-
ние дает множитель V — объем ящика. А интеграл по импульсам
гауссов, что приводит к результату
F = V(2ir/3)-3/2. (22.34)
Здесь F зависит от /3, а также от параметров Qi, Q2,..., Qd толь-
ко через объем V. В этом частном случае определим равновесные
состояния как
P/3,Q = (22.35)
где F = F(/3, Qi, Q2? • • • ? Qd) задается формулой (22.33).
Давайте определим
Z - log Е (22.36)
Можно вычислить dZ/dfl, дифференцируя (22.33) под знаком
интеграла, и получить
dZ/d(3 = F~xdF/d/3 = F"1 [ -Не~рн dqr dq2 dq3 dPl dp2 dp3
Jr6
= - j HP/3,Q dqi dq2 dq3 dP1 dp2 dp3 = -E(H; P/3>q) (22.37)
или
dZ/дв = -U. (22.38)
Вернемся к понятиям работы и обратимой кривой. Предпо-
ложим, что мы медленно двигаем один из поршней, скажем,
Q1. Соответственно изменяется энергия 7Z, и возникает функция
dH/dQ\ на пространстве 7И, которая имеет смысл силы. Для лю-
бого заданного состояния р мы должны вычислить среднее зна-
чение и получить обобщенную силу
EtfH/dQ^p).
Обратимость процесса означает, что мы ограничиваем состояния
р требованием, что они принадлежат множеству равновесных со-
стояний. Следовательно, форма для работы имеет вид
cv - E(dH/dQr,p) dQi + E(dH/dQ2-p) dQ2 + • • •
+ E(dH/dQk-,p)dQk.
22.8. Наблюдаемые, ожидания и внутренняя энергия 1157
Дифференцируя Z по Qi, получим
-/За; - (dZ/dQ^dQx + (dZ/dQ2) dQ2 + * • • + (dZ/dQk) dQk
(22.39)
или в более символической форме
dQZ = -/За;, (22.39а)
где dQ обозначает правую часть формулы (22.39), т. е. мы вычис-
ляем оператор d в направлениях Q (при фиксированном значении
/3), Заметим, что при выводе уравнений (22.37)-(22.39) мы нигде
не использовали явный вид Н. Если же теперь предположить,
что рассматривается «свободный газ в ящике», где функция F и,
следовательно, Z зависят только от Qi через объем V, то можно
написать dZ/dQi = (dZ/dV)(dV/dQi), и формула (22.39) превра-
щается в
-/3u; = (dz/dv)dv.
Конечно, увеличение V вызывает уменьшение Н (поскольку точ-
ки, которые раньше были за пределами ящика, где У = +сю,
теперь оказываются внутри ящика, где V — 0). Как обычно, дав-
ление считается положительным, из чего следует, что — —pdV.
Тогда последнее уравнение принимает вид
dZ/dV =/Зр = щ
а это показывает, что Z обладает всеми свойствами функции
Массье.
Итак, у нас теперь есть общий рецепт вычисления функции
Массье. Для заданной системы (М, Л, р) и функции 77, опреде-
ленной на пространстве М и называемой «энергией», определим
функцию разбиения F выражением
F = У е~0Нц. (22.40)
Функция Н и, следовательно, F могут зависеть от дополнитель-
ных переменных Q1? Q2, ..., Qk. Кроме того, интеграл в формуле
(22.40) будет сходиться только в определенной части простран-
ства (/3, Qi, Q2, * •., Qk)- Определим внутреннюю энергию форму-
лой (22.32), равновесные состояния — формулой (22.35) (где F
1158
Глава 22. Термодинамика
определяется формулой (2240)) и функцию Массье — форму-
лой (22.36). Тогда справедлива формула (22.38), и форма для
работы ш задается формулой (22.39). Это и есть рецепт для пе-
рехода от «микроскопической модели», закодированной функци-
ей Н. к «макроскопическим равновесным явлениям», описывае-
мым функцией Массье. Получен четкий рецепт, но его еще надо
обосновать. Это можно будет сделать, когда мы поймем вероят-
ностное определение энтропии, которым займемся в следующем
параграфе.
Есть еще одно небольшое обобщение наших рассуждения, ко-
торое окажется полезным. Предположим, что мы хотим рассмот-
реть не одно наблюдаемое, а несколько наблюдаемых (Jj,..., Jn)
сразу. В этом случае можно ввести J = (Ji,..., Jn) — векторное
наблюдаемое, значения которого лежат в пространстве Rn, т.е.
наблюдаемое, принимающее значения в векторном пространстве
W. Наблюдаемое со значениями в W — это просто функция из
М в W (удовлетворяющая соответствующему условию измери-
мости, как и в случае R). Понятие интеграла от вектор-функции
определено, поэтому определение (22.28) для математического
ожидания вектор-наблюдаемого в данном состоянии сохраняет-
ся без изменения. Точно так же можно говорить про вероятность
(в данном состоянии) наблюдаемого J лежать в некотором под-
множестве W. Но нам не придется этим заниматься.
22.9. Энтропия
Введем понятие энтропии состояния. Пусть (М, А, /л) — систе-
ма. Мы хотим каждому состоянию системы р приписать число
Ent(p), которое будет измерять меру «беспорядка» состояния р по
отношению к р. Таким образом, Ent будет функцией, определен-
ной на пространстве всех состояний. Чтобы оправдать такое опре-
деление, сначала рассмотрим пространство конечной выборки,
т. е. случай А из параграфа 22.6. Если М = {ei,..., е^}, то состо-
яние р определяется заданием к вещественных чисел Pi = p(ej,
i ~ l,...,fc. Тогда pi есть вероятность события {еД. В теории
информации энтропия состояния р — (pi,...,Pfc) определяется
22.9. Энтропия
1159
равенством
k
Entfe(p) = - pi log ft. (22.41)
i=l
Эта функция обладает различными свойствами, делающими
ее мерой «беспорядка» или недостатка информации. Выпишем
некоторые из них.
(i) Entfc(pi,... ,pfc) симметрична по (pi,... ,pfc). Это соответ-
ствует требованию, что мера беспорядка не зависит от спо-
соба индексации результата.
(ii) Ent&(l,0,... ,0) — 0. (Здесь мы определяем xlogx = 0 для
х = 0 в силу непрерывности.) Это соответствует утвержде-
нию, что если в данном состоянии результат предопределен,
то оно имеет нулевой беспорядок.
(iii) Entfc+i(pi,... ,рь0) — Entfc(pi,... ,pfc). Это означает, что
если нашу систему М — заменить на систему
Mf = {ei,..., efc, efc_|_i}, но при этом рассматривать толь-
ко состояния, в которых е&_|_1 невозможны, то энтропия не
изменяется. Другими словами, добавление фиктивной аль-
тернативы не изменяет недостаток информации.
1 1А| а
—, • • , — I, где будет строгое нера-
гС К /
венство^ если pi 1/к для некоторого значения г.
Таким образом, недостаток информации достигает максиму-
ма, когда все альтернативы равновероятны. Для доказательства
этого утверждения заметим, что для всех х > 0 справедливо усло-
вие
xlogx х — 1.
Равенство будет только для х = 1, что легко проверяется диф-
ференцированием обеих частей. При х 0 это условие можно
переписать в виде
— log г х-1 — 1.
(iv) Entfe(pi,... ,pfc) Ent
1160
Глава 22. Термодинамика
Тогда
1 ( 1 1А 1 Pi ( fc-1 Л 1
-Pilogp— -Pilogy = -Pilvg—r < -Pi---------------1 = ~y+Pi-
\ к/ k~L \ pi / к
При вычислении суммы по i справа получается 0, потому что
£3(l/fc) = 1 = Y^Pi' Итак, мы имеем
- log?* - 52^ log 1 = - log 1 = - 22 1 log 1
Заметим, что Ent(pi,... ,р&) отражает недостаток знания
до выполнения эксперимента, который скажет нам, какие из
к возможностей реализуются на самом деле. В этом смысле
Ent(pi,... ,pfc) представляет количество информации, получен-
ной при выполнении эксперимента.
(v) Предположим, что М — Mi х М2, где Mi содержит k эле-
ментов {ei,...,efc}, а М2 содержит I элементов, так что
М состоит из к1 элементов Предположим, что р =
Pl X Р2, так что р({(вг,Л)}) = Pi<lj- Тогда
EntfeZ(p) = - ^PiQi log(piqj)
= - £р^з(1оёрг + log?,)
= - 22р* log Pi - 22 log Qi.
Но поскольку Pi — 52 Qj — мы имеем
Entfe/(pi x p2) = Entfe(pi) + Entz(p2).
Другими словами, если мы проведем два независимых экс-
перимента, то полное количество полученной информации
будет равно сумме информаций, полученных от каждого
эксперимента.
Оказывается, что свойства (i)—(iv) вместе с более сильным ва-
риантом утверждения (v) определяют функцию Ent с точностью
22.10. Равновесие в статистических системах
1161
до постоянного множителя. Таким образом, в пространстве ко-
нечной выборки есть только один способ измерения «беспоряд-
ка» состояния, если эта мера беспорядка удовлетворяет несколь-
ким разумным аксиомам. Мера беспорядка задается выражени-
ем (22.41). Это выражение можно переписать таким образом, что
оно будет иметь смысл для любой системы.
По определению, для произвольной системы (Л/, Л, р) и про-
извольного состояния р имеем
Ent(p) = — у* plogpp, (22.42)
при условии, что этот интеграл сходится.
22.10. Равновесие в статистических системах
Итак, у нас есть определение меры «беспорядка» в системе. Пред-
положим, что нам задана система и последовательность вещест-
венных наблюдаемых Ji,..., Jn. Мы можем наблюдать ожидае-
мые значения этих наблюдаемых в любом состоянии. Соберем на-
блюдаемые в векторную конструкцию J = (Ji,..., Jn). Используя
принцип максимальной энтропии, рассмотрим состояние «стати-
стического равновесия», в котором «беспорядок» достигает мак-
симума в соответствии с нашим знанием ожидаемого значения J.
Сначала поставим точную математическую задачу.
Пусть J : М —► V — векторное наблюдаемое системы, и пусть
J — произвольное возможное ожидаемое значение J. Рассмотрим
следующую проблему.
Среди всех состояний р, обладающих свойством
E(J; р)~ У pJ^ = J,
найти такое, в котором энтропия достигает своего мак-
симума.
Иначе говоря, нужно решить задачу на условный максимум
Ent(p) при ограничении f рЗр = J.
1162
Глава 22. Термодинамика
Оказывается, что если для системы (М, Л, и наблюдаемого
J выполняются ряд предположений, то эта задача имеет един-
ственное решение. Итак, начнем.
Пусть V* обозначает пространство, дуальное к V. Тогда эле-
мент 7 Е V* ~ линейная функция на пространстве V. Пусть 7 • v
обозначает значение 7 на векторе v. Тогда для любых 7 G 7* и
т Е М можно рассмотреть 7-J(m), что является числом, завися-
щим от 7 и т. Но тогда 7 • J — числовая функция на множестве
М. Запишем интеграл
F(7) = [ е~^р.
JM
Отсюда видно, что 0 < F(7) +оо (интеграл может расходиться
к +оо). Предположим, что 7 таково, что интеграл F(7) конечен.
Тогда
<22-«)
определяет состояние системы. Действительно, ру — положитель-
ная функция, и по определению F(7) мы имеем J рур = 1. Для
каждого значения 7, когда F(7) < +00, мы получаем состоя-
ние Ру. Итак, мы получили набор состояний, параметризованный
подмножеством V*. Заметим, что если < +00, то Ent(p7)
конечна. Действительно,
- У P~f log P~fP = - У Р-/(- log F(7) - 7 • J)m-
Здесь F(7) постоянна, если рассматривать ее как функцию на
множестве М. Поэтому
У log F(y)p = log F(7).
Кроме того,
j pyjp = F(J; py)
есть просто ожидаемое значение векторного наблюдаемого J в
состоянии р. Поэтому можно написать
р77-Jl/ = 7.E(J;p7).
22.10. Равновесие в статистических системах
1163
Но тогда
Ent(p^) = log F(7) + 7 • Е(3; ру). (22.44)
Давайте теперь учтем, что функция J может также зависеть
от некоторых «конфигурационных» параметров Q. Если напи-
сать 5(7,Q) = Ent(p7,Q) и Z(7,Q) = logF(7,Q), то равенство
(22.44) принимает вид
5-Z + 7-J(7, Q)-
В частном случае, когда J = Н, это равенство совпадает с (22.24).
Но формула (22.24) представляет собой комбинацию первого и
второго законов термодинамики.
Предположим, что для заданного значения J Е V мы можем
найти такое 7 Е V*, что
Jр~ур — £/( J*, р7) “ J •
(При этом предполагается, что J Зрур сходится абсолютно.)
Тогда утверждается, что р — единственное решение экстре-
мальной задачи. Другими словами, справедлива
Теорема. Пусть 7 G V* таково, что < +00 и справедливо
равенство (22.44), где ру определено формулой (22.43). И пусть
Р ~ другое состояние, для которого
(22.45)
Тогда
Ent(p) Ent(p-y),
причем мы имеем строгое неравенство, если р и ру отличаются
на множестве с положительной мерой р.
Доказательство. Здесь мы повторяем аргументы, которые
приводили для доказательства, что (1/fc,..., 1/к) дает максимум
энтропии в конечной системе. Итак, для любого состояния р и
любого т Е М мы имеем
-p(m) log р(т) - (-p(m) log р-у(тп)) р7(т) - р(ш). (22.46)
pjp — J.
1164
Глава 22. Термодинамика
В самом деле, если р(тп) = 0, то левая часть равенства равна
нулю, а правая положительна. Если р(т) > 0, то
- p(m) log p(m) - (-p(m) log p7(m)) = p(m) log[p(m)/p7(m)]
sj p(m)([p7(m)/p(m)] - 1) = p7(m) - p(m),
при этом используется неравенство — log х < ж”1 — 1.
Интегрирование по пространству М дает
J р log рр - У р log p-pi < О,
потому что
Р-/М = 1-
Но
logp-y = - log F(7) - 7 * J,
а следовательно,
= log F(7) + 7 • J = Ent(p7)
поскольку E(J; р7) — J.
Таким образом,
Ent(p) С Ent(p-y).
(Заметим, также, что из неравенства (22.46) следует, что
-plogp < -p[logF(7) + 7 J] + ру - р,
причем правая часть этого неравенства — абсолютно интегриру-
емая функция. Итак, если — J plogpp, расходится, то это проис-
ходит на —оо.)
Неравенство (22.46) будет строгим, если p(m)/p7(m) 1. Тог-
да, если р(т) / р^(т) для множества с положительной мерой,
то мы имеем Ent(p) < Ent(p7), что и требовалось доказать.
В качестве следствия этой теоремы мы дадим статистическое
определение равновесного состояния.
22.10. Равновесие в статистических системах
1165
Определение. Пусть J — наблюдаемое в системе (М, Л, д). Если
7 таково, что F(~y) — J < оо, то
о —____1
“ Г(7)
называется равновесным состоянием системы (относительно на-
блюдаемого J).
Мы должны показать, что (при соответствующих предполо-
жениях) для любого значения J существует состояние для
которого E(J;p^) — J. Из доказательства теоремы следует, что
если такое состояние ру существует, то оно единственно. Мы вер-
немся к этому вопросу позднее. А сначала дадим несколько при-
меров равновесных состояний, используя системы, введенные в
примерах параграфа 22.6.
А1. Пусть М = {ei,..., е&} и р точно такие же, как и в при-
мере А параграфа 22.6. Пусть V = R — одномерное пространство
и пусть J : М —* R задается условием J(e$) = где £* ~ веще-
ственные числа (мы будем считать их «энергетическими уровня-
ми»). Без потери общности для элементов множества М введем
индексы
£1 £2
Тогда V* = R и для любого /3 Е V* мы имеем
к
F(/3) =
так что равновесное состояние р@ задается формулой
°
Оно называется «распределением Максвелла-Больцмана».
Вспомним вычисление ожидаемого значения «энергии»
1166
Глава 22. Термодинамика
или короче
E<J’w) -------
(Как мы уже видели, это последнее равенство дает общее прави-
ло.) Тогда
dE(J;pp)
дР
причем будет строгое неравенство, если только не все ер равны
между собой. (Если же все равны, то существует только одно
возможное значение для J, равное этому общему значению всех
Si. Тогда все рр одинаковы и равны p^(ej = 1/fc. Таким образом, в
этом случае теорема сводится к утверждению (iii).) Если Si
то Е{3\рр) — строго убывающая функция от /3. Очевидно, что
lim Е(3]рд)=ек и lim Е^рр)^^.
р—^—оо р~>4-оо
Итак, любое значение J такое, что ei < J < £&, может быть
получено только единственным выбором /3. Для любого значения
/3 мы имеем
Ent(pp) = -p3(ei)logp/3(ei)
р I
= - ZL у—~рГр logfV) - 1о§ 13 е“^
г ^Р \ j
- + log F(P) = /3 • J + log F(P).
Это, конечно, частный случай формулы (22.24).
А2. Рассмотрим случай конечной системы Л/, элементы ко-
торой для удобства обозначим ео?.*.,вь так что в ней насчи-
тывается к + 1 элемент. Пусть J = (Ji,..., Jk) отображает М в
22.10. Равновесие в статистических системах
1167
пространство где
Таким образом, J отображает М в вершины симплекса в прост-
ранстве заданного базисными векторами.
В этом случае 7 = (71,..., 7^) и
F(7) = 1 + е“71 + • • • + е~^к
сходится для всех значений 7 с
1 е“71 е~Ук
^(е°) = F\yY = 7(т)’ ' ‘’ Р'1^ = '
Если мы обозначим через то понятно, что в любую точ-
ку р = (pi,... ,pfc) внутри симплекса можно попасть с помощью
соответствующего выбора 7$. В этом случае все состояния, соот-
ветствующие внутренней точке р, являются равновесными состо-
яниями.
Отображение 7 —> E(J; p-у) переводит все элементы простран-
ства Rn = V* во внутреннюю область единичного симплек-
са. Читатель может проверить, что это отображение взаимно-
однозначно и имеет дифференцируемое обратное.
В. Пусть (R, Д, д) — вещественная прямая с обычной мерой.
Если J — тождественное отображение J(x) = х, то соответствую-
щая функция 2(7) — JZ^oe~7X dx расходится для всех значений
7. Однако, если рассмотреть отображение J : R —> R2, задан-
ное равенством J(x) = (т,х2), то для всех 7 — (71,72) с 72 > 0
функция
2
= / e~^x~^x v
J—00
сходится. Соответствующее равновесное состояние
_ 2?^)-le7i/472e-(x+Tl/272)2/2(l/272)
имеет нормальную плотность, математическое ожидание т =
—71/272 и дисперсию21 а = (272) Очевидно, что для любого
21 Напомним, что дисперсия случайной величины (функции на пространст-
ве с вероятностной мерой) f с математическим ожиданием т определяется
как математическое ожидание величины (/ — т)2. — Прим. ред.
1168
Глава 22. Термодинамика
сг > 0 и любого т можно найти такой вектор 7 = (71,72), что
Р-у(ж) =
1 „-(ar-m)2/2<т2
<Т\/27Г
Итак, для всех случайных величин с производными, имеющих
заданные математическое ожидание и дисперсию, энтропия мак-
симальна при нормальных распределениях. Чтобы вычислить эн-
тропию, заметим, что в силу трансляционной инвариантности
можно считать, что т = 0. Тогда
2 1
-log27r + log<r +^2 dx
Ent(p,) = -1= [
ау/Ък J
= log а + log 2-7Г + 1.
Энтропия стремится к —оо при а 0. Это соответствует тому,
что при сг 0 состояние р становится более сосредоточенным
вокруг точки и поэтому требуется «бесконечное количество ин-
формации, чтобы выделить эту точку из континуума».
С. Давайте рассмотрим наблюдаемые — х и J2 = logx в
пространстве R+. Тогда 7 = (71,72), J ~ (Л, Л) и
F(7)= f°° £-71^-72 logТ dx = [°°e-^xx-^dx
Jo Jo
сходится при 7i > 0 и 72 < —1.
Если положить к — —72 + 1 и у = ух, то интеграл принимает
вид
F(7) = [°° е-71^^-1 dx = У Г° е~уук-х dy = 7ffcr(fc).
Jo Jo
Соответствующие распределения называются гамма-распре-
делениями. В этом случае плотность равна
л — 1 р"71^-72 log X
' угы
Мы хотим вычислить векторное ожидаемое значение
E(J) = (E(Ji),E(J2)).
22.10. Равновесие в статистических системах
1169
При этом мы имеем
E(Ji) = [°° xe-^x~^ogx dx
Jo
и
E(J2) = [ log Ж • 6-71^-72 log x dx.
Jo
Тогда
E(Ji)= [°° x1-'ne~''ix dx.
Jo
Сново оббозначим у ~ ^xnk = 1 — 72? что дает
/*ОО
Е(Ji) = 71-1 / е~уук dy = 7i-1r(fc + 1).
Jo
Вычисление E^Jz) оставляем читателю в качестве упражнения.
D. Пусть J “ наблюдаемое, заданное формулой J(A;) = к, а
(3 € R1. Тогда мы видим, что ряд
сходится для всех значений /3. Введем величину е~~@ = А; тогда
F(J3) = е\ (Параметр А часто называют «активностью».) Тогда
Поэтому
РгоЬрр/э = fc} = е-Л—.
Это распределение вероятностей называется распределением
Пуассона. Заметим, что
E(J’,pp) = -dlogF(/?)/d/? = —де~$/д(3 = е~е
или
Е(3;р/з) = А.
Другими словами, параметр А показывает ожидаемое число ча-
стиц в ящике.
Давайте теперь еще раз перечислим полученные теоретиче-
ские результаты.
1170
Глава 22. Термодинамика
• Система (7И, Д, р) является пространством с мерой.
• Состояние — неотрицательная функция р на М с условием
f рр = 1-
• Энтропия состояния есть Ent(p) — — f plogp/z.
• Наблюдаемое есть (векторная) функция на пространстве М.
• Ожидаемое значение наблюдаемого К в состоянии р есть
Е(К;р) = J Крр.
Если J — наблюдаемое со значениями в пространстве V, то функ-
ция разбиения, связанная с J, есть функция, определенная для
7 € V* условием
Г(7) = I е~^р.
Она определена на подмножестве С пространства V*, где этот
интеграл сходится.
Функция Массье Z определена на С условием Z — logF.
Равновесные состояния относительно J — это состояния вида
= F(7)-1e-Tj
для 7 G С. С помощью функции Массье можно вычислить ожи-
даемое значение J в состоянии при условии, что 7 находится
внутри подмножества С, по формуле
Ji = -dZ/dyi,
что для краткости можно записать в виде
J = -dZIfrt.
Тогда
£(7) = Ent(p.y) = Z + 7 • J.
В частности, 7 можно получить из J по формуле
7 = dS/dJ.
22.11. Квантовые и классические газы
1171
Здесь мы рассматриваем S как функцию от J, поскольку у мож-
но выразить как функцию от J, обращая заданную функцию
J = J(7). Наблюдаемое J может зависеть от дополнительных
координат Qi,..., Qd- т. е. J может быть функцией на простран-
стве М х В, где В — пространство с координатами Qi,..., Qd-
Тогда функция F и равновесные состояния ру также зависят от
этих дополнительных координат.
В случае, когда одной из компонент J является Н — «энер-
гия», внутренняя энергия состояния р дается Е(Н\р). Имея все
эти определения и после обсуждения работы в параграфе 22.8
(см. (22.39а)), мы подготовились в переходу от «микроскопиче-
ской» модели к «макроскопически» наблюдаемым явлениям.
22.11. Квантовые и классические газы
Начнем со сравнения функций разбиения для трех систем D, Е и
F, рассмотренных в параграфе 22.8. Как и раньше, для каждой
из этих систем будем рассматривать двумерное наблюдаемое J =
(N,H), где N — «число заполнения», Н — «уровень энергии»,
причем N и Н связаны соотношением
Н = Ns,
где г — «энергия одного заполненного состояния». В предыдущем
параграфе мы уже проделали вычисления для случая D, а теперь
сделаем все сразу в виде таблицы 22.2.
Во всех трех случаях мы вычисляем последний столбец по
формуле E(N) = — 51ogF/cty?i. Сумма, возникающая при вычис-
лении случая F, является геометрической прогрессией, а в слу-
чае Е — это просто сумма двух слагаемых. Во всех трех случаях
E(N) мала тогда и только тогда, когда велика Тогда
мы пренебрегаем слагаемым ±1, появляющимся в знаменателе
выражения для Z. Но тогда распределения вероятностей наблю-
даемого N очень близки. В таблице 22.3 мы введем обозначение
Л =
Если рассматривать ожидаемое число заполнения как ме-
ру «концентрации», то для «разреженных» систем распределе-
ния вероятностей Больцмана, Ферми-Дирака и Бозе-Эйнштейна
1172
Глава 22. Термодинамика
Таблица 22.2
Система Функция разбиения E(N)
D 1/fc! ехр[е-^1+^2£)] e^~s^T = ехр[е(м-е)/т]
Е М(0) = м(1) = 1 1 + e-^+W ^(Ь)7т ц(&) = 0, k > 1 =1 + е^~£^т
F 1 I 1 — е-(01+/32S) е-(м-е)/Т_1 - 1 — 1 - е^-£)/г
Таблица 22.3
Система Название Prob(N = fc)
D Больцмана-Пуассона е~хХк/к\
Е Ферми-Дирака Prob(./V = 0) = 1/(1 + А) Prob(W = 1) = A/(l + А) Prob(7V > 1) = 0
F Бозе-Эйнштейна (1 - A)Afe
очень близки, т. е. все члены в правом столбце таблицы 22.3 бу-
дут близки друг к другу, когда А очень мало. Но для больших
«концентраций» они сильно отличаются. На рис. 22.16 изображе-
ны графики трех функций е-*, 1/(е* + 1) и 1/(е* — 1). Заметим,
что при t > 2 кривые почти сливаются, но при малых значениях
t они сильно расходятся.
Давайте рассмотрим ситуацию, когда имеется d экземпляров
одной из этих систем, причем каждая имеет различное значе-
ние энергии одного заполненного состояния, так что мы имеем d
значений Si,..., Система представляет собой прямое произве-
дение
М — Mi х • • • х Md.
22.11. Квантовые и классические газы
1173
Рис. 22.16. Графики ожидаемых значений числа частиц для рас-
пределений Больцмана, Ферми-Дирака и Бозе-Эйнштейна в за-
висимости от (д — е)/Т = t
Мы предполагаем, что «энергия взаимодействия» пренебрежимо
мала, т. е.
Н ^Нг + . ' + Hd.
Кроме того, определим
N - М + • • + Nd.
Тогда функция разбиения всей системы есть просто произведение
функций разбиения всех компонент:
F = Fi х - * • х Fd,
где
Я = ге< (&,&).
В таблице 22.2 мы должны в выражениях для функций разбиения
вместо е подставить
Давайте еще раз обсудим, что это означает. У нас есть d си-
стем. Мы собрали их в одну систему. Следовательно, они мо-
гут «взаимодействовать». Равновесные состояния г-й подсисте-
мы определялись бы ее собственными параметрами /Зц и Тот
факт, что системы находятся в равновесии, означает, что у нас
1174
Глава 22. Термодинамика
имеются общие для всех значения /31 и /З2. Таким образом, мы
еще раз открыли критерий Гиббса (22.26).
До сих пор шел весьма абстрактный разговор, и мы не да-
вали физического описания компонент нашей системы. Сейчас
рассмотрим следующую модель «газа в ящике» (отличную от
прежней модели). В фазовом пространстве рассмотрим подоб-
ласть В х □, где В С R3 — наш ящик и □ Е R3 — небольшой ку-
бик с центром в точке р в пространстве импульсов. Итак, когда
мы говорим, что молекула находится в нашей области, то имеем
в виду, что она находится в ящике и ее импульсы близки к р.
Подсистемы «взаимодействуют» посредством столкновений, т. е.
за счет обмена импульсами. Предположим, что энергия одной ча-
стицы в выбранной подобласти есть ее кинетическая энергия, т. е.
г(р) = |||р||2 = |(р2+р? + р2)-
Это и есть «энергия заполненного состояния» для подсистемы с
центром в точке р. Согласно утверждению Больцмана-Пуассона
«ожидаемое число частиц в нашей подсистеме» пропорционально
ехр (м- |||Р||2) jТ
Это и есть распределение Максвелла-Больцмана, где дополни-
тельный параметр /л зависит от плотности газа. Конечно, мы пе-
репрыгнули через две техниченских ступени — мы рассмотре-
ли бесконечное число подсистем, заполняющих все фазовое про-
странство, и устремили размер ячейки в фазовом пространстве к
нулю. Но это не представляет большой сложности.
Эти же соображения можно было бы применить к стати-
стикам Ферми-Дирака и Бозе-Эйнштейна. Тогда вместо распре-
деления Максвелла-Больцмана мы получили бы распределение
Ферми-Дирака
ехр[(|||р||2 ~ц)/Т] + 1
Аналогичная замена происходит и в случае статистики Бозе-
Эйнштейна.
22.12. Определители и следы
1175
22.12. Определители и следы
Давайте перепишем формулу
F(fa fa) = Ffafafa) х F2(ft,ft) х - х Ffafafa) (22.47)
(в каждом из трех случаев) на первый взгляд странным образом,
но так, чтобы из нее были видны следствия. Пусть V = и X
— диагональная матрица, г-й элемент которой равен ег.
Сначала рассмотрим случай Больцмана-Пуассона. Посколь-
ку произведение экспонент равняется экспоненте от суммы, мы
имеем
Ffjfafa) = ехр[е~<Л+^е1> + • • • +
= exp(tre-^1I+^2X))
= Det(expe-^1I+^2X^).
Здесь использовано, что для любой матрицы имеет место равен-
ство Det(exp А) = exp(tr А).
Давайте рассмотрим случай Ферми-Дирака. Поскольку опре-
делитель диагональной матрицы равен произведению ее диаго-
нальных элементов, можно написать
fFfafafa) 0 ••• 0 \
О F2(Jfafa) О
F(fafa) = Det
о О ••• Fd(jfafa)J
(22.48)
Матрица, стоящая справа, — это матрица
и поэтому
F = Det(I + е-(Л1+/?2Х)).
Аналогично, в случае Бозе-Эйнштейна соответствующее равен-
ство имеет вид
F = Det[I - е-С/М+ДгХ)]-!.
Другими словами, мы получили таблицу 22.4.
1176
Глава 22. Термодинамика
Таблица 22.4
Система Функция разбиения
Больцмана Det (exp е~ Е+^2Х))
Ферми-Дирака Det(I +
Бозе-Эйнштейна Det[I — -1
Если сравнить таблицы 22.2 и 22.4, то увидим, что изменение
состоит в том, что скаляр Z?i + foe заменяется на матрицу +
(ЗъХ и вычисляется определитель.
Опишем несколько по-другому процедуру взятия определите-
ля. Но сначала сделаем ряд замечаний относительно линейной
алгебры. Пусть V — векторное пространство, и А — его линейное
преобразование. Тогда А индуцирует линейное преобразование
А ® А пространства V ® V согласно формуле
(А 0 А)(и 0 v) = Аи 0 Av.
Если А = etY, то, дифференцируя уравнение
etY 0 etY (и 0 v) = etYu 0 etYv
no t в точке t = 0, получаем
(d/dt)[etY 0 etY(u 0 v)]|t==o = Уи Ф v + и 0 Yv
= (У 01 +10 У)[п 0v].
Это показывает, что etY 0 etY — exp(tZ), где Z — оператор,
определенный равенством
Y 01 + К 0 Y.
Другими словами,
etY ®etY =
Аналогично, если рассмотреть индуцированное действие на V 0
V 0 V, то получим
etY etY etY =
22.12. Определители и следы
1177
Далее идут аналогичные выражения для V 0 V 0 V 0 V ит.д.
Введем обозначение Dk(Y) для матрицы, стоящей в экспоненте
справа. Тогда
D2(Y) = У0К + 10У на V® V,
2?з(У) = У0Я0Я + 10У01[ + 1[010У на V 0 V 0 V
и т. д. Например, если взять t == 1 на V 0 V 0 V, то получим
еу®еу®еу = е°з(П
Вычисление следа матрицы, стоящей слева, дает (trey)3, по-
скольку tr(A ® В ® С) = (tr A)(trB)(trС), т.е. под знаком тен-
зорного произведения следы умножаются. Итак,
(trey)3=treD3(y).
Давайте положим
£>о(Г) = О, Р1(Г) = У,
так что для всех к
(trY)k = tr eDk('Y\
Теперь функцию разбиения для больцмановской составной
системы можно написать в виде
Det(expe-^1I+^2X^) = exp(tre“'^1I+^2X^)
- J2(tr[e-^n+^2x>])fe/fc!
= 52(l/fc!) tr{exp(Dfe[-(/?iI + &*)])},
где мы взяли Y = е_^1Я+^2Х\ Запишем эту формулу более ком-
пактно. Пусть 2fc(V) — /с-кратное тензорное произведение V на
себя, так что
Т0(у) = R,
Ti(V) = V,
T2(V) = V ® V,
T3(V) = V ® V ® V, ит.д.
1178
Глава 22. Термодинамика
Рассмотрим полную тензорную алгебру
T(V) = T0(V) Ф T^V) ф T2(V) Ф • •
(Это бесконечномерное пространство, но не надо беспокоиться.)
Любая матрица на этом пространстве разлагается на блоки
^00
>110
Л2о
-^30
Л01
Ди
Л31
Д)2 Д>3 • •
А12 Дз • • •
Л22 Л2з • •
Л32 Л33 • • •
где Лоо — преобразование 7b(V) (т. е. скаляр), Ли — линей-
ное преобразование Т1(У), Л22 — линейное преобразование T2(V)
и т. д. Определим
^Л = £(1Д!)егЛи.
Конечно, это выражение не обязательно сходится. Мы будем счи-
тать, что оно определено только для бесконечных рядов, сходя-
щихся абсолютно.
Для любого оператора Y в пространстве V можно записать
(Do(Y) 0 0 0 -\
0 Di(Y) 0 0
D(Y) = 0 0 D2(K) 0
0 0 0 Рз(П •••
’ /
Полагаем теперь Dq(Y) — 0 и Di(Y) ~ Y. Тогда получаем
tr® е£>(Г) __ tr exp{Dfc(Y)},
следовательно,
22.12. Определители и следы
1179
Построим аналогичную конструкцию для случая Ферми-
Дирака. Вместо T(V) (тензорной алгебры) рассмотрим A(V)
(внешнюю алгебру). Например, давайте посмотрим на Л2(К) —
V Л V — пространство внешних 2-векторов над V. В этом случае
определим Dz(Y) как линейное преобразование Л2(У) согласно
формуле
D2(Y)(u Av) = Yu Av + иА Yv.
Это та же формула, что и раньше, только знак ® заменен на Л.
Как и раньше, мы имеем
еу Л еу = eD2^ на Л2(У).
Точно так же определяем
D3(Y) = Y Л1А1 + 1ЛУ Al+lAlA V на Л3(У)
и т. д. Так же, как и раньше, мы определяем D(Y) как прямую
сумму всех Di(Y) — матрицу на Л(У), диагональные компонен-
ты которой суть £>г(У). Если V — конечномерное векторное про-
странство, то теперь это конечная матрица.
Предположим, что Z — диагонализуемая матрица, собствен-
ные значения которой равны ^i,...,zj, а соответствующие соб-
ственные векторы — ei,...,е^. Тогда мы знаем, что векторы
ei A где i < j, образуют базис пространства Л2(И) и
(Z Л Z){ei A ej) = Zei A Zej ~ ziZjei А
так что Z{Zj для i < j — собственные значения Z A Z на A2(V).
Аналогично, Z{ZjZ^ для г < j < к — собственные векторы Z А
Z Л Z на A3(V) и т. д. Поэтому, если ZA обозначает прямую
сумму рассмотренных операторов, т. е. оператор на пространстве
Д(У) = R ф V ф (v Л V) ф • • •, где
/I 0 0 0 • \
0 Z 0 0
гл = 0 0 ZAZ 0
0 0 0 Z A Z Л Z
1180
Глава 22. Термодинамика
то
tr 7Л = 1 + Zi + ZiZj + У2 zizizk + ••
= fI(l + zi) = Det(I + Z).
Пусть Z = eY. Воспользуемся формулой
(/)Л = еОД
которая является прямой суммой всех формул
1 — е° = е^оСУ) на ]ц,
eY = eD^ HaV,
еу/\ еу — е°2^ на Л2(У) ит,д.
Тогда получаем
trA eD^ = Det (К + еу),
где в левой части уравнения мы использовали оператор trA, что-
бы отразить то, что след вычисляется в пространстве Л(У). Если
ВЗЯТЬ Y — е-(/М+02Х), то получим
Det(I + e-(/W/?2X)) = trA e-~D(f3^/32x)t
Давайте еще раз обсудим странные математические манипу-
ляции, которыми мы здесь занимались. Начнем с простой сис-
темы, которая может находиться в d состояниях с «энергиями»
£1,... ,£d. Соответствующая функция разбиения имеет вид
Z(/3) = e~^£1 + + е-Р£*.
Если X — диагональная матрица с собственными значениями
£1,..., то эту формулу можно переписать в виде
Z(J3) = tre~0X. (22.49)
Пусть V обозначает векторное пространство Rd, и след есть про-
сто след матрицы. Мы хотим рассмотреть более сложную систе-
му, в которой на каждом «энергетическом уровне» может нахо-
диться различное число частиц — «оккупантов». У нас есть две
22.12. Определители и следы
1181
равновесных наблюдаемых — полное число оккупантов и полная
энергия. Теперь функция разбиения зависит от двух переменных,
и переход от простой системы к этой сложной состоит в следую-
щем:
Заменяем V на T(V), и тогда
^(/31,32) — tr0 (статистика Больцмана-Пуассона);
заменяем V на Л(И), и тогда
~ trA e-D(M+02X} (статистика Ферми-Дирака).
Таким образом, различие между случаями Больцмана-Пуас-
сона и Ферми-Дирака состоит в том, что используется внешняя
алгебра Л(У) вместо полной тензорной алгебры Т(У). В слу-
чае Бозе-Эйнштейна мы заменяем внешнюю алгебру симметри-
ческой алгеброй 5(У) (алгеброй всех полиномов на пространст-
ве V*). Используются те же соображения, что и в случае Ферми-
Дирака, но теперь у нас будет
trsym Z == Det(I - Z)-1.
Все полученные результаты собраны в таблице 22.5.
Таблица 22.5
Система Векторное пространство Функция разбиения
Простая V ехр(—ДХ)
Больцмана-Пуассона T(V) tr0 e~D(Prf+fhX) = Det(e”^11I+/32X))
Ферми-Дирака Л(У) trA e-D^+p2x) = Det(I + e~№K+^2X))
Бозе-Эйнштейна Ж) trsym e~D(^il+(32X) = Det (I —
1182
Глава 22. Термодинамика
22.13. Квантовые состояния и квантовая
логика
Давайте еще раз рассмотрим построения предыдущего парагра-
фа в простейшем случае. Пусть система будет конечным мно-
жеством, в котором р приписывает одинаковые веса всем точкам,
т.е. систему А из параграфа 22.6. В такой системе «интегриро-
вание» есть просто суммирование. Наблюдаемое — это функция,
определенная на этом конечном множестве, а состояние — неотри-
цательная функция, сумма значений которой равна 1. Но в этот
раз мы будем записывать функции как диагональные матрицы,
так что суммирование становится вычислением следов этих мат-
риц. Итак, состояние р записывается в виде
р = /р(1) 0 0 0 Р(2) 0 0 0 • р(3) . 7
и наблюдаемое J аналогично
р(1) 0 0 ...\
0 J(2) 0
J — 0 0 J(3)
1 ;
так что
£(J;p) = trJp. (22.50)
Функция разбиения задается в форме
F(0) = tre~^x, (22.51)
где
X = • • • о о £> © .S' о ••• S <=> <=> < '
22.13. Квантовые состояния и квантовая логика
1183
Тогда равновесные состояния имеют вид
0 о -Х
0 е-/?е2 0
Рр = Ffjir1 0 0 е ~0ез . . .
• •7
или
Рр = F(/3) (22.52)
Переход от простой системы к случаю с числами заполнения
состоял в замене конечномерного векторного пространства V на
одно из более широких пространств T(V), A(V) или S(V), в за-
висимости от того, какая «статистика» исследуется. При этом
все рассматриваемые матрицы были диагональными, поэтому ис-
пользование матриц казалось весьма искусственным. Здесь же
давайте рассмотрим эту роль матриц более серьезно.
Пусть V ~ векторное пространство, где определено скаляр-
ное произведение. (В силу важных физических причин мы будем
рассматривать комплексное векторное пространство V, где (•,•)
— положительно определенное скалярное произведение, так что
V является унитарным пространством. В реальных задачах час-
то приходится рассматривать бесконечномерное пространство V.
Но для понимания ключевых идей нет необходимости включать
сюда еще и технические проблемы теории (унитарных) гильбер-
товых пространств, поэтому все понятия мы продемонстрируем
на конечномерном пространстве.) Вспомним, что оператор А в
пространстве V называется самосопряженным^ если
(Ли, v) — (и, Лу) для всех и, v Е V.
Рассуждения, приведенные в параграфе 4.3 (выполненные для
комплексного векторного пространства), показывают, что лю-
бой самосопряженный оператор можно привести к диагональ-
ному виду, т. е. что существует такой ортонормированный базис
ei,... , е^, что
Лег — z — 1, *.., б?,
где Xi — вещественные числа. (В случае бесконечномерного про-
странства соответствующая теорема, модифицированная опреде-
ленным образом, называется спектральной теоремой.) Оператор
1184
Глава 22. Термодинамика
А называется неотрицательным, или А > 0, если все Аг 0. Дру-
гими словами, А неотрицателен, если и только если
(Ли, и) 0 для всех и е V,
что можно легко проверить, записав и в виде линейной комбина-
ции всех ег. Теперь можно ввести следующие определения.
Квантовая система ~ унитарное (гильбертово) простран-
ство V.
Квантовое (статистическое) состояние — неотрицатель-
ный самосопряженный опрератор р, для которого
tip = 1.
Энтропия состояния р задается формулой
Ent(p) = — trplogp.
Квантовое наблюдаемое — самосопряженный оператор.
Ожидаемое значение наблюдаемого А в состоянии р задается
формулой
Е(Л;р) = tr Ар.
Пусть k коммутирующих наблюдаемых, т.е.
предположим, что
Ji Jj = JjJi для всех i и j.
Пусть /3 ~ (/31,... ,/3&), где Д — вещественные числа, и пусть /3J
— наблюдаемое
[33 ~ [3\J\ + • • • + (З^Зк-
Тогда соответствующая функция разбиения определяется выра-
жением
F(/3) = tre-^J, (22.53)
и равновесные состояния рр определяются выражением
Рв = F^e-^.
22.13. Квантовые состояния и квантовая логика
1185
Итак, ожидаемое значение наблюдаемого А в равновесном состо-
янии, соответствующем /3, имеет вид
= F(/3)-1tr Ае~^3. (22.54)
Уравнения (22.53) и (22.54) являются теоретическим базисом
квантовой статистической механики. Приведем цитату с первой
страницы книги Фейнмана «Статистическая механика»: «Это
фундаментальное соотношение является вершиной статистиче-
ской механики; остальное ее содержание есть либо спуск с верши-
ны, когда основные принципы применяются к частным вопросам,
либо восхождение на нее, когда выводятся основные соотноше-
ния ...»
В случае, когда V — бесконечномерное пространство, след
оператора становится бесконечным рядом, который может и не
сходиться. Поэтому не все операторы имеют след. Соответствен-
но, функция F(/3) будет сходиться только в ограниченной области
/3. Сейчас мы оставим эти проблемы в стороне и займемся моде-
лью конечномерного пространства V.
Основное различие между квантовой и классической систе-
мами состоит в том, что в классической системе наблюдаемая
является функцией (на конечном множестве), которую будет диа-
гональной матрицей, а для квантовой системы мы допускаем все
(самосопряженные) матрицы. На первый взгляд это может пока-
заться только технической модификацией (которая подтвержда-
ется экспериментами на протяжении шестидесяти лет). На самом
же деле это наиболее глубокая революция в истории науки, пото-
му что она изменяет элементарные правила логики. Давайте это
объясним.
Опять начнем с классической системы. Наблюдаемое типа «да
или нет» является функцией /, принимающей значения 0 или 1.
Это соответствует любому эксперименту, в котором ответ зада-
ется неким индикатором (например, выключателем или светом),
включен он или нет. Когда мы говорим, что функция f прини-
мает значения 0 или 1, — это то же самое, что
/(m)2 = /(т)
для всех т, или короче
/2 = /• (22.55)
1186
Глава 22. Термодинамика
Каждая такая функция соответствует подмножеству В С М мно-
жества, где f = 1. Поэтому для любого заданного подмножества
В мы имеем функцию22 /в, для которой
/в(тп) = 1» если m 6 В, и /в = 0, если т £ В.
Если / и д — две такие функции «да или нет», то в классической
системе
fg — тоже функция «да или нет». (22.56)
Действительно, если С и D — подмножества, то
fcfD - /спр, (22.57)
поскольку /с(^)/р(т) = 1, если и только если для обеих функ-
ций мы имеем /с(т) = 1 и /р(т) = 1- Такое умножение функций
соответствует пересечению подмножеств, т. е. логической конъ-
юнкции — точка принадлежит подмножеству СпП, если и толь-
ко если она принадлежит и С, и D. Например, подмножества С
и D не пересекаются, т. е.
С П D = 0, если и только если fcfD ~ 0.
Если С и D не пересекаются, то
fc + fD = fcvD, (22.58)
поскольку обе части равенства равны 1, когда аргумент принад-
лежит С или D (и не существует точек, принадлежащих обоим
подмножествам). Дистрибутивный закон умножения
fetfc + /р) = fBfc + /в/р. (22.59)
— это перевод дистрибутивного закона теории множеств
В П (С и D) - (В ПС) и (В П D), (22.60)
что, в свою очередь, является записью дистрибутивного закона
логики. Пусть В обозначает утверждение т Е В и т.д., тогда О
22называемую характеристической функцией, или индикатором множест-
ва В. — Прим. ред.
22.13. Квантовые состояния и квантовая логика
1187
обозначает конъюнкцию: формула В П С утверждает, что и В, и
С верны. Аналогично, U обозначает (неисключающую) дизъюнк-
цию, т. е. формула CUD означает, что верно либо С, либо D, либо
и то, и другое. (Далее мы будем употреблять «или» в неисклю-
чающем смысле, не уточняя «или оба».) Итак, дистрибутивный
закон просто отражает элементарный логический принцип:
Если мы говорим, что верны В и (С или D), то это то
же самое, что сказать: верно (В и С) или (В и D).
Рассмотрим соответствующую ситуацию в квантовых системе.
Наши наблюдаемые уже являются не функциями, а самосопря-
женными операторами. Мы уже не можем говорить о «значени-
ях» наблюдаемых, а только о их собственных значениях. Поэто-
му назовем самосопряженный оператор тг наблюдаемым типа «да
или нет», если его собственные значения равны 0 или 1. Это про-
изойдет, если и только если
%2 - тг, (22.61)
что аналогично (22.55). Условие (22.61) означает, что тг является
проекцией. Более того, если ei,... ,ej — собственные векторы тг,
то тг — ортогональная проекция на подпространство, натянутое
на собственные векторы, соответствующие собственному значе-
нию 1. Таким образом, каждое наблюдаемое «да или нет» соот-
ветствует подпространству (вместо подмножества), и можно пи-
сать 7гд, обозначая ортогональную проекцию на подпространство
А. Заметим, что теперь нулевой оператор соответствует ортого-
нальной проекции на нулевое подпространство {0} и
тгстгр — 0, если и только если С П D = {0}, (22.62)
поэтому нулевое подпространство {0} играет роль, аналогичную
пустому множеству. Заметим, что если ttcttd — 0, то, перейдя к
сопряженным операторам, имеем
о = (тгстгр)* = 7Гр7Г^ =
откуда получаем, что тгртгс = 0 и
(тгс + ТГр)2 = 7Г^ Ч- 7Гр = 7ГС + Яр.
1188
Глава 22. Термодинамика
Таким образом, тгс + тгр является наблюдаемым «да или нет».
Очевидно, что это ортогональная проекция на прямую сумму
С ф D ортогональных подпространств С и D. Итак, условие
тгс + = 7ГСФР, если 7VC7TD = 0 (22.63)
является полной аналогией (22.58), где ф заменяет U. Однако
(22.56) полностью нарушается. Вообще говоря, для произволь-
ных подпространств С и D равенство itc^d = ттртгс не выполня-
ется, и поэтому оператор не является самосопряженным, и,
следовательно, он не является наблюдаемым. Например, если С
и D — две неортогональные прямые на плоскости, то Ф 0.
Но образом тгс^Р является С, а образом тгртгс — D. Поэтому
/ 'Kd'kc- Проблема возникает из некоммутативности умно-
жения матриц. Заметим, что аналогом дистрибутивного закона
теории множеств являлось бы утверждение
В А (С Ф D) - (В А С) © (В А В),
которое верно далеко не всегда. Действительно, если в качестве
С взять ось х, а в качестве D — ось у на плоскости, то С ф D —
вся плоскость, и поэтому В А [(С ф В) = В для любой прямой В
на этой плоскости. Но если В -- любая прямая, отличная от осей
х иу, то В А С = В A D — {0}, поэтому (В А С) ф (В А В) =
{0} ф {0} = {0}, и мы уже не имеем равенства двух частей.
Итак, в квантовой логике не выполняется дистрибутивный за-
кон. Как уже упоминалось, на протяжении многих лет экспери-
ментально подтверждается справедливость квантовой механики.
Поэтому эксперимент показывает, что, работая с квантовыми на-
блюдаемыми, необходимо отказаться от одного из наиболее дра-
гоценных принципов логики.
Резюме
А. Формулировка Каратеодори второго закона
термодинамики
Вы должны уметь объяснить, при каких обстоятельствах сущест-
вуют точки в окрестности точки Р, которые нельзя соединить с
ней нулевой кривой 1-формы а.
Задачи
1189
Вы должны уметь формулировать и объяснять формулу Ка-
ратеодори для второго закона термодинамики.
Вы должны уметь объяснять понятия абсолютной темпера-
туры и энтропии в терминах дифференциальных форм и кон-
турных интегралов, уметь описывать, как эти величины можно
вычислять по экспериментальным данным.
Задачи
22.1. Пусть а = (у3 + у) + dy. Дайте характеристику множе-
ству точек в пространстве R2, которые можно соединить с точкой
[ 1) с помощью нулевой кривой.
22.2. Пусть о = ydx + xdz. Найдите нулевую кривую формы о, кото-
/1\
рая соединяет начало координат с точкой 1^1? где Ъ > 0 и с > 0.
\с /
Кривая не должна проходить через какие-либо точки, у которых
х, у или z равны нулю, за исключением начала координат.
22.3. Пусть а ~ xdy. Покажите, что любые две точки в пространстве
R3 можно соединить нулевой кривой формы а, несмотря на то,
что о Л da = 0. Покажите, что для формы /3 = (1 + х2) dy две
точки с различными координатами у не могут быть соединены
нулевой кривой.
22.4. Форму а = 2уех dx запишите в виде а — f dg и в виде а = F dQ,
где F не пропорционально /.
22.5.
Рассмотрите один моль одноатомного газа, для которого pV ~
3
RT и U — -pV. Предположим, что начальные параметры газа:
р = 32, V = 1, но потом он расширяется до параметров: р = 1,
V = 8. Вычислите работу, совершенную газом, и количество
тепла, поглощенного им, в следующих процессах.
(а) Сначала газ охлаждается при постоянном объеме, и его дав-
ление р понижается до 1; затем объем V увеличивается до
8 при постоянном давлении.
(Ь) Сначала газ изотермически расширяется до объема V = 8;
потом при фиксированном объеме давление снижается до 1.
(с) Происходит процесс, в ходе которого рК5//3 = 32.
1190
Глава 22. Термодинамика
22.6. Для одноатомного идеального газа из упражнения 22.5 напиши-
те форму для тепла в виде а = Т dS, Определите энтропию S (с
точностью до аддитивной константы) как функцию р и V. Про-
верьте, что dT /\dS — dp Л dV.
22.7. Сосуд объема V заполнен электромагнитным излучением при
температуре Г, давлении р = (где @ ~ пост°янная). Его
энергия U = 3pV.
(а) Записав форму тепла dU + р dV в виде а = TdS, найдите
выражение для S через р и V.
(Ь) Предположим, что начальный объем сосуда равен Vo, а тем-
пература То. Объем увеличивается адиабатически до вели-
чины 64Vq. Определите конечную температуру и работу, вы-
полненную при расширении.
22.8. (а) В машине Карно тепло поглощается при температуре 4То,
а отдается при температуре То- Какова максимальная доля
поглощенного тепла, которая может быть преобразована в
полезную работу?
(Ь) Предположим, что эта же машина работает как холодиль-
ник. Если тепло Q поглощается при более низкой темпера-
туре То, то какую работу необходимо затратить для этого
холодильника?
22.9. Система из N протонов, каждый из которых имеет магнитный
дипольный момент д, помещена во внешнее магнитное поле Н.
Разумно полагать, что Н — единственная конфигурационная пе-
ременная. Магнитный момент системы протонов М и соответ-
ствующая энергия U при больших температурах Т хорошо ап-
проксимируются формулами
Np?H _ ЛГ(цН)2
кТ ’ “ кТ
Работа, совершенная системой, определяется выражением W =
J М dH, Поглощенное тепло равняется ДС7 + W. Получите выра-
жение для энтропии S через Т и Н,
22.10. Рассмотрим систему, у которой объем V — единственная конфи-
гурационная переменная. Докажите следующие соотношения.
дТ
адиабат.
др\
/ V—const
Задачи
1191
I'M
I /ил / I rYT1 /
\^v / изотерм. / V=const
(Указание: используйте равенство dT /\dS = dp A dV.)
22.11. «Свободная энергия Гельмгольца» F для системы связана с внут-
ренней энергией U соотношением F ~ U — TS.
(а) Покажите, что если система взаимодействует с окружени-
ем изотермически, то свободная энергия F равна работе,
совершенной над системой.
(Ь) Предположим, что F записана как функция V и Т. Вычис-
лите ее частные производные по этим переменным.
(с) Найдите функцию F(V\ Т) для идеального одноатомного га-
за из упражнения 22.5.
dV Л dT
22.12. Пусть К = у обозначает изотермическую сжимаемость,
dV Л dp
и a = у.—^. обозначает коэффициент теплового расширения
при постоянном давлении. Докажите соотношение
а2
Cp = Cv+VT—.
Л
22.13. Для одноатомного газа из упражнения 22.5 получите явное выра-
жение для функции Z(/3, V). Вычислите ее частные производные
и покажите, что они равны — U и /Зр соответственно.
22.14. Предположим, что энтропия системы S зависит только от ее
внутренней энергии U согласно формуле S = N(U/Uq)1/2. Полу-
чите выражения для теплоемкостей этой системы в зависимости
от температуры.
22.15. Рассмотрим систему трех частиц. Две из них — неразличимые
бозоны, а третья — какая-то другая частица. Каждая частица
может находиться в одном из трех состояний, причем все они
имеют одинаковую энергию.
(а) Какова вероятность того, что все три частицы находятся в
одном состоянии?
(Ь) Какова вероятность того, все три частицы находятся в раз-
ных состояниях?
1192
Глава 22. Термодинамика
22.16. Для классического магнитного диполя с моментом д в магнит-
ном поле Н энергия равна U = —pH cos (9, где 0 — угол между
этими векторами. Вычислите функцию разбиения этой системы,
интегрируя по всевозможным направлениям.
22.17.
22.18.
Рассмотрим систему, у которой есть три состояния с энергиями
—е, 0 и е. Предположим, что ожидаемое значение энергии равно
— Определите вероятности этих трех состояний.
Предположим, что в системе есть одно состояние с энергией —г,
два состояния с энергией 0 и одно состояние с энергией в. Если
1
ожидаемое значение энергии равно — -е, то каковы вероятности
этих состояний?
22.19. Пусть в системе есть только два состояния: одно с энергией —г,
другое с энергией г. Найдите функцию разбиения этой системы
и используйте ее для определения энергии U и энтропии S в
зависимости от температуры Г.
Приложение: доказательство теоремы
о нормальной форме
1. Ранг 1-формы
Сначала определим ранг 2-формы. Пусть Q — 2-форма. Для
каждого положительного целого числа к можно рассмотреть
2/с-форму
Qk ~ Q Л Q Л • • • Л Q (к раз).
Для каждой точки х пусть к будет таким неотрицательным це-
лым числом, что 0, но = 0. Вообще говоря, целое
число к может меняться от точки к точке. Ранг формы Q в точке
х равен 2к. Нам, главным образом, интересны формы постоянно-
го ранга, когда 2к не зависит от х. Если 2к = 0, то Q = 0. Тогда
форма Q — dx Л dy имеет ранг 2, поскольку Q 0, в то время как
Q2 = 0. Форма
Q = dx Л dy + du Л dv
имеет ранг 4, поскольку
Q2 = 2dx Л dy Л du Л dv 5^ 0,
Приложение
1193
но Q3 = 0. (Здесь мы предполагаем, что х, у, и, v и т.д. —
независимые функции.)
А теперь определим ранг 1-формы. Это немного сложнее, по-
этому воспользуемся индукцией. Если си = 0 в точке х, то мы
говорим, что ранг си в х равен 0. Если сиж / 0, но dcvx = 0, то мы
говорим, что ранг си в точке х равен 1. Если сих 0 и dwx ± 0,
но сих Л dcux = 0, то ранг си в точке х равен 2. В общем случае мы
ищем такое положительное целое число /с, что
шх Л / 0,
но
шх Л (dcu)* - 0.
В этой ситуации существует две возможности.
Если (dcu)£ ф 0, то ранг си в точке х равен 2k.
Если (dcu)£ = 0, то ранг си в точке х равен 2к — 1.
Конечно, таким образом ранг си определен в каждой точке х. Нам
интересны только те случаи, когда ранг постоянный. Поэтому
на самом деле мы имеем в виду, что: ранг си равен 2к + 1, если
cu Л (dcu)* нигде не обращается в нуль, a (dcu)fe+1 тождественно
равна нулю; ранг си равен 2к, если (dcu)fc нигде не обращается в
нуль, но везде выполняется тождество cuA(dcu)fc = 0. Если к этому
тождеству применить оператор d, то (dcu)fc+1 тождественно равна
нулю. Итак, если 1-форма си имеет ранг 2к или 2к +1, то 2-форма
dcu имеет ранг 2к.
Примеры. Нулевая форма имеет ранг 0; dx$ имеет ранг 1, по-
тому что d(dxo) = 0, откуда следует к — 0; Xi dx2 имеет ранг 2
в области Xi 1, потому что форма d(xi dx2) ~ dxi Л dx2 имеет
к = 1 и ад dx2 Л dxi Л dx2 = 0; dxo + dx2 имеет ранг 3, потому
что d(dxo + xi dx2) = dx\ Л dx2 имеет к — 1, в то время как
(dxo 4- xi dxs) Л dxi Л dx2 = dxo Л dxi Л dx2 ф 0.
В общем случае очевидно, что
dxQ 4“ х^ dx2 4- хз dx^ 4- * * * 4~ X2k—1
1194
Глава 22. Термодинамика
имеет ранг 2к 4-1, а
Xi dx2 4- Хз dx4 4-F Х2к~ 1 dx2k
имеет ранг 2к в области, где не все #26-1 равны нулю.
В этом приложении мы хотим доказать, что это фактически
единственные примеры. А именно, если си ~ линейная дифферен-
циальная форма постоянного ранга 2 А;, то всегда можно найти
такие локальные координаты #i, #2,..., #26» что
си = #1 dx2 4- #з dx^ 4-F #26-1 dX2k,
а если ранг си равен 2к 4~ 1, то всегда можно найти такие коорди-
наты #о, #1, #2, • • • ,#26? ЧТО
cu = d#o 4- #1 d#2 + Хз dx^ 4-1- #26-1 dx2k-
Это и есть тот факт, по модулю которого мы доказали теорему
Каратеодори.
2. Сведение к теореме Дарбу
Как можно заключить из предыдущей теоремы, всегда можно
ввести такие координаты, что
dw — dxi Л d#2 4- d#3 Л d#4 4- • • • 4- d#26-i A dx2k-
Теорема Дарбу (ее мы докажем позднее в этом приложении)
утверждает, что если Q ~ любая замкнутая 2-форма постоянного
ранга 2 А:, то всегда можно ввести такие координаты, что
Q = dx± Л d#2 4- d#3 Л d#4 4--F dx2k-i Л d#26-
Давайте допустим, что эта теорема доказана, и с ее помощью
получим теорему о нормальной форме. Если ранг си нечетный,
то это совсем просто. Действительно, dw — замкнутая 2-форма
ранга 2А:, поэтому можно записать ее в виде
dw — dxi Л d#2 -F dx3 Л d#4 4- • • • 4- d#26-i Л d#26
= d(#i dx2 + #3 dx4 4---F #26-1 dx2k,
так что
d(w - (#i dx2 4- #3 dx4 4----F #26-1 dx2k)) = 0.
Приложение
1195
Откуда, в силу леммы Пуанкаре, имеем
ш - (xi dx2 + Хз dx4 4--I- X2k-1 dx2k) ~ dxo,
где Xq — некоторая функция. Тогда
UJ dxQ “I- Xi dx% 4~ Х3 dx± ~Н * * * 4“ Х2Д;—1 dX2k*
Но мы предположили, что
си Л (dcu)fc = dxQ Л dxi Л dx2 Л • • • Л dx2fc-i Л dx2k
не равняется нулю. Следовательно, dxg не зависит от остальных
dxij и можно использовать xo,xi,X2, •.. ,X2fc в качестве коорди-
нат. Итак, с учетом теоремы Дарбу о замкнутых 2-формах, это
доказывает теорему о нормальной форме для линейных диффе-
ренциальных форм нечетного ранга.
Для форм четного ранга доказательство несколько сложнее.
Мы докажем, что если форма о; имеет постоянный ранг 2k, то
можно найти такую положительную функцию /, что
W = /ст,
где форма а имеет ранг 2& — 1. Если теперь применить теорему
о нормальных формах нечетного ранга, то можно написать
a = dxo + wi dx2 4----h w2fc-3 ^2fc-2,
где xo, wi, X2, W3 и т. д. — координаты. Тогда
w = f dxo 4- /wi dx2 4-
= Xi dX2 + X3 dx^ 4---1- X2k-1 dX2k,
если положить
Xl^fwly X3 = fW3, ^2fc-3 = /W-3,
^2/c—1 “ /> *^2/c = ^0 •
В силу того, что ф 0, внешнее произведение всех dx^ не
равно нулю, так что dxi линейно независимы во всех точках, и х«
1196
Глава 22. Термодинамика
образуют часть системы координат. Следовательно, мы должны
доказать, что си = /сг, где а имеет ранг 2к—1 и / положительна. С
этой целью воспользуемся теоремой Дарбу (пока не доказанной)
и напишем
dw = dyi Л dy2 + dy3 Л dy4 + • • + dy2k-i A dy2k,
где yi,... ,уп — подходящие локальные координаты. Можно ис-
пользовать эти координаты и написать
си = dyi + а2 dy2 Ч-----И ап dyn.
Тогда поскольку си Л (dcu)fc = 0, все щ = 0 для i > 2k. Из записи
формы dcu следует, что все щ для i 2 А; не зависят от переменных
2/2fc+i, • • •, Уп, поскольку иначе в выражении для dcu мы получили
бы ненулевые коэффициенты при dyi Л dyj, где i 2к и j > 2к.
Итак, доказывая теорему о нормальных формах четного ранга
2/с, можно предположить, что мы работаем в пространстве R2fc.
(Все остальные переменные роли не играют.) Итак, си Л (dcu)^'1
— ненулевая форма степени 2к — 1 в пространстве R2fe. Следо-
вательно, в каждой точке своей области определения она задает
прямую, т. е. одномерное пространство всех решений уравнения
= 0.
Таким образом, ш Л (dw)fc-1 определяет «элемент поля направле-
ний», другими словами, систему обыкновенных дифференциаль-
ных уравнений. Давайте выберем (2к — 1)-мерную поверхность
и будем рассматривать точки этой поверхности как начальные
условия. Тогда каждая точка вблизи гиперповерхности лежит на
единственной кривой решения, и поэтому соответствует опреде-
ленному моменту времени t (параметр кривой) и определенной
точке (начальное условие) на гиперповерхности.
Если на гиперповерхности ввести координаты 21,..., то
£, ., z2k-i будут локальными координатами в пространстве
В2/с. В этих координатах £ = Э/сИ. Другими словами, формы
си Л (dcu)*1”1 и dzi Л dz2 Л • • • Л dz2k~i
определяют один и тот же элемент поля направлений. Тогда
cu Л (dcu)fc-1 — gdzi Л dz2 Л • • • Л d^fc-i,
Приложение
1197
где д — функция, нигде не обращающаяся в нуль. Можно при
необходимости заменить z\ на — z\ и считать, что д — положи-
тельная функция. Пусть fk = д. Если определить форму а ра-
венством w ~ fa, то
dw — df Ла + f da,
откуда
w Л dw — f2a Л da.
Далее, находим
w Л (dw)k~1 = fka Л — gdz± A dz2 A • • • A dz2k-i-
Тогда
a A (dcr)*-1 = dz\ A dz2 A * • A dz2k-l-
Действуя оператором d на обе части этого уравнения, получаем
(dcr)fc = 0.
Другими словами, а — форма ранга 2к — 1. Это доказывает тео-
рему о нормальной форме в предположении теоремы Дарбу.
3. Доказательство теоремы Дарбу
Для доказательства этой теоремы сделаем ряд редукций. Нач-
нем с замкнутой 2-формы Q ранга 2к в n-мерном пространстве.
Предположим, что п > 2к. Можно выбрать такое векторное поле
£, что i(£)Q = 0. Тогда, как и раньше, можно (решая систему
обыкновенных дифференциальных уравнений) ввести координа-
ты yi,..., Уп-i Д такие, что £ = d/dt. Поскольку г(£)П тожде-
ственно обращается в нуль, форма П не содержит dt, если запи-
сать ее в этих локальных координатах, т. е.
Q = dyi Л dyj.
Но тогда уравнение с/П = 0 означает, что все da^/dt == 0, так как
иначе в d£l будут несокращаемые члены (da^/dt) dt Л dyi Л dyj.
Таким образом, зависят только от yi,... Другими сло-
вами, на самом деле Q — 2-форма в (п — 1)-мерном пространстве
1198
Глава 22. Термодинамика
координат уг. Если п — 1 > 2к, то можно повторить процедуру
и убрать дополнительные координаты, т.е. при доказательстве
теоремы Дарбу можно предположить, что 2к — п.
Утверждается, что это условие означает, что форма Q несин-
гулярна в каждой точке в том смысле, что если
~ о
для касательного вектора £р в точке р, то £р = 0. Действительно,
из этого уравнения очевидным образом следует, что
= о.
к раз
Но [Q Л Q Л • • • Л Q]p — n-форма в n-мерном пространстве, а
пространство n-форм одномерно. Поскольку мы предположили,
что n-форма [Q A Q Л • • • Л 0, то = 0. (Это следует
на самом деле из того, что в n-мерном пространстве условие
несингулярности Q эквивалентно условию, что эта форма имеет
ранг п.) Сказать, что Q несингулярна, можно и по-другому: п х п
матрица (% (у)), возникающая в выражении Q = 52 aij dyi Л dyj,
несингулярна для всех у.
Доказательство теоремы Дарбу разобъем на две части.
(а) Дифференциально-геометрическая часть, в которой утвер-
ждается, что всегда можно провести локальную замену коорди-
нат так, чтобы в новых координатах матрица (а^(у)) была по-
стоянной, т. е. все матричные элементы не зависели от у.
(Ь) Алгебраическая часть, в которой утверждается, что мож-
но сделать линейную замену координат так, чтобы постоянная
матрица (а^ ) имела вид
’о1 0% ••• 0 \
0 ? ’о1 ••• О
\ 0 о ••• ° "7
Это — теорема о кососимметричных билинейных формах в век-
торном пространстве, которую мы докажем по индукции.
Приложение
1199
Предположим, что V — двумерное векторное пространство
и Q - невырожденная билинейная форма в этом пространстве.
Пусть и — произвольный ненулевой вектор в V, Тогда линейная
форма
i(u)H — Q(u, •)
является ненулевой линейной формой в силу невырожденности
П. Следовательно, можно найти такой вектор v, что
П(и, v) = 1.
Если в качестве базиса пространства V взять и и v, a dy± и dy%
образуют дуальный базис, то
П = dyi Л dy2,
что мы и хотели получить. Пусть теперь V — n-мерное простран-
ство, и п — четное число > 2. Возьмем те же и и v, что и раньше,
и пространство Vi, натянутое на эти вектора. Тогда
V = viev^,
где Vf*- обозначает ортогональное дополнение по отношению к
П. Ограничение П до невырождено. Поэтому желаемый ба-
зис пространства V/- можно найти по предположению индукции.
Тогда разложение в прямую сумму вместе с результатом для дву-
мерного случая доказывает теорему для пространства V.
Получим теперь геометрический результат (а). Если матрич-
ные элементы а^-(у) зафиксировать в какой-то точке уо, то полу-
чим невырожденную 2-форму По, совпадающую с W в точке уо.
Таким образом, достаточно доказать следующее.
Пусть Qi и По — две замкнутые невырожденные 2-формы,
которые совпадают, например, в 0. Тогда существует диффео-
морфизм /, определенный в окрестности 0, для которого выпол-
няется равенство
/*П1 = По.
Докажем это утверждение, снова решая дифференциальные
уравнения. Но здесь потребуется некоторая подготовка. Пусть
= (1 — t)Ho + tHi — По + ter, где сг = Hi — По-
1200
Глава 22. Термодинамика
Тогда da ~ 0 и а равно нулю в 0. Поскольку По несингулярна,
то и ПДО) = По несингулярна для всех t. Следовательно, мож-
но найти окрестность начала координат, где И* несингулярна для
всех 0 < t 1. Переходя к меньшей окрестности (если это необ-
ходимо) можно предположить, что наша окрестность является
звездной областью. Следовательно, существует определенная в
этой окрестности 1-форма /3 такая, что
а = £(0) = 0.
Следовательно, форма Не невырождена, и существует единствен-
ное (зависящее от t) векторное поле £f, для которого
i(£t№t = -0.
Поле мы рассматриваем как зависящую от времени систе-
му обыкновенных дифференциальных уравнений. Решение этих
уравнений дает нам однопараметрическое семейство диффеомор-
физмов ft, для которого /о = id и касательный вектор к кривой
Д(х) в момент времени t есть £t(A(x))- Кроме того, Д(0) = 0 для
всех t. А теперь из фундаментальной формулы дифференциаль-
ного исчисления форм (глава 18) мы имеем
= ft (+ *(&) dat + = 0,
tit \ Civ /
поскольку
d
dftt — 0, — Ht = a
dt
и
dz(£jHt = ~d(3 — —a.
Следовательно,
f1 d
/1*n1-Q0 = №-m= / T(f^dt = o.
Jo dt
Итак, мы получили искомый диффеоморфизм Д, что завершает
доказательство теоремы Дарбу и вместе с ней доказательство
теоремы о нормальной форме, на которую мы ссылались при
доказательстве теоремы Каратеодори.
Рекомендуемая литература
Повторим, что приведенный ниже перечень книг следует счи-
тать не библиографией, а дополнительной литературой. Книга
Loomis and Sternberg еще заметнее, чем в случае тома I, пре-
тендует на роль параллельного учебника. Мы ссылаемся на нее,
когда нужны точные (или более абстрактные) математические
доказательства. Точно так же Фейнмановские лекции мож-
но считать универсальным справочником по физике.
Основное алгебраическое содержание тома II составляет пере-
ход от линейной алгебры к полилинейной. Книга GREUB является
ясным и аккуратным введением в эту область. В частности, в ней
дается подробное описание тензорной алгебры, симметрической
алгебры и алгебр Клиффорда, которых мы только касаемся.
Главы 12 и 13 посвящены теории электрических цепей. Клас-
сический учебник по теории цепей — это Guillemin. В книге
Lorrain and Corson обсуждаются теоремы о цепях из гла-
вы 8. Мы рекомендуем ознакомиться с вероятностным аспектом
теории цепей опять-таки по книге Doyle and Snell, а для бо-
лее серьезного изучения почитать Kelly. По теории графов и ее
приложениям мы рекомендуем книгу Bondy AND Murty.
В главе 14 мы даем определения гомологий и когомологий с
целью ввести соответствующий язык и не вдаемся в подробности.
Для знакомства с этой областью на уровне этой книги см. кни-
гу Giblin, а на более высоком математическом уровне находит-
ся книга MUNKRES. После ее прочтения можно перейти к кни-
ге Вотт AND Ти, которая представляет собой великолепную и
элегантную трактовку многих глубоких вопросов алгебраической
1202
Рекомендуемая литература
топологии с точки зрения внешнего исчисления. Еще раз реко-
мендуем книгу Guillemin and Pollack как геометрически ин-
туитивное и математически строгое изложение дифференциаль-
ной топологии. Приложения внешнего исчисления, изучаемого в
главе 15, можно найти в книге Sternberg.
Главы 16-19 посвящены электричеству и магнетизму. Есть
много замечательных книг по этому предмету. Наиболее доступен
на уровне этой книги учебник Purcell, элегантно и предельно
ясно написанный, но в нем изложение ведется по принципу, от-
личному от нашего. В книге Misner ет al. электромагнетизм
обсуждается с использованием дифференциальных форм.
Имеется две серии книг, где математическая физика излага-
ется на существенно более высоком уровне, чем у нас. Это Reed
and Simon и Thirring. Первая из них математическая, вто-
рая физическая. Обе серии читать нелегко, но они того стоят.
В Thirring используется внешнее исчисление.
Классическим учебником по комплексному анализу является
Ahlfors; его полезно прочитать после нашей главы 20. Еще од-
на хорошая книга — POLYA AND Latta. Конечно, есть и многие
другие. Про асимптотические методы и их связь с комплексным
анализом можно прочитать в книге Olver, имеющейся в боль-
шой и маленькой версии. Книга Guillemin and Sternberg бе-
рет обсуждение асимптотики излучения из главы 21 в качестве
отправной точки для изложения современной теории интеграль-
ных операторов Фурье и геометрической теории асимптотик. При
этот от читателя требуется весьма серьезная математическая под-
готовка.
Имеются сотни книг по термодинамике и статистической ме-
ханике. История этой науки в форме иконоборчества имеется
в книге TRUESDELL. Кстати, он категорически не разделяет ту
точку зрения на термодинамику, которая принятая у нас здесь.
Книга BORN является классическим полупопулярным изложени-
ем указанных тем. Наша трактовка статистической механики до-
вольно близка к весьма объемной книге Tribus. Книга Kittel не
такая толстая и более элементарна, чем наше изложение. Стан-
дартным учебником является Reif, а в книге THOMPSON хорошо
Рекомендуемая литература
1203
изложены различные вопросы с более выраженных математичес-
ких позиций.
В этом курсе мы не занимались квантовой механикой, не счи-
тая краткого упоминания о квантовой логике в самом конце. Луч-
шее введение в этот предмет с математической точки зрения —
книга Mackey. Подробное обсуждение квантовой логики на вы-
соком научном уровне содержится в Varadarajan. Книга Вонм
— это сбалансированное и выверенное изложение, затрагиваю-
щее многие приложения. Другое доступное введение в данную
область — SUDBERY.
Хинчин А. Я. Математические основания теории информации. — Физ-
матгиз, 1954.
Ahlfors L. V. Complex Analysis. An Introduction to the Theory of Func-
tions of One Complex Variable. — New York: McGraw-Hill, 1978 (3rd ed.).
(International Series in Pure and Applied Mathematics.)
BOHM A. Quantum Mechanics: Foundations and Applications. — New
York: Springer, 1993 (3rd ed.); reprinted 2001. (Texts and Monographs
in Physics.)
Bondy J. A. AND Murty U.S.R. Graph Theory with Applications. —
New York: American Elsevier, 1976.
Born M. The Natural Philosophy of Cause and Chance. — Oxford Univ.
Press, 1964.
Bott R. and Tu L. W. Differential Forms in Algebraic Topology. — New
York: Springer, 1982. (Graduate Texts in Mathematics, 82.)
Русский перевод: Ботт P., Ту Л. В. Дифференциальные формы в
алгебраической топологии. — М.: Наука, 1989.
Doyle P.G. and Snell J.L. Random Walks and Electric Networks.
— Washington, DC: Mathematical Association of America, 1985. (Carus
Mathematical Monographs, 22.)
Feynman R. P., Leighton R. B. and Sands M. The Feynman Lectures
on Physics. Vol. 1-3. — Reading, MA: Addison-Wesley, 1963-1965.
Русский перевод: Фейнман P. П., Лейтон Р. Б. и Сэндс М. Фейн-
мановские лекции по физике. Вып. 1-9. — М.: Мир, 1965-1967.
Feynman R. Р. Statistical Mechanics. A Set of Lectures. — Reading, MA:
Perseus Books, 1998 (reprint of the 1972 original).
Giblin P. J. Graphs, Surfaces and Homology. An Introduction to Algebraic
Topology. — London: Chapman & Hall, 1981 (2nd ed.).
1204
Рекомендуемая литература
Greub W. Multilinear Algebra. — New York: Springer, 1978 (2nd ed.).
(Universitext.)
Guillemin E. A. Introductory Circuit Theory. — Wiley, 1953.
Guillemin V. W. and Pollack A. Differential Topology. -- Englewood
Cliffs, NJ: Prentice-Hall, 1974.
Guillemin V. W. and Sternberg S. Geometric Asymptotics. — Provi-
dence, RI: Amer. Math. Soc., 1977. (Mathematical Surveys, 14.)
Русский перевод: Гийэмэн В. и Стернберг Ш. Геометрические
асимптотики. — М.: Мир, 1981.
Kelly J.P. Reversibility and Stochastic Networks. — Chichester: Wiley,
1979. (Wiley Series in Probability and Mathematical Statistics.)
Kittel C. Thermal Physics. — W. H. Freeman, 1980.
Lax P. D. and Phillips R. S. Scattering Theory. — Academic Press,
1967; 1989 (2nd ed.).
Русский перевод: Лакс П. Д. и Филлипс Р. С. Теория рассеяния. —
М.: Мир, 1971.
Loomis L. Н. and Sternberg S. Advanced Calculus. — Boston, MA:
Jones and Bartlett, 1990 (revised ed.).
Lorrain P. and Corson D. R. Electromagnetic Fields and Waves. —
W.H.Freeman, 1988 (3rd ed.).
Mackey G. W. The Mathematical Foundations of Quantum Mechanics.
- Mineola, NY: Dover, 2004 (reprint of the 1963 original).
Marion J. B. and Heald M. A. Classical Electromagnetic Radiation. —
New York: Academic Press, 1980 (2nd ed.).
Misner C. W., Thorne K. S. and Wheeler J. A. Gravitation. — San
Francisco, CA: W.H.Freeman, 1973.
Русский перевод: МизНЕР Ч., Торн К. и Уилер Дж. Гравитация.
Т. 1-3. - М.: Мир, 1977.
Munkres J. R. Elements of Algebraic Topology. — Menlo Park, CA:
Addison-Wesley, 1984.
Olver F.W.J. Asymptotics and Special Functions. — Wellesley, MA:
A К Peters, 1997 (reprint of the 1974 original).
Русский перевод: Олвер Ф. Асимптотика и специальные функции. —
М.: Наука, 1990.
POLYA G. and Latta G. Complex Variables. — New York: Wiley, 1974.
Purcell E. Electricity and Magnetism. — McGraw-Hill, 1965.
Reed M. and Simon B. Methods of Modern Mathematical Physics.
Vol. I-IV. — New York: Academic Press, 1972-79.
Рекомендуемая литература
1205
Русский перевод: Рид М. И САЙМОН Б. Методы современной матема-
тической физики. Т. 1-4. — М.: Мир, 1977-82.
Reif F. Fundamentals of Statistical and Thermal Physics. — McGraw-Hill,
1965.
Ross S. M. Introduction to Probability and Statistics for Engineers and
Scientists. — Burlington, MA: Academic Press, 2000 (2nd ed.).
Scott W. Physics of Electricity and Magnetism. — Wiley, 1977.
Sommerfeld A. Electrodynamics. Lectures on Theoretical Physics,
Vol. III. — New York: Academic Press, 1952.
Sternberg S. Lectures on Differential Geometry. — New York: Chelsea,
1983 (2nd ed.).
Русский перевод: Стернберг Ш. Лекции по дифференциальной гео-
метрии, — М.: Мир, 1970.
Sudbery A. Quantum Mechanics and and the Particles of Nature. —
Cambridge University Press, 1986.
Thirring W. A Course in Mathematical Physics. Vol. 1-4. — New York-
Vienna: Springer, 1978-83.
Thompson C. J. Mathematical Statistical Mechanics. — Princeton Univ.
Press, 1972; reprinted 1979.
Tribus M. Thermostatics and Thermodynamics. - Van Nostrand, 1961.
Truesdell C. A. The Tragicomical History of Thermodynamics, 1822-
1854. — New York-Berlin: Springer, 1980. (Studies in the History of Math-
ematical and Physical Sciences, 4.)
Varadarajan V. S. Geometry of Quantum Theory. — New York: Springer,
1985 (2nd ed.).
Предметный указатель
а-алгебра, 1137
fc-форма, см. дифференциальная
форма степени к
0-коцепь, 604
0-цепь, 591
1-коцепь, 604
1-форма, см. дифференциальная
форма линейная
— критическая, см. экстремаль
1-цепь, 591
2-форма, 386, 412
4-импульс, 228
—, закон сохранения, 229
4-потенциал, 983
А
аберрация, 436
— сферическая, 437
абсолютная константа, см.
скорость света
абсолютная температура, 1097,
1111
абстрактная температура, 1103
адиабатическая кривая (адиабата),
1104
адиабатически замкнутая система,
1104
алгебра, 948
— Хг-градуированная, 958
— ассоциативная, 928, 948
— внешняя (A(V)), 947, 952
— Дирака, 931
— измеримых множеств, 1137
— кватернионов, 930
— Клиффорда, 928, 951
— матриц (и линейных
преобразований), 34
— с единицей, 948
— тензорная (T(V)), 949
алгебраическое дополнение
элемента матрицы, 560
ампер, 576
Ампера закон (второй), 886
— в форме Максвелла, 971
аналитическая функция, 1004
аналитическое продолжение, 1025
аннулирующее пространство
(аннулятор), 492, 606
ансамбль статистический, 1154
антикоммутативность, 756
анти коммутационные соотношения,
926
аппроксимация дискретного
распределения непрерывным,
819
атлас карт многообразия, 790
аффинная плоскость, 2
аффинное преобразование, 23
аффинное пространство
(ассоциированное с векторным
пространством), 12
Б
базис, 14, 55, 488
— дуальный, 491
— ортонормированный, 177
1208
Предметный указатель
базисы
— подобные, 398
— противоположные, 398
Бесселя функция, 1087, 1088
биения,194
билинейная функция, 379, 750
билинейное отображение, 937
близнецов парадокс, 217
Бозе-Эйнштейна распределение,
1172
бозоны, 1142
Больцмана-Пуассона
распределение, 1172
борновское разложение, 270
Ботта периодичность, 968
бутылка Клейна, 723
В
вакуум
—, диэлектрические свойства, 840
—, конститутивные соотношения,
972
вариационный принцип, 984
вариация постоянных, 149
ведущий элемент строки матрицы,
507
Вейля метод ортогональных
проекций, 645, 848
вектор
— касательный, 286
— Пойнтинга, 987
— энергии-импульса, см. 4-импульс
векторное поле, 866
векторное произведение, 934, 937
векторное пространство, 6, 10, 476
—, базис, 488
— двумерное, 55
— дуальное, 479
— касательное, 290
— линейных преобразований, 944
—, натянутое на множество
векторов, 484
— одномерное, 13
—, подпространство, 480
—, размерность, 486
— свободное над множеством, 941
— симплектическое, 461
— универсальное, 942
вероятность (мера), 1139
вечный двигатель второго рода,
1113
взаимодействие, 1101
— адиабатическое, 1104
вихрь (rot), 934
внешнее произведение, 383, 756
внешняя алгебра (А(У)), 947, 952
внешняя производная, 379
внешняя степень, 749, 754, 946
внутреннее произведение, 872
внутренняя энергия, 1096, 1105,
1171
— состояния, 1154
волна
— обратная (падающая), 990, 993
— прямая (испускаемая), 990
— распространяющаяся, 988
— расходящаяся, 992
волновой оператор, 974
волновой пакет, 1080
волновой фронт, 988
вольт, 576
вольт-амперная характеристика,
577
время
— истинное (по Ньютону), 15
— собственное, 372
вторичное излучение, 993, 1085
второй закон термодинамики, 1097,
1107
вынужденные колебания, 148
—, резонанс, 154
вырожденная матрица, см.
линейное преобразование
сингулярное
вычет функции, 1012
Г
газовая постоянная, 1123
Галилея преобразование, 221
Гамильтона теорема, 452
Гамильтона уравнения, 452
Гамильтона-Кэли теорема, 86
Предметный указатель
1209
гамма-распределение, 1168
гамма-функция, 1066
гармоническая функция, 844
— сопряженная, 1053
Гаусса закон (о потоке поля), 663,
731, 825
гауссово разложение, 448
гауссово распределение, 1039
Гельмгольца формула, 991, 1084
генри, 577
геометрия
— конформная, 932
— риманова, 933
гессиан, 313
Гиббса принцип минимальной
энергии, 1132
гиперболические синус и косинус,
213
главная ветвь, 1036, 1039
главное значение Коши, 1042
главные плоскости, 448
голоморфная функция, 1004
гомеоморфные пространства, 715
гомологии, 709
градиент (grad), 934
Грама Шмидта процесс, 176
граница, 708
граница области, 415
граничное отображение, 591
граничный оператор, 707, 820
Грина оператор, 678
Грина теорема взаимности, 657
Грина формула, 415
— вторая, 843
— дискретная, 679
— дискретная вторая, 682
— первая, 842
Грина функция, 851
— дискретная, 678
групповая скорость, 1080
Гюйгенса принцип, 993
— в формулировке Френеля, 1086
д
давление, 1106
Дарбу теорема (о 2-формах), 1194
движение евклидово, 213
двухступенчатый фильтр, 634
дельта-функция Дирака, 823
дерево, 597
— максимальное, 599
детерминант, см. определитель
дефект линейного преобразования,
503
диаграмма Моллье, 1126
диатермальный контакт, 1101
дивергенция (div), 758, 934
Дирака алгебра, 931
Дирака дельта-функция, 823
Дирихле задача, 830, 849
— дискретная (для цепи), 668
дискриминант квадратичной
формы, 184
дисперсия, 1167
дифракция, 434
дифференциал, 250, 254
дифференциальная форма
— замкнутая, 367, 385, 792
— комплекснозначная, 1003
— линейная (1-форма), 277
— степени к, 749, 757
— степени 2 (2-форма), 386, 412
— точная, 363, 792
дифференциальное уравнение
—, интегральная кривая, 135
— Лапласа, 317
— линейное неоднородное, 148
— —, установившееся решение, 152
— линейное однородное, 125
— —, начальные условия, 128
— , общее решение, 127
—, фазовый портрет, 135
дифференцируемое отображение,
250
—, регулярная точка, 524
—, сохраняющее ориентацию, 401
диэлектрическая постоянная, 840
диэлектрическая проницаемость,
579, 836
длина
— вектора, 166, 371
----лоренцева, 372
1210
Предметный указатель
— кривой, 372
— оптическая, 452
доктрина скрытого и явного тепла,
1117
дуальное пространство, 479
дуальный базис, 491
Е
евклидова плоскость, 165
евклидово преобразование, 23, 166
единичная матрица, 35
емкость, 577
3
задача
— Дирихле, 830, 849
---дискретная (для цепи), 668
— Пуассона
---дискретная (для цепи), 669
закон
— Ампера (второй), 886
---в форме Максвелла, 971
— Гаусса (о потоке поля), 663, 731,
825
— Кеплера второй, 274
- - об отсутствии «магнитных
зарядов», 886
- сложения скоростей, 214
— Снеллиуса, 436
---линеаризованный, 442
— сохранения, 986
---4-импульса, 229
---углового момента, 273
---энергии, 987
— термодинамики
---второй, 1097, 1107
---нулевой (о равновесии), 1103
---первый, 1096, 1104
— умножения определителей, 559
- - Фарадея, 731, 969
законы
- - идеального газа, 1123
— Кирхгофа, 580, 592, 612, 882
запаздывающие потенциалы, 982
заплатки, см. атлас карт
многообразия
зародыш коцепи, 746, 817
заряд, 576
-- «магнитный», 886
—, распределение (плотность), 818
—, скорость потока, 875
затухание
— апериодическое, 146
— критическое, 145
звездное множество, 799
звездный оператор (*), 837, 903
Зоммерфельда условия излучения,
992
И
идеал, 950
идеальный газ, 1123
идемпотентный оператор, 650
излучение
— вторичное, 993, 1085
—, Зоммерфельда условия, 992
— монохроматическое, 993
измеримое пространство, 1137
—, произведение, 1144
изоморфизм векторных
пространств, 14, 56
изотерма, 1104
изотропная среда, 837
импеданс, 590
инволюция, 956
индекс строки матрицы, 507
индикатор (функция), 1186
индуктивность, 577
индуктор, 576
интеграл
—, главное значение Коши, 1042
— двойной
----абсолютный (первого рода),
391
----от 2-формы (второго рода),
389
— криволинейный
- - — абсолютный (первого рода),
371
Предметный указатель
1211
----от 1-формы (второго рода),
355
— Лебега, 1139
— несобственный, 428
— от к-формы, 765, 774
—- по мере, 1138
— Френеля, 1039
интерференция, 435
источник питания, 612
К
калориметр, 1095
«калорическая» функция, 1095
каноническое преобразование, см.
симплектическое отображение
Каратеодори теорема, 1094
Карно цикл, 1114
касательное пространство, 290
касательный вектор, 286
квадратичная форма, 184
квадратичная функция, 191
квазистатический процесс, 1106
квантовая логика, 1187
квантовая система, 1184
кватернионы, 930
кельвин (градус), 1123
Кеплера закон второй, 274
Кирхгофа законы, 580, 592, 612, 882
Кирхгофа теорема, 603, 626
Клейна бутылка, 723
Клиффорда алгебра, 928, 951
коаксиальный луч, 438
когомологии, 731
--- де Рама, 793
кограница, 793
кограничное отображение
ограниченное, 608
кограничный оператор, 729
количество информации, 1160
коммутатор пары матриц, 271
комплекс
— двумерный, 705
— одномерный, 590
— размерности п, 706
— связный, 595
композиция отображений, 20
конденсатор, 577
конститутивные соотношения (для
вакуума), 972
контакт, 1131
— диатермальный, 1101
конфигурационные переменные,
1104
конформная геометрия, 932
конформная матрица, 80
кососимметричность, 750, 752
коцепь, 604, 728
коцикл, 792
Коши теорема интегральная, 1003
Коши теорема о вычетах, 1012
Коши формула интегральная, 1015
Коши-Римана уравнения, 1005
Коши-Шварца неравенство, 233
коэффициент
— полезного действия (КПД), 1114
— преломления, 436
— сжимаемости, ИЗО
— теплового расширения, ИЗО
кривая
— адиабатическая, 1104
— нулевая, 1090
— обратимая, 1106
кривизна, 441, 443
круговой ток, 601
кулон, 576
Л
Лагранжа множитель, 318
лагранжево подмногообразие, 1128
лагранжиан, 983
Лапласа принцип, 1072
Лапласа уравнение, 317
лапласиан, 317
911
— дискретный (для цепи), 664
— ограниченный, 666
Лебега мера и интеграл, 1139
Лежандра полиномы, 180
Лейбница правило, 881
Лейбница формула (производная
произведения функций), 263
1212
Предметный указатель
лемма
— Морса, 339
— Пуанкаре, 797
линейная зависимость векторов, 9,
47, 483
линейное преобразование, 28, 57
—, изменяющее ориентацию, 401
— конформное, 77, 1007
— Лоренца, 210
----собственное, 209
—, матрица, 29
—, норма, 308
— ортогональное, 166
— регулярное (несингулярное), 28
— симплектическое, 231, 460
— сингулярное, 28
— скорости, 221
— сопряженное, 526
—, сохраняющее ориентацию, 400
— транспонированное, 183
линза
— тонкая, 443
—, фокальные плоскости, 445
—, фокусное расстояние, 444
лист Мёбиуса, 723, 737
Лиувилля теорема, 1021
логики дистрибутивный закон,
1186, 1187
Лорана ряд, 1051
Лоренца преобразование, 210
— собственное, 209
Лоренца сила, 988
М
магнитная восприимчивость, 886
магнитная индукция, 885
магнитное поле (возбуждение,
напряженность), 886, 971
магнитные силовые линии, 885
Максвелла методы анализа цепей,
580
Максвелла распределение, 1152
Максвелла уравнения, 972, 984
Максвелла-Больцмана
распределение, 1165, 1174
Маркова процесс, 93
—, матрица вероятностей перехода,
95
масса покоя, 228
Массье функция, ИЗО, 1157, 1170
масштабное преобразование, 932
математическое ожидание, 1151
матрица
—, ведущий элемент строки, 507
— вероятностей перехода, 95, 684
— вращения, 564
— Гессе, 313
— единичная, 35
— емкостных коэффициентов, 688
— замены базиса, 58, 490
—, индекс строки, 507
— конформная, 80
— линейного преобразования, 29
----, зависимость от базиса, 29
— обратная, 45
—, определитель, 549
— оптическая
----, гауссово разложение, 448
----общего вида, 448
----преломления, 442
----распространения, 441
— ортогональная, см. линейное
преобразование ортогональное
— потенциальных коэффициентов,
688
— присоединенная, 562
—, редукция по строкам, 506
— симплектическая, см. линейное
преобразование
симплектическое
— сингулярная (вырожденная), см.
линейное преобразование
сингулярное
— транспонированная, 183
—, функция от, 115
- Якоби, 303, 407
Мёбиуса лист, 723, 737
мера, 1137
— «беспорядка», 1159
— вероятностная, 1139
Предметный указатель
1213
— гауссова (дискретная и
непрерывная), 1143
— Жордана, 767
— Лиувилля, 1143
-, перенос (pushforward), 1146
мероморфная функция, 1012
метод
— вариации постоянных, 149
— Гаусса, см. редукция по строкам
— Кирхгофа расчета цепи, 650
— круговых токов (Максвелла),
587, 613, 622
— множителей Лагранжа, 317
— Ньютона, 323
— ортогональных проекций Вейля,
645, 848
— Пикара, 325
— узловых потенциалов
(Максвелла), 588, 614, 624
— эквивалентных сопротивлений,
584
механический эквивалент тепла,
1105
Минковского расстояние, 216
многообразие, см. подмногообразие
— равновесных состояний, 1101
Моллье диаграмма, 1126
Морса лемма, 339
Муавра теорема, 81
Н
наблюдаемое, 1149, 1170
— «да или нет», 1185, 1187
— квантовое, 1184
накрытие, 1035, 1039
напряжение, 576
— холостого хода, 612
напряженность
— магнитного поля, 971
— электрического поля, 824
неравенство
--- Коши-Шварца, 233
— треугольника, 216
----обратное, 217
Нётер теорема, 985
низкочастотный фильтр, 632
нильпотент, 54
норма линейного преобразования,
308
нормальная мода, 628
нормальное распределение, 1039
нормальные колебания, 192
нулевая кривая, 1090
нулевой вектор, 9
нулевой конус, см. световой конус
Ньютона метод, 323
Ньютона уравнение (оптическое),
450
Ньютона-Лейбница формула, 362,
415
О
область
— абсолютного будущего, 208
— влияния, 976
— зависимости, 976
— звездная, 366, 799
— односвязная, 1053
обобщенные функции, 823
образ
— линейного преобразования, 51,
502
— отображения, 18
обратимая кривая, 1106
обратная матрица, 45
обратное отображение, 19
обратное преобразование Фурье,
989, 1083
однородная среда, 837
ожидаемое значение, 1151, 1170,
1184
оккупанты, см. число заполнения
ом, 577
оператор
- волновой, 974
— — приведенный, 990
— граничный, 707, 820
— Грина, 678
— звездный (*), 837, 903
— идемпотентный, 650
— кограничный, 729
— Лапласа, см. лапласиан
1214
Предметный указатель
— линейный дифференциальный
первого порядка, 921
— рождения фермионов, 926
— самосопряженный, 1183
— уничтожения фермионов, 926
— формально сопряженный, 920
определитель (детерминант), 42,
549
оптика
— волновая (теория Френеля), 434
— гауссова, 437
— геометрическая, 436
— линейная, 436
оптическая ось, 438
оптическая сила, 443
ориентация
- векторного пространства, 399,
902
— комплекса, 726, 778
— многообразия, 791
— области (на плоскости), 389, 416
— параллелограмма, 387
— поверхности (в пространстве),
391
~ траектории, 351
ориентированная площадь
(параллелограмма), 387
ориентированный граф, 590
ориентированный объем (п-мерного
параллелепипеда), 547
ортогональная проекция, 179, 235
ортогональное преобразование, 166
ортогональность векторов, 166
ортонормированный базис, 177
ортонормировочная процедура, см.
Грама -Шмидта процесс
основная теорема алгебры, 1022
особая точка
— полюс, 1012
— существенная, 1030
— устранимая, 1018
осциллятор
— без затухания, 144
— с затуханием, 145
отображение, также функция,
оператор, преобразование, 18
— аффинное, см. аффинное
преобразование
— биективное, 19
— билинейное, 937
— вычисления, 939
— граничное, 591
— дифференцируемое, 250
----, регулярная точка, 524
----, сохраняющее ориентацию, 401
— евклидово, см. евклидово
преобразование
— измеримое, 1145
— инъективное, 19
— Клиффорда, 951
— кограничное ограниченное, 608
— конформное, 1006
— кососимметричное, 945
— линейное, см. линейное
преобразование
— обратное, 19
— ограниченное, 250
— открытое, 1031
— полилинейное (&-линейное), 945
— симплектическое, 467
— сюръективное, 19
— универсальное, 937
— экспоненциальное, 1086
П
пакет волновой, 1080
параллельное соединение, 580
параметризация траектории, 352
первый закон термодинамики,
1096, 1104
перенос
— меры (pushforward), 1146
— формы (pullback), 402, 761, 763
— функции (pullback), 291
периодичность Ботта, 968
перпендикулярность, см.
ортогональность векторов
Пикара метод, 325
Планка постоянная, 1082
Планка функция, 1127
Предметный указатель
1215
плоскость
— аффинная, 2
- - проективная, 72
плотность, 393
— заряда, 818
— тока (скорость потока заряда),
875
поверхность
— риманова, 1035
— эквипотенциальная, 832, 1091
подкомплекс, 596
подмногообразие
векторного пространства, 523
— лагранжево, 1128
- - ориентируемое, 791
подпространство векторного
пространства, 480
Пойнтинга вектор, 987
показатель преломления, 438
полюс функции, 1012
поляризация света, 436
полярные координаты, 291, 370
порядок
— нуля, 1026
— полюса, 1012
последовательное соединение, 582
постянная Планка, 1082
потенциал
— запаздывающий, 982
— Льенара-Вихерта, 983
— химический, 1134
— электростатический, 686
поток, 868
— энергии, 987
правило
— Лейбница, 881
— фаз, 1136
преобразование
— масштабное, 932
— Фурье, 1076
----обратное, 989, 1083
приближение Борна (первое), 270
принцип
— вариационный, 984
— Гюйгенса, 993
----в формулировке Френеля, 1086
— Дирихле (минимума энергии),
849
— Лапласа, 1072
— максимальной энтропии, 1132
— максимума (для гармонических
функций), 846
- - минимальной энергии Гиббса,
1132
--- причинности, 976
-- устранимых особенностей, 1018
— Ферма (наименьшего времени),
457
— электрической экранировки, 831
присоединенная матрица, 562
проводимость, 580, 864
проективная плоскость, 72
проекция, 52
— ортогональная, 179, 235
произведение матриц, 31
производная
— внешняя, 379, 881
— Ли (по направлению), 288, 880
— многомерная (отображения
векторных пространств), см.
также дифференциал, 247
— произведения функций, см.
Лейбница формула
— смешанная (вторая), 282
— частная, 275
производящая функция, 1129
простой (порядка 1) нуль или
полюс, 1026
пространство
-- fc-форм, 754, 946
— аннулирующее, 606
— билинейных функций, 750
— гомологий, 709
— границ, 593, 708
— когомологий, 731
— циклов, 708
пространство-время, 205
противоположный вектор, 10
процесс
— ГрамаШмидта, 176
— квазистатический, 1106
1216
Предметный указатель
— Маркова, 93
----, матрица вероятностей
перехода, 95
прямая сумма векторных
пространств, 596
Пуанкаре лемма, 797
Пуанкаре преобразование, 213
Пуассона распределение, 1169
Пуассона уравнение, 837, 915
— дискретное (для цепи), 664
— ограниченное, 664
Пуассона формула интегральная,
855, 1055
Пуассона ядро, 680
Р
работа, 1095, 1156
— силового поля, 349
равновесие тепловое, 1102
равномерная дифференцируемость,
326
равномерная сходимость
последовательности
голоморфных функций, 1047
радиус сходимости, 1050
разбиение единицы, 785
разложение
— борновское, 270
— гауссово, 448
размерность векторного
пространства, 486
ранг
— дифференциальной (1- или 2-)
формы, 1192
— линейного преобразования, 503
распределение
— БозеЭйнштейна, 1172
— Больцмана-Пуассона, 1172
— гамма-, 1168
— гауссово (нормальное), 1039
— Максвелла, 1152
— Максвелла-Больцмана, 1165,
1174
— Пуассона, 1169
— Ферми-Дирака, 1172
распространяющаяся волна, 988
расстояние Минковского, 216
регулярная точка
(дифференцируемого
отображения), 524
редукция по строкам, 506
резистор, 577
резисторный порт, 659
резонанс, 154, 194
резонансная частота, 628, 633
риманова геометрия, 933
риманова поверхность, 1035
род поверхности, 722
росток голоморфной функции, 1025
ротор (rot), 934
Руше теорема, 1028
Ряд
— Лорана, 1051
— степенной, 116
— — абсолютно сходящийся, 119
----сходящийся, 118
— Тейлора, 1020, 1049
— Фурье, 1052
С
световой конус, 210
свободное векторное пространство,
941
связное множество, 846
сила
— Лоренца, 988
— обобщенная, 1156
силовое поле, 348
—, работа, 349
силовые линии магнитные, 885
сименс, 580
симплектическая группа, 232, 461
симплектическая форма, 461
симплектическое векторное
пространство, 461
симплектическое отображение, 467
сингулярная (вырожденная)
матрица, см. линейное
преобразование сингулярное
система, 1100, 1170
— адиабатически замкнутая, 1104
— квантовая, 1184
Предметный указатель
1217
скалярное произведение, 167
— в пространстве &-форм, 900
— дуальное (1-форм), 899
— евклидово, 175
— из векторного анализа (dot
product), 934
—, свойства, 169
— симплектическое, 231
скорости преобразование, 221
скорость
— групповая, 1080
— звука, 1119
— потока заряда, 875
— света, 206, 973
сложения скоростей закон, 214
случайное блуждание (по графу),
684
смещение, см. трансляция
аффинная
Снеллиуса закон, 436
— линеаризованный, 442
собственное время, 372
собственное значение, 82
собственный вектор, 82
сопротивление, 577
— комплексное, см. импеданс
— нелинейное, 578
— удельное, 864
сопряженное отображение, 526
сопряженные плоскости, 443
состояние, 1100, 1140, 1170
— квантовое, 1184
— равновесное, 1101, 1165, 1170,
1184
специальная теория
относительности, 206
статистика (Бозе-Эйнштейна,
Ферми-Дирака), см.
распределение
Стирлинга формула, 1065
Стокса теорема, 757, 777
суперкоммутативность, 756
существенная особенность, 1030
Т
Тейлора ряд, 1020, 1049
Тейлора формула (многомерная),
311
телескоп астрономический, 447
телесный угол, 822
Теллегена теорема, 605
температура
— абсолютная, 1097, 1111
— абстрактная, 1103
— эмпирическая, 1103
тензор
- типа (А:, 0), 754
— энергии-импульса, 988
тензорная алгебра (T(V)), 949
тензорное произведение, 940, 945
— скрученное, 958
теорема
— алгебры основная, 1022
— взаимности Грина, 657, 687
— Гамильтона, 452
— Гамильтона-Кэли, 86
— Грина, см. Грина формула
— Дарбу (о 2-формах), 1194
— Каратеодори, 1094
— Кирхгофа, 603, 626
— Коши интегральная, 1003
— Коши о вычетах, 1012
— коэффициентов Морзе, 457
— Лиувилля, 1021
— Муавра, 81
— Нётер, 985
—- о кососимметрических
билинейных формах, 1198
— о неявной функции, 334
— о нормальной 1-форме, 1099,
1194
— о постоянном ранге, 517
— о ранге и дефекте, 503
— о среднем значении, 305
----гармонической функции, 845
----многомерная (неравенство),
309
— об обратной функции, 332
— Радона-Никодима, 1149
— Руше, 1028
— спектральная (для операторов),
1183
1218
Предметный указатель
— Стокса, 757, 777
— Теллегена, 605
— Эйлера для комплекса, 714
тепло, 1095
— механический эквивалент, 1105
— скрытое (латентное), 1118
тепловое равновесие, 1102
теплоемкость, 1117
термометр, 1103
ток, 576
— короткого замыкания, 612
— круговой, 601
— через поверхность, 864
тонкая линза, 443
тор, 718
точечная характеристика
(оптической системы), 452
точка ветвления, 1035
траектория
— кусочно-дифференцируемая, 352
— ориентированная, 351
—, параметризация, 352
— простая (в цепи), 585
трансляция аффинная, 6, 25
транспонирование, 183
— формальное (оператора), 821
трилинейная функция, 752
У
увеличение
— линзы, 446
— телескопа угловое, 447
угловой момент, 272
—, закон сохранения, 272
угол между векторами, 167
удельное сопротивление, 864
умножение матриц, 31
универсальное отображение, 937
универсальное пространство, 942
уравнение
— волновое
----неоднородное, 981
----одномерное (колебаний
струны), 974
----приведенное (Гельмгольца),
991
----трехмерное, 977
— дифференциальное, см.
дифференциальное уравнение
— Лапласа, 317
----двумерное, 317, 665
----дискретное (для цепи), 664
— Ньютона (оптическое), 450
— Пуассона, 837, 915
----дискретное (для цепи), 664
----ограниченное, 664
— характеристическое, 83
уравнения
— Гамильтона, 452
— Коши-Римана, 1005
— Максвелла, 972, 984
условия излучения Зоммерфельда,
992
условный экстремум, 317
устранимая особенность, 1018
Ф
фаз правило, 1136
фаза волны, 988
факторалгебра, 950
факторпространство, 497
фарад, 577
Фарадея закон, 731, 969
Ферма принцип (наименьшего
времени), 457
Ферми-Дирака распределение, 1172
фермионы, 1142
фильтр
— двухступенчатый, 634
— низкочастотный, 632
фокальные плоскости, 445
фокусное расстояние, 444
формальное сопряжение, 920
формальное транспонирование
(оператора), 821
формула
— Гельмгольца, 991, 1084
— Грина, 415
----вторая, 843
— — дискретная, 679
----дискретная вторая, 682
----первая, 842
Предметный указатель
1219
— де Бройля, 1081
— дифференциального исчисления
фундаментальная, 881
— замены переменных в fc-мерном
интеграле, 768
- - Кирхгофа, 993
— Коши интегральная, 1015
— Лейбница (производная
произведения функций), 263
— Ньютона-Лейбница, 362, 415
— обратного преобразования
Фурье, 1083
— Пуассона интегральная, 855,
1055
— стационарной фазы, 1074
— Стирлинга, 1065
— Тейлора (многомерная), 311
— Эйнштейна, 1081
Френеля интеграл, 1039
фронт волновой, 988
функция
— аналитическая, 1004
— Бесселя, 1087, 1088
— билинейная, 379, 750
— гамма-, 1066
— гармоническая, 844
----сопряженная, 1053
— голоморфная, 1004
— Грина, 851
----дискретная, 678
— Дирака (дельта-), 823
— Дирихле (разрывная
интегрируемая), 1139
— «калорическая», 1095
— квадратичная, 191
— комплекснозначная
дифференцируемая, 999
— Массье, ИЗО, 1157, 1170
— мероморфная, 1012
— обобщенная, 823
— от матрицы, 115
— Планка, 1127
— производящая, 1129
— разбиения, 1157, 1170, 1184
— с компактным носителем, 818
— трилинейная, 752
— характеристическая, 1186
— Хевисайда, 1141
Фурье преобразование, 1076
— обратное, 989, 1083
Фурье ряд, 1052
Фурье-образ, 1083
X
характеристический полином, 83
характеристическое уравнение, 83
химический потенциал, 1134
ц
цепное правило, 256
цепь комплекса, 591
цикл, 593, 708
—- Карно, 1114
циркуляция магнитного поля, 971
Ч
частная производная, 275
число заполнения, 1141
Э
эйконал, см. точечная
характеристика
Эйлера теорема для комплекса, 714
эйлерова характеристика, 714
эквипотенциальная поверхность,
832, 1091
экспоненциальное отображение,
1086
экстремаль (лагранжиана), 983
электрическое смещение, 825
электродвижущая сила (ЭДС), 578
электростатическая энергия, 842,
849
электростатический потенциал, 686
эмпирическая температура, 1103
энергии-импульса тензор, 988
энергия
— взаимодействия, 1131
— внутренняя, см, внутренняя
энергия
1220
Предметный указатель
— кинетическая, 1151
— свободная Гельмгольца, 1191
— электростатическая, 843, 849
энтальпия, 1125
энтропия, 343, 1097, 1108, 1159,
1170, 1184
эффективность (КПД), 1114
Я
ядро
— линейного преобразования, 52,
502
— Пуассона, 680
якобиан, см. матрица Якоби
ячейка
— комплекса, 706
— электрической цепи, 585, 592