ΤΙ Τ"
ΠΛ I
3 я0
*"*■
Г" mf
- О
/Ч i
**.

Предлагаемый курс лекций
известных профессоров
Гарвардского университета
П. Бамберга и Ш. Стернберга
пользуется большой
популярностью среди физиков и
инженеров, считающих для
себя необходимым освоить
основные элементы
современной математики.
Помимо традиционных
■опросов этот курс содержит
изложение основ топологии и
геометрии, топологический
смысл уравнений Максвелла,
комплексный анализ,
асимптотический метод Лапласа и
нвчала термодинамики.
Объединение всех этих
рвзделов математики и
физики в одной монографии,
несомненно, полезно для
студентов и аспирантов
российских университетов
и позволит им быстро
включиться в проходящие
во всём мире исследования
в теоретической и
математической физике.
Я. Г. Синай и
на ступенях МГУ ι
(фото,
Я. Г. Синай
академик РАН

История преподавания
математического анализа,
начиная с его изобретения
Ньютоном, изобиловала крутыми
поворотами. К середине XX века
традиционные изложения стали
отличать полное исключение
всех геометрических понятий и
представлений, с одной стороны,
и полный отрыв от физики и всех
приложений, с другой.
Предлагаемая книга знаменует
возвращение преподавания
математики к
естественнонаучному подходу, для которого
характерны явная
геометричность и прямое представление
математики как части физики,
непосредственно пригодной для
многочисленных приложений
как в естествознании,так и
в инженерном деле.
Это возвращение математики
в русло естественных наук
происходит сейчас и на уровне
новых научных исследований, а
его проявление в преподавании
давно стало абсолютно
необходимым.
В. И. Арнольд
академик РАН

Пол БАМБЕРГ
Шломо СТЕРНБЕРГ
КУРС МАТЕМАТИКИ
для
СТУДЕНТОВ-ФИЗИКОВ
Том I
Главы 1-11
ПЕРЕВОД С АНГЛИЙСКОГО
к.ф.-м. н., доц. Л.П.Котовой (МФТИ)
ПОД РЕДАКЦИЕЙ
к.ф.-м.н., доц. Е.В.Майкова (МГУ)
Φ
МОСКВА
2006

УДК 51 Издание осуществлено при поддержке
Центрального аэрогидродинамического
<Г~"ТДДГИГ—— института имени Η. Ε. Жуковского,
директор В. Г. Дмитриев
и
Фонда «КНИГА-НАУКА-КУЛЬТУРА»,
директор В. Б. Филиппов
Бамберг П., Стернберг Ш.
Курс математики для студентов-физиков. Том I, главы 1-11.
Перев. с англ. Л. П. Котовой под ред. Е. В. Майкова.
- М.: ФАЗИС, 2006. 592c.(i-xvni, 1-574)
ISBN 5-7036-0109-6
Paul Bamberg & Shlomo Sternberg
A Course in Mathematics for Students of Physics
© Cambridge University Press 1988 (Vol. 1)
Издательство ФАЗИС
123557 Москва, Пресненский вал, 42-44
e-mail: publisher@phasis.ru /iiip://www.phasis.ru
Типография «Наука» Академиздатцентра РАН
121099 Москва Г-99, Шубинский пер., 6
Заказ № 3638
ISBN 5-7036-0109-6
© ФАЗИС, 2006

Оглавление тома I
Предисловие VII
От издателя русского перевода XVII
Глава 1. Линейные преобразования плоскости 1
1.1. Аффинные плоскости и векторные пространства 1
1.2. Векторные пространства и их аффинные пространства 10
1.3. Функции и аффинные функции 18
1.4. Евклидовы и аффинные преобразования 23
1.5. Линейные преобразования 25
1.6. Матрица линейного преобразования 29
1.7. Умножение матриц 31
1.8. Алгебра матриц 34
1.9. Площади и определители 37
1.10. Обратные матрицы 45
1.11. Сингулярные матрицы 50
1.12. Двумерные векторные пространства 55
Добавление: фундаментальная теорема аффинной геометрии 60
Резюме 64
Задачи 64
Глава 2. Собственные векторы и собственные значения 77
2.1. Конформные линейные преобразования 77
2.2. Собственные векторы и собственные значения 82
2.3. Процессы Маркова 93
Резюме 101
Задачи 102
Глава 3. Линейные дифференциальные уравнения на плоскости 115
3.1. Функции матриц 115
3.2. Экспонента от матрицы 119
3.3. Вычисление экспоненты от матрицы 127
3.4. Дифференциальные уравнения и фазовые портреты 135
3.5. Применения дифференциальных уравнений 142

IV Оглавление тома I
Резюме 155
Задачи 156
Глава 4. Скалярные произведения 165
4.1. Скалярные произведения в евклидовом пространстве 165
4.2. Процесс Грама-Шмидта 171
4.3. Квадратичные формы и симметричные матрицы 181
4.4. Нормальные колебания 189
4.5. Нормальные моды в многомерном пространстве 195
4.6. Специальная теория относительности 205
4.7. Группа Пуанкаре и группа Галилея 218
4.8. Импульс, энергия и масса 222
4.9. Антисимметричные формы 230
Резюме 232
Задачи 233
Глава 5. Дифференциальное исчисление на плоскости 243
Введение 243
5.1. «О» большие и «о» малые 247
5.2. Дифференциальное исчисление 254
5.3. Примеры на цепное правило 262
5.4. Частные производные и дифференциальные формы 274
5.5. Производные по направлению 285
5.6. Операция переноса 291
Резюме 299
Задачи 299
Глава 6. Теоремы многомерного дифференциального исчисления 305
6.1. Теорема о среднем значении 305
6.2. Производные высших порядков и формула Тейлора 310
6.3. Максимум и минимум 314
6.4. Теорема об обратной функции 321
6.5. Поведение функции вблизи критической точки 336
Резюме 339
Задачи 339
Глава 7. Дифференциальные формы и криволинейные интегралы 347
Введение 347
7.1. Ориентированные траектории 351
7.2. Криволинейные интегралы 355
7.3. Точные дифференциальные формы 362
7.4. Замкнутые дифференциальные формы 366
7.5. Перенос дифференциальной формы и интегрирование 368
7.6. Абсолютный криволинейный интеграл. Длина кривой 370
Резюме 373
Задачи 373
Глава 8. Двойные интегралы 379
8.1. Внешняя производная 379

Оглавление тома I V
8.2. 2-формы 386
8.3. Интегрирование 2-форм 388
8.4. Ориентация 397
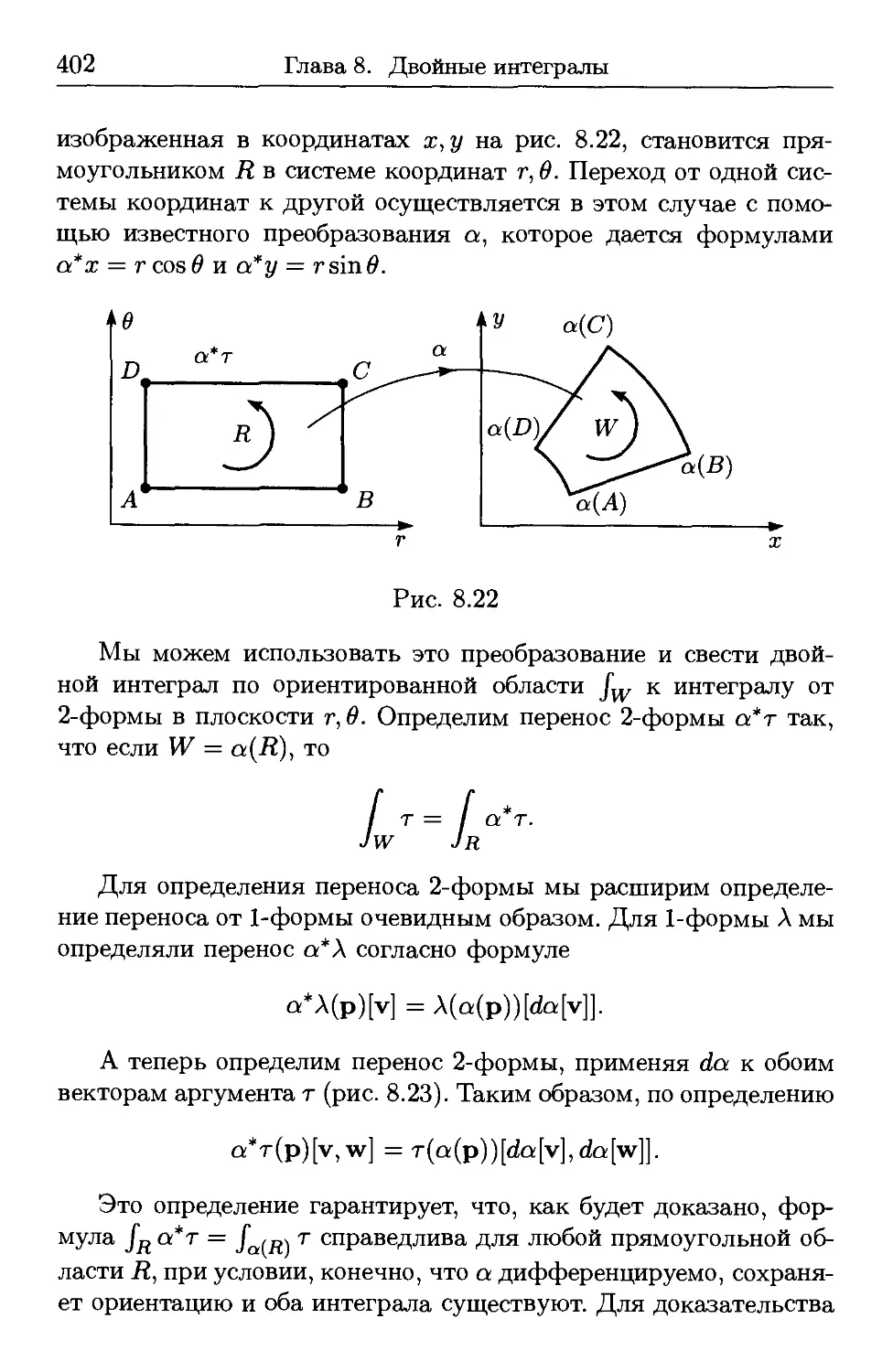
8.5. Перенос и интегрирование 2-форм 401
8.6. 2-формы в трехмерном пространстве 411
8.7. Различие между 2-формами и плотностями 413
8.8. Формула Грина на плоскости 415
Резюме 425
Задачи 426
Глава 9. Гауссова оптика 433
9.1. Оптические теории 433
9.2. Матричные методы 438
9.3. Метод Гамильтона в гауссовой оптике 451
9.4. Принцип Ферма 455
9.5. От гауссовой оптики к линейной 458
Резюме 468
Задачи 468
Глава 10. Векторные пространства и линейные преобразования 475
Введение 475
10.1. Свойства векторных пространств 476
10.2. Дуальное пространство 479
10.3. Подпространства 480
10.4. Размерность и базис 482
10.5. Дуальный базис 491
10.6. Факторпространство 493
10.7. Линейные отображения 502
10.8. Редукция по строкам 506
10.9. Локальная структура дифференцируемого отображения 517
10.10. Сопряженное отображение 526
Резюме 531
Задачи 532
Глава 11. Определители 547
Введение 547
11.1. Аксиомы для определителей 549
11.2. Закон умножения и другие следствия аксиом 557
11.3. Существование определителя 560
Резюме 562
Задачи 562
Рекомендуемая литература 565
Предметный указатель 569

I

Предисловие
В этой книге излагается курс математики, который мы
преподавали в Гарварде в течение восьми лет. Курс предназначен
для студентов, интересующихся физикой и имеющих хорошую
подготовку по математическому анализу функций одной
переменной. Полезно некоторое знакомство с линейной алгеброй, но
это не обязательно. Большинство наших студентов
одновременно с этим курсом изучают сложные курсы по физике, так что
они могут соединить излагаемые здесь сведения со своими
физическими знаниями. Такое совмещение полезно, но не
обязательно. Основное содержание нашего, курса — теория и
физические приложения линейной алгебры и математического анализа
функций нескольких переменных, включая внешнее исчисление.
Наш педагогический метод — изложение по «спирали», т. е. мы
рассматриваем одну и ту же тему несколько раз, возвращаясь к
ней на все более высоком уровне, одновременно расширяя
области ее применения. Такое построение мы предпочитаем
«прямолинейному» строгому логическому порядку. Надеемся, что при
этом мы избежим логических ошибок типа «порочного круга»,
но часто будем начинать с простого случая того или иного
понятия, а затем возвращаться к нему для обобщений, делая это
только после ознакомления с родственными понятиями и, как
следствие, приобретения более широкого взгляда на предмет.
Такой подход требует от студентов определенного доверия и
терпения. Но мы надеемся, что, в конце концов, они будут
вознаграждены более глубоким интуитивным пониманием предмета
в целом.

VIII
Предисловие
Теперь расскажем о содержании книги более детально. Цель
первых четырех глав — познакомить читателя с алгеброй и
анализом квадратных матриц. Таким образом, изучив эти главы,
студент должен научиться думать о матрицах как о
самостоятельных объектах, а не просто как о наборе чисел, выстроенных
по квадрату. В этих главах мы рассматриваем почти
исключительно матрицы 2x2, когда самые сложные вычисления сводятся
к решению квадратных уравнений. Но каждый раз мы
формулируем результаты, имея в виду матрицы более высокого порядка.
Глава 1 начинается с объяснения связи закона умножения
матриц 2 х 2 и геометрии прямых линий на плоскости. Далее
излагается алгебра матриц 2x2, обсуждается детерминант и его
отношение к плоскости и ориентации. Мы вводим определение
абстрактного векторного пространства в общем случае,
объясняем понятие базиса и замены базиса в одномерном и двумерном
векторном пространстве.
В главе 2 мы обсуждаем конформную линейную геометрию
на плоскости, т.е. геометрию линий и углов и их связь с
определенного вида матрицами 2x2. Кроме того, вводятся понятия
собственных значений и собственных векторов, столь важные в
квантовой механике. Мы пользуемся этими понятиями, чтобы
построить алгоритм вычисления степеней матрицы. В качестве
примера, где это применяется, обсуждаются основные свойства цепей
Маркова.
Основная задача главы 3 — показать, что система
однородных линейных дифференциальных уравнений с постоянными
коэффициентами может быть записана в виде du/dt = Аи, где А
— матрица, а и — вектор, и что решение этой системы имеет вид
е^'ио, где ио задается начальными условиями. При этом,
конечно, требуется объяснить, что означает экспонента, в показателе
которой стоит матрица. Кроме того, описывается качественное
поведение решений в неоднородном случае, в том числе
обсуждается явление резонанса.
Глава 4 посвящена изучению скалярных произведений и
квадратичных форм. В ней имеется много физических приложений, в
том числе обсуждение нормальных форм и детальное изложение
специальной теории относительности.

Предисловие
IX
В главах 5 и 6 изложены основные положения
дифференциального исчисления.
В главе 5 определяется дифференциал отображения
одного векторного пространства на другое, обсуждаются его
основные свойства, в частности, правило дифференцирования
композиции. В качестве физических приложений рассматриваются
задача Кеплера и приближение Борна. Мы даем определения
частной производной и производной по направлению, определяем
линейные дифференциальные формы.
В главе 6 продолжается изложение дифференциального
исчисления. Мы представляем в векторной форме теорему о
среднем значении, формулу Тейлора и теорему об обратном
отображении. Обсуждаем поведение критических точек и множители
Лагранжа.
Главы 7 и 8 знакомят читателя с интегральным исчислением.
Глава 7 посвящена изучению линейных дифференциальных
форм и их интегралов. Особое внимание уделено замене
переменных. Кроме того, обсуждаются и другие одномерные интегралы,
например, длина дуги.
Глава 8 посвящена изучению внешних форм второй степени
и соответствующих им двумерных интегралов. Вводится понятие
внешней производной и подчеркивается инвариантность
относительно замены переменных. Доказывается двумерный вариант
теоремы Стокса, т. е. теорема Грина. Рассматриваются
поверхностные интегралы в трехмерном пространстве.
В главе 9 результаты первых восьми глав используются при
построении физической теории — оптики. Вся глава посвящена
приложениям, и ее можно опустить без ущерба для понимания
последующего материала.
В главе 10 мы возвращаемся назад и доказываем основные
свойства конечномерных векторных пространств и их линейных
преобразований. Обычно это непосредственное обобщение
результатов, полученных в первых четырех главах в двумерном случае.
Но при этом дан новый алгоритм редукции матрицы по строкам.
Вводятся два новых понятия — дуальное пространство и фак-
торпространство (в начале курса их было трудно определить).
В дальнейшем эти понятия окажутся чрезвычайно важными.

χ
Предисловие
Глава 11 посвящена свойствам детерминантов матриц η χ п.
Тема рассмотрена аксиоматически, показаны основные
вычислительные алгоритмы.
Главы 12-14 знакомят читателя с математикой формы, т. е. с
алгебраической топологией.
В главе 12 мы начинаем изучение электрических цепей. При
этом рассматриваются два аспекта. Во-первых, изучаются
«провода» цепи, т. е. как соединяются между собой различные ветви.
На математическом языке это называется топологией
одномерных комплексов. Во-вторых, мы изучаем реакцию цепи в целом,
если нам известно поведение отдельных ветвей, в частности
изменение мощности и энергии. Мы приводим несколько примеров
цепей, интересных с физической точки зрения.
В главе 13 мы продолжаем изучение цепей. Исследуем
краевые задачи, связанные с емкостными цепями, и применяем
изложенные методы для решения ряда классических задач
электростатики, включающих проводники.
В главе 14 мы кратко показываем, как результаты,
полученные в главах 12 и 13 в одномерном случае, обобщаются на случай
большего числа измерений.
Главы 15-18 посвящены разработке внешнего
дифференциального исчисления, рассматриваемого как непрерывная версия
дискретной теории комплексов.
В главе 15 излагаются основные сведения о внешнем
исчислении: внешняя алгебра, fc-формы, замена переменных, внешняя
производная и теорема Стокса.
Глава 16 посвящена электростатике. Мы рассматриваем
диэлектрические свойства вакуума как непрерывный аналог
емкости цепи, причем эти диэлектрические свойства определяют
евклидову геометрию в трехмерном случае. Излагаем основные
положения теории потенциалов.
В главе 17 мы продолжаем изучение внешнего
дифференциального исчисления. Основные темы: векторные поля и потоки,
внутренние произведения и производные Ли. Полученные
результаты применены для решения задач магнитостатики.
Глава 18 заканчивает изучение внешнего исчисления
углубленным обсуждением общего случая звездного оператора.

Предисловие
XI
Главу 19 можно считать кульминацией всего курса. В ней
результаты, полученные в предыдущих главах, применяются для
исследования уравнений Максвелла и связанных с ними
волновых уравнений.
Главы 20 и 21 никак не связаны с главами 9-19, и их можно
читать независимо. Обычно они не включаются в наш годовой
курс. А вот главы 1-9, 20 и 21 могут составить самостоятельный
краткий курс математики.
Материал главы 20 представляет собой относительно
стандартное изложение теории функций комплексного переменного,
которое вполне доступно для студентов, подготовленных к
чтению этой книги.
В главе 21 обсуждаются простейшие аспекты асимптотик.
В главе 22 показано, как, следуя идеям Бора и Каратеодори,
внешнее исчисление можно использовать в классической
термодинамике.
Большинство математиков и все физики, результаты которых
представлены в этой книге, работали в первом десятилетии
двадцатого века. Это значит, что изложенному материалу уже по
крайней мере 90 лет. И, тем не менее, он еще не вошел в наши
элементарные курсы математики, хотя большая его часть (за
исключением, может быть, теории цепей) должна изучаться
современными физиками, что они и делают на определенном этапе
своей карьеры. Причины этого, в значительной мере, исторические.
У. Гамильтону (1805-1865) было очевидно, что вещественных и
комплексных чисел недостаточно для глубого изучения
геометрического анализа, что в декартовой геометрии дву- и
трехмерного пространства возникает желание рассматривать числа
парами и тройками, как самостоятельные объекты с
собственными алгебраическими свойствами. Для этого он разработал
алгебру кватернионов, которая была очень популярна в Англии в
середине девятнадцатого века. Однако, теория имела ряд
изъянов: кватернионы более естественны в пространстве четырех,
а не трех измерений. Геометрия трех измерений возникала как
часть более общей конструкции, а не как самостоятельная теория.
Кроме того, кватернионы имели слишком сложную
алгебраическую структуру. Например, очень громоздкой была связь между

XII
Предисловие
умножением кватернионов и геометрическими построениями в
трехмерном пространстве. (Конечно, первый недостаток сегодня
считался бы не очень серьезным, но вместо него возникло бы
другое возражение: теория ограничена четырьмя измерениями.)
В конце концов, векторная алгебра в трехмерном пространстве
с ее скалярным и векторным произведениями была очищена от
теории кватернионов. Ее объединили с необходимыми
дифференциальными операциями, в результате чего появился векторный
анализ, окончательно разработанный Дж. Гиббсом (1839-1903) и
обнародованный им в своей знаменитой книге «Элементы
векторного анализа», оказавшей сильное влияние на дальнейшее
развитие науки.
Итак, векторный анализ с его операциями grad, div, curl и т. д.
стал стандартным языком изложения геометрических законов
физики. Однако, несмотря на то, что векторный анализ
прекрасно описывает геометрию трехмерного пространства, он тоже
имеет ряд существенных недостатков. Первый — и наименее
серьезный — состоит в том, что в нем не просматривается очень важное
единство: например, не ясно, что фундаментальная теорема
исчисления одна — сейчас ее называют общей теоремой Стокса, а
теоремы Грина, Гаусса и классическая теорема Стокса являются
ее частными случаями. В рамках векторного анализа мы не
можем это увидеть. Более серьезный недостаток состоит в том, что
фундаментальные операторы (например, grad, div)
предполагают евклидову структуру пространства, т. е. подразумевают
трехмерное пространство и ориентацию (например, curl). Это значит,
что теория работает только в трехмерном ориентированном
евклидовом пространстве. При этом возникает еще одна
проблема — при произвольном изменении координат операторы ведут
себя неприятно, их выражения в неортогональных координатах
очень громоздкие. Уже А. Пуанкаре (1854-1912) в своих
фундаментальных научных и философских работах,
предшествовавших теории относительности, подчеркивал необходимость делать
различие между «топологическими» законами геометрии и
физики, т. е. законами, которые зависят только от дифференциальной
структуры пространства и поэтому инвариантны относительно
гладких преобразований, и законами, зависящими от геометри-

Предисловие
XIII
ческой структуры, например, от понятия расстояния. Теория
относительности оказала огромное влияние на развитие
математики главным образом потому, что она поощряла изучение теории
многомерных пространств, которая уже существовала в
математической литературе, но не считалась важной для изучения
геометрии. Кроме того, необходимо было исследовать произвольные
изменения координат. Векторный анализ не мог решить эти две
задачи и поэтому позднее его дополнили тензорным анализом.
Но и тензорный анализ с его обилием индексов тоже имеет много
серьезных недостатков. Главный изъян состоит в том, что
невероятно трудно сказать, какие операции имеют общее
геометрическое значение, а какие связаны только с данной системой
координат. Таким образом, тензорный анализ очень хорош для
вычислений, но трудно сказать, что именно вычисляется. Вся работа,
начатая еще Гамильтоном и направленная на создание
математического аппарата, в котором объекты имеют геометрический
смысл, оказалась напрасной. Для того, чтобы заставить теорию
работать, необходимо было ввести аффинную связь —
довольно изощренную геометрическую конструкцию. Но даже с такой
конструкцией геометрическое значение операций не стало
прозрачным. По существу интуитивно ясный векторный анализ так
и не был вытеснен тензорным анализом из программ начального
университетского обучения.
Математики в основном уже согласились, а физики
постепенно привыкают к тому, что самым удобным аппаратом для
геометрического анализа является внешнее дифференциальное
исчисление Грассмана и Картана. Его преимущество состоит в том,
что наряду с простыми и четкими правилами вычисления все
объекты имеют прозрачный геометрический смысл. Внешнее
исчисление работает при любом числе измерений, хорошо себя
ведет при отображениях и изменениях системы координат,
обладает существенным единством основных теорем и четко различает
«топологические» и «метрические» свойства. В рамках
внешнего анализа геометрические законы физики принимают простую и
элегантную форму. Чтобы это продемонстрировать, полезно
привести таблицу, взятую из книги «Курс математической физики»,
написанную Тиррингом.

XIV
Предисловие
Таблица 1. История записи уравнений Максвелла.
Константы с, μ0, и ео положены равными 1.
Однородное уравнение Неоднородное уравнение
Самая ранняя форма
дВх , дВ^ дВ^ _ п
дх "·" ду "·" dz — и
dEz _ аЕу_ _ _ А
dy dz x
дЕх дЕг R
Λζ dx — °У
дЕу _ дЕх. _ _ ή
дх ду ζ
дЕх ,§Ε^ 9Εζ _ .
дх ^ ду ^ dz — Ρ
-fa дТ = ίχ + Цх
~af ~ ~~d£ = h + еу
дВу дВх _ ■ . ρ
dx ~~dy — Jz ~r &z
Конец
VB = 0
V χ Ε = -В
XIX века
V-E = p
V χ Β =j + Ё
Начало XX века
*FPa,a = 0
FP<*,a = JP
Середина XX века
dF = 0
SF = J
В 1844 году Г. Грассман (1809-1877) опубликовал книгу «Aus-
dehnungslehre». Математическое сообщество не оценило эту
работу и ведущие немецкие математики того времени
проигнорировали ее. Фактически, Грассман так никогда и не получил
место в университете; всю свою жизнь он преподавал
математику в школе. Однако, похоже, что он прожил счастливую и
плодотворную жизнь. У Грассмана была большая семья и он
считался признанным экспертом по санскритской литературе.
В конце жизни он попробовал еще раз выпустить новое
издание «Ausdehnungslehre», но оно также не имело успеха. Толь-

Предисловие
XV
ко немногие из математиков того времени оценили его работу.
Среди них был К.Мебиус (1825-1908). Тем не менее, в книге
«Ausdehnungslehre» впервые появились ключевые в современной
математике понятия и большинство алгебраических структур,
используемых в этой книге. В ней были определены: векторное
пространство, внешняя алгебра, внешнее и внутреннее
произведение, теорема Стокса в обобщенной форме.
В настоящее время общепризнано, что Э.Картан (1869-1951)
является крупнейшим специалистом по геометрии в XX веке. Его
ранние работы, относящиеся к группам Ли и дифференциальным
уравнениям в частных производных, имеющие огромное значение
для современной математики, тоже сначала не были поняты. Но
в 1920 году они стали известны широкому кругу ученых. К
этому времени теория групп Ли начала играть ключевую роль в
математике и физике, и Г. Вейль заново представил их в своих
статьях. В настоящее время работы Картана по основным
узлам и связям (известные под общим названием «калибровочные
теории») являются основой теории элементарных частиц. В 1922
году Картан опубликовал книгу «Лекции по интегральным
инвариантам», где показал, что изобретенное им внешнее
дифференциальное исчисление является гибким инструментом не только
для геометрии, но и для вариационного исчисления с широким
кругом физических приложений. Как уже было сказано,
признание пришло не сразу, но сегодня и физики, и математики
считают, что внешнее исчисление позволяет наилучшим образом
формулировать геометрические законы физики. И нам кажется, что
пришла пора заменить им векторное исчисление в программах
начального университетского обучения.
Необходимо пояснить, почему в книге так много внимания
уделено теории электрических цепей, хотя обычно эта тема не
входит в учебные программы по математике. Прежде всего, это
оправдано с педагогической точки зрения. Данная тема
всегда нравится студентам. Она позволяет на очень приземленном
уровне ввести понятия дуального пространства и факторпро-
странства. Иначе эти понятия кажутся студентам слишком
абстрактными и поэтому трудно воспринимаются ими. Кроме того,
в дискретном, алгебраическом подходе к теории цепей теорема

XVI
Предисловие
Стокса появляется, по существу, как естественное определение,
что позволяет понять роль оператора d и теоремы Стокса при
формулировке внешнего исчисления. Конечно, есть более
глубокие, философские причины, почему мы приняли решение
подробно рассказать о теории цепей. Уже почти сто лет, как люди
думают, что силы, удерживающие макроскопические тела,
имеют электрическую природу. Таким образом, понятие твердого
тела и отсюда евклидова геометрия вытекают из
электростатики (конечно, в нерелятивистском приближении, когда понятия
твердого тела и геометрия Евклида имеют смысл). Физические
исследования как предельно малых объектов (элементарных
частиц) , так и предельно больших (космология) заново ставят
фундаментальные вопросы о геометрии пространства и времени. Мы
полагаем, что разумно уже в самом начале изучения математики
дать студентам представления о связи геометрии и физики. Без
сомнения, сторонники компьютеров и ряда современных теорий
в физике зададут вопросы о дискретности,
противопоставляемой непрерывному характеру пространства и времени
(проблема, поднятая Риманом в его диссертации об основах геометрии).
Надеемся, что наше обсуждение может быть полезно тем, кто в
будущем станет решать эту проблему.
Наш курс математики читается в течение одного года, и
поэтому мы вынуждены были опустить некоторые важные темы.
Мы не обсуждаем бесконечномерные векторные пространства,
в частности, гильбертовы пространства; не даем определения и
не изучаем абстрактные дифференцируемые многообразия и их
свойства. Наш опыт показал, что эти темы слишком сложны для
студентов, и усилия, которые необходимо затратить на их
объяснение, лучше использовать по-другому. Конечно, в книге есть
места, где нам приходится компенсировать отсутствие этих
понятий. Однако, более серьезно то, что в книге нет подробного
обсуждения гармонического анализа Фурье, классической
механики и теории вероятностей. Мы только слегка касаемся этих
тем, не давая подробного изложения. Нас может извинить только
то, что каждая из этих тем потребовала бы семестрового курса,
а их подробное изложение на современном уровне легко найти.
В конце книги приводится список рекомендуемой литературы.

От издателя русского перевода
XVII
Нам приятно поблагодарить профессора Даниэла Гороффа,
тщательно прочитавшего рукопись, за многочисленные
исправления и полезные предложения. Мы искренне благодарим Джин
Моррис за отличное качество набора, за то, что она внимательно
сопровождала производство книги на протяжении восьми лет —
с самого начала проекта до его завершения.
От издателя русского перевода
Еще восемь лет потребовалось для выхода в свет русского
варианта этой книги, выполненного типографским способом. На
пути русского издания оказалось много препятствий.
Невыполнение Российским фондом фундаментальных исследований своих
уставных обязанностей по финансированию издания выигравших
конкурс произведений (проект №98-01-14152), последствия
преступного дефолта августа 1998 года, — эти и другие финансовые
трудности были преодолены благодаря энтузиазму тех, кто
работал над русским переводом двухтомника.
Однако не только финансовые проблемы снижали скорость
подготовки русского издания. Оказалось, что английский
оригинал содержит изрядное количество неточностей и ошибок.
Поэтому необходимо особо отметить труд переводчика и
редакторов, которые провели тщательную работу по адаптации данного
курса к практике российского образовательного процесса. Часть
ошибок была найдена Л. П. Котовой уже при переводе. Многие
неточности и ошибки устранены Е. В. Майковым при его
скрупулезном редактировании первого тома. Некоторые исправления
в первый том внес и редактор второго тома А. Н. Якивчик; его
же трудами в списке рекомендуемой литературы указаны теперь
точные библиографические данные последних изданий.

XVIII От издателя русского перевода
Тем не менее, не исключено, что наш уважаемый Читатель
заметит в книге отдельные опечатки, неточности, ошибки. И
хотя кое-кто считает, что не следует устранять опечатки, чтобы
не лишать читателя удовольствия находить ошибки*, мы все же
постоянно ведем работу по уточнению текста книги и будем
признательны читателям за соответствующие замечания (наш адрес:
publisher@phasis.ru).
Москва, май 2006
*См., например: «Задачи Арнольда» (М.: ФАЗИС, 2000, с. X).

Глава 1
Линейные преобразования
плоскости
В главе 1 мы рассказываем о связи закона умножения
матриц 2 χ 2 с геометрией прямых на плоскости.
Излагаем алгебру матриц 2x2, изучаем определитель и его
связь с площадью и ориентацией. Вводим понятие
абстрактного векторного пространства в общем случае,
объясняем понятия базиса и замены базиса в случае
одномерного и двумерного векторного пространства.
1.1. Аффинные плоскости
и векторные пространства
Евклидова плоскость, знакомая из школьной планиметрии,
возникла на раннем этапе развития математики. Физические
эксперименты на столе или школьной доске легко демонстрируют ее
свойства. Благодаря использованию линейки и транспортира мы
привыкаем считать «длину» и «угол» такими же
фундаментальными понятиями, как «точка» и «прямая». Занимаясь чистой
математикой или ее приложениями к физике и другим
дисциплинам, мы часто рассматриваем плоскости, для которых прямые
определены, но нет общего определения длины, или когда
обычное евклидово определение длины не работает. Такая плоскость
может быть изображена на листе бумаги, но физическое
расстояние между двумя точками, измеренное линейкой, или угол между

2 Глава 1. Линейные преобразования плоскости
двумя прямыми, измеренный транспортиром, может не иметь
никакого смысла.
В качестве примера приведем плоскость, где графически
изображается движение частицы вдоль оси χ (рис. 1.1). Точки Ρ и Q
на этой плоскости представляют физическое понятие события,
определяемого местом и временем. Линия I тоже имеет
физический смысл; она соответствует движению частицы, на которую не
действует никакая сила. Мы можем сравнивать длины отрезков
вдоль оси t (временные интервалы) или вдоль оси χ (расстояния).
Однако измеренное линейкой расстояние между точками Ρ и Q
лишено всякого физического смысла. Точно так же не имеет
физического смысла начало координат такой плоскости, т. е. точка
пересечения осей.
Рис. 1.1
Такой ситуации (и многим другим «двумерным» ситуациям)
соответствует математическое понятие действительной
аффинной плоскости, т. е. такой плоскости, которая представляет много
двумерных ситуаций. Точки на аффинной плоскости обозначаем
заглавными латинскими буквами Р, Q и т. д., а прямые линии,
в дальнейшем называемые просто прямыми, строчными буквами
I, m и т.д. Следуя Декарту, считаем, что аффинную плоскость
образует множество всех пар действительных чисел. Точка на
такой плоскости — упорядоченная пара действительных чисел, обо
VI
значаемая . Эти числа называют координатами точки. Такую

1.1. Аффинные плоскости и векторные пространства 3
плоскость назовем АЖ2 (рис. 1.2). Здесь А говорит нам, что
плоскость аффинная, и мы не выделяем на ней начала координат.
Буква R соответствует множеству действительных чисел, а
верхний индекс два указывает, что мы рассматриваем пары
действительных чисел. (Как обычно, изображая плоскость на бумаге, мы
откладываем χ по горизонтальной оси, а у определенного вида —
вертикально вверх вдоль перпендикулярной оси. Однако, в
настоящий момент понятия «перпендикулярности» или величины
угла не определены. С одинаковым успехом можно откладывать
χ и у вдоль любых1 осей.) Прямая — это определенного вида
множество точек. Мы предполагаем, что в результате изучения
геометрии читатель знаком с прямыми и, в частности, знает, как
описываются прямые в аналитической геометрии.
Ук
Рис. 1.2
Прямые на аффинной плоскости АШ2 могут описываться по-
разному. Например, уравнением, которому удовлетворяют все
точки, лежащие на прямой,
I
< ах + by = с>
\[у\ I
Формулу следует читать так: «/ — это множество точек
координаты которых удовлетворяют уравнению ах + by = с».
Предполагается при этом, что а и b одновременно не равняются
нулю.
Такой способ описания прямой не очень удобен, потому что
параметры прямой а, Ь, с не определяются прямой однозначно.
Не параллельных друг другу. — Прим. ред.

4 Глава!. Линейные преобразования плоскости
Например, формулы
< ах + by = с > и < Sax + ЗЬу = Зс >
IbJ J I bJ J
определяют одну и ту же прямую. Вообще параметры га, rb, гс
при г φ 0 описывают ту же прямую, что и а, Ъ, с.
Второй способ задания прямой состоит в том, что на
плоскости АЖ2 выбираются две различные точки Р0 =
,Ρι
и через них проводят прямую. Тогда точки, лежащие на такой
прямой, определяются формулой
х0 + t(xi - х0)
yo + t(yi -уо).
где параметр t — любое действительное число. Это описание
прямой еще более громоздко, чем предыдущее: мы можем заменить
выбранные точки Pq и Ρχ любой другой парой точек,
принадлежащих этой прямой.
Есть более удобный способ описания прямой
(«динамический» в отличие от «статического» описания). Мы задаем точку
на прямой и «направляющий вектор прямой». Таким образом,
набор точек, определяемых по формуле < +М Ι ί €R>,
{[Уо] \vj J
где ( Ι ψ ( I — заданный вектор, и есть прямая. (Представим
себе частицу, движущуюся вдоль этой траектории с вектором
скорости
, находившуюся в точке
XQ
Уо
в нулевой момент
времени). Здесь для описания прямой мы используем четыре
параметра. При этом можно умножить I I на не равный нулю
скаляр и получить ту же прямую (это будет движение с другой
х0
скоростью) или можем сдвинуть начальную точку
2/0
вдоль
прямой. В этом случае мы имеем два избыточных параметра.

1.1. Аффинные плоскости и векторные пространства 5
Конечно, эта формула переходит в формулу, полученную
вторым способом,
и = χι - х0,
v = y\- у\.
Ну, а теперь опишем четвертый, привычный способ задания
прямой. В нем нет избыточных параметров, его неудобство состоит
в отсутствии единообразия записи для различных прямых. Если
а и b — любые действительные числа, то набор точек
I = { у = ах + Ь>
\[У\ )
задает прямую, пересекающую ось у в точке
и имеющую
«угловой» коэффициент а, т.е. для всех точек прямой увеличение χ
на единицу влечет за собой увеличение у на величину а.
Прямая задается простым уравнением, параметры а и Ъ определяют
геометрические свойства прямой. Но не все прямые могут быть
заданы таким образом. Необходимо добавить прямые,
параллельные оси у:
НИИ}-
Следуя строгой логике, мы должны принять один из этих
четырех способов описания за определение прямой. Например,
следует сказать: по определению, прямая I — это набор точек
на плоскости АШ2,
I = < ах + by = с> ,
\[У\ )
где три параметра а, бис- действительные числа, причем а
и b одновременно не равны нулю. Теперь нам следовало бы
доказать, что этот же набор точек может быть получен и в трех
других способах описания. Но здесь мы не станем углубляться в
логические тонкости, которые можно реализовать в рамках
элементарной аналитической геометрии.

6 Глава 1. Линейные преобразования плоскости
Важно помнить, что в аффинной плоскости не выделено
начало координат, и бессмысленно складывать точки на такой плос-
не имеет особого значения, и мы устоим перед
кости. Точка
соблазном складывать точки
и
суммируя их
координаты. Однако, существует близкое понятие двумерного векторного
пространства, где операция сложения определена. Мы построим
векторное пространство из аффинной плоскости, вводя для
любой пары ее точек вектор смещения PQ, такой, что «хвост»
вектора находится в точке Р, а его «голова» — в точке Q (рис. 1.3).
Такие векторы будем обозначать жирными строчными латинскими
буквами v, w и т. д. Вектор ν определяется парой
действительных чисел, например, ν = I ) . (Заметим, что для векторов мы
используем круглые скобки ( ), а для точек — квадратные [ ]).
Ρ Ρ
Рис. 1.3 Рис. 1.4
Например, вектор ν =
которое переводит точку
следует понимать как смещение,
в точку
, и вообще, произвольную точку Ρ =
точку
-3
2
в точку Q =
в точку
'х + Ъ
У + 2
Таким образом, вектор ν определяет некое преобразование
аффинной плоскости, а именно, жесткую трансляцию всей
плоскости. Если Ρ — любая точка аффинной плоскости, то смещенную

1.1. Аффинные плоскости и векторные пространства 7
точку Q обозначаем Ρ "+" ν: знак "+" обозначает действие
вектора на точки. Таким образом, вектор ν переводит точку Ρ в
точку Q = Ρ "+" v. В координатной форме это выглядит так:
если Ρ
и ν = " , то Ρ "+" ν =
χ + а
У + Ь
Мы ставим кавычки вокруг знака "+", потому что в этом
случае операция производится над объектами различной природы,
над точками и векторами, и поэтому отличается от обычной
процедуры сложения. Далее, для любой пары точек Ρ viQ определим
единственный вектор ν = Q "—" Ρ такой, что
Ρ «+" ν = Q.
Вокруг знака минус мы тоже ставим кавычки, потому что здесь
тоже участвуют объекты разного рода — из пары точек
получается вектор. Нарисовав несколько примеров на бумаге в клеточку,
вы можете самостоятельно убедиться, что две пары точек Р, Q и
R, S определяют один и тот же вектор (т. е. Q "—" Ρ = S "—" R)
тогда и только тогда, когда векторы PQ и RS являются
противоположными сторонами параллелограмма (рис. 1.4). Поэтому
часто говорят, что вектор определяется величиной и направлением.
Но здесь мы не будем вводить понятия величины и направления
вектора, потому что они не являются инвариантными.
По определению, суммой двух векторов и =
является вектор
и + ν =
И V =
Заметим, что
а + с
b + d
Ρ "+" (u + ν) = (Ρ "+" u) "+" ν,
(1.1)
так как, если и =
иР =
вая части равенства (1.1) определяют точку
то и левая, и пра-
. Форму-
I — /
а + с + χ
b + d + y
л а (1.1) означает, что смещение, соответствующее и + ν, может
быть получено последовательным применением операций
смещения и и v. При этом заметим, что и + ν = ν + и. Мы можем

I

I

10 Глава!. Линейные преобразования плоскости
в обозначениях между Ш и АШ . Дело в том, что в пространстве
R2 точка I I имеет особое значение (нейтральный элемент), и
имеет смысл сложение двух векторов. В пространстве АШ2 ничего
этого нет.
1.2. Векторные пространства
и их аффинные пространства
Легко проверить, что операция сложения векторов в
пространстве R2 и операция умножения векторов на действительные числа
удовлетворяют следующим аксиомам.
Сложение векторов
Ассоциативность сложения: (u + v) + w = и + (ν + w).
Коммутативность сложения: и + ν = ν + и.
Существование нулевого элемента: существует такой вектор О,
что 0 + ν = ν для всех векторов v.
Существование противоположного элемента: для любого
вектора ν существует —ν такой, что ν + (—ν) = 0.
Умножение векторов на действительные числа
Свойство числа 1: 1ν = ν для любого v.
Ассоциативность и дистрибутивность умножения на число:
для любых действительных чисел г и s и любых векторов и и ν
(rs)v = r(sv),
(г + s)v = rv + sv,
r(u + v) = ru + rv.
Эти аксиомы известны как аксиомы векторного
пространства. По определению, векторное пространство — это такое
множество V объектов, называемых векторами u, v и т.д., в котором
введены операция сложения, означающая, что каждой паре
векторов и и ν соответствует третий вектор и + ν, и операция
умножения такая, что каждому действительному числу t и каждому
вектору ν соответствует вектор ίν. При этом должны
выполняться вышеперечисленные аксиомы.

1.2. Векторные пространства и их аффинные пространства 11
Итак, мы показали, что R2 является векторным
пространством. В качестве второго примера рассмотрим пространство R3,
в котором вектор является триплетом, состоящим из
действительных чисел:
Сложение векторов производится сложением компонент, как и в
пространстве R2:
(аЛ /α2\ /αϊ + а2
bi и v2 = Ь2 , то vi + v2 = I Ъ\ + Ь2
С\) \С2/ \С1+С2
Пространство R3 — это знакомое нам трехмерное
пространство векторов. Понятие размерности пространства мы обсудим
позднее.
Все действительные числа тоже можно рассматривать как
векторное пространство R = R1, в котором процедурами
сложения и умножения являются обычные операции сложения и
умножения чисел. Когда мы определим понятие размерности
пространства, станет ясно, что R1 — это пример одномерного
векторного пространства.
В качестве другого примера векторного пространства
рассмотрим множество всех полиномов. Мы умеем складывать
полиномы, просто складывая коэффициенты при одинаковых
степенях х, например:
(1 + Зх + 7х2) + (2 - х2 + х4 - х6) = 3 + Зх + 6х2 + х4 - х6,
Мы умеем умножать полиномы на действительное число:
7(1 + Зх + Зх2) = 7 + 21х + 21х2.
Легко проверить, что в этом случае все аксиомы векторного
пространства тоже выполняются. Далее, можно рассматривать
пространство полиномов не выше заданной степени. Например,
наиболее общий вид полинома не выше второй степени таков:
Ρ = ах2 + Ьх + с.

12 Глава 1. Линейные преобразования плоскости
Сумма двух полиномов
Ρι = αγχ2 + Ъ\х + с\ и Р2 = а2х2 + Ь2х + с2
равна
Р\+Р2 = (αϊ + а2)х2 + (bi + Ь2)х + (ci + с2).
Например, если
Pi = Зх2 + 2х + 1, Р2 = 7х2 - 10х + 2,
то
Рг+Р2 = Юх2 - 8х + 3.
Множество всех полиномов степени не выше двух также
является векторным пространством. Заметим, что оно похоже на
R3, в том смысле, что предыдущие равенства можно записать в
виде
(Η-ί)-Κ)·
В дальнейшем мы еще вернемся к этому вопросу.
Предположим, что задано векторное пространство V;
например, это может быть R1, R2 или R3. Аффинным пространством,
ассоциированным с V, мы называем множество А, состоящее из
точек Р, Q, и т. д., при этом операция "+" означает, что каждой
точке Ρ € А и каждому вектору ν € V в аффинном пространстве
А соответствует другая точка, обозначаемая Ρ "+" v. При этом
должны выполняться следующие аксиомы.
Ассоциативность: (Р "+" и) "+" ν = Ρ "+" (и + ν) для Ρ € А
и и, ν € V.
«Нуль» действует как тождественное отображение:
Ρ "+" 0 = Ρ для любой точки Ρ £ А.
Транзитивность: для заданных Ρ и Q € А существует ν € V
такой, что Ρ "+" ν = Q.
Точность: если для любой точки Ρ выполняется Ρ"+" и =
Ρ "+" ν, то и = v.
Комбинируя две последних аксиомы, можно сказать, что для
любых заданных точек Ρ и Q существует единственный вектор

1.2. Векторные пространства и их аффинные пространства 13
ν такой, что Ρ "+" ν = Q. Иногда это удобно записывать как
ν = Q "-" Р.
Концепция векторного пространства и ассоциированного с
ним аффинного пространства привлекает внимание физиков на
протяжении трех столетий. Началось это еще с ньютоновской
механики, затем продолжалось в специальной теории
относительности и в квантовой механике. Цель этой главы — исследуя на
интуитивном уровне простой случай двумерного2 векторного
пространства R2, продемонстрировать ключевые идеи, необходимые
для изучения таких структур. Начнем, однако, с одномерного
случая, концепция которого настолько очевидна, что подробное
обсуждение может показаться слишком педантичным. Однако
стоит постараться.
Векторное пространство V называется одномерным, если оно
удовлетворяет следующим двум условиям: (i) в нем существует
вектор ν φ 0; и (ii) если ν φ 0, то любой вектор и € V может
быть записан как u = rv, где г — некоторое действительное
число. Заметим, что число г единственное: если riv = r2V, то
обязательно т\ = г2- Действительно, равенство riv = T2V можно
переписать в виде
(п - ^2)ν = 0.
Если Г\ — Г2 φ 0, тогда, вводя обозначение s = {т\— Гъ)_1, имеем
О = s[(n - Γ2)ν] = (s(ri - Γ2))ν = lv = ν,
т. е. ν = 0, что противоречит начальному предположению ν φ 0.
(Проверьте самостоятельно, какую из аксиом векторного
пространства мы использовали на каждом этапе рассуждений.)
Итак, если выбрать в одномерном пространстве вектор ν φ Ο,
то для каждого вектора и можно указать вещественное число г,
и —> г такое, что u = rv.
Если ui = r\v и U2 = r2V, to ui + U2 = (π + ^v. Таким
образом, вектору ui + U2 соответствует число Т\ + г2- Аналогично,
Мы дадим строгое определение термина «двумерный» в разделе 1.12,
термина «одномерный» на следующей странице, а общее понятие
размерности векторного пространства — в главе 10. — Прим. ред.

14 Глава!. Линейные преобразования плоскости
если u = rv и t — любое действительное число, то iu = (ir)v, т. е.
вектору iu соответствует число tr. Итак, каждый вектор
соответствует вещественному числу, и векторные операции
соответствуют операциям в пространстве R1. В этом случае мы
говорим, что имеется изоморфизм одномерного векторного
пространства V с пространством R1. Такое сопоставление пространства V
пространству R1 зависит от выбора вектора v. Выбор вектора ν
называется выбором базиса V, а число г, связанное с и
соотношением u = rv, называется координатой вектора и относительно
базиса v. Предположим, что мы выбрали другой базис ν'. Здесь
ν' = αν, где а — действительное число, не равное нулю. Если
и = rv, то
u = (ra-1)av,
поэтому
u = r'v', г' = а~ г.
Таким образом, изменение базиса посредством замены ν на αν
вызывает замену координаты любого вектора г на а~1г. Выбор
базиса в одномерном пространстве очень похож на выбор
системы единиц для физической величины. Если один килограмм
(единицу массы) мы заменим на новую единицу массы — один
грамм, то вес тела, равный 1.3 кг, станет равным 1300 г. Отличие
состоит в том, что для многих обычных физических величин
измерение объектов производится с помощью положительных (или
нулевых) значений. Бессмысленно говорить, что тело имеет
отрицательный объем, массу и т. д. Есть исключение только в
теории электричества, где электрический заряд может быть
положительным и отрицательным. Например, мы можем представить
себе ситуацию, когда в качестве единицы измерения выбран
заряд электрона. В таком базисе электрон будет иметь заряд +1, а
не —1.602191 х Ю-19 Кл, где кулон (Кл) — стандартная единица,
т. е. базис, принятый международным соглашением.
Пусть А — аффинное пространство, ассоциированное с
одномерным векторным пространством V ■ Если мы выберем точку
О в А, то каждая точка Ρ определяет вектор и = Ρ "—" О.
Если в пространстве V выберем базис ν, то каждой точке Ρ будет
соответствовать число х{Р),
Р = 0 "+" ζ(Ρ)ν.

1.2. Векторные пространства и их аффинные пространства 15
Значение х(Р) назовем координатой точки Р. Теперь у нас есть
две возможности: можно взять точку О в качестве начала
координат, и тогда считать другие точки векторами; либо выбрать
базис в пространстве V, и тогда отождествить векторы с
числами. Если мы заменим базис ν на αν, то χ перейдет в х' согласно
формуле
х'(Р) = a^xiP).
Если, кроме того, мы заменим начало О на О', где О' = О "+" w,
то получим
Ρ «_» О' = (Р "-" О) - w.
Если w = bv, то это равносильно замене х' на х" по формуле
х"(Р) = a^xiP) - Ъ.
Сравним вышеприведенные рассуждения с концепцией
абсолютного времени, введенной Ньютоном. Ньютон писал:
Абсолютное, истинное, математическое время или
длительность течет равномерно в соответствии со
своей внутренней природой, независимо от каких-либо
внешних условий. Относительное, кажущееся,
обычное время есть некоторая мера длительности,
измеренная посредством движения (например, движения
стрелки часов). Оно обычно используется вместо
истинного времени.
В нашей терминологии мысль Ньютона можно изложить так:
есть понятие абсолютного времени, и множество всех
абсолютных времен обладает структурой одномерного аффинного
пространства. Идея гладкого и равномерного течения времени
делает математически точным утверждение, что для множества
абсолютных времен в одномерном векторном пространстве V
существует операция "+". Именно эта постулированная операция
позволяет нам сравнивать различные интервалы времени.
Ньютон различает истинное и обычное время. В нашей дискуссии это
соответствует степени произвольности при определении
координат на аффинной прямой.

16 Глава 1. Линейные преобразования плоскости
Давайте сделаем небольшую паузу и еще раз обдумаем этот
абстрактный постулат Ньютона, который является
краеугольным камнем в физике двух последних столетий. Каждый из нас
имеет собственное психологическое восприятие времени. Наше
психологическое время во многих отношениях отличается от
абсолютного времени Ньютона. Основное отличие в том, что для
нас время имеет определенное направление. Будущее в какой-
то степени неизвестно и подвержено нашим желаниям и
нашему вмешательству. Во многих европейских языках, например,
будущее время указывается словами, выражающими желание или
необходимость (по-английски I will go — я хочу идти или по-
французски j'irai — я должен идти). А вот прошлое в какой-то
степени мы знаем и помним. Однако законы Ньютона не зависят
от изменения направления времени. Если бы мы прокрутили
кинофильм ньютоновской планетарной системы (во всех
отношениях реальной) в обратном направлении, то не обнаружили бы
противоречий с законами Ньютона. Второе существенное отличие в
том, что психологическое время не течет гладко и равномерно, по
крайней мере так, как это происходит с ньютоновским
абсолютным временем. У нас есть определенные физические функции,
повторяющиеся периодически, которые побуждают нас ввести
понятие временного интервала: через определенный промежуток
времени после еды мы опять хотим есть. Но величина такого
промежутка сильно меняется, она определяется уровнем сахара в
крови, который, в свою очередь, зависит от того, что мы
съели, что делали, от нашего психологического состояния в целом
и т. д. Кроме того, сильно меняется психологическое восприятие
временных интервалов. Время летит быстро, когда нам
интересно, и мы увлечены тем, что делаем, и наоборот, оно тянется очень
медленно, если нам скучно. И тем не менее, оказывается, что наш
внутренний ритм как-то коррелирует с периодичностью мира
вокруг нас. Из самых древних источников мы знаем, что измерение
внешнего времени для ведения календаря или для научных
целей всегда основывалось на вращении небесных тел. В качестве
стандарта временного интервала суток обычно использовали
видимое вращение Солнца, т. е. интервалы между
последовательными прохождениями Солнцем зенита. Египтяне разделили сутки

1.2. Векторные пространства и их аффинные пространства 17
на 24 равных промежутка (24 часа), а греки делили периоды от
восхода до заката солнца на двенадцать одинаковых часов,
аналогично делили ночные периоды. Эти временные интервалы
отмечались с помощью разных приборов, например, с помощью
водяных часов, а днем с помощью солнечных часов. Те, кто принял
греческую систему, должны были оборудовать водяные часы
специальным компенсирующим приспособлением, чтобы
модифицировать временные интервалы в соответствии со временем года.
(Длительность календарного, или солнечного, дня в течение года
непостоянна из-за неравномерности движения Солнца на
небесной сфере. Простейшая, относительно точная мера времени —
это звездный день. Он определяется по вращению Земли вокруг
своей оси и измеряется наблюдением за какой-то фиксированной
звездой: период между двумя последовательными
прохождениями фиксированной звезды определенного меридиана называют
звездным днем. Календарный день в среднем на четыре минуты
длиннее звездного дня.)
Самые первые часы, по-видимому, появились в Европе в
тринадцатом веке, но они были очень неточными. Первый крупный
шаг в деле усовершенствования часов был сделан в XVII веке,
когда Галилей обнаружил, что период колебаний маятника
(измеренный, например, по нормальному сердечному пульсу)
постоянен. Но Галилей, похоже, мало использовал это открытие на
практике и только изобрел небольшой прибор для врачей,
чтобы измерять пульс у пациентов. Однако говорят, что его сын
использовал маятник для создания часов. Во всяком случае, с
этого времени усовершенствование механических часов
происходило стремительно. Таким образом, во времена Ньютона уже
существовал метод, согласно которому, в принципе, можно было
делить время на произвольно малые равные интервалы.
Следует отметить, что направление движения стрелок механических
часов совершенно условно, и оно легко обратимо. Простой
заменой зубчатой передачи мы можем заставить стрелки вращаться в
противоположном направлении. Интересно пофантазировать на
тему: как развитие механических часов связано с ньютоновской
концепцией времени?

18 Глава 1. Линейные преобразования плоскости
1.3. Функции и аффинные функции
В нескольких следующих параграфах мы будем рассматривать
те отображения АШ2 на себя, при которых прямые линии
преобразуются в прямые линии. Начнем с общего обсуждения понятий
«отображения» или «функции».
Пусть W и X — некоторые множества. Правило / : W —►
X, согласно которому элементу w множества W соответствует
элемент f(w) € X, называется функцией (или отображением,
картой, оператором), переводящей множество W в множество
X. Множество W называется областью определения f. Если А —
подмножество W, то f(A) обозначает подмножество X, состоящее
из элементов f(w), где w € А:
f(A) = {/И \weA}.
Множество f(W) называется образом /, оно является
подмножеством X.
Например, допустим, что / — это отображение R2 на себя,
определяемое равенством f(P) = Ρ "+" ν, где ν —
фиксированный вектор. Тогда f(A) получается из А переносом А на вектор
v. Если А = I = {Р + iu} — прямая, то /(/) = {Ρ + ν + tu} —
другая прямая (рис. 1.7).
Рис. 1.7
Это очень общее и мощное определение функции. Уточним,
что считать результатом действия функции. Например,
невозможно иметь функцию / : R —► R, обладающую свойствами:

1.3. Функции и аффинные функции
19
/(1) = 2 и /(1) = 3, но все будет в порядке, если для функции
/ : R —► R2 мы будем иметь /(1) =
Следует знать стандартную терминологию, касающуюся
области определения и образа функции /.
1. Если два различных элемента w\, и>2 € W всегда
отображаются в различные точки х\, Х2 € X, то /
называют инъективным отображением. Другими словами, /
инъективно, если из равенства f(w\) = /(it^) следует,
что w\ = и>2-
2. Если образ f(W) составляет все множество X, то /
называется сюръективным (иногда говорят, что /
является отображением на X). Другими словами, если
уравнение /(го) = χ имеет по крайней мере одно
решение для каждого χ € X, то / сюръективно.
3. Если отображение / и инъективно, и сюръективно, то
оно называется биективным. Другими словами, /
называется биективным, если уравнение f(w) = χ имеет
единственное решение w для каждого элемента χ € X.
В этом случае существует обратная функция /_1 :
X —► W, которая отображает каждый элемент χ € X в
единственный и>, для которого f(w) = χ.
Эти свойства отображений проиллюстрированы на рис. 1.8.
Во многих случаях мы можем описать функции с помощью
формул. Существует два способа записи соответствующих
формул. Например, операцию возведения в квадрат F : R —► R мы
можем записывать как F(x) = χ2 или
F : χ у-> х2.
При любой форме записи χ — немой символ. Та же функция
может записываться как
F(t) = t2
или
F : а н-> а .
з>

20 Глава 1. Линейные преобразования плоскости
Рис. 1.8. (а) Отображение сюръективно, но не инъективно.
Невозможно определить /_1(х). (Ь) Отображение инъективно, но не
сюръективно. Нет определения для /_1(хз)· (с) Отображение
биективно. /_1(xi) = w\ и /_1(х2) = и>2-
Формула для описания функции может содержать несколько
численных аргументов, например,
G(x, у) = 2х + Зу или G : (х, у) \—> 2х + Зу.
Такая функция G упорядоченную пару чисел (х, у) переводит в
2х + Зу.
Определим еще одно понятие, относящееся к функциям —
композицию. Пусть W, Χ,Υ, Ζ — некоторые множества, и
допустим, что у нас есть функции
f-w-^x,
g-.X-^Y,
h:Y -» Ζ.

1.3. Функции и аффинные функции
21
Рассмотрим функцию, которая берет w € W, действует на этот
элемент посредством /, в результате чего получается элемент
f(w) множества X; затем на этот элемент f(u)) действует д,
производя элемент множества Υ. Такую функцию обозначим д о /
и назовем ее композицией д с /. Короче: (д о f)(w) = g(f(w)).
Заметим, что композиция
ho д о f : W —* Ζ
(сначала действует /, потом д, потом h) совпадает с
отображениями h о (д о /) и (h о д) о /. Таким образом, для композиций
выполняется такой же «ассоциативный закон», как и для
умножения действительных чисел.
Теперь рассмотрим функции, определенные на аффинных
прямых, плоскостях и векторных пространствах. Начнем с
одномерных примеров, которые, конечно, очень важны, но при этом
достаточно просты для изучения.
Пусть А — аффинная прямая, изображенная на рис. 1.9. Мы
можем выбрать некоторое начало и направление и приписать
координату каждой точке на этой прямой.
PR Q
Рис. 1.9
На математическом языке это значит, что мы выбрали начало
координат О на прямой А и базис ν в пространстве V, как это
сделано в предыдущем параграфе. Таким образом, мы построили
аффинную координатную функцию
χ : А -» R.
Конечно, на прямой существует много возможных аффинных
координатных функций, которые можно построить в зависимости
от выбора начала координат и единицы измерения. Мы называем
χ координатной функцией, потому что она обратима: зная х(Р),
можно восстановить Р. Заметим, что χ сохраняет
«интерполяционное свойство» действительной аффинной прямой: если
R = (1 - t)P + tQ,

22 Глава 1. Линейные преобразования плоскости
то
x(R) = (1 - t)x(P) + tx(Q).
В частности, если R — средняя точка отрезка PQ, то
x(R) = \х(Р) + \x{Q).
Вы, вероятно, никогда раньше не думали об χ как о функции.
Вы не можете написать для нее формулу. Однако без этой
функции невозможно изучать физику, потому что именно она
позволяет вам записывать другие функции на прямой в виде формул.
Например, сила, действующая на частицу, которая находится на
прямой, является функцией положения частицы
/ : А -» R;
причем вы не можете написать формулу для /, но можете ввести
аффинную координату
χ : А -» R
и функцию F : R —> R, после чего написать
f(P) = F(x(P)) = (FoX)(P).
Именно такая композиция, например, формула «сила = sin x», и
применяется для представления функции на прямой.
Время — это тоже аффинная прямая, точками которой
являются «мгновения». Аффинная координатная функция t : А —► R
приписывает каждому мгновению число. Чтобы узнать t, мы
смотрим на часы. Часы, отсчитывающие время с разной
скоростью, дают различные функции ί, но любые «хорошие» часы
производят аффинную функцию. В то же время плохие часы,
например, часы, у которых длина маятника меняется с температурой,
произведут неаффинную функцию.
Движение частицы по прямой линии определяет зависимость
одной действительной аффинной прямой At (время) от другой
действительной аффинной прямой Ах (пространство). Такая
функция / : At —► Ах каждому моменту времени Ε ставит в
соответствие точку Ρ на прямой, так что Ρ = f(E). Мы не
можем записать формулу для /, потому что £ и Ρ не являются

1.4. Евклидовы и аффинные преобразования 23
числами. Поэтому, если мы хотим иметь формулу для описания
движения частицы, то должны ввести аффинные координатные
функции t и х. После этого можно написать
х(Р) = F(t(E)),
где F : R —> R может быть представлена формулой типа,
например, F{a) = хо + vqQ! + \аа2.
1.4. Евклидовы и аффинные
преобразования
Отображение / : R2 —► R2 называется евклидовым
преобразованием, если оно сохраняет расстояние. Это значит, что расстояние
между двумя любыми точками Р\ =
иР2 =
Х2
2/2
равняется
расстоянию между /(Pi) и /(Лг)· Если мы выразим / через две
функции <^:12^1и^:М2-^1 так, что
/
Ф{х,.у)
ф(х,у)
то из условия сохранения расстояния получим равенство
[Ф(Х2,У2)-Ф(Х1,У1)}2 + [Ф(Х2,У2)~Ф(Х1,У1)}2 = 02-Ζΐ)2 + (2/2-2/ΐ)2,
которое должно выполняться для всех значений х\, у\, Х2, 2/2·
Можно считать, что евклидова геометрия изучает свойства
тех подмножеств плоскости, которые инвариантны при любом
евклидовом преобразовании. Например, если А — окружность
и / — евклидово преобразование, то f(A) — тоже окружность.
Если / — прямая, то /(/) — тоже прямая. Из определения ясно,
что если / и g — евклидовы преобразования, то композиция go f
тоже будет евклидовым преобразованием.
Отображение / : R2 —► R2 называется аффинным
преобразованием, если оно переводит прямые в прямые. Таким образом,
для любой прямой / образ /(/) — тоже прямая. Например, пусть
преобразование / задается как
/
2х + у + 1
у — χ + 5

24 Глава 1. Линейные преобразования плоскости
Самое общее выражение для прямой на плоскости записывается
уравнением
ах + by + с = 0.
Это значит, что
"{
ах + by + с
-}
Поэтому
/(0
Г W
Ik
w = 2х + у + 1, ζ = у — х + Ъ и ах + by + с
Мы можем решить уравнения
w = 2х + у + 1,
ζ = у — χ + 5
-}■
для х и у, выразив их через юиг:
у = -(w - 1) + -(ζ - 5).
Тогда условие
αχ + by + с = 0
можно переписать в виде
I(tt,_l)_I(2_5)
+ ь
i(u,-l) + |(z-5)
+ с = 0,
или иначе:
-(а + b)w + ί -Ь - -а 1 2 + с + -о - — Ь = 0.
Другими словами,
ew + gz + h
-о}.

1.5. Линейные преобразования
25
где
1 , 2и 1 4 11
е = -{а + Ь), д = -Ъ--а, nh = c+-a-—b.
Мы видим, что в результате отображения / получилась снова
прямая.
Заметим, что / из этого примера не является евклидовым
преобразованием. Аффинная геометрия изучает те свойства
подмножеств плоскости, которые инвариантны при всех
взаимнооднозначных аффинных преобразованиях. Таким образом,
если А — окружность, то f(A) не обязана быть окружностью
(позднее мы увидим, что это всегда эллипс).
Предположим, что / и есть такое аффинное преобразование.
Тогда, по определению, / преобразует прямые в прямые и
поскольку различные точки переходят в различные точки, то
параллельные прямые переходят в параллельные прямые. Поэтому
преобразование / переводит параллелограммы в
параллелограммы. Таким образом, в аффинной геометрии существует понятие
параллелограмма — рис. 1.10, но нет понятий прямоугольника и
квадрата — рис. 1.11.
а
Рис. 1.10
Рис. 1.11
1.5. Линейные преобразования
Простейшим случаем аффинных (и евклидовых) преобразований
являются трансляции
χ + а
У + Ъ
С помощью трансляций любую точку пространства можно
переместить в любую другую. Прежде чем переходить к
дальнейшему, давайте ограничимся аффинными преобразованиями, при

26 Глава 1. Линейные преобразования плоскости
которых одна точка, скажем
неподвижна, т. е.
Производя трансляцию, мы сможем из этой точки перейти в
любую другую.
Пусть / — взаимно-однозначное аффинное преобразование,
о Го'
при котором начальная точка и =
бую точку Ρ =
жения ν =
неподвижна. Теперь лю-
можно задавать с помощью вектора поло-
, так что Ρ = О "+" v. В дальнейшем мы будем
опускать обозначение [ ], тем самым не будем различать АШ2 и R2.
Из того, что / преобразует параллелограмм в параллелограмм,
немедленно следует, что если вектор положения точки Q есть
ν + w, то вектор положения f(Q) будет /(v) + /(w). Поэтому
/(ν + w) = /(ν) + /(w) при ν φ w.
(1.2)
£iv) №)
ν + w
Рис. 1.13

1.5. Линейные преобразования
27
Теперь можно показать, что преобразование / сохраняет
отношение длин отрезков на любой прямой. Если параллелограмм
натянут на векторы w, ν, ν + w и 2v, то из рис. 1.12, 1.13 видно,
что
/(2v) = 2/(v),
и уравнение (1.2) выполняется при ν = w. Повторяя те же
аргументы, получаем
/(ην) = η/ (ν)
для любого целого числа η > 0. Проводя такое же рассуждение
для вектора (l/ra)v, в результате получим
/(αν) = α/(ν)
для любого рационального числа α > 0.
Из рассмотрения параллелограмма с вершинами О, w, —v+w,
—ν видим, что
/(-ν) = -/(ν),
поэтому
/(αν) = α/(ν)
для любого рационального числа а, положительного и
отрицательного, и для всех v.
Если мы предположим, что / — непрерывное преобразование,
то получим, что
/(αν) = α/(ν)
для всех вещественных чисел а. Но оказывается, такое
предположение излишне. Действительно, из свойств системы
вещественных чисел и из того, что / преобразует прямую на плоскости в
другую прямую, следует, что / — непрерывное преобразование.
Это значит, что равенство /(αν) = α/(ν) справедливо для всех
вещественных чисел α и всех векторов v. Доказательство этого
утверждения несколько искусственно, мы приведем его в
добавлении в конце этой главы. А сейчас ограничимся только теми
аффинными преобразованиями, для которых условие /(αν) = α/(ν)
выполняется при всех вещественных числах а, хотя, как уже было

28 Глава 1. Линейные преобразования плоскости
сказано, здесь нет никакого ограничения. Для таких
преобразований / имеем тождество
/(av + bw) = a/(v) + b/(w), (1.3)
справедливое для любых вещественных чисел а, Ь и для любых
векторов v, w в пространстве R2.
Отображение / ". R2 —► R2, удовлетворяющее условию (1.3),
называется линейным преобразованием плоскости. Таким
образом, изучение аффинных преобразований R2, при которых
фиксировано начало координат, мы свели к изучению линейных
преобразований векторного пространства R2.
По определению, любое отображение R2 —► R2,
удовлетворяющее условию (1.3), линейно. Но не каждое линейное
преобразование является взаимно-однозначным. Например, преобразование,
которое отображает каждый вектор пространства R в нулевой
вектор:
, (х\ /0\ (х\
/ = η Для всех >
линейно, но не взаимнооднозначно.
Если / — линейное преобразование, то
/(v + tw) = /(v)+t/(w).
Если /, кроме того, взаимно-однозначно, то из условия w φ
О следует, что /(w) φ 0. Таким образом, / преобразует
прямую {v + iw I t € R} в прямую {/(ν) + i/(w) | t € R}, т.е.
/ всегда прямые преобразует в прямые. Следовательно, любое
взаимно-однозначное линейное преобразование является
аффинным преобразованием. Взаимно-однозначное линейное
преобразование называется регулярным или несингулярным. Линейное
преобразование, не являющееся взаимнооднозначным,
называется сингулярным. Мы уже видели, что любое регулярное линейное
преобразование является аффинным. Покажем, что сингулярные
преобразования переводят всю плоскость в прямую или в
начальную точку.
Очевидно, что если / и g — линейные преобразования
(регулярные или нет), то g о / — тоже линейное преобразование.

1.6. Матрица линейного преобразования
29
Действительно, поскольку / линейно, то (д о /)(αν + bw) =
g(a/(v) + b/(w)), и поскольку д линейно, это выражение
равно ад о /(v) + bg о /(w), из чего следует линейность д о /.
Итак, по определению, преобразование / линейно, если
условие (1.3) выполняется для всех пар векторов ν и w и для всех
вещественных чисел а и Ъ. Аффинное преобразование — это
взаимнооднозначное отображение пространства R2 в себя,
переводящее прямые в прямые. Любое аффинное преобразование
может быть записано как регулярное линейное преобразование с
последующей трансляцией, т. е. для любого аффинного
преобразования / выполняется
аффинно.
/(w) = l(w) + ν,
ание. Берне
вид, то оно
где I — регулярное линейное преобразование. Верно и обратное
утверждение: если преобразование / имеет такой вид, то
1.6. Матрица линейного преобразования
Пусть / : R2 —* R2 — линейное преобразование. На плоскости
У)
'х
каждый вектор I I можно записать в виде
I =iw4?
/iiWfiW'0
так что
у) \°J V1
Последняя формула показывает, что преобразование /
полностью определяется тем, во что оно переводит базисные векторы
θ) И (!)■ nPe^0™™' что / (J) = (с) и / (?) = (J)·
Тогда / полностью определяется четырьмя числами а, Ъ, с и d
?х\ _ (αχ + by^
f
\yl \cx + dy

30 Глава 1. Линейные преобразования плоскости
Запишем эти числа в форме квадратной матрицы
а Ь^
Mat (/) =
d
где первый столбец есть образ вектора I ), а второй — образ
вектора ( 1 I · Тогда образ любой точки I J задается формулой
a b\ (х
с d) \y
ах + Ьу\
сх + dy) '
(1.4)
причем соотношение (1.4) рассматривается как определение
умножения матриц. Оно показывает, как вектор I I умножать на
матрицу I , ], чтобы получить другой вектор. Согласно
этому правилу для получения каждой компоненты вектора надо
«умножить строку на столбец». Подробнее, верхняя компонента
αχ+by вектора справа в (1.4) получена умножением верхней стро-
х
ки матрицы (а, Ь) на столбец I I, аналогично получена нижняя
компонента.
Например, пусть Re есть поворот на плоскости против часовой
стрелки на угол Θ. Тогда (рис. 1.14)
Re
COS0
sin#
Рис. 1.14

1.7. Умножение матриц
31
*(iwr/
а поворот ϋβ имеет матрицу
cos θ — sin θ
sin θ cos 0
Образ любой точки I J имеет вид
cos# — sin#\ (х\ _ (х cos θ — у sin θ
sin# cos# J \yj \x sin 0 + у cos 0
Формула (1.4) показывает соответствие между линейными
преобразованиями и матрицами, т. е. матрицы 2x2 можно
отождествить с линейными преобразованиями пространства R2.
1.7. Умножение матриц
Допустим, что F — линейное преобразование, которому
соответствует матрица I , ), а линейному преобразованию G соответ-
(е А
ствует матрица I , I. Мы знаем, что преобразование F о G
тоже линейно и ему соответствует матрица, в которой первый
столбец равен
FoG,A=Ffe\-fa b\ (Л _ fae + ь9
. ОI \д) \с dj \gj \ce + dg
а второй столбец равен
\) \hj \с dj \hj \cf + dh
Мы определим умножение матриц так, чтобы их произведение
соответствовало композиции линейных преобразований: (MatF) x
(Mat G) = Mat F о G. Итак, правило умножения матриц таково:
a b\ (е /\ _ (ае + Ъд af + bh
с dj \g h) \ce + dg cf + dh

32 Глава 1. Линейные преобразования плоскости
Каждый элемент матрицы-произведения получается
умножением той или иной строки первой матрицы на некоторый столбец
второй.
Например, если R$ есть поворот против часовой стрелки на
угол Θ, а 11ф есть аналогичный поворот на угол ф, то R$ · Яф =
Щ+ф и
(cos θ — sin θ\ /cos φ — sin φ
sin θ cos θ J ysin φ cos φ
(cos θ cos φ — sin θ sin φ —со
sin θ cos ^ + cos θ sin ^ cos
Сравнение этого выражения с матрицей Ro+φ
/cos(0 + <£) -sin(0 + <£)\
Vsin(0 + <£) cos(0 + <£) у
дает стандартные тригонометрические формулы для cos(# + φ) и
sin(# + φ). Таким образом, уже нет необходимости помнить
формулы для синуса и косинуса суммы углов. Вы можете получить
их из более общего правила умножения матриц.
Заметим, что, вообще говоря, умножение матриц не
коммутативно. Например,
/1 2\ /4 0\ /4 Ю\
V0 зу [р ъ) ~ [р is/ '
а произведение этих же матриц в обратном порядке дает другой
результат:
/4 0\/1 2\ = /4 8\
\0 Ъ) \0 Зу \0 15J
(Два поворота в пространстве R2 коммутируют между собой,
потому что не важно, на какой угол мы поворачиваем сначала.
Но в общем случае коммутативности нет.)
В качестве другого примера умножения матриц докажем
утверждение о разложении матрицы в произведение трех
матриц. Позже это утверждение нам пригодится. Мы докажем, что
)
is θ sin φ — sin θ cos φ
θ cos φ — sin θ sin φ

177T Умножение матриц
33
любая матрица ( , I при а φ 0 может быть записана как
тройное произведение в виде
fa Ь\ (\ 0\ [г 0\ /1 χ
с d) \y I) \0 sj \0 1/ ' ^"^
Чтобы это доказать, мы просто предложим способ вычисления
констант у, г, s, χ. Сначала умножим две матрицы, стоящие
в (1.5) справа. Получаем:
г 0\ (\ х\ __ (г гх
О s) [θ Ι) ~ [θ s
Мы хотим, чтобы выполнялось равенство
a b\ _ (\ 0\ (г гх\ _ (г гх
с d) \у 1/ \0 s ) \ry rxy + s
Приравняем соответствующие элементы матриц справа и слева.
Сначала получаем а = г, и по нашему предположению а ф О,
г φ 0. Далее, имеем Ь = гх и, следовательно, χ = b/r = b/a
(напомним, что о ^ 0). Аналогично, с = гу, поэтому у = с/г =
с/а. И наконец, d = rxy + s, и, следовательно,
s = d — rxy = d — r{b/r)(c/r) = d — (be)/a.
Аналогичное разложение матрицы, важное при изучении систем
линз, имеет вид
с d) \0 \) \е 0J \0 1
Это разложение, возможное для любой матрицы при с φ 0,
доказывается столь же просто: достаточно выполнить умножение в
правой части формулы и приравнять соответствующие элементы
в обеих частях равенства.

34 Глава 1. Линейные преобразования плоскости
1.8. Алгебра матриц
Пусть F и G — линейные преобразования в пространстве R2.
Определим их сумму равенством:
(F + G)(v) = F(v) + G(v).
Заметим, что
(F + G)(av + bw) = F(av + bw) + G(av + bw)
= aF(v) + ftF(w) + aG(v) + ftG(w)
= a(F(v) + G(v)) + b(F(v) + G(v))
= a(F + G)(v) + ft(F + G)(w).
Таким образом, сумма преобразований F + G есть тоже линейное
преобразование. Очевидно, что такая операция сложения
обладает свойствами ассоциативности, коммутативности, нулевое
преобразование имеет вид O(v) = 0 для всех ν, условие (—F)(v) =
—.F(v) определяет противоположное к F преобразование (-F),
т. е. (-F) + F = О, где О обозначает нулевое линейное
преобразование.
Если Η — третье линейное преобразование, то композиция,
представляющая произведение матриц, обладает свойством:
Ho(F + G)(v) = H[(F + G)(v)}
= H[F{v) + G(v)]
= H[F(v)} + H[G(v)}
= (Η ο F)(v) + (Η ο G)(v),
справедливым для всех v. Это можно записать кратко
Ho(F + G) = HoF + HoG.
Аналогично,
(F + G)oH = FoH + GoH.
Это значит, что умножение матриц дистрибутивно по отношению
к введенной операции сложения.

1.8. Алгебра матриц
35
Из определения суммы линейных преобразований
непосредственно следует, что если имеются матрицы F и G:
Mat(F) = (« ») и Mat(G) = (<{),
то для матрицы преобразования F + G имеем
Mat(F + G) = (° + ед J + {) = Mat(F) + Mat(G).
Другими словами, при сложении матриц мы складываем их сот-
ветствующие элементы. Матрицу можно умножать на число: на-
пример, 2^ J) = (1с 2d)-3aMeTHM'4TO
о (а Ь\ - (2а 2Ь\ - (2 °\ (а Ь
\с d)~ \2с 2d) ~ \0 2) \с d
Итак, мы определили сложение и умножение матриц 2x2;
правила сложения и умножения матриц точно такие же, как
большинство известных правил сложения и умножения чисел. Таким
образом,
о сложение ассоциативно, коммутативно, существуют нулевое
и противоположное преобразования;
о умножение матриц ассоциативно, дистрибутивно по отно
А $\ 3
шению к сложению, существует единичная матрица 1„ I.
Однако, у матриц есть два существенных свойства, отличающие
их от чисел.
1. Умножение матриц некоммутативно.
2. Произведение двух ненулевых матриц может
равняться нулю, так что закон сокращения при умножении
матриц работает не всегда:
О 1\ /0 1\ /О О
о о; х Ιο ο;~ Ιο о
Имеется в виду, что умножение любой матрицы Μ на матрицу ( 1 I
(и слева, и справа) дает Μ. — Прим. ред.

36 Глава 1. Линейные преобразования плоскости
И тем не менее, во многих отношениях с линейными
преобразованиями можно работать так же, как и с числами.
Теперь рассмотрим линейные преобразования не в R2, а в
векторном пространстве R3. Векторы пространства R3 описываются
(Х\ И Ρ
столбцами I у I. Существуют три базисных вектора 0 1, 1
W W Ц
0 I. Наиболее общее линейное преобразование в пространстве
описывается матрицей 3x3:
(а\\ α12 αι3'
«21 «22 «23
^«31 «32 «33 ,
где первый столбец является образом первого базисного вектора
0 1 и т. д. Формула умножения таких матриц имеет вид
,0/
'«η αΐ2 αΐ3\ (Ъц 6i2 &1з\ /сц ci2 ci3N
«21 Я22 «23 J X Ь2\ Ь22 &23 I = I &1\ С22 С2з
^«31 аз2 «зз/ \h\ Ь32 Ьзз/ \сз1 с32 сзз,
где для любых г, j, принимающих значения 1, 2, 3, элемент
результирующей матрицы равен
Cij = anbij + ai2b2j + a^b^j-
Таким образом, как ив!2, для получения любого элемента
произведения надо строку первой матрицы умножать на столбец
второй. Например, пусть г = 2 и j = 3. Тогда написанная выше
формула условно изображена на рис. 1.15.
При сложении матриц 3x3 матричный элемент
результирующей матрицы равен сумме соответствующих матричных
элементов. При этом сохраняются все свойства, которыми обладают
матрицы 2x2: ассоциативность и коммутативность для
сложения; ассоциативность и дистрибутивность по отношению к
сложению — для умножения.

1.9. Площади и определители
37
ι 1
«21 «22 «23
1 i
1
I
bis '
ί>23
&33
C23
I
Рис. 1.15
Аналогично, мы можем рассматривать матрицы 4 χ 4, 5 х 5 и
вообще матрицы η χ п.
Можно умножить вектор в пространстве R3 на матрицу 3x3:
^а Ъ с\ ix\ Iax + by + cz\
d e / \ \у = \dx + еу + fz ,
^д h г) \z) \gx + hy + iz)
в общем случае можно умножить вектор в пространстве Rn на
матрицу η χ п.
1.9. Площади и определители
Опять вернемся к плоскости. Пусть / — несингулярное линейное
преобразование плоскости. Поскольку /(v + iw) = /(ν) + i/(w),
преобразование / прямые переводит в прямые, следовательно,
/ является аффинным преобразованием и квадраты переводит в
параллелограммы. Далее, пусть Dv — единичный квадрат, левый
нижний угол которого находится в ν (рис. 1.16):
°·=Η(ί)+'(!)
= {ν + w I w € Do} .
0<s< 1, 0 < ί < 1
}
та
В результате преобразования / получается образ квадра-
Dv, обозначаемый /(Dv), который может быть получен

38 Глава 1. Линейные преобразования плоскости
1
0
]
ν>^
Рис. 1.16
Рис. 1.17
трансляцией образа /(По) квадрата Do:
/(Dv) = {/(v) + /(w)|w€D0}
= {/(v) + u|ue/(D0)}.
Это значит, что /(Πν) имеет ту же самую площадь, что и /(Do)·
Очевидно, что то же самое справедливо не только для
единичного квадрата, но и для квадрата любого размера. С другой
стороны, можно разделить единичный квадрат на четыре
конгруэнтных квадрата (рис. 1.17). Соответствующие образы тоже будут
конгруэнтны и сложенные вместе образуют образ Do, т.е. образ
каждого из них имеет площадь, равную \ х (/(Do)) (рис. 1.18).
Рис. 1.18
Продолжив деление квадратов дальше, можно сделать вывод,
что для квадрата D, длина стороны которого l/2fe, отношение
площадь/(D)
площадь D

1.9. Площади и определители
39
есть число, не зависящее от D (или от величины 2к). Обозначим
это число Аг(/), т.е.
= площадь/(D)
площадь D
Пусть D — некоторое «хорошее» подмножество на
плоскости (рис. 1.19), т.е. подмножество, которое можно с любой
степенью точности аппроксимировать объединением описанных выше
квадратиков (рис. 1.20). (Строго говоря, следовало бы
аппроксимировать D изнутри и снаружи. Если мы можем покрыть
границу множества D конечным объединением квадратиков сколь
угодно малой суммарной площади, то общую площадь их
образов тоже можно сделать сколь угодно малой. Именно такие
аппроксимации нам необходимы, и именно их возможность
подразумевается нашим термином «хорошее» множество ). Для таких
множеств также будет выполняться5 равенство
площадь/(D)
площадь D
= Аг(/)·
Рис. 1.19
Рис. 1.20
Итак, Аг(/) есть коэффициент, показывающий, как
изменяется площадь в результате преобразования /. Если fug — два
43десь авторы фактически предполагают знакомство читателя с
понятием площади для довольно широкого класса подмножеств плоскости,
называемых «измеримыми по Жордану», или «квадрируемыми». Именно такие
множества авторы называют «хорошими». Читатель должен также знать
понятие «границы множества» и ее простейшие свойства. — Прим. ред.
5При очевидном условии, что (площадь D) φ 0. — Прим. ред.

40 Глава 1. Линейные преобразования плоскости
несингулярных линейных преобразования, то
площадь (/ о д)(\3) _ площадь / о д(П) площадь д(0)
площадь D площадь д(0) площадь D
и, следовательно,
Ar(/o5) = (Ar(/))x(Ar(p)).
Теперь вычислим коэффициенты Аг(/) для нескольких
линейных преобразований специального вида, а затем используем
полученные результаты, чтобы получить этот коэффициент в
общем случае. Заметим, что Аг(/) = площадь [/(Do)] = площади
образа единичного квадрата в результате действия
преобразования /.6
Случай 1а. Преобразование / задается матрицей
F = (/)=(o 5)' r>0' s>0·
Тогда, как видно из рисунка 1.21(a), Ar(/) = rs.
Рис. 1.21(a)
Случай lb. Преобразование / задается матрицей
F=(S °)' г<0' *>0.
Тогда (рис. 1.21(b)) Аг(/) = \rs\.
6Если принять, что площадь единичного квадрата Do равна единице. —
Прим. ред.

1.9. Площади и определители
41
Рис. 1.21(b)
Из рассмотрения этих двух случаев видно, что Ar(/) = \rs\
для любой диагональной матрицы F.
Случай 2а. Преобразование / задается матрицей F = I
Рис. 1.22(a)
Заштрихованный треугольник (см. рис. 1.22(a)) с вершинами
1\ /l\ fl + x^
1/'
можно получить из заштрихованного
треугольника с вершинами
0\ /О
О/' VI
χ
трансляцией, прибавляя
к каждой вершине вектор I I. Поэтому образ единичного
параллелограмма имеет ту же площадь, что и сам единичный
параллелограмм. Это значит, что при таком преобразовании сдвига
площадь не изменяется и коэффициент Аг(/) = 1.
Случай 2Ь. Преобразование / задается матрицей F = I ).

42 Глава 1. Линейные преобразования плоскости
Рис. 1.22(b)
И в этом случае два заштрихованных треугольника имеют
одинаковую площадь, т.е. коэффициент Аг(/) — 1.
Теперь поговорим о связи между свойствами линейного
преобразования и определителем его матрицы.
Определителем матрицы F
с d
Det F = ad- be.
Докажем важную формулу:
Ar(/) = |DetF|,
называется число
(1.6)
(1.7)
где F обозначает матрицу преобразования /. Чтобы доказать эту
формулу, воспользуемся важным свойством определителей:
Det(F о G) = (Det F) х (Det G).
Оно проверяется простым умножением: если G =
h
то
Det(F о G) = Det
ае + bg af + bh
се + dg cf + dh;
= (ae + bg)(cf + dh) - (af + bh){ce + dg)
= (ad - bc)(eh - fg) = (Det F) χ (Det G).
Принимая во внимание два правила,
Ar(/ о g) = (Ar(/) χ Ar(p)) и Det(F oG) = (Det F) χ (Det G),

1.9. Площади и определители
43
получаем, что формула
Аг(/) = |DetF|
верна для любого преобразования, которое можно записать как
композицию преобразований, для которых уже проверена ее
справедливость. В разделе 1.7 мы доказали, что если α φ Ο,
можно записать (см. (1.5)):
α Ь\ - (1 °\ (г °\ = (1 х
с d)-\y l) \0 s)~[p 1
Таким образом, формула доказана для всех α φ 0. Если α = 0,
мы можем действовать двумя способами:
1. Непосредственной проверкой: Arl ) = |6c|= Detl ,1
Доказательства предоставляем читателю .
2. Воспользоваться непрерывностью8: заметим, что и Аг(/) и
Det F — непрерывные функции коэффициентов матрицы F
(т.е. если мы мало изменяем эти коэффициенты, то
значения Аг(/) и DetF тоже изменяются мало.) Если матрица
, ; несингулярна, то для достаточно малых е матрица
е Ь\ π
, I тоже несингулярна. Далее, поскольку мы знаем, что
равенство
°< \
выполняется для всех е, близких к нулю, то оно верно при
е = 0.
7Легкое доказательство: если с = 0, то преобразование сингулярно, если
же с φ 0, то (° J) = (° J) χ (J d(C). - Прим. ред.
8 Следующее рассуждение использует не определенные ранее понятия
непрерывной зависимости от параметра нескольких объектов:
преобразования, его матрицы и функций от них. — Прим. ред.

44 Глава 1. Линейные преобразования плоскости
Перейдем к выяснению геометрического смысла знака Det F,
если Det F φ 0. (Смысл модуля этого определителя мы уже
обсудили.) Смысл знака DetF лучше всего показать на
примере (рис. 1.23). Преобразование ( п 1 ) — это отражение
плоскости относительно оси х.
0 -1
ш
tt
\ ->.·
\
: I
.·' /
• /
Рис. 1.23
Результатом отражения является изменение направления
вращения против часовой стрелки на вращение по часовой
стрелке. Таким образом, тот факт, что определитель отрицателен,
означает изменение ориентации плоскости на противоположное,
см. рис. 1.23.
В качестве иллюстрации давайте рассмотрим евклидово
линейное преобразование плоскости, обозначаемое F. Поскольку
вектор F I ] имеет единичную длину, то для некоторого угла
θ можно написать
COS0
sin#
Так как F | I тоже имеет единичную длину, и он перпендику-
/cos#
лярен вектору I . . ], у нас есть две возможности:
-sin#
COS0
или
sin#
COS0

1.10. Обратные матрицы
45
В первом случае мы имеем дело с поворотом на угол Θ:
'cos# -sin#\
. а /> и DetF= 1.
sm 0 cos θ J
г. ,. „ fcos9 sin#\
Во втором случае преобразование г — I . д д I, для
которого Det F = — 1, является отражением относительно вектора
/cos0/2\
I . д /9 ) · Действительно, из тригонометрических формул
следует, что
/cos 6» sin θ λ /cos0/2\ _ /cos0/2\
\sin0 -cos0/ ^sin0/2/ ~~ ^sin0/2/ '
Поэтому вектор I . '. I после преобразования F остается на
месте и прямая, проведенная из начала вдоль этого вектора,
отображается сама в себя. Далее FoF = I
F действительно является отражением.
ражается сама в себя. Далее FoF = { I, т. е. преобразование
1.10. Обратные матрицы
Пусть F = I , 1 — любая матрица порядка 2x2.
Матрица G называется обратной к F, если GF = FG
1 0^
0 1у
Если Det F = 0, то матрица F не имеет обратной, поскольку
(DetF) · (DetG) = Det \\ °) = 1 φ 0. Если же DetF φ 0,
то мы найдем обратную к F матрицу G с помощью следующего
построения.
Определим матрицу Fa согласно формуле
ра=( d -Ь
— с а

46 Глава 1. Линейные преобразования плоскости
Непосредственное умножение показывает, что
Поэтому ясно, что в качестве матрицы, обратной к F, можно
взять
G = (DetF)_1Fa.
Таким образом, мы доказали теорему: матрица F имеет
обратную тогда и только тогда, когда Det F φ 0. В этом случае для
обратной матрицы F-1 справедлива формула
F-^( 65*ί& -Ь,^ТЛ (1-8)
-c(DetF)-1 a(DetF)"
Нам следует понять геометрический смысл F-1; эта матрица
«уничтожает» действие матрицы F. Если сначала мы произведем
операцию F, а потом F-1, то вернемся в исходное состояние9,
поскольку FF~l = I n I — соответствует тождественному
отображению.
Заметим, что если F сингулярна, то она не имеет обратной
матрицы, потому что для любой матрицы F, имеющей обратную,
из Fv = Fw следует F~lFv = F~lFw, т.е. ν = w.
Тот факт, что условие условия DetF — 0 соответствует
сингулярности F, можно интерпретировать в терминах площадей.
Действительно, пусть параллелограмм имеет одну вершину в
начале и стороны, параллельные векторам I I и I , I.
Параллелограмм имеет площадь, не равную нулю, если эти вектора не
лежат на одной прямой, проходящей через начало. Это значит, что
равен площади этого
Det ( 1^0, потому что Det I ,)
параллелограмма. В этом случае существует обратная матрица,
и мы можем написать
Здесь и иногда далее авторы не делают различия между линейным
преобразованием и его матрицей. — Прим. ред.

1.10. Обратные матрицы
47
То же самое можно написать по-другому: I
I — f [ ) + ^ ( j ) · А эт0 значит, что любой вектор на
плоскости может быть представлен как линейная комбинация
ЛЛ fb\ f
векторов I I и I , I, где е, j, д и η — просто числа.
Вспомним (см. параграф 1.1), что вектора и и ν называются
линейно зависимыми, если существуют вещественные числа г и
s, не равные нулю, такие, что
ru + sv = 0.
Если векторы u, v не являются линейно зависимыми, то их
называют линейно независимыми.
Пусть и = I I и ν = I I. Вектора и и ν линейно
независимы тогда и только тогда, когда матрица
М= .
КУ t
несингулярна. Действительно, матрица Μ переводит единичные
вектора I I и II в и и ν соответственно. Таким образом, и
и ν будут лежать на одной прямой (а это и означает их линейную
зависимость) тогда и только тогда, когда матрица Μ
преобразует единичный квадрат в вырожденный параллелограмм нулевой
площади, т. е. при условии, что Det Μ = 0.
Предположим, что и и ν линейно независимы, и мы имеем
матрицу М, определенную выше. Пусть w есть любой вектор на
плоскости R2. Поскольку Μ несингулярна, то мы можем
построить обратную матрицу М-1 и взять вектор M_1w. Этот вектор
определен на плоскости R2 и, следовательно, можно написать
Умножаем обе части этого уравнения на Μ и получаем
MM-1w = w = аМ ( А + ЬМ ( А = аи + bv.

48 Глава 1. Линейные преобразования плоскости
Таким образом, если и и ν линейно независимы, то любой
вектор на плоскости может быть записан как линейная комбинация
этих векторов. Обратно, допустим, что любой вектор на
плоскости можно записать в виде линейной комбинации векторов и и v.
Очевидно, что и и ν не могут лежать на одной прямой,
проходящей через начало, так как это означало бы, что любой вектор на
плоскости лежит на той же прямой. Таким образом,
векторы и и ν линейно независимы тогда и только
тогда, когда любой вектор на плоскости может быть
представлен как линейная комбинация и и v.
Допустим, что F — матрица, a ui и U2 — два линейно
независимых вектора. Параллелограмм, построенный на векторах ui и U2,
имеет ненулевую площадь, следовательно, ^(ui) и F(\i2) будут
линейно независимы тогда и только тогда, когда Det F φ 0.
Подытожим сказанное.
Все утверждения, приведенные ниже, эквивалентны.
1. Матрица F = I ,1 имеет обратную.
2. DetF^O.
3. Векторы I I и I , I не лежат на одной прямой, проходящей
через начало координат.
4. Любой вектор на плоскости можно записать в виде
линейной комбинации I и ,
5. Для некоторой пары векторов ui, U2 соответствующие
вектора F(\i\) и F(\i2) линейно независимы.
6. Для любой пары линейно независимых векторов νχ, V2
вектора .F(vi) и .F(v2) линейно независимы.
7. F — несингулярная матрица.
Давайте используем эти результаты для иллюстрации ряда
положений из аффинной геометрии. Для начала отметим, что в

1.10. Обратные матрицы
49
рамках аффинной геометрии не имеет смысла не только длина
отрезка, но и относительные длины двух отрезков, не лежащих
на одной прямой. Действительно, если и и ν — два линейно
независимых вектора, то существует единственное линейное
преобразование /, которое выполняет операции: и и ru и ν н sv, где
г и s — любые числа, не равные нулю. Таким образом, подбирая
s/r, мы можем сделать любым отношение длин /(и) и /(ν).
С другой стороны, отношение длин отрезков, лежащих на
одной прямой, в аффинной геометрии имеет смысл. Действительно,
раз трансляции сохраняют длину, мы можем предположить, что
прямая I и ее образ /(/) проходят через начало. Так как вращения
тоже сохраняют длину, то мы можем сделать поворот и считать,
что f(l) = l. Но тогда, если 0 φ и € I, образ /(и) тоже лежит на
прямой I, поэтому /(и) = си, где с — постоянный коэффициент.
Следовательно, /(v) = cv для любого вектора ν с /. Это
значит, что / изменяет длины всех отрезков на прямой I одинаково,
умножая их на \с\.
Следует также отметить, что для заданных треугольников
Δι и Дг существует аффинное преобразование /, для
которого /(Δι) = Δ2- На самом деле, с помощью трансляций одну из
вершин треугольника Δ ι можно поместить в начало. Пусть
концы векторов ui и ν χ находятся в двух других вершинах. Вектора
ui и vi линейно независимы, поэтому вершины треугольника О,
ui, vi не лежат на одной прямой. Аналогично можно считать,
что вершинами треугольника Δ2 являются точки О, U2, V2. Но
тогда существует единственное линейное преобразование /, для
которого /(ui) = U2 и /(vi) = V2. Теперь мы можем
сформулировать теорему: для любого треугольника три прямые,
соединяющие вершины со средними точками противоположных сторон,
пересекаются в одной точке.
Понятие средней точки в рамках аффинной геометрии
существует, поэтому утверждение, что эти три прямые
пересекаются в одной (общей) точке, имеет смысл. Чтобы доказать эту
теорему, достаточно рассмотреть один треугольник, потому что
мы можем найти аффинное преобразование, переводящее один
треугольник в другой. Поэтому, если теорема справедлива для
одного треугольника, то она будет справедливой и для любого

50 Глава!. Линейные преобразования плоскости
другого. Теорема очевидна для равносторонних треугольников.
Поэтому можно считать, что она доказана и в общем случае.
1.11. Сингулярные матрицы
Давайте разберемся, что происходит, когда DetF = 0. В этом
случае возможны два варианта:
-(и) ™^(SS)·
Если F — нулевая матрица, то каждый вектор она отображает
в 0, вся плоскость стягивается в начальную точку. В другом
случае, когда F — не нулевая матрица, но Det F = 0, справедливы
следующие утверждения.
1. Существует такая прямая I, что F(u) € I для каждого
вектора и на плоскости R2. Более того, каждый вектор ν € I
является образом некоторого и € R2, т.е. ν = F(u).
Другими словами, матрица F стягивает плоскость в прямую I.
2. Существует такая прямая к, что .F(w) = 0 тогда и только
тогда, когда w € к. Другими словами, матрица F стягивает
прямую к в начальную точку и не переводит в 0 ни одного
вектора, не принадлежащего прямой к.
Докажем утверждение 1. Пусть
Ч:И(©) — ОНО
образуют два столбца матрицы F =
Поскольку F — ненулевая матрица, с ι и С2 не могут
одновременно быть равными 0. С другой стороны, если ci и С2 не
лежат на одной прямой, то из утверждений 2 и 3 предыдущего
параграфа следует, что Det F φ 0, что противоречит исходному
предположению. Таким образом, ci и С2 лежат на одной прямой.
α Ь
с d

1.11. Сингулярные матрицы
51
Обозначим ее I. Любой вектор u € R2 можно представить в виде
х\ /1\ /О
поэтому .F(u) = xci + 2/C2 лежит на той же прямой I.
Если ci φ О, то любой вектор ν € I равен ν = же ι, где χ —
некоторое число. Следовательно, ν = F II 11. Если же С2 φ О,
то ν = ус2 и вектор ν = F II )). Таким образом, мы доказали
утверждение 1.
Теперь докажем утверждение 2. Пусть b>i и Ь2 — первый и
второй столбцы матрицы Fa, т.е.
1 и Ь2 = (
-с) V α
Поскольку DetFa = DetF = 0 и из (7) мы знаем, что b>i и Ь2
линейно зависимы. Кроме того, они не могут быть одновременно
равны 0, т. к. мы предположили, что исходная матрица F φ 0.
Значит, эти вектора порождают прямую, которую мы обозначим
к. Простое вычисление показывает, что Fbi = Fb2 = 0.
Следовательно, каждый вектор w € к удовлетворяет соотношению
Fw = 0.
Обратно, пусть вектор w = I J удовлетворяет условию
Fw = 0, и пусть хотя бы одно из чисел а, Ь не равно нулю. Тогда
координаты вектора w удовлетворяют уравнению ах + by = 0,
которое, очевидно, задает прямую к. Если же a = b = 0, то хотя
бы одно из чисел с, ci не равно нулю, и выполняется равенство
сх + dy = 0, что снова является уравнением прямой к. В обоих
случаях мы получили w € к, что и доказывает утверждение 2.
Обозначим Im(F) подмножество R2, состоящее из всех
элементов вида .F(u). Запишем это символически:
Im(F) = {ν Ι ν = F(u) для некоторого и}.
Читается обозначение Im(F) так: «образ отображения F».

52 Глава 1. Линейные преобразования плоскости
Аналогично определяем «ядро отображения F», обозначая
его символом Ker(F). Так мы будем обозначать множество
векторов, которые преобразование F переводит в 0. Запишем это
формулой:
Ker(F) = {w I /(w) = 0}.
Такм образом, в зависимости от коэффициентов матрицы F
существует три возможности.
1. Det F φ 0. Тогда Im(F) = R2 и Ker(F) = {0}.
2. Det F = 0, но F — ненулевая матрица. Тогда Im(F) = I
есть прямая и Ker(F) = к тоже прямая. Другими словами,
Im(F) и Ker(F) образуют одномерные векторные
пространства (рис. 1.24).
3. F — нулевая матрица. Тогда Im(F) = {0} и Ker(F) = R2.
Если рассматривать {0} как векторное пространство нулевой
размерности, то можно написать общее выражение
размерность Im(F) + размерность Ker(F) = 2.
Специальные случаи сингулярных преобразований.
Сейчас мы изучим несколько частных случаев сингулярных
линейных преобразований.
Рис. 1.24
1. Проекции. Будем называть преобразование ρ проекцией, если
оно обладает свойством:
если ν есть вектор из образа р, то p(v) = v.

1.11. Сингулярные матрицы
53
Для произвольного сингулярного преобразования / : R —> R
можно было бы лишь сказать, что при ν € Im(/) вектор /(ν)
лежит на той же прямой, что и ν, τ. е. /(ν) = αν для некоторого
числа а. Если w — произвольный вектор, то ν = p(w)
принадлежит образу ρ и
{pop)(w) =p(v) = v = p(w).
Отсюда следует, что ρ op = ρ, и поэтому матрица Р,
представляющая проекцию, удовлетворяет условию Р2 = Р. Таким образом,
ία Ъ\ ία Ъ\ _ ία2 + be ab + bd\ _ ία b\
\c d) \c d) " \ac+cd be + d2) ~\c d) '
Поэтому ab + bd = b, и для b φ 0 получаем α + d = 1. Далее,
ас + cd = с, для с φ 0 снова получаем α + d = 1. В случае, когда
b = 0 и с = 0, мы имеем а2 = а, d2 = d и Det P = ad = 0, т. е.
либо а = 1, d = 0 либо а = 0, d = 1, либо Ρ = 0. Поэтому, кроме
случая Ρ = 0, след Р, обозначаемый Тг Ρ = α + d, должен быть
равен 1.
Итак, ненулевая (сингулярная) проекция ρ удовлетворяет
условию pop = ρ] матрица Ρ удовлетворяет условию Ρ = Ρ
и имеет нулевой определитель (ad — be = 0) и единичный след
(a + d = l).
Обратно, предположим, что ad — bc = 0na + d = 1. Тогда
ab+bd = (a+d)b = b и ac+cd = с, кроме того, a2+bc = a2+ad = а и
bc + d2 = d. Таким образом, Ρ2 = Ρ и ρ есть проекция на прямую.
В общем случае будем называть оператор ρ проекцией, если
ρ ο ρ = р. Тогда у нас есть три возможности.
1. Ρ несингулярна. В этом случае обе части уравнения Р2 = Ρ
можно умножить на Р-1 и получить
В этом случае ТгР = 2 = dim(Im(P)), где dim обозначает
размерность.
2. Ρ сингулярна, но не равна нулю. Мы уже рассмотрели этот
случай раньше. Здесь Ρ отображает R2 на прямую и Тг Ρ =
1 = dim(Im(P)).

54 Глава 1. Линейные преобразования плоскости
3. Ρ = I п п 1, поэтому Ρ стягивает всю плоскость в
начальную точку и Тг Ρ = 0 = dim(Im(P)).
Во всех трех случаях выполняется равенство Τι Ρ = dim(Im(P)).
2. Нилыготенты. Для произвольной сингулярной матрицы
определены две прямые Im(F) и Ker(F). Рассмотрим частный
случай, а именно, преобразование п, для которого прямые его
образа и его ядра совпадают. Действуя преобразованием η на
произвольный вектор w, получаем вектор ν = n(w), который
принадлежит одновременно образу и ядру преобразования п.
Отсюда следует, что η(ν) = η о n(w) = 0. Таким образом,
преобразование поп стягивает всю плоскость в начальную точку
и матрица ./V, определяющая п, удовлетворяет условию ./V2 = 0.
Поэтому
fa Ъ\ /а Ъ\ = ία2 + be ab + bd\ = /θ 0\
\c d) \c d) ~ \ac + cd be + d2) ~ \0 0J '
В частности ab + bd = 0 и ас + cd = 0, поэтому если b φ 0 или
с φ 0, то α + d = 0. Если Ъ = с = 0, то а2 = d2 = 0 и N =
В любом случае матрица ./V имеет нулевой след. И обратно, если
ΊτΝ = а + d = 0 и OetN = ad - be = 0, то Ν2 = 0.
Будем называть матрицу нильпотентом, если Nk = 0 для
некоторого к. У такой матрицы необходимо Det./V = 0, т.к.
Oet{N)k = (Det N)k. Итак, ad - be = 0 и, следовательно,
ία b\2 = i(a + d)a (a + d)b\
\c d) ~ \(a + d)c (a + d)d) '
Тогда
k=({a + df-1a {a + df-lb\
\{a + d)k-lc (a + df-ld)-
Эта матрица становится нулевой, если α + d = 0. Но в этом
случае уже ./V2 = 0. Таким образом, на плоскости матрица ./V
является нильпотентом тогда и только тогда, когда выполняется
условие ./V2 = 0, а оно выполняется тогда и только тогда, когда
Det N = 0 и Тг N = 0.

1.12. Двумерные векторные пространства 55
1.12. Двумерные векторные пространства
Векторное пространство V называется двумерным, если в V мы
можем найти такие два вектора щииг, что каждый ν € V можно
единственным способом представить в виде
ν = aiui + a2U2.
«Единственность» означает, что если
ν = aiui + a2U2 и ν = biui + b2u2,
то необходимо выполняются равенства
αϊ = Ь\ и а2 = Ь2.
Упорядоченная пара векторов ui, u2, обладающая описанным
свойством, называется базисом векторного пространства V.
Выбор базиса определяет отображение L = LUl)U2 векторного
пространства V на плоскость R2
такое, что если
ν = α\\λι + а2и2, то L(v) = ( 1
Предполагаемая единственность гарантирует, что отображение L
однозначно определено, компоненты αχ и а2 полностью
определяются вектором v. Отображение L сюръективно: при любых
заданных I I для ν = aiui + a2U2 равенство L(v) = I
Va2/ \a2
удовлетворяется очевидным образом10.
Отметим некоторые свойства отображения L.
Если ν = aiui + a2U2 и w = biui + b2u2, то
ν + u = aiux + a2U2 + biui + b2u2 = (ai + bi)ui + (02 + 62)42,
Следовало бы еще отметить инъективность отображения L. — Прим. ред.

56 Глава 1. Линейные преобразования плоскости
и, следовательно,
L(v + w) = L(v) + L(w).
Аналогично,
L(rv) = rL(v)
для любого вещественного числа г и любого вектора ν в
пространстве V.
Имея в виду все эти свойства, мы говорим, что L —
изоморфное11 отображение (или изоморфизм) пространства V на R2. Это
позволяет нам все свойства и операции векторного пространства
V отождествить с соответствующими свойствами и операциями
в R2 — так же, как в одномерном случае свойства векторного
пространства мы перенесли на R1. Конечно, как и в одномерном
случае, изоморфизм L зависит от выбора базиса. Таким образом,
выбор базиса {ui,U2} есть двумерный аналог «выбора единиц
измерения». Нас будут интересовать только те свойства, которые
не зависят от выбора базиса и имеют истинно геометрическую
природу.
Давайте коротко изучим, как изменяется L при замене
базиса. Сначала рассмотрим, как, зная L, можно восстановить базис
{ui, U2 }. Действительно,
Таким образом, задание базиса равнозначно заданию
изоморфизма, L : V —> R2. Выбрав L, мы можем из этих уравнений получить
базисные вектора ui и U2- Поскольку любой вектор в R2 может
быть однозначно записан в виде линейной комбинации векторов
I „ I и I 1 I и поскольку L — изоморфное отображение, то
каждый вектор в V может быть однозначно записан в виде линейной
ПВ математике термин «изоморфизм» означает взаимно однозначное
(биективное) отображение, сохраняющее все относящиеся к делу структуры.
Для векторных пространств V и W мы говорим, что отображение L
пространства V h&W является изоморфизмом, если оно линейно, инъективно и
сюръективно (т.е. биективно).

1.12. Двумерные векторные пространства 57
комбинации векторов ui, U2. Таким образом, изоморфизм,
связанный с {ui,U2}, очевидно, есть L.
Линейным преобразованием F : V —► V называется
отображение, удовлетворяющее знакомому тождеству
F(au + bv) = aF(u) + bF(v).
Выбрав базис в пространстве V, определяющий отображение L :
V —► R2, мы можем определить линейное преобразование
пространства R2 следующим образом:
LFL~l.
Здесь L"1 : R2 -» V, F : V -» V и L : V
лучше всего видеть на диаграмме:
Эту ситуацию
V
V
Преобразование LFL~l : R2 —► R2, соответствующее нижней
линии, получается после трех последовательных преобразований:
вверх по левой линии диаграммы, вправо по верхней линии и
вниз по правой. Линейное преобразование R2 —► R2 задается
матрицей. Таким образом, выбрав базис L, мы определяем
соответствующую матрицу преобразования F
MatL(F) = Mat (LFL~l)
для любого линейного оператора F : V
другое линейное преобразование, то
LGFL~l = LGL~lLFL-
V. Если G : V -» V
поэтому
MatL(G о F) = MatL(G)MatL(F).
Другими словами, композиции линейных преобразований
соответствует умножение их матриц. Аналогичный вывод можно

58 Глава 1. Линейные преобразования плоскости
сделать для сложения линейных преобразований. Таким
образом, алгебра линейных преобразований двумерного векторного
пространства преобразуется в алгебру матриц 2x2.
Пространство R является векторным пространством. Оно
имеет «естественный» базис, состоящий из векторов I I и
Если / : R2 —► R2 — линейное преобразование, то, пользуясь
языком предыдущих параграфов, соответствующая
естественному базису матрица — это F. Отображение L : R2 —► R2,
соответствующее этому базису — просто тождественное отображение /.
Таким образом, связь между / и F следует записать в виде
F = Mat/(/).
Следуя строгой логике, нам следовало бы с самого начала
использовать обозначение Mat/(/) вместо F, но это было бы слишком
громоздко. С настоящего момента, владея понятием линейного
преобразования произвольного векторного пространства, мы не
будем делать различие между большими и малыми буквами в
скобках.
Привязка Matl(F) к F зависит от выбора базиса. Давайте
посмотрим, что произойдет, если базис изменить. Предположим,
что у нас есть два базиса. Это значит, что нам заданы два
изоморфизма: L : V —у R2 и Μ : V —► R2. Рассмотрим матрицу
В = ML-1 : R2 —► R2, обладающую свойством
M = BL.
Эту ситуацию легко видеть на диаграмме:
R2 ^ ^r2
Матрица В называется «матрицей замены базиса»
(устанавливает связь между базисами L и М). Это двумерный аналог
множителя 1000, на который мы должны умножать численные
значения масс при переходе от килограммов к граммам в новой
©■

1.12. Двумерные векторные пространства 59
системе единиц. Итак, повторяем: L(v) и M(v) — это две точки
в R2, соответствующие одной и той же точке ν в пространстве V
для двух различных базисов L и М. Эти две точки в R2 связаны
между собой матрицей замены базиса:
M(v) = BL(v).
Матрица В задает изоморфизм R2 —► R2 (это композиция
двух изморфизмов), т.е. она не сингулярна. (Ясно, что если мы
имеем изоморфизм L и дана любая несингулярная матрица В,
то можно определить Μ = BL, при этом матрица Μ — это
изоморфизм V —у R2. Итак, коль скоро мы выбрали базис, т.е.
имеем отображение L : V —► R2, то множество других базисов
в пространстве V параметризуется множеством всех обратимых
матриц 2x2, обозначенных у нас В.)
Пусть F : V —у V — некоторое линейное преобразование.
Тогда MatL(F) = LFL~l и MatM(F) = MFM'1.
Следующая выкладка приводит к важной формуле:
MFM~l = {BL)F(BL)-1 = BLFL^B-1 = B{LFL-l)B~l,
поэтому
MatM (F) = BMatL(F)B~1.
Эта формула показывает, как две матрицы одного и того же
преобразования связаны в разных базисах между собой, если мы
знаем матрицу замены базиса В.
Для заданного линейного преобразования F : V —► V
можно выбрать такой базис L, что Matl(F) имеет наиболее
удобную форму. Например, допустим, что F : V —► V стягивает все
пространство V в прямую и эту прямую преобразует в точку 0.
Другими словами, пусть ImF = KerF. Возьмем вектор U2, не
принадлежащий KerF; обозначим ui = F(u2), так что ui φ Ο,
a F(ui) = 0. Вектора Ui и U2 выберем в качестве базиса. Тогда
-1 ίλ\ - ΓΕΎ,,.ϊ - τ(ς\\ - ЛЛ „ ri?r-l ^°
LFL-1 ГА = LF(ui) = L(0) = ГА и LFL^ ГА = LF(u2) =
L(ui) = I 1. При таком выборе базиса матрица преобразования

60 Глава 1. Линейные преобразования плоскости
F имеет следующий вид:
MatL(F) = (° j). (1.9)
В ходе этих рассуждений ничто не мешает нам рассмотреть
случай, когда векторное пространство V есть R2. Используя
стандартный базис, мы задали линейное преобразование в виде
матрицы. Другими словами, когда в параграфах 1.5 и 1.6 мы писали
F, на самом деле следовало писать Mat/(F). Например, пусть
./V — ненулевая нильпотентная матрица. Тогда ./V = Mat/ (F), где
F — линейное преобразование R2 с KerF = ImF. (Это значит,
что ./V есть матрица линейного преобразования F в стандартном
базисе.) Предыдущие рассуждения позволяют нам найти другой
базис L, для которого выполняется (1.9). Формула замены базиса
(переходим от базиса L к базису /) дает нам
N = B§ J) Б- (1.10)
Итак, мы доказали следующее: задав любую ненулевую нильпо-
тентную матрицу ./V, можно найти такую обратимую матрицу В,
что выполняется (1.10). В следующей главе мы еще к этому
вернемся (в частности, рассмотрим, как получить В).
Важные физические приложения результатов этой главы
изложены в главе 9. В ней мы покажем, как гауссова оптика
сводится к изучению матриц 2x2. Однако, большую часть главы 9
можно читать, только зная материал главы 1.
Добавление: фундаментальная теорема
аффинной геометрии
Мы хотим доказать следующее:
Пусть f — аффинное преобразование R2,
удовлетворяющее условию / I I = I n I. Тогда f линейно.
Для доказательства этой теоремы сделаем ряд упрощений.
Заметим, что если g — обратимое линейное преобразование, то g о f

Добавление: фундаментальная теорема аффинной геометрии 61
линейно тогда и только тогда, когда / линейно. Пусть вектора
/ I 1 и / I 1 не лежат на одной прямой, проходящей через
начало координат, т. е. они линейно независимы, и, следовательно,
мы можем построить линейное преобразование д,
обеспечивающее равенства д о f IA = (A и д о f 11А\ = ΙΑ. Таким
образом, с учетом замены / на д о / нам достаточно доказать
следующее:
Пусть f — аффинное преобразование,
удовлетворяющее условиям /ίί0)) = (о)' М(о)) = (θ) U
/ ((J)) = (J). Тогда / - тождественное преобра-
зование.
Доказательство. Из параграфа 1.5 мы знаем, что / (( 1
* (( 0 ) W ((1)) = ( 0 ) + (1) = (1)' (П° сУЩествУ' мы Доказали,
что /II )) = ( ) для любых рациональных чисел г и s.)
Таким образом, / переводит оси х, у и прямую χ = у,
проходящую через точки I I и I I, в самих себя.
Итак, для любого вещественного числа α
'αΥ\ _ [Ф(аУ
^\0)) \ О
где φ — некоторая функция. (Мы хотим доказать, что ф(а) =
а для всех а.) Аналогично / II , II = I ,,,-. I для некоторой
функции ψ. Поскольку
'<« -ЧЙМЙ
мы имеем
/
а\\ (Ф(а)\
bjj Km;

62 Глава 1. Линейные преобразования плоскости
Мы утверждаем, что ψ и φ — одна и та же функция.
Действительно, возьмем прямую χ = а (рис. 1.25). Она параллельна оси
у и, следовательно, ее образ при преобразовании / должен быть
параллелен оси у, т. е. образ должен быть χ = ф(а). Прямая χ = а
пересекает прямую χ = у в точке I 1, а прямая χ = φ(α)
пересекает прямую χ = у в точке
ф(а)
ф(а)
f
. Следовательно,
ф(а)\
ф(а) '
т. е. ф(а) = V'(fl) Для всех а.
Мы знаем, что
О )) VV°>
ф(а + Ъ)= ф(а) + ф(Ъ).
т.е.
Воспользуемся аргументами из параграфа 1.2 и докажем
удивительное равенство
ф(аЪ) = ф{а)ф{Ъ).
Действительно, давайте посмотрим на рис. 1.26. Прямая, со-
Ί\ (Ь
единяющая точки
и | ], параллельна прямой,
соединяющей точки { ~ I и I ™" ). Таким образом, значение аЬ может быть

Добавление: фундаментальная теорема аффинной геометрии 63
х = у
Рис. 1.26
получено графически с помощью параллельных и пересекающих
'Ф(а)
О
ся прямых. Поэтому, рисуя аналогичную диаграмму для
[Ф(Ъ)\
и I I, мы получим
ф(аЬ)\ = f /αδλ = Ша)ф(Ь)\
откуда следует, что
ф(аЪ) = ф{а)ф(Ъ).
Вещественное число χ положительно тогда и только тогда, когда
χ = у2 при некотором положительном у. Поэтому ф(х) = ф(у2) =
ф{у)2, и из неравенства χ > 0 следует, что ф(х) > 0. Итак, из
α — Ь > 0 вытекает, что ф(а) — ф(Ь) > 0. И если г < а < s, то
ф(г) < ф(а) < </>(s). Для любого вещественного числа α мы можем
найти рациональные числа г и s, удовлетворяющие условию г <
а < s, сделав величину s — г сколь угодно малой. Однако, для
рациональных чисел ф(г) = г и <fi(s) = s. Отсюда
г < ф(а) < s.
Следовательно, \а — ф(а)\ < s — г. Поскольку число s — г может
быть выбрано сколь угодно малым, то для всех вещественных
чисел выполняется ф(а) = а. Этим заканчивается наше
доказательство.

64 Глава 1. Линейные преобразования плоскости
Резюме
A. Преобразования плоскости
Прочитав эту главу, вы должны усвоить определения аффинного
преобразования, линейного преобразования и евклидова
преобразования.
Вы должны уметь определять геометрические свойства,
которые сохраняются при аффинных преобразованиях, и свойства,
которые сохраняются при евклидовых преобразованиях.
B. Алгебра матриц
Вы должны уметь складывать и умножать квадратные
матрицы одинакового ранга, вычислять определители матриц 2 х 2 и
писать обратную матрицу для обратимой матрицы 2x2.
C. Матрицы и линейные преобразования
Имея достаточную информацию о линейном преобразовании
плоскости, вы должны уметь писать матрицу 2x2,
определяющую это преобразование.
Вы должны понимать связь между умножением матриц и
композицией линейных преобразований и уметь пользоваться
этой связью.
Вы должны уметь определять матрицы 2x2, которые
представляют частные случаи преобразований (преобразования
вращения, отражения, проекции, нильпотентные преобразования).
Задачи
1.1. Ниже приводятся несколько теорем евклидовой геометрии
плоскости. Разберитесь, какие из них справедливы для аффинной
геометрии плоскости.
(a) Все медианы треугольника пересекаются в одной точке и
делятся этой точкой в отношении 2 : 1 (считая от вершины
угла).
(b) Длины биссектрис равнобедренного треугольника равны.
(c) Диагонали ромба взаимно перпендикулярны.
(d) Диагонали параллелограмма в точке пересечения делятся
пополам.

Задачи
65
(е) Пусть PQR и P'Q'R' — два таких треугольника, что
параллельны следующие три пары прямых: PQ и P'Q', QR и Q'R',
PR и P'R'. Тогда три прямые РР', QQ' и RR' либо
параллельны друг другу, либо пересекаются в одной точке.
1.2. (а) Пусть Αι и Аг — аффинные прямые, χ — аффинная
координата на Αι, а у — аффинная координата на Аг- Далее,
пусть / : Αι —> Аг — аффинное отображение, а
соответствующая ему функция F : R —► Ш. такова, что если Q = f(P), то
y(Q) = Fox(P). Покажите, что наиболее общий вид функции
F есть F(a) = га + s.
(b) Пусть χ' = αχ + Ь, у' = су + d, где χ' и у' — новые
аффинные координаты на А\ и Аг соответственно, и пусть
y(Q) = F о х(Р), где F(a) = га + s. Получите формулу для
такой функции F'(/3), чтобы y'(Q) = F' о х'(Р).
1.3. Функцию и : R2 —► Ш. назовем аффинной, если она аффинна
для каждой прямой в плоскости и для любого параллелограмма,
изображенного на рис. 1.27, выполняется равенство u(P)+u(R) =
u(Q) + u(S). Пусть и : R2 —► Ш — аффинная функция и известны
следующие ее значения: и
1"
2
= 3, и
з"
8
= 8, и
' 2"
-1
9.
(a) Получить формулу для и
(b) Нарисовать R2 и показать прямые и = const.
1.4. Для линейного преобразования, представленного каждой из
матриц, следующих ниже, получить образ прямоугольника ABDE,
изображенного на рис. 1.28. Вычислить определители
преобразований и проверить, что они правильно предсказывают площади
и ориентации образов прямоугольника.
(а) Вращение Rn/2 = ( 1 Q j.

66 Глава 1. Линейные преобразования плоскости
D
В
Ε
О
Рис. 1.28
(b) Вращение Λπ/4 = -fe ( χ 1 j.
(c) «Искажение» D2 = ί η ι /г>) ■
(d) Преобразование Лоренца Li = I „ ,. _ ,. J.
(e) Сдвиг SY = ί 0 1J.
(f) Сдвиг SI = (}[2/2 J/2).
(g) Отражение М0 = ( Q _1 J.
(h) Отражение Μπ/4 = I , η Ι.
(ί) Проекция Ρπ/4 = ί Λ2 ^,Δ-
(j) Нильпотентное преобразование No = L .-. J.
(k) Нильпотентное преобразование Νπ/4 = Ι ι /ο ι /ο /·
1.5. Алгебраически вычислите произведения матриц, определенных
в предыдущем упражнении, и дайте геометрическую
интерпретацию полученных преобразований:
(а) R-π/ίΙΙπ/2ι
(Ъ) si

Задачи
67
(c) Л^/гМо,
(d) Pl/v
(e) К/*-
1.6. Для каждой из следующих матриц вычислите обратную матрицу
и дайте геометрическую интерпретацию полученного результата:
(a) Λ*/4 = 7ΐ( 1 1 )'
(b) i2 - ^з/4 5/4у
(c) Si=(j J),
1.7. Для каждой из следующих матриц, имеющих нулевой
определитель, найдите образ (Im) и ядро (Кег):
Ы Рм-Л/2 1/2\
,,. Лг /-1/2 1/2\
(Ь) ^π/4=^_1/2 1/2J.
1.8. В параграфе 1.7 доказано разложение матрицы в произведение
трех множителей. Представьте матрицу
(2 4
в виде
Ί 0\ /г 0\ /1 χ
ку I) \0 s) \0 1
1.9. Найдите процедуру, представляющую любую матрицу I ,1
при с φ О в виде произведения
1 у\ /О Л Л ι
О lj \е О/ [0 1

68 Глава 1. Линейные преобразования плоскости
О помощью этой процедуры разложите матрицу I
произведение трех множителей.
ι m π . /О Ь\ ^ , /Ό Ь
1.10. Докажите, что Ar I
Det,
с а
(a) путем прямой проверки (найдите образ квадрата);
(b) используя разложение из предыдущего упражнения, которое
справедливо даже при а = 0.
1.11. Постройте матрицы 2x2, которые представляют следующие
преобразования плоскости:
(a) преобразование Р, удовлетворяющее условию Р2 = Р,
которое всю плоскость отображает на прямую у = 2х, а прямую
у = — 2х отображает в начало координат;
(b) преобразование сдвига S, которое каждую точку прямой у =
2х отображает в себя, ось у отображает в прямую у = — χ и
удовлетворяет условию (S — I)2 = 0;
ι \ л ίΛ ί2\ ( Λ А/2>
(c) преобразование, переводящее „ в . , а о)в( л
(d) нильпотентное преобразование N, удовлетворяющее
условию N2 = 0, для которого прямая у = Зх является
одновременно образом и ядром.
1.12. Упражнение на умножение матриц 3x3. Возьмите две матрицы
17 =
0 1 0\
0 0 1,
0 0 0/
L =
/0 0 0
10 0
\0 1 0
и вычислите UL, LU, £73.
1.13. Известно, что определитель матрицы 3x3 равен:
(an an αΐ3Ν
0,21 0,21 α23
ο3\ «32 οζζ)
= a„Detfa22 "23Va12Detfa21 aA + a13Det (a21 U22)
\a32 a33J \a31 a33J \a3i a32J
= θηα,22θ33 — αιια,23α32 — a\2u2\a33
+ 012^23^31 + 013021032 — θ\3θ22θ3\.

Задачи
69
Докажите, что
Det(F о G) = Det F x Det G.
1.14. Покажите, что если матрица
fan α12 аиу
«21 0*22 0*23
^«3ΐ азг «ззу
удовлетворяет условиям ац φ 0 и ацагг —Я12Я21 Φ 0, то ее можно
записать в виде произведения трех матриц
1 0 0\ /е 0 0\ /1 х\2 ζΐ3Ν
2/21 1 0 0/00 1 Х2г
КУ31 2/32 1/ \0 0 <// \0 0 1
1.15. В пространстве R3 мы можем определить VolF для любого
несингулярного линейного преобразования F так же, как мы
определяли Аг на плоскости. Таким образом,
Vq1F= объем F(D)
объем D
для любой области D. Кроме того,
Vol(FoG) = VolFxVolG
и VolF = объем F(D), где D — единичный куб. Докажите, что
VolF=|DetF|.
1.16. Рассмотрите аффинное преобразование, которое не оставляет
начало координат на месте:
где А — аффинное преобразование, оставляющее начало
координат на месте. Покажите, что такое преобразование может быть
представлено матрицей 3x3:
а
Ъ
0 0 '

70 Глава 1. Линейные преобразования плоскости
где А — матрица 2x2, при условии, что вектор на плоскости
х\ (Л
I представляется трехкомпонентным вектором I у I.
Докажите следующие утверждения.
(a) Такая матрица 3x3 имеет определитель, равный Det А.
/А
(b) Когда такая матрица 3x3 действует на вектор I у I, третья
W
компонента результирующего вектора равна 1.
/1 0 а\
(c) Матрицы Т(а, Ь) ξ I 0 1 Ь ], представляющие чистые
\о о ι)
трансляции, удовлетворяют закону
Т(а, Ъ)Т(с, d) = T(a + c,b + d).
Это упражнение может быть интерпретировано
геометрически. Рассмотрим аффинную плоскость как плоскость ζ = 1 в
пространстве R3. Группу аффинных преобразований этой
плоскости отождествим с группой линейных преобразований в прост-
ранстве R3. Точку у I на плоскости ζ = 1 отождествим с пря-
W
мой, соединяющей эту точку с началом координат. Любая
точка на плоскости определяет единственную такую прямую. Если
прямая, проведенная из начальной точки, пересекает плоскость
ζ = 1, то она пересекает ее в единственной точке (рис. 1.29).
Таким образом, мы можем говорить, что каждой точке на нашей
аффинной плоскости соответствует прямая в пространстве R3,
выходящая из начальной точки и пересекающая плоскость ζ = 1.
Такая геометрическая интерпретация позволяет нам подойти к
определению понятия перспективы: две плоские фигуры в
пространстве R3 (не содержащие начало) перспективно совпадают,
если они определяют одно и то же семейство прямых,
выходящих из начала координат (рис. 1.30).
Это позволяет нам рассмотреть новую геометрию, в которой
«точки» — это прямые в пространстве R3, проходящие через
начало; мы не требуем, чтобы прямая пересекала плоскость ζ = 1.

Задачи
71
Рис. 1.29
Рис. 1.30
Новые «точки», которые мы добавили, соответствуют тем
прямым в пространстве R3, которые лежат в плоскости ζ = 0 и
проходят через начальную точку. Пусть I Ь Ι φ 10 1 — точка
W W
пространства R3, лежащая в плоскости ζ = 0. Буквой Ρ
обозначим прямую, проходящую через начальную точку и точку
b I, т. е. Ρ — это одна из наших «новых» точек. Таким образом,
ί (Λ \
Ρ = < I bt I >. С точки зрения пространства R3, где Р явля-
IWtaJ
ется прямой, мы можем аппроксимировать Ρ семейством прямых
Ре, проходящих через начальную точку (рис. 1.31) и задаваемых
формулой
Ре =
teR<
В некотором смысле Ре —> Ρ при е —► 0. Но Ре пересекает плос-
а/е\
кость 2 = 1 при t = 1/е в точке b/e I.
V1/
Точки прямых Р€, принадлежащие аффинной плоскости,
стремятся к бесконечности при е —► 0 в определенном направлении,

72 Глава 1. Линейные преобразования плоскости
ζ к /
А
У
Ч Х^7
1^
X
Рис. 1.31
задаваемым вектором ( , I. Поэтому будем считать, что новая
«точка» Ρ — это точка, лежащая на бесконечности в аффинной
плоскости. Понятие о таких бесконечно удаленных точках было
впервые введено в пятнадцатом и шестнадцатом веках
художниками и геометрами, изучавшими перспективу.
Итак, мы определили новое пространство Р2, называемое
проективной плоскостью. «Точка» в пространстве Р2 — это прямая,
проведенная из начальной точки в пространстве R3. Давайте
теперь посмотрим, как определить «прямую» в Р2. С точки
зрения пространства R3 «прямая» на аффинной плоскости ζ = 1
состоит из прямых, проходящих через начало координат и
пересекающих плоскость ζ = 1 во всевозможных точках некоторой
прямой (рис. 1.32).
Рис. 1.32

Задачи
73
Такое семейство прямых образует плоскость в
пространстве R3. Другими словами, с точки зрения пространства R3,
прямая на аффинной плоскости есть линия пересечения плоскости в
пространстве R3, проходящей через начальную точку, и
плоскости ζ = 1. Теперь ясно, что делать дальше. Мы опускаем
условие пересечения плоскостей и определяем «прямую» на Р2 как
плоскость в пространстве R3, проходящую через начальную
точку. Существует только одна плоскость в пространстве R3,
проходящая через начало и не пересекающая плоскость ζ = \. Это
плоскость ζ = 0. Нам осталось добавить к множеству прямых
на аффинной плоскости «бесконечно удаленную прямую». Точка
Ρ принадлежит «прямой» I, если прямая, проведенная из
начала, лежит в плоскости, проходящей через это начало. Две
разные «точки» Ρ и Q (т. е. две разные прямые, проведенные через
начало) определяют единственную плоскость, проходящую через
начало, т. е. две различные «точки» определяют единственную
«прямую». Две различные плоскости, проходящие через начало
в пространстве R3, пересекаются по прямой, проходящей через
начало. Таким образом, две разные «прямые» на плоскости Р2
всегда пересекаются в «точке». (Заметим, что здесь проявляется
различие с аффинной геометрией, где две прямые могут быть
параллельны. Две параллельные прямые, принадлежащие
аффинной плоскости, пересекаются «на бесконечности» в проективной
плоскости.)
Выводы: любая «точка» на плоскости — это прямая,
проходящая через начало в пространстве R3; любая «прямая» на
плоскости Р2 — это плоскость, проходящая через начало в
пространстве R3; две различные «прямые» пересекаются в единственной
«точке».
Любая обратимая матрица 3x3, действуя в пространстве
R3, переводит прямые, проходящие через начало, в прямые,
тоже проходящие через начало; переводит плоскости, содержащие
начало, в плоскости, тоже содержащие начало.
1.17. (а) Покажите, что любая обратимая матрица 3x3
определяет взаимно-однозначное преобразование проективной
плоскости Р2, переводящее «прямые» в «прямые».

74 Глава 1. Линейные преобразования плоскости
(Ь) Покажите, что две обратимые матрицы А и В третьего
порядка определяют одно и то лее преобразование плоскости
Р2 тогда и только тогда, когда А = сВ для вещественного
числа с, не равного нулю.
1.18. Три вектора u, v и w в пространстве R3 называются линейно
независимыми, если уравнение
au + bv + cw = 0
не может выполняться, если только не все числа а, Ь, с равны
нулю. Покажите, что если u, v и w линейно независимы, то
существует единственная обратимая матрица А третьего порядка,
для которой
Av=\l\, Aw
(Обобщение этой теоремы для любого конечномерного
векторного пространства будет доказано позже.)
1.19. (а) Пусть Pi, Рг, Рз — различные «точки» на плоскости Р2,
определяемые прямыми, проходящими через начальную точку, и
(Л (°\ (°\
векторами 10 1, 111 и 101 соответственно. Пусть Q\, Q2,
w w w
<5з — три любые другие различные «точки» Р2. Покажите,
что существует обратимая матрица 3x3, которая
преобразует точку Qi в Pi, <Эг в Рг и <5з в Р3.
(b) Пусть Qi,Q2, <9з> Qi — «точки» на плоскости Р2, из которых
никакие три не лежат на одной прямой. Пусть R\, R2, R3,
R4 — другой набор четырех «точек», из которых никакие три
не лежат на одной прямой. Покажите, что существует такая
матрица 3x3, которая преобразует Qi в Р1; <5г в Р2, <5з в
Р3 и Qi в Р4.
(c) Докажите фундаментальную теорему проективной
геометрии: любое взаимно-однозначное преобразование плоскости
Р2, переводящее «прямые» в «прямые», осуществляется
матрицей 3x3. (Подсказка: сведите все к фундаментальной
теореме аффинной геометрии, доказанной в приложении к этой
главе.)

Задачи
75
1.20. В качестве иллюстрации применения упражнения 1.19(b)
докажите теорему Фано (рис. 1.33). Пусть А, В, С, D — четыре точки,
из которых никакие три не лежат на одной прямой, и пусть Ρ —
точка пересечения прямых АВ и CD, Q — точка пересечения
АС и BD, R — точка пересечения AD и ВС. Тогда Р, Q и R не
лежат на одной прямой. (Подсказка: рассмотрите частный
случай, например, пусть А, В, С — три вершины равностороннего
треугольника, a D — его центр.)
Рис. 1.33

I

Глава 2
Собственные векторы
и собственные значения
Во второй главе мы обсудим конформную линейную
геометрию на плоскости, т. е. геометрию прямых,
углов и их связь с матрицами 2x2 определенного вида.
Обсудим очень важные для квантовой механики
понятия собственных векторов и собственных значений1.
С помощью этих понятий получим алгоритм
вычисления степеней матрицы. В качестве приложения
изучим основные свойства цепей Маркова.
2.1. Конформные линейные преобразования
Мы рассмотрим такие линейные преобразования / пространства
R2, которые
(1) сохраняют угол,
(2) сохраняют ориентацию, т. е. Det F > О,
где F — матрица, представляющая /. Заметим, что если / и д —
два таких преобразования, то их композиция до f обладает теми
же свойствами.
1Конечно, эти понятия не менее важны в самых различных разделах
математики и ее приложениях. — Прим. ред.

78 Глава 2. Собственные векторы и собственные значения
Допустим, что / сохраняет угол и ориентацию (рис. 2.1). Мы
можем найти такой поворот г-в, что г-в о / переводит I
точку на положительной оси х. Но раз преобразование г-в ° /
сохраняет углы и Det(r_e о /) > 0, то Г-е ° / ( ( ι ) ) находится
на положительной оси у.
Рис. 2.1
Таким образом, матрица, представляющая г-в о/, имеет вид:
г-*о/=(о I
где г > 0, s > 0. Так как г-в о / сохраняет углы, прямая, иду-
1, переходит в себя. Если мы говорим, что
щая вдоль вектора
г 0\ /1
лежит на прямой, заданной вектором
0 s) \1
чит, что г = s. Следовательно,
, это зна-
г 0
0 г
г-в о / =
Поэтому матрица, представляющая /, имеет вид
F =
г 0
0 г
cos θ — sin θ
sin θ cos θ
r cos θ
rsin#
-rsin#
rcos#
α — b
b a
где α = r cos θ, b = rsin#. Ясно, что любая такая матрица
удовлетворяет условию Det F = а2 + Ь2 = г2 > 0.

2.1. Конформные линейные преобразования 79
Обратное утверждение: любая ненулевая матрица ( ,
α -Ь \ 2,12
сохраняет угол и ориентацию, потому что взяв
Ь а" «2 + ^°>
можно положить г2 = а2 + Ъ2 и потом найти такой угол Θ, при
котором
cos θ = ar~ , sin θ = br~ ,
поскольку α < г и sin2 0 + cos2 0 = (a2 + b2)/r2 = 1. Следовательно,
матрица принимает вид
α — b\ _ frcosO —rs'm6
b a J yrs'me rcosO
Итак, в общем случае матрица
" ) , где а2 + Ь2 φ О,
о a J
сохраняет угол и ориентацию, причем
Очевидно, что произведение двух таких матриц дает матрицу
такого же вида. Кроме того, заметим, что
а -Ь\(а! -V\ _ (аа'-Ы/ -(Ьа! + аЬ')
Ь а) \У а!) " \Ьа! + аУ ао! - W
а' -ЬГ\ (а -Ь
У а')\Ь а
т. е. в этом случае произведение матриц коммутативно. Более
того, при ненулевых значениях α и b существует обратная матрица
(т. к. определитель матрицы равен а2 + Ь2). Наконец, если мы
сложим две матрицы
α -Ь\ fa' -У\_(а + а' -(Ъ + У)\
Ь а [У а' ~{Ъ + У а + а' Г

80 Глава 2. Собственные векторы и собственные значения
то сумма будет опять матрицей типа ( , ]. Это
замечательное свойство не следует прямо из определения. Матрицу типа
, J будем называть конформной. (При этом мы
допускаем возможность, что α = b = 0. Таким образом, ненулевыми
конформными матрицами называются такие матрицы, которые
сохраняют угол и ориентацию.)
Итак, мы доказали, что множество всех конформных
матриц замкнуто относительно операций сложения и умножения.
Для таких матриц умножение является коммутативной
операцией. Каждая ненулевая конформная матрица имеет обратную. Это
значит, что поведение конформных матриц во многом похоже на
поведение чисел.
Любую конформную матрицу можно записать в виде
а -Ь\ (I 0\ ,/0 -1
Ъ а)=а{0 l)+b{l 0
Заметим, что ( 1 „I есть поворот на девяносто градусов и что
0 -1\2 /-1 0\ /10
1 0/ V 0 -1/ \0 I)'
Введем обозначения:
I для
1 ДЛЯ
Тогда
где
α — Ъ
Ъ а
1 0
0 1
0 -1
1 0
= αϊ + Ы,
Ϊ2 = -I

2.1. Конформные линейные преобразования 81
Другими словами, множество конформных матриц можно
отождествлять с множеством комплексных чисел.
Обычное представление комплексного числа в виде точки
на плоскости есть просто отождествление комплексного числа
Τ
с образом точки I „ I при преобразовании, задаваемом матри-
„ (а -б\ _ , (а\
цеи I , I. Для конформных матриц точка I , I определяет
(а -Ь
матрицу .
у о α
Легко вычислить n-ю степень конформной матрицы.
Действительно, если мы запишем
/а -Ь\ _ (г 0\ /cosθ -sinθ
1 b a) ~\0 r) Vsintf costf
то, учитывая, что I „ I коммутирует со всеми матрицами 2x2,
получим
дп ir 0\n/cos^ — sin#\n (rn 0\ f совпв — sinn#
n0 r) \ sin θ cos θ J \ 0 rn) \ sin ηθ cos ηθ
Итак,
rcos# —rsin#\n _ /rncosn# — rnsinn#
rsin# r cos θ J yrnsmn9 rncosn0
На языке комплексных чисел это значит, что если
ζ = г (cos θ + isin#),
то
zn = rn(cos ηθ + i sin ηθ);
это равенство известно как теорема Муавра.
Другой способ вычисления матрицы Ап состоит в применении
биномиальной формулы. Учитывая, что
(о ΐ)=α(1 ?) и (б "оЬ)=ь(? "о1)'

82 Глава 2. Собственные векторы и собственные значения
вычисляем
*■=<·<;; W! "о1
-*·(;?)+«-*(; -^„-«.-νβ -)2+
Но ( ι η ) = 1 η ϊ ). поэтому
10/ \ 0
«λ 71-1 L ΛΛ „71-3l3 ■ \ /Ό -1
4W*6Ч»Г * + Αϊ ο
В следующем параграфе мы покажем процедуру вычисления
степеней произвольной матрицы 2x2 (не обязательно конформной).
Для этого потребуется понятие собственных значений, играющее
ключевую роль в квантовой механике.
2.2. Собственные векторы
и собственные значения
Пусть F — линейное преобразование. Зададим вопрос: может ли
оно перевести прямую, проходящую через начальную точку, в
себя? (Ни один нетривиальный поворот не обладает таким
свойством, а вот любое ненулевое сингулярное преобразование
переводит свой образ в себя.)
Если ν — ненулевой вектор, лежащий на такой прямой, то
должно выполняться равенство
F(v) = λν,
где λ — вещественное число. Если это уравнение выполняется
для некоторого ν φ 0, то λ называется собственным значением
преобразования /, соответствующим собственному вектору v.
Последнее уравнение можно переписать в виде
'-<Ч
v = 0.

2.2. Собственные векторы и собственные значения 83
Так как вектор ν не равен нулю, мы получаем равенство
Det(F-A(o Ό)=ο'
представляющее собой уравнение относительно λ.
**-» -(:ί)-«"·-4ϊ?)-(β.λΛ)·
и предыдущее уравнение можно записать так:
Det (α с λ d - λ ) = (fl-A)(d-A)-bc = A2-(a+d)A+(ad-bc) = О,
или
A2-(TrF)A + DetF = 0.
Полином
Р(Х) = X2 - (а + d)X + (ad - be)
fa b\
называется характеристическим полиномом матрицы I , I, а
уравнение
Ρ(λ) = О
называется характеристическим уравнением. Это уравнение
будет иметь вещественные корни
λ = -[(a + d) ± v/{(a + d)2-4(ad-bc)}]
= -[(a + d)± у/{{а - d)2 + 4Ьс}]
тогда и только тогда, когда
(а - d)2 + 4Ьс > 0.
В этом случае мы можем проверить, что
α — λ Ъ \/d — λ
А \ I \ ' =0
d — А/ V —с

84 Глава 2. Собственные векторы и собственные значения
α-λ Ь \( Ь \_
с d-Xj\-(a-X)J ~
Поэтому, если I _ ) или ( , _ .. ) не равны нулю, то они
являются собственными векторами; они лежат на одной прямой,
поскольку
-С_-СА -(Лл))=-°- (β;λΛ)=*
Если же они оба равны нулю, τοα = λ, b = c = 0nd = \, поэтому
fa Ь\ (\ 0N
с dj~\0 \J> F = λΙ'
и каждый (ненулевой) вектор на плоскости является собственным
вектором.
Рассмотрим возможные варианты собственных значений
линейных преобразований.
Случай 1. Характеристическое уравнение имеет
различные вещественные корни. В случае, когда (а — d)2 + 4bc > 0,
существуют два различных вещественных собственных значения
λι и λ2· Тогда F φ λΐ и, следовательно, есть только две
прямые, проходящие через начало координат и не меняющиеся при
таком преобразовании, каждая из которых задается собственным
вектором vi = I ) или vo = I ). Мы можем записать
W W
α b\ /хЛ = λ ίχ\
с d) \yi) ι \υχ
а Ъ\ (х2\ _ ч (х2
— А
с dj \у2) \У2
Возьмем матрицу
В
Х\ Х2
У\ 2/2

2.2. Собственные векторы и собственные значения 85
Она несингулярна, потому что векторы
принадле-
жат разным прямым. Тогда уравнение для собственных векторов
можно записать в виде
где Λ =
О
λ2
FB = ΒΑ,
, или, окончательно,
F = ВАВ-
А =
λι О
О λ2
Обратное утверждение: если F = ВАВ 1 при Λ = I . ),
то
В
= ВАВ~1В
= ВА(п)=ВХ1
= ХлВ
так что первый столбец матрицы В является собственным
вектором преобразования F, соответствующим собственному
значению λι, и второй столбец — собственный вектор для собственного
значения λ2.
Случай 2. Характеристическое уравнение имеет кратный
вещественный корень. В случае, когда (а — d)2 + 4bc = 0 и
полином Р(Х) = 0 имеет два одинаковых корня λ, ситуация
немного сложнее. Рассмотрим две матрицы
О О
О О
О 1
О О
Для этих матриц характеристический полином Р(Х) = X2
имеет два равных корня λ = 0. Каждый ненулевой вектор на
плоскости является собственным вектором первой матрицы, и
только векторы I J будут собственными векторами второй.
Заметим, однако, что обе матрицы удовлетворяют уравнению F2 = 0,
которое можно записать как P(F) = 0, т. е. мы заменяем F

86 Глава 2. Собственные векторы и собственные значения
(как будто это число) на его характеристический полином и
получаем ноль. В общем случае это утверждение называется теоремой
Гамильтона-Кэли.
Если Р(Х) — характеристический полином матрицы F, то
P(F) = О,
т. е.
а Ьч2
с d
<°+Ч° 5)+(«*-")^ ?)=·■
В случае матриц 2x2 эта теорема проверяется вычислением.
Действительно,
га Ь\ _ ία2 + bc ab + bd
чс dj \ca + cd cb + d2
, ,, fa b\ _ fa2 + ad ab + bd
^ ' \c d) ~ \ca + cd ad + d2
«•^4 ?R"" «A)
поэтому
2
a b
с
ί)-<·+0+<4-*>(ί ;)-α
Если полином Р(Х) имеет кратный корень, то
Ρ(Χ) = (Χ-λ)2,
следовательно,
При этом существуют две возможности
F-λβ ;)-0, тогда F-β °

2.2. Собственные векторы и собственные значения 87
или
'-Μίϊ'*
Пусть ( ) — собственный вектор преобразования F, а
ненулевой вектор I ) не является собственным вектором F. Тогда
вектор
F-X
1 О
О 1
будет собственным вектором F, потому что ( F — I . ] ] = О,
и он должен быть пропорционален вектору ( _ ). Действительно,
умножая ( ) на соответствующую ненулевую константу, можно
\У2)
получить
Ί 0Ν
F-X
О 1
τι ι-> (χ1 χ2\
И в этом случае матрица В = I I несингулярна, а преды-
дущее уравнение можно записать в виде
FB = B
X 1
О λ
или^ = Б(о 1х)в~1-
Обратное утверждение: любая матрица вида
F=Bii гк1
обладает свойством
F-X
1 О
О 1
= 0, но при этом
*■-*(;;)*.,
что можно легко проверить.

88 Глава 2. Собственные векторы и собственные значения
Случай 3. Комплексные корни. Иногда нам приходится
работать с преобразованиями, не имеющими вещественных
собственных значений и собственных векторов. Наиболее очевидные
примеры таких преобразований: повороты на угол, не кратный π;
конформное преобразование, которое состоит из поворота
плоскости и последующего однородного «растяжения».
Давайте посмотрим, что получится, если мы попытаемся
найти собственные значения и собственные векторы конформной
матрицы2
У х
Характеристическое уравнение этой матрицы имеет вид
С='Х ~У
Далее получаем
(х - λ)2 + у2 = 0.
(λ - χ)2 = -у2,
λ — χ = алу
λ = χ ± \у.
В параграфе 2.1 мы отметили, что конформная матрица
χ — ν \
1 может быть применена для представления комплекс-
У х
ного числа χ + \у. Сейчас мы видим, что это комплексное число
является собственным значением матрицы. Более того, для
любой пары комплексно сопряженных чисел x + 'iy, x — iy существует
вещественная конформная матрица, для которой эти числа
являются собственными значениями. Конечно, мы не можем дать
геометрическую интерпретацию комплексных собственных
значений, потому что соответствующие собственные векторы имеют
комплексные компоненты и не могут рассматриваться как
векторы на вещественной плоскости.
2В дальнейшем предполагается, что у φ 0. — Прим. ред.

2.2. Собственные векторы и собственные значения 89
Покажем, что любая матрица F с собственными значениями
χ ± \у может быть записана в форме
F = BCB-\ С=(Х У\
\У х )
Доказательство. Рассмотрим матрицу G = F — xl. Согласно
теореме Гамильтона-Кэли, имеем
{F - xl)2 + уЧ = 0.
Таким образом,
G2 = -уЧ.
Возьмем произвольный вектор ν χ φ 0 и определим новый вектор
V2 по формуле
v2 = y~lGvi.
Тогда
Gv2 = y-xG2vi = -yvi,
а по определению вектора v2
Gvi = yv2.
Пусть В — матрица со столбцами ν χ и ν2. Тогда ν χ = В I
ν2 = Β I 1 I, и, следовательно,
СВ§=УВ§ „ ОВ§~уВ§.
" 1 Vwil«,„nr. r-.rr.TT ЛплттштттЛИТХг. ттл. С? 1
поэтому GB = В I J I. Умножая эти соотношения на В ,
получаем, что G = В I ) Б-1. Итак, матрицу F можно
записать в виде
0 -У \ п-1 _ d^d-1 , 0 /Ό -У \ „_ι
F = xI + jB(y 0 J^^^W^ + ^U 0 )Б
= Б
χΙ+(° -»
в-\

90 Глава 2. Собственные векторы и собственные значения
а так как В(хТ) = (хТ)В, то
F = B(X 'У )в-\
у χ
что и требовалось доказать.
Например, для простоты выберем ν χ = В ( п ), хотя можно
было бы сделать и другой выбор. Тогда
V2 = y~lG\i = y~lG
т.к. Gv\ = 2/V2. Это значит, что νχ (первый столбец матрицы В)
Τ
равен I I, а второй столбец этой матрицы V2 — это первый
столбец матрицы G, деленный на у.
Подведем итог: если F = ( . ) имеет собственные значе-
Vе dJ
ния, равные χ ± iy, причем у φ 0, то F = ВС В 1, где
В=[\ (α-χ)/*Λ и С-(Х -у
0 с/у J \у χ
А матрица G = F — х! удовлетворяет уравнению G2 = — у21.
В качестве примера рассмотрим матрицу г = I I,
имеющую TrF = 6 и DetF = 13. Характеристическое уравнение
λ2 — 6λ + 13 = 0 имеет корни
2
Таким образом, χ = 3, у = 2. Матрица
'4 -10
G = F-3I=.2 _4
как и ожидалось, удовлетворяет уравнению G2 = —41. Чтобы
получить второй столбец матрицы В, нам следует первый столбец
G разделить на у:
ΚίΗΟ-

2.2. Собственные векторы и собственные значения 91
Следовательно, В = ( „ 1 ) и
"=">* -4ίϊ βΐίΐ
Степени матриц. Предположим, что нам задана матрица F, и
мы хотим вычислить F™ для разных значений η (или для очень
больших п). В следующем параграфе мы дадим пример, когда
возникает такая проблема.
Случай 1. Различные вещественные корни. Если
% О
Л=10 А2
тогда очевидно, что
А"-Л" °
Это значит, что вычисление степеней диагональной матрицы
сводится к вычислению степеней вещественных чисел. Если
F = ВкВ~1,
то
F2 = BAB-i-BAB'1 = ВА2В~1
и тогда по индукции
рп _ ΒχηΒ-1_
Случай 2. Равные вещественные корни. Рассмотрим
матрицу
Ά Л А о\ /о Г
о х) \о х) + Vo о

92 Глава 2. Собственные векторы и собственные значения
Матрица ( „ . ) коммутирует со всеми матрицами 2x2. Далее
мы имеем
О 1
О О
= 0,
поэтому можно воспользоваться формулой бинома:
λ 1
0 λ
A 0\/0 1
о χ \о о
λ оу (х оу-1Л) ι
0 λ +η(θ Α (θ 0
т. к. все остальные члены в биномиальном разложении равны
нулю. Следовательно,
λ 1
0 λ
Хп пХ71-1
0 Хп
Поэтому если
F-B,.o 1.1в~'
то
F" = BixQ ])Пв-' = в(^ ^Ги-1
Случай 3. Комплексные корни. Пусть, наконец,
F = ВСВ~\
χ -у ч
где С =
У х
конформная матрица. Тогда
где Сп вычисляется одним из двух методов, изложенных в конце
параграфа 2.1.
Итак, вычислив собственные значения матрицы F и найдя
матрицу В замены базиса, мы получаем простой метод
вычисления степеней матрицы F, который применим во всех случаях

2.3. Процессы Маркова
93
(разные вещественные собственные значения, два одинаковых
вещественных или два комплексно-сопряженных собственных
значения) .
На самом деле для двух последних случаев у нас нет
необходимости вычислять В: если собственные значения вещественны и
равны, то матрица N = (F — λΐ) удовлетворяет условию ./V2 = О,
следовательно, используя формулу бинома, получаем
F" = (λΐ + N)n = Xnl + nXn~lN.
Для комплексно-сопряженных собственных значений χ ± \у
имеем равенство
F-xI = уН, где Я2 = -I.
Следовательно,
F71 = (xl + уН)п = хЧ + пхп-1уН +(ПЛ хп~2у2Н2 + ■■■
= (?- © хП~2у2 + ■ ■ )1+ ((?) х^у- (з) хП~3у3+- ■ )н-
2.3. Процессы Маркова
В этом параграфе мы покажем, как умножение матриц
применяется в вероятностных задачах. При этом мы не собираемся
писать подробное введение в теорию вероятностей. Мы просто
приведем основные положения этой теории. Каждому «событию» А,
В и т. д. ставится в соответствие «вероятность события» —
вещественное число р(А), р(В) и т.д., так что выполнены некоторые
условия:
0<р(А)<1, 0<р(Я)<1, ...
в соответствии с определенными правилами:
• вероятность достоверного события равна 1;
• вероятность невозможного события равна 0;

94 Глава 2. Собственные векторы и собственные значения
• если событие А может произойти к взаимно исключающими
способами А\,...,Ак, что мы записываем как
А = Ai\J---\JAk, AiDAj = 0, при гфз,
то
p{A)=p{Ai) + --- + p{Ak).
В частности, если Ас обозначает «дополнительное событие»,
означающее, что событие А не произойдет, то A U Ас достоверно
(событие А либо произойдет, либо нет), и А П Ас = 0, поэтому
р(А) + р(Ас) = 1. Кроме того, применяется понятие «условной
вероятности»:
р(В\А) — условная вероятность события В при заданном А.
Таким образом, если событие А значит, что «сегодня идет дождь»,
а событие В значит, что «завтра будет ясно», то р(В\А) есть
вероятность того, что завтра будет ясно, если известно, что сегодня
идет дождь. Тогда у нас есть правило
р(АПВ)=р(В\А)р(А),
т. е. вероятность двух событий А и В равна произведению
условной вероятности события В при заданном А на вероятность
события А.
В частности, если А^,...,Ак — взаимно исключающие друг
друга события, AiHAj = 0, и событие В может произойти только
при условии, что произойдет одно из событий Ai, то:
В = (ВГ\А1)и---и(ВГ)Ак),
тогда
р(В) =р{ВГ)А1) + ---+р{ВГ)Ак),
следовательно,
р(В) = ρ(β|Λι)ρ(Λι) + · · · + р(В\Ак)р(Ак).

2.3. Процессы Маркова
95
Теперь рассмотрим систему, которая может находиться в
одном из двух состояний. Например, прибор выключен или
включен; или игра в бадминтон: состояние 1 означает ситуацию, когда
подает первый игрок, а в состоянии 2 подает второй игрок. При
этом один «шаг» соответствует переходу подачи от одного игрока
к другому. Таким образом, во время игры в бадминтон система
может находиться в одном состоянии (игрок получил очко и
продолжает подавать), потом происходит переход из одного
состояния в другое (игрок проиграл очко, и подача переходит к
противнику). Итак, пусть подает первый игрок, с вероятностью 0.8 он
может выиграть очко, а с вероятностью 0.2 может его проиграть.
Когда подает второй игрок, то он выигрывает очко с
вероятностью 0.7, а проигрывает с вероятностью 0.3. В реальной игре для
каждого игрока вероятность выиграть очко зависит от
множества факторов (от его желания победить, от степени его усталости,
деморализации и т.д.). Мы же сделаем радикальное
упрощающее предположение: развитие игры зависит только от того, кто в
данный момент подает, и ни от чего другого. Все перечисленные
выше вероятности можно организовать в матрицу
/0.8 0.3\
V0.2 0.7у '
Таким образом, 0.8 есть условная вероятность системе
находиться в состоянии 1 после шага, если до выполнения шага она
находилась также в состоянии 1; 0.2 есть условная вероятность системе
находиться в состоянии 2 после шага, если до него она была в
состоянии 1.
Вообще, в случае дискретного времени и стационарной
системы с двумя состояниями процесс Маркова — это процесс, когда
состояния могут изменяться в дискретные моменты времени, а
вероятность перехода из одного состояния в другое зависит
только от состояния самой системы и не зависит от прошлой истории
системы и от времени перехода между состояниями. Таким
образом, все определяется только четырьмя «вероятностями
перехода», которые могут быть организованы в матрицу

96 Глава 2. Собственные векторы и собственные значения
где
α = вероятность перехода из состояния 1 в состояние 1;
Ь — вероятность перехода из состояния 2 в состояние 1;
с = вероятность перехода из состояния 1 в состояние 2;
d = вероятность перехода из состояния 2 в состояние 2.
Предположим, что мы не знаем, в каком состоянии находится
система в данный момент времени. Знаем только, что с
вероятностью ρ система находится в состоянии 1 и с вероятностью
q = 1 — ρ в состоянии 2. Такое распределение вероятностей
может быть представлено вектором ν =
После одного шага,
согласно закону для условной вероятности, мы получаем
вероятность быть
в состоянии 1
' после одного шага
вероятность пере-
> = < хода из состояния 1
в состояние 1
[вероятность
χ < быть в
состоянии 1
(вероятность
перехода из состояния 2
в состояние 1
(вероятность
быть в
состоянии 2
> = ар + bq.
Аналогично, вероятность находиться в состоянии 2 после
выполнения одного шага равна
ср + dq.
Другими словами, новый вектор вероятности равен
= Av.
ар + bq\ _ ία b
ср + dq) \c d
Давайте проиллюстрируем это на примере игры в бадминтон.
Предположим, мы знаем, что первый игрок начинает игру. Век-
Т
тор vo
является вектором вероятности в начале игры.
После первой подачи вектор вероятности становится
vi = Av0 :
0.8 0.3
0.2 0.7
0.8
0.2

2.3. Процессы Маркова
97
. ,0.8 0.3\ /0.8\ f0.7\ 2
v2 = Ανι = _ 0 п _ _ 0 = п , = A v0.
После второй подачи он равен
Ό.8 0.3
^0.2 0.7J V0.2/ ~ V0.3
После третьей подачи
/0.8 0.3\ /0.7\ /0.65\ .3
v3 = Av2 = ^ 0 ?j i^3j = (^ 35J = A vo
и так далее. В результате η шагов появляется матрица Ап.
Интуиция позволяет сделать вывод, что после большого числа
шагов вектор вероятности практически не будет зависеть от
начального состояния, т. е. вероятность того, что первый игрок
подает, чтобы выиграть пятнадцатое очко, вряд ли сильно зависит
от того, кто подавал в первый раз. Эта гипотеза подтверждается
вычислением. Действительно,
А2 =
А* =
А8 =
0.8 0.3\ /0.8 0.3\ = /0.7 0.55
0.2 0.7у \0.2 0.7/ ~ V0.3 0.45
0.7 0.55\2 /0.63 0.56
0.3 0.45у V0·37 °·44
0.63 0.5б\2 _ /0.602 0.598
0.37 0.44/ ~ 10.398 0.402
16 _ /0.602 0.598\ = /0.600006 0.599994\
~ \0.398 0.402; \0.399994 0.400006;
Теперь можно предположить, что
Ό.6 0.6
lim Ап - . . . . .
п-*оо \0Л 0.4
В общем случае легко показать, что если Ь и с одновременно
не равны 0 или 1, то ϋπΐη-,οο Αη существует. Надо только найти
собственные значения и собственные векторы матрицы А.
Учитывая, что а + с= 1, b + d = 1, можно написать
1-е Ь
с 1-Ь

98 Глава 2. Собственные векторы и собственные значения
ТаккакТгА = 2-(Ь + с) и Det А = 1 - b-c + be- be = 1 - (6 + с),
характеристическое уравнение имеет вид
λ2 - [2 - (ft + с)]Х + 1 - (ft + с) = О,
или
(А-1)(А-(1-Ь-с)) = 0.
Из этого уравнения получаем собственные значения λ ι = 1, λ2 =
1 — (ft + с). Заметим, что |Aa| < 1, где равенство выполняется
только если ft = с = 0 или ft = с = 1.
Собственные векторы легко получаются из рассмотрения
матрицы
Ядро этой сингулярной матрицы пропорционально собственному
вектору, соответствующему λχ = 1. Нормируем этот вектор так,
чтобы его компоненты в сумме давали 1. В результате получаем
'Ъ
VI
ft + с Vе
Образ А — λιΐ пропорционален собственному вектору,
соответствующему λ2, который удобно выбрать в виде V2 = I 1
Операция А может быть наглядно представлена через эти
собственные значения и собственные векторы. Проведем отрезок
прямой, соединяющий точки и I I. Тогда конец вектора
vi лежит на нем. Любой вектор, конец которого лежит на этом
отрезке, может быть записан в виде ν = νχ + α ( I. Учитывая,
что Av\ = vi и А ( J = Aq I I, получаем (рис. 2.2)
Αν = vi + αλ2 ( 1

2.3. Процессы Маркова
99
Рис. 2.2
или для произвольной степени η
Αην = νι + a(X2)r
Из того, что |λ2| < 1, очевидно, следует, что, независимо от
того, каким был начальный вектор v, lim Anv — νι.
Выразим матрицу А явным образом через диагональную. Для
этого запишем А — BhB~l, где
R_/6/(6 + c) -1
*-{с/(Ъ + с) 1
в-1 =
-с/{Ъ + с) 6/(6 +с) Г
Л =
о
Тогда
Учитывая, что
v0 λ2
Ап = ВАпВ~1
получим
lim#_/V(b + c) -l\/l θ\/ 1 1
п1™,^ -\с/(Ъ + с) l)\p Oj\-c/(b + c) 6/(6 +с)
= /6/(6 +с) -Л /1 1\ _1__ /b 6
\с/(6 + с) 1 у [p OJ b + c \c с

100 Глава 2. Собственные векторы и собственные значения
Таким образом, если v — I ) при ρ + q — 1, то
^Anh = (b/l + Ci)-
п-*оо \qj \c/{b + c)J
Итак, если А — стохастическая матрица 2 х 2, т. е. А — I ,
с условием α > 0, b > 0, с > 0, d > 0, а + с=1, b + d — 1, то ее
собственные значения равны 1 и 1 — (Ь + с), а соответствующие
соответственно. Если все входящие в матрицу параметры строго
положительны, то повторное действие А заставляет систему стре-
fb/(b + c)\
миться к предельному состоянию I .), . Переход от
состояния в данный момент к этому предельному состоянию
осуществляется умножением на λ2 при каждом шаге. Вернемся к игре в
* г. л /0.8 0.3\ .
бадминтон. В этом случае матрица А = \ , Аг = 0.5 и
/0.б\ „
предельное состояние I I. Это значит, что после розыгрыша
большого числа очков первый игрок имел 60% подач.
л /о Л
Пусть теперь матрица А = ( I — стохастическая и не
удовлетворяет условиям строгой положительности. Очевидно,
что
если η — четное число,
Ап
если η — нечетное число.
Смысл матрицы А очевиден. Она представляет безусловный
переход в другое состояние. В этом случае нет предела Ап при
η —► оо. (Однако, в некотором «усредненном» смысле мы
ожидаем, что система проводит в каждом состоянии половину
времени.)
Несложно сделать обобщение на случай процессов Маркова
для систем с большим числом состояний. Процессы с тремя
состояниями описываются матрицами 3 χ 3 и т. д. Параметры
каждого столбца должны быть неотрицательными и в сумме дают 1.

Резюме
101
Такова, например, стохастическая матрица 3x3
/0.5 0 0.1\
А = 0.3 0.6 0 .
\0.2 0.4 0.9/
С некоторыми поправками сохраняются важные свойства матриц
2x2. Например, матрица
0.5 0.3 0 0\
0.5 0.7 0 0
О 0 0 1
0 0 10/
представляет систему, в которой невозможны переходы из
первых двух состояний в два последние и наоборот. Вектор
вероятности, ограниченный первыми двумя состояниями, имеет предел.
Вектор, ограниченный двумя последними состояниями (т. е.
первые две компонеты равны 0) предела при η —► оо не имеет, и
его величина зависит от четности п. Нетрудно понять, как все
это будет звучать на языке матричных элементов матрицы А. За
исключением этих случаев n-мерная матрица дает то же самое,
что и двумерная. Матрица имеет собственное значение, равное
1, соответствующий собственный вектор определяет предельное
состояние. Все другие собственные значения меньше единицы, и
lim^-too An является сингулярной матрицей, преобразующей
любой вектор вероятности в собственный вектор, соответствующий
λ = 1.
Резюме
А. Конформные матрицы
Вы познакомились в этой главе с определением конформной
матрицы и с геометрической интерпретацией преобразования,
которое она представляет.
Вы должны уметь установить и применять изоморфизм
между конформными матрицами и комплексными числами.

102 Глава 2. Собственные векторы и собственные значения
B. Собственные значения и собственные векторы
Вы должны уметь писать характеристическое уравнение
матрицы 2 χ 2 и использовать его для определения собственных
значений матрицы; уметь получать собственные векторы,
соответствующие вещественным собственным значениям матрицы 2x2,
уметь описывать действие матрицы на языке собственных
значений и собственных векторов.
C. Подобие матриц
Для данной матрицы А (2x2) вы должны уметь построить такую
матрицу В, что А — ВСВ~1, где С диагональна, если А имеет
разные вещественные собственные значения; С конформна, если
А имеет комплексно-сопряженные собственные значения и С =
I, если А имеет два равных собственных значения, но при
этом Α φ λΐ. В каждом случае вы должны дать геометрическую
интерпретацию столбцов матрицы В.
D. Процессы Маркова
Вы должны уметь написать матрицу η χ п, представляющую
процесс Маркова для η состояний.
Для матрицы А (2 χ 2), представляющей процесс Маркова, вы
должны уметь связывать собственные значения и собственные
векторы с поведением вероятностей двух состояний.
Задачи
2.1. Рассмотрим две конформные матрицы
*-(ϊΐ) -«-(-ϋ)·
(a) Напишите комплексные числа ζ ι и гг, соответствующие этим
матрицам.
(b) Выразите матрицы Fi и F2 B виде произведения числа на
единичную матрицу и на матрицу поворота. Используя
тождество ειθ = cos# + isin#, запишите z\ и Ζι в полярных
координатах ζ = relfl'.

Задачи
103
(c) Вычислите F^1, потом вычислите zj"1, домножая числитель
и знаменатель на сопряженное число а — bi. Сравните
полученные результаты.
(d) Вычислите F^F2 и F2Fi. Потом вычислите ζγζ2 и сравните
результаты.
2.2. Проверьте теорему Муавра на примере двух конформных матриц
F\ и F2 из первого упражнения, т. е. вычислите Ff hF23.
2.3. (а) Покажите, что матрица Д = I „'„ " I представляет
поворот против часовой стрелки приблизительно на 37°.
Вычислите Д-1.
/1 2\
(b) Матрица S = I „ .. ) представляет сдвиг вдоль оси х.
Вычислите 5-1 и дайте геометрическую интерпретацию
результата.
(c) Вычислите А = Д5Д-1 и дайте геометрическую
интерпретацию результата. То же самое сделайте для А-1, В =
RS-ЧГ1 и В"1.
/ η ig\
2.4. Матрицу F = I „ „ I приведите к диагональному виду
согласно процедуре:
(a) напишите характеристический полином Ρ(λ), приравняйте
его к нулю и найдите собственные значения матрицы F.
(Ответ: λι =2,λ2 = -1.)
(b) Проверьте, что в соответствии с теоремой Гамильтона-Кэли
P(F) = 0.
(c) Для каждого собственного значения получите собственные
векторы. Пусть для каждого собственного вектора у = 1.
(d) Постройте матрицы В и В-1 так, чтобы F = ВАВ~1.
2.5. Матрицу лоренцева преобразования L2 = I „ ,. J,, I приведите
к диагональному виду, записав ее как L2 = BAB-1, где В есть
матрица вращения, а Λ диагональна. Дайте геометрическую
интерпретацию результата.
2.6. Получите такую обратимую матрицу В и такую диагональную
матрицу D, чтобы выполнялось равенство
в( \ iW'-в.

104 Глава 2. Собственные векторы и собственные значения
/-1 9\
2.7. Матрица F = I ^ I имеет равные собственные значения.
Приведите ее к диагональному виду, следуя процедуре:
(а) напишите характеристический полином Ρ(λ) и найдите
собственные значения;
(Ь) получите собственный вектор матрицы F в форме
(c) постройте матрицу G = F — λΐ. Покажите, что из теоремы
Гамильтона-Кэли следует уравнение G2 = 0. Получите ядро
и образ матрицы G;
(d) получите вектор I 1 I,такой, что
с(?) = (Ж11)-Построй-
те матрицы В и В-1 так, чтобы выполнялось равенство
2.8. Диагонализуйте матрицу
/ 3/5 1/5
Г ~ ^-4/5 7/5
имеющую равные собственные значения. Получите образ и
ядро матрицы G = F — λΐ, дайте геометрическую интерпретацию
преобразования F.
2.9. Пусть А есть матрица с собственными значениями \\ > Аг > 0.
(a) Диагонализуя матрицу Л, опишите процедуру
вычисления матрицы Gn = Х[пАп. Покажите, что матрица F =
1ш1п_оо Gn сингулярна.
(b) Проделайте эту процедуру для матрицы А = I 1 „ I,
вычисляя явно матрицы Gn и F. Найдите собственные значения
и собственные векторы матрицы А, ядро и образ
преобразования F и свяжите их с собственными векторами матрицы А.
2.10. Для любой матрицы А след (ТгЛ) определяется как сумма
матричных элементов, стоящих на главной диагонали. Таким
образом, если j4=( , I, то Тт Λ = α + d.
(а) Докажите, что для двух матриц Л и β (2 χ 2) Tr (AB) =
Тг (ΒΑ), даже если Л и β не коммутируют друг с другом.

Задачи
105
(b) Докажите, что Тг А равен сумме собственных значений
матрицы А. Докажите, что если А = SBS~l, то ТгЛ = ТгВ.
(c) Используя результат пункта (а), докажите, что
Tr {ABC) = Тг {ВСА) = Тг {CAB).
2.11. Матрицу F= { ^ _1 ), имеющую комплексно-сопряженные
собственные значения, запишите в форме F = ВСВ~1, следуя
процедуре, описанной ниже.
(a) Найдите собственные значения матрицы F.
(b) Постройте конформную матрицу С, имеющую те же
собственные значения, что и F.
(с) Постройте матрицу В в виде ( „ , I.
2.12. Пусть А = ( 1 „I. Постройте такую конформную матрицу С
и такую матрицу сдвига S, чтобы А = SCS~l.
2.13. Пусть F = I ,1 — матрица с различными вещественными
собственными значениями λ ι и Аг, и пусть
ζ=2(λι+λ2), У= ^ι-^)-
(a) Покажите, что Η = F — xl удовлетворяет уравнению
Я2 = уЧ.
(b) Покажите, что матрица S = I I имеет те же
собственные значения, что и F.
(c) Постройте матрицу В, у которой первый столбец I „ ). При
этом должны выполняться условия Η = В I ^).В-1и
f = b(x у)в-к
\у χ;
(d) Постройте такую матрицу R, чтобы выполнялось равенство

106 Глава 2. Собственные векторы и собственные значения
Докажите, что BR (J ] и BR (°Л являются собственными
векторами матрицы F.
2.14. Пусть F есть матрица 2 χ 2 с различными вещественными
собственными значениями λι и λ2. Определим
р =F-\2I p =Fj-Xil
λι — λ2 λ2 — λι
Докажите следующие свойства Pi и Р2:
(a) Pi и Р2 являются проекциями: Р2 = Pi, Р2 = Р2;
(b) ΡιΡ2 = Ρ2Ρι=0;
(c) Ρ = λιΡι+λ2Ρ2;
(d) Ρη = λίιΡι+λ2ιΡ2.
(e) Вычислите Pi и Р2 для случая F = ( _1 _п)·
Воспользовавшись этим результатом, вычислите F7.
2.15. Пусть F — матрица 2x2, характеристическое уравнение которой
имеет корни λ = χ ± iy. Можно переписать это в полярных
координатах χ ± iy = ге±1в, где г = \/(х2 + у2) и ε±ιθ = cos θ ± isin θ.
Если F — конформная матрица, то она поворачивает плоскость
на угол θ и однородно растягивает ее с коэффициентом г. В этой
задаче нет необходимости требовать конформность матрицы F.
(a) Покажите, что матрица Fn пропорциональна единичной
матрице для целых чисел η тогда и только тогда, когда
ηθ = τηπ для целого числа т. В этом случае
(Подсказка: F = ВСВ~1, где С — конформная матрица.)
(b) Запишите матрицу F = Ι ι ) в виДе ВС В-1.
Найдите наименьшее число п, для которого Fn пропорциональна
единичной матрице. Проверьте ответ прямым вычислением.
(c) Покажите, что этот ответ соответствует теореме Гамильто-
на-Кэли.
(d) Получите «квадратный корень» матрицы G = I „ ._ I,
т. е. найдите такую матрицу А, чтобы выполнялось условие

Задачи
107
А2 = G. Напоминаем формулы:
θ 1 θ λ
cos2 - = -(1 + cos#), sin2 - = -(1 — cos#).
2.16. Композитор-модернист Але А. Тори3 создает музыкальные
произведения из двух нот, следуя теории процессов Маркова.
1. Если (п — 1)-я нота есть Фа, тогда вероятность рп того, что п-я
нота тоже Фа, будет равна 3/4, а вероятность qn того, что п-я
нота Соль, равна 1/4.
2. Если (п — 1)-я нота есть Соль, то вероятность рп того, что п-я
нота Фа, равна 1/2, а вероятность qn того, что п-я нота Соль,
тоже равна 1/2.
(a) Постройте матрицу А (2x2), которая преобразует
вероятности ( I в вероятности (
\qn~ij \qn
(b) Допустим, что первая нота есть Фа. С помощью матрицы
А найдите, чему равна вероятность третьей ноте тоже быть
Фа.
(c) Получите собственные значения и соответствующие
собственные векторы матрицы А.
(d) Допустим, что первая нота есть Фа. Это значит, что
?ί) = (о
Покажите на диаграмме последовательность векторов
и получите предел этой последовательности, интерпретируя
его через собственные значения матрицы А.
2.17. Один студент, успешно изучавший теорию вероятностей и
увлекавшийся футболом, придумал игру со следующими правилами.
1. Если в (п — 1)-й раз некоторый игрок дал пас другому игроку, то
в n-й раз он делает пас с вероятностью рп = 1/6 и ведет мяч сам
с вероятностью qn = 5/6.
Непереводимая игра слов: aleatory — случайный. — Прим. ред.

108 Глава 2. Собственные векторы и собственные значения
2. Если в (п — 1)-й раз игрок повел мяч сам, то вероятность паса на
п-м ходу равна рп = 2/3, а вероятность самостоятельного прохода
равна qn = 1/3.
(a) Постройте матрицу Л, которая преобразует вероятности
I в вероятности \^п
Чп-iJ \qn
(b) Для матрицы А найдите собственные значения и
соответствующие им собственные векторы. Покажите на диаграмме,
как А действует на собственные векторы.
(c) Никто не знает, что капитан сделает, получив мяч в первый
раз. Однако, видеозапись игры показала, что при втором
ходе в половине случаев он отдавал пас, а в другой половине
случаев вел м», сам. Каковы вероятное™ (*) для „ерво™
хода?
2.18. Профессор Константин Байес много лет читает курс
«Стохастические методы в классической археологии». Всем известно, что
Байес подбирает экзаменационные вопросы, вытаскивая
разноцветные шарики из древнегреческих урн, стоящих в его
кабинете, но содержание урн он держит в секрете. Однако, анализируя
вопросы Байеса, заданные им на выпускных экзаменах в течение
многих лет, а все они хранятся в библиотеке Ламонта, студенты
выяснили следующее:
1. Если на выпускном экзамене в (N — 1)-м году профессор
спрашивал о статуях, то на выпускном экзамене N-ro года вероятность
получить вопрос о статуях равнялась 1/2, и вероятность
получить вопрос о керамике тоже равнялась 1/2;
2. Если на выпускном экзамене в (N — 1)-м году профессор задавал
вопрос о керамике, то в N-м году вопрос о статуях на выпускном
экзамене можно было получить с вероятностью 1/4, а вопрос о
керамике — с вероятностью 3/4.
(а) Напишите матрицу М, преобразующую распределение веро-
„„осей вопросов о схатуях „ о керамике (»-) в рас-
пределение вероятностей вопросов на выпускных экзаменах
следующего года
(b) Найдите собственные значения и собственные векторы
матрицы Μ и запишите ее в форме SDS~l, где D —
диагональная матрица.

Задачи
109
(с) Заходя регулярно в кабинет Байеса, студенты, наконец,
поняли метод профессора. У Байеса было две урны, но он
пользовался ими дважды: один раз для себя, предварительно,
а потом еще раз для окончательного экзаменационного
вопроса, так что матрица Μ представляет собой два шага
марковского процесса. Диагонализуя матрицу М, найдите две
возможные матрицы N для одного шага процесса.
2.19. Джон и Илья играют в мяч, который может быть либо в лунке
Н, либо в лунке У. Джон предпочитает мяч в лунке Н, а Илья —
в лунке У. Джон получает ход. Если мяч лежит в Н, он не
делает ничего. Но если мяч оказывается в У, то он пытается
перекатить его в Н. Это не так просто. Вероятность того, что
Джону удается перекатить мяч, равна 2/3, но с вероятностью
1/3 мяч скатывается обратно в лунку У. Когда Илья получает
ход, он ничего не делает, если мяч лежит в лунке У, и пытается
перекатить, если мяч находится в Н. Илья играет хуже Джона,
и вероятность удачи равна только 1/2.
(a) Мяч лежит в лунке У и играет Джон. Чему равна
вероятность мячу быть в лунке Η после второго хода Джона?
(b) Джон играл η раз, а Илья (п— 1) раз. Чему равна вероятность
того, что после η-го хода Джона мяч окажется в Н?
(c) Допустим, что игра продолжается «очень долго». Вы
смотрите на игру после хода Ильи. Чему равна вероятность
увидеть мяч в лунке ΗΊ Сколько надо сделать ходов, если мы
хотим быть уверенными в этой величине вероятности с
точностью до 0.001?
2.20. Банк разработал правила, согласно которым очередь в окно не
должна быть длиннее двух человек. Если появляется третий
клиент, то все трое сопровождаются в кабинет менеджера и
обслуживаются по высшему разряду. Перед окном нет никакой очереди.
Более того, вооруженный охранник на входе в банк не
пропускает более одного клиента в минуту (именно столько времени
требуется для тщательной проверки клиента). В результате длина
очереди в окно определяется процессом Маркова, описывающим,
что происходит в течение одной минуты.
1. Если нет очереди, то с вероятностью 1/2 клиент появится в
течение одной минуты и с вероятностью 1/2 не появится.
2. Перед окном стоит один человек. С вероятностью 1/6 этого
клиента обслужат, и он уйдет; с вероятностью 1/3 появится второй
клиент и с вероятностью 1/2 ничего не изменится.

110 Глава 2. Собственные векторы и собственные значения
3. Перед окном в очереди два человека. С вероятностью 1/6
одного клиента обслужат, и он уйдет; с вероятностью 1/6 появится
третий клиент, и все трое уйдут в кабинет менеджера, и с
вероятностью 2/3 ничего не изменится.
(a) Постройте матрицу М, преобразующую распределение веро-
(рЛ
ятностей I р2 I в момент t в распределение вероятностей в
W
момент (t + 1).
(b) Когда банк открывается в 9 часов утра, pi = 1. Каково
(рЛ
распределение вероятностей I рг I через три минуты?
W
(c) Получите собственные значения и собственные векторы
матрицы М.
(рЛ
(d) Какое будет распределение вероятностей I рг I после многих
W
часов работы банка? Оцените, через какое время
вероятности ρι, рг и рз будут совпадать с предельными значениями с
точностью до 0.001.
(e) Сколько, в среднем, посетителей обслуживается в течение
одной минуты? Сколько клиентов приглашаются в кабинет
менеджера?
Модель Эренфеста. Предположим, что у нас есть два
ящика и iV шаров. Пусть г шаров лежат в первом ящике и N — г
во втором. Состояние системы определяется целым числом г, т. е.
система имеет η + 1 состояние: г = 0, г = 1, ..., г = N. В каждый
временной интервал из одного ящика вынимают шар (с
вероятностью 1/Ν) и перекладывают его в другой. Таким образом, г
принимает значения г — 1 или г + 1, в зависимости от того,
берут шар из первого ящика или кладут в него. Вероятности таких
переходов равны гЛ/--1 и (Л/- — г)Л/"-1 соответственно. Итак,
Pi-i,i =iN~1,
pi+i,i = (N-i)N-\

Задачи
111
Например, если N = 4, то матрица 5x5 равна
/0
1
0
0
V>
1/4
0
3/4
0
0
0
1/2
0
1/2
0
0
0
3/4
0
1/4
0\
0
0
1
<7
Заметим, что Ρ преобразует состояние с четным г в состояние с
нечетным г и наоборот. А преобразование Р2 переводит четные
состояния в четные и нечетные состояния в нечетные, так как
матрица Р2 имеет вид
Pi-2,i = i(i-l)N-2,
Pi,i = [i(N - г + 1) + (Ν - г)(г + 1)]ЛГ2,
^+2,, = (ЛГ-г)(ЛГ-г-1)ЛГ2,
Pj,i = 0, ίφϊ-±2,ι.
В случае, когда N = 4, соответствующая матрица равна
Р2 =
/1/4 0 1/8 0 0 \
0 5/8 0 3/8 0
3/4 0 3/4 0 3/4
0 3/8 0 5/8 0
V 0 0 1/8 0 1/4/
Так как Р2 осуществляет переходы только между состояниями с
одинаковой четностью, можно рассматривать отдельно состояния
с четными значениями г = 0, 2,4,... и с нечетными г = 1,3,5,...
Это значит, что из выписанной матрицы можно выделить четно-
четные позиции и нечетно-нечетные в две отдельные матрицы
Ί/4 1/8 0
Q = | 3/4 3/4 1/4
0 1/8 3/4,
и Я =
5/8 3/8
3/8 5/8
2.21. (а) Для матрицы Q покажите, что I 6 1 является собственным
W
вектором, соответствующим собственному значению 1; для

112 Глава 2. Собственные векторы и собственные значения
матрицы R покажите, что
является собственным
вектором, соответствующим собственному значению 1.
(Ь) Повторите предыдущее упражнение для случая N = 5.
Покажите, что «четный» собственный вектор для собственного
значения 1 пропорционален | 10 | и «нечетный»
собственный вектор пропорционален
(с) Докажите в общем случае, что «четные» и «нечетные»
собственные векторы для собственного значения 1
пропорциональны вектору, где элементы столбца суть четные и
нечетные биномиальные коэффициенты соответственно с четными
и нечетными номерами. Другими словами, докажите, что
\ : /
четные
собственные векторы
\ : /
нечетные
собственные векторы.
2.22. Числа Фибоначчи.
Числовая последовательность 0,1,1,2,3,5,8,13... называется
последовательностью Фибоначчи. Эти числа появляются при
изучении многих интересных физических и математических
задач, от роста растений до механики небесных тел (см. например
книгу D'Arcy Thompson On Growth and Form). Рекуррентная
формула для этой последовательности имеет вид
ХП+2 = Хп+1 + ХП, Х0 =0, Χι = 1.
(a) Вычислите отношение χη+ι/χη для η от 1 до 8. Имеет ли эта
последовательность предел?
(b) Найдите такую матрицу А, чтобы выполнялось равенство
ХП+2
Хп+1
= А
Хп+1
Хп

Задачи
113
С помощью матрицы А выразите ( п+ I через (
'XI
(c) Получите явное выражение для хп через а;ι и xq. (Подсказка:
приведите матрицу А к диагональному виду.)
(d) Покажите, что существует предел lim χη+ι/χη и вычислите
п~*оо
его.
(e) Используя величину этого предела, что молено сказать о
бесконечной дроби
1
1 + : ?
1 +
1 +
1 +
! + ■■
(f) Существуют ли такие хо и χ ι, что lim χη+ι/χη отличается
п~*оо
от значения, полученного в упражнении (d)?

I

Глава 3
Линейные дифференциальные
уравнения на плоскости
Основная цель этой главы — объяснить, что система
однородных дифференциальных уравнений с
постоянными коэффициентами может быть записана в форме
du/d t = Аи, где А — матрица и и — вектор, и что ре-
At
шение этого уравнения имеет вид е ио, где Uo
определяется начальными условиями. При этом, конечно,
надо объяснить, что такое экспонента, показателем
которой является матрица. Кроме того, обсуждается
качественное поведение решений в неоднородном случае,
в том числе явление резонанса.
3.1. Функции матриц
Обсуждая теорему Гамильтона-Кэли, мы уже встречались с
матричным полиномом. В общем случае, пусть Q(X) — любой
полином. Если
Q(X) = апХп + αη-ιΧη~ + · · · + αιΧ + αο,
то можно определить матрицу Q(F) как
Q(F) = anF71 + dn^F71'1 + ■ ■ ■ + aiF + αο-
Мы можем перемножить два полинома и получить третий
полином: {Q\Q2){X) = Q\{X)Q2{X)· Аналогично, для матриц
(QiQ2)(F) = Q1(F)Q2(F).

116 Глава 3. Линейные дифференциальные уравнения ...
Здесь не возникает проблемы из-за некоммутативности
матричного умножения, так как степени фиксированной матрицы всегда
коммутируют друг с другом в соответствии с ассоциативным
законом:
pkpl _ pk+l _ plpk
Аналогично,
(Qi+Q2)(F)=Q1(F) + Q2(F).
Короче говоря, при вычислении матричного полинома действуют
обычные законы алгебры.
Мы хотим перейти к изучению функций от матриц более
общего вида. С этой целью сделаем небольшое отклонение и
поговорим о степенных рядах.
Выражение вида
R(X) =а0 + агХ + а2Х2 + ■■■ + апХп + ■■■ ,
где коэффициенты α^,ί = 0,1,... — вещественные числа, & X —
некий символ, называется формальным степенным, рядом.
Сложение степенных рядов производится по правилу
(αο + αιΧ + а2Х2 + ···) + (bo + hX + Ъ2Х2 + ■■■)
= (ао + Ьо) + (αϊ + bi)X + (а2 + b2)X2 + ■■■ ,
т. е. мы складываем коэффициенты при одинаковых степенях
X. Для умножения степенных рядов воспользуемся правилом
ХкХ1 = Χ +ι. Тогда, собирая члены с одинаковыми степенями
X, получаем
(αο + αλΧ + а2Х2 + ■ ■ ■ )(Ь0 + hX + Ь2Х2 + ■■■)
= аоЬо + («1^0 + αο^ι)^" + (а2Ьо + «ι^ι + аф2)Х2 -\ .
Таким образом, например,
(1 + X + X2 + ■ ■ ■ )(1 + X + X2 + ■ ■ ■) = 1 + 2Х + ЗХ2 + ■ ■ ■ .
Легко проверить, что обычные свойства сложения и умножения
полиномов сохраняются и для степенных рядов.

3.1. Функции матриц
117
Пусть t — любое вещественное число. По определению,
формальный степенной ряд для exp (tX) имеет вид
exp (tX) = l + tX+ У2Χ2 + ^t3X3 + ^ί4Χ4 + · · · . (3.1)
Тогда
exp (sX) exp (tX) = (l + sX+^s2X2 + - ■ ·Υΐ+ίΧ+^ί2Χ2 + ·
= 1 + (s + t)X + ^(s2 + 2st + t2)X2 + · · · ,
где коэффициент при Хп определяется формулой
i (sn + nsn-H + n^^-sn-2t2 + --+A,
которая, по формуле бинома Ньютона, равна просто (l/n!)(s+i)n.
Так как по определению
l + (s + t)X + ^(s + t)2X2 + ^(s + t)3X3 + ■ ■ ■ = exp (s + t)X,
то можно сделать вывод, что равенство
exp (sX) exp (tX) = exp (s + t)X (3.2)
выполняется тождественно для формальных степенных рядов.
В отличие от полиномов, мы в общем случае не можем
вычислить R(X) для какого-нибудь числа г или матрицы F.
Действительно, если в формальный степенной ряд
R(X) = oq + αιΧ + а2Х2 + ■ ■ ■
вместо символа X подставить вещественное число г, то получится
бесконечная сумма
«о + а\т + а*2Г2 -\ ,
которая в таком виде не имеет смысла. Один способ придать
такой сумме смысл сводится к обрезанию бесконечного ряда на

118 Глава 3. Линейные дифференциальные уравнения ...
каком-то слагаемом. Может оказаться, что такая конечная сумма
не будет сильно зависеть от места обрыва ряда, если мы оставим
достаточное количество слагаемых. Величину, полученную как
«предельное значение» конечной суммы, обозначим R(r).
Объясним эту процедуру более аккуратно. Пусть из бесконечной суммы
мы оставили Μ слагаемых. Обозначим RM{r) соответствующую
конечную сумму:
RM(r) = a0 + air + a2r2 + ■■■ + амгМ ■
Мы будем говорить, что степенной ряд R(X) сходится для
данного числа г, если при сколь угодно малом положительном ε можно
найти достаточно большое число Mq, такое, что для любых целых
Μ и Ν, больших Мо, выполняется неравенство
\RM(r)-RN(r)\<e.
Другими словами, если мы учтем достаточно большое число
слагаемых, то все значения R (г) будут отличаться на малое
значение ε. Чем больше членов мы учитываем, тем ближе конечная
сумма RM(r) к предельному значению, обозначаемому Д(г)1.
Точно такое же определение можно ввести для матриц. Для
любой матрицы F конечная сумма
RM(F) =ao + aiF + --- + aMFM
имеет смысл. Разность RM (F) — RN(F) — тоже матрица. Тогда
условие
\RM(F)-RN(F)\ <ε
означает, что все матричные элементы матрицы RM (F) — RN (F)
по модулю меньше ε. Итак, мы говорим, что R(X) сходится для
1 Авторы проявляют здесь некоторую непоследовательность.
Предположив в начале книги, что читатели владеют одномерным математическим
анализом, было бы естественно считать, что они знают понятие предела
числовой последовательности. Тогда сумму Щг) ряда можно определить как
lim RM(r), если, конечно, этот предел существует. Рассуждения авторов
М—>оо
здесь нечетким образом используют «критерий Коши» (теорему о
равносильности сходимости последовательности и ее фундаментальности). Кстати,
предел последовательности чисел (и матриц!) уже использовался авторами
в главе 2. — Прим. ред.

3.2. Экспонента от матрицы
119
матрицы F, если при любом ε > 0 существует такое значение
Мо, что условие \RM (F) — RN(F)\ < ε выполняется для всех Μ
и Ν, больших Mq. В этом случае каждый матричный элемент
RM(F) стремится к предельному значению2. Таким образом, мы
получаем матрицу предельных значений матричных элементов,
которую обозначаем R(F).
Очевидно, что если Ri(X), R2{X) и Rs(X) — формальные
степенные ряды, для которых справедливо равенство
Ri(X)R2(X) = Дз(Х),
и, если все три степенных ряда сходятся для матрицы F, то
R1(F)R2(F) = R3(F).3
Аналогично для сложения: если Ri(X) + R2(X) = Rs{X), и все
ряды4 сходятся для матрицы F, то R\(F) + R2(F) = Rz(F).
3.2. Экспонента от матрицы
Мы уже ввели формулой (3.1) формальный степенной ряд для
экспоненциальной функции и показали, что для нее выполняется
равенство (3.2). Сейчас докажем, что степенной ряд для exp (tX)
будет сходиться в случае, когда символ X заменяется матрицей
2x2, обозначаемой буквой А. В качестве первого шага проведем
доказательство того, что ряд сходится абсолютно5, если вместо
X подставить произвольное вещественное число к. Рассмотрим
степенной ряд
ехр г/ = ι + г/ + —г/2 + —г/3 ч— , (з.з)
2 Это следует из упомянутого в предыдущем примечании критерия
Коши. — Прим. ред.
3Вряд ли стоит называть очевидным утверждение, являющееся
следствием одной тонкой теоремы Абеля. — Прим. ред.
4 Здесь достаточно предположить сходимость первых двух рядов. — Прим.
ред.
5Говорят, что ряд сходится абсолютно, если сходится другой ряд,
составленный из модулей слагаемых первого ряда. В этом случае первый ряд тоже
сходится. — Прим. ред.

120 Глава 3. Линейные дифференциальные уравнения ...
где у = \tk\. При положительных значениях у все слагаемые этого
ряда положительны. Если мы покажем, что ряд (3.3) сходится,
будет доказана абсолютная сходимость ряда для exp tk.
Для доказательства сходимости ряда (3.3) покажем, что
фрагмент rm>n, получающийся при суммировании членов с номерами
от т до (т + п), может быть сколь угодно малым, если выбрано
достаточное большое значение т. Это легко сделать, сравнивая
фрагмент
11 1
m! m!(m + l) m!(m+l)(m + 2)
+ ym+n
ml (m + 1) · · · (m + n)
ym+n.
Очевидно, что Тчтп < Sjtjji для всех т. Сумму smn
геометрической прогрессии можно вычислить явно:
с геометрической прогрессией
Sm,n = —.Ут + -\~ym+l + -^Ут+2 + ■
ml т\т т\т*
1
1 1 и
т\тп
s -У—
т!
.п+1
= (!-(-) )sm,
где
_Ут 1
1+у. + (уЛ\(у\\... + (у\п
т \т/ \т/ \т/
(-)
\т/
т\ 1 — у/т
Итак, мы доказали, что
Γτη,η ^ Sj;
Предположим, что мы выбрали т > 2у. В этом случае
1 <^U = 2.
1 - у/т 1 - 1/2
Тогда sm < 2ут/т\. Каждый раз, увеличивая т на единицу,
мы умножаем sm на множитель, меньший 1/2. Очевидно, что

3.2. Экспонента от матрицы
121
выбрав достаточно большое значение т, можно сделать величину
sm сколь угодно малой. А так как rm>n < sm, то и значение rm>n
может быть сделано сколь угодно малым. А это означает, что ряд
expifc = 1 + tk + 2\(Щ2 + 7у(Щ3 + ■■■
сходится абсолютно. Между прочим, хорошо известное
доказательство абсолютной сходимости степенного ряда
ао + <ЧУ + о-2У2 + а3у3 + ■··
с учетом оценки предела
т-*оо атут
основывается на тех же аргументах, которые мы только что
использовали6.
Перейдем теперь к матричному случаю. Возьмем матрицу
л (о, Ь\
Ι Α ι' в котоР°й каждый элемент по модулю меньше, чем
к/2. Матричные элементы матрицы А2 = Г , , состоят
из двух слагаемых, причем эти слагаемые по модулю меньше,
чем (к/2)2 = к2/4. Таким образом, матричные элементы А2 по
модулю меньше, чем к2/2. Легко показать, что все матричные
элементы Л3 по модулю меньше, чем к3/2, и далее, по индукции,
элементы матрицы Ат по модулю меньше, чем кт/2. Теперь,
если мы будем суммировать ряд
ехр(М) = I + tA + Ь-А2 + 1-А3 + ■ ■ ■ ,
то все слагаемые в четырех матричных элементах получающейся
матрицы меньше, чем соответствующие слагаемые ряда
к ί^ ί3^
1 + ί2 + 2! 2 +3! 2 +'" '
6В русскоязычной литературе последний прием составляет содержание
признака Даламбера. — Прим. ред.

122 Глава 3. Линейные дифференциальные уравнения ...
Из этого следует, что для любого вещественного числа t и
любой матрицы Л (2 х 2) ряд exp (tA) сходится. Используя те же
аргументы, заменив только к/2 на к/п, можно показать, что
экспоненциальный ряд сходится и в случае, когда матрица А имеет
размер η х п.
Итак, для экспоненциальной функции от матрицы мы
получили фундаментальное тождество
exp (s + t)A = exp (sA) exp (tA).
Вы можете спросить: а как обстоит дело с тождеством
ехр (А + В) = (ехр Л) (ехр В),
где А и В — произвольные матрицы? Чтобы понять, что
происходит в этом случае, разложим в ряд обе части этого равенства:
ехр (А + В) = I + А + В + ± (А + В)2 + ■ ■ ■
= I + А + В + \(А2 + АВ + ВА + В2) + ■ ■ ■
1 12 , \ /π , о , 1 о2
(ехрЛ)(ехР5) = (I + А + -ΑΔ + ■ ■ ■ 1 I I + В + -Βζ + ■ ■
= I + А + В + ( )-А2 + АВ + Ιβ2] +■■■ ,
где многоточия обозначают слагаемые более высоких степеней по
А и В. Если мы сравним слагаемые второй степени в этих двух
выражениях, то увидим, что они равны только при условии
\(АВ + ВА) = АВ,
т. е. если
АВ = В А.
Итак, если матрицы А и В не коммутируют, то нет оснований
ожидать, что выполняется тождество
ехр (А + В) = (ехр Л)(ехр В),

3.2. Экспонента от матрицы
123
и на самом деле оно не всегда верно. Рассмотрим конкретный
пример. Возьмем матрицу
А-(° 1
А~ [θ О
В этом случае А2 = 0 и, следовательно, все слагаемые более
высоких степеней в разложении ехрЛ равны нулю. Получаем
простую формулу:
ехРЛ = 1 + Л=^ j'
Возьмем теперь другую матрицу 5=1 „ ), для которой тоже
В2 = 0. Тогда
ехрВ = 1 + В=(] °
А теперь перемножим две получившиеся матрицы:
Ί 1\ /1 0\ (2 1
(ехрЛ)(ехр5) = VQ γ . ^ γ. - . χ χ
С другой стороны, А + В = I „ ) и, соответственно, (А + В)
. Отсюда получаем, что
1 0>
0 1,
exp(A + B) = I + (A + B) + |l + ±(A + B) + ±1 + ■ ■ ■
= (1 + h. + i + -)l+(1 + h + h + -){A+B)-
Множители в скобках можно упростить7
, 1 1 !/ -и
7 Это делается с использованием тождеств
1+ϊι + έ + έ+"'=θχρ1=6'
1-π + έ-έ+-=6χρ(-1)=6-1·

124 Глава 3. Линейные дифференциальные уравнения ...
, 111 1/ -ь
1+3! + 5! + 7!+··· = 2(6-6 >■
Окончательно, получаем, что
I (e + e l e — е"
ехр(Л + В) = ^\^'_ \_λ ^ + g_i W (ехр Л)(ехр5).
Справедливость формулы
exp(s + t)A = exp(si4) exp(tA)
связана с тем, что матрицы sA и tA коммутируют.
Показав, что exp(i.A) определяется степенным рядом, мы
теперь обобщим на матричный случай хорошо известную формулу
— [exp(ifc)] = kexp(tk). (3.4)
Определим производную функции exp(tA) по вещественной
переменной t следующим образом
— [ехр(М)] = lim -[exp((i + h)A) - ехр(М)].
α τ n—tO n
Предел в правой части равенства означает матрицу, элементы
которой являются пределами соответствующих элементов
зависящей от t матрицы, стоящей под знаком lim. Поскольку
А—»0
exp((i + К)А) = exp(hA) exp(tA),
получаем
— [exp(tA)} = lim r[exp(M.) - Ilexp(M).
a t h->o h
В то же время
h2A2 h3A3
exp(hA) -l = hA + -^- + —^- +
следовательно,
1, tUA, ^ А НА2 h2A3
-(exp(M) -1) = A + — + -gj- +

3.2. Экспонента от матрицы
125
Ит£[ехр(М)-1] = А8
h—+0 ΓΙ
j
— [ехр(М)] = Aexp(tA).
Эта формула похожа на (3.4), но справа подразумевается
матричное умножение.
Выберем на плоскости фиксированный вектор vq = I ] и
определим зависящий от времени вектор ν(ί) формулой
v(i) = exp(iA)v0, где А = ί ° А.
Определим производную по времени ν(ί) вектора ν(ί):
v(i) = Umi[v(i + h)-v(i)].
Если ν(ί) = ( , Μ, то производная этого вектора по времени,
fx(t)\
очевидно, может быть записана в виде ν(ί) = I ., ' I. Так как
Vo — постоянный вектор, то
ν(ί) = lim r[exp((i + h)A) - exp(ii4)]v0,
т. e.
*(') = -τ7βχρ(Μ)ν0.
at
Отсюда
v(t) = i4exp(M)v0 = Av(t).
Итак, мы показали, что ν(ί) удовлетворяет дифференциальному
уравнению
ν(ί) = Av(t), v(0) = ν0·
8 Здесь следовало сослаться на теорему о почленном переходе к пределу,
которая требует проверки некоторых условий, например, равномерной
сходимости ряда (это понятие авторы даже не упоминают). — Прим,, ред.

126 Глава 3. Линейные дифференциальные уравнения ...
Записав, как и выше, ν(ί) = 1 ).{), получаем
(±(t)\_(a b\(x(t)
\т)~\с d)\y(t)
т.е.
Итак, формула
x(t) =ax(t) +by(t),
y(t) = cx(t) + dy(t).
χ®λ = e^tA) (Xo
y(t)J ~ «^ \yQ
дает решение системы линейных дифференциальных уравнений
первого порядка, написанной выше.
Легко доказать, что любое решение дифференциального
уравнения ν(ί) = Av(t) имеет вид v(i) = exp(i.A)vo. Для
доказательства возьмем вектор w(i) = ехр(—tA)v(t). Тогда9
w(i) = —(exp(-M))v(t) + exp(-M)v(t).
В то же время
— ехр(-М) = -Aexp(-tA)
at
и, кроме того,
v(t) = Av(t).
Следовательно,
w(i) = -;4exp(-M)v(t) + exp(-tA)Av(t) = О,
так как матрицы А и exp(-tA) коммутируют. Из этого следует,
что w — постоянный вектор (обозначенный vo), и мы получаем
vo = ехр(—Μ)ν(ί)
Следующая далее выкладка использует упоминавшуюся ранее формулу
дифференцирования переменного вектора w(t), заданного как образ другого
переменного вектора v(t) при преобразовании, также зависящем от t. —
Прим. ред.

3.3. Вычисление экспоненты от матрицы 127
или
v(i) = exp(ii4)vo-
Итак, мы показали, что последняя формула с экспонентой
ехр(М) определяет общее 'решение системы дифференциальных
уравнений с постоянными коэффициентами. Поэтому важно
обсудить различные методы вычисления exp(iA).
3.3. Вычисление экспоненты от матрицы
Предположим, что матрицы F и G связаны между собой
соотношением
F = BGB~\
Тогда при любом к
рк = ВскВ~1
и из разложения ехр(М) в степенной ряд следует, что
exp(iF) = 5exp(iG)5-1.
Случай 1. Матрица F имеет разные вещественные
собственные значения. Мы уже научились приводить матрицу
2 χ 2 к диагональному виду. Допустим, что матрица F имеет
разные вещественные собственные значения λ ι и λ2· Тогда можно
записать, что при некоторой матрице В
Очевидно, что
/% 0 \η А? О \
и из разложения экспоненциальной функции в степенной ряд
следует, что
Ait 0 \ (ех^ 0 \
Тогда
exp(iF) = В (^ JJ, 4) В-\

128 Глава 3. Линейные дифференциальные уравнения ...
Приведем конкретный пример. Характеристический полином
матрицы F = I J имеет вид λ2 — 2λ — 3 = 0, откуда
получаем собственные значения \\ = 3, λ2 = — 1. Рассматривая
(F — 31) = I J, найдем собственные векторы ν χ = I I
(ядро матрицы F — 31) и V2 = I „I (образ матрицы F — 31).
Таким образом, можно взять
в=[ ; -iV b-^J2 l
-1 2/' VI 1
и записать матрицу F в виде
'-(:!-ί)(ί-ϊ)(ϊ!
Отсюда следует, что
1 -l\ (еы 0 \ /2 1
exp(tF) = l_1 2д0 e-*Al !
Перемножив эти матрицы, получаем
,.т ( 2е*-е^ е^-е-1 \
exp(iF)=^_2e3t + 2e_t _est + 2e-t)-
Выбрав вектор vo, определяющий начальные условия, т.е.
значение ν в момент t = О, мы можем написать частное решение
уравнения ν(ί) = Fv(t). Пусть, например, vo = I ). Тогда
vW=exp(iF)(;) = (_3^r+2Ie"'.)·
Дифференцирование этого вектора дает
9e3i + 2е~*
-9e3i - 4е
V(*) - I _Q„3i _ Ao-t

3.3. Вычисление экспоненты от матрицы 129
Прямым вычислением легко проверяется равенство
и· ил _ ( 7 л f3e3i -2e-i \ - f9e3i+2e_i "\
b VW - ^_8 _5 J ^_3e3i + Ae-tj - ^_9e3i _ ie-t) ,
т. е. справедливость уравнения ν = Fv.
Случай 2. Одинаковые собственные значения. Метод,
описанный выше, работает, когда F имеет разные собственные
значения. Допустим теперь, что F имеет два одинаковых
собственных значения λ. Тогда либо F = I . I, когда можно писать
exp(iF) = (е* е°А^,либо^ = В^ ]^В-\
Пусть в показателе экспоненты стоит матрица I „ . I.
Сначала преобразуем ее к виду
Ао'л'()— Чоо
Если матрицы С и D коммутируют, то, как мы знаем,
ехр(С + D) = (ехр С) (ехр D).
Поскольку λΐ коммутирует с любой матрицей, мы имеем
ехр(Ао λί) =ехр(м) ^ (о о'
0 /о Л2 /о о\
В то же время I „ „ ] = I „ „ ], поэтому степенной ряд для
соответствующей экспоненты сводится к
/о г\л (\ о\ /о А
ехр \П П ) \ 0 1 J + Ι Ω n)+ слагаемые> Равные нулю,
О А (\ t
т. е. ехр ( „ I = I „ и, следовательно,
'λί t λ fext 0 \ /1 A fext tex"
expU λί =(θ е*Но- 1 =U e*

130 Глава 3. Линейные дифференциальные уравнения ...
Итак, мы получили, что
если F = b(). ])в-\ то exp(iF) = В (*? **%) В~1
В качестве примера рассмотрим систему уравнений
χ = х + у,
у = -х + Зу.
( 1 Λ
Матрица F = I _ I имеет характеристическое уравнение
λ2 - 4λ + 4 = 0, имеющее два равных корня λ = 2. Рассматривая
(F — 21) = I I, получаем собственный вектор νι = I ) и
вектор V2 = I ), для которого (F — 21) V2 = νχ. Отсюда
'-(ίί)(?ί)(-!!
(2t t\ (e2t te2t\
Поскольку exp I „ J = I „ 2t )» мы имеем
ИЛИ
'(1 - t)e2t te2t
-te2t (1 + t)e
exp(tF) = (yi_X (л^„
Если, например, мы хотим найти решение нашей системы
дифференциальных уравнений с начальными условиями xq = 2, у о = 1,
то следует построить вектор
'2\ _ (2e2t - te2t'
1 -\e2t-te2
exp(iF) J = <% _ + o(
Легко проверить, что
ι
2e2t - e2t - 2te2t = -x + 3y.
χ = 4e2i - e2t - 2te2t = x + y,

3.3. Вычисление экспоненты от матрицы 131
На самом деле в случае равных собственных значений λ необя-
А 1\„_1-Со_
зательно записывать матрицу F в виде F = В I . I В
гласно теореме Гамильтона-Кэли (F — λΙ)2=0, поэтому матрица
G = F — XI является нильпотентом. Поскольку λΐ и G
коммутируют, из равенства F = G + XI следует:
exp(iF) = exp(Ail) exp(iG).
Но exp(iG) легко вычисляется разложением в степенной ряд:
exp(iG) = I + tG,
поскольку (tG)2 и все последующие слагаемые ряда равны нулю.
Следовательно,
exp(iF) = (e^ jL)(I + tG).
О е
В предыдущем примере, где F =
G = F-2l--
1 1
-1 3
-1 1
-1 1
получаем
/e2i
exp(iF)=(J0
О
„2ί
1 0\ f-t t
о ι +\-t t
(l-i)e
2ί
te
2ί
-te
2ί
(l+i)e
2ί Ι»
что и следовало ожидать.
Случай 3. Комплексно-сопряженные собственные
значения. Ранее мы доказали, что если матрица F имеет комплексно-
сопряженные собственные значения а ± ίβ, то ее можно
представить в форме F — ВСВ*1, где С = L
матрица. Перед нами стоит задача получить экспоненту, в
показателе которой стоит С.
Заметим, что конформная матрица С может быть записана в
ниде С = αϊ + β J, где J = ( t n I. Матрица J удовлетворяет
— конформная
1
О

132 Глава 3. Линейные дифференциальные уравнения ...
уравнению J = —I и соответствует комплексному числу i. Так
как αϊ и β J коммутируют, мы имеем равенство
exp(iC) = exp(ial) exp(i/3J),
где
exp(ial) =
Чтобы вычислить exp(tp\7), воспользуемся разложением в
степенной ряд:
exp(ipV) = I + tpj + ^y(ipV)2 + ±(tpj)3 + ^j(i/9J)4 + · ■ ■ ·
Поскольку J2 = —I, J3 = —J, J4 = I, J5 = J и т.д., получаем
exp(ipV) = I + ipV - ±(tp)4 - ^m3J + \,{ίβγΐ + ■■■
-{ι-φ + φ + ·--)*+{»-φ + ---)*
Воспользуемся тем, что коэффициент при матрице I в
последнем выражении — степенной ряд для cos/ft, а коэффициент при
матрице J — степенной ряд для sin/ft. Следовательно, можно
записать
exp(ipV) = cos βί Ι + sin βί J = ( °°S (? " аП β1 \ .
v ' γ sin pi cos pi J
Полученная матрица является матрицей вращения, зависящей от
времени. Отождествляя матрицу J с комплексным числом i, мы
можем получить известную формулу
ei/3i = cos/3i + isin/3i.
Итак, если С = ( п |, то
\β а)'
и™ feat 0 \ /cos/ft -sin/?t\
«P(*C)=(o **)\*ηβί cos/3iJ·
feat 0 \
I 0 eat)

3.3. Вычисление экспоненты от матрицы 133
И если F = ВС В 1, то exp(iF) можно вычислить по формуле
exp(iF) =5exp(iC)5-1.
В качестве примера возьмем матрицу I ^ I.
Характеристическое уравнение этой матрицы λ2 + 2λ + 5 = 0 имеет
корни λ = -1 ± 2i. Тогда F = ВСВ~\ где С = ' ~1 ~2
2 -1
конформная матрица. Как описано в параграфе 2.2, в качестве
первого столбца матрицы В можно взять ( η Ι, тогда второй
столбец В равняется первому столбцу F — αϊ, деленному на β,
т. е. столбцу - I „ ) = ( ι ) · Следовательно, В = ( ) и
F=l)l ι)(η ι)' В°спользовавшись
изложенной выше процедурой, вычислим exp(iC):
tm (е~1 ° λ /cos2i -sin2i\
exp(iC) = (^0 e-t)[sin2t cos2iJ·
(\ 2\ (\ -2\
Из равенства exp(iF) = I I exp(iC) I I, перемножая
матрицы, получаем
, „ _ /e_i(cos2i + 2sin2i) -5e-isin2i \
exp(·* >~\ е~* sin 2ί е~г (cos 2i - 2 sin 2i) J '
Можете самостоятельно проверить, что
— exp(iF) =Fexp(iF).
at
И в этом случае нет необходимости явно выписывать
разложение на множители F = ВСВ~1. Пусть F имеет собственные
шачения a±i/3, так что характеристическое уравнение имеет вид
(А - α)2 + β2 = 0.
Согласно теореме Гамильтона-Кэли
(F - αϊ)2 + β21 = 0,

134 Глава 3. Линейные дифференциальные уравнения ...
поэтому матрица G = F — αϊ, след которой равен нулю,
удовлетворяет уравнению G2 = —β21. Из равенства F = al+G получаем,
что
exp(iF) = exp(ail) exp(iG).
Экспоненту, в показателе которой стоит tG, запишем в виде ряда
, ^ π ^ t2G2 i3G3 i4G4
exp(iG) =I + tG+ —+ — + — + ■■·.
Используя уравнение G2 = —β21, получаем
exp(tGf)=I + tG-^1-^ + ^1+-...
Коэффициент при матрице I — это степенной ряд для cos/3i, a
коэффициент при матрице G равен
βΗ3 βΗ5 1 / βψ βΗ5 \ sin/ft
3! 5! β V 3! 5! У /3 '
Следовательно,
exp(iG) = cos/ft I + [(sin/%)//?](?,
и
exp(iF) = (^ ei) exp(iG).
Возвращаясь к матрице F = I I, для которой α = — 1,
/3 = 2, построим матрицу (7 = F + I = I .), имеющую след,
равный нулю и удовлетворяющую уравнению G2 = —41. Тогда
urr. fcos2t 0 \ , 1 . _. /4 -10
exp(iG) = ^ 0 cos2iJ + 2^2^2 _4
, ™ _ /cos2i + 2sin2i -5sin2i
exp(,tG j - ^ gin 2f cog 2f _ 2 gin 2f
/e-i 0 \
Умножив последнее равенство на exp(ail) = I _t I,
получим ранее вычисленную exp(iF), но затратив гораздо меньше
усилий.

3.4. Дифференциальные уравнения и фазовые портреты 135
3.4. Дифференциальные уравнения
и фазовые портреты
Мы уже показали, что дифференциальное уравнение ν(ί) = Αν
с начальным условием v(0) = vq имеет единственное решение
ν(ί) = exp(ii4)v0.
Это решение ν(ί) определяет функцию от времени в двумерном
векторном пространстве. Поскольку ехр(М) определена как для
положительных ί, так и для отрицательных, область определения
векторной функции ν(ί) — вся вещественная ось: —оо < t < оо.
Изображая на графике положение конца вектора ν для всех
значений t, мы получаем интегральную кривую дифференциального
уравнения (рис. 3.1). Эта кривая изображает траекторию
частицы, движущейся в плоскости, вектор ν(ί) = Αν(ί) касается
траектории и изображает скорость частицы в момент времени t. Через
каждую точку плоскости проходит единственное решение
уравнения, а преобразование exp(i А) задает движение по этой кривой
в зависимости от времени t.
Рис. 3.1
Нарисовав семейство интегральных кривых, мы можем
создать фазовый портрет, отражающий важные свойства
решений дифференциального уравнения. Хотя матрицы А, задающие

136 Глава 3. Линейные дифференциальные уравнения ...
дифференциальное уравнение ν(ί) = Αν, могут быть самыми
разными, но они порождают ограниченное число различных
типов фазовых портретов. Скажем конкретнее: если матрицы А
и F — сопряженные, т.е. А = BFB~l, то интегральные
кривые уравнения ν(ί) = Αν получаются из решений уравнения
w(i) = Fw линейным преобразованием v(i) = Bw(t).
Доказательство очень простое: матрица В не зависит от времени,
поэтому v(i) = Bw(t). Следовательно, если w(i) = Fw, то
ν = Bw = BFw = BFB^v = Αν.
Таким образом, если А и F — сопряженные матрицы, то
фазовые портреты для уравнения ν(ί) = Αν, по существу, совпадают
с фазовыми портретами w(i) = Fw. Поэтому можно (с
точностью до линейного преобразования) определить фазовые
портреты, рассматривая различные возможные собственные значения
матрицы А.
Сначала отметим, что если vq — собственный вектор А,
соответствующий собственному значению λ, то
v(i) = exp(ii4)vo =
ι + ίλ + 1(ίλ)2 + ··
νο
ν0 = extv0.
В этом случае интегральная кривая представляет собой прямую,
проходящую через начало координат по направлению вектора vq.
Если λ положительно, то с ростом t конец вектора ν(ί)
экспоненциально удаляется от начала координат. Если же λ отрицательно,
то частица, движущаяся по закону ν(ί), при t —> +00
экспоненциально приближается к началу координат. Наконец, когда λ = О,
v(i) = vq для всех t. Поэтому все точки на прямой, проходящей
через начало координат и vq, остаются неподвижными.
Теперь мы можем перечислить все возможные случаи.
Случай 1. Матрица А пропорциональна единичной
матрице.
1а. А = I „ _ ), ехр(Ы) = I „ ). Поэтому все точки
неподвижны.

3.4. Дифференциальные уравнения и фазовые портреты 137
. Каждый вектор является
1Ь'Л=(о α)'6ΧΡ^=(60 е°,
собственным, поэтому все интегральные кривые — это прямые
линии, проходящие через начало координат. Если λ > 0, то при
t —► +00 каждая точка плоскости экспоненциально удаляется от
начала координат (рис. 3.2(a)); если λ < 0, то точки движутся в
обратном направлении, к началу координат (рис. 3.2(b)).
Рис. 3.2(a). λ > О
Рис. 3.2(b). λ <0
Случай 2. Матрица А имеет разные вещественные
собственные значения λ χ и λ2· Тогда
А = В
λι
О
О
λ2
в-
2а. λι и λ2 положительны и λι > λ2· В частном случае, если
В = 1, интегральные кривые изображены на рис. 3.3(a). Оси χ и
у являются интегральными кривыми. Далее, поскольку решения
задаются формулами
eXltx0
ех*у0
и λι — λ2 > 0, отношение х/у = e^Xl~X2^ растет при t —► +00, а
при t —► — 00 кривые входят в начало координат, касаясь оси у.
В случае произвольной матрицы В пусть νχ и vq —
собственные векторы матрицы А. Прямые, идущие вдоль векторов νχ и
V2, являются интегральными кривыми. Поскольку λχ > λ2,
другие интегральные кривые становятся почти параллельными νχ

138 Глава 3. Линейные дифференциальные уравнения ...
Рис. 3.3(a). А =
Рис. 3.3(b). А = 5
λι
О
О
λ2
5
-1
при t —► +оо и касаются v2 при t —> — оо, как это показано на
рис. 3.3(b).
2Ь. λχ и λ2 отрицательны и |λι| < |λ2|. Этот случай похож на
случай 2а, но все стрелки направлены в противоположную
сторону. При t —► +оо все интегральные кривые движутся к началу
координат.
2с. λχ положительно, а λ2 отрицательно. В частном случае, когда
5 = 1, оси χ и у опять являются интегральными кривыми. С
ростом t значение |х| растет, а значение |у| убывает.
Другие интегральные кривые стремятся к оси χ при t —► +оо
и к оси у при t —> —оо, как это показано на рис. 3.4(a).
В случае произвольной матрицы В пусть вектор νχ
соответствует собственному значению λχ > 0, а вектор ν2 —
собственному значению λ2 < 0. Точки, расположенные на прямой,
проходящей через vi, удаляются от начала координат, а точки на
прямой, порожденной вектором v2, движутся к началу
координат. Кривые решений стремятся к прямой, проходящей через vi,
при t —> оо, и к прямой, проходящей через V2, при t —► — оо, как
это изображено на рис. 3.4(b).
2d. λι положительно, λ2 равно нулю. В частном случае, когда
5 = 1, координата у на каждом решении не зависит от времени.
Точки оси у неподвижны. Интегральными кривыми являются

3.4. Дифференциальные уравнения и фазовые портреты 139
Рис. 3.4(a). А =
у) ~ \eX2ty0
λι Ο
О λ2Γ
Рис. 3.4(b). А = В
λι О
О λ2
в-
прямые, параллельные оси х. При t —* +00 точки удаляются от
оси у, а при t —> — 00 приближаются к ней (рис. 3.5(a)).
Рис. 3.5(a). А
χ \ ι eXltx0
λι Ο
О О
2/0
Рис. 3.5(b). А = В f^1 °q) В'1
В случае произвольной матрицы В, пусть вектор vi
соответствует собственному значению λι > 0, a v2 — собственному
значению λ2 = 0. Прямые, проходящие через начало координат

140 Глава 3. Линейные дифференциальные уравнения ...
вдоль вектора V2, состоят из неподвижных точек.
Интегральными кривыми являются прямые, параллельные вектору vi. Точки
удаляются от прямой, проходящей через V2, при t —► оо и
приближаются к ней при t —► — оо (рис 3.5(b)).
2е. λι отрицательно, λ2 равно нулю. Все стрелки имеют
направление, противоположное предыдущему случаю. При t —► +00
вся плоскость проектируется на прямую, проходящую через
вектор V2-
Случай 3. Собственные значения матрицы А равны, но
А ф XI. При этом А = В (* 1jB-\exp{tA) = BeXl(1Q [jB'1.
В этом случае преобразование А имеет только один собственный
вектор vi.
За. λ > 0. Если В = I, то собственный вектор vi лежит на
оси х. Ось χ является интегральной кривой. На любом решении
при t —► +00 |х| становится много больше \у\; соответственно
интегральные кривые, задаваемые формулой
х\ =ем (хо + tyo
становятся «почти параллельными» оси χ (рис. 3.6(a)). При t —►
—00 знак χ противоположен знаку у. Все кривые пересекают ось
у при t = -хо/уо-
Рис. 3.6(a). А =
λ 1
0 λ
Рис. 3.6(b). А = В (* Μβ
-1

3.4. Дифференциальные уравнения и фазовые портреты 141
В случае произвольной матрицы В интегральной кривой
является прямая, проходящая через начало координат вдоль
вектора vi. При t —► оо все другие кривые становятся
«параллельными» этой прямой, причем пересекаются они в начале координат.
ЗЬ. λ < 0. Стрелки меняют направление на противоположное по
сравнению с предыдущим случаем.
Зс. λ = 0. В частном случае, когда В = I, ось χ состоит из
неподвижных точек. Интегральными кривыми являются прямые,
параллельные этой оси. Для произвольного значения t функция
ехр(<Л) является преобразованием сдвига (см. рис. 3.7(a)).
ехр(*Л) =
1 t
0 1
Рис. 3.7(a). А=(^0 J), Рис. 3.7(b). А = В (^ ^
В
-1
В случае произвольной матрицы В прямая, проходящая
через начало координат вдоль вектора νχ, остается
неподвижной. Все точки плоскости сдвигаются параллельно этой прямой
(рис. 3.7(b)).
Случай 4. Матрица А имеет комплексно-сопряженные
собственные значения а ± Ίβ. В этом случае собственные
векторы отсутствуют.
4а. а = 0. В частном случае, когда В = I, интегральными
кривыми будут окружности с центром в начале координат. Одно из

142 Глава 3. Линейные дифференциальные уравнения ...
решений — неподвижное начало координат (рис. 3.8(a)).
Преобразование ехр(М) является вращением:
ехр(<Л) =
cos βί — sin βί
sin βί cos βί
Решения — периодические с периодом 2π/β.
Рис. 3.8(a). А =
exp(tA) =
cos/3i
sin/3i
-β
О
- sin βί
cos/3i
Рис. 3.8(b). А = в(°д 0^ В'1
В общем случае интегральные кривые являются эллипсами.
Решения — периодические с периодом 2π/β (рис. 3.8(b)).
4Ь. а > 0. Интегральные кривые — это спирали, закрученные
против часовой стрелки (рис. 3.9(a), (Ь)). При t —► +оо точки
удаляются от начала координат, а при t —► — оо приближаются к
нему.
4с. а < 0. То же самое, что и в предыдущем случае, но спирали
закручиваются к центру при t —► +оо.
3.5. Применения дифференциальных
уравнений
На рис. 3.10 изображена физическая система, поведение
которой описывается дифференциальным уравнением только что
рассмотренного типа.

3.5. Применения дифференциальных уравнений 143
а -0
Рис. 3.9(a). А = Γβ -П, «р(М) = <- I ~£ ~£
cos /?ί — sin βί
Рис. 3.9(b). А = В (° fj В''
|->QQQQr-
к
Рис. 3.10

144 Глава 3. Линейные дифференциальные уравнения ...
Масса Μ движется под действием пружины, создающей силу
—кх, пропорциональную смещению х; линейный буфер создает
силу — zu, пропорциональную скорости и, с которой движется
эта масса. Второй закон Ньютона говорит, что Ми = — кх — zu,
где скорость определена как χ = и. Состояние системы
полностью описывается вектором w = I J, компонентами которого
являются положение и скорость массы М. Поскольку
χ = и,
к ζ
Μ Μ
можно написать дифференциальное уравнение
w = i4w,
где
л- ( ° Л 2_ к г_ ζ
Движение системы определяется собственными значениями
матрицы А. Характеристическое уравнение матрицы имеет вид
λ2 + Γλ + ωΐ = О,
решая которое, получаем следующие собственные значения:
Таким образом, существуют четыре возможности.
1. Если Г = 0 (отсутствует трение), то λ = ±.\wq. Такая
система движется, не затухая, совершая колебания около положения
равновесия {осциллятор без затухания). Фазовый портрет
соответствует случаю 4а из предыдущего параграфа. Кривыми
решения являются эллипсы в плоскости хи (рис. 3.11(a)). Уравнение
для каждого из эллипсов имеет вид ^кх2 + \Ми2 = const, что
означает сохранение энергии. Период движения равен 2π/ωο-

3.5. Применения дифференциальных уравнений 145
Рис. 3.11(a)
Рис. 3.11(b)
2. Если Г > 0 и при этом Г2 — 4a>Q < 0, то собственные
значения равны
λ =
Такая система называется осциллятором с затухающими
колебаниями. Фазовый портрет соответствует случаю 4с.
Интегральными кривыми являются спирали, закручивающиеся к началу
координат (рис. 3.11(b)).
3. Если Г2 = 4и>о, то характеристическое уравнение имеет
два одинаковых корня λ = —Г/2. Такую систему называют
осциллятором с критическим затуханием, его фазовый портрет
соответствует случаю ЗЬ (рис. 3.11(c)).
Запишем явно матрицу
А-\1 =
Г/2
-Г2/4
1
-Г/2
ч-Г/2
ров матрицы А. Это значит, что если
Отсюда видно, что wi
один из собственных векто-
хо\ _ ζο
щ \-(Г/2)хо1 '

146 Глава 3. Линейные дифференциальные уравнения ...
и
Рис. 3.11(c)
Рис. 3.11(d)
то в процессе движения отношение координат χ и и остается
постоянным.
4. Если Г2 > 4и>о, то характеристическое уравнение имеет
отрицательные вещественные корни
Х = -Г/2±у/гЩ-ш1
Такое поведение системы называется апериодическим
затуханием; его фазовый портрет соответствует случаю 2Ь (рис. 3.11(d)).
Чтобы лучше понять эти четыре типа движения, давайте для
каждого из этих случаев найдем и нарисуем зависимость
координаты χ от времени ί.
Случай 1. Осциллятор без затухания. Мы имеем:
А =
О 1
-"о °
_ шо
-1/2
ω.
О
-1/2
следовательно,
ехр
-Шп
-1/2
cos u>oi sin ωοί
— sin UQt cos ujQt
ω,
-1/2

3.5. Применения дифференциальных уравнений 147
Отсюда зависимость χ от t имеет вид
χ = mcosu>oi + nsinu>oi,
где тип определяются из начальных условий. Введем параметр
р, удовлетворяющий равенству
2,2 2
т + η = ρ
и определим φ из соотношений
т = ρ sin φ, η = ρ cos φ.
Тогда можно написать
x(t) = /9cos(u>oi + φ)-
Такая кривая представляет собой синусоиду с частотой ω$. Фаза
φ и амплитуда ρ зависят от начальных условий (рис. 3.12).
Рис. 3.12
Случай 2. Осциллятор с затухающими колебаниями. Нам
известно, что в этом случае
/± л\ i-> fe~rtcosujit -e_risino;1A „_i
exp(tA) = B[ _Tt . \ _Tt \)В \
где
ωλ = ^4α,2-Γ2.
Таким образом, зависимость χ от t имеет вид
x(t) = pe~Tt cos(ujit + φ),

148 Глава 3. Линейные дифференциальные уравнения ...
Рис. 3.13
где риф зависят от начальных условий. Графиком этой
зависимости является экспоненциально затухающая синусоида
(рис. 3.13).
Случаи 3 и 4. Здесь у графика x(t) не существует
синусоидальной составляющей в траектории, координата χ экспоненциально
затухает со временем t и может пересекать линию χ = 0 не
больше одного раза (рис. 3.14 и 3.15).
я*
О
Рис. 3.14
Рис. 3.15
Вынужденные колебания. Очень часто дифференциальные
уравнения, возникающие при решении физических задач, явля-

3.5. Применения дифференциальных уравнений 149
ются неоднородными уравнениями типа
ν - Αν = b(i),
где b(i) не равняется тождественно нулю. Чтобы понять, как
появляется член b(i), рассмотрим управляемый осциллятор: на
массу Μ помимо пружины и буфера действует внешняя
вынуждающая сила F(t) (рис. 3.16).
Рис. 3.16
Тогда уравнения χ = и и тй = —кх — Zu + F(t) можно
записать в форме
\й) ~ \-к/М -Z/Mj [и) = \F(t)/Mj '
Чтобы получить решение неоднородного уравнения ν—Αν = b(i),
обобщим метод, называемый вариацией постоянных. Этот
метод хорошо известен для решения линейных
дифференциальных уравнений от одной переменной. В случае одной неизвестной
функции для решения уравнения
χ — кх = b(t)
пользуются тем, что функция ekt является решением однородного
уравнения χ — кх = 0. Тогда решение неоднородного уравнения
можно искать в виде x(t) = ektu(t). Подставляя это выражение в
неоднородное уравнение χ — кх = 6(ί), получаем
kektu(t) + ektu(t) - kektu(t) = b(t),
откуда
u(t) = e~ktb(t).

150 Глава 3. Линейные дифференциальные уравнения ...
Интегрируя это равенство по времени, получаем в качестве
одного из решений
t t
u(t) = I e~ksb(s) ds, x(t) = ektu(t) = ekt f e-ksb(s) ds
или
t
:(t) = /e'«->6Wrf,
о
Это решение получено для начального условия х(0) = 0. Чтобы
получить решение для произвольного начального условия хо, мы
просто добавляем соответствующее решение однородного
уравнения ektXQ. Тогда решение уравнения χ — кх = b(t) с начальным
условием х(0) = xq можно записать в виде
τ
(t)= iek^-sh(s)ds + ektx0.
Этот метод можно применить и для решения векторного
уравнения ν—Aw = b(i). Действительно, функция exp(i.A)vo является
решением однородного уравнения ν — Αν = 0. Мы можем
заменить постоянный вектор νο на функцию w(i) и искать решение
неоднородного уравнения в виде v(i) = exp(i.A)w(i). Подстановка
этой функции дает
Aexp(tA)w(t) + exp(M)w(i) - Aexp(M)w(i) = b(i).
Отсюда следует, что
w(i) = exp(-M)b(i).
Интегрируя по времени, получаем, как одно из решений,
τ
(ί) = / exp(-sA)b(s)ds.

3.5. Применения дифференциальных уравнений 151
Итак,
v(i) = exp(M)w(t),
τ
r(t) = / exp[(i - s)A]b(s) ds.
Очевидно, это решение удовлетворяет условию v(0) = ί „ J.
Чтобы получить решение с произвольными начальными условиями,
добавим общее решение однородного уравнения. Тогда получаем
векторную функцию
ί
ν(ί) = / exp[(i - в)Л]Ь(в) ds + exp(M)v0,
о
которая удовлетворяет условию v(0) = νο·
В учебниках по физике при обсуждении осциллятора с
вынуждающей силой обычно рассматривают в качестве функции
b(i) синусоиду с постоянной частотой ω. Например,
/sin^ + cosci
Тогда b(i) удовлетворяет уравнению b = — u;2b. В этом случае
мы можем в общем решении, полученном выше, провести
интегрирование по частям. Применим тот же трюк, который
используют для вычисления неопределенного интеграла f e~ks sin sds:
проинтегрируем два раза по частям и получим уравнение для
неизвестного интеграла. Пусть
ί
ν = / exp[(i - s)i4]b(s) ds.
о
Интегрируем один раз по частям и, предполагая, что А —
несингулярная матрица, получаем
ί
v= [-exp[(i-s)i4]i4_1b(s)]* + ί exp[(t - s)A}A-1b(s)ds.

152 Глава 3. Линейные дифференциальные уравнения ...
Еще раз интегрируем по частям:
ν = [- ехр[(* - в)Л]Л_1Ь(в)]* - [exp(i - в)уГ2Ь(в)1*
t
+ / ехр[(< - s)A]A~2b(s) ds.
Заменив b на — ω b, видим, что последний член равен —Α λω ν.
Итак,
ν + Α~2ω2ν = - [exp[(i - s)A] U_1b(s) + yT2b(s)'
или
(A2 + ω2Ι)ν = - exp[(i - s)A] b(s) + Ab(s)
it
Кроме случая, когда А имеет собственные значения ϋω (тогда
матрица (А2 + ω2Τ) сингулярна), обе части последнего равенства
умножаем на (Л2+о;21)_1 и получаем решение уравнения в явном
виде
ν = -(А2 + ω2!)'1 [b(i) + ЛЬ(*) - exp(tA) (b(0) + ЛЬ(0))| .
Член, содержащий exp(i.A), обеспечивает выполнение начального
условия v(0) = 0. Если Г > 0, то умножение на ехр(М) приводит
к тому, что любой вектор стремится к нулю при t —► +оо. Таким
образом, при больших значениях t этот член можно опустить и
мы получаем установившееся решение:
ν = -(А2 + ω2!)'1 [b(i) + Ab(t) .
Чтобы проверить этот результат, заметим, что
ν = -(А2 + ω2!)'1 [b(i) + Ab(t)
и
Αν = -(Α2 + ω2!)'1 [^ϊ)(ί) + A2b(t)

3.5. Применения дифференциальных уравнений 153
Тогда
ν - Αν = -{А2 + ω2!)"1 [u;2b(i) + A2b(t)] = b(i).
Эта проверка показывает, что результат правильный, даже если
матрица А сингулярна!
Например, мы хотим найти решение для
Здесь
А =
-1 -2
2 -1
-1 -2
2 -1
Ь(«) =
sin3i
cos3i
sin3i
cos3i
и b(i) = -32b(i), т. е. ω = 3. Тогда
А2 + ω21 =
(Α2 + ω21)~1 =
-1 -2
2 -1
52
6 -4
4 6
-1 -2
2 -1
= λ(3
26 V2
+
6 4
-4 6
ν =
26
J_
26
-2
-2
3
3 cos 3ί \ /— sin 3i — 2 cos 3i
—3 sin 3tJ \ 2 sin 3i — cos 3i
cos 3i — sin 3i \ _ J_ /sin 3i — 5 cos 3i
— cos3i — sin3tl 26 \5sin3i + cos3i
Это есть установившееся решение исходного дифференциального
уравнения. Заметим, что компоненты вектора ν(ί) — опять
синусоидальные функции от t с той же частотой, что и вынуждающий
член. Однако, амплитуды компонент ν и соответствующие фазы
(положение гребней и впадин волны) изменились.
Рассмотрим установившееся решение для физической
системы, описанной в начале параграфа, с синусоидальной
вынуждающей силой. Пусть
А =
О
-utf
1
-Г
ь(«)
о
sinujt

154 Глава 3. Линейные дифференциальные уравнения ...
Тогда
2 _ / ~wg
Τω2 Γ2-ω,
Далее,
Α2 + ω4=(ω2-?Ζ р2 ~Г 2
\_ Гц; Тг + ωζ - ω^
и
Det(^2+o;2I) = (ω2 -ω$)2 + Γ2(ω2 -ω$) + Γ2ω$ = (ш2-ш02)2+Г2ш2.
Поэтому
М2!^2^-1 1 Λ^ + ^-α;2 Γ \
(Л + о, Л) - (ω2 _ ^)2 + Γ2α;2 ^ _Γω2 ω2 _ „2 J ,
и мы получаем формулу для установившегося поведения системы
-(^2 + o;2I)-1(b(i) + ^b(i))= X
(ω2 - ωΐ)2 + Τ2ω2
χ (Γ2+ω2-ω2 Γ \ Π 0 \/ sinu,i
у — Γα>ο ω2 — ujqJ \\ujcosujtJ y—Tsinut
Таким образом, закон движения определяется формулой
Χ(ί) = ~ {ω2 - ω2)2 + Τ2ω2 \-ωΤο08ωί + (ω* ~ ωο) smut]
= psin(u;i + φ),
где
Ρ = ,, 9 2ч9 ^9 9, ^ = агетш(-Ги;/р) = arccos(u;g - ω2)/ρ.
V (^ — ωο) + νΔωΔ
Заметим, что если Г мало, то для значения ω, близкого к и>о, в
амплитуде появляется большой множитель. Это явление
называется резонансом (рис. 3.17).
Обратите также внимание, как изменяется фазовый сдвиг φ от
нуля при малых значениях ω2 до —π/2 для ω2 = ω$. Для больших
значений ω2 фазовый сдвиг равен arccos(—1) = —π (рис. 3.18).

Резюме
155
Рис. 3.17. Резонансная кривая Рис. 3.18. Фазовый сдвиг
Резюме
А. Экспонента от матрицы
Изучив эту главу, вы должны научиться выражать
экспоненциальную функцию expiX в виде формального степенного ряда,
уметь вычислить эту функцию в тех случаях, когда степени
матрицы X имеют простую форму.
Вы должны уметь объяснить смысл производной (d/dt)etx и
показать, что она равна Xetx.
В. Линейные дифференциальные уравнения
Вы должны уметь показать, что все решения уравнения ν = Αν
At
имеют вид ν = е vq.
Вы должны уметь вычислять eAt для любой матрицы А (2x2)
и решать уравнение ν = Αν с заданными начальными условиями.
Вычислив собственные значения матрицы А (2x2), вы
должны уметь рисовать фазовый портрет, представляющий
интегральные кривые для уравнения ν = Л v.
С. Неоднородные уравнения и гармонический осциллятор
Вы должны уметь преобразовывать дифференциальное
уравнение второго порядка, описывающее осциллятор, к виду ν — Αν =
b, где А — матрица 2x2 иЬ — вектор, зависящий от времени.
Вы должны уметь решать это уравнение и связывать решение
с поведением осциллятора при наличии затухания и резонанса.

156 Глава 3. Линейные дифференциальные уравнения ...
Задачи
3.1. (а) Напишите разложение в степенной ряд для (1 — Х)~1 и для
(1-Х)"2.
(Ь) Перемножьте два полученных ряда и сравните результат с
разложением в степенной ряд (1 — Х)~3.
3.2. (а) Пусть F = (^ j^j. Докажите, что F2 = F/2 и Fn =
F/2n~1. Используя этот результат, получите разложение в
ряд матрицы (I—F)-1. Получите обратную матрицу прямым
вычислением и сравните результаты.
/3/2 1/2\-1
(Ь) Вычислите матрицу, обратную I 1',_ „',_ I , записав ее в
виде (I + Р)~1, где Ρ — проекция I '._ '._ I, и
воспользовавшись разложением в ряд матрицы (1 + Χ)~γ. Обратите
внимание на то, что ряд расходится, несмотря на
существование обратной матрицы.
3.3. (а) Для матрицы Νπ/^ = I _1 ,„ 1 ,„ ) справедливо условие
Ν2,4 = 0. Используя это, вычислите F(t) = βχρ(ίΝπμ) и
проверьте, что F'(t) = Νπ/4Ρ(ί).
(b) Матрица Ρπ/4 = f jy2 /2 J удовлетворяет условию P2/4 =
Ρπ/4- Вычислите G(t) = exp(iP7r/4), воспользовавшись этим
свойством, и проверьте, что G^/4 = P^/iG{t).
3.4. Пусть матрица Ρ удовлетворяет уравнению Р2 = ЗР.
(a) Какие собственные значения имеет Р? Приведите свои
аргументы.
(b) Используя разложение экспоненты в степенной ряд,
покажите, что exp(iP) может быть записана в виде
exp(iP) = I + g(t)P.
Найдите явное выражение для функции g(t).
3.5. Допустим, что В есть матрица 2 χ 2 с одинаковыми собственными
значениями λ.
(а) Покажите, что матрица N = В — XI является нильпотентом,
т.е. Ν2 = 0.

Задачи
157
(b) Записав В = N + XI и воспользовавшись разложением
экспоненты в степенной ряд, покажите, что
ехр(Ш) = (1+ ίΛΓ)βχρ(ίλΙ).
3.6. Воспользовавшись результатом задачи 3.5, решите систему
уравнений
x = x{t) -y(t),
у = x{t) + 3j/(i)
с произвольными начальными условиями
3.7. Вычислите «xp(iyl) для следующих матриц и проверьте, что
(d/dt)exp(tA) = Aexp{tA):
<а)Л=(:< «).
/_1 д\
(Ь) А = I _1 _). (Подсказка: А = 21 +N, где N — нильпотент-
ная матрица.)
3.8. Пусть А — матрица 2x2, имеющая два разных вещественных
собственных значения λι и Аг, соответствующие собственным
векторам ν ι и V2.
(a) Покажите, что матрица Pi = (А — Аг1)/(А1 — Аг) задает
проекцию на прямую, задаваемую собственным вектором vi:
Pi = Pi, образ Pi есть λνι, а ядро Pi есть λν2.
(b) Покажите, что матрица Рг = (А — ΑιΙ)/(λ2 — Αι) задает
проекцию на прямую, задаваемую V2. Покажите, что
ΡιΡ2 = Р2Р1 = 0, Pi + Р2 = Ι, ΑιΡι + λ2Ρ2 = Α.
(c) Используя разложение экспоненты в степенной ряд,
покажите, что
βχρ(ίλιΡι + ίλ2Ρ2) = eAltPi + βλ2ίΡ2.
(d) Воспользовавшись этим результатом, решите систему
уравнений
x(t) = -4x(t) + 5y(t),
y(t) = -2x(t) + 3j/(i)
Й- ■

158 Глава 3. Линейные дифференциальные уравнения ...
с произвольным начальным условием
3.9. Пусть А — матрица 2 χ 2, у которой след равен нулю и
определитель равен 1.
(a) Напишите характеристическое уравнение матрицы А. Что
молено сказать о матрице А2 в этом случае?
(b) Используя разложение exp(iyl) в степенной ряд, получите
формулу
exp(tA) = F{t)l + G(t)A,
где матрицы F(t) и G(t) содержат тригонометрические
функции от t.
(c) Кривой решения уравнения ν = Αν с начальным условием
ν = vq является эллипс, изображенный на рис. 3.19.
Докажите, что все хорды, соединяющие exp(iyl)vo с ехр(—tA)v0
параллельны Ανο, и что средняя точка каждой хорды лежит
на диаметре эллипса, на котором лежит вектор vq .
Рис. 3.19
3.10. Допустим, что матрица G имеет след, равный нулю и
определитель, равный — β2.
(a) Чему равняется G2 (примените теорему Гамильтона-Кэли)?
(b) Используя разложение экспоненты в степенной ряд,
покажите, что матрица exp G+exp(—G) пропорциональна единичной

Задачи
159
матрице. Найдите такую функцию /, чтобы выполнялось
равенство
exp(G) + exp(-G) = /(/3)I.
(c) Умножив это тождество на expG и применив теорему Га-
мил ьтона-Кэли, покажите, что Det(exp(G)) = 1, и получите
выражение для следа матрицы exp G.
(d) Пусть F = XI + G. Используя результаты, полученные выше,
покажите, что Det(expF) = expCTrF).
3.11. Для каждой системы дифференциальных уравнений,
представленных ниже, найдите, какой из фазовых портретов, полученных
в параграфе 3.4 (случаи 1(а)-4(с)), наилучшим образом
описывает поведение общего решения. Решите эти системы для
начального условия I °) = ( ι ) ПРИ ί = 0.
(a) х = -4у,
у = х- 4у;
(b) χ = χ — 2у,
у = —2х + 4ух — 4у;
(c) χ = Ах — 5у,
у = 4х- 4у;
(d) χ = 2х + у,
У = -х + 4у;
(e) χ = χ — Ъу,
у = 2х- 5у;
(f) χ = -2х + 4у,
У=-х + 2у.
3.12. Решите системы уравнений, приведенные ниже, с начальными
условиями I ° I = I I. В каждом случае определите, какой
фазовый портрет наилучшим образом представляет общее
решение системы.
(a) х = Ъу,
у = х- 2у;
(b) χ = -х + у,
у = -5х + Ъу;
(c) х = Ъх + у,
у=-х + у;

160 Глава 3. Линейные дифференциальные уравнения ...
(d) χ = —5а; + 4у,
у = -8х + 7у;
(e) χ = —Ах — 2у,
у = 5х + 2у;
(f) х = х + 2у,
у = 2х — 4у.
3.13. Обобщив на случай матрицы 3x3 то, что вам известно о
вычислении и применении экспоненты, в показателе которой стоит
матрица 2x2, решите систему дифференциальных уравнений
х = у,
ζ = —6х — Ну — 6ζ
(х\ I 1\
с начальными условиями I у I = I 2 I при t = 0. (Примечание:
W V-1/
возникнет проблема вычисления обратной матрицы 3x3. Это
можно сделать «в лоб», если рассмотреть задачу решения трех
систем линейных уравнений.)
3.14. Обобщив известную технику, решите систему уравнений
χ = χ + у — ζ,
у = -х + Ьу + ζ,
ζ = -2х + 2y + 4z
(Л (Л
с начальными условиями I у I = I 1 I при t = 0.
ν; ν;
3.15. Введя величину ν = χ, преобразуйте дифференциальное
уравнение второго порядка
χ + Ίχ + 5х = 0
в систему уравнений первого порядка. Решите эту систему для
хо^
произвольных начальных условии
3.16. (а) Дифференциальное уравнение для гармонического
осциллятора с критическим затуханием (единицы выбраны так, что
ω2 — 1) имеет вид
χ + 2х + χ = 0.

Задачи
161
Решите это уравнение матричным методом, вводя υ = χ в
качестве новой переменной. Запишите решение для начальных
условий Pj = i^°j и (ζ) = (), нарисуйте фазовые
портреты этих и других решений. Покажите, что каждое из
равенств χ = О или υ = О может выполняться не больше, чем
в одной точке.
(b) Есть другой способ решения этого уравнения. Сначала
ищутся решения уравнения х+2х+(1—е2)х = О при ε > О, что
приводит к матрице с разными вещественными собственными
значениями, а затем рассматривается предельный переход
ε —► 0. (Физически это соответствует использованию слегка
ослабленной пружины.) Выполните всю процедуру для
начальных условий I '~ I и I J. Покажите, что произойдет с
фазовыми портретами при ε —► 0.
(c) Еще один способ решения того же уравнения. Сначала
решается уравнение χ+2ж+(1+ε2)χ = 0, что приводит к матрице с
комплексно-сопряженными собственными значениями, после
этого ε —> 0. Проделайте вычисления для начальных условий
I „ I и I I, нарисуйте фазовые портреты решении и
покажите, что происходит с фазовыми портретами при ε —> 0.
3.17. Рассмотрим функцию cos ία;.
(a) Разложите функцию в формальный степенной ряд и
покажите, что
■j-^ (cos ία;) = —α; cos ία;
и
— (cos tx) = 0 при ί = 0.
(b) Пусть I .. J = — В I J, где матрица В имеет квадратный
корень А (т.е. А2 = В). Покажите, что cos(iyl) I \Л I есть
решение дифференциального уравнения второго порядка
^v(t) = A2v(t)

162 Глава 3. Линейные дифференциальные уравнения ...
с начальными условиями г>(0) = г>о и dv/dt(0) = О.10
(5/2 —3/2\
—4/9 ^/9 )' Найдите такую матрицу А,
которая имеет положительные собственные значения и
удовлетворяет уравнению А2 = В. (Указание: диагонализуйте
матрицу В.)
(d) Для построенной таким образом матрицы А вычислите
cos(iyl). (Указание: Матрица А уже приведена к
диагональному виду. Воспользуйтесь той же процедурой, что и для
вычисления ехр(£Л).)
(e) Используйте полученные выше результаты для решения
системы уравнений
5 3
Х=-2Х+2У'
.. 3 5
У=2Х~2У
с начальными условиями
±(0) = jr(0) = 0, ι(0) = хо, 2/(0) = ι/ο-
3.18. Рассмотрим систему дифференциальных уравнений
χ = 4βχ — у
ν = 9χ + β,
где β — вещественный параметр.
(a) Решите систему с произвольными начальными условиями
при /3 = 0.
(b) Найдите два критических значения параметра βγ < 0 и
/?2 > 0, при которых меняется характер решения.
Обсудите случаи β = βι и β = β2.
(c) Нарисуйте фазовые портреты, которые качественно
описывают природу решений для β < βι, βι < β < β2 и β > β2.
3.19. Пусть Α = (~22 _}
10Авторы имеют в виду, что матрица cos(tA) должна быть получена как
сумма формального степенного ряда для cos ia;, где вместо числа χ
подставлена матрица А. Разумеется, необходимо убедиться в сходимости полученного
ряда. (Молено доказать, что он сходится для всех t при любой матрице А.)
См. также указания авторов к задаче 3.17 (d). — Прим. ред.

Задачи
163
(a) Найдите такие матрицы D ш В, чтобы выполнялось
соотношение А = BDB~l (D — диагональна).
(b) Постройте решение дифференциального уравнения ν = Αν
для произвольных начальных условий νο = I I при t = 0.
(c) Нарисуйте фазовый портрет решения уравнения ν = Αν.
Получите образ и ядро матрицы
F = lim exp(yli),
ί—»оо
объясните их значения в связи с фазовыми портретами.
(d) Выбрав пробное решение в виде ν = exp(yli)w, получите
решение дифференциального уравнения ν — Αν = I „ I.
3.20. (а) Введя и = χ в качестве новой переменной, преобразуйте
χ + 2х - Зх = 3 sin 2ί + 2 cos 2ί
к уравнению вида
'*)-AQ=bw-
(b) Решите это уравнение с начальными условиями х(0) = 0,
it(0) = 0, воспользовавшись результатами, полученными в
параграфе 3.4.
3.21. Когда к незатухающему осциллятору приложена вынуждающая
сила, частота которой равна собственной частоте осциллятора,
обычные методы решения не работают. В этом случае они не
дают установившегося решения. Однако, мы получили формулу
τ
v(t) = / exp[(i - s)A]b(s)ds,
которая прекрасно работает. С помощью этой формулы получите
решение уравнения
*\- ( ° Л(х\ = ( °
й) \—ω2 Оу \uj \^sina;i
для начальных условий х(0) = 0, и(0) = 0.

I

Глава 4
Скалярные произведения
Глава 4 посвящена изучению скалярных произведений
и квадратичных форм. В ней много физических
приложений, в том числе обсуждение нормальных мод и
подробное изложение специальной теории
относительности.
4.1. Скалярные произведения
в евклидовом пространстве
Как вы помните, на аффинной плоскости мы располагаем очень
ограниченным понятием длины: мы можем сравнивать длины
отрезков на параллельных прямых, но для прямых, которые не
параллельны, это сделать нельзя. Например, можно говорить,
что на рис. 4.1 длина отрезка QR (или Q'R') в два раза больше
длины отрезка PQ, но мы не имеем права сравнивать длины
отрезков PQ' и PQ.
Евклидова плоскость — это аффинная плоскость, где
определена функция расстояния, которая каждой паре точек
приписывает неотрицательное вещественное число D(P,Q), называемое
расстоянием между этими точками. Эта функция расстояния
совместима с ограниченным понятием длины в аффинной
геометрии, например, на рис. 4.1 D(Q',R') = 2D(P,Q). Кроме
того, она позволяет сравнивать длины непараллельных отрезков,
таких как PQ и PQ''. На евклидовой плоскости R2 расстояние

166
Глава 4. Скалярные произведения
Рис. 4.1 Рис. 4.2
между двумя точками определяется хорошо известной формулой
D(P,Q) = sJ(xQ-xp)2 + (yQ-yp)2.
Евклидовым преобразованием / : R2 —► R2 называется аффинное
преобразование, сохраняющее функцию расстояния, т. е.
удовлетворяющее условию D(f(P),f(Q)) = D(P,Q).
Обратим внимание на векторное пространство смещений на
евклидовой плоскости. Мы видим, что функция расстояния
позволяет определить длину каждого вектора. Действительно,
длина вектора — это просто расстояние от его «головы» до
«хвоста». Длину вектора ν будем обозначать ||ν||. Очевидно, что если
ν = I ), то ||v|| = \Jx2 + у2 (рис. 4.2).
Вообще говоря, линейные преобразования векторного
пространства R2 не сохраняют длины векторов. Линейные
преобразования, сохраняющие длину, называются ортогональными
преобразованиями. Это могут быть вращения вокруг начала
координат или отражения относительно прямых, проходящих через
начало координат.
Поскольку евклидово преобразование плоскости сохраняет
длины, то оно каждый треугольник переводит в конгруэнтный
треугольник (рис. 4.3) и, следовательно, сохраняет не только
длины, но и углы. В частности, в евклидовой геометрии
приобретает смысл понятие «перпендикулярности» (это понятие не
определено в аффинной геометрии). Мы будем говорить, что два
вектора ν и w перпендикулярны или ортогональны друг другу,

4.1. Скалярные произведения в евклидовом пространстве 167
Рис. 4.3
если для треугольника, который они определяют, справедлива
теорема Пифагора, т.е. ||v]|2 + ||w]|2 = ||v — w||2 (рис. 4.4).
Рис. 4.4
Рис. 4.5
Теперь, имея понятия длины и угла в евклидовом
пространстве, мы можем определить скалярное произведение двух векторов.
Пусть даны два вектора, ν = I I и ν' = I , I. Их скалярное
произведение, обозначаемое (ν, ν'), определяется равенством
(ν, ν') = 1|ν|| -llv'Hcostf,
где θ — угол между этими векторами.

168
Глава 4. Скалярные произведения
Геометрически это можно истолковать так (рис. 4.5): мы
берем проекцию вектора ν' на прямую, на которой расположен
вектор v. Затем мы умножаем полученную проекцию на длину
вектора v. Берем это произведение со знаком плюс, если направление
спроектированного вектора совпадает с направлением вектора ν,
и со знаком минус, если проекция имеет противоположное
направление. Поскольку скалярное произведение определено в
терминах евклидовой геометрии плоскости, то любое линейное
преобразование, сохраняющее длину, должно сохранять и скалярное
произведение, т. е. линейное преобразование, сохраняющее длину
векторов и угол между ними, сохраняет скалярное
произведение этих векторов. Другими словами, если есть ортогональное
преобразование М, то (Μν,Μν') = (ν, ν') для любой пары
векторов ν' и v. Ниже мы приведем алгебраическое доказательство
этого утверждения. Обратно, поскольку (ν, ν) = ||ν||2, то любое
преобразование М, сохраняющее скалярное произведение любых
векторов ν' и ν, является ортогональным.
Допустим, что мы зафиксировали вектор v. Рассмотрим
(ν, ν') как функцию вектора ν'. Мы утверждаем, что (ν, ν')
является линейной функцией от ν', т.е. (ν, αν' + bw') = α (ν, ν') +
b(v,w') для любых чисел а и Ъ и для любых векторов ν' и w'.
Самый простой способ доказать это состоит в следующем.
Сначала рассмотрим частный случай, когда вектор ν = I J лежит
на оси х. Тогда для вектора ν' = I ,1 скалярное произведение
(ν, ν') = сх'. Очевидно, что это выражение зависит линейно от
ν', что доказывает наше утверждение в частном случае. Теперь
пусть у нас вектор ν произволен. Можно найти
преобразование вращения М, совмещающее вектор ν с осью х. При этом
(ν,ν') = (Μν,Μν') линейно зависит от Μν' и Μν' линейно
зависит от ν', что и требовалось доказать. Сделаем это
доказательство более подробно.
(ν, αν' + bw') (= (Mv,M{av' + bw')) = (Μν,αΜν' + bMw')
= a{Mv, Μν') + b{Mv, Mw') = a(v, v') + b(v, w'),
где (α) следует из ортогональности Μ, (b) — из линейности Μ,

4.1. Скалярные произведения в евклидовом пространстве 169
(с) — доказано в частном случае, что Mv лежит на оси х, (d)
также следует из ортогональности М. Так как скалярное
произведение (ν, ν') симметрично по ν и ν', то (ν, ν') будет линейной
функцией ν при фиксированном ν'. Это позволяет нам получить
формулу для скалярного произведения. Пусть мы имеем два
вектора:
-(:)-(ί)+'(ϊ)-"-(?)-<ί)+^°
Базисные вектора I ) и I ) ортогональны друг другу и имеют
длину, равную единице. Тогда
(Ь) ,//14 /l\\ , ,//1\ /О
ι ίίι\ /Ό\\ tff°\ ί°
(с) / , /
= хх + уу .
Обоснования: (α) следует из линейности по ν, (Ь) следует из
линейности по ν', (с) — использованы соотношения
Таким образом, мы получили удобную формулу для скалярного
произведения двух векторов, лежащих в одной плоскости:
(ν, ν') =χχ' + уу'.
Перечислим важные свойства скалярного произведения в
евклидовом пространстве:

170
Глава 4. Скалярные произведения
1. симметрия: (ν, ν') = (ν', ν);
2. линейность: (ν, αν' + bw') = α(ν, ν') + b(v, w');
3. положительная определенность: (ν, ν) > 0 и (ν, ν) = 0,
только если ν = 0.
Воспользовавшись этими свойствами, можно выразить скалярное
произведение через длины векторов. Рассмотрим тождество:
||ν — w||2 = (ν — w, v — w).
Скалярное произведение линейно по обоим векторам, поэтому
||v — w||2 = (ν, ν) — (v,w) — (w, ν) + (w,w).
Так как (ν,ν) = ||ν||2, (w, w) = ||w||2 и (v,w) = (w, ν), мы
получаем
2(v,w) = ||v||2 + ||w||2 — ||v — w||2.
Следовательно,
(ν, w) = -{||v||2 + ||w||2 - ||v - w||2}.
(4.1)
Эта формула показывает, что евклидово скалярное произведение
определяется евклидовым понятием длины. Если мы напишем
(v, w) = ||v|| · ||w||cos# и посмотрим на рис. 4.6, то увидим, что
формула 4.1 — это просто завуалированная теорема косинусов.
Рис. 4.6

4.2. Процесс Грама-Шмидта
171
4.2. Процесс Грама-Шмидта
Пусть V — абстрактное двумерное векторное пространство.
Допустим, что в нем дано положительно определенное скалярное
произведение (·, ·)γ. Другими словами, допустим, что у нас есть
функция, которая каждой паре векторов νχ, V2 из V
приписывает вещественное число (vi,V2)y, удовлетворяющее условиям
симметричности, билинейности и положительной
определенности. Тогда мы утверждаем, что существует линейный
изоморфизм1 L : V —► R2 такой, что
(vi,v2)v = (LvbLv2).
Другими словами, выбрав правильный базис, можно сделать так,
чтобы скалярное произведение (·, -)у в пространстве V выглядело
так же, как евклидово скалярное произведение (·, ■) в
пространстве R2. Для доказательства этого утверждения выберем в
пространстве V ненулевой вектор w. Так как \\vf\\v = (w,w)y > 0,
длина вектора
w
llwllv
равна единице, т. е.
||ei||2 = (ei,e2)v = 2 (w,w)v = 1.
Ilwllv
Теперь пусть и — вектор в пространстве V, линейно
независимый от βχ. Так как это пространство двумерно, то такой вектор
существует. Пусть
u2 =u- (u,ei)yei.
Вектор и2 перпендикулярен ei, т. е. (u2,ei)v = 0. Действительно,
(u2,ei)v = (u - (u,ei)vei,ei)v
= (u,ei)v - (u,ei)v(ei,ei)v
= (u,ei)v - (u,ei)v = 0,
1 Напоминаем, что в параграфе 1.12 мы определили понятие
изоморфизма: L — линейное, взаимно-однозначное, сюрьективное преобразование, и,
следовательно, имеющее обратное линейное преобразование.

172
Глава 4. Скалярные произведения
так как (ei,ei)y = 1. Кроме того, U2 φ О, так как в противном
случае вектора ei и и были бы линейно зависимы. Определим
вектор
1
в2 = Т. 7Г- U2.
||u2||v
Тогда (β2,βι)ν = (1/||ιΐ2||ν)(ιΐ2,βι)ν = 0 и ||β2|| = 1. Выберем эти
векторы βι, β2 в качестве базиса в пространстве V. Тогда любой
вектор в этом пространстве можно представить в форме
ν = xei + уе2.
Заметим, что χ = (ν,βι), так как (β2,βι) = 0 и (βι,βι) = 1.
Аналогично, у = (ν,β2)·
Пусть
vi =xiei + j/ie2,
V2 = Χ2βΐ + 2/2β2·
Возьмем отображение L : V —► R2 в нашем базисе
LVi = (XA и Lv2=fX2
Тогда
(νι,ν2)ν = (xiei+2/ie2, X2ei + y2e2)v = Х1Х2 + У1У2 = (Lvi,Lv2),
т.к. (ei,e2)v = (e2,ei)v = 0 и (ei,ei)y = (e2,e2)v = 1. Наше
утверждение доказано.
Определим евклидово скалярное произведение в пространстве
R3 формулой
XlX2 + 2/12/2 + Z\ Z2-
х\
Как и в двумерном случае, если ν = I у I, то ||ν||2 = (ν, ν)
является квадратом евклидовой длины вектора v. Приведенные выше

4.2. Процесс Грама-Шмидта
173
соображения показывают, что, воспользовавшись формулой 4.1,
по длине вектора можно восстановить скалярное произведение:
(v,w) = -(||v||2 + ||w||2 - ||v - w||2).
Таким образом, вращения в трехмерном пространстве сохраняют
скалярное произведение. В частности, если нам даны два вектора
ν и w, то можно повернуть плоскость, в которой они
расположены, так, чтобы она совпала с плоскостью ζ = 0. Для векторов в
такой плоскости скалярное произведение сводится к скалярному
произведению в пространстве R2. А для таких векторов мы уже
получили, что
(v,w) = ||v|| · ||w||cos#,
и, следовательно, это справедливо для любой пары векторов
(поскольку обе части равенства инвариантны относительно
вращений).
Векторное пространство V называется трехмерным, если
любые четыре вектора линейно зависимы, но существуют три
линейно независимых. Это значит, что для любых четырех векторов νχ,
v2; V3, V4 можно найти четыре числа 01,02,03,04, не все равные
нулю, при которых выполняется равенство
αϊ vi + α2ν2 + 03V3 + α4ν4 = 0,
и при этом существуют три вектора u, v, w такие, что равенство
au + bv + cw = 0
выполняется только при условии α = b = с = 0.
Допустим, что в пространстве V есть положительно
определенное скалярное произведение (·, -)γ. Повторим построение,
приведенное выше для двумерного случая. Выберем ненулевой
вектор. Обозначим его ei. Выберем другой вектор и, линейно
независимый с вектором ei. Положим
u2 = u- (u,ei)yei,
1
е2 = τι—тг~ и2·
||u2||v

174
Глава 4. Скалярные произведения
Векторы ei и е2 удовлетворяют условиям
||ei||y = ||е2||у = 1, (ei,e2)y=0.
Множество векторов вида xei + уе2 изоморфно R2 и,
следовательно, образует двумерное векторное пространство. Оно не
заполняет все пространство V, так как в этом множестве мы не
можем найти три линейно независимых вектора. Таким образом,
в пространстве V существует вектор w, который нельзя записать
в форме xei + уе2. Значит, вектор
w3 = w - (w,ei)yei - (w,e2)ye2
не равен нулю. Определим вектор
1
е3 = 71 H~w3·
llw3||v
Тогда
||ei||v = ||e2||v = ||е3||у = 1,
(ei,e2)v = (ei,e3)v = (e2,e3)y = 0.
Если ν — произвольный вектор в пространстве V, то мы
утверждаем, что
ν - (v,ei)yei - (v,e2)ye2 - (v,e3)ye3 = 0.
Действительно, воспользовавшись теми же соображениями, что
и раньше, положим
ν4 = ν - (v,ei)ei - (v,e2)e2 - (v,e3)e3.
Тогда
(v4,ei)v = (v4,e2)v = (v4,e3)v = 0.
Если предположить, что v4 φ 0, то можно доказать, что векторы
ei, e2, e3, v4 линейно независимы. В самом деле, пусть выполнено
равенство
αιβι + а2е2 + а3е3 + α4ν4 = 0.
Домножим обе его части на βχ, е2 и е3. В результате получим,
что а\ = 0, а2 = 0, а3 = 0. Следовательно, если ν4 φ 0, то

4.2. Процесс Грама-Шмидта
175
u4 = 0. Но это противоречит исходному предположению, что
пространство V трехмерное.
Итак, любой вектор в пространстве V может быть записан в
форме
ν = xei + уе2 + ze3, где x = (v,ei), y=(v,e2), z = (v,e3).
Точно также, как и в двумерном случае, определим отображение
L : V —► R3 равенством
Mv) = I У I 7 если v = xei + Уе2 + гез-
Это отображение является линейным, взаимнооднозначным
отображением V на пространство R3 и
(u,v)v = (Lu,Lv)R3.
Аналогичное утверждение можно доказать и для случаев
четырех, пяти, ..., η измерений.
В пространстве Шп определим евклидово скалярное
произведение
ίίχΛ /V \\
: , : = χινυι + ■■■ + xnwn.
Векторное пространство V называется n-мерным, если
существует η линейно независимых векторов, при этом любой набор
из η + 1 векторов является линейно зависимым. Общую теорию
n-мерных векторных пространств мы будем изучать в главе 10.
Если V — n-мерное пространство, имеющее положительно
определенное скалярное произведение, то в нем можно найти
ортогональный базис ei,...,еп, т.е. можно найти η векторов ei,...,еп,
обладающих свойствами
Ilei||v = Ile2||v = · · · = ||en||v = 1
и
(е»,е,-)у=0, г Ф 2-

176
Глава 4. Скалярные произведения
Любой вектор ν в пространстве V может быть записан в форме
ν = xxei Η +хпеп, Xi = (v,ej).
Соответственно определяется отображение L : V —> R"
ί χι
L(v)
\3-n
Тогда
(v,w)v = (Lv, Lw).
Итак, если у нас есть η независимых векторов νχ,... νη, то
векторы е^ можно последовательно получить с помощью следующего
алгоритма:
ei =
vi
Tvb
U2 = v2 - (v2,ei)eb
e2 =
u2
Г"2,
"3 = v3 - (v3,ei)ei - (v3,e2)e2,
1
ез
"3
г"з,
и так далее. Этот алгоритм называется ортонормировочной
процедурой Грома-Шмидта.
Покажем начало процедуры Грама—Шмидта в применении к
векторам vi, v2, V3, V4 пространства R4, где
vi
/ 1\
1
1
V-i/
v2 =
/з\
3
5
(Мы сделаем только два первых шага, поэтому векторы V3, V4
нам не потребуются.) Скалярное произведение в пространстве

4.2. Процесс Грама-Шмидта
177
R4 определяется, как обычно. Иными словами, мы предполагаем,
что векторы
/Л /о\ /о\ /о\
W W W V1/
образуют ортонормированный базис.
Первый шаг состоит в преобразовании вектора νχ к
единичному вектору:
(vbVl) = l2 + l2 + l2 + (-l)2=4,
поэтому
>/(νι,νι)=2,
следовательно,
βι = gvi =
/ 1/2 \
1/2
1/2
V-1/2/
Далее, из вектора v2 вычитаем его проекцию на вектор ei:
w2 =
/3\ //3\ / 1/2 \\
3 _ 3 1/2
5 5 ' 1/2
\3) \\3) V-1/2//
/3\
3
5
/ 1/2 \
1/2
1/2
V-1/2/
/ 1/2 \ /Л
1/2 _ 1
1/2 ~ 3
V-1/2/ \5/
(3/2 + 3/2 + 5/2 - 3/2)
И наконец, преобразуем вектор w2 в единичный вектор:
//1\ /1\\
( \ 1 1
(w2,w2) = з ' 3
VW \5//
= I2 + I2 + З2 + 52 = 36,

178
Глава 4. Скалярные произведения
поэтому
в2 = τ w2 = -
о о
В качестве проверки заметим, что
/Л
1
3
W
// Л
1
1
1
3
= 0.
VV-1/ W/
Заметим, что любой вектор ν в пространстве R4 можно
записать как сумму вектора πν, который является линейной
комбинацией векторов ei, е2 (и, следовательно, векторов νχ и V2), и
вектора, перпендикулярного ei и е2. Например, возьмем вектор
/ 4\
0
-1
V 7/
Определим вектор πν следующим образом:
πν = (v,ei)ei + (v,e2)e2,
ν =
// 4\
πν =
/ 1\\
0 1
-1 ' 1
νν υ \-ι//
/ Λ
= ι(-4)
1
1
V-1/
+ 3636
/ Λ
1
1
/Λ
1
1
+ 36
3
W
-1
-1
V ι/
+
// 4\ /1\\ /1\
0 1 1
— 1 ' 3 3
VV υ \5// W
/-1\ /1\ /0\
1 = 0
3 ~ 2
W V6/
Можно проверить, что вектор
/ 4\
0
ν — πν =
V 7/
/0\
о
2
V6/
/ 4\
0
-3
V ι/

4.2. Процесс Грама-Шмидта
179
перпендикулярен векторам βχ и β2· (Это можно сделать прямой
проверкой ортогональности этого вектора исходным базисным
векторам νχ и V2, либо ортонормированной системе векторов ei
и β2·) Мы будем говорить, что преобразование π, переводящее
вектор ν в πν, есть ортогональная проекция на подпространство
W, натянутое на векторы ν χ и V2.
В качестве второго примера применения процедуры Грама-
Шмидта рассмотрим четырехмерное пространство полиномов
степени < 3, где скалярное произведение определяется
формулой
(f,E) = J f(t)g(t)dt.
(Проверьте, что эта формула действительно определяет
скалярное произведение!) Начнем со степенного базиса
vi = 1, ν2=ί, ν3 = ί2, ν4=ί3.
(Если бы начали с других базисных элементов, либо с теми же
элементами, но в другом порядке, то могли бы получить другой
ортонормированный базис.) Сначала вычислим
(vi,vi)= J at = 2
и преобразуем вектор νχ к единичному вектору:
ei = vi-y(vi,vi) = 1/\/2.
Затем вычислим
(ei,v2)= I (t/V2)dt = 0,
откуда следует, что вектор V2 уже ортогонален вектору ei.
Поскольку
(v2,v2) = J i2 <ft = 2/3,
то получаем β2 = ί/^/(2/3) = -^(3/2)ί.

180
Глава 4. Скалярные произведения
Теперь можно вычислить вектор W3:
w3 = v3-ei(ei,v3) -e2(e2,v3)
1 Ζ*1 3 Ζ"1
= t2 - - / t2dt- -t t3dt
2 У-1 2 J_i
Вычисляем скалярное произведение
(w3>w3) = / (*2"§) di =
45
и получаем третий нормированный базисный вектор
9 1
t2 - -
3_./45/+2 l\_./5,o+2
V45
Наконец, вычисляем вектор w4:
w4 = v4-ei(ei,v4) -e2(e2,v4) -e3(e3,v4)
= tz-\ Ρ tzdt- ft I1 t4dt - |(3i2 - 1) f1 (3i5 -t3)dt
2 У-i 2 y_! 8 J_i
= t2_0-|t.?-0 = t3-|t.
Разделив его на \/(w4, w4), получаем четвертый нормированный
вектор
β4 = -^== = ν^(5ί3-3ί).
V(w4,w4) V 8
Очевидно, что действуя таким образом, мы можем
построить последовательность ортогональных полиномов более
высоких степеней. Эти полиномы, известные как полиномы Лежанд-
ра, появляются при решении задач электростатики в
сферических координатах. На самом деле, обычно при решении
физических задач векторные пространства функций, получающихся

4.3. Квадратичные формы и симметричные матрицы 181
при решении дифференциальных уравнений, имеют
ортогональный базис, возникающий естественным образом из физических
соображений. Поэтому на практике не так уж часто приходится
прибегать к громоздкой процедуре Грама-Шмидта.
4.3. Квадратичные формы и симметричные
матрицы
В параграфах 4.1 и 4.2 мы изучали евклидовы скалярные
произведения, обладающие тремя свойствами: они билинейны,
симметричны и положительно определены. Сейчас мы займемся
изучением «скалярных проиизведений» более общего вида, когда
положительная определенность не обязательна. Эти скалярные
произведения играют центральную роль в теории относительности.
Возвращаемся в пространство R2. Допустим, что в этом
пространстве нам дано скалярное произведение (·,·), которое не
обязательно будет положительно определенным. При этом мы
полагаем, что оно
билинейно: (v, au + bw) = α(ν, u) + b{v, w)
и симметрично: (u, ν) = (v,u)
для всех векторов u, v, w и всех вещественных чисел α и Ь.
Интересно сравнить скалярное произведение (·, ·) с евклидовым
скалярным произведением (·,·)· Начнем с элементарной леммы.
Пусть / : Ш2 —► R есть линейное отображение. Тогда
существует единственный вектор w, для которого
/(v) = (v, w) для всех ν из R2.
Действительно, I определяется матрицей 1 χ 2: (а Ь), т.е.
/I ) = ах + by для любого ν = ( ) € R2.
\yj \yJ
Выберем вектор
«О-

182
Глава 4. Скалярные произведения
Тогда
(v,w) = ((i)'(b))=ax + by'
что мы и хотели доказать. Очевидно, что w — единственный
вектор в пространстве R2, обладающий таким свойством. Теперь
рассмотрим (u, v) как функцию ν при фиксированном векторе
и. Это скалярное произведение линейно по ν, следовательно,
существует такой вектор w, для которого
(и, ν) = (ν, w) для всех ν € V.
Вектор w зависит от и, поэтому в этом уравнении следует писать
w(u). Итак, w(u) — это такой вектор, для которого евклидово
скалярное произведение с любым вектором ν равно (u, v). Пусть
Ui и U2 — два вектора, а им соответствуют w(ui) и w(u2)- Тогда
(aui + bu2, ν) = (ν,αιίι + bu2)
= a(v,ui) + b(v,u2)
(c)
= a(ubv) + b(u2,v)
= a(v,w(ui)) + b(v,w(u2))
= (v,aw(ui) + bw(u2)),
где (a) — следствие симметрии, (Ь) — следствие билинейности,
(с) — следствие симметрии. Таким образом,
w(aui + bu2) = aw(ui) + bw(u2).
Другими словами, w линейно зависит от и. Но тогда можно
написать w(u) = Ли, где А — линейное преобразование. Вводя
прежние обозначения w(u) = Ли, получаем:
(и, ν) = (ν, Ли)
для всех и и ν в пространстве R2. До этого момента мы
использовали только билинейность (и, ν), т. е. линейность по и при
фиксированном ν и линейность по ν при фиксированном и. (Здесь, по

4.3. Квадратичные формы и симметричные матрицы 183
существу, использована также симметрия (·,·).) Симметрия (·, ·)
позволяет записать
(и, ν) = (ν, и),
следовательно,
(ν, Ли) = (u,;4v).
Однако, (и, ν) = (ν, и), поэтому
(ν, Ли) = (Αν, и)
для всех векторов и и ν в пространстве V. Посмотрим, что из
этого можно получить для матрицы Л.
Для любой матрицы В выражение (i?v, u) линейно в
отдельности по и и по v. Воспользовавшись предыдущими аргументами,
можно показать, что существует единственное линейное
преобразование (обозначим его Вт), которое удовлетворяет условию
(Sv,u) = (v,STu)
для всех векторов и и ν в пространстве V. Это преобразование
называется транспонированным по отношению к В. Вычислим
ВТ, приняв обозначения
-(;)·-(?)·-С О-
Тогда
(Влг, и) = (еж + fy)x' + (дх + hy)y'
— ехх' + fyx' + дху' + hyy'
= х{ех' + ду') + y{fx' + hy'),
следовательно,
ят /V\ _ fex' + gy'\
\y')-\fx' + hy')>
или
Другими словами, транспонированная матрица Вт получается
отражением матрицы В относительно главной диагонали.

184
Глава 4. Скалярные произведения
Отсюда для матрицы А, определяющей наше «скалярное
произведение», следует, что
А = АТ,
т. е. матрица А симметрична. Значит, А может быть записана в
виде
Если мы обозначим
Q(v) = <v,v>,
тогда, как и в параграфе 4.1, можем получить тождество
<u,v) = ^(Q(u) + Q(v)-Q(u-v)),
и если ν = ( I , то
Q(v) = (Αν,ν) = αχ2 + 2bxy + су2.
Такая функция Q называется квадратичной формой. Таким
образом, предыдущие формулы показывают, что квадратичная
форма Q определяет (■,■), и обратно, каждое скалярное
произведение определяет квадратичную форму.
Коэффициенты а, 26, с в квадратичном полиноме Q(v)
определяют матрицу А. Другими словами, Q определяет А и,
следовательно, (■,■).
Характеристический полином для матрицы А имеет вид
х2 — (а + с)х + ас — Ь2,
при этом выполнено условие
(а + с)2 - 4(ас - Ь2) = (а - с)2 + 4Ь2 > 0.
Выражение (а — с)2 + 4Ь2 называется дискриминантом
квадратичной формы Q. Дискриминант равен нулю в том и только том
случае, если α = с и Ь = 0. Тогда

4.3. Квадратичные формы и симметричные матрицы 185
и
(u, v) = a(u,v).
В этом случае (·,-) пропорционально (■,■)■
Предположим, что А имеет различные собственные значения
λ ι φ λ2, соответствующие собственным векторам νι и V2-
Докажем, что вектор νι перпендикулярен вектору V2, т. е. (νχ, V2) = 0.
Это очень просто: (Avi,V2) = (νι,Αν2), т.к. А
симметрична; (AiVi,V2) = (vi,A2V2), т.к. νι, V2 — собственные векторы;
λι(νι,ν2) = λ2(νι,ν2), т.к. скалярное произведение линейно;
(vi, V2) = 0, потому что λχ φ λ2·
Докажем обратное утверждение: пусть собственный вектор
νι матрицы А соответствует собственному значению \\. Пусть
вектор V2 не равен нулю и перпендикулярен νι, т. е. (νχ, V2) = 0.
Тогда
(νι,Αν2) = (Ανι,ν2) = λι(νι,ν2) = 0,
следовательно, i4v2 перпендикулярен νι. Но существует только
одна прямая, перпендикулярная вектору νχ, и вектор V2 φ 0
лежит на ней. Это значит, что i4v2 пропорционален V2, т.е. i4v2 =
A2V2 для некоторого собственного значения λ2·
Итак, мы доказали, что любая симметричная матрица А
имеет два ортогональных собственных вектора νχ и V2. Умножив
векторы νι и V2 на соответствующие скаляры, можно сделать их
(Хл ЗСо \ ( Хл
I, где νι = I
ίχΛ -
и V2 = I , является матрицей вращения.
\У2)
Таким образом, можно записать А = R I .1 R~l, где
R — матрица вращения. Для ортогональной матрицы Μ
выполняются соотношения (Μν, Μν) = (ν, ΜτΜν) = (ν, ν) для всех
векторов v. Отсюда следует, что МТ = М~1, и мы можем
написать равносильное равенство:
Предположим, что мы выбрали собственные векторы так, что
λι > λ2· Тогда собственный вектор νχ, уже преобразованный к

186
Глава 4. Скалярные произведения
единичной длине, отличается от всех других векторов единичной
длины ν тем, что Q(v) принимает максимальное значение.
Вектору V2, тоже имеющему единичную длину, соответствует
минимальное значение Q(v), т. е.
Q(vi) > Q(v) > Q(v2)
для любого вектора ν единичной длины ((ν, ν) = 1). Чтобы
доказать это утверждение, запишем ν = vi cos# + v2 sin# (рис. 4.7).
Векторы vi и v2 ортогональны и имеют единичную длину,
следовательно,
(v, v) = (v!,vi)cos2^ + (v2,v2)sin20 = 1.
Рис. 4.7
Тогда
Q(v) = (Av,v)
= (Ανι cos θ + Αν2 sin θ, νχ cos θ + v2 sin θ)
= (λι νχ cos θ + λ2ν2 sin θ, νχ cos θ + v2 sin Θ)
= Ai(vi,vi)cos2^ + A2(v2,v2)sin20 (т.к. (vbv2) = 0)
= λι cos2 θ + λ2 sin2 θ
= λι-(λι -A2)sin20.
Очевидно, что Q(v) имеет максимум при sin2 θ = 0, т. е когда
ν = ±νι, и принимает минимальное значение при sin2 θ = 1, т. е.
когда ν = ±ν2.

4.3. Квадратичные формы и симметричные матрицы 187
Теперь понятно, как нарисовать линию Q(v) = (.Αν, ν) =
const. С помощью матрицы вращения Д приведем А к
диагональному виду:
<?W = I я ГЛ' °)я-Ч,у
Тогда
П(,А - Ι Ρ I
χ χΟ Ч
Матрица Д ортогональна, поэтому RT = Д-1, и мы получаем
β(ν)=((θ λ2'Λ V'R
χ \ ~-ΐ Ι Χ \ _ ρ_ι
Если записать Ι , Ι = Д ( Ι = Д ν, το
Vl/7 W
. ,λ2 г/7 Лу
Если оба собственные значения λ ι и λ2 положительны, то
линия C?(v) = к — это эллипс при /с > 0, начало координат при
к = 0 и пустое множество при к < 0. Если λχ и λ2
отрицательны, то линия будет эллипсом при к < 0. Если λι и λ2 имеют
противоположные знаки, то линия Q(v) = к будет гиперболой,
вырождающейся в две прямых при к = 0. Вершины эллипса или
гиперболы, в которых расстояние от точки на кривой до начала
координат имеет локальный экстремум, лежат на прямых,
задаваемых собственными векторами матрицы А.
Рассмотрим пример, когда А = I I. Тогда
Q(v) = 9х2 + Аху + 6у2.
Собственные значения матрицы А таковы: λχ = 10, λ2 = 5.
Соответствующие им собственные векторы: ( ) и ( _ I. Мы можем
. _ /10 0\ _ ι
написать А = К I I Д , где матрица вращения Д равна
*~7l(i 2

188
Глава 4. Скалярные произведения
Введем новые координаты
= Я~
1 / X
J_ / 2 1
V5V-1 2
т. е.
х' = -^(2х + у),
В новых координатах
Q(v) = Юх'2 + Ъу'2.
График множества Q(y) = 1, т. е.
Юх'2 + Ъу'2 = 1,
является эллипсом, у которого малая ось — y^l/ΙΟ, а большая
равна yl/5. Оси расположены вдоль собственных векторов
матрицы А : I ) и ί _ ), см. рис. 4.8.
Рис. 4.8
Рис. 4.9
Предположим, что помимо вращения, изменяющего
координаты, возможно неортогональное преобразование вида: х" = ах'
и у" = βρ'. Тогда, введя новые координаты х" и у", получим
π, ν. Αχ „2 , λ2 „2

4.4. Нормальные колебания
189
Если λι φ О, то можно выбрать α2 = |λι|. Тогда \\/а2 = ±1.
Аналогичную процедуру проделаем и для λ2· Мы приходим к
следующему результату.
Пусть Q — любая квадратичная форма в пространстве R2.
Мы можем найти такие координаты х" и у", для которых Q
определяется одной из следующих формул:
ιιΐ , ιιΐ
х" + у" ,
ill
Χ ,
<?(V) = Κ 0' ,,2
-X
J&
-χ
Il2
..«2
Если обе координаты входят в формулу со знаком плюс, то Q(v)
имеет минимум при ν = 0 (рис. 4.9). Если они входят со знаком
минус, то Q(v) имеет в этой точке максимум. Если одна
координата входит со знаком плюс, а другая со знаком минус, то Q(v)
не имеет ни максимума, ни минимума, а седловую точку в начале
координат, как это показано на рис. 4.10.
Рис. 4.10
4.4. Нормальные колебания
Теория связанных осцилляторов является одним из самых
важных приложений результатов предыдущего параграфа. Чтобы

190
Глава 4. Скалярные произведения
это продемонстрировать, рассмотрим механическую систему,
состоящую из двух незатухающих осцилляторов (рис. 4.11),
которые мы соединим пружиной с константой упругости к (рис. 4.12).
Уравнения движения, определяемые законами Ньютона, имеют
вид
т\Х\ = —к\х\ — к{х\ — Х2),
т2Х2 = ~к2Х2 - к(х2 —Xl),
или
χι \ _ н Ι χι
Х2) \Х2
где Τ и Η — симметричные матрицы:
Τ = ( TOl Μ н ^ fki+k -к
0 То2/ ' V — к к2 + к
pro-4· «^шн
Κι
Рис. 4.11. Несвязанные осцилляторы
fci к &2
■>· XI ► Xl
Рис. 4.12. Связанные осцилляторы
Наша задача — попытаться одновременно диагонализировать
матрицы Τ и Н, чтобы «развязать» уравнения.
Давайте обсудим общий случай. Мы рассматриваем две
симметричные матрицы Τ и Н, причем Τ положительно определена.
Сначала покажем, что можно найти положительно определенную
матрицу В, удовлетворяющую уравнению
Т = В2.

4.4. Нормальные колебания
191
Действительно, если Τ диагональна, как в нашем примере, то
можно взять
"(? -■<·)
С другой стороны, можно найти такую матрицу вращения R$,
что
Τ = ReARe , где Δ — диагональная матрица.
Пусть Δ = С2, где С положительно определена. Тогда матрица
В = RgCRj симметрична, положительно определена и
удовлетворяет условию В2 = Т.
Теперь определим
w = Bv,
откуда
ν = β_1\ν.
Тогда ν = i?_1w, и наше уравнение Tv = — Ην принимает вид
ТВ'1™ = -ΗΒ~ι\ν,
или
Bw = -HB^w,
так как Τ = В2. Теперь получаем
w = -Aw, где А = В'1 Η В'1.
Заметим, что А — тоже симметричная матрица. Таким образом,
мы свели задачу к случаю, когда Г = I. (Проницательный
читатель, должно быть, заметил, что с геометрической точки зрения
мы просто перешли в систему координат, в которой квадратичная
функция, связанная с Т, приведена к нормальному виду χ + у .)
Чтобы решить уравнение w = — Aw, найдем собственные
значения и собственные векторы матрицы А. Предположим, что
vi — собственный вектор матрицы А с положительным
собственным значением ω2. Тогда очевидно, что функция
w(i) = pcos(u>ii + α)νι

192
Глава 4. Скалярные произведения
является решением при произвольной амплитуде ρ и фазе а.
Аналогично, второй собственный вектор и собственное значение
дадут pcos(u)2t + а). Эти решения называются нормальными
колебаниями осциллирующей системы.
Запишем матрицу А в виде
А=RDR~\
где D — диагональная матрица. Тогда, определив вектор и
равенством
w = Ди,
получаем уравнение
w = Ru = -RDR^Ru,
или
VL = -£>U.
Так как матрица D диагональна, для каждой компоненты
вектора и получается независимое дифференциальное уравнение.
Предположим, что оба собственных значения матрицы А
положительны. Пусть они равны ω\ νίω\. Тогда общее решение
уравнения
Vi= -£>U
имеет вид
(щ\ = /ViCos(u>it + αι)\
\U2 ) \f>2COs(tjJ2t + а.2)) '
Если собственные векторы матрицы А равны
νι = *(θ)' V2 = 4O'
то общее решение уравнения w = — Aw можно записать в форме
w(i) = pi cos(u>it + αι)νχ + ρ2 cos(u2t + α2)ν2.
Таким образом, общее решение является «суперпозицией»
нормальных колебаний.

4.4. Нормальные колебания
193
В качестве примера рассмотрим две одинаковые связанные
между собой пружины, т. е. предположим, что т\ = rri2 = га,
ki = &2- В отсутствие связи каждая пружина описывается
уравнением
χ = — ujqX, ω§1 = k\/m\ = к2/гп2-
При наличии связи получаем систему уравнений
Х\ = —(uJq + s)xi + SX2, Х2 = SXi — (Jq + s)x2, S = к/т
ИЛИ
ν = -Αλτ, Α = ° 2 , .
Из соображений симметрии получаем, что собственные векторы
матрицы А равны
для собственного значения ω0
и
для собственного значения ω0 + 2s.
Эти векторы задают два вида нормальных колебаний нашей
системы. В первом случае шарики движутся в одну сторону, а во
втором — в противоположных направлениях (рис. 4.13).
\\п
Рис. 4.13
(u;jj + 2s)1'2 ~ ωο + s/ωο, если s/ojq мало.
Общее решение нашей системы дифференциальных
уравнений имеет вид
xi = Pi cos(u>oi + αχ) + р2 cos(u/i + α2),
Χ2 = ρ\ cos(u>oi + αχ) - β2 cos(u/i + α.2).
(0
-0

194
Глава 4. Скалярные произведения
Изучим частное решение нашей системы, когда мы натянули
одну пружину и отпустили ее в t = 0. Иными словами, зададим
начальные условия
zi(0) = C, xi(0) = 0,
х2(0) = 0, х2(0) = 0.
Из общего решения для данных начальных условий получаем
Pi = Р2 ~ С/2 и αχ = Q2 = 0. Таким образом, частное решение
имеет вид
χι = -C(cosu>oi + cosu/t),
Δ
Х2 = -C(cosujQt — cos α; t).
Δ
Вспомним, что cos α = \{ега + е~га). Отсюда можно получить
известные формулы:
^ до (<*-β\ ία + β
cos α + cos ρ = 2 cos I —-— I cos
cos a — cos ρ = —2 sin I sin
Подставив α = (jjQt и β = ω'ί, получаем наше частное решение в
форме
χι = Ccos(u/ — u>o)i coso^oi,
Х2 = — Csin(u/ — u)o)t sinu>oi.
В случае слабой связи, т. е. при малой константе s, величина
ω' — ωο мала. На рис. 4.14 изображены графики движения обеих
пружин как функции от времени. Колебания каждой пружины
(с собственной частотой о>о) модулируются. Биения определяются
модулирующими множителями cos(u/ — u>o)t, sin(u/ — u>o)t.
Энергия переходит от одной пружины к другой. Когда одна пружина
колеблется с максимальной амплитудой, вторая отдыхает, и
наоборот. Это явление называется резонансом.
Если пружины не одинаковы, но отличие невелико
(«неточная настройка»), то поведение системы будет почти таким же.

4.5. Нормальные моды в многомерном пространстве 195
Рис. 4.14
По-прежнему колебания каждой пружины модулируются.
Вторая пружина отдыхает через определенные промежутки времени,
а первая осциллирует даже в то время, когда вторая
осциллирует с максимальной амплитудой. Неточность «настройки»
приводит к неполной передаче энергии от первой пружины ко второй.
Мы не будем говорить об этом более подробно. Детали
исследования здесь просты, хотя и несколько утомительны. Вычисление
собственных векторов и собственных значений матрицы А
предоставим читателю в качестве упражнения.
4.5. Нормальные моды
в многомерном пространстве
Пусть V — n-мерное векторное пространство с положительно
определенным скалярным произведением. Кроме того, имеется
другое, не обязательно положительно определенное скалярное
произведение (·, ■). Аргументы, изложенные в параграфе 4.3,
показывают, что существует линейное преобразование А : V —► V,
при котором
(и, ν) = (Ли, ν) для всех и, ν в пространстве V,

196
Глава 4. Скалярные произведения
где А симметрично, т. е.
(Au,v) = (u,Av).
Действительно, из параграфа 4.2 мы знаем, как найти
изоморфизм V пространства R", чтобы (■, ■) преобразовалось в
евклидово скалярное произведение. Тогда без изменения можно
воспользоваться аргументами параграфа 4.3 и показать, что А —
симметричная матрица.
С помощью аргументов параграфа 4.3 можно показать, что
матрица А имеет η взаимно перпендикулярных собственных
векторов. Действительно, рассмотрим квадратичную форму
<3(ν) = (ν,ν) = (Λν,ν)
на единичной сфере
{ν|ΙΜ| = ι}.
Эта функция непрерывна и ограничена. Если для всех
матричных элементов Aj выполняется неравенство |Aj| < М, где Μ —
некоторое число, то для
\Хп)
мы имеем ||ν||2 = Σχ\ = 1, следовательно, |xj| < 1 при всех
значениях г и
(Av, v) = ^AijXiXj.
Откуда следует
|(Av,v)|<^|Aj|<nM.
Пусть ν определяет точку на поверхности единичной сферы,
где Q(v) принимает максимальное значение. (В этом месте мы
реально используем свойства системы вещественных чисел,
которые гарантируют, что на самом деле существует точка на
сфере, где Q принимает максимальное значение.) Утверждается, что

4.5. Нормальные моды в многомерном пространстве 197
ν является собственным вектором матрицы А. Действительно,
определим вектор w формулой
w = Αν — (Αν,ν)ν.
Покажем, что если в точке ν квадратичная форма Q принимает
максимальное значение, то w = О. Так как (ν, ν) = 1, то вектор
w перпендикулярен вектору ν, τ. е.
(w,v) = 0,
и, следовательно,
(i4v,w) = ||w||2.
Тогда для любого вещественного числа s
||v + sw||2 = (ν + sw, v + sw) = ||ν||2 + s2||w||2 = 1 + s2||w||2
и
(i(v + sw),v + sw) = (Αν,ν) + s(Aw,v) + s(Av,w) + s2(Aw,w).
Однако, (Av,w) = (w, Αν), следовательно,
(A(v + sw), ν + sw) = (Av, v) + 2s(Av, w) + s2(Aw, w)
= (Av, v) + 2s||w||2 + s2(iw,w).
Домножим вектор ν + sw на число, чтобы получить вектор
единичной длины:
1 ι
U = -(V + SW).
V + SW
Возьмем функцию
d f I
Us) = (Ли,и) = iT7r(i4(v + sw),v + sw)
J v ' v ' ||v + sw||2V v '
((Αν,ν) + 2s||w||2 + s2(Aw, w)).
1 + s2||w
'9то выражение представляет дифференцируемую функцию
переменной s. По нашему предположению она имеет максимум в

198
Глава 4. Скалярные произведения
точке s = О, поэтому первая производная /'(0) при s = 0 должна
обращаться в нуль: /'(0) = 2||w||2. Отсюда следует, что w = 0.
Таким образом, мы доказали, что
Αν = (Αν,ν)ν.
Другими словами, ν является собственным вектором А для
собственного значения (Αν, ν). Обозначим этот вектор νχ, а
соответствующее ему собственное значение (Αν ι, νι) = λι.
Теперь рассмотрим пространство всех векторов ζ в V,
которые перпендикулярны вектору ν ι (рис. 4.15), т. е. для всех
векторов ζ должно выполняться условие
(ζ,νι) = 0.
Для таких ζ мы имеем
(Αζ,νι) = (ζ, Avi) = λι(ζ,νι) = 0, λι = (Λνι,νι).
Рассмотрим множество всех ζ единичной длины, т. е. таких ζ, для
которых справедливы равенства
||ζ|| = 1, (ζ,νι) = 0.
Рис. 4.15
Пусть V2 определяет точку, где Q принимает максимальное
значение. Запишем
Av2 = (Αν2, ν2)ν2 + w2.

4.5. Нормальные моды в многомерном пространстве 199
Из того, что (ν2,νι) = 0 и (Αν2,νι) = 0, получаем (w2,vi) = 0.
Как и раньше, мы делаем вывод, что (w2,V2) = 0. Тогда
(A(v2 + sw2), (v2 + sw2))
ΐ({Αν2, v2) + 2s||w2||2 + s2(Aw2,w2))
|v2 + sw2||2
1
l + s2 + ||w2|
имеет максимум при s = 0 и, следовательно, W2 = 0, а вектор V2
является собственным вектором матрицы А.
Мы можем продолжить наши рассуждения: рассмотрим
векторы ζ, удовлетворяющие условию (ζ, νχ) = (ζ, V2) = 0 и ||ζ|| = 1,
и так далее. Каждый раз мы будем находить новый
собственный вектор матрицы А, перпендикулярный ко всем предыдущим.
Когда этот процесс закончится? Когда мы выберем все ненулевые
векторы, перпендикулярные νι,...,ν^. Это произойдет только
при условии к = п. Действительно, к не может быть больше п, так
как тогда векторы νχ,..., νη+ι будут взаимно перпендикулярны
и, следовательно, линейно независимы. Но это противоречит
исходному предположению, что в пространстве V нет η + 1 линейно
независимых векторов (мы предположили, что пространство V
n-мерно). С другой стороны, если к < п, то уравнения
(vi,w) = 0,
(vfc,w) = 0
в пространстве R" образуют систему к однородных линейных
уравнений с η неизвестными. Такие системы всегда имеют
решение. В общем случае мы докажем это в главе 10. Здесь мы
докажем существование вектора w φ 0. Если η-компонентный
вектор ν*, не равен нулю, т. е.
то последнее уравнение системы имеет вид
XlWi -I + XnWn = 0.

200
Глава 4. Скалярные произведения
Из этого уравнения вектор wn выразим через wi,..., wn_i:
Wn = (xiWi H h Xn-lWn_i).
Xn
Подстановка этого вектора в предыдущее уравнение дает
систему к — 1 уравнений с η — 1 неизвестными. Процедура может быть
продолжена. Если n-я компонента любого из векторов νι,..., vjt
не равна нулю, мы можем проделать то же самое — взять вектор
Vj с ненулевой n-й компонентой и получить wn. Если n-я
компонента всех векторов νχ,..., νη равна нулю, то решением является
вектор
w =
(все первые η — 1 компонент обращаются в 0).
Таким образом, продолжая этот алгоритм, мы получим η
попарно ортогональных собственных векторов.
Нормальные колебания как волны
Поработаем с интересным примером в пространстве η
измерений. Представим себе последовательность равных точечных масс,
где каждая соединена с ближайшими соседками пружинками,
причем все пружинки одинаковые. Тогда сила, действующая на
г-ю точечную массу, равна
-к(Х{ - Xi+i) + k(Xi - Xi-l).
Запишем уравнения Ньютона
mxi = —k(2xi - Xj-i - Xi+i).
Предположим, что первая и последняя точки также соединены
пружинкой. Система изображена на рис. 4.16.
Введем частоту ω2 = к/т и перепишем уравнения движения
в форме
χ = —ω2 Ах,

4.5. Нормальные моды в многомерном пространстве 201
где
А =
( 2
-1
0
V-1
Рис. 4.16
-1 0
2 -1
-1 2
0 -1\
-1
2/
Наша задача — найти собственные значения и собственные
векторы матрицы А. Прежде чем рассматривать общий случай, начнем
с рассмотрения случая η = 3. Из равенства
[Л
следует, что I 1 I — собственный вектор этой матрицы, соответ-
W
ствующий собственному значению 0. Мы знаем, что другие соб-
[Л
ственные векторы должны быть ортогональны I 1 I. Попробуем
W

202
Глава 4. Скалярные произведения
вектор
-1 I. Тогда
0,
яв-
/ 1\ / 0'
Значит, вектор I —1 I и, аналогично, третий вектор 1
V о/ \-it
ляются собственными векторами с собственным значенем 3.
Таким образом, собственные значения равны 0 и 3, причем значение
3 реализуется дважды.
Перейдем к случаю η = 4:
/ 2 -1
1 2
0 -1
0
Тогда
V-1
1
1
как и раньше. Кроме того,
1\
-1
1
1/
о
-1
2
-1
/о\
о
о
W
/ Λ
-1
1
W/
л
о
-1
2/
Остающиеся собственные векторы должны быть ортогональны
этим двум. Попробуем вектор

4.5. Нормальные моды в многомерном пространстве 203
Получаем
/ 2
-1
0
-1
2
-1
0
0
-1
2
-1
■Л / Л
о о
-1 -1
2/ V 0/
/ Л
о
Находим последний собственный вектор
/ 2
-1
0
V-i
-1
2
-1
0
О
-1
2
-1
1\
О
-1
/ о\
1
о
= 2
2/ V-1/
/0
0
0
1
0
0
0
1
0 ··
0 ·
■ °^
• 1
Итак, мы получили четыре собственных значения: 0, 4 и два раза
появилось собственное значение 2.
Чтобы рассмотреть n-мерный случай, заметим, что наша
система инвариантна относительно поворота, когда первая точка
становится на место n-й, вторая на место первой, и т.д. Такой
поворот осуществляется матрицей
S =
Легко проверить, что SA = AS. Найдем собственные векторы
матрицы 5. Если Sw = Aw, то SAw = ASw = A(Aw) = XAw.
Поэтому, если w является собственным вектором матрицы 5 для
собственного значения λ, то Aw — тоже собственный вектор с
тем же собственным значением. Ниже мы получим η различных
собственных значений матрицы S. Тогда если Sw = Aw, то
вектор Aw должен быть пропорционален w, т. е. быть собственным
вектором матрицы А.
Окажется, что «собственные значения» матрицы S и
координаты «собственных векторов» будут комплексными числами.
Вещественные и мнимые части этих векторов будут собственными
векторами матрицы А. Приведем это доказательство.

204
Глава 4. Скалярные произведения
Пусть τ = е27Г1/п, откуда тп = 1. Тогда
/1 \
τ
τ2
=
(τ \
τ2
ν)
=
τ2
= τ
/1 \
τ
τ2
/ ! ^
τ2
τ4
τ6
^T2(n-l)y
= τ2
( Χ \
τ2
τ4
τ6
^т2("-1)у
и так далее. Все собственные значения 1, τ, τ2, ..., τ
.71-1

различны. Таким образом, каждый собственный вектор матрицы 5
должен быть собственным вектором матрицы А. Обозначим эти
«собственные векторы» βχ,... ,еп. Мы знаем, что
Аек = Хкек
для некоторых λ^, которые нам предстоит вычислить. Вторая
координата вектора Аек равна
(\\
(-12 -10 ... 0)
Лк
\ '■ I
= -1 + 2тк-т2к = {-т'к + 2 - тк)тк = 2(1 - cos{2nk/п))тк.
Отсюда следует, что к-е собственное значение равно
Хк = 2(1 - cos(27rfc/n)).

4.6. Специальная теория относительности 205
Мы получаем одинаковые собственные значения для к и η — к.
Тогда, складывая и вычитая собственные векторы для к и η — к,
мы можем получить вещественные собственные векторы. Итак,
векторы
/ 1 \
cos(2nk/n)
cos(47rfc/n)
cos(6nk/n)
\
ί 0 \
sin(2nk/n)
sin(4nk/n)
sm(6nk/ri)
J
\
)
являются собственными векторами для собственного значения
2(l + cos(2nk/n)).
Если η = 2т — четное число, то второй столбец равен нулю при
/с = га. Во всех остальных случаях собственные векторы не равны
нулю. Таким образом, каждую нормальную моду системы можно
рассматривать как волну сжатия (синус или косинус).
4.6. Специальная теория относительности
В этом параграфе мы подробно рассмотрим геометрию
двумерного векторного пространства с квадратичной формой Q(y) =
(ν, ν), которая может принимать как положительные, так и
отрицательные значения. Как мы уже знаем, это пространство можно
идентифицировать с R2, а квадратичную форму Q определить
соотношением
χ
Q
= tz
X
Мы увидим, что геометрия этого пространства (рис. 4.17)
обеспечивает хорошую модель для понимания специальной
теории относительности. Слово модель мы применяем в следующем
смысле. Наше обычное пространство трехмерно. Поэтому,
если добавить время в качестве дополнительного измерения, мы
получим четырехмерное пространство-время. В нашей
модели мы будем считать пространство одномерным, поэтому наше
пространство-время вместо четырехмерного будет двумерным.

206
Глава 4. Скалярные произведения
<Э = 0
Αζ- ► t
/ \ Q = 0
Рис. 4.17
В этом случае мы сможем нарисовать все геометрические
конструкции. На самом деле, большая часть того, что будет сказано,
работает в обычном четырехмерном мире, с некоторой
модификацией нашей двумерной модели.
Первый постулат специальной теории относительности
подтверждает закон Ньютона: частицы, на которые не действуют
никакие силы, движутся вдоль прямых линий. Таким образом,
геометрия нашего пространства-времени среди всех возможных
кривых выделяет прямые линии. Наше пространство-время
является аффинной плоскостью с некоторыми дополнительными
геометрическими структурами.
Второй постулат — конечная абсолютная константа. Таким
образом, в каждой точке пространства-времени существуют две
определенные линии, изображающие распространение света
влево или вправо. Пространственная и временная инвариантность
скорости света означает, что при смещении точки Ρ в точку Q
два световых луча, проходящие через точку Р, преобразуются в
два световых луча, проходящих через точку Q (рис. 4.18).
Мы будем исследовать такие аффинные преобразования,
которые световые лучи переводят в световые лучи. Трансляции
попадают в это категорию. Поэтому задача сводится к изучению
линейных преобразований, которые сохраняют световые лучи,
проходящие через начало координат. Итак, у нас есть две прямые
χ = ±ct. Требуется найти такие линейные преобразования,
которые сохраняют эти прямые. Для дальнейших вычислений удобно
ввести естественные единицы длины и времени, для которых

4.6. Специальная теория относительности 207
X
Л\
Рис. 4.18
скорость света равна единице. Например, мы могли бы измерять
t в годах, а х в световых годах. Или если мы выберем
наносекунду (Ю-9 секунд) в качестве единицы времени, то
соответствующая единица длины, с великолепной точностью, будет один фут.
Поэтому в качестве естественных единиц t можно измерять в
наносекундах, а х в футах.
Итак, мы будем изучать такие линейные преобразования,
которые сохраняют изображенную на рис. 4.19 фигуру,
определяемую линиями χ = t и χ = — t.
\ 1
ix /
Рис. 4.19
Получив эти линейные преобразования, мы определим все
преобразования пространства-времени, которые сохраняют
прямые линии и скорость света.
На самом деле, мы хотели бы, по крайней мере временно,
исключить из рассмотрения определенные типы преобразований.

208
Глава 4. Скалярные произведения
Например, преобразования отражения
-*
χ
Рис. 4.20
и преобразование инверсии (рис. 4.22).
Рис. 4.21
-*
—χ
=>
Рис. 4.22
Эти преобразования все прямые χ = ±ί переводят в χ = ±ί,
при этом возможна перестановка линий. На рисунках показано,
как эти преобразования переставляют четыре области на
плоскости. Поэтому, умножая на одно из них, можно сделать так, чтобы
необходимые нам преобразования сохраняли бы каждую из этих
четырех областей. Таким образом, мы будем искать
преобразования F, которые сохраняют прямые χ = t, x = —t и переднюю
область (область абсолютного будущего): t2 > x2, t > 0.
Чтобы получить такие преобразования, перейдем к новым
координатам, для которых эти прямые становятся осями координат
(рис. 4.23):
Ρ
Я,
= R-
R =
ΒΓι =
2 V-l

4.6. Специальная теория относительности 209
«=§(* + *)
^
р= Ux-t)
Рис. 4.23
Таким образом, RrlFR должно сохранять координатные оси
и положительный квадрант, и преобразование R~lFR является
диагональной матрицей
R-lFR =
а 0
0 d
а > 0, d > 0.
Введем обозначения: ad = s2 и a/d = г2 выбрав s > 0, г > 0.
Тогда
Значит, мы доказали, что
где
F = SLr,
s 0
5 =
0 s
является преобразованием смены масштаба и
R
г 0
0 г
)-1
(4.2)
Преобразование Lr называется собственным преобразованием
Лоренца с параметром г. Мы утверждаем, что для любой пары
некторов vi, V2
' ' (4-3)
(Lrvi,Lrv2) = (νι,ν2).
Действительно, по аналогии с формулой (4.1) для скалярного
произведения (-, ■), достаточно доказать, что
^(v) = Q(Lrv).

210
Глава 4. Скалярные произведения
В нашем случае
и, если ν' = Lrv = ί / I, то
Q(v) = t2 - хг = -4pq
f
Ρ
rp
д')-\г-%> и G(v') =-4pV =-4w = Q(v),
что и требовалось доказать .
χ
Рис. 4.24.
— ljr
Результат преобразования масштаба 5 состоит в том, все
длины и время умножаются на множитель s. Существование
атомных часов вместе с определенными спектральными линиями
показывает, что природные явления не инвариантны относительно
преобразования 5 при s φ Ι.
Линейное преобразование Л, которое сохраняет
квадратичную форму Q в том смысле, что
Q(Av) = Q(y) для всех ν в пространстве V,
называется преобразованием Лоренца. Такое преобразование А
должно переводить световой конус (называемый также нулевым
конусом)
{ν | Q(v) = 0}
2Инвариантность Q(v) при преобразовании Лоренца проиллюстрирована
на рис. 4.24. — Прим. ред.

4.6. Специальная теория относительности 211
в себя, т. е. множество {χ = ±ί} должно сохраняться. Если, кроме
того, А преобразует область абсолютного будущего в себя же, то
оно является собственным преобразованием Лоренца А = Lr для
некоторого числа г.
Производя ряд преобразований Лоренца, собственные
преобразования Лоренца могут быть непрерывно сведены к
тождественному. В этом состоит их отличие от других преобразований
Лоренца. Действительно, пусть A(t) есть семейство
преобразований Лоренца, удовлетворяющее условиям А(0) = I, А(1) =
А. Пусть ν указывет точку в области абсолютного
будущего. Тогда A(t)v не может пересекать световой конус, потому
что Q(A(t)v) = Qiy) > 0. Для любого преобразования Лорен-
Ό ι
ца Det Л = ±1, т.к. А, умножаемое на матрицу вида .
или I -li)> есть собственное преобразование Лоренца и
Det L = 1 для собственного преобразования Лоренца L. Таким
образом, поскольку Det A(t) непрерывно изменяется со временем
t и Deti4(0) = 1, мы должны иметь Deti4(i) = 1, следовательно,
Det A = 1. Но если А может быть непрерывным образом сведено
к тождественному преобразованию, значит, А является
собственным преобразованием Лоренца. С другой стороны, если А = Lr,
то положим A(t) = Ltr, так что Л(0) = I и Л(1) = А.3
Собственные преобразования среди всех преобразований Лоренца можно
охарактеризовать возможностью перевести их в тождественное отображение
непрерывным изменением в классе всех преобразований Лоренца. Точнее,
для того, чтобы А было собственным преобразованием Лоренца, необходимо
и достаточно существование семейства А(т) преобразований Лоренца,
непрерывно зависящего от τ при 0 < τ < 1, такого, что А(0) = I, -<4(1) = А.
Докажем это. Необходимость доказывается совсем просто: если А = Lr,
то в качестве А(т) можно взять А(т) = LTr. Докажем достаточность.
Пусть ν — произвольная точка из передней области. Поскольку при всех τ
Q(A(t)\) = Q(v) > 0, то точка .<4(τ)ν не может пересечь световой конус,
т. е. и при τ = 1 находится внутри передней области. Далее, детерминант
любого преобразования Лоренца равен +1 или —1, поскольку такое
преобразование может быть получено из собственного домножением на матрицу
Но поскольку Det Л(0) = 1, то из соображений непрерывности
(" ±°>
Dot Л (τ) = 1, откуда Det А = 1. Из этих фактов следует, что А — собственное
преобразование Лоренца. — Прим. ред.

212
Глава 4. Скалярные произведения
Произведение двух собственных преобразований Лоренца
тоже является собственным преобразованием Лоренца.
Действительно, если
Lr = R\0 г-1)1*1 И Lr'=RiQ ^-lJR'1,
то
(s °-0дЧ
LrLr — R
О r'-^R
так что
Ij'pijj. ±Jrrt .
(4.4)
Удобно обозначить г = еа и положить
Тогда
2 \е
eQ + e"
LQ-LQ =L
Q+Q
(4.5)
Если ввести в рассмотрение гиперболические функции cosh α =
-(eQ + е~а), sinha = -(eQ — e~a), то можно написать
Δ Δ
та _ /cosha sinha\
у sinh a cosh a y
Теперь по своей записи преобразование Лоренца La очень похоже
на преобразование вращения Rq\
та _ /cosh a sinh α λ „ _ /cos# — sin#\
у sinh a cosh α у ' ysin# cos θ J '
Похожие формулы получаются для произведений
преобразовании:
Lai ■ La2 = LQ1+Q2, в то время как R9l ■ Щ2 = ϋθ1+θ2·
При изменении параметра α точка L°V движется вдоль
гиперболы, за исключением пограничного случая, когда ν лежит на

4.6. Специальная теория относительности 213
световом конусе. В этом случае точка L°V движется к вершине
светового конуса или от нее (кроме ν = 0, когда LQv = 0 для всех
а). Именно поэтому функции sinh, cosh называются
гиперболическим синусом и гиперболическим косинусом. Если изменяется
параметр Θ, то точка Rqv движется по окружности, кроме случая
ν = 0, когда она остается неподвижной. Поэтому функции cos,
sin называются круговыми.
Евклидово движение плоскости — это преобразование вида
I —► R I ) + (/,)> гДе -^ ~~ ортогональное преобразование;
другими словами, евклидово преобразование состоит из
трансляции и ортогонального преобразования. Евклидова геометрия
изучает свойства подмножеств плоскости, которые инвариантны
при всех евклидовых преобразованиях. Преобразование Пуанкаре
на плоскости есть преобразование вида I I —► L I ] + I ,
где L — преобразование Лоренца. Геометрия специальной теории
относительности изучает свойства, инвариантные относительно
всех преобразований Пуанкаре. Свойство прямой I быть
параллельной оси у не является евклидовым свойством прямой I.
Действительно, если / параллельна оси у, то RI не будет параллельна
у для всех вращений R, кроме поворотов на 0° и 180°.
Аналогично, свойство прямой быть параллельной оси χ не является
свойством, которое определяет специальная теория относительности.
Если I параллельна х, то LI не будет параллельной оси χ для
всех преобразований L, кроме тождественного. Это утверждение
обычно формулируется так: «в рамках специальной теории
относительности понятие одновременности не имеет смысла».
Точно так же не имеет смысла утверждение, что «частица
покоится». Нам хотелось бы сказать, что линия χ = 0 (ось ί)
представляют частицу, покоящуюся в начале координат. Но преобра-
чование Лоренца Lr переводит эту линию в другую, проходящую
через начало координат, и
Lr( θ) "2Г-Г1

214
Глава 4. Скалярные произведения
Таким образом, преобразование Lr переводит ось t в прямую
χ — vt, где ν
γ _ γ 1 Г2 — 1
г + ι—1 г2 + 1
Результат похож на траекторию частицы, движущейся с
постоянной скоростью v. Мы можем решить уравнение
υ = (г2 - 1)/(г2 + 1),
выразив г через ν:
r = y/(l + v)/(l-v),
что легко проверяется. При желании мы можем использовать ν
в качестве параметра для описания L: определим
L(v) = Lr = Lec,
где
г = y/(i + v)/(i-v) = ea,
г — г
-1
V =
еа — е а sinh α
r _|_ r i ea_|_ea cosh α
= tanha.
Заметим, что
L(v)L(v') = Lrr,, r = y/(i + v)/{l-v), r' = y/(l + v')/(l - v').
При этом произведение тт' можно записать в виде
гг =
1 +
ν + ν'
1 + υυ'
ν + ν'
1 + υυ' _
1/2
так что
L(v)L(v') = L
ν + ν'
1 — vv'
(4.6)
Эта формула представляет закон сложения скоростей в
специальной теории относительности.

4.6. Специальная теория относительности 215
Итак, мы пользуемся тремя способами параметризации
одного и того же преобразования Лоренца:
Lr = La = L(v),
где
г = еа = y/(l + v)/(l-v).
В зависимости от выбора параметризации умножение
преобразований определяется формулами (4.4), (4.5) и (4.6).
Мы показали, что линейные преобразования специальной
теории относительности сохраняют квадратичную форму Q(v). Но
мы еще не дали физической интерпретации Q(v). Приведем такой
пример: у нас есть световые лучи и часы. Рассмотрим (рис. 4.25)
точки ίι и ί2 на оси t, которые соединены с точкой I |
световыми лучами (прямыми, параллельными t = χ и t = —χ).
Тогда
так что
Рис. 4.25
t — t\ = x или ίι = t — χ,
<2 — t = X ИЛИ ί2 = t + Χ,
Μ2 = ζ?(ν) ДЛЯ V
11аблюдатель находится в точке I n I ■ Он покоится или движется
(· постоянной скоростью и хочет связаться с точкой v. Он
излучает световой сигнал в момент времени ίχ и регистрирует время

216
Глава 4. Скалярные произведения
<2 возвращения к нему отраженного сигнала. Произведение ίιί2
называется расстоянием Минковского — интервалом между
двумя событиями. Отметим, что если ν лежит на линии χ = О, то
ίι = ί2 = ί, потому что передача сигнала происходит мгновенно.
Если ν лежит на световом луче, проходящем через точку I ],
то ίι = 0. Если Q(v) < 0, то ίι < 0 и ί2 > 0 (рис. 4.26).
Рис. 4.26
Еще одно важное свойство геометрии пространства
Минковского. Вспомним, что в геометрии Евклида у нас есть
неравенство треугольника
||и + ν|| < ||u|| + ||v||,
причем равенство будет только в случае, когда и и ν лежат на
одной прямой в одном направлении. Это проиллюстрировано на
рис. 4.27.
c = a + b, a = ||u||, b=||v||.
Очевидно, что ломаная линия длиннее прямой. Это значит,
что в геометрии Евклида прямая линия есть кратчайшее
расстояние между двумя точками.
А теперь рассмотрим аналогичную диаграмму для
пространственно-временной геометрии, когда окружности
\\А-Р\\2 = а2 и \\В - Д||2 = Ь2

4.6. Специальная теория относительности 217
Рис. 4.27
заменяются гиперболами Q(A — Ρ) = а2 и Q(B — R) = b2
(рис. 4.28). Но в этом случае для любых отрезков I и га,
образующих ломаную линию между точками Ρ и R, мы имеем
Q(l) < а2 и Q(m) < Ь2.
L^-^^^ \/ \т
Ρ I R
Q(B-R) = b2l \Q{A-P)=a2
Рис. 4.28
Здесь Q(l) равняется квадрату временного отрезка, который
показывают часы, движущиеся с постоянной скоростью вдоль
линии I. Итак, в этом случае мы имеем обратное неравенство
треугольника.
Время, измеренное по часам, движущимся с постоянной
скоростью из точки Ρ в точку R будет больше, чем время,
измеренное по часам, движущимся вдоль любой ломаной линии, соеди-
пящей точки Ρ и R.
Это явление называют эффектом близнецов: близнец,
двигающийся вдоль ломаной линии, (если он выживет на ухабах)
будет моложе другого близнеца, который двигается с постоянной

218
Глава 4. Скалярные произведения
скоростью из точки Ρ в точку R. Этот эффект называют
также парадоксом близнецов. Конечно, здесь нет никакого
парадокса, мы имеем просто очевидное следствие обратного неравенства
треугольника.
4.7. Группа Пуанкаре и группа Галилея
До сих пор мы описывали преобразования геометрии Евклида и
специальной теории относительности в терминах естественных
единиц. Точки в пространстве-времени называют событиями.
Они отмечают, где и когда что-то произошло. Если мы
зарегистрируем все события, случившиеся с одним человеком (скажем,
за 70 лет) в секундах и возьмем несколько сотен или тысяч
метров, тоже измеренных в секундах4, то мы получим множество
событий, протяженность которого вдоль временной оси
примерно в 1018 раз больше, чем в направлении пространственных осей
(рис. 4.29)5.
Рис. 4.29
Авторы имеют в виду световую секунду, т. е. расстояние, проходимое
светом за 1 секунду. — Прим. ред.
5Расчет авторов ошибочный: 70 лет/1000 метров « 2 · 1014. — Прим. ред.

4.7. Группа Пуанкаре и группа Галилея 219
Получив такую вытянутую вдоль временной оси область,
возникает желание измерять расстояния в более мелких единицах
(например в метрах), чем те единицы (секунды), которые мы
применили для измерения времени. Конечно, если единица
измерения будет меньше, то значение измеряемой велинины станет
больше. Поэтому в «обычной» системе единиц пространственные
расстояния будут сильно увеличены по сравнению с временными
интервалами. Конкретно это значит, что мы будем рассматривать
новые переменные Τ и X, связанные с естественными единицами
t и χ соотношениями Τ = t и X = сх, т. е.
Χ) = \0 с) \х
где с — большое число. Световой конус |х| = |ί| в новой системе
единиц преобразуется в с_1|Х| = |Г| или |Х| = с\Т\.
Мы будем говорить, что «в обычных единицах скорость света
равна с». Аналогично, гипербола t2 — χ2 = к преобразуется в
кривую Т2 — с2Х2 = к (рис. 4.30). «Времениподобные гиперболы»,
соответствующие к > 0, становятся менее кривыми, при малых
значениях X они становятся почти вертикальными прямыми
линиями.
Выразим преобразования Лоренца через обычные единицы.
/Т\
Для этого проделаем следующее: возьмем точку Ι γ I и найдем
точку
х) = \ъ ο-ή{χί
Подействуем на нее преобразованием Лоренца L и получим
Выразим этот новый вектор через обычные единицы, умножив
(4Ό на матрицу I I. В результате получим:
0 c)L(o с-Ч [х

220
Глава 4. Скалярные произведения
Рис. 4.30
Итак, в терминах обычных единиц преобразование Лоренца пе-
реводит вектор I „ вМ γ ], где матрица Μ равна
»=И>0>;
Пусть L = La. Перемножив матрицы, получаем
М =
cosh а с l sinh a
с sinh a cosh α
Эта формула справедлива для любого значения а. Вернемся к
преобразованию Лоренца L, для которого параметр α мал.
Введем tanha = sinh a/ cosh a = ν /с, где, по нашему
предположению, с — большая скорость, а υ — обычная скорость, так что
a — очень маленький параметр. Тогда
Μ =
или
cosh a
с tanh α cosh α
Μ = cosh α
с tanh α cosh α
cosh α
1 υ/c2
ν 1

4.7. Группа Пуанкаре и группа Галилея 221
где
^(Тз^№ = (1-*2^1/2'
(1 - tanh2 α)
Разложение в ряд по малому параметру ν2/с2 дает
cosh α = 1 + -ν2/с2 + · · · .
Δι
Подставив это разложение в формулу для М, получаем
или
где элементы матрицы Ε имеют порядок величины С2. Матрица
Gv~\v 1
называется преобразованием скорости, соответствующим
значению скорости, равному v. Это преобразование сохраняет
прямые Τ = const, т.к. Gv Ι γ J = I у _ J. Таким образом, мы
видим, что преобразования скорости можно рассматривать как
«предельный случай» преобразований Лоренца при малом
значении а. Иными словами, предполагая обычную скорость малой
но сравнению со скоростью света, мы получаем, что временипо
добные гиперболы превращаются в вертикальные прямые линии,
а преобразования Лоренца становятся преобразованиями
скорости.
Множество преобразований скорости образует группу,
элементы которой обладают свойством GVlGV2 = GVl+V2, что можно
легко проверить. Для этой группы сохраняется понятие
одновременности.
Преобразования типа у ~* ^» у + J называются
преобразованиями Галилея. Итак, преобразования Галилея — это

222
Глава 4. Скалярные произведения
композиции трансляций и преобразований скорости. Механика
Ньютона основана на принципе относительности Галилея; ее
основные понятия инвариантны относительно преобразований
Галилея. Гениальность открытий Лоренца, Пуанкаре и Эйнштейна
состояла в том, что они поняли приближенный характер
понятия одновременности: это понятие справедливо только на малых
расстояниях и для малых скоростей. А преобразование скорости
Gv = I ) следует рассматривать как аппроксимацию
преобразований Лоренца (в обычной системе единиц):
(l/yJ\-V2/C2 v/c2y/l-V2/c2\
\v/y/l-v2/c2 1/v/l - ν2/с2 J '
4.8. Импульс, энергия и масса
Переход от группы Галилея к группе Пуанкаре потребовал
переопределения базисных понятий механики. Основные контуры
такой теории Пуанкаре изложил в обращении к Всемирной
Выставке, проходившей в 1904 году в Сент-Луисе. После этого он и
работавший независимо А. Эйнштейн опубликовали в 1905 году
серию фундаментальных работ. Опишем некоторые идеи из этих
работ.
В классической механике существуют два фундаментальных
закона, используемых при изучении движения частиц, — закон
сохранения импульса и закон сохранения энергии. Например, мы
изучаем столкновение двух частиц А и В. Импульс частицы А
до столкновения обозначим рд, а после столкновения р'А,
аналогично для частицы В. Закон сохранения импульса говорит, что
РА + РВ = ΡΑ +Р'в-
Столкновение называется упругим, если полная кинетическая
энергия сохраняется. Пример неупругого столкновения: в
результате столкновения двух частиц получается одна. Обратная
ситуация: пусть в начальный момент две покоящиеся частицы были

4.8. Импульс, энергия и масса
223
связаны, потом произошел взрыв, в результате которого две
частицы разлетаются. Это можно рассматривать как процесс,
«обратный» столкновению. Если бы мы записали его на пленку и
прокрутили в обратном направлении, то увидели бы
столкновение двух частиц, в результате которого получается одна частица.
Полная кинетическая энергия не сохраняется — до взрыва она
была равна нулю, а стала больше нуля. Энергия, освободившаяся
при взрыве, преобразовалась в кинетическую энергию. В
обратном процессе мы полагаем, что когда из двух частиц получается
одна, кинетическая энергия преобразуется либо в потенциальную
энергию, либо в тепло. Для неупругих столкновений выполняется
закон сохранения импульса. А для упругих столкновений, когда
нет преобразования кинетической энергии в другие формы
энергии, полная кинетическая энергия тоже сохраняется:
ЕА + ЕВ = Е'А + ΕΪΒ,
где Ед — кинетическая энергия частицы А до столкновения,
Е'А — кинетическая энергия той же частицы после столкновения
и т.д.
Оказывается, что в специальной теории относительности
законы сохранения энергии и импульса выполняются, как и в
механике Ньютона. Что необходимо изменить в определениях энергии
и импульса?
Импульс частицы в механике Ньютона равен
ρ = mv,
где ν — скорость движущейся частицы и т — ее масса.
Скорость (и, следовательно, импульс) является вектором в
трехмерном пространстве. В нашей модели мы будем рассматривать его
как одномерный. (Другими словами, мы ограничимся
рассмотрением частиц, движущихся вдоль одной прямой. Массу можно, в
принципе, измерить, проделав следующие эксперименты.
Рис. 4.31

224
Глава 4. Скалярные произведения
Допустим, у нас есть несколько объектов — например,
шарики, сделанные из разных материалов. Пусть два удерживаются
вместе и покоятся. Далее происходит взрыв или отпускается
пружина, и шарики разлетаются в разные стороны. Один полетит
вправо, другой влево (рис. 4.31). Если шарики сделаны из одного
материала и имеют одинаковый размер, то их движение должно
быть симметричным. Например, если на равных расстояниях от
точки, где покоились шарики, поместить две отражающие
стенки, следует ожидать, что после отражения шарики столкнутся в
той же точке. Этот эксперимент можно проделать и убедиться,
что все будет происходить именно так. А теперь возьмем
шарики, сделанные из одного материала, но имеющие разные размеры.
Пусть правый шарик будет больше. Мы можем убедиться, что
после отражения шарики столкнутся правее центра, т. е. меньший
шарик пройдет большее расстояние. Тот же эксперимент
можно проделать с шариками, сделанными из разных материалов.
Например, пусть шарики имеют одинаковый размер, но правый
сделан из свинца, а левый из алюминия. В этом случае
столкновение произойдет справа от центра. Однако, если свинцовый
шарик будет очень маленький, а алюминиевый того же размера, то
столкновение произойдет левее центра. Если у нас много
свинцовых шариков разных размеров, то среди них можно найти такой,
который будет точно соответствовать алюминиевому шарику (в
том смысле, что столкновение будет происходить в центре).
А теперь давайте сравнивать свинцовые шарики с медными.
Допустим, мы нашли свинцовый шарик, соответствующий
алюминиевому, и медный шарик, соответствующий свинцовому.
Теперь мы можем сравнить алюминиевый шарик с медным.
Эксперимент покажет, что они соответствуют друг другу. И это не
логический вывод, а закон природы6. Теперь мы можем
определить понятие массы: два объекта имеют одинаковую массу, если
в нашем эксперименте они соответствуют друг другу. Закон
природы, который мы обсуждаем, позволяет корректно определить
понятие массы. Если А ж В имеют одинаковую массу, а масса В
6Повернем наш прибор на 180°, т. е. поменяем местами правую и левую
стороны. Этот поворот не отразится на свойствах шариков соответствовать
друг другу. И это тоже закон природы.

4.8. Импульс, энергия и масса
225
равна массе С, то Л и С имеют одинаковые массы. В
эксперименте можно проверить закон природы: если шарик А\ соответствует
шарику В\ и шарик А2 соответствует i?2, то, экспериментируя с
парами шариков: Αι и А2 против В\ и i?2, можно убедиться, что
А\ и Αι соответствуют В\ и Βι (рис. 4.32).
| · # 1
ι О О 1
ι О—«О 1
Рис. 4.32
Экспериментально можно также убедиться, что масса шарика
пропорциональна его объему: если свинцовый шарик с радиусом
г а соответствует медному шарику с радиусом г в, то свинцовый
шарик с радиусом Зга будет соответствовать 27 медным шарикам
с радиусом г в-
Это позволяет нам ввести единицу массы: выберем один
объект, скажем свинцовый шарик объемом 1см3. Тогда мы можем
сравнивать с ним другие объекты, масса которых будет кратна т
(массе выбранного свинцового шарика). Таким образом, мы
получим численное значение любой массы. Первоначально в
метрической системе единиц за единицу массы — 1 грамм — была взята
масса 1 кубического сантиметра воды при 4°С. Поскольку нам
сложно проводить эксперименты по столкновениям с водой при
■1°С, мы могли бы определить 1 грамм как массу медного шарика
объемом 0.11... см3. Интересно отметить, что во всех описанных
экспериментах не было потребности в каких-либо инструментах
нчмерения времени.
Вернемся к закону сохранения импульса. В механике
Ньютона, если мы определим импульс частицы
ρ = mv,
то полный импульс сохраняется. (Нетрудно показать, что такая
<|н>рмулировка закона сохранения импульса является следствием
нашего определения массы и предположения, что законы
природы инвариантны относительно группы преобразований Галилея.

226 Глава 4. Скалярные произведения
См. Лекции по физике Фейнмана, главу 10, где дается четкое
изложение этого утверждения.) В специальной теории
относительности такое определение импульса не имеет смысла, потому что
не имеет смысла скорость] Ведь по определению скорость равна
dx
ν = τν
при этом предполагается, что мы выбрали координатные оси χ
и ί и решили параметризовать движение частицы временем t.
Именно поэтому мы записываем траекторию частицы с
помощью функции x(t). Если мы сделаем преобразование Лоренца,
то получим новые координатные оси t', χ' и, следовательно,
новую скорость ν'. Поставим задачу немного по-другому. Допустим,
что траектория частицы описывается третьим нейтральным
параметром s. Например, в роли s могут быть показания неких
внутренних часов, которые частица несет вместе с собой.
Тогда траектория частицы на пространственно-временной плоскости
дается вектором
■«-(30·
В некоторый момент so мы можем вычислить касательную к этой
кривой (рис. 4.33)
du _ (dt/ds\ _ _ fa\
ds ~ \dx/ds) ~W~\bJ-
Тогда в системе координат ί, χ скорость ν = dx/dt равна
ν = b/a.
Очевидно, что для вектора
-С)
отношение ν = b/a не имеет физического смысла. Если мы
заменим w на
w' = Lw

4.8. Импульс, энергия и масса
227
А
t
Рис. 4.33
и напишем
w'=(b')' υ' = 6'/α/'
то ν' не будет равно ν, за исключением случаев, когда ν = ±1 или
L = I. При преобразованиях Лоренца сохраняется одно свойство
вектора w — величина
Q(w) = а2 - Ь2.
Условие <5(w) > 0 эквивалентно условию |υ| < 1. Поскольку
в нашей системе единиц скорость света равна 1, это значит, что
скорость ν меньше скорости света.
Опыт показывает, что все частицы с положительной массой
покоя (будет определена ниже) движутся со скоростями,
меньшими скорости света, т. е. для них всегда Q(w) > 0. Обозначим
Q(w) = μ2 > 0,
так что
а2-Ъ2 = μ2,
и пусть
Ъ/а = ν
в определенном секторе пространства-времени. Заметим, что
соотношение Ь/а = ν не определяет сами величины а, Ь. (Это —
w

228
Глава 4. Скалярные произведения
отражение того факта, что мы не конкретизировали наш
мистический параметр s для кривой u(s).) Теперь можно решить два
уравнения а2 — Ь2 = μ2, b/a = ν и получить
Μ b= №
VT^v2' VT^v2
для данного сектора пространства-времени. Для малых значений
ν можно воспользоваться разложением в ряд Тейлора
так что
1 2
а = μ+ -μν +··· ,
1 3
Ь = μν + -μν + · · · .
Δι
Отметим, что разложение величины b очень похоже на ρ =
mv, если мы идентифицируем μ с т и отбросим члены более
высокого порядка по v. Точно так же второй член в
разложении α похож на выражение для кинетической энергии в механике
Ньютона. Итак, мы подошли к возможности переопределить
понятия энергии и импульса. Каждому объекту соответствует
определенное значение величины μ. Во избежание путаницы
обозначим эту величину гщ и назовем ее массой покоя данного
объекта. Если оказывается, что объект покоится в некотором секторе
пространства-времени, то масса покоя совпадает (с точностью до
выбранной системы единиц) с массой покоя, определенной выше
экспериментально. Допустим, что то > 0 (мы это все время
подразумевали). Тогда для движущегося объекта вводится вектор
энергии-импульса (А-импульс)
такой, что
Q(w) = E2 -p2 = m2Q

4.8. Импульс, энергия и масса
229
и w есть произведение ύ = du/ds на скалярный множитель,
где u(s) — траектория объекта, движущегося в пространстве-
времени.
В данном секторе пространства-времени, где траектория
объекта задается формулой
соответственно
U(s) =
*>-(£!)·
mQV
р Vi -ν2'
( t{s) \
dx x(s)
V ~ dt ~ i(s)
F,- Ш0
Vi-v2
мы получаем
В частности, если объект покоится, так что ν = 0, то
ρ = О, Ε = rtiQ
в данной системе координат.
Закон сохранения энергии-импульса в новой формулировке
выглядит как закон сохранения для векторов в пространстве-
времени при любом столкновении:
ЕЛ /БЛ/ВЛ/В,
PA J \PbJ \PaJ \Рв
Эти уравнения записаны в естественной системе единиц,
когда скорость света равна 1, a v — число. Поэтому выражение
\/1 — ν2 имеет смысл. Если же мы будем работать с
«психологическими единицами», то ν не будет числом, а будет скоростью,
выраженной, например, в см/сек. Тогда выражение \/1 — υ2 уже
не имеет смысла. В этом случае \/1 — ν2 следует заменить на
y/l — v2/c2. Соответственно изменяется выражение для р:
_ ТПрУ
Р~ Vl-v2/c2'

230
Глава 4. Скалярные произведения
При малых значения ν мы получим ньютоновское выражение для
импульса. Аналогично изменяется формула для энергии Е:
Ε = moc2
ν/1 - ν2 /с2
Для покоящейся частицы мы получаем известную формулу
Эйнштейна
Ε = т0с2.
4.9. Антисимметричные формы
В предыдущих параграфах мы рассмотрели два типа скалярных
произведений на плоскости. Первое — евклидово скалярное
произведение, определяемое формулой
(w, w') = хх' + уу', где w = ( х J и w' = ( Х, J
/ '
второе — лоренцево скалярное произведение
(ν, ν') = tt' — хх', где ν = I J и ν' = I , J .
Оба типа скалярных произведений билинейны, т. е. если один
вектор зафиксировать, то произведение будет линейной функцией от
другого вектора:
(awi + 6w2, w') = a(wi, w') + 6(w2, w').
Оба скалярных произведения симметричны:
(w, w') = (w',w) и (ν,ν') = (ν',ν).
Введем третий тип произведения между двумя векторами на
плоскости, который будет по-прежнему билинейным, но
вместо симметричности обладает свойством антисимметрии. Именно,
определим следующую функцию от двух векторов:
ω(ν, ν'} = qp' - q'p = Det (« £) , где ν = (j) и V = (fy .

4.9. Антисимметричные формы
231
Здесь выполняется тождество
ω(ν,ν') = -ω(ν',ν),
которое мы и называем антисимметричностью.
Рис. 4.34
Геометрический смысл ω(ν,ν') понятен: это
ориентированная площадь параллелограмма, построенного на векторах ν и ν'
(рис. 4.30). Очевидно, что функция ω(ν, ν') билинейна. Величина
ω называется симплектическим скалярным произведением.
Линейное преобразование А называется симплектическим,
если оно сохраняет симплектическое скалярное произведение ω.
Таким образом, А симплектично тогда и только тогда, когда для
любых ν, ν'
ω(Αν,Αν') = ω(ν,ν').
Матрица, столбцы которой Αν и Αν', получается умножением
матрицы А на матрицу I , ]. Отсюда
\Р Ρ J
u;(Av,Av') = Oet
q q'
Ρ Ρ'
= Det A Det
q q'
Ρ Ρ'
= Det^w(v,v').
Следовательно, преобразование А является симплектическим
тогда и только тогда, когда Det Л = 1. Очевидно, что любая
симплектическая матрица имеет обратную, которая также сим-
илектична, и произведение двух симплектических матриц
тоже всегда симплектично. Это означает, что совокупность всех

232
Глава 4. Скалярные произведения
симплектических матриц образует группу, называемую
(двумерной) симплектической группой. Симплектическая группа играет
очень важную роль в оптике, мы увидим это в главе 9.
Резюме
A. Евклидово скалярное произведение
Изучив эту главу, вы должны усвоить понятие евклидова
скалярного произведения и научиться пользоваться его свойствами.
Вы должны уметь транспонировать матрицу и применять
операцию транспонирования в связи со скалярным
произведением и евклидовыми преобразованиями.
Вы должны знать, как в векторном пространстве двух и
более измерений с евклидовым скалярным произведением
применить процесс Грама-Шмидта для построения ортонормирован-
ного базиса и для получения ортогональной проекции вектора на
подпространство.
B. Квадратичные формы
Вы должны уметь выразить квадратичную форму Q(v) через
симметричную матрицу А и связать максимальные и
минимальные значения Q с собственными векторами и собственными
значениями А.
Если на плоскости задана квадратичная форма Q, то вы
должны уметь ввести такие координаты ж' и у', в которых она
имеет вид
Q = Χιχ'2 + \2у'2\
и воспользоваться этими координатами для построения графика
Q = const.
C. Связанные колебания
Вы должны уметь свести задачу о двух связанных осцилляторах
к уравнению w = — Aw и выразить нормальные колебания через
собственные векторы и собственные значения А.
D. Лоренцево скалярное произведение
Вы должны уметь вычислять лоренцево скалярное произведение

Задачи
233
двух векторов, определять преобразования Лоренца, которые
сохраняют это скалярное произведение. Применять эти понятия в
специальной теории относительности.
Задачи
4.1. (а) Используя три свойства скалярного произведения
(симметричность, линейность, положительная определенность),
докажите неравенство Коши-Шварца
(v, w) < v/(v,v)(w,w)
для любой пары векторов ν и w. ("Указание: рассмотрите
скалярное произведение (ν — aw, ν — aw). Этот
квадратичный полином по α не может иметь вещественных корней,
кроме случая ν = aw.)
(b) Докажите неравенство треугольника
||v + w||<||v|| + ||w||,
где ||ν||2 = (ν, ν). (Указание: возведите неравенство в
квадрат и примените неравенство Коши-Шварца из пункта (а).)
4.2. (а) На плоскости заданы два вектора ν и ν'. Покажите, что
поворот Re на угол Θ, для которого
COS0= -^
V(v,v)(v',v')'
сделает вектор ν пропорциональным вектору ν'. Найдите
'2\ / 4Ч
угол между векторами [ I и , „
(Ь) В двумерном пространстве-времени заданы два вектора ν и
ν'. Оба вектора либо пространственноподобны, либо време-
ниподобны вперед или времениподобны назад. Покажите,
что собственное преобразование Лоренца La, для которого
, {ν,ν'}
cosh a =
V{v,v}{v',v'}'
переводит вектор ν в вектор, пропорциональный вектору ν'.

234
Глава 4. Скалярные произведения
Воспользуйтесь этим результатом и найдите
преобразование Лоренца, переводящее вектор ( л ) в вектор,
пропорциональный вектору
Какая проблема возникнет, если вектор ν — пространствен-
ноподобный, а вектор ν' — времениподобный? Если вектор
ν — времениподобный вперед, a v' — времениподобный
назад? Если векторы ν и ν' находятся на световом конусе?
4.3. Чтобы научиться вычислять лоренцевы скалярные
произведения, поработайте с векторами в двумерном
пространстве-времени. (Первая координата соответствует времени ί, а вторая оси х.)
vi=(i)' ^=(~з)' V3=G)'
V4=(;), v5=(_?), vo=(?)·
Вычислите лоренцево скалярное произведение каждого
вектора на самого себя {ν, ν}. В системе координат х, t
изобразите каждый вектор и разберитесь, к какому типу он
относится: пространственноподобный, времениподобный вперед
или назад, лежит на световом конусе вперед или назад.
Вычислите лоренцевы скалярные произведения {v2,V3},
{v5,v6} и {v3,v6}.
Найдите векторы wi,..., W6, в которые переходят векторы
vi,..., V6 под действием преобразования Лоренца
_ /5/4 3/4λ
L2-(,3/4 5/4J·
Изобразите полученные векторы в системе координат х, t.
(d) Вычислите скалярные произведения {w2,W2}, {w6,w6},
{w2, W3}, {W5, W6} и {w3, wj}. Они должны совпадать с
соответствующими скалярными произведениями векторов v.
4.4. Пусть матрица S симметрична и имеет положительные
собственные значения. Введем новое скалярное произведение [v, w]s,
определяемое уравнением [v, w]§ = (5v, w).
(а) Покажите, что это скалярное произведение симметрично,
билинейно и положительно определено.
(а)
(Ъ)
(с)

Задачи
235
(b) Покажите, что матрица С сохраняет это скалярное
произведение (т. е. [Cv, Cw]s = [v, w]s) тогда и только тогда, когда
CFSC = S).
(c) Опишите процедуру построения матрицы В, обладающей
следующим свойством: если v' = B-1v, w' = B_1w, то
[v,w]s = (v',w'). Объясните как, имея одну матрицу В,
обладающую этим свойством, молено построить много
других.
Л к ТТ С ι37 09\
4.5. Пусть в предыдущем упражнении Ь = I „ Q 1 „ I.
(a) Получите вектор ν, ортогональный вектору w = ( _. I,
для скалярного произведения, определенного матрицей S
так, что [v, w]s =0.
(b) Постройте матрицу В, обладающую свойствами,
описанными в задаче 4.4(c). Проверьте, что для векторов ν и w из
пункта (а) выполняется равенство (B-1v, B_1w) = 0.
(c) Постройте матрицу ортогонального проектирования Р,
удовлетворяющую уравнению Р2 = Р, чей образ состоит
из векторов, пропорциональных вектору w = I _. I.
Проверьте, что для всех векторов ν выполняется равенство
[w,Pv]s = [w,v]5-
(d) Постройте матрицу С, которая сохраняет скалярное
произведение, определяемое матрицей S, и удовлетворяет
уравнению С2 = —I. (Указание: матрица R = I 1 „I
удовлетворяет уравнению R2 = — I и сохраняет обычное скалярное
произведение.
4.6. Для квадратичной формы
<3(v) = 8х2 + 12ху + 17у2
проделайте следующие операции.
(a) Запишите Q в виде (Αν, ν), где А — симметричная матрица.
(b) Найдите собственные значения матрицы А.
(c) Представьте матрицу А в форме
% 0 λ „_!
A = R°(Xl л°2)^

236
Глава 4. Скалярные произведения
(d) Найдите такие координаты х' и у', для которых
квадратичная форма Q принимает вид
Q(v) = 20а;'2 + Ъу'2.
(e) Нарисуйте линию Q(v) = 20. Отметьте на ней
координатные оси х, у и х', у'.
4.7. (а) Найдите собственные значения λι и Аг матрицы 5= I „ „ I,
определите собственные векторы νι и V2, соответствующие
этим собственным значениям.
(b) Постройте такую матрицу вращения Д, чтобы выполнялось
равенство S = RAR"1, где Л — диагональная матрица.
Проверьте, что R на самом деле осуществляет поворот!
(c) Найдите новые координаты х', у', являющиеся линейными
функциями χ и у, для которых
9а;2 + 4ху + 6у2 = Aia;'2 + Х2у'2.
4.8. (а) Найдите собственные значения и собственные векторы
матрицы
'10 6'
А —
л~ ' 6 10
(b) Постройте матрицу вращения R и диагональную матрицу
Л, для которых выполняется соотношение А = ЛЛД-1.
(c) Нарисуйте график уравнения 10а;2 + \2ху + 10у2 = 24.
4.9. (а) Найдите такие координаты а;', у', чтобы квадратичная
форма
Q(v) = -а;2 + бху + 7у2
приняла вид
Q(v) = λίχ'2 + Х2у'2.
Нарисуйте линию <2(ν) = 40.
(b) Пусть χ и у лежат на окружности единичного радиуса, так
что χ = cos0, у = sin#. Найдите значения углов Θ, при
которых Q принимает максимальное и минимальное
значение. Вычислите эти значения. Какова связь между этими
результатами и результатами, полученными в предыдущем
пункте?

Задачи
237
4.10. Предположим, что Μ и К — симметричные матрицы 2x2.
(a) Приведите пример, показывающий, что М~1К не
обязательно симметрична.
(b) Опишите, как построить такую симметричную матрицу В,
чтобы выполнялось равенство В2 = М-1. Покажите, что
матрица S = ВКВ симметрична, и, следовательно, ее
можно записать в форме S = RAR"1, где R — матрица враще-
л Αι О'
ния, а Л = ( _
0 λ2,
(с) Покажите, что если А = BR, то M~lK = AAA"1. Это
доказывает, что М-1 К имеет вещественные собственные
значения.
V
(d) Найдите новые координаты х' и у' из условия
Л-1 ( I. Покажите, что если ν = ( I, то
W \у)
(Μν, ν) = χ'2 + у'2, a (KV, ν) = λιζ'2 + Х2у'2.
(Указание: В — симметричная матрица, поэтому (Bv, w) =
(ν, Bw). R — ортогональная матрица, следовательно,
(Rv,w) = (v,R~lw).)
4.11. (а) Покажите, что если А = ( „ ), то exp(iyl) является
преобразованием Лоренца.
(Ь) В релятивистской механике полная энергия Ε и импульс ρ
частицы, имеющей массу т и движущейся вдоль прямой,
образуют вектор ν = ( I, при этом (ν, ν) = Ε2 — ρ2 = τη2.
Если частица движется так, что ее ускорение всегда равно а
с точки зрения наблюдателя, который видит частицу
покоящейся в данный момент времени, το Ε ш ρ связаны между
собой уравнениями
dE dp
-=ар, -=аЕ,
где τ — время, измеренное по часам, движущимися вместе
с частицей. Решите эту систему уравнений с начальными
/Μ π fE(r)\
условиями I I при τ = U и получите вектор I ,> / I .

238
Глава 4. Скалярные произведения
4.12.
Допустим, что расстояния вдоль двух взаимно
перпендикулярных осей на плоскости измеряются в единицах, которые
отличаются большим множителем с. Например, у нас есть
сверхскоростная прямая дорога. Ее проекция на ось χ равна 1000 километрам,
а проекция на ось у только 1000 сантиметрам. Мы можем ввести
новые координаты X = χ и Υ = су, где с = 105. Теперь X
измеряется в километрах, a Y в сантиметрах. Постройте матрицу
поворота на угол θ в системе координат Χ, Υ. Покажите, что для
прямых, чей наклон Χ/Υ порядка единицы, матрица вращения
превращается в матрицу сдвига в пределе с —» оо. Объясните это
явление геометрически, рассмотрев, что происходит с
окружностями х2 + у2 = к. (Замечание: выполнив это упражнение, еще
раз прочитайте в параграфе 4.3 обсуждение предела с
преобразований Лоренца.)
оо для
4.13. Вычислите симплектическое скалярное произведение ω(νι,ν2)
для векторов
i)' V2 = U
Vl
Проверьте непосредственно, что это скалярное произведение
сохраняется при действии на него симплектической матрицы
А =
5 3
-2 -1
4.14. Рассмотрите конструкцию, состоящую из масс и пружин,
изображенную на рис. 4.35.
Ш
-ЙЧ
м
I ►
XI
I ►
Х2
Рис. 4.35
(а) Покажите, что если ΐι и Ϊ2 задают смещения масс
вправо от положения равновесия, то уравнение движения этой
системы имеет вид
= -Н

Задачи
239
где
Т =
4 О
О 1
и Я =
4 -1
-1 1
(b) Пусть В — диагональная матрица с положительными
матричными элементами, удовлетворяющая уравнению В2 =
Т. Постройте матрицу А = В~1НВ~1. Найдите ее
собственные значения и собственные векторы, используйте их для
нахождения общего решения уравнения w = — Aw.
(c) Опишите нормальные колебания системы, определив их
частоту через ωο = у/{К/М) и отношение Х2/х\-
4.15. Рассмотрите систему масс и пружин, изображенную на рис. 4.36.
Пусть х\ и Х2 обозначают смещение масс вправо от положения
равновесия.
'Л ш
'Л
2М
W
м
I ►
χι
ι—►
Рис. 4.36
(a) Определите частоты нормальных колебаний и>а иц. Для
каждого колебания получите отношение xijx\.
(b) Пусть в начальный момент смещения масс равны х\ = А,
Х2 = 0, и они покоятся. Потом их отпускают. Найти
выражения xi(t) и X2(t), определяющие дальнейшее движение
системы.
4.16. Частица с 4-импульсом
подвергается действию
преобразования Лоренца L с матрицей
г + г
г — г'
г + г'
Покажите, что при этом сумма энергии и импульса
умножается на г, а их разность делится на г. Объясните этот результат в
терминах собственных значений и собственных векторов
преобразования L.

240
Глава 4. Скалярные произведения
4.17. Масса частицы равна 15 (в произвольных единицах), а ее
скорость равна и = 12/13 (с = 1). Эта частица сталкивается с
покоящейся частицей, масса которой равна 6, и они образуют одну
частицу.
(а) Получите 4-импульсы I I всех трех частиц, участвующих
в реакции. Определите массу и скорость образовавшейся
частицы.
(Ь) Возьмите преобразование Лоренца L = I .'. _'.„ I,
со-
4
ответствующее скорости —с. Определите 4-импульсы каж-
(Е'\
дой частицы I , в системе координат, движущейся со
4
скоростью -с.
5
4.18. Допустим, что две частицы имеют 4-импульсы wi = ( I и
(Е2\
W2 = I I соответственно, где
m\=El~p\, т\ = Е\-р\.
(a) Напишите лоренцево скалярное произведение этих
векторов {wi,W2} = mirri2Cosha. Покажите, что υ = tanha =
V cosh α — 1/ cosh α представляет скорость одной из частиц
в системе покоя другой частицы.
(b) Определите скорость ν для двух случаев:
13\ /5
wi=l _5I, w2-
13\ /5
Wl=> 5 ' W2=\3
4.19. В системе единиц, где с не равняется 1, матрица преобразования
Лоренца, действующая на 4-импульс I ), равна
cosh а (1/с) sinh a
с sinh a cosh a

Задачи
241
жется со скоростью -.
5
(a) Покажите, что на 4-импульс ( I действует матрица,
транспонированная этой.
(b) Покажите, что та же матрица L действует на 4-импульс,
если мы представим его в виде строки, т. е.
(E\p') = (E,p)L.
4.20. В системе единиц, где с = 1, энергия фотона равна его импульсу,
т.е. 4-импульс фотона равен Ε ( 1 I или Ε ( _. I в зависимости
от направления его движения.
(a) Допустим, что покоящаяся частица с массой 2т
распадается на частицу с массой т и фотон. Используя закон
сохранения 4-импульса, получите скорость частицы с массой т и
энергию фотона.
(b) Используйте преобразование Лоренца для описания этого
распада в системе координат, где частица с массой 2т дви-
3
5'
4.21. Фотон имеет энергию ΕΊ; соответственно, в системе координат,
где с = 1, 4-импульс фотона равен I F7 ) ■ Фотон сталкивается с
неподвижной частицей (масса mi), и образуется одна частица с
массой гаг- Покажите, что
mj-mj
Ει~ — г
7 2ту
4.22. Используя скалярное произведение (/, д) = /0°° f(t)g(t) dt,
постройте ортонормированный базис для пространства функций,
удовлетворяющих дифференциальному уравнению
χ + Ъх + 2х = 0.
■1.23. Постройте ортонормированный базис для подпространства R4,
определяемого векторами
VI =
ί2\
2
1
V2 =
(4\
0
1
ν3 =
ί°
4
1
Vo,
\о,
\2,

242
Глава 4. Скалярные произведения
4.24. В пространстве R2 определите скалярное произведение согласно
формуле (vi,V2) = 4a;ia;2 + yii/2· Постройте матрицу Ρ (2 χ 2),
которая осуществляет ортогональную проекцию любого вектора
ν (по отношению к скалярному произведению, определенному
выше) на прямую, порожденную вектором I 1 I. Покажите, что
(I — Ρ)ν ортогональна Ρν.

Глава 5
Дифференциальное исчисление
на плоскости
В главах 5 и б излагаются основы
дифференциального исчисления. В главе 5 мы определим
дифференциал отображения одного векторного пространства на
другое, обсудим его основные свойства, в частности,
цепное правило. Дадим примеры физических
приложений, в частности, движение Кеплера и
приближение Борна. Дадим определение частной производной,
производной по направлению и линейных
дифференциальных форм.
Введение
Наша первая задача — разработать дифференциальное
исчисление для четырех типов отображений:
(i) R1 -»R2,
(ii) R2-^R\
(iii) R1-^R1,
(iv) R2 -»R2.
Отображения первого типа R1 —► R2 можно изобразить, как
кривые на плоскости (рис. 5.1), функции R2 —► R1 — как
поверхности в трехмерном пространстве (рис. 5.2). Функции R1 —► R1
'шакомы читателю с первого года изучения математического
анализа. В главе 1 рассмотрены линейные отображения R2 —► R2.

244 Глава 5. Дифференциальное исчисление на плоскости
Рис. 5.1. Функция из R1 в R2 Рис. 5.2. Функция из R2 в R1
Сейчас мы хотим расширить изучение и включить в
рассмотрение нелинейные отображения одной плоскости в другую
(рис. 5.3). Чтобы не рассматривать каждый случай отдельно,
введем некоторые единообразные обозначения. В дальнейшем буквы
V, W, Ζ и т. д. будут обозначать либо R1, либо R2. Поэтому, когда
мы пишем
f:V-^W
(читайте «/ отображает V в W», или, другими словами, «/ есть
отображение из V в W»), то это значит, что рассматривается
любой из четырех случаев: V — это R1 или R2, и W — это R1
или R2.
•
Ρ
R2
Рис. 5.3
На самом деле наши обозначения и доказательства будут
таковы, что позволят множествам V, W и т. д. быть пространствами
Rn, т. е. они могут быть любыми конечномерными
вещественными векторными пространствами или аффинными
пространствами (эти пространства мы будем изучать в главе 10). В этой главе

Введение
245
мы проделаем некоторые общие вычисления, далее не имея в
распоряжении всех формальных определений.
Сначала отметим факт, вероятно, уже известный читателю,
который следует из простого обобщения нашего обсуждения в
главе 1: линейное отображение пространства Rp в Жя
определяется матрицей, имеющей q строк и ρ столбцов. Итак, матрица
'5 2 10 1
4 1-10 3
3 0 110
задает линейное отображение R5 в
/0\
1
о
о
W
Если
В
/1\
0
0
0
W
/5
= 4
\з
и т.д.
т.е. В отображает R3 —► R4, то В А отображает R5 —► R4 и,
следовательно, является матрицей, имеющей четыре строки и пять
столбцов, причем матричные элементы вычисляются по обычным
правилам умножения матриц.
/■
ВА =
Л
χ
V
7
В нашем примере
х = (2)(1) + (6)(-1) + (Ю)(1).
В частности, линейное отображение Rp —► R1 = R (обычно
называемое линейной функцией) определяется матрицей, у которой

246 Глава 5. Дифференциальное исчисление на плоскости
одна строка и ρ столбцов. Такую матрицу называют вектором-
строкой. Итак, I = (1,2,3,4) является линейным отображением
R4 -» R, так что
2, и т. д.
Результат действия этого отображения на произвольный вектор
задается формулой
/1\
0
0
W
= 1, I
/о\
1
0
W
У
ζ
χ + 2у + Sz + 4w.
Еще пример: пусть вектор-строка I = (a,b,c,d) действует на
вектор-столбец
/х\
У
ζ
\wj
Согласно обычным правилам умножения матриц, мы получаем
один матричный элемент
I(v) = ах + by + cz + dw.
Если А : W -» Rq и I : R« -» R, то I о А : Ш? -» R определяется
матричным умножением: матрица I x q умножается на матрицу
q χ р. Например, если q = 3, ρ = 5, I = (1,2,3),
'5 2 1 О Г
4 1-10 3
3 0 110
то
5 2 10 1'
Ы = (1,2,3) | 4 1 -1 0 3
3 0 110
(22,4,2,3,7).

5.1. «О» большие и «о» малые
247
Еще небольшое напоминание об обозначениях из
параграфа 4.1. В пространстве Жк мы имеем евклидово скалярное
произведение (■, ■) и соответствующую норму || ■ || > 0, определяемую
формулой
м м2 / \ 2,2, ,2
1М| = (v, v) = xl+x2 + --- + xk
для
(χι
ν =
\Xkt
Неравенство треугольника утверждает, что при любых и и ν
llu + vll < llull + llvll.
5.1. «О» большие и «о» малые
В одномерном дифференциальном исчислении говорится, что
функция /, зависящая от одной переменной, имеет производную
А в точке х, если / определена в некоторой окрестности точки χ
и разностное отношение
f(x + v)- f(x)
V
определенное для всех достаточно малых ν φ 0, имеет предел А
при ν —> 0. Мы хотели бы обобщить это определение на
отображения / : V —► W. Первое препятствие состоит в том, что
деление на вектор не имеет смысла, и мы не можем использовать
понятие разностного отношения. Поэтому в многомерном случае
обойдемся без дробей:
/(χ + ν)-/(χ) = Αν + 0(ν). (5.1)
По определению, А будет производной / в точке х, если
поправочный член φ(ν) стремится к нулю «быстрее, чем ν». Утверждению
в кавычках можно придать точный смысл, потребовав, чтобы
lim^ и =0 ПРИ ΙΙνΙΙ-^°· (5·2)

248 Глава 5. Дифференциальное исчисление на плоскости
Подробнее: для любого значения ε > 0 существует такая
величина δ > О, что
||<Ην)||<ε||ν|| (5.3)
для всех ν, удовлетворяющих условию ||ν|| < δ.
В формулах (5.2) и (5.3) выражение ||ν|| обозначает длину
вектора ν в пространстве V, что следует отразить в
обозначении, записав ||v||y. Аналогично, ||^(v)|| обозначает длину вектора
φ(ν) в пространстве W, что следует обозначить ||<Kv)||w· Тогда
неравенство (5.3) приобретет вид
||<Hv)||w <ε||ν||ν.
Нижние индексы делают обозначения слишком громоздкими,
поэтому мы не будем их использовать, а будем писать, как в
формулах (5.2) и (5.3).
Например, пусть / и, следовательно, φ — отображения R2 на
пространство R1. Наиболее общее выражение для вектора ν в
пространстве R2 имеет вид ν = I ). Для типографского
упрощения запишем φ(ν) как ф(х,у). Тогда ||ν|| = (χ2 + у2)1/2 и
||^)(ν)|| = \φ(χ, у)\. В этом случае условие (5.3) можно прочитать
следующим образом:
Для любого заданного значения ε > 0 существует
такая величина δ > 0, что неравенство
\φ(χ,υ)\<ε(χ2 + υ2γ/2
выполняется для всех хну, удовлетворяющих
условию
(χ2+ν2γ/2<δ.
Функцию φ : V —> W, определенную в малой окрестности
вокруг начала координат, удовлетворяющую условию (5.3),
называют «"о" малое от ν». Символически мы говорим «0 есть ο(ν)»
или, несколько злоупотребляя обозначениями, пишем φ = ο(ν).
Теперь условие того, что А является производной функции / в
точке х, можно записать в виде
/(χ + ν)-/(χ) = Αν + <Κν),

5.1. «О» большие и «о» малые
249
где φ(ν) есть ο(ν), или φ(ν) = ο(ν), или более кратко:
/(χ + ν)-/(χ) = Λν + ο(ν). (5.4)
С точки зрения логики этот вариант записи слегка хромает, но
из соображений удобства мы будем его часто использовать. Член
ο(ν) в формуле (5.4) на самом деле обозначает «некоторую
функцию φ(ν), являющуюся ο(ν)». Очень часто остаточный член φ
нас не будет интересовать, нам достаточно будет знать, что он
удовлетворяет условию (5.3). Именно поэтому удобно не вводить
отдельный символ для каждой подобной функции ф.
Чтобы прочувствовать понятие ο(ν), давайте докажем лемму:
Предположим, что φ : V -^>W — линейное преобразование и что
ф(у) = o(v). Тогда
ф = 0. (5.5)
Доказательство. Ввиду линейности φ для любого вещественного
числа г справедливо равенство φ{τν) = νφ(ν). Для любого ε > О
выберем такое δ, чтобы выполнялось неравенство ||^(ν)|| < ε||ν||,
когда ||ν|| < δ. Теперь для произвольного вектора w φ 0 выберем
г = ||w||/5 и запишем
w = rw'.
Тогда ||w'|| = δ, следовательно,
||^(w)|| = r||^(w')|| < re||w'|| = ετδ = e||w||.
Итак, для каждого w φ 0
№(w)|| <e||w||
(очевидно, что ввиду линейности φ это справедливо и для w = 0).
Но это неравенство должно выполняться для всех ε.
Следовательно, φ = 0.
Из леммы следует, что если справедливо равенство (5.4), то
производная А, стоящая в нем, определена однозначно.
Действительно, предположим, что
/(χ + ν) - /(χ) = Αν + φ(ν)

250 Глава 5. Дифференциальное исчисление на плоскости
и
/(x + v)-/(x) = A'v + 4>'(v),
где и φ и ф' являются ο(ν). Тогда
(Α'-Α)ν = φ(ν)-φ'(ν).
Но мы утверждаем, что сумма или разность двух функций,
каждая из которых есть ο(ν), тоже является функцией ο(ν).
Действительно, для любого ε > 0 можно найти такие δι > 0 и fo > 0,
чтобы выполнялись неравенства
1№(ν)|| < 2ε\\ν\\ Для llvll ^ *ι
и
μ'(ν)||<^|ΜΙ Для ||ν||<ί2.
Теперь, выбрав δ, равное наименьшему из двух чисел δι и #2, из
неравенства треугольника мы получаем при ||ν|| < δ
\\Φ(ν)±φ'(ν)\\<\\φ(ν)\\ + \\φ'(ν)\\<ε\\ν\\.
Мы получили, что линейное преобразование А' — А есть ο(ν)
и, следовательно, является тождественно нулевым, т. е. А = А'.
Повторим, что отображение /, удовлетворяющее условию
(5.4) для некоторого (единственного) А называется
дифференцируемым в точке х. В этом случае линейное преобразование А
называется дифференциалом / в точке χ и обозначается dfx.
Повторяем еще раз: дифференциал / в точке χ есть единственное
линейное отображение V на W, которое аппроксимирует
истинное изменение отображения / в точке χ для малых ν, что может
быть записано как
/(x + v)-/(x) = d/x[v]+o(v).
Для того, чтобы доказать основные теоремы
дифференциального исчисления, нам необходимо собрать сведения о функциях,
которые попадают в категорию o(v). Для этого удобно ввести
следующие обозначения.

5.1. «О» большие и «о» малые
251
Подпространство 5 пространства V называется
окрестностью нуля, если оно содержит некоторый шарик с центром в
начале координат, т. е. если для некоторого δ > 0 оно содержит
множество всех ν, удовлетворяющих условию ||ν|| < δ. Очевидно,
что пересечение двух окрестностей тоже является окрестностью
(просто возьмем меньший из двух шариков, он находится в
пересечении). Точно так же можно говорить об окрестности любой
точки х. Это будет множество, которое содержит некоторый
шарик вокруг точки х, т. е. содержит множество {у | ||у — х|| < δ}.
Если А — обратимое линейное преобразование из V в W (V и
W имеют одинаковую размерность), тогда можно найти
константы fci и fc2 > 0, для которых выполняются неравенства
||Av|| < fci||v|| и ||A_1w|| < fc2||w||,
или, положив w = Αν, неравенство
fc^HvH < ||Λν||.
Таким образом, образ шарика с радиусом г содержится в шарике
с радиусом k\r, внутри которого содержится шарик с радиусом
Щ г (рис. 5.4). В частности, А преобразует окрестности в
окрестности, этим же свойством обладает А~1.
Рис. 5.4
Давайте рассмотрим общий случай, когда размерности V и
W не совпадают. Введем обозначение o(V, W) для пространства

252 Глава 5. Дифференциальное исчисление на плоскости
функций, попадающих в категорию o(v), т. е. функция φ
принадлежит o(V, W), если φ = ο(ν). Более подробно: φ € o(V, W), если
φ определена в некоторой окрестности вокруг начала координат
и удовлетворяет условию (5.3).
Функция ψ принадлежит категории Ο(ν) (следует читать *ψ
есть "О" большое от ν»), если она определена в некоторой
окрестности 0 и существует такая постоянная к > О, для которой
неравенство
l№(v)||<fc||v||
справедливо для любого ν в этой окрестности. Например,
линейное отображение автоматически является Ο(ν). Очевидно, что
любая функция, попадающая в категорию ο(ν), заведомо
является Ο(ν). Пусть 0(V,W) обозначает пространство всех функций,
попадающих в категорию O(v), и пусть J(V, W) обозначает
пространство функций, определенных вблизи 0 и стремящихся к О
при ν —► 0. Иначе говоря,
χ € I(V, W), если χ определена в некоторой
окрестности вокруг начала координат и для каждого значения
ε > 0 существует такое значение δ > 0, что
||χ(ν)||<ε, когда ||ν|| < δ.
Очевидно, что
o(V, W) С 0(V, W) С I(V, W).
Если, например, мы возьмем V = W = R1 и определим ф(х) = х2,
ф{х) = χ и χ(χ) = l^l1/2, то
φ£ο(ν,\¥),
il>GO(V,W), но ψ£ο(ν,\ν)
и
Xel(V,W), но xtO(V,W).
Следовательно, выписанные выше включения — строгие.
Выше мы доказали, что сумма двух функций, являющихся
o(V, W), по-прежнему попадает в категорию o(V, W). Аналогично

5.1. «О» большие и «о» малые
253
доказывается, что сумма двух функций, являющихся 0(V,W),
также есть 0(V, W). То же — для I(V, W).
Рассмотрим поведение этих пространств при композиции.
Пусть X обозначает третье пространство. Докажем следующие
утверждения.
Если φι € 0(V, W) и ф2 € 0{W,X), το φ2οφι € 0{V,X). (5.6)
Если ^i€0(V,W) и ф2€о(\¥,Х), то φ2οφι е o(V,X). (5.7)
Если ^i€o(V,W) и φ2€θ{\¥,Χ), το ψ2°ψι £ o(V,X). (5.8)
Доказательство. Если ||ι/Ί(ν)|| < ^ι|ΙνΙΙ Для llvll < ^1 и
ll^iw)!! < fc2||w|| для ||w|| < δ2, то композиция ф2 о φι будет
определена для ||ν|| < δ, где δ есть меньший из двух параметров
δι и δ2/Ηι. Для таких ν мы имеем
||V>2°Vi(v)|| = №2(^1 (ν))|| < fc2||Vi(v)|| < fcafciH,
что доказывает (5.6). Если ф2 € o(W, X), мы можем сделать &2
сколь угодно малым, выбирая δ2 (и, следовательно, δ) малым.
Это доказывает утверждение (5.7). Если φι € o(V,W), то мы
можем сделать сколь угодно малым значение hi, выбирая δι (и,
следовательно, δ) достаточно малым, что доказывает (5.8).
Если φ — отображение изУв\¥ид: V—>M.— функция с
вещественными значениями, то произведение ρ(ν)φ(ν) имеет смысл
только для тех ν, которые лежат в пересечении областей
определения φ и д. Так получается функция дф, которая отображает V
naW.
Если φ G 0(V,W) и де1(уЛ), то дф € o(V,W). (5.9)
Доказательство. Мы знаем, что существует такое значение
к, для которого Hi/H^OH ^ ^llvll B некоторой окрестности вокруг
начала координат. Задав произвольное значение ε > 0, выберем
δ настолько малым, чтобы ||ρ(ν)|| < ε/к для всех ν при условии
||ν|| < δ. Тогда для таких ν
\\дШЫ\\<Ш\\ФМ\\<Ф1

254 Глава 5. Дифференциальное исчисление на плоскости
что и доказывает утверждение (5.9). Аналогично доказываются
следующие утверждения.
Если ipeI(V,W) и деО(У,Щ, то gipGo(y,W). (5.10)
Если φ € o(V, W) ид — ограниченная функция из V —► R, то
gipeo(V,W). (5.11)
Если отображение ψ из V в W, определенное в некоторой
окрестности вокруг начала координат, ограничено и д € o(V,R), то
<^€o(V,W). (5.12)
(Когда мы говорим, что отображение ψ : V —► W ограничено, это
значит, что существует некоторое положительное вещественное
число fc, такое, что HVK^OIIw < ^ для всех ν из V.)
Итак, мы собрали все необходимые леммы, чтобы приступить
к изучению дифференциального исчисления.
5.2. Дифференциальное исчисление
Пусть / : V —► W определена в некоторой окрестности точки
χ € V. Определение функции Vx/ дается формулой
Vx/(h) = /(x + h)-/(x).
Она определена для всех значений h в некоторой окрестности
О и показывает изменение / относительно ее значения в точке
х. Функция / непрерывна в точке х, если Vx/ € I(V,W). (Это
значит, что Vx/(h) стремится к 0 при h —► 0, так что /(х + h) —►
/(χ).) Напоминаем, что функция / дифференцируема в точке х,
если существует линейное преобразование ci/x : V —► W такое,
что
Vx/(h) = d/x[h]+o(h).
Это уравнение единственным образом определяет линейное
преобразование ci/χ, называемое дифференциалом / в точке х.
Любая линейная функция относится к категории 0(V,W); сумма

5.2. Дифференциальное исчисление
255
функции типа 0(V, W) и функции типа o(V, W) тоже относится
к 0(V, W). Отсюда можно сделать вывод:
если / дифференцируема в точке х, то Vx/ € 0(V, W). (5.13)
(В частности, из того, что 0(V, W) С I(V, W), следует, что если
функция / дифференцируема в х, тогда она обязательно
непрерывна в точке х.)
Если / — линейная функция, т.е. /(х) = Ах, то Vx/[h] =
А(х + h) — Ах = Ah. Следовательно, линейная функция /(х) =
Ах дифференцируема во всех точках. Ее дифференциал дается
формулой d/χ = А и не зависит от х.
Если / — постоянная функция, то Vx/ = 0 и формула (5.4)
справедлива при А = 0. Следовательно, постоянная функция
дифференцируема везде, и ее производная тождественно равна
нулю.
Теперь мы можем сформулировать и доказать .правило
вычисления дифференциала суммы двух функций.
Если / и д — две функции из V на W, и обе функции
дифференцируемы в точке х, то дифференциал суммы равен
d(f + g)* = dh + dg*. (5.14)
Доказательство. Очевидно, что Vx(/ + 9) — Vx/ + Vx5- Из
того, что
Vx/= <#х + <£ι и Vx5 = d9x + ^2,
где ф\ и 4>2 — функции типа o(V,W), следует, что
Vx(/ + 9) = 4fx + <*Ях + Φι + Φι-
Так как (φι + (fo) € o(V, W), формула (5.14) доказана.
Если мы умножим функцию д, значения которой
принадлежат R, на функцию /, значения которой принадлежат W, то
получим функцию, значения которой принадлежат W.
Сформулируем правило вычисления производной произведения функций.
Предположим, что /: V —> W и д : V -^Ш дифференцируемы в
точке х. Тогда произведение gf тоже дифференцируемо в точке
χ и
<%/)x[h] = S(x)#x[h] + (dffx[h])/(x).

256 Глава 5. Дифференциальное исчисление на плоскости
Доказательство.
Vx(s/)[h] = 5(х + h)/(x + h) - р(х)/(х)
= р(х + h)(/(x + h) - /(χ)) + (р(х + h) - р(х))/(х)
= р(х)(/(х + h) - /(χ)) + (р(х + h) - р(х))/(х)
+ (5(x + h)-p(x))(/(x + h)-/(x))
= р(х) Vx /И + (Vx5[h])/(x) + (VxS[h])(Vx/[h])
= 5(x)(d/x[h]+o(h)) + (d5x[h])+o(h))/(x)+0(h)0(h),
так как / и д дифференцируемы в точке χ и, следовательно, оба
дифференциала Vx/ и 4x9 суть o(h) из (5.13). Из (5.9) следует,
что произведение двух функций типа o(h) есть функция типа
o(h). Обе функции / и д ограничены вблизи х, т. е. g(x + h) — ρ (χ)
и /(χ + h) — /(x) стремятся к нулю. Произведение ограниченной
функции и функции типа o(h) есть тоже функция типа o(h).
Используя это в последнем равенстве, получаем
Vx(s/)[h] = 5(x)d/x[h] + (dflx[h])/(x) + o(h),
что и требовалось доказать.
А теперь сформулируем очень важную теорему.
Цепное правило. Предположим, что / : V —► W
дифференцируема в точке xS7hj:W-»I дифференцируема в точке
у = /(х) € W. Тогда д о / : V —> X дифференцируема в точке χ
и ее дифференциал определяется формулой:
4о/)х = (%х))'Ш· (5.15)
(В правой части этого выражения стоит композиция двух
линейных преобразований: dpy(x) : W -^ X и dfx : V —► W. В левой
части стоит композиция д и /.)
Доказательство.
Vx(W)[h]=5(/(x + h))-5(/(x))
= s(/(x) + Vx/[h])-5(/(x))
= V/(x)5[Vx/[h]]
= d5/(x)[d/x[h]] + dgf{x)[o[h}} + (φ ο V>)(h),

5.2. Дифференциальное исчисление
257
где φ ζ o(V, X) (происходит от остаточного члена в V/(x)5)j a
Ψ = Vx/ € 0(V,W), что следует из (5.13). Согласно (5.8), эта
композиция относится к категории o(V,X). Кроме того, d<?/(x)
линейна и, следовательно, относится к категории 0(W,X).
Таким образом, второе слагаемое есть композиция элемента типа
0(W, X) и элемента типа o(V, W). Согласно (5.7) эта композиция
имеет тип o(V,W). Поэтому
Vx(5 о /)[h] = (dgf{x) о d/x)[h] + o(h),
что и требовалось доказать.
Примеры
Приведем несколько примеров на вычисление
дифференциалов и на цепное правило. Для функций а : R1 —► R1
дифференциал dax, вычисленный для h € R, определяется умножением на
производную а'(х), т.е.
dax[/i] = a'(x)h.
Это выражение является определением производной а'(х).
Например, пусть а : R1 —► R1 и β : R1 —► R1 имеют вид
<*(у) = гЛ β(χ) = 5х3 +1,
так что
αοβ(χ) = (5χ3 + 1)2.
Тогда
da.y соответствует умножению на 2у,
άβχ соответствует умножению на 15х2,
d(a о β)χ соответствует умножению на 2(5х3 + 1)(15х2).
В соответствии с цепным правилом dap^ о άβχ = d(a о β)χ.
Поэтому мы имеем:
^а/3(х) соответствует умножению на 2(5х3 + 1),
άαβ/χ\ ο άβχ соответствует умножению на 15х2, а потом
на 2(5х3 + 1), или
da0(x) ° άβχ соответствует умножению на 2(5х3 + 1)(15х2).

258 Глава 5. Дифференциальное исчисление на плоскости
Очевидно, что эти обозначения довольно громоздкие.
Обозначения Лейбница для функций одной переменной лучше.
Если α — функция от у, то ее производная записывается как
а = —— или аа = а dy.
dy
Последнее равенство показывает, что для каждого значения у
day(h) = a'(y)h.
Другими словами, dy является фиктивным символом, вместо
которого мы подставляем значение h. Тогда
d(y2) = 2у dy, d(5x3 + 1) = 15х2 dx.
Согласно цепному правилу, подставляем
у = (5х3 + 1) и dy = 15х2 dx
в формулу для d(y2) и получаем выражение для d[(5x3 + I)2]. В
обозначениях Лейбница цепное правило становится механической
подстановкой.
Мы, тем не менее, продолжим вычисление других
примеров в наших, более громоздких обозначениях, надеясь прояснить
смысл выполняемых операций.
Пусть / : R1 —► R2 и д : R2 —► R1 определены формулами
Чтобы вычислить dfx, заметим, что
Vxf[s] = f(x + s)-f(x)
= HI + ( о )
Таким образом, dfx представляется матрицей d/:
(?)·

5.2. Дифференциальное исчисление
259
Аналогично,
Ч(у)9
(ж + s)2{y + ί) - х2у
= x2t + 2sxy + 2sxt + s2y + s2t
поэтому матрица для dgtx\ имеет вид
d9(x) = (2ху,х2).
Композиция д о / : R1 —> R1 дается формулой
ρο/(χ) = (χ2 + 1)2(2χ-1),
так что
d(g о f)x = 2(х2 + 1)(2ж)(2ж - 1) + 2(х2 + I)2.
Согласно цепному правилу, это выражение должно быть
равно матричному произведению cip/(x) о dfx. Действительно,
<%(*) ° dfx = (2(х2 + 1)(2х - 1), (х2 + I)2) (2*\
= 2(х2 + 1)(2х - 1)(2х) + 2(х2 + I)2,
а это равняется d(g о f)x.
Мы можем также построить композицию этих функций в
другом порядке, / о д : R2 —» R2, определяемую формулой
Подробно вычислим d(f о д)/ху.
V(S)(/°5) (WJ = (2(x + ,)2(y+i) - ij - [Jy- \

260 Глава 5. Дифференциальное исчисление на плоскости
(z4 + 4x3s + 6x2s2 + 4xs3 + s4)(y2 + 2yt + t2) - x4y2
2(x2 + 2xs + s2)(y + t)- 2x2y
(2x4yt + 4x3y2s
\ 2x2t+4xys
fxH2 + 4x3s(2yi + i2) + (6zV + 4xs3 + s4)(y + i)2
\ 4xst + s2y + s2t
fW Уу)(8^+0((*
\ ixy 2xz J \tj \\t
Следовательно,
,,. , /4x3y2 2x4y\
d{f °9\y) = { ixy 2x2)
Согласно цепному правилу, это должно быть равно df (/χ\\ °
dg/x\, определяемому формулой
df9((Xy))°d9(Xy)={2X2y)(2Xy>x2)
4х3у2 2х4у
4ху 2х2
Как и следовало ожидать, мы получили ту же матрицу.
Еще один пример на цепное правило. Пусть F : R2
G : R2 —► R2 заданы формулой
х\\ fx2 + y\ g((X^ = (Зху2
У )) \ ху ) ' \\1/// V х
Вычислим дифференциалы отображений F и G в отдельности.
Для отображения F имеем
V7x F((*\i-((* + *)2 + l3l + t)\ (Х2+У\
Ч(У)ГЬ))~\ (x + s)(y + t) )-\ ху )
_ f2xs + t\ is2
\xt + sy) \st
'ϊί)(;)4;

5.2. Дифференциальное исчисление
261
откуда
Аналогично,
V(v)G((
откуда
для от
;))
Композиция
Fc
■°(
1 =
=
=
Fo
I:
лр (2х
dF(x\ =
Ы V У
i)
ображения G имеем
fS(x + s)(y + t)2
V (х + s)2
(Ssy2 + Sxy(2t)\
\ 2xs J
/32/2 6ху\ (s\
\2х 0 J \t)
dG(y) = \2х
)-
>♦(
+ 0
бху
0
G : R2 -» R2 задается
/9x2y4+x2
~ 1 Эх3?/2
-(
)·
ο?)
'3xi2 + 3s(22/i + i2)\
J
(С))·
)·
формулой
(Зх2/2)2 + х2\
Зх2/2а;2 /
Найдем дифференциал композиции F о G.
9х22/4 + χ2
Эх3?/2
'9(x + s)2(2/ + i)4 + (x + s)2N
3(x + s)3(2/ + i)2
'9(2zs)2/4 + 9χ2(42/3ί) + 2xs4
3(3x2s)2/2 + 3x3(22/i)
/9χ2(62/2ί2 + 4yi3 + 4i) + l8xs[(y + 1)4 _ y4] + gs2(y + ^4
+ V 3x3i2 + 3(3xs2 + s3)(2/ + i)2 + 9x2s(2yt + t2)
_fl8xy4 + 2x 36x2y3\fs\ ((V
"V 9x22/2 ^y )\t)+0\ti
Отсюда
/18х2/4 + 2х 36x22/3N
у 9х22/2 6x32/
d(FoGf)(*)

262 Глава 5. Дифференциальное исчисление на плоскости
Согласно цепному правилу, это должно быть равно dFQiix\\ о
dGix\. Проверяем:
\у)
dFo((Xy))°dG(Xy) = { х2 Зху2)\2х 0
18ху4 + 2х 36x2y3'
3x2y2 + 6x2y2 6x3y
= d(FoG)Cyy
В следующих параграфах мы займемся некоторыми
важными следствиями цепного правила. Но сначала рассмотрим еще
несколько более «абстрактных» примеров на применение
цепного правила и введем несколько обозначений.
5.3. Примеры на цепное правило
Рассмотрим отображение умножения д : R2 —► R1, заданное
формулой
Если ν = ( ) и h = I |, то
.У/ Vs,
g(v + h) = (χ + r)(y + s) = xy + xs + yr + rs
= g(v) + xs + yr + o(h).
Откуда
dgv(h) =xs + yr,
а соответствующая матрица (с одной строкой и двумя столбцами)
равна
(у, χ)·
Пусть задано отображение / : R1 —► R2. Его можно изобразить
как кривую на плоскости или, что проще, представить как две
вещественных функции от одной вещественной переменной, т. е.

5.3. Примеры на цепное правило
263
Тогда
ш , м _ М* + Ь) \ (x(t) + x'(t)h + o(h) \
S{t+ > - \y(t + h)J - \y(t) + y>(t)h + o(h))>
следовательно,
/(* + Л)-/(*) = л(^[*)))+о(Л),
или
fit) = (x'{t)
Умножение матрицы
dgm = (y(t),x(t)) на df* = /'(*) = (y'(J)
дает
d(g о f)t = (d ο /)'(ί) = x'(t)y(t) + x(t)y'(t).
Ho (g ο /)(ί) = x(t)y(t). Таким образом, в этом случае цепное
правило можно истолковать как применение формулы Лейбница
для производной от произведения двух функций.
Прежде чем двигаться дальше, удобно ввести некоторые
новые обозначения. Вместо того, чтобы писать
dgv(h) = уг + xs, где ν= (Х) , h=iM, g (ίζ j\ = xy,
удобно всю информацию заключить в формулу
d{xy) = ydx + xdy.
В этом уравнении символ dx в правой части следует понимать как
линейное отображение R2 —► R1: отображение, приписывающее
каждому вектору его первую координату. Итак,
dx(h) = г, если h = I
и аналогично
dy(h) = s.

264 Глава 5. Дифференциальное исчисление на плоскости
В выражении у dx символ у — это функция вектора ν, приписыва-
ющая вектор, ν - β) его вх„рую координату. Следовательно,
члены типа у dx зависят от переменных двух типов, от
переменной ν, говорящей нам, где вычисляется производная, и от
переменной h, являющейся мерой небольшого отклонения. Стоящее
в левой части формулы выражение d{xy) есть краткая запись
dgv, где функция д определяется условием д (ν) = ху для
вектора ν — I ). Используя цепное правило по аналогии с первым
примером, мы говорим:
Рассмотрим χ как функцию1 в пространстве R2,
которая каждому вектору приписывает его первую
координату. Тогда, по определению нашего отображения
/, можно написать (хо/)(() = x(t). Согласно цепному
правилу, d((x о f)t = x'(t) dt, функция x'(t)
вычисляется в той точке ί, где требуется найти
дифференциал, dt определяет малое приращение. Следовательно,
когда мы рассматриваем χ как функцию t, заданную
отображением /, мы производим «замену» dx = χ' dt,
где χ' зависит от t. Аналогично, если мы
рассматриваем у как функцию от ί, задаваемую отображением /,
цепное правило приписывает нам сделать подстановку
dy = y'dt.
Тогда можно написать
d{g ° /) = ух' dt + ху' dt,
где справа величины х,у, х' и у' следует заменить явными
функциями от t.
Например, положим x(t) = t + sini, y(t) = e2t. Тогда
dg = d(xy) = ydx + xdy, df = d Ι β? J = ί ^f J dt
1 Вероятно, полезно еще раз прочитать то место в параграфе 1.3, где
подробно обсуждается, как координату χ молено рассматривать в качестве
функции.

5.3. Примеры на цепное правило
265
и
d(gof) = d((i + sini)(e2i)) = (e2i(l + cosi) + 2e2i(i + sin*)) dt.
Давайте изобразим цепное правило на диаграмме (рис. 5.5).
Нам даны два дифференцируемых отображения / : V —> W и
д : W —► Z, из которых можно составить композицию д о / : V —►
Z. На некоторую точку ν в пространстве V действуем
отображением / и получаем /(ν), потом действуем отображением д и
получаем ρ(/(ν)). При вычислении дифференциала d(g о /)v(h)
мы можем двигаться последовательно, сначала подействовав
линейным отображением dfv на вектор h и затем подействовав
линейным отображением cip/(v) н& полученный образ.
9°f
Рис. 5.5
А теперь давайте выполним более сложные вычисления с
цепным правилом. Рассмотрим векторные пространства V,W и т.д.
большого числа измерений. Конечно, формально говоря, нам бы
следовало отложить эти вычисления, пока не изучен
соответствующий раздел линейной алгебры. Но мы, тем не менее,
рекомендуем разобрать их сейчас. Начнем с вычисления производной от
произведения двух матриц. Пусть V есть векторное
пространство, образованное парами матриц η χ п. Вектор в таком
пространстве имеет вид
-(5)·

266 Глава 5. Дифференциальное исчисление на плоскости
где А и В — матрицы размера пхп. Векторы в этом пространстве
складываются и умножаются на скаляр покомпонентно.
Если ν = ί β J Ην'=ίβ/
то v + v=^ + 5#j и av=l^aB
Очевидно, что пространство V имеет размерность 2п2.
Пусть W обозначает другое векторное пространство матриц
размером пхп. Определим отображение д : V —> W формулой
Если v= Uh= L· ,то
5(v + h) - д(у) = (А + Х){В + Y)-AB
= ХВ + AY + XY = ХВ + AY + o(h).
Следовательно,
dgv(h) = Χ Β + AY. (5.16)
В процессе вычислений будем для удобства пользоваться
обозначениями, где опущены индекс ν и аргумент h. Тогда уравнение
(5.16) имеет вид
d(AB) = (dA)B + A(dB). (5.17)
В этих обозначениях величина АВ в левой части уравнения —
это удобное обозначение функции д. Величина dA справа есть
производная функции, кохорая векхор, (*) c« в _
ствие матрицу А. Эта производная, вычисленная в точке I
для вектора I v J дает значение X. Таким образом, dA —
линейное отображение, которое каждому вектору I v ) ставит в
соответствие величину X. Поэтому, например, (dA)B есть линейное

5.3. Примеры на цепное правило
267
отображение, которое вектору Ι ν I ставит в соответствие
значение ХВ. В этом смысле уравнение (5.17) есть краткая запись
уравнения (5.16).
Далее, пусть / обозначает отображение из W в V согласно
формуле
f(A)=U^
A J ■
Так как / — линейное отображение, то его производная не
зависит от А, является линейным отображением, и вычисление дает
dfA(X) = (*
В дифференциальных обозначениях это следует записать так:
А\ (dAs
d\Aj ~ \dA
где опять dA — линейное отображение, которое любому элементу
X ставит в соответствие значение X.
А теперь рассмотрим отображение h:W—* W, определяемое
формулой
h(A) = A2.
Очевидно, что h(A) = g(f(A)) или h = д о /. Действие цепного
правила в этом случае изображено на рис. 5.6.
W ^ ХА+АХ
Рис. 5.6
Это значит, что
dhA(Z) = d(gof)A(Z) = dgf{A)(dfA(Z)) = dgm (ΐ) = ZA+AZ.

268 Глава 5. Дифференциальное исчисление на плоскости
Мы могли бы записать эту выкладку в «дифференциальных»
обозначениях, а именно, в уравнении (5.17) сделаем «замены»:
А = АиВ = А. В результате получаем
d(A2) = (dA)A + A(dA).
(Отметим еще раз: вследствие некоммутативной природы
матричного умножения эта формула дает правильное обобщение
формулы d(x2) = 2xdx. Формула d(A2) = 2AdA неверна!)
Разложение Борна
Рассмотрим отображение (inv), которое каждой обратимой
матрице ставит в соответствие ее обратную, т. е.
(inv)(A) = А~\
Отображение (inv) определено только на подмножестве W,
состоящем из всех обратимых матриц. Предполагая, что (inv)
дифференцируемо в области определения, покажем, как вычислять
производную (inv), используя цепное правило. Пусть
отображение / задано формулой
или, символически,
_ / (id) \
J-\(inv))·
Напоминаем, что отображение д, как и выше, определено
формулой
Тогда (gof)(A) = ΑΑ~λ = I, где I — единичная матрица. Другими
словами, композиция gof постоянна и, следовательно, d(gof) = 0.
Согласно цепному правилу,
dfA(x)-(dA{id){x))-( х λ
<УА{Л) - ydA{inv){X)J - \d(inv)A(X)) ■
Воспользуемся цепным правилом еще раз:
0 = [df{A)9](dAf(X)) = ΧΑ-1 + A(dA(inv)(X)).

5.3. Примеры на цепное правило
269
Умножая это уравнение слева на А 1 и решая его относительно
da (inv) (X), получаем
dA{inv){X) = -Α'1 ΧΑ'1.
В дифференциальных обозначениях эта процедура записывается
следующим образом. Так как АА~1 = I, мы имеем d{AA~l) = 0.
Заменяя А и А~1 на А и В в формуле d(AB) = {dA)B + A{dB),
получаем
0 = d{AA~l) = {dA)A~1 + Ad{A~1).
Решая это уравнение относительно d{A~1), получаем формулу
d(A-1) = -A-\dA)A-1. (5.18)
(Соотношение (5.18) дает правильное обобщение формулы
дифференциала d(l/x) = —(l/x2)dx на случай матриц.) Дадим
немного другое объяснение формуле (5.18). Предположим, что
А — обратимая матрица, т. е. Det А ф 0. Тогда, если X является
матрицей, элементы которой достаточно малы и Det(A + X) φ Ο,
то матрица А + X тоже обратима. В этом случае можно написать
А + X = (I + ХА~1)А.
Если X достаточно мала, то матрица ХА~1 тоже будет малой и
ряд
(I + ΧΑ'1)'1 = I - (ΧΑ'1) + (ХА~1)2 - (XA~lf + ■■■
будет сходиться. Тогда мы получим
{А + Χ)'1 = [(I + ΧΑ-ι)Α]-λ = A-\l + ΧΑ-1)-1
= A'1 {I - {ΧΑ'1) + {ΧΑ'1)2 )
или
{А + Χ)'1 = А'1 - Α'1 Χ А'1 + А'1 X А'1 X А'1
- Α'1 ΧΑ'1 ΧΑ'1 ΧΑ'1 + ■■■ .

270 Глава 5. Дифференциальное исчисление на плоскости
В физической литературе этот ряд называется борновским
разложением по имени известного физика-теоретика Макса Борна.
Формула (5.18) получается из разложения Борна, если опустить
все члены более высокого порядка малости, чем X. В физической
литературе формула (5.18) известна как первое борновское
приближение, играющее чрезвычайно важную роль в теории
рассеяния. Как мы уже показали, нам не надо знать все борновское
разложение для получения первого борновского приближения. Его
можно получить непосредственно из цепного правила.
С другой стороны, разложение Борна означает, что
(А + Χ)'1 - А'1 = -А~1ХА~1 + о(Х).
Это доказывает, что функция (inv) дифференцируема. Именно
это нам пришлось предположить, когда мы применяли цепное
правило.
Пусть В — постоянная матрица. Рассмотрим отображение
f(A) = ABA'1. Тогда
d{ABA~l) = (dA)BA~1 + AB{dA~l)
= {dA)BA~l - ABA~\dA)A-\
Это можно записать по-другому:
dAf(X) = X В А'1 - ΑΒΑ'1 Χ Α'\
Предположим, что t —> A(t) есть некоторая дифференцируемая
кривая в пространстве матриц. Пусть
C{t) = A(t)BA(t)-\
где В — постоянная матрица. Кроме того, предполагаем, что A(t)
обратима для всех ί. Применяя цепное правило и предыдущие
формулы, получаем
C'(t) = A'i^BAit)'1 - A(t)BA(t)A'(t)A(t)-\
Допустим, что А(0) = I и А'(0) = X. Тогда, полагая t = 0 в
предыдущей формуле, имеем
С'(0) = ХВ- ВХ.

5.3. Примеры на цепное правило
271
Это весьма важная формула в математике и физике. Правая
часть называется коммутатором матриц X и В и обозначается
[Х,В],т.е.
[X, В] = ХВ- ВХ.
В качестве примера возьмем A(t) = expiX. Тогда
A(t) = I + tX + -t2X2 + ■ ■ ■ .
Δ
Очевидно, что А(0) = I и А'(0) = X, поэтому можно
воспользоваться полученной формулой. Итак, мы имеем
Ait)'1 = (expiX)"1 = exp(-tX) =I-tX + \t2X2 + ■■■ ,
Δ
поэтому
A{t)BA{t)~l = (I + tX + \t2X2 + ■■■ )B(I -tX + \t2X2 + ■■■)
Δ Δ
= B + t(XB - ВХ) + \t2{X2B - 2XBX + ВХ2) + ■■■ .
Собрав вместе члены порядка два и выше по ί, получаем
A(t)BA(t)~l = B + t[X, В] + o(t).
Движение Кеплера
Мы уже видели, что цепное правило влечет правило Лейбница
для производной произведения, причем это верно и для
произведения матриц, когда операция умножения не обладает свойством
коммутативности. Давайте используем ту же аргументацию для
векторного произведения в пространстве R3. (Сейчас мы
напомним это определение.) В качестве следствия мы получим второй
закон Кеплера, описывающий движение планет.
В трехмерном пространстве векторное произведение
определено следующим образом:
Если ν = \ у I и w =
Р\
q)
г
, то
V X W =
lyr-zq
1 zp — xr
\xq-yp

272 Глава 5. Дифференциальное исчисление на плоскости
Из этого определения вытекают свойства векторного
произведения:
(V1+V2) XW = Vi XW+V2 XW, VX (W1+W2) = V XW1+VXW2,
(αν) х w = ν χ (aw) = α(ν χ w) и ν χ ν = 0.
Из первых трех уравнений следует, что знак « χ» действует как
знак умножения. Можно доказать, что
d(v xw)=dvxw + vx dw.
В частности, если ν(ί) и w(i) — кривые в пространстве R3, и если
мы положим
u(i) = ν(ί) х w(i),
то
u'(i) = ν'(ί) χ w(i) + ν(ί) χ w'(i).
Допустим, что r(i) обозначает положение частицы в момент
времени ί, и пусть ρ(ί) обозначает импульс этой частицы в
момент t. Тогда вектор
μ(ί) = ρ(ί) Χ r(i)
называется угловым моментом частицы относительно начала
координат (в момент времени ί). Предположим, что частица имеет
массу т, и на нее действует сила F(i) = c(i)r(i), направленная
вдоль вектора, идущего от начала координат к частице.
Поскольку r(i), ρ(ί) и F(i) связаны формулами
r'(i) = (l/m)p(t) и ρ'(ί) = F(i) = c(i)r(i),
то
μ'(ί) = ρ'(ί) χ г + ρ(ί) χ r'(i)
= c(i)r(i) χ r(i) + (l/m)p(t) x ρ(ί) = 0.
Другими словами, вектор μ должен быть постоянным. Этот
закон называется законом сохранения углового момента. Для
простоты предположим, что μ φ 0. Из определения векторного
произведения легко показать, что для любых векторов ν и w
выполняется соотношение (ν χ w) · w = 0. Так как μ = ρ(ί) χ r(i), мы

5.3. Примеры на цепное правило
273
получаем, что μ ■ r(i) = 0 для всех значений ί. Другими словами,
частица всегда двигается в фиксированной плоскости, которая
перпендикулярна вектору μ. В пространстве R3 повернем
систему координат так, чтобы μ был направлен вдоль оси ζ, тогда
частица будет двигаться в плоскости ху. Итак,
r(i) = y(t) , тогда ρ(ί) =
О
и μ = πι Ι 0
x'(t)y(t)-x(t)y'(t)
Таким образом, условие сохранения μ значит, что выражение
x'(t)y(t) — x(t)y'(t) постоянно. Чтобы понять смысл этого
условия, нарисуем траекторию частицы в плоскости ху (рис. 5.7).
С точностью до членов o(h) область, ограниченная траекторией
fx(t)\ fx(t + h)\
Ι , ( Ι и вектором I ) Л I, совпадает с площадью
треугольника
fx(t)\ fx(t + h)\
, построенного на векторах I ) ( I и I ) , Μ, т. е. с этой
точностью мы можем пренебречь площадью, заштрихованной на
рис. 5.7.
r(i + h)
Рис. 5.7
С точностью до знака площадь треугольника равна
^(x(t + h)y(t)-x(t)y(t + h)).

274 Глава 5. Дифференциальное исчисление на плоскости
Но
x(t + h) = x(t) + hx'(t) + o(h) и y(t + h) = y(t) + hy'(t) + o(h).
Тогда площадь треугольника равна
l-(x'(t)y(t)-x(t)y'(t))h + o(h).
Это значит, что скорость изменения площади, описываемой
радиусом-вектором движущейся частицы, постоянна. Так
формулируется второй закон Кеплера. Используя цепное правило, мы
видим, что второй закон Кеплера и то, что частица движется в
фиксированной плоскости, является результатом действия силы,
направленной вдоль ее радиуса-вектора. Тот факт, что движение
планет происходит в фиксированных плоскостях и за равные
промежутки времени их радиусы-векторы описывают равные
площади, определяется тем, что действующая на них сила направлена
к Солнцу. Изложенный вывод второго закона Кеплера
принадлежит Ньютону.
5.4. Частные производные
и дифференциальные формы
В этом параграфе мы введем понятия и обозначения, удобные для
применения цепного правила. Рассмотрим дифференцируемую
функцию / : Шк —► R. Например, пусть к = 3 и
xVz4-
Тогда dfv есть линейное отображение R3 —► R. Следовательно, dfv
можно рассматривать как вектор-строку. Утверждается, что для
(х\
любой точки ν = \ у I вектор-строка определяется формулой
dfv = (2xy3z4, 3x2y2z4, 4x2y3z3).

5.4. Частные производные и дифференциальные формы 275
Чтобы убедиться в этом, вычислим его проекции на каждый из
векторов [01,[11и[01. Например,
W W V1/
/Iv + Ло) J -/(v)=d/v|oj +0(5)
Это следует из определения dfv и из того факта, что
дифференциал ci/v[h] линеен по h. Тогда
и предел этого выражения при s —► 0 является производной / по
переменной χ при фиксированных у и ζ. Он называется частной
производной f по χ и обозначается df /дх. Если
то элементарное вычисление дает
1[[\\\^>
Таким образом,

276 Глава 5. Дифференциальное исчисление на плоскости
Аналогично, dfv [ [ 1 I I = — и dfv I I 0 I I = —. Итак, для
функции / мы получаем формулу
At (dfl Л df< Л df< Л
d/v=V^(v)'^(v)'^(v)J·
Непосредственная проверка для / = x2y3z4 дает тот же
результат. Есть более удобный способ организации этой информации.
Напоминаем, что мы уже имели обозначение dx для линейной
функции, приписывающей каждому вектору его первую
компоненту, т. е. dx задается матрицей
(1, 0, 0)
и, аналогично, для dy и dz — матрицы
(0, 1, 0) и (0, 0, 1).
Теперь можно записать равенство
= ^(v)(l, 0, 0) + g(v)(0, 1, 0) + ^(ν)(0, 0, 1)
в форме
df = -J-dx + -J-dy+-J-dz.
дх ду dz
Таким образом,
d(x2y3z4) = 2xy3z4 dx + 3x2y2z4 dy + 4x2y3z3 dz.
Справа стоит сумма трех членов, являющихся функциями,
умноженными на dx, dy и dz. Такая сумма называется линейной
дифференциальной формой. Смысл этой формы в том, что она
определяет правило, по которому каждой точке пространства R3
приписывается вектор-строка.

5.4. Частные производные и дифференциальные формы 277
Это формула естественна в том смысле, что если взять
функцию
то
df , df n df n
— = 1 — = 0 — = О
дх ' ду ~ ' dz - '
и тогда мы получаем
df = cix.
С этими обозначениями цепное правило сводится к
формальным подстановкам. Покажем, что мы имеем в виду. Рассмотрим
отображение φ : R2 —> R2, определяемое формулой
г \\ /г cos θ
Φ"Θ)Ι Vrsintf
Пусть / : R2 —> R есть некая функция, скажем,
/к;Цз+д·
Тогда
/««MiflJJ^cosi?.
Отображение άφιτ\ будет матрицей размера 2x2, скажем,
<%) = (с d
Чтобы найти верхнюю строку этой матрицы, мы должны
умножить ее слева на вектор (1, 0). Тогда
(1, 0) (« J) = (а, Ь).
В нашем случае (1, 0) есть dx. Согласно цепному правилу,
^((S))°#(S)=d(s°#)(S)·

278 Глава 5. Дифференциальное исчисление на плоскости
Но ю^ = г cos θ, следовательно, мы получаем вектор-
строку
ά(χ о ф), г \ = cos θ dr — г sin θ άθ
= (cos#, — rsin#).
Итак, α = cos#, b = —rsin#. Аналогично
(cd) = (o,i)(° J)=^((5))°^(5)
= d(y о ф)/г\ = sinOdr + rcosOde = (sin#, rcos#).
Откуда следует, что άφιτ\ задается матрицей
(cos# —rsin#
sin θ r cos θ
Тогда
df = (Зх2 + у2) dx + (2ху) dy
и
d(f оф) = 3r2 cos ваг-г3 sin θ άθ.
В принципе, согласно цепному правилу, можно перемножить
матрицы и получить матрицу для дифференциала d(f о ф):
/г, 2 2 л 2 · 2Л ^ 2 · Л Л> / COS θ —rsm6 \
(3r^cos^0+ r^sm20,2r2sm0cos0) [ . Л л
v ' у sinfl г cost? )
= (3r2cos0, -r3 sin θ).
Конечно, это правильно. Однако, можно сделать иначе —
подставить
£ = rcos#, άχ = cosO ar — rsvaOaO,
у = г sin#, dy = sin θ dr + r cos θ άθ
в выражение
df = (Зх2 + у2) άχ + (2ху) ay,
после этого все перемножить, собрать вместе коэффициенты и
получить то же самое выражение для a(f о ф).

5.4. Частные производные и дифференциальные формы 279
Другими словами, можно считать, что отображение φ
превращает χ в функцию г и Θ, т.е. χ надо заменить на функцию
х о φ = г cos θ и вычислить ее дифференциал.
Чтобы проделать эти вычисления, полезно вспомнить, что
d(gh) = gdh + hdg.
Например, в пространстве R2
дд , дд .
d9=dx-dX+dydy>
откуда
L 99 , ,дд,
hag = h-— αχ + η-— ay.
οχ ay
Тогда
d[{gh) о φ] = (до φ) d(h ο φ) + (ho φ) d(g ο φ).
Таким образом, в нашем примере
F U J = =gh\y
где д = х2 + у2 и h = χ. Тогда / о φ = г2 -г cos θ и, следовательно,
d(f о ф) = (г cos в)2г dr + r2(cos θ dr - r sin θ άθ)
= 3r2 cos θ dr- r3 sin θ άθ.
Эта процедура легко обобщается: пусть у\,..., у ι обозначают
координатные функции в пространстве Ж1, где точка задается
столбцом
' У\
У1
Пусть / : R* —► R есть дифференцируемая функция. Тогда
df = ^— dyi + ■ ■ ■ + — dyt.
dyi dyt

280 Глава 5. Дифференциальное исчисление на плоскости
Предположим, что х\,...,х^ обозначают координаты в
пространстве Шк. Пусть φ : Шк —► Ш1 — дифференцируемое отображение.
Определим ф\ = у\ о ф, ф2 = У2 ° φ и так далее. Тогда
^(ν) =
^ι(ν)
<Mv)
где ν
χι
Хк
Далее можно написать
άφι =
θφι , θφι ,
-αχι Η h -ζ—axk,
дх
дхк
δφι
δφι
ι , υΨΙ ι υΨΙ 1
άφι = -5— dxi + ■■■ + -5— dxk,
σχι охк
и линейное отображение άφν задается матрицей
я-(ν)
σχι
9φι, .
\dx~i{v)
дф\, .
^(ν)
\
или в более простой форме
άφ
( θφι
dxi
дф±
\ dxi
θφι , .
dx-k(v)/
θφι \
дхк
дфх_
дхк )
df
Согласно цепному правилу,
d(f °Ф) = ^—о φάφι + ■ ■ ■ + ^- о φάφι,
ОУ1 ОУ1
АХ 9& А , , д& А
где использованы выражения αφι = —— αχι + · · · + —— ахк.
οχι охк

5.4. Частные производные и дифференциальные формы 281
Закончим этот параграф доказательством двух теорем.
Чтобы определить частную производную, мы использовали
дифференцируемость / в точке р. Можно показать, что
существование частных производных по χ и по у еще не означает
дифференцируемость / в р. Достаточные условия дифференцируемости
/ в точке ρ дает следующая теорема.
Теорема: Пусть f : R2 -» R1
df df
производные —— и п
дх ду
имеет непрерывные частные
в точке р. Тогда f дифференцируема в
их иу
точке р.
Доказательство. Если / дифференцируема в р, то линейное
отображение dfp должно иметь вид
dfp
Итак, если существуют
= s
а/
дх
_а/
дх
а/
ду
df
ду
, то / дифференцируема в
точке ρ тогда и только тогда, когда
W/ ((;))■
дх
+ t
а/
ду
+ о(ШгЖ).
Запишем приращение функции / в виде
VP / И? ]] = f(xp + s,yp + t)- /(хр, ур)
= f{xP + s,yp + t)- f(xp, ур + t) + f(xp, Ур + t)- f(xp, yp).
По теореме Лагранжа о среднем значении из одномерного
дифференциального исчисления можно записать:
f(xp + s,yp + t)- f(xp, yp + t) = s—
f(xP, Ур + t)- f(xP, Ур) = t—
(l/p+i)

282 Глава 5. Дифференциальное исчисление на плоскости
для некоторых xq и уо, удовлетворяющих условиям хр < хо <
хр + s и ур < уо < ур + t. Тогда
Vp/ ,
= S
дх
+ t
(уХЛг) * (Й)
EL
ду
так что
= s
а/
дх
df
— s
-EL
дх
id-L
ду
( χ0 \ ΟΧ (Χρ\
\yP+t) \Ур) >
ду
ft) ^ft)J
> .
Если
стремится к нулю, то ввиду непрерывности функций
df /дх и df /ду коэффициенты при s и t тоже стремятся к нулю,
т.е. относятся к категории /(R^R1). Поскольку обе функции s
и t являются Οζβ^,Μ.1), то все выражение есть o(R2,R1), что и
требовалось доказать.
Теорема: Пусть f : R2 —► R1 дифференцируема в точке ρ и име-
д (df\ д (df
era непрерывные смешанные производные — I —— I и — ( —
в точке р. Тогда
ду \дх) дх \ду
д_Ш
ду \дх
д (df
дх \ду
Интуитивная идея, лежащая в основе доказательства этой
χ
важной теоремы, очень проста. Возьмем четыре точки
χ + s
так:
χ
Ύ ~\~ S
,, , , . и | , ). Они расположены на плоскости
у У' \y + tj \y + t '
χ
χ
У

5.4. Частные производные и дифференциальные формы 283
Рассмотрим выражение, составленное из значений функции / в
этих точках:
/
-лг;')+/((;^]]-/
Его можно сгруппировать двумя способами: либо
либо
- /
X
y + t
-(/((*£'))-/
X
y + t
χ
Очевидно, что они равны. Выражение (5.20) равно
у(^)К(°0)~у(*До))·
Учтем, что
д
дх
V(y+t)f{l))
X7(y)f{So))=S%
+ o(s)
(y+t)
+ o(s).
(у)
(5.19)
(5.20)
Если бы мы могли «пренебречь» поправочными членами o(s), то
мы бы имели
='*«>(£)С)-*Ш)+"*>·
Если те же операции проделать с выражением (5.19), то получим
<4(!)(;ι^>·

284 Глава 5. Дифференциальное исчисление на плоскости
Разделив полученные ответы на st, получаем (без учета
последних, «малых» слагаемых)
д_д]_ _ д_д]_
дх ду ду дх
Чтобы приведенное рассуждение стало строгим, нам
необходимо внимательно исследовать поправочные члены. Мы можем
сделать это с помощью теоремы о среднем значении из
дифференциального исчисления функций одной переменной. Положим
^'((т))-'((:))·
Функция g дифференцируема по у и выражение (5.20) равно
9(v + t) -9{У)·
Согласно теореме о среднем значении
9(y + t)-g{y)=tg'{y),
где у — некоторая точка между у и у + t. Далее,
g'{y) = lira-(д(у +ε)-д{у))
-aK4;++:H("i1-'((.:.)>4;D)
По предположению теоремы функция df /dy дифференцируема.
Еще раз воспользуемся теоремой о среднем значении
ыг))-1А(;))=°т(т·
Таким образом, выражение (5.20) равно

5.5. Производные по направлению
285
По условию теоремы функция —— ( —— I непрерывна. Поэтому
дх \ду)
для любого ε > 0 можно найти такое δ > О, что
dxdyJ \\yJJ dxdyJ \\y
< ε, если \s\ + \t\ < δ.
Таким образом, (5.20) преобразуется к
"(£(£И;Ь
где |γι| < ε, если \s\ + \t\ < δ. Аналогично получаем, что (5.19)
равняется
чшхсь
Будем считать, что \st\ > 0. Разделив полученные результаты на
st, получаем неравенство
д_д£ ((х\\_д_?1 ((х
дхду\\у)) дудх\\у
<г3,
где
|т*з| < ΙΓι| + \г2\ < 2ε, если \s\ + \t\ < δ.
Левая часть неравенства есть просто разность между двумя
числами, она не зависит от δ, следовательно, гз может быть сделано
сколь угодно малым и, мы получаем равенство смешанных
производных, т. е.
д_д]__д_д]_
дх ду ду дх'
5.5. Производные по направлению
Пусть / — интервал в пространстве R1, содержащий 0. Возьмем
7 : / —► V, дифференцируемую в 0. (Как обычно, в качестве
V можно взять любое векторное пространство, для наглядности

286 Глава 5. Дифференциальное исчисление на плоскости
представляйте себе случай V = R2.) Предположим, что 7(0) = х,
и пусть 7'(0) обозначает вектор с^7о(1), т.е.
7'(0) = d7o(l) = Jim[(l/i)(7(i) - 7(0))]·
Вектор 7'(0) называется касательным вектором к кривой η в
точке t = 0. Если 71 — вторая кривая, для которой выполняются
условия 71 (0) = 7(0) и 7ι(0) = 7'(0) (рис. 5.8) то мы будем
говорить, что 7 и 7ι касаются при t = 0, или что они согласуются
в нуле с точностью первого порядка.
Рис. 5.8
Если 7 касается 71 в нуле, и 71 касается 72 в нуле, то
очевидно, что 7 касается 72 в нуле. Другими словами, мы определили
отношение эквивалентности для дифференцируемых кривых: две
кривые эквивалентны, если они согласуются в нуле с точностью
первого порядка. Если 7'(0) = ν, то пара {χ, ν} определяет класс
эквивалентности. Мы представляем этот класс эквивалентности
как вектор ν с началом в точке х, и называем этот вектор
касательным вектором в точке х. Любые χ и ν определяют
некоторый класс эквивалентности, потому что всегда можно взять
прямую линию
7(ί) = х + ίν,
для которой выполняются условия 7(0) = χ и У(0) = v. Иногда
мы будем пользоваться греческой буквой, например, ξ, для
обозначения касательного вектора в точке х, т. е. ξ обозначает пару
χ и v.

5.5. Производные по направлению
287
Предположим, что V = R2, тогда кривая η задается двумя
функциями χ о 7 и у о 7, обычно обозначаемыми x(t) и y(t).
Например,
x(t) = isini + 1
y(t) = е*
определяют кривую
,,-. /isini + l\
7(ί) = { е* J
с начальными условиями
7(0) =(J) и 7'(0) = (J).
Заметим, что
d(x 07) = d(i sin ί + 1) = (sini + icosi) dt
d(yo7) = d{el) = eldt.
Поэтому функция
,,.-. /sini + icosi λ
может быть восстановлена по коэффициентам при dt в ci(x о 7) и
<%о7).
Пусть функция / : V —» R определена в некоторой
окрестности точки р. Для каждой кривой η, удовлетворяющей условию
7(0) = р, функция / о 7 определена вблизи 0 в пространстве R.
Если / — дифференцируемая функция в ρ и 7 дифференцируема
в нуле, то, согласно цепному правилу, /°7 будет (вещественной)
функцией, дифференцируемой в нуле, и ее производная
определяется формулой
(/o7)'(0) = d/P(7'(0)).
Используя обозначения, принятые для дифференциальных
форм в пространстве R2, в выражении для df заменим d(x о 7) на

288 Глава 5. Дифференциальное исчисление на плоскости
dx и ά(η о 7) на dy. Например, если взять
df = 2xdx + 2у dy,
d(/o7) = 2(*зт* + 1)(8т* + *со8*)Л + 2е* ■ егdt
= 2(ί sini + l)(sini + ί cosi) di + 2e2i di.
Коэффициент при di равен (/ ο j)'(t). Полагая t = О, получаем
(/°7)'(0).
Заметим, что (/ о 7)'(0) зависит от ρ и 7'(0)> но при этом
не требуется другая информация о кривой η, т.е. эта величина
зависит только от касательного вектора ξ. Обозначим эту
величину D^f и будем называть ее производной по направлению ξ от
функции /. Итак,
Dtf = dfp(v), £ = {p,v}.
Например, если ν = ί Q J, то D$f = -~-(p)· Пусть /ι и /2 —
две функции, дифференцируемые в точке х, и пусть / = /ι + /г-
Кривая 7 проходит через точку х, причем ее касательный вектор
в ρ есть ξ. Из курса дифференциального исчисления функций
одной переменной мы знаем, что
(/°7)'(0) = (/iO7)'(0) + (/2°7)'(0).
Следовательно,
Щ(/г + /2) = Я€Л + Я€/2-
Аналогично, если мы возьмем h = /1/2, то элементарные
вычисления дают
(h о 7)'(0) = (/ι о 7)'(0)(/2 о 7)(0) + (/ι о 7)(0)(/2 о 7)'(0)
= (/i°7)'(0)/2(x) + /i(x)(/2O7)'(0),
так как (/ι °7)(0) — /ι (7(0)) = /ι(χ) и т0 же самое для f2. Таким
образом, мы можем записать
Dz(hf2) = (Dzh)f2 + h(D(:f2).

5.5. Производные по направлению
289
Еще один пример на вычисление производной по направлению.
Пусть 7 : R -» R2, где
Тогда df/x\ и ξ = {7(0)) 7'(0)} определяются формулами
ог/(х} = (2ху,х2 + Зу2), ξ = | Г"2) , (з) } ·
Отсюда
D,(f) = 4f(-i) ((J)) = (-4,13) (^ = -4 + 26 = 22.
Покажем, что это равно (/ о j')(0). Для этого заметим, что
/ о 7(ί) = (ί - 1)2(ί2 + 2ί + 2) + (ί2 + 2ί + 2)3,
(/ ο 7)'(ί) = 2(ί - 1)(ί2 + 2ί + 2) + (ί - 1)2(2ί + 2)
+ 3(ί2 + 2ί + 2)2(2ί + 2).
Следовательно,
(/ ο 7)'(0) = 2(-1)(2) + (-1)2(2) + 3(2)2(2) = 22.
Вычислим производную по направлению от произведения
двух функций. Пусть д : R2 —► R, где д II II = х2 — у2. Тогда
отображение произведения fg : R2 —> R имеет вид
ж\\ _ t ίίχ^\ „ ίίχ\\ _ tJl„, , „.3v~2
Дифференциалы Gig и ci(/p) равны
dg^xj= (2x,-2y)
d(/5)( J) = (2xy(x2 - 2/2) + (x22/ + 2/3)(2x), (z2 + 3y2)(x2 - y2)
+ (x22/ + 2/3)(-2y)).

290 Глава 5. Дифференциальное исчисление на плоскости
Тогда мы имеем
D,(f9) = d(f9){-2i)([l))
= (-4(-3) + Ю(-2), 13(-3) + Ю(-4))
= -8 - 158 = -166.
Согласно правилу дифференцирования произведения,
производная D^(fg) должна быть равна
Di(fg) = De(f)g ("J) + / ("2) D&),
где
9 ("г) = (_1)2 - 22 = -3' f ("2) = (-1)22 + 23 = 10
ЗД)=^(-21)((;))=(-2,-4)(;)=-Ю.
Следовательно,
Dt(fg) = 22(-3) + 10(-10) = -166,
что совпадает с ранее полученным результатом. Множество
касательных векторов в точке χ удобно рассматривать как векторное
пространство, называемое касательным пространством в точке χ
и обозначаемое TV*. Тогда если ξ = {χ, ν} и η = {χ, w} — два
касательных вектора в точке х, то их сумма равна ξ+η = {x,v+w}.
Кроме того, если ξ = {χ, ν} и α — произвольное вещественное
число, то αξ = {χ, αν}. Таким образом, пространство TV*
похоже на пространство V, за исключением того, что все выражения
имеют немой индекс х. Сейчас читателю эти обозначения могут
показаться слишком громоздкими, но позднее станет ясно,
насколько они удобны.
Если ξ = {χ, ν} и η = {x,w}, то
Οξ+τ,ί = d/x[v + W] = d/xx[v] + d/x[w] = D€/ + Dvf,

5.6. Операция переноса
291
следовательно,
Dt+r,f = Dzf + Dvf.
Аналогично,
Daif = aD^f.
5.6. Операция переноса
Пусть φ : V —► W, где ф(х.) = у — дифференцируемая функция.
Если / : W —► R определена в окрестности у, то функция / о φ
определена в окрестности х. Чтобы подчеркнуть точку зрения,
которая будет центральной в этой книге, обозначим эту функцию
ф* / и назовем ее переносом2 функции / с помощью ф. Таким
образом,
ΦΊ = ί°Φ,
(4>7)(χ) = НФЫ).
Будем считать функцию φ фиксированной, а / переменной, так
что ф* переводит все функции на пространстве W в функции на
пространстве V (назад). Заметим, что
Φ*(ίΐ + ί2)=ΦΊΐ+ΦΊ2
И
<№/2) = (ΦΊύ(ΦΊ2),
следовательно, ф* сохраняет все алгебраические операции.
Если, например, φ : R2 —> R2 — отображение, задающее
переход от полярных координат к декартовым согласно формуле
4;))=С^)·
2В английском оригинале эта операция имеет выразительное название
pullback, что в буквальном переводе означает отступление, отход назад.
Русский термин перенос несколько менее информативен, так как в нем нет
указания на то, что область определения функции / под действием переноса
перемещается в направлении, противоположном перемещению точек при
отображении ф. — Прим. ред.

292 Глава 5. Дифференциальное исчисление на плоскости
то можно написать
4>*x = rcos9, φ* у = г sin θ.
Здесь нам хотелось бы остановиться и объяснить смысл этих
уравнений. У нас есть две плоскости: гв и ху (рис. 5.9). Пусть
отображение φ каждой точке плоскости гв ставит в соответствие
точку на плоскости ху. Мы рассматриваем χ как функцию на
плоскости ху: каждой точке плоскости эта функция ставит в
соответствие координату х.
θ у
Φ
IIIId^
r _
Рис. 5.9
Тогда ф*х становится функцией на плоскости гв, т.е.
ф*х = гсовв, и, аналогично, ф*у = rsin#.
Теперь мы хотим определить перенос с помощью φ для
дифференциальных форм. Начнем с определения переноса для
базисных форм dx и dy. По определению,
φ*άχ = ά(φ*χ) = cos в dr — r sin θ άθ,
ф*ау = а(ф*у) = sin θ dr + r cos θ άθ.
Тогда для любой линейной дифференциальной формы типа
х2 dx + у2 dy
можно определить
ф*{х2 dx + у2 dy) = φ* (χ2) -φ*άχ + ф*(у2)ф* dy
= (r2 cos2 θ) (cos θ dr - r sin θ άθ) + (r2 sin2 θ) (sin θ dr + r cos θ άθ)
= r2(cos30 + sin3 θ) dr + r3(sin2 θ cos θ - cos2 Θ sin θ) άθ.

5.6. Операция переноса
293
Другими словами, для дифференциальной формы
adx + bdy,
где α и Ъ — функции, определяем
φ*{αάχ + bdy)= φ*{α)φ*(άχ) + ф*(Ъ)ф*(ау),
где потом следует собрать вместе коэффициенты при dr и άθ.
Заметим, что если / — произвольная функция на плоскости ху,
то
df=dx-dX+dy-dy-
Откуда, воспользовавшись цепным правилом, получаем
= (^оф)а(хоф)+(^оф)\а(уоф)
= ά(/οφ)
И
так,
φ*άί = ά{φ*ί).
Эта формула справедлива в общем случае для
дифференцируемых отображений Rfe -^ R'.
В качестве примера рассмотрим отображение φ : R2 —► R3,
заданное формулой
Тогда если х, у, ζ обозначают координаты в пространстве R , то
ф*х = г2, отсюда ф* dx = 2rdr,
φ*у = sr, отсюда φ* dy = sdr + r ds,
φ*ζ = s2, отсюда φ* dz = 2s ds.

294 Глава 5. Дифференциальное исчисление на плоскости
Для любой функции / в пространстве R справедлива
формула
df = d/dX + d/dy+d7fdZ
ох ду dz
и мы можем вычислить 4>*(df) двумя способами: вычислять
ά(ΦΊ)
или
ф*т=ф* шф*dx+ф* {%)ф*dy+ф* {%)ф*dz-
Например, пусть
у2 — xz.
Тогда
df = —zdx + 2ydy - χ dz.
Подстановка дает
^7 = 0
и
4>*df = d(<t>*f) = o.
Если вычислять <j)*df непосредственно, получаем
ф* df = —s2 -2rdr + 2sr(sdr + rds) — г2 ■ 2s ds
= [-s2 ■ 2r + 2s2r] dr + [-r2 ■ 2s + 2r2s] ds = 0.
Теперь понятно, как поступать в общем случае. Если х\,... ,х^
— координаты в пространстве Шк и у\, ■ ■ ■ ,yi — координаты в
пространстве R*, то дифференцируемое отображение φ : Rfe —► R*
определяется формулой
(XI

5.6. Операция переноса
295
Тогда
Ф*У\ = Φι, Φ* dyi = άφι = -^ dxi + · · · + -^ dxk,
Φ* VI = Φι, Φ*άρι=άφι.
Операция φ* переносит функции на пространстве Μ.1 в
функции на пространстве R , соответственно она переводит линейные
дифференциальные формы из пространства Ш.1 в линейные
дифференциальные формы пространства Шк. При этом перенос ф*
сохраняет все алгебраические операции: сложение и умножение
двух функций, сложение двух форм, умножение функции на
форму. Более того, согласно цепному правилу,
Φ*ά/ = ά(φ*η
для любой функции / в пространстве Ж1.
Предположим, что мы имеем φ :V -^>W ж-ф :W -^> Ζ. Можно
сделать композицию двух отображений и получить
ψοφ·.ν->Ζ.
Если д — произвольная функция на пространстве Ζ, то можно
образовать
Ф*д = доф,
т. е. функцию на пространстве W, и тогда
Φ*(Ψ*9) = (90,Ф)0Ф
является функцией на пространстве V. Согласно ассоциативному
закону, для композиции имеем
(д о ψ) о φ = д о (ψ о ф).
Следовательно,
(фоф)*д = ф*(ф*д),
так что
(φοφΥ =φ*οψ*.

296 Глава 5. Дифференциальное исчисление на плоскости
Обратите внимание на обратный порядок функций!
Допустим, что V = Rk, W = ΜΪ и Ζ = Rm. В каждом из
пространств определены координаты х1,... ,хк; у1,..., у1; ζ1,..., zm
соответственно. Тогда если
ω = αχ dzl + ■ ■ · + ат dzm
дифференциальная форма в пространстве Rm, то φ*ω будет
дифференциальной формой в пространстве Ш1, а φ*ψ*ω -
дифференциальной формой в пространстве Жк. Из цепного правила следует,
что
ф*Г df = φ*(ά(ΨΊ)) = ά(φ*φ*/) = d[(V ο φ)*ί].
Операции ф* и ψ* сохраняют все алгебраические действия, то же
самое можно сказать и про (ψ ο φ)*,
Φ*ψ*{9άί) = {ψοφγ{9άί).
Наиболее общий вид дифференциальной формы представляется
суммой членов типа gdf, т.е.
αχ dzl + h amdzm,
следовательно, уравнение
(ψοφγ(ω)=φ*ψ*ω (5.21)
справедливо для всех линейных дифференциальных форм.
Пусть 7 : R -* У — кривая, проходящая через точку х, т. е.
7(0) = х, а кривая φ ο η проходит через точку у. Если η —
дифференцируемая функция в нуле, то φ ο η тоже дифференцируема
в нуле и, согласно цепному правилу,
(^о7)'(0) = #х(7,(0)).
Правая часть этого уравнения зависит только от касательного
вектора ξ, относящегося к кривой η. Поэтому άφ* отображает
касательные векторы в точке χ в касательные векторы в точке
<Ях):
άφχ:Τνχ-^Τ\νφ{χ),

5.6. Операция переноса
297
где мы определили
άφχξ = {<КХ), άφχ(ν)}, если ξ = {χ, ν}.
Дифференциал άφ* можно истолковать как преобразование ин-
финитезимальных кривых, проходящих через точку х, в инфи-
нитезимальные кривые, проходящие через ^(х).
Пусть теперь функция / : W —> R дифференцируема в ^(х).
По ассоциативному закону для композиции имеем:
(Ф*Л о7 = /о^о7 = /о(^о7).
Дифференцируя это уравнение при ί = О, получаем
ЭД7) = Α^ξ/· (5.22)
Это значит, что мы можем перенести функцию / назад с
помощью φ и потом вычислить производную по направлению ξ, или
мы можем пройти вперед с помощью άφ* и потом взять
производную по направлению от / по άφχξ. В обоих случаях мы получим
один и тот же ответ.
Положив ξ = {χ, ν}, полученное равенство можно переписать
в виде
•D{x,v}(^*/) = %(χ),#χ[ν](/).
или, равносильно,
<i(/^)x[v]=%)[#x[v]].
Последнее равенство означает, что
d(f °ф)х = d/фм о άφχ,
а это не что иное, как частный случай цепного правила.
В качестве примера на применение этого равенства возьмем
f : W —>Ж и φ : V —* W, определяемые формулами

298 Глава 5. Дифференциальное исчисление на плоскости
Тогда
,, _ fcos6 —rsin#'
άφ(θ)~\ζΐηθ г совв J'
и мы получаем, что
%((θ))Μθ)Μ}{Ι) = άΙΦ(θ)οάφ(θ)[ν]
= (2(rcos0)(rsin0), (rcosfl)2) IC0S* -rsin^ IVA
= (2r2cos0sin0, r2cos20) (4cos0-^sin0\
' \ vr sin θ + rvg cos θ J
= 2r2 cos θ sin θ(ντ cos θ — vvq sin Θ) + r2 cos2 6{vr sin 0 + rvg cos 0)
= 3r2 cos2 0 sin 0 vr + r3 (-2 cos θ sin2 0 + cos3 θ)νβ.
Теперь надо показать, что последнее выражение равно
Для этого заметим, что
*V((«)) =/((rll)) = (rcos0)2rsin0 = r3cos20sin0.
Следовательно,
d{4>*f),T-, = (3r2cos26»sin6», r3(2cos0(-sin0)sin0 + cos30)).
Отсюда, наконец, получаем:
«{«wwvi-wto ((:))=
= 3r2 cos2 0 sin 0 vr + r3(-2 cos θ sin2 0 + cos3 θ)νθ.

Резюме
299
Резюме
A. Дифференциалы и частные производные
Вы должны уметь давать определение дифференциала df
функции / в терминах «о» и «О».
Вы должны знать и уметь применять правила
дифференцирования суммы, произведения и композиции функций.
Вы должны уметь выражать дифференциал функции через
частные производные и уметь строить матрицу, представляющую
дифференциал функции / : R2 —► R2.
B. Преобразования координат
Для заданного преобразования, которое вводит новые
координаты на плоскости, надо уметь пользоваться цепным правилом для
выражения дифференциалов и частных производных в этих
новых координатах.
C. Применения дифференциалов
Вы должны знать, как получить уравнение прямой или
плоскости, касательной к графику функции в выбранной точке.
Вы должны уметь пользоваться цепным правилом для
решения задач с участием функций от нескольких переменных.
Задачи
5.1. Покажите, что если / : V —► W дифференцируема в точке а и
Τ : W —► Ζ линейна, то композиция Τ о / дифференцируема в
точке α и
d(Tof)a=Todfa.
5.2. Пусть F : V —> R дифференцируема в α и функция / : R —► R
имеет производную в а = F(a). Докажите, что f о F
дифференцируема в точке α и
d(foF)a = f'(a)dFa.
5.3. Пусть F : V —> W n G : W —> V — непрерывные отображения,
причем G о F(v) = ν и F о G(w) = w для всех ν в пространстве

300 Глава 5. Дифференциальное исчисление на плоскости
V и для всех w в пространстве W. Допустим, что F
дифференцируема в точке a, a G дифференцируема в точке β = F(a).
Докажите, что
dG0 = (dFn)-1.
5.4. Пусть функция / : V —► R дифференцируема в точке а.
Покажите, что д = fn дифференцируема в точке α и что
dga = nfn~1dfa.
5.5. Пусть -γ : IR —>■ IR2 обозначает кривую ^(t) = ( . I. Пусть
sini
F : Rz —► R2 — отображение, где
(a) Вычислите вектор, касательный к кривой -у при ί = 0 и
t = -к 12.
(b) Найдите производную по направлению отображения F для
каждого из полученных касательных векторов.
5.6. Пусть / : R2 —► R2 и д : R2 —* R2 определены формулами
Проверьте цепное правило для отображ;ения д о / : R2 —> R2
ffx\\ ( х2еу
5.7. Пусть д : V —* W — отображение, где д II ]] = I
λ : R —у V — прямая линия
w=(-?)+* О
(a) Найдите касательный вектор в точке I л I для кривой
до\.
(b) Производную по направлению D / з \ /1 \ (д) вычислите дву-
{-ί)Λ2)
мя способами.

Задачи
301
5.8. Пусть φ : V —> W — отображение, задаваемое формулой φ :
(Т \ IT COS θ \
„ J ь-► Ι . η ), а функция / : W —> R определена формулой
/ : Ι ι-» ι3!/4. Проверьте, что
ОД*/) = Af*a«)/
для всех касательных векторов ξ = (α, ν).
5.9. Определим отображения F : R2 -> R2, G : R2 -> R2, / : R1 -> R2
и д : R2 —► R1 равенствами
у JJ \ ху ) \\УJJ \ У
Проверьте, что:
(a) d(FoG)(Xj = dFG^x^odG(Xj
(b) d(GoF)(X)=dGF((*))odF(x)
(c) d(g о /)(t) = d5/(t) o dF(t)
(d) d(fog){*)=dfg{{*))odg{*y
5.10. Пусть функция / : R2 —► R дифференцируема в некоторой
окрестности I I и удовлетворяет условию /II II φ 0.
Покажите, что в некоторой окрестности I I отображение
д II II = 1// (( )) дифференцируемо и что
*(й) = -<у(й)/(/((2))У
5.11. Функция / определена на плоскости через аффинные
координаты χ и у следующим образом:
/(Р) = vl^reCP)!·

302 Глава 5. Дифференциальное исчисление на плоскости
(a) Непрерывна функция / в начале координат Ро(х = 0, у = 0)
или нет? Дайте точный ответ через определение
непрерывности.
(b) Дифференцируема ли функция / в начале координат? Дайте
точный ответ через определение дифференцируемости.
5.12. Так называемые параболические координаты на плоскости
выражаются через декартовы координаты χ и у согласно формуле
и\ _ ( \Jx2 + у2 - χ
ν ) ~ \ ^/χΐ + у2 + х
по-
(a) Выразите ( , I через I , I, используя матрицы 2x2
/ dx \ ( du\
том обратите эти матрицы и выразите I , I через I , 1.
(b) Получите обратное преобразование координат, выразив
I через I I. Выразите дифференциал I , I через
du
dv
(c) Покажите, что кривые и = const и υ = const являются
параболами, перпендикулярными друг другу в точке
пересечения. Нарисуйте семейства этих кривых.
(d) Рассмотрите функцию /, определенную на плоскости
формулой /(р) = 1/(и(р) + г>(р)). Выразите d4f, где q — точка
с координатами и = 4 и ν = 16, сначала через du и dv, a
потом через dx и dy.
(e) Предположим, что траектория движущейся частицы
определена формулами: α : R —► R2, где
dx \ ft2+t
dyj°a=\ ί3
Вычислите производные от юа, у о а, и о а и ν о а при
ί = 2.
5.13. Пусть координаты на плоскости и я υ связаны с декартовыми
координатами χ и у уравнениями
х\ ( 2uv
у I \ и2 - ν2

Задачи
303
(a) Вычислите производную (матрицу Якоби) этого
преобразования в точке и = 2, ν = 1 (т. е. выразите I , I через I , I
в этой точке).
(b) Рассмотрите функцию f(u,v) = и2υ3. В координатах χ и
у получите уравнение касательной к кривой f(u,v) = 4 в
точке и = 2, υ = 1 (т. е. χ = 4, у = 3). (Не пытайтесь искать и
и ν как функции χ и у; просто используйте цепное правило.)
(c) Предположим, что частица движется вдоль траектории
А _ ( <3/2 \
В момент времени t = 2 частица проходит через точку
и\ /2\ _
О какой скоростью изменяются координаты
ν) \1
и и υ, т. е. чему равны du/dt и dv/dt в этот момент?
5.14. Пусть А обозначает аффинную плоскость. Точка Pq лежит на
этой плоскости. Постройте функцию / : А —> R, для которой
/(Ро) = 0, такую, что для произвольных аффинных координат
s(P), t(P) частные производные (df/ds)t и (df/dt)s определены
и равны нулю в точке Ро, но при этом / не дифференцируема
в Pq. (Указание: если заменить термины «дифференцируема»
на термин «непрерывна» и «частная производная» на «предел
функции от одной переменной», то ответ был бы
{0 в точке Ро,
х2У
—г-—- в других точках,
ж4 -I- у1
где х(Ро) и у(Ро) равны нулю.)
5.15. Для некоторого кратера высота над уровнем моря определяется
формулой
z(x, у) = -\/х2 + Ay2 (χ, у, ζ измерены в километрах).
Температура по Фаренгейту находится из уравнения
Т(х,у) = 100 +2а; - jx2y2·
(а) Выразите dz и dT через dx и dy в точке χ = 3, у = 2.

304 Глава 5. Дифференциальное исчисление на плоскости
(b) Получите уравнение касательной плоскости к кратеру в
точке χ = 3, у = 2.
(c) Вдоль какого направления температура изменяется быстрее
всего в точке χ = 3, у = 2? Если двигаться вдоль этого
направления, то с какой скоростью изменяется температура
в зависимости от высоты над уровнем моря (с точностью до
градуса на километр)?

Глава б
Теоремы многомерного
дифференциального
исчисления
В этой главе мы продолжаем изучение
дифференциального исчисления. Приводим векторные варианты
теоремы о среднем значении, формулы Тейлора и
теоремы существования обратной функции. Обсуждаем
поведение в окрестности критической точки и
множители Лагранжа. Эту главу можно прочитать быстро,
не очень вникая в детали доказательств, но
упражнения надо проделать.
6.1. Теорема о среднем значении
Это одна из немногих теорем, которые для функций нескольких
переменных мы не сможем доказать с такой же степенью
строгости, как это делается для функций, зависящих только от одной
переменной. Сначала вспомним формулировку теоремы для
случая одной переменной. Утверждается, что если / — непрерывно
дифференцируемая функция на некотором отрезке [а,Ь], то
существует точка ζ, лежащая внутри этого отрезка, такая, что
f(b)-f(a) = f'(z)(b-a). (6.1)
Значение ζ в общем случае трудно определить явно, поэтому
обычно теорема о среднем значении используется в несколько

306 Глава 6. Теоремы ... дифференциального исчисления
ином виде, как неравенство:
Если f'(x)<m для всех х£[а,Ь], то /(b) — /(а) < т(Ь — а).
(6.2)
Так как f'(z) < m, то это неравенство немедленно следует из
теоремы о среднем значении, сформулированной выше. В то же
время его легко доказать непосредственно с помощью
фундаментальной теоремы интегрального исчисления. Действительно,
f(b)
rb rb
f(a) = / f'(s)ds< / mds<m(b-a). (6.3)
J a J a
Чтобы обобщить теорему на случай большего числа измерений,
удобно немного переписать аргумент функции в (6.3):
f(b)~f(a)= ( ^-f(a + t(b-a))dt = f f'(a + t(b-a))(b-a)dt
Jo di Jo
<(b-a) I f'(a + t(b - a)) dt < m(b - a). (6.4)
Jo
(Заметим, что второе равенство следует из цепного правила.)
Преимущество записей (6.2) или (6.4) по сравнению с (6.1)
состоит в том, что их можно сразу же распространить на случай,
когда / является отображением из R в R . Предположим, что /
— именно такое отображение:
/(*)
Тогда f'(t) = lim^0(l/h)(f(t + h) - f(t)) = dft[l]. Здесь мы
рассматриваем 1 как вектор в пространстве R1, если использовать
ранее введенное обозначение. Очевидно, что вектор f'(t)
определяется формулой
(№'
№ = ;
U(*).

6.1. Теорема о среднем значении
307
Для этого вектора можно написать равенство, аналогичное (6.4),
т. е.
f(b)-f(a) = J jtf(a+t(b-a))dt=(J f (a + t(b - a)) dt\ (b-a).
(6.5)
Под интегралом от векторной функции д мы подразумеваем
вектор, компонентами которого будут интегралы от его компонент:
если д = I I , то / g(t) dt = I
\9kJ \Jgk(t)dt/
Конечно, у нас есть определение интеграла в виде предела
аппроксимирующей суммы:
Jo
g(t)dt= lim(l/n)V5(i/n).
г=1
Поскольку каждая компонента этой аппроксимирующей суммы
векторов есть аппроксимирующая сумма для интеграла от
соответствующей компоненты функции, то оба определения
интеграла для векторной функции от одной переменной совпадают.
Для векторов существует неравенство ||νι + V21| < ||νι|| + ||v2||.
Аналогичное неравенство можно написать для
аппроксимирующей суммы и, переходя к пределу, мы получаем неравенство для
интеграла
yg(t)dtj<J\\g(t)\\dt.
Положим д = f и подставим в (6.5). Тогда
\\f(b) — f(a)\\<m(b — a), если ||/'(t)|| < m для всех t G [а,Ь].
(6.6)
Именно здесь можно увидеть трудность, возникающую при
попытке обобщить (6.1) на функцию, определенную в пространстве
R . Мы можем применить (6.1) к каждой компоненте fj функции
/. Для каждой компоненты мы получим
/,(Ь)-/,(а) = /'(^)(Ь-а).

308 Глава 6. Теоремы ... дифференциального исчисления
Однако значения Zj могут быть разными для разных j.
Вообще говоря, не существует такой точки ζ, которая подошла бы
для всех компонент fj. Поэтому аналогия с (6.1) в многомерном
случае не проходит. Что касается формулы (6.5), она остается
верной.
Давайте обобщим утверждение (6.6) на случай, когда / есть
отображение V —■> W, при этом V — не обязательно одномерное
пространство. Мы уже знаем, что обобщением f'(x) является dfx.
Пусть dfx — линейное преобразование. Нам необходимо понять,
что значит || Л ||, если А — линейное преобразование из V в W■ По
определению,
||Л|| = max ||Ли||
||u|| = l"
или, что то же самое,
\\м\
- max ———.
v^o ||v||
Тогда ||^4ν|| < ||Л|| · ||v|| для всех ν и ||Л|| будет наименьшим
числом, обладающим этим свойством1, т.е. если
||Av|| < Ar||v|| для всех ν, то \\А\\ < к.
Если А\ и ^2 — два линейных преобразования из V и W, то
||(Λι + Λ2)ν|| = ||i4iv + i42v|| < ||Λιν|| + ||Λ2ν|| < (||i4i||+i42||)-||v||,
откуда
ЦЛ1 + Л2Ц < ||i4i|| + ||i42||. (6.7)
Пусть [a, b] обозначает отрезок прямой, соединяющей любые
точки а и b в пространстве V (рис. 6.1). Это значит, что отрезок [а, Ь]
состоит из всех точек вида a+i(b —а) для 0 < t < 1 (естественное
обобщение одномерных обозначений). Мы хотим доказать
следующее. Предположим, что / : V —■> W дифференцируема во всех
точках [а, Ь], и дифференциал функции ci/x является
непрерывной функцией от χ на этом отрезке. Далее, предположим, что
1И/х|| < "г для всех χ € [а, Ь].
1 Число ||А|| называют нормой линейного преобразования А : V —> W.
Прим. ред.

6.1. Теорема о среднем значении
309
Рис. 6.1
Тогда
||/(b)-/(a)||<m||b-a||. (6.8)
Доказательство. Пусть h : [0,1] —* [а, Ь] — отображение,
заданное формулой
h(t) = a + i(b-a).
Обозначим F = f о h, так что F(t) = /(а + i(b — а)). Тогда F —
дифференцируемое отображение [0,1] —■> W и, согласно цепному
правилу,
dFt = dfh(t) о dht.
Далее, dht[l] = b — а, значит,
F\t) = dFt[l} = dfh{t)[h-a\.
Отсюда
/(b)-/(a) = F(l)-F(0)= / F'(t)dt= f dfh(t)[b-a]dt.
Jo Jo
Следовательно,
/(Ь)-/(а) = Л(Ь-а), (6.9)
где А — линейное преобразование
Л= ! dfh{t)dt. (6.10)
Jo
В формуле (6.10) мы интегрируем функцию, которая каждому
значению t приписывает линейное преобразование dfh(t) ■ Мы
можем толковать эти интегралы точно так же, как мы
толковали векторные интегралы. Например, так как в пространствах
V и W имеются стандартные базисы, то каждое линейное
преобразование можно определять матрицей. Интеграл от
матричной функции д, где g(t) = {gij(t)), задается матрицей, у которой

310 Глава 6. Теоремы ... дифференциального исчисления
ij-й матричный элемент есть интеграл от численной функции д^.
Или, как и раньше, интеграл можно рассматривать как предел
от аппроксимирующих сумм. Тогда из (6.7) следует, что
\jg{t)dt\< J\\g(t)\\dt.
В частности, выполнив такую оценку (6.10) и предположив, что
||4/х|| < т для всех χ € [a, b], можно сделать вывод:
||Л||<т,
и с учетом свойств нормы ||Л|| из равенства (6.9) получаем
справедливость оценки (6.8).
6.2. Производные высших порядков
и формула Тейлора
Пусть / : R2 —► R — дифференцируемая функция. Если частные
производные df /dx и df /ду непрерывно дифференцируемы, то
можно образовать конструкции
±(%), обозначая
дх \дх )
*Ш, обозначаем
ду \ду)
SL(°f), обозначается
дх \ду)
что
d2f д df
дхду ду дх
d2f
дх2'
d2f
ду2'
d2f
дхду
Мы уже знаем, что
Аналогично можно определить частные производные более
высоких порядков, если они существуют, и получить соответствующие
равенства для смешанных производных. Например,
А (1. f9!)) = JL(JL f9!)) = JL(JL f9!))
дх \ду \дх) ) ду \дх \дх) ) дх \дх \ду) )

6.2. Производные высших порядков и формула Тейлора 311
и так далее. Значение производных второго и более высоких
порядков связано с формулой Тейлора, которую мы сейчас получим
и докажем.
Для упрощения обозначений пока сформулируем ее для
начала координат. Предположим, что / имеет непрерывные про-
ί°\ тт
изводные первого и второго порядков в окрестности ( I. Для
удобства мы будем писать fix-, у) вместо /II II. Тогда
/(х,у) = /(0,0) + J jtf(tx,ty)dt
= /(0,0) + J (^{tx,ty)x+^(tx,ty)yjdt.
Пусть
С1 df f1 df
fi{x,y)= I Tj-(tx,ty)dt и f2(x,y)= — (tx,ty)dt.
Тогда
f(x, У) = /(0,0) +xh(x,y) + yf2(x,y),
где /ι и /2 — дифференцируемые2 функции, или, более
компактно,
/ = /(0,0) + χ/ι + ι//2.
Отметим, что
/i(0,0) = g (0,0) и /2(0,0) = g(0,0).
Те же самые соображения применим для f\ и /2:
/ι (ж, у) = /i(0,0) + xfu(x,y) + у/12 (х, У),
где
/■1 β г /·1 β ι
fn(x,y)= / -jr^(tx,ty)dt и fu(x,y)= / -rr^(tx,ty)dt.
2Разумеется, это требует доказательства. — Прим,, ред.

312 Глава 6. Теоремы ... дифференциального исчисления
Аналогично
/2(ж, у) = /2(0,0) + ж/21 (ж, У) + уЫ(х, У)·
Итак,
/ = /(0,0) + χ/ι(0,0) + у/2 (0,0) + х2/и + xy(fl2 + /21).
Если / имеет непрерывные3 производные вплоть до третьего
порядка, мы можем повторить процедуру еще раз и получить:
/ =/(0,0) + x/i(0,0) + у/2(0,0) + х2/ц(0,0)
+ xy(f 12(0,0) + /2i(0,0)) + 2/2/22(0,0)
+ Ж3/ш + X2y(f 112 + /l21 + /211)
+ Xy2{fl22 + /212 + /22l) + У3/222,
где все функции /ш, /т, и т.д. непрерывны. Вычислив вторые
производные от обеих частей этого уравнения, получаем
d2f
2/п(0,0) = ^2" (0,0),
/12(0,0)+ /2i(0,0)
df
дхду
(0,0),
2/22(0,0) ^(Ο,Ο).
Итак, мы доказали, что
f(x,y) = /(0,0) +х^(0,0) + 1/^(0,0) + ^20(О,О)
а2/
1 2d2f,
~2УЪу~2
+ ^^(°'°) + оГ^±(0,0) + О
(6.11)
3Авторы опускают здесь доказательство непрерывности, так лее, как
ниже в формуле (6.11) опускают оценку остатка, записанного сразу как
О
С)
Прим,, ред.

6.2. Производные высших порядков и формула Тейлора 313
Очевидно, что если / имеет непрерывные производные более
высоких порядков, то эту процедуру можно продолжать и дальше.
Понятно также, что подобные соображения применимы не
только в R2, но и в произвольном пространстве Жк. Наконец, начало
координат I „ 1 можно заменить любым вектором и и I J
заменить на u + v. В результате придем к следующей теореме:
Пусть функция / : R —► R имеет непрерывные частные
производные вплоть до порядка η + 1. Тогда существует такой
полином Рп, зависящий от координат вектора ν, что
/(u + v) = Pn(v) + 0(||v|r1).
Коэффициенты Ρη{ν) определяются путем последовательного
дифференцирования по ν этого тождества и последующей
подстановки ν = О.4
Если / : R2 —■> R1, то матрица, составленная из частных
производных второго порядка,
Яр(/)
/a2/. d2f \
называется матрицей Гессе, а соответствующая квадратичная
форма называется гессианом и обозначается d /p. Если функция
/ и точка ρ зафиксированы, матрицу Hp(f) будем обозначать
просто Н. Итак, формулу (6.11) можно переписать в форме
/(Ρ + ν) = /(р) + d/p(v) + ^2/ρ(ν) + ο(||ν||2), (6.12)
где
d2fp = vTHv = (ы,Ь2)Н l·1) . (6.13)
4Можно доказать, что в условиях этой теоремы все частные производные
от остатка О (||ν||η+1) до порядка η включительно при ν = 0 равны нулю. —
Прим. ред.

314 Глава 6. Теоремы ... дифференциального исчисления
Гессиан d2fp является квадратичной формой, и поэтому к нему
применим анализ, изложенный в главе 4. Например, если f(P) =
[χ (Ρ)]2 у (Ρ), то в точке χ = 2, у = 3 частные производные равны
df df η
d2f _ _ d2f _ _ d2f _
дх2 ' дхду ' ду2
Следовательно, дифференциал df в точке ρ = ( 1 определяется
числами (12,4), а гессиан — матрицей (
6.3. Максимум и минимум
Гессиан особенно полезен при анализе поведения функции в
окрестности критической точки, т. е. точки, где df равен нулю.
Если ро = ( ) — критическая точка, то
/(ρο + ν)=/(ρ0) + ^2/ρ(ν).5
Если квадратичная форма d?fp положительно определена
(в этом случае Η имеет два положительных собственных
значения), то из формулы Тейлора следует, что /(ро + ν) > /(ро) для
достаточно малых v/Ои функция / имеет минимум в точке ро-
Если d?fp отрицательно определена (Н имеет два
отрицательных собственных значения), то /(ро + ν) < /(ро) и / достигает
максимума в ро- Наконец, если собственные значения Η имеют
5Авторы опустили в этой формуле остаток О
У)
так что
написанное равенство — приближенное, а не точное. Поэтому, хотя
сформулированные в следующем абзаце утверждения верны, приведенные рассуждения
следует считать лишь наводящими соображениями, а не строгим выводом
достаточных условий максимума, минимума и седловой точки. — Прим. ред.

6.3. Максимум и минимум
315
разные знаки, то d2f(v) может иметь и положительные, и
отрицательные значения. В этом случае точка ро является седловой
точкой функции /. Если одно или два собственных значения Η
равны нулю, т. е. гессиан — сингулярный, то чтобы установить,
будет ли функция / иметь максимум или минимум в точке р0,
мы должны исследовать производные более высокого порядка.
Рассмотрим пример использования гессиана. Мы должны
найти и классифицировать критические точки функции
/ = Зх2 + 2у3 - бху.
Вычислим частные производные по χ и по у и приравняем их к
нулю.
fi(x>y) = 6х-6у = 0, т.е. χ = у,
ίτίχι У) = 6У2 - 6х = 0, т. е. χ = у2.
Следовательно, функция / имеет критические точки: χ = 0, у = О
и χ = 1, у = 1. Чтобы построить гессиан, вычислим частные
производные второго порядка:
d2f _ d2f _ d2f _
дх2 ' дхду ' ду2
Следовательно, в точке χ = 0, у = 0 матрица гессиана равна
Определитель этого гессиана отрицательный, следовательно, его
собственные значения имеют противоположные знаки, и
функция /(х, у) имеет в начале координат седловую точку. Чтобы
проверить это, заметим, что / имеет положительные значения при
у = 0 и малых х. А при χ = у функция имеет отрицательные
значения в окрестности начала координат.
В точке χ = 1, у = 1 матрица гессиана равна
Н = ( -6 12 ) '
°1
дх
а/
ду

316 Глава 6. Теоремы ... дифференциального исчисления
Определитель этого гессиана положителен, поэтому собственные
значения имеют одинаковый знак. Так как след определителя
положителен, то собственные значения гессиана положительны.
Следовательно, в точке χ = 1, у = 1 функция имеет локальный
минимум.
На аффинной плоскости дифференциал второго порядка d?f
обладает одним свойством, которое не зависит от выбора
системы координат, а именно, число положительных, отрицательных
и нулевых собственных значений гессиана. На евклидовой
плоскости функция / обладает еще одним свойством, не зависящим
от выбора системы координат. Чтобы получить его, сравним
значение функции, усредненное по малой окружности вокруг точки
Ро, со значением функции в точке ро (рис. 6.2).
h cos θ
hs'm6
Рис. 6.2
Из формулы (6.12) следует, что
/(Ро + ν) = /(ро) + df[v] + -d2f{v) + остаток.
Поскольку df[—ν] = — d/[v], среднее значение df[v] для
любой окружности с центром в точке ро равно нулю. Чтобы
усреднить -ci2/(v), положим ν = I . . I. Воспользуемся
формулой (6.13):
Ь., ч 1,, Л L . nJ d2f/dx2 d2f/dxdy\fhcose
-A*
d2f d2 f d2f'
-4 cos2 θ + 2—-|- cos θ sin θ + ^4 sin2 θ
οχΔ oxoy oyz

6.3. Максимум и минимум
317
Средние значения cos2 θ и sin2 θ на отрезке [0, 2π] равны -, сред-
нее значение cos θ sin θ равно нулю. Поэтому
{2d /(v)) = lh [d^ + W\ ·
Следовательно,
</(po + v)> = /(po) + ^2 ^ + ^2 J + остаток.
Величина d2f/dx2 + d2f /ду2, определяющая «в среднем»
поведение функции / при движении от точки ро, называется
лапласианом /. Для любой системы координат, полученной
вращением системы х, у, лапласиан имеет одинаковое значение. Поэтому
уравнение
0V + 0V=o
дх2 ду2
называемое уравнением Лапласа, описывает свойство функции
на евклидовой плоскости, не зависящее от выбора системы
координат. Не удивительно, что такое уравнение часто описывает
функции, имеющие физический смысл: электрический
потенциал, температура и т. д.
Прежде чем закончить исследование вопроса о максимуме и
минимуме функции на плоскости, рассмотрим проблему
условного экстремума: найти максимум и минимум функции /(р) на
кривой, заданной уравнением уравнением g(p) = const. 6
Необходимое условие того, что функция достигает
условного экстремума в точке ро, имеет вид: dfPo(v) = 0 для любого
вектора ν, касательного к кривой g(p) = const (рис. 6.3). Но
такой вектор удовлетворяет уравнению dg(v) = 0. Следовательно,
в точке ро, где достигается максимум или минимум исследуемой
функции, значение dfPo должно быть пропорционально dgpo, т.е.
df = Xdg. Таким образом, проблема условного экстремума
привела нас к методу, известному как метод множителей Лагранэюа.
6В дальнейшем используется, что /, д дифференцируемы, а также
условие, что dgPo не равен тождественно нулю. — Прим. ред.

318 Глава 6. Теоремы ... дифференциального исчисления
д = const
Рис. 6.3
Рассмотрим функцию / — Хд, где λ — неопределенный скалярный
коэффициент, называемый множителем Лагранжа. Если в
точке ро достигается максимум или минимум, то в этой точке при
некотором λ должно выполняться равенство d(f — Хд) = 0. Кроме
уравнения д = const, это дает еще два, из которых
определяются неизвестные значения х, у и λ. Чтобы выяснить, какой
экстремум (максимум или минимум) мы получили (или никакого),
сначала найдем вектор ν, для которого dg(v) = 0. Этот вектор
будет касательным к кривым / = const и д = const в критической
точке ро· Затем рассмотрим функцию h = f — Хд, у которой, по
построению, точка ро будет критической на плоскости. Найдем
наилучшее квадратичное приближение к h в окрестности этой
критической точки и вычислим его для нашего вектора v. Если
величина -d2h(v) положительна, то h(p) > h(po) во всех точках
Δι
кривой вблизи ро- Действительно, зададим кривую д = 0
параметрически: ρ = p(t), т.е. мы возьмем функцию ρ : R —■> R2, для
которой
g{P{t))=0, р(0)=ро, ρ'(0)=ν.
(Это всегда можно сделать, как следует из теоремы о неявной
функции, которую мы докажем в следующем параграфе.) Тогда
h о ρ = f о ρ, так как д о ρ = 0.
Далее,
(/iop)'(0) = d/ipo(v)=0,
(/op)" = (hop)"(0)=<i2V(v).

6.3. Максимум и минимум
319
Если (h о р)"(0) > 0, то / имеет минимум в точке р0 на линии
д = 0. Аналогично, / имеет максимум на линии д = 0, если
d2h(v) < 0.
Например, мы хотим найти экстремум квадратичной формы
Q(x, у) = 8х2 - \2ху + Пу2
на окружности G(x,y) = χ2 + у2 = 1. Положив дифференциал
Q — XG равным нулю, получаем
16х - 12у - 2\х = 0,
-12х + 34у - 2\у = 0.
Исключив из этих уравнений λ, получаем
16-12(ι//χ) = -12(χ/ι/)+34
или
(х/у) - (у/х) = 3/2.
Отсюда
х2 ~ 2ХУ ~ У2 = °>
и, следовательно,
(ж - 2у) (х + -у\ = 0.
Таким образом, квадратичная форма Q может принимать
экстремальные значения в точках пересечения прямых χ = 2у и
χ = — -у с окружностью х2 + у2 = 1 (рис. 6.4), т. е. в точках
Δι
— га " —(-$)■
Исследуем теперь, имеются ли экстремумы в этих точках, и
какие именно. Вычислим дифференциалы
dQ = (16ж - 12у) dx + (-12ж + 34у) ciy,
ciG = 2xdx + 2у dy.

320 Глава 6. Теоремы ... дифференциального исчисления
х = 2у
Рис. 6.4
В точке pi, где χ = 2у, получаем
dQ = 10х dx + Ъх dy, dG = 2xdx + χ dy.
Как мы и ожидали, dQ пропорционален dG с множителем λ = 5.
Вектор ν, для которого dQ(v) = dG(v) = 0, равен I J. В этом
случае гессиан квадратичной формы Q — 5G равен
3 -6Ч
IT
' -6 12
Вычисляем (1, —2) I ) I _ ) = 75 и приходим к выводу,
что Q имеет минимум на окружности в точке pi.
В другой критической точке р2, где у = — 2х, получаем
dQ = 40х dx — 80х dy, dG = 2xdx — 4х dy,
следовательно, λ = 20. Вектор, для которого dQ(v) = dG(v) =
0, равен ( 1 ) · Вычислив гессиан функции Q — 20(? для этого
вектора, получаем
значит, Q имеет локальный максимум на окружности х2 + у2 = 1
в точке р2-

6.4. Теорема об обратной функции
321
6.4. Теорема об обратной функции
Пусть ί/ и V — векторные пространства одинаковой размерности
и пусть / : U —► V — дифференцируемое отображение с условием
/(Ро) — Чо- Мы хотели бы знать, при каких условиях существует
такое отображение д :V —* U, что д ° f = (id). Прежде чем дать
формулировку соответствующей теоремы, исследуем сначала ряд
необходимых ограничений этой проблемы.
Если мы ожидаем, что отображение д тоже должно быть
дифференцируемым, то согласно цепному правилу
ά9}{ρ) ° dfp = (id).
Тогда линейное отображение dfp должно быть обратимым. Если
это так, то справедлива формула
d9f(p) = [dfp]'1-
\ \у I
χ
Рис. 6.5
Обсудим случай, когда df не является обратимым
отображением: U = V = R1 и f(x) = χ2 (рис. 6.5). В начале координат
dfo = 0, и возникает проблема с д(у) = у/у вблизи у = 0. По
существу, возникают три разных проблемы. Прежде всего, у/у не
определен (в области вещественных чисел) для у < 0. Более точно, не
существует точки у < 0, являющейся образом /. Во-вторых,
корень квадратный из у определен неоднозначно: для данного у > 0

322 Глава 6. Теоремы ... дифференциального исчисления
существует два значения х, удовлетворяющих уравнению χ = у.
И последнее: производная у/у неограниченно растет при у —■> 0.
Чтобы обойти вторую из перечисленных трудностей, проделаем
следующую процедуру.
Рис. 6.6
Предположим, что мы взяли некоторое значение xq φ 0, для
которого х\ = уо. Для определенности, пусть хо > 0. Тогда в
достаточно малой окрестности точки уо (настолько малой, чтобы
не включать у = 0) существует единственная обратная функция:
квадратный корень, удовлетворяющая конкретному требованию:
значения функции должны быть достаточно близки к xq. (В этом
случае слова «достаточно близки» значат, что функция не может
быть отрицательной. Если мы выбрали положительное значение
корня, то функция определена однозначно (рис.6.6).)
Мы можем не только утверждать существование
квадратного корня, но и дать алгоритм его вычисления с любой наперед
заданной точностью. Здесь приводится один из возможных
алгоритмов — метод Ньютона, который формулируется в общем
случае.
Допустим, что у нас есть отображение /:[/—► V с условием
/(Ро) = Чо- Пусть задано некоторое значение q вблизи qo, и мы
хотим найти такое ρ вблизи р0, что /(р) = q. Найти ρ — это то
же самое, что найти ρ — ро· Итак, мы хотели бы иметь равенство
/(Ро + Ρ - Ро) = q

6.4. Теорема об обратной функции
323
Однако,
/(Ро + Ρ - Ро) = /(Ро) + <#ρο(Ρ - Ро) + о(р - Ро)
= Qo + <#ρο(Ρ - Ро) + о(р - Ро)·
Если опустить член о(р — ро), то получится приближенное
уравнение
q-q0 = ci/p0(p-po),
или, так как dfPo имеет обратное отображение,
P = Po + d/P01(q-qo)·
Это значит, что мы получили
pi = Po + ci/p01(q-qo)
в качестве приближенного решения. Теперь определим
qi = /(pi)
и начнем все сначала. На следующем шаге получим
Р2 =Pi + ci/p11(4-4i)'
и так далее7. В этом и состоит метод Ньютона.
Вернемся к рассмотренному выше примеру. Пусть U = V =
R1 и f(p) = ρ2. Тогда dfp есть умножение на 2р и, следовательно,
df~l(w) = w/2p. В этом случае
Р\ =Ро + 1г-{я-Чо)·
2ро
Например, если взять Ро = 3, то qo = 9 и q = 10. Тогда
Р1 =3+^(10-9) = 3.1666..., qi = р\ = 10.02777...
При выполнении некоторых условий последовательность ρι,Ρ2, ■ ■ ·,
вычисляемая по формуле Pi+i = Pi + d/fT.^q — Qi)i имеет предел ρ, который
является решением уравнения /(р) = q. Авторы говорят об этом ниже, в
пункте «Сходимость метода Ньютона». — Прим. ред.

324 Глава 6. Теоремы ... дифференциального исчисления
(Заметим, что р\ дает значительно лучшее приближение для V10,
чем ро = 3.)
Следующее приближение:
P2=3l6+dui(10-iao2?>
= 3.1622816...
При этом
q2 = v\ = 10.000024,
а число р2 дает ответ с точностью до четырех десятичных знаков
(>/Ϊ0 = 3.1622776... )■
Рассмотрим еще пример. Пусть U = V = R2 и отображение /
дается формулой
Тогда df/ χ \ есть линейное преобразование, матрица которого рав-
Зх2 -3y2N
на
Пусть ро = ( 1 ) ■ Тогда
qo
2у 2х
8-1W7
2-2-1 I U
dUo - у 2 i) ' ^/ро) Х ~ 54 V-2 12
Возьмем q = I ' I и будем решать уравнение /(р) = q по
методу Ньютона. Тогда
pi = po + (ci/po)-1(q-qo)
2\ J_ / 4 3\ / 0.5\ _ /2.026
1 У + 54 V -2 12 ) V —0.2 ) ~ I 0.937

6.4. Теорема об обратной функции
325
(7.493 \
)' чт0 Уже Достаточно близко
/2.026643.. Л „
к точному решению: ρ = I „ 007^10 ) ■ ^аметим> чт0 каждый
последующий шаг этого алгоритма означает вычисление
значений преобразования (d/Pi)_1 в различных точках pi-
Ниже мы сформулируем математическую теорему, согласно
которой при некоторых предположениях относительно / метод
Ньютона дает последовательность точек pi, которая сходится к
решению р, когда /(р) = q при условии, что q достаточно близко
к q0.
Существует другой алгоритм вычисления квадратного корня,
называемый методом Пикара. Однако сходится он гораздо
медленнее метода Ньютона. Согласно методу Пикара, полагаем
L = (d/ροΓ1
и тогда
pi =p0 + L(q-q0), qi=/(pi),
Р2 = pi + L(q-qi), q2 = /(P2), и так далее.
Например, для / : R —■> R с f(p) = ρ2, q = 10 и ро = 3 мы
имеем
pi = 3.16, qi = 10.027,
как и в методе Ньютона. Однако
р2 = 3.16 + -(-0.027) = 3.162036,
92 = 9.9984817 и так далее.
Преимущество метода Пикара в том, что L вычисляется один раз.
Сравнительно легко доказать сходимость методов Пикара и
Ньютона при небольших ограничениях на /. Получение хорошей
оценки скорости сходимости метода Ньютона потребует, как мы
увидим, более сильных ограничениях на /.
Доказательства сходимости. Здесь мы сформулируем
предположения относительно функции /, которые нам необходимы для

326 Глава 6. Теоремы ... дифференциального исчисления
доказательства сходимости обоих методов. Напоминаем, что мы
называем функцию / дифференцируемой в точке р, если
/(Р1) = /(Р) + d/pip1 - Ρ) + «(ρ1 - ρ).
Это значит, что для любого данного ε можно найти такое δ, что
НДр1) - Яр) - d/pip1 - р.)|| < ^IIp1 - Р|| (б.н)
при условии, что Цр1 — р|| < δ. Величина δ, стоящая в этом
неравенстве, может зависеть от точки р. Предположим, что /
равномерно дифференцируема в том смысле, что для любого ε
можно найти такое δ, что (6.14) выполняется для всех точек ρ и
р1, принадлежащих небольшому шарику с центром в ро- Итак,
мы предполагаем, что существует такое α > 0, что для данного ε
можно найти такое δ, чтобы неравенство (6.14) выполнялось при
условии:
IIf»1 — f»II < <^, ||р-ро||<а, Цр1 - poll < α.
Предположим также, что df~l равномерно ограничена, т. е. что
существует некоторая постоянная К, для которой
1И/р" 111 < к для всех Up ~~ Poll < α· (6.15)
Кроме того, будем считать, что и сама функция dfp равномерно
ограничена, т. е. что
\\dfp\\ < Μ для всех ||р — ро|| < а.
Наконец, для метода Пикара предположим, что dfp непрерывна
в том смысле, что для любого ε > 0 существует такое δ, что
\\dfp~dfpAl < 2ε>
если ||р> — р11| < <5, ||р - ро|| < а, Цр1 — р0|| < а, (6.16)
и нам потребуется только существование (с(/р0)-1·
Сходимость метода Ньютона. Рассмотрим метод Ньютона.
Переход от точки р^ к точке pi+i определяется формулой
Pi+i = pi + (d/pj-^q - /(Pi))· (6-17)

6.4. Теорема об обратной функции
327
Дифференцируемость /(р) в точке рг_1 означает, что
/(Рг) = /(Рг-1 + Рг - Pi-l)
= /(pi-l) + d/p^Pi - Pi-l) + «(Рг - Pi-l) (6-18)
Равенство (6.17) можно переписать в виде
4/рДРг+1 - Рг) = q - /(pi),
откуда заменой г на (г — 1) мгновенно получается, что сумма
первых двух слагаемых в правой части (6.18) равна q, поэтому
из (6.18) следует, что
/(Pi) - Я = o(pi -Pi-i).
Это значит, что для любого ε > 0 можно подобрать δ > 0 так,
чтобы при ||Pi — Pi-i || < δ выполнялось неравенство
ll/(Pi)-q|| <e||Pi-Pi-i||·
С учетом равенства (6.17) и оценки (6.15) из только что
написанной формулы можно получить следующую оценку:
||Pi+i - Pill < -K^llPi - f»*—ill- (6·19)
В дальнейшем будем считать, что число ε взято таким, что
Κε<\.
Перейдем к оценке скорости сходимости метода Ньютона.
Прежде всего,
Pi = ро + d/po1 (q - qo), qo = /(ρο)·
Поэтому, если ||q — qo|| < δ/Κ, то ||р — Ро|| < δ. Если δ < α/2,
точка pi будет удовлетворять неравенству
„ 1
||Pi "Poll < 2α·
Поскольку ρ! лежит внутри области определения /, то можно
воспользоваться алгоритмом (6.17) и получить р2· Из
неравенства (6.19) следует, что
|Р2-Р1||<^<Ща),

328 Глава 6. Теоремы ... дифференциального исчисления
следовательно,
и и и и и Л \ 1
||Р2-Ро|| < ||Ρ2-ρι|| + ||Pi -Poll < ( 2 + 1 I ^a<a.
Итак, точка р2 опять лежит внутри шарика радиуса α и опять
можно воспользоваться алгоритмом (6.17). Получаем
||рз-Р2||<^||Р2-Р1||<^,
и, следовательно,
||Рз-ро|| - ( 4 + 2 + J 2α~α'
и так далее. По индукции можно доказать, что при всех г
||Pi-Pt-i|| <i/2i_1
и
||Pi " Poll < ^ + 2ΪΤΙ + · · · + 1J 2α - 2 " 2° " α·
Последовательность точек р^ сходится8 к некоторой точке р, т. к.
1 / 1 1 Л г 1 г п
p,-+fr — р,- < —г-τ —г Η ;—г + ■ ■ ■ Η— ) 0 < —г-^-д —■> О
MVt+fc У1\\ - 2г_! ^2fc "Г 2fc_! τ -г 2у _ 2г_х
при г —► оо.
Наконец,
l|q - /(Pi)ll = Цсг/рДрг+ι - р*)|| < мцРт - Pi|| -+ о,
т. е. limj^oo /(pi) = q. Так как функция / непрерывна, то
Яр) = q-
Единственность решения. Рассмотрим проблему
единственности решения уравнения /(р) = q. Заметим, что величина К
83десь авторы используют классическое необходимое и достаточное
условие сходимости, известное как «критерий Коши». — Прим,, ред.

6.4. Теорема об обратной функции
329
определяется функцией /. При желании мы можем выбрать еще
меньшее значение а, не изменяя при этом К. Сделать это можно
за счет выбора δ и, следовательно, меньшего значения δ/К. В
частности, предположим, что α выбрано настолько малым, что
(6.14) выполняется для любой пары точек ρ и р1, и при этом
ε К < 1. Тогда для любой пары точек имеем
Ир - р1!! = ШиГ'Шр - р1))!! < K\\dfp(P - Pl)\\.
Если /(р) = /(р1), то неравенство (6.14) значит, что
Шр'-рН^Ир'-рЦ,
и тогда, комбинируя эти два неравенства, получаем
Цр-р1!! < εΚ\\ρ -ρ1!!, εΚ < 1.
Это неравенство справедливо только в случае ||р — р1!! = 0, т.е.
ρ = ρ1. Таким образом, для ||р —Ро|| < я может быть только одно
уравнения решение /(р) = q.
Сходимость метода Пикара. Рассмотрим метод Пикара. Пусть
L = Иро)-1· Тогда
Рг+1 = Рг + £(q - /(Рг))
= Рг + L(q - /(Рг-l) + dfp^Pi - Pi_i) + o(pj - Рг-l)),
как и раньше. Теперь
q - /(Pi-l) + dfp0{pi - Ρί-l) = О,
следовательно,
l|q - /(ρ·-ι) + d/pi_i(Pi - Pi-i)ll = \\i.dfpi-i - dfpo){pi - Pi-i)||
ε
< 2 IIP*- Pi-l II
при условии, что выбранное значение α достаточно мало. Кроме
того, мы можем выбрать δ настолько малым, чтобы в неравенстве
(6.14) можно было ε заменить на -ε. Тогда
и , Л „ „ 1 и
||Pi+i -Рг|| < к Ι 2εΙΐΡ» -Ρ*-ιΙΙ + οεΙΙρί "Ρ*-1!
< Κε\\ρί -pi_i||,

330 Глава 6. Теоремы ... дифференциального исчисления
так что неравенство (6.19), где сделана замена К = \\L\\,
выполняется, как и раньше. На самом деле можно воспользоваться
теоремой о среднем значении, чтобы изменить обоснование
метода Пикара, и таким образом избежать необязательного
предположения о равномерной дифференцируемости. Действительно,
рассмотрим отображение
Мр) = р + Цч-/(р)),
где L = (ci/po)-1. Непрерывность дифференциала dfp позволяет
выбрать значение α настолько малым, чтобы выполнялось
неравенство
\\dhp\\ = \\I-Ldfp\\<±.
Тогда, воспользовавшись теоремой о среднем значении, получаем
||Рг+1 - Pt|| = НМРг) - MPi-l)ll < gill* ~ Pi-lll>
и дальше можно рассуждать, как и раньше.
Теперь обсудим, почему на самом деле метод Ньютона
сходится гораздо быстрее, чем это видно из доказанных выше оценок.
Предположим, что / имеет две непрерывные производные. Тогда
из формулы Тейлора следует, что
1ДР1) - Яр) - d/pip1 - р)| < сЦр1 -р|
2
где постоянная с определяется максимумом |ci2/|· Это
неравенство значительно сильнее, чем (6.14). Возвращаясь назад к
доказательству (6.17) и использовав это неравенство, получаем
||Рг+1 - Pl|| < Щ\Рг ~ Pi-l||2·
Если, например, мы начали со столь малого значения ||ρι — ро||,
что Κ\\ρι — РоЦ1^2 < 1 (и ||ρι — poll < 1), то из последнего
неравенства следует
||Pi+i - Pill < K\\pi - Pi-i||1/2 · Up» - Pi-i||3/2·
Тогда
|Pt+i -pt|| < IIpi -po
I(3/2)"

6.4. Теорема об обратной функции
331
т. е. мы получаем экспоненциальную скорость убывания вместо
геометрической прогрессии Црг+ι — Pt|| < (^-^)n||pi — Ро||ι
получающейся в методе Пикара.
Итак, резюмируем, что мы выяснили. Мы показали, что при
соответствующих условиях вокруг точки qo = /(ро) существует
шарик В, а вокруг точки ро шарик С, такие, что для каждой
точки q € В существует единственная точка ρ € С, для которой
/(р) = Q (рис. 6.7). Другими словами, мы определили такое
отображение д : В —* С, что / о д = (id) и д о / = (id).9
Дифференцируемость решения. Докажем, что функция д
дифференцируема. Заметим, что из единственности д вытекает
ее непрерывность. Итак, предположим, что g(q) = p. Нарисуем
шарик с центром в точке р. А теперь воспользуемся
результатами, уже полученными для точек ρ и q. Это значит, что
существуют шарик с центром в точке q, и функция, обратная к /,
отображающая его в шарик с центром в точке р.
В С
Рис. 6.7
Однако, в силу единственности, эта обратная функция
должна совпадать с д. Следовательно, д отображает небольшой шарик
с центром q в небольшой шарик с центром р, т. е. она непрерывна.
Тогда
v = /(5(q + v))-/(5(q))=rf/p(5(q + v)-5(q))+0(5(q + v)-5(q)).
Применим отображение (rf/p)_1 к обеим частям этого равенства.
9Последнее предложение, означающее биективность отображения д,
требует уточнения: для биективности д следует его рассматривать как
отображение д : В —> Ci, где С\ = д(В) — образ шарика В при отображении д,
который содержится в С, но не обязательно заполняет все С. — Прим. ред.

332 Глава 6. Теоремы ... дифференциального исчисления
В результате получим
(d/P)-1(v) = g(q + v) - p(q) + o(p(q + ν) - p(q)).
В силу непрерывности функции д мы можем выбрать ν настолько
малым, что ||o(p(q + v)-(/(q))|| будет меньше -||p(q + v)-p(q)||.
Из написанного выше равенства следует, что
iKrf/p)"1^)!! + IKiKq + ν) - p(q))|| > ||p(q + ν) - p(q)||,
откуда
ll5(q + v)-p(q)||<2||(Ci/p)-1(v)||,
т. е. g(q + ν) — g(q) = O(v). Но тогда
o(g(q + v) - p(q)) = o(0(v)) = o(v).
Следовательно, мы получили, что
5(q + v)-p(P)-(d/Pr1(v) + o(v))
т. е. функция д дифференцируема в точке q, и ее производная
равна
<%(р) = (.dfp)'1-
Тем самым мы доказали следующую теорему10.
Теорема об обратной функции. Пусть f : U —► V —
непрерывно дифференцируемая функция, где /(ро) = qo> и
отображение dfPo обратимо. Тогда вокруг точек qo и ро существуют
такие шарики В и С, что имеется единственное отображение
g : В —► С, для которого f о g — (id). Это отображение
непрерывно дифференцируемо и
d9f(P) = (d/ρΓ1·
Теорема о неявной функции. Давайте рассмотрим некоторые
следствия теоремы существования обратной функции.
Предположим, что G : R2 -+ R1, G(x0, у0) = 0 и
9G , п .
— ψ О в точке (х0, уо).
ду
DB связи с формулировкой этой теоремы см. сноску 9. — Прим. ред.

6.4. Теорема об обратной функции
333
Речь будет идти о том, чтобы решить (хотя бы локально)
уравнение д{х, у) — 0 относительно у.
Определим отображение / : R2 —* R2 формулой
ί Ъ)) ~ \G{x,y))
Тогда
1 О
df=\dG_ <κ?
dx dy
является матрицей, несингулярной в точке I ° ). Согласно
теореме существования обратной функции, можно найти
отображение д, для которого / о д = [id). Тогда можно написать
u\\ = (F(u,v)
vj) \H(u,v)
и уравнение / о д = (id) преобразуется к виду
F(u,v) = и,
G(F(u,v),H(u,v)) =υ.
Подставив первое уравнение во второе, получим
G(u,H(u,v)) = ν,
а выбрав ν = 0 и обозначив h(u) = H(u, 0), имеем
G(u,h(u)) =0.
Функция h(u) дифференцируема и является единственным
решением этого уравнения. Единственность и дифференцируе-
мость функции h составляет содержание теоремы
существования неявной функции. Таким образом, теорема существования
неявной функции от одной переменной есть следствие теоремы
существования обратной функции, зависящей от двух
переменных. Сформулируем эту теорему еще раз.

334 Глава 6. Теоремы ... дифференциального исчисления
Теорема о неявной функции. Пусть G — дифференцируемая
функция, для которой G(xQ,yo) = 0 и (dG/dy)(xo,yo) φ 0. Тогда
существует единственная функция h(x), определенная вблизи
χ — Xq, удовлетворяющая условиям: h(xo) — уо и G(x,h(x)) = 0.
Функция h дифференцируема и h'(x) = — (dG/dx)/(dG/dy).
Предыдущую аргументацию можно сформулировать
по-другому. Простейшее отображение из R2 —► R1 (за исключением
постоянного отображения), которое можно придумать, есть
проекция на одну из осей:
Пусть G : R2 -♦ R1 - любое непрерывно дифференцируемое
отображение и предположим, что dGPo сюръективно (что в
нашем случае одномерной области значений означает dGP0 φ 0).
Утверждается, что существуют локальные замены координат,
т.е. отображения g : R2 —-► R2, которые локально определены
и имеют дифференцируемые обратные отображения, так что
Go g = π.
Действительно, поскольку dGPo φ 0, мы можем сначала линейной
заменой добиться, чтобы dG/dy φ 0. Тогда вышеприведенные
соображения позволяют построить отображение д, для которого
Gog = π. Таким образом, если допускаются произвольные замены
координат, то самое общее непрерывно дифференцируемое
отображение, у которого dGp сюрьективно, есть проекция на одну из
осей. На рис. 6.8 вы видите пример функции G{x, у) = (х2 + у2)1/2
(изображены линии д(х,у) = const), которая после перехода к
полярным координатам имеет вид Gog(6,r) = г, т.е. задает
проекцию точки (Θ, г) на ось г.
Теперь поговорим об отображениях из R1 в R2. Простейшее
нетривиальное отображение такого вида — это отображение г,
которое вставляет пространство R1 в R2 как ось х:
г-.Ш'-^Ж2, г(*)=(о)·
Мы утверждаем, что если G : R1 —► R2 — любое непрерывно
дифференцируемое отображение с условием dGPo φ 0, то локально

6.4. Теорема об обратной функции
335
G(x,y) = (х2 + у2)Ь
G о д(в,г) = г
R
г cos θ
г sin θ
Рис. 6.8
можно найти замену координат, т. е. непрерывно
дифференцируемое отображение /, имеющее дифференцируемое обратное, так
что (см. рис. 6.9)
foG = i.
vl:
Рис. 6.9
Действительно, сначала можно выполнить линейное
преобразование переменных на плоскости так, чтобы в новой состоме
координат отображение G имело вид
Теперь определим F : R2 —■> R2 формулой
Gi(u)
G2(u) + ν

336 Глава 6. Теоремы ... дифференциального исчисления
Тогда
dF,
G(po)
1 О
О 1
и, следовательно, F имеет (локально) непрерывно
дифференцируемое обратное отображение. Из определения F и г следует, что
™=(£)-а
Поэтому, взяв / = .F-1, получаем
i = foG.
Итак, изменяя систему координат, можно локально «выпрямить
любую кривую».
6.5. Поведение функции вблизи
критической точки
Предположим, что / : R2 —■> R имеет критическую точку в ро,
т. е. ci/po = 0. Будем считать, что мы уже сделали преобразование
координат так, что теперь ро = 0 в R2. Допустим, что d2fo
невырождена, т.е. Det(ci2/o) Φ 0. Другими словами, предположим,
что симметричная матричная функция
Н =
I &£
d2f
\дх\дх2
d2f \
дх\дх2
дх\
I
невырождена в 0. Из результатов параграфа 4.2 мы знаем, что
можно найти такое линейное преобразование координат L, что
LH(0)LT может быть принять одну из трех форм:
LH(0)L2
1 0
,0 1
-1 0
0 1
'-1 0
0 -1

6.5. Поведение функции вблизи критической точки 337
Допустим, что мы уже сделали линейное преобразование
координат, и d2fo уже записывается в виде одной из этих стандартных
форм. Из доказательства разложения Тейлора мы знаем, что
/О, У) = /(0) + Ьц(х, у)х2 + 2Ь12(х, у)ху + Ь22(х, у)у2
'Ьц bi2\ (V
.У.
= /(о) + (*,»)в(*),
где bij — непрерывные функции χ и у, а матричная функция В,
вычисленная в начале координат, равна d2/o, т. е.
В(0) = Я(0)
или
M0) = g(0), МО) = |^(0), МО) = 0(0).
Матрица В симметрична. Применим процедуру Грама-Шмидта
к В(х) и В(х) ). Из непрерывности В ясно, что
произведения
(1,0)Я(х)^), (1,0)Б(х)(^, (0,l)l?(x)(j
непрерывно зависят от х. Следовательно, для х, достаточно
близких к нулю, можно найти такую обратимую матрицу <5(х)
(заданную процедурой Грама-Шмидта), что
Я(х) = 3(χ)τ£(0)3(χ).
Алгоритм Грама-Шмидта обеспечивает дифференцируемость
функции <5(х)- Таким образом,
Дх) = /(0) + хтд(х)тЯ(0)д(х)х,
или
/(х) = /(0) + утЯ(0)у,

338 Глава 6. Теоремы ... дифференциального исчисления
где
у = #(х)х.
Отображение хну, заданное этой формулой, обратимо согласно
теореме об обратной функции! Более подробно·, пусть φ : R2 —■> R2
определена формулой
ф(х) = Q(x)x.
Тогда, дифференцируя произведение, получаем
#о(х) = (dQo(x))0 + Q(0)x
или
ci^o = (id).
Таким образом, теорема существования обратной функции
гарантирует, что φ имеет дифференцируемую обратную
χ = v(y)-
Но тогда (ip*f)(y) = Дх), поэтому
Г/(У) = /(0) + УТЯ(0)у.
Другими словами, функция ip*(f — /(0,0)) — квадратичная
форма! Итак, мы доказали, что вблизи любой невырожденной
критической точки можно ввести такие координаты у\, у2, что
/(l/i.I/2) = /(0) + Q(i/i,ifc).
где
(3(2/1.2/2) = ±(yl + 1/2) или (5(2/1,2/2) =-2/1+2/2·
Что выбрать из этих трех вариантов, определяется нормальной
формой (числом отрицательных собственных значений) второго
дифференциала d2fo-
Это доказательство имеет общий характер, оно применимо
для любой размерности. Итак, если 0 — невырожденная
критическая точка /, то можно найти такие координаты, в которых
/(y) = /(0) + Q(y),

Резюме
339
где
Q(y) = ±y2l±y22 + --- .
Число знаков минус в этой формуле (называемое индексом Q),
равно числу отрицательных собственных значений матрицы cfifo-
Этот результат известен как лемма Морса. Мы воспользуемся
этой леммой при изучении асимптотических интегралов в
главе 21.
Резюме
A. Производные высших порядков
Вы должны уметь писать разложение Тейлора для функции,
определенной на плоскости, через частные производные
первого и второго порядка.
Вы должны уметь применять цепное правило, чтобы
выразить частные производные второго порядка или уравнения в
частных производных второго порядка через новые координаты.
B. Критические точки
Надо уметь находить критические точки функции, определенной
на плоскости, и классифицировать их, т. е. определять максимум,
минимум и седловую точки.
Надо уметь пользоваться методом множителей Лагранжа для
нахождения условных критических значений функции
нескольких переменных.
C. Обратные функции
Вы должны знать формулировку теоремы существования
обратной функции и уметь пользоваться ей.
Вы должны уметь применять метод Ньютона для нахождения
приближенного решения уравнения /(р) = q, где / : R2 —► R2.
Задачи
(О для χ = у = 0;
х3у
—ζ ςτ в других точках.
χΔ + у*

340 Глава 6. Теоремы ... дифференциального исчисления
(a) Вычислите dF/dx и dF/dy. Непрерывны ли они в (0,0)?
(b) Вычислите d2F/dxdy и d2F/dydx. Непрерывны они в (0,0)
или нет? (Замечание: если эти производные не непрерывны
в (0,0), то их нельзя вычислить, получая общую формулу и
устремляя χ и у к нулю!)
(c) Покажите, что d2F/dxdy(0,0) ф d2F/dydx(0,0).
(d) Придумайте гладкую кривую, которая проходит через
начало координат и определяется формулами χ = X(t), у = Y(t)
с условием Х(0) = Y(0) = 0 так, чтобы функция
G(t) = F(X(t),Y(t))
была не дифференцируема в начале координат.
6.2. Найдите и проклассифицируйте все критические точки функции
F : R2 —» R, определенной формулой
F(x, у) = х3+у3- Ъху.
6.3. Пусть F(x, у) = х2у — Ъху + \х2 + у2.
(a) Найдите уравнение плоскости, касательной к функции ζ =
F(x, у) в точке χ = 2, у = 2, ζ = 2.
(b) Функция F(x, у) имеет три критические точки, две из
которых лежат на прямой χ = у. Найдите эти критические
точки и выясните, где будет максимум, минимум или сед-
ловая точка.
6.4. Функция F в пространстве R2 определена формулой
F(x, у) = х2 — 4ху + у2 — 6ж-1.
(a) Получите уравнение плоскости, касательной к ζ = F(x, у) в
точке χ = —1, у = —2.
(b) Найдите критические точки этой функции и выясните их
природу.
6.5. Найдите и проклассифицируйте все критические точки
функции F(x, у) = у2 + (х2 — Ъх) log у, определенной в верхней
полуплоскости у > 0.
6.6. Покажите, что функция F(x, у) = у(е4х — 1) + 9ж2 + 6у2 имеет
критическую точку в начале координат и определите природу
этой точки. Опишите линии уровня F(x, у) в окрестности начала
координат. Нарисуйте пару типичных кривых. Опишите линии
уровня F(x, у) в окрестности точки χ = 0, у = 1 и нарисуйте
типичные кривые.

Задачи
341
6.7. Найдите критические точки функции
F(x, у) = 5х3 - Ъх2у + Qxy2 - Ay3 - 21х + 27у
и определите их природу. (Критические точки имеют целые
координаты.)
6.8. (а) Найдите критические точки функции F(x, у) = ху2е~^х+у\
(b) Определите природу тех критических точек, которые не
находятся в начале координат. Нарисуйте как молено точнее
несколько кривых уровня вблизи каждой точки.
(c) Если критическая точка совпадает с началом координат, то
в ней гессиан равен нулю. Выясните природу критической
точки в начале координат и нарисуйте несколько кривых
уровня в его окрестности.
6.9. Пусть χ тл у — обычные аффинные координатные функции на
плоскости. Определим другую пару координатных функций в
правой полуплоскости (х > 0):
и = х2 — у2, ν = 2ху.
(a) Выразите du и dv через dx и dy. Напишите матрицу, вы-
(du \ (dx \ г,
ражающую I , I через I , I в точке Ρ с координатами
χ = 2, у = 1, и = 3, ν = 4.
(b) Найдите приближенные значения координат χ и у для такой
точки Q, что u(Q) = 3.5, v(Q) = 4.
(c) Пусть φ обозначает электрический потенциал на плоскости.
Для выбранной точки Р(х = 2, у = 1, и = 3, ν = 4),
где (дф/ди) = 2 и дф/dv = — 1, вычислите дф/дх и дф/ду.
Найдите направление, по которому функция φ изменяется
быстрее всего.
(d) В той же точке выразите д2ф/дудх через частные
производные φ по и и υ. Конечно, ответ может включать явный
вид функций от χ и у.
6.10. Предположим, что координаты и тл ν выражаются через χ тл у
согласно формуле
и\ _ /cosa — sina\ (x
υ J ~ I sin α cos a J \y

342 Глава 6. Теоремы ... дифференциального исчисления
Пусть / — дважды дифференцируемая функция на плоскости.
Покажите, что
ди2 dv2 дх2 ду2
6.11. Полярные координаты г, θ связаны с декартовыми координатами
соотношением
х\ _ ( г cos 0 s
у J ~~ \ г sin θ
Предположим, что функция / : R2 —» Ш удовлетворяет
уравнению Лапласа:
дх2 ду2
Выразите это уравнение через производные / по г и Θ.
6.12. Пусть / : R2 —» R — дважды дифференцируемая функция и
пусть I I = I ■ а )■ Выразите d2f/3Θ2 через частные
производные / по χ и у.
6.13. Пусть / : R2 —► Ш. — дважды дифференцируемая функция.
Пусть, далее, х^Ои
г\ = ( yjx2 + у2
θ J у arctan(y/a;)
Выразите д2 f /дх2 через частные производные / по г и Θ.
6.14. Дано, что df /дх = f + df /ду- Покажите, что
d2f/dx2 - д2Цду2 = } + 2(д//ду).
6.15. Воспользуемся полярными координатами, данными в
упражнении 6.11.
(a) Пусть функция / определена на плоскости. Допустим, что
в точке с координатами χ = 3, у = 4 частные производные
равны df /дх = 2 и df /ду = 1. Вычислите df/dr и df/δθ в
этой точке.
(b) Предположим, что / удовлетворяет уравнению в частных
производных
дг2 г дг г2 дв2
Преобразуйте его в уравнение, содержащее только частные
производные / по χ и у.

Задачи
343
6.16. Предположим, что на плоскости определена функция /,
удовлетворяющая уравнению Лапласа d2f/dx2 + d2f/dy2 = 0.
Преобразуйте это уравнение к координатам, приведенным в упражнении
5.13. В него могут войти d2f/du2, d2f/dv2, d2f/dudv, df/ди,
df/dv, и и ν, но не должны входить х, у и частные производные
по χ и у.
6.17. Пусть есть отображение φ : R2 —> R2:
*α-(?ΐί)-
Покажите, что для φ в окрестности любой точки можно получить
обратную функцию. Вычислите якобиан обратного отображения.
6.18. В пространстве R3 рассмотрите поверхность ζ = F(x,y), где
F(x, у) = χ2 - 2ху + 2у2 + 3х + 4у.
(a) Получите наилучшее аффинное приближение к F в
окрестности точки
(b) Напишите уравнение плоскости, касательной к поверхности
в точке
(c) Получите уравнение линии, перпендикулярной к
поверхности в этой же точке.
(d) Уравнение F(x,y) = 8 определяет функцию у = д(х).
Вычислите д'(1).
6.19. В статистической механике существует важная проблема.
Рассмотрим физическую систему, которая может иметь энергии +Е,
0 и — Е. Пусть χ обозначает вероятность системе иметь энергию
+Е и пусть у обозначает вероятность системе иметь энергию —Е.
Тогда вероятность системе иметь нулевую энергию равна 1-х—у.
Получите максимум энтропии S, если она определена
соотношением
S(x, у) = -х log χ - у log у - (1 - χ - у) log(l - χ - у)
при условии, что средняя энергия равна £Ό, τ. е.
F(x,y)=xE-yE = E0.
Решите эту задачу, введя множитель Лагранжа β. Покажите, что
вероятность χ пропорциональна е~@Е, а вероятность у
пропорциональна е^Е. Найдите коэффициенты пропорциональности.

344 Глава 6. Теоремы ... дифференциального исчисления
6.20. Рассмотрите функцию а : R2 —» R2, определенную формулой
(a) Вычислите матрицу якобиана 2x2, которая
представляет линейную часть наилучшего аффинного приближения к
функции а вблизи точки I ) = ( ι ) ■ Вычислите прибли-
женное значение F 11 1 л 11, воспользовавшись этой
матрицей.
(b) С помощью той же матрицы получите приближенное реше-
ние уравнения F ((*)) = (( £2
6.21. Пусть f(x, у) = л/х2у4 + 9х2.
(a) Получите наилучшее аффинное приближение к этой
функции вблизи точки χ = 1, у = 2.
(b) Возьмем точку χ = 1, у = 2. По какому направлению
скорость изменения функции f(x, у) максимальна?
(c) Решением системы уравнений
f(x,y) = 5,
χ + у = 3
является точка χ = 1, у = 2. Получите приближенное
решение уравнения
f(x, у) = 5.34,
χ + у = 3.05,
используя наилучшее аффинное приближение, полученное
в первом пункте.
6.22. Функции s и t определены через аффинные координаты функций
χ и у в области χ > 0, у > 0 следующими формулами:
s = xy, t = log у — log x.
(а) Выразите дифференциалы ds и dt через dx и dy в точке
а; = 1, I/ = 2.

Задачи
345
(b) В точке χ = 1, у = 2 значения функций s и t равны s = 2,
t = log 2 « 0.693. Используйте матрицу Якоби в этой точке
и получите приближенные значения координат хну для
точки, где s = 2.02 и t = 0.723.
(c) Пусть / — дважды дифференцируемая функция,
определенная на плоскости. Выразите df/дх, df/dy и д2}/дудх
через х, у и частные производные / по s и t.

I

Глава 7
Дифференциальные формы
и криволинейные интегралы
Главы 7 и 8 являются введением к изучению
многомерного интегрального исчисления. Глава 7
посвящена линейным дифференциальным формам и
соответствующим криволинейным интегралам. Особое
внимание уделено замене переменных в
криволинейных интегралах. Обсуждаются некоторые другие
одномерные интегралы, в частности, вычисление длины
кривой.
Введение
В этой главе мы выясним геометрический смысл линейных
дифференциальных форм, в частности, объектов, которые предстоит
интегрировать по ориентированным траекториям, в результате
чего получаются числа. Начнем с примеров. Рассмотрим форму
ω = -(xdy - ydx).
По определению, эта форма задает правило, которое каждой
точке I I ставит в соответствие вектор-строку \{—у, х)-
Далее, вектор-строка понимается как линейная функция векторов
нашего пространства. В рассматриваемом случае вектор-строка

348 Глава 7. Дифференциальные формы ...
\{—у, х) ставит в соответствие вектору h = ( )
w(*)[h] = ^(xs-yr),
φ Ί
(рис. 7.1).
число
которое равно ориентированной площади треугольника с верши-
х\ ix + rs
нами в нуле и в точках
Рис. 7.1
Предположим (рис. 7.2), что у нас есть кривая α(ί) =1 /.\ 1 ■
Выберем на этой кривой точки pi и пусть hi = Pi+i — Pi-
Тогда сумма Σ ωΡί [hi] даст нам полную ориентированную площадь
изображенных на рис. 7.2 треугольников.
В пределе ломаная линия, соединяющая точки pi,
аппроксимирует кривую. Мы ожидаем, что эта сумма будет стремиться
к пределу — ориентированной площади, заметенной радиусом-
вектором, движущимся вдоль нашей кривой. Мы уже
встречались с этим понятием, когда изучали второй закон Кеплера.
Второй пример. В нем появляется понятие силового поля.
Силовое поле
ω = Fdx + Gdy + Η dz
в каждой точке трехмерного пространства определяет линейную
функцию с матрицей
(F, G, Я).

Введение
349
Рис. 7.2
Эта линейная функция задает элемент работы инфинитезималь-
ного движения, т. е. любому вектору смещения ν в точке ρ ставит
в соответствие
(F, G,H)lvy\= Fvx + Gvy + Hvz.
Мы ожидаем, что эта величина может быть проинтегрирована
вдоль любой траектории Г, в результате чего получается §^ω
— работа, совершенная при движении вдоль траектории Г.
Заметим, что хотелось бы уметь получать работу при движении вдоль
всех траекторий. Представим себе двумерное пространство, где
действует силовое поле
ω = Fdx + Gdy.
Рис. 7.3
Например, на рис. 7.3 изображено влияние гравитации при
движении по поверхности ζ = f(x, у). В этом случае силовое поле

350 Глава 7. Дифференциальные формы ...
пропорцио нально
At W A ^9f А
u = df = -dx+-dy.
Допустим, что у нас есть идеально обратимый электрический
автомобиль. (Идеально обратимый означает, что вся энергия
торможения возвращается в аккумуляторную батарею, при этом не
учитывается ни сопротивление воздуха, ни любое другое
сопротивление.) Будем измерять, сколько энергии поступает в батарею
и сколько расходуется. Разницу между начальным и конечным
показаниями батареи обозначим В ρ — В\. Кроме того, введем
кинетическую энергию автомобиля в начале и в конце пути — ΚΕι
и К Ер. Из закона сохранения энергии следует, что
КЕр - ΚΕι + Βρ-ΒΙ= ί ω,
что равно работе, выполненной при движении. (В этом
рассуждении мы предполагаем, что силы не зависят от скорости, т. е. мы
рассматриваем такое силовое поле, для которого силы зависят
только от пространственных координат.)
Отметим некоторое отличие от использования понятия силы в
законах Ньютона. Если мы пустили камень катиться по
поверхности, то законы Ньютона предсказывают, как он будет двигаться
дальше: движение камня определяется уравнениями
dp
— = F, ρ = mv — импульс, ν — скорость.
Рис. 7.4
В нашем обсуждении мы интересуемся величиной энергии,
использованной при движении вдоль данной кривой. Силовое поле
ω приписывает энергии траекториям Г. Если ω = df, то полная

7.1. Ориентированные траектории
351
работа, совершенная при движении вдоль траектории, есть
разность потенциалов
f(Q)-f(P),
где Ρ и Q — начальная и конечная точки нашего пути (рис. 7.4).
Ну а теперь, имея в виду все эти соображения, перейдем на
математический язык.
7.1. Ориентированные траектории
Ориентированной траекторией на плоскости (или в
пространстве R ) мы будем называть кривую, на которой выбрано
определенное направление движения. Траектория вида Γχ (рис. 7.5),
начальная и конечная точки которой не совпадают, имеет
определенное начало (точка Ра) и определенный конец (точка Рь).
Перестановка начальной и конечной точек изменяет ориентацию
кривой на противоположную. Замкнутая кривая вида Г2 (рис. 7.6)
не имеет определенных начальной и конечной точек. Любая
точка Ρ может быть началом траектории и одновременно ее концом.
Для таких замкнутых траекторий, тем не менее, можно задать
направление движения, т. е. ориентацию. Тогда для любого
фрагмента такой траектории определится его начало и конец.
О
Рис. 7.5 Рис. 7.6
Физически это можно истолковать так: мы имеем траекторию
движения частицы, причем известно, через какие точки проходит
частица и в каком порядке, но скорость ее движения мы не знаем.
Вполне возможно, что какие-то отрезки пути проходятся два или
более раз. Например, частица может пройти два раза по
окружности единичного радиуса против часовой стрелки, или (рис. 7.7)

352 Глава 7. Дифференциальные формы ...
пройти от точки Ра до точки Q, обратно до точки R и только
потом к точке Рь- Такие траектории, может быть, трудно
изображать кривыми с соответствующими стрелками, но они имеют
физический смысл и, как мы скоро увидим, их легко описывать
на языке функций.
Рис. 7.7
Рис. 7.8
Здесь мы ограничимся рассмотрением только
кусочно-дифференцируемых траекторий — непрерывных кривых, для которых
существуют касательные во всех точках, за исключением их
конечного числа (рис. 7.8). Такая траектория может быть описана
как образ отрезка вещественной прямой при непрерывном
отображении
а : R -♦ R2,
которое дифференцируемо везде, кроме конечного числа точек.
Функция а называется параметризацией траектории (рис. 7.9).
Физически можно считать, что функция а определяет
положение частицы в каждый момент времени. Мы можем задавать
а, определяя перенос а* координатных функций, т. е.
записывать формулы, которые дают численные значения координат χ
и у в зависимости от времени. Например, если частица движется
вдоль круговой дуги с радиусом К из точки в точку I „
(рис. 7.10), то ее траекторию можно представить в форме
а : t
Rcost
Rsint
или
0 < 2ί < π,
а*х = Rcost, а* у = Rsint.
Каждая траектория может быть параметризована по-разному,

7.1. Ориентированные траектории
353
Рис. 7.9
Рис. 7.10
причем каждый способ физически будет соответствовать
прохождению траектории с различными скоростями в разные
промежутки времени. Например, отрезок гиперболы у2 — х2 = 1 от точки
I до точки I /jr I (рис. 7.11) может быть параметризован
следующими способами:
a*x = t, а*у = Vt2 - 1, 0 < ί < 1,
а*х = sinhi, а* у = coshi 0 < t < arcsinh 1,
а*х = tani, a*y = seci 0 < 4ί < π.
Траектории, на которых отдельные участки кривой
проходятся более одного раза, удобно записывать в параметрической
форме. Например, параметризация
a*x = cosi, а*у = sini, 0 < t < 4π
описывает путь, проходимый частицей вдоль окружности
единичного радиуса против часовой стрелки два раза, а
параметризация
а*х = sin2 ί, а*у = sin2 ί, 0 < t < 3π/2
f°\
описывает движение по отрезку прямой от точки I „ I вперед к
точке
обратно к I I и потом еще раз вперед к точке

354 Глава 7. Дифференциальные формы ...
Рис. 7.11
Рис. 7.12
*РЬ = Ра
Pn = Pbj
Рис. 7.13
В практических вычислениях каждый дифференцируемый
отрезок пути параметризуется отдельно. Например, на рис. 7.12
изображен путь, который можно параметризовать в виде: сначала
a*x = t, a*y = t, 0<ί<1,
а потом
a*x = y/2cos(ir/A-t), a*y = \/2sm(7r/4 - ί), 0 < t < π/4.
Кусочно-дифференцируемый путь можно аппроксимировать
последовательностью векторов, уложенных вдоль него (рис. 7.13).
Разобьем кривую на отдельные участки, расставив на ней по ходу
движения точки Pq, Pi, P2, .. ■, Pn, где Лэ ~ начало пути, а Ρ/ν
— его конец. При этом необходимо включить в это подразбиение

7,2, Криволинейные интегралы
355
все точки, где кривая не имеет касательной. Затем можно ввести
векторы смещения
v0 = РоРь vi = PiP2, vjv-i = Pn-iPn-
Выбрав точки Pj достаточно близко, мы можем
аппроксимировать любую кусочно-гладкую траекторию с помощью ломаной
линии, заданной последовательностью векторов с любой наперед
заданной точностью. Следует заметить, что есть пути, которые
нельзя хорошо аппроксимировать таким способом, но они не
могут быть параметризованы дифференцируемыми функциями, и
мы не будем их рассматривать.
7.2. Криволинейные интегралы
Теперь опишем естественный способ, когда заданная
дифференциальная форма приписывает траектории некоторое
вещественное число. Пусть отрезок пути характеризуется точкой Pj с
соответствующим вектором Vj. Дифференциальная форма ω
приписывает этому отрезку вещественное число u;(Pi)[vj]. Вычислим
сумму этих чисел по всем отрезкам пути:
JV-1
/лг = £>(Рг)М.
г=0
Эта сумма очень похожа на римановскую сумму для обычного
интеграла. Пусть число точек Р| растет так, что все вектора V|
стремятся к нулю1. Вычислим предел суммы In в этом случае.
Если такой предел существует и не зависит от выбора
последовательности точек, то он называется криволинейным интегралом2
Точнее говоря, следует потребовать, чтобы стремилось к нулю число,
равное maxi||vi||. — Прим. ред.
2В русскоязычной литературе такие интегралы иначе называют
криволинейными интегралами второго рода. Конструкция «абсолютного» интеграла
по кривой, рассматриваемая авторами в конце этой главы, в русскоязычной
литературе называют криволинейными интегралами первого рода. — Прим.
ред.

356 Глава 7. Дифференциальные формы ...
от дифференциальной формы ω по пути Г. Его обозначают fruj,
т. е.
. JV-1
ω = lira V>(P;)[Vi].
i=0
Мы докажем скоро, что для кусочно-дифференцируемых путей
написанный предел существует и не зависит от выбора точек
деления пути. Дадим формулу для /Γω, используя операцию
переноса дифференциальной формы.
Из определения суммы дифференциальных форм и
произведения дифференциальной формы на вещественное число следуют
три очевидных свойства криволинейных интегралов /Γω.
(1) Интеграл линеен по ω, т.е. если ω = ω\ + u>2, то fru; =
/Γωι + Jruj2- Если ω = Χω', το fru> = λ/Γα/.
(2) Если Г состоит из двух участков Γχ и Г2, то
ι ω = ω + ω.
Jr Jtx Jt2
Это значит, что всегда можно разделить
кусочно-дифференцируемую траекторию на дифференцируемые фрагменты, как это
показано на рис. 7.14, и свести интегрирование по всей кривой к
вычислению интегралов по этим фрагментам.
Рис. 7.14 Рис. 7.15
(3) Если Г отличается от Г' только ориентацией, то
/ ω = — / ω.
Jr Jt

7.2. Криволинейные интегралы
357
Это следует из того, что, изменяя ориентацию Г, мы меняем
направление всех векторов V|, а поскольку ω — линейная форма,
то
ЦДН-Vi] = -ω(Ρ0[ν4].
Перейдем к задаче нахождения численного значения
криволинейного интеграла. Наша цель состоит в том, чтобы свести эту
задачу к вычислению обычного интеграла по параметру,
введенному вдоль пути интегрирования. Параметризация а : R —► R2
отображает отрезок вещественной прямой [а, Ь] в траекторию Г.
Предположим, что точка α (нижняя граница интервала [а,Ь])
отображается в начальную точку пути Ра, а верхняя граница Ъ
— в конечную точку пути Р&. Рассматривая отдельно гладкие
участки нашего пути, будем считать, что а задается
дифференцируемыми функциями
a*x = X(t), a*y = Y(t),
для которых, согласно цепному правилу,
a* dx = X'(t) dt, a* dy = Y'(t) dt.
Пусть разбиение пути соответствует следующему разбиению
отрезка:
а = to < ti < ■ ■ ■ < tn = Ь,
так что
« = "<« = (?&')■
Возьмем дифференциальную форму
ω = gdx + hdy.
Тогда криволинейный интеграл может быть аппроксимирован

358 Глава 7. Дифференциальные формы ...
суммой
5>(Р4)[а(*4+1)-а(*0]
г
= Σ{9(Ρί) dx[a(ti+1) - a(h)} + h(Pi) dy[a(ti+1) - α(ί4)]}
г
= ^{д(а(и))[Х(и+1) - X(U)] + h(a(U))[Y(ti+1) - Y(U)}}.
(7.1)
Вспомним, что α*ω = / dt, где
f(t) = g(a(t))X\t) + h(a(t))Y'(t).
Покажем, что (при соответствующих предположениях
относительно a, f и д) приближенное выражение (7.1) стремится к
! fdt, (7.2)
J a
когда длина отрезков разбиения пути стремится к нулю. Итак, мы
хотим сравнить (7.1) и (7.2) для данного разбиения и показать,
что их разность стремится к нулю, когда maxi(ii+i —ί,) стремится
к нулю. Можно написать
X(ti+l) - X(U) = Г+1 X\s)ds
и
Y(ti+1)-Y(U)= ft+1Y'(s)ds.
J и
Тогда сумма (7.1) имеет вид
£ (g(a(ti)) J l+1 X'(s) ds + h(a(U)) J l+1 Y'(s) ds\ ,
a (7.2) можно написать в виде
fti+l
Ε / /wds
= Σ {[+1 9Hs))X\s) ds + £+1 h(a(s))Y'(s) ds} .

7.2. Криволинейные интегралы
359
Разница между этими выражениями в том, что для (7.1) мы
имеем g(a(ti)) или h(a(ti)), стоящими перед знаком интеграла в
каждом слагаемом, а в (7.2) функции g(a(s)) и h(a(s)) стоят под
знаком интеграла. Интуитивно ясно, что для непрерывных
функций дики гладком отображении а эта разница пренебрежимо
мала при достаточно мелком разбиении. Сделаем ряд
предположений, чтобы получить точную оценку разницы между (7.1) и
(7.2). (Можно было бы сделать и более слабые предположения,
но тогда потребовалось бы более сложное доказательство.)
(i) Предположим, что д и h равномерно3 непрерывны, т. е.
что для любого ε > 0 существует такое η > 0, что из неравенства
\\P-QW <η следует \д(Р) - g(Q)\ <еи \h(P)-h(Q)\ <ε. Это -
предположение относительно ω. По теореме Лагранжа о среднем
значении оно будет выполняться (при ηΝ = ε), если производные
dg и dh удовлетворяют неравенствам \\dg\\ < N и \\dh\\ < N во
всех точках.
(ii) Допустим, что существует такая постоянная М, что
|Χ'(ί)|<Μ и |Υ"(ί)|<Μ
для всех значений t. Это — предположение относительно пути а.
По теореме о среднем значении можно найти такое δ > 0, что
для любых t' и t" из условия
|ί' - t"\ < δ
вытекает неравенство
\a(t')-a(t")\<V.
Разделим весь путь на отрезки так, чтобы для всех г выполнялось
неравенство |ij+i— U\ < δ . Согласно предположению (i), мы будем
иметь
\g(a(s)) - g(a(U))\ < ε для U < s < ti+i.
Аналогичную оценку можно получить для h. Тогда
g(a(U)) ! l+1 X'(t) dt- f 1+1 g(a(s))X'(s) ds
3Известно, что непрерывная на компакте функция всегда равномерно
непрерывна. — Прим. ред.

360 Глава 7. Дифференциальные формы ...
< [1+1\9(а(и))-д(а(з))\.\Х'(8)\аз
< sM\ti+i - U
Просуммировав эти неравенства по всем отрезкам (с учетом
аналогичной оценки для членов с h), можно увидеть, что разность
между (7.1) и (7.2) не больше, чем
^εΜ|ίί+ι - U\ + eM\ti+\ - Ц = 2еМ\Ь - а\.
Выбирая длину разбиения с достаточно малым δ, можно
получить эту оценку со сколь угодно малой величиной ε. Тем самым
доказано равенство нашего криволинейного интеграла и
определенного интеграла (7.2).
Поскольку / dt = α*ω, можно написать
pb rb
/ fdt= α*ω,
J a J a
где правая часть равенства равна левой по определению. В
результате получаем:
Ιω=Ια"ω-
В этом равенстве левая часть имеет очевидный интуитивный
смысл, а правая удобна для вычисления.
Пример. В качестве применения этого результата вычислим
интеграл / от
0\ /1
ω = xydx + х2 dy
вдоль двух различных путей, соединяющих точку I I с . „
Первый путь Γι идет вдоль параболы у = 1-х2, а путь Г2 — вдоль
прямолинейного отрезка, соединяющего эти точки (см. рис. 7.16).
Для параметризации Γι введем функцию
α:ί^(ΐ^2), 0<*<1,

7.2. Криволинейные интегралы
361
т. е.
откуда следует, что
Рис. 7.16
а*х = ί, а*у = 1 — ί2,
a* dx = dt, a* dy = —It dt.
Направление движения, задающего ориентацию на кривой,
соответствует увеличению параметра t: начало кривой — это точка
а(0) = I ), а ее конец — точка а(1) = I
Тогда
α*ω = ί(1 - ί2) dt + t2(-2tdt) = (t - 3i3) dt
и интеграл от ω по этой кривой равен
[ ω= j\t
7γι Jo
3t3)dt =
2 4
Jo
Для параметризации кривой Г2 введем функцию
β-.t* ' Ь
т. е.
1-tJ '
β*χ = t, P*y = l- t.

362 Глава 7. Дифференциальные формы ...
Следовательно,
β* dx = dt, β* dy = -dt
и
β*ω = ί(1 -t)dt + t2(-dt) = {t- 2i2) dt.
Тогда для этого пути получаем
1
J ω= Ι (ί - 2ί2) dt =
Jr2 Jo
1 ι
Jo
7.3. Точные дифференциальные формы
В предыдущем примере величина криволинейного интеграла
зависит от формы пути, по которому он вычисляется, при
фиксированном положении начальной и конечной точки. В общем
случае это правильно, но есть один важный частный случай
дифференциальных форм, для которых величина криволинейного
интеграла полностью определяется начальной и конечной точками
кривой Г. Допустим, что дифференциальная форма ω имеет вид
ω = df. В этом случае
[df= f a*(df)= f d(a*f).
Jr Ja Ja
Согласно фундаментальной теореме интегрального исчисления
(формула Ньютона-Лейбница)
/ d(a*f) = a*f(b)-a*f(a).
Ja
Однако, a*f(b) = f(a(b)) = /(Рь), где Рь — конечная точка пути
Г, и аналогично a*f(a) = f(Pa)- Отсюда следует вывод, что если
начало и конец пути Г, т. е. точки Ра и Рь, фиксированы, то
интеграл
jdf = f{Pb)-f{Pa)
определяется этими точками и не зависит от выбора пути Г.

7.3. Точные дифференциальные формы 363
Итак, этот результат в комбинации с предыдущими
вычислениями показывает, что не любая дифференциальная форма
имеет вид ω = df. Действительно, легко написать необходимое для
этого условие: допустим, что
ω = G dx + Η dy = df = ~ dx + тг dy.
ox dy
Поскольку смешанные производные равны4, т.е. d2f/dxdy =
d2f/dydx, мы имеем
dG _ дН
ду дх '
В вышеприведенном примере G = ху и Η = χ2, поэтому
— - ^ — -2
ду дх
Дифференциальная форма ω, которую можно представить в виде
ω = df, называется точной.
Сейчас мы докажем, что локально условие
dG _ дН
ду дх
достаточно, чтобы дифференциальная форма ω = Gdx + Η dy
имела вид ω = df для некоторой функции /, определенной с
точностью до константы.
Сначала зафиксируем точку Ра, и пусть f(Pa) = 0. Теперь
определим функцию / по формуле f(P) = /гш, где Г —
специально выбранная траектория, соединяющая точки Ра и Р.
Конечно, к / можно добавить любую константу без изменения ее
дифференциала df. Выбор точки Ра определяет эту константу.
Давайте проделаем эту процедуру в декартовых координатах.
Допустим, что
ω = G(x, у) dx + Η (χ, у) dy.
При дополнительном условии непрерывности этих производных. —
Прим. ред.

364 Глава 7. Дифференциальные формы ...
Для простоты пусть Ра совпадает с началом координат.
Следовательно, / (( п )) = 0. В качестве Г выберем путь,
соединяющий начало координат и точку ( ] прямолинейным отрезком
(рис. 7.17), который легко параметризовать:
а : t к-* ( Xtt ] 0 < ί < 1.
Рис. 7.17
Поскольку буквы χ и у обозначают у нас координаты конечной
точки пути Г, то для обозначения переменных интегрирования
используем буквы χ и у. Таким образом,
а*х = xt, a*y = yt,
a* dx = χ dt, a* dy = у dt
Тогда
α* ω = G(xt, yt)x dt + H(xt, yt)y dt.
f(P) = Ι αV
Jo
и, следовательно, формула
f(x, y)= f [xG{xt, yt) + yH{xt, yt)} dt (7.3)
Jo

7.3. Точные дифференциальные формы 365
позволяет построить функцию / по дифференциальной форме ω.
Заметим, что это можно сделать только при условии, что
функции G и Η определены на всем пути Г.
До сих пор мы не делали никаких предположений
относительно формы ω, кроме того, что она должна быть определена
вдоль траектории интегрирования. Поэтому, вообще говоря, мы
не ожидаем, что df = ω. Поэтому сейчас мы должны сделать ряд
предположений. Давайте вычислим df/dx. В определении
функции / продифференцируем по χ под знаком интеграла5:
d_i
дх
= / G(xt,yt)dt + lxt—{xt,yr) + ty—(xt,yt)jdt.
Теперь воспользуемся тождеством
d ЗС дН
— (tG(xt,yt)) = G{xt,yt) + tx—(xt,yt) + ty—(xt,yt).
Из него следует:
/■ι d
G(x, у) = [tG{xt, yt)]l = J - (tG{xt, yt)) dt
= / (G(xt,yt) + tx—{xt,yt)+ty—(xt,yt)jdt.
Подставив это выражение в df /дх, получим
Предположим, что вдоль всего пути
3G _ ЗН
Зу дх
Тогда —— = G. Аналогично —- = Н. Поэтому ω = df, т. е.
дх ду
дифференциальная форма ω является точной.
Для этого достаточна непрерывная дифференцируемость подинтеграль-
ной функции. — Прим. ред.

366 Глава 7. Дифференциальные формы ...
Рассмотрим пример восстановления функции по ее
дифференциалу в явном виде. Пусть
ω = 2ху3 dx + Зх2у2 dy.
Поскольку ω определена везде и
£-{2ху3) = 6ху2 = -^(Зх2у2),
то ω = df. А теперь вычислим /:
f(x,y)= I [xG(xt,yt)+yH(xt,yt)]dt,
Jo
f(x,y) = I {2x2y3 + 3x2y3)t4dt = x2y\
Jo
Действительно,
d(x2y3) = 2xy3 dx + 3x2y2 dy.
7.4. Замкнутые дифференциальные формы
В предыдущем параграфе мы показали, что если ω определена
в области R, имеющей форму звезды, все точки которой
можно соединить с некоторой точкой О, лежащей внутри R,
отрезками прямых, также лежащими в R (рис. 7.18), то условие
dG/dy — дН/дх достаточно для того, чтобы форма ω была
точной. Если области определения G и Η не удовлетворяют условию
звездности, то такой вывод может оказаться неверным.
Например,
У а , х а
ω = —γ-—^ dx + -х-—5 dy
χΔ + у* χΔ + у
удовлетворяет условию dG/dy = дН/дх, но ω не определена в
точке χ = 0, у = 0. В этом случае в плоскости с «проколотой

7.4. Замкнутые дифференциальные формы 367
Рис. 7.18
точкой» I ) не существует функции /, для которой ω = df.
Действительно, если ω — точная форма, то интеграл от нее по
замкнутому пути должен быть равен нулю. Но легко показать,
что интеграл от нашей формы по окружности Г единичного
радиуса с центром в начале координат не равен нулю. Возьмем
а х = cost, а у = sini,
a*dx = — sini dt, a*dy = costdt,
так что
Тогда
α* ω = sin2 tdt + cos2 tdt = dt.
Iu=I
Jr Jo
2тг
dt = 2π.
Дифференциальная форма ω = Gdx + Hdy, определенная
в некоторой области пространства R2, называется замкнутой,
если dG/dy = дН/дх. Если область имеет форму звезды, то мы
доказали, что замкнутая форма является точной. В общем случае
это не так.
В последующих главах мы вернемся к рассмотрению этих
идей, имеющих важнейшее значение для теории
электромагнитного поля.

368 Глава 7. Дифференциальные формы ...
7.5. Перенос дифференциальной формы
и интегрирование
Поскольку определение линейного интеграла fru; не зависит от
выбора параметра вдоль пути Г, очевидно, что численное
значение интеграла не зависит от параметризации. Полезно
продемонстрировать эту независимость в явном виде. Предположим, что
путь Г параметризован двумя способами: с помощью переменных
s и t.
a b s a(a) a(b) t
Рис. 7.19
Тогда существует взаимно-однозначное отображение а
отрезка s-прямой на отрезок ί-прямой, как это показано на рис. 7.19.
Следовательно, параметризацию пути Г можно записать в виде
Ρ = /?(*) и P = /?(a(s))=/?oa(s).
Используя параметр s, цепное правило и формулу для замены
переменных в обычных определенных интегралах, вычислим
ρ гЬ рЬ Го{Ь)
ω= / (βοα)*ω= / α*(β*ω) = / β*ω.
■/Γ Ja Ja Ja(a)
Это в точности совпадает с тем, что мы получили бы,
вычисляя интеграл с помощью параметра t. С вычислительной точки
зрения это значит, что использование разных параметризаций
эквивалентно замене переменных в интеграле.
Криволинейный интеграл, заданный в одной плоскости,
можно преобразовать в равный ему интеграл в другой плоскости,
как это показано на рис. 7.20. Символ β обозначает
взаимнооднозначное отображение пути Г на плоскости А в путь /3(Г) на

7.5. Перенос дифференциальной формы и интегрирование 369
плоскости В. Выбрав дифференциальную форму ω на плоскости
В, мы определяем ее перенос согласно формуле
β*ω(Ρ)[ν}=ω(β(Ρ))[άβρ[ν}}.
Рис. 7.20
Мы утверждаем, что
/ ω= [ β*ω.
Jeer) J г
Действительно, по определению криволинейного интеграла
ЛГ-1
β*ω = \\πίγ^β*ω(Ρί)[ν]
L
г=0
ЛГ-1
= \ιταΥ^ω(β(Ρί))[άβρί[^}}.
г=0
Заметим, что при N —► оо векторы άβ\ν^ располагаются вдоль
пути β(Γ) все более близко. Следовательно, последняя сумма в
пределе N —► оо становится интегралом /л(Г) ω. Действительно,
если мы параметризуем Г с помощью отображения а, то согласно
цепному правилу получим
ί β*ω= ! α*(β*ω)= ί (βοα)*ω.
Jr Ja Ja
Однако, βοα есть параметризация пути β(Τ), поэтому последний
интеграл равен /я(Г\ ω, что и требовалось доказать.

370 Глава 7. Дифференциальные формы ...
Пример. Смысл последнего результата состоит в том, что для
вычисления интеграла можно вводить любую удобную систему
координат. Например, если мы хотим вычислить интеграл от ω =
1
χ dy—у dx по полуокружности единичного радиуса от точки
до точки
на плоскости ху (рис. 7.21), эту полуокружность
можно заменить на направленный отрезок Г в полярной системе
'г \ (г cos θч
координат с помощью отображения β : I ' I —► I """" I. Тогда
β*ω = (г cos θ) d(r sin θ) - (r sin θ) d(r cos θ) = r2 άθ.
Рис. 7.21
Для отрезка Г значение г = 1 и поэтому
ί β*ω= ί άθ = π.
Ясно, что вычисление foir\ ω с помощью параметризации t
cosi4
sini
дает то же самое значение интеграла.
7.6. Абсолютный криволинейный интеграл.
Длина кривой
До сих пор мы рассматривали направленные криволинейные
интегралы, вычисляемые вдоль ориентированных путей на
плоскости, где скалярное произведение может быть не определено.

7.6. Абсолютный криволинейный интеграл. Длина кривой 371
Рис. 7.22 Рис. 7.23
Если скалярное произведение определить, то становится
возможным определение абсолютного криволинейного интеграла6
от функции / по пути Г. Чтобы определить такой интеграл
Jr / ds, разобьем путь Г на короткие отрезки с векторами Vj =
РгРг+ι (рис. 7.22), после этого вычислим длину каждого отрезка
по формуле для скалярного произведения Sj = ||vj|| = \/(vj, v^).
Тогда интеграл снова определяется как предел суммы
/ fds = lim £/(P<K
Очевидно, что в этом случае ориентация пути Г не имеет
значения, так как длина вектора Vj равна длине вектора (—Vj).
Для вычисления абсолютного криволинейного интеграла
удобно, как и выше, параметризовать путь Г. Пусть
а*х = X(t), a*y = Y(t),
откуда
a* df = X'(t) dt, a* dy = Y'(t) dt.
Тогда вектор щ = iiij+i отображается в вектор
аа[щ] = ( r,y jdt[ui].
Если мы имеем дело с обычным евклидовым скалярным
произведением, то длина этого вектора равна
||ά*[ΐϋ]|| = у/Х'(и)2 + ¥'(и)2<И[щ].
В русскоязычной литературе такие интегралы называют
криволинейными интегралами первого рода. — Прим. ред.

372 Глава 7. Дифференциальные формы ...
По определению
f(Pi) = f(a(U)) = Q*/(ii),
что позволяет7 написать
JV—ι
! fds= lim V а*/(и)^Х>(П)1 + У>(и)Ци+1-Ь). (7.4)
/ Λί—>оо *—'
J i=0
Это приводит нас к формуле вычисления абсолютного
криволинейного интеграла с помощью параметризации:
J fds = J ^fitWx'iuf + Y'it^dt
Если f(P) = 1, то интеграл f ds определяет длину кривой Г.
В более общем случае, если f(P) задает линейную плотность
массы тонкой проволоки, имеющей форму кривой Г, то f f ds
представляет полную массу проволоки.
Есть интересный с точки зрения применения в физике пример
абсолютного линейного интеграла, построенного с помощью
неевклидова скалярного произведения. Это вычисление
собственного времени, связанного с мировой линией движущейся частицы
(рис. 7.24), когда прошедшее время измеряется по часам,
движущимся вместе с частицей. В этом случае значение времени t
вдоль мировой линии всегда растет. Его можно использовать в
качестве параметра и написать
a*t = t, а* (х) = X(t),
откуда
a* dt = dt, a*(dx) = X'(t) dt.
Тогда лоренцева длина вектора
da[ui] = I x,,t, J dt[ui
7Ha самом деле длина Si вектора Vj не обязана равняться ||e£a[ui]||, и
правая часть следующего равенства (7.5) не совпадает с правой частью (7.4).
Правда, при непрерывности f(t) и частных производных X'(t), Y'(t) пределы
этих правых частей все лее равны, но доказательство этого факта требует
кропотливых оценок. — Прим. ред.

Резюме
373
Рис. 7.24
равна y/l — X'(t)2 М[щ]. Поскольку X'(t) есть скорость частицы
ν, то получаем интеграл
f \/l-v2 dt,
определяющий собственное время движущейся частицы.
Резюме
A. Криволинейные интегралы
Вы должны уметь объяснить смысл линейного интеграла /Γω,
знать его свойства и уметь пользоваться ими.
Вы должны знать процедуру вычисления линейного
интеграла с помощью переноса дифференциальной формы, уметь
вводить соответствующую параметризацию для заданных
траекторий и вычислять криволинейные интегралы.
B. Дифференциалы и дифференциальные формы
Для заданной дифференциальной формы ω, определенной на
плоскости, вы должны уметь выяснять, можно ли представить
ее как дифференциал функции / и, если такая функция
существует, уметь найти ее.
Задачи
7.1. Пусть ω = (у cosxy + ех) dx + (χcosxy + 2у) dy.

374 Глава 7. Дифференциальные формы ...
(а) Вычислите /Γω вдоль участка параболы у = х2 от точки
_ °0 ) до ( } ). Используйте параметризацию ф, задаваемую
переносом
' '*х
(b) Вычислите /г ω, если Г — прямая линия, соединяющая
начало координат с точкой I „ I. Вычислите тот же интеграл,
если путь Г состоит из отрезка 0 < χ < а вдоль оси χ и
отрезка χ = а, 0 < у < β.
(c) Найдите такую функцию f{x,y), чтобы выполнялось
условие ω = df.
7.2. Пусть снова ω = (у cosху + ех) dx + (χ cosxy + 2у) dy.
(а) Вычислите /г ω вдоль участка параболы Г, определенного
формулами
: - и
2 / ДЛЯ 0 < t < 1.
(b) Найдите такую функцию f(x, у), чтобы ω = df.
7.3. Пусть ω = ydx — xdy.
(a) Вычислите /Γ ω вдоль полуокружности Г от точки I „ I
до точки ( п ) ■ Путь Г определен формулами
х\ /-cosi\ η^ί^
= . , для 0 < t < έ.
у) \ suit J ^ ~ ~
(b) Покажите явно, что выбрав другую кривую, соединяющую
-1\ /Г
те ж;е точки , η ι " ι η
ние интеграла от той же формы.
7.4. Пусть ω = (15х2у2 — Зу) dx + (10х3у — За;) dy. Вычислите /г ω, где
Г — путь от (—1,0) до (1,0) вдоль полуокружности х2 + у2 = 1,
У>0-

Задачи
375
7.5. (а) Вычислите /г ω, где ω = dx + 2х dy, Г — участок параболы
χ = 1 — у2 между у = —1 иу = +1, как это показано на
рис. 7.25.
(Ь) Найдите такие константу α и функцию /, для которых
выполняется равенство еауи> = df.
У ,
1<
-1
1
1 1
X
Рис. 7.25
Рис. 7.26
7.6. (а) Пусть ω = (χ2 — 2xy)dx + (у2 — 2xy)dy. Вычислите /Γω,
где путь Г проходит вдоль участка параболы у — х2 между
точками (—1,1) и (1,1).
(Ь) Пусть σ = 30х2у5 dx + 40x3y4dy. Найдите целое число η
и функцию /, для которых выполняется равенство df =
(χν)ησ.
7.7. Пусть ω = 10у2 dx + Axy dy.
(a) Вычислите /Γω, где путь Г проходит по дуге единичного
(Л ί°\ (ν
радиуса между точками I „ I и I I. (Указание: введите
параметр θ — см. рис. 7.26.)
(b) Найдите такое целое число η и функцию /, чтобы
выполнялось равенство хпи> = df.
7.8. (а) Покажите, что дифференциальная форма
ω = Зху dx + 2x dy
не является дифференциалом никакой функции /.

376 Глава 7. Дифференциальные формы ...
(b) Найдите уравнение семейства кривых, зависящих от одного
параметра и обладающих свойством ω (ν) = 0 для
любого вектора ν, касательного к какой-либо из этих кривых.
(Указание: если у = F(x) и ν = I ,-,,, , , то вы можете
написать дифференциальное уравнение для F(x).)
(c) Найдите функции f(x,y) и д(х,у), для которых
выполняется равенство df = дш. (Указание: функция / должна
быть постоянной вдоль кривых, полученных в предыдущем
упражнении.)
7.9. (а) Нарисуйте полуэллипс, заданный уравнением в полярных
координатах
о
для 0 < θ < тт.
5—4 cos θ
Вспомнив, что χ = г cos θ и у = г sin θ, покажите, что этот
полуэллипс есть участок кривой
(*~4)2 у2
25 9
(b) Дифференциальную форму
ху dy — у2 dx
χΔ +у*
выразите в полярных координатах через г, Θ, dr и άθ.
(c) Вычислите /г ω, где путь Г — полуэллипс из первого пункта
этого упражнения. Воспользуйтесь полярными
координатами, где θ — удобный параметр.
(d) Вычислите /Γω в координатах χ та у. Удобную
параметризацию определяет отображение
4 +5 cos Α η^ί^
„ , , 0 < t < π.
3cosi J ' — —
7.10. (а) Предположим, что и и ν — криволинейные координаты в
области D на плоскости. Соответствующий якобиан
Det (duldx duldy\
\ dv/dx dv/dyJ

Задачи
377
7.11.
нигде в области D не обращается в нуль. Пусть ω — гладкая
дифференциальная форма, определенная в области D, а Г
— кривая в этой области. Покажите, что /г ω имеет
одинаковое значение, если ω и Г выражать через переменные х,
у или через и та υ. (Предыдущая задача является примером
этого утверждения.)
(Ь) Пусть путь Г определен в полярных координатах
согласно формулам: ρ = F(6), при этом F(6) > 0 и F(2tt) = F(0).
Покажите, что площадь, заключенная внутри этого
замкнутого пути, равна /Γω, где ω = ^р2 άθ. (Указание: Форму ω
выразите в декартовых координатах.)
Состояние газа, заключенного в цилиндр, можно представить
точкой на плоскости, где декартовыми координатами являются Ρ
(давление) и V (объем). Количество тепла, поглощенного газом
в некотором процессе, заданном траекторией Г, равно Q
где
Lj = \pdV + \vdP.
2 2
/г
Р<
32-
24-
16
8-
(1,32)
Ι ι
1
1Г/
1л
Г\(8,1)
8
V
Рис. 7.27
Рис. 7.28
(а) Вычислите /г ω, где путь Г проходит вдоль ломаной линии,
изображенной на рис. 7.27. Линия последовательно
соединяет точки V = 1, Ρ = 32, затем V = 1, Ρ = 8 и V = 8,
Р = 1.

378 Глава 7. Дифференциальные формы ...
(b) Вычислите интеграл /г, ω вдоль пути Г', проходящем вдоль
кривой PV5/3 = 32 от точки V = 1, Ρ = 32 к точке V = 8,
Р = \.
(c) Найдите такую функцию S, чтобы выполнялось равенство
dS = ω/PV.
7.12. (а) Имеется однородная проволока с массой М, согнутая в
полуокружность с радиусом R, как это показано на рис. 7.28.
Найдите у-ю координату центра масс этой проволоки и
вычислите ее момент инерции относительно оси х.
(Ь) Решите ту же задачу в случае, когда линейная плотность
проволоки пропорциональна у, но ее полная масса по-
прежнему равна М.
7.13. Запишите в форме интеграла длину кривой у = (х — 2)3,
соединяющей точки _1 ) и I . I на евклидовой плоскости.
7.14. Рассмотрите дифференциальную форму
ω = 5ydx + 3xdy.
(a) Найдите такие целые числа тип, для которых
выполняется равенство d{xmynuj) = 0.
(b) Для этих целых чисел найдите такую функцию /, чтобы
выполнялось равенство df = xmynuj.
(c) Отобразим плоскость uv на плоскость ху так, чтобы
а\ ( α2+β
Перенесите форму ω на плоскость uv.
(d) Вычислите J ω вдоль путей Γι и Гг, соединяющих точки
( π ) и ( ι )" Путь Γι состоит из двух прямых отрезков и
проходит через точку I _ J, а путь Г2 проходит по двум
прямым отрезкам через точку I .
(e) Вычислите абсолютный криволинейный интеграл/г ||ω|| ds.
(В ответе один член можно оставить в виде обычного
определенного интеграла.)

Глава 8
Двойные интегралы
Глава 8 продолжает изучение интегрального
исчисления. Она посвящена внешним 2-формам и
двумерным интегралам, которые им соответствуют.
Вводится определение внешней производной и отмечается ее
инвариантность относительно переноса.
Доказывается двумерный вариант теоремы Стокса, известный как
теорема Грина. Исследуются поверхностные
интегралы в трехмерном пространстве.
8.1. Внешняя производная
Мы уже знаем, что дифференциал функции / дает наилучшее
линейное приближение к приращению значения функции при
перемещении ее аргумента от точки Ρ к точке Ρ + v. Это можно
записать в форме
#(P)[v]=/(P + v)-/(P) + 0(v),
где при ν —у О поправочный член o(v) стремится к нулю
быстрее, чем длина вектора v. Можно представлять себе, что df
является линейной функцией, значение которой на конце вектора
ν определяется значениями самой функции / на концах
отрезка, заданного вектором ν «в пределе», когда ν становится очень
малым.
Воспользовавшись аналогичным подходом, можно из 1-формы
τ построить 2-форму dr, которая будет называться внешней
производной от т. Эта 2-форма в каждой точке Ρ будет билинейной

380
Глава 8. Двойные интегралы
функцией двух векторов ν и w. Именно, выбрав точку Р,
упорядоченную пару векторов ν и w и 1-форму, мы можем получить
число, проинтегрировав τ по параллелограмму, построенному на
векторах ν и w, двигаясь сначала «вперед» от Ρ вдоль
первого вектора ν, а в конце пути «назад» вдоль второго вектора w
(рис. 8.1).
Рис. 8.1 Рис. 8.2
Если векторы ν и w достаточно малы и поведение формы τ
в окрестности точки Ρ достаточно хорошее, то можно ожидать,
что значение этого интеграла будет приблизительно билинейно,
т. е. оно будет зависеть приблизительно линейно от ν (при
фиксированном векторе w) и линейно от w (при фиксированном ν).
Обозначим P(h, к) параллелограмм, заданный векторами hv и
few (рис. 8.2). Хотелось бы определить άτ(Ρ) формулой
/ τ = hkdr(P)[v, w] + остаток, (8.1)
JP{h,k)
где (мы надеемся) остаточный член стремится к нулю быстрее,
чем h при h —* 0 (значение к фиксировано) и быстрее, чем к при
к —* 0 (значение h фиксировано)1.
Если 2-форма άτ(Ρ) существует, то она единственна.
Доказательство практически совпадает с доказательством утверждения,
что дифференциал функции единственен. Предположим, что
1 Обычно требуется более сильное условие: дробь остаток/hk должна
стремиться к нулю при одновременном стремлении к нулю обоих чисел h, к (см.
раздел 8.8). — Прим. ред.

8.1. Внешняя производная
381
уравнение (8.1) справедливо для двух разных билинейных
функций άτ и άτ. Пусть σ обозначает их разность. Тогда мы имеем
О = hka[v, w] + остаток.
Разделим это равенство на hk и устремим h к нулю. Тогда
получаем
О = a[v,w] + — lim(oeraTOK//i).
к h—>о
Но остаток стремится к нулю быстрее h, следовательно,
σ[ν, w] = 0. Это значит, что άτ не может отличаться от άτ.
А теперь займемся проблемой вычисления άτ(Ρ) и
доказательством существования 2-формы. Для простоты сначала
предположим, что τ имеет вид / dx, где / — дважды
дифференцируемая функция в окрестности точки Р. В этом выражении dx
является формой, которая каждому касательному вектору
приписывает его х-ю компоненту. В частности, dx[hv] = hdx[v] = hvx,
если ν = I x J. Вклад в интеграл, получаемый при движении
(рис. 8.3) вдоль одной стороны параллелограмма, скажем, от
точки Ρ к точке Ρ + hv, получаемый с помощью параметризации
t —> Ρ + thv, равен
/ f(P + thv)x'(t)dt= ι f(P + thv)dx[hv]dt
Jo Jo
= hdx[v] f f(P + thv)dt.
Jo
P + fcw
Рис. 8.3

382
Глава 8. Двойные интегралы
Вклад противоположной стороны от точки Ρ + hv + kw к
точке Ρ + kw получается аналогично. Он равен
-hdx[v] / /(Ρ + thv + kw) dt.
Jo
Складывая оба члена, мы получаем
(Ρ + thv + kw) - /(Ρ + thv)] dt.
-hdx[v] f [/(I
Jo
Поскольку мы предположили, что / — дважды
дифференцируемая функция, то можно воспользоваться формулой Тейлора
/(Р + thv + kw) - /(Ρ + kw) = df{P+thv)[kw] + 0(k2)
и записать суммарный вклад от двух сторон в виде
-hdx[v] dfrp+thv)[kw]dt + 0(hk2).
Jo
Вычисление интеграла вдоль других двух сторон дает
выражение
+kdx[w] / ci/(p_|_tfcW) [hv]dt + 0(kh2).
Jo
Собирая вместе все члены, получаем
/ τ = -hk dfrp+thv)[w] dt ■ dx[v]
J-p{h,k) Jo
+ hk I df{P+tkw)[v]dt ■ dx[w] + 0(kh2) + 0(hk2).
Jo
Здесь ^/(ρ+ίλν) является вектором-строкой
(Ιϊ(ρ+*,"·!<ρ+**))·
Согласно нашему предположению о функции /, ее частные
производные дифференцируемы. Следовательно, по теореме о
среднем значении
|ί(Ρ + ί/,ν) = |(Ρ)+0(Λ),

8.1. Внешняя производная
383
откуда
#(P+tfcv)M = 4fp[w] + 0(h).
Интегрирование этого выражения дает
/ 4f(p+tfcv)[w] dt = 4fp[w] + O(h).
JO
Подставим это в наш интеграл по контуру параллелограмма и
получим
/ т = hk(dfP[v] dx[w] - d/P[w] dx[v]) + 0(h2k) + 0(hk2).
J-p{h,k)
Таким образом, мы можем получить выражение (8.1), если
положим
drp[v, w] = d/p[v] dx[w] - d/p[w] dx[\].
Из этого выражения видно, что dr является антисимметричной
функцией своих аргументов, т.е. dr[w, ν] = —dr[v, w].
2-форма dr может быть записана короче, если ввести
понятие внешнего произведения двух 1-форм. По определению, это
внешнее произведение равно
(σ Λ λ)[v, w] = a[v]A[w] - σ[\ν]λ[ν],
где σ и λ являются 1-формами, a v и w — векторами. Тогда
можно написать
άτρ [ν, w] = (d/p Λ dx) [ν, w],
или еще короче
dr = df Л dx.
Из определения внешнего произведения ясно, что
λΛ σ = —σ Λ λ,
т. е. оно антисимметрично. В частности, σ Λ σ = —σ Λ σ = 0, т. е.
произведение 1-формы на себя равно нулю.
Кроме того, очевидно, что
(σ + ω) Λ λ = (σ Λ λ) + (ω Λ λ),

384
Глава 8. Двойные интегралы
т. е. внешнее произведение дистрибутивно по отношению к
операции сложения.
Теперь рассмотрим 1-форму общего вида: / dx + gdy. Те же
самые соображения, примененные к д dy, дают
d{g dy) =dg/\ dy.
Поскольку интеграл от ω линеен по ω, мы получаем
d(f dx + g dy) = df A dx + dg A dy.
Это выражение можно доказать непосредственно, исходя из
определения d. Теперь выразим df и dg через dx и dy:
df=d-xdx + Yydm d9 = -£dx+dydy-
Поскольку dx A dx = 0 и dy A dy = 0, мы имеем
df , , dg ,
dr = — dy /\dx + — dx Λ dy.
dy ox
И наконец, поскольку dy Adx = —dx Л dy, получаем
dT=^x-9/y^dxAdy-
В качестве примера возьмем 1-форму
τ = χ у dx + χ у dy.
Тогда
dr = d(x2y2) Adx + d(x3y) Л dy
= (2xy2 dx + 2x2y dy) Adx + (3x2y dx + x3 dy) Л dy
= 2x2y dy Adx + 3x2y dx A dy = x2y dx A dy.
В частном случае, когда 1-форма τ точная, т. е. τ = άφ, мы
получаем, что dr = 0. Это видно из определения dr: поскольку
dr[v, w] является наилучшим линейным приближением к
интегралу по контуру параллелограмма Jt, и поскольку интеграл

8.1. Внешняя производная
385
от полного дифференциала по замкнутому контуру равен
нулю, то ά(άφ) = 0. Этот результат можно установить и прямым
вычислением:
,. дф , дф ,
τ = άφ = — dx + — dy,
ox dy
дгф д2ф
dr = ——- dyAdx+ ^-^- dxAdy = 0,
oyox oxoy
потому что смешанные частные производные второго порядка
равны. Заметим, что попутно мы получили короткий вариант
определения замкнутой формы: форма τ является замкнутой
тогда и только тогда, когда
dr = 0.
Итак, мы показали, что если / дифференцируема и χ —
координатная функция, то d(f dx) = df Л dx. Используем этот
результат для доказательства более общей формулы
d(fr) = dfAT + fdT,
где / — дифференцируемая функция, а т — дифференцируемая
1-форма. Записав τ = gdx + h dy, мы получим /т = (fg) dx +
(fh) dy и, следовательно,
d(fr) = d(fg) Adx + d(fh) Л dy.
Поэтому
d(fT) = gdf /\dx + f dg /\dx + hdf /\dy + f dh /\dy
и мы видим, что
d(fr) = df Л (gdx + hdy) + f(dg A dx + dh A dy),
т. e.
d(fr) = dfAT + fdr.

386
Глава 8. Двойные интегралы
8.2. 2-формы
Поскольку общий вид 1-формы на плоскости — это выражение
f dx + g dy, то самый общий вид произведения двух 1-форм будет
некоторой функцией F(x,y), умноженной на dx Л dy. Назовем
такое выражение 2-формой и будем писать
σ = F(P) dx Л dy = F(x, у) dx Л dy.
Значение 2-формы в точке Р, т. е. F(P) dx Л dy, мы будем
рассматривать как правило, которое каждой паре векторов
приписывает определенное число.
Чтобы лучше понять смысл «постоянной» 2-формы dx Л dy,
вычислим ее сначала для пары единичных векторов (ех,еу). По
определению
dx Л dy[ex, еу] = dx[ex] dy[ey] - dx[ey] dy[ex] = 1-1 — 0-0=1.
Более общая формула:
dx Л dy[hex, key] = hk.
Очевидно, что это — площадь (с некоторым знаком)
прямоугольника, построенного на векторах hex и кеу, если площадь
прямоугольника, построенного на векторах ех и еу, принимается за
единицу (рис. 8.4).
Рис. 8.4
Мы можем вычислить dx Л dy для любой упорядоченной пары
векторов (v, w). Запишем ν = аех + сеу, w = bex + dey. Если
ввести матрицу А
А =
v = A
w = A

8.2. 2-формы
387
то
dx Л φ/[ν, w] = dx[w\ dy[w] — dx[w] dy[v]
= ad - bc = Det A.
В общем случае 2-форма σ является функцией трех
переменных: Ρ, ν и w. Для фиксированной точки Ρ она билинейна и
антисимметрична относительно векторов ν и w. Если σ = F dxAdy,
то
a(P)(v,w) = F(P)Det A,
где ν, w и А определены выше. Итак, каждому параллелограмму
с вершиной в точке Ρ 2-форма σ(Ρ) приписывает площадь с
определенным знаком — ориентированную площадь.
dx /\dy[ex,ev] = +1 dx /\dy[ey,ex} =
Рис. 8.5
Очень важно помнить, что величина dx Л dy для данного
параллелограмма зависит от его ориентации, которая определяется
порядком векторов, задающих его. Для ориентированного
прямоугольника, соответствующего векторам [ex,ev], dxAdy = 1, а
dy Л dx = — 1. Для того же прямоугольника, но с
противоположной ориентацией, соответствующей порядку [ev,ex], dxAdy = — 1
и dy Л dx = +1 (см. рис. 8.5). В общем случае, чтобы получить
2-форму τ для параллелограмма, построенного на векторах ν и
w, надо задать его ориентацию, т. е. выбрать, какой вектор будет
«первым», а после этого вычислять либо r[v, w], либо r[w, v].

388
Глава 8. Двойные интегралы
8.3. Интегрирование 2-форм
Итак, 2-форма τ приписывает число каждому малому
ориентированному параллелограмму (паре векторов), точно так же,
как 1-форма приписывает число каждому малому
направленному отрезку линии (вектору). Поэтому мы можем
интегрировать 2-формы по области R подобно тому, как мы интегрировали
1-формы по путям.
-*>
R
\
)
/
Рис. 8.6
Приступим к построению такого интеграла. Возьмем
прямоугольник R, ориентированный так, как показано на рис. 8.6,
разбиваем его на NxNy маленьких прямоугольников и составляем
римановы суммы
Nx-lNv-l
snxnv = Σ Σ σ(ρ^
i=0 j=0
b — a d — с
Если
σ = F(x, у) dx Л dy,
то
где
SnxNv = -Τΐ y~ Σ Σ F(xi'%')'
У i=0 j=0
**"* Nx Nu
1 Ί
Xi = a+—(b-a), yj=c+—(d-c).
X у

8.3. Интегрирование 2-форм
389
Теперь определим интеграл от 2-формы τ по ориентированной
области R согласно формуле
/.
Т= Jim SNxNy,
ц Nx—>oo
при условии, что предел не зависит от характера измельчения
разбиения2.
Двойной интеграл от F(x, у) dx Л dy по области R можно
вычислять как «повторный» интеграл. Чтобы вычислить
выражение
Ь-а d-cNx~lNy~l
Ny^<x> У г=0 3=0
сначала просуммируем по j для каждого фиксированного
значения г и прежде, чем суммировать по г, устремим Ny —> оо. По
определению обычного риманова интеграла от функции одной
переменной
d - с АГ"~1 fd
lim —— V F{xi,yj)= j F(xi,y)dy.
y^°° "у ^ Jc
Следовательно,
Nx-l
Рассматривая предел этой римановой суммы как интеграл,
мы можем написать
= I F(x, у) dy J dx,
2Авторы не останавливаются на вопросе о том, для каких функций F(x, у)
написанный предел существует. На самом деле для этого достаточно, чтобы
F(x,y) была непрерывной на прямоугольнике R. То лее самое относится к
рассматриваемому ниже вопросу о сведении двойного интеграла к
повторному. — Прим. ред.

390
Глава 8. Двойные интегралы
т. е. наш двойной интеграл / мы выразим через «повторный»
интеграл, который можно вычислять методами интегрального
исчисления функций одной переменной. Точно так же мы можем
сначала просуммировать по г, а потом по j. В результате получим
I = J (J F(x,y)dx)dy.
При вычислении интеграла от 2-формы τ по ориентированной
области R мы должны думать об ориентации прямоугольника.
Если R ориентирован так, что χ будет «первой» координатой, а у
— «второй», как это показано на рис. 8.7(a), мы должны писать
τ = F(x, у) dx Л dy и вычислять повторный интеграл
/ ( / F(x, у) dy J dx или / ί / F(x, У)dx) dy.
кУ
d-
a ■■
(a)
5)
*>
kV
d-
(b)
^
a ■■
г
Рис. 8.7. (а) Координата χ — первая. (Ь) Координата у — первая.
Если R ориентирован так, что первой координатой будет у,
как это показано на рис. 8.7(b), мы можем написать
τ = G(y,x)dy Adx (где G(y,x) =-F(x,y))
и вычислять повторный интеграл
αι:
G(y, x) dy J dx или
f(/:
G(y,x)dx) dy.

8.3. Интегрирование 2-форм
391
Изменение ориентации прямоугольника R приводит к изменению
знака интеграла.
В случае криволинейных интегралов понятие ориентации (и
почему изменяется знак при изменении ориентации)
интуитивно ясно. (Например, для случая силового поля криволинейный
интеграл дает работу, выполняемую при движении вдоль пути.
Прибор регистрирует разность энергий Ев — Ε а- При изменении
направления движения прибор будет показывать изменение
энергии Ε а — Ев-) Важно иметь аналогичный интуитивный пример
для наших двумерных интегралов. Вот такой пример.
Ориентация плоскости изменяется в зависимости от того, смотрим мы на
нее сверху или снизу. Предположим, что в трехмерном
пространстве есть плоскость ху при ζ = 0. Мы смотрим на эту плоскость
сверху и видим вращение по часовой стрелке. Но если смотреть на
эту же плоскость снизу, то то же самое вращение мы будем видеть
как вращение против часовой стрелки (рис. 8.8). Можно сказать,
что выбор ориентации плоскости в трехмерном пространстве
тесно связан с выбором «стороны» этой плоскости. Допустим, что
через поверхность течет какое-то вещество. Например,
поверхность — это клеточная мембрана, и нам интересно знать, какое
количество ионов проходят через нее.
Рис. 8.8
Конечно, используя слово «через», мы должны сделать
выбор: переход в каком направлении мы считаем со знаком «+», а
в каком — со знаком «—». Итак, для измерения полного потока
через поверхность мы должны задать ее ориентацию. Изменение
ориентации приводит к изменению знака потока и,
соответственно, знака нашего интеграла.
Абсолютные двойные интегралы. Часто необходимо
вычислять абсолютный двойной интеграл, который вычисляется по

392
Глава 8. Двойные интегралы
области, не имеющей ориентации3. Если, например, σ обозначает
плотность плоской пластины (массу на единицу площади),
имеющей форму прямоугольника R, то масса всей пластины
определяется двойным интегралом
Μ
-L
σάΑ.
Очевидно, что Μ должна быть положительным числом, и
ориентация прямоугольника R не имеет значения (рис. 8.9). В этом
интеграле dA можно считать функцией, которая любому
малому параллелограмму приписывает его обычную геометрическую
площадь, т. е. абсолютное значение его ориентированной
площади. В качестве координат выберем χ и у. Тогда dA = dxdy или
dA = dydx, порядок координат не важен.
♦ У
d
Рис. 8.9
Абсолютный интеграл fRF(x, у) dx dy вычисляется как
повторный интеграл
F(x,y)dy) dx,
или как
ι: а:
jf GO
у) dx ) dy.
Важно отметить, что существуют два разных типа
геометрических объектов: выражения типа σάΑ, которые можно называть
В русскоязычной литературе такие интегралы называют интегралами
первого рода. Интегралы, рассматривавшиеся выше, в русскоязычной
литературе называют интегралами второго рода. — Прим,, ред.

8.3. Интегрирование 2-форм
393
плотностями, при этом интегрирование по области R не зависит
от ее ориентации; и 2-формы τ = Fdx Ady, интеграл от которых
зависит от ориентации. У них совершенно различный физический
смысл. Позднее мы увидим, что они по-разному ведут себя при
замене переменных или переносе.
Двойные интегралы по произвольной области как
повторные интегралы. Двойные интегралы можно вычислять
как повторные для любой области, ограниченной прямыми χ =
const и графиками функций, которые не пересекаются.
Например, на рис. 8.10 изображена область, ограниченная слева
прямой χ = а, справа прямой χ = Ь, сверху линией у = ф(х) и снизу
линией у = ψ(χ).
Рис. 8.10
В этом случае справедлива формула4:
г ή ι гФ{х) \
/ F(x,y)dxdy= / / F{x,y)\dydx.
JR Ja \J4>{x) J
В качестве примера вычислим интеграл I = fR 2xy dx dy по
четверти круга, ограниченной прямыми χ = 0, χ = а, у = 0 и дугой
4Отсутствующее у авторов определение левой части этой формулы
можно дать так: дополним область R до координатного прямоугольника R и
доопределим функцию F(x, у) нулем вне R, получим функцию F на R.
Тогда можно свести дело к предыдущему понятию, определив /я F dx dy как
JfcFdxdy. Для следующего ниже равенства достаточны непрерывность и
ограниченность на R функции F и непрерывность ψ(χ) и ф(х). — Прим. ред.

394
Глава 8. Двойные интегралы
У л
а
с
1
χ = а(у)/
/
~7
1χ = β(ν)
\
X
Рис. 8.11
Рис. 8.12
у — л/а2 — х2 (рис. 8.11). Интегрируя сначала по у, а потом по х,
получаем
га I r^/(a2-x2) \
1=1 [ I 2ху dy J dx
= fa[xy2]fa2-x2)dx= Γχ(α2-χ2)άχ = \αζ.
Jo Jo 4
Иногда двойной интеграл легче вычислять, если изменить
порядок интегрирования и сначала выполнить интегрирование по
х. Например, интеграл / = fs F(x,y)dxdy по области 5,
изображенной на рис. 8.12 (который совсем не просто получить, если
сначала проинтегрировать по у), может быть вычислен так:.
fd ( Γβ{ν) \
I=[ F{x,y)dx)dy.
J с \ Ja(v) I
>а{у)
Даже для областей, не имеющих форму прямоугольника,
двойной интеграл часто можно вычислять как повторный
интеграл при обоих порядках интегрирования. Предположим,
например, что нам надо вычислить / = fRydxdy по области R,
заключенной между параболой у = х2 и прямой у = χ (рис. 8.13).
Сначала проинтегрируем по у, а потом по х:
1 - ί (/»dx=I! [И>=\1У -xi)dx - π

8.3. Интегрирование 2-форм
395
Рис. 8.13
Рис. 8.14
Эту же область можно заключить между прямой χ = у и
параболой χ = у/у, тогда сначала интегрируем по х, затем по у:
1 = 1 (/ dx)ydy = J (Vy-y)ydy = j (y3/2-y2)dy = ~.
Иногда, чтобы изменить порядок интегрирования, имеет
смысл рассматривать повторный интеграл как двойной.
Например, интеграл
/■1 / /-1
„2
га1-*
dy I dx
довольно сложно вычислять в таком виде. Однако, его можно
записать как двойной интеграл
"/.
е у dxdy,
где область R заключена между прямыми χ = 0, у = 1 и у = χ
(рис. 8.14).
В этом двойном интеграле проще сначала проинтегрировать
по х, а потом по у:
dx ) dy.
Тогда
■/о \Jo
1 = J ye-y2dy = J l-e-udu=\(l-e-1).

396
Глава 8. Двойные интегралы
Заметим, что в этом примере исходный интеграл можно вы-
2
числить по-другому. Введем первообразную функции е~у
G(y) = fVe-t2dt,
Jo
так что
Тогда
С (у) = е-У\
1= ! dx ! е-у2 dy= [ (G(l) - G(x)) dx.
JO Jx JO
Интегрирование по частям дает
/ = [(G(l) - G(x))x]l - ! x(-G'(x))dx.
Jo
Первый член в правой части равенства обращается в нуль на
обоих пределах. Поскольку G'{x) = е~х , мы получаем
J= / xe-x2dx=\(l~e~l),
Jo 2
что совпадает с результатом, полученным ранее.
Иногда для вычисления интеграла по χ и у необходимо
разделить область интегрирования на части.
Рис. 8.15

8.4. Ориентация
397
Например, чтобы вычислить f F(x,y)dxdy по сектору R,
изображенному на рис. 8.15, разделим его на области Я ι и i?2-
Тогда можно написать
/ F(x,y)dxdy = / F(x,y)dxdy + / F(x,y)dx
JR ifii JR2
dy
и каждый интеграл свести к повторному. Существует более
естественный способ вычисления этого интеграла — ввести полярные
координаты. Важную проблему замены переменных мы обсудим
в разделе 8.5.
8.4. Ориентация
Мы уже знаем, что знак криволинейного интеграла зависит от
ориентации пути, а знак интеграла от 2-формы зависит от
ориентации плоскости. Надеемся, что у читателя появилось
интуитивное ощущение того, что означает ориентация. В то же
время мы понимаем, что необходимо дать точное математическое
определение, что и будет сделано в этом разделе. Прежде чем
углубиться в абстрактные математические определения, давайте
рассмотрим пример. Интуитивно ясно, что на плоскости имеются
две возможные ориентации (рис. 8.16).
уп
О
У"
о
Рис. 8.16
Мы не можем дать внутренние характеристики этих
ориентации, но точно знаем, что они разные и что их только две. То
же самое можно сказать о прямой (рис. 8.17) или о трехмерном
пространстве, где существуют правая и левая системы координат
(рис. 8.18).

398
Глава 8. Двойные интегралы
Рис. 8.17
и Ζ
Рис. 8.18
Сначала рассмотрим плоскость, где нам известно (раздел 1.9),
что невырожденная матрица А сохраняет ориентацию или
изменяет ее на противоположную в зависимости от знака Det А. Это
дает нам ключ для общего определения5.
Пусть V — абстрактное двумерное векторное пространство.
Как мы уже видели в конце главы 1, задание базиса в
пространстве V равносильно заданию изоморфизма L : V —► R2. Если L и
V — два таких базиса, то
И = BL,
где В — невырожденная матрица 2x2 (рис. 8.19).
Рис. 8.19
Назовем базисы L и V подобными, если Det В > 0, и
противоположными, если Det В < 0. Утверждается, что множество всех
базисов в пространстве V распадается на два подмножества,
которые обозначим Т\ и Тг- Все базисы подмножества Т\ взаимно
5Позднее мы увидим, что это определение работает в га-мерном векторном
пространстве при любом га.

8.4. Ориентация
399
подобны, так же, как и все базисы подмножества Тг- Каждый
базис из Т\ противоположен каждому базису из Т2- Действительно,
выберем базис L\. Пусть подмножество Т\ содержит базисы вида
BLi, DetS>0,
а подмножество Т2 — базисы вида
BLi, DetS<0.
Любой базис принадлежит одному из этих подмножеств. Если
два базиса L и V принадлежат Т\, то
L = BLi, L' = B'Li, Det В > 0, Det В' > О,
следовательно,
I/ = B'B~lL и Det B'B~l = Det В'(Det B)~l > О,
а это значит, что L и V подобны. Если в этих выражениях
Det В < 0 и Det В' < 0, то базисы L и V подобны. В случае, когда
один определитель положителен, а другой отрицателен, базисы L
и V противоположны. Итак, если Τ обозначает множество всех
базисов в пространстве V, то мы имеем
T = TiUT2, ΤιΠΤ2 = 0.
Выбор ориентации в пространстве V означает выбор одного
из этих подмножеств. Другими словами, по определению
ориентация в пространстве V — это такое подмножество базисов V,
что любые два базиса из подмножества подобны, и любой базис,
подобный базису из подмножества, тоже принадлежит этому
подмножеству. Отметим, что выбор базиса L в пространстве V
определяет ориентацию пространства, т. е. множество всех базисов,
подобных L. Итак, пусть мы выбрали ориентацию пространства
V. Тогда базис V называется хорошим или положительным,
если он принадлежит выбранному подмножеству базисов, и плохим
или отрицательным, если нет. Таким образом, раз мы выбрали
ориентацию, то любой базис становится либо хорошим, либо
плохим. (Конечно, другой выбор ориентации изменяет эту
классификацию на противоположную.)

400
Глава 8. Двойные интегралы
V
V-
Μ
■+»w
Μ
Рис. 8.20
Рис. 8.21
Пусть W — другое векторное пространство и пусть А : V —►
W — линейный изоморфизм, т. е. существует обратное линейное
отображение A~l : W —► V (см. рис. 8.20). Предположим, что мы
выбрали ориентацию Оу в пространстве V и ориентацию <Э\у в
пространстве W. Пусть Μ € 0\у — хороший базис в
пространстве W. Тогда Μ : W —► R2, следовательно, Μ о А — изоморфизм,
т. е. задает базис в пространстве V. Итак, существуют две
возможности — базис Μ о А либо хороший, либо плохой. Давайте
посмотрим на эту альтернативу по-другому. Пусть L — хороший
базис в пространстве V. Обозначим
С = MatL,M(4) = MAL~l
Матрица С = MAL~l — это матрица перехода от базиса Μ А
к базису L (рис. 8.21); другими словами,
Μ А = CL.
Итак, базис Μ А будет хорошим тогда и только тогда, когда
DetC > 0. Если базис L заменить на V = B\L (Detf?i > 0) и
Μ заменить на М' = В2М (Det B2 > 0), то
С = M'AL'~l = B2MAL~lB^1 = В2СВ^\
Тогда
Det С" = Det B2 Det С Det B{
-1
имеет тот же знак, что и DetC. Таким образом, знак DetC не
зависит от частного выбора L € Оу и Μ € Ow-
Если DetC > 0, мы будем говорить, что отображение А
сохраняет ориентацию (или положительно). Если же DetC < 0,

8.5. Перенос и интегрирование 2-форм 401
мы говорим, что А изменяет ориентацию (или отрицательно).
А А'
Предположим, что V —► W и W —► Ζ — два линейных
изоморфизма, и мы выбрали ориентацию во всех трех пространствах.
Тогда легко проверить, что
о если А и А' сохраняют ориентацию, то А'о А тоже сохраняет
ориентацию;
о если оба изоморфизма А ж А' меняют ориентацию, то А' о А
ее сохраняет;
о если один изоморфизм сохраняет ориентацию, а другой
изменяет, то А' о А изменяет ориентацию.
Пусть φ : V —> W — дифференцируемое отображение. Тогда
в каждой точке ρ € V дифференциал άφρ '· V —► W — линейное
отображение. Мы говорим, что φ сохраняет ориентацию, если в
каждой точке дифференциал άφρ является линейным
отображением, сохраняющим ориентацию. (В частности, мы предполагаем,
что άφρ — линейный изоморфизм для каждой точки р.)
До сих пор мы предполагали, что пространство V —
двумерное. Но это не имеет значения. Например, если V — трехмерное
пространство, то все определения работают. Просто надо знать,
что матрица 3x3 обратима тогда и только тогда, когда ее
определитель не равен нулю, что любые три линейно независимые
вектора в трехмерном пространстве V образуют базис, т. е.
определяют изоморфизм с R3. Тогда все рассуждения, приведенные в
конце главы 1, применимы и здесь. Такая же ситуация в п-мерном
пространстве — требуется определение размерности η и
определителя матрицы η χ п. Эти вопросы мы будем обсуждать в
главах 10 и 11. (В пространстве одного измерения базисом является
ненулевой вектор, матрица 1x1 — это просто число а, которое
рассматривается как определитель этой матрицы.)
8.5. Перенос и интегрирование 2-форм
Чтобы упростить вычисление двойного интеграла, часто
вводятся новые, более удобные координаты. Например, область W,

402
Глава 8. Двойные интегралы
изображенная в координатах х, у на рис. 8.22, становится
прямоугольником R в системе координат г, Θ. Переход от одной
системы координат к другой осуществляется в этом случае с
помощью известного преобразования а, которое дается формулами
а* х = г cos θ и а* у = г sin θ.
Рис. 8.22
Мы можем использовать это преобразование и свести
двойной интеграл по ориентированной области fw к интегралу от
2-формы в плоскости г, Θ. Определим перенос 2-формы а*т так,
что если W = a(R), то
Jw Jr
т.
Для определения переноса 2-формы мы расширим
определение переноса от 1-формы очевидным образом. Для 1-формы λ мы
определяли перенос а*\ согласно формуле
α*λ(ρ)[ν]=λ(α(ρ))[Α*[ν]].
А теперь определим перенос 2-формы, применяя da к обоим
векторам аргумента τ (рис. 8.23). Таким образом, по определению
a*r(p)[v,w] = T(a(p))[da[v],da[w]].
Это определение гарантирует, что, как будет доказано,
формула JR а* т = / (д\ τ справедлива для любой прямоугольной
области R, при условии, конечно, что α дифференцируемо,
сохраняет ориентацию и оба интеграла существуют. Для доказательства

8.5. Перенос и интегрирование 2-форм 403
1
W
л
а*т
^Г"
Рис. 8.23
Рис. 8.24
мы будем аппроксимировать интеграл fR а* т римановой суммой
по большому числу малых прямоугольников (рис. 8.24).
Вклад в эту сумму прямоугольника с вершиной в точке ρ
равен a*r(p)[hv, few]. По нашему определению переноса 2-формы
это равно τ (α (ρ)) [da [h ν], da [few]], т.е. значению формы т на
параллелограмме, который является наилучшим линейным
приближением к образу прямоугольника, построенного на векторах hv
и few при преобразовании а.
Конечно, образ прямоугольника при преобразовании а не
является точным параллелограммом (рис. 8.25) и величина
r(a(p))[da(hv), da(kw)]
не будет точно равна интегралу от τ по образу прямоугольника.
Таким образом, у нас возникнут погрешности двух типов: мы
заменяем образ прямоугольника на параллелограмм (обозначим
его Р), так что
0) /«(прямоуг.) заменяем на /р,
и
(ii) fp заменяем на T(a(p))[da(hv),da(kw)].
da(v)

404
Глава 8. Двойные интегралы
Рис. 8.25
Если τ непрерывна, то погрешность типа (ii) будет o(hk). Если
τ имеет равномерно ограниченные первые производные во всей
области, ограниченные, скажем, числом к, то
|r(q) - τ(α(ρ))| < n(h2 + k2)1/2 для любого q в P.
Тогда погрешность типа (ii) будет не больше, чем
K(h2 + k2)l/2hk.
Погрешность типа (i) можно оценить, исходя из формулы
Тейлора, заменив, например, искривленный образ каждой стороны на
аппроксимирующую прямую линию. Предполагая, что первая и
вторая производные а ограничены в области R, можно получить,
что погрешность оценивается сверху суммой слагаемых вида h2k
и hk2, умноженных на некоторую константу. Отсюда можно
получить оценку
a*(r(pj))[/iv, hw] = I τ + погрешность,
■/«(прямоуг.)
где
|погрешность| < C(h2 + k2)1/2 x (площадь R).
Суммируя по всем прямоугольникам, получаем
y]a*(r(pi))[hv, hw] = / τ + погрешность,
Ja{R)
где
|погрешность| < C(h2 + к2)1/2 χ (площадь R).

8.5. Перенос и интегрирование 2-форм 405
Если мы будем неограниченно измельчать разбиение, то сумма
слева стремится к fR а*т, а погрешность справа стремится к
нулю. Отсюда следует, что
/ а*т = т.
JR Ja{R)
Более аккуратное доказательство этого важного результата,
не требующее таких строгих ограничений на а и т, справедливое
для всех п, читатель может найти в книге Loomis and Sternberg,
Advanced Calculus, раздел 8.11. Мы вообще рекомендуем для
изучения теории интегрирования главу 8 этой книги (ее можно
читать независимо от других).
Теперь необходимо разработать процедуру вычисления
переноса от 2-форм. Поскольку любая 2-форма на плоскости
выражается в виде произведения двух 1-форм, сначала вычисляем
α* (λ Λ σ), где λ и σ обозначают 1-формы. По определению
α*(λΛσ)[ν,\ν] = (λ Λ σ)[da[ν], da[w]]
= A[da[v]]a[da[w]] - A[da[w]]a[da[v]].
С другой стороны,
(α*λΛα*σ)[ν,\ν] = a*A[v]a*a[w] - α*λ[\ν]α*σ[ν].
Согласно определению переноса для 1-формы, α*λ[ν] = A[da[v]].
Отсюда следует, что
α*(ΑΛσ) = α*\Λα*σ,
т. е. операция переноса коммутирует с внешним произведением.
Поскольку самый общий вид 2-формы на плоскости ху — это
τ = F dx Л dy,
мы немедленно получаем, что
а*т = (a*F) d(a*x) Л d(a*y).

406
Глава 8. Двойные интегралы
Если, например, а*х = rcos#, а*у = rsin#, то
d(a*x) Л d(a*y) = (cos θ dr - r sin θ άθ) Λ (sin θ dr + r cos θ άθ)
= rdr /\άθ.
Итак, мы установили, что формула перехода от декартовых
координат к полярным имеет вид
/ (a*F)(r, в)г dr/\d6= j F(x, у) dx Л dy.
2-форма г drAdO каждому маленькому параллелограмму на
плоскости г, θ ставит в соответствие не его ориентированную площадь
(что делает dr Л άθ), а ориентированную площадь его образа в
плоскости ху, получившегося в результате преобразования а.
Теперь мы можем получить формулу замены переменных для
ориентированных двойных интегралов в общем случае. Пусть
R — ориентированная область в плоскости uv, которую
дифференцируемое преобразование а переводит в ориентированную
область a(R) на плоскости ху (рис. 8.26).
Рис. 8.26
Преобразование а задается с помощью переноса для
координатных функций χ и у:
а*х = Х(и, ν), а*у = Y(u, v).
Тогда
,, * λ д(а*х) , д(а*х) дХ , ЭХ ,
d(a χ) = — du Η dv = -pr— du + —— dv,
ou ov ou dv
,. , λ д(а*у) , д(а*у) дУ дУ ,
d(a*y) = -Цг-^ du + \ "' dv = -rr-du+ — dv.
ou ov ou ov

8.5. Перенос и интегрирование 2-форм 407
2-форма τ на плоскости ху записывается в виде τ = F(x, у) dx Л
dy. Перенос этой 2-формы равен
а* т = a*Fd(a*x) Л d(a*y)
= a*F
д(а*х) д(а*у) д(а*х) д(а*у)
ди dv
dv ди
du Л dv,
или
a*T = F(X(u,v),Y(u,v))
дХдУ
ди dv
дХдУ
dv ди
du Л dv.
Множитель в квадратных скобках является детерминантом
матрицы Якоби (якобиана) J, который выражает da в выбранных
координатах,
_ [д(а*х)/ди d(a*x)/dv\ (дХ/ди dX/dv
~ \д\а*у)/ди d(a*y)/dv) ~ \dY/du dY/dv
Следовательно, мы можем написать
/ Fdx/\dy= / а"
Ja{R) JR
FDetJduAdv.
Это равенство совершенно естественно. Поскольку Det J
является множителем, «преобразующим площадь» для линейного
преобразования da, то Det J du Adv каждой малой области на
плоскости uv ставит в соответствие ориентированную площадь его
образа в плоскости ху. Если порядок unv определяется
ориентацией R, а порядок χ и у — ориентацией а(К), причем а сохраняет
ориентацию, то якобиан J будет иметь положительный
определитель. Изменение порядка и и ν (или порядка хну) соответствует
изменению ориентации на плоскости uv (на плоскости ху). При
этом столбцы или строки J меняются местами, что вызывает
изменение знака Det J.
В качестве примера рассмотрим вычисление площади
ориентированной области W, ограниченной осью х, прямой у = тх,
гиперболой х2 — у2 = 1 и гиперболой х2 - у2 = 4 (рис. 8.27, 8.28).
Чтобы это сделать, напишем W = a(R), где а*х = u cosh υ и

408
Глава 8. Двойные интегралы
а* у = u sinh υ. Отображение а переводит ориентированный
прямоугольник R, заданный неравенствами
1 < и <2, 0<t>< arctanhm,
в область W. Например, вертикальный отрезок прямой и = 2
отображается в кусок гиперболы х2 — у2 = 4.
Рис. 8.27
Рис. 8.28
Поскольку в ориентации области W первой координатой
является х, ее площадь А = fw dx Л dy. Выполнив перенос,
получаем А = fRa*(dx Л dy) = Jρ Det Jdu Л dv. Здесь a*(dx Л
dy) = d(u cosh v) Л d{u sinh v) = (cosh ν du + sinh ν dv) Λ (sinh ν du +
и cosh ν dv) = и cosh2 vdu /\dv + и sinh2 vdv f\du = udu Л dv,
следовательно,
tanh J m
f f2 f
A= I udu Adv = I udu I
Jr J\ Jo
С другой стороны, мы можем вычислить
ι ° 1-1
dv = - tanh m.
т^ χ τ τ^ χ /cosh t> usmhtA
Det J = Det I . , , J =
у sinh ν и cosh ν J
и получить тот же самый интеграл А = fRudu/\dv.
Мы видим, что секрет полезности преобразования
координат состоит в том, что границы области W становятся
образами сторон прямоугольника на плоскости uv. Если, например, W
— треугольник, заключенный между осями координат и прямой

8.5. Перенос и интегрирование 2-форм 409
а(А),а(В) 1 χ
Рис. 8.29
χ + у = 1, то полезным преобразованием координат будет
такое, которое переводит отрезки прямых и = const с
фиксированным интервалом по υ в отрезки χ + у = const между осями
координат. Такое преобразование координат описывается
формулами: а*х = uv, а*у = и(1 — ν), которые обладают свойством
а*(х + у) — и. Читателю рекомендуется проверить, что а
преобразует квадрат единичной площади R на плоскости uv в область
W. Если в ориентации R сделать ν первой координатой, то
ориентация a(R) будет согласована с ориентацией W. Итак, если ν
— первая координата, то якобиан
J =
d(a*x)/dv д(а*х)/ди
d(a*y)/dv д(а*у)/ди
ν
1 -ν
имеет положительный определитель, равный и, что
подтверждает предыдущее утверждение. (Если первой координатой считать
и, то Det J = — и.)
Используем это преобразование для вычисления интеграла
= / — dx Л dy,
Jw у/хУ
который довольно сложно получить как повторный интеграл по
χ и у. Перейдем к новым переменным. Получаем
а
' е-(*+!/) \
1
у/ху J yfu2v(l - ν) и у^(1 - ν)

410
Глава 8. Двойные интегралы
и a*(dx Л dy) = (udv + vdu) Л (-udv + (1 - v)du) = udv Л du.
Тогда на плоскости uv имеем
JR \/v(l - V)
dv Λ du.
ν4ι - ν)
Порядок дифференциалов dv Л du под знаком интеграла связан с
тем, что в ориентации R первой координатой является v.
Окончательно получаем
1= Г e~udu С . dV = (1 - e-1^.
Jo Jo y/v(l - v)
(При вычислении второго интеграла мы воспользовались
формулой
dv , „ ,. .
= - arcsm(-2t> + 1).)
/
y/v{\ - ν)
Наконец, перейдем к задаче замены переменных для
вычисления абсолютного двойного интеграла / = fw F dx dy. Для этого
сначала преобразуем этот интеграл в ориентированный двойной
интеграл JWF dx Л dy, соответствующий ориентации W, для
которой первой координатой является х.
Рис. 8.30
Теперь напишем W как a(R) и зададим ориентацию R
(χ ν\
—— ) положителен, то выберем на R
u,vj
ориентацию, при которой первой координатой является и. Тогда
J= I a*F(DetJ)duAdv= i a*F(DetJ)
( R ) ( R )
\ и первая ) \ неориент. )
dudv.

8.6. 2-формы в трехмерном пространстве 411
/ χ у \
Если Det J I —— ) отрицателен, то зададим на R ориентацию,
\u,vj
при которой первой координатой является v. Тогда
/= I a*F(OetJ)dvAdu = - f a*F(OetJ)dudv.
( R ) ( cR )
\ ν первая ) \ неориент. /
В обоих случаях можно брать абсолютное значение Det J:
'x,ys
JR
Det J
u, ν
dudv.
При этом не возникает вопроса об ориентации или о порядке
переменных интегрирования. Перестановка χ и у или и и ν не
влияет на абсолютное значение Det J.
В главе 15 мы обсудим интегрирование форм более высоких
степеней.
8.6. 2-формы в трехмерном пространстве
В предыдущем параграфе мы определили понятие переноса для
2-форм. При этом правила вычисления очень простые: если ωχ и
и>2 — линейные дифференциальные формы, то
ф*(и>1 Л UJ2) = Ф*Ш\ Л ф*Ш2-
Если / — функция и τ — 2-форма, то
Φ*(Μ = Φ*(ΩΦ*τ.
Если τι и Т2 — 2-формы, то
Φ*(τι + τ2) = φ*τ1 + φ*τ2.
Таким образом, при работе с дифференциальными формами
сохраняются все обычные свойства алгебраических операций.
Кроме того, мы определили линейный оператор d, преобразующий
1-формы в 2-формы:
d(fdg) = df Adg,

412
Глава 8. Двойные интегралы
или в более общем виде:
d(fuj) = df Α ω + f άω,
удовлетворяющий условию
ά(ωι + u>2) = djjj\ + dui2-
Перенос ф* коммутирует с оператором d в том смысле, что
φ*(ά/) = άφ*/, где / — функция
и
φ*άω = άφ*ω, где ω — 1-форма.
2-формой в трехмерном пространстве (в декартовых
координатах х, у, ζ) мы по определению будем называть выражение
вида
a dx Л dy + b dx Л dz + с dy Л dz,
где а, Ь и с — функции. Если дана 1-форма
ω = A dx + В dy + С dz,
то правила для внешней производной d и для внешнего
умножения дают
άω = d А Л dx + dB Л dy + dC Л dz
(дА , дА , dA,\J
= —— dx + -^— dy + —-dz ] /\dx
\ox ay dz )
(dB , dB J dB \ J
+ {dx-dX+dyJdy + ~^dZ)Ady
fdc , эс J dc /\ J
+ —— ctx + —— dy + —— dz ) Adz
\ox ay dz )
(ЭВ дА\ , , (ЭС дА\ J J
= {-dx--dy')dxAdy+{-dx'--^)dxAdz
fdC dB\ J ,
Если ^ : R2 —y R3 и τ — 2-форма в пространстве R3, то ф*т будет
2-формой в пространстве R2.

8.7. Различие между 2-формами и плотностями 413
Рис. 8.31
Если R — некоторая область в R2 и мы выбрали в ней
ориентацию, то можно написать §оф*т, который рассматривается как
интеграл от τ по ориентированной поверхности a(R).
8.7. Различие между
2-формами и плотностями
Вернемся в двумерное пространство. Мы помним, что перенос
а*т определен для любой 2-формы т. Другими словами, если а
отображает плоскость uv в плоскость ху, то
а*(/ dx Л dy) = (a*f) · (Det J) du A dv,
(8.2)
где якобиан перехода J определяется матрицей
J =
dai/ди dai/dv
да2/ди dcLijdv
a =
α2
Эта формула верна для любого дифференцируемого
отображения а. Кроме того, мы доказали, что если α —
взаимнооднозначное отображение, сохраняющее ориентацию, то
/ <**(т) = I т.
JR Ja(R)
(8.3)
Это верно для интегралов от 2-форм, когда ориентация имеет
значение. Предположим, однако, что мы хотим вычислить
абсолютный интеграл. Тогда выбор ориентации не имеет значения,
но формула для замены переменных или перенос для выражения

414
Глава 8. Двойные интегралы
/ dA или fdxdy не будет совпадать с (8.2). Давайте вернемся
назад, к доказательству формулы замены переменных. Тогда
интеграл /в(прямруг0 мы заменяли на
r(P)[da(hv),da(kw)]
= f(P) x ориентированную площадь прямоугольника.
Очевидно, что в случае вычисления абсолютного интеграла мы
должны заменить ориентированную площадь на абсолютное
значение этой площади. Таким образом, в формуле (8.2) надо
написать
a* (fdxdy) = a*f -\DetJ\dudv. (8.4)
Читателю предлагается проверить в качестве поучительного
упражнения, что если а — взаимно-однозначное отображение,
то
/ a*(fdxdy) = / fdxdy
JR Ja{R)
независимо от ориентации.
Итак, 2-формы τ = / dx Л dy и плотности / dx dy являются
совершенно разными объектами — при замене переменных они
преобразуются по-разному. Например, плотность может быть
положительной и отрицательной (плотность электрического
заряда): если / > 0, то при замене переменных fdxdy становится
а*(/)| Det J\ dudv и a* f ■ | Det J\ по-прежнему положительна
(если Det J φ 0, что выполняется при дифференцируемое™ а-1).
Однако, не имеет смысла задавать вопрос о знаке 2-формы т,
потому что Det J, входящий в (8.2), может быть и положительным,
и отрицательным. Плотности и 2-формы совпадают, только если
мы выбрали ориентацию и делаем замену переменных,
сохраняющую эту ориентацию (для них Det J > 0).

8.8. Формула Грина на плоскости
415
8.8. Формула Грина на плоскости
Рассматривая криволинейные интегралы, мы уже встречались с
обобщением фундаментальной теоремы интегрального
исчисления — формулы Ньютона-Лейбница, а именно, с формулой
fdf = f(B)-f(A),
J1
где криволинейная трактория η проходит от точки А к точке В
(рис. 8.32). Эта теорема связывает интеграл от df по
одномерной области (т. е. по пути 7) со значениями самой функции / в
конечных точках траектории.
А
Рис. 8.32
Аналогичный результат, связывающий двумерную область и
ее одномерные границы, известен как формула Грина. Эта
теорема утверждает, что для любой дифференцируемой 1-формы τ
и любой ориентированной области на плоскости R справедливо
равенство
/ dr= I т.
JR JdR
Слева 2-форма άτ интегрируется по области R, а справа 1-форма
τ интегрируется по пути dR, являющимся границей области R.
6Для того, чтобы обе части этой формулы существовали, область Д и ее
граница dR должны удовлетворять некоторым требованиям, например, R
ограничена, dR кусочно-непрерывно-дифференцируема. — Прим,, ред.

416 Глава 8. Двойные интегралы
Ориентация R определяет направление движения по dR.
Например, если R — кольцевая область, ориентированная против
часовой стрелки, как показано на рис. 8.33, то dR состоит из
внешней окружности, по которой движение происходит против
часовой стрелки, и внутренней окружности, проходимой по часовой
стрелке.
Рис. 8.33
Прежде чем формально доказывать теорему Грина, имеет
смысл еще раз вспомнить определение оператора d,
действующего на 1-форму. Это поможет понять, почему должна быть такая
теорема. Мы определяли άτ как антисимметричную билинейную
функцию пары векторов v, w, обладающую свойством
dr(P)[hv, few] = / τ + погрешность,
P(h,k)
где P(h, к) есть параллелограмм, построенный на векторах hv и
few, причем погрешность стремится к нулю быстрее, чем
произведение hk, т. е. быстрее площади параллелограмма.
Рассмотрим область, состоящую из ./V параллелограммов,
каждый из которых построен на векторах hv и few (рис. 8.34).
Тогда мы имеем
Ν Ν . Ν
\]dT(Pi)[hv, few] = 2_\ / т + /^(погрешность)^.
г=1 г=1 о г=1
В сумме криволинейных интегралов по контурам
параллелограммов вклады от внутренних сторон, принадлежащих
одновременно двум параллелограммам, взаимно уничтожаются, так как они

8.8. Формула Грина на плоскости
417
Рис. 8.34
проходятся в противоположных направлениях. Таким образом,
остается один криволинейный интеграл по границе области R:
Ν . Ν
У] dr(Pj) [hv, few] = / τ + У](погрешность)г.
i=l dR t=l
Если h и к стремятся к нулю, то сумма в левой части равенства
стремится к fRd,T. Поскольку число N пропорционально 1/hk
и каждый поправочный член стремится к нулю быстрее, чем
hk, сумма поправочных членов стремится к нулю при Ник,
стремящихся к нулю. В результате мы получаем
R dR
для любой области, состоящей из параллелограммов.
Чтобы доказать теорему Грина более строго, рассмотрим
сначала частный случай, когда τ = G(x,y)dy, и вычислим
криволинейный интеграл JdR τ по контуру прямоугольника, стороны
которого параллельны осям χ и у (рис. 8.35).
Вклад в интеграл дает только сторона χ = а, проходимая от
у = 0 до у = Ь, и сторона χ = 0, проходимая от у = Ъ к у — 0.

418
Глава 8. Двойные интегралы
Рис. 8.35
Можно записать:
Iт= I G(a,y)dy + I G(0,y)dy
J Jo Jb
8R
= I (G(a,y)-G(0,y))dy.
Jo
Согласно фундаментальной теореме интегрального исчисления
последнее подинтегральное выражение можно записать так:
га ft(~i
G(a,y)-G(0,y) = J —(x,y)dx.
Поэтому криволинейный интеграл JdR τ можно записать как
повторный интеграл
Ιο\ΐο^(Χ'ν)άΧ)^
который равен ориентированному двойному интегралу
/.
дх
(х, у) dx Λ dy.

8.8. Формула Грина на плоскости
419
Аналогичные соображения для 1-формы F(x, у) dx дают
I F(x,y)dx= I ( —(x,y))dxAdy
dR
Га f BF
= - / (F(x, b) - F(x, 0))dx = - / — dx Λ dy.
Jo J oy
R
Сложив это с предыдущим результатом, получаем
/Г ВС BF
F(x,y)dx + G(x,y)dy = / —(x,y)dx- —(x,y)dxAdy.
dR R
Поскольку для дифференциальной 1-формы
τ = F(x, у) dx + G(x, y) dy
внешняя производная равна
BF. ., , BG, 4J
dr = - — {x,y)dx/\dy + —{x,y)dx/\dy,
By Bx
то последнее равенство с интегралами означает справедливость
формулы Грина для координатного прямоугольника R:
R dR
А теперь докажем теорему Грина в более общем случае,
когда область на плоскости является образом прямоугольника при
гладком биективном отображении а. Стратегия уже знакома: мы
перенесем интегралы /дга( mi τ и Ja,R\ dr на плоскость st, где
рассматриваемая область интегрирования является
прямоугольником (рис. 8.36).
Мы будем пользоваться условием, что образом границы
области R является граница a(R). Следовательно,
/ T = /aV
9{a{R)] dR

420
Глава 8. Двойные интегралы
t,
'
dR
■ э ■
ι
s
д[а(Щ
Рис. 8.36
Однако, для прямоугольной области R мы уже доказали, что
Iа*т= fd(a*r).
dR R
Более того, согласно определению переноса, мы имеем
! dr= Ia*(dr).
*(Я)
я
Следовательно, для доказательства равенства fd, ,„-,, τ = J ,R\ dr
достаточно показать, что
a*(dr) = ά(α*τ).
Это легко сделать прямым вычислением. Пусть τ = / dx +
gdy. Используя равенства a*(dx) = d(a*x), a*(dy) = d(a*y),
получаем, что а*т = (а*/) d(a*x) + (a*g) d(a*y). Далее, из формулы
d(f dh) = df Adh имеем
d(a*r) = d(a*f) A d(a*x) + d(a*g) A d(a*y).
С другой стороны, мы знаем, что
dr = df Adx + dg A dy.
Правило α*(σ Α ω) = α*σ Α ο*ω дает нам
a*dr = a*(df) A a*(dx) + a*(dg) A a*(dy),

8.8. Формула Грина на плоскости
421
следовательно,
a*dr = d(a*f) Л d(a*x) + d(a*g) Л d(a*y).
Из сравнения этого выражения с (8.2) получаем то, что нам
требовалось:
d(a*r) = a*(dr).
Таким образом, мы имеем
J τ = I а*т = I d(a*r) = ! a*(dr) = I dr,
Ja{dR) JdR JR JR J a{R)
т.е. формула Грина доказана для любой области, которая
является образом прямоугольника.
Добавим еще доказательство этой формулы для случая,
когда область является многоугольником. На плоскости любой
многоугольник можно разложить на треугольники. Действительно,
любой многоугольник разбивается на выпуклые
многоугольники (рис. 8.37). А любой выпуклый многоугольник разлагается на
треугольники, если взять точку внутри него и соединить эту
точку со всеми вершинами (рис. 8.38).
Рис. 8.37 Рис. 8.38
Если бы мы знали формулу Грина для треугольников, то она
была бы нам известна для всех многоугольников, так как
интегралы, вычисленные по внутренним границам треугольников,
взаимно уничтожаются (рис. 8.39).
Итак, мы должны доказать теорему для треугольников.
Аффинное преобразование переводит любой треугольник в
треугольник. Следовательно, инвариантность интегралов при
гладком (в частности, аффинном) преобразовании означает, что
теорему достаточно доказать для какого-либо одного треугольника.

422
Глава 8. Двойные интегралы
Рис. 8.39
Рис. 8.40
Итак, на плоскости ху рассмотрим треугольник (рис. 8.40)
Т0 = {0 < χ < у < 1}.
Мы можем рассмотреть четырехугольник
Τε{0 < χ < у, ε < у < 1},
где 0 < ε < 1. Очевидно, что если мы докажем теорему Грина для
Τε, она будет верна в предельном случае для треугольника То,
поскольку криволинейные интегралы и интегралы по площади
внутри малой области при ε —> 0 стремятся к нулю. Область Τε
для ε > 0 есть образ прямоугольника {0 < г* < 1, г<г;<1}на
плоскости uv, полученный в результате отображения
χ = uv
у = ν.
Это отображение имеет гладкое обратное
и = х/у,
v = y,
если у > ε > 0. Следовательно, мы свели теорему к случаю,
который уже доказан, т.е. к образу прямоугольника (рис. 8.41).
В качестве иллюстрации применения формулы Грина
рассмотрим интеграл от 1-формы
τ = χ dy
по замкнутому пути dR (рис. 8.42), образованному отрезком
прямой от точки
Г
к точке
к точке
параболой у = 1 — х2 от точки
и отрезком от точки
к точке
'(Г

8.8. Формула Грина на плоскости
423
Рис. 8.41
Рис. 8.42
Прямолинейные отрезки, как нетрудно проверить, не дают
вклада в интеграл. Параметризуя параболу
β*χ = 1-ί, P*y = l-(l-t)2 = 2t~t2, 0<ί<1,
получаем
β*τ = (1 - ί)2(2 - 2ί) dt = 2(1 - ί)3 dt,
и
[ т= f 2{l-tfdt = \.
JdR JO l
По формуле Грина интеграл от dr = 2xdx A dy по области R
должен давать то же самое. Вычисляем этот интеграл как повторный
и получаем
-1-х2
dy
/■1 /-1-х2 /-1 γ
I 2xdx I dy = 2(1 - x2)xdx = -,
Jo Jo Jo 2

424
Глава 8. Двойные интегралы
что и следовало ожидать.
Формулу Грина можно использовать для вычисления
площадей через криволинейные интегралы. Например, если τ = xdy,
то άτ = dx /\dy и
JdR Jr
dx /\dy = площади R,
предполагая, что R ориентирована против часовой стрелки.
Конечно, любая 1-форма т' = xdy + df, где / — произвольная
дифференцируемая функция, обладает этим свойством, так как
dr' = d{x dy) + d(df) = dx /\dy = dr.
Например, выберем / = — \xy. Тогда получаем
τ' = xdy - -xdy - -ydx = -{xdy -ydx).
Вводя полярные координаты согласно формулам7
а*х = г cos θ, о*у = г sin θ,
мы можем получить
qV = \ν2άθ,
Δι
откуда следует хорошо известная формула
Г-27Г
Μ
для площади, ограниченной замкнутой кривой, заданной в
полярных координатах.
7В практических вычислениях символ а* часто опускают и пишут просто
χ = г cos θ, у = r sin θ.

Резюме
425
В заключение выпишем основные формулы этой главы:
λ Λ σ = —σ Λ λ,
(u>i + u>2) Λ σ = ω\ Λ σ + и>2 Л σ,
d(fui) = df Λ ω + /(Ζω,
α*(λΛσ) = α*λΛα*σ,
α*(η + Τ2) = α*τι + α*Τ2,
a* dr = da* τ,
JR Ja
ί τ= Ι dr.
JdR JR
т для α, сохраняющего ориентацию,
(Я)
Резюме
A. 2-формы
Для заданной на плоскости дифференциальной 1-формы τ надо
уметь давать определение ее внешней производной dr и
вычислять dr в координатах х, у.
Вы должны знать определение и уметь вычислять интеграл
от 2-формы по ориентированному прямоугольнику на плоскости.
B. Двойные интегралы
Вы должны уметь вычислять двойные интегралы по заданным
на плоскости областям, сводя их к повторным интегралам с
соответствующими пределами интегрирования; уметь изменять
порядок интегрирования в повторном интеграле, преобразуя его к
двойному интегралу.
Выбрав преобразование одной области на плоскости в другую,
надо уметь вычислять интегралы по второй области с помощью
переноса. Надо уметь находить такое преобразование, в
результате которого упрощается вычисление двойного интеграла.
С. Формула Грина
Надо знать формулу Грина на плоскости и уметь применять ее.

426
Глава 8. Двойные интегралы
Задачи
8.1. В трех случаях, перечисленных ниже, и и υ являются
функциями на плоскости, а χ и у — аффинные координаты.
Выразите dx Л dy через du Л dv. Нарисуйте графики типичных кривых
и = const и ν = const в первой четверти плоскости (х, у > 0) и
попробуйте дать геометрическую интерпретацию соотношениям
между dx Л dy и du Л dv на примере параллелограмма, стороны
которого касательны к кривым и = const и ν = const.
(a) х = ucosv, у = usmv.
(b) χ = ucoshv, у = usinhv.
(c) χ — и2 - ν2, y = 2uv.
8.2. Вычислите интеграл ffs x2y2 dx dy, где область S расположена в
первой четверти и находится между гиперболами ху = 1, ху = 2
и прямыми линиями у = х, у = 4а;.
8.3. (а) Изменяя порядок интегрирования, покажите, что
Г ( Г ет^-х^1{х) dx) dy = Г (а - x)em^a-^f(x) dx,
где α и т — постоянные и α > 0.
(b) Покажите, что
du J dv = - / {χ - t)2f{t) dt.
Если делать это последовательно в два шага, то вам не
придется рассматривать тройной интеграл!!
8.4. Вычислите повторный интеграл
1=1 у{[1У s^dx)dy'
представив его как двойной по соответствующей области W.
После этого вычислите интеграл как повторный, изменив порядок
интегрирования. Нарисуйте график области W.
8.5. Рассмотрите отображение, определенное формулами
χ = и+ ν, у = v — u2.
I (J. ILmdt

Задачи
427
(a) Вычислите якобиан этого отображения в переменных unv.
(b) Треугольник Τ лежит на плоскости uv и имеет вершины в
точках: (0,0), (2,0), (0,2). Нарисуйте образ этого
треугольника S на плоскости χ у.
(c) Вычислите площадь S как двойной интеграл по области S
и как двойной интеграл по области Т.
(d) Вычислите интеграл
//.
dxdy
s(x-y+l)2'
(а) Пусть S обозначает единичный квадрат на плоскости uv
(рис. 8.43). Опишите и нарисуйте образ S при отображении
На рисунке покажите ф(А), ф{В) и ф(С)
uv
(2-й2)
У А
2-"
(b) Вычислите интеграл J J у dx dy по этой области на плоскости
ху.
(c) Вычислите этот же интеграл, интегрируя соответствующую
функцию по квадрату S на плоскости uv.
(а) Вычислите интеграл
/(
Jw
(х + 2у) dx dy
для треугольной области W, изображенной на рис. 8.44.

428
Глава 8. Двойные интегралы
Рис. 8.44
(Ь) Вычислите этот же интеграл в переменных и и υ,
определенных формулами χ = 2uv, у = u — uv.
8.8. Вычислите интеграл
/ I/ \А2 + у2 dy ) dx
сначала как повторный интеграл по у и х, а потом в полярных
координатах.
8.9. (а) Вычислите повторный интеграл
/ ( / u5v9 du I dv.
(b) Интерпретируйте этот интеграл как двойной по
соответствующей области на плоскости uv. Нарисуйте эту область,
выписав в явном виде ограничивающие кривые. (Не
беспокойтесь здесь и в дальнейшем, что область не ограничена8.)
(c) Полученный двойной интеграл еще раз перепишите как
повторный с другим порядком интегрирования и вычислите
его.
(d) Выполните в двойном интеграле замену переменных и =
х2у~3 и ν = х~1у2. Получите новый двойной интеграл на
плоскости ху. Нарисуйте область интегрирования для этого
нового интеграла.
(e) Преобразуйте полученный двойной интеграл в повторный и
вычислите его.
Здесь появляется несобственный двойной интеграл. Определение этого
понятия и изучение свойств несобственных интегралов составляет
самостоятельный раздел математического анализа. — Прим. ред.

Задачи
429
.11.
(f) Покажите, что χ и у являются дифференцируемыми
функциями в первой четверти плоскости uv.
.10. (а) Вычислите интеграл
JL
ydA,
где Q — первая четверть круга единичного радиуса. Этот
интеграл преобразуйте в повторный по переменным χ и у.
(А обозначает обычную площадь на плоскости ху.)
(b) Введите полярные координаты г и θ обычным способом и
преобразуйте данный интеграл в интеграл по
соответствующей области на плоскости гв. Дайте описание этой
области. (Под плоскостью г θ подразумевается новое
пространство R2, где декартовыми координатами являются г и Θ.)
(c) Преобразуйте полученный интеграл в повторный в
переменных г, θ и вычислите его еще раз.
(а) Вычислите интеграл / = Jw 2y dx Л dy как сумму двух
повторных интегралов на плоскости ху. Область W (рис. 8.45)
ограничена прямыми у = х/2, у = 2х и гиперболами ху = 2,
ху = 8.
υΑ
2 и
Рис. 8.45
(b) На плоскости uv найдите такой прямоугольник R, чтобы W
была образом R после преобразования а, заданного
формулами: а*х = 2uv, а*у = u/v.
(c) Вычислите а* (2у dx Л dy).
(d) Вычислите интеграл / как интеграл по области R.

430
Глава 8. Двойные интегралы
В.12. (а) Вычислите криволинейный интеграл J[(2y2+3x) dx+2xy dy]
по кривой 7, изображенной на рис. 8.46, которая состоит из
прямолинейных отрезков 0 < а; < 2, 0 < у < 2 и дуги
окружности х2 + у2 = 4 при χ > 0 и у > 0.
(Ь) Постройте такой двойной интеграл по области,
ограниченной кривой 7, чтобы он был равен криволинейному
интегралу, вычисленному в предыдущем пункте. Вычислите этот
двойной интеграл, преобразуя его к полярным
координатам.
Рис. 8.46
(с) Найдите функцию f(x), обладающую свойством
/ f(x)[(2y2 + Зх)dx + 2xydy] = 0,
когда интеграл вычисляется по любой замкнутой кривой на
плоскости.
.13. Один из способов замены переменных в ориентированном
интеграле / = fwfdx Л dy, где W = 0(5), состоит в том, чтобы
воспользоваться формулой Грина и преобразовать интеграл / в
криволинейный интеграл по замкнутому пути dW. Затем
преобразовать результат в криволинейный интеграл на плоскости uv,
еще раз применить формулу Грина и выразить / как двойной
интеграл на плоскости uv. Воспользовавшись этим подходом,
получите формулу замены переменных для двойного интеграла.
8.14. Пусть и и υ будут функциями на плоскости, у которых первые
и вторые производные по χ и у непрерывны. Пусть S — связная

Задачи
431
область на плоскости, границу которой обозначим dS. Покажите,
что
dv ди .
I If ^i — qi J θ£β _1_ f qi _
Jas ΙΛ dx dx) V ду " ду t
=4L{u^y-v^k)dxdy-
Рис. 8.47
5. (а) Тонкая пластина S (рис. 8.47) имеет постоянную плотность
σ (здесь σ — масса на единицу площади). Момент инерции
пластины относительно оси χ равен
h = σ / у2
Js
dxdy.
Покажите, что Ιχ = σ Jgs xy2 dy, где dS — граница
пластины, проходимая против часовой стрелки.
(Ь) Момент инерции пластины относительно оси у равен
1У = σ Ι χ2 dx dy.
Js
Найдите две дифференциальные формы ω и т, для которых
справедливо равенство
1У — σ ω = σ Ι τ.
Jas Jas
las Jas
(с) Момент инерции пластины относительно оси ζ равен
Ιζ = σ / (χ2 + у2) dx dy = Ix + Iy.
Js

432
Глава 8. Двойные интегралы
Найдите такую дифференциальную форму Ω, для которой
выполняется равенство Ιζ = σ fgs Ω. Форму Ω запишите в
полярных координатах г и Θ.

I

Глава 9
Гауссова оптика
В главе 9 дан пример использования результатов
Первых восьми глав в физической теории — оптике. Она
состоит целиком из приложений, и ее пропуск при
чтении никак не отразится на понимании последующего
материала.
9.1. Оптические теории
В истории физики часто случается, что старая теория
вытесняется новой, но при этом старая остается справедливой, становясь
либо приближением к новой, которое пригодно при
определенных ограничениях, либо частным случаем новой теории. Так,
ньютоновская механика может рассматриваться как
приближение к релятивистской механике, справедливое при скоростях,
малых по сравнению со скоростью света. Аналогично, ньютоновская
механика может рассматриваться как приближение к квантовой
механике, когда изучаемые объекты достаточно велики. Законы
Кеплера, описывающие движение планет, являются частным
случаем законов Ньютона, когда сила взаимодействия между телами
обратно пропорциональна квадрату расстояния между ними.
Законы Кеплера можно также считать приближением к
уравнениям движения Ньютона, когда мы пренебрегаем влиянием одной
планеты на движение других.

I

436
Глава 9. Гауссова оптика
распространения луча. Это явление называется поляризацией
света, и его можно наблюдать, например, используя специальные
поляроидные фильтры.
Геометрическая оптика является приближением к волновой
оптике, в котором пренебрегают волновой природой света. Это
можно делать, когда размеры апертур велики по сравнению
с длиной волны света и когда мы не интересуемся тем, что
происходит в фокусах и в окрестности тени.
Линейная оптика является приближением к геометрической
оптике, когда исследуются малые углы. В рамках линейной
оптики делаются приближения: sin# = θ, tan# = θ, cos# = 1 и т. д.,
т. е. отбрасываются все выражения, квадратичные (и более
высоких порядков) по углам. Например, в геометрической оптике
справедлив закон Снеллиуса, согласно которому, если свет
проходит область с коэффициентом преломления η (относительно
вакуума) и попадает в область с коэффициентом преломления
п', то η sin г = η'sin г', где г я г' — углы, которые составляет
направление распространения луча с нормалью к поверхности,
разделяющей эти области (рис. 9.3). В линейной оптике этот
закон упрощается: га = nV, потому что углы гиг' малы. (Этот
приближенный закон был известен еще Птолемею.)
Рис. 9.3
Различие между геометрической оптикой и ее линейным
приближением называется (геометрической) аберрацией. Например,

9.1. Оптические теории
437
Рис. 9.4. Сферическая аберрация
пусть пучок параллельных лучей падает на сферическое зеркало
(рис. 9.4). Тщательное наблюдение отраженных лучей
показывает, что не все они пересекаются в одной точке. Только лучи,
распространяющиеся вблизи диаметра, пересекаются вблизи
фокуса1 зеркала. В рамках линейной оптики мы ограничиваемся
рассмотрением лучей, которые близки к диаметру, так что
можно считать, что они пересекаются в фокусе. (Это отклонение от
фокуса сферического зеркала называется сферической
аберрацией.)
Гауссова оптика является частным случаем линейной оптики,
когда предполагается, что все рассматриваемые поверхности
обладают вращательной симметрией относительно некоторой
центральной оси. Это очень важный частный случай, потому что
все линзы и большинство полированных зеркал обладают этим
свойством. Наше обсуждение оптических теорий изображено на
схеме:
«Фокус» в данном случае расположен в середине радиуса сферы,
параллельного направлению лучей. — Прим. ред.

438
Глава 9. Гауссова оптика
Гауссова оптика
частный случай
при наличии вращательной
симметрии
Линейная оптика
приближение,
пренебрегающее аберрацией
Геометрическая оптика
приближение
пренебрегающее
коротких волн,
дифракцией, интерференцией
и поляризацией
Волновая оптика
частный случай,
когда не рассматривают
излучение света
Электродинамика Максвелла
приближение,
пренебрегающее квантовыми эффектами
Квантовая электродинамика
9.2. Матричные методы
В рамках гауссовой оптики мы изучаем траекторию светового
луча, когда он проходит через различные преломляющие
поверхности оптической системы (или отражается от отражающих
поверхностей) . Введем систему координат, в которой ось ζ
(направленная слева направо) совпадает с оптической осью (осью
симметрии системы). Мы ограничимся исследованием коаксиальных

9.2. Матричные методы
439
лучей — лучей, лежащих в одной плоскости с оптической осью2.
В силу вращательной симметрии очевидно, что можно
ограничиться изучением лучей, лежащих в одной выбранной
плоскости. Траектория луча, проходящего через систему
преломляющих поверхностей, будет представлять собой последовательность
прямых линий. Наша задача состоит в том, чтобы связать
прямолинейный луч, выходящий из системы, с прямолинейным лучом,
падающим на нее. Для этого мы должны получить метод
описания прямых линий. Выберем фиксированное значение ζ = zq
и плоскость, перпендикулярную оптической оси, которую будем
называть плоскостью отсчета. Тогда прямая линия определяется
двумя параметрами: высотой q над осью ζ и углом Θ,
определяющим наклон линии к оптической оси (рис. 9.5). Угол θ будем
измерять в радианах и считать положительным, если вращение
против часовой стрелки совмещает положительное направление
оси ζ с направлением луча. На каждой стадии вычислений
следует выбирать удобную плоскость отсчета.
Рис. 9.5
Например, если свет падает на оптическую систему слева и
выходит направо (рис. 9.6), мы должны выбрать одну плоскость
отсчета ζ\ слева от системы линз и вторую плоскость отсчета ζ-ι
справа. Луч, входящий в систему по прямой линии с параметрами
<7ι и θ\ при ζ = ζ\, выходит из системы по прямой линии с
параметрами qi-, #2 при ζ = ζι· Наша задача состоит в том, чтобы
для любой системы линз найти связь между (92,^2) и (<7ι,#ι).
Хотя это и является упрощающим предположением, на самом деле
молено доказать, что линейность означает изучение произвольных лучей, потому
что их можно свести к коаксиальным лучам, проектируя на два взаимно
перпендикулярных направления.

440
Глава 9. Гауссова оптика
Рис. 9.6
Теперь надо сделать очень простой, но чрезвычайно важный
шаг — главный в геометрической оптике и механике.
Переменную θ заменим на ρ = ηθ, где η обозначает
показатель преломления среды в плоскости отсчета. (В механике это
соответствует замене скорости на импульс.)
V
Тогда световой луч может быть описан вектором
и мы
должны найти вектор ( I как функцию ( ). Мы
пренебрегаем квадратичными членами и членами более высоких
порядков, следовательно, в нашем приближении I ) будет линейной
функцией от
т. е.
Р2
q^=M2llqi
Pi
где Μ2ι — некоторая матрица. Главным результатом выбора ρ
вместо переменной θ является
DetM2i = 1.
Другими словами, изучение гауссовой оптики сводится к
изучению группы вещественных матриц 2x2, имеющих определитель,
равный единице, т. е. группы 51(2, R). Чтобы доказать это
утверждение, заметим, что если луч последовательно проходит три
плоскости отсчета ζ\, z2 и 23, то по определению матрица
перехода
М31 =Мз2М21.

9.2. Матричные методы
441
Таким образом, если оптическая система состоит из двух или
более блоков, мы должны только проверить, что Det Μ = 1 в
отдельности для каждого блока. Для упрощения изложения
предположим, что в системе нет зеркал.
Основные процессы в оптике
Прохождение света через систему линз можно рассматривать
как совокупность основных оптических процессов,
(а) Распространение (трансляция): луч движется по прямой
между двумя плоскостями отсчета, лежащими в одной и той же среде.
Для описания этого процесса расстояние между плоскостями
обозначим ί, показатель преломления среды п. Очевидно, что при
таком движении светового луча угол Θ, и, следовательно, р, не
изменяются: (р2 = pi), и <?2 = <?ι + (ί/η)ί>ι (рис. 9.7).
^,—rtC"1
Z\
Ях
t
Z2
Ч2\
η
2
Рис. 9.7
Введем приведенное расстояние Τ = t/n. Тогда
Τ
1
Det
Τ
1
= 1.
(b) Преломление на границе между двумя областями с разными
показателями преломления. Показатели преломления двух сред
обозначим щ и П2- Естественно, надо учитывать кривизну
поверхности раздела сред. Выбираются две плоскости отсчета,
слева и справа вблизи от этой поверхности. На поверхности раздела
величина q не изменяется, а вот угол и, следовательно, ρ
изменяются согласно закону Снеллиуса (его линеаризированному
варианту). В закон Снеллиуса входит наклон касательной к
поверхности в точке, где происходит преломление. В нашем
приближении мы пренебрегаем квадратичными членами в этом наклоне и
членами третьего и более высокого порядка в уравнении
поверхности. Таким образом, мы предполагаем, что линия пересечения

442
Глава 9. Гауссова оптика
этой поверхности с нашей плоскостью будет параболой:
ζ - ζλ = -kq.
Тогда производная ζ по q, т.е. z'(q) = kq, будет tan(7r/2 — ψ),
где ψ — угол, изображенный на рис. 9.8.
Рис. 9.8
Для малых углов Θ, т.е. для малых значений q, угол ψ будет
близок к π/2, и тогда tan(7r/2 — ψ) можно заменить на π/2 — ψ,
если мы готовы опустить члены более высокого порядка по q и
р. Таким образом, в гауссовом приближении π/2 — ψ = kq. Угол
между падающим лучом и касательной равен (π/2 — ii). Из того,
что сумма внутренних углов треугольника равна π, следует, что
(π — ψ) + θ\ + (π/2 — i\) = π или
i\ = θ\ + kq.
Аналогично получаем
«2 = #2 + kq,
где q = q\ = q2 определяют точку на преломляющей поверхности,
в которую падает луч. Первое уравнение умножим на п\, а второе
на П2. Используя приближенную формулу для закона Снеллиуса
n\i\ = Π2«2> получаем
\р1) = \-Р iJW'

9.2. Матричные методы
443
константа Ρ = (п2 — гц)-к называется оптической силой
преломляющей поверхности.
Сопряженные плоскости
Итак, движение луча в любой гауссовой оптической системе
между двумя плоскостями отсчета соответствует матрице
М=(с L)) ' Где AD~BC = !·
Теперь можно составить словарь, переводящий свойства матрицы
в оптические свойства.
Например, две плоскости z\ и z2 называются
сопряженными, если для любого значения q\ все лучи, выходящие из q\, Z\,
сходятся в точку q2, ^2· Это значит, что значение q2 не должно
зависеть от р\, т. е. что
В = 0.
Тонкие линзы
Заметим, что произведение двух матриц вида I pi)
имеет тот же вид, т. е.
1 0\ / 1 0\ _ / 1 О
-Pi I) \-Р2 I) - \-{Ρι + Ρ2) 1
Это позволяет написать уравнение для так называемых тонких
линз, состоящих из преломляющих поверхностей с
пренебрежимо малым расстоянием между ними (рис. 9.9)3. В этом случае
плоскости отсчета ζ\ и ζ2 удобно брать совпадающими с
плоскостью линз. При этом с плоскостью ζ\ связывают лучи, падающие
слева, а с плоскостью ζ2 — лучи, выходящие из линз и
распространяющиеся направо.
3На рис. 9.9 преломляющие поверхности изображены не параболами, как
делалось выше, а дугами окружностей. Молено доказать, что уравнение
окружности радиуса R с центром на оси ζ справа от точки ζ\, в которой эта
/ 2\ Я2
окружность пересекает ось ζ, с точностью до o(q ) имеет вид ζ — ζ\ = — ·
2R
Поэтому константа к из предыдущего построения в этом случае равна 1/R.
Заметим, что число к = 1/R называют кривизной окружности радиуса R. —
Прим. ред.

444
Глава 9. Гауссова оптика
Рис. 9.9
Матрица для левой преломляющей поверхности равна
/ 1 0\
\ Rx )
Соответственно, матрица для правой преломляющей поверхности
равна
( 1 °\
п\ - п2
Я2
1
(Заметим, что на рис. 9.9 значение R2 отрицательно.)
Перемножив эти матрицы, мы получаем матрицу для тонкой линзы
1 О
-V/ ι
где Ι^-ηΟί^-^
Число / называется фокусным расстоянием линзы. Мы будем
предполагать, что линзы находятся в вакууме, так что щ = 1 и
П2 > 1· Если Ri положительно, a R2 отрицательно
(двояковыпуклая линза), то фокусное расстояние / положительно, поскольку
п2- п\> 0.
/
/
Fi
F2
Рис. 9.10

9.2. Матричные методы
445
Вычислим матрицу для тонкой линзы, задающую движение
луча между плоскостью отсчета Fi, расположенной слева на
расстоянии / от линзы, и плоскостью отсчета F2, расположенной
справа на расстоянии / от нее (рис. 9.10):
(о i)(-i// ι До ij = (-i// о)'
Плоскость i*i называется первой фокальной плоскостью. Если
луч, падающий на линзу, проходит через эту плоскость в точке
<7ι = 0 под углом ρι, то выходящий луч имеет параметры
т.е. выходящий луч параллелен оси ζ. Обратное утверждение:
если падающий луч параллелен оси ζ, то выходящий луч имеет
параметры
UJ = (-1// oj(oJ = (-gi//j'
т. е. пересекает ось ζ во второй фокальной плоскости. В общем
случае, можно видеть, что р2 не зависит от р\, следовательно,
лучи, проходящие через фиксированную точку в первой фокальной
плоскости, выходят из линзы параллельным пучком под одним и
тем же углом к оси ζ. Далее, q2 не зависит от q\, т. е. все
параллельные друг другу до линзы лучи проходят через одну точку во
второй фокальной плоскости.
Рассмотрим простой пример использования матричного
метода фокусировки. Пусть плоскость отсчета z\ находится слева от
тонкой линзы на расстоянии s\, а плоскость отсчета z2 находится
справа от линзы на расстоянии s2. Матрица, задающая движение
луча между этими плоскостями, такова:
(I S2\( 1 0\ /1 sA_{l-S2/f S2 + S1-WA
{о i)\-i/f 1Д0 1;-^ -1// i-Sl// )■
Плоскости будут сопряженными, если верхний правый
матричный элемент равен нулю. Мы получаем хорошо известное
уравнение тонкой линзы \/s\ + \/s2 = 1//· Запишем его в виде
s\ + s2 - Psis2 = 0, где Ρ = 1//.

446
Глава 9. Гауссова оптика
Уравнение можно решить относительно S2 при условии, что
si φ 1/Р- Таким образом, кроме случая si = /, любая плоскость
имеет единственную сопряженную плоскость. Если же si = /,
т. е. z\ совпадает с первой фокальной плоскостью, то все лучи,
проходящие в этой плоскости через фиксированную точку q,
выходят из линзы параллельным пучком. Значит, плоскость,
сопряженная первой фокальной плоскости, «лежит в бесконечности».
Аналогичные рассуждения можно провести для второй
фокальной плоскости.
Для si φ f и значения S2, соответствующего сопряженной
плоскости, увеличение дается уравнением
^ = 1-^ = 1-^(1 + 1) = -^.
<?i / \si s2J si
Если s\ и S2 положительны (объект находится слева от линзы,
а изображение справа), то увеличение отрицательно. Это значит,
что изображение перевернуто.
Умножая матрицы, можно построить матрицу для любой
комбинации тонких линз. Например, пусть есть две линзы с
фокусными расстояниями /ι и /2, расположенными на расстоянии I
друг от друга (рис. 9.11). В этом случае для плоскостей отсчета
ζ\ (первая линза) и ζ-ι (вторая линза) получается матрица
1 О
-1//2 1
1 I
О 1
1
ι - IIк
Ч hh - VS2 -
1//1
i/h
Рис. 9.11

9.2. Матричные методы
447
Телескоп
Очень интересная ситуация возникает с парой линз, когда
I = /i + J2- В этом случае матрица имеет вид
А
О
В
D
т.е. С = 0. Это значит, что р2 = Dpi, т.е. направление
выходящего луча зависит только от направления падающего луча. Это
условие выполняется в конструкции, которая называется
астрономическим телескопом. Он состоит из линзы (объектива) с
большим положительным фокусным расстоянием /ι и окуляра с
малым положительным фокусным расстоянием /2,
расположенных на расстоянии /ι + /2 друг от друга (рис. 9.12). Такой
телескоп преобразует параллельные лучи, идущие от далекой звезды,
в параллельные лучи, попадающие в глаз наблюдателя.
Рис. 9.12
Угловое увеличение телескопа равно отношению наклона
выходящего луча к наклону падающего луча, что равняется
D = \-
1-
/1+/2
/2"
h /2
Это увеличение отрицательно (образ перевернут), и его величина
равна отношению фокусного расстояния объектива к фокусному
расстоянию окуляра.

448
Глава 9. Гауссова оптика
Общий случай
Здесь мы хотим показать, что любая матрица Μ = I „ „ )
с Det Μ = 1 описывает некоторую оптическую систему.
Пусть сначала С φ 0. В этом случае матрицу Μ можно
представить в виде произведения трех оптических матриц:
2£)-(ίί)(*ϊ)(ί0· <->
Непосредственной проверкой можно убедиться, что это равенство
\-А 1-D
выполняется при s = ———, τ = ———, и только при этих s, t.
С О
Если С = 0 (при этом А ф 0), то, домножив матрицу Μ слева
на ρ 1 I (берем Ρ φ 0), получим матрицу
м>=(1 °)(А В) = (Л в
\Р 1J \0 D) \РА PB + D
у которой левый нижний элемент — не нуль, поэтому М' —
оптическая матрица, а поскольку Μ = I pi) Μ', то Μ — тоже
оптическая матрица.
Гауссово разложение
Из формулы (9.1) вытекает, что для любой матрицы Μ =
\ Г П ) с ^е* Μ = I и С φ 0 существуют и единственны числа
s, t такие, что
1 Л (А В\ /1 А _ /1 0\
0 \) \С D) [θ 1) \С I) ·
Таким образом, для любой не телескопической оптической
системы существуют такие две плоскости, что матрица,
описывающая движение луча между ними, имеет вид I ~ I. Эти
плоскости сопряжены между собой, и соответствующее увеличение
равно 1. Гаусс назвал их главными плоскостями. Если начать

9.2. Матричные методы
449
с оптической матрицы
между двумя главными плоско-
1 О
С 1
стями, то так же, как и в случае тонких линз, для любой
плоскости можно найти сопряженную. Для этого достаточно написать
С — —Р = —1//· Например, справа и слева от главных
плоскостей находятся фокальные плоскости с фокусным расстоянием /:
1 /
О 1
1 О
-ι// ι
ι /
О 1
о /
■ι// о
Гаусс так интерпретировал этот результат.
z\
Вторая
главная плоскость
Рис. 9.13
Пусть луч I * I, параллельный оси, входит в оптическую
систему при ζ = ζ\ (рис. 9.13). Этот луч приходит ко второй
главной плоскости на той же высоте, но с наклоном —q/f (вектор
Я
-q/f
) и фокусируется на оси во второй фокальной точке F2-
Аналогично, луч, выходящий из первой фокальной точки с
любым наклоном в первой главной плоскости, преобразуется в луч,
распространяющийся параллельно оси, и приходит в z-i на той же
высоте, какую он имел в первой главной плоскости.
Итак, мы видим, что произвольная не телескопическая
оптическая система может быть описана тремя параметрами:
положением двух главных плоскостей и фокусным расстоянием.
(Мы уже знали, что должно быть три независимых параметра
— три элемента матрицы 2x2, потому что четвертый
матричный элемент определяется из условия, что определитель матрицы
равен 1.)

450
Глава 9. Гауссова оптика
Если мы знаем положение главных плоскостей, то положение
фокальных плоскостей мы получаем из равенств
Hi-F1 = /, F2-H2 = f.
Если фокальные плоскости рассматриваются как плоскости
отсчета в оптической системе, то из определения фокальной
плоскости мы знаем, что оптическая матрица должна иметь нуль в
верхнем левом и в нижнем правом углах. Таким образом,
матрица распространения луча между двумя фокальными плоскостями
имеет вид
(-V/ о)·
Теперь возьмем (рис. 9.14) две другие плоскости у\ и у2,
связанные с фокальными плоскостями соотношениями
Fi-yi = n\x\ и у2 - F2 = щх2.
У\
4—П1Ж1-*
Fi
F2
4—П2Х2-*·
V2
Рис. 9.14
Матрица, соответствующая этим плоскостям, будет равна
(I х2\( 0 Л/1 xA_{-x2/f f-(xix2/f)\
\о ι ) {-iff о До ι)-{ -ι// -т// ) ■
Отсюда видно, что плоскости у\ и у2 сопряжены тогда и только
тогда, когда Х\х2 = /2 (это уравнение называется уравнением
Ньютона). Тогда увеличение дается формулой
т = -x2/f = -f/x\.

9.3. Метод Гамильтона в гауссовой оптике 451
Например, пусть У2 находится справа от i<2, так что Х2
положительно. Тогда, если фокусное расстояние / положительно, то
увеличение т отрицательно, т. е. изображение оказывается
перевернутым.
Давайте перечислим полученные результаты. Пусть 51(2, R)
обозначает группу матриц 2 χ 2 с определителем, равным 1.
В этом разделе мы показали изоморфизм между 51(2, R) и
системами гауссовой оптики. Каждая матрица соответствует
оптической системе. Умножение матриц соответствует композиции
оптических систем.
А теперь перейдем к изложению идей Гамильтона в самой
простой форме.
9.3. Метод Гамильтона в гауссовой оптике
Предположим, что в нашей оптической системе ζ\ и Ζ2 — не
сопряженные плоскости. Это значит, что элемент В в оптической
матрице не равен нулю. Тогда из уравнений
(?2 = Aqi + Връ
Р2 = Cqi + Dpi
мы можем выразить р\ и р2 через q\ и q^.
Pl = (l/B)(q2-Aqi),
Р2 = (l/B)(Dq2 - gi),
где мы воспользовались условием AD — ВС = 1. Этот результат
можно интерпретировать геометрически. Выбираем точку q\ на
плоскости z\ и точку <?2 на плоскости Z2- Существует
единственный луч, соединяющий эти точки. (Для сопряженных плоскостей
это не так. Если <?2 — изображение точки q\, то имеется
бесконечное число лучей, соединяющих точки q\ и q2, т. е. все лучи,
выходящие из точки <?1, попадают в точку <?2. Если <?2 не является
изображением точки q±, то лучей, соединяющих точки qi и q2, не
существует.) Пусть функция W = W(qi,q2) имеет вид
W(qi,q2) = (1/2Я)(Лд? + Dq\ - 2qiq2) + К,

452
Глава 9. Гауссова оптика
где К — постоянная. Тогда р\ и р2 выражаются в форме
Pl = -(dW/dq1) и р2 = (dW/dq2).
Гамильтон назвал эту функцию точечной характеристикой
системы. В современной физической литературе иногда ее
называют эйконалом. Предположим, что мы выбрали плоскости z\, z-i
и 2з, причем ни одна пара плоскостей не является сопряженной.
Пусть Ζ\ < ζι < 23 и 22 не совпадает с преломляющей
поверхностью. Обозначим W21 точечную характеристику системы z\ — 22,
а Wj,^ ~~ системы 22 — z%. Утверждается, что точечная
характеристика системы Z\ — 23 (с точностью до произвольной аддитивной
постоянной) дается формулой
W3i(gi,93) = W21 (91,92) + ^32(92,93),
причем луч, распространяющийся из точки q\ в точку 93,
проходит через точку 92 = 92(91, 9з) на плоскости Z2-
Чтобы убедиться в справедливости этой формулы, заметим,
что раз плоскость z-i не совпадает с преломляющей поверхностью,
то она не изменяет направление луча. Тогда
р2 = (dW2i/dq2)(qi,q2) = -{dWZ2/dq2)(q2,qz)-
А теперь применим цепное правило и получим, что
dWsi/dqi = -р\ и dW3i/dq3 = рз-
Итак, функция W определена с точностью до аддитивной
постоянной. Гамильтон показал, что при соответствующем выборе
этой постоянной можно сделать так, что W(91,92) будет
оптической длиной луча, соединяющего точки q\ и 92·
Понятие оптической длины определяется следующим
образом. Для отрезка пути / в среде с постоянным коэффициентом
преломления η оптическая длина пути равна nl. Пусть путь η
является ломаной линией, где каждый отрезок li лежит в среде с
постоянным коэффициентом преломления щ. Тогда оптическая
длина пути 7 равна

9.3. Метод Гамильтона в гауссовой оптике 453
Докажем теорему Гамильтона в рамках гауссовой оптики.
В этом приближении в производных функции W сохраняются
только члены, линейные по ρ и q. Таким образом, для
вычисления оптической длины в функции W мы должны учитывать
члены не выше квадратичных. Итак, световой луч, падающий на
плоскость z\, определяется параметрами I ), а луч,
выходящий из плоскости z2, — параметрами ( I. Тогда оптическая
\P2j
длина пути
L(7) = L0 + -{p2q2 - Ml),
где L0 обозначает оптическую длину вдоль оси системы между
плоскостями z\ и 22 [р\ = q\ = 0 = р2 = ^г)· Если мы докажем эту
формулу, то предположив, что z\ и z2 не являются сопряженными
плоскостями, значения р\ и pi можно выразить через 9ι и q%, т. е.
подстановка р\ = (1/B)(q2 - Aq{) и р2 = (l/B)(Dq2 - 91) в L(7)
даст выражение для W, если принять К = L0.
Прежде чем доказывать формулу для 1/(7), заметим, что она
правильно себя ведет для случая комбинированной системы: если
мы взяли ζ\, ζ2 и 2з, то очевидно, что длина вдоль оси
складывается:
2^292 - Ρΐ9ι) + 2^з9з - V242) = -^{рзЯз - Ρΐ9ι)·
Следовательно, мы должны доказать формулу в двух
фундаментальных случаях.
(1) Если коэффициент преломления η постоянен, d —
проекция луча на ось ζ, то в этом случае
L(7) = n(d2 + (g2-9i)2)1/2
7 ln/ ч2
= nd +--(q2 - qi)
= nd + \id
(92 - 91) (?2 - 9i)
= nd+ -p(q2 -91),
где p2 = pi = ρ = -(92 - 9i).

454
Глава 9. Гауссова оптика
(2) Пусть теперь коэффициент преломления слева от пре-
!, 2
ломляющеи поверхности ζ — ζ = -kq равен щ, а справа η-ι
(рис. 9.15).
-^"""^
2
J>^V
W/
2"
Рис. 9.15
Предположим, что слева от преломляющей поверхности
выбрана точка 2з, а справа z±. Если бы п\ равнялось П2, то
оптическая длина между этими точками была бы равна n\lz + η2(1 + Ц),
где £з ~~ длина отрезка слева от выбранной плоскости, а I + Ц
— длина отрезка справа, причем Ц — отрезок справа от
преломляющей поверхности. (Мы нарисовали картину для к > 0, но то
же самое справедливо и для к < 0.) Если П2 Φ η\, то nil\ будет
другим, но его можно вычислить по формуле случая (1) между
точками ζ и 24- Кроме того, влияние преломляющей поверхности
приведет к замене nil на ηι( в выражении для длины пути, и
вклад преломляющей поверхности будет равен
(щ - п2)1
Итак,
/ = {z" — z)cosec#i,
где ζ" находится из системы уравнений
ζ" - ζ = -kq"2
2 н
q" = (ϊΆ·αθι)(ζ" - ζ) + q.

9.4. Принцип Ферма
455
Очевидно, что с точностью до членов более высокого порядка
мы можем взять ζ" = ζ' = -kq2 + ζ и cosec#i заменить на 1.
Δι
Следовательно,
(ηι - n2)l = -k(m - n2)q2 =
= -j[k{ni -n2)q]q
= ^(p2-pi)q,
поскольку на преломляющей поверхности q2 = q\ = q и p2 =
pi — Pq, где Ρ = k(n2 — п\). Итак, наша формула доказана.
9.4. Принцип Ферма
Рассмотрим преломляющую поверхность с оптической силой Ρ =
(п2 — п\)к, расположенную в некотором ζ. Здесь Ρ может
обращаться в нуль. Пусть плоскость ζ\ находится слева, а плоскость
ζ2 справа от ζ (рис. 9.16). Предположим, что коэффициенты
преломления среды на участках от ζ\ до ζ и от ζ до ζ2 постоянны.
Пусть q\ — точка на плоскости z\, q2 — точка на плоскости z2 и
q — точка на плоскости ζ. Рассмотрим траекторию, состоящую
из трех участков: луч от точки q\ движется к точке q, второй
qi,
Л—τ
V
Я2
Ζ\ Ζ Ζ2
Рис. 9.16
= —2т

456
Глава 9. Гауссова оптика
участок — через преломляющую поверхность в точке q, и потом
опять световой луч от q до точки <?2.
Поскольку q выбрана произвольно, то, вообще говоря, эта
траектория не будет оптическим путем. Однако оптическая длина
этой траектории
П\1\ + nl + П2^2
в гауссовом приближении состоит из трех членов:
L(qi,q,q2) = L0 + -(pi(q - <?ι) + p2(<?2 - <?) - Pq2),
как было показано в предыдущем разделе. В этом выражении
п\, п2, ч
р\ = -j-(q-qi) и р2 = —(<?2 - <?)·
Следовательно, мы можем написать
1 (ά\ 2 . d2 2 D 2\
2 \щ n2 /
Предположим, что мы фиксировали точки q\ и q2. Найдем
положение точки q, когда L достигает экстремума. Другими
словами, мы хотим решить уравнение dL/dq = 0 для фиксированных
значений q\ и q2. Вычисляя производную по q от L и учитывая,
что dpi/dq = n\/d\ и dp2/dq = — n2/d2, получаем уравнение
pi - р2 - Pq = 0.
Откуда имеем
р2 = Pq + pi.
Но это в точности то же самое соотношение между р\ и р2,
которое определяется из матрицы преломления в точке ζ.
Итак, мы доказали следующий факт. Фиксируем точки q\ и <?2·
Рассмотрим траектории, соединяющие точки q\ и q2, состоящие
из двух отрезков: от точки q\ до q' и от q' до <?2. Из всех
возможных траекторий световой луч распространяется вдоль той, где L
достигает экстремума, т. е. выполняется условие

9.4. Принцип Ферма
457
Это и есть знаменитый принцип наименьшего времени Ферма
(в гауссовом приближении). Давайте подставим
п\, , п2, .
Pi = ^-(g-9i) и р2 = ^-№-9)
в формулу для L. Получим еще одно выражение для L:
L = n\d\ + пъаъ + -
id
£(,-«)' +£<*-«>'-*
Коэффициент при q2 равен n\/d\ + η2/ά2 — Р- Таким образом,
оптический путь минимален при условии
d\ d2
и максимален при условии
d\ с<2
Если Ρ > 0, то мы получаем минимум при малых значениях
d\ и cfe и максимум при больших значениях d\ и с?2- Ситуация
становится неопределенной, когда
^i + ^2 =р
т.е. мы не можем найти решение для q'. Это условие означает,
что соответствующие плоскости являются сопряженными. Итак,
мы получаем минимум, если плоскость, сопряженная к ζ\, не
лежит между z\ и 22, и максимум в противном случае. Тот факт,
что L достигает минимума только до первой сопряженной
точки, справедлив и для произвольной оптической системы, где он
известен как теорема коэффициентов Морзе.
Рассмотрим интуитивно ясный пример этого явления. Пусть
свет отражается от вогнутого сферического зеркала. Возьмем
точку Q на оси ζ внутри сферы. Луч распространяется вдоль
диаметра сферы и, отражаясь, попадает в точку Q. Очевидно,
что расстояние от зеркала до точки Q будет локальным
минимумом, если точка Q расположена между зеркалом и центром, в
противном случае это расстояние будет локальным максимумом.

458
Глава 9. Гауссова оптика
9.5. От гауссовой оптики к линейной
Что произойдет, если мы не будем предполагать наличие
вращательной симметрии оптической системы, но по-прежнему будем
учитывать только члены первого порядка по углам и
расстояниям? Прежде всего для описания луча нам необходимо иметь
четыре переменных: qx и qy — координаты точки, в которой луч
пересекает плоскость, перпендикулярную оси ζ; два угла θχ и
ву, определяющие направление луча. Направление в трехмерном
пространстве задается единичным вектором ν = {ух, vy, vz).
Если направление этого вектора близко к положительному
направлению оси ζ, то можно считать, что он имеет вид ν = (θχ, ву, νζ),
где υζ = 1 — ~{θχ + ву) = 1, при условии, что углы θχ и ву малы.
Δι
Угловые переменные θ заменим на р, определяемые формулами
рх = ηθχ и ру = пву. (Если среда анизотропна, например, для
некоторых кристаллов, то соотношение между вир становится
более сложным. Но здесь мы не будем рассматривать такие
среды.) Конечно, все происходит в некоторой фиксированной
плоскости, перпендикулярной оси ζ. Если мы будем рассматривать
две плоскости ζ\ и Ζ2, то лучу будут соответствовать два вектора
для каждой плоскости соответственно:
f 9x2 \
Яу2
Рх2
\ Ъ2 J
Наша задача — найти соотношение между ui и U2· Поскольку
мы пренебрегаем членами порядка выше первого, можно
написать
U2 =Mui,
где Μ — матрица размера 4x4.
Наша задача — установить, какие матрицы 4x4
возникают в линейной оптике. Первая очевидная мысль, что это
матрицы, удовлетворяющие условию DetM = 1. Однако это не так.
Безусловно, верно, что все оптические матрицы должны иметь
единичный детерминант, но не верно, что все матрицы 4 χ 4 с
U1
/ Чх\ \
Ы
Рх\
V Pyi J
И U2 =

9.5. От гауссовой оптики к линейной 459
единичным детерминантом могут быть матрицами
преобразований в линейной оптике. Должно быть более строгое ограничение.
Чтобы объяснить, в чем состоит это более строгое ограничение,
вернемся назад и еще раз сформулируем условие, при котором
матрица 2x2 имеет определитель, равный единице. После этого
можно будет вернуться к соответствующему условию для случая
четырех переменных. Пусть на плоскости даны два вектора:
В разделе 4.9 мы определили антисимметричное произведение
u;(w, w') между двумя векторами согласно формуле
w(w,w') = qp' — q'p.
Геометрический смысл u;(w,w') — это ориентированная
площадь параллелограмма, построенного на векторах w и w' (см.
рис. 9.17). Из определения и из геометрического смысла следует
антисимметрия ω:
u;(w,w') = — u;(w',w).
Рис. 9.17
Матрица 2x2 сохраняет площадь и ориентацию тогда и только
тогда, когда ее определитель равен 1, т.е. DetM = 1 тогда и
только тогда, когда
w(Mw,Mw') = ω(\ν, w')

460
Глава 9. Гауссова оптика
для всех w и w'. А сейчас предположим, что в четырехмерном
пространстве есть два вектора
и =
/ Qx \
%
Рх
\Ру )
/ Ях\
И U =
Я'у
Р'х
\Ру/
Введем по определению
ш(и, и') = qxp'x - q'xpx + qyp'y - q'ypy.
Произведение ω по-прежнему остается антисимметричным:
w(u',u) = -и(и,и'),
но геометрический смысл его не очень понятен.
Оказывается, что матрица Μ (4 χ 4) может быть матрицей
преобразования в линейной оптике только при выполнении
условия
ш(Ми, Ми') = ш(и, и')
для всех векторов и и и'. Матрицы такого типа называются в
физической литературе линейными каноническими
преобразованиями, а в математической литературе они называются линейными
симплектическими преобразованиями. Эти матрицы (и их
обобщения на случай большего числа измерений) играют важнейшую
роль в теоретической механике и геометрии.
Сначала сформулируем ряд основных сведений относительно
линейных симплектических преобразований в пространстве
четырех переменных. Тогда мы сможем увидеть, что наши
рассуждения, показывающие, что гауссова оптика эквивалентна
группе 51(2, R), могут быть использованы для демонстрации
эквивалентности линейной оптики группе Sp(4, R) — группе линейных
симплектических преобразований в пространстве четырех
измерений.
В общем случае пусть V обозначает векторное (вещественное
конечномерное) пространство. Билинейная форма Ω в
пространстве V — это любая функция Ω : V х V —> R, линейная по каждой
переменной при условии, что другая фиксирована, т. е. Ω(ιι, ν) —

9.5. От гауссовой оптики к линейной
461
линейная функция ν при фиксированном и и линейная функция
и при фиксированном v. Мы говорим, что Ω антисимметрична,
если Ω(ιι,ν) = — Ω(ν, и) для всех и и ν в пространстве V. Мы
говорим, что Ω невырождена, если при любом фиксированном
и линейная функция Ω (и, ·) не тождественный нуль (если только
сам вектор и не равен нулю). Антисимметричная невырожденная
билинейная форма в пространстве V называется симплектиче-
ской формой. Векторное пространство, снабженное данной сим-
плектической формой, называется симплектическим векторным
пространством, говорят, что оно имеет симплектическую
структуру. Пусть V — симплектическое векторное пространство с сим-
плектической формой Ω и пусть А — линейное преобразование
пространства V в себя; тогда мы говорим, что А —
симплектическое преобразование, если Ω(Α\ι, Αν) = Ω(ιι,ν) для всех и и
ν в пространстве V. Существует теорема (Guillemin, Sternberg,
Symplectic Techniques in Physics, Chapter II), утверждающая, что
каждое симплектическое векторное пространство должно быть
пространством четного числа измерений, и что каждое
симплектическое линейное преобразование должно иметь детерминант,
равный единице, а значит, быть обратимым. Очевидно, что
преобразование, обратное к симплектическому преобразованию,
должно быть симплектическим, и что произведение любых двух сим-
плектических преобразований тоже должно быть
симплектическим. Множество всех симплектических линейных
преобразований называется симплектической группой в пространстве V и
обозначается Sp(V).
Предположим, что V = Ш.п + Ш.п. Это — пространство, в
котором вектор можно записать в виде
Симплектическая форма Ω определяется формулой
Ω(ιι, и') = ρ q' - ρ' q,
где символ · обозначает обычное скалярное произведение в
пространстве Шп. Если использовать запись скалярного произведения

462
Глава 9. Гауссова оптика
и · u' = q · q' + ρ · ρ', то форму можно переписать по-другому
П(и,и') = и'· Ju,
где J — матрица 2η χ 2η вида I _ ), а I — единичная матрица
η х п. Повторим: линейное преобразование Τ в пространстве V
симплектично тог
няется равенство
симплектично тогда и только тогда, когда для всех и и и' выпол
П(Ти,Ти') = П{и,и').
Это можно переписать в виде
Г* JTu · u' = Ju · и',
где Г* обозначает транспонированную матрицу (т. е. матрицу,
сопряженную к Τ по отношению к скалярному произведению в
пространстве V). Поскольку это равенство выполняется для всех и
и и', мы получаем
TlJT = J.
Отображение Τ можно записать в виде
q\ _ f Aq + Bp
T'pJ \Cq + DpJ>
где А, В, С и D — матрицы η х п, т. е.
Т=(А В
\С D
Тогда
rpl
t_lAt С'"
Bt Dt ι,
где А1 обозначает матрицу, транспонированную к Л, и т. д.
Условие TlJT = J переходит с совокупность условий: А1 С = С*А,
B*D = D*B, и AlD — С1 В — I. Заметим, что матрица Т-1,
которая также симплектична, имеет вид
,_ι _ / D* -Bt
-С1 А
Τ — \ ^<t At

9.5. От гауссовой оптики к линейной
463
причем выполняются условия:
DC1 = CD1 и ΒΑ1 = АВК
А теперь вернемся к проблеме доказательства того, что
группа линейных симплектических преобразований (в пространстве
четырех измерений) совпадает с множеством всех
преобразований в линейной оптике. Как и в случае гауссовой оптики,
доказательство распадается на две части. Первая, физическая часть
доказательства показывает, что (в линейном приближении) мат-
( 1 °\ и Ы
рица Ι ρ _ I, где Ρ = Ρ — симметричная матрица,
соответствует преломлению на поверхности раздела между двумя
областями с постоянным коэффициентом преломления (для каждой
поверхности появляется своя матрица Р), и что матрица
соответствует движению в среде с постоянным коэффициентом
преломления, где d — оптическая длина вдоль оси. Вторая часть
доказательства (математическая) позволяет доказать, что любая
симплектическая матрица может быть записана как
произведение матриц этого вида.
Здесь мы не будем заниматься математическим
доказательством, которое является довольно хитроумным обобщением
доказательства, приведенного в разделе 9.2. Читатель может найти
его в книге Guillemin, Sternberg, Symplectic Techniques in Physics,
стр. 27-30. Давайте рассмотрим физическую часть этой задачи.
Напомним, что мы определяем падающий луч заданием его
направления ν = (vx,vy,vz), ||v|| = v%. + Vy + v"l = 1, и точкой, где
луч пересекает плоскость, параллельную плоскости ху и
находящуюся в точке ζ на оптической оси. Тогда
Мы предполагаем νχ и vy малыми и поэтому пренебрегаем
квадратичными членами. Пусть
Рх = nVx, py = ПУу,
где η — коэффициент преломления. Смещение на расстояние t
вдоль оптической оси — это с точностью до квадратичных членов
I Л
0 I

464
Глава 9. Гауссова оптика
по vx и vy то же, что и смещение на расстояние t вдоль вектора v.
Следовательно,
Я2х - Qix = tvx
Тогда мы имеем
<?2у - Ч\ у = tvy.
q2\ = (ι л\ /V
V2 [о iMpW'
где d = t/n (см. рис. 9.18).
Рис. 9.18
Теперь перейдем к преломлению света. Предположим, что
преломляющая поверхность квадратична и определяется
формулой
Z -2=-fcqq,
где к — симметричная матрица 2x2. Нормаль к этой поверхности
в точке q определяется формулой
u= (fcq,-l).
(С точностью до членов порядка выше первого вектор и имеет
единичную длину.) Проекция вектора ν на плоскость,
касательную к поверхности в точке q, равна
ν - (ν · u)u.

9.5. От гауссовой оптики к линейной
465
Запишем ν = (vx, vy, 1) = (ν, 1), тогда ν · u = fcq · ι/ — 1и
ν — (ν · и)и = (и, 1) - (fcq · и - l)(fcq, -1).
Откуда, пренебрегая квадратичным членом fcq · и, получаем для
проекции выражение
(i/ + fcq,0).
Закон Снеллиуса говорит, что п\(у\ — (vi-u)u) = ri2(v2 — (v2-u)u).
В линейном приближении и с учетом того, что pi = пи\ и р2 =
ra>2i получаем
pi - nifcq = р2 - r^fcq
или
Р2 = Pi - Pq,
где
~(щ - П2)к.
Итак, мы получили матрицу преломления
I О
-Р I
. Таким
образом, мы показали, что группа преобразований линейной оптики
совпадает с группой 5p(4,R).
Есть еще один заслуживающий внимания момент в гауссовой
оптике. Предположим, что оптическая система обладает
вращательной симметрией. Тогда на каждой преломляющей
поверхности матрица оптической силы Ρ имеет вид Ρ = ml, где m —
скалярный коэффициент и I — единичная матрица 2x2. Оче-
Ί el
видно, что произведение таких матриц на матрицу вида
О I
может быть записано в виде
матрица действует на вектор
αϊ Ы
cl Л
Заметим, что когда такая
Чу
Рх
\PyJ

466
Глава 9. Гауссова оптика
то получится то же самое, когда матрица I ,) действует
отдельно на I х ) и I y I. Итак, когда мы изучали гауссову
оптику, то не обязательно было ограничиваться изучением
коаксиальных лучей. Можно было рассматривать произвольные лучи,
разложив их на х- и у-компоненты. Это является следствием
принятого линейного приближения.
Основная формула для оптической длины
L = L0 + -(p2-q2-pi -qi)
(где теперь ρ и q — векторы) доказывается так же, как и в
гауссовом случае, проверяя, что происходит с базисными
компонентами. Нет смысла повторять это еще раз.
Две плоскости называются несопряженными, если оптическая
матрица В, связывающая их, несингулярна. Тогда можно решить
уравнения
q2 = Асц + βρι
и
Р2 = Cqi + £>ρι
относительно pi и р2, которые оказываются равны
Р1 = -В^Ащ + В~1Ч2
и
pa = (С - DB-lA)(n + DB'1^-
Теперь можно написать
L = L0 + W(qi,q2),
где
W(qi,q2) = \ \DB-X4l ■ q2 + Я-1Ац ■ qi - (2Bt)-\1 · q2] .
(При выводе этой формулы мы использовали тождество
-(В*)'1 =C-DB~1A,

9.5. От гауссовой оптики к линейной
467
которое следует из несингулярности В и условия А1Б — В1С = I.)
Прямое вычисление (с использованием этого тождества) дает (в
очевидном смысле)
dL dL
^—=Р2 и —- = -ρι.
<9q2 aqi
Таким образом, знание L дает возможность выразить pi и р2
через qi и q2.
Мы можем теперь коротко описать переход к (нелинейной)
геометрической оптике. Сформулируем условие симплектично-
сти матрицы А немного по-другому. В пространстве R4
рассмотрим 2-форму
ω = dqx Λ dpx + dqy Λ dpy.
Линейное отображение А : R4 —► R4 симплектично тогда и только
тогда, когда
Α*ω = ω.
Другими словами, перенос формы ω в результате действия А дает
снова ω. Поэтому дадим следующее определение:
дифференцируемое отображение φ называется симплектическим, если
φ*ω = ω.
Мы не требуем здесь, чтобы φ было линейно. (В старой
литературе симплектические отображения назывались каноническими
преобразованиями.) Гамильтон показал, что отображения в
геометрической оптике (от входа до выхода) являются в точности
симплектическими отображениями. Кроме того, он показал, что
в предположении неконгруэнтности симплектическое
отображение определяется характеристической функцией L, где L(qi,q2)
есть оптическая длина пути, соединяющего точки qi и q2-
(Конечно, в этом случае формула для L будет гораздо сложнее.)
Примерно через десять лет после написания
фундаментальных работ по оптике Гамильтон сделал потрясающее наблюдение:
тот же самый формализм применим и в механике точечных
частиц. Пусть (ft,..., qn — обобщенные координаты системы частиц,
a pi,... ,рп — их обобщенные импульсы. Вместо оптической оси ζ

468
Глава 9. Гауссова оптика
рассматривается время. Тогда преобразование от начальных
координат и импульсов к конечным всегда будет симплектическим.
В XIX веке это открытие привело к громадному прогрессу в
теоретической механике. А почти столетием позже, в 1920 году,
аналогия между оптикой и механикой, обнаруженная Гамильтоном,
сыграла ключевую роль в развитии квантовой механики.
Резюме
A. Матричная формулировка гауссовой оптики
Вы должны уметь использовать двухкомпонентный вектор для
описания луча, проходящего через плоскость отсчета.
Вы должны уметь получать и использовать матрицы 2x2
для описания эффектов распространения, преломления света и
тонкой линзы.
B. Система линз
Вы должны уметь вычислять матрицу для системы
преломляющих поверхностей или системы тонких линз между двумя
плоскостями отсчета.
Для данной системы линз надо уметь находить главные и
фокальные плоскости. Надо уметь пользоваться ими для
нахождения изображения объекта.
C. Гамильтонова оптика
Для гауссовой оптической системы надо уметь находить
точечные характеристики Гамильтона между плоскостями отсчета и
использовать их для определения траектории луча,
соединяющего две точки в двух плоскостях.
Задачи
9.1. На рис. 9.19 изображены фокальные и главные плоскости для
тонкой линзы. Лучи, падающие слева параллельно оси системы,
преломляются и проходят через фокус в плоскости F^. Лучи,
выходящие из фокуса в плоскости F\, преломляются и выходят
параллельными оси. Главные плоскости Ну и Ή.2 связаны с
фокальными плоскостями Fi и F2 соответственно.

Задачи
469
(a) С помощью луча Ri, изображенного на рисунке,
определяется положение в плоскости ζ. Нарисуйте ход луча Ri и еще
двух других лучей.
(b) Вычислите координаты изображения из предыдущего
пункта с помощью уравнения Ньютона относительно любой из
плоскостей, изображенных на рис. 9.19.
(c) Постройте матрицу оптической системы между
плоскостями ζι и Z2- С помощью этой матрицы определите положение
и наклон луча Ri, выходящего из линзы в плоскости Ζ2·
ζι Fi H2 #iz2 F2
#1
1см"
г (cm)
Рис. 9.19
9.2. На рис. 9.20 изображена толстая линза, сделанная из стекла с
показателем преломления η = 3/2. Постройте матрицу
распространения луча между плоскостями отсчета ζ\ и гг. Определите
положение фокальных плоскостей F\ и F2, главных плоскостей
Hi и Η2 и покажите их на рисунке. Нарисуйте ход лучей и
определите положение изображения объекта, находящегося слева от
ζ\ на расстоянии 1 см. Используя уравнение Ньютона, проверьте
полученные результаты.
6 см
Ζ2
\R\ = 4 см
|Д| = 6см
Рис. 9.20

470
Глава 9. Гауссова оптика
9.3. Предположим, что ход лучей считается фундаментальной
характеристикой свойств тонкой линзы, т.е. предположим, что
пересечение луча, проходящего через центр линзы, с лучом,
параллельным оси слева от линзы и проходящим через ее фокус справа,
определяет пересечение всех лучей от выбранного объекта.
(a) Используя это допущение, получите уравнение тонкой
линзы. Рассмотрите только тот случай, когда р, q и /
положительны.
(b) Используя это допущение, докажите, что тонкая линза
может быть описана матрицей 2 χ 2 и получите вид этой
матрицы.
9.4. Шарик радиуса 6 см (рис. 9.21) сделан из стекла с показателем
преломления η = 3/2. Для лучей, проходящих вблизи диаметра,
этот шар ведет себя как линейная толстая линза (толстая линза —
это цилиндрическая сердцевина, осью которой является диаметр
шара). Постройте матрицы для этой линзы между плоскостями
отсчета ζ ι и гг, между фокальными и главными плоскостями.
Покажите эти плоскости на рисунке.
/ =
1
'
12 см
/ =
I
'
чш
'
8 см
1
'
Ζ\
Ζ2
Рис. 9.21
Рис. 9.22
9.5. (а) Для системы из двух собирающих линз, изображенной на
рис. 9.22, постройте матрицу для движения луча между
ПЛОСКОСТЯМИ Ζι И Z2-
(Ь) Найдите положение фокальных плоскостей z[ и z'2,
используя уравнение тонкой линзы и матрицу этой оптической
системы. Постройте матрицу между двумя фокальными
плоскостями.

Задачи
471
(c) Найдите положение главных плоскостей #χ и Ич и
постройте соответствующую матрицу. Это легко сделать, учтя тот
факт, что фокусное расстояние / = 6 см и каждая
главная плоскость находится на расстоянии 6 см от
соответствующей фокальной плоскости. Обратите внимание, что обе
главные плоскости лежат между линзами, и в этом случае
Η ι находится справа от Ή.2 ·
(d) На рисунке покажите положение фокальных и главных
плоскостей этой системы.
(e) Пусть плоскость гз находится на расстоянии 12 см слева
от z\. Четырьмя способами найдите плоскость,
сопряженную этой: (1) перемножая матрицы, (2) дважды используя
уравнение тонкой линзы, (3) используя уравнение Ньютона
х\.Х2 = /2 и (4) рисуя ход лучей.
9.6. Оптическая система состоит из двух тонких линз с фокусными
расстояниями /ι и /2, расположенными на расстоянии t друг от
друга (рис. 9.23). Первая фокальная плоскость находится слева
от первой линзы на расстоянии ίχ; вторая фокальная плоскость
находится справа от второй линзы на расстоянии \ч- Докажите,
что фокусное расстояние / этой системы удовлетворяет
уравнению /2 — tf — lih = 0. Имея в виду, что все параметры ίχ, /г, /, /χ
и /г могут иметь любой знак, определите, какой из корней этого
квадратного уравнения имеет физический смысл.
ίχ>·4
<-к
Fi /x h
Рис. 9.23
9.7. Придумайте систему тонких линз, оптическая матрица которой
β °\ tv
имеет вид I _ _ I. (Указание: система состоит из нескольких
линз. Можно начать с построения системы, матрица которой
удовлетворяет уравнению М2 = I.)

472
Глава 9. Гауссова оптика
9.8. На рис. 9.24 изображена оптическая система. В плоскости z\
падающий луч имеет координаты I ) = ( о ) · Найдите
координаты луча, выходящего из плоскости ζ2·
ζι /=1 / = -1 /=1
Рис. 9.24
Z2
*1.
9 см
,Z2
\R\ = 6см
|Д| = 9см
Рис. 9.25
9.9. На рис. 9.25 изображена толстая линза, сделанная из стекла с
показателем преломления η = 3/2.
(а) Постройте матрицу, соответствующую движению луча
между плоскостями ζι и ζ-ι.
' Ч\
Pi
«2\_/1/2\
р2) \1/б)-
(Ь) Выясните, какой падающий луч
в плоскости Z2 с координатами
выходит из системы
9.10. На рис. 9.26 изображена собирающая линза с фокусным
расстоянием / = 10 см. Она сделана из стекла с показателем
преломления η = 1.4. Выпуклые поверхности линзы имеют одинаковый
радиус кривизны R.
(а) Вычислите радиус кривизны R, найдите зависимость
толщины линзы b от расстояния q от оси. (Указание: 6(2) = 0.)

Задачи
473
(b) Луч проходит через точку Л, потом по линии ACF.
Покажите, что время движения вдоль этой траектории
минимально по сравнению с любой траекторией, которая
проходит через линзу с другими значениями q.
(c) Покажите, что время движения луча вдоль траектории
АСВ максимально по сравнению со временем движения
по любой траектории, связывающей точки А и В.
(d) Напишите функцию W(qA, 9р) для плоскостей А и F.
Покажите, что уравнения Гамильтона дают правильный наклон
луча, заданного параметрами qA = 1 и qp = 0. Сделайте
то же самое для плоскостей А я В. Используйте функцию
W(qA,qe) Для определения траектории луча, проходящего
через А и В.
Рис. 9.26
9.11. Пусть vi = ( ] и vi = { _ I обозначают два луча, входящие
в произвольную гауссову оптическую систему. Симплектическое
скалярное произведение этих векторов определяется формулой
ω(νι,νι) = qipi - ξιΡι.
(a) Покажите, что это скалярное произведение сохраняется
при прохождении оптической системы, т.е. что o;(v2,V2) =
ω(νι,νι).
(b) Покажите, что ω(νι, vi) = 0, если Vi и νχ обозначают лучи,
пересекающиеся на оптической оси.

474
Глава 9. Гауссова оптика
(с) Допустим, что два луча проходят через одну точку qi в
плоскости отсчета z\ с углом ф\ между ними. Если эти лучи
пересекаются в сопряженной плоскости гг с углом фг между
ними, то чему равно расстояние от оси q{l (Пусть η = 1 в
ПЛОСКОСТЯХ Ζ\ И Ζ2.)

Глава 10
Векторные пространства
и линейные преобразования
В главе 10 мы возвращаемся назад и доказываем
основные свойства конечномерных пространств и их
линейных преобразований. Здесь, главным образом,
обобщаются результаты, полученные в первых
четырех главах для двумерного пространства. Излагается
новый алгоритм — редукция по строкам. Вводятся
два новых понятия: понятие сопряженного
пространства и факторпространства. (Их было сложно ввести
раньше.) Эти понятия будут играть решающую роль
в дальнейшем1.
Введение
Мы уже довольно подробно изучили двумерное пространство. Но
при этом рассматривались только две конкретные модели.
Векторное пространство V было либо множеством перемещений в
аффинной плоскости, либо это было пространство R2 —
множество упорядоченных пар вещественных чисел. Вводя координаты,
*В параграфе 10.9 авторы выходят за пределы линейной алгебры и
доказывают важную теорему о локальной структуре дифференцируемого
отображения. — Прим. ред.

476
Векторные пространства ...
мы могли отождествить любое двумерное пространство с
пространством R2, в котором линейное преобразование
представлялось матрицей 2x2.
Сейчас мы начнем изучение произвольного векторного
пространства в абстрактном виде с аксиоматической точки зрения.
Преимущество такого подхода состоит в том, что мы сможем
рассматривать векторные пространства, которые не определяются
ни через геометрические понятия, ни как множество наборов из
η вещественных чисел. Окажется, что такое векторное
пространство, содержащее только конечное число линейно независимых
элементов, может быть отождествлено с пространством Шп для
некоторого целого числа п, так что в конечном счете мы вернемся
к изучению пространства Жп и использованию матриц для
описания линейных преобразований. В последующем надо все время
иметь в виду известную двумерную геометрическую модель
векторного пространства, чтобы напоминать себе, что последующие
аксиомы и определения вполне разумны. Однако, мы специально
будем давать примеры векторных пространств без
геометрического содержания. Такие векторные пространства являются
частью естественного математического языка в различных
областях физики, особенно в электромагнитной теории и квантовой
механике.
10.1. Свойства векторных пространств
Начнем с повторения основных определений.
Векторное пространство V, иногда называемое линейным
пространством, состоит из элементов — векторов, для которых
справедливы ряд аксиом. Эти пространства будем обозначать
заглавными буквами, напрмер, V, W*, С\, а их элементы — строчными
буквами жирным шрифтом, например, v, W2, b1.
В векторном пространстве V вводится правило, согласно
которому любым двум элементам νχ и V2 ставится в соответствие
третий элемент ν, называемый их суммой и обозначаемый vi+V2-
Эта операция удовлетворяет тем же аксиомам, что и сложение
вещественных чисел:

10.1. Свойства векторных пространств 477
Коммутативный закон:
νι + ν2 = ν2 + νι. (10-1)
Ассоциативный закон:
(vi + v2) + v3 = vi + (v2 + v3)
Существование нуля: существует такой элемент 0, что
ν + 0 = ν для всех v. (10.3)
Существование противоположного: для любого ν
существует такой элемент —ν, что
_ν + ν = 0. (10.4)
В некоторых случаях сложение определяется прямо через
сложение вещественных чисел, поэтому сразу бывает ясно, что эти
аксиомы выполняются. Например, в пространстве R2 мы
определяем
Va2/ yh) \a2 + b2)'
Аналогично, можно рассматривать двумерное векторное
пространство всех функций, определенных на двухточечном
множестве {А, В}, где сложение определяется отдельно для каждой
точки, т. е. h = f + g — функция, обладающая свойствами
h(A) = f(A) + g(A),
h(S) = f(S)+g(S).
В качестве еще одного примера рассмотрим пространство всех
непрерывных функций на отрезке [0,1], где также сложение
определяется отдельно для каждой точки. Если f и g — элементы
этого пространства, то их суммой будет функция h, задаваемая
формулой h(x) = f(x) + g(x)· В этом случае важно отметить, что
для любых f и g сумма h будет также непрерывной функцией и
поэтому принадлежит векторному пространству.
Ясно, что во всех этих примерах нулевой элемент и
противоположный элемент существуют и единственны. Это верно для
(10.2)

478
Векторные пространства ...
любого векторного пространства, что легко доказывается, исходя
из приведенных аксиом. Читателю предоставляется возможность
сделать это самостоятельно.
В векторном пространстве должна быть определена еще одна
операция: умножение вектора на скаляр. В этой главе мы
всегда будем считать, что скаляр — вещественное число. Поэтому
векторное пространство будет вещественным векторным
пространством. Позднее рассмотрим комплексные векторные
пространства, в которых элементы могут умножаться на
комплексные числа. И в этом случае должны быть справедливы аксиомы
обычного умножения, а именно: если с\ и с2 — скаляры, а νχ и
V2 — векторы, то справедливы
Ассоциативный закон:
ci(c2v) = (cic2)v
Дистрибутивные законы:
(ci + c2)v = civ + c2v,
/ ч (10.6)
c(vi + v2) = cv\ + cv2.
Умножение на 1 дает тождество:
lv = ν для всех v. (10.7)
Поскольку аксиомы сложения и умножения на скаляр в
векторном пространстве точно такие же, как и в арифметике, то
в векторной алгебре сохраняются все арифметические свойства.
Они легко доказываются, исходя из аксиом. Ниже приводится
перечень этих свойств. Подумайте и постарайтесь доказать их, так
как в определениях они не содержатся.
(a) 0·ν = 0.
(b) с· 0 = 0.
(c) (-c)-v=-(c-v) = c-(-v).
(d) v + ν = 2ν, ν + ν + ν = 3ν, и т. д.
(e) Если α · ν = 0, то либо α = 0, либо ν = 0.
(f) - (ν + w) = -ν + (-w).
(10.5)

10.2. Дуальное пространство
479
10.2. Дуальное пространство
Для выбранного векторного пространства V можно рассмотреть
множество всех линейных функций из V в R. Сейчас мы покажем,
что они образуют векторное пространство, называемое дуальным
пространством, сопряженным к пространству V, и
обозначаемое V*. Элементы этого пространства будем обозначать
греческими буквами жирным шрифтом и договоримся писать у них
индексы сверху, в отличие от элементов пространства V. Таким
образом, vi, V2,... — элементы пространства V, а а1, а2,... —
элементы пространства V*. Действие элемента из V* на элемент
из V будем обозначать «[ν].
Сумму двух элементов пространства V* определим как для
функций, т. е. для любого ν € V положим (α1 + α2)[ν] = α1 [ν] +
α2[ν]. Поскольку сумма линейных функций — тоже линейная
функция, а1 + а2 является элементом пространства V*. Легко
видеть, что все аксиомы сложения (10.1)—(10.4) выполняются;
нулевым элементом V* будет нулевая функция, которая, конечно,
линейна. Аналогично определяется умножение на скаляр:
(с <*) Μ = c(a[v]).
Очевидно, что с а — линейная функция, и что для введенной
таким образом операции умножения на скаляр выполняются все
аксиомы умножения.
Приведем несколько очень разных примеров определения
элементов дуального пространства.
1. Пусть V — двумерное пространство R2. Элементы
этого пространства обозначены ν = I J. Тогда можно считать,
что элементами пространства V* будут вектор-строки.
Например, a = (a, b), причем α [ν] = (a, b) I J = ax + by.
2. Пусть V — пространство всех функций множества,
состоящего из двух элементов {А, В}. Тогда правило а : V —► R
приписывает каждому элементу f € V его значение на
элементе А, т.е. αΑ[ΐ] = ΐ(Α) будет элементом множества V*. В этом
случае общий вид элемента из V* можно записать в форме
a[f] = αϊ (Α) + М(В)

480
Векторные пространства ...
для произвольных α и Ь. В этом примере интересно то, что мы
идентифицировали А с а и В с ав. Выражение аА+ЪВ
бессмысленно, а выражение аа. + Ъав определяет элемент пространства
V*. Таким образом, мы получили процедуру, связывающую
векторное пространство с любым конечным множеством так, чтобы
все элементы множества стали векторами. Для этого надо взять
дуальное пространство к пространству функций на этом
множестве. Такая конструкция оказывается очень полезной в теории
электрических цепей.
3. Пусть V — пространство дифференцируемых функций f (ί)
на отрезке [0,1]. Тогда все выписанные ниже отображения будут
элементами пространства V*:
α : f .-► f (0),
β: f->f(0),
7: f ■-► / t(t)dt,
Jo
δ: f ■-► / if (i) dt,
Jo
«: f"f(i)+i·
10.3. Подпространства
Часто векторное пространство W является частью большего
векторного пространства V, причем процедуры сложения и
умножения на скаляр определены в них одинаково. Поскольку известно,
что V удовлетворяет всем аксиомам векторного пространства, то
нет необходимости проверять их для W- Чтобы показать, что
подпространство W является векторным пространством, достаточно
доказать, что W замкнуто по отношению к операциям сложения
и умножения, т.е. что сумма двух любых элементов wi, W2 € W,
равная wi + W2, является элементом W, и для произвольного
вещественного числа с и любого w € W элемент cw принадлежит
W. В частности, нулевой вектор должен быть элементом W.
На практике подпространство обычно определяется одним из
6)-С
if (i) dt.

10.3. Подпространства
481
двух методов: конкретизируется некоторое множество элементов
из V, либо множество элементов из V*.
Метод 1. Пусть wi,W2,...,wjt — векторы в пространстве V.
Тогда множество W всех линейных комбинаций вида
к
W = Σ C;W;
t=l
образует подпространство пространства V. (Конечно, это может
быть и все пространство V.)
Метод 2. Пусть а1, а2,..., ак — элементы V*. Тогда множество
W элементов ν € V, удовлетворяющих условиям
α1[ν] = 0,
α2 [ν] = 0,
afc[v]=0,
образует подпространство пространства V. Это доказывается
очень просто. Пусть wi и W2 — два вектора из множества W.
Тогда вследствие линейности функций а}, а2,... мы получаем
α1 [ν/1 + w2] = a'[wi] + аг[л\г2] =0, i = 1,2,... ,k,
так что wi + W2 € W. Точно так же, если w € W, то
a'[cw] = ca'[w] = 0,
следовательно, cw € W. Таким образом, мы показали, что
множество W замкнуто по отношению к операциям сложения и
умножения на скаляр, т. е. является подпространством. (Конечно, это
может быть {0} — нулевое подпространство, состоящее из
единственного элемента — нулевого вектора.)
Хорошо известный пример применения этих двух методов
дает построение плоскости, проходящей через начало координат в
пространстве R . Согласно методу 1, плоскость задается двумя

482
Векторные пространства ...
векторами, например,
(!) - (!) или G) - (1)·
Согласно методу 2, плоскость описывается линейным
уравнением, например,
2х - 2у + ζ = О,
которое соответствует a[w] = 0, где
α = (2,-2,1) и w= ly J .
Рассмотрим еще один пример: пространство V образовано
множеством полиномов, степень которых < 2. Элемент этого
множества имеет вид
/(*) = a + bt + ct2.
Согласно методу 1, в качестве одномерного подпространства W
можно рассматривать пространство всех полиномов, имеющих
вид умноженной на любую константу функции 1 — ί2.
Согласно методу 2, это же подпространство можно определить двумя
условиями
/(1) = 0 и /(-1) = 0,
или, более замаскированно, условиями
/'(0) = 0 и / f(t)dt = 0.
Jo
10.4. Размерность и базис
Чтобы двигаться дальше в изучении векторных пространств, нам
необходимы понятия линейной зависимости и линейной
независимости набора векторов. Говорят, что множество векторов

10.4. Размерность и базис
483
{vi, V2,..., ν*;} линейно зависимо, если существуют такие
вещественные числа λι, Аг,..., Ajt, не все равные нулю, что
Avi + λ2ν2 Η h AfcVfc = 0.
Если это равенство выполняется только для Αχ = А2 = · · · = Ajt =
О, то такое множество векторов линейно независимо.
Приведем несколько примеров, иллюстрирующих эти важные
понятия.
1. Пусть V — пространство R3. Рассмотрим
Векторы, образующие набор {vi,V2,V3}, линейно зависимы,
потому что
С другой стороны, набор векторов {νχ,ν2} линейно независим,
потому что
Αι I 1 1 + А2 I 2 I = Ι Αι + 2А2
Очевидно, что результирующий вектор равен нулю, только если
Αι = 0 и А2 = 0.
2. Пусть V — пространство функций на отрезке [0,2π].
Рассмотрим
vi = cos2 ί, ν2 = sin2 i, V3 = cos 2ί.
Этот набор линейно зависимый, потому что νχ — v2 — V3 = 0.
3. Пусть V — пространство функций на множестве {А, В}.
Рассмотрим
fl
h
h
W) = 1, h{B) = 2,
f2(A) = 2, f2(B) = -3,
/3(Л) = -3, /з(Я) = 1.

484
Векторные пространства ...
Функции этого набора линейно зависимы, потому что fi + f2 + f3 =
О (т.е. мы получили нулевую функцию).
4. Пусть V — пространство полиномов степени < 2.
Рассмотрим следующие элементы пространства V*:
α : f -+ J if (i) dt,
β: f-*f'(0).
Написав f(i) = A + Bt + Ct2, мы получим
α
[f] = J\m
1 Λ
+ Bt2 + Ct3) dt = -^-B
/3[f] = B.
Следовательно, Ι α ——β J [f] = 0, и набор векторов {ex, β}
линейно зависим.
Из приведенных примеров, вероятно, стало понятным, что
существуют ситуации, когда не очевидно, является ли некоторый
набор векторов линейно зависимым или нет. Поэтому мы должны
разработать процедуру исследования этого вопроса.
Мы говорим, что пространство V натянуто на множество
векторов {yi,V2,..., vjt}, если V состоит из векторов, которые
можно записать как линейную комбинацию Σ^=ιμίνί· (Набор
векторов {vi, V2,..., ν*;} может быть линейно зависимым, но
тогда коэффициенты μι, μ2,..., μ& определены неоднозначно.)
Рассмотрим следующие примеры.
1. Пусть V — пространство R3. Очевидно, что набор векторов
порождает пространство R3, потому что любой элемент
μι

10.4. Размерность и базис
485
этого пространства может быть записан в виде
= μι | 0 I + μ2 1 1 + μ3 ί 0
Менее очевидно, что набор векторов
тоже порождает пространство R3, а вот набор
пространство К не порождает.
2. Пусть V — пространство функций f (ί) на интервале [0, оо),
удовлетворяющих дифференциальному уравнению
f" + 3f' + 2f = 0.
Векторы e-i и e~2t порождают пространство V, потому что общее
решение уравнения имеет вид
f (*) = Ае~г + Be~2t.
3. Пусть V — пространство функций вида f(i) = А + Bt3.
Тогда векторы
a: f-»f(0),
β: f-» i tf(t)dt
порождают дуальное пространство V*. В самом деле,
<*[f] = A,
β[ΐ] = f{At
+ Bt4)dt= -В.

486
Векторные пространства ...
Однако любой элемент 7 € V* должен иметь вид 7[f] = οΆ + ЬВ,
5
где α и b — некоторые постоянные. Таким образом, 7 = асх + -Ь/3,
Δι
а и β определяют пространство V*.
Пусть vi, V2,..., ν„ — конечный линейно независимый набор
векторов, порождающих векторное пространство V. Число
векторов η называется размерностью пространства V. Чтобы
установить, что размерность определяется однозначно, т. е. что все
такие наборы для данного пространства содержат одинаковое
количество элементов, мы должны доказать следующую теорему.
Теорема. Пусть набор векторов vi, V2,..., vjt порождает
векторное пространство V. Тогда любой набор к + 1 векторов
в этом пространстве V линейно зависим.
Теорему будем доказывать по индукции: сначала проверим
ее для к = 1, потом покажем, что если теорема верна для
пространства, натянутого на к — 1 вектор, то она справедлива и для
пространства, натянутого на к векторов.
Итак, пусть к = 1. Теорема в этом случае утверждает, что
если V натянуто на один вектор ν, то любые два вектора в этом
пространстве V линейно зависимы. Действительно, рассмотрим
два таких вектора Wi и W2. Так как ν порождает пространство V,
то существуют такие вещественные числа μι и μ2, что wi = μι ν
и W2 = //2V. Тогда очевидно, что
M2Wi - Miw2 = M2Miv - μιμ2ν = 0,
откуда ел едут линейная зависимость векторов wi и W2.2
Теперь предположим, что теорема верна для любого
набора к векторов в пространстве, натянутом на к — 1 вектор.
Рассмотрим набор к + 1 векторов {wi,..., w^+i} в пространстве,
определенном векторами νι,.,.,ν*. Мы можем написать wi =
αηνι + ai2V2 + ■ ■ · + aifcVfc, потому что векторы {ν^}
порождают пространство V. Если wi = 0, то rwi = 0, где г φ 0, дает
нетривиальную связь между векторами w,, и тогда все
доказано. Поэтому предположим, что wi φ 0. В этом случае молено
2Определение линейной зависимости векторов {wi, W2} требует, чтобы по
крайней мере одно из чисел μι, μ2 не равнялось нулю. На случае μι = μ2 = 0
авторы не останавливаются. Молено порекомендовать читателю рассмотреть
его в качестве самостоятельного (очень простого) упражнения. — Прим. ред.

10.4. Размерность и базис
487
упорядочить векторы vi, V2,..., Vfc так, что ац φ 0. Тогда
1 , «12 а*\к
—wi = vi Л v2 Л 1 vfc.
ац ац ац
Далее, пусть
W2 = 021V1 + U22V2 Л + a2fcVfc.
Можно написать равенство
«21 / а21«12\ , , / a21«lfc\
W2 Wi = θ22 V2 + ■ ■ · + I a2Jfc Vfc.
ац у оц / V «и /
Qq-I
Аналогично, можно выразить W3 wi и т. д. через к — 1 вектор
ац
из набора v2,..., Vfc. Но мы предположили, что теорема верна для
к — 1 векторов. Следовательно, набор /с векторов
Г «21 «31 a(fc+l)l \
J W2 Wi, W3 Wi, . . . , Wfc+i i -Wi >
L ац ац ац J
линейно зависим. Это значит, что существуют такие константы
λ2,..., Ajt+i, не все равные нулю, что
λ2 ( w2 —wi ) + λ3 ( w3 —wi J + · ■ ·
V an J V an /
_l \ ( a{k+l)l \ _
+ Afc+i Wfc+l i LWi = 0.
V an /
Отсюда вытекает, что набор векторов {wi, w2,..., Wfc+i} линейно
зависим, что и требовалось доказать.
Теперь мы можем легко показать, что размерность
векторного пространства определена однозначно. Предположим, что у нас
есть набор линейно независимых векторов {vi,..., Vfc}, на
который натянуто пространство V. Кроме того, есть еще один набор
{wi,..., wn}, на который тоже натянуто это пространство. Из
только что доказанной теоремы следует, что η < к. В противном
случае векторы {wi,..., wn} будут линейно зависимы. С другой
стороны, по той же теореме, к < п. Иначе векторы {vi,..., Vfc}

488
Векторные пространства ...
будут линейно зависимы. Следовательно, к = п, и любой
конечный набор линейно независимых векторов, определяющих
пространство V, содержит одинаковое число элементов. Это число и
называется размерностью пространства V.
На самом деле в векторном пространстве V, имеющем
размерность п, любой набор η линейно независимых векторов
порождает это пространство. Действительно, пусть {vi,..., νη} —
набор линейно независимых векторов в пространстве V, и пусть
w — произвольный вектор, не равный нулю. Множество векторов
{w,vi,..., νη}, состоящее их η + 1 элементов, должно быть
линейно зависимым. Следовательно, существуют такие постоянные
λ0, λι,.. .,λη, что
A0w + λινι Η h ληνη = 0.
В этом выражении константа λο не может быть равна нулю,
так как иначе векторы {νχ,..., νη} будут линейно зависимы, что
противоречит начальному предположению. Поэтому можно
написать
w = —— (λινι + ■ · · + ληνη).
Таким образом, произвольный ненулевой вектор w выражен как
линейная комбинация векторов {vi,..., νη}, порождающих
пространство.
Линейно независимый набор векторов {νχ,..., νη},
порождающий векторное пространство V, записанный в определенном
порядке, называется базисом пространства V. Таким образом,
наборы {vi,V2,V3,... ,ν„} и {v2,vi,V3,... ,νη} являются разными
базисами.
Рассмотрим векторы wi,..., wjt (k < η) в n-мерном
векторном пространстве V. Мы всегда можем найти вектор w^+i,
который не принадлежит подпространству {wi,..., w^}. Продолжая
этот процесс η — к раз, мы получим базис в пространстве V,
который включает векторы wi,...,wjfc. В частности, для данного
векторного пространства V с размерностью п, содержащего
подпространство W с размерностью /с, мы всегда можем построить
такой базис для V, что его первые к векторов будут базисом
подпространства W. Эта процедура называется расширением
базиса подпространства W до базиса пространства V.

10.4. Размерность и базис
489
Пусть в пространстве V выбран базис {βχ,... ,еп}. Тогда
любой элемент этого пространства может быть единственным
образом записан как линейная комбинация базисных векторов:
V = Χιβι + £2^2 Η + Χη&η·
Числа χι,... ,хп называются компонентами вектора ν в данном
базисе. Чтобы показать единственность такого разложения,
допустим, что ν может быть записан по-другому:
ν = yiei + у2е2 -\ h упеп-
Вычтем из первого равенства второе и получим
О = (χι - yi)ei + (х2 - ί/2)β2 + ■■■ + (хп- Уп)еп-
Поскольку базисные векторы линейно независимы, то
Х1-У1=Х2-У2 = ---=Хп-Уп = 0,
что и доказывает единственность компонент вектора v.
Из сказанного видно, что с помощью базиса в пространстве V
можно определить изоморфизм L пространства V с R", положив
Lvi
/Л
о
о
Lv2 =
/0\
1
о
и т.д.
W W
Обратно, если L — такой изоморфизм, то набор векторов
vi = ΖΓ1
/Л
о
о
W
, v2 = L-x
/0\
1
о
и т.д.
является базисом пространства V. Таким образом, мы можем
отождествить базис {νχ,..., νη} с соответствующим
изоморфизмом L точно так же, как мы делали в главе 1 в двумерном случае.

490
Векторные пространства ...
Пусть L : V —► R™ и V : V —► W1 — два базиса в одном
n-мерном пространстве V.
Тогда В = V о L~l — линейный изоморфизм R™ —> Шп, т.е.
обратимая матрица η х п- Эта матрица называется матрицей
замены базиса.
Пусть V — векторное пространство размерности к, a W —
векторное пространство размерности I, и пусть Τ : V —> W —
линейное преобразование. Предположим, что мы выбрали базисы
в пространствах V и W. Тогда у нас есть изоморфизмы L : V —►
Шк и Μ : W —► R', и мы можем определить отображение
MTL-1 : Шк -» R'.
Выражение MTL~l можно рассматривать как матрицу, у
которой / строк и к столбцов. Мы называем MTL~X матрицей
отображения Τ относительно базисов L и Μ и обозначаем ее Matl,m{T),
т. е.
MatLM{T) = MTL~l.
Эта ситуация может быть изображена на диаграмме
τ
Ma.tLiM{T)
Если мы выберем другие базисы: V = PL в пространстве V
и М' = QM в пространстве W, то
L'~1 = L~1P-1, так что M'TL''1 = QMTL~lp-1,
ИЛИ
Mati/iAf/(r) = Q(MatL,Af (T))P-\
т. е. получена формула для замены базисов, из которой видно, как
матричное представление линейного преобразования изменяется
при такой замене.

10.5. Дуальный базис
491
10.5. Дуальный базис
Построив базис векторного пространства V, мы можем
приступить к построению дуального базиса для дуального пространства
V*. Пусть {βι, β2,..., еп} — базис в пространстве V. Тогда любой
вектор ν € V может быть записан единственным образом
V = xid + £2^2 "Ι + Хп^п-
Пусть α — элемент дуального пространства V*. Поскольку а. —
линейная функция в пространстве V, мы имеем
α [ν] = χια[βι] + Χ2«[β2] Η 1- Χη«[βη]·
Это значит, что α полностью определяется своими значениями
на базисных векторах {βι,β2, · · · , еп}. Введем в пространстве V*
систему векторов е1,..., еп, задаваемых равенствами
и , / 1, i = j,
ег[еЛ = <
Чтобы доказать линейную независимость этой системы,
рассмотрим Σ ^|€г · Применив эту линейную функцию к е^, получаем
η
i=l
Таким образом, если ^ А|€г является нулевым элементом в V*, то
Xj = 0 для всех j. Это доказывает, что набор векторов {е1,..., еп}
линейно независим.
Для любого элемента α € V* можно написать
α = οφιΐε1 + а[е2]е2 + ■ ■ ■ + а[еп]еп.
Очевидно, что обе части этого равенства имеют одинаковое
значение для любого базисного вектора е^, т. е. являются одним и тем
же элементом дуального пространства V*. Это доказывает, что
пространство V* натянуто на векторы е1,..., еп, которые, кроме
того, линейно независимы. Из этого следует, что пространство V*

492
Векторные пространства ...
имеет ту же размерность п, и набор векторов {е1,... ,еп}
является базисом в пространстве V*.
Этот базис можно использовать, чтобы идентифицировать V
с пространством Шп*. Если мы разложим элемент α € V* по
дуальному базису
*
α
λχε1 + λ2ε2 + · ■ ■ + Хпеп,
то обнаружим, что удобно рассматривать элементы Ш.п* как
векторы-строки. Тогда а. отождествляется с вектором-строкой
(λι, λ2, · · ·, λη). Преимущество такого обозначения в том, что
действие α на ν описывается обычными правилами умножения
матриц
«Μ = (λΐ,λ2,...,λη)
Х2
\Хп/
λιΧχ + λ2Χ2 + ■ · ■ + \пХп-
Важно не забывать, что эта техника применима только в случае,
когда базис, определяющий соответствие между V* и R"*,
является дуальным к базису, определяющему соответствие между V
иЕ".
Предположим, что у нас есть n-мерное пространство V и
fc-мерное подпространство W■ В пространстве V мы можем
выбрать такой базис, что его первые к векторов образуют базис
подпространства W:
{vi,...,vfc;vfc+1,...,vn}.
После этого построим дуальный базис
{α1>...>α*;α*+1>-·.,αη},
так что
αΜν,-l =
Подпространство в V* размерности η — к, натянутое на
векторы {ак+1,..., а71}, называется аннулирующим пространством

10.6. Факторпространство
493
для W и обозначается W^. Если α € W и w € W, то a[w] = 0,
т. е. W"1- «аннулирует» подпространство W. Отсюда и
происхождение этого термина. То, что мы раньше называли методом 2
для описания подпространства, по существу, было описанием ан-
нулирущего пространства. Например, вектор (а, Ь, с) определяет
одномерное подпространство W1- дуального пространства R3*.
Подпространство W пространства R3, аннулированное W^,
будет двумерным: это плоскость ах + by + cz = 0. Если мы выберем
два независимых элемента дуального пространства R3*,
например, (ai,bi,ci) и (а2,Ь2;С2), Т0ГДа подпространство R3,
аннулированное ими, будет одномерным: это будет прямая, задаваемая
системой уравнений
αχχ + b\y + c\z = 0,
CL2X + ЪъУ + C2Z = 0.
Заметим, что аннулирующее пространство W1- подпространства
W С V не зависит от конкретного выбора базиса пространства V.
Мы вводили базис только для того, чтобы было удобно вычислить
размерность W^.
Пока нам недостает систематической процедуры вычисления
размерности подпространства, натянутого на определенные
элементы векторного пространства, или размерности
подпространства, аннулированного конкретными элементами дуального
векторного пространства. Эту процедуру, которая называется
редукцией по строкам, мы опишем позднее.
10.6. Факторпространство
Продолжим рассмотрение n-мерного векторного пространства V,
содержащего подпространство W с размерностью к.
Кажется естественным, что должно существовать
подпространство с размерностью η — к, которое в некотором смысле
будет «разницей» между V и W. Такое подпространство
называется факторпространством и обозначается V/W. Однако, его
элементы не будут элементами пространства V. Они являются
множествами элементов пространства V и называются классами
эквивалентности. Прежде чем дать определение этих классов,

494
Векторные пространства ...
нам следует сначала увидеть, почему что-то более простое не
будет достаточным.
В качестве конкретного примера пространства V с
подпространством W рассмотрим плоскость R2 и прямую W на этой
плоскости, как это изображено на рис. 10.1. «Разностью» между
V и W могло бы быть множество элементов V, не входящих в
W. Но ведь они порождают всю плоскость. На рис. 10.1 видно,
что векторы vi и V2, не лежащие на прямой W, порождают всю
плоскость.
Рис. 10.1
Можно попробовать поступить по-другому — взять к
базисных векторов подпространства W и расширить это множество до
базиса пространства V. Тогда у нас добавится η — к базисных
векторов, не входящих в W. Возникает подпространство нужной
размерности, но оно зависит от выбора базисных векторов и
поэтому «плохо» определеноГНапример, на рис. 10.1 мы взяли w в
качестве первого базисного вектора. После этого в качестве
второго базисного вектора можно брать ν χ, V2 или V3. При этом мы
каждый раз будем получать новое пространство. Если бы в
пространстве V было определено скалярное произведение, то можно
было бы выбрать подпространство, ортогональное к W. Но у нас
нет скалярного произведения, поэтому и нет возможности
определить процедуру предпочтительного получения второго базисного
элемента.

10.6. Факторпространство
495
Работающая конструкция дает определение классов
эквивалентности (по модулю W) как множеств, каждое из которых
состоит из векторов в пространстве V, разность между которыми
лежит в W. Класс эквивалентности вектора ν будем обозначать
черточкой над вектором. Таким сбразом, ν обозначает
множество векторов вида ν + w, где ν — заданный элемент множества V,
aw — произвольный элемент W.
W
^з/ о/ /vi
/ V3 /
/ \ /v2
начало γ^ , /
координата vi У
Рис. 10.2
Например, на рис. 10.2 видно, что 0 (класс эквивалентности
нулевого вектора) есть подпространство W, т. е. прямая,
проходящая через начало координат. Векторы νχ и V2, отличающиеся
на элемент подпространства W, принадлежат одному и тому же
классу эквивалентности, который можно обозначать ν ι или V2-
Этот класс эквивалентности является прямой, не проходящей
через начало координат. Класс эквивалентности V3 будет другой
прямой, которая тоже не проходит через начало координат. В
этом случае классы эквивалентности составляют семейство
прямых, параллельных W. В более общем случае мы можем считать
подпространство W fc-мерной гиперплоскостью3, проходящей
через начало координат n-мерного пространства V. Тогда классами
эквивалентности по модулю W будет семейство гиперплоскостей,
параллельных ей.
3В русскоязычной математической литературе термин «гиперплоскость»
обычно относят только к случаю к = η — 1. — Прим. ред.

496
Векторные пространства ...
Чтобы ввести операцию сложения классов эквивалентности,
сначала рассмотрим арифметику целых чисел по модулю 4, с
которой читатель, возможно, уже знаком. В этом случае есть
четыре класса эквивалентности:
О ={0,4,-4, 8,-8,... } = {4п},
ϊ = {1,5,-3, 9,-7,...} = {4п + 1},
2 = {2,6,-2,10,-6,... } = {4п + 2},
3 = {3,7, -1,11, -5,... } = {4п + 3}.
Чтобы сложить два класса эквивалентности, выбираем любое
целое число из каждого класса, складываем их и получаем класс
эквивалентности суммы. Например, чтобы сложить 2 и 3,
выбираем число 6 из 2 и число 3 из 3. Складываем эти числа 6+3 = 9 и
видим, что сумма принадлежит классу эквивалентности 1. Таким
образом, 2 + 3 = 1. Любой другой выбор, скажем, —2+ (—1) = —3,
дает тот же результат. Значит, процедура сложения классов
эквивалентности определена корректно.
Сложение классов эквивалентности векторов по модулю под-
пространства W определяется аналогично. По определению, νχ +
V2 = (νχ + V2), т. е. складываем любые два вектора из классов νχ
и V2 и находим класс, к которому принадлежит сумма.
Допустим, что мы взяли νχ + wi из класса νχ и V2 + W2 из класса
V2, где wi и W2 — произвольные элементы подпространства W.
Тогда сумма νχ + V2 есть класс эквивалентности, содержащий
(νχ + V2) + (wi + W2), т. е. класс (ν χ + V2) не зависит от выбора
Wi И W2-
Процедура сложения изображена геометрически на рис. 10.3.
Сумма νϊ + V2 = V3 независимо от того, какую пару векторов
— νχ и V2 или ui и U2 — мы брали в качестве представителей
классов νϊ и V2-
Аналогично определим операцию умножения класса
эквивалентности на скаляр: cv\ = (ενχ), т.е. умножая произвольный
элемент из класса νχ на с, мы получаем класс эквивалентности
произведения. Результат единственный, потому что W является
подпространством.

10.6. Факторпространство
497
W V! V2 V3 = V! + V2
Рис. 10.3
Нетрудно проверить, что классы эквивалентности
пространства V по модулю W образуют векторное пространство. Это
пространство и называется факторпространством V/W.
Чтобы построить для него базис, возьмем базис
подпространства W и расширим его до базиса во всем пространстве V. Итак,
пусть базисными элементами V являются векторы wi, W2,.. ■, w^
(элементы W) и νχ, V2,..., ~vn-k (не являются элементами W).
Утверждается, что классы эквивалентности vi, V2,..., νη_£
образуют базис для V/W. Чтобы это доказать, мы должны
показать, что они линейно независимы и на них натянуто
пространство V/W.
Сначала рассмотрим проблему линейной независимости.
Допустим, что vi, V2,..., νη_£ линейно зависимы. Тогда
существуют такие константы λι, Аг,. · ·, Ап_^, что выполняется равенство
Aivi + λ2ν2 + ■ ■ ■ + An_fcvn_fc = 0.
Значит,
Aivi + λ2ν2 + · ■ ■ + \n-kVn-k € W,
что противоречит нашему предположению о линейной
независимости векторов {wi,W2,...,Wjfc;Vl,V2,...,Vil_jfc}.
Любой вектор ν € V можно записать как сумму векторов
ν = xivi + x2V2 Η + хп-кУп-к + элемент из W,

498
Векторные пространства ...
откуда следует, что
V = Ж!VI + X2V2 + ■ · · + Xn-kVn_k.
Это доказывает, что классы эквивалентности v"i, v~2,..., vn-k
порождают пространство V/W. Таким образом, v"i, V2,.. ■ , vn_fc
образуют базис V/W и
dim (V/W) = dim V - dim W.
(Здесь и в дальнейшем dim обозначает размерность
пространства.)
А теперь приведем несколько примеров факторпространств.
Пример 1. Пусть пространство V — это R3, а одномерное под-
/1\ /1\ /О'
пространство W натянуто на вектор 1 I . Векторы [11,11
\о/ \о/ \о.
и [ О I порождают пространство R3. Поэтому векторы [ 1
1/ \0
и | 0 | могут быть базисными векторами факторпространства
V1/
V/W. Например,
= 3
Следовательно,
Класс эквивалентности любого вектора в пространстве R3 можно
выразить как линейную комбинацию векторов 1 I и I О I .
\0/ \1/

10.6. Факторпространство
499
Заметим, между прочим, что векторы 0 I и 1 I не мо
W W
гут быть базисом V/W. Сумма этих векторов является
элементом W, поэтому они не будут линейно независимыми элементами
факторпространства V/W:
(НИ!)·поэтому 6Н)=*
Пример 2. Пусть V — пространство полиномов f (ί) степени < 2,
и пусть двумерное подпространство W образовано полиномами,
удовлетворяющими условию f(l) = 0. Базисными полиномами
W будут fi = 1 — t и Ϊ2 = 1 — ί2. Базисом факторпространства
V/W будет класс эквивалентности 1. В этом случае общий вид
элемента пространства V — это
f (*) = А + Bt + Ct2,
или, что то же самое,
f (ί) = A + B + C-B(l-t)-C(l- ί2).
Это означает, что
Щ=(А + В + С)1.
Если элементами факторпространства V/W считать плоскости,
то подпространство W — это плоскость f (1) = 0, и класс
эквивалентности любой функции f(i) определяется значением f(l).
А теперь воспользуемся понятиями дуального пространства и
факторпространства и получим очень важный результат.
Раньше мы обнаружили, что если W является подпространством V,
то аннулирующее пространство W1- является подпространством
дуального пространства V*. Предположим, что α — элемент W^,
и рассмотрим его действие на класс эквивалентности v.
Поскольку a[w] =0 для всех w € W и α линейно, то
α[ν + w] = α [ν].

500
Векторные пространства ...
Это значит, что α имеет одинаковое значение для любого
элемента класса эквивалентности и поэтому может рассматриваться
как линейная функция в пространстве классов эквивалентности.
И обратное утверждение: любая линейная функция в V/W
может считаться линейной функцией в пространстве V. Определим
/3[ν] формулой
/3[ν]=/3[ν].
Тогда /3[w] = /3[0] = 0. Следовательно, /3 является элементом
W^~. Поэтому W может быть отождествлено с дуальным
пространством факторпространства V/W. Вспомним, что W1-
и V/W имеют одинаковую размерность: dim V — dim W.
Аналогично можно рассмотреть факторпространство V*/W^,
элементами которого являются классы эквивалентности /3,
элементы которых, в свою очередь, отличаются на элементы W^,
т.е.
/3 = {/3 + а : α € WL].
Определим действие /3 на вектор w € W согласно формуле
/3[w] = /3[w]. Это вполне законно, потому что для любого а € W1-
мы имеем (/3 + a)[w] = /3[w]. Если /3[w] =0 для всех w € W, то
/3[w] = 0 для всех w € W. А это значит, что /3 € W1- или /3 = 0.
Следовательно, /3 полностью определено линейной функцией,
заданной в подпространстве W ■
Обратное утверждение: каждый элемент 7 € W* имеет вид
7 = β для некоторого β € V*. Действительно, выберем
базис wi,..., wjt в подпространстве W и расширим его до базиса
wi,... , wjt, vi,..., vn_fc пространства V.
Пусть /3 — произвольная линейная функция,
удовлетворяющая условию /3[wi] = 7[wi] для всех г, и пусть /3 принимает
любые значения для всех Vj. Тогда /3 = 7- Поэтому мы можем
пространство этих классов эквивалентности, т. е. фактор-
пространство V*/W-L, отождествить с дуальным
пространством W*.
Этот результат можно изобразить на следующей схеме:
V*/WL «- V* <- W±,
W-^V -»V/W.

10.6. Факторпространство
501
Здесь пространства, дуальные друг другу, расположены одно над
другим: V и V* (размерность n), W и V*/W1- (размерность к),
V/W и W1- (размерность η — к).
На этой теореме основывается много результатов линейной
алгебры и ее применений в теории электрических цепей, что,
безусловно, заслуживает более тщательного рассмотрения.
Приведем один пример. Пусть пространство V образовано
полиномами f(i) степени < 2, а двумерное подпространство W —
четными полиномами. Тогда факторпространство V/W будет
одномерным, базисный элемент, обозначаемый h0, — это класс
эквивалентности функции f(i) = t. Таким образом, если f(i) =
A + Bt + Ct2, то? = Bh0.
В этом случае аннулирующее пространство W1- тоже
одномерно. Базисный элемент может быть выбран в виде линейного
оператора
α : f ^ / if (i) dt.
Поскольку
/ t(A + Bt + Ct2) dt = \b,
то а на самом деле аннулирует любой четный полином и
приписывает значение 2/3 полиному f(i) = ί, который определяет
базисный элемент ho факторпространства V/W- Таким образом,
За/2 — это базисный элемент, дуальный к ho-
Мы можем расширить а до полного базиса V*, добавив
базисные элементы
01 : f-f(0),
β2: f ~ |f(0),
действие которых состоит в выборе коэффициентов А и С
соответственно, т. е.
βλ[Α + Bt + Ct2] = А,
fi2[A + Bt + Ct2]=C.

502
Векторные пространства ...
Классы эквивалентности βλ и /32, образующие базис V*/W^,
также образуют базис W*, поскольку они являются дуальными
базисными элементами для базисных элементов 1 и ί2
подпространства четных полиномов пространства W ■
10.7. Линейные отображения
Рассмотрим линейное преобразование
А : V -» W,
где V — векторное пространство размерности п, &W —
пространство размерности к. Как мы уже знаем, линейность отображения
Л означает, что A(c\Vi + C2V2) — c\Av\ + C2Av2.
С линейным отображением А : V —► W связаны два
подпространства: ядро А и образ А.
Ядро А, в дальнейшем обозначаемое Кег А, — это по
определению множество всех таких векторов ν € V, что Αν = 0.
Проверим, что Кег Л является подпространством пространства V.
Заметим, что если vi и v2 принадлежат ядру А, то A{c\V\ +C2V2) =
ciAvi + C2AV2 = 0, откуда следует, что c\V\ + C2V2 € Кег Л. Это
и значит, что ядро А является подпространством.
Образ А, в дальнейшем обозначаемый Im A, — это множество
всех векторов w € W, которые имеют вид Αν для каких-либо
ν € V. Если wi и W2 — два вектора из множества 1тЛ, то
wi = Av\ и W2 = Av2 для некоторых vi, V2 € V. Поскольку
отображение А линейно, мы имеем
А(С\\\ + C2V2) = C\Avi + C2AV2 = C1W1 + C2W2,
откуда видно, что элемент ciwi + C2W2 является элементом
множества Im А. Это доказывает, что А является подпространством
пространства W.
Размерности пространств Кег Л и Im Л, как мы сейчас
докажем, связаны соотношением
dim(Im Л) + dim(Ker Л) = dim V.
(10.8)

10.7. Линейные отображения
503
Размерность образа А называется рангом отображения Л, а
размерность ядра А — дефектом отображения А. Соотношение
(10.8) называется теоремой о ранге и дефекте. Читатель уже
знаком с этой теоремой в частном случае преобразований плоскости
в себя. Вспомним, что в этом случае было три возможности для
А : R2 -» R2:
1. Образом преобразования А является вся плоскость и
отсутствует ненулевой вектор, который преобразуется в нулевой
(ранг равен 2, дефект равен 0);
2. А преобразует плоскость в прямую, а прямую — в начало
координат (ранг равен 1, дефект равен 1);
3. А переводит всю плоскость в начало координат (ранг равен
0, дефект равен 2).
Чтобы доказать эту теорему в общем случае в пространстве V,
выберем удобный базис. Допустим, что dim V = η и dim(Ker A) =
к. Выберем базис ui, U2,..., щ для Кег А и расширим его до
базиса всего пространства V, выбрав г = п — к векторов νχ, ν2, ■.., vr.
Для удобства упорядочим этот базис в виде:
{vi,v2,...,vr;ui,u2,...,ujfc},
где первые г векторов не принадлежат подпространству Кег Л.
Теперь надо показать, что г векторов вида {.Ανι,.Αν2,..., Avr}
являются базисом Im A
Сначала покажем, что векторы {Ανχ, Λν2, ■ ■., ΑνΓ} линейно
независимы. Предположим противное:
г
Σ KAwi = 0.
i=l
Преобразование А линейно, что означает
^(X>iVi]=0.

504
Векторные пространства ...
Отсюда сразу же следует, что Σ[=1 ^iVj € Ker А Однако,
векторы {vi} вместе с векторами {щ} образуют базис V. Поэтому из
равенства
г
/J \vi = u> гДе ч € Кег Л,
г=1
следует, что все λ| равны нулю, и вектора {Ανι,Αν2, ■ · · , ΑνΓ}
линейно независимы.
Теперь надо показать, что вектора {Av\, Av2,..., Avr}
порождают ImA Для этого рассмотрим произвольный вектор w €
ImA Существует такой вектор ν € V, для которого w = Αν.
Тогда мы можем написать
г к
i=l 3=1
Однако, все базисные вектора Uj принадлежат множеству Кег Л,
значит,
(г к \ г
ΣaiVi+Σ bJuJ = Σ α^Αν*)>
i=l j=l / i=l
т. е. любой вектор w можем быть записан в виде линейной
комбинации векторов {^4νι, ^4ν2, · ■., Avr}.
Отсюда мы делаем вывод, что г векторов {Avi, Av2,..., Avr}
образуют базис ImA Кроме того, dim(Imi4) — г = η — к, где
dim V = η и dim(Ker A) = к. Таким образом, dim(Im A) = dim V —
dim(Ker.A), что равносильно формуле (10.8).
Теорема о ранге и дефекте доказывает еще один факт об ан-
нуляторе подпространства, о котором читатель, возможно, уже
догадался. Предположим, что {а1, а2,... , а.п} — элементы
пространства V*. Определим линейное преобразование
А : V -» R"
формулой
/α1[ν]\
α2 [ν]
Aw =

10.7. Линейные отображения
505
На векторы {сх1, сх2,..., схп} натянуто подпространство U1- С
V*, которое аннулирует подпространство Кег А Доказанная
нами теорема говорит, что dim(Im.A) = dim V — dim(Ker А). Но в
параграфе 10.4 мы показали, что
dimtt/-1-) = dim V - dim(Ker A),
откуда следует, что
dim(Imi4) = dim [/"К
На языке матриц каждый элемент схг является строкой
матрицы и dimf/-1- есть размерность подпространства V*, натянутого
на строки матрицы. В тоже время dim(Imi4) есть размерность
подпространства W, натянутого на столбцы матрицы. Обе эти
размерности равны (обозначим их г), и число г называется
рангом матрицы.
Представление строк матрицы как элементов дуального
пространства V* особенно полезно для решения системы линейных
уравнений. Например, система уравнений
χ + у + ζ = 0,
χ + 2у + Sz = 0,
2х + Зу + 4г = 0
может быть записана в форме Αν = 0, где
41 ii)· 4)-
Здесь в строках матрицы А записаны коэффициенты каждого
уравнения. Поскольку третье уравнение является суммой первых
двух, то три строки определяют только двумерное
подпространство пространства V*, ранг матрицы А равен 2, и ее дефект
(размерность ядра) равен 3 — 2 = 1. Поэтому Кег Л — одномерное
подпространство, и существует одномерное подпространство
решений уравнения Л ν = 0.

506
Векторные пространства ...
10.8. Редукция по строкам
Рассмотрим линейное отображение
Τ : V -» W,
где V — векторное пространство размерности т, a W —
пространство размерности п. Отображение Τ имеет ранг г. Мы уже
видели, что при выборе базисов для Ки1У отображение Τ
представляется в виде матрицы. В качестве базиса пространства V
выберем векторы
{vi,v2,...,vr;vr+i,...,vm},
где последние т — г векторов являются базисом Кег Т. Тогда
Tvr+1 = Tvr+2 = ... = Tvm = 0.
Следовательно, векторы Tvi, TV2,... ,ΤνΓ являются базисом
ImT. Теперь выберем векторы
wi = 7Vi, w2 = Tv2, ..., wr = Tvr
в качестве базиса ImT и расширим этот этот набор до базиса
всего пространства W- В этих базисах матричное представление
преобразования Τ имеет очень простой вид:
\ °)} η строк (10.9)
т столбцов
В левом верхнем углу по диагонали этой матрицы стоят г единиц,
а все остальные матричные элементы равны нулю.
Увы, обычно отображение Τ описывается матрицей А,
которая представляет его в других, менее удобных базисах. Важная
задача — найти такую замену базисов для пространств V и W,
которое преобразует матрицу А, заданную в произвольном базисе,
к I,.. Наиболее эффективно эта задача решается с помощью
редукции по строкам,, что, по существу, является систематической
процедурой решения линейных уравнений методом исключения

10.8. Редукция по строкам
507
неизвестных4. Сначала мы покажем процедуру на конкретном
примере, а потом объясним, почему таким образом решается
задача в общем случае.
Предположим, что нам дана матрица
/0 4 -4 8\
М= 2 4 0 2 ) .
\3 0 6 -9/
Назовем индексом любой строки матрицы М, где не все элементы
равны нулю, положение первого ненулевого элемента,
называемого ведущим элементом этой строки. Для первой строки нашей
матрицы Μ индекс равен 2, а ведущий элемент равен 4. Для
третьей строки индекс равен 1, а ведущий элемент равен 3.
В качестве первого шага определим строку с минимальным
индексом, переместив ее вверх матрицы, переставляя строки, и
разделив ее на ведущий элемент. Для данной матрицы Μ мы
переставляем первую и вторую строки:
2 4 0 2\
0 4-4 8
3 0 6 -9/
и делим верхнюю строку на ее ведущий элемент:
1 2 0 1\
0 4-4 8 1.
3 0 6 -9/
В качестве второго шага мы должны «очистить» столбец под
ведущим элементом верхней строки. Для этого первая строка
умножается на соответствующий коэффициент и вычитается
последовательно из нижних строк. В нашем случае мы умножаем
первую строку на 3 и вычитаем из третьей строки:
12 0 1\
0 4-4 8 ] .
0-6 6 -12/
Другое название этой процедуры, принятое в русскоязычной литературе,
— метод Гаусса. — Прим,, ред.

508
Векторные пространства ...
Теперь у матрицы есть ведущий элемент 1 в верхней строке,
а все другие строки имеет более высокий индекс. Далее,
передвигаем строку со следующим по величине индексом на вторую
позицию и делим ее на ведущий элемент. В нашем примере
вторая строка уже имеет следующий по величине индекс, поэтому
нам остается разделить ее на ведущий элемент 4. В результате
получаем
12 0 1\
0 1-1 2 1.
0-6 6 -12/
Теперь надо очистить столбец, соответствующий ведущему
элементу второй строки, умножая вторую строку на
соответствующий коэффициент и вычитая ее из других строк. В нашем случае
мы умножаем вторую строку на 2 и вычитаем ее из первой
строки, потом умножаем вторую строку —6 и вычитаем ее из третьей
строки. Получаем матрицу
1 0 2 -3\
0 1-1 2 ] . (10.10)
0 0 0 0/
Теперь первый и второй столбцы содержат по единственному
ненулевому элементу, равному 1, которые являются ведущими
элементами соответствующих строк.
В общем случае мы снова переставляли бы строку со
следующим по величине индексом на третью позицию и делили бы ее
на ведущий элемент. Далее умножали бы третью строку на
соответствующие коэффициенты и вычитали бы из остальных строк,
чтобы очистить третий столбец. И так далее. В нашем случае
больше нет ненулевых строк, и мы получили матрицу в
редуцированной форме. Перечислим свойства редуцированной
матрицы, которые молено увидеть из (10.10).
(a) Все нулевые строки, если они есть, находятся внизу.
(b) Ненулевые строки расположены в порядке возрастания
индексов.

10.8. Редукция по строкам
509
(с) Все элементы столбца, содержащего ведущий элемент (он
равен 1) ненулевой строки, равны нулю, (кроме,
естественно, этого ведущего элемента).
Каждая операция в процедуре редукции по строкам может
быть получена умножением слева на обратимую матрицу η х п.
Например, умножение нашей матрицы слева на матрицу
Si
приводит к перестановке первой и второй строк:
-4 8\ /2 4 0
0 2 1 = 10 4 —4
6 -9/ \3 0 6 -9.
Умножение слева на матрицу
соответствует делению первой строки на 2:
2\ /12 0
8 = 0 4 -4
-9/ \3 0 6-9
Умножение слева на матрицу
соответствует трехкратному вычитанию первой строки из
третьей:
1\ /12 0 1'
8
-12
1
0
3
0 0\
1 0
0 1/
/1
0
\з
2
4
0
0
-4
6
1
0
0
2
4
-6
0
-4
6

510
Векторные пространства ...
Таким образом, редуцированная по строкам матрица В может
быть записана в виде
В = 5fc5fc_i · · · 53525ιΜ
ИЛИ
В = SM,
где 5 — обратимая матрица η χ п. Заметим, что поскольку 5
обратима, dim Im В = dim Im M.
Образ и ядро редуцированной матрицы В легко определить.
Очевидно, что образ является r-мерным подпространством,
соответствующим г ненулевым строкам матрицы В и натянутым на
столбцы
/Л /о\
w v°y
которые содержат ведущие элементы всех ненулевых строк.
Согласно теореме о ранге и дефекте, ядро матрицы В имеет
размерность т — г, равную числу столбцов, которые не содержат
ведущих элементов. Базис для Кег В будем искать следующим
образом. Возьмем векторы, имеющие 1 в одной из т — г
позиций, соответствующих столбцам с неведущими элементами, и
нулю в остальных т — г — 1 позициях. Для нахождения первых г
компонент этих векторов умножим поочередно строки матрицы
В на эти векторы-столбцы, приравняем результаты к нулю и из
получившихся уравнений найдем компоненты, соответствующие
ведущим элементам столбцов.
Например, очевидно, что для матрицы
10 2 -3N
В= ί 0 1 -1 2
0 0 0 0,
ί'\ (°\
базисом Im В являются вектора I 0 I и I 1 I . Третий и четвер-
W W
тый столбцы не содержат ведущих элементов. Поэтому базисные

10.8. Редукция по строкам
511
вектора Кег В ищем в форме
Ul
и и2 —
2/2
0
Положив Ви^ — О, получаем
χι + 2 = 0, х2 - 1 = 0.
Следовательно,
Ul
/-2\
1
V о/
Положив Ви.2 = О, получаем
2/1-3 = 0, 2/2 + 2 = 0
/ 3\
-2
U2= 0
V 1/
Конечно, нам интересно знать ядро и образ первоначальной
матрицы М, а не редуцированной по сторокам матрицы В.
Однако, В = SM, где 5 — обратимая матрица. Тогда
Μ = S~lB.
Из двух последних равенств видно, что любой вектор из ядра
отображения В принадлежит ядру М. Поэтому получив ядро В,
тем самым, мы получаем ядро Μ. Чтобы найти образ М, надо
обратить 5 и подействовать матрицей 5-1 на образ В. Итак, мы
имеем В = SM, Кег В = Кег Μ и dim Im В = dim Im M.
Предположим, что нам надо решить уравнение
Mv = w.

512
Векторные пространства ...
Проделаем процедуру редукции по строкам с обеими частями
этого уравнения:
SMv = Sw или Bw = u,
где В — редуцированная по строкам матрица, a u = Sw. Это
уравнение имеет вид
1
η
0
η
1
0
2
-1
0
-л
А
о)
(χΛ
Х2
хз
\х4;
Оно может быть исследовано и решено следующим образом.
1. Если хотя бы одна компонента вектора и, соответствующая
нулевой строке В, отлична от нуля, то уравнение не имеет
решения.
2. Если все компоненты вектора и, соответствующие нулевым
строкам В, равны нулю, то
ν0
/«Л
U2
О
является частным решением уравнения.
3. Общее решение уравнения имеет вид νο + ν, где ν € Ker M.
Решая конкретную задачу, прежде чем проводить редукцию
по строкам, удобно объединить матрицу Μ и вектор w в одну
таблицу так, чтобы проводить редукцию одновременно.
Приведем пример. Нам надо решить уравнение
Mv
w,
где
Μ
И W =

10.8. Редукция по строкам
513
Объединяем Μ и w в таблицу
2 2
2 0
-2 8
и проводим редукцию, получая последовательно
Так мы получаем частное решение нашего уравнения
/ 2\
-1
0
V о/
Чтобы найти общее решение, мы должны построить базис
ядра М. Один базисный вектор имеет 1 на третьей позиции и 0 на
/ Л
. Другой имеет 0 на третьей позиции
четвертой, он равен
V 0/
и 1 на четвертой, он равен
Mv = w будет
/-з\
1
о
V Ч
Поэтому решением уравнения
/ 2\
-1
0
V V
+ λι
( Л
-1
1
1 о
+ λ2
/-з\
1
0
Ι ι/

514
Векторные пространства ...
где λχ и λ2 — произвольные вещественные числа.
Отметим характерную форму решения относительно
столбцов редуцированной матрицы, которые не содержат ведущих
элементов строк (в нашем случае это третий и четвертый столбцы).
Частное решение уравнения имеет нули на третьей и четвертой
позициях. А вот базисные вектора ядра Μ имеют ненулевой
элемент (единицу) ровно на одной из этих позиций. Общее решение
уравнения можно записать многими способами, но этот вид —
самый простой.
Для несингулярной квадратной матрицы А эта техника дает
эффективный метод получения обратной матрицы.
Преобразование S, которое редуцирует по строкам матрицу А к единичной, и
есть А~λ. Поэтому обратная матрица может быть получена, если
каждый отдельный шаг процедуры редукции применять к
матрице, которая получается добавлением к матрице А справа единич-
/ 1 2 Л
ной матрицы. Допустим, что -<4 = I 2 3 3 1. Эту матрицу и
V-i -ι о)
единичную матрицу объединим в одну таблицу
1
2
1
2 1
3 3
-1 0
1 0
0 1
0 0
0
0
1
Первую строку умножим на —2 и сложим со второй, потом
прибавляем первую строку к третьей:
1
0
0
2 1
-1 1
1 1
1 0
-2 1
1 0
0
0
1
Умножим вторую строку на —1:
1 2
0 1
0 1
1
-1
1
1
2
1
0 0
-1 0
0 1

10.8. Редукция по строкам
515
Вторую строку умножим на —2 и прибавим к первой, потом
вычтем вторую строку из третьей:
Разделим третью строку на 2:
3
-1
1
-3 2 0'
2-10
-1/2 1/2 1/2,
Третью строку умножим на —3 и сложим с первой, потом
прибавим третью строку ко второй:
-3/2
3/2
-1/2
1/2 -3/2N
-1/2 1/2
1/2
1/2,
Отсюда следует, что матрица А 1 равна:
Вернемся теперь к случаю прямоугольной матрицы. Вместо
того, чтобы выполнять редукцию по строкам, мы можем
выполнить редукцию по столбцам. Процедура точно такая же, только
слово «строка» надо заменить на «столбец». В результате
получим матрицу
С = МТ,
где Τ — обратимая квадратная матрица, а С — матрица,
редуцированная по столбцам. Отметим свойства матрицы,
редуцированной по столбцам.
(а') Все нулевые столбцы матрицы С, если они есть,
расположены справа.
(V) Ненулевые столбцы матрицы С расположены в порядке
возрастания индекса. (Индекс ненулевого столбца равен
номеру первого ненулевого элемента.)

516
Векторные пространства ...
(с') Каждая строка, содержащая ведущий элемент ненулевого
столбца, имеет ведущий элемент, равный 1, а все остальные
элементы строки равны нулю.
Отметим, что
1тС = 1тМ,
и г ненулевых столбцов матрицы С будут линейно независимы.
Следовательно, они образуют базис ImM. Таким образом,
подведем итоги.
Чтобы найти базис ImM, применяется редукция по
столбцам. Базисом являются ненулевые столбцы
получившейся матрицы С.
Чтобы найти базис КегМ, применяется редукция по
строкам. Получившиеся строки редуцированной
матрицы В = SM дают систему г уравнений для Кег В,
с помощью которых затем и находится ядро Μ и его
базис.
Мы можем также проделать редукцию и по строкам, и по
столбцам. Например, допустим, что надо сделать редукцию по
столбцам с матрицей, редуцированной по строкам:
В
Первый столбец умножим на 2 и вычтем из третьего, потом
первый столбец умножим на 3 и вычтем из четвертого. В результате
получим
10 0 0'
0 1-12
0 0 0 0,
Теперь второй столбец сложим с третьим, потом второй столбец
умножим на 2 и прибавим к четвертому. Получаем матрицу
1 0 0 0Ч
0 10 0
0 0 0 0,
1 0
0 1
0 0
2 3
-1 2
0 0

10.9. Локальная структура дифференцируемого отображения 517
В общем случае, проводя редукцию по столбцам с матрицей В,
редуцированной по строкам, мы делаем так, чтобы ведущими
столбцами стали первые г столбцов. (В нашем примере этого не
надо было делать.) Затем, умножая первые г столбцов на
соответствующие коэффициенты и вычитая их из остающихся т — г
столбцов, мы получаем матрицу, у которой на главной диагонали
стоят г единиц, а остальные элементы равны нулю, т. е. матрицу
вида (10.9). Итак, мы описали эффективный метод получения
таких матриц S и Т, что матрица SMT имеет вид (10.9).
10.9. Локальная структура
дифференцируемого отображения
Если собрать вместе результаты предыдущего параграфа с
результатами параграфа 6.3, то можно получить очень важную
информацию о структуре дифференцируемых отображений. Пусть
V и W — векторные пространства размерности тип
соответственно, и пусть О — некоторая (открытая) область в
пространстве V. Далее, предположим, что / : О —► W — дифференцируемое
отображение. В каждой точке ρ € О мы можем вычислить
дифференциал dfp. Этот дифференциал является линейным
отображением V на W, и поэтому мы можем вычислить его ранг.
Конечно, этот ранг может зависеть от точки р. Сейчас мы докажем
следующую теорему.
Теорема о постоянном ранге. Предположим, что
существует такое постоянное целое число г, что ранг dfp равен г для
всех ρ € О. Тогда для любого χ € О существует такое
взаимнооднозначное дифференцируемое отображение ф, преобразующее
окрестность χ в некоторую окрестность в Шт, такое, что φ
имеет обратное дифференцируемое. Кроме того, можно найти
такое взаимно-однозначное дифференцируемое отображение ψ,
преобразующее окрестность /(х) в пространстве W в
некоторую окрестность в Шп, причем оно таксисе имеет обратное
дифференцируемое. При этом композиционное отображение
гро}оф-1:Жт-^Жп
является линейным отображением с матрицей вида (10.9).

518
Векторные пространства ...
Короче говоря, эта теорема утверждает, что для
дифференцируемых отображений постоянного ранга выполняется основная
теорема о редукции по строкам: мы можем «сделать такие замены
переменных», т. е. найти такие отображения φ и ψ, что
выполняется равенство
{Ф° f'
W
Доказательство. Сделав трансляцию в пространстве V, мы
можем считать, что χ = 0. Сделав еще одну трансляцию в
пространстве W, можно предположить, что /(х) = 0. Иными словами,
чтобы упростить обозначения, можно считать, что /(0) = 0, и
мы интересуемся отображениями / в окрестности 0. Проделав
редукцию по строкам, мы можем привести линейное
отображение dfo к виду (10.9), т. е. мы можем найти обратимые линейные
отображения R : W —► Шт и S : V —> Rn, для которых
d(RfS-1)0 = Rdf0S-1
имеет вид (10.9). Тогда можно рассмотреть отображение
/ Л \
RfS-1 =
/г
/г+1
\ fn J
где матрица
dfi
t=l,...,r

10.9. Локальная структура дифференцируемого отображения 519
есть единичная матрица в 0. Следовательно, она обратима в
некоторой окрестности точки 0. Рассмотрим отображение д,
определенное вблизи 0 в пространстве Rm формулой
/ Λ \
/г
хг+1
\ %т J
Здесь первые г компонент отображения д — это введенные выше
функции /ι,.. ., /г, а остальные m — r компонент равны
соответствующим координатам. Заметим, что матрица
/
\
ддЛ _
dXj)
<
dxj
0
\
1
0
г
зтолбцс
в
0
ч
г
строк
т — г
строк
т — г
столбцо!
»
обратима в 0 и, следовательно, обратима в окрестности 0.
А теперь применим теорему об обратной функции из
параграфа 6.3 к отображению д. Еще раз рассмотрев то
доказательство, мы видим, что оно работает для произвольных
конечномерных пространств. (Заметим также, что сохраняется и
доказательство теоремы о неявной функции, если χ и у рассматривать
как векторные переменные, а условие неравенства нулю
производной dg/ду (вместо нее теперь матрица) становится
требованием обратимости матрицы.)
Вернемся к нашей задаче. Мы можем найти обратное
преобразование для д. Пусть
h = (RfS-l)og-

520
Векторные пространства ...
Тогда
Следовательно,
(RfS-1)
//*ι
vv
/г
xr+l
\ %τη J
((
У\
\\У*
У\
Ут
9г+\{у)
V 9п{у) )
при некоторых функциях gr+i,... ,дп, определенных в
пространстве Rm в окрестности 0. Воспользуемся цепным правилом и
получим
dh4 = d(fl/pS_1) о dg~l, где q = g(Sp).
Отсюда получаем, что в некоторой окрестности 0 ранг dh4
тождественно равен г. Рассмотрев матрицу
dh\
дУз)
—
/ 1г
V '
г
С1
олбц
ов
0 \
dgi
дУз /
η — г
столбц(
г
строк
η — г
строк
эв

10.9. Локальная структура дифференцируемого отображения 521
мы видим, что это может случиться, только если все частные
производные, появляющиеся в правом нижнем углу,
тождественно обращаются в нуль. Это значит, что последние η—r компонент
отображения h зависят только от первых г координат у, т.е.
9r+i =5r+i(yi>·-· ,Уг,0,... ,0), и т.д.
Введем преобразование Η в пространстве R" согласно формуле
// Ζ1 \\ /Zl \
Я
Zr+l
zr+i - 9r+i(zi,... ,ζ,.,0,... ,0)
\\ Ζη II \Ζη - 9n{zi,...,zr,0, ...,Ο) J
Это гладкое отображение, определенное в окрестности 2 = 0
в R". Очевидно, что оно обратимо — обратное преобразование
определяется формулой
Н~
W\
\
wr
Тогда
wr+i +gr+i(wi,...,Wr,0,... ,0)
\wn + gn(wi,...,wr,0,...,0) J
(Η oh)
\°/
Подставив определение h = (RfS х) о д 1 ъ Η oh, получаем
Hoh = (HR)ofo(S-1g-1).

522 Векторные пространства ...
Определяя
и
Φ = д ° S,
видим, что φ о / о ф~1 имеет требуемую теоремой форму
2/1 \
Ут
О '
°/
что и требовалось доказать.
Наиболее важное применение этой теоремы относится к
случаю г = η (напомним, что η — это размерность пространства W).
Если дифференциал dfp непрерывен в некоторой точке ρ и
имеет ранг п, то утверждается, что он имеет ранг η во всех точках,
достаточно близких к р. Действительно, с помощью редукции по
строкам мы можем найти такие R и 5, что RdfpS^1 имеет вид
(10.9) с г = п. Если q достаточно близко к р, то верхний
левый блок матрицы RdfpS-1 будет близок к единичной матрице.
Следовательно, размерность образа ci/q не меньше п. Поскольку
размерность этого образа не может быть больше dim W = η, мы
делаем вывод, что ранг дифференциала ci/q тождественно равен
η для всех q в некоторой окрестности р. Из теоремы о постоянном
ранге мы делаем следующий вывод.
Теорема о множестве решений. Предположим, что f :
О —> W — непрерывно дифференцируемое отображение и что
dfp сюръективно в точке р, га. е. что ранг dfp равен dim W.
Тогда мы можем найти дифференцируемые отображения: ф,
отображающее окрестность ρ в Rm, и ψ, отображающее
окрестность /(р) в Шп, так что оба отображения имеют непрерывно-
дифференцируемые обратные, причем ф(р) = 0 в Шт, ^(/(ч)) =
2/1
ψο f оф х

10.9. Локальная структура дифференцируемого отображения 523
О в Шп и локально выполняется равенство
((xi
ΜΦ~ι
νν
Хт
о
V° /
В частности, точка χ является решением уравнения
/(х) = /(р) (х вблизи р)
тогда и только тогда, когда
-1
(( ° Υ\
0
Ут+1
νν уп 11
χ = ψ
причем все Ут+1>Утп+2> ■ ■ ■ ,Уп лежат в окрестности 0.
Введем несколько терминов, чтобы сделать теорему о
множестве решений более краткой. Пусть Нт-п обозначает
подпространство
, определенное условиями
х\ = 0,
х„. = 0.
(Здесь предполагается, что η должно быть < т.) Подмножество
Μ m-мерного векторного пространства V называется
подмногообразием коразмерности п, если оно обладает следующим
свойством: около каждой точки χ € Μ мы можем найти
окрестность О в пространстве V и дифференцируемое отображение
φ : О —> Жт с 0(х) = 0, так что φ взаимно-однозначным
образом отображает О в окрестность U вблизи 0, при этом ф~1
дифференцируемо и
Ф(м ηθ) = υη ят_,

524
Векторные пространства ...
Н-тп—п
Рис. 10.4
Другими словами, это условие на Μ означает, что вблизи
каждой точки χ € Μ мы можем найти такую гладкую деформацию
всей окрестности, задаваемую отображением ф, что Μ
«уплощается» и становится куском гиперплоскости. Например,
окружность х2 + у2 = 1 является подмногообразием коразмерности 1 в
пространстве R2, потому что мы можем ввести отображение
*(x'y)=(ar<L~(y/s)
во всех ее точках с χ φ 0 (с последующим сдвигом в вертикальном
направлении к началу координат образа). В точках, где χ = 0,
мы можем пользоваться функцией arctan(x/y). А вот периметр
квадрата не является подмногообразием, потому что не
существует гладкого способа выпрямить углы.
Пусть / : О —► W — непрерывно-дифференцируемое
отображение. Точка ρ € О называется регулярной точкой отображения
/, если dfp сюръективно, т. е. если ранг dfp равен dim W■ Точка,
которая не является регулярной, называется критической точкой.
Если W = R, то ρ будет критической точкой при условии dfp = 0.
Это согласуется с нашими предыдущими обозначениями.
Точка q € W называется регулярным значением, если все
точки ρ в /_1(q) являются регулярными точками. Теперь дадим
еще одну формулировку нашей теоремы.
Если q — регулярное значение /, то /_1(q) —
подмногообразие.
Приведем несколько примеров.

10.9. Локальная структура дифференцируемого отображения 525
(а) Пусть η = 1 и / : Rm —► R1 = R определено формулой
/7*ι
/
= А + ■ ■ ■ + 4г
VV
Тогда dfp φ 0, если ρ φ 0. Таким образом, любое ненулевое
значение / будет регулярным значением. Для с > 0, /_1(с) есть
сфера радиуса у/с. Значит, сферы являются подмногообразиями.
(Ь) Пусть М(к) обозначает векторное пространство всех
матриц к х к, тогда т = dim V = к2. Пусть W = S(R) обозначает
векторное пространство всех симметричных матниц к х к, т. е.
матриц D, удовлетворяющих условию Dt = D. Тогда
n = dimW = ~к(к+ 1).
Δι
Рассмотрим отображение / : V —> W, где f(A) = AAf. Легко
проверить, что с$а{В) = ВАТ + АВ*. Мы утверждаем, что
единичная матрица I является регулярным значением отображения
/. Для доказательства этого утверждения следует проверить, что
dJA сюръективно, если ААЬ = I. Другими словами, при каждом
А уравнение
В А1 + АВ* = С
относительно В должно иметь решение для любой симметричной
матрицы С. Действительно, пусть В = С А/2. Тогда
ВАЬ + АВ1 = \ СААг + \ АА1СЬ
Δι Δ
= \с+\с\ т.к. АА1 = А1А = 1
Δ Δ
= С, т.к. С = СК
Итак, множество всех ортогональных матриц, т. е. матриц,
удовлетворяющих условию АА* = I, является подмногообразием
пространства всех матриц.

526
Векторные пространства ...
10.10. Сопряженное отображение
Изучая отображения одной аффинной плоскости в другую, мы
пользовались понятием переноса функции (pullback). Вспомним,
что при отображении φ аффинной плоскости А в другую
аффинную плоскость В естественным образом возникало линейное
отображение функций, определенных на плоскости В, в
функции, определенные на плоскости А. Эта ситуация изображена на
рис. 10.5. Перенос определенной на плоскости В функции /,
обозначаемый ф*/, является функцией на плоскости А,
определяемой соотношением
(ΦΊ)(Ρ) = КФ(Р)У
Рис. 10.5
Понятие переноса может быть расширено на случай отображений
одного векторного пространства V в другое векторное
пространство W. Нам особенно интересен перенос линейных функций в
пространстве W (т.е. элементов дуального пространства W*),
возникающий как следствие линейного отображения А
пространства V в W. В этом случае перенесенное отображение из W* в
V* называется отображением, сопряженным к А. Мы будем
обозначать его А*. Его действие на элемент β € W* определяется
формулой
(Α*β)[ν]=β[Αν].
Доказательство того, что таким образом определенное
отображение А* линейно по /3, точно такое же, как доказательство

10.10. Сопряженное отображение
527
того, что вообще перенос — линейное отображение. Если
элементы /З1 и /3 являются элементами W*, то
(А*{сф1 + c2/32))[v] = (d/31 + €2β2)[Αν]
= εφ^Αν] + ε2β2[Αν]
= αΑ*β1[ν]+ο2Α*β2[ν].
Отсюда получаем равенство
А\сф1 + с2/32) = ολΑ*βι + ο2Α*β2,
которое и означает линейность А*. Отметим, что из линейности А
и β следует линейность функции Α*β по ν, τ. е. что действительно
Α*β находится в пространстве V*.
Важно отметить, что сопряженное отображение А* действует
«в направлении, противоположном» А. Это значит, что если А
преобразует вектор ν € V в вектор Av € W, то сопряженное
отображение А* преобразует вектор β € W* в вектор Α*β € V*.
На схеме это выглядит так:
ν* £- w*,
ν ^ w.
Рассмотрим пример сопряженного отображения: пусть V —
трехмерное пространство четных полиномов степени < 4 и пусть
W — двумерное пространство нечетных полиномов степени < 3.
Тогда операция дифференцирования определяет линейное
отображение D из V в W:
D: fh-*f.
Пусть элемент пространства W* таков:
β: gi-*g(l).
Например, /3(ί + 2ί3) = 1 + 2 = 3. Чтобы вычислить Ό*β,
воспользуемся определением
L>*/3[f]=/3[L>f].

528
Векторные пространства ...
В нашем случае Όΐ = f' и /3[£)f] = f'(l). Отсюда следует, что D*β
— линейная функция в пространстве V (элемент пространства
V*):
Ό*β : f -» f (1).
Возьмем другой элемент пространства W*:
а. : g ι—>
Тогда
/ g(t)dt-
■/о
D*a[f\ = a[Df\ = f f'(t) dt = f(1) - f(0),
Jo
т. e. D*a — линейная функция
D*ol : f к-* f (1) - f (0).
Если ввести базисы в пространствах V, W, V* и W*, то
описание сопряженного отображения становится особенно
простым. Предположим, что V — m-мерное пространство с
базисом {vi, V2,.. . , vm}. Введем дуальный базис {а1, а2,... , а.™} в
дуальном пространстве V*. Аналогично, пусть {wi, W2,..., wn}
и {β1, β2 ... ,βη} будут базисами пространств W и W*
соответственно. Если А — линейное отображение из V в W, то
η
Awi = y^ajjWj,
3=1
где величины {ац,а2г, ■ ■ ■ ,ani} образуют г-й столбец матрицы,
задающей отображение А. Вычислим, как А* действует на
базисный элемент пространства W*:
(Л*/3*)[у4]=/3*[Лу4]=/3*
3=1
Поскольку базис {β ,β2 ... ,βη} дуален базису {wi, W2,. ■. , wn},
мы имеем
' 1, 3 = к,
β>Α =
0, j^k,

10.10. Сопряженное отображение
529
т. е.
(Л*/3*)Ы=аы.
Итак, мы можем выразить Α*β через базисные вектора
{а1, а.2,..., α"1} в пространстве V*:
η
Α*β* = ΣαΜ<χι.
ί=ι
Величины {аы} = {afci,«fc2> ■ ■ ■ >«fcm} образуют к-й столбец
матрицы, задающей отображение А*, но одновременно они
являются к-й строкой матрицы, задающей А. Это значит, что матрица
отображения А* является транспонированной матрицей
отображения А. Например, если V — трехмерное пространство, W —
двумерное и А : V —► W представляется матрицей
а _ ι «li «12 «13
^21 «22 «23,
то сопряженное отображение А* : W* —► V* задается матрицей
(an «2iN
«12 Я22
αΐ3 «23 у
Вспомним, что элементы дуального пространства могут быть
записаны в виде векторов-строк. В нашем примере элемент
пространства W* можно записать в виде двухкомпонентного
вектора-строки:
/3 = (λι,λ2),
а элемент пространства V — как трехкомпонентный вектор-
столбец:
V2
Тогда (i4*/3)[v] = /3[Av] можно записать как произведение
(λι,λ2)(αΐ1 °12 °13'
\α2ι α22 Я23

530
Векторные пространства ...
Естественное истолкование этого произведения: матрица А,
действуя сначала на столбец, расположенный от нее справа, дает Αν,
на который уже действует β. С другой стороны, можно думать,
что матрица сначала действует на вектор-строку, стоящую слева:
(Ai.AaH"11 "12 °13 ) = (μι,μ2,μ3),
\«21 «22 «23/
где (μι,μ2,μζ) представляет вектор (Α*β) € V*, который потом
действует на ν € V. Таким образом, если мы изменим обычные
правила умножения матриц и позволим матрице сначала
действовать налево на вектор-строку, то одна и та же матрица будет
представлять А и А*. Если же мы хотим записывать А*
традиционно, т. е. в виде матрицы, действующей на столбец справа, то
мы должны писать
μΐ \ /«11 «21
М2 I = I Я12 Я22
μζ)) \«ΐ3 Я2з
И мы видим, что матрица, представляющая А*, будет
транспонированной матрицей А.
Исследуем теперь ядро и образ сопряженного отображения
А*. Если β € W* и принадлежит ядру А*, то Α/3[ν] = 0 для всех
ν € V, т. е. /3[Av] = 0. Это значит, что β аннулирует все вектора
вида Αν. Отсюда можно сделать вывод, что ядро А* аннулирует
образ А.
Предположим, что α € V* и принадлежит образу А*, т. е.
α = Α*β для некоторых β € W*.
Предположим, что ν есть элемент Кег А Тогда
α [ν] = Α*β[ν] = β[Αν] = 0.
Отсюда следует, что образ А* аннулирует ядро А.
Объединив эти результаты с общими результатами для
дуальных пространств и факторпространств, доказанными в конце
параграфа 10.5, мы можем построить две схемы, изображающие

Резюме
531
общую картину векторных пространств и линейных
преобразований. Итак, для подпространств V и V* мы имеем
V*/lmA* ^V* ^1тЛ*,
ΚβτΑ-^V -^V/КетА.
Эта схема отражает тот факт, что факторпространство V*/lmA
может быть идентифицировано с сопряженным к Ker Л, а образ
А* сопряжен с V/Ker Л.
Для подпространств W и W* мы получаем схемы:
W*/K&c А* <- W* ^КегЛ*,
Inu4-»W ->W/lmA.
Здесь W* /Ker А* может быть идентифицировано с дуальным
Im A, a Ker А* дуально к W/Im А. Многочисленные примеры этих
соотношений будут нами рассмотрены при изучении теории
электрических цепей.
Резюме
A. Векторные пространства
Вы должны знать аксиомы векторных пространств и уметь
применять их.
Для данного базиса векторного пространства надо уметь
находить дуальный базис для дуального пространства.
Для данного подпространства U векторного пространства V
надо уметь строить базисы для аннулирующего пространства U
и факторпространства V/U и использовать их.
B. Линейные преобразования
Вы должны уметь писать матрицу, представляющую линейное
преобразование А : V —► W в заданных базисах.
Вы должны знать формулировку теоремы о ранге и дефекте,
уметь доказывать и применять ее.
Для данной матрицы линейного преобразования А надо уметь
пользоваться редукцией по строкам для определения базисов для
Ker А и Im Л и получать общее решение уравнения Л ν = w.

532
Векторные пространства ...
Вы должны знать определение сопряженного отображения А*
для линейного преобразования А. Надо знать формулы,
доказывать и применять соотношения между ядром и образом А, между
ядром
применять соотношения между ядром и образом А, между
и образом А*.
Задачи
10.1. Рассмотрите пятимерное векторное пространство V полиномов
f(t) степени < 4. Выясните, будет ли подпространством
множество в каждом из перечисленных ниже примеров. Если нет,
то объясните, почему. Если да, то найдите базис.
(a) Полиномы удовлетворяют условию f(t) = /(—t).
(b) Полиномы удовлетворяют условию /(0) = 1.
(c) Полиномы удовлетворяют условию /(1) =/(—1).
(d) Полиномы удовлетворяют условию J_i tf(t) dt = 0.
10.2. (а) Найдите базис для подпространства R3, определенного
условием α [ν] =0, где
α = (2,-3,1).
(b) Найдите базис для подпространства R3, определенного
условиями α [ν] = 0 и /3[ν] =0, где
α = (2,-3,1) и /3 = (2,1,-1).
(c) Найдите базис аннулирующего пространства для
подпространства W С R3, натянутого на вектора
10.3. (а) Покажите, что множество функций f(t), удовлетворяющих
уравнению /" + 5/' + 6/ = 0, является векторным
пространством V.
(Ь) Возьмем три элемента пространства V*, дуального к этому
пространству:
<*1. /-/(0),
а2: /-/'(0),
/• + 00
а3 : / ь-> / e'/(i) dt.
Jo

Задачи
533
Найдите соотношение между а1, а2 и а3, показывающее,
что они линейно зависимы.
(с) В качестве базиса пространства V выберем вектора
Vl = e~2t + e~3t,
v2=2e-2t-e-3t.
Выразите дуальные базисные элементы β и β через а1 и
а2, определенные в предыдущем пункте.
10.4. (а) Покажите, что если S и Τ — подпространства векторного
пространства V, то их пересечение S П Τ (множество
элементов, общих для S и Т) является подпространством V.
(b) Покажите, что S + Τ (множество векторов, являющихся
линейными комбинациями векторов из S и Т) будет
подпространством V.
(c) Покажите, что dim(5 + T)= dim(5) + dim(T) - dim(5 П Τ).
(Указание: начните с базиса Sf)T и расширьте его до базиса
S + T.)
/J\
(d) Предположим, что V есть R4, S натянуто на векторы I 1
\0/
'2\ /!\ /°\
и , 0
1
о
о/
По-
, а Т соответственно на векторы I ..
,1/
стройте базисы для S Г)Т, S + Τ и для пространства,
аннулирующего S + Т.
10.5. Пусть W — подпространство R3, натянутое на вектор | 2
(а) Покажите, что ei = | 1 I и e2 = I 1 J образуют базис
0/ \1
1\ /0'
факторпространства R3/V7. Выразите вектора [ 0 I, I 1
0/ \0

534
Векторные пространства ...
и I 0 ) в виде линейных комбинаций этих базисных векто-
V1
ров.
(Ь) Покажите, что α = (2,-1,0) и β = (4,0,-1), будучи
элементами дуального пространства к R3, являются базисом
аннулирующего пространства W-1. Для W1- постройте
базис {е^е2} через элементы α и /3, который будет дуален
базису {е1,ег} факторпространства R3/W.
10.6. (а) Пусть W — подпространство векторного пространства V.
Пусть U — подпространство W. Докажите, что W/U явля-
т/т VIU
ется подпространством V U и что естественно
совпаду Ζ"
дает cV/W.
(b) Пусть векторное пространство V есть R3, W — плоскость
x + y + z = 0,a,U — прямая линия, определенная вектором
Л
-2 1. Получите явный вид базисов для этих пространств.
(c) Разберитесь, что происходит в дуальном пространстве, т. е.
постройте подпространства V*, которые будут дуальными
или аннулирующими пространствами для всех пространств,
перечисленных в пункте (а). Сначала сделайте это в общем
виде, а потом для частного случая, описанного в пункте (Ь).
10.7. Рассмотрите пространство V, образованное функциями вида
/(t) = At + B/t, заданными на отрезке [1,2]. Пусть базисные
вектора имеют вид vi = t и V2 = l/ί. Два элемента дуального
пространства V* равны
/З1 :/(*)-/(!),
β2 : /(*) -ч /(2).
Выразите базисные элементы {а1,а2}, дуальные к {νι,ν2}, в
виде линейной комбинации β и β .
Прежде чем выполнять упражнения 10.8-10.12, перечитайте
параграф 4.2 о процессе Грама-Шмидта.
10.8. (а) Найдите размерность пространства тригонометрических
полиномов, натянутого на
{1, sin2 ж, cos2 ж, sin4 ж, sin2 a;cos2 ж, cos4 ж}.

Задачи
535
(b) Пусть скалярное произведение в этом пространстве равно
1 Г
(f,9) = - f{x)g{x)dx.
π Jo
С учетом этого определения постройте ортонормированный
базис.
10.9. (а) Рассмотрите векторное пространство нечетных полиномов
степени < 3 с базисом {t,t3} и скалярным произведением
/о f(t)9(t) dt. Постройте ортогональный базис (его не надо
нормировать).
(b) Для линейного оператора / : V —► V, определенного
формулой f(p(t)) = tp'(t), постройте матрицу А, которая
представляет / в базисе {ί,ί3}, и матрицу Л, которая
представляет / в ортогональном базисе, построенном в предыдущем
пункте.
(c) Три элемента дуального к V пространства V* можно задать
в виде: а1\р] = р(1), а2\р] = р'(0) и а3\р] = J^tp(t)dt.
Получите соотношение между α1, α2 и а3, показывающее
в явном виде, что они линейно зависимы.
10.10. Пусть V — двумерное векторное пространство функций,
являющихся линейными комбинациями /ι = 1 и /2 = cos21.
Определим скалярное произведение в этом пространстве (/, д) =
rj2f{t)№dt.
(a) Постройте ортонормированный базис для пространства V.
2 ίπΙ2 1 2 /"Г/2 3
(Замечание: — / cos2 tdt = -, — / cos4icii = -.)
π Jo 2 π J0 8
(b) Три элемента дуального пространства V* равны:
/•т/2
а1 : / -> /(т/2)> а2:/^/ /(t) cos tdt,
Jo
а3
Ό
/•π/2
/•τ/·4
/ -> / /(t) sin tdt.
Jo
/о
Покажите в явном виде, что они линейно зависимы.
10.11. Рассмотрите трехмерное пространство V, элементами которого
будут полиномы степени < 2, умноженные на e_2t. Базисом этого
пространства будут три вектора:
V! = e"2t, v2 = te"2t, v3 = t2e~2t.

536
Векторные пространства ...
(a) В этом базисе напишите матрицу D, представляющую
операцию дифференцирования, т. е.
Df(t) = f\t).
(b) Постройте матрицу D2 + 4D + 41. (В этой матрице будет
много нулей!)
(c) Общее решение уравнения χ + 4х + 4х = e~2t лежит в
векторном пространстве V. Получите его с помощью матрицы,
построенной в пункте (Ь).
10.12. Векторное пространство решений уравнения
χ + Зх + 2х = 0
обозначим через V. Определим скалярное произведение в этом
пространстве равенством
/- + 0О
(f,g)=/ {(t)g(t)dt.
Jo
(Учтите, что $0+°°e-Xtdt = 1/λ.)
(a) Пусть fi = e_2i — первый базисный вектор пространства V.
Постройте второй вектор Ϊ2, ортогональный к fι.
(b) В базисе {fi, £2} постройте матрицу D, которая
представляет операцию дифференцирования по t. Проверьте, что
D2 + 3D + 21 = 0. Пусть три элемента дуального
пространства V* имеют вид
αϊ И = f(0),
a2[f]=f(0),
/■+00
a3[f]=/ f(t)dt.
Jo
(c) Объясните из общих соображений, почему существуют
числа λι, Аг, Аз (не все равные нулю), для которых
выполняется соотношение
λιαι + λ2α2 + А3аз = О.
Получите λι, λ2 и λ3.

Задачи
537
(d) С помощью αϊ и с*2 постройте базис {/31; /32} для V*,
который будет дуальным к базису {fi, £2}, полученному в
пункте (а).
Пусть V — четырехмерное векторное пространство полиномов
степени < 3 с базисными элементами 1,ί,ί2,ί3. Пусть D —
дифференциальный оператор, действующий в этом пространстве:
Df(t) = f'(t) и пусть Та — оператор трансляции: Taf(t) = f(t+a).
(a) В этом базисе постройте матрицы D я Та и покажите, что
Та = I + Da + \ϋ2α2 + Ιϋ3α3.
(b) Докажите, что если V — пространство полиномов степени
< п, то Та = exp(Da). (Указание: вспомните формулу
Тейлора, и тогда не придется строить матрицы.)
Пусть V — пространство 1-форм на плоскости, для которых
коэффициенты при dx и dy — квадратичные функции. Базисом
такого пространства V будут х2 dx, xy dx, у2 dx, x2 dy, xy dy, у2 dy.
Любая кривая Г, лежащая на плоскости, определяет элемент ар
дуального пространства V* согласно формуле
"г Μ = /
ω.
г
(a) Найдите нетривиальную кривую Г, для которой аг будет
нулевым элементом V*.
(b) Получите базис для подпространства V, которое
аннулируется элементом аг, где Г — любая замкнутая кривая.
(c) Пусть Γι, Гг и Гз — три произвольные замкнутые кривые
на плоскости. Докажите, что а^, «г2 и аг3 линейно
зависимы. (Указание: воспользуйтесь теоремой Грина, чтобы
преобразовать криволинейные интегралы к двойным.)
(d) Найдите такие кривые Г χ, Г 2,. ■., Гб (это могут быть
отрезки прямых линий), чтобы аг1,скг2,... ,агв были базисом
для V*, дуальным к базису, данному в условии задачи.
Например,
[ x2dx = l, остальные / х2 d, = О О" = 2,3,4,5,6);
/ xydx=l, остальные / xydx=0 (j = 1,3,4,5,6).
JT2 JTj

538
Векторные пространства ...
10.15. Рассмотрите линейное преобразование / из пространства
пространство R3, матрица которого имеет вид:
1 2
1 0
0 1
0
2
-1
1
-3
2
(a) Получите базис для ядра / и найдите общее решение
уравнения
/м-Ц
(b) Пусть N обозначает ядро /; пусть G — факторпростран-
ство R4/./V. Постройте базис для G и объясните, почему
полученные базисные вектора будут линейно независимыми
элементами G.
10.16. Рассмотрите линейное преобразование / из К4 в R3, с матрицей
(а) Получите базис ядра / и найдите общее решение уравнения
/(v) =
(b) Напишите базис образа /.
(c) Два элемента факторпространства Η имеют вид:
hi = I 1 I и h2 =
W
Покажите в явной форме, что hi и h2 линейно зависимы.
(Указание: вернитесь к первому пункту этого упражнения.)
10.17. Линейное преобразование / : R4 —» R4 представляется матрицей
I 11 ') Л _С

Задачи
539
(a) С помощью редукции по строкам получите ранг матрицы А
и найдите базис ядра этой матрицы. Обозначьте этот базис:
vi,..., Vfc, где к = dimKer А.
(b) Найдите решения wi,..., Wfc уравнений ylwj = Vj.
(c) Будут ли вектора w\,..., w/., vi,..., Vfc базисом
пространства R4? Что означает ответ на этот вопрос для
преобразования /?
(d) Найдите базис Im А и выразите этот базис через вектора Wj
и Vj. Как этот результат связан с результатами
предыдущего пункта?
10.18. Нам дана матрица 4x4:
/2 4
' 1 2
3 6
\0 0
2
0
5
3
2\
2
1
-3/
(а) С помощью редукции по строкам получите базис ядра А и
базис образа А. Найдите общее решение уравнения
Λν
(b) Получите базисные вектора щ и иг для факторпростран-
/ 4\
ства U = М4/КегЛ. Вектор
3
4
\-зУ
выразите через
полученные Ui И U2.
10.19. Пусть W — векторное подпространство в R4, натянутое на
вектора
!\ /3\ ί1\
, w2 =
Wi =
w3 =
Скалярное произведение в R4 — обычное евклидово,
(а) Постройте ортонормированный базис для W.

540
Векторные пространства ...
(b) Запишите вектор ν = I в виде суммы вектора из
7/
пространства W и вектора, ортогонального к W.
(c) Пусть / : R4 —► R3 определено формулой
/(wi,v)\
/(v)= (w2lv) .
\(w3,v)/
Запишите матрицу, представляющую преобразование /.
С помощью редукции по строкам получите общее решение
уравнения
/(ν) = ( 6
10.20. С помощью редукции по строкам получите базис
подпространства U S Ж5, аннулирующее пространство которого Vх- натянуто
на вектор-строки
а1 = (1,2,0,-1,2),
а2 = (2,4,3,4,4),
а3 = (0,0,1,2,1).
а4 =(3,6,5, 7,8).
Получите общее решение для системы линейных уравнений
αχ[ν] = 5, α2[ν] = 16, α3[ν] = 3, α4[ν] = 27.
10.21. С помощью редукции по строкам получите матрицу, обратную к
1
-2
1
-2
5
-4
1
-4
6
10.22. Пусть V — пространство функций / на Ж2, обладающих
свойством f(Xx,Xy) — \3f(x,y). Базисные вектора пространства V
имеют вид
{vi=a;3, v2 = x2y, v3 = xy2, v4 = у3}.

Задачи
541
Пусть W — пространство 1-форм на плоскости, являющихся
квадратичными функциями χ и у. Базис этого пространства
имеет вид
wi = χ dx, W2 = xydx, W3 = у dx,
w4 = χ2 dy, w5 = xy dy, w6 = y2 dy.
Оператор d является линейным преобразованием из V в W.
(a) Напишите матрицу, представляющую оператор d в
заданных базисах.
(b) Получите базис для образа d и для факторпространства
G = W/(lmd).
,
1
-1
уУ
'
*
'
'а1
1
X
■а2
Рис. 10.6
(c) Два элемента дуального пространства W* обозначаются а1
и а2. Причем а1 приписывает любому элементу ω S W
значение интеграла f г ω, где а1 является квадратом
единичной площади 0<а;<1,0<у<1, проходимым против
часовой стрелки, а для элемента а2 берется другой квадрат
0 < а; < 1, — 1 < у <0 (рис. 10.6). Получите векторы-строки,
представляющие а1 и а2. Найдите линейные комбинации
а1 и а2, образующие дуальный базис для базиса
пространства G.
(d) Пусть U обозначает пространство 2-форм на плоскости,
которые зависят линейно от χ и у. Базисом этого пространства
являются вектора
{ui = χ dx Л dy, 112 = у dx Л dy}.

542
Векторные пространства ...
Постройте матрицу, представляющую оператор d из W в U.
Что является ядром этого оператора?
10.23. Пусть А — линейное преобразование из V в W; и пусть А*—
сопряженное преобразование из W* в V*. Предположим, что
мы имеем произвольные (не обязательно дуальные) базисы для
V и V*: базис {νι , V2,..., vm} для пространства V и базис
{а1, а2,... ,ат} для пространства V*, где α*[ν^] = Sij.
Числа Sij образуют га χ га матрицу S. Аналогично у нас есть базисы
{wi, w2,..., wn} и {β1, β2,..., βη} для W и W* соответственно,
где β [w(] = Ты- Числа Ты образуют η χη матрицу Т. (Если бы
мы выбрали дуальные базисы, то Τ и S были бы единичными
матрицами.)
Если А — матрица отображения в базисах {vj} и {wj}, то какова
будет А* — матрица сопряженного отображения в базисах {β1}
и {с*г}? Ответ выразить через транспонированную матрицу Л* и
матрицы S и Т.
10.24. Для векторного пространства V, где определено скалярное
произведение (νι, ν2), сопряженное преобразование А* для
линейного преобразования А : V —► V тоже будет линейным
преобразованием А* : V —* V, определяемым формулой
(τΓνι,ν2) = (νι,Αν2).
(a) Покажите, что это определение следует из определения А*,
как преобразования из V* в V*, с учетом обычной
идентификации V* cV, которая следует из скалярного
произведения5.
(b) Покажите, что в ортонормированном базисе {ei, е2,..., еп}
матрица, представляющая А*, будет транспонированной к
матрице А.
(c) Пусть π обозначает линейную операцию ортогонального
проектирования из V на подпространство W, т.е. для
любого veF вектор πν принадлежит подпространству W и
вектор ν — πν ортогонален вектору πν. (Операция π есть
преобразование из V в V, причем Ιπιπ = W.) Покажите,
что π* = π.
5Напомним, что упомянутая идентификация означает, что каждому
вектору u G V ставится в соответствие линейная функция а € V, действующая
по формуле л (ν) = (и, ν). — Прим. ред.

Задачи
543
(d) Пусть V — пространство полиномов степени < 2, где
определено скалярное произведение (f, g) = /0 f (i)g(i) dt.
Выберем базис vi = 1, V2 = t, V3 = t2. (Этот базис не ортонорми-
рован.) Пусть А — линейное преобразование, определенное
формулой
Af(t) = f(t+l).
В этом базисе постройте матрицу, представляющую А*.
10.25. Рассмотрите линейное преобразование из четырехмерного
векторного пространства V в трехмерное векторное пространство
W, которое представляется матрицей
11 0 3
2 12 2
2 3 -2 10у
(a) Пусть Μ обозначает образ А. Покажите, что вектора mi =
Л (Л
2 I и тг = I 1 I образуют базис подпространства М.
,v W
(b) Пусть Η = W/M. Покажите, что базис этого факторпро-
странства состоит из одного вектора hi = 10 1, кото-
W
рый является классом эквивалентности, содержащим все
(Л
вектора I 0 1 + т, где т — элемент М. Покажите, что
\0/
°\ ι
11=— -hi, т. е. найдите такой элемент m из простран-
ства М, чтобы выполнялось равенство
'(Г
Выразите | 0 ] через hi.

544
Векторные пространства ...
(с) Пусть N обозначает ядро А. Один элемент из N равен ηι =
. Найдите второй вектор пг, так чтобы η ι и п2 были
базисом пространства N.
Указание: Сначала проведите редукцию по строкам для
л I b
матрицы А, а потом ищите вектор вида I 1
(d) Пусть G обозначает факторпространство V/N. Базисные
вектора этого пространства имеют вид: gi = I п и 82 =
Покажите, что
= 2gi - 2g2, и выразите | Q
.1/
о
,0/
через gi и g2.
(e) Получите несингулярную 2x2 матрицу С, которая
представляет А как преобразование от G (с базисом gi, g2) к Μ
(с базисом mi, тг).
(2\
(f) Вектор I 1 I выразите через mi и тг. (Указание: сделай-
W
те те лее операции, которые выполняются при редукции по
строкам.) После этого примените С-1, т.е. решите уравне-
(2
ние Αν = I 1 ], записав ответ в виде ν = agi + bg2 =
\7
+ η, где η — произвольный элемент из N.
10.26. Пусть /* обозначает сопряженное отображение для / в
предыдущей задаче. Отображение /* является отображением дуального
пространства W* в дуальное пространство V* и задается
формулой /*/3(ν) = /3(/ν), где β и ν — произвольные элементы из
W* и V. Если взять базисы, дуальные к исходным базисам в

Задачи
545
пространствах V и W, то /* представляется матрицей,
транспонированной к А:
/1 2 24
Л I 0 2 -2 "
\3 2 10/
(a) Покажите, что образ /* сопряжен с пространством G. Пусть
εί и εϋ> ~ элементы V*, дуальные к gi ид2- Каждый столбец
в матрице А* выразите через g£ и g£.
(b) Покажите, что ядро /* сопряжено с пространством Н.
Пусть элемент 7' дуален hi, т.е. 7'(hi) = 1- Пусть /З1 —
элемент W*, выбирающий первую компоненту вектора, т. е.
а\
β I Ь I = а. Выразите β через 7'- Сделайте то же самое
Vе/
для β и β , которые выбирают вторую и третью
компоненты вектора соответственно.
(c) Найдите такие вектора а1 и а2 в пространстве W*, что
f*cx1 = β1, f*a2 = β2. Покажите, что α1, α2 и j' образуют
базис для W*.

I

Глава 11
Определители
Глава 11 посвящена доказательствам основных свойств
определителей матриц пх п. Сначала приводятся
аксиомы для определителей, потом даются методы их
вычисления.
Введение
В этой главе мы обсудим свойства определителей матриц размера
η χ п. Пусть А — матрица пх п. Столбцы этой матрицы будем
обозначать А\,..., Ап. Для единичной матрицы I размера η χ η
столбцы имеют вид:
h =
(Л
О
U
h=
1
u
и т.д.
Тогда для произвольной матрицы А
Ai=Ah, ..
An — ■Λ-'τΐ)
другими словами, Αι является образом Ц, т. е. г-го вектора
стандартного базиса в R" при отображении А.
Мы хотели бы определить Det А как ориентированный
объем параллелепипеда, построенного на векторах Αχ,...,Αη.
Наши знания, полученные в главах 1 и 4, позволяют говорить, что

548
Глава 11. Определители
этот ориентированный объем будет полилинейным, т. е.
линейным по А\ при фиксированных Αι-, ■ ■., Ап, линейным по А2 при
фиксированных А\, А%,..., Ап, и так далее. Вследствие наличия
ориентации мы ожидаем, что Det А антисимметричен по
столбцам, т. е. перестановка любых двух столбцов матрицы изменяет
знак определителя. Мы должны дать определение определителя
и доказать, что он обладает требуемыми свойствами. Материал
излагается классически, начиная с основных аксиом для
определителей. Мы выпишем основные свойства, которыми должны
обладать определители, и покажем, что эти свойства задают его
однозначно. Другими словами, покажем, что существует не более,
чем одна функция от элементов матрицы с требуемыми
свойствами. Затем получим правила вычисления определителей и
покажем, что функция, удовлетворяющая аксиомам, существует.
Потом дадим другие определения определителей и убедимся, что
все определения дают одну и ту же функцию.
В последующем мы будем рассматривать функцию от
матриц. Если эта функция вычисляется для конкретной матрицы А,
то пишем D(A) или D(A\,... ,Ап), чтобы подчеркнуть, что это
функция от η векторов Αι,..., Ап. Если все столбцы, кроме fc-ro,
фиксированы, то мы получим функцию одного столбца, которую
будем обозначать D^. Например, будем писать
(Строго говоря, в обозначении Dk мы должны отразить постоян-
ные векторы А\= \ — 2 I и Лз = I 9|и писать
3/ 1-1
ЧЖ)
но это обозначение слишком громоздко.)

11.1. Аксиомы для определителей
549
11.1. Аксиомы для определителей
Функция матриц D называется определителем, если она
удовлетворяет следующим условиям.
о Каждая функция Dk линейна:
Dk(Ak + A'k) = Dk(Ak) + Dk(Ak),
Dk{cAk) = cDk{Ak).
Другими словами, D линейна по каждому столбцу, когда
другие столбцы фиксированы.
о Если два соседних столбца матрицы А равны, то
D(A)=0. (11.2)
Наконец,
£>(!) = 1. (11.3)
Предположим, что функция D, удовлетворяющая свойствам
(11.1) и (11.2), существует. Что из этого следует?
Если один столбец умножить на какое-то число и
прибавить его к соседнему, то значение функции D не изменится.
Доказательство. Прибавим к (к + 1)-му столбцу fc-й,
умноженный на с. Получим
D(Ai, ...,Ак, сАк + Ак+Ъ Ак+2, ...,Ап)
= D(Ai,..., Ак,Ак+1, Ак+2 ...,Ап)
+ cD(Ai, ...,Ak,Ak, Ак+2, ...,Ап)
= D(Al,...,An). (11.4)
Здесь использовались условия (11.1) и (11.2). Например,
1 4-4-1 7
= D || 2 5-4-2 8||=D
3 6-4-3 9
Чтобы получить еще одно свойство определителя, прибавим fc-й
столбец к (к + 1)-му, получившийся (к + 1)-й столбец вычтем из

550
Глава 11. Определители
fc-ro столбца, потом еще раз прибавим полученный к-й столбец к
(к + 1)-му. В результате получим:
Ак, Ак + Ак+1, Ак+2, ■ ·., Ап)
Ак-(Ак + Ак+1),Ак + Ak+\i■.., Ап)
-Ак+1,Ак + Ак+1,Ак+2,..., Ап)
~Ак+\, Ак + Ак+\ — Ак+\,..., Ап)
~Ак+1,Ак, Ак+2, ■ · ■, Ап)
D(A) = D(A1,.
= П(АЪ.
= D(A1,.
= D(A1,.
= П(АЪ.
■■■>Ак-ъ
■ ■ ,Ak-i,
·■ ,Ak-i,
■■ ,Ak-i,
■· ,Ak-i,
= —D(Ai,..., Ak-ι, Ak+i, Ак, Ак+2,..., Αη).
(11.5)
Таким образом, перестановка двух соседних столбцов изменяет
знак определителя D(A). Отсюда немедленно следует, что
если два столбца матрицы А равны, то D(A)=0. (П-6)
Действительно, если у матрицы есть два одинаковых
столбца, то мы можем переставлять соседние столбцы до тех пор, пока
наши столбцы не станут рядом. После этого остается
воспользоваться свойствами (11.2) и (11.5). Ссылки на свойства (11.1) и
(11.6) приводят нас к еще одному следствию.
Если умножить один столбец на число
и прибавить его к другому столбцу,
то величина D(A) не изменяется.
(11.7)
Продолжим наш пример вычисления определителя. Мы
получили:
III 4 7\\ III 0 7-
D\\2 5 8 =£> 2 -3 8
\\3 6 9JJ \\3 -6 9,
Теперь 1-й столбец умножим на 7 и вычтем из 3-го, а затем 2-й
столбец умножим на 2 и вычтем из 3-го:
по свойству (11.1).

11.1. Аксиомы для определителей
551
Сделаем еще один пример.
D
= D
2-й столбец умножим на 2
и вычтем из 1-го
1-й столбец умножим на 2
и сложим со 2-м
= D I I — 1 0 ill 1-й столбец прибавим к 3-му
= D
2-й столбец умножим на 4
и вычтем из 3-го
= £) 11 — 1 0 0)1 воспользуемся аксиомой (11.1)
= -9D
3-й столбец умножим на 2
и вычтем из 2-го
= — 9D I I —1 0 Oil меняем местами 1-й и 2-й столбцы
= 9D [10 —1 Oil воспользуемся аксиомой (11.1)
= -9D
Если теперь использовать аксиому (11.3), то получаем

552
Глава 11. Определители
Заметим также, что из (11.7) следует (доказывается как в (11.5)),
что
перестановка двух любых столбцов изменяет знак D(A).
(11.8)
Можно также получить, что
если столбцы А линейно зависимы, то D(A)=0. (П-9)
Действительно, если \iA± + · · · + ХпАп = 0 и некоторое значение
\i φ 0, то можно разделить это соотношение на \ и получить
Ai-c\A\ спАп = 0, Cj = 0.
Поэтому вычитание с\А\ и т.д. из г'-го столбца не изменяет D(A)
(следствие (11.7)) и приводит к матрице с нулевым г-м столбцом.
Тогда вследствие (11.1) D(A) = 0. В частности, мы знаем, что
любые η векторов вида
//0\\
«2
\\anJJ
(с нулем в первой строке) линейно зависимы. Поэтому
если все элементы верхней строки матрицы А
равны нулю, то D(A) = 0.
Предположим, что хотя бы один элемент в верхней строке
матрицы А не равен нулю. Переставляя столбцы, если это надо,
всегда можно сделать так, что первый столбец имеет ненулевой
элемент в верхней строке. Следовательно,
D(A) = ±D{B), где Ьц^О.
Но тогда
D(B) = bnD(B'),
где для матрицы В' первый столбец В[ = (\/Ъ\{)В\.

11.1. Аксиомы для определителей
553
Умножая первый столбец на соответствующий коэффициент
и вычитая из остальных столбцов, можно сделать так, чтобы все
остальные элементы в первой строке были равны нулю, т. е.
где
(В') =
/ 1
Щ\
Wl
D(B"),
0 ... 0\
С
)
в" =
Рассмотрим D(B") как функцию матрицы С. Очевидно, что
аксиомы (ИЛ) и (11.2) удовлетворяются. Кроме этого, если бы С
была единичной матрицей (п—1)х(п — 1), мы могли бы, не
изменяя значения D(B"), сделать все элементы первого столбца Ь'^ъ
&31 и Т-Д- равными нулю (умножая остальные столбцы на
соответствующие множители и вычитая из первого). Например,
2-й столбец умножаем на 2
и вычитаем из 1-го
3-й столбец умножаем на 3
и вычитаем из 1-го
4-й столбец умножаем на 4
и вычитаем из 1-го

554
Глава 11. Определители
Другими словами, функция
D
(( 1
В2\
^W'i
0
С
0\\
//
как функция от С удовлетворяет всем аксиомам для
определителя матриц (п — 1) χ (η — 1). Следовательно,
D(B") = D(C),
где справа стоит £)-функция (если она существует) для матриц
(п - 1) χ (η - 1).
Еще раз повторив предыдущие рассуждения, мы приходим к
выводу, что или D{C) = 0 (если все элементы в первой строке
равны нулю) или D(C) можно выразить как £)-функцию матриц
(п — 2) χ (η — 2). И так можно спускаться, пока не дойдем до
матриц 1x1, для которых из аксиом (11.1) и (11.3) следует, что
D(a) = a(D(l)) = а.
Таким образом, мы доказали, что £)-функция, если она
существует, единственна, и получили правило для ее вычисления.
Например, пусть
/ 0 3 -1 4\
2 4 15
-4 7 2 8
\ 2 9 3 2/
Можно показать, что D(A) = —D(B), где
В =
/-1 3 0 4\
14 2 5
2 7-48
\ 3 9 2 2/

11.1. Аксиомы для определителей
555
а дальше получаем, что D(B) = —D(B"), где
В" =
( 1
-1
-2
О
7
13
\-3 18
Далее, D{B") = D(C), где
С =
Наконец,
D(C) = 2D
= -2D
= -2D
= -2D
= -2 · 27D
= -2 · 27D
1 3
11/27 I
1 О
11/27 5-34-11/27
= -2 · 27(5 - 34 · 11/27) = 478.
В следующем параграфе мы дадим другое доказательство
единственности D(A) и другой рецепт его вычисления. Но нам
еще надо показать, что D(A), удовлетворяющий условиям (11.1),
(11.2) и (П.З), существует.
Из приведенного способа вычисления определителя А можно
получить важное следствие. Предположим, что матрица А имеет

556
Глава 11. Определители
вид
(L Μ
где L есть матрица к х к, N — матрица (п — к) χ (η — fc) и Μ —
матрица, у которой fc строк и (п — к) столбцов. Другими
словами, предположим, что первые к столбцов матрицы А имеют нули
в последних η — к позициях. В этом случае первые к столбцов
матрицы А линейно зависимы или линейно независимы тогда и
только тогда, когда столбцы матрицы L линейно зависимы или
линейно независимы, т.е. последние η — к нулевых элементов не
влияют на линейную зависимость или независимость этих
столбцов. Если эти столбцы линейно зависимы, то
D(A) = 0 и D(L) = 0.
Если же они линейно независимы, то применяя вышеизложенный
метод, можно использовать первые к столбцов и заменить
матрицу Μ нулевой матрицей, не изменяя при этом элементы матрицы
N. В этом случае
Ό(θ %)=D(L)D(N). (11.11)
Эта формула является обобщением на пространство η
измерений формулы вычисления площади параллелограмма (рис. 11.1).
В двумерном случае мы получаем
Это ориентированная площадь параллелограмма, построенного
на векторах и ), причем она равна ориентированной
χ
площади параллелограмма, построенного на векторах
(Г
ν,
В трехмерном случае
= D[[Xy Uv))D{{r)),

11.2. Закон умножения и другие следствия аксиом 557
Рис. 11.1 Рис. 11.2
а интерпретация та же самая (рис. 11.2).
11.2. Закон умножения
и другие следствия аксиом
Рассмотрим еще некоторые следствия из свойства (11.8) о
перестановке двух столбцов определителя. Пусть {у\,..., νη) —
произвольная перестановка чисел (1,...,п). Возьмем определитель
матрицы с переставленными столбцами
и будем попарно переставлять их до тех пор, пока не вернемся к
исходному порядку. На каждом шаге будем применять свойство
(11.8) и придем к выводу, что
D{{AVl,...,AVn))=±D{{Al,...,An)),
(11.12)
где знак + или — не зависит от конкретных значений
матричных элементов матрицы А. Если (11.12) применить к единичной
матрице, то получим
D((I„1,...,Il/n)) = ±l
и, следовательно,
D((Avl,...,AVn)) = D((Ivl,...,IVn))D(A). (11.13)

558
Глава 11. Определители
Пусть В = ipij) — другая матрица η χ η и пусть
С = АВ.
Столбцы матрицы С равны
Ск = 6ifci4i + ЪъкМ Η l· bnkAn.
Для вычисления D{C) мы можем сначала применить (11.1) к
первому столбцу С и получить сумму некоторых слагаемых; потом
можно проделать то же самое со вторым столбцом, и так далее.
Например, в трехмерном случае
С\ = bUAl+h2A2 + bi3A3,
С2 = ЬиМ + Ь22А2 + &32^3,
С3 = 6l3-^l + Ь23А2 + Ь33А3
Тогда
D{CUC2,C3)
= bnD(AuС2,С3) + b21D(A2,C2, С3) + b31D(A3, C2, С3)
= bll{b12D{A1,Al,C3) + b22D{Al,A2,C3) + b32D{Al,A3,C3)}
+ b21{b12D(A2, АЪС3) + b22D{A2, A2,C3) + b32D{A2, А3, С3)}
+ b31{b12D{A3, Αλ, С3) + b22D(A3, А2, С3) + b32D{A3, А3, С3)}.
Прежде чем двигаться дальше, можно исключить слагаемые с
повторяющимися столбцами. Очевидно, что останутся только
выражения типа D((AU1,AU2, AU3)), а они в силу (11.12) равны ±D(A).
Таким образом, в общем случае мы видим, что
D{C) = D{A) Σ ±bwllbW22... bVnn, (11.14)
где берется сумма по всем перестановкам и знак ± соответствует
(11.12).
Предположим, что А = I. Из (11.14) следует, что С = В и
D(B) = Y^±bVll...bVnn. (11.15)
Таким образом, мы получили явный вид D(B), что еще раз
доказывает единственность определителя, если он существует. Если

11.2. Закон умножения и другие следствия аксиом 559
(11.15) подставить в (11.14), то получается важный закон
умножения определителей:
D(AB) = D(A)D(B). (11.16)
Каждый член в (11.15) содержит только один элемент из
каждой строки матрицы В. Поэтому
D(B) — линейная функция каждой строки
при фиксированных других строках.
Выведем еще одно свойство определителя, связанное с его
строками. Пусть для некоторого значения 1 < г < η матрица
А имеет вид
Ak = h, кфг,ъ + \,
А% = 1{ + Ц+1,
Ai+i = 0.
Например, для п=3иг = 2у нас была бы матрица
Заметим, что в матрице АВ все строки, кроме (г+1)-й, совпадают
со строками матрицы В, а (г + 1)-я строка заменена на г-ю. В
нашем примере мы получили бы
Ί 0 0\ /1 5 9\ /1 5 9^
0 1 02 6 8 = 2 6
^0 1 0/ \3 7 4/ \2 6 8у
Кроме того, D(A) = 0, потому что один столбец этой матрицы
нулевой. С помощью подобного построения можно прийти к
выводу, что
если В имеет две одинаковых соседних строки, то D(B) = 0.
(11.2')

560
Глава 11. Определители
Это значит, что Ώ(Βι) удовлетворяет аксиомам (11.1) и (11.2),
потому что замена В на транспонированную матрицу В1 приводит к
перестановке роли строк и столбцов. Поскольку £)(!*) = D(I) = 1,
то функция Ό{Βι) удовлетворяет аксиомам (11.1)—(11.3) и
вследствие единственности определителя должна совпадать с D(B).
Другими словами,
D(B*) = D(B). (11.17)
11.3. Существование определителя
Теперь, наконец, мы должны доказать существование
определителя, т. е. построить функцию матриц пх п, которая
удовлетворяет (11.1), (11.2) и (11.3)1.
Для η = 1 положим по определению D((a)) = а.
Для η = 2 определим D (I , )) = ad — be. Легко
проверить, что аксиомы (11.1)—(11.3) в этих случаях
выполняются. Предположим, что существуют определители матриц размера
(п — 1) χ (η — 1). Пусть А = (aik) — матрица пхп. Возьмем
некоторый матричный элемент а^ из г-й строки и fc-ro столбца.
Вычеркнем из матрицы А г-ю строку и к-й столбец. Теперь рассмотрим
определитель для получившейся матрицы (п — 1) χ (η — 1). Этот
определитель, умноженный на (— 1)г+к, называется
алгебраическим дополнением элемента а^ и обозначается А&. Знак (—\)г+к
распределен в шахматном порядке, а именно:
+ - + -
- + - +
+ - + -
- + - +
*На самом деле существование такой функции стало очевидным ранее,
когда была получена формула (11.15) — явное выражение D(B) через
элементы матрицы В. В этом параграфе приводится несколько других важных
понятий и формул: алгебраические дополнения и вычисление
определителей с их помощью, присоединенная матрица, способ нахождения обратной
матрицы. — Прим. ред.

11.3. Существование определителя
561
Пусть г — некоторое фиксированное число от 1 до п.
Рассмотрим следующую функцию D от матрицы А:
D = <щАц + ai2Ai2 -I \- ainAin. (11.18)
Ее структура — сумма произведений всех элементов г-й строки
на их алгебраические дополнения.
Рассмотрим зависимость D от заданного столбца, скажем, от
Ак- Для ν φ к Aiv зависит линейно от Ak, а а^ не зависит
от него; для ν — к А^ не зависит от Ak, но а^ является
элементом этого столбца, т. е. это слагаемое также линейно зависит
от столбца Ak- Таким образом, аксиома (11.1) выполняется.
Далее, предположим, что два соседних столбца А^ и Ак+\ равны.
Для ν φ к, к + 1 мы имеем два одинаковых столбца в AiV, т. е.
Aiu = 0. При вычислении А^ и Αι^+ι используются одинаковые
определители, но с противоположными знаками. Следовательно,
Aik = — Aifi+i, а α^ — difr+i- Таким образом, D — 0 и
выполняется аксиома (11.2). В частном случае Av = Iv (u = 1, 2,... , η) мы
имеем a,iv = 0 для ν φ г и ац = 1, Ац — 1. Следовательно, D = 1,
что означает выполнение аксиомы (11.3). Таким образом, мы
доказали существование определителя матрицы η χ η и выполнение
формулы (11.18), так называемое разложение определителя по
элементам г-й строки. Формулу (11.18) можно обобщить. В
определителе заменим г-ю строку на j-ю и разложим определитель
по этой новой строке. Для г\ф j определитель равен нулю, а для
г — j он равен D, т. е.
Г D i = г
щАц + aj2Ai2 + · · · + ajnAin = I Q ' -J. ' (11.19)
Если мы поменяем ролями строки и столбцы, то получим
Г D h — к
aihAik + a2hA2k ^ \-anhAnk = i ' ^ , fc' (11.20)
Составим из алгебраических дополнений элементов ац
матрицы А матрицу В = (Aji). (Обратим внимание, что алгебраическое
дополнение элемента ац, стоящего на пересечении г-й строки и
j-ro столбца, находится на пересечении j'-й строки и г-ro столбца.)

562
Глава 11. Определители
Матрица В называется присоединенной матрицей к матрице А.
Из уравнения (11.20) следует, что
АВ = В А = D(A)l.
Мы уже доказали, что если А сингулярна (столбцы А линейно
зависимы), то D(A) — 0. Если же D(A) φ 0, то предыдущее
уравнение дает формулу для А~1. Таким образом, мы доказали,
что
матрица А обратима
тогда и только тогда, когда D(A) φ 0.
Если D(A) φ 0, то Л-1 = jyjzB,
где В — матрица, присоединенная к матрице А
(Для η = 2 это правило совпадает с методом, изложенным
в главе 1.) При η > 2 это правило не очень удобно, лучше
использовать алгоритм, изложенный в главе 10. И тем не менее, эта
формула важна с теоретической точки зрения. Например, она
показывает, что все элементы матрицы А"1 являются частным от
деления полинома от матричных элементов А на определитель.
Резюме
А. Определители
Вы должны знать аксиомы для определителей и пользоваться
этими аксиомами для вычисления определителей.
Вы должны уметь вычислять определители с помощью
алгебраических дополнений.
Вы должны знать и уметь применять метод вычисления
обратной матрицы для несингулярной квадратной матрицы.
Задачи
Напишите несколько матриц размера ЗхЗи4х4и вычислите
для них определители. Вы увидите, что уже для случая 4x4
(11.21)

Задачи
563
выражения (11.15) и (11.18) становятся очень громоздкими (при
вычислении по формуле (11.15) приходится выполнить 3-4!
умножений и 4! — 1 сложений). А вот метод, описанный в параграфе
11.1, вполне приемлем. Ниже даются определители, для которых
надо проверить ответы.
(а)
Det
= -2.
(Ь)
Det
= 12.
(с)
Det
(d)
Det
/11 1 1
2 3 5 6
4 9 25 36
\8 27 125 216,
72.
11.1. Обобщая пример (Ь), покажите, что
Det
'Γι α α α\
b Γ2 α α
b b гз α
b b b Γ4 /
bf(a) - af(b)
, если афЪ,
где f(x) = (γι - ж)(г2 - x)(r3 - ж)(г4 - ж).

564
Глава 11. Определители
Указание: рассмотрите определитель матрицы, выписанной
ниже, его значение обозначим F(x):
Ь —χ у4 — χ )
F(x) линейно зависит от х, потому что мы можем вычесть первую
строку из остальных, исключив χ из всех строк, кроме первой.
Следовательно,
F(x) = А + Вх,
где А и В — некоторые постоянные. При этом F(a) = /(α)
и F(b) = f(b). Наш исходный определитель, очевидно, равен
F(0) = А. Чему он будет равен при а = Ы
11.2. Обобщая пример (с), покажите, что
Dethr „ h h =(a-x)(b-y)(c-z).
11.3. Обобщая пример (d), покажите, что
1 1 1 1\
= (у - x)(z - x)(w - x)(z - y)(w - y)(w - ζ).
χ у ζ w
χ2 у2 ζ2 w2
с3 у3 ζ3 w3 /
Выпишите и докажите соответствующую формулу, если число 4
заменить на п.
11.4. Покажите, что
|Det(Ai,...,An)| < ||Λι|| ■ · · ||Λη||.
Когда будет равенство?
Указание: воспользуйтесь интерпретацией | Det | как объема.
11.5. Покажите, что если О — ортогональная матрица (т.е. ОО* = I),
то Det О = ±1.
11.6. Матрица R будет матрицей вращения, если RR* = I и Deti? =
+ 1. Покажите, что вращение в пространстве нечетного числа
измерений всегда сохраняет неподвижным по крайней мере один
ненулевой вектор, т. е. число 1 является собственным значением
матрицы R. Указание: рассмотрите определитель Det(i? — I).

Рекомендуемая литература
В конце тома мы даем короткий перечень книг, не
являющийся, конечно, библиографией. Это скорее дополнительная
литература, полезная студентам, изучающим наш курс. Книгу LOOMIS
and Sternberg можно считать параллельным учебником, хотя
изложение материала более формально и абстрактно, с акцентом
на математические доказательства. Содержание, по существу,
такое же, как и в нашей книге, но гораздо больше внимания
уделяется формальным определениям, строгой аргументации и
математической изощренности. Во втором томе мы несколько раз
будем отсылать читателя к этой книге за детальным
доказательством некоторых ключевых теорем.
В данной книге одним из главных разделов математики
является линейная алгебра. Поэтому мы рекомендуем
классический учебник HALMOS, где имеется уклон к расширению
конечномерной теории в направлении гильбертова пространства. Книга
Lang обсуждает этот предмет с точки зрения абстрактной
алгебры, в то время как в книге STRANG акцент делается на
вычислительной технике и приложениях, которые мы здесь почти
не рассматриваем. Чтобы получить полное представление о
линейной алгебре, правильная стратегия — прочитать все три эти
книги.
В главе 1 мы обсуждаем геометрию прямых. Далее,
естественный шаг — проективная геометрия. Мы немного говорим о ней в
добавлении к главе 1 и в задачах 1.16-1.20. В книге HARTSHORNE
дается введение в проективную геометрию.

566
Рекомендуемая литература
В конце главы 2 мы только слегка касаемся теории
вероятностей. Этот важный раздел не получил серьезного обсуждения,
что является одним из главных наших пробелов. Хорошее
введение в теорию вероятностей без математических сложностей
читатель может найти в трех томах HOEL, PORT AND Stone.
Теория вероятнотей легко приводит к довольно изощренной
математической «кухне», например, к теории меры и тонким
вопросам Фурье-анализа. Достоинством этих книг является изложение
важных идей без глубокого погружения в трудную математику.
Книга MORAN уже сложнее для чтения, но на нее стоит
потратить усилия. В книге KEMENY AND Snell обсуждаются
конечные цепи Маркова, и ее следует читать как продолжение главы 2.
Книга Doyle and Snell дает краткое введение и в теорию цепей
Маркова, и в теорию сетей, которые мы будем изучать во втором
томе.
В главе 3 мы даем начальные сведения о дифференциальных
уравнениях. Учебник HlRSCH AND Smale здесь будет вполне
естественным, так как наши точки зрения довольно близки.
Книга BRAUN излагает материал более стандартно. (Экспонента от
матрицы появляется там только на с. 321!) Однако, ее следует
прочитать, поскольку в ней есть много полезных деталей и
приложений. Книга Simmons довольно традиционная, но в ней много
интересной исторической информации. Две классические книги
АРНОЛЬДА очень приятно читать. Во взаимодействии геометрии
и анализа видна уверенная рука крупного специалиста в этом
вопросе.
В главе 4 два параграфа посвящены теории относительности.
На эту тему мы рекомендуем три книги. Во-первых, большая и
сложная, богатая идеями книга Misner, ThOrne and Wheeler.
Во-вторых, короткая, захватывающая, с минимумом
математики книга Taylor and Wheeler. И, наконец, книга Spacetime,
Geometry, Cosmology, написанная Burke, обсуждает
математические идеи, которые мы пытаемся объяснить в нашей книге, и
дает прекрасное изложение физики относительности.
Другая книга BuRKE вместе с книгами FLANDERS и SPIVAK
могут быть рекомендованы как параллельное и дополнительное
чтение.

Рекомендуемая литература
567
В главе 6 и потом еще раз в параграфе 10.9 мы касаемся
вопросов, относящихся к курсу дифференциальной топологии.
Книга Guillemin AND Pollack написана как лекционный курс, в
котором, помимо формального изложения теории, автор
использует интуитивный подход и много рисунков. А вот книга BrOCKER
and Lander совсем другая. В ней минимум обсуждений, а
главным образом точные формулировки теорем и доказательств. И,
конечно, ее непросто читать. Эти книги посвящены несколько
различным проблемам, и поэтому мы рекомендуем изучить обе.
АРНОЛЬД В. И. Обыкновенные дифференциальные уравнения. — М.:
Наука, 1984 (3-е изд.).
Арнольд В. И. Дополнительные главы теории обыкновенных
дифференциальных уравнений. — М.: Наука, 1978.
Braun Μ. Differential Equations and their Applications. An Introduction
to Applied Mathematics. — New York: Springer-Verlag, 1993 (4th ed.).
Brocker Th. and Lander L. Differentiable Germs and Catastrophes. —
Cambridge, UK: Cambridge University Press, 1975. (London Mathematical
Sociaty Lecture Note Series, 17.)
Burke W.L. Spacetime, Geometry, Cosmology. A Series of Books in
Astronomy. — Mill Valley, CA: University Science Books, 1980.
Burke W.L. Applied Differential Geometry. — Cambridge, UK:
Cambridge University Press, 1985.
Doyle P.G. and Snell J. L. Random Walks and Electric Networks.
— Washington, DC: Mathematical Association of America, 1985. (Carus
Mathematical Monographs, 22.)
Feynman R. P., Leighton R. B. and Sands M. The Feynman Lectures
on Physics. Vol. 1-3. - Reading, MA: Addison-Wesley, 1963-1965.
Русский перевод: Фейнман Р. П., Лейтон Р. Б. и Сэндс М. Фейн-
мановские лекции по физике. Вып. 1-9. — М.: Мир, 1965-1967.
Flanders Η. Differential Forms with Applications to the Physical
Sciences. — New York: Dover, 1989 (2nd ed.). (Dover Books on Advanced
Mathematics.)
Guillemin V. W. and Pollack A. Differential Topology. — Englewood
Cliffs, NJ: Prentice-Hall, 1974.
Guillemin V. W. and Sternberg S. Symplectic Techniques in Physics.
— Cambridge, UK: Cambridge University Press, 1984 (2nd ed.).

568
Рекомендуемая литература
Halmos P. F. Finite-Dimensional Vector Spaces. — New York: Springer-
Verlag, 1974 (reprint of the 1958 2nd edition). (Undergraduate Texts in
Mathematics.)
Русский перевод: Халмош П. Конечномерные векторные
пространства. — М.: Физматгиз, 1963; Ижевск: РХД, 2002.
Hartshorne R. Foundations of Projective Geometry. Lecture Notes,
Harvard University, 1966/67. — New York: W. A. Benjamin, 1967.
Hirsch M. W. AND SmaleS. Differential Equations, Dynamical Systems
and Linear Algebra. — New York: Academic Press, 1974. (Pure and Applied
Mathematics, 60.)
Hoel P.G., Port S.C. and Stone C.J. Introduction to Probability;
Introduction to Statistical Theory; Introduction to Stochastic Processes. —
Boston, MA: Houghton Mifflin, 1971; 1971; 1972. (The Houghton Mifflin
Series in Statistics.)
Kemeny J. G. and Snell J.L. Finite Markov Chains. — New York:
Springer-Verlag, 1976 (reprint of the 1960 original). (Undergraduate Texts
in Mathematics.)
LANG S. Linear Algebra. — New York: Springer-Verlag, 1987 (3rd ed.).
(Undergraduate Texts in Mathematics.)
Loomis L. H. AND Sternberg S. Advanced Calculus. — Boston, MA:
Jones and Bartlett, 1990 (revised ed.).
Misner С W., Thorne K. S. and Wheeler J. A. Gravitation. — San
Francisco, CA: W. H. Freeman, 1973.
Русский перевод: Мизнер Ч., Торн К. и Уилер Дж. Гравитация.
Т. 1-3. - М.: Мир, 1977.
Moran P. A. P. An Introduction to Probability Theory. — Oxford:
Clarendon Press, 1968; corrected reprint 1984.
Simmons G. F. Differential Equations with Applications and Historical
Notes. — New York: McGraw-Hill, 1972. (International Series in Pure and
Applied Mathematics.)
Spivak M. Calculus on Manifolds. A Modern Approach to Classical
Theorems of Advanced Calculus. — New York: W. A. Benjamin, 1965.
Strang G. Linear Algebra and its Applications. — New York: Academic
Press, 1980 (2nd ed.).
Русский перевод: Стрэнг Г. Линейная алгебра и ее применения. — М.:
Мир, 1980.
Taylor Ε. F. and Wheeler J. A. Spacetime Physics. — New York:
W.H. Freeman, 1992 (2nd ed.).

Предметный указатель
1-форма, см. дифференциальная
форма линейная
2-форма, 386, 412
4-импульс, 228
—, закон сохранения, 229
А
аберрация, 436
— сферическая, 437
абсолютная константа, см.
скорость света
алгебра матриц (и линейных
преобразований), 34
алгебраическое дополнение
элемента матрицы, 560
аннулятор (аннулирующее
пространство), 492
аффинная плоскость, 2
аффинное преобразование, 23
аффинное пространство
(ассоциированное с векторным
пространством), 12
Б
базис, 14, 55, 488
— дуальный, 491
— ортонормированный, 177
базисы
— подобные, 398
— противоположные, 398
биения, 194
билинейная функция,379
близнецов парадокс, 217
борновское разложение, 270
В
вариация постоянных, 149
ведущий элемент строки матрицы,
507
вектор
— касательный, 286
— энергии-импульса, см. 4-импульс
векторное пространство, 6, 10, 476
—, базис, 488
— двумерное, 55
— дуальное, 479
— касательное, 290
—, натянутое на множество
векторов, 484
— одномерное, 13
—, подпространство, 480
—, размерность, 486
— симплектическое, 461
внешнее произведение (1-форм),
383
внешняя производная (от
1-формы), 379
время
— истинное (по Ньютону), 15
— собственное, 372
вынужденные колебания, 148
—, резонанс, 154
вырожденная матрица, см.
линейное преобразование
сингулярное

570
Предметный указатель
Г
Галилея преобразование, 221
Гамильтона теорема, 452
Гамильтона уравнения, 452
Гамильтона—Кэли теорема, 86
гауссово разложение, 448
гессиан, 313
гиперболические синус и косинус,
213
главные плоскости, 448
Грама-Шмидта процесс, 176
граница области, 415
Грина формула, 415
д
движение евклидово, 213
детерминант, см. определитель
дефект линейного преобразования,
503
дискриминант квадратичной
формы, 184
дифракция, 434
дифференциал, 250, 254
дифференциальная форма
— замкнутая, 367, 385
— линейная (1-форма), 277
— степени 2 (2-форма), 386, 412
— точная, 363
дифференциальное уравнение
—, интегральная кривая, 135
— Лапласа, 317
— линейное неоднородное, 148
, установившееся решение, 152
— линейное однородное, 125
, начальные условия, 128
, общее решение, 127
—, фазовый портрет, 135
дифференцируемое отображение,
250
—, регулярная точка, 524
—, сохраняющее ориентацию, 401
длина
— вектора, 166, 371
лоренцева, 372
— кривой, 372
— оптическая, 452
дуальное пространство, 479
дуальный базис, 491
Ε
евклидова плоскость, 165
евклидово преобразование, 23, 166
единичная матрица, 35
3
закон
— Кеплера второй, 274
— сложения скоростей, 214
— Снеллиуса, 436
линеаризованный, 442
— сохранения
4-импульса, 229
углового момента, 273
— умножения определителей, 559
затухание
— апериодическое, 146
— критическое, 145
И
изоморфизм векторных
пространств, 14, 56
индекс строки матрицы, 507
интеграл
— двойной
абсолютный (первого рода),
391
от 2-формы (второго рода),
389
— криволинейный
абсолютный (первого рода),
371
от 1-формы (второго рода),
355
— несобственный, 428
интерференция, 435
К
каноническое преобразование, см.
симплектическое отображение
касательное пространство, 290

Предметный указатель
571
касательный вектор, 286
квадратичная форма, 184
квадратичная функция, 191
Кеплера закон второй, 274
коаксиальный луч, 438
коммутатор пары матриц, 271
композиция отображений, 20
конформная матрица, 80
Коши-Шварца неравенство, 233
коэффициент (показатель)
преломления, 436
кривизна, 441, 443
Л
Лагранжа множитель, 318
Лапласа уравнение, 317
лапласиан, 317
Лежандра полиномы, 180
Лейбница формула (производная
произведения функций), 263
лемма Морса, 339
линейная зависимость векторов, 9,
47, 483
линейное преобразование, 28, 57
—, изменяющее ориентацию, 401
— конформное, 77
— Лоренца, 210
собственное, 209
—, матрица, 29
—, норма, 308
— ортогональное, 166
— регулярное (несингулярное), 28
— симплектическое, 231, 460
— сингулярное, 28
— скорости, 221
— сопряженное, 526
—, сохраняющее ориентацию, 400
— транспонированное, 183
линза
— тонкая, 443
—, фокальные плоскости, 445
—, фокусное расстояние, 444
Лоренца преобразование, 210
— собственное, 209
Μ
Маркова процесс, 93
—, матрица вероятностей перехода,
95
масса покоя, 228
матрица
—, ведущий элемент строки, 507
— вероятностей перехода (в
процессе Маркова), 95
— вращения, 564
— Гессе, 313
— единичная, 35
— замены базиса, 58, 490
—, индекс строки, 507
— конформная, 80
— линейного преобразования, 29
, зависимость от базиса, 29
— обратная, 45
—, определитель, 549
— оптическая
гауссово разложение, 448
общего вида, 448
преломления, 442
распространения, 441
— ортогональная, см. линейное
преобразование ортогональное
— присоединенная,562
—, редукция по строкам, 506
— симплектическая, см. линейное
преобразование
симплектическое
— сингулярная (вырожденная), см.
линейное преобразование
сингулярное
— транспонированная, 183
—, функция от, 115
— Якоби, 303, 407
метод
— вариации постоянных, 149
— Гаусса, см. редукция по строкам
— множителей Лагранжа, 317
— Ньютона, 323
— Пикара, 325
Минковского расстояние, 216
Морса лемма, 339
Муавра теорема, 81

572
Предметный указатель
Η
неравенство
— Коши-Шварца, 233
— треугольника, 216
обратное, 217
нильпотент, 54
норма линейного преобразования,
308
нормальные колебания, 192
нулевой вектор, 9
нулевой конус, см. световой конус
Ньютона метод, 323
Ньютона уравнение (оптическое),
450
Ньютона-Лейбница формула, 362,
415
О
область абсолютного будущего, 208
образ линейного преобразования,
51, 502
образ отображения, 18
обратная матрица, 45
обратное отображение, 19
определитель (детерминант), 42,
549
оптика
— волновая (теория Френеля), 434
— гауссова, 437
— геометрическая, 436
— линейная, 436
оптическая ось, 438
оптическая сила, 443
ориентация
— векторного пространства, 399
— области (на плоскости), 389, 416
— параллелограмма, 387
— поверхности (в пространстве),
391
— траектории, 351
ориентированная площадь
(параллелограмма), 387
ориентированный объем (гг-мерного
параллелепипеда), 547
ортогональная проекция, 179, 235
ортогональное преобразование, 166
ортогональность векторов, 166
ортонормированный базис, 177
ортонормировочная процедура, см.
Грама-Шмидта процесс
осциллятор
— без затухания, 144
— с затуханием, 145
отображение, также функция,
оператор, преобразование, 18
— аффинное, см. аффинное
преобразование
— биективное, 19
— дифференцируемое, 250
, регулярная точка, 524
, сохраняющее ориентацию, 401
— евклидово, см. евклидово
преобразование
— инъективное, 19
— линейное, см. линейное
преобразование
— обратное, 19
— ограниченное, 250
— симплектическое, 467
— сюръективное, 19
Π
параметризация траектории, 352
перенос (pullback)
— 2-формы, 402
— функции, 291
перпендикулярность, см.
ортогональность векторов
Пикара метод, 325
плоскость
— аффинная, 2
— проективная, 72
плотность (распределение по
площади), 393
подмногообразие векторного
пространства, 523
подпространство векторного
пространства, 480
показатель преломления, 438
поляризация света, 436
полярные координаты, 291, 370
приближение Борна (первое), 270

Предметный указатель
573
принцип Ферма (наименьшего
времени), 457
присоединенная матрица, 562
проективная плоскость, 72
проекция, 52
— ортогональная, 179, 235
произведение матриц, 31
производная
— внешняя (от 1-формы), 379
— многомерная (отображения
векторных пространств), см.
также дифференциал, 247
— по направлению, 288
— произведения функций, см.
Лейбница формула
— смешанная (вторая), 282
— частная, 275
пространство-время, 205
противоположный вектор, 10
процесс
— Грама-Шмидта, 176
— Маркова, 93
, матрица вероятностей
перехода, 95
Пуанкаре преобразование, 213
Ρ
работа силового поля, 349
равномерная дифференцируемость,
326
разложение
— борновское, 270
— гауссово, 448
размерность векторного
пространства, 486
ранг линейного преобразования,
503
расстояние Минковского, 216
регулярная точка
(дифференцируемого
отображения), 524
редукция по строкам, 506
резонанс, 154, 194
ряд степенной, 116
— сходящийся, 118
абсолютно, 119
С
световой конус, 210
силовое поле, 348
—, работа, 349
симплектическая группа, 232, 461
симплектическая форма, 461
симплектическое векторное
пространство, 461
симплектическое отображение, 467
сингулярная (вырожденная)
матрица, см. линейное
преобразование сингулярное
скалярное произведение, 167
— евклидово, 175
—, свойства, 169
— симплектическое, 231
скорости преобразование, 221
скорость света, 206
сложения скоростей закон, 214
смещение, см. трансляция
аффинная
Снеллиуса закон, 436
— линеаризованный, 442
собственное время, 372
собственное значение, 82
собственный вектор, 82
сопряженное отображение, 526
сопряженные плоскости, 443
специальная теория
относительности, 206
Τ
Тейлора формула (многомерная),
311
телескоп астрономический, 447
теорема
— Гамильтона, 452
— Гамильтона-Кэли, 86
— Грина, см. Грина формула
— коэффициентов Морзе, 457
— Муавра, 81
— о неявной функции, 334
— о постоянном ранге, 517
— о ранге и дефекте, 503
— о среднем значении, 305

574
Предметный указатель
многомерная (неравенство),
309
— об обратной функции, 332
тонкая линза, 443
точечная характеристика
(оптической системы), 452
траектория
— кусочно-дифференцируемая, 352
— ориентированная, 351
—, параметризация, 352
трансляция аффинная, 6, 25
транспонирование, 183
У
увеличение
— линзы,446
— телескопа угловое, 447
угловой момент, 272
—, закон сохранения, 272
угол между векторами, 167
умножение матриц, 31
уравнение
— дифференциальное, см.
дифференциальное уравнение
— Лапласа, 317
— Ньютона (оптическое), 450
— характеристическое, 83
уравнения Гамильтона, 452
условный экстремум, 317
Φ
факторпространство, 497
Ферма принцип (наименьшего
времени), 457
фокальные плоскости, 445
фокусное расстояние, 444
формула
— Грина, 415
— Лейбница (производная
произведения функций), 263
— Ньютона-Лейбница, 362, 415
— Тейлора (многомерная), 311
функция
— билинейная, 379
— квадратичная, 191
— от матрицы, 115
X
характеристический полином, 83
характеристическое уравнение, 83
ц
цепное правило, 256
Ч
частная производная, 275
Э
эйконал, см. точечная
характеристика
энтропия, 343
Я
ядро линейного преобразования,
52, 502
якобиан, см. матрица Якоби