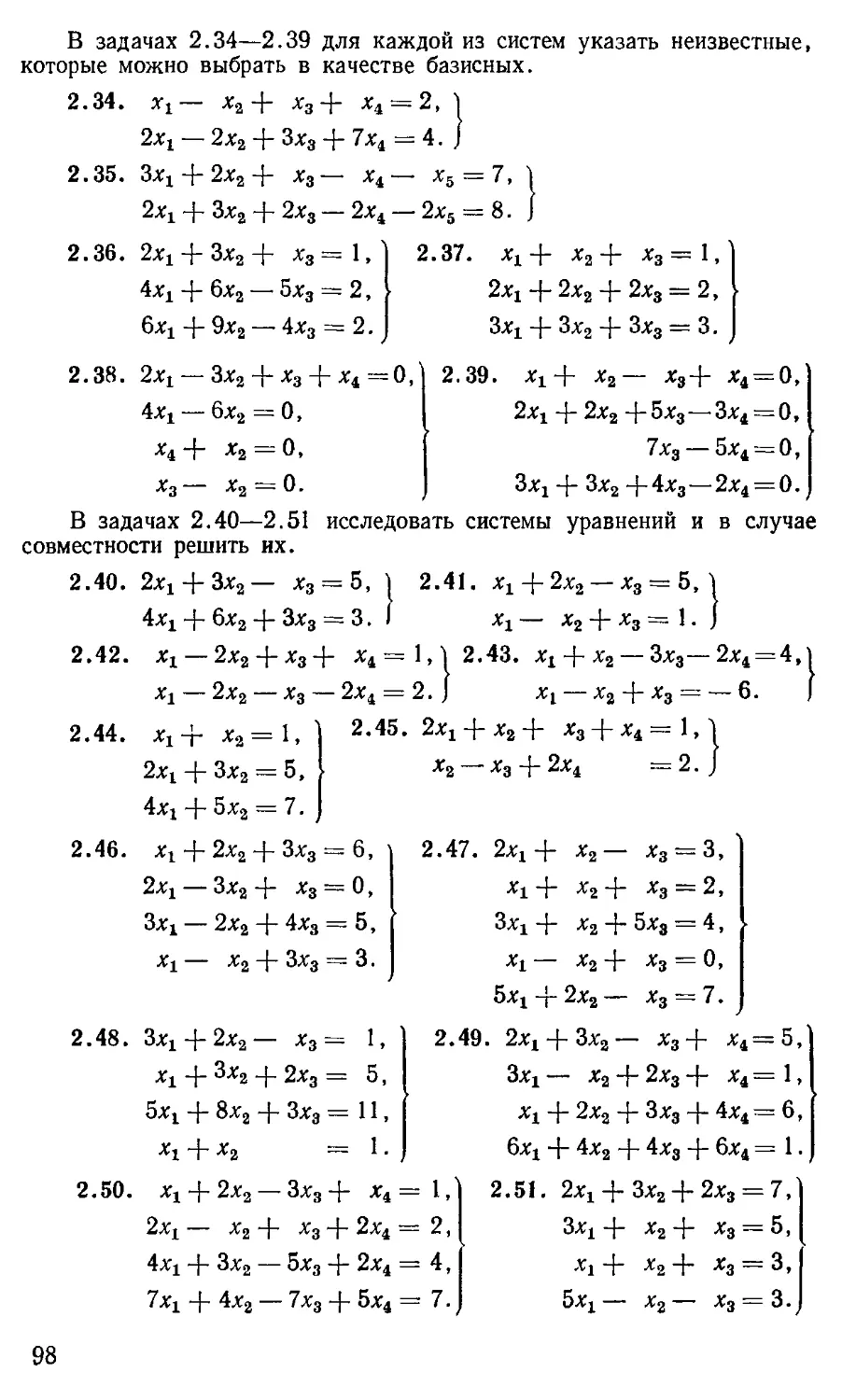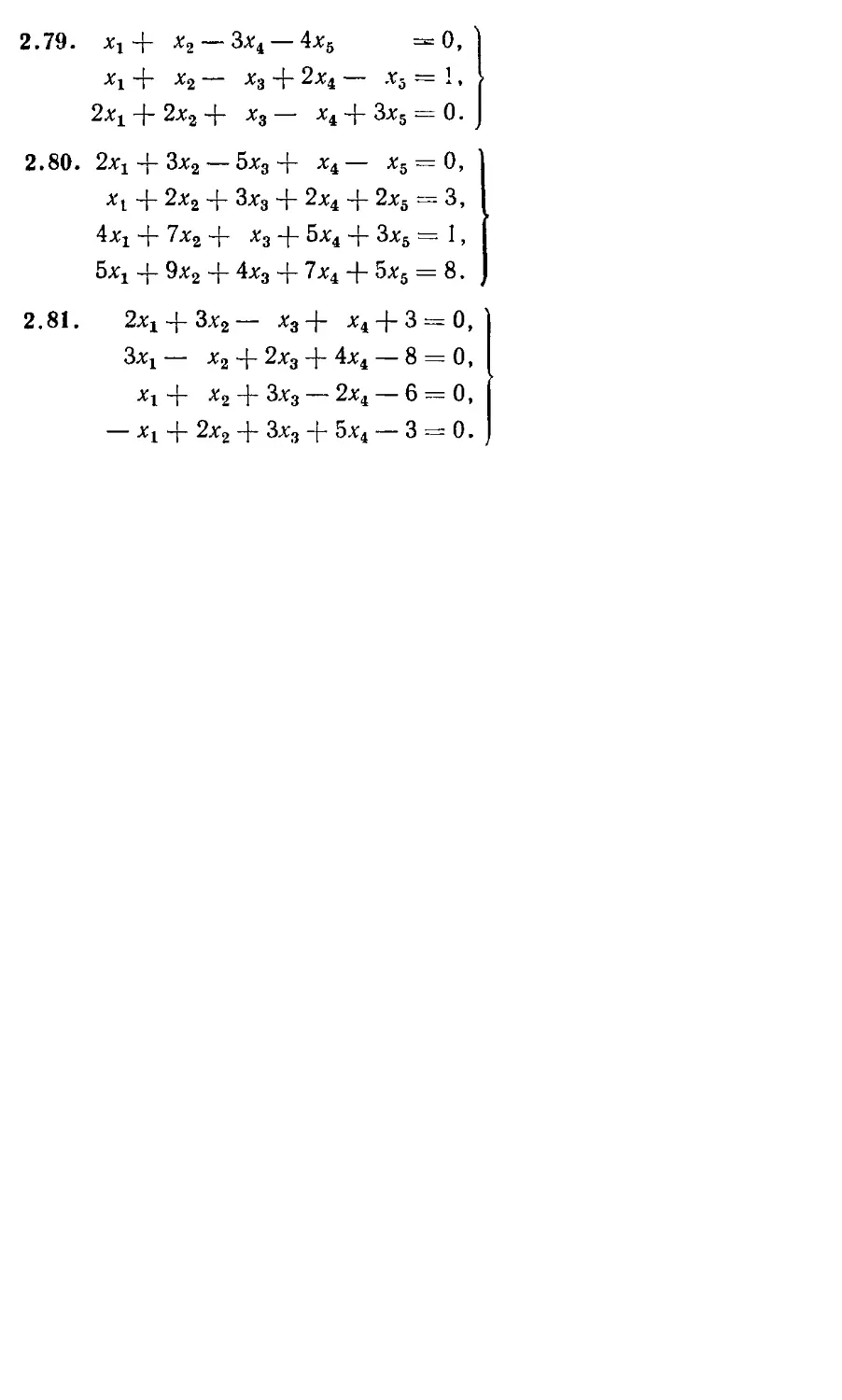ЭЛЕМЕНТЫ
ЛИНЕЙНОЙ
АЛГЕБРЫ

ЭЛЕМЕНТЫ
ЛИНЕЙНОЙ
АЛГЕБРЫ
Под общей редакцией Р. Ф. Апатенок
Допущено Министерством высшего и среднего спе-
специального образования БССР в качестве учебного по-
пособия для студентов инженерно-технических специ-
специальностей высших учебных заведений
-¦-
МИНСК
«ВЫШЭЙШАЯ ШКОЛА»
1977

517.1
Э45
УДК 512.8@75.8)
Рецензенты:
кафедра высшей математики Кишиневского политехнического
института им. С. Лазо и канд. физ.-мат. наук, доц. кафедры
высшей математики Белорусского института инженеров желез-
железнодорожного транспорта В. Г. Виляцер
Элементы линейной алгебры. Под общ. ред.
345 Р- Ф- Апатенок. Мн., «Вышэйш. школа», 1977.
256 с. с ил.
На обороте тит. л. авт.: Р. Ф. Апатенок, А. М. Маркина,
Н. В. Попова, В. Б. Хейнман
В учебном пособнн излагаются все вопросы раздела «Линейная
алгебра», предусмотренные программой курса «Высшая математика»
для инженерно-технических специальностей вузов. Содержится большое
количество задач для самостоятельного решения.
Пособие предназначено для студентов инженерно-технических спе-
специальностей вузов,
20203—177 ,,,,
Э М304@5)-77 30~77 5ПЛ
© Издательство «Вышэйшая школа», 1977 г.
Рогнеда Федоровна Апатенок, Александра Матвеевна Маркина, На-
Наталья Васильевна Попова, Валентина Борисовна Хейнман
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ. Под общей редакцией
Рогнеды Федоровны Апатенок
ИБ № 296
Редактор Е. В. Сукач. Мл. редактор Т. С. Канцлер. Худож. редактор А. Н. Зво-
нарёв. Техн. редактор П. В. Фрайман. Корректор А. П. Берлина.
Сдано в набор 15/VI-1977 г. Подписано к печати 21/XI 1977 г. Бумага 84Х108'/з2.
тип. № 1. Печ. л. 8 A3,44). Уч.-нзд. л. 13,41. Изд. № 75-212. Тип. зак. 311,
Тираж 15 000 экз. Цена 65 коп..
Издательство «Вышэйшая школа» Государственного комитета Совета Минист-
Министров БССР по делам издательств, полиграфии и книжной торговли. Редакция
литературы по математике, физике и энергетике. 220004. Минск, Парковая
магистраль, 11. Ордена Трудового Красного знамени типография ЦК КП
Белоруссии. Минск, Ленинский пр., 79.

ПРЕДИСЛОВИЕ
В последние годы существенно воз-
возросла роль линейной алгебры в различ-
различных разделах математики и техники. Это
нашло отражение в новой программе по
курсу высшей математики для втузов, в
которой значительно расширен раздел
линейной алгебры.
Настоящее учебное пособие предна-
предназначено для студентов технических вузов
всех специальностей. В нем содержатся
все вопросы раздела «Линейная алгебра»,
предусмотренные программой курса
«Высшая математика» для инженерно-
технических специальностей высших
учебных заведений, рассчитанной на
510 часов. Пособие может быть исполь-
использовано аспирантами инженерно-техниче-
инженерно-технических специальностей втузов, а также сту-
студентами не математических факультетов
университетов.
Учебное пособие содержит пять глав:
«Матрицы и определители», «Системы
линейных уравнений», «Линейные про-
пространства», «Линейные преобразования»,
«Квадратичные формы». В каждой главе
имеется достаточное количество задач и
примеров для самостоятельного решения,
снабженных ответами. Таким образом,
данное пособие может быть использовано
и в качестве задачника.

При написании данной книги авторы
основывались на написанных ими посо-
пособиях, изданных в Белорусском политех-
политехническом институте («Матрицы и систе-
системы линейных уравнений», 1971, «Линей-
«Линейные пространства», 1973, «Квадратичные
формы», 1973, «Канонические формы мат-
матриц», 1974, «Задачник по линейной алгеб-
алгебре», 1975), которые в течение ряда лет
используются студентами Белорусского
политехнического института и некоторых
не математических факультетов Белорус-
Белорусского государственного университета.
Авторы выражают искреннюю благо-
благодарность доценту кафедры высшей мате-
математики Кишиневского политехнического
института им. С. Лазо, канд. физ.-мат.
наук П. К- Осматеску и доценту кафедры
высшей математики Белорусского инсти-
института инженеров железнодорожного транс-
транспорта, канд. физ.-мат. наук В. Г. Виляце-
ру, сделавшим ряд ценных замечаний
при рецензировании пособия, а также
К- Ф. Беганской, Н. В. Мадорской,
И. Я. Скорикову и Н. Ф. Юранову за по-
помощь, оказанную при оформлении ру-
рукописи.
Все отзывы и пожелания просим при-
присылать по адресу: 220004, Минск, Парко-
Парковая магистраль, 11, Дом книги, издатель-
издательство «Вышэйшая школа».
Авторы

Глава 1
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
§ 1.1. Матрицы. Основные определения
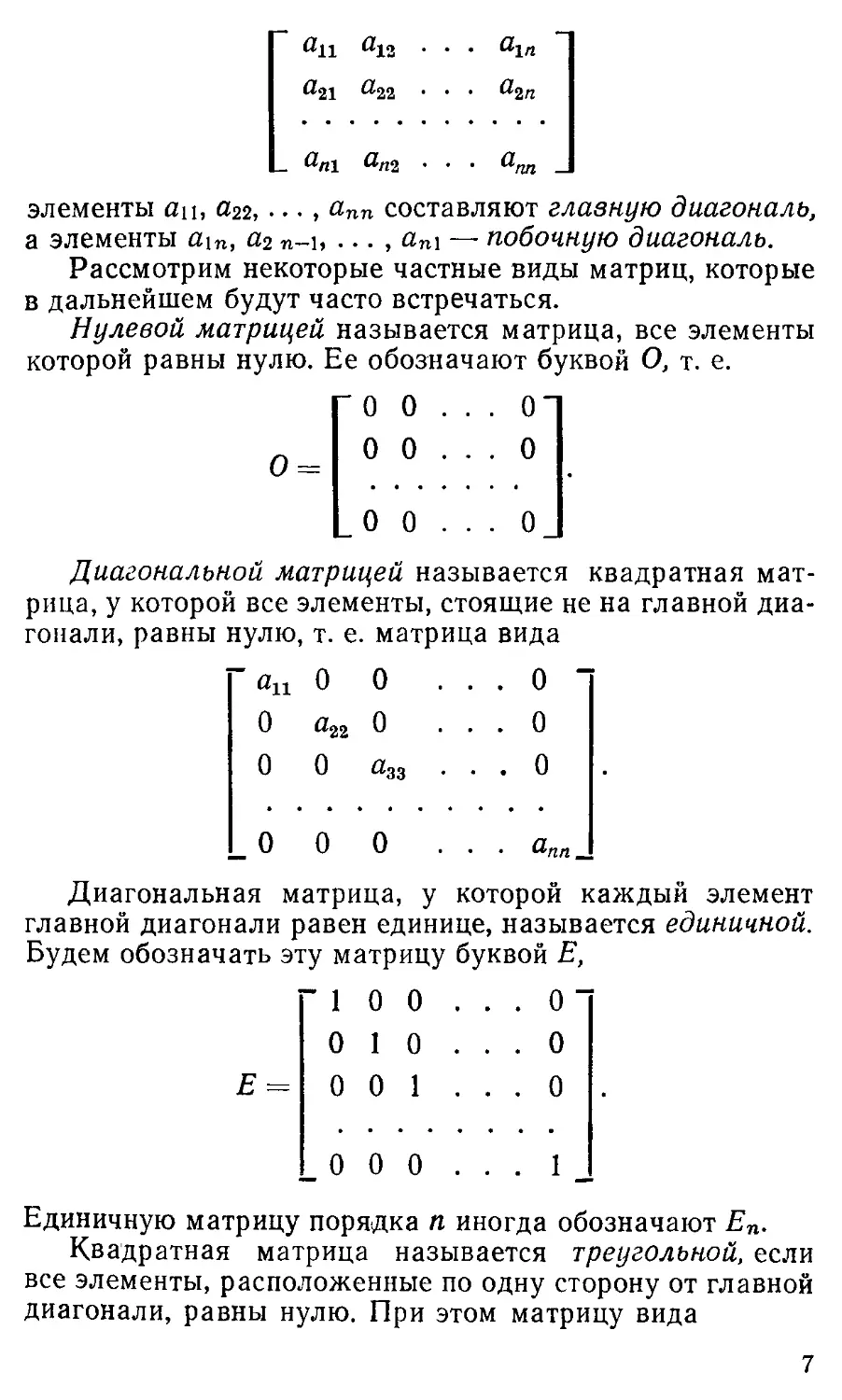
Рассмотрим прямоугольную таблицу из тп чисел:
ап я12 . . . аы
#21 #22 • • • ®гп
«ml «m2
#„
Эта таблица называется матрицей (точнее, числовой мат-
матрицей) размеров пгХп (пг на п). Для матрицы размеров
тХп обычно употребляются следующие обозначения:
ап а12
/«11
I «21
\« 1
~«11
«21
-«ml
«12
«22
«m2
«12
«22
«m2
(X
• • • «m«/
• • • «in
... a2n
• • • amn-
\
\
1
: (
«ml «m2
t = l, 2, ... , т;
] — 1, z, . .. , п.
Иногда матрицу обозначают одной буквой, например
•42
#<.. #«
«1
a»
L"ml
Если хотят указать размеры матрицы, то пишут АтХп-
Числа, из которых составлена матрица, называются
элементами матрицы.

Если все элементы матрицы—вещественные (действи-
(действительные) числа, то матрица называется вещественной.
Элементы аи, ai2, ..., ain составляют 1-ю строку, а эле-
элементы ац, a2j, . •. , ami — /'" столбец матрицы; ац — эле-
элемент матрицы, который находится в t-й строке и ;-м
столбце.
Матрица, состоящая из одной строки, называется
матрицей-строкой или строчной матрицей. Такая матрица
имеет вид
[ап ai2
Матрица
¦41
состоящая из одного столбца, называется матрицей-
столбцом или столбцевой матрицей.
Строки и столбцы матрицы называют ее рядами. Под
двумя параллельными рядами будем понимать две стро-
строки или два столбца матрицы.
Две матрицы называются равными, если они одина-
одинаковых размеров и элементы одной матрицы равны соот-
соответствующим элементам другой. Таким образом, АтХп =
= BpXk, если т = р, п = k и а,, = Ьи («=1,2 т;
/=1, 2, .... я).
Матрица, у которой число строк равно числу столбцов
(т = п), называется квадратной. Порядком квадратной
матрицы называется число ее строк (или столбцов).
Матрицы
[Oil.
«12 1
«22 J
«U
«21
«31
«12
«22
«32
«13
«23
«33
являются квадратными матрицами соответственно первого,
и третьего порядков.
Будем говорить, что в квадратной матрице
второго

an a12
«21 «22
L ««I
а„
элементы йц, агг, • • • , ^nn составляют глазную диагональ,
а элементы йщ, «2 п-ь ... ,ап\ — побочную диагональ.
Рассмотрим некоторые частные виды матриц, которые
в дальнейшем будут часто встречаться.
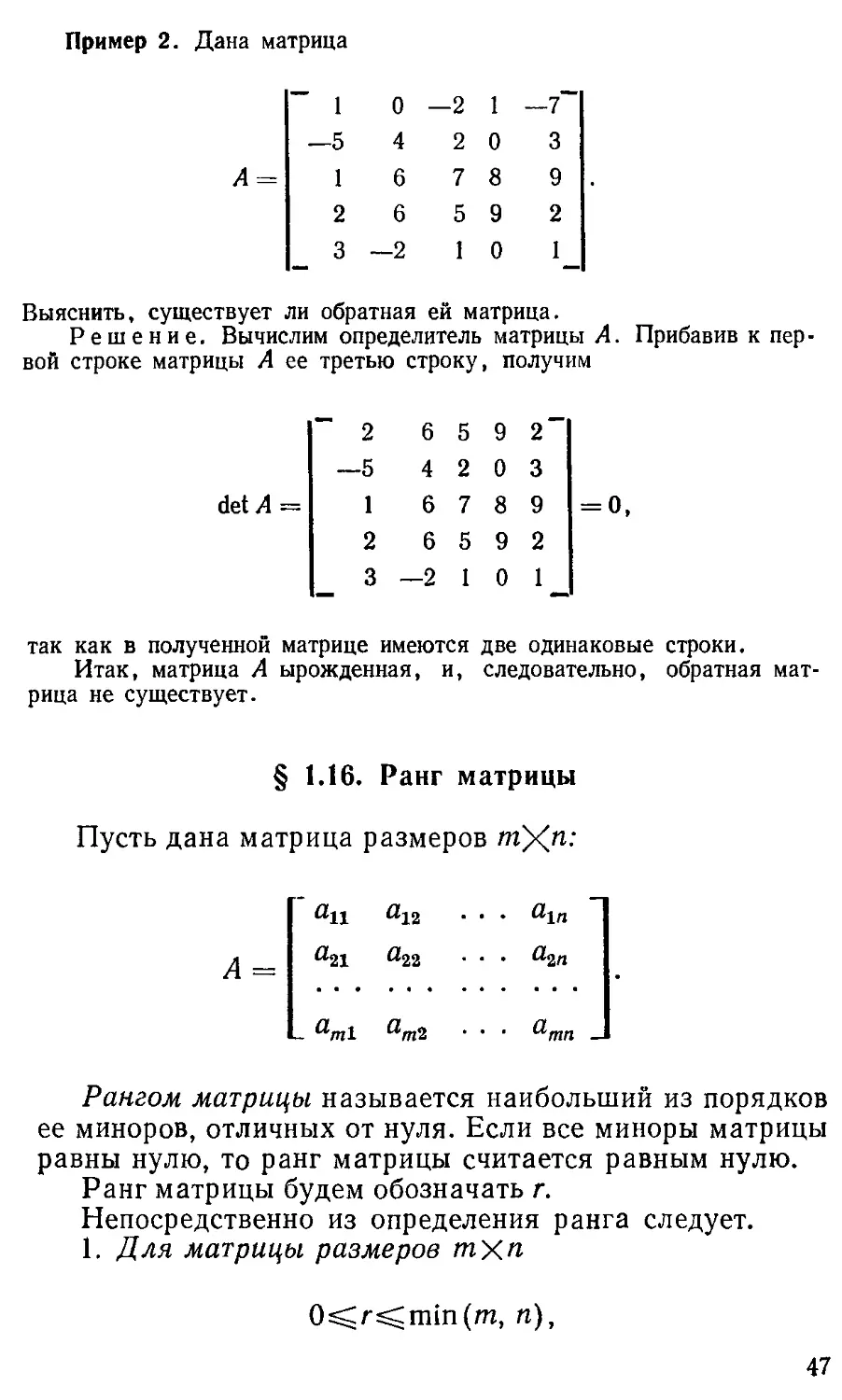
Нулевой матрицей называется матрица, все элементы
которой равны нулю. Ее обозначают буквой О, т. е.
О 0 ... О
0 =
О О
О
О О
О
Диагональной матрицей называется квадратная мат-
матрица, у которой все элементы, стоящие не на главной диа-
диагонали, равны нулю, т. е. матрица вида
0 0 . . . О
п
О
О
аг
О
О
«33
О
О
_ 0 0 0 . . . ап,
Диагональная матрица, у которой каждый элемент
главной диагонали равен единице, называется единичной.
Будем обозначать эту матрицу буквой Е,
1
0
0
0
1
0
0
0
1
. . . 0
. . . 0
. . . 0
0 0 0
1
Единичную матрицу порядка п иногда обозначают Еп.
Квадратная матрица называется треугольной, если
все элементы, расположенные по одну сторону от главной
диагонали, равны нулю. При этом матрицу вида

au
0
0
«12
я22
0
«13
«23
«33
• • • «1л
. . . агп
. . . asn
_ О О О ... ап__ _
называют верхней треугольной, а матрицу вида
~ ап О О ... О
«21 «22 О ... О
а31 а32 а33 ... О
«
лз
• «лл_
нижней треугольной.
Назовем матрицу произвольных размеров трапецие-
трапециевидной, если она имеет вид
«и
0
0
0
«12
«22
0
0
«13
«23
0
0
. . . alr .
. . . air .
. . . arr .
... 0
Ct
¦ ¦ «2Л
¦ • arn
. . 0
_ 0 0 0 ...0 ...0_
где ац, О22, ..., йгг отличны от нуля.
§ 1.2. Линейные операции над матрицами
Сложение матриц
Операция сложения вводится только для матриц оди-
одинаковых размеров.
Суммой двух матриц АтХп = (%) и ВтХп = (fy/) на-
называется матрица Ступ = (с;/-) такая, что ci{ — ац -\- Ьц
(/= 1, 2, ... , т; /= 1, 2, ... , и).
Сумма матриц Л и В обозначается Л + fi.
Сумма А + В + С трех матриц — матрица, которая по-

лучается последовательным сложением данных матриц,
т. е.А + В + С=(А + В) + С.
Аналогично определяется А\+А2+ ... +Ап для м>3.
Умножение матрицы на число
Произведением матрицы Атхп = (аи-) на число а (или
числа а на матрицу Атхп) называется матрица ВтХп =
= (Ьц) такая, что Ьи = ааи- (г=1, 2, .... т;
/= 1, 2, ... , л).
Произведение матрицы А на число а обозначается Аа
или аЛ.
Пример. Произведение матрицы
[-3 0 7
на число а = — 3 есть матрица
-3 -6 -9
Г
Аа=[ 9 0 -21
Матрицу (—1) А будем называть матрицей, противо-
противоположной матрице А, и обозначать —А.
Легко проверить справедливость следующих свойств.
1. А + В = В+А (коммутативность).
2. (А + В) + С=А + (В + С) (ассоциативность).
3. А + О=А.
4. Л + С—А) = О.
5. \А=А.
6. а(рЛ) = (сф)Л (ассоциативность относительно ум-
умножения чисел).
7. а(А + В) = аА + аВ (дистрибутивность умножения
на число относительно сложения матриц).
8. (а+р)Л = аЛ + рЛ (дистрибутивность умножения
на матрицу относительно сложения чисел).
Разность матриц А—В можно определить следующим
образом: Л— В=А + (—В).
§ 1.3. Умножение матриц
Прежде чем рассматривать умножение матриц, вве-
введем понятие согласованности матриц. Матрицу Л будем
называть согласованной с матрицей В, если число столб-
столбцов матрицы Л равно числу строк матрицы В. (Из согла-

сованности матрицы Л с В не следует, вообще говоря, сог-
согласованность матрицы В с А.)
Пример 1. Даны матрицы
A =
«21 °22 %
> с —
C21 C22
C31 C32
Матрица А согласована с матрицей В, так как число столбцов мат-
матрицы А равно числу строк матрицы В. Матрица В не согласована
с матрицей А, так как матрица В имеет один столбец, а число строк
матрицы А равно двум. Матрица А не согласована с матрицей С, но
матрица С согласована с матрицей А. Матрица В не согласована
с матрицей С, и матрица С также не согласована с матрицей В.
Легко заметить, что если А и В — квадратные матри-
матрицы одинакового порядка, то матрица А согласована с В
и В согласована с А.
Произведение матрицы А на матрицу В вводится толь-
только в том случае, когда матрица А согласована с матрицей
В, т. е. если А есть матрица размеров ту^п, а В — разме-
размеров пХ&-
Произведением матрицы АтХп = (%) на матрицу
Ь) называется матрица CmXk = (сц) такая, что
S=l
Произведение матрицы А на матрицу В обозначается
АВ.
Из определения следует, что элемент матрицы АВ,
стоящий в i-й строке и /-м столбце, равен сумме произве-
произведений элементов t'-й строки матрицы А на соответствую-
соответствующие элементы /-го столбца матрицы В.
Произведение АВ часто называют произведением мат-
матрицы А на матрицу В справа или произведением матрицы
В на матрицу А слева.
Заметим, что если матрицу А можно умножить на мат-
матрицу В, то отсюда не следует, что матрицу В можно
умножить на А, так как из согласованности матрицы А
с В, вообще говоря, не следует согласованность матрицы
В с А.
Следует иметь в виду, что если матрицу А можно ум-
10

ножить на матрицу В и В можно умножить на А, то, во-
вообще говоря, АВфВА. Если АВ = ВА, то матрицы назы-
называются перестановочными или коммутативными.
Произведение двух ненулевых матриц может быть ну-
нулевой матрицей (для произведения чисел этого быть не
может).
Пример 2. Найти произведение АВ, если
А = Га" °1г 31
2X3 " U21 Й22 023 У
5ЗХ2 —
Решение. Матрица А2хз согласована с матрицей #3x2* по"
этому существует произведение ^2хз^зх2:
.Умножить матриц1
Пример 3.Умножить матрицу А на матрицу В:
— 10 3
1 2 —9
Решение. Используя определение, находим
2-1 1-0 + 2-2 1 3 +- 2 (—9)"I Г1 4 —151
•1 —3-0 + 4-2 — 3-3 +4(—9)J = L7 8 — 45J*
Пример 4. Пусть
1 —2 0
'-[-?
1
3
— 1
7'
4
0
Тогда
М—6 + 0
В=[з —3 —5
1 -+- 21 —2 —
3+12 —6 —
-1+0 2+
7
21
7
4
0
-8 + 01 Г
-4 + 0J L
0 + 35"
0 + 20
0 + 0
Г
=
— 5
— 5
22
15
— 1
ir]'
— 9
— 10
2
35
20
0
Таким образом, мы видим, что АВ ф ВА.
Пример 5. Пусть
-СП-

Тогда
ГЫ + 1(_
ГО 01
Lo oj
м.1 + (-1I Ы + (-1I] ГО 01
[(-i)i + i.i (-i)i + i-ij Lo oj
В этом случае АВ = В А.
Из определения операции умножения матриц следует,
что
АЕ = ЕА=А, АО = ОА = О.
Если матрица А согласована с матрицей В, а матрица
АВ согласована с матрицей С, то под произведением ABC
трех матриц понимаем матрицу, полученную последова-
последовательным умножением данных матриц, т. е. матрицу
(АВ)С.
Аналогично определяется произведение k матриц (к —
натуральное число, &>3).
Имеют место следующие свойства (при условии, что
указанные операции имеют смысл).
1. (АВ)С=А(ВС) (ассоциативность).
2. а(АВ) = (аА)В=А(аВ) (обозначается аАВ).
3. (А + В)С=АС + ВС (дистрибутивность умножения
справа относительно сложения матриц).
4. С(А + В) = СА + СВ (дистрибутивность умножения
слева относительно сложения матриц).
Докажем первое свойство. Левая часть рассматривае-
рассматриваемого равенства имеет смысл только в том случае, когда
матрица А согласована с матрицей В, а матрица АВ
согласована с матрицей С, т. е. если А =АтХп, В = Вп\к,
С = Ckxt- Тогда матрица (АВ) С имеет размеры тХ I.
Обозначим ее Н. Легко убедиться, что произведение А (ВС)
также имеет смысл и матрица Н = А (ВС) имеет те же раз-
размеры, что и матрица Я. Докажем, что соответствующие
элементы h^ и h^ матриц Я и Я равны между собой.
Введем обозначение АВ = DmXk- Элемент этой матрицы
dM = ? avsbS9,
s=l
а элемент матрицы Я имеет вид
12

-2
или
k n k n
p=l S = l p=ls = l
n k n k
|iS "Sp ?pv
S=l p = l S = \ p=l
Очевидно, что
P=l
есть элемент матрицы ВС = G, стоящий в s-й строке и v-m
столбце. Тогда
В правой части этого равенства стоит элемент ц-й строки
и v-ro столбца матрицы Н = (h^) — AG. Следовательно,
К* = %,,.
В справедливости остальных свойств предлагаем чита-
читателю убедиться самостоятельно.
Замечание. Произведение двух верхних треугольных матриц
есть верхняя треугольная матрица. Аналогичное утверждение спра-
справедливо и для нижних треугольных матриц.
§ 1.4. Многочлены от матриц
Целой положительной степенью Ah (&>1) квадратной
матрицы А называется произведение k матриц, каждая
из которых равна А. Согласно определению,
k раз
Очевидно, что матрица Ah имеет тот же порядок, что
и матрица А.

Нулевой степенью А0 квадратной матрицы А
называется единичная матрица Е того же порядка, что
и А, т. е. А°=Е.
Первой степенью А1 матрицы А называется сама мат-
матрица А, следовательно, Ах—А.
Многочленом или полиномом степени k (k — целое не-
неотрицательное число) от квадратной матрицы А называ-
называется выражение вида
... +akA°,
где ceo, ctj, ... , as — любые числа, причем ссо=И=О.
Будем обозначать многочлен от матрицы А через
Р(А). Таким образом,
+ ... +ahA°
или
P(A) = a(>Ah + alAh-l+ ... +ahE.
Из определения следует, что многочлен от матрицы
может быть получен, если в обычный многочлен
i+ ... +ak
вместо х подставить квадратную матрицу (при этом надо
учесть, что as = сс&л:0).
Пусть дан многочлен Р(х). Если Р(А) есть нулевая
матрица, т. е. Р(А) = О, то матрица А называется корнем
многочлена Р(х), а многочлен Р(х) — аннулирующим
для матрицы А.
Пример. Показать, что матрица
Ч-з:;]
является корнем многочлена
Р(х) = х* + х— 14.
Решение. Подставив в данный многочлен вместо х матрицу А,
получим
Р(А) = А* + А— 14 ? =
Г13 41 Г 1 —41 Г —14 01 ГО
= [3 ieJ + l-3 -2J + l 0 -14j = [o j
Следовательно, матрица А является корнем данного многочлена.
14

§ 1.5. Транспонирование матрицы
Матрица, полученная из данной заменой каждой ее
строки столбцом с тем же номером, называется матри-
матрицей, транспонированной к данной.
Матрицу, транспонированную к матрице А, будем
обозначать А' или Лт. Таким образом, для
А =
Лт =
Операция нахождения матрицы, транспонированной
к данной, называется транспонированием матрицы.
Заметим, что если Л — матрица размеров mXn> то Лт
имеет размеры пу^пг.
Имеют место следующие свойства.
2.
3.
4.
В справедливости свойств 1—3 читатель может легко
убедиться самостоятельно.
Докажем свойство 4. Следует заметить, что левая
часть рассматриваемого равенства имеет смысл только
в том случае, когда матрица Л согласована с матрицей В,
т. е. если Л = Атхп и В = Bnxi. Очевидно, что тогда
матрица ВТ согласована с матрицей Лт и произведение
ВТАТ имеет смысл.
Для доказательства справедливости свойства 4 пока-
покажем, что матрицы (АВ)Т и ВТАТ одинаковых размеров
и их соответствующие элементы равны.
Произведение АВ является матрицей размеров m X I,
следовательно, (АВ)Т — матрица размеров lXm. Матрица
ВТАТ также имеет размеры / X тп, так как Вт — В]¦ , Лт =
«= Лт
ПХШ'
15

Пусть c'tj — элемент матрицы (АВ)Т, стоящий в /-й
строке и /-м столбце. Этот элемент равен элементу с;1,
стоящему в /-й строке и i-м столбце матрицы АВ, т. е.
Cf — CH- Согласно правилу умножения матриц,
s=l
где aJg и bsl — соответственно элементы матриц А и В,
Так как ajs = a'sj, bs[ = b'is (a'sj и b'is — соответственно эле-
элементы матриц Лт и Вт), то
с . ^
' s=l ' s=l
Последнее выражение, представляющее собой сумму про-
произведений элементов г-й строки матрицы Вт на соответст-
соответствующие элементы /-го столбца матрицы Лт, является эле-
элементом матрицы ВТАТ, стоящим в г-й строке и j-u столбце.
Таким образом, соответствующие элементы матриц (АВ)Т
и ВТЛТ равны. Свойство 4 доказано.
Заметим, что свойство 4 состоит в том, что при тран-
транспонировании произведения двух матриц сомножители
транспонируются и меняются местами.
Для произведения трех матриц имеем
Следовательно,
Аналогично для п сомножителей
(ЛИ2 ¦•¦ Ап^Апу = А1А1_х ...
§ 1.6. Блочные матрицы
А\А\.
До сих пор мы рассматривали матрицы, элементами
которых являются числа. Можно рассматривать матри-
матрицы, элементами которых в свою очередь являются матри-
матрицы. К таким матрицам относятся блочные матрицы.
Пусть дана матрица
16

•Hi
A =
2
Goo
L "ml "m2 • • • "nw
Разобьем ее горизонтальными и вертикальными прямыми
на ряд матриц. Полученные при этом матрицы называют-
называются блоками (клетками) матрицы А.
Данную матрицу можно записать в виде матрицы,
элементами которой являются блоки. В этом случае бу-
будем говорить, что матрица записана в виде блочной мат-
матрицы. Очевидно, что данная матрица может быть запи-
записана в виде блочной не единственным образом.
Пример 1. Пусть данная матрица А разбита на блоки следующим
образом:
А =
«11
«21
«31
«41
«12
«22
«32
«42
13
«23
«33
«43
«14
«24
«34
«44
«15
«25
«35
«45 _
Введем обозначения:
B=Bix2 = [«it«i2];
Г «21 «22 1.
2 L «31 «32 J
1 = О1Х2==[«41 «42];
D —
= С1ХЗ = [а13«14«1в];
_ р _ Г а*3 йы
L «33 «34
= ^1X3 = [«43 «44 «45^
«25 1.
«35 J
Тогда матрицу А можно записать в виде блочной:
В
1X2
'1X3
¦^2X2 -^2X3
О
1X2
или А =
В С
D F
G К
Чхз.
Эту же матрицу можно записать в виде следующей блочной
матрицы:
где
"~ "" "" """ "~«14 «15
«21
«31
«41
«12
«22
«32
«42
«13
«23
«33
«43
О —
» ч. —
«24 «25
«34 «35
аы а15
17

Блочная матрица, каждая строка которой содержит
v блоков, а каждый столбец — ц блоков, называется блоч-
блочной матрицей размеров X
I O22 023 O24
В примере 1 матрица А сначала представлена в виде блочной
матрицы размеров 3X2, а затем —размеров 1X3.
Будем говорить, что две матрицы одних и тех же раз-
размеров одинаковым образом разбиты на блоки, если их со-
соответствующие блоки имеют одни и те же размеры.
Например, матрицы
"«и
А =
. «31 j «32 аЗЗ °24 .
одинаковым образом разбиты на блоки.
Линейные операции (сложение, вычитание и умноже-
умножение на число) над блочными матрицами могут быть све-
сведены к соответствующим операциям над блоками. При
этом следует иметь в виду, что при сложении и вычитании
матрицы должны быть одинаковым образом разбиты на
блоки.
Прежде чем свести операцию умножения матриц
к операциям над блоками, введем понятие согласованно-
согласованности блочных матриц.
Блочная матрица А]= А^Х1 называется согласованной
с блочной матрицей В — ВхХ\, если v = х и блоки 1-й
строки матрицы А согласованы с соответствующими бло-
блоками /-го столбца матрицы В при любых i, / (/=1,
2 р; J=l, 2, .... Я).
Пусть матрицы А и В представлены в виде блочных
матриц Лр.х» и ВхХ\ так, что матрица А^? согласована
с матрицей ВхХ\. Тогда произЁедение АВ — С может быть
представлено в виде блочной матрицы С^х\, блок кото-
которой, стоящий в /-й строке и /-м столбце, есть матрица,
равная сумме произведений блоков /-й строки матрицы
Лр.х„ на соответствующие блоки /-го столбца матрицы ВхХ\.
Пример 2. Пусть матрицы А и В представлены в виде блочных
матриц следующм образом:
18

A =
¦ 1 1
1 1
- ' 1
— 1
0
0
0
0
3
' — 2
4
0
0 '
1
1
или
где
Mill- 421-
Л4 = [0 3], Bx = [-2 0], Д2 =
Легко показать, что блочная матрица А согласована с блочной
матрицей В. Следовательно,
АВ=
=\А% АЛ \ВЛ = \А^ + А*ВА
[А3 А,\ [В,\ [АА + А&У
Так как
то
—4 —
Г-6 -П
~L-4 о]1
= [2 O] + [O 0] = [2 0],
— 6 —1
— 4 0
Заметим, что если данные матрицы А и В представить в виде
блочных матриц следующим образом:
1
2
— 1
— 1
0
0
0
0
3
D
— 2
4
0
0"
1
0.
то блочная матрица А не согласована с блочной матрицей В, и, сле-
следовательно, АВ нельзя найти, оперируя этими блочными матрицами.
§ 1.7. Перестановки
Для того чтобы ввести понятие определителя матри-
матрицы, нам понадобятся некоторые сведения о перестановках.
Перестановкой из п натуральных чисел 1, 2, 3,... , п
19

называется любое их расположение в определенном по-
порядке.
Произвольную перестановку из п чисел будем записы-
записывать в виде (си; аг; ... ; а„), где каждое сц — одно из чи-
чисел 1, 2,..., п и щфа.] при 1ф\.
Две перестановки из п чисел называются различными,
если они отличаются расположением хотя бы одного
числа.
Например, A; 3; 2; 4; 5) и B; 1; 5; 4; 3) —две различные пере-
перестановки из чисел 1, 2, 3, 4, 5.
Подсчитаем число различных перестановок из чисел
1, 2, 3, ... , п. Так как на первом месте можно поместить
любое из п данных чисел, на втором — любое из (п—1)
оставшихся чисел и т. д., то получаем п-(п— 1)х
X(п—2)• ... -2-1 различных перестановок.
Итак, число различных перестановок из чисел 1, 2,
3, ... , п равно произведению 1-2-3- . .. -(п—\)-п, которое
обозначается п! («эн факториал»).
Будем говорить, что два числа образуют инверсию
в перестановке, если большее число стоит перед меньшим.
Например, в перестановке A; 4; 5; 3; 2) инверсию образуют сле-
следующие пары чисел: 4 и 3, 4 и 2, 5 и 3, 5 и 2, 3 и 2. Итак, в рассмат-
рассматриваемой перестановке пять пар чисел образуют инверсию, т. е. име-
имеется пять инверсий.
Число инверсий в перестановке (ец; аг; ... ; а„) будем
обозначать через k (а\, аг, ... , ап).
Легко заметить, что
k(a\, иг, ... , а„) =k\ + k2+ . . . +&n-i,
где ki (t=l, 2, ... , п—1) — число чисел, стоящих перед
числом i в перестановке, полученной из данной зачерки-
зачеркиванием чисел, меньших числа i (если таковые имеются).
Пример. Найти число инверсий в перестановке C; 1; 2; 4).
Решение. Перед 1 стоит одно число, следовательно, k\ = \. За-
Зачеркнем число 1. Теперь перед числом 2 стоит одно число, следова-
следовательно, k2=\. Аналогично получаем &3=0. Следовательно,
/еC, 1,2, 4) = 1 + 1+0=2.
Заметим, что если числа в перестановке записаны в
порядке возрастания, то число k инверсий равно нулю.
Если число инверсий в перестановке четное, то она на-
20

зывается четной, если нечетное, то перестановка называ-
называется нечетной.
Если в данной перестановке поменять местами два
числа щ и а_,-, при условии, что остальные числа остаются
на своих местах, то будем говорить, что новая перестанов-
перестановка получена из данной транспозицией чисел m и щ. Будем
считать, что две перестановки имеют разный характер
четности, если одна из них — четная, а другая — нечет-
нечетная.
Теорема. Данная перестановка и перестановка, полу-
полученная из нее одной транспозицией, имеют разный харак-
характер четности.
Доказательство. Возможны следующие случаи.
1. Переставляемые числа а; и а3- стоят в перестановке
рядом, т. е. перестановка имеет вид
(сц; а2; ... ; сц; а,; ... ; а„). A.1)
Применив к перестановке A.1) транспозицию чисел m
и a,j, получим перестановку
(cti; ot2; ... ; а/, а,; ... ; ап). A.2)
Числа сц и otj со всеми остальными числами в обеих
перестановках образуют одно и то же число инверсий.
Если числа щ и щ в перестановке A.1) не образуют ин-
инверсию, то в перестановке A.2) эти числа образуют
инверсию, и наоборот. Следовательно, в любом случае
число инверсий в перестановке A.1) отличается на едини-
единицу от числа инверсий в перестановке A.2), т. е. переста-
перестановки A.1) и A.2) имеют разный характер четности.
2. Между переставляемыми числами щ и otj в пере-
перестановке имеется s чисел (s>0), т. е. перестановка имеет
вид
(cti; ot2; ... ; Щ-и щ; Pi; р2; ... ; ps; а/, ... ; а„). A.3)
Применив к перестановке A.3) транспозицию чисел ott
и otj, получим перестановку
(сц; а2; ... ; ct,-_i; щ; Рг, р2; ... ; ps; а,; ... ; а„). A.4)
Перестановка A.4) может быть получена из перестанов-
перестановки A.3) следующим образом. Осуществим в перестановке
A.3) транспозицию чисел at и Pi, в полученной переста-
21

новке — транспозицию чисел а, и Рг и т. д. Этот процесс
продолжаем до получения перестановки
(сц; а2; ... аг-ь рг, р2; ... ; Р«; ац а»; ... ; а„). A.5)
При этом осуществим s+1 транспозиций. Далее в пере-
перестановке A.5) осуществим транспозицию чисел а;- и ps,
в полученной перестановке — транспозицию чисел ctj
и ps-i и т. д. Этот процесс продолжаем до получения пе-
перестановки A.4). При этом осуществим s транспозиций.
Таким образом, перестановка A.4) получается из пе-
перестановки A.3) с помощью 2s+l транспозиций рядом
стоящих чисел. Так как каждая транспозиция рядом
стоящих чисел приводит к перестановке, имеющей другой
характер четности, то перестановки A.3) и A.4) имеют
различный характер четности. Щ*
Читатель легко убедится в справедливости того, что
из любой перестановки (аг, а2; ... ; ап) может быть по-
получена перестановка A; 2; ... ; п) с помощью последова-
последовательного применения конечного числа транспозиций. (Ес-
(Если в данной перестановке произведена транспозиция
и в полученной перестановке также произведена транспо-
транспозиция, то будем говорить, что последняя перестановка по-
получена из данной последовательным применением двух
транспозиций.)
§ 1.8. Определители матриц
Понятие определителя матрицы вводится только для
квадратной матрицы. Пусть дана квадратная матрица по-
порядка п:
~ап а12 ... а1п'
А =
\_ап1 ап2 ... ат
Рассмотрим произведения элементов этой матрицы,
взятых по одному и только по одному из каждой ее стро-
строки и каждого столбца. Любое такое произведение будет
содержать п сомножителей и может быть записано в виде
ai4a2a, ... апа. . A.6)
п
* Знак ¦ означает конец доказательства.
22

Здесь для удобства сомножители расположены так, что
первые индексы (номера строк) следуют в порядке воз-
возрастания, вторые индексы си, а2, ... , а„ (номера столб-
столбцов) представляют собой натуральные числа 1, 2, ... , п,
расположенные в некотором порядке. Таким образом,
(аг, аг; ... ; ап) есть перестановка из п чисел.
Два произведения вида A.6) будем считать различ-
различными, если соответствующие им перестановки из вторых
индексов различны. Различных произведений будет
столько, сколько можно составить различных перестано-
перестановок из п чисел, т. е. п!.
Далее будем оперировать только с различными произ-
произведениями. Умножив каждое из п\ этих произведений на
(—l)*(«i ап), получим произведения вида
(— 1 )*«-.«« e«>flleifl»«.
A.7)
Сумма п\ произведений вида A.7) называется опре-
определителем матрицы А порядка п. Каждое из выражений
A.7) называется членом определителя.
Определитель матрицы А порядка п называется опре-
определителем п-го порядка и обозначается
ап а12
Й21 «22
¦Чп
а,
'¦п%
Таким образом, согласно определению,
а
п
а21 а22
а1п
а2п
пп1
= 2 (—1 )«•»•«•¦
(«г, «,;...; О
A.8)
где сумма содержит все слагаемые, для которых переста-
перестановки (<ц; аг; ... ; ап) различны.
Употребляются также следующие обозначения опре-
определителя:
|Л|, A, detЛ, detCa«).
Иногда определитель называют детерминантом.
Заметим, что определитель матрицы есть число, так
23

как мы рассматриваем матрицы, элементами которых яв-
являются числа.
Элементы, строки, столбцы и диагонали матрицы на-
называют соответственно элементами, строками, столбцами
и диагоналями определителя матрицы. Так же, как и для
матрицы, строки и столбцы определителя называют его
рядами.
Рассмотрим следующие частные случаи.
1. Определитель матрицы первого порядка
содержит, согласно выражению A.8), одно слагаемое
(_l)*(«ofllei.
Здесь аг = 1 и k(a1) = 0. Следовательно,
det Лх = det (ап) = аи.
2. Определитель матрицы второго порядка
«11 Й12
«21 #22
содержит, согласно выражению A.8), 2! = 2 слагаемых
вида
Для первого слагаемого возьмем а1=1, a2 = 2. Тогда
k(l, 2) = 0. Для второго слагаемого 0^ = 2, а2=1,
/гB, 1) = 1.
Таким образом, определитель второго порядка
«12
«22
т. е. равен произведению элементов главной диагонали
минус произведение элементов побочной диагонали.
3. Определитель матрицы третьего порядка
ап а12 а13
а21 а22 а23
- «31 «32 «33
содержит 3! = 6 слагаемых вида
(—1)* (««.«•¦ «.)aieifl2«1a3«,.
24

Чтобы записать эти слагаемые, выпишем все перестановки
из вторых индексов: A; 2; 3), B; 3; 1), C; 1; 2), C; 2; 1),
B; 1; 3), A; 3; 2). Число k инверсий в них соответ-
соответственно равно 0, 2, 2, 3, 1, 1.
Таким образом, определитель третьего порядка
ап
31 Й32 Я3
а1га23а31 + а13а21а32 — а13а2га31 —
— а12а21а33 — а1га23а32. A.9)
Существует ряд правил, облегчающих составление
выражения, стоящего в правой части формулы A.9).
Рассмотрим некоторые из них:
1) слагаемые составляются по следующей схеме:
ч
,/
В этой схеме плюс означает, что произведения указанных
элементов берутся со своими знаками, а минус — с про-
противоположными. Это правило называется правилом тре-
треугольников;
2) слагаемые составляются по схеме
^21
/
Х22
\
Л
25

В этой схеме используется матрица, полученная из мат-
матрицы определителя приписыванием справа первых двух
ее столбцов.
Пример. Вычислить определитель
— 2 3
Д =
5
3
— 3
1—1
4 1
Решение. По правилу треугольников получим
Д =(-2) (_1)(_3)+5-1 • 1+3-3-4—5 (—1) 4-3-1 (—3)—(—2) 3-1=70.
Пользуясь вторым правилом, составим матрицу
¦
и получим
Д=(-2) (-1) (-3) + 3-3-4+5-1 • 1-5 (-1) 4-(—2K-1—3-1(—3)=70.
Теорема. Если аа1р,аа,р, • • • аа р — произведение эле-
элементов матрицы
А =
an an
взятых по одному и только одному из каждой строки
и каждого столбца, то
является членом определителя матрицы А.
Доказательство. Переставим в произведении
^•Р.Яс.р, ••• Яапр„ A-10)
26

множители так, чтобы перестановка, составленная из пер-
первых индексов, имела вид A; 2; ... ; п). Тогда указанное
произведение запишется в виде
a\^fi2U .. ¦ <V[ , A-11)
где (yi; Y2; • • ¦; Yn) — перестановка из чисел 1,2 пи
(—1)*(т..т тя)а,71а2т, ... а«Тл
есть член определителя матрицы А. Так как
то для доказательства теоремы достаточно показать, что
Перестановки
К;
(Pi;
A;
(Yi;
р2; ••
2; ..
y2; ••
•; <*„),
•; Р„),
• ; п)
• ; y«)
A.14)
A.15)
A.16)
A.17)
являются перестановками, составленными из первых
и вторых индексов соответственно произведений A.10)
и A.11).
Из равенства A.12) видно, что перестановка A.16)
получена с помощью некоторого числа транспозиций из
перестановки A.14), а перестановка A.17)—из A.15)
с помощью такого же числа транспозиций. Отсюда сле-
следует, что
k(yi, Y2, ¦ ¦ • , Y«) +k{\, 2, ... ,п) =/?(yi, Y2. • • • , Yn)
/г(аь а2, .. . ,
имеют один и тот же характер четности и, следовательно,
равенство A.13) имеет место. ¦
Следствие. Если
А =
«21 «22
In
27

тд
где (c^; а2; ... ; ая) и (p\; p2i • • •! P«) — перестановки из
n чисел; ая.рА.р, ... aa p — произведение элементов опре-
определителя, взятых по одному и только по одному из
каждой строки и каждого столбца матрицы А.
§ 1.9. Свойства определителей
1. Определитель матрицы, полученной из данной
транспонированием, равен определителю данной мат-
матрицы.
Доказательство. Пусть
А =
ап
"и
и Ат — транспонированная к А матрица. Тогда, согласно
следствию § 1.8,
<МЛ = 2(— 1)М1*2 «> + *<««.»« ««»fli«,fl2., ... amnl
Отсюда det A = det A\ Щ
Это свойство называется свойством инвариантности
определителя относительно транспонирования матрицы.
2. Если все элементы некоторого ряда определителя
равны нулю, то определитель равен нулю.
3. Если все элементы некоторого ряда определителя
имеют общий множитель, то его можно вынести за знак
определителя.
Например, если все элементы г'-й строки определителя имеют
множитель %, то
л
ап
an
«in
28

Следствие. Если матрица В получена из матрицы А
умножением некоторого ряда на число К, то det В =
= XdetA (Умножить ряд матрицы на число k значит
умножить на k все элементы этого ряда.)
4. Определитель, у которого каждый элемент некото-
некоторого ряда является суммой двух слагаемых, равен сумме
двух определителей, у первого из которых в указанном
ряду стоят первые слагаемые, а у второго — вторые сла-
слагаемые; остальные ряды, параллельные указанному, у
всех определителей одинаковы.
Например, если каждый элемент /-го столбца определителя явля-
является суммой двух слагаемых, то
«11
«21
ч/
anJ + anJ
«11
a2J
«in
«2/1
««
«11
«21
¦м/
12/
«П
unj
Свойства 2—4 следуют непосредственно из определе-
определения определителя.
5. Если матрица В получена из матрицы А переста-
перестановкой двух параллельных рядов, то det Л = —det В.
Доказательство. Пусть матрица В получена из-,
матрицы А перестановкой двух рядом стоящих столбцов;
с номерами щ и схг+ь Тогда
det А = 2 (— l)ftiaia, ... aia..ai+\ а{+1 ... a«v
где
р
= k(alt ..., alt ai+l an>,.
= k(alt ..., al+u ait ..., aj,
b b аи..
Так как перестановка (ai; ... ; щ; щ+и,....... ;¦ ап] после
применения транспозиции чисел щ и at+i дает переста-
29

новку (ai; ... ; a*+i; a,; ... ; an), то k[ и k2 имеют разный
характер четности, и, следовательно, det Л =—det В.
Пусть матрица В получена из матрицы Л перестанов-
перестановкой i-ro и /-го столбцов (i<j), между которыми содер-
содержится т столбцов (j=i + m + l). Очевидно, что г'-й стол-
столбец можно поместить на место /-го, а /-й — на место i-ro
путем последовательной перестановки рядом стоящих
столбцов 1т + 1 раз. Поэтому
det S= (— lJm+!det Л = —det Л.
Справедливость этого свойства для строк следует из
свойства инвариантности определителя относительно
транспонирования матрицы.¦
6. Если матрица А имеет два одинаковых параллель-
параллельных ряда, то det Л=0.
Доказательство. Поменяв местами два одина-
одинаковых параллельных ряда матрицы и учитывая свойство
5, получим det>4 = —det Л, откуда det Л = 0. И
7. Если матрица А имеет два параллельных пропор-
пропорциональных ряда, то det Л = 0.
Доказательство. Пусть в матрице Л элементы
некоторого ряда равны соответствующим элементам па-
параллельного ряда, умноженным на К. Тогда, вынося К за
знак det Л, получим det Л = A det В, где В — матрица
с двумя одинаковыми параллельными рядами. Так как
detS = O, то и det Л = 0. И
8. Если матрица В получена из матрицы А прибавле-
прибавлением к некоторому ряду другого, параллельного ему ря-
ряда, умноженного на К, то det Л = det В. (Прибавить к дан-
данному ряду другой, параллельный ему ряд,—значит к эле-
элементам данного ряда прибавить соответствующие эле-
элементы параллельного ему ряда.)
Это следует из свойств 4 и 7.
§ 1.10. Миноры и алгебраические дополнения
Пусть дана матрица размеров т\п. Выберем в ней
произвольно s строк и s столбцов, причем каждая строка
и каждый столбец могут быть выбраны только один раз
(l^s^min(m, n), где min(m, n) —меньшее из чисел
тип). Элементы, стоящие на пересечении выбранных
строк и столбцов, образуют матрицу порядка s. Опреде-
30

литель этой матрицы называется минором порядка s дан-
данной матрицы.
Для квадратной матрицы наряду с понятием минора
вводится понятие дополнительного к нему минора.
Пусть дана квадратная матрица порядка л и ее ми-
минор М порядка s. Минором М', дополнительным к мино-
минору М, называется определитель матрицы, оставшейся
после вычеркивания тех s строк и s столбцов данной мат-
матрицы, которые входят в минор М.
Очевидно, что дополнительным к минору М' будет
минор М.
Пример 1.
Дана
матрица
" «и
«21
«31
«41
«12
«22
«32
«42
013
023
«33
043
014
024
«34
«44
«15
«25
«35
«45
«52 «53 «54 «55 _
Выбрав в ней 2-ю и 3-ю строки и 3-й и 5-й столбцы, получим минор
2-го порядка:
023
«33 «35
Дополнительным мннором к минору М будет
«И °12 «14
М'
а.
а,
а.,
1 2 4
«51 «52 4
Миноры квадратной матрицы называют также мино-
минорами ее определителя.
Алгебраическим дополнением минора называется до-
дополнительный к нему минор, умноженный на (—1)", где
а — сумма номеров строк и столбцов данной матрицы,
которые входят в рассматриваемый минор.
Пример 2. Найти алгебраическое дополнение М* минора М, рас-
рассмотренного в примере 1.
Решение. На основании определения получим
где а = 2 + 3 +3 + 5 = 13. Следовательно.
«11 «12 «14
М* = — а,
41
а.
44
«51 «52 «54
31

Каждый элемент ац матрицы n-го порядка является
минором 1-го порядка. Дополнительный минор является
определителем порядка (п—1). Этот дополнительный
минор будем называть минором элемента ац и обозна-
обозначать Мц.
Алгебраическое дополнение элементов ац будем обоз-
обозначать Aij. Из определения алгебраического дополнения
следует, что
Пример 3. Дана матрица
2 —3 1
4 0—5
7—2 3
Алгебраическим дополнением элемента — 3, стоящего в первой
строке и втором столбце, будет
4~5 = — A2 + 35)= —47.
§ 1.11. Разложение определителя по элементам ряда
Теорема. Определитель матрицы равен сумме произ-
произведений элементов некоторого его ряда на алгебраиче-
алгебраические дополнения этих элементов.
Доказательство. Пусть дана матрица А, опре-
определитель которой
det Л =
2
Чп
Докажем теорему для случая, когда в качестве ряда
взята некоторая строка, т. е. докажем справедливость ра-
равенства
det А = ацАц+а{2А{2+ ...
... +ацАц+ ... +ainAin, A.18)
где i — некоторое фиксированное число, l^Ci^Cn.
Так как Aij является определителем порядка (п— 1),
то aijAij состоит из (п.— 1)! cyiaraeMiix. и, следовательно,.
3-2

правая часть равенства A.18) содержит п - (п— 1)! = п!
слагаемых.
Докажем, что все слагаемые, входящие в ацА^, явля-
являются членами определителя det Л.
Если i=/=l, то uijAij — auAu. Согласно определению
определителя,
Ли = 2 (— 1)*(а вл>а211а3*, ... а„
а,,,.
Следовательно,
(«.; ...; «„)
Ясно, что (—1)*A> а ал)апа2а,аза, ... ап^п является чле-
членом определителя det А. Но k A, а2, ..., ап) = & (а2, ...,
ая), поэтому все слагаемые, входящие в аиЛш являются
членами определителя det Л.
Если i, }'—любые числа (l^Ci^Cn; 1^/^n), то пре-
преобразуем матрицу Л = (ciij) в матрицу Я= faij) так, чтобы
элемент ац находился в первой строке и первом столбце,
т. е. чтобы а,\\ = а,ц, и чтобы миноры Мц и Мц рассматри-
рассматриваемого элемента матриц Л и Л" совпадали. Для этого t-ю
строку будем последовательно менять местами с рядом
стоящей сверху строкой до тех пор, пока t'-я строка не ста-
станет первой. При этом потребуется произвести (i—1) та-
таких перестановок. Затем /-й столбец меняем последова-
последовательно местами с рядом стоящим слева столбцом, пока
j-й столбец не станет первым. При этом потребуется про-
произвести (/—1) перестановку. Следовательно,
det Л = (- 1) (i-i)+O-J)det Л = (-1) wdet Л
или
det Л = det Л"(—1)^+^" A.19)
ацли = аи (- iy+Ш,, = (- 1I+'апМп = (- 1){+'апАп.
Согласно доказанному выше, слагаемые, входящие
в йцАц, являются членами определителя det Л. Следова-
Следовательно, в силу равенства A.19), заключаем, что слагае-
слагаемые, входящие в ctijAij, являются членами определителя
33

Справедливость теоремы для случая, когда в качестве
ряда выбран некоторый столбец, следует из свойства ин-
инвариантности определителя относительно транспонирова-
транспонирования матрицы.
Пример. Вычислить определитель
3—5 2
1
8 4
5 —3 1
разлагая его по элементам второго столбца.
Решение.
1 4
5 1
3 2
1 4
3 2
5 1
121.
Рассмотренная теорема является частным случаем бо-
более общей теоремы — теоремы Лапласа, которую мы
приведем здесь без доказательства.
Теорема Лапласа. Определитель порядка п равен сум-
сумме произведений всевозможных миноров k-го порядка
(k<n), которые можно составить из произвольно выб-
выбранных k параллельных рядов, на алгебраические допол-
дополнения этих миноров.
§ 1.12. Теоремы замещения и аннулирования
Теорема замещения. Сумма произведений произволь-
произвольных п чисел d\, d% ... , dn на алгебраические дополнения
элементов некоторого ряда матрицы порядка п равна оп-
определителю матрицы, которая получается из данной за-
заменой элементов указанного ряда на числа d\, d2, ..., dn.
Доказательство. Пусть дана матрица
А =
"*12
Щ—\ 2
0-а.
2
аи ... а.
34

Возьмем любые п чисел du d2, ... , dn и алгебраиче-
алгебраические дополнения элементов i-й строки Аи, А12, ... , Аы-
Докажем, что
nAin = dei Au
A.20)
где
det
«11
ac-1 i
dx
ai+i ,
an . .
ai-i 2 -
d2
Qi+\ 2
• "in
¦ • ««-In
• • da
• • ai+ln
Разложив определитель det Л] по элементам 1-й стро-
строки, получим
det Al = d1Di + d2D2+ ... +dnDn,
где D\, D2, ..., Dn — алгебраические дополнения соответ-
соответственно элементов dit d2,..., dn.
Так как Di=An, D2=Ai2, ... , Dn=Ain, то detЛх =
= diAii+d2Ai2-\- ... +dnAin и равенство A.20) доказано.
Аналогично доказывается теорема для случая, когда
числа d\, d2, ... , dn умножаются на алгебраические до-
дополнения элементов некоторого столбца. ¦
Теорема аннулирования. Сумма произведений эле-
элементов адного из рядов матрицы на алгебраические до-
дополнения элементов другого, параллельного ему ряда,
равна нулю.
Доказательство. Пусть дана матрица А — (о,ц)
порядка п. Докажем, что
kn = Q, B.21)
Левая часть равенства A.21) есть сумма произведе-
произведений алгебраических дополнений элементов k-n строки
матрицы А на числа аи, ai2, ... , ain- На основании тео-
теоремы замещения эта сумма есть определитель det Л] мат-
матрицы Аи полученной из матрицы А путем замены элемен-
35

тов k-и строки числами an, ai2, ... , щп- Следовательно,
определитель det Л1 имеет две одинаковые строки и пото-
потому равен нулю, т. е.
det Ai = ciuAili-\-ai2Ah2-\- . ¦ ¦ -\-ttinAiin = 0.
Аналогично доказывается теорема для столбцов. Н
§ 1.13. Некоторые методы вычисления определителей
и-го порядка
Разложение определителя по элемен-
элементам строки или столбца
Теорема о разложении определителя по элементам
строки или столбца позволяет свести вычисление опреде-
определителя n-го порядка (ft>l) к вычислению п определите-
определителей порядка п—1.
Если определитель имеет равные нулю элементы, то
удобнее всего разлагать определитель по элементам той
строки или столбца, который содержит наибольшее чис-
число нулей.
Используя свойства определителей (см. § 1.9), можно
преобразовать определитель n-го порядка так, чтобы все
элементы некоторой строки или столбца, кроме, может
быть, одного, равнялись нулю. Таким образом, вычисле-
вычисление определителя n-го порядка, если он отличен от нуля,
сводится к вычислению одного определителя (п—1)-го
порядка.
Пример 1. Вычислить определитель
Д =
Решение. Прибавив ко второй строке первую, к третьей —
первую, умноженную на 2, к четвертой — первую, умноженную на —5,
получим
Д =
1
1
2
5
2
3
1
2
7
— 1
2
— 1
5
2
3
3
1
0
0
0
2
5
5
— 8
7
6
16
— 36
5
7
13
— 22
36

Разлагая определитель по элементам первого столбца, имеем
5 6 7
5 16 13 =-252,
_8 —36 —22
Приведение определителя к треуголь-
треугольному виду
Определителем треугольного вида называется опреде-
определитель треугольной матрицы, т. е. определители
«11 «12 «13 • • • «1„
О
Ai =
«22 «23
О 0 а33
¦Чп
0
«11
«21
«31
0
0
«22
«32
0
0
0
«33
... а,
. . . 0
. . . 0
. . . 0
"П2 «Л3 • • • "ял
Определитель треугольного вида равен произведению
элементов его главной диагонали, т. е.
Al = Л2 = «П«22«33 • • • «пп-
Действительно, разлагая определитель Ai по элемен-
элементам первого столбца, имеем
«22 «23 • • • «2
О а33 . . . а3
= а
п
0 0
Полученный определитель вновь разлагаем по элементам
первого столбца. Тогда
«33 «34 • • • «Зп
0 а,, ... а.
— «Ц«22
Чп
О О
37

Продолжая этот процесс, получим
Аналогично можно показать, что
1
1
— 1
2
2
5
2
4
— 1
6
3
— 2
5
3
5
8
Таким образом, иногда удобно при вычислении опре-
определителя предварительно привести его к треугольному
виду, используя свойства определителей.
Пример 2. Вычислить определитель
А =
Решение. Приведем определитель к треугольному виду. Для
этого из второй строки вычтем первую, к третьей строке прибавим
первую, из четвертой строки вычтем первую, умноженную на 2.
Получим
Д =
Так как определитель треугольного вида равен произведению эле-
элементов главной диагонали, то
А = 1 -3-2 (— 2) = — 12.
Разложение определителя
потеореме Лапласа
Теорема Лапласа позволяет свести вычисление опре-
определителя порядка п к вычислению определителей более
низких порядков. Этой теоремой удобно пользоваться
тогда, когда в определителе имеются равные нулю мино-
миноры. В этом случае при вычислении определителя удобно
выделять в нем те k строк или столбцов, которые содер-
содержат наибольшее число миноров k-vo порядка, равных
нулю.
1
0
0
0
2
3
0
0
— 1
7
2
0
5
— 2
10
— 2
38

Пример 3. Вычислить определитель
2 3 0 0 0
4 7 0 0 0
Д= —8 2 10 0
25 17 0 I 0
17 8 0 0 1
Решение. Выделив в определителе две первые строки и при-
применив теорему Лапласа, получим
А =
2
4
3
7
1
0
0
0
1
0
0
0
1
= 2.
Метод опорного элемента
Метод опорного элемента заключается в последова-
последовательном применении формулы, выражающей определи-
определитель порядка п через определитель порядка (п—1), эле-
элементами которого являются определители второго по-
порядка.
Если элемент данного определителя, стоящий в левом
верхнем углу, отличен от нуля, то эта формула имеет вид
«11 «12 «13 • • • «1л
«21 «22 «23
«31 «32 «33
«2„
п—2
и
«И
«21
Oil
«31
Й12
«22
«12
«32
«11
«21
«11
«31
«13
«23
«13
«33
«11
«21
«11
«31
«1л
«2л
«in
«3„
ап а
13
«„1 «лЗ
«И «1„
«nl «я
• A-22)
«11 «12
«Л1 «„2
Элемент аи в этом случае называется опорным. В ка-
качестве опорного элемента можно взять любой отличный
от нуля элемент данного определителя.
39

При п = 3 формула A.22) имеет вид
аи
«21
«31
«12
2
Й32
flu
П
3
«33
1
«11
an
«21
flu
«31
«12
Й22
flu
Й32
Oil
«21
«11
«31
fll8
Й23
flu
ЙЗЗ
A.23)
Докажем справедливость этого равенства. Умножим
вторую и третью строки данного определителя на опор-
опорный элемент аи. Так как при этом определитель умно-
умножится на а2п, то
а
12
а
13
«22 «23
-*32
а
33
1
«12
ЙЦ«
Ц«21
Вычитая в последнем определителе из второй строки
первую, умноженную на а21, а из третьей — первую,
умноженную на а31, получим
1
fl?1
a
0
0
ЙЦ
«12
«13
«11«32 «12«31 «11«33 «13«31
Разлагая полученный определитель по элементам первого
столбца и учитывая, что
ап
aii
ап
«31
flu
Й22
Й12
Й32
ап
«13
flu
«31
«21
Й23
«13
«33
«11«32 — «12«31 =
приходим к равенству A.23).
Аналогично доказывается справедливость формулы
A.22).
Применяя последовательно формулу A.22), мы при-
приводим данный определитель к определителю второго по-
порядка. Таким образом, вычисление определителя порядка
п сводится к вычислению некоторого числа определите-
определителей второго порядка.
40

Пример 4. Вычислить определитель
— 12 7 5
13—12
2 1 2 3
— 5 2—13
Д =
Д =
Решение. Согласно формуле A.22),
—12 —1 7
13 1—1
—12 —1 7
(—IJ 2 1 2 2
—12 —1 7
_5 2 —5 —1
—5 —6 —7
_5 —16 —13
8 36 22
— 1 5
1 2
— 1 5
2 3
— 1
— 5
А =
Применив еще раз формулу A.22), получим
5 —6
1
_5 —6 —7
_5 —16 —13
8
36
22
—5
— 5 —16
8
50 30
— 132 —54
— 5
— 5
— 5
36
= — 252.
7
— 13
— 7
22
§ 1.14. Определитель произведения матриц
Теорема. Определитель произведения двух квадрат-
квадратных матрац одинакового порядка равен произведению
определителей перемножаемых матриц.
Доказательство. Приведем доказательство тео-
теоремы для матриц второго порядка. Пусть даны матрицы
*i
Ъ,
ап а12
->гг
Произведением этих матриц будет матрица
i" «22^21 021*
12
41

Докажем, что
det (AB) = det A det В.
Рассмотрим вспомогательную матрицу
аи я12 О О
а21 % О О
— 1 О 6ц Ьи
О —1 Ьи Ь%2
с =
Выделив, например, в определителе матрицы С две пер-
первые строки и применив теорему Лапласа, получим
detC = (— 1I+2+1+2
an
или
det С = det A det B.
A.24)
Вычислим det С другим способом. Для этого в мат-
матрице С к третьему столбцу прибавим первый, умножен-
умноженный на Ь\\, и второй, умноженный на 621, к четвертому
столбцу прибавим первый, умноженный на Ь\ч, и второй,
умноженный на Ь22- Тогда
detC =
flll «12
«21 «22
— 1 О
О —1
anb
nb12
a12b,
22
0
0
0
0
Выделив в полученном определителе последние две стро-
строки и применив теорему Лапласа, получим
—1 О
detC=(—
О —1
или
Сравнивая выражения A.24) и A.25), имеем
A.25)
Аналогично эта теорема доказывается для матриц
произвольного порядка. ¦
42

Замечание. Теорема справедлива и для случая произведения
п матриц (п>2).
§ 1.15. Обратная матрица
Матрица В называется обратной квадратной матрице
А, если АВ = ВА=Е, где Е— единичная матрица. Из оп-
определения следует, что обратная матрица может сущест-
существовать только для квадратной матрицы.
Прежде чем рассматривать вопрос существования
обратной матрицы, введем некоторые понятия.
Невырожденной или неособенной матрицей называет-
называется квадратная матрица, определитель которой отличен от
нуля.
Если определитель матрицы равен нулю, то матрица
называется вырожденной или особенной.
Пусть дана квадратная матрица
А =
«11 «12
«21 «22
и1п
а
л2
Матрицей, союзной или присоединенной к матрице А,
называется матрица
А12 л22 . . . АП2
С =
4ХЛн **-с>
где Aij — алгебраическое дополнение элемента ац данной
матрицы А.
Обратим внимание на то, что в матрице С алгебраи-
алгебраические дополнения к элементам i-й строки матрицы А
расположены в t-м столбце.
Лемма. Если А — квадратная матрица порядка п, а
С — союзная к ней матрица, то
где Е — единичная матрица порядка п.
Доказательство. Обозначим через D произве-
произведение АС, т. е.
43

«И «12
«21 «22
л
«2л
ып2
Аи А,
А,
].2
К
А„
А„
Согласно определению произведения матриц, элемент
dij матрицы D равен сумме произведений элементов г-й
строки матрицы А на соответствующие элементы /-го
столбца союзной матрицы С. Для элементов da, стоящих
на главной диагонали, получим сумму произведений эле-
элементов t-й строки матрицы А на их алгебраические до-
дополнения, что равно det А (по теореме о разложении оп-
определителя по элементам ряда). Для остальных элемен-
элементов da (i?=j) получим сумму произведений элементов t-й
строки на алгебраические дополнения элементов /-й стро-
строки, что равно нулю (по теореме аннулирования). Следо-
Следовательно,
det Л 0 0 ... О
О det Л 0 . . . О
О
1 О О
О 1 О
О
О
О
О
0 0 0 . . . 1
det Л
det A = E det А.
Аналогично можно доказать, что СА = Е det Л.
Таким образом,
АС = СА=Е det Л.¦ A.26)
Теорема 1. Для того чтобы существовала матрица В,
обратная матрице А, необходимо и достаточно, чтобы
матрица А была невырожденная.
Доказательство. Необходимость. Пусть для
матрицы А существует обратная матрица В. Тогда АВ =
=Е и, следовательно, det (AB) = det E. Используя теоре-
теорему об определителе произведения матриц, имеем
det Л det B = det E. Так как det ?"= 1, то deM^O и, сле-
следовательно, матрица Л невырожденная.
Достаточность. Пусть матрица Л невырожденная,
44

т. е. йе[АфО. Докажем, что матрица , .С, где С-
союзная матрица к Л, является обратной матрице А.
Из A.26) имеем
или
det Л
С =
det Л
_J
det Л
1
С Л = Е,
откуда следует, что матрица , С является обратной
матрице А, т. е.
1
В =
det Л
-С.
В процессе доказательства теоремы получен способ
нахождения матрицы, обратной данной.
Матрицу, обратную матрице А, будем обозначать А~1.
Из теоремы следует, что
Л Л
1
det Л
121
*22
"V2
• • • А
A.27)
Теорема 2. Для невырожденной матрицы существует
единственная обратная матрица.
Доказательство. Пусть Л] и Л^1 — матрицы,
обратные невырожденной матрице А. Имеет место
равенство
ААТ1 = Е.
Умножив обе его части на Л^1 слева, получим
С другой стороны
АТ!ААТ] = (A^A)AT1=EAi1 =
Следовательно,
45

Очевидно, что для невырожденных матриц имеют
место следующие свойства.
1. detA = ....
det А
2. (Л~1)-1 = Л.
3. (Л*) = (Л)*.
4. (АВУ1 = 5-М-1.
Пример 1. Дана матрица
А =
5 —2
1 —3
6
7 —3
Выяснить, существует ли обратная ей матрица А ',
вует, то найти ее.
Решение. Определитель матрицы А
и если сущест-
det Л =
3 5—2
1—3 2
6 7—3
= 10 ф 0.
Следовательно, данная матрица невырожденная и Л существует
Согласно формуле A.27),
1
То"
3
Найдем алгебраические дополнения Ац элементов данной матрицы.
Получим:
11 =
Л21=-
31 =
-3
7
;
5
2
—3
2
—3
2
2
Тогда
1
10
— —5, Л|2
= 1,
" —5 1
15 3
25 9
—14
1
6
3
6
3
1
-
2
—3
—2
—3
2
2
=
= 15,
= 3,
' — 0
1
2
2
о
о,
,5
,5
,5
А*
з —
0,
0,
0,
=
1
3
9
6
3
6
3
1
—
—3
7
5
7
5
—3
0,4
0,8
1.4
=25,
=9,
=—14.

Пример 2. Дана матрица
1
—5
1
2
3
0
4
6
6
2
—2
2
7
5
1
1
0
8
9
0
7
3
9
2
1
Выяснить, существует ли обратная ей матрица.
Решение. Вычислим определитель матрицы А. Прибавив к пер-
первой строке матрицы А ее третью строку, получим
2 6 5 9 2
-5 4 2 0 3
1 6 7 8 9
2 6 5 9 2
3—2101
= 0,
так как в полученной матрице имеются две одинаковые строки.
Итак, матрица А ырожденная, и, следовательно, обратная мат-
матрица не существует.
§ 1.16. Ранг матрицы
Пусть дана матрица размеров тУ(п:
А =
an
«21
«12
«22
а„
Рангом матрицы называется наибольший из порядков
ее миноров, отличных от нуля. Если все миноры матрицы
равны нулю, то ранг матрицы считается равным нулю.
Ранг матрицы будем обозначать г.
Непосредственно из определения ранга следует.
1. Для матрицы размеров пгХп
n),
47

где. min (m, n) — меньшее из чисел тип.
2. г —0 тогда и только тогда, когда все элементы мат-
матрицы равны нулю.
3. Для квадратной матрицы п-го порядка г — п тогда
и только тогда, когда матрица невырожденная.
Пример. Найти ранг матрицы
10 2 0
3 0 6 0
5 0 10 0
Решение. Среди миноров первого порядка (элементов матри-
матрицы) есть отличный от нуля, значит, г>0. Очевидно, что все миноры
второго и третьего порядков равны нулю. Следовательно, г=1.
Отметим свойство миноров матрицы, которым пользу-
пользуются при нахождении ранга матрицы.
Если все миноры порядка k данной матрицы равны
нулю, то все миноры более высокого порядка также рав-
равны нулю. Это следует, например, из теоремы о разложе-
разложении определителя по элементам ряда.
Из указанного свойства ясно, что если среди миноров
порядка k данной матрицы есть отличные от нуля, а все
миноры порядка й+1 равны нулю или не существуют, то
г = й. Отсюда следует, что ранг г матрицы может быть
найден следующим образом.
Если все миноры первого порядка (элементы матри-
матрицы) равны нулю, то г=0. Если хотя бы один из миноров
первого порядка отличен от нуля, а все миноры второго
порядка равны нулю, то г=\. В том случае, когда есть
минор второго порядка, не равный нулю, исследуем мино-
миноры третьего порядка. Так поступаем до тех пор, пока не
случится одно из двух: либо все миноры порядка k равны
нулю, либо миноры порядка k не существуют. Тогда
r = k-\.
Указанный метод нахождения ранга матрицы не всег-
всегда бывает удобным, так как он часто связан с вычисле-
вычислением большого числа определителей. Ниже будут рас-
рассмотрены другие методы вычисления ранга матрицы.
Очевидны следующие свойства ранга матрицы.
1. Ранг матрицы, полученной из данной вычеркива-
вычеркиванием какого-либо ряда, равен рангу данной матрицы или
меньше его на единицу.
2. Ранг матрицы, полученной из данной приписывав
48

наем к ней ряда, элементами которого являются произ-
произвольные числа, равен рангу исходной матрицы или боль-
больше его на единицу.
3. Если вычеркнуть из матрицы или приписать к ней
нулевой ряд, т. е. ряд, все элементы которого равны ну-
нулю, то ранг матрицы не изменится.
4. Ранг матрицы, полученной из данной транспониро-
транспонированием, равен рангу данной матрицы.
§ 1.17. Элементарные преобразования матрицы
Элементарными преобразованиями матрицы назовем
следующие преобразования:
1) умножение некоторого ряда матрицы на число, от-
отличное от нуля;
2) прибавление к одному ряду матрицы другого, па-
параллельного ему ряда, умноженного на произвольное
число;
3) перестановку местами двух параллельных рядов
матрицы.
Если матрица В получена из матрицы А некоторым
элементарным преобразованием, а матрица С в свою оче-
очередь получена из матрицы В также элементарным преоб-
преобразованием, то говорят, что матрица С получена из мат-
матрицы А последовательным применением этих преобра-
преобразований.
Если матрица В получена из матрицы А путем эле-
элементарного преобразования, то будем писать А-*-В.
Легко убедиться в том, что если матрица В получена
из матрицы А путем элементарного преобразования, то
и матрица А получается из матрицы В путем элементар-
элементарного преобразования.
Лемма. Элементарное преобразование 3, заключаю-
заключающееся в перестановке двух параллельных рядов матрицы,
может быть получено последовательным применением
элементарных преобразований 1 и 2.
Доказательство. Пусть дана матрица
. . аи . . . аи ...
А= ¦ • ¦ ам ¦ • ¦ <hi • • •
¦ ¦ ami ¦ ¦ ¦ ami ¦ ¦ ¦
49

Прибавив к i-му столбцу матрицы А /-й столбец, умно-
умноженный на — 1, получим
au — au
a<ii — #2/
Прибавив к /-му столбцу матрицы Л2 /-й столбец, имеем
А-*-А, —
• au
. . . a,.
... a
•21
• • • ami —
Прибавив к i-му столбцу матрицы Л2 /-и столбец, умно-
умноженный на — 1, получим
¦а-ц . . . ax
¦a»,- . . . a2
¦ ¦ ¦ —"mi • • • ami
Умножив /-й столбец матрицы А3 на — 1, имеем
хи
а.
а2/ ... и21
а„г . . . а„
которая получается из данной матрицы А перестановкой
i-ro и ;-го столбцов.
Аналогично проводится доказательство для строк. ¦
Теорема 1. Любое элементарное преобразование, про-
производимое над столбцами матрицы А порядка п, эквива-
эквивалентно умножению матрицы А справа на матрицу, полу-
полученную из единичной матрицы порядка п с помощью того
же элементарного преобразования.
Доказательство. Пусть дана матрица
50

Oil «12
«al «22
au
a9l
au
¦ • "in
• • «2П
0,i
¦Ijl Uj2
au
*jn
*n2
*m
Возможны три случая.
1. Пусть матрица К получена из матрицы А умноже-
умножением t-ro столбца на число %ф®. Обозначим через В мат-
матрицу, полученную из единичной матрицы Е порядка п
умножением i-ro столбца на К. Тогда
X
«и
«21
«Д
<
" 1
0
0
_ 0
an a
«21 «
«;
l a
«12
«22
«i2 •
0 .
1 .
0 .
0 .
12 • •
22 • •
B ¦ •
• • «li
• • Й2;
• • «u
. . 0 .
. . 0 .
. . X .
. . 0 .
. Xau
¦ Xa2i
¦ *"«
. . .
. . .
. . .
. . 0
. . 0
. . 0
. . 1
. . .
. . .
. . .
Mm
«2Л
ain
i
«in "
«2П
11
«П2
uni
= А.
2. Пусть матрица К получена из матрицы А прибав-
прибавлением к ?-му столбцу /-го столбца, умноженного на А,, а
51

С — матрица, полученная из Е прибавлением к г'-му
столбцу /-го столбца, умноженного на К. Тогда
ап а12
<h\ «22
X
1 0
О 1
_0 О
«и аи •
a2l a22 .
aa ai2
ап а/а
flit
/
«2/
. аи
• • • ain
an aj2 . . . aH ... an . . . ajn
... a,
л/
О
О
. . . 0
. . . 0
... а,
. О"
. О
... О
¦«
a2i
Xa
2j
!/
a2j
. . . au
. . . aLj
. . . a,-
m 4-
. anj
X
пп _
00 ...1 ...О ...О
00 . . . К ...1 ...О
1
. aln'
. a2n
.. ain
. a
nn _
3. Так как перестановка двух параллельных рядов
матрицы равносильна последовательному применению
рассмотренных выше преобразований, то теорема верна
и при перестановке двух столбцов матрицы А. Ш
Теорема 2. Любое элементарное преобразование, про-
производимое над строками матрицы А порядка п, эквива-
эквивалентно умножению матрицы А слева на матрицу, полу-

ченную из единичной матрицы порядка п с помощью то-
того же элементарного преобразования.
Теорема доказывается аналогично предыдущей.
Теорема 3. Всякая невырожденная матрица может
быть приведена к единичной матрице с помощью элемен-
элементарных преобразований только над столбцами (стро-
(строками).
Доказательство. Для невырожденной матрицы
первого порядка теорема очевидна. Предположим, что
теорема верна для любой невырожденной матрицы
(п— 1)-го порядка. Пусть дана невырожденная матрица
А =
ап а
„
а1п
ап2
*nn _
Среди элементов первой строки есть хотя бы один, отлич-
отличный от нуля. Не нарушая общности, будем считать, что
Умножив первый столбец матрицы А на , получим
а
ап
матрицу
а12
Й22
_ап\ апг ... ап
Прибавив ко второму столбцу полученной матрицы пер-
первый столбец, умноженный на —а\% к третьему столбцу —
первый, умноженный на —а12, и т. д., получим матрицу
вида
1 0 0 ... 0
Й21 Ь22 Ь23 ... Ь2п
А =
Lam bni bn3 ... bnn j
Полученная матрица является невырожденной, следова-
следовательно, и матрица

Ь,
23
в
невырожденная. Согласно индуктивному предположению,
матрица В с помощью элементарных преобразований
только над столбцами может быть приведена к единич-
единичной матрице. Следовательно, матрица А приводится
к виду
1
«21
Й31
0
1
0
0 .
0 .
1 .
. . 0
. . 0
. . 0
_а'п\ О О
1
Значит, и матрица А может быть приведена к этому виду.
Прибавив к первому столбцу полученной матрицы второй
столбец, умноженный на —a'2i, третий столбец, умножен-
умноженный на — а'г\, и т. д., п-й столбец, умноженный на — а'п\,
получим единичную матрицу порядка п.
Аналогично можно доказать, что невырожденная мат-
матрица приводится к единичной матрице с помощью эле-
элементарных преобразований только над строками. ¦
Следствие. Любая невырожденная матрица может
быть получена из единичной матрицы путем элементар-
элементарных преобразований только над столбцами (строками).
Теорема 4 (об инвариантности ранга матрицы относи-
относительно элементарных преобразований). Ранг матрицы,
полученной из данной элементарными преобразованиями,
равен рангу данной матрицы. (Иногда для краткости го-
говорят: элементарные преобразования не меняют ранга
матрицы или ранг матрицы инвариантен относительно
элементарных преобразований.)
Доказательство. Дана матрица
А =
аи
ап1 ¦ • • aml • • ¦ amn
Достаточно доказать, что ранг матрицы не меняется
при элементарных преобразованиях 1 и 2.
54

Докажем, что преобразование 1, т. е. умножение неко-
некоторого ряда матрицы на число X, отличное от нуля, не ме-
меняет ранга.
Пусть матрица
in ... Хаи . . . а1п
Laml . . . Xami ... amnJ
получена из матрицы А умножением /-го столбца на
\фО. Миноры матрицы В, не содержащие элементов 1-го
столбца, совпадают с соответствующими минорами мат-
матрицы А, а содержащие элементы t-го столбца, равны со-
соответствующим минорам матрицы А, умноженным на X.
Так как КфО, то миноры матрицы В равны нулю или от-
отличны от нуля вместе с соответствующими минорами мат-
матрицы А. Следовательно, ранг матрицы В равен рангу
матрицы А.
Докажем, что преобразование 2, т. е. прибавление
к одному ряду матрицы другого, параллельного ему ряда,
умноженного на число X, не меняет ранга.
Рассмотрим матрицу
С =
аи + Хаи . . . аи . . . аы
<hi + каг! . . . аГ] ... а2п
-ат\ ¦ ¦ ¦ ami+^ani • ¦ ¦ ami • • • amn_i
полученную из матрицы А прибавлением к Z-му столбцу
/-го столбца (i?*j), умноженного на X.
Пусть ранг матрицы А равен г, т. е. среди миноров по-
порядка г матрицы А есть хотя бы один, отличный от нуля,
а все миноры порядка г+1 равны нулю.
Докажем, что среди миноров порядка г матрицы С
также есть хотя бы один, отличный от нуля. Возможны
следующие случаи.
1. Среди миноров порядка г матрицы А, не содержа-
содержащих элементов /-го столбца, есть минор М, отличный от
нуля. Так как матрица С отличается от матрицы А толь-
только /-м столбцом, то минор М является минором матрицы
С. Следовательно, у матрицы С есть минор порядка г,
отличный от нуля.
2. Все миноры порядка г матрицы А, не содержащие
55

элементов i-ro столбца (если такие имеются), равны ну-
нулю. Тогда у матрицы А есть минор М, отличный от нуля
и содержащий элементы i-ro столбца. Рассмотрим минор
Mi матрицы С, расположенный в матрице С так же, как
минор М в матрице А. Так как элементы i-ro столбца
матрицы С являются суммой двух слагаемых, то М\ =
=М+М2. Минор М2 = 0. Действительно, если элементы
/-го столбца содержатся в миноре Мь то минор М2 имеет
два пропорциональных столбца. Если же элементы /-го
столбца не входят в минор Ми то минор М2 равен нулю,
так как является умноженным на % минором матрицы А
(возможно с переставленными столбцами), не содержа-
содержащим элементов /-го столбца матрицы А.
Итак, в любом случае М[=М и, следовательно, матри-
матрица С имеет минор порядка г, отличный от нуля.
Аналогично можно доказать, что все миноры порядка
г+\ матрицы С равны нулю.
Таким образом, матрица С имеет ранг г, равный рангу
матрицы А.Щ
Рассмотренную теорему удобно использовать при вы-
вычислении ранга матрицы. Для этого при помощи элемен-
элементарных преобразований данную матрицу преобразуют
в матрицу, ранг которой легко находится.
Можно показать, что с помощью элементарных преоб-
преобразований любая ненулевая матрица А может быть при-
приведена к трапециевидной
В =
bn
0
0
0
&12
022
0
0
»13
023 •
0
0
. . blr .
. . b2r .
. . brr .
. . 0
. . bln
h
• • t/2/J
• • bra
. . 0
0 0 0
о
о
где Ь\\, Ь22,... ,ЬГТ отличны от нуля.
Вычеркнем в матрице В строки, все элементы которых
равны нулю. Ранг полученной матрицы, состоящей из г
строк, равен г, так как минор порядка г, стоящий в верх-
верхнем левом углу, отличен от нуля. Следовательно, и ранг
матрицы В равен г.
56

Так как матрица В получена из А путем элементар-
элементарных преобразований, то ранг матрицы А также равен г.
Пример. Найти ранг матрицы
Г1 2
Л= 3 —1
5 3
3
4
10
5
2
8
Решение. Ко второй строке прибавим первую, умноженную
на —3, а к третьей строке—первую, умноженную на —5. Получим
2 3 5
.7 —5 — 17
.7 —5 —17
К третьей строке полученной матрицы прибавим вторую, умножен-
умноженную на —1, тогда
2 3 5"
0 —7 —5 —17
0 0 0 0
Мы получили трапециевидную матрицу, ранг которой равен 2. Сле-
Следовательно, ранг матрицы А также равен 2.
Всякую ненулевую матрицу при помощи элементар-
элементарных преобразований можно привести к виду
0 0 ... 0 0 . . . О'
010 ...00 ...0
0
0
0
0
0 .
0 .
. . 1
. . 0
0 .
0 .
. . 0
. . 0
0 0 0
о о
о
Такая матрица является частным случаем трапециевид-
трапециевидной. Ранг этой матрицы равен числу ее единиц.
Теорема 5. Если матрицу А умножить слева или
справа на невырожденную матрицу В, то ране получен-
полученной матрицы будет равен рангу матрицы А, т. е. если
detB^O, то rAB = rBA = rA.
Доказательство. Так как любая невырожден-
невырожденная матрица может быть получена из единичной путем
элементарных преобразований только над столбцами, то
57

умножение матрицы А справа на невырожденную мат-
матрицу В равносильно применению элементарных преобра-
преобразований над столбцами матрицы А. Так как элементар-
элементарные преобразования не меняют ранга матрицы, то
Гав = Га-
Аналогично можно доказать, что гВа — Га-Ш
§ 1.18. Нахождение обратной матрицы при помощи
элементарных преобразований
Известно, что невырожденная матрица путем элемен-
элементарных преобразований только над столбцами или стро-
строками приводится к единичной матрице.
Теорема. Если к единичной матрице порядка п приме-
применить те же элементарные преобразования только над
столбцами (строками) и в том же порядке, с помощью ко-
которых невырожденная матрица А порядка п приводится
к единичной, то полученная при этом матрица будет об-
обратной матрице А.
Доказательство. Пусть А — невырожденная
матрица. Осуществим над столбцами матрицы А элемен-
элементарные преобразования, приводящие ее к единичной мат-
матрице. Те же преобразования и в том же порядке осущест-
осуществим над матрицей Е. Если при этом матрица Е перейдет
в матрицу В, то матрица А перейдет в матрицу АВ=Е,
откуда следует, что В = А~К Ш
Доказанная теорема дает способ нахождения матри-
матрицы, обратной данной. При этом удобно записывать матри-
матрицы А и Е рядом через черту и одновременно производить
элементарные преобразования над строками матриц. Ес-
Если преобразования производятся над столбцами, то мат-
матрицу Е подписывают под матрицей А.
Пример. С помощью элементарных преобразований найти матрицу
I
л-I
обратную матрице
2 0 4
1—1—2
-1 2 3
Запишем матрицы А и Е рядом через черту:
2 0 4 [ 1 0 0
1 —1 —210 1 О
— 1 2 з!о о 1
58

1
Умножив первую строку на -«-, получим
О 21-тгО О
1 —1
¦21010
— 1
2 3 \ 0 0 1
Ко второй строке прибавим первую строку, умноженную на — 1,
а к третьей строке — первую строку. Имеем
1
1
0
0—1—4
0 О
--L 1 О
-г0
Умножив вторую строку на — 1, получим
1 0 2
О 1 4
0 2 5
— О о'
— 1 О
-2- 0 1
Далее, прибавив к третьей строке вторую, умноженную на — 2,
получим
1
0
0
0
1
0
2
4
— 3
2
1
2
1
2
0
j
2
0
0
1
Умножив третью строку на —-д—, имеем
1 0 2 ' J- О О
1
О 1 4
О О 1
1 _ 1
Т
о
1
59

К первой строке прибавим третью, умноженную на —2, а ко второй-
третью, умноженную на —4. Получим
1 0 0 [ JL
I
о 1 о I -4- Л- Л-
i
0 0 11 _ —_ — —
Отсюда следует, что
1
тг
1
6
1
6
1
6
1
6
1
6~
4
3
5
3
2
~з~
4
Т
5
3
2
~?
2 "
3
4
3
1
~зГ_
2 "
~з"
4
3
1
3
§ 1. 19. Теорема о базисном миноре
Если в матрице некоторый ряд может быть представ-
представлен в виде суммы k других параллельных ему рядов, ум-
умноженных соответственно на числа сц, аг, ... , аи, то бу-
будем говорить, что данный ряд является линейной комби-
комбинацией указанных рядов.
Будем говорить, что / параллельных рядов матрицы
линейно-зависимы, если хотя бы один из этих рядов явля-
является линейной комбинацией остальных. В противном слу-
случае параллельные ряды называются линейно-независи-
линейно-независимыми.
Например, в матрице
1
2
3
0
2
3
8
5
0
2
4
4
третья строка является линейной комбинацией первых двух строк,
так как она может быть получена сложением первой строки со вто-
второй, умноженной на 2. Следовательно, три первые строки этой мат-
матрицы являются линейно-зависимыми.
Очевидно, что если в матрице А размеров ту^
торая строка является линейной комбинацией k
п неко-
некодругих
60

строк, где k<m—1, то эта строка является линейной ком-
комбинацией всех строк матрицы, кроме данной. Таким об-
образом, если в матрице s строк линейно-зависимы, то все
строки матрицы линейно-зависимы. Аналогичные утвер-
утверждения имеют место для столбцов матрицы.
Если n-й столбец матрицы Атхп является линейной
комбинацией остальных ее столбцов, то это означает, что
существуют такие числа сц, аг, ... , ап-ь что
2
«21
2
«22
«1 л-1
«2 л-1
&т л— 1
а„_1.
Аналогичная запись имеет место для любого ряда
матрицы, если он является линейной комбинацией осталь-
остальных параллельных ему рядов.
Рядами, проходящими через минор М матрицы А, бу-
будем называть ряды этой матрицы, на пересечении кото-
которых стоят элементы минора М.
Минором, окаймляющим минор М порядка k матрицы
А, называется минор порядка k+\ этой матрицы, содер-
содержащий минор М.
Теорема 1. Если в матрице имеется минор М, отлич-
отличный от нуля, а все окаймляющие его миноры (если они
существуют) равны нулю, то любой ряд этой матрицы, не
проходящий через минор М, является линейной комбина-
комбинацией параллельных ему рядов, проходящих через М.
Доказательство. Так как теорема доказывает-
доказывается аналогично для строк и столбцов, то проведем доказа-
доказательство, например,только для столбцов.
Пусть матрица
«11 «12
й21 а22
«2Л
А =
имеет отличный от нуля минор М порядка k.
Рассмотрим случай, когда существуют миноры, окайм-
окаймляющие минор М, т. е. &<min (m, п). Не нарушая общно-
общности, можно считать, что минор М расположен в левом
верхнем углу данной матрицы.
61

Зафиксируем /
и рассмотрим определители
Al7=
п
а1г
a22
alk
ak2
akj
(* = 1, 2,
m).
akl
aa aiZ . . . aik
Если хотя бы одно из чисел i или / не больше k, то оп-
определитель Ajj = O, так как в определителе имеются два
одинаковых параллельных ряда. При i>k, а также j>k
определитель AtJ = 0, так как он является минором матри-
матрицы А, окаймляющим минор М. Разлагая A,j по элемен-
элементам последней строки, получим
Aij = anai + ai2a2+ ... +flihah+a,-jaft+i, A-29)
где ai, (Z2, ... , а&, а&+1 — алгебраические дополнения эле-
элементов последней строки определителя Aij, причем оче-
очевидно, что числа ai, аг, ... , аи не зависят от i, г ah+i = M
не зависят ни от i, ни от /. Учитывая что A,j=O и МФО,
из равенства A.29) имеем
A.30)
(t=l,2, .... т),
(/=1, 2 k).
Равенство A.30) показывает, что /-й столбец матрицы
А является линейной комбинацией столбцов, проходящих
через минор М.
В случае, когда минор М не имеет окаймляющих ми-
миноров, теорема доказывается аналогично. ¦
Базисным минором матрицы назовем отличный от ну-
нуля ее минор, порядок которого равен рангу матрицы.
Для ненулевой матрицы существует базисный минор
(вообще говоря, не единственный).
Пусть для данной матрицы выбран базисный минор.
Строки и столбцы, на пересечении которых стоят элемен-
элементы базисного минора, называются базисными.
Теорема (о базисном миноре). 1. Любая строка (стол-
(столбец) матрицы является линейной комбинацией базисных
строк (столбцов). 2. Базисные строки (столбцы) матрицы
линейно-независимы.
Доказательство. 1. Пусть М — базисный минор
матрицы А, ранг которой равен г. Тогда все миноры по-
62

рядка г+1 (если они существуют), в том числе и миноры,
окаймляющие минор М, равны нулю. Следовательно, сог-
согласно теореме 1, всякая не базисная строка (столбец)
является линейной комбинацией базисных строк (столб-
(столбцов). Тот факт, что всякая базисная строка (столбец)
представляется в виде линейной комбинации базисных
строк (столбцов), является очевидным.
2. Предположим, что базисные строки (столбцы) мат-
матрицы линейно-зависимы. Тогда одна из базисных строк
(столбцов) матрицы является линейной комбинацией
остальных базисных строк (столбцов); следовательно,
одна из строк (столбцов) базисного минора является ли-
линейной комбинацией остальных его строк (столбцов). От-
Отсюда и из свойств определителей следует, что базисный
минор равен нулю, что противоречит его определению. ¦
Следствие 1. Всякий не базисный ряд матрицы, явля-
является линейной комбинацией всех параллельных ему рядов
этой матрицы.
Следствие 2. Максимальное число линейно-независи-
линейно-независимых параллельных рядов матрицы равно рангу матрицы.
Следствие 3 (критерий равенства нулю определите-
определителя). Для того чтобы определитель матрицы был равен
нулю, необходимо и достаточно, чтобы некоторый его ряд
был линейной комбинацией других параллельных ему
рядов.
§ 1.20. Метод окаймляющих миноров для вычисления
ранга матрицы
Из результатов предыдущего параграфа следует: если
в матрице А имеется минор М порядка г, отличный от
нуля, а все миноры матрицы А, окаймляющие минор М
(если они существуют), равны нулю, то ранг матрицы А
равен г. Значит, для определения ранга матрицы доста-
достаточно найти отличный от нуля минор М, все окаймляю-
окаймляющие миноры которого равны нулю. Тогда ранг матрицы А
равен порядку минора М.
Пример. Найти ранг матрицы
А —
1
— 2
0
7
1
— 3
4
— 2
— 15
1
2
3
7
— 7
5
5
1
11
2
6
63

Среди элементов матрицы А имеются отличные от нуля, например
элемент, стоящий в левом верхнем углу. Среди миноров, окайм-
окаймляющих этот элемент, также есть отличные от нуля, например
1 —3
— 2 4 '
Среди миноров, окаймляющих М, т. е. среди миноров
М =
1
— 2
0
—
—
—
1
2
7
3
4
2
—
2
3
7
3
4
15
5
1
2
1
— 2
0
—
—
—
1
2
1
3
4
2
5
1
11
-3
4
1
t
2
3
5
1
2
7
—
—
—
1
2
1
3
4
15
— 3
4
1
—
5
1
6
2
3
7
нет отличных от нуля. Следовательно, ранг матрицы А равен 2.
Задачи
1.1. Даны матрицы
'2
3
5
j
0
4
, в =
' — 1
2
7
3
5
8
?
" 0
12
7
4
5
13
Найти:
а) 2А + ЗВ; б) А — 2В + ЗС.
1.2. Найти А + А\ где
А =
1.3. Для каких матриц А — Атхп существует А + АТ?
1.4. Каким условиям должны удовлетворять элементы матрицы
ап а12
021 fl22
*Я1 "Л2
чтобы А-\-Ат = О, где О — нулевая матрица порядка я?
1.5. Дана матрица
ч: -;
Найти матрицу X, удовлетворяющую условию:
а) ЗА + X = О; б) ЧА + ЗХ = Е.
64

Г-1 8 4 3]
'[ 0 5 -1 а]'
1.6. Даны матрицы
5 —1 4 01 _ Г— 1 8
1 3 7_Г =L 0 5
Найти матрицу X, удовлетворяющую условию:
а) ЗА — -g-X = B; б) А + 5 Х = О; в) X — 2В = О.
1.7. Известно, что А3х5Втхп = С3х4. Найти тип.
1.8. Известно, что Атх3 Bnx4=C5xfe. Найти т, п, k.
1.9. Даны матрицы
2 —Г
3 4
А =
г
— 1
3
Существуют ли произведения:
а) ЛВ; б) ВЛ; в) АС; г) СЛ; д) ВС;
е) СВ; ж) ОЛ; з) AD; и) ЛВС; к) BAD;
л) СВЛ; м) ЛСВ; н) ВСА?
1.10. Найти /4В, если
'-[-?:]¦-[;]•
В задачах 1.11 — 1.16 найти произведения матриц.
— 1
4
6
1.11.
Г 2 01 ГЗ 21 1.12. Г1
[-1 4J 1.0 б]' [4
1.13.
3
5
1
— 1
6
— 2
4
0
3
2
0
0
0
— 1
0
0
0
3
1.14.
1.15.
— 1
5
4
3 4
• 9 13
7 12
•1 2
5
0
8
— 3
О О
О О
о о
о о
о о
3
5
О
7
2
5
— 1
A 2 3).

1 . ID.
1.17.
Л =
2—1 3
1 3—1
_ 4 5 1
Даны матрицы
ап а12 . . .
Я21 «22 • • •
ап1 ап2 .. .
—
агп
впп _
8
5
7
. D =
dt О
О d2
ш- 0 0
а) Найти В = AD и С = DA;
б) указать условия, при которых AD = DA.
1.18. Даны матрицы
Л =
Найти элемент матрицы D = ЛВ, стоящий во второй строке
и третьем столбце.
1.19. Дано
— 1
8
3
5
9
7
10
— 8
7
5
2
5
2
5
1
1
0
— 1
2
— 1
0
8
4
3
1
4
2
Найти ВА — АВ.
1.20. Проверит^ имеет ли место равенство (Л + ВJ = Л2 +
2ЛВ + В2, если:
б) Л =
2 3
—2
1.21. Показать, что если матрицы А к В перестановочны, то:
а) (А + ВJ = А2 + ЧАВ + В2;
б) (Л + В) (Л — В) = Л2 — В2;
В) (л + бK = Л3 + ЗЛ2В + ЗЛВ2 + В3.
1.22. Найти:
а)
-1 5
2 З
Г-1
L 2
в) ГО 1 *
[ 0 0 J '
б)

0
0
0
1
0
0
0
1
г)
cos a — sin а
sin а cos а
66

1.23. Найти (ABf, если
-i 3
1.24. Найти (АВK, если
В задачах 1.25 — 1.27 для данных А и / (х) найти / (А).
1.25. Л = [3 о]1
3 О
О 1 О
О 0 1
0 0 0
1.26. /4 =
1.27. A =
1.28. Найти f(AB), если
, / (jc) = Ъхъ — 4х4 —
— 7.
, / (х) = х3 — Зх2 + 4а- — 1.
1.29. Доказать, что матрица
1 2 —2
1 0 3
1 3 О
является корнем полинома / (х) = Xs — хг — 9х -\- 9.
1.30. Доказать, что матрица
1 О О'
А= 0 1 О
0 0 3
является корнем полинома / (х) = х3 — 5х2 + 7х — 3.
1.31. Дано
— 1 2
О 3
Найти 2f(A) — Зф(Л).
67

1.32. Дано
I f(x) = x
!j ф(ж) = :
1 2j ф(х) = Зл: + 5.
Найти/(Л) — 2ср(Л).
1.33. Найти (/(Л))а, если
ГО 1 -1-1
=2 -1 3 ,
LO -I -lj
В задачах 1.34 — 1.39 найти число инверсий в перестановках.
1.34. 1, 5, 7, 2, 4, 3, 6.
1.35. 2, 3, 1, 4, 5.
.36. 1, 2, 7, 8, 5, 6, 4, 3.
1.37. 5, 4, 3, 2, 1.
1.38. 1, 3, 5, 7, ... , Bп—1), 2, 4, 6, 8, ... , 2я.
1.39. 2, 4, 6, ... , 2п, 1, 3, 5 Bя—1).
1.40. Пусть k — число инверсий в данной перестановке. Найти
число &J инверсий в перестановке, полученной из данной переменой
местами двух рядом стоящих чисел.
1.41. Пусть k — число инверсий в данной перестановке, а кг —
число инверсий в перестановке, полученной из данной переменой
местами двух чисел, между которыми имеется / чисел. Выяснить,
четным или нечетным будет А1? если к:
а) четное; б) нечетное.
В задачах 1.42—1.48 выяснить, является ли членом определи-
определителя пятого порядка каждое из указанных выражений.
1.42.
1.43.
1.44. —
1.45.
1.46.
1.47.
1.48. —
1.49. При каких значениях k и т является членом определителя
шестого порядка выражение:
а) —
б)
1.50. Существует ли значение k, при котором является членом
определителя пятого порядка выражение:
68
б) —
В задачах 1.51, 1.52 вычислить определители

1.51.
— 1 3
2 — 2
4 5
1.52.
1
0
0
2
4
0
3
5
6
В задачах 1.53 — 1.55 решить указанные уравнения.
1.53.
1.55.
1-х
1
1 — л:
О
О
1
3 — х
1
2-х
О
= 0.
2
3
3 — х
1.54.
= 0.
х
3
х — 5
1
1
1
2
1
2
— 1
1
3
В задачах 1.56—1.61 вычислить указанные определители, поль-
пользуясь их свойствами.
1.56.
1.58.
1.60.
2
4
О
3
2
3
4
2
361
2
363
— 1
7
О
— 1
3 4
4 5
6 8
3 7
273
2
275
3
12
О
2
5
6
10
8
568
2
570
5
— 2
О
4
1.57.
1.59.
1.61.
2
О
О
О
5
7
8
9
1273
1272
— 3
6
6
2
4
2
6 '
8
2273
2272 '
1.62,
Дана матрица
Г —2 —1
5
-7
2
1
3
2
14
5
1
4"
4
13
4
2
Найти:
а) минор, дополнительный к минору, стоящему на пересечении
первой и третьей строк, первого и второго столбцов;
б) алгебраическое дополнение к минору третьего порядка, стоя-
стоящему в правом верхнем углу;
в) алгебраическое дополнение к минору, стоящему на пересече-
пересечении первой и второй строк, второго и четвертого столбцов.
1.63. Дана матрица
' 5 0
4 —1
2 1
69

Найти:
а) миноры элементов второй строки;
б) алгебраические дополнения элементов второй строки;
в) алгебраические дополнения элементов третьего столбца.
В задачах 1.64—1.66 вычислить определители, используя теорему
о разложении определителя по элементам ряда.
1.64.
1.66.
2 3
О 1
О О
О О
О О
3
О
— 1
1
— 2
5
3
0
0
1
4
— 3
5
0
0
1
4
— 7
20
1.65
— 2 1 1
1 2 0
2 4 2
— 3 0 0
0 0 2 0 0
0 1 5—1 О
2—3 7 2 3
1 0—4 2—0
-1 2 0—1 2
В задачах 1.67—1.69 вычислить определители, используя их
свойства и теорему о разложении определителя по элементам ряда.
1.67.
2 —3 1
— 2 3 5
4 7—2
1.68.
1 2 —1
5—3 7
2 4 8
1.69. 2-3 4-2
2—1 3 1
12—1 0
3 1 4—1
В задачах 1.70, 1.71 вычислить определители, используя теорему
Лапласа.
1.70.
3
0
0
1
0
1
0
2
5
2
2
3
— 1
3
3
— 1
2
0
0
0
1
2
0
0
0
1.71.
1
3
0
0
0
0
2
4
0
0
0
0
0
0
2
6
0
0
0
5
1
1
0
0 -
0
0
5
6
9
-1
2
3
1
8
10
2
В задачах 1.72—1.74 вычислить определители, приведя их
к треугольному виду.
70

1.72.
1.74.
¦1 3
5 7
1 2
1.73.
¦12 2
3 6 0
6 6 4
5
2
10
15
— 2 3
7 1
— 1 5
— 6 13
В задачах 1.75, 1.76 вычислить определители методом опорного
элемента.
1.75. 2—1 3 0 '-76.
112 3
0 4—1—5
0 2 18
В задачах 1.77 — 1.79 вычислить определители
1.77. n I _i 1 1.78.
2
7
3
1
1
1
— 1
3
1
3
1
2
0
1
2
1
0 1—1 1
1 2 3—1
0 4 3 2
1—1 12
218 178 201
220 180 199
4 4 4
1.79.
2 3
3 1
5 4
•1 О
1 О
1 3
— 1 О
О 4
О 3
3 1
1.80. Найти det (AB), если det A = 2, det S = — 3.
1.81. Найти det (AB), если
о
1.82. Найти det (ЛВС), если
— 1 2 1~| Г—1
1 О 3 , В= 7
3—4 1 17
=[ ° Ч-
L-1 2J
5
13
— 8
12
148
25
Q
3 5 7
12—8—1
О 15 2
71

1.83. Найти det
2 О
4 1
1 1
I, если det A = 3,
— 1 — 2 О
С = —3 —4 —1
— 1 —1 —1
В задачах 1.84—1.91 найти матрицы, обратные данным (если
они существуют).
1.85.
1.84. Г2 —П 1.85. ГО П
L3 5]' [з -2У
1.86.
1.88.
1.90.
— 1
1
4
2—3 0
-1 1 4
3—2 5
1.87.
1.89.
2 —3
-1 5
3 —1
1 0 1
0 0 2
— 13 1
•1
1
3
2
2 3
— 1 О
— 5 —1
1 О
4
0
3
3
1
.91.
1111
0 111
0 0 11
0 0 0 1
1.92. Доказать, что матрицы А + Е и Е — А невырожденные
и взаимно-обратные, если А2 = О.
1.93. Доказать, что матрицы Л + ? и Аг-\-Е — А невырожден-
невырожденные и взаимно-обратные, если А3 — О.
1.94. Доказать, что если А, В, С — невырожденные матрицы,
то ABC и С~1В~1А~1—взаимно-обратные.
В задачах 1.95—1.99 найти матрицу X из уравнений.
1.95. |
1.97. Г
1.98.
— 2
3
— 1
О
= 2С, где
1
0
0
1
1
0
1
1
1
1 —1
О 3
-2 О
— 1
О
2"
4
-1
3
— 3
— 1
72

1.99. XA — 25 =
1—1 3"
Л=
2
— 1
5 7
12
где
,6=
1 3 —2
— 1 2 О
3-1 4
В задачах 1.100, 1.101 определить, при каких значениях Я, су-
существует матрица, обратная данной.
1.100.
•2 2
3 О
1 1
1.101.
к 2 О
2 А, 1
О 1 к
В задачах 1.102—1.107 найти ранг матрицы.
1.102
. Г 1 21 1.103. Г 1 21
1.3 -lj" [з б]'
1.104.
1.106.
О 1 3
0 3—1
0 2 О
1 3 2
2 6 4
_1 _з —2
1.105.
1.107.
1 —2 3
2—4 6
5 1 4
1—240
— 1 3 5 1
2—140
В задачах 1.108—1.111 найти ранг матрицы, используя элемен-
элементарные преобразования.
1.108.
1.110.
—10 3—2
2 3—1—3
3 6 1—8
— 2 Г
1 —1
4 1
О О
1.109.
1.111.
13 5 3 7
40 16 10 22
54 22 14 30
1 2'
7 3 5
11 5 8
15 7 11
В задачах 1.112—1.116 найти ранг матрицы методом окайм-
окаймляющих миноров.
1.112.
110 0 0
2 3 0 0 0
0 0 5 0 0
0 0 0 6 0
О 0 0 0 8
1.113.
12 3 4-
— 13 0 1
2 4 18
17 6 9
О 10 1 10
73

1
1
1
имеет
1.
1.
1.
1.
равен:
а)
114.
116.
117. 1
ранг,
118. 1
1
2
1

0
0
0
1
1
1ри
1
2 —
1
1 2
2 1
0 3
0 0
3 6
3 3
каких
равный 1?
1ри
119. При
120. При
121. При
1;б)
2; 1
каких
каких
каких
каких
з) 3?
3 3
2"
1—14
3 3 2
3 — 1"
2 2
3 —3
4 0
12 —2
5 1
1.115
*
2
— 1
1
значениях X матрица
[:
значения?
А =
значения}
А =

2
1
зничениях
Л =
значениях

С
А
2J
: % ранг
\ 0
3 4
1 —1
' % ранг
0
к-2
0
к ранг
" 1 0 X
2 3 4
0 0 8
X ранг
% 2"
> 1 4
1 2 8
матрицы
1
1
2
?
матрицы
— Г
3
4
?
матрицы
>
матрицы
4 —2
— 2 1
2 —1
А равен
Л равен
Л равен
3
1
4
2,
3,
3,
3 1
7 2
10 3
если
если
если
74

Глава 2
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
§ 2.1. Матричная запись системы линейных уравнений
Линейной системой m уравнений с п неизвестными
х\, х% ..., хп называется система вида
B.1)
где uij, ft,(t = l, 2 m; /=1, 2, ... , /i) —числа. Заме-
Заметим, что ац — коэффициент при неизвестном Xj в i-u
уравнении системы; hi — свободный член в этом урав-
уравнении.
Матрица
~ап а12 ... аы
составленная из коэффициентов при неизвестных системы
B.1), называется матрицей или основной матрицей си-
системы, а матрица
А =
ап
aln
L"ml
которая получается из матрицы А приписыванием столб-
столбца из свободных членов, называется расширенной мат-
матрицей системы.
Для того чтобы записать систему B.1) в матричной
форме, наряду с матрицей системы рассмотрим матрицы
75

_*«_
К
„К.
Так как матрица А согласована с матрицей X, можно
найти произведение АХ:
-f- a12xa -{-•••+ ainXn
~~\~ CL22X2 ~T~ • • • 1 &2nXn
АХ =
Элементами полученной столбцевой матрицы являются
левые части уравнений системы B.1). На основании оп-
определения равенства матриц систему B.1) можно запи-
записать в виде
АХ = Н. B.2)
Такая запись системы называется матричной.
Каждой системе B.1) соответствует единственная па-
пара матриц Л и Я, и наоборот. Систему B.1) можно запи-
записать также в виде
ап
«14-
-атп-
к
.К-
. B.3)
§ 2.2. Решение системы. Эквивалентные системы
уравнений
Упорядоченная система чисел (ci; с2; ... ; сп) назы-
называется решением системы B.1), если каждое из уравне-
уравнений B.1) обращается в верное равенство после подста-
подстановки вместо Х\, х% хп соответственно чисел С\,
С2, . . . j Cw
Матрица
С =
76

называется вектор-решением данной системы. Матрица С
удовлетворяет уравнению B.2).
Если существует хотя бы одно решение системы B.1),
то она называется совместной, в противном случае — не-
несовместной. Совместная система называется определен-
определенной, если она имеет единственное решение. Система, име-
имеющая более одного решения, называется неопределенной.
В дальнейшем будет показано, что неопределенная систе-
система всегда имеет бесконечно много решений.
Решить систему — это значит выяснить, совместна
она или несовместна, и в случае совместности найти все
ее решения (множество решений).
Например, система
2лгх = 3,
имеет единственное решение:
_3_ _J_
2 ; 8
и, следовательно, является совместной и притом определенной.
Система, состоящая из одного уравнения
является совместной, но неопределенной. Действительно, положив,
например, *i=Ci, Хг=Съ где С\ и с2 — произвольные числа, из данного
уравнения находим, что
дг3=4-2с1+3с2.
Таким образом, множество решений данной системы бесконечно
и имеет вид
{Ci; с2; 4 — 2c1-\-Zc2 | для любых~с1( с2€ Я}.
Система
„ t „ л
¦^lT ¦*! — "»
Х1 "Г Х2 — °
несовместна.
Очевидно, что если в системе B.1) Cjj = O, t = 1,2, ... , m;
/ = 1, 2, ... , п, то: 1) при Л,=0, i=l, 2, ... , т множество
решений системы бесконечно; 2) если хотя бы одно из
Aj^=O, то система несовместна.
Две системы называются эквивалентными или раено-
сильными, если всякое решение одной из них является ре-
решением другой и наоборот, т. е. если они имеют одно и то
7?

же множество решений. Всякие две несовместные систе-
системы являются эквивалентными.
Элементарными преобразованиями системы назовем
следующие преобразования:
1) умножение некоторого уравнения системы на от-
отличное от нуля число;
2) прибавление к одному уравнению системы другого
ее уравнения, умноженного на произвольное число;
3) перестановку местами двух уравнений системы.
Легко заметить, что при элементарных преобразова-
преобразованиях системы соответствующие элементарные преобразо-
преобразования производятся над расширенной матрицей си-
системы.
Можно доказать, что при элементарных преобразова-
преобразованиях системы приходим к системе, эквивалентной данной.
§ 2.3. Решение невырожденных линейных систем.
Формулы Крамера
Пусть дана система п линейных уравнений с п неизве-
неизвестными
+ «12*2 + • ¦ • + аыхп = hlf
~Ь «22*2 ~Ь • ¦ ¦ 4" агпХП = h2,
anlxx + апгх2
или в матричной форме
аппхп = hn
АХ = Н.
B.4)
B.5)
Матрица А такой системы является квадратной матрицей
порядка п. Определитель этой матрицы
д = det A =
ап
называется определителем системы B.4).
Если определитель системы отличен от нуля, то она
называется невырожденной, в противном случае система
называется вырожденной.
Найдем решение системы B.4) в случае, когда она не-
невырожденная. В этом случае матрица А невырожденная
и для нее существует единственная обратная матрица
78

¦

?22 ... л
Un ... A
лл J
Умножив обе части уравнения B.5) слева на матрицу
А~\ получим
Так как
то
Х=А-Ш. B.6)
Формула B.6) является матричной записью решения
рассматриваемой системы. Матричное равенство B.6)
можно записать в виде
. . . Л„, ~ ~ hx
1
¦ • ¦ Кп- -К-
h,
ИЛИ
X,
А
... 4-
'•in"! "г • • • ~Т "лл"л _
откуда следует, что для любого / (/ = 1, 2, ... , п)
1
В силу теоремы замещения (см. § 1.12),
Л Pi i A Pi \ \ /X Pi — Л
1/ "Г / ~Г • • • ~Г "л/"п — п1'
где Д/ — определитель, полученный из определителя А за-
заменой /-го столбца столбцом из свободных членов системы.
79

Таким образом, имеем
х- А/
Х1 л"
(/=1, 2 n).
B.7)
Выражения B.7) называются формулами Крамера. Фор-
Формула B.6) представляет собой матричную запись фор-
формул Крамера.
Итак, невырожденная система п линейных уравнений
с п неизвестными имеет единственное решение, которое
может быть найдено по формулам Крамера.
Пример. Решить матричным способом систему
6*!+ 7*, — 3*3 = й3-
Решение. Матрица системы имеет вид
3 5 — 2
1 —3
7 —3
Она невырожденная, так как
3
1
6
5 —2
—3
7 —3
= 10^0,
и, следовательно, решение системы может быть найдено по фор-
формуле B.6).
Обратная матрица
Г—5 1 4
1
10
15 3 —8
25 9 —14
(см. пример § 1.15). В данном случае матричное равенство B.6)
может быть записано в виде
— 0,5 0,1 0,4
1,5 0,3 —0,8
2,5 0,9 —1,4
Л,
откуда
*! = — 0,5 Ах
, lft, + 0,4Л3.
Лз — 0,8А3,
80

§ 2.4. Теорема Кронекера — Капелли
Будем рассматривать систему B.1), т. е. произволь-
произвольную систему т линейных уравнений с п неизвестными.
Имеет место следующая теорема.
Теорема Кронекера—Капелли. Для совместности си-
системы B.1) необходимо и достаточно, чтобы ранг матри-
матрицы системы был равен рангу ее расширенной матрицы.
Доказательство. Запишем систему B.1) в виде
B.3).
Необходимость. Пусть система совместна. Докажем,
что ранг гА матрицы
Чп
равен рангу
A =
йтп .
расширенной матрицы
«1л <
\_атХ ... атп hm
Так как система совместна, то имеется совокупность
чисел съ с2, ... , сп такая, что
а
п
«22
т. е. последний столбец матрицы А является линейной
комбинацией остальных ее столбцов. Вычитая из послед-
последнего столбца матрицы А указанную линейную комбина-
комбинацию остальных столбцов, получим матрицу
. . с. О
ап
а12
Jml ат2 • • • атп О
Ранг матрицы Ах равен рангу матрицы А и рангу ма-
матрицы А.
81

Достаточность. Пусть rA = r~ — г. Докажем, что си-
А
стема совместна. Так как гА = г^, то существует минор
А
М, являющийся базисным минором как матрицы А, так
и матрицы А. На основании теоремы о базисном миноре,
последний столбец матрицы А является линейной комби-
комбинацией базисных столбцов, а следовательно, и всех столб-
столбцов матрицы А. Это значит, что существуют числа alt
"Ail
К
-К-
ап такие,
«и
«21
а х
что
«i +
«12
«22
I
а 2
а2 + ... +
fl2n
;
О-тп
Сравнивая последнее равенство с равенством B.3), зак-
заключаем, что (cti; ссг; ... ; ап) является решением системы
B.1). Таким образом, система B.1) совместна. В
§ 2.5. Решение произвольных линейных систем
Теорема 1. Если ранг матрицы совместной системы
равен числу неизвестных, то система имеет единственное
решение.
Доказательство. Пусть система B.1) совместна
и гА — г~ = п. Тогда существует минор М, который
А
является базисным как для матрицы А, так и для А. Так
как каждая не базисная строка матрицы А является ли-
линейной комбинацией ее базисных строк, то система B.1)
эквивалентна системе, состоящей из тех п уравнений этой
системы, коэффициенты при неизвестных в которых обра-
образуют базисный минор М. Последняя система есть невы-
невырожденная система п уравнений с п неизвестными и имеет
единственное решение. Следовательно, и данная система
имеет единственное решение. В
Теорема 2. Если ранг матрицы совместной системы
меньше числа неизвестных, то множество решений системы
бесконечно.
Доказательство. Пусть система B.1) совместна
82

и га = г~ = т < п. Обозначим через Л4 базисный минор
матриц А к А. Не нарушая общности, можно считать,
что базисный минор М расположен в левом верхнем углу
матрицы А, в противном случае можно изменить нумера-
нумерацию неизвестных и порядок уравнений в системе. Таким
образом,
Так как каждая не базисная строка матрицы А явля-
является линейной комбинацией ее базисных строк, то данная
система эквивалентна системе
ахххх
а1гхг + ах г+ххг+1
иЛ, = V
аг1х
г1хх
или
ахххх
arrxr + arr+ixr+i
аХгхг = /?! —
= К
— ... — alnxn,
B.8)
алхх
— ... — arnxn,
состоящей из первых г уравнений системы B.1). Придав
неизвестным хг+\, ..., хп системы B.8) произвольные зна-
значения сг+ь ... , Сп, получим систему г уравнений с г неиз-
неизвестными:
ах1хх
alrxr =:hx —
— ... — alncn,
arlxx
arr+icr+1 — ... — arncn.
B.9)
Определитель этой системы А=МфО, следовательно, при
фиксированных cr+h ... , сп система B.9) имеет решение
Х\ = сь х2 = с2, ... , хт = ст. Очевидно, что (си с2; ... ; ст;
сг+1; ... ; сп) является решением системы B.8). Так как
числа Сг+и ... , сп могут быть взяты произвольно, то мно-
множество решений системы B.8), а следовательно, и систе-
системы B.1) бесконечней!
Из теорем 1 и 2 вытекают следующие теоремы.
аз

Теорема 3. Если система имеет единственное решение,
то ранг матрицы системы равен числу неизвестных.
Теорема 4. Если множество решений системы беско-
бесконечно, то ранг матрицы системы меньше числа неизввг-
стных.
Базисными неизвестными совместной системы, ранг
матрицы которой равен г, назовем г неизвестных, коэффи-
коэффициенты при которых образуют базисный минор. Осталь-
Остальные неизвестные назовем свободными.
Так как базисный минор может быть выбран не един-
единственным образом, то и совокупность базисных неизвест-
неизвестных может быть выбрана не единственным образом.
В доказательстве теоремы 2 содержится способ на-
нахождения решений неопределенной системы (гл = л~ =
А
= г<Сп), состоящий в том, что систему B.1) заменяем
эквивалентной системой B.8). Решение системы находим,
придавая свободным неизвестным произвольные значения
и находя значения базисных неизвестных из системы B.8).
Докажем, что этим способом можно получить любое
решение неопределенной системы. При этом будем поль-
пользоваться обозначениями, принятыми в теореме 2.
Пусть (cti; а.2', ... ; ctn) —решение рассматриваемой
системы, а следовательно, и эквивалентной ей системы
B.8), т.е.
а1пап>
B.10)
В системе B.8) положим xr+i = ar+i, xr+2~-
= аг+2, • • •, хп = а„. Имеем
апх2
+1— ... — а1пап,
B.11)
— arr+iar+i — ... —o,maa.
Сравнивая системы B.10) и B.11), получаем, что
(cti; аг; ... ; аг) — решение системы B.11). Так как систе-
система B.11) невырожденная^ то это решение едицственн.ое.

Следовательно, указанным способом мы нашли решение
(аг, аг; . •. ; ап) системы B.1).
Из доказанных теорем следует, что решение системы
линейных уравнений производится следующим образом.
1. Находим г а — ранг матрицы системы и г~ — ранг
расширенной матрицы. Если гАфг,
то
А
система
несов-
несовместна.
2. Если
г а = г~ = г, то выделяем базисный минор
А
и базисные неизвестные.
3. Данную систему заменяем равносильной ей систе-
системой, состоящей из тех г уравнений, в которые вошли эле-
элементы базисного минора.
4. Если число базисных неизвестных равно числу не-
неизвестных системы, то система имеет единственное реше-
решение, которое можно найти по формулам Крамера.
5. Если число базисных неизвестных меньше числа не-
неизвестных системы, то из системы, полученной в пункте 3,
находим выражение базисных неизвестных через свобод-
свободные, используя, например, формулы Крамера. Придавая
свободным неизвестным произвольные значения, получим
бесконечно много решений исходной системы. Отсюда,
в частности, следует, что неопределенная система имеет
бесконечно много решений.
Пример 1. Решить систему
*i — 5*2 + х3 = 12,
2*! + 4л:2 = — 6,
2*i + *2 + 3*з = 3,
5*!+ 4л:3 = 9.
Решение. 1. Находим ранги матриц
3 -1 Г
1 —5 1
2 4 0
2 1 3
.5 0 4.
и А =
3 —1 1
1 —5 1
2 4 0
2 1 3
.5 0 4
6
12
-6
3
9
Получим
, =^ = 3. Следовательно, система совместна.
А

2. В качестве базисного минора можно взять, например, минор
1 —5 1
2 4 0
2 1 3
так как М ф 0 и его порядок равен тА = Ъ. Базисными неизвестными
являются *х, *2, *з-
3. Данная система равносильна системе
*s —5*2 + х3 = 12,
, = — 6,
, = 3.
4. Число базисных неизвестных равно числу неизвестных системы,
и система имеет единственное решение: *j= 1, *2 =— 2, *3 = 1.
Пример 2. Решить систему
Решен
А =
' 1
2
5
ие.
2
4
10
2*i +
5*i+l
Находим
— 3
5 -
7
4*2
+
0*2+"
ранги
4"
1
2
и
5*3 —
*4
Г*3 + 2*4
матриц
Л =
1
2
5
= 2,
= 11
2
4
10
•J
— 3
5
7
4
— 1
2
7
2
11
Получим гд = г^ = 2. Следовательно, система совместна.
м =
В качестве базисного минора можно взять, например, минор
2 —3
4 5 '
так как МфО и его порядок равен тА = 2. При таком выборе ми-
минора УИ базисными неизвестными являются хг, х3.
Данная система равносильна системе
*i + 2*2 — 3*з + 4*4 = '
2*i + 4*2 J
или
2*2 — Здг3 = 7 -
4*2 + 5*3 = 2 -
По формулам Крамера находим:
7 — *! — 4*4 — 3
2 — 2*! + *4 5
-*! —4*4,
-2*х+*4.
2 —3
4 5
41 —ll*t—17*4
22
86

2 7 — л^ — 4лг4
4 2 — 2x1 + x4
— 24+18*4
22
2 —3
4 5
Следовательно, множество решений имеет вид
41 — llci— 17c2. 9с2 — 12
22 11 ' '
При вычислении рангов гА и
для любых сх, с2 ? Л | •
„ удобно использовать
метод окаймляющих миноров, так как при этом сразу
находится и базисный минор. Удобно также использовать
элементарные преобразования только над строками матрицы
А, приводя ее к трапециевидной форме.
§ 2.6. Системы однородных линейных уравнений.
Фундаментальная система решений
Система линейных уравнений называется однородной,
если свободный член в каждом уравнении равен нулю.
Однородная система имеет вид
«12*2
+ ат2х2 +
атяха = 0-
B.12)
Система однородных линейных уравнений является
частным случаем системы B.1). Она всегда совместна,
так как ранг ее матрицы равен рангу расширенной мат-
матрицы. Очевидно, что
Xi = x2= ... =Хп = 0 B.13)
является решением системы B.12).
Решение B.13) называется нулевым или тривиальным
решением. Система B.12), кроме тривиального, может
иметь и другие решения (нетривиальные).
Из § 2.5 следует, что однородная система имеет лишь
тривиальное решение тогда и только тогда, когда ранг
матрицы системы равен числу неизвестных (г = п). В ча-
частности, если число уравнений равно числу неизвестных
(т=п), то для того чтобы система имела только три-
тривиальное решение, необходимо и достаточно, чтобы опре-
определитель системы был отличен от нуля.
87

Пример 1. Решить систему
—3*4=0.
Решение. Число уравнений меньше числа неизвестных. Сле-
Следовательно, множество решений системы бесконечно.
Ранг матрицы системы равен двум, так как среди ее миноров
второго порядка есть отличный от нуля, например минор
2 —1
4 1
Следовательно, данная система эквивалентна системе
о у y = х X
4*1 + *3 = — 2*г + 3*4.
Отсюда
— 3*2 + 2*4 _5_
*i= g ' ч~ 3 **•
Следовательно, множество решений системы имеет вид
6 3
5
для любых ct, са € Я J.
Если ранг матрицы системы однородных линейных
уравнений меньше числа неизвестных, то множество ре-
решений системы бесконечно.
Пусть Си С2,..., Ck — вектор-решения системы одно-
однородных линейных уравнений, a cti, ct2, ... , а& — некото-
некоторые числа. Тогда
а1С1 + а2С2+ ... +ahCh B.14)
называется линейной комбинацией вектор-решений Clt
С2> ..., Ck, а alf a2, ... , ak — коэффициентами этой
k
комбинации. Если ^ 1аИ=0» то линейная комбинация
B.14) называется тривиальной.
Вектор-решения С\, С% ... , Ck называются линейно-
зависимыми, если хотя бы одно из них является линейной
комбинацией остальных. В противном случае эти вектор-
решения называются линейно-независимыми.
88

Имеют место следующие свойства.
1. Любая линейная комбинация конечного числа век-
вектор-решений системы однородных линейных уравнений
является вектор-решением этой системы.
В справедливости этого свойства читатель легко убе-
убедится самостоятельно.
2. Пусть для системы линейных однородных уравне-
уравнений г<п, где г — ранг матрицы системы, п — число неиз-
неизвестных. Тогда существует п—г линейно-независимых
вектор-решений С\, С2, . ¦., С„_г данной системы и любое
вектор-решение системы является линейной комбинацией
С\, Сг, ..., Сп_г.
Доказательство. Пусть в системе B.12) г<Сп.
Тогда данная система имеет п—г свободных неизвестных.
Не нарушая общности, можно считать базисными неиз-
неизвестными Х\, х% . ¦. , хт. Выразим базисные неизвестные
через свободные. Получим
x1 — d^Xr^-i -j- ... -j- dy n—rXn,
n-rxn, \
п—гХп, {
хг = dnxr+1 + ... +d2
xr = driXr+i -f- ... -\- dr n—rXn.
B.15)
Тогда любое вектор-решение данной системы можно за-
записать в виде
С=
Cr+l
B.16)
где cr+i, ... , с„ — произвольные числа; х\,
ределяются равенствами B.15) при
. . , Xr 0П-
Рассмотрим вектор-решения
89

dm
drl
1
0
0
2
^22
L
0
1
_ 0
d2n-r
drn~r
0
0
• B-17)
1
Очевидно, что эти вектор-решения линейно-независимы,
и для любого вектор-решения С имеем
C — Crjr\C\ -\-Cr-\-2C1-\- . . . + CnCn—r,
т. е. вектор-решение B.16) является линейной комбина-
комбинацией
С\, Сг, .... Сп-г-Ш
Можно доказать, что максимальное число линейно-
независимых вектор-решений системы B.12) (в случае
г<п) равно п—г. В этом случае вводится понятие фунда-
фундаментальной системы решений.
Фундаментальной системой решений системы одно-
однородных линейных уравнений называется совокупность
максимального числа линейно-независимых вектор-реше-
вектор-решений.
Совокупность решений B.17) является фундаменталь-
фундаментальной. Эта совокупность решений называется нормирован-
нормированной фундаментальной системой решений системы B.12).
Пример 2. Найти нормированную фундаментальную систему ре-
решений для системы, заданной в примере 1.
Решение. Было получено:
_ — Зх2 + 2хЛ 5
кх— 6 , х3 — 3 хх.
Используя формулы B.17), в данном случае получаем вектор-решения
1 -
— 2
1
0
Г|
о L
" 1 "
3
0
5
3
1
образующие нормированную фундаментальную систему решений.
90

§ 2.7. Метод последовательного исключения
неизвестных (метод Гаусса)
Дана система т уравнений с п неизвестными:
«12*2 + ¦ • • + а\пх„ = А],
«22*2 + • • •
««2*2
B.18)
Для решения этой системы, кроме вышеизложенных, су-
существуют другие методы. Рассмотрим один из них (метод
Гаусса).
Среди коэффициентов при Xj имеется хотя бы один, от-
отличный от нуля. Не ограничивая общности, можно счи-
считать, что ai 1=^=0, так как всегда можно принять за первое
уравнение системы то, в котором коэффициент при Xj от-
отличен от нуля, а затем перенумеровать неизвестные.
Исключим неизвестное Х\ из всех уравнений, кроме пер-
первого (если таковые имеются). Если ац = 0, то i-e уравне-
уравнение не содержит хп если 0,1 = 0, то к t-му (г = 2, ... , т)
уравнению системы, умноженному на —, прибавим
«
первое уравнение. Получим систему вида.
«и
+ «12*2 + • • • + «!„*„ = Alt
B.19)
эквивалентную системе B.18). Назовем переход от си-
системы B.18) к системе B.19) первым шагом. В резуль-
результате осуществления первого шага могут иметь место сле-
следующие случаи.
1. Среди уравнений системы B.19) имеется хотя бы
одно такое, у которого все коэффициенты при неизвест-
неизвестных равны нулю, а свободный член отличен от нуля. Тог-
Тогда система B.19), а следовательно, и B.18) несовместны.
2. Все коэффициенты а\Р и свободные члены h[X) равны
нулю. Тогда система B.19) состоит из одного первого
уравнения. Если в этом уравнении все коэффициенты,
91

кроме au, равны нулю, то система имеет единственное
решение. В противном случае система неопределенна.
3. Среди коэффициентов а,-/' найдется хотя бы один,
отличный от нуля. В этом случае переходим ко второму
шагу. Не ограничивая общности, можем считать, что
аЩ ф 0. Исключим неизвестное х2 из всех уравнений
системы B.19), начиная с третьего (если таковые
имеются). Получим систему
anxx +
aB2
+
+ .
1
= hi
эквивалентную исходной системе B.18).
В результате второго шага могут иметь место случаи,
аналогичные тем, которые получились в результате пер-
первого шага. Если имеет место третий случай, то переходим
к третьему шагу.
Продолжаем данный процесс, пока это возможно. Ес-
Если мы проделаем (р—1) шагов, то получим систему
Яаз-^з +
^гз-^з "т*
• • • 1 &1пХп
• • ¦ + b2nxn =
... + с3пхп =
к
h% ,
Лз ,
0 =
(P-I)
B.20)
О = fl
, A) B) . „\Р— Ч
Где 0<ц = Й2/ > C3j = Язу > • • • 1 <*ру = Upj
Переход от системы B.18) к эквивалентной ей системе
B.20) называется прямым ходом метода Гаусса.
Возможны следующие случаи.
1. Хотя бы одно из Лр+i", .... /im~" отлично от
92

нуля, тогда система B.20), а следовательно, и система
B.18) несовместны.
2. Все h)p~X) (/ = р + 1, ... , т) равны нулю. Очевидно,
что последние т — р уравнений, левые и правые части
которых равны нулю, не влияют на решение системы,
и их можно отбросить.
Система B.20) может иметь один из двух видов:
треугольный (при р = п):
• • + а1пхп = hlt
апхх + а12х2
l
B.21)
или трапециевидный (при р < п):
апхг + аХ2х2 + ... + а1пхп =
dppxp
*n = h\T1},
B.22)
где flu, 622, • • •, dpp отличны от нуля.
Нахождение неизвестных хи х2, ... , хп из системы
B.21) или B.22) называется обратным ходом метода
Гаусса.
Система B.21), а следовательно, и исходная система
имеют единственное решение. Так как йппФ0, то из пос-
последнего уравнения B.21) хп определяется единственным
образом. Подставляя найденное значение хп в пред-
предпоследнее уравнение, получим единственное значение для
х„_ь так как 1п-\ п-\Ф®. Продолжая этот процесс, нахо-
находим последовательно хп-2, ¦ ¦ ¦ , Х\.
В системе B.22) число неизвестных больше числа
уравнений. Так как йррф0, то из последнего уравнения
этой системы хр единственным образом выражается че-
через Xp+i, .... Хп, Осуществляя обратный ход, выразим
единственным образом неизвестные xp_i, хр-2, ... , Х\ че-
через Хр+п Хр+2, ... , хп. Придавая последним произволь-
произвольные значения ср+ь ср+2, ... , сп, получим бесконечное
множество решений системы B.22), а следовательно, и
системы B.18).
93

Заметим, что при применении метода Гаусса на праю-
тике имеет смысл вместо преобразований системы произ-
производить соответствующие преобразования над строками
расширенной матрицы системы, т. е. приводить расширен-
расширенную матрицу системы к трапециевидной с помощью эле-
элементарных преобразований над строками.
Пример. Решить методом Гаусса систему
4*1 + 2х2+ х3= 7,
2*! + 3*2 — 3*з = И,
4*i+ х2— х3= 7.
Решение. Расширенная матрица системы имеет вид
4 2 1 7'
1—1 1—2
2 3—3 11
4 1—1 7
Прибавив последовательно ко второй строке, умноженной на —4,
к третьей, умноженной на —2, и к четвертой, умноженной на —1, пер-
первую строку, получим
Разделим вторую строку на 3:
4
0
0
0
за
4
0
0
0
2
6
. 4
1
3:
2
2
—4
1
1
—3
7
2
1
— 1
7
2
7
15
—15
0
7
5
—15
0
Прибавив последовательно к третьей строке, умноженной на 1/2, и к
четвертой, умноженной на —2, вторую строку, получим
4
0
0
0
2
2
0
0
1
1
5
2 '
—5
7
5
5
~ 2
5
94

Этой матрице соответствует система
Oy v — Ч
?л2 — л3 — О,
~2~ *s = — ~2~
-5*з = 5.
Осуществляя обратный ход, находим х3 = —• 1, *2 = 2, хх = 1,
Задачи
В задачах 2.1—2.6 записать в матричной форме каждую из ука-
указанных систем линейных уравнений.
2.1. 5*! —
у Q
.+ ж,= 5.
2.3. *,—4*»
2.2.
+ х3
— хг
=5,
= 1,
= 0.
х3= 0, ] 2.4. *!— *2 —5 = 0,
о v «, 1 Q v Л I О v ^ v L I Л
2.5. *i = 0, 2.6. 2*j —4*2+1 = 0,
Xj — Х2 === ' » -^2 "^1 == ^»
*3 + 4 =0. 3*!+ х2 =—1.
В задачах 2.7—2.10 перейти от матричной записи систем к обычной.
2.7. Г 1 -31Г*,1 ГП 2.8. Г 1 0~\[xt-\ ГЗ-
.7. Г1 -3] Г*!] [11 2.8. Г1 0
L4 oJL*1Js=L2j- [о -i
2.9.
2
4
1
1
0
1
3
—2
5
"*х
*2
*3
=
0
0
0
2.10.
= 0.
2.11. Решения каких из приведенных ниже систем можно найти
по формулам Крамера:
а) 2*—3(/ = 5,
в) * + 2(/ — Зг = 1,
*- у+ г = 2,
4х + Зг/ — z = 0;
б) * — 2#= 2,
3*-
: —2i/= 2, |
: —6t/ = 61; J
г) * —2(/+3z = 0,
4* + 7г/+ г = 0,
Зг/ + 6* + 7z = 0?
95

В задачах 2.12—2.21 решить системы уравнений, используя фор-
формулы Крамера.
2.12.
2.14.
2.13.
s— *з= 4,1 2.15.
*з= 8,
*х + 2*2 + 2*з= 5,
3*! +4*2 —5*з= 2.
2.16. 2*!+ *2— *3= 0,
6=0,
= 1.
2.18. 3*з+ *2+ 6 = 0,1 2.19. *!•
Xi — ZA2 — Л3 — О f
3*2 — 2*j — 3*3 = — 5,
3*! — 4*2 + 5*3"= 10.
2.17. 2*x —3*2— *3 + 6 = 0,
3*i + 4*2 + 3*з + 5 = 0,
2— *3 —*4 =
3*!
— 2*з= 13. J
j —3*4
=—6,
=2.
2.20. 2*!+3*з+ 8*4= 0,
2.21. 3*!+
2*! + 3*2 — *4 = 0,
= 1, ^ + 5*2 — 3*3 =7,
= — 24. 3*2 + 2*3+ *4 =2.
В задачах 2.22—2.25 решить системы уравнений матричным
собом.
2.22. 2*!— *2 =Л1.
*i + 2*2— x3 = h2,
спо-
спогде:
a) hx = —1, Л2 = — 2, Л3 = — 2;
б)Л1= 0, Л2 = —2, А3 = —5;
в)Л1= О, Л2= 1, А3= 0.
2.23. 4
где:
a) ftx= 0,
б)Л1 = 12,
— -^3 === »
=1, А3 = —3;

2.24. 2*t + *3 + 3*4 = А,,
2х2 — *х — х3 — 2*4=Л2,
xi— *2 + 4*i =h3,
*t + 2*2 + *3 + 3*4 = Л4,
где:
a) Лх = 0, А2 = А3 = 2, Л4 = 3;
6)/t!= О, Л2 = Л3 = — 4, Л4 = — 6;
!})&! = — 5, А2 = 8, А3 = — 9, Л4 = —2.
2.25. *x + *2 + *3 = Л1
2х1 — *2 + 3*з + *4 = Л2
2*2
3*4
=Л3,
где:
а) Л, = О, /i2 = — 2, Л3 =
Л4 = — 2;
в)А1= 3, A2= 7, A3 = — 2, Л4= 7.
В задачах 2.26—2.33 выяснить, совместна или несовместна каж-
каждая из указанных систем.
2.26. 2*х + 3*2 = 5, ] 2.27. хх — *2 + *3 —2*4=1,
у, \ v О I Ц v ^ v I Q v 7 v . ^
Л| ~т~ Ао — ¦* • I иЛ1 '-'Ло ~Т" ОЛд / Л/л v •
2.28. 2*! +2*2 —3*3 + *4 = 1, | 2.29. *!—2,
2*! —2*2+ *3 — *4=3. / 4*] — 2;
2.30. *х + 2*2 — 3*з — 4*4 = 1.) 2.31.
*1 + 3*2 — *3 + 2*4 = 1 ,
4*х — 4*2 — 3*3 — 3*4 = — 7.
2.32. 2*! + 3*2 + 3*3 — 3*4 + *5=Ю,
*2 + 2*3 + 4*4 — 8*5 = 2,
4*3 + *4 — *5 = 3.
2.33. 3*! + *2 + *3 = 5,
4*, - 3*2 + *3 = 2.
з
= 6,
2хх + 3*2 -
*1 — *2 " *3 ==
= 12,

В задачах 2.34—2.39 для каждой из систем указать неизвестные,
которые можно выбрать в качестве базисных.
2.34. *!— *2
2*! — 2*2
2.35. 3*х + 2*2
2*х + 3*2
*3 + *4 = 2,
7*4 = 4.
х3— *4
х4 — 2*5 = 8.
2.36. 2^ + 3*2+ х3= 1,
—4*3 = 2.
2.37.
3*2
*з=
3*3 = 3.
2.38. 2*! —
2.39. *i+ *a— *3+ *4 = 0,
2*t + 2*2 + 5*з—3*4 = 0,
В задачах 2.40—2.51 исследовать системы уравнений и в случае
совместности решить их.
2.40. 2*1 + 3*2— *3 = 5, | 2.41. *х + 2*2 — *3 = 5, "I
2.42. *,—2*„-
h 2*4-4,1
, = -6. !
2.44.
2.45.
2*! + 3*2 = 5,
4*!+ 5*2 = 7.
2.46. *t + 2*2 + 3*з = 6,
3*! —2*2 + 4*з = 5,
*j — *2 + 3*з = 3.
=2.
2.47. 2*х+ *2— *3 = 3,
2.48.
— *3=
8*2
= 5,
= 1.
3*i+
*!— *2+ *3 = 0,
5*!+ 2*2— *3 = 7.
2.49. 2*x + 3*2— *3+ *4=5,
3*i— *2 + 2*3+ *4= 1,
*x + 2*2 + 3*3 + 4*4= 6,
6*t + 4*2 + 4*3 + 6*4 = 1 .
2.50. ^ + 2*2 — 3*3+ *4=1,
2Xl- x2+ *3 +2*4=2,
4*!+ 3*2 — 5*3 + 2*4=4,
7*! + 4*2 — 7*3 + 5*4 = 7.
2.51. 2*! +3*2 + 2*з = 7,
3*i+ *2+ *з = 5,
*1 + *2+ *3 — 3,
С« у у __ О
98

В задачах 2.52—2.61 решить однородные системы уравнений.
L + *2 + *3 = О,
i — х2 — *3 = О,
. + 3*2 + х3 = 0.
2.52. *! + 2*2 + 3*з= 0, ) 2.53.
2*! + 3*2 + 4*з = О,
3*i + 4*2 + 5*з = 0.
2.54. 3*г — 4*2 + х3 — *4 = °.
6л:! — 8*2 + 2х3 + 3*4 = 0.
2.55. *х —2*2 + 3*3 —
*1 + -«а— *3 +
*t — 5х2 + 8л:3
= 0.
2.56.
3*! —2*2+ ^3 = 0.
^ + 4*2 —7*3 = 0.
2.58. 2^+3*2+2*3 = 0,
3*! + *2 + -«з = 0.
*!+ *2+ *3 = 0.
5*!— *2— *3 = 0.
2.57. 3*! — х2 + 2a;3 + *4 = О,
*1 + *2 — -«з — *4 = °>
5*j + *2 — *4 =0.
2.59. 2*i —*2+ *3+3*4 = 0,
Х1 + Хг+ 3*3 + *4 = О,
4*1 + *2 + 7*3 + 5*4 = О,
5*! — *2 + 5*3 + 7*4 = 0.
2.60. 3*! + *2+ *3 —6*4—12*5 + 3*в = О,
х\ + Х2 + *3 — 2*4— 6*5+ *ц = О,
у J y *\y О
*1 — *2 + Х3—4*5 — *б = 0.
2.61. *! + 3*2— *з+4*4 —*5=0,
v i^ ov „ (^ v i^ у л
¦*1 Ч~ |-'-*2 Л3 "Т~ 4 ~Г* Л5 — w»
2^ + 6*2 — 2*3+ *4 =0,
о*1 ~\- У*2 *Э^з 1~ "^4 "Т" Х$ —— " •
В задачах 2.62, 2.63 выяснить, существует ли фундаментальная
система решений для каждой из указанных систем.
2.62. *! —2*2 = 0, | 2.63. 4*! —2*2+ *3 = О,
3*! +4*2 = 0. | *2 —2*х —3*3 = 0.
2.64. 4*! — 3*2 + 2*з = О,
8*! —6*2+ *з = 0,
2.65.
3*1— *
5*! —
*! — 2Л
2 + 4*3
*3
2 + 9*3
= о,
= 0,
= 0.
99

В задачах 2.66—2.69 найти фундаментальную систему решений
каждой из указанных систем.
2.66. *! + .«2 —5*3 —3*4 = О,
2хх — *а — Ч = 0.
2.67. Xj — 2*3 + *3 — 4*4 + *5 = О,
2х1 — 4*2 — х3 + *4 —2*5 = 0.
2.68. *!+ л2 — Зд;3 =0,
*1 — *2 + *3 + 2*4 = О,
2*i + -«2 — 4д:з+ *4 = 0,
х1-\-2х2 — 5х3— *4 = 0.
2.69. — 2*1 + д:2+ д;3— х4 = О,
*! Д;2 *3 — 2*4 = О,
5*j — х2 — 3*з — 2*4 = 0.
В задачах 2.70—2.73 по данным общим решениям однородных си-
сгем найти нормированные фундаментальные системы решений.
2.70. *! = су + с2 — с3,
Ч = q + 2с2 + с3,
2.71. *1 = 2с1-
*2= clf
С2 —С3,
*4 = С2,
2.72. *!= clt
*2 = 2сх— с2,
*3 = 3ct + 5с2,
2.73.*,=
^^
*2 = Су — С2,
-«з = 3ci +2c2,
4 * *4= Clf *5 = C2.
В задачах 2.74—2.81 решить системы методом Гаусса.
2.74.
2.76. 2^ — 3*2 + 5*3= 11,
3*1— *2 + 3*з = 10,
*1 + 2*2 —4*з = —7.
2.75. 3*! + 2*г — 3*з + 4*4 = 1,
2*х + 3*2 — 2*з + 3*4 = 2,
4*! + 2*2 — 3*з + 2*4 = 3.
2.77. 2.Xi —J— #2 — -^з == *¦*»
*! —3*2 +3*з = 7,
5*! — 3*2 + Зх3 = 7.
2.78. 3*х —2*2+ *3— *4 = 0,
3*i — 2*2 — *з + л'4 = 0,
100

2.79. *i + *2 —3*4 —4*6 =0,
2.80. 2*j+ 3*2 —5*з+ *4— *5 = 0,
4*x + 7*2 + *3 + 5*4 + 3*5 = 1,
5*j + 9*2 + 4*3 + 7*4 + 5*5 = 8.
2Q1 Ov I ^v v I v I Q Л
, ol i ***^1 "i~ ^-*o -^g ~~r~ JCi —г— О === U,
Qv v i 9v 1 Иv Q П
V J_ V _4_ *Чг 9v fi П
— *! + 2*2 + 3*3 + 5*4 — 3 = 0.

Глава 3
ЛИНЕЙНЫЕ ПРОСТРАНСТВА
§ 3.1. Определение линейного пространства
и подпространства
Рассмотрим непустое множество V элементов х, у,
г, ... и R — множество всех вещественных чисел.
Пусть задан закон, в силу которого каждой паре х, у
элементов множества V ставится в соответствие опреде-
определенный элемент z этого же множества. В этом случае го-
говорят, что на множестве задана внутренняя операция, или
операция сложения; элемент z называют суммой и пишут
x+y=z.
Кроме того, будем считать, что определена внешняя
операция, или операция умножения элементов множества
V на число, т. е. задан закон, в силу которого каждому
элементу jteV и произвольному числу ае R ставится
в соответствие определенный элемент zeV. Будем назы-
называть z произведением числа а на элемент х и писать
ax=z или xa=z.
Предположим, что для введенных операций выпол-
выполняются следующие аксиомы.
I. х+у=у+х для любых х, уеК
II. (x+y)+z=x+ (y+z)=x+y+z для любых х, у,
III. В множестве V существует элемент, который бу-
будем называть нулевым и обозначать о, такой, что х+о = х
для любого л:е V.
IV. Для каждого элемента x^V существует элемент,
который будем называть противоположным элементу х
и обозначать —х, такой, что х+ {^х) =о.
V. Для любого x^V \-x=x.
Для любых чисел а, ре R и любых х,
VI. а(р*) = (ар)х.
VII. а(х+у)=ах+ау.
VIII. (
102

Множество V, в котором определены операции сложе-
сложения (внутренняя операция) элементов множества и умно-
умножения (внешняя операция) элементов множества на про-
произвольные числа из Л и эти операции удовлетворяют ука-
указанным выше аксиомам I—VIII, называется веществен-
вещественным линейным или векторным пространством.
Если множество образует линейное пространство, то
элементы х, у, z, ... этого множества будем называть эле-
элементами пространства или векторами и обозначать
х.у.г,...
Аналогично определяется комплексное линейное про-
пространство. В этом случае вместо множества R берется
множество всех комплексных чисел.
В дальнейшем будем часто употреблять термин «ли-
«линейное пространство», опуская слова «вещественное» или
«комплексное» в тех случаях, когда речь идет о свойст-
свойствах, справедливых как для вещественных, так и для ком-
комплексных линейных пространств.
Из определения линейного пространства вытекают
следующие утверждения.
1. В линейном пространстве существует единственный
нулевой элемент (вектор).
Предположим, что в линейном пространстве V суще-
ствуют два нулевых вектора о\ и о2. Тогда O2 + Oi = o2, так
как О] — нулевой элемент и Oi + o2 = oi, так как о2— ну-
нулевой элемент. Сравнивая эти равенства и учитывая ак-
СИОМу I, ПОЛУЧИМ О] = О2.
2. В линейном пространстве для каждого элемента х
существует единственный противоположный ему эле-
элемент — х.
Предположим, что для элемента х имеются два проти-
-> ->
воположных ему элемента —хх и —х2. Тогда
J J lJci)) +:(-Jca) =
С другой стороны,
x+ (-*i) +i(-*2) =x+(-x2) + (-*i) =
(-*!) =0+ (-xi) = -Xi.
103

Сравнивая результаты, имеем
3. Для элемента —х противоположным является эле-
элемент х. Это свойство очевидно.
4. Произведение числа 0 на любой элемент х есть ну-
нулевой элемент.
Действительно,
= 0х+,(х+ (-*)) =
= (Ох+х) + (-~х) = @+1)х+ (—Зс) = 1х+ (-л-) =
= л:+ ( — л;) =о.
5. Произведение —\х равно элементу —х.
Действительно,
= (-1 + l)J^=OJ?=:o!
Поэтому элемент — \х противоположен элементу х и, сле-
следовательно, — \х=~х.
6. Произведение любого числа а на нулевой элемент
есть нулевой элемент.
Действительно,
( ) ( — ax) =o.
7. Если
ах = о C.1)
и a ?= 0, то л; = о.
Действительно, умножив равенство C.1) почленно на
I/a, получим
1 . ~. 1 -
— (ах) = — о
a a
или х = о.
104

8. Если
ах=о C.2)
и хфо, то а=0.
Предположим, что а=7^=0. Тогда, умножив равенство
C.2) почленно на 1/а, получим х = о, что противоречит
условию.
Из утверждений 4, 6—8 следует, что в линейном про-
странстве произведение числа а на элемент х равно нуле-
нулевому элементу тогда и только тогда, когда а = 0 или
х=о.
В дальнейшем сумму х-\-(— у) будем обозначать
х—у и называть разностью элементов х и у.
Пример 1. Пусть М — множество свободных векторов, знакомых
читателю из курса аналитической геометрии в пространстве. Опреде-
Определим операции сложения векторов и умножения вектора на веществен-
вещественное число так, как это было сделано в курсе аналитической геомет-
геометрии. Так как при сложении векторов и умножении вектора на число
получается также вектор, то введенные операции являются опера-
операциями на множестве М. Они удовлетворяют аксиомам I—VIII. Следо-
Следовательно, множество М с введенными выше операциями является ве-
вещественным линейным пространством.
Если из множества М выделить множество Mi векторов, лежа-
лежащих в некоторой плоскости, и определить операции сложения векто-
векторов и умножения вектора на вещественное число так же, как в мно-
множестве М, то М\ будет также линейным вещественным пространством.
Пример 2. Рассмотрим множество S всех вещественных матриц
размеров тХп. Легко видеть, что если ввести операции сложения
матриц и умножения матрицы на вещественное число так, как это
сделано в матричном исчислении, то эти операции удовлетворяют
аксиомам I—VIII. Следовательно, множество S с введенными опера-
операциями является вещественным линейным пространством.
Пример 3. Рассмотрим множество Si всех вещественных матриц
размеров IXи. Введем операцию сложения матриц так, как это сде-
сделано в матричном исчислении. Операцию умножения на число введем
следующим образом: если x=[xi хг ... хп], то аж=[ал;1 х2 ... хп].
Легко проверить, что аксиомы I—VII выполняются, а аксиома
VIII не выполняется. Следовательно, множество Si не является ли-
линейным пространством.
Пусть V — линейное пространство. Рассмотрим мно-
жество всевозможных пар (х, у), где х, !/еУ, Это мно-
множество будем обозначать VX V и назовем декартовым
произведением линейных пространств.
105

В множестве Vyy определим внутреннюю и внеш-
внешнюю операции так:
1) (*ь У\) + (хг, Уг) =
2) а(х,у) = (ах,ау).
Легко показать, что введенные таким образом опера-
операции удовлетворяют аксиомам I—VIII. Следовательно,
VX V является линейным пространством.
Множество V\ элементов линейного пространства V
называется подпространством пространства V, когда вы-
выполняются следующие условия:
1) в множестве V\ операции сложения элементов
и умножения элемента на число определяются так же,
как в множестве V;
2) если х, y^Vi, то
-* -».
3) если x^Vi, то ax^.V\, где а — вещественное число,
если V — вещественное пространство, и комплексное, ес-
если V — комплексное.
Очевидно, что всякое подпространство Vi линейного
пространства является линейным пространством, т. е.
в V\ выполняются аксиомы I—VIII.
Действительно, в подпространстве V\ имеется нулевой
-¦>• -> ->
вектор, так как если x^Vu то 0* = ое1Л. Для любого
элемента x^V\ в подпространстве V\ имеется противопо-
ложный элемент —х, так как если x^V\, то —\х=
Справедливость остальных аксиом I—VIII очевидна.
Заметим, что нулевой элемент о линейного простран-
пространства V образует подпространство этого пространства. Са-
Само пространство V можно рассматривать как подпрост-
подпространство пространства V.
В примере 1 рассмотрены пространства М и Mi. Оче-
Очевидно, что Mi является подпространством линейного про-
пространства М.
§ 3.2. Линейная зависимость и линейная независимость
векторов
-> -> -*•
Рассмотрим векторы (элементы) хи х^, ..., хт некото-
некоторого линейного пространства V. Вектор
106

.. +arxT,
где <ii, O2, ... , ar — числа (вещественные, если V — ве-
вещественное пространство, и комплексные, если V— комп-
комплексное), принадлежит также пространству V (в этом
случае говорят что вектор у линейно выражается через
векторы х\, х2, ... , хг). Этот вектор называется линейной
комбинацией векторов Х\, х2, ... , хг, а числа ai,
аг, ... ,аг — коэффициентами этой комбинации.
Если все коэффициенты линейной комбинации векто-
векторов равны нулю, то такая комбинация называется три-
тривиальной и представляет собой нулевой вектор.
Если хотя бы один из коэффициентов cti, аг, ... , ar
отличен от нуля, то комбинация векторов называется
нетривиальной.
Следует иметь в виду, что и нетривиальная линейная
комбинация может быть нулевым вектором.
Система векторов называется линейно-независимой,
если только тривиальная линейная комбинация этих век-
векторов является нулевым вектором.
Система векторов называется линейно-зависимой, ес-
если существует нетривиальная линейная комбинация этих
векторов, которая является нулевым вектором.
Из приведенных выше определений следует, что воп-
рос, является ли данная система векторов х\, х2, ... , хт
линейно-зависимой или линейно-независимой, сводится
к выяснению того, при каких ai, аг, ... , ar возможно ра-
равенство
aiA,-i + a2*2+ • • • +OrXr=o. C.3)
Если это равенство справедливо лишь при ai = a2=
= ... =ar=0, то векторы линейно-независимы. Если же
существуют числа ai, аг, ... , аг, из которых хотя бы одно
отлично от нуля, и для этих чисел имеет место равенство
C.3), то векторы линейно-зависимы.
Система, состоящая из одного ненулевого вектора, ли-
-> -> -> -*•
нейно-независима, так как равенство ах —о при хфо
возможно лишь при а=0.
Система, состоящая из одного нулевого вектора, ли-
107

нейно-зависима, так как равенство ао = о имеет место
и при а=т^0.
Пример. В линейном пространстве М примера 1 § 3.1 любые два
ненулевых коллинеарных вектора являются линейно-зависимыми.
Действительно, из аналитической геометрии известно, что для колли-
неарных векторов х и у существует число Л такое, что х = Ху или
х — Ху—о. Таким образом, нетривиальная линейная комбинация
aix + a2y, где (Xi=l, a2=— X, является нулевым вектором.
Для векторов линейного пространства имеют место
следующие свойства.
1. Если к системе г линейно-зависимых векторов при-
присоединить любые m векторов, то получим систему r + m
линейно-зависимых векторов.
-> -> -*¦
Доказательство. Пусть х\, х2, ... , хт — линей-
линейно-зависимые векторы, т. е. существуют числа а\, ol2, • • • »
аг, из которых хотя бы одно отлично от нуля, такие, что
->¦ -> -> ->
01X1 + 02X2+ .•• +arxr — o. C.4)
Присоединим к данным векторам xh х2, ... , хг произ-
произвольные векторы у\, У2, ... , ут- Полученная система век-
векторов
хи х2, .. . , хг, Уи г/2, • ¦ • , Ут
линейно-зависима, так как, учитывая равенство C.4),
имеем
. . . +агл:г+Ог/1+Ог/2+ .. . +0ут=о,
где среди чисел аь аг, ... , а,, есть хотя бы одно, отличное
от нуля. ¦
2. Если из системы г линейно-независимых векторов
отбросить любые пг векторов (пг<г), то оставшиеся век-
векторы образуют линейно-независимую систему.
Доказательство. Пусть векторы
Х\, Х2, ¦ ¦ ¦ , Хт,
линейно-независимы. Рассмотрим систему векторов
Хт+\, Хт+2, ¦ ¦ ¦ , хг, C-6)
полученную из данной отбрасыванием первых т векто-
108

ров. Система векторов C.6) является линейно-независи-
линейно-независимой, так как если бы она была линейно-зависимой, то, на
основании предыдущего свойства, была бы линейно-зави-
линейно-зависимой и система C.5), так как она получается из системы
C.6) присоединением векторов х\, х%, ... , хт, а это про-
противоречит условию. ¦
Следующие свойства предлагаем читателю доказать
самостоятельно.
3. Если среди векторов Х\, х2, ... , хг имеются Хи
и xt(k=?l) такие, что xh = 'kxi, где К — число, то векторы
Х\, х2, ... , хг линейно-зависимы.
-> -»- ->-
4. Если среди векторов Х\, х2, . ¦ . , хг имеется нулевой,
то эти векторы линейно-зависимы.
Теорема. Для того чтобы векторы Х\, х% .. . , хт (г> 1)
были линейно-зависимы, необходимо и достаточно, чтобы
хотя бы один из этих векторов являлся линейной комби-
комбинацией остальных.
Доказательство. Необходимость. Пусть векто-
ры х\, Х2, ¦ ¦ ¦ , хг линейно-зависимы. Тогда существуют
числа cti, <i2, ... , <zr, среди которых хотя бы одно отлично
от нуля,такие, что
Предположим что a^ =7^=0. Тогда
(=1
т. е. вектор Xh является линейной комбинацией остальных
векторов данной системы.
Достаточность. Пусть один из векторов данной систе-
->•
мы, например хи, является линейной комбинацией
остальных векторов, т. е.
г г
** = 2 М;или ** — 2 $ixi= °-
1=1 1=1
10©

Таким образом, нетривиальная линейная комбинация
-*¦-*¦ ->
векторов Х\, х% ... , хт является нулевым вектором и, сле-
следовательно, эти векторы линейно-зависимы. ¦
Два вектора линейного пространства называются кол-
линеарными, если они линейно-зависимы, и неколлинеар-
ными, если они линейно-независимы.
Три вектора линейного пространства называются ком-
компланарными, если они линейно-зависимы, и некомпланар-
некомпланарными, если они линейно-независимы.
Введенные таким образом понятия коллинеарности
и компланарности векторов совпадают в пространстве М
(см. пример 1 § 3.1) с известными из аналитической гео-
геометрии понятиями коллинеарности и компланарности
векторов.
§ 3.3. Размерность и базис линейного пространства.
Изоморфизм
Пусть в линейном пространстве V выполняются сле-
следующие условия:
1) существует п линейно-независимых векторов;
2) любая система я + 1 векторов линейно-зависима.
Тогда число п называется размерностью пространства
V. Если пространство состоит из одного нулевого элемен-
элемента, то его размерность будем считать равной нулю.
Размерность пространства V будем обозначать dim V
(от французского слова dimension — размерность).
Пространство V размерности п будем называть п-мер-
ным пространством.
Базисом п-мерного пространства V называется любая
упорядоченная система п линейно-независимых векторов
этого пространства.
Теорема 1. Если ех, е2, ¦ ¦. , еп — базис п-мерного про-
->
странства V, то любой вектор х этого пространства ли-
-> -> ->
нейно выражается через векторы в\, е% ¦ ¦. , еп, т. е.
->-*¦-> ->
x=a.ie\ + a.2e2+ ... +апеп.
Доказательство. Пусть х — произвольный век-
вектор пространства V. Так как рассматриваемое простран-
ство n-мернре, то. система векторов ей е%, • • • , ец, х ли-
U0

нейно-зависима, т. е. существует нетривиальная линейная
комбинация
такая, что
Plfil + Р2б2 + ... + РгЯг + Р„+1Х = О. C.7)
Легко показать, что Pn+i^O. Действительно, если
pn+i = 0, то среди коэффициентов Pi, р2, ... , рп есть от-
личные от нуля, и векторы е\, е2, ... , еп линейно-зависи-
линейно-зависимы. Так как pn+i=^=0, то из равенства C.7) следует, что
где
а,= Pf_(/=1, 2, ... , п).Ш
Рл+1
Теорема 2. Если е\, е2, ¦ ¦ ¦, еп — система линейно-неза-
висимых векторов пространства V и любой вектор х это-
-> -*• ->
го пространства линейно выражается через в\, е2, ... , еп,
то пространство V является п-мерным.
-> -> -*• ->
Доказательство. Пусть Х\, х2, ... , хп, xn+i —
произвольные векторы пространства V. Докажем, что они
линейно-зависимы, т. е. что существует нетривиальная
линейная комбинация
такая, что
Рл + Рг*2+ ... +Р„^п + Рп+1^п+1 = о! C.8)
Так как по условию теоремы
Xn+l =
то
111

(Pian
en.
Так как elt e2, ... , en линейно-независимы, то соот-
соотношение C.8) возможно только тогда, когда
aiiPi + a2iP2 + • ¦ • + an+i iPn+i = 0
ai2Pi + a22P2 + • ¦ ¦ + an+i 2Pn+i = °
+ a2«P2 + • • • + an+l лРл+1 = 0.
Мы получили систему п линейных однородных уравнений
с п+\ неизвестными Pi, P2, ... , Рп+ь Как известно, такая
система имеет ненулевое решение. Следовательно, суще-
существуют числа Pi, р2, ... , Рп, Рп+ь среди которых хотя бы
одно отлично от нуля, такие, что имеет место равенство
C.8). ¦
Из доказанных теорем следует, что если в пространст-
пространству
ве V существует п линейно-независимых векторов в\,
е2, ... , еп таких, что любой вектор х этого пространства
линейно выражается через еь е2, ... , еп, то пространство
является n-мерным, а векторы еи е2, ... , еп — базисом.
Пример. В пространстве М примера 1 § 3.1 векторы /, /, k обра-
образуют базис. Действительно, эти векторы линейно-независимы, так как
они некомпланарны, и любой вектор этого пространства линейно вы.
ражается через i, j, k (как известно из аналитической геометрии).
Размерность этого пространства dimAl=3.
Заметим, что любые три некомпланарных вектора
пространства М образуют базис этого пространства, а
112,

любые два неколлинеарных вектора пространства М\
свободных векторов на плоскости образуют базис этого
пространства.
Пространство, в котором имеется базис, состоящий из
конечного числа векторов, называется конечномерным.
Линейное пространство называется бесконечномер-
бесконечномерным, если в нем существует любое число линейно-незави-
линейно-независимых векторов.
Примером бесконечномерного пространства может служить про-
пространство всех непрерывных иа отрезке [а, Ь] вещественных функций
вещественного аргумента, в котором операции сложения функций
и умножения функции на вещественное число определены так же, как
в математическом анализе.
Пусть даны два линейных пространства V и V. Если
между элементами этих пространств установлено взаим-
но-однозначное соответствие, причем xeV соответствует
-> -> ->
x'^V, то будем писать х+-+х'.
Два линейных вещественных (комплексных) простран-
пространства V и V называются изоформными, если между эле-
элементами можно установить взаимно-однозначное соответт
ствие такое, что если x1*->xi и хг*->хч, где xlt
то
axx *-> a*i,
где a — вещественное (комплексное) число.
Теорема 3. Два линейных вещественных (комплекс-
(комплексных) пространства изоморфны тогда и только тогда, ког-
когда они имеют одинаковую размерность.
Эту теорему предлагаем читателю доказать самостоя-
самостоятельно.
§ 3.4. Координаты вектора
В этом и последующих параграфах будем рассматри-
рассматривать конечномерные пространства.
-> -> ->
Теорема. Если еь е2, . ¦. , еп — базис линейного про-
странства, то для любого вектора х этого пространства
113

существует единственная система чисел си, a2, . • • , ап та-
такая, что
^ = aiei + a2?2+ ... +а^еп. C.9)
Доказательство. Из определения базиса сле-
следует существование системы чисел аь аг, ... , ап такой,
что имеет место равенство C.9). Допустим, что сущест-
существует также система чисел Pi, р2, • • • . Рп такая, что
Тогда
или
(ai—Pi)^i + (a2— p2)"e2+ ... + (an—Pn)X.=o.
Так как векторы е\, е2, ... , еп линейно-независимы, то
последнее равенство имеет место только при условии
ai—Pi = 0, a2—p2=0, ... , а„—pn = 0,
откуда
ai = Pi, a2=p2, ... , an = pn.H
Выражение C.9) будем называть разложением век-
тора х по базису еи е2, ... , еп, а числа ai, a2, ... , an —
координатами вектора в этом базисе. Если вектор х имеет
в некотором базисе координаты ai, a2) ... , an, то будем
писать *(ai, аг, • • • , ап).
В пространстве М, рассмотренном в примере 1 § 3.1,
в качестве базиса возьмем векторы i, j, k. Координатами
->
вектора х в этом базисе будут декартовы прямоугольные
координаты этого вектора.
Пример. Пусть V — пятимерное линейное пространство с базисом
«1. еа, е3, е4, е5. Найти координаты векторов ег и х = Ъех —
в данном базисе.
Решение. Вектор х представим в виде
следовательно, д;C, 0, —1, 2, 0).
114

Аналогично
72 = 0?! + 1еа + 0% + 0?4 + 0е6,
откуда 72 (О, 1, 0, 0, 0).
Имеют место следующие свойства.
1. Вектор является нулевым вектором пространства
тогда и только тогда, когда все его координаты в любом
базисе равны нулю.
Доказательство. Если все координаты вектора
->•->¦ ->
в некотором базисе е\, еч, ..., еп равны нулю, то
•.. +0еп = о.
Если х=о и в некотором базисе е\, вг, ¦.., еп
-*¦-*•-*• -*•
... +апеп,
то
Векторы е\, е2, ... , еп линейно-независимы, следова-
следовательно, ai = a2= ... =an = 0. И
2. Координаты суммы двух векторов в некотором ба-
базисе равны сумме соответствующих координат этих век-
векторов в том же базисе.
Доказательство. Пусть в некотором базисе
-*¦ -> ->
ей е2,..., еп
Тогда
... +апеп)
Учитывая аксиомы I, II, VIII линейного пространства,
имеем
Получено разложение вектора х+у по базису ей
115

e2, ... , en. Так как разложение по базису единственно, то
координатами вектора х+у будут ai + Pi, C12+P2, ... , an +
¦
Следующие свойства предлагаем читателю доказать
самостоятельно.
3. Координаты произведения вектора на число в неко-
некотором базисе равны произведению соответствующих ко-
координат данного вектора в том же базисе на это число.
->
4. Вектор х является линейной комбинацией векторов
Х\, Х2, ¦ ¦ ¦ , хг тогда и только тогда, когда каждая коорди-
координата вектора х в некотором базисе является такой же ли-
линейной комбинацией соответствующих координат векто-
векторов Х\, х2,..., хг в том же базисе.
5. Два вектора равны между собой тогда и только
тогда, когда равны между собой их соответствующие ко-
координаты в одном и том же базисе.
Указанные свойства позволяют свести операции над
векторами к соответствующим операциям над их коорди-
координатами.
->
Пример. В некотором базисе даны векторы хB, — 1, 3, 5) и
(/( — 1, 4, 0, —2). Найти координаты вектора 2х—Ъу.
Решение. Учитывая свойства 2 и 3, заключаем, что вектор
—> —>•
2.V—3i/ имеет координаты G, —14,6, 16).
§ 3.5. Матрица системы векторов
Пусть дана система векторов
хх(ап, а21, ... , ап1),
х2 (а12, а22, ... , ап2), | C.10)
->
хт (а1т, аШ апт)
ft-мерного линейного пространства, координаты которых
даны в одном и том же базисе. Поставим в соответствие
этой системе векторов матрицу
116

A =
«11 «12 • • • СЦт
^21 22 • • • 2ff|
C.
в /-М столбце которой стоят координаты вектора х,-.
Матрицу А будем называть матрицей системы векто-
ров Х\, Х2, . ¦., хп в данном базисе.
Обратно, если наперед задана матрица C.11), то ей
можно поставить в соответствие систему C.10) m векто-
векторов я-мерного пространства.
Согласно свойству 4 § 3.4, будем говорить, что столб-
столбцы матрицы C.11) линейно-зависимы, если соответству-
соответствующие им векторы линейно-зависимы, и наоборот.
Теорема. Для того чтобы m векторов п-мерного ли-
линейного пространства были линейно-независимы, необхо-
необходимо и достаточно, чтобы ранг г матрицы системы векто-
векторов был равен т.
Доказательство. Необходимость. Пусть систе:
ма векторов C.10) линейно-независима. Тогда среди век-
векторов этой системы нет нулевых и ранг г матрицы А си-
системы больше нуля. Предположим, что г<пг. На основа-
основании теоремы о базисном млноре, в матрице А имеется не-
небазисный столбец, который является линейной комбина-
комбинацией всех остальных столбцов. Тогда вектор, соответству-
соответствующий этому столбцу, является линейной комбинацией
остальных векторов, чего не может быть, так как данные
векторы линейно-независимы.
Достаточность. Пусть ранг г матрицы А данной систе-
системы m векторов равен т. Тогда в матрице А есть базис-
базисный минор М порядка т. Предположим, что векторы ли-
линейно-зависимы. Тогда один из столбцов матрицы А яв-
является линейной комбинацией остальных ее столбцов, а
значит, и соответствующий столбец минора М является
линейной комбинацией остальных его столбцов. Отсюда
следует, что М = 0, чего не может быть, так как М — ба-
базисный минор. ¦
Следствие 1. Для того чтобы система п векторов п-
мерного линейного пространства была линейно-независи-
линейно-независимой, необходимо и достаточно, чтобы матрица этой си-
системы векторов была невырожденной.
117

Следствие 2. Если ранг матрицы системы m векторов
равен г, то максимальное число линейно-независимых
векторов этой системы равно г.
Пример. Найти максимальное число линейно-независимых векторов
в системе векторов хх B, 3, —1, 4), х2{— 1. 1, 2, 0), *3@, 0, 1, 1),
*4A, 4, 1,4), х,B. 3, 0, 5),
Решение. Матрица данной системы векторов имеет вид
2
3
—1
4
—1
1
2
0
0
0
1
1
1
4
1
4
2
3
0
5
Так как ранг этой матрицы равен 3, то максимальное число линейно-
независимых векторов данной системы векторов равно 3.
§ 3.6. Пространство решений однородной системы
линейных уравнений
Рассмотрим однородную систему m линейных уравне-
уравнений с п неизвестными:
Xn = 0,
Xn = 0,
Хп = 0.
C.12)
Пусть (аг, а2; ... ; а„) и (Рг, р2; ... ; Рп) — два реше-
решения системы C.12). Тогда
i; a2+p2; ... ; a»+pn); C.13)
i; ka2: ... ; ^an), C.14)
где k — любое число, также являются решениями систе-
системы C.12). Назовем решение C.13) суммой решений,
а C.14) — произведением решения на число.
Очевидно, что множество решений системы C.12)
с введенными таким образом операциями образует ли-
линейное пространство, которое назовем пространством ре-
решений однородной системы линейных уравнений и обоз-
обозначим U.
Теорема. Пространство U является пространством
размерности п—г, где г — ранг матрицы системы C.12).
Доказательство. Докажем, что в пространстве
118

U имеется система п—г линейно-независимых векторов.
Нормированная фундаментальная система решений си-
системы C.12) состоит из п—г решений:
/r(l). r(D. . ,,A). 1. П. . т.
\Х\ , Х2 , ... , хг , 1, и, .. . , и;,
„B).
B).
<2 , . . . i Xr , U, U, . . . , I).
C.15)
Система C.15) является системой векторов простран-
пространства U. Известно, что эта система векторов является ли-
линейно-независимой и всякое решение системы C.12) есть
линейная комбинация нормированной фундаментальной
системы решений (см. § 2.6). Следовательно, пространст-
пространство U имеет размерность п—г. ¦
§ 3.7. Матрица перехода от одного базиса к другому
Рассмотрим в линейном пространстве V два базиса:
ей е2,... ,еп C.16)
еи е2, ... , еп. C.17)
Матрицей перехода от базиса C.16) к базису C.17)
называется матрица системы векторов е\, е2, ... , е„ в ба-
базисе ~еи ~ег, ... , 7п.
Из определения следует, что если
il
'22 •••
(ЗЛ8)
_ *nl 'Я2 • • • 'лл _
есть матрица перехода от базиса C.16) к базису C.17), то
б1 = ^11е1 + ^21е2 + • • • + ^Л1ел»
-*•# -¦•-¦• -*•
б2 = ^2^1 + tub + •¦¦ + tn%en, C.19)
-*, ->• -*• -*
^л = txtfii -f" '2n^2 T • • • Т trirfin-
119

Из теоремы § 3.5 следует, что матрица перехода от од-
одного базиса к другому является невырожденной и всякую
невырожденную матрицу порядка п можно рассматри-
рассматривать как матрицу перехода от одного базиса к другому
в /г-мерном пространстве.
Очевидно, что матрица Т~1, обратная матрице C.18),
является матрицей перехода от базиса C.17) к базису
C.16).
Пример. Рассмотрим в линейном пространстве Мг примера 1 § 3.1
базис i, /, а также базис еи ег (рис. 3.1). В этом случае
е1 = i cos ф + / sin ф,
е2 = — i sin ф -j- / cos ф.
Рис. 3.1
Матрицей перехода от базиса г, /' к базису et, e2 является матрица
Г cos (р — sin ф 1
[ sin ф cos ф J'
§ 3.8. Преобразование координат вектора
Задача преобразования координат заключается в на-
нахождении зависимости между координатами вектора
в разных базисах. При этом предполагается, что связь
между базисами известна.
120

Формулы, связывающие координаты вектора в раз-
разных базисах, называются формулами преобразования
координат.
Теорема. Если alt а2, ... , ап — координаты векто-
вектора х в базисе еъ е2, ..., еп, а а[, а2, ..., а'п — коорди-
наты этого же вектора в базисе е\, е2, ... , еп, то имеет
место следующее соотношение:
а2
или
где
Х=ТХ'
X =
а2
Т — матрица перехода от базиса еъ е2, ... , еп к базису
е\, е2, ... , еп.
Доказательство. Из условия теоремы следует, что
х = а^х + а2е2 +... + апеп, C.20)
х = a\e'i + а'2е2 + ... + a'nei C.21)
Если матрица Т имеет вид C.18), то из равенства
C.21), учитывая соотношения C.19), получим
х = а\ (tne1+ t%1e2 + ... + tnen) +
+ «2 (^2ei + t22e2 + ... + tnien) + ...
¦ ¦¦ + a'n {tlnex + t2ne2 + ... + tmen) =
121

• • • + t2nan)
Сравнивая этот результат с равенством C.20), имеем
а1 = ^11«1 + *12а2 + • • • + tlrfln,
а2 = t21a.i -f- t%2a2 + ... + t2nan,
• • • + tma'n
C.22)
или в матричной форме
«1
<z2
= T
"a',"
a2
C.23)
Соотношение C.23) можно записать в виде
си
a2
= Т

an
C.24)
Формулы C.22) — C.24) являются формулами преоб-
преобразования координат.
**¦ -> ->
Пример. Пусть вектор х в базисе ех, е2 имеет координаты 1, —2.
Найти координаты этого вектора в базисе е\ =elt e'2=el-\-e2.
Решение. Матрица перехода от базиса е1г ег к базису е^, е2
имеет вид
]•
Искомые координаты <Х|, а2 находим по формуле C.24). Имеем
Следовательно, a'j = 3, а'2 = — 2.
122

§ 3.9. Определение евклидова пространства
Рассмотрим линейное вещественное пространство V.
Наряду с имеющимися в этом пространстве операциями
(сложения векторов и умножения вектора на число) вве-
введем еще одну операцию следующим образом. Каждой
паре векторов х, у этого пространства поставим в соот-
соответствие вещественное число, обозначаемое (х, у), так,
что для любых х, у, геУ и любого ЯбЕ-R выполняются
следующие аксиомы.
I. (xjy)^(y, х)^^
II. (х+у, г) = (х, г)^+ (у, г).
III. (U, #)=МХ У)-
-»• ->
IV. (х, х) ^0, причем равенство имеет место только
в том случае, когда х=о.
Введенную операцию назовем скалярным умножением
векторов, а число (х, у) — скалярным произведением.
Скалярное произведение (х, х) называется скалярным
квадратом вектора х и обозначается х2, т. е. (х, х) =х2.
Заметим, что если хотя бы один из векторов нулевой,
то скалярное произведение равно нулю. Действительно,
Евклидовым пространством называется линейное ве-
вещественное пространство, в котором задана операция ска-
скалярного умножения векторов.
Если м-мерное линейное пространство — евклидово,
то будем называть его евклидовым п-мерным пространст-
пространством, а базис линейного пространства — базисом евклидо-
евклидова пространства.
Пример 1. Пусть М — пространство свободных векторов (см.
§ 3.1). В аналитической геометрии для векторов определена операция
скалярного умножения, которая удовлетворяет аксиомам I—IV. Сле-
Следовательно, пространство М с введенной операцией скалярного умно-
умножения векторов является евклидовым пространством.
Пример 2. В линейном пространстве S вещественных матриц раз-
размеров nXl (см. § 3.1) каждой паре матриц
123

X —
поставим в соответствие число
x1
Ч
X
, Y =
У\
Уг
-Уп-
(X, К) =
C.25)
Выражение C.25) является скалярным произведением, так как ак-
аксиомы I—IV выполнены. Следовательно, пространство S с введенной
операцией скалярного умножения есть евклидово пространство.
Легко убедиться в том, что линейное пространство ве-
вещественных матриц размеров IX" также является евкли-
евклидовым, если скалярное произведение введено по формуле
C.25).
Два евклидовых пространства Е и Е' называются
изоморфными, если изоморфны соответствующие линей-
ные пространства и, кроме того, если х, у^Е, х',
и х~х\ !/<->«/', то (х, у) = (х', у').
§ 3.10. Длина вектора
Длиной (или модулем) вектора х евклидова простран-
пространства называется арифметическое значение квадратного
корня из скалярного квадрата вектора х.
Длину вектора х будем обозначать \х\. Таким образом,
|
Имеют место следующие свойства.
1. \х\ =0 тогда и только тогда, когда х = о.
2. \1х\ = \К\ \х\, где К — вещественное число.
3. \(х, у) | ^ \х\ \у\ (неравенство Коши — Буняков-
ского).
4. |х+(/| ^ |л:| + \у\ (неравенство треугольника).
В справедливости свойств 1 и 2 читатель легко убе-
убедится самостоятельно. Докажем справедливость свойст-
свойства 3.
124

Если хотя бы один из векторов нулевой, то свойство
очевидно. Пусть х и у — произвольные ненулевые векто-
векторы евклидова пространства, а к— любое вещественное
число. В силу аксиомы IV § 3.9, имеем
(кх—1/J^0 C.26)
или, учитывая аксиомы I—III,
к2х2—21(х,у)+~у2^0.
Так как к — любое вещественное число, а левая часть
последнего неравенства есть квадратный трехчлен отно-
относительно к, то это неравенство справедливо только тогда,
когда дискриминант трехчлена неположителен, т. е.
Так как обе части неравенства неотрицательны, то
V(
(x,
или
\Сх,У)\^Й\~У\- C.27)
Замечание. В соотношении C.27) равенство достигается тог-
да и только тогда, когда векторы хну коллинеарны.
Действительно, пусть векторы х и у коллинеарны. Тогда у = Ъ.х,
и поэтому
Следовательно,
|(*. T)l = 1*11^1- C-28
—> ->
Пусть имеет место равенство C.28). Предположим, что х и у не-
коллинеарны. Тогда \х—уфо при любом X. При этом в соотношении
C.26), а следовательно, и C.27) имеет место строгое неравенство,
что противоречит условию C.28). Следовательно, х и у коллинеарны.
Для доказательства свойства 4 рассмотрим равенства
, х+у) =х2 + у2 + 2(х, у)
125

(\x\ + \y\)*=\x\'+\y\*+2\x\ \y\.
Из неравенства Коши—Буняковского имеем
(х,Й«?|*| \у\.
Следовательно,
l^/l2^ (Й + \у\J или \х+у\ <\х\ + \у\.
Заметим, что введенное понятие длины вектора в про-
пространстве свободных векторов (см. пример 1 § 3.8) сов-
совпадает с понятием длины, рассматриваемым в векторной
алгебре.
§ 3.11. Угол между векторами
Из неравенства Коши—Буняковского следует, что для
ненулевых векторов
\x\\y\ \x\\y\
Число
(х, Ъ
\х\\У\
можно рассматривать как косинус некоторого угла q>.
Угол ф, для которого
-> ->
(^ У} , 0<ф<2я,
^ }
\x\\y\
-¦• ^>
назовем углом между векторами х и у.
Два вектора называются ортогональными, если их
скалярное произведение равно нулю.
Очевидно, что нулевой вектор ортогонален любому
другому вектору.
Из определения следует, что для того чтобы ненуле-
вые векторы х и у были ортогональны, необходимо и до-
достаточно, чтобы cos ф = 0, т. е. ф = я/2 или ф = Зя/2.
126

Для того чтобы ненулевые векторы х и у были колли-
неарны, т. е. у = 1кх, необходимо и достаточно, чтобы
cos ф= ± 1, т. е. ф=0 (при Х>0) или ф = я (при Я,<0).
Действительно, если в соотношении C.27) имеет ме-
-¦• ~> -> ->
сто равенство, т. е. | (л:, у) \ = \х\ \у\, то cosф=±1, отку-
откуда ф=0 или ф=я. Но, как отмечалось ранее, в соотноше-
соотношении C.27) равенство достигается тогда и только тогда,
когда векторы коллинеарны.
Заметим, что введенное понятие угла между вектора-
векторами в пространстве свободных векторов (см. пример 1
§ 3.8) совпадает с понятием угла, рассматриваемым
в векторной алгебре. Ортогональность векторов в этом
пространстве означает их перпендикулярность.
§ 3.12. Ортонормированный базис
> >
Система векторов х\, Х2, ... , хп (п^2) называется
ортогональной, если эти векторы попарно ортогональны,
т. е. (Xi, Xj)=0 при i=f=\.
Теорема 1. Ортогональная система ненулевых векто-
векторов линейно-независима.
Доказательство. Пусть х\, х%, ... , хп — ортого-
ортогональная система ненулевых векторов. Предположим, что
она линейно-зависима. Тогда существуют числа си,
<Х2, ... , ап, среди которых хотя бы одно отлично от нуля,
такие, что
Пусть <ii#O. Тогда скалярное произведение
{х{, сцл:1+ • • • +a{Xi+ ... +апхп) =0
или
а\{хи xi)+ . . . +щ(х{, Хг)+ . .. +an(Xi,xn)=0.
Так как (х^ х,) =0 при 1ф\, то
откуда \х\\ =0, т. е. х% — нулевой вектор, что противоре-
противоречит условию теоремы.И
127

Вектор х называется нормированным или единичным,
если |*| = 1.
Если х — ненулевой вектор, то
*° = -?-. C.29)
1*1
C.30)
-1*1
есть нормированный вектор.
Нахождение для данного вектора нормированного
вектора по формуле C.29) или C.30) называется нор-
нормированием данного вектора, а множитель
1
±1*1
называется нормирующим множителем.
Система векторов Х\, х2, ... , хп (п~^2) называется
ортонормированной, если она ортогональна и каждый
вектор является нормированным, т. е. если
0 при 1ф\,
1 при / = /,
где i, /=1,2,..., п.
Очевидно что если х\, х2, ... , хп — ортогональная си-
система ненулевых векторов, то система, полученная из
данной нормированием каждого вектора, также является
ортогональной.
Базис евклидова м-мерного пространства называется
ортонормированным, если базисные векторы составляют
ортонормированную систему.
Теорема 2. Во всяком евклидовом п-мерном простран-
пространстве (и^2) существует ортонормированный базис.
Доказательство. Пусть gu g2, ¦ ¦ ¦ , gn — некото-
некоторый базис данного евклидова пространства. Составим
ортогональную систему вектора fu f2, ... , fn следующим
образом.
128

Положим /х = g-L. В качестве /2 возьмем вектор /2 =
= g2 + M2)gi. где Я*2' —число. При любом К\2) вектор/2
ненулевой, так как gt и g% линейно-независимы. Подберем
%\2) так, чтобы (flt Д.) = 0, т. е.
(ft. g« + M2)gi)=-o.
Отсюда
(ft. ft) + M2)(ft. ft)-=0
или
(ft. ft)+M2)|gi|f = 0.
Так как 1^1=^0, то
,<2) (gi. ga)
Л2 = ц: .
В качестве /3 возьмем вектор
7. = F. + M8Oi + ^8O,, C.31)
где >ti3), Я,23> —числа. При любых ЯA3), Я,23) ^— ненулевой
вектор (в этом легко убедиться, подставив в равенство
C.31) вместо /х и /2 их выражения через gx и g2). Под-
Подберем М3> и Я23) так, чтобы Gi. /,) = 0 и (f2, 7з) = 0, т. е.
G.,
Отсюда
-о,
(?2. ft) + ^ (Та. /i) + ^23)G2. 7а) = 0.
Так как &, 7.) = Gа. 7i) = 0, a Gi, 7i) = \Ъ\*фО и (/„
), то
(fit Ss) лC) (/г> ёз)
-, М = —
11 12 11 ia
I/11 I /2 I
129

Пусть найдены векторы flt /2, ... , fk-i- В качестве fk
возьмем вектор
где X\k\ xt\ ... , Aj^i — числа. Легко убедиться в том,
что при любых A,f'(/ = 1, 2, ... , k—1) вектор fk — нену-
ненулевой. Находя Я(/( (/ = 1, 2, ... , k — 1) из условий
G/. 7*) = 0 (/=1,2, ... , ft-1),
получим
Итак, построена ортогональная система ненулевых
векторов f[, /2, ... , fn- Пронормировав каждый вектор
этой системы, получим ортонормированную систему век-
векторов
ei, е2 еп,
которая является ортонормированным базисом. ¦
Процесс построения по данному базису ортонормиро-
ванного базиса называется ортогонализацией данного
базиса.
В процессе доказательства теоремы получен метод
ортогонализации базиса.
В одномерном пространстве любой ненулевой вектор
составляет базис. За ортонормированный базис естест-
естественно принять любой единичный вектор.
Пример. Рассмотрим пространство 5 в случае m = 1, п = 3. В ка-
качестве базиса возьмем линейно-независнмые векторы gi = [l —1 1](
ft=[2-3 4].ft = [2 2 6].
Построим по данному базису ортонормированный базис. Положим
?i = ?i = [l -1 П. T2 =
где
(gi.g«)
.B) _ (gi.g«) 2 + 3 + 4
Л[ — _>. — п О-
Il1 3
130

Следовательно,
7» = 1-1 0 1].
Далее находим
/ з = ёз + А1
где
(Т2. ?з)
^C) у/1' бз^ __2 х.C) = —¦
' l?il2 ' 2 |Ыа
Таким образом,
73=[2 4 2].
Нормируя векторы flt f2, f3, получим ортонормированныи базис
1 2 1
§ 3.13. Выражение скалярного произведения через
координаты в ортонормированном базисе
Пусть в м-мерном евклидовом пространстве задан не-
некоторый ортонормированныи базис еи е% . ¦. , еп. Рас-
смотрим в этом пространстве векторы х и у, координаты
которых в данном базисе соответственно равны <ц,
аг,.. . , ап и fh, Рг, • • • , Рп, т. е.
--> -> -> ->
... +а„е„,
Скалярное произведение этих векторов
(х, ~у) = (а^ + a2e2 + • • • + «A- Piei +
(л \ л л
аЯ. 21 Ра = 21 21
1=1 / ft=l 1=1
131

Так как elt e2, ..., еп — ортонормированный базис, то
_ ^ f 0 при k Ф i,
{е"' в'> = ( 1 при k = /.
Следовательно,
(х, i0 =
Таким образом, если векторы заданы координатами
в ортонормированном базисе, то их скалярное произве-
произведение равно сумме произведений одноименных координат.
Так как \х\ — V (х, х), то
|x| = V a? + a|
и для этого вектора нормирующий множитель
1
1 ,-1/2,2. i 2
^r I/ (Xj -p (Л2 ~p • . . ~f~ Ctrt
где ai, O2, ... , an — координаты вектора х в ортонорми-
ортонормированием базисе.
§ 3.14. Аффинное пространство
Пусть дано множество U элементов произвольной при-
природы, которые будем называть точками и обозначать
большими буквами латинского алфавита, а также ли-
линейное пространство V. Пусть выполняются следующие
аксиомы.
I. Каждой упорядоченной паре точек М, N^Ucono-
ставлен вектор x^V. При этом будем писать x=MN.
II. Для каждой точки М^ U и каждого вектора xeV
найдется единственная точка Afe Uтакая, что MN=x.
III. Для любых трех точек М, N, P^.U имеет место
соотношение MN+NP=MP (соотношение Шаля). Тог-
Тогда множество U называется аффинным пространством,
связанным с линейным пространством V.
Если линейное пространство V /г-мерное, то и связан-
связанное с ним аффинное пространство U называется п-мер-
ным.
132

Зафиксируем в аффинном пространстве {/некоторую
точку О. Тогда каждой точке М этого пространства будет
-*¦ —>
соответствовать единственный вектор x=OM^V, назы-
называемый радиус-вектором точки М. Обратно, каждый век-
вектор хеУ можно рассматривать как радиус-вектор един-
единственной точки М^ U. Таким образом, множество всех
радиус-векторов точек аффинного пространства совпа-
совпадает с линейным пространством V.
Следует заметить, что всякое линейное пространство
V можно рассматривать как аффинное пространство U
Для этого достаточно векторы пространства V назвать
точками пространства Uи каждой упорядоченной паре
точек х, у сопоставить вектор у—х.
Из определения аффинного пространства вытекают
следующие утверждения.
1. Каждой паре совпадающих точек из пространства
U соответствует нулевой вектор из V.
Действительно, пусть точкам М, Me ^/сопоставлен
-> —>-
вектор xQ=MM^V. Рассмотрим произвольный вектор
. В силу аксиомы II существует единственная точка
i/такая, что MN=x. На основании аксиомы III
ММ+Ш=Ш
или
хо+х=х,
откуда х0 — нулевой вектор линейного пространства V.
—>¦->—>- ->
2. Если MN=x, то NM=—х.
Согласно аксиоме III,
или
x+NM=o,
откуда NM = — х.
Пример. Пусть U — множество точек, рассматриваемых в аналити-
аналитической геометрии; V — линейное пространство свободных векторов, рас-
рассмотренное в примере 1 § 3.1. Очевидно, что для рассматриваемого мно-
множества аксиомы I—III выполняются и f/является трехмерным аффинным
пространством, связанным с линейным пространством V.
133

§ 3.15. Аффинные координаты
Системой координат или репером в аффинном прост-
пространстве называется совокупность фиксированной точки
О этого пространства и базисных векторов е\, е2, ... , еп
связанного с ним линейного пространства. Такой репер
-* ->¦ ->
будем обозначать (О; е\, е2, .. ., еп)- Фиксированную точ-
точку О назовем началом координат.
Каждой точке М аффинного пространства соответ-
соответствует радиус-вектор ОМ. Координаты вектора ОМ в
указанном базисе называются аффинными координата-
координатами точки М в заданной системе координат.
Очевидно, что каждой точке /г-мерного аффинного
пространства в заданном репере соответствует единствен-
единственная упорядоченная совокупность п чисел, являющихся
аффинными координатами точки, и наоборот, каждой
упорядоченной совокупности п чисел соответствует един-
единственная точка «-мерного аффинного пространства в не-
некотором репере.
Если точка М в некотором репере имеет аффинные ко-
координаты х\, х2,..., хп, то будем писать М (хи х2, ... , хп).
Пусть даны точки М(х\, х2, . . . , х„), N(yu у2, . . . , уп)
в репере (О; е\, е2, .. ¦ , еп). Тогда координатами соот-
соответствующего этим точкам вектора MN в базисе е\,
<?2, • • • , еп будут yi—xu У2—Х2, ¦ ¦ ¦ , Уп—Хп.
Действительно, согласно аксиоме III,
откуда
mn=on—6m.
Так как координатами векторов ON и ОМ являются
соответственно координаты точек W и М, то координатами
вектора MN будут у\—хъ у2—х2, .... уп—хп.
Рассмотрим два репера:
(О;7,,е2,...,еп), C.32)
(О'; 7и ?2, ... , Z). C.33)
134

Пусть hlt h2, ... , hn — координаты точки О' в репере
C.32). Найдем зависимость между координатами хи х2,
... , хп точки М в репере C.32) и координатами х\,.х2,
... , хп этой же точки в репере C.33), если Т — матрица
перехода от базиса е1г е2, ... , еп к базису е\, е2, ... , еп.
Пусть У — матрица-столбец из координат вектора
—> -> -> ->
О'М в базисе еь ег, ..., еп. Тогда
Y = X-H, C.34)
где
X =
С другой стороны, согласно формулам преобразования
координат вектора, имеем
Y=TX', C.35)
где
Х' =
•«I
Сравнивая равенства C.34) и C.35), имеем
X—Н = ТХ'
или
Х = ТХ' + Н. C.36)
Формула C.36) есть формула преобразования координат
точки при переходе от одного репера к другому.
->/ *> ~>/ -»•
В частном случае, если в репере C.33) е\ = elt e2 = еъ
... , ^ = е„, говорят, что репер (О'; еь е2, ... , 7п) полу-
получен из репера (О; еъ е2, . .. , е„) параллельным переносом
на вектор 00'. При этом формула C.36) принимает вид
Х = Х'
135

и называется формулой преобразования координат при
параллельном переносе.
Система координат (О; в\, ег, ... , еп) называется
прямоугольной, если базисные векторы в\, вг, ... , еп —
ортогональны, и декартовой прямоугольной, если базис-
базисные векторы ортонормированные.
Задачи
В задачах этой главы будем считать, что для элементов рассмат-
рассматриваемых множеств действия введены так, как это делается в соот-
соответствующих разделах математики (если нет специальных указаний).
3.1. Является ли множество R всех вещественных чисел:
а) вещественным линейным пространством;
б) комплексным линейным пространством?
3.2. Является ли множество С всех комплексных чисел:
а) вещественным линейным пространством;
б) комплексным линейным пространством?
3.3. Является ли множество всех целых чисел:
а) вещественным линейным пространством;
б) комплексным линейным пространством?
3.4. Является ли множество всех рациональных чисел:
а) вещественным линейным пространством;
б) комплексным линейным пространством?
3.5. Каким должно быть число а, чтобы множество, состоящее
из одного этого числа, являлось вещественным линейным простран-
пространством?
3.6. Является ли множество всех линейных функций одного
переменного с вещественными коэффициентами:
а) вещественным линейным пространством;
б) комплексным линейным пространством?
3.7. Является ли множество всех многочленов от одного пере-
переменного второй степени с вещественными коэффициентами веществен-
вещественным линейным пространством?
3.8. Является ли множество всех алгебраических многочленов от
одного переменного не выше второй степени с вещественными коэф-
коэффициентами вещественным линейным пространством?
3.9. Является ли комплексным линейным пространством мно-
множество всех алгебраических многочленов от одной переменной с комп-
комплексными коэффициентами:
а) степени не выше я;
б) степени п;
в) степени выше я?
3.10. Является ли множество всех вещественных матриц размеров
тХп:
а) вещественным линейным пространством;
б) комплексным линейным пространством?
3.11. Является ли множество всех комплексных матриц разме-
размеров тХп:
а) вещественным линейным пространством;
б) комплексным линейным пространством?
136

3.12. Является ли множество всех вещественных диагональных
матриц порядка п:
а) вещественным линейным пространством;
б) комплексным линейным пространством?
3.13. Является ли множество всех матриц вида
где а, Ь, с — любые вещественные числа, вещественным линейным
пространством?
3.14. Является ли множество всех матриц вида
V '
[Ь с
где а, Ь, с — любые вещественные числа, вещественным линейным
пространством?
3.15. Является ли множество всех вещественных матриц вида
вещественным линейным пространством?
3.16. Является ли множество всех невырожденных вещественных
матриц порядка п вещественным линейным пространством?
3.17. Является ли вещественным линейным пространством мно-
множество всех свободных векторов, рассматриваемых в курсе аналити-
аналитической геометрии в пространстве?
3.18. Является ли множество всех матриц вида [о 0], где а —
любое вещественное число, вещественным линейным пространством?
3.19. Является ли множество всех матриц вида [а 2], где а —
любое вещественное число, вещественным линейным пространством?
3.20. Доказать, что множество всех вещественных функций, не-
непрерывных на отрезке [а, Ь] числовой оси, является вещественным
линейным пространством.
3.21. Является ли вещественным линейным пространством мно-
множество всех вещественных функций, непрерывных во всех точках
отрезка [а, Ь] числовой оси, кроме точки хо^[а, Ь]?
3.22. Является ли вещественным линейным пространством мно-
множество функций вида:
а) «/=а+ In
б) у=\п B+)
где х — вещественное переменное; а — любое вещественное число.
3.23. Пусть М — множество всех степенных рядов с одним и тем
же радиусом сходимости R. При каком R это множество является
вещественным линейным пространством?
3.24. Показать, что множество всех решений системы п алгеб-
алгебраических линейных однородных уравнений с п неизвестными является
вещественным линейным пространством.
3.25. Показать, что множество всех решений однородного линей-
линейного дифференциального уравнения n-го порядка с постоянными
коэффициентами является вещественным линейным пространством.
3.26. Пусть М—множество всех вещественных матриц вида
137

[a, a2], в котором операция сложения определена обычным способом
(как в матричном исчислении), а операция умножения на любое
число а определяется равенством
a[«i a2] = [ai aa2].
Выяснить, является ли множество М вещественным линейным прост-
пространством.
3.27. Пусть М — множество, состоящее из одного элемента а.
Определим операции сложения и умножения на любое число а соот-
соответственно равенствами
а-\-а = а, аа = а.
Выяснить, является ли множество М линейным пространством.
3.28. Являются ли подпространствами линейного вещественного
пространства всех вещественных Ч1?сел:
а) множество всех четных чисел;
б) множество всех нечетных чисел;
в) множество всех целых чисел?
3.29. Является ли множество всех вещественных чисел подпрост-
подпространством:
а) линейного вещественного пространства всех комплексных
чисел;
б) линейного комплексного пространства всех комплексных
чисел?
3.30. Является ли подпространством линейного вещественного
пространства всех вещественных матриц порядка п:
а) множество всех вещественных невырожденных матриц
порядка я;
б) множество всех вещественных диагональных матриц
порядка п;
в) множество всех вещественных матриц вида
«12
0
0
«12
«22
0
«13
«23
«33 • • •
«in
«2Я
«з-
О 0 0 ... а„
г) множество всех вещественных матриц порядка п, опре-
определитель каждой из которых равен единице?
3.31. Является ли подпространством линейного вещественного
пространства всех вещественных матриц размеров 1Хя множество
всех вещественных матриц вида:
а) [2 а2аъ ... а„];
б) [а\О2 ... ап], где at>0 (i'=l, 2, ... , п)\
в) [а, а2 ... ап], где ai+a2+ ... +ап=0;
г) [а! а2 ... ап], где ai + a2+ ... +а„ = 3?
3.32. Является ли множество всех векторов, рассматриваемых
в аналитической геометрии на плоскости, подпространством линей-
линейного пространства всех векторов, рассматриваемых в аналитической
геометрии в пространстве?
3.33. Дано линейное пространство всех векторов, рассматривае-
рассматриваемых в аналитической геометрии в пространстве. Пусть а — некоторый
138

вектор этого пространства. Является ли множество всех векторов ka,
где k — любое вещественное число, подпространством данного про-
пространства?
3.34. Является ли множество всех вещественных невырожденных
матриц второго порядка подпространством пространства всех вещест-
вещественных матриц второго порядка?
3.35. Доказать, что если к совокупности г линейно-зависимых
векторов некоторого линейного пространства присоединить любые
т векторов этого пространства, то получим систему г-\-т линейно-
зависимых векторов.
3.36. Доказать, что в пространстве вещественных матриц второго
порядка матрицы
О П ГО О"
Г, 01 ГО П ГО 01
[о oj [о оj Lо 1J
являются линейно-независимыми.
3.37. Пусть L — вещественное линейное пространство многочленов
не выше второй степени. Выяснить, является ли линейно-независимой
каждая из следующих систем векторов данного пространства:
а) 1,х; б) 1, х, х2;
в) 1, х, х2, 2х2+3; г) 1, (х-2),(х-2J.
3.38. Пусть Mi — вещественное линейное пространство вещест-
вещественных матриц размеров 1 Х4. Выяснить, является ли линейно-зави-
линейно-зависимой каждая из следующих систем векторов этого пространства:
а) [1 0 0 0], [0 1 0 0];
б) [1 0 0 0], [0 1 0 0], [0 0 1 0];
в) [1 0 0 0], [0 1 0 0], [0 0 1 0], [0 0 0 1];
г) [1 1 1 1], [0 2 3 1], [0 0 4 -5], [0 0 0 7];
д) [1 0 0 0], [2 0 0 0], [12 3 4];
е) [2 1 -5 4], [3 0 7 2], [1 2 -17 6].
3.39. Пусть Л'г — вещественное линейное пространство вещест-
вещественных матриц третьего порядка. Выяснить, является ли линейно-
зависимой каждая из следующих систем векторов этого пространства:
1 0 0~1 Г0 1 0
б)
в)
0 0 0
0 0 0
2-11
0 0 0
0 0 0
0 2 —1
3 2 0
1 —2 4
1 2 3
—2 0 0
1 —1 3
0 0 0
0 0 0
0 0 0
-3 1 2
0 0 0
0 —4 2
6 4 0
2—4 8
2 —2
0 0
1 0
0 0 0
0 0 0
1 1 4
—1 2 0
0 1 0
3 —1 1
0
0
0
0
0
0
0
0
0
4 3 5
2—2 0
0 0 1
0 —1 Г
1 0 0
0 1 0
139

3.40. Пусть Vz — вещественное линейное пространство свободных
векторов, рассматриваемых в курсе аналитической геометрии на
плоскости. Выяснить, является ли линейно-независимой каждая из
следующих систем векторов:
а) "?=Т+27; 6=2?+?
б) ~a=4i—2j', ~b=~J—2i;
в) "а=3?— 7, ~b=2t, t=J—T.
3.41. Пусть Vz — пространство, рассматриваемое в задаче 3.40.
Доказать, что:
—>¦ ->
а) векторы I и / линейно-независимы;
б) любые два коллинеарных вектора линейно-зависимы;
в) любые три вектора линейно-зависимы.
3.42. Пусть Vs — вещественное линейное пространство свободных
векторов, рассматриваемых в курсе аналитической геометрии в про-
пространстве. Выяснить, является ли линейно-независимой каждая из
следующих систем векторов:
а) a = i+j— k, b =
б) ¦?=?— 3/+ *, ~Ь=Т+ J;
в)"а=2?—?+3fc, 7=7+4?—?, c"=5fe— 9/;
г) "а =7+27, 7 = 3?—7+ ?, с"=7+Х
д) а = 2?—?, =7+7—X 7 = 27 + 3?, d=?—ft.
3.43. Пусть Уз — пространство, рассматриваемое в задаче 3.42.
Доказать, что:
~> ->¦ ^v
а) векторы I, /, k лииейно-независимы;
б) любые два коллинеарных вектора линейно-зависимы.
3.44. Пусть Vs — пространство, рассматриваемое в задаче 3.42.
Доказать, что линейно-зависимы:
а) любые три компланарных вектора;
б) любые четыре вектора.
В задачах 3.45—3.51 выяснить, какова размерность каждого из
указанных линейных пространств, и указать один из базисов.
3.45. L — линейное пространство, рассмотренное в задаче 3.37.
3.46. Mi — линейное пространство, рассмотренное в задаче 3.38.
3.47. Мг — линейное пространство, рассмотренное в задаче 3.39.
3.48. V2 — линейное пространство, рассмотренное в задаче 3.40.
3.49. V3 — линейное пространство, рассмотренное в задаче 3.42.
3.50. У — линейное пространство всех решений линейного одно-
однородного дифференциального уравнения n-го порядка.
3.51. Р — линейное пространство всех многочленов от одного
переменного не выше п-й степени с вещественными коэффициентами.
3.52. Показать, что линейное пространство всех степенных рядов
с бесконечным радиусом сходимости является бесконечномерным.
3.53. Показать, что линейное пространство всех вещественных
функций, непрерывных на отрезке [а, Ь], является бесконечномерным.
3.54. Чему равны координаты каждого из указанных векторов
в базисе elf"e2, es, e4:
140

в базисе
a) a =3^— e2+ 5e3—4e4;
в) с= е1 — e3;
r) ej?
3.55. Найти координаты матрицы
ГЗ -М
L.2 -2\
Г 1 01 ГО 1"] 0 01 ["О 01
[о oj' [о oj' I oj' Lo ij"
3.56. Найти координаты каждого из указанных многочленов
в базисе 1, х, х2:
а) 2+Зх+4х2; б) Зх2-2;
в) (х+Б)(дс-3) + 1;г) 2+(х-1J.
3.57. Найти координаты каждого из указанных многочленов в ба-
базисе 1, (х—2), (х—2J:
а) 2-3(х-2)+5(л-2J; б) х+1;
в) *2+Зх+4; г) 2х-4.
В задачах 3.58—3.61 векторы заданы координатами в одном
и том же базисе.
3.58. Найти 2Н-3"б, если "а (—1, 3, 2), ?E, 0, —3).
3.59. Найти а"—26+Зс, если а B, —1, 3, 4), 6*@, 1, 2, 2,),
Г@, 0, 0, 1).
«* -+¦ ¦¦ -> *¦¦ *+
3.60. Найти вектор х, если 2а + 3х = 56, а B, —I, 4), 6 (— 1,
2, 0).
3.61. Найти вектор х, если За — 5х = 6, а@, 2, 7, 0, 0), 6B,
О, 0, 5, —10).
3.62. Даны векторы а = 2ех+ е2, 6 = ех — 2е2, где «х, е2 — базис
линейного пространства.
а) Доказать, что векторы а, Ь образуют базис;
б) найти координаты вектора с—3et+2e2 в базисе а, 6.
3.63. Даны векторы а = е1 + е2 + е3, 6=2е2+3е3> с = е2 + 5е3,
->¦->¦->¦
где ег, е2, е3 — базис линейного пространства.
а) Доказать, что векторы а, Ь, с образуют базис;
б) найти координаты вектора d=2el — е2-\-е3 в базисе а, Ь, с.
В задачах 3.64—3.67 даны векторы в некотором базисе. Показать,
что данные системы векторов линейно-зависимы, и выяснить, является
ли вектор 6 линейной комбинацией остальных векторов.
3.64. "ох B, 0, —1),"оаC, 0, —2), "o3j(—1, О, 1J, б"A, 2, 0).
141

3.65. Oi(—2, 0, 1), oa(l, —1, 0), o3@, 1, 2), 6B, 3, 4).
3.66. oi(—1, 2, —4), 02B, 1, 5), 0^C, —1, 5), ^l, 1, 1).
3.67. o^(l, 1, 1, 1, 1), ?2B, 2, 2, 2, 2), б"C, —3, 4, 5, 2).
3.68. В некотором базисе даны векторы:
a) 3iB, 1), ?(-1, 3);
6)^B, 1), ^D, 2).
Найти все значения Я, при которых вектор 6A, Я) в том же базисе
—>¦ —>
линейно выражается через векторы аг и о2.
В задачах 3.69—3.74 рассматриваются векторы alt a2, а3, 6 в не-
некотором базисе. Найти все значения Я, при которых вектор 6 линейно
выражается через векторы ах, о2, а3.
3.69. oi(l, 2- —1), Оа(—2, 1, 3), Оз@, 1, —1), б"A, Я, 2).
3.70. 0^A, —2, 3), ^2 @, —1, Я), ^зО, О, 1), C, —1, 2).
3.71. 0^B, 3, 0), oj A. 36- 0), ~а3(— 1. 2, 0),"б@, Я, 5).
3.72. о*,A, 2, 1), ?2B, 1, 1), а3(—1, —2, —1), ~Ь {2, 3, Я).
3.73. ^B, 3, 7), ОаC, —2, 4), ?а (— 1, 1, —1), б"A, Я, 3).
3.74. о^A, 2, 4), 02B, 1, 5), ~а3C, —1, 5), б"A, Я, Я,).
3.75. Найти матрицу перехода от базиса elt e2, е3 к базису е2,
3.76. Найти матрицу перехода от базиса elt е2, е3, е4 к базису
3-77. Дана матрица
["ii
перехода от базиса ex, e2 K базису е,, е2- Найти координаты векто-
векторов e'j, e2 в базисе elt ег.
3.78. Дана матрица
" 1 2 —Г
3 1 О
2 О 1
перехода от базиса ~ех, ~е2, е3 к б.азису е(', е2, е'ъ. Найти координаты
вектора ej в базисе ех, ег, е3.
142

3.79. Дана матрица
1 2 3
— 10 4
3 1 -5
перехода от базиса elt е2, е3 к базису е[, е'2, е%. Найти координаты
->, -> *> ->
вектора е3 в базисе elt е2, е3.
-*¦->•->
3.80. Найти матрицу перехода от базиса ег, е2, е3 к базису
~е[ = 2ех — е3 + е2, ~е% = Зех — е2 +~е3, ~е'г ="е3.
3.81. Найти матрицу перехода от базиса elt e2> ез к базису
3.82. Найти матрицу перехода от базиса е1г е2, е3, е4 к базису
= 2еа+ з1 +"е*. ^2 = ^1 — 2^2 + Зе3—?4, "е^ =^i + е4. е4 =
3.83. Дана матрица
перехода от базиса ех, ег к базису е(, е2- Найти координаты векто-
ров ег,' е2 в базисе ех, е2,
3.84. Дана матрица
Г2 -11
L3 5J
перехода от базиса elt e2 к базису е[, е2. Найти координаты векто-
векторов elt e2 в базисе elt e2.
3.85. Дана матрица
~1 — 1 3
5 1 2
1 4 —1
[
перехода от базиса е1? ег, е3 к базису е[, е2, е3. Найти координаты
-»¦ -*,->•, ->,
вектора е2 в базисе вр е2- ез*
3.86. Дана матрица
1 О Г
0 0 2
-1 3 1 ^
143

перехода от базиса elt е2, е3 к базису е,, е2, е3. Найти координаты
->• *> —*¦ ->/ *>/ —>¦/
векторов et, е2, е3 в базисе е1? е2, е3-
3.87. Дана матрица
1 1 1 1
0 111
0 0 11
0 0 0 1
перехода от базиса ех, е2, е3, ех к базису е[, е'2, е'ъ, е'4. Найти коор-
-* -* -»¦/-»¦, -»,—-i,
динаты векторов ег, е3 в базисе elt е2, es, e4,
->¦ -*¦->¦
3.88. Вектор х в базисе ех, е2 имеет координаты 1, —2. Найти
координаты этого вектора в базисе е[ = е{ -\- 2е2, е2 = — ех + е2.
^+- -*•-*¦
3.89. Вектор* в базисе е1г е2 имеет координаты —3, 1. Найти
->, -*¦ -»¦ *>/ -»¦
координаты этого вектора в базисе е, =—2е1-\-е2, е2 = е2.
3.90. Вектор х в базисе elt е2, е3 имеет координаты —1, 2, 0.
Найти координаты этого вектора в базисе е[ = 2е1—еа-|-Зез1 е'2 =
= — Зех + еа — 2е3! е^ = 4г2 + 5е3.
-+¦ -*-*-+¦
3.91. Вектор х в базисе et, е2, е3 имеет координаты 1, —1, 0.
->/ ->¦-»- -»- ->,
Найти координаты этого вектора в базисе е, =3^+62 + 6^3, е2 =
= 5?! — З"е2+ 7?3. "е3' = — 2?i + 2«2— 3^.
3.92. Вектор х в базисе е1г е2, е3 имеет координаты 4, 0, —12.
Найти координаты этого вектора в базисе е, = ех + 2еа + ез. е2 =
= 2e"j, + Зе + 4t3, е3' = 3ei + 4е2 + 3?3.
3.93. Вектор х в базисе е1( е2. ез> е\ имеет координаты 0, 1,
—>/ ~> ->¦
—1, 0. Найти координаты этого вектора в базисе е, =
= — 2?! — 4Т2 — Зе3— 6е^.
3.94. В базисе еи е2, е3 заданы векторы аA, 2, 3), 6@, 3,
1), с @, 0, 2), dD, 3, 1). Доказать, что векторы а, Ь, с образуют
базис, и найти координаты вектора d в этом базисе.
->••-> •-> *> -*•
3.95. В базисе еи е2 даны векторы аB, —1), 6C, 1), сB, 1).
-*¦ —*•
Доказать, что векторы а, Ь образуют базис, и найти координаты век-
вектора с в этом базисе.
144

3.96. Даны два базиса: а = е1 + 3е2, Ь=—4е1+е2 и с = 5<?2
d = ех + Зе2 • Является ли матрица
матрицей перехода от базиса a, b к базису с, d?
3.97. Даны два базиса: а = 2ех + е2, b = et— 2е2 и
+ 10е2, d = — 5е! + 5е2. Является ли матрица
= Ъе1-\-
Г 4 11
L-3 -з]
матрицей перехода от базиса a, b к базису с, d?
3.98. Даны два базиса: а = 3et+ 2ег + е3,
— ех— 2е2-\-е3,
и а1 =
1+2+3
Является ли матрица
0,5
—0,15
—0,1
0,1 0,8
0,1 —0,4
—0,6 0,3
матрицей перехода от базиса а, Ь, с к базису alt blt c{t
3.99. Даны два базиса: a = ex+eg — es, * = e1-f-es, c = 2e,
•*-*¦-*¦-*¦ _».->¦-¦.»¦-+.->.
и aJ = e1 — eit bl = 2e1—eti c1=e1-f-e8 — e3. Является ли матрица
-1 1 3'
2 4—5
1 2 0
матрицей перехода от базиса а, Ь, с к базису аг, blt cx?
3.100. Является ли евклидовым пространством линейное про-
пространство свободных векторов, рассматриваемых в аналитической
геометрии в пространстве, если каждой паре векторов х, у этого про-
пространства поставлено в соответствие число |je| \y\ cos<p, где <р—угол
•-»¦ -*•
между векторами х, у?
3.101. Пусть в вещественном линейном пространстве веществен-
ных матриц размеров 1Х« паре векторов х=[Х[ х2 ... хл], у*=
= [{/i Уг ¦ ¦ ¦ Уп] поставлено в соответствие число Х\У1+х2у2+.. .+хпуп.
Является ли данное пространство с введенной таким образом опера-
операцией евклидовым?
3.102. Является ли евклидовым пространством множество всех
функций вида ан cos kx-\-bh sin kx, где k — любое натуральное число,
Он, bk — любые вещественные числа, если каждой паре функций
145

а„ cos nx-\-bn sin nx, am cos mx-\-bm sin mx поставлено в соответствие
число
Г р (х) (ап cos пх + bn sin /«) (ат cos m* -(- *ш sin mx) dx,
—тс
где р(х) —фиксированная положительная непрерывная на отрезке
[ — л, л] функция?
3.103. Является ли евклидовым вещественное линейное простран-
пространство вещественных функций, непрерывных на отрезке [а, Ь] (а<6),
если каждой паре функций f(x), g(x) этого пространства поставлено
в соответствие число:
а) (I (x) g (x) dx; б) fp(x)}(x)g(x)dx,
где р(х)—фиксированная положительная непрерывная на отрезке
[а, Ь) функция?
3.104. В евклидовом пространстве, рассмотренном в задаче 3.102,
положив р(х) = 1, найти:
а) длину вектора cos x+sin x;
б) скалярное произведение векторов sin 2x, sin Зх;
в) угол между векторами sin x и cos x.
3.105. В евклидовом пространстве, рассмотренном в задаче
3.103, а, найти:
а) длину вектора f(x) =x;
б) скалярное произведение векторов f(x)=x, g(*)=ex;
в) угол между векторами f (х) = 1, g(x) —x;
г) записать неравенство Коши — Буняковского для функций
!(х)< g(x) этого пространства;
д) записать неравенство треугольника.
3.106. В евклидовом пространстве, рассмотренном в задаче 3.101,
положив п = 4, найти:
а) длину вектора [1—10 2];
б) скалярное произведение векторов [1—10 2], [1 —3 0 2]
и угол между векторами [1—10 2], [1 —3 0 2].
3.107. В евклидовом пространстве, рассмотренном в задаче 3.101,
найти:
а) длину вектора [1 1 ... 1];
б) скалярное произведение векторов [1 1 ... 1], [3 3 ... 3];
в) скалярное произведение векторов [11 .. 1], [1 2 ... я]
и угол между ними;
г) угол между векторами [\ I ... Ц, [а а ... а], если а-фО;
д) записать неравенство Коши — Буняковского для векторов
[Xi x2 ... хп], [ух 1/2 ... Уп]\
е) записать неравенство треугольника для векторов [хх хг ... хп],
[У\ 1/2 .-• Уп].
3.108. В евклидовом пространстве, рассмотренном в задаче 3.103,
даны функции
=1. 2
(полиномы Лежандра). Положив а= — 1, Ь=\, найти:
146

а) длины векторов Ро{х), Pi(x), Рг(х), Рз(х), Pi(x);
б) скалярные произведения (Pi(x), Рг(х)), (Pi(x), P3{x)).
3.109. Выяснить, являются ли ортогональными в евклидовом про-
пространстве вещественных матриц размеров 1ХЗ следующие системы
векторов:
а) [1 0 0], [0 2 3];
б) [0 1 1], [0 -1 3];
в) [1 0 0], [0 2 0], [0 0 3];
г) [1 1 2], [ -1 -1 1], [2 2 -2].
3.110. Установить, образует ли каждая из указанных систем век-
векторов ортогональный базис в евклидовом пространстве вещественных
матриц размеров 1x4:
а) [2 0 0 0], [0 3 0 0], [0 0 0 5];
б) [2 0 0 0], [0 3 0 0], [0 0 0 5], [0 0 -1 0];
-1 2 0 0], [2 -1 1 1], [-2 -1 3 0], [0 1 1 1];
J_ _L _L _Ll [_L _L —-1 — _Ll li. — _L _L — J_l
2 2 2 2 J' [2 2 2 2 j' 1.2 2 2 2J
в)
г)
L 2 2 2 2
3.111. Даны векторы % = [1 0 0], х3=[1 —3 2], ха = [0 — 1 0 0],
-* Г 19 ч 1 -> ->¦ Г ч 4 1
х4= _0 — , х5 = [2 0 0 0 1], л:6= _ _ . Какие из них яв-
1_ 13 13 j L 5 5 j
ляются нормированными?
3.112. Пронормировать следующие векторы:
а) [-1 1 1]; б) [0 2 0 3];
в) [3 0 4]; г) [12 0 0 5].
3.113. В евклидовом пространстве вещественных функций, непре-
непрерывных на отрезке [—1, 1], выяснить, какие из данных систем век-
векторов являются ортогональными:
а) х, х2; б) х, х3;
в) 1, sin nx, cos nx, sin 2nx, cos2n;t, ... , sin nnx, cos nnx;
г) полиномы Лежандра Ро(х), Pi(x), Рг(х), Рз(х).
3.114. В евклидовом пространстве вещественных функций, непре-
непрерывных на отрезке [—1, 1], пронормировать следующие векторы:
а) х; б) х2; в) sin x; г) полином Лежандра Яо(х) = 1.
3.115. В евклидовом пространстве вещественных матриц разме-
размеров 1X3 по данному базису построить ортонормированный базис:
а) ft = [1 2 3], ?2 = [0 2 0], ft = [0 0 3];
б) ft = [1 0 0], ?2 = [° 1 —1]. 7з= I1 ! М-
3.116. В евклидовом пространстве вещественных матриц размеров
1X4 по данному базису построить ортонормированный:
a) ft = [l 1 0 0], g2 = [0 0 1 1], ft = [l 0 1 1], g^ = [0 1 0 —1];
6)ft = [10I2], ft = [-10-10], ? = [0021],
?« = [0 1 1 1].
3.117. В евклидовом пространстве многочленов степени не выше
первой, рассматриваемых на отрезке [—1, 1], по данному базису
gt = 1, ga = x построить ортонормированный.
147

3.118. В евклидовом пространстве многочленов степени не выше
второй, рассматриваемых на отрезке [—1, 1], по данному базису
-*¦ -> ->
gi = 1( Ёг=х, ga = xi построить ортонормированный.
В задачах 3.119—3.121 проверить, что следующие системы век-
векторов попарно ортогональны, и дополнить их до ортогональных
базисов.
3.119. [1 -2 0 1], [0 1 0 2].
3.120. [2 2 1 0], [2 -3 2 4].
3.121. [3-1 1 1], [-1 -1 1 !]•
3.122. Даны векторы elt е2, е3, образующие ортогональный ба-
зис. Найти (х, у) и |х|, \у\, если:
а) х = 2^—372 +473, ^=/i + 73 — б73; | 7j | = 1, |72|=2,
|73|=2;
б) 7=7^+472—Ja.J^eg —е^; |7!|=^, |72|=^, |73|=1;
в) 7=472+^, 7=7!+з73; |7i|=5, |72| = 1, |^| = 2.
3.123. Даны векторы в!, е2> ез> е4. е5> образующие ортонорми-
ортонормированный базис. Найти (х, у) и |дс|, \у\, если:
а) 7=7^—2еН-75^7= з7и-73—7t + 2e^;
б) 7 = 2?! + з72 — Зе3, ~у = «5 — 213;
в) 7 = б7х — З"ег + 4е4 + е5, ~у = г72 —73 +74.
3.124. Даны векторы e1( ег, е3> ei> образующие ортогональный
базис. Найти угол между векторами хну, если:
а) 7=7Х —272+^ + ej, «Г=^+2^ —74; | ej = 3, |72|=2,
I 7,|=1, |74| = 2;
б) 7=2?!—72+73, 7 = 72 + 7,— 74; |^| = 2, |е2| = 3,
1^1 = 3, Ы=/2-^ ^ _ ^
в) 7=37X+^ —273+74, 7=27г+272 — Зе3 + е4; 1 ег | = 1,
|72| = 2^|^| = 3, |^| = 1^
г) х = е1 — е2 — 4е4, </ = ^ + 2е3 + е4; |е1| = 2, |е2| = 3,
|73| = 1, |74| = 1.
3.125. Даны векторы е1, е2, е3, образующие ортонормированный
базис. Найти угол между векторами х и у, если
а) х = <?!— 2еа + 3е3, У = е2— 4ех;
б) л = Зе2— е3, г/ = 4et + е2 — 2е3;
в) х = 5в! + е3. У = Ч + ег + еа-
148

Глава 4
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
§ 4.1. Определение линейного преобразования
Рассмотрим некоторое линейное пространство V. Если
задан закон, по которому каждому вектору х пространст-
пространства поставлен в соответствие единственный вектор у это-
этого же пространства, то будем говорить, что в данном про-
пространстве задано преобразование (отображение, опера-
оператор) f или преобразование пространства V в себя, и пи-
писать f'.V-+-V.
Вектор у назовем образом вектора х, а х — прообра-
прообразом вектора у. В этом случае будем говорить, что преоб-
-* -* -*¦•*¦
разование переводит вектор х в вектор у, и писать y=f(x).
Из определения преобразования следует, что каждый
вектор имеет единственный образ, но не каждый вектор
имеет прообраз, а если имеет, то этот прообраз, вообще
говоря, не единственный.
Преобразование называется взаимно-однозначным
(биективным), если каждый вектор имеет прообраз и
притом единственный.
Преобразование называется линейным, если для лю-
любых векторов пространства и произвольного числа Я (ве-
(вещественного, если пространство вещественное, и комплек-
комплексного, если комплексное), удовлетворяются следующие
условия:
1) f(x,+x2)=/(?)+/(x2); 2) f(Xx)=lf(x).
Из определения следует, что для линейного преобра-
преобразования справедливо следующее соотношение:
f(a?, + px2)=af(xI)+p/(u, D.1)
где аир — любые числа (вещественные или комплекс-
комплексные).
149

Справедливо и обратное: если имеет место равенство
D.1), то преобразование / является линейным.
Из определения линейного преобразования также сле-
следует, что линейное преобразование переводит нулевой
вектор в нулевой. Действительно, f(o)=f(x—x)—f(x)—
-/(*)= о"
Преобразование называется тождественным, если оно
каждому вектору пространства ставит в соответствие этот
же вектор, т. е. f(x) =x.
Очевидно, что тождественное преобразование являет-
является линейным.
Пример 1. В линейном пространстве М\ свободных векторов на
плоскости определим преобразование следующим образом: каждому
вектору х поставим в соответствие вектор }(х), полученный из векто-
У
0
J
ml
A{(x)-f(Ax)
/ N
ее
Рис. 4.1
ра х поворотом на один и тот же угол ф (преобразование вращения
на угол ф). Это преобразование является линейным (рис. 4.1).
Пример 2. В пространстве М\ вектору х поставим в соответствие
—*• —> —*¦
вектор f(x) = \x\x. Заданное таким образом преобразование не явля-
является линейным. Действительно,
|*i |*i+ \хг\хг.
образом, вообще говоря,
15Q

В дальнейшем будем рассматривать только конечно-
конечномерные пространства.
Пусть линейное преобразование f данного пространства
переводит некоторый базис еъ е2, ..., еп этого простран-
—*¦ —V —>¦ —v
ства соответственно в векторы e'v e'2, ..., е'п, т. е. е\ =
—V
Образ любого вектора х данного пространства при
рассматриваемом преобразовании можно выразить через
образы базисных векторов. Действительно, так как
то
f(x)=f (
= <hf &i)
Отсюда следует, что линейное преобразование простран-
пространства вполне определено, если заданы образы базисных
векторов этого пространства.
§ 4.2. Матрица линейного преобразования
Пусть / — линейное преобразование некоторого про-
странства, переводящее базис еъ е2, ..., еп в векторы
? 4 % ^i ^2» • • •. ~еп — базис, то
?,, 4> ••••'%• Так как
Матрица
«2А
-f
a12
a22
aln
151

называется матрицей линейного преобразования в базисе
е\, е2,..., еп, ранг г матрицы А — рангом преобразования
f, а п—г — дефектом этого преобразования.
Заметим, что в j-m столбце матрицы А стоят коорди-
координаты вектора ~e't = f(е,) в базисе 7и ~ег, ..., ~еп.
Таким образом, каждому линейному преобразованию
соответствует матрица преобразования в данном базисе.
Справедливо и обратное: всякой матрице порядка п соот-
соответствует линейное преобразование л-мерного простран-
пространства.
Пример. В пространстве Мх рассмотрим преобразование вращения
на угол ф (см. пример 1 § 4.1) и найдем матрицу этого преобразова-
преобразования в базисе i, j.
У'.
N
0
--#
/ \
АЛ \
м "Г '«
1^
р
у
У
о
т
S
Рис. 4.2
Из рис. 4.2 видно, что
f (Т) =dAf+0&=7cos ф+fsin ф,
f (/) =OP+OS= -7sin ф +7cos ф.
Следовательно, искомая матрица имеет вид
Г cos ф — sin ф ]
[ 8Н1ф СОЭф J'
Матрица тождественного преобразования в любом
базисе является единичной матрицей, и наоборот, всякой
единичной матрице порядка п соответствует тождествен-
тождественное преобразование n-мерного линейного пространства.
152

§ 4.3. Связь между координатами вектора и его образа
Пусть вектор х имеет координаты х\, х2, ¦ ¦. , хп в ба-
базисе еи ег,...,вп, т. е.
x = xlei + x2e2+ ... +хпеп.
Рассмотрим линейное преобразование / с матрицей
А =
an a12 ... aln
^21 ^22 * • * ^2/i
anl an2 ... am
в базисе еь ег, ... , еп и найдем координаты у\, у2 уп
вектора f(x) в том же базисе. Имеем
f(x)=y\ei+y2e2+ ... +упеп. D.2)
С другой стороны,
f (x) =f(xiei+x2e2+ ... +хпеп) =
= xif(ei) +x2f(e2) + ... +xnf(en) =
= xi(ane1+a2le2+ .^. +anlen) +x2(al2e1 +
+a22e2+ ... +an2en) + ... +xn(i
-\-a2ne2-\- ... -!гО.ппеп) = (п\\Х\-\-п\2х2-\- ..
... +a2nXn)e2+ ...
•¦• \йппХп)&п.
Сравнивая это выражение с равенством D.2), получим
#i = ai
D.3)
Формулы D.3) можно записать в матричном виде:
Y=AX, D.4)
153

где
Х =
ч
хг
Хп
Y =
Ух
Уг
- Уп -
А =
а
12
«21 «22
лп2
Если y = f(x), где f — линейное преобразование, име-
имеющее в некотором базисе матрицу А, то будем писать
у=Ах.
Если учесть уравнение D.4), то условия 1 и 2, содер-
содержащиеся в определении линейного преобразования, мож-
можно записать в виде
А{Х{ + Х2)=АХХ+АХ2,
А(ХХ)=К(АХ).
Пример. Пусть в двумерном пространстве линейное преобразова-
преобразование f в базисе е\, е2 задано матрицей
Г 3 21
= L-1 б]"
Найти f(x), где х=4в[—Зег-
Решение. По формуле D.4) имеем
Следовательно,
Если переменные х\, х2, ... , хп связаны с переменны-
переменными у и у2, ... , уп соотношениями D.3), то будем говорить,
что задано линейное однородное преобразование перемен-
переменных с матрицей А, переводящее переменные х\, х2, ... , хп
в переменные у\, у2, ... , уп- Оно обладает теми же свой-
свойствами, что и линейное преобразование векторного про-
пространства.
§ 4.4. Зависимость между матрицами одного и того же
преобразования в различных базисах
Теорема. Если
е\, е2,..., еп
D.5)
154

e\, e'v ..., e'n— D.6)
два базиса некоторого линейного пространства и А —
матрица линейного преобразования f в базисе D.5), то
матрица В этого преобразования в базисе D.6) имеет вид
В = Т~1АТ,
где Т — матрица перехода от базиса D.5) к базису D.6).
Доказательство. Пусть вектор х имеет коорди-
координаты аь а2, . .., ап в базисе D.5) и а',, а^, ..., а^ в
базисе D.6), а вектор у = / (х) имеет координаты ръ j32,
..., Р„ в базисе D.5) я $\, $'2, ..., $'п в базисе D.6).
Тогда
Х=ТХ', D.7)
Y=TY' D.8)
Y=AX, D.9)
Y' = BX'. D.10)
Умножив равенство D.7) слева на матрицу А, полу-
получим АХ=АТХ' или, учитывая выражения D.8) и D.9),
TY'=ATX'. Отсюда Y' = T-'-ATX'. Сравнивая последнее
равенство с D.10), имеем В = Т~1АТ. ¦
Следствие. Если линейное преобразование имеет в не-
некотором базисе невырожденную матрицу, то и в любом
другом базисе матрица этого преобразования является
невырожденной.
Действительно, пусть А и В — матрицы данного пре-
преобразования в двух различных базисах, причем det Л=^0.
Так как В = Т~ХАТ, где Т-—невырожденная матрица, то
detB = detT-1det^ detr#O.
Пример. В базисе elt e2 преобразование f имеет матрицу
Найти матрицу преобразования / в базисе е\—ei — 2е2, е' =2е1+е2.
155

Решение. Матрица перехода
Тогда
Искомая матрица
—21 Г 17
и;н:
§ 4.5. Характеристическое уравнение линейного
преобразования
Теорема. Если линейное преобразование f в некотором
базисе
61,62 вп D.11)
имеет матрицу Айв базисе
\ \ •••> < D-12)
матрицу В, то
det{A-XE)=det(B-KE),
где К — произвольное число; Е — единичная матрица по-
порядка п.
Доказательство. Пусть Т — матрица перехода
от базиса D.11) к базису D.12). Тогда В = Т~ХАТ
(см. § 4.4). Следовательно,
det(B-hE) =detG-M7-X?) = det (T^ AT-%
Заметим, что det (Л — %Е) является многочленом сте-
степени л относительно К. Этот многочлен называется ха-
характеристическим многочленом матрицы А или преобра-
преобразования f.
Характеристическим уравнением линейного преобра-
преобразования называется уравнение
det(A-XE)=O, D.13)
где А — матрица этого преобразования в некотором ба-
базисе.
156

Уравнение D.13) называется также характеристиче-
характеристическим уравнением матрицы А, а его корни — характеристи-
характеристическими числами линейного преобразования, а также мат-
матрицы А.
Матрица линейного преобразования меняется при пе-
переходе от одного базиса к другому, а характеристический
многочлен, как следует из доказанной теоремы, не зави-
зависит от выбора базиса.
Пусть линейное преобразование f имеет в некотором
базисе матрицу
^12
_anl an2 ... an
Характеристическое уравнение этого преобразования
имеет вид
1 0 ... О'
det
ап а12 ...
<hn
-ап\
— X
О 1 ... О
О 0 ... 1
= 0
или
ап — % ап
а21 а22 ¦
а
¦in
... а„„ — %
= 0.
Пример. Найти характеристический многочлен и характеристиче-
характеристические числа матрицы
[0 _2 —3 
—2 0 —3
2 2 5 J
Решение. Характеристический многочлен данной матрицы
имеет вид
I _х _2 —3
ф(Х) = 1—2 —Я, —3
I 2 2 5—Я,
Для нахождения характеристических чисел решаем уравнение
157

Его можно записать в виде
или
Корни этого уравнения, т. е. характеристические числа: Xi=l,
Л2=Лз=::=2.
§ 4.6. Произведение линейных преобразований
Пусть к вектору х применено преобразование /, пере-
переводящее вектор х в вектор у, т. е.
УЧИ.
Применим к вектору у преобразование g, переводящее
вектор у в вектор z, т. е.
z=g(y)-
В этом случае говорят, что вектор z получен из вектора
х последовательным применением преобразований fug.
Преобразование, заключающееся в последовательном
применении преобразований f и g, называется произведе-
произведением преобразования f на преобразование g или компози-
композицией преобразований и обозначается g ° /. (Преобразо-
(Преобразование, которое применяется первым, записывается
справа.)
Таким образом,
g°f(*)=g(fW)-
Теорема 1. Произведение линейных преобразований
есть линейное преобразование.
Доказательство. Пусть f и g — линейные пре-
преобразования некоторого пространства. Следовательно,
для любых х\ и Х2 этого пространства
g (aJel + рх2) = ag (x,) + $g {x2),
где a, p — любые числа. Тогда
158

gof (ax, + px2) = g (a/ (X) + p/ (?)) = ag
+ I
Таким образом,
откуда следует, что gof — линейное преобразование.¦
Теорема 2. Если линейные преобразования fug имеют
соответственно матрицы А и В в некотором базисе, то
преобразование gof имеет матрицу В А в том же базисе.
Доказательство. Пусть
Следовательно,
z = go f(x).
Тогда
Y=AX, Z=BY, D.14)
Z=CX, D.15)
где С —матрица преобразования g° f в данном базисе.
Из уравнения D.14) следует, что
Z=BAX. D.16)
Сравнивая уравнения D.15) и D.16), имеем С = ВА. ¦
Пример. Даны два линейных преобразования / и g соответственно
с матрицами
2—14
А = I 0 1 3|, В= | 3 0 1
5 2 2
Г1 0-2-1
.= 0 1 3,
L0 —1 2j
в некотором базисе. Найти матрицы С и D соответственно преобразо-
преобразований gof и fog в том же базисе.
Решение. Согласно теореме 2,
4] Г 1 0
10 1
|
Г1 0 -2-1 Г
D = АВ = 0 1 3
I 0 -1 2 I L
159

§ 4.7. Сумма линейных преобразований
Суммой преобразований fug некоторого пространства
называется преобразование А такое, что для любого век-
тора х этого пространства
А(х) =/(*)+*(*).
Сумму преобразований / и g будем обозначать f+g.
Очевидно, что f+g=g+f.
Теорема 1. Сумма линейных преобразований есть ли-
линейное преобразование.
Доказательство. Пусть f и g — линейные пре-
преобразования некоторого пространства. Следовательно,
-¦ ->
для любых х\, х2 этого пространства
g(axi + Р*2) = ag (xi) + $g (x2),
где а, р — любые числа. Тогда
(f+g) (cai^
Итак,
A (axi + pjc2) = ah (xi) + pA (x2),
откуда следует, что h=f+g — линейное преобразова-
преобразование. ¦
Теорема 2. Если линейные преобразования fug имеют
соответственно матрицы А и В в некотором базисе, то
преобразование f+g имеет матрицу А + В в том же ба-
базисе.
Доказательство. Пусть
~y = f(x), ~z=g(x).
Следовательно,
h(x) = (f+g)(x)=y+z.
160

Тогда
Y=AX, Z=BX, D.17)
Y+Z=CX, D.18)
где С — матрица преобразования h в данном базисе. Из
уравнений D.17) следует, что
Y+Z=(A + B)X. D.19)
Сравнивая равенства D.18) и D.19), имеем С=А + В. Ш
§ 4.8. Невырожденные линейные преобразования
Линейное преобразование называется невырожден-
невырожденным, если его матрица невырожденная. В противном слу-
случае преобразование называется вырожденным.
Теорема 1. Невырожденное линейное преобразование
является взаимно-однозначным. И, обратно, всякое вза-
взаимно-однозначное линейное преобразование является не-
невырожденным.
Доказательство. Пусть f — невырожденное ли-
линейное преобразование. Докажем, что для каждого век-
тора у* (у*, у\, ..., у*п) существует единственный вектор
х такой, что /(х) = у* или
AX=Y*, D.20)
где Л — матрица данного преобразования, а X, Y* —
столбцы соответственно из координат векторов х и у*.
Так как система D.20) — невырожденная, то она имеет
единственное решение: х\, х*2, ..., х\ Следовательно,
вектор у* имеет единственный прооораз х* (х\, х\, ..., х*п).
Докажем обратное. Пусть / — взаимно-однозначное ли-
линейное преобразование, имеющее в некотором базисе мат-
->
рицу А. Так как каждый вектор у* (г/*, у\, .... г/*) имеет
->
единственный прообраз х, то система D.20) имеет единст-
единственное решение. Следовательно, det Л # О^и преобразова-
преобразование / — невырожденное. ¦
Теорема 2. Для того чтобы линейное преобразование
было невырожденным, необходимо и достаточно, чтобы
оно переводило ненулевой вектор в ненулевой.
161

Доказательство. Необходимость. Пусть данное
преобразование / — невырожденное. Всякое линейное
преобразование переводит нулевой вектор в нулевой,
а так как невырожденное преобразование взаимно-одно-
взаимно-однозначно, то оно переводит ненулевой вектор в ненулевой.
Достаточность. Пусть данное линейное преобразова-
преобразование f с матрицей А переводит любой ненулевой вектор
в ненулевой. Предположим, что преобразование / вырож-
вырожденное, т. е. det Л = 0. Тогда система АХ=0 имеет нетри-
нетривиальное решение х\, х*2, ..., х*п. Следовательно, преобра-
преобразование f переводит ненулевой вектор х* (х*, х*2, ..., х*п)
в нулевой, что противоречит условию.В
Теорема 3. Произведение двух невырожденных ли-
линейных преобразований есть невырожденное преобразо-
преобразование.
Доказательство. Пусть даны линейные невы-
невырожденные преобразования f и g соответственно с матри-
матрицами А и В в некотором базисе. Произведение f ° g дан-
данных преобразований имеет в том же базисе матрицу АВ.
Так как произведение невырожденных матриц А и В есть
невырожденная матрица, то преобразование f ° g являет-
является невырожденным. В
§ 4.9. Преобразование, обратное данному линейному
преобразованию
Линейное преобразование ф называется обратным
данному линейному преобразованию f, если для любого
вектора х имеют место равенства
f°<p(*) = <po/(*) = *, D.21)
т. е. фо/ и /оф — тождественные преобразования.
Из определения следует, что если преобразование ф
является обратным преобразованию f, то / — преобразо-
преобразование, обратное ф. Преобразования / и ф, удовлетворяю-
удовлетворяющие условию D.21), называются взаимно-обратными.
Если преобразования f и ф имеют в некотором базисе
соответственно матрицы А к В, то из равенств D.21) сле-
следует, что АВ = ВА = Е, т. е. А и В — взаимно-обратные
матрицы.
162

Из сказанного выше вытекают следующие утверж-
утверждения.
1. Для того чтобы линейное преобразование имело об-
обратное преобразование, необходимо и достаточно, чтобы
оно было невырожденным.
2. Для данного линейного невырожденного преобра-
преобразования с матрицей А в некотором базисе существует
единственное обратное преобразование, причем матрица
обратного преобразования равна матрице А~1 в том же
базисе.
Пример. Дано преобразование переменных
у у == 1хх — Зх2,
Найти преобразование, обратное данному, если оно существует.
Решение. Матрица
В-
данного преобразования невырожденная, так как det
Матрица обратного преобразования
5 3
7фО.
Следовательно, преобразование, обратное данному, имеет вид
_5_ _3_
_J_ _2_
Х2 — 7 Ух + 7 Уг
§ 4.10. Собственные векторы линейного преобразования
Вектор х линейного пространства называется собст-
собственным вектором линейного преобразования f этого про-
пространства, если этот вектор ненулевой и существует число
k такое, что
f(x)=kx. D.22)
При этом k — вещественное, если линейное пространство
является вещественным, и комплексное, если пространст-
пространство комплексное.
163

Число k называется собственным числом вектора отно-
относительно преобразования f.
Равенство D.22) можно записать в матричном виде:
AX^kX, D.23)
где А — матрица преобразования f в некотором базисе;
X — матрица-столбец из координат вектора х в том же
базисе.
Ненулевую матрицу-столбец X, удовлетворяющую
условию D.23), назовем собственным вектор-столбцом
матрицы А с собственным числом k.
Пример 1. Пусть линейное преобразование / линейного двумерного
пространства в базисе е1( ег имеет матрицу
Л = [з Г
—> -+• —>
Вектор х = ех — Зе2 является собственным вектором этого преоб-
-¦¦
разования с собственным числом k = — 1. Действительно, вектор х —
ненулевой и
т. е / (х) = — х.
Имеют место следующие свойства.
1. Собственный вектор линейного преобразования
имеет единственное собственное число.
Доказательство. Пусть k\ и &2 — собственные
числа собственного вектора х относительно преобразова-
преобразования f. Тогда
f(x)=klx, f(x)=
откуда
k\X — kiX ИЛИ (k\ — k2)x = O.
Так как х— ненулевой вектор, то k\ = k2. Ш
^>
2. Если х — собственный вектор линейного преобра-
преобразования f с собственным числом k и Я — любое отличное
->
от нуля число, то Ъх — также собственный вектор преоб-
преобразования f с собственным числом k.
164

Доказательство. Если х — собственный вектор
с собственным числом к, то
f (кх) = If (х) = I (kx) = k (Кх).
Таким образом, ненулевой вектор Кх удовлетворяет
условию D.22) и, следовательно, является собственным
вектором преобразования f с собственным числом k. В
3. Если Х\ и Х2— линейно-независимые собственные
векторы линейного преобразования f с одним и тем же
собственным числом k, то Х\+х2—также собственный
вектор этого преобразования с собственным числом k.
Доказательство. Если %\ и Хч— линейно-неза-
линейно-независимые собственные векторы, то х\ + Хг—ненулевой
вектор
=f{xi) +f{x2) =k
т. e.
f(xi+x2)=k(xi+x2).m
Следствие. Если x\, x2, ... xr — линейно-независимые
векторы линейного преобразования f с одним и тем же
собственным числом k, то любая нетривиальная линейная
комбинация этих векторов является собственным векто-
вектором этого преобразования с собственным числом k.
Это следует из свойств 2 и 3.
-»• ->¦
4. Если х\ и х2 — собственные векторы линейного пре-
преобразования f соответственно с собственными числами k\
и k2, причем k\=?k2, то Х\ и х2 — линейно-независимые
векторы.
—»•
Доказательство. Предположим, что векторы Х\
и х2 — линейно-зависимые. Следовательно, существует
нетривиальная линейная комбинация ai*i + a2x2 такая,
¦ *-*
что aiX\ + a2x2=o. He ограничивая общности, можно счи-
считать, что cii=^0. Тогда
хх = ^-х2 = сх2, D.24)
165

где сфО, так как х\ — ненулевой вектор. Согласно свой-
ству 2, вектор сх2 является собственным вектором преоб-
преобразования f с собственным числом k% Учитывая свойство
1, из равенств D.24) заключаем, что ki = k2, что противо-
противоречит условию теоремы. ¦
Легко доказать, что свойство 4 справедливо и для г
векторов (г>2), т. е. собственные векторы преобразова-
преобразования с попарно различными собственными числами линей-
линейно-независимы. Обратное утверждение, вообще говоря, не
является справедливым, так как существуют линейно-
независимые собственные векторы с одинаковыми собст-
собственными числами.
Теорема 1. Для того чтобы линейное преобразование
комплексного линейного пространства имело собственный
вектор с собственным числом k, необходимо и достаточно,
чтобы k было корнем характеристического уравнения это-
этого преобразования.
Доказательство. Для того чтобы линейное пре-
преобразование / комплексного линейного пространства име-
имело собственный вектор с собственным числом k, необходи-
мо и достаточно, чтобы для некоторого вектора хфо
имело место соотношение AX = kX или
(A-kE)X=O, D.25)
где А — матрица преобразования f в некотором базисе;
Е— единичная матрица; X — матрица-столбец из коор-
координат вектора х в том же базисе.
Уравнение D.25) представляет матричную запись од-
однородной системы линейных уравнений, в которой число
уравнений равно числу неизвестных. Для того чтобы эта
система имела нетривиальное решение, необходимо и до-
достаточно, чтобы det(A — kE)=0, т. е. чтобы k являлось
корнем характеристического уравнения. Щ
Заметим, что собственными числами линейного преоб-
преобразования вещественного пространства являются только
вещественные корни характеристического уравнения.
Собственные числа линейного преобразования назы-
называются также собственными числами матрицы этого пре-
преобразования.
Собственное число называется пг-кратным, если оно
является m-кратным корнем характеристического урав-
166

нения. В частности, собственное число называется про-
простым, если оно является простым корнем характеристи-
характеристического уравнения.
Пусть
ап а
п
"In
лп2
матрица линейного преобразования f, a k — собственное
число этого преобразования. Тогда координаты собствен-
собственного вектора преобразования f с собственным числом k
можно найти из системы D.25), которая может быть за-
записана в виде
(an — k)x1 + aVix2 + ... + а1пхп = 0,
а21хх + (а22 — k) х.2 + ... + а^х,, = О,
«„Л + ««2^2 + • ¦ • +(««„ — k) хп = 0.
D.26)
Пример 2. Найти собственные числа собственных векторов пре-
преобразования f, заданного в некотором базисе матрицей
2
3
О
Решение. Характеристическое уравнение преобразования /
имеет вид
1-Я,
1
1
2
0—Я.
3
—2
3
о—я.
— 0
или A—К) (к2—9)=0. Решая это уравнение, находим характеристи-
характеристические числа Я,1 = 1, ?Ь2 = 3, %г — —3, которые являются собственными
числами собственных векторов рассматриваемого преобразования.
Теорема 2. Пусть k — собственное число линейного
преобразования f с матрицей А п-мерного пространства.
Если г — ранг матрицы А — \Е, то имеется п—г линей-
линейно-независимых собственных векторов преобразования f
с собственным числом k.
Доказательство. Если
167

an a12 ... aln
a21 a22 ... a2n
i_anl an2 ... am_
матрица линейного преобразования, то координаты соб-
собственного вектора с собственным числом k можно найти
из системы D.26). Так как матрица А—kE этой системы
по условию теоремы имеет ранг г, то пространство реше-
решений системы D.26) (см. § 3.6) является (п—г)-мерным
и, следовательно, существует п — г линейно-независимых
собственных векторов с собственным числом k. Щ
Заметим, что пространство решений системы D.26)
совпадает с множеством, состоящим из нулевого вектора
и всех собственных векторов преобразования f с собствен-
собственным числом k. Это пространство назовем пространством
собственных векторов данного преобразования с собст-
собственным числом k. Размерность п — г этого пространства
не превышает кратности собственного числа k.
§ 4.11. Нахождение собственных векторов линейного
преобразования
Из теорем § 4.10 вытекает следующий метод нахож-
нахождения собственных векторов линейного преобразования
f, имеющего в некотором базисе матрицу А.
1. Составляем характеристическое уравнение данного
преобразования и находим его корни Яь fa, ¦ ¦ ¦ , Яп, т. е.
характеристические числа.
2. Выделяем только те характеристические числа, ко-
которые являются собственными числами данного преобра-
преобразования.
3. В системе D.26) полагаем k равным одному из соб-
собственных чисел данного линейного преобразования,
например, & = Яг, и находим ненулевое решение
(<хг, <хг;... ; ап) этой системы.
4. Записываем вектор х (аи аг, ... , ап), который яв-
является собственным вектором данного преобразования
с собственным числом Яг.
Аналогично поступаем с другими собственными числа-
числами данного преобразования.
168

Пример. Найти собственные векторы линейного преобразования,
заданного в некотором базисе матрицей
Г 1-4-8 1
.= -4 7 -4 .
L —8 —4 1 J
Решение. 1. Характеристическое уравнение данного преобра-
преобразования имеет вид
1-Я, _4 —8
—4 7—Х —4
—8 —4 1-Я,
= 0.
Корни этого уравнения следующие: A,i=A,2=9, X3=—9.
2. Все корни являются собственными числами.
3. Чтобы найти собственный вектор с собственным числом ?|=9,
полагаем в системе D.26) k=9. Получим
—8лгх — 4л:2 — 8х3 = 0,
—4^ — 2^ — 4^3 = 0,
—8.*! —4л:2 —8*3 = 0.
Решение этой системы можно записать в виде
Xi=su л:2= — 2si—2s2, jt3=S2.
4. Вектор x(slt —2sx — 2s2, s2), где Sj и s2 — любые числа,
удовлетворяющие условию Sj-J-s|^-O, является собственным векто-
вектором данного преобразования с собственным числом fex = 9.
->
Аналогично находим, что вектор yBt, t, 2t), где / — любое от-
отличное от нуля число, является собственным вектором данного пре-
преобразования с собственным числом ?2=— 9.
§ 4.12. Приведение матрицы преобразования
к диагональному виду
Теорема 1. Для того чтобы матрица А преобразования
-* -»• -»•
/ в базисе е\, ег, ..., еп была диагональной, необходимо
и достаточно, чтобы каждый базисный вектор был соб-
собственным вектором преобразования f.
Доказательство. Необходимость. Пусть матри-
-> -> ->•
ца А преобразования f в базисе в\, е% ... , еп диагональ-
диагональная, т. е.
Л 0 ••• 0
0 Л, ... 0
А =
0 0
169

Тогда f(e,)=A,iei (i=l, 2, ...,«). Таким образом, нену-
->
левой вектор ег- удовлетворяет условию D.22) и, следова-
следовательно, является собственным вектором преобразования /
с собственным числом Ki.
-> -> -»-
Достаточность. Пусть еь е2, . ¦ ¦ , еп — базис простран-
пространства, состоящий из собственных векторов преобразования
соответственно с собственными числами к\, Яг, ..., Кп, т. е.
f(ег) =А,гбг 0=1, 2, ... , /г). Следовательно, в рассмат-
рассматриваемом базисе преобразование / имеет диагональную
матрицу
,х О ... О
.0 0 ...I
Квадратная матрица А называется приводимой к диа-
диагональному виду, если существует невырожденная мат-
матрица Т такая, что матрица Т~ХАТ — диагональная.
Характеристические многочлены матриц А и Т~1АТ
совпадают, и характеристические числа диагональной
матрицы равны ее диагональным элементам. Поэтому ес-
если матрица А приводима к диагональной матрице В, то
"Ях 0 ... 0
о к ... о
о о
где К\, %2, ¦ • ¦ , Кп — характеристические числа мат-
матрицы А.
Теорема 2. Для того чтобы матрица А линейного пре-
преобразования f п-мерного линейного пространства была
приводима к диагональному виду, необходимо и доста-
достаточно, чтобы существовал базис этого пространства, со-,
стоящий из собственных векторов преобразования f.
Доказательство. Необходимость. Рассмотрим
преобразование /, имеющее в некотором базисе
ей е2, ... ,еп D.27)
матрицу А. Пусть матрица А приводима к диагональному
виду, т. е. существует такая невырожденная матрица Т,
170

что B = T~lAT— диагональная матрица. Так как Т — не-
невырожденная матрица порядка п, то ее можно рассматри-
рассматривать как матрицу перехода от базиса D.27) к некоторому
базису
W .... е;. D.28)
В базисе D.28) преобразование f имеет матрицу
В = Т~1АТ, которая является диагональной. Следователь-
Следовательно, согласно теореме 1, базис D.28) состоит из собствен-
собственных векторов преобразования f.
Достаточность. Пусть А — матрица преобразования f
в базисе D.27) и существует базис
7 7 7 D.29)
состоящий из собственных векторов преобразования f.
Тогда в базисе D.29) преобразование f имеет диагональ-
диагональную матрицу D. Обозначим через Т матрицу перехода от
базиса D.27) к базису D.29), тогда Т — невырожденная
матрица и D = T~XAT, т. е. матрица А приводима к диаго-
диагональному виду. ¦
Из теоремы 2 следует, что если преобразование f
имеет в базисе D.27) матрицу А, приводимую к диаго-
диагональному виду, т. е. существует невырожденная матрица
Ттакая,что
ях
0
0
0 .
я2 .
0 .
.. о -
.. 0
•• К-
где Я,ь Яг, ¦.. Дп — характеристические числа матрицы А,
то Т является матрицей перехода от базиса D.27) к бази-
базису D.28), состоящему из линейно-независимых собствен-
собственных векторов преобразования f соответственно с собствен-
собственными числами К\, кг, ... , Кп. Так как столбцами матрицы
перехода от базиса D.27) к базису D.28) являются коор-
динаты векторов е\, е'2, ..., е'п в базисе D.27), то для
построения матрицы Т достаточно найти собственные
векторы матрицы А.
Теорема 3. Пусть собственные числа Яь Яг, ... , Я»
матрицы А порядка п, кратности которых соответственно
171

равны ти т2, ... , tns (mi+m2+ ... +ms = n), по-
попарно различны. Если mi = n — ri,...,ms—n — rs, где
Г\, г2, ¦ ¦ ¦ , rs — соответственно ранги матриц А — %\Е, ...
... , А—KSE, то матрица А приводится к диагональному
виду.
Доказательство. Рассмотрим линейное преоб-
преобразование f с матрицей А. Координаты Х\, х2, ... , хп соб-
собственного вектора преобразования f с собственным чис-
числом Xi (t=l, 2, ... , п) находятся из матричного урав-
уравнения {A-XiE)X=O, где
X =
Так как ранг Л — К%Е равен rt, то фундаментальная
система решений состоит из /г — n = mi вектор-решений.
Таким образом, имеется 1щ линейно-независимых собст-
собственных векторов преобразования f с собственным числом
%1. Поскольку собственные векторы с различными собст-
собственными числами линейно-независимы, то имеется
s
п=
i линейно-независимых собственных векторов пре-
образования /, которые и составляют базис пространства.
Следовательно, на основании предыдущей теоремы, мат-
матрица А приводится к диагональному виду.Н
Следствие. Если все собственные числа матрицы по-
попарно различны, то матрица приводится к диагональному
виду.
Пример. Матрица
Г 1-4-8 1
-4 7-4
L —8 —4 1 J
имеет характеристические числа ^=9, Х2=—9, кратность каждого из
которых соответственно равна mi=2, m2=l. Ранг г\ матрицы А—%\Е
равед 1, и и—/=3—1=2=ть Ранг г2 матрицы А—мЕ равен 2,
и п—г2 = 3—2=1=тг. Таким образом, условие теоремы 3 выполне-
выполнено, и матрица А приводится к диагональному виду, например
В =
Г9 О О"]
0 9 0 .
Lo 0 —9J
172

Найдем матрицу Т, удовлетворяющую условию Т~ХАТ=В. Соб-
Собственными векторами матрицы А с собственным числом A.i=9 будут
x(su — 2si—2s2, s2), а с собственным числом Х2= —9—(/B/, t, 2t)
(см. § 4.11). Положив Si = 0, s2=l и Si=l, s2=0, /=l, получим соб-
собственные векторы х\ @, —2, 1), х2 A, —2, 0), х3 B, 1, 2), составляю-
составляющие базис. Следовательно,
Г 0 1 2-1
= —2 —2 1 .
L 1 0 2J
§ 4.13. Ортогональные матрицы
Вещественная квадратная матрица
А
ап
«22
\-ип1
называется ортогональной, если соответствующая ей си-
стема векторов х\{аи, а2\, ... , ani), ... , хп(ащ, а2п, ¦ ¦.
... , апп) ортонормированная. При этом предполагается,
-*¦ ->
что векторы Х\, ... , хп являются элементами евклидова
пространства, в котором скалярное произведение опре-
определено следующим образом:
п
(х1г х,) = 2<а*«%-
Из определения следует, что если А — ортогональная
матрица, то
при i =
D.30)
для любых фиксированных i и / (i= 1, 2, ... , п; /=
Пример. Ортогональными являются следующие матрицы:
"I 0 01
0,6 -0,8
cos« -Sina
Очевидно, что единичная матрица любого порядка
является ортогональной.
173

Теорема 1. Необходимым и достаточным условием
ортогональности матрицы А является условие
А*А = Е, D.31)
где Ат — матрица, транспонированная к матрице
А=(ац)\ Е — единичная матрица того же порядка, что
и Л.
Доказательство. Необходимость. Пусть матрица
А — (ац) ортогональная, а Лт = (а'..) — транспонированная
к ней. Найдем
Согласно правилу умножения матриц,
си =
k=\
но так как a'lk = aki, то
В силу условий D.30),
Следовательно,
1 при i = /,
О При /=
С =
1 О О ... О
О 1 О ... О
О О О ... 1
= ?.
Достаточность. Пусть АТА = Е. Докажем, что Л — ор-
ортогональная матрица. Обозначим матрицу АТА через
С = (Cij). По условию С = Е, т. е.
( 1 при i = /,
ч = \
{ 0 при i-ф].
С другой стороны,
Следовательно,
174
и
= Zi

1 при i = },
т. е. условие D.30) выполняется и матрица А ортогональ-
ортогональная. ¦
Следствие 1. Определитель ортогональной матрицы по
абсолютной величине равен единице.
Действительно, из условия D.31) следует, что
т. е.
(det ЛJ= 1 или detЛ = ± 1.
Обратное утверждение, вообще говоря, не имеет места,
т. е. если det Л = ± 1, то матрица А не обязательно орто-
ортогональная.
Следствие 2. Ортогональная матрица является невы-
невырожденной. Это следует из предыдущего.
Следствие 3. Произведение двух ортогональных мат-
матриц есть ортогональная матрица.
Доказательство. Пусть А и В — ортогональные
матрицы одинакового порядка. Тогда
(АВ)?(АВ) = EМТ) (АВ) =В*(А*А)В =
= ВТЕВ = В*В—Е.
Таким образом, для матрицы АВ выполняется условие
D.31) и она является ортогональной.В
. Заметим, что сумма ортогональных матриц не являет-
является ортогональной матрицей.
Следствие 4. Необходимым и достаточным условием
ортогональности матрицы А является условие
А*=А-К
Следствие 5. Если матрица А ортогональная, то Лт
также ортогональная.
Действительно,
Следствие 6. Если матрица А ортогональная, то А~1
также ортогональная.
Замечание. Необходимым и достаточным условием ортого-
ортогональности матрицы А наряду с условием D.31) является также
условие
175

Теорема 2. Матрица перехода от одного ортонормиро-
ванного базиса к другому является ортогональной.
Доказательство. Пусть
i, ег, ... , еп
D.32)
е1> е2 en
D.33)
два ортонормированных базиса евклидова простран-
пространства, а
Т =
'
• • • h
11 ^12 • • • hn
Hi Нг • • • hn
матрица перехода от базиса D.32) к базису D.33). Тогда
е\ = ^iei + ^21^2 + • •. + tnlen,
Рассматриваемые базисы ортонормированные, следо-
следовательно,
1, если i = /,
О, если
Так как
k=\
1> если 1' = '
то
и, следовательно, матрица Т ортогональная.
176

§ 4.14. Ортогональные преобразования
Линейное преобразование евклидова пространства
называется ортогональным, если в некотором ортонорми-
ортонормированием базисе его матрица ортогональна.
Теорема 1. Для того чтобы линейное преобразование
евклидова пространства было ортогональным, необходи-
необходимо и достаточно, чтобы оно ортонормированный базис пе-
переводило в ортонормированный.
Доказательство. Необходимость. Пусть f —
ортогональное преобразование евклидова пространства,
имеющее в некотором ортонормированном базисе
e2, ... , en матрицу
A =
1
c21
Lanl an2 ... amJ
Тогда координаты вектора е'( = / (е;) (i = 1, 2, ...,«) рас-
расположены в i-м столбце матрицы А. Так как матрица А
ортогональная, то
П, если / = /,
если ij
Следовательно, векторы е\, е'2, ..., е'п образуют ортонор-
ортонормированный базис.
Достаточность. Пусть преобразование f переводит
ортонормированный базис D.32) в базис D.33). Тогда
матрица А преобразования f в базисе D.32) является мат-
матрицей перехода от базиса D.32) к базису D.33). Следо-
Следовательно, матрица А ортогональная и преобразование /
является ортогональным. В
Теорема 2. Ортогональное преобразование не меняет
скалярного произведения векторов.
-> ->¦ -¦¦
Доказательство. Пусть в\, ег, ... , еп — орто-
ортонормированный базис евклидова пространства, и
...+xnen,
... +упеп —
177

два произвольных вектора этого пространства. Тогда
(х, y)=xiyi+x2y2+ . • • +хпуп-
Если / — ортогональное преобразование, то
f(x) =xifGi) + x2f(e2) + ... +xnf(en),
f(y) =У\\{е\) +Уг!(е2) + ... +ynf(en),
где f(ei), f(e2), ... , f(en) — ортонормированный базис.
Следовательно,
(fW. f(y))=xiyi+x2y2+ ... +xnyn,
т.е. (f(x),fQ)) = (x,y).M
Следствие 1. Ортогональное преобразование f не ме-
меняет длины вектора, т. е. \х\ = \f (x) \.
Следствие 2. Ортогональное преобразование не ме-
меняет угла между векторами.
Ортогональные преобразования обладают следующи-
следующими свойствами.
1. Ортогональное преобразование— невырожденное.
2. Для ортогонального преобразования существует
обратное преобразование, которое также является орто-
ортогональным.
3. Если А — матрица ортогонального преобразования,
то Ат — матрица преобразования, обратного данному.
4. Произведение ортогональных преобразований так-
также является ортогональным.
Эти свойства следуют из свойств ортогональных
матриц.
§ 4.15. Построение ортогонального преобразования
Для того чтобы построить ортогональное преобразова-
преобразование и-мерного евклидова пространства, достаточно найти
ортогональную матрицу порядка п, т. е. построить систе-
систему из п ортонормированных «-мерных векторов. Это по-
построение можно осуществить следующим образом.
Сначала построим п попарно ортогональных ненуле-
ненулевых /г-мерных векторов. В качестве координат первого
вектора Х\ возьмем п произвольных вещественных чисел
178

an, Я21, • ¦ • , am, среди которых хотя бы одно отлично от
нуля.
Координаты t\, t2, . ¦. , tn второго вектора х2 найдем
из условия ортогональности его с вектором Х\, т. е. из
условия
... +anltn = O.
Мы получим уравнение первой степени с п неизвест-
неизвестными U, t2,... , tn, среди коэффициентов которого имеется
отличный от нуля. Множество решений такого уравне-
уравнения бесконечно. Одно из них (ненулевое)
ti = ui2, t2 = Ct22, ¦ • • , tn — O-ni
возьмем в качестве координат вектора х2.
Покажем, как построить xu+i, если построены
хи х2, ... , Xh (\<k<n). Координаты Z\, z2, ... , zn век-
вектора Xh+\ находим из условий попарной ортогональности
его с векторами х\, ... , хь., т. е. из системы
Я1Л + a21z2 + • ¦ • + anlzn = 0, '
«12^1 + a2222 + ¦ • • + an2zn = О,
alkzx + a2kz2 + ... + ankzn = 0.
Это система k линейных однородных уравнений с п не-
неизвестными, в которой число неизвестных больше числа
уравнений. Множество решений такой системы бесконеч-
бесконечно. Одно из них (ненулевое)
возьмем в качестве координат вектора
Пронормировав векторы х\, х2, ... , хп, получим орто-
пормированную систему векторов
л,,
Матрица, в столбцах которой расположены соответ-
ственно координаты векторов х\, х*2, ..., х*п, и будет
искомой.
179

Из изложенного способа построения ортогональной
матрицы следует, что существует бесчисленное множест-
множество ортогональных матриц порядка п.
Пример. Построить ортогональное преобразование трехмерного
евклидова пространства, отличное от тождественного.
Решение. Построим сначала ортогональную матрицу третьего
порядка. Возьмем произвольный ненулевой вектор, например (—2, 1,
->
2). Координаты ti, t2, t3 вектора Х2 найдем из уравнения
Общее решение этого уравнения запишем в виде
tt=2ti-2ts,
где ti и U — любые числа. Положив /i = l, h=\, получим /2=0. Ta-
-*¦
ким образом, х2 A, 0, 1).
-*.
Координаты 2Ь z2, z3 вектора Хз найдем из системы
, = 0.
Общее решение этой системы имеет вид
1 2
О 1
2 —2
Zi =
1
2
1
1
k = k,
= — k,
где k — любое число, отличное от нуля. Положив k=l, имеем
xz(\t 4* —1). Пронормировав векторы Хц x2i x3i получим
X, —
Матрица
180

является ортогональной матрицей третьего порядка, следовательно,
преобразование f, имеющее в ортонормированием базисе матрицу А,
является ортогональным.
Задачи
В задачах 4.1—4.14 координаты векторов х и f (x) заданы в одном
я том же базисе. Выяснить, являются ли указанные преобразования
линейными.
->
4.1. Преобразование f, переводящее всякий вектор x(ai, аг, аз)
-> -*
в вектор f(x) =«/B<Zi—а3, аз, ai—аг).
•->
4.2. Преобразование f, переводящее всякий вектор х(аь аг, аз)
->¦ ->
в вектор f(x)=y(aiu2, агаз, а1аз).
->
4.3. Преобразование f, переводящее всякий вектор x(at, аг, аз, оч)
в вектор f(x)=y(ai+2, a2, а3, а4).
4.4. Преобразование /, переводящее всякий вектор x(ai, аг) в век-
вектор /W=jyBai, 0).
4.5. Преобразование f, переводящее всякий вектор x(ai, аг)
в вектор f(x) =t/(ai2, a22). ^
4.6. Преобразование f, переводящее всякий вектор x(ai, аг, аз)
в вектор f(х) =«/(аг—2аз, аг+ai, ai).
4.7. Преобразование f евклидова пространства, переводящее каж-
-> -*¦->->-> ^>
дый вектор х в вектор {(х) = (х, а)а, где a — фиксированный вектор
этого пространства.
4.8. Преобразование f, переводящее каждый вектор х в вектор
-> -> ->
х+a, где а — фиксированный вектор.
4.9. Преобразование f евклидова пространства, рассматриваемого
в курсе аналитической геометрии в пространстве (см. задачу 3.100),
переводящее каждый вектор х в вектор, равный векторному произве-
произведению вектора х на фиксированный вектор а этого пространства.
4.10. Преобразование f линейного пространства многочленов сте-
степени не выше п, переводящее каждый многочлен этого пространства
в его производную.
4.11. Преобразование / вещественного линейного пространства,
*> ->
переводящее каждый вектор x=(ai аг ... а„) в вектор у=-(ри
Рг ... Рп), если
.. .-\-ainan,
.. .+annan)
где <Hj(i—l, 2, ...,»; /=1, 2, ... , п) —фиксированные веществен-
вещественные числа.
181

4.12. Преобразование f евклидова пространства, рассматривае-
рассматриваемого в курсе аналитической геометрии на плоскости, переводящее
вектор г в вектор:
а) симметричный вектору г относительно оси Ох;
—>•
б) kr, где k — фиксированное вещественное число, отличное
от нуля.
4.13. Преобразование f, переводящее всякий вектор х в вектор
f(x)=x (тождественное преобразование).
—>
4.14. Преобразование f, переводящее всякий вектор х в нулевой
(нулевое преобразование).
4.15. Пусть а — фиксированное вещественное число, В— фикси-
фиксированная вещественная матрица второго порядка. Выяснить, является
ли линейным преобразование / вещественного линейного пространства
вещественных матриц второго порядка, переводящее каждую мат-
матрицу А этого пространства в матрицу:
а) аА; б) АВ; в) ВА; г) А+В.
4.16. Найти матрицу линейного преобразования, переводящего
любой вектор х(аи а2) в вектор t/Bai+3a2, аг—ai), в том базисе,
—>• —>¦
в котором даны координаты векторов х и у.
4.17. Найти матрицу линейного преобразования, переводящего
любой вектор *(<zi, аг, аз) в вектор «/(ai+a2—аз, 2аз, 2а2+5аз),
в том базисе, в котором даны координаты векторов х и у.
4.18. Найти матрицу линейного преобразования f евклидова про-
странства, переводящего каждый вектор х в вектор f(x) = (x, a)a,
в ортонормированном базисе е\, ег, ез, если:
->->-*¦->
а) а=3в1+4е2+5ез;
б) a = ei—е2+ез",
в) a = 2ei—е3.
4.19. Найти матрицу линейного преобразования f евклидова про-
пространства, переводящего каждый вектор х в вектор f(x) = (x, a)a,
в ортогональном базисе еи е2, е3, где |е-»] =У2, |е2|=3, |е3| = 1,
если:
-> ->->¦-»¦
а) a = 2ei—e2—е3;
->- *->- ->
б) а=е2+3е3;
в) а = е3—2ei.
4.20. Найти матрицу линейного преобразования f евклидова про-
пространства, рассматриваемого в курсе аналитической геометрии в про-
странстве, переводящего каждый вектор х в вектор у=[х, а] (век-
торное произведение), в ортонормированном базисе i, /, k, если:
а) a=2i+3j—k;
182

б) a = i+j—k;
в) ~Z=-7+j+k.
4.21. Найти матрицу линейного преобразования / линейного про-
пространства многочленов не выше третьей степени, переводящего каж-
каждый многочлен этого пространства в его производную в базисе:
а) I, х, х2, х3;
б) 1, (х—1), (х-1J, (х—IK;
в) 2, 2х, Ахг, %х\
4.22. Найти матрицу линейного преобразования f вещественного
->
линейного пространства, переводящего каждый вектор jc(<zi, аг, ¦ ¦ ¦ ,
->
а„) в вектор y($i, fb, ... , |3п), если
ауос/ («= 1, 2, . . ., п, ац — произвольные числа)
в том базисе, в котором заданы координаты векторов х и у.
4.23. Найти в произвольном базисе еь е2, ..., е„ матрицу линей-
линейного преобразования «-мерного линейного пространства, переводя-
переводящего каждый вектор х в вектор kx, где k — вещественное число.
Записать в указанном базисе матрицы тождественного и нулевого
преобразований.
¦?¦ ¦?¦
4.24. Найти в ортонормированном базисе i, j матрицу линейного
преобразования евклидова пространства, рассматриваемого в анали-
аналитической геометрии на плоскости, переводящего вектор г в вектор:
а) kr, где k — фиксированное вещественное число, отличное от
нуля;
б) симметричный вектору г относительно оси Ох;
в) симметричный вектору г относительно оси Оу.
4.25. Найти в базисе
1 01 ГО 11 ГО 01 ГО 01
o о J* Lo oj' [1 oj' [о ij
матрицу линейного преобразования линейного пространства вещест-
вещественных матриц второго порядка, переводящего каждую матрицу А
этого пространства в матрицу:
В задачах 4.26—4.33 даны в некотором базисе матрица А линей-
линейного преобразования / и вектор х. Найти в этом базисе координаты
вектора у = / (х).
183

4.26. A =
4.27. A =
4.28. A =
4.29. A =
4.30. A =
4.31. A =
4.32.
4.33. A =
2 —1
3 4
—1 О
2 1
3 О
0 0 1-1
112
. 1 2 1 J
10 0 0
0 10 0
0 0 10
0 0 0 1
—1 1
2 1
1 ОТ
о о]'
1 , ^=
}¦
xB, -1).
x{\, 2, —1, 0,3).
3 01 -
2 3 J' Х{
•2 О О О ОН
0 2 0 0 0
0 0 2 0 0
0 0 0 2 0
.00002.
В задачах 4.34—4.37 даны в некотором базисе матрица А линей-
линейного преобразования / и векторы х, у. Найти в том же базисе вектор
4.34. А =
4.35. Л =
, 1B, -1), ?C, 2), о=1, Р = 2.
, —1, 1), а = 2.
" 1 2 3-1
—1 0 2 , х{— 1, 1, —1),
L 1 1 и
Г 1 0 2-1
.36. А= —1 2 0 , х{2, 0, —1),
L 2 1 _lj
, 2, 3), а = 3,
4.37. /4 =
а=1, р=1.
184
10 0 2
—2300
0 2 11
0 0 12
(-1, 0, 2, 0), 1/@, 2, 0, 1),

В задачах 4.38—4.48 даны два базиса ех, е2, . . ., еп и е^, е2,
—>¦,
.... еп линейного пространства и матрица линейного преобразова-
ния в базисе eit е2, . ¦ ., еп. Найти матрицу этого преобразования
в базисе е[, е'2, . . ., е'п.
4.38.
4.39.
_] J, ~*е\ =
=\ +Т,.
г] (Л -*, -> -*
4.40. А = \ , е1=3е1 + 2е2,
3 1 0 , ~*е\ = Зв! +"
2—1 1 J
2е3, ^=2
4.42. Л =
2 0 10
3 2 0 1
0 1—12
10 0 3
е. =elt e2=
2, e, =
4.43. Л =
¦2^, % = 3e
4.44. А =
2—1 О
О 1 —1
О 0 1
4.45.
Г—1 41 -> -
4.46. Л =
1 2 —3
0 3 1
—12 5
е3, е2 = 2ei —
185

4.47. A =
4.48. А =
2—1 0 1
О 1 —1
О 0 1
0—10 2'
2 0 0 1
—3 10 0
0 0 2 0
= 2e1 +62 — ез, ea = 2e,—
+ е2 + ез, e4 = ei+62+ез
4.49. В евклидовом пространстве, рассматриваемом в курсе ана-
->- -> -v -*¦
литической геометрии на плоскости, даны векторы a=3i+4/, 6 =
-> -> ->- ->
= — 2i'+7/, образующие базис. Найти в базисе а, 6 матрицу:
а) преобразования симметрии относительно оси Ох;
б) преобразования симметрии относительно оси Оу;
в) преобразования, ортогонально проектирующего всякий век-
->
тор г этого пространства на ось Ох;
г) преобразования, ортогонально проектирующего всякий век-
~>
тор г этого пространства на ось Оу.
4.50. В евклидовом пространстве, рассматриваемом в курсе ана-
-> ->->->
литической геометрии в пространстве, даны векторы a = i—j, b =
-> ->-> -> -> ->->->
=/+2й, с = 2(+у. Найти в базисе а, Ь, с матрицу:
а) преобразования, переводящего всякий вектор г этого про-
-*¦
странства в вектор кг, где k — фиксированное вещественное число,
отличное от нуля;
б) преобразования, ортогонально проектирующего всякий век-
вектор г этого пространства на плоскость хОу;
в) преобразования, ортогонально проектирующего всякий век-
вектор г этого пространства на плоскость уОг;
г) преобразования, переводящего всякий вектор г этого про-
пространства в вектор, симметричный вектору г относительно пло-
плоскости xOz.
4.51. В евклидовом пространстве, рассматриваемом в аналити-
аналитической геометрии на плоскости, задана прямоугольная декартова
система координат. Найти характеристическое уравнение и характе-
характеристические числа каждого из следующих преобразований:
а) симметрии относительно оси Оу;
б) преобразования, ортогонально проектирующего всякий век-
->¦
тор г на ось Ох;
в) преобразования, ортогонально проектирующего всякий век-
->
тор г на ось Оу.
186

4.52. В евклидовом пространстве, рассматриваемом в аналитиче-
аналитической геометрии в пространстве, задана прямоугольная декартова
система координат. Найти характеристическое уравнение и характери-
характеристические числа каждого из преобразований, указанных в пунктах
а — г задачи 4.50.
4.53. Найти характеристическое уравнение и характеристические
числа линейного преобразования f, если:
а) / (ei) = 2ei, / (<?2) = $4 + 3<?2, / (е3) = Зех + 4е2 — 6<?3, где ех,
е2> е3 — базис пространства;
—>¦ —»- —>¦ —> —>¦ -*¦—>¦—>¦->
f (е4) — ех -\- 7е2 + 4е3 + 6е4. где Si, e2, е3, е4 — базис пространства;
в) / (ег) — 2ех -\- 2е3, f (е2) = 2е, |- 2е2, / (е3) ^^ — 2е2 -f- 2e3,
где е,, е2, е3—¦ базис пространства.
4.54. Даны два линейных преобразования / и g соответственно
с матрицами
5 —2 ОН Г 1 1 3'
1—1
2 0
— 1
2
О 2
3 4
в некотором базисе. Найти матрицу преобразования:
а) / + g; б) 2/ + 3g;
в) f-2g; г) 3/-4§.
4.55. Пусть преобразование / в базисе е1( е2 имеет матрицу
3 5
¦ 1 4
Л =
а преобразование g в базисе е' = ех—е2. е'^ = ех-\- 2е2 — матрицу
Найти матрицу преобразования:
а) / + g в базисе ех, е2;
б) / + g B базисе e'lt e^
—> -*¦
в) 2/ — 3g в базисе е,, е3»
г) 3/ — 2g в базисе е[, е'2.
4.56. Пусть преобразование / в базисе elt ег, е3 имеет матрицу
А =
2 0 —2
1 1 О
3 0—1
187

а преобразование g в базисе е' =е1 + 2е2, е' —ег—е3, вд=е2 + е3—
матрицу
0 3 0
в =
0 1 —2
1 2 О
Найти матрицу преобразования:
а) /+Я в базисе е^ е2, е3;
б) / + g в базисе е', е', е';
12 3
в) 3/ —g в базисе в,, е2, е3;
г) / — 2g в базисе е', е', е'.
12 3
4.57. Дано евклидово пространство, рассматриваемое в аналити-
аналитической геометрии на плоскости. Пусть преобразование / есть симмет-
симметрия относительно оси Ох, преобразование g — поворот на угол а,
преобразование h — симметрия относительно оси Оу, преобразование
Ф — симметрия относительно биссектрисы первого и третьего коорди-
координатных углов.
1. По данному вектору г построить вектор:
a) r1 = fogr; 6)r2 = gofr; в)г3 = /оЛг; r)rt=hofr,
Д) гъ = (/ ° §) ° h г; е) /^ = ф о А г; ж) г, = g о (ф о А) г;
2. В базисе i, j найти матрицы преобразований: a) f°g; б) go/;
в) /оЛ; г) Ао/; д) (fog) oh; e) фоА; ж) ?о(фоА).
4.58. Дано евклидово пространство, рассматриваемое в аналити-
аналитической геометрии в пространстве. Пусть преобразование / есть сим-
симметрия относительно плоскости хОу, g—преобразование подобия,
А — преобразование, ортогонально проектирующее всякий вектор на
плоскость yOz. В базисе i, /, k найти матрицу преобразования:
a) f°g; б) go/; в) foh; г) Ао/; д) goA; e) f°(gof); ж) (b/) = g.
4.59. Даны два линейных преобразования / и g соответственно
с матрицами
10 0 0
2 10 0
0 110
0 0 0 2
3 2 0 0
0 0 10
0 0 5 0
2 0 0 1
в некотором базисе. Найти матрицу преобразования: a) /»g; б) fof.
4.60. Пусть преобразование / в базисе elt e2 имеет матрицу
— 1 2'
0
А =
Г Ч
L о 1J*
188

а преобразование g в базисе е' =2е1
, е' =е1 — е2,— матрицу
3 — 2
1 О
Найти матрицу преобразования:
—>¦•¦> -> ->
a) fog в базисе ех, ег; б) g°/ в базисе е1( е2;
в) / ° g в базисе е', е'; г) g • f в базисе е', е'.
4.61. Пусть преобразование / в базисе еи е2, е3 имеет матрицу
2 —1 О
А= 0 1 1
— 2 0 3
а преобразование
матрицу
в базисе е' =е1-\- е3, е' = — е3
0 0 4
-10 0
О 1 2
Найти матрицу преобразования:
a) fog в базисе ех, е2, е3; б) go/ в базисе ех, е2, е3;
в) fog вбазисее', е', е'; г) go/ в базисе е', е', е'.
12 3 12 3
4.62. В евклидовом пространстве, рассматриваемом в аналити-
аналитической геометрии на плоскости, задана прямоугольная декартова
система координат. Найти собственные векторы и собственные числа К
каждого из следующих преобразований:
а) симметрии относительно оси Ох;
б) симметрии относительно оси Оу;
в) преобразования подобия с коэффициентом подобия k;
г) преобразования, ортогонально проектирующего любой вектор
на ось Ох;
д) преобразования, ортогонально проектирующего любой вектор
на ось Оу;
е) преобразования вращения на угол <р.
4.63. В евклидовом пространстве, рассматриваемом в аналитиче-
аналитической геометрии в пространстве, задана прямоугольная декартова
система координат. Найти собственные векторы и собственные числа К
каждого из следующих преобразований:
а) симметрии относительно плоскости хОу;
б) симметрии относительно плоскости уОг;
в) преобразования, ортогонально проектирующего любой вектор
на плоскость хОу;
г) преобразования, ортогонально проектирующего любой вектор
на ось Ох.
189

В задачах 4.64—4.67 в некотором базисе даны матрица А преоб-
->¦ -> ->
разования / и векторы х1з х2, х3. Определить, какие из указанных
векторов являются собственными векторами преобразования / .
4.65. А =
4.66. А =
4.67. А =
1
— 6
о о
2 О
О 2
О
6
3
— 1
2
2~
О
О,
01
2
1
-1"
1
3
—>¦
> Х2 =
' 1 "
0
5
. х3 =
' 2
2
2
"— Г
2
0
- г
0
— 3
, *з =
"—4
0
1
4.68. Пусть л: — собственный вектор линейных преобразований/
и ф соответственно с собственными числами Хх и Хг. а) Доказать,
что х является собственным вектором преобразования /°ф.
Указать собственное число собственного вектора х преобразования
/оф; б) доказать, что х является собственным вектором преобразова-
преобразования / + ф. Указать собственное число собственного вектора х пре-
преобразования / + ф.
4.69. Пусть хг и х2 — собственные векторы линейного преобра-
преобразования / соответственно с собственными числами Я,х и Х2. Является ли
вектор хх -f- хг собственным вектором преобразования /?
В задачах 4. 70—4.79 найти собственные векторы линейного пре-
преобразования, заданного в некотором базисе матрицей А.
2 *¦ 4.7..
4.70. А =
4.72. А =
4.74. А
4.76.
— 1 —3
]. «.„.,-[_;
1
1
1
1
0
1
1
0
0
0
2
0
3
1
2
0
0
2
0
0
1
0
0
0
2"
3
0
8^
0
1 _
0
3
—1
0
4.73. Л =
4.75. А =
4.77. А =
1 0
0 3
0 0
2
1
— 1
1
1
2
j
2
0
0
0
3
0
(
:
-6"
-2
1
) 0
—4
-4 7
э Л
j ^
190

4.78. A =
0
4
— 2
0
1
4
1
0
0
0
2
0
1
— 1
1
1
4.79. A =
4 —1 — Г
1 2—1
1—1 2
В задачах 4.80—4.95 выяснить, приводится ли к диагональному
виду каждая из указанных матриц в вещественном пространстве.
В случае приводимости записать диагональный вид матрицы.
J.80. Г
4.82.
4.84.
4.86.
4.88.
4.90.
4.92.
4.94.
2
0
0
5
3
0
3
4
-6
1 О О
3 0 1
2
— 1
1
О О
О 2
2 О
" —1
О
о
о
4.J
4.83.
4.85.
4.87.
4.91.
2
3
2
2
3
О
3

О
О -
¦ 5
4
— 4
" 1
О
О
]
1
4
5
— 4
0 1
1 1
— 1 1
4.93.
4.95.
1
1
— 1
— 1
1
1
1
— 1
5 6
6 5
— 6 —6
— 1
— 1
1
9
9
10
В задачах 4.96—4.107 в некотором базисе линейное преобразова-
преобразование задано матрицей А. В вещественном линейном пространстве най-
найти базис, d котором это преобразование имеет диагональный вид.
191

4.98. 4 =
4.100. Л =
4.102. Л =
4.104. А =
4.106. Л =
2—2 0
— 2 1 —2
0—2 0
" — 10 54 36
0—1 0
— 3 18 11
100
10 0 0
0 0 0 1
0 0 10
1 —2
— 2 2
0 —2
0 2 —4
0 12—4
0 0 3—4
0 0 2—3
4.99. Л =
4.101. Л =
4.103. Л =
4.105. Л =
5—6 2
6—7 2
6 —6 1
0 —2
— 2
2
— 1
1 1
1 1
3
О —3
2 5.
10 0 0'
110 0
2 5 2 1
1 0 3_
0
0
4.107. Л =
0 0 2
1 0 0
6 7 6
—9 —9 —8 —3
0 0 0—2

Глава 5
КВАДРАТИЧНЫЕ ФОРМЫ
§ 5.1. Основные определения
Пусть даны п переменных Х\, х% .. ¦, хп, принимающих
числовые значения. Рассмотрим всевозможные парные
произведения д^г,- (i= 1, 2, ... , п; /= 1, 2 п) и со-
составим сумму
+ «12*Л + ••• +а1пх1хп +
•2 _
где aij — некоторые числа, среди которых хотя бы одно
отлично от нуля. Эта сумма называется квадратичной
формой п переменных Х\, х2, ... , хп и обозначается
L (X\, X2, . ¦ ¦ , Хп).
Таким образом,
L{хи х2, ..., хп) =
Числа ац называются коэффициентами квадратичной
формы. В дальнейшем будем рассматривать квадратич-
квадратичные формы с вещественными коэффициентами. Такие
формы называются вещественными. Кроме того, будем
считать, что областью изменения каждой из переменных
Xi (t=l, 2, ... , п) является множество всех веществен-
вещественных чисел.
Квадратичную форму можно записать в таком виде,
193

чтобы коэффициенты при xtXj и XjXt {ьф}) были равны
между собой. Действительно, так как XjXi=XiXj, то
+ aHxlxi = (аИ + ан) xixi = ~ (аЧ + att) xixi +
В дальнейшем будем считать, что в квадратичной фор-
форме E.1)
ац = а}г. E.2)
Из коэффициентов квадратичной формы составим
матрицу
~ап а1а ... а1п
агх а22 ... а2п
А =
L«nl
В силу равенства E.2), в матрице А равны между собой
элементы, расположенные симметрично относительно
главной диагонали.
Матрица, у которой равны элементы, расположенные
симметрично относительно главной диагонали, называет-
называется симметрической.
Для того чтобы матрица была симметрической, необ-
необходимо и достаточно, чтобы АГ=А, где Лт — матрица,
транспонированная к матрице А.
Из вышесказанного следует, что всякой квадратичной
форме соответствует единственная симметрическая мат-
матрица. Всякой симметрической матрице соответствует
единственная квадратичная форма с точностью до обоз-
обозначения переменных.
Симметрическую матрицу
А =
«11 «12
«12 «22
<hn
составленную из коэффициентов квадратичной формы,
будем называть матрицей этой квадратичной формы.
194

Заметим, что вещественной квадратичной форме со-
соответствует матрица с вещественными элементами.
Рангом квадратичной формы называется ранг ее мат-
матрицы.
Квадратичная форма называется невырожденной, ес-
если ее матрица невырожденная.
Очевидно, что ранг невырожденной квадратичной
формы равен числу переменных этой формы.
Так как квадратичные формы являются функцией п
независимых переменных с одной и той же областью оп-
определения, то две квадратичные формы L\{x\, х%, .... , хп)
и L2(xi, х2, ..., хп) равны тогда и только тогда, когда они
имеют одинаковые матрицы.
Пример 1. Квадратичная форма
2, х3) = 4хj —
х\ —
имеет матрицу
4 -1 т
— 1
~Y o-з
и ранг ее равен 3.
Пример 2. Матрице
1—2 3"
— 2 5—1
3—1 0.
соответствует квадратичная форма
L(xlt xit xs) = x21+5xl—4x1xi + <
переменных xlt хг и х3.
— 2х2х3
§ 5.2. Матричная запись квадратичной формы
Пусть дана квадратичная форма
L (х1г х2, .... j;n) =
auxixr
Матрица А этой квадратичной формы согласована со
столбцевой матрицей
195

x2
X =
— n —
Произведение AX является столбцевой матрицей раз-
размеров п\1. Матрица XT=(xi x2 ... хп) согласована
с матрицей АХ. Произведение ХТАХ представляет матри-
матрицу первого порядка, единственный элемент которой равен
n
2
т. е. данной квадратичной форме.
Таким образом,
X?AX=(L(xux2 хп)).
Матрицу первого порядка (flu) часто отождествляют
с ее элементом «п. Учитывая это, можно записать
Выражение ХТАХ представляет матричную запись квад-
квадратичной формы. Заметим, что выражение ХТАХ является
матричной записью квадратичной формы и в том случае,
когда А — несимметрическая матрица. Однако в этом
случае А не является матрицей квадратичной формы.
Пример 1. Дана квадратичная форма
L(xlt *2, xs) = 2x2l-3x22 + xl + 8x1x2 + 2x1x3.
Записать ее в матричном виде.
Решение. Матрица данной квадратичной формы
A =

4 -
_1
Следовательно
Lj [X^ у Х% i ™3/ — L 1 2 3J
4
-3
0

4
1
1
0
1
—
4
3
0
1
0
1
196

Пример 2. Дана квадратичная форма
Записать ее в виде E.1).
Решение. Произведение
Следовательно,
[х 1
= 2;cf — Злг| + 5x1x2.
§ 5.3. Изменение квадратичной формы при линейном
однородном преобразовании переменных
Пусть переменные х\, х2, ... , хп получены из перемен-
переменных у\, у2, ... , уп линейным однородным преобразова-
преобразованием Рв с матрицей В, т. е.
• • • +Ь1пУп>
. + Ь22у2 + . . • + Ь2пуп. .g 3^
или в матричном виде X — BY.
Рассмотрим квадратичную форму
п п
L (хи ь, .... ха) = 2 2 аИхЛ E-4)
ИЛИ
L(xu x2, ... , хп)=Х*АХ.
Если в квадратичную форму E.4) вместо переменных
хи х%,..., хп подставить их выражения через у\, Уг, •• • ,Уп
из соотношений E.3), то получим квадратичную форму
Li{yi, У2, ¦ ¦ ¦ , Уп) с некоторой матрицей С. Будем гово-
говорить, что квадратичная форма Ь(хи х2, ... , хп) преобра-
преобразованием E.3) переводится в Li(yu у2, ... , уп).
Если L(xlt х2, ..., хп) переводится в Lx(ylt y2. ...,
уп) невырожденным линейным однородным преобразова-
преобразованием Рв, то существует невырожденное линейное одно-
однородное преобразование PB-i, которое переводит L1(y1,
у2, ..., уп) в /,(*!, х2, ..., хп).
197

Две квадратичные формы называются конгруэнтны-
конгруэнтными, если существует невырожденное линейное однородное
преобразование, переводящее одну из них в другую.
Если L(xu x2, ... , хп) и Li(«/b y2, ... , Уп) конгруэнт-
конгруэнтны, то будем писать L (хи х2, ... , хп) ~LX (yu у2, ... , уп).
Имеют место следующие свойства.
1. L(xi,x2, ... ,xn)~L(xhx2,.. .,хп).
Действительно, невырожденным однородным линей-
линейным преобразованием, переводящим квадратичную фор-
форму в самое себя, является тождественное преобразование.
2. Если
L(xu x2, ... ,xn)~Li(yu y2, ..., Уп)
и
1\{У\,У2, ... , Уп) ~ L2(zu z2, ... ,zn),
то
L(xu x2, ... , хп) ~L2(zh z2, ... , zn).
Справедливость этого свойства следует из того, что
произведение невырожденных линейных однородных пре-
преобразований есть также невырожденное линейное одно-
однородное преобразование.
Теорема 1. Матрица квадратичной формы L\(y\, у% . ¦.,
уп), полученной из квадратичной формы L{X\, х% ..., хп)
линейным однородным преобразованием X—BY, равна
ВТАВ, где А — матрица квадратичной формы L.
Доказательство. Подставив X = BY в данную
квадратичную форму
L(xux2, ... ,хп)=Х'гАХ,
получим
или
где С =
Так как
(АВ)т (Бт)т = ВТА ТВ = ВТАВ = С,
то С — симметрическая матрица. Таким образом, матри-
матрица С = ВТАВ является матрицей квадратичной формы
и(у\,у2,...,уп).Ш
198

Следствие. Определители матриц конгруэнтных невы-
невырожденных квадратичных форм имеют одинаковые знаки.
Так как матрицы А я С двух конгруэнтных квадратич-
квадратичных форм связаны соотношением С=ВТАВ, где В— не-
невырожденная матрица, то
det C = detEM5) =det BT det A det ?= (det BJ det A.
Следовательно, det С и det А имеют одинаковые знаки.
Теорема 2. Конгруэнтные квадратичные формы имеют
одинаковые ранги.
Справедливость этой теоремы следует из теоремы 1
и из того, что ранг матрицы не меняется при умножении
ее слева или справа на невырожденную матрицу.
Пример I. Дана квадратичная форма
L (х1, хг) = 2х\ + 4*i*2 — 3*2 •
Найти квадратичную форму, полученную из данной преобразованием
Решение. Матрица данной квадратичной формы
а матрица преобразования
Следовательно, матрица искомой квадратичной формы
а квадратичная форма имеет вид
?-1 (Уи Уз) = 1 Зг/f — Щ1Уа + Ъу\.
Пример 2. Дана квадратичная форма
L (xlt х2) = 17*, + 12^*2 + 8*|.
Найти квадратичную форму, полученную из данной преобразованием
6 |
199

Решение. Матрица данной квадратичной формы
17
а матрица преобразования
т
o
J
Следовательно, матрица искомой квадратичной формы
С =
1 О
17
1
17 6
6 8
а квадратичная форма имеет вид
J _
0
100
6 "
1
2
17
0
0
100
17
§ 5.4. Приведение квадратичной формы
к каноническому виду
Квадратичная форма
называется канонической (иначе говоря, имеет канониче-
канонический вид), если все аг\/ = 0 при 1ф\.
Следовательно, каноническая квадратичная форма
имеет вид
апх] + а22х\
... +аппх2п =
t —1
а се матрица является диагональной.
Заметим, что любая квадратичная форма одной пере-
переменной
L (xj) = аах\
является канонической.
Квадратичная форма
L (хх, х2) = 2x2l -f-
». %п
200

не является канонической, а форма
L {хъ х2) = Ъх\ + 2х\
является.
Каноническая форма называется нормальной, если
каждый ее коэффициент, отличный от нуля, по абсолют-
абсолютной величине равен единице.
Например, каноническая форма
L (Х), х2, х3, хЛ) = — Xj -|- Х2 — #4
является нормальной. Здесь аи = — 1, а22 = 1, а33 = 0, а41 = — 1.
Нахождение по данной квадратичной форме кон-
конгруэнтной ей канонической квадратичной формы назы-
называется приведением квадратичной формы к каноническо-
каноническому виду.
Теорема 1. Для любой квадратичной формы сущест-
существует конгруэнтная ей каноническая квадратичная форма.
Доказательство. Для квадратичной формы одной
переменной L (xL) — axix\ теорема справедлива в силу
свойства 1 (§ 5.3).
Для доказательства теоремы применим метод полной
математической индукции. Предположим, что теорема
справедлива для всех квадратичных форм пг переменных,
где пг^.п—1. Докажем, что она справедлива для квадра-
квадратичной формы п переменных.
Для квадратичной формы
L{хи хг, ..., хп) = 2 2 aUxixl
возможны два случая.
1. Хотя бы один из коэффициентов аи (при квадратах
переменных) отличен от нуля. Не нарушая общности,
можно считать, что ацфО. Этого всегда можно добиться
соответствующей перенумерацией переменных.
В данной квадратичной форме выделим члены, содер-
содержащие х\, и запишем ее в виде
L(л*, х2 хп) = (апх\ + 2a12x1xi + 2а13х1х3 + ...
... + 2alnxixj) + Lx(*2, x3, .... xn),
где L](x2, x3 xn) — квадратичная форма, вообще го-
говоря, (п—1)-й переменной. (В частном случае
201

Li(x2, ... , хп) может быть квадратичной формой пере-
переменных, число которых меньше п—1.)
Выражение, стоящее в скобке, преобразуем следую-
следующим образом:
... +2а1пхгхп =
... + а1пхп) +
^2— («12*2+«13*3 + ••• + ainXnJ — -ZT~ («12*2 +
11
+ «1з*з + ... + alnxnJ\ =
Следовательно,
1
*1 + «12*2 + «13*3 + • • •
3. • • • . *„)•
a12x2
alnxnf
X3>
где L3 (x2, x3, .... х„) = Lx (x2, x3 xn) + L2 (x2, x3) ..
.... xn).
Заметим, что (aux! + а12л;2 + ... + аыхп) = -у -g^-.
По индуктивному предположению, для формы
^з(*2. ••• , *п) существует конгруэнтная каноническая
форма. Следовательно, существует невырожденное ли-
линейное однородное преобразование Рв
11 = hi Y . I ¦ h Y . I ¦ I . h у
c?2 22 2 4^ L/23 3 4^ • • • i^ 2/i, л*
^3 = ^32*2 + ^33*3 + • • • + &3/i*n»
Уп = ЬП2х2 + Ь*,х3+ . . . +Ьппхп,
переводящее Ьъ{х2, ..., хп) в каноническую форму. Тогда
преобразование
E.6)
. . . -\-а1пхп,
У2 == ^22-^2 "Г • • • ~Г пХп'
Уп = Ьп2х2+ . . . +brmxn
202

переводит данную квадратичную форму в каноническую:
я
U (уи Уг, . • • , Уп) = ^ ЪУг E-7)
i=l
Преобразование E.6) является невырожденным, так
как его матрица
~аи а12 . . . а1п
О Ь22 . . . Ь2п
.0 bn2 . . . &„„_,
невырожденная. Следовательно,
L(x\, X2, ... , хп) ~Li(y\, У2, .. ¦, Уп)¦
2. Все коэффициенты а,ц = 0. Этот случай сводится к
предыдущему.
Пусть некоторый коэффициент ацфЪ) {^Ф'])- Суще-
Существует невырожденное преобразование, например, преоб-
преобразование
хх = Уи
yt + y]t
= Ус+it
xn Уп'
переводящее квадратичную форму E.5) в квадратичную
форму, у которой коэффициент при yj отличен от нуля. ¦
Легко показать, что в квадратичной форме E.7) чис-
число коэффициентов at, отличных от нуля, равно рангу г
квадратичной формы. Поэтому любую квадратичную
форму можно привести к. каноническому виду
(=1
где &{ф0 (t=l, 2, ... , г); г — ранг квадратичной фор-
формы.
203

Заметим, что если квадратичная форма L(x\, х2, ... ,
хп) является невырожденной, то конгруэнтная ей канони-
каноническая форма имеет вид
где все аг#О.
Теорема 2. Для любой вещественной квадратичной
формы существует конгруэнтная ей нормальная форма.
Доказательство. Пусть квадратичная форма
L(x\, х2, . .. , хп) приведена к каноническому виду
U (Уи «/г. • • •, Уп) = М? + • • • + ЬггУг>
где г < п и Ьи ф 0 ({ = 1, 2, ..., г).
Применив невырожденное преобразование
— Уг+1
2п = Уп>
получим нормальную каноническую форму L2{z\, z2, ... ,
zn). Следовательно,
L(xu x2,..., xn) ~L2(zu z2,..., zn). Ш
При доказательстве теоремы 1 получен практический
способ приведения квадратичной формы к каноническому
виду, называемый способом Лагранжа. Невырожденное
преобразование, приводящее квадратичную форму к ка-
каноническому виду, при этом может быть получено как
произведение преобразований, применяемых в методе
Лагранжа.
Итак, для любой вещественной квадратичной формы
существует не единственная конгруэнтная каноническая
форма.
Пример 1. Привести к каноническому виду квадратичную форму
L (xj х2 х3) =х\ —
х\.
204

Решение. Так как среди коэффициентов ац есть отличные от
нуля, то приведение к каноническому виду можно осуществить сле-
следующим образом. Данную квадратичную форму представим в виде
и х2, х,) =
4
- 4x3) + -j- (Здг2—4AT3)aJ -
1 / 3 \2
— -т- (Зхг — 4лг3J + 2х2х3 + лг| = I xt — -к-х2 + 2х3) —
2 п .
I О» у- ____ О „* I j. ^__
9 / о 32 256
¦•)-
32
9
+
81
64 2 2
9 *з Зл:з
*2 37
9 / 16
— Т Vе* ~ Т
Невырожденное преобразование
i/l — *1— 2 X2-f-"X3, у2 — ДГ2— g Х3, у3 — Хя
приводит данную квадратичную форму к каноническому виду
2
У\
37
2
МЛ. Уг, Уз)=У\—^У^
Пример 2. Привести к каноническому виду квадратичную форму
L (*!, хг, х3) = 4х1лга — 5дг2дг3.
Решение. Так как все коэффициенты ац = 0, то сначала при-
приб
меним преобразование
В результате получим
Так как в этой квадратичной форме коэффициент при у\ отличен от
нуля, то
i-i (ffi. Уъ, Уз) =\Ух — " 0з
Применив преобразование
5
гх = 0i — "Z" Уз.
Уг +
5 \2
Т0з]-
?а =
205

получим
= z\— г\— 0г|.
Итак, невырожденное преобразование
zi == xi ~Ь -*а Т~ хз>
_
Х1
5
Х2~\ д
приводит данную квадратическую форму к каноническо-
каноническому виду.
Кроме метода Лагранжа, существуют и другие мето-
методы приведения квадратичной формы к каноническому ви-
виду. Рассмотрим метод Якоби, который применим в случае,
когда все главные миноры матрицы квадратичной формы
отличны от нуля. Этот метод заключается в следующем.
Пусть дана квадратичная форма
Предположим, что главные миноры Аь ... , А„ матрицы
А отличны от нуля. Можно доказать, что тогда существует
единственное невырожденное однородное пребразование
переменных вида
#2 — У г + а32#3 + • • • + апгУл>
х3= у3+ • • • И
хп = Уп>
приводящее данную квадратичную форму к каноническо-
каноническому виду
где
4 — &\> Лу — —г-; , / = z п.
E.8)
Коэффициенты этого преобразования определяются по
формуле
206

aJi —
A/-
1 i
E.9)
где Aj-н — минор матрицы А, расположенный на пересе-
пересечении строк этой матрицы с номерами 1,2,...,/—1
и столбцов с номерами 1,2,..., i—1, i+1, ... , /.
Пример 3. Привести к каноническому виду квадратичную форму
L (xlt х2, ха) = 2х\ + Ъх\ + х\ —
— 2дгадг3.
Решение. Матрица данной квадратичной формы имеет вид
2 —2 Г
— 2 3 —1
1—1 Г
а ее главные миноры Ax = 2, Д2 = 2, А3 = 1. По формулам E.8)
имеем:
1
Следовательно, данная квадратичная форма приводится к канони-
каноническому виду
п п 1 п
Преобразование, приводящее данную квадратичную форму к кано-
каноническому виду, имеет вид
Уз- .
Использовав формулы E.9), получим
М.1
«зг = (-1L
— 2
~~ 2
— 2 1
3 —1
= 1,
2.2
«*- = (-l)t—^
2 1
2 ]
• = О
Таким образом,
207

§ 5.5. Закон инерции квадратичных форм
Для данной квадратичной формы существуют различ-
различные конгруэнтные ей канонические формы. Однако все
канонические формы, конгруэнтные данной, обладают
рядом общих свойств. Рассмотрим одно из этих свойств,
выражающее так называемый закон инерции квадратич-
квадратичных форм.
Теорема. Все канонические формы, конгруэнтные дан-
данной квадратичной форме, имеют: 1) одно и то же число
нулевых коэффициентов, 2) одно и то же число положи-
положительных коэффициентов; 3) одно и то же число отрица-
отрицательных коэффициентов.
Доказательство. 1. Так как в любой канониче-
канонической форме, конгруэнтной данной квадратичной форме,
число коэффициентов, отличных от нуля, одно и то же
(равное рангу формы), то и число нулевых коэффициен-
коэффициентов одно и то же.
2. Пусть
L(xu х%. .., х„) ~Li (г/,, г/а, ..,, Уп)
L(xu х2,..., хп) ~L2{zu z2,..., zn),
где
i. У% Уп) =
, z2 zn) =
Ку1
1+р>
E.10)
72 —
E.11)
%, .... aH, Pi, ..., pp, Yi, • • •, Ys» 8i. ..., 8q — положи-
положительные числа. Докажем, что k — s.
Предположим, что k<s. Пусть форма E.10) получе-
получена из L(xu х2,..., хп) преобразованием
. +Ь1пхп,
Уп = Ki
• •- • +bknxn,
• • • +bmxn,
E.12)
208

а форма E.11) —преобразованием
zl = + +
га — CslXl "Ь • • ¦ "f" CsnXn>
E.13)
Возьмем k первых уравнений системы E.12) и п—s
последних уравнений системы E.13). Положим в этих
уравнениях
и рассмотрим полученную вспомогательную систему
k+(n—s) однородных линейных уравнений с п перемен-
переменными XU X2, . .. , Хп.
Так как k-\- (n — s) = n— (s — k)<n, то число
уравнений меньше числа неизвестных и, следовательно,
вспомогательная система имеет ненулевое решение, на-
например х\, х*2, .... х\.
Подставляя х\, х*2, ..., х*п в преобразование E.12), по-
получим у*, у\ у\, где у\ = у\ = ... = утк = 0.
Среди y*k+l, y*k+2, .... у*п есть отличные от нуля, что
следует из невырожденности преобразования E.12). Из
выражения E.10) следует, что
Lx(y\, У\ ^)<°- E-14)
Аналогично из преобразования E.13) находим г*,
г', .... г'п, где 2S'+, = z*+2 = ... = z'n = 0, а среди г^,
г*, ..., г* есть хотя бы один отличный от нуля.
Из выражения E.11) получим
Мгр г;, ...,г;)>0. E.15)
Так как
'-•1 \i/i> ?/2» • • • > Уп) — ^ \xi> Х2> • • . , Хп),
*- \?i> '2' ' " " » П' — \ 1' 2' • • • > хп'у
ТО
l2(г;, г*. ..., z;) = La{y\, у;, ..., у*п),
209

что противоречит соотношениям E.14) и E.15). Следова-
Следовательно, k не может быть меньше s. Аналогично доказы-
доказывается, что k не может быть больше s. Следовательно,
k = s.
3. То, что все рассматриваемые канонические виды
данной квадратичной формы имеют одно и то же число
отрицательных коэффициентов, следует из доказанного
в пунктах 1 и 2. ¦
Следствие. Любая квадратичная форма имеет единст-
единственную конгруэнтную нормальную форму (с точностью
до обозначения переменных).
§ 5.6. Знакоопределенные квадратичные формы
Совокупность значений переменных Х\, х%, ... , хп на-
назовем нулевой, если xi = X2= ... =х„=0, и ненулевой, ес-
если среди значений переменных есть хотя бы одно, отлич-
отличное от нуля.
Очевидно, что для любой квадратичной формы
L(xu х2, ..., хп) имеем L@, 0 0) =0.
Квадратичная форма L (хъ х2, ..., хп) называется по-
положительно-определенной, если для любой ненулевой со-
совокупности значений переменных х], х\, ..., х*п имеем
L(x\, x*v ..., х*) >0, и отрицательно-определенной, если
для любой ненулевой совокупности значений переменных
х\, х\, ..., х*п имеем L (х\, х\, ..., х*п) < 0.
Положительно- и отрицательно-определенные квадра-
квадратичные формы называются знакоопр еде ленными.
Пример. Квадратичная форма
L(xlt xit x3) = 2x\ + 3xl + 4xl
является положительно-определенной, а
L(xlt xj) = — x\ — 2x\
отрицательно-определенной.
Квадратичная форма
L (Xi, Х2, Х3) = х\ + 2Х^2 + 2*1*3 + *2 + 2Х2Х3 + Х3 =
не является знакоопределенной, так как существует ненулевая сово-
210

купность значений переменных, например ^=1, х2 = —-дг,
1 / 1 I \
х3 = — -g", такая, что L II, — -g—, —-g—1 = 0.
Теорема 1. Если квадратичная форма положительно-
определенная, то любая конгруэнтная ей квадратичная
форма также является положительно-определенной.
Доказательство. Пусть L(х\, х2, ... , хп) — по-
положительно-определенная квадратичная форма и
L\ (у и Уъ ¦ ¦ ¦ , Уп) ~ L (хи х2, ... , хп).
Предположим, что Lx (уъ у2, . .., уп) не является
положительно-определенной формой. Тогда существует
ненулевая совокупность значений переменных у\, у*2, ...,
г/*) такая, что
Рассмотрим невырожденное однородное линейное
преобразование
E.16)
переводящее форму Lx (ylt y2 уп) в L (х1г х2, .... хп).
Положив в соотношениях E.16) УХ = У\, Уг*=У*2> •••>
Уп = У*п> получим невырожденную неоднородную систему
уравнений, которая имеет единственное ненулевое реше-
решение х\, х\, ..., х*п. Так как
MV* V* V* \ ... ¦ Г ///* /I* //*\
Лр л2, . . . , лп) — Ь]Дг/|, у2> • • • > Упп
а
Mtf. Уг ••"•. ^)<0,
то и
что противоречит условию. ¦
Теорема 2. Если квадратичная форма отрицательно-
определенная, то любая конгруэнтная ей квадратичная
форма также является отрицательно-определенной.
211
C12^2 + • • • + С1пХп>
Уг = сг1хг + с22х2 + . . .

Доказательство аналогично доказательству предыду-
предыдущей теоремы.
Теорема 3. Знакоопределенная квадратичная форма
является невырожденной.
Доказательство. Пусть L(x\, хг, ... , хп) — зна-
знакоопределенная квадратичная форма. Предположим, что
она вырожденная, т. е. ее ранг г<п. Тогда она может быть
приведена к канонической форме
?-1 (г/i. Уъ • • •» Уп) = 2 а&Ъ ai^° l = ]' 2' • • •' г>
t=\
конгруэнтной форме L(xu хг, ..., хп).
Существует ненулевая система, например у* = г/* =
= ••• = У* = 0, у'+1 = ... = у*п = 1, для которой Lt\y\,
у\, ..., у*п) = 0. Следовательно, форма Lx{уъ у2, ..., уп)
не является знакоопределенной, что противоречит тео-
теореме 1. Таким образом, предположение неверно и г — п. Щ
§ 5.7. Критерии знакоопределенности
квадратичных форм
Во многих случаях необходимо выяснить, является ли
квадратичная форма знакоопределенной. Рассмотрим
теоремы, выражающие критерии знакоопределенности
квадратичных форм.
Теорема 1. Для того чтобы каноническая квадратич-
квадратичная форма была положительно- (отрицательно-) опреде-
определенной, необходимо и достаточно, чтобы все ее коэффи-
коэффициенты были положительны (отрицательны).
Доказательство. Необходимость. Пусть кано-
каноническая форма
Ь(х1У х2, ..., хп) = 2 aix1 E.17)
i=l
является положительно-определенной. Так как всякая
положительно-определенная форма — невырожденная, то
все а,- Ф 0. Докажем, что все а,. > 0. Для любой ненулевой
совокупности х*, ..., х*п имеем
iXf>0, EЛ8)
212

X2 —
= x~ = U, из
Положив, например, х\ = 1,
условия E.18) видим, что ах > 0. Аналогично доказы-
доказывается, что а2 > 0, ..., ал > 0.
Достаточность. Если в квадратичной форме E.17) все
коэффициенты щ>0, то очевидно, что эта форма являет-
является положительно-определенной.
Аналогично проводится доказательство для отрица-
отрицательно-определенной формы. ¦
Доказанная теорема дает возможность исследовать
знакоопределенность любой квадратичной формы путем
предварительного приведения ее к конгруэнтной канони-
канонической форме.
Существует критерий знакоопределенности квадратич-
квадратичной формы, не требующий приведения ее к канонической
форме. Рассмотрим некоторые вспомогательные теоремы.
Теорема 2. Если квадратичная форма положительно-
определенная, то определитель ее матрицы положителен.
Доказательство. Пусть L (х\, Хъ ... , хп) — по-
положительно-определенная форма с матрицей А. Тогда
в конгруэнтной ей канонической форме
все а, > 0.
Матрица этой формы
с =
0 а,
0
0
0 0
и det C=aia2 ... а„>0. Следовательно, det/4>0 (см.
следствие теоремы 1 из § 5.3). ¦
Обратное утверждение, вообще говоря, не является
справедливым, т. е. из того, что определитель матрицы
квадратичной формы положителен, не следует, что форма
положительно-определенная.
Теорема 3. Если квадратичная форма п переменных
отрицательно-определенная, то при п четном определи-
определитель ее матрицы положительный, а при нечетном — отри-
отрицательный.
Доказательство. Пусть L(xu х2, ... , хп) — от-
отрицательно-определенная квадратичная форма с матри-
213

цей А. Тогда — L(x\, х2, ... , хп) — положительно-опреде-
положительно-определенная форма с матрицей (—А). Следовательно, по тео-
теореме 2, det(—Л) >0.
Так как общий множитель всех элементов ряда опре-
определителя можно вынести за знак определителя, то
det(-4) = (-l)"deM. Следовательно, (— 1)" det Л>0,
откуда при п четном det Л>0 и при нечетном det Л<0. В
Теорема 4. Если квадратичная форма знакоопреде-
ленная, то все главные миноры ее матрицы отличны от
нуля.
Доказательство. Пусть
А =
«11 «12
ax
a»
[_а1п а
¦2л
матрица знакоопределенной квадратичной формы
Ь(х\, х% ... , хп). На основании теорем 2, 3 det АфО.
Рассмотрим вспомогательные квадратичные формы:
Lx (Xl) = L (xl7 0 0) = anx\,
^г (*i. x2) — L {xy, x2, 0, .... 0) = anx\
%, . . . , Xn— l) =
n—1 n— 1
= L(xlt x2, ..., xn-u 0) =
aUxixh
матрицы которых соответственно
= (flu), ^2 =
«11 «
12
«12 «22
ап
¦42
«12
«22
«l,n-l
Й2, n-1
_«l,n—1 «2. n—1
«n— l.n—1_
Легко заметить, что поскольку L(xb x2, ..., xn) —
знакоопределенная форма, то Li(xi), ^(лгь х2), ... ,
Ln_i(xi, х2, ... , xn-i) также являются знакоопределенны-
ми формами, и на основании теорем 2, 3 определители их
214

матриц отличны от нуля, т. е. главные миноры матрицы А
отличны от нуля. ¦
Теорема 5 (критерий Сильвестра). Для того чтобы
квадратичная форма была положительно-определенной,
необходимо и достаточно, чтобы все главные миноры мат-
матрицы этой формы были положительны. Для того чтобы
квадратичная форма была отрицательно-определенной,
необходимо и достаточно, чтобы главные миноры четного
порядка матрицы этой формы были положительны, а не-
нечетного — отрицательны.
Доказательство. Необходимость. Пусть
L(xh х2, ... , хп) — знакоопределенная квадратичная
форма. Тогда, на основании теоремы 4, все главные ми-
миноры матрицы А данной квадратичной формы отличны
от нуля и, следовательно, L(x\, %%,..., хп) методом Яко-
би приводится к каноническому виду
где Хг (i= 1,2,... ,п) определяются по формулам E.8).
Если L{x\, X2, ... , хп) — положительно-определенная
квадратичная форма, то Xi>0 (t=l, 2, ... , га), и из
формул E.8) следует, что все главные миноры матрицы
А положительны.
Если L{x\, X2, ... , хп) —отрицательно-определенная
квадратичная форма, то Я,,<0 (i=l, 2, ... , п), и из
формул E.8) получаем: Ai = A,i<0, A2=A,2Ai>0 и т. д.
Достаточность. Пусть все главные миноры матрицы А
положительны, т. е. А,>0 (t=l, 2, ..., п). Тогда из
формул E.8) следует, что kt>0 (i=l, 2, ..., п), т. е.
данная квадратичная форма положительно-определен-
положительно-определенная. ¦
Пусть Ai<0, A2>0 и т. д. Тогда из формул E.8) сле-
следует, что Яг<0 (i=l, 2, ..., п), т. е. данная квадратич-
квадратичная форма отрицательно-определенная.
Пример. Исследовать на знакоопределенность следующие формы
Li (*i. х2) = 2х\ + х22 —
Ц (*i, х2, х3) = х\ -f 4*2 + х\
Квадратичная форма Lx (х1, х2) не является знакоопределенной,
так как для ее матрицы
215

[-1 -I]
главные миноры Дх = 2, Д2 = — 7.
Матрица формы L2 (x±, х2, х3) имеет вид
1 2 ~y
2 4 2
1
¦г»
Для этой матрицы Л1=1, Д2 —0. Следовательно, эта форма не
является знакоопределенной.
§ 5.8. Свойство корней характеристического уравнения
симметрической вещественной матрицы
Если С — матрица, элементы которой, вообще говоря,
являются комплексными числами, то можно ввести поня-
понятие матрицы, сопряженной.данной.
Матрицей С, сопряженной матрице С, называется мат-
матрица, элементами которой являются числа, сопряженные
соответствующим элементам матрицы С.
Из определения следует, что если элементы матрицы
С будут Ckj = akj -f- фу, то элементами матрицы С являются
числа сщ = akj — i$kJ, где i = Y — l.
Легко видеть, что имеют место следующие соотно-
ношения.
1. С = С, если С — вещественная матрица.
2. (Г+В=_С + В.
3. СВ =СВ.
4. КС = КС, где К — число.
Теорема. Корни характеристического уравнения ве-
вещественной симметрической матрицы являются вещест-
вещественными числами.
Доказательство. Если А — вещественная сим-
симметрическая матрица порядка п, то А=А и АТ=А.
Пусть % — корень характеристического уравнения
этой матрицы. Рассмотрим собственный вектор
х(хи Х2, ... , хп) матрицы А с собственным числом К.
216

(Координаты вектора х, вообще говоря, могут быть ком-
комплексными числами.) Тогда
Х =
Х2
является собственным столбцом матрицы А с собствен-
собственным числом А,.
Найдем произведение ХТАХ двумя способами. С одной
стороны,
ХТАХ = ХТАХ = ХМХ = ХГШ = ХТАХ = Х7(ХТХ).
С другой стороны,
ХМХ = ХТЛТХ = (АХУХ = (ХХУХ = % (ХТХ).
Таким образом,
или
Но
— А.)(ХТХ) = О.
E.19)
ХГХ - [Xlx2 ... хп]
х„ха]
или
Х*Г=(|х,|2+|х2|2+ ... +\хп\2), E.20)
где \xh\ — модуль числа xh (k= 1,2,... , «).
Так как X — ненулевой столбец, то из выражения
E.20) следует, что Х^ХфО. Тогда из равенства E.19)
имеем к=к, т. е. к — вещественное число. И
217

§ 5.9. Свойства собственных векторов симметрической
вещественной матрицы
Теорема 1. Вещественная симметрическая матрица
имеет только вещественные собственные вектор-столбцы.
Доказательство. Если X — собственный вектор-
столбец с собственным числом А, вещественной симметри-
симметрической матрицы А, то его координаты х\, лг2) ... , хп, как
известно, находятся из системы уравнений
(йи — А,) хг + апх2 + . . . +а1пхп = 0,
+ («22 — Я.) х2 + . . . + а2пхп = О,
an2x2+ . . . +(am — А,)
Так как К — вещественное число (см. § 5.8), то вы-
вышеуказанная система имеет вещественные коэффициенты
и, следовательно, вещественные решения. ¦
Если для вектор-столбцов размеров «XI введем опе-
операцию скалярного умножения так, как в примере 2 § 3.9,
то имеет место следующая теорема.
Теорема 2. Два собственных вектор-столбца вещест-
вещественной симметрической матрицы, соответствующих раз-
различным собственным числам, ортогональны.
Доказательство. Пусть Х1г Х2 — собственные
вектор-столбцы вещественной симметрической матрицы А
порядка п, собственные числа которых %г и А.2 различны.
Подсчитаем Х]АХ2 двумя способами.
С одной стороны,
Х]АХ2 = Х\ (АХ2) = X] (А,2Х2) = Х2Х]Х2,
с другой стороны,
Х]АХ2 = {Х\А) Х2 = (Х]А?) Х2 =
Сравнивая полученные результаты, имеем
или
(Я, —Xi)XTX, = O
Но ^т^^г» следовательно, Х\Хг = 0.
218

§ 5.10. Ортогональное преобразование, приводящее
квадратичную форму к каноническому виду
Ранее было доказано, что при помощи невырожденно-
невырожденного линейного однородного преобразования всякую веще-
вещественную квадратичную форму можно привести к кано-
каноническому виду. Докажем, что вещественную квадратич-
квадратичную форму можно привести к каноническому виду при по-
помощи ортогонального преобразования.
Теорема 1. Если существует ортогональное преобразо-
преобразование, приводящее вещественную квадратичную форму
L (х\, х2, ... , хп) к каноническому виду
1ЛУъ г/2, • • •, Уа) = КУ\ + ЪУ\ + ¦ ¦ ¦ + КУЪ E-21)
го Ль Яг, ... , Хп — характеристические числа матрицы А
квадратичной формы L (xi, х2, ..., хп).
Доказательство. Пусть ортогональное преобра-
звание X=CY приводит квадратичную форму
L(xu х2, ... , хп) к каноническому виду E.21). Тогда мат-
матрица D формы L] (г/ь г/2,- ¦ ¦, Уп) имеет вид
,х 0 ... 0
о о2
Так как С — ортогональная матрица, то СТ = С~1
и D=C~1AC, поэтому Хг — характеристические числа
матрицы А. ¦
Теорема 2. Если существует ортогональное преобразо-
преобразование с матрицей С, приводящее вещественную квадра-
квадратичную форму L{x\, х2, .. . , хп) с матрицей А к канони-
каноническому виду
Уп)-
то столбцами матрицы С являются собственные вектор-
столбцы матрицы А с собственными числами Х\, %ь • ¦ ¦, Хп.
Доказательство. Пусть ортогональное преобра-
преобразование X=CY, где С= (Cij) (i, /= 1,2,..., п), приводит
форму L (х\, х2,..., хп) к каноническому виду
Kyi + ^i+ ... + Ку1-
219

Тогда
СТАС =
Л О ... О
О X, . . . О
о о . . . к
Умножая обе части этого равенства на С слева и учиты-
учитывая, что ССТ = Е, получим
Л 0 ... О
О Я2 . . . О
О 0 . . . K
Согласно правилу умножения матриц, для элементов
da (i= I, 2,.... и) матрицы D = AC имеем
dij = ajiCij + ai2c2j+ ... +aincnj.
С другой стороны,
dij^d-Kj.
Следовательно,
т. е.
апси + anc2j
«2 А/ + аггсг]
= Ь]Сц (t=l, 2, ... , п),
. . . + а1псп1 =
. . . -f a2ncn] =
или в матричной форме
А
Следовательно, /-й столбец (/=1, 2, ... , п) матрицы
С является собственным вектор-столбцом матрицы А
с собственным числом Xj. ¦
220

Теорема 3. Для любой вещественной квадратичной
формы, существует ортогональное преобразование, приво-
приводящее ее к каноническому виду.
Доказательство. Для квадратичной формы одного
переменного L (хг) — аг1х\ искомым преобразованием явля-
является тождественное преобразование, матрица которого
ортогональна, Предположим, что теорема справедлива для
всех квадратичных форм k переменных, где k = 1, 2, ...,
п—1, и докажем, что она справедлива для квадратичной
формы п переменных.
Пусть L(X\, х2, ... , хп) — квадратичная форма с мат-
матрицей А = (ац) (i, /= 1, 2, ... , п), % — одно из собствен-
собственных чисел матрицы А и
1-21
E.22)
нормированный собственный вектор-столбец этой матри-
матрицы с собственным числом X.
Построим ортогональную матрицу С=(сц), первым
столбцом которой является столбец E.22). Рассмотрим
квадратичную форму L\(t/i, У2, ¦ ¦ ¦ , Уп), полученную из
данной путем преобразования
X=CY.
Матрица D формы L\ (у\, ..., уп) имеет вид
E.23)
Найдем сначала первую строку матрицы В = СТА. Для
элементов Ь^ (}= 1, 2,..., п) этой строки имеем
Ьц=спаи +c2ia2j+ ... +cnlanj (/=1, 2, .... п).
Так как E.22) является собственным вектор-столбцом
матрицы А с собственным числом К и матрица А симмет-
симметрическая, то
следовательно, Ьц—ксц.
221

Теперь найдем первую строку матрицы D = BC. Для
элементов dij (j= 1,2,... , п) этой строки имеем
Так как матрица С ортогональная, то
К при У = 1,
dlj \0 при }=?1.
Матрица D — симметрическая, следовательно, она
имеет вид
X 0 ... О
О dM . . . d.
О d d
и л • • • ит
Поэтому форму L\ B/1, ... , уп) можно записать в виде
Lx (уг Уп) — ^У\ + ^2 (#2> • ¦ •» Уп)-
Квадратичная форма L2(y2, ¦ ¦ ¦ , Уп) является, вообще
говоря, формой п—1-й переменной, и для нее, согласно
индуктивному предположению, существует ортогональное
преобразование
г2 = h22y2 + h23y3 + . . . +h2nyn,
+ hn3y3+ . . . +hnnyn,
приводящее ее к каноническому виду
Преобразование
Zi = Уъ
E.24)
является ортогональным и приводит квадратичную форму
?-1 (Уи У2, ¦ ¦ ¦ , Уп) к каноническому виду.
Таким образом, квадратичная форма L(xu х2, ... , хп)
приводится к каноническому виду последовательным при-
222

менением ортогональных преобразований E.23) и
E.24). ¦
Теорема 4. Любая вещественная симметрическая мат-
матрица приводима к диагональному виду.
Доказательство. Пусть А — вещественная сим-
симметрическая матрица порядка п. Рассмотрим квадратич-
квадратичную форму L от п переменных с матрицей А. По теоре-
теореме 3 существует ортогональное преобразование, приводя-
приводящее форму L{x\, х2, ... , хп) к каноническому виду. Пусть
Т — матрица этого преобразования. Тогда TTAT—D, где
D — диагональная матрица. Так как матрица Т ортого-
ортогональная, то ТГ = Т~1 и T~lAT = D. Следовательно, матри-
матрица А приводима к диагональному виду. ¦
Из доказательства теоремы 4 следует, что для всякой
вещественной симметрической матрицы А существует ор-
ортогональная матрица Т, такая, что Т~ХАТ— диагональная
матрица.
Теорема 5. Если линейное преобразование веществен-
вещественного линейного пространства в некотором ортонормиро-
ванном базисе имеет вещественную симметрическую мат-
матрицу, то существует ортонормированный базис, состоящий
из собственных векторов этого преобразования.
Доказательство. Пусть линейное преобразова-
преобразование f в ортонормированном базисе е\, е%,... , еп имеет ве-
вещественную симметрическую матрицу А. По теореме 4,
существует ортогональная матрица Т такая, что Т~1АТ —
диагональная матрица. Таким образом, преобразование
с матрицей Т переводит данный базис в ортонормированный
-» -> -»-
базис е[, е'г ... , е'п, в котором матрица преобразования f
-»--»¦ -»-
является диагональной. Следовательно, е\, е'2, ..., е'п —
собственные векторы преобразования f. ¦
§ 5.11. Нахождение ортогонального преобразования,
приводящего квадратичную форму к каноническому виду
Из теорем, рассмотренных в предыдущих параграфах,
вытекает следующее правило нахождения ортогонального
преобразования, приводящего квадратичную форму п пе-
переменных к каноническому виду.
1. Записываем матрицу А данной квадратичной фор-
формы и находим характеристические числа этой матрицы.
223

2. Находим ортонормированную систему собственных
вектор-столбцов матрицы А.
3. Составляем искомое ортогональное преобразо-
преобразование.
Пример 1. Найти ортогональное преобразование, приводящее
к каноническому виду квадратичную форму
Решение. 1. Матрица данной квадратичной формы
-г. :]¦
Характеристические числа матрицы А являются корнями уравнения
17 — X 6
8 —Я
= 0.
Решая это уравнение, находим A,t = 20, A,2 = 5.
2. Сначала найдем нормированный собственный вектор-столбец
матрицы А с собственным числом X = 20. Для этого составим систему
из которой находим ax = 2a2. Следовательно, при любом /, отличном
от нуля, столбец
является собственным вектор-столбцом матрицы А. Столбец
2
1
является нормированным собственным вектор-столбцом матрицы А.
Координаты 1>! и и2 собственного вектор-столбца матрицы А
с собственным числом А,2 = 5 находим из системы
Решая эту систему, получаем v% = — 2vt. Следовательно, при любом
s, отличном от нуля, столбец
U1
224

является собственным вектор-столбцом матрицы А. Столбец
1
~ VT
2
является нормированным собственным вектор-столбцом матрицы А.
3. Составляем матрицу
2 1
1
Т/Т
2
ут ут
Искомым преобразованием является следующее:
2 1
У г-
Пример 2. Найти ортогональное преобразование,
к каноническому виду квадратичную форму
приводящее
xti Хз) = Х1 — 8ххХ2 — iua^s Т'Л2 — °-»2А3 "Г Л3'
Решение. 1. Матрица данной квадратичной формы
1 _4 —8'
А= —4 7 —4
— 8 —4 1
Характеристическим уравнением матрицы А является уравнение
1_Х —4 —8
— 4 7-х —4 =;о(
— 8 -4 1-Х
корни которого Я,х = — 9, Х2 = А,3 = 9.
2. Координаты хи хг, х3 собственного вектора
ным числом %i = — 9 находятся из системы уравнений
10*! —4х2 —8х3 = 0,
— 4х1+16ха —4*3 = 0,
— 8хг — 4х2 + 10л:3 = О
с собствен-
собствен225

или
5*! —2x2 — 4.*:s =
4*x -J- 2*2 — 0*3= 0.
Ранг матрицы этой системы равен двум, и поэтому система имеет не-
ненулевые решения. Для их нахождения решаем систему
5*г —2*2 —4*3 = 0,
*! —4*2 + *з = 0.
Имеем: *х = — 18*. *2 = — 9/, *3 = —18/.
Таким образом, вектор-столбец
— 18
— 9
— 18
при любом значении /, отличном от нуля, является собственным
вектор-столбцом матрицы А с собственным числом Хх = — 9.
Пронормировав вектор Xt, получим вектор-столбец
- 2_ -
3
3
_2_
3
Чтобы найти собственные вектор-столбцы матрицы А с собствен-
собственным числом К = 9, составим систему
— 8ui — 4u2 — 8tt3 = 0,
Ранг матрицы этой однородной системы равен 1, и поэтому имеются
два свободных неизвестных. Следовательно, решение можно записать
в виде йх = slt и2 = — 2s! — 2s2, u3 = s2-
Таким образом, вектор-столбцы
- 2Sl - 2ц
E.25)
при любых st и s2, удовлетворяющих условию s\-{-s\ ф 0, лвляются
собственными для матрицы А с собственным числом к = 9.
226

Существуют два ортогональных собственных вектор-столбца Х%
иХ, с собственным числом Я, = 9. Для нахождения Х2 положим
в вектор-столбце E.25), например, s1 = l, s2 = 0. Получим
Х.=
Чтобы найти вектор-столбец Х3, определим st и s2 в вектор-
столбце E.25) так, чтобы выполнялось условие ортогональности Х2
и Х3, т. е. чтобы sx + 4sj -f- 4s2 = 0 или sx =—-g- s2.
Положив, например
Пронормировав
, s2 = 5,
векторы
1
У"
2
у~
0
находим
Y
—
—
Х2 и Л,
5
А~
2
5
получим
3
3
1
4
У У
2
У 5
/ 5
3
Ортонормированной системой собственных вектор-столбцов матрицы
является система векторов
у* —
А, —
у* —
Л2 —
/У
о
3 V 5
2
'з /У
1 У
3. Искомым преобразованием является следующее:
1
КУ
2
"Ту
~ з/У1'3'
3/5
227

§ 5.12. Упрощение уравнений фигур второго порйдка
на плоскости
Пусть на плоскости задана прямоугольная декартова
система координат (О; еи е2). Если х и у — координаты
произвольной точки на плоскости в данной системе ко-
координат, то, как известно,
х2 Ф
(I) уравнение —^—|—^— = 1 определяет эллипс;
х2 и2
(II) уравнение —^—| 1^— = 0 — точку;
х2 иг
(III) уравнение —^—I—%— = — 1—пустое множество
точек (мнимый эллипс);
х2 ф
(IV) уравнения —^ js~ = — 1 — гиперболы;
хг иг
(V) уравнение —^ ~— = 0 — пару пересекаю-
пересекающихся прямых;
(VI) уравнение у2 = 2рх (х2 = 2ру), р Ф 0, — параболу;
(VII) уравнение у2 = а2 (х2 = а2), афО, — пару парал-
параллельных прямых;
(VIII) уравнение у2 = 0 (х2 = 0) —пару слившихся прямых;
(IX) уравнение у2 = — а2(х\= — а2), афО, —пустое
множество точек.
Уравнения (I) — (IX) называются каноническими
уравнениями фигур второго порядка на плоскости.
Уравнения (I) — (III) определяют фигуру эллиптиче-
эллиптического типа, уравнения (IV), (V) —гиперболического ти-
типа, уравнения (VI) — (IX) —параболического типа.
Рассмотрим уравнение второго порядка
ax2 + bxy + cy2 + dx + gy + f = 0, E.26)
где а2 + Ъг + с2 Ф 0. Множество точек плоскости, коор-
координаты х, у которых удовлетворяют уравнению E.26),
образует некоторую фигуру. Покажем, что это уравнение
определяет одну из фигур (I) — (IX). Для этого найдем
уравнение фигуры E.26) в системе координат (О;
228

e'j, e^), где векторы et и е^ получены из векторов е1 и е2
ортогональным преобразованием с матрицей
т. е.
Т =
e\ =
12
22 J
При этом формулы преобразования координат точек бу-
будут иметь вид
х = tnx' + tny',
У = hiX' + кгУ'-
Подставив эти значения хир уравнение E.26), по-
получим уравнение данной фигуры в системе координат
(О; X, ~е'2)-
Сумма первых трех членов
ах2 + Ьху + су2 E.27)
является квадратичной формой двух переменных х, у, ко-
которую мы будем называть квадратичной формой, соответ-
соответствующей уравнению E.26). Матрица этой формы имеет
вид
Ь_
2
А =
Пусть выбранное преобразование приводит квадратич-
квадратичную форму E.27) к каноническому виду (как известно,
такое преобразование всегда существует)
где Xi и %2 — корни характеристического уравнения мат-
матрицы Л. Тогда уравнение E.26) примет вид
т-/ = 0, E.28)
229

где di =
Возможны следующие случаи.
1. detA>0. Так как определитель матрицы квадра-
квадратичной формы не меняется при ортогональном преобразо-
преобразовании, то ii?i2>0, т. е. Xi и %2 имеют одинаковые знаки.
В уравнении E.28) дополняем до полного квадрата
члены, содержащие х'2 и х', а также члены, содержащие
г/'2 и у'. После этого уравнение можно записать так:
M*'-fti)8 + M0'-A.)" = fi- E-29)
Осуществим параллельный перенос репера (О; e'v e'2)
—> -> -*¦
на вектор 00', координатами которого в репере (O;ej, е'2)
—> -> ->
являются hx и 1г2, т. е. на вектор 00' — кхех + h2e'2).
Тогда уравнение E.29) в репере (О'; e'v e'2) примет вид
hx + Хьу = fv E.30)
Если /i=#=0, то уравнение E.30) приводится к виду (I)
или (III), если /i = 0 — к виду (II).
2. det А<0, следовательно, и ХД2<0, т. е. Xi и fa —
разных знаков.
Как и в первом случае, уравнение E.28) можно при-
привести к виду E.30). В этом случае, если }\ФО, уравнение
E.30) приводится к виду (IV), если fi=0 — к виду (V).
3. det А = 0, следовательно, /\Д2 = 0, т. е. одно из чисел
Х\, %2 равно нулю. Не нарушая общности, будем считать,
что Х\фО, /\,2=0. Дополняя в уравнении E.28) члены, со-
содержащие х'2 и х', до полного квадрата, получим
'ki{x'-hly + gly'+f=b. E.31)
Если g\=?0, то уравнение E.31) можно записать
в виде
X1(x'-hiy=-g1(y'-h2). E.32)
Осуществим параллельный перенос репера (О; е[, е'2) на
вектор 00' = h^e[ + h^'r Уравнение E.32) в репере (О';
e'v e'2) примет вид
230

Это уравнение приводится к виду (VI).
Если gi = 0, то уравнение E.31) имеет вид
Осуществив параллельный перенос репера (О; е\, е'2) на
вектор 00' = hxe'v получим в репере (О'; е\, е'2) урав-
уравнение
XlX + h = 0.
Это уравнение при fi#0 приводится к виду (VII) или
(IX), при/,=0 —к виду (VIII).
Итак, если det Л >0, то уравнение E.26) определяет
фигуру эллиптического типа; если det/l<0 — гиперболи-
гиперболического; если deM=0 — параболического типа.
Операция перехода от уравнения E.26) к уравнению
E.28) называется отнесением фигуры к главным осям.
Если фигура, определяемая уравнением E.26), являет-
является эллипсом или гиперболой, то новые оси координат па-
параллельны осям симметрии кривой.
Уравнение E.26) в случае det АфО определяет фигу-
фигуру, называемую центральной. Если det Л = 0, то фигура,
определяемая уравнением E.26), называется нецентраль-
нецентральной.
К центральным относятся фигуры эллиптического
и гиперболического типов, к нецентральным — параболи-
параболического типа.
Главными направлениями фигуры, заданной уравне-
уравнением E.26), назовем направления ортогональных собст-
собственных векторов матрицы квадратичной формы, соответ-
соответствующей этому уравнению.
Из сказанного выше следует, что существует декарто-
декартова прямоугольная система координат, в которой уравне-
уравнение E.26) принимает канонический вид. Чтобы найти эту
систему координат, поступаем следующим образом.
1. Находим ортогональное преобразование, приводя-
приводящее квадратичную форму, соответствующую данному
уравнению, к каноническому виду.
2. По этому преобразованию находим главные направ-
ления фигуры, т. е. векторы е[, е'2 — ортонормированные
собственные векторы матрицы квадратичной формы, соот-
соответствующей данному уравнению.
231

3. Находим уравнение данной фигуры в репере
(о-, 1;, X).
4. В полученном уравнении производим дополнения
до полных квадратов так, как это было указано выше.
Находим координаты точки О', которая является нача-
началом искомой системы координат.
В найденной системе координат (О'; е\, е'2) уравнение
данной фигуры имеет канонический вид.
Пример. Привести к каноническому виду уравнение
17л? + \2ху + 8у* + 20 У~Ьх + 20 = 0
и построить фигуру, определяемую этим уравнением.
Решение. Квадратичная форма, соответствующая данному
уравнению, имеет вид
L (х, у) = 17л;2 + 12ху + 8у*.
В примере 1 §5.11 было найдено ортогональное преобразование
2 , !
х' —
' +
5 E.33)
приводящее квадратичную форму L (х, у) к каноническому виду.
Базисные векторы е' и е', полученные в результате ортого-
ортогонального преобразования из базисных векторов ех и ег, задаются
формулами
E.34)
Найдем уравнение данной фигуры, отнесенное к главным осям,
т. е. ее уравнение в системе координат @; е', е'). Для этого под-
подставим в данное уравнение значения х, у из соотношений E.33).
Получим уравнение
20*'2 + Ъул + 40*' — 20#' + 20 = 0,
которое можно записать в виде
^Ф^ + -^-=1. E.35)
232

Осуществляя параллельный перенос системы (О; е'. е') на век-
тор 00' = — е'+2е', получим систему (С; е', е'), в которой
уравнение E.35), а следовательно, и данное уравнение принимает
канонический вид
v//2 */'2
_?_ + _?_ = 1. E.36)
Рис. 5.1
Таким образом, данное уравнение задает эллипс.
Для того чтобы построить этот эллипс, нужно построить фигуру,
определяемую уравнением E.36) в системе (О'; е' е'), которая по-
->¦ -»• —>•
лучается из (О; е', е') параллельным переносом на вектор 00' =
-*¦ —>
= — е'' + 2е'. При этом вместо векторов E.34) можно строить
векторы
ОМ\ =
На рис. 5.1 изображена кривая, определяемая данным уравнением.
§ 5.13. Упрощение уравнений фигур второго порядка
в пространстве
Рассмотрим общее уравнение фигуры второго порядка
E.37)
233

где хотя бы один из коэффициентов atj (t=l,2, 3;
/=1, 2, 3) отличен от нуля.
Сумма первых шести членов этого уравнения
апх2 + а22У2+аззг2 + 2а\2ху+2а1зхг+2а2зуг E.38)
является квадратичной формой трех переменных х, у, г,
которую будем называть квадратичной формой, соответ-
соответствующей уравнению E.37). Матрица этой формы имеет
вид
А =
«11
а13
а22
«13
а23
Известно, что существует ортогональное преобразова-
преобразование, приводящее квадратичную форму E.38) к канониче-
каноническому виду.
Упрощение уравнения E.37) и построение фигуры, оп-
определяемой этим уравнением, производится способом,
аналогичным способу, изложенному в § 5.12.
Пример. Построить фигуру, заданную уравнением
9*2 + 20jr2 + 20г2 — Щг — 36* — 4 /~2</ + 4 УЪ + 4 = 0.
Решение. Квадратичная форма, соответствующая этому урав-
уравнению, имеет вид
9л;2 + 20(/2 + 20г2 — 40уг,
и ее матрица
А =
9
0
0
0
20
— 20
0
-20
20
Характеристические числа этой матрицы Х1=9, %г = 40, Х3 = 0,
следовательно, канонический вид квадратичной формы будет таким:
Найдем ортогональное преобразование, приводящее квадратичную
форму, соответствующую данному уравнению, к каноническому виду.
Элементы собственного вектор-столбца, соответствующего собствен-
собственному числу А,! = 9, находим из системы
0и+ Пи — 20w = 0,
Оы — 20ч + 11ш =
234

следовательно, собственный вектор-столбец имеет вид
где / — любое число, отличное от нуля.
Чтобы найти элементы собственного столбца с собственным числом
%2 = 40, составим систему
0« — 20u — 20ш = 0,
из которой находим, что
О
s
— s
является искомым собственным столбцом.
Собственным столбцом матрицы А с собственным числом Х3 = 0
является столбец
('/0),
элементы которого найдены из системы
20у — 20w = О,
— 20и + 2(Ъ = 0.
Пронормировав собственные столбцы, получим матрицу искомого пре-
преобразования:
С =
1
0
О —¦
235

Итак, преобразование
v v'
Л = А ,
E.39)
является ортогональным преобразованием, приводящим квадратичную
форму, соответствующую данному уравнению, к каноническому виду.
Это преобразование переводит базисные векторы е1г еа, еа в векторы
е\ =
E.40)
Найдем уравнение данной фигуры в системе координат @; е',
е' , с'). Подставив в данное уравнение значения х, у, г из соотно-
2 3
шений
или
E
.39),
получим
9а:'2 + 40(/'2
(х' — 2J
3,6
— 36*'
, (У
"г
-8у' +
— 0,1)г
0,81
4
= 0
Осуществляя параллельный перенос системы (О; е\,
е^1, "бд) на вектор 00'= 2?j + 0,1бг' получим систему
(О'; ej, fig. ез)> в К0Т0Р°й уравнение данной фигуры
имеет вид
У"
где a = У^З.б, Ъ = 0,9. Это уравнение, а следовательно,
и данное уравнение определяют эллиптический цилиндр
с образующей, параллельной е'у Для того чтобы построить
этот цилиндр, наряду с системой координат (О; ev ez,
236

е3) построим систему координат (О'; е\, е'2, е3'). При этом
—> -*¦
вместо векторов E.40) можно строить векторы ОМг = е1г
= е2 —е3, ОМ3 = е2+'е3.
2"
Лз:
На рис. 5.2 изображен цилиндр, определяемый данным
уравнением.
Задачи
В задачах 5.1 —5.3 записать матрицу каждой из данных квадра-
квадратичных форм.
5.1. х 1 +*|
5.2. 2*2 + 3(/2 — г2
5.3. 4л:] + хз — 2*
В задачах 5.4 — 5.6 найти ранг каждой из данных квадратич-
квадратичных форм.
5.4. х21+х22 + х1 + 2х1х2.
5.5. 2х\ — х\ + 3x1 + 2*i*2 + 6*Л•
5.6. 2х2 -f- 4l/2 + 9г2 + 4ху + 6л:г + 120г.
237

В задачах 5.7 —5.9 записать каждую из квадратичных форм
в матричном виде.
5.7. 3*^ + х\ — хххг.
5.8. х^ + *з — 2ххх2 ~\-Ьхгх3.
5.9. 2х\ + Ъх\ — 2х\ + ххх2 + 2ххх3 + Зх2ха.
В задачах 5.10, 5.11 записать матрицу каждой из данных ква-
квадратичных форм.
Л2
Х3
5.11. [хх х2 х3]
-10
2 4
3 0 —
В задачах 5.12 — 5.14 найти квадратичную форму, полученную
из данной указанным преобразованием.
5.12. L(xx, хг) = Ъх\ — х
5.13.
,, д:3) =
Уг-
_ х\
5.14. L(xlt
В задачах 5.15—5.18 исследовать
каждую из данных квадратичных форм.
5.15. х
на знакоопределенность
5.16. 2х\ — х\ —
5.17. х\ + х\ + х
5.18. 3xf + 3xf + 4.ВД1 + 4*iX3 — 2хгха.
В задачах 5.19 — 5.21 исследовать, при каких значениях пара-
параметра К является знакоопределенной каждая из данных квадратич-
квадратичных форм.
5.19. %х\ + х\
238

5.20. 2x\ + Zx\ + 2Xxtx2 + 2*1X3 — ix2x3.
5.21. Xx\ — x\—4xtx2-\- 6xxx3-\- 10x2x3.
В задачах 5.22 —5.29 найти ортогональное преобразование, при-
приводящее к канонь .ескому виду каждую из квадратичных форм,
и записать канонический вид квадратичной формы.
5.22. L(xx, *г) = х* + *| + 4*1*2.
5.23. L (xlt х2) — Ъх\ + \2ххх2.
5.24. L (хи х2) = 7х\ + Злг| + 6 у'Твд,.
5.25. L (хи х2, х3) = 2х\ + х\ + Ъх\ — 4 УТх2х3 .
5.26. L(xlt x2, X3) = 5x2i+9l l
5.27. 1(*1( л:а, л:3) = 4jci +
5.28. L (х1( ж2, %) = 5xf + 2
5.29. L(xt, x2, x3) = 3x21-\-
В задачах 5.30 — 5.37 построить на плоскости фигуру, опре-
определяемую каждым из данных уравнений, приводя предварительно
уравнение к каноническому виду.
5.30. 2ху— 6х + 4у — 20 = 0.
5.31. 5х* + *ху + 8уа — 32* — Жу + 80 = 0.
5.32. 8у2 + бху — 12* — 26у + 11 = 0.
5.33. 48*2 + Мху + 32* + 16у + 5 = 0.
5.34. 5*2 + 6*1/+ 5#а — 16* — 16#+ 16 = 0.
5.35. *2 + 2*(/ + #2 — 8* + 4 = 0.
5.36. 8*2 — 4ху + 5у2 + 4х — Юг/+ 41 = 0.
5.37. *а — 8ху+7у2 + 6х — 6у=0.
В задачах 5.38 — 5.40 построить в пространстве фигуру, опреде-
определяемую каждым из данных уравнений, приведя предварительно урав-
уравнение к каноническому виду.
5.38. *2 — 2i/2 + г2 + Аху — 8г* — iyz —14* — 4(/+ 14г + 16 = 0.
5.39. *2 + у2 — Зг2 — бг/г — бгх — 2ху + 2* + 2у + 4г = 0.
5.40. б*2 — 2#2 + 6г2 + 4*г + 8* — 4(/ — 8г + 1 = 0.

Ответы
Глава 1
1.1. а)
1
12
31
7
15
32
б)
*
4
35
12
5"
5
27
1.2. Г 2 — З"! 1.3.
• L-3 Щ
А = А„
( 0, (
1.4. ац = \
1.5. а) Г— 6 31 б)
[-12 of
О, если i = /;
если i ф /; i = 1, 2, ... , я; / = 1, 2, ... , я.
[32 —22 16 — 6]
- 4 20 38
б)
б)
1
5
1
5
—1
8
~ 3
4
~ 5
3
~ 5
2
3
1
3
1.6. а) Г32 —22 16 — 6~|
[12 — 4 20 38J5
в) Г—2 16 8 6"]
[ 0 10 —2 4J'
1.7. т = 5, я = 4. 1.8. т = 5, я = 3, k = 4. 1.9. а) Нет; б) да:
в) да; г) нет; д) да; е) да; ж) нет; з) нет; и) нет; к) нет; л) да;
м) да; н) нет. 1.10. Г8] 1.11. Г 6 4] 112 Г 9 6]
Ы
1.13.
6
10
2
1
—6
2
12"
0
9
1
•
.14.
I. Г 6 4] 1.12. Г 9 6]
[-3 18j* L 0 13J*
1.15. Нулевая матрица
3 6 9
5 10 15
0 0 0
_7 14 21 _
размеров 4x2. 1.16. Нулевая матрица размеров 3x1. 1.17. а) В =
(h) (d)С () (d) A12 / 12 )
рр у р рр )
= (hj) = (aijdj), С = (су) = (at]dt) A=1,2, ... п; / = 1, 2, ... я);
б) либо А — нулевая, либо dx = d^ =... =dn. 1.18. d23 = 92.
1.19. Г 3 —3 "] 1.20. а) Да; б) нет. 1.22. а) Г 11 10 "
_ L 9 _-3 J[
б)
1 О О
О 1 О
О 0 1
в)
О О] г) Г co
О Oj' [ si
cos
sin
За
За
— sin
cos
За"
За
1 I
Г
.23.
L 4
Г 21
-12
19
— 9
12
240

1.24. Г—76 21] 1.25. Г
[-28 -69J" [-
ГО 01 1.28. Г
Lo о]1 [
15—8
12 11
1.27.
1.33.
1 0
[о i
1 1.26.
J'
Г—18 401 1732. Г—8 —
[о 62.Г [-6 -
3 2 2
2 —1 —2
—2 О —3
1.31. Г—18 40
[о 62
1.34. 8. 1.35. 2.
—7 0 3
0—7 О
О 0—7
—8 — 6"
20.
1.36. 13. 1.37. 10.
1.38.
1.39.
1.40. fex =
если перестав-
перестав2 ' •""'• 2
ляемые числа не образуют инверсию; kt = k—1, если образуют.
1.41. a) kt нечетное; б) kx четное. 1.42. Да. 1.43. Да. 1.44. Нет.
1.45. Нет. 1.46. Нет. 1.47. Да. 1.48. Да. 1.49. а) 6=1; б) k=\,
m = 3. 1.50. а) Нет; б) да. 1.51. 111. 1.52. 24. 1.53. х = 2.
1.54. jc=11. 1.55. х1 = \, *2 = 2, х3=3. 1.56. 0. 1.57. 0. 1.58. 0.
1.59. 0. 1.60. 0. 1.61. 1000. 1.62. а) 30; б) 2; в) 13. 1.63. а) 5,
—2, —12; б) —5, —2, 12; в) 6, 12, —18. 1.64. 600. 1.65. —22.
1.66. 32. 1.67. —156. 1.68. —130. 1.69. 44. 1.70. 32. 1.71. 224.
1.72. 15. 1.73. —84. 1.74. 108. 1.75. —261. 1.76. 5. 1.77. —32.
1.78. 640. 1.79. —54. 1.80. —6. 1.81. —3. 1.82. 0. 1.83. 0.
\Л
"¦¦•4-
— 9 11—5
7—4 13
19—5 6
1.87. Не существует.
1.88. —¦
25
13 15
17 10
— 1 — 5
1.89. Т
6—3 0
—2 —2 2
0 3 0
1.90. Не существует. 1.91.
0
0
0
— 5 2 "] 1.97.
13
1 —1
1
0
0
1.98.
1 Г 1 0 I 1.96. Г — 5 2 "I 1.97. Г 6 —
ITl-a 6J- I 13 -5J- In -
—12
— 8
— 1
0 0=
1 0
1 —1
0 1
—3
•2
—5
4
4
16 —8
- 7 5
1
2
1.99. тн
—21
—21
51
45 —156
15 — 21
20 — 79
1.100. % ф-г.
1.101. кфО, Ъф±УЬ. 1.102. 2. 1.103. 1. 1.104. 2. 1.105. 2.
1.106. 1. 1.107. 3. 1.108. 2. 1.109. 2. 1.110. 3. 1.111. 2. 1.112. 5.
1.113.3. 1.114.2. 1.115. 2. 1.116.4. 117. Х= — -j. 1.118. А, = -§-.
1.119. X Ф1. 1.120. к — любое. 1.121. а) К = у, б) к ф у; в) ни
при какой &.
241

Глава 2
2.1.
5 —3
1
2
2.3.
Г
—1
1
—4
—1
*!
Ч
х3
~| Г„
' 1 1 1
"—Г
0
5
-Й
2.2.
0 1
1 —1
—5 О
2.5.
0
—1
0
0
0
1
Xi
*2
*з
=
0
1
—4
2
.6.
2 —4
— 1 1
3 1
Xl
х2
=
"—Г
5
—1
2.7. *! — 3*2 =
4*, = 2. )
2.8.
-*2 = 4.
2.9. 2,Х-^ — Xg —р л^з ==='
4*! —2*з = 0,
2.10.
2.12.
2.15.
= 0, *2 = 0, ... , *л = 0. 2.11. а) Да; б) нет; в) да; г) да.
1 v . О О 1Q v , v О iA v v v 1
~"~ 1 , А2 С» Л. Ю. А^ * Л2 — 1 . ?i. 1*1. Л^ —— Л» A3 1 •
= 1, *2 = 2, х3 = о. 2.16. *i = 1, *2 =—2, *з = 0. 2.17. *i==
= — 2,"*2=1, *3 = —1. 2.18. *! = 3, *2 = 0, *3 =—2. 2.19. *х = 0,
„ 1 v 1 v . О О 9ft v 1Q v 9А v 11 v ^
А2 === J » -*3 — 1 1 Л^ — *•% ?• * &\J* Л^ — iij* Л2 — ^'-'» -*3 — И | Л^ — О •
2 1I „ 1 v 1 v 1 v 1 О ОО rt\ v v v 1 •
1 2 2
б) -^1 == — * i ^2 == — ^» ^3 == — ^» ^) ^1 == 7 i ^2 == "у"» -^3 == — ~~7~ *
2.23. а) *! = 1, *2 = — 1, *3 = 2; б) *х = 3, *2 = 1, *3 = 2; в) *j =
„ л ,. •? п съЛ гъ\ v ^ 1 ^ ь» 1 . t^\ 1* 1* О
Л3 —- yJ , Л2 — I. 6.A1. dl Л-j Лз "~~ ^ , Ло —¦ А4 1, UI Л1 —¦ Л3 —• ?i,
„ v Q. _\ v ___ 1 ^. Q v , 1 v су О ОС л\ *- Л
Л2 Лл ^) О) Л\ 1 , <Л-2 — л/, Л3 ~~~ 1 , Ал *^~ ?j. ^ . ^О . ЛI Лл U ,
*2 = 1, *з = — 11 *4 == 2; б) *i = *2 = *з == — 1, *4 == 0» в) *i = 2,
*з=1, *2 = *4 = 0. 2.26. Совместна. 2.27. Несовместна. 2.28. Сов-
Совместна. 2.29. Совместна. 2.30. Совместна. 2.31. Совместна. 2.32. Сов-
Совместна. 2.33. Совместна. 2.34. Любая пара неизвестных, кроме х1г *2.
2.35. Любая пара неизвестных, кроме пар: *3, *4; *з. х5; *4, *5-
2.36. *х, *3 или *2, a;3- 2.37. Любое неизвестное. 2.38. Любые
три неизвестных. 2.39. Любая пара неизвестных, кроме xlt x2.
18—15с 7
2.40.*! = jo , *2 = с, *3 = —-д—, где с — любое число.
7 — с 4 + 2с
о 41 у = * = х = с 2 42 * = с х с
*3 = — Зсх + 6с2 + 4, *4 = 2^1 — 4с2 — 3. 2.43. *г= ct + с2 — 1, *2 =
= 2ci + c2 + 5, *3 = С!, *4 = с2. 2.44. *1 = —2, *2 = 3. 2.45. хх =
= -j(—2с! + с,—1), *2 = Ci —2c2+2, *3 = q, *4 = с2. 2.46. *х =
= *2 = *з = 1. 2• 47¦ *! = *2 = 1, *з=:0. 2*48. *j=^c — 1, *2 = 2—с,
*з=с. 2.49. Несовместна. 2.50. *i = c, *2 = 7(с—1), х3<=Ь{с— 1),
*4 = 0. 2.51. *1 = *2 = *з = 1. 2.52. *! = с, *2 = —2с, *3 = с.
о го „ _ „ _ х _ л or4 v- 4Cl~Ca v _г j, -л г -П
4?<QO* Л^ Л2 Л| Ui 6iv7i А^ —— о у «2 — **\i  2 * 4
242

1 3
2.55. x1 = — ~4~c, x2 = с, x3 = ~r c, л?4 = 0. 2.56. л?1 = 5е, *2=llc,
x3 = 7c. 2.57. Д?! = —-j-cX) Af2 = -^Ci + c2, *3 = <a. *4 = <V
4 1
2.58. x1 = xa = x3 = O. 2.59. xx = — -y (c± + c2), хг = "g-fo — 5ci).
*з = с1. *4 = c2. 2.60. jc1 = 2c1 + 3c2 —c3, х2 = сх-\-Съ — с3, х3 =
= —c1 + 2ca + c3, x4 = ct, x., = c2, x6=c3. 2.61. «,=6!, x2 = c2,
% = Ci + 3c2> x4 = x5 = 0. 2.62. Нет. 2.63. Да. 2.64. Нет. 2.65. Да.
2.66. xt=2, х2 = 3, х„=1, «4 = 0; *г = ж4 = 1, *2 = 2, х3 = 0.
2.67. х1 = 1, *2 = д:5 = 0, *3 = 3, a;4=1; *i = 2, жа=1, х3 = х4 =
1 4
= лг5 = 0; *1=-з, *2 = *4 = °. *з = —"тр -«s = 1 • 2-68- *i = *s=l.
*2 = 2, a;4 = 0; ^ = — 1, х2 = аг4 = 1, х3 = 0. 2.69. лх = д:2 = 1,
х3 = 2, *4 = — 1. 2.70. *, = х2 = лг3 = 1, xt = л;5 = 0; ж, = *4 = 1,
*2 = 2, х3 = х& = 0, *! = — 1, a;2 = x5=1, х3 = 0, х4 = 0. 2.71. % = 2,
а;2=1, *3 = 3, а;4 = д;5 = 0; % = — 3, л:2 = л;5 = 0, х3 = л;4=1;
a;1 = a;5 = 1, >;2 = а;4 = 0, a;3 = — 1. 2.72. Jtt = 1, дс2 = 2> ^з = 3»
х4 = 0; ^1 = 0, х2 = — 1, д;3 = 5, ж4=1. 2.73. д^ = дса = дс4= 1,
лг3 =: 3, дг5 = 0; Xi = "g", аг2 = — 1, х3 = 2, дс4 = 0, л;5 = 1. 2.74. Xj =
= х, = дс3= 1. 2.75. xtv=— 10с + 10, ха = с, х3 = — 16с+ 15, л;4 =
= 4—5с. 2.76. Х!=1, хг = 2, х3 = 3. 2.77. Несовместна. 2.78. xt =
= 14с, лга = 21с, ж3 = х4 = с. 2.79. хх = -jq C — 2са) — ct, xa = clt
х, = —-g- —4ca, x4 = -jQ-A — 14са), х5 = са. 2.80. Несовместна.
2.81. хг==1, х, = —1, ха = 2, х4 = 0.
Глава 3
3.1. а) Да; б) нет. 3.2. а) Да; б) да. 3.3. а) Нет; б) нет.
3.4. а) Нет; б) нет. 3.5. а=0. 3.6. а) Да; б) нет. 3.7. Нет. 3.8. Да.
3.9. а) Да; б) нет; в) нет. 3.10. а) Да; б) нет. 3.11. а) Да; б) да.
3.12. а) Да; б) нет. 3.13. Да. 3.14. Нет. 3.15. Да. 3.16. Нет. 3.17. Да.
3.18. Да. 3.19. Нет. 3.21. Нет. 3.22. а) Нет; б) да. 3.23. R = oo.
3.26. Нет. 3.27. Да. 3.28. а) Нет; б) нет; в) нет. 3.29. а) Да; б) нет.
3.30. а) Нет; б) да; в) да; г) нет. 3.31. а) Нет; б) нет; в) да; г) нет.
3.32. Да. 3.33. Да. 3.34. Нет. 3.37. а) Да; б) да; в) нет; г) да.
3.38. а) Нет; б) нет; в) нет; г) нет; д) да; е) да. 3.39. а) Нет; б) нет;
в) нет; г) да. 3.40. а) Да; б) нет; в) нет. 3.42. а) Нет; б) да; в) нет;
г) да; д) нет. 3.45. dim L = 3; 1, х, х*. 3.46. dimM1 = 4;
[10 0 0J, [0 1 0 0], [0 0 1 0], [0 0 0 1] 3.47. dim M2 =
= 9;
"l
0
0
0
0
0
о'
0
0
0
0
0
1
0
0
о"
0
0
"о
0
0
0
0
0
1
0
0
"о
1
0
0
0
0
о"
0
0
"о о о"|
0 10,
О О 0J
243

"о
0
0
0
0
0
о"
1
0
"о
0
1
0
0
0
о"
0
0
"о
0
0
0
0
1
(Г
0
0
0
0
0
0
0
0
0
0
1
. 3.48.
= 2; i, /.3.49. dimV3 = 3; '. /. *• 3.50. dimK = n; ylt
Уг> ••¦ . Уп — фундаментальная система решений. 3.51. dim P =
= л+1; 1, х, х*, ... , хп. 3.54. а) 2"C, — 1, 5, — 4); б) Г(—5,
1, 2, 3); в) *сA, 0, — 1, 0); г); ?A, 0, 0, 0). 3.55. C, — 1,
2, —2). 3.56. а) B, 3, 4); б) (—2, 0, 3); в) (—14, 2, 1);
г) C, —2, 1). 3.57. а) B, —3, 5); б) C, 1, 0); в) A4, 7, 1);
г) @, 2, 0). 3.58. A3, 6, —5). 3.59. B,-3, —1, 3).
3.60. х ( — 3, 4, — —). 3.61. х — —
V 5
-3, 4, — __|.
О
"Г*
3.62. б) 7 (—, — —). 3.63. бOB,— 2,1). 3.64. Нет. 3.65. Да.
\ 5 5 /
3.66. Да. 3.67. Нет. 3.68. а) При любом X; б) % = -?-. 3.69. При
5
любом X. 3.70. %ф\. 3.71. Ни при каком Я. 3.72. X = -у.
3.73. Я,= 1. 3.74. Ни при каком X. 3.75.
"о
1
0
0
0
1
Г
0
0
3.76.
1, 0).
3.81
'о о о Г
0 0 10
10 0 0
0 10 0
3.79.
3.77. 7' (—1, 2), 7' A, 0). 3.78. е'2 B,
C, 4, —5). 3.80.
3.82.
О
2
3
l 1
2 V 3.84.
5
1 1
— 2 О
3 О
— 1 1
2 3
1 -1
-1 1
3.83. "ej
1
5
13
41
_L
_5^
41
3.86. е
1,4-.°).
13'
-X' "г)"  Г "Г1 Т 3'87' еЛ~1' L0, о),ег,(о, -1,
244

2 ' 2
3.90. x (—0,68; —0,12; 0,36). 3.91. л; (— 0,6; 1,2; 1,6).
3.92. x (— 4, — 8, 8). 3.93. x G, — 3, 3, —1). 3.94. d 4;
— A, — itV 3.95. "c(— 0,2; 0,8). 3.96. Нет. 3.97. Нет.
3.98. Нет. 3.99. Нет. 3.100. Да. 3.101. Да. 3.102. Да. 3.103. а) Да;
в) -|-. 3.10
(а + Ь) У~Е
б) да. 3.104. а) У 2л; б) 0; в) -|-. 3.105. a) I/63 ~ °3; б) е6 F—
— 1) — е" (а — 1); в) arccos
2 /а2 + а& +
ff(x).g(x)dx
Г Ь ь
<У jU(x)Lx-j (g(x))*dx; д)
а а
<Л/ I (f (x)J dx -\- I/ letxW
• а "а
l/
U (х) + g
dx
3.107. a) /«; 6) 3»; в)
п(п+1)
е. 3.106. а)/6, 6)8, -р=г.
arccos \ ^(Ъп-V 1)' ^ °*
если а > 0; л, если а < 0; д)
I =]/¦§•; e)(Pi(x),
) = 0. 3.109.а)Да;
б) нет; в) да; г) нет. 3.110. а) Нет; б) да; в) нет; г) да. 3.111. xlt
/ 1 1 1 \ / 1 1
3.1.2. «)(-^ ^7Т Jrf) или ^O= -^
°
/13
в) (J- 0 -1-) или
\ 5 5 /
3 \ / 2 3 \
4 • -4-) "
2_
лт
_12_
13
"
или |— 12 0 0 — ). 3.113. а) Является; б) не является;
13 13 /
245

в) является, г) является. 3.114. а) х 1/ _; б) х* 1/—_;
_L _5_ __3\ f__L_ о -4=-!; 6,A О О),
X 35 У 35 |/35 /' V У Ю У10 ' ' v ;
1 1
\ 2
О 0 —L- —tL-I, I-tV --t=- ° °1.
/ 1 1 \ / 1 1 2
0 ° ,/-7Г — ,/-ГГ '. б) ,/- 0
jpL о -_^_ J^-V (—4=- о -^ о|.
1
f- ' о
@100). 3.117. y=-, x ]/-|— 3-118'
a; "b'—3—, _1_ Cxa— 1) У"ГО. 3.119. Можно дополнить векто-
векторами (—5—2 1 1), E 2 30—1). 3.120. Можно допол-
дополнить векторами (—3222), (—2—8 20 —15). 3.121. Можно
дополнить векторами @ 1 1 0), @ —1 1 — 2). 3.122. а) (х, у) =
= -90, 1^1 = 2/26, |у|=-У105; б)?, у)--10, |7|=/74,
^ = /Т5; в) A, у) = 12, |х| = 2УТ, М = УбТ. 3.123. а) (*,
Й=-4. \x\=VT, |?| = /ТН; б) (J, у)-в, 1*1=^22, |у|-
= /Б; в) ?, у) = 7, | х | - V51, | П = /6. 3.124. a) arccos (-
_]Q2); б) " ; в) arccos -™; г) " . 3.125. a) arccos (_ »\
6/2 10/51 2 V /238/
б) arccos ]/-^-; в) arccos
Глава 4
4.1. Да. 4.2. Нет. 4.3. Нет. 4.4. Да. 4.5. Нет. 4.6. Да.
4.7. Да. 4.8. Нет. 4.9. Да. 4.10. Да. 4.11. Да. 4.12. а) Да;
б) да. 4.13. Да. 4.14. Да. 4.15. а) Да; б) да; в) да; г) нет.
4.16. Г 2 3] 4.17. Г1 1 —1"] 4.18. а) Г 9 12 15 
|_ 1 1J* ° ° 2 Г 12 16 20 ;
L 0 2 5 J L 15 20 25 J
246

4 0 —21 4.19. а)
б) Г 1 -1 П в) Г 4 0 -21
_1 1 —1 ; оо о
L 1 -1 lj L-2 0 lj
10 001 в) Г 80—2] 4.20. а) Г 0 —1
0 9 3; 000. 1 0
0 27 9 J L -4 0 1 J L 3 —2
ГО —1 —I! в) Г 0 1-1-1
1 О -1 ; -10 -1 .
Ll -1 Oj L 1 1 Oj
б)
О 1 —I"! 4.21. а)
б)
0 10 0
О о 2 О
0 0 0 3
0 0 0 0
в)
0 10 0
0 0 4 0
0 0 0 6
.0 0 0 0-
4.22.
4.23. kE, Е, О, где Е и О — соответственно единичная и
матрицы порядка п. 4.24. а) Г А 0"[_ б)
0
гнно единичная и
Г1 01 в) Г
1.0 -lj' L
4.25. а)
2 0 0 0
0 2 0 0
2 0
0
г)
0 0
.0 О
2 О
3 0
2
б)
-15 0 01
3 0 0 0
0 0—15 ;
0 0 3 oJ
в)
4 0
О 4
—1 0
0—1
а„„ -
нулевая
-1 О
О 1
1 О
О 1
2 О
О 2
О 0
1
0 0—1
°1
° •
2 •
3J
Д)
10 0 0
0 10 0
0 0 0 0
.0000
4.26.^B,3).
4.27. у (-4, 7, 7). 4^28. у(\, 3, 4).^ 4.29. уB, 1, -1,1).
4.30. И^ Г
—2, 0,
16). 4.
—3, 3). 4.31.^C,0). 4.32. «Г(-3, 19). 4.33.1/B,4,
6). 4.34. (—2, 9). 4.35. (—10, —5, —5). 4.36. G, —3,
.37. A, 8, 7, 4). 4.38. Г—2 31 4.39. Г —3 14П
[ J [_3 8J'
4.40.
4.43.
4.46.
Г
[—
—1 18 —3
-18
—2 10
5 3 4 3
_3 —2 —1 —2
_1 о —1 —2
L 1 1 1 4J
4.45.
6] 4.41. Г—85— 59 18 1 4.42.
—в!' 121 84-25 .
L—13 —9 3J
—2 11 7 1 4.44. ГЗ 3] 4.45. Г 2 71
-4 14 8 . [о 2j- L2 -3j
5 -15 -8J
3 Т 4.47. Г 3 —10 —8 1
0. —1 84.
2 J L 2 —13 —7 J
247

4.48.
в)
б)
J
—1
—3
L 0
29
12
29
2
П
1 —1
1 —2
2 —2_
14 "
29
8
29 .
4.49
•
г)
• а)
" 8
29
12
- 29
28_
29
J!
29 J
4.50.
6)
13
9
24
29
[k 0
0 k
0 0
2
0
0
0
в)
4.51.
в'
6)
0
0
a) A2—1 = 0,
0
1
— " 0 "
2~
0
1
3
r)
»
_1_
3
0
_2_
"
28"i
29
113
29 J
0
0
k
3
0
_1_
T
)
в) А,» — Я = 0,
б) А, (Л— 1J =
х == — 1,
А2=1.
0 А
А2=1; б)
4.52. а)
А 1
4.53. a) (A + 6) (A —2)(A —3) = 0,
6) a+1) (A-5) (A2-9A-2) = 0,
9 + T^§9
= —±4- ; в) A3 — 6A2 + 12A = (
в) MA-
pi — — О, Л2 — ^*
i = -l. Ь2 = 5,
T, Л Л 1 .
4.54.
6)
Г 13
5
L 0
в)
6)
в)
ГЗ -4 —6"
6 1—5
[_7 _4 _8
б)_1_Г 1 1
3 [_4 2
4.58. а)
-10 —12"] 4.55. a) J_[
3 —11 . 3 I
—6 —16 J
12"! г) Г 1 231 4.56. а) Г
ej: [-9 isJ-
—4 4] в) Г 2 2 —61 г) Г-
12 —8 ; —12 10 —7 ;
17 -7 J \} 4 2 -7J L
[cosa —sin a 1 б) Г cos a sin a"] в) Г
— sin a — cos a J' [ sin a — cos a J' [
e) Г 0 1] ж) Г si
[-1 0j: [-се
0 0"] в)Г00 0"l
k 0 ; 0 1 0 ;
0 —k\ Lo 0 -lj
Ik 0 0
0A0
0 0 ?
г) Г-1 ОТ д) Г
L 0 -lj' [
[k 0 0
0 k 0
0 0 —A
10 0 ОТ Д)
0 1 0 ;
0 0 -lj
—cos a —sin a]
sin a —cosaj'
k
0
0
—2
—6
2
—13
9
11
—1
0
sin a
—2'
7
3
4:
—2
—7.
—1
cosa
-cos a sin a

0
0
0
k
0
6)
0
0
k
10 0 0T
0 k 0 ;
0 0 -k\
248

4.59. a)
б) Г-1 7
3 2 0 0
6 4 10
0 0 6 0
4 0 0 2J
б)
10 0 0
4 10 0
2 2 10
L0 О О 4
—10
4
4.60. а)
Г-1 71 в) _1_Г—1 -2] г) J_ Г7
L 0 2j* 3[_7 4]' 3 [i
Г-4 2 4] в) Г 1-2 8-1
4 2 0; —2—40;
L 2 4 5J [ 1 1 6 J
4.62. а) Любой ненулевой вектор, коллинеарный оси Ох, с к=\ и лю-
любой ненулевой вектор, коллинеарный оси Оу, с Я= — 1; б) любой
ненулевой вектор, коллинеарный оси Ох, с А, = —1 и любой ненуле-
ненулевой вектор, коллинеарный оси Оу, с Х=\; в) любой ненулевой вектор
с Я=й; г) любой ненулевой вектор, коллинеарный оси Ох, с Х=\
и любой ненулевой вектор, коллинеарный оси Оу, с Х = 0; д) любой
ненулевой вектор, коллинеарный оси Ох, с Х=0 и любой ненулевой
вектор, коллинеарный оси Оу, с Я=1; е) любой ненулевой вектор
при ф = ягс («=0, ±1, ±2, ...), если п — четное, то К=1, если п —
нечетное, то К= — 1, при ф=й=ял собственных векторов нет. 4.63. а) Лю-
Любой ненулевой вектор, параллельный плоскости Оху, с Я=1 и любой
ненулевой вектор, перпендикулярный плоскости Оху, с Я= — 1; б) лю-
любой ненулевой вектор, параллельный плоскости Оуг, с %=\ и лю-
любой ненулевой вектор, перпендикулярный плоскости Оуг, с к= — 1;
в) любой ненулевой вектор, параллельный плоскости Оху, с Х=\
и любой ненулевой вектор, перпендикулярный плоскости Оху, с Х=0;
г) любой ненулевой вектор, коллинеарный оси Ох, с А,= 1
и любой ненулевой вектор, перпендикулярный оси Ох, с А, = 0.
4.64. хг, х3. 4.65.
4.70. Г
нуля. 4.71.
нуля. 4.72.
j. 4.66. х3- 4.67. *2. 4.69. Является, если Xi = X2.
где s, t — любые числа, отличные от
где s, ? — любые числа, отличные от
где с, t, s — любые
где с, t—любые
1 \с,
1
числа, отличные от нуля. 4.73. Г —21
0|с,
1
числа, отличные от нуля. 4.74.
где с, t, s — любые числа, отличные от нуля. 4.75. Г0
t,
249

[3
4.76.
где t, s, с — любые числа, отличные от нуля.
-— 1"
0
1
- 0-
с,
"
0
0
-0.
отличные от нуля.
t,
АЛ.
где с, t, s — произвольные числа,
" 0
t
— 2(t + k)
- k
0
2
1
2 _
где с, t, k, s — любые числа такие, что с ф 0, s ф 0, <2 + № ф 0.
4.78.
с,
. 4.79.
2/
s
LOJ
сфО,
где с, rf, s—любые числа такие, что сфО.
где с, t, s—любые числа такие, что
. 4.80. Приводится Г1 0 ] с точностью до по-
Г1 01
LO 5j
рядка диагональных элементов. 4.81. Не приводится. 4.82. Не
приводится. 4.83. Приводится Г1 ОТ с точностью до порядка диа-
[о 4J
тональных элементов. 4.84. Приводится
—6 О ОТ
0 2 0
О 0 з]
о точностью до порядка диагональных элементов. 4.85. Не приводится.
4.S6. Не приводится. 4.87. Приводится
~2 0
— 1—
0
о
-1+/2
с точностью до порядка диагональных элементов. 4.88. Не приво-
приводится. 4.89. Приводится
Г1 О ОТ
0 10
0 0 3
250

с точностью до порядка диагональных элементов. 4.90. Приводится
-2 0 ОТ
0 2 0
О О 2J
с точностью до порядка диагональных элементов. 4.91. Не приво-
приводится. 4.92. Приводится
1
0
0
п
0
5
0
0
0
9-1'
2
п
89
S
0
0
0
1 + /~89~
с точностью до порядка диагональных элементов. 4.93. Приводится
-2 0 0 о"
0 2 0 0
0 0 2 0
0 0 0 2
с точностью до порядка диагональных элементов,
дится. 4.95. Приводится
4.94. Не приво-
с точностью до порядка диагональных элементов. 4.96. е1 =
= (— el-\-e2)t, е2 = (et -j-2e2) s, где t, s — любые вещественные
числа, отличные от нуля. 4.97. el=(e1— 2e2)t, е2 = (^i + е2) s,
где t, s — любые вещественные числа, отличные от нуля.
4.98. !>[ = Й + 2е + 2е3) t, ~%'2 = Bё1-\-'ег — 2е3) s, ~е'3 = 2^ — 2е2 +
+е3) k, где t, s, k — любые вещественные числа, отличные от нуля.
4.99.
+1272
числа,
(е, = ех + е2 + е
+ 3(t2—s2)e3.
причем
s)k,
где
k
Ч
S2
е2
«1.
k
h
h
s2.
/
3(<i
\ 2
tu t2
-si)
-s.)
! + 3 Cl — sl) e3 > e3 = S2el+
k — любые вещественные
ФО.
4.100. е,
+ Sxe2 +
= Fs2
ех + s2e2 + <2
251

e'3 = 3kex -f- kes, где sx, s2, tlt t2, ft — любые вещественные числа,
причем
6s2 + .
3ft
s2
?=0.
4.101. V, =
—T3) ft, 1; = B/j + 3S
> --> —>¦
= B/2+3x2N!—2Aje2 — 2s2e3, где sx, s2,
венные числа, причем
ft ft —ft
—любые вещест-
вещест+ 3s2 — 2t% — 2s2
4.102. в| = — t^e^ -f- t^e2 -f- $1ез — sie4> e2 == —
-> ->/ ->->->-> ->/ -> ->
где <ц /2, Sj s2, ftlt plt ft2, p2 — любые вещественные числа, причем
— Г2 Г2 ^2 — ^2
К fti Pi Pi
ft2 ft2 p2 p2
4.103. e'j = B4ej — 12e2+ e3 + 9e4) s, e2 = (~2e2 + 9ез + ei) ^. ез=
= ke3, e4 = (e3-|- e4) p, где у, /, ft, p — любые вещественные числа,
~>/ —>¦ —»¦—>- —>-, —> —>
отличные от нуля. 4.104. е, = Bej-)-2е2 + е3) s, е2 = Bе1 — е2 —
— 2е3)?, e'z = (e1 — 2e2-)-2e3)ft, где ft, s, t — любые вещественные
числа, причем
2s 2s s
2t — t —2t
ft — 2ft 2ft
фО.
4.105. e1=ke1 — ke2, e2 = ^
где ft, ty, t2, slt s2 — любые вещественные числа, причем
—ft О
s2e3,
t2 s2
4.106. e , = slel
e3 =
2e3 + ft2e4,
e3 + ft3e, "e4 = (e[ + ^ + T3 + Tt) p, где s1; s2,
рлюбые вещественные числа, причем
252

4.107. e\ =
где
5.1.
5.3.
f s'i
+ рЛ—G
-
—
4
1
" 2
0
4
s2
/1
h
0
0
1
1
a
О

—
Si
s2
*1
ft,
1
2
0
0
5
2
->
«2-
. ft,
3"
2
1
0
0
1
0
Sl
s2
S3
p
-(
-f 2
h
h
h
P
h +
2/^ &!
2fe2 fe2
2fe3 k3
P P
Si)"e3.
. Pi. Pi
-(
-(
fi +
'2 +
Pi
Pa
— любьк
Si) 0
s2) 0
% =
=v2
#
+
L + S2e2 — (^2
: вещественные числа
-C*x+
Глава 5
4
5
2
0
-2
5.2.
5.4. /
*i +
2
2
—3
- = 2
Pi)
2Pi
2
3
5
. 5
)
#0.
—3"
5
—1
5. r = 2. 5.
+ %)"e3.
- 2p2)!4,
, причем
6. r=2.
5.7.
-"о 1
X
5.11.
5.9.
— 11 -7Г
2 -7Г
5 ~
2
1 4 -7Г
г 3
2
5.12.
5.8.
1
_3
2
— 2
1 —1 -ft
— 1
_5_
2
5.10.
0 0
0 1
x
253

5.13. L, (ylt y2, y3) = 22</2 + 12*/2, + 3</|
5.14. Lid/!, </2, Уз)=7у1-}-9у1 — Зу1у2-\-5у1у3. 5.15. Положи-
Положительно-определенная. 5.16. Отрицательно-определенная. 5.17. Не
является знакоопределенной. 5.18. Не является знакоопределенной.
5.19. Ни при каком К не является отрицательно-определенной. При
Я>4— положительно-определенная. 5.20. Ни при каком X не является
знакоопределенной. 5.21. Ни при каком К не является знакоопреде-
знакоопределенной .
5.22. Lx ((/!, j/2) = Ъу\ — у\; хх = -= У1 + —= у2, хг = —^ уг —
1 3 2
523 M ) 9f 4|
54" Ll(i/1' У2) = l2y*~2y*'' Xi =
з) = 2г/, + 5#2 — г/з= *i = Уи X2= y^f У2 + У -|- Уз. 4 =
j/-|- й + ^7y </з- 5-26. Li ((/!, y,, y3) = 9jrJ
5
2 3 1
¦y-g-J/i +,/™#2+,, —A Уз- 5.27. ^((/l i/a, Уз) = .
2 1 6 1 2
yi4 й+ ут Уг~~уШ Уз> X2 = -yuyi+JT
3 3 5
+=Уз- 5.28. ^(«/1( (/2, Уз) = Ъу\
2 1 111
+
Ill о
o,l 1 1 1
1 1 1 2
+

ОГЛАВЛЕНИЕ
Предисловие 3
Глава 1. Матрицы и определители
§ 1.1. Матрицы. Основные определения E). § 1.2. Линейные опе-
операции над матрицами (8). § 1.3. Умножение матриц (9).
§ 1.4. Многочлены от матриц A3). § 1.5. Транспонирование ма-
матрицы A5). § 1.6. Блочные матрицы A6). § 1.7. Перестановки
A9). § 1.8. Определители матриц B2). § 1.9. Свойства определи-
определителей B8). § 1.10. Миноры и алгебраические дополнения C0).
§ 1.11. Разложение определителя по элементам ряда C2).
§ 1.12. Теоремы замещения и аннулирования C4). § 1.13. Неко-
Некоторые методы вычисления определителей и-го порядка C6).
§ 1.14. Определитель произведения матриц D1). § 1.15. Обрат-
Обратная матрица D3). § 1.16. Ранг матрицы D7). § 1.17. Элементар-
Элементарные преобразования матрицы D9). § 1.18. Нахождение обратной
матрицы при помощи элементарных преобразований E8). § 1.19.
Теорема о базисном миноре F0). § 1.20. Метод окаймляющих
миноров для вычисления ранга матрицы F3). Задачи F4).
Глава 2. Системы линейных уравнений
§ 2.1. Матричная запись системы линейных уравнений G5).
§ 2.2. Решение системы. Эквивалентные системы уравнений G6).
§ 2.3. Решение невырожденных линейных систем. Формулы Кра-
Крамера G8). § 2.4. Теорема Кронекера — Капелли G8). § 2.5. Ре-
Решение произвольных линейных систем (82). § 2.6. Системы одно-
однородных линейных уравнений. Фундаментальная система реше-
решений (87). § 2.7. Метод последовательного исключения неизвестных
(метод Гаусса) (91). Задачи (95).
Глава 3. Линейные пространства
§ 3.1. Определение линейного пространства и подпространст-
подпространства A02). § 3.2. Линейная зависимость и линейная независимость
векторов A06). § 3.3. Размерность и базис линейного простран-
пространства. Изоморфизм (ПО). § 3.4. Координаты вектора A13).
§ 3.3. Матрица системы векторов A16). § 3.6. Пространство ре-
решений однородной системы линейшлх уравнений A18). § 3.7. Ма-
Матрица перехода от одного базиса к другому A19). § 3.8. Преоб-
255

разованне координат вектора A20). § 3.9. Определение евклидо-
евклидова пространства A23). § 3.10. Длина вектора A24). § 3.11. Угол
между векторами A26). § 3.12. Ортонормированный базис A27).
§ 3.13. Выражение скалярного произведения через координаты в
ортонормированием базисе A31). § 3.14. Аффинное простран-
пространство A32). § 3.15. Аффинные координаты A34). Задачи A36).
Глава 4. Линейные преобразования
§ 4.1. Определение линейного преобразования A49). § 4.2. Матри-
Матрица линейного преобразования A51). § 4.3. Связь между коорди-
координатами вектора и его образа A53). § 4.4. Зависимость между
матрицами одного и того же преобразования в различных бази-
базисах A54). § 4.5. Характеристическое уравнение линейного преоб-
преобразования A56). § 4.6. Произведение линейных преобразова-
преобразований A58). § 4.7. Сумма линейных преобразований A60). § 4.8.
Невырожденные линейные преобразования A61). § 4.9. Преобра-
Преобразование, обратное данному линейному преобразованию A62).
§ 4.10. Собственные векторы линейного преобразования A63).
§ 4.11. Нахождение собственных векторов линейного преобразо-
преобразования A68). § 4.12. Приведение матрицы преобразования к диа-
диагональному виду A69). § 4.13. Ортогональные матрицы A73).
§ 4.14. Ортогональные преобразования A77). § 4.15. Построение
ортогонального преобразования A78). Задачи A81).
Глава 5. Квадратичные формы
§ 5.1. Основные определения A93). § 5.2. Матричная запись ква-
квадратичной формы A95). § 5.3. Изменение квадратичной формы
при линейном однородном преобразовании переменных A97).
§ 5.4. Приведение квадратичной формы к каноническому ви-
виду B00). § 5.5. Закон инерции квадратичных форм B08).
§ 5.6. Знакоопределенные квадратичные формы B10). § 5.7. Кри-
Критерии знакоопределенности квадратичных форм B12). §5.8. Свой-
Свойство корней характеристического уравнения симметрической ве-
вещественной матрицы B16). § 5.9. Свойства собственных векторов
симметрической вещественной матрицы B18). § 5.10. Ортогональ-
Ортогональное преобразование, приводящее квадратичную форму к канони-
каноническому виду B19). § 5.11. Нахождение ортогонального преобра-
преобразования, приводящего квадратичную форму к каноническому
виду B23). § 5.12. Упрощение уравнений фигур второго порядка
на плоскости B28). § 5.13. Упрощение уравнений фигур второго
порядка в пространстве B33). Задачи B37).
Ответы 240