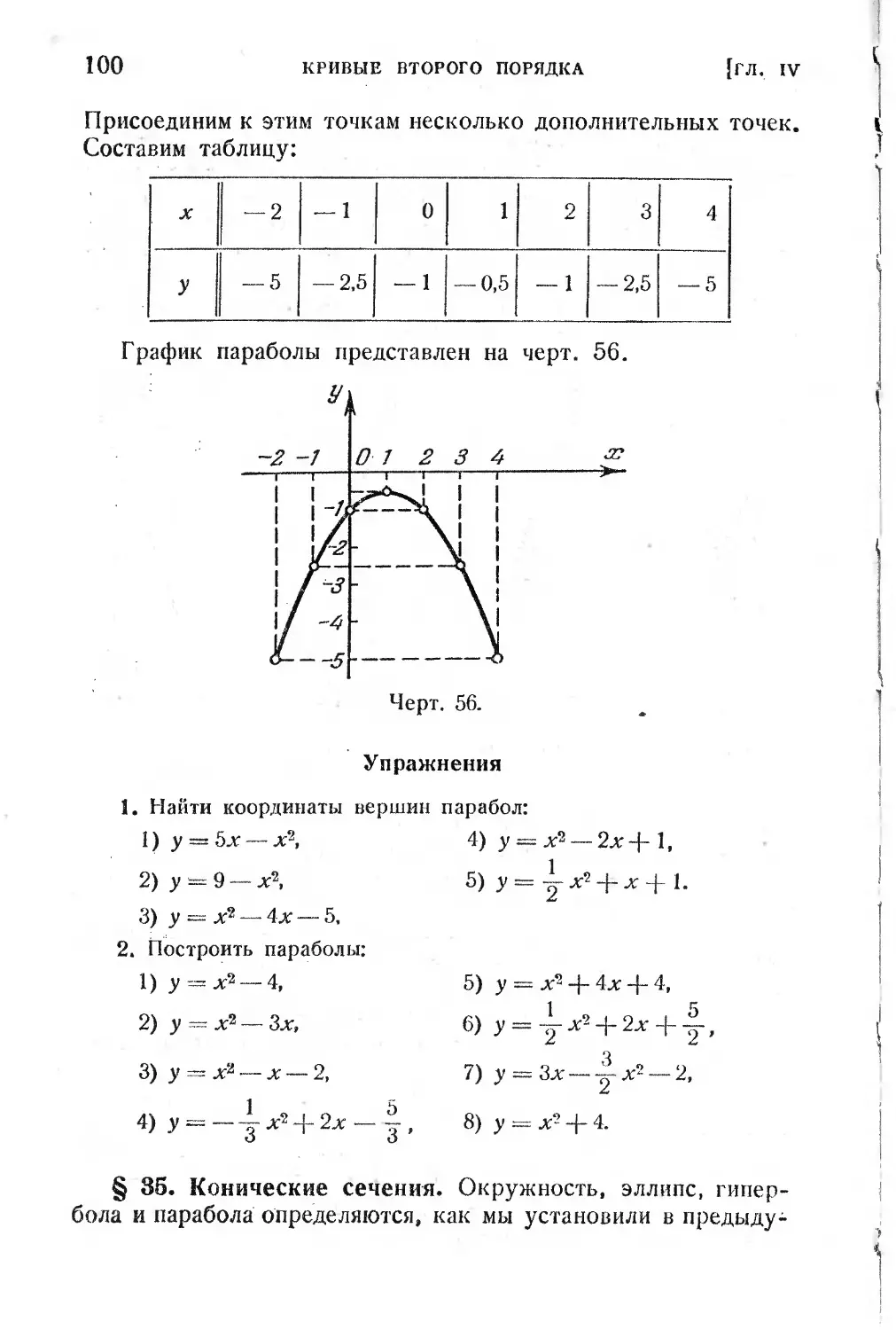
Текст
ВЫСШЕЙ
МАТЕМАТИКИ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА-1958
И. Л. ЗАЙЦЕВ
КУРС
ВЫСШЕЙ МАТЕМАТИКИ
ДЛЯ ТЕХНИКУМОВ
Под редакцией Г. С. Б А Р А Н Е Н К О В А
ИЗДАНИЕ ТРЕТЬЕ,
ПЕРЕРАБОТАННОЕ
Допущено Управлением средних
специальных учебных заведений
Министерства высшего образования СССР
в качестве учебника для техникумов
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1958
Зайцев Иван Лазаревич.
Курс высшей математики для техникумов.
Редактор И. А. Угарова.
Технический редактор С. Н. Ахламов. Корректор М. М. Шулименко.
Сдано в набор 19/Ш 1958 г. Подписано к печати 2/VII 1958 г. Бумага 84х108'/32
Физ. печ. л. 11,63. У слови. печ. л. 19,06.Уч.-изд. л. 18,20. Тираж 75 000 экз. Т-03985.
Цена книги 6 р. 45 к. Заказ № 3032.
Государственное издательство физико-математическо-й литературы
Москва, В-71, Ленинский проспект, 15.
Типография № 2 им. Евг. Соколовой УПП Ленсовнархоза,
Ленинград, Измайловский пр., 29
ОГЛАВЛЕНИЕ
Из предисловия к первому изданию................... 9
Предисловие к третьему изданию.................... 10
ЭЛЕЛ1ЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
НА ПЛОСКОСТИ
Глава I. Метод координат............................... 11
§ 1. Предмет аналитической геометрии................ 11
§ 2. Декартова прямоугольная система координат на
плоскости............................................ 11
§ 3. Расстояние между двумя точками................. 14
§ 4. Деление отрезка в данном отношении............. 16
Глава II. Линии и их уравнения.......................... 20
§ 5. Постоянные и переменные величины............... 20
§ 6. Функциональная зависимость между переменными
величинами................... . ................... 21
§ 7. Линии и их уравнения .......................... 22
Глава III. Прямая линия................................. 27
§ 8. Уравнения прямых, параллельных осям координат . 27
§ 9. Уравнения осей координат....................... 28
§ 10. Уравнение прямой, проходящей через начало коор-
динат ............................................... 29
§11. Уравнение прямой с угловым коэффициентом и на-
чальной ординатой.................................... 32
§12. Общее уравнение прямой......................... 36
§13. Уравнение прямой в. отрезках................... 40
§ 14. Уравнение пучка прямых......................... 42
§ 15. Уравнение прямой, проходящей через две данные
точки.............................................. 44
§ 16. Угол между двумя прямыми....................... 47
§ 17. Условие параллельности прямых.................. 50
§ 18. Условие перпендикулярности прямых.............. 51
§19. Пересечение прямых............................ 53
1*
4
ОГЛАВЛЕНИЕ
Глава IV. Кривые второго порядка........................ 60
§ 20. Окружность и ее уравнение..................... 60
§ 21. Уравнение окружности как частный вид общего урав-
нения второй степени ............................... 62
§ 22. Эллипс и его уравнение........................ 65
§ 23. Исследование уравнения эллипса................ 68
§ 24. Эксцентриситет эллипса........................ 71
§ 25. Связь эллипса с окружностью................... 73
§ 26. Гипербола и ее уравнение...................... 75
§ 27. Исследование уравнения гиперболы.............. 78
§ 28. Эксцентриситет гиперболы...................... 80
§ 29. Асимптоты гиперболы .......................... 81
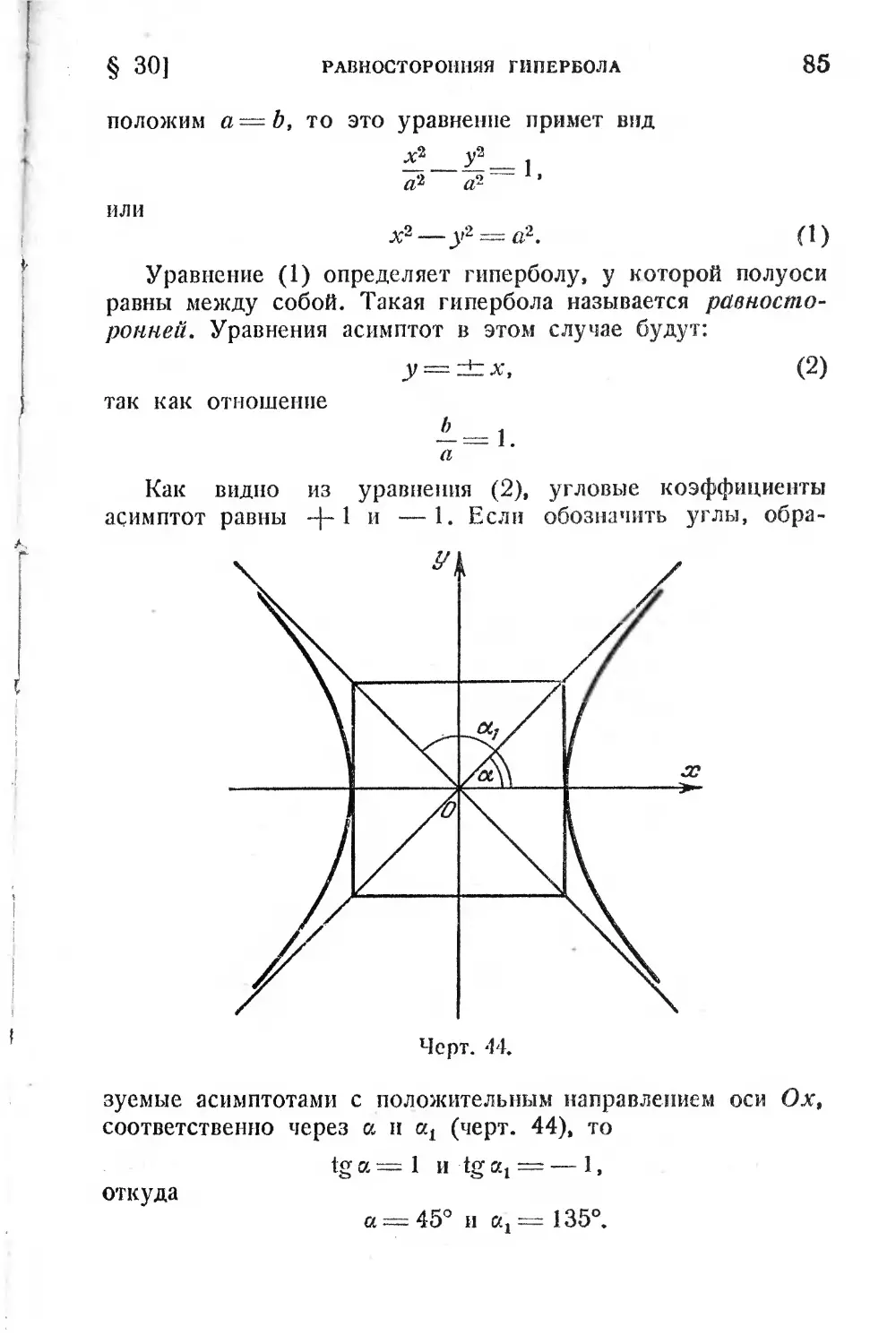
§ 30. Равносторонняя гипербола...................... 84
§ 31. Уравнение равносторонней гиперболы, отнесенной
к асимптотам........................................ 86
§ 32. Парабола и ее простейшее уравнение............ 88
§ 33. Исследование уравнения параболы............... 90
§ 34. Уравнение параболы со смещенной вершиной и
осью, параллельной оси Оу.......................... 94.
§ 35. Конические сечения............................100
ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОГО
И ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЙ
Глава V. Теория пределов................................105
§ 36. Абсолютная величина и соотношения, связанные с ней 105
§ 37. Последовательность. Характер изменения переменной
величины............................................107
§ 38. Бесконечно малая величина.....................109
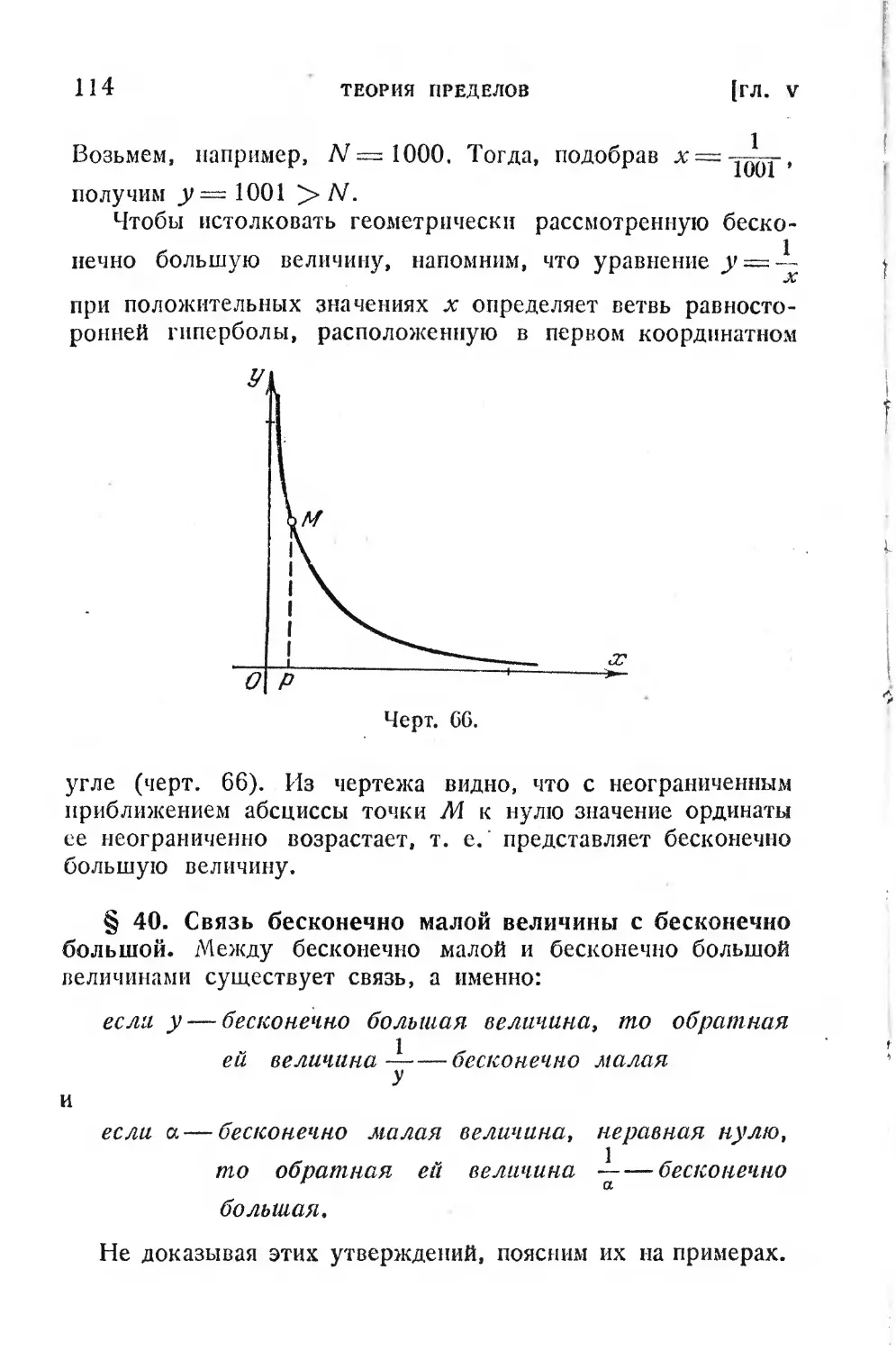
§ 39. Бесконечно большая величина...................112
§ 40. Связь бесконечно малой величины с бесконечно
большой............................................ 114
§ 41. Понятие о пределе переменной..................115
§ 42. Свойства бесконечно малых величин.............118
§ 43. Теоремы о пределах............................120
§ 44. Предел функции................................124
§ 45. Предел отношения при л->0.....................130
§ 46. Эквивалентные бесконечно малые величины.......132
/ 1 \п
§ 47. Предел выражения 11-}-“) при п->со............133
§ 48. Натуральные логарифмы.........................134
Глава VI. Функция и ее простейшие свойства..............136
§ 49. Символика функциональной зависимости..........136
§ 50. Частное значение функции. Область существования
функции . ..........................................137
§ 51. Геометрическое изображение функций............138
§ 52. Приращение функции............................141
ОГЛАВЛЕние
5
§ 53. Геометрическое изображение приращений аргумента
и функции......................................143
§ 54. Непрерывность функции.........................145
§ 55. Свойство непрерывной функции..................149
§ 56. Классификация функций.........................150
Глава VII. Понятие о производной функции................152
§ 57. Равномерное движение и его скорость...........152
§ 58. Неравномерное движение и его скорость.........153
§ 59. Скорость изменения функции....................155
§ 60. Производная функции...........................157
§ 61. Связь дифференцируемости функции с непрерыв-
ностью .............................................160
§ 62. Понятие о касательной.........................161
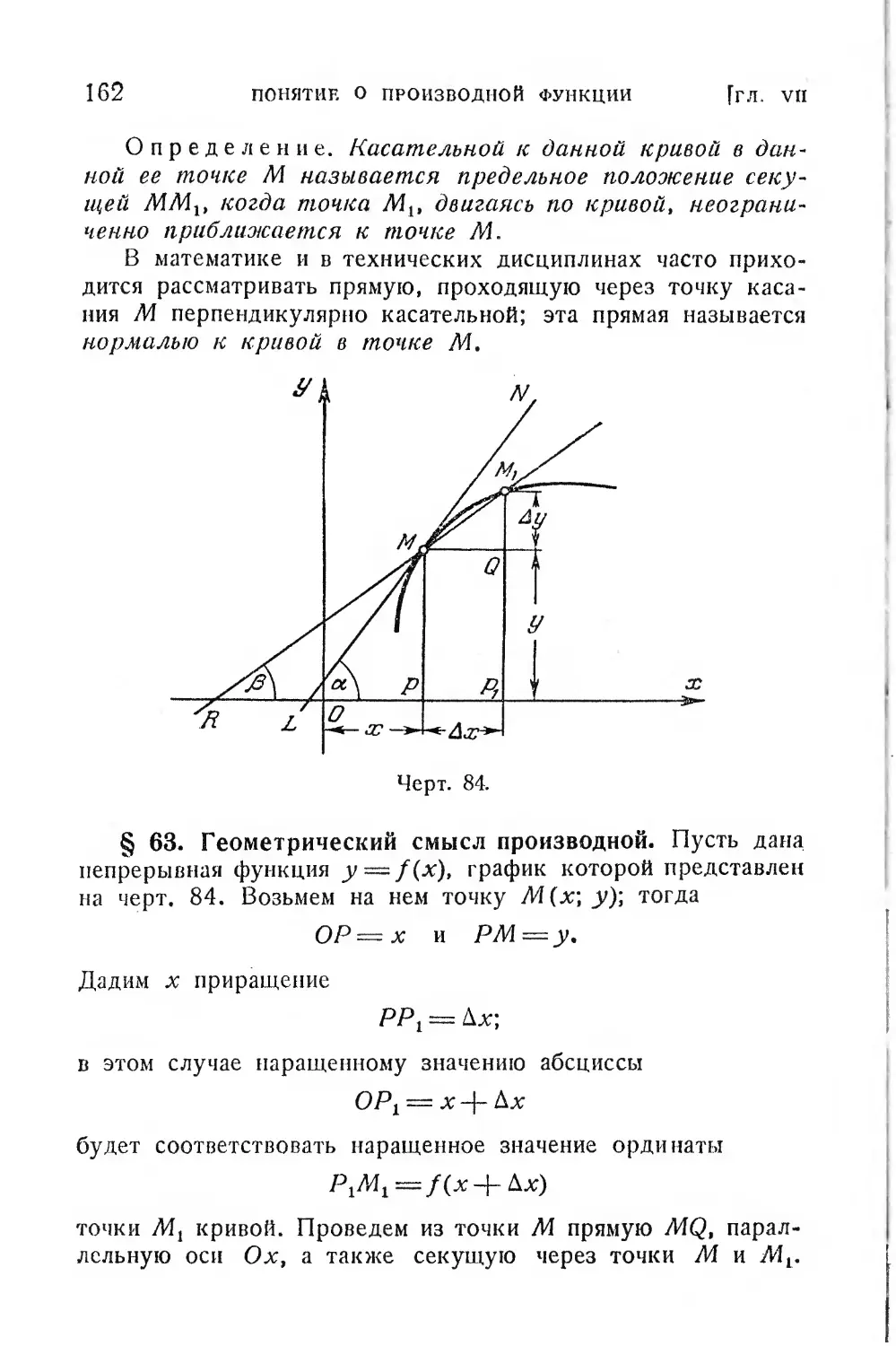
§ 63. Геометрический смысл производной..............162
Глава VIII. Формулы дифференцирования...................166
§ 64. Производная постоянной........................166
§ 65. Производная функции у = х.....................167
§ 66. Производная алгебраической суммы функций .... 167
§ 67. Производная произведения двух функций.........168
§ 68. Производная произведения постоянной на функцию 170
§ 69. Производная степени с целым положительным пока-
зателем ............................................170
§ 70. Производная функции у = ..................171
§ 71. Производная функции у ==—.....................171
§ 72. Производная частного...........................171
§ 73. Применение формул дифференцирования............172
§ 74. Функция от функции (сложная функция)...........177
§ 75. Производная сложной функции............^ ... . 178
§ 76. Производные тригонометрических функций.........181
§ 77. Производная логарифмической функции............186
§ 78. Производная степени при любом показателе .... 190
§ 79. Производная показательной функции..............190
§ 80. Производные обратных тригонометрических функций 192
§ 81. Производная неявной функции....................196
§ 82. Производная второго порядка ...................198
§ 83. Механический смысл второй производной..........198
Т л а в а IX. Приложения производной....................201
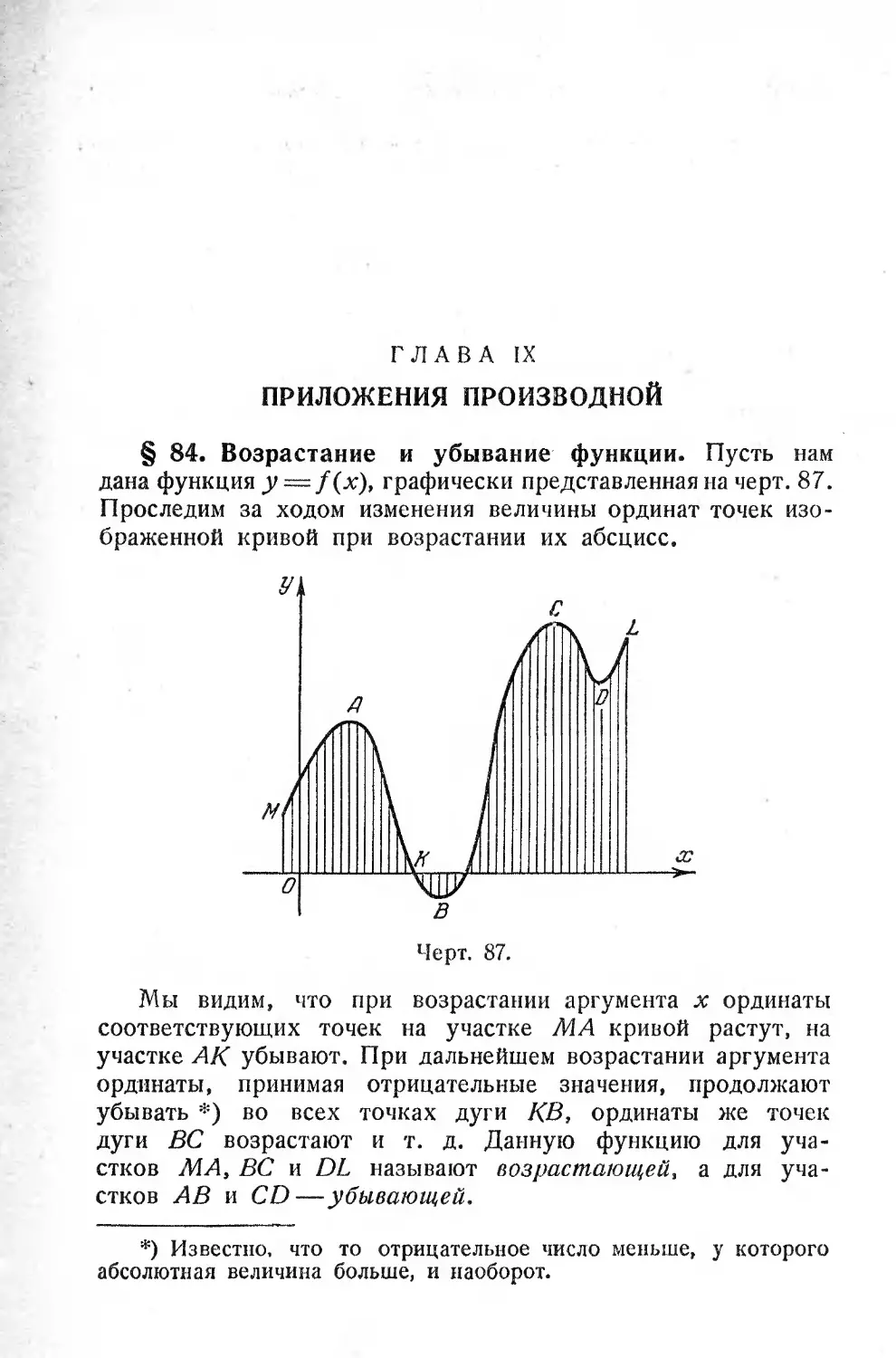
§ 84. Возрастание и убывание функции................201
§ 85. Признаки возрастания и убывания функции .... 202
§ 86. Максимум и минимум функции....................204
§ 87. Признаки максимума и минимума функции........205
§ 88. Правило нахождения максимума и минимума функции 207
§ 89. Выпуклость и вогнутость кривой................212
§ 90. Признаки выпуклости и вогнутости кривой.......213
§ 91. Нахождение точки перегиба.....................214
6
ОГЛАВЛЕНИЕ
§ 92. Второе правило нахождения максимума и минимума
функции.............................................216
§ 93. Задачи на максимум и минимум функции......218
§ 94. Графики функций............................223
Глава X. Дифференциал...................................227
§ 95. Сравнение бесконечно малых величин между собой.
Понятие о дифференциале.............................227
§ 96. Геометрическое изображение дифференциала .... 231
§ 97. Дифференциал второго порядка...............232
§ 98. Приложение дифференциала к приближенным вычи-
слениям ............................................233
§ 99. Кривизна кривой...............................238
§ 100. Кривизна окружности..........................240
§ 101. Радиус кривизны кривой.......................241
Глава XI. Интеграл......................................244
§ 102. Понятие о неопределенном интеграле...........244
§ 103. Основные свойства неопределенного интеграла . . . 246
§ 104. Основные формулы интегрирования..............247
§ 105. Определение постоянной интегрирования.......250
§ 106. Определенный интеграл........................252
§ 107. Основные свойства определенного интеграла .... 254
§ 108. Геометрический смысл определенного интеграла . . 256
§ 109. Интегрирование способом подстановки..........259
§ 110. Вычисление определенного интеграла ;с помощью
подстановки.........................................267
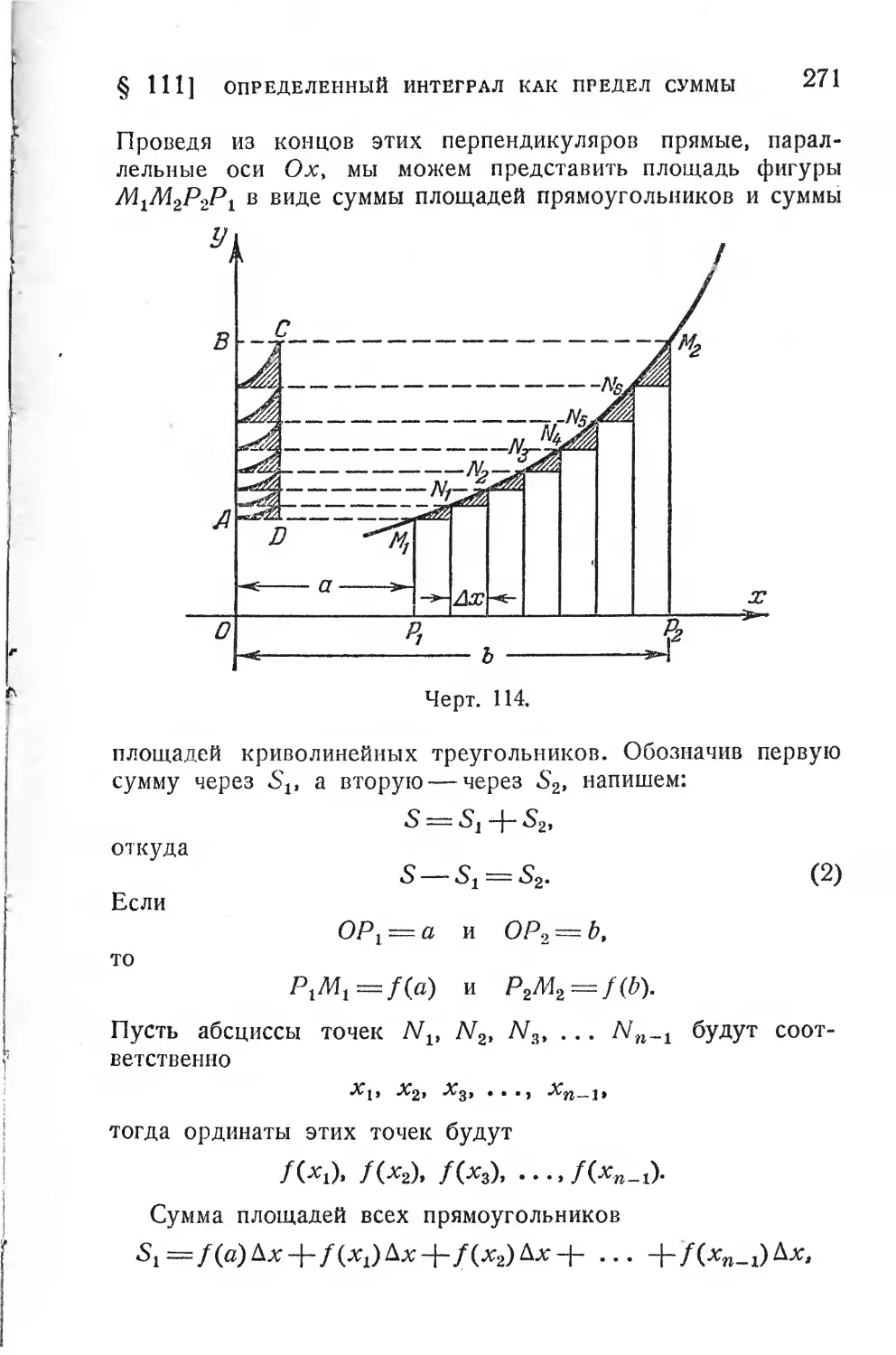
§ 111. Определенный интеграл как предел суммы.......270
Глава XII. Приложения интеграла.........................275
§ 112. Площади фигур................................275
§ ИЗ. Объем тела вращения..........................278
§ 114. Путь, пройденный телом.......................287
§ 115. Работа силы..................................290
§ 116. Работа, совершаемая при поднятии груза......292
§ 117. Давление жидкости............................296
ДОПОЛНЕНИЯ
Глава ХШ. Дифференциальные уравнения.................301
§ 118. Общие понятия..............................301
§ 119. Дифференциальные уравнения первого порядка
с разделяющимися переменными......................302
г-
§ 120. Дифференциальные уравнения вида = /(*) • • ЗОэ
Глава XIV. Ряды......................................310
§ 121. Понятие о рядах............................310
§ 122. Необходимый признак сходимости ряда........311
§ 123. Достаточные признаки сходимости ряда.......313
ОГЛАВЛЕНИЕ 7
§ 124. Признак сходимости знакочередующихся рядов . . 316
§ 125. Абсолютно сходящиеся ряды....................318
§ 126. Функциональные ряды..........................319
§ 127. Степенные ряды...............................320
§ 128. Ряд Маклорена................................322
§ 129. Примеры разложения функций в ряд.............323
§ 130, Приложение степенных рядов к приближенным
вычислениям.........................................326
§ 131. Ряды с комплексными членами..................327
§' 132. Формулы Эйлера..............................328
Глава XV. Гармонический анализ.........................331
§ 133. Графики функций вида у = A sin <лх...........331
§ 134. Гармонические колебания......................333
§ 135. Тригонометрические ряды......................335
§ 136. Коэффициенты Фурье. Ряд Фурье................336
§ 137. Возможность разложения непериодической функции
в ряд Фурье.........................................338
§ 138. Условия Дирихле. Теорема Дирихле.............339
§ 139. Интегрирование по частям.....................310
§ 140. Примеры разложения функций в ряд Фурье .... 343
§ 141. Ряды Фурье для четных и нечетных функций . . . 347
Ответы к упражнениям...................................357
ИЗ ПРЕДИСЛОВИЯ к ПЕРВОМУ ИЗДАНИЮ
Настоящий учебник написан согласно программе по мате-
матике для техникумов, утвержденной Министерством высшего
образования в 1952 г. Исключение составляют два раздела:
кривизна кривой и дифференциальные уравнения, которые
помещены в учебник по той причине, что сведениями из этих
разделов часто пользуются преподаватели общетехнических
и специальных дисциплин.
Кроме изложения теории, в учебнике приведены примеры
и задачи. Количество и степень трудности их решения рас-
считаны на прочное закрепление изучаемого материала.
При написании учебника обращалось особое внимание на
доступность излагаемого материала пониманию учащихся,
имеющих возраст 16—17 лет и подготовку, соответствующую
8—9 классам средней школы. Для достижения этой цели
изложение велось по возможности простым языком, выяснение
математических основ проводилось индуктивным способом.
Так, например, изложение теории прямой линии начинается
с частных случаев положения прямых, параллельных осям
координат; ознакомлению с понятиями дифференциала и инте-
грала предпосылаются примеры и т. п.
Учитывая уровень подготовки учащихся техникума, а также
крайне ограниченное число часов (90 часов), отводимое про-
граммой для прохождения высшей математики в техникумах,
строгие выводы, представляющие большие трудности для
усвоения, я опускал, ограничиваясь в таких случаях геометри-
ческими иллюстрациями или рассмотрением примеров.
Пользуясь случаем, приношу искреннюю благодарность
В. П. Минорскому, давшему мне много методических советов.
Автор
ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
В третьем издании учебника «Курс высшей математики
для техникумов» я учел опыт преподавания по первым двум
его изданиям, а также принял во внимание критические
замечания преподавателей и их пожелания.
Мною были подвергнуты существенной переработке не-
которые главы курса: «Функция и ее простейшие свойства»,
«Понятие о производной функции», «Приложения производ-
ной», «Интеграл», «Приложения интеграла».
Кроме того, рассмотрены некоторые вопросы, не затро-
нутые в первых изданиях: область существования функции,
второе определение непрерывности функции, сравнение беско-
нечно малых величин между собой, элементы гармонического
анализа.
В некоторых параграфах добавлены примеры и задачи
для упражнений.
Чтобы улучшить изложение, в текст внесены некоторые
стилистические исправления.
Автор
ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
НА ПЛОСКОСТИ
ГЛАВА 1
МЕТОД КООРДИНАТ
§ 1. Предмет аналитической геометрии. Предметом
аналитической геометрии служит изучение свойств геометри-
ческих образов (линий, фигур, тел, поверхностей и т. п.)
с помощью особого метода, называемого методом коорди-
нат. При этом широко используется алгебра.
В элементарной геометрии также прибегают иногда к ме-
тодам алгебры, например, при определении площади тре-
угольника по трем сторонам или при вычислении стороны
вписанного в окружность правильного многоугольника и т. п.
Однако область приложения методов алгебры к геометрии
стала наиболее широкой со времени введения метода коорди-
нат, который позволил изучать не только форму и размеры
геометрических образов, но и их положение на плоскости
и в пространстве.
Аналитическая геометрия состоит из двух частей. Первая
часть — аналитическая геометрия на плоскости, вторая
часть — аналитическая геометрия в пространстве.
Здесь мы дадим элементарное изложение только аналити-
ческой геометрии на плоскости.
§ 2. Декартова прямоугольная система координат на
плоскости. Возьмем на плоскости две взаимно перпендику-
лярные прямые Ох и Оу (черт. 1) и произвольную точку Л4.
Опустим из нее перпендикуляры MN и МР на Оу и Ох.
Выбрав какую-нибудь единицу масштаба и измерив ею
отрезки NM и РМ, получим числа:
x=NM=OPt
у = PM ON.
12
МЕТОД КООРДИНАТ
[гл. I
Эти числа х и у, определяющие положение точки М по от-
ношению к заданным прямым Оу и Ох, называются коорди-
натами точки Л4. Их обычно записывают в скобках рядом
с обозначением точки: М (х; у), причем сначала выписывают
координату х, а потом координату у.
Пусть, например, х = OP— 1 единице выбранного мас-
штаба, а у — ON = 2 единицам того же масштаба. Тогда
говорят, что точка /14 имеет координаты /14(1; 2).
Возникает, однако, вопрос, нет ли на плоскости еще точек,
имеющих те же координаты, что и точка /14. На черт. 2
показано, что каждая из точек /И, Л4Р /И2 и 7И3 удалена
на 1 единицу масштаба от прямой Оу и на 2 единицы
масштаба от прямой Ох. Получается неопределенность: четыре
точки имеют одинаковые координаты (1; 2). Чтобы устранить
этот недостаток, уточним определение прямоугольных коор-
динат точек на плоскости.
Координатой х точки /И называется число, измеряю-
щее расстояние точки М от прямой Оу и взятое со
знаком -j-, если М удалена вправо от Оу, и со знаком—,
если /14 удалена влево от Оу.
Координатой у точки М называется число, измеряющее
расстояние точки /14 от прямой Ох и взятое со знаком
если /14 удалена вверх от Ох, и со знаком —, если М
удалена вниз от Ох.
§ 2] ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ 13
Теперь точки Л4, Mlf Л42 и Л43 на черт. 2 имеют уже
различные и вполне определенные координаты: тИ(1; 2),
Mt(— 1; 2), М2(— 1; —2), Ж3(1; —2).
Таким образом, чтобы определить положение любой точки
на плоскости координатами х и у, нужно задать:
1) две взаимно перпендикулярные прямые Ох и Оу, назы-
ваемые осями координат, точку О пересечения которых
принято называть началом координат',
2) единицу масштаба;
3) направление на каждой из осей координат, принимаемое
за положительное (на чертеже принятое положительное на-
правление на осях отмечается стрелками).
Все эти данные называются декартовой системой пря-
моугольных координат на плоскости [по имени французского
математика Декарта (1596—1650) — создателя аналитической
геометрии].
Координату х называют абсциссой, а координату у—ор-
динатой.
Как выше показано, в декартовой системе прямоугольных
координат на плоскости каждой точке плоскости соответ-
ствует пара действительных чисел х и у (ее координат),
определяющих положение точки на плоскости, и наоборот,
каждой паре действительных чисел х и у соответствует
одна точка плоскости. Вследствие указанного соответствия
между точками и координатами этих точек принято го-
ворить: «дана точка ЛЦа; Ь)» вместо «даны координаты
точки М», «найти точку М (х; J)» вместо «найти коорди-
наты точки М».
Упражнения
1. Построить точки А (3; 5), В (— 3; 4), С (5; — 1), D (— 2; — 4),
£(0; 2), В (2; 0), /<(—3; 0), А(0; — 4) и О (0; 0).
2. Дана точка А (3;2). Найти координаты точки В, симметричной
с А относительно оси Ох, и точки С, симметричной с В относительно
оси Оу; построить эти три точки.
3. Стороны прямоугольника равны 6 см и 10 см. Найти коорди-
наты его вершин, приняв за оси координат прямые, параллельные
его сторонам и делящие эти стороны пополам.
4. Дан квадрат со стороной, равной 8 см. Приняв его диагонали
за координатные оси, найти координаты вершин квадрата.
14
МЕТОД КООРДИНАТ
[ГЛ. 1
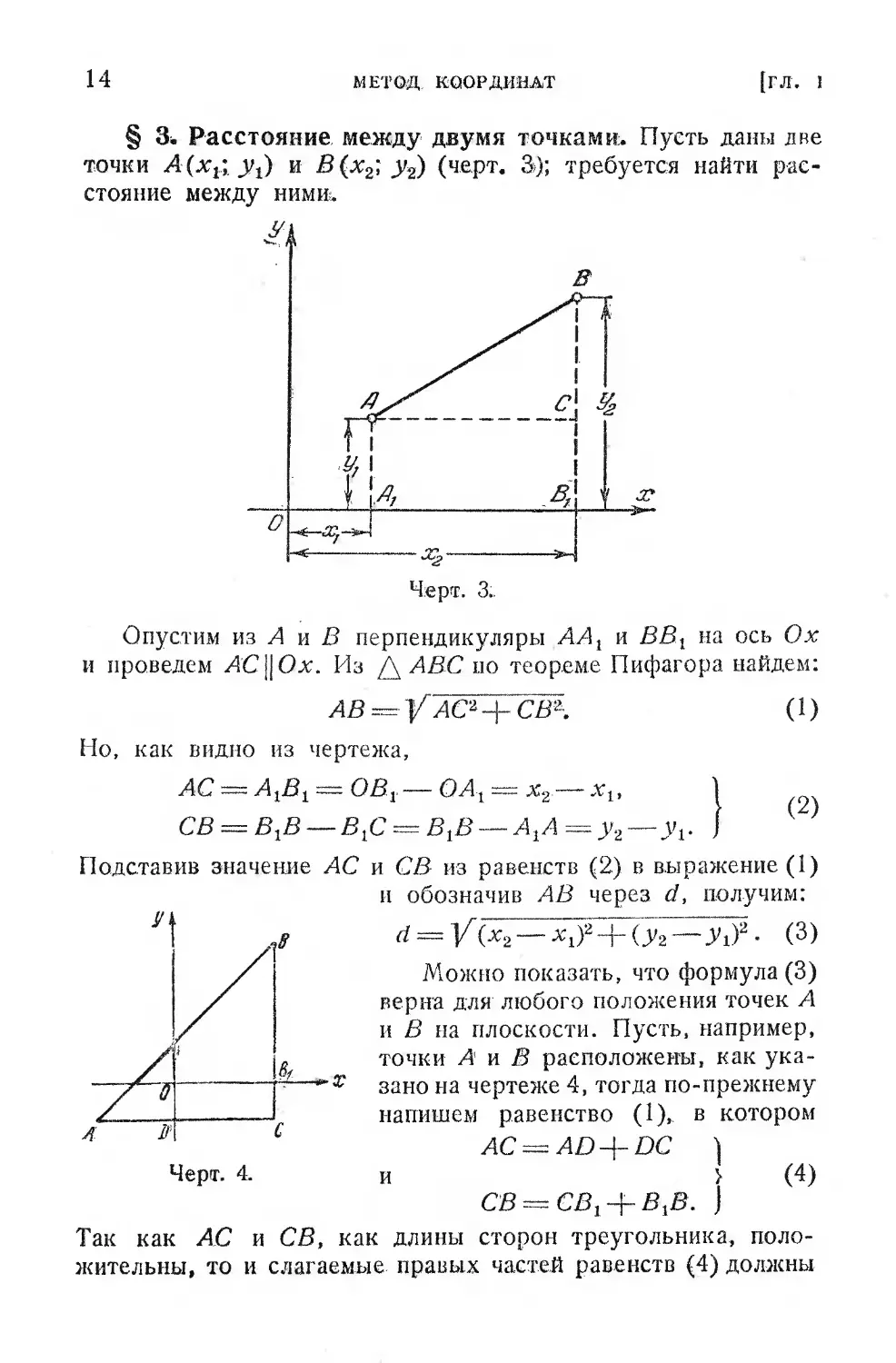
§ 3'. Расстояние между двумя точками. Пусть даны две
точки А(х£. и В(лг2; у2) (черт. 3); требуется найти рас-
стояние между ними.
Опустим из А и В перпендикуляры АА1 и ВВЛ на ось Ох
и проведем ЛСЦОх. Из Д АВС по теореме Пифагора найдем:
АВ = V ЛС24- СВ2-. (1)
Но, как видно из чертежа,
AC = АГВХ = ОВЛ — ОАГ = х2 — хг,
СВ = ВгВ — В£ = ВХВ — Аг А = у2 — уР
Подставив значение АС и СВ из равенств (2) в выражение (1)
и обозначив АВ через d, получим:
а = У{х2—х^+(у2—у^- (3)
Можно показать, что формула (3)
верна для любого положения точек А
и В на плоскости. Пусть, например,
точки А и В расположены, как ука-
зано на чертеже 4, тогда по-прежнему
напишем равенство (1), в котором
АС АО + DC )
И > (4)
CB^CB^BiB. J
Так как АС и CBt как длины сторон треугольника, поло-
жительны, то и слагаемые правых частей равенств (4) должны
§ 3] РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ 15
быть положительными. Но координаты точки А
xY < 0 и уг < 0;
следовательно,
AD —— xt и СВ1~—yv
Отрезки же
DC = х2 и ВгВ = у2.
Итак,
АС = — + х2 = х2 —
СВ =-------------------yt -}-^2 — У‘2-Л*
После замены АС и СВ в равенстве (1) их *’значениями по-
лучим ту же формулу (3).
Пример. Найти расстояние между точками А(—3; 5)
и В(1; 2).
Решение. По условию хг =— 3, уг — 5, х2— 1,
у2— 2. Подставив эти координаты в формулу (3), получим:
АВ = ]/[!—(— 3)12 + (2 —5)2 = ]Л42-|-(—З)2 = У 25 = 5.
Решим тот же пример графически. Для этого построим
данные точки Л и В (черт. 5) и, измерив отрезок АВ,
найдем АВ—5.
Если одной из точек будет начало координат 0(0; 0),
а другой М(ус; у), то формула (3) примет вид
d — Y х2 + У2*
(5)
16
МЕТОД КООРДИНАТ
[гл. I
Упражнения
1. Найти расстояние точки М (6;—8) от начала координат.
2. Найти расстояние между точками: 1) А (14; 12) и В (8; 4),
2) М (— 2; 4) и N (2; 1), 3) С (0; 4) и D (3; 0).
3. Найти аналитически и графически длину отрезка, соеди-
няющего точки А (— 10; — 10) и В (2; — 1).
4. Найти длины сторон треугольника с вершинами А (3; 2),
1; _ 1) и С (11; — 6).
5. Показать, что треугольник с вершинами А (— 5; 2), В (3; 6)
и С (4; — б) равнобедренный.
6. Показать, что треугольник с вершинами Л(1; 2), В (3; 4) и
С(—1; 4) прямоугольный.
7. На оси абсцисс найти точку А, удаленную от точки В (4; 6)
на 10 единиц. Пояснить графически, почему получаются два ре-
шения.
8. Даны две вершины равностороннего треугольника О (0; 0)
и А (2У*3; 0). Найти третью вершину В.
9. Найти точку, равноудаленную от точек О (0; 0), А (— 4; 0)
и В (0; 8).
10. На оси ординат найти точку, равноудаленную от точек
А (10; 8) и В (—6; 4).
11. Найти точку, удаленную на 10 единиц и от оси Ох и от
точки А (— 5; 2).
12. Найти точку, находящуюся на равных расстояниях от ссей
координат и от точки Л(1; 2).
§ 4. Деление отрезка в данном отношении. Пусть даны
точки и В(х2; у2) (черт. 6). Требуется найти
точку (х; у), делящую отрезок АВ в отношении:
AM : 714В = т : п *).
Опустим из точек А. М и В перпендикуляры AAlt MMt
и ВВХ на ось Ох и проведем прямые Лб?||Ох и Л4О||0х.
Из подобия треугольников АМС и MBD найдем:
АС ___ СМ ____ AM ___ т z.x
~MD~^DB ~ ~МВ~~п' ' '
*) Отношение — имеет положительное значение, так как
п
точка М находится внутри отрезка АВ. В случае, если точка М
расположена на продолжении отрезка АВ. величина — имеет
отрицательное значение (см. Привалов И. 1L, Аналитическая
геометрия, 1958, гл. 1, § 6).
§ 4] ДЕЛЕНИЕ ОТРЕЗКА В ДАННОМ ОТНОШЕНИИ 17
Но
АС = A1Ml — ОМ1 — OAt = х— xlt
MD = OB, — OMt = x2 — xt
CM = M,M — M tC = M,M — A j A = у — j/p
DB = B,B — B,D = B,B — M,M = y2 — v.
Подставив (2) в (1), получим:
x — хг у — т~
х2— х у2 — у п '
Для краткости положим — = Х. Тогда , из равенств (3)
получим два уравнения:
Решив уравнения (4) и (5) относительно х и у, получим:
г________________ Х1 + v________У1 -Г ^Уз
* —у ~ " 1+1 ’ w
Формулы (6) служат для определения координат точки
М{х\у), делящей отрезок между точками и B(x2i у2)
в отношении т : /г = X.
Можно показать, что формулы (6) справедливы для любого
положения точек А и В на плоскости.
2 Зак. 3032. И. Л. Зайцев
18
МЕТОД КООРДИНАТ
[гл. I
В частном случае, при делении отрезка АВ пополам, т. е.
в отношении 1:1, получим X = 1 : 1 = 1, и поэтому
у Xf+ X‘2 _ Уг+Уэ /7к
X— 2 , у — 2 . V)
Если в формулах (6) заменить X отношением ~, то по-
лучим:
v __ ЯХ| + _ пух + ту2
Х~'...n + m~’ У~ (8>
Формулы (8) часто применяются в механике для опреде-
ления положения центра тяжести однородного тела или оты-
скания центра параллельных сил.
Пример. Даны точки Л(7; 4) и В(10; —2). Точка 44
делит отрезок АВ в отношении AM : 44В=0,2. Найти точку М.
Решение. По условию ~ 7, = 4, х2= 10, — 2,
Х=0,2. Подставив эти данные в формулы (6), получим:
7 + 0,2-10 9 „ с
-T+oJ-^^7,5,
4 + 0,2 (— 2)_„3,6_о
1+0,2 ~1,2~~’б*
Итак, искомая точка будет 44(7,5; 3).
Решим тот же пример графически. Для этого построим
точки А и В (черт. 7) и разделим отрезок АВ на шесть рав-
ных частей. Отложив одну такую часть от точки Л, получим
У
§ 4 J ДЕЛЕНИЕ ОТРЕЗКА В ДАННОМ ОТНОШЕНИИ 19
точку Л4, которая и разделит АВ в отношении 1:5 = 0,2.
Измерив отрезки ОР и РМ, найдем координаты точки М:
ОР = х — 735', РМ=у = 3.
Упражнения
1. Определить координаты середины отрезка, соединяющего
две точки А и В.
1) Л(3; 5) и В (7; 9), 2) Л (0; — 12) и В (8; 0).
2. Даны координаты четырех вершин параллелограмма:
Л(— 1; — 1), 25(1; 1), <7(2;—1) и Г>(0; — 3).
Найти длины диагоналей АС и BD, а также точку их пересечения.
3. Даны координаты трех вершин треугольника АВС:
Л(3;7), В (5; 2) и С(— 1; 3).
Найти длину медианы, проведенной из вершины В.
4. Найти конец В отрезка АВ, если дано: начало его А (7; —4)
и середина С (— 1; 3).
5. Даны две смежные вершины параллелограмма А (4; 2)
и В (5; 7) и точка пересечения диагоналей 3^. Найти
остальные его вершины.
6. На отрезке, соединяющем точки Л (6; 4) и В(1; 9), лежит
точка ЛТ, делящая данный отрезок так, что AM: МВ — 2:3. Найти
точку М. Дать аналитическое и графическое решения.
7. Найти точки, делящие отрезок между точками М(—3; —7)
и 7V (10; 2) на три равные части.
8. Точка С (—2; 1) делит отрезок АВ в отношении АС: СВ — 2.
Найти координаты конца В отрезка, если начало его Л имеет коор-
динаты (10; 5).
9. В точке Л (2; 5) сосредоточена масса 2 кг, в точке В (12; 0) —
масса 3 кг. Найти центр этих масс.
10. Найти координаты точки пересечения медиан треугольника,
зная координаты вершин Л (1; 4), В(—5; 0) и С(—2; —1).
11. Даны вершины треугольной однородной пластинки Л (4; — 2),
j5(1; 5> и С(—2; 0). Найти центр тяжести этой пластинки.
12. Найти центр тяжести треугольной однородной пластинки,
вершины которой лежат в точках Л (хг; уг), В (л2; у2) и С (х3; у3).
13. Даны координаты двух вершин треугольника Л (0; 5),
В (5; 3) и точка пересечения его медиан М (1; 3). Найти коорди-
наты третьей вершины треугольника.
2*
ГЛАВА II
ЛИНИИ И ИХ УРАВНЕНИЯ
§ 5. Постоянные и переменные величины. В практиче-
ской деятельности, в технике, при исследовании какого-либо
процесса мы встречаемся с величинами двух родов: постоян-
ными и переменными.
Постоянной величиной называется такая, которая при изу-
чении какого-либо процесса не меняет своего значения. На-
пример, длина радиуса одной и той же окружности, темпе-
ратура кипения чистой воды при постоянном давлении — вели-
чины постоянные.
Постоянные величины принято обозначать первыми буквами
латинского алфавита: a, b, с, d и т. д.
Переменной величиной называется такая, которая в усло-
виях изучаемого процесса меняет свое значение. Например,
периметр правильного вписанного в окружность многоуголь-
ника при увеличении числа его сторон, длина металлического
стержня при его нагревании — величины переменные.
Переменные величины принято обозначать последними бук-
вами латинского алфавита: х, у, г, а также /, ut v> w.
Часто бывает, что одна и та же величина при одних усло-
виях является постоянной, при других — переменной. Напри-
мер, в правильном вписанном в окружность многоугольнике
апофема — величина постоянная; при неограниченном удвоении
числа сторон этого многоугольника апофема становится вели-
чиной переменной.
Среди постоянных величин имеются, однако, и такие, ко-
торые сохраняют свое значение при любых условиях; они на-
зываются абсолютными постоянными. Например, сумма
внутренних углов треугольника, отношение длины окружности
к диаметру.
§ 6]
ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ
21
§ 6. Функциональная зависимость между переменными
величинами. Переменные величины в математике играют
важную роль: они служат средством изучения явлений при-
роды и технических процессов. При этом используются
переменные величины не в отрыве друг от друга, а в их
взаимной связи, в определенной зависимости между ними.
Рассмотрим случай зависимости двух переменных величин
между собой.
Две переменные величины могут быть взаимосвязаны так,
что каждому данному значению одной из них соответствует
вполне определенное значение другой. Возьмем, например,
уравнение
S —4,9/2, (1)
в котором S означает расстояние, пройденное падающим
телом, a t — время падения. Дадим времени t какое-либо
числовое значение, тогда величина пройденного расстояния S
получит соответствующее значение; например,
если t — 2, то S — 4,9 • 22== 19,6,
„ /==3, „ S = 4,9 • 32= 44,1,
„ ^ = 4, „ S = 4,9 -42 — 78,4 и т. д.
Переменная величина t, которой мы давали произвольные
значения, называется независимой переменной или аргумен-
том', другая же переменная 5, изменяющаяся в зависимости
от изменения t, называется зависимой переменной или
функцией. Связь между этими переменными носит название
дъункционалъной зависимости.
Следует отметить, что хотя аргументу мы даем произ-
вольные значения, однако эти значения выбираются только
такими, которые допускаются условиями задачи. Так, в разо-
бранном примере время t может принимать только поло-
жительные значения или нуль, ибо время, выраженное отри-
цательным числом, здесь смысла не имеет.
Заметим также, что выбор независимой переменной
диктуется условиями задачи. Если, например, нас интересует
время, в течение которого тело прошло то или иное рас-
стояние, то в уравнении (1) мы должны давать <S числовые
значения, которым будут соответствовать определенные зна-
чения /; при этом условии S явится уже аргументом,
22 ЛИНИИ И ИХ УРАВНЕНИЯ [гл. п
a t— функцией. В таком случае для удобства вычисления
функции t уравнение (1) следует переписать так:
Определение. Переменная величина у называется
функцией переменной х, если каждому допустимому
значению х соответствует определенное значение у.
Функция, определяемая таким образом, называется одно-
значной.
В математике рассматриваются и такие функции, которые
имеют несколько значений, соответствующих одному значению
аргумента, например у ==zt]/"x2—1, y==Arctgx и г. п.
Такого рода функции, называемые многозначными, в нашем
курсе рассматриваться не будут.
Пример 1. Площадь круга
S=7zr2.
Каждому значению г в этом равенстве соответствует
определенное значение 5; следовательно, площадь круга есть
функция радиуса, а само равенство выражает функциональную
зависимость между этими переменными.
Пример 2. Путь, пройденный телом в прямолинейном
движении с постоянной скоростью V,
S — vt.
Здесь путь S получает определенное значение, соответ-
ствующее значению /; поэтому S — функция времени t.
Пример 3. Согласно закону Бойля — Мариотта дав-
ление р и объем v газа связаны формулой:
где с — постоянная величина для данной массы и температуры
газа. С изменением объема v изменяется и давление /?; сле-
довательно, давление р газа есть функция его объема v.
§ 7. Линии и их уравнения. Из курса алгебры известно,
что по уравнению, определяющему функцию, можно построить
линию, называемую графиком функции.
Пусть, например, дано уравнение у — х2> определяющее у
как функцию х.
§ 7]
ЛИНИИ И ИХ УРАВНЕНИЯ
23
Составим таблицу значений х и соответствующих значений у:
соответствует точка плоскости. Построив эти точки (черт. 8)
и соединив их плавной линией,
мы получим график функции
у=х2. Этот график, как вид-
но, представляет линию, все
точки которой обладают оди-
наковым свойством, а именно:
ордината каждой из них равна
квадрату соответствующей абс-
циссы. Линия, все точки кото-
рой обладают одним и тем же
свойством, называется геомет-
рическим местом таких точек.
Наш пример показывает,
что уравнению с переменными
х и у соответствует на плос-
кости некоторая линия как
геометрическое место точек, координаты которых удов-
летворяют этому уравнению.
Обратно, линии на плоскости, представляющей геоме-
трическое место точек, соответствует некоторое урав-
нение с переменными х и у. Покажем это на примере.
Пусть дана на плоскости окружность с центром в начале
координат и радиусом, равным 5 (черт. 9). Из элементарного
курса геометрии известно, что эта окружность есть геоме-
трическое место точек, удаленных от центра на 5 единиц.
Возьмем на окружности произвольную точку М(х;у). По
условию, ОМ —5; с другой стороны, по формуле (5) § 3
ОМ = /х2 + >2.
Следовательно, для любой точки нашей окружности должно
быть
У X* -4- у 2 = 5,
24
ЛИНИИ И ИХ УРАВНЕНИЯ
[гл. п
или
х2+д/2=25. (1)
Итак, окружности с радиусом, равным 5, и с центром
в начале координат соответствует уравнение (1).
Уравнение (1) вполне определяет данную окружность,
а потому оно называется уравнением этой окружности.
Имея уравнение (1) окружности, можно узнать, лежат ли
на ней какие-нибудь данные точки, например Л(—3; 4) и
В(—1; 3). Для этого нужно проверить, удовлетворяют ли
координаты точек А и В уравнению (1). Подставив их в урав-
нение (1) на место х и у, получим:
для точки А:
(_ 3)2 + 42= 9 + 16 = 25,
для точки В:
(— 1)24- 32= 1-Ь9=#25.
Координаты точки А удовлетворяют уравнению (1), зна-
чит, точка А лежит на данной окружности; координаты же
точки В не удовлетворяют этому уравнению, значит, точка В
на этой окружности не лежит (черт. 9).
Определение. У равнением линии называется уравне-
ние с переменными х и у, которому удовлетворяют коор-
§ 7J ЛИНИИ И ИХ УРАВНЕНИЯ 25
динаты любой точки этой линии и не удовлетворяют
координаты любой точки, не лежащей на линии.
Переменные х и у, входящие в уравнение линии, назы-
ваются текущими координатами.
Таким образом мы установили, что между линиями и их
уравнениями существует связь, поэтому принято говорить:
«дана линия» вместо «дано уравнение линии»,
«найти линию» вместо «найти уравнение линии».
Установленная выше связь между линиями и их уравне-
ниями позволяет изучать свойства линий путем анализа урав-
нений, соответствующих этим линиям. Отсюда и название
изучаемого нами предмета — аналитическая геометрия.
Пример 1. Лежит ли точка А ( — 2; 4) на линии у = х2?
Решение. Подставив вместо х и у в данное уравнение
координаты точки А( — 2; 4), получим тождество:
4 = ( — 2)2 = 4.
Следовательно, точка А лежит на данной линии.
Пример 2. Дана линия у =— и точка на
ней с абсциссой, равной—1. Определить ординату точки Л.
Решение. Так как точка А лежит на данной линии, то
ее координаты должны удовлетворять данному уравнению.
Одна координата х ——1. Чтобы найти вторую, т. е. у, мы
подставим в уравнение вместо х его значение. Получим:
j = -3(—1)+1^4.
Итак, ордината точки А равна 4.
Упражнения
1. Дана линия у —~х-|-2. Узнать, лежат ли па ней точки
А (2; 3), В(3; 3) и С (4; 4)?
2. На линии 4х — 5у = 8 лежат точки А (2; у) и В (х; 4). Найти
неизвестную координату каждой точки.
3. Написать уравнение линии, все точки которой одинаково уда-
лены от осей координат. Построить эту линию.
4. Ординаты любой точки некоторой линии в 4 раза больше ее
абсциссы. Написать уравнение этой линии и построить ее.
26
ЛИНИИ И ИХ УРАВНЕНИЯ
[гл. п
5. Написать уравнение линии, все точки которой удалены от
точки О (0; 0) на одинаковое расстояние, равное 2. Какой вид имеет
эта линия?
6. Написать уравнение линии, все точки которой удалены от
точки Л4(2; —3) на одинаковое расстояние, равное 4.
7. Точки некоторой линии одинаково удалены от двух точек
Л(— 2; 1) и В(— 1; —3). Написать уравнение этой линии.
8. Написать уравнение линии, по которой движется точка М (х; у)
так, что ее расстояние от оси Ох остается все время равным рас-
стоянию ее от точки F(Q; —2).
9. Определить траекторию точки М (х; у), которая при своем
движении остается вдвое ближе от точки А (1; 0), чем от точки В (4; 0).
ГЛАВА III
ПРЯМАЯ ЛИНИЯ
§ 8. Уравнения прямых, параллельных осям координате
Возьмем прямую линию, параллельную оси Оу и проходящую
на расстоянии а от нее
(черт. 10).
Все точки этой прямой
одинаково удалены от оси
ординат на расстояние, рав-
ное а. Следовательно, для
каждой точки прямой AM
абсцисса одна и та же,
а именно:
х = а, (1)
ордината же различна. Та-
ким образом, уравнение (1)
вполне определяет прямую,
параллельную оси Оу, а потому оно является ее уравнением.
Возьмем прямую, параллельную оси Ох, на расстоянии,
равном Ъ от нее (черт. 11). Все точки этой прямой одина-
ково удалены от оси Ох на расстояние, равное Ь, т. е.
28
ПРЯМАЯ ЛИНИЯ
[гл. ш
любая точка прямой ВМ имеет постоянную ординату,
а именно:
(2)
абсциссу же различную. Как видно, уравнение (2) вполне
определяет прямую, параллельную оси Ох, а потому оно
является ее уравнением.
По уравнениям (1) и (2)
можно построить соответствую-
щие им прямые. Пусть, напри-
мер, дана прямая х — — 4.
Отложив на оси Ох отрезок
О А — — 4 (черт. 12) и проведя
через точку А прямую, парал-
лельную оси Оу, получим иско-
мую прямую.
§ 9. Уравнения осей коор-
динат. Возьмем уравнение пря-
мой, параллельной оси Оу:
х— а
и станем в нем уменьшать абсолютную величину а, тогда
прямая, определяемая этим уравнением, будет приближаться
к оси Оу, оставаясь все время ей параллельной, и при а = 0
сольется с ней. Уравнение
х — О
является уравнением оси Оу.
Если же в уравнении
У — Ь
прямой, параллельной оси Ох, будем уменьшать абсолютную
величину Ь, то эта прямая станет приближаться к оси Ох,
оставаясь ей параллельной, и при b — 0 с ней совпадет.
Таким образом, уравнение
= О
будет уравнением оси Ох.
§ 10] ПРЯМАЯ, ПРОХОДЯЩАЯ ЧЕРЕЗ НАЧАЛО КООРДИНАТ 29
Упражнения
1. Построить прямые:
1) х = 3, 2) х = — 5, 3) у = 3, 4) у — — 2.
2. Написать уравнение прямой, параллельной оси Ох и отсекаю-
щей на оси Оу отрезок, равный —5.
3. Написать уравнение прямой, параллельной оси Оу и отсекаю-
щей на оси Ох отрезок, равный —2.
4. Составить уравнение прямой, проходящей через точку
А (— 3; 2) и параллельной оси Ох.
5. Составить уравнение прямой, параллельной оси Оу и прохо-
дящей через точку А( — 3; —1).
6. Сторона квадрата равна 12. Написать уравнения всех его
сторон, если за оси координат принять прямые, параллельные его
сторонам и проходящие через центр квадрата.
7. Стороны прямоугольника, равные 6 и 8, совпадают с осями
координат. Написать уравнения сторон этого прямоугольника для
случая, когда он расположен в первом координатном углу.
§ 10. Уравнение прямой, проходящей через начало
координат. Проведем прямую через начало координат под
углом а (а =# 90°) к оси Ох (черт. 13). Принято положи-
тельный угол а отсчитывать от положительного направления
оси абсцисс в сторону, противоположную движению часовой
стрелки (черт. 13), а отрицательный — по часовой стрелке.
Возьмем на проведенной прямой произвольную точку
М (х; у). Опустив перпендикуляр МР на ось Ох, получим
прямоугольный треугольник ОМР, из которого найдем:
PM — OPtga. (1)
30 ПРЯМАЯ ЛИНИЯ 1ГЛ. ш
Но
ОР — х и РМ — у,
поэтому равенство (1) перепишется так:
у = х tgа.
Положим
tga = /s, (2)
тогда получим:
у = kx. (3)
Координаты любой точки прямой ОМ удовлетворяют
полученному уравнению; можно показать, что координаты
любой точки, не лежащей на прямой CW, не удовлетворяют
ему; поэтому оно является уравнением прямой ОМ. Итак,
у<— kx
есть уравнение прямой, проходящей через начало коор-
динат. В нем х и у — текущие координаты, a k— угло-
вой коэффициент.
Определение. Угловым коэффициентом прямой
называется тангенс угла наклона этой прямой к положи-
тельному направлению оси Ох.
Величина k может быть как положительной, так и отри-
цательной. Если угол сс острый, то тангенс его имеет поло-
жительное значение; если же угол а тупой,—то отрица-
тельное. Поэтому величина k в уравнении прямой будет
положительной, если а — острый угол, и отрицательной, если
тупой.
Заметим, что при а = 90° углового коэффициента не суще-
ствует, так как tg 90° не имеет числового значения.
Зная угловой коэффициент прямой y — kx, можно опре-
делить ее положение.
Пусть требуется построить прямую у — 2х.
Для этого найдем угол а из условия
k = tga= 2,
откуда
а=63е26'.
§ 10] ПРЯМАЯ, ПРОХОДЯЩАЯ ЧЕРЕЗ НАЧАЛО КООРДИНАТ
31
точке О найденный
Построив при
искомую прямую (черт. 14).
Построение этой прямой
Известно, что положение
прямой определяется двумя точ-
ками, поэтому для решения за-
дачи нужно знать их коорди-
наты. В нашем же случае доста-
точно определить координаты
одной точки, так как вторая
(начало координат) нам из-
вестна. Для этого дадим х
произвольное значение, напри-
мер х=2, тогда из уравнения
прямой найдем:
= 2 • 2 = 4.
Значения х = 2 и у = 4
и будут координатами точки,
угол, мы и получим
лежащей на .данной прямой. Построив эту точку, проведем
через нее и начало координат прямую линию (черт. 14).
Упражнения
1. Написать уравнение прямой, проходящей через начало коор-
динат и образующей с положительным направлением оси Ох один
из следующих углов:
1) 45°, 2) 30°, 3) 135°, 4) 0°, 5) 180°.
2. Прямая задана уравнением у = kx. Каково будет положение
прямой при 1) k — 0, 2) & = 1, 3) k~— 1?
3. Под каким углом к положительному направлению оси Ох
наклонены следующие прямые:
1)у = Узх, 2)у=-|л, 3) у = — 2л?
4. Построить прямые: 1) у — 2х, 2) у ~ х, 3) у = —2xt
лч 1
4) У = —2 х.
5. Дана прямая у = Зх. Лежат ли на ней точки А (1; 3), В (2; 5),
6. На какой из прямых у = 4х, у = — Зх и у = 2х лежит
точка А (~~ 2; — 4)?
32
ПРЯМАЯ ЛИНИЯ
1гл. ш
7. Дана прямая у = 1,5х и точки па ней А(х; 6) и В(—2; у).
Найти неизвестные координаты этих точек.
8. Прямая у — kx проходит через точку А(—1; 5). Найти ее
угловой коэффициент.
9. Написать уравнение прямой, проходящей через начало коор-
динат и точку А (2; — 4).
10. Вершина острого угла равнобедренного прямоугольного
треугольника совпадает с началом координат, а катет, равный 10, —
с положительным направлением оси Ох. Найти уравнения его сторон.
11. Построить точки А (—6; 0) и В (0; 3) и прямоугольник ОАСВ.
Написать уравнения сторон прямоугольника и его диагонали ОС,
12. Сила приложена к началу координат и составляющие ее
по осям Ох и Оу соответственно равны 5 и —2. Написать уравне-
ние прямой, по которой направлена сила, и построить эту прямую.
§ 11. Уравнение прямой с угловым коэффициентом
и начальной ординатой. Пусть дана прямая ОС, проходя-
щая через начало координат под углом а к положительному
направлению оси Ох (черт. 15). Ее уравнение имеет вид
у = kx,
где k— tga (§ 10).
Проведем прямую ЛВЦОС, отсекающую на оси Оу отре-
зок ОВ — Ь, Прямая АВ составляет с положительным напра-
влением оси Ох тот же угол а. Пусть М(х\у) — произволь-
ная точка прямой АВ. Из черт. 15 найдем:
y — PM = PMl~\- b. (1)
Но
PMt — kx’t
§ 111
ПРЯМАЯ С УГЛОВЫМ КОЭФФИЦИЕНТОМ
33
подставив значение PMY в равенство (1), получим уравне-
ние прямой АВ в виде
y — kx-\~bt (2)
где k—угловой коэффициент, а b называется начальной
ординатой.
Заметим, что прямая y~kx-\-b получается смещением
всех точек прямой y = kx (черт. 15) на отрезок b вверх
(при положительном Ь) и вниз (при отрицательном Ь).
Уравнение y = kxt определяющее прямую, проходящую
через начало координат, является частным случаем уравне-
ния (2) при b — Q.
Зная угловой коэффициент k и начальную ординату /?,
можно определить положение прямой. Пусть, например, тре-
буется построить прямую
_у = х4-4.
Из данного уравнения имеем:
tga= 1,
откуда
а = 45°.
Проведем через начало координат прямую MN под углом
в 45° к положительному направлению оси Ох (черт. 16).
Но прямая у = х-|“4, как видно из уравнения ее, пере-
секает ось Оу на расстоянии ОС, равном 4 единицам мас-
3 Зак. 3032. И. Л. Зайцев
34
ПРЯМАЯ ЛИНИЯ
[гл. ш
штаба от начала координат. Поэтому прямая АВ, проведен-
ная через точку С параллельно прямой Л'Ш, и будет искомой.
Однако проще построить указанную прямую по двум ее
точкам. Удобнее для этого брать точки пересечения прямой
с осями координат. Одна из них — точка С пересечения пря-
мой с осью Оу— дается самим уравнением, а именно С(0; 4).
Для нахождения точки D пересечения этой прямой с осью Ох
положим в данном уравнении _у = 0, получим х — — 4; зна-
чит, прямая пересекает ось Ох в точке £)(—4; 0). Строим
точки С и D и проводим через них искомую прямую.
Пример. Найти уравнения прямых АВ, CD и EF, изо-
браженных на черт. 17.
Решение. Чтобы написать уравнения данных прямых,
нужно определить величины /г и Ь, а затем подставить их
значения в уравнение у — kx-\-b.
Для прямой АВ k = tg 60° = ]Лз, & —3;
» » CD /? = tg(180° — 45°) = tg 135° = — 1,
= —3;
» » Л/7 Л == tg 150°=== — tg 30° —— Xp-, /> — 2.
§ И]
ПРЯМАЯ С УГЛОВЫМ КОЭФФИЦИЕНТОМ
35
Следовательно, уравнения данных прямых будут:
АВ: j’^/Зх + З,
CD: у — х 3,
EF: у=^х+2.
Упражнения
1. Построить прямые
1) у = Зх + 2, 3) у ~ — Зх 4- 2,
2) у = Зх — 2, 4) у — — Зх — 2.
2. На какой из прямых
5 1
1)у = — Зл+1, 2)у = ух-у, 3) у = — 8лг—10
лежит точка А (— 1; — 2)?
3. Дана прямая у = 5х — 2 и точка на ней с абсциссой, рав-
ной 1. Определить ее ординату.
4. На прямой у — — 2x-j-l лежит точка, ордината которой
равна 5. Найти ее абсциссу.
5. Даны прямые: 1) у = 4х — 2, 2) у = —Зх — 6. Найти точки
пересечения этих прямых с осями координат.
6. Составить уравнение прямой, образующей с положительным
направлением оси Ох угол в 135° и отсекающей на оси Оу отрезок,
равный — 5.
7. Написать уравнение прямой, проходящей через точку А под
углом а к положительному направлению оси Ох, если дано:
1) А (0; 2), а == 45°; 2) А (0; — 3), а = 135°; 3) А (0; 4), а = 150°.
8. Найти углы, образуемые с положительным направлением
оси Ох прямыми: 1) у = У 3 х -|- 2; 2) у ~ — х — 3; 3) у — ф- б.
9. Написать уравнение прямой, проходящей через точку А (2; 5)
и образующей с положительным направлением оси Ох угол:
1) а = 0°, 2) а = 90°, 3) а = 180°.
10. Найти уравнение прямой, проходящей через точку А(1;—3)
и образующей с положительным направлением оси Ох угол, рав-
* ный arc tg (— 2).
11. Найти угловой коэффициент прямой, проходящей через
точку А и отсекающей на оси Оу отрезок, равный Ь, если дано;
1) Л(3;4), 6 = —2; 2) А (— 2; 5), b = 5.
12. Две стороны квадрата совпадают с положительными напра-
влениями осей координат. Написать уравнения диагоналей квадрата,
если сторона его равна 12.
13. Написать уравнения сторон квадрата, диагонали которого
служат осями координат. Длина стороны квадрата равна 4.
3*
36
ПРЯМАЯ ЛИНИЯ
[гл. III
14. Сторона квадрата равна 4 V 2. Найти уравнения его сто-
рон и диагоналей, если одна из его вершин лежит в начале коор-
динат, а диагональ совпадает с положительным направлением оси Оу.
§ 12. Общее уравнение прямой. В предыдущих пара-
графах были выведены следующие виды уравнения прямой:
уравнение прямой, параллельной оси Оу:
х — а, где а =/= 0, (1)
уравнение прямой, параллельной оси Ох:
у — Ь, где b Ф 0, (2)
уравнение оси Оу:
х=0, (3)
уравнение оси Ох:
у = 0, (4)
уравнение прямой, проходящей через начало координат:
У = kx, (5)
уравнение прямой с угловым коэффициентом и началь-
ной ординатой:
у = Рх-\-Ь. (6)
Уравнения (1) — (6) исчерпывают все возможные положе-
ния прямой, поэтому можно сказать, что
всякая прямая линия определяется уравнением первой
степени относительно текущих координат.
Покажем теперь, что указанные виды уравнения прямой
можно получить из уравнения
Ах-\-Ву + С = Ъ (7)
при некоторых частных значениях коэффициентов Л, В и С.
I. Если В —0, то уравнение (7) обратится в следующее:
Лл: + С = 0,
откуда
С
х— Д.
Положив
получим:
х~ а.
§ 12] ОБЩЕЕ УРАВНЕНИЕ ПРЯМОЙ 37
Уравнение Ах~{-С = 0 есть уравнение прямой, парал-
лельной оси II. Если Оу. А — 0, то
отсюда С У — ~~ В-
Положив с h -~в=ь’
получим: у = Ь.
Уравнение Ву-{-С—0 определяет прямую, параллельную
оси Ох.
III. Если В — 0 и С — 0, то Ах~ 0,
• отсюда х— 0.
IV. Если /1 = 0 и С — 0, то Ву — 0,
отсюда > = о,
V. Если С = 0, то . Ах-+-Ву = 0,
отсюда А У = -~вх-
Положим А / — В ~ k‘
тогда У~ kx.
Уравнение Ах~\-Ву = 0 определяет прямую, проходящую
через начало координат.
VI. Если ни один из коэффициентов уравнения (7) не равен
нулю, то и в этом случае его можно преобразовать в зна-
комую нам форму уравнения прямой. Найдем из уравнения (7)
значение у*. А С у~~~вх~~в'
38 ПРЯМАЯ линия [гл. ш
Положив
(8)
и
С .
В ~Ь'
можем написать:
у — kx~\~b.
Следовательно, уравнение
Ах + Ву + С = О
включает в себя все рассмотренные нами ранее уравнения
прямой; поэтому оно называется общим уравнением прямой.
Итак, всякое уравнение первой степени
АхАгВуАгС = ^
при любых значениях коэффициентов Л, В и С, исклю-
чая одновременное равенство А и В нулю, определяет
прямую линию.
Пример 1. Построить прямую 2х— 5у-]-^0 = 0.
Решение. Проще всего построить прямую по двум ее
точкам пересечения с осями координат. Положив в данном
уравнении у — 0, получим х = — 5; координаты (—5; 0) и
будут определять положение точки пересечения прямой
с осью Ох. Для нахождения точки пересечения прямой
с осью Оу положим в том же уравнении х — 0, тогда най-
дем у = 2; координаты искомой точки будут (0; 2).
Построив эти точки, проводим <Я|)ез них прямую
2х — 5у-|- 10 = 0 (черт. 18).
Пример 2. Найти угловой коэффициент и начальную
ординату прямой 4х 4~ бу — 3 — 0.
Решение. Преобразуем это уравнение к виду у — kx-\-b*t
для этого находим:
бу = — 4x4-3,
отсюда
2 . 1
Сравнив полученное уравнение с уравнением у = kx-\-b,
найдем:
. 2 А 1
§ 12]
ОБЩЕЕ УРАВНЕНИЕ ПРЯМОЙ
39
Угловой коэффициент можно найти и из равенства (8).
Для этого, как видно, нужно коэффициент при х общего урав-
нения прямой разделить на коэффициент при у и частное
взять с противоположным знаком. Таким образом, в дан-
ном примере
Упражнения
1. Построить прямые:
1) Зх — 4у + 12 = 0, 2) 4х + 5у + 20 = 0, 3) Зх — 4у = 0.
2. Даны прямые 5х — Зу 4~ 2 = 0 и 4х 4~ Бу = 0. Какая из них
проходит через начало координат?
3. Даны прямые:
1) бх —Зу + 10==0, 2) 5х + 8у — 15 = 0.
Преобразовать их к виду у — kx Ь,
4. Даны прямые:
Q 9
1)у==_|х, 2)у=7х-4.
Представить данные уравнения в общем виде.
5. Определить угловые коэффициенты прямых:
1) 2х —Зу+5 = 0, 2) х4-2у = 0.
6. Найти начальную ординату прямых:
1)2х —9у —6 = 0, 2) 5хф-2у = 0.
40
ПРЯМАЯ ЛИНИЯ
[гл. III
7. Найти начальную ординату и угол наклона к положительному
направлению оси Ох прямой 5х -|- бу — 15 = 0.
8с Показать, что геометрическое место точек, равноудаленных
от двух точек А (2; 4) и В(—3; 1), есть прямая линия.
9. Показать, что геометрическое место точек, равноудаленных
от любых двух точек, есть прямая линия.
§ 13с Уравнение прямой в отрезкахв Как мы уже знаем,
положение прямой определяется или двумя точками или одной
точкой и углом наклона прямой к оси Ох. Если прямая не
параллельна ни одной из координатных осей и .не проходит
через начало координат, то ее положение может быть опре-
делено и другими данными, например отрезками, которые
она отсекает на осях. Выведем уравнение прямой для этого
случая.
Пусть дана прямая, отсекающая на координатных осях
отрезки ОА — а и ОВ = Ь (черт. 19).
Возьмем на этой прямой произвольную точку Ж (х; у) и
проведем МР | Ох. Из подобия треугольников РМА и ОВА
имеем:
РМ _ РА
О В “ О А’
или
у___ а — х
b а *
Разделив а — х почленно на а, будем иметь:
У. _ 1 ±
Ь а 9
§ 13] УРАВНЕНИЕ ПРЯМОЙ В ОТРЕЗКАХ
41
откуда
а 1 b
(D
Можно показать, что координаты любой точки нашей пря-
мой будут удовлетворять этому равенству, а потому его нужно
рассматривать как уравнение прямой АВ.
В уравнение (1) входят отрезки а и bt отсекаемые пря-
мой на осях; поэтому оно называется уравнением прямой
в отрезках.
Величины а и b могут быть как положительными, так и
отрицательными в зависимости
начала координат откладывают-
ся отрезки а и Ь.
Пусть, например, дана пря-
мая АВ (черт. 20). Здесь
а = — 2, Ь — — 3; следова-
тельно, уравнение прямой АВ
запишется в таком виде;
или
_.£_2 — 1
2 3 ‘
По уравнению вида (1)
очень просто строится прямая.
Для этого нужно только отл(
взятые из уравнения, и через их концы провести прямую.
Заметим, что уравнение в отрезках легко получается
из общего уравнения прямой: Лх-|- By А-С— 0, если все
коэффициенты общего уравнения отличны от нуля (иначе
уравнение в отрезках не имеет смысла).
Упражнения
1. Построить прямые:
+ | = 2)-у + 7 = 1.
Х У 1 Л\ Х У 1
1.
42
ПРЯМАЯ ЛИНИЯ
[гл. III
2. Прямая проходит через точки А и В:
1) Л (0; 2), В (4; 0), 2) А (—2; 0). В (0; —1); 3) Л(0; 3), В (—2; 0).
Написать уравнение прямой в отрезках.
JC у
3. Определить длину отрезка прямой = 1, заключен-
ного между точками пересечения прямой с осями координат.
4. Преобразовать следующие уравнения прямой в форму урав-
нения прямой в отрезках:
1)2^Д-Зу —6 = 0, 2) х — 6уД-6 = 0, 3)2х — у — 1=0.
5. Определить площадь треугольника, заключенного между
осями координат и прямой —= 1.
6. Диагонали ромба совпадают с осями координат. Определить
площадь ромба, если одна из сторон его задана уравнением
2L + 2 = 1.
2,5 10
7. Две смежные вершины ромба лежат в точках А (5; 0) и
В (0; 8). Написать уравнения в отрезках для всех его сторон, если
диагонали ромба совпадают с осями координат.
8. Отрезок прямой, заключенный между осями координат, равен
3 У2 и наклонен к положительному направлению оси Ох под
углом 135°. Написать уравнение этой прямой в отрезках (два случая).
§ 14. Уравнение пучка прямых. Пусть прямая АВ про-
ходит через точку ^(х^Ух) и образует угол а с положи-
тельным направлением оси Ох (черт. 21). Составим для пря-
мой АВ уравнение вида
(I)
Для этого нужно найти величины k и Ь, определяющие пря-
мую АВ> а затем подставить в уравнение (1) их значения.
Так как угол ос дан, то величина k определится из равенства
k — iga.
Для нахождения b воспользуемся тем, что точка М лежит
на прямой (1) и, следовательно, ее координаты удовлетво-
ряют уравнению этой прямой.
Подставив в уравнение (1) вместо х и у их значения
xt и а величину /г полагая известной, получим:
-+ b,
откуда
b — yt — kxl.
§ 14] УРАВНЕНИЕ ПУЧКА ПРЯМЫХ 43
Уравнение (1) можем теперь записать в виде
у = kx + уг — kxt
или
у—y^kix — Xi). (2)
Таково искомое уравнение прямой АВ; в нем k имеет
одно, вполне определенное значение.
Допустим, что через ту же точку ЛЦлу, j/J проходит
несколько прямых; тогда угол а наклона этих прямых к оси Ох,
а также множитель k в урав-
нении (2) будут иметь раз-
личные значения.
В таком случае уравне-
ние (2) будет определять
уже не одну прямую, про-
ходящую через данную точ-
ку 7И, а множество прямых,
пересекающихся в этой
точке.
Совокупность всех пря-
мых, проходящих через одну
точку М, называется пучком
прямых с центром в точ-
ке М. Таким образом, урав-
нение (2) с переменным k
можно рассматривать как уравнение пучка прямых, прохо-
дящих через данную точку, исключая прямую, параллельную
оси ординат (так как tg90° не имеет числового значения)
(черт. 21).
Чтобы выделить из этого пучка прямую, образующую
заданный угол с осью Ох, нужно в уравнении (2) вместо k
подставить его числовое значение. Пусть, например, пучок
прямых проходит через точку 7И(2;—5), тогда его уравне-
ние будет;
j/ + 5 = /e(x —2). (3)
Выделшм из этого пучка одну прямую, которая наклонена
к положительному направлению оси Ох под углом а = 45°;
тогда
k — tg 45°= 1,
44
ПРЯМАЯ ЛИНИЯ
[гл. III
и уравнение (3) обратится в следующее:
= х — 2,
или
х—у — 7 — О.
Упражнения
1. Дано уравнение пучка прямых у + 2 = k(x— 6). Найти коор-
динаты центра этого пучка прямых.
2. Дано уравнение пучка прямых у — 4 = k (х 3). Проходят
ли эти прямые через точку М (—3; 4)?
3. Написать уравнение пучка прямых, проходящих через точку
Af(—6; —9).
4. Из пучка прямых, проходящих через точку М (2: —7). одна
прямая образует с положительным направлением оси Ох угол 60°,
а другая — угол 150°. Написать уравнения этих прямых.
5. Написать уравнение прямой, проходящей через точку
М(—1; 8) и образующей с положительным направлением оси Ох
один из углов: 45°, 30°, 135°, 180°.
6. Написать уравнение прямой, проходящей через точку
М (10; —2) и образующей с положительным направлением оси Ох
угол, равный
1) arctg3, 2) arctg(—2).
7. Высота равнобедренного треугольника совпадает с положи-
тельным направлением оси Оу, а основание — с осью Ох. Написать
уравнения боковых сторон треугольника, если одна из них обра-
зует с положительным направлением оси Ох угол в 135°, а высота
его равна 5.
8. Высота равностороннего треугольника, равная 6 У 3, совпа-
дает с положительным направлением оси Оу, а основание — с осью Ох.
Написать уравнения боковых сторон треугольника.
9. Написать уравнения сторон равнобедренной трапеции, зная,
что основания ее равны 10 и 6, а боковые стороны образуют с осно-
ванием угол в 60°. За оси координат взяты большее основание (ось Ох)
и ось симметрии трапеции (ось Оу). Рассмотреть два случая.
§ 15. Уравнение прямой, проходящей через две данные
точки. Пусть даны две точки A (xt; у±) и В(х2; у2У требуется
найти уравнение прямой, проходящей через эти точки.
Если взять одну точку, например А, то через нее можно
провести пучок прямых, уравнение которого будет:
у — yt = k{x—Xj), (1)
где каждому значению k отвечает одна прямая.
§15] ПРЯМАЯ, ПРОХОДЯЩАЯ ЧЕРЕЗ ДВЕ точки 45
Выделим из этого пучка прямую, которая проходит и
через вторую точку В (черт. 22). Чтобы найти ее уравнение,
необходимо определить угловой коэффициент. Для этого
примем во внимание, что точка В лежит на искомой прямой,
а потому ее координаты должны обращать уравнение (1)
в тождество при kt равном угловому коэффициенту этой пря-
мой. Подставив в уравнение (1) вместо текущих координат
х и у координаты точки В, получим:
у 2—— ^i);
отсюда находим угловой коэффициент искомой прямой:
х2 — xt
Уравнение (1) можно переписать так:
у—л=—xi)-
Х2 — -Ч
Преобразуем это уравнение, разделив обе части его на
У2—Уъ получим:
У2 — У1 *2 — л'1 '
где х и у — текущие координаты. Равенство (2) является
уравнением прямой, проходящей через две данные точки.
Это, как и уравнение в отрезках, частный случай общего
уравнения прямой.
46
ПРЯМАЯ ЛИНИЯ
[гл. III
Если хг — х2 или yt = y2, то формула (2) теряет смысл,
так как делить на нуль нельзя. В этих случаях точки А и В
лежат либо на прямой, параллельной оси Оу, либо на пря-
мой, параллельной оси Ох. В первом случае уравнение пря-
мой запишется в виде
х = xlf
а во втором — в виде
У = У1-
Пример 1. Написать уравнение прямой, проходящей
через две точки:
Л (—4; 6) и В (2; —3).
Решение. Имеем:
хг — —4, х2~ 2
и
^t==6. л = —3.
Подставим эти значения в уравнение (2); получим:
у — 6 __ х4~4
LZ3TZ6 — ‘2 4Г4 >
или
у — 6 ___ х4-4
—9 “ Г"*
Умножив обе части последнего уравнения на —18, будем
иметь:
2у — 12 = — Зх— 12,
откуда
ЗхН-2у = 0.
Пример 2. Через две точки Л(3;2) и В (5; 2) прохо-
дит прямая. Написать ее уравнение.
Решение. Так как ординаты данных точек равны, то
заключаем, что искомая прямая параллельна оси Ох, а потому
ее уравнение будет у — 2.
Упражнения
1. Написать уравнение прямой, проходящей через две точки А
и В, если даны:
1) А (1; 2) и В (4; 3), 3) А (0; 0) и В (4; —1),
2) А (—2; 3) и В (5; —3), 4) А (—2; —3) и В (—2; 5).
§ 16] УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ 47
2. Даны вершины треугольника ЛВС:
А (3; —1), В (4; 2) и С (—2; 0).
Написать уравнения его сторон.
3. На план участка нанесено положение двух вех, координаты
которых в прямоугольной системе (30; 40), Л42 (50; 80). Найти угол
наклона прямой к положительному направлению оси абсцисс
плана.
4. Определить отрезки, отсекаемые на координатных осях пря-
мою, проходящей через две точки Л (2; 3) и В (4; 1).
5. Даны координаты вершин треугольника АВС:
Л (4;—2), В(—1;5) и С (—5;— 3).
Написать уравнение медианы, проведенной из вершины А.
6. Дан треугольник с вершинами
Л (2; 4), В (0; 2) и С (4; —2).
Написать уравнение прямой, проходящей через середины сто-
рон АС и ВС треугольника.
7. Даны координаты трех вершин параллелограмма ABCD:
А (—1; 2), В (—2; —2) и С (5; — 2).
Найти уравнения его диагоналей АС и BD.
8. Написать уравнение прямой, проходящей через точку А (3; —2)
и отсекающей на оси Ох отрезок, равный 5.
9. Точка, двигаясь прямолинейно, в некоторые моменты зани-
мала положения А (5; 2) и В (—1; —2). Определить положение этой
точки в момент нахождения ее на оси Ох.
§ 16. Угол между двумя прямыми. Пусть даны уравне-
ния двух прямых:
у —
y=k2x-{-b2t
где kit k2, и b2 имеют вполне определенные значения.
Выведем формулу для определения угла между этими пря-
мыми.
Обозначим углы, образуемые данными прямыми с поло-
жительным направлением оси Ох, через и а2, а угол между
этими прямыми через ср (черт. 23).
Угол а2, как внешний угол треугольника АВС, будет
равен сумме внутренних, с ним не смежных, т. е.
«2 = ai + «P.
откуда
ср ™ а2 — ах.
48
ПРЯМАЯ ЛИНИЯ
[гл. тп
Если углы равны между собой, то и тангенсы Их равны
друг другу, поэтому
tg? = tg(a2 —«О-
Применяя формулу для тангенса разности двух углов, получим:
Черт. 23.
SY 1+tgattga/
Но
tg al = kl 11 tg a2 — ^2>
поэтому
(1)
Определив tg <p no
формуле (1), можно найти
и самый угол ср.
Пример. Опреде-
лить угол между прямыми:
2х — Зу -|- 6 — О
и
х Ц— ^у — 2 :==: 0.
Решение. Из данных уравнений найдем угловые коэф-
фициенты этих прямых [(8) § 12]:
/Ci = -y и /г2 = —у.
Согласно формуле (1) имеем:
_1___ *3
откуда
ср — arctg (— 1) = 135°.
Полученный угол между прямыми тупой. Но если принять
/ 1 1 2
— — т- и /г2 = -у,
А о о
§ 16]
УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ
49
то, вычисляя tg cpj по той же формуле (1), получим:
2_ £ 13
3 + 5 _ 15
О U <
, J” “ Тз— ь
1 15 15
откуда срл = 45°. Получился угол острый, смежный с ранее
Черт. 24.
найденным тупым углом (черт. 24). Первое и второе значе-
ние угла будет ответом па вопрос задачи.
Упражнения
1. Определить острый угол между прямыми:
1) у = 2х+3и у = х-2, 3) |-^=1 и * + JL=l,
2) Зх — у -f” 6 = 0 и х — у + 4 — 0, 4) у 4“ 5 = Зх и у — 2 = 0.
2. Найти угол между прямой 2х— Зу4-6 = 0 и прямой, про-
ходящей через точки А (4; —5) и В (—3; 2).
3. Под каким углом пересекаются прямые:
1) х — 2у — 2 = 0 и у==-1-х4-3,
2) Зх + у — 2 = 0 и х — Зу + 1 = 0?
4. Две прямые пересекаются в точке А (2; —1). Одна из них
проходит через начало координат, другая же через точку В (5; 1).
Найти острый угол между этими прямыми.
4 Зак. 3032. И. Л. Зайцев
50
ПРЯМАЯ ЛИНИЯ
[гл. ш
§ 17. Условие параллельности прямых. Если прямые
параллельны между собой, то они образуют одинаковые
углы cq и а2 с положительным направлением оси Ох (черт. 25).
Из равенства углов cq
и а2 следует
tg «1 = tg «2
или
= k2.
Обратно, если = k2i
т. е. tg = tg а2, то
СС^ —— Otg»
а это значит, что данные
прямые параллельны.
Итак, если прямые па-
раллельны между собой,
то их угловые коэффициен-
ты равны (и наоборот).
Пример. Написать уравнение прямой, проходящей че-
рез точку А (—2; 6) и параллельной прямой 5х Зу— 7 = 0.
Решение. Через точку А проходит пучок прямых, среди
которых находится искомая прямая. Следовательно, прежде
всего пишем уравнение пучка прямых [(2) § 14], проходя-
щих через точку А:
у.— 6 — р (х 2).
Затем находим из данного в задаче уравнения прямой ее
угловой коэффициент; применяя равенство (8) § 12, получим;
5
k = —
Согласно условию параллельности угловой коэффициент
5
искомой прямой тоже равен------.
о
5
П одставим найденное значение k = — в уравнение
о
пучка:
у — 6 =-----^-(х + 2).
§18] УСЛОВИЕ ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМЫХ 51
Выполнив необходимые преобразования, получим искомое
уравнение прямой:
5х —Зу — 8 = 0.
Упражнения
1. Параллельны ли прямые:
1) 2х + 3у —7 = 0 и 2х4-Зу + 9 = 0,
2) у = 2х + 3 и 4у — 8х = 1,
3) Зх — 5у = 0 и 6х-|-10у 4-5 = 0?
2. Чему равно а в уравнении прямой у = ях4-4, которая па-
раллельна прямой 2у — Зх — 5 = 0.
3. Написать уравнение прямой, проходящей через точку А (2; 3)
и параллельной прямой у = 2x4-5.
4. Прямая проходит через точку А (—2; —1) и параллельна
прямой 2х — у = 5. Написать ее уравнение.
х у
5. Точка движется по прямой, параллельной данной ~ 1,
4 о
и в некоторый момент времени проходит точку А (—1; 8). Найти
уравнение прямой, по которой движется точка.
6. Даны точки А (3; 5)иВ(—3; 4). Написать уравнение прямой,
проходящей через точку С(—2; 1) параллельно АВ.
7. Написать уравнение прямой, проходящей через точку А (2; 5)
и параллельной прямой, на которой лежат точки В (—4; 3) и
С (-4; 1).
8. Прямая, параллельная прямой 4х — 5у — 9 = 0, пересекает
ось Оу на расстоянии, равном 3 единицам масштаба вверх от начала
координат. Написать уравнение этой прямой.
9. Написать уравнение прямой, отсекающей на оси Ох отрезок,
равный 5, и параллельной прямой = 1.
§ 18. Условие перпендикулярности прямых. Пусть две
прямые взаимно перпендикулярны и образуют с положитель-
ным направлением оси Ох углы ах и а2 (черт. 26).
В этом случае
а2 = 90°4-сс1,
отсюда
tgct2 = tg(90°-]-a1).
Но
tg (90° 4- а,) = — ctg а, = — .
Следовательно,
1
tg а9 = -— ----
4*
52
ПРЯМАЯ ЛИНИЯ
[гл. ш
или
Обратно, если
a2 =—-L, /гг
то tg«2— tg»!-" ctg«i —tg(90oH-at).
Отсюда
а2 = 90° -J- сер
т. е. данные прямые взаимно перпендикулярны.
Таким образом, если прямые взаимно перпендикулярны,
то их угловые коэффициенты обратны по абсолютной
величине и противоположны по знаку {и наоборот).
Так, например, если у одной прямой угловой коэффициент
2 5
равен то у перпендикулярной ей прямой он равен —
Пример. Написать уравнение прямой, проходящей через
точку А (—3; 5) и перпендикулярной прямой 4х — Ъу—10 == 0.
Решение. Через точку А проходит пучок прямых, среди
которых находится и искомая прямая. Поэтому напишем сна-
чала уравнение этого пучка
у — 5 = k (х —I- 3). (2)
Чтобы выделить из него нашу прямую, нужно найти ее угло-
вой коэффициент связанный с угловым коэффициен-
§ 19]
ПЕРЕСЕЧЕНИЕ ПРЯМЫХ
53
том k2 данной прямой равенством (1). Но k2 — ~^-f следова-
, 3
тельно, kl =----
Подставив в уравнение (2) вместо k найденное его зна-
чение kit получим:
у-5 = -4(хЧ-3).
Это и есть искомое уравнение прямой. Преобразовав его,
найдем:
4у —20 = —Зх~9,
или
Зх4_4д;_11 =0.
Упражнения
1. Перпендикулярны ли прямые
1) Зх— у — 3 = 0 и х-|~3у — 17 = 0,
2)2х + 5у — 6 = 0 и 5х + 2у — 3 = 0?
2. Написать уравнение прямой, проходящей через точку Л (2; 7)
перпендикулярно к прямой Зх — 2у — 8 = 0.
3. Из точки А(—2; —3) на прямую х — 2у-|-3 = 0 опущен
перпендикуляр. Написать его уравнение.
4. Написать уравнение прямой, проходящей через данную точку
Л(—2; —1) перпендикулярно к прямой — —~ = 1.
5. Написать уравнение прямой, отсекающей на оси Оу отрезок,
х у
равный 5, и перпендикулярной к прямой =
о 4
6. Даны координаты вершин треугольника АВС:
А (3; 4), В (2; 5) и С (7; 6).
Написать уравнение высоты, опущенной на сторону АС.
7. Написагь уравнение прямой, проходящей через середину
отрезка, соединяющего точки А (4; 3) и В (—2; 5), перпендикулярно
к нему.
8. Противоположные вершины ромба лежат в точках Л (5; 7)
и С (3; 3). Написать уравнения его диагоналей.
§ 19. Пересечение прямых. Пусть даны две прямые,
определяемые уравнениями:
Лх4-Ву+ С = 0,
А jX —= 0.
Требуется найти точку их пересечения.
54 ГПРЯМАЯ линия [гл. III
Так как точка пересечения данных прямых есть их общая
точка, то ее координаты должны удовлетворять как первому,
так и второму уравнению, т. е. эти координаты должны
быть общими корнями данных уравнений.
Чтобы найти эти корни, нужно, как известно из алгебры,
решить совместно данные уравнения, рассматривая их как
систему уравнений.
Пример 1. Найти точку пересечения прямых
2х-|-Зу—12 — 0 и х—у—1=0.
Решение. Решим данные уравнения как систему. Умно-
жив второе уравнение на 3 и сложив результат с первым
уравнением, получим:
2х4-3у— 12 = 0
~"^3х —3 у — 3 = 0
Ъх —15 = 0,
откуда
х = 3.
Зная х, находим у, например, из второго уравнения:
у — х— 1=3— 1=2.
Пример 2. Найти точку пересечения прямых
2х— 5_у —8 = 0 и 4х—10у — 3 = 0.
Решение. Умножив все члены первого уравнения на —2
и сложив полученное уравнение со вторым, найдем:
— 4,v-f-10y— 16 = 0
+ 4х— 10у — 3 = 0
— 19 = 0,
что невозможно. Значит, данная система уравнений решений
не имеет, а потому прямые, определяемые этими уравне-
ниями, не имеют общих точек, т. е. данные прямые парал-
лельны.
К этому же заключению можно прийти, сравнивая угло-
вые коэффициенты данных прямых.
§ 19]
ПЕРЕСЕЧЕНИЕ ПРЯМЫХ
55
Упражнения
1. Найти координаты точки пересечения прямой 4х— Зу—
— 10 = 0:
1) с осыо Ох, 2) с осью Оу.
2. Найти точку пересечения двух прямых:
1) Зх — 2у — 4 = 0 и х 4~ Зу — 5 = 0;
2) х — 5у 4-7 = 0 и 15у— Зх— 4 = 0.
3. Показать, что прямые 7х — 9у4~15 = 0и 13x4- 12у — 20 = О
пересекаются в точке, лежащей на оси Оу.
4. Определить координаты вершин треугольника, если даны
уравнения его сторон:
у = 2х—1, 2у— х = 3, Зу4-2х — 5 = 0.
5. Найти точку, в которой прямая, соединяющая точки А (4; 1)
и В (—1; —4), пересекает ось абсцисс.
6. Написать уравнение прямой, проходящей через точку А (2; 5)
и через точку В, в которой пересекаются прямые
Зх — у = 0 и 2х + 5у — 17 = 0.
7. Через точку пересечения прямых
2х — у — 3 = 0 и х — Зу — 4 = 0
проведена прямая, параллельная прямой х4~У — 1. Написать урав-
нение проведенной прямой.
8. Через точку пересечения прямых
х 4~ 2у -|- 2 = 0 и Зх 4- 4у 4“ 9 = 0
проведен перпендикуляр к прямой 2х 4- Зу — 6 = 0. Написать урав-
нение этого перпендикуляра.
9. Даны уравнения сторон треугольника:
2х — 5у = 3, х 4- Зу = 7 и Зх — 2у 4~ 1 = 0.
Написать уравнение высоты, проведенной на сторону 2х — 5у = 3.
10. Дан треугольник, уравнения сторон которого суть
Зх 4~ 2у — 5 = 0, Зх — у — 11=0, Зх 4- У — 1 = 0.
Написать уравнение перпендикуляра, восставленного к стороне
Зх 4“ 2у — 5 = 0 в ее середине.
11. Диагонали ромба пересекаются в точке Л4(5; 1). Уравнения
одной из диагоналей и одной из сторон его соответственно
у — х + 4 = 0 и Зу — х — 6 = 0.
Найти координаты вершин ромба.
56
ПРЯМАЯ ЛИНИЯ
[гл. ш
Смешанные задачи
1. Найти точки пересечения прямой Зх-f- 4у = 8 с осями коор-
динат.
2. Показать, что прямые
4х + Зу — 5 = 0, Зх — у + 6 = 0 и 2х — у 5 = 0
проходят через одну точку.
3. Прямая, параллельная оси Ох и проходящая выше ее на
расстоянии, равном 4, пересекает прямую Зх— 4у-|-5 = 0. Найти
точку пересечения этих прямых.
4. Показать, что прямая, на которой лежат точки Л(—3; 6) и
В (2; —4), проходит через начало координат.
5. Написать уравнение прямой, проходящей через точку А (3; —5)
в отсекающей на оси Ох отрезок, равный —2.
6. Проверить, лежат ли на одной прямой точки
Я(1; 3), Я (5; 7) и С (10; 12).
7. Найти длину отрезка прямой 4х-|- Зу + — 0, заключенного
между осями координат.
8. Какую ординату имеет точка С (5; у), лежащая па той же
прямой, что и точки А (—8; —6) и В(—3; —1)?
9. Написать уравнение прямой, проходящей через точку А (—3; 4)
и параллельной биссектрисе первого координатного угла.
10. На биссектрисе первого координатного угла найти точку,
расстояние которой от точки М (—2; 0) равно 10.
11. При каком значении т прямая у = /7?х-|-3 проходит через
точку пересечения прямых 2х — у -|- 1 = 0 и у = х + 5?
12. Противоположные вершины квадрата лежат в точках
А (—2; 5) и С (2; 8). Найти длину и уравнения его диагоналей.
13. Две смежные вершины квадрата ABCD лежат в точках
А (—5; 4) и D (—3; 2), а диагональ его АС параллельна оси Ох,
Определить координаты двух других вершин квадрата.
14. Даны уравнения сторон треугольника:
х-|-2у — 2 = 0, 2х + у — 13 = 0 и х — 2у-|-6 = 0.
Показать, что этот треугольник прямоугольный, и определить ра-
диус окружности, описанной около него.
15. Нужно провести прямую, проходящую через точку /И (30; 50)
и образующую с положительным направлением оси Ох угол 45°.
На каком расстоянии от оси Ох нужно взять две точки, отстоя-
щие от оси ординат на расстоянии 1 и 3, чтобы искомая прямая
проходила через них?
16. Определить углы наклона к положительному направлению
оси Ох сторон треугольника АВС, вершины которого находятся
в точках А (1; 3), В (6; 1) и С(—1; —3).
17. Две прямые пересекаются в точке А (2; —5). Найти острый
угол между ними, если одна из них проходит через точку В (1;—3),
а другая — через точку С (4; 1).
18. Даны две прямые y = 2x-f-l и Зх — 2у — 5 = 0. Опреде-
лить расстояние между точками, в которых они пересечены прямой
х — у — 3 — 0.
§ 19]
СМЕШАННЫЕ ЗАДАЧИ
57
19. Через точку А(—5; 3) проведена прямая так, что ее отре-
зок, заключенный между координатными осями, делится в этой
точке пополам. Написать уравнение этой прямой.
20. Через точку А (—4;—3) проведена прямая так, что опа отсекает
на осях координат равные отрезки. Написать уравнение этой прямой.
21. Сторона треугольника, равная 10, лежит на оси Ох, а одна
из его вершин — в точке А (4; 6). Найти уравнения сторон тре-
угольника, если одна из боковых сторон его отсекает на оси абс-
цисс отрезок, равный — 2 (два случая).
22. Дан треугольник АВС с вершинами
А (8; 4), В (—2; 6) и С (4; 0).
Из точки £), делящей сторону ВС в отношении BD : DC ==2:1,
проведена прямая через середину Е стороны АВ. Найти уравнение
и длину отрезка DE.
23. Даны две точки А (—4; —3) и В (1; 2). Написать уравнение
прямой, проведенной перпендикулярно к прямой АВ через точку С,
делящую отрезок АВ в отношении АС: СВ = 1:2.
24. Две вершины треугольной однородной пластинки лежат
в точках А (6; 0) и В(—8; —2), а ее центр тяжести в точке М (1; 2).
Найти координаты третьей вершины этой пластинки.
25. В трех точках А(—1; 0), В(—2; 4) и С (4; —5) помещены
грузы соответственно в 30 кг, 50 кг и 70 кг. Найти центр тяжести
этой системы.
26. Дай треугольник АВС с вершинами
Л(—5; —1), В(—1; 4) и С(3; 2).
Через вершину А проведена прямая, параллельная ВС, а через вер-
шину В — прямая, перпендикулярная к ВС. Найти координаты точки
пересечения проведенных прямых.
27. По какой линии должна двигаться точка, начальное поло-
жение которой определено координатами (3; 8), чтобы дойти крат-
чайшим путем до прямой у — -^х— 1? В какой точке она достигнет
этой прямой и как велик будет пройденный путь?
28. Две прямые пересекаются в точке, лежащей на оси Ох, под
углом 45° друг к другу; прямая с меньшим наклоном к положи-
тельному направлению оси Ох имеет уравнение 2х — Зу — 6 = 0.
Написать уравнение второй прямой.
29. Даны уравнения сторон треугольника
2х —Зу+11=0, Зх-{-у —11=0, х+4у = 0.
Найти угол, образованный с положительным направлением оси Ох
медианой, проведенной на сторону х -|- 4у = 0.
30. Отрезок прямой х -|- 2у — 6 = 0, заключенный между осями
координат, разделен на три равные части и в точках деления вос-
ставлены перпендикуляры к этой прямой до пересечения с осью Оу.
Найти координаты точек пересечения.
31. В треугольнике АВС даны середины его сторон 1),
Ai2(3; —5) и Л43(5; —3). Составить уравнения сторон треуголь-
ника АВС.
58
ПРЯМАЯ ЛИНИЯ
[гл. ш
32. Даны две вершины Л(3; —1) и В (5; 5) треугольника АВС
и точка N (6; 2) пересечения его высот. Найти координаты третьей
вершины треугольника.
33. Даны уравнения сторон треугольника:
х 4" у — 3 = 0, х = 0, 2х -1- у — 1 = 0.
Найти длину высоты, проведенной на сторону х-]-у — 3 = 0.
34. Определить площадь параллелограмма, зная уравнения его
сторон:
у = 2х-|-1» У = 2х— 5, у == х — 2, у = х4~2.
35. Определить площадь ромба, зная уравнения его сторон:
пл 4 4 20
У = 0, у = 4, у = -^х, У==ТХ~~"3'
36. Один из катетов равнобедренного прямоугольного треуголь-
ника параллелен оси Ох и отстоит от нее на расстоянии, равном 8,
а продолжение гипотенузы проходит через начало координат. На-
писать уравнения сторон этого треугольника, если его катет равен 6
и треугольник расположен в первом координатном углу (два случая).
37. Две стороны квадрата определяются уравнениями:
х4~3у 4-10 = 0 и Зх — у — 20 = 0,
а его центр лежит в точке Л4 (3; —1). Найти уравнения диагона-
лей квадрата.
38. Гипотенуза равнобедренного прямоугольного треугольника
параллельна оси Ох. Вершина прямого угла лежит в точке А (8; 20),
а одна из вершин острого угла расположена на оси Оу. Написать
уравнения сторон этого треугольника (два случая).
39. Одна из сторон правильного треугольника параллельна оси Оу
и отсекает па оси Ох отрезок, равный —4, а противоположная
вершина лежит в точке А (2; 0). Найти уравнения высот треуголь-
ника.
40. Гипотенуза прямоугольного треугольника пересекает оси
координат в точках А (—5; 0) и В (0; 5); а один из катетов — в точ-
ках С (—2; 0) и D (0; 1); продолжение же другого катета отсекает
на оси Ох отрезок, равный 4. Найти координаты вершин этого
треугольника.
41. Две стороны и диагональ, исходящие из одной вершины
параллелограмма, определяются соответственно уравнениями
х— у 4-4 = 0, у = 5 и 5х4~2у— 15 = 0.
Написать уравнения двух других сторон параллелограмма, если
точка пересечения его диагоналей лежит на оси Ох.
42. Две противоположные вершины ромба ABCD лежат в точ-
ках >4(1; 3) и С (5; 9), а сторона AD определяется уравнением
х — у 4- 2 = 0. Найти координаты двух других вершин его.
43. Две противоположные вершины прямоугольника ABCD
лежат в точках Л (1; 4) и С (5; 6), а сторона CD наклонена к поло-
жительному направлению оси Ох под углом 45°. Найти площадь
этого прямоугольника.
§ 191
СМЕШАННЫЕ ЗАДАЧИ
59
44. Одна из сторон ромба проходит через начало координат
и образует с положительным направлением оси Ох угол, равный
4
arctg-тг, а другая сторона определяется уравнением у = 8. Найти
о
уравнения остальных сторон ромба, если его диагонали пересе-
каются между собой в точке, лежащей на оси абсцисс.
45. Дан треугольник АВС с вершинами
Л(4;1), В (7; 5) и С(—4; 7).
Найти точку пересечения биссектрисы угла А с противоположной
стороной ВС.
46. Даны вершины треугольника:
А (—2; —8), В (3; —8) и С (3; —5).
Написать уравнение биссектрисы угла В.
47. Из точки А (6; 9) направлен луч света под углом 45° к по-
ложительному направлению оси Ох\ дойдя до оси Ох, он отра-
жается от нее. Найти уравнения падающего и отраженного лучей.
48. Луч света направлен по прямой у — — 4; дойдя до
оси Ох, он от нее отражается. Определить уравнение отраженного
луча.
49. Луч света, выйдя из точки А (2; 3), отражается от оси Ох
и попадает в точку В (5; 8). Найти уравнения падающего и отра-
женного лучей.
50. Луч света, проходящий через точку А (3; 4), отражается
от прямой ху— 2 = 0 и после отражения проходит через точку
В (5; 2). Найти уравнения падающего и отраженного лучей.
ГЛАВА IV
КРИВЫЕ ВТОРОГО ПОРЯДКА
§ 20. Окружность и ее уравнение. Окружностью на-
зывается геометрическое место точек, одинаково удален-
ных от одной точки, называемой центром.
Пользуясь этим определением, выведем уравнение окруж-
ности. Пусть радиус ее равен г, а центр находится в точке
01 (а\ Ь). Возьмем на окружности произвольную точку М (х; у)
(черт. 27).
По формуле расстояния между двумя точками можем
написать:
OtM = г = У(х —c)24-(_v —Z?)2,
или, после возведения обеих частей равенства в квадрат,
(x — af + (y — bj = r*. (1)
§ 20] УРАВНЕНИЕ ОКРУЖНОСТИ 61
Так как точка М нами взята произвольно, а радиус г —
величина постоянная, то равенство (1) справедливо для всех
точек окружности, т. е. координаты любой ее точки удовле-
творяют этому равенству. А если так, то равенство (1) нужно
рассматривать как уравнение окружности.
В уравнении (1) а и b — координаты центра окружно-
сти, ахи у — текущие координаты.
Если положить а—0, то уравнение (1) обратится в сле-
дующее:
х2 + (у — Ь)2 = г2
и будет определять окружность с центром на оси Оу
(черт. 28).
При 6 = 0 уравнение (1) примет вид
(х — а)2 + у2 — г2
и будет определять окружность с центром на оси Ох
(черт. 29).
зуется в следующее:
х2 у2 — г2
и будет определять окружность с центром в начале коор-
динат (черт. 30).
Можно построить окружность, имея ее уравнение. Пусть,
например, требуется построить окружность
(x-2)’- + (j, + 3)2=9.
62
КРИВЫЕ ВТОРОГО ПОРЯДКА
[гл. IV
Перепишем это уравнение в следующем виде:
(* — 2)2+Ьу— (-3)р = 9; '
сравнивая это уравнение с(1), видим, что координаты центра Ot
окружности суть (2;—3) и радиус ее г = 3. Построив
точку Ot(2; —3), опишем из нее радиусом, равным 3 еди-
ницам масштаба, искомую окружность (черт. 31).
§ 21. Уравнение окружности как частный вид общего
уравнения второй степени. Раскрыв скобки в уравнении (1)
§ 20, можем написать:
х2 — 2ах + а2 + у2 — 2by + b2 = г2,
или
x2 + j/2_2^x — 2by-\~a2Arb2 — г2 —0.
Умножив все члены последнего равенства на Л, получим:
Ах2 + А у2 — 2 Аах — 2 A by + Аа2 + А Ь2 — Аг2 = 0. (1)
Положим:
— 2Aa = D,
— 2АЬ = Е,
Aa2~\-Ab2 — Ar2—F;
тогда уравнение (1) окружности примет вид
Ах2 + Ау2 4- Dx + 4- F = 0. (2)
§ 21] УРАВНЕНИЕ ОКРУЖНОСТИ 63
Уравнение (2) является частным случаем общего уравнения
второй степени с двумя переменными. В самом деле, сравним
уравнение (2) с общим уравнением второй степени с двумя
переменными, имеющим, как известно, следующий вид:
Ax2-±Bxy + Cy2-}-Dx + Ey + F^Q. (Ъ)
Мы видим, что уравнение (2) отличается от уравнения (3)
только тем, что у первого коэффициенты при х2 и у2 оди-
наковы и отсутствует член, содержащий произведение ху.
Таким образом, окружность определяется общим урав-
нением второй степени с двумя переменными, если в нем
коэффициенты при х2 и у2 равны между собой и отсут-
ствует член с произведением ху.
Обратно, уравнение вида (2), вообще говоря, определяет
окружность. Убедимся в этом на примере. Пусть дано урав-
нение
х2 у2 4Х — — 5 — 0.
Перепишем его в следующем виде:
(х2 4Х) + (у _ 8^) = 5
и преобразуем двучлены, стоящие в скобках, в полные квад-
раты суммы и разности, прибавив к первому 4, ко второму 16.
Чтобы равенство при этом не нарушилось, увеличим и правую
часть его на сумму 4+16. Получим:
(х2+4х + 4) + (у2 —8у+ 16) = 5 4- 4-4- 16,
или
(х 4- 2)2 + (у — 4)2 = 25.
Последнее равенство является уравнением окружности,
имеющей радиус, равный 5, и центр в точке Ог (—2; 4).
Бывают однако случаи, когда уравнение (2) при некото-
рых значениях коэффициентов не определяет окружности;
например, уравнению х24и->2 = 0 удовлетворяют координаты
единственной точки (0; 0), а уравнению х24~У2 —— 4 не
удовлетворяют координаты ни одной точки, так как сумма
квадратов действительных чисел не может иметь отрицатель-
ного значения.
Пример. Дана окружность х24~У2— 4x-j-2y—15 = 0
и хорда Х-4-.У — 7 = 0. Найти длину этой хорды.
Решение. Так как концы хорды являются общими точ-
ками окружности и хорды, то их координаты удовлетворяют
64 КРИВЫЕ ВТОРОГО ПОРЯДКА [гл. IV
как уравнению первой, так и уравнению второй линии. По-
этому, чтобы найти эти координаты, нужно решить совместно
уравнения окружности и хорды. Подставив значение
_V = 7 — х
в уравнение окружности, получим:
Л24-(7_ х)2 —4х + 2(7 — х)~ 15 = 0,
или
Х2_р49_14х^.х2_4д._|_ 14_2х—15 = 0,
или, наконец,
х2— 10% +24 = 0.
Отсюда
Х12 = 5 dz /25 — 24 = 5 ± 1,
Xi = 5 — 1 = 4, Х2== б *+ 1 = 6.
Находим значение у:
yt = 7 — xt = 7 — 4 = 3,
у 2 — 7 — х2 — 7 — 6=1.
Итак, концами хорды служат точки с координатами (4; 3)
и (6; 1).
По формуле расстояния между двумя точками можем
определить искомую длину хорды
d = /(4 —6)2+(3—1/ == У 4^4 = 2 /2.
Упражнения
1. Написать уравнение окружности с центром в точке и с ра-
диусом г, если даны:
1) 01 (—1; 2), г = 5, 2) Ot (—2; —3), г = /б , 3) Ot (0; 5), г = 6.
2. Построить окружности:
1) (х + ЗГ + (У~2)— 16, 2) (х-2)2 + (у + 1)2-9,
3) л2 + (у — 4)2 — 25.
3. Дана окружность (х — З)2 + (у + 5)2 = 16. Лежат ли на ней
точки:
Л (3; —1), В (3; —9) и С(0; —3)?
4. Дана окружность (х2)2(у 4~3)2 = 13 и точка на ней
с ординатой, равной нулю. Найти ее абсциссу.
§ 22] ЭЛЛИПС И ЕГО УРАВНЕНИЕ 65
5. Написать уравнение окружности с центром в точке <?г и про-
ходящей через точку Л, если даны:
1) Ох (2; 1), А (5; 5), 2) Ot (—3; 2), А (— 4; 0).
6. Написать уравнение окружности, проходящей через две
точки: Л (—5; 5) и В (1; 3) и имеющей радиус г = 1^10.
7. Написать уравнение окружности, проходящей через две
точки: А (2; 4) и В (—2; 0), и имеющей центр па оси Ох.
8. Составить уравнение окружности, касающейся оси Ох в на-
чале координат и проходящей через точку А (0; —8).
9. Найти координаты центра и длину радиуса окружности
X2 — 8у == 0.
10. Построить окружности:
1) х2 + у24-4х — бу — 3 = 0, 3) х2 + у2-~12у-|-11 =0,
2) x2 + y2 + Sx + 7 = 0, 4) 4х24-4у2 — 16x4» 8у —5 = 0.
11. Даны окружности
х2 -j- у2 — 6х+8у = 0 и х2-\-у2-\-2х—12у+ 1 = 0.
Написать уравнение их линии центров (т. е. уравнение прямой, про-
ходящей через центры данных окружностей).
12. Найти расстояние между центрами окружностей х24~У2~1б
и х2-\-у2 — 12x4-11 =0.
13. Написать уравнение диаметра окружности х2 у2 4- 6х 4-
4- 8у = 0, параллельного оси Оу.
14. Дана окружность х2 4~ у2 — 8х — 4у — 5 = 0. Написать урав-
нение ее диаметра, образующего с осью Ох угол 45°.
15. Дана окружность х2 4- у2 — 2х 4~ бу — 6 = 0. Написать урав-
нение ее диаметра, перпендикулярного к хорде 2х — у 4~ 3 = 0.
16. Найти координаты точек, в которых окружность х24~ У2—
— 6x4-8у 4-5 = 0 пересекает ось Ох.
17. Написать уравнение радиуса, проведенного в точку Л(1; 4)
окружности х2 4~ У2 — 4у — 1 = 0.
18. Написать уравнение касательной, проведенной к окружно-
сти х2 4- У2 — 12х 4- 2у 4- 12 = 0 в точке ее А (9; 3).
19. Найти координаты точек пересечения прямой у = х—1
с окружностью х2 4* У2 — Зх — 4у — 5 = 0.
20. Найти точки пересечения прямой х = 3 с окружностью
х2 4~ у2 + Зх — бу — 9 = 0.
21. Как расположена прямая у — 6 = 0 по отношению к окруж-
ности х2 4~ У2 — Зх — 9 = 0?
22. Написать уравнение общей хорды окружностей х24~у2 = 16
и х24-у-— 10х— 10у4-30 = 0.
§ 22. Эллипс и его уравнение. Эллипсом называется
геометрическое место точек, сумма расстояний каждой
из которых от двух данных точек, называемых фокусами,
есть величина постоянная (и большая, чем расстояние
между фокусами).
5 Зак. 3032. И. Л. Зайцев
66
КРИВЫЕ ВТОРОГО ПОРЯДКА
[гл. IV
Пусть, например, на эллипсе взяты точки Л1г, ТИ2, Л43, Л14
и т. д. (черт. 32). Если фокусы обозначить через F и F1?
то согласно данному определению можно написать:
F1Mi + FMi = РгМ2 + РМ2 = РгМ% + FM* =
= FiM4 -4- FM4 = const. (1)
Геометрическое место точек, обладающих вышеуказанным
свойством (1), и есть эллипс.
На основании определения эллипса составим его уравне-
ние. Для этого выберем систему координат следующим обра-
зом. За ось Ох примем прямую, проходящую через фо-
кусы F и Fl9 а за ось Оу — прямую, перпендикулярную
к FFt и проведенную через середину отрезка FFL (черт. 33).
Обозначим расстояние f\F между фокусами через 2с, тогда
координаты фокусов будут:
Р(с\ 0) и Л(— с;0).
§ 22] ЭЛЛИПС И ЕГО УРАВНЕНИЕ 67
Возьмем на эллипсе произвольную точку /И (х; у). Обозначим
постоянную величину суммы расстояний каждой точки от
фокусов через 2а, тогда
F/W + FlM — 2a. (2)
По формуле расстояния между двумя точками найдем:
FM = —0)2 = У(х —c)2+j>2 ,
= У(x + ^ + Cj' —О)2 = У(х+с)2+У.
Теперь равенство (2) перепишется следующим образом:
]Л(х—с)2+у*+1Л*4-£)2+У2 = (3)
и будет представлять уравнение эллипса в принятой системе
координат.
Упростим уравнение (3). Для этого перенесем один из
радикалов в правую часть уравнения:
]/*(х — с)2 4 у2 — 2а — У (х 4~ с)2 + у2.
Возведем обе части этого равенства в квадрат:
(х — с)2 4- J/2 = 4а2 — 4а '|/’(л- + ^)2 + У2 + (* + О2 4“У2-
Раскроем скобки:
х2 — 2cx + c24-j/2 =
= 4я2— 4а Ух2-]- 2cx~|-c24"j24- х24~ 2сх 4 с2 4у2.
Приведем подобные члены:
— 2с х = 4а2 — 4« ]/х2 4 %сх 4~6'2 + У2 4 х>
или
4а Ух2 4 %сх 4 62 У2 — 4&2 4 4сх.
Сократив на 4 и снова возведя в квадрат обе части ра-
венства, получим:
а2 (х2 4 %сх + с2 + У2) — (а2 4- ех)2>
или
а2х2 2а2сх 4 а2с2 4 а2у2 = а4 4 2а2сх 4 с2х2.
5*
68
КРИВЫЕ ВТОРОГО ПОРЯДКА
[гл. IV
Перенесем все члены, содержащие х и у, в левую часть
равенства, остальные члены — в правую:
а2х2--С2Х2 а2у2 — а1----а2С2,
ИЛИ
(а2 — с2) х2 + а2у2 = а2 (а2 — с2). (4)
Но согласно определению эллипса
2с < 2а,
отсюда
с < а.
Из последнего неравенства следует, что а2 — с2 > 0, а по-
тому эту разность можно обозначить через Ь2. Подставив это
обозначение в равенство (4), найдем:
b2x2^a2y2—d2b2. (5)
Наконец, разделим все члены последнего равенства на а2Ь2',
окончательно получим:
(6)
где х и у— текущие координаты точек эллипса, а
Ь2 = а2 — с2. (7)
Уравнение (6) и есть простейший вид уравнения
эллипса *).
§ 23. Исследование уравнения эллипса. Определим сна-
чала у из уравнения (5) § 22:
2 а2Ь2 _ ь2х2 _ Ь2 (а2 — х2)
у д2 ,
отсюда
(1)
*) Уравнение (6) получилось в результате двукратного возведе-
ния в квадрат уравнения (3), благодаря чему, вообще говоря, воз-
можно появление посторонних корней. Можно показать, что уравне-
ние (6) не имеет посторонних корней, т. е. любая точка, координаты
которой удовлетворяют уравнению (6), лежит па эллипсе.
§ 23] ИССЛЕДОВАНИЕ УРАВНЕНИЯ ЭЛЛИПСА 69
Из того же уравнения (5) найдем:
следовательно,
x = (2)
Рассмотрим теперь равенства (1) и (2).
I. Пусть
| х | < а *).
Тогда под корнем в равенстве (1) получится положительное
число, а потому у будет иметь два значения, равные по аб-
солютной величине, но с противоположными знаками. Это
значит, что каждому значению х соответствуют две точки
эллипса, симметричные относительно оси Ох.
Пусть теперь
Ь1<*.
Тогда каждому значению у, как мы видим из равенства (2),
отвечают два значения х, равные по абсолютной величине,
но с разными знаками. Отсюда следует, что каждому значе-
нию у соответствуют на эллипсе две точки, симметричные
относительно оси Оу.
у2
Из сказанного заключаем: эллипс —4-~=1 симмет-
а2 1 Ь2
ричен относительно координатных осей.
II. Найдем точки пересечения эллипса с осью Ох. Пусть
тогда из равенства (2) имеем:
х = zt у Y ь2 — — а-
Отсюда следует: эллипс пересекает ось Ох в двух точ-
ках, координаты которых (я; 0) и (— а\ 0) (точки А и
на черт. 34).
:1:) | х | означает, что х берется по абсолютной величине; таким
образом, запись | х | < а нужно читать так: х по абсолютной вели-
чине меньше чем а.
70
КРИВЫЕ ВТОРОГО ПОРЯДКА
1гл. IV
III. Найдем точки пересечения эллипса с осью Оу. Пусть
х = 0;
тогда из равенства (1) имеем:
Отсюда заключаем, что эллипс пересекает ось Оу в двух
точках, координаты которых (0; Ь) и (0; —Ь) (точки В
и на черт. 35).
IV. Пусть х принимает такие значения, что
|х(>а; (3)
тогда выражение под корнем в равенстве (1) будет отрица-
тельным, и, следовательно,- у будет иметь мнимые значения.
А это значит, что не существует точек эллипса, абсциссы
которых удовлетворяют условию (3), т. е. эллипс расположен
внутри полосы, заключенной между прямыми х — и
х —— а (черт. 34, прямые KL и PQ).
Если же положить
(4)
то из равенства (2) получим для х мнимые значения. Это
говорит о том, что точки, удовлетворяющие условию (4), на
эллипсе не лежат, т. е. эллипс заключен между прямыми
yz=^-b и у —— b (черт. 35, прямые РК и QL).
§ 24]
ЭКСЦЕНТРИСИТЕТ ЭЛЛИПСА
71
Из сказанного следует, что все точка эллипса лежат
внутри прямоугольника, стороны которого параллельны
координатным осям и имеют длины, равные 2а и 2b, а
диагонали пересекаются в начале координат (черт. 36).
Эллипс имеет форму, показанную на черт. 37.
Точки А, В и Вг называются вершинами эллипса, а
точка О — его центром. Отрезок AtA = 2a называется его
большой осью, а отрезок ВгВ = 2Ь— малой осью. Отрезки
FM и FrM носят название фокальных радиусов точки М.
§ 24. Эксцентриситет эллипса. Эксцентриситетом эл-
липса называется отношение расстояния между его фо-
-ч ~ 2с с
кусами к длине большой оси. т. е. — = —.
2а а
72 КРИВЫЕ ВТОРОГО ПОРЯДКА [гл. IV
Эксцентриситет обычно обозначают буквой е. Таким об-
разом,
е = -. (1)
а v
Но согласно формуле (7) § 22
с =/«2—^.
Поэтому для определения эксцентриситета может служить
следующее равенство:
Так как 0 < с < а (§ 22), то эксцентриситет эллипса есть
положительная величина, меньшая единицы.
Эксцентриситет характеризует форму эллипса, что легко
усмотреть из формулы (2). Например, если уменьшить вели-
чину Ь, не изменяя а, то разность а2— Ь2 увеличится, отчего
увеличится и дробь правой части формулы, а следовательно,
и е станет больше. Эксцентриситет также возрастет, если
увеличить а. оставив b постоянной величиной.
Мы рассмотрели эллипс, у которого b < а. При b > а
уравнение (6) § 22 представляет эллипс, фокусы которого
лежат на оси Оу\ в этом случае его большая ось равна 2/?,
а малая 2п. В соответствии с этим формула (7) § 22 и
формулы (1) и (2) настоящего параграфа примут такой вид:
с
е — ~Ь'
_ у 6‘.>_Я2
е-~ ь
П р и м е р. Дан эллипс 16х2 -ф- 25у2 — 400. Определить
длину его осей, координаты вершин и фокусов, а также ве-
личину эксцентриситета.
Решение. Разделив обе части данного уравнения на
400, получим:
Отсюда
а2 =25, Z>2=16
и
я = 5, b~4.
§ 25J связь эллипса с окружностью 73
Итак, большая ось эллипса AtA — 2^=10, а малая —
В1В = 2&—8 (черт. 38).
Координаты вершин его будут:
Л (5; 0), Лх(— 5; 0), В(0;4), В,(0;—4).
Чтобы найти координаты фокусов, нужно узнать величину
OF—с, Из равенства (7) § 22 имеем:
с = ]Лв2 —*2 = /25— 16 = 3.
Следовательно, координаты фокусов будут:
F(3; 0) и Л(—3; 0).
Наконец, по формуле (1) настоящего параграфа находим:
С 3 Г\ г»
6» = —= -- = 0,6.
а 5
§ 25. Связь эллипса с окружностью. Положим, что
полуоси эллипса равны между собой, т. е. а — b» тогда урав-
нение эллипса примет вид
или —
1 аи
Полученное уравнение, как известно, определяет окруж-
ность радиуса, равного а.
74 КРИВЫЕ ВТОРОГО ПОРЯДКА [гл. IV
Посмотрим, чему будет равен эксцентриситет в этом
случае; полагая в формуле (2) § 24
а — Ь,
получим:
е = А^£. = 0.
а
Отсюда заключаем, что окружность есть частный слу-
чай эллипса, у которого полуоси равны между собой, а
следовательно, эксцентриситет равен нулю.
Упражнения
1. Написать простейший вид уравнения эллипса, если даны его
полуоси а = 5 и b ~ 4.
х2 у2
2. Дан эллипс —Определить его оси и расстояние
между фокусами.
3. Определить длину осей и координаты фокусов эллипса 49х2 -|-
Д-24у2 = 117(5.
4. Составить уравнение эллипса, если две его вершины нахо-
дятся в точках А (8; 0) и (— 8; 0), а фокусы имеют координаты
(± 5; 0).
5. Написать уравнение эллипса, координаты фокусов которого
(± 3; 0), а длина большой оси равна 12.
6. Написать уравнение эллипса, у которого длина малой оси
равна 6, а фокусы имеют координаты (0; ±: 4).
7. Найти эксцентриситет эллипса 4х2 Д- 9у2 = 180.
8. Написать простейший вид уравнения эллипса, если даны
2с = 8 и е ~ 0,<8.
9. Написать уравнение эллипса, у которого фокусы имеют коор-
динаты (0; ± 5), а эксцентриситет равен —.
о
10. Написать простейший вид уравнения эллипса, если сумма
полуосей его равна 10, а расстояние между фокусами равно 4]/" 5-
х2 у2
И. Проверить, лежат ли на эллипсе — Д- — = 1 точки Л(0;2),
В (3; 0), С(1; 2).
X2 V2
12. Дан эллипс -^ + -pj==l и течка на нем с абсциссой, рав-
ной 3. Найти ее ординату.
13. Написать простейший вид уравнения эллипса, проходящего
через точку’ Д(3; "К 2) и имеющего большую ось 2а = 2уг 15.
14. Эллипс с центром в начале координат и фокусами па оси Ох
проходит через две точки А и В; написать его уравнение, если даны:
1) А (У~5;/6), В (0; — 2/2); 2)Л(2/б; 2 / 3), В (— 5; — 3).
ГИПЕРБОЛА И ЕЕ УРАВНЕНИЕ
75
§ 26]
15. Найти длину хорды, проходящей через фокус и перпенди-
у^
кулярной к большой оси эллипса +
16. Найти точки пересечения эллипса 4х2 -1- 9у2 = 36 с прямыми:
1)2л4-3у —6 = 0, 2) 2х4-ЗУ З.у= 12, 3)у = х —6.
17. Прямая 2х -J- У — 14 = 0 пересекает эллипс 4У2 + у2 = 100.
Найти длину отрезка этой прямой, заключенного внутри эллипса.
18. Определить траекторию точки Л4, которая при своем движе-
нии остается втрое ближе от точки Л(1; 0), чем от прямой х = 9.
19. Определить эксцентриситет эллипса, если отрезок между
фокусами виден из конца малой оси под прямым углом.
20. Отрезок прямой линии движется так, что концы его сколь-
зят по осям координат. Показать, что при указанном движении
любая точка этого отрезка, кроме середины и концов его, описы-
вает эллипс.
§ 26. Гипербола и ее уравнение. Гиперболой назы-
вается геометрическое место точек, разность расстоя-
ний каждой из которых от двух данных точек, назы-
ваемых фокусами, есть величина постоянная (эта постоян-
ная берется по абсолютному значению, причем она меньше
расстояния между фокусами и не равна нулю).
Пусть, например, точки Mlt Л42> Л43, Л44 лежат на ги-
перболе, фокусы которой находятся в точках F и Ft (черт. 39).
Тогда, согласно данному выше определению, можно написать:
F^ — FMr = FXM2 — FM2 = FjAfg — FM3 =
^FJWi— FM4 = const. (1)
Пользуясь определением гиперболы, выведем ее уравнение.
76 КРИВЫЕ ВТОРОГО ПОРЯДКА [гл. IV
Примем за ось Ох прямую, проходящую через фокусы
и F (черт. 40), а за ось Оу — прямую, перпендикуляр-
ную к отрезку FXF и делящую его пополам.
Положим F1F=2ct тогда координаты фокусов будут
F(c;0) и Fx(— с;0).
Возьмем на гиперболе произвольную точку Ж (х; у) и
обозначим величину разности расстояний каждой точки от
фокусов через тогда
FyM — FM = + 2a*). (2)
По формуле расстояния между двумя точками найдем:
FrM = У(хЧ-с)2 + (з/—
FM = ]Л(х —с)24-(.у—-О)2 = У(х —с)24-_у2
и, заменив в равенстве (2) FtM и FM их выражениями, на-
пишем:
V(хН-с)2Н-у — /(х —с)24-_у2 = ± 2а. (3)
Это и есть уравнение гиперболы относительно выбранной
системы координат, так как оно согласно равенствам (1)
справедливо для любой ее точки.
*) Знак -|- берется в случае, если FiAf>FA4, и знак —,
если F12W<FM
§ 26] ГИПЕРБОЛА И ЕЕ УРАВНЕНИЕ 11
Упростим уравнение (3). Для этого перенесем один из
радикалов в правую часть уравнения:
У*(Х + с)2 -Н у2 — dz 2а + V (х — с)2+у2.
Возведем обе части уравнения в квадрат:
(х 4- с)2 4~ У2 = 4а2 -+~ 4а ]Л(х — с)2 4~ у2 4~ (х — с)2 + у2.
Раскроем скобки:
х2 2с X + с2 + у2 = 4&2 ± 4а V х2 — 2сх + с2+у2 +
4~х2 —2сх4~с24~у2.
Приведем подобные члены:
2с х — 4а2 dz 4а х2 — 2сх 4~ с2 4~ У2 — 2сх,
или
4сх — 4а2 = dz 4я ]Лх2 — 2сх 4~ с2 4~ у2.
Сократив на 4, снова возведем в квадрат обе части урав-
нения; получим:
(сх — а2)2 — а2 (х2 — 2с х 4~ с2 4~ У2).
Раскроем скобки:
с2х2 — 2а2сх 4~ а4 = а2х2 — 2а2сх 4~ а2с2 4" а2у2,
или
с2х2 4- а4 = а2х2 4~ а2с2 4~ а2у2.
Перенесем в левую часть члены, содержащие х и у,
а остальные члены в правую:
с2х2 — а2х2 — а2у2 — а2с2 — a41
отсюда
(С2 _ ^2) Х2 _ а2у2 ^2 2 _ ^2). (4)
Согласно определению гиперболы
2с > 2а,
отсюда
с > а. (5)
При условии (5) разность с2 — а2 имеет только положи-
тельное значение, а потому ее можно обозначить через Ь2.
Сделав это в равенстве (4), получим:
Ь2х2 — а2у2 = а2Ь2. (6)
78
КРИВЫЕ ВТОРОГО ПОРЯДКА
[ГЛ. IV
Разделив последнее равенство на а2Ь2,
тельно:
1
а2 ь2 ~ ’
найдем оконча-
(?)
где х и у— текущие координаты точек гиперболы, а
Ь* = с2—а2. (8)
Равенство (7) представляет собой простейший вид урав-
нения гиперболы.*).
§ 27. Исследование уравнения гиперболы. Из уравне-
ния (6) § 26 имеем:
отсюда
и
а2у2~Ь2х2 — а2Ь2»
_ Ь2х2 — а?Ь2 (х? — а2)
а2 а2
У = -ч-А]/х2 — а2,
а г
(1)
Из этого же уравнения (6) § 26 находим:
_ а2у2 + а2Ь2 __ а2(у2^Ь2)
ft —
И
x = ±~Vy2-[-b'.
(2)
Исследуем уравнения (1) и (2) для выяснения геометри-
ческой формы гиперболы.
I. Найдем точки пересечения гиперболы с осью Ох.
Для этого полагаем у = 0 и из уравнения (2) получаем:
Отсюда следует: гипербола пересекает ось Ох в двух
точках» координаты которых («; 0) и (— 0) (черт. 41,
точки А и Д).
П. Положим в уравнении (1)
|х|<«; (3)
*) Как и в случае эллипса, можно показать, что уравнение (7)
равносильно уравнению (3), т. е. не имеет посторонних корней.
§ 27]
ИССЛЕДОВАНИЕ УРАВНЕНИЯ ГИПЕРБОЛЫ
79
тогда у получит мнимое значение, а это значит, что на
гиперболе нет точек, удовлетворяющих условию (3). Следо-
вательно, в полосе между
(прямые KL и PQ на
черт. 41) нет точек гипер-
г х2 У2 1
болы —-г — -77Г — 1.
а2 Ь2
прямыми х — -\~а и х —— а
Ш. Пусть
| х | > а\
тогда из равенства (1) най-
дем для каждого х два дей-
ствительных значения у,
равных по абсолютной ве-
личине, ио с противополож-
ными знаками. А это значит,
Черт. 41,
что каждому значению х,
удовлетворяющему неравенству (4), соответствуют на нашей
кривой две точки, симметричные относительно оси Ох.
X*2 V2
Следовательно, гипербола-^.-------“-=1 симметрична
относительно оси Ох.
С другой стороны, для каждого значения у из равен-
ства (2) найдем два действительных значения х, равных по
абсолютной величине, но противоположных по знаку, т. е.
каждому значению у на гиперболе соответствуют две точки,
симметричные относительно оси Оу.
х2 у2
Следовательно, гипербола симметрична
относительно оси Оу.
IV. Если в уравнении (1) давать х значения, заключен-
ные между и 4-сю, то величина у будет изменяться
от 0 до ztzoo, т. е. в этом случае каждому значению х соот-
ветствуют на кривой две точки, симметричные относительно оси
Ох и отстоящие друг от друга тем дальше, чем больше вели-
чина абсциссы. Таким образом, можно сказать, что гипер-
бола имеет бесконечную ветвь, расположенную справа от
прямой х = а.
Если же давать х значения, заключенные между —а и
— сю, то у будет изменяться опять от 0 до ±оо, а это
80
КРИВЫЕ ВТОРОГО ПОРЯДКА
[гл. IV
значит, что, как в предыдущем случае, гипербола имеет
бесконечную ветвь, но идущую влево от прямой х —— а.
Итак, гипербола есть кривая, состоящая из двух вет-
вей, простирающихся в бесконечность.
Из всего изложенного следует, что гипербола —— ^=1
состоит из двух симметричных относительно оси Оу бес-
конечных ветвей, одна из которых расположена справа от
прямой х — Д- а, а другая слева от прямой х = — а.
Каждая из этих ветвей симметрична относительно оси Ох
(черт. 42).
Точки А (а; 0) и Лх( — а; 0) называются вершинами гипер-
болы, а точка О (0; 0) — ее центром.
Отрезок /Л1 = 2^ носит название действительной или
вещественной оси гиперболы в отличие от оси ВВХ — 2b,
называемой мнимой *).
Отрезки У7!М и FM— фокальные радиусы точки Л1.
§ 28. Эксцентриситет гиперболы. Эксцентриситетом
гиперболы называется отношение расстояния между
фокусами к длине вещественной оси, т. е.
*) Отрезок ВВ\~^2Ь называется мнимой осью, так как на нем
нет точек гиперболы.
§ 29] АСИМПТОТЫ ГИПЕРБОЛЫ
81
Эксцентриситет гиперболы, так же как и для эллипса,
обозначается буквой е\
Но согласно равенству (8) § 26
с = /о2-Ь^,
поэтому формулу (1) можно представить в следующем виде:
в — —----!---.
а
Так как для гиперболы с > а (§ 26), то дробь
- > 1,
а
а потому эксцентриситет гиперболы больше единицы.
§ 29. Асимптоты гиперболы. Построим на осях гипер-
болы
1
а2 д2 “
прямоугольник LQRS со сторонами, равными 2а и 2bt и
проведем его диагонали LR и QS, продолжив их по обе
стороны (черт. 43).
Прямая LR проходит через начало координат, поэтому
ее уравнение будет:
у— kx. (1)
6 Зак. 3032. И. Л. Зайцев
82 КРИВЫЕ ВТОРОГО ПОРЯДКА [гл. IV
Но угловой коэффициент
Заменив в уравнении (1) k найденным его значением, полу-
чим уравнение прямой LR в следующем виде:
= (2)
Прямая QS также определяется уравнением (1), но угло-
вой коэффициент ее будет уже другой, а именно:
k = tg LA0S = tg (180°— ^SOAJ =
= tg (180° — a) == — tg a = — ~.
Таким образом, уравнение прямой QS будет:
= (3)
Обычно уравнения (2) и (3) записывают следующим
образом:
У = (4)
Между прямыми, представленными уравнениями (4), и
гиперболой существует связь; выясним ее.
Решим совместно способом подстановки уравнения (4) и
уравнение гиперболы — 1 •
Будем иметь:
х2 Ь2х2 _ 1
а2 а-Ь2
или
х2—х2—a2 f
что невозможно, так как а =/= 0. Таким образом, прямые (4)
и гипербола 1 не имеют общих точек, т. е. пря-
мые (4) не пересекают гиперболу.
Возьмем на прямой LR и на гиперболе точки М и 7V,
расположенные в первом координатном углу и имеющие
одну и ту же абсциссу. Ординатой точки М служит РМ;
обозначим ее через Y в отличие от ординаты точки N> ко-
§ 29] АСИМПТОТЫ ГИПЕРБОЛЫ 83
торую обозначим буквой у. Из уравнения (2) можно напи-
сать:
л/ Ь
Y- — х.
а
Из уравнения гиперболы имеем:
у — — Ух2 — а2,
а*
Составим разность
Y — у = х — — ]/х2 — а2 = -~(х — У х2 — а2)
a av a v г '
и посмотрим, как она будет изменяться при возрастании
абсциссы. Для этого умножим и разделим правую часть
последнего равенства на выражение x-j-Ух2— а2; получим:
Z>(x—У х2 — а2) (х+Ух2 — а2)
a(x-j- У х2 — а2)
Ь\х2 — (х2 — а2)]
а^ + Ух2 —а2)
b (х2 — х2 4- л2) _ Ьа2 _______ ab
«(х+’Ух2^-^) ~~ « (х + У х2“— l^j “ * + У х2 — а2 ’
Итак,
(5)
Пусть величина х в равенстве (5) бесконечно возрастает,
тогда знаменатель дроби также бесконечно растет, а сама
дробь уменьшается, приближаясь к нулю. Таким образом,
гипотенуза NM и, следовательно, катет NT в прямоугольном
треугольнике MN7 стремится к нулю. Из сказанного делаем
вывод: при неограниченном возрастании абсциссы х ги-
пербола приближается к прямой LR как угодно близко,
нигде ее не пересекая.
Так как прямые LR и QS, а также точки гиперболы
симметричны относительно оси Ох, то можно сказать, что
и часть гиперболы, расположенная в четвертом координат-
ном углу, как угодно близко подходит к прямой QS, нигде
ее не пересекая.
Вывод, сделанный для правой ветви гиперболы, справед-
лив и для ее левой ветви благодаря той же симметричности
прямых (4) и гиперболы относительно координатных осей.
6*
84
КРИВЫЕ ВТОРОГО ПОРЯДКА
[гл. IV
Прямые
£
а
называются асимптотами гиперболы.
Из сказанного в настоящем параграфе можно сделать
заключение, что гипербола расположена всеми своими точ-
ками внутри вертикальных углов, образуемых асимптотами,
и нигде не выходит за их границы. Этим обстоятельством
можно воспользоваться для построения гиперболы в случае,
если не требуется точного, а достаточно только приближен-
ного ее изображения; для этого, начертив асимптоты, нужно
провести плавную кривую линию, постепенно приближая ее
к асимптотам.
X2 V2
Пример. Дана гипербола ~ — 1. Узнать, ле-
жит ли точка А (2; 1,5) на какой-либо ее асимптоте.
Решение. Из данного уравнения имеем:
а = /Тб = 4,
Ь = У9'=3.
Следовательно, уравнения асимптот будут:
, 3
У = ~ -4 х-
Так как точка А лежит согласно условию в первохм
координатном углу, то она может принадлежать только
асимптоте, определяемой уравнением
3
У = ~4Х-
Подставив в него вместо х и у координаты точки А, полу-
чим тождество:
1,5=4-2 = 1,5.
Значит, точка А лежит на указанной асимптоте гиперболы.
§ 30. Равносторонняя гипербола. Если в уравнении
гиперболы
л2 1А
§ 30]
РАВНОСТОРОННЯЯ ГИПЕРБОЛА
85
положим а — Ь, то это уравнение примет вид
X2__________________________у2__ .
или
(1)
Уравнение (1) определяет гиперболу, у которой полуоси
равны между собой. Такая гипербола называется равносто-
ронней. Уравнения асимптот в этом случае будут:
у — (2)
так как отношение
Как видно из уравнения (2),
асимптот равны -ф-1 и —1. Если
угловые коэффициенты
обозначить углы, обра-
зуемые асимптотами с положительным направлением оси Ох,
соответственно через а и at (черт. 44), то
tg I и tgat = — 1,
откуда
а =45° и 135°.
86 КРИВЫЕ ВТОРОГО ПОРЯДКА [ГЛ. IV
Следовательно, угол между асимптотами будет:
с^ —а = 135° —45°= 90°.
Отсюда заключаем: асимптоты равносторонней гипер-
болы взаимно перпендикулярны.
§ 31. Уравнение равносторонней гиперболы, отнесен-
ной к асимптотам. Так как асимптоты равносторонней ги-
перболы взаимно перпендикулярны, то их можно принять за
оси прямоугольной системы координат и рассматривать ги-
пербол}' по отношению к этим новым осям. Выведем урав-
нение равносторонней гиперболы для этого случая.
Пусть дана равносторонняя гипербола. Тогда ее уравне-
ние по отношению к координатным осям Ох и Оу (черт. 45)
Черт. 45.
выразится, как было пока-
зано в § 30, в виде
х2—= (1)
Взяв на гиперболе произ-
вольную точку Л1 (х; у) и
построив ее координаты,
будем иметь:
х—ОА, у = АМ.
Примем теперь за оси коор-
динат асимптоты гиперболы:
ОХ—за ось абсцисс, OY —
за ось ординат. Опустив
перпендикуляр МС на но-
вую ось абсцисс, найдем:
X—ОС, Y—CM.
Выразим новые координаты X и Y точки М через старые
х и у. Для этого из точки А проведем АВ±_СМ и
AO.LOX. Обратим внимание на то, что в образовавшихся
прямоугольных треугольниках АМВ и AOD
^АМВ = £_AOD
как углы, образованные взаимно перпендикулярными пря-
мыми. Но £_AOD — 45°, поэтому
Д АМВ = ДДОО = 45°.
§ 31] УРАВНЕНИЕ ГИПЕРБОЛЫ, ОТНЕСЕННОЙ К АСИМПТОТАМ 87
Из чертежа имеем:
Х= ОС = OD—CD = OD—BA = О A cos 45° —AM sin 45° =
=^.г_у/,=^(л._л (2)
F=CM==CB4-BM=D71+J3AI=OXsin450+/Afcos 45°=
— —2~ лгН—2~у — —2~ (х-\-у), (3)
Перемножив равенства (2) и (3) и приняв во внимание ра-
венство (1), получим:
XY=~(x2—y2) = ~a2. (4)
Положим для краткости
тогда равенство (4) перепишется так:
XY = m, (5)
где т — постоянная величина.
Таково уравнение равносторонней гиперболы, если за оси
координат принять ее асимптоты.
Как видно из уравнения (5), переменные X и Y—вели-
чины обратно пропорциональные, а потому можно сказать,
что равносторонняя гипербола ху — т представляет со-
бой график обратно пропорциональной зависимости
между переменными величинами.
Упражнения
1. Написать уравнение гиперболы, если даны:
1) а = 6, 6 = 2; 2) а = 4, с = 5; 3)6 = 5, с = 13.
у2
2. Дана гипербола —-g- = 1. Определить ее оси и расстоя-
ние между фокусами.
У"
3. Найти координаты вершин и фокусов гиперболы = 1.
144 20
4. Написать уравнение гиперболы, у которой фокусы имеют
координаты (± 4; 0) и вещественная ось равна 6.
5. Дана гипербола 24л2 — 25у2 = 600. Определить координаты
ее фокусов, длину осей и эксцентриситет.
88
КРИВЫЕ ВТОРОГО ПОРЯДКА
[l Л. IV
6. Написать уравнение гиперболы, если даны:
1) с = 7, 2) 6 = 9, <?=1,25.
7. Написать уравнение гиперболы, у которой
а 3
Т“Т’
с = 15.
8. .Лежат ли на гиперболе
16 36
следующие точки А (8; 61^3), В (6; 3)^5) и С(3; 21^6)?
9. Написать простейший вид уравнения гиперболы, проходящей
через точку А (9; —4), если ее вещественная полуось равна 3.
10. Написать простейший вид уравнения гиперболы, проходя-
шей через две точки А (4; 5) и В (—4 ^3; 5).
11. Написать уравнения асимптот, а также найти величину
эксцентриситета гиперболы л*2 — 2у2 = 6.
12. Написать уравнения асимптот гиперболы, у которой веще-
ственная ось равна 8, а расстояние между фокусами, лежащими на
оси Ох, равно 1(1
13. Написать уравнение ишерболы, если расстояние между
фокусами, расположенными на оси Ох, равно 10 У 2, а уравнения
3
асимптот у == Н- — х.
~~ 4
14. Написать уравнение
жат прямые
гиперболы, асимптотами которой слу-
У=± 5Х
И
фокусы которой имеют координаты
(±2; 0).
15. Точка А (10; 4,5) лежит на гиперболе, а точка В (4; 3) на
одной из ее асимптот. Написать простейший вид уравнения гипер-
болы.
16. Найти точки пересечения гиперболы х2— 2у2 = 18 с прямой
х = 6.
17. Найти точку пересечения гиперболы х2— 2у2 = 4 и прямой
Зх — 4у = 2.
18. Найти острый угол между асимптотами гиперболы 4х2-—
- 5у2 = 100.
19. Найти эксцентриситет гиперболы, у которой угол между
асимптотами равен 60°.
20. Определить траекторию точки М (х; у), которая при своем
движении остается вдвое ближе к прямой х=1, чем к точке (4; 0).
§ 32. Парабола и ее простейшее уравнение. Парабо-
лой называется геометрическое место точек, каждая
из которых одинаково удалена от точки, называемой
фокусом, и от прямой, называемой директрисой (при
условии, что фокус не лежит на директрисе).
§ 321
ПАРАБОЛА И ЕЕ ПРОСТЕЙШЕЕ УРАВНЕНИЕ
89
Пусть точки ТИ2, Л43, Ж4 лежат на параболе (черт. 46).
Если точка F изображает фокус, а прямая АВ — директрису,
то согласно данному выше определению можем написать:
FM. —lt
FM2—M2N2,
FM3 M3N3t
fm^m\n4.
Выведем уравнение параболы, пользуясь ее определением.
Для этого выберем систему координат, приняв за ось Ох
прямую, проведенную через
точку F (фокус) перпендику-
лярно к директрисе АВ, а за
ось Оу — прямую, проходящую через середину отрезка KF
перпендикулярно к последнему (черт. 47).
Обозначим
KF — p\
тогда координаты фокуса F будут . Возьмем на пара-
боле произвольную точку М (х; у); расстояния ее от фо-
куса F и от директрисы АВ будут выражаться соответ-
ственно отрезками FM и MN. Согласно определению пара-
болы, можем написать:
FM = AW.
(1)
90 КРИВЫЕ ВТОРОГО ПОРЯДКА [гл. IV
Применяя формулу расстояния между двумя точками и при-
няв во внимание, что точка N имеет координаты
найдем:
™ + О' - О)2 = |/" (* - f )’ -Г у,
MN= |/Г(х+|)Ч(3'—= +
Заменив FM и MN в равенстве (1) их выражениями,
получим:
= (2)
Это и есть уравнение параболы относительно выбранной
системы координат, так как оно справедливо для любой ее
точки.
Упростим уравнение (2). Для этого возведем обе части
его в квадрат:
(х — Q -4- Д/2 = (х _j_ .
Раскроем скобки:
о I р2 । 9 9 1 I р2
X-—рх -4- = X14- рх.
Приведя подобные члены, получим простейшее уравнение
параболы
у2 = 2рх *). (3)
Величина р называется параметром параболы-
§ 33. Исследование уравнения параболы. Из уравне-
ния (3) § 32 найдем:
у — ^У^рх. (1)
Исследуем уравнение (1) для выяснения геометрической
формы пашей кривой, полагая р > 0.
*) Можно показать, что уравнение (3) равносильно уравне-
нию (2).
§ 33]
ИССЛЕДОВАНИЕ УРАВНЕНИЯ ПАРАБОЛЫ
91
I. Положим
х — 0;
тогда
j = -0 = 0.
Отсюда следует: парабола у2—2рх проходит через
начало координат.
II. Если х < 0, то у — мнимое число. А это значит, что
парабола у2= 2рх не имеет точек с отрицательными абсцис-
сами и, следовательно, распо-
ложена справа от оси Оу.
III. Если х > 0, то у имеет
два действительных значения,
равных по абсолютной величи-
не, но с разными знаками. Это
значит, что каждому положи-
тельному значению х на пара-
боле соответствуют две точки,
расположенные симметрично
относительно оси Ох.
Следовательно, парабола
у2—2рх симметрична отно-
сительно оси Ох.
IV. Пусть х неограниченно возрастает, тогда и |д/| будет
неограниченно расти, т. е. точки параболы с перемещением
вправо от оси Оу неограниченно
удаляются вверх и вниз от оси Ох.
Итак, парабола у2=2рх со-
стоит из бесконечных ветвей.
Вышеизложенное позволяет пред-
ставить параболу, как показано на
я черт. 48.
Точка О называется вершиной
параболы, отрезок FM— фокаль-
ным радиусом точки /И параболы,
а бесконечная прямая Ох является
ее осью
Если
местить
пат, то
на чертеже 49. При этом абсциссы
0, а
Черт. 49.
симметрии.
директрису параболы по-
сирава от начала коорди-
фокус и ветви ее располо-
жатся как показано
точек параболы будут удовлетворять условию х
92
КРИВЫЕ ВТОРОГО ПОРЯДКА
[гл. IV
потому ее уравнение примет вид:
у2 = — 2рх.
Парабола может быть симметрична и относительно оси Оу;
в этом случае фокус ее будет лежать на оси ординат,
а директрисой будет прямая, параллельная осп Ох. Как видно,
при этом условии координатные оси поменяются ролями, и
уравнение параболы примет вид
х2=2ру, (2)
если ветви ее направлены вверх (черт. 50), и
х2 — — 2ру,
(3)
если ветви направлены вниз (черт. 51).
Пример 1. Дана парабола
у2 = 12х.
Найти координаты ее фокуса и написать уравнение дире-
ктрисы.
Решение. Данная парабола симметрична относительно
оси Ох и расположена направо от оси Оу. Из уравнения
находим:
2р — 12,
откуда
р^в.
§ 33] ИССЛЕДОВАНИЕ УРАВНЕНИЯ ПАРАБОЛЫ 93
Т. 1 Р
Расстояние фокуса от начала координат равно , по-
этому абсцисса фокуса будет ^=у=3. Итак, фокус нахо-
дится в точке
F(3; 0).
Директрисой служит прямая, параллельная оси Оу и
отстоящая от последней на расстоянии ~ = 3. Следовательно,
уравнение директрисы параболы будет х —— 3.
Пример 2. Фокус параболы с вершиной в начале коор-
динат лежит в точке F(0; —4). Написать уравнение этой
параболы.
Решение. Согласно условию данная парабола симме-
трична относительно оси Оу, а ветви ее направлены вниз,
поэтому искомое уравнение найдется из (3). Так как
то
р = 8
и уравнение параболы будет:
Х2 = _16л
Упражнения
1. Написать уравнения четырех парабол с вершиной в начале
координат, зная, что координаты их фокусов равны:
1) Л(4; 0), 2) f(— 2; 0), 3) А(0; 3), 4)Д(0;—5).
2. Определить координаты фокусов следующих парабол:
1) у2 == 10х, 2) у2 = — 12jc, 3) х- = 8у, 4) х2 = — 10у.
3. Найти координаты фокуса параболы 2у2 — 5х = 0.
4. Написать уравнение директрисы и найти координаты фокуса
каждой из парабол:
1)у2 = 4х, 2)л2 = — 8у.
5. Написать уравнения парабол с вершиной в начале координат,
для которых директрисами служат прямые:
1)х = — 2, 2) х = 3, 3) у = 2,5, 4)у = —4.
6. Директрисой параболы с вершиной вначале координат слу-
жит прямая 2x-f-5 = 0. Написать уравнение и определить коорди-
наты фокуса этой параболы.
94 КРИВЫЕ ВТОРОГО ПОРЯДКА [гл. IV
7. Проверить, лежит ли
1) точка Л (2; —2) па параболе у2~2х,
2) » В(—1; /5) » » у2 = 5х?
8. Из отверстия бака, находящегося на поверхности земли,
вытекает вода струей, представляющей ветвь параболы ,г2 =— бу.
На каком расстоянии от края бака падает струя на землю, если
высота отверстия равна 1,5 м>
9. Найти высоту арки моста длиной 21 м, если арка имеет вид
параболы, уравнение которой х2 = — 48у.
10. Написать уравнение параболы, имеющей вершину в начале
координат, симметричной относительно оси Ох и проходящей через
точку А (4; — 2).
11. Написать уравнение параболы с вершиной в начале коорди-
нат, симметричной относительно оси Оу и проходящей через точку
А (-4; -2).
12. Через фокус параболы у2—Юх проведена хорда перпенди-
кулярно к ее оси. Найти длину хорды.
13. Найти точки на параболе у2 = 5х, имеющие равные коор-
динаты.
14. Через фокус параболы у2 = 8х и через ее точку, абсцисса
которой равна 4,5, а ордината положительна, проведена секущая.
Составить уравнение этой секущей.
15. Найти точки пересечения параболы у2 = с прямыми:
1)у = 2х+1, 2)2у —Зл —3 = 0, 3) у = Зл;1.
16. Найти длину общей хорды двух парабол:
у2 = 4х и х2 ~ 4у.
17. Через фокус параболы у2 — —4х проведена прямая под
углом 135° к положительному направлению оси Ох. Написать урав-
нение прямой и найти длину образовавшейся хорды.
§ 34. Уравнение параболы со смещенной вершиной и
осью, параллельной оси Оу. Возьмем уравнения параболы
(2) и (3) § 33 и запишем их в следующем виде:
х2 = -ь- 2ру.
Отсюда
>=4Л (1)
Положив в уравнении (1)
получим:
у = Ах2. (2)
§ 34] УРАВНЕНИЕ ПАРАБОЛЫ СО СМЕЩЕННОЙ ВЕРШИНОЙ
95
Уравнение (2) определяет параболу, ветви которой направлены
вверх, если А > О,
вниз, если А 0.
В дальнейшем мы будем часто пользоваться уравнением (2),
представляющим параболу с вершиной в начале координат
и с осью симметрии, сов-
падающей с осью ординат.
Рассмотрим параболу,
у которой вершина лежит
в точке Ot(a; Ъ), ось сим-
метрии параллельна оси Оу,
а ветви направлены вверх
(черт. 52).
Возьмем на параболе про- 4
извольную точку М(х\ у).
Опустив из нее перпендику-
ляр МР на ось Ох, будем ____
иметь: О
ОР~х, РМ~у.
Проведем через Ot прямые Черт. 52.
ОгХ и QY, параллельные
координатным осям Ох и Оу, и положим временно, что прямые
ОхХ и OtY служат осями новой системы координат. Обо-
значим координаты точки 714 в этой системе через X и Y,
т. е.
OJ\^X и PXM—Y.
Уравнение параболы в новой системе координат напишется
следующим образом:
Y — АХ2, (3)
где А > 0.
Чтобы найти ее уравнение относительно прежних осей
Ох и Оу, нужно X и Y выразить через х и у. Так как
OQ = a и 0Ог — Ь,
то
X=OiP1 = QP—OP — OQ—x — a,
Y^P.M — PM — РРк = PM — QO^y — b.
96
КРИВЫЕ ВТОРОГО ПОРЯДКА [ГЛ. IV
Подставив в уравнение (3) найденные значения X и Y,
получим:
у — Ь = А(х — а)2,
или
у—А(х—я)2 + &. (4)
Упростим уравнение (4); для
примет следующий вид:
этого раскроем в нем скобки.
Получим:
у —Ах2— 2Аах-\- Аа2-\-Ь.
(5)
Обозначим:
— ЪАа = В, (6)
Аа2~}-Ь — С', (7)
тогда уравнение (5) примет
вид
у = Ах2-}- Вх-}- С. (8)
Это—уравнение пара-
болы с вершиной, лежащей
в любой точке плоскости, и с осью симметрии, парал-
лельной оси Оу.
Рассмотрим частные случаи.
Пусть абсцисса вершины параболы я = 0; тогда вели-
чина В в равенстве (6) также будет нулем и уравнение (8)
у=^Ах2АгС.
Полученное уравнение определяет параболу, у которой вер-
шина лежит на оси Оу, являющейся в то же время и ее
осью симметрии (черт. 53).
Положим, что одна из точек параболы (исключая ее вер-
шину) лежит в начале координат; тогда координаты (0; 0)
должны удовлетворять уравнению (8). Заменив в нем х и у.
нулями, найдем С ~ 0. В этом случае уравнение (8) полу-
чит вид
у — Вх
§ 34] УРАВНЕНИЕ ПАРАБОЛЫ СО СМЕЩЕННОЙ ВЕРШИНОЙ
97
и будет определять параболу, проходящую через начало
координат (черт. 54).
Заметим, что и уравнение (2) можно рассматривать как
частный случай уравнения (8). Действительно, положив
в равенствах (6) и (7)
У.
а ~ 0 и b — О,
получим:
В = 0 и С=0,
вследствие чего уравнение
преобразуется в следующее:
д/ — Ах2.
(8)
Из сказанного следует, что Черт. 54.
парабола, у которой ось сим-
метрии параллельна оси Оу ила совпадает с ней, опре-
деляется уравнением
у = Ах2 —Зх —J— С
при любых значениях Л, В и С, кроме Д = 0.
Убедимся на примере, что справедливо и обратное утверж-
дение: всякое уравнение вида (8) определяет параболу с осью
симметрии, параллельной оси Оу.
Пусть дано уравнение
у — 2х2—4х — 3.
(9)
Преобразуем его следующим образом:
у = 2х2— 4х — 3 = 2х2—4х + 2 — 5 =
= 2(х2 — 2х+ 1)—5 = 2(х — I)2—5.
Отсюда
_у-4-5 = 2(х— I)2. (10)
Положим
_у + 5=Г,
х—1=Х;
тогда уравнение (10) примет вид:
Y=2X2. (11)
7 Зак. 3032. И. Л. Зайцев
98 КРИВЫЕ ВТОРОГО ПОРЯДКА (гл. IV
Уравнение (11) имеет такой же вид, как и уравнение (2),
поэтому оно, а следовательно, и уравнение (9) определяют
параболу, у которой ось симметрии параллельна оси Оу.
Для построения параболы, определяемой уравнением вида
(8), можно использовать обычный прием, применяемый для
вычерчивания графиков функций, а именно: дав х ряд зна-
чений, вычислить значения у, а затем, построив точки по
найденным координатам, провести через них плавную линию.
Пример 1. Построить параболу у — х2— 4х.
Решение. Прежде всего найдем абсциссы точек пере-
сечения данной параболы с осью Ох; положив у— О, получим:
х2 — 4х — 0, откуда хх = 0, х2 — 4.
Так как найденные точки симметричны относительно оси па*
раболы, то вершина последней, находясь на этой оси, имеет
0-1-4
абсциссу, равную —g— = 2; ордината же ее
у=22 — 4 • 2 = — 4.
Этих трех точек достаточно для приближенного изображения
параболы.
Для более точного ее представления нужны дополнитель-
ные точки. Составим следующую таблицу:
X — 1 0 1 2 3 4 5
У 5 0 — 3 — 4 — 3 0 5
Построив эти точки и проведя через них плавную линию,
получим искомую параболу (черт. 55).
Пример 2. Построить параболу у =—
Решение. Корни уравнения
— у х2 + х — 1 = 0
мнимые, а потому ось Ох не пересекает данную параболу.
В этом случае следует найти абсциссы точек пересечения
§ 34] уравнение параболы со смещенной вершиной 99
параболы с прямой
У = — 1
(—1—свободный член данного уравнения параболы).
Решая для эгой цели систему уравнений
j у= — ’ V-24-X— 1,
I у = — 1,
будем иметь:
-р+х-1=-1,
или
х2— 2х — О,
откуда
Xj=0, х2 — 2.
Полученные точки симметричны относительно оси параболы,
поэтому абсцисса ее вершины равна —~—= 1; ордината же ее
1 1
7*
100 КРИВЫЕ ВТОРОГО ПОРЯДКА [гл. IV '
Присоединим к этим точкам несколько дополнительных точек. I
Составим таблицу: J
X | | —2 — 1 0 1 2 3 4
у i — 5 — 2.5 — 1 — 0,5 — 1 — 2,5 — 5
График параболы представлен на черт. 56.
Упражнения
1. Найти координаты вершин
1) у = 5х — х2,
2) у == 9 — х\
3) у = х2 — 4х— 5,
2. Построить параболы:
1) у х2 — 4,
2) у — х2 — Зх,
3) у = х2 — х — 2,
4)
парабол:
4) у = х1 2 — 2х+ 1,
5) у ~ ~2 4~х 4"
5) у = х2 + 4х + 4,
6) у = ^л2 + 2х + Т’
7) у = 3х — 2-
8) у = х2 4.
§ 35. Конические сечения. Окружность, эллипс, гипер-
бола и парабола определяются, как мы установили в предыду-
§ 35]
КОНИЧЕСКИЕ СЕЧЕНИЯ
101
щих параграфах, уравнениями второй степени относительно
текущих координат; поэтому их называют кривыми второго
иорядка. Они были известны еще древним грекам, которые
изучали эти кривые, рассматривая их как результат сечения
прямого кругового конуса плоскостью в следующих четырех
случаях.
I. Секущая плоскость перпендикулярна к оси конуса;
в сечении получается окружность (черт. 57).
П. Секущая плоскость образует с осью конуса угол, не
равный 90°, и пересекает все его образующие по одну
сторону от вершины <$; в сечении получается эллипс
(черт. 58).
III. Секущая плоскость параллельна какой-либо образую-
щей конуса; при этом получается кривая, называемая пара-
болой (черт. 59).
IV. Секущая плоскость пересекает обе полости конуса;
при этом получаются две бесконечные ветви, образующие
гиперболу (черт. 60).
Окружность, эллипс, гипербола и парабола называются
коническими сечениями.
Конические сечения изучались в древности исключительно
геометрическим путем, что представляло большие трудности,
и только со времени Декарта, давшего метод координат,
изучение их значительно упростилось.
102 КРИВЫЕ ВТОРОГО ПОРЯДКА [гл. IV
Смешанные задачи
1. В окружности х2 4- у2 — 6х бу — 50 — 0 проведена хорда,
параллельная оси Оу па расстоянии, равном 5, от нее. Найти длину
хорды.
2. На гиперболе 5х2— 4у2= 180 взята точка с абсциссой, рав-
ной 10. Определить расстояние ее от фокусов гиперболы.
3. Расстояния одного из фокусов эллипса до концов его боль-
шой оси равны 7 и 1. Написать простейший вид уравнения эллипса.
4. Составить уравнение окружности, концы одного из диаметров
которой находятся в точках Л(—2; 1) и В(0; 3).
5. Определить эксцентриситет равносторонней гиперболы.
6. Написать уравнения диаметров окружности х2 + у2 -(- 8х -|-
J-4у—16 — 0, перпендикулярных к осям координат.
7. Даны окружности х2 -j- у2 4х — 2у — 15 = 0 и х2 -f- у2 —
— 6х + 2у — 7 = 0. Как велик угол, образуемый линией центров
этих окружностей с положительным направлением оси Ох?
8. Разность полуосей эллипса равна 2, координаты фокусов
суть (± 2 У 6; 0). Найти уравнение эллипса.
9. Фокусы эллипса находятся на оси Ох и делят его большие
полуоси пополам. Написать уравнение этого эллипса, если его малая
ось равна 4 У* 3.
10. В эллипс вписана окружность х2 +У2 == 16, пересекающая
большую ось эллипса в фокусах, лежащих на оси абсцисс. Написать
уравнение эллипса.
11. Найти величину осей гиперболы, если расстояние между ее
фокусами равно 8, а угол между асимптотами прямой.
12. Написать уравнение гиперболы, имеющей общие фокусы
с эллипсом х2-|-2у2 = 18 и эксцентриситет, равный 1,5.
13. Найти длину хорды, проходящей через фокус и перпенди-
кулярной к действительной оси гиперболы 9х2—16у2=144.
14. Найти длину хорды, проведенной через фокус перпепдику-
х2 у2
лярно к большой оси эллипса —х-4- = 1.
r a2 b2
15. Через фокус параболы у2 = 2рх проведена хорда, перпен-
дикулярная к ее оси симметрии. Найти длину хорды.
х2 у2
16. На гиперболе ——-~g- = l взята точка с абсциссой, рав-
ной 12. Найти фокальные радиусы этой точки.
17. Вычислить длину сторон правильного треугольника, вписан-
ного в параболу у2 = 4х.
18. На параболе у2 = Зх взята точка, ордината которой равна 2.
Найти расстояние этой точки от фокуса.
19. Мнимая полуось гиперболы больше действительной на 2,
одна из асимптот ее проходит через точку 4(10; 14). Написать
уравнение гиперболы.
20. Написать уравнение гиперболы, если ее асимптоты даны
, 3
уравнениями y = ±-g-x и известно, что гипербола проходит через
точку А (10; — ЗУ"3).
§ 35]
СМЕШАННЫЕ ЗАДАЧИ
103
21. Окружность х2 + у2 — 9 проходит через фокусы гиперболы.
Написать уравнение последней, если ее асимптота образует с поло-
жительным направлением оси Ох угол, равный arc tg 2.
22. В окружность х2 -|- У2 = 25 вписан эллипс с фокусами, лежа-
щими па оси Ох. Радиус окружности, проведенный в ее точку
А (4; 3), делится эллипсом пополам. Написать уравнение этого эллипса.
X2 V2
23. В эллипс ~ = 1 вписан прямоугольник, две про-
100 75 г
тивоположпые стороны которого проходят через фокусы. Найти
длину его сторон.
24. В эллипс 9х2+ 1бу2 = 144 вписан квадрат. Найти длину его
сторон.
25. Под влиянием некоторой силы точка М двигалась по окруж-
ности х2 + у2 — 10х + бу 4- 9 = 0. Действие силы прервалось в тот
момент, когда точка М совпала с точкой А (2; 1) окружности. Опре-
делить дальнейшую траекторию точки.
26. Даны уравнения двух окружностей:
л2 + >2___Съг„2у — 3 = 0 и л2 + у2 — 4х — бу + 3 = 0.
Показать, что линия их центров перпендикулярна к их общей хорде.
27. Камень, брошенный с крыши дома параллельно горизонту,
упал на землю, описав параболу л2 =— Бу. На каком расстоянии
от вертикали упал камень на землю, если высота дома 20 ж?
28. Парабола, симметричная относительно оси Оу, с вершиной
у начале координат пересекает эллипс x2-j-4y2~ 16 в точках, лежа-
щих па хордах, проходящих через его фокусы перпендикулярно
к большой оси. Написать уравнение параболы.
29. Фокальные радиусы точки эллипса равны 2,6 и 7,4; хорда,
выходящая из этой точки и перпендикулярная к большой оси его,
равна 4,8 и определяется уравнением х — 3 = 0. Написать уравне-
ние эллипса.
30. Камень, брошенный под острым углом .к горизонту, описал
дугу параболы и упал на расстоянии 16 м от начального положе-
ния. Написать простейшее уравнение параболы, зная, что наиболь-
шая высота подъема камня равна 12 м.
31. Параболическое зеркало рефлектора Симеизской обсерва-
тории имеет диаметр 1,02 м\ расстояние его фокуса от вершины
равно 5 м. Найти глубину параболической выемки, которую приш-
лось сделать при изготовлении зеркала из плоского стекла.
32. На параболе у2 = 8х найти точку, расстояние которой от
фокуса равно 20.
33. Парабола с вершиной в начале координат расположена сим-
метрично относительно оси Ох. Определить фокальный радиус ее
точки Л4(2; 4).
34. Фокальный радиус точки М параболы у2 = 12х равен б.
Найти координаты точки Л4.
35. На параболе у2 = 4,5х взята точка 44, находящаяся от
директрисы на расстоянии 9,125. Найти расстояние этой точки от
вершины параболы.
104 КРИВЫЕ ВТОРОГО ПОРЯДКА [гл. IV
36. Определить эксцентриситет эллипса, если расстояние между
фокусами его равно расстоянию между концами большой и ма-
лой с сей.
37. Найти эксцентриситет эллипса, у которого большая ось
втрое больше малой.
38. Земной меридиан приближенно представляет собой эллипс,
отношение осей которого равно 299:300. Определить эксцентриси-
тет земного меридиана.
39. Прямая х—10 = 0 пересекает гиперболу и ее асимптоту
соответственно в точках А и В. Написать уравнение этой гипер-
болы, если ордината точки В равна 5, а длина отрезка данной пря-
мой, заключенного внутри гиперболы, равна 8.
40. Найти острый угол, образуемый каждой из асимптот гипер-
болы с ее действительной осью, если вершины гиперболы отстоят
2
от ее центра на — расстояния фокусов от центра.
х^ у2
41. Две вершины эллипса —1 лежат в фокусах гипер-
болы, вершины которой находятся в фокусах данного эллипса.
Составить уравнение гиперболы.
42. К окружности а:2 -|- у2 — 4х -f- Зу -}~ 5 == 0 проведена секущая
х — 2у — 3 — 0. Написать уравнения сторон прямоугольника, впи-
санного в данную окружность и имеющего стороной внутренний
отрезок данной секущей.
43. Найти расстояние от центра окружности л2-(-у2— 6х —
— 4у 5 = 0 до прямой 2х + у — 3 = 0.
44. Из точки С (5; 4) окружности х2 + у2 — 8у— 9 = 0 опущен
перпендикуляр на диаметр АВ. конец которого лежит в точке
В (3; 8). Найти длину этого перпендикуляра.
ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОГО
И ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЙ
ГЛАВА V
ТЕОРИЯ ПРЕДЕЛОВ
§ 36. Абсолютная величина и соотношения, связанные
с ней. В дальнейшем изложении курса нам встретится необхо-
димость рассматривать соотношения между абсолютными вели-
чинами некоторых выражений. Поэтому напомним определе-
ние абсолютной величины числа и соотношения, связанные
с этим понятием.
Определение. Абсолютной величиной положитель-
ного числа называется само это число; абсолютной вели-
чиной отрицательного числа называется это число, взятое
с противоположным знаком.
Абсолютная величина числа а обозначается так: |а|.
Таким образом,
181 = 8;
и=-£.
| —8| = 8;
если b > 0;
если b < 0.
1. Абсолютная величина алгебраической суммы меньше
или равна сумме абсолютных величин слагаемых.
Например:
а) | 2 4-4-4- 6 | =| 12| = 12,
|2|4-|4| 4-| 6| = 2 4-44-6 = 12,
следовательно, |24~44“6|=|2|4~|4[4~|6|;
б) I — 5 — 2| = | — 7| = 7,
| —5| + | —2| = 5 + 2==7,
106
ТЕОРИЯ ПРЕДЕЛОВ
[ГЛ. V
следовательно, | — 5 — 21 — | — 51 —J— | — 2 [;
в) |_5^2| = | — 3 ] = 3,
| —5 | +121=5+ 2^7,
т. е.
i-5 + 2|<|-5| + |2|.
2. Абсолютная величина разности двух чисел больше
или равна разности абсолютных величин уменьшаемого и
вычитаемого.
Например:
а) |7 — 9] = |—- 2| = 2,
[ 7 | | 9 | ~ 7 _ 9 ~ _ 2,
т. е.
|7 — 9| > 171 —19|;
б) |9 — 71 = [ 2 | = 2,
19 | — | 7 | = 9 — 7 = 2,
т. ё.
|9 — 7|=|9| — | 7 ].
3. Абсолютная величина произведения конечного числа
со множите лей равна произведению их абсолютных величин.
Например:
|(_3).5.(— 2)| = | 30 | = 30,
] —3 [ - | 5[ - [ — 2| = 3-5.2 = 30,
т. е.
1(—3) • 5 • (—2)| = | — 3|.|5|.| — 2|.
4. Абсолютная величина частного равна частному
абсолютных величин делимого и делителя.
Например:
a) ^1| = 1_5| = 5,
— 15 | 15 g
т. е.
I — 20 | _ 20
§ 37] ХАРАКТЕР ИЗМЕНЕНИЯ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ 107
т. е.
I — 201_ I — 2°|
I -5 |~ |—-5| •
§ 37. Последовательность. Характер изменения пере-
менной величины. I. Пусть дано множество чисел, располо-
женных в определенном порядке, например,
2; 4; 8; 16; 32; 64; . .. 2П ...; (1)
тогда каждому числу этого множества можно приписать
помер места, которое оно занимает. Так, число 8 занимает
третье место, 32 — пятое, и т. д.
Определение. Числовой последовательностью или
просто последовательностью называется занумерованное
множество чисел, расположенных в порядке возрастания
номеров.
Совокупность чисел (1) служит примером последователь-
ности. Обычно последовательность записывают в общем виде
так:
Z/j f .<£ • • • ZZ^ • • • >
где un называется общим членом последовательности.
Зная формулу общего члена последовательности, можно
найти любой се член. Например, десятый член последова-
тельности (1)
= 210 = 1024.
Пример 1. Найти восьмой член последовательности
1 . 2 . 3 . п
2 ; 3 ; 4 ; I ’ ’
Решение.
_ 8 _ 8
"s— 8+ 1 ~ 9 •
Пример 2. Найти седьмой член последовательности
X. 2. A-
2 ’ 4 ; 8 ; • 2“* ' ’
Реше н и е.
__ J _ 7
«7— 27'— 128 •
II. Мы знаем (§ 5), что в математике и ее приложениях
встречаются величины постоянные и величины переменные.
108 ТЕОРИЯ пределов [гл. V
На координатной оси Ох (черт. 61) постоянной величине а
соответствует неподвижная точка А, а переменной величине
х — движущаяся вправо или влево точка Л4.
Переменная величина может изменяться весьма разнооб-
разно: возрастать, убывать, переходить от возрастания к убы-
ванию и т. д. Закон изменения переменной величины можно
задать последовательностью числовых значений, которые опа
принимает. Пусть, например, переменная х принимает число-
вые значения последовательности (1). Закон изменения здесь
состоит в том, что каждое новое значение переменной х
вдвое больше предыдущего.
О Л
Ь<--------<27 ------>4
Черт. 61.
Как видно, переменная в этом примере изменяется скачко-
образно; однако очень часто рассматриваются переменные,
изменяющиеся непрерывно; например, время, путь, проходи-
мый телом, и т. п.
Переменная величина, которая в процессе изменения
постоянно возрастает или постоянно убывает, называется
монотонной. Примером такой величины служит переменная,
принимающая значения (1).
Всякая величина, меняющаяся не монотонно, называется
колеблющейся. Например, переменная величина, изменяющаяся
но закону последовательности
1- о- 2- _!• А- £• JL-
b 3 ’ 3 ’ 9 ’ 9 ’ 27 ’ ’ ’ ”
члены которой попеременно увеличиваются вдвое и умень-
шаются втрое, является колеблющейся.
Переменные величины по характеру изменения еще делятся
па ограниченные и неограниченные.
Определение. Переменная величина у называется
ограниченной, если, начиная с некоторого ее значения,
выполняется неравенство
И<М,
где Л1 — какое-либо постоянное положительное число.
§ 381
БЕСКОНЕЧНО МАЛАЯ ВЕЛИЧИНА
109
Например, tgx — ограниченная переменная в промежутке
значений аргумента от х —— 45° до х = 45°, так как в этом
случае | tg х| 1.
Наряду с ограниченными переменными величинами встре-
чаются и такие, которые не удовлетворяют вышеуказанному
определению. Возьмем, например, tg х в промежутке значений
аргумента от 0 до 90°. Какое бы большое положительное
число N мы ни взяли, найдется в первой четверти дуга xt
для которой tgx>N. Такая переменная величина называется
неограниченной.
§ 38. Бесконечно малая величина. Возьмем переменную
величину а, принимающую последовательно значения:
1 1- 1- 1- I-
2 ’ 3 ’ 4; 5 ’ 6 ’ ‘ ”
или
_J_. __L. __L. _JL.
2 ’ 3 ’ 4 ’ 5’ 6 ’ • • •
(1)
(2)
По мере увеличения номера места, занимаемого членами этих
последовательностей, абсолютная величина а уменьшается,
и какое бы малое положительное число е мы ни выбрали,
в каждой из указанных последовательностей найдется число,
начиная с которого абсолютная величина значений а будет
меньше выбранного е. Пусть, например, е —0,001. В соот-
ветствующем удалении от начала каждой из данных после-
довательностей найдем число, по абсолютной величине мень-
шее чем 0,001, причем абсолютное значение членов, сле-
дующих за найденным, остается меньше этой дроби. Если
возьмем еще меньшую дробь, например, s = 0,0001, то и
в последовательности (1) и в последовательности (2), если
достаточно удалиться от их начала, найдется число по абсо-
лютному значению меньшее, чем 0,0001, причем последую-
щие члены тоже будут меньше чем 0,0001.
В этом случае говорят, что величина а неограниченно
приближается к нулю или, иначе, стремится к нулю.
Этот факт записывают так: а->0.
Геометрически процесс изменения величины а, принимаю-
щей значения последовательности (1), можно представить
изменением абсциссы точки Л, перемещающейся по коорди-
натной оси в направлении, указанном стрелками на черт. ,62.
110
ТЕОРИЯ ПРЕДЕЛОВ
[ГЛ. V
Какое бы малое положительное число мы ни взяли, наступит
момент, когда абсцисса точки А станет и в дальнейшем
останется меньше выбранного числа.
Процесс изменения величины а, принимающей значения
последовательности (2), представится изменением абсциссы
точки Bt перемещающейся по координатной оси в направлении,
указанном на черт. 62. И в этом случае абсцисса точки В
по абсолютной величине сделается и останется меньше наперед
заданного положительного числа, как бы мало оно ни было.
В ------ -е- -
—ч-----------1--1—Hi--1----Hi—i--F
-7 ~1 _1ЛЛ О 111 1
2 3 4 5 54 3 2
Черт. 62.
/7
/‘
Определение. Бесконечно малой величиной назы-
вается переменная а, которая при последовательном
изменении по абсолютному значению становится и при
дальнейшем изменении остается меньше любой наперед
заданной как угодно малой положительной величины е,
т. е. а —>0.
Не следует смешивать бесконечно малую величину с ни-
чтожно малой. Так, например, при сравнении длины в 1 см
с расстоянием Земли от Солнца (150 000 000 км) первую вели-
чину по отношению ко второй можно считать ничтожно малой,
но назвать ее бесконечно малой нельзя, так как она не
меняет своего значения, между тем как бесконечно малая
величина — переменная.
Как видно, никакая постоянная величина не может быть
бесконечно малой, так как она по абсолютной величине не
может сделаться меньше любой наперед заданной как угодно
малой величины. Однако нуль составляет исключение из всех
постоянных величин; нуль всегда меньше любого сколь угодно
малого положительного числа. Поэтому нуль относят к бес-
конечно малым величинам.
Пример 1. Переменная а — ~
при п — 0; 1; 2; 3; 4; .. .
получает значения:
±- ±. ±. JL-
2 ’ 4 ’ 8 ’ 16 ’ ’ * ‘
§ 38] БЕСКОНЕЧНО МАЛАЯ ВЕЛИЧИНА
111
Какое бы малое положительное число мы ни взяли, в данной
последовательности найдется число, меньшее взятого. Выберем,
например, дробь При п— 10 будем иметь:
__ 1 _ 1 1
° — 2Ю — Ю24 < 1000 •
Таким образом, переменная а —при указанных выше зна-
чениях п есть бесконечно малая величина.
Пример 2. Возьмем окружность радиуса, равного еди-
нице (черт. 63). Обозначив угол АОМ в радианной мере
через а, будем иметь:
sin а
ОМ 1
По, как видно из чертежа,
или
Поэтому
PM < — AM,
РМ<а.
sin а < а.
Если а неограниченно приближается к нулю, то тем более
sin а стремится к нулю. Следовательно, sin а при а~>0 — бес-
конечно малая величина.
Тот же вывод получим, если угол имеет отрицательное
значение —-а. В этом случае при а~>0 абсолютная величина
sin( — а) также стремится к нулю, а потому sin( — а) при
а->0— величина бесконечно малая.
Пример 3. Давление газа р и его объем v связаны
функциональной зависимостью
с
p=v-
где с = const. Как видно, с увеличением объема v давление р
уменьшается. Если объем v увеличивать неограниченно, то
давление р будет неограниченно уменьшаться. Какое бы малое
положительное число е мы ни взяли, можно подобрать вели-
чину v настолько большой, что дробь станет меньше е.
112
ТЕОРИЯ ПРЕДЕЛОВ
[ГЛ. V
Следовательно, давление газа р—величина бесконечно малая,
если объем его v неограниченно растет.
§ 39. Бесконечно большая величина. Пусть переменная
величина у принимает последовательно значения:
2; 4; 6; 8; 10; 12; ... (1)
или
—2; —4; —6; —8; —10; —12; ... (2)
Как видно, с увеличением номера места, занимаемого членами
написанных последовательностей, абсолютная величина у воз-
растает. Положим, что этот процесс возрастания идет неогра-
ниченно; тогда какое бы большое положительное число W
мы ни взяли, в каждой из указанных последовательностей
найдется член, начиная с которого все последующие члены
по абсолютному значению больше 7V. Зададим, например,
число N= 1000. В последовательностях (1) и (2) найдем
число, абсолютная величина которого больше 1000, причем
последующие члены также больше 1000.
-7/7 ~8 -6 ~4 -2 0 2 4 6 8 10
Черт. 64.
Геометрически изменение величины у можно представить
изменением абсциссы точки, удаляющейся в бесконечность по
координатной оси:
в первом случае направо от начала Q (черт. 64),
во втором » налево » » » (черт. 64).
Определение. Бесконечно большой величиной назы-
вается переменная у, которая при последовательном изме-
нении по абсолютной величине становится, а в дальней-
шем и остается больше наперед заданной полоэюительной
величины N, как бы велико N ни было.
Бесконечно большую величину не следует смешивать
с очень большим числом, так как последнее постоянно, бес^-
конечно большая же величина — переменная.
§ 39] БЕСКОНЕЧНО БОЛЬШАЯ ВЕЛИЧИНА
113
Если у — бесконечно большая величина, то условились
записывать
у —> оо
и читать: «игрек стремится к бесконечности».
Необходимо помнить, что символ бесконечности не выра-
жает определенного числа, а указывает только на характер
изменения переменной величины, а именно на его неограни-
ченный рост. Поэтому с символом
обращаться осторожно, чтобы не
впасть в ошибку.
Пример 1. Рассмотрим изме-
нение переменной y — igx при
Взяв окружность радиуса
/?=1 (черт. 65), можем написать:
tgx = -^-==-j—=
Если дуга х, находясь в первой чет-
верти, приближается к то АЛ1,
а следовательно, tgx неограничен-
но растут. Действительно, какое бы
большое положительное число N мы
бесконечности нужно
Черт. 65.
ни выбрали, найдется
в первой четверти дуга, тангенс которой будет больше N,
а потому tg х останется и подавно больше А?,если дуга уве-
личится.
Итак, tgx при х——бесконечно большая
Пример 2. Переменная величина у — —
. 1111
при х=1;
величина.
принимает соответственно значения:
1; 2; 3; 4; 5; ...
Если х неограниченно уменьшается (х—>0), то у неограни-
ченно возрастает, т. е. будет бесконечно большой величиной,
так как какое бы большое положительное число N мы ни
взяли, найдется такое малое значение х, при котором у > N.
8 Зак. 3032. И. Л. Зайцев
114
ТЕОРИЯ ПРЕДЕЛОВ
[ГЛ. V
Возьмем, например, А/ = 1000. Тогда, подобрав x =
получим у — 1001 > N.
Чтобы истолковать геометрически рассмотренную беско-
нечно большую величину, напомним, что уравнение ^ = 2,
при положительных значениях х определяет ветвь равносто-
ронней гиперболы, расположенную в первом координатном
угле (черт. 66). Из чертежа видно, что с неограниченным
приближением абсциссы точки 7И к нулю значение ординаты
ее неограниченно возрастает, т. е.‘ представляет бесконечно
большую величину.
§ 40. Связь бесконечно малой величины с бесконечно
большой. Между бесконечно малой и бесконечно большой
величинами существует связь, а именно:
если у — бесконечно большая величина, то обратная
ей величина ~-------------бесконечно малая
У
и
если а — бесконечно малая величина, неравная нулю,
г - 1
то обратная ей величина ~---------бесконечно
большая.
Не доказывая этих утверждений, поясним их на примерах.
§ 41] ПОНЯТИЕ О ПРЕДЕЛЕ ПЕРЕМЕННОЙ
115
1. Пусть у — бесконечно большая величина, принимающая
значения:
1, 10, 100, 1000, ... ~>оо;
1
тогда — получит соответственно значения:
1; 0,1; 0.01; 0,001; ... ->0,
т. е. будет бесконечно малой величиной.
2. Пусть а — бесконечно малая величина, принимающая
значения:
1; 0,1; 0,01; 0,0001; ... ->0;
тогда — примет соответственно значения
1; 10; 100; 1000; ... оо,
т. е. будет бесконечно большой величиной.
§ 41. Понятие о пределе переменной. Пусть перемен-
ная х, изменяясь, неограниченно приближается к числу 3 и
при этом принимает значения:
3,1; 3,01; 3,001; 3,0001; ...
или
2,9; 2,99; 2,999; 2,9999; ...
В этих случаях абсолютная величина разности х—3 стре-
мится к нулю. В самом деле, при указанных выше значе-
ниях переменной х
|х — 3 | = 0,1; 0,01; 0,001; 0,0001; ... -> 0,
т. е. разность х — 3 есть величина бесконечно малая.
Число 3 в нашем примере называется пределом пере-
менной х.
Предел обозначается символом lim (от французского слова
limite, что значит предел). Таким образом, в пашем случае
можно написать:
lim х = 3.
Употребляют также и такую запись: х—>3.
Определение. Постоянная а называется пределом
переменной х> если разность между ними есть бесконечно
малая величина а, т. е. \imx~a, если х — а —а.
8*
116
ТЕОРИЯ ПРЕДЕЛОВ
[ГЛ. V
Отсюда следует, что предел бесконечно малой величины
равен нулю, т. е.
lim а — 0.
Если переменная х неограниченно возрастает, то говорят,
что она стремится к бесконечности; в этом случае усло-
вились писать:
lim х = оо.
Пример 1. В треугольнике АВС (черт. 67) положим
/_АСВ = х, /_BCD — a;
тогда
х-]-а= 2d,
откуда
2d — х== а.
(2)
Если вершина В движется равномерно и безостановочно по
прямой, параллельной AD, то углы х и а становятся пере-
Че рт. 67.
менными, причем а будет бесконечно малой. Таким образом,
в равенстве (2) разность между постоянной величиной 2d и
переменной х стремится к нулю, а потому согласно опре-
делению предела
lim х = 2d.
Пример 2. В окружность вписан правильный /г-угольник
(черт. 68).
§ 41]
ПОНЯТИЕ О ПРЕДЕЛЕ ПЕРЕМЕННОЙ
117
Обозначив
АВ = ап, OA — R и OK = hn>
имеем из треугольника АО К'.
О А — ОК < АК,
или
к___h
2
(3)
Будем неограниченно увеличивать число п сторон этого много-
угольника. Тогда hn и станут переменными величинами,
Черт. 68.
чина (§ 38), 2nR — постоянный мно-
житель. В § 42 будет доказано, что
произведение постоянной величины на
также бесконечно малая; поэтому
2л/?. 1->о,
п
бесконечно малую—
т. е. ап и, следовательно, — бесконечно малые величины.
Из неравенства (3) следует, что в таком случае разность
R—hn также будет бесконечно малой величиной, а потому
согласно определению предела имеем:
lim hn — R,
п у со
П р и м е ч а п и е. Всякая переменная величина, имеющая
конечный предел, в частности, бесконечно малая, является
ограниченной переменной.
118
ТЕОРИЯ ПРЕДЕЛОВ
[ГЛ. V
§ 42. Свойства бесконечно малых величин.
Первое свойство. Произведение бесконечно малой
величины а на постоянную а {а Ф 0) есть величина бес-
конечно малая.
Для доказательства возьмем произвольное положительное
число е. Так как а — бесконечно малая величина, то |а|
при изменении а может сделаться и остаться меньше любой
положительной дроби, а следовательно, и меньше т. е.
I а)
с некоторого момента будет
или
| аа | < е.
Значит, произведение аа— бесконечно малая величина.
Рассмотренное свойство справедливо и в случае а — 0,
как будет показано в этом же параграфе.
Пример. Умножив бесконечно малую величину
а — I; 0,1; 0,01; 0,001; . . . -> 0
на —8, получим:
— 8а = — 8; —0,8; —0,08; —0,008; ... (1)
Произведение — 8а также бесконечно малая величина, так
как какое бы малое положительное число г мы ни взяли,
в последовательности (1) найдется дробь, абсолютное значе-
ние которой меньше е. Например, абсолютная величина — 8а
может сделаться меньше 0,0001; 0,00001; 0,000001 и т. д.
Следствие. Произведение ограниченной переменной
на бесконечно малую величину есть бесконечно малая.
Так как ограниченная переменная меньше некоторой по-
стоянной (§ 37), доказанное свойство бесконечно малых можно
распространить и на случай произведения ограниченной пере-
менной величины на бесконечно малую.
Это следствие справедливо и для произведения двух
бесконечно малых величин, а также для произведения нуля
на бесконечно малую, так как бесконечно малые величины
относятся к ограниченным переменным (примечание § 41j,
а нуль есть частный случай бесконечно малой (§ 38).
Второе свойство. Алгебраическая сумма двух бес-
конечно малых есть величина бесконечно малая.
§ 42J СВОЙСТВА БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИН 1 19
Возьмем произвольное положительное число е. Так как а
и р — величины бесконечно малые, то |а| и |р| каждая в от-
дельности с некоторого момента сделается и будет оставаться
меньше любого положительного числа е и даже у, т. е.,
начиная с некоторого момента, будет
1«|<1 и |И<|-
Сложив эти неравенства, получим:
1«Ц-|?|<-2-+у или |а| +1РI < s-
Но на основании § 36, (1)
[яЧ~р|<С 1а1 + ! Pl-
Поэтому, начиная с некоторого момента, будет
la+N <£-
Следовательно, а+р— величина бесконечно малая.
П р и м е р. Сложим две бесконечно малые величины:
а = —2; —0,2; —0,02; —0,002; ...-> 0,
и
р ——14; —1,4; —0,14; —0,014; . . . -> 0;
получим:
= —1,6; —0,16; —0,016; ... (2)
Результат сложения а -р— тоже бесконечно малая величина,
так как какое бы малое положительное число е мы ни взяли,
среди членов последовательности (2) найдется дробь, абсо-
лютная величина которой меньше с; например, |а-|-р| может
сделаться меньше 0,0001; 0,00001; 0,000001 и т. д.
Следствие. Алгебраическая сумма конечного числа
бесконечно малых есть величина бесконечно малая.
Пусть требуется сложить бесконечно малые величины
ссг, а2, . ..,аи. Согласно второму свойству, имеем:
ai + a2 — бесконечно малая
(ax + а2) — бесконечно малая
(at + a2 + a3) — бесконечно малая
(с?! a2-j- a3 + ... -{- — бесконечно малая, ч. т. д.
120
ТЕОРИЯ ПРЕДЕЛОВ
[ГЛ. V
Нужно помнить, что это свойство доказано нами только
для того случая, когда количество бесконечно малых сла-
гаемых конечное, хотя бы и очень большое. Если же нужно
сложить бесконечно большое число бесконечно малых вели-
чин, то указанное свойство может оказаться неверным. Так,
например, при неограниченном удвоении числа сторон пра-
вильного вписанного в окружность многоугольника длины
этих сторон будут бесконечно малыми (см. пример 2 § 41),
однако их сумма, в пределе равная длине окружности, не
есть бесконечно малая величина.
§ 43. Теоремы о пределах.
Теорема I. Переменная величина не может иметь
двух различных пределов.
Доказательство. Допустим, что переменная х имеет
два разных предела Л и В. В таком случае согласно опре-
делению предела (§ 41) разность между переменной и ее
пределом должна быть бесконечно малой, т. е.
X — А = а,
х— в~ р,
где а и р— бесконечно малые величины.
Вычтя из первого равенства второе, получим:
х— А — х-\- В = а — р,
или
а — р = В — А.
Левая часть этого равенства как разность двух бесконечно
малых величин есть величина бесконечно малая; правая же
часть — величина постоянная. Но бесконечно малая величина
может равняться постоянной только в том случае, если эта
постоянная равна нулю (§ 38); следовательно, В — Д = 0,
отсюда А —В, т. е. переменная величина имеет один предел.
Следствие. Если две переменные величины, имею-
щие пределы, при всех своих изменениях равны между
собой, то равны и их пределы.
В самом деле, каждая из переменных по доказанному
имеет по одному пределу, но так как переменные равны
между собой при всех изменениях, то они и стремятся к оди-
наковой постоянной, т. е. имеют равные пределы.
§ 43] ТЕОРЕМЫ О ПРЕДЕЛАХ 121
Теорема II. Предел суммы конечного числа пере-
менных величин, имеющих пределы, равен сумме преде-
лов этих переменных.
Доказательство. Возьмем две переменные величины
х и у, имеющие пределами соответственно А и В, т. е.
limx = A, |
limy — В. ]
Согласно определению предела (§ 41) разности х — А и
у — В суть бесконечно малые величины, т. е.
х — А — а,
у-в^,
где а и р— бесконечно малые величины.
Сложив эти равенства, получим:
(Х~Ь У) — (Л 4“ В) = а4~р.
В левой части последнего равенства имеем разность между
переменной x-j-J и постоянной А-]-В, в правой же части
бесконечно малую величину (см. второе свойство в § 42).
Следовательно, согласно определению предела имеем:
у) = А В.
Учитывая равенства (1), можем написать:
lim 4~ у) = lim х Hm у.
Точно так же можно доказать эту теорему для трех, че-
тырех и любого конечного числа переменных.
Теорема III. Предел разности переменных, имею-
щих пределы, равен разности пределов этих переменных.
Как известно, разность можно рассматривать как алге-
браическую сумму, а потому теорему 11 можно распростра-
нить и на разность.
Теорема IV. Предел произведения конечного числа
переменных, имеющих пределы, равен произведению пре-
делов этих переменных.
Доказательство. Возьмем две переменные величины
х и у, имеющих пределами соответственно А и В, т. е.
Ишх = А,
lim у = В.
122 ТЕОРИЯ ПРЕДЕЛОВ [гл. V
По определению предела [(1) § 41], можем написать:
X Л —а,
где а и р —бесконечно малые величины.
Перемножив эти равенства, получим:
откуда
ху — А В = р А 4- аВ 4- ар.
В левой части последнего равенства имеем разность между
переменной ху и постоянной АВ, в правой же части каждое
слагаемое — бесконечно малая величина (см. первое свойство
в § 42), а потому сумма их — также величина бесконечно
малая (следствие второго свойства § 42). Таким образом,
разность ху — АВ — бесконечно малая величина, а потому,
по определению предела,
lim ху — АВ,
или
lim ху = lim х lim у.
Эту теорему можно доказать для любого конечного числа
переменных сомножителей.
Следствие 1. Предел произведения постоянной
величины на переменную, имеющую предел, равен про-
изведению постоянной на предел переменной, т. е.
lim ах — a lim х,
где а — постоянная, а х — переменная.
Если а — постоянная величина, то, очевидно,
lim а — а.
Поэтому согласно теореме IV получим:
lim ах = lim a lim х = a lim х.
Следствие 2. Предел степени переменной, имею-
щей предел, равен той же степени предела переменной,
т. е.
lim хт — (lim x)w.
§ 431
ТЕОРЕМЫ О ПРЕДЕЛАХ
123
В самом деле, хт можно представить как произведение т
одинаковых сомножителей; тогда
lirn хт=\im (х • х • х... x)-~iim х lim х lim х... lim х—(lim х)т.
Выведенное следствие, как доказывается в подробном
курсе анализа, справедливо для любого значения т.
Пользуясь этим, можно сказать, что предел корня из
переменной, имеющей предел, равен корню этой же сте-
пени из предела переменной, т. е.
яп яп
lim Ух — Уlim х.
яп 1
Действительно, представив Ух в виде степени хт, по-
лучим:
ЯП 1 1 ЯП
lim У х = lim х w = (lim х) w = Уlim х.
Теорема V. Предел частного от деления двух пе-
ременных, имеющих пределы, равен частному от деле-
ния пределов делимого и делителя при условии, что
предел делителя не равен нулю.
Доказательство. Пусть
lim х — А 1
И limj/ = BJ,
причем В Ф 0. Примем без доказательства существование
предела -у ввиду сложности этого вопроса; докажем только,
что он равен частному от деления пределов х и у.
Положим
— = Z,
У
(3)
откуда
X — у Z.
Приняв во внимание, что х, у и z имеют пределы, приме-
ним теорему о пределе произведения:
limx= limj/lim^
или
А = В lim z,
откуда
V А
limz = -и-.
£>
124
ТЕОРИЯ ПРЕДЕЛОВ
[ГЛ. V
Согласно равенствам (2) и (3) имеем:
при условии
lim у Ф 0.
§ 44. Предел функции. Пусть дана функция
У = х2 — 4. (1)
О пределе функции можно говорить только при условии
задания предела, к которому стремится ее аргумент х; без
этого условия вопрос о пределе функции не имеет смысла.
Положим, что х—>3; посмотрим, существует ли при
этом условии предел данной функции и если существует,
то какой *).
Говоря о пределе переменной в § 41, мы показали, что
эта переменная может стремиться к своему пределу, изме-
няясь разными способами.
Пусть в нашем примере х принимает такую последова-
тельность значений:
3,1; 3,01; 3,001; 3,0001; . . . ->3;
тогда функция (1) получит соответственно значения:
5,6; 5,06; 5,006; 5,0006; ...->5.
Мы видим, что данная функция при х->3 имеет предел,
равный 5. Это записывают так:
lim (х2— 4) — 5.
х -> 3
Если в равенстве (1) аргументу дать значения:
2,9; 2,99; 2,999; 2,9999; . ..->3,
то и в этом случае предел нашей функции будет тот же,
в чем легко убедиться соответствующими вычислениями.
Итак, функция (1) имеет предел при х~>3.
*) В полных курсах анализа дается определение понятия пре-
дела функции. Ввиду сложности этого определения мы не находим
возможным здесь его приводить.
§ 44]
ПРЕДЕЛ ФУНКЦИИ
125
Показанный выше способ нахождения предела функции
громоздок, поэтому на практике он не применяется. Доказан-
ные нами теоремы о пределах (§ 43) позволяют упростить
решение этой задачи.
I. Пример 1. Найти lim (х2—4).
х -> з
Решение. Применяя теорему III и следствие 2 теоремы
IV о пределах, получим:
lim (х2 — 4) = lim х2 — lim 4 — ( lim х)2 —lim 4 = З2—4=5.
х > з х -> з х -> з
Этот предел равен ранее найденному нами для функции
у == х2 — 4.
—I— Зх
Пример 2. Найти lim 9 ^7......г.
X -> 2 « 1
Решение. Прежде чем применить теорему о пределе
частного, нужно узнать, не будет ли предел делителя равен
нулю при х —>2. Пользуясь теоремой II и следствием 1 тео-
ремы IV о пределах, найдем:
lim (2х~4~ 1) — 2 lim x-J-lim 1—2«2-]-1=5.
2 X -> 2
Предел делителя не равен нулю, поэтому теорема V о пре-
делах может быть применена к нашей функции. Таким
образом,
lim х2 + 3* — Пга
^22х+Г— 11т(2х+1У-
х -> 2
Но
Пт (л2 3х) = ( Нт х)2 -f- 3 lim х.
х~> 2 X -> 2 а? -> 2
Следовательно,
,, х2-|-Зх (Нт х)2 + 3lim х_22-|-3-2____10___Q
J1™Ух+ Г “ Fliinx + Ит Г ~ 2-2-1-1 ~ Т ~
Х Х 2 х->2
Подставив в выражения функций в последних примерах
вместо х его предельное значение, мы получим те же резуль-
таты. В полных курсах анализа доказывается законность такой
подстановки при условии, что к функции, предел которой
находится, применимы теоремы о пределах.
В дальнейшем мы будем пользоваться этим приемом, так
как он значительно ускоряет процесс отыскания предела
функции.
126
ТЕОРИЯ ПРЕДЕЛОВ
[ГЛ. V
II. Разберем примеры, в которых предел делителя равен
нулю и, следовательно, теорема о пределе частного непри-
менима; при этом может представиться два случая.
а) Предел делимого не равен нулю.
3
Пример 3. Найти lim -и-------
х->з 2х —6
Решение. Найдем предел делителя, заменяя х его пре-
дельным значением:
lim (2х — 6)^2.3 — 6 = 0.
х -> 3
Как видно, теорему о пределе частного в данном примере
использовать нельзя (деление на 0 недопустимо). Мы знаем,
что если lim (2х — 6) = 0, то 2х— 6 есть бесконечно малая
х -> 3
величина, а обратная ей величина есть бесконечно большая
(§ 40). Поэтому ПРИ а следовательно, и про-
изведение т;——• 3 — бесконечно большая величина, т. е.
2х — 6 *
б) Предел делимого равен нулю.
Пример 4. Найти lim *
Решение. Предел делителя
lim (х2 + х)=024-0 = 0
х -> о
и предел делимого
lim (х2+ 2х) = О22 • 0 = 0.
х -> О
о О
В этом случае получим выражение —, не имеющее смысла.
Однако отсюда не следует, что данная функция нс имеет
предела; для его нахождения нужно предварительно преоб-
разовать функцию, разделив числитель и знаменатель на х^
что возможно, так как до перехода к предельному значению
х ф 0, т. е.
-р 2х_х -р 2
+ { )
§ 44]
ПРЕДЕЛ ФУНКЦИИ
127
К выражению -
так как предел
дроби .
теорема о пределе частного применима,
его делителя не равен пулю. Найдем предел
.. х + 2 0 + 2 Q
lim —Н- = _ 2.
Приняв во внимание равенство (2) и следствие теоремы I
§ 43, будем иметь:
.. х2 + *х ..
11П1 —-------— 11Ш
2.
Этот результат можно подтвердить и вычислением зна-
чений данной функции при значениях аргумента, близких
к нулю, например при
х = 0,1; 0,01; 0,001; 0,0001; ...
Следующая таблица показывает характер изменения функции
х2 + 2х п
—— при х->0:
У
X 0,1 0,01 0,001 0,0001 1 ... •—> 0
х1 + 2х А'2 + X 1,9 1,99 1,999 1,9999 ... —> 2
Пример 5. Найти lim -------у-.
а?-> 3 х 6
Решение. И в даннотл случае пределы делимого и
делителя равны нулю, поэтому функцию необходимо пред-
варительно преобразовать, сократив ее на х — 3, что допу-
стимо, так как до перехода к предельному значению х—3 + 0.
Итак,
.. х2 —9 .. (х + 3)(х —3) о I о
lim —— = 11 щ -—!—------------ = lim (х + 3) == 3 + 3—6.
а? -> 3 х а? -> 3 х 6 а? -> 3
ГТ с u Н 1- л + з — 2
Пример 6. Найти lim --------!—=—.
os > 1 х 1
Решение. Как и в * предыдущих примерах, данная
функция должна подвергнуться преобразованию. Для этой
128
ТЕОРИЯ ПРЕДЕЛОВ
{гл. V
цели освободим числитель от иррациональности, умножив
оба члена дроби на ]/ х 4~ 3 4~ 2, и сделаем необходимые
упрощения:
•• £1±±± — нт СГ7+~з-2)СГ7+~з+2)
«,->» JC~1 (х-1)(/х + ЗЧ-2)
= lim ----------------=
х->\ (х—1)(Ух + 3 + 2)
.. X— 1 .. 1
— |1П1 ---------------— hm ———
ж->1 (X— 1)(Ух+3+2) -|Лл^з+2
1 1
“ УТ+3 + 2 “ 4 *
III. Разберем примеры отыскания предела функции при
2
Пример 7. Найти lim -........у 9 •
Ж -> ОО I
Решение. Делитель 3x4” 2 при х —> со неограниченно
растет, т. е. представляет бесконечно большую величину;
обратная же ей величина л..\ а — бесконечно малая (§ 40).
OX Z
Следовательно, произведение -..• 2 стремится к нулю,
оХ *т*
если х сю ;
V 2 л
Inn ~=0.
с -> оо Зх 2
Пример 8. Найти lim -~гМ~г.
X -> ОО “"Г *
Решение. Делимое и делитель данной функции при
X-+OQ — бесконечно большие величины, а их отношение не
имеет смысла. Поэтому преобразуем данное выражение,
разделив делимое и делитель на х:
Зх~р5 3~1~ х
^"r“7Z± ’
’ X
5 1
Но — и — при х-»оо — бесконечно малые величины,
х х г
а потому пределы делимого и делителя будут соответственно
равны 3 и 4, а предел функции 0,75.
§ 44]
ПРЕДЕЛ ФУНКЦИИ
129
Процесс нахождения предела данной функции запишется
так:
lim — lim
? -> со ™ ‘ х -> С
5
х 3 -р 0
Т~ = 4+"б =
0,75.
Пример 9. Найти lim —-тгт-— *
х->™ ^ + 4
Решение. Разделив оба члена дроби на
о п . 1
х2, получим:
2л3 ~р Зл - л
о 1
При х —» со отношения —
неограниченно растет; следовательно,
4
-у стремятся к
нулю, а 2х
се
lim
1,
а вся дробь
2л ~р 3 “4" ~—
-> со
Итак,
.. 2л3+Зл2-4-л
11Ш ---L_—L— — ilm
2x4-34-4-
4
л2
— со
Найти:
Упражнения
Е lim (2л2 — Зл + 4).
х -> 2
4. Нт
х -> о 1 + 2 л2
2. lim
х i 2л — 1
5. lim ...........
х -> о л — 1
8. lim
х -> о л
3. lim
ж-х) 5
6. lim .
х->о 2л2 5
2л3 ~р ~р х
4
и
и
4
9 Зак. 3032. И, Л. Зайцев
130
ТЕОРИЯ ПРЕДЕЛОВ
[ГЛ. V
9. lim _L±£±2L,
х -> о 2-V 4~ х2 4~ х*
12. lim 24±М
х ->о
10.
lim
х-\-х2
х -> о Злг
13. lim 5—-1
х -> 1 х — 1
ll.lim2^3^.
х ->э 2х
14. lim 4а2.~х'.:..
ж->2а X — 2а
15. lim ^ + х-в.
х 2 X 2
17. lim 4~РЛ + 6
х —> 2 х—12х4“20
19. lim . ,.-------.
х -> з х* — Ьх 4" 0
16. lim j±+4*-5,.
Ж >-Г> X + 5
18. lim .
х -> — з х 4” з
20. lim
x О X
21. lim +
22.
24. lim (44- —-----Ц.
Ж->со\ 1 x x1}
23. lim
x->o 4x
25. lim _J______. 26. lim £±2. 27. lim -..2jL_.
X > 00 X2 -j- X x -> co X x -> CO X 1
28. lim ...Lz: 4. 29. lim — + 4 . 30. lim 4 — 4-.
X -> 00 1 4~ x -> 00 X^ 4“ x -> co X“ 4“ & *
§ 45. Предел отношения
sin x
X
при x->0. Так как
в данном случае limx = 0, то для нахождения предела отно-
sin х п
шения при х —> 0 нельзя при-
менить теорему о пределе частного;
нельзя также сделать никаких пре-
образований для вычисления предела
данного отношения. Поэтому ис-
пользуем геометрические сообра-
жения.
Возьмем окружность радиуса R
и центральный угол х, выраженный
в радианной мере (черт. 69). Прове-
дем хорду AM и касательную AN,
пересекающую продолжение радиу-
са ОМ в точке N. Из чертежа видно:
Площ. Д АОМ < площ. сектора АОЛ4 < площ. Д AON.
Выражая площади треугольников и сектора по форму-
лзхМ, можехм переписать:
О А • РМ ОЛ • AM ОА • .
~ ” 2 2 ‘ 2 ’
131
о л Гт Ь1Н -л- /Л
§ 45] ПРЕДЕЛ ОТНОШЕНИЯ ----- ПРИ X —> О
ОА
после сокращения на у получим:
PM AM < AN.
Разделим все члены последних неравенств на /?:
Но
PM AM AN
R < R < R *
(1)
PM
== sin X
R
AN
R
tg*»
AM
R
поэтому неравенства (1) принимают вид:
sin х < х < tg х,
или
sin x < x
sin x
cos x
Так как x — острый угол, то sinx— величина положительная;
-------1----------1-------1------н-—>-
Z2 cosx s&M'. 7
х
Черт. 70.
I- разделив полученные неравенства на sin х, найдем;
1 " х 1
sin х cos х
или
. . sin X .
1 >-----> cos х (2)
х 7
Положим теперь, что х —> 0; тогда
cos х —> 1.
I I Shl X
Но так как отношение -у- согласно неравенствам (2) заклю-
чено между единицей и cosx, то оно и подавно стремится
г к единице.
132
ТЕОРИЯ ПРЕДЕЛОВ
[гл. V
ГЧ O1U Л.
Это стремление отношения —— к единице хорошо выяс-
няется, если величины, содержащиеся в неравенствах (2},
представить на координатной оси (черт. 70).
Итак,
sin х .
lim ----------------------= 1.
ж -> о х
§ 46. Эквивалентные бесконечно малые величины.
Эквивалентными называются бесконечно малые величины,
предел отношения которых равен единице.
В § 45 был рассмотрен предел отношения двух беско-
нечно малых величин sin х и х, причем этот предел оказался
равным единице; поэтому sinx и х — эквивалентные беско-
нечно малые при х—>0.
Можно указать и на другие эквивалентные бесконечно
малые величины, например tgx и х при х-> 0. В самом деле,
sin х
.. tgx .. cos х .. sin х .. /sin x 1
lim ~lim----------— lim -------— hm ------------ —
Ж § X Я? -> 0 X ж о x cos x ж -> o ' x cos x'
В подробных курсах анализа доказывается, что при оты-
скании предела отношения двух бесконечно малых величин
каждую из них можно заменить ей эквивалентной.
sill2 у
Пример 1. Найти lim —5—.
Ж >0 Х
Решение. Мы уже показали, что sin х и х при х -•> 0 —
эквивалентные бесконечно малые величины; поэтому в данном
выражении можно sin заменить его аргументом . Сделав
это, получим:
lirnl
2. Найти
,. sin ах
11П1
Я, > о Sin bx
£
4 ’
Пример
§ 47}
ПРЕДЕЛ ВЫРАЖЕНИЯ ПРИ /2—> CXD
133
Решение. При х —>0 также ах—>0 и 7>х->0; по-
этому sin ах и sin bx— бесконечно малые величины. Заменяя
sin ах и sinfrx эквивалентными бесконечно малыми величинами
соответственно ах и Ьх, получим:
lim
х > 0
sin ах
sin bx
lirn
х > о
ах
bx
а а
lim -г — -г
b b
Найти:
Упражнения.
1. lim ~—.
._>osinx
sin ‘2х
hm —х----.
Зх
5.
2. lim -------
„ . n cos X
„ sin#x
6. hm ------
bx
„ х sin3 -ту
9. lim 10.
Ж->0 X3
sin X
12. lim 13.
Л‘>0 tg*
15
sin x cos
hm-----------
lim
X ->o
lim xctgx.
ж->0
18.
lim
x 0
sin 3x
3 sin x *
19.
o o sin 2x
3. hm---------.
ж->о x '
sin2x
hm —5—
sin2 x
x3
16. hm
x ->0
lim
x -> 0
11
lim
14. lim
x ->0
sin x + tg x
X
sin 3x
sin 2x ’
sin
4. lim --------
cc->o x
8.
lim
sin22x
x2
sin 2x 4~ sin 3x
x
sin 2x sin x
X2
17.
sin 2x
hm —:------.
•p->o
tg2x 1 — cosx
20. hm ——•. 21. hm-*—
x x+0 X^
§ 47. Предел выражения +~y при п->оо. В по-
/ 1 \n
дробных курсах анализа доказывается, что предел
при п —> со существует, что он больше 2 и меньше 3 и
выражается иррациональным числом. Для пояснения сказанного
/ 1
составим следующую таблицу значений выражения 11 ~Ьур1
при возрастающих значениях nt
п 1 2 3 4 5 10 100 1000
/ 1 \п \ п / 2 2,25 2,37 2,44 2,49 2,59 2,705 2,717
134
ТЕОРИЯ ПРЕДЕЛОВ
[ГЛ. V
Из таблицы видно, что по мере возрастания п выражение
/ 1 \п
также возрастает, замедляясь в росте.
/ 1 \«
Предел (1 + пРи я->со, равный приближенно 2,718,
принято обозначать буквой е.
Итак,
1 V*
-Ц = е^2,718.
§ 48. Натуральные логарифмы. В высшей математике
число е имеет очень важное значение, которое можно срав-
нить со значением тс в геометрии. Число е принимают за осно-
вание натуральных, или неперовых *), логарифмов, имеющих
большое применение в математическом анализе, так как
с их помощью многие формулы можно представить в более
простом виде, чем при пользовании десятичными логариф-
мами. Для натурального логарифма установлен символ In.
Натуральный и десятичный логарифмы одного и того же
числа связаны простым соотношением, позволяющим пере-
ходить от десятичного логарифма числа к натуральному, и
наоборот.
Для вывода этого соотношения возьмем число N и пред-
ставим его в виде двух степеней, приняв за основания их
числа 10 и е\
/V = 10ж
и
N = еу,
где х и у, как известно, называются логарифмами числа /V,
причем х — десятичным, у — натуральным. Из написан-
ных равенств следует
10ж^Л
Прологарифмировав обе части этого равенства по основа-
нию 10, получим:
х lg 10 = у 1g е,
*) Натуральные логарифмы названы неперовыми по имени шот-
ландского математика Непера, впервые применившего логарифми-
ческие вычисления.
§ 48]
НАТУРАЛЬНЫЕ ЛОГАРИФМЫ
135
или
откуда
Заменяя х и у соответственно через lg N и In/V, напишем:
1 V lg'V
In TV -—- —— .
В таблице логарифмов найдем:
1g е = 0,4343.
Поэтому
lnA/=lgAZ.-~ = lgAZ- -^ = ^.2,303, (1)
т. е. натуральный логарифм числа равен произведению
десятичного логарифма этого числа на множитель, рав-
ный 2,303.
Отсюда следует, что натуральный логарифм числа больше
десятичного в 2,303 раза.
Из равенства (1) находим:
lg TV = In TV • 0,4343,
т. e. десятичный логарифм числа равен произведению на-
турального логарифма этого числа на множитель, рав-
ный 0,4343.
Пример. Найти In 2;
Решен и е. in 2 = 1g 2 • 2,303 = 0,3010.2,303 0,693.
Найти:
1. 1пЗ.
5. In 0,2.
Упражнения
2. In 12. 3. In 4,5. 4. In 10,5.
6О In 0,16. 7. 1п0,84. 8. 1110,1.
ГЛАВА VI
ФУНКЦИЯ И ЕЕ ПРОСТЕЙШИЕ СВОЙСТВА
§ 49. Символика функциональной зависимости. Как
указывалось (§ 6), переменная у называется функцией пере-
менной х, если каждому допустимому значению х соответ-
ствует вполне определенное значение у, Задать функцию
аналитически —значит указать действия, которые нужно про-
извести над аргументом х, чтобы получить соответствующее
значение у.
Пусть, например, функция задана уравнением
х2 + 2У"х— 1
у — —!----------.
X
Этим самым нам даются и те действия, которые необходимо
совершить над х, чтобы получить у.
Часто бывает, что одна и та же функция, заданная иногда
сложным уравнением, не раз встречается в изложении одного
и того же вопроса. Условились для краткости записи пра-
вую часть уравнения, задающего функцию, обозначать симво-
лом f(x) и писать:
y = f(x).
Это равенство читается так: «игрек равен эф от икс» или
«игрек есть функция от икс».
Иногда нас будет интересовать не какая-нибудь конкрет-
ная функция с известной совокупностью действий над аргу-
ментом, а только факт, что одна переменная величина зави-
сит от другой переменной величины. В этом случае также
принято писать y — f(x), разумея под символом /(^неиз-
вестную совокупность действий над аргументом х.
Если в одном и том же вопросе речь идет о нескольких
различных функциях, то, чтобы не смешивать их, символы
этих функций обозначают разными буквами, например: F, <?, ф.
§ 50] ОБЛАСТЬ СУЩЕСТВОВАНИЯ ФУНКЦИИ 137
§ 50. Частное значение функции. Область существо-
вания функции. I. Пусть функция у задана уравнением
у—х2— х. (1)
Дадим х ряд значений, например хх = 1, х2 = 3, х3 = 5
и т. д.; тогда у получит соответствующие значения: <у1 = 0,
у2 = 6, у3 = 20 и т. д.
Величины xlt х2, х3 называются частными значениями
аргумента, а уи у2, у3—частными значениями функции.
Если совокупность действий над аргументом функции (1)
обозначить символом f(x'), то можно написать:
/(х) = х2 — х.
В этом случае найденные значения функции запишутся гак:
/(1) = 0, /(3) = 6, /(5) = 20.
Пример. Дана функция /(х) = 2х2 -(- х — 1. Найти:
1)7(—1), 2)/(0), 3)/(2), 4) f(a).
Решение. 1) /(—1) = 2(— 1)2 + (—1)— 1 =
= 2 —1 — 1=0,
2) /(0) = 2 • 0-|~0 — 1 =— 1,
3) /(2) =2.22+2— 1 =9,
4) /(а)=2я2-|-я—1.
II. Как видно, функция в разобранном примере имеет
действительные значения при любых действительных значе-
ниях х. Однако часты случаи, когда функция при некоторых
значениях аргумента не имеет числовых значений или, как
говорят, не существует. Например, функция у = •— при
л 1
х = 0 не существует, так как не выражается никаким
числом; функция у — ]^х при х < 0 не существует: она
имеет мнимые значения при х < 0.
Определение. Совокупность всех действительных
значений аргумента, при которых функция имеет дей-
ствительные значения, называется областью существо-
вания функции.
138 ФУНКЦИЯ И ЕЕ ПРОСТЕЙШИЕ СВОЙСТВА [ГЛ. VI
Например, областью существования функции у — х2
является совокупность всех действительных значений х, т. е,
— оо < х < ос;
для функции —1 область существования состоит
из действительных значений х, абсолютная величина которых
не меньше единицы, т. е.
Упражнения
1. Дана функция f(x)~2x—1. Определить
1)/(2), 2)/(0), 3)/(—1).
2. Дана функция f(x) = Зх2Д- 1. Определить
1) Z(— 2), 2)/(5), 3) / (2а), 4)/(zz—1).
3. Показать, что для функции f(x) = Зх4 — 2х2 -J- 1 справедливо
равенство f (— 3) = /(3).
4. Дана функция f(x) = х*— х. Доказать, что /(—х) = —/(•*)•
5. Как записать, что числа 2 и — 3 служат корнями уравнения
/(л) “О?
6. Найти область существования функций:
1) 4),= ^
1 У х 5) у — In х;
2) У = J7ZT]! 6) у =
3) 7)y = arcsinx
§ 51. Геометрическое изображение функций. Пусть дана
функция у = f (х). Из аналитической геометрии мы знаем,
что уравнение y=f(x)t вообще говоря, определяет некото-
рую линию, которую называют графиком функции. Этот
график дает нам наглядное представление о характере изме-
нения данной функции.
Пример 1. Построить график функции у — х3.
Решение. Полагая х — —1,2; —1; —0,5; 0; 0,5;
1; 1,2, найдем соответствующие значения функции у и запи-
шем результаты вычисления в таблицу:
X — 1.2 — 1 — 0,5 0 0,5 1 1.2
У — 1,7 — 1 — 0,1 0 0,1 1 1,7
§ 51] ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ ФУНКЦИЙ 139
Рассматривая каждую пару найденных значений х и у как
координаты точек плоскости, построим эти точки и, соединив
их плавной линией, получим кривую, называемую кубической
параболой (черт. 71).
Пример 2. Построить кривую, заданную уравнением
у2 = х3.
Р ешение. Найдем у из данного уравнения
у — ± ]/\3.
Мы видим, что уравнением у*=х3 заданы две функции:
v = ± И у — — У X3,
область существования которых х^>0. Составим следующую
таблицу значений х и у> вычисляя Ух3:
X 0 0,5 1 2
У 0 ±0,35 ±1 ±2,3
140
ФУНКЦИЯ И ЕЕ ПРОСТЕЙШИЕ СВОЙСТВА
[ГЛ. VI
Построив точки по найденным координатам и соединив их
кривую, называемую полукубиче-
ской параболой (черт. 72).
Пример 3. Построить гра-
фик функции
{х, если х^>0,
— х, если х < 0.
Решение. Здесь функция
задана двумя уравнениями: у — х,
где х имеет только положитель-
ные значения и нуль, и у = — х,
где х имеет только отрицатель-
ные значения. Таким образом,
область существования данной
функции состоит H3fBcex действи-
тельных чисел, график же ее пред-
ставляет ломаную линию, состоя-
Черт. 72. щую из биссектрис первого и вто-
рого координатныхуглов (черт. 73).
Пример 4. Построить график функции
1, если х^>0;
— 1, если х < 0
Решение. Область существования данной функции
составляют все действительные числа, а график ее состоит
из двух полупрямых параллельных оси Ох (черт. 74).
Примечание. Как известно из алгебры, функция
может быть задана тремя способами: аналитическим, таблич-
ным и графическим. Эти три способа задания функции мы
§ 52]
ПРИРАЩЕНИЕ ФУНКЦИИ
141
имели в первых двух разобранных примерах. Хотя каждый
из этих способов имеет применение в математике, однако
аналитическое задание функции играет особо важную роль.
§ 52. Приращение функции. Если переменная величина х
изменила свое значение от до х2, то разность между
новым ее значением и первоначальным называется прираще-
нием переменной и обозначается символом Ах *) (читается:
«дельта икс»).
Таким образом,
Ах = х2-— Хр
отсюда
х2 — Xi + Ах.
Величина х2 иначе называется наращенным значением
переменной.
Приращение переменной может быть как положительным,
так и отрицательным числом. Если, например, значение х
изменяется от 5 до 5,2 то
Ах = 5,2 —5 = 0,2,
а если оно изменяется от 10 до 9,7, то
Ах = 9,7 — 10 = — 0,3.
Пусть дана функция
- у = х2.
Предположим, что аргумент ее имел первоначальное зна-
чение Xi = 3, а потом изменил свое значение на х2 = 3,5;
тогда
Ах = 3,5 — 3 = 0,5.
Найдя значения функции сначала при Xj = 3, а потом при
х2 —3,5, получим:
Л = 3*=9,
Л=^3,52= 12,25.
Величина у} называется первоначальным значением функ-
ции, у2 — новым или наращенным ее значением, а разность
*) Заметим, что Дх нельзя рассматривать как произведение
двух множителей; символ Д неотделим от х, как, например, в вы-
ражении sin х символ sin неотделим от х.
142 ФУНКЦИЯ И ЕЕ ПРОСТЕЙШИЕ СВОЙСТВА [ГЛ. VI
у2 — ух— приращением функции. Согласно принятому сим-
волу для приращений можем написать:
&у—у2—ух — 12,25 — 9 = 3,25.
Найдем приращение Ду функции у — х2 при любом изме-
нении х.
Положим, что аргумент ее имеет любое первоначальное
значение х; тогда первоначальное значение данной функции
будет:
у = %2. (1)
Допустим теперь, что х получает приращение Дх; тогда
новое (наращенное) значение аргумента будет х-ф-Дх. Чтобы
найти новое (наращенное) значение функции, нужно в дан-
ное выражение функции вместо х подставить х-ф- Дх; получим:
у-ф-Ду = (х-ф-Дх)2. * (2)
Вычтя из равенства (2) равенство (1), найдем:
__ у -ф- Ду — (х + Дх)2
у = X2
Ду — (х -ф- Дх)2 — х2,
или после преобразования
Ду — х2 4~ 2х Дх -ф- (Дх)2 — х2 = 2х Дх + (Дх)2. (3)
Мы нашли приращение данной функции в общем виде.
Чтобы получить приращение этой функции для частного
случая, который мы имели в начале параграфа, можно в ра-
венстве (3) х и Дх заменить соответственно числами 3 и 0,5,
после чего найдем:
Ду = 2 - 3 • 0,5 + (0,5)2 = 3 + 0,25 = 3,25.
Последний результат совпадает с ранее найденным.
Таким образом, для нахождения приращения функции
нужно:
1) в данном выражении функциональной зависимости
заменить х на х-ф-Дх, а у на у-ф-Ду;
2) из полученного выражения вычесть почленно данное.
Если функция задана в общем виде у = /(х), то согласно
высказанному правилу ее приращение можно написать по
формуле
(4)
Ду = /(х4-Дх)—/(*).
§ 53] ИЗОБРАЖЕНИЕ ПРИРАЩЕНИЙ АРГУМЕНТА И ФУНКЦИИ 143
Пример 1. Найти приращение функции у — 2х24~ 3.
Решение. 1. у4~Ду — 2(х4~Д-42~Н 3 =
= 2х2 4~ 4х Дх 4~ 2 (Дх)2 4- 3.
2. у 4-Ду = 2х24~ 4х Дх4-2(Дх)24~ 3
у =2х24-3__________________
&у = 4х Дх 4~ 2 (Дх)2
Пример 2. Найти приращение функции у = —.
х
Решение 1. у 4~ ^У — •
2. у4~Ду =—Д—
х 1 х 4 Ах
~ 1
х + Ах х х{х + Ах) х (х + Ах) ‘
Упражнения
1. Дана функция у = 2x4-1. Найти ее приращение, если х
изменяется: 1) с 4 на 4,3; 2) с 0 на 0,2; 3) с 2 на 1,5.
2. Найти приращение функции у = 2х2, если х изменяется:
1) с 1 на 1,3; 2) с —0,2 на 3) с на а-
3. Найти приращение функции у = х2—1, если известно:
1) х^ = 2, Ах = 0,5; 2) хг = 3, Ах = — 0,6.
4. Найти приращение функции у = 2х2 —- х + 1, если даны:
1) xt = — 3, Ах = 0,5; 2) xt = а, h.
12
5. Дано v = , рг = 1, А/? = 0,4; найти Av.
6. Дано у = sin х, Xi = , Ах = — ; найти Ау.
7. Найти в общем виде приращение функций:
1) у = Зх 4- 2, 2) у = 2х2 — 1, 3) у = Зх2 — 2х,
4) у =- — х- — Зх, 5) у = х3, 6) у = 2х3 — 2х2,
7) у-х-1.
§ 53. Геометрическое изображение приращений аргу-
мента и функции. Пусть дана функция у —/(х), график
которой представлен на черт. 75.
Положим, что отрезок ОРХ = х изображает первоначаль-
ное значение аргумента; тогда значение функции при этом
144 ФУНКЦИЯ И ЕЕ ПРОСТЕЙШИЕ СВОЙСТВА [ГЛ. VI
значении аргумента будет f(x) и геометрически представится
ординатой точки Alp
PlM1 — f(x), (1)
Дадим аргументу х приращение
Р,Р2 = кх-9
тогда новое значение х будет:
ОР2 — х -4- Ах;
новое же значение функции будет f{x 4- Дх) и геометрически
представится ординатой Р2^2 точки М2:
P2M2 — f(x-\-&x). (2)
Проведя из точки М{ прямую, параллельную ОР2, до пере-
сечения с прямой Р2М2 в точке УУ, имеем:
ДМ42 = Р2М2 — P2N = Р2М2 —
или согласно равенствам (1) и (2)
NM2 — /(x-f-Ax) — f(x\
Полученная в правой части разность равна &у [см. фор-
мулу (4) § 52], а потому
NM2 — ky.
§ 54]
НЕПРЕРЫВНОСТЬ ФУНКЦИИ
145
Следовательно, геометрически приращение аргумента
изображается приращением абсциссы точки кривой, а при-
ращение функции — приращением ординаты этой точки.
§ 54. Непрерывность функции. Пусть дуга АВ есть
график функции y — f(x) (черт. 76). Возьмем на этой дуге
произвольную точку М (х; у) и дадим х приращение
РР1==Дх,
тогда у получит приращение
QMt — Ду.
Положим, что Дх—>0 и пусть при этом Ду—>0, т. е.
lim Ду = 0.
Ьх ->0
Это значит, что если Дх -» 0, то ордината PtМ, неограни-
ченно приближается к РМ, а точка к точке Л4 и, следова-
тельно, на дуге АВ найдется точка, сколь угодно близкая
к Л1. В этом случае говорят, что функция у — /\х) непре-
рывна при данном значении х.
Определение. Функция y — f(x) называется не-
прерывной при данном значении х, если бесконечно малому
10 Зак. 3032. И. Л. Зайцев
146
ФУНКЦИЯ И ЕЕ ПРОСТЕЙШИЕ СВОЙСТВА
[ГЛ. VI
приращению х соответствует бесконечно малое прира-
щение у9 т. е. если
lim Ду = 0. (1)
Дж->0
При соблюдении этого условия для любого значения
аргумента в промежутке от х — а до х — Ь функция назы-
вается непрерывной в указанном промежутке. Отсюда следует,
что дугу АВ графика непрерывной функции можно начертить
непрерывным движением карандаша, не отрывая его от
бумаги.
Однако не все функции и не при всяком значении х не-
прерывны. Возьмем, например, функцию = Из анали-
тической геометрии мы знаем, что графиком этой функции
(черт. 77) является равносторонняя гипербола, состоящая
из двух ветвей. Непрерывным движением карандаша можно
описать любую дугу на левой ветви и любую дугу на правой,
но нельзя, не отрывая карандаша от бумаги, прийти по кри-
вой от точки А на левой ветви к точке В па правой. Это
иллюстрирует нам непрерывность функции = ~ - при
любом х, кроме х=0, где данная функция, как говорят,
имеет разрыв.
§ 54] непрерывность функции 147
В рассмотренном примере разрыв заключается в том, что
при переходе аргумента через х — 0 (слева направо) функ-
ция изменяется с —оо на -)-оо.
Подобные разрывы имеют вообще дробные функции при
тех значениях xt при которых знаменатель обращается в нуль,
а значения функции неограниченно возрастают (у —> оо).
Например, функция y — j^yg имсет> РазРыв ПРИ х=3;
, 10 о о
функция у — при xi==2 и х2 = — 2 и т. п.
Существуют и другого рода разрывы, когда функция
меняет одно конечное значение на другое, тоже конечное.
Подобный пример представляет функция
если х^>0,
— 1, если х < 0,
график которой изображен на чертеже 74. Здесь при пере-
ходе аргумента через х = 0 (слева направо) функция меняет
значение с — 1 на 1.
Пример. Исследовать непрерывность функции у = х2.
Решение. Дадим х приращение Ах; тогда функция у
получит приращение (формула (3), § 52]:
Ду = 2х &х 4- (Дх)2.
Найдем предел Ду при Дх—>0:
lim Ду = lim [2х Дх + (Дх)2] = 2х • 0 -Ц— О2 = 0.
Да?->0
Полученное равенство справедливо при любом конечном
значении х; поэтому функция у = х2 непрерывна при любом
значении х. Представление о непрерывности функции у = х2
дает ее график (черт. 8).
Рассмотрим другое определение непрерывности функции, тесно
связанное с данным выше.
Найдем приращение функции у=/(х) при изменении аргу-
мента от х — с до х = с + Ах; согласно формуле (4) § 52 имеем:
Ду=/(с + Дх)-/(с).
Если данная функция непрерывна при х = с, то, заменив в ра-
венстве (1) Ду найденным его выражением, напишем:
lim Ду = lim [/ (с + Дх) — / (с)] = 0.
Да? -> о Да? -> О
10*
148
ФУНКЦИЯ И ЕЕ ПРОСТЕЙШИЕ СВОЙСТВА
[ГЛ. VI
По теореме о пределе разности (§ 43) будем иметь:
lim [J (с + Дх)— / (с)] = lim / (с + Дх)— lim /(с)-~0
Да; -> о Дж -> о Дж -> О
ИЛИ
lim /(с4-Дх)— lim /(с).
Дж-> о
дж -*•>
По /(с) — постоянная величина, поэтому
в1йп /(с4~ Дх) = ]{с).
Дж->0
Если
с 4- Дх — х,
(2)
то из условия Дх -»0 следует; х -> с; равенство (2) примет вид:
lim f(x) (3)
Ж ->с
Таким образом, из равенства (1) вытекает равенство (3). Можно
показать, что, наоборот, из (3) следует (1).
Отсюда видно, что равенство
Черт. 78.
(черт. 78) и точка с абсциссой
соответственно будут:
PM^f(c) и /W
(3) выраж^т условие непрерыв-
ности функции при данном х,
равносильное рассмотренному
в начале параграфа.
О п р е д е л е и и е. Функ-
ция y~f(x) называется не-
прерывной при х~ с. если
предел этой функции при
х с равен значению функ-
ции при х — с.
Если равенство (3) выпол-
няется для любого значения
аргумента от х = а до х = Ь,
то функция называется непре-
рывной в указанном проме-
жутке.
Поясним сказанное гео-
метрически. Пусть на графике
непрерывной функции у = /(х)
дана точка М с абсциссой х = с
х = с 4~ А-*, тогда их ординаты
= ./ (с 4- Дх)=/(х).
Так как функция непрерывна, го при Дх->0 и Ду -> 0, а точка М2
неограниченно приближается к М. Но при этом, как видно,
с 4~ Дх = х —> с
и ордината Р2Л42=/(х) стремится к ординате PAI—/(с).
Если взять точку с абсциссой х = с — йх, то и в этом
случае при Дх->0 и Ду->0, а точка неограниченно прибли-
§ 55] СВОЙСТВО НЕПРЕРЫВНОЙ ФУНКЦИИ
149
жается к М. Но тогда, очевидно,
с — Дх = х -> с
и ордината PiM1=f(x) стремится к ординате РЛ4=/(с).
Мы видим, что, если данная функция y=f(x) непрерывна,
при х = с, то равенство (3) выполняется при стремлении х к с как
с правой стороны, так и с левой. Очевидно, верно и обратное утвер-
ждение: если равенство (3) выполняется при стремлении х к с как
справа, так и слева, то функция у — / (х) непрерывна при х — с.
Если это условие нарушается, то функция имеет разрыв. Так,
на графике 74 мы имеем при х = 0 разрыв функции: здесь предел
ее при стремлении аргумента к нулю справа равен + 1, а слева
он имеет уже другое значение, равное — 1.
Заметим, что равенство (3) подтверждает справедливость ска-
занного в § 44 о том, что для нахождения предела функции доста-
точно подставить вместо аргумента его предельное значение.
Упражнения
Исследовать непрерывность следующих функций:
1. у — 2х. 2. у = х2 — 3. 3. у — х — 2х2.
4. у == х3. 5. у = sin х. 6. у = cos х.
Указать точки разрыва функций:
„ 1 о Х n 2х
7.у=-.------. 8. у =-----х- 9. у =—гт- Ю. y = tgx
7 1—х J х —2 J х-f-l л 6
§ 55. Свойство непрерывной функции. Непрерывная
функция может изменить знак только при переходе через
нуль. Это свойство непрерывной функции легко выясняется
геометрически. В самом деле, пусть
/(х)>0 при х~а (черт. 79, точка /1),
/(х)<0 при х = Ь (черт. 79, точка В).
150
ФУНКЦИЯ И ЕЕ ПРОСТЕЙШИЕ СВОЙСТВА
[ГЛ. V!
Если изменять непрерывно значение абсциссы от а до Ь, то
график функции в силу его непрерывности должен пересечь
ось Ох. В точке же пересечения кривой с осью абсцисс
значение функции равно нулю.
Если непрерывная функция меняет знак подряд несколько
раз, то график ее пересекает ось Ох столько же раз (черт. 80).
Ясно, что эта функция сохраняет один и тот же знак в про-
межутке между двумя соседними точками пересечения ее гра-
фика с осью Ох (между А и В отрицательный, между В и С
положительный), а также для всех точек налево от А (поло-
жительный) и направо от С (отрицательный).
§ 56. Классификация функций.
Явные и неявные функции. Функции делятся на
явные и неявные. Функция называется явной, если уравне-
ние, задающее ее, разрешено относительно этой функции.
Например, в уравнении у = 2х2 — хЦ-3 у есть явная
функция.
Функция называется неявной, если задающее ее урав-
нение не разрешено относительно этой функции.
Например, в уравнении х24~у2 — 25 функция у дается
в неявном виде. Однако функцию, заданную последним урав-
нением, можно представить и в явном виде; действительно,
решив это уравнение относительно у, получим у = z±z 25—х2.
Но в более сложных случаях часто бывает невозможно сде-
лать такое преобразование.
§ 56]
КЛАССИФИКАЦИЯ ФУНКЦИЙ
151
Классификация явных функций. Явные функции
делятся на два класса: алгебраические и трансцендентные
функции.
Алгебраической называется такая функция, над аргу-
ментом которой производится конечное число алгебраиче-
ских операций (сложение, вычитание, умножение, деление
и возвышение в рациональную степень).
Например, у — 2х2— 3]/х-|-1, у — ^-^~
раические функции.
суть алгеб-
Трансцендентной называется всякая неалгебраическая
функция.
Например, у = ах, y — logax, у — sin х, у/= arcsin х
суть трансцендентные функции.
Трансцендентные функции делятся на несколько видов,
простейшие из которых следующие:
1. Показательная функция у = аж, где аргумент является
показателем степени.
2. Логарифмическая функция y = \ogax.
3. Тригонометрические функции', у — sin х, j = cosx,
у = tg х, у = ctg х, у = sec х, у — cosec х.
4. Обратные тригонометрические функции*, у — arcsin х,
у = arccos х, у = arctg х, у — arcctg х, у — arcsec х,
у = arccosec х.
Взаимно обратные функции. Пусть дано урав-
нение
У — хъ, (1)
где у — функция х. Выразим отсюда х через у.
х = у. (2)
Заменив в уравнении (2) х на у, а у на х, получим:
У = ]Хх. (3)
Функция у, заданная уравнением (3), называется обратной
по отношению к функции у, заданной уравнением (1); обе
же функции (1) и (3) взаимно обратны.
Например, y = sinx и у— arcsinх\ у — аж и у— logax
суть попарно взаимно обратные функции.
ГЛАВА VII
ПОНЯТИЕ О ПРОИЗВОДНОЙ ФУНКЦИИ
§ 57. Равномерное движение и его скорость. Пусть
тело движется равномерно и прямолинейно. Это значит, что
в каждую единицу времени оно проходит одно и то же рас-
стояние, называемое скоростью этого движения. Закон рав-
номерного движения выражается формулой
s=-vt s0,
представляющей собой функцию первой степени, а геометри-
чески — прямую линию.
Обратно, всякая линейная функция вида
s = vt-y s0, (Г)
где v и s()— постоянные величины, выражает закон равномер-
ного прямолинейного движения. Чтобы в этом убедиться,
найдем расстояния, пройденные телом к моментам и t2.
Подставив в равенстве (1) вместо t значения tx и /2> получим:
= vtx -|~ So,
$2 = vt2 $0*
Отсюда
s2 — = {vt2 + s0) — (vtt + s0) = v (t2 — Q
и
$2--
Обозначив приращение пути s2— sx через As, а приращение
времени t2 — tv через А/, напишем:
§ 58]
НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ И ЕГО СКОРОСТЬ
153
Равенство (2) показывает, что отношение пройденного телом
пути к промежутку времени, в течение которого этот путь
r-Т Д$
совершен, величина постоянная. Поэтому представляет
скорость равномерного движения.
Следовательно, линейная функция s = vt-\-SQ выражает
закон равномерного прямолинейного движения, причем v
есть скорость этого движения.
§ 58. Неравномерное движение и его скорость. Кроме
равномерного движения в природе имеет место и неравномер-
ное движение. Закон его выражается уже не уравне-
нием первой степени, а более сложным уравнением.
Пусть, например, дана функция ''°
выражающая закон падения тела. Так как падение
тела — движение неравномерное, то возникает вопрос,
как определить его скорость в какой-нибудь момент
времени. Поступим следующим образом.
Допустим, что в начале падения тело было в
точке О (черт. 81). По истечении времени t оно прой-
дет путь, равный
5] = 4,9/2,
и окажется в точке А, а по прошествии времени
t4~ Дг от начала движения совершит путь
/7
'В3
Вг
В,
В
$2 = 4,9(/-Н-Д/)2
Черт. 81.
и будет в точке В, Отрезок пути, пройденный телом за
время Д£, будет:
АВ = s2 — = 4,9 (t + Д/)2 — 4,9z2 —
= 4,9/2 + 9,8/Д£ 4- 4,9 (Д/)2 — 4,9f2 =
= 9,8^ 4-4,9 (ДО2.
Разделив пройденный путь s2 — slt равный Д$, на время Д/.
получим:
Д/ Д/ ’ v
Результат деления ~ называется средней скоростью паде-
ния тела на участке пути АВ — Д$,
154 ПОНЯТИЕ О ПРОИЗВОДНОЙ ФУНКЦИИ [гл. VH
Однако средняя скорость движения тела не выражает ис-
тинной скорости в любой момент времени. Так, например,
когда говорят, что поезд идет со скоростью 50 км в час, то
это не значит, что он движется с этой скоростью во всех
точках своего пути; отходя от станции, поезд по-
степенно увеличивает скорость, доводит ее до наибольшей
величины, затем замедляет движение, пока не остановится на
следующей станции. Таким образом, на одном участке пути
его скорость меньше 50 км в час, на другом — больше, в сред-
нем же — 50 км в час.
Средняя скорость тем лучше характеризует движение, чем
меньше участок пути, на котором она определена; поэтому
положим, что промежуток времени А/ падения тела умень-
шается, тогда и путь АВ = As будет уменьшаться, становясь
равным ABlt AB2i АВ3 и т. д. (черт. 81), и для каждого
нового значения Аг отношение будет определять среднюю
скорость падения тела на участке пути, все более и более
коротком. Положим, что А/—>0, тогда /-|~А£—>/, а отно-
шение ™ будет стремиться к величине, называемой скоростью
в данный момент времени t, что соответствует скорости
в точке А.
Обозначив эту скорость через vt будем иметь:
Нт (2)
Д£->0
Таким образом, скорость прямолинейного движения
тела в данный момент времени t есть предел средней
скорости в промежутке времени от t до когда
Д/—>0.
Приняв во внимание равенства (1) и (2), найдем скорость
падения тела в момент /:
v = lim (9,8/-j-4,9A/)= 9,8/.
м > о
Итак,
г/= 9,8/.
Упражнения
1. Найти скорость тела, движущегося по закону
s ~ 31 — 5.
§ 59] СКОРОСТЬ ИЗМЕНЕНИЯ ФУНКЦИИ 155
2, Найти среднюю скорость движения тела, совершаемого по
закону
s — 2 А
для промежутков времени:
1) от — 2 до /2 = 4,
2) от = 6 до /2 = 10.
3, Закон движения тела выражается формулой:
s = /2 + 1.
Найти среднюю скорость движения тела для промежутка времени
/2 — А если:
1) tt = 2, /2 = 3; 3) = 2, t2 = 2,01;
2) t± = 2, /2 = 2,1; 4) = 2, t2 = 2,001.
Результаты вычислений записать в таблицу и проследить за изме-‘
пением средней скорости. #
4. Найти скорость движения тела в момент времени t = 2, если
закон движения дан формулой:
5 = 4/5 — 3.
5. Закон движения тела дан формулой
5 = 3/5.
Найти: 1) среднюю скорость движения за промежуток времени
от /1 = 2 до /2 ~ 5;
2) скорость движения в моменты /(= 2 и t2 = 5.
§ 59. Скорость изменения функции. Определять ско-
рости приходится не только в случае движения, но и при
изменении любой переменной величины, имеющей физическое
содержание (скорость испарения жидкости, скорость реакции
и т. д.).
Пусть переменная величина у, характеризующая какой-либо
процесс изменения, есть линейная функция другой перемен-
ной х, т. е.
у = /гх*4“
Ду
тогда отношение как и в случае равномерного движения
(§ 57), будет постоянной величиной, равной /г, т. е.
^ = /г. (1)
кх 4 7
Величина k, показывающая, сколько единиц приращения
линейной функции приходится па единицу приращения
156 ПОНЯТИЕ О ПРОИЗВОДНОЙ ФУНКЦИИ [гл. VII
аргумента, называется скоростью изменения линейной функ-
ции при любом х.
Если же величина у представляет функцию иного вида,
то отношение по аналогии с неравномерным движением (§ 58)
определяет среднюю скорость изменения у для промежутка
значений аргумента от х до х-|-Дх. При Ах —> О будем
иметь: x-\-kx—> х, а средняя скорость изменения функции
стремится к величине, называемой скоростью изменения
функции при данном х. Обозначив эту скорость через v,
напишем:
= I'm (2)
Аж->0
Таким образом, скорость изменения функции при дан-
ном х есть предел средней скорости ее для промежутка
аргумента от х до х-|-Дх, когда Дх->0.
Разберем несколько примеров.
Пример 1. Вес Р в килограммах однородного стержня
выражается формулой Р = 0,5/, где I — длина стержня в мет-
рах. Определить скорость изменения веса стержня с измене-
нием его длины.
Решение. Так как Р — функция первой степени отно-
сительно длины /, то в данном случае имеет место равно-
мерное изменение. Следовательно, скорость изменения веса
Р при любом значении длины I будет согласно формуле (1)
^=0,5.
Это значит, что при удлинении стержня на 1 м вес его уве-
личивается на 0,5 кг.
Пример 2. При нагревании тела температура его Т
изменяется в зависимости от времени нагревания t по закону
Г—0,4/2.
С какой скоростью нагревается тело в момент t— 10 сек.?
Решение. Данная функция второй степени и выражает
закон неравномерного изменения, а потому для решения
задачи применим формулу (2), причем для нахождения пре-
дела поступим так же, как это мы делали при определении
скорости падающего тела (§ 58).
§ 60]
ПРОИЗВОДНАЯ ФУНКЦИИ
157
В момент 7—10 температура тела Г, = 0,4 • 102 = 40.
» » /=10 + Д/ » » 7'2 = 0,4(10-|-Д/)2.
Вычтя из Т2 значение Т\, получим приращение температуры
Д7" за время Д/:
ЬТ= Тг—7\ = 0,4(10 + ДО2 — 40 =
= 40 + 8Д/ + 0,4 (Д/)а — 40 = 8Д/ + 0,4 (ДО2,
отсюда
^ = 8 + 0,4Д^
II
Частное есть средняя скорость нагревания тела за время
от /=10 до t = 10-|- &t.
Чтобы определить скорость нагревания тела в момент
/-10 сек., найдем предел средней скорости нагревания при
условии, что Д/ —> 0. Получим:
lim -*7= Ит (8 + 0,4Д/)=8.
Д/>0 Д/->0
Итак, в момент t— 10 сек. тело нагревается на 8° в еди-
ницу времени. Это значит, что если бы, начиная с момента
t— 10 сек., тело нагревалось равномерно, то в каждую еди-
ницу времени температура его увеличивалась бы на 8°.
Упражнения
1. Найти скорость изменения функции у = 2х — 1 при любом х.
2. Объем v газа при температуре t определяется формулой:
v = 1 + 0,0075/.
Определить скорость изменения объема газа при любой температуре.
3. Найти скорость изменения функции у == х2 при 1) х — 1,
2) л—3
4. Сила тока в амперах изменяется в зависимости от времени
по закону
/ = 0,2/2,
где / — секунды. Найти скорость изменения силы тока в конце чет-
вертой секунды.
§ 60. Производная функции. Величина lim являю-
Дж+о
щаяся основным понятием математического анализа,
носит специальное название производной функции по аргу-
менту х.
158
ПОНЯТИЕ О ПРОИЗВОДНОЙ ФУНКЦИИ
[гл. VII
Определение. Производной функции у = f(x) по
аргументу х называется предел отношения приращения
функции &у к приращению аргумента &х, когда Дх—>0.
Для производной функции у =f(x) приняты обозначения:
У («игрек штрих»),
/'(*) («эф штрих от икс»),
dy /
—; («дэ игрек по дэ икс»),
ух («игрек штрих по икс»).
В целях упрощения производную функции, заданной ма-
тематическим выражением, записывают в виде скобок, заклю-
чающих данную функцию, со штрихом с правой стороны.
Например, производную функции у — 2х2—Зх —{— 1 можно
записать так;
(2х2 — ЗхД- О'.
Из определения производной следует правило:
Для отыскания производной функции у — /(х) по аргу-
менту х нужно найти:
1) наращенное значение функции, т. е. _у4-А_у;
2) приращение функции, т. е. Ду;
3) отношение приращения функции к приращению аргу-
су
мента, т. е.
Ьх ’
4) предел этого отношения при Дх->0, т. е. .
Дж->0
Нахождение производной называется дифференцированием
функции. Раздел математического анализа, занимающийся
вопросами, связанными с производной, называется дифферен-
циальным исчислением.
Пример 1. Найти производную функции у — х2 4~
Решение. 1-й шаг:
у 4- Ду — (х 4- Дх)2 4- (х 4- Дх).
2-й шаг:
Ду = (у 4- Ду) — у = (х4- Дх)24- (х4- Дх)— (х24- х) =
— х2 4- 2хДх 4- (Дх)2 4- х 4“ — х =
— 2xAx-j- (Ах)2 4“
§ 60] ПРОИЗВОДНАЯ ФУНКЦИИ 159
3-й шаг:
Ду = 2хЛх + (ДхГ + Дх = 2% + Дд. + j.
Д х /\х
4-й шаг:
у' — Пт — = lini(2x + Дх-|- 1) — 2х-|- 1.
Да?->0 &Х Дд?->0
2
Пример 2. Продифференцировать функцию у = --.
Решение. 1-й шаг:
। л 2
3' + АУ = Т+ДГ’
2-й шаг:
9 2
= (у + Ду) —у = - =
2х — 2х —2Дх ___ 2Дх
х (х 4~ Дх) х (х + Ьх) *
3-й шаг:
Ду 2Дх * 2
Дх х (х Дх) ’ х (х +
4-й шаг:
/ 1. Ду Г 2 1 2
у = hm -~~= lim----------—=---------.
дж->о &х a.t)->oL x(x~pAx)J х
Производная функции y — f(x) является также функцией
аргумента х.
Определение. Значение производной функции
у = /(х) при данном х называется частным значением
производной.
Пример 3. Найти частное значение производной
функции
f (х) = х2 4~ х при х — 3.
Решение. Подставив в найденную уже производную
данной функции (см. пример 1) х = 3, получим:
/'(3) = 2.3+ 1 = 7.
В связи с данным выше определением производной можно
сформулировать определения рассмотренных нами скорости
движения (§ 58) и скорости изменения функции (§ 59) следую-
щим образом.
160
ПОНЯТИЕ О ПРОИЗВОДНОЙ ФУНКЦИИ
[гл. VII
Скорость прямолинейного движения тела в данный
момент равна производной пути по времени, вычисленной
для данного момента.
Скорость изменения функции при данном значении
аргумента равна производной функции при этом значе-
нии аргумента.
Найти производные
1. у = 4х — 5.
4. /(х) = — 2х2 + х.
7. v = и3 — и.
Упражнения
следующих функций:
2. у = 5х2 4- 1. 3. у = 4х2 — (2х.
5. f(x) = 3х2-- 2x4-5. 6. /(/) = —2/з
8. v^=—
Р
9. Дана функция /(х) = х2— 5х. Найти:
1)/'(3), 2)/'(2,5), 3)/'(0), 4)/'(-1).
§ 61. Связь дифференцируемости функции с непре-
рывностью.
Теорема. Если функция у — /(х) имеет производ-
ную при каком-нибудь значении х, то при этом значе-
нии х данная функция непрерывна.
Доказательство. Пусть при каком-нибудь значе-
нии х функция у — /(х) дифференцируема, т. е. имеет про-
изводную (§ 60)
/ v Ду
У = 1П1 Дл ’
Да?->0
тогда по определению предела можем написать:
Ду / ।
= у -4- а,
Дх J ‘
где а->0 при Дх—>0. Отсюда
&у = у' &х -Ь а &х
и
lim Ду = lim (у' Дх)+ lirn (а Дх)= 0
Да? -> о Да? > о Да; •> о
[Ит(у'Дх) = 0 как предел произведения постоянной на бес-
конечно малую и Пт(аДх)=0 как предел произведения
бесконечно малых]. Но мы знаем (§ 54), что если при дан-
ном значении аргумента выполняется равенство
lim Ду = 0,
Да? >0
F
§ 62]
ПОНЯТИЕ О КАСАТЕЛЬНОЙ
161
то функция при этом значении аргумента непрерывна. Тео-
рема доказана.
Обратное же утверждение не всегда бывает верно, так
как существуют функции, всюду непрерывные, но при неко-
торых значениях х не имеющие производной.
§ 62. Понятие о касательной. Касательную к окружности
мы определили как прямую, имеющую с ней одну общую точку.
Такое определение годится не для любой кривой линии. На-
пример, прямая 'MN касается кривой в точке А (черт. 82),
но имеет с этой кривой не одну, а две общие точки.
Чтобы определить касательную к данной кривой в точке М
(черт. 83), возьмем на ней еще одну точку Мг и проведем
секущую ТИ/Ир Если будем перемещать точку по кривой
так, чтобы она приближалась к Л4, стремясь с ней слиться,
то секущая ЛШ, будет поворачиваться вокруг точки Л4,
стремясь занять положение прямой MN, называемой каса-
тельной.
]] Зак. 3032. И. Л. Зайцев
162
ПОНЯТИЕ о ПРОИЗВОДНОЙ ФУНКЦИИ
[гл. VII
Определение. Касательной к данной кривой в дан-
ной ее точке Л4 называется предельное положение секу-
щей когда точка двигаясь по кривой, неограни-
ченно приближается к точке 714.
В математике и в технических дисциплинах часто прихо-
дится рассматривать прямую, проходящую через точку каса-
ния 714 перпендикулярно касательной; эта прямая называется
нормалью к кривой в точке 714.
§ 63. Геометрический смысл производной. Пусть дана
непрерывная функция у = /(х), график которой представлен
на черт. 84. Возьмем на нем точку М(х\ у\, тогда
ОР = х и РМ — у.
Дадим х приращение
РР^кх',
в этом случае наращенному значению абсциссы
ОР1 — х + kx
будет соответствовать наращенное значение ординаты
P^^ftx+kx)
точки кривой. Проведем из точки М прямую MQ, парал-
лельную оси Ох, а также секущую через точки М и 7141.
§ 63] ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ 163
В полученном прямоугольном треугольнике M^MQ
MQ—kx,
QMt = РгМ j — PM = f (x + Дх)—f(x) = ky.
Обозначим угол наклона секущей М^ к положительному
направлению оси Ох через р; тогда
^M,MQ= £MRP = $.
Из треугольника MtMQ имеем:
или
&у = Axtg р,
откуда
Из равенства (1) видно, что отношение приращения функции
к приращению аргумента равно тангенсу угла наклона секу-
щей к положительному направлению оси Ох.
Пусть Дх—>0, тогда Ду->0, так как данная функция
непрерывна (§ 54). Вследствие этого точка Мг будет неогра-
ниченно приближаться к М, а секущая MtR — вращаться
вокруг точки М, стремясь занять положение касательной NL
(§ 62).
Найдем предел обеих частей равенства (1) при условии
Дх —> 0; получим:
Hm Hm tg₽. (2)
Да?->о
Так как наклон секущей к оси Ох при ее повороте изме-
няется, то р становится переменной величиной и в пределе
стремится к величине угла, образованного касательной NL
с положительным направлением оси Ох; поэтому, обозначив
£NLP буквой а, можем написать:
lim tg р = tg а.
Д.Х'->0
Равенство (2) можно теперь переписать так:
limir=tga- (3)
Дя:->0 *Х
и*
164 ПОНЯТИЕ О ПРОИЗВОДНОЙ ФУНКЦИИ [гл. VII
Левая часть равенства (3) есть производная данной функции
(§ 60), а правая часть — угловой коэффициент k касатель-
ной NL (§ 10):
У = k- (4)
Обозначив абсциссу точки М через а, можно равен-
ство (4) сформулировать так: Производная функции у — f(x)
при х = а равна угловому коэффициенту касательной,
проведенной к графику данной функции в его точке,
с абсциссой х —а.
Задача. Написать уравнение касательной, проведенной
к кривой j/ = x2-|-x в точке ее А1 с абсциссой, равной 2.
Решение. Найдем ординату точки М кривой:
у = 22 4-2 = 6.
Искомая касательная находится в пучке прямых, прохо-
дящих через точку М (2; 6) и определяемых уравнением
у — 6 = k(x— 2).
Остается определить угловой коэффициент касательной,
для чего следует найти производную данной функции. Эта
производная нами была уже найдена: она равна 2x4- 1 (см.
§ 60, пример 1) и определяет угловой коэффициент касатель-
ной, проведенной в любой точке данной кривой. Чтобы иметь
угловой коэффициент касательной, проведенной в данной
точке М (2; 6), нужно в выражение
У = 2х 4- 1
вместо х подставить его значение, равное 2. Получим:
* = 2-24-1=5.
Искомое уравнение касательной напишется в следующем
виде:
у — 6 = 5(х— 2),
или
у = 5х— 4.
Упражнения
1. Найти угловой коэффициент касательной, проведенной к кри-
вой у — Зх2 в точке ее, абсцисса которой х равна: 1) х — 1, 2) х = 0.
2. Определить угол наклона к положительному направлению
§ 63] ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ 165
оси Ох касательной к кривой у = 2х2 в точке ее с абсциссой,
равной .
3. Под каким углом к положительному направлению оси Ох про-
ведена касательная к кривой у ~ —- х2 в точке ее с абсциссой,
о
3 _
равной — у ?
4в Написать уравнение касательной, проведенной к кривой
у^х2 — 2 в точке ее с абсциссой, равной 2.
5. К кривой у = Зх2 4- х в точке ее с абсциссой х = — 1 про-
ведены касательная и нормаль. Написать их уравнения.
ГЛАВА VIII
ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ
В § 60 было дано основное правило нахождения произ-
водной. Однако применение его занимает много времени, а
во многих случаях представляет большие трудности. Поэтому
выгодно иметь такие правила, которые позволяли бы находить
производные проще, с минимальной затратой времени. Дей-
ствительно, такие правила имеются, причем они выводятся
из основного правила дифференцирования.
§ 64. Производная постоянной. Пусть С — постоянная
величина; тогда равенство
У = С
можно рассматривать как выражение функции, не меняющей
своего значения с изменением аргумента. В справедливости
этого можно убедиться, представив это равенство графически,
т. е. в виде прямой линии АВ, параллельной оси Ох (черт. 85).
Действительно, с изменением абсциссы точек этой прямой
ординаты их остаются постоянными.
§ 66| ПРОИЗВОДНАЯ АЛГЕБРАИЧЕСКОЙ СУММЫ ФУНКЦИЙ 167
Для нахождения производной функции у = С применим
основное правило дифференцирования:
1-й шаг: _у + Д_У = С.
2-й шаг: Ду = Су+Ду)—у—с—с = о.
3-й шаг: ^ = JL = o. Дх Дх
4-й шаг: у' = Пт = lim 0 = 0. (С)' = 0, (I)
т. е. производная постоянной равна нулю.
Не следует производную постоянной смешивать с пределом
постоянной, который, как известно, равен самой постоянной.
§ 65. Производная функции у = х. Применяя основное
правило дифференцирования, получим:
1-й шаг: у 4~ Ду = х + Ах.
2-й шаг: Ду — (у 4~ Ду)—у = х 4“ Дх — х — Lx.
3-й шаг: &у &Х J Дх Дх
4-й шаг: / = Кт = lim 1 = 1. Дя»0 (х)'=1, (II)
т. е. производная функции у = х равна единице, или: про-
изводная независимой переменной равна единице.
§ 66. Производная алгебраической суммы функций.
Возьмем функцию
у = и-\-<и — w,
где и, v и w— функции от х и имеющие производные
по х. Если аргументу х дать приращение Дх, то и функции и,
и w получат приращения, соответственно равные Lut Lv и
Aw, а потому у также получит приращение &у.
По основному правилу находим:
1-й шаг: у4~ Ду = (zz —Azz) —|—(т/&и)— (w~|~Aw).
2-й шаг: Ду = (у 4-Ду)— у ==(« +Д/г) + (^ +Д^)—
— (w 4- Aw) — (я 4~ — w) — 114~ + v + —
— и — v 4~ w = Azz 4~
168
ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ
[ГЛ. VIII
3-й шаг:
4-й шаг:
Ду Д« Ди Aw
Lx Lx ‘ Lx Lx *
Г 1- 1-
у = hm lim
Да?->0 Да?->0
/Lu । Lv Lw\
\Lx Дх Дх/
lim д—}- lim -r------------lim
Дж->()АХ Да?->0^-^ Да?->9
Lw
Lx *
Слагаемые правой части последнего равенства являются
производными функций и» v и w. Указанное равенство можно
переписать:
у' = и' 4~ v' — <w't
или
{и 4- v — w)' — и' -}-v' — <w',
(Ш)
т. е. производная алгебраической суммы конечного числа
функций равна алгебраической сумме производных каж-
дой из них.
§ 67. Производная произведения двух функций. Пусть
дана функция
у = uvt
где и и v — функции от х, имеющие производные по х.
Дадим аргументу х приращение Дх; тогда согласно основ-
ному правилу будем иметь:
1-й шаг: у 4- &У — (а 4- Дй) О 4“ А-и).
2-й шаг: Ду = (у4~Ау)—У = (w4~ Azz)(^~4~ Lv) — uv —
— uv 4~ a Lv 4- у Lu 4“ Aw Дг> — uv — и Lv-}~v Lu-}- Lu Lv,
o .. Ду и Lv . v Lu . Lu Lv Lv , Lu , A Lv
3-й шаг: = -г------k ~r--—г— — и-r—k v-?—k Lu-r-.
Дх Lx ’ Lx 1 Дх Lx 1 Дх 1 Дх
4-й шаг: у'= lim lim Hm
да?>од* дя?>(Л д^/ дж-><Л LxJ^
4~ Hm (Lu^-\.
дж>о\ &xj
§ 67] ПРОИЗВОДНАЯ ПРОИЗВЕДЕНИЯ ДВУХ ФУНКЦИЙ 169
Но и и v не зависят от Дх, а потому их нужно считать
постоянными *) при Дх > 0; согласно следствию 1 теоремы IV
§ 43 можем написать:
,. / Дс/ \ .. Дv
hm (и -г—) = и hm
Да? -> 0 ' ^х' Да? -> О ^х
/ Дм \ .. д«
hm (г/ -г— I —'i/hrn -т—.
Да? > 0 \ / Да? -> 0
Приращение же функции Дм меняется с изменением Дх,
поэтому согласно теореме IV § 43 имеем:
hm |Дм-г--) = hm Дм hm -г—.
Да? -у О ' &Х • Да? -> О Да? -> О ^Х
Таким образом,
/ = м lim ^-4-^ lim Ит Дм Нт
Да? -> О ^х йх >0 &х Да? ->о Да? -> О &х
Но
lim
Да?-> О
Дг
Дх
= 7?',
Ит
Да?->0
Дм
— = U
Далее, так как и дифференцируема, то она непрерывна (§ 61),
следовательно,
lim Дм = 0.
Да? ->0
*) Это можно иллюстрировать на черт. 86. Здесь ОР^-х,
РМ = м. Если Дх -> 0, то РМ = м не меняется.
170 ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ [гл. VIII
Поэтому
yf =z uvf + Vu' + 0 • v' = uv' 4- vu'.
Итак,
(uv)' = uv' + vu', (IV)
т. e. производная произведения двух функций равна сумме
произведений первой функции на производную второй и
второй функции на производную первой»
§ 68. Производная произведения постоянной на функ-
цию. Возьмем функцию
у = Си,
где
С = const, u—f(x),
причем функция и имеет производную по х.
Применяя правило (IV), получим:
у' — (Си)' = Си' 4- иС' = Си' 4~ я • 0 = Си',
(Си)' = Си', (V)
т. е. производная произведения постоянной на функцию
равна произведению постоянной на производную функции.
§ 69. Производная степени с целым положительным
показателем. Возьмем сначала функцию
у = х2.
Представив ее в виде произведения и применяя правило (IV),
получим:
у' = (х2)' ~ (хх)' ~ х (х)' + х (х)' — х 4~ х — 2х.
Найдем производную новой функции:
у = х3.
Заменив ее произведением х2х и опять применяя то же пра-
вило (IV), найдем:
У = (х3)' = (х2х)' — х2 (х)' 4” х (х2)' = х2 • 1 4“ х • 2х — Зх2.
Поступив точно так же с функцией
у = х4,
найдем:
у = (х4)' == (х3х)' = х3 (х)' 4~ х (х3)' — х3 • 1 4" Зх2 = 4х3.
ПРОИЗВОДНАЯ ЧАСТНОГО
171
§ 72]
Если продолжать дифференцирование функций хъ, л6, х7
и т. д. этим способом, то получим результаты, подчиняю-
щиеся одной и той же формуле:
(хт)' — тх™-1. (VI)
Таким образом, производная степени хт, где т— целое
положительное число, равна произведению показателя
степени на основание х в степени, на единицу меньшей
чем данная.
Однако выведенное правило справедливо для любого
показателя т, что мы и докажем в § 78.
§ 70. Производная функции у —]Аг. Представив функ-
цию у — х в виде степени с дробным показателем и при-
меняя правило (VI), получим:
Таким образом,
(VII)
т. е. производная функции у — равна единице, делен-
ной на удвоенную функцию.
§ 71. Производная функции у — ~. Заменив ~ па х^1
и дифференцируя по правилу (VI), получим:
у'=(т/=у=-1 • х~2=- i
(VIII)
т. е. производная дроби ~ равна отрицательной дроби,
равной единице, деленной на квадрат знаменателя.
§ 72. Производная частного. Возьмем функцию
где и и v — функции от х, имеющие производные по х,
причем v Ф 0 при значении х, при котором находится
производная. Применим основное правило дифференцирования.
172 ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ [гл. VIII
1м I А П
1-й шаг: у 4-Ду ——.
s 1 л v 4- Дг>
п « л / । л \ «+ Д« и
2-й шаг: Ду = (у 4- Ду)— у =— -----------=
__ tiv -|- V Ьи — UV — и bv V Д/z — и bv
v (v + bv) v (v 4~ Av)
Д/z Ду
v----и
_ o Ду v bu— и bv A Дх Дх
3-й шаг: —гпгт : Дх — ————.
Дх v (v 4- Av) V (v 4- Av)
4-й шаг: применяя теоремы V, III, II и следствие 1 тео-
ремы IV § 43, находим:
.. / bu bv\ / bu\ / Ду\
. lim I v т-----и -г— ) lim I v -г- | — lim и г -)
z by _ \ Дх Дх/ \ Дх/_____\ Дх/ __
У Ах lim [у (у 4~ Av)] lim \v (у 4~ Av)] “
Дж>() Джх)
bu „ bv
v lim -7---и hm — . . . ,
bx bx _ vu — uvr _ vw — uv'
'v [lim v4-Hm Ду] ' v(v + 0) v2
Дж ~>0
Здесь, как и при выводе формулы (IV), нужно считать и
и v не зависящими от Дх, a lim Ду —0.
Итак,
vw — uv*
V2
(IX)
т. е. производная частного равна дроби, знаменатель
которой есть квадрат делителя, а числитель есть раз-
ность между произведением делителя на производную
делимого и произведением делимого на производную де-
лителя.
§ 73. Применение формул дифференцирования. Рас-
смотрим несколько примеров на применение выведенных
правил.
Пример 1. Продифференцировать функцию
у — 2х3 — 4х2 + 5х — 3.
Решение. По правилу (III) имеем:
у' = (2х3)' — (4х2)' -+- (5х)' — (ЗУ.
§ 73]
ПРИМЕНЕНИЕ ФОРМУЛ ДИФФЕРЕНЦИРОВАНИЯ
173
Применяя к первым трем слагаемым правило (V), а к послед-
нему— правило (I), получим:
у' — 2 (х3)' — 4 (х2)' 4- 5 • х' — 0.
Согласно правилам (VI) и (II) будем иметь:
У = 2 • Зх2 —4 • 2x4-5 • 1 ==:6х2 —8x4-5.
Пример 2. Продифференцировать функцию
У = (х2+1)(2х4"3).
Решение. По правилу (IV) имеем:
У = (х24~ 1)(2х4-ЗУ + (2х4~3)(х^+ 1)'.
По правилу (III):
У = (Х2 + J} [(2х)' + (3)'] + (2х 4- 3) Цх2)' 4- (1У].
По правилам (V), (II), (I) и (VI):
у' = (х2 4- 1) (2 4- 0) 4- (2х 4- 3) (2х 4- 0) =
= 2х2 4- 2 4- 4х2 4- 6х = 6х2 4- 6х 4- 2.
Этот пример можно решить иначе: сначала перемножить
выражения в скобках, а затем продифференцировать получен-
ную сумму:
У = (х2 4- 1) (2х 4- 3) = 2х3 4- Зх2 4- 2х + 3,
У = (2х3 4- Зх2 4“2х4- ЗУ = 6х2 4- 6х 4- 2.
2х х
Пример 3. Продифференцировать функцию у == ——— .
Решение. Преобразуем данную функцию следующим
образом:
£
у = Ц1Д = == .
Применяя правила (V) и (VI), будем иметь:
174
ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ
[ГЛ. VIII
Пример 4. Продифференцировать функцию
Решение. Представим данную функцию в следующем
виде:
1 - 1
у —2 З/х + 4 • х 3.
Применяя правила (III) и (V), получим:
У = 2(1)'— 3 (/х)' + 4 U) .
По правилам (VIII)» (VII) и (VI) имеем:
2 3 4 _ / 2 . 3 4 \
~ *2 2 Ух 1“ U2^21<x +3ъ^ ) ’
Зх3 ' '
Пример 5. Продифференцировать функцию
У 2х
Решение. По правилу (IX) имеем:
,__2х (х2 -р х — 3)' — (х2 + х — 3) (2х)'
У — (2х)2 ‘
Дифференцируя сумму по правилу (III), получим:
, _ 2х [(х2У + (хУ - (3)'] - (х2 + х - 3) (2х)'
У — 4х2
Наконец, по правилам (VI), (II), (I) и (V) найдем:
2х(2хЧ-1) — (х24-х —3)-2 _4х2 + 2х — 2х2—2x4-6
У ~ 4х2 “ 4х2
2х2-|-6 _хг + 3
—' 4х2 2х2 ’
Можно иначе продифференцировать данную функцию,
разделив в правой части данного уравнения почленно
§ 731
ПРИМЕНЕНИЕ ФОРМУЛ ДИФФЕРЕНЦИРОВАНИЯ
175
числитель на знаменатель, получим:
Упражнения
Найти производные функций.
1. у = 3, 2. f(x) = ах, 3. у = х5. 4. /(х) = хр.
5. у = 5х3. 6. 5 = — З/4. 1. /(х) = — ах\
8. f(x) = —х"+1. 9. у = 2ха — Зх. 10. s = 4- V — -Ъ- + 2г.
п 4~1 4 2
1 3
11. у (х) =-- х'5 -f- — х- — 2х 4“ 1- Найти f (3).
о 2
2 1
12. f (х) = ^n+1 - 2Й х2П' 13- У = х (х + 1).
14. s = Z2 (3/ — 2). 15. /(х) = 2х (Зх2 — х Н- 5). Найти f (— 2).
16. s = t (t J- 1) (t + 2). 17. /(«•) = (2и2 H- и.) (4«2 — 1).
18. s = 2yrx. 19. у — —У^х2. 20. s = r],rr.
21. v = M2fz‘w. 22. v=2-. 23./(r)=-L. Найти/'(—2).
op Г“
1 ' и V
24. у = • 25. /(«) = . Найти f' (8). 26. f (v) = .
jzx2 V и v
27. y = — ^. 28. y = xVxVx. 29. s = ^4^“.
Vx^ Vi
30. 31. y= “ X-"Vx.
"+1
176 ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ [гл. УШ
32. у = /(/? + !). 33. s = ^^=A±-l.
ол 2л?Н-Зл-|-1 QE Зха —2х —4
34. у =----. 35. у ==----------г,-----=-.
z х +1 J 2х — 1
2 1
36^=^- 38./(г) = ^.
39. У =----40. f(x) = —£-^4-1. 41. у = 1±1^£.
J х(14-х) 1—-х2 X J 1—у\
42. Точка движется прямолинейно по закону
5 = 1 уг.
Найти ее скорость в момент t = 2,25.
43. Точка, двигаясь по кривой
у = х2 — 8х 4- 15,
сорвалась с нее в тот момент, когда оказалась на прямой х = 6.
Найти уравнение дальнейшего пути точки.
44. Найти уравнения касательной и нормали к кривой
ху = 2
в точке ее Л (2; 1).
45. К кривой
у == Зх9 — 6х + 5
проведена,, касательная, параллельная оси Ох. Найти координаты
точки касания.
46. В какой точке кривой
у = 2х9 — х 4- 1
надо провести касательную, чтобы она была параллельна прямой
у г» Зх -Н 5.
47. Тело вращается вокруг оси, причем закон изменения угла f
в зависимости от времени t задан формулой
?^0,1А
Найти угловую скорость вращения тела в момент / = 5.
48. Колесо вращается так, что угол поворота пропорционален
квадрату времени. Первый оборот был сделан колесом за 8 секунд.
Определить угловую скорость колеса через 32 секунды после
начала вращения.
49. Написать уравнения касательной и нормали к кривой
х
У ~ 1 + jfl
в точке ее А (0; 0).
50. В уравнении параболы
у = х9 4~ Ьх 4- с
определить b и с» если парабола касается прямой у =* х в точке
с абсциссой х = 2.
§ 74] функция от функции (сложная функция) 177
§ 74. Функция от функции (сложная функция). Пусть
нам даны две функции:
У==и3 (1)
и
м=2х2 —3x4-1. (2)
Если в (1) заменить и его выражением из (2), то получим:
> = (2х2 —3x4- I)3. (3)
Из уравнений (1) и (2) видно, что у есть функция от «, но
и в свою очередь функция от х; таким образом, функция у
зависит от функции и — 2х2—3x4-1. Функцию (3) назы-
вают функцией от функции или сложной функцией.
Всякую сложную функцию можно представить в виде
нескольких простых. Разберем примеры. ______
Пример 1. Представить функцию у = х2 — х 4~ 1
в виде двух простых.
Р е ш е н и е. Положим
и = х2 — х 4~ 1 >
тогда
Мы получили две функции и и у более простого вида,
чем данная.
Пример 2. То же для функции y==sin3x.
Решение. Положим
и — sin х;
тогда
у — и3.
Упражнения
Представить каждую функцию двумя простыми:
1. у = (Xs — 2x4-5)4. 2. у = Ух=4-'2х. 3. у =У1х4-5.
4 ____________
4. у = 2 ух3 — 2х2 + 1. 5. s = cos4/. 6. v = 4 sin "ад.
7. у = У sin х. 8. у == У 3 cos х. 9. у = 4 И cig х.
10. 5 = sin to/. ll.s —2tg3/. 12. « ==3 cos
12 Зак. 3032. И. Л. Зайцев
178
ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ
[ГЛ. УШ
§ 75. Производная сложной функции. Возьмем функцию
причем
J = (О
« = ? (х). (2)
Пусть функция (2) имеет производную при данном х;
тогда при Дх->0 и ДиО (§ 61). Пусть также и функция
(1) имеет производную при значении и, соответствующем
тому же значению х.
Напишем тождество
Ду Ду Ди
Дх Ди Дх’
Применяя к правой части тождества (3) теорему о пре-
деле произведения (теорема IV § 43), получим:
.. Ду .. Ду ..
Inn у~~= hm hm
Д.г -> О Ли -> 0 Да? -> и
Ди
Дх ’
(4)
Но, как известно (§ 60),
lim Да? ->0 Ду_ Дх Ух
lim д» -> 0 Ду_ Ди У'и>
lim Да? > 0 Ди Дх “'а,-
Поэтому равенство (4) можно переписать:
у' = у' -и'. (5)
-44 X ' '
Формула (5) служит для дифференцирования сложной
функции, составленной из двух простых.
Пример. Продифференцировать функцию
у = (3х2—2Х-4-4)5.
Решение. Представим данную функцию в виде сле-
дующих двух:
и = Зх2 — 2х -ф- 4,
у =
§ 75] производная сложной функции 179
Найдем сначала у'и (т. е. производную функции у по
аргументу и), а затем и' (т. е. производную функции и по
аргументу х):
Ум = (м6)' = 5м*,
и'х = (Зх2 — 2х 4~ 4)' = 6х — 2.
Искомая производная будет:
_j/=5«4 (6-V — 2),
или, заменяя и его значением,
у'х = 5 (Зх2 — 2х 4- 4)4 (6х — 2) =
= 10(Зх2 — 2х+ 4)4 (Зх — 1).
Как видно из формулы (5), производная сложной функ-
ции выражается произведением производных простых функ-
ций и, конечно, перестановка сомножителей не изменит
результата. Однако удобней находить эти сомножители
в одной определенно выбранной последовательности, которую
полезно запомнить как правило. Так, например, для разо-
бранного случая степенной функции это правило можно вы-
сказать следующим образом:
для дифференцирования сложной степенной функ-
ции *) нужно взять производную сначала от степени по
основанию (принимая основание за аргумент), а потом от
выражения, стоящего в основании, по независимой пере-
менной и результаты перемножить.
Если у = ит—сложная степенная функция, то ее про-
изводная согласно этому правилу запишется так:
(ит)^тит^и^ (6)
Пусть, например, требуется найти производную функции
у = (х3— 4х+ О3*
Положив
и — х3 — 4x4“ 1
*) Под сложной степенной функцией будем разуметь степень,
основание которой есть функция от х.
12*
180
ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ
[ГЛ. VIII
и, применяя правило (6), будем иметь:
У =3(х3 — 4х+ 1)2(х3 — 4х+ 1/ =
и и
= 3(х3—4х+ 1)2(3х2 —4).
В дальнейшем для каждого особого случая будут даваться
аналогичные правила, устанавливающие свою последователь-
ность дифференцирования.
Разберем еще пример. Пусть требуется найти производ-
ную функции
у = У х2 + х.
Разбив ее на две простые функции, получим:
и = х2 + х,
отсюда
«' = 2x4-1,
, _ 1 _ 1
Уи ~ 2 У « ~ 2 ‘
Следовательно,
у' = —У = (2х + 1) = ~ +1 .
И здесь можно установить последовательность в нахож-
дении производной, которая выразится следующим правилом:
для дифференцирования сложной функции у = У и
нужно сначала взять производную от этой функции по
подкоренному выражению и (считая и аргументом), а потом
от подкоренного выражения по независимой переменной
и результаты перемножить] таким образом, считая и функ-
цией от xt получаем:
Так, например, производная функции
= —Зх + 4
§ 76] ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ 181
по вышеуказанному правилу найдется так:
у' =---- -...J-.._....- . (2х2 — Зх + 4)' =
2/2х2 —3x4-4 .---------
У U
\х — 3
и
= . ...1.:-,- (4х — 3) = _________
2/2x2 —3x4-4 2/2x2 —Зх-Ь4
Если дан корень другой степени, то его нужно предва-
рительно преобразовать в степень с дробным показателем и
применить правило для дифференцирования сложной степен-
ной функции. Например,
(/ х2 +1)' = [(х2+1)2 ] == f (X2-4-1) 3 (£+2,)' =
и и
1 2х
-з(х2+1) - /
Упражнения
Найти производные функций:
1. y = (x-f-2)l
4. /(х) = (х2 —2х)2
6. / (и) = 5 (3«2 _ и 4- 4)1.
9./(х)=Ух2+-1-
П.г/=/ (2 —х) (3 + 2х).
13. /(X) = /X2 — Зх2 4- 1.
15. s = /2/4T^3.
17. у = (х4- 1)2/Т=Т.
Q Y* Q у_ 1
,9-/w^7Ff- ^/W 21
22. /(х) = . 23. /(х) = •
X У А'ф!
2. s = (3/ — 2)2. 3. у=(х2—1 )5.
5. 5 = (/2 — /4-1у.
7. s = / / 4* 1. 8. у="/ 2х -^1.
10. /(х) = 2 /Т+2х=^2.
12.
14.
г = V /— 1.
У = (3х-1)2(х4-1>г
16. у = (х—1)/х2+1.
I8.0==Wzl4\
?2
§ 76. Производные тригонометрических функций.
1. у = sin х.
По общему правилу дифференцирования находим:
1-й шаг:
у ~|- Ду == sin (х -ф Дх).
182
ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ
|ГЛ. VIII
2-й шаг:
Д.У = (.У + Ду)— У = sin(x-f~ Дх) — sin х.
Преобразуя разность синусов, будем иметь:
л • / । л ч • п хЧ-ДхЧ-х . х-4-Дх— х
Ду = sin (х + Д*) — sin х — 2 cos —!!— sin —1—g-=
п / . Дх\ . Дх
— 2 cos (х )sin ~2 ’
3-й шаг:
/ Дх\ , Дх
. 2 cos x 4~ -rr sln —
Ду__ \ ' 2 / 2
Дх ‘ Дх
После деления числителя и знаменателя дроби на 2 по-
лучим:
2 2
4-й шаг:
~ Дх ~
А у A X Sin ТГ •
г ..Ду .. / . Дх\ 2
у — lull “ == Ьш COS X-f-v -------------- =
Л Дх-->0 Д* Дх >0 \ 2 ' Дх
2
Дх
ZjM,. s п "2"
— Inn cos|xH--n-l hm —х—.
д»->о \ 2 / Дж ->-0
2
Но
. Дх
sin —
lim ^-=1 (§ 45) и Hm cos(x-[- — cos х;
д.г -> о ™ д о -> о \ /
2
поэтому
у' =Z cos X • 1 — cos X.
Следовательно,
(sin х)' — cos х. (X)
2. у — cos х.
По формуле приведения можно написать:
• / я
У = COS X — Sin ( --------х
§ 76J ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ 183
отсюда
У = (cos х)' — [sin -.
Для дифференцирования сложной функции у =sin —х
представим ее в виде двух простых:
7С
и^-Х,
у — sin /л
Согласно формуле (5) § 75 имеем:
j/ = (sin и)' — cos и — cos — xj — sin х,
у = sin х • (— 1) — — sin х.
Следовательно,
(cos х)' — — sin х. (XI)
3. ^ = tgx.
Заменив tgx отношением -------- и применяя правило диф-
COS jc
ференцирования частного, получим:
,___/sin х \'_cos х (sin х)' — sin х (cos x)' ___
(tg X) \C0S xj — COS2 x
cos x-cos x — sinx(—sin x) _ cos2x-|-sin2 x 1
COS2 X cos2 x cos2 X
Итак, имеем:
(ХП)
4. j/ = ctgx.
Как и в случае 3, имеем:
z х к/ /cos х\' sin х (cos xY — cos x (sin xY
1-----si,^...........—
sin x (— sin x) — cos x • cos x _ — sin2 x — cos2 x_
sin2 x sin2 x
sin2x 4- cos2x 1
sin2 x sin2 x *
Таким образом,
<XH|)
184
ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ
[ГЛ. VIII
В п. 2 настоящего параграфа мы дифференцировали
сложную функцию (у— xj, пользуясь формулой (5) § 75.
Однако эту операцию можно произвести и по следующему
правилу:
для дифференцирования сложной тригонометрической
функции *) нужно сначала взять производную от триго-
нометрической функции по выражению, стоящему под
ее знаком (принимая его за аргумент), а потом от этого
выражения по независимой переменной и результаты
перемножить] поэтому, считая и функцией от х, получаем:
(sin uY — cos и • и', v Л» .е (1)
(cos U)’x — —sin U • u'x, (2)
(3)
(ctg«£- sin2„-<- (4)
Пользуясь правилом (1), процесс дифференцирования функ-
ции sinf-^--х^ можно записать таким образом:
Пример 1. Продифференцировать функцию
/< । 1 \
^ = cos^l + —)•
Решение. Согласно правилу (2) настоящего параграфа
найдем:
у = [cos (1 + ±)]' = - Sin (1 + ±) (1 + |)' =
и и и
*) Под сложной тригонометрической функцией будем понимать
тригонометрическую функцию сложного аргумента.
§ 76] ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ 185
Пример 2. Продифференцировать функцию у = sin2 Д/ х»
Решение. Переписав функцию в виде у — (sin Ух)2,
найдем по правилу (6) § 75
У = [(sin Ух)2]' = 2 sin Ух • (sin Ух)'.
и и и
Но sin ]/~ х—сложная тригонометрическая функция, а потому
согласно правилу (1) настоящего параграфа имеем:
(sin ]/ х)' = cos Ух (Ух)' = cos Ух —.
—V— -V-* —V— 2 у х
и и и
Следовательно,
/ л • 1/“’ 1 sin 2 Ух
у' = 2 SIH |/ X COS У X • -jrzz =-.
Л У 2 У х 2 У х
Процесс дифференцирования данной функции можно за-
писать следующим образом:
yf = (sin2 Ух)'==2 sin Уx (sin Уx)'=2 sin Уx cos У х(У x)'=
n • 1/“ 1 sin 2 Ух
— 2 Sin У X COS У X • -.
v v 2УX 2 УX
Упражнения
Найти производные функций:
у — х — sin х. 2. 6 = cos 3. v = sec и,
4. /(Z) = sin t cos Z. 5. /(x) =s tg x—ctg x. 6. s = tg 0 — 0.
7, 0 = <p-f-ctg <p. 8. s—a (1—cos Z). 9./(0)=(14-cos 0) sin 0.
1 - COS t , . xzftx 1 + tg 0 1 a 9
= lh/(0)==“vF- 12. y = Ys^x.
13. v= — ~COS4W. 14./(f)~“-Ctg5<p. Найти15./(<p)~sln 2<p.
16. /(«>) = y cos 2<o. 17. у = sin x^. 18. y= — a cos Z^ .
19. s = cos (1 — 2<p). 20. f (u>) = -1- tg оЛ 21. Z == 2 sin (<f>2 — <p).
22. /(0) у sin У~б. 23. s— — У cos Z. 24. у = 4 tg 2 У x.
25. у = У sin x. 26. s — cos . 27. s ~ sin “.
1 r_______________________
28. У = -g- sec2 с». 29. у = У sec x. 30. у = sin3 x cos x.
186
ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ
[ГЛ. VIII
31 ./(/) = 2 sin 2/ cos21. 32. f (0) = 2 sin2 6 cos2 0.
33. > = sin(x4-«)cos(x — а). 34. у=|/
35. 0 = sin22<p. 36. у = cos2 . 37. s ~ У sin 2%>.
38. y = -i“tg3 —. 39. у = Vsin 2x. 40. 0 = l^sin2 2<o .
J 3 ъ x
41. r = -Ltg3^.—tgy. 42. у ==ytg5xbytg3x + tgx.
§ 77. Производная логарифмической функции. Пусть
дана функция
у = in х.
Для ее дифференцирования применим общее правило.
1-й шаг:
у 4- Ду — In (х + Дх).
2-й шаг:
Ду/ = (у 4- Ду/)—у/ — 1п(х4-Д*)—In х,
3-й шаг:
. , х-Ь-кх . /1 । Д*\
— = |п^1 +—J
(1)
Положим
кх___4
п
отсюда
(2)
Подставив значения — и Дх в равенство (1), получим:
или, после потенцирования,
§ 77] ПРОИЗВОДНАЯ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ 187
Из равенства (2) следует, что
Дх —> 0, если
п —> оо .
(3)
4-й шаг. Принимая во внимание условие (3), напишем:
у'= ,im lim [x,n(1+v)T
Дж -> 0 п -> СО L х \ / J
лл 1
Множитель — не зависит от п> поэтому его можно считать
постоянным при п —> оо ; следовательно,
, 1 1- 1
у — — lim In
X
71 -> со
(4)
В подробных курсах анализа доказывается теорема: пре-
дел логарифма переменной величины равен логарифму
предела этой же переменной величины} поэтому
Hm In
71 -> ОО
— 1П
Но, согласно § 47,
Нт
П -> оо
Равенство (4) будет иметь вид
7 1 1 1 У “ЗГ n | Г .. /i . 1 \и] 1 . 1 < 1 lim (1 Н ) = — 1п£ — —. 1 = —. Lzt -> со \ п / J х х х
Следовательно, (lnx)' = ±, (XIV)
т. е. производная натурального логарифма равна еди-
нице, деленной на аргумент.
Если дан десятичный логарифм, то его нужно предвари-
тельно выразить через натуральный. Мы знаем (§ 48), что
1g х = 0,4343 In х.
Дифференцируя обе части последнего равенства, получим:
(1g ху = 0,4343 (In х)' = 0,4343 • ,
ИЛИ
(1g *)'
0,4343
X
(XV)
188 ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ [гл. VIII
т. е. производная десятичного логарифма равна произве-
дению производной натурального логарифма на постоян-
ный множитель 0,4343.
Пример 1. Продифференцировать функцию
у — 1п(2х-)~ О-
Решение. Данная функция сложная; положим
и = 2х + 1;
тогда
у — In zz.
Отсюда согласно формуле (5) § 75 имеем:
Ух У и ' их 7Г ’ + I ‘
Производную сложной логарифмической функции *) можно
найти и по следующему правилу:
для диффе ренцирования сложной логарифмической
функции нужно сначала взять производную от логариф-
ма по выражению, стоящему под знаком логарифма
(принимая его за аргумент), а потом от выражения, стоя-
щего под знаком логарифма, по независимой переменной
и результаты перемножить', поэтому, считая и функцией х,
получаем:
(\п а)'= Л- и' . (5)
х и х
Пример 2. Продифференцировать функцию
у — In cos(l —х).
Решение. Согласно правилу (5) найдем:
у' = [In cos(l—x)l' = cos J::: tcos<1 ~~ *)!'•
и '-' .и
и
Но cos (1—х) — сложная тригонометрическая функция; при-
меняя к ней правило (2) § 76, получим:
[cos (1 — х)]' — — sin (1 — х)(1 — х)' —
и и и
= — sin (1 — х)( — 1) = sin (1 — х),
*) To-есть логарифмической функции сложного аргумента.
§ 77| ПРОИЗВОДНАЯ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ 189
[In COS (1 — X)]' = [COS (1 - X)]' =
= соз(1-х) I - si n <1 - X) 1 <1 - x)'=
—----_J---- sin (1 — x) = tg (1 — x).
cos (1 — x) v 7 sv 7
Пример 3. Продифференцировать функцию v~-ln
Решение. Преобразуем сначала данную функцию, при*
менив правила логарифмирования корня и дроби:
у = -1 [In х— In (1 4- х)].
Продифференцировав
вилу (XIV), а 1п(1 + х)
полученную функцию [In х по пра-
по правилу (5)], найдем:
/ 1 f 1 1 /1 । 1 / 1
У~ 21 х 14-х ( 2
_ 1 1 4-х — х _ 1
“ 2 ’ х(1 4-х) 2х(1 4-х) '
1 4- х)
Упражнения
Найти производные функций:
1. у == х In л. 2. 0 = i (In t — I). 3. f(u) = .
4. у = 1g 2x
6. 5 = In (/2 — 1).
9. у = — In cos t.
5./(л) = 21g (x 4-I). Найти /'(I).
7. U = In 1. 8. t =» In sin a.
v
10. /(/)== In (2 cos 0-
11, /(0) = in tg 0. Найти /'
12. у = In2 x.
13. и = 10 In . 14. /(%) = In , 15. у == In3 sin x.
4 "t~ t G> X
16. f(u) = In sin . 17. s = In tg ~ . 18. у — In2 V x.
19. у = / in tg л*. 20.
22. f{x) = In V & 4- x\
24. y^lnyj±^.
s = in cos2 (1 — /)• 21. у = in sec2 x.
23. у = In (x 4- /1 4- x«).
25. y^lnX^+L-^
Ух^+1+х
190 ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ [гл. VIII
§ 78. Производная степени при любом показателе.
В § 69 мы вывели формулу
(хт)'=мхт-'
для т целого положительного. Докажем теперь справедли-
вость этой формулы для любого показателя.
Положим, что в равенстве
у—хт
т имеет любое постоянное значение; логарифмируя это
равенство по основанию е* получим:
lny = mlnx. (1)
Приняв во внимание, что In у — сложная функция (In у зави-
сит от у, а у зависит от х), дифференцируем обе части
равенства (1) по х:
1 / 1
.— у == щ • —,
у х*
отсюда
у хш
у =: m • — = m ----= пгхт~х,
х х
Следовательно,
(xw)z = шУ"1.
§ 79. Производная показательной функции. Дана пока-
зательная функция
у — ах. (1)
Прологарифмировав равенство (1) по основанию е, получим:
In у — х In а.
Дифференцируем это равенство по х, считая 1п_у сложной
функцией:
1 / 1
— . у = In я,
У
отсюда
У = у In а — 1п а.
Следовательно,
(ахУ == ах In а,
(XVI)
§ 79] ПРОИЗВОДНАЯ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ 191
т, е. производная показательной функции ах равна произ-
ведению самой функции на натуральный логарифм осно-
вания.
Если дана показательная функция
у = ех,
где е — основание натурального логарифма, то производная
ее найдется по формуле (XVI):
(ех)' = ех In е = ех ,
или
(ex)' = ext (XVII)
т. е. производная показательной функции ех равна самой
функции.
Пример 1. Продифференцировать функцию у — ^siQ х.
Решение. Заменив данную сложную функцию двумя
простыми, получим:
и — sin х,
у — еи.
Согласно формуле (5) § 75 имеем:
у я = — eU cos х = £sln х cos х.
Данную функцию можно дифференцировать и по следую-
щему правилу:
для дифференцирования сложной показательной функ-
ции *) нужно сначала взять производную от показатель-
ной функции по выражению, стоящему в показателе
(считая его аргументом), а потом от выражения, стоящего
в показателе, по независимой переменной и результаты
перемножить*, поэтому, считая и функцией от х, получаем:
(аи)'х = аи\паих, (2)
(еи)х = еЧ • их. (3)
Пример 2. Продифференцировать функцию у —
Решение, По правилу (3) настоящего параграфа
у —(etgz) =^>(tg<2x)'.
и
*) To-есть показательной функции сложного аргумента.
192
ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ [ГЛ. VIII
Но согласно правилу (3) § 76
, 1 , 2
(tg 2х/ =-------(2х)' — —.
__ cos2 2x cos2 2л
и и
и
Следовательно,
(е*« 2®у _ etS2a,(tg. 2х/ — е>яга —1 (2х)' = -2<?-*У
v 7 v ь cos2 2х 7 cos2 2х
Упражнения
Найти производные функций:
1. у = хех — ех. 2. s = & In t.
px__________1
4-У = -^+Т’ 5.Р = ^.
3. f(x) =
pX^l
ex
7. у = хе2®,
10. у = хпп®.
13. f (/) = sin е*.
рю
I6. /(и)) = 1п____
19с /(х) = V cos
22. v == tg е~*?,
х
25. у = (е а — е
8. О = 0-ф2.
11. s = In е*.
14. /(/)== 02 sin«.
17.0 = sinM.
20. f(t) = In е™***
i
m —
23. R = e
X
“)•
6. f(x) =
i
9. и = a p *
12. 5==^.
15. у =
18. r- cos .
21. f(x) = coseVx
24. у == ясов x sin x.
pX___p—X
27. 0 = 02(p cos 2<p. 28. у = eax (sin ax — cos ax).
px
29. у = In —------7
V1 +
§ 80. Производные обратных тригонометрических
функций.
1. у == arcsin х.
В силу определения арксинуса получаем:
sinj/ = x. (1)
Здесь sin у представляет сложную функцию (sinj/ зависит
от у, а у зависит от х; дифференцируя обе части этого
равенства по х, напишем):
(sinj>)/ = (x)/.
§ 80] ПРОИЗВОДНЫЕ ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ 193
ИЛИ
cosy. у — 1,
откуда
у' —------.
s cos у
Приняв во внимание, что
cosy = У1 — sin2j/ *),
а также равенство (1), получим:
/ = 1 1 — 1
У cos у У1 — sin2 у У1 — х2 '
или
(arcsin х)' — уу==. (XVIII)
2. у = arccos х.
Согласно определению арккосинуса имеем:
COS У = х.
Дифференцируя обе части этого равенства по х, считая
cos .у сложной функцией, найдем:
(cos у)' = (х)',
или
— sin у. у — 1,
отсюда
, 1
у =---------.
sin у
Но
sin у = У1 — cos2y **) = УI — х2;
поэтому
у=_________
У1—
ИЛИ
(arccos х)' =---(XIX)
У 1 — X2 ‘
*) Здесь радикал берется с плюсом, так как значения arcsin х
заключены между — у и , а в этом промежутке cos у имеет
положительные значения.
**) И здесь радикал берется с плюсом, так как значения
arccos х заключены между 0 и я; в этом же промежутке sin у
имеет положительные значения.
13 Зак. 3032. И. Л. Зайцев
194
ФОРМУЛА ДИФФЕРЕНЦИРОВАНИЯ
[ГЛ. VIII
з. y/ = arctgx.
Согласно определению арктангенса имеем:
tgj = x. (2)
Дифференцируя обе части этого равенства no х, как и
в предыдущих случаях, получим:
(tg-У)' = (*)',
ИЛИ
cos2 у
отсюда
у' = cos2 у.
Но
cos У sec2 у 1 + tg2 у
Приняв во внимание равенство (2), получим:
, 2 1
У =QQ^y--—-------
у 1 4- х2
Следовательно,
(arctgх)' = • (XX)
4. у — arcctg х.
Для данной функции имеем:
ctgy — x.
После дифференцирования этого равенства получим:
(ctg>)' = (х/,
или 1 . у/ — 1
sin2 у *
отсюда у' = — sin2 у'.
Но
sltl У cosec2 у 1 4- ctg2 у 1 4* х2
Следовательно,
т. е.
(arcctg х)' —-------• (ХХ1)
§ 80] ПРОИЗВОДНЫЕ ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ 195
Пример 1. Продифференцировать функцию у — arctg-L
Решение. Заменим данную сложную функцию двумя
простыми:
и — —,
х
у — arctg и.
Согласно формуле (5) § 75 имеем:
/ _ г г _ 1 / 1 \
ух — yutix — J Х2 ) —
1___/____1_\ _ _ 1 __ 1
1+-V л2(1+ДЛ 1 +
1 X* \ ХЧ
Для дифференцирования этой функции можно восполь-
зоваться и следующим правилом:
для дифференцирования сложной обратной тригоно-
метрической сфункции*) нужно сначала взять производную
от обратной тригонометрической функции по выраже-
нию, стоящему под ее знаком (принимая его за аргумент),
а потом от этого же выражения по независимой пере-
менной и результаты перемножить', таким образом, считая
и функцией от %, получаем:
(arcsin и)' — ——♦ и';, (arctg uY — —-— * и';
(arccos //У —-• и'; (arcctg uY — — -—J— • и'.
к 1 - - и2 4 ь l + zz2
Пример 2. Продифференцировать функцию у =
— arcsin 2х.
Решение. Данная функция — обратная тригонометри-
ческая и притом сложная; применяя вышеуказанное правило
для производной arcsin и, найдем:
yg=(a,cs,nes)'=/n^-(0^
*) To-есть обратной тригонометрической функции сложного
аргумента.
13*
196
ФОРМУЛ Ы ДИФФ ЕР Е И ЦИР ОВ АН ИЯ
[ГЛ. VIII
1
У*2л ’
-.-2 =
2 У 2х
Но У2х— тоже сложная функция; согласно правилу (7)
§75 имеем:
(/2х) = —— (2хУ
11 —— и
и
Следовательно,
у' — (arcsin У2х)' — -=2==?
J V V1 — 2х
(/2х)' =
_____ (2х/ — - ——- 2 — . ,
У1 — 2х .2 У 2х У1 — 2х 2 У 2х У2х — 4х2
Упражнения
Найти производные функций:
1. у == arcsin 2х. X 2. у = arccos у. 3. у = arctg Зх.
4. f (t) = arctg у. 5. /(х) = arcsin V r*x*. 6. и ~ arctg 'У v •
7. $ = arcsin /2. 8. 0 = arctg е'?. 9. s = arcsin-^-.
10. ср = (arcsin х)2 It. y = ^arct-aJ. 12. у = arcsin У"ех .
13. f(x) = (arccos Зх)2. 14. y = ln^arcsiQaJ.
15. у = arcsin У 1 - - X2. 16. s = In cos £arccos 1
17. f(x) = х arcsin х + У* 1 — х2. Вычислить /' .
18. и = a arcsin ~4" — /2. 19. s — /arctg —----In (a2-{-t2).
20. f(x) = arctg 21. 9 = arctg
§ 81. Производная неявной функции. Пусть неявная функ-
ция у задана уравнением
ху — х— 1=0. (1)
Найдем производную у', полагая, что опа существует. Для этого
дифференцируем обе части уравнения (1), применяя правило для
производной алгебраической суммы, получим:
(ху)'-(х)'-(1)' = 0. (2)
Так как ху — произведение переменных величин, то:
(ху)' = х (у)' + у (х)'.
197
§ 81] ПРОИЗВОДНАЯ НЕЯВНОЙ ФУНКЦИИ
Таким образом, равенство (2) примет вид
или
Ху' 4- у — 1 == 0.
Решая последнее уравнение относительно у', найдем'.
(3)
Для дифференцирования данной функции можно было бы сначала
выразить у через х, а потом уже найти производную от явной функ-
ции. В самом деле, из уравнения (1) имеем:
откуда
По внешнему виду этот результат отличается от найденного
ранее, но если мы в равенстве (3) подставим значение у, то по-
лучим:
Таким образом, результаты дифференцирования в обоих слу-
чаях оказались одинаковыми. Однако переход от неявной к явной
функции можно делать только в простейших случаях. Встречаются
неявные функции, которые обратить в явные очень трудно и даже
невозможно. Например, функцию у, заданную уравнением ху
+ х = sin у, явно выразить нельзя. Поэтому приходится дифферен-
цировать такие функции как неявные.
Разберем другой пример. Пусть требуется найти производную
неявной функции у, заданной уравнением
у2 —8х = 0.
Применяя правило дифференцирования алгебраической суммы,
имеем:
(y2)'-(W-0. (4)
Но у2— сложная функция (у2 зависит от у, а у зависит от х). По
правилу дифференцирования сложной степенной функции [(6) § 75]
имеем:
(у2)' = 2уу'.
Следовательно, равенство (4) примет вид
2уу' — (8л)' = 0,
или
2уу' — 8 = 0,
откуда
8 4
У 2У У ‘
198
ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ
[ГЛ. VIII
Упражнения
Найти производные функций:
1.
4.
7.
10.
13.
16.
2у — Зх23 = 0. 2. у2 —4х = 0. 3. 2у2 — 6х +1 = 0.
х — у у2 _ 5. х2 У2 = г2. 6. 2х2 + Зу2 — 4яу — 0.
8. ху = 4. 9. х? — 2ху — 6 = 0.
а2 1 Ь2
х2у 4- ху2 = 4.
ху — sin у.
arc sin у = х2.
11. (1—у)2—ах. 12. siny = l—х.
14. х2 = еу. 15. ху = ех+у.
§ 82. Производная второго порядка. Пусть функция
у = /(х) имеет производную yf — f' (х). Производная от f' (ус)
по х, если она существует, называется второй производной
или производной второго порядка.
Вторую производную функции у = f(yc) принято обозна-
чать так:
у", у"х, /"(*)•
Пример. Найти вторую производную функции у —
Решение, у'= = (х~2)' =— 2х-3,
У = ( — 2х-3У = - 2 (- Зх-*) =
Упражнения
Найти вторые производные от функций:
1. у = 4х + 1. 2. у = х3.
4. Q = 2Vu. 5./(0=~.
7. / (а) = у cos 2«. 8. f (t) = Уа *.
3. s = 3fl + 2t — 1.
6. у = (x2— I)2.
9. s = 2-ln g-qy-.
§ 83. Механический смысл второй производной. Пусть
тело движется прямолинейно по закону
В § 60 мы установили, что скорость v движения тела в дан-
ный момент t определяется как производная пути по времени,
т. е.
V — s'.
§ 83] МЕХАНИЧЕСКИЙ СМЫСЛ ВТОРОЙ ПРОИЗВОДНОЙ 199
Если тело движется неравномерно, то скорость v с тече-
нием времени изменяется и за промежуток времени полу-
чает приращение До. В этом случае величина отношения
показывающая изменение скорости в единицу времени,
называется средним ускорением в промежутке времени от t
до
Положим, что Д/-—> О, тогда а среднее уско-
До
рение — стремится к величине, которая называется уско-
рением в данный момент времени t. Обозначив это уско-
рение через у, будем иметь;
J = ,lm л7 — v = (s ) = s •
Ai->0
Таким образом, ускорение прямолинейного движения
тела в данный момент равно второй производной пути
по времени, вычисленной для данного момента.
Прим е р. Точка движется прямолинейно по закону
s=2£2— 3/-1~ 5. Найти скорость и ускорение точки в мо-
мент t — 5.
Решение. Для определения скорости нужно найти пер-
вую производную данной функции при г = 5. Таким образом:
v = s' = (2/2 — 3t + 5)' = 4/ —- 3
и
vf=6 = 4.5 —3 = 17.
Ускорение J равно второй производной функции при
t = 5, т. е.
j=s" = (s')' = ^t — 3)' = 4.
Величина ускорения оказалась постоянной для любого значе-
ния /, значит, движение точки по заданному закону происхо-
дит с постоянным ускорением.
Упражнения
Определить ускорение точки в указанные моменты времени /,
если скорость точки, движущейся прямолинейно, задается нижесле-
дующими уравнениями.
l.v = ^ + 2/, Z = 3. 2. о = 3/ —/з t = 2.
3.0 = 4510-77, t-==^. 4. v = 2 cos 3/,
2 3 о
200
ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ
1ГЛ. VIII
Найти в указанные моменты времени t скорость и ускорение
точки, движущейся прямолинейно по закону, заданному следующими
уравнениями:
5. s = Ze-y2Z2 Z=s2. 6. s = 2Z —Z2, Z=l.
7. s = 2sin Z, I« — » 8. s = 3cos , Z = 1.
4 9 3 ’
9, Путь, пройденный клетью подъемной машины, определяется
из уравнения h = 4 + 5Z. Найти скорость и ускорение в любой мо-
мент времени.
10. Определить момент Z, когда ускорение прямолинейного
движения, совершаемого по закону s = —— Za~|- 3Z2— 5, равно нулю.
Какова при этом скорость?
Таблица формул
I. (су=о.
п. (х)'=1.
ш. (и —wy = = и' -у v' — w'.
IV. (uv)' = UV' -+ VU'*
V. (си)' = си'.
VI. (xV1)' =
VII. (/*)'= 1. 2 у л
VIII. \ х) X2
IX. / и V vu' — uvr \ V / V2
X. (sin х)' = cos х.
XI. (cos х)' = — sin х.
XII. (tg х/ = —1—• v ь 7 COS2 X
дифференцирования
XIII. .. ч, 1
(ctg X) — sin? x .
XIV. (\nx)' = ~.
XV. 0,4343 (Ig-v)== x •
XVI. (д«У = ax In a.
XVII. (ex)' = ex.
XVIII. (arcsin xy = y=L=.
XIX. (arccos x)' = 1
Vl —X2
XX. (arctg x)' =1тр2-
XXI. (arcctg x)' = 1
“ 14- x2 ‘
ГЛАВА IX
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
§ 84. Возрастание и убывание функции. Пусть нам
дана функция у — f(x), графически представленная на черт. 87.
Проследим за ходом изменения величины ординат точек изо-
браженной кривой при возрастании их абсцисс.
Черт. 87.
Мы видим, что при возрастании аргумента х ординаты
соответствующих точек на участке /ИД кривой растут, на
участке АК убывают. При дальнейшем возрастании аргумента
ординаты, принимая отрицательные значения, продолжают
убывать *) во всех точках дуги КВ, ординаты же точек
дуги ВС возрастают и т. д. Данную функцию для уча-
стков МА, ВС и DL называют возрастающей, а для уча-
стков АВ и CD—убывающей.
*) Известно, что то отрицательное число меньше, у которого
абсолютная величина больше, и наоборот.
202
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
[гл. IX
Определение. Функция y = f(x) называется возра-
стающей в данном промежутке значений х, если при
увеличении аргумента х в этом промежутке соответ-
ствующие значения у возрастают, и убывающей, если при
увеличении х значения у убывают.
В дальнейшем изложении данной главы изменения
аргумента будут рассматриваться только возрастаю-
щие, а функция и ее первая и вторая произ-
водные— только непрерывные при всех рассматри-
ваемых значениях аргумента.
§ 85. Признаки возрастания и убывания функции.
Теорема. Если производная функции у = /(х) в дан-
ном промежутке значений х положительна, то функция
возрастает в этом промежутке, а если производная
отрицательна, то функция убывает.
Черт. 88а.
Не доказывая этой теоремы, поясним ее геометрически.
I. Пусть в данном промежутке значений х
/'(*)> о.
Приняв во внимание геометрический смысл производ-
ной (§ 63), можно утверждать, что угловой коэффициент
касательных, проведенных к графику функции j/ = /(x),
в рассматриваемом промежутке положителен. Иначе говоря,
касательные образуют с положительным направлением оси Ох
острый угол (черт. 88а и 886), а это наблюдается в том
§ 85] ПРИЗНАКИ ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИИ 203
случае, когда график в данном промежутке поднимается, т. е«
функция возрастает.
П. Положим, что в данном промежутке значений х
Г(х)<0.
Это значит, что угловой коэффициент касательных, прове-
денных к графику функции y = f(x)t отрицателен. Иначе
говоря, касательные образуют тупой угол с положительным
направлением оси Ох (черт. 89а и 896), а это бывает
204
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
[гл. IX
в случае, когда график в рассматриваемом промежутке опу-
скается, т. е. функция убывает.
Пример. Определить промежутки возрастания и убыва-
ния функции у — х2.
Решение. Найдем про-
изводную данной функции
У = (х2)' = 2х.
Величина 2х имеет положи-
тельное значение при вся-
ком положительном х и от-
рицательное — при любом
-г отрицательном его значении.
Отсюда следует, что данная
функция убывающая при
Черт. 90. х < 0 и возрастающая при
х> 0 (черт. 90).
§ 86. Максимум и минимум функции. Рассматривая ход
изменения функции на черт. 87, мы можем отметить, что
ординаты точек на участках МА и ВС возрастают, достигая
в точках А и С кривой наибольшей величины сравнительно
со значениями ординат ближайших к ним точек, и убывают
на участках АВ и CD до наименьшей величины в точках
В и D сравнительно со значениями ординат соседних к ним
точек.
Те значения аргумента, при которых функция имеет
наибольшую или наименьшую величину, называются соответ-
ственно точками максимума или минимума функции,
а значение функции при этих значениях аргумента — макси-
мумом или минимумом ее.
Как видно, точка максимума служит границей перехода
от возрастания функции к ее убыванию, а точка мини-
мума— границей перехода от убывания функции к ее возра-
станию.
Определение 1. Функция у = f(x) имеет максимум
при х — а, если при всех х, достаточно близких к а,
выполняется неравенство
f(a)>f(x).
Определение 2. Функция у ~ f(x) имеет минимум
при х=а, если при всех х, достаточно близких к а
§ 87] ПРИЗНАКИ МАКСИМУМА И МИНИМУМА ФУНКЦИИ 205
выполняется неравенство
f(d)<f(x).
§ 87. Признаки максимума и минимума функции.
I. Пусть точке А графика функции y = f(x) соответствует
максимум при х—а (черт. 91). Как видно из чертежа, во
всех точках, расположенных левее А, касательные образуют
с положительным направлением оси Ох острые углы. Поэтому
Черт. 91.
тангенс этих углов, а согласно геометрическому смыслу
производной (§ 63) и f'(x) в указанных точках имеет поло-
жительное значение.
В точках же, лежащих правее А, касательные образуют
с положительным направлением оси Ох тупые углы, а потому
тангенс этих углов, а также первая производная имеет отри-
цательное значение.
Так как производная функции непрерывна, то ее значение
должно меняться без скачков, и, следовательно, при переходе
от положительных значений к отрицательным пройдет при
х—а через нуль (§ 55), т. е. в точке А
f(a) = 0.
Если функция у == f(x) при х — а имеет максимум, то
1)/'(я) = 0 и
2) f(x) при переходе аргумента через
х—а меняет знак с 4- на —.
(1)
206
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
[гл. IX
И. Положим, что точке В графика функции y — f(x)
соответствует минимум при х — а (черт. 92). Рассуждая так
же, придем к выводу, что в этом случае первая производная
при возрастании х меняет отрицательные значения на поло-
жительные и, будучи непрерывной, обращается при х — а
в нуль, т. е. в точке В
Таким образом, если функция у — f(x) при х—а имеет
минимум, то
1) /'(<*) = О и
2) f'(x) при переходе аргумента через '
х—а меняет знак с — на .
(2)
Справедливы обратные утверждения.
Функция = при х — а имеет максимум, если
1) /'(«) = 0 и )
2) /'(х) при переходе аргумента через < G*)
х — а меняет знак с + на —. J
Функция у = f (х) при х — а имеет минимум, если
1)/'(о) = 0и I
2) при переходе аргумента через < (2*)
х—а меняет знак с — на J
§ 88] ПРАВИЛО НАХОЖДЕНИЯ МАКСИМУМА И МИНИМУМА ФУНКЦИИ 207
Признаки (1*) и (2*) являются достаточными признаками
максимума и минимума функции, т. е. такими признаками,
наличие которых влечет за
собой или максимум или ми-
нимум функции.
Как видно из равенства
f(a) — 0, касательная, про-
веденная в точках А м В
графиков, параллельна оси
Ох *).
III. Может, однако, слу-
читься, что первая производ-
ная функции, обращаясь
в нуль при х — а, не меняет
знака при переходе аргу-
мента через х — а. В этом
случае функция не имеет
ни максимума ни минимума. На черт. 93 показано, что
касательная в точке А кривой у — f(x) параллельна оси Ох,
т. е. f'(a)=0, но tga!>0 и tga2>0. Следовательно,
первая производная функции y = f(x) при переходе аргу-
мента через х — а не меняет знака. Функция, как по-
казывает чертеж, не имеет при х—а ни максимума ни ми-
нимума.
Значения аргумента, обращающие первую производную
в нуль, будем называть критическими значениями аргу-
мента.
§ 88. Правило нахождения максимума и минимума
функции. Пусть дана функция y — f(x). Для исследования
ее на максимум и минимум прежде всего нужно решить
уравнение f (х) — 0 для нахождения критических значений
аргумента. Пусть действительными корнями этого уравнения
будут xlt х2, х3 и т. д. **).
*) Бывают случаи, когда в точках кривой, соответствующих
максимуму или минимуму функции, касательная параллельна не
оси Ох, а оси Оу. Такие функции исключаются нами из рас-
смотрения.
**) Этих корней будет ограниченное число, если мы исключим
из рассмотрения бесконечно колеблющиеся функции.
208
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
[гл. IX
Затем нужно исследовать знак /'(х) для найденных кри-
тических значений х, начиная с xt (наименьшего); с этой
целью определяют знак производной сначала для х < хр
подставляя какое-либо число, меньшее Xj (производная при
всех значениях х < не обращается в нуль, а потому ее
знак в силу непрерывности сохраняется неизменным при х < xt
как это следует из выводов § 55).
После этого определяют знак производной при каком-
либо значении х в промежутке между х{ и х2 (в промежутке
между х, и х2 производная сохраняет один и тот же знак
по тому же свойству непрерывной функции).
Найдя таким образом знаки производной для значений х,
сначала меньшего, а потом большего чем хп устанавливают,
существует ли при этом значении х = xt максимум или мини-
мум функции или нет ни того ни другого (см. § 87).
Точно так же исследуют знак /'(х) для остальных крити-
ческих значений х.
Первое правило. Таким образом, для исследования
функции y — f(x) на максимум и минимум нужно:
I. Найти производную функции y' = f'(x).
II. Приравняв ее нулю, найти действительные корни
полученного уравнения} пусть они будут х19 х2, х3 и т, д.
III. Расположив значения хп х2, х3, ... в порядке их
возрастания, подставить в производную сначала какое-
либо число, меньшее хр затем подставить число, заклю-
ченное в промежутке между xt и х2;
если при этом знак производной меняется на — *
то при х — Xj имеет место максимум}
если с— на~\~ , то при х — xt имеет место минимум}
если эюе знак производной не меняется, функция при
x — xt не имеет ни максимума ни минимума}
таким же образом определить знак производной до х2
и после х2 и т. д.
IV. Найти максимальные и минимальные значения
функции, т. е. вычислить /(xj, /(х2), /(х3) и т. д.
Четвертый пункт этого правила нужен только в том слу-
чае, если есть необходимость знать положение точек на кри-
вой, соответствующих максимуму и минимуму функции.
Рассмотрим несколько примеров.
Пример 1. Исследовать на максимум и минимум функ-
цию у = х2— 1.
§ 88] ПРАВИЛО НАХОЖДЕНИЯ МАКСИМУМА И МИНИМУМА ФУНКЦИИ 209 .
i
lb
и
b
J
Решение I. Находим производную функции:
у'=(х2— 1)' — 2х.
II. Приравниваем ее нулю:
2х = О,
откуда э
х — 0.
III. Определяем знак производной для значения х < 0, ’
например для х — —1:
4-.=2(-1)=~2.
Теперь находим знак производной
для х= 1:
.у' =2-1 = 2.
Изменение знака производной
с минуса на плюс показывает, что
данная функция при х = 0 имеет
минимум.
IV. Находим минимальное зна-
чение функции, т. е. /(0):
например
для х > 0,
у,
О т
>(О;-7)
Черт. 94.
/(0)=02— 1= — 1.
Теперь мы можем представить на чертеже положение най-
денной точки Л (0; — 1) и вид кривой вблизи нее (черт. 94).
Пример 2. Исследовать на максимум и минимум
функцию
у = ~х3 — А х2 — 4х~р 6.
о Л
Решение. Согласно правилу имеем:
I. У —— у х2— 4х-]-6^ — х2—Зх— 4.
II. х2 — Зх — 4 = 0,
откуда
3±Т<9+Тб 3±5 . 1 . и
2- 2 -- 2 ’ 1
14 Зак. 3032. И. Л. Зайцев
210
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
1гл. IX
III. 1) Исследуем критическое значение =—1. Берем
значение х < — 1, например х =— 2; тогда
Х-=-2 = (— 2)2— 3(— 2) — 4 = 4 + 6 — 4=6.
Возьмем значение — 1, например х = 0; тогда
,У^_0= О2 —3 • 0 —4 = — 4.
Перемена знака производной с плюса на минус показы-
вает, что функция при х = —1 имеет максимум.
2) Исследуем критическое значение х2 = 4. Беря для
х<4 значение х—0, а для х>4 значение х=5, имеем:
У = —4, У = 25 — 15 — 4 — 6.
-Лх’=0 Лг=5
Следовательно, при х — 4 функция имеет минимум.
IV. Максимальное и минимальное значения функции будут:
^=-t=|(-D3—4(-1)2 — 4(-1)+6 = 8
1 Q 9
Ух^ =±43 — 4.42—4.4 + 6 = — 12 4-
О Z о
Результат вычисления запишем в таблицу:
Критические значения аргумента Знак производной Поведение функции Значения функции при критиче- ском значении аргумента
до критического значения аргумента после критиче- ского значения аргумента
— 1 + — макс. 4
4 — + мин. >—* го Сс| ЬО
Обозначив точки графика функции, соответствующие
максимуму и минимуму ее через А и Bt напишем:
л(— 1; 8-4) и В (4; — 12 44
\ о / \ о /
Положение точек А и В и вид кривой вблизи них пред-
ставлены на черт. 95.
§ 88] ПРАВИЛО НАХОЖДЕНИЯ МАКСИМУМА И МИНИМУМА ФУНКЦИИ 21 1
А-<%'
4
~О Г
оди-
фупк-
X
Черт. 95.
Пример 3. Исследовать на максимум и минимум
цию у = х3.
Решение I. у' — (х3)' — Зх2.
[I. Зх2 = 0, откуда Xi, 2 = 0;
III. Для х < 0, например для ;
= — 1,
^=_1 = 3(-1^ = 3;
для х > 0, например для х=1,
у' =3- 12=3.
Знаки производной оказались
наковыми при переходе через крити-
ческое значение х = 0; следовательно,
данная функция при х — 0 не имеет
ни максимума ни минимума (черт. 71).
Упражнения
1. Дана функция у = 2х2. Узнать, будет
ли она возрастать или убывать при значе-
нии аргумента: 1) х— 1, 2) х = — 1. Про-
верить результат на графике.
2. То же для функции у = — х24-х—1 при значении аргу-
мента: 1) х — — 2, 2) х ~ 0, 3) х — 2.
3. Найти значения аргумента, при которых возрастают или
убывают функции: 1) у = 5x-f- 1, 2) у = 4 — Зх.
4. Найти промежутки возрастания или убывания функций:
1) у = х2 — Зх 4* 1, 2) у = — 2х2 + 8х — 1.
Найти максимум и минимум функций:
5,
8.
11.
у = х2 — 2х, 6. у = — х2 -|- 4х. 7, у == 2х2 Зх -|- 4.
у =— 5х2 — 2x4-2. 9. v == 6/ — Z2 — 7. 10. у = х4.
1 9
у=ух4— 2х. 12. у ~ х3х2— 5.
y = —X. 14. s = 4-f —4 ^4-6/ —7.
О О 2
у ~ А х3— 2х2-|-Зх—1. 16. у = х3 + х2 — 5х — 6.
17. s = 2/3 — /2 — 4/ + 5. 18. v
19. у = г-^-т>. 20. у = 3х —~--.
z 1 -j- х2 J 2 — х
21. Показать, что следующие функции не имеют ни максимума
ни минимума:
13.
15
и*
14. s =
27
З/?2 — 9/7 -}- 4.
I) 3X2_|_9X_2,
О
2) у = 6л* — 15х4 + Ю*3
212
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
[гл. IX
§ 89. Выпуклость и вогнутость кривой; Рассмотрим
кривую, изображенную на черт. 96. Проведя касательную,
например АВ, мы видим, что точки кривой, смежные с точ-
кой касания А и лежащие по обе стороны от нее, распола-
гаются ниже касательной. В таком случае говорят, что кри-
вая выпукла вверх в точке А\ если часть кривой между
точками М и N удовлетворяет этому условию, то эту часть
кривой называют выпуклой вверх или просто выпуклой.
Возьмем кривую, изображенную на черт. 97. Здесь мы
наблюдаем другое явление, а именно: точки кривой, близкие
к точке касания С и расположенные по разным сторонам от
нее, лежат выше касательной CD. В этом случае говорят,
что кривая в точке С вогнута вверх и часть кривой между
точками Р и Q, удовлетворяющей этому условию, называют
вогнутой вверх или просто вогнутой^
§ 90] ПРИЗНАКИ ВЫПУКЛОСТИ И ВОГНУТОСТИ КРИВОЙ
213
Бывают случаи, когда кривая в одной своей части выпукла,
а. в другой вогнута; так, например, синусоида (черт. 98)
имеет и выпуклость (выше оси Ох) и вогнутость (ниже оси Ох)»
причем точка А служит границей между ними. Касательная,
проведенная к кривой в этой точке, является общей для
выпуклой и вогнутой части ее; эта касательная в то же время
пересекает кривую в точке касания; поэтому синусоида
в точке А ни выпукла ни вогнута. Эта точка носит название
точки перегиба.
§ 90. Признаки выпуклости и вогнутости кривой.
Теорема. Если вторая производная функции у — f(x)
в данном промежутке значений х положительна» то
кривая вогнута в этом промежутке» а если отрица-
тельна» — то выпукла.
Поясним эту теорему геометрически.
I. Пусть в данном промежутке значений х
Г(х)>0. (1)
Так как f"(x) является производной функции f'(x)» то, при-
меняя признак возрастания и убывания к функции f'(x)(§ 85),
скажем, что при условии (1) f'(x) возрастает с возраста-
нием х в данном промежутке. Но тогда согласно геометри-
ческому смыслу первой производной (§ 63) возрастает и
угловой коэффициент касательных, проведенных к графику
функции y=f(x) в точках данного промежутка, т. е. растет
тангенс угла наклона этих касательных, а следовательно, и
угол их наклона к положительному направлению оси Ох.
Итак, при условии (1) с возрастанием х угол,
образованный касательными к кривой у = f(x) с положи-
тельным направлением оси Ох» растет, а это наблюдается
только в случае, когда касательные проведены в точках,
лежащих на вогнутом участке кривой (черт. 99).
II. Пусть в данном промежутке значений х
Г(Х)<О (2).
При этом условии с возрастанием х функция f (х) убывает,
а потому убывает и угловой коэффициент касательных, про-
веденных к графику функции у = f(x) в точках данного
промежутка, т. е. убывает тангенс угла наклона этих каса-
тельных, а следовательно, и угол их наклона к положитель-
ному направлению оси Ох.
214 ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ [гл. IX
Таким образом, при условии (2) с возрастанием .г
угол между касательными к кривой y = f(x) и положитель-
ным направлением оси Ох убывает, а это имеет место
только в случае, когда касательные проведены на выпуклом
участке кривой (черт. 100).
Пример. Узнать, выпукла или вогнута кривая у — х3
в точке, абсцисса которой равна —2.
Решение. Находим вторую производную данной функ-
ции и определяем ее знак при х =— 2:
у' — (х3)' = Зх2,
у" — (Зх2)' — 6х,
^=-2 = 6.(-2) = -^12.
Вторая производная отрицательна; следовательно, кривая
у — х3 в данной точке выпукла (черт. 71).
§ 91. Нахождение точки перегиба.
Определение. Точкой перегиба кривой называется
точка, которая отделяет выпуклую часть кривой от
вогнутой.
Если график функции у — /(х) меняет выпуклость на
вогнутость или наоборот, то при этом вторая производная
данной функции должна менять свой знак, обращаясь в нуль
в точке перегиба.
§ 91] НАХОЖДЕНИЕ ТОЧКИ ПЕРЕГИБА 215
Легко показать, что справедливо и обратное утверждение:
если при данном х вторая производная функции у — f(x)
равна нулю и при переходе аргумента через данное зна-
чение х меняет знак, то при этом график функции имеет
точку перегиба.
Это является достаточным признаком точки перегиба.
Отсюда имеем следующее правило.
Чтобы найти точку перегиба кривой у — f(x), нужно*.
I. Отыскать вторую производную функции y — f(x),
II. Приравняв ее нулю, решить полученное уравнениех
пусть действительными корнями его будут xt, х2, х3
и т, д. *).
III. Расположив значения хг, х2, х3, ... в порядке их
возрастания, подставить во вторую производную сначала
любое число, меньшее х}, затем — любое число, заклю-
ченное между хг и х2; если в обоих случаях получатся
разные знаки, то при х — хх имеется точка перегиба,
если же одинаковые, то точки перегиба нет-, таким же,
образом определить знак второй производной до и после х2
и т. д.
IV. Найти ординаты точек перегиба, т, е. вычислить
функцию для тех значений аргумента, для которых
имеет место перегиб.
Пример. Найти точку перегиба кривой у = х3.
Решение. Согласно правилу находим:
I. у' = (х3У=Зх2, y" = (3x2Y=Qx.
II. 6х = 0, откуда х = 0.
III. Определяем знак:
^=1 = 6.1^+б.
Как видно, при х—О имеет место точка перегиба.
IV. у = 03 = 0.
Кривая у — х3 имеет точку перегиба в начале координат
и здесь меняет выпуклость на вогнутость, как это видно из
чередования знаков второй производной (черт. 71).
*) Предполагается, что уравнение имеет ограниченное число
корней.
216
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
[гл. IX
Упражнения
1. Узнать, выпукла или вогнута кривая у = х3 — 5х2 Зх — 1
в точках, абсциссы которых: 1) х-= 1, 2) х = 2.
2. Выпукла или вогнута кривая у = х4— 4х3-|-8х— 2 в точ-
ках, абсциссы которых: 1) х — 2) х = — 2.
3. В каких точках выпуклы или вогнуты кривые:
1) у^х2 — Зх--|-6, 2) у = 2 — Зх — х2?
Найти точки перегиба следующих кривых:
4. у = ±х3-х. 5. у — х3-|-Зх2 —5х — 6.
6. у = 2х3 — Зх2 — 4х + 9. 7. у = —х3 + 6х2 — 15x4-10.
8. у — х4. 9. у — х4 — 12х3 + 48х2 — 50.
10. у = х + 36х2 — 2х’ — 11. у = ^х4 + -|х2.
12. у = 12х4 — 12x2. 13. у = 3x5 — 5х»+ 1.
Найти промежутки выпуклости и вогнутости кривых:
14. у = х3—4х2— 2х-}-1. 15. у = х4—~ х2— 4х.
§ 92. Второе правило нахождения максимума и мини-
мума функции.
Теорема. Если для некоторой функции у — /(х)
/'(«)=о.
то данная функция при х — а имеет
максимум, если f" (а) < 0
и минимум, если f" (а) > 0.
Покажем справедливость теоремы следующими сообра-
жениями.
При условии /' (а) — 0 функция у — /(х) имеет максимум
или минимум или точку перегиба (§ 87). Но согласно теореме
f" (#)^=0, поэтому точка перегиба исключается.
При f" (а) < 0 точка с абсциссой х = а лежит на выпу-
клой части графика функции, а при /z/(«)>0—на вогнутой
его части (§ 90). Следовательно, в первом случае имеет место
максимум, во втором — минимум, что и требовалось показать.
Может однако случиться, что при f' (а) — 0 также и
/"(#)= 0, тогда при помощи второй производной нельзя
установить, что имеет функция: максимум или минимум.
В этом случае для решения вопроса нужно прибегнуть к пер-
вому правилу (§ 88).
§ 92] ВТОРОЕ ПРАВИЛО НАХОЖДЕНИЯ МАКСИМУМА И МИНИМУМА 217
Таким образом» имеем второе правило для нахож-
дения максимума и минимума функции:
Найти вторую производную функции и подставить
в нее каждое из критических значений аргумента} если
в результате подстановки одного из них вторая про-
изводная будет отрицательной^ то при этом значении
аргумента функция имеет максимум' если положитель-
ной'— то минимум' а если же вторая производная обра-
щается в нуль, то для решения вопроса нужно обра-
титься к первому правилу.
Рассмотрим несколько примеров.
Пример 1. Исследовать на максимум и минимум функцию
у = х2— 4х-4~ 9.
Решение. Согласно правилу имеем:
I. у = (х2 —4х4~ 9)'== 2х—4.
II. 2х—4 = 0, откуда х=2.
III. у' = (2х — 4)'= 2.
Вторая производная оказалась положительной; следова-
тельно, при х—2 имеет место минимум.
Пример 2. Исследовать на максимум и минимум функцию
91
у=х3—-^-х24-30х4-15.
Решение. 1.у' — ^х3—х24~ 30x4“ 15^ —
= 3х2—21x4-30.
II. Зх2—21x4" 30 = 0 или х2—7х4-Ю = 0, откуда
7 7 -ч- 3
х1(2 —у—у ю — у—2;
Xj 2,
х2 = 5.
III. У' = (Зх2—21x4-30)'= 6х—21.
Подставим во вторую производную вместо х поочередно
значения 2 и 5:
>L2=6.2-2I=-9.
j;=5 = 6.5-2l= + 9.
218 ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ [гл. IX
Как видно, при х—2 функция имеет максимум, при х —
— 5 — минимум.
Пример 3. Исследовать на максимум и минимум
функцию
у= X4.
Решение. I. у' — (х4)' — 4х3.
И. 4х3=0, откуда х— 0.
III. у" = (4х3)' = 12х2.
Подставив значение х=0, получим:
зСо=12-°2 = о-
Вторая производная оказалась равной нулю, поэтому ука-
занным способом установить максимум и минимум нельзя.
Обратившись к первому правилу, будем иметь:
^=1 = 4.Р = + 4.
Перемена знака первой производной показывает, что при
х=0 функция имеет минимум.
Упражнения
Исследовать на максимум и минимум функции:
1.у = 3х2 2. у = 4х2—12. 3. у ==х2 —6х + 3.
4. у = — 2х2 + 8х — 5. 5. у = х3 — 12х2 4~ Збх — 10.
6. у = х» — 2х2 —4x4-3. 7. у = 2_X3_|__Lx2_6x4-1.
о 2
8. у ==— -^-х3 + ™х2 — 6x4-2. 9. у =—~ х3 4~ х2 4~ Зх — 4.
10. у = х4 — 8х34~22х2 — 24x4-12. 11. у = х\
Найти промежутки возрастания и убывания функций:
12. у = х3—12х —4. 13. у =— х3 4" х2 + Зх — 6.
Имеют ли максимум и минимум следующие функции:
< л 1 г 4х2 4“ 23
14. у = —. 15. у =--~.
х 10х
§ 93. Задачи на максимум и минимум функции. Тео-
рия максимума и минимума функции имеет большое приме-
нение как в самой математике, так и в технических дисци-
плинах. Решим несколько задач.
Задача 1. Разбить число 20 на два слагаемых, произве-
дение которых имело бы наибольшее значение.
§ 93] ЗАДАЧИ НА МАКСИМУМ И МИНИМУМ ФУНКЦИИ 219
Решение. Будем искать эти слагаемые. Обозначим одно
из них буквой х; тогда другое слагаемое выразится в виде
20 — х. Произведение этих слагаемых есть переменная вели-
чина, меняющаяся с изменением слагаемого х. Обозначая
произведение буквой у, запишем:
у — х(20 — х).
Мы получили функцию, выражающую зависимость про-
изведения у от величины слагаемого х. В задаче требуется
найти такое х, при котором у принимает наибольшее зна-
чение, т. е. задача свелась к нахождению максимума функ-
ции. Поступим по правилу, изложенному в § 92.
I. у = [х (20 — х))' = (20х — х2)' = 20 — 2х.
II. 20 — 2х = 0, откуда х=10.
Ш. у" — (20 — 2х)' = — 2.
Следовательно, при х=10 функция имеет максимум.
Число 20 нужно разбить на два равных слагаемых, тогда
их произведение будет наиболь-
шим.
Задача 2. Найти высоту
конуса наибольшего объема, ко-
торый можно вписать в шар ра-
диуса, равного R,
Решение. Обозначив радиус
основания, высоту и объем конуса
соответственно буквами г, h и
запишем:
1 9Z
V = -у- КГ-h.
о
Это равенство выражает зави-
симость v от двух переменных г
и Zz; исключим одну из этих ве-
Черт. 101.
личин, а именно г. Для этого из прямоугольного треуголь-
ника ABD (черт. 101) выводим (по теореме о квадрате пер-
пендикуляра,
гипотенузу):
вершины прямого угла на
опущенного из
АО2 = ВО * DOt
или
г2^Л(2/? —/г).
220
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
[гл. IX
Подставив значение г2 в формулу объема конуса, получим:
v — (2/? — h).
о
Мы видим, что объем v конуса, вписанного в шар
радиуса R, есть функция от высоты этого конуса h. Найти
высоту, при которой вписанный конус имеет наибольший
объем, это значит найти такое /г, при котором функция v
имеет максимум.
Ищем максимум функции v*.
I. v' — C^-itRh2—^ — nRh — ти/z2.
\3 3/3
II. —nRh — -л/г2—0, откуда /г.=0 и /z2==-^/?.
о о
III. = (~vRh— rJi2\ ^^-nR— 2ith,
\ о /о
4
Подставив вместо h сначала /z1 = 0, а потом h2 = -^R>
получим:
" 4 о
®л=0 = -у«^»
V 4 =4 --2тг • 4 R =-X- T.R.
h~-~ Ro о 3
В первом случае имеем минимум, во втором — искомый
максимум.
Следовательно, при h — ~R
конус, вписанный в шар радиуса R,
имеет наибольший объем.
Задача 3. Окно имеет форму
прямоугольника, завершенного полу-
кругом; периметр фигуры окна ра-
вен 6 м. Каковы должны быть его
размеры, чтобы оно пропускало
максимум света (черт. 102).
Решение. Как известно, коли-
чество света, проходящего через
окно, тем больше, чем больше площадь окна. Обозначим:
AD— х\
тогда длина полуокружности ВтС будет равна ~~, а высота
§ 93] ЗАДАЧИ НА МАКСИМУМ И МИНИМУМ ФУНКЦИИ
221
в__ пх
6 — AD — ВтС Х 2 12 —2х —тех п
окна АВ =---------о-------=------2----~--------*-----• 11л0"
4
2
щадь всего окна состоит из площадей прямоугольника ABCD
и полукруга ВтС. По соответствующим формулам найдем:
с 12 — 2х— кх 12х— 2х?— лх2
одвСР —-----4---- ’ х —----J------
И
ВвтС
7СХ2
~е
Обозначив площадь окна буквой у, получим:
12х — 2х2 — тех2 , тех2
У = :-------4--------=
__ 24х — 4х2 — 2тсх2 -J- ^х2 __ 24х — 4х2 — тех2
_ _ — • §
Мы видим, что площадь окна у в условиях нашей задачи
является функцией его основания х, и задача свелась к на-
хождению максимума функции у.
Исследуем полученную функцию на максимум:
. , /24х — 4х2 — тсх2\х 24 — 8х — 2тсх 12 — 4х — пх
L У =(------8-------) =-------8-----=------4-----•
12 — 4х — тех п 12
II . ----л----=0, откуда х = -г-.—.
4 J 4~|- тс
,, /12 — 4х — тсх\' —4—тс 4-1-тс
ш. _/' = (-----) =—4-------------------f-.
Вторая производная оказалась отрицательной, значит, при
12 *
х — — площадь окна наибольшая.
4 4- ТС
Для прохождения наибольшего количества света через
окно с контуром в 6 м нужно, чтобы ширина его была равна
12
44-тс
1,68 м.
Упражнения
1. Разбить число 12 на два слагаемых, произведение которых
имело бы максимальное значение.
2. Разбить число 10 на два слагаемых, чтобы сумма их квадра-
тов была наименьшая.
3. Число 8 разбить на два слагаемых так, чтобы сумма их
кубов была наименьшая.
222 ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ [гл. IX
4. Для какого числа разность между этим числом и его квад-
ратом наибольшая?
5. Какой из прямоугольников с периметром, равным 50 см,
имеет наибольшую площадь?
6. Прямоугольный участок земли в 10 000 м2 нужно окопать
вдоль всей границы рвом. Как выбрать размеры участка, чтобы
длина рва была наименьшая?
7. Сумма основания и высоты треугольника равна 10 см.
Каковы должны быть размеры основания, чтобы площадь треуголь-
ника была наибольшая?
8. Из квадратного листа железа, сторона которого равна 30 см,
нужно вырезать по углам четыре квадратика так, чтобы из остав-
шейся части после сгибания получить коробку наибольшей емкости.
Каковы при этом размеры вырезанных квадратиков?
9. Из листа картона прямоугольной формы размером 30 X 30 см2
нужно вырезать по углам квадратики так, чтобы из оставшейся
части после сгибания получить коробку наибольшей боковой по-
верхности. Подсчитать размеры вырезанных квадратиков.
10. Окно имеет форму прямоугольника, который сверху заканчи-
вается правильным треугольником. Периметр окна равен 3 м. Каково
должно быть основание прямоугольника, чтобы окно имело наи-
большую площадь?
11. Сечение шлюзового канала имеет вид прямоугольника,
заканчивающегося полукругом. Периметр сечения равен 4,5 м.
При каком радиусе полукруга сечение будет иметь наибольшую
площадь?
12. Требуется изготовить ящик с крышкой, объем которого
равен 72 дм\ а стороны основания относятся как 1 :2. Каковы
должны быть размеры всех сторон его, чтобы полная поверхность
ящика была наименьшей?
13^ Объем правильной четырехугольной призмы равен 8 дм\
Какова должна быть сторона основания призмы, чтобы полная по-
верхность ее была наименьшей?
14. Резервуар емкостью в 4 ж3 с квадратным основанием, от-
крытый сверху, нужно выложить оловом. Каковы должны быть его
размеры, чтобы олова пошло для этого минимальное количество?
15. Найти величину радиуса основания и высоту цилиндра,
имеющего объем 27к см*, у которого полная поверхность наи-
меньшая.
16о Какими нужно взять размеры цилиндрического сосуда ем-
костью в 1 л, открытого сверху, чтобы на его изготовление по-
требовалось наименьшее количество материала.
17. В равнобедренный треугольник с основанием 20 см и высо-
той 8 см вписан прямоугольник. Какова должна быть высота прямо-
угольника, чтобы он имел наибольшую площадь?
18. Из проволоки длиной 120 см нужно сделать модель прямо-
угольного параллелепипеда с квадратным основанием. Какова должна
быть сторона основания, чтобы полная поверхность параллелепи-
педа была наибольшей?
19. Из проволоки длиной 90 см нужно сделать модель призмы
с правильным треугольником в основании. Какова должна быть1
§ 94]
ГРАФИКИ ФУНКЦИЙ
223
сторона основания призмы, чтобы боковая поверхность ее была
наибольшей?
20. Требуется изготовить коническую воронку с образующей,
равной 20 см. Какова должна быть высота воронки, чтобы ее объем
был наибольший?
21. Найти высоту цилиндра с наибольшим объемом, вписан-
ного в шар радиуса R.
22. В конус, радиус основания которого 6 см и высота 15 см,
требуется вписать цилиндр, имеющий наибольшую полную поверх-
ность. Определить радиус цилиндра.
23. На параболе у1 = 2х найти точку, ближайшую к точке
Л(3; 0).
24. Электрическая лампочка висит над центром круглого стола.
На какую высоту нужно ее поднять, чтобы она наиболее ярко
освещала предмет, лежащий на столе на расстоянии 1 м от центра?
(Яркость освещения прямо пропорциональна синусу угла, образо-
ванного лучом, падающим на предмет, с крышкой стола, и обратно
пропорциональна квадрату расстояния предмета от источника света,
z _ sin ср ч
т. е. Z = .)
25. Картина в 1,4 м высотой висит на стене так, что ее ниж-
ний край на 1,8 м выше глаза наблюдателя. На каком расстоянии
от стены должен стать наблюдатель, чтобы его положение было
наиболее благоприятным для осмотра картины (т. е. чтобы угол
зрения был наибольший)?
§ 94. Графики функций. В настоящей главе мы позна-
комились с тем, как изучаются свойства функции с помощью
ее производных. Знание этих свойств позволяет нам полу-
чить представление о функции, а также построить ее график.
1 2
Пример. Построить график функции > =-g-х3—х2 + у.
Р е ш е и и е. Исследуем данную функцию на максимум и
минимум.
(1 9 V 1
-g- х3— х2 —|— — ~х2— 2х.
II. у х2— 2х = 0, или х2 — 4х==0,
откуда Х1 = 0 и х2 = 4.
III. у/ = ^ух2 — 2х^ —х — 2,
^=о = О-2 = -2,
у"^ = 4-2 = + 2.
При х = 0 функция имеет максимум, при х = 4— ми-
нимум.
224
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
[гл. IX
IV. Найдем ординаты точек, соответствующих максимуму
и минимуму функции:
1 2 9
1 ,9 . 2 32 , 2 .2
^ = К-43“42+у=з-1б+з=-4з-
Координаты
искомых точек
4;
Исследуем теперь данную функцию на точку перегиба;
для этого найденную вторую производную приравняем нулю:
откуда
х — 2 = 0,
х — 2.
Чтобы убедиться, что при х=2 имеет место перегиб,
определим знаки второй производной для х < 2 и для х > 2;
в результате получим:
-У^=з ~ 3 —2 — + 1.
Смена знаков второй производной показывает, что аргументу
х = 2 соответствует точка перегиба. Найдя ее ординату,
будем иметь:
^=1- 23-22+1=4-4+1=-2.
и координаты точки перегиба (2; —2).
Чтобы яснее представить график данной функции, вычис-
лим координаты еще нескольких точек *). Положив, напри-
мер, х = — 2 и х = б, получим:
1 2
4 Л , 2 .2
==___ —_ 4_,
1 9 9 9
=зб-зб+4=4.
*) Часто бывает полезно найти точки пересечения кривой с осями
координат, однако это нередко связано с большими трудностями
при решении уравнений высших степеней.
§ 94]
ГРАФИКИ ФУНКЦИЙ
225
Координаты дополнительных точек суть —2; —
(б; . Составим таблицу найденных значений координат
точек:
X — 2 0 2 4 6
У -4 2 3 — 2 СЧ [со 2 3
Построим все эти точки и проведем через них плавную
линию (черт. 103).
Для построения графика функции следует придерживаться
такой схемы.
1. Найти значения х, при которых данная функция имеет
максимум или минимум.
2. Найти значения х, при которых график функции имеет
точки перегиба.
3. Вычислить значения ординат точек, соответствующие
найденным значениям абсцисс; присоединив к этим точкам
еще несколько дополнительных, записать найденные значения
х и у в таблицу.
4. Построить найденные точки и провести через них
плавную линию.
15 Зак. 3032. И. Л. Зайцев
226
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
[гл. IX
Упражнения
Построить графики функций:
1. У=уХ24-2. 2. у = 2х24~6х. 3. у = — 2х24-4х.
4. у = х2 — 6х + 5. 5. у = — у х2 + 4х — 3,5.
6. у = х4. 7. у = х5. 8. у — х3 + х.
9. у = х3— Зх. 10. у = -|-х3—4.
о
11. у = — 2-хЗ_|_2х2 — 1. 12. y=-Lx3— 3x4-2.
13. у = -1х3 — х4-3. 14. у = 2х3 — 9х24-12х4-1.
15. у = -^-х4— 8х. 16. у = х4 — 2х34~3.
ГЛАВА X
ДИФФЕРЕНЦИАЛ
§ 95. Сравнение бесконечно малых величин между
, собой. Понятие о дифференциале. I. В § 42 мы рассмот-
рели действия над бесконечно малыми величинами и показали,
что в результате сложения, вычитания и умножения их
получаются также бесконечно малые величины. Однако част-
ное от деления двух бесконечно малых друг на друга может
быть не только бесконечно малой величиной, но и беско-
нечно большой и конечной.
В самом деле, пусть, например, а — бесконечно малая,
тогда а2 и 2а будут также бесконечно малыми. При деле-
нии их друг на друга возможны следующие случаи:
1) отношение
— = а —бесконечно малая величина,
а
2) отношение
А —1—бесконечно большая величина,
а- а
3) отношение
2а п
— — 2 — конечная величина.
а
Первое отношение показывает, что бесконечно малая а2
составляет ничтожно малую часть от а и, следовательно,
стремится к нулю значительно быстрее, чем а.
Второе отношение указывает на то, что а, неограниченно
уменьшаясь, остается значительно больше, чем а2, т, е. стре-
мится к нулю медленнее величины а2.
15*
228 ДИФФЕРЕНЦИАЛ [гл. X
Сказанное молено иллюстрировать следующей таблицей:
а 1 0.1 0.01 0,001 0,0001 ... — 0
а2 1 0,01 0.0001 0.000001 0,00000001 ... — -> 0
а2 а 1 0,1 0,01 0,001 0,0001 ... — -> 0
а а2 1 10 100 1000 10000 ... — -> оо
Принято бесконечно малую а2 по отношению к а назы-
вать бесконечно малой высшего порядка, а а по отношению
к а2 — бесконечно малой низшего порядка.
Что касается третьего отношения, то из него следует, что
бесконечно малые 2а и а стремятся к нулю с одинаковой
2а
скоростью, так как при их изменении отношение — остается
постоянным. Такие бесконечно малые имеют, как говорят,
одинаковый порядок малости.
Таким образом, частное от деления двух бесконечно ма-
лых величин позволяет сравнивать их между собой. Это
сравнение особенно полезно в приближенных вычислениях,
где отбрасывание бесконечно малых высшего порядка при-
водит к значительному упрощению вычислений.
П. Возьмем функцию у = х2; ее приращение
Ду = 2х Дх + (Дх)2 [(3) § 52].
Множитель при Дх есть производная данной функции,
а потому последнее равенство можно переписать так:
Ду = у' Дх 4~ (Дх)2. (1)
Сравним изменение величины обоих слагаемых правой
части равенства (1) с уменьшением Дх. Положив, например,
§ 95] СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИН 229
х — 2 и, следовательно, у' = 4, составим следующую таблицу
значений этих слагаемых:
Дх 1 0,1 0,01 0,001
у' Дх 4 0,4 0,04 0,004
(Дх)2 1 0,01 0,0001 0,000001
Как видно из таблицы, слагаемые у'Lx и (Дх)2 умень-
шаются с уменьшением Дх, причем первое пропорцио-
нально Дх, второе же значительно быстрее.
Покажем, что то же самое справедливо для любой диф-
ференцируемой функции /(х).
Пусть дана функция y — f(x). Ее производная
z .. Ду
у = hm .
Дж->о к-Х
Согласно определению предела переменной (§ 41) имеем:
Ду z .
= у 4- а,
кх 1
где а — бесконечно малая величина при Дх~>0. Отсюда
Ду = у Дх 4- а Дх. (2)
И здесь при уменьшении Дх первое слагаемое УДх умень-
шается пропорционально Дх, второе же слагаемое аДх умень-
аДх а
шается быстрее, так как отношение—y-v———у — бесконечно
1 у' Дх у'
малая величина при У =# 0, т. е. по отношению к у'Lx ве-
личина аДх — бесконечно малая высшего порядка. Поэтому
выражение УДх называют главной частью приращения
функции у — f(x).
Определение. Главная часть у'Lx приращения
функции y — f(x) называется дифференциалом функции.
Дифференциал функции y—j\x) принято обозначать
символом dy. Таким образом
dy — y'Lx, (3)
Дифференциал аргумента dx принимают равным прираще-
нию аргумента Дх, т. е.
dx — Дх.
230 ДИФФЕРЕНЦИАЛ [гл. X
Поэтому равенство (3) можно переписать в следующем виде:
dy — y'dx, (4)
т. е. дифференциал функции равен произведению произ-
водной функции на дифференциал аргумента.
Из формулы (4) следует:
(5)
Равенство (5) показывает, что производная функции есть
отношение дифференциала функции к дифференциалу
аргумента. На этом основании производную функции часто
dy
выражают в виде и читают: «дэ игрек по дэ икс».
III. Заменив в равенстве (2) у'&х символом dy, напишем:
Ду == dy + а Дх. (6)
Как было показано выше, аДх— бесконечно малая высшего
порядка по отношению ку'кх—dy, а потому, отбросив
в равенстве (6) слагаемое аДх, получим:
Ду dy. (7)
В практических вопросах часто используют формулу (7),
т. е. берут дифференциал функции вместо ее приращения,
делая при этом незначительную ошибку и тем меньшую,
чем меньше Дх.
Примечание. В случае линейной функции ky~dy.
В самом деле, для функции y = kx-\-b приращение будет:
by — Z?(x+ Дх)+/> — (/гх4-£) =
— kx-\-k Дх-j-^ — kx — b — khx.
Множитель k есть производная линейной функции; поэтому
правая часть последнего равенства выражает дифференциал
данной функции, т. е.
k \х — dy.
Итак, в случае линейной функции
Ду = dy.
§ 96] ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ ДИФФЕРЕНЦИАЛА 231
§ 96. Геометрическое изображение дифференциала.
Возьмем функцию у — f(x), график которой изображен на
черт. 104. Пусть абсцисса точки М
ОР—х\
тогда ордината ее
PM=y — f(x).
Дадим аргументу х приращение PPt = dx и восставим
в точке Рг перпендикуляр Р^М^ к оси Ох, а из точки М
проведем 7WQ||dx. Тогда, как известно (§ 53),
= Д>.
Проведем в точке М касательную к кривой; полученный
при этом отрезок QN, равный приращению ординаты точки Mt
движущейся по касательной, называется приращением орди-
наты касательной. Из прямоугольного треугольника MNQ
имеем:
Q7V = 2l4Qtg£ NMQ.
Но
MQ = PPV — dxt
а, согласно геометрическому смыслу производной (§ 63),
tg£ WMQ==tga=y.
Поэтому
QN — у' dx.
Но
у' dx = dy [(4) § 95].
232 ДИФФЕРЕНЦИАЛ [гл. X
Следовательно,
= dy.
Таким образом, если в точке М кривой у = f(x) провести
касательную, то дифференциал функции y — f(x) в этой
точке изобразится приращением ординаты касательной,
соответствующим приращению ее абсциссы на dx.
Дифференциал функции в данной точке может быть как
меньше приращения ее (черт. 104), так и больше (черт. 105).
§ 97. Дифференциал второго порядка. Дифференциал dy
функции у — f(x), называемый первым дифференциалом или
дифференциалом первого порядка, представляет собой также
функцию х, а потому и от него можно найти дифференциал,
который называют вторым дифференциалом или дифферен-
циалом второго порядка. В этом случае пишут d(dy) или
короче d2y и читают: «дэ два игрек».
Найдем выражение дифференциала второго порядка от функ-
ции через ее производную. Для этого продифференцируем
по х равенство , , ,
dy — ydx,
считая dx постоянным множителем (так как dx не зависит
от х):
d2y = d (у' dx) — d {у') dx.
Но согласно формуле (4) § 95
d (у') = (у')' dx — y"dx.
Поэтому
d2y = у7 dx • dx = y” dx2,
(1)
§ 98] ДИФФЕРЕНЦИАЛ И ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ 233
т. е. дифференциал второго порядка равен произведению
второй производной функции на квадрат дифференциала
аргумента.
Из равенства (1) следует
Это дает основание для выражения второй производной
. d?y
функции в виде отношения которое читают так: «дэ два
игрек по дэ икс квадрат».
§ 98. Приложение дифференциала к приближенным
вычислениям. Рассмотрим несколько примеров использования
дифференциала в приближенных вычислениях.
а) Определение приращения функции.
Пример 1. Найти приближенно приращение функции
j = 2x24-3 при х — 2 и Дх = 0,001.
Решение. Так как приращение аргумента — величина
малая, то согласно формуле (7) § 95 можем приращение
функции заменить ее дифференциалом.
Дифференциал же данной функции
dy = (2х2 + 3)' dx — 4х dx. (1)
Заменив в равенстве (1) х и dx их значениями, получим:
dy — 4- 2-0,001=0,008.
Следовательно,
Ьу^ 0,008.
Посмотрим, какую ошибку мы делаем, беря дифференциал
вместо приращения. Для этого найдем точное значение при-
ращения функции (см. пример 1, § 52):
&у = 4х &х 4~ 2 (Дх)2 =
= 4-2.0,001 + 2 (0,001 )2 = 0,008 + 0,000002 = 0,008002.
Сравнивая полученное точное значение &у с приближенным,
видим, что допущенная ошибка равна 0,000002. Выражая ее
в процентах, найдем:
0,00023 = 0,025%.
Ошибка оказалась очень малой.
234
ДИФФЕРЕНЦИАЛ
[ГЛ. X
Пример 2. Шар радиуса = 20 см был нагрет, отчего
радиус его удлинился на 0,01 см. Насколько увеличился
при этом объем шара?
Решение. Объем шара определяется по формуле
4 ГУ?
V —
о
Каждому значению R по закону, заданному этой форму-
лой, отвечает одно определенное значение vt т. е. v есть
функция от R. Следовательно, наша задача сводится к опре-
делению приращения функции v при заданном приращении
аргумента /?. Так как приращение аргумента мало (Д/? =
^-dR~ 0,01), то мы можем приращение функции заменить
ее дифференциалом [(7) § 95].
Находим дифференциал функции v\
4
dv = 4 т: • З/?2 dR = 4т:/?2 dR.
о
Но
R = 20 и d/? = 0,01.
Поэтому
dv — 4 тс • 202 • 0,01 = 16тс см3.
б) Нахождение числового значения функ-
ци и. Пусть требуется найти приближенное значение функции
/(х)=2х24~3
при Xi = 2,001, т. е. найти величину /(2,001).
Представим хг в виде суммы
Xl = 24-0,001,
где 0,001 будем рассматривать как приращение аргумента.
Из формулы для приращения функций
&У=f(x 4- Дх)—f (х)
найдем:
/(х + Дх) = /(х)4-Ду.
Полагая Дх малой величиной, можем Ду заменить вели-
чиной dy\ тогда последнее равенство перепишется в виде
/(х + Дх)?«/(х) + </у. (2)
§ 98] ДИФФЕРЕНЦИАЛ И ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ 235
Применив равенство (2) к данному примеру, можем на-
писать:
/(2 + 0,001)^/(2) + ^.
Но
dy = 4х dx = 4.2 • 0,001 = 0,008,
/(2) —2 • 22 + 3= 11.
Поэтому
/(2 + 0,001) = /(2,001)^ 11 + 0,008 — 11,008.
Равенство (2) может служить формулой для приближенного
вычисления значения функции.
в) Вычисление по п р и б л и ж е п н ы м ф о р м у л а м.
Пользуясь формулой (2), выведем приближенные формулы
для вычисления некоторых выражений.
1) Возьмем функцию
у — sin х
и положим, что угол х, равный нулю, получает весьма ма-
лое приращение а. Применим формулу (2), полагая в ней
х — 0 и dx — а. Получим:
/(0 + а)^/(0)+^.
Но
dy = (sin х)' dx — cos х • dx — cos 0 • а — а
и
/(0) = sin0 = 0.
Поэтому
/(0 + а)^0 + а,
или
sin а а.
Отсюда следует, что синус очень малого угла приближенно
равен самому углу; при этом нужно помнить, что угол дол-
жен быть выражен в радианной мере. Так, например,
sin 0,003 0,003. В самом деле, выразив данный угол в гра-
дусной мере, найдем:
а
sin 10'^0,003.
236
ДИФФЕРЕНЦИАЛ
[ГЛ. X
2) Возьмем функцию у = хп и положим, что х, равный 1,
получает весьма малое по сравнению с единицей приращение
Дх = а. Тогда согласно формуле (2) имеем:
Но
dy — (х11)' dx — nxtl~l dx = ti • 1 n'“i • a = na
и
/(l)=lw=l.
Поэтому
f(l+a)^l+na,
или
(1 + a)w 1 + zza. (3)
Точно так же можно вывести равенство
(1 — a)n 1 — па. (4)
По формулам (3) и (4) можно быстро найти приближен-
ную степень числа, близкого к единице; например:
1,0152==(1 +0,015)2 1 4-2 • 0,015 = 1,03,
0.9883 = (1 — 0,012)3 1 — 3 • 0,012 = 0,964.
3) Выведем формулу для приближенного вычисления выра-
п -------
жения у 1 + а, где а имеет малое значение по сравнению
п г----------------------------------
с единицей. Для этого представим у 1 + а в виде степени
п ____ JL
у 1 + a = (1 + а) п.
Но по формуле (3)
ИЛИ
п г--------------------- 1
/1+а=1+4а- (5)
Аналогично выводится формула
П ----- 1
1 — a = 1---™ а. (6)
§ 98] ДИФФЕРЕНЦИАЛ И ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
237
По формулам (5) и (6) можно легко найти приближенное
значение корня из числа» близкого к единице; например:
/1,03 = /1 4- 0.03 « 1 ч- у • 0,03 = 1,015,
1^0,964 == ]Х1 —0,036 « 1 — у • 0,036 = 0,988.
Упражнения
Найти первый дифференциал функции:
1 -1Г- О 1 —z О 12
1,у = хУх 2. 5 = г—г— 3. t7=7r COS —.
1 -j“ t Z <0
4. у — sin2 Y x. 5. и = In2—*. 6. у = In .
7. у = arctg
8. Найти дифференциал пути, выраженного уравнением s = 5Z3,
если t = 4 и А/ = 0,01.
9. Вычислить приближенно приращение функции у=ха—5х2-|-80
ври переходе аргумента от х = 4 к х = 4,001.
10. Сторона квадрата равна 5 см. Найти приближенное прира-
щение площади его при увеличении его стороны на 0,01 см.
11. Найти приближенное приращение площади круга, если
радиус его изменяется с 50 см на 50,1 см.
12. Сторона куба, равная 1 м, удлинилась на 10 см. Насколько
при этом увеличился объем куба?
13. В прямоугольном параллелепипеде с квадратным основанием
сторона основания равна 20 см, а высота равна 10 см. Насколько
увеличится его объем, если сторону основания удлинить на 0,02 см?
14. В конусе радиус основания равен 15 см, а высота содер-
жит 20 см. Насколько увеличится его объем, если радиус основания
удлинить на 0,04 см?
15. Шар радиуса R = 9 см был нагрет, вследствие чего объем
его увеличился на 32,4л см\ Узнать удлинение радиуса шара.
16. Куб со стороной а = 10 см при нагревании увеличился
на 0,06 своего объема. Узнать удлинение ребра куба.
17. Объем шара при нагревании увеличился на 0,0024 своей
величины. На сколько процентов увеличилась длина его радиуса?
18. Какой процент будет составлять ошибка, полученная при
вычислении площади круга, если при измерении радиуса его сделана
ошибка в 1%?
19. Объем куба увеличился на 6% своей величины. На сколько
процентов увеличилось при этом его ребро?
Найти- приближенное значение следующих функций:
20. у = х2 + х ПРИ х = 3,01.
21. у = Зх2 + 2х — 1 при х = 2,03.
22. у = х3-|~ х2 — 2х при х = 2,01.
238
ДИФФЕРЕНЦИАЛ
[ГЛ. X
23. у = ~ х% — 5л2 + х — 1 при X = 2,1.
24. у = х% — 2х 4- 1 при х = 0,02.
25. у — х3 — 4х2 -j- 1 при х = — 2,03.
26. у = ....?..х—- при х = 4,2.
V х2 + 9
§ 99. Кривизна кривой. Пусть дана кривая, определяемая
уравнением y=f(x) (черт. 106). Возьмем на ней две точки А и В
и проведем в них касательные к кривой. При переходе от точки А
к точке В касательная меняет угол наклона к положительному
направлению оси абсцисс на некоторую величину. Если обозначим
угол наклона касательной в точке А к оси Ох через а, то угол
наклона касательной в точке В к той же оси, получив прираще-
ние Да, будет равен а Да. а угол между самими касательными,
как видно из чертежа, будет Да. Величину Да можно рассматривать
как угол отклонения касательной от первоначального ее положения.
Разделив Да на длину дуги АВ = As, получим среднюю величину
угла отклонения, приходящегося на единицу длины дуги. Отно-
Да . .. .
шение -у- называется средней кривизной кривой на ее участке АВ.
Средняя кривизна кривой на разных ее участках может быть раз-
личной.
Допустим теперь, что точка В, двигаясь по кривой, неограни-
ченно приближается к точке А и As уменьшается, стремясь к нулю;
Да
тогда предел отношения -д^- будет определять кривизну кривой
в точке А. Обозначив кривизну кривой в точке буквой /<, будем
иметь;
,, .. Да
/< = lim -т— .
Да -> 0 .
§ 99]
КРИВИЗНА КРИВОЙ
239
Определение. Кривизной кривой в данной ее точке А
называется предел, к которому стремится средняя кривизна
дуги АВ при неограниченном приближении точки В к А.
Согласно определению производной (§ 60)
Да da
lim —— = ——:
Да о $S
поэтому
„ flfa
(1)
Преобразуем правую часть этого равенства, выразив da и ds
через производные данной функции у=/(х).
Согласно геометрическому смыслу производной (§ 63) имеем
где а — угол наклона касательной к кривой y=f(x) в точке А
к положительному направлению оси абсцисс (черт. 106); отсюда
а = arctg у'.
В этом равенстве arctg у' — функция от функции, так как arctg у'
зависит от у', a у* зависит от х. Продифференцируем последнее
равенство по аргументу х; получим:
da 1 у"
dx ~ (arclg у } ~ 1 + (У)2 (У ) ~ 1 + (У)2 ’
отсюда
_ у" dx
1 +W
Найдем выражение ds через производную функции у ==/(х).
Для этого возьмем снова тот же участок АВ кривой (черт. 107). Будем
(2)
рассматривать длину АВ как приращение дуги М0А, соответствую*
гцее приращениям PQ = Дх и RB = Ду. Если Дх достаточно мало,
то отрезок дуги АВ можно считать прямолинейным; в этом случае,
применяя теорему Пифагора, получим:
АВР — А№ + RBP,
240
ДИФФЕРЕНЦИАЛ
(ГЛ. X
ИЛИ
(Д5)2 = (Дх)2 + (Ду)2.
Разделив обе части равенства на (Дх)2, найдем:
отсюда
/ Д5 \2 / Ду \2
\Дх/ ~ +\Дх/ ’
Положим, что Дх->0; тогда
.. As ..
hm = hm
Да? > 0 &Х > о
Применяя
получим:
теоремы о пределе корня, суммы и степени (§ 43),
lim
Да?->0
As
Дх
lim 1 + Нт (—
дж->о дж->о\Ах
= 1/* 1+( Нт 4М2- (3)
F W>o Дх/ v '
Но
.. As ds
hm —~ =
дж о Дх dx
г ДУ /
и hm = у,
Да?~>0 &х
поэтому равенство (3) примет вид
~ = rr+W2.
откуда
ds^VV+ty^dx.
Подставив значение da и ds в выражение (1), получим:
/< = • У’Г+ (у7)2 dx =z
л ds 1 + (yz)2 ’ F {У > ах
у" у"
(4)
(5)
[I + (3'z)2] VI + (У)"2 [1 + (У)2]а/а ’
vz/
/<=________у______,
11 + (У)2Г/з
Формула (5) позволяет найти кривизну кривой, определяемой урав-
нением у = f(x), в любой ее точке.
§ 100. Кривизна окружности. Кривизну окружности можно
определить по формуле (5) § 99, но гораздо проще ее найти из сле-
дующих рассуждений.
§ 101] радиус кривизны кривой 241 ’
Проведем касательные в двух точках А и В окружности
(черт. 108). Обозначив дугу АВ через As, найдем среднюю кривизну
Да _
на этом участке; она выразится дробью Проведя радиусы
в точки касания, получим:
Z АОХВ ~ Да,
так как углы и Да образованы взаимно перпендикулярными
прямыми. Но, как известно, угол в радианной мере измеряется
отношением длины дуги к радиусу; следовательно,
откуда
Да _ 1
As ~ 7? '
Ясно, что такой же вывод мы получим, взяв другой какой-либо
участок окружности. Следовательно,
Да 1 1
11Ш -7— = 11П1 — = ~
Да ~> О Да -> О К
для любой точки окружности, т. с. кривизна окружности по-
стоянна во всех ее точках и равна обратной величине ее радиуса.
§ 101. Радиус кривизны кривой. При изучении кривизны
кривой подбирают такую окружность, кривизна которой равна кри-
визне кривой в той или иной ее точке. Центр этой окружности на-
зывается центром кривизны кривой в соответствующей точке,
радиус—радиусом кривизны кривой в этой точке, а сама окруж-
ность— окружностью кривизны (черт. 109).
16 Зак. 3032. И. Л. Зайцев
242
ДИФФЕРЕНЦИАЛ
[гл. X
Определение. Окружностью кривизны в точке М кривой
называется окружность, проходящая через точку М и имеющая
с кривой одинаковую кривизну и общую касательную.
Заметим, что центр окружности кривизны всегда располагается
со стороны вогнутости кривой.
Кривизна окружности, как мы знаем (§ 100),
отсюда
Следовательно, и радиус кривизны
кривой в точке ее определяется тем же
равенством.
Заменив К его значением, взятьем
из равенства (5) § 99, получим формулу
для определения радиуса кривизны кри-
вой в любой ее точке:
(1)
Применяя эту формулу к прямой линии, заданной, например
уравнением у = kx 4- b, получим:
,<.<1+^^.
так как у' = k и у" ~ 0.
Это значит, что прямую линию можно рассматривать как окруж-
ность бесконечно большого радиуса.
Пример. Найти радиус кривизны кривой у — 2х2 в точке,
V2
абсцисса которой равна —:
Решение. Найдем сначала первую и вторую производные
У 2*
функции у = 2х2 для точки с абсциссой х = :
, 1/" 2 г —
У = (2^)' = 4х, и у' v- = 4^ = 2V2,
у" = (4х)' = 4 для всех х.
Подставив значения у' и у" в формулу (1), получим:
Il+(2/2nS/l (1 —8)3/з У 9з 27
Е =--------------=---------= __ = _ = 6,7q.
§ 1011
РАДИУС КРИВИЗНЫ КРИВОЙ
243
Упражнения
Найти радиус кривизны следующих кривых:
1. у = х2 -f- х в точке 0 (0; 0).
2. у — х2— х 4~ 1 в точке, абсцисса которой х= -%.
3. ху = 4 в точке А (2; 2).
4. у2 = 4х3 в точке /1(1; 2).
5. у2 = л3 4-х в точке, абсцисса которой х= 1.
6. у = ех в точке А (0; 1).
7. у = sin х в точке, абсцисса которой х = .
(71
2" ’ / *
9. Найти точку иа кривой у = ™ х2, в которой радиус кривизны
наименьший.
ГЛАВА XI
ИНТЕГРАЛ
§ 102. Понятие о неопределенном интеграле. Имея
функцию, можно по известным нам правилам найти
ее производную, что, как мы знаем, имеет большое
практическое значение. Так, по данному закону движения
тела мы находим скорость его, как производную пути по
времени (§ 58 и § 60); по данному уравнению кривой опре-
деляем при помощи производной угловой коэффициент
касательной, проведенной к этой кривой (§ 63), и т. п.
Однако часто приходится решать и обратную задачу:
по известной скорости движения тела устанавливать закон
его движения, по данному угловому коэффициенту касатель-
ной к кривой находить уравнение этой кривой и т. п., иначе
говоря, по данной производной отыскивать функцию, от
которой произошла эта производная. Поэтому нам необходимо
познакомиться с правилами решения указанной задачи.
Заметим, что находить функцию можно не только по
данной ее производной, но и по ее дифференциалу, так как
производная функции и ее дифференциал связаны простым
соотношением |(4) § 95]. Практически же отыскивать функ-
цию удобнее по ее дифференциалу, поэтому в дальнейшем
изложении мы и будем пользоваться дифференциалом для
решения обратной задачи.
Пусть функция
У^Р(х) (1)
имеет производную f(x)t тогда ее дифференциал
dy — f(x)dx. (2)
Функция (1) по отношению к ее дифференциалу (2) назы-
вается первообразной.
§ 102J ПОНЯТИЕ О НЕОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 245
Определение. Первообразной функцией для выра-
жения f(x)dx называется функция F(x), дифференциал
которой равен f(x)dx.
Однако дифференциалу функции соответствует не един-
ственная первообразная, а множество их, причем они отли-
чаются друг от друга постоянным слагаемым. Действительно,
взяв, например, несколько функций
у = х2,
j/ = x2 + 2,
у — х2— 5,
у = х2 -И С,
где С = const, мы замечаем, что дифференциал каждой из
них один и тот же:
dy — 2х dx.
Но, как видно, этому дифференциалу соответствует мно-
жество первообразных функций вида х2 + С, где С — любая
постоянная.
Выражение х2-\-С называется неопределенным инте-
гралом для дифференциала 2xdx и обозначается симво-
лом J* 2xdx9 т. е.
J* 2х dx — х2-\-С.
Определение* Совокупность всех первообразных
функций F(x)-\-C для дифференциала f(x)dx называется
неопределенным интегралом и обозначается j* f(x)dx.
Таким образом, можно записать
J/(х) dx — F(x)-\-Ct
где f(x)dx называется подынтегральным выражением,
а С — произвольной постоянной интегрирования.
Процесс нахождения первообразной функции называется
интегрированием, а раздел математики, занимающийся во-
просами, связанными с интегрированием,—интегральным
исчислением.
Из сказанного видно, что интегрирование есть
действие, обратное дифференцированию.
246
ИНТЕГРАЛ
[ГЛ. XI
103. Основные свойства неопределенного 'интеграла.
Первое свойство. Дифференциал неопределенного
интеграла равен подынтегральному выражению, т. е.
J / f(x) = ^х'
Это свойство следует из определения неопределенного ин-
теграла.
Второе свойство. Неопределенный интеграл от
дифференциала функции равен этой функции, сложенной
с произвольной постоянной.
Пусть
dF(x) — f(x)dx.
Если возьмем интеграл от обеих частей этого равенства, то
получим:
J* dF(x) = f f(x) dx.
Но по определению
f f(x)dx = F(x)-}-C,
следовательно,
f dF(x) = F (х)-{-С.
Примем без доказательства еще следующие свойства
неопределенного интеграла.
Третье свойство. Постоянный множитель можно
выносить за знак интеграла, т. е.
J* af(x) dx — a J*/(х) dx,
где а — постоянный множитель.
Четвертое свойство. Интеграл алгебраической
суммы функций равен алгебраической сумме интегралов
каждой из них, т. е.
/ l/iW+AW—/з(*)1 dx =
= J fi(x)dx + $ f2(x)dx—у f,(x)dx.
§ 104] ОСНОВНЫЕ ФОРМУЛЫ ИНТЕГРИРОВАНИЯ 247
104. Основные формулы интегрирования. Для нахож-
дения неопределенного интеграла необходимо знать основные
формулы интегрирования.
Выведем сначала формулу для интегрирования степени.
Для этого возьмем функцию хп+1 и найдем ее дифференциал:
Взяв интеграл от обеих частей этого равенства, получим:
J d (хи+1) = J (/г +’ 1) хп dx.
Применяя второе свойство интеграла к левой части последнего
равенства и третье свойство к правой, найдем:
хп+1 + С, = (п 4- 1) у Хп dx,
отсюда при п~\~ 1 #= 0
Г ПА I Су
I xndx ——,—7-4----т-Ц-.
J п + 1 1 п + 1
С
Обозначив постоянное слагаемое буквой С, будем иметь
окончательно: /* vn+i
J *”^=^тг+с-
Выведенная формула справедлива для любого значения п,
кроме п — — 1. В последнем случае эта формула теряет смысл.
Аналогично можно вывести другие простейшие формулы.
Но они могут быть получены и проще.
Г dx
Пусть, например, нам нужно найти J — . Зададимся во-
просом, какая функция имеет своим дифференциалом выра-
dx '
жение —. Такой является функция Inx-j-C, так как
следовательно, /» dx
J — =
Приводим следующую таблицу основных формул, легко
получаемых из соответствующих формул дифференцирования
248
ИНТЕГРАЛ
[гл. XI
путем их обращения, как это
*"^=4т+с со
при п — 1.
= (II)
e*dx = e*-\-C. (Ill)
j axdx— (IV)
J" sinxdx——cosx4-C. (V)
было сделано для вывода у ™:
J* cos х dx = sin х ~|~ С. (VI)
///**
55iT=tgx + C. (VII)
/ж?-=-с18' + С- <VIII>
/• dx
J — arcsin x+C. (IX)
/r^^arctgx+c- (X)
Разберем несколько примеров.
Пример 1. Найти J*(5х4— 4х34-3х2—l)dx.
Решение. Применяя четвертое и третье свойства инте-
грала, а затем формулу (1) и второе свойство, получим:
j (5х4 — 4х3 + Зх2 — l)dx =
~ j' 5x4dx— J* 4x3rfx+ f Зх2dx— ("dx —
= 5 J* x4 dx — 4
= 5^- —4^4-3-^ —x4-C=x5—x*4-x3 —xH-C.
Здесь С является алгебраической суммой четырех произволь-
ных постоянных слагаемых, входящих составной частью
в каждый интеграл,
Легко проверить правильность интегрирования; для этого
найдем дифференциал от полученной в ответе функции:
d(xb — х4 + х3 — х + С) = (5х4— 4х34--3х2— l)dx.
В результате получили подынтегральное выражение; следо-
вательно, интеграл найден верно.
Пример 2. Найти
Решение. Данный интеграл не подходит ни под одну
из табличных формул, поэтому подынтегральное выражение
J2x У х iZx
Ух
§ 104] ОСНОВНЫЕ ФОРМУЛЫ ИНТЕГРИРОВАНИЯ 249
преобразуем следующим образом:
J 2х. — = 2 J хх7х~7 dx = 2 J х«~ dx.
Применяя формулу (I)» получим:
13
г6 19 е г- 12 6 г—
хМх = 247--]-С = ^/ х» -ЬС=^х2/х4-С.
ГО 1О 10
6“
/Г? • 1
—~—dx.
Решение. Представим подынтегральное выражение в
виде суммы двух дробей, разделив числитель почленно на х:
f ^r~dx=f{x^^)dx’
Разбив последний интеграл на сумму интегралов и применяя
формулы (I) и (II), получим:
dx — J*xdx-{- J* = 4~ Н~ С*
Мы разобрали простейшие примеры, в которых функции
могли быть выражены путем несложных преобразований в
виде, позволяющем применить для нахождения интеграла таб-
личные формулы. Очень часты случаи, когда таких простых
преобразований сделать нельзя и для интегрирования прихо-
дится применять особые приемы, иногда довольно сложные.
Таким образом, для интегрирования недостаточно про-
стого знания формул, нужен еще опыт, который накапли-
вается постепенно в процессе решения примеров. Интегри-
рование в отличие от дифференцирования требует от нас
известной изобретательности и смекалки.
Упражнения
1. J х dx. 2. J х1 dx.
5. J* a dy. 6. J4 2х dx.
9. J* (Зх — х2) dx.
12. J (4х»4-4х— 3)dx.
10. J" (а <р2) d<?.
13. J х2 (1 4- 2х) dx.
4. J 5 dx.
8. J* (2—x)dx.
11. J 3(х—2)dx.
250
ИНТЕГРАЛ
[гл. XI
f(^-^+3^x2)dx-
28. p-tg-rfv.
J I v
30. f2ecos<prf<p. 31. f JgL 32.
J J cos20 J sin2 и *
33. I (1 + cos t) dt.
34. J* (2 — 3 sin x) dx.
35. I (3x2 — 2 cos x) dx.
- ,/'U
3 \
sin2 <?/ aV*
37. J Зе™ du.
40. § (2et — 3 cos t) dt.
43. / Y+x*' 44.
46, J sin2/ dt'
48. I sec2x dx.
(* 3dx l*2 cos2 v -|~ 1
J 4 "j/T — x2 ‘ 45‘ J cos2 v dv-
I* _|_ ex sin x
47. J --------~x------dx.
49. ftg’xdx. 5O.f-~~.
§ 105. Определение постоянной интегрирования.
В § 102 было установлено, что в равенстве
J f(x) dx — F(x)-[-C
постоянное слагаемое С имеет произвольное значение, а по-
тому неопределенный интеграл представляет собой множе-
ство первообразных функций, отличающихся друг от друга
постоянным слагаемым. Чтобы из совокупности первообраз-
§ 105] ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ ИНТЕГРИРОВАНИЯ 251
пых функций найти одну, отвечающую задаче, нужно иметь
дополнительное условие.
Пусть, например, требуется найти уравнение кривой, про-
ходящей через точку 7И (1; 3), если известно, что угловой
коэффициент касательной, проведенной в любой точке кри-
вой, равен 2х.
Согласно геометрическому смыслу производной (§ 63)
напишем:
откуда
dy — 2х dx.
Взяв интеграл от обеих частей последнего равенства, получим:
У dy — J 2х dx
или
у = х^С. (1)
Равенство (1) не может служить ответом на вопрос
задачи, так как оно содержит неопределенное постоянное С.
Чтобы получить определен-
ный ответ (т. е. единствен-
ную первообразную функ-
цию для данного дифферен-
циала), воспользуемся до-
полнительными данными
задачи, а именно координа-
тами точки, лежащей на
кривой, уравнение которой
ищется. Положив в уравне-
нии (1) х= 1 и у — 3, бу-
дем иметь:
з= 1-4-с,
откуда
С=2.
Итак, искомое уравне-
ние кривой (т. е. искомая
первообразная функция, удовлетворяющая данному дополни-
тельному условию), будет
у = х2+2. (2)
252
ИНТЕГРАЛ
[ГЛ. XI
Построив графики первообразных функций, определяемых
уравнением (1), мы получим множество (семейство) парабол
(черт. 110), каждая из которых имеет вершину на оси Оу.
Задав дополнительное условие (при х—1 иу = 3), мы тем
самым из множества парабол выделили одну параболу (2),
на которой лежит точка с координатами х—1 и у=3.
В самом деле, подставив в уравнение (2) вместо х и у
соответственно 1 и 3, получим тождество.
Если изменить дополнительное условие, то и С изменится,
а соответственно с этим мы получим другую первообразную
функцию, графиком которой будет другая парабола того же
семейства. Например, если кривая проходит через точку
/V(l; 1), то С = 0 и у — х2 (черт. 110).
Упражнения
1. Найти J* (х — 3) dx, если при х = 2 первообразная функция
равна 9.
2. Найти J* (sin х + cos .v) dx, если при х = у первообразная
функция равна 2.
3. Найти J (~^ — 1^dx, если при х=1 первообразная функ-
ция равна 2.
4. Найти j* — cos х^ dx, если при л: = 0 первообразная
, 1
функция равна
5. Найти У 1) ^х, если при х = 0 первообразная
функция равна 0.
§ 106. Определенный интеграл. Пусть в интеграле
J* 2xdx = х2-]~С
аргумент изменяется от х = 2 до х = 4, тогда приращение
первообразных функций x2-j-C в указанном промежутке
значений х будет:
424~С —(224-С)= 16 —4= 12.
§ 106] ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 253
Полученное приращение первообразных функций называется
4
определенным интегралом и обозначается символом J* 2х dx.
2
Определение. Приращение F(b)— F(a) любой из
первообразных функций F(x)-\~C при изменении аргумента
от х = а до х — b называется определенным интегралом
ь
и обозначается J* f(x)dx.
а
При этом предполагается, что функция f(x) непрерывна
в промежутке значений аргумента от а до Ь.
Таким образом,
ъ
f f(x)dx = F(b) — F(a). (1)
а
Левая часть этого равенства читается так: «определенный
интеграл от а до b эф от икс дэ икс».
Значение а называется нижним пределом определенного
интеграла, значение b — верхним его пределом.
Из равенства (1) вытекает следующее правило:
б
Для вычисления определенного интеграла Jf(x)dx
а
нужно найти соответствующий неопределенный интеграл,
в полученное его выражение подставить вместо х сна-
чала верхний, а затем нижний пределы определенного
интеграла и из первого результата подстановки вычесть
второй.
Чтобы подчеркнуть два действия при отыскании опреде-
ленного интеграла — нахождение неопределенного интеграла
и подстановку пределов, — пишут формулу (1) в следующем
виде:
ь ъ
f f(x)dx = \F(x) — F(b) — F(a).
а а
+ 1
Пример L Вычислить f (х2-1-1) dx.
— 1
254
ИНТЕГРАЛ
[гл. XI
Решение. Согласно правилу имеем:
2
Пример 2. Вычислить £ 4 cos х dx.
Т
Р е ш е и и е:
к п
~2 ~2
J 4 cos х dx — J 4 sin x — 4 ^sin ~ — sin ~ ) =>
8 T
= 4(1 —121)^4(1—0,865) = 4-0,135 = 0,54.
13
Пример 3. Вычислить j .
1
P e ш e н и e:
i 3 V з*
I — j arctg x — arctg )/3 — arctg 1 —
1 1
§ 107. Основные свойства определенного интеграла.
В § 103 мы рассмотрели четыре основных свойства неопре-
деленного интеграла. В подробных курсах высшей матема-
тики доказывается, что третьим и четвертым из них обладает
и определенный интеграл. Кроме этих свойств, для опре-
деленного интеграла справедливо и следующее:
Если переставить пределы определенного интеграла,
то его знак изменится на противоположный.
§ 107] ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 255
В самом деле, вынеся за скобку множитель — 1 в правой
части равенства
ъ
J*/(х) dx — F(b}— F(a),
а
получим:
6
f /(х) dx = — IF (fl) — F 0)1.
a
Но разность в квадратных скобках есть тот же определенный
а
интеграл, только с переставленными пределами, т. е. J f(x)dx.
ь
Следовательно,
J/(х) dx =
а
Упражнения
Вычислить определенные интегралы:
2 з
1. j' xdx. 2, J* х'dx.
1 о
о
5. J (3x24-l)rfx.
-1
1 1
3. J* x'^dx. 4. J*(2x+1)/Zx.
1 о
*2
4-1
6. +
+4
7. У 3(«24-l)rffl.
1
2
8. У 2к (1 4- х2) dx.
Г 2dt~'
J cos21 *
о
dx.
cos dy. 13. J sin у dy.
о о
256
ИНТЕГРАЛ
[ГЛ. XI
тс
Т
Г 2 dO *
J sin2 0 *
7С
т
16.
2
*2 ...
-g- COS t dt.
sin 0 dO.
2
18. J* (cos у + sin ?) d<f>.
о
тс
”2
fL2-
J \ COS2 X
0
dx.
1___
sin2 х
М? — cos x) dx.
6
2
./ 5x ‘
x cos x 4- 1 '
---------’--- ^x.
7C
0,5
/* 2 dx
3 dx
~2
dx
2
3
о
о
з
,/ 2 V1 — x‘‘ ’
К 2 r
2
§ 108. Геометрический смысл определенного интеграла.
Пусть дана кривая, определяемая уравнением у = f(x)> причем
Черт. Hi.
/(х) — функция непрерывная и положительная при рассма-
триваемых значениях х (черт. 111). Возьмем на кривой
§ 108] ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 257
точку 7И0 с постоянной абсциссой OPQ = a и точку Ж,
меняющую свое положение в зависимости от изменения
абсциссы ОР^х. Тогда площадь фигуры M^MPPq, назы-
ваемой криволинейной трапецией, будет переменной величи-
ной, зависящей от х. Обозначим ее через S. Дадим аргу-
менту х приращение РРХ = Дх; тогда площадь S получит
приращение AS, равное криволинейной площади
Проведя прямую 7I4Q||Ох, а также А^Д/ЦОх до пересечения
с продолженной ординатой РМ, будем иметь:
площ. MQP±P < AS < площ. TVAl^P,
или, выражая площади прямоугольников по формулам:
РМ • РР± < AS < РгМг - PPt. (1)
Но
PPt = Дх,
РМ = /(х),
поэтому неравенства (1) перепишутся так:
/(х) Дх < AS < /(х Дх) Дх.
Разделив полученные неравенства на положительную вели-
чину Дх, получим:
(2)
Пусть Дх—>0, тогда /(x-j-Дх)—>/(х). Так как величина
заключена между /(х) и /(х-|-Ах), как видно из нера-
венств (2), то и подавно
AS ч
или
.. ft X
hm 7—=/(x).
TT f i
Ho lim -г--------производная функции s; следовательно,
Дя?->0
^=/<*)>
откуда
dS = f(x) dx.
(3)
17 Зак. 3032. И. Л. Зайцев
258
ИНТЕГРАЛ
(ГЛ. XI
Взяв интеграл от обеих частей равенства (3), получим:
J'dS — J' j\x)dxt
или
S-bC,= f/(x)dx. (4)
Пусть F(x) — первообразная функция для дифференциала
f{x)dx> тогда
jf(x)dx = F(x) + C2. (5)
Сравнив равенства (4)
и (5), получаем:
5 Ci = F (х) С2,
или
S = С, (6)
где
С = С2 — Ср
в равенстве (6) х — а, тогда,
площ. MqMPPq = S — 0;
будем иметь:
0 = F(a) + C.
Отсюда С = — F(a) и равенство (6) перепишется так:
S=F(x)— F(a).
Но по определению (§ 106)
F(x)—F(a)= j" f(x)dx.
Следовательно,
S = f f(x)dx. (7)
Для определения С положим
как видно из чертежа 111,
Эта формула определяет переменную площадь 2И0МРР0.
§ 109] ИНТЕГРИРОВАНИЕ СПОСОБОМ ПОДСТАНОВКИ 259
Чтобы получить постоянную площадь в про-
межутке значений х от а до b (черт. 112), нужно й равен-
стве (7) положить х=Ь\ тогда площадь
ъ
= $ f(x)dx = F(b)—F (а).
а
прямыми х—а а х — Ь,
Итак, площадь фигуры, ограниченной кривой y=f(x)t
где f(x) > 0, осью Ох и двумя
выражается определенным
ъ
интегралом J*f(x) dx.
к
а
Таков геометрический
смысл определенного ин-
теграла.
Пример. Определить
площадь фигуры, заключен-
ной между ветвью кривой
у — х2, осью Ох и пря-
мыми х — 0 и х=3.
Решение. Согласно
геометрическому смыслу оп-
ределенного интеграла иско-
мая площадь (черт. 113)
з з
S = f х2 dx = | = 9.
и о
0 7 2 3
Черт. 113.
§ 109. Интегрирование способом подстановки. Если
заданный интеграл простейшими преобразованиями трудно
привести (или совсем нельзя привести) к табличному, то для
его отыскания применяются особые приемы. Рассмотрим один
из них, называемый интегрированием способом подстановки.
Пример 1. Найти J*(1 х)5dx.
Решение. Положим
1 -j- х — z>
(I)
17*
260
ИНТЕГРАЛ
[ГЛ. XI
где z—новое переменное. Возьмем дифференциал от обеих
частей равенства (1); получим:
dx — dz.
Заменив в искомом интеграле 1 + х и dx их найденными
значениями и применив формулу (1) § 104, будем иметь:
У* (14~x)5rfx = f z*dz = ~- + C.
Но ответ должен быть представлен как функция от пере-
менной х; поэтому, подставив вместо z его значение из равен-
ства (1), получим:
pl + X)S rfx =4 (1 + х/4-С.
Для проверки решения найдем дифференциал получен-
ного выражения, рассматривая его как сложную степенную
функцию:
+х)6 + с] = 4 • 6(1 +x)5rfx = (l 4~x)5rfx.
В результате получилось подынтегральное выражение; следо-
вательно, интегрирование было произведено верно.
Пример 2. Найти ]^2%4-3dx.
Решение. Положим
2х-\- 3 — zt
отсюда 2dx — dz и dx = -^-„
Подставив в подынтегральное выражение вместо 2х-{~3
и dx их значения, заменив корень степенью с дробным пока-
зателем и применив формулу (I) § 104, будем иметь:
У /2х + 3^х = У /7.^ = 1 У Z*dz =
3
4f+c=l^+c-
2
§ 109] ИНТЕГРИРОВАНИЕ СПОСОБОМ ПОДСТАНОВКИ 261
Перейдя к прежнему переменному х, получим:
J'/2x4-3 dx = - j- /(2х4-3)3 4- С.
Пример 3. Найти J" sin (а 4- bx) dx.
Решение. Положим
а + bx = zy
откуда
dz
bdx — dz и dx~—r^
b
Сделав подстановку, как в предыдущем примере, и применяя
формулу (V) § 104, получим:
j sm(a-^-bx)dx— I sinz*-^- =— -—cosz-\-C —
= —— cos (& —j- Z?x) -j— C.
Пример 4. Найги ,
Решение. Положим
1 -j- x3 = z,
откуда
3x2^x — dz и x2 dx = ~,
Сделав необходимую замену и применив формулу (II) § 104,
будем иметь:
-nSW 4 = 41пИ-С^11п(14-хЗ)+С.
Пример 5. Найти J*sin2xcosx6?x.
Решение. Положим
sinx — z\
тогда
cos xdx— dz
и
J sin2 xcos xdx — j z2dz — ^-^C = “Sin3 x*4~C.
2G2
ИНТЕГРАЛ
(ГЛ. XI
Пример 6. Найти Г
J У 1 — cos х
Решение. Положим
1 —COSX— z\
тогда
sin xdx = dz
sin х dx ______ f* dz _
V1 — COS X J У z
2Z r_______
—pc = 2/1— cosx+C.
У
Пример
- т_т м Г dx
'• Найти J (Г~
Решение. Положим
тогда
и
1 — ех = z\
ех dx — — dz
= —2 . £ZL-|-c = -4-c= , 2 - ч-с.
— 1 1 z 1 1 — ех 1
Пример 8. Найти J -g-qy^.
Решение. Так как искомый интеграл напоминает таб-
личный [(X) § 104], нужно соответствующими преобразова-
ниями привести его к виду, позволяющему применить ука-
занную формулу. Для этого вынесем за знак интеграла мно-
1
житель -у-.
Получим:
/dx 1 j dx 1 I dx
§ 109J ИНТЕГРИРОВАНИЕ СПОСОБОМ ПОДСТАНОВКИ 263
Положим теперь
•‘тогда dXz=z$dz
= у arctg z 4- С — у arctg + С.
Пример 9. Найти / •====.
F F J Уз — 5л2
Решение. Этот интеграл приводится к табличному
[(IX) § 104] следующими преобразованиями:
Положим
z~7^ax = dz,
V з
отсюда
Следовательно,
264
ИНТЕГРАЛ
[ГЛ. XI
или
dx 1 . V 5 .
г ....=з ~7Г= arcsin х -н С.
/з — Зх* /5 /3
Пример 10. Найти J tgxdx.
Решение.
/. Г sin х dx
tgxdx — I --------
b J cos x
Положим
cos x = z\
тогда
sin x dx = — dz
и
----у = — In z + C = — In cos x -|- C.
Пример 11. Найти J* cos2 x dx.
Решение. Заменим cos2 x по формуле
o 14- cos 2x
cos2 x — —;
тогда
/* Г 1 4- cos 2x . Г11 . 1 o \ .
/ cos2xdx = / -—-t;---dx==. I (y 4~y cos2x) б/х =
~J у cos2xrfx = y x+y У cos2xdx.
Для нахождения JcosZxdx положим:
. 2x — z,
откуда
dx= у dz
и
у У cos 2х^х==уУ* cosz • у dz = -~J* coszdz —
= -i sin z 4“ С = у sin 2x C.
Следовательно,
У cos2xtfx = y x + ysin2x-|-C.
§ 109] ИНТЕГРИРОВАНИЕ СПОСОБОМ ПОДСТАНОВКИ 265
Пример 12. Найти J*Уа2— x2dx.
Решение. Положим:
x = asin£, (2)
тогда
dx = acoszdz
и
У а2 — х2 — Уа2 — a2 sin2 z — а У1 — sin2 z = a cos z.
Таким образом,
J* У а2 — x2dx — fa cos z a cos z dz — a2 f cos2 zdz.
Взяв f cos2zdz из примера 11, напишем:
f У a2 — x2dx = a2^y^ + “Sin2^j+C, (3)
Из равенства (2) находим:
х
sin г — —,
а
откуда
. х
z — arcsin — .
Кроме того,
sin 2г = 2 sin z cos z — 2 sin z У1 — sin2 z ~
= 2—1/~ 1 — -4 = /а2 —JC2.
a¥ a2 a? v
Подставив значения z и sin 2г в равенство (3), получим:
j Уа2 — х2 dx — a2 (—arcsinу * ~гУа2 — х2^-\-С —
— arcsinа2 — х2 + С.
Итак,
У У а2 — х2 dx = arcsin -у + *у У а2 — х2 + С.
266
ИНТЕГРАЛ
[гл. XI
Упражнения
1. {(3 + 5x)idx. 4. f V х+ 2dx. 2. f* J* (a + bx)™ dx. 3 3 Z
•./ (3x4-1)2' p 3
5- / 2 У4x — 3 dx. 6. J V(3x+l)2dx.
п f 3 dx 9. / dx
Ze / 4 . f(2 — 3x)2 *’ l+2x *
У 3x4-5
10 f 11. f sin 2x dx. 12. J* cos 4x dx.
10- J 3 —4х ’
13. J sin(l— i) dt. 14. j* cos + 2^ dy.
Г / х , п \ , Г dx 17. f - ..... J sin2 3x
j 1-о 3 / ’J cos2 2x ’
18 Г dX 19. § <?2c? dy. 20. f dQ.
J cos2 (1 — 2х) J
с ~Г“+1 21. i 2е d<». 22. /£• I !— ^x.
J J
24. J 3-г+2 di. Г 2xdx Г 2tdt
J 14-x2' J (2/2—I)2’
97 /* 28. Г ‘J* 29. /* x2dx
• J (2-v^y р . j У2хЗ-1
30. I х V х2 4* 1 dx. 31. J flV 14-2/3^.
9 Г cos х dx 6 J 1 + sin x * 33. Г sin у rfy Г sin t dt
J 2 — 3 cos у ’ 3 ’ J cos2^ *
o_ C cos <o dm 35. / •——; • J Sin4 co 36. Г cos x dx Г cos i dt
J (2 — sin^)2’
у 1 -J- sin t
38. J* sin a cos a da. 39. I sin3 у cos у dy.
40. p У” cos '0 sin 0 dQ. 41. J COS a (1 4- Sin a)2 da.
42. J* x2 sin 3x3 dx. 43. J ecosa!sinxdx.
44. J* ctgxdx. p 45. Г . 46. J 14-^- Г 49 f 2ex dx
J (2 4-^)2 •
47. e^yl+e^dx. 48. 1 x&^ dx.
J V2 + eu-
§ ПО] ВЫЧИСЛЕНИЕ ИНТЕГРАЛА С ПОМОЩЬЮ ПОДСТАНОВКИ 267
т Г cos 2х dx
50- J 1 +sin 27-
53. Г
J 2-^x2
59 /* sin (р cos <р dtp
J У" i +sln2
62. J* tg2x dx.
Г in х dx
6э. / ------.
J х
63. / ---^=-.
J 14- / х
71. J” V1 + eos х dx.
sin2 х dx.
du
у 9 — 4tz2
dx
55. Г = =.
J /1-4/2
58. Г-JL^.
J V 3 — 402
I dx.
J V1 —x2
67. p sin3 x dx.
Г Y x dx
cos x dx
1 4- sin2 x
§ 110. Вычисление определенного интеграла с по-
мощью подстановки. Для вычисления определенного инте-
грала с применением подстановки поступают так же, как
указано в разобранных примерах § 109. Но в этом случае
есть одна особенность, на которую нужно обратить внима-
ние. Как мы уже выяснили, метод подстановки заключается
в том, что для приведения заданного неопределенного инте-
грала к табличному выражают аргумент через новое пере-
менное, затем находят неопределенный интеграл и получен-
ный результат снова выражают через первоначально заданное
переменное (аргумент). В случае же определенного интеграла
нет необходимости возвращаться к первоначально заданному
переменному.
Разберем несколько примеров.
А
*2
Пример 1. Найти /* z .
1 г е/ (1 — х^у
о
Решение. Положим
1 —x2 — z\
(1)
тогда
— 2х dx — dz,
268
ИНТЕГРАЛ
(ГЛ. XI
откуда
, dz
xdx =---j-.
Так как мы ввели новое переменное, связанное с преж-
ним равенством (1), то границы изменения переменного z,
т. е. пределы интегрирования по переменному г, будут уже
другие. Они найдутся из равенства (1) заменой аргумента х
его значениями 0 и ~. Сделав эту замену, получим:
1 —0= 1
(нижний предел),
(верхний предел).
Таким образом, мы нашли, что пределам изменения х
п 1
от 0 до j соответствуют пределы изменения нового пере-
3
менного z от 1 до Заменив в заданном интеграле 1—х2
и xdx их выражениями через новое переменное и изменив
соответственно пределы интегрирования, можем записать ре-
шение данного примера следующим образом:
Пример 2. Найти / 9 j.^2.
Уз
4
з
Решение. Вынесем множитель ~ за знак интеграла:
§ ПО] ВЫЧИСЛЕНИЕ ИНТЕГРАЛА С ПОМОЩЬЮ ПОДСТАНОВКИ 269
Положим 4х=z- (2) о
тогда 4 , -~dx = dz, о
откуда л 3 , dx — -rdz. 4
Находим новые пределы:
_ 4 Уз _ Уз
Za~ 3 * 4 — 3
_ 4 3 .
Z&~ 3 ‘ 4 ~~ L
Следовательно,
Т 1 3 1 1
. 1 Г _ 1 3 Г 1 I агсН~-
J 9+16л2~ 3 J 14-2-2- 3 4 J 1-]-2-2 4 L Ь
Уз Уз Уз Уз
4 Т 3 3
1 ( , . . Уза 1 (к к\ л
= т (^arctg 1 — arctg-g-J = т —g) = s.
Упражнения
1. У V1 — х dx.
о
dx
2. /* 7
J УЗх+1
G
Зл
~2
_ Г х .
5. / cos -j dx.
о
0
/• dx
(l-2x)»
-2
9
2 dx
3 cos2 Зх
х dx
l+x2*
х dx
2 У1 + jc2
12
3
‘ J У16 +A-2
0
х^ dx
3 + 2ха ‘
—-1
2х dx
(2x2 ^1)2 •
Г 6x2 dx
J 1 + 2Л*
0
270
ИНТЕГРАЛ
[ГЛ. XI
13.
15х dx
(х2—1)3
4
14. f xfx2 — 7dx.
2V2
2
15. J (x2 — 1)* xdx.
1
sin x dx
(1 — cos x)2 ’
7
Г cos x dx
1 -j- sin x
У cos x dx
sin3 x ’
7U
7
К
T
20. § 4 sin3 x cos x dx.
7C
T
T
21. J sin x cos2 x dx.
0
0,4
99 Г $X
’ J 4 + 25x2 *
0
+R
25. j V R^j?dx.
-й
dx
V 4 —Л2 *
dx
3 + x2’
§ 111. Определенный интеграл как предел суммы.
Возьмем функцию у = /(х), непрерывную в промежутке зна-
чений х от а до Ь. Положим для простоты, что эта функ-
ция в указанном промежутке положительная и возрастающая.
Рассмотрим площадь фигуры TWjAIg/V3! ограниченной
дугой графика данной функции, прямыми х = а и
х = Ь и осью Ох (черт. 114). Согласно геометрическому
смыслу определенного интеграла (§ 108) эта площадь
ъ
S= j* f(x)dx.
а
(1)
Разделим отрезок РХР2 на п равных частей, каждую из
которых обозначим через Дх, и в концах полученных отрез-
ков восставим перпендикуляры до пересечения с кривой.)
§ 111] ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ КАК ПРЕДЕЛ СУММЫ
271
Проведя из концов этих перпендикуляров прямые, парал-
лельные оси Ох, мы можем представить площадь фигуры
714^2^2^1 в виде суммы площадей прямоугольников и суммы
Черт. 114.
площадей криволинейных треугольников. Обозначив первую
сумму через а вторую — через S2t напишем:
£ = <^+£2,
откуда
S—Sj = S2. (2)
Если
ОР1 = а и ОР2 = Ь,
то
PxMi=f{a) и P2M2 — f(b).
Пусть абсциссы точек Nlt N2t N3, ... Nn-i будут соот-
ветственно
•^1» *^2» ^3’ • • •> 1»
тогда ординаты этих точек будут
/(«^2)» /(^з)» • • •»
Сумма площадей всех прямоугольников
I
272 ИНТЕГРАЛ [гл. XI
или
ъ '|
51==2/(х)Дх. (3)
а
В равенстве (3) 2 (сигма) — символ суммы; /(х)Дх ука-
зывает, какого вида выражения складываются; буквы а и Ь,
стоящие внизу и вверху символа говорят о том, то
значения аргумента при этом берут в границах от х= а
до х — Ь.
Если число делений п отрезка РгР2 неограниченно уве- г
личивать, то Ах > О и величины и S2 станут переменными.
Покажем, что S2 при этом условии — величина бесконечно
малая. Для этого передвинем криволинейные треугольники
параллельно оси Ох, расположив их в прямоугольнике ABCD,
основание которого V
AD— кх
и высота
AB=P2M2 — P1Ml = f(b)—f(a).
Площадь прямоугольника ABCD будет равна <
[/(*)— /0)1 Дх.
Как видно из черт. 114
52<[/(^)— /(^)]Ах. (4)
Если Дх->0, то [/(/>)—f(a)\kx как произведение по-
стоянной на бесконечно малую есть величина бесконечно У
малая, а потому согласно неравенству (4) S2— также бес-
конечно малая величина..
Таким образом, в левой части равенства (2) мы имеем
разность между постоянной S и переменной а в пра-
вой— бесконечно малую. Следовательно, по определению
предела (§ 41), |-
— lim Sj,
Дя?->0
или согласно равенствам (1) и (3)
Ь Ь 1
f f(x)dx— lim V/ (х) Дх. (5) ?
a a i
§ 111] ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ КАК ПРЕДЕЛ СУММЫ
273
Сумма, стоящая под знаком предела в равенстве (5),
называется интегральной суммой.
Таким образом, определенный интеграл с конечными
пределами равен пределу интегральной суммы, число сла-
гаемых которой неограниченно
растет, а каждое слагаемое
стремится к нулю.
Можно показать, что к тому
же результату мы придем, если
возьмем функцию положительную
и убывающую в рассматриваемом
промежутке значений х, или по-
ложительную, но на одних участ-
ках возрастающую, а на других
убывающую, или, наконец, отри-
цательную функцию, т. е. такую,
график которой расположен ниже
оси Ох.
Полученный вывод показывает,
что интегрирование можно рас-
сматривать как процесс сумми-
рования, т. е. нахождения целого
сложением его частей. В связи
с этим интеграл и получил свое
название от латинского слова
integer (целый), да и символ его
Черт. 115.
(удлиненная буква S, которой обычно обозначается сумма)
связан с вышеуказанным свойством определенного интеграла.
В главе XII мы подробно остановимся на приложении
формулы (5); здесь же разберем только одну задачу вычис-
ления объема пирамиды с помощью интеграла.
Возьмем пирамиду с площадью основания Q и высотой Н
и разобьем ее на п пластинок плоскостями, параллельными
основанию ее (черт. 115). Если количество этих пластинок
неограниченно увеличивать, то толщина каждой из них будет
бесконечно малой величиной; в этом случае пластинки можно
принять за призмы. Выделив одну из них, например
обозначим площадь ее основания, высоту и объем соответ-
ственно через q, Ду и Дг>; тогда
Lv — q Ду.
(6)
18 Зак. 3032. И. Л. Зайцев
274
ИНТЕГРАЛ
(ГЛ. XI
Так как площадь основания пластинки зависит от расстоя-
ния ООх—у, выразим q через у. По известной теореме
о свойстве сечения, параллельного основанию пирамиды,
можем написать:
Я _
Q /72
откуда
д = ^Н-у^.
Теперь равенство (6) перепишется так:
Дг> = ^(Я—у)^у.
Величина Д-у бесконечно малая, так как Ду —> О при п —> оо;
таким образом, объем v пирамиды представится как предел
суммы бесконечно малых величин вида —у)2 Ду, т. е.
я
•V = lim ^(Я —_у)2Ду,
дг/ -> 0
или согласно формуле (5) настоящего параграфа
я
^(Я—у)*ау.
О
Вычисляя этот интеграл по известным правилам, находим:
н н
2НУ+>2) аУ = /Я | (у2У - Hyi + у)=
о о
Итак,
® = 1<2Я.
т. е. объем пирамиды равен одной трети произведения
площади ее основания на высоту.
ГЛАВА XII
ПРИЛОЖЕНИЯ ИНТЕГРАЛА
§ 112. Плсщади фигур. В § 108 мы доказали, что если
/(х) > 0 в промежутке значений х от а до Ь, то площадь
фигуры, заключенной между графиком кривой y=f(x),
осью Ох и прямыми х—а и x = bf определяется по фор-
муле
(1)
Можно показать, что в слу-
чае /(х)< 0 формула (1) дает
отрицательное число, равное
по абсолютной величине иско-
мой площади, т. е.
Пример 1. Найти пло-
щадь фигуры, заключенной
между осью Ох и кривой Черт. 116.
у=х2—4х (черт. 116).
Решение. Точки О и В пересечения параболы у —
= х2— 4х с осью Ох имеют абсциссы, равные 0 и 4. Как
видно из чертежа, искомая площадь (она заштрихована) ог-
раничена сверху осью Ох, снизу параболой, слева и справа
прямыми х=0 и х —4, от которых парабола и ось Ох
отсекают отрезки нулевой длины. Заданная функция отри-
цательна в промежутке значений х от 0 до 4: поэтому,
18*
276
ПРИЛОЖЕНИЯ ИНТЕГРАЛА
[гл. XII
применяя формулу (2), получим:
Пример 2. Найти площадь фигуры, заключенной между
кривой у — х3, прямыми х = —1, х= 2 и осью Ох (черт. 117).
Решение. Искомая площадь, как видно из чертежа,
состоит из двух площадей AOD и ВОС, расположенных
по разные стороны оси Ох,
В промежутке значений х от 0 до 2 функция у — х3
положительна, поэтому площадь AOD вычисляем по фор-
муле (1)
2
Saod^J x*dx = |^=1 = 4.
В промежутке значений х от —1 до 0 функция у — х3
отрицательна, поэтому по формуле (2) имеем:
Sboc — / dx
-1
1° zi =1-11 = 1.
Lx 4 1.41 4
§ Н2]
ПЛОЩАДИ ФИГУР
277
Таким образом, вся искомая площадь
S = Saqd + Sboc = 4 .
Пример 3. Найти площадь фигуры, заключенной между
линиями у~х2 и у ==х (черт. 118).
Решение. Заданные линии пересекаются в начале ко-
ординат и в точке А (1; 1) (координаты точек пересечения
находим, решив совместно уравнения обеих линий). Опустим
из точки А на ось Ох перпендикуляр АВ. Он является от-
резком прямой х=1. Искомая площадь (черт. 118) равна
разности между площадями треугольника ОАВ и фигуры
ОтАВ, т. е.
S От А — S ОАВ S От АВ*
(3)
Площадь ОАВ заключена между графиком функции у — х,
прямыми х=0 и и осью Ох.
Площадь ОтАВ заключена между кривой у — х2, пря-
мыми X— О И X ~ 1 и осью Ох. Функции у ~ X и у = X2
положительны в промежутке значений х от 0 до 1.
Следовательно, по формуле (1), учитывая равенство (3),
имеем:
1 ill
х^_ |^_1_ 1_ 1
2 I 3 ““ 2 3 ~ 6 ’
О О 0 0
х2 dx =
Упражнения
1. Найти площадь фигуры, ограниченной прямыми у = 5х, х = 2
и осью Ох.
2. Найти площадь фигуры, заключенной между прямыми у --
= 4х — 5, х = —3, х ~ —2 и осью Ох.
3. Найти площадь фигуры, ограниченной кривой у = 2х2, осью Ох
и прямыми х — 2 и х = 4.
4. Найти площадь фигуры, ограниченной кривой у2 = 9х и пря-
мыми х~ 1 и х — 9.
5. На кривой у2 = 4х дана точка, ордината которой равна 6.
Найти площадь фигуры, заключенной между данной кривой, осью Оу
и прямой у = 6.
6. Найти площадь фигуры, заключенной между кривой у — х2—х,
ссыо Ох и прямыми х = 0 и х = 2.
7. Дана кривая у == 2х2— х + 2. Найти площадь фигуры, за-
ключенной между данной кривой, осями координат и прямой х = 3.
8. Определить площадь параболического сегмента, основание
которого а — 6, а высота h = 8.
278 ПРИЛОЖЕНИЯ ИНТЕГРАЛА [гл. хп
9. Найти площадь фигуры, ограниченной осью Ох и линиями;
1) у = 2х— х2, 2) у = 9 — х2, 3) у = х2— 5x4-4.
10. Найти площадь, ограниченную одной волной синусоиды и
осью Ох.
11. Найти площадь фигуры, ограниченной осями координат и
кривой у = 4 (1 — хв).
12. Найти площадь, заключённую между линиями:
1) у — 2х — х2 и у = х,
2) у = у х2 и у — 4 — х,
3) х2 — 9у = 0 и х — Зу 4~ 6 = 0,
4) 4у — х3 — 0 и у — х = 0.
13. Найти площадь, заключенную между следующими кривыми:
1) у2 == х и у — х2,
2) у = х2 и у = 1 — х2,
3) 4х2 — 9у4~18 = 0 и 2х2 —9у4-36 = 0,
4) х2 4- у2 = 8 и у2 = 2х.
§ 113. Объем тела вращения. Пусть дана кривая, опре-
деляемая уравнением y—ffyc), и на ней две точки А и В
Черт. 119.
с абсциссами ОР = а и OQ — Ъ (черт. 119). Если вращать
фигуру ABQP вокруг оси Ох, то образуется некоторое тело
вращения.
§ 113]
ОБЪЕМ ТЕЛА ВРАЩЕНИЯ
279
Разделим отрезок PQ на п равных частей, каждую из
которых обозначим через Дх, и в точках деления восставим
перпендикуляры к оси Ох до пересечения с кривой. Проведя
из этих точек пересечения прямые, параллельные оси Ох, до
встречи с соседними перпендикулярами, мы разобьем фи-
гуру ABQP на п прямоугольников и криволинейных треуголь-
ников. При вращении фигуры ABQP вокруг оси Ох каждый
из прямоугольников образует цилиндр, а сумма объемов этих
цилиндров даст приближенную величину объема рассматрива-
емого тела вращения. Подсчитаем эту сумму объемов цилин-
дров. Для этого возьмем один из них, например CDFE. Как
видно из чертежа, радиусом основания этого цилиндра будет:
Cfi=y=f(,x),
а высотой
= Дх.
Следовательно объем указанного цилиндра равен
тсу2 Дх,
а сумма объемов всех цилиндров будет
ъ
2 ъу2
а
Это выражение и представляет собой приближенную величину
объема тела вращения, т. е.
ь
v ~ 2 ^у2 •
а
Положим теперь, что число делений отрезка PQ неогра-
ниченно возрастает; тогда Дх, а следовательно, и произве-
дение ку2Дх будут бесконечно малыми величинами.
Перейдя к пределу, получим:
&
v = Hm
Дж->0 а
или согласно формуле (5) § 111
& ъ ь
lim ^пу2кх = f Tzy2dx — r. f у2 dx.
Да?->0 а * J
а а
280
ПРИЛОЖЕНИЯ ИНТЕГРАЛА
[гл. хп
Поэтому
ъ
v — тс J* y2dx. (1)
а
Пример. Фигура, ограниченная линиями у2 — 4х, х = 0,
х = 4 и у — 0, вращается вокруг оси Ох. Найти объем по-
лученного тела (черт. 120).
Решение. Полученное тело называется параболоидом
вращения. Согласно формуле (1) имеем:
4 4 4
у2 dx — к J* 4х dx — тг j 2х2 — к • 2 • 42 = 32тс.
о 6 о
Пользуясь формулой (1), можно вывести формулы объема
конуса, шара и его частей.
Объем прямого кругового конуса. Прямой
круговой конус получается от вращения прямоугольного тре-
угольника О АР вокруг оси Ох (черт. 121). Составим урав-
нение прямой ОА, образующей при своем вращении кониче-
скую поверхность.
Обозначив
ОР — Н, PA — R,
напишем искомое уравнение прямой ОА:
. , РА uR
_y = fcx = tga х = =
§ 113] ОБЪЕМ ТЕЛА ВРАЩЕНИЯ 281
Применяя формулу (1), будем иметь:
н н
Г (R у. /?2 Г 9 ,
v — тс / йх = ъ-^ I х-ах~
и о
н
_ ^1*!—L^H
Я2 | 3 Нъ' 3 3™"'
о
v = ^-itR^H. (2)
О
Объем усеченного конуса. Усеченный конус
можно получить, вращая прямоугольную трапецию АВСО
вокруг оси Ох (черт. 122). Найдем уравнение прямой АВ,
образующей коническую поверхность. Для этого положим:
ОА — г, CB — R, ОС = Н
и напишем уравнение АВ в виде у = kx-{-b.
Как видно из чертежа,
/ а , BD R — r
b = r, k = tga = -^5=—7r.
Таким образом, искомое уравнение будет:
R — г
282
ПРИЛОЖЕНИЯ ИНТЕГРАЛА
[гл. XII
Согласно формуле (1) найдем:
н
Г /R — г . \2 ,
v-к I—dx.
и
Вычислим определенный интеграл способом подстановки.
Положим
/? —г .
z = —— х -г,
тогда
, R — r,
dz = —dx,
отсюда
, Hdz
dx = -о-.
R — r
Новые пределы интеграла будут:
ги = ^^.0 + г = /-, z^B^LH^-r = R.
Следовательно,
= ~ И <*2 + +Rr+r2>-
W=^(/?2 + /?r_|_r2). (3)
Объем шара. Шар получается от вращения полукруга
с центром в начале координат вокруг оси Ох (черт. 123).
Уравнение окружности радиуса R, представленной на чертеже,
имеет вид
x2^_y2=R2f
откуда
у2, = R2 — х2.
§ 1131
ОБЪЕМ ТЕЛА ВРАЩЕНИЯ
283
Черт. 123.
284
ПРИЛОЖЕНИЯ ИНТЕГРАЛА
[ГЛ. ХИ
Согласно формуле (1) найдем:
+-R +-Я R
v = k f = j* (Я2—х2) dx~2n J (Z?2 — x2)dx —
— R -r о
R
= 2rc |(/?2x — ^\ = 27r(/?3 —~) = 4к/?3-
I \ ” / \ о J о
0
4
—yTC/?3. (4)
Объем шарового сегмента. Шаровой сегмент
можно получить, вращая половину кругового сегмента АВС
вокруг оси Ох (черт. 124). Обозначив высоту РВ шарового
сегмента через Я, а радиус круга через R, будем иметь:
R R R
v~~t: J y2dx = K J (R2— x2)dx — K | (r2x — "yj —
R-H R-H R-H
= ЯI (/?2 • R —f) — [/?2(7? — H) —(АгЯ)"] | =
= те(2 + =
= - J (2#> — ЗЯ3 + 3R2H + R8 — 3/?2H -j- SRH2 — H3) =
= 4(ЗЯ№ — H3) = khRr — Rh\.
v=«H2(R—±h). (5)
Объем шарового сектора. Шаровой сектор можно
представить как тело, полученное от вращения кругового
сектора ОАВ вокруг оси Ох (черт. 125). Как видно из чер-
тежа, объел! шарового сектора равен сумме объемов конуса О АС
и шарового сегмента АВС. Применяя формулы (2) и (5),
найдел! объем шарового сектора:
1 / РВ\
v =±кРА2 • ОР+ тг. РВ2(ОВ—^).
о \ о /
Обозначим
РВ = Н, ОВ = R;
тогда
OP — R — H
§ 1131
ОБЪЕМ ТЕЛА ВРАЩЕНИЯ
285
286
ПРИЛОЖЕНИЯ ИНТЕГРАЛА
[гл. хп
и из треугольника ОАР
РА2 = _ Я)2 = 2RH— И2.
Подставив значения РВ, OB, ОР, РА2 в выражение объема
шарового сектора, получим:
V = ± л (2RH — Я2) (Я — Я) + гсЯ2 (д _
= гс (-1 R2H—4 RH2 — 1W -j-1 Я3 + RH2 —1- нЛ=
о
9
V=~vR2H. (6)
Объем шарового слоя. Шаровой слой получается
в результате вращения фигуры ACQP вокруг оси Ох, где
АС—дуга окружности с центром в начале координат(черт. 126).
Положим:
OA — OC — R, OP = hy
PA — rlf PQ = H\
QC — r2,
тогда согласно
OQ
v=zk j* y2 dx
OP
формуле (1) объем шарового слоя
H+h H+h
= к f (R2— x2)dx = n |
h
X3\ _
h
з
(R* — h2 — Hh —
— дя +
Но так как R2 = r\ + Л2 (из треугольника ОАР) и
R2 — rl-{-(H-}-h)2 (из треугольника OCQ), то
Г1 —h = Г 2 “р (^ ~F »
или
r2t + h2 = r22 + Н2 4- 2Я/г + h2,
§ Н4]
ПУТЬ, ПРОЙДЕННЫЙ ТЕЛОМ
287
отсюда
Hh =
Подставив найденные значения
объема шарового слоя, получим:
R2, Hh в выражение
v = кН и + li — h2
2
— т.Н
/f Г 2 —
2
^2_1/72
1 \
— //2 _
3 /
г? 4-
— тс//——
.2
2
v~kH
-2, 2
Г1~ГГ2
2
И3
(7)
2
н*
Упражнения
1. Фигура, ограниченная прямыми у = — х 4- 3, х = О, х = 3 и
у — О, вращается вокруг оси Ох. Найти объем полученного тела
вращения.
2. Фигура ограничена кривой у — ~ и прямыми х — 2, х = Зи
у — 0. Найти объем тела, полученного от вращения ее вокруг оси Ох.
3. От шара радиуса R = 5 см отсечен сегмент с высотой Д=2 см.
Найти объем этого сегмента,
4. Найти объем сферического сектора, у которого радиус осно-
вания г — 3 см, а радиус шара R = 5 см.
5. Найти объем сферического слоя с радиусами оснований
~ 5 см и г2 = 8 см и высотой h — 3 см.
6. Вывести формулу объема эллипсоида вращения вокруг
оси Ох.
7. Найти объем параболоида вращения, у которого диаметр
основания равен 60 см, а высота равна 50 см.
8. Найти объем тела, образуемого вращением вокруг оси Ох
фигуры, ограниченной кривой у = sin х и прямыми х — 0 и х — к.
9. Найти объем тела, полученного от вращения вокруг оси Ох
фигуры, ограниченной осью абсцисс и кривой:
1) у = 2х — х2, 2) у — х2 — 4.
10. Найти объем тела, полученного от вращения вокруг оси Ох
фигуры, ограниченной линиями:
у == х2 + 1 и у = 2.
§ 114. Путь, пройденный телом. Путь $, пройденный
телом за время t в прямолинейном движении с постоянной
скоростью vt определяется по формуле
ь' = <ut.
(1)
288
ПРИЛОЖЕНИЯ ИНТЕГРАЛА
[ГЛ. ХП
Если тело движется неравномерно, то скорость его ме-
няется в зависимости от времени /, т. е.
^=/(0-
Чтобы найти в этом случае путь тела за время от t = tx
до / = /2, разделим промежуток времени t2—tx на п рав-
ных и очень малых частей Д/. Положим, что в течение каж-
дого из промежутков времени Д/ скорость тела остается
постоянной, меняясь скачком в конце каждого проме-
жутка Д£. Пусть, например, t2 — мы разбили на проме-
жутки Д£= 1 сек. Согласно сделанному допущению в первую
секунду тело движется равномерно и в конце ее меняет ско-
рость, продолжая в течение второй секунды двигаться равно-
мерно с полученной скоростью; затем в конце второй се-
кунды приобретает новую скорость, с которой и движется
равномерно в течение третьей секунды и т. д.
Поэтому путь тела за время Д/ найдется по формуле (1)
и будет приближенно равен а за время t2 — путь
его
^2
tl
Будем увеличивать число делений п, тогда Д£, а также
и скачки в изменении скорости в конце каждого проме-
жутка Lt будут все меньше и меньше. Если п -> оо, то
Д£->0, а, следовательно, и f(t)Lt~-+Q. При этом условии
скорость тела меняется уже не скачкообразно, а непрерывно,
и путь его будет равен:
А»
$ = Ит 2/(0^»
дг->о г,
или согласно формуле (5) § 111
lim У/(ОД/= f/(t)dt,
М + О™ *
s = J/ЮЛ.
(2)
§ 1И]
ПУТЬ, ПРОЙДЕННЫЙ ТЕЛОМ
289
Пример. Скорость движения тела задана уравнением
а — 2/2 1 см!сек.
Найти путь, пройденный им за 6 сек. от начала движения.
Решение. Согласно формуле (2) имеем:
6 G
5 = 4 (2/2-+-/)Л = |(-|/3 + ~/2) =
о о
9 1
= 4-63+4-62= 162 см.
О Z
Упражнения
1. Скорость падающего в пустоте тела определяется по фор-
муле
v — 9,8 / м/сек.
Какой путь пройдет тело за первые 10 сек. падения?
2. Найти формулу пути падающего тела в пустоте, если скорость
его падения
v = gt м/сек.
3* Скорость движения тела определяется по формуле
v = (З/2 — 2/) см/сек.
Какой путь тело пройдет за 5 сек. от начала движения?
4. Скорость движения тела
v — ^4/ —см/сек.
Определить путь его за третью секунду.
5. Два тела начинают движение одновременно из одной и той же
точки: одно со скоростью
v = З/2 м/мин,
другое со скоростью
v = 2/ м/мин.
На каком расстоянии друг от друга они будут через 10 мин., если
они движутся по прямой линии в одном направлении?
6. Два тела движутся по одной и той же прямой линии: одно со
скоростью
v = (З/2 2/) м/сек,
второе со скоростью
v = (8/ 4-1°) м/сек.
Если в начале движения они были вместе, то когда и на каком рас-
стоянии от начала движения они опять будут вместе?
19 Зак. 3032. И. Л. Зайцев
290 ПРИЛОЖЕНИЯ ИНТЕГРАЛА [гл. XII
*.
7. Найти путь, пройденный телом от начала движения до оста-
новки, если скорость его определяется по формуле
v = (6/ — 2Z2) см/сек.
8. Камень брошен с земли вертикально вверх. Найти наиболь-
шую высоту подъема камня, если скорость его
v = (19,6 — 9,8Z) м/сек.
9. Мяч брошен вертикально вверх с начальной скоростью 20 м/сек.
На какую наибольшую высоту он поднимется?
§ 116. Работа силы. Пусть тело движется по прямой
линии под действием постоянной силы F; тогда работа Р,
совершаемая этой силой на пройденном пути, равном х,
найдется по формуле
P = Fx, (1)
где х выражается в метрах, F—в килограммах, а Р — в кило-
граммометрах.
Но если движение тела происходит под действием пере-
менной силы, то ее работа определяется сложнее. Выведем
формулу для этого случая.
Допустим, что тело, находящееся в точке О в состоянии
покоя, начинает двигаться по прямой линии (черт. 127) под
О Д В
Черт. 127.
действием переменной силы F, изменяющейся в зависимости
от пройденного пути х, т. е.
Г = /(х).
Пусть в некоторые моменты времени тело оказалось в точ-
ках А и В> причем
О А — а и ОВ = Ь.
Покажем, как определить работу, совершаемую данной силой
на отрезке пути АВ — b — а.
Для этого разобьем его на п равных и очень малых
отрезков Дх. Положим, как и в задаче § 114, что на каж-
дом отрезке Дх сила остается постоянной, изменяясь скачком
в конце каждого отрезка Дх. Тогда по формуле (1) работа
§ 115] РАБОТА СИЛЫ 291
силы па отрезке пути Дх будет приближенно равна /(х)Дх;
работа же силы на всем пути АВ = Ь — а.
ь
P^fMAx.
а
Если число делений п неограниченно увеличивать, то Дх
а, следовательно, и f(x)kx станут бесконечно малыми вели-
чинами. При этом условии сила будет меняться не скачками,
а непрерывно, и искомая работа ее будет равна
ь
р== lim S/(-v)Ax>
Да?->0 а
или согласно формуле (5) § 111
ь ь
Р = Ит V/(x)Ax = f/(x)<Zx,
а а
b
Р— f f(x)dx. (2)
а
Пример. Сила в 1 кг растягивает пружину на 3 см.
Какую работу она при этом производит?
Решение. По закону Гука сила пропорциональна растя-
жению или сжатию пружины, т. е.
F — kxt
где х—величина растяжения или сжатия ее, a k — коэффи-
циент пропорциональности.
Чтобы найти значение k для нашей задачи, подставим
данные величины в уравнение, выражающее закон Гука;
получим:
1 = & - 0,03,
откуда
ь— 1
* —0,03 ’
Следовательно, сила, растягивающая нашу пружину, выразится
в следующем виде:
19*
292
ПРИЛОЖЕНИЯ ИНТЕГРАЛА
[ГЛ. ХП
Так как сила начинает действовать на пружину; находя-
щуюся в состоянии покоя, то нижний предел интеграла
в формуле (2) а —О, верхний же предел £> = 0,03. Следо-
вательно, искомая работа будет:
0,03 0,03
О Г 1 , 1 I х2 1 0,032 0,03 ПП1-
Р~,1 0,03х dx~0,03 I 2 ~0,03' 2 ~~ 2 “ 0,015/сглг.
о о
Упражнения
1. Сила в 6 кг растягивает пружину на 8 см. Какую работу она
производит?
2. Вычислить работу, производимую при сжатии пружины па
4 см, если для сжатия ее на 1 см нужна сила в 1 кг.
3. Пружина растягивается на 6 см под действием силы в 3 кг.
Какую работу она производит, растягивая ее па 10 см?
4. Найти работу, производимую при' сжатии пружины на 3 см,
если известно, что для сжатия ее на 0,5 см нужно приложить
силу в 1 кг.
5С Сила в 6 кг достаточна, чтобы растянуть пружину на 2 см.
Первоначальная длина пружины 14 см. Какую работу нужно совер-
шить, чтобы растянуть ее до 20 см?
6. Растягивая пружину па 4 см, произвели работу в 10 кгм.
Какая работа будет произведена при растяжении пружины на 10 см>
7. Чтобы растянуть некоторую пружину на 2 см, нужно произ-
вести работу в 20 кгм. Насколько можно растянуть пружину,
затратив работу в 80 кгм?
8. Пружина в спокойном состоянии имеет длину 20 см. Груз
в 10 кг растягивает ее на 2,5 см Какую работу надо совершить,
чтобы растянуть ее от длины в 25 см до длины в 35 еж?
§ 116. Работа, совершаемая при поднятии груза. Из
физики известно, что при поднятии груза на некоторую высоту
совершается работа, равная произведению веса, выраженного
в килограммах, на высоту подъема, выраженную в метрах.
При этом сама работа измеряется в килограммометрах. Решим
несколько задач.
Задача 1. Из цилиндрического бака нужно выкачать
воду, наполняющую бак до края. Какая работа при этом со-
вершается, если радиус основания бака R — 0,6 м, а высота
его Н= 3 м?
Решение. Если бы мы подняли на некоторую высоту
бак вместе с водой, то работу, необходимую для этого,
нашли бы легко простым умножением веса груза на высоту
подъема. Но работа, совершаемая при выкачивании жидкости,
§ 116] РАБОТА, СОВЕРШАЕМАЯ ПРИ ПОДНЯТИИ ГРУЗА 293
определяется сложней, так как жидкость в этом случае под-
нимается не вся сразу, а по частям, слоями, причем высота
подъема у разных слоев жидкости разная.
Для решения задачи разобьем цилиндр плоскостями, па-
раллельными его основанию, на тонкие слои (черт. 128).
Выделив один из них на глубине
001= у
и обозначив его толщину и объем
соответственно через &у и Дт/, бу-
дем иметь:
Д-ц = tcR2 Ду м3.
Вес воды Д<2 в найденном объеме
будет:
AQ — тгР2 Ду т,
так как 1 .м3 воды весит 1 т. Вы-
разив Др в килограммах, получим:
Др = 1000тгР2Ду кг.
Чтобы выкачать воду, находящуюся в рассматриваемом
слое, его нужно поднять до края бака, т. е. на высоту
Ofi = y.
Работа ДР, совершаемая при этом, выразится так:
ДР = Др . 1000тиР2уДу/^. (1)
При последовательном поднятии до края бака каждого
слоя, начиная с первого и кончая последним, совершается
в каждом случае работа, определяемая равенством (1); при
этом величина у имеет для каждого слоя свое значение
в границах от 0 до Н. Работа же, необходимая для поднятия
всей воды, выразится в виде
я
5 1000и#2_уДу.
Но полученная величина работы —только приближенная.
Чтобы найти искомую работу, будем неограниченно увеличивать
294
ПРИЛОЖЕНИЯ ИНТЕГРАЛА
[ГЛ. XII
число делений цилиндра плоскостями; тогда вся работа
н
Р= lim 2 1000л/?2_уДу,
Д?/ -> О и
или согласно формуле (5) § 111
н
Р= f 1ОООтг/?2_уб(у== 1000к/?2
О
772
= ЮООтс/?2. fZ_ = 500тс/?2Я2.
п
У1-
2 ~
о
Заменив и Н их значениями, найдем:
Черт. 129.
Р = 500тс • 0,62.32= 1620тс кгм.
Задача 2. Резервуар коничес-
кой формы, расположенный верши-
ной на поверхности земли и име-
ющий высоту 7Y=3j/ и радиус
основания R — 90 см, наполнен
водой. Какую работу нужно произ-
вести, чтобы выкачать из него всю
воду?
Решение. Как и в первой зада-
че, разобьем конус на тонкие слои
и каждый из них примем за цилиндр.
Выделим один из них на глубине 00 х—
= 3/(черт. 129). Обозначив толщину
выделенного слоя и его объем соот-
ветственно через Дд/ и напишем:
А-и = тс • ОГВ2 ку м3. (2)
Выразим ОХВ через у; из подобия треугольников O2OtB и
О2ОА имеем:
О\В__О2О\
ОА—"О£)’
откуда
о,в = • 0,0, = §^(О2О - ООО=£(И-у).
Заменив в равенстве (2) О,В найденным значением, получим:
= у)2ДуЛз.
§ 116] РАБОТА, СОВЕРШАЕМАЯ ПРИ ПОДНЯТИИ ГРУЗА
295
Вес воды AQ в объеме Д^ будет:
AQ = (Н—by т = 1 000 (Я—у? Ьу кг.
Работа ДР, совершаемая при поднятии воды весом в LQ кг
на высоту
(\О=у,
выразится так:
ДР = Д(2 . OYO — 1000т: “ у (Н—у)2 &у кгм.
Работа же, необходимая для поднятия всей воды, будет
приближенно равна
н
2 1000к^2Д/(Я-^ДЛ
о
Если неограниченно увеличивать число делений конуса,
то искомая работа
н
Р — lim ЮООтг—У)2 ^У
или согласно формуле (5) § 111
н
Р=f 1000^^ У щ—ууау=
О
II
=1000лI (H2y~2Hy2-\-y3)dy =
О
II
= ЮООтг-7—7
/7“ I \ Z
О
W* у4х_
3 ~Г" 4 /
100(W /Я4 2Я4 //4 \ _ lOOCW 7-/4 _ 250тсР2/Р
“ И2 \ 2 3 4 / И2 ’ 12 ~ 3
или после замены R и И их значениями
п 250к • 0,92 • З2 к
р =-------»-----== 607,5к кгм.
з
Упражнения
1. Бак с прямоугольным основанием 50 см X 80 см и высотой,
равной 60 см, наполнен водой. Какую работу нужно совершить,
чтобы выкачать всю воду из бака?
296
ПРИЛОЖЕНИЯ ИНТЕГРАЛА
[ГЛ. XII
2. Цилиндрический сосуд с диаметром основания D = 50 см и
высотой Н — 70 см наполнен водой. Какую работу нужно произвести,
чтобы выкачать всю воду из сосуда?
3. Вычислить работу, необходимую для того, чтобы выкачать ке-
росин, наполняющий цистерну с радиусом основания R = 2 м и вы-
сотой Н=3м. (Удельный вес керосина d == 0,8.)
4. Какую работу нужно затратить, чтобы поднять всю воду из
цилиндрической цистерны с диаметром 2 м и глубиной 4м на вы-
соту 15 м над верхним краем цистерны?
5. Канат длиной 50 м, площадью поперечного сечения 2 еж2, из-
готовленный из материала, плотность которого 6,4 г/см\ извлекается
из шахты на поверхность земли. Определить работу, которая при
этом совершается.
6. Резервуар конической формы с вершиной, обращенной книзу,
наполнен водой. Какую работу нужно совершить, чтобы выкачать из
него всю воду, если радиус основания конуса R — 50 см, а высота
Н~ 1 м!
7. Какую работу нужно произвести, чтобы насыпать кучу песку
конической формы, радиус основания которой 1,2 м, а высота 1 ж?
(Удельный вес песка 2 г/см3', песок поднимается с поверхности земли.)
8. Резервуар, имеющий форму усеченного конуса, наполнен
водой. Какую работу нужно произвести, чтобы выкачать из резер-
вуара всю воду, если радиусы его оснований R = 2 м и г = 1 м,
а высота Н = 3 м?
§ 117. Давление жидкости.
Задача 1. Прямоугольная пластинка с размерами
20 см X 30 см погружена в воду так, что меньшая сторона
ее лежит на поверхности
воды, а большая занимает
вертикальное положение.
Найти давление воды на
пластинку.
Решение. Пусть дан-
ная пластинка ABCD распо-
ложена, как указано на
черт. 130, где MN — по-
верхность воды. Если бы эта
пластинка находилась в го-
ризонтальном положении, то
давление воды на нее было
бы равно весу столба жид-
кости, имеющего основа-
нием данную пластинку,
а высотой — глубину ее расположения от поверхности жидко-
сти. Но по такому закону нельзя рассчитать давление воды
§ 117]
ДАВЛЕНИЕ ЖИДКОСТИ
297
на вертикальную площадку, так как давление на единицу пло-
щади изменяется с глубиной.
Для решения задачи разобьем пластинку на большое
число полосок, параллельных AD. Выделив одну из них, на-
пример abcd> на глубине
ВЬ=у
и обозначив ширину ее через Ду, а площадь через As, найдем
As = ad • ab — 20 Ду см2. (1)
Горизонтальная площадка 1 см2 на глубине ВЬ испытывает
давление, равное весу столба воды, имеющего основание в 1 см2
и высоту Bb~yt т. е. давление, равное у г.
По закону Паскаля давление жидкости передается во все
стороны с одинаковой силой; поэтому давление ее на 1 см2
вертикально расположенной полоски abed будет приближенно
тоже у г. На всю же полоску abed давление ДР выра-
зится так:
Др = у As г,
или после замены As согласно равенству (1)
АР = 20уДуг. (2)
Находя таким же образом давление воды на каждую из
полосок, составляющих пластинку ABCDt мы получим в каж-
дом случае величину этого давления, определяемую равен-
ством (2), в котором у имеет значение, соответствующее глу-
бине расположения той или иной полоски. Давление же воды
на всю пластинку ABCD будет приближенно равно
30
2 20у Ьу.
О
Будем неограниченно увеличивать число делений пластинки
ABCD*, тогда искомая величина давления
30 30 30
Р = lim V 20у Ду — f 20у dy — 20 ~ —
J о о о
= 10.302 = 9000 г = 9 кг.
Задача 2. Пластинка в виде прямоугольного треуголь-
ника АВС с катетами АВ = 12 см и АС =9 см опущена
298
ПРИЛОЖЕНИЯ ИНТЕГРАЛА
[ГЛ. XII
в ртуть так, что катет АВ занимает вертикальное положе-
ние, а вершина В находится на 3 см ниже уровня ртути.
Найти давление ртути на эту
пластинку. (Удельный вес рту-
ти 13,6 г!см3).
Решение. Расположение
пластинки указано на черт. 131,
где MN—уровень ртути. Как
и в задаче 1, разобьем пла-
стинку АВС на большое число
полосок, параллельных АС,
каждую из которых примем за
прямоугольник. Выделим одну
из этих полосок, например abed,
на глубине Db.
Обозначив ВЬ через у, а ширину и площадь полоски abed
соответственно через &у и AS, найдем:
AS = be • Ад/ см2. (3)
Согласно закону Паскаля давление ртути на площадку 1 см2,
расположенную на глубине
Db = Bb-\- DB = у + 3,
равно приближенно
. 13,6/9/9:= 13,6(j4-3)?,
а на всю полоску abed давление АР выразится так:
AP=13,6(j4-3)AS2,
или согласно равенству (3):
ДР= 13,6(д/4-3)- • Ду/ = 13,6 . Ьс(уАтЪ)куг. (4)
Выразим длину полоски Ьс через у; для этого рассмотрим
треугольники АВС и ЬВс\ из их подобия следует
Ьс ВЬ
АС АВ ’
или
Ьс__ у
"9“ 12’
откуда
, 9 3
=_у.
§ И71
ДАВЛЕНИЕ ЖИДКОСТИ
299
Теперь равенство (4) перепишется:
ДР = 13,6 + 10,2(»-f-З» Ду г. (5)
Давление на каждую из остальных полосок будет опреде-
ляться равенством (5), в котором у принимает значения
в границах от 0 до 12. Суммируя все эти давления, мы полу-
чим величину давления на пластинку АВС, приближенно
равную
12
2 10,2 (.у* 4-3» Ду.
О
При неограниченном увеличении числа делений пластинки АВС
искомая величина давления на нее будет равна
12
Р = lim У 10,2 (.у2 4-3» Ду =
Дг/->о^
12 12
= f 10,2(»+3»rfy=10,2 + =
О о
= 10,2 4- = 10,2 (576 4- 216) =
= 10,2 • 792 = 8078,4 г«8,08 кг.
Упражнения
1. Найти давление воды, наполняющей аквариум, на одну из
его стенок, имеющую длину 60 см и высоту 20 см.
2. Найти давление воды на боковые стенки аквариума, наполнен-
ного водой до высоты 0,5 м, если дно имеет размеры 1,2 м X 1,3 м.
3. Найти давление воды па вертикально стоящий прямоугольник
с размерами 3 ж X 2 м, если его большая сторона вертикальна,
а верхняя на 1,5 м ниже поверхности воды.
4. В боковой стенке резервуара имеется прямоугольное отверстие
с размерами 60 см X 40 см. С какой силой вода прижимает клапан,
закрывающий отверстие, если большая сторона прямоугольника го-
ризонтальна и расположена на 2 м ниже поверхности воды?
5. Пластинка в виде ромба со стороной 5 см и одной из диаго-
налей 8 см погружена вертикально в воду. Найти давление воды на
эту пластинку, если:
1) сторона ее лежит па поверхности воды;
2) верхняя сторона ее лежит на 2 см ниже поверхности воды.
6. Пластинка в виде треугольника, основание которого 2 см,
а высота 1,5 см, погружена вертикально в воду. Найти давление,
испытываемое этой пластинкой, если:
300 ПРИЛОЖЕНИЯ ИНТЕГРАЛА [ГЛ. ХП
1) вершина ее лежит на поверхности воды, а основание парал-
лельно ей;
2) вершина лежит- на 0,5 см ниже поверхности воды, а основа-
ние параллельно ей.
7. Вычислить давление воды на плотину, имеющую форму тра-
пеции, верхнее основание которой равно 6,4 м, нижнее 4,2 л/,
а высота 3 м, если вода доходит до верха плотины.
8. Передняя часть дамбы имеет форму параболы с вершиной
внизу; основание дамбы а — 3,2 л/, высота ее h — 1,6 м. Определить
давление воды на дамбу, если вода доходит до верхнего края дамбы.
9. На какой глубине нужно провести горизонтальную линию
на стейке аквариума, имеющего длину 60 см, а высоту 25 см, чтобы
давления на нижележащую и вышележащую части стенки были
равны?
ДОПОЛНЕНИЯ
ГЛАВА XIII
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§ 118. Общие понятия. Дифференциальным уравнением
называется уравнение, содержащее производные от искомой
функции или ее дифференциалы. Так, например, х dy — ‘2y dx
или = — дифференциальные уравнения.
Решить дифференциальное уравнение, значит найти такую
функцию от Ху которая удовлетворяет данному уравнению, т. е.
обращает это уравнение в тождество при подстановке
ее в уравнение вместо у.
Уравнение, содержащее производные или дифференциалы
не выше первого порядка, называется дифференциальным
уравнением первого порядка.
Дифференциальные уравнения имеют большое применение
в геометрии, механике, физике и других дисциплинах, а также
в технике.
Пример решения дифференциального уравнения мы имели
в § 105, отыскивая уравнение кривой по заданному угло-
вому коэффициенту касательной. В результате решения диф-
ференциального уравнения
мы получили уравнение
v-хЧС (2)
которое носит название общего решения дифференциального
уравнения. Подставив вместо х и у соответственно 1 и 3,
мы нашли уравнение
у z= х2 -4- 2,
называемое частным решением дифференциального урав-
нения *).
*) Общее решение дифференциального уравнения всегда со-
держит произвольное постоянное С, в частном же решении это по-
стоянное заменено определенным числом.
302 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII'
Данные значения х = 1 и у — 3 называются начальными
условиями. Начальные условия задаются для того, чтобы из
общего решения дифференциального уравнения получить его
частное решение.
Правильность решения дифференциального уравнения легко
проверить, подставив выражение (2) в уравнение (1). В ре-
зультате получим:
dx
или
2х dx ~
——= 2х,
ах
т. е.
2х — 2х,
что говорит о правильности решения уравнения (1).
§ 119. Дифференциальные уравнения первого порядка
с разделяющимися переменными. Если каждая часть диф-
ференциального уравнения представляет собою произведение
некоторого выражения, зависящего от одной переменной, на
дифференциал этой переменной, то говорят, что переменные
в уравнении разделены; например, х dx = у dy. В этом слу-
чае уравнение можно интегрировать почленно.
Уравнения, в которых переменные разделяются, назы-
ваются дифференциальными уравнениями с разделяющимися
переменными-.
Для того чтобы решить дифференциальное уравнение
с разделяющимися переменными, нужно произвести разделе-
ние переменных, а затем взять интеграл от обеих частей
уравнения.
Рассмотрим несколько примеров.
Пример 1. Решить уравнение xdy=ydx, если при
х~- 5 у = 10.
Решение. Для разделения переменных обе части уравне-
ния поделим на произведение ху, получим:
dy _dx
У “ т •
Интегрируя обе части последнего уравнения, найдем:
§ 119] ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 303
ИЛИ
lnjy = ln Х-|-1пС.
В правой части прибавлено постоянное в виде In С для
облегчения потенцирования. Освобождаясь от символа лога-
рифма, т. е. потенцируя, получим общее решение:
у = Сх.
Для определения постоянного С подставим в полученное
решение начальные условия х = 5 и у —10:
10 = 5С,
откуда
С=2.
Следовательно, искомое частное решение будет:
у= 2х.
Таким образом, из всех прямых (семейства прямых), про-
ходящих через начало координат, мы выделили одну, на
которой лежит точка с координатами (5; 10).
Пример 2. Решить уравнение — = 2 (у — 3), если при
х = 0 j —4.
Решение. После разделения переменных получим:
у —3
отсюда
или
In (у — 3) — 2х С.
Находим значение С из условия х — 0 и у = 4; сделав
подстановку, получим:
1п(4 — 3)=2 * О-4-С,
откуда
С==1п1 =0.
Итак,
In (у — 3) — 2х.
(1)
304
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ. XIII
Для потенцирования нужно и правую часть последнего
равенства написать со знаком логарифма. Пользуясь опре-
делением логарифма, будем иметь:
2х=1п^;
следовательно, решение (1) можно переписать:
In (у — 3)=1п^,
отсюда, потенцируя, получаем: у—3 — е2х, или
Упражнения
Найти частные решения уравнения:
1. ds = (4/ — 3) dt, если при t = 0 s = 0.
2. dx = (2t2 — 5)dt, если при t = 1 x — — 4.
3. х dx = dy, если при X = 1 y = 0.
4. x dx == у dy, если при X = 2 У = 1-
5. x2 dx ф- у dy = 0, если при X --- 0 y = l.
6. (/ — 1) dt ф- 5 ds = 0, если при t = 2 s = 0.
7 2 Q V X если при X — 1 y = V"2.
8.4>+^=o, если при X 0 у = 2.
2x у
9. 2s dt — t ds, если при t = 1 s = 2.
10. x2 dy — y2 dx = 0, если при X = 0,2 у = 1.
11. x^dy = y'*dx, если при X У У y = V"2.
12. 4^- = 1 + dx если при X 0 y==0.
13. dy 4~ x dx = 2dx, если при х = 1 у = 1,5.
14. x2 dy—1-уЗдГх — О, если при X = — -1 У - 1
15. (/4- V)dx = 2xdt, если при t = l х = 4.
16. У x dy — У у dx ~ 0, если при х = 0 У = 0.
dy . , dx 17. —-= + dx = —== , Vy V* если при х = 0 У = 1.
18.-g- — dx = 0, если при х = 0 У=^ 3.
19. (1 4" У) dx — (l — x) dy == 0, если при х = 0 у^ 1.
20. 2yf = y, если при х = 0 У == 1.
§ 120] дифференциальные уравнения вида d2y)dx2 = f (х) 305
21.^4-^==-^-, У + 1 dy если при х = 5 У = 0.
22. tg х • yz = 1 Jr у, если при х = ~ - У = —
23. (l-^)-g- + xy = 0, если при х = 0 У = 4.
24. dy~yytgxdx~$> если при х = 0 У = 1.
25. cos л sin у dy — — cos у sin x dx = 0, если При X = тс У = ТС.
Найти общие решения уравнений:
/У у
26. (jcy + x) — = 1. 27. (xy2 + x)dx+(x2y — y)dy = O.
28. (у — х2у) dy-j-(x A- ху2) dx = 0.
29. (1 + х2) dy — (ху ~t~x)dx = 0. 30. у dx -j- (1 — у) х dy = 0.
31. x2dyA~(y— l)dx = 0. 32. 2 (ху + у) dx = х dy.
33. (х2 + 1) dy = у dx. 34. х2у' — 2ху = Зу.
35. Тело движется по оси абсцисс, начиная движение от точ-
ки А (10; 0) со скоростью
v = 2/ —А
Найти уравнение движения тела.
36. Написать уравнение линии, проходящей через точку А (— 1; 0)
и всюду имеющей касательную с угловым коэффициентом, равным 2.
37. Найти уравнение кривой, проходящей через точку Л(3; 1)
и имеющей касательную, угловой коэффициент которой равен
2х—1.
38. Найти уравнение кривой, проходящей через точку Л (4; 4)
2
и имеющей касательную с угловым коэффициентом k = —.
39. Написать уравнение кривой, проходящей через точ-
ку А —1; и имеющей касательную с угловым коэффициен-
том k = у.
40. Координаты точек некоторой кривой связаны уравнением
лу'= (л+1)у.
Написать уравнение этой кривой, если она проходит через точку (1; е).
41. Тело движется по кривой, имеющей касательную с угловым
коэффициентом./? = х2. Найти изменение ординаты точки при изме-
нении абсциссы с 2 до 5.
d2v
§ 120. Дифференциальные уравнения вида
Уравнение, содержащее производные или дифференциалы
второго порядка, называется дифференциальным уравнением
второго порядка. Простейшее из этих уравнений имеет вид
d2y г, ч
= оно решается двукратным интегрированием.
20 Зак. 3032. И. Л. Зайцев
306
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[гл. XIH
Пример 1. Решить уравнение 1— 2х.
Решение. Согласно определению второй производной
можно написать
Положим теперь
dx *
тогда
d(£L\
dx2 dx dx ’
и данное уравнение перепишется следующим образом:
или
dp = (l —2x)dx.
Интегрируя последнее уравнение, найдем: i
J dp =z J* (1 — 2x) dx
и
P— X X2 + Cjl.
Ho
dy _
dx
поэтому
~~ — x — x2 4~ Cj, dx in
или
dy — (x — x2 4* Ct) dx.
Снова интегрируем и получаем:
У = y(x_x2+Ci)6?x = ^_^ + C1x+C2. (1)
Мы нашли общее решение данного уравнения.
Чтобы получить частное решение его, необходимо найти
числовые значения постоянных Сх и С2; для этого нужно
иметь начальные условия. Пусть кривая, определяемая частным
§ 120] дифференциальные уравнения вида d2y/dx2=f (х) 307
решением, проходит, например, через точки с координа-
тами (0; 1) и тогда, подставив значения х и у
в уравнение (1), получим следующую систему уравнений
относительно Сг и С2:
1 • о + с2,
111
(1=4-4+с>+с-
откуда
Ct = — 1 и С2=1.
Следовательно, частное решение данного дифференциаль-
ного уравнения при указанных начальных условиях будет:
у = ~ х2-----~х3— х-ф-1.
Для проверки правильности решения найдем вторую про-
изводную этой функции:
^- — (}-х2--U3— x-j-l/j — х— х2—1,
dx \ 2 d 1 /
g = (x_x2_iy=i_2x.
Мы пришли к исходному уравнению, что говорит о том, что
оно решено правильно.
В разобранном примере начальные условия были даны
в виде координат двух точек кривой, уравнение которой
является частным решением дифференциального уравнения.
Однако начальные условия могут быть даны и в иной форме,
например, при х = х0, y — yQ и у'— у'^. Это значит, что
мы задаем точку кривой и направление касательной в этой
точке.
Пример 2. Ускорение прямолинейного движения тела
равно 2 см! сек2. Выразить путь s тела как функцию вре-
мени t.
Решение. Согласно механическому смыслу второй про-
изводной функции (§ 83) имеем:
d&
20*
308 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. ХШ
Обозначив
ds
иг=р-
напишем:
Л ds\
d2s _ \ dt ) _ dp _~
dt2 dt ~~dT~Zi
откуда
dp — 2 dt
и
р = 2/Ч-СР
Заменив р его выражением, получим:
е
+ (2)
ИЛИ
ds — (2t-\-Cx)dtt
отсюда
s=/'(2/ + С1)Л = /2 + С/ + С2. (3)
Для получения частного решения нужны начальные уело-
ds
вия. Пусть при Z = 0, s = 0 и — —0 (предполагаем, что
„ ds
в начальный момент движения путь 5 и скорость равны
ds
нулю). Заменив t, s и — в уравнениях (2) и (3) нулями,
получим:
с{ =0, С2 = 0.
Таким образом, искомая зависимость будет s — t2.
Упражнения
Найти частные решения уравнений:
6?‘2У
1, ~~х- =0, если при
dx2 1
d^y
2. -т-4 = 5, если при
dx2 *
о ” л
3. ух = х, если при „q и при
А d2s t — 0
4- = еСЛИ ПРИ 5 = 2
х == 0
1 и
у=1
х = 2
к и
у = 5
прй у = 0.
ПрИ у = 11.
х = 2
у -2.
ds II
И ~dt
§ 120] дифференциальные уравнения вида d2y!dx2—f(x) 309
^0 о со = 0 4/0 3
5. = со2, если при и — = ~~
da2 0 = 0 //со 4
Найти общие решения уравнений:
_ 0 d2y о _ 4/20 фо"
6. х2~х = 2. 7. —= е*. 8. у = cos х
dx2 dy2 х
9,^.= ,0.е,.^ = 1.
11. Поезд, выйдя со станции, спустя t часов имеет ускорение
j = 3t2 — 42/ -j- 80 км/час2.
Найти скорость в конце 2-го часа и расстояние, пройденное за это
время.
12. Ускорение прямолинейного движения пропорционально вре-
мени. Найти зависимость между пройденным расстоянием и време-
нем, если при / = 0 v — 0 и $ = 0, а также при / = 1 s = -^-.
о
13. Ускорение прямолинейного движения пропорционально квад-
рату времени. Найти зависимость между s и /, если при 1 — 0
v = 0, s = 1 и при / = 1 s = 2.
ГЛАВА XIV
РЯДЫ
§ 121. Понятие о рядах. Выражение вида
ui 4“ и2 4~ из 4~ • • • 4“ ип 4~ • • • >
(О
где ut, u2i и3, ... —члены некоторой бесконечной последо-
вательности, называется бесконечным рядом или просто
рядом.
Член ип называется общим членом ряда.
Обозначим сумму п первых членов ряда (1) через Sn, т. е.
4- и2 4~ из 4~ 4“ • • • 4“ ип
Сумма Sn называется частичной суммой ряда. При измене-
нии п меняется и Sn\ при этом возможны два случая:
1) величина Sn при и —> оо имеет предел S, т. е.
lim Sn = S\
п~> со
2) величина Sn при п —> оо предела не имеет или предел
ее равен сю.
В первом случае ряд называется сходящимся, а число
S = Hm Sn— его суммой. Во втором случае ряд называется
П->со
расходящимся', такой ряд суммы не имеет. Например, ряд
представляющий -собой бесконечно убывающую геометриче-
скую прогрессию, есть ряд сходящийся, так как по извест-
ной формуле для такой прогрессии
§ 122] НЕОБХОДИМЫЙ ПРИЗНАК СХОДИМОСТИ РЯДА 311
Ряд же
2 4- 22 + 23Н-24+ ...4-2п-+
представляющий собой бесконечно возрастающую геометри-
ческую прогрессию, — расходящийся. В самом деле,
aq^-a 2.2”-2
11Ш = 111Т1 —----г-= НП1 —о----.— =
>*' л _ ] у _ I
П -> со п - > со " п > со
= lim (2”+1— 2) = оо.
П->оо
§ 122. Необходимый признак сходимости ряда. Пусть
дан сходящийся ряд
lhA~ и2~\~ + + • • • (О
Найдем сумму п—1 и п его членов:
*Sn-l = ZZl~l“ZZ2~bZZ3+ • • ‘ +/Zn-P
4~ и2 + и3 4“ ... + ип_1 + ип*
Вычтя из второго равенства первое, получим:
(2)
Возьмем предел от обеих частей равенства (2) при п сю:
lim (6\ — = Ит ип,
л - > оо п -> оо
ИЛИ
lim Sn— lim Sn_1 — lim un, (3)
n -> co n > co n -> co
Так как ряд (1), по условию, сходящийся, то
lim Sn— lim =
n -> co n > co
Равенство (3) можно переписать так:
S — S— lim un,
П -> co
или
lim ttn = 0. (4)
n -> co
Это дает необходимое условие сходимости ряда, т. е.
такое условие, без наличия которого ряд не может сходиться.
Однако оно не является достаточным. Покажем это на
примере.
312
РЯДЫ
[гл. XIV
Возьмем так называемый гармонический ряд
- +4+
Для него условие (4) выполняется, так как
lim и,„ — lim — — О,
п п
п->со п->оо
между тем этот ряд расходится.
Чтобы убедиться в этом, воспользуемся равенством (§ 47)
(1 \п
14- — ) = е,
1 п
"J
где
/ 1 \п
(1+^)<- <5>
Прологарифмировав обе части неравенства (5) по осно-
ванию et напишем:
п In ^1 4" е —
отсюда
Но
1П (1 4“ — In — In (п 4“ 1) — In п,
поэтому неравенство (6) примет вид:
In о? 4~ 1) — 1п п < (7)
Положив в неравенстве (7) п—1, 2, 3, 4, 5, будем
иметь:
In 2 — In 1 < 1
In 3 — In 2 < у
In4 — 1n3 < v
In 5 — In 4 < -i
In(/? 4- 1)—Inn <4
I
j
i
i
>
§ 123] ДОСТАТОЧНЫЕ ПРИЗНАКИ СХОДИМОСТИ РЯДА 313
Сложив эти неравенства, найдем:
In (п -Р 1) < 1 у 4~ . 4~ ™.
Пусть п —> сю, тогда
1 . .. _|___> in (п 1) —> оо.
Следовательно, гармонический ряд расходится.
§ 123. Достаточные признаки сходимости ряда.
1. Сравнение рядов. Будем сравнивать два ряда
с положительными членами:
4~ 112 ~Ь из 4~ • • • 4~ ип 4“ • • • (О
и
Vj 4- v2 4~ 4~ • • • 4“ vn 4~ • • - (2)
1) Пусть ряд (2) сходится и каждый член ряда (1) меньше
соответствующего члена ряда (2); тогда и ряд (1) сходится.
2) Пусть ряд (2) расходится и каждый член ряда (1) больше
соответствующего члена ряда (2); тогда и ряд (1) расходится.
Примем указанные признаки без доказательства.
Пример 1. Для установления сходимости ряда
1-2.з+ 1 -2.3-4-*- ' ‘ + (л 4- 1)! + • ’ ’
сравним его с убывающей геометрической прогрессией
2*4“ 22 4" 2з 4“ • • • 4~2й + • • • (4)
Каждый член ряда (3), начиная со второго, меньше соответ-
ствующего члена ряда (4); кроме того, как мы знаем, бес-
конечно убывающая геометрическая прогрессия — сходящийся
ряд. Следовательно, и ряд (3) — сходящийся.
Пример 2. Возьмем ряд
1+-Д+-Д+•••+-4+(5)
*) Принято произведение 1-2«3. ../п записывать символом ml
и читать «эм факториал» (по определению 0! — 1).
314
РЯДЫ
[гл. XIV
и сравним его с гармоническим рядом
1+4+4+...+|+... и
Так как каждый член ряда (5), начиная со второго, больше
соответствующего члена ряда (6), а ряд (6) — расходящийся
(§ 122), то и ряд (5) тоже расходящийся.
2. Признак Даламбера. Если в ряде с положи-
тельными членами
ui + и2 + из + • • • +^п+ • • •
выполняется условие
lim ^ = 1,
п -> со
то данный ряд сходится при I < 1 и расходится при
l> 1.
Примем этот признак без доказательства.
Пример 3. Исследовать сходимость ряда
1,3.5. .2/2 — 1,
2 • 22 ’ 23 * * * * * ’ * * * ‘ 2П
Решение.
_ 2п — 1 . _ 2п + 1 в
ип — {2п 9 10 un+i 2n+1 ’
ип+1 2п 4- 1 в 2/г — 1 2/2 4- 1
ип ~ 2п+1 ' 2п ~~ 2(2/2 —1) ’
Применяя признак Даламбера, находим:
lim
П -> оо
zzn+l
ип
2/2 4-1
2(2/2 —1) “
2 + -
.. /2
hm -------
СО 2___L
п
Данный ряд сходится.
Пример 4. Исследовать сходимость ряда
1 , 1 • 2 , 1 • 2 • 3 ( . п\ .
10 ‘ IO2 "Т" юз “+-••• "Г i0n ~Г •
§ 123] ДОСТАТОЧНЫЕ ПРИЗНАКИ СХОДИМОСТИ РЯДА
315
Решение.
1.2-3 ... п , _ 1 - 2-3 ... л (и-pi),
Un 10n ’ UnAA 10n+1 ’
nn+1 1 -2-3 ... n (n -pl) . 1-2.3... n n -p 1
10n+l ’ 10" ~ 10 ’
lim ^±1 — Hm —4т— — co.
n->OO n->oo
Данный ряд расходится, так как найденный предел оказался
больше единицы.
При исследовании ряда на сходимость может оказаться
Ит ^”±1=1.
п -> со
В этом случае признак Даламбера ответа не дает, а потому
для исследования ряда нужно применить другие приемы.
Упражнения
Исследовать сходимость рядов
1в Ь2~^ 2^22 + зТ2з + •“
2 J___|__1___I__1__к ... -I_5______и
1.2 3 - 22 5.2:^ (2лг — 1) 2П ‘ ‘
з 1 -Р + --+ -1- п -1
’ 2.22 3.23 4 - 24 (n-pi)2n+1
4 4. о,оо1 + УбЖ+^(^ + ... + У^^ + ---
_ 10 . 102 юз ця
6< Т+П2+Ь27з+---+-71Г+-"
) 3 | 32 , 38 , 34 , , 3“ ,
'• 1 +1.2+1-2.3+1.2-3.4+'" + л!+-"
8. ч—U-н—Р-н—р+..ч—Р+..
2^2 31<3 4^4 nV п
9 1_] Ь2 1-2.3 1-2.3-4 п!
»• 2 22 о" 23 т 24 т — Т2» Т —
316
РЯДЫ
[гл. XIV
И* 1.2 + 2.3 + 3.4 + 4-5+ ” +л(« + 1)
2 22 23 2п
12' Ккй + 200о + з00б+ 1000л + '"
§ 124. Признак сходимости знакочередующихся рядов.
Знакочередующимся рядом называется ряд вида
z/i — ^2 + — и4: + — ив + • • • + (— 1 )П И ип “Ь • • •» (1)
где и±, и2, и3...—числа положительные. Докажем следую-
щую теорему:
Если в знакочередующемся ряде каждый член по абсо-
лютной величине меньше предшествующего и если
lim ип = 0,
П -> оо
то ряд сходится.
Доказательство. Обозначив буквой т четное число
членов ряда (1), напишем сумму т его членов:
— их — U2~\-tl3 — Il -----UQ~\~ ... 4“ ит^1---ит>
Эту сумму можно представить в следующем виде:
$т = (и1 ^) + (^з—+ —йб)+ • • • +(^7?г-1—ит) (2)
ИЛИ
' (^2 ^з) (^4 ^б) • • • (^етг-2 ^т— 1) (3)
Согласно условию, разности в скобках равенства (2)
положительны; следовательно, сумма 8т с возрастанием т
возрастает. Разности в скобках равенства (3) также положи-
тельны; поэтому
^1*
Sm, возрастая при т —> оо, остается меньше up значит, 8)П
имеет предел, т. е.
lim Sm = 8. (4)
m-> 00
Мы доказали, что сумма четного числа членов 8т имеет
предел при т —> оо.
Докажем, что сумма нечетного числа членов тоже
имеет предел при т —> оо и притом тот же самый. Отсюда
§ 124] ПРИЗНАК СХОДИМОСТИ ЗНАКОЧЕРЕДУЮЩИХСЯ РЯДОВ 317
будет следовать, что сумма любого числа п членов ряда (1)
Sn имеет предел при п -> оо.
ВозьмелМ сумму нечетного числа /п —|— 1 членов ряда (1);
тогда
Перейдя к пределу при т —> оо, получим:
lim Sm+l= lim + lim um+1.
in -> oo in > CO in -> OO
Приняв во внимание равенство (4) и условие теоремы, на-
пишем:
Hm SOT+) = SH-0 = 5.
in -> ОО
Таким образом, при всяком п, как четном, так и нечетном,
предел суммы членов ряда (1) при п -> со один и тот же,
т. е. существует
lim Sn — S.
П -> оо
Следовательно, ряд (1) сходится.
Доказанная теорема служит достаточным признаком
сходимости знакочередующихся рядов.
П р и м е р. Исследовать сходимость ряда
1 _ J - 1 _1с±_ I
1 2" ‘ 3 4 ‘ ‘ ‘ п
Решение. Так как
и
то согласно доказанной теореме данный ряд сходится.
Упражнения
Исследовать сходимость рядов:
У 2 У 3 У 4 Уп
1 1 1 (— 1V1+1
2‘ 1-“Г2+ Ь2Тз~1-2-3-4 й Ь
о 1 2 3 4 (-!)«+*„
3. + 2ra_j +••.
318
РЯДЫ
[гл. XIV
§ 125. Абсолютно сходящиеся ряды. Пусть дан ряд
4“ ^2+ ^3 + ^4+ • • • + ^н + • • • > (О
членами которого служат как положительные числа, так и
отрицательные. Напишем новый ряд, состоящий из абсолют-
ных величин членов ряда (1):
I и\ I +1 и2 [ +1 из 1 +1 и41+ • • • +1 ип\ + • • • (2)
Можно доказать, что если ряд (2) сходится, то схо-
дится и ряд (1).
Определение. Ряд называется абсолютно сходя-
щимся, если сходится ряд, составленный из абсолютных
величин всех его членов.
Пример. Ряд
абсолютно сходящийся, так как ряд
составленный из абсолютных величин членов ряда (3), схо-
дится.
Однако не всякий сходящийся ряд есть ряд абсолютно
сходящийся. Например, ряд
(4)
сходится (см. пример § 124); но ряд, составленный из абсо-
лютных величии его членов
1 +т+4+4+4+4+••• •••’
есть гармонический, а потому расходится (§ 122).
Ряд (4) называется не абсолютно или условно сходящимся.
Определение. Сходящийся ряд называется не абсо-
лютно или условно сходящимся, если расходится ряд,
составленный из абсолютных величин всех его членов^
§ 126]
ФУНКЦИОНАЛЬНЫЕ РЯДЫ
319
Упражнения
1.
2.
Выяснить, абсолютно или не абсолютно сходятся ряды:
1 2 I 3 А_Ц »(-I)"*1 ,
2 4 8 16 ‘ ” ”1" 2« ’
__1 + J____L + J__...+±d£ - .
§ 126. Функциональные ряды. Пусть дан ряд
/.i(x) + /2W + /3 W+ • • • +fn W+ • • - CD
членами которого служат не числа, а функции аргумента х.
Такой ряд называется функциональным. Примером функцио-
нального ряда может служить ряд
1 +х-ь-х24-^3+ ...•+*”+ ...» (2)
представляющий собой геометрическую прогрессию. Если
дать аргументу х какое-либо численное значение, то функ-
циональный ряд обратится в числовой.
Может оказаться, что функциональный ряд при одних
значениях х сходится, при других расходится. Совокупность
всех значений х, при которых ряд (1) сходится, называется
областью сходимости ряда.
В пределах сходимости ряда, сумма его членов будет
функцией х.
Обозначив эту сумму через /(х), можем записать:
f (х) — Л (х) + /2(х) + /з (х)+ • * • +А(х) + • • •
Написанное равенство справедливо только для значений х
в области сходимости ряда; в этом случае оно представляет
собой разложение функции /(х) в ряд функций /.(х), /2(х),
/з(х), ... Разберем пример.
Ряд (2) при | х | < 1 является бесконечно убывающей
геометрической прогрессией, а потому сходится; при |х|> 1
этот ряд, представляющий собой бесконечно возрастающую
геометрическую прогрессию, расходится. Данный ряд рас-
ходится и при | х | = 1. Таким образом, областью сходимости
ряда (2) является | х| < 1 или иначе — 1 < х < 1. Найдя
сумму членов ряда (2), как бесконечно убывающей геоме-
трической прогрессии получим:
320
РЯДЫ
[гл. XIV
Теперь мы можем написать равенство
* ==l+x + x2 + x3+... + xn+..>
справедливое только при значениях аргумента |х| < 1. Это
равенство представляет собой разложение функции -у-^—
JL — X
в ряд по степеням х.
§ 127. Степенные ряды. Степенным рядом называется
функциональный ряд вида
а^ ~Н <4* “Ь" ^2^^ + а3х* —j— а^х* —... —j— а.пхп -j— ..., (1)
где я0, аи а2> а3, а^ ... — постоянные коэффициенты.
Если в ряде (1) дать аргументу х какое-нибудь значение,
то получим числовой ряд, который будет сходиться или рас-
ходиться в зависимости от значения х. В полных курсах
анализа доказывается, что для любого степенного ряда суще-
ствует непрерывная область значений х, при которых этот
ряд сходится. Эта область значений х обычно называется
промежутком сходимости степенного ряда *). Применяя
известные нам признаки, можно найти этот промежуток
сходимости.
Пример. Исследовать сходимость ряда
X । X"1 । Х^ । Х^ I I X 1 /О\
Т+ + + т + • • • + ~/Г + ” • ' '
Решение. Применим признак Даламбера к ряду
Pd I I I •«"! [ /ох
1 -t- 2 ' 3 4 *” • • • “I" n “r • * ’ W
Для этого ряда имеем:
\хп\ _ ип+г | хп^ | . | xn | = л |x|
n 9 n -f-1 * an n -p 1 n n -J-1
*) Иногда промежуток сходимости состоит из одной точки
(х = 0), в этом случае ряд сходится только при х = 0.
СТЕПЕННЫЕ РЯДЫ
321
§ 127]
Отсюда находим:
lim ^±1
П->ОО
lim
= | х | lim -----р = | х |.
п-> оо 1 _г 2_
п
Для сходимости ряда (3) достаточно, чтобы
lim < 1, т. е. | х | < 1,
п -> оо
или иначе
— 1 <х< 1.
Отсюда следует, что ряд (2) сходится абсолютно при значе-
ниях х, удовлетворяющих последним неравенствам, т. е.
при всех значениях х между —1 и +1, исключая крайние
значения
х — — 1 и х = 4"
Вопрос о том, будет ли ряд (2) сходиться при х = — 1
и х = 4- 1, нужно исследовать особо.
Положив в исследуемом ряде х =—1 и = полу-
чим два ряда:
^2 3^4 п - 1
И
1 +т+4+4+ • ••+4+ • • •
Первый ряд знакочередующийся, он удовлетворяет теореме
§ 124, а потому сходится, второй же ряд гармонический,
а потому расходится. Итак, исследуемый ряд сходится при
— 1 х < 1, причем при — 1 < х < 1 сходится абсолютно.
Дифференцируя ряд (1), получим также степенной ряд:
^4-2^2-^+ Зя3х24~ 4я4х34~ ... 4~ папхп-г 4~ • • •
В полных курсах анализа доказывается следующая теорема:
степенной ряд можно почленно дифференцировать и
интегрировать сколько угодно раз, при этом полученные
ряды имеют тот же промежуток сходимости, что и
пе рв оначале ный.
Примем эту теорему без доказательства.
21 Зак. 3032, И. Л. Зайпев
322
РЯДЫ
[гл. XIV
Упражнения
q Х I I X*
• 1 ' 1*2 ' 1-2-3
Исследовать сходимость рядов:
у2 у4 «гЗ
1-т+^ + т+-+^г +
х™
Vn
, хп
* п!
4,1.2"^1.2.3.4‘*' 1 - 2-3-4.5-6
х™
(2/г)!
5. х + 2х2 + Зх3 4х4 ••• + пхП + • • •
§ 128. Ряд Маклорена. Возьмем функцию f(x)> разла-
гающуюся в степенной ряд:
У(х) = а0 + агх+а2х2 а3х3 + ... + апхп + ... (1)
Согласно теореме § 127 ряд (1) можно почленно дифферен-
цировать любое число раз, при этом полученные ряды будут
иметь тот же промежуток сходимости, что и ряд (1). Про-
дифференцируем ряд (1) п раз, будем иметь:
f (х) = at 4- 2а2х + Зя3х2 + 4я4х3
... +папхп^1+ • -
f" (х) = 2а2 + 2 • З«3х + 3 • 4я4х2 + ...
... -]-(л— 1)папхп^2
/'"(х) = 2 • Зл3-|- 2 • 3 • 4^4х+ ...
... +(и — 2)(^ — 1)папхп~3 + ...
(2)
и т. д.
Положив в равенствах (1) и (2) х = 0, получим:
/(0)=-йо. отсюда «о=/(0).
отсюда
//(0)=2а2, отсюда а «2— 1-2 ,
/да(0) = 2" За3> отсюда °3 ~ 1 • 2 • 3
и т. д.
§ 129]
ПРИМЕРЫ РАЗЛОЖЕНИЯ ФУНКЦИЙ В РЯД
323
Подставив найденные значения коэффициентов в равен-
ство (1), будем иметь:
/(х)=/(0) + Г (0) X + ^ + ... *”+••• (3)
Равенство (3) представляет собой ряд Маклорена, позво-
ляющий разложить функцию у — f(x) в ряд по степеням х.
§ 129. Примеры разложения функций в ряд.
Пример 1. Разложить в степенной ряд Маклорена
/(х) = ех.
Решение, Для этого находим:
f'(x) — ex, f"(x) = ex, f"(x) — ex и т. д.
Положив х = 0, получим:
/(0)=1, /'(0) = 1, /"(0)== 1, /'"(0) = 1 и т. д.
Таким образом,
у2 уЗ у71
‘”=1 + *+га+пЬ+---+у+--- <>
Ряд (1) сходится при любом значении х (см. упражнение 3
§ 127).
Пример 2. Разложить в степенной ряд Маклорена
/(х) = sin х.
Решение. Находим:
и
и
/(x) = sinx и
f (х) — cos х и
f (х) = — sin х и
f" (х) = — cos х и
/(0) = 0,
/'(0)=1,
Г(0) = 0,
Г(0)=-1,
И /<lv>(0) = 0,
и /<v)(0)=l,
/(•V)(x) = sinx и /<lv>(0) = 0,
/(V) (х) — cos X и /<V) (0) = 1,
f<VI>(x) = —sinx и /(VI)(O) = O,
/(VII)(x) = —COS X И /(vu>(0)=—1
И т. д.
Таким образом,
Xs . х3 х7 . . (—1)” !х2п 1 .
sinx—х зг+и”"71+• • • + (2л —1)1
21*
324
* РЯДЫ
[гл. XIV
Составив ряд из абсолютных величин членов ряда (2)>
исследуем его на сходимость. Применим признак Даламбера;
1л2"-1! . _ |х2"+1| .
“п ~ (2п — 1)! ’ "n+1 ~ (2л + 1)! ’
ап+1
lim =
« -> оо ип
~ (2/2 + 1)! '• (2/2 — 1)! 2/2 (2/2 + 1) ’
X2 1
lim —гтг —-£2 Ит -а—тй—г"тт- = О«
-> оо “Ь 1) п -> оо 2/2 (“/2 4“ 1)
Последнее равенство справедливо при любом х; следо-
вательно, ряд (2) сходится абсолютно при всяком значении х.
Пример 3. Разложить в степенной ряд Маклорена
/(х) = cos х.
Решение. Данная функция разлагается в ряд таким же
приемом, как и sinx. Однако ряд для cosx можно получить
проще. Так как степенной ряд (2) сходится при всех зна-
чениях х, то, дифференцируя его, получим степенной ряд,
сходящийся при том же условии (теорема § 127). Взяв про-
изводную от обеих частей равенства (2), найдем:
, Зх2 , 5х< 7хв , | (—l)x2n-2 ,
COsx= 1----т+—- —+ ... +------------------
или
, X2 . X4 Xе .
cosx 1 2!-Ь‘4| 6! ~Ь • • '
(—1)” х2п
(2л)!
(3)
Пример 4. Разложить в степенной ряд Маклорена
/(х) = (1 + х)та.
Решение. Имеем:
f (х) = (1 + хЛ
/ (х)=ш(1+х)™-1.
f" (X) = т (т — 1)(1 + х)т~2,
f" (х) = т (т — 1 )(т — 2) (1 + х)т'3,
f (0)=т;
f"(0)^=т (т — — 2)
н т. д.
§ 129] ПРИМЕРЫ РАЗЛОЖЕНИЯ ФУНКЦИЙ В РЯД 325
Таким образом,
(1 +хГ = 1 +отх4-^^^ + ”г(теТ* 19)(7-^хЗ+-..
1 • Z 1 • Z • о
I l)(m —2) ... [m — (n — 1)1 n . /4x
Если in— натуральное число, то ряд (4) обрывается на
(т+1)-м члене, так как последующие коэффициенты обра-
щаются в нуль; при т дробном или отрицательном этот ряд
бесконечный. Применяя признак Даламбера, можно показать,
что бесконечный ряд (4) сходится при |х| < 1.
Пример 5. Разложить /(х)= arcsin х в степенной ряд.
Решение. Применим формулу (4) к функции :
* = = (1 — = 1 + (_ В (_ Х2} _|_
]/ 1 — х2 \ 2 /
_±/_1 Л
о \ 9 I
-I---------'(-*2)2 +
_]--П—j —/ (_ Х2)3 4- ... =
1 • Z • О
==1+|х2+3.х4+^х6+ ... (5)
Интегрируя это равенство в пределах от 0 до х, будем
иметь:
X XXX X
f dx+if x2dx+lf x*dx+if х^х+--
о r о о о о
X x x X X
| arcsinx = |x + -|-|x3 *+^| x5 + j^| x7+ ....
0 0 0 J 0
. x3 . Зх5 , 5x7 .
arcsin x = x + — 4- -40+-П2+ ••• (6)
Так как ряд (5) сходится при |х| < 1, то и ряд (6) согласно
теореме § 127 также сходится при |х|<1.
326
РЯДЫ
[гл. XIV
Пример 6. Разложить в степенной ряд /(х) = arctgх.
Решение. Согласно формуле (4) имеем:
TJ—2 = (1 + = 1 + (-1) Х2 + ~ 1 X4 +
X -j- X 1 •
+ ~~1(~11~?2?з"1 — х6+ • • • = !— х2 + х*~Xе4- ... (7)
Умножив равенство (7) на dx и интегрируя в пределах от О
до х, получим:
X XX X X
J 1 f — J‘ x2dx-|~ J x4dx — j xGJx-(- ...»
о о о о и
отсюда
X X X X X
|arctgx = 1 x — i | x3 + -|-1 x6 —7 | x7 +
о OVOO
или
arctgx = x—-y+y — ... (8)
Ряд (8) сходится при | х | < 1, так как ряд (7) сходится при
| х | < 1 (теорема § 127).
§ 130. Приложение степенных рядов к приближенным
вычислениям. Степенные ряды имеют большое приложение
к приближенным вычислениям. Покажем это на примерах.
Пример 1. Вычислить sin 18°.
Решение. Угол 18° в радианной мере равен 0,3142.
Подставив значение х — 0,3142 в формулу (2) § 129, получим:
0 31423
sin 18° = sin 0,3142^0,3142 —
0,3142 — 0,0052 == 0,3090.
Пример 2. Вычислить -к.
Решение. Положив в равенстве (6) § 129 х = -^
и учитывая, что arcsin ~ , получим •— ~-f-
3
+ 2^40’ °ТСЮДа
я~3 + 1+ 9^^з + о, 125 + 0,0141 «3,14.
О • лХ)
§ 131]
РЯДЫ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ
327
1
П р и м е р 3. Вычислить ^~-dx,
о
Решение. Неопределенный интеграл данного вида не
может быть выражен в элементарных функциях. Однако его
можно в указанных пределах вычислить приближенно с по-
мощью рядов. Разделим обе части равенства (2) § 129 на х:
sin х
х
х2 t х4
3! + 5! ’
отсюда
i 11 1
f f — 4l f x^dx —
0 oo о
§ 131. Ряды с комплексными членами. Возьмем ряд
(ах М 4~ (а2 Ч~ • • • + (ап 4“ Ьп1) + .. • > (1)
состоящий из комплексных чисел вида an-\-bnlt где а и b —
действительные числа, a I — ]/—1. Ряд (1) называется схо-
дящимся, если ряды
^1 + ^2+ ^з + ••• ~ЬапЧ" ••• (2)
и
bi + #2 + b3 + ... + Ьп + ..., (3)
состоящие из действительных частей и коэффициентов при
мнимых членах ряда (1), сходятся. Пусть суммы рядов (2)
и (3) соответственно равны А и В; тогда сумма ряда (1)
будет равна А-[-В1. Например, сумма членов ряда
(1 + tz)+(4+4z)+ •" + (^4+^z)+ •••
328
РЯДЫ
[ГЛ. XIV
равна
(1 +-д-+у + <^+ ... 4-^7+ ..•) +
+ ••• +F1+ •')Z =
1
— ---2—I---—Г“ Z = y4~Z= 1,5 z.
1—L 1 L z
3 2
Докажем теорему:
Ряд с комплексными членами сходится, если сходится
ряд, составленный из модулей его членов.
Доказательство. Пусть сходится ряд
• • • + /4ЙЙ^+ • •
(4)
составленный из модулей членов ряда (1). Как видно,
Поэтому члены рядов (2) и (3) не превышают соответствую-
щие члены ряда (4). Следовательно, ряды (2) и (3) сходятся
и притом абсолютно (§ 125), а потому сходится и ряд (1).
Теорема доказана.
В некоторых случаях рассматриваются степенные ряды
c04-C4Z-ba2z2-|-a32:3-|- ... Н-«п^ге+ ....
где а$, alt а2, а3 ... — действительные или комплексные числа»
а z — комплексное переменное вида х-\-1у. Пользуясь дока-
занной теоремой и известными нам признаками сходимости,
можно исследовать сходимость и таких рядов.
§ 132. Формулы Эйлера. В § 129 мы представили пока-
зательную функцию ех в виде ряда (1) для действительных
значений показателя. В полных курсах высшей математики
доказывается, что ряд (1) не теряет смысла и в случае ком-
плексного показателя. Таким образом, можно написать:
e,=x+z+~+t-+-+-+... +7S+.. „(1)«)
где z — комплексное переменное вида x-J-Zy.
*) Можно показать, что этот ряд абсолютно сходящийся для
всех значений г.
§ 132]
ФОРМУЛЫ ЭЙЛЕРА
329
В частном случае, положив в равенстве (1) z = iyt по-
лучим:
W)n
п\
1пуп
п\
или
1 . . I /2У2 . Ру8 , /4У4 , /5У5
с’?' = 1 +1у+4-^-4-
Но
/2==—1, 13 = —1, /4=1, fi — i и т. д.»
е{У
гЗ
поэтому
^=14-Zy—...
е 2! 3! ’ 4! ‘ 5|
Выделив действительные и мнимые члены, напишем:
I (-РУ” , \ I
1 •”+• (2п)1 "Г •• J-T-
(2л—1)! “*"•••
Приняв во внимание формулы (3) и (2) § 129, получим:
e*v — cos у + i sin у.
Заменив в равенстве (2) у на —у, напишем:
e-w = cos(—j/)4-/sin(— y)t
(2)
или
(3)
е~Щ — cos у— I sin у.
Равенства (2) и (3) ввфажают связь между показательной и
тригонометрическими функциями. Эти равенства были даны
Эйлером.
Решив равенства (2) и (3) относительно cosj/ и sin у,
будем иметь:
j4±.e-iy . eiy — e-iy
cos у =-------- и sin у —------.
Заметим, что из равенства (2) легко получить новый вид
записи комплексного числа, имеющего модуль г и аргумент у,
а именно:
г (cos у -|-1 sin у) — ге^У.
330
РЯДЫ
[гл. XTV
Таким образом, комплексное число может быть записано
в трех формах: в алгебраической, тригонометрической и
показательной. Например,
1 4- //3 = 2^cos у 4-Z sin = 2е* г.
Формулы Эйлера позволяют установить периодичность
показательной функции. Действительно, заменив в равен-
стве (2) у на _у-|-2к, найдем:
^(?/+2л) г _ cos 2к) 4- i sin (у 4" 2^) = cos у 4~ Z sin у — е^.
Таким образом,
e(ij+2n) г _ егу>
или
eiy+2ni — eiy* (4}
Равенство (4) показывает, что е^ — периодическая функция
с мнимым периодом 2к/.
ГЛАВА XV
ГАРМОНИЧЕСКИЙ АНАЛИЗ
§ 133. Графики функций вида у== A sin сох. В даль-
нейшем изложении нам придется использовать функции вида
v = Л sin сох, а также их графики. Покажем на примерах,
как строятся графики таких функций.
Пример 1. Построить график функции у~ sin Зх.
Решение. Данная функция— периодическая; областью
ее существования служат все действительные числа. Построим
график этой функции для значений аргумента от х = 0 до
х = составив предварительно следующую таблицу зна-
чений х и у.
X 0 ТС т тс "3 7С 2" 2п: ”з“ 5тс 6 тс 7?С 6 4 тс т Зтс Т 5тс ”3 lh 6 2тс
У 0 1 0 — 1 0 1 0 ~ 1 0 1 0 — 1 0
Рассматривая каждую пару значений х и у как коорди-
наты точек графика данной функции, построим эти точки
и, проведя через них плавную линию, получим график функ-
ции j/ = sin Зх, представленный на чертеже 132 в виде сплош-
« 2*
ной линии —синусоиды с наименьшим периодом -у.
Как видно из чертежа, этот график можно получить
из графика функции у — sinx, изображенного на том же
чертеже пунктирной линией, уменьшив масштаб по оси Ох
в три раза.
Пример 2. Построить график функции у — 3 sin 2х.
332
ГАРМОНИЧЕСКИЙ АНАЛИЗ
[ГЛ. XV
Р е ш е н ие. Составим таблицу значений х и у.
X 0 7С ~4 7С 7 Зл 7С “Г Т 7п V 2я
У 0 3 0 — 3 0 3 0 — 3 0
График, построенный по точкам с вычисленными коор-
динатами, представляет синусоиду с наименьшим периодом
— = к (на чертеже 133 эта синусоида изображена сплош-
ной линией).
§ 134]
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
333
График функции y = 3sin2x можно получить и из гра-
фика функции у = sin х, представленного на том же чертеже
пунктирной линией, уменьшив масштаб по оси Ох вдвое и
увеличив его по оси Оу втрое.
§ 134. Гармонические колебания. I. Простые гар-
монические колебания. В естествознании и технике
часто наблюдаются периодические процессы, т. е. такие яв-
ления, которые повторяются через определенный промежуток
времени. Например, колебания маятника, явления переменного
тока и др.
Простейшее периодическое явление — гармоническое коле-
бание, совершаемое по закону
у = A sin (wt -4- <р0). (П
В равенстве (1) постоянный множитель А, представляющий
наибольшую величину, которую может иметь у, называется
амплитудой колебания, (ш/ -1~ ср0)— фазой колебания, а
со — частотой колебания.
Функция (I) — периодическая с наименьшим периодом—,
от прибавления которого к аргументу t функция не меняет
своего значения. В самом деле,
у — A sin + cpoj=Xsin(cn^-f~27u+<po)==24siti((D/4~cPo)’
Величина — определяет время, в течение которого про-
исходит одно колебательное движение, поэтому ее называют
периодом колебания. Обозначив ее буквой Т, можно на-
писать:
у.___2тс
а> *
откуда
Так как Т—время одного колебания, то -у------------число коле-
баний за время 2тг. Таким образом, величина со определяет
частоту колебаний. Преобразуем равенство (I), применяя
формулу для синуса суммы двух углов:
A sin (W <р0) — A (sin cos ср0 + cos wt sin<р0) =
— A cos ср0 sin (о/ + Л sin ср0 cos (о/.
334 ГАРМОНИЧЕСКИЙ анализ [гл. XV
Обозначив
а = A cos ср0 и b — A sin <р0,
получим:
у = a sin о/ b cos о/. (2)
Колебательное движение, происходящее по закону функ-
ции (1) или, что то же, по закону функции (2), называется
простым гармоническим колебанием, а график его — про-
стой гармоникой.
II. Сложные гармонические колебания. Не
всякий периодический процесс можно рассматривать как
простое гармоническое колебание. Очень часты случаи,
Черт. 134.
когда периодическое явление есть результат сложения несколь-
ких простых гармонических колебаний. Полученное результи-
рующее движение называется сложным гармоническим
колебанием, а график его — сложной гармоникой.
Итак, сложная гармоника есть результат сложения
нескольких простых гармоник или иначе — результат
наложения простых гармоник друг на друга.
Рассмотрим пример. Пусть даны две простые гармоники,
определяемые уравнениями:
у — sin/
и
у — sin 31.
На чертеже 134 эти гармоники изображены пунктирными
линиями, сложная же гармоника, являющаяся графиком
функции
у — sin/4" sin ЗА
§ 135] ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ 335
представлена сплошной линией. Любая точка сложной гармо-
ники имеет ординату, равную сумме ординат точек, лежа-
щих на простых гармониках и имеющих одну и ту же
абсциссу. Так, например,
АВ = АВ. + В.В = АВ. + ЛВ2,
CD = CD. — DD. = CD. — CD2 = CD. 4~ (— CD2).
Как видно из чертежа, результирующая гармоника будет
повторяться через каждый промежуток t = т. е. будет
периодической, но по своей форме она уже теряет харак-
тер синусоиды.
Можно доказать, что вообще при сложении простых
гармоник с разными частотами получается сложная гармоника
не синусоидального вида, а при сложении гармоник с одина-
ковыми частотами — гармоника того же вида, что и простые.
§ 135. Тригонометрические ряды. Как было указано
в § 134, наблюдаются периодические процессы, которые
нельзя рассматривать как простые колебательные явления.
Положим, что какое-либо периодическое движение задано
при помощи некоторой периодической функции, отличной
от (1) § 134. Чтобы иметь представление о характере этого
движения, данную функцию разлагают в ряд простых гармо-
ник, имеющий следующий вид:
4- (a. cos со/ 4“ b. sin со/) 4~ (^2cos 2ю/ 4" ^2 s*n 2co/) 4“ • • •
... 4-(tfwcos nut 4- bnsm /zco/)4~ ... (1)
Ряд (1) называется тригонометрическим рядом.
а числа а., а2 ... b.t b2.....—коэффициентами ряда.
Положим для простоты
х = со/
и будем считать, что ряд (1) сходится при всех действи-
тельных значениях х к данной функции |т. е. сумма ряда
равна функции /(х)], тогда можно написать:
/(х) = 4- (a. cos х 4~ b. sin х) 4~ (а2 cos 2х 4“ b2 sin 2х)4~. • •
• • • + (ап cos пх 4" bn sin пх) 4~ • • •
336
ГАРМОНИЧЕСКИЙ АНАЛИЗ
[ГЛ. XV
или короче
оо
/(*)=-??+ У (% cos их 4~ bn sin их).
2, давя
(2)
Как видно, функция /(х)— периодическая с периодом 2~,
так как прибавляя к х (или вычитая из х) 2тс целое число
раз, мы не изменим величины каждого члена ряда (2), а,
следовательно, не изменим и величины суммы (2).
Отсюда следует, что тригонометрический ряд достаточно
рассматривать только для значений х от 0 до 2к (или от — тс
до-|-7г), так как за пределами указанного промежутка зна-
чений аргумента величина каждого члена ряда будет периоди-
чески повторяться.
Чем больше простых гармоник ряда (2) мы сложим,
тем точнее результирующая гармоника будет представлять
периодическое движение, заданное функцией /(х). По-
этому вопрос о разложении функции в тригонометрический
ряд приобретает очень важное значение в прикладных
науках.
Процесс разложения функции, представляющей сложное
периодическое движение, в тригонометрический ряд назы-
вается гармоническим анализом.
§ 136. Коэффициенты Фурье. Ряд Фурье. Чтобы раз-
ложить периодическую функцию /(х) с периодом 2тс в тригоно-
метрический ряд, нужно найти коэффициенты этого ряда.
Мы приводим здесь без вывода формулы, по которым про-
изводится вычисление этих коэффициентов:
4-тс
= f{x)dx,
— ГС
ап—^ j* f(x)cQsnxdxt !•
— гс
+ ТС
Ьп = -i- У* /(х) sin пх dx,
—тс
(1)
где п — 1, 2, 3, 4, ...
§ 136]
КОЭФФИЦИЕНТЫ ФУРЬЕ. РЯД ФУРЬЕ
337
Числа, полученные по формулам (1), называются коэф-
фициентами Фурье*), а тригонометрический ряде этими
коэффициентами — рядом Фурье.
Определение. Ряд
где
со
^+2 (flncoszzx + ^nslnzzx)»
п-1
4-7С
ао=-^ J f(x)dx,
—те
ап—~ j*f(x)cosnxdx,
— те
4-7С
дп = ~ I f(x)sinnxdx
— к
л=1,2, 3,4
1
называется рядом Фурье функции f(x).
Если ряд Фурье сходится к функции f(x), то можно записать:
со
7(*) = -тг + 2 (anCOSiix-[- bnsinnx). (2)
n = t
Следует заметить, что величина интегралов в формулах (1)
не изменится, если пределами их взять 0 и 2тг. В этом слу-
чае формулы для определения коэффициентов Фурье можно
написать в следующем виде:
2тс
а0=^~ f f(x)dx,
О
2 те
cos пх dx,
о
2те
~ j* f (х) sin пх dx,
о
где п — 1, 2, 3, 4 ...
*) Формулы (1) были даны еще Эйлером (1707—1783), но широко
использовал их французский математик Ж. Фурье (1768—1830).
22 Зак. 3032. И. Л. Зайцев
338 ГАРМОНИЧЕСКИЙ анализ [гл. XV
Формулы (3) представляют иногда большие удобства,
чем формулы (1). *
§ 137. Возможность разложения непериодической функ-
ции в ряд Фурье. Периодическая функция, как мы уже
знаем, определяет колебательное движение. Однако бывают [
колебательные явления, которые совершаются по закону
непериодической функции. Поэтому для изучения колеба-
тельного движения, подчиняющегося непериодической функ-
ции, выгодно разложить эту функцию в ряд Фурье, что
оказывается возможным при некоторых условиях, о кото-
рых скажем в § 138.
Пусть, например, задана функция
/(х) —уХ при —тс<^х<^тс, (1)
график которой изображен на чертеже 135 отрезком прямой ЛВ.
Покажем, что для разложения данной функции в ряд Фурье
можно и к ней применить правила § 136. Для этого введем
вспомогательную периодическую функцию ср (х) с периодом 2тс
при условии:
<р(х) = /(х) в промежутке значений х от —к до -|-тс, (2)
за пределами же указанного промежутка <р (х) /(х).
К функции <р (х), как к периодической, можно применить
формулы § 136. Но мы знаем, что тригонометрический ряд
достаточно рассматривать для промежутка значений аргумента
от —тс до +тс (§ 135), поэтому формулы § 136 имеем право
применить не только к функции ср (х), но, согласно усло-
вию (2), и к заданной.
§ 138]
УСЛОВИЯ ДИРИХЛЕ. ТЕОРЕМА ДИРИХЛЕ
339
Величина суммы ряда Фурье, полученного для функции (1),
вследствие периодичности его членов будет повторяться через
каждый промежуток, равный 2тс, и принимать значения дан-
ной функции (1). Поясним это геометрически. С этой целью
перенесем отрезок АВ (черт. 135), сохраняя его направление,
вдоль оси Ох на расстояния, равные 2тс, 4тс и т. д., вправо
и влево от начала координат или, как говорят, продолжим
периодически график функции (1). Возьмем значение х внутри
промежутка от —тс до -j-тс, например,
x=0D = 2,
тогда ордината
DC = /(2) = 4>2==1
даст величину суммы ряда Фурье функции (1) при х = 2.
Ясно, что при
x=OD2 = 2 + 2k
или
х — ODr — 2 — 2тс
величина ординат D2C2 и а следовательно, и сумма
ряда при тех же значениях х не изменится и будет равна
по-прежнему единице.
Обратим внимание, что для значений х вне промежутка
от —тс до -f-тс сумма ряда Фурье функции (1) и значения
этой функции не равны между собой. Действительно, сумма
этого ряда при х = 2-|--2тс, как мы узнали, равна 1, а зна-
чение функции
/(2+ 2тг) = D2M = 1 (2+ 2к) = 1 + к.
Все сказанное выше подтверждает мысль, что ряд Фурье
функции имеет смысл рассматривать только в промежутке
—тс х тс.
§ 138. Условия Дирихле. Теорема Дирихле. Как было
уже сказано, функция /(х) с областью существования —тс<^
может быть разложена в ряд Фурье, сходящийся
к данной функции /(х) при определенных условиях. Эти
22*
340 ГАРМОНИЧЕСКИЙ АНАЛИЗ [гл. XV
условия, называемые условиями Дирихле, заключаются в сле-
дующем:
1) функция должна быть непрерывной в промежутке
значений х от —тс до 4-тс или может иметь в указан-
ном промежутке разрывы первого рода, но только в ко-
нечном числе;
2) функция должна иметь конечное число максимумов
и минимумов или не иметь их совсем.
Одной из основных теорем, применяемых при исследова-
нии рядов Фурье, является теорема Дирихле.
Теорема Дирихле. Если функция /(х) с областью
существования —тс<^х<^тс удовлетворяет условиям Ди-
рихле, то
1) ряд Фурье функции f(x) сходится в указанном
промежутке значений х;
2) сумма этого ряда сходится к функции f(x) во всех
точках ее непрерывности;
3) в каждой точке разрыва функции сумма ряда равна
половине скачка функции;
4) при х — тс и х — — тс сумма ряда одинакова и равна
/(--*) + /(*)
2
Примем указанную теорему без доказательства.
Заметим, что в дальнейшем изложении мы будем пользо-
ваться только функциями, удовлетворяющими условиям Ди-
рихле, а потому в каждом разбираемом примере не будем
останавливаться на этих условиях.
Прежде чем перейти к разложению функций в ряды
Фурье мы должны познакомиться с методом интегрирования по
частям, без которого нельзя определять коэффициенты Фурье.
§ 139. Интегрирование по частям. Пусть и и v— диф-
ференцируемые функции х, тогда по правилу IV § 67 имеем:
или
d (ttv) — udv-\-v du,
откуда
udv — d (uv) — v du.
(1)
§ 1391
ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ
341
Взяв интеграл от обеих частей равенства (1), получим:
J udv~ J* d(uv)— j*v du
или
§udv=ztiv— J* vdu. (2)
Равенство (2) служит формулой интегрирования по
частям.
Пример 1. Найти J* xcosxdx.
Реш ен ие. Положим
тогда
и — х,
dv — cos х dx,
du — dx,
v== I cosxdX" sin x
(3)
(произвольное постоянное интегрирования напишем в окон-
чательном результате).
Подставив (3) во (2), получим:
х cos х dx — х sin х — I sin x dx — x sin x 4" cos x 4~ c.
Пример 2. Найти j x cos nxdx.
Решение. Положим
и — x,
dv — cos nx dx,
тогда
du = dx,
v— Jcos nx dx.
( , dz\
nx — z, dx — —j, получим:
v— I cos nxdx —— sin 2 = — sin/гх.
J fi ll
342
ГАРМОНИЧЕСКИЙ АНАЛИЗ
[ГЛ. XV
Согласно формуле (2) имеем:
, X sin пх
х cos пх dx =-------------
п
j* sinnxdx *) =
х sin пх 1
п п
— cos пх . х sin ил; . cos их .
------------р с = ------------------к- с. (4)
п 1 п 1 п2 • v
Аналогично можно найти:
X cos пх , sin их
х sin пх dx —-----------5—
п 1 п2
Пример 3. Найти J* х2 cos их dx.
Решение. Положим
(5)
откуда
и — х2,
dv = cosnxdx,
du — 2х dx.
, sin пх ,
CQsnx dx ——-—(см. пример 2)<
Подставив (6) во (2), получим:
о , х2 sin пх 1
х2 cos nxdx —----------/
х2 sin их 2, . .
—--------------/ х sinnxdx.
n nJ
2x sin nx .
---------dx —
n
Приняв во внимание равенство (5), будем иметь;
, х2 sin пх 2 / х cos пх . sin пх
J x^osnxdx = —-------------------------
_ х2 sin пх f 2х cos пх 2 sin пх ,
п ' п2 п%
Таким же образом найдем:
/о . х2 cos пх . 2х sin пх . 2 cos пх .
х2 sin пх dx —--------------------------------------5----Н с,
п 1 п2 1 п* 1
*) Применяется подстановка пх = z и dx — —.
§ 140] ПРИМЕРЫ РАЗЛОЖЕНИЯ ФУНКЦИЙ В РЯД ФУРЬЕ
343
§ 140. Примеры разложения функций в ряд Фурье.
Пример 1. Разложить в ряд Фурье функцию:
/(*) =
х при —
О при 0 < х те.
Решение. По формулам (1) § 136 найдем коэффициенты
Фурье
Но
О dx — с, так как de = 0 • dxt
кроме того,
dx~c — с = 0.
Поэтому
Приняв во внимание равенство (4) § 139, получим:
cos(—пя) 11 _
Jj~
1 I J s^n Лтс cos nrz \ _
7C \ ' пЧ n П2 )
I /1 7C • 0
П \n2 n
COS ПК
n2
-L-(l—cos«k).
344
ГАРМОНИЧЕСКИЙ АНАЛИЗ
[гл. XV
Отсюда
^=^(1-cos’c)=i(1 + 1)=T'
°2 ~ ~ COS 2к) = st (1 ~ 1 > = °’
«з = 5Гз?(1 — cos Зя)=it(1 ~ cos K) = it(I + П=
o< = cos = it(1 ~ cos 0) == it(1 —= 0
и т. д.
Как видно, при четном значении п коэффициенты ап равны
нулю.
sin пх
о
xsin nx dx + -~ j
о
—
Согласно равенству (5) § 139 получим:
} ( — x cos nx I sln nx
\ n
— 0» cos 0 t sin 0
n ' n2
л . л тг cos пк
.0 =
n2
Г7C COS (—ПК} . sin (—Птс)
| п п2
sin пк 1 / к cos пк .
' n * n2 ) к \ n . '
7C COS пк\ _ COS ПК
n ) n •
^2
^3
и т. д.
*4=
Отсюда
, COS 7C <
/>,==--— = 1,
cos 2u 1
2 ~ —T*
cos Зтс cos 7C 1
3 ~ 3-’
cos 4k cos 0 1
4 4 4
Искомый ряд напишется так:
~ т+4cos х+itcos Зх+itcos 5х + • • •
sin 2х , sin Зх sin 4х
...+SlaX------2---1---g-------4-
§ 140] ПРИМЕРЫ РАЗЛОЖЕНИЯ ФУНКЦИЙ В РЯД ФУРЬЕ 345
Согласно теореме Дирихле этот ряд сходится к данной
функции во всех точках промежутка значений х от —тс до
-4-тс, кроме х — — к и х = тс. В самом деле, при х — —тс
/(—тО+УС11) —те 4-0 те
м х — п сумма ряда равна —--------' 1 = —
между тем как значения функции при х — — тс и х = тс
соответственно равны —тс и 0, т. е. не совпадают с сум-
мой ряда.
Таким образом, можно написать:
х те , 2 / . cos Зх . cos 5х , \ .
/ (х) = — т+ ~^С08хЧ-------------------г •••; +
. / . sin 2х . sin Зх sin 4х . \ .
+ -----g---1---g----------H. J при — K<
Пример 2. Разложить в ряд Фурье функцию
f(x) — при 0 < х < 2тс.
Решение. Здесь для определения коэффициентов Фурье
используем формулы (3) § 136.
*) I cos пх dx находится подстановкой: пх = z и dx = —.
346
ГАРМОНИЧЕСКИЙ АНАЛИЗ
[ГЛ. XV
Приняв во внимание равенство (4) § 139, будем иметь:
. 1 |2к (х sin пх , cos пх'
sxnnx—тг (---------------------9—
|0 2 |0 \ п /г2 ,
1 j тс , . л . лч 1 / 2тс sin 2тстг ,
— — (sin 2тиг — sin 0)— -77 (------------------к
71 [2п 4 ' 2 \ п 1
I cos 2тги 0 • sin 0 cos 0 \ 1 __
' п2 п п2 /J
I / тс . л тс sin 2тстг cos 2ти/г . л
— — (<т- sin 2тс/г-------------------------Р 0 -
7t \2п п 2п2 1
1 / тс ~ тс • 0 1
Т\2л* п 2п2
1
2zz2,
Таким образом, все коэффициенты aQt а19 а2> . равны
нулю.
bn = iJ (y-y)sinnx^ =
о
sin пх dx —
2тс
cos пх 1 Г
----------Y / xsin nxdx
о
Применяя к I хsin nxdx формулу (5) § 139, получим:
§ 141] РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ 347
Искомое разложение будет:
. sin 2х , sin Зх
sin хЧ--------1----—
Полученный ряд сходится к функции у — - ~~ при всех
значениях х в промежутке от 0 до 2к, кроме х — 0 и х = 2тг>
как это и следует из теоремы Дирихле.
Таким образом,
~— = sin х
sin 2х
sin Зх
~3~
при 0 < х < 2к.
§ 141. Ряды Фурье для четных и нечетных функций.
Функция f(x) называется четной, если при подстановке
вместо х величины — х знак функции не меняется, т. е.
/(—х) = /(х). Например, х2, cosx— четные функции, так
как (— х)2 = х2, cos (-- х) = cos х.
Функция /(х) называется нечетной, если при подста-
новке вместо х величины — х знак функции меняется на
противоположный, т. е. f(—x) — —f(x). Например, х3,
sin х— нечетные функции, так как (— х)3 = — х3, sin (— х)=
—---sin
Заметим, что произведение двух четных или двух не-
четных функций есть четная функция, а произведение
четной функции на нечетную есть функция нечетная.
В самом деле,
(—х)2 cos (—х) = х2 cos х—произведение двух четных функций,
(—х)3 sin (—х) = х3 sin х— „ „ нечетных „ ,
cos (—х) sin (—х) = — cos х sin х — произведение четной функ-
ции на нечетную.
График четной функции симметричен относительно оси Оу,
график нечетной функции симметричен относительно начала
координат. Примеры таких графиков даны на чертеже 136
для четной функции, на чертеже 137 — для нечетной.
Если /(х)—четная функция, то
J f{x)dx = 2/(xjdx,
—а О
348
ГАРМОНИЧЕСКИЙ АНАЛИЗ
[ГЛ. XV
если /(х)—нечетная функция, то
а
У /(х)<7х = 0,
—а
Эти равенства можно подтвердить геометрическими сооб-
(I
ражениями. Пусть J* f(x)dx выражает площадь фигуры,
заключенной между графиком функции /(х), двумя прямыми
х —— а и х = а и осью Ох,
тогда в случае четной функ-
ции /(х) эта площадь равна
удвоенной площади фигуры,
Черт. 136.
Черт. 137.
образованной тем же графиком, осью Ох и прямыми х = 0
и х~~а (черт. 136); в случае нечетной функции площадь
равна нулю, так как она состоит из двух равных площадей
с противоположными знаками (черт. 137).
Приняв во внимание сказанное, можно упростить фор-
мулы (1) § 136, написав их в следующем виде:
для случая четной функции
ао—~1
u nJ
о
(1)
а”~ J
О
bn = G,
cos nxdx,
§ 141] РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ 349
для случая нечетной функции
ао=0 и яп = 0,
2 Г <2 *)
/ /(x)sin nxdx.
о
Как видно, ряд Фурье (2) § 136 для четной функции
будет состоять только из косинусов, т. е.
= + 2 ancosnx>
72 = 1
а для нечетной функции — только из синусов, т. е.
/(*)= 2 bn sin пх.
п-1
Пример 1. Разложить в ряд Фурье функцию
f (х) = | х | при — тс х тс.
Решение. Функция у— |х|— четная (см. черт. 73),
а потому согласно формулам (1) имеем:
2 f , 2 Гх2 1 z ,
I х dx = — тг — — (тс2 — 0) — тс,
° тс J тс L 2 тс4 * * 7
о
тс
2 Г
ап = — I х cos пх dx.
о
Приняв во внимание равенство (4) § 139, найдем:
_____ 2 р (х sin пх t cos пх\ __
п к 1о \ п ‘ л2 /
2 Гтс sin итс cos тгтс /0 • sin 0 . cos 0\~J __
тс L п и2 \ п ’ п2 /J
cos птс 1 \
п2 п2)
2 /тс « 0 cos птс 0 1 \____ 2 /
тс \ п * п2 п п2) тс \
2
---^"(COSHTC-----1).
TC/Z2 v 7
350
ГАРМОНИЧЕСКИЙ АНАЛИЗ
[ГЛ. XV
Отсюда
Gj = —=5 (cos к — 1) = — (—1 — 1) = — —,
1 тс • I2 4 ' тс 4 ' тс ’
2 2
c2 = -A-2(cos 2-— 1) = _±_(1 — 1) = 0,
2 тс • 22 х 7 ТС • 22 4 7
2 2
fl3 = ^32(cos Зя— l) = ^(cos~—1) =
2 4
т: • З2 4 ' тс • З2
«4 = ^742(cos 4я— 1) = ^L(cosO— 1) =
9
= 7^(1—1) = ° и т- «•
7С • 4Z 4 '
Искомое разложение будет:
тс 4 4 о 4 £
vr---cos х----cos Зх-------^cos5x— ... =
2 тс ТС • З2 ТС • 52
тс 4 / . cos Зх . cos 5х , \
= 2-k\cosx4—да—Ь-52—I-...).
Применяя теорему Дирихле, можно показать, что получен-
ный ряд сходится к данной функции при всех значениях х
от —ТС до 4~тг.
Следовательно, можно написать:
при —тс<^ х<^тс.
Пример 2. Разложить в ряд Фурье функцию
/(х) — | sin х | при — тс х к.
Решение. Данная функция четная; применяя формулы (1),
получим:
— cosx =
2 , 2 f t 4
—------(cos тс — cosO) =---------(— 1 —1) = —
тс 4 z тс 4 ' тс
§ 141] РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ 351
Положив п — 1 в формуле для ап, будем иметь:
тс те
sin х cos х dx = — / 2 sin x cos x dx —
1 7C J П J
0 0
1 f • П Л 1 |TC cos 2x 1 I"
= — / Sin 2X£?X — — ——= —— cos2x =
я J к |0 2 21Z Io
0
— — J-(cos 2k— cos 0) = — — (1 — 1) = 0.
Для n = 2, 3, 4 ... получим:
тс те
an—dLj* sinxcosnx dx-=^^ J 2 sin x cos nx dx.
о о
Представим произведение 2 sin x cos пх в следующем виде:
2 sin x cos nx — sin(/z + V)x — sin(n— l)x$),
тогда
тс
an=2-1 [sin(/z—{— l)x — sin (/г— l)x]Jx =
о
1 |TC Г COS (n + 1) X . cos (n — 1) X~1 **)
к Io L n + 1 ‘ n — 1 J
1 Г C0S (n4~l) | COS (n — 1) к / cos 0 . cos 0 \1
TL zz —|— 1 n — 1 \ n + 1 ’ n — 1 /j
1 Г C0S (^ + 1) I cos (/r—1)k 1_________________1 J ___
"к" [ n 4~ 1 * n — 1 ' n + 1 n — 1] “
1 Г cos (zz —1) re . cos (n — 1) к_______2 "|
К L «4-1 ‘ n — 1 —1J *
*) Это равенство легко проверить, применив к правой части
его формулу для разности синусов двух углов.
**) | sin (п 4- 1) х dx находится подстановкой: (п 4~ 1) х = z и
dz
dx = • Аналогичную
J sin (п — l)xdx.
подстановку применяем и
к
352
ГАРМОНИЧЕСКИЙ АНАЛИЗ
[ГЛ. XV
Отсюда
1 / cos 7л , cos 5л 2\_ 1 / cos л . cos л 2^_
^6 — V \ 7 ’ 5 35/ “ V 7 “Г“ ”~5 35Г~
2/J____1_1А —______1-
л \ 7 5 35/ 35л И 1 ’ ,й”
Искомое разложение напишется так:
2 4 п 4 л 4 г
----— cos 2х— тт— cos4x — -гр— cos bx— ... —
л Зл 1ол Зол
2 4 /cos 2х । cos Ах f cos 6х f \
“Т Т\ЬЗ ' ~3^~5 Н~ТГ7 Г • • J-
Согласно теореме Дирихле полученный ряд сходится к дан-
ной функции при — л х л, поэтому
. . । 2 4 /cos 2х , cos 4х , cos 6х . \
| sin х I = - - - -57^ + • • •)
при всех значениях х указанного промежутка.
Пример 3. Разложить в ряд Фурье функцию
f(x) = x при —Л-^Х-^Л.
Решение. Применим формулы (2), так как функция
f(x) = x нечетная.
1С
х sin пх dx.
§ 141] РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ
353
Согласно равенству (5) § 139 найдем:
. 2 |тс/ х cos пх । sin пх \ 2 17 тс cos л тс . sin лгтс\
"тс L\ й ‘ и2 / тс L\ п ' п2 /
/ 0* cos 0 . sin 0\“|_ 2 / тс cos птс\__ 2coshtc
\ п ‘ п2 /J тс \ п / п
Отсюда
£1==_ = _ 2(— 1) = 2,
, 2 cos 2тс „ 2*1 .
д 2 cos Зтс 2 cos тс 2
, 2 cos 4тс 2 cos 0 1
-----г- =-------4- = -2 ИТ. д.
Искомое разложение таково:
2 1
2 sin х — sin 2x4- sin Зх —ту-sin + . ==
о Z
п/ . sin 2х . sin Зх sin 4х
= 2(sinx-------g--1-----g-------—
Этот ряд представляет функцию /(х) — х при всех значе-
ниях х промежутка от —тс до 4 тс, кроме х — ±тс. Дей-
ствительно, по теореме Дирихле при х = dz к сумма ряда ’
/(—тс) 4-/ (тс) —тс 4-тс п
равна —-----2 значения же функции
при х =— тс и х — тс соответственно равны —тс и тс, т. е.
не совпадают с суммой ряда.
Таким образом,
х — 2 (sin х
sin 2х . sin Зх sin 4х .
_ - |_
при---ТС < X < тс.
Пример 4. Разложить в ряд Фурье функцию
/(х) =
— Y при —тс<^х<^0,
тс
4* при
О < х тс.
23 Зак. 3032, И. Л. Зайцев
354
ГАРМОНИЧЕСКИЙ АНАЛИЗ
[ГЛ. XV
Решение. Данная функция — нечетная, а потому, при-
меняя формулу (2), получим:
тс it
к 2 Г п . 1 Г . 1
-г sin пх— I sinnxJx = Tr
п тс J 4 2 J 2
о о
cos пх
п
1
2л
I cosnx =
10
— — CQ3 0) = —
1 / n
-(cos як-1).
Отсюда
/>1 = _ _1_(COSK— 1) = —y(— 1 — 1)=1,
^2 = —272 (cos2k—!) = -Id —!) = (),
b3 =— (cos 3k— 1) — — ~(cos к— 1) —
=- ±(-i-i)=4,
b4 = — 2^4 (COS 1)= —-|(cosO— 1) =
— —-|-(1 — l) = 0 и т. Д.
Разложение напишется следующим образом:
. sin Зх , sin Зх
Sin АН--------5-----h----н
1 о ' о
При х =— к, х = 0 и х — к сумма полученного ряда не
совпадает со значениями данной функции, поэтому указан-
ный ряд сходится к функции f(x) при —тс<х<0 и
0 < х < к.
Следовательно,
тс . , sin Зх , sin 5х , . . А
--~ = sin X Н---------g-1------1- . . . при -К < X < 0,
тс . . sin Зх . sin 5х . А . .
— = sin%4----------з-1---§“-F • • • ПРИ 0 < х < л.
Покажем на примере разложения в ряд этой функции,
что по мере увеличения числа слагаемых (простых гармо-
ник) частичная сумма ряда (результирующая гармоника) все
лучше и лучше представляет данную функцию.
§ 141] РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ 355
На чертеже 138 I показана первая гармоника (sinx) ряда.
На чертеже 138 II изображены первые две гармоники
ряда (sinx и sin?~— пунктирные линии) и их сумма
На чертеже 138 III показаны найденная сумма двух пер-
... sin Зх ,
вых гармоник (sinx-J-----§-----пунктирная линия) и третья
гармоника (sin 5-У — пунктирная линия), а также сумма трех
и
, . , sin Зл , sin 5л ч
первых гармоник (sin х ~|--g---1---g----сплошная линия)*
23*
356
ГАРМОНИЧЕСКИЙ АНАЛИЗ
[ГЛ. XV
На чертеже 138 IV—найденная сумма трех первых гар-
z . , sin Зх , sin 5х ч
моник (sin х—|--g---1---g----пунктирная линия), четвер-
тая гармоника (—?-----пунктирная линия) и сумма первых
z . . sin Зх । sin 5х . sin lx
четырех гармоник (sin х-1-g----1---g---1---?----сплош-
ная линия).
Продолжая операцию сложения простых гармоник и
дальше, мы будем получать результирующую гармонику
(частичную сумму ряда), все больше и больше приближаю-
щуюся к двум параллельным отрезкам, изображающим дан-
ную функцию.
Вследствие периодичности ряда Фурье данной функции
результирующая гармоника будет точно повторяться через
каждый промежуток значений х, равный 2тс.
Упражнения
Разложить в ряд Фурье следующие функции:
1.
2.
/(х) = х2 при
О при
х при
— ТС X < ТС,
— тс х О,
О < х < тс.
== |
ОТВЕТЫ К УПРАЖНЕНИЯМ
§ 2
3. (5; 3), (— 5^3), (— 5; — 3)J5; — 3); или (3; 5), (— 3; 5)Д—3; —5),
(3; — 5). 4. (4 V 2; 0), (0; 4 / 2), (—4 / 2; 0), (0; —4 / 2).
§ 3
I. 10. 2. 1) 10, 2) 5, 3) 5. 8. 15. 4. 5; 13 и 8 У 2. 7. Д (—4; 0),
А, (12; 0). 8. (V 3; ±3). 9. (—2; 4). 10. (0; 14). И. (1; 10) и
(—11; 10). 12. (1; 1) и (5; 5).
§ 4
I. 1) (5; 7), 2) (4; —6). 2. 3 и /17; Q-; —1). 3. 5.
4. (—9; 10). 5. (—3; 4) и (—4; —1). 6. (4; 6). 7. (1-1; —4^
и (б-|; —1). 8. (—8; —1). 9. (8; 2). 10. (—2; 1). И. (1; 1).
12. х = *1 + -^ + -^ > у = У1 + №±Уз . |3> (_ 2.
«3 о
§ 7
I, А и С лежат, В не лежит. 2. у = 0, х = 7. 3. у = х и
у = — X. 4. у = 4х. 5. х2 + у2 = 4. 6. х2 + у2 —4х~Ь6у — 3 = 0.
7. 2х —8у —5 = 0. 8. х2 + 4.у + 4 = 0. 9. х2 + у2 = 4.
§ 9
2. у = —5. 3. х = —2. 4. у = 2. 5. х = —3. 6. х = 6,
х = — 6, у = 6, у = — 6. 7. х = 0, х = 8, у = 0, у = 6 или х = О,
х = 6, у = 0, у = 8.
§ ю
' 1/*"з
1. 1) у = х, 2) у = х, 3) у == — х, 4) у = 0, 5) у = 0.
2. 1) совпадает с осью Ох, 2) делит первый координатный угол
пополам, 3) делит второй координатный угол пополам. 3. 1) 60°,
2) 33°42', 3) 116°34'. 5. А и С лежат, В не лежит. 6. На прямой
у = 2х. 7. х==4, у = — 3. 8. £ = —5. 9. у = —2х. АО. х = 10,
у = 0, у — х или х = 10, у = 0, у = — х. II. х = 0, у = 0, х =—6,
у — 3; уравнение диагонали у = —~ х. 12. у = — 0,4х.
24 Зак. 3032. И. Л. Зайцев
358
ОТВЕТЫ К УПРАЖНЕНИЯМ
§ И
2. На прямой у = —8х —10. 3. у = 3. 4. х =— 2.
5. 1) 0-; 0) и (0; —2), 2) (—2; 0) и (0; —6). 6. у = —х —5.
7. 1) у = л + 2, 2) у == — X —3, 3) у = —Д~х + 4. 8. 1)60°,
2) 135°, 3) 26О34Л 9- 1) у = 5, 2) х = 2, 3) у = 5. 10. у = — 2х-4.
11.1)2,2)0. J2- У = х и У_ = — * + 12. 13^у = х-|-2У 2,
у ~ — л + 2 У" 2, у — х — 2 У 2, у = — х — 2 У 2. 14. Уравнения
сторон: у — х, у — — * + 8, у — х + 8, у = — х. Уравнения диаго-
налей: у — 4, х = 0.
§ 12
2. 4х + 5у = 0. 3. Г)у = 2х+™, 2)у = -^х + ^.
2 1
4.1) Зх + 4у = 0, 2) 2х — Зу —12 = 0. 5.1)4, 2)
О Z
6. 1) — 4, 2) 0. 7. b = 2,5; а = 140°12'.
О
§ 13
2.1) 4 + 4 = 1. 2)-4~у = 1, 3)-4 + 4 = 1. 3.10.
4.1)4+4=!,2) _¥+у=1’ 3)o3_>,==L s-9- ®-50-
§ И
I. (6; —2). 2. Проходит^ 3. у + 9 = Л(х + 6). 4. 1) У Зх—
_у_7 — 2У 3 = 0, 2) У 3xJ-Зу + 21 — 2 У 3 = 0. 5. х — у +
+ 9 = 0; У Зх —Зу + 24+У 3 = 0; х+у—7 = 0; у=8. 6. 1)3х—
— у —32 = 0, 2) 2х + у —18 = 0. 7. х + у —5 = 0, х —у + 5 = 0.
8. У Зх + у —бУ 3 = 0, У Зх — у + бУз = 0. 9. 1)у = 0,
у=2У 3,_у = У Зх + 5У 3,_ у = —УЗх + 5УЗ£_ 2) у = 0,
у = —2У 3, у = У Зх —5У‘3, у = —У Зх —5У 3.
§ 15
1. 1) х — Зу + 5 = 0, 2) 6х + 7у — 9 = 0, 3) х + 4у = 0,
4)х + 2 = 0. 2. Зх —у—10 = 0, х —Зу + 2 = 0, х + 5у + 2 = 0.
3. arctg 2. 4. 5 и 5. 5. Зх + 7у + 2 = 0. 6. х — у — 2 = 0.
7. 2х + 3у —4 = 0, х —2у —2 = 0. 8. х —у —5 = 0. 9. (2; 0).
ОТВЕТЫ К УПРАЖНЕНИЯМ
359
§ 16
1. 1) arctg-у, 2) arctgу, 3) arctg 12, 4) arctg3. 2. arctg5
или arctg (—5). 3. 1) 0°, 2) 90°. 4. arctg 1,75.
§ 17
I. 1) Да, 2) да, 3) нет. 2. 1,5. 3. 2х— у —1=0. 4. 2х — у4~
+ 3 = 0. 5. 2х + у — 6 = 0. 6. х — 6у + 8 = 0. 7. х = 2. 8. 4х —
— 5у + 15 = 0. 9. 4х + 3у —20 = 0.
§ 18
I. 1) Да, 2) нет. 2. 2х + 3у —25 = 0. 3. 2х + у + 7 = 0. 4. 2х+
+ Зу + 7 = 0. 5. Зх — 4у + 20 = 0. в. 2х+у —9 = 0. 7. Зх —
_у + 1=0. 8. 2х — у — 3 = 0, х + 2у — 14 = 0.
§ 19
3. Точка пересечения (0; -5-). 4.
I. 1) (2,5; 0), 2) (0; —yj. 2. 1) (2; 1), 2) нет пересечения.
У
5. (3; 0). 6. 2х — у+1=0. 7. х + у = 0. 8. Зх — 2у + 18 = 0.
9. 5х + 2у —9 = 0. 10. 2х —Зу + 1 =0. II. (1; — 3), (7; — 1),
(9; 5), (3; 3).
.>.(4+).
Смешанные задачи
и (0,2). 2. Общая точка (—1; 3). 3. (3~; 4J.
4. Уравнение прямой у —— 2х. 5. х + у + 2 — 0. 6. Лежат на
прямой х—у + 2 = 0. 7. 5. 8,7. 9- х — у + 7 = 0. 10» (6; 6)
и (—8; —8). И. 1,5. 12» Длина диагонали 5; уравнения диаго-
налей: 8х + 6у— 39 = 0, Зх — 4у + 26 = 0. 13. (—3; 6) и (—1; 4).
14. — 5,6. 15. 21 и 23. 16. arctgy, arctg 3, arctg (--0,4). 17. 45°.
I.
18. 3 V" 2. 19. Зх — 5y+30 = 0. 20. x+y+7=0 или
x — у + 1 = 0. Указание. Через данную точку можно провести
две прямые, отсекающие на осях координат равные отрезки.
21. 1) у = 0, х—у + 2 = 0, Зх + 2у—24 =_0; 2) у = 0, х—у + 2 = 0,
Зх — 8у + 36 = 0. 22. Зх —у —4 = 0; /10. 23. Зх + Зу + 11 =0.
24. (5; 8). _25. (1; —1). 26. (—3,8; —1,6). 27. 2х+у — 14 = О,
(6; 2), 3 У 5. 28. 5х— у— 15 = 0. 29. arctg2,5. 30. (0; — 2) и
(0;—7)^31. х —у = 0, х + у + 2 = 0, Зх + у —12 = 0. 32. (9; 1).
33. У 2. 34. 24. Указание. Площадь параллелограмма можно
определить двумя способами- по основанию и высоте (т. е. s = ah)
и по двум сторонам и углу между ними (т. е. 5 = ab sin а). 35. 20.
36. 1) у = х, у = 8, х = 14; 2) у = х, у = 8, х = 2. 37. 2х + у —
— 5 = 0, х — 2у — 5 = 0. 38. 1) у = 12, у = х+12, у = ~х + 28,
2) у = 28, у = —х + 28, у = х+12. 89. у = 0, /Зх + у +
+ 2 У 3 = 0, /Зх — у + 2 V 3 = 0. 40. (—8; —3), (1; 6), (2,8; 2,4).
41. х —у —10 = 0, у = —5. 42. В (2,4; 6,4), D (3,6; 5,6). 43.6.
24*
360
ОТВЕТЫ К УПРАЖНЕНИЯМ
44. 4х —Зу —80 = 0, у = — 8, 4х —Зу = О. 45. ^3 ~; 5 ~ j.
46. х у + 5 = 0. 47. х — у 4- 3 = О, х + у + 3 = 0. Указание.
2
Угол падения луча равен углу его отражения. 46. у = —х 4- 4.
о
49. 11x4-Зу = 31, Пх — 3у = 31. Указание. Провести из
течки А перпендикуляр к с си Ох до пересечения его с продолжен-
ным в обратную сторону отраженным лучом и рассмотреть полу-
ченные прямоугольные треугольники.
Зх- 7у — 1 = 0.
50. 7х — 3у — 9 = 0,
§ 21
1. 1) (х + 1Г + (у-2Г = 25; 2) (х 4~ 2)2 * * * * + (У 4~ З)2 = 5;
3) х2 -1- (у — 5)2 = 36. 6. А и В лежат, С не лежит. 4. xt = 0,
х9 = —4. 5. 1) (х — 2)2 + (у — 1)2 = 25; 2) (х + З)2 + (у — 2)2 = 5.
6; (х + 2)24-(у —4)2=10. 7. (х —2)2 + у2 = 16. 8. х24-
4-(у + 4)2 = 16. 9. (3; 4), г = 5. И. 5x4- 2у — 7 = 0. 12.6.
13. х4-3 = 0. 14. х —у —2 = 0. 15. х4-2у4-5 = 0. 16. (5; 0)
и (1; 0). 17. 2х —у 4-2 = 0. 18. Зх 4-4у — 39 = 0. 19. (7; 6)
и (0; — 1). 20. Касательная в точке (3; 3). 21. Вне окружности.
22. х 4- У — 4 = 0.
§ 25
I. *1_|_ -У = 1. 2. 2а = 26, 2Ь = 24, 2с = 10. 3. 2а = 4У£
Ли 10
у2 м2 у2 м2
2»_14, Л0;±5>. + 5.ж + А, = 1.
„ X2 , у2 , , Уб о X2, у2 , X2 У2 , '
6" 9 ”* 25 — 1’ 7‘ е 3 • 8’ 25+ 9 -1 ИЛИ 9 + 25 ’
9. 36х2 + 20у2 =1125. 10. 4х2 + 9у2 = 144 или 9х2 + 4у2 = 144.
11. А и В лежат, С не лежит. 12. ±3. 13. х2 4~3у2 = 15.
14. 1) 2х24~5у2 = 40, 2) Зх24-5у2= 120. 15. 4. 16. 1) (3; 0) и (0; 2);
2) касательная в точке У 3^, 3) нет пересечения. 17. Уб.
У"2
18. 8х2 4- 9у2 = 72. 19. .
§ 31
2. 2д = 6, 2Ь = 10, 2с = 2 У 34. 3. А (± 12; 0), В(± 13; 0).
4. 7х2 —9у2 = 63. 5. F(±7; 0), 2а = 10, 26 = 4 У 6, 2 = 1,4.
6. 1) 25х2 — 24у2 = 600, 2) 9х2 — 16у2 = 1296. 7. 16х2 — 9у2 = 1296.
8. А и В лежат, С не лежит. 9. 2х2 — 9у2 = 18. 10. 5х2 — 8у2 = 40.
11. у = ±П?х, е= 12. у = ±-|х 13. 9х2— 16у2 = 288.
14. 153х2 — 425у2 = 459. 15. 9х2—16у2 = 576. 16. (6; ±3).
ОТВЕТЫ К УПРАЖНЕНИЯМ
361
17. Точка касания (6; 4). 13. tg<p = 4y 5. 19. —'
20. Зх2 — у2 = 12.
§ 33
I. 1)у2 = 16х, 2)у2 = — 8х, 3)х2 = 12у, 4) х2 = —2Эу.
2. 1) (21; о), 2) (-3; 0), 3) (0; 2), 4) (в; -2-1). 3. (|; о).
4. 1)х=—1, F(1;O); 2) у = 2, >(0;—2). 5.1)у2 = 8х, 2) у2=-12х,
3) х2 = —10у, 4) х2 = 16у. 6. у2 = 10х, г(|; о). 7. 1) Лежит,
2) нет. 8, 3 м. 9. 3 м. 10. у2 = х. И. х2 = — 8у. 12. 10. 13. (0; 0)
и (5; 5). 14. 12х —5у —24 = 0. 15. 1) (1; 3) и 0-; у), 2) (1; 3) —
точка касания, 3) нет пересечения. 16. 4 У 2. 17. х + у +1 = 0; 8.
§ 34
!. 1) (2,5; 6,25), 2) (0; 9), 3) (2; —9), 4) (1; 0), 5) (— 1; 0,5).
§ 35
1. 16. 2. 9 и 21. 3. 7х2 + 16у2 = 112 или 16х2 + 7у2 = 112.
4. х2 + у2Н-2х —4у + 3 = 0. 5. У 2. 6. х + 4 = 0 и у + 2 = 0.
7. arctg (— 0, 4). 8. 25х2 + 49у2 = 1225. 9. Зх2 + 4у2 = 48.
10. х2 + 2у2 = 32. II. 4 У 2. 12. 5х2 — 4у2 = 20. 13.4,5.
2Z>2 г— 1 х2 V2
14. 15. 2р. 16. 7 и 23. 17. 8 У 3. 18. 2^. 19. — ^ = 1.
20. 9х2 — 25у2 = 225. 21. 20х2 — 5у2 = 36. 22. Зх2 + 28у2 = 75.
23. 10 и 15. 24. 4,8. 25. Зх —4у —2 = 0. 26. у = —2х + 7,
у = А-х + -|-. 27. Юж. 28. х2=12у и х2 = —12у. 29. 9х2 +
+ 25у2 = 225. 30. х2 = — = у. 13 мм. 32. (18; 12) и (18; —12).
О
33. 4. 34. (3; ±6). 35. 10. 36. . 37. 4 У 2. 35f- ^<=^0,08
О о
V~5
39- х2 — 4у2 = 36. 40- arctg-^. 41. 9х2 —7у2 = 63.
42- х-~2у — 3 = 0, х — 2у — 7 = 0, 2х + у—1 = О, 2х + у — 4 = 0.
43. У 5. 44. 4.
§ 44
I. 6. 2- 1. 3. 0. 4- 1. 5- 0. 6- 0. 7- со. 8- оо. 9- со.
IO. 1 11. 0. 12. со. 13. 2. 14. — 4а. 15. 5. 16. —6. 17. -1
о о
18.27. 19.СО. 2О.Х^. 21. 22. 4. 23. -1 24.4.
2а а 4
25- 0. 26-1. 27- 2. 28. --0,5. 29- 0. 30. оо.
362
ОТВЕТЫ К УПРАЖНЕНИЯМ
§ 46
1.1. 2.0. 3.2. 4.1. 5.у. в. -у. 7.1. 8.4. 9.1.
IO. оо. II. 5. 12. 1. 13. 1. 14. 2. 15. 1. 16. 2. 17. 2. 18. 1.
19. 1,5. 20. 2. 21. 0,5.
§ 48
1. 1,098. 2. 2,485. 3. 1,504. 4. 2,352. 5.-1,610. 6.-1,833.
7.-0,174. 8.-2,303.
§ 50
I. 1) 3; 2) — 1; 3) — 3. 2.1) 13; 2) 76; 3) 12л2 + 1; 4) За2 — 6а + 4.
5И/(2) — 0, /(—3) = 0. 6. 1) Все значения х* кроме х =— 1;
2) все значения х, кроме х — ±1; 3) х"^>1; 4) 5) х>0;
6) — со < х + оо; 7) — 1 < х < + 1.
§ 52
2. 1) 1,38;
— 6; 2) 2Л2 + 4дЛ — й.
2) 4а Да 4-2 (Да)9;
2) 0; 3) 2а2. 3. 1) 2,25;
5. — Зу. 6. ~ —0,13.
3) 6а Да — 2Да 4~ 3 (Да)2;
4) — 2а Да —ЗДа —(Да)2; 5) За2 Да 4-За (Да)2 4-(Да)3; 6) 6а2 Да 4-
+ 6а (Да)2 - 2 (Да)2 - 4а Да 4- 2 (Да)* 7) х2 Ах + х О.^±..Д-£.
I. 1) 0,6; 2) 0,4; 3) — 1.
2)—3,24. 4.1)
7. 1) ЗДа;
§ 54
7« х ~ 1. 8- х = 2. 9. х = — 1. 10. х = 4-
§ 58
I. 3. 2. 1) 12; 2) 32. 3. 1) 5; 2) 4,1; 3) 4,01; 4) 4,001.
4. 16. 5. 1) 21; 2) 12 и 30.
§ 59
I. 2. 2. 0,0075. 3. 1) 2; 2) 6. 4. 1,6.
§ 60
I. 4. 2. 10а. 3. 8а —2. 4. — 4а 4-1. 5. 6а —2. 6. — 6ft
4
7. За2—1. 8. -Д-. 9. 1) 1; 2) 0; 3) —5; 4) —7.
§ 63
I. 1) 6; 2) 0. 2.45°. 3.135°. 4.4а — у — 6 = 0.
5. 5а + у + 3 = 0, а — 5у4-11=0.
§ 73
1.0, 2. а. 3. 5а4. 4. рХР~\ 5.15а2. 6. —12ft 7. 6 а а7.
8.2а". 9. 6а2 —3. IO. З/3—/4-2. II.—2. 12. 2а2" — а2"-4
13. 2а4- 1. 14. 9/2 — 4/. 15. 90. 16. 3/24-6/4-2. 17. 32м34- 12а2 —
— 4м —1. 18.1^. 19.—111-. 20.1,5/7. 21.1“]^“-
X ОХ о
ОТВЕТЫ К УПРАЖНЕНИЯМ
363
22-- зл'" 23- 0'25' 254-
6 __ 6 _ 12 _
27.1^. 28.-^-]Л*А 29-30-1^-. ЗА. 2xV^.
32.
36.
39.
42.
ЗУ Z + 2
2
х (4 — х)
?2-х)2 ’
2х24~2х-}-1
х2(1 + х)2 •
t____9
33. -^F-. 34. 2.
Г5
37.
40.
2
Зх2—1
х2 (1 — х2)2 *
35.
6х2 — 6х + 10
(2х—I)2
38.
2v
(*2 + I)2 ‘
лаи ____!______
ух(1 — У х)2
1. 43. у = 4х —21. 44. х + 2у — 4 = 0, 2х — у — 3 = 0.
45. (1; 2). 4S. (1; 2). 47. 1.
50. b = — 3, с = 4.
48. 2л. 49. у = xt у = — х.
§ 74
fl. и = х3—2х + 5, y = w4 2. & = х24-2х, у = У
3 - 4г~
3. rz —4х-|-5, у—у и. 4. и — х3 — 2х2-]-1, у — 2 у и.
5. и = cos Л s и*. 6. и = sin со, и — 4и3. 7. и = sin х, у = У и.
8. и = 3 cos х, у — У и. 9. и = ctg х, у = 4 У и. АО. и = со/,
5 == sin и. АА. и = 3/, $ = 2 tg и. А2. г = у , и = 3 cos г.
§ 75
I. 4(х + 2)3 2. 9(3/—2)2. 3. 10х(х2—I)4. 4. 6(х2—2х)2(х—1).
5, 4(/2_/_|_ 1)3(2/ —1). в. 20(3«2 —«4-4)->(6н —1). 7. - y-L^z..
1 — 4х
. 9.
Х (1 •У) gg___________
У2х+Т’ " УхЧ7!* 1 У 1+2х—х2’ 2У(2—х)(3+2х)‘
n2 v2 О jr
12. ----- 13. —....-. 14. 3(3х—1)(5х+1)(х+1р.
У (Р3_ 1)2 V(xi— 3x2 + 1)2
2/(5/-3) 2x2 —x-Н 5x2-f-2x —3 2(4^-1)
ЕЭ. —г , —zzr . ВО. г... ——. А/. '-г. .... — . 1<5|
У4/ —3 Ух2+1 2Ух —1
х — 2 x-j-2 а2 __
19. г —. 20. г- --^т. 21. - 22,
У(Х— 1)' у (х2+1)3 у (а’+х2)’
(х+1)Ух2—1 '
Т3
а?
а2
364
ОТВЕТЫ К УПРАЖНЕНИЯМ
§ 76
1. 1 — cos х. 2. cos с₽—ср sin ср. 3. sin-—-. 4. cos 2/. 5. 4 cosec2 2л.
1 1 1 cos2 и
6. tg2 6. 7. — ctg2 <f>- 8. a sin t. 9. cos 0 + cos 26. 10. —.
T 1 (1 + cos /)2
I!.-------- . 12. 4-sin2x 13. cos3 co sin co. 14. 10. 15. 2 cos 2<p.
sin2 6 2 T
16. — sin 2«. 17. у cos t8- ~ sin 19. 2 sin (1 — 2<p).
cos 0
20. <osec2 <t>2. 21. 2(2<f —l)cos(<f2 —?). 22.
23. 4 tg/УсозТ. 24. -7——----------------25. — ctg л sin x.
2 Ух cos2 2 У x 3 ____
__ 1 . 1 __ я ci „ __ sin x У cos x
26. ^-sin-p 27. —^cosy. 28. tgcosec2®. 29. 2cos2x ...................•
30. sin2 x (3 cos2 x — sin2 x). 31. 4 cos t cos 3/. 32. sin 46. 33. cos 2л.
34. i—t. 35. 2 sin 4c. 36. —4 sin x. 37. ctg 2? У sin 2<p.
cos x — 1 T 4
38. —~o tg2 - sec2 —. 39. — ctg 2л sin 2л. 40. 4- ctg 2<o Ysin2 2co.
X& X X О о
COS co
41.---------. 42. sec6 л.
2 cos4-^-
§ 77
A « 1 — In и _ 0,4343 e n .o.o
1.1 4-In л. 2. In Z. 3. -X---. 4. . 5. 0,4343.
1 u2 л
6. 1^-T. 7.-1. 8. ctga. 9. tg/. to. - tg/. 11. 2. 12.
13. —14, 15. 3 ctg л in2 sin x. 16. — ctg ~ .
4 +1 — xL о о
.н . .a to 1^” x .n cosec 2x on о in и /ч
17. cosec/. 18. -----. 19. .. . 20. 2tg(l—/).
X у In tg X
§ 79
. n e* (1 + / In /) _ = о 9b
1. xe^. 2. - 7------'• 3" e 4' (e^ + iy- 5‘ 2e '
C.—a-^lna. 7. (1 + 2x). 8. — 2<?е“У 9. — 4-ayln«.
ОТВЕТЫ К УПРАЖНЕНИЯМ
365
10. Х1пл). 11. 1.
12. 1®в et cos et' I*" 2tf2sinif cos t.
15. е®1па,(1+1пл). 16. T-г—. 17. ^81п2Л 18. — 4- У sin /<?«>.
' 1 ' 1 -|- e°> 2
1 _____ cfn
19. — -=- ex tg e® У cos ex. 20. — sin t. 21.-----«—==—.
2 * 2/x
22.------.......-. 23. — — / ®. 24. <?С08Ж(cos x — sin2л).
cos2 г"2? x
(X x\
_ ^+e~°). 2«.(„
27. 2tf2?(cos 2<p — sin 2<p) или
2 У 2e2? sin (45° — 2<p). 28. 2aeax sin ax.
29 1
§ 80
1. ~f== • 2. - -7==- .
/1—4л2 /4 —л2
3_ M ... a ___________t__
14-9л2’ 4 + /2’
5.—.
2 V x — x2
tV t2—i
6. -.lv-..
2v(l+v)’
2 arcsin x
10. r .
/1 —X2
It.
2/
УП^Г’
^arctg x
1 + Л2’
12.
6 arccos Зл л _ 1
----- • • 14. —,.=r~.
У1 — 9x2 У 1 -Г x2
8" 1+е2ф '
Уё®
2У 1—e® ’
1
У1—X2 '
„arccos t tcT „arccos t
16. e.-- -14=-----. n. 4.
у 1—t2 6
20, i+xa •21, r+v •
18. л/~
r a -j-1
19. arctg — .
a
7.
I. 3x
b2x
d2y *
2. 2
У
§ 81
_ 3 1
3' 2y • 1—2y
8. —9. -—. 10.
X X
5. —
У
2xy 4- y2
2xy + x2 *
R 2X
2a — Зул
11. ——
2(У-1)’
12. —secy. 13_____. 14. —. 15. 16. 2x У1 — у2-
J cos у — X x x — xy
§ 82
1. 0. 2. 6x. 3. 6. 4.
5 -2
2«2 /з •
6.12x2—4. 7,—2 cos 2a
8. esm 1 (cos21 — sin t). 9. „ ..а .
"T~
366
ОТВЕТЫ К УПРАЖНЕНИЯМ
§ 83
I. 8. 2, — 9. 3. У 3. 4. —6. 5. v = 20, j = 16. 6. v = 0, j = —2.
7. v = Y2,J=-V2. 8. v = -^-Y3, j = _*.n2 9. v==5>
j = 0, 10. t = 6, v = 18.
§ 88
1. 1) Возрастает, 2) убывает. 2, 1) Возрастает, 2) возрастает,
3) убывает. 3. 1) Возрастает при всех х, 2) убывает при всех х.
4. 1) Убывает при х<-^-, возрастает при х>-^-; 2) убывает
Л л
при х>2, возрастает при х<2. 5. Мин. (1; —1). 8. Макс. (2; 4).
7. Мин. (— 4: j) • 8- Макс- (~°’2; 2>2)- 9' Макс- 2)- ,0- Мин-
(0; 0). it. Мин. (1; —4V |2« Мнн- (0; — 5), макс. |
14. Макс.
, мин. (3; — 1); 16. Макс.
4).
МИН.
— 15. Макс.
13'
МИН. |
(— 4’27)’ мин-
(1; 2). 18. Макс. (—1; 9), мин. (3; —23). 19. Мин. (— I; —0,5),
макс. (1; 0,5). 20. Макс. (—1; —12), мин. (5; 24).
§ 91
1. 1) Выпукла, 2) вогнута. 2. 1) Выпукла, 2) вогнута. 3. 1) Во-
гнута во всех точках, 2) выпукла во всех точках. 4. Точка перегиба(0; 0).
7. Точка
перегиба (2; —4). 8. Точки перегиба нет. 9. Точки перегиба (2; 62)
и (4; 206). 10. Точки перегиба (— 3; 294) и (2; 114). 11. Точки перегиба
— 4) • <3. Точ-
14. Выпуклость
__Л
2 '
i7. Макс. (--J-: S§),
МИН.
19. Мин. (—1; —0,5),
5. Точка перегиба (— 1; 1). 6. Точка перегиба 6~^.
.от х (V 6 5\ ? У
нет. 12. Точки перегиба g— I — -уJ и — ~-
ки перегиба (—0,7; 2,2), (0; 1) и (0,7; —0,2).
4 4
при X < -х- , вогнутость При X 4> — . 15. Вогнутость при X
о о
1 1 1
выпуклость при — у < х< -тр вогнутость при X > -g- .
§ 92
1. Мин. (0; 0). 2. Мин. (0; —12). 3. Мин. (3; —6). 4. Макс. (2; 3).
5. Макс. (2; 22), мин. (6; — 10). 6. Макс. ~ ; 4 , мин. (2; —5).
7. Макс. (—3; 14,5), мин. 12;—61). 3. Мин. (1; —
ОТВЕТЫ К УПРАЖНЕНИЯМ
367
макс. (6; 20). 3» Мин. (—1; — 5-|-^, макс. (3; 5). SO. Мин. (1; 3),
макс. (2; 4), мин. (3; 3). 18. Нет ни максимума, ни минимума. 82. Воз-
растает при х < — 2, убывает при — 2 < х < 2, возрастает при х > 2.
83. Убывает при х<— 1, возрастает при — 1<х<-~-, убывает
о
5
при х>-~-. 84. Мин. (1; е). 85. Мин. (2,5; 2), макс. (—2,5; —2).
§ 93
1. 6 и 6. 2. 5 и 5. 3. 4 и 4. 4. 0,5. 5. Квадрат. 6. 100 X 100 л3.
7. 5 см. 8. 5 X 5 см\ 9. 10 X Ю слА 10. ~ 0,7 м. 11. ~ 0,63 м.
12. ЗХ6Х4<ЭлД 13.25л. 14.2X2X1 м*. 15. 2R = Н = 3 fl см.
16. R = H= — У^дм. 17. 4 см. 18. 10 см. 19. 7,5 см.
20. /1 см. 21. -j- R Уз. 22. 5 см. 23. (2; ± 2). 24. ~ 0,71 м.
25. 2,4 м.
§ 98
- з г- 2dt ъ 1 . 2 . sin 2 х
I. tfV xdx. 2. —3. -tv sin — dw. 4- -------==—dx.
% О + 02 0)2 CO 2 V x
2 1 dx dx
5.-^Inyrf/. 6. -g. 7. g*--. 8.0,4. 9. ~ 0,008.
10. ~0,1 слА 11. 12. ~0,ЗлА !3.~8слА 14.~ 8- см*
15. —0,1 см. 16. ~0,2 см. 17. ~0,08%. 18. ~2%. 19. — 2°/о-
20. —12,07. 21. ~ 15,42. 22. ~8,14. 23.-16,3. 24. ~0,96.
25.---23,84. 26. ~ 0,814.
§ 101
I. У 2. 2. 0,5. 3.2/2 4. /Тб. 5.3 Уб. 6.2/2
О
7. —-|/3. 8. со. 9. (0; 0).
§ Ю4
I. уХ34-С. 2. ух54-С. 3. f-x’i-j-C. 4. 5х + С. 5.«<? + С.
6. х3 + С. 7. ^3+С. 8. 2х— уА^+С. 9.-|х2 —jX3 + C.
10. а? + 4<р3 + С. И. ^-х^ — бх + С. 12. х<Ч-2х2 —Зх + С.
О Z
13. 4-х34-1x4 +С. 14. 4*3 + Зх3 + 9х + С. 15. ^х3—8х2+
о 2 о о
+ 4х + С. 16. 4х4—|-х3+4х2 + С. 17.4-х/х + С.
4 о z о
18. -|-х/х3 + С. 19. —4 + С. 20. 2/й+С. 21. з/х + С.
368
ОТВЕТЫ К УПРАЖНЕНИЯМ
22. ^х» + С. 23. |хУх-|-С. 24. х +С. 25.~ ху
+ С. 26. jx^x2 —8/х — ^ + С. 27. — Зх + С.
28. 4- С. 29. — 4cos x-j-C. 30. Ча sin cf -f-C.
31. 2 tg 0 4- C. 32. — 3a ctg и 4- C. 33. 14- sin 14- C. 34. 2x 4-
+ 3 cos x + C. 35. л3 — 2 sin x -f- C. 36. 2 tg у + 3 ctg -j-
37. 3e«4-C. 38. j~ + C. 39. j x2—5e^+C. 40. 2e*—3sin/-|-C
41.-|ln/4-C. 42. 21nx — lx24-C. 43. 6arctgx4-C.
з
44. -j- arcsin x + C. 45. 2у -f- tg v + C. 46. t -j- 2 ctg t + C.
47. ex — cos x + C. 48. tg x + C. 49. tg x — x + C. 50. x —
— arctg x + С. Указание. Представить x2 dx в виде (лЛ-J-l—1) dx.
§ 105
I.-i-x2 — 3x4-13. 2. slnx—cosx4-l. 3. 21nx —x4-3.
4. -g-e® — slnx. 5. 5arctgx4-x.
§ 107
1. 1,5. 2. 9. 3. . 4. 2. 5. 2. 6. 2 4- 7. 3,25. 8. 9. 6 ~ .
64 3 3 3
10. 4. 11. 0,8. 12. 1. 13. 2. 14. 2. 15. 2. 16. 11. 17. 0,75. 18. 2.
19. ~3,96. 20.------0,68. 21. e*—l. 22. ~ 0,277. 28. ~ —0,31.
24. -5-. 25. -j-. 26. =77.
3 4 24
§ 109
1.1(3 + 5л)> + С. 2. JJlni(, + (^>+c,
1 О _______ 9 _____________________
’“W+o + c- *-3 ’ <-' + 2’’ + c- »- зГ(«х-3)< + С.
S. 41'13^3- !) 4- c. 7. 4 У (3x + 5)s + С. в. У3л — 2 ; с.
9. у In (1 4- 2х) 4- С. 10. — i In (3 — 4х) + С. 11. — ~ cos 2х 4- С.
12. -1 sin 4x4- С- 13. cos (1 — t) 4- С. 14. 2stn^¥4-2^4-C.
15. 3 sin 4 + 4- cos 3x4- С. 16. 4 <g 2x4- С. 17. —4 ctg Зх 4- С.
о и ; Z . о
ОТВЕТЫ К УПРАЖНЕНИЯМ
369
18. -l-tg(2x — 1)4-С. 19. ^e1 2'f + C. 20. — <Г30 + С.
2 2 о
21. —4е 2“+1 + С. 22. —-L4-C. 23. х — е~х + С.
2ех
М-“Т33-,+' + С- 25- М1+*’)-|-С. 26.
2’' 3(г1<.у + С- 2“- - ТТ^ + С. 26. 1 Г 2^Г+ С.
30. 4 V(Jt:2 -J- 1)3-4- с. 81. 1 У (1 + 2^8)3 4- С. 32. In (1 -f-sin х)±С.
33. 4-In (2 — 3 cos ?) + <?. 34. -Lj-f-C. 35. — 5-Д; 1- С.
3 7,1 cos/ 3 sin3 со 1
36. яi-------FC. 37. 4^(1 + Sin /)« + С. 38. 4 Sin2 a 4- C,
• 2— sinx 1 2 v 1 71 2 ‘
или —— cos2 a 4- С, или —cos 2a 4- C. 39. — sin4 ср 4 C.
2 4 4
40. — 4 COS 6 У cos e 4- C. 41. 4(1 + sina)84-C.
О о
42. — 4-cos.lr<4-C. 43. — eG0SX + C. 44. In sinx 4-C.
45. In (1 4-^)4-C. 46. ~44+C 47.
z -f- о
48. 2У2 + ^4-С. 49. ~e^+C. 50. 1 In(1 4-sin2x) 4- C.
11 1 r 1 r
51. 4 X — 4- sin 2x+C. 52. 4 arctg 4 + C. 53. — arctg ~4= + C.
2 4 1 2 2 1 2 V 2
54. arctg -^= + C.
10 У 5
1 arcsin v + C. 58.
2 о
57.
60.
63.
ln(x2 — 3x)-\-C. 6fii
i in (x2 + 1) + arctg x + C.
55. -i- arcsin 2t -j- C. 56. arcsin 4 + £*•
2 о
i arcsin4- C. 59. У1 -f- sin^ <p 4- C.
arctg (sin x) + C. 62. —~ In cos 2x -j- C.
64. 3 arcsin x — 2 У1 — X2 + C,
1 n ___________ 1
65. 2-In2x + C. 66. 4 У (14-lnx)!4-C. 67. vcos3x—cosx4-C.
2 о о
Указание. Заменить: sin3 х = sin х • sin2 х = sin х (1 — cos2 х).
68. 2 (Ух 4-1) — 2 in (Ух 4- 1)4- С. Указание. 1 У ~х = г.
Показать, что полученный ответ можно представить в виде:
2Ух — 21п(Ух+1) + С1. 69. х —In(14-х)4-С. Указание.
370
ОТВЕТЫ К УПРАЖНЕНИЯМ
Представить х dx в виде: (х-р—1) dx. 70- 2 (У х — arc tg У*х)-\-С.
Указание. У х = z. 71. 2 У 2 sin ~ + С. Указание. Заме-
нить: 1 cos х = 2 cos2 ~. 72- tg ~ 4- С.
§ но
2 2
I. 4. 2. 4. 3. 0,24. 4. 3. 5. 3. 6. -/0,16. 7. -/0,46. 8. 0,5.
о о
1 2 1
9. 2. 10. —/0,27. 11. 4. 12. -/1,1. 13. 0,4. 14. 84- 15- Ю—.
У о о
16. 0,5. 17. -/0,29. 18. 0,5. 19. 2 4- 20- 21-4- 22. -/0,39.
О 10 о
23. ~ 0,78. 24. ~ 0,45. 25. — л/?2.
§ П2
1. 10. 2. 15. 3. 371. 4. 104. 5. 18. 6. 1. 7. 19,5. 8. 32.
О
4 1
9. 1) 4; 2) 36; 3) 4,5. 10. 4. II. 3. 12. 1) 4; 2) 18; 3) 13,5; 4) 2.
О о
13. 1) 4; 2) -1-/2’; 3) 8; 4) ~7,6i.
о о
§ 113
I. 9л. 2. 4-л. 3. |-л слЛ 4. ~Л СМ\ 5. 138л смХ 6. 4 лай
ООО о
7. 22 500л см*. 8. Тл2 9. 1) ~ л; 2) ^л. 10. ^л.
2 15 '15 15
§ 114
I. 490 м. 2. S = -i- gt2. 3. 1 м. 4. 9 см. 5. 900 м. 6. t = 5 сек.,
S = 150 м. 7. 9 см. 8. 19,6 м. 9. ~ 20,4 м.
§ 115
1. 0,24 кгм. 2. 0,08 кгм. 3. 0,25 кгм. 4. 0,09 кгм. 5. 0,54 кгм.
6. 62,5 кгм. 7. 4 см. 8. 4 кгм.
§ П6
I. 72 кгм. 2. — 48,1 кгм. 3. — 45216 кгм. 4. — 213 500 кгм.
5. 1600 кгм. 6. — 65,4 кгм. 7. — 753,6 кгм. 8. 12750 л кгм.
§ П7
1. 12 кг. 2. 625 кг. 3. 18 т. 4. 528 кг. 5. 1) 57,6 г, 2) 105,6 г.
6. 1) 1,5 г, 2) 2,25 г. 7. 22,2 т. 8. 2185 кг. 9. — 17,7 см.
ОТВЕТЫ К УПРАЖНЕНИЯМ
371
§ 119
2 1 1
I. s = 2/2 —3/. 2.x = -g /3— 5/ + у,3. у=±(х2 — 1). 4.x2—
— у2 = 3. 5. 2х3 + 3у2 = 3. 6. s2-2/-H2 = 0. 7. у2 = 2х. 8. у2 =
= 4 —2х2. 9. s=2A 10. у = -г^7-. И. у^ = 7^—. |2. у =
J 1 — 4х J 6 + х2
3 х —I— х^ 1 х
= 13. у = 2х-^х\ 14. 15. х = (1+02.
16. у = х. 17. 2 /у —2 Ух + х = 2. 18. у = Зе2®. 19. у = j-±-^.
20. уз = ех. 21. 3 (у + 1) == У 2х — 1. 22. у = sin х — 1. 23. у ~
=z 4 У 1 — х2 24. у — cos х. 25. у = х и у = 2тс — х, 20. у =
а?
= Се*—1. 27. (х2 —1) (у2 + 1) = С. 28. у2 = С(1 — х2)—1.
£
29. у = С VT+jfi — 1. 30. ху = Сеу. 31. у = Се03 + 1. 32. у =
•=Сх2е2®. 33. y = CearotgiB. 34. у = Сх2<?~®. 35. х = — £:1 г
-4-Z2-+-1O. 36. у—2х-\-2. 37. у = х2 —х —5. 38. у2 = 4х.
39. у = еж, 49. у = хех. 41. 39.
§ 120
1. у = 1— х. 2. у = |х2- 12x4-19. 3. у = 1x3+Ах — 1.
4. s = 1/3+vz2-7TZ + 2- 5- е = Г5“4+4“- 6. у = -21пх +
Сх Ср 0 = в*? -j— Су * р Ср 9. у = — cos х Сх -j— Ср 9. 5 =
= 1^+8^/ + » + ^. 10. у = l<?-® + Cx + Q. И. v = 84km,
s = 108 км. 12. s = 11\ 13. s = + 1.
О
§ 123
I. Сходится. 2. Сходится. 3. Сходится. 4. Расходится. 5. Рас-
ходится. 6. Сходится. 7. Сходится. О. Сомнительный случай. 9. Рас-
ходится. 10. Сходится. И. Сомнительный случай. 12. Расходится.
§ 124
I. Сходится. 2. Сходится. 3. Расходится.
§ 125
I. Сходится абсолютно. 2. Сходится неабсолютно.
ш
ОТВЕТЫ К УПРАЖНЕНИЯМ
§ 127
1. Сходится при — 1<х<1. 2. Сходится при —1
3» Сходится при — оо<<х< + оо. 4. Сходится при —оо<\
5. Сходится при — 1 < х < 1.
§ 141
_ л2 . /cos х cos 2x . cos 3x cos 4x
I. x2 = y-4(-f2-----§2---Г—32------42“
„ к 2 [ , cos Зх , cos 5х
2. /(x) = -T--^cosx+^- + -35-
sin 2х , sin Зх sin 4х ,
+ sin х-g--1--if----4--Ь •*
1.
х<я).