ANNALS OF MATHEMATICS STUDIES
Number 76
CHARACTERISTIC CLASSES
BY
John W. Milnor
AND
James D. Stasheff
PRINCETON UNIVERSITY PRESS
and
UNIVERSITY OF TOKYO PRESS
Princeton, New Jersey
1974
Дж. Милнор,
Дж. Сташеф
ХАРАКТЕРИСТИЧЕСКИЕ
КЛАССЫ
С приложением работы
Дж. Манкрса
«ЭЛЕМЕНТАРНАЯ ДИФФЕРЕНЦИАЛЬНАЯ
топология»
Перевод с английского
М. А. ШТАНЬКО
Под редакцией
В. М. БУХШТАБЕРА
С предисловием
М. М. ПОСТНИКОВА
ИЗДАТЕЛЬСТВО «МИР»
Москва 1979
УДК 513.83
Современное изложение важного раздела алгебраической
топологии — теории характеристических классов как аппарата
для изучения гладких многообразий. Оно дополнено переводом
небольшой книги Дж. Манкрса «Элементарная дифференциальная
топология», удачно сочетающейся с основным текстом.
Книга интересна не только топологам, но и специалистам по
дифференциальным уравнениям, динамическим системам, слое-
. ниям, геометрии, группам Ли, а также физикам-теоретикам. Она
доступна студентам старших курсов математических факуль-
тетов.
Редакция литературы по математическим наукам
1702040000
20203—006
041 (01)-79
6-79
«Characteristic Classes» by J. W. Milnor and
J. D. Stasheff:
© 1974 by Princeton University Press
«Elementary Differential Topology» by J. R. Mun-
kres:
© 1963, 1966 by Princeton University Press
© Составление, перевод на русский язык, «Мир»,
1979
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
Характеристические классы — одна из самых центральных
тем современной топологии, и книгу Милнора и Сташефа, ей
посвященную, почти двадцать лет с нетерпением ожидали все
топологи. Еще в 1957 году Дж. Милнор прочитал в Принстоне
курс лекций о характеристических классах и в том же году
записки этих лекций, сделанные Дж. Сташефом, были выпу-
щены в виде препринта (их русский перевод опубликован в
сборниках «Математика», 3:4, с. 3—53, и 9:4, с. 3—40). Однако
окончательное издание книги задержалось до 1974 года.
Эта книга, в отличие от других источников, специально по-
священа теории характеристических классов. Участие в ней та-
кого превосходного автора, как Дж. Милнор, определило стиль
и характер изложения. Книга предназначена в первую очередь
для начинающих и она не претендует на широту и полноту
охвата темы; ее главная цель — подробное и тщательное изло-
жение основ теории. И эта цель блестяще достигнута. -
Однако теория характеристических классов находится на
стыке целого ряда математических дисциплин, в том числе —
топологии гладких многообразий, теории когомологических опе-
раций и римановой геометрии. Это определяет интерес и значи-
мость теории, но вместе с тем существенно осложняет ее изуче-
ние. Чтобы хотя бы частично помочь читателю овладеть этой
теорией в достаточно полном объеме, было решено, с любезного
согласия авторов, дополнить русское издание книги Милнора и
Сташефа переводом небольшой книжки Дж. Манкрса «Элемен-
тарная дифференциальная топология», которая содержит акку-
ратное и подробное изложение элементарной (= не использую-
щей алгебраико-топологических методов) теории гладких много-
образий. Манкрс доводит изложение до теоремы Уайтхеда о три-
ангулируемости, в учебной литературе до него не освещавшейся
(если не считать трудно читаемой книги X. Уитни). Это допол-
нение будет полезно молодым топологам и независимо от тео-
рии характеристических классов.
6 Предисловие к русскому изданию
В целях сокращения объема при, переводе книги Манкрса
опущен один параграф, мало связанный с остальным ее текс-
том, а также удалено предисловие.
Перевод книги Манкрса (как и перевод основного текста)
осуществлен М. А. Штанько, а его редактирование — А. В. Чер-
навским.
Л1. М. Постников
ПРЕДИСЛОВИЕ
Текст настоящей книги основан главным образом на лекциях,
прочитанных в Принстонском университете в 1957 г. Старший
из авторов приносит извинения за задержку публикации.
Начало теории характеристических классов было положено
в 1935 г. почти одновременно работами ХАССЛЕРА УИТНИ в
Соединенных Штатах и ЭДУАРДА ШТИФЕЛЯ в Швейцарии.
Штифель в своей диссертации, написанной под руководством
Хайнца Хопфа, ввел и изучил некоторые «характеристические»
гомологические классы, определенные при помощи касательного
расслоения гладкого многообразия. Уитни (работавший тогда
в Гарвардском университете) исследовал случай произвольного
расслоения, слоем которого является сфера. Чуть позднее он
изобрел язык теории когомологий, а тем самым и само понятие
характеристического когомологического класса и доказал фун-
даментальную теорему о произведении.
В 1942 г. в Московском университете ЛЕВ ПОНТРЯГИН на-
чал изучать гомологии многообразий Грассмана, используя их
клеточное разбиение, предложенное Шарлем Эресманном. На
этом пути ему удалось построить новые важные характеристи-
ческие классы. (Выдающиеся достижения Понтрягина в мате-
матике тем более замечательны, что в 14 лет он полностью ли-
шился зрения в результате несчастного случая.)
В 1946 г. в Институте высших научных исследований
ЧЖЕНЬ ШЕН-ШЕНЬ, незадолго до этого приехавший в Прин-
стон из Куньмина (юго-западный Китай), определил характе-
ристические классы для комплексных векторных расслоений.
Он показал, что в действительности комплексные многообразия
Грассмана имеют когомологическую структуру намного более
простую, чем вещественные многообразия Грассмана. Это при-
вело к значительному прояснению теории вещественных харак-
теристических классов.
Мы счастливы сообщить, что все четыре творца теории ха-
рактеристических классов остаются и по сей день активными
математиками: Уитни — сотрудник Института высших научных
8 Предисловие
исследований в Принстоне, Штифель — директор Института
прикладной математики при Федеральном технологическом ин-
ституте в Цюрихе, Понтрягин — заведующий отделом Матема-
тического института им. В. А. Стеклова в Москве и Чжень—
сотрудник Калифорнийского университета в Беркли.
Эта книга посвящается им.
Джон Милнор
Джеймс Сташеф
§ 1. ГЛАДКИЕ МНОГООБРАЗИЯ
Этот параграф содержит краткое введение в теорию гладких
многообразий и их касательных пространств.
Пусть R" — координатное пространство, состоящее из всех
наборов x=(xi, хп) по га вещественных чисел. В частном
случае п = 0 условимся, что R0 состоит из одной-единственной
точки. Само поле вещественных чисел будем обозначать R.
Термин «гладкий» будет у нас означать «дифференцируе-
мый класса С°°». Таким образом, функция, определенная на от-
крытом множестве U с R", со значениями в R* является глад-
кой, если ее частные производные всех порядков существуют и
непрерывны.
Иногда удобно использовать координатное пространство R4,
которое может быть и бесконечномерным. Пусть А — произволь-
ное множество индексов и RA— векторное пространство всех
функций х из А в R1. Значение функции xg R4 при а е А бу-
дем обозначать ха и называть а-й координатой вектора х. Ана-
логично для любой функции f: Y -+ RA будем а-ю координату
вектора f(y) обозначать fa(y).
Топологию в пространстве RA введем как топологию пря-
мого произведения А экземпляров пространства R. Любое под-
множество М с R4 мы наделяем относительной (индуцирован-
ной) топологией. Таким образом, отображение f: Y -♦ Al с R4
непрерывно тогда и только тогда, когда непрерывна каждая из
ассоциированных функций fa: Y R; здесь Y — произвольное
топологическое пространство.
ОПРЕДЕЛЕНИЕ. Для U с R” отображение f: U-*-MczRA
называется гладким, если каждая ассоциированная функция fa:
£7 —R гладкая. Если отображение f является гладким, то част-
ная производная df/ди, может быть определена как гладкое
отображение U -*• RA, у которого a-я координата есть dfa/dui,
i = 1, .... п.
1 Очевидно, наше предыдущее понятие координатного пространства R"
можно получить как частный случай этого более общего понятия, если в ка-
честве Д взять множество целых чисел от 1 до п.
10 Дж. Милнор и Дж. Сташеф
Классическими и наиболее известными примерами гладких
многообразий служат кривые и поверхности в координатном
пространстве R3. Обобщая классическое понятие кривой и по-
верхности, введем следующие n-мерные объекты в координат-
ном пространстве ИЛ.
ОПРЕДЕЛЕНИЕ. Подмножество Me RA называется глад-
ким многообразием размерности п 0, если для каждой точки
х е М существует гладкое отображение
h: U-*RA,
определенное на некотором открытом подмножестве U cz R", та-
кое, что
1) й гомеоморфно отображает U на некоторую открытую
окрестность V точки х в М и
2) для каждой точки и е U матрица [dha(u)/duj] имеет
ранг п (другими словами, п векторов dh/dui, ..., dh/dun, вы-
численные в точке и, должны быть линейно независимы).
Образ h(U)=V такого отображения будем называть коор-
динатной окрестностью в М, а тройку (U, V, й)— локальной
параметризацией1 многообразия М.
Лемма 1.1. Пусть (U, V, h) и (U', V', h') — две локальные
параметризации многообразия М, такие, что V f| V' непусто.
Тогда соответствие
и'(и'))
определяет гладкое отображение открытого множества
(й')-1 (КП К') о: R" в открытое множество й-1 (КП К')с R".
Доказательство. Пусть х — h(u) = й' («')— произвольная
точка из VQK'. Выберем индексы аь .... апеА так, чтобы
«X «-матрица [дйа(./5«/], вычисленная в точке й, была невырож-
денной. Тогда из теоремы об обратной функции следует, что мы
можем представить и\....ип в виде гладких функций
«/ = fi (Ч (и), .... йвп(и))
для и из некоторой окрестности точки й (см., например, [Уитни,
1957]). Записывая эти равенства в векторной форме
« = /(йа,(м)> han(u)) и полагая й(и) —й'(м'), получаем, что
функция
и' h~l й' («') = f (й'а, («').h'an («'))
1 Обратное отображение h-': V -* U с R" часто называют локальной
координатной системой или картой для AJ,
§ 1. Гладкие многообразия 11
является гладкой в некоторой окрестности точки и', чем лемма
и доказана. 
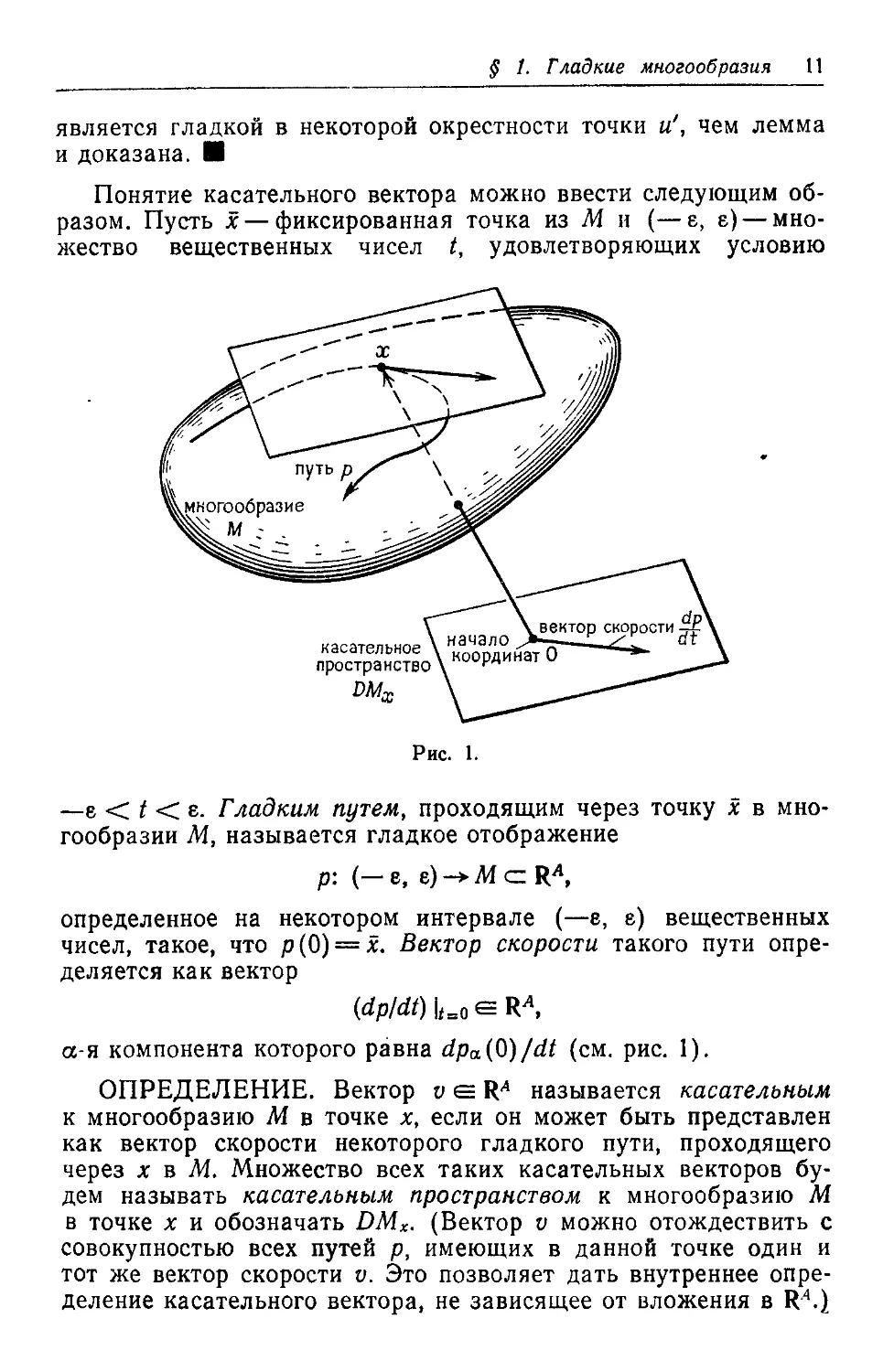
Понятие касательного вектора можно ввести следующим об-
разом. Пусть х — фиксированная точка из М и (—е, е) — мно-
жество вещественных чисел t, удовлетворяющих условию
—е < t < е. Гладким путем, проходящим через точку х в мно-
гообразии М, называется гладкое отображение
р: (— е, е) -> М с RA,
определенное на некотором интервале (—е, е) вещественных
чисел, такое, что р(0) = х. Вектор скорости такого пути опре-
деляется как вектор
(dp/dt) |/=oeRA,
a-я компонента которого равна dpa(Q)/dt (см. рис. 1).
ОПРЕДЕЛЕНИЕ. Вектор и е RA называется касательным
к многообразию М в точке х, если он может быть представлен
как вектор скорости некоторого гладкого пути, проходящего
через х в М. Множество всех таких касательных векторов бу-
дем называть касательным пространством к многообразию М
в точке х и обозначать DMX. (Вектор v можно отождествить с
совокупностью всех путей р, имеющих в данной точке один и
тот же вектор скорости v. Это позволяет дать внутреннее опре-
деление касательного вектора, не зависящее от вложения в RA.)
12 Дж. Милнор и Дж. Сташеф
В терминах локальной параметризации (U, V, h), где /г(«) =
= х, касательное пространство может быть описано следующим
образом.
Лемма 1.2. Вектор ое R'1 является касательным к М в точке
х тогда и только тогда, когда его можно представить в виде
линейной комбинации векторов
dh	dh
•^7^......
Таким образом, касательное пространство DM* есть п-мерное
векторное пространство над полем вещественых чисел.
Доказательство непосредственно следует из определений. 
Касательное многообразие для М определяется как подпро-
странство
DM czMX R4,
состоящее из всех пар (х, v), где хеМ, veDMx. Из леммы 1.2
легко вытекает, что DM, рассматриваемое как подмножество
в R4 X R4, является гладким многообразием размерности 2га.
Рассмотрим теперь два гладких многообразия М с R4 и
WcR8 и отображение f: M-+N. Пусть х — точка из М и
(U, V, h) — локальная параметризация многообразия М, причем
х = h(U).
ОПРЕДЕЛЕНИЕ. Отображение f называется гладким в точ-
ке х, если композиция 1
foh:
является гладким отображением в некоторой окрестности
точки й.
Из леммы 1.1 следует, что это определение не зависит от
выбора локальной параметризации.
ОПРЕДЕЛЕНИЕ. Отображение f: M-*-N называется глад-
ким, если оно гладко в любой точке хеМ. Отображение f;
M-+N называется диффеоморфизмом, если оно есть взаимно
однозначное отображение на и если одновременно и f, и обрат-
ное отображение f~l: N-+M являются гладкими.
Лемма 1.3. Тождественное отображение всякого многообра-
зия М на себя гладко. Далее, композиция двух гладких отобра-
жений М-1+М' -U М" гладка.
1 Для композиции двух отображений Л Д У -+ Z будем использо-
вать обозначение f»g.
§ 1. Гладкие многообразия 13
Доказательство аналогично доказательству леммы 1.1. По-
дробности мы опускаем. 
Любое гладкое в точке х отображение f: M-+N определяет
линейное отображение Dfx: DMX-+ DN;lx} касательных про-
странств следующим образом. Пусть дан вектор ое DMX. Пред-
ставим его в виде вектора скорости
v = (dp/dt) |,_0
некоторого гладкого пути p(t), проходящего через точку х, в М
и определим Dfx(y) как вектор скорости
{d(fop)/dt)\t_0
пути fop: (—е, е)-> N. Легко видеть, что это определение не за-
висит от выбора пути р и что Dfx— линейное отображение. На
самом деле в терминах локальной параметризации (U, V, /г)
имеет место явная формула
Dfx (Е Ci dhfdut) = Е ctd (f о h)/dut
для любых вещественных чисел Ci....сп.
ОПРЕДЕЛЕНИЕ. Линейное преобразование Dfx называется
произвобной или якобианом отображения f в точке х.
Предположим теперь, что отображение f: M-+N является
гладким всюду. Объединяя все якобианы Dfx, получаем ото-
бражение
Df: DM-+DN,
где Df(x, v) = (j(x), Dfx(v)).
Лемма 1.4. D есть функтор 1 из категории гладких многооб-
разий и глабких отображений в себя.
Другими словами: (1) если М— гладкое многообразие,
то DM — гладкое многообразие; (2) если f — гладкое отображе-
ние из М в N, то Df — гладкое отображение из DM в fW;
(3) если / — тождественное отображение многообразия М, то
DI — тождественное отображение многообразия DM, и (4) если
композиция fog двух гладких отображений определена, то
D(f ° g) = (Df) ° (Dg). Все это непосредственно вытекает из опре-
делений. 
Немедленным следствием леммы 1.4 является такое утверж-
дение: Если f — диффеоморфизм из М в N, то Df —диффеомор-
физм из DM в DN.
1 Определение категории и функтора см., например, в [Эйленберг, Стин-
род, гл. IV].
14 Дж Милнор и Дж. Сташеф
Замечания. Согласно нашим определениям, касательное про-
странство DR? координатного пространства R" в точке х совпа-
дает с самим векторным пространством R". В частности, для лю-
бого вещественного числа и касательное пространство DRU равно
R. Таким образом, если /: М~*R — гладкая вещественнозначная
функция, то производную Dfx: DMX-+ DRf(X) = R можно рассма-
тривать как элемент двойственного векторного пространства
Нотц (DA!*, R).
Этот элемент Dfx двойственного пространства, иногда называе-
мый «полным дифференциалом» функции f в точке х, более тра-
диционно обозначается через dj(x).
Заметим, что справедливо правило Лейбница:
D (fg)x = f (х) Dgx + g (х) Dfx,
где fg обозначает произведение функций: х>—»f(x)gr(x).
Для любого касательного вектора v е DMX вещественное чи-
сло Dfx(v) называется производной вещественнозначной функ-
ции f в точке х по направлению v *. Если мы зафиксируем пару
(х, и) и разрешим f пробегать векторное пространство С°°(М, R),
образованное всеми вещественнозначными функциями на М, то
получим линейный дифференциальный оператор
X: С°°(М, R)->R,
задаваемый формулой X(f) = Dfx(v). Правило Лейбница в этом
случае принимает вид
X(fg) = f(x)X(g) + X(f)g(x).
Во многих изложениях рассматриваемой теории касательный
вектор (х, о) отождествляют с этим линейным оператором X.
Данные выше определения имеют тот недостаток, что глад-
кость многообразия М оказывается зависящей от выбора кон-
кретного вложения М в координатное пространство. Однако для
каждого гладкого многообразия М существует каноническое вло-
жение этого многообразия в каноническое для него координат-
ное пространство.
А именно, для данного многообразия М cz R4 обозначим че-
рез F — C°°(M, R) множество всех гладких функций из М в R.
Определим вложение
Z: M->RF,
положив if (х) — f(x). Пусть Mi — образ г (Al) ед R'’.
1 Правильнее было бы говорить о «дифференциале функции [ в точке х
при приращении V». — Прим. pedt
§ I. Гладкие многообразия 15
Лемма 1.5. Этот образ М\ является гладким многообразием
в Rf, и каноническое отображение i: M-*Mi есть диффеомор-
физм.
Доказательство непосредственно следует из определений. 
Таким образом, любое гладкое многообразие имеет канони-
ческое вложение в ассоциированное с ним координатное про-
странство. Это приводит к следующему определению.
Пусть М — некоторое множество и F — совокупность веще-
ственнозначных функций на М, которая разделяет точки (т. е.
для каждой пары различных точек х и у из М существует функ-
ция feF, такая, что f (х) ф f (у)). Тогда М может быть отож-
дествлено со своим образом при каноническом вложении i:
ОПРЕДЕЛЕНИЕ. Множество F называется структурой глад-
кости на М, если подмножество Z(Af)czRF является гладким
многообразием и если F в точности совпадает с множеством
всех вещественнозначных гладких функций на этом гладком
многообразии 1>2.
Замечание. Это определение гладкости аналогично тому,
которое дано в книге [Номидзу]. С классической точки зрения
«структура гладкости» многообразия задается как совокупность
локальных параметризаций (см., например, [Стинрод, 1951]).
Имеется другой способ определения «структуры гладкости», в
котором используются совокупности гладких функций на откры-
тых подмножествах (см. [де Рам]). Все эти определения экви-
валентны.
В заключение мы предлагаем читателю три задачи. Первые
две из них будут играть важную роль в последующих пара-
графах.
Задача 1.А. Пусть Mi сс R4 и М2 с RB — гладкие многообра-
зия. Показать, что Mt X М2 <z. R4 X R° — гладкое многообразие
и что касательное многообразие ГЦМгУ^Мц) канонически диф-
феоморфно произведению L)Mi X DM2. Обратим внимание, что
функция %•—>(fi(x), /г(х)) из М в MiX,M2 является гладкой
тогда и только тогда, когда одновременно и fi: M-*-Mi, и f2:
М-*-М2 являются гладкими.
Задача 1.В. Пусть Рп — множество всех прямых, проходящих
через нуль, в координатном пространстве R"+1. Определим
1	Если выполнено только первое условие, то F можно назвать «бази-
сом» для структуры гладкости на М.
2	Таким образом, дано определение гладкого многообразия, не завися-
щее от вложения в координатное пространство. — Прим. ред.
16 Дж. Милнор и Дж. Сташеф
функцию
<7: R"+I \ {0}->Р",
положив <?(x) = Rx (прямая, проходящая через х). Пусть F—
множество всех функций f: Pn-*-R, таких, что композиция f«q
гладка.
а)	Показать, что F— структура гладкости на Рп. Получаю-
щееся гладкое многообразие называется вещественным проек-
тивным пространством размерности п.
Ь)	Показать, что функции fz/(Rx) = х/х//£ х| определяют
диффеоморфизм между Рп и подмногообразием в R<n+1>!, обра-
зованным всеми симметричными (га + 1)Х(п-|- 1)-матрицами А
со следом 1, удовлетворяющими условию АА — А.
с)	Показать, что многообразие Рп компактно и что подмно-
жество V cz Рп открыто тогда и только тогда, когда открыто
Задача 1.С. Показать, что для любого гладкого многообра-
зия М совокупность F = C°°(M, R) всех гладких вещественно-
значных функций на М представляет собой кольцо, такое, что
любая точка хеМ определяет кольцевой гомоморфизм F->R
и, следовательно, определяет максимальный идеал в F. Пока-
зать, что если многообразие М компактно, то любой максималь-
ный идеал кольца F можно получить таким образом при по-
мощи некоторой точки из М. Более общо, показать, что если
существует счетный базис топологии на М, то этим путем может
быть получен любой кольцевой гомоморфизм F->R. (Исполь-
зовать функцию f 0 из F, для которой каждое множество
f-1 [0, с] компактно.) Таким образом, гладкое многообразие М
полностью определяется своим кольцом F. Показать, что для
данной точки хеЛ4 всякое R-линейное отображение X: F->R,
удовлетворяющее условию X(fg) = X(f)g(x) +f(x)X(g), имеет
вид X(f)~ Dfx(v), где v & DMX — некоторый однозначно опре-
деленный вектор.
§ 2. ВЕКТОРНЫЕ РАССЛОЕНИЯ
Пусть В обозначает фиксированное топологическое простран-
ство, которое будет называться базисным пространством.
ОПРЕДЕЛЕНИЕ. Вещественное векторное расслоение | над
базисным пространством (или базой) В состоит из:
1)	топологического пространства Е = Е(£), называемого про-
странством расслоения,
2)	непрерывного отображения л: Е-+В, называемого проек-
цией, ц
§ 2. Векторные расслоения 17
3)	заданной для каждого b е В структуры векторного про-
странства 1 над вещественными числами в множестве л-1 (б).
При этом должно удовлетворяться следующее условие ло-
кальной тривиальности: для каждой точки b е В существуют
окрестность U с В, целое число п О й гомеоморфизм
h:
такие, что соответствие х>—>h(b, х) определяет изоморфизм век-
торных пространств R" и л-1 (б).
Такую пару (U, h) будем называть локальной координатной
системой для £ в окрестности точки Ь. Если можно взять U рав-
ным всему базисному пространству, то | называется тривиаль-
ным расслоением.
Векторное пространство л-1(&) называется слоем над Ь. Оно
будет обозначаться F& или Еб(|). Заметим, что Fb никогда не
пусто, хотя и может состоять из одной-единственной точки. Раз-
мерность п слоя Fb, вообще говоря, является (локально посто-
янной) функцией от б; однако в большинстве интересных слу-
чаев эта функция постоянна. Тогда говорят, что £ есть п-мерное
векторное расслоение.
Аналогично может быть определено понятие гладкого век-
торного расслоения. Нужно дополнительно потребовать, чтобы
В и Е были гладкими многообразиями, л было гладким отобра-
жением и для каждой точки бе В существовала локальная ко-
ординатная система (U, h), b^U, в которой h есть диффео-
морфизм.
Замечание, n-мерное векторное расслоение представляет со-
бой весьма специальный пример косого произведения в смысле
Стинрода (см. [Стинрод, 1951]2). В терминологии Стинрода,
n-мерное векторное расслоение — это косое произведение со
слоем R" и полной линейной группой GL„(R) от и переменных
в качестве структурной группы.
Рассмотрим теперь два векторных расслоения | и г| над од-
ним и тем же базисным пространством В.
ОПРЕДЕЛЕНИЕ. Говорят, что | изоморфно ц (запись:
£ ц), если существует гомеоморфизм
f: £(|)-+£(п)
1 Формально эту структуру векторного пространства можно было бы за-
дать, указав подмножество в R X R X Е X Е X Е, состоящее из всех пятеро^
Pi, /2, eh е2, е3), где л pi) = л(е2) = л(е}) и е3 —	+ /2е2.
2 Или [Хьюзмоллер]. — Прим, ред..
18 Дж. Милнор и Дж Сташеф
пространств расслоений, который изоморфно отображает каж-
дое векторное пространство Fb(l) на соответствующее вектор-
ное пространство /7ь(т)).
Пример 1. Тривиальное расслоение с пространством расслое-
ния В X R", проекцией n(b, х)= b и структурой векторного про-
странства в слоях, определяемой формулой
/i (b, xi) + /2 (b, х2) = (b, tiXi + t2x2),
будет обозначаться е". Заметим, что какое-либо другое «-мер-
ное расслоение над В тривиально тогда и только тогда, когда
оно изоморфно «д.
Пример 2. Касательное расслоение гладкого многообра-
зия М. Пространством расслоения является многообразие
DM, состоящее из всех пар (х, о), где хе Л! и о — касательный
вектор к М в точке х. Проекция
л: DM->M
задается формулой л(х, v) = x, а структура векторного про-
странства в слое л-1(х)— формулой
6 (х, t»i) + t2 (х, П2) = (*. tlVi + t2v2).
Условие локальной тривиальности проверяется без труда. За-
метим, что тм есть пример гладкого векторного расслоения.
Если тм представляет собой тривиальное расслоение, то мно-
гообразие М называется параллелизуемым. Например, пусть
М— открытое подмножество в R". Тогда DM можно отожде-
ствить с М X R" и М, очевидно, параллелизуемо.
Единичная двумерная сфера S2 с: R3 дает пример многооб-
разия, которое не параллелизуемо (см. задачу 2.В). Действи-
тельно, как мы увидим в § 9, параллелизуемое многообразие
должно иметь нулевую эйлерову характеристику, а у двумерной
сферы эйлерова характеристика равна 4-2 (см. следствие 9.3
и теорему 11.6).
Пример 3. Нормальное расслоение v гладкого многообразия
М cz R" получается следующим образом. Пространство расслое-
ния E(v) есть подмножество
Е cz М X R",
состоящее из всех пар (х, v), таких, что вектор v ортогонален
касательному пространству DMX. Проекция л: Е^>-М и струк-
тура векторного пространства в слоях л-1(х) определяются
точно так же, как и в примерах 1 и 2, формулами л(х, п) = х
§ 2. Векторные расслоения 19
и Л(х, ui)+ t2(x, v2) — (x, tivi + t2v2). Доказательство того,что v
удовлетворяет условию локальной тривиальности, мы отложим
до § 3 (см. 3.4).
Пример 4. Вещественное проективное пространство Рп мо-
жет быть определено как множество всех неупорядоченных пар
{х,—х}, где х пробегает единичную сферу Sn cz R"+1; оно на-
деляется топологией факторпространства сферы S".1
Пусть Е (у^) — подмножество в Рп X Rn+1, состоящее из
всех пар ({±х}, и), в которых вектор v кратен вектору х.
Определим проекцию л: Е(у*)->Р", полагая л({±х}, и) = {±х}.
Тогда слой л-1({±х}) можно отождествить с прямой, проходя-
щей через х и —х в R"+1. Каждая такая прямая несет обычную
структуру векторного пространства. Получившееся одномерное
векторное расслоение Y„ называется каноническим линейным
расслоением над Рп.
Доказательство того, что расслоение у^ локально-триви-
ально. Пусть U с S” — открытое множество, настолько малое,
что оно не содержит никакой пары антиподальных точек, и
пусть Ui — образ U в Рп. Тогда гомеоморфизм
/г:
задается формулой
/г({±х}, /) = ({±х}, tx)
для каждой пары (х, ()eUXR- Очевидно, (U\,h) есть ло-
кальная координатная система, поэтому расслоение у1п локаль-
но-тривиально.
Теорема 2.1. Расслоение у1п над Рп не тривиально ни при ка-
ком п 1.
Этот факт мы докажем, изучив сечения расслоения у^.
ОПРЕДЕЛЕНИЕ. Сечением векторного расслоения £ с ба-
зисным пространством В называется всякое непрерывное ото-
бражение
s: В-+Е®,
которое переводит точку бе В в соответствующий слой Рь(Л).
Сечение называется всюду ненулевым, если для каждой точ-
ки b вектор s(b) в Fb(l) ненулевой.
1 Иначе пространство Рп может быть определено как множество пря-
мых, проходящих через начало координат в Rn+I (см. задачу 1.В). Это при-
водит к тому же самому, поскольку любая такая прямая высекает на S"
две антиподальные точки.
20 Дж Милнор и Дж. Сташеф
(Сечение касательного расслоения к гладкому многообразию
М обычно называют векторным полём на /И.)
Очевидно, тривиальное одномерное расслоение обладает
всюду ненулевым сечением. Покажем, что расслоение у^ не
имеет таких сечений. Пусть
— произвольное сечение. Композиция
переводит точку х е 8п в некоторую пару
({±х}, 1(х)х)^Е(у1п).
Ясно, что /(х) есть непрерывная вещественнозначная функция
от х и
t (— х) = — t (х).
Так как пространство Sn связно, то из теоремы о промежуточ-
ном значении следует, что /(хо) = О для некоторой точки хо.
Рис. 2.
Следовательно, s({±xo}) = ({±xo}, 0). Доказательство завер-
шено. В
Интересно рассмотреть более подробно пространство Д(у„)
для случая п = 1. В этом случае каждую точку e=({±x},t>)
из Е (у^) можно записать в виде
e=({±(cos0, sin 0)}, Z(cos0, sin 0)),
0	0 л, t e R. Такое представление однозначно, за исклю-
чением того, что для каждого t пары ({± (cos 0, sinO)}, f(cos 0,
sinO)) и ({±(cos л, sin л)},—t(cos n, sin л)) соответствуют од-
ной и той же точке. Другими словами, пространство £ (у}) мо-
§ 2. Векторные расслоения 21
жег быть получено из полосы [0, л] X R в (G,t -плоскости
отождествлением левой границы [0]XR с правой границей
[n]XR при помощи соответствия (0, t)>—»(л,—t). Таким обра-
зом, Е (у{) есть открытый лист Мёбиуса (см. рис. 2).
Это описание дает другое доказательство того, что расслое-
ние у] нетривиально, так как лист Мёбиуса, конечно, не гомео-
морфен цилиндру Р1 X R-
Рассмотрим теперь некоторую конечную совокупность
{si, ..., s„} сечений произвольного векторного расслоения |.
ОПРЕДЕЛЕНИЕ. Сечения sb ..., sn называются всюду не-
зависимыми, если для каждой точки be В векторы Si(b), ...
..., sn(b) линейно независимы.
Теорема 2.2. п-мерное расслоение £ тривиально тогда и толь-
ко тогда, когда £ допускает п всюду независимых сечений
$1» • • • , Sn*
Доказательство опирается на следующий основной результат.
Лемма 2.3. Пусть g и г]— векторные расслоения над В и
[: £(|)->Д(т]) — непрерывное отображение, которое изоморфно
переводит каждое векторное пространство Еь(1,) в соответ-
ствующее векторное пространство Еь(т\). Тогда f является го-
меоморфизмом и, следовательно, £ изоморфно г).
Доказательство. Для заданной точки Ьо е В выберем ло-
кальные координатные системы (U, g) для £ и (V, h) для ц,
где Ьо е U П V. Нам надо показать, что композиция
(U П V) X R” (U Л V) X R"
есть гомеоморфизм. Положим
h~l(f(g(b, x))) = (b, у).
Очевидно, вектор y = (yi...уп) можно представить в виде
У1= Z fll&X!,
где [fo(6)] — невырожденная вещественная матрица, элементы
fij(b) которой непрерывно зависят от Ь. Обозначим через
обратную матрицу. Ясно, что
g~l°r1 °h(b, y) = (b, х),
где
Xj = S Fji (b) yt.
22 Дж. Милнор и Дж. Сташеф
Так как матричные элементы Рц(Ь) непрерывно зависят от
матрицы [///(£>)], то они непрерывно зависят от Ь. Таким обра-
зом, отображение g"1 °f~' ° h непрерывно, чем и завершается
доказательство леммы 2.3. 
Доказательство теоремы 2.2. Пусть ..., sn — всюду не-
зависимые сечения. Зададим отображение
f; BXRn-*E
формулой
f (b, х) = X1S1 (i>) + ... + xnsn (b).
Очевидно, f является непрерывным и изоморфно отображает
каждый слой тривиального расслоения е" на соответствующий
слой g. Следовательно, f есть изоморфизм расслоений и потому
расслоение £ тривиально.
Обратно, предположим, что g — тривиальное расслоение с
координатной системой (В,Л). Определим сечение s,, положив
s{(b) = h(b, (0, .... О, 1, 0, ..., 0))6Fb©
(1 стоит на i-м месте). Ясно, что сечения si, ..., sn всюду не-
зависимы. Доказательство завершено. 
Примеры. Касательное расслоение к окружности S1 с R2
допускает всюду ненулевое сечение s(x), показанное на
рис. 3. (Стрелки идут от х <= S1 к х + и, где s(x) — (x, и) =
— ((*ь х2), (—Х2, xi)). Значит, S1 параллелизуемо. Аналогично,
трехмерная сфера S3 с R4 допускает три всюду независимых
векторных поля S;(x) = (x, $/(х))> где
$1 W = (— Х2, Xh — Xi, х3),
s2 (х) = (— х3, х4, X,, — х2),
«з W = (— Xi, — х3, Х2, Xi).
$ 2. Векторные расслоения 23
Поэтому многообразие S3 параллелизуемо. (Эти формулы воз-
никают из формул умножения кватернионов в R4, см. [Стин-
род, 1951, п. 8.5].)
Евклидовы векторные расслоения
Для многих целей важно изучать векторные расслоения, у
которых каждый слой имеет структуру евклидова векторного
пространства.
Напомним, что вещественнозначная функция р на конеч-
номерном векторном пространстве V называется квадратичной,
если она может быть представлена в виде
р (») = X It (о) It (о),
где все /,• и // — линейные функции на V. Каждая квадратич-
ная функция определяет симметричное билинейное спаривание
v, w и-* v • w из V X V в R, где
v • w = у (р (о + w) — р (о) — р (да)).
Заметим, что о-» = р(п). Квадратичная функция р называется
положительно определенной, если р(и)>0 для всех о =/= 0.
ОПРЕДЕЛЕНИЕ. Евклидовым векторным пространством
называется вещественное векторное пространство V вместе с
положительно определенной квадратичной функцией
р: V->R.
Вещественное число v-w называется скалярным произведением
векторов» и да. Число о-» = р(и) обозначается также через | v |2.
ОПРЕДЕЛЕНИЕ. Евклидовым векторным расслоением на-
зывается вещественное векторное расслоение g вместе с непре-
рывной функцией
И:
такой, что ограничение р на каждый слой расслоения g яв-
ляется положительно определенной квадратичной функцией.
Сама функция р называется евклидовой метрикой на векторном
расслоении
В случае касательного расслоения тм гладкого многообра-
зия евклидова метрика
р: DM->R
называется римановой метрикой, а М вместе с р— римановым
многообразием. (Обычно требуют, чтобы р было гладкой функ-
24 Дж. Милнор и Дж. Сташеф
цией. Для римановой метрики часто употребляют обозначение
ц = ds2.)
Замечание. В терминологии Стинрода евклидова метрика на
| задает редукцию структурной группы расслоения | от полной
линейной группы к ортогональной группе (см. [Стинрод, 1951,
п. 12.9]).
Примеры. На тривиальном расслоении eg можно задать
евклидову метрику
р(Ь, х) = х2 + ... + х2.
Так как касательное расслоение к R" тривиально, то R" как
гладкое многообразие допускает стандартную риманову мет-
рику |х. Для любого гладкого многообразия М с. R" компози-
ция
DMcDRnJi>R
превращает М в риманово многообразие.
Априори существует два различных понятия тривиальности
для евклидовых векторных расслоений; однако следующая
лемма показывает, что они совпадают.
Лемма 2.4. Пусть g — тривиальное векторное расслоение
размерности п над В и ц — произвольная евклидова метрика
на g. Тогда существует п сечений Si, ..., sn расслоения g, ко-
торые являются нормированными и ортогональными в том
смысле, что
St (b) • Sj (b) = 6ц (символ Кронекера)
для каждого Ь Е В.
Таким образом, расслоение | тривиально и как евклидово
векторное расслоение. (См. задачу 2.Е ниже.)
Доказательство. Пусть s], .... s' —любые п сечений, ко-
торые всюду независимы. Применяя процесс Грама — Шмид-
та 1 к векторам s' (6)..s' (b), мы получим ортонормирован-
ный базис si(i>), .... sn(b) для Fb(%). Получающиеся таким
образом функции st, ..., sn от b, очевидно, непрерывны, чем
и завершается доказательство. 
В заключение параграфа шесть задач для читателя.
Задача 2.А. Показать, что единичная сфера Sn нечетной раз-
мерности допускает всюду ненулевое векторное поле. Пока-
! См. любое руководство по линейной алгебре.
§ 2.. Векторные расслоения 25
зать, что нормальное расслоение к Sn с Rn+1 тривиально для
всех п.
Задача 2.В. Пусть сфера Sn допускает всюду ненулевое век-
торное поле. Показать, что тогда тождественное отображение
сферы S" гомотопно антиподальному отображению. Показать,
что антиподальное отображение сферы Sn четной размерности
гомотопно отражению r(xi......хя+1) = (—xi, Х2,	x»+i) и,
следовательно, имеет степень —1 (см. [Эйленберг, Стинрод]).
Комбинируя эти факты, показать, что многообразие Sn не па-
раллелизуемо для четных п 2.
Задача 2.С. Теорема существования евклидовой метрики.
Используя разбиение единицы, показать, что любое векторное
расслоение над паракомпактной базой может быть наделено
евклидовой метрикой. (См. § 5.8 или [Келли].)
Задача 2.D. Линия Александрова L (иногда называемая
также «длинной линией») есть гладкое связное одномерное
многообразие, которое не паракомпактно (см. [Кнезер]). Пока-
зать, что L не может быть наделено римановой метрикой.
Задача 2.Е. Теорема об изометрии. Пусть ц и ц/ — две раз-
личные евклидовы метрики на одном и том же векторном рас-
слоении Доказать, что существует гомеоморфизм /: £(|)->-
^-Е(£), изоморфно переводящий каждый слой в себя, так что
композиция р.о|-. E(£)->R равна ц'. [Указание. Использовать
тот факт, что любую положительно определенную матрицу А
можно однозначно представить в виде квадрата положительно
определенной матрицы д/Д. Разложение в степенной ряд
д/(/Т+ТУ=д/Г(/ + -^х--^гх2 + ...)
справедливо при условии, что собственные числа матрицы
И + X лежат между 0 и 2t. Это показывает, что функция
А д/Д является гладкой.]
Задача 2.F. Как и в задаче 1.С, пусть F— алгебра гладких
вещественнозначных функций на М. Для каждой точки х е М
обозначим через Irx+l идеал всех функций из F, производные
которых порядка равны нулю в точке х. Элемент фактор-
алгебры FIIr^1 называется г-джетом. вещественнозначной функ-
ции в точке х (см. [Эресманн, 1952]). Построить локально-
тривиальное «расслоение алгебр» #1$ над М с типичным слоем
26 Дж, Милнор и Дж. Сташеф
§ 3.	ПОСТРОЕНИЕ ИЗ ВЕКТОРНЫХ РАССЛОЕНИЙ НОВЫХ РАССЛОЕНИЙ
В этом параграфе будет описано несколько основных кон-
струкций, связанных с векторными расслоениями.
(а)	Ограничение расслоения на подмножество базисного про-
странства. Пусть £ — векторное расслоение с проекцией л: Е —♦
и В — некоторое подмножество базисного пространства В.
Полагая Е = л-1 (В) и обозначая через
п: Е-*-В
ограничение проекции л на Е, мы получим новое векторное
расслоение, которое будем обозначать £|Д и называть ограни-
чением расслоения g на В. Каждый слой Fb(g|S) равен соот-
ветствующему слою Fb(|) и имеет ту же самую структуру
векторного пространства.
Например, если М — гладкое многообразие и U — открытое
подмножество в М, то касательное расслоение ти равно | U.
Имеется следующая более общая конструкция.
(Ь)	Индуцированные расслоения. Пусть £ — то же, что и
выше, и Bi — произвольное топологическое пространство. Для
заданного отображения f: Bi -> В можно построить индуциро-
ванное расслоение f*l над Пространство Ei индуцирован-
ного расслоения f*l есть подмножество с: Bi X Е, состоящее
из всех пар (Ь, е), таких, что
f(b) = n(e).
Проекция ли Ei—определяется равенством ni(£>,e) = Ь. Та-
ким образом, имеет место коммутативная диаграмма
Ei-^E
Bi-^B
где f(b,e)—e. Структура векторного пространства в слоелр1(&)
задается формулой
(^> ei) + 4 (b, е2) = (b, tiei + /гф)"
Таким образом, f изоморфно отображает каждое векторное
пространство	на векторное пространство Ff(b)(£).
Пусть (I/,Л)—какая-либо локальная координатная система
расслоения £. Положим Ui — f-^U) и определим отображение
<5 3. Построение новых расслоений VI
формулой hi (b, х) — (b, h х)). Тогда (Ui,hi) будет, оче-
видно, локальной координатной системой расслоения f*i. Это
доказывает, что индуцированное расслоение [*£ локально три-
виально. (Отсюда, в частности, следует, что если расслоение g
тривиально, то и индуцированное расслоение тривиально.)
Замечание. Можно показать, что, если £ — гладкое вектор-
ное расслоение и f — гладкое отображение, то Ех—гладкое
подмногообразие в Bi X Е, и поэтому f*l- также является глад-
ким векторным расслоением.
Рассмотренная выше коммутативная диаграмма наводит на
мысль ввести следующее априори более общее понятие. Пусть
£ и т] — векторные расслоения.
ОПРЕДЕЛЕНИЕ. Послойным отображением г| в £ назы-
вается непрерывное отображение
g- E(n)-E(g),
которое изоморфно переводит каждое векторное пространство
Еь(т\) в одно из векторных пространств Fb'(g).
Ясно, что, если положить g(b)=b', то получающееся ото-
бражение
g" В(п)->В(|)
непрерывно.
Лемма 3.1. Пусть g-. Е(т])->-Е(£)— послойное отображение
и g: В(т])-»-В(£) — соответствующее отображение базисных
пространств. Тогда расслоение г| изоморфно индуцированному
расслоению g*%.
Доказательство. Определим отображение h: Е (т\)Е (g*£,)
формулой
Л(е) = (л(е), g(e)),
где л — проекция расслоения rj. Так как h является непрерыв-
ным и изоморфно отображает каждый слой Fb(r}) на соответ-
ствующий слой Fb(g*Z), то из леммы 2.3 следует, что h — изо-
морфизм. 
(с)	Прямое произведение. Пусть gi и — два векторных рас-
слоения с проекциями л<: Ei-^-Bi, i— 1,2. Прямым произведе-
нием £i X & называется расслоение с пространством Е{ X В2
и проекцией
Л1 X л2: Ei X Е2 -+ Bi X В2,
где каждый слой
(л, х я,)м-здхма
28 Дж. Милнор и Дж. Сташеф
наделен очевидной структурой векторного пространства. Ясно,
что расслоение gi X I2 локально тривиально.
Например, если М = Afi X М2 — произведение гладких мно-
гообразий, то касательное расслоение тм изоморфно прямому
произведению тМ1 X (ср. с задачей 1.А).
(d)	Сумма Уитни. Рассмотрим два расслоения g2 над од-
ним и тем же базисным пространством В. Обозначим через
d: В-+ВХВ
диагональное вложение. Индуцированное расслоение d*(£i X
XI2) над базисным пространством В называется суммой
Уитни расслоений gi и g2 и обозначается £i ф |2. Заметим, что
каждый слой ФЬ) канонически изоморфен прямой сум-
ме F6(|l)©Fft(|2).
ОПРЕДЕЛЕНИЕ. Рассмотрим два векторных расслоения £
и т] над одним и тем же базисным пространством В, удовлет-
воряющих условию E(g)cz Е(т]). Расслоение g называется под-
расслоением расслоения ц (запись: gczr]), если каждый слой
Fj(g) является векторным подпространством соответствующего
слоя Fb(r]).
Лемма 3.2. Пусть £1 и £2 — подрасслоения расслоения л, та-
кие, что каждое векторное пространство равно прямой
сумме подпространств F<>(5i) и Fj(g2). Тогда т] изоморфно
сумме Уитни gi ф £2.
Доказательство. Определим отображение f: Д(?1Ф?2)->-
->Е(т]) формулой f(6; ci, е2)= 61 + е2. Тогда из леммы 2.3 сле-
дует, что f — изоморфизм. 
(е)	Ортогональное дополнение. Естественно возникает воп-
рос, существует ли для данного подрасслоения | с: ц дополни-
тельное к нему подрасслоение, такое, что расслоение q пред-
ставляется как их сумма Уитни? Если расслоение q снабжено
евклидовой метрикой, то такое дополнительное к g слагаемое
можно построить1 следующим образом.
Пусть Fb^1) обозначает подпространство в слое ^(ц), со-
стоящее из всех векторов v, таких, что v • w = 0 для всех w е
^Fb(l), и пусть Е(^1)с Е(т\) — объединение пространств
Fjd1) по всем Ь е В.
1 В случае когда базисное пространство В — паракомпакт, расслоение ч
всегда может быть наделено евклидовой метрикой (задача 2.С), поэтому
всякое подрасслоенне 1 с ц является слагаемым некоторой уитниевской
суммы. Если не требовать, чтобы В было паракомпактным, это уже не так
(можно дать контрпример).
§ 3. Построение новых расслоений 29
Теорема 3.3. Е^1) является пространством некоторого под-
расслоения cz т], и расслоение г| изоморфно сумме Уитни
т1.
ОПРЕДЕЛЕНИЕ. Подрасслоение называется ортого-
нальным дополнением подрасслоения £ в расслоении т).
Доказательство. Ясно, что каждое векторное пространство
Еь(т]) есть прямая сумма подпространств Гб(?) и	Та-
ким образом, задача состоит только в том, чтобы доказать, что
расслоение g1 удовлетворяет условию локальной тривиально-
сти.
Пусть Ьо е В — некоторая точка и U — такая окрестность
этой точки, что расслоения £| U и т] | U одновременно являются
тривиальными. Выберем ортонормированные сечения Si, sm
расслоения и s{, .... s'n расслоения т}|{7, где пг и п — раз-
мерности слоев расслоений | и ц соответственно (см. 2.4). Тогда
m X и-матрица
(*о) • < (6о)]
имеет ранг пг. Перенумеровав, если надо, сечения s', мы мо-
жем считать, что первые пг столбцов матрицы линейно неза-
висимы.
Пусть V cz U — открытое множество, состоящее из всех то-
чек Ь, для которых первые пг столбцов матрицы [sz (А) • s't (6)]
линейно независимы. Тогда п сечений
Sl> S2...Sm< Sm+l.....Sn
расслоения будут линейно независимы в любой точке из
V. (Действительно, линейная зависимость в какой-нибудь точ-
ке b е V означала бы, что некоторая ненулевая линейная ком-
бинация векторов Si(6), .... sm(b) является также линейной
комбинацией векторов s'm+i(b), ..., s'n(b) и, следовательно, ор-
тогональна векторам s[(ft), ..., s'm(b).) Применяя процесс орто-
гонализации Грамма — Шмидта к этому набору сечений, полу-
чаем ортонормированные сечения si, ..., sm, $m+i, ..., sn рас-
слоения т] | V.
Далее, формула
A (b, х) =	(Ь)	xn_msn (b)
задает локальную координатную систему
A: VXR'“'"->£(rL)
расслоения £-4 Тождество
й-1 (?) = (ле, (е • sm+i (ле), .... е • sa (ле)))
30 Дж. Милнор и Дж. Сташеф
показывает, что отображение h есть гомеоморфизм, чем и за'
вершается доказательство теоремы 3.3, 
Для примера рассмотрим гладкие подмногообразия М <=
cz N cz R-4 и предположим, что N наделено римановой метри-
кой. Тогда касательное расслоение тм является подрасслоением
ограничения tjv|Af. В этом случае ортогональное дополнение
cz rN | М называется нормальным, расслоением v подмного-
образия М в N. Таким образом, справедливо
Следствие 3.4. Для любого гладкого подмногообразия М
гладкого риманова многообразия N определено нормальное
расслоение v, и
1Л4.
Более общим образом, гладкое отображение f: M-+N глад-
ких многообразий называется погружением, если якобиан
отображает касательное пространство DMX инъективно (т. е.
с нулевым ядром) для каждой точки х е М. [Из теоремы о
Рис. 4.
неявной функции следует, что локально погружение является
вложением многообразия М в N, однако глобально образ М
в N может иметь самопересечения. Типичное погружение ок-
ружности в плоскость показано на рис. 4.]
Предположим, что N— риманово многообразие. Тогда для
каждой точки х е М касательное пространство DNfw разби-
вается в прямую сумму образа Dfx(DMx) и его ортогонального
дополнения. Соответственно, индуцированное расслоение
над М разбивается в сумму Уитни подрасслоения, изоморфного
гм, и дополнительного подрасслоения Vf. Итак, имеем
Следствие 3.5. Для любого погружения f: М —> N, где N —
риманово многообразие, существует разложение в сумму Уитни
§ 3. Построение новых расслоений 31
Это расслоение Vf называется нормальным расслоением по-
гружения f.
(f)	Непрерывные функторы от векторных пространств и век-
торных расслоений. Операция взятия прямой суммы, пожалуй,
наиболее важный метод построения из заданных векторных
пространств новых, тем не менее и многие другие подобные
конструкции играют важную роль в дифференциальной геомет-
рии. Например, любой паре V, W вещественных векторных про-
странств можно сопоставить:
1)	векторное пространство Hom(V, W) линейных отображе-
ний из V в W;
2)	тензорное произведение 1 V ®
3)	векторное пространство всех симметричных билинейных
отображений из V X V в W и т. д.
Всякому векторному пространству V можно сопоставить:
4)	двойственное векторное пространство Hom(V, R);
5)	k-ю внешнюю степень 1 Л*У;
6)	векторное пространство всех 4-линейных отображений
К: VXVXVXV-»-R, удовлетворяющих следующим соотно-
шениям симметрии:
K(vi, v2, о3, о4) = /С(о3> и4, 01, о2) = — Л(оь о2, о4, о3)
и
К(»1, V2, о3, о4) + К(оь о4, о2, о3) + К(оь о3, о4, о2) = 0.
(Последний пример мог бы показаться искусственным, не будь
он важен в теории римановой кривизны.)
Эти примеры наводят на мысль рассмотреть общее понятие
функтора от нескольких переменных — векторных пространств.
Пусть У обозначает категорию, состоящую из всех конеч-
номерных вещественных векторных пространств и всех изомор-
физмов между такими пространствами. (Ковариантным2)
функтором Т-, УУУУ-*У называется операция, сопоставляю-
щая
1)	каждой паре векторных пространств V, W <= У— вектор-
ное пространство Т(У, IT)е У и
2)	каждой паре изоморфизмов f: V-+V', g: W-^W' — изо-
морфизм
T(f, g): T(V, W)-+T(Vf, W')
1 См., например, [Ленг, 1965].
! Различие между ковариантными и контравариантными функторами
здесь не важно, так как мы имеем дело только с изоморфизмами.
32 Дж. Милнор и Дж. Сташеф
так, что
3)	Т (idy> = idr и
4)	Т (fi о f2, gi ° gii — T (fi, gi) ° T (f2, g2).
Такой функтор будем называть непрерывным, если Т (f, g) не-
прерывно зависит от f и g. Это определение имеет смысл, так
как на множестве всех изоморфизмов одного конечномерного
векторного пространства в другое существует естественная то-
пология.
Аналогично определяется понятие непрерывного функтора
Т; У°Х ••• Х^-от k переменных. Заметим, что в примерах
1—3 мы имеем непрерывные функторы от двух переменных, и
в примерах 4—6 — непрерывные функторы от одной перемен-
ной.
Пусть Т: X Х^’_>^’— непрерывный функтор от k пе-
ременных и gi, ...,	— векторные расслоения над общим ба-
зисным пространством В. Построим новое векторное расслое-
ние над В следующим образом. Для каждой точки b е В по-
ложим
Fb = T(Fb(li), ..., FbO.
Обозначим через Е дизъюнктное объединение векторных про-
странств Fb и определим отображение л: Е -> В условием
n(Fb)=b.
Теорема 3.6. Существует каноническая топология на мно-
жестве Е, превращающая Е в пространство векторного рас-
слоения с проекцией л и слоями Fb.
ОПРЕДЕЛЕНИЕ. Это расслоение будем обозначать
Т(Ъ.....Ы.
Например, данная конструкция для функтора тензорного
произведения определяет тензорное произведение g ® ц двух
векторных расслоений, для функтора прямой суммы — сумму
Уитни | © г) двух расслоений. Для функтора двойственности
Уь->Нот(У, R)
мы получаем функтор
£ i-> Hom (g, в'),
сопоставляющий каждому векторному расслоению двойственное
ему векторное расслоение.
Дадим лишь набросок доказательства теоремы 3.6. Пусть
(U,hi), .... (U,hk) — локальные координатные системы для
расслоений £i....соответственно, все с одним и тем же
открытым множеством U. Для каждой точки b е U определим
§ 3. Построение новых расслоений 33
изоморфизм
формулой Л/й(х) = ЛД&, х). Тогда определен изоморфизм
T(hlb, hkb):	.....Rnk)-^Fb.
Соответствие
(b, x)^T(hib, hkb)(x)
задает взаимно однозначное отображение
h: UXtIiC1, .... Rnft)->n-1(tf).
Утверждение. Существует единственная топология на Е, в
которой каждое такое отображение h является гомеоморфиз-
мом, а каждое множество n~l(U)— открытым подмножеством
в Е.
Доказательство. Единственность очевидна. Чтобы доказать
существование, достаточно показать, что если две такие <коор-
динатные системы» (U, h) и (U',h') перекрываются, то преоб-
разование
(ипи')хт(r"1, .... Rn0 (Uпи')хт(r"1, .... R"*)
непрерывно, но это следует из непрерывности функтора Т.
Теперь ясно, что л: Е-+В непрерывно и что получающееся
в результате векторное расслоение T(gi, .... gt) удовлетво-
ряет условию локальной тривиальности. 
Замечание 1. Эту конструкцию можно .следующим образом
описать в терминологии Стинрода. Пусть GLn = GLn(R) обо-
значает группу автоморфизмов векторного пространства R".
Тогда Т определяет непрерывный гомоморфизм из произведе-
ния групп GLni X • • • X GLnk в группу GL' автоморфизмов век-
торного пространства tCr"1, ..., Rnft). Следовательно, для дан-
ных расслоений gi, ..., g* над В со структурными группами
GLnp ..., GLnk соответственно существует отвечающее этому
гомоморфизму расслоение Т (gi, ...,£») со структурной груп-
пой GL' и слоем Т (R"1....Rn*). Дальнейшее обсуждение см.
в [Хирцебрух, 1966, § 3.6].
Замечание 2. Для расслоений &, .... & над различными
базисными пространствами аналогичная конструкция дает век-
торное расслоение f(gi, ..., gs) над B(gi)X ••• ХВ(^) со
слоем Т(Fbi (gj), ..., Fbk (gfc)) Это определяет функтор Т в себя
2 Дж. Милнор, Дж. Сташеф
34 Дж. Милнор и Дж. Сташеф
категории векторных расслоений с морфизмами — послойными
отображениями. Например, взяв функтор прямой суммы ф на
категории Т, получаем функтор прямого произведения
П1—®П = £Хт]
для векторных расслоений.
Замечание 3. Если ...,&. являются гладкими вектор-
ными расслоениями, то на расслоении T(gi, ..., можно так-
же задать структуру гладкого расслоения. Доказательство ана-
логично доказательству теоремы 3.6. При этом надо использо-
вать тот факт, что изоморфизм Т(ft, ..., fk) есть гладкая
функция от изоморфизмов fi, ..., fn. (См. [Шевалле].)
Для иллюстрации пусть f: МN— гладкое отображение.
Тогда Нот(тм, будет гладким векторным расслоением
над М. Заметим, что производная Df задает гладкое сечение
этого векторного расслоения.
В качестве другого примера рассмотрим вложение
с нормальным расслоением v, где N — гладкое риманово мно-
гообразие. Тогда «вторая фундаментальная форма» может
быть определена как гладкое симметрическое сечение расслое-
ния Нот(тм ®тм, v). (См. [Бишоп и Криттенден], а также за-
дачу 5.В.)
В заключение шесть задач для читателя.
Задача З.А. Гладкое отображение f: М -> W гладких много-
образий называется наложением, если каждый якобиан
Dfx-- DMx-+DNfM
сюръективен (т. е. является отображением на). Построить век-
торное расслоение Xf с базой М и слоем, равным ядру Dfx. По-
казать, что если М — риманово многообразие, то
Гм£!Х(ф|Ч#.
Задача З.В. Для данных расслоений £ сц ц определить фак-
торрасслоение т|/£ и проверить, что оно локально тривиально.
Показать, что если т] имеет евклидову метрику, то
Задача З.С. Более общим образом, пусть £, т] — произволь-
ные векторные расслоения над В и f — сечение расслоения
Hom(g, н). При условии, что ранг линейного отображения
локально постоянен как функция от Ь, определить ядро х, cz |
и коядро Vf и доказать, что они суть локально тривиальные
расслоения.
§ 4. Классы Штифеля — Уитни 35
Задача 3.D. Показать, что если векторное расслоение ? на-
делено евклидовой метрикой, то оно изоморфно своему двой-
ственному расслоению Нот(?, е1).
Задача З.Е. Показать, что множество классов изоморфных
друг другу одномерных векторных расслоений над В образует
абелеву группу относительно операции тензорного умножения.
Показать, что данное одномерное расслоение £ можно наде-
лить евклидовой метрикой тогда и только тогда, когда оно
представляет собой элемент порядка ^2 в этой группе.
Задача 3.F. (Ср. [Сван].) Пусть В — тихоновское простран-
ство1 и R(B)— кольцо непрерывных вещественнозначных функ-
ций на В. Для векторного расслоения ? над В через S(?) обо-
значим R (В)-модуль всех сечений расслоения ?.
а)	Показать, что S(? ф я) = 5(?) ф 5(ц). Далее, показать,
что расслоение ? тривиально тогда и только тогда, когда мо-
дуль S(?) свободен.
Ь)	Показать, что если расслоение ?©я тривиально, то S(?)
есть конечно порожденный проективный модуль2. Обратно, по-
казать, что если Q—конечно порожденный проективный R(B)-
модуль, то Q S (?) для некоторого расслоения ?.
с)	Показать, что ? = я тогда и только тогда, когда S(?)s
= 5(я).
§ 4. КЛАССЫ ШТИФЕЛЯ —УИТНИ
В этом параграфе мы начнем изучение характеристических
классов, введя четыре аксиомы, которые характеризуют кого-
мологические классы Штифеля — Уитни векторных расслоений.
Существование и единственность когомологических классов,
удовлетворяющих этим аксиомам, будут установлены в после-
дующих параграфах3.
Выражение Н‘(В-, G) обозначает ью группу сингулярных
когомологий пространства В с коэффициентами в G. Краткий
очерк основных определений и теорем теории сингулярных ко-
гомологий читатель может найти в приложении А. В данном
параграфе группой коэффициентов G всегда будет Z/2, группа
целых чисел по модулю 2.
1 Топологическое пространство называется тихоновским, если оно хаус-
дорфово и для любой точки х и не содержащего ее замкнутого множества А
существует непрерывная вещественнозначная функция, отделяющая х от А
(см. [Келли]).
2 Модуль называется проективным, если он является прямым слагаемым
некоторого свободного модуля (см., например, [Маклейн и Биркгоф]).
3 В § 8 — существование, в § 7 — единственность. — Прим, перев.
2*
36 Дж. Милнор и Дж. Сташеф
АКСИОМА 1. Для каждого векторного расслоения g суще-
ствует последовательность когомологических классов
W®; Z/2), i = 0, 1, 2, ....
называемых классами Штифеля — Уитни расслоения Класс
©о(£) равен единичному элементу
1еЯ°(В®; Z/2),
и классы Wi(l) равны нулю для I больших, чем п, если £ есть
n-мерное расслоение.
АКСИОМА 2. Естественность. Если отображение f: В(|)->
накрывается некоторым послойным отображением
£->Т], то
wt (|) = f*w{ (n).
АКСИОМА 3. Теорема Уитни о произведении. Если £ и
т] — векторные расслоения над одним и тем же базисным про-
странством, то
k
wk (£Ф п) = Z wt © wk-i (п)-
<-о
Например,
W1 (g ф П) = Wi (g) + ©! (л),
®2 (| ф п) = W2 (|) + W1 (£,) W] (л) + W2 (п).
(Мы будем опускать символ умножения в когомологиях о вся-
кий раз, как это будет удобно.)
АКСИОМА 4. Для линейного расслоения1 у* над окруж-
ностью Р1 класс Штифеля — Уитни	(у{) ненулевой.
Замечания. Характеристические гомологические классы для
касательных расслоений гладких многообразий были опреде-
лены Штифелем в 1935 г. [Штифель]. В том же году Уитни
определил классы wi для любого расслоения над симплициаль-
ным разбиением, слоем которого является сфера [Уитни].
(Расслоения на сферы получаются из евклидовых векторных
расслоений, если в пространстве расслоения брать лишь век-
торы единичной длины.) Теорема Уитни о произведении при-
надлежит Уитни и У2 [Уитни, 1940, 1941], [У, 1948]. Данное
выше аксиоматическое определение классов Штифеля — Уитни
было предложено Хирцебрухом в работе [Хирцебрух, 1966],
где дано аналогичное определение классов Чженя.
1 См. § 2, пример 4. — Прим, перев.
’ Иногда пишут также By. (Полное имя: У Вэнь-цзунь.)—Прим. ред.
§ 4. Классы Штифеля — Уитни 37
Вовсе не очевидно, что классы удовлетворяющие ука-
занным четырем аксиомам, могут быть определены. Тем не ме-
нее мы будем предполагать всюду в этом параграфе, что такие
классы существуют, и выведем некоторое число следствий из
этого предположения.
Следствия из приведенных выше четырех аксиом
Из аксиомы 2 непосредственно вытекает
Предложение 1. Если § изоморфно т], то wi(Z,)= о^(т]).
Предложение 2. Если в — тривиальное векторное расслоение,
то Wi(e) = 0 для i > 0.
Действительно, если расслоение s тривиально, то существует
послойное отображение е в векторное расслоение над точкой.
Сопоставляя эти факты с теоремой Уитни о произведении,
получаем
Предложение 3. Если расслоение 8 тривиально, то wi(e ф
фт])= ®,(т]).
Предложение 4. Если § — некоторое п-мерное расслоение с
евклидовой метрикой, обладающее всюду ненулевым сечением,
то о)п(?)==0. Если g обладает k всюду линейно независимыми
сечениями, то
©n-A+l(S)“a'n-A+j(l)“ ••• “ММ-
В самом деле, из теоремы 3.3 следует, что в этом случае
расслоение £ разбивается в сумму Уитни вфв1, где расслое-
ние s тривиально, а в1 имеет размерность п — k.
Особенно интересное следствие теоремы Уитни о произведе-
нии получается в случае, когда сумма Уитни ? ф г] тривиальна.
Тогда соотношения
©1 (5) + (П) = 0,
©2 (I) + ®i (?) ®i (n) + w2 (п) = 0,
®з (?) + (?) (п) + ®1 (?) «Ъ (n) + w3 (ц) = О,
могут быть рекуррентно разрешены, так что класс оуг (т)) вы-
разится в виде полинома от классов Штифеля — Уитни рас-
слоения £. Удобно ввести следующий формализм.
ОПРЕДЕЛЕНИЕ. Обозначим через ЯП(В, Z/2) кольцо всех
формальных бесконечных рядов
а = а0 + Я1 + а2 + ....
38 Дж. Милнор и Дж. Сташеф
где сц е Hl(B', Z/2). Операция умножения в этом кольце
задается формулой (а0 + ai + а2 + ...) (Ьо + 61 4* 62 + .. .) =
= (лоМ +	+ aobi) 4-(а26о4- 0161 + аоМ+ • Это ум-
ножение коммутативно (так как всё делается по модулю 2) и
ассоциативно. Аддитивно кольцо //П(В; Z/2) представляет со-
бой просто прямое произведение групп Н‘(В-, Z/2).
Полный класс Штифтеля — Уитни «-мерного расслоения g
над В — это по определению элемент
w® »= 1+ ®1 ® + w2© + ... +	+ о 4- О ...
кольца //п (B;Z/2). Заметим, что теорема Уитни о произве-
дении может быть теперь выражена простой формулой
да(£фг]) = да(|)да(г|).
Лемма 4.1. Совокупность всех бесконечных рядов
w = 1 4* + ©2 4* ... s 77 п (В; Z/2),
начинающихся с единицы, образует коммутативную группу по
умножению.
(Это в точности группа единиц кольца Bn(B;Z/2).)
Доказательство. Обратный к заданному элементу w элемент
w — 1 + й>1 + й>2 + й>з + • • 
можно построить рекуррентно по формуле
wn = w1wn_i + w2wn_2+ ••• +wn_Iw1 + wn.
Таким образом, мы получаем
W1 = и>1,
w2 = wf 4- w2,
w3 = w34- w3,
w4 = w4t 4- wfw2 4- w22 4- w4
и т. д., что и доказывает нашу лемму. 
Иначе обратный элемент w может быть вычислен при по-
мощи разложения в ряд:
да = [1 4- (oij 4- W2 4- w3 4- .. .)]’ ==
= 1 — (да]4- w2 4- ®з 4- ...) 4~	4- ®2 4- • • .)2 —
— (а/t 4- w2 4- .. .)3 4- — • • • =
s= 1 — да, 4- (да* — w 4- (— ю3 4-	— к>3) 4- ..,
§ 4. Классы Штифеля — Уитни 39
(где знаки, конечно, не имеют значения). Это приводит к точ-
ному выражению (и + ... +t*)!/ii! ... ik\ для коэффициента
при ... w1^ в разложении w.
Рассмотрим теперь два векторных расслоения £ и г, над од-
ним и тем же базисным пространством. Из леммы 4.1 следует,
что уравнение
может быть однозначно разрешено относительно ьу(т|):
w (ц) = w (g) w (£®П)-
В частности, если расслоение £ ® г) тривиально, то
w (т|) = w (£).
Отметим один важный частный случай:
Лемма 4.2 (теорема двойственности Уитни). Пусть хм— ка-
сательное расслоение многообразия М, лежащего в евклидовом
пространстве, a v — его нормальное расслоение. Тогда
U>i (v) = Wi (хм).
Вычислим теперь классы Штифеля — Уитни в некоторых
частных случаях. При этом нам часто будет удобно использовать
краткое обозначение w (М) для полного класса Штифеля —
Уитни касательного расслоения хм многообразия М.
Пример 1. Для касательного расслоения х единичной сферы
Sn класс w(x) = w(Sn) равен 1. Другими словами, с помощью
классов Штифеля — Уитни расслоение т нельзя отличить от
тривиального расслоения над S".
Доказательство. Для стандартного вложения Sn с: Rn+*
нормальное расслоение v тривиально. Так как о» (т) да (v) = 1 и
w(v) — 1, отсюда следует, что и w(x) = 1.
Другое доказательство (без использования теоремы Уитни
о произведении). Каноническое отображение
f: Sn-+Pn
сферы на проективное пространство является Локальным диф-
феоморфизмом. Поэтому индуцированное отображение
Df: DSn-*DPn
касательных расслоений есть послойное отображение. Приме-
няя аксиому 2, получаем равенство
fX(H = ^(sn),
где гомоморфизм
/*: Нп(Рп- Z/2) -+Hn(Sn-, Z/2),
40 Дж. Милнор и Дж. Сташеф
как хорошо известно, нулевой (см. замечание ниже). Таким
образом, wn(Sn)= 0, что и завершает доказательство. В
В оставшейся части § 4 мы будем иметь дело с расслое-
ниями над проективным пространством Рп. Прежде всего не-
обходимо описать когомологии проективного пространства Рп
с коэффициентами в Z/2.
Лемма 4.3. Группа Hi(Pn-,Z/2) представляет собой цикли-
ческую группу порядка 2 для 0 i п и равна нулю для
бдлыиих значений i. Далее, если а — ненулевой элемент из
№(P";Z/2), то каждая группа H‘(Pn-,Z/2) порождается 1-крат-
ным ^-произведением а1.
Таким образом, кольцо Н*(Рп-, Z/2) является алгеброй с
единицей над полем Z/2 с одной образующей а и одним соотно-
шением ап+1 = 0.
Доказательство читатель может найти в книгах [Хилтон и
Уайли, п. 4.3.3] или [Спеньер]. См. задачи 11.А и 12.С (ср. с 14.4).
Замечание. Эту лемму можно использовать для вычисления
гомоморфизма
Г: Нп (Рп-, Z/2) -> Нп (S'1-, Z/2)
в случае, когда п > 1. Действительно, элемент f*(an) = (j*a)n
равен нулю, так как f*a е Я1 (Sn; Z/2) = 0.
Пример 2. Полный класс Штифеля — Уитни канонического
линейного расслоения у1п над Рп задается формулой
W (у1п) = 1 + а-
Доказательство. Стандартное вложение /: Pl сд Рп, очевид-
но, накрывается послойным отображением расслоения у} в у^.
Следовательно,
Ч (Yi) = “’1 (Y1) ¥= 0.
Итак, класс w1 (у£) не равен нулю, а значит должен быть ра-
вен а. Поскольку по аксиоме 1 остальные классы Штифеля —
Уитни расслоения у^ равны нулю, то это завершает доказатель-
ство. 
Пример 3. По определению линейное расслоение у1 над Ря
содержится как подрасслоение в тривиальном расслоении еп+1
(см. § 2, пример 4). Обозначим через у1 ортогональное допол-
нение к подрасслоению у^ в en+1. (Таким образом, пространство
§ 4. Классы Штифеля — Уитни 41
Е(ух) расслоения у1 состоит из всех пар
({± х}, v)<=PnX Rn+1,
где v е Rn+1— вектор, ортогональный к х.) Тогда
w (у1) = 1 + а + а2 + • • • + ап.
Доказательство. Так как расслоение у„®ух тривиально, то
о, (у1) = w (у^) = (1 + а)-1 — 1 + а + а2 + ... 4- ап. 
Этот пример показывает, что классы Штифеля — Уитни
«-мерного расслоения могут быть ненулевыми во всех размер-
ностях.
Пример 4. Пусть т — касательное расслоение проективного
пространства Рп.
Лемма 4.4. Касательное расслоение т проективного прост-
ранства Рп изоморфно расслоению Нот (у1п, у1).
Доказательство. Пусть L — прямая, проходящая через на-
чало координат в Rn+1 и пересекающая сферу Sn в точках ±х,
и Р с Rn+1 — ортогональная к ней «-мерная плоскость. Пусть
далее f: Sn-+Pn— каноническое отображение, f(x) = {±х}. За-
метим, что два касательных вектора (х, к) и (—х, —о) в DSn
имеют один и тот же образ при отображении
Df: DSn-+DPn,
индуцированном f (см. рис. 5). Таким образом, касательное
многообразие DPn может быть отождествлено с множеством
всех пар {(х, о), (—х,—v)}, удовлетворяющих условиям
х • х = 1, х • и = 0.
Но каждая такая пара определяет линейное отображение
Z:
где
I (х) = о,
и обратно, каждое линейное отображение /: L-+L1, где L —
прямая, проходящая через точки ±х (х-х=1), определяет
вектор v, такой, что х-о = 0. Таким образом, касательное про-
странство к Р" в точке {±х} канонически изоморфно вектор-
ному пространству Hom (А,!1). Следовательно, касательное
векторное расслоение тр„ канонически изоморфно расслоению
Hom (yj,, у-1-). 
42 Дж. Милнор и Дж. Сташеф
При помощи этой леммы нельзя непосредственно вычислить
класс w(Pn), так как мы не знаем пока соотношений, связы-
вающих классы Штифеля — Уитни расслоения Hom (у„> Yx) с
классами Штифеля — Уитни расслоений у1п и у-1-. Однако это
вычисление может быть проведено следующим образом. Пусть
в1 — тривиальное линейное расслоение над Рп.
Рис. 5
Теорема 4,5. Сумма Уитни т ® е1 изоморфна (п 4- \)-крат-
ной сумме Уитни Y„ ® Y„ ® • • • © Y„ • Следовательно, полный
класс Штифеля — Уитни проективного пространства Рп равен
,.	/ n + 1 X Zn-f-lX
w (Р") = (1 + а)+= 1 -Ц j ja-Ц 2 Ja‘2+..
Доказательство. Расслоение Hom (y„, Y„) тривиально, так
как оно является линейным расслоением с каноническим всюду
ненулевым сечением. Следовательно,
Hom (y^, Yx)®Hom (y„, Y„).
Написанное справа расслоение, очевидно, изоморфно расслоению
Нот (ухп, y1® Yi) = Нот (y„, en+1)
и, следовательно, изоморфно (п + 1)-кратной сумме Уитни
Нот(у„> е’Ф ••• ® s') ss Hom (у^> в1)® ... ®Hom(Y^, в’).
§ 4. Классы Штифеля — Уитни	43
Но расслоение Hom (y„> е1) изоморфно у„> так как Y„ имеет
евклидову метрику (см. задачу 3. D). Это доказывает, что
тфе1^ ••• ®Yi-
Используя теперь теорему Уитни о произведении, получаем, что
класс ш(т)= ®(т фе1) равен
••• w(Y;) = (l+a)n+1.
Применение теоремы о биноме завершает доказательство тео-
ремы 4.5. И
Ниже приводится таблица биномиальных коэффициентов
mod 2, 0 i п + 1, для п 14:
1
1 1
Р1:'	1	0 1
Р2:	1111
Р3:	1 0 0 0 1,
Р4.-	.10 0 11
р5:	10 10 10 1
Р6:	11111111
р7:	1 0 0 0 0 0 0 0 1
Р8:	1	1 0 0 0 0 0 0 11
р’:	1	0 10 0 0 0 0 10 1
р10:	111100001111
р";	1 О О О 1 О О О 1 О О О 1
р12:	11001100110011
р'З;	101010101010101
р14;	1111)11111111111
Правую сторону этого треугольника, т. е.
n+ 1 X
, , I, можно не
л 1 J
принимать во внимание, так как Hn+l(Pn-, Z/2) = 0. Например,
мы имеем
w (Р2) — 1 + а + а2,
w(P3) = l,
йу(Р4)=1+а + а4.
Следствие 4.6 (Штифель). Класс w(Pn) равен 1 тогда и
только тогда, когда п+ 1 является степенью двух. Таким обра-
зом, параллелизуемыми могут быть только следующие проек-
тивные пространства: Р\ Р3, Р7, Р'5, ... .
44 Дж. Милнор и Дж. Сташеф
Чуть погодя в теореме 4.7 мы увидим, что Pl, Р3 и Р7 дей-
ствительно параллелизуемы. С другой стороны, известно, что
проективные пространства больших размерностей Р16, Р31, ...
не параллелизуемы (см. [Ботт, Милнор], [Кервер, 1958],
[Адамс, I960]).
Доказательство. Из равенства (а + Ь)2 = а2 + 62(mod2)
вытекает, что
(1+а)2г=1+а<
Следовательно, если п + 1 = 2Г, то
w(Pn) = (l+a)n+l=l+an+1=l..
Обратно, если n-j-l=2rm, где пг нечетно, пг> 1, то
w (Р") = (1 + a)n+1 = (1 + а2Т = 1 + та2' +	° а2'2' + ...
так как 2r < n-j-1. Это завершает доказательство. 
Алгебры с делением
Параллелизуемость проективных пространств тесно связана
с вопросом о существовании вещественных алгебр с делением.
Теорема 4.7 (Штифель). Предположим, что существует би-
линейная операция умножения1
р: КПХКЛ->КП
без делителей нуля. Тогда проективное пространство Рп~1 па-
раллелизуемо и, следовательно, п должно быть степенью чи-
сла 2.
Известно, что такие алгебры с делением существуют для
п=1, 2, 4 и 8, а именно алгебры вещественных чисел, ком-
плексных чисел, кватернионов и чисел Кэли. Следовательно,
проективные пространства Р1, Р3 и Р7 параллелизуемы. То, что
для п > 8 вещественных алгебр с делением не существует, до-
казано в работах, указанных выше, где шла речь о непаралле-
лизуемости проективных пространств размерности п^ 15.
Доказательство. Пусть bi....bn — стандартный базис век-
торного пространства Rn. Заметим, что соответствие
у р (у, Ьх)
1 Не требуется, чтобы эта операция умножения была ассоциативной или
имела единицу.
$ 4. Классы Штифеля — Уитни 45
определяет изоморфизм R" на себя. Следовательно, формула
vt (р (у, Ь^) = р (у, bi)
определяет линейное отображений
vp. Rn->Rn,
такое, что уДх), ..., vn(x) линейно независимы для х#=0, при-
чем ui (х) = х.
Отображения и%(х), ..., Vn(x) определяют п—1 линейно
независимых сечений векторного расслоения
V-i = Hom (yLp Vх).
Действительно, для каждой прямой L, проходящей через начало
координат, определим линейное отображение
vt: L-+Ll
следующим образом. Для вектора xeL пусть б,(х) обозначает
образ вектора у»(х) при ортогональной проекции Rn—*L1. Ясно,
что th = 0, a V2, ..., vn всюду линейно независимы. Таким об-
разом, касательное расслоение является тривиальным рас-
слоением. Это завершает доказательство теоремы 4.7. 
Погружения
В качестве последнего приложения теоремы 4.5 исследуем
вопрос о том, какие проективные пространства допускают по-
гружение в евклидово пространство данной размерности.
Если многообразие М размерности п может быть погружено
в евклидово пространство R"+ft, то, согласно теореме двойствен-
ности Уитни
w{ (у) — W( (М),
двойственные классы Штифеля — Уитни wi(M) равны нулю для
i > k.
В качестве типичного примера рассмотрим проективное про-
странство Р9. Поскольку
ау(Р9) = (1 +а)10=1 +а2 + а8,
то
ш(Р9) = 1 +а2 + а4 + а®.
Таким образом, если Рэ может быть погружено в R9+ft, то k дол-
жно быть не меньше 6.
Еще более эффектный результат получается, когда размер-
ность проективного пространства Рп является степенью двух.
46 Дж. Милнор и Дж. Сташеф
Если п = 2Г, то
w(Pn) = (l 4-fl)'l+1 = l +а + ап,
следовательно,
w (Рп') = 1 + а + а~ + ... 4- ал-1.
Итак, справедлива
Теорема 4.8. Если проективное пространство Р2* может быть
погружено в R2 +к, то k не меньше, чем 2Г — 1.
С другой стороны, Уитни доказал, что любое гладкое ком-
пактное многообразие размерности п > 1 может быть погру-
жено в R2"-1 (см. [Уитни, 1944]). Таким образом, теорема 4,8
дает наилучшую возможную оценку.
Заметим, что из теоремы 4.8 следуют также оценки и для
других проективных пространств. Например, поскольку Р8 не
может быть погружено в R14, то и подавно Р9 не может быть
погружено в R14. Мы заново получили известную оценку для Р9
(см. [Джеймс]).
Обширная и красивая теория погружений многообразий
была разработана Смейлом и Хиршем. Интересующегося чита-
теля отсылаем к работам [Хирш, 1959] и [Смейл, 1959].
Числа Штифеля — Уитни
Теперь мы опишем один полезный инструмент, позволяющий
сравнивать некоторые классы Штифеля — Уитни двух различ-
ных многообразий.
Пусть М — замкнутое, возможно несвязное, гладкое п-мер-
ное многообразие. Поскольку используются гомологии с коэф-
фициентами в Z/2, существует единственный фундаментальный
гомологический класс
Цл1еЯ„(Л1; Z/2)
(см. приложение А). Поэтому для любого когомологического
класса v е Нп(М-, Z/2) определен индекс Кронекера
(о,	€= Z/2.
Мы будем иногда употреблять для него сокращенное обозначе-
ние и[М].
Пусть и, Гг, ..., гп — неотрицательные целые числа, такие,
что г\ + 2г2	... 4- пгп = п. Для любого векторного расслое-
ния £ мы можем образовать моном
®1(ЮГ‘ ... w„(|)rn
§ 4. Классы Штифеля — Уитни 47
в группе когомологий Hn(B(l), Z/2). В частности, мы можем
сделать это для касательного расслоения хм многообразия М.
ОПРЕДЕЛЕНИЕ. Соответствующий индекс Кронекера
(да1 (тм)'1 • • • wn(rM)n> Рм) или сокращенно ... wrn" [Af]
(являющийся вычетом по модулю 2) называется числом Шти-
феля— Уитни многообразия М, отвечающим классу оу,1 ... wrnn
При изучении этих чисел нас будет интересовать вся сово-
купность всевозможных чисел Штифеля — Уитни данного много-
образия. Таким образом, мы говорим, что два различных много-
образия М и М' имеют одинаковые числа Штифеля — Уитни,
если w,1 ... wrnn [АГ] = о,'1 ... wrnn [АД] для любого класса wTf ...
... wnn полной размерности п. (См. п. 6.6 и задачу 6.D.)
Для примера попытаемся вычислить числа Штифеля — Уит-
ни проективного пространства Рп (чуть ли не единственного
многообразия, для которого мы в данный момент в состоянии
решить эту задачу). Пусть т — касательное расслоение Рп. Если
п четно, то когомологический класс шл(т) = (/г 4-1)а” ненуле-
вой и, следовательно, число Штифеля — Уитни wn [Рп] ненуле-
вое. Аналогично, поскольку а>1(т) = (п 4* 1)а =/= О, то w" [Prt] =#0.
Если п есть степень двух, то w(x)= 1 4* а 4- ап, и, значит, в
этом случае все остальные числа Штифеля — Уитни проектив-
ного пространства Рп равны нулю. В общем случае, даже когда
п не является степенью двух, остальные числа Штифеля — Уит-
ни могут быть, конечно, эффективно вычислены в виде произ-
ведения биномиальных коэффициентов.
С другой стороны, если п нечетно, скажем п = 2k — 1, то
и?(т) = (1 4-а)2* =(1-|-а2)*, поэтому w/(r) = 0 для любого не-
четного /. Так как каждый моном полной размерности 2k—1
должен содержать сомножитель W/ нечетной размерности /’, то
все числа Штифеля — Уитни нечетномерного проективного про-
странства Р2к~1 равны нулю. Это дает представление о том, как
много деталей структуры многообразий не улавливает этот ин-
вариант.
Важность чисел Штифеля — Уитни вытекает из следующей
теоремы и ее обращения.
Теорема 4.9 (Понтрягин). Пусть В — гладкое компактное
(п 4- \)-мерное многообразие, границей которого является мно-
гообразие ЛГ (см. § 17). Тогда все числа Штифеля — Уитни мно-
гообразия М равны нулю.
48 Дж. Милнор и Дж. Сташеф
Доказательство. Обозначим фундаментальный гомологиче-
ский класс пары (В, М) через
ЦВЕ//Л+1(Й, М)-
подразумевается, что группой коэффициентов служит Z/2. Тогда
естественный гомоморфизм
д: Hn+i(B, М)-+Нп(М)
переводит цв в цм (см. приложение А). Для любого класса
v е Нп (М) справедливо тождество
(о, <Эр.в) = (бо, цв),
где 6 — естественный гомоморфизм Hn(M)-*-Hn+l(B, М) (мы
здесь не учитываем знаки, так как имеем дело с коэффициен-
тами в группе Z/2). Рассмотрим ограничение на М касатель-
ного расслоения тв и в нем подрасслоение тм. Вводя евклидову
метрику на расслоении тв, можно построить векторное поле,
сопоставляющее точке из М единственный направленный на-
ружу нормальный вектор, натянуть на это поле тривиальное ли-
нейное расслоение е1 и получить тем самым, что
тв |М = тЛ1фе1.
Поэтому классы Штифеля—Уитни расслоения xB|Af совпадают
с классами Штифеля — Уитни W/ расслоения хм- Используя точ-
ную последовательность
Нп (fl) _£> Нп (М) Нп+1 (В, М),
где i* — гомоморфизм, индуцированный вложением г. М-+-В,
получаем,что
б (w,1 ... wrn") — О
и, следовательно,
<Эцв> = (б (ш[‘ ... <«), цв) =- 0.
Таким образом, все числа Штифеля — Уитни многообразия М
равны нулю. 
Обратная теорема, принадлежащая Тому, доказывается мно-
го труднее.
Теорема 4.10 ([Том]). Если все числа Штифеля — Уитни
многообразия М равны нулю, то М является границей некото-
рого гладкого компактного многообразия.
Доказательство можно найти в монографии [Стонг].
Например, дизъюнктное объединение двух экземпляров
Многообразия М, у которого, очевидно, все числа Штифеля —»
§ 4. Классы Штифеля — Уитни 49
Уитни нулевые, служит границей цилиндра MX [О, 1]. У нечет-
номерного проективного пространства Р2*-1 также все числа
Штифеля — Уитни нулевые. Читатель может поразвлекаться,
попытавшись непосредственно доказать, что многообразие Р24-1
является границей.
Теперь мы введем понятие класса кобордизма.
ОПРЕДЕЛЕНИЕ. Два гладких замкнутых n-мерных много-
образия Mi и М2 принадлежат одному и тому же классу (не-
ориентированного) кобордизма, если их дизъюнктное объедине-
ние Mi UM2 служит границей некоторого гладкого компактного
(п + 1)-мерного многообразия.
Из теорем 4.9 и 4.10 непосредственно вытекает следующее
важное
Следствие 4.11, Два замкнутых п-мерных многообразия при-
надлежат одному и тому же классу кобордизма тогда и только
тогда, когда все их соответствующие числа Штифеля — Уитни
равны между собой.
В заключение пять задач для читателя.
Задача 4.А. Показать, что классы Штифеля — Уитни пря-
мого произведения вычисляются по формуле
k
Wk (g X П) = E Wi (g) x wk-i (n).
i-0
Задача 4.B. Доказать следующую теорему Штифеля. Если
п + 1 = 2rm, где m нечетно, то на проективном пространстве Рл
не существует 2Г всюду линейно независимых векторных полей *.
Задача 4.С. Говорят, что многообразие М допускает поле
касательных 6-мерных плоскостей, если его касательное рас-
слоение имеет подрасслоение размерности 6. Показать, что про-
ективное пространство Рп допускает поле касательных одномер-
ных плоскостей тогда и только тогда, когда п нечетно. Пока-
зать, что Р4 и Р6 не допускают поля касательных двумерных
плоскостей.
1 См. [Штифель, 1936], [Стинрод и Уайтхед], [Адамс, 1962].
50 Дж. Милнор и Дж. Сташеф
Задача 4.D. Показать, что если «-мерное многообразие М
может быть погружено в R'*+l, то каждый класс te?f-(Af) равен
i-кратному ^-произведению класса Wi(M) на себя. Показать,
что если проективное пространство Рп может быть погружено
в R/,+I, то число п должно иметь вид 2Г — 1 или 2Г — 2.
Задача 4.Е. Показать, что множество Л’п всех классов не-
ориентированных кобордизмов гладких замкнутых «-мерных
многообразий может быть наделено структурой аддитив-
ной группы. Эта группа кобордизмов Лп конечна в силу 4.11
и, очевидно, является модулем над Z/2. Используя многообра-
зия Р2 X Р2 и Р\ показать, что содержит по крайней мере
четыре различных элемента.
§ 5. МНОГООБРАЗИЯ ГРАССМАНА И УНИВЕРСАЛЬНЫЕ РАССЛОЕНИЯ
В классической дифференциальной геометрии встречается
понятие «сферического образа» кривой А!1 с R*+1. Это образ
кривой М' при отображении
t:
которое сопоставляет каждой точке кривой единичный касатель-
ный вектор в этой точке. Аналогично Гаусс определил сфери-
ческий образ гиперповерхности Mk cr Rft+1 как ее образ при ото-
бражении
h\ Mk-+Sk,
которое сопоставляет каждой точке гиперповерхности Мк нор-
мальный вектор в этой точке (см. рис. 6 и 7). Для того чтобы
уточнить знак касательного или нормального вектора, надо за-
фиксировать ориентацию кривой АР или гиперповерхности М*
(см. § 9). Однако и без введения ориентации можно определить
$ 5. Многообразия Грассмана и универсальные расслоения 51
соответствующее отображение многообразия М* в вещественное
проективное пространство Рк.
Более общо, пусть М — гладкое многообразие размерности п
в пространстве R'l+4. Тогда каждой точке х многообразия М
можно сопоставить касательное пространство DMX с И"*4 в этой
точке х. Гиперплоскость DMX мы будем рассматривать как точ-
ку некоторого нового топологического пространства G^fR"4"4).
Рис. 7.
ОПРЕДЕЛЕНИЕ. Многообразием Грассмана Gn(R.n+k) на-
зывается множество всех n-мерных плоскостей, проходящих че-
рез начало координат в пространстве Rrt+4. В этом множестве
вводится топология факторпространства следующим образом.
Будем называть п-репером в R"4"4 всякий набор из п линейно
независимых векторов пространства Rn+4. Совокупность всех
n-реперов в R'l+4 образует открытое подмножество п-кратного
прямого произведения R"4"4 X R”+4 X • • • X R"+4 и называется
многообразием Штифеля Vn(R"+4) (см. [Стинрод, п. 7.7]). Су-
ществует каноническое отображение
Я- V„(R"+*Wn(Rn+4),
сопоставляющее каждому n-реперу натянутую на него п-мерную
плоскость. Введем в множестве Gn(R',+4) фактортопологию: под-
множество U cz Gn(R"+4) открыто тогда и только тогда, когда
открыт его прообраз <7-1(t/)c: Vn(R"+4).
С другой стороны, пусть V°n (Rn+fe) — подмножество много-
образия Штифеля Vn(R"+4), состоящее из всех ортонормирован-
ных n-реперов. Тогда Gn(R',+4) может быть также рассмотрено
как факторпространство пространства V'h (Rn+*). Обе эти кон-
струкции приводят к одной и той же топологии для многообра-
82 Дж. Милнор и Дж. Сташеф
зия Грассмана Gn(R',+ft), в чем можно убедиться с помощью
следующей коммутативной диаграммы:
процесс ортогонализации
Здесь qo — ограничение отображения q на подмножество
V„(R"+a).
Лемма 5.1. Многообразие Грассмана Gn(Rn+k') является ком-
пактным топологическим многообразием1 размерности nk. Со-
ответствие Х>—>ХХ, сопоставляющее каждой п-мерной плоско-
сти ее ортогональное k-мерное дополнение, определяет гомео-
морфизм многообразий Gn(R"+ft) и G4(R"+ft).
Замечание. В случае k= 1 многообразие Грассмана Gi(R"+1).
совпадает с вещественным проективным пространством Рп. Сле-
довательно, многообразие Gn(Rn+1) всех n-мерных плоскостей
(n + 1)-мерного пространства канонически гомеоморфно проек-
тивному пространству Рп.
Доказательство. Для того чтобы показать, что Gn(R/,+ft) яв-
ляется хаусдорфовым пространством, достаточно построить для
любых двух точек разделяющую их непрерывную вещественно-
значную функцию. Для фиксированной точки w е R"+* обозна-
чим через pw(X) квадрат евклидова расстояния от этой точки
до гиперплоскости X. Пусть Xi, ..., хп — ортонормированный
базис в X. Из равенства
pw(X) — ww — (w Xi)2 — ... — (w • х„)2
видно, что композиция
v°n Gn(Rn+k) R
непрерывна, а значит, и функция рш непрерывна. Пусть теперь
X и Y — различные n-мерные плоскости и точка w принадлежит
X, но не принадлежит У. Тогда pw (X) ф рш (У). Это доказывает,
что Gn(R"+ft) — хаусдорфово пространство.
Множество (Rn+ft) ортонормированных n-реперов является
замкнутым ограниченным подмножеством прямого произведе-
1 Топологическим многообразием размерности d называется хаусдорфово
пространство, у которого каждая точка имеет окрестность, гомеоморфную
евклидову пространству R*
g В. Многообразия Грассмана и универсальные расслоения 53
ния R"+* X ••• X R"+4 и потому компактно. Следовательно, про-
странство
G„(Rn+ft) = z?0(lZ°(R"+ft))
также компактно.
Доказательство того, что всякая точка Хо пространства
Gn(R',+4) имеет окрестность U, гомеоморфную Rnft. Представим
евклидово пространство R',+4 в виде прямой суммы ХофХ^-
Пусть U — открытое подмножество в Gn(R"+ft), состоящее из
всех n-мерных плоскостей У, таких, что ортогональная проекция
р: ХофХ^Хо
отображает У на Хо (т. е. U состоит из всех У, таких, что
У П -Xq- = 0). Тогда каждую гиперплоскость У е V можно рас-
сматривать как график линейного отображения
Т(уу. х0-*х0\
Это определяет взаимно однозначное соответствие
Т: G->Hom(X0, Xo’JasR"*.
Покажем, что Т — гомеоморфизм.
Пусть Xi.....хп — фиксированный ортонормированный ба-
зис в гиперплоскости Хо. Каждая гиперплоскость У s U имеет
базис у\.....уп, однозначно определяемый требованием
p(*/i) = *i..рЫ = х„.
Легко проверить, что n-репер (pi, ..., уп) непрерывно зависит
от У.
Теперь заметим, что имеет место тождество
У1 ~xi + Т (У)хг.
Так как вектор yi непрерывно зависит от У, то и образ
Т (У) х{ е Х^ вектора х,- при отображении Т(У) непрерывно за-
висит от У. Следовательно, линейное отображение Т(У) непре-
рывно зависит от У.
С другой стороны, указанное выше равенство показывает,
что n-репер (у\, .... уп) непрерывно зависит от Т(У) и, следо-
вательно, что У непрерывно зависит от Т(У). Таким образом,
отображение Т-1 также непрерывно. Это завершает доказатель-
ство того, что Gn(R',+4)— многообразие.
Доказательство того, что У1 непрерывно зависит от У. Пусть
(xi, ..., Хй) — фиксированный базис в гиперплоскости Х£. Опре-
делим отображение
f: q~'U->Vk(Rn+k')
54 Дж Милнор и Дж. Сташеф
следующим образом. Для каждого п-репера (z/i, .... уп)^.д~хи
применим процесс ортогонализации Грама — Шмидта к набору
векторов (t/i...уп, х\....хь). Тогда получим ортонормиро-
ванный (п 4- k)-репер (у[, ..., г/'+Д в котором у'п+1.у'п+к <=
еУ1. Полагаем f ........Уп)==(Уп+г •••• /„+*)• Нетрудно убе-
диться, что диаграмма
q-'U-Ц
«I
V
иЛ
Q
Gk(Rn+k)
коммутативна. Далее, отображение f непрерывно и, следова-
тельно, q of непрерывно, поэтому соответствие У*—>У1 также
должно быть непрерывным. Это завершает доказательство лем-
мы 5.1. 
Каноническое векторное n-мерное расслоение	над
многообразием Грассмана Gn(R"+ft) строится следующим обра-
зом. Пространство
f = £(Yn(R"+ft))
этого расслоения определяется как множество всех пар 1
(n-мерная плоскость в Rn+ft, вектор в этой плоскости).
В множестве Е вводится топология, индуцируемая его вложе-
нием в Gn(R"+ft)X R"+ft. Проекция л: £->Gn(R"+ft) определяет-
ся условием л(Х, х) = Х. Структура векторного пространства в
слое над «точкой» XeGn(Rz,+ft) задается формулой ti(X, Xi) +
+ t2(X, х2) — (Х, fiXi + t2Xzf. (Заметим, что расслоение v*(R',+I)
совпадает с линейным расслоением у1п, определенным в при-
мере 4 § 2.)
Лемма 5.2. Построенное выше расслоение yn(Rnvk) удовле-
творяет условию локальной тривиальности.
Доказательство. Пусть U — окрестность точки Хо е Gzl(R/,+ft),
такая же, как при доказательстве леммы 5.1. Определим коор-
динатный гомеоморфизм
й: UXXQ-+n-4J
следующим образом. Положим h(У, х) = (У, у), где у — одно-
значно определенный вектор в У, переходящий в х при ортого-
* Здесь, как и всюду в книге, термин «л-мерная плоскость» означает
линейное подпространство размерности л. Таким образом, мы рассматриваем
только те л-мерные плоскости, которые проходят через начало координат.
$ 5. Многообразия Грассмана и универсальные расслоения 55
нальной проекции
р: R"+*->Xo.
Тождества
й(У, х) = (У, х + Г(У)х)
и
h~\Y, y) = (Y, ру)
показывают, что отображения й и h~l непрерывны. Тем самым
лемма доказана. 
Для данного гладкого n-мерного многообразия М a R"+*
обобщенное гауссово отображение
g: M->Gn(Rn+k)
определяется как отображение, которое ставит в соответствие
каждой точке х <= М касательное пространство DMX^ Gn(Rn+k).
Обобщенное гауссово отображение накрывается послойным ото-
бражением
S' £(TAf)->f(Yn(R'l+4)),
где g(x, v) — (DMx, v). Мы будем использовать для этого ото-
бражения сокращенную запись
g-
Ясно, что оба отображения g и g непрерывны.
Не только касательные расслоения, но и большинство дру-
гих «-мерных расслоений могут быть отображены в расслоение
7/,(R',+4), если только число k достаточно велико. По этой при-
чине y',(R,,+ft) называют универсальным расслоением. (См. тео-
ремы 5.6 и 5.7, а также [Стинрод, § 19].)
Лемма 5.3. Для любого п-мерного расслоения £ над ком-
пактным базисным пространством В существует послойное ото-
бражение g->v"(R"+ft), при условии что k достаточно велико.
Для того чтобы построить послойное отображение
£->V'!(R'n), достаточно построить отображение
f: £(£)->Rm,
которое на каждом слое расслоения ? линейно и инъективно
(т. е. имеет нулевое ядро). Требуемое отображение / тогда мо-
жно определить условием
f(e) = (f (слой, содержащий вектор е), f(e)).
Непрерывность отображения f нетрудно проверить, используя
локальную тривиальность расслоения
56
Дж. Милнор и Дж. Сташеф
Доказательство. Выберем открытые множества U\.......Ur,
покрывающие В и такие, что каждое расслоение £| Ui триви-
ально. Поскольку базисное пространство В нормально, найдутся
открытые множества Vi, .... Vr, покрывающие В и такие, что
P/ct/f (см. [Келли]). Здесь Г, обозначает замыкание множе-
ства Vi. Аналогично выбираются открытые множества Wi,..., Wr,
удовлетворяющие условию IF,- с Vt. Пусть
Хг: B->R
— непрерывная функция, равная 1 на ТРг и 0 вне Vi.
Так как расслоение l\Ui тривиально, то существует отобра-
жение
htt n-lU{-^Rn,
которое является линейным изоморфизмом на каждом слое.
Определим отображение hi: E(g)->Rn формулами
t (	0, если л (е) ф Рг,
(е)	| X/ (л (a)) ht (е), если л (а) е [7г.
Очевидно, hi непрерывно и линейно на каждом слое. Теперь
определим отображение
f: E(g)->Rn© ... ©R^R™,
положив f (е) = (ftf(a), hh(e).h'r(e}). Отображение f также
непрерывно и на каждом слое инъективно. Это завершает дока-
зательство леммы 5.3. 
Бесконечные многообразия Грассмана
Аналогичные рассуждения проходят также в случае, когда
база В паракомпактна и конечномерна (см. задачу 5.Е). Однако
если мы хотим охватить и расслоения с более экзотическими
базисными пространствами, то нужно позволить размерности
евклидова пространства Rn+ft бесконечно возрастать, и это при-
водит к бесконечным многообразиям Грассмана Gn(R<x>).
Пусть R00 обозначает векторное пространство, состоящее из
всех бесконечных последовательностей
х = (хь х2, х3, ...)
вещественных чисел, в которых лишь конечное число членов от-
лично от нуля. (Таким образом, R°° гораздо «меньше», чем про-
странства с бесконечным числом координат, использовавшиеся
в § 1.) Для любого фиксированного k подпространство в R00,
состоящее из всех последовательностей вида
(х}, х2, .... xk, 0, 0, ..
§ 5. Многообразия Грассмана и универсальные расслоения 57
будем отождествлять с координатным пространством R*. Тогда
R1 cz R2 cz R3 cz ... и объединение всех R* равно R00.
ОПРЕДЕЛЕНИЕ. Бесконечным, многообразием, Грассмана
Gn-Gn(W°)
называется множество всех n-мерных линейных подпространств
пространства R°°, наделенно топологией прямого предела1
следующей последовательности многообразий:
G„ (Rn) <= G„ (Rn+1) с G„ (Rn+2) с ....
Другими словами, подмножество пространства Gn открыто
[соотв. замкнуто] тогда и только тогда, когда его пересечение
с Gn(R'!+ft) открыто [соотв. замкнуто] как подмножество в
Gn(R"+ft) для каждого k. (Это определение имеет смысл, так
как Gn(R°°) равно объединению подмножеств Gn(R"+ft).)
В частности, бесконечное проективное пространство Р°° —
= Gi(R°°) —это прямой предел последовательности P*czP2cz
с. Р3 cz ... .
Аналогично само R°° может быть наделено топологией пря-
мого предела последовательности R1 cz R2 cz ... .
Универсальное расслоение у"
Каноническое расслоение у" над бесконечным многообра-
зием Грассмана G„ строится точно так же, как и в конечномер-
ном случае. А именно, пусть
E(yn)<=GnXK°
—множество всех пар вида
(n-мерная плоскость в R°°, вектор в этой плоскости)
с топологией, индуцированной из прямого произведения. Опре-
делим проекцию л: E(yn)-+Gn условием я(Х, х) = Х и введем
структуру векторного пространства в слоях, как и прежде.
Лемма 5.4. Так построенное векторное расслоение уп удовле*
творяет условию локальной тривиальности.
1 Обычно в алгебраической топологии топологию прямого предела моно-
тонно возрастающей последовательности пространств называют «слабой»,
причем под слабой топологией понимается та, в которой много открытых
множеств. Такое словоупотребление неудачно, ибо в анализе термин «слабая
топология» используется точно в противоположном смысле. С другой сторо-
ны, термины «тонкая топология» или «уайтхедовская топология» вполне при-
емлемы.
58 Дж. Мцлнор и Дж. Сташеф
Доказывается эта лемма по существу так же, как и лем-
ма 5.2. Однако нужна следующая техническая лемма (см.
[Уайтхед, 1961, п. 18.5]).
Лемма 5.5. Пусть 410:42 с: ... и BioB2o ... — последо-
вательности локально компактных пространств с прямыми пре-
делами А и В соответственно. Тогда топология прямого произве-
дения на А X В совпадает с топологией прямого предела после-
довательности 41X^1 cz Д2ХВ2С ••• .
Доказательство. Пусть множество W открыто в топологии
прямого предела, и пусть (а, Ь)—некоторая точка из W. Пред-
положим, что (а, 6)<= Д, Х Bi. Выберем компактные окрестно-
сти Ki точки а в Ai и Ц точки b в Bi так, чтобы Ki X LiCzW.
Далее, можно (чуть потрудившись) выбрать компактные окре-
стности Ki+i множества Ki в 4,+1 и Li+i множества L,- в B(+i
так, чтобы Ki+i X Li+t о W. Продолжая по индукции, построим
последовательность окрестностей Kt о Ki+\ о К/+2 о: ... с объ-
единением U и последовательность окрестностей Li <0 Li+\ <0
с Li+2 о: ... с объединением V. Множества V и U открыты, и
(a, b) е U X V с= W.
Таким образом, множество W открыто и в топологии прямого
произведения, что и завершает доказательство леммы 5.5. 
Доказательство леммы 5.4.Пусть AqcR00 — фиксированная
n-мерная плоскость и UcGn— множество всех n-мерных пло-
скостей У, которые проектируются на Хо при ортогональной
проекции р: R°°-*-Xo. Это множество U открыто, потому что для
каждого k пересечение
Uk = Uf\Gn^n+k),
как мы знаем, открыто. Определим координатное отображение
й: UXX0^n-lU,
как в лемме 5.2. Тогда, согласно этой лемме, отображение
h\ UkXKo непрерывно для каждого k. Используя теперь лем-
му 5.5, получаем, что отображение h непрерывно на всем множе-
стве иххй.
Как и прежде, из тождества й-1 (У, «/) = (У, ру) следует не-
прерывность обратного отображения й-1. Таким образом, й —
гомеоморфизм. Это завершает доказательство того, что рас-
слоение у" локально тривиально. 
Следующие две теоремы показывают, что расслоение уп над
Gn является «универсальным» n-мерным расслоением,
§ 5. Многообразия Грассмана и универсальные расслоения 59
Теорема 5.6. Всякое п-мерное расслоение £ над паракомпакт-
ной базой допускает послойное отображение
Два послойных отображения f, g-. называются по-
слойно гомотопными, если существует однопараметрическое
семейство послойных отображений
такое, что ho — f, h\ = g и h непрерывно как функция от двух
переменных £ и t, т. е. ассоциированное отображение
h-. £©Х[0, 1]-*W)
непрерывно.
Теорема 5.7. Любые два послойных отображения данного
п-мерного расслоения I в расслоение у" послойно гомотопны.
Паракомпактные пространства
Прежде чем приступать к доказательству теорем 5.6 и 5.7,
дадим обзор определений и основных теорем, касающихся пара-
компактности. Более подробные сведения читатель может найти
в книгах [Келли] или [Дугунджи].
ОПРЕДЕЛЕНИЕ 5.8. Топологическое пространство В назы-
вается паракомпактным, если оно хаусдорфово и для любого его
открытого покрытия {£7а} существует такое открытое покрытие
{Ер}, что
1) покрытие {Ер} вписано в {t/a}, т. е. каждое открытое мно-
жество Ер содержится в некотором Ua,
2) покрытие {Ер} локально конечно, т. е. каждая точка про-
странства В имеет окрестность, пересекающуюся лишь с конеч-
ным числом множеств Ер.
Почти все обычно используемые топологические простран-
ства паракомпактны. Например (см. указанные выше книги):
Теорема А. Стоуна. Всякое метрическое пространство пара-
компактно.
Теорема Мориты. Если регулярное топологическое простран-
ство является счетным объединением компактных подмножеств,
то оно паракомпактно.
Следствие. Прямой предел последовательности Ki с К2 cz
с. Кзс. ... компактных пространств паракомпактен. В частно-
сти, бесконечное многообразие Грассмана Gn паракомпактно.
Действительно, как следует из результатов работы [Уайт-
хед, 1961, п. 18.4], такой прямой предел является регулярным
60 Дж. Милнор и Дж. Сташеф
пространством. (Читателю не составит особого труда доказать
это самостоятельно.)
Теорема Дьёдонне. Всякое паракомпактное пространство нор-
мально.
Доказательство теоремы 5.6 основано на следующей лемме.
Лемма 5.9. Для любого расслоения £ над паракомпактной
базой В существует локально конечное счетное покрытие про-
странства В открытыми множествами Ui,Ui,U3, такими,
что расслоение || Ut тривиально для каждого i.
Доказательство. Выберем локально конечное открытое по-
крытие {Уа}, такое, что каждое расслоение £|Уа тривиально, и
открытое покрытие {1Уа}, такое, что W’aCzVa для каждого а
(см. [Келли]). Пусть Ха:	— непрерывная функция, кото-
рая принимает значение 1 на замкнутом множестве и зна-
чение 0 вне открытого множества Va. Для каждого непустого
конечного подмножества S множества индексов {а} обозначим
через U(S) множество всех точек бе В, для которых
min Ха (б) > max Ха (б).
aeS	аф S
Пусть Uk — объединение тех множеств C/(S), для которых S
состоит точно из k элементов. Ясно, что Uk — открытое множе-
ство и что
B = t/iUC/2Ut/3U ....
Действительно, если для данной точки Ь^В ровно k чисел
(б) положительны, то б е Uk-
Заметим, что если а — элемент множества S, то
U(S)cVa.
Так как покрытие {Уа} локально конечно, то и покрытие {{/*}
локально конечно. Далее, так как расслоение £|Уа тривиально,
то и каждое расслоение £[ U(S) тривиально. Но множество Uk
равно дизъюнктному объединению своих открытых подмножеств
U(S). Следовательно, расслоение также тривиально. 
Послойное отображение f: |->,уп можно теперь построить
так же, как при доказательстве леммы 5.3 (подробности предо-
ставляем читателю). Этим завершается доказательство теоре-
мы 5.6. 
Доказательство теоремы 5.7. Каждое послойное отображе-
ние f:	определяет отображение
f: W->IT,
5 5. Многообразия Грассмана и универсальные расслоения 61
ограничение которого на каждый слой расслоения £ линейно и
инъективно. Обратно, каждое отображение f определяет послой-
ное отображение	по формуле
f (e) = (f (слой, содержащий е), f(e)).
Пусть f, g:	— любые два послойных отображения.
Частный случай. Предположим, что вектор f(e)eR°° не ра-
вен отрицательному кратному вектора g(e) ни для какого
е =/= 0, е е Е (£). Тогда формула
определяет гомотопию между f и Чтобы доказать, что ассо-
циированное отображение И: В(|)Х[О, 1]->R°° непрерывно, до-
статочно показать, что в R00 непрерывны операции векторного
пространства (т. е. сложение векторов и умножение их на ска-
ляры). Но это легко следует из леммы 5.5. Очевидно, что
й((е)#=0 для любого ненулевого вектора из £(|). Следователь-
но, мы можем определить послойную гомотопию h\ £(£)Х
Х[0, 1]^-£(у”) формулой
ht (е) = (ft (слой, содержащий е), fit (е)).
Чтобы доказать, что отображение h непрерывно, достаточно
показать, что соответствующее отображение базисных про-
странств
й: В® ХЮ. 1]->G„
непрерывно. Пусть U — открытое подмножество базисного про-
странства В(1), такое, что расслоение Jj| U тривиально, и
si, .,,, Sn — всюду линейно независимые сечения расслоения
£| U. Тогда отображение Н| UX[0, 1] можно представить в виде
композиции следующих двух отображений:
1) непрерывного отображения b, ti—>(fitsi(b), ..., fitsn(b))
произведения £7 X [0, 1] в бесконечное многообразие Штифеля
Vn(R°°)c: R°°X ••• XR“ (п сомножителей) и
2) канонической проекции q: Vn(R°°)-> Gn.
Применяя лемму 5.5, заключаем, что проекция q непрерывна.
Поэтому отображение Н непрерывно и, следовательно, послой-
ная гомотопия h между f и g непрерывна.
Общий случай. Пусть f, g:	— два произвольных по-
слойных отображения. Обозначим через
df. y”->y”
послойное отображение, индуцированное линейным преобразо-
ванием R°°-*R°°, переводящим г-й базисный вектор в (21—1)-й.
62 Пж Милнор и Дж. Сташеф
Аналогично, обозначим через d2. уп ->уп послойное отображе-
ние, индуцированное линейным преобразованием, переводящим
i-й базисный вектор в (2/)-й. Теперь заметим, что, используя
конструкцию рассмотренного выше частного случая, можно по-
строить следующие три послойные гомотопии:
f~ di ° f ~ d2 ° g ~ g.
Следовательно, f~g. В
Характеристические классы
вещественных n-мерных расслоений
Используя теоремы 5.6 и 5.7, можно дать общее определение
характеристического класса. Сначала заметим следующее.
Следствие 5.10. Любое n-мерное расслоение £ над параком-
пактной базой В определяет единственный гомотопический
класс отображений
h- B->Gn.
Доказательство. Пусть fe. — одно из послойных ото-
бражений, существующих по теореме 5.6, и \ — соответствую-
щее отображение базисных пространств. Единственность гомо-
топического класса отображения следует из теоремы 5.7. В
Пусть теперь А — некоторая область коэффициентов, являю-
щаяся группой или кольцом, и
c^Hl(Gn- А)
— некоторый класс когомологий. Тогда расслоение £ вместе с
классом с определяют когомологический класс
Н(с)еЯг(В; А).
Этот класс будет кратко обозначаться с(£).
ОПРЕДЕЛЕНИЕ. Класс с(£) называется характеристиче-
ским когомологическим классом расслоения £, определяемым
классом когомологий с.
Заметим, что соответствие >с(£) обладает свойством есте-
ственности относительно послойных отображений (ср. с аксио-
мой 2 § 4). Обратно, если
— соответствие, естественное относительно послойных отобра-
жений, TQ
с(|) = Нс (у").
£ 5. Многообразия Грассмана и универсальные расслоения 63
Таким образом, приведенная конструкция когомологических ха-
рактеристических классов является наиболее общей. Коротко
говоря, кольцо всех характеристических когомологических клас-
сов п-мерных расслоений над паракомпактным базисным про-
странством с кольцом коэффициентов Л канонически изоморфно
кольцу когомологий H*(Gn', Л).
Эта конструкция придает особое значение задаче вычисле-
ния когомологий многообразия Грассмана Gn. В следующих двух
параграфах будет дан метод вычисления когомологий этого мно-
гообразия, по крайней мере для кольца коэффициентов Z/2.
Замечание. Используя «теорему о накрывающей гомотопии»
(см. [Дольд], [Хьюзмоллер]), можно усилить следствие 5.10
следующим образом: два п-мерных расслоения £ и т] над пара-
компактным пространством В изоморфны тогда и только тогда,
когда отображения \ и из следствия 5.10 гомотопны.
В заключение пять задач для читателя.
Задача 5.А. Показать, что многообразие Грассмана Gn(Rn+*)
может быть следующим образом наделено структурой гладкого
многообразия: функция ф. Gn(Rn+A)-*R принадлежит совокуп-
ности F гладких вещественнозначных функций (см. § 1) тогда
и только тогда, когда композиция fo q: Vn(R'I+*)-> R является
гладкой функцией.
Задача 5.В. Показать, что касательное расслоение многообра-
зия Грассмана Gn(Rn+*) изоморфно расслоению Hom(y/I(R'I+/i),
у1), где у1 обозначает ортогональное дополнение к расслоению
^n(Rn+*) в тривиальном расслоении еп+*. Далее, рассмотрим
гладкое многообразие М cz Rn+* с нормальным расслоением v.
Показать, что отображение .
Dg: DM^DGa($l'rk'),
индуцированное обобщенным гауссовым отображением g-. М-+
-> Gn (R"+*), определяет сечение расслоения
Hom(TM, Нот(тл1, v)) s* Hom (tm® xm, v).
(Это сечение называется «второй фундаментальной формой»
многообразия М.)
Задача 5.С. Показать, что многообразие Грассмана Gn(R'ra)
диффеоморфно гладкому многообразию всех симметричных
идемпотентных m X m-матриц со следом п. Показать также, что
отображение
(хь ..., хп) xi А ... А ,хп
64 Дж. Милнор и Дж. Сташеф
многообразия Штифеля Vn(R"') во внешнюю степень Л" ОТ)
пространства Rm дает возможность построить гладкое вложение
многообразия Грассмана Gn(Rm) в проективное пространство
Gi (A’CR'”))^^") \(См. [Ван дер Варден, 1939, § 7].)
Задача 5.D. Показать, что многообразие Грассмана Gn(Rn+ft)
обладает следующим свойством однородности. Для любых двух
n-мерных плоскостей X, Y a Rn+* существует ортогональный ав-
томорфизм пространства Rn+\ который переводит X в У.
Дж. Г. К. Уайтхед [Уайтхед Дж. Г. К., 1961] определил угол
а(Х, У) между л-мерными плоскостями X, У как максимум по
всем единичным векторам х е X угла, образуемого вектором х
с плоскостью У. Показать, что а есть метрика на топологиче-
ском пространстве Gn(Rn+*) и что
а(Х, У) = а(Х±, У-*-).
Задача 5.Е. Пусть g— некоторое n-мерное расслоение над
пространством В.
1)	Показать, что векторное расслоение т] над В, такое, что
расслоение £ © т] тривиально, существует тогда и только тогда,
когда существует послойное отображение
(для больших k). Расслоение g, для которого такое отображе-
ние существует, будем называть расслоением конечного типа.
2)	Предположим теперь, что пространство В нормально. По-
казать, что расслоение g имеет конечный тип тогда и только
тогда, когда В обладает конечным открытым покрытием
U\, .... Ur, таким, что расслоения g|Ui тривиальны для всех i.
3)	Показать (используя рассуждения из доказательства
леммы 5.9), что если пространство В паракомпактно и имеет
конечную размерность по покрытиям, то всякое расслоение g
над В имеет конечный тип.
4)	Используя классы Штифеля — Уитни, показать, что век-
торное расслоение у1 над Р°° не является расслоением конеч-
ного типа.
§ 6. КЛЕТОЧНАЯ СТРУКТУРА МНОГООБРАЗИЙ ГРАССМАНА
В этом параграфе мы опишем данное в [Эресманн] канони-
ческое клеточное разбиение бесконечного многообразия Грас-
смана Gn (R00). Каждое конечное многообразие Грассмана
Gn(Rn+J!!) появляется при этом как конечное подразбиение. Эта
клеточная структура многообразия Грассмана была использо-
вана в [Понтрягин] и в [Чжень] в качестве основы для по-
§ 6. Клеточная структура многообразий Грассмана 63
строения теории характеристических классов. За дальнейшими
сведениями читатель может обратиться к этим источникам, а
также к работе [У]. Подробное изложение теории клеточных
разбиеии имеется в книге [Ланделл и Вейнграм]. Многообра-
зия Грассмана впервые появляются в этой книге на стр. 17.
Сначала напомним некоторые определения. Пусть D” обо-
значает единичный шар в Rp, состоящий из всех векторов v, та-
ких что | v |	1. Внутренность единичного шара £>р определяет-
ся как множество всех векторов о, таких, что |v|< 1. В особом
случае р = 0 будем считать, что шар D₽ и его внутренность со-
стоят из одной-единственной точки.
Любое пространство, гомеоморфное шару D?, называется
замкнутой р-мерной клеткой, а любое пространство, гомеоморф-
ное его внутренности, — открытой р-мерной клеткой. Например,
само Rp есть открытая р-мерная клетка.
ОПРЕДЕЛЕНИЕ 6.1 ([Дж. Г. К. Уайтхед, 1949]). Клеточ-
ное разбиение1 * 3 состоит из хаусдорфова пространства К, назы-
ваемого пространством разбиения, и семейства {ео} его непере-
секающихся подмножеств, покрывающих К и таких, что выпол-
нены четыре условия:
1)	Каждое ea представляет собой топологическую открытую
клетку размерности п(а)^0, для которой существует непре-
рывное отображение
f: Dn(a)->K,
гомеоморфно отображающее внутренность шара на клетку
еа. (Такое отображение / называется характеристическим ото-
бражением для клетки еа.)
2)	Каждая точка х; принадлежащая замыканию ёа клетки
еа, но не принадлежащая самой этой клетке, должна лежать
в некоторой клетке ер меньшей размерности.
Если клеточное разбиение конечно, т. е. имеется лишь ко-
нечное число клеток ев, то этих двух условий уже и достаточно.
В общем же случае нужны еще два условия. (Конечным) под-
разбиением разбиения К называется всякое разбиение, состоя-
щее из замкнутого подмножества пространства К и покрываю-
щего это подмножество (конечного) подсемейства клеток еа.
3)	Конечность замыкания. Каждая точка пространства К
принадлежит некоторому конечному подразбиению.
4)	Топология Уайтхеда. Топология в пространстве К совпа-
дает с топологией прямого предела его конечных подразбиений.
Это означает, что подмножество пространства К замкнуто
1 В оригинале используется термин «СИ7-сотр1ех». Подробное изложение
теории клеточных разбиений имеется в книге [* Постников] (звездочка отсы-
лает к списку литературы, добавленной при переводе). — Прим, перев.
3 Дж. Милнор, Дж, Сташеф
66 Цж. Милнор и Иж. Сташеф
тогда и только тогда, когда его пересечение с каждым конеч-
ным подразбиением замкнуто.
Заметим, что замыкание ёа клетки еа пространства К не обя-
зано быть клеткой. Например, сферу Sn можно рассматривать
как СЦ^-комплекс с одной 0-мерной клеткой и одной п-мерной
клеткой. В этом случае замыкание n-мерной клетки равно всей
сфере S".
Теорема Миядзаки утверждает, что любое клеточное разбие-
ние есть паракомпактное пространство ([Миядзаки], ср. [Ду-
гунджи]).
Клеточное разбиение многообразия Грассмана Gn(Rm) стро-
ится следующим образом. Напомним, что пространство Rm со-
держит подпространства
R°c R1 с R2c ... cRn,
где Rfe состоит из всех векторов вида v — (vi, ..., Vk, 0, ...,0).
Каждая n-мерная плоскость X с: Rm задает последовательность
целых чисел
О < dim (X Л R1) < dim (X Л R2X . . . < dim (X Л Rm) = n.
Два соседних числа в этой последовательности различаются не
более чем на 1. Этот факт доказывается при помощи точной
последовательности
О -> X Л R*-1 -> X Л R*	R.
Таким образом, в указанной выше последовательности целых
чисел имеется в точности п «скачков».
Символом Шуберта a=(oi, ..., оп) называется всякая по-
следовательность целых чисел, удовлетворяющая условию
1	01 < ст2 < ... < стя пг.
Для каждого символа Шуберта о обозначим через е(о)с:
cz Gn(Rm) множество всех п-мерных плоскостей X, таких, что
dim(хЛR°z) — i, dim(xnR°z *) = /—1,
i = l, 2, ..., n. Очевидно, каждая плоскость XeG„(R'ra) при-
надлежит в точности одному из множеств е(о). Мы увидим
вскоре, что множество е(о) является открытой клеткой1 раз-
мерности d(a) = (oi — 1)4-(аг — 2)-J- ... 4-(®п — п).
1 Ее замыкание ё(о) называется многообразием Шуберта (ср. [Шу-
берт]). В обозначениях Чженя и У клетка е(о) индексируется не последо-
вательностью о = (Оь ...,ап), а модифицированной последовательностью
(01 — 1, 02 — 2, ..., Ол — п), что во многих случаях более удобно.
$ 6. Клеточная структура многообразий Грассмана 67
Пусть Hk cz Rm обозначает открытое полупространство, со-
стоящее из всех векторов вида x=(gi, %k, 0,	0), где
> 0. Заметим, что n-мерная плоскость X принадлежит е(а)
тогда и только тогда, когда она обладает базисом Ху.хп,
таким, что
Xi&H0', .... хп^Н°п.
Действительно, если в X имеется такой базис, то из указанной
выше точной последовательности следует, что
dim (х Л R°z) > dim (х Л Ro<~‘)
для i=l, п и поэтому Xse(o), Обратное утверждение
доказывается аналогично. На языке матриц, n-мерная пло-
скость X принадлежит е(о) тогда и только тогда, когда ее мож-
но представить как пространство, натянутое на векторы-строки
некоторой п X m-матрицы [х,/] вида
“•...*10...000...000...0”
*...***. ..*10. ..000. ..о
.***... *10... о
где в i-й строке о/-й элемент положителен (скажем, равен 1), а
все последующие равны нулю.
Лемма 6.2. Каждая n-мерная плоскость Хее(о) обладает
единственным ортонормированным базисом (xi, xj, .... хп), та-
ким, что Х| еЯ ..., хп е Н ".
Доказательство. Вектор xi должен принадлежать одномер-
ному векторному пространству X Л RCT| и быть единичным. Это
дает только две возможности для выбора вектора xj, а условие,
что его О1-я координата должна быть положительной, оставляет
лишь одну из них. Далее, вектор Хг должен принадлежать дву-
мерному векторному пространству X Л R°’ и быть единичным и
ортогональным к хь Снова мы получаем только две возможно-
сти для выбора вектора xj, и условие, что его Ог-я координата
должна быть положительной, оставляет лишь одну из них. Про-
должая по индукции, получаем, что, векторы хз, х«, ..., хп так-
же однозначно определены. 
Определение. Пусть е' (о) — Vn (Rm) Л (я”1 X ... X Яст") обо-
значает множество всех ортонормированных п-реперов
(xi, ..., хя), таких, что каждый вектор Xi принадлежит откры-
3*
68 Дж. Милнор и Дж. Сташеф
тому полупространству Н°*. Пусть ё'(о) обозначает множество
всех ортонормированных реперов (xi.....х„), таких, что каж-
тт°1
дый вектор Xi принадлежит замкнутому полупространству Н \
Лемма 6.3. Множество ё'(о) представляет собой замкнутую
клетку размерности d(o) = (ai — 1) + (а2 — 2)4- ... 4-(°« — п\
с внутренностью е'(р). Далее, q гомеоморфно отображает откры-
тую клетку е'(о) на е(а).
Таким образом, е(а) действительно является открытой клет-
кой размерности d(o), причем отображение
<7|ё'(о): e'(a)-*Gn(Rm)
служит характеристическим отображением этой клетки.
Доказательство проведем индукцией по п. Для п = 1 множе-
ство e'(ai) состоит из всех векторов
X1~(X11’ Х12> •••>	0....0)>
таких, что £хц= 1, х10 ^0. Очевидно, что это множество есть
замкнутая полусфера размерности Oi — 1 и, следовательно, го-
меоморфно шару D01-1.
Для двух данных единичных векторов и, v е R'”, таких, что
и ф — v, обозначим через Т (и, v) однозначно определенное
вращение пространства Rm, которое переводит вектор и в век-
тор v и оставляет на месте все векторы, ортогональные одновре-
менно кино. Таким образом, Т(и, и) — тождественное отобра-
жение и Т(о, и) — Т(и, о)-1. Иначе вращение Т(и, о) может
быть определено формулой
Т(и, о) х = х — ^^.’VX (и 4- и) 4- 2 (и • х) о.
Действительно, отображение Т(и, о), определенное таким обра-
зом, линейно и действует нужным образом на векторы и, о и
векторы, ортогональные к и и и. Из этой формулы следует, что
1) вектор Т(и, о)х непрерывно зависит от совокупности трех
переменных и, и, х и
2) если и, о е R*, то Т(и, v) х&з х (mod Rft).
Пусть bt^H — вектор, у которого oi-я координата рав-
на 1, а все другие равны нулю. Таким образом, (&i, ..., 6л)е
ее'(а). Для любого n-репера (хь ..., хл)её'(о) рассмотрим
вращение
т = Т (Ьп, хп) ° Т х„_1) о ... о Т (bl, Xi)
§ 6. Клеточная структура многообразий Грассмана 69
пространства Rm. Это вращение переводит п векторов bi, ..., bn
в векторы xi....хп соответственно. В самом деле, каждое из
вращений T(b\, xi), T(bi-i, x(-i) оставляет вектор bi не-
подвижным, так как bi-b) = bi-х/ = 0 для i> /; вращение
T(bi, xi) переводит bi в хр, и наконец, вращения 7'(&;+i, Xt+\), ...
..., Т (bn, хп) оставляют вектор xi неподвижным.
Для данного целого числа an+i > ал обозначим через D мно-
жество всех единичных векторов ы е Н л+1, таких, что
Ь^ и =...== Ьп • и = 0.
Очевидно, D является замкнутой полусферой размерности
Ол+i — п — 1 и, следовательно, топологически представляет со-
бой замкнутую клетку. Построим гомеоморфизм
f- e'(oi...an)XD-+e' (ai, .... ct,!+i).
А именно, определим f формулой
f((xi...хп), u) = (xi...хп, Ти),
где Т — построенное выше вращение, зависящее от xi, ..., хп.
Чтобы доказать, что (п -(-l)-penep (xi, .... хя, Ти) действитель-
но принадлежит множеству ё'(<Т1, .... a«+i), заметим, что
Xi •Tu==Tbi • Ти = bi • и — 0.
ДЛЯ и что
Ти • Ти — и • и — 1
(ГиеЯ°л+1, так как T« = u(mod Ra,t)). Очевидно, что f непре-
рывно отображает множество ё' (аь ..., ап) X D в ё' (оь ..., <тя+1).
Аналогичным образом формула
« = 7’-1хл+1 = 7’(х1, bi)о ... о7’(х„, bn)xn+leD
показывает, что обратное отображение f~l определено и непре
рывно.
Итак, множество e'(oi.....on+ij гомеоморфно произведе-
нию ё'(аь ..., dn)XD. Рассуждая по индукции, мы получим,
что каждое множество ё'(о) есть замкнутая клетка размерно-
сти d(a). Аналогичное рассуждение по индукции показывает,
что каждое множество е'(а) является внутренностью клетки
ё'(о). Действительно, гомеоморфизм
f: ё'(оь .... on)XD-^e'(oi...о„+1)
отображает произйедение e'(oi, .... on)X(внутренность D) на
множество e'(<Ji...сгп+О-
Доказательство того, что отображение
q\e'(o): e'(a)->e(o)
70 Дж. Милнор и Дж. Сташеф
— гомеоморфизм. Согласно лемме 6.2, q взаимно однозначно
отображает е'(о) на е(о). С другой стороны, если п-репер
(хь .... Хп) принадлежит «границе» ё'(а)\е'(а), то п-мерная
плоскость X=*q(x\.....хп) не принадлежит е(а), ибо хотя бы
один из векторов xi должен лежать на границе R полупрост-
ранства Следовательно,
dim(xnRo<"l)>Z,
и поэтому X ф е (а).
Пусть теперь Лсе'(о) — относительно замкнутое подмноже-
ство. Тогда АПе'(о) = Л, причем замыкание Ас.ё'(о) есть ком-
пакт и, значит, q (А) — замкнутое множество. Из результатов
предыдущего параграфа следует, что <?(А)Пе(о) — q(A), поэто-
му q(A)cz е(о) представляет собой относительно замкнутое мно-
жество. Таким образом, q гомеоморфно отображает клетку
е'(о) на множество е(а). 
( m \
Теорема 6.4. Совокупность из I I множеств е(о) образует
клеточное разбиение, пространством которого является много-
образие Грассмана	Аналогично, взяв прямой предел при
пг-^-оо, мы получим бесконечное клеточное разбиение, про-
странством которого является бесконечное многообразие Грасс-
мана G„(R°°).
Доказательство. Прежде всего надо показать, что каждая
точка границы клетки е(а) принадлежит некоторой клетке е(т)
меньшей размерности. Так как ё'(о)— компакт, то образ qe'(o)
равен ё(а). Следовательно, любая n-мерная плоскость X из гра-
ницы ё(о)\е(о) имеет базис (xi, .... хл), принадлежащий
множеству ё'(а)\е'(п). Очевидно, что векторы хь ..., хп орто-
нормировании и х( е RCT*. Значит, dim (X П R°z) i для каждого
i и, таким образом, символ Шуберта (п, .... тя), ассоцииро-
ванный с плоскостью X, должен удовлетворять условиям
хп (Тл.
Однако, как и выше, хотя бы один из векторов х< должен в
действительности принадлежать пространству RCTi-I> поэтому
соответствующее целое число т/ должно быть строго меньше сн.
Следовательно, d(x)< d(a). С учетом леммы 6.3 это завершает
доказательство того, что многообразие Грассмана Gn(Rm) яв-
ляется конечным клеточным разбиением.
Аналогично доказывается, что бесконечное многообразие
Грассмана Gn(R°°) является клеточным разбиением. Условие ко-
нечности замыкания выполняется здесь, так как каждая «точка»
§ 6. Клеточная структура многообразий Грассмана 71
Хе Gn(R00) принадлежит некоторому конечному подразбиению
Gn(Rm). Наконец, пространство Gn(R°°) по определению имеет
топологию прямого предела. 
Поучительно рассмотреть частный случай п = 1.
Следствие 6.5. Бесконечное проективное пространство Рх —
= Gi(R°°) есть клеточное разбиение, имеющее по одной г-мер-
ной клетке е (г + 1) для каждого целого г 0. Замыкание
ё(г+ 1) равно конечному проективному пространству Рг.
Доказательство. Это непосредственно следует из теоремы
6.4. 
Теперь подсчитаем количество r-мерных клеток в многообра-
зии Грассмана Gn(Rm) для произвольного числа п. Для этого
удобно использовать язык разбиений.
ОПРЕДЕЛЕНИЕ 6.6. Разбиением целого числа г 0 назы-
вается всякая неупорядоченная последовательность i\iz ... it
положительных целых чисел, в сумме дающих г. Число разбие-
ний числа г обычно обозначается р(г). Следующая таблица
указывает значения р(г) для г 10.
г	0	1	2	3	4 5	6	7	8	9	10
Р(г)	1	1	2	3	5 7	И	15	22	30	42
Например, число 4 имеет пять разбиений, а именно: 1111, 112,
2 2, 1 3 и 4. Число 0 имеет в точности одно разбиение (пустое).
(Как показали Харди и Рамануджан, функция р(г) имеет асим-
птотику ехр(л-у/2г/3)/4г V3 при г-*-оо. Более подробные све-
дения можно найти в [Остманн].)
Каждому символу Шуберта (oi, ..., сгл) с d(o) = г и ол tn
соответствует разбиение i\iz ... is числа г, где й, .... й — по-
следовательность, получаемая из последовательности Oi—1, ...
..., оп — п удалением нулей, которые могут иметься в ее на-
чале. Ясно, что
1 < А < А is ш — п
и s^n. Таким образом:
Следствие 6.7. Число r-мерных клеток многообразия Грасс-
мана Gn(Rm) равно числу разбиений числа г на не более чем п
целых положительных чисел, каждое из которых не больше чем
пг — п.
К Дж. Милнор и Дж. Сташеф
В частности, если оба числа п и m — л не меньше г, то число
r-мерных клеток в Grt(Rm) равно р(г).
Заметим, что это следствие остается верным, если разрешить
пг принимать значение + °°<
В заключение пять задач для читателя.
Задача 6.А. Показать, что клеточное разбиение конечно то-
гда и только тогда, когда его пространство является компак-
том.
Задача 6.В. Показать, что для р < k гомоморфизм ограни-
чения
Г: ЯР(СП(К~))-*Я₽(ОЛ(НП+*))
есть изоморфизм (при любой области коэффициентов). (См.
описание когомологий клеточного разбиения, данное в прило-
жении А.)
f
Задача 6.С. Показать, что соответствие X*—*"R фА опреде-
ляет вложение многообразия Грассмана Gn(Rm) в Gn+i(R‘®
$Rm)ss.Gn+l(Rm+1) и что f накрывается послойным отобра-
жением
81®Yn(Rm)->Yn+,(Rm+1).
Показать, что f Переводит r-мерные клетки многообразия Грас-
смана Gn(Rm), соответствующие данному разбиению h ... it
числа г, в r-мерные клетки многообразия Грассмана G„+i(R'n+1),
соответствующие тому же разбиению й ... is.
Задача 6.D. Показать, что число различных чисел Шти-
феля — Уитни ... te£n [Al] всякого л-мерного многообразия М
равно р(л).
Задача 6.Е. Показать, что число r-мерных клеток многооб-
разия Грассмана Gn(Rn+*) равно числу r-мерных клеток мно-
гообразия Грассмана Gs(Rn+*) (или, более того, показать, что
вти два клеточных разбиения в действительности изоморфны).
§ 7. КОЛЬЦО КОГОМОЛОГИЙ Н*(6Я; Z/2)
В этом параграфе, по-прежнему в предположении, что клас-
сы Штифеля — Уитни существуют, мы вычислим когомологии
по модулю 2 бесконечного многообразия Грассмана Gn =
= Gn (R°°) и докажем теорему единственности классов Шти-
феля— Уитни. Напомним, что каноническое n-мерное расслое-
ние над G„ обозначается через у".
$ 7. Кольцо когомологий Н*(Оп; Zf2) 73
Теорема 7.1. Кольцо когомологий H*(Gn;2/2) является ал-
геброй полиномов над полем 2/2, свободно порожденной
классами Штифеля — Уитни ®i(yn), .... и’л(?п).
Для доказательства этой теоремы установим сначала сле-
дующий результат.
Лемма 73. Между элементами wi(yn) нет никаких полино-
миальных соотношений.
Доказательство. Предположим, что существует соотношение
вида p(wi(yn), ..., wn("tn)) — 0, где р — полином от п перемен-
ных с коэффициентами в Z/2. По теореме 5.6 для любого
n-мерного расслоения £ над паракомпактной базой существует
послойное отображение g: i -* у". Следовательно,
М£)=£’(Муп))>
где g — отображение базисных пространств, индуцированное g.
Отсюда вытекает, что когомологические классы должны
удовлетворять соответствующему соотношению
p(®i(g), .... wn®) = g*p(wi(yn), ..., wn(yn)) — 0.
Таким образом, чтобы доказать лемму, достаточно найти ка-
кое-нибудь n-мерное расслоение g, между характеристическими
классами ®i(£), .... wn(£) которого нет никаких полиномиаль-
ных соотношений.
Рассмотрим каноническое линейное расслоение у1 над бес-
конечным проективным пространством Ра>. Напомним (см.
лемму 4.3), что /f*(P°°;Z/2) является алгеброй полиномов над
полем Z/2 с одной образующей а размерности 1 и что полный
класс Штифеля — Уитни w(?')= 1 + а. Взяв теперь п-кратное
прямое произведение X = Р°° X • • • X Р00, получаем, что его
кольцо когомологий Н*(Х\ 2/2) представляет собой алгебру по-
линомов от п одномерных образующих at, ..., ап (см. прило-
жение А, теорему А.6 или [Спеньер]). Здесь образующий эле-
мент ai может быть определен как образ л* (а) при гомомор-
физме, индуцированном проекцией пг. Х-*-Р°° на i-й сомножи-
тель. Рассмотрим n-кратное прямое произведение
£ = V' X ... Ху’ ^(лУ)Ф ...
Ясно, что g есть n-мерное расслоение над X = Р°° X ... X Р“
и его полный класс Штифеля — Уитни
w(g) —а>(у’)Х ... Xo’(V,) = «I(a'(v1)) ... <(®(у‘))
равен n-кратному произведению
(1+а)Х	Х(1+«) = (!+aI)d+«?) ... (1+а„).
74 Дж. Милнор и Дж. Сташеф
Другими словами,
Wi (|) = at + 02 + ... + ап,
® == «1^2 + «103 + • •• +aian+ ... +ап-{ап,
wn(^ — aX02 ... ап
и вообще класс представляется в виде элементарного
симметрического полинома от а\......ап. В учебниках по ал-
гебре доказывается, что п элементарных симметрических по-
линомов от п независимых переменных над полем не удовлет-
воряют никаким полиномиальным соотношениям (см., напри-
мер,.[Ленг, 1965] или [Ван дер Варден]). Таким образом, классы
wi(j), ..., wn(S) алгебраически независимы над Z/2, а отсюда,
как отмечалось выше, следует, что классы Wi(t"), .... и?«(ул)
также алгебраически независимы. 
Доказательство теоремы 7.1. Мы показали, что алгебра
Я*(Оя) над Z/2 содержит подалгебру, являющуюся алгеброй
полиномов над Z/2, свободно порожденной элементами
а>1(уп), ..., а>п(ул). Используя соображения, связанные с под-
счетом числа образующих, покажем, что в действительности эта
подалгебра совпадает со всей алгеброй
Напомним (см. следствие 6.7), что число r-мерных клеток
клеточного разбиения Gn равно числу разбиений числа г на не
более чем п целых положительных чисел. Следовательно, ранг
группы Hr(Gn, Z/2) не превосходит этого числа разбиений.
(Действительно, пусть С'— группа r-коцепей по модулю 2 этого
клеточного разбиения, a Zr zz>Br — соответствующие группы ко-
циклов. и кограниц. Тогда число r-мерных клеток равно рангу
группы Сг, а
ранг (Сг) > ранг (Zr) > ранг (Z'IBr) — ранг (Яг).)
С другой стороны, число различных мономов вида
Wi (упУ1 • • - W (уп)г>1 в группе Hr(Gn‘, Z/2) в точности равно числу
разбиений числа г на не более чем п целых положительных
чисел. В самом деле, каждой последовательности rit ..., гп не-
отрицательных целых чисел, таких, что
п + 2г2+ ... +пгп = г,
можно поставить в соответствие разбиение числа г, получаемое
из набора п чисел
rn> гп + гп-ъ •••, r„ + rn_i+ ... + Г1
удалением нулей, если таковые имеются, и обратно.
Как известно, эти мономы линейно независимы над Z/2, и
поэтому указанные выше неравенства должны быть в действи-
§ 7. Кольцо когомологий H*(Gn; Z/2)	75
тельности равенствами: группа Hr(Gn-,Z/2) как Z/2-модуль
имеет ранг, равный числу разбиений числа г на не более чем п
целых положительных чисел, и базис этой группы состоит
из всевозможных мономов Wi (у")Г| ... wn (v")'" полной раз*
мерности г. Это завершает доказательство теоремы 7.1. 
Между прочим, попутно доказано, что естественный гомо-
морфизм g*: H*(Gn)->	... X Р°°) изоморфно отобра-
жает алгебру когомологий H*(Gn) на подалгебру, образован-
ную всеми полиномами от переменных он, ..., ап, инвариант-
ными относительно любых перестановок этих п переменных.
Единственность классов Штифеля — Уитни
До сих пор мы еще не доказали, что существуют классы
Штифеля — Уитни удовлетворяющие аксиомам из § 4.
Прежде чем доказывать существование, докажем единствен-
ность.
Теорема единственности 7.3. Существует не более одного
соответствия g *—> w (g), сопоставляющего каждому векторному
расслоению над паракомпактным базисным пространством по-
следовательность когомологических классов, удовлетворяющих
четырем аксиомам для классов Штифеля — Уитни.
Доказательство. Предположим, что существует два таких
соответствия, скажем I н-> да (g) и g н-* w (g). Для канонического
линейного расслоения yj над Р1 имеем
да (у}) = да (у}) = 1 + а
по аксиомам 1 и 4. Вкладывая у{ в линейное расслоение у1 над
бесконечным проективным пространством Р°°, получаем, что
w (у1) = да (у1) = 1 + а,
согласно аксиомам 1 и 2. Переходя к n-кратному прямому про-
изведению
g = у1 X ... Ху1 = njy'® ... фл^у1,
находим, что
t0(g) = ®(g) = (l +«i) ••• (1 +ап).
в силу аксиом 2 и 3. Используя теперь существование послой-
ного отображения g-^y" и тот факт, что алгебра Я*(ОЛ) изо-
морфно отображается на подалгебру в Я*(Р“Х ... ХР°°),
заключаем, что да (ул) = да (ул).
Для произвольного n-мерного расслоения п над параком-
пактной базой, взяв какое-нибудь послойное отображение f: т]->
76 Дж. Милнор и Дж. Сташеф
-* у", немедленно получаем, что
w (n)e f*® (Vn) = f*w (Vn) = w (т|)- 
Замечание. Используя по существу те же самые рассужде-
ния, нетрудно доказать теорему единственности классов Шти-
феля — Уитни и для существенно меньшей категории гладких
векторных расслоений и их гладких послойных отображений
над паракомпактными гладкими многообразиями. Намного
труднее было бы доказать этот результат, используя только ка-
сательные расслоения многообразий (ср. [Блантон и Швей-
цер]).
В заключение три задачи для читателя. Первые две осно-
ваны на задаче 6.С.
Задача 7.А. Указать в явном виде коциклы в группе
Cr(Gn)& Hr(Gn), соответствующие классам Штифеля — Уитни
аМу").
Задача 7.В. Показать, что алгебра когомологий
Н* (Gn (R"+ft), Z/2) порождается классами Штифеля — Уитни
а>ь ...» &п универсального расслоения у" и двойственными
классами йц, ..., Wk, подчиненными лишь следующим п 4- k
определяющим соотношениям:
(14- 4- ... + аУл) (1 4- + • • • 4- й»л) = 1
(ем. [Борель, 1953]).
Задача 7.С. Пусть gm и т)п — векторные расслоения над па-
Йакомпактным базисным пространством. Показать, что классы
1тифеля — Уитни тензорного произведения ® т)л (или изо-
морфного ему расслоения Horn(gm,if1)) могут быть вычислены
следующим образом. Если размерности слоев /пип обе рав-
ны 1, то
W1 (g1 ® Т]1) = И», (g1) 4- Wi (п1).
В общем случае имеет место универсальная формула вида
W ® п") — Pm, п (йУ1 (£т)...Wm (im). 0У1 ОТ)...(п")).
где полином рт,п от т 4- п переменных можно описать так.
Пусть ffi, ..., от — элементарные симметрические полиномы
от переменных /1.....tm и о[......а' — элементарные симмет-
рические полиномы от переменных t\.....tn, тогда
т п
Рт,п(°1> •••• ат> •••’ <) = Д /Ц (1 4- tt 4- Q.
§ 8. Существование классов Штифеля — Уитни 77
[Указание. Когомологии произведения Gm X Gn могут быть вы-
числены при помощи теоремы Кюннета А.6 (приложение А).
Формулу для класса 0 rf) нужно проверить сначала для
частного случая, когда расслоения и г]п являются суммами
Уитни линейных расслоений.]
§ 8. СУЩЕСТВОВАНИЕ КЛАССОВ ШТИФЕЛЯ — УИТНИ
Дадим теперь доказательство существования классов Шти-
феля— Уитни, построив их при помощи известных операций.
Для любого n-мерного расслоения £ с пространством рас-
слоения Е, базисным пространством В и проекцией я обозна-
чим через Еа множество ненулевых векторов из Е и через Fq —
множество ненулевых векторов типичного слоя F = n~'(b).
Ясно, ЧТО Fq — F П Eq.
Используя теорию сингулярных когомологий и тот или иной
технический прием (например, спектральные последовательно-
сти или прием, указанный в § 10), находим, что
,	С 0 для i=£n,
Hl (F, Fq‘, Z/2) = \
'	'	(.	Z/2 для t = n,
И
,	(	0 для I < n,
Я (£, £0; Z/2) = |	z/2) для
(Интуитивно, хотя и нестрого, этот факт можно объяснить
следующим образом. Единичный n-мерный шар является де-
формационным ретрактом пространства R", а единичная
(п —>1) -мерная сфера — деформационным ретрактом простран-
ства R" с выколотым нулем (Rn \ 0) = Ro • Как известно, если
базисное пространство В паракомпактно, то в пространство
расслоения Е можно ввести евклидову метрику. Тогда подмно-
жество Е' cz Е, состоящее из всех векторов х е Е, таких, что
х-х 1, будет деформационным ретрактом Е. Аналогично под-
множество Е" cz Е, состоящее из всех векторов х е Е, таких,
что х-х — 1, представляет собой деформационный ретракт про-
странства Ео. Следовательно, Н* (Е', Е") & Н* (Е, Ео). Теперь
предположим, что В есть клеточное разбиение с настолько мел-
кими клетками, что ограничение расслоения £ на каждую клет-
ку ck является тривиальным расслоением. Тогда прообраз
ft-мерной клетки с* в Е' будет произведением клеток размерно-
стей ft и п. Таким образом, пространство Е' может быть полу-
чено из подпространства Е" присоединением клеток размер-
ностей >п, по одной (n +ft)-мерной клетке на каждую ft-мер-
ную клетку базы В. Отсюда следует, что Н1(Е',Е") = 0 для
78 Дж. Милнор и Дж Сташеф
i < п. С меньшей очевидностью отсюда следует также изомер*
физм Нп+к (Е', Е") & Нк (В).)
Строго и подробно мы докажем в § 10 следующее утверж-
дение. Далее, как и выше, рассматриваются когомологии с
коэффициентами в Z/2.
Теорема 8.1. Группа Н‘(Е,Е0) является нулевой для i < п,
а группа Нп(Е,Е0) содержит единственный класс и, такой, что
для каждого слоя F — л-1 (Ь) ограничение
u\(F, F^Hn(F, Fq)
является единственным ненулевым классом в Hn(F,Fo). Далее,
соответствие х^хии определяет изоморфизм Нк(Е)-*-
—>Нк+п(Е,Е0) для любого k. (Мы назовем класс и фунда-
ментальным когомологическим,классом.)
С другой стороны, проекция л: Е-+В, очевидно, индуцирует
изоморфизм Нк(В)-+ Нк(Е), так как нулевое сечение задает
вложение базисного пространства В в пространство Е в каче-
стве деформационного ретракта с ретракцией л.
ОПРЕДЕЛЕНИЕ 8.2. Изоморфизмом Тома ф: Нк(В)-*-
-> Нк+п(Е, Ео) называется композиция двух изоморфизмов
Нк (В) X Нк (Е) Нк+п (Е, Ео).
В дальнейшем мы будем использовать стинродовские квад-
раты в Н*(Е,Е0). Эти операции характеризуются следующими
четырьмя основными свойствами (см. [Стинрод, Эпстейн]). Об-
ластью коэффициентов по-прежнему предполагается Z/2.
(1)	Для каждой пары пространств X зэ У и каждой пары
неотрицательных целых чисел п, i определен аддитивный гомо-
морфизм
Sqz: Нп(Х, Y)^Hn+t(X, Y)
(называемый стинродовским квадратом степени i).
(2)	Естественность. Если f: (X, Y)-*-(X', Y')—непрерывное
отображение пар, то Sq‘ = Sq‘.
(3)	Если a&Hn(X,Y), то Sq°(a)=a, Sqn(a)=a\ja и
Sq‘(a) = 0 для i>n. (Таким образом, наиболее интересны те
стинродовские квадраты, у которых 0 < I < п.)
(4)	Формула Картана. Для любых а, Ь, для которых опре-
делено а о Ъ, имеет место тождество
Sqk(a^b) = £ Sq‘(a)^Sq‘(b).
t+i-k
Используя стинродовские квадраты и изоморфизм Тома, оп-
ределим классы Штифеля — Уитни Wi(?)s//'(B) формулой
§ 8. Существование классов Штифеля — Уитни 79
Тома
Другими словами, а><(£) —это однозначноопределенный когомо-
логический класс в Н‘(В), образ которого при изоморфизме
Тома	—	и равен стинродовскому квадрату
Sq‘ 0(l)= Sq' и.
Для многих целей удобно ввести полный стинродовский
квадрат
Sq(a)=a + Sq,(a) + Sq2(a)+ ... +Sqn(a),
где а^Нп(Х, Y). Заметим, что формулу Картана можно при
этом выразить равенством
Sq (а Ь) — (Sq a) (Sq b).
Аналогично, соответствующее равенство для стинродовских
квадратов Х-умножения 1 также становится более простым:
Sq (а X b) — (Sqa) X (Sq &)•
В терминах полного стинродовского квадрата полный класс
Штифеля — Уитни векторного расслоения, очевидно, задается
формулой
^(£) = </>"1Sq^(l) = </>-1Sq(u).
Проверка аксиом
Для данного выше определения четыре аксиомы классов
Штифеля — Уитни проверяются следующим образом.
АКСИОМА 1. Из свойств (1) и (3) стинродовских квадра-
тов следует, что	где и»о(ь)в 1 и и>,(£)=0, если
i больше размерности слоя п.
АКСИОМА 2. Любое послойное отображение f: g -> оче-
видно, индуцирует отображение g: (Е, Е0)-*(Е', Е'о). Далее, из
определения класса и (см. 8.1) следует, что если и' — фунда-
ментальный когомологический класс в Нп (Е', Е'о), то класс
g*(u') равен классу и е Нп (Е, Ео). Теперь легко видеть, что
изоморфизмы Тома ф и ф' удовлетворяют условию естествен-
ности
g* ° Ф' =
1 В оригинале cross product (крест-произведение); см. приложение А;
X-умножение называется также внешним когомологическим умножением
(см. [Дольд]).— Прим, перво.
80 Дж. Милнор и Дж. Сташеф
Следовательно, используя свойство (2) стинродовских квадра-
тов, получаем
что и требовалось.
АКСИОМА 3. Сначала вычислим классы Штифеля — Уитни
прямого произведения |" = g X где g" — расслоение с проек-
цией л X л': Е X Е' -* В X В'. Рассмотрим фундаментальные
классы
и s Hm (Е, Ео) и и' е Нп (Е', Е'о)
расслоений £ и £'. Так как пространство Ео открыто в Е, а
Е'о открыто в Е', то определено Х-произведение
иХи'^Нт+п(ЕХЕ', EXE'oUE.XE')
(см. приложение А). Заметим, что открытое подмножество
(Е X Е'о) U (Ео X Е') в пространстве Е" = EX Е' расслоения g"
есть в точности множество Eq ненулевых векторов из Е". Мы
утверждаем, что класс и X «' в точности равен фундаменталь-
ному классу и" е Нт+п(Е", Е%). Для того чтобы доказать это,
достаточно показать, что ограничение
uXu'\(F", Fq)
равно ненулевому когомологическому классу из Нт*п(р", F")
для любого слоя F” = FX F' расслоения £ . Но это ограниче-
ние, очевидно, равно Х-произведению u|(F, Fq) и u'\(F',F'q
и поэтому является ненулевым классом, согласно теореме А.5
приложения А.	>
Легко видеть, что изоморфизмы Тома расслоений £, g' и g"
связаны тождеством
Действительно, если положить а = л* (а) е//*(£) и 5 —
— л'* (b) €= Н*(£'), то справедливость этого тождества следует
из равенства
(а X Ь) v {и X и') = (а о и) X (Ь и').
Здесь мы не обращаем внимания на знаки, так как коэффи-
циенты берутся по модулю 2.
Далее, полный класс Штифеля — Уитни расслоения мо-
жет быть вычислен по формуле
Ф" (w (g")) = Sq (и") = Sq (и X «') = Sq («) X Sq («').
Полагая правую часть равной
t (W (g)) X (W (Г)) = Г 0) X W (!'))
§ 8. Существование классов Штифеля — Уитни 81
и применяя затем (Ф")~1 к обеим частям нового равенства, на-
ходим, что
Предположим теперь, что £ и являются расслоениями над
одним и тем же базисным пространством В. «Поднимая» обе
стороны доказанного равенства обратно на В при помощи диа-
гонального вложения В -> В X В, получаем требуемую фор-
мулу1
w (£ ф z) == w (g) w (£').
АКСИОМА 4. Пусть у}, как обычно, — нетривиальное ли-
нейное расслоение над окружностью Р1. Тогда пространство
векторов длины в пространстве расслоения Е = Е (у;), оче-
видно, является листом Мёбиуса М, ограниченным окруж-
ностью дМ. Так как М есть деформационный ретракт Е и
дМ — деформационный ретракт Ео, то
Н* (М, дМ) И* (Е, Ео).
С другой стороны, если вложить двумерную клетку D2 в про-
ективную плоскость Р2, то замыкание пространства P2\D2 бу-
дет гомеоморфно листу Мёбиуса М. Используя теорему о выре-
зании из теории когомологий, получаем, что
Н*(М, дМ)о&Н*(Р2, ЕР).
Следовательно, существуют естественные изоморфизмы
Н1 (Е, Ео) -> Н{ (М, дМ) «- Н1 (Р2, ЕР) -► Н1 (Р2)
для любого i У= 0. Фундаментальный когомологический класс
а е № (Р, Eq) , очевидно, ненулевой, поэтому при изоморфизме-
композиции он должен соответствовать образующей а е
еЯ’(Р2). Следовательно, класс Sq1(u) = u^>u должен соот-
ветствовать классу Sq'(a)= a\j а. Однако a а =/= 0 по лем-
ме 4.3. Таким образом, класс
должен быть также ненулевым. Это завершает проверку всех
четырех аксиом. 
В заключение две задачи для читателя.
Задача 8.А. Из теоремы 7.1 следует, что когомологический
класс Sq*a>m(B) можно представить в виде полинома от клас-
1 Здесь используется также тот факт, что когомологическое Х-умно-
жение переходит при диагональном отображении в ^-умножение (см., на-
пример, [Дольд]). — Прим, перев.
82 Дж Милнор и Дж. Сташеф
сов и>1(£).....wm+*(5).	Доказать явную формулу У
.	( k — m
Sq (wm) = wkwm + j
(k — m\
]WoWm+k
( ( x\ \
I где, как обычно, I J — x(x— 1) ... (x — i + l)/il I, рассуждая
следующим образом. Показать, что, если формула верна для
расслоения g, то она верна для расслоения | X У*. Таким обра-
зом по индукции она верна для у1 X ... X у1 и, следователь-
но, для всех расслоений
тот факт, что
Задача 8.В. Показать, что, если и>(£)#= 1, то наименьшее
п > 0, такое, что wn(5)¥= 0, есть степень двух. (Использовать
х
k
k = 2'.)
J нечетно, если х — нечетное кратное числа
§ 9. ОРИЕНТИРОВАННЫЕ РАССЛОЕНИЯ И КЛАСС ЭЙЛЕРА
До сих пор в качестве области коэффициентов для групп
когомологий использовалась только группа Z/2. При этом, ко-
нечно, многие интересные структуры выпадают из поля зрения.
Теперь для более тщательного изучения предмета мы возьмем
в качестве группы коэффициентов кольцо целых чисел Z. Од-
нако для того чтобы сделать это, необходимо ввести в наши
векторные расслоения дополнительную структуру ориентации.
В частности, нам нужна ориентация для того, чтобы построить
фундаментальный когомологический класс и <= Нп(Е, Ео) с це-
лыми коэффициентами.
Прежде всего рассмотрим случай одного-единственного век-
торного пространства.
ОПРЕДЕЛЕНИЕ. Ориентацией вещественного векторного
пространства V размерности п > 0 называется класс эквива-
лентности его (упорядоченных) базисов, причем два базиса
У!....vn и .... v'n считаются эквивалентными тогда и
только тогда, когда матрица [az/], определяемая равенствами
и' = У, atlvjt имеет положительный определитель. Очевидно, у
всякого конечномерного векторного пространства V в точности
две различные ориентации. Заметим, что координатное про-
странство R" обладает канонической ориентацией, задаваемой
его каноническим упорядоченным базисом.
В алгебраической топологии принято определять ориента-
цию симплекса при помощи выбора некоторого упорядочения
§ 9. Ориентированные расслоения и класс Эйлера 83
его вершин. Наше понятие ориентации связано с понятием
ориентации симплекса следующим образом. Пусть — неко-
торый n-мерный симплекс, вложенный в n-мерное векторное
пространство V, с упорядоченными вершинами До, Ai, .... Ал.
Тогда, взяв вектор, идущий из точки До в точку Д1, в качестве
первого базисного вектора, вектор, идущий из точки Д1 в точку
Д2, — в качестве второго и т. д., мы получим соответствующую
ориентацию векторного пространства V.
Отметим, что выбор ориентации векторного пространства V
соответствует выбору одной из двух возможных образующих
группы сингулярных гомологий Hn(V, V0;Z). Действительно,
пусть Д»— стандартный n-мерный симплекс с каноническим
порядком вершин. Выберем некоторое сохраняющее ориента-
цию линейное вложение
о: An->V,
которое переводит барицентр симплекса Д'» в нулевой вектор
(и, следовательно, отображает границу симплекса Д" в Vo).
Тогда а будет сингулярным n-мерным симплексом, представ-
ляющим некоторый элемент в группе относительных п-мерных
циклов Zn(V, Vo;Z). Класс гомологий этого цикла а дает от-
меченную образующую цу группы гомологий Hn(V, Vo;Z).
Аналогично группа когомологий Нп(V, Vo; Z), отвечающая
ориентированному векторному пространству V, имеет отмечен-
ную образующую (которую мы обозначим символом uv), опре-
деляемую равенством <«у, р.у>= +1.
Теперь рассмотрим векторное расслоение g со слоем размер-
ности п > 0.
ОПРЕДЕЛЕНИЕ. Ориентацией расслоения g называется
функция, ставящая в соответствие каждому слою F этого рас-
слоения некоторую ориентацию и удовлетворяющая следую-
щему условию локальной согласованности: для любой точки Ь»
базисного пространства существует локальная координатная
система (N, h), где b0 е N и h: N X R" -* л-1 (N), такая, что для
каждого слоя F = n~}(b), b&N, гомоморфизм xi—>h(b,x) яв-
ляется сохраняющим ориентацию изоморфизмом R" на F. (Или,
эквивалентно, существуют сечения Si, ...,	та-
кие, что базис s\(b), ..., sn(b) определяет требуемую ориента-
цию в слое л-’ (&) для каждой точки b е N.)
В терминах когомологий это означает, что для каждого слоя
F существует отмеченная образующая
ureHn(F, Fo; Z).
Из условия локальной согласованности вытекает, что для лю-
бой точки базисного пространства существуют окрестность N и
84 Дж. Милнор и Дж. Сташеф
класс когомологий
и (= Нп (л-1 (N), Jt-‘(A0o; Z),
такие, что для любого слоя F над N ограничение
u\(F, F0)eHn(F, Fo; Z)
равно up. Доказательство проводится непосредственно.
В § 10 будет доказан следующий важный результат (ср. с
теоремой 8.1).
Теорема 9.1. Пусть g— ориентированное п-мерное расслое-
ние с пространством расслоения Е. Тогда группа когомологий
Н1(Е, £о‘, Z) является нулевой для i <п, а группа Нп(Е, Ео; Z)
содержит один и только один когомологический класс и, огра-
ничение которого
u\(F, F0)(=Hn(F, Fo; Z)
совпадает с отмеченной образующей ир для любого слоя F рас-
слоения g. При этом соответствие уь-ъ-у^и представляет со-
бой изоморфизм группы Hk(E\Z) на группу Hk+n(E, До; Z) для
любого целого k.
На более техническом языке эта теорема утверждает, что
кольцо Н*(Е, До; Z) является свободным Я*(Д; Z)-модулем с
одной образующей и степени п. (В качестве области коэффи-
циентов здесь можно было бы использовать вообще любое
кольцо с единицей.)
Из теоремы 9.1 следует, конечно, что группа когомологий
Hn+k(E, E0-,Z) изоморфна группе когомологий Hk(B, Z) базис-
ного пространства.
Фактически изоморфизм Тома
ф-. Hk(B-, Z)^Hk+n(E, Е9\ Z)
может быть определен формулой
W = (я*х) и
точно так же, как в § 8.
Теперь мы подготовлены к тому, чтобы определить новый
важный характеристический класс.
Для данного ориентированного n-мерного расслоения g вло-
жением (Д, пустое множество) с: (Д, До) индуцируется гомомор-
физм ограничения
Н'(Е, Ео; г)->/Г(Д; Z),
который мы обозначим через у*—>у\Е. В частности, применяя
этот гомоморфизм к фундаментальному классу иеНп(Е, До;
§ 9. Ориентированные расслоения и класс Эйлера 85
Z), мы получаем новый когомологический класс
и|£еД“(£; Z).
Но группа Нп{Е\1) канонически изоморфна группе когомоло-
гий Нп(В-, Z) базисного пространства.
ОПРЕДЕЛЕНИЕ. Классом Эйлера ориентированного п-мер-
ного расслоения g называется когомологический класс
е®е=Нп(В', Z),
соответствующий классу и\Е при каноническом изоморфизме
л*:Нп(В] Z)-+Hn(E\ Z).
Мотивировку выбора названия «класс Эйлера» читатель най-
дет на стр. ПО. Укажем некоторые основные свойства класса
Эйлера.
Свойство 9.2 (естественность). Если отображение В-+В'
накрывается послойным отображением g -> i', сохраняющим
ориентацию, то е(£) =
В частности, если g — тривиальное n-мерное расслоение, то
e(g)=O. Действительно, в этом случае в качестве расслоения
можно взять расслоение над точкой.
Свойство 9.3. Если обратить ориентацию расслоения то
класс Эйлера в (|) изменит знак.
Доказательство этих свойств проводится непосредственно. 
Свойство 9.4. Если размерность слоя расслоения £ нечетна,
то е(5)+ е(£) = 0.
По этой причине, применяя классы Эйлера, мы будем обыч-
но предполагать, что слой имеет четную размерность.
Доказательство. Любое нечетномерное векторное расслое-
ние допускает обращающий ориентацию автоморфизм (b, o)i—>
—о). Поэтому требуемое равенство е(&) =—е(&) следует
из 9.3. 
Другое доказательство. Изоморфизм Тома ^(х) = (л*х)ч> и,
очевидно, отображает е(£) в когомологический класс
(л’еО и »= (u |£) и •= и о и.
Другими словами, е (?) = (и о и). Но из тождества
a^& = (-l)<dlme>(dlraW^a
86 Дж, Милнор и Дж. Сташеф
видно, что, если размерность пкласса « нечетна, то и и имеет
порядок 2. 
Свойство 9.5. Естественный гомоморфизм Hn(B,,Z)-*-Hn(B-,
Z/2) переводит класс Эйлера e(g) в старший класс Штифеля —
Уитни wn(l).
Доказательство. Если мы применим этот гомоморфизм (ин-
дуцированный эпиморфизмом колец коэффициентов Z -► Z/2)
к обеим сторонам равенства e(g) = 0~’(u w)> то> очевидно, це-
лочисленный класс и перейдет в Z/2-когомологический класс и
(описанный в § 8) и поэтому класс u\ju перейдет в Sqn(«).
Следовательно, класс ф~1 (и и) отображается в класс
^-1Sq"(u)= wn(l). 
Несколько важных свойств характеристического класса
wn(l) относятся в равной степени и к классу е(%).
Свойство 9.6. Класс Эйлера суммы Уитни расслоений g и
g' вычисляется по формуле e(g ф g')= e(g) о e(g')- Анало-
гично класс Эйлера прямого произведения дается формулой
e(gXg')=e(g)Xe(H.
Здесь необходимо отметить, что по определению прямая
сумма F ф F' двух ориентированных векторных пространств
наделяется ориентацией, задаваемой при помощи ориентирую-
щих базисов для F и F', записанных один за другим.
Доказательство. Пусть слои расслоений g и g' имеют раз-
мерности шип соответственно. С учетом соглашения о знаках,
описанного в приложении А, нетрудно проверить, что фунда-
ментальный когомологический класс прямого произведения вы-
ражается формулой
«ахг)=(-1)тяи(1)хи(&').
(Ср. с проверкой аксиомы 3 в § 8. Если бы мы использовали
классическое соглашение о знаках, как, например, в [Спеньер],
то знаковый множитель в этой формуле отсутствовал бы.) При-
меняя гомоморфизм ограничения
Hm+n (Е ХЕ', (ЕХ Ло) -> Нп+п (Е X Л « Нп+п (В X Л
к обеим частям последнего равенства, легко получаем, что
X £') = (- i)m"e(g) Хе (£'),
причем знаковый множитель может быть опущен, так как в
случае, когда т или п нечетно, в правой части стоит элемен”
второго порядка.
§ 9. Ориентированные расслоения и класс Эйлера 87
Теперь предположим, что В — В'. Перенося обе части полу-
ченного равенства на пространство В с помощью диагональ-
ного вложения В-*йХВ, получаем формулу e(g©g') =
= e(g)^ e(g') для класса Эйлера суммы Уитни. 
Замечание. Хотя эта формула очень похожа на соответ-
ствующую формулу ф g') =	w(g') для полных клас-
сов Штифеля — Уитни, между ними имеется существенное раз-
личие. Полный класс Штифеля — Уитни w(g) является едини-
цей кольца ЯП(В; Z/2), и потому можно разрешить написанное
выше равенство относительно w(g') и представить этот класс в
виде функции от классов w(%) и	(см. лемму 4.1).
Однако класс Эйлера е(1), конечно, не является единицей в
кольце целочисленных когомологий базы Вив действитель-
ности вполне может оказаться нулем или делителем нуля. По-
этому из уравнения e(g ф g')= e(g) e(g'), как правило, нель-
зя найти класс е(£') как функцию от классов e(g) и e(g®g').
Рассмотрим одно применение свойства 9.6. Пусть г] — век-
торное расслоение, для которого 2е(г])#=0. Тогда г] не может
быть представлено в виде суммы Уитни двух ориентированных
нечетномерных векторных расслоений. Например, пусть М —
гладкое компактное многообразие. Предположим, что каса-
тельное расслоение т многообразия М ориентировано и что
е(т)¥=0. Тогда т не содержит никакого нечетномерного вектор-
ного подрасслоения. В самом деле, если бы такое подрасслое-
ние g существовало и было ориентируемо, то класс Эйлера
е(т) = е(1) о e(g1) должен был бы быть элементом порядка
два в свободной абелевой группе Нп(М\ Z) (см. приложе-
ние А). В случае, когда подрасслоение g неориентируемо, надо
перейти к подходящему двукратному накрытию многообразия
М. Подробности предоставляем читателю.
Свойство 9.7. Если ориентированное векторное расслоение
g допускает всюду ненулевое сечение, то класс Эйлера e(g)
равен нулю.
Доказательство. Пусть з: В -> Ео — сечение, так что компо-
зиция
является тождественным отображением базисного простран-
ства В. Тогда композиция индуцированных гомоморфизмов
Нп (В) X Нп (£) -► Нп (£0) X Нп (В)
будет тождественным отображением кольца Нп(В). По опреде-
лению гомоморфизм л* отображает класс Эйлера e(g) в огра-
88 Дж. Милнор и Дж. Сташеф
ничение и\Е. Следовательно, первые два гомоморфизма в этой
композиции отображают класс е(£) в ограничение (м|Е) |Е0>
которое равно нулю, так как композиция
Нп(Е, Ео)Нп (Е)-* Нп (Ео)
есть нулевой гомоморфизм. Применяя гомоморфизм $*, полу*
чаем, что е(%) = s* (0) = 0. 
(Если расслоение £ допускает евклидову метрику, то можно
дать другое доказательство. А именно, пусть 8 — тривиальное
одномерное расслоение, натянутое на сечение s расслоения £.
Тогда
е(|) = е(в)^е(8х)
согласно свойству 9.6, но класс е(в) равен нулю по свой-
ству 9.2.)
В заключение параграфа дадим несколько примеров рас*
слоений с ненулевым классом Эйлера (см. также § 11 и 15).
Задача 9.А. Напомним, что у" обозначает каноническое п-
мерное расслоение над бесконечным многообразием Грассмана
Gn(R°°). Показать, что у” фу" является ориентированным век-
торным расслоением с ®2п(у" ф у")т^0 и, следовательно,
е (уя ф у")	0. Показать, что, если п нечетно, то 2е(у"фуя) =
= 0.
Задача 9.В. Рассмотрим комплексное многообразие Грасс*
мана ОП(С°°), состоящее из всех комплексных векторных под-
пространств комплексной размерности п в бесконечномерном
комплексном координатном пространстве (см. § 14). Поскольку
любое комплексное n-мерное расслоение можно рассматривать
как вещественное ориентированное 2п-мерное расслоение, то
существует каноническое ориентированное 2п-мерное расслое-
ние £2я с базой Gn(C°°). Показать, что ограничение расслоения
|2п на вещественное многообразие Грассмана Gn(R°°)cz Gn(С00)
изоморфно уяфуя и, следовательно, е(£2п)^=0. (Замечание.
Фактически группа когомологий //2я(6/1(С00)'; Z) является сво-
бодной абелевой группой, а класс е(£2я)—одной из ее образую-
щих, см. теорему 14.5 ниже.)
Задача 9.С. Пусть т касательное расслоение n-мерной сфе-
ры и A <=. Sn X Sn — антидиагональ, состоящая из всех пар ан-
типодальных единичных векторов. Используя стереографиче-
скую проекцию, показать, что пространство расслоения Е =
= Е (%) канонически гомеоморфно пространству 5я X 5Я\А
Применяя этот результат, а также аксиомы вырезания и гомо-
§ 10. Теорема Тома об изоморфизме 89
топии, показать, что
И* (Е, Ео)« И* (Sn X Sn, S" X Sn \ диагональ)« H* (Sn X Sn, A) c
с/Г($"Х-$п)
(ср. с § 11). Предположим теперь, что п четно. Показать, что
класс Эйлера е(т) = ^“*(и о и) равен дважды взятой обра-
зующей группы Hn(Sn-, Z). Вывести отсюда как следствие, что
расслоение т не содержит никакого нетривиального вектор»
ного подрасслоения.
§ 10. ТЕОРЕМА ТОМА ОБ ИЗОМОРФИЗМЕ
В этом параграфе мы сначала дадим полное доказательство
теоремы Тома об изоморфизме для неориентированного случая
(см. теорему 8.1), а затем укажем изменения в доказательстве,
требующиеся в ориентированном случае (см. теорему 9.1).
В первой половине этого параграфа будет предполагаться, что
областью коэффициентов служит поле Z/2.
Мы начнем с краткого изложения некоторых конструкций,
более подробно описанных в приложении А (см., в частности,
А.5). Пусть Ro обозначает множество ненулевых векторов в R".
Для п = 1 группа когомологий №(R, Ro) изоморфна Z/2. Пусть
е1 — ненулевой элемент этой группы. Тогда для любого тополо-
гического пространства В соответствие yt-где X — опе-
рация Х-Умиожеиия в когомологиях, задает изоморфизм когомо-
логий
Яг(В)-Я/+1(ВХК. BXRo)-
Это доказывается при помощи точной когомологической после-
довательности тройки (В X R, В X Ro, В X R-), где R_ обозна-
чает множество отрицательных вещественных чисел.
Пусть теперь В' — открытое подмножество пространства В.
Тогда для каждого когомологического класса у е Н> (В, В')
определено Х-произведение у X и
yXe’a^^XR, B'XRU BXRo).
Используя лемму о пяти гомоморфизмах *, можно показать, что
соответствие у i—* у X определяет изоморфизм
Н‘ (В', В1) Hl+1 (В X R, В' X R U В X Ro).
Отсюда следует по индукции, что n-кратная композиция
t/*-*!/XeIi->yXeIXe1i->...i-*yXe1X...Xe1
1 См., например, [Спеньер].
90 Дас. Милнор и Дж. Сташеф
также определяет изоморфизм (подробности см. в приложе-
нии А). Полагая
е',-в1Х...Хе1бЯ’(Г, Rg),
получаем следующий результат.
Лемма 10.1. Для любого топологического пространства В и
любого п 1 соответствие у i—» у X еп определяет изоморфизм
групп когомологий
Н1 (В) -> Я/+п (в х R", в х Ro). 
Теперь напомним утверждение теоремы Тома. Пусть £ —
некоторое n-мерное расслоение с проекцией л: Е-*-В.
Теорема об изоморфизме 10.2. Существует один и только
один когомологический класс ие Нп(Е,Е0) с коэффициентами
по модулю 2, ограничение которого на группу когомологий
Н" (F, Fo) является ненулевым для любого слоя F. Далее, соот-
ветствие уу и определяет изоморфизм группы когомоло-
гий Н1 (Е) на группу когомологий Н1+п(Е,Е0) для любого це-
лого j.
В частности, беря . / < 0, видим, что когомологии пары
(£, Ео) тривиальны в размерностях, меньших чем п.
Доказательство разобьем на четыре случая.
Случай 1. Предположим, что £ — тривиальное векторное
расслоение. Тогда Е можно отождествить с произведением
В X R". Поэтому группа когомологий Нп (Е, Ео) = Нп(в X R”
В X R”) канонически изоморфна группе Н°(В) по лемме 10.1.
Чтобы доказать существование и единственность класса и, до-
статочно показать, что существует один и только один когомо-
логический класс	ограничение которого на каждую
точку пространства В является ненулевым. Но очевидно, что
единичный элемент 1 е Н°(В) — это единственный класс, удов-
летворяющий этому условию. Следовательно, класс и суще-
ствует и равен 1 X е".
Далее, так как любой когомологический класс в НЦВ'Х, R")
может быть единственным образом записан как Х-произведе-
ние z/X 1, где у^НЦВ), то в силу леммы 10.1 соответствие
у X 1 (У X 1)	и = (у X 1)	(1 X еп) = у X еп
определяет изоморфизм. Это завершает доказательство для
случая 1.
Случай 2. Предположим, что В — объединение двух откры-
тых множеств В' и В", таких, что утверждение теоремы 10.2
§ !0 Теорема Тома об изоморфизме 91
выполнено для расслоений-ограничений g|B', g|B" и £|В'ПВ".
Введем сокращенные обозначения: Впдля пересечения В' Г) В"
и Е', Е" и £ п соответственно для прообразов подмножеств В',
В" и В'(]В" базы В в пространстве расслоения £ = £(£). Мы
будем использовать следующую точную последовательность
Майера — Вьеториса:
... -+Н1~1(Еп, Ео)~+Н1(Е, Е0)^Н{(Е', £о)ф
©Н1 (Е", Eq) ->И1 (Еп, £о) -* ...
Об этой последовательности можно прочитать, например, в
книге [Спеньер].
Из принятого предположения следует, что существуют одно-
значно определенные когомологические классы и' е Нп (Е', Eq)
и и" е Нп (Е", Eq), ограничения которых на каждый слой яв-
ляются ненулевыми.
Применяя часть теоремы, касающуюся единственности, к
расслоению 51В11, видим, что классы и' и и" имеют один и тот
же образ в Нп(Еп, Eq). Следовательно, они служат образом
некоторого общего класса и е Нп (Е, Ео). Этот класс однозначно
определен, так как Hn~l (£п, Ео) = 0.
Теперь рассмотрим последовательность Майера — Вьеториса
... -» Н{~1 (£п) -> Н1 (£) -> Н1 (Е')®Н’ (£") -> Н1 (£п) -> ....
где j + п = I. Отображая эту последовательность в предыду-
щую последовательность Майера — Вьеториса при помощи со-
ответствия у •—> у и и применяя лемму о пяти гомоморфиз-
мах, получаем,что
Н’(Е)-^+ Н1+п(Е, Ео).
Это завершает доказательство для случая 2.
Случай 3. Предположим, что у базисного пространства В
имеется конечное открытое покрытие множествами В\, ..., Вц,
такими, что для каждого В, расслоение g| Bi тривиально. Дока-
жем индукцией по числу k, что и в этом случае утверждение
теоремы 10.2 выполнено для расслоения £. Для k = 1 наше
утверждение, конечно, верно. Если k > 1, то мы можем пред-
положить по индукции, что утверждение теоремы верно для
расслоений g|(BiU ... U#t-i) и g|(BiU ••• UBs-OH#*- Сле-
довательно, используя случай 2, можно провести шаг индук-
ции, и мы получаем, что доказываемое утверждение верно для
расслоения g.
Общий случай. Пусть С — произвольное компактное под-
множество базисного пространства В. Тогда, очевидно, расслое-
92 Дж. Милнор и Дж. Сташеф
ние £|С удовлетворяет предположениям случая 3. Так как объ*
единение любых двух компактных множеств компактно то мы
можем взять прямой предел
lim Я, (С)
групп гомологий, где С пробегает множество всех компактных
подмножеств базисного пространства В, и соответствующий об-
ратный предел lim Н1 (С) групп когомологий.
Напомним следующий результат.
Лемма 10.3. Естественный гомоморфизм
И1 (В) ->lim Н1 (С)
есть изоморфизм. Аналогично группа НЦЕ,Е0) отображается
изоморфно на lim Н Дя-1 (С), л-1 (С)о).
Предостережение. Эти утверждения верны только для слу-
чая, когда группа коэффициентов является полем. Для цело-
численных коэффициентов они заведомо неверны.
Доказательство леммы 10.3. Соответствующее утверждение
для групп гомологий, и именно утверждение, что группа
lim Hj(С) изоморфна группе Н/(В), справедливо, очевидно, для
произвольных коэффициентов, так как любая сингулярная цепь
на В содержится в некотором компактном подмножестве про-
странства В. Аналогично группа lim Hf (л"1 (С), л_|(С)0) отобра-
жается изоморфно на группу Hi(E,E0). Однако, согласно тео-
реме А.1 приложения А, группа когомологий И1 (В) с коэффи-
циентами в поле Z/2 канонически изоморфна группе
Нот (///(В); Z/2). Вместе с легко проверяемым изоморфизмом
Hom (lim Ht (С); Z/2) lim Нот (Я7 (С); Z/2),
это доказывает лемму 10.3. Я
В частности, группа когомологий Нп(Е, Eq) отображается
изоморфно на обратный предел групп Н^лтЦС), л_1(С)0). Но
каждая из этих последних групп содержит один и только один
класс «с, ограничение которого на каждый слой является нену-
левым. Отсюда немедленно следует, что группа Нп(Е,Е0) со-
1 Здесь мы неявно предполагаем, что базисное пространство В хаусдор-
фово. Это не является необходимым. Доказательство точно так же проходит
для нехаусдорфовых пространств, надо только «компактность» всюду заме-
нить на «квазикомпактность» (которая характеризуется условием: любое от-
крытое покрытие содержит конечное подпокрытие),
§ 10. Теорема Тома об изоморфизме 93
держит один и только один класс и, ограничение которого на
каждый слой ненулевое.
Рассмотрим теперь гомоморфизм и: Н> (£)-> Н1+п(Е, Ео).
Ясно, что для каждого компактного подмножества С базисного
пространства В имеет место коммутативная диаграмма
Н1 (Е)^“»Н1+п(Е, Ео)
4	4
Н‘ (л’1 (С)) -> Н1+п (л’1 (С), л"1 (С)о)
Переходя к обратному пределу (С пробегает множество всех
компактных подмножеств), получаем, что гомоморфизм ии
является изоморфизмом. Это завершает доказательство тео-
ремы 10.2. 
Таким образом, мы имеем, наконец, полное доказательство
существования и единственности классов Штифеля — Уитни.
Теперь попытаемся провести аналогичное доказательство в
случае, когда группой коэффициентов служит произвольное
кольцо Л. (Конечно, как всегда, предполагается, что Л — ассо-
циативное кольцо с единицей.) Точно такие же, как и выше,
рассуждения показывают, что группа когомологий Нп (Rre, R"; Л)
является свободным Л-модулем с единственной образующей
еп = ei X ... X ei (см. теорему А.5 приложения А).
Пусть g — ориентированное n-мерное расслоение. Тогда в
каждом его слое F мы можем выбрать отмеченную образую-
щую
uFsHn(F, Fo- Z)
(см. § 9). Используя канонический кольцевой гомоморфизм
Z->A, мы получаем соответствующую образующую для груп-
пы Hn(F,F0-, Л), которую также будем обозначать символом Uf.
Теорема об изоморфизме 10.4. Существует один и только
один когомологический класс «е Нп(Е, £0; А), ограничение ко-
торого на пару (F, Fq) равно uf для любого слоя F. Далее,
соответствие у ► у и изоморфно отображает группу когомо-
логий НЦЕ’,Л) на группу когомологий Н<+п(Е,Е0-, Л) для лю-
бого целого j.
Если кольцо коэффициентов Л является полем, то доказа-
тельство этой теоремы полностью аналогично доказательству
теоремы 10.2. (Провести его во всех деталях предоставляется
читателю.) Также и в случае, когда базисное пространство В
компактно, доказательство снова вполне аналогично доказа-
тельству теоремы 10.2. (Сходные рассуждения годятся для
любого расслоения g конечного типа, см. задачу б.Е.)
94 Дж. Милнор и Дж. Сташеф
Трудность распространения результата на общий случай
связана с тем, что лемма 10.3 несправедлива, вообще говоря,
если группа коэффициентов когомологий — не поле. Фактически
обратный предел из леммы 10.3 может вести себя очень плохо.
Однако построение фундаментального класса и проходит без
особых сложностей. Нам понадобится следующая
Лемма ЮЛ. Группа гомологий Hn-.i(E,Eo;Z) является ну-
левой.
Предположим на некоторое время, что эта лемма доказана.
Тогда из теоремы А.1 приложения А следует, что группа
когомологий //"(£, £0;Z) канонически изоморфна группе
Нот(Нп(Е, Ео-, Z), Z). Поэтому точно так же, как и в доказа-
тельстве леммы 10.3, мы получаем, что группа Hn(E,E0;Z)
канонически изоморфна обратному пределу групп
Нп(п~1(С), л~*(С)0; Z),
где С пробегает множество всех компактных подмножеств ба-
зисного пространства В. Поскольку теорема 10.4 уже доказана
для векторных расслоений над компактным базисным простран-
ством С, отсюда следует, что существует однозначно опреде-
ленный когомологический класс и е Нп(Е, Eq; Z).
Замечание. Важно отметить, что для любого кольца Л при
каноническом кольцевом гомоморфизме Z->A фундаменталь-
ный класс из группы Нп(Е, Ео; Z) переходит в фундаменталь-
ный класс из группы Нп(Е, Ео; Л).
Для доказательства того, что взятие ^-произведения е
фундаментальным классом и индуцирует изоморфизм когомо-
логий, используем следующую формальную конструкцию.
ОПРЕДЕЛЕНИЕ. Свободным цепным комплексом над Z
называется последовательность свободных Z-модулей Кп и го-
моморфизмов
...
подчиненных условию д о д = 0. Цепным отображением f: К—*К'
степени d называется последовательность гомоморфизмов
Ki -*• Кл+а, удовлетворяющих условию д' °f = (—l)df.od.
Лемма Ю.6. Пусть	— некоторое цепное отображе-
ние, где К и К' — свободные цепные комплексы над Z. Если f
индуцирует изоморфизм когомологий
Г-	Л)
$ tO. Теорема Тома об изоморфизме 05
для любого поля коэффициентов Л, то f индуцирует изомор-
физм гомологий и когомологий с произвольной областью коэф-
фициентов.
Доказательство. Рассмотрим конус К! отображения f, т. е.
свободный цепной комплекс, построенный следующим образом.
Положим = Ki-d-i ® Ki и зададим граничный гомоморфизм
df: /С; -» формулой
d'(x, x') = ((-I)d+1dx, f(«)+d'x')
(ср. [Спеньер]). Очевидно, что цепной комплекс Kf включается
в короткую точную последовательность
О-»#' —
цепных отображений. Далее, граничный гомоморфиз.м
д':
в ассоциированной точной последовательности гомологий сов-
падает с Таким образом, группы гомологий	яв-
ляются нулевыми тогда и только тогда, когда f индуцирует
изоморфизм ННв целочисленных гомологиях.
В нашем случае дано, что f индуцирует изоморфизм когомо-
логий Н* Л)-»- //*(/<; Л) для произвольного поля коэффи-
циентов Л. Используя точную последовательность когомологий,
получаем, что Н* (КЦ Л)=0. Но группа когомологий Нп(Ю', К)
канонически изоморфна группе	® Л); Л), согласно
теореме А.1 приложения А. Следовательно, векторное простран-
ство гомологий Нп(К! 8 Л) является нулевым. Действительно,
в противном случае существовало бы нетривиальное Л-линей-
ное отображение этого векторного пространства в поле коэффи-
циентов Л.
В частности, группа рациональных гомологий Hn(Kf 8 Q)
нулевая. Значит, для любого цикла geZn(Af) некоторое его
целочисленное кратное будет границей. Поэтому группа цело-
численных гомологий Нп(К.!) может состоять только из элемен-
тов конечного порядка.
Для доказательства того, что группа нулевая, доста-
точно показать, что любой элемент простого порядка равен
нулю. Пусть I; е Zn(Kf) —некоторый цикл, представляющий го-
мологический класс простого порядка р. Тогда
р£^дк
для некоторого элемента xe/fn+i. Таким образом, х является
Циклом по модулю р. А поскольку группа гомологий
Hn+i(Kf 8 Z/p), как известно, нулевая, то мы видим, что х яв-
96 Дж. Милнор и Дж. Сташеф
ляется границей по модулю р, скажем
к = дк + р%".
Следовательно, pZ = ди равняется рдк”, а, значит, £ = дк”.
Итак, элемент £ представляет тривиальный гомологический
класс, и тем самым доказано, что Н^К1) — 0.
Отсюда легко следует теперь, что комплекс Kf имеет триви-
альные гомологии и когомологии для произвольной области
коэффициентов (см. [Спеньер]). Например, так как группа
Zn-i свободная, то точная последовательность
является расщепляющейся и, следовательно, остается точной
после тензорного умножения на произвольную аддитивную
группу Л. Без труда проверяется, что последовательность
... ...
также точна, и поэтому ®Л)=0. Это завершает дока-
зательство леммы 10.6. 
Доказательство теоремы 10.4 проводится теперь следующим
образом. Мы будем использовать операцию г\-умножения. (Оп-
ределение и основные свойства г\-умножения см. в приложении
А ’.) Доказывая теорему 10.4, мы по ходу дела докажем сле-
дующий результат. Предполагается, что кольцом коэффициентов
служит Z.
Следствие 10.7. Соответствие т] н-> и г\ т] определяет изомор-
физм целочисленных групп гомологий
Hn+i(E, E0)^Ht(E).
Доказательство. Выберем какой-нибудь сингулярный коцикл
zeZ'l(E, Ео), представляющий фундаментальный когомологи-
ческий класс и. Тогда отображение yi—>zr\y из группы цепей
Cn+i(E, Ео) в группу цепей С;(Е) удовлетворяет тождеству
д(ггх Y) = (-l)nzr>(dY).
Следовательно, гомоморфизм
С.(Е, Е0)->С.(Е)
является цепным отображением степени —п. Учитывая тожде-
ство
(с, z Г\ у) = (с z, у),
мы видим, что индуцированное коцепное отображение
(гп)*: С* (Е; А)->С*(Е, Ео; А)
1 См. также [Дольд]. — Прим, перев.
§11. Некоторые вычисления на гладких многообразиях
97
задается соответствием с *—> с z. Здесь Л может быть произ-
вольным кольцом. Если кольцо коэффициентов Л — поле, то
это коцепное отображение индуцирует изоморфизм когомологий
согласно уже доказанному частному случаю теоремы 10.4. Сле-
довательно, мы можем применить лемму 10.6 и получить, что
гомоморфизмы
«гл; Ht+n(E, Ео;	л)
и
«: Н' (Е-, Л) -> Hl+n (Е, Ео; Л)
являются в действительности изоморфизмами для произволь-
ного кольца Л. В частности, используя изоморфизм о и:
Н°(Е-, Л)-»Нп(Е, Ео, Л), мы можем убедиться в единственности
фундаментального когомологического класса и с коэффициен-
тами в кольце Л.
Это завершает доказательство теоремы 10.4 и следствия
10.7 — при условии, что мы сумеем сделать одни пропущенный
выше шаг. А именно, надо еще доказать, что Hn-i(E, Ео’, Z)=0
(лемма 10.5). 
Доказательство леммы 10.5. Предположим сначала, что ба-
зисное пространство В компактно. Тогда, как уже было отме-
чено, теорема 10.4 верна независимо от леммы 10.5. Точно так
же и доказательство следствия 10.7 для этого частного случая
проходит без привлечения леммы 10.5. Таким образом, мы мо-
жем свободно использовать следствие 10.7 в этом частном слу-
чае и заключить, что
Я„_, (Е, Ео; Z) H_t (Е; Z) = 0.
Доказательство для общего случая получается немедленно при
помощи изоморфизма гомологий
ИтЯДл-'(С), л-'(С)о; Z)-^Ht(E, E0;Z),
где С пробегает множество всех компактных подмножеств ба-
зисного пространства В (см. 10.3). 
§11. НЕКОТОРЫЕ ВЫЧИСЛЕНИЯ НА ГЛАДКИХ МНОГООБРАЗИЯХ
Нормальное расслоение
Пусть М = Мп — гладкое многообразие, гладко вложенное
в риманово многообразие А = А"+*. Для изучения характери-
стических классов нормального расслоения многообразия М в
А нам понадобится следующий геометрический результат.
4 Дж. Милнор, Дж3 Сташеф
98 Дж. Милнор и Дж. Сташеф
Теорема 11.1. (о существовании трубчатой окрестности). Су-
ществует открытая окрестность многообразия М в А, диффео-
морфная пространству нормального расслоения многообразия
М в А при диффеоморфизме, который переводит каждую точку
х из М в нулевой нормальный вектор в этой точке.
Такая окрестность называется открытой трубчатой окрест-
ностью многообразия М в Д.
Доказательство. Чтобы упростить изложение, проведем до-
казательство во всех деталях только для того частного случая,
когда многообразие М компактно. Этого частного случая будет
достаточно для почти всех наших применений. Доказательство
для общего случая дано, например, в книге [Ленг, 1962].
Пусть Е обозначает пространство нормального расслоения
v*. Каждому вещественному числу е > 0 поставим в соответ-
ствие открытое подмножество Е (в) cz Е, состоящее из всех пар
(х, v)eE, таких, что <8. Здесь х — точка многообразия М,
a v — нормальный вектор к многообразию М в точке х.
(Или, более общим образом, любой гладкой вещественно-
значной функции х I—> е (х) > О поставим в соответствие откры-
тое множество £(в), состоящее из всех пар (х, v)e£, таких,
что |v|<a(x). Эта более общая конструкция существенна,
когда мы имеем дело с некомпактными многообразиями.)
Мы будем использовать так называемое экспоненциальное
отображение
Exp: Е (в) -> А,
столь употребительное в римановой геометрии, которое соотно-
сит каждой паре (x,t')e£, где |и] достаточно мало, концевую
точку у(1) параметризованной дуги геодезической
у: [О, 1]->Д
длины |v| с начальной точкой у(0), совпадающей с х, и век-
тором скорости dy/dt\t=o, равным v. Например, если объемлю-
щее риманово многообразие А является евклидовым простран-
ством, то у — это просто отрезок прямой и экспоненциальное
отображение задается формулой Exp (х, и) = х + и.
Из обычных теорем существования, единственности и глад-
кости решения для дифференциальных уравнений следует, что
отображение Ехр(х, и) определено и является гладким как
функция от (х, и) в некоторой окрестности нулевого сечения
МХ0с£ (см., например, [Бишоп, Криттенден]). Отсюда лег-
ко следует, что отображение Ехр определено и является глад-
ким на окрестности Е(е) при достаточно малом в.
Далее, применяя теорему об обратной функции в произволь-
ной точке (х, 0) нулевого сечения, мы видим, что некоторая ее
§ 11. Некоторые вычисления на гладких многообразиях 99
открытая окрестность в Е(е) диффеоморфно отображается на
открытое подмножество в А.
Утверждение. Если е достаточно мало, то экспоненциальное
отображение осуществляет диффеоморфизм всего открытого
множества Е (е) на некоторое открытое множество Ne <= А.
Доказательство в предположении, что многообразие М ком-
пактно. Так как экспоненциальное отображение, ограниченное
на Е(е), является локальным диффеоморфизмом при малых е,
то достаточно установить, что оно взаимно однозначно. Но если
бы это было не так, то для каждого целого i > 0, взяв е = 1 /i,
мы получили бы, что в окрестности E{\/i) существуют две раз-
личные точки (xz, =/= (Хр v'^, для которых Ехр (Хр —
= Exp (Хр и'^. Поскольку многообразие М компактно, отсюда
следовало бы, что существуют сходящиеся подпоследователь-
ности [Х1^ И {Х/у}> ТаКИе> ЧТ0
lim (x(f,	= (х, 0), lim (x't/, v'^ = (x', 0).
Очевидно, что предельная точка х = Ехр (х, 0) = lim Exp (xt,
должна была бы совпадать с предельной точкой х'. Но тогда
равенства Ехр (х{ , и(.р = Ехр (х^, v'(^ для достаточно больших
/ противоречили бы тому, что экспоненциальное отображение
является взаимно однозначным отображением в окрестности
точки (х,0).
Таким образом, окрестность £(е) диффеоморфна своему об-
разу Ne для достаточно малых е. Чтобы завершить доказатель-
ство теоремы 11.1, остается заметить, что окрестность Е(е) диф-
феоморфна также всему пространству расслоения Е-, этот диф-
феоморфизм осуществляется, скажем, отображением
(х, v)>-^(x, v/Vl — | v 12/е(х)2). 
Теперь сделаем дополнительное предположение, что много-
образие М с А является замкнутым как подмножество тополо-
гического пространства А. Конечно, это предположение авто-
матически выполняется, если М — компактное многообразие.
Следствие 11.2. Если многообразие М замкнуто в многообра-
зии А, то кольцо когомологий Н* (Е, Eq\ А), ассоциированное
с нормальным расслоением многообразия М в А, канонически
изоморфно кольцу когомологий Н*(А, А\М; А).
Здесь А может быть любым кольцом коэффициентов.
4*
100 Дж. Милнор и Дж. Сташеф
Доказательство. Так как трубчатая окрестность Ne и допол-
нение А \ М являются открытыми подмножествами с объеди-
нением, равным А, и пересечением, равным Ne \ М, то имеет
место изоморфизм вырезания
И* (А, А\М)-> Н* (Ne, Ne \ М)
(см., например, [Спеньер]). Следовательно, вложение
Ехр: (£(в), £(е)0)->(Яе, Ne\M)cz(A, А\М)
индуцирует изоморфизм
Ехр*: Я* (Л, А \ М) Н* (Е (в), Е (в)0).
Взяв его композицию с изоморфизмом вырезания
Н* (£(в), £(в)0)~Я*(£, £0),
получаем требуемый изоморфизм, который, очевидно, не зави-
сит от выбора е. И
Замечание. Этот изоморфизм Н*(А, А\М)-+Н*(Е, Eq) не
зависит даже и от выбора римановой метрики на А. Чтобы при-
дать смысл этому утверждению, надо сначала дать определение
«нормального расслоения», основанное на точной последова-
тельности
0 -> гм -> тА | М -> vk -> 0,
которое не зависит от выбора конкретной римановой метрики
на А. (Ср. с задачей З.В). Так как любые две римановы метрики
Но и щ могут быть соединены гладким однопараметрическим
семейством римановых метрик (1 —	+ то легко видеть,
что соответствующие экспоненциальные отображения гомо-
топны.
В качестве приложения следствия 11.2 получаем, что фунда-
ментальный когомологический класс «е//‘(£, £о; Z/2) соответ-
ствует каноническому когомологическому классу, который мы
обозначим символом
и'е=Нк(А, А\М-, Z/2).
Аналогично, если нормальное расслоение ук ориентируемо, то
любая фиксированная ориентация ук определяет соответствую-
щий класс и'^Нк(А, А \ Л4; Z) с целочисленными коэффици-
ентами.
Теорема 11.3. Если многообразие М вложено как замкнутое
подмножество в А, то композиция двух гомоморфизмов ограни-
чения
Hk (А, А \ М) Нк (А) -> Нк (М)
<5 11. Некоторые вычисления на гладких многообразиях 101
с коэффициентами по модулю 2 отображает фундаментальный
класс и' в старший класс Штифеля — Уитни Wk(Qk) нормального
расслоения v*.
Аналогично, если расслоение vk ориентировано, то соответ-
ствующая композиция групп когомологий с целочисленными
коэффициентами отображает фундаментальный класс и' в класс
Эйлера e(yk).
Доказательство. Пусть s: М-+-Е— нулевое сечение расслое-
ния vk. Оно индуцирует канонический изоморфизм Н*(Е)-+-
-+Н*(М). Заметим прежде, что композиция
Нк (Е, Ео) Hk (£) Нк (М)
с коэффициентами по модулю 2 отображает фундаментальный
класс и в класс Штифеля — Уитни ay«(v4) (ср. 9.5). Действи-
тельно, образ з*(ц|Е) при изоморфизме Тома
ф-. Hk (М)-> Н2к (Е, Ео)
равен n*s* («| £) о и = (и | Е) о и = и и — Sqk (и) и, следова-
тельно, элемент s*(u | Е) равен $~lSqk(u) = Wk(vk).
Далее, заменяя пару (£, Ео) диффеоморфной парой
(Ne, Ne\M), получаем, что композиция двух гомоморфизмов
ограничения
Нк (Ne, Ne \ М) -> Нк (Ne) -> Нк (М)
отображает класс, соответствующий фундаментальному классу
и, в класс Штифеля — Уитни Wt(vk). Доказываемое утвержде-
ние вытекает теперь из рассмотрения коммутативной диаграммы
Нк (Л, А \ М) -> Нк (Л)
1“ 1
Hk(Ne, Ne\M)-+Hk(M)
Доказательство в ориентированном случае совершенно ана-
логично. 
ОПРЕДЕЛЕНИЕ. Образ класса и' в группе когомологий
Нк(А) называется двойственным когомологическим классом
подмногообразия MczA коразмерности k. (Ср. с задачей 11.С.)
Если этот двойственный класс м'|Л является нулевым, то из
этого следует, конечно, что старший класс Штифеля — Уитни (и
соответственно класс Эйлера) нормального расслоения vk дол-
жны равняться нулю. Один частный случай этого утверждения
особенно заслуживает внимания.
102 Дж. Милнор и Дж. Сташеф
Следствие 11.4. Если многообразие М = Мп гладко вложено
как замкнутое подмножество в евклидово пространство Rn+*,
те Wk(yk) = 0. В ориентированном случае e(yk) = 0.
Доказательство. Двойственный класс и' |Rn+ft принадлежит
группе когомологий Hk(Rn+*), которая является нулевой. 
По теореме двойственности Уитни (лемма 4.2) класс Wk(vk)
равен характеристическому классу ш*(тм) касательного рас-
слоения многообразия М. Поэтому следствие 11.4 можно пере-
формулировать следующим образом: если ш(тм)^=0, то много-
образие М нельзя гладко вложить как замкнутое подмножество
в евклидово пространство Rn+ft.
Например, если п — степень двух, то вещественное проектив-
ное пространство Рп не может быть гладко вложено в R2"-1.
(Ср. с теоремой 4.8. Как показал Уитни, любое гладкое «-мер-
ное многообразие, топология которого имеет счетный базис, мо-
жно гладко вложить в евклидово пространство R2" ([Уитни,
1944]). Весьма вероятно, что оно может быть вложено в R2n
как замкнутое подмножество, хотя Уитни и не удалось доказать
этого.)
, Замечание. В утверждении следствия 11.4 существенно то,
что многообразие М не имеет границы и вложено в евклидово
пространство как замкнутое подмножество. Например, откры-
тый лист Мёбиуса (см. рис. 2) можно, конечно, вложить в R3,
однако нельзя вложить как замкнутое подмножество, посколь-
ку ассоциированный класс Штифеля — Уитни шЦт) является
ненулевым. Точно так же существенно то, что многообразие М
вложено (без самопересечений), а не просто погружено в Rn+ft.
Например, согласно одной теореме Боя вещественная проектив-
ная плоскость Р2 может быть погружена в R3 ([Бой]; см. также
[Гильберт и Кон-Фоссен]), однако и здесь двойственный класс
Штифеля — Уитни ©Цт) не равен нулю.
Касательное расслоение
Пусть М — риманово многообразие. Тогда произведение
М X М также имеет структуру риманова многообразия, причем
длина касательного вектора
(и, о) е DMX XDMy^D(M\ М\х>
определяется формулой
1(«, о)Г = 1ыр4-|ор,
а скалярное произведение двух касательных векторов — форму-
лой
(ы, о) • (и', v') = u> и' + о •»'.
§ 11. Некоторые вычисления на гладких многообразиях 103
Заметим, что диагональное отображение
X >—> Д (х) = (х, х)
дает гладкое вложение многообразия М в качестве замкнутого
подмножества в М%М. (Это диагональное вложение является
почти изометрией: оно увеличивает все длины в д/2 раз.)
Лемма 11.5. Нормальное расслоение vn, ассоциированное а
диагональным вложением многообразия М в М\М, канониче-
ски изоморфно касательному расслоению М.
Доказательство. Очевидно, что вектор (и, о) ® DMX X DMy as
asZ)(Af Х-М)(Х,х) касателен к подмногообразию Д(уЙ) тогда и
только тогда, когда и = v, и нормален к Д(М) тогда и только
тогда, когда « + и = 0. Таким образом, каждому касательному
вектору v е DMX однозначно соответствует нормальный вектор
(— v, u) ® D (М X М.) (*, х). Это соответствие
(х, и) ((х, х), (— v, и))
диффеоморфно отображает касательное многообразие DM =
= £(тм) на пространство нормального расслоения Е(уп). 
Мы будем особо интересоваться римановыми многообра-
зиями М, у которых касательное расслоение тм ориентировано.
Лемма 11.6. Ориентация касательного расслоения хм глад-
кого многообразия М порождает ориентацию соответствующего
топологического многообразия М, и обратно, ориентация много-
образия М порождает ориентацию его касательного расслое-
ния Хм-
Доказательство. Как определено в приложении А, ориента-
цией топологического многообразия М называется функция, со-
поставляющая каждой точке х е М отмеченную образующую
бесконечной циклической группы гомологий Нп (М, М \ х) с це-
лочисленными коэффициентами. Требуется, чтобы эта отмечен-
ная образующая непрерывно зависела от х в том смысле, что
Их соответствует ру при изоморфизмах
Нп(М, М\х)*-Нп(М, М \ N) -* Нп(М, М\у),
где N— хорошо вложенная n-мерная клеточная окрестность
точки х и у — произвольная точка из N.
Аналогично ориентацию векторного расслоения хм можно за-
дать, сопоставив отмеченную образующую р' бесконечной цик-
лической группы Hn(DMx, DMx\0) каждой точке хеМ. Эти
образующие ц' должны непрерывно зависеть от х в том смысле,
104 Дж. Милнор и Дж. Сташеф
что ц' соответствует ц' при изоморфизмах
Нп (DMX, DMX \ 0) -* (DN, DN\ (NX 0)) *- (DMy, DMy \ 0),
где N обозначает n-мерную клеточную окрестность точки х в
многообразии М н у е N. (Ср. § 9.)
Однако группа гомологий Нп(М, MW х) канонически изо-
морфна группе Нп (DMX, DMX \ 0), в чем можно убедиться, при-
меняя следствие 11.2 к 0-мерному многообразию х, вложенному
в М как замкнутое подмножество с нормальным расслоением
DMX. Нетрудно доказать, что функция непрерывно зависит
от х тогда и только тогда, когда соответствующая функция р'х
непрерывно зависит от х. Действительно, так как эта задача
чисто локальная, то достаточно рассмотреть частный случай,
когда М— евклидово пространство со стандартной метрикой.
Подробности предоставляются читателю. 
Обратимся теперь к задаче изучения гомологий и когомоло-
гий многообразия М с коэффициентами в некотором фиксиро-
ванном коммутативном кольце Л. Мы будем предполагать, что
либо многообразие М ориентировано, либо A = Z/2. Тогда из
следствия 11.2 вытекает, что существует фундаментальный кого-
мологический класс1
и'^Нп(МХМ, М%М\ЦМ))
с коэффициентами в Л. В силу теоремы 11.3 и леммы 11.5 огра-
ничение класса и' на диагональное подмногообразие &(М)&М
равно классу Эйлера
е (vn) = е (тм)
с коэффициентами в кольце Л в ориентированном случае или
классу Штифеля — Уитни
«'n(vn) = syn(TAI)
в случае коэффициентов по модулю 2.
Этот когомологический класс и' можно описать более явно
следующим образом. Заметим, что каждая группа когомологий
Нп(М, М\ х) имеет отмеченную образующую их, определяемую
условием
{их, Цх)= 1.
(В случае коэффициентов по модулю 2 образующая их является
единственным ненулевым элементом группы Нп(М, М\х).)
1 Определение класса и' с коэффициентами в Z и Z/2 см. перед теоре-
мой 11.3. — Прим, перев.
$ И. Некоторые вычисления на гладких многообразиях 105
Определим каноническое вложение
jxt (М, М\х)-^(МХМ, МХМ\Д(М)),
полагая jx(y) = (x, у).
Лемма 11.7. Класс и' еНп(МХМ, МХМ \ Д(2И)) одно-
значно характеризуется тем свойством, что его образ fx(u')'
равен отмеченной образующей их для любой точки хеМ.
Доказательство. Из построения когомологического класса и'
(см. теоремы 10.2, 10.4 и следствие 11.2) вытекает, что он мо-
жет быть однозначно охарактеризован следующим образом.
Для любой точки х и любой малой окрестности N нуля в каса-
тельном пространстве DMX рассмотрим вложение
(N, #\0)-*(А«ХЯ МХЛ4\Д(А4)),
определяемое при помощи экспоненциального отображения по
правилу
v t—► (Ехр (х, — о), Ехр (х, v)).
Тогда индуцированный гомоморфизм когомологий должен ото-
бражать элемент и' в отмеченную образующую модуля
nn(N, N \ 0)&Hn(DMx, DMX \ 0).
Применение гомотопии v, >(Ехр(х, —tv), Ехр(х, о)),
0< / < 1, показывает, что мы можем с равным успехом исполь-
зовать вложение (N, N\Q) в (МХМ, МХМ \ Д(М)), зада-
ваемое правилом
рн>(х, Ехр(х, о)).
Но это вложение представляет собой композицию канонического
вложения /х с каноническим вложением
Ехр: (N, N\Q)^(M, М\х),
которое использовалось при доказательстве леммы 11.6, откуда
и следует доказываемое утверждение. 
Диагональный когомологический класс в Н^МХМ)
Мы по-прежнему предполагаем, что либо многообразие М
ориентировано, либо кольцом коэффициентов Л является группа
Z/2, так что определен фундаментальный класс
И'еЯл(МХЯ МХМ\Д(М)).
Заметим, что гомоморфизм ограничения
#Л(/ИХЯ МХМ\ЬМ))^Нп(МХМ)
106 Дж. Милнор и Дж. Сташеф ,
переводит класс и' в когомологический класс u'jMXM, «двой-
ственный» диагональному подмногообразию в MX М.
ОПРЕДЕЛЕНИЕ. Этот когомологический класс и'\МХМ
будет кратко обозначаться и” н называться диагональным кого-
мологическим классом в Нп(МХМ).
Мы хотим описать более явно диагональный когомологиче-
ский класс и”. Предварительно докажем лемму, которая выра-
жает алгебраически тот факт, что класс и" «сосредоточен» иа
диагонали A (Af) cz М X М.
Лемма 11.8. Для любого когомологического класса а&
е Н* (М) произведение (а X1) v и" равно (1 X а) и".
Доказательство. Пусть Nt — некоторая трубчатая окрест-
ность диагонального подмногообразия Д(ЛГ) в МХМ. Очевид-
но, что Д(ЛГ) является деформационным ретрактом этой окрест-
ности. Определим две проекции
рь р2: МХМ-+М
формулами pi(x, у) = х, рз(х, у) = у. Поскольку pi и р2 совпа-
дают на Д(ЛГ), то ограничение pi\Ne гомотопно ограничению
p2|/Ve- Таким образом, два когомологических класса р*(а) =
= аХ 1 и pj(a)=!Xa имеют один и тот же образ при гомо-
морфизме ограничения Н‘(МХМ)->Н1(И,). Из рассмотрения
коммутативной диаграммы
Н1 (МХМ)---------> Hl (Nt)
АГе\Д(М))
Hl+n (М х Я М X м \ Д (М)) s* Hi+n (Ne, JVe\& (М))
вытекает теперь, что (а X 1)= (1 X а) Переходя с по-
мощью гомоморфизма ограничения от класса и' к классу и", по-
лучаем наше утверждение. 
Мы будем использовать операцию /-умножения'
НР+ч (J х У) ® Нч (Y) -+ Нр (X)
с коэффициентами в Л. В частном случае, когда X и У — конеч-
ные комплексы, а Л — поле, так что
H*(XXY)&H*(X)®H*(Y),
1 В оригинале slant product operation (дословно: операция косого про-
изведения); /-умножение называют также косым гомологическим умноже-
нием (см. [Дольд]),—- Прим, tiepea.
§ И. Некоторые вычисления на гладких многообразиях 107
/-умножение определяется очень просто. А именно, рассмотрим
гомоморфизм
Н* (X) ® Я* (У) ® Н, (У) -> Я* (X),
задаваемый формулой	а®&®0н->а<&, р>. Подставляя
Я*(ХХ У) вместо Я*(Х)® Я*(У), получаем искомую операцию
Я‘(ХХП®ЯДУ)-Я,(Х),
которая записывается так: р ® р*—>р/р. Эта операция удовле-
творяет тождеству
(aXW—a(b, р)
и характеризуется им. Заметим, что для каждого фиксирован-
ного ре Я* (У) гомоморфизм pi—>р/р является левым Я*(Х)-
линейным отображением в том смысле, что ((йХ1)ир)/₽ =
= а и (p/р) для любого а еЯ*(1) и р е Я* (XX У) •
Определение /-умножения в общем случае можно найти в
книгах [Спеньер] или [Дольд].
Лемма 11.9. Предположим, что многообразие М компактно,
так что определен фундаментальный когомологический класс
р^Нп(М). Тогда диагональный когомологический класс и"&
£Нп(МХ^) и фундаментальный гомологический класс ц свя-
заны тождеством и"/р — 1 е Я0(Л!) .
Мы предполагаем, что область коэффициентов является по-
лем, хотя в ориентированном случае доказательство проходит
на самом деле для любого кольца коэффициентов.
Доказательство. Вычислим для произвольной точки хеМ
образ элемента и"/р при гомоморфизме ограничения Н°(М)—»
-»Я°(х)^А. Воспользуемся коммутативной диаграммой
Нп(МХМ)-^Н°(М)
I 1
Я" (х X-М)Я0 (х)
Заметим, что левая вертикальная стрелка отображает когомо-
логический класс и" в класс 1 X С (и")’ Где
Zx: М-+МХМ
обозначает вложение у>->(х, у). Применяя тождество
(аХ£)/и = а<6, р>, получаем, что значение (и"/р)|х равно
индексу Кронекера (/’ (и"), р), умноженному на 1 е Я0 (х).
Как указано в приложении А, фундаментальный гомологиче-
ский класс р однозначно характеризуется тем свойством, что
108 Дж. Милнор и Дж. Сташеф
для каждой точки х е М естественный гомоморфизм
Нп(М)-*Нп(М, М\х)
отображает ц в отмеченную образующую Используя отобра-
жения
М с. (М, М\х)
М х м <= (М х М, МХМ\ЩМ))
где jx также переводит у в (х, у), заключаем на основании
этого определяющего свойства фундаментального класса ц, что
индекс Кронекера (1*х(и"), ц) = (/*(«') |М, р.) равен (/*(«')>
Согласно лемме 11.7, (/* («')> Их) = 1 и, следовательно,
(«"/ц)|х=1 <=Я°(х).
Так как это равенство верно для любой точки х, отсюда, оче-
видно, следует, что класс и"/ц равен единичному элементу груп-
пы Н°(М). 
Двойственность Пуанкаре и диагональный класс
Пусть М — компактное гладкое многообразие. Мы будем
изучать когомологии многообразия М с коэффициентами в поле
Л, по-прежнему предполагая, что либо многообразие М ориен-
тировано, либо Л = Z/2.
Теорема 11.10 (о двойственности Пуанкаре). Для каждого
базиса bi...br векторного пространства когомологий Н*(М)
существует соответствующий двойственный базис bf, ...,&*
для Н*(М) , удовлетворяющий тождествам
(b, о bf, у,) = у _	...
\ <	1 *7 (о при i ф ].
Отсюда следует, что ранг векторного пространства Hk(M)
равен рангу векторного пространства /7n-ft(Af). Действительно,
если базисный элемент bi имеет размерность k, то двойственный
базисный элемент Ь1* должен иметь размерность п — k. Факти-
чески из теоремы следует, что векторное пространство
ЯЙ(М) изоморфно двойственному векторному пространству
НотА(Яп-*(Л1), Л), причем этот изоморфизм осуществляется
отображением ан-»/га, где ha(b) — (a Ь, ц>. (Другие форму-
лировки теоремы двойственности Пуанкаре даны в задаче 11.В
и приложении А, а также в книгах [Спеньер], [Дольд].
§ 11. Некоторые вычисления на гладких многообразиях 109
Доказывать теорему 11.10 мы будем одновременно с доказа-
тельством явной формулы для когомологического класса и" е
^Нп(МХМ).
Теорема 11.11. Пусть {6J и {£>*} те же, что и выше. Тогда
диагональный когомологический класс и" равен
u"^i(-\fmbtb(XbT.
/-i
Доказательство 'теорем 11.10 и 11.11. Используя формулу
Кюннета
Я* (М X М) « Н* (М) ® Н* (М),
легко проверить, что наш диагональный класс можно предста-
вить в виде суммы г слагаемых
u" = blXci + ... +brXcr,
где Ci, ..., сг — некоторые вполне определенные когомологиче-
ские классы в Н* (М), такие, что
dim b{ + dim ct = п.
Применим гомоморфизм /и к обеим частям тождества
(аХ1)^«" = (1Хв)^Л
В левой части, используя линейность слева /-умножения, полу-
чаем
((а X 1) «")/н = а о (и'7|х) = а.
В правой части, подставляя вместо и" сумму У bj х Oj, полу-
чаем
Z (- l)dlm а dlm Ь1 (Ь, х (а О С,))/Р = z (- DdIm “dIm Ь1Ь, (avcj, р>.
Следовательно, это последнее выражение должно равняться а.
Подставляя bi вместо а, находим, что коэффициент
(-l)dlm4'dta6/<fez^C/, и)
при bj должен равняться 4-1, если i — /, и 0, если i=£j. Полагая
&* = (-l)dim6/C6
легко убеждаемся в справедливости доказываемых утверж-
дений. 
НО Дж. Милнор и Дж. Сташеф
Класс Эйлера и эйлерова характеристика
Эйлерова характеристика конечного клеточного разбиения К.
определяется как альтернированная сумма
Х(Ю = Ё(-1)йгапкЯй(К),
где в качестве области коэффициентов используется какое-ни«
будь поле. Известная теорема утверждает, что эйлерова харак*
теристика равна альтернированной сумме
£(— l)fe (число A-мерных клеток)
и, следовательно, не зависит от выбора поля коэффициентов
(см. [Дольд]).
Следствие 11.12. Если М — гладкое компактное ориентиро-
ванное многообразие, то индекс Кронекера (е (тм), р> по рацио-
нальной или целочисленной областям коэффициентов равен эй-
леровой характеристике ч(М). Аналогично для неориентирован-
ного многообразия М число Штифеля—Уитни <шп(тм), р> =
= wn[M] равно приведенной по модулю 2 эйлеровой характе-
ристике х(ЛГ).
Доказательство. В силу теоремы 11.3 и леммы 11.5, класс
Эйлера касательного расслоения многообразия М равен
е(тм) = Д*(И.
В случае рациональных коэффициентов подставляем вместо и"
его выражение
и получаем равенство
Применяя к обеим его сторонам гомоморфизм < ,(л>, приходим
к требуемой формуле
<е(хм), p) = E(-l)d,m6‘ = x(M).
Рассуждение для случая коэффициентов по модулю 2 совер-
шенно аналогично. 
Формула У для классов Штифеля — Уитни
Пусть Wi = есть i-й класс Штифеля — Уитни каса-
тельного расслоения гладкого многообразия М, или, что то же
самое, i-й класс Штифеля — Уитни нормального расслоения
диагонали в произведении М X М. Применяя формулу Тома
§ 11. Некоторые вычисления на гладких многообразиях 111
(см.§ 8)
Sqz (ы) = (л*Ш/) о и
вместе с изоморфизмом
Н* (Е, Ео) ~ Я* (ЯЕ, N, \ А (М)) £*Н*(МХМ, МХМ\Ь (М))
(следствие 11.2), легко получаем, что
Sq* (и') = (wt X 1) о и'.
Ограничение на Я*(Л1Х-М) дает формулу
Sqz(u") = HXD^w".
Мы снова будем использовать тот факт, что гомоморфизм
/-умножения
/Р: Н* (X XY)-* Н* (X)
является Н* (X) -линейным слева для любого элемента р е
еЯ,(У), В частности, /-произведение
X 1) и")/ц
равно
W{ V (u"/n) = Wi.
(Ср. с доказательством теоремы 11.11.) Так как это произведе-
ние равно также Sq*(u")/n, то мы приходим к следующему ре-
зультату.
Лемма 11.13. Классы. Штифеля — Уитни гладкого компакт-
ного многообразия М определяются формулой
wt = Sq* (ы")/ц. 
В качестве следствия получаем, что, если два многообразия
Mi и М2 имеют один и тот же гомотопический тип, то их классы
Штифеля — Уитни должны совпадать при соответствии, опреде-
ляемом индуцированным изоморфизмом H*(Mi)sz Н*(М2). Это
следует из выражения для класса и", данного в теореме 11.11.
В действительности можно, следуя У, дать явный рецепт вы-
числения классов wt, использующий только кольцо когомологий
Н*(М) с коэффициентами по модулю 2 и действие стинродов-
ских квадратов на Н*(М). Рассмотрим аддитивный гомомор-
физм
х (Sq* (х), ц)
из группы когомолегий Hn~k(M) в Z/2. Привлекая теорему
двойственности Пуанкаре, легко показать, что существует один
и только один когомологический класс
vke=Hk(M),
112 Дж. Милнор и Дж. Сташеф
который удовлетворяет тождеству
(vkux, pi) = (Sq*(x), |i>
для любого x^Hn~k(M). (Фактически, если рассматривать мно-
гообразие М как дизъюнктное объединение его связных компо-
нент, то, как нетрудно проверить, элемент Уй удовлетворяет бо-
лее сильному условию
uft<7X = Sqft(x)e//n(Al)
для любого х е Hn~k(M). Конечно, класс Vk равен нулю, если
k > п — k.) Определим полный класс У
уеЯп(М) = Я°(Л1)ф//1(М)ф ...
как формальную сумму
V = 1 + yt 4- у2 + ... + vn.
Ясно, что класс v удовлетворяет тождеству
(y^x, iO = (Sq(x), |х),
справедливому для любого когомологического класса х, и ха-
рактеризуется им. Здесь Sq обозначает полный стинродовский
квадрат Sq° + Sq1 + Sq2
Теорема 11.14. (У). Полный класс Штифеля — Уитни w ка-
сательного расслоения хм многообразия М равен Sq(y). Дру-
гими словами,
wk= Z Sq'^y).
i+j-k
Доказательство. Выберем базис {&,} для mod 2-когомологий
Н*(М) и двойственный базис {&*}> как в теореме 11.10. Тогда
для любого когомологического класса хеЯп(Л1) имеет место
легко проверяемое тождество
х = Z bi (х v bf, ц).
Применяя это тождество к полному классу У v, получаем
v = Z bi (v bf, ц) = <Sq (б*). ц).
Следовательно, класс Sq(y) равен
Е Sq (bi) <Sq (tf).	= S (Sq (bt) X Sq (bf))/p = Sq (u")/n
по теореме 11.11. Таким образом, Sq(y) = ty, что и утвержда-
лось. 
Укажем одно конкретное применение, иллюстрирующее тео-
рему У. Пусть М — компактное многообразие, кольцо mod 2-ко-
$ 11. Некоторые вычисления на гладких многообразиях ИЗ
гомологий которого порождается одним-единственным элемен-
том as k 5* 1. Таким образом, когомологии Я*(А!)
имеют базис {1,а,а2.....ат} и размерность многообразия М
должна быть равной km, где т — некоторое целое число, т 1.
Следствие 11.15. Если многообразие М, такое, как указано
выше, то полный класс Штифеля — Уитни w(xm) равен
,, fm+l\	/т4-1\ „
(1+а)т+1 = Ц-( 1 Ja+ ... +( m Ja .
Например, предположениям следствия 11.15, очевидно, удо-
влетворяет сфера Sk, для которой m = 1 и ш =(1а)2 = 1.
Им также удовлетворяет вещественное проективное простран-
ство Pm = Pm(R) с когомологической образующей а в размер-
ности k = 1 (см. теорему 4.5). В § 14 мы увидим, что этим пред-
положениям удовлетворяет комплексное проективное простран-
ство Рт(С), которое является многообразием вещественной раз-
мерности 2m с когомологической образующей в размерности
k — 2. Аналогично им удовлетворяет кватернионное проектив-
ное m-мерное пространство, представляющее собой многообра-
зие вещественной размерности 4m с когомологической образую-
щей в размерности Л = 4 (см., например, [Спеньер]). Наконец,
этим предположениям удовлетворяет плоскость Кэли, являю-
щаяся многообразием М вещественной размерности 16 с кого-
мологической образующей аеЯ8(Л4) и полным классом Шти-
феля— Уитни w = (1 + а)3 = 1 + а + а2 (см. [Борель, 1950]).
Это по сути дела и все существующие примеры. Действи-
тельно, как показано в [Адамс, 1960], если пространство X
имеет mod 2-когомологии, порожденные одной образующей а е
^Hk(X), k 1, причем а2=й=0, то k может быть только одним
из чисел 1, 2, 4, 8. Далее, если а3 0, то, как показано в [Адем,
1952], k может быть только одним из чисел 1, 2, 4. Таким обра-
зом, описанные выше многообразия — это единственно возмож-
ные многообразия, для которых кольцо когомологий с коэф-
фициентами в Z/2 является кольцом усеченных полиномов
от одной образующей. (Ср. обсуждение близких вопросов на
стр. 44, 45).
Доказательство следствия 11.15. Действие стинродовских
квадратов на когомологиях Я*(Л1), очевидно, задается фор-
мулой
Sq (а) = а 4- а2,
и поэтому
Sq (а1) = (а а2)' = а1 (1 + а)\
114 Дж. Милнор и Дж. Сташеф
Отсюда следует, что индекс Кронекера <Sq(a'),|i> равен бино-
(i \
_ .] • Применение формулы
<Sq (az),	=	|л>
показывает, что коэффициент при элементе am~l в выражении
/ i’ \
полного класса У v должен быть также равен I _ .]. Следо-
вательно,
»=у( 1
\m — U
Заменяя т — i на /, получаем более удобную запись для
v* (т
класса У v= у )а • Следовательно,
o> = Sq(u) = ^^ . JSqft?).
Поскольку мы знаем, как вычислять элемент Sq(a>), остается
только провести явное вычисление с биномиальными коэффици-
ентами. Например, если т — 5, то
0 = Х(5 j =
следовательно,
w = Sq (1 + а2) — 1 + а2 + а4.
В общем случае ясно, что необходимые вычисления, которые
нужно выполнить для того, чтобы получить выражение класса
w в виде полинома от а, зависят только от числа т и совсем не
зависят от размерности k элемента а. А это дает нам возмож-
ность обойтись совсем без вычислений. Действительно, для k—\
мы уже знаем, что вычисления должны приводить к формуле
w — (1 4-a)m+1 (согласно теореме 4.5). Очевидно, что точно та-
кие же вычисления, примененные к образующей а большей раз-
мерности, должны привести к той же самой формуле. 
В заключение задачи для читателя.
Задача 11.А. Доказать лемму 4.3 (т. е. вычислить mod 2-ко-
гомологии проективного пространства Рп) индукцией по п, ис-
пользуя теорему двойственности Пуанкаре 11.10 и следствие 6.5
(о клеточной структуре проективного пространства).
Задача 11.В. Еще одна теорема двойственности Пуанкаре.
Показать, что для компактного многообразия Af в случае, когда
область коэффициентов — поле, гомоморфизм
W"/: Нц_к(М)-+Нк(М)
$ 11. Некоторые вычисления на гладких многообразиях 115
является изоморфизмом. Используя операцию гл-умножения
(см. приложение А), показать, что обратным изоморфизмом
служит отображение
умноженное на (—1)*п.
Задача 11.С. Пусть М = Мп и А=А>>— компактные ориен-
тированные многообразия и i: М—>А — гладкое вложение. По-
ложим k = р — п. Показать, что изоморфизм двойственности
Пуанкаре
Hk(A)^Hn(A)
отображает когомологический класс и'[А, «двойственный» к
многообразию М, в гомологический класс (—1)nki* (цм). (Мы
предполагаем, что нормальное расслоение vk ориентировано,
так что расслоение ф v* ориентированно изоморфно расслое-
нию тд|Л4. При доказательстве использовать следующую ком-
мутативную диаграмму:
Hk (Л, А\М)®Нр (A)+Hk (Л, А\М)®Нр (Л, A\M)stHk (N, N\M)®Hp (N, АГ\Л1)
Hk (Л) ® Нр (Л)-----Нп (Л)«---------------Нп (АГ)
где N — трубчатая окрестность многообразия М в А.)
Задача 11.D. Доказать, что все числа Штифеля — Уитни лю-
бого трехмерного многообразия равны нулю.
Задача 11.Е. Доказать следующий вариант формулы У.
Пусть
Sq: ЯП(М)->ЯП(М)
— отображение, обратное кольцевому автоморфизму Sq. Пока-
зать, что двойственные классы Штифеля — Уитни Wi(xM) опре-
деляются формулой
(Sq(x), |x) = (t0ox, ц),
которая имеет место для любого когомологического класса х.
Показать, что юп = 0. Показать, что если п не есть степень
ДВУХ, TO Wn-i = 0.
Задача 11.F. Определяя операции Стинрода
Sq': Hk(X)-*Hk_{(X)
в mod 2-гомологиях тождеством
U Sq'(₽)) = (S?(x), Р>,
116 Дж. Милнор и Дж. Сташеф
показать, что
Sq (а ₽) — Sq (а) Sq (0)
и
Sq(«'7₽) = Sq(^/Sq(₽).
Доказать формулы Sq (ц) = w р, и Sq (р) = v р.
§ 12, ПРЕПЯТСТВИЯ
В первоначальных работах Штифеля и Уитни характеристи-
ческие классы были определены как препятствия к существова-
нию некоторых полей линейно независимых векторов. Аккурат-
ное изложение вопроса с этой точки зрения было дано Стинро-
дом в [Стинрод, 1951, разделы 25.6, 35 и 38]. В общих чертах
соответствующую конструкцию можно изложить следующим об-
разом.
Пусть | — некоторое n-мерное расслоение с базисным про-
странством В. Для каждого слоя F расслоения £ рассмотрим
многообразие Штифеля Vk(F), состоящее из всех 6-реперов в F.
Здесь под k-репером мы понимаем просто набор (th, .... и*),
состоящий из k линейно независимых векторов пространства F,
где 1 k п. (Ср. § 5. Стинрод использовал ортонормирован-
ные 6-реперы, однако это видоизменение не влияет на рассуж-
дения.) Эти многообразия Vk(F) можно рассматривать как слои
некоторого нового расслоения, которое мы будем обозначать
V*(g) и называть ассоциированным, расслоением на многообра-
зии Штифеля над базой В. По определению пространство рас-
слоения 14(g) состоит из всех пар (х, (tq,...,о*)), где х —
точка из В, a (th, ..., Vk) — 6-репер в слое Fx над х. Заметим,
что сечение этого расслоения на многообразии Штифеля есть не
что иное, как набор 6 линейно независимых сечений расслое-
ния g.
Теперь предположим, что базисное пространство В является
клеточным разбиением *. Например, если базисное простран-
ство— гладкое паракомпактное многообразие, то, согласно тео-
реме Дж. Г. К. Уайтхеда, оно допускает гладкую триангуляцию,
а потому в нем и подавно можно ввести структуру клеточного
разбиения (см. [Манкрс]).
Стинрод показал, что слой Vk(F) является (п —6 — ^-связ-
ным, так что легко построить сечение расслоения Vs(g) над
(п —6)-остовом базы В. Сечение же над (п — 6+1)-остовом
базы В существует тогда и только тогда, когда равен нулю не-
который вполне определенный примарный препятствующий
1 Стинрод рассматривал только случай конечных клеточных разбиений,
однако полезно и не намного труднее иметь дело с произвольными клеточ-
ными разбиениями.
$ 12. Препятствия 117
класс, лежащий в группе
Hn-k+i(B- {n„_ftVft(F)}).
Здесь рассматриваются когомологии с локальными коэффици-
ентами. Символ	используется для обозначения си-
стемы локальных коэффициентов (т. е. пучка абелевых групп),
которая сопоставляет каждой точке хе В группу nn-kVk(Fx).
(В случае п — k = 0 группа яоХ определяется как группа при-
веденных сингулярных гомологий /?0(Х; Z).)
Полагая j — n — /?+1, будем использовать для этого при-
ма рного препятствующего класса обозначение
Если / четное и меньше п, то, как показал Стинрод, группа
nj~iVn~j+i(F) является циклической порядка 2. Следовательно,
она канонически изоморфна группе Z/2. Если / нечетно или
/ = п, то группа	(F) будет бесконечной циклической.
Однако она не будет канонически изоморфна группе Z. Система
локальных коэффициентов {n/_iVn_/+i(F)}, вообще говоря, яв-
ляется скрученной.
В любом случае существует, конечно, единственный нетриви-
альный гомоморфизм h группы n/-iVn-/+i(B) в Z/2. Поэтому мы
можем привести систему коэффициентов по модулю 2 и по-
лучить индуцированный когомологический класс /i*0/(g)e
e=W(B; Z/2).
Теорема 12.1. Описанная выше редукция по модулю 2 пре-
пятствующего класса 0/(g) равна классу Штифеля — Уитни
№/(В).
Доказательство. Прежде всего рассмотрим универсальное
расслоение у" над многообразием Грассмана Gn — Gn(R°°). Так
как кольцо H*(Gn, Z/2) является алгеброй полиномов с обра-
зующими Wt(yn)......wn(yn), то
V/ (Yn) = fi fai (y")..(y")).
где fi — некоторый полином от n переменных. Поскольку и пре-
пятствующий класс и классы Штифеля — Уитни естественны от-
носительно послойных отображений (см. [Стинрод, п. 35.7]), то
М/(Г) = //(№1(Ю, .... ®„(1))
для любого n-мерного расслоения £ над клеточным разбиением.
Так как fj(wi, ..., wn) — когомологический класс размерно-
сти / п, то полином fi можно, очевидно, однозначно предста-
вить в виде суммы
fi&i.....=	......И1/.0 4-
118 Дай. Милнор и Дж. Сташеф
где f'n - некоторый полином, а коэффициент X = X/, п ра-
вен 0 или 1.
Чтобы вычислить f', рассмотрим n-мерное расслоение i) =
= у/-1 ф 8"-/+1 над многообразием Грассмана G/-i, где ел-/+1—
тривиальное расслоение. Поскольку расслоение i) допускает
п — / + 1 линейно независимых сечений, то препятствующий
класс
0/(т1)еЯ/(В;	(F)})
должен быть нулем. Следовательно, приведенный по модулю 2
класс
М/ (П) = f' (wi (n)..Wj_i (tj)) + kWj fa) =
= f (ybi)........ay/_I (Y/-1)) о
также равняется нулю. Так как классы	..., Щ/-1(у/_|)
алгебраически независимы, то это доказывает, что f' = 0. Таким
образом,
М (£) = Щ ($)
для любого «-мерного расслоения
Докажем теперь, что коэффициент X = Х/)П равен 1. Сначала
рассмотрим случай / = «. Возьмем в качестве £ ограничение у}*
универсального расслоения у" на многообразие Грассмана
G„(Rn+1) всех «-мерных плоскостей в («+ 1)-мерном простран-
стве. Отождествляя Gn(Rn+1) с вещественным проективным про-
странством Рп (см. замечание к лемме 5.1), можно описать это
расслоение у" следующим образом.
Точке, соответствующей паре антиподальных точек {и, —и}
единичной сферы S", сопоставляется слой, состоящий из всех
векторов v пространства Rn+1, таких, что ti-v = 0:
Формула {«,—u} f—>и0 — (и0. и) и задает сечение расслоения у",
которое является ненулевым всюду, за исключением одной-един-
§ 12. Препятствия 119
ственной точки {«о, —«о} проективного пространства Р”:
Выбирая точку «о посредине n-мерной клетки проективного про-
странства Рп (см. следствие 6.5), получаем сечение расслоения
Vt (у“) над (п — 1) -остовом, и препятствующий коцикл, очевид-
но, сопоставляет n-мерной клетке образующую циклической
группы
Лп-1 V1 (р) *= лп_1 (Р \ 0) е* Z.
Таким образом, hton(yfy 0 и, следовательно, коэффициент
Хп, п должен быть равен 1.
Доказательство для случая j < п проводится совершенно
аналогично. Нужно использовать расслоение у(феп-/ над мно-
гообразием Грассмана О/(Р/+1)е=£ Р1 и описание образующей в
группе л/-1 Vn-f+i (Rn), данное в [Стинрод, п. 25, 6]. 
Замечание. С теорией препятствий тесно связано любопыт-
ное описание классов Штифеля — Уитни многообразия М, вы-
сказанное в виде гипотезы Штифелем и впервые доказанное
Уитни. Если выбрать на многообразии М произвольную глад-
кую триангуляцию, то сумма всех симплексов первого барицен-
трического подразделения является циклом 1 по модулю 2, пред-
ставляющим гомологический класс wryp, двойственный по
Пуанкаре полному классу Штифеля — Уитни касательного рас-
слоения гм- Доказательство этого результата было недавно опу-
бликовано в работе [Гальперин, Тол ед 6^.
Пусть нам заданы классы Штифеля — Уитни w/(§) некото-
рого n-мерного расслоения |. В какой мере можно восстановить
по ним препятствующие классы 0/(£)? Если число / = 2i четно
и меньше п, то группа коэффициентов n/-iVn-/+i(^) имеет по-
рядок 2, и поэтому мы можем, не опасаясь двусмысленности,
написать
о2/ (g) = w2i (Ю Для 21 < п.
1 Следует иметь в виду, что под циклом здесь понимается сумма циклов
разных размерностей. — Прим, перев.
120 Дж. Милнор и Дж. Сташеф
Далее, согласно (Стинрод, п. 38.8], класс Огж (&) можно пред»
ставить как образ 6*02/(&), где б* — некоторая надлежащим об-
разом подобранная когомологическая операция. Таким образом,
препятствующие классы о/ (?) для нечетных j или j < п вполне
определяются классами Штифеля — Уитни расслоения £.
Ниже мы докажем, что старший препятствующий класс оп(£)
может быть отождествлен с классом Эйлера е(|), когда рас-
слоение ориентировано. Для доказательства нам понадобятся
две важные конструкции.
Последовательность Гизина для векторных расслоений
Пусть g —некоторое n-мерное расслоение с проекцией я:
Е -* В. Ограничив отображение я на пространство Ео ненулевых
векторов в Е, мы получим ассоциированную проекцию яо: Ео—* В.
Теорема 12.2. Для любого ориентированного п-мерного рас-
слоения £ имеет место точная последовательность вида
... ^Н‘(В)^Н{+п(В)-Хн1+п(Е0)^>Н‘+1(В)^Л
где группы когомологий берутся с целочисленными коэффици-
ентами.
Символ v? е обозначает здесь гомоморфизм а»—>а<>е(£).
Доказательство. Начнем с когомологической точной после-
довательности
... -+Hf(E, Ео)-> Н} (Е)~* Н1 (Ео) -Л Яж (Е, Ео)-> ...
пары (Е, Ео). Используя изоморфизм Тома
uu: Н,~п(Е)-+Н1 (Е, Ео)
из § 10, заменим в ней группу Н'(Е, Ео) изоморфной группой
Н1~п(Е). В результате получим точную последовательность
... Н'~п (Е) Н1 (Е) -► Н1 (Ео) Я/-л+’ (Е)
где
g (х) == (х и) |Е = х о (и |Е).
Теперь подставим вместо кольца Н*(Е) изоморфное ему кольцо
когомологий Н*(В). Так как когомологический класс и[Е из
группы Нп(Е) соответствует классу Эйлера е(£) в группе Нп(В),
то мы придем к требуемой точной последовательности
... -^ Н‘~п (В) Н1 (В) -> Н1 (Ео) -► н'~п+1 (В) — ... 
Аналогично для неориентированных расслоений существует
соответствующая точная последовательность с коэффициентами
§ 12. Препятствия 121
по модулю 2, использующая класс wn(l) вместо класса Эйлера
(ср. с доказательством теоремы 11.3). Для примера рассмотрим
скрученное линейное расслоение у„ над проективным простран-
ством Рп. Так как пространство Д0(у„) может быть отождеств-
лено с Rn+1 \ 0, то оно содержит единичую сферу S" как дефор-
мационный ретракт. Таким образом, мы получаем точную после-
довательность
... -> Н‘~' (Рп) Н1 (Рп) -> Н1 (Sn) -> Н1 (Р") -> ...
с коэффициентами по модулю 2, где wl = (у£).
Более общо, рассмотрим произвольное двукратное накрытие
В —* В. Это значит, что каждая точка пространства U обладает
открытой окрестностью U, прообраз которой состоит из двух от-
крытых дизъюнктных экземпляров U. Тогда мы можем по-
строить одномерное расслоение g над пространством В, про-
странство расслоения которого получается из прямого произве-
дения В X R отождествлением каждой пары (х, t) с парой
(х', —t), где х и х' — две различные точки пространства В, ле-
жащие над одной и той же точкой пространства В. Очевидно,
что открытое подмножество Ео содержит В как деформацион-
ный ретракт. Таким образом, мы доказали следующее утверж-
дение.
Следствие 12.3. Для любого двукратного накрытия В-+В
имеет место точная последовательность вида
... ...»
где группы когомологий берутся с коэффициентами по моду-
лю 2 и w\= ач(|). 
Ориентированное универсальное расслоение
Пусть Gn(Rn+A!) обозначает многообразие Грассмана, состоя-
щее из всех ориентированных п-мерных подпространств (п-|-£)-
мерного пространства. Точно так же, как и в § 5, его можно на-
делить топологией факторпространства многообразия Штифеля
V«(Rn+'!). Ясно, что (jn(Rn+ft) является двукратным накрываю-
щим пространством над многообразием Грассмана Gn (Rn+ft)
всех неориентированных п-мерных подпространств. Легко про-
верить, что 6f„(Rn+ft) представляет собой компактное клеточное
разбиение размерности nk. Переходя к прямому пределу при
k-*oo, получаем бесконечное клеточное разбиение Gn = C„(R°°).
(Пространства Оп и Gn обычно обозначаются через ВО(п) и
BSO (п) соответственно.)
122 Дж. Милнор и Дж. Сташеф
Универсальное расслоение уя над Gn поднимается до ориентир
рованного «-мерного расслоения над Gn. Мы. будем обозначать
это универсальное ориентированное расслоение символом уяг
Ясно, что для любого ориентированного «-мерного расслоения |
каждое послойное отображение £-*у" однозначно поднимается,,
до сохраняющего ориентацию послойного отображения £ —»уя.
Когомологии пространства Gn с коэффициентами по модулю 2
могут быть вычислены следующим образом (ср. § 7).
Теорема 12.4. Кольцо когомологий H*(Gn', Z/2) является алге-.
брой многочленов над полем Z/2, свободно порожденной класса-,
ми Штифеля — Уитни wz( у"), ..., wn(у")•
В частности, группа H'(Gn; Z/2) нулевая. Отсюда следует,
что а>1( уя) = 0 и, значит, ^1(^) = 0для любого ориентируемого
векторного расслоения £ над паракомпактным базисным про-
странством (ср.с задачей 12.А.)
Доказательство. Согласно следствию 12.3, существует точная
последовательность
... Д'-1 (G„) Н1 (Gn)	Н1 (Gn) -> Н1 (Gn)
где с — первый класс Штифеля — Уитни линейного расслоения, •>
ассоциированного с двукратным накрытием р: Gn-+Gn. Этог
класс с не может быть нулевым. Действительно, если бы он был •
нулевым, то из точности последовательности
О Н° (Gn) Н° (Gn) -> Д° (G„) ^...	»
вытекало бы, что пространство Сп имеет две компоненты связ- '*
ности, а это противоречит тому очевидному факту, что любое
ориентированное «-мерное подпространство в R“ можно вепре-
рывно деформировать в любое другое ориентированное «-мер-
ное подпространство. Используя теорему 7.1, заключаем, что
с = ®1(уя), и доказательство завершается непосредственным
образом. 
Класс Эйлера как препятствие
Теперь в нашем распоряжении имеются все предварительные
конструкции, необходимые для изучения старшего препятствую-
щего класса
ориентированного «-мерного расслоения £. Используя ориента-
цию в слоях F, можно показать, что каждая коэффициентная
группа
п„_,У, (Л =	(F \ 0) a (F \ 0; Z) & Нп (F, F \ 0; Z)
§ 12. Препятствия 123
канонически изоморфна группе Z. Поэтому следующее утверж-
дение имеет смысл.
Теорема 12.5. Если расслоение £ является ориентированным
п-мерным расслоением над клеточным разбиением, то препят-
ствующий класс оя(£) равен классу Эйлера e(g).
Доказательство. Исходя из проекции по: Ео-+В, образуем
индуцированное расслоение njg над пространством Ео. Ясно, что
это индуцированное расслоение имеет всюду ненулевое сечение,
и поэтому
"о оп © = оя (л$ = 0.
Используя точную последовательность Гизина
Н°(В)^Нп(В)-Хнп(Е0)
с целочисленными коэффициентами, заключаем, что
для некоторого элемента Zs№(B). Это рассуждение приме
нимо, в частности, к универсальному расслоению уя над Оп. Из
рассмотрения последовательности Гизина
На(бп)^Нп(Сп)Лнп(Еот
вытекает, что оя( у") ~ Хяе(у”) для некоторого целого числа Хя.
Следовательно, по свойству естественности оя(£) = Хяе(£) для
любого ориентированного «-мерного расслоения £ над клеточ-
ным разбиением.
Приводя теперь обе стороны этого равенства по модулю 2,
получаем, что
wn(yn) = Knwn(yn)
в силу теоремы 12.1 и свойства 9.5. Так как ®я (?")=/’ 0, п° тео-
реме 12.4, то отсюда следует, что Кп нечетно.
Если размерность п нашего расслоения £ нечетна, то класс
Эйлера е(£) сам имеет порядок 2, согласно свойству 9.4, и, та-
ким образом, мы получаем, что в этом случае оя(£) = е(%).
Если размерность п четна, то нам надо показать, что Хя =
— 4-1. Пусть т — касательное расслоение «-мерной сферы, где «
четно. Тогда индекс Кронекера <е(т), |х> равен эйлеровой ха-
рактеристике %(5Я)= -j-2 по следствию 11.12. Аналогичным об-
разом справедливо равенство
<оя(т), р) = 4-2
(см. [Стинрод, п. 39.6]; его легко можно проверить и непосред-
ственно, используя векторное поле на сфере Sn, указанное при
124 Дж. Милнор и Дж. Сташеф
доказательстве теоремы 12.1). Следовательно, коэффициент кп
должен быть равен +1. И
В заключение задачи.
Задача 12.А. Доказать, что векторное расслоение £ над кле-
точным разбиением ориентируемо тогда и только тогда, когда
®1(Ю = 0.
Задача 12.В. Используя формулу У (теорема 11.14) и тот
факт, что jt2V2(R3) = Л2£О(3) = 0 [Стинрод], доказать теорему
Штифеля, утверждающую, что любое компактное ориентируе-
мое трехмерное многообразие параллелизуемо.
Задача 12.С. Применив следствие 12.3, дать другое доказа-
тельство того, что кольцо когомологий Н*(Рп; Z/2) таково, как
указано в 4.3.
Задача 12.D. Показать, что ffn(R',+*) является гладким ком-
пактным ориентируемым многообразием размерности nk. Пока-
зать, что отображение, которое сопоставляет n-мерной плоско-
сти с ориентированным базисом bi, ..., bn вектор Ь\ Л ...
... A Л ... /\Ьп\, осуществляет гладкое вложение
ff«(R"+ft) во внешнюю степень A"R',+*.
§ 13. КОМЛЕКСНЫЕ ВЕКТОРНЫЕ РАССЛОЕНИЯ
И КОМПЛЕКСНЫЕ МНОГООБРАЗИЯ
Часто бывает полезным рассматривать векторные расслое-
ния, в которых каждый слой является векторным пространством
над полем комплексных чисел.
Пусть В — некоторое топологическое пространство.
ОПРЕДЕЛЕНИЕ 13.1. Комплексное векторное расслоение о
комплексной размерности п над В (или, кратко, комплексное
n-мерное расслоение) состоит из топологического пространства
Е и проекции я: Е-+В, причем в каждом слое л~! (Ь) задана
структура комплексного векторного пространства и должно удо-
влетворяться следующее
Условие локальной тривиальности. Для каждой точки из В
существует окрестность U, такая, что прообраз л-1([/) гомео-
морфен прямому произведению U X Сп при некотором гомео-
морфизме, комплексно-линейно отображающем каждый слой
л-1 (b) на произведение b X С".
Здесь Сп обозначает координатное пространство, состоящее
из всех наборов по п комплексных чисел, a b X С" превращает-
ся в комплексное векторное пространство игнорированием «ко-
ординаты» Ь,
§ 13. Комплексные векторные расслоения 125
Точно так же, как в § 3, мы можем образовывать из задан-
ных комплексных векторных расслоений новые комплексные
векторные расслоения, например сумму Уитни, или тензорное
произведение (над С), или индуцированные расслоения.
Один из методов построения комплексного n-мерного рас-
слоения состоит в том, чтобы для данного вещественного 2п-
мерного расслоения попытаться ввести в каждом его слое до-
полнительную структуру комплексного векторного простран-
ства.
ОПРЕДЕЛЕНИЕ. Комплексной структурой на вещественном
2п-мерном расслоении £ называется непрерывное отображение
J:
пространства расслоения на себя, R-линейно переводящее каж-
дый слой в себя и такое, что для каждого вектора v е Е(£)
/(/(«)) = -V-
Если на расслоении £ задана комплексная структура, то мы
можем превратить каждый слой в комплексное векторное
пространство, полагая
(х + iу) v = xv + J (yv)
для любого комплексного числа х + iy. Условие локальной три-
виальности из определения 13.1 легко проверяется, так что рас-
слоение | действительно становится комплексным векторным
расслоением.
Верно, конечно, и обратное: если нам дано комплексное
n-мерное расслоение ®, то мы можем просто забыть о комплекс-
ной структуре и рассматривать каждый слой как вещественное
векторное пространство размерности 2п. Таким образом мы по-
лучаем лежащее в основе вещественное 2п-мерное расслоение
соц. Заметим, что это вещественное расслоение <or и первона-
чальное комплексное расслоение ® оба имеют одно и то же про-
странство расслоения, одно и то же базисное пространство и
одну и ту же проекцию.
Пожалуй, наиболее важными примерами комплексных век-
торных расслоений служат касательные расслоения «комплекс-
ных многообразий». Рассмотрим сначала один частный случай.
Пример 13.2. Пусть U — открытое подмножество координат-
ного пространства С". Тогда касательное расслоение ту с про-
странством расслоения DU — U'X.Cn имеет каноническую ком-
плексную структуру /о, определяемую формулой
J0(u, v) — (u, iv)
для любых и е U и с е С".
126 Дж. Милнор и Дж. Сташеф
Пусть далее f: U-+ U' — какое-нибудь гладкое отображение,
где U' <=. Ср также является открытым подмножеством некото-
рого комплексного координатного пространства. Можно спро-
сить, не будет ли 7?-линейное отображение Dfu: DUu-> DU'f(u}
в действительности комплексно-линейным для всех и, так что
(Df) о J0 = J0°Df.
В случае, когда производная Df является комплексно-линейной,
говорят, что отображение f удовлетворяет условиям (или урав-
нениям) Коши — Римана или что f является голоморфным (или
комплексно-аналитическим) отображением. Стандартная тео-
рема комплексного анализа утверждает, что отображение f мо-
жет быть тогда локально представлено в виде суммы сходяще-
гося комплексного ряда (см. [Хёрмандер] или [Ганнинг, Росси]).
Пусть М — гладкое многообразие размерности 2п. Комплекс-
ную структуру на касательном расслоении многообразия М ино-
гда называют почти-комплексной структурой на многообра-
зии М.
ОПРЕДЕЛЕНИЕ 13.3. Комплексной структурой на много-
образии М называется комплексная структура J на касательном
расслоении тм, удовлетворяющая следующему чрезвычайно
сильному условию: каждая точка из М должна обладать откры-
той окрестностью, диффеоморфной открытому подмножеству
комплексного пространства Сп при диффеоморфизме h, произ-
водная которого всюду является комплексно-линейной: dh° J =
= /о о dh.
Пара (М, J) называется в этом случае комплексным много-
образием комплексной размерности п. Обычно, чтобы не пере-
гружать обозначения, мы будем использовать для обозначения
комплексного многообразия просто символ М.
ОПРЕДЕЛЕНИЕ. Гладкое отображение f: M-+N комплекс-
ных многообразий называется голоморфным, если производная
Df комплексно-линейна, т. е.
(Df)°J = J°Df.
Замечания. Фундаментальная теорема Ньюлэндера — Нирен-
берга ([Ньюлэндер, Ниренберг]) утверждает, что гладкая поч-
ти комплексная структура / является «настоящей» комплексной
структурой тогда и только тогда, когда она удовлетворяет не-
которой системе квадратичных дифференциальных уравнений в
частных производных первого порядка. Используя скобки Ли
векторных полей, эти уравнения можно записать так:
[Jo, /су] = J [о, 7w] + J [/v, w] + [o, w],
§ 13. Комплексные векторные расслоения 127
где v и w — произвольные гладкие векторные поля иа многооб-
разии М.
Самая классическая (и часто самая удобная) процедура вве-
дения комплексной структуры на гладком многообразии состоит
в следующем. Задается совокупность диффеоморфизмов
ha: Ua->Va,
где Ua — открытые подмножества в Сп, a Va — открытые под-
множества, образующие покрытие нашего многообразия, и надо
только проверить, что каждая композиция
является голоморфным отображением *.
В заключение несколько задач для читателя.
Задача 13.А. Показать, что комплексная структура J: Е(£)^>-
на вещественном векторном расслоении автоматически
удовлетворяет комплексному условию локальной тривиальности
из определения 13.1.
Задача 13.В. Показать, что если М — комплексное многооб-
разие, то DM также является комплексным многообразием. Ана-
логично, показать, что если отображение f; M-+N голоморфно,
то Df: DM —► DN — также голоморфное отображение.
Задача 13.С. Показать, что если М — компактное комплекс-
ное многообразие, то любое голоморфное отображение f: М —> С
является константой.
Задача 13.D. Показать, что проективное пространство РЯ(С),
состоящее из всех комплексных прямых, проходящих через на-
чало координат в Ся+1, может быть наделено структурой ком-
плексного многообразия. (Заметим, что Р1 (С) можно отожде-
ствить с комплексной прямой С, пополненной одной-единствен-
ной точкой в бесконечности.) Более общо, показать, что про-
странство С*(СЯ) всех комплексных ^-мерных подпространств,
проходящих через начало координат в Ся, является комплекс-
ным многообразием комплексной размерности k(n — k).
Задача 13.Е. Пусть у1п обозначает каноническое комплексное
линейное расслоение над РЯ(С). Таким образом, пространство
расслоения Е(у^) состоит из всех пар (L, у), где L — комплекс-
ная прямая, проходящая через начало координат в Ся+1, а
1 Примеры, иллюстрирующие взаимоотношение понятий: гладкое ве-
щественное многообразие, почти-комплексное многообразие и Комплексное
многообразие, — можно найти в книге [*Уэллс]. — Прим, перед.
128 Дж. Милнор и Дж. Сташеф
veL, Показать, что у расслоения нет никаких голоморфных
сечений, отличных от нулевого. Показать, однако, что двой-
ственное расслоение Нотс (у^, С) имеет по меньшей мере
п + 1 голоморфных сечений, линейно независимых над С.
Задача 13.F. Если М — комплексное n-мерное многообразие,
то вещественное векторное расслоение HomR (Тлр R) касатель-
ных ковекторов не обладает никакой естественной комплекс-
ной структурой. Показать, однако, что его комплексификация
HomR (тм, R) 8rCs HomR (тЛ1, С)
является комплексным 2п-мерным расслоением, которое кано-
нически расщепляется в сумму Уитни
НошсСгм, С) ® Ноше (тль С).
Здесь Нотс (Хи, С) обозначает комплексное векторное простран-
ство сопряженно-линейных отображений (Л(Хо) = Л,/г(о)). По-
казать, что, если U с: Ся — открытое множество с координат-
ными функциями zi.....гя: U -> С, то полные дифференциалы
dz\(u)....dzn{u) образуют базис пространства Home{DUU, С),
a dzi(u), ..., dzn(и) — базис пространства Homc(DC/„, С).
Отсюда следует, что, если /—произвольная гладкая (необя-
зательно голоморфная) комплекснозначная функция на U, то
ее полный дифференциал df можно единственным образом за-
писать как линейную комбинацию дифференциалов dzi, ...
..., dzn, dz\, ..., dzn с коэффициентами, которые также яв-
ляются гладкими комплекснозначными функциями на U. Эти
коэффициенты принято обозначать через dfldz\, ..., df/tfen,
df/diii, ..., df/diin соответственно. Таким образом, полный диф-
ференциал df может быть однозначно представлен в виде сум-
мы df 4- df, где df — J} (dfldzi) dz/ есть сечение расслоения
Нотс(тль С), adf — ^(df/dzf) dz{ — сечение расслоения Нотс (тм,
С). Показать, что, если положить г, = X/ + iyf, то производ-
ная df/dzj равна ~ {df/dXj + i dffdyf). Показать, что уравнения
Коши — Римана для функции f можно записать так: df/dzj — О
или, кратко, df = 0.
Задача 13. G. Показать, что комплексное векторное про-
странство, натянутое на дифференциальные операторы
d/dzi, ..., d/dzn в точке г, канонически изоморфно касатель-
ному пространству DU2.
$ 14. Классы Чженя 129
§ 14. КЛАССЫ ЧЖЕНЯ
Прежде всего докажем следующее утверждение.
Лемма 14.1. Для всякого комплексного векторного расслое-
ния со его овеществление ®r обладает канонической отмечен-
ной ориентацией.
Применяя эту лемму к частному случаю касательных рас-
слоений, мы получаем, что любое комплексное многообразие
обладает канонической отмеченной ориентацией. Действитель-
но, согласно лемме 11.6, ориентация касательного расслоения
гладкого многообразия однозначно определяет ориентацию са-
мого многообразия.
Доказательство. Пусть V — произвольное конечномерное
комплексное векторное пространство. Выберем какой-нибудь
базис Яь ..., ап пространства V над С. Тогда векторы Oi, iait
а%, Ш2, .... ап, ian образуют вещественный базис лежащего
в его основе вещественного векторного пространства Vr. Этот
упорядоченный базис и определяет искомую отмеченную ориен-
тацию пространства Vr. Для того чтобы показать, что эта
ориентация не зависит от выбора комплексного базиса, доста-
точно заметить, что полная линейная группа GL(n, С) является
связной. Поэтому мы можем переходить от любого данного
комплексного базиса к любому другому комплексному базису
при помощи непрерывной деформации, которая не изменяет
индуцированной ориентации.
Пусть теперь со — комплексное векторное расслоение. При-
меняя описанную конструкцию к каждому его слою, получаем
искомую ориентацию вещественного расслоения ®r. 
В качестве приложения леммы 14.1 заметим, что для лю-
бого комплексного «-мерного расслоения ® над базисным про-
странством В однозначно определен класс Эйлера
е(а>к)е//2я(В; Z).
Отметим, что, если со' — комплексное m-мерное расслоение
над тем же базисным пространством В, то
e((®©m%)==e(<oR)e(c^).
Действительно, если а\, ..., ап — базис для слоя F расслоения
® и Ъ\, ..., bm — базис для соответствующего слоя F' расслое-
ния и', то упорядоченный базис ait ia\, .... ап, ian слоя Fr
вместе с выписанным вслед за ним упорядоченным базисом
di, ibi, ..., bm, ibm слоя Fr дают упорядоченный базис ait
iai, .... ian, bi, ibi, ..., ibm, определяющий отмеченную ориен-
5 Дж. Милнор, Дж. Сташеф
130 Дж. Милнор и Дж. Сташеф
тацию слоя (F©F')R. Таким образом, расслоение ®r©<or
ориентированно изоморфно расслоению (<o®ci/)R» откуда
и следует требуемое утверждение.
Эрмитовы метрики
Подобно тому как при изучении вещественных векторных
расслоений важную роль играют евклидовы метрики, для комп-
лексных расслоений важную роль играют аналогичные эрмито-
вы метрики. По определению эрмитова метрика на комплекс-
ном векторном расслоении <о — это евклидова метрика
>| v
(см. стр. 23) на овеществленном расслоении ®R, удовлетво-
ряющая тождеству
I iv I == I v |.
Нетрудно показать, что для каждой такой эрмитовой метрики
существует одно и только одно комплекснозначное скалярное
произведение
(и, w) =* у (| v + w р — | v |2 — | w |2) + i (| v + lw р — | v |2 — | iw I2),
определенное для векторов v и w из одного и того же слоя
расслоения о, которое
(1)	комплексно-линейно по v при фиксированном w;
(2)	антилинейно по w при фиксированном v (т. е. <о,
*=Х<и, w));
(3)	обладает свойством <v, v>==|v|2.
Два вектора v и w называются ортогональными, если их
скалярное произведение <v, w) равно нулю. Легко проверяется
тождество Эрмита	_____
{w, о) = (о, w),
следовательно, вектор v ортогонален к w тогда и только тогда,
когда w ортогонален v.
Если базисное пространство В паракомпактно, то любое
комплексное векторное расслоение над В допускает эрмитову
метрику (ср. с задачей 2.С).
, Построение классов Чженя
Дадим теперь индуктивное определение характеристических
классов комплексных n-мерных расслоений ®. Прежде всего
нам нужно построить каноническое (п—1)-мерное расслоение
(По над «разрезанным» пространством расслоения Е'о. (Как и в
вещественном случае, Е’о = Е’о (®) обозначает множество всех
§ 14. Классы Чженя 131
ненулевых векторов в пространстве расслоения Е (со) = Е (coR).)
Точка пространства Ео определяется заданием слоя F расслое-
ния со вместе с ненулевым вектором v из этого слоя. Предпо-
ложим сначала, что на расслоении со задана эрмитова метрика.
Тогда слоем расслоения соо над точкой veE0 является по оп-
ределению ортогональное дополнение к вектору v в простран-
стве F. Это дополнение есть комплексное векторное простран-
ство размерности п—1, и эти пространства, очевидно, можно
рассматривать как слои нового векторного расслоения соэ
над Ео.
Иначе, без использования эрмитовой метрики слой расслое-
ния <оо над точкой у(У=0) может быть определен как фактор-
пространство Г/(Су), где Су — одномерное комплексное под-
пространство, порожденное вектором у. Ясно, конечно, что при
наличии эрмитовой метрики это факторпространство канони-
чески изоморфно ортогональному дополнению к вектору у в
пространстве F.
Напомним (см. теорему 12.2), что любое вещественное
ориентированное 2п-мерное расслоение обладает точной после-
довательностью Гизина
... -> //г"2л (В) И1 (В) Н1 (Ео) -> Hl~2n+l (В)-+...
в когомологиях с целочисленными коэффициентами. Для I <
< 2п—1 группы Н'~2п(В) и Я,-2п+1(В) нулевые и, следова-
тельно, гомоморфизм nJ: Н‘(В) -*Н1 (Ео) является изоморфизмом.
ОПРЕДЕЛЕНИЕ. Классы Чженя ct(cn)& H2i(B,Z) опреде-
ляются при помощи индукции по комплексной размерности п
расслоения со следующим образом. Старший класс Чженя сп(а)
равен классу Эйлера e(wR). Для 1<п полагаем
Ci (со) = nj-’c^ (<0о).
Выражение справа имеет смысл, так как гомоморфизм п0:
H2i (В) -> Н2{ (Ео) есть изоморфизм для i < п. Наконец, для i>n
классы с, (и) полагаются равными нулю.
Формальная сумма с (со) = 1 + Ci (со) 4- ... 4-сп (со) в кольце
№(B;Z) называется полным классом Чженя расслоения со.
Ясно, что с (о) является единицей (обратимым элементом)
кольца Нп(В- Z), так что определен обратный класс
с (со)-1 = 1 — С! (со) + (ci (со)2 — с2 (со)) + . . .
Лемма 14.2. (Естественность.) Если отображение f: В —» В'
накрывается некоторым послойным отображением комплекс-
ного п-мерного расслоения со над В в комплексное п-мерное
расслоение со' над В', то с(со) = f*c(co') .
5*
132 Дж. Милнор и Дж. Сташеф
Доказательство (индукцией по п). Старший класс Чженя
удовлетворяет свойству естественности ся(ш) = f*cn(a/), так
как классы Эйлера естественны (см. 9.2). Для того чтобы до-
казать соответствующее утверждение для младших классов
Чженя, заметим, что послойное отображение ®->®/ опреде-
ляет отображение
f0: Ео(®)-+Ео(®'),
которое, очевидно, накрывается послойным отображением
расслоений размерности п—1. Поэтому Q (®о) =(®о)
по предположению индукции. Используя коммутативную диаг-
рамму
Е0^)-^Е0((о'),
|«0	|л0
В -1* В'
и тождества с{ (<»о) = яос£ (©),	(®о) — яо’с/(©z)> гДе яо и п'о*—
изоморфизмы для i < п, получаем, что ct (®) = f*ct (o'), как и
утверждалось. 
Лемма 14.3. Если ек — тривиальное комплексное k-мерное
расслоение над базисным пространством В = В (о), то
с(шфе*) = с(®).
Доказательство. Достаточно рассмотреть частный случай
k = 1, так как утверждение для общего случая легко доказы-
вается тогда по индукции. Пусть <р = <о©е1. Так как у («+ 1)-
мерного расслоения <р имеется всюду ненулевое сечение, то, со-
гласно свойству 9.7, старший класс Чженя сл+1 (<р) = е (<pR) яв-
ляется нулевым и, следовательно, равен классу ся+1(о). Пусть
s: В —► £o(® фе1) — очевидным образом определяемое сечение.
Ясно, что отображение s накрывается некоторым послойным
отображением <о -»• фо, и поэтому
S*Ci (фо) =	(®),
согласно лемме 14.2. Подставляя (ф) вместо сДф0) и ис-
пользуя соотношение s*onj = id, получаем сДф)= сДо), что и
требовалось. I
Комплексные многообразия Грассмана
Продолжая строить наш комплексный аналог теории веще-
ственных векторных расслоений, определим комплексное много-
образие Грассмана Gn(C"+*) как множество всех комплексных
n-мерных плоскостей, проходящих через начало координат в
§ 14. Классы Чженя 133
комплексном векторном пространстве Сп+к. Точно также как и
в вещественном случае, это множество имеет естественную
структуру гладкого многообразия. В действительности Оп(Сп+к)
имеет естественную структуру комплексно-аналитического мно-
гообразия комплексной размерности nk. Далее, существует ка-
ноническое комплексное n-мерное расслоение над Gn(Cn+k),
которое мы обозначаем через уп = уя(С"+*). По определению
пространство этого расслоения состоит из всех пар (X, v), где
X — комплексная n-мерная плоскость, проходящая через начало
координат в Сп+к, и v — вектор, лежащий в X.
В качестве примера рассмотрим частный случай п = 1. Мно-
гообразие Грассмана Gj(C*+1) известно также как комплексное
проективное пространство Рк(С). Мы хотим вычислить кольцо
когомологий Я*(Р*(С); Z) (ср. с задачей 12.С).
Применяя последовательность Гизина к каноническому ли-
нейному расслоению у1 = у1 (С*+1) над Р*(С) и используя тот
факт, что Ci (у1) = е (у0, получаем следующую точную после-
довательность:
Hi+' (Ео) -> И1 (Рк (С)) Hl+2 (Рк (С))	Н1+2 (Ео) .
в когомологиях с целыми коэффициентами. Пространство Ео —
= Е0(у'(Ск+1)) представляет собой множество всех пар вида
(прямая, проходящая через начало координат в С*+’, ненуле-
вой вектор на этой прямой). Оно может быть отождествлено с
пространством С*+1\0 и, следовательно, имеет гомотопический
тип единичной сферы S2ft+I. Таким образом, наша точная по-
следовательность Гизина сводится к точной последовательности
О -> Н1 (Рк (С)) Hl+2 (Рк (С)) -► О
для О г 26 — 2. Поэтому
(Рк (С)) “ Я2 (Р* (С))	~ Н* (Рк (С)).
Так как пространство Рк(С), очевидно, связно, то отсюда сле-
дует, что каждая группа Н2‘(Рк(С)), i 6, является бесконеч-
ной циклической, порожденной элементом с\(ух)1. Аналогично
Я1 (Pk (С)) ~ Я3 (Рк (С)) s ... а Н2к~х (Рк (С)),
и, используя часть
... -> Н~х (Pk (С)) -► Н' (Рк (С)) Н1 (Ео) -+ ...
точной последовательности Гизина, мы видим, что все нечетно-
мерные группы когомологий — нулевые. Итак, мы доказали сле-
дующий результат.
134 Дж. Милнор и Дж. Сташеф
Теорема 14.4. Кольцо когомологий H*(Pk(C);Z) является
кольцом усеченных полиномов, порожденным классом Чженя
Ci = ci (у1 (С*+‘)) с условием cf+l=O. 
Устремим теперь число k к бесконечности. Каноническое
n-мерное расслоение уп(С”) над бесконечным комплексным
многообразием Грассмана 0я(С”) будет кратко обозначаться
уп. Из теоремы 14.4 следует, что кольцо f/*(Gi(C°°)) является
кольцом полиномов, порожденным классом Чженя сДу1). Более
общим образом, справедлива
Теорема 14.5. Кольцо когомологий H*(Gn(C°°)',Z) является
кольцом полиномов над Z, порожденным классами Чженя
С](у"),	сл(у"). Между этими п образующими нет никаких
полиномиальных соотношений.
Доказательство (индукцией по п). Мы можем считать, что
п 2, так как для п — 1 теорема уже установлена. Рассмот-
рим точную последовательность Гизина
...-+Н1 (Gn) Ht+2n (Gn) Hi+2n (£0) -> H,+l (Gn) - ...
в когомологиях с целыми коэффициентами, ассоциированную
с расслоением уп.
Покажем прежде всего, что кольцо когомологий Н*(Е0)
можно отождествить с кольцом 7/*(Gn-i). Для этого следую-
щим образом построим каноническое отображение f: Ео —► Gn-i.
По определению точка (X, о) пространства До представляет со-
бой n-мерное комплексное подпространство X в С°° вместе с
ненулевым вектором о, лежащим в X. Пусть f(X, о)=Х П v1 —
ортогональное дополнение к вектору о в X относительно стан-
дартной эрмитовой метрики
<(V1, V2, . . .) (ПУ1, ПУ2. •••)) = S VjWj
в пространстве С°°. Тогда f(X,v) есть однозначно определенное
(п—1)-мерное комплексное подпространство в С".
Для доказательства того, что отображение f индуцирует
изоморфизм когомологий, удобно перейти к подрасслоению
yn(CN)cc уп, состоящему из комплексных п-мерных подпро-
странств JV-мерного пространства, где N — большое, но конеч-
ное число. Пусть £0(yn(Cw))-* Gn-i(Cw)—соответствующее
ограничение отображения f. Очевидно, что для любой (п— 1)-
мерной плоскости Y из Gn-i (Ск) прообраз
состоит из всех пар (X, о), где о G О — ненулевой вектор, пер-
пендикулярный к У, и X — У + Со — гиперплоскость, опреде-
§ 14. Классы Чженя 135
ляемая о и У. Таким образом, отображение fN можно отож-
дествить с проекцией
E0^N-n+l)-^Qn_ACN),
где а1/-п+1 — комплексное векторное расслоение, слой которого
над yeG„-i(CJV) есть ортогональное дополнение к У в CN.
Используя последовательность Гизина для этого нового век-
торного расслоения, получаем, что отображение fn индуцирует
изоморфизм когомологий в размерностях ^2(2V— п). Переходя
к пределу при N -> оо, убеждаемся, что отображение f инду-
цирует изоморфизм когомологий во всех размерностях.
Таким образом, мы можем подставить Gn-i вместо Ео в по-
следовательности Гизина и получить новую точную последова-
тельность вида
(Qn) Hi+2a (Gn) Hi+2n (G„_,) -> (Gn) ->...,
где A =
Нам надо показать, что этот гомоморфизм А, = (/*)”'nJ ото-
бражает класс Чженя Ci(yn) в класс Ci(y"-1). Это утверждение
очевидно для i = п, поэтому можно предположить, что I < п.
По определению классов Чженя образ л£сДуя) равен сг(уя)
Но, как легко видеть, отображение f: Eo-+Gn-i накрывается
некоторым послойным отображением yj -> у'1-1. Поэтому
Гс<(У“-1) = с/(Уо) по лемме 14.2 и, следовательно, класс
Асг (уп) = (П_1^г(уя)
равен классу с1(уя-1), что и утверждалось.
Теперь воспользуемся предположением индукции. Так как
кольцо H*(Gn~i) порождается классами Чженя Ci(y"~'), ...
..., сп-i(yn-1), то гомоморфизм % является эпиморфизмом, так
что наша последовательность сводится к короткой точной по-
следовательности
О -+ И1 (Gn) Hi+2n (Qn) — Hl+2n (G„_1) ->0.
Используя эту последовательность, мы докажем при по-
мощи вспомогательной индукции по t, что любой элемент хе
е Hl+2n[Gn) можно единственным способом представить в виде
полинома от классов Чженя Cj(уя), .... с„(уя). Конечно, образ
А. (х) можно единственным способом представить в виде поли-
нома р(С1(ул-1), .... сп-\ (у”-1)), согласно нашему основному
предположению индукции. Следовательно, элемент х —
— р(с1(уя-1), ..., c„_i(yn-1)) принадлежит ядру гомоморфизма
X и поэтому может быть представлен в виде произведения
усп (уя) для некоторого однозначно определенного элемента
136 Дж. Милнор и Дж. Сташеф
уеН‘{Оп)- Но у можно однозначно представить в виде поли-
нома q(ci(yn), .... сп(уп)), согласно нашему вспомогательному
предположению индукции, следовательно,
x = p(cj(y'1), .... cn_i (у")) + сп (ул) q (ci (у”), ..., с„(Уя))-
Полиномы в правой части этого равенства определены одно-
значно. Действительно, если бы элемент х был представим так-
же в виде
р'(С1 (Vя)..ся-1(Уя)) + с„(уя)/(с1(уя)....с„(Уя)),
то, применяя гомоморфизм А, мы получили бы, что р = р', а
разделив затем разность двух выражений для х на класс
с« (Vя), — чт0 я — я'- 
Точно так же, как для вещественных n-мерных расслоений
(см. теорему 5.6), можно доказать следующий результат.
Теорема 14.6. Для любого комплексного п-мерного расслое-
ния над паракомпактным базисным пространством существует
послойное отображение в каноническое комплексное п-мерное
расслоение уп = уя(С°°) над Gn = Gn(C°°). 
Другими словами, любое комплексное n-мерное расслоение
над паракомпактным базисным пространством В изоморфно
индуцированному расслоению /*(уя) для некоторого отобра-
жения f: В —► Gn. Фактически точно так же, как и в веществен-
ном случае, можно доказать более сильное утверждение, что
два индуцированных расслоения f* (уя) и g* (уя) изоморфны
тогда и только тогда, когда f гомотопно g. По этой причине
расслоение уя = уя(С°°) называется универсальным комплекс-
ным n-мерным расслоением, а его базисное пространство
G„(C°°)— классифицирующим пространством для комплексных
n-мерных расслоений. (В литературе для обозначения этого
классифицирующего пространства часто используется символ
BU(n).)_
'	Теорема о произведении для классов Чженя
Рассмотрим два комплексных векторных расслоения со и ср
над общим паракомпактным базисным пространством В. Мы
хотим доказать формулу
(14.7)	с(со©ф) = с(со)с(<р),
которая выражает полный класс Чженя суммы Уитни со ф ср
через полные классы Чженя расслоений со и ср. В качестве пер-
вого шага в этом направлении докажем следующую лемму.
§ 14. Классы Чженя 137
Лемма 14.8. Существует один и только один полином
Pm,n = Pm,n{CV Cm> CV •••’ <)
с целыми коэффициентами от т-\- п независимых переменных,
такой, что для любых комплексных расслоений со и ср размер-
ности тип соответственно над общим паракомпактным ба-
зисным пространством В справедливо тождество
с(®®ф) = рт,„(С1(ш)....cm (®); ci (<₽), .... сп (<р)).
Доказательство. Возьмем в качестве универсальной модели
для пары комплексных векторных расслоений над общим ба-
зисным пространством два векторных расслоения у™ и у" над
пространством Gm X Gn, построенные следующим образом.
Пусть yj" = nJ (ут), где л^ Gm X Gn -> Gm — проекция на первый
сомножитель. Аналогично У2 = л^(уя), где лг: GmX Gn-+ Gn —
проекция на второй сомножитель. Таким образом, сумму Уитни
” ®уя можно отождествить с прямым произведением расслое-
ний ут X у".
Воспользуемся тем фактом, что внешнее когомологическое
Х-умножение
a, b I—> а X b — л'а лгЬ
индуцирует изоморфизм
H*(Gm)®H'(Gn)^H*(GmXGn)
колец целочисленных когомологий. Действительно, для случая
конечных клеточных разбиений К к L прй условии, что H*(L)—
свободная абелева группа, изоморфизм Кюннета
И* (К)®
установлен в приложении А. Соответствующее утверждение для
наших бесконечных клеточных разбиений Gm и Оп следует от-
сюда непосредственно, так как каждый остов пространств От
и Gn конечен.
Таким образом, кольцо когомологий H*(GmXGn) является
кольцом полиномов над Z от алгебраически независимых обра-
зующих
njcz(у”1) = cz (yj"),	и n2ct (уя) = ct (уя), 1 </<п.
Следовательно, полный класс Чженя расслоения у^фуя может
быть единственным образом представлен в виде полинома
с (Vf ® V?) = Рт,п (ct (УГ). • • • > ст (у«); с, (уя), ..., с„ (у2я)).
138 Дж. Милнор и Дж. Сташеф
Если теперь со— комплексное /n-мерное расслоение над В и
Ф — комплексное n-мерное расслоение над В, то мы можем
выбрать отображения f: В -* Gm и g: В —► Gn, такие, что
Г(ут)-со> g*(Yn) = q>.
Определив отображение h: B-*GmXGn формулой h(b) =
= (f(b), g(b)), замечаем, что следующая диаграмма коммута-
тивна:
В
Отсюда вытекает, что
h* (у"1) s о, h* (у") <р
и, следовательно,
с (со ф ф) = h*c (у™ ф у") = pm п (fj (со), ...,	(®); Cj (ф), .... сп (ф)),
что и требовалось доказать. 
Чтобы в явном виде вычислить эти полиномы рт, п, мы про-
ведем индукцию по сумме т + п следующим образом. Примем
индуктивное предположение, что класс с(у^-1фу") равен
(1 + ci (у«->) + • • • + ст_х (уГ *)) (1 + сх (у«) + ... + сп (у«)).
Рассмотрим два векторных расслоения у^-'фе1 и у" над
Gm-\ X Gn, где е1 — тривиальное комплексное линейное расслое-
ние. По лемме 14.8
с(у5""1фе1фу«) =
= Рт, п (с! (Y?-1 © е').‘Гт(УГ,®е1);С1(У").....cn(Y?))-
Но, согласно лемме 14.3, слагаемое е1 всегда можно игнори-
ровать, поэтому справедлива также формула
С (УГ ‘ © Y5) = с (у™~1 ф е1 ф у») ==
.....C1(Y2")..................С„(у»)).
Используя индуктивное предположение и подставляя перемен-
ные ci и с} вместо алгебраически независимых элементов сДу^-1)
§ 14. Классы Чженя 139
и сДУг). приходим к формуле
Л»,. (Л....0;<..............<)	=
-(!+<:, + ...+с,_, )(!+<+. •+<).
Вводя новую переменную ст, получаем, что имеет место срав-
нение
Рт.п(С1....Ст> С1> •••> Cn)s
= (1 + С,+ . • • + О ( 1 + с\ + ... + с'п) (mod ст)
в кольце полиномов Z[^cl.....ст; с',	с']. Аналогичное ин-
дуктивное рассуждение показывает, что эти два полинома срав-
нимы также по модулю с'п. Поскольку кольцо Z[cp ..., cm;
с,, ..., с'] является областью с однозначным разложением на
множители, отсюда следует, что эти полиномы сравнимы и по
модулю стс'п, т. е.
и (1 > • • • 9 @... у @ f 9 • • • ,	"
~tn, п \ р ’ т1 и ’ nj
= (1 + Ci + ... + ст) (1 + с' + ... + с') + истс'п
для некоторого полинома и. Здесь полином и должен иметь ну-
левую размерность и, следовательно, быть целым числом, так
как в противном случае сумма Уитни у^фу" имела бы нену-
левые классы Чженя в размерностях, больших чем 2(ffi-f-n).
Но старший класс Чженя Ст+л(й®ф) может быть отож-
дествлен с классом Эйлера
e((®©<P)R) = e(®R®<PR)
и, следовательно, равен ст(ш)сп(ф) (см. свойство 9.6 и обсуж-
дение после леммы 14.1). Таким образом, коэффициент и дол-
жен быть нулем, и мы тем самым доказали формулу произведе-
ния (14.7). 
Двойственные и сопряженные расслоения
Пусть со — комплексное векторное расслоение. Сопряженное
расслоение ш определяется как комплексное векторное расслое-
ние с тем же самым овеществлением
®R = ®R.
но с «противоположной» комплексной структурой. Таким обра-
зом, тождественное отображение /:£(<»)—£(©) является анти-
линейным, т. е.
f = xf (о)
140 Дж. Милнор и Дж. Сташеф
для любого комплексного числа % и любого вектора v е Е (и)
(здесь X обозначает число, комплексно сопряженное с X).
В частности, f(iv) — —if(v).
Для примера рассмотрим касательное расслоение т1 комп-
лексного многообразия Р*(С). (Если игнорировать комплекс-
ную структуру, то это — в точности касательное расслоение
к двумерной сфере.) Расслоение т1 не изоморфно своему со-
пряженному расслоению т1. Действительно, изоморфизм т1 ->
-> т1 задавал бы для каждой касательной плоскости к двумер-
ной сфере отображение на себя, «обращающее» комплексную
структуру. Очевидно, что каждое такое отображение получает-
ся при помощи отражения относительно некоторой однозначно
определенной прямой в этой касательной плоскости. Однако,
как следует из свойства 9.3, двумерная сфера не допускает не-
прерывного поля касательных прямых.
Классы Чженя сопряженного расслоения можно вычислить
следующим образом.
Лемма 14.9. Класс Чженя с*(й) равен классу (—1)*с*(со).
Следовательно, с(й)=1— ci(®) + ^(®)-------1- ... ±сл(®).
Доказательство. Для произвольного слоя F расслоения ш
выберем базис t»i, ..., vn над С. Тогда базис Di, iv\, .... vn,ivn
лежащего в его основе вещественного векторного пространства
Fr определяет отмеченную ориентацию FR. Аналогично базис
Vi, —lOi, .... vn, —ivn определяет отмеченную ориентацию со-
пряженного векторного пространства. Таким образом, два
ориентированных вещественных векторных расслоения ®R и йк
имеют одну и ту же ориентацию, если п четно, и противопо-
ложные ориентации, если п нечетно. Отсюда сразу следует,
что старший класс Чженя
c„(®) = e(®R)
равен (—1)"с„(й). Чтобы вычислить класс с*(й) для k < п,
напомним, что по определению ck (и) = (по)-1 ck (и0), где ®о —
каноническое (п—1)-мерное расслоение над пространством
ЕоС.Е(<й). Легко проверить, что сопряженное расслоение ®в
канонически изоморфно расслоению (й)о, поэтому непосред-
ственная индукция показывает, что
Сь (й) = (— 1)* ск (и)
для всех k. 
С понятием сопряженного расслоения й тесно связано по-
нятие двойственного расслоения Homc (®, С) . По определению
§ 14. Классы Чженя 141
это — комплексное векторное расслоение над тем же базисным
пространством, типичный слой которого является двойствен-
ным комплексным пространством Homc (F, С) для соответствую-
щего слоя F расслоения со (ср. с аналогичной конструкцией для
вещественных векторных расслоений в § 3, п. (f)). Для упро-
щения обозначений мы будем обычно опускать индекс С.
Заметим, что, если комплексное векторное расслоение со
обладает эрмитовой метрикой, то его двойственное расслоение
Hom(<o, С) канонически изоморфно сопряженному расслоению
ш. Действительно, если мы имеем эрмитово скалярное произве-
дение
<V1, о2) е= С
на типичном слое F, линейное по первому переменному и ан-
тилинейное по второму, то соответствие
•-> < ,v2)
задает изоморфизм сопряженного векторного пространства Р
с двойственным векторным пространством Hom(F, С) .
Касательное расслоение
комплексного проективного пространства
В качестве приложения рассмотрим касательное расслоение
тя проективного пространства РЯ(С).
Теорема 14.10. Полный класс Чженя с(хп) равен (1 -|-а)я+1,
где а — соответствующим образом выбранная образующая груп-
пы когомологий Я2(Р2(С); Z).
В действительности, как мы увидим ниже, элемент а равен
взятой со знаком минус образующей сДу1), использованной
в теореме 14.4.
Доказательство. Пусть у1=у1(Ся+1)— каноническое линей-
ное расслоение над проективным пространством РЯ(С) и <ап —
его ортогональное дополнение, построенное при помощи стан-
дартной эрмитовой метрики в комплексном пространстве С”*1,
так что сумма Уитни у1 ф <оя является тривиальным комплекс-
ным (и + 1)-мерным расслоением над РЯ(С). М.ы утверждаем,
что комплексное векторное расслоение
Нотс(у’, ®")
можно отождествить с касательным расслоением х" проектив-
ного пространства РЯ(С). Действительно, если L — комплекс-
ная прямая, проходящая через начало координат Ся+1, и LL —
ее ортогональное дополнение, то векторное пространство
142 Дж. Милнор и Дж. Сташеф
Hom(L, L1) можно отождествить (комплексно-аналитически)
с окрестностью прямой L в пространстве Рп(С), состоящей из
всех прямых L', которые могут служить графиками линейных
отображений прямой L в пространство L1 (см. леммы 4.4 и 5.1,
а также задачу 5.В). Отсюда легко следует, что касательное
пространство многообразия РЛ(С) в точке L можно отождест-
вить с пространством Hom(L,L1) и, следовательно, расслоение
тл изоморфно расслоению Нот (у1, о").
Добавляя теперь тривиальное расслоение е1 Нош (у1, у1)
к обеим частям соотношения хп а* Нот (у1, со"), получаем, что
тпфе’s* Нот (у1, ю"фу') “ Нот (у1, е1 ф ... фе1),
откуда ясно, что расслоение т” ф е1 может быть отождествлено
с суммой Уитни п + 1 экземпляров двойственного расслоения
Нош(у1, е1) = у1. Таким образом, согласно лемме 14.9, полный
класс Чженя с(тл) = с(хп ф е1) равен с(у1)л+1 =(1 —
— С1(у1))»+1.
Чтобы завершить доказательство, остается положить а =
= —сДу1). 
Замечание. Из теоремы 14.10 следует, что старший класс
Чженя сп(хп) равен (п + 1)а". Следовательно, число Эйлера
е [Рп (С)] = сп [Рп (С)] = {сп (тп), ц2„)
равно n + 1 со знаком sign<a'1, ц2л>== ±1. Здесь ц2л обозначает
фундаментальный гомологический класс многообразия РЛ(С).
Вычисляя это число Эйлера согласно следствию 11.12, полу-
чаем, что оно равно
Z(- 1)г ранг Яг(Р"(С)) = п+ 1
и, следовательно, знаковый множитель sign<a'1, ц2л> в действи-
тельности равен +1. Таким образом, элемент ап в точности сов-
падает с образующей группы когомологий Н2л(Рл(С); Z), со-
гласованной с отмеченной ориентацией комплексного многооб-
разия РЛ(С).
В заключение несколько задач для читателя.
Задача 14.А. Используя лемму 14.9, дать другое доказа-
тельство того, что касательное расслоение многообразия Р1 (С)
не изоморфно своему сопряженному расслоению.
Задача 14.В. Доказать по индукции, используя свойство 9.5,
что коэффициентный гомоморфизм Н‘(В- Z)-* Н‘(В; Z/2) ото-
бражает полный класс Чженя с (со) в полный класс Штифеля —
Уитни tw(coR). Показать, в частности, что нечетномерные клас-
сы Штифеля — Уитни вещественного расслоения coR равны нулю,
§ 15. Классы Понтрягина 143
Задача 14.С. Пусть Vn-q(Cn) обозначает комплексное много-
образие Штифеля, состоящее из всех комплексных (п — q) -ре-
перов в комплексном n-мерном пространстве С", где 0 q < п.
Согласно [Стинрод, п. 25.7], это многообразие 2^-связно и
n2q+lVn-q (С”) = Z.
Для данного комплексного n-мерного расслоения © над кле-
точным разбиением В с типичным слоем F построить ассоции-
рованное расслоение Vn-^w) над В с типичным слоем Vn-q(F).
Показать, что первое препятствие к существованию сечения
расслоения ’[/„_,(©) равно когомологическому классу из группы
H2q+2(B- {n2q+1Vn_q(F)}),
который можно отождествить с классом Чженя с^+^ю).
Задача 14.D. По аналогии с § 6 построить клеточное раз-
биение комплексного многообразия Грассмана Gn(C°°) с числом
клеток в размерности 2k, равным числу разбиений числа k
на не более чем п целых положительных чисел.
Показать, что класс Чженя Ck(yn) соответствует коциклу,
который принимает значение ±1 на клетке Шуберта, отвечаю-
щей разбиению 11 ... 1 числа k, и нуль — на всех других клет-
ках. (Ср. с задачей 6.С.)
Задача 14.Е. Показать по аналогии с конструкцией классов
Чженя, что можно определить классы Штифеля — Уитни веще-
ственных n-мерных расслоений по индукции при помощи фор-
мулы Wi (£) = (otq)-1 Wt (g0) для i <. n. Старший же класс Шти-
феля— Уитни дал(|) должен быть построен в соответствии с
процедурой, указанной в § 9 на стр. 85, как mod 2-аналог клас-
са Эйлера. [При таком подходе возникает некоторая трудность
при доказательстве того, что класс wn-\ (£0) принадлежит об-
разу гомоморфизма л0*. Достаточно показать, что ограничение
класса twn-i(5o) на каждый слой Го равно нулю, или, эквива-
лентно, что для касательного расслоения т (п— 1)-мерной сфе-
ры класс Штифеля — Уитни о>п-1(т) равен нулю (ср. пример 1
на стр. 39). В этом месте существенно, что рассматриваются
коэффициенты по модулю 2, поскольку, вообще говоря, е(т)^
Ф 0.] Используя эту конструкцию классов Штифеля — Уитни,
проверить аксиомы из § 4 без привлечения квадратов Стин-
рода.
§ 15. КЛАССЫ ПОНТРЯГИНА
Для дальнейшего изучения вещественных векторных рас-
слоений нам будет нужна следующая конструкция. Пусть V —
вещественное векторное пространство. Тогда тензорное произ*
144 Дж. Милнор и Дж. Сташеф
ведение V ® С = V ® RC пространства V на поле комплексных
чисел С представляет собой комплексное векторное простран-
ство, называемое комплексификацией V. Применяя эту кон-
струкцию к каждому слою F вещественного n-мерного расслое-
ния £, мы получаем комплексное n-мерное расслоение с типич-
ным слоем F ® С над тем же базисным пространством. Мы
будем обозначать это новое расслоение | ® С и называть комп-
лексификацией вещественного векторного расслоения |.
Заметим, что любой элемент комплексного векторного про-
странства F ® С может быть однозначно записан в виде суммы
х + iy, где х, у е F. Используя это разложение в веществен-
ную прямую сумму
F®C = F®iF,
заключаем, что овеществленное векторное расслоение (| ® С) r
канонически изоморфно сумме Уитни £ ф
Очевидно, что комплексная структура на расслоении | ® С
соответствует комплексной структуре
I (х, у) = (— у, х)
на сумме Уитни В ф
Лемма 15.1. Комплексификация | ® С вещественного век-
торного расслоения £ всегда изоморфна своему сопряженному
расслоению g ® С.
Доказательство. Соответствие f: х + iy i—> х — iy определяет
гомеоморфизм пространства расслоения Е (| ® С) на себя, ко-
торый на каждом слое R-лйнеен и удовлетворяет тождеству
f (i (х + iy)) = —if (х + iy). 
Теперь рассмотрим полный класс Чженя
с & ® С) = 1 + Ci (| ® С) + е2(| ® С) + ... + сп(& ® С)
этого комплексифицированного n-мерного расслоения. Прирав-
нивая его классу
c(f®C)=l-cI(|® С) + с2а® С)-+ ... ± c„(g®C)
(см. лемму 14.9), получаем, что все нечетномерные классы
Ч ясеня
М£®С), Сз(£®С), ...
являются элементами порядка 2 (см. задачу 15.D).
ОПРЕДЕЛЕНИЕ. Игнорируя эти элементы порядка 2, опре-
делим i-й класс Понтрягина
р^)^ни(в-,г)
§ 15. Классы Понтрягина 145
вещественного расслоения | равным целочисленному когомо-
логическому классу
Знак (—1)‘ вводится здесь для того, чтобы избежать появления
знакового множителя в последующих формулах (см. при-
мер 15.6 и следствие 15.8). Очевидно, что для i > п/2 класс
p_z(£) нулевой. Полный класс Понтрягина полагается равным
следующей единице кольца ЯП(В; Z):
р (|) = 1 + Pl (£) + ... + рМ2] (|).
Здесь [п/2] обозначает целую часть (наибольшее целое число,
меньшее или равное) п/2.
Лемма 15.2. Классы Понтрягина естественны относительно
послойных отображений. Далее, если ek — тривиальное k-мер-
ное расслоение, то р(| ф е*)= р(|).
Доказательство. Это немедленно следует из лемм 14.2 и
14.3. 
Хотелось бы, чтобы по аналогии с другими уже изученными
характеристическими классами и классы Понтрягина удовлет-
воряли формуле произведения. Здесь, однако, существует неко-
торая трудность, связанная с тем, что нечетномерные классы
Чженя расслоения | ® С были нами отброшены, и самое луч-
шее, что мы можем получить, это следующее утверждение.
Теорема 15.3. Полный класс Понтрягина р (В ф я) суммы
Уитни двух вещественных расслоений | и г] сравним с произ-
ведением р(В)р(л) гао модулю элементов порядка 2. Другими
словами,
2 (р (| Фп) “ Р (I) Р (П)) = 0.
Доказательство. Так как расслоение (£фт1)®С, очевидно,
изоморфно (£ ® С)® (п ® С), то
М(1®п)®С)= L с(а®С)с/(п®С).
i+1—k
Отбрасывая нечетномерные классы Чженя, которые являются
элементами второго порядка, получаем сравнение
c2fe((l®n)®C)^ S c2i&® С)с2/(|®С)
i+i-k
по модулю элементов второго порядка. Умножая обе стороны
этого сравнения на коэффициент (—l)fe=(—1)‘(—1)/, полу*
146 Дж. Милнор и Дж. Сташеф
чаем требуемую формулу
i+1-k
Пример. Для касательного расслоения т" «-мерной сферы
сумма Уитни т" ® v1 а* г" ® 81 тривиальна, и из леммы 15.2
следует, что полный класс Понтрягина р(т") равен 1.
Таким образом, классы Понтрягина касательного расслое-
ния сферы не интересны. Чтобы получить интересные примеры,
рассмотрим комплексные проективные пространства. Но сна-
чала нам надо несколько глубже изучить связь между классами
Понтрягина и классами Чженя.
Мы имеем перед собой ситуацию, которую схематически
можно изобразить следующей диаграммой:
вещесг-
Отправляясь от вещественного «-мерного расслоения мы мо-
жем образовать соответствующее комплексное «-мерное рас-
слоение | ® С. Затем, «забывая» комплексную структуру, мы
получаем лежащее в основе вещественное 2«-мерное расслое-
ние (£ ® C)R с канонической отмеченной ориентацией. Наконец,
«забывая» ориентацию, мы приходим к вещественному 20-мер-
ному расслоению, которое можно просто отождествить с сум-
мой Уитни £ ф
Ясно, однако, что указанная процедура представляет собой
замкнутый цикл, и мы можем с одинаковым успехом начать
наши построения с любого другого места. После полного об-
хода по циклу мы получим новое расслоение того же типа
(комплексное или ориентированное), что и исходное расслое-
ние, но удвоенной по сравнению с ним размерности. Предполо-
жим, например, что мы начинаем с комплексного расслоения.
Лемма 15.4. Для любого комплексного векторного расслое-
ния со комплексификация coR ® С его овеществления канони-
чески изоморфна сумме Уитни со ф <а.
Доказательство. Напомним, что для любого вещественного
векторного пространства V его комплексификация V ® С цано-
§ 15. Классы Понтрягина 147
нически изоморфна прямой сумме V ® V, которая превращает-
ся в комплексное векторное пространство введением комплекс-
ной структуры J (х, у) = (—у, х).
Теперь предположим, что V = FR, где F — типичный слой
некоторого комплексного векторного расслоения. Легко прове-
рить, что соответствие g-. х ь->(х,—гх) определяет комплексно-
линейное отображение F в V ф V, т. е. g(ix) = J(g(x)). Ана-
логично соответствие
h: х ь—> (х, ix)
определяет антилинейное отображение F в V ф V. Так как лю-
бая точка (х, у) пространства = FR ® С может быть од-
нозначно представлена как сумма
4^)+4-4^)
элемента из g(F) и элемента из h(F), то мы видим, что про-
странство Fr ® С канонически изоморфно как комплексное век-
торное пространство прямой сумме F ф F. Поскольку это верно
для каждого слоя F расслоения со, то мы получаем требуемый
канонический изоморфизм комплексных векторных расслоений
сор ® С = софй. 
Следствие 15.5. Для любого комплексного п-мерного рас-
слоения со классы Понтрягина pk (coR) определяются через клас-
сы Чженя Ct (со) по формуле
1 — pi + р2 — + • • • ±Рп =
= (1 — С1 + с2-Ь • • • ± С„) (1 + С?! + С2 + . . . + Сп).
Таким образом, класс Понтрягина pk (coR) равен
ck (со)2 — 2cft_i (со) cft+i (©) + —... ± 2ci (со) c2fe_i (со) Т 2c2fe (со).
Доказательство. Это непосредственно следует из леммы 15.4,
если учесть теорему 14.7 и лемму 14.9. И
Пример 15.6. Пусть т — касательное расслоение комплекс-
ного проективного пространства Р"(С). Так как полный класс
Чженя с(т) равен (1 + a)n+1 (см. теорему 14.10), то классы
Понтрягина задаются формулой
1 — Pl + Р2-Ь • • • ± Рп =
= (1 — ci 4— ... ± сп) (1 4- с, 4-... 4- сп) =
== (1 - a)”+1 (1 4- а)П+‘ = (1 - а2)л+1.
148 Дж. Милнор и Дж. Сташеф
Следовательно, полный класс Понтрягина 1 + pi + ... + рп
равен (1 + а2)л+1. Другими словами,
рИ^(С)) = (я^1)а2й
для 1 k п/2, а классы Понтрягина более высокой размер-
ности равны нулю, ибо Я4*(Р”(С)) = 0 для k > п/2. Мы ис-
пользуем здесь сокращение р*(Л1) для классов Понтрягина
pk (т (M)R) комплексного многообразия М. Таким образом,
р(Р*(С)) = 1,
р (Р2 (С)) = 1 + За2,
р (Р3 (С)) = 1 + 4а2,
р (Р4 (С)) = 1 + 5а2 + 10а4,
р (ре (С)) = 1 + ба2 + 15а4,
р (ре (С)) = 1 + 7а2 + 21а4 + 35а6
и т. д. Из этих примеров видно, что классы Понтрягина вполне
могут быть ненулевыми.
Теперь предположим, что мы начинаем с ориентированного
n-мерного расслоения £. Комплексифицируя, а затем овеществ-
ляя, мы получаем 2п-мерное расслоение (£®C)R с отмеченной
ориентацией (согласно лемме 14.1).
Лемма 15.7. Вещественное 2п-мерное расслоение (S, ® C)R изо-
морфно сумме Уитни | ф | при изоморфизме, который либо
сохраняет, либо обращает ориентацию, в зависимости от того,
четно или нечетно число п(п — 1) /2.
Доказательство. Пусть vi, ..., vn — упорядоченный базис
типичного слоя F расслоения Тогда векторы th, ivi..........vn,
ivn образуют упорядоченный базис, определяющий отмеченную
ориентацию пространства (F ® C)R. Отождествляя это про-
странство с вещественной прямой суммой F ф iF F ф F, по-
лучаем, что базис ui, ..., vn для F с выписанным следом за
ним базисом iv\, ..., ivn для IF задают тот же, но по-другому
упорядоченный базис для (F ® C)R. Очевидно, что перестанов-
ка, которая переводит один упорядоченный базис в другой,
имеет знак (—l)('I-1)+(n-2)+...+i = (—i)n(«-i)/2 g
Следствие 15.8. Для всякого ориентированного 21г-мерного
расслоения g класс Понтрягина рь(£>) равен квадрату класса
Эйлера е(£).
§ 15. Классы Понтрягина 149
Доказательство. По определению класс Понтрягина pfe(&) ра-
вен (— 1)& c2k (I ® С) = (— 1)& е ((£ ® C)R). Однако, согласно лем-
ме 15.7 и свойству 9.6, класс Эйлера e((£®C)R) равен классу
е(£ф|) = е(£)2, умноженному на коэффициент (—1)2/г(2*-1)/2;=
-(- 1)< 
Когомологии ориентированного многообразия
Грассмана
Напомним, что Gn = <5n(R°°) обозначает пространство ориен-
тированных п-мерных линейных подпространств в R00. (Обычно
для этого классифицирующего пространства используется обо-
значение BSO(n).) Мы будем изучать когомологии простран-
ства Gn. с коэффициентами в некоторой области целостности
А, содержащей 'Д. Такой выбор области коэффициентов обес-
печивает избавление от 2-кручения. «Универсальным» приме-
ром такой области А служит кольцо Z^/s]. Однако наши рас-
суждения могут быть с одинаковым успехом проведены и когда
область коэффициентов есть поле рациональных чисел Q или
вообще любое поле характеристики =/=2. Результат будет лишь
чуть сложнее, чем в случае колец//*(Gn(R“); Z/2),/7*(G„(R00);
Z/2) и Н*(Gn(C°°y, Z), которые мы уже вычислили1.
Теорема 15.9. Если А — область целостности, содержащая
’/г, то кольцо когомологий /Z*(<52m+i(R°°); А) является кольцом
полиномов над А, порожденным классами Понтрягина
Pi(v2rn+I). •••, Pm(y2m+1).
Аналогично кольцо когомологий H*(<?2m(R°°); А) представ-
ляет собой кольцо полиномов над А, порожденное классами
Понтрягина Р1(у2т), ...» pm-i(y2m) « классом Эйлера е(уЯт).
Другими словами, для любого значения п, четного или не-
четного, кольцо Я*(дл;А) порождено характеристическими
классами ..., р[„/2] и е. Эти образующие подчинены только
следующим соотношениям:
е = 0, если п нечетно,
е2 = рп/2, если п четно
(ср. с 9.4 и 15.8). Относительно соответствующего результата
для целочисленной области коэффициентов см. задачу 15.С.
Доказательство (индукцией по п). Для п = 1 пространство
Gi (Rw), очевидно, гомеоморфно единичной сфере SN~X и, сле-
1 См. соответственно теоремы 7.1, 12.4 и 14.5 —- Прим, перев.
150 Дж. Милнор и Дж. Сташеф
довательно, имеет когомологии точки в размерностях — 2.
Переходя к пределу при N —► оо, получаем, что пространство
<?i(R°°) имеет когомологии точки во всех размерностях.
Предположим, что утверждение теоремы выполнено для
пространства Gn-i. Точно также как в комплексном случае (см.
теорему 14.5), имеет место точная последовательность
...-+Н1 {Qn} --	фJ	Hi+n	Hi+l	t
где е обозначает класс Эйлера е(у") и кольцевой гомоморфизм
Л = (/*)“'nJ переводит классы Понтрягина расслоения у" в
классы Понтрягина расслоения у"-1- Подразумевается, что
кольцом коэффициентов служит Л.
Случай 1. Если п четно, то рассуждения совершенно анало-
гичны рассуждениям, примененным при доказательстве теоре-
мы 14.5. Данная точная последовательность сводится к корот-
кой точной последовательности
0 -> И1 (Gn)	Hi+n (Gn)	Hi+n (Gn.!) -> 0,
где группа когомологий пространства Gn-i является кольцом
полиномов, порожденным классами pi, р2, ..., p<n/2)-i. Отсюда
легко следует, что кольцо H*(Gn) есть кольцо полиномов от
требуемых образующих pi......P(n/2)-i и е.
Случай 2. Предположим, что п нечетно, скажем п — 2m + 1.
Тогда класс Эйлера е(ул) с коэффициентами в Л равен нулю,
поэтому наша точная последовательность сводится к короткой
точной последовательности
0 -> Н1 (Gw) Н1 (G2m) -> Н1'2"1 (G2m+I) -> 0.
Следовательно, кольцо Н*((52т+1) можно рассматривать как
подкольцо кольца H*(G2m).
Нам будет удобно ввести сокращенное обозначение А* для
подалгебры полиномов A[pi(y2m)..........pm(y2m)]c: Я*(б2т).
Очевидно, Л* с Х(Я*(б2т+1)). Наша задача — доказать, что на
самом деле здесь имеет место равенство.
Ясно, конечно, что для каждой размерности j справедливо
неравенство
(1)	ранг А'<ранг Н1 (G2m+i).
(Здесь под рангом Л-модуля понимается максимальное число
линейно независимых над Л элементов; см. [Эйленберг, Стин-
род].)
Используя предположение индукции, легко получаем, что
любой элемент группы	может быть однозначно запи-
§ 15. Классы Понтрягина 151
сан в виде суммы а + еа', где а е А1, а' е А1-2"1. (Здесь е обо-
значает класс Эйлера расслоения у2т\ е2 — рт.) Из этого раз-
ложения в прямую сумму	А> ф А>~2т вытекает, что
(2)	ранг Н! (О2т) = ранг А1 + ранг Л/~2,п-
С другой стороны, из рассмотрения указанной выше короткой
точной последовательности видно, что
(3)	ранг Н1 (G2m) = ранг Н> (G2m+I) + ранг Hl~2m (G2m+1).
Комбинируя формулы (1) — (3), получаем
ранг А1 = ранг Н1 (G2m+i).
Но отсюда следует, что группа А1 в действительности равна
образу к (Н1' (G2m+i)). Действительно, в противном случае этот
образ содержал бы сумму а + е(у2т) а', где а' #= 0. Между
этим новым элементом и базисными элементами из А! не мо-
жет существовать никакого линейного соотношения, и поэтому
неравенство (1) должно было бы быть строгим, что приводит
к противоречию. 
Как обычно, приведем в заключение несколько задач для
читателя.
Задача 15.А. Используя задачу 14.В, доказать, что приве-
денный по модулю 2 класс Понтрягина равен квадрату
класса Штифеля — Уитни u»2i(g).
Задача 15.В. Показать, что кольцо когомологий H*(Gn(R°°);
Л) является кольцом полиномов над Л, порожденным клас-
сами Понтрягина Pi(y"), .... Р[л/2](у"). [Более общо, показать,
что для любого двукратного накрытия Я—*Х с накрывающей
трансляцией t: ЯX группа когомологий Я*(Х;Л) может
быть отождествлена с множеством неподвижных точек инволю-
ции t*-. Н*(Х- А)^Н*(Х- Л).]
Задача 15.С. Вычислить когомологии коцепного комплекса
Д*(0гт+1(К“); Z/2) относительно дифференциала Sq’. [То есть
вычислить группу ker Sq’/im Sq1. Для этого полезно предста-
вить кольцо когомологий #*(G2m+i (R°°); Z/2) в виде тензор-
ного произведения кольца полиномов от образующей Wi и
кольца полиномов от образующих w2i и Sq1 w2t, 1 i т.]
Доказать, используя точную последовательность Бокштейна
...~>Н'(-, Z)-^H‘(-, Z)-^>Hi(-, Z/2) Hl+i (•, Z)-> ...,
где pop = Sq’ (см. [Стинрод, Эпстейне, стр. 2]), что кольцо
Н* (G2m+i (R°°); Z) аддитивно расщепляется в прямую сумму
152 Дж. Милнор и Дж. Сташеф
кольца полиномов Z[pi, pm] и образа гомоморфизма р. До-
казать аналогичное утверждение для многообразий Грассмана
G2m(R°°) и C„(R°°).
Задача 15.D. Используя предыдущую задачу, доказать, что
нечетномерные классы Чженя расслоения £ ® С вычисляются
по формулам
^2/+1 (5 ® С) = ₽ (®2i (I) ®2« + 1 О'
Аналогично доказать, что для ориентированного (2k -j- ^-мер-
ного расслоения |
е (|) = Рш2й (£).
§ 16. ЧИСЛА ЧЖЕНЯ И ЧИСЛА ПОНТРЯГИНА
По аналогии с числами Штифеля — Уитни компактного мно-
гообразия, введенными в §4, в этом параграфе будут введены
числа Чженя компактного комплексного многообразия и числа
Понтрягина компактного ориентированного многообразия. Все
многообразия предполагаются гладкими.
Разбиения
Напомним, что, согласно определению 6.6, разбиением не-
отрицательного целого числа k называется всякая неупорядо-
ченная последовательность / = iit2 ... ir положительных це-
лых чисел, в сумме дающих k. Пусть / = iii2 ... ir — разбие-
ние числа k и J — ji j2 ... js — разбиение числа /. Тогда «объ-
единенная» неупорядоченная последовательность
IJ = iii2 ... iriij2 ... Is
будет разбиением числа k +1. Эта операция композиции двух
разбиений ассоциативна, коммутативна и имеет в качестве еди-
ничного элемента пустое разбиение нуля, которое мы будем
обозначать символом пустого множества 0. (На более техни-
ческом языке, множество всех разбиений всех неотрицатель-
ных целых чисел можно рассматривать как свободный комму-
тативный моноид с образующими 1, 2, 3......)
В множестве всех разбиений можно следующим образом
ввести отношение (частичного) порядка. Измельчением разбие-
ния iii2 ... ir называется всякое разбиение, которое можно
записать как композицию IJ2 ... Ir, где каждое // является
разбиением числа i/. Если jij2 ... js — измельчение разбиения
i\i% ... ir, то, конечно, s г,
§ 16. Числа Чженя и числа Понтрягина 153
Числа Чженя
Пусть Кп — компактное комплексное многообразие комп-
лексной размерности п. Для каждого разбиения / = й/г ... ir
числа п определим /-е число Чженя
c,m^c ...Ci [Г]
1	г
как целое число, равное
<с{1(тп) ...	Ц2„).
Здесь тл обозначает касательное расслоение многообразия Кп,
а Ц2л — фундаментальный гомологический класс, определяемый
отмеченной ориентацией. Примем соглашение, что с/[Кп] равно
нулю, если / есть разбиение целого числа, отличного от п.
Например, для комплексного проективного пространства
Р«(С)
для любого разбиения i[i2 ... ir числа п, так как cz(t")==
а{ и (ап, М'2п) = +1> согласно теореме 14.10.
Всякое комплексное одномерное многообразие № имеет
только одно число Чженя, а именно эйлерову характеристику
С1[№].
У комплексных двумерных многообразий К2 существует два
числа Чженя, а именно CiCj[№] и эйлерова характеристика
с2[№]. В общем случае комплексное n-мерное многообразие
имеет р(п) чисел Чженя, где р(п)— число различных разбие-
ний числа п (см. определение 6.6). Как мы увидим ниже (см.
теорему 16.7), эти р(п) чисел Чженя линейно независимы, т. е.
между ними нет никаких линейных соотношений, которые вы-
полнялись бы одновременно для всех комплексных п-мерных
многообразий.
Существует иной подход к классам Чженя, важный во мно-
гих случаях. Заметим, что группа когомологий №n(Gn(C°°); Z)
является свободной абелевой группой ранга р(п). Произведе-
ния классов Чженя cii (Vя) ••• cz^(Y )> где ц ... ir пробегает
всевозможные разбиения числа п, образуют базис этой груп-
пы. Для каждого комплексного многообразия К” касательное
расслоение т” «классифицируется» отображением
/; Кп-*Оп(С°°),
154 Дж. Милнор и &ж. Сташеф
таким, что /* (у")	т". При помощи этого классифицирующего
отображения f фундаментальный гомологический класс ц2л
многообразия К.п определяет некоторый гомологический класс
f«(P2n) в свободной абелевой группе Я2п(бл(С°°); Z) ранга
р(п). Чтобы найти этот класс /*(ц2п), достаточно вычислить
р(п) индексов Кронекера
поскольку всевозможные произведения (у") ... с( (уп) обра-
зуют базис соответствующей группы когомологий. Но каждый
такой индекс Кронекера равен числу Чжеия
<f(4(Yn)---%(Yn)} H2n> = ^.-.^m
Этот подход показывает, что не обязательно использовать
базис (Yn) ••• cif (у")} группы Я2л(Сл(С°°); Z). Любой дру-
гой базис был бы так же хорош. Позднее мы как раз будем
использовать другой базис этой группы.
Числа Понтрягина
Теперь рассмотрим гладкое компактное ориентированное
многообразие М4л. Для каждого разбиения I — ii ... ir числа п
определим I-& число Понтрягина
Р7[Л14п] = рг1 ...pjM4"]
как целое число, равное
(рг1(т4л) ... pir (т4л),
Здесь т4л обозначает касательное расслоение, а — фунда-
ментальный гомологический класс многообразия Min.
Например, комплексное проективное пространство Р2л(С),
если забыть о его комплексной структуре, представляет собой
компактное ориентированное многообразие вещественной раз-
мерности 4га. Числа Понтрягина этого многообразия задаются
формулой
Г 2n Т ( “Ь 1	/2/1 “J” 1 \
(С)]-( (1	,г ).
что легко проверить, используя пример 15.6.
Заметим, что, если обратить ориентацию многообразия 2И4л,
то классы Понтрягина не изменятся, а фундаментальный гомо-
логический класс р4п изменит знак. Следовательно, каждое
§ 16. Числа Чженя и числа Понтрягина 155
число Понтрягина
?/,•••	••• Pir> Pin)
также изменит знак. Таким образом, если хоть одно число Пон-
трягина pit ... Ptr[M4n] отлично от нуля, то у многообразия
М4п не существует диффеоморфизма на себя, обращающего
ориентацию.
Например, у комплексного проективного пространства
Р2п(С) не существует диффеоморфизма на себя, обращающего
ориентацию. (С другой стороны, комплексное проективное про-
странство Р2п+1(С) обладает обращающим ориентацию диф-
феоморфизмом, который порождается операцией комплексного
сопряжения.)
Такое поведение чисел Понтрягина прямо противоположно
поведению числа Эйлера е[М2п], остающегося неизменным при
изменении ориентации. Скажем, четномерная сфера S2n, у кото-
рой e[S2”] =/= 0, очевидно, допускает диффеоморфизм, обращаю-
щий ориентацию.
Далее, если некоторое число Понтрягина р{ ... pt [М4п] не
равно нулю, то, рассуждая точно так же, как в случае теоремы
4.9, мы убеждаемся, что многообразие М4п не может быть гра-
ницей никакого гладкого компактного ориентированного
(4n+1)-мерного многообразия с границей (ср. § 17). Напри-
мер, проективное пространство Р2п(С) не может быть ориенти-
рованной границей. Более того, дизъюнктное объединение
Р2л(С)+ ... +Р2п(С) любого числа экземпляров многообразия
Р2п(С) не может быть ориентированной границей, поскольку /-е
число Понтрягина такого /г-кратного объединения равно /-му
числу Понтрягина самого многообразия Р2л(С), умноженному
на k. И опять это рассуждение не проходит для случая Р^+^С).
(Фактически проективное пространство Р2л+1(С) является про-
странством расслоения над кватернионным проективным про-
странством со слоем-окружностью и, следовательно, служит гра-
ницей ассоциированного расслоения со слоем-диском.)
Соответствующее утверждение для числа Эйлера и в этом
случае неверно. Так, e[S2'1] =£0, хотя сфера S2n, очевидно, яв-
ляется границей ориентированного многообразия.
Все эти наблюдения принадлежат Понтрягину.
Симметрические функции
Описываемая ниже классическая алгебраическая техника
даст нам возможность определить некоторые полезные линей-
ные комбинации чисел Чженя или чисел Понтрягина и работать
с ними.
156 Дж. Милнор и Дж. Сташеф
Пусть fi, .... tn — независимые переменные. Полином
f(ti, tn), скажем с целыми коэффициентами, называется
симметрической функцией, если он инвариантен относительно
всех перестановок переменных t\....tn. Таким образом, сим-
метрические функции образуют подкольцо
!?<=Z[tt, .... tn].
Хорошо известная фундаментальная теорема общей алгебры ут-
верждает, что это подкольцо £? само является кольцом полино-
мов от п алгебраически независимых образующих:
^ = Z[a,.....а„],
где <jk = ok(ti, .... tn) обозначает k-ю элементарную симметри-
ческую функцию, однозначно характеризуемую следующим
условием: есть однородный полином степени k от переменных
t\, .... tn и
1 4- <Г1 + 02 + • • • + = (1 + й) (1 + Q • • • (1 + Q
(ср. с леммой 7.2).
Если мы превратим кольцо Z[fi, ..., tn) в градуированное
кольцо, полагая, что степень каждой переменной ti равна 1, то,
очевидно, симметрические функции образуют градуированное
подкольцо ^’*=Z[oi.....ап], где каждый полином ok имеет
степень k. Таким образом, мономы
где й, .... ir пробегает все разбиения числа k на целые положи-
тельные числа, не превосходящие п, образуют базис аддитив-
ной группы 9>k, состоящей из однородных симметрических поли-
номов степени k от переменных й, ..., tn.
Другой и весьма полезный базис может быть построен сле-
дующим образом. Назовем два монома от переменных й, /2, ...
..., tn эквивалентными, если некоторой перестановкой перемен-
ных t\, ..., tn один из них преобразуется в другой. Обозначим
через X t°' ... t°r сумму всех мономов от переменных й, ..., tr,
эквивалентных моному ... tar'. Используя это обозначение,
мы можем, например, записать аА — У, t{t2 ... tk.
Лемма 16.1. Полиномы ... tarr, где а{ ... аг пробегает
все разбиения числа k длины г п, образуют аддитивный ба-
зис группы 9>к однородных симметрических полиномов степени
k от переменных й, ..., tn.
Доказательство не составляет труда. И
§ 16. Числа Чженя и числа Понтрягина 157
Теперь для любого разбиения I = 1\ ... ir числа k определим
полином Si от k переменных следующим образом. Выберем
п k, так что элементарные симметрические функции Ст], ..., ст*
от переменных 6, ..., tn алгебраически независимы, и положим
$/ = $;	< равным однозначно определенному полиному от k
переменных cq, ..., а*, для которого
si (ai...=	•••
Этот полином не зависит от п, что легко проверить, вводя до-
полнительные переменные/„+1 = ... ==/„'==0. В действитель-
ности, даже если п < k, соответствующее тождество
s/(ap ..., <т„, 0, ..., 0) = £/р ...I1/
остается верным, что проверяется аналогичными рассужде-
ниями.
Если п k, то очевидно, что p(k) полиномов .........or*)
являются линейно независимыми и образуют базис группы 5’*.
Первые двенадцать таких полиномов выписаны ниже:
{$W
{$1 (<У1)
Г s2 (аР а2)
t Sn (orb о2)
' *з(а1’ °2> аз)
 $12 (Оъ 02, О3)
 $111 fab а2, °з)
= 1,
= СГ1,
= of - 2ст2,
=	02,
= ст’ — ЗСТ]СТ2 + Зо3,
===	^1^2 — 3(Уз,
=	<Уз>
S4 (GP °2> G3- a4) = ai - SCT2 + 2(T2 + 4(Tia3 “ 4(T4>
S13 (aP G2> a3> О =	^2 - 2a2 ~ ai°3 + 4(TP
S22 (°P a2- °3- a4) =	°2 “ 2(T1CT3 + 2<T4>
$112 (al> °2, °3, <Ч) =	ОдОз — 4ОГ4,
$1111 (Cl, 02, 03, O4)—	СГ4.
Относительно дальнейшей информации см. задачу 16.А, а также
[Ван дер Варден, гл. 26, особенно упражнения] и [Макмахон].
Применение этих понятий к классам Чженя и классам Пон-
трягина вполне аналогично применению их к классам Штифе-
ля— Уитни, данному в § 7. Так, если комплексное n-мерное рас-
слоение © разбивается в сумму Уитни гц © ... линейных
расслоений, то формула
1 + С1 (©) + ... + сп(и) = (1 + d (тц)) ... (1 + с, 01п))
158 Дж. Милнор и Дж. Сташеф
показывает, что класс Чженя с^(©) может быть отождествлен
с k-й элементарной симметрической функцией <Ул(С1(т}1), ...
..., Ci(Лп))• «Универсальный» пример суммы Уитни линейных
расслоений доставляется n-кратным прямым произведением
V1 X • • • X V1 над произведением комплексных проективных
пространств Р°°(С)Х ••• ХВ°°(С). Заметим, что кольцо кого-
мологий этого произведения является кольцом полиномов
Z[ai, ..., ап], где каждая образующая at имеет степень 2 и
c(y1X...XY,) = (l+a1) ... (1+Оп).
Так как элементарные симметрические функции алгебраически
независимы, то кольцо когомологий Я*(Сп(С°°); Z) классифи-
цирующего пространства изоморфно отображается на кольцо
9* <=. Z [аь ..., ап]
симметрических полиномов (это теорема Бореля [Борель, 1953];
ср. с доказательством леммы 7.2). Таким образом, наш новый
базис для 9* задает новый базис
{«Де,, ..., ck)}
группы когомологий №fe(G„(C°°); Z).
Формула произведения
Пусть со — комплексное n-мерное расслоение с базисным про-
странством Вис полным классом Чженя с = 1 + ci + - • • +сп.
Для любого целого числа k 0 и любого разбиения 1 числа k
класс когомологий
S1(Cl, .... Cfe)eH2A(B; Z)
будем кратко обозначать символом s/(c) или $/(с(©)).
Лемма 16.2 (Том). Характеристический класс (с (©©©'))
суммы Уитни © © ©' равен
S Sj(c(aitosK(c(to%
1К=1
где суммирование ведется по всем разбиениям J и К, компози-
ция IK которых равна I.
Например, поскольку разбиение числа k, состоящее из одно-
го-единственного элемента, можно представить в виде компо-
зиции лишь двумя тривиальными способами, то мы получаем
следующий результат.
Следствие 16.3. Характеристический класс (с(со ©со')) сум-
мы Уитни © © ©' равен Sk (с (©)) + sA (с (©')). 
$ 16. Числа ЧЭкеня и числа Понтрягина 150
Доказательство леммы 16.2. Рассмотрим кольцо полиномов
Z[/i..../гп] от 2га независимых переменных, и пусть о* (соотв.
о£) есть k-я элементарная симметрическая функция от пере-
менных ti, ..., tn (соотв. /n+i, .... t2n). Положим
k
Ясно, что полином ст" в точности равен А-й элементарной сим-
метрической функции от переменных Л, ...» t2n. Мы докажем,
что для каждого разбиения I = п ... ir числа k справедливо
тождество
S/«. .... <')== Е зД<гр <т2, ...)зД<, <т2', ...).
Так как классы Ор ..., ak, <Гр ..., ^алгебраически независи-
мы (в предположении k п, которое мы можем принять), то
из этого тождества вместе с теоремой о произведении для клас-
сов Чженя легко следует утверждение нашей леммы.
По определению элемент
....<)eZ[/p...U2n]
равен сумме всех мономов, которые могут быть записаны в виде
... t*r, где си, ..., аг — попарно различные целые числа,
“1	“г
заключенные между 1 и 2п. Для каждого такого монома обо-
значим через J (соотв. К) разбиение, образованное теми пока-
зателями iq, для которых 1 ач п (соотв. п + 1 ад 2л).
Сумма всех таких мономов, отвечающих данному разложению
JK.=I, равна
зД<Ур ст2,	о» -
Поскольку каждое такое разложение встречается, это завер-
шает доказательство. 
Теперь рассмотрим компактное комплексное многообразие
Кп комплексной размерности п. Для каждого разбиения / чис-
ла п характеристическое число
<3/ (с (тп)), р,2„> е Z
будем обозначать 3/(с)[7<л] или, кратко, «?[/<"]. Это характери-
стическое число равно, конечно, некоторой линейной комбина-
ции чисел Чженя.
160 Дж. Милнор и Дж. Сташеф
Следствие 16.4. Характеристическое число s/[7(mX^“] про-
изведения комплексных многообразий равно
£ sjrXlL'1],
/л=/
где суммирование ведется по всем разбиениям Ц числа m и Д
числа п, композиция 1\1г которых равна I.
Доказательство. Касательное расслоение произведения мно-
гообразий Km X Ln расщепляется в сумму Уитни
tXt's (л‘т) ф (njx'),
где Л1 и яг — проекции на сомножители. Следовательно, харак-
теристическое число
(s; (т X т'), Ц2т X
равно
11*2 — 1
В этой формуле нет знаков, так как все фигурирующие в ней
классы четномерны. 
В качестве очевидного частного случая получаем
Следствие 16.5. Для всякого произведения Km X Ln комплекс-
ных многообразий размерностей т, п =£0 характеристическое
число sот+п[Кт X £"] равно нулю. 
Это следствие указывает на важность характеристических
чисел sm [Km]. Приведем пример, показывающий, что это харак-
теристическое число не всегда равно нулю.
Пример 16.6. Пусть т — касательное расслоение комплекс-
ного проективного пространства РЛ(С). Так как с(т) = (1+а)"+1,
то £-й класс Чженя с*(т) равен &-й элементарной симметриче-
ской функции от n + 1 экземпляров элемента а. Следовательно,
класс Sk(c\, .... сь) равен сумме п-j-l экземпляров элемента
ak, т. е.
Взяв k — п, находим
sn[Pn(C)] = n+l¥=0.
Таким образом, многообразие РЛ(С) нельзя представить в виде
прямого произведения комплексных многообразий.
Совершенно аналогичные формулы верны для классов Пон-
трягина и чисел Понтрягина. Если | — вещественное векторное
расслоение над базисным пространством В, то для каждого раз-
§ 16. Числа Чженя и числа Понтрягина 161
биения 1 числа п характеристический класс
...» р„(Ю)еЯ4п(В; Z)
кратко обозначается S/(p(£)). Из доказательства леммы 16.2
следует, очевидно, справедливость сравнения
/к—/
по модулю элементов порядка 2. Поэтому имеет место соответ-
ствующее равенство
st (р) [Л4 X ЛГ] =	st (р) [М] зк (р) [ АГ]
для характеристических чисел. В частности, эти характеристи-
ческие числа многообразия MXN равны нулю, если размер-
ность хотя бы одного из многообразий М или У не делится на 4.
Линейная независимость чисел Чженя
и Понтрягина
Следующий основной результат показывает, что между чис-
лами Чженя не существует никаких линейных соотношений.
Теорема 16.7 (Том). Пусть ..., Кп — комплексные много-
образия, такие, что st(c) [К*]=5^ 0. Тогда р(п)У^р(п)-матрица
чисел Чженя, где й ... tr и j\ ... js пробегают множество всех
разбиений числа п, является невырожденной.
Согласно примеру 16.6, мы можем взять, например, Кг *=
= Р'(С).
Аналогично справедлива
Теорема 16.8 (Том). Если М\ ..., М4п— ориентированные
многообразия, такие, что sk(p) [ЛГ**] =/= 0, то р(п)Хр(п)-матрица
Дм4'1 х... X
чисел Понтрягина, где ii ... ir и ji ... js пробегают множество
всех разбиений числа п, является невырожденной.
Снова мы можем взять в качестве многообразия Л14А ком-
плексное проективное пространство P2fe(C), так как р(т)=«
= (1 + а2)2А+* и, следовательно,
s*(p)[^(C)] = 2fe + l ^0.
в Дж. Милнор, Дж. Сташеф
162 Дж. Милнор и Дж. Сташеф
Рассмотрим сначала один пример. Для комплексной размер-
ности 2, взяв 7<П = РП(С), мы получаем матрицу
с1С1[№] = 9-|
L с2[Л1ХЮ] = 4	c2[№] = 3j
чисел Чженя с определителем, равным —12. Ясно, что такой
лобовой подход, состоящий в непосредственном вычислении
матрицы, бесперспективен в общем случае.
Доказательство теорем 16.7 и 16.8. Вместо самих чисел
Чженя мы можем использовать их линейные комбинации $/(с).
В качестве очевидного обобщения следствия 16.4 имеем фор-
мулу
«/к'*х...хк/’]= X кЧ    S; кЧ,
где суммирование ведется по всем разбиениям /1 числа Д, Л
числа /2, .... /<? числа jq, композиция Л/2 ... Iq которых равна I.
Таким образом, характеристическое число s, к ,1Х...Х^]
равно нулю, если разбиение I = 1\ ... ir не является измельче-
нием разбиения ji ... jQ. В частности, оно равно нулю, если
г <. q. Таким образом, если разбиения й ... ir и Д ... jq соот-
ветствующим образом упорядочить, то матрица
будет треугольной с нулями всюду выше диагонали. Но каж-
дый диагональный элемент s, , k*1 X • • • X К г] очевидно,
ч ••• ’г
равен произведению
•	^к'*]... «>7кЧ^о.
Следовательно, наша матрица не вырождена.
Доказательство теоремы 16.8 совершенно аналогично. 
В заключение задачи для читателя.
Задача 16.А. Подставляя — ti вместо х в тождество
(х 4- h) ... (х 4- tn) = хп + олх""1 4- ... 4-
и затем суммируя по I, доказать формулу Ньютона
sn — GlSn_ I 4- <Ы„-2 — . . . Т <y„_iS! ± ПСп = 0.
При помощи этой формулы можно индуктивно вычислять поли-
номы Sn(CTi, . . . , On).
§ 16. Числа Чженя и числа Понтрягина 163
Взяв логарифм от обеих частей тождества
(1+6) ... (1+/п)=1 + (о1+ ... +оп),
доказать формулу Жирара
(-l)kSk/k =
il+2ii+ ... +kik-k	1	*
Задача 16.В. Характер Чженя ch (со) комплексного «-мерного
расслоения ® определяется как формальная сумма
«+ £ зА(с(®))//г!еЯп(В; Q).
k*" 1
Показать, что характер Чженя характеризуется свойством ад-
дитивности
ch (<в ф <в') =» ch (<о) + ch (со')
вместе со свойством, что ch(r)1) равен формальному степенному
ряду ехр(с](т]1)) для любого линейного расслоения ц1. Пока-
зать, что характер Чженя является также мультипликативным:
ch (© ® <в') =>= ch (со) ch (со').
(Как и в задаче 7.С, рассмотреть сначала случай двух линей-
ных расслоений.)
Задача 16.С. Показать, что, если 26 ... 21г— разбиение чи-
сла 2k на четные целые положительные числа, то 4£-мерный ха-
рактеристический классу 2i (с(со)) комплексного векторного
расслоения со равен характеристическому классу s( t
его овеществления <br. В качестве примеров проверить, что 4/г-
мерный класс $2...2(с(со)) равен классу pk (coR), и показать, что
характеристическое число s2n(c)[№n] комплексного 2п-мерного
многообразия равно числу sn(p) [№я].
Задача 16.D. Показать, что, если комплексное многообразие
Кп комплексно-аналитически вложено в Л?+1 и ие№(/(л+1; Z) —
когомологический класс, двойственный подмногообразию К", то
полный класс Чженя с(К.п) касательного расслоения многооб-
разия Кп равен ограничению на Кп когомологического класса
с (кя+1)
и • Показать, что для любого когомологического класса
х е №я(/(я+1; Z) индекс Кронекера <х|/Ся, ц2п> равен <хи, ц2л+2>.
(См. определение двойственного когомологического класса и'
в § 11 и задачу 11.С) Используя эти конструкции, вычислить
6*
164 Дж. Милнор и Дж. Сташеф
полный класс Чженя с(Ап) неособой алгебраической гиперпо-
верхности К.п степени d в комплексном проективном простран-
стве РП+1(С) и доказать, что характеристическое число s„[/Cn]
равно d(n + 2 — dn). (Алгебраической гиперповерхностью сте-
пени d называется множество нулей однородного полинома сте-
пени d.)
Задача 16.Е. Аналогично, доказать, что если Нт,п— неосо-
бая гиперповерхность степени (1, 1) в произведении Рт(С)Х
ХРП(С) комплексных проективных пространств, где т, п^2,
то характеристическое число 5т+л-1[Ят>п] равно —(т + п)\/
/т\п\. Доказать, используя дизъюнктное объединение гиперпо-
верхностей, что в каждой размерности п существует комплекс-
ное многообразие Кп, такое, что 5п[Ал] = р, если п + 1 есть сте-
пень простого числа р, или sn[An] = 1, если n + 1 не является
степенью простого числа. (Теорема Милнора — Новикова ут-
верждает, что эти многообразия А1, №, №, ... свободно порож-
дают кольцо, состоящее из всех «классов кобордизма» многооб-
разий с комплексной структурой на стабильном касательном
расслоении т ф е*; см. [Стонг].)
Задача 16.F. Провести соответствующие вычисления для
тос!2-характеристических чисел Si(wi, .... wn)[Mn], где I про-
бегает множество всех разбиений числа п. Используя веще-
ственные алгебраические гиперповерхности степени (1, 1) в про-
изведении вещественных проективных пространств, доказать,
что существуют многообразия Yn, такие, что sn(w) [Ул]#= 0, если
п + 1 ие является степенью двух. Показать, что для нечетных п
многообразие У" ориентируемо. Пусть, как и в задаче 4.Е, Л’п —
векторное пространство над полем Z/2, состоящее из классов
кобордизма неориентированных п-мерных многообразий. Пока-
зать, что произведения У*1 X ••• ХУ*Г» где й ... ir пробегает
множество всех разбиений числа п на целые положительные
числа, неимеющие вида 2fe — 1, линейно независимы в JCn. (Со-
гласно одной теореме Тома, такие произведения в действитель-
ности образуют базис векторного пространства JCn, так что
кольцо кобордизмов Л9, является алгеброй полиномов, свободно
порожденной многообразиями У2, У4, У5, У6, У8..)
§ 17. КОЛЬЦО ОРИЕНТИРОВАННЫХ КОБОРДИЗМОВ Я.
В следующих двух параграфах мы определим и изучим коль-
цо кобордизмов Тома Й». Данный параграф содержит основные
определения и некоторые предварительные результаты. Полное
изложение теории кобордизмов читатель может найти в книге
[Стонг].
§ 17. Кольцо ориентированных кобордизмов Q. 185
Гладкие многообразия с границей
Дадим сначала точное определение этого понятия, которое
уже мимоходом использовалось в §§ 4 и 16. В качестве универ-
сальной модели для многообразия с краем возьмем замкнутое
полупространство Н", состоящее из всех точек (xi, ..., хп) в ев-
клидовом пространстве R", таких, что xi 0. Подмножество
XczR'1 называется гладким п-мерным многообразием с грани-
цей, если для каждой точки хеХ существует гладкое отобра-
жение
h:
гомеоморфно отображающее некоторое относительно открытое
множество U cz Н" на окрестность точки х в X и такое, что
матрица из первых производных [dha/duj] всюду имеет ранг п
(ср. с определением гладкого многообразия в § 1).
Точка хеХ называется внутренней, если существует ло-
кальная параметризация ft: £/-> R-4 многообразия X в точке х,
такая, что множество U является открытым подмножеством в
R" (а не в Н"). Очевидно, что множество внутренних точек об-
разует гладкое «-мерное многообразие, являющееся открытым
подмножеством в X. Множество невнутренних точек образует
гладкое («—1)-мерное многообразие, являющееся замкнутым
подмножеством в X. Оно называется границей многообразия X
и обозначается через дХ.
Касательное расслоение хп гладкого многообразия X с гра-
ницей дХ представляет собой гладкое «-мерное расслоение над
X. Определение его совершенно аналогично тому, которое дано
в примере 2 § 2. Это n-мерное расслоение обладает некоторой
дополнительной структурой, которую можно описать следую-
щим образом. Если х — граничная точка многообразия X, то
слой DXx содержит («—1)-мерное подпространство D(dX)x,
состоящее из векторов, касательных к границе. Эта гиперпло-
скость D(dX)x разбивает касательное пространство на два от-
крытых подмножества, состоящих соответственно из векторов,
направленных «внутрь» многообразия X и «наружу». По опре-
делению вектор v^DXx, не принадлежащий D(dX)x, направ-
лен внутрь многообразия X, если v служит вектором скорости
(dp/dt) t=o некоторого гладкого пути
р: [0, в)->Х
с р(0) = х. Аналогично, вектор v направлен наружу, если v слу-
жит вектором скорости в точке t = 0 некоторого пути р:
(—е, 0]—*Х с р(0) = х.
Теперь предположим, что касательное расслоение т" много-
образия X является ориентированным n-мерным расслоением.
166 Дж. Милнор и Дж. Сташеф
Тогда касательное расслоение т"-1 границы дХ имеет следую-
щую индуцированную ориентацию. Выберем ориентирующий
базис ui, ..., vn в касательном пространстве DXx произвольной
граничной точки х так, чтобы вектор th был направлен наружу,
а векторы о2, •••> Un были касательными к границе дХ. Тогда
упорядоченный базис v?, vn определяет требуемую ориен-
тацию пространства D(dX)x.
[В стоящем особняком случае одномерных многообразий с
границей эту конструкцию надо несколько модифицировать.
А именно, «ориентация» точки х нульмерного многообразия
дХ — это просто выбор знака +1 или —1, и мы приписываем
точке х ориентацию +1 или —1 в соответствии с тем, куда ука-
зывает положительное направление в DXx, наружу или внутрь
X.]
Нам понадобится следующее утверждение.
Теорема о цилиндрической окрестности1 17.1. Для всякого
гладкого паракомпактного многообразия с границей X суще-
ствует открытая окрестность границы дХ в X, диффеоморфная
произведению <9ХХ[0, 1).
Доказательство аналогично доказательству теоремы 11.1.
(Точно так же как в теореме 11.1, это утверждение фактически
нужно нам только для того частного случая, когда граница дХ
компактна.) Подробности предоставляются читателю. 
Ориентированный кобордизм
Для гладкого ориентированного многообразия М через —М
будем обозначать то же самое многообразие, но взятое с проти-
воположной ориентацией. Символом + будем обозначать опе-
рацию взятия дизъюнктного объединения (называемого также
топологической суммой) гладких многообразий.
ОПРЕДЕЛЕНИЕ. Два гладких компактных ориентирован-
ных п-мерных многообразия М и М' называются ориентирован-
но кобордантными или принадлежащими одному и тому же
классу ориентированного кобордизма, если существует гладкое
компактное ориентированное многообразие X с границей, такое,
что граница дХ, взятая с индуцированной ориентацией, ориен-
тированно диффеоморфна многообразию М+ (— М').
Лемма 17.2. Отношение ориентированной кобордантности
рефлексивно, симметрично и транзитивно.
1 В оригинале collar neighborhood (воротниковая окрестность). См. тео
рему 5.9 дополнения. — Прим, перев.
§ 17. Кольцо ориентированных кобордизмов О. 167
Доказательство. Дизъюнктное объединение М + (—М), оче-
видно, диффеоморфно границе многообразия [0,1] ХЛ1 при не-
котором диффеоморфизме, сохраняющем ориентацию. Далее,
если М4~(—М')^дХ, то, очевидно, М'4-(—М)^д(—X). На-
конец, если М + (—М')^дХ и М'4-(—M")^dY, то, исполь-
зуя теорему 17.1, можно «склеить» структуры гладкости и ори-
ентации многообразий X и Y по общей части М' их границы так,
что получится новое гладкое ориентированное многообразие с
границей М 4- (— М").
Подробности мы предоставляем читателю. 
Множество Qn, состоящее из всех классов ориентированного
кобордизма n-мерных многообразий, очевидно, является абеле-
вой группой относительно операции дизъюнктного объединения
+. Нулевым элементом этой группы служит класс кобордизма
пустого многообразия.
Далее, операция взятия прямого произведения многообразий
М™, Мг 1—> М? X М2 порождает ассоциативную билинейную
операцию умножения
~m X “* ^m+n-
Таким образом, последовательность
Q, = (Q0, Qb Q2, ...)
групп ориентированных кобордизмов имеет структуру градуиро-
ванного кольца. Это кольцо обладает двусторонним единичным
элементом 1 е Qo. Легко проверить, что прямое произведение
Мд X Мг изоморфно как ориентированное многообразие много-
образию (—l)”1" М2 X М™. Следовательно, наше кольцо ориен-
тированных кобордизмов коммутативно в градуированном смы-
сле.
Числа Понтрягина служат основным инструментом для изу-
чения этих групп кобордизмов. Как уже отмечалось в § 16,
имеет место следующее утверждение.
Лемма 17.3. (Понтрягин). Если M*k — граница гладкого
компактного ориентированного (4/г 4- 1) -мерного многообразия,
то любое число Понтрягина р^ ... рг [М4А] равно нулю. 
Так как, очевидно, справедливо тождество р/[М14~М2] =
= pi [Mi] 4- pi [М2], то отсюда вытекает
Следствие 17.4. Для каждого разбиения i = i\ ... ir числа k
соответствие
определяет гомоморфизм группы кобордизмов в группу Z. 
168 Дж. Милнор и Дж. Сташеф
Применяя теперь теорему 16.8, получаем
Следствие 17.5. Произведения комплексных проективных про-
21	21
странств Р 1 (С) X • • • XР т(С), где ц ... ir пробегает множе-
ство всех разбиений числа k, определяют линейно независимые
элементы группы кобордизмов й4л. Поэтому группа й4* имеет
ранг не меньший, чем число p(k) разбиений числа k. И
В § 18 мы докажем, следуя Тому, что этот ранг в точности
равен p{k).
В заключение этого параграфа укажем, не приводя доказа-
тельств, фактическое строение первых нескольких групп ориен-
тированных кобордизмов (см. [Уолл, 1960, стр. 309]).
Qo = Z. Всякое компактное ориентированное 0-мерное много-
образие— это просто конечное множество точек, снабженных
знаками, и сумма этих знаков служит полным инвариантом ко-
бордизма.
Qi = 0, так как любое компактное одномерное многообразие
является, очевидно, границей.
Q2 = 0, так как любое компактное ориентированное двумер-
ное многообразие является границей.
Из = 0. В противоположность случаю меньших размерностей
это утверждение, впервые анонсированное Рохлиным [Рохлин],
нетривиально. Насколько нам известно, оно никогда не было
доказано непосредственно1.
Q4 Z, образующая — класс комплексной проективной пло-
скости Р2(С).
й5 Z/2, образующая — класс многообразия УБ из задачи
16.F.
Qe = 0.
Q? = 0.
Q8 = Z®Z, образующие — классы многообразий Р4(С) и
Р2(С)ХР2(С).
QgS=Z/2®Z/2, образующие — классы многообразий У9 и
У5ХР2(С).
Qio = Z/2, образующая — класс многообразия У5 X У5.
Qn^Z/2, образующая — класс многообразия У11.
В качестве многообразия У5 (соотв. У9, У11) можно взять не-
особую гиперповерхность степени (1,1) в произведении Р2ХР4
(соотв. Р2 X Ps, Р* X Р8) вещественных проективных про-
* В работе [*Ликориш] дано элементарное доказательство того, что лю-
бое ориентируемое трехмерное многообразие является краем четырехмерного
многообразия, получающегося приклейкой к границе четырехмерного шара
ручек индекса два. — Прим, перев.
§ 18. Пространства Тома и трансверсальность 189
странств. Используя произведения указанных выше образую-
щих, легко показать, что все группы кобордизмов больших раз-
мерностей являются ненулевыми.
§ 18. ПРОСТРАНСТВА ТОМА И ТРАНСВЕРСАЛЬНОСТЬ
В этом параграфе описываются некоторые конструкции, не-
обходимые для фактического вычисления групп кобордизмов.
Мы разовьем теорию настолько, чтобы быть в состоянии вычис-
лить строение кольца Q, по модулю кручения.
Пространство Тома
евклидова векторного расслоения
Пусть £ — некоторое A-мерное расслоение с евклидовой мет-
рикой и А <= Е (£)—подмножество пространства расслоения, со-
стоящее из всех векторов и, таких, что | v | ;> 1. Тогда фактор-
пространство Е(£)/А, получающееся в результате «сжатия>
множества А в одну точку, называется пространством Тома
Т(1) расслоения £. Таким образом, Т(£) имеет отмеченную ба-
зисную точку, обозначаемую to, и дополнение Т (£) \ to состоит
из всех векторов v е Е (£), таких, что | и | < 1.
Замечание. Если базисное пространство расслоения | ком-
пактно, то пространство Тома Т(£) можно отождествить с одно-
точечной компактификацией Александрова пространства Е(£).
Действительно, соответствие v н-> o/Vl — | о Р диффеоморфно
отображает Ё(|)\А на Е(|), индуцируя требуемый гомеомор-
физм Т (£)->£(£) U 0°.
В следующих двух леммах выясняется топологическое строе-
ние пространства Тома Т(£).
Лемма 18.1. Если базисное пространство В является клеточ-
ным разбиением, то пространство Тома Т (£) представляет со-
бой (k—1)-связное клеточное разбиение, имеющее помимо ба-
зисной точки to по одной (п + k) -мерной клетке на каждую
п-мерную клетку пространства В.
В частности, если В — конечное разбиение, то Т($) — также
конечное разбиение.
Доказательство. Для каждой открытой n-мерной клетки е9
пространства В прообраз л-1 (еа)П(Е\А) является открытой
клеткой размерности п + k\ эти клетки попарно не пересекаются
и покрывают все множество Е \ А & Т \ to Заметим, что клеток
в размерностях от 1 до k — 1 нет.
170 Дж. Милнор и Дж. Сташеф
Пусть Dn — замкнутый единичный шар в Rn, и f: Dn-> В
характеристическое отображение для клетки еа (см. определе-
ние 6.1). Тогда индуцированное евклидово векторное расслое-
ние f*(i) тривиально по теореме о накрывающей гомотопии
[Стинрод, п. 11.6], и поэтому множество векторов длины ^1
в пространстве E(f*(£)) гомеоморфно произведению DnXDk.
Композиция
DnXDkcE(r®)^E®-+T(£)
дает теперь требуемое характеристическое отображение для про-
образа л-1(еа) в пространстве Тома Т’(^). Дальнейшие детали
доказательства предоставляются читателю. И
Нам надо вычислить (или по крайней мере оценить) гомо-
топические группы пространства Тома 7(g). В качестве первого
шага на этом пути дадим описание гомологий.
Лемма 18.2. Если £ — ориентированное k-мерное расслоение
над В, то каждая группа целочисленных гомологий Нк+\(Т(£,),
to) канонически изоморфна группе Hi (В).
ДоказлтЕльство. Очевидно, что базисное пространство В
вложено как нулевое сечение в пространство Е \ A Т \ t0.
Пусть То~Ео/А обозначает дополнение к нулевому сечению
в пространстве Тома Т. Ясно, что пространство То стягиваемо,
и поэтому из точной последовательности тройки (7, То, to) сле-
дует, что
Нп(Т, t0)^Hn(T, То).
Но несложное рассуждение с применением аксиомы вырезания
показывает, что
Нп(Т, to)~Hn(E, Ео).
Вместе с изоморфизмом Тома
Нп(Е, E0)~Hn_k(B)
(см. теорему 10.7) это завершает доказательство. 
Гомотопические группы по модулю
Для того чтобы связать группы гомологий с гомотопическими
группами, мы используем некоторые результаты Серра [Серр].
Пусть & обозначает класс всех конечных абелевых групп. Го-
моморфизм h: АВ абелевых групп называется &-изоморфиз-
мом, если одновременно и ядро hr1 (0), и коядро B/h(A) при-
надлежат классу
§ 18. Пространства Тома и трансверсальность 171
Теорема 18.3. Пусть X — конечное (k—1)-связное клеточное
разбиение, k 2. Тогда гомоморфизм Гуревича
лг(Х)->Нг(Х- Z)
является ^-изоморфизмом для г <Z2k— 1.
Доказательство. Эта теорема будет установлена путем СО'
поставления нескольких результатов Серра. Заметим прежде
всего, что теорема верна для того частного случая, когда X есть
n-мерная сфера Sn, n^k, ибо гомотопические группы Пг(5")
конечны для г < 2п—1, г #= п (см., например, [Спеньер]).
Далее, заметим, что теорема верна также для любого ко-
нечного букета сфер. Действительно, если она верна для двух
(k— 1)-связных комплексов X и У, то, в силу теоремы Кюннета,
она верна для произведения XX У. Поэтому, применяя отно-
сительную теорему Гуревича для пары (XX У, XV У), мы ви-
дим, что лг(Х УУ)^л,(ХХУ)£л,(Х)®л,(У) при г <26—1,
а отсюда легко следует, что теорема верна и для букета XV У.
Наконец, рассмотрим произвольное (6—1)-связное конеч-
ное клеточное разбиение X. Так как гомотопические группы
Лг(Х) конечно порождены [Спеньер], то мы можем выбрать ко-
нечный базис свободной части абелевой группы пг(Х) для каж-
дого г < 26. Представляя каждый базисный элемент отображе-
нием S'lX-+, сохраняющим отмеченную точку, соединяем эти
отображения в единое отображение букета сфер
f: S*1 V ... V Srp-*X.
Поскольку для этого букета сфер теорема уже установлена,
мы легко видим, что отображение f индуцирует ^-изоморфизм
гомотопических групп в размерностях, меньших 26—1, и ^-эпи-
морфизм в размерности 26—1. Следовательно, согласно обоб-
щенной теореме Уайтхеда [Спеньер], отображение f также ин-
дуцирует ^-изоморфизм групп гомологий в размерностях мень-
ших, чем 26—1. Итак, из того, что теорема верна для букета
сфер, следует, что она верна и для клеточного разбие-
ния X. 
Другое доказательство.В [Серр] доказано соответствующее
утверждение для когомотопических групп и групп когомологий.
Отсюда по двойственности Спеньера — Уайтхеда [Спеньер,
Уайтхед] сразу следует справедливость доказываемой тео-
ремы. 
Следствие 18.4. Если Т — пространство Тома ориентирован-
ного k-мерного расслоения над конечным клеточным разбив-
172 Дж. Милнор и Дж. Сташеф
наем В, то для всех размерностей n<k — 1 имеет место ^-изо-
морфизм
nn+k(T)-^Hn(B; Z).
Доказательство. Это немедленно вытекает из леммы 18.2
и теоремы 18.3. 
Теперь покажем, как применить это следствие к вычисле-
нию групп кобордизмов.
Регулярные значения и трансверсальность
Пусть Af и N — гладкие многообразия размерности /пип
соответственно, и пусть f: М -> N — гладкое отображение. Го-
ворят, что точка у е N является регулярным значением ото-
бражения f или что отображение f трансверсально к у, если
для каждой точки х е (у) индуцированное отображение ка-
сательных пространств
Dfx: DMX-*DN„
есть эпиморфизм. [Более общо, будем говорить, что отображе-
ние [ имеет точку у своим регулярным значением вдоль некото-
рого подмножества XczM, если это условие удовлетворяется
для любой точки х g f~l (у) П X.] Заметим, что, если многооб-
разие Af компактно, то множество регулярных значений яв-
ляется открытым подмножеством многообразия N.
Конечно, если размерность m меньше, чем п, то указанное
выше условие может выполняться лишь бессодержательным
образом: точка у е N будет регулярным значением отображе-
ния f, только если множество /-1 (у) пусто. Однако при m п
множество f-1 (у) вполне может быть непустым.
Если у — регулярное значение отображения f, то прообраз
f~l(y) является (возможно пустым) гладким многообразием
размерности пг — п. Это утверждение легко следует из теоремы
о неявной функции (см., например, [Грейвс]).
Следующая чрезвычайно полезная теорема принадлежит
Артуру Б. Брауну и (в несколько усиленном варианте) Ар-
туру Сарду.
Теорема Брауна. Пусть f: W -* R" — гладкое (т. е. бесконеч-
но дифференцируемое) отображение, где W — открытое подмно-
жество пространства Rm. Тогда множество регулярных значений
отображения f всюду плотно в R".
Различные доказательства можно найти, например, в рабо-
тах [Браун], [Сард], [Стернберг], [Милиор, 1965].
$ 18. Пространства Тома и трансверсальность 173
Из теоремы Брауна легко следует, что для любого гладкого
отображения f: М-+ N множество регулярных значений при
единственном предположении, что у топологии многообразия М
существует счетная база, является счетным пересечением всюду
плотных открытых множеств и, следовательно, всюду плотно в N.
Теперь предположим, что нам дано гладкое подмногообра-
зие У с N размерности п — k. Гладкое отображение
называется трансверсальным к У, если для любой точки х е
еГ(У) композиция
Dfx
DMX DNy -> DNyIDYy
сюръективно отображает касательное пространство в точке х
в нормальное пространство в точке f(x) = y. [Более общо, f
называется трансверсальным к У вдоль некоторого подмноже-
ства X с М, если это условие выполняется для любой точки
хеНВД
Используя теорему о неявной функции, можно проверить,
что для трансверсального к У отображения f прообраз f~l(Y)
является (возможно пустым) гладким многообразием размер-
ности m — k.
Если vft — нормальное расслоение подмногообразия У в N,
то, как нетрудно показать, расслоение над f~l(Y), индуциро-
ванное из v* при помощи отображения f, можно отождествить
с нормальным расслоением подмногообразия f~l(Y) в М. От-
сюда следует, в частности, что, если vk — ориентированное век-
торное расслоение и М — ориентированное многообразие, то
f~'(Y) также является ориентированным многообразием.
Действительное построение таких трансверсальных отобра-
жений мы осуществим в два этапа, отправляясь от теоремы
Брауна. Рассмотрим снова открытое множество W cz Rm и
гладкое отображение f: W -> R*. Предположим, что начало ко-
ординат в R* является регулярным значением отображения f
вдоль некоторого относительно замкнутого подмножества
X с W. Пусть К — компактное подмножество в W.
Лемма 18.5. Существует гладкое отображение g: W -> R*,
которое совпадает с f вне некоторого компактного множества
и имеет начало координат регулярным значением вдоль Х\) К.
Фактически мы можем выбрать отображение g равномерно
близким к отображению f, т. е. для любого е > 0 можно по-
добрать g так, чтобы |f(x)— g(x) | <8 для всех х.
Доказательство. Используя гладкое разбиение единицы, по-
строим гладкое отображение X: W-* [0,1], принимающее зна-
чение 1 на некоторой окрестности компакта К и обращающееся
174 Дж. Милнор и Дж. Сташеф
в нуль вне некоторого большего компактного множества К'с:
G W. Пусть у — произвольное регулярное значение отображе-
ния f, такое, что |у|<: е. Тогда отображение g, определяемое
формулой
g W = f (х) — Л (х) у,
очевидно,
(а)	имеет 0 своим регулярным значением вдоль /С;
(Ь)	совпадает с f вне К'\
(с)	удовлетворяет неравенству |g(x) — f(x) | < е. Согласно
теореме Брауна, точка у может быть выбрана как угодно близ-
кой к началу координат 0. Мы утверждаем, что если она вы-
брана достаточно близкой к 0, то для отображения g 0 также
будет регулярным значением вдоль пересечения К' Г) %- Дей-
ствительно, выбирая |z/| достаточно малым, мы можем гаран-
тировать не только то, что отображение g будет равномерно
близким к /, но и то, что частные производные dgi/dxj будут
равномерно близки к производным dft/dxt. Отсюда следует,
что, если отображение f имеет 0 своим регулярным значением
вдоль компактного множества К.' П %, то и g также имеет 0
своим регулярным значением вдоль /СП-К (см. задачу 18.А).
Вместе с (а) и (Ь) это дает, что точка 0 является регулярным
значением для g вдоль объединения К (J X, что и требовалось
доказать. 
Пусть теперь £ — некоторое гладкое ориентированное ^-мер-
ное расслоение. Его базисное пространство В гладко вложено
как нулевое сечение в пространство расслоения Е(£) и, следо-
вательно, в пространство Тома Т = Т(£).
Для данного произвольного непрерывного отображения f
сферы Sm в пространство Тома Т мы хотели бы прежде всего
подобрать аппроксимирующее его «гладкое» отображение. Это
намерение не совсем корректно, так как пространство Тома Т
не является многообразием. Однако дополнение к базисной
точке T\t0 имеет, очевидно, структуру гладкого многообразия,
и поэтому нетрудно аппроксимировать отображение f гомотоп-
ным ему отображением /о, которое совпадает с f на множестве
^-I (f0)« f”1 (/0) и гладко на всем его дополнении /7* (Т \ Zo). Не-
обходимая техника описана, например, в [Стинрод, п. 6.7].
Теорема 18.6. Всякое непрерывное отображение f: Sm-+T (£)
гомотопно некоторому отображению g, гладкому на
gTx(T(^)\to) и трансверсальному к нулевому сечению В.
Класс ориентированного кобордизма получающегося гладкого
(m — k) -мерного многообразия g~l (В) зависит только от гомо-
§ 18. Пространства Тома и трансверсальность 175
топического класса отображения g. Следовательно, соответ-
ствие
задает гомоморфизм гомотопической группы nm(T(g),/o) в
группу ориентированных кобордизмов Clm—k.
Доказательство. Как было замечено выше, мы можем сна-
чала аппроксимировать f отображением fo, гладким всюду на
множестве/7* \^о)- Возьмем какое-нибудь покрытие ком-
пактного множества {В) открытыми подмножествами Wi, ...
..., Wr пространства fo' (Т \ t0), столь малыми, что каждый
образ
fo(W{)^T\toczE®
содержится в некоторой локальной координатной системе
векторного расслоения £. Здесь U, обозначает открытое под-
множество базисного пространства В, которое является на-
столько малым, что расслоение £|£Л тривиально.
Выберем компактные множества Д7 cz Wi так, чтобы мно-
жество fo' (В) содержалось во внутренности объединения
Ki U . • • U Кг. Последовательно изменяя отображение fo на от-
крытых множествах Wi, W2, ..., Wr, мы построим последова-
тельность отображений fi, f2, .... fr, удовлетворяющих следую-
щим трем условиям.
(1)	Каждое отображение Д-гладко на множестве f^l(T \/0)=з
— h1 \ Q и совпадает с f,-i вне некоторого компактного
множества из Wi.
(2)	Каждое f> трансверсально к В вдоль множества
Ki U К2 U • . U Ki.
(3)	Проекция n(f;(x))eB равна n(f0(x)) для всех хе
sf0“ (Г\^)- При этом мы будем выбирать каждое отображе-
ние ft «близким» к fi-i в смысле, который уточним позднее.
Приступим к построению. Предположим по индукции, что
уже выбрано отображение f,_i, удовлетворяющее условиям
(1)—(3). Из условия (3) следует, что f/_i должно переводить
открытое множество Wi в координатную окрестность л-1 (17,).
Используя структуру прямого произведения
введем проекцию р(: л-1 (£//)-> R* на второй сомножитель. Мы
хотим построить новое отображение xt—>f((x) для всех хе W<.
176 Дж. Милнор и Дж. Сташеф
Первая координата n(fi(x)) уже определена условием (3), по»
этому иам нужно только выбрать вторую координату pt(fi(x)).
Так как p-i удовлетворяет условию (2), то, как легко ви»
деть, для композиции xi—>pi(fi-i(x)) начало координат про»
странства R* является регулярным значением вдоль относи»
тельно замкнутого в Wi подмножества (/G U ... UKj-i) По-
следовательно, по лемме 18.5, мы можем аппроксимировать эту
композицию отображением из Wi в Rfe, которое
(а)	совпадает с pi°fi-i вне некоторого компактного подмно-
жества множества Wi и
(Ь)	имеет начало координат своим регулярным значением
вдоль (Кл U ... иК/)П№/.
Запишем это аппроксимирующее отображение в виде
piofi. Ввиду условий (1) и (3) ясно, что fi(x) определено для
всех х. Кроме того, ясно, что это новое отображение fi будет
удовлетворять условию (2).
Таким образом, по индукции мы можем построить отобра-
жения fi, f2, .... fr, удовлетворяющие условиям (1) —(3). По-
ложим g = fr. Очевидно, что отображение g трансверсально
к В вдоль компактного множества Ki U • • • U Кг. Если мы смо-
жем теперь гарантировать, что весь прообраз g~'(B) содер-
жится в объединении К\ U • • • U Кг, то мы можем быть уверены,
что g трансверсально к В всюду, что нам и требуется.
Для каждого вектора t^T\to = E\A обозначим через
|f|, 0С|И< 1» его евклидову норму, так что |/| = 0 тогда и
только тогда, когда t е В. Удобно положить | /0| = 1.
Поскольку множество Kill UKr является окрестностью
множества (В) в компактном пространстве Sm, то найдется
константа с > 0, такая, что
I fo(x) |>с
для всех х ф. Ki U - - • U Кг- Предположим, что каждое отобра-
жение ft выбрано настолько близким к ft—i, что
\fi(x) — ft_l(x)\<c/r
для всех х. Тогда, очевидно,
1я(*) —foWKc-
Следовательно, |я(х) |#=0 для x^Kil) ... IIКг, и весь про-
образ g~} (В) должен содержаться в Ki U • • • (JKr. Значит, ото-
бражение g трансверсально к В всюду и прообраз g~l(B)
есть гладкое компактное ориентированное (tn — k) -мерное мно-
гообразие. Это доказывает первую часть теоремы 18.6.
Пусть теперь мы имеем два гомотопных отображения g и
g' сферы Sm в пространство Тома Т, оба гладкие на прообразе
§ 18. Пространства Тома и трансверсальность 177
T\to и оба трансверсальные к В. Тогда нетрудно построить
гомотопию
hot SmX[0, 3]->Т,
гладкую на Л^’(Т\/0) и удовлетворяющую следующим усло-
виям:
Ло (х, t) — g (х) при t s [0, 1],
ho (х, I) = g' (х) при t е [2, 3].
Поступая точно так же, как и выше, мы можем построить но-
вое отображение A: SmX [0, 3]-» Г, которое совпадает с Ло вне
некоторого компактного подмножества в SmX(0>3) и транс-
версально к В. Построение отображения h можно произвести
индуктивно, проверяя на каждом шаге, что трансверсальность
вдоль множества Sm Х[0,1](J Sm Х[2,3] не нарушается. Про-
образ Л-1 (В) при этой новой гомотопии осуществляет ориен-
тированный кобордизм между многообразиями g~l (В) и g'~l (В).
Таким образом, класс ориентированного кобордизма многооб-
разия g~l(B) зависит только от гомотопического класса ото-
бражения g.
Так как операция сложения в гомотопической группе
nm(T, t0), очевидно, соответствует операции дизъюнктного объ-
единения многообразий g~!(B), то соответствие g>—*g~l(B)
определяет гомоморфизм гомотопической группы лт(Т,/0) в
группу ориентированных кобордизмов Qm-k- Я
Основная теорема
Возьмем в качестве гладкого ориентированного А-мерного
расслоения, фигурирующего в теореме 18.6, универсальное
ориентированное A-мерное расслоение yk над <?*(R°°). Следую-
щий результат лежит в основе теории Тома.
Теорема Тома. Для k > п -f- 1 гомотопическая группа
Лл+л(Г(у*), to) универсального пространства Тома канонически
изоморфна группе ориентированных кобордизмов Q„. Анало-
гично гомотопическая группа nn+k(T(yk), to) пространства Тома
универсального неориентированного расслоения канонически
изоморфна группе неориентированных кобордизмов Лп.
Замечание. Том использовал для этих двух универсальных
пространств обозначения MSO(k) и MO(k). Это отвечает стан-
дартным обозначениям BSO(k) и BO(k) для соответствующих
универсальных базисных пространств.
Чтобы упростить наше изложение, мы не станем доказы-
вать всей теоремы Тома, а докажем только следующую ее
178 Дж. Милнор и Дж. Сташеф
часть. Пусть Yp = Yfe(Rfe+₽) ~ Расслоение ориентированных k-
мерных подпространств (k + р) -мерного пространства.
Лемма 18.7. Если k п и р п, то гомоморфизм
из теоремы 18.6 является эпиморфизмом.
Доказательство. Пусть Мп — произвольное гладкое ком-
пактное ориентированное n-мерное многообразие. Тогда по тео-
реме Уитни [Уитни, 1944] многообразие Мп может быть вло-
жено в евклидово пространство R"+ft. Согласно теореме 11.1, мы
можем выбрать трубчатую окрестность U многообразия Л4Л в
пространстве Rn+ft, которая диффеоморфна пространству Е (ук)
нормального расслоения v*. Используя гауссово отображение,
получаем отображение
• U &Е (О -*Е(у*) с Е(ук),
взятие композиции которого с каноническим отображением
£ (у*) -> Т (у£) дает отображение g: U-+Т	трансверсальное
к нулевому сечению В и удовлетворяющее условию g~'(B) =
= Мп.
Далее, продолжим g на одноточечную компактификацию
Rn+* U °° = 5n+ft, отображая дополнение Sn+k\U в базисную
точку to. Получающееся отображение & Sn+k~^T (yty, оче-
видно, задает по правилу, указанному в теореме 18.6, класс ко-
бордизма многообразия Af". И
Теперь мы можем доказать наш главный результат.
Теорема 18.8. (Том). Группа ориентированных кобордизмов
конечна для пфО mod4, а в случае п = 4г является ко-
нечно-порожденной группой ранга, равного числу р(г) разбие-
ний числа г.
Доказательство. По лемме 18.7 группа fi„ есть гомоморф-
ный образ гомотопической группы nn+ft (Т (ур\) Для достаточно
больших k и р, а, согласно следствию 18.4, эта последняя груп-
па ^-изоморфна группе гомологий Hn(Ck(Rk+p)-,Z). Но, в силу
теоремы 15.9, эта последняя группа является конечной для
п (mod 4) и конечно-порожденной ранга р(г) для п = 4г.
Следовательно, группа fi„ конечна для n^0(mod4), а й4,
есть конечно-порожденная группа ранга ^р(г). Но согласно
следствию 17.5, ранг (й4г)^р(г), откуда и следует утвержде-
ние теоремы. Н
§ 19. Мультипликативные последовательности 179
Если мы убьем кручение, тензорно умножив кольцо кобор-
дизмов Q* на поле рациональных чисел Q, то произведения
Р2(>(С)Х...ХР2;ЧС),
где ii ... ir пробегает множество всех разбиений числа k, бу-
дут, очевидно, линейно независимы и, следовательно, будут об-
разовывать базис векторного пространства 0 Q (ср. со след-
ствием 17.5). Отсюда вытекает
Следствие 18.9. Тензорное произведение Q* 0 Q представ-
ляет собой алгебру полиномов над Q с независимыми образую-
щими Р2(С), Р4(С), Р6(С).....И
Вот другое непосредственное следствие.
Следствие 18.10. Пусть Мп— гладкое компактное ориенти-
рованное многообразие. Некоторое положительное кратное
Мп + ... + Мп многообразия Мп является ориентированной
границей тогда и только тогда, когда каждое число Понтря-
гина р;[Мп] равно нулю.
Действительно, в противном случае в группе Qn существо-
вало бы слишком много линейно независимых элементов. I
Ч. Уолл доказал следующее гораздо более сильное утверж-
дение [Уолл].Многообразие Мп является ориентированной гра-
ницей тогда и только тогда, когда все его числа Понтрягина
и все числа Штифеля — Уитни равны нулю. Таким образом,
группа кобордизмов Qn всегда есть прямая сумма некоторого
числа экземпляров группы Z/2 и (если nsflmodl) некото-
рого числа экземпляров группы Z.
В заключение одна задача для читателя.
Задача 18.А. Предположим, что, как в доказательстве лем-
мы 18.5, начало координат служит регулярным значением ото-
бражения f вдоль некоторого компактного множества К" cz
cz W a: Rm. Показать, что, если отображение g равномерно
близко к f и производные dgt/dxt равномерно близки к произ-
водным dft/dxj, то и для отображения g начало координат
является регулярным значением вдоль К".
§ 19. МУЛЬТИПЛИКАТИВНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
И ТЕОРЕМА О СИГНАТУРЕ
Материал этого параграфа заимствован из книги [Хирцеб-
рух, 1966].
Пусть А — фиксированное коммутативное кольцо с едини-
цей (обычно это кольцо рациональных чисел). Символом
А* = (А°, А1, А2, ...)
180 Дж. Милнор и Дж. Сташеф
будем обозначать градуированную Л-алгебру с единицей, ком-
мутативную в классическом смысле (ху = ух независимо от
того, каковы степени х и у). В большинстве приложений Аа
будет группой когомологий Hin(B\ Л).
Каждой такой алгебре А* мы сопоставим коммутативное
кольцо Ап, состоящее из всех формальных сумм а0 4- а1 4-
4- аг -f- ..., где at е А1 (ср. с определением кольца НП(В-,
Z/2) в § 4). Нас будет особенно интересовать мультипилика-
тивная группа единиц кольца Лп, состоящая из всех элементов
вида
а — 1 4~ Я] 4- ^2 4- • • •»
с операцией умножения
(1 4~ 4~ <*2 4~ •••)(! + 4-62+ . ..)в
= 1 4" (ai 4" М 4- (<% 4-	4" Ьг) 4~ •. •
Рассмотрим последовательность полиномов
Ki(xi), К.2{хь x2), K3(xh хг, х3), ...
с коэффициентами в Л, такую, что, если переменной х, припи-
сать степень i, то
(1) каждый полином Кп(Х\, .... хп) является однородным
степени п.
Пусть дано кольцо Ап указанного выше вида. Для всякого
элемента ае АП, начинающегося с 1, определим новый элемент
К(а)е4п, который тоже начинается с 1, по формуле
К (а) — 1 4- Ki (Д1) 4* Кг (#ь 02) 4" • • • •
ОПРЕДЕЛЕНИЕ. Будем говорить, что полиномы Кп обра-
зуют мультипликативную последовательность, если для всех
Л-алгебр А* и для всех элементов а, b еЛп, начинающихся с 1,
выполняется тождество
(2) К(а6) = К(а)К(6).
Пример 1. Для любой заданной константы полиномы
1	Kn(.Xi, ...» Хл) = Л Хц
образуют мультипликативную последовательность, причем
К(14_О14~й2 4~ • •.) — 1 4~	4“ ^202 4“ • • • •
Особый интерес представляют случаи Х=1 (когда К(а) = а)
и X = —1 (см. лемму 14.9).
§ 19. Мультипликативные последовательности 181
Пример 2. Тождество К(а) = а-1 отвечает мультипликатив-
ной последовательности
Ki С*л)	= — *1
/С2 (Хр х2)	— Xj х2,
/С3 (Хр х2, х3)	= — х] + 2х/2 — х3,
^4	^2’ ^3’ ^4)	*” 3XjX2 2Х[Х3 "4" х2 хп,
общий член которой имеет вид
к.- Z	<-*>'
<,+2^+ ... +«<„-»«
При помощи этих полиномов можно выразить связь между
классами Понтрягина (соответственно классами Чженя, клас-
сами Штифеля — Уитни) двух векторных расслоений, сумма
Уитни которых является тривиальным расслоением (см.
стр. 37—39).
Пример 3. Полиномы K2n+i — 0 и /C2n(*i..........х2п) =
= х£ — 2х„_1хп+1 + ... + 2х1х2п_1 ± 2хл образуют мультипли-
кативную последовательность, при помощи которой может быть
выражена связь между классами Чженя комплексного вектор-
ного расслоения <в и классами Понтрягина его овеществления <вц
(см. следствие 15.5).
Следующая лемма дает простую классификацию всех воз-
можных мультипликативных последовательностей. Пусть Л* —
градуированное кольцо Л[/], где t — независимая переменная
степени 1. Тогда любой элемент кольца Лп, начинающийся с 1,
может быть представлен как формальный степенной ряд
f (0 = 1 + М + W2 + V + • • •
с коэффициентами в Л. В частности, 1 -f-1 есть такой элемент.
Лемма 19.1 (Хирцебрух). Для данного формального степен-
ного ряда f(t)= 14-М + W2 + ... с коэффициентами в Л су-
ществует одна и только одна мультипликативная последова-
тельность {/<„} с коэффициентами в Л, удовлетворяющая усло-
вию
Я(1+/)-/(/),
или, эквивалентно, условию, что коэффициент прих* в каждом
полиноме K.n(xi...хл) равен Хп.
182 Дж. Милнор и Дж. Сташеф
ОПРЕДЕЛЕНИЕ. Эта последовательность {/(„} называется
мультипликативной последовательностью, принадлежащей сте-
пенному ряду f(t).
Примеры. Три мультипликативные последовательности, при-
веденные выше, принадлежат соответственно степенным рядам
1 + 4 1—/+/2 —/3+ ... , 1 + /2.
Замечание. Если мультипликативная последовательность
{/Сп} принадлежит степенному ряду f(t), то для любой алгебры
Л* и любого элемента ai е Л1 выполнено тождество
К (14 ai) = /(«!).
Конечно, это тождество перестает быть верным, если вместо а\
подставить какой-нибудь элемент степени #= 1.
Доказательство единственности. Выбрав произвольное поло-
жительное целое число п, возьмем в качестве А* кольцо поли-
номов Л[6, ..., tn] от алгебраически независимых переменных
ti степени 1 и положим
<т = (1+б) ... (1НМП
Тогда
/С(а)в/С(1 + 6) ... K(l+Q = F(/i) ... f(tn).
Выделяя однородную часть степени п, заключаем, что поли-
ном /Сп(<Т1, .... Оп) однозначно определен степенным рядом /(/).
Поскольку элементарные симметрические функции агь .... <уп
алгебраически независимы, это доказывает единственность каж-
дого полинома Кп-
Доказательство существования. Для сокращения записи бу-
дем для всякого разбиения /= й ... ir числа п обозначать че-
рез X; произведение Л/, ... Л;г. Приняв это соглашение, опреде-
лим полиномы Кп формулой
Kn(<h, <*2> •••> Од)=	..., СГп),
где сумма берется по всем разбиениям I числа п. Здесь si обо-
значает полином из леммы 16.1, удовлетворяющий условию
sj (<Тр •. • > 0П)== Е й1 • • •
Точно так же, как в лемме 16.2, имеем тождество
sz(a6)= Е sH(a)si(b),
HJ-I
где суммирование ведется по всем разбиениям Н и J, компози-
ция HJ которых равняется I. Следовательно,
К(а6) = Е ^iSi(ab)
§ 19. Мультипликативные последовательности 183
равно
S S sn (а)s; (fi) = hffSff (a)kjSj(b).
I HJ-I	H, J
Но последнее выражение, очевидно, равно К{а)К(Ь), что и тре-
бовалось доказать. 
Теперь рассмотрим некоторую мультипликативную последо-
вательность полиномов {Kn(xi...хп)} с рациональными ко-
эффициентами. Пусть Мт — гладкое компактное ориентирован-
ное m-мерное многообразие.
ОПРЕДЕЛЕНИЕ. К-род /<[Л4т] многообразия Мт полагает-
ся равным нулю, если размерность т не делится на 4, и равным
рациональному числу
^т=(к„(рь.... рп), |х4д
если т = 4п, где pt обозначает i-й класс Понтрягина касатель-
ного расслоения многообразия М. Таким образом, К-род К[Л4т]
есть определенная рациональная линейная комбинация чисел
Понтрягина многообразия Мт.
Лемма 19.2. Для любой мультипликативной последователь-
ности {Кп} с рациональными коэффициентами соответствие
Afi—»К[Л4] определяет кольцевой гомоморфизм кольца кобор-
дизмов Q* в кольцо рациональных чисел Q.
Очевидно, что это соответствие задает гомоморфизм алгебр
й*® Q-»Q.
Доказательство. Ясно, что указанное соответствие аддитив-
но и что /(-род многообразия, являющегося границей, равен
нулю. Полный класс Понтрягина произведения многообразий
М X М' сравним с классом р X р' по модулю элементов поряд-
ка 2, поэтому К{рХ р') = К(р)ХК(р') и, следовательно,
{К(р X р'), рХЮ = (- Dmm' (Р), и) {К(/), и').
Поскольку знаковый множитель в этой формуле, конечно, ра-
вен + 1, когда размерности ш, ш' делятся на 4, то мы полу-
чаем, что
Я[Л4ХМ'] = /С[Л4]К[М'],
как и требовалось. 
Используем эту конструкцию для вычисления одного важ-
ного инварианта гомотопического типа многообразия М.
ОПРЕДЕЛЕНИЕ. Сигнатура о компактного ориентирован-
ного многообразия Мт полагается равной нулю, если размер-
184 Дж. Милнор и Дж. Сташеф
ность m не кратна 4, а если m — 4k, определяется так. Выберем
базис d, аг векторного пространства H2k(Mik; Q), в кото-
ром симметричная матрица
«а, о а,, ц>]
диагона льна. Тогда сигнатура равна разности числа по-
ложительных и числа отрицательных диагональных элементов.
(Другими словами, о есть сигнатура рациональной квадратич-
ной формы ан»(а о а, ц>, а е H2k(Mik-, Q).)
Это число а часто называют также индексом многообразия
М, особенно в старых работах.
Лемма 19.3 (Том). Сигнатура обладает следующими тремя
свойствами-.
(1)	<т(М4-Л1') = аСМ) + ст(ЛГ);
(2)	<т(Л4ХМ') = <т(Л4)а(ЛГ);
(3)	если многообразие М является ориентированной грани-
цей, то о(М) = 0.
Доказательство. Утверждение (1) тривиально. Утверждение
(2) можно доказать, используя изоморфизм Кюннета
Н*(МХ.М'; Q)“/f*(Af; Q)® Н*(М'-, Q), а утверждение (3) —
используя теорему двойственности Пуанкаре для многообразий
с границей. Детали можно найти в книгах [Хирцебрух, § 8] или
[Стонг]. 
Из свойств (1) и (3) немедленно следует, что сигнатура мно-
гообразия может быть представлена как линейная функция от
его чисел Понтрягина. Более точно, как показал Хирцебрух,
имеет место следующая теорема.
Теорема о сигнатуре 19.4. Пусть {Lk(p\, .... pk}} — мульти-
пликативная последовательность полиномов, принадлежащая
степенному ряду
VF/thV7 = l + j/-4-/2+- ... +(-1)й-‘22^/(2/г)1 + ....
Тогда сигнатура ст(Л44*) любого гладкого компактного ориенти-
рованного многообразия Mik равна его L-роду L [Л44А].
Здесь Bk обозначает k-e число Бернулли (см. приложе-
ние В):
=	Вг=1/у), BA — i/i2......
§ 19. Мультипликативное последовательности 1Й8
Первые четыре L-полинома выглядят так:
^2 ~ ЧЁТ (7р2 “ Р1)’
= 945 (82^з	1 Зр2Р] + 2р|),
L4 = 14175’ (381^ “ 7Ш - 19?2 + 22М - 3Р1)-
Доказательство теоремы о сигнатуре. Так как оба соответ-
ствия А4>—>о(Л1) и М н-> L [М] задают гомоморфизм алгебр из
й* ® Q в Q, то достаточно проверить эту теорему на множестве
образующих алгебры Q* ® Q. Согласно следствию 18.9, такую
систему образующих доставляют комплексные проективные про-
странства Р2*(С).
Для вычисления сигнатуры многообразия Р2А(С) достаточно
заметить, что векторное пространство №ft(P2*(C); Q) имеет
единственную образующую ak, такую, что
{ak ак, р) = 1
(см. теоремы 14.4 и 14.10). Следовательно, сигнатура о(Р2А(С))
равна + 1.
Теперь вычислим L*[P2ft(C)]. Напомним (см. пример 15.6),
что полный касательный класс Понтрягина р комплексного про-
ективного пространства Р2*(С) равен (1 + а2)2*+1. Так как
мультипликативная последовательность {£*} принадлежит сте-
пенному ряду f (t) = Vt /th	то
L(l+a2 + 0+ . ..) = V^/th V^2
и, следовательно,
L(p) = (a/tha)2*+>.
Таким образом, L-род (А(р), ц) равен коэффициенту при а2* в
этом степенном ряде.
Если заменить а на комплексную переменную z, то коэффи-
циент при z2k в разложении Тэйлора функции (z/thz)2*+i мож-
но вычислить, поделив эту функцию на 2niz2*+1 и проинтегриро-
вав затем по замкнутому контуру вокруг начала координат.
Подстановка и = th z, для которой
dz = T^- = (l+«2 + «4+ ...)du,
показывает, что интеграл
1 A dz _ 1 с (1 + »2 + u4+ ...}du
2ш з (thz)2ft+1 2ni J и2А+1
186 Дж. Милнор и Дж. Сташеф
равен 4- 1. Следовательно, L[P2*(C)] = + 1 — о(Р2*(С)), а зна-
чит, L[Af] = ог(Л1) для всех многообразий М. 
Более прямое доказательство теоремы о сигнатуре было
дано Атьёй и Зингером [Атья, Зингер, § 6] как приложение
«теоремы об индексе» для эллиптических дифференциальных
операторов.
Следствие 19.5. L-pod любого многообразия является целым
числом.
Действительно, сигнатура а всегда целое число. 
Отсюда следует, например, что число Понтрягина pi [Л44]
делится на три, а число 7р2 [Af8] — pf [Л18] делится на 45.
Следствие 19.6. L-род L [Л4] зависит только от ориентирован-
ного гомотопического типа многообразия М.
Действительно, сигнатура о(М), очевидно, инвариантна от-
носительно гомотопической эквивалентности, сохраняющей ори-
ентацию. 
Как показано в работе [Кан], L-род и его рациональные
кратные — это единственные рациональные линейные комбина-
ции чисел Понтрягина, являющиеся инвариантами ориентиро-
ванного гомотопического типа.
Мультипликативные характеристические классы
В оставшейся части параграфа мы очень коротко остано-
вимся на еще одном применении мультипликативных последо-
вательностей.
Пусть Л — область целостности, содержащая ‘Д и пусть
{Кп} — мультипликативная последовательность с коэффициента-
ми в Л. Полагая
МЫМ................?Л))
для любого вещественного векторного расслоения мы, оче-
видно, получаем последовательность «характеристических клас-
сов»
/гп(5)еЯ4«(В; Л),
которые естественны относительно послойных отображений и
удовлетворяют формуле произведения
*ЛФп) = Z МШ)-
<+/=»
J 19. Мультипликативные последовательности 187
Здесь предполагается, что Ло(£) = 1. [Вводя /г(£) = X М£)> мы
можем, конечно, записать формулу произведения кратко в виде
Ш©п) = *Шад.]
Обратно, если дана последовательность характеристических
классов &п(£), обладающая указанными свойствами, то, как не-
трудно показать, kn(%) — Kn{pi (g)....P«(D) Для некоторой
однозначно определенной мультипликативной последовательно-
сти {/(„} (см. теорему 15.9 и задачу 15.В). При этом не важно,
требуется или нет, чтобы расслоение | было ориентированным
или ориентируемым.
Для того чтобы точно указать мультипликативную последо-
вательность, соответствующую заданной последовательности
характеристических классов {&„(£)}, мы поступим следующим
образом. Пусть у1 — каноническое комплексное линейное рас-
слоение над Р°°(С). Напомним, что
Р1(у$ = а*е=Н*(Р°°(С)-, Z)
(см. теоремы 14.4 и 14.10 и следствие 15.5). Определим фор-
мальный степенной ряд f(t), полагая f(a2) равным &(у^) =
==Х^п(^к)' Тогда ясно, что искомая последовательность
{Кп} есть мультипликативная последовательность, принадлежа-
щая этому степенному ряду.
Для иллюстрации рассмотрим случай A = Z//, где I — фик-
сированное нечетное простое число. Пусть
НЦХ; Z/l)^H{+irk (X; Z/Z)
— приведенная l-я степенная операция Стинрода, где г =
= (1 —1)/2 (см. [Стинрод, Эпстейн]. Следуя [У, 1955], опреде-
лим по аналогии с определением классов Штифеля — Уитни,
предложенным Томом (см. § 8), новый характеристический
класс
Z/Z)
формулой Цп(1) — ф~'0>пф(Д), где £ — произвольное ориентиро-
ванное расслоение. Точно так же, как в § 8, легко проверить,
что классы qn являются естественными и удовлетворяют фор-
муле произведения. Следовательно,
а)Km (pi (&).....ргп®),
где {К,} — некоторая однозначно определенная мультипликатив-
ная последовательность с коэффициентами по модулю I.
Чтобы вычислить эту мультипликативную последователь-
ность, достаточно рассмотреть частный случай, когда £ есть век-
торное расслоение y’R над бесконечным комплексным проектив-
ным пространством Р°°(С). Пространство Ео ненулевых векто-
ров в пространстве расслоения ^(vlR) имеет гомологии точки.
188 Дж. Милнор и Дж. Сташеф
Поэтому существует естественный кольцевой изоморфизм
Н* (Е, Ео) Н* (Е, point) ~ Н* (Р°° (С), point).
Фундаментальный когомологический класс ие№(£, Ео) соот-
ветствует классу
е(у>)-С1(у!) = -аеЯ2(Р°°(С))
(см. теорему 14.10). Следовательно, элемент 0,1(м)=и' (см.
[Стинрод, Эпстейн, стр. 76]) соответствует элементу (—а)1, и
поэтому
ft (Yr) = (— а)'-1 = а2г.
Поскольку элементы 0* (и) равны нулю для k > 1 по размер-
ностным соображениям, отсюда вытекает, что формальный сте-
пенной ряд f (а2) = У qk (у^) равен 1 + а2г. Тем самым мы до-
казали следующую теорему.
Теорема 19.7 (У). Если l = 2r-j-l— нечетное простое чи-
сло, то характеристический класс по модулю I
равен Krn(pi(%), •••» ргп(%)), где {Ki) — мультипликативная по-
следовательность, принадлежащая степенному ряду f(t) =
= 1 + t'. 
Например, для 1 — 3 мы получаем, что класс qn(li) равен
классу Понтрягина рп{1), приведенному по модулю 3, а для
1 = 5,— что класс ft(£) равен классу р2 — 2рп_{рп+1 Ч— ... ±
± 2р2п, приведенному по модулю 5.
Точно так же, как в mod 2-случае, можно показать, что ха-
рактеристический класс qi{xn) касательного расслоения тп ком-
пактного ориентированного многообразия является инвариантом
гомотопического типа (ср. с теоремой 11.14). Фактически
ft = ft+ 0’4-1+04-2 + •••>
где классы У V/ характеризуются тождеством
(01х, р.) = {х о v{, р)
для всех хе Hn~iri(Mn-, Z/l). Отсюда, в частности, следует, что
классы Понтрягина по модулю 3 суть инварианты гомотопиче-
ского типа. Доказательства предоставляем читателю.
Эти характеристические классы ft(|) играют важную роль в
теории расслоений со слоем, гомотопически эквивалентным сфе-
ре, см. [Милнор, 1968], [Сташеф], [Мэй].
В заключение предлагаем читателю следующие три задачи
(все они взяты из книги [Хирцебрух]).
$ 20. Комбинаторные классы Понтрягина 189
Задача 19.А. Пусть {Тп} — мультипликативная последова-
тельность полиномов, принадлежащая степенному ряду f(t) —
= t/(\—е~*). Род Тодда Т[ЛГ] комплексного «-мерного
многообразия определяется как характеристическое число
<Т„(сь сп),р,2п>. Доказать, что Т[РЛ(С)] = 1 и что {Тп} —
единственная мультипликативная последовательность с этим
свойством.
Задача 19.В. Пусть {К„} — мультипликативная последова-
тельность, принадлежащая ряду f (/) = 1 + Kit -f- K2t2 + ... .
Выразим явно зависимость от коэффициентов X;, положив
Кп(хь ..., хп) = /гп(Л1,	..., Кп, Ху ..., хя),
где kn — полиномы от 2га переменных с целыми коэффициента-
ми. Рассмотрев случай, когда К\...Кп суть элементарные сим-
метрические функции от п независимых переменных, доказать
свойство симметрии
^п(^1> •••> ^п» К\, . .., ХЯ) = /5Я(ЛЬ Кп> Xi, • «>, Хп).
В частности, показать, что у полинома Kn(xi, хп) коэффи-
циент при х ' xir равен stt... ir (Ki...Кп).
Задача 19.С. Используя тождество Коши
f (О= 1 -1= 1+ X<- D'5/(Ч .... к^1,
доказать, что коэффициент при рп в L-полиноме Ln(pi, рп)
равен 22*(22А-1— l)B*/(2fe)! =/= 0 (см. приложение В).
§ 20. КОМБИНАТОРНЫЕ КЛАССЫ ПОНТРЯГИНА
Для любого триангулированного многообразия Мп Том опре-
делил классы k е Н4‘(Мп; Q), которые являются комбинатор-
ными (т. е. кусочно-линейными) инвариантами ([Том, 1958];
см. также [Рохлин, Шварц, 1957]). В случае гладкого многооб-
разия, надлежащим образом триангулированного, эти классы
совпадают с классами Хирцебруха Ц(р\, ..., pt) касательного
расслоения тл многообразия М.
Напомним (см. задачу 19.С), что коэффициент при pi у по-
линома Li(pi, ..., pi) ненулевой. Отсюда следует по индукции,
что уравнения li = Li(pi, ..., pi) можно однозначно разрешить
относительно классов Понтрягина pi, выразив их как полиномы
от классов /1, ..., /(. Например,
Pi = 3Zb
p2=(45Z2 + 9Z2)/7,
р3 = (6615Z3 + 1 755Z2Zj - 27Z|)/434.
190 Дж. Милнор и Дж. Сташеф
Следовательно, рациональные классы Понтрягина pi(%n)e
е H4i(Mr;Q) суть кусочно-линейные инварианты. Данный па-
раграф посвящен изложению этих результатов.
В 1965 г. С. П. Новиков доказал значительно более сильное
утверждение о том, что рациональные классы Понтрягина яв-
ляются топологическими инвариантами ([Новиков, 1966]; см.
также заключение). Мы не можем входить здесь в обсуждение
этого более сильного результата.
Гладкий случай
Для того чтобы мотивировать комбинаторное определение
классов Хирцебруха, предварительно дадим новую интерпрета-
цию классов Щр\......pi) гладкого «-мерного многообразия.
При этом вначале будем предполагать, что 41 <(«— 1) /2.
Пусть Мп — гладкое компактное «-мерное многообразие и
f; Mn-*Sn~4i— гладкое (т. е. бесконечно дифференцируемое)
отображение.
Лемма 20.1. Существует всюду плотное открытое подмноже-
ство сферы Sn~4i, состоящее из точек у, таких, что прообраз
f-1(t/) является гладким 41-мерным многообразием с тривиаль-
ным нормальным расслоением в Мп.
Доказательство. По теореме Брауна и Сарда (см. § 18) мно-
жество регулярных значений отображения f всюду плотно в
S'1-4*. Это множество открыто, так как его дополнение есть об-
раз компактного подмножества многобразия Мп. Но для каж-
дого регулярного значения у прообраз f-'(y) является гладким
компактным подмногообразием в Мп с тривиальным нормаль-
ным расслоением, так как последнее индуцировано из нормаль-
ного расслоения для точки у в S'1-4'. 
Теперь предположим, что многообразие Мп ориентировано.
Тогда ориентации на Мп и Sn-4‘ определяют ориентацию на
Н(у), если использовать разложение в сумму Уитни
r4i(f-4y))®Qn-4! = ^\f-^y).
Ниже и и |1л обозначают стандартные образующие групп
Я*(5*; Z) и Hn(Mn-,Z) соответственно, а хп — касательное рас-
слоение многообразия Мп. Класс Li(pi (тп), ..., pi(xn))<=
е= H4i(Mn', Q) будем кратко записывать как £,(тл).
Лемма 20.2. Для любого гладкого отображения f: Мп —* Sn~4i
и любого регулярного значения у индекс Кронекера
{Ц(^)^Г(и), |i„)
§ 20. Комбинаторные классы Понтрягина 191
равен сигнатуре а многообразия M4i = f~l{y). В случае
41 <(«—1)/2 класс Li(xn) однозначно характеризуется этим
свойством.
Доказательство. Пусть т4‘— касательное расслоение много-
образия М4‘ и /: М41->М"— отображение вложения. Ясно, что /
накрывается послойным отображением x4i © vn~4i -> т". Так как
нормальное расслоение v"-41' тривиально, то класс Li{x4i) равен
j*Li(xn). Следовательно, сигнатура
o(A449 = <Li.(t4‘), ^} = {ГЦ{хГ),
равна <L/(r"), /#(ц4<)>.
Теперь рассмотрим когомологический класс /*(и) е
е//n-4;(Afn; Z). Из коммутативной диаграммы
sn-4i Д
I	I
Нп~41 (мп, Мп \ М41) -> Нп~41 (Мп)
видно, что этот класс может быть отождествлен с «двойствен-
ным когомологическим классом» (см. стр. 101) подмногообра-
зия М4‘ с: Мп.
Далее, воспользуемся изоморфизмом двойственности Пуан-
каре а>—ъ-аоцп группы Hn~4i(Mn) на группу Нц(Мп), опреде-
ляемым при помощи операции лл-умножения (см. стр. 229). Со-
гласно задаче 11.С, этот изоморфизм переводит двойственный
когомологический класс f*{u) в гомологический класс /«(по-
следовательно, сигнатура o(Af4i)= <^г(тп), /»(р.40> равна
(т"), Г {и) и„> = {Ц (г") Г (и), ц„).
Это доказывает первую половину леммы.
Чтобы доказать вторую ее половину, применим теорему
Серра [Серр] о когомотопических группах Борсука — Спенье-
ра. Если п < 2k — 1, то множество всех гомотопических
классов отображений f: Мп ->• Sk образует абелеву группу, обо-
значаемую л* (АР1) и называемую &-й когомотопической группой
многообразия Мп. Серр доказал, что соответствие /*—*/*(«) ин-
дуцирует ^-изоморфизм
nk(Mn)^Hk{Mn- Z).
(Ср. стр. 170—172. Этот результат двойствен в смысле Спенье-
ра — Уайтхеда теореме 18.3.) В частности, образы f*(u) порож-
дают подгруппу конечного индекса в группе Hk{Mn', Z). Произ-
ведем теперь подстановку k = n— 41. Указанное выше размер-
ностное ограничение п < 2k—1 принимает тогда вид 41 <
< {п— 1) /2. Если это ограничение выполнено, то по двойствен-
105 Дж. Милнор и Дж. Сташеф
ности Пуанкаре (см. теорему 11.10) рациональный когомологи-
ческий класс Li(T”) однозначно определяется множеством всех
индексов Кронекера <1г(т")ч> f*(w), |in>. 
Замечание. Как метод вычисления классов Lt(xn) лемма 20.2,
пожалуй, непригодна. Однако утверждение, что число <Lj(rn)v>
рп> является целым для любого (/) е л"-41’(ЛГП), может
оказаться полезным при вычислении когомотопических групп.
Например, для комплексного проективного пространства Рт(С)
полный класс Хирцебруха L (%2т) равен
Wth0)"« - 1 + J + 5т‘ +Л" - о* + ....
О	VU
Отсюда следует, что при m^2(mod3) образ гомоморфизма
я2т-4 (рт	^т-4 (рт
делится на 3, а если т » 0 (mod 3), то образ
п2т-& (рт	я2т-8 (рт
делится на 9, и т. д.
Комбинаторный случай
Введем один класс объектов, с которым удобно работать.
Пусть К — локально-конечное симплициальное разбиение1.
ОПРЕДЕЛЕНИЕ. Разбиение К называется л-мерным рацио-
нальным гомологическим многообразием, если для каждой точ-
ки х из К локальная гомологическая группа
Ht(K, К\х; Q)
равна нулю для iVn и изоморфна Q для i — п.
Это условие эквивалентно требованию, что граница звезды
любого симплекса разбиения К является рациональной гомоло-
гической (л—1)-мерной сферой. Если К—рациональное гомо-
логическое «-мерное многообразие, то, как легко проверить,
каждая его компонента есть «простой «-мерный цикл» (см. Эй-
ленберг, Стинрод]). В частности, каждый («—1)-мерный сим-
плекс из К инцидентен в точности двум л-мерным симплексам.
Такое разбиение К называют ориентированным, если можно так
ввести ориентацию в каждом л-мерном симплексе, чтобы сумма
всех л-мерных симплексов образовывала л-мерный цикл. По
1 Определение симплициального разбиения см. в § 7 дополнения.—
Прим, перво.
§ 20. Комбинаторные классы Понтрягина 193
По определению этот цикл представляет фундаментальный го-
мологический класс р,еЯп(К; Z).
Ориентированные рациональные гомологические многообра-
разия удовлетворяют теореме двойственности Пуанкаре с ра-
циональными коэффициентами (см., например, [Борель, I960]).
Аналогично можно ввести понятие n-мерного гомологическо-
го многообразия с границей. В этом случае граница дК будет
гомологическим (п—1)-мерным многообразием, и ориентация
определяет относительный гомологический класс ц^Нп(К., дК;
Z) и определяется им.
Напомним некоторые стандартные определения. Пусть К —
симплициальное разбиение. Под (прямолинейным) подразделе-
нием разбиения К понимается симплициальное разбиение К'
вместе с гомеоморфизмом s: К'-+К, который является линей-
ным на симплексах, т. е. линейно отображает каждый симплекс
из К' в некоторый симплекс из К- Отображение f: K—-L сим-
плициальных разбиений называется кусочно-линейным, если су-
ществует подразделение $: К.'-* К., такое, что композиция f°s
линейна на симплексах.
Отображение называют симплициальным, если оно
линейно на симплексах и переводит каждую вершину из К в
какую-либо вершину из L. Можно показать, что, если комплекс
К компактен, то для любого кусочно-линейного отображения f:
K.-+L существуют подразделения s: К' —и t: L'—tL, такие,
что композиция	К' — L' симплициальна (см., например,
[Рурк, Сандерсон]).
Пусть обозначает границу стандартного (г + 1)-мерного
симплекса. Наша ключевая лемма состоит в следующем.
Лемма 20.3. Пусть Кп — компактное рациональное гомологи-
ческое n-мерное многообразие и f: К.п-*И>Г — кусочно-линейное
отображение, причем п — г = 41. Тогда для почти всех у е2'
прообраз f~l(y) является компактным рациональным гомологи-
ческим 41-мерным многообразием. Если заданы ориентации на
Кп и 2Г, то определена индуцированная ориентация гомологи-
ческого многообразия f~x(y) и сигнатура o(f_’(y)) этого ориен-
тированного гомологического многообразия не зависит от точки
у для почти всех у.
Здесь слова «для почти всех у» можно понимать так: «за ис-
ключением точек у, принадлежащих некоторому подразбиению
меньшей размерности».
Для этого общего значения сигнатуры a(f~l(y)) удобно вве-
сти сокращенное обозначение o(f). (Имеется известная анало-
гия между этим определением инварианта o(f) и определения-
7 Дж. Милнор, Дж, Сташеф
194 Дж. Милнор и Дж. Сташеф
ми таких классических гомотопических инвариантов, как «сте-
пень» или «инвариант Хопфа» отображения f.)
Лемма 20.4. Целое число o(f) зависит только от гомотопи-
ческого класса отображения f. Далее, если 4i <(«—1)/2, так
что определена когомотопическая группа лг(Кп), то соответ-
ствие (f)>—>o(f) определяет гомоморфизм ur(Kn)-+Z.
Доказательство лемм 20.3 и 20.4 основано на следующей
лемме.
Лемма 20.5. Если f: К-* L — симплициальное отображение и
точка у принадлежит внутренности U некоторого симплекса Д
из L, то прообраз гомеоморфен произведению
Соответствующее утверждение для всего замкнутого сим-
плекса, конечно, неверно.
Доказательство. Пусть Aq.....Аг — вершины симплекса Д
и у = /(До + ... + trAr, где ti — положительные числа, в сумме
равные 1. Очевидно, что любая точка	может быть
однозначно представлена в виде суммы
X = SqAo 4“ -• • + Sr Аг,
где каждая точка At является граничной точкой наименьшего
симплекса разбиения К, содержащего точку х, и f (Л{) = Ai. За-
метим, что /(х) = $оДо + ... +«гА-. Искомый гомеоморфизм
f-1 (С/)-»- С/ X f-1 (у) определяется теперь формулой
X ь-* (f (х), tgAo + . . . + trAr). 
Из доказательства леммы 20.5 попутно следует, что f~l(y)
гомеоморфно f-1 (у') для любых у и у' из U.
Доказательство леммы 20.3. Подразделим разбиения Кп и
2У так, чтобы отображение f стало симплициальным. Это воз-
можно, так как разбиение Кп компактно. Предположим, что точ-
ка у принадлежит внутренности U некоторого симплекса Дг
старшей размерности подразделния Sr. Тогда, согласно лемме
20.5, у множества U X f^1 (у) локальные рациональные гомоло-
гические группы такие же, как у некоторого «-мерного много-
образия. Поскольку U имеет локальные гомологические группы
H*(U, U \ х) такие же, как у некоторого r-мерного многообра-
зия, отсюда легко следует, что у множества f~{(y) локальные
рациональные гомологические группы такие же, как у некото-
рого многообразия размерности п — г = 4/.
В этом множестве f~'(y) может быть задана структура сим-
плициального разбиения. Действительно, произведя дальнейшее
подразделение так, чтобы точка у была вершиной подразделен-
§ 20. Комбинаторные классы Понтрягина 195
ного разбиения Sr, получаем, что f-1 (у) является подразбиением
соответствующего подразделения разбиения Кп.
Если заданы ориентации на U и на V X f-1 (</), то нетрудно
построить индуцированную ориентацию на f-1(z/), используя,
например, операцию гомологического Х-умножения. Поэтому
определена сигнатура о (f~'(y)). Но, как мы уже отмечали выше,
f-1 (у') гомеоморфно f~l (у) для всех у' е U. Следовательно,
целочисленная функция o(f-1(i/)) не зависит от у для y^U.
Предположим, что / и g— гомотопные кусочио-линейные
отображения разбиения Кп в разбиение 2Г. Возьмем какую-ни-
будь кусочно-линейную гомотопию
h: КпХ[0,
затем подразделим наши разбиения так, чтобы отображение h
стало симплициальным, и выберем точку у ffi U, как и выше.
Аналогичными рассуждениями можно показать, что множество
h~l (у) будет рациональным гомологическим многообразием с
границей, ограниченным дизъюнктным объединением £-1(у) +
+ (—Так как сигнатура всякой границы равна нулю,
это доказывает, что
о (Г1 (!/)) = о (g~l (у))
для почти всех точек у.
Теперь предположим, что нам даны две различные точки
yi и t/а сферы Sr, каждая из которых удовлетворяет условию,
Что функция i/i—> о (/-'(«/)) является постоянной в некоторой
окрестности точки у,. Выбрав кусочно-линейный гомеоморфизм
и: Sr—>2Г, гомотопный тождественному и такой, что u(«/i) = «/2,
получаем, что композиция u°f гомотопна отображению f и, еле*
довательно, что равенство
о (Г (г)) = а (Г1 (г))
выполнено для почти всех точек z е Sr. Если выбрать точку г
достаточно близкой к уз, то точка и-1(г) будет достаточно
близка к точке yi и, следовательно, мы получим
о (Г* (У1)) =“ (Г* (4/г))>
что и требовалось доказать. 
Доказательство леммы 20.4. Из доказательства предыду-
щей леммы немедленно следует, что целое число a(f) зависит
только от гомотопического класса отображения f. Покажем, что
соответствие (/)>—>о(/) аддитивно. Напомним, как устроена
групповая операция в когомотопической группе лг(Л?). Если
даны два отображения f, g\	то мы можем образовать
7*
196 Дж. Милнор и Дж. Сташеф
из них отображение (f, g): xt—>(/(х), g(x)) разбиения К.п в пря-
мое произведение 2r X Sr. При п < 2г это отображение может
быть продеформировано на подразбиение
Sr V 2r = (2r X point) U (point X S') X Sr,
причем в случае п <. 2г—1 получающееся отображение Кп->
-> V определено однозначно с точностью до гомотопии.
(Предположение, что (f, g) отображает разбиение К.п в 2r V Ег,
эквивалентно предположению, что для любой точки хе
либо f(x), либо g(x) является отмеченной точкой.) Отображая
теперь X Sr на Ег при помощи «складывающего отображе-
ния», которое тождественно на каждом экземпляре разбиения
Sr, мы получаем составное отображение h: Кп ->• Sr, представ-
ляющее искомую сумму (/) + (g).
Если отображения f и g выбраны в своих гомотопических
классах так, что для всех х либо f(x), либо g(x) есть отмечен-
ная точка, то h определяется просто формулой
( f (х), если f (х) #= отмеченной точке,
' '	(. g (х), если f (х) = отмеченной точке.
Следовательно, множество ft-I(t/) является дизъюнктным объ-
единением множеств f-I(t/) и g~'(y) для любой точки у, не
равной отмеченной точке, откуда немедленно следует, что
o(/i)=a(f)+oU). 
Теперь мы можем доказать основной результат этого па-
раграфа. Мы продолжаем предполагать, что конечное симпли-
циальное разбиение Кп есть ориентированное рациональное го-
мологическое многообразие.
Теорема 20.6. При 4К.(п—1)/2 существует один и только
один когомологический класс
Q),
который удовлетворяет тождеству
для любого отображения f: К" 2п-4/.
Ясно, что этот класс h = k (Кп) инвариантен относительно
кусочно-линейных гомеоморфизмов.
Доказательство. Как уже было замечено, гомоморфизм
лп-и(кп)->Нп~и(Кп; Z),
определенный соответствием (f)v->f*(u), является ^-изомор-
физмом (см. стр. 191). Отсюда легко следует, что существует
§ 20. Комбинаторные классы Понтрягина 197
один и только один гомоморфизм
o': Нп~и{кп‘, Z)->Q,
замыкающий следующую диаграмму до коммутативной:
п',-4г(/Сл)->Яп-4'(кп; Z)
!• ?
Z с Q
Но по теореме двойственности Пуанкаре
о' (х) = {Ц х, |1„)
для некоторого однозначно определенного рационального кого-
мологического класса Ц. 
Сравним «комбинаторное» и «гладкое» определения. Нам
понадобится следующий важный результат Дж. X. К. Уайтхеда.
Пусть М — Мп — гладкое многообразие. Гладкой триангуля-
цией многообразия М называется всякий гомеоморфизм
t: К-»М
(где К — некоторое симплициальное разбиение), такой, что огра-
ничение t на каждый замкнутый симплекс комплекса К является
гладким отображением всюду максимального ранга.
Теорема Уайтхеда. Любое гладкое паракомпактное много-
образие обладает гладкой триангуляцией. Если М — гладкое
паракомпактное многообразие с границей, то любую гладкую
триангуляцию Ко~*~дМ можно продолжить до гладкой триан-
гуляции К-* М, где К — некоторое симплициальное разбиение,
содержащее Ко как подразбиение. Наконец, если tr.Ki-*~M и
t2: Kz^-M — две различные гладкие триангуляции многообра-
зия М, то гомеоморфизм tzl 0 Л: Ki~+ Kz гомотопен некоторому
кусочно-линейному гомеоморфизму из К\ в Kz.
Таким образом, гладкому многообразию М отвечает симпли-
циальное разбиение К, которое определено однозначно с точ-
ностью до кусочно-линейного гомеоморфизма. Доказательства
можно найти в [Уайтхед, 1940] и в дополнении.
Рассмотрим теперь характеристический когомологический
класс li(K). Используя изоморфизм t*;	Hil(K), полу-
чаем соответствующий класс
Г‘МХ)еЯ4'(М),
198 Дж. Милнор и Дж. Сташеф
по-прежнему в предположении, что 4i<(n—1)/2. Этот класс
не зависит от выбора гладкой триангуляции. Действительно,
если t\:	— другая гладкая триангуляция, то композиция
/j-1»/ гомотопна некоторому кусочно-линейному гомеоморфизму
и, следовательно,
Этот однозначно определенный рациональный класс мы будем
Кратко обозначать через /<(М).
Теорема 20.7. Класс определенный для гладкого мно-
гообразия при помощи описанной выше комбинаторной про-
цедуры, равен классу Хирцебруха Li(pi, ..., pi) касательного
расслоения многообразия М.
Доказательство. Пусть f: Mn-*-Sr — гладкое отображение.
Мы построим коммутативную с точностью до гомотопии диаг-
рамму
I* |<
Lr-^Sr
где § — кусочно-линейное отображение, a t, s —гладкие триан-
гуляции, такую, что
для у, принадлежащих некоторому непустому открытому мно-
жеству в Sr, и z, принадлежащих некоторому непустому от-
крытому множеству в Lr. Разбиение L' обязано быть кусочно-
линейно гомеоморфным разбиению Sr. Ввиду леммы 20.2 и тео-
ремы 20.6 отсюда будет следовать наше утверждение.
Пусть Wo a Sr — какое-нибудь регулярное значение отобра-
жения f. Нетрудно проверить, что если В — достаточно малый
Шар с центром в точке уо, то прообраз Н(В) диффеоморфен
проивведению f_1(«/o)XB при диффеоморфизме, который сохра-
няет проекцию на В. Выберем какие-либо гладкие триангуля-
ции
К К^ГЧуо)
и
t2’ К2~*В.
Тогда гладкая триангуляция
h X 4: Ki X K2^f~' (Уо) ХВсяМп
при ограничении дает гладкую триангуляцию
К1ХдК2-*Г1(Уо)ХдВ
§ 20. Комбинаторные классы Понтрягина 199
границы многообразия /-1(Уо)Х^> которая по теореме Уайтхеда
продолжается до гладкой триангуляции
К3 -> АГ \ внутренность (f-1 (z/0) X В)>
дополнительной к внутренности многообразия f-1(y0)XB об-
ласти. Полагая Кп — Ki X Кг U Кз (и производя, если надо, со-
ответствующее продразделение), мы получим гладкую триан-
гуляцию t: Кп Мп. Аналогично триангуляция £2 может быть
продолжена до гладкой триангуляции s: Lr -> Sr.
Далее, проекцию Ki X Кг -*• Кг с Lr можно продолжить до
кусочно-линейного отображения g'.Kn^-Lr таким образом,
чтобы дополнение к разбиению К\ X Кг отображалось на до-
полнение к разбиению Кг. Легко проверить, что композиция
s°g гомотопна f °t. Более того,
f-\y)~g-\Z)
для каждой точки у е В и каждой точки z е Кг, так что сиг-
натура сг(/—1 (г/)) равна, очевидно, сигнатуре or(^-1(z)). 
До сих пор предполагалось выйолненным условие 41 <
< (п—1)/2. Однако для заданного рационального гомологи-
ческого многообразия Кп мы всегда можем образовать прямое
произведение KnX2m, где m достаточно велико. Класс li(Kn}
можно тогда определить как класс, индуцированный классом
ЦК"Х2т) при помощи естественного вложения. Нетрудно по-
казать, что этот новый класс однозначно определен и имеет
нужные свойства. В частности, индекс Кронекера </ДК4/),
всегда равен сигнатуре о(К4/).
Легко также обобщить все это на случай гомологических
многообразий с границей. Надо только в предыдущих рассуж-
дениях рассматривать относительные когомотопические группы
лп~4‘(Кп, дКп) и привлечь теорему двойственности Лефшеца.
Некоторые приложения
Начнем с одного примера, который открыли независимо
Том [Том, 1955—56, стр. 81], Тамура [Тамура, 1957] и Симада
[Симада, 1957]. Нам будут нужны две леммы.
Лемма 20.8. Для всякого гладкого векторного расслоения
с проекцией л: Е —> В касательный класс Понтрягина р(Е)==
= Р(те) пространства расслоения Е(%) равен л*(р(£)р(тв))
с точностью до 2-кручения.
Доказательство. Выберем какую-нибудь риманову метрику
на многообразии Е. Тогда касательное расслоение тв, очевидно,
расщепляется в сумму Уитни расслоения, образованного век-
200 Дж. Милнор и Дж. Сташеф
торами, касательными к слоям и расслоения, образованного
векторами, нормальными к слоям Утверждение леммы сле-
дует из того, что эти расслоения изоморфны соответственно
л* (£) и л* (тв). 
Пусть ue//4(S4) обозначает стандартную образующую
группы когомологий.
Лемма 20.9. Существует ориентированное 4-мерное расслое-
ние £4 над сферой S4, такое, что pi(£4) =—2и и е(^) — и.
Доказательство. Пусть Н обозначает некоммутативное поле
кватернионов. (Буква Н выбрана в честь Уильяма Рауэна Га-
мильтона (W. R. Hamilton).) Мы можем построить проективное
пространство Рт(Н) кватернионных прямых, проходящих через
начало координат в кватернионном координатном пространстве
Нт+1. Это — гладкое 4/п-мерное многообразие. Существует кано-
ническое «кватернионно-линейное» расслоение у над Рт(Н), про-
странством £(у) которого служит множество всех пар (L,v),
состоящих из кватернионных прямых Lc Hm+l и векторов
Пространство единичных векторов из £(у) может быть отожде-
ствлено с единичной сферой S4m+3 с Н'"+1.
Используя естественные вложения R с Сс Н, мы получаем,
что для расслоения у существуют лежащие в его основе комп-
лексное двумерное расслоение уэ и вещественное четырехмерное
расслоение yR над тем же базисным пространством Рт(Н). Из
точной последовательности Гизина для yR видно, что кольцо
когомологий Я*(Р*(Н)) с целыми коэффициентами является
кольцом усеченных полиномов, порожденным классом Эйлера
или классом Чженя
е(у^ = с2(ус)^Н\Рт(Н)).
Если для краткости обозначить эту когомологическую обра-
зующую через и е= Я4(Рт(Н)), то полный класс Чженя равен
с(ус)=1 +“
и, следовательно, полный класс Понтрягина равен
Р (Yr) = (1 — «)2 == 1 - 2и + и2
(согласно следствию 15.5). Таким образом, для частного слу-
чая одномерного кватернионного проективного пространства
Р1(Н) S4 мы имеем
Pi(Yr) = -2«, e(YR)=u,
как и утверждалось. Е
§ 20. Комбинаторные классы Понтрягина 201
Из этой леммы следует, что для любого целого четного чис-
ла k существует векторное 4-мерное расслоение g над сферой
S4 с pi (£) = ku. Можно просто взять £ = f (yR), где /*: S4 —» S4 —
какое-нибудь отображение степени —k/2. Это наилучший воз-
можный результат, поскольку класс Pi(?) не может быть нечет-
ным кратным элемента и, согласно задаче 15.А.
(Для векторных расслоений над сферой Sim соответствую-
щий наилучший возможный результат заключается в том, что
класс Понтрягина может быть равен любому кратному
элемента (2m—1)! (н.о. д. (m + 1, 2))и. Доказательство этого
утверждения основано на теореме о периодичности Ботта (см.
[Ботт, 1958—59]).)
Пример 1. Пусть — гладкое n-мерное расслоение над сфе-
рой S4. Для удобства будем считать, что п > 5. Выбрав ка-
кую-нибудь евклидову метрику, обозначим через с£(|”)
множество векторов длины и через дЕ'— множество век-
торов длины, равной 1.
Учитывая сделанное выше замечание, мы видим, что
pi(ln) = ku, где k может быть произвольным четным числом1.
Следовательно,
Р1(£(Г)) = ^*(«)
по лемме 20.8. Так как многообразие дЕ' имеет тривиальное
нормальное расслоение в Д(|п), то отсюда следует, что
где и' <= Н4 (дЕ') — стандартная образующая, которая соответ-
ствует элементу и при гомоморфизме
Я4($4)->Я4(д£')
из точной последовательности Гизина для расслоения
Поскольку класс Понтрягина pi гладкого многообразия дЕ'
является комбинаторным инвариантом, то и четное число |/г|
также будет комбинаторным инвариантом. Таким образом,
варьируя k, мы получаем бесконечное множество гладких мно-
гообразий дЕ' фиксированной размерности п +3	8, которые
все комбинаторно различны.
С другой стороны, как показали И. М. Джеймс и Дж.
X. К. Уайтхед [Джеймс, Уайтхед], для любого фиксированного
п эти многообразия дЕ' принадлежат лишь конечному числу
(а именно 13) различных гомотопических типов. Следователь-
но, для любой фиксированной размерности п 8 существуют
два гладких односвязных многообразия, которые имеют один
1	= £ Ф е"-4. — Прим, перев.
202 Дж. Милнор и Дж. Сташеф
и тот ясе гомотопический тип, однако не являются кусочно-ли-
нейно гомеоморфными. (Размерность 8 может быть легко пони-
жена до 7.)
Используя теорему Новикова о том, что рациональные клас-
сы Понтрягина являются топологическими инвариантами, полу-
чаем, что эти многообразия не будут даже гомеоморфными*.
Совершенно другой пример многообразий, которые имеют
один и тот же гомотопический тип, но не гомеоморфны, по-
является при изучении фундаментальной группы, например
трехмерного линзового пространства (см. [Броди], [Чепмэн]).
Наш следующий пример принадлежит Тому ([Том, 1958];
см. также [Милнор, 1956] и [Симада]). Сначала мы должны
усилить лемму 20.9.
Лемма 20.10. Для любых целых чисел k, I, удовлетворяющих
условию k =z 21 (mod 4), существует ориентированное 4-мерное
расслоение £ над сферой S4, такое, что pi(%) = ku, е(%)=1и.
(Эти целые числа k и I в действительности определяют
класс изоморфизма расслоения g, так как гомотопическая
группа л4(б4)=£ n3(SO4) изоморфна Z®Z.)2
Доказательство. Напомним, что через 6f4 мы обозначаем
пространство ориентированных 4-мерных подпространств в R°°.
Для каждого гомотопического класса (f) в гомотопической
группе л4(С4) мы можем образовать когомологический класс
Р1(П4) = ГР1(у4)
в группе когомологий 774(S4) с целыми коэффициентами, пере-
неся универсальное расслоение у4 на четырехмерную сферу и
взяв затем его класс Понтрягина. Это соответствие (f)i—>
*->pi(f*y4) задает аддитивный гомоморфизм группы л4(б4) в
группу //4(S4)aZ, что легко увидеть, если заметить, что
MV), P4> = <P1(V4).
где соответствие
есть хорошо известный гомоморфизм Гуревича. Аналогично
класс Эйлера задает аддитивный гомоморфизм
(f)^e(fV)
группы л4(б4) в группу #4(S4)^ Z. * 1
1 Имеется общая формула Сулливана, описывающая'-все негомеоморф-
ные замкнутые топологические многообразия размерности п 5, гомотопи-
чески эквивалентные заданному замкнутому односвязному топологическому
многообразию, см. [Сулливан, 1975]. — Прим, перев.
1 См. [Стинрод]. — Прим, ред.
§ 20. Комбинаторные классы Понтрягина 203
Далее, касательное расслоение к сфере S4 изоморфно рас-
слоению f[у4, а расслоение yR из леммы 20.9 — расслоению fffl,
для подходящих отображений fi, f2: S4->G4. Таким образом,
Pi (W = 0,	e(f[y4) = 2«,
Pi C2Y4) = - 2u, e(fjY4) = u.
Взяв соответствующую линейную комбинацию (/) классов (fi)
и (fs) в группе лДбч), мы можем, очевидно, добиться того,
чтобы
Р1(Н4) = £ц, е(Гу4) = /«,
где числа k и I удовлетворяют условию k s 21 (mod 4). 
Пример 2. В силу леммы 20.10, для любого целого числа
fe = 2(mod4) существует ориентированное 4-мерное расслое-
ние £ над S4, такое, что
Pi (Ю = ku, е (|) = и.
Используя последовательность Гизина для легко показать,
что пространство дЕ' единичных векторов пространства рас-
слоения Е(%) имеет гомотопический тип сферы S7. В действи-
тельности это многообразие дЕ' гомеоморфно семимерной сфе-
ре. Как гладкое многообразие, оно может быть получено отож-
дествлением границ двух экземпляров единичных семимерных
шаров при помощи некоторого подходящего (возможно, экзоти-
ческого) диффеоморфизма между этими границами (шестимер-
ными сферами). Этот факт был доказан прямым методом в ра-
боте [Милнор, 1956] и является также следствием обобщенной
гипотезы Пуанкаре, как показано в [Смейл, 1961]. Далее, от-
правляясь от какой-нибудь гладкой триангуляции граничной
6-мерной сферы и продолжая ее до триангуляции наших двух
«склеенных» 7-мерных шаров, мы легко получаем, что много-
образие дЕ' даже комбинаторно эквивалентно 7-мерной сфере *.
Рассмотрим пространство Тома Т = Т(£). Очевидно, что оно
может быть отождествлено с многообразием, полученным из
Е' присоединением некоторого конуса над дЕ'. Выбирая какую-
нибудь гладкую триангуляцию многообразия Е' и учитывая то
обстоятельство, что дЕ' является комбинаторной сферой, ви-
дим, что Т = Т(£) можно триангулировать как кусочно-линей-
ное многообразие. Это означает, что его можно триангулиро-
вать так, чтобы каждая его точка имела окрестность, кусочно-
линейно гомеоморфную пространству R8.
1 То есть дЕ' кусочно-линейно гомеоморфно 7-мерной сфере, — Прим,
перев.
204 Дж. Милнор и Дж. Сташеф
Согласно лемме 18.1 или лемме 18.2, группы гомологий мно-
гообразия Т — бесконечные циклические в размерностях 0, 4, 8
и нулевые в других размерностях. Таким образом, сигнатура
а(Т) должна быть равна ±1, и, выбирая ориентацию подходя-
щим образом, мы можем считать, что о(Т) = 4-1.
В силу леммы 20.8, касательный класс Понтрягина pi(E')
равен k раз взятой когомологической образующей. Следова-
тельно, класс pi(T) равен некоторой образующей, умноженной
на k, и число Понтрягина р2 [Т] должно быть равно k2. Тео-
рема о сигнатуре дает
откуда следует, что второе число Понтрягина равняется
Рг [Г] = (45 4- k2)/7.
Здесь k может быть любым целым числом, сравнимым с 2 по
модулю 4. Однако если k ^±2 (mod 7), то число (45±А2)/7
не будет целым. (Например, при k — 6 число р2(Л не будет
целым.) Так как числа Понтрягина гладких многообразий
должны быть целыми, то мы доказали тем самым следующее
утверждение.
Для k ^±2 (mod 7) триангулированное 8-мерное многооб-
разие Т — Т(%) не обладает гладкой структурой, согласован-
ной с заданной триангуляцией.
Отсюда как следствие вытекает, что гладкое 7-мерное мно-
гообразие дЕ' (которое гомеоморфно сфере S7) не диффео-
морфно S7. Действительно, в противном случае на многообра-
зии Т, очевидно, можно было бы ввести согласованную гладкую
структуру.
Закончим одной задачей для читателя.
Задача 20.А. Пусть т — касательное расслоение кватернион-
ного проективного пространства Рт(Н) (см. доказательство
леммы 20.9). Используя изоморфизм т Нотн (у, у-1-) веще-
ственных векторных расслоений, показать, что
т® Нотн (у, у) Нотн (у, Нт+1)
и, следовательно, р(т) = (1 4-и)2т+2/(1 4-4«) (см. [Шчарба],.
а также теорему 14.10).
ЗАКЛЮЧЕНИЕ
Мы дадим здесь очень краткий обзор некоторых наиболее
важных результатов в теории характеристических классов, по-
лученных после того, как были прочитаны и записаны лекции,
послужившие основой этой книги. О других результатах чита-
тель сможет узнать из работ [Хьюзмоллер], [Адамс, 1972] и
[Атья] *.
Негладкие многообразия
Теория вещественных векторных расслоений идеально при-
способлена для изучения гладких многообразий точно так же,
как теория комплексных векторных расслоений приспособлена
для изучения комплексных многообразий. Если мы имеем дело
с какой-нибудь другой категорией многообразий, то полезно
подыскать подходящий для этой категории тип расслоений. Рас-
смотрим, например, категорию всех кусочно-линейных много-
образий и их кусочно-линейных отображений. Подходящий тип
расслоений для этой категории может быть описан следующим
образом. Пусть В — локально-конечное симплициальное разбие-
ние.
ОПРЕДЕЛЕНИЕ. Ку сочно-лине Иное п-мерное расслоение
над В состоит из симплициального разбиения Е и кусочно-ли-
нейного отображения р: Е-+В, удовлетворяющего следующему
условию локальной тривиальности. Каждая точка базисного
пространства В должна обладать открытой окрестностью U,
такой, что множество p~l(U) кусочно-линейно гомеоморфно
прямому произведению U X R" при гомеоморфизме, который
согласован с проекцией на U. (Открытое множество U имеет
структуру симплициального разбиения по теореме Рунге, см.
[Александров, Хопф].)
Кусочно-линейное касательное расслоение кусочно-линей-
ного «-мерного многообразия М может быть построено следую-
1 См. также [*Коннер, Флойд, 1969], [*Стонг 1973], [*Каруби, 1977],
[*Бухштабер, 1975], [*Бухштабер, 1978] (напоминаем, что звездочка отсы-
лает к списку литературы, добавленной при переводе). — Прим, перев.
206 Дж. Милнор и Дж. Сташеф
щим образом. Согласно теореме Б. Мазура (к сожалению, не-
опубликованной) * *, существует окрестность Е диагонали в про-
изведении М X М, такая, что проекция (х, у)н->х этой окрест-
ности на Af является кусочно-линейным n-мерным расслоением.
Кроме того, это расслоение единственно с точностью до изо-
морфизма. (По поводу аналогичной теоремы в топологической
категории см. [Кистер].) Если не использовать теорему Мазура,
то можно было бы провести все рассмотрения, основываясь на
менее известном понятии кусочно-линейного микро расслоения
(см. [Милнор, 1964]).
Кусочно-линейные n-мерные расслоения над В классифици-
руются отображениями базисного пространства В в некоторое
«универсальное базисное пространство» или «классифицирую-
щее пространство», которое обозначается BPL(ri). Таким об-
разом, теория характеристических классов для кусочно-линей-
ных многообразий сводится к вычислению когомологий
H*(BPL(ri)).
Переходя к прямому пределу при га-»-оо, можно2 построить
каноническое отображение
BO^BPL.
Здесь ВО обозначает стабильное многообразие Грассмана
lim ВО (n) = lim Gn(R°°). Как показали Хирш и Мазур (см.
[Хирш] *), относительная гомотопическая группа
nk(BPL, ВО)
изоморфна группе П-ь состоящей из всех классов ориентиро-
ванного диффеоморфизма скрученных (А—1)-мерных сфер
(т. е. гладких многообразий, полученных склеиванием границ
двух замкнутых (k—1)-мерных шаров). Эта группа тривиаль-
на для k < 7 и конечна для всех k (см. [Кервер, Милнор] и
[Серф]). Отсюда следует, что рациональные когомологии
H*(BPL; Q) изоморфны рациональным когомологиям Н*(ВО;
Q), которые представляют собой алгебру полиномов, порож-
денную классами Понтрягина (см. § 20). Заметим, однако, что
для когомологий с целочисленными коэффициентами отобра-
жение Я*(BPL)/torsion-*Н*(ВО)/torsion не является эпимор-
физмом (см. условия целочисленности в примере 2 § 20). По
поводу когомологий пространства BPL с другими коэффициен-
тами см. [Вильямсон] и [Брамфил,.Мадсен, Милграм].
1 См. [*Кюйпер, Лашеф, ч. 1]. — Прим, перев.
8 См. [*Хирш, Мазур]. — Прим, перев.
* А также [*Хирш, Мазур]. — Прим, перев. ,
Заключение 207
Фундаментальная теорема Хирша и Манкрса [Хирш, 1963],
[Манкрс, 1964—1968]1 утверждает, что кусочно-линейное мно-
гообразие М. обладает согласованной гладкой структурой тогда
и только тогда, когда классифицирующее отображение
M-+BPL
стабильного касательного расслоения многообразия М подни-
мается до отображения М -> ВО (ср. [Милнор, 1964]), или,
эквивалентно, тогда и только тогда, когда каждая последова-
тельность препятствий, лежащих в группах Hk(M; Г*_ i), нуле-
вая.
Теория топологических п-мерных расслоений и топологиче-
ских касательных расслоений совершенно аналогична. В этом
случае классифицирующее пространство обозначается ВТОР (и).
Существует каноническое отображение
BPL(ri)->BTOP (п).
Что касается предела при п->оо, то поразительная теорема,
принадлежащая Кёрби и Зибенманну [Кёрби, Зибенманн, 1969]2,
утверждает, что относительная гомотопическая группа
nk (ВТОР, BPL)
является нулевой для k^iu циклической порядка 2 для k —4.
Далее, они показали, что топологическое многообразие М раз-
мерности ^5 может быть триангулировано как кусочно-линей-
ное многообразие тогда и только тогда, когда классифицирую-
щее отображение
М-+ВТОР
стабильного касательного расслоения многообразия М подни-
мается до отображения
M-+BPL,
или, эквивалентно, тогда и только тогда, когда единственный
топологический характеристический класс в группе
Я4(М; Z/2)
равен нулю.
Из этого, между прочим, следует, что кольцо Н* (ВТОР; Л)
топологических характеристических классов изоморфно кольцу
когомологий H*(BPL;K) для любого кольца коэффициентов Л,
содержащего ’/2. Отсюда, конечно, вытекает теорема Новикова
о том, что рациональные классы Понтрягина являются тополо-
гическими инвариантами.
1 См. также [*Хирш, Мазур]. — Прим, перев.
’ См. также [*Кёрби, Зибеиманн, 1977]. — Прим, перев.
208 Дж. Милнор и Дж. Сташеф
Еще более широкую категорию «многообразий» доставляет
класс всех пространств Пуанкаре, т. е. клеточных разбиений М,
которые удовлетворяют теореме двойственности Пуанкаре
(с произвольными локальными коэффициентами в неодносвяз-
ном случае) относительно некоторого фундаментального гомо-
логического класса ц е Нп(М-, Z).
Чтобы изучать такие объекты, мы должны ввести совсем
иной тип расслоений. А именно, будем говорить, что непре-
рывное отображение р: Е -* В является расслоением в смысле
Гуревича1 над В или что оно удовлетворяет аксиоме о накры-
вающей гомотопии, если для любого пространства X и любого
непрерывного отображения f:X —► Е всякая гомотопия отобра-
жения р о f может быть накрыта гомотопией отображения f (см.
[Гуревич, 1955], [Дольд, 1963]). Такое расслоение называется
k-сферическим, если каждый слой р-1(6) имеет гомотопический
тип A-мерной сферы.
Как показал Спивак, любое односвязное пространство Пуан-
каре М допускает по существу единственное сферическое рас-
слоение Е —► М, обладающее тем свойством, что старший гомо-
логический класс в ассоциированном пространстве Тома Т при-
надлежит образу гомоморфизма Гуревича 2
лп+Л+1 (?) ~* Hn+k+i (Г; Z)
(см. [Спивак]). Более точно, это расслоение, называемое нор-
мальным расслоением Спивака комплекса Пуанкаре М, един-
ственно с точностью до стабильной послойной гомотопической
эквивалентности, которую мы не будем здесь определять3.
В работах [Сташеф, 1963], [Сташеф, 1968] доказано, что
такие сферические расслоения над М классифицируются с точ-
ностью до стабильной послойной гомотопической эквивалентно-
сти отображениями в некоторое классифицирующее простран-
ство BF. Существуют канонически определенные с точностью до
гомотопии отображения
ВО -> BPL -> ВТОР -» BF.
Как установили Браудер и Хирш [Браудер, Хирш, 1966], одно-
связное пространство Пуанкаре М формальной размерности
п 5 имеет гомотопический тип замкнутого кусочно-линейного
1 В оригинале fibration. (Термину «расслоение» отвечает английское
bundle.)—Прим, перев.
2 Ниже п — размерность фундаментального гомологического класса ком-
плекса Пуанкаре М, a k — размерность сферического слоя; k — достаточно
большое число. — Прим, перев.
3 См. [*Браудер, 1972]. Теорему существования и единственности расслое-
ния Спивака для неодносвязного случая см. в работах [* Уолл, 1967], [* Брау-
дер, 1972]. — Прим. nepeet
Заключение 209
многообразия М' тогда и только тогда, когда классифицирую-
щее отображение М —* BF поднимается до отображения М —►
-+BPL. (Проблема единственности многообразия М', впервые
исследованная Новиковым для гладкого случая [Новиков,
1964], здесь намного сложнее.)
Гомотопическая группа n.t(BF) для i^2 изоморфна ста-
бильной (i—1)-й гомотопической группе сфер ллг+<--1 (SN) и,
следовательно, всегда конечна. Когомологии классифицирую-
щего пространства BF изучали Милграм [Милграм, 1970], Мэй
[Мэй, 1972] и другие.
При вычислении когомологий H*(BPL) и H*(BF) приме-
няются совсем другие технические методы, чем развитые в этой
книге. Вместо того чтобы вычислять эти группы, используя
особые характеристические классы, анализируют гомотопиче-
ский тип в терминах ассоциированных расслоений или в терми-
нах дополнительных внутренних структур. Например, Сулливан
[Сулливан, 1970] показал, что «по нечетным простым числам»
пространство ВО имеет гомотопический тип слоя расслоения
BPL -> BF.
В работах [Бордман,Фогт, 1968], [Мэй, 1972], [Сигал, 1974]
было показано, что стабильные классифицирующие простран-
ства BPL, ВТОР и BF все имеют гомотопический тип бесконеч-
ных пространств петель и поэтому для их изучения может быть
привлечена не только алгебра Стинрода, но также и ее гомоло-
гический аналог — алгебра Дайера — Лашефа. Хотя классы У
из § 19 и их образы при гомоморфизме Бокштейна по-прежнему
играют важную роль (см. [Милнор, 1968], [Сташеф, 1968]), по-
явились и другие классы, интерпретация которых в терминах
геометрии расслоений пока далеко не ясна (см. [Равенель,
1972]).
Гладкие многообразия
с дополнительной структурой
Помимо негладких многообразий можно еще рассматривать
гладкие многообразия, наделенные некоторой дополнительной
структурой. Например, мы можем потребовать, чтобы «струк-
турной группой» касательного расслоения нашего п-мерного
гладкого многообразия (см. [Стинрод], [Хьюзмоллер]) была та
или иная подгруппа общей линейной группы GL(n, R) (или,
эквивалентно, ортогональной группы О(п)). Важный пример
доставляет унитарная группа Щп)с О(2п)\ это приводит к
изучению почти-комплексных многообразий и близко с ними
связанных комплексных многообразий (см. § 13). Другие при-
меры доставляют специальная унитарная группа SU(n) с О (2п)
и компактная симплектическая группа Sp (n)az О(4п).
210 Дж. Милнор и Дж. Сташеф
Аналогично можно потребовать, чтобы структурная группа
касательного расслоения сводилась к двукратному накрытию
Spin(n)->SO(п). Обсуждение теорий кобордизмов, ассоцииро-
ванных с различными такими редукциями, см. в книге [Стонг].
Другое направление основано на определении характеристи-
ческих классов при помощи дифференциальных форм (см. при-
ложение С). Так определяемые классы оказываются особенно
хорошо приспособленными для изучения многообразий с та-
кими дополнительными структурами, как слоение или риманова
метрика. Обращение в нуль этих классов в определенных слу-
чаях дает возможность построить новые характеристические
классы, впервые изученные с других точек зрения в работах
[Чжень, Саймонс] и [Годбийон, Вей] *. Некоторые из этих клас-
сов зависят, например, от конформной структуры риманова мно-
гообразия. Некоторые из характеристических чисел, соответ-
ствующих новым характеристическим классам, могут прини-
мать произвольные вещественные значения ([Ботт, 1972],
[Баум], [Тэрстон]), что говорит о большом богатстве таких
структур. В настоящее время эта ветвь теории характеристиче-
ских классов находится в стадии очень быстрого и интенсив-
ного развития. Современный обзор работ по этой тематике в
статье [Ботт, Хэфлигер], дальнейшие результаты представлены
в сборнике [Am. Math. Soc. 27] *.
Обобщенные теории когомологии
До сих пор мы обсуждали обобщения, получающиеся, когда
используется обычная теория когомологий, но различные экзо-
тические типы расслоений. Совершенно другое обобщение воз-
никает, если мы используем обычные векторные расслоения, но
зато привлекаем обобщенные когомологии.
По определению обобщенная теория когомологий — это
функтор (X, A)i—>2&* (X, А) из категории пар пространств в ка-
тегорию градуированных аддитивных групп, который удовлет-
воряет первым шести аксиомам Эйленберга — Стинрода, но не
обязан удовлетворять аксиоме размерности (утверждающей,
что № (точка) = 0 для k ф О)2.
Первый и наиболее важный пример такой обобщенной тео-
рии когомологий доставляет К-теория.
ОПРЕДЕЛЕНИЕ. Для любого компактного пространства X
аддитивная группа №(Х) задается следующими образующими
и соотношениями. Имеется по одной образующей [£] на каждый
* См. также обзор [*Фукс]. — Прим, перед.
* Ср. [Дайер]. — Прим, перев.
Заключение 211
класс изоморфных друг другу комплексных векторных рас-
слоений £ над базисным пространством X и по одному соот*
ношению
[|®п] = И + [п]
на каждую пару комплексных векторных расслоений. Для
пг "> 0 группа К~т (X) может быть определена как коядро есте-
ственного эпиморфизма
№ (Sm X X) -> К° ((отмеченная точка) X X).
Операция тензорного умножения для комплексных векторных
расслоений порождает операцию умножения
К~т (X) ® К~п (У) -> К~т~п (X X У).
Теорема периодичности Ботта утверждает, что умножение на
стандартную образующую группы К~2 (точка) дает изомор-
физм
(Это тесно связано с утверждением, что классифицирующее
пространство BU имеет гомотопический тип своего двукратного
пространства петель.)
Кольцо ХО*(Х) определяется аналогично, с той лишь разни-
цей, что вместо комплексных расслоений используются веще-
ственные. В этом случае имеет место теорема периодичности
Ботта
КО_'"(Х)-^ХО“'П"8(Х).
За иллюстрациями силы методов К-теории мы отсылаем чита-
теля к работам [Атья, 1967] и [Адамс, 1962—1972] ‘.
Аналогично можно определить обобщенную теорию гомоло-
гий. Важным примером служат стабильные гомотопические
группы
где SkX обозначает А-кратную надстройку над пространством
X. Другой пример — группы ориентированных бордизмов (X)
(см. [Коннер, Флойд]2). По определению два отображения
ff. Afi-^X, f2: М2->Х
гладких замкнутых компактных ориентированных п-мерных
многообразий Afi, Л12 в пространство X называются бордант-
ными, если существуют гладкое компактное ориентированное
1 См. также [*Каруби, 1977]. — Прим, перев.
’ См, также [* Коннер, Флойд, 1969], — Прим, перев.
212 Дж. Милнор и Дж. Сташеф
многообразие N с границей dN — М> -j-(—Ah) и отображение
продолжающее отображения ft и fs. Классы бордизмов
таких отображений образуют группу Q„(X). Заметим, что груп-
па Qn (точка) есть в точности группа кобордизмов из § 17.
С каждой такой обобщенной теорией гомологий связана соот-
ветствующая обобщенная теория когомологий. См. [Уайтхед
Дж. У., 1962]!.
Чтобы изучать характеристические классы со значениями
в обобщенной теории когомологий, например такой, как К*{В),
надо сначала вычислить группу К* от соответствующего класси-
фицирующего пространства. В случае комплексной /(-теории
Атья и Хирцебрух установили изоморфизм между K*(BG) для
компактной группы Ли G и пополненным кольцом ее представ»
лений ([Атья, Хирцебрух]; относительно соответствующих ре»
зультатов для КО-теории см. [Андерсон]).
Точно так же, как при изучении гомологий многообразий,
важную роль играет ориентация многообразия, использующая
классическую теорию гомологий Z7»(; Z), ее аналог — ориента-
ция в /(-теории— играет основную роль в /(-теории многообра-
зий (см. [Ши]). Например, Сулливан доказал удивительный ре-
зультат, что PL-расслоения — более или менее то же самое, что
и сферические расслоения, снабженные /(О-ориентацией [Сул-
ливан, 1970].
Для любого /(-ориентированного расслоения можно опреде-
лить характеристические классы в /С-теории, используя под-
ход, описанный в § 8 и 19, и соответствующие /(-операции вме-
сто операций Стинрода. Эта идея была предложена Боттом
[Ботт, 1962] и широко развита Адамсом [Адамс, 1965].
В качестве типичной иллюстрации полезности этих обоб-
щенных характеристических классов укажем работу [Андерсон,
Браун, Петерсон] о спинорных кобордизмах. Предположим, что
дано ориентированное односвязное многообразие М с и)2(М) —
= 0. Для того чтобы узнать, будет ли многообразие А1 грани-
цей некоторого ориентированного многообразия с w2 = 0, нуж-
но проверить не только то, что все его числа Штифеля — Уитни
и числа Понтрягина равны нулю, но и то, что все его /(О-ха-
рактеристические числа равны нулю.
Коннер и Флойд [Коннер, Флойд, 1966] ввели классы типа
классов Чженя для теории когомологий, соответствующей комп-
лексным бордизмам. Алгебраический аппарат в этой ситуации
оказался особенно гибким, что привело к быстрому развитию
теории, в которое внесли свой вклад сразу несколько авторов,
в особенности С. П. Новиков (см. [Новиков, 1967], а также
[Адамс, 1967]).
1 А также [Стоит]. — Прим, ред.
ПРИЛОЖЕНИЕ А
СИНГУЛЯРНЫЕ ГОМОЛОГИИ И КОГОМОЛОГИИ
В этом приложении будут даны краткие доказательства
ряда теорем из теории сингулярных когомологий, которые ис-
пользовались в основном тексте. Чтобы фиксировать обозначе-
ния и соглашения о знаках, начнем с основных определений.
Несмотря на это, мы предполагаем у читателя некоторое зна-
комство с теорией гомологий и когомологий. В частности, мы
предполагаем, что читатель знаком с теми фундаментальными
свойствами, которые суммированы в аксиомах Эйленберга и
Стинрода [Эйленберг, Стинрод, 1958].
За время, прошедшее с тех пор, как были прочитаны лек-
ции, послужившие основой этой книги, появилось несколько
руководств, излагающих теорию гомологий и когомологий на
нужном нам уровне, из которых отметим [Хилтон, Уайли,
1966], [Спеньер, 1971] и [Дольд, 1976].
Основные определения
Стандартным п-мерным симплексом называется выпуклое
множество Ал с: Rn+1, состоящее из всех наборов (to, Л, .... tn)
из п + 1 вещественных чисел, таких, что
to + t\ + ... -j-Zn=l.
Всякое непрерывное отображение симплекса А” в топологиче-
ское пространство X называют сингулярным п-мерным симп-
лексом в X; i-й гранью сингулярного n-мерного симплекса
о: Ал -> X называется сингулярный (п — 1) -мерный симплекс
ooq)z: А"-1 ->Х,
где ф/: Ал-1 Ал — линейное вложение, задаваемое формулой
Фг (to> • • • > ti_\, ti+i, ..., tn) — (to, . •., //_i, 0, t[+i, .... tn).
Для каждого n^O группой сингулярных цепей Сп(Х\ Л.)
с коэффициентами в коммутативном кольце А называется сво-
бодный A-модуль, имеющий по одной образующей [о] для каж-
214 Дж. Милнор и Дж. Сташеф
дого сингулярного «-мерного симплекса о в пространстве X.
При п < 0 группа СП(Х; Л) по определению считается нулевой.
Граничный гомоморфизм
д: Сп(Х; А^С^Х-, Л)
определяется формулой
д [о] = [о о Фо] — [о о ф1] + — ... 4- (—1)л [а о фп].
Легко проверяется тождество д о д = 0. Поэтому мы можем
определить «-мерную группу сингулярных гомологий Нп(Х;А)
как фактормодуль Zn(X-, А)/Вп(Х; А), где Zn(X;A)—ядро го-
моморфизма д: Сп(Х\ А)—► Сп-1 (X; А), а Вп(Х-, А) — образ гомо-
морфизма д: Сп+1 (X; А)-> Сп(Х; А). Здесь и всюду в этом при-
ложении слово «группа» фактически означает «левый А-мо-
дуль».
Группа коцепей С”(Х;А) — это по определению двойствен-
ный модуль Нотл(Сп(Х; А), А), состоящий из всех А-линейных
отображений группы СЛ(Х;А) в А. Значение коцепи с на цепи
у будет обозначаться (с, у>еА. Кограница коцепи с£Сл(Х;
А) — это по определению коцепь бс е Сп+1(Х; А), значение ко-
торой на каждой («4* 1)-мерной цепи а определяется тожде-
ством
(бс, а) 4- (—1)" (с, да) — 0.
Таким образом, мы получаем соответствующие модули
Нп (X; А) = Zn (X; А)/Вп (X; А) = (ker 6)/(im б),
которые называются группами сингулярных когомологий про-
странства X.
Замечание. Выбор знака в формуле, определяющей коцепь
бс, основан на следующем соглашении. Всякий раз, когда пе-
реставляются два символа размерностей тип, вводится знак
(—l)”1”. При этом операторы д и б рассматриваются как имею-
щие размерность соответственно —1 и 4-1. Таким образом,
наше соглашение о знаках такое же, как и в книгах [Маклейн,
1966] и [Дольд, 1976], но отличное от того, которое принято
в книгах [Эйленберг, Стинрод, 1958] и [Спеньер, 1971].
В некоторых случаях, особенно в теории препятствий, важно
рассматривать когомологии с коэффициентами в произвольном
A-модуле. Однако в этом приложении мы будем рассматривать
лишь когомологии с коэффициентами в самом кольце А.
Приложение А. Сингулярные гомологии и когомологии 215
Соотношение
между гомологиями и когомологиями
С этого момента будем предполагать, что Л есть область
главных идеалов (например, кольцо целых чисел или некоторое
поле). Чтобы упростить обозначения, мы будем опускать сим-
вол Л всякий раз, когда это только возможно, например писать
НпХ вместо Ял(Х;Л). Для обозначения полной последователь-
ности групп (НйХ, Н\Х, Н2Х, ...) часто будет использоваться
сокращенная запись Н*Х.
Теорема А.1. Предположим, что группа Нп-\Х нулевая или
является свободным Л-модулем. Тогда группа НпХ канонически
изоморфна модулю НошЛ(ЯпХ, Л), состоящему из всех А-ли-
нейных отображений НпХ в Л.
Справедливо соответствующее утверждение для пар {X, Л).
(См. [Маклейн] или [Спеньер].) Заметим, что предположе-
ние теоремы всегда удовлетворяется, если Л — поле.
Доказательство. Для заданных элементов х е НпХ и | е
е НпХ определим «индекс Кронекера» <х, £>е Л следующим
образом. Выберем какой-нибудь представляющей коцикл г е
е ZnX элемента х и какой-нибудь представляющий цикл £ е
ZnX элемента £ и положим <х, £> равным <z, £>е Л. Чита-
тель может проверить, что это значение не зависит от выбора
представителей z и Теперь определим гомоморфизм
k: Ял(Х)->НотЛ(Я„Х, Л),
полагая k(x) (g)=<x, £>.
Доказательство того, что k есть гомоморфизм на. Прежде
всего заметим, что подмодуль ZnX с СпХ является прямым сла-
гаемым. Это следует из того, что фактормодуль
Сп (X)/Zn (X) ~ Bn_t (X) с С„_, (X)
является подмодулем свободного модуля и, следовательно, сам
свободен (см., например, [Капланский] *). Следовательно, лю-
бой гомоморфизм ZnX—► А можно продолжить на СпХ.
Пусть f — произвольный элемент модуля Нотд(ЯпХ, А).
Композиция
Z„X->tfnX-UA
продолжается до гомоморфизма F: СпХ -* А. Так как гомомор-
физм F обращается в нуль на границах, то 6F = 0. Пусть х е
» А также [Ленг, 1965, стр. 432]. — Прим, перед.
216 Дж. Милнор и Дж. Сташеф
е Н"Х — класс когомологий коцикла F: Тогда для любого эле-
мента £ е НпХ с представителем £ е ZnX мы имеем
<x,g> = F (□ = /«).
Таким образом, k(x) = f, чем и доказано, что k есть гомомор-
физм на.
Доказательство того, что k имеет нулевое ядро. Пусть zo е
^ZnX — такой коцикл, что <z0, £>= 0 для всех циклов
е ZnX. Нам надо показать, что z0 является кограницей.
Поскольку коцикл Zo обращается в нуль на циклах, то ком-
позиция Zo<?-1: Bn-iX-+ Л однозначно определена. Так как фак-
тормодуль
Zn_lX/Bn_lX = Hn_lX
по предположению свободен, то отсюда следует, что группа
Вп-1Х является прямым слагаемым группы Zn-iX и, следова-
тельно, прямым слагаемым группы Cn-iX. Таким образом, гомо-
морфизм год~' может быть продолжен на Cn-iX. Пусть
Л
— такое продолжение; тогда
<6/, [а]) = ± (f, д [ст]) = ± zQd~l (д [ст]) = ± (zo, [ст]).
Следовательно, коцикл ±z0 равен когранице коцепи f, что и
требовалось установить. 
Гомологии клеточных разбиений
Пусть К — пространство некоторого клеточного разбиения
(см. определение 6.1) и К" с К обозначает п-мерный остов
(т. е. объединение всех клеток размерностей ^п).
Лемма А.2. Относительная группа гомологий Hi{Kn, Л"-1) с
коэффициентами в кольце Л равна нулю, если i^= п, а для
i = п является свободным модулем с одной образующей на
каждую п-мерную клетку разбиения К.
Отсюда вытекает в силу теоремы А.1, что группа когомоло-
гий Н1(Кп, Кп~1) также нулевая для i п.
Доказательство. Мы предполагаем, что читатель знаком с
тем основным фактом, что группа гомологий //,(Rn. R"\0)
равна нулю для i п и изоморфна Л при i п. (См., напри-
мер, [Дольд, 1976]; ср. с теоремой А.5 ниже. Так как единич-
ный шар Dn является деформационным ретрактом пространства
R", а единичная сфера S"-1 — деформационным ретрактом про-
Приложение А. Сингулярные гомологии и когомологии 217
странства Rn\0, то группа гомологий /7,(R", Rn\0) изоморфна
группе Hi(Dn,Sn~l), которая вычисляется в книгах [Эйленберг,
Стинрод] или [Спеньер].)
Пусть S — дискретное множество, которое состоит из точек
Se, выбранных по одной внутри каждой n-мерной клетки Е раз-
биения К. Тогда, как нетрудно видеть, разбиение Л71-1 будет
деформационным ретрактом пространства A"\S. Используя
точную последовательность тройки (Кп, Kn\S, Кп~1), мы полу-
чаем, что
Hi (К", К"-1) ~ Hi (к", Ка \ S).
По аксиоме вырезания эта последняя группа изоморфна группе
Hi(\JE, \J(E\se)), где U-Е обозначает дизъюнктное объединение
всех п-мерных клеток разбиения К. Но i-я группа гомологий
такого дизъюнктного объединения открытых подмножеств про-
странства К.п, очевидно, является прямой суммой групп гомо-
логий Hi(E, E\se) = Hi(Rn, R"\0), последняя же группа в раз-
мерности i = п является свободной с одной образующей, а во
всех других размерностях — нулевой. 
Следствие А.З. Группа HiKn равна нулю для 1>п и изо-
морфна группе HiK для i < п. Аналогичное утверждение вер-
но для когомологий.
Доказательство. Для гомологий. Разумеется, HiK° = 0 для
I > 0. Используя точную последовательность
HiKn~' -> HtKn -> Hi (кп, /с"*1),
получаем индукцией по п, что Н,(Кп) — 0 для i > п. Если i < п,
то применение аналогичной последовательности дает изомор-
физм HiKn s* HiKn+i, и, следовательно, по индукции
HiKn ~ HtK.n+l ~ HiK^2
Если К— конечномерное разбиение, то это завершает доказа-
тельство. В общем случае нужно воспользоваться теоремой о
том, что группа изоморфна прямому пределу при г -> оо
групп HiKr. Этот факт следует из того, что как любой сингу-
лярный симплекс в К содержится в некотором компактном под-
множестве этого пространства и, значит, содержится в некото-
ром Кг (см. [Уайтхед, 1949], § 5 (D)).
Для когомологий. Аналогичным образом показывается, что
относительная группа Hi (К., Кп), будучи изоморфна группе
К"), является нулевой для I п. Следовательно,
Н‘(К, Кп) — 0 для i^n по теореме А.1, и используя точную
когомологическую последовательность пары (К, Кп1, мы видим,
218 Дж. Милнор и Дж. Сташеф
что н1 (К) Н1 (Кп) для i < п. Доказательство того, что
Н‘ (К.п)— 0 для i> п, проводится точно так же, как соответ-
ствующее доказательство для гомологий. 
ОПРЕДЕЛЕНИЕ. Свободный модуль Нп(Кп, Кп~1) будем
называть группой п-мерных цепей клеточного разбиения К и
обозначать ^пК =	(Л; Л). Аналогично модуль
Я" (Г, Л"’1) ~ Ношд Л)
будем называть группой п-мерных коцепей и обозначать
«Граничный» гомоморфизм дп: ffn+iK -* 'S’nK. получается из
точной гомологической последовательности тройки (К"+1, Ка,
/С"-1). Аналогично определяется «кограничный» гомоморфизм
Теорема А.4. Группа гомологий 3£пК/$пК цепного комплекса
канонически изоморфна группе сингулярных гомологий
НпК. Аналогично, группа когомологий ZnK/f8nK коцепного
комплекса Ч?*К. канонически изоморфна группе сингулярных
когомологий НпК-
Доказательство. Рассмотрим следующую коммутативную
диаграмму:
О
Горизонтальная строка в этой диаграмме является частью точ-
ной гомологической последовательности тройки (Ап+1, К.п,
а вертикальная — частью точной последовательности тройки
(Ка, /С"-1, К"-2). Из диаграммы следует, очевидно, что
Г’2)
и
ад„^я„(кп+1, Г-2).
Но ь силу следствия А.З
Нп (КЛ+1, Кп~2) HnKn+i нпк.
Доказательство для когомологий совершенно аналогично. 
Приложение А. Сингулярные гомологии и когомологии 219
^-умножение
Для заданных коцепей с е СтХ и с' е СпХ произведение
сс' = с с' е Ст+пХ определяется следующим образом. Пусть
а: Ат+п->Х— сингулярный симплекс. Передней т-мерной
гранью симплекса о называется композиция аоат' Ат-+Х, где
®т(А)» •••> tm)— (fot •••» ^m> 0, •••» 0)«
Аналогично, задней п-мерной гранью симплекса а называется
композиция о о Ал -> X, где
Pn(^m> 6п+1» •••» 1т+п) == (0, • ••» 0, tm, • ••» tm+n)'
Мы определяем произведение сс' = с с' тождеством
<с< [а]> = (- 1Г*{с, [ао<хт]>(с', [Ооря]>еЛ.
Эта операция умножения коцепей билинейна и ассоциативна,
но не коммутативна. Постоянный коцикл 1 е С°Х служит еди-
ничным элементом для этой операции. Легко проверяется фор'
мула
б (сс') = (бс) с' + (—1)"* с (бс').
Отсюда вытекает существование соответствующей операции
умножения НтХ ® НпХ -* Нт+пХ классов когомологий. На уро,
вне когомологий эта операция умножения уже коммутативна с
точностью до знака (см., например, [Спеньер]). Фактически
для элементов а е НтХ, b е НпХ имеет место формула Ьа =
= (—i)mnab. В теории градуированных групп это свойство на-
зывают коммутативностью. Таким образом, мы можем сказать
коротко, что когомологии Н* (X) = (HQX, Н'Х, НаХ, ...) обра-
зуют коммутативное градуированное кольцо.
Теперь предположим, что дана пара пространств X А. Если
коцепь с принадлежит подмножеству Ст(Х, А) с СтХ (т. е. если
с[о] = 0 для любого сингулярного симплекса о: Ат—►АсХ) и
если с' е СпХ, то, очевидно, коцепь сс' принадлежит Ст+п(Х, А).
Это дает возможность построить операцию умножения
Нт(Х, А)®НпХ->Нт+п(Х, А).
Волее общим образом, рассмотрим два подмножества А, ВсХ,
которые удовлетворяют следующему предположению.
ПРЕДПОЛОЖЕНИЕ. Оба множества А и В являются отно-
сительно открытыми как подмножества объединения A U В.
Тогда операцию умножения
Нт(Х, А)®Нп(Х, В)->Нт+п(Х, АО В)
220 Дж. Милнор и Дж. Сташеф
можно определить следующим образом1. Пусть Cn(X; A, B)cz
cz С‘(X) обозначает пересечение подмодулей С'(Х, Л) и С{(Х, В)
модуля С‘(Х). Ясно, что для данных коцепей сеСт(Х, Л) и
с' е С"(Х, В) произведение сс' принадлежит пересечению
Cm+"(X; А, В) = Ст+п(Х, А)(]Ст+п (X, В).
Очевидно, имеет место короткая точная последовательность ко-
цепных комплексов
0->С*(Х, Д11В)->(?(Х; /В) ->С*(Л1|В; А, В)->0.
Но стоящий справа в этой точной последовательности коцепной
комплекс ацикличен (см. [Эйленберг, Стинрод] или [Спеньер]).
Поэтому вложение
С*(Х-, Л11В)->С*(Х; А, В)
индуцирует изоморфизм групп когомологий. Следовательно, мы
получаем операцию ^-умножения со значениями в требуемой
группе когомологий Нт+п(Х, A U В).
Когомологии произведения пространств
Пусть RS обозначает дополнение к началу координат в про-
странстве Rn. Мы хотим доказать, что для любого простран-
ства X
НтХ ~ Bm+" (X X R", X X Ro).
Этот изоморфизм лучше всего описать при помощи операции
когомологического ^.-умножения. Предположим, что даны кого-
мологические классы
а<=Нт(Х, Л), b<==Hn(Y, В),
где А — открытое подмножество пространства X, а В — открытое
подмножество пространства У. (Если В пусто, то А не обяза-
тельно должно быть открытым, и наоборот.) Используя проек-
ции
pi‘- (ХХУ, AXY)-+(X, А),
Рг- (XXГ, ХХВ)»(У, В),
j 1 Возникающие здесь трудности связаны с тем фактом, что
Сг (X, Л) П с1 (X, В) С1 (X, А и В),
так как сингулярный симплекс в X может лежать в A U В и при этом не
лежать ни в А, ни в В.
Приложение А. Сингулярные гомологии и когомологии 221
определим ^-произведение (или внешнее когомологическое про-
изведение) а X b как когомологический класс
(pja) (р;&) е Нт+п (X X Y, (А X П U (X X В)).
Иногда будет удобно использовать для пары (X X Y,
(AX^)U(XX5)) сокращенную запись (X, А)Х(У, В). Заме-
тим для примера, что при этом соглашении пару (R*, Ro) мож-
но записать в виде n-кратного произведения (R, Ro)X •••
... X(R.R).
Выберем специальную образующую еп свободного модуля
Нп (Rn, Ro) следующим образом. Пространство Ro = R\O мо-
жет быть представлено как дизъюнктное объединение двух по-
лупрямых R-UR+. Пусть ee//’(R, Ro) — элемент, отвечающий
тождественному элементу 1 е H°R+ при изоморфизме выреза-
ния и кограничном изоморфизме:
77°R+^_№(R0, R_)_^tfl(R, Ro),
где 6 — кограничный гомоморфизм из точной последователь-
ности тройки (R, Ro, R-). Через е” е Нп (Rn, Ro) мы обозначим
n-кратное Х-произведение е X • • • Хе.
Теорема А.5. Для любой пары (X, А), где А — открытое под-
множество в X, соответствие а>—>а‘Хеп определяет изоморфизм
Hm (X, А) -> Нт+п ((X, А) X (R", Ro)).
Доказательство. Прежде всего заметим, что достаточно рас-
смотреть случай п= 1. Общий случай получается по индукции,
если воспользоваться законом ассоциативности:
а X еп — (а X ел-1) X е.
Случай 1. Предположим, что п — 1 и что А пусто. Для фикси*
рованного элемента а е НтХ имеем диаграмму
Я° (R+) ч-----Н° (Ro, R_)--—* Hl (R, Ro)
|ах Jax Jex
НтХ^Нт (XXR+)«^- tfm(XXRo, XXR_) Л- Hm+X (XXR, XXRo).
которая коммутативна с точностью до знака. Гомоморфизм i* —
это изоморфизм вырезания. Гомоморфизм б' взят из точной ко-
гомологической последовательности тройки (XX R> XX Ro,
XXR-). Он является изоморфизмом, так как оба пространства
X X R и X X R- содержат в качестве деформационного ретракта
подмножество X X (точка) .
222 Дж. Милнор и Дж. Сташеф
Обходя эту диаграмму, мы видим, что элемент аХее
е Hm+l (X X R, XX Ro) есть образ элемента а е НтХ при ком-
позиции изоморфизмов. Этим доказано наше утверждение для
случая 1.
Случай 2. Предположим, что п = 1 и что А непусто. Пусть
zeZ^R, Ro)—коцикл, представляющий когомологический
класс е. Рассмотрим следующую коммутативную диаграмму:
О-------► Ст (X, Л)-----> Ст (X)-----► Ст (А)-----► О
1Хг 1хг |хг
0->Cm+I (XXR; XX Ro, XXR)~>Cm+1 (XXR,XXRo)->C'n+1 (XXR, 4XRo)->0
Непосредственные рассуждения показывают, что горизонталь-
ные последовательности являются точными. Далее, все верти-
кальные гомоморфизмы коммутируют с кограничным операто-
ром:
б (a X г) = (ба) X z.
Таким образом, имеет место соответствующая коммутативная
диаграмма групп когомологий
...-Л.//т(Х, Л)----->НаХ-------*нтА-±+...
|х • |х * |х *
..Лнт+1 (X,X)X(R,Яо))->Ят+1 (XXR,XXRo)->//m+1 MXRMXRo) Л...
(см., например, [Спеньер]). Согласно случаю 1, две правые вер-
тикальные стрелки суть изоморфизмы. Следовательно, по лемме
о пяти гомоморфизмах и левая вертикальная стрелка также
изоморфизм.
Итак, мы доказали теорему А.5 для случая, когда п— 1. Но,
как замечено в начале доказательства, отсюда следует, что она
верна для всех п. В
Теперь рассмотрим два пространства X и У. Операция
X-умножения определяет гомоморфизм
X: Ф Я'ХвЯ'У-^Я'ЧХХУ).
i+i-n
Хотелось бы, конечно, доказать, что гомоморфизм X есть изо-
морфизм, но это в общем случае не так. Это не так, например,
если X и У— вещественные проективные плоскости (для кого-
мологий с целочисленными коэффициентами) или если X и У —
бесконечные дискретные пространства (для когомологий с про-
извольной областью коэффициентов).
Теорема А.6. Пусть X и Y — такие клеточные разбиения, что
каждая группа когомологий Н1Х является К-модулем без кру-
Приложение А. Сингулярные гомологии и когомологии 223
чения *, a Y имеет лишь конечное число клеток в каждой раз-
мерности. Тогда прямая сумма ф Н‘Х ® H!Y изоморфно ото-
i+i-=-n
бражается на Нп(ХХ У).
Аналогичный результат может быть доказан для пар (X, А)
и (У, В). Утверждения этого типа известны как теоремы Kjoh-
нета, ибо их прототипом служит теорема, доказанная в 1923 г.
X. Кюннетом. Один более сильный вариант теоремы см. в книге
[Спеньер].
Доказательство. Сначала предположим, что У — конечное
клеточное разбиение. Тогда нашу теорему можно доказать ин-
дукцией по числу клеток разбиения У. Конечно, теорема верна,
если У состоит из одной-единственной точки.
Пусть Е — открытая клетка в У наивысшей размерности и
У1 = У \ Е. Предположим по индукции, что гомоморфизм
X': ф Я'Х®Я/У1->ЯЛ(ХХУ1)
i+!-n
является изоморфизмом. Рассмотрим коммутативную с точ-
ностью до знака диаграмму
... ->ф Н1Х ® H‘Y ->фН1Х ® Я'У1 ->ф Я'Х ® Яж (У, У1) -> ...
Iх	|Х-	|х-
... ->Я'1(ХХ1,)->Яп(ХХГ1)->Ял+1(ХХУ, ХХУ1)-> ...
Верхняя строка в этой диаграмме получена из точной последо-
вательности пары (У, У1) при помощи тензорного умножения на
группу когомологий Н‘(Х) с последующим взятием прямой сум-
мы по всем I, j, таким, что i + / = п. Так как модуль Н1Х не
имеет кручения, то эта последовательность остается точной (см.
[Маклейн] [Картан, Эйленберг]).
По предположению X' является изоморфизмом. Используя
теорему А.5 вместе с изоморфизмами
Н> (У, У1) <- Н! (У, У \ точка)) -> Н> (Е, Е \ точка)
и
Hn(XXY, ХХУ1)<-ЯЛ(ХХГ, х х (У \ точка)) ->
-> Ял (XX Е, XX (Е\ точка)),
мы видим, что X" — также изоморфизм. Следовательно, по
лемме о пяти гомоморфизмах X есть изоморфизм. Этим завер-
шается доказательство для случая, когда У — конечное разбие-
1 Конечно, это предположение автоматически выполняется, если Л —
поле. Предположение, что X представляет собой клеточное разбиение, не
обязательно, оно принято лишь для упрощения доказательства.
224 Дж. Милнор и Дж. Сташеф
ние. (Мы даже не использовали предположение, что X является
клеточным разбиением.)
Если разбиение У бесконечно, но каждый его остов Уг коне-
чен, то приведенные выше рассуждения применимы к произве-
дениям X X Уг- Однако, как легко вытекает из следствия А.З,
вложения
УГ->У, XXYr-+XXY
индуцируют изоморфизм групп когомологий в размерностях,
меньших г. Таким образом, теорема А.6 верна для п < г. По-
скольку г может быть выбрано сколь угодно большим, это за-
вершает доказательство. В
Гомологии многообразий
Мы докажем здесь некоторые предварительные результаты,
которые нам понадобятся при построении фундаментального
гомологического класса многообразия и доказательстве теоремы
двойственности Пуанкаре (см. лемму 11.5).
Пусть М — фиксированное n-мерное многообразие, не обяза-
тельно компактное. Изучим прежде всего группы Hi (М, М \ К),
где К — какое-нибудь компактное подмножество многообразия
М. Если К a L cz М, то естественный гомоморфизм
Ht(M, М \L)-+ Ht(M, M\K)
будем обозначать через рк. Образ рх(а) можно представлять
себе как «ограничение» элемента а на подмножество К.
Лемма А.7. Группы гомологий Hi(M, М\К) являются нуле-
выми для i > п. Гомологический класс а е Нп (М, М\К) равен
нулю тогда и только тогда, когда для любой точки х^К равно
нулю ограничение
рх(а)(= Я„(М, М\х).
Доказательство разобьем на шесть шагов.
Шаг 1. Предположим, что М = R" и К — компактное выпук-
лое подмножество.
Пусть х — точка компакта К и S — достаточно большая
(п—1)-мерная сфера с центром в х. Тогда S является дефор-
мационным ретрактом одновременно и Rn \ х и Rn \ К. Отсюда
следует, что
Ht (Rn, Rn\K)-^ Hi (Rn, Rn \ x)
для всех i, чем доказана справедливость нашей леммы в рас-
сматриваемом случае.
Приложение А. Сингулярные гомологии и когомологии 225
Шаг 2. Предположим, что К — К\ U Кг, причем известно, что
утверждение леммы выполнено для Ki, Кг и К\ П Кг.
Воспользуемся относительной последовательностью Майе'
ра — Вьеториса
м\(^и/с2))Хядм, М\К)-±>
->Яг(М, М\К1)®Н{(М, М\Кг)-> ....
где гомоморфизм s определяется равенством
s (а) = P^(a)®Pj<, (“)
(см., например, [Эйленберг, Стинрод] или [Спеньер]). Распо-
лагая такой последовательностью, легко можно доказать желае-
мый результат для нашего случая. Детали предоставляем чи-
тателю.
Опишем вкратце, как строится эта последовательность. Обо-
значим открытое множество М \ К> через Up Далее, по анало-
гии с рассуждениями на стр. 220 обозначим через Ui, I72)
факторгруппу	+ CiU2), где CiU1 + CiU2 a:
cz Ci(Ui u t/2)— свободный модуль, порожденный всеми сингу-
лярными i-мерными симплексами, которые лежат либо в Up
либо в U2. Тогда естественный гомоморфизм
СДМ; Ub U2)-+C,(M, Ui\)U2)
индуцирует изоморфизм групп гомологий (ср. с рассуждениями
на стр. 220). Коммутативная диаграмма
позволяет теперь построить короткую точную последователь*
ность
0 -> Ct (М,	U U2) Ct (М, Ui) ® Ct (М, U2)
-+С{(М-, иь U2)^0.
Ассоциированная длинная точная последовательность групп го-
мологий дает требуемую относительную последовательность
Майера — Вьеториса.
Шаг 3. Подмножество К <= R" является конечным объедине-
нием Ki U ... U Кг компактных выпуклых подмножеств.
8 Дж. Милнор, Дж. Сташеф
226 Дж. Милнор и Дж. Сташеф
В этом случае лемма может быть доказана индукцией по
числу г при помощи шагов 1 и 2.
Шаг 4. Пусть К— произвольное компактное подмножество
пространства R".
Для данного элемента	Rn \ К) выберем компакт-
ную окрестность N множества К и класс a'eHi(R\ Rn \ N)
так, чтобы рк(а') = а. Это возможно, ибо мы можем выбрать
такую цепь у е C(R", образ которой по модулю R" \ К будет
циклом, представляющим а. Граница этой цепи у имеет «носи-
телем» компактное подмножество, не пересекающееся с К, и
надо только подобрать окрестность Л/ настолько малую, чтобы
она не пересекалась с этим «носителем».
Покроем множество К конечным набором замкнутых шаров
Bi....Вг, таких, что BiCiN и Bi (] К. = 0. Если i > п, то
PbjU ив (а) ~ 0 (шаг слеД°вательно, а = 0. Если I = п и
Рх(а) = 0 для каждой точки хе К, то ясно, что рх(а')=0 для
любой точки х е В] U ... U Вг (см. шаг 1). Значит, опять
Рв,и ... ив,(а,) = 0 и поэтому а = 0.
Шаг 5. Пусть компактное подмножество К с М настолько
мало, что имеет окрестность U, гомеоморфную R".
Так как по аксиоме вырезания имеет место изоморфизм
Н,(М, М \	U \ К), то наше утверждение следует в
этом случае из шага 4.
Шаг 6. Компактное подмножество К cz М произвольно.
Тогда К — Ki U ... U Кг, где каждое из подмножеств Kj до-
статочно «мало», как на шаге 5. Доказательство получается те-
перь индукцией по числу г с использованием шага 2. Это пол-
ностью завершает доказательство леммы А.7. 
Фундаментальный
гомологический класс многообразия
Далее мы будем использовать в качестве области коэффи-
циентов бесконечную циклическую группу Z. Напомним, что для
каждой точки х е М группа гомологий
Hi (М, М \ х; Z) Ht (Rn, R" \ 0; Z)
является бесконечной циклической для i = п и нулевой для
i ф п.
ОПРЕДЕЛЕНИЕ. Локальной ориентацией многообразия
М в точке х называется выбор одной из двух возможных обра-
зующих группы Нп(М, М \ х; Z).
Приложение А. Сингулярные гомологии и когомологии 227
Заметим, что локальная ориентация рх в точке х определяет
локальную ориентацию ру для всех у из достаточно малой окре-
стности точки х. Более точно, если В — шар с центром в х (от-
носительно некоторой локальной координатной системы), то
для каждой точки у е В изоморфизмы
ЯДЛ4, Л4\х)-^-Я.(ЛГ, М \ В)-4 ЯДЛГ, М\у)
определяют локальную ориентацию р».
ОПРЕДЕЛЕНИЕ. Ориентацией многообразия М называется
функция, сопоставляющая каждой точке х е М локальную ори-
ентацию рх> которая непрерывно зависит от х в следующем смы-
сле: для каждой точки х должны существовать компактная
окрестность N и класс р№ Нп(М., М\ N), такие, что рй(^) =
= р? для всех у е N.
Пара, состоящая из многообразия и ориентации, называется
ориентированным многообразием.
Теорема А.8. Для любого ориентированного многообразия М
и любого компактного подмножества КсМ существует один и
только один класс рк е Нп(М, М\К), удовлетворяющий усло-
вию рх (рх) = Цх для каждой точки х^Д.
В частности, если многообразие М само является компакт-
ным, то существует один и только один гомологический класс
Рм е Нп (М) с требуемым свойством. Этот класс р = рм назы-
вается фундаментальным гомологическим классом многообра-
зия М.
Доказательство. Единственность класса рк немедленно вы-
текает из леммы А.7. Доказательство существования разобьем
на три шага.
Шаг 1. Если подмножество К содержится в достаточно ма-
лой окрестности некоторой заданной точки, то существование
класса рх следует из определения ориентации.
Шаг 2. Предположим, что К = Ki U К2, причем классы рх, и
Рх2 существуют. Как и в доказательстве леммы А.7, рассмот-
рим точную последовательность
...	М\К)-^Нп(М, M\Ki)QHn(M, М\К2)
~^Нп(М,	....
где
s(a) = pKi(a)®p/<(a)>
^(Р®¥) = Рд1ПД.(Р)-Рк1Пд1(¥).
8*
228 Дж. Милнор и Дж. Сташеф
По теореме единственности, примененной к компакту K.Y П Кг,
имеем / (рЛ1фрА!) = 0, следовательно, рЛ1 ф рЛг = s (а) для неко-
торого однозначно определенного элемента а^Нп(М, М \ К).
Этот элемент а и есть искомый класс рк.
Шаг 3. Компактное подмножество К с: М произвольно. То-
гда К = Kill ••• II Кг, где соответствующие классы рК/ суще-
ствуют согласно шагу 1, и класс рк строится при помощи ин-
дукции по числу г. 
Замечание 1. Для любой области коэффициентов Л канони-
ческий гомоморфизм Z-*A задает класс в группе Нп(М, М \ К;
Л), который также будет обозначаться рЛ. Особенно важен
случай Л = Z/2, так как mod 2-гомологический класс
рх<=Я„(М, М\К; Z/2)
может быть непосредственно построен для любого многообра-
зия, без каких бы то ни было предположений об ориентируе-
мости.
Замечание 2. Аналогичные рассмотрения применимы к ори-
ентированному многообразию М с границей. Для каждого ком-
пактного подмножества К с Л1 существует однозначно опреде-
ленный класс рк е Нп (М (М \ К) U дМ), такой, что рх(рк) = рх
для любой точки х е К П (Af \ дМ). В частности, если многооб-
разие М компактно, то существует единственный фундаменталь-
ный гомологический класс рмеЯп(Л1, дМ) с требуемым свой-
ством. Можно показать, что естественный гомоморфизм
д'. Нп(М, дМ)->Нп-у(дМ)
переводит класс рм в фундаментальный гомологический класс
многообразия дМ. (См. [Спеньер].)
Когомологии с компактными носителями
Говорят, что коцепь с s С‘М имеет компактный носитель,
если существует компактное множество КаМ, такое, что ко-
цепь с принадлежит подмодулю С1 (М, М \ К) <=. С1 (М). Дру-
гими словами, коцепь с должна обращаться в нуль на любом
сингулярном симплексе из М \ К- Коцепи с компактными носи-
телями образуют подмодуль, который будет обозначаться
CcompAI cz С1М. Группы когомологий соответствующего комплек-
са CcompAI будут обозначаться KcompAf. Непосредственные
рассуждения показывают, что группа ЯсотрА! изоморфна пря-
мому пределу групп Н‘(М, М\К), где К пробегает направлен-
ное множество, состоящее из всех компактных подмножеств
Приложение А. Сингулярные гомологии и когомологии 229
многообразия М (см. [Спеньер]). Заметим, что, если М ком-
ПаКТНО, ТО ЯсотрМ НГМ.
В случае когда многообразие М ориентировано, существует
важный гомоморфизм
ЯсотрМ->Л,
который будет записываться как а -* а ГЛ4] и называться инте-
грированием на многообразии М. Если М компактно, то этот го-
моморфизм можно задать формулой
а[М] = (а, Цм>еЛ.
В общем случае надо выбрать некоторый представитель а' е
е Нп(М, М \ К) элемента а и положить
а[М] = « Ик>.
Читателю следует проверить, что это определение не зависит
от выбора К и а'.
«''-умножение
Для любого пространства X и любой области коэффициентов
существует билинейная операция спаривания
rv ClX®CnX~^Cn_iX,
которую можно описать следующим образом. Для каждой ко-
цепи b s С‘Х и каждой цепи | е СпХ о-произведение b r\ £ —
это однозначно определенный элемент в группе цепей Cn-iX, та-
кой, что
(1)	<a,b^l) = {ab,l>
для всех аеСя-,Х. Более явно, для каждой образующей [о]
группы цепей СпХ /^-произведение &г>[о] может быть опреде-
лено как произведение элемента кольца, коэффициентов
(—[задняя /-мерная грань симплекса о]}
на сингулярный симплекс
[передняя (п —/)-мерная грань симплекса а]1.
Комбинируя тождество (1) со стандартными свойствами
гл-произведения, можно вывести следующие правила;
(2)	=
(3)	1^ = £,
(4)
1 Определение передней и задней граней симплекса см. в пункте <о-
произведение» этого приложения. — Прим, перев.
230 Дж. Милнор и Дж. Сташеф
Из формулы (4) следует, что существует соответствующая one-
рация умножения
Н1 (X)® Нп(Х)Hn-i (X),
которая также будет обозначаться символом гл.
Используя эту операцию, мы можем теперь сформулировать
теорему двойственности для компактных многообразий при про-
извольной области коэффициентов.
Теорема двойственности Пуанкаре. Если многообразие М
компактно и ориентировано, то соответствие ai—>ar\pM задает
изоморфизм группы когомологий Н‘(М) с группой гомологий
Hn-iM.
Для неориентируемых многообразий теорема двойственности
также верна, но только при условии, что используется область
коэффициентов Z/2.
Доказательство, которое мы проведем, связано с рассмотре-
нием более общей ситуации и фактически дает более общую
теорему двойственности. А именно заметим, прежде всего, что
для любой пары (X, А) /^-умножение задает спаривание
Cl(X, А)®Сп(Х, A)-*Cn_tX
и, следовательно, спаривание
Hl(X, А)®Нп(Х, A)-+Hn_tX.
(Более общим образом можно определить спаривание
Н1(Х, А)®Нп(Х, A[)B)->Hn_i(X, В)
для случая, когда А и В открыты в A [JB.) Далее, пусть много-
образие М ориентировано, но не обязательно компактно. Опре-
делим отображение двойственности
D-. Н1сотрМ-*Нп_1М
следующим образом. Для любого элемента аеЯсотрЛ4 =
= lim Н1 (М, М\К) выберем какой-нибудь представитель
а' е Н1 (М, М \ К) и положим
Д(а) = а'гч ji*.
Это определение корректно, так как если KczL, то диаграмма
Н'(М.М\К) --------
Приложение А. Сингулярные гомологии и когомологии 231
очевидно, коммутативна. Отметим, что в том частном случае,
когда многообразие М компактно, D(a) = а г\ р,м.
Теорема двойственности А.9. Гомоморфизм D изоморфно
отображает еруппу когомологий Н1^ М на группу гомологий
В случае когда многообразие М компактно, мы получаем,
что гомоморфизм г\ цм изоморфно отображает группу Н‘М на
группу как и утверждалось выше.
Доказательство разобьем на пять шагов.
Шаг 1. Предположим, что М = R".
Для любого заданного шара В мы, очевидно, имеем
//n(R", Rrt\.8) = А, с образующей (см. лемму А.7, шаг 1).
Следовательно, //"(R", R" \ В)&£ Л, согласно теореме А.1, с об'
разующей а, такой, что <а, р,в> = 1. Тождество
(1а, Рв) = <1.
показывает теперь, что элемент а г\ цв является образующей
группы #oRn Л. Таким образом, гомоморфизм оцв изоморф’
но отображает группу 7f*(R", Rn \ В) на группу /f,(Rn), застав’
ляя шар В расти и переходя к прямому пределу, мы получаем,
что гомоморфизм D изоморфно отображает Я’отр (/?") на
группу Н, (R").
Шаг 2. Предположим, что М = U V, причем теорема вер-
на для открытых множеств U, V и U П V.
Мы построим коммутативную диаграмму
. . . Hlaomp (U П Ю -► ЯсотрС/ ® Яеотр V -> ЯеотрМ Л- . . .
Hn_t (U п ю -> Hn_t (U) ® Нп_{ (V) -+ Hn_t (М)	,
в которой нижняя строчка является последовательностью Май-
ера — Вьеториса (см. [Эйленберг, Стинрод]). Построение этой
нижней последовательности аналогично тому, которое было дано
в доказательстве леммы А.7. Чтобы построить верхнюю точную
последовательность, заметим, что для любых компактов KcU
и L с: V существует относительная последовательность Майе»
ра — Вьеториса	,
...	M\K(]L)-+Н1 (М,	M\L)->
M\KUL)-+ ....
232 Дж. Милнор и Дж. Сташеф
такая же, как указанная в доказательстве леммы А.7. Согласно
аксиоме вырезания, эту последовательность можно переписать
в виде
... v, ипу\япп-*яг(я,с;\л)®я'(7, v\D-»
...
Переход к прямому пределу при возрастании К и L дает тре-
буемую последовательность.
Применяя лемму о пяти гомоморфизмах к получившейся
диаграмме, приходим к утверждению теоремы для рассматри-
ваемого случая.
Шаг 3. Пусть многообразие М является объединением семей-
ства вложенных открытых множеств Ua, для каждого из кото-
рых наша теорема двойственности верна.
Тогда ЯсотрЛ! = Inn//compt/a И Hn-lM = Пт Hn-iUa,. (Оба эти
утверждения легко следуют из того, что любое компактное под-
множество многообразия М содержится в некотором Ua.) Но
прямой предел изоморфизмов есть изоморфизм.
Шаг 4. Многообразие М — произвольное открытое подмно-
жество в Rn.
Если М выпукло, то оно гомеоморфно Rn и доказываемое
утверждение имеет место согласно шагу 1. В общем случае вы-
берем последовательность выпуклых открытых множеств
Vi, Vz....объединение которых равно М. Применяя шаг 2,
можно по индукции доказать, что теорема верна для каждого
конечного объединения Vi U Vz U • • • U V*. Переходя к прямому
пределу при k—>оо, мы получаем, что она верна для всего мно-
гообразия М.
Шаг 5. Многообразие М произвольно.
Покроем М открытыми множествами Va, каждое из которых
диффеоморфно открытому подмножеству пространства R", и
выберем какое-нибудь полное (линейное) упорядочение в мно-
жестве индексов. (Если М имеет счетный базис, то в качестве
индексов можно использовать целые положительные числа.) Не-
посредственная трансфинитная индукция, использующая шаги
2—4, показывает, что теорема верна для каждого частичного
объединения (J Va. Следовательно, согласно шагу 3, она вер-
а<р
на для всего многообразия М. 
В заключение предлагаем читателю две задачи.
Задача А.1. Для ориентированного многообразия с грани-
цей построить изоморфизм двойственности
Н^отвМ->Нп-1(М, дМ).
Приложение А. Сингулярные гомологии и когомологии 233
Либо, полагая по определению
Ясотр (М, дМ) = lim Н1 (Af, (М \ Я) U дМ),
построить изоморфизм
Я‘отр(М, дМ)-+Нп_{М.
Задача А.2 (двойственность Александера). Пусть /С — ком-
пактное подмножество сферы S", являющееся ретрактом неко-
торой своей окрестности. (Это предположение нужно, посколь-
ку мы используем сингулярные когомологии, а не когомологии
Александрова — Чеха.) Показать, что группа когомологий Н1К
изоморфна прямому пределу lim HlU, где U пробегает множе-
ство всех окрестностей компакта К. Показать, что группа кого-
мологий H‘(Sn, К) изоморфна группе
lim Н1 (Sn, U) ~ Я*отр (Sn \К)~ Hn_t (Sn \ К).
Наконец, показать, что для заданных точек хе К и y^Sn\K
Н‘~1(К, х)^нп_^8п\к, у).
ПРИЛОЖЕНИЕ В
ЧИСЛА БЕРНУЛЛИ
поп как появилась теорема Хирцебруха о сигнатуре и
С т®1иенная теорема Римана —Роха, для топологов стало
его обоО з атЬ КОе-что о числах Бернулли и их теоретико-чис-
полезны*1 В этом приложении будут описаны некоторые
ловых с0°Й“рТВ
из этих сВ° 3„уЛЛИ Bi В2, ... могут быть определены как ко-
эффЧиц»е«™ Разложе"М " "еПеНН0Й РЯД
, =г,Л4Ь'»1 + 4г<2х>’—&<ЭД’ + 4г(2х>'-+ •••
tE7 sh*
й„_ «пи Ixl •< л), или, эквивалентно, разложения
(СХОДЯИ1И0СЯ при 1 I /
'' г 1	3-i--^-z2 — —z4 + —z6 — 4-
« — ssl--2+ 2! Z 4! Z 6! z 1- ••••
в 1
na„a гвязаны между собой легко проверяемым тожде-
Эти два Ряда свяв
СТВОМ	х  2х .
обозначениях читателю следует иметь в виду, что для
В этих 0 ли широко используются и другие обозначения1;
чисел у ьких первых чисел Бернулли таковы:
значения	1	___L	691
1 В2»Тп.	^4— 30’ °5	66’	2730’
6	„	7 о 3617
В8==-51о--
были впервые введены Яковом Бернулли, старшим
Эти чиСЛИ0г0 семейства математиков, в работе, опубликован-
из известно^
в 1713 г. Их можно вычислить, например, дей-
ной выполняя деление соответствующих степенных ря-
ствитель» домощи процедуры, основанной на докавываемой
дов или Р в J
ниже лем 00дСТвенные классические разложения в степенные
МногИ Р д ь вЫведены из указанных выше. Например, тож-
ряды могу
--------^пример, [*Воревич, Шафаревич, стр. 436]. — Прим. рвд.
1	См*»
Приложение В. Числа Бернулли 235
дество
1 _ 1 1
sh 2х	th х th 2х
приводит к ряду
^=1-(2>-2)Аи“ + (2*-2)-£<.<- + ...
(см. задачу 19.С), а тождество
thx=____2-_____-
11	х th 2х th х
— к ряду
thx = 22(22 -l)^-x- 24(24 - 1)>х3 + ~ ....
С этим рядом тесно связан ввиду равенства th iy = itgy сле-
дующий ряд:
tg у = 22(22 - 1) у + 24(24 - 1)^ у* + ....
При помощи этого последнего ряда можно доказать один инте-
ресный теоретико-числовой факт.
Лемма В.1. Для каждого п число 22п(22п — 1)Вп/2п — поло-
жительное целое.
Доказательство. Из приведенного выше разложения Тэй-
лора следует, что число 22п(22п—1)Вп/2п равно значению в
нуле (2п—1)-й производной от функции tg г/. Однако тожде-
ство
d (tgm y)/dy = m (tg"*-1 у + tgm+1z/)
вместе с непосредственной индукцией показывают, что (2п—1) -я
производная от функции tg у равна
апй + ащ tg2 у + ... + tg2ra у,
где коэффициенты апо, ап\, .... апп — некоторые положитель-
ные целые числа. В частности, значение в нуле равно положи-
тельному целому числу агао- И
Более общим образом, имеет место
Лемма В.2 (Липшица — Сильвестра). Для любого целого чи-
сла k выражение k2n(k2n— l)Bn/2n является целым числом.
Доказательство. Рассмотрим функцию
f(x) = 1 +е* + е2х+ ... +е(*-1)« = (е**_ 1)/(ех — 1).
236 Дж. Милнор и Дж. Сташеф
Заметим, что f(Q) — k и что все производные от / в нуле суть
целые числа. Возьмем логарифмическую производную от fi
(log - 1) - log (е* - 1) =
f (х) dx	eRX — 1 ех — 1
Используя разложение Тэйлора
е*  1 х ________1 (। _1_	_1_ г2_^2. у4 j_\
ех — 1 х е~х — 1 х\ 2	2!	4!
получаем, что
^ = (^1)у4Л*2-1)>••••
Следовательно, (2п—1)-я производная от функции f (х) /f (х)
в нуле равна ±(&2"— \)Вп/2п. Непосредственная индукция по-
казывает, что эта производная может быть представлена в виде
полинома от f(x), f'(x), .... f(2n)(x) с целыми коэффициентами,
поделенного на f(x)2n. Если положить х = 0, то это дает равен-
тво
(k2n — 1)Вп/2п = (целое число)/£2л,
что и требовалось доказать. 
В следующих двух теоремах содержится более точная тео-
ретико-числовая информация. Первая из них была доказана
независимо Т. Клаузеном и К. Г. К. фон Штаудтом в 1840 г.
Теорема В.З. Рациональное число (—\)пВп сравнимо по
модулю Z с числом	где суммирование производится по
всем простым р, таким, что р — 1 делит 2п. Следовательно, зна-
менатель числа Вп, представленного в виде несократимой дроби,
равен произведению всех простых чисел р, таких, что (р—1) |2п.
Таким образом, Знаменатель числа Вп всегда «свободен от
квадратов» и делится на 6. Он делится на простое число р > 3
тогда и только тогда, когда п кратно числу (р— 1)/2. Доказа-
тельство читатель может найти в книгах [Харди, Райт], § 10,
или [Боревич, Шафаревич].
Вторая теорема была доказана фон Штаудтом в 1845 г.
Теорема В.4. Простое число делит знаменатель числа Вп/п
(представленного в виде несократимой дроби) тогда и только
тогда, когда оно делит знаменатель числа Вп-
Теперь легко вычислить знаменатель числа Вп[п в явном
виде. Для любого простого р, такого, что (р—1) [ 2п, обозна-
чим через pi* наивысшую степень числа р, делящую п. Тогда,
очевидно, p^+1 равно наивысшей степени р, делящей знамена-
Приложение В. Числа Бернулли 237
тель числа В„/п. Например, для и =14 условию (р—1)|2л
удовлетворяют лишь следующие простые числа: 2, 3, 5, 29, и по»
этому знаменатель числа Вц/14 равен 22-3-5-29.
Замечание. Это вычисление интересно для теории гомотопий
ввиду теоремы, утверждающей, что образ стабильного /-гомо-
морфизма
Л4И_1+^(Sw)
является циклической группой порядка, равного знаменателю
числа Вп/Ьп (см. [Милнор, Кервер, 1958], [Адамс, 1965] и [Ма-
ховальд]).
Доказательство теоремыВ.4. Пусть р — произвольное простое
число. Если оно делит знаменатель числа Вп, то оно, конечно,
делит и знаменатель Вп/п. Если р не делит знаменатель Вп, то
2п Ф 0 (mod р— 1) согласно теореме В.З. Выберем какой-нибудь
первообразный корень k по модулю р, т. е. такое число k, что
kr = 1 (mod р) тогда и только тогда, когда г кратно р — 1. Тогда
Л2" Ф1 (mod р),
и потому целое число k2n(k2n—1)/2 взаимно просто с р. Сле-
довательно, число Вп/п, будучи равным целому числу
Л2л(й2л— 1)В„/2п, деленному на £2л(/г2л— 1)/2, имеет знамена-
тель, взаимно простой с р. 
Вычислить числитель дроби Вп/п значительно труднее. Для
малых значений п он представлен в следующей таблице:
П	<5	6	7	8	9	10	11	12
Числитель	1 дроби Вп/п	691	1	3617	43 867 174 611	77 683	236 364 091
Замечание. Этот числитель представляет интерес для диффе-
ренциальной топологии ввиду теоремы о том, что группа, со-
стоящая из всех классов диффеоморфных друг Другу экзотиче-
ских (4п— 1)-мерных сфер, ограничивающих параллелизуемые
многообразия, является циклической группой порядка
22л-2(22л-1 — 1) (числитель дроби (4В„/п))
для п^2 (см. [Кервер, Милнор, 1963]). Он представляет ин-
терес и для теории чисел, так как Куммер доказал в 1850 г.
справедливость большой теоремы Ферма для каждого простого
показателя р, который не делит числитель никакой (несократи-
238 Дж. Милнор и Дж. Сташеф
мой) дроби Вп/п (см. [Боревич, Шафаревич]). Такие простые
числа р называют «регулярными». Наименьшее нерегулярное
простое число равно 37, оно делит числитель 7709321041217 чи-
сла Ви. Куммер доказал, что если два целых числа шип удо-
влетворяют условиям m = n^Q(mod(p—1)/2) для некото-
рого нечетного простого р, то р делит числитель числа
(—l)mBm/rn — (—1)"В„/п.
Следовательно, для того чтобы проверить регулярность данного
простого р, достаточно рассмотреть числа Бернулли Вп, для ко-
торых 1 п < (р — 1) /2.
Числитель дроби Вп/п нетривиален для всех п>8 и очень
быстро растет с ростом п. Чтобы увидеть это, воспользуемся
знаменитой формулой Эйлера
• + ^г + ^г + ^г +	=B»(2«W2(2»)I
см. задачу В.4 ниже). Применение формулы Стирлинга
,	zn!	1112m
. 1 < —-—m	.... < е
m e~m
(см. [Артин]) дает неравенства
Вп > 2 (2п)!/(2«)2« > 4 (^)2л V™
(где все три выражения асимптотически равны между собой
при и->оо). Следовательно,
Л вп^вп	4 ( п	,
числитель дроби — > — > —I —)	>1
п п	уе \пе /
для всех п > ле = 8.539 ....
Дальнейшие сведения о числах Бернулли можно найти в
книгах [Нильсен] или [Боревич, Шафаревич].
В заключение несколько задач для читателя.
Задача В.1. (Дж. Ф. Адамс). Показать, что если все простые
множители числа п имеют вид 6k + 1, то знаменатель дроби
Вп/п равен 6.
Задача В.2 (Дж. Ф. Адамс). Показать, что для заданной
константы N > log2(4n) наибольший общий делитель целых
чисел
2W(2a»-l), 3лг(32л— 1), 4W(42” — 1), ...
равен знаменателю дроби Вп/Ьп.
Приложение В. Числа БернулЯи 239
Задача В.З. Пусть D = d/dt обозначает дифференциальный
оператор f(0|—*Г(0> применяемый к произвольным полино-
мам f(t). Показать, что оператор
eD==l+D + ^-Z)2+ ... переводит f(/) в f (t + 1), а оператор
—2—= 1-1р+^д2_+ ...
eD - 1	2	21
переводит f(t) в полином
g ю=f (о - 4 г (о+4г f" (о - 4г f"" (о+-...,
который удовлетворяет разностному уравнению
Используя эти факты, доказать формулу суммирования Эйле-
ра — Маклорена
f'(O) + f'(l)+ ... +f'(k-V = g(k)-g(0).
Задача В.4. Для f(t) = tm/m\ соответствующий полином
g (/) = tmlrn\ - /т~7(т - 1)! +	- 2)1 - + ...
можно назвать /n-м полиномом Бернулли pm(t). Показать, что
эти полиномы Бернулли допускают следующее индуктивное
описание: если начать с p0(t)=l, то каждый полином pm(t),
т 1, есть первообразная от полинома pm-i(f), удовлетворяю-
щая условию рт (0 dt = 0. Применяя интегрирование по час-
о
тям, вычислить по индукции интеграл
1
§ Pm(t) e~2nikt dt = — l/(2nlk)m
о
для k ф 0, т 1 и тем самым установить разложение в рав-
номерно сходящийся ряд Фурье
рт® = ~ Z
fe’H’O
для т 2, 0 t 1. Подставляя сюда i = 0, получить фор-
мулу Эйлера
В„/(2п)! = 2 £ 1/(2^)’'*.
А-=1
ПРИЛОЖЕНИЕ С
СВЯЗНОСТИ, КРИВИЗНА
И ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
В этом приложении мы наметим в общих чертах подход
Чженя — Вейля к описанию характеристических классов с ве-
щественными или комплексными коэффициентами в терминах
форм кривизны (см. [Чжень] или [Ботт, Чжень, § 2]). Мы бу-
дем предполагать, что читатель знаком с основами внешнего
дифференциального исчисления и теории когомологий де Рама,
например, в объеме книги [Уорнер] '. Однако наше соглашение
о знаках (см. приложение А) отличается от того, которое при-
нято у Уорнера и других авторов. Ниже мы вернемся к этому
вопросу.
Начнем со случая комплексного векторного расслоения.
Пусть £— гладкое комплексное n-мерное расслоение над глад-
ким базисным пространством М и
tJ. — HomR (т, С)
— комплексицированное кокасательное (т. е. двойственное к
касательному) расслоение многообразия М. Тогда (комплекс-
ное) тензорное произведение т* также будет комплексным
векторным расслоением над М. Векторное пространство глад-
ких сечений этого расслоения будем обозначать С°° (тс ® £)•
ОПРЕДЕЛЕНИЕ. Связностью на расслоении £ называется
всякое С-линейное отображение
V:
удовлетворяющее формуле Лейбница
V(fs) = df®s + fV(s)
для любого сечения s е С°°(£) и любой функции f е С°°(М, С).
Образ V(s) называется ковариантной производной сечения з.
Опишем вкратце основные свойства связностей. Заметим
прежде всего, что соответствие st—>V(s) уменьшает носитель.
Это означает, что если сечение з обращается в нуль на некото-
ром открытом подмножестве U с М, то его образ V (з) также
1 Или [Стернберг]. — Прим, перев.
Приложение С, Связности, кривизна и характеристические классы 241
обращается в нуль на U. Действительно, для произвольной за-
данной точки х е U мы можем подобрать гладкую функцию f,
которая равна нулю вне U и тождественно равна 1 вблизи точ-
ки х. Тождество
df ®s + fV(s) = V(fs) = O,
примененное к точке х, показывает, что V(s) равно нулю в х.
Замечание. Всякое линейное отображение L: С°°(£)—>С00(т]),
которое уменьшает носители, называют локальным оператором,
так как значение сечения L(s) в точке х зависит лишь от зна-
чений сечения s в точках из произвольно малой окрестности
точки х. (Теорема Петре (см. [Петре]) утверждает, что любой
локальный оператор является дифференциальным оператором,
т. е. может быть представлен как конечная линейная комбина-
ция частных производных с коэффициентами в С°°(г)).)
Так как связность — локальный оператор, имеет смысл го-
ворить об ее ограничении на открытое подмножество многооб-
разия М. Если совокупность открытых подмножеств Ua покры-
вает многообразие М, то глобальная связность однозначно оп-
ределена своими ограничениями на Ua.
Если открытое множество U настолько мало, что расслое-
ние t, | U тривиально, то совокупность всех возможных связно-
стей на | можно описать следующим образом. Пусть Si,
.... sn — какой-нибудь базис сечений расслоения £|С7, так что
любое сечение может быть однозначно записано как сумма
fi$i + ...	fnsп, где коэффициенты fi являются гладкими комп-
лекснозначными функциями.
Лемма 1. Связность V на тривиальном расслоении £ | U од-
нозначно определяется своими значениями V($i).....V(Sn), ко-
торые могут быть совершенно произвольными гладкими сече-
ниями расслоения х*с<3)^\ U. Каждое сечение V(«<) единственным
образом записывается в виде суммы^&ц®sj, где матрица
[©//] может быть произвольной п X п-матрицей комплексных
1-форм на U класса С00.
Мы принимаем соглашение, что знак У обозначает сумми-
рование по всем дважды встречающимся индексам.
Доказательство. Если заданы значения y(si), .... V(sn),
то мы можем определить значение связности на произволь-
ном сечении формулой
V (Л«1 + ... + fnSn) — У (df{ ® S/ + fiV($i)).
Подробности предоставляем читателю. 
242 Дж. Милнор и Дж. Сташеф
В частности, существует одна и только одна связность, та-
кая, что все ковариантные производные V(«i), ...» У(зп) рав-
ны нулю (или, другими словами, такая, что матрица связ-
ности [со//] является нулевой). Она задается формулой
V (2 fiSi) = ^t st. Эта специальная «плоская» связность за-
висит, конечно, от выбора базиса {з,}.
Совокупность всех связностей на расслоении £ не имеет ка-
кой-либо естественной структуры векторного пространства. За-
метим, однако, что если V] и V2— две связности на расслоении
£ и g— гладкая комплекснозначная функция на многообразии
М, то линейная комбинация gVi +(1 —g)V2 также будет кор-
ректно определенной связностью на £.
Лемма 2. На любом гладком комплексном векторном рас-
слоении над паракомпактным базисным пространством можно
ввести связность.
Доказательство. Выберем покрытие базисного простран-
ства открытыми множествами Ua, такими, что расслоения £|t/e
тривиальны, и затем гладкое разбиение единицы {Ха} с
supp{Xa}c Ua. Каждое ограничение £|t/a обладает некоторой
связностью Va по лемме 1. Взяв линейную комбинацию J]ZaVa,
получим корректно определенную глобальную связность. 
Теперь рассмотрим случай индуцированного векторного рас-
слоения. Для любого гладкого отображения g: М' -*• М мы мо-
жем образовать индуцированное векторное расслоение t,' =
— g*Z- Заметим, что существует каноническое С°° (Л1, С)-линей-
ное отображение
g*:
Далее, любая 1-форма на многообразии М индуцирует форму
на многообразии М', так что существует каноническое
С°° (А/, С) -линейное отображение
g*: С°° (т* (АТ) ® Q ->	(г* (М') ® Q.
Лемма 3. Каждой связности V на расслоении £ соответ-
ствует одна и только одна связность V' = g*V на индуцирован-
ном расслоении t,', такая, что следующая диаграмма комму-
тативна:
С“©^С“(<(Л1)®£)
Доказательство. Пусть заданы сечения sb ..., sn над от-
крытым множеством U многообразия Af, причем V(s<)=^©//®s/.
Приложение С. Связности, кривизна и характеристические классы 243
Тогда мы можем построить индуцированные 1-формы <o'lt и
индуцированные сечения s'{ над g~lU, Если искомая связ-
ность V' существует, то, очевидно,
Дальнейшие подробности предоставляем читателю. 
Попробуем для заданной связности V на расслоении £ по-
строить что-то вроде связности на расслоении rj,®^. Мы будем
использовать помимо V еще оператор внешнего дифференциро-
вания
d:
Лемма 4. Для заданной связности V существует одно и
только одно С-линейное отображение
V: С~(т’®0 = С~(Л2т’®£),
удовлетворяющее формуле Лейбница
V (0 ® s) = dO ® s — 0 Д V (s)
для любой 1-формы 0 и любого сечения s е С°°(5). Кроме того,
V удовлетворяет тождеству
V (f (0 ®s)) = df Д (0®з) + /V(0®з).
Доказательство. В терминах локального базиса сечений
«1, .... sn мы должны иметь тождество
V (01 ® $i + ... + 0n ® sn) = Z 8 Si — 0i Л V (зг)).
Взяв эту формулу в качестве определения V, легко проверить
требуемые тождества. И
Теперь рассмотрим композицию /C = V°V двух С-линейных
отображений
С00 ($)	С°° (т* ® Q С°° (Л2т* ® ?).
Лемма 5. Значение сечения K{s)=\(V(s)) в точке х зави-
сит только от s(x) и не зависит от значений сечения s в дру-
гих точках многообразия М. Следовательно, соответствие
s (х) *—> Д ($) (х)
определяет гладкое сечение комплексного векторного расслое-
ния Нот (С,Л2т‘с ® 0.
244 Дж. Милнор и Дж. Сташеф
Определение. Это сечение К = векторного расслоения
Нот (£, Л2Тд ® £) = Л2Тс ® Нот (£, £) называется тензором кри-
визны связности V.
Доказательство леммы 5. Ясно, что К. является локальным
оператором. Небольшое вычисление:
V (V (fs)) = V (df ® s + fV (s)) = 0 - df Д Vs + df Д Vs + [V (V (s))
— показывает, что композиция V» V = К в действительности яв-
ляется С°°(М, С)-линейным отображением: K(fs) — fK(s). Да-
лее, если s(x) = s'(x), то в терминах локального базиса сечений
si, ..., s„ мы имеем вблизи точки х равенство
S ~- S = fi$i “|" ... 4“ ftiSnt
где fi (х) = ... = fn (х) = 0. Следовательно, сечение К. (s') —
— К. (s) — "ZfiK. (s,) равно нулю в точке х, чем и завершается
доказательство. 
В терминах базиса Si, .... sn сечений расслоения для
которого V(sj) = S®i/®5/, мы имеем явную формулу
К (Si) = V (£ G>ii ® S/) = £ Qz/ ® Sj,
где положено
Q/y = datif — £ ®Za Д ©0/.
Таким образом, тензор кривизны К может быть локально опи-
сан п X «-матрицей й = [й,7] 2-форм примерно таким же об-
разом, как оператор связности V локально описывается матри-
цей и =[©«/] 1-форм. В матричной записи имеем
й — da — со А ©•
Фундаментальная теорема, которую мы не будем здесь дока-
зывать, утверждает, что тензор кривизны К равен нулю тогда
и только тогда, когда в окрестности каждой точки многообра-
зия М существует базис si.....sn сечений расслоения £, такой
что V(si)= ... =V(Sn)=0 (см. [Бишоп, Криттенден] или
[Кобаяси, Номидзу]). Более того, если многообразие М одно-
связно и К = 0, то существуют глобальные сечения Si, .... sn,
такие, что V(si)=; ... = V(s«) = 0. В этом случае £ будет, ко-
нечно, тривиальным расслоением. Если тензор кривизны К =>
— Кхт нулевой, то связность V называют плоской.
Замечание. В терминологии Стинрода расслоение с плоской
связностью может быть описано как расслоение с дискретной
структурной группой. Чтобы увидеть это, рассмотрим два раз-
Приложение С. Связности, кривизна и характеристические классы 245
личных локальных базиса, скажем si, ..., sn s U) и
у,, .... s'е С°° (£ | У), каждый из которых состоит из сечений
с нулевыми ковариантными производными. На пересечении
U f] V мы можем положить =	Уравнение V (sz) ==
—У ^ац ®s/ ~ 0 показывает, что функции перехода ац локально
постоянны. Следовательно, ассоциированное отображение
[а0]: U(]V-^GL(n, С)
непрерывно, даже если линейная группа GL(n, С) наделена дис-
кретной топологией.
Отправляясь от тензора кривизны К, мы можем следующим
образом построить характеристические классы. Пусть Af„(C)
обозначает алгебру всех комплексных п X п-матриц.
ОПРЕДЕЛЕНИЕ. Инвариантным полиномом на алгебре
Af„(C) называется всякая функция
Р: М„(С)->С,
представимая в виде комплексного полинома от матричных
элементов и удовлетворяющая условию
P(XY) — P(YX)
или эквивалентному условию
Р (TXT"1) = Р (X)
для любой невырожденной матрицы Т.
(Ясно, что первое тождество следует из второго, когда Y
является невырожденной матрицей, а в общем случае это вер-
но по непрерывности, ибо любая вырожденная матрица может
быть аппроксимирована невырожденными матрицами.)
Примеры. Хорошо известными примерами инвариантных по-
линомов на алгебре Л!Л(С) служат след	У Хц и опре-
делитель det.
Пусть Р — инвариантный полином. Определим внешнюю
форму Р(К) на базисном пространстве М следующим образом.
Выбрав какой-нибудь локальный базис Si, ..., sn для сечений
вблизи точки х, запишем 2<($г) = У Qz/Элементы матрицы
Q = [Q;/] принадлежат коммутативной алгебре над полем С,
состоящей из всех внешних форм четной степени. Следователь-
но, мы можем придать точный смысл вычислению значения на-
шего комплексного полинома Р в матрице Q, причем этим зна-
чением будет некоторый элемент указанной алгебры форм.
246 Дж. Милнор и Дж. Сташеф
Этот элемент Р(й) не зависит от выбора базиса si, .... sn, так
как замена базиса переводит матрицу й в матрицу вида
ТЙТ-1, где Т — невырожденная матрица функций перехода. По-
скольку Р(7’Й7’~1)= Р(й), то все эти локальные дифференци-
альные формы Р(й) определены однозначно. В совокупности
они определяют дифференциальную форму на всем многообра-
зии М, которую мы будем обозначать Р(К).
Замечание 1. Если Р— однородный полином степени г, то,
очевидно, Р(К) является внешней формой степени 2г. В общем
случае Р есть сумма однородных полиномов различных степе-
ней и соответственно Р(К) будет суммой внешних форм раз-
личных четных степеней. Примем обозначения
р (К) <= с°° (л®<) = фс00 (л%).
Замечание 2. Более общо, вместо инвариантного полинома
можно с равным успехом использовать инвариантный формаль-
ный степенной ряд вида
Р = Ро + Л + Р2+ ....
где Рг — инвариантный однородный полином степени г. Значе-
ние Р(Л) по-прежнему будет корректно определено, так как
РГ(К)—О для 2r > dim(Al). (Достойным внимания примером
инвариантного формального степенного ряда служит характер
Чженя ch (Д) = tr (е4/2я‘).)
Основная лемма. Для всякого инвариантного полинома (или
инвариантного формального степенного ряда) Р внешняя фор-
ма Р(К) является замкнутой, т. е. dP(K)= 0.
Доказательство. Для любого заданного инвариантного по-
линома или формального степенного ряда Р(Д) = Р([Д//]), где
Aq — элементы матрицы А, мы можем образовать матрицу
[дР/дД,/] формальных первых производных. Нам будет удоб-
но обозначать символом Р'(Д) не саму эту матрицу, а транспо-
нированную к ней.
Пусть теперь й — [йг;]— матрица кривизны относительно
некоторого локального базиса сечений расслоения £|£Л Оче-
видно, внешний дифференциал dP(Q) равен
X(dP/dQu)dQ{l.
В матричной записи мы можем переписать это выражение в
виде
1)	dP(fi) = tr(P'(Q)dQ).
Приложение С. Связности, кривизна и характеристические классы 247
Матрицу 3-форм dQ можно вычислить, взяв внешний диф-
ференциал от матричного уравнения
Q = do — © /\ <в
и подставив это уравнение в получившийся результат. Мы по-
лучим тождество Бьянки
(2)	dQ. — © Л Q —• Q Д о.
Нам понадобится следующее наблюдение. Для любого ин-
вариантного полинома или степенного ряда Р транспонирован-
ная матрица первых производных Р' (Д) коммутирует с А. Для
доказательства этого утверждения рассмотрим матрицу [Я/,],
у которой (/, 0-й элемент равен 1, а все остальные равны нулю.
Дифференцируя уравнение P((I + tE/{)A)^> P(A(I + tE/i)) по
t и полагая затем /=0, находим £ А[а (дР/дА1а)=*=^ (дР/дАа1)Аа1.
Таким образом, матрица А коммутирует с матрицей, транспо-
нированной к [дР/дАц], что и утверждалось.
В частности, беря в качестве А матрицу Q,
(3)	ЙЛР,(2) = /’/(0)ЛЙ.
Нам будет удобно обозначить внешнее произведение Р'(П)’А'о
через X. Подставляя тождество Бьянки (2) в (1) и используя
(3), приходим к равенству
dP (Q) = tr (X Д Q - Q Д X) = £ (Xtl Д Q}[ - Д Xl7).
Так как каждый элемент Хц коммутирует с 2-формой Q,/, то
эта сумма равна нулю, чем основная лемма и доказана. 
Итак, внешняя форма Р(/С) замкнута, другими словами,
является коциклом в смысле де Рама и, значит, представляет
некоторый элемент, который мы обозначим (Р (/()), в полном
кольце когомологий де Рама Я® (Л1; С)= фЯ‘(Л4; С).
Следствие. Когомологический класс (P(/C))=«(P(/CV)) не
зависит от выбора связности V.
Доказательство. Пусть Vo и Vi — две различные связности
на расслоении £. Отображая М X R в М при помощи проекции
(х, мы можем образовать индуцированное расслоение £/
над М X R с индуцированными связностями V', V, и составить
линейную комбинацию
v-=/v; + (i-0v;.
Таким образом, форма Р(Ку) является коциклом де Рама на
многообразии М X R.
248 Дж. Милнор и Дж. Сташеф
Теперь рассмотрим отображение ie:	е) многообразия
М в М X R, где е равно 0 или 1. Очевидно, что индуцирован-
ная связность (ie)*V на расслоении (ie)*£' может быть отожде-
ствлена со связностью Ve на расслоении Следовательно,
m/w))=(p (М)-
Но отображение io гомотопно ii, поэтому когомологический
класс (Р (Kvo)) равен когомологическому классу (Р (К?,)). 
Итак, всякий инвариантный полином (или степенной ряд)
Р определяет характеристический когомологический класс в
Н*(М-,С), зависящий только от класса изоморфизма вектор-
ного расслоения £. Если отображение g: М' —> Л1 индуцирует
расслоение % = g*^ с индуцированной связностью V', то, оче-
видно,
Таким образом, эти характеристические классы обладают свой-
ством естественности относительно индуцированных расслоений.
Однако мы уже знаем из § 14, что любой характеристиче-
ский класс комплексных векторных расслоений может быть
представлен как полином от классов Чженя. Таким образом,
перед нами встают следующие два вопроса: какие существуют
инвариантные полиномы и как ассоциированные с ними харак-
теристические классы явно выразить через классы Чженя?
На первый вопрос ответить нетрудно. Для любой квадрат-
ной матрицы А пусть сгДЛ) обозначает k-ю элементарную сим-
метрическую функцию от собственных значений матрицы А, так
что
det (/ + tA) = 1 + t<h (Л) + . • • + /'Ч (Л).
Лемма 6. Всякий инвариантный полином на алгебре Мп(С)
может быть представлен в виде полинома от 04, ..., оп.
Доказательство. Для заданной матрицы ЛеА4п(С) мы
всегда можем подобрать матрицу В, такую, что матрица ВАВ~1
будет верхней треугольной; действительно, матрицу Л можно
привести к жордановой канонической форме. Заменяя В на
diag(e, е2, ..., в") В, мы можем сделать элементы вне диаго-
нали произвольно близкими к нулю. Отсюда по непрерывности
следует, что значение полинома Р(Л) зависит только от диаго-
нальных элементов матрицы ВЛВ-1, или, другими словами, от
собственных значений матрицы Л. Так как Р(Л), очевидно,
должно быть симметрической функцией от этих собственных
значений, то применение классической теории симметрических
функций завершает доказательство. Я
Приложение С. Связности, кривизна и характеристические классы 249
Позднее мы увидим, что характеристический класс (щ(А))
равен некоторому комплексному кратному класса Чженя сг(£).
Оставив этот вопрос на время в стороне, обратимся к соот-
ветствующей теории вещественных векторных расслоений. По-
нятия связности
V: С00®-^00^*®?)
на вещественном векторном расслоении £ и ее тензора кри-
визны
К е Сх (Hom (g, AV ® |)) ~ С°° (AV ® Нот (g, £))
определяются точно так же, как и выше, просто везде надо за-
менить комплексные числа вещественными. Всякий инвариант-
ный полином Р на алгебре матриц Aln(R) порождает характе-
ристический когомологический класс (Р(Л))е Н*(М\ R).
Самый классический и самый известный пример связности —
это связность Леви — Чивиты на касательном или кокасатель-
ном расслоениях риманова многообразия. Сейчас мы дадим
эскиз этой теории.
Рассмотрим вещественное векторное расслоение | над мно-
гообразием М, снабженным евклидовой метрикой. Тогда, если
s и s' — гладкие сечения расслоения £, то их скалярное произ-
ведение <s, s') представляет собой гладкую вещественнознач-
ную функцию на многообразии М.
ОПРЕДЕЛЕНИЕ. Связность V на расслоении £ называется
согласованной с метрикой, если справедливо тождество
d (s, s') = (Vs, s') + (s, Vs')
для всех сечений s и s'.
Здесь предполагается, что скалярные произведения в пра-
вой части определяются условиями
<0 ® s, s') = {s, 0 ® s') = <s, s') 0
для всех 0 е С°°(т*) и всех s, s' е С°°(£). К сожалению, такая
запись может иногда приводить к путанице. Надежнее исполь-
зовать следующий критерий.
Лемма 7. Пусть si, ..., sn — ортонормированный базис для
сечений расслоения так что {st,Sj)=§if. Связность V на
расслоении ||U согласована с метрикой тогда и только тогда,
когда соответствующая матрица связности [ащ] (определяемая
равенством V (si)='^(£>ll®st') кососимметрична.
250 Дж. Милнор и Дж. Сташеф
Доказательство. Если связность V согласована с метрикой,
то
0 = d(s/( sJ) = {^si, sl) + {si, Vs/) =
= (E©ife®Sfe, s/) + (sz,	'=»«/ + ©/<•
Доказать обратное утверждение предоставляем читателю. 
Замечание. Появление здесь кососимметричных матриц свя-
зано, конечно, с тем фактом, что алгебра Ли ортогональной
группы О(п) равна подалгебре Ли всех кососимметричных мат-
риц в Af„(R).
Теперь рассмотрим поближе частный случай, когда рас-
слоением | является кокасательное расслоение т* над многооб-
разием М.
ОПРЕДЕЛЕНИЕ. Связность V на расслоении т* называется
симметричной (или не имеющей кручения), если композиция
С00 (т*) X- С" (т‘ ® т*) А С°° (A V)
равна внешнему дифференциалу d.
В терминах локальных координат х1.....х", если положить
V(dxfc) = Er?/dxi®dx/,
это означает, что образ ^T/yrix* Д dx1 дифференциала dxk при
композиции !Д о V должен быть равен его внешнему дифферен-
циалу d(dxft)=0. Следовательно, символы Кристоффеля Г*/
должны быть симметричны относительно I, j. Более общим об-
разом, справедливо следующее легко проверяемое утверждение.
Утверждение. Связность V на расслоении т* симметрична
тогда и только тогда, когда вторая ковариантная производная
любой гладкой функции f является симметричным тензором.
Другими словами, в терминах локального базиса 91, .... 9П се-
чений расслоения т*. должно выполняться тождество Vd (f) =
где аИ = ац.
Лемма 8. Кокасательное расслоение т* риманова многооб-
разия обладает одной и только одной симметричной связ-
ностью, согласованной с его метрикой.
Эта специальная связность V называется римановой связ-
ностью или связностью Леви— Чивиты.
Доказательство. Пусть 91, .... 9Л — какой-нибудь ортонор-
мированный базис сечений расслоения т*|£Л Мы покажем, что
Приложение С. Связности, кривизна и характеристические классы 251
существует одна и только одна кососимметричная матрица
1-форм [юл/], такая, что
d®k = Е ®ft/ Л 9/-
Если определить связность V над U условием
V (0ft) = X ®ft/ ® 9/,
то очевидно, что V представляет собой единственную симмет-
ричную связность на расслоении т* | U, согласованную с метри-
кой. Из единственности так построенных локальных связностей
следует, что они совпадают на пересечениях U П U' и в сово-
купности дают требуемую глобальную связность на всем мно-
гообразии.
Нам понадобится следующее комбинаторное наблюдение.
Каждый п'Хп'Х n-массив вещественнозначных функций Ацк
можно единственным образом записать в виде суммы массива
Bi/n, симметричного по I, j, и массива Cijk, кососимметричного
по j, k. В самом деле, существование таких массивов Btfk и С//*
доказывается непосредственной проверкой явных формул
— у	~~	~ Akn + Ари + Aft/)»
Cl}k — (А/ft — A(ft + Ami + ^kfi — Alki ~
а единственность очевидна, поскольку, если массив Ощ, одно-
временно симметричен по I, j и кососимметричен по j, k, то
равенства О^з ~ ^231 = —-D231 = —-Оз21 — ^312 = ^132 == —^123-
показывают, что его типичный элемент D123 равен нулю.
Выбрав теперь функции Aijk так, чтобы dQk — Е A/j0< л 0/»
и записав массив Aijk в виде Ацк — Btik + Сцк, как указано
выше, получаем, что о!0* = Есг/А Д 0/. Очевидно, что 1-формы
®ft/ = Ecz/ft0z задают единственную кососимметричную матрицу,
такую, что dQk = Е ®ft/ Л 9/. Лемма доказана. 
Рассмотрим частный случай двумерного ориентированного
риманова многообразия. Относительно ориентированного ло-
кального ортонормированного базиса 01, 02 для 1-форм мат-
рицы связности и кривизны имеют вид
[О (012 "j	Г 0	^12 1
— ®12 0 J	L — Й12 0 J ’
где dfi>12 = QI2. Тождество
[cos t	sin t ] Г 0	&i2 1 [cos t — sin t 1	[ 0	QI21
— sin/ cos/JL — Qu Ojlsin/ cos/ J —L—Qla oj
252 Дж. Милнор и Дж. Сташеф
показывает, что внешняя 2-форма Qi2 не зависит от выбора
ориентированного ортонормированного базиса. Следовательно,
мы имеем вполне определенную глобальную 2-форму.
ОПРЕДЕЛЕНИЕ. Эта форма Qj2 называется 2-формой Гаус-
са — Бонне на рассматриваемой ориентированной поверхности.
Обозначая 2-форму —01$ 02 ориентированной площади кратко
символом dA, мы можем записать Qi2 = WdA, где Ж — некото-
рая скалярная функция, называемая гауссовой кривизной.
Так как обе формы Qi2 и dA изменяют знак, если обратить
ориентацию поверхности, то функция X не зависит от выбора
ориентации.
Замечание о знаках. Наш выбор знака для формы dA мо-
жет показаться читателю странным. Приведем доводы в его
защиту. Следуя Маклейну (см. [Маклейн]), мы, как это уже
отмечалось в приложении А, вводим знак (—1) тп всякий раз,
когда объект размерности т переставляется с соседним объек-
том размерности п. Поэтому, если 1п обозначает единичный куб
с упорядоченными координатами t\, ..., tn и каноническим
ориентирующим классом ц е//«(/", д/я), то мы полагаем
/ 1 1 \
{dtx Д ... Л dtn, ц> = (dtx Л ... Л dtn, $ ... § ) =
\	f|-o <„-о/
==(_1)П+(П-1)+...+1 J	J Л„ = (-1)лП+1)/2.
Л-0	*л-о
Другими словами, п-форма ориентированного объема на Iя по
определению равна у нас (—1 )п(я+Л* ... f\dtn. Такой
выбор знака приводит к следующему варианту теоремы Стокса:
Ш р> + (- l)dlmT <ф,	= О,
в согласии с приложением А. Читатель, который предпочитает
использовать классическое соглашение о знаках, как в книгах
[Спеньер], [Уорнер] или в статье [Ботт, Чжень], может забыть
все сказанное об этих знаках, однако ему следует заменять К.
на — К всюду, где тензор кривизны К встречается в наших фор-
мулах для характеристических классов.
Чтобы сделать осязаемее данное выше несколько абстракт-
ное определение, выполним одно явное вычисление. В некото-
рой окрестности U любой точки риманова двумерного многооб-
разия можно ввести геодезические координаты х, у так, чтобы
метрический квадратичный дифференциал в С°° (т* ® т* | U)
Приложение С. Связности, кривизна и характеристические классы 253
принял вид dx 0 dx + g(x, y)2dy ® dy. Полагая
6i = dx, Q2 = gdy,
мы получим ортонормированный базис для 1-форм на U. Урав-
нения
= в>12 Д 02,
d02 = — ©12 Л 01
имеют единственное решение ©12 = gxdy, где нижций индекс х
обозначает частное дифференцирование. Отсюда следует, что
£12 = gxx dx /\dy = (— gxx/g) dA.
Таким образом, гауссова кривизна выражается формулой
•ft —	gxxlg'
Например, беря в качестве координат на единичной сфере дол-
готу и широту, мы имеем g(x, у) = cos х и, следовательно,
1.
Теорема Гаусса — Бонне, Для любого замкнутого ориенти-
рованного риманова двумерного многообразия М интеграл
равен 2ле[Л4].
Доказательство. Более общим образом рассмотрим произ-
вольное ориентированное вещественное двумерное расслоение
£ с евклидовой метрикой. Оно имеет каноническую комплекс-
ную структуру /, которая поворачивает каждый вектор на угол
л/2 в направлении «против часовой стрелки». В терминах
ориентированного’локального ортонормированного базиса si.sj
для сечений мы имеем Jsi(x) = s2(x).
Выбрав какую-нибудь согласованную связность V на рас-
слоении g, мы можем записать
V«1 — ©12 ® S2,
Vs2= —©12®«1-
Очевидно, что V задает связность на получающемся комплекс-
ном линейном расслоении где
VS1 = ©12 ® К] = £©12 ® Si
и, следовательно, V(isi)= iV(«i) = —©12 ® si. Таким образом,
матрицей этой комплексной связности служит 1 X 1-матрица
[1'012], а матрицей кривизны будет [££12]. Используя инва-
риантный полином ci = tr, мы получаем замкнутую 2-форму
tr [££12] "—= ££12,
254 Дж. Милнор и Дж. Сташеф
которая представляет некоторый характеристический когомо-
логический класс в Н2(М-, С). Однако характеристическим клас-
сом в Н2( ; С) для комплексного линейного расслоения £ мо-
жет быть только класс Чженя Ci(£;)=e(£R) (или его кратные).
Следовательно,
(ZQ12) = aCi (£) = %?(£),
где а — некоторая комплексная константа.
Чтобы вычислить эту константу а, достаточно подсчитать
обе стороны равенства для какого-нибудь частного случая.
Предположим, например, что £ является кокасательным рас-
слоением т* замкнутого ориентированного двумерного рима-
нова многообразия М. Так как (iQ12) = ае(т*), то имеет место
равенство
Ш12 = ае [АТ],
или, другими словами,
Вычисляя обе части последнего равенства для единичной дву-
мерной сферы, мы видим, что а = 2ni. Это завершает доказа-
тельство. 
Теорема. Пусть £ — комплексное векторное расслоение со
связностью V. Тогда когомологический класс	равен
(bdycrft).
Доказательство. Для случая комплексного линейного рас-
слоения проведенные выше рассуждения показывают, что
(а1(Ю) = ас1($) = 2л/с1(^).
Таким образом, если определить инвариантный полином с
формулой
с (Л) = det (/ + Л/2ш) = Е (Л)/(2л/)*.
то для всякого комплексного линейного расслоения коцикл
£(/()== 1 +<МЮ/(2лг)
представляет когомологический класс с(£)= 1 + Ci(£).
Теперь рассмотрим любое расслоение £, которое расщеп-
ляется в сумму Уитни @ ... ©линейных расслоений. Если
заданы связности Vi, .... Vn на расслоениях £/, то существует,
очевидно, их «сумма Уитни» — связность на расслоении £. Вы-
бирая локальные сечения sj расслоений вблизи точки х, мы
Приложение С. Связности, кривизна и характеристические классы 255
можем рассматривать $1, ..., sn как локальные сечения рас-
слоения £. Соответствующая локальная матрица кривизны диа-
гональна:
й== diag(Qb ..Qn),
и поэтому
£ (Q) = с (QJ ... с (□„).
Отсюда следует, что соответствующие глобальные внешние фор-
мы обладают тем же самым свойством:
£(/C)=£(^) ... С(КП).
Но правая часть этого равенства представляет полный класс
Чженя
c(Ci)...c(C„) = c(£).
Таким образом, равенство с(£) = (с(/С)) верно для любого рас-
слоения которое является суммой Уитни линейных расслое-
ний.
Утверждение для общего случая получается теперь стан-
дартными рассуждениями (см. [Хирцебрух, § 4.2] или доказа-
тельство единственности для классов Штифеля — Уитни, дан-
ное в § 7). Если у1 обозначает универсальное линейное расслое-
ние над m-мерным комплексным проективным пространством
Р«(С), где m достаточно велико, то для Х-произведения п
экземпляров расслоения у1 выполняется равенство
С (у1 X ... X Y1) = (С (К (Y1 X ... X у1))).
Так как в размерностях когомологий базисного простран-
ства С„(С°°) универсального расслоения у" отображаются в ко-
гомологии произведения Рт(С)Х ... ХА»(С) мономорфно, то
с(уп) = (£(/С(уп))).
Следовательно, равенство с(£) = (£(/((£))) верно и для произ-
вольного расслоения £. 
Следствие 1. Для любого вещественного расслоения £ ко-
цикл де Рама о2*(Л) представляет когомологический класс
(2n)2ltpk(l) в R), а класс О2а+1(Ю) является кограницей.
Другими словами, полный класс Понтрягина 1 +pi(g) +
+ ра(ё)+ ••• в кольце когомологий H*(A4; R) соответствует
инвариантному полиному j)(A) = det (7 + А/2л).
Доказательство. Это немедленно следует из доказанной
теоремы и определения классов Понтрягина. 
256 Дж. Милнор и Дж. Сташеф
Замечание. Можно дать прямое доказательство того, что
O2fe+i(K) является кограницей. Выберем какую-нибудь евкли-
дову метрику на расслоении | и согласованную с ней связность
V. Тогда матрица связности относительно локального ортонор-
мированного базиса сечений будет кососимметричной, откуда
легко вытекает, что ассоциированная матрица кривизны й так-
же кососимметрична: й* = —й. Следовательно,
Таким образом, для нечетных m коцикл Wv) нулевой. Отсюда
следует, что для произвольной (т. е. неметрической) связности
V' коцикл	представляет собой кограницу.
Следствие 2. Если вещественное (соотв. комплексное) век-
торное расслоение обладает плоской связностью, то все его
классы Понтрягина (соотв. Чженя) с рациональными коэффи-
циентами равны нулю.
Доказательство очевидно. 
Замечание. Из следствия 2 вытекает, что если группа го-
мологий	с целыми коэффициентами является конечно-
порожденной, то классы Понтрягина (или классы Чженя) рас-
слоения с плоской связностью суть элементы конечного поряд-
ка. Эти элементы конечного порядка, вообще говоря, не нуле-
вые. Ботт и Хайтч недавно построили вещественное (и также
комплексное) векторное расслоение с дискретной структурной
группой, классы Понтрягина (соотв. классы Чженя) которого
в группе Н* (В\ Z) не являются элементами конечного порядка
и не удовлетворяют никаким полиномиальным соотношениям
(см. [Ботт, Хайтч]). В этом случае, конечно, группа гомологий
Н*(В‘, Z) не может быть конечно-порожденной.
Бросается в глаза, что в предыдущем обсуждении отсутст-
вует одна вещь. А именно, мы не дали выражения для класса
Эйлера ориентированного 2п-мерного расслоения в терминах
кривизны (за исключением одного весьма специального по-
строения для случая п=1). Это не просто случайность. Позд-
нее мы увидим на примере, что и не может быть никакой фор-
мулы, выражающей класс Эйлера через кривизну для расслое-
ний с произвольной связностью. Ситуация, однако, изменяется,
если потребовать, чтобы связность была согласована с евкли-
довой метрикой на расслоении.
Нам понадобится следующая классическая конструкция.
Лемма 9. Существует один и с точностью до знака только
один полином с целыми коэффициентами, сопоставляющей
каждой кососимметричной 2п X 2п-матрице А над некоторым
Приложение С. Связности, кривизна и характеристические классы 25?
коммутативным кольцом элемент Pf(A) этого кольца, квадрат
которого равен определителю матрицы А. При этом
Pf(BAB^Pf(A) det (В)
для любой 2п X 2п-матрицы В.
Для определенности выберем знак полинома из условия
Pf(diag(S, ..., S))=+1, где S обозначает 2 X 2-матрицу
Г 0 11
I Q Получающийся полином Pf называется пфаффиа-
ном.
Например,
а пфаффиан кососимметричной 4 X 4-матрицы [ау] равен
U12Й34 — <2136124 + U 14^23.
Доказательство леммы 9*. Будем работать с кольцом
A = Z[A 12,	А2П-12П, Вц, ..., Вгпгп], в котором в качестве
независимых переменных выступают все элементы кососиммет-
ричной матрицы А=[Ау], лежащие выше диагонали, и все
элементы матрицы В = [By]. Над полем частных кольца Л
нетрудно найти матрицу X, такую, что ХАХ1 = diag(S, ..., S).
Следовательно, полином detAeA равен det(X)-2, т. е. яв-
ляется квадратом в поле частных кольца Л. Так как Л — коль-
цо с однозначным разложением на множители, то отсюда вы-
текает, что det А будет квадратом и в самом кольце Л.
Аналогично из тождества det (BAB*)— det (A) det (В)2 сле-
дует, что Pf (ВАВг)= ±Pf (A) det В; полагая В = 1, мы видим,
что знак должен быть равен +1. 
Пусть теперь g— ориентированное 2п-мерное расслоение с
евклидовой метрикой. Выбрав какой-нибудь ориентированный
ортонормированный базис сечений расслоения g над некоторой
координатной окрестностью U, мы получим матрицу кривизны
Q = [йу], которая является кососимметричной, так что опре-
делен пфаффиан
Pf(Q)eC°°(A2V|t/)2.
Если мы выберем другой ориентированный ортонормированный
базис сечений над U, то Pf(Q) заменится на РцХЙХ-1), где
матрица X ортогональна (X-1 = Х‘) и сохраняет ориентацию
(det X = 1). Следовательно, наш пфаффиан не изменится. Та-
1 Подробности см. в [Бурбаки], гл. IX, § 5, п. 2.
9 Дж. Милнор, Дж. Сташеф
258 Дж. Милнор и Дж. Сташеф
ким образом, из всех этих локальных форм мы можем обра-
зовать единую глобальную 2п-форму
Pf (К) е С°° (д2"?*).
(Тем самым для случая п = 2 мы еще раз доказали утвержде-
ние, что 2-форма Гаусса —Бонне Qi2 = Pf(ft) корректно опре-
делена глобально.) Точно так же, как и раньше, мы можем
проверить, что матрица формальных частных производных
[d Pf (Л) /dAtj] коммутирует с А и, значит,
d Pf (К) = 0.
Следовательно, 2п-форма Pf (К) представляет некоторый ха-
рактеристический когомологический класс в	Пере-
ходя к расслоению у, универсальному в размерностях и
учитывая, что квадрат класса Pf(/C(y)) представляет когомо-
логический класс (det(/C(y))) = (23i)2npn(y), мы видим, что
(Pf(/С(у)))= ±(2л)"е(у), а потому
(Р{(Л(ё))) = ±(2я)"е(|)
для любого ориентированного 2п-мерного расслоения |. Фак-
тически знаковый множитель равен +1; это можно показать,
вычислив левую и правую части для некоторой суммы Уитни
двумерных расслоений. Таким образом, нами доказана следую-
щая
Обобщенная теорема Гаусса — Бонне. Для любого ориен-
тированного 2п-мерного расслоения | с евклидовой метрикой и
группы Ли G с алгеброй Ли g кольцо когомологий Н®(Ва-, R)
представляет класс Эйлера е (|).
Замечание. Эта теорема иллюстрирует общий результат
Чженя — Вейля, состоящий в том, что для любой компактной
группы Ли G с алгеброй Ли g кольцо когомологий Я®(В0; R)
классифицирующего пространства Ва изоморфно алгебре всех
полиномов g -* R, инвариантных относительно присоединенного
действия группы G. Для некомпактных групп, таких, как
SL (2п, R), этот общий результат уже неверен.
Для примера рассмотрим кокасательное расслоение т* еди-
ничной сферы S2" со связностью Леви — Чивиты. Если выбран
какой-нибудь ориентированный ортонормированный базис
91, .... 0л сечений расслоения т*|U, то, как показывают вы-
числения,
— Q// = 91 А 9/.
(Это равенство выражает тот факт, что у единичной сферы
кривизна в двумерном направлении тождественно равна +1.)
Приложение С. Связности, кривизна и характеристические классы 239
Далее,
(-l)nPf(Q) = Pf[0£ Л9/] =
= (1.3-5.7- ... .(2п-1))01Д ... Л 02л-
Интегрируя по сфере S2", находим
Jpf(K) = (l .3-5- ... -(2n—1) объем (S2")-
Полагая это выражение равным (2л)"е[52п] =£(2n)n, мы полу-
чаем новое доказательство равенства
объем (S2") = 2 (2л)"/1 • 3 • 5 • ... • (2п - 1).
В заключение этого приложения покажем, что класс Эйлера
не может быть определен по тензору кривизны произвольной
(не согласованной с метрикой) связности. Мы приведем при-
мер ориентированного векторного расслоения с плоской связно-
стью, для которого класс Эйлера с вещественными коэффициен-
тами ненулевой (см. [Милнор, 1958] и [Вуд]). Предположим,
что задан некоторый гомоморфизм фундаментальной группы
11 = 311 (АТ) многообразия М в специальную линейную группу
SL(n, R). Тогда группа П действует на универсальном накры-
тии М и, следовательно, действует диагонально на произведении
М X R" Нетрудно видеть, что естественное отображение
(MXR")/n->M/n = M
является проекцией некоторого «-мерного расслоения g с пло-
ской связностью (или, эквивалентно, с дискретной структурной
группой). Мы хотим построить пример, когда е(£)=/= 0.
Пусть М — компактная риманова поверхность рода g > 1.
Тогда универсальное накрытие М конформно диффеоморфно
верхней комплексной полуплоскости Н (см., например, [Сприн-
гер]). Каждому элементу группы П преобразований накрытия
соответствует дробно-линейное преобразование полуплоскости
Н вида
мы имеем гомоморфизм h группы П в факторгруппу
z (az + b)/(cz + d),
где матрица
Га b I
L JeSL(2,R)
определена однозначно с точностью до знака. Таким образом,
PSL(2, R) = <SL(2, R)/{±/}.
в*
260 Дж. Милнор и Дж. Сташеф
Покажем, что этот гомоморфизм h поднимается до гомомор-
физма n-*SL(2, R), который индуцирует искомое двумерное
расслоение над римановой поверхностью М.
Группа PSL (2, R) действует естественно на вещественной
проективной прямой /’'(R), которую можно отождествить с
границей R U 00 полуплоскости Н. Поэтому h индуцирует рас-
слоение т) над многообразием М со слоем Р1 (R) и проекцией
(М х р‘ (R))/n -> М/П = М.
Будем рассматривать я как расслоение со структурной груп-
пой PSL(2, R), наделенной дискретной топологией. Это инду-
цированное расслоение т] можно отождествить с расслоением,
имеющим в качестве слоя окружность, ассоциированным с каса-
0	f(z.v) R
Рис. 8.
тельным расслоением многообразия М. Действительно, каждый
ненулевой касательный вектор v в точке z^H является каса-
тельным к некоторой единственной ориентированной дуге окруж-
ности (или вертикальному прямолинейному отрезку), идущей
из точки z в точку f(z, v) на границе RU ео и пересекающей эту
границу ортогонально (см. рис. 8). Получающееся отображение f
инвариантно относительно действия группы П (т. е. f(az, Daz(v))~
= af(z,v) для аеП) и, следовательно, индуцирует требуемый
изоморфизм пространства касательных направлений к много-
образию М на (R U оо)-расслоение т). (Здесь D — производная,
см. стр. 13). Отсюда следует, что число Эйлера е (т]) [Л4"| равно
2 2g =£ 0.
Пусть £0— пространство расслоения т), а Е — пространство
ассоциированного расслоения, слоем которого является тополо-
гический двумерный диск. Так как класс е(г]) делится на 2,
то w2(л) — 0. Поэтому из точной последовательности пары
(£, £0) следует, что фундаментальный класс и е Н2(Е, Ео; Z/2)
представляет собой образ некоторого когомологического класса
ае Н1(Е0', Z/2), ограничение которого на каждый слой яв-
ляется ненулевым. Пусть Ё0-*Е0 — двукратное накрытие, ассо-
циированное с этим когомологическим классом а. Тогда компо-
зиция ~Ёо~*Ео—*М задает новое расслоение т) над М, имеющее
Приложение С. Связности, кривизна и характеристические классы 261
слоем окружность. Используя, скажем, определение класса Эй-
лера как препятствия (см. § 12), мы видим, что e(fj) = -|-e(ii).
Таким образом, эйлерово число расслоения т) равно 1 —g ф 0.
Структурной группой этого нового расслоения fj служит,
очевидно, двукратная накрывающая группа SL(2, R) группы
PSL(2, R), действующей на двукратном накрытии проективной
прямой ^‘(R). (Это ясно, ибо группа PSL(2, R) в действитель-
ности имеет тот же гомотопический тип, что и пространство
^(R), на котором она действует.) Но у расслоения т) дискрет-
ная структурная группа, значит, и у расслоения т) тоже. По-
этому можно считать, что f| индуцировано некоторым подходя-
щим гомоморфизмом II->SL(2, R). Ассоциированное ст) дву-
мерное расслоение имеет, очевидно, плоскую связность и в то
же время ненулевое число Эйлера (равное 1 —g). 
СПИСОК ЛИТЕРАТУРЫ1
Адамс Дж. Ф. (Adams J. F.) On the non-existence of elements of Hopf
invariant one, Ann. Math., 1960, 72, 20—104. [Русский перевод: О несущество-
вании отображений с инвариантом Хопфа, равным единице. — Математика,
1961, б: 4, 3—86.]
— Vector fields on spheres, Ann. Math., 1962, 75. [Русский перевод: Векторные
поля на сферах. — Математика, 1963, 7: 6, 48—79.]
— On the groups J(X). II; IV, Topology, 1965, 3, 137—171; 1966, 6, 21—71.
[Русский перевод: О группах 7 (л). II, IV. — Математика, 1967, 11:4, 3—
41; 1968, 12:3, 37—97.]
— S. Р. Novikov’s work on operations on complex cobordism, Lecture Notes,
Univ, of Chicago, 1967.
— Quillen’s work on formal groups and complex cobordism, Lecture Notes,
Univ, of Chicago, 1970.
— Algebraic Topology: a student’s guide, Cambridge Univ. Press, 1972.
Адем Дж. (Adem J.) The iteration of the Steenrod squares in algebraic topo-
logy, Proc. Nat. Acad. Sci. U.S.A., 1952, 38, 720—726.
Александров П. С., Хопф X. (Alexandroff P„ Hopf H.) Topologie, Springer-
Verlag, 1933.
Андерсон Д. У. (Anderson D. W.) The real К-theory of classifying spaces,
Proc. Nat. Acad. Sci. U.S.A., 1964, 51, 634—636.
Андерсон Д. У., Браун'Э., Петерсон Ф. П. (Anderson D. W„ Brown Е.,
Peterson F. Р.). The structure of the Spin cobordism ring, Ann. Maht., 196?,
86, 271—298.
Артин Э. (Artin E.) The Gamma Function, Holt, Rinehart and Winston, 1964.
[Translated from Hamburg Math. Einzelschr. 1, 1931.]
Атья M. (Atiyah M.) Лекции по К-теории. — M.: Мир, 1967 (1967).
Атья M., Зингер И. (Atiyah М., Singer I.) The index of Elliptic operators,
III, Ann. Math., 87, 1968, 546—604. [Русский перевод: Индекс эллиптических
операторов. Ill, УМН, 1969, 24, № 1, 127—182.]
Атья М., Хирцебрух Ф. (Atiyah М„ Hirzebruch F.) Vector bundles and homo-
geneous spaces, Proc. Symp. Pure Math., Ill, 7—38, Amer. Math. Soc„ 1961.
1 Для переводных книг в круглых скобках стоит год оригинального
издания. Если он больше года выхода перевода, то это означает, что пере-
вод делался с более раннего издания, чем то, которое указывает автор. —
Прим, перев.
Список Литературы 263
[Русский перевод: Векторные расслоения и однородные пространства. — Ма-
тематика, 1962, 6 : 2, 3—39.]	,
Баум П. (Baum Р.) Chern classes and singularities of complex foliations,
Proc Symp. Pure Math. 27, Differential Geometry, Amer. Math. Soc., 1975.
Бишоп P., Криттенден P. (Bishop R. L., Crittenden R. J.) Геометрия много-
образий.— M.: Мир, 1967 (1964).
Блантон Дж. Д., Швейцер П. (Blanton J. D., Schweitzer Р. A.) Axioms for
characteristic classes of manifolds, Proc. Symp. Pure Math. 27, Differential
Geometry, Amer. Math. Soc., 1975.
Бой В. (Boy W.) Uber die Curvatura Integra und die Topologie geschlossener
Flachen, Math. Ann., 1903, 57, 151—184.
Бордман Дж., Фогт P. (Boardman J. M„ Vogt R.) Homotopy Everything
Я-spaces, Bull. Amer. Math. Soc., 1968, 74, 1117—1122.
—	Гомотопически инвариантные алгебраические структуры на топологиче-
ских пространствах. — М.: Мир, 1977 (1973).
Боревич 3. И., Шафаревич И. Р. Теория чисел. — М.: Наука, 1964.
Борель A. (Borel A.) Le plan projectif des octaves et les spheres comme
epaces homogenes, C. R. Acad. Sci. Paris, 1950, 230, 1378—1380.
—	La cohomologie mod 2 de certains espaces homogenes, Comm. Math. Helv.,
1953, 27, 165—197. [Имеется перевод первой главы этой работы: Класси-
фицирующие пространства ортогональных групп; многообразия Штифеля. —
В ки.: Расслоенные пространства. М.: ИЛ, 1958, с. 282—292.]
—	Sul la cohomologie des espaces fibres principaux et des espaces homogenes
de groupes de Lie compacts, Ann. Math., 1953, 57, 115—207. [Русский пере-
вод: О когомологиях главных расслоенных пространств и однородных про-
странств компактных групп Ли. — В кн.: Расслоенные пространства. М.: ИЛ,
1958, с. 163—246.]
—	Topology of Lie groups and characteristic classes, Bull. Amer. Math. Soc.,
1955, 61, 397—432.
— Seminar on Transformation Goups, Ann. Math. Studies, 46, Princeton
Univ. Press, 1960.
Ботт P. (Bott R.) The space of loops on a Lie group, Mich. Math. J., 1958, 5,
35—61.
—	The stable homotopy of the classical groups, Ann. Math., 1959, 70, 313—337.
— A note on the АО-theory of sphere bundles, Bull. Amer. Math. Soc., 1962,
68, 395—400.
—	The periodicity theorem for the classical groups and some of its appli-
cations, Advances Math., 1970, 4, 353—411.
—	On a topological obstruction to integrability, Proc. Symp. Pure Math., 16,
Amer. Math. Soc., 1970, 127—132.
—	The Lefschetz formula and exotic characteristic classes, Symposia Math.,
10, Differential Geometry, Rome, 1972.
Ботт P., Милнор Дж. (Bott R., Milnor J.) On the parallelizability of spheres,
Bull. Amer. Math. Soc., 1958, 64, 87—89.
Ботт P., Хайтч И. (Bott R., Heitsch J.) A remark on the integral cohomology
of ВГ„ Topology, 1972, 11, 141—146.
Ботт P., Хэфлигер A. (Bott R., Haefliger A.) On characteristic classes of Г
foliantions, Bull. Amer. Math. Soc., 1972, 78, 1039—1044.
Ботт P., Чжень Шен-шень (Bott R., Chern S. S.) Hermitian vector bundles
and the equidistribution of the zeroes of their holomorphic sections, Acts
Math., 1965, 114, 71—112.
264 дж Милнор и Дж. Сташеф
Брамфил Г., Мадсен И., Милграм Р. Дж. (Brumfiel G., Madsen I., Mil-
gram R. J.) PL-characteristic classes and cobordism, Bull. Amer. Math. Soc.,
1971, 77, 1025—1030 (подробное изложение: Ann. Math., 1973, 97, 82—159).
Браудер У., Хирш M. (Browder W., Hirsch M. W.) Surgery on piecewise linear
manifolds and applications, Bull. Amer. Math. Soc., 1966, 72, 959—964.
Браун А. Б. (Braun A. B.) Functional dependence. Trans. Amer. Math. Soc.,
1935, 38, 379—394.
Броди Э. (Brody E. J.) ^Typological classification of lens spaces, Ann. Math.,
1960, 71, 163—184.
Бурбаки H. (Bourbaki N.) Elements de Math., Algfibre, Hermann, Paris,
1942 — ...
Ван дер Варден Б. Л. (Van der Waerden В. L.) Einfuhrung in die Alge-
braische Geometrie, Springer-Verlag, Berlin, 1939.
- Алгебра, —M.: Наука, 1976 (Vol. 1: 1971; Vol. 2: 1967).
Вильямсон P. У. (Williamson R. W.) Cobordism of combinatorial manifolds,
Ann. Math., 1966, 83, 1—33.
Вуд Дж. (Wood J.) Bundles with totally disconnected structural group, Comm.
Math. Helv., 1971, 46, 257—273.
Гальперин С., Толедо Д. (Halperin S., Toledo D.) Stiefel-Whitney homology
classes, Ann. Math., 1972, 86, 511—525.
Ганнинг P., Росси X. (Gunning R. C., Rossi H.) Аналитические функции
многих комплексных переменных. — М.: Мир, 1969 (1965).
Гильберт Д., Кон-Фоссен G (Hilbert D., Cohn-Vossen S.) Наглядная гео-
метрия.— Л.—М.: Гостехиздат, 1951 (1956).
Годбийон К., Вей Ж. (Godbillon С., Vey J.) Un invariant des feuilletages de
codimension 1, C. R. Acad. Paris, 1971, 273, 92—95.
Грейвс Л. (Graves L.) Theory of functions of real variables, 2nd ed., McGraw-
Hill, N. Y„ 1956.
Гуревич В. (Hurewicz W.) On the concept of fibre space, Proc. Nat. Acad.
Sci. U.S.A., 1955, 41, 956—961.
Дайер Э. (Dyer E.) Cohomology Theories, Benjamin, N. Y., 1969.
Джеймс И. (James I. M.) Euclidean models of projective spaces, Bull. Lon-
don Math. Soc., 1971, 3, 257—276.
Джеймс И., Уайтхед Дж. Г. К. (James I. М., Whitehead J. Н. С.) The
homotopy theory of sphere bundles over spheres. I. Proc. London Math. Soc.,
1954, 4, 196—218.
Дольд A. (Dold A.) Partitions of unity in the theory of fibrations, Ann. Math.,
1963, 78, 223-255.
— Лекции по алгебраической топологии.—M.: Мир, 1976 (1972).
Дугунджи Дж. (Dugundji J.) Topology, Allyn and Bacon Boston, 1966.
Каи П. (Kahn P. J.) A note on topological Pontrjagin classes and the
Hirzebruch index formula, Illinois J. Math., 1972, 16, 243—256.
Капланский И. (Kaplansky I.) Infinite Abeliangroups, Univ. Michigan Press,
1954.
Картан А., Эйленберг C. (Cartan H., Eilenberg S.) Гомологическая алгеб-
ра.—M.: ИЛ, 1960 (1956).
Карубй M. (Karoubi М.) Cobordisme et groupes formels (d’apres D. Quillen
et T. tom Dieck), Seminaire Bourbaki 1971/72. 408, Lecture Notes in Math.
317, Springer-Verlag, 1973.
Квиллен Д. (Quillen D.) The Adams conjecture, Topology, 1971, 10, 67—80.
— Elementary proofs of some results of cobordism theory using Steenrod •
operations, Advances Math., 1971, 7, 29—56.
Список литературы 266
Келли Дж. (Kelley J. L.) Общая топология. — М.: Наука, 1968 (1955).
Кервер М. (Kervaire М.) Non-parallelizability of the n-sphere for n > 7,
Proc. Nat. Acad. Sci. U.S.A., 1958, 44, 280—283.
Кервер M., Милнор Дж. (Kervaire M., Milnor J. W.) Groups of homotopy
spheres. I, Ann. Math., 1963, 77, 504—537.
Кёрби P., Зибенманн Л. (Kirby R., Siebenmann L.) On the triangulation of
manifolds and the Hauptvermutung, Bull. Amer. Math. Soc., 1968, 75, 742—749.
Кистер Дж. (Kister J. M.) Microbundles are fibre bundles, Ann. Math., 1964,
80, 190—199.
Киезер X. (Kneser H.) Analytische Struktur und AbzShlbarkeit, Ann. Acad.
Sci. Fenn. Ser. A. I, 1958, 251/5.
Кобаяси С., Номидзу К. (Kobayashi S., Nomizu K.) Foundations of differen-
tial geometry. I, Interscience, New York, 1963.
Коннер П., Флойд Э. (Conner P., Floyd E.) The relation of cobordism to
К-theories, Lecture Notes in Math., 28, Springer-Verlag, 1966. [Имеется пе-
ревод: О соотношении теории кобордизмов и К-теории. — В кн.: Коннер П.,
Флойд Э. Гладкие периодические отображения.— М.: Мир, 1969 (1966).]
Ланделл Э., Вейнграм С. (Lundell А. Т., Weingram S.) The Topology of CW
Complexes, Van Nostrand Reinhold, 1969.
Лашеф P., Ротенберг M. (Lashof R. K., Rothenberg M.) Microbundles and
smoothing, Torology, 1965, 3, 357—388.
Ленг C. (Lang S.) Алгебра.—M.: Мир, 1968 (1965).
—	Введение в теорию дифференцируемых многообразий.— М.: Мир, 1967
(1962).
Маклейн С. (MacLane S.) Гомология. — М.: Мир, 1966 (1963).
Маклейн С., Биркгоф Г. (MacLane S., Birkhoff G.) Algebra, MacMillan, 1967.
Макмахон П. (Macmahon P. A.) Combinatory Analysis, Cambridge Univ.
Press, 1915—16.
Маикрс Дж. (Munkres J. R.) Elementary Differential Topology, revised ed.,
Ann. Math. Studies, 54, Princeton Univ. Press, 1966. [Переведено на рус-
ский в виде дополнения в настоящей книге.]
—	Obstructions to imposing differentiable structures, Illinois J. Math., 1964,
8, 361—376; 1968, 12, 610—615.
Маховальд M. (Mahowald M.) The order of the image of the /-homomorphism,
Bull. Amer. Math. Soc., 1970, 76, 1310—1313.
Милграм P. Дж. (Milgram R. J.) The mod 2 spherical characteristic classes,
Ann. Math., 1970, 92, 238—261.
Милнор Дж. (Milnor J. W.) On manifolds homeomorphic to the 7-sphere,
Ann. Math., 1956, 64, 399—405. [Имеется перевод: О многообразиях, гомео-
морфных семимерной сфере.— Математика, 1959, 1 : 3, 35—42.]
—	On the existence of a connection with curvature zero, Comm. Math: Helv.,
1958, 32, 215—223.
—	Microbundles. I, Topology, 1964, 3 (Suppl. 1), 53—80.
—	Topology from the Differential Viewpoint, Univ. Press Va., Charlottes-
ville, 1965. [Переведено на русский в виде одной из двух частей книги:
Милнор Дж., Уоллес А. Дифференциальная топология. Начальный курс.—
М.: Мир, 1972 (1968).]
—	On characteristic classes for spherical fibre spaces, Comm. Math. Helv.,
1968, 43, 51—77.
Милнор Дж., Кервер M. (Milnor J. W , Kervaire M.) Bernoulli numbers, ho-
motopy groups, and a theorem of Rohlin, Proc. Int. Cong. Math., Edinburgh
1958, Cambridge Univ. Press, 1960, p. 454—458.
266 Дж. Милнор и Дж. Сташеф
Миядзаки X. (Miyazaki Н.) Paracompactnees of С IF complexes, Tohoku
Math. J., 1952, 4, 309—313.
Мэй Дж. П. (May J. P.) Geometry of interated loop spaces, Lecture Notes
in Math. 271, Springer-Verlag, 1972. [Имеется перевод: Геометрия итери-
рованных пространств петель. — В кн.: Бордман Дж., Фогт Р. Гомотопиче-
ски инвариантные алгебраические структуры. — М.: Мир, 1977 (1972).]
Нильсен Н. (Nielsen N.) Traite elementaire des nombres de Bernoulli,
Gauthier-Villars, Paris, 1923.
Новиков С. П. Гомотопически эквивалентные гладкие многообразия. I. — Изв.
АН СССР, сер. мат. 1964, 28, № 2, 365—474.
— О многообразиях со свободной абелевой фундаментальной группой и их
применения. — Изв. АН СССР, сер. мат., 1966, 30, № 1, 71—96.
— Методы алгебраической топологии с точки зрения теории кобордизмов. —
Изв. АН СССР, сер. мат. 1967, 31, 855—951.
Номидзу К. (Nomizu К.) Группы Ли и дифференциальная геометрия. — М.:
ИЛ, 1960 (1956).
Ньюлэндер Э., Нупенберг Л. (Newlander A., Nirenberg L.) Complex analytic
coordinates in almost complex manifolds, Ann. Math., 1957, 65, 391—404.
Остманн X. (Ostmann H.) Additive Zahlentheorie, Springer-Verlag, 1956.
Петерсон Ф. (Peterson F. P.) Some results on sohomotopy groups, Amer.
J. Math., 1956, 78, 243—258.
—	Some results on PL-cobordism, J. Math. Kyoto U., 1969, 9, 189—194.
—	The mod p homotopy type of BSO and F/PL, Bol. Soc. Math. Mex., 1969,
14, 22-27.
— Twisted cohomology operations and exotic characteristic classes, Advances
Math., 1970, 4, 81—90.
Петерсон Ф., Тода X. (Peterson F. P., Toda H.) On the structure of H* (BSF\
Zp), J. Math. Kyoto U., 1967, 7, 113—121.
Петре Я. (Peetre J.) Une caracterization abstraite des operateurs differentials,
Math. Scand., 1959, 7, 211—218; 1960, 8, 116—120.
Понтрягин Л. С. Характеристические циклы дифференцируемых многообра-
зий.—Мат. сб. н. с., 1947, 21 (63), 233—284.
Равенель Д. (Ravenel D.) A definition of exotic characteristic classes of
spherical fibrations, Comm. Math. Helv., 1972, 47, 421—436.
де Рам Ж. (de Rham G.) Дифференцируемые многообразия. — M.: ИЛ, 1956
(1955).
Рохлин В. А. Трехмерное многообразие — граница четырехмерного.—ДАН
СССР, 1951, 81, № 3, 355—357.
Рохлин В. А., Шварц А. С. О комбинаторной инвариантности классов Пон-
трягина,—ДАН СССР, 1957, 114, № 3, 490—493.
Рурк К. П., Сандерсон Б. (Rourke S. Р., Sanderson В. J.) Введение в ку-
сочно-линейную топологию. — М.: Мир, 1974 (1972).
Сард A. (Sard A.) The measure of the cricital values of differentiable maps,
Bull. Amer. Math. Soc., 1942, 48, 883—890.
Сван P. (Swan R.) Vector bundles and projective modules, Trans. Amer.
Math. Soc., 1962, 105, 264—277.
Серр Ж.-П. (Serre J.-P.) Groupes d’homotopie et classes des groupes abeliens,
Ann. Math., 1953, 58, 258—294. [Имеется перевод: Группы гомотопий и
классы абелевых групп. — В кн.: Расслоенные пространства. М.: ИЛ, 1958,
с. 124—162.]
Серф Ж. (Cerf J.) Sur les diffeomorphismes de la sphere de dimension trois
(Г4 = 0), Lecture Notes in Math. 53, Springer-Verlag, 1968,
Список литературы 267
Сигал Г. (Segal G.) Categories and cohomology theories, Topology, 1974, 13,
293—312.
Симада H. (Shimada N.J Differentiable structures on the 15-sphere and
Pontrjagin classes of certain manifolds, Nagoya Math., J., 1957, 12, 56—69.
Смейл C. (Smale S.) The classification of immersions of spheres in Euclidean
space, Ann. Math., 1959, 69, 327—344.
— Differentiable and combinatorial structures on manifolds, Ann. Math., 1961,
74, 498—502.
Спеньер Э. (Spanier E. H.) Алгебраическая топология. — M.: Мир, 1971
(1966).
Спеиьер Э., Уайтхед Дж. Г. К. (Spanier Е. Н., Whitehead J. Н. С.) Duality in
homotopy theory, Mathematika, 1955, 2, 56—80.
Спивак M. (Spivak M.) Spaces satisfying Poincare duality, Topology, 1967, 6,
77—101.
Спрингер Дж. (Springer G.) Введение в теорию римановых поверхностей.—
М.: ИЛ, 1960 (1957).
Сташеф Дж. (Stasheff J. D.) A classification theorem for fibre spaces, Topo-
logy, 1963, 2, 239—246.
— More characteristic classes for spherical fiber spaces, Comm. Math. Helv.,
1968, 49, 78—86.
Стернберг Ш. (Sternberg S.) Лекции по дифференциальной геометрии. — Мл
Мир, 1970 (1964).
Стинрод Н. (Steenrod N.) Топология косых произведений. — М., ИЛ, 1953
(1951).
Стинрод Н., Уайтхед Дж. Г. К- (Steenrod N., Whitehead J. Н. С.) Vector field
on the n-sphere, Proc. Nat. Acad. Sci. U.S.A., 1951, 37, 58—63.
Стиирод H., Эпстейн Д. В. Э. (Steenrod N., Epstein D. B. A.J Cohomology
Operations, Ann. Math. Studies 50, Princeton Univ. Press, 1962.
Стонг P. (Stong R. E.) Заметки по теории кобордизмов. — M.: Мир, 1973
(1968).
Сулливан Д. (Sullivan D.) Геометрическая топология. — М.: Мир, 1975
(1970).
Тамура И. (Tamura I.) On Pontrjagin classes and homotopy type of mani-
folds, J. Math. Soc. Japan, 1957, 9, 250—262.
Том P. (Thom R.) Espaces fibres en spheres et саггёз de Steenrod, Ann. Sci.
Ecole Norm. Sup., 1952, 69, 109—181.
— Quelques proprietes globales des varietes diffferentiables, Comm. Math.
Helv., 1954, 28, 17—86. [Имеется перевод: Некоторые свойства в целом диф-
ференцируемых многообразий. — В кн.: Расслоенные пространства. М.: ИЛ,
1958, с. 291—348.]
— Les singularites des applications differentiables, Ann. Inst. Fourier, Gre-
noble, 1955—56, 6, 43—87.
— Les classes charact^ristiques de Pontrjagin des varietes triangulees, Sym-
posium Internacional de Topologia Algebraica, Mexico, La Universidad Natio-
nal Autonoma de Mexico у la Unesco, 1958, p. 54—67.
Томас Э. (Thomas E.) On tensor products of n-plane bundles, Archiv der
Math., 1959, 10, 174—179.
— On the cohomoloqy of the real Grassman complexes and the characteristic
classes of n-plane bundles, Trans. Amer. Math. Soc., 1960, 96, 67—89.
— On the cohomology groups of the classifying space for the stable spinor
group, Bol. Soc., Math. Mex., 1962, 57—69.
— The torsion Pontrjagin classes, Proc. Amer. Math. Soc., 1962, 13, 485—488.
268 Дж. Милнор и Дж. Сташеф
Тэрстон У. (Thurston W.) Non-cobordant folations of S’, Bull. Amer. Math.
Soc., 1972, 78, 511—514.
У	4 Вэнь-цзунь (Wu Wen-tsun) On the products of sphere bundles and the
duality theorem modulo two, Ann. Math., 1948, 49, 641—653.
—	On Pontrjagin classes. II, Scientia Sinica, 1955, 4, 455—490.
—	A theory of embedding, immersion, and isotopy of polytopes in a Euclidean
space, Science Press, Peking, 1965.
Уайтхед Дж. Г. К. (Whitehead J H. C.) On C4-complexes, Ann. Math., 1940,
41, 809—824.
—	Combinatorial homotopy. I, Bull. Amer. Math. Soc., 1949, 55, 213—245.
—	Manifolds with transverse field in Euclidean space, Ann. Math., 1961, 73,
154—212.
Уайтхед Дж. У. (Whitehead G. W.) Generalized homology theories, Trans.
Amer. Math. Soc., 1962, 102, 227—284.
Уитни X. (Whitney H.) Sphere spaces, Proc. Nat. Acad. Sci., 1935, 21,
462—468.
—	On the theory of sphere bundles, Proc. Nat. Acad. Sci. U.S.A., 1940, 26,
148—153.
—	On the topology of differentiable manifolds, Lectures in Topology, Univ,
of Michigan Press, 1941, 101—141.
—	The self-intersections of a smooth n-manifold in 2n-space, Ann. Math.,
1944, 45, 220—246.
—	The singularities of a smooth n-manifold in (2n — 1)-space, Ann. Math.,
1944, 45, 247—293.
—	Геометрическая теория интегрирования. — M.: ИЛ, 1960 (1957).
Уолл Ч. (Wall С. Т. С.) Determination of the cobordism ring, Ann. Math.,
1960, 72, 292—311.
Уорнер Ф. (Warner F.) Foundations of Differentiable Manifolds and Lie
Groups, Scott, Foresmann and Co., Glenview, Illinois, 1971.
Харди Г., Райт Э. М. (Hardy G. Н., Wright Е. М.) Ап Introduction to the
Theory of Numbers, 3rd ed., Clarendon Press, Oxford, 1956.
Хёрмандер JI. (Hormander L.J Введение в теорию функций нескольких ком-
плексных переменных. — М.: Мир, 1968.
Хилтон П., Уайли С. (Hilton Р. J„ Wylie S.) Теория гомологий. Введение в
алгебраическую топологию. — М.: Мир, 1966 (1960).
Хирцебрух Ф. (Hirzebruch F.) On Steenrod’s reduced powers, the index of
inertia and the Todd genus, Proc. Nat. Acad. Sci. U.S.A., 1953, 39, 951—956.
— Uber die quaternionalen projekctiven Raume, S.-Ber. math.-naturw. KI.
Bayer. Akad. Wiss. Munchen, 1953, 301—312.
—	Топологические методы в алгебраической геометрии. — М.: Мир, 1973
(1966).
Хирш М. (Hirsch М. W.) Immersions of manifolds, Trans. Amer. Math. Soc.,
1959, 93, 242—276.
—	Obstruction theories for smoothing manifolds and maps, Bull. Amer. Math.
Soc., 1963, 69, 352—356.
Хьюзмоллер Д. (Husemoller D.) Расслоенные пространства.—M.: Мир, 1970
(1966).
Хэфлигер А., Уолл Ч. (Haefliger A., Wall С. Т. С.) Piecewise linear bundles
in the stable range, Topology, 1965, 4, 109—214.
Чепмэн T. (Chapman T. A.) Compact Hilbert cube manifolds and the inva-
riance of Whitehead torsion, Bull. Amer. Math. Soc., 1973, 79, 52—56.
1 Часто пишут также By. — Прим, перев.
Список литературы 269
Чжеиь Тен-шень (Chern S. S.) On the multiplication in the characteristic
ring of a sphere bundle, Ann. Math., 1948, 49, 362—372.
—	Geometry of characteristic classes, to appear.
Чжень Шен-шеиь, Саймонс Дж. (Chern S. S„ Simons J.) Some cohomology
classes in principal fiber bundles and their application in Riemannian geo-
metry, Proc. Nat. Acad. Sci. U.S.A, 1971, 68, 791—794.
—	Characteristic forms and geometric invariants, Ann. Math., 1974, 99, 48—69.
Шевалле К. (Chevalley С.). Теория групп Ли. I.— M.: ИЛ, 1948 (1946).
Ши В. (Shih W.) Une remarque sur les classes de Thom, C. R. Acad. Sci.
Paris, 1965, 260, 6259—6262.
Ши В., Сингх Варма X. О. (Shih W., Singh Varma H. O.) Sur les AO-classes
characteristiques de fibres reels, C. R. Acad. Sci. Paris, 1971, 273-A, 1212—
1214.
Штифель Э. (Stiefel E.) Richtungsfelder und Fernparallelismus in Manni-
gfaltigkeiten, Comm. Math. Hels., 1936, 8, 3—51.
Шуберт X. (Schubert H.) Kalkfll der abzahlenden Geometric, Teubner, Leip-
zig, 1879.
Шчарба P. (Szczarba R.) On tangent bundles of fibre spaces and quotient
spaces, Amer. J. Math., 1964, 86, 685—697.
Эйленберг С., Стинрод H. (Eilenberg S., Steenrod N.) Основания алгебраи-
ческой топологии. — M.: Физматгиз, 1958 (1952).
Эресманн Ш. (Ehresmann С.) Sur la topologie de certains espaces homogenes,
Ann. Math., 1934, 35, 396—443.
—	Sur la topologie de certains variates algebriques r6els, J. Math. Pures
Appl., 1937, (9), 16, 69—100.
—	Introduction a la theorie des structures infinitfesimales et des pseudo-groupes
de Lie, Colloque de topologie et geometric differentielle, Strasbourg. 1952
No. 11, La Bibliotheque Nationale et Universitaire de Strasbourg, 1953.
American Math. Soc., Proceedings Sumposia in Pure Math. 27, Differential
Geometry, 1975.
ДОПОЛНЕНИЕ
Дж. Манкре
ЭЛЕМЕНТАРНАЯ
ДИФФЕРЕНЦИАЛЬНАЯ ТОПОЛОГИЯ1
ГЛАВА I
ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ
§ 1. ВВЕДЕНИЕ
Этот параграф посвящен определению таких основных по-
нятий, как дифференцируемое многообразие, дифференцируе-
мое отображение, погружение, вложение и диффеоморфизм, и
доказательству теоремы о неявной функции.
Мы рассматриваем евклидово пространство Rm как про-
странство всех бесконечных последовательностей вещественных
чисел х—(х1,х2, ...), таких, что х1 = 0 для i > т; евклидово
полупространство Нт— это подмножество Rm, состоящее из то-
чек х, для которых хт 0. Таким образом, R"1-1 cz Н"1 cz Rm.
Мы обозначаем д/(*')2 + ••• + (хт)2 через ||х||, а тах|х'| че-
рез |х|. Единичная сфера S"1-1 — это подмножество точек х
пространства Rm, для которых ||х|| = 1; единичный шар Вт—
это подмножество точек х, для которых ||х||^ 1; т-мерный
r-куб Ст(г)— это подмножество точек х, для которых | х| г,
т. е. куб со стороной 2г. Часто мы рассматриваем Rm просто
как пространство всех наборов из т чисел (х1, .... хт), если
это не может вызвать недоразумений.
ОПРЕДЕЛЕНИЕ 1.1. (Топологическим) многообразием М
называется всякое хаусдорфово пространство со счетной ба-
зой, удовлетворяющее следующему условию: существует целое
число т, такое, что каждая точка х е М имеет окрестность, го-
меоморфную некоторому открытому подмножеству простран-
ства Rm или полупространства Нт.
Если h: U -> Нт (или Rm) — гомеоморфизм окрестности U
точки х на открытое подмножество в Н"1 или в Rm, то пару
(U, h) часто называют координатной окрестностью в М. Если
1 Elementary Differential Topology, by James R. Munkres, Lectures given
at Massachusetts Institute of Technology, Fall, 1961, Revised ed., Ann. Math.
Studies, 54, Princeton, New Jersey, Princeton University Press, 1966.
§ 1. Введение 271
h(U) открыто в Н"1 ий(х)е R"1-1, то точка х называется крае-
вой (или граничной) точкой многообразия М. Множество всех
таких точек называется краем (или границей) многообразия М
и обозначается через BdM1. Если множество BdM пусто, то
мы говорим, что многообразие М есть многообразие без края.
(В литературе чаще применяется иная терминология: слово
«многообразие» используют, только когда край BdAf пуст; а в
общем случае говорят о «многообразии с краем».) Множество
M\BdA4 называется внутренностью многообразия М и обозна-
чается Int М. (Если А — подмножество топологического про-
странства X, то мы используем символ Int Л также для обозна-
чения множества Х\С1 (Х\Л), однако это не должно вызывать
недоразумений.)
Чтобы оправдать эти определения, нам надо еще показать,
что, если hi:	и Л2: Uz—> Hm суть гомеоморфизмы ок-
рестностей точки х на открытые подмножества в Нт и /ц(х)е
е Rm~1, то также й2(х)е R"*-1. Но действительно, в противном
случае отображение осуществляло бы гомеоморфизм не-
которого открытого множества в Rm с некоторой окрестностью
точки р == hi (х) в Нт. Последняя окрестность, конечно, не яв-
ляется открытой в Rm, и мы получаем противоречие с теоремой
Брауэра об инвариантности области [2].
Можно также проверить, что число m однозначно опреде-
лено для всякого многообразия М; оно называется его размер-
ностью, а М называют m-мерным многообразием. Проверить
это можно, либо используя теорему Брауэра об инвариантно-
сти области, либо применяя теорему теории размерности, ут-
верждающую, что топологическая размерность многообразия М
равна m [2]. Строго говоря, чтобы применять последнюю тео-
рему, мы должны знать, что М является сепарабельным метри-
зуемым пространством; однако это следует из стандартной
метризационной теоремы теоретико-множественной топологии
[17].
Так как М есть локально-компактное сепарабельное метри-
ческое пространство, то М паракомпактно [17]. Напомним чита-
телю, что это означает, что для любого открытого покрытия зФ
пространства М существует другая совокупность & открытых
множеств, покрывающих Л4, со свойствами:
(1) Покрытие вписано в покрытие т. е. любой эле-
мент покрытия $ содержится в некотором элементе покрытия
1 Bd — от boundary (граница). В основном тексте использовалось другое
обозначение, дМ-, мы решили сохранить в каждом случае авторские обозна-
чения. — Прим, перев.
272 Дополнение. Дж. Манкрс
(2) Покрытие & локально-конечно, т. е. любая точка из М
имеет окрестность, пересекающуюся лишь с конечным числом
элементов покрытия 93.
Заметим, между прочим, что, поскольку М обладает счетной
базой, любое локально-конечное открытое покрытие простран-
ства М должно быть счетным.
Упражнение1 (а). Показать, что для всякого m-мерного многообра-
зия М край Bd М либо пуст, либо является (т—1)-мерным многообразием
без края.
Упражнение (Ь). Пусть М— некоторое «-мерное многообразие с не-
пустым краем и Ма = М X 0 и Mt = М X 1 — Два экземпляра многообра-
зия М. Удвоение2 многообразия М, обозначаемое D(Af),—это топологическое
пространство, получающееся из Мо U Mi отождествлением точки (х, 0) с точ-
кой (х, 1) для каждого х е Bd М. Доказать, что D(/W) является «-мерным
многообразием без края.
Упражнение (с). Если М и N — многообразия размерности « и п
соответственно, то М X N — многообразие размерности «-j- п и
Bd (М X N) = ((Bd М) X N) U (М X (Bd (N)).
ОПРЕДЕЛЕНИЕ 1.2. Пусть U — открытое подмножество
пространства Rm. Отображение f:U-+Rn называется диффе-
ренцируемым класса Сг (или Сг-отображением), если каждая из
его координатных компонент ф, ..., fn обладает в U непрерыв-
ными частными производными всех порядков до г включитель-
но. В случае когда отображение f является дифференцируемым
класса Сг для любого конечного г, говорят, что оно имеет
класс С°°.
Пусть А — произвольное подмножество пространства R"1.
Отображение ф. А -* R" называется дифференцируемым класса
Cr (1 г оо), если для каждой точки хеЛ существует та-
кая окрестность Ux точки х, что f| (А П Ux) можно продолжить
до отображения класса Сг на Ux.
Для всякого дифференцируемого отображения ф. А —► R" и
всякой точки хеА через Df(x) обозначается матрица Якоби
отображения f в точке х — матрица, элементы которой имеют
вид atj = дф/дх1. Для этой матрицы мы используем также обо-
значение дф, ..., ф1/д(х1, ..., хт). Разумеется, здесь, прежде
чем определять частные производные, надо продолжить отобра-
жение f на некоторую окрестность точки х; в представляющих
интерес случаях частные производные не зависят от выбора
продолжения (см. упр. (Ь)).
1 Упражнения, результат которых (или его доказательство) представляют
особый интерес (или особую трудность), именуются у Манкрса задачами. Уп-
ражнения и задачи, несущественные для общей логической линии изложения,
помечены звездочкой. — Прим. ред.
2 J3 оригинале double. Отсюда обозначение D(A1).— Прим, перев.
§ 1. Введение 273
Напомним еще цепное правило1 для дифференцирования,
которое утверждает, что D(fg) = Df-Dg, где fg— композиция
отображений2, а точка обозначает умножение матриц3 *.
Упражнение (а). Проверить, что дифференцируемость определена
корректно, т. е. что дифференцируемость отображения ft А -» Rn не зависит от
того, какое объемлющее пространство R“ выбрано для А.
Упражнение (Ь). Пусть U — открытое подмножество в R” и С/с
сЛсЦ Показать, что, если ft А -+ R" — отображение класса С1 и хеЛ, то
Df(x) не зависит от выбора продолжения отображения f на окрестность точки
х в пространстве Rm.
Замечание. Наше определение дифференцируемости отобра-
жения f: А —» R" является существенно локальным. Ниже мы
дадим эквивалентную глобальную формулировку свойства диф-
ференцируемости (см. теорему 1.5).
Лемма 1.3. Существует функция ср: Rm —►R1 класса С°°, рав-
ная 1 на Ст(}/2), положительная внутри 0(1) и равная нулю
вне 0(1).
Доказательство. Положим f(t) = e~lli для t > 0 и /(/) = 0
для t 0. Тогда функция f имеет класс О и положительна
при t > 0. Далее, возьмем g(t) = f (t)/(f (/)+ f (1 — /)). Тогда g
будет функцией класса О, такой, что g(t) = O для t О,
g'(t) > 0 для 0 < t < 1 и g(t)= 1 для t 1.
Пусть теперь	= g(2t + 2)g(—2t-f-2). Ясно, что h яв-
ляется функцией класса О, причем й(/) = Одля И 5s 1,Л(0>
>0 для |^|^1 и h(t)= 1 для |/|^1/2. Наконец, полагаем
^(х1, ..., xm) = h(x1)h(x2) ... h(xm). 
Упражнение (а). Обобщить предыдущую лемму следующим образом.
Пусть и — открытое подмножество пространства Rm и С — компактное под-
•Правило дифференцирования сложной функции. — Прим, перев.
2 Ниже fg обозначает то композицию, то поточечное произведение функ-
ций. Это не должно вызвать затруднений у читателя. — Прим. ред.
3 Заметим, что матрица Dg вычисляется в рассматриваемой точке х, a
матрица Df — в точке g(x). — Прим, ред,
Дополнение. Дж. Манкрс
множество в U. Существует вещественнозначная функция ф класса С“, опре-
деленная на Rm, положительная на С и равная нулю в некоторой окрестности
дополнения к U.
Замечание. Всякий раз, когда мы будем говорить, что индек-
сированное семейство {С,} подмножеств пространства X ло-
кально-конечно, мы будем понимать под этим, что любая точка
пространства X имеет окрестность, пересекающуюся с Ci только
для конечного числа значений I. Это соглашение удобно, ибо
оно гарантирует, что ни одно множество не встретится в по-
следовательности С\, Cz, ... бесконечное число раз.
Лемма 1.4. (1) Пусть {(/>•}—открытое1 покрытие параком-
пактного пространства X. Существует локально-конечное от-
крытое покрытие {Vi} пространства X, такое, что Vi a Ui для
каждого i.
(2) Пусть {V,}—локально-конечное открытое покрытие нор-
мального пространства X. Существует замкнутое покрытие {CJ
пространства X, такое, что Ci cz Vi для каждого i.
Доказательство. Пусть &— локально-конечное покрытие,
вписанное в покрытие {J7J. Для каждого элемента В покры-
тия & выберем индекс j(B) из условия В cz Ukb). Определим
V/ как объединение тех элементов В, для которых j(B) — j.
Каждая точка имеет окрестность, пересекающуюся лишь с ко-
нечным числом элементов покрытия В; эта окрестность пересе-
кается лишь с конечным числом множеств V/.
Построим теперь замкнутое покрытие {С/} по индукции.
Пусть Wi — открытое множество, которое содержит X\(V2U
и Кз и . -.) и замыкание которого содержится в Уь Положим
Ci = Fi.
Предположим, что Wt U ... U Wj-i U Vt U Vj+i U ... = X.
Пусть W, — открытое множество, которое содержит X\(FiU
(J ... U F/-i U V/+i U • • •) и замыкание которого содержится в
V/. Положим Cj = Wj.
Чтобы доказать, что совокупность {F/} покрывает X, заме-
тим, что любая точка х принадлежит лишь конечному числу
множеств Vj. Следовательно, для некоторого / точка х не при-
надлежит объединению V/ U V/+i U ... . Но тогда по индуктив-
ному предположению точка х должна принадлежать объедине-
нию Wi и ... U Wj-I. 
Теорема 1.5. Пусть А — подмножество пространства Rm.
Всякое отображение f: A -*R.n класса Сг можно продолжить
до отображения класса Сг, определенного на некоторой окре-
стности множества А.
1 Счетное. — Прим. ред.
§ 1. Введение 275
Доказательство. По предположению для каждой точки х е
еЛ существует такая ее окрестность Ux, что f\A П Ux может
быть продолжено до отображения класса С на Ux. Не умень-
шая общности, можно считать Ох компактом. Пусть М есть
объединение множеств Ux по всем хеЛ. Ясно, что М — от-
крытое подмножество пространства Rm. Пусть {К} — локально-
конечное открытое покрытие множества М, вписанное в по-
крытие {Ux}, л пусть {С;} — покрытие множества М замкну-
тыми множествами, такими, что С, а V, для каждого I. Пусть
далее ф, для каждого i — функция класса С°°, определённая
на Rm, положительная на Ci и равная нулю в некоторой окрест-
ности дополнения к Vi. (Здесь мы используем упр. (а) п. 1.3.)
Тогда £ф/(х) будет функцией класса С°° на М, ибо эта сумма
фактически является конечной в некоторой окрестности любой
заданной точки множества М. Положим <pz (х) = фг (х)/^ ф/ (х).
Тогда Z <рг (х) == 1.
Для каждого i пусть fi — какое-нибудь отображение класса
Сг, продолжающее /|ЛП Vi на К; если Л Л К пусто, то пусть ft
равно нулю. Произведение <р,/7 можно продолжить до отображе-
ния класса Сг на М, положив его равным нулю вне Vi. Опреде-
лим отображение f равенством
f(x) = Z Ф/ (х) fi (х).
Выражение справа является конечной суммой в некоторой окре-
стности любой данной точки х е М и, следовательно, есть ото-
бражение класса Сг на М. Далее, если х е А, то fi(x) = f(x) для
любого г, так что
f (х)= Z<p,(x)f (x) = f(x).
Таким образом, f представляет собой искомое продолжение
класса Сг отображения f на окрестность М множества А в Rm.
ОПРЕДЕЛЕНИЕ 1.6. Дифференцируемое т-мерное много-
образие класса Сг — это m-мерное многообразие М вместе с
дифференцируемой структурой 2D класса Сг на М. Дифференци-
руемой структурой класса Сг на многообразии М называется
всякая совокупность координатных окрестностей (U, h) на мно-
гообразии М, удовлетворяющая следующим трем условиям:
(1)	Координатные окрестности из 2) покрывают М.
(2)	Если (t/i, hi) и (U2, й2) принадлежат 0, то
М2-1: й2 (Ui П U2) -> Rm
есть дифференцируемое отображение класса Сг.
(3)	Совокупность 2D является максимальной относительно
свойства (2), т. е. если любую координатную окрестность, не
276 Дополнение. Дж. Манкрс
принадлежащую Я), присоединить к S), то свойство (2) пере-
стает выполняться.
Элементы из совокупности S) часто называют координатны-
ми системами на дифференцируемом многообразии М.
Упражнение (а). Пусть 3)' — совокупность координатных окрестно-
стей на многообразии М, удовлетворяющая только условиям (1) и (2). До-
казать, что существует единственная дифференцируемая структура класса Сг,
содержащая 3)'. (Мы называем ЗУ базисом структуры 3) по аналогии с тер-
мином «базнс топологии».)
Указание. Взять в качестве 3) совокупность всех координатных окрест-
ностей (U,h) на многообразии М, «дифференцируемо класса С' пересекаю-
щих» каждый элемент из ЗУ', это означает, что для каждого элемента (1У,
hi) е ЗУ отображения
Л1Л"1: h (U f| Ui) -> Rm
и
ЙЙГ1: hi (U П СЛ) -> R”1
являются дифференцируемыми класса Сг. Некоторая осторожность требуется
при рассмотрении координатных окрестностей точек из Bd М.
Упражнение (Ь). Пусть М— дифференцируемое многообразие класса
С'. (Мы часто будем опускать упоминание о дифференцируемой структуре 3,
когда это не может вызвать недоразумений.) Тогда М можно естественным об-
разом рассматривать также как дифференцируемое многообразие класса С'-1—
нужно просто принять совокупность 3> в качестве базиса дифференцируемой
структуры ЗУ класса Сг~* на М. Проверить, что включение 3 с 3\ является
собственным ’. Это доказывает, что класс С' дифференцируемого многообразия
однозначно определен.
Мы видим, таким образом, что класс данного дифференцируемого много-
образия М можно понизить насколько угодно простым добавлением новых ко-
ординатных систем к дифференцируемой структуре. Обращение этого утвер-
ждения также верно, однако доказательство требует большого труда 2.
’.Упражнение (с). Пусть М — дифференцируемое многообразие. Ка-
кие трудности возникают пришв еденни дифференцируемой структуры на
D(M)?(D(M) было определено в упражнении (Ь) п. 1.1.)
ОПРЕДЕЛЕНИЕ 1.7. Пусть М и N — дифференцируемые
многообразия размерности тип соответственно и класса по
крайней мере Сг. Пусть далее А — некоторое подмножество мно-
гообразия М и f: A-+N. Говорят, что f есть отображение клас-
са Сг, если для любой пары (U, h) и (V, k) координатных си-
стем на М и N соответственно, для которой f (А П с V, ком-
позиция
kf/Г1: h(AQU)-H-Rn
имеет класс Сг. (Заметим, что отображение класса С2 является
также отображением класса С1, но многообразие класса С2 не
1 То есть 3\ \ 3) =/= 0. — Прим. ред.
2 См. следствие 4.9 ниже. — Прим, перев.
§ 1. Введение 277
является многообразием класса С1, пока дифференцируемая
структура не изменена.)
Рангом отображения f в точке р е М называется ранг ма-
трицы D(kfh~x) в точке й(р), где (U, h) и (V, k)—координат-
ные системы в точках р и f(p) соответственно. Это число вполне
определено при условии, что существует открытое подмноже-
ство IF многообразия М, такое, что W a A cz W. Действительно,
если (U\, hi) и (Vi, ki) — другие такие же координатные систе-
мы, то мы имеем
D (kifhT1} = D (Ы-1) • D • D (ййГ1).
Требования на дифференцируемую структуру обеспечивают, что
оба отображения kik~l и kk7l будут дифференцируемыми, так
что матрица D(k\k~l) является невырожденной, имеющей в ка-
честве обратной матрицу D (k, &~1). Аналогично матрица
£)(й/гГ') невырожденна, так что матрицы D(kifh\X} и D (kfh~l)
имеют один и тот же ранг. 
Упражнение (а). Стандартная дифференцируемая структура класса
С" на Rm имеет в качестве базиса единственную координатную систему i:
Rm->Rm. Аналогично для Нт. Проверить, что понятия дифференцируемости,
введенные в определениях 1.2 и 1.7, согласованы между собой.
ОПРЕДЕЛЕНИЕ 1.8. Пусть f: M-+N— дифференцируемое
отображение класса Сг, причем М nN имеют размерность т и
п соответственно. Если ранг отображения f равен т в каждой
точке р е М, то говорят, что f является погружением. Если ото-
бражение f является одновременно гомеоморфизмом в и погру-
жением, то f называется вложением. Если отображение f — од-
новременно гомеоморфизм М на N и погружение, то f назы-
вается диффеоморфизмом; в этом случае, конечно, т — п.
Упражнение (а). Заметим, что Bd Нт = Rm-1 и включение Rw-'c: Н”
представляет собой вложение. Обобщить этот результат следующим образом.
Если М — дифференцируемое многообразие класса Сг, то существует одно-
значно определенная дифференцируемая структура класса Сг на Bd М, такая,
что включение Bd М -> М является Сг-вложением.
Упражнение (Ь). Показать, что композиция двух погружений есть
погружение.
Упражнение (с). Пусть М и N — многообразия класса С', причем
М — многообразие без края. Построить дифференцируемую структуру класса
С' на М X N, такую, что естественные включения М и W в М X " СУТЬ вложе-
ния. Почему мы требуем, чтобы М не имело края?
’Упражнение (d). Построить дифференцируемую структуру класса
С“ на Н1 X Н1, такую, что включение i: Н1 X H'-»-R2 является дифференци-
руемым. Какие трудности возникают при введении дифференцируемой струк-
туры на произведении М X N в общем случае?
278 Дополнение. Дж. Манкрс
‘Упражнение (е). Построить С°°-погружение окружности S1 в пло-
скость R2, переводящее S1 в «восьмерку». Можно ли такое погружение продол-
жить до погружения В2 в R2?
•Упражнение (f). Доказать, что две дифференцируемые структуры
класса Сг на топологическом многообразии М совпадают тогда и только тогда,
когда тождественное отображение одного из них на другое есть С'-диффео-
морфизм.
•Упражнение (g). Построить две различные дифференцируемые
структуры класса С" на многообразии R1, такие, что получающиеся диффе-
ренцируемые многообразия дифферморфны.
*3адача 1.9. Доказать, что любые две дифференцируемые
структуры на R1 дают диффеоморфные многообразия.
(Долгое время стояла следующая классическая проблема:
всегда ли две различные дифференцируемые структуры на од-
ном и том же топологическом многообразии размерности т бу»
дут давать диффеоморфные дифференцируемые многообразия?
Недавно оказалось, что ответ положителен, если т^З [9, 15],
и отрицателен, если т = 1 [5]. Кроме того, ответ положителен
для R", если п Ф 4 [13]. Известны и другие результаты1, но
еще много предстоит сделать.)
Задача 1.10. Пусть f: M-+N — диффеоморфизм класса Сг.
Доказать, что f~l — тоже диффеоморфизм класса Сг.
Указание. Доказательство нужно проводить в несколько эта'
пов. Пусть g— отображение открытого подмножества U про-
странства Rm в пространство R".
(1)	Dg(x) существует, если существуют матрицы А и мат»
ричная функция jR(xi), такие, что
g М — g (х) = А • (xi — х) + R (xi)
(где g, х и xi записываются в виде столбцов) и
Ш)\11х>—х|| —> 0, когда xi —>х. Отсюда следует, что
A = Dg{x}.
(2)	Если отображение g имеет класс С1 на U и А — компакт»
ное подмножество в U, то
g (*i) — g (х) = Dg (х) • (xi — х) 4- R (хь х),
где jR(xi, х)/|| xi — х || -> 0 равномерно, когда || хх — х||->0,
причем точки xi, х принадлежат подмножеству А. (Это утверЖ'
дение является даже более общим, чем нам в действительности
будет нужно.)
(3)	Если g — отображение класса С1 на U, имеющее ранг т
в точке х, то оно удовлетворяет двустороннему условию Лип»
1 См. основной текст, § 20 и заключение. — Прим, перев.
§ 1. Введение 279
шица: существуют 6 > 0 и константы I и L, такие, что
0</<U(x1)-g(x)||/||x1-x||<L
при 0 < || xi — х || < 6.
(4)	Пусть g— гомеоморфизм открытого подмножества U
пространства Rm на некоторое открытое подмножество про-
странства Rm, причем g — класса С1 на U и имеет ранг т в точ-
ке х. Тогда матрица D(g~}) существует в точке g(x) и равна
обратной к матрице Dg(x).
Замечание. Выше мы привлекали теорему Брауэра об инва-
риантности области, чтобы доказать, что край и размерность
многообразия корректно определены. Если ограничиться рас-
смотрением многообразий, на которых существуют дифференци-
руемые структуры (а недавно Кервером [3] было показано,
что это действительно ограничение1), то обращения к теореме
Брауэра можно до некоторой степени избежать, воспользовав-
шись следующей теоремой, которая имеет некоторое сходство с
теоремой об инвариантности области.
Теорема 1.11. Пусть f есть С{-отображение открытого подмно-
жества U пространства Rm в Rm, имеющее ранг пг в точке х.
Тогда f является гомеоморфизмом некоторой окрестности точ-
ки х на соответствующую окрестность в пространстве Rm точ-
ки f(x).
Доказательство. Мы можем считать, что точки х и f(x) ле-
жат каждая в начале координат и что Df(O)=^I (где I — еди-
ничная матрица. (Почему?) Выберем г настолько малым, чтобы
куб Cm(r) содержался в окрестности U и чтобы максимальное
абсолютное значение элементов матрицы Df(x) — I не превосхо-
дило 1/2т для xeCm(r). Если положить g(x) — f(x)— х, то
для точек xi и х2 из Ст (г) выполняются неравенства
. I g (xi) — g (х2) К 4 1 “ *2 I
И
I / (*1) — / (х2) |> 41 х‘ — Х2 !•
Прежде всего мы покажем, что любая точка у е Int Ст(г/2)
является образом при отображении f некоторой точки х е
е Int Ст (г). Чтобы сделать это, положим хо = 0, xi = у и во-
обще
хп+\ = у — g (хп)
1 См. также § 20 основного текста. — Прим, перев.
280 Дополнение. Дж. Манкрс
при условии, что точка хп лежит в области определения отобра-
жения g. Заметим, что
I %п+1 %п I= I §	S (%п—1) I "g I Хл Хл_[ 1>
так что
I *п+1 хп I /2) I xl ~~ Х0 I == 2п । У I"
Суммируя эти неравенства, находим, что
I Хп+1 хт I < ~2tn 21 У |
для т п. В частности, |xn+i— х0| < 2|«/| < г. Следователь-
но, точка Xn+i должна принадлежать Int Cm(r) и поэтому лежать
в области определения отображения g. Таким образом, точки
хп определены для всех п. Отсюда также следует, что последо-
вательность хп есть последовательность Коши. Пусть х — ее
предел. Тогда |х— хо|^2|«/|, так что хе Int Ст(г). Очевид-
но, что х — у — g(x), а значит f(x) — y, что и требовалось по-
казать.
Далее заметим, что существует только одна точка xeCm(r),
такая, что f(x)== у. В противном случае мы получили бы проти-
воречие с тем фактом, что |f (xi) — f(x2) |	*/2|xi — х2| для лю-
бых точек xi, х2 е Ст (г).
Наконец, мы видим, что обратное отображение f~l:
IntO(r/2)-»Cm(r) непрерывно, ибо |«/i — z/2| >('/г) If2'1 (</i) —
—f~l (Уг) I для любых точек yi, у2 е Int Ст (г/2).
Таким образом, отображение f является гомеоморфизмом от-
крытого множества f-1 (Int Ст(г/2))П Int Ст(г) на открытое мно-
жество Int Ст(г/2). 
Следствие 1.12 (теорема об обратной функции). Пусть f —
отображение класса С' открытого подмножества U простран-
ства Rm в R"1, имеющее ранг m в точке х. Тогда f есть Сг-диф-
феоморфизм некоторой окрестности точки х на некоторую окре-
стность ее образа f(x) в пространстве Rm.
Доказательство. Поскольку мы уже знаем, что отображение
f является гомеоморфизмом на некоторой окрестности, нам ну-
жно только сократить эту окрестность до меньшей, на которой f
имеет ранг пг. Это возможно, так как множество тех точек х,
для которых detDf(x)^ 0, открыто. 
Следствие 1.13 (теорема о неявной функции). Пусть
(х1, .... хп, у\ ..., г/р) обозначает общую точку произведения
R" X Rp, и пусть f есть Сг-отображение некоторой окрестности
нуля U в пространстве Rn X Rp в пространство Rp, причем
§ 1. Введение 281
f(0) = 0 и матрица df1, р/д(У1,	У”) невырожденна в
точке 0. Тогда существует однозначно определенное отображе-
ние g класса Сг некоторой окрестности нуля в пространстве R"
в пространство R^, такое, что f(x, g(x)) = 0 для точек х из этой
окрестности и g(0) = 0.
Доказательство. Определим отображение F: U -*R”+p ра-
венством
F (х, у) = (х', .... хп, f'(x, У).fp(x, У))-
Поскольку матрица DF (х) имеет вид
Г I 0 1
L<№ df/dyj
она невырожденна в начале координат. Следовательно, отобра-
жение F имеет локальное обратное G вблизи 0. Если мы хотим,
чтобы f(x, g(x)) = Q, то надо, чтобы
F(x, g(x)) = (x, f(x, g(x))) = (x, 0),
так что
GF (х, g (х)) = (х, g (х)) = G (х, 0).
Поэтому мы должны взять g(x) = xG(x, 0), где л — проекция
Rn X Rp на R₽. Мы предоставляем читателю проверить, что так
определенное отображение g(x) будет удовлетворять требова*
ниям теоремы. 
Следствие 1.14. Пусть U — открытое подмножество простран-
ства Rm и f: U-*R.n — отображение класса Сг, имеющее ранг пг
в начале координат, причем /(0) = 0. Существует Сг-диффео-
морфизм g некоторой окрестности начала координат в R” на
другую окрестность нуля в R", такой, что
gfix1, ..., х"!) = (х1, ••• хт, 0, .... 0).
Доказательство. Мы можем считать, что подматрица df1, ...
..., fm/d(х1...хт) матрицы Df невырожденна в 0 (так как
по условию хотя бы одна невырожденная подматрица размера
т X т в матрице Df имеется). Определим отображение F;
U X Rn~m -> R" формулой
F^1, .... х^-^Цх1,..., xw) + (0......0,	xm+1, .... x«).
Ясно, что F имеет ранг л в 0, а матрица
DF имеет вид
df/dx
° 1
I J
Следовательно, отображение F имеет локальное обратное g. Это
отображение g является Сг-дифФеомоРФизмом некоторой окрест*
282 Дополнение. Дж. Манкрс
ности начала координат пространства R" в R" и
gf(xl....xm) = g(F(xl, хт, 0, ...» 0) =
= (х1, .... хт, О, .... 0). 
Замечание. Утверждение следствия выполнено также, если U
является открытым подмножеством полупространства Нт. Ну-
жно просто продолжить f на какое-нибудь открытое подмноже-
ство в Rm и применить только что доказанный результат.
§ 2. ПОДМНОГООБРАЗИЯ И ВЛОЖЕНИЯ
В этом параграфе мы определим, что такое подмногообразие
дифференцируемого многообразия, и докажем, что любое диф-
ференцируемое многообразие является подмногообразием неко-
торого евклидова пространства.
ОПРЕДЕЛЕНИЕ 2.1. Пусть N является n-мерным многооб-
разием класса по меньшей мере Сг, и пусть N' обозначает мно-
гообразие класса Сг, получающееся из N добавлением (если это
необходимо) новых координатных систем. Пусть далее Р— не-
которое подмножество в Int/V. Оно называется подмногообра-
зием класса Сг (или Сг-подмногообразием) многообразия N,
если существует покрытие подмножества Р координатными си-
стемами (Ui, hi) из N', такое, что каждое hi(UiftP) есть от-
крытое подмножество в Нр или в Rp для некоторого фиксирован-
ного числа р.
Сразу видно, что координатные окрестности ([//ПЛ hi) об-
разуют базис дифференцируемой структуры класса Сг на Р и
что относительно этой структуры на Р включение i: P—>N яв-
ляется Сг-вложением.
Стоит здесь отметить, что мы используем термин «подмного-
образие» в смысле, отличном от того, какой придается ему диф-
ференциальными геометрами. Для них подмногообразие — это
взаимно-однозначное погружение f: P-*N одного многообразия
в другое, а не образ при вложении.
Заметим, что при нашем определении подмногообразия чи«
ело г отвечает подмногообразию Р неоднозначно. Например, ве-
щественная прямая R1, рассматриваемая как подмножество
С°°-многообразия R2, является подмногообразием в R2 класса С'
для любого г, заключенного между единицей и бесконечностью.
Упражнение (а). Показать, что Вт и Sm-1 суть С“-подмногообразия
в R"1.
"Упражнение (Ь). Пусть R2 наделено естественной С “-структурой.
Построить для 1 г < оо подмножество в R2, которое является С'-подмного-
образием, но не является С'+'-подмногообразием.
$ 2. Подмногообразия и вложения 283
Теорема 2.2. Если отображение f: Af-* Int TV представляет со-
бой &-вложение, то f(M) есть подмногообразие класса Сг мно-
гообразия N.
Доказательство. Пусть реМ, (U, h) — какая-нибудь коор-
динатная система в точке р и (V, k)— какая-нибудь координат-
ная система в точке f(p). Будем считать, что точки h(p) и kf(р)
лежат каждая в начале координат (почему это возможно?). Со-
гласно следствию 1.14, существует диффеоморфизм g некоторой
окрестности точки kf (р) в R" на открытое множество в R", та-
кой, что
gkfh~l(xl, ..., xm) = (x1, ..., xm, О, .... 0).
Координатная система (V',gk) будет требуемой координатной
системой в точке f(p)', она переводит окрестность точки f(p) в
fM на открытое множество в Н"1 или в R"1. Я
•Упражнение (а). Показать, что эта теорема неверна, если f — лишь
С'-гомеоморфизм.
*3адача 2.3. Пусть /: Rn—>R' — отображение класса Сг и
Р— множество точек х, для которых /(х) = 0. Предположим,
что grad/ = df/dfx1.....хл) является ненулевым в каждой
точке х е Л Доказать, что Р есть подмногообразие без края в
R" класса Сг и размерности п—-1.
Сформулировать и доказать обобщение этого утверждения
на случай, когда / отображает R" в R"1.
Замечание. Предыдущее утверждение показывает, что диф-
ференцируемые многообразия очень естественно появляются как
подмногообразия евклидова пространства. Сразу возникает во-
прос, может ли так быть получено любое дифференцируемое
многообразие. Ответ на этот вопрос утвердительный, как мы
сейчас увидим. Сначала рассмотрим один частный случай.
Теорема 2.4. Пусть М — компактное m-мерное многообразие
класса Сг. Тогда существует Сг вложение М в некоторое евкли-
дово пространство.
Доказательство. Для каждой точки р е М выберем коорди-
натную систему ([/, h) в точке р, такую, что h(U) содержит
0(1) и h(p) лежит в начале координат. (Почему это возмож-
но?) Если peBdAf, то мы потребуем, чтобы h(U) содержало
0(1)0 Н"1. Пусть V обозначает h~l (Int 0(1)), a W обозначает
/г-1 (Int О(*/2)). Множества W покрывают М; выберем конеч-
ное подсемейство этих множеств Wi, ..., Wn, которое покры-
вает М\ соответствующие индексы согласованно припишем h,
U и V.
284 Дополнение. Дж. Манкрс
Пусть <р — функция, определенная в лемме 1.3. Для i =
= 1, ..., п положим
( ф (й/ W) при х е и,
Ф/ w — Q ПрИ х s \ V.
Каждое ф/: М -* R1 есть отображение класса С“, так как оно
имеет класс С" на двух открытых множествах U и М \ V и со-
гласовано на их пересечении. Пусть отображение Ф: М -»/?"
задается равенством
Ф(х) = (Ф1(х)....ф„(х)).
Определим отображение f: М -> R" X Rm X • • • X Rm = Rn X
X(Rm)n равенством
f (x) = (Ф (x), Ф1 (x) • fti (x), .... ф„ (x) • hn (x)).
Конечно, отображение ф/(х)-й/(х) определено, только когда
х s Ui, однако если положить его равным нулю вне Ui, то оно
становится С°°-отображением на всем М; мы будем предпола-
гать это выполненным.
Отображение f, очевидно, имеет класс Сг. Чтобы доказать
его взаимную однозначность, предположим, что f(x) = f(y) для
x=#z/. Тогда ф<(х)= ф;(у) для любого i, так что, если х принад-
лежит Vi, то у также принадлежит Vi. Из того, что <р» (х) -Л/(х) =
= Ф« (у)  hi (у), и того, что ф; (х) = ф/ (у) > 0, следует, что ht (х) =
= hi(y), в противоречие с тем фактом, что отображение hi вза-
имно-однозначно.
Поскольку М компактно, f является гомеоморфизмом. Нако-
нец, нам надо показать, что f имеет ранг т. Пусть Хо е Wk, и
пусть мы используем координатную систему (Uk, hk) для вы-
числения ранга f в точке х0. Нам нужно показать, что матрица
D(fhkl) содержит невырожденную матрицу размера пг X
Пусть hk(x) = (ux......ит) = и и hk(xa) — uq. Мы имеем
Фа(х)-hk(x)~ hk(x) в некоторой окрестности точки Хо, так что
т X m-подматрица <Э(фЙ(/г^' (и)) • и^ди матрицы	яв-
ляется единичной матрицей при и == м0. И
Замечание. Данное выше доказательство непосредственно
обобщается на некомпактный случай, однако возникает несколь-
ко дополнительных трудностей. Одна из них связана с нахожде-
нием конечного числа координатных систем, покрывающих мно-
гообразие М, другая — с тем, что в некомпактном случае из
взаимной однозначности не следует гомеоморфизм. Эти труд-
ности последовательно преодолеваются в леммах и задачах
2.6—2.9; провести оставшуюся часть доказательства общей тео-
ремы мы предоставляем читателю (задача 2.10) .
§ 2. Подмногообразия и вложения 285
ОПРЕДЕЛЕНИЕ 2.5. Пусть <р — неотрицательная функция,
определенная на многообразии М. Носителем supp <р функции ф
называется замыкание множества точек х, для которых ф(х)>
> 0. Разбиением единицы класса Сг на многообразии М назы-
вается совокупность неотрицательных функций ф; класса Сг,
определенных на М, таких, что множества С/ = зиррф/ обра-
зуют локально-конечное покрытие многообразия М, причем
Ф, (х) = 1 для любой точки х g М. Это определение приме-
нимо и для произвольного топологического пространства, исклю-
чая условие дифференцируемости, которое в этом случае не
имеет смысла.
Задача 2.6. Пусть {£Л} —локально-конечное открытое покры-
тие Сг многообразия М. Существует Сг-разбиение единицы {ф/},
такое, что зиррф(<г£Л для каждого t; при этом говорят, что
разбиение единицы {ф;} подчинено покрытию {[/;}. В случае
г = 0 это верно для произвольного пространства X (как всегда,
сепарабельного и метрического).
Упражнение (а). Пусть {CJ — локально-конечное покрытие сепара-
бельного метрического пространства X компактными множествами не/ — по-
следовательность положительных постоянных. Существует вещественнозначная
функция в(х), определенная на X и такая, что 6(х) < е< для х е Ci.
Лемма 2.7. Пусть М есть m-мерное многообразие и — его
открытое покрытие. Существует локально-конечное открытое по-
крытие, вписанное в покрытие которое является объедине-
нием совокупности m 4- 1 систем открытых множеств ...
..., S%m, причем множества, принадлежащие каждой данной си-
стеме $1, попарно не пересекаются.
Доказательство. Применим следующую фундаментальную
теорему теории размерности: если М — m-мерное многообразие,
то в любое открытое покрытие пространства М вписано по-
крытие такое, что любая точка многообразия М принадлежит
не более чем m + 1 элементам покрытия &. Доказательство для
случая, когда М компактно, можно найти в [2]. Это доказатель-
ство легко может быть распространено на некомпактный слу-
чай, однако столь же легко доказать эту теорему заново. Это
сделано в 2.12—2.15.
Пусть = {Uj}—заданное открытое покрытие, {У/}—ло-
кально-конечное открытое покрытие, такое, что V/ сг Uj для
каждого /, и {ф/} — С'-разбиение единицы, которое подчинено
покрытию {V/} (см. задачу 2.6). Пусть задано целое число п,
такое, что 0 п т. Рассмотрим произвольное множество
to, .... in различных положительных целых чисел. Обозначим
через 117(г0, ..., in) открытое множество, состоящее из тех точек
286 Дополнение. Дж. Манкрс
х, для которых
<Р( (х) < min (ф,о (х), .... <р/п (х))
для всех значений I, отличных от io, ..., in. По определению
система открытых множеств состоит из всех таких множеств
W (io....in).
Нам надо доказать, что элементы попарно не пересекают-
ся. Пусть io, .... in и /о, jn — различные множества индек-
сов; предположим, что число k принадлежит первому множеству
и не принадлежит второму и что число I принадлежит второму
множеству и не принадлежит первому. Если точка х принадле-
жит множеству W(io.......in), то ф/(х)< ф*(х); если же х при-
надлежит W(j0, .... jn), то ф4х)<ф/(х). Следовательно, эти
два множества не пересекаются, что и требовалось показать.
Докажем теперь, что объединение ^ = ^oU ••• U покры-
вает М. Пусть х е М. Выберем индексы io, ..., in, для которых
фг(х)>0. Хотя бы один такой индекс существует, так как
£ фг (х) = 1; согласно выбору покрытия Uj, таких индексов су-
ществует не более т+ 1, Тогда ф<(х)=0 для всех других ин-
дексов, так что хеК7 (io, ..., in) •
То, что покрытие $ локально-конечно, доказывается анало-
гично. Каждая точка х имеет окрестность U, на которой все
функции ф,-, за исключением лишь конечного числа, тождествен-
но равны нулю. Пусть io, ..., im — те индексы, для которых
функция фг не равна тождественно нулю на U. Если множество
W(jo.....jk) пересекается с U, то множество индексов jo, ..., jk
является подмножеством множества {io, ..., im}', но таких под-
множеств только конечное число. I
’Упражнение (а). Пусть М — некоторое симплициальное разбиение1
в плоскости с вершинами гч, Vj..Пусть далее Vi—(открытая) звезда
точки Vi и <р;(х)—барицентрическая координата точки х относительно Щ.
(Она, конечно, равна нулю, если точка х не принадлежит V/.) Провести пре-
дыдущую конструкцию в этом случае и описать получающиеся множества
W(i0) и IF(toii).
Это упражнение должно прояснить идею доказательства предыдущей тео-
ремы.
Задача 2.8. Пусть М — (^-многообразие размерности т. До-
казать, что оно может быть покрыто т + 1 координатными си-
стемами (Ut, hi). При этом Ui можно выбрать так, чтобы оно
было объединением счетной совокупности попарно непересе-
кающихся открытых множеств Vtj, таких, что hi (Уц) есть огра-
ниченное подмножество в Rm.
1 Определение снцплициального разбиения см. ниже на стр. 325. — Прим,
перев.
§ 2. Подмногообразия и вложения 287
ОПРЕДЕЛЕНИЕ 2.9. Пусть X и Y — сепарабельные метри-
ческие пространства и f: X -> У — непрерывное отображение.
Предельным множеством отображения f называется множество
всех точек у е У, таких, что для некоторой последовательности
хп в X, не имеющей сходящихся подпоследовательностей, f(xn)
сходится к у. Это множество обозначается L(f)1.	,
У пражнение (а). Доказать, что, если пространство X локально-ком-
пактно, то предельное множество L(f) отображения f: Х-*У замкнуто в У.
Упражнение (Ь). Пусть отображение f: X-► У непрерывно и взаимно-
однозначно. Доказать, что пересечение L(f)fl f(X) пусто тогда и только тог-
да, когда f есть гомеоморфизм, а образ f(X) замкнут в У тогда и только тог-
да, когда L(f)c:f(X).
Задача 2.10. Пусть М — Сг-многообразие размерности т. До-
казать, что многообразие М допускает Сг-вложение в качестве
замкнутого подмножества в евклидово пространство размерно-
сти (т -j- I)2.
Замечание. Эта теорема показывает, что любое дифферен-
цируемое многообразие является подмногообразием некоторого
евклидова пространства. Этот факт будет иметь для нас ре-
шающее значение в § 4 2
Естественно теперь поставить вопрос: является ли необходи-
мым использование евклидова пространства такой высокой раз-
мерности, для того чтобы вложить в него заданное многообра-
зие М? Ответ — нет, не является. Это классический результат
Уитни, утверждающий, что достаточно R2/"+l [16] .В записи лек-
ций Милнора [6] содержится прозрачное доказательство этой
теоремы Уитни3.
В действительности достаточно даже R2m, однако доказать
это гораздо труднее.
*3адача 2.11. Пусть М — ^-многообразие размерности т.
Показать, что, если А — замкнутое подмножество в М и hi —
Сг-вложение некоторой окрестности U множества А в Rp, то су-
ществует Сг-вложение f многообразия М в некоторое евклидово
пространство, совпадающее с hi на А. При этом образ f(M) мо-
жет быть выбран замкнутым, если hi(A) замкнуто.
Указание. Покрыть множество М \ А координатными систе-
мами (th, hi), i = 2, ..., т + 2. Пусть U\ = U и <pi, ..., <pm+2 —
какое-нибудь Сг-разбиение единицы, подчиненное покрытию
Ui, .... t/m+2- Затем поступать так, как в теореме 2.4.
1 L •— от limit. — Прим, перев.
2 См. теорему 4.8 и следствие 4.9. — Прим, перев.
• См. [Уитни, 1957] и [“Понтрягин, 1976]. — Прим, перев.
288 Пополнение. Дж. Манкрс
ОПРЕДЕЛЕНИЕ 2.12. Пространство А имеет размерность
по покрытиям, не превосходящую пг, если в любое открытое по-
крытие пространства А можно вписать покрытие порядка не
больше т (это означает, что любая точка хе А лежит не более
чем в т + 1 элементах вписанного покрытия). Если А —замк-
нутое подмножество пространства X, то это определение экви-
валентно утверждению, что в любое открытое покрытие про-
странства X можно вписать покрытие, ограничение которого на
А имеет порядок, не больший т. Если А' — замкнутое подмно-
жество множества А и А имеет размерность по покрытиям, не
превосходящую т, то и А' имеет размерность по покрытиям, не
превосходящую т.
Лемма 2.13. Пусть Ап — замкнутые подмножества простран-
ства X, такие, что A„c:IntAn+i и (Мл = X. Если А] и каждое
множество Cl (A„+i \ А„) имеют размерность по покрытиям, не
большую т, то и X имеет размерность по покрытиям, не боль-
шую пг.
Доказательство. Для данного открытого покрытия простран-
ства X пусть — вписанное в него покрытие, такое, что любой
элемент из $0, пересекающийся с А,-, лежит в А,+1. Пусть далее
— вписанное в покрытие, ограничение которого на Ai
имеет порядок не выше пг. Для удобства будем считать, что Ао
пусто.
Предположим , что является вписанным в покрытием,
ограничение которого на А„ имеет порядок не выше т. Пусть
— вписанное в покрытие, ограничение которого на
Cl(An+J \ А„) имеет порядок не выше т. Определим покрытие
^л+1 следующим образом.
(1)	Если U лежит в $п и пересекается с An—i, то U входит
в $л+1.
(2)	Для каждого элемента который пересекается с Ап
и не пересекается с А„_ь выберем элемент	содержа-
щий V. Тогда для каждого элемента U пусть t/'e^n+],
где U' обозначает объединение тех элементов \!е^, для кото-
рых f (V) определено и равно U.
(3)	Каждый элемент V е <ё>, не пересекающийся с А„, пусть
принадлежит &п+\-
Легко проверяется, что система открытых множеств 6Sn+i по-
крывает пространство X и что ее ограничение на A„+i имеет по-
рядок не выше пг. Пусть $ состоит из тех открытых множеств,
которые принадлежат всем $п, за исключением, быть может,
конечного их числа. Тогда будет покрытием порядка не
выше пг. 
§ 3. Отображения и аппроксимации 289
Следствие 2.14. Если Bt и В2— замкнутые подмножества про-
странства Y, имеющие размерность по покрытиям не выше т,
то и их объединение Bi\J В2 имеет размерность по покрытиям
не выше т.
Доказательство. Пусть Ai — Bt и Ап = X = Bt (J В2 для
п 2. Так как множество С1(Дг \ Л) содержится в А2, его раз-
мерность по покрытиям не больше т. Теперь применяем лем-
му. 
Теорема 2.15. Любое т-мерное многообразие М имеет раз-
мерность по покрытиям не выше т.
Доказательство. (1) Любое компактное подмножество В про*
странства Rm имеет размерность по покрытиям не выше т. Дей-
ствительно, В лежит в некотором кубе Ст, который в свою оче-
редь является полиэдром 1 некоторого симплициального разбие-
ния К размерности т. Для данного открытого покрытия st- куба
Ст существует подразделение К' разбиения К настолько мелкое,
что совокупность звезд вершин разбиения К' вписана в st. По-
лученное таким образом покрытие имеет порядок т.
(2) Покроем многообразие М локально-конечной совокуп-
ностью множеств Bi, гомеоморфных компактным подмноже-
ствам пространства Rm. Пусть Ai = Вь Если множество А" =
= Bi U ... U Bq уже построено, то выбираем целое число р > q,
такое, что czz Int (Bi (J ... иД>), и полагаем Ап+1 = BiU ...
... UВ₽. Согласно следствию 2.14, каждое множество Ап имеет
размерность по покрытиям не выше т. Теорема следует теперь
из леммы 2.13. 
§ 3. ОТОБРАЖЕНИЯ И АППРОКСИМАЦИИ
В этом параграфе мы определим, что такое сильная С'-ап-
проксимация дифференцируемого отображения одного много-
образия в другое (определение 3.5); для того чтобы сделать
это аккуратно, необходимо сначала построить касательное рас-
слоение дифференцируемого многообразия. После этого мы до-
кажем важную аппроксимационную теорему (теорема 3.10), ут-
верждающую, что, если f: М —> N — погружение, вложение или
диффеоморфизм, то то же самое можно сказать о любой доста-
точно близкой сильной С1-аппроксимации g отображения f.
(В случае диффеоморфизма следует еще предположить, что
g(BdM)cBdtf.)
1 Определение симплициального полиэдра см. ниже на стр. 326,— Прим,
перев,
10 Дж. Милнор, Дж.. Сташеф
290 Дополнение. Дж. Манкрс
ОПРЕДЕЛЕНИЕ 3.1. Пусть М — ^-многообразие размер-
ности т и х0— точка в М. Касательный вектор v к многообра-
зию М в точке Хо — это соответствие, сопоставляющее каждой
координатной системе (U, h) в точке xq матрицу а размера
m X 1 и обладающее следующими свойствами:
Если (U, h) и (V,k) — две координатные системы в точке Хо,
а а и а — соответствующие m X 1-матрицы, то
а = D («о) • а>
где Uo = h(xo). Элементы матрицы а называются компонен-
тами вектора v в координатной системе ((/, h).
Если f: [a,Z?]—* М есть Сг-отображение (где [а, 6] — интер-
вал прямой R1), то f называется (параметризованной) кри-
вой на многообразии М. Пусть f((o) = xo. Если мы определим
v как соответствие, сопоставляющее координатной системе
(U, h) матрицу D(hf)(t0), то v будет касательным вектором
к многообразию М в точке Хо, как читатель может проверить
непосредственно. Этот вектор называют вектором скорости для
параметризованной кривой f.
Заметим, что любой касательный вектор v к многообразию
М в точке хо является вектором скорости для некоторой пара-
метризованной кривой. Действительно, пусть (а1, .... а"1) —
компоненты вектора v в координатной системе (U,h), причем
й(хо) = 0. Положим —	.....amt). Если xoeInt7H,
то отображение f корректно определено на некотором интер-
вале [—е, е] с центром в 0; если х0 е Bd М, то f определено
либо на интервале [—е, 0], либо на интервале [0, е]. В любом
случае вектор v будет вектором скорости для кривой f в
точке х0.
Касательные векторы к многообразию М в данной точке
Хо образуют m-мерное векторное пространство; чтобы сложить
векторы v и w, нужно просто взять их компоненты в коорди-
натной системе (U, h) и произвести покомпонентное сложение.
Можно проверить, что это определение не зависит от выбора
координатной системы. Это векторное пространство называется
касательным пространством к многообразию М в точке хо.
ОПРЕДЕЛЕНИЕ 3.2. Пусть М — (^-многообразие. Обозна-
чим через Т(М) множество всех касательных векторов к мно-
гообразию М, и пусть л:Т(М)-*М — отображение, переводя-
~>
щее вектор v в точке хо в точку хо. Пространство Т (М) назы-
§ 3. Отображения и аппроксимации 291
вается касательным расслоением многообразия М, а л — проек-
цией.
Если (U,h) — координатная система на многообразии М, то
определим Н: л-1 (£/) —► Rm X R"1 или Hm X Rm равенством
h (v) = /гл (v) X (а1, .а"1),
где (а1, .... аш)—компоненты вектора v в координатной си-
стеме (U,h). Требование, чтобы множество л-1(£/) было от-
крытым и /г было гомеоморфизмом, немедленно вводит тополо-
гию на множестве Т(/И), которая является хаусдорфовой и сепа-
рабельной (см. упр. (а)).
Пространство Т (Л!) представляет собой 2т-мерное многооб-
разие с краем ir'(BdM) и координатными окрестностями
(л-1 (С/), Я).
Если (U, h) и (V, £) —перекрывающиеся координатные ок-
рестности многообразия М, то
kh~{ (х, а) = (kh~l (х), D (й/i-1) (х) • а)
на множестве h (U П V) X Rm, где а записывается как mXi-
матрица. Таким образом, kh~l есть отображение класса С''-1,
так что совокупность пар (л-1 (U), И) служит базисом диффе-
ренцируемой структуры класса Сг~1 на Т (/И).
Всякий раз, когда мы будем рассматривать пространство
Т (М), мы будем наделять его этой дифференцируемой струк-
турой (если г > 1).
Отображение включения	переводящее точку х
в нулевой вектор в точке х, и проекция л являются отображе-
ниями класса Сг~\
Упражнение (а). Пусть {U, h) и (V, k)—две перекрывающиеся ко-
ординатные системы на многообразии М. Показать, что kh~l есть гомеомор-
физм h(U П V) X Rm на k(U Г) V) X Rra. Вывести отсюда, что топология на
множестве Т(М) корректно определена Показать далее, что она сепарабельна
и хаусдорфова.
’Упражнение (Ь). Показать, что для некоторой окрестности V точки
х е М существует диффеоморфизм g: л-1 (У) -» VX Rm, такой, что отображе-
ние л§-1 является естественной проекцией V X Rm У, причем g есть линей-
ный изоморфизм касательного пространства в точке х на xXRm-
Это показывает, что л: Т(М)-+М является расслоением со слоем Rm и
невырожденными линейными преобразованиями пространства Rm в качестве
структурной группы (см. [12]).
ОПРЕДЕЛЕНИЕ 3.3. Пусть М и N — многообразия класса
по меньшей мере Сг и g: М —> N — отображение класса Сг. Су-
ществует индуцированное отображение dg: Т(М)-+Т(N) клас-
са С1'-1, определяемое следующим образом. Пусть v — вектор
в точке хо с компонентами а в координатной системе (U, h) и
10*
292 Дополнение. Дж. Манкрс
w— вектор в точке g(x0) с компонентами [3 в координатной
системе (V,k). Мы полагаем
dg(v) — w,
если
$ = D(kgh~v) -а.
Заметим, что dg является линейным отображением на каждом
касательном пространстве; оно называется дифференциалом ото-
бражения g.
Упражнение (а). Проверить, что дифференциал определен корректно,
т. е. не зависит от выбора координатных систем.
Упражнение (Ь). Показать, что, если /: [а,	— кривая с векто-
ром скорости о, то dg(v) является вектором скорости для кривой gf: [а, 6] -► N,
Упражнение (с). Пусть f: [а, 6]->Л1 есть С'-отображенне. Интер-
претировать дифференциал df геометрически, имея в виду, что f отображает
одномерное многообразие [а, 61 в М. Предыдущее упражнение утверждает
тогда просто, что d(gf)= dg-df. Обобщить эту формулу на случай, когда
отображение f определено на многообразии размерности, большей чем 1.
•Упражнение (d). Пусть g — погружение, вложение или диффеомор-
физм. Как это отражается на отображении dgt
ОПРЕДЕЛЕНИЕ 3.4. Пусть Л4 — ^-многообразие. Предпо-
ложим, что на каждом касательном пространстве к многооб-
разию Л1 определено скалярное произведение (о, te>), являю-
щееся дифференцируемым класса Сч, 0 q <Z г, в том смысле,
что отображение Т(М) в R, переводящее v в (v, v), имеет класс
С’. Такое скалярное произведение называется римановой мет-
рикой на многообразии М. Как обычно, || v || обозначает д/(о, о).
Заметим, что вещественная функция (о, w} непрерывна на под-
пространстве произведения Т(AfjX Т(Л4), состоящем из всех
пар (о, w), таких, что л (v) = п (w). Это следует из тождества
(V, w) =|||« + Й2— jllu — ®IP-
Упражнение (а). Существует стандартная риманова метрика на мно-
гообразии Rn; нужно просто взять компоненты а1 и й1 векторов о и w от-
носительно стандартной координатной системы /: R" -> R” и определить
(о, го) как обычное скалярное произведение ^Га*Рг.
Пусть М — Сг-многообразие и f: М -> R" — некоторое С’+1 -погружение.
Если v и w — касательные векторы к многообразию М в точке х, то поло-
жим (о, ш) равным обычному скалярному произведению в Т (Rn) векторов
df (о) и df (to). Проверить, что это — риманова метрика на М. Почему не-
обходимо, чтобы / было погружением?
§ 3. Отображения и аппроксимации 293
•Упражнение (Ь). Пусть (о, w) — риманова метрика на многообра-
зии М, {U, h) — какая-то координатная система на М и а и Р — матрицы ком-
понент векторов v и w в этой координатной системе. Показать, что сущест-
вует единственная матричная функция G (х) класса С9, определенная иа U,
которая симметрична, положительно определена и такова, что 1
(у, ш) = р* • G (х)  а.
Пусть G(x)—матричная функция, соответствующая координатной системе
(V, k); показать, что
G (х) = D (hk'1)* -GW-D
Всякое соответствие, сопоставляющее каждой координатной системе (U, Л) в
точке Хо некоторую матрицу G, такое, что матрицы G и G связаны этим урав-
нением, называется (в классической терминологии) ковариантным тензором
второго порядка.
ОПРЕДЕЛЕНИЕ 3.5. Пусть v — касательный вектор к про-
странству R" в точке х и а — его компоненты в координатной
системе i: R" —»R'i. Соответствие щ->(х, а) задает гомеомор-
физм между Т(R") и R" X R", который является изоморфизмом
касательного пространства в точке х на произведение х X R".
Мы будем для удобства отождествлять 7’(R't) и RnXRn и пи-
сать v =(х, а). Если f-. М -> R" есть С'-отображение и v — ка-
сательный вектор к многообразию М в точке, х, то определим
dof(v) соотношением
df{v) = (f(x), dof(v)).
Рассмотрим пространство F1 (М, R") всех (^-отображений
многообразия М в R". Топология в атом пространстве вводится
следующим образом.
Выберем какую-нибудь риманову метрику на М. Для задан-
ного С*-отображения f: М —» R" и заданной положительной не-
прерывной функции б(х) на М обозначим через W(f, б) множе-
ство всех (^-отображений g: М —> R", таких, что
II f W — g (х) || < б (х)
и
II dof (о) — dQg (о) II < б (х) II о И
для каждой точки х е М и каждого вектора и 0, касатель-
ного к М в х. Если отображение g принадлежит W(f, б), то оно
называется 8-аппроксимацией отображения f. О таких отобра-
жениях говорят также как о сильных С1-аппроксимациях ото-
бражения f. Множества W (f, б) образуют базис некоторой то-
1 Ниже символ t обозначает транспонирование, — Прим, перев.
294 Дополнение. Дж. Манкрс
пологий на пространстве F1 (М, R"); эта топология называется
тонкой С1-топологией.
Пусть N— заданное дифференцируемое многообразие. Вло-
жим его дифференцируемо в некоторое евклидово пространство
R". Тонкая С'-топология на F'(M,N) определяется как топо-
логия, индуцированная из тонкой С'-топологии на Fl(M, R").
Эта топология не зависит от выбора римановой метрики на М
и вложения N в R" (см. упр. (Ь) п. 3.6).
Чтобы получить грубую С'-топологию, нужно изменить оп-
ределение, потребовав выполнения указанных неравенств толь-
ко для точек х из некоторого компактного множества А, и за-
тем рассмотреть множества W(f, б, Д) как базис топологии. Мы
не будем существенно использовать грубую С’-топологию.
Упражнение (а). Проверить, что множества W(f,8) образуют базис
топологии.
Упражнение (Ь). Тонкая С°-топология на Р°(Х, У) (пространствевсех
непрерывных отображений сепарабельного метрического пространства X в се-
парабельное метрическое пространство У) определяется следующим образом.
Для заданного отображения f: X -> У и заданной положительной непрерывной
функции S на X пусть окрестность отображения f состоит из всех отображе-
ний g, таких, что g(x)) < S(x) для всех х, где р— (топологическая ’)
метрика на У. Отображение g называется сильной С°-аппроксимацией f (или
просто Са-6-аппроксимацией) отображения f. Проверить, что эти множе-
ства образуют базис топологии на F°(X, У).
Лемма 3.6. Пусть N является р-мерным подмногообразием
в R" и f: Mm —» Np — некоторое С1-отображение. Пусть, далее,
(U,h) — координатная система на М; С — компактное подмно-
жество в U и (V, k) — координатная система на N, содержащая
f(C). Какого бы ни было е > 0, найдется такое б > О, что,
если отображение g: М-* N удовлетворяет условиям
g(C)<= V,
Г \kfh-'(y)-kgh-1(y)\<6,
[ \D{kfh~l) (у) — D(kgh~l) (у)\ < д
для всех y^h (С), то
( II f (X) — g (х) II < с,
1
I IMof (о) — dOg(t>)|| < 8 II У II
для каждого ненулевого вектора V, касательного к М в точке
х е С.
Доказательство. Предположим, что заключение леммы не
выполнено. Тогда для каждого п найдутся такое отображение
1 То есть исходная метрика метрическою пространства У.—Прим, перев.
§ 3. Отображения и аппроксимации 295
gn и такой вектор vn =£ 0, касательный к Л4 в точке хп е С, что
неравенства (*) выполнены для g = g„, y = yn = h(xn) и
б = 1/п, однако неравенства (**) не выполнены для g — gn,
х = хп и v — vn для всех достаточно больших га. Переходя, если
надо, к подпоследовательности и производя перенумерацию, мы
можем считать, что хп х и у„/ ||v„ || = ип -> и, где и — некото-
рый единичный касательный вектор к многообразию М в точке
х. Имеем \kf(xn) —- kgn(xn) | < 1/га, так что kf(xn) и kgn(xn)
сходятся к kf(x.) Таким образом, обе последовательности f(xn)
и gn(Xn) сходятся к f(x), так ЧТО ||f(Xn) — gfrt(Xn) II ->0.
Пусть dh(un) = (уп, аП) — запись соответствующего вектора
в пространстве Rm X Rm = Т(Rm). Тогда
| D (kfhT1) (Уп) 'V-n — D (kgnh~l) (уп) • а„ | < m| a„ |/га,
II dok (df (un)) — dok (dgn (un)) || < pm \\dh (un) ||/ra.
Так как правая часть последнего неравенства стремится к нулю,
то и левая тоже стремится к нулю. Следовательно, обе после-
довательности dok (df (ип)) и dok (dgn (ип)) сходятся к dok (df (и)),
так что dk (df (ип)) и dk (dgn (ип)) сходятся к dk (df (и)). Поскольку
отображение непрерывно, то последовательности df (ип)
и dgn(un) сходятся к df (и), так что || dof (ип) — dagn (ип) || -> 0.
Полученное противоречие доказывает лемму. |
Упражнение (а). Доказать обращение этой леммы: для всякого
6 > 0 найдется е > 0, такое, что если условие (♦*) выполнено, то выполнено
и условие (*).
Упражнение (Ь). Пусть f: M-+N — дифференцируемое отобра-
жение и {С<-} — локально-конечное покрытие многообразия М компактными
множествами. Рассмотрим координатные системы (Ui, h-t) и (V/, kF), содер-
жащие С/ и f(Ct) соответственно. Введем множество X(f,8i), состоящее из
всех таких отображений g: M-+N, что g(Ct) <= Ui, (у) —	(у) |<б(
и |D(W1)(y)-Z)(MV1)^l <6i для всех у s ht (С(.). Показать, что
эта система окрестностей отображения f эквивалентна системе тонких С'-ок-
рестностей этого отображения. Вывести отсюда, что тонкая С'-топология на
F'(M,N) не зависит от римановой метрики на М и вложения N в евклидово
пространство.
Упражнение (с). Пусть X(f, б,) определено, как в предыдущем уп-
ражнении, за тем исключением, что опускается второе неравенство (в котором
фигурируют производные от /). Показать, что получающаяся система окрест-
ностей отображения f эквивалентна системе тонких С°-окрестностей этого ото-
бражения. Вывести отсюда, что тонкая С°-топология на F°(M, N) не зависит
от выбора метрики для N.
* Упражнение (d). Показать, что топология на множестве F'(M, N),
индуцированная из тонкой С°-топологии вложением Fl(M, N) cz F«(M, N),
строго грубее, чем топкая С’-топология.
298 Дополнение. Дж. Манкре
•Упражнение (е). Выше была определена грубая С'-топология на
Fl(M, N). Сформулировать другое определение, аналогичное тому, которое
дано в утверждении леммы 3.6, и доказать, что эти два определения эквива-
лентны.
•Упражнение (f). Рассмотрим множество F1(R.R) в тонкой С’-топо-
логии, в грубой С'-топологин и в равномерной топологии, элементами базиса
которой являются множества вида W (f, е), где f: R -* R, е > 0, н W(f, е) —
множество всех g, таких, что sup |/(х) —g(x)| < е. Описать компоненты ли-
нейной связности нулевой функции в каждом из этих трех случаев.
Задача 3.7. Пусть f: М -»• N и g: N -♦ Р суть С'-отображения.
(1)	Для заданной функции е(х)>0, определенной на М,
доказать существование такой функции б(х)>0, что, какова
бы ни была б-аппроксимация J отображения f, gf будет е-ап-
проксимацией отображения gf.
(2)	Пусть f вкладывает многообразие М в качестве замкну-
того подмножества в многообразие N. Доказать существование
61 (х) >0 иб2(х)> 0, таких, что, каковы бы ни были бгаппрок-
симация f отображения f и б2-аппроксимация g отображения
g, gf является е-аппроксимацией отображения gf.
(3)	Пусть f— диффеоморфизм. Показать, что для всякой
заданной функции в (у) > 0 существует такая функция б (х) >
> 0, что, если f— б-аппроксимация отображения f и диффеомор-
физм, то J-1 есть е-аппроксимация отображения f~l.
•Упражнение (а). Показать, что утверждение (2), вообще говоря,
неверно, если f — ие гомеоморфизм или если f(M) не замкнуто.
ОПРЕДЕЛЕНИЕ 3.8. Рассмотрим множество Fr(M,N) всех
Сг-отображений М в N. Определение тонкой С’-топологии, дан-
ное в лемме 3.6, естественно обобщается до определения тон-
кой Сг-топологии в этом пространстве. А именно, берется то же
самое определение, только второе неравенство (требующее бли-
зости первых частных производных) заменяется требованием,
чтобы частные производные отображения kigtii1 вплоть до по-
рядка г аппроксимировали соответствующие частные производ-
ные отображения kifhT1 с точностью б; для точек х из С,. Тон-
кая С°°-топология на F°°(M,N) определяется с помощью базиса,
получающегося объединением Сг-топологий по всем конечным г.
Нам не представится случая использовать эти топологии.
ОПРЕДЕЛЕНИЕ 3.9. Пусть fo и ft суть ^-отображения М
в N. Регулярной ^-гомотопией между отображениями f0 и ft
называется всякое непрерывное отображение f: М X R —> N, та-
кое, что 1
1 Как обычно, для произвольного фиксированного t е R через ft обозна-
чается отображение М-+ N, x-+f(x,t).— Прим. ред.
£ 3. Отображения и аппроксимации 297
(1)	для некоторого е>0 выполнены соотношения: ft — fo
при t <. е и ft = ft при t > 1 — е;
(2)	ft является С-отображением для каждого t\
(3)	отображение dfe. Т (М)Х R -* T(N) непрерывно.
Гомотопия ft называется дифференцируемой С’-гомотопией,
если отображение f:M\R—N имеет класс С1; это условие
сильнее, чем условия (2) и (3). Гомотопия ft называется диф-
ференцируемой Сг-гомотопией, если она имеет класс Сг.
В случае когда fo и f i — погружения, мы всегда будем пред-
полагать выполненным стандартное соглашение, что регуляр-
ная (или дифференцируемая) гомотопия ft между ними обла-
дает тем свойством, что ft является погружением при любом t.
Если fo и fi — вложения, то регулярная (или дифференцируе-
мая) гомотопия ft называется изотопией, если ft есть вложение
при любом t.
Понятия регулярной и дифференцируемой гомотопии в дей-
ствительности различаются очень незначительно. Ниже чита-
тель найдет задачу, в которой требуется доказать, что сущест-
вование регулярной гомотопии между f0 и fi влечет за собой
существование дифференцируемой гомотопии. Не ясно, однако,
какому понятию отдать предпочтение как более естественному.
Регулярная гомотопия весьма естественна в том смысле, что
она эквивалентна существованию пути Ф: R — Fl (М, N), соеди-
няющему отображения fo и fi, где в качестве топологии в про-
странстве отображений берется грубая С^-топология. Однако на
практике обычно строят дифференцируемые, а не просто регу-
лярные гомотопии. Так будет и в нашем случае, поэтому нам
почти не представится поводов применить более слабое понятие.
Упражнение (а). Пусть ft — гомотопия между fo и fi, gt — гомото-
пия между go н и f 1 = go- Определим h: MXVt,-+N формулой
Г /2«М ПРИ
I g2<_i (*) при
1/2,
Показать, что ht является регулярной (или дифференцируемой) С1-гомото-
пией, если таковы ft и gt.
•Упражнение (Ь). Построить регулярную С’-гомотопию, которая не
является дифференцируемой С1 — гомотопией.
•Упражнение (с). Пусть ft — регулярная С*-гомотопия. Определим
отображение Ф: R -> F1 (Af, N) равенством
Ф(/)(х) = Л(х).
Показать, что Ф непрерывно, если пространство Р(М, N) наделено
грубой С-топологией. Сформулировать и доказать обратное утверж-
дение.
298 Дополнение. Дж. Манкре
Теорема 3.10. Пусть f: М -♦ N — С1-отображение. Если f —
погружение или вложение, то существует тонкая С1-окрестность
отображения f, состоящая только из погружений или вложений
соответственно. Если f — диффеоморфизм, то существует тон-
кая Сх-окрестность отображения f, такая, что, если g лежит
в этой окрестности и переводит Bd М в Bd N, то g есть диффео-
морфизм.
Доказательство. Пусть {CJ — локально-конечное покрытие
многообразия М компактными множествами, такое, что множе-
ства Int С, также покрывают М и (Ui, hi), {Vt,ki) являются ко-
ординатными системами, содержащими С,- и ЦСг) соответ-
ственно.
(1)	Предположим, что f—погружение. Тогда матрица
£)(й^йГ')(*) имеет ранг m = dim М для всех точек хейДС,).
Обозначим через М (р, q\ г) множество всех р X «/-матриц ранга
г; оно рассматривается как подпространство в Rpi?. Множество
М (т, п; т) открыто в Rmn. Действительно, если сопоставить
каждой матрице сумму квадратов определителей всех ее т X
X m-подматриц, то указанное множество будет прообразом от-
крытого множества R \ {0} при этом непрерывном отображе-
нии.
Матрицы D (kifh'i'r) (х), где хейДС,), образуют компактное
подмножество Ki пространства М(т, п\ т). Поэтому существует
б,, такое, что 6«-окрестность множества Ki лежит в М(т, п;т).
Этот выбор б/ определяет нужную тонкую С1-окрестность ото-
бражения f, как в лемме 3.6.
(2)	Пусть f — вложение. Как мы только что доказали, су-
ществует тонкая С*-окрестность Wt отображения f, состоящая
из погружений. Докажем, что в ней содержится тонкая С'-ок-
рестность W2 отображения f, состоящая из отображений g, вза-
имно-однозначных на каждом С/.
Предположим противное. Тогда найдутся число I и после-
довательность gn, такие, что gn сходится к f и dgn сходится к
df равномерно на С,-, однако gn(xn) — gn(yn) для некоторых
двух различных точек х„ и уп из Ci. Переходя к подпоследова-
тельностям и производя перенумерацию, мы можем считать, что
хп-+х и уп-^у. Так как f(x!l)-^f(x), то gn(xn)->- f(x); анало-
гично gn(Уп)-+ f(у). Следовательно, f(x) = f(y)-, так как /
взаимно-однозначно, то х = у.
Представим f и g в координатных системах; пусть fl
= йДй;1, = kgh;', хп = й£ (х„), уп = й, (уп). Тогда
О = (*,) - gln (уп) = Dgln (zn> г) • (х„ - у„),
§ 3. Отображения и аппроксимации 299
где zn, i — некоторая точка, лежащая на прямолинейном от-
резке, соединяющем точки хп и уп. Переходя к подпоследова-
тельностям и производя перенумерацию, мы можем считать, что
(хп — Уп)/\\хп — /М -> «• Тогда, поскольку гп, i —> х, мы имеем
О = Df1 (х) • и
для каждого i в противоречие с тем фактом, что матрица
D/(x) невырожденна.
(3)	Пусть f — вложение. Как мы только что доказали, су-
ществует тонкая С'-окрестность W2 отображения f, состоящая
из погружений, которые взаимно-однозначны на каждом Ci. Те-
перь мы докажем, что существует тонкая С°-окрестность ото-
бражения /, пересечение которой с W2 состоит из отображений,
взаимно-однозначных глобально; это пересечение будем обозна-
чать через IV's. Мы определим эту окрестность при помощи не-
которой непрерывной функции б(х); таким образом, мы пред-
полагаем, что на N задана топологическая метрика р. Суще-
ствует покрытие Di многообразия М компактными множе-
ствами, такими, что Did Int С/ для каждого i (см. лемму 1.4).
Пусть е> — расстояние в N от f(Di) до f(M\Int С,); так как
/ — гомеоморфизм, это расстояние положительно. Пусть б(х) —
непрерывная функция на М, которая меньше е,-/2 на Ci (см.
упр. (а) п. 2.6). Пусть далее g—какая-нибудь С°-б-аппрок-
симация отображения f, лежащая в W2. Предположим, что
g( х) = £(«/), где xd Di, yd Dj и e< «С еЛ Тогда
P (f (x), f (y)) < ez/2 + ez/2 < e,.
Так как g взаимно-однозначно на Cjt точка x не лежит в С/,
так что р(/(х), /(у))^е/. Полученное противоречие доказывает
существование окрестности
Наконец, докажем существование тонкой С°-окрестности
отображения f, пересечение которой с состоит из гомеомор-
физмов. Так как / — гомеоморфизм, то L(/)Q/(M) пусто. Пусть
е; меньше 1/t и меньше, чем расстояние в N от компактного
множества f(Cj) до замкнутого множества L(/). Выберем не-
прерывную функцию б(х) на М, такую, что б(х)< е, для хе С,-,
и пусть g — какая-нибудь С°-б-аппроксимация отображения /,
лежащая в №3.
Покажем прежде всего, что L (/) = L {g}. Если хп — после-
довательность в М, не имеющая сходящихся подпоследователь-
ностей, то каждое компактное множество Ci содержит лишь
конечное число членов этой последовательности. Это означает,
что p(/(x„), g(x„))->0, ибо р(/(хп), g(xn))< \/i, если хп е Ct.
Следовательно, f(xn)-+y тогда и только тогда, когда g(xn)-*-y,
так что L(/) = L(g).
300 Дополнение. Дж. Манкрс
Отсюда следует, что L(g)f|g(Al) пусто. Если xsG, то
p(g(x), f(x)) < ei, так что точка g(x) не лежит в множестве
L(f), которое равно L(g). Следовательно, g— гомеоморфизм.
Заметим, что g(M) является замкнутым подмножеством много-
образия N тогда и только тогда, когда таковым является ДМ).
(4)	Пусть f — диффеоморфизм. Мы доказали, что сущест-
вует тонкая С'-окрестность W4 отображения f, состоящая из
вложений. Приводимая ниже лемма 3.11 показывает, что су-
ществует тонкая С°-окрестность отображения f, такая, что, если
g лежит в пересечении W4 с этой окрестностью и g(BdM)cz
cz Bd N, то g есть диффеоморфизм. 
Упражнение (а). Пусть f— гомеоморфизм пространства X на про-
странство У и {CJ — локально-конечное покрытие пространства X компактны-
ми множествами, такими, что множества Int Сг тоже покрывают X. Доказать,
что существует тонкая С°-окрестность отображения f, такая, что, если ото-
бражение g лежит в этой окрестности и взаимно-однозначно на каждом Ci,
то оно является гомеоморфизмом. (Здесь X и У, как всегда, — сепарабельные
метрические пространства.)
’Упражнение (Ь). Пусть М и N — С’-многообразия, и пусть ft — ре-
гулярная гомотопия между двумя отображениями fo и ft многообразия М в
N. Доказать, что, если ft — погружение для каждого t, то для некоторой функ-
ции 6(х) >0 любая С’-регулярная гомотопия Ft между f0 и fb являющаяся
6-аппроксимацией отображения ft для каждого t, также будет погружением
для каждого t. Доказать аналогичное утверждение для случая, когда каждое
ft — вложение, а М компактно или когда каждое ft — диффеоморфизм много-
образий без края.
Указание. Обобщить доказательство теоремы 3.10. При этом построение
(1) достаточно для случая погружения, построение (2) — для случая вложе-
ния; для случая диффеоморфизма построения (3) и (4) могут быть приме-
нены к отображению F: М X R-> определяемому равенством F(x. t) =
- (ftW.t).
•Упражнение (с). Показать, что в предыдущем упражнении пред-
положение компактности многообразия М для случая, когда ft — вложение,
является необходимым.
Лемма 3.11. Пусть f — гомеоморфизм М на N, где М и N —
топологические многообразия. Существует тонкая (^-окрест-
ность отображения f, такая, что, если g лежит в этой окрестно-
сти и #(Bd Af) cz Bd N, то g переводит M на N.
Доказательство. Рассмотрим сначала случай, когда край
Bd М пуст. Выберем локально-конечное покрытие многообразия
М множествами Ct, такими, что для некоторой координатной
системы (У<, kt), содержащей множество ktf(Ci) представ-
ляет собой m-мерный шар Вт и множества Int С/ также покры-
вают М (см. упр. (а)).
Выберем 6, настолько малым, чтобы шар Вт(1 4-6,) ра-
диуса 1 + б» содержался в Ai(Vi), а множества Di =*
=** (Вт (I — все еще покрывали М (см. лемму 1,4).
Тогда множества f (D<) покрывают N.
§ 3. Отображения и аппроксимации 301
Пусть g:M-*N— такое отображение, что ||й/§(х)—
— A/f(x)||< fi/ при хе Ci для всех i. Докажем, что g является
отображением на, а именно докажем, что g(C,) содержит
Другими словами, композиция отображений h =(kig) яв-
ляется корректно определенным отображением, переводящим
Вт в Rm, и образ единичной сферы S'"-1 = Bd Вт при отобра-
жении h лежит вне шара Вт(1—б/); мы докажем, что h(Bm)
содержит шар Вт (1 — б/).
Предположим, что точка г принадлежит шару Вт (1—6/),
но не принадлежит h(Bm). Пусть Л— радиальная проекция из
точки z, отображающая Rm\z на S'"-1. Тогда Л/г переводит
шар Вт в S'"-1.
С другой стороны, рассмотрим отображение h\Sm~': Sm~l-*
-* R"1. Оно гомотопно тождественному: можно просто взять
Ft(х) = th(х) + (1 — /)х, хе S”1-1. Эта гомотопия переводит
точку Л(х) по прямолинейному отрезку в точку х, так что Г/(хУ
лежит вне шара В'"(1—б/). Следовательно, KFt является кор-
ректно определенной гомотопией между отображением
S'"-1 -*• S'"—1 и тождественным отображением.
Рассмотрим гомологическую последовательность пары
(Вт, S'"-1) и ее гомоморфизм в себя, индуцированный отобра-
жением Л/г:
0 -> Нт (Вт, S'”"1) Нт_х (S'”"1) -> 0
О -> нт (вт, s'"-1) -> ят_! (s'”-1) -> о
Гомоморфизм (Л/г), представляет собой нулевой гомоморфизм
бесконечной циклической группы Нт(Вт, S'"-1), поскольку ЛЛ
отображает Вт в S'""1. Гомоморфизм (AA|S'"—1) е является тож-
дественным гомоморфизмом бесконечной циклической группы
302 Дополнение. Дж. Манкре
так как отображение	гомотопно тожде-
ственному. Это противоречит коммутативности приведенной
выше диаграммы. (Это — единственное место в наших замет-
ках, где используется немного алгебраической топологии.)
Теперь рассмотрим случай, когда край BdAf непуст. Пусть
D(Af) — удвоение многообразия М (см. упр. (Ь) п. 1.1), а
D(W) — удвоение многообразия N, и пусть f: D (М)—- D (N) —
гомеоморфизм, индуцированный отображением /. Выберем ка-
кую-нибудь метрику р на D(W). По уже доказанному, суще-
ствует положительная непрерывная функция е(х) на D(A1),
такая, что, если g: D(A1)—► D(W) и p(f(x), g(x)) <. е(х), то
g является гомеоморфизмом на.
Поскольку D(Af) = AfoU-Mi, функция е определяет две по-
ложительные непрерывные функции ео и ej на М. Аналогично
метрика, р индуцирует две метрики ро и pi на N. Пусть g: М -*
->N— гомеоморфизм, такой, что g(BdAf)c: Bd N. Тогда g ин-
дуцирует отображение g: D(Af)—* D(W). Если мы потребуем,
чтобы g было ео-аппроксимацией относительно метрики ро и
ei-аппроксимацией относительно метрики pi, то g будет е-ап-
проксимацией отображения f и, следовательно, гомеоморфиз-
мом на. Тогда g также должно быть гомеоморфизмом на. 
Упражнение (а). Доказать существование множеств С,, используемых
в процессе доказательства леммы.
Упражнение (Ь). Пусть А — замкнутное подмножество многообразия М
без края и В — замкнутое множество, содержащее А в своей внутренности.
Доказать, что существует положительная непрерывная функция б(х), опреде-
ленная на В и такая, что, если f: В-+М является С°-6-аппроксимацией то-
ждественного отображения, то f(B) содержит А.
§ 4.	СГЛАЖИВАНИЕ ОТОБРАЖЕНИЙ И МНОГООБРАЗИЙ
Теперь мы подошли к двум главным теоремам этой главы.
Первая из них утверждает, что, если М и N С°°-многообразия
и	— погружение, вложение или диффеоморфизм, то f
может быть аппроксимировано С°°-погружением, вложением
или диффеоморфизмом соответственно. Доказательство дано в
пп. 4.2—4.5, исключая случай, когда f является диффеомор-
физмом, а М имеет край; этот случай разобран в § 5 (см. тео-
рему 5.13).
Вторая теорема утверждает, что любая дифференцируемая
структура класса С1 на многообразии М содержит некоторую
С°°-структуру. Доказательство для случая, когда М — многооб-
разие без края, дано в пп. 4.7—4.9; случай, когда М имеет край,
рассмотрен в § 5 (см. теорему 5.11).
Основным инструментом для доказательства этих теорем
служит следующая лемма о сглаживании.
§ 4. Сглаживание отображений и многообразий 303
Лемма 4.1. Пусть U — открытое подмножество в Нт или в
R"1 и А — компактное подмножество открытого множества V,
удовлетворяющего условию V сг U. Пусть далее f: U -> R" есть
С'-отображение, 1 г, и 6 — положительное число. Существует
отображение fa U ->• R", такое, что-.
(1)	fi имеет класс Сх в некоторой окрестности множе-
ства А;
(2)	fi равно f вне V;
(3)	|fi(x) — f(x) | < б и |Dfi (х) — Df (х) | < б для всех х;
(4)	fi имеет класс Ср на любом открытом множестве, на ко-
тором f имеет класс Ср, 1 р оо;
(5)	существует дифференцируемая Сг-гомотопия ft между
отображениями fQ = f и fa такая, что ft удовлетворяет усло-
виям (2) — (4) для каждого t.
Доказательство. Достаточно рассмотреть случай, когда U —
открытое подмножество в R"1, так как другой случай сводится
к этому, если отображение f продолжить на какую-либо окрест-
ность U в Rm. Мы можем также считать, что V—компакт.
Пусть W — открытое множество, содержащее А и такое, что
W cz V, и пусть ф — какая-нибудь С°°-функция на Rm, равная 1
на некоторой окрестности множества Л и 0 вне W. (Берем раз-
биение единицы, подчиненное двухэлементному покрытию
{№,	тогда в качестве ф можно взять функцию, отвечаю-
щую F.)
Положим g(x) — ф(х)-f(x), так что g: U-*• R". Продолжим
отображение g на Rm, полагая его равным нулю вне W. Тогда
g: Rm —► R" будет отображением класса Сг.
Пусть ф(х)—С°°-функция на Rm, положительная на
Int Cm(e) и равная нулю вне Int Cm(e). Здесь 8 — положитель-
ное число, значение которого мы уточним позднее. Мы также
предполагаем, что
\ Ф (х) dx — 1,
ибо этого всегда можно добиться умножением ф на подходя-
щую константу. Положим
Л(х) = j q(y)g(x + y)dy
Cm (e)
для x e Rm. Выберем e так, чтобы число fame было меньше,
чем расстояние от W до Rm\V. Тогда й(х)=0 для точек
х е \ V. Положим
fi (х) = f (х) (1 — ф (х)) 4- h (х),
304 Дополнение. Дж. Манкрс
Так как (х) и h(x) обращаются в нуль при x^Rm\V, то ус*
ловие (2) выполняется.
Поскольку -ф(х) = 1 в некоторой окрестности множества А,
то fi(x)— h(x) для точек х из этой окрестности. Но h является
отображением класса С". Действительно,
ft(x) =	4>(y)g(x + y)dy = jj <p(z — x)g(z)dz =
Cm (в)	X + C (8)
= j <p (z — x) g (z) dz,
Rm
ибо <p(z — x)= 0, если z не принадлежит множеству x-f- Cm(eJ.
Так как q> — функция класса С°°, то и ft имеет класс С°°. Таким
образом, выполнено условие (1).
Поскольку fi = f(l — ip)+ft и отображение ф и й имеют
класс С00, класс отображения ft на любом открытом множестве
не меньше, чем класс отображения f. Следовательно, выпол-
няется условие (4).
Далее, fi(x) =/(х) + (Л(х)— g(x)). Выберем е настолько
малым, чтобы ft было б-аппроксимацией отображения g. Тогда
по теореме о среднем значении имеем
h‘ (х) == g‘ (х + у{)
и
57 « = 57 <* + «»).
где точки ус и уу принадлежат кубу Ст(е). Функции gc и
dgl/dx! равномерно непрерывны, поэтому, если мы выберем 8
так, чтобы |g'(x) —£г(х*) | и \dgl/dxf (х)— dgt/dxifx*) | были
меньше б, когда |х — х*|< 8, то условие (3) будет выполнено.
Наконец, пусть а — монотонная С°°-функция, такая, что
а (0 = 0 для t */з и а(0= 1 для t 2/з (см. лемму 1.3). По-
ложим
А(х) = а(0Л(х) + (1-а(0)/(х).
Ясно, что ft есть Сг-дифференцируемая гомотопия между
отображениями f и fa. Вне V имеем fa == f, а значит, и ft = f.
Подобным же образом
1Л-Л = а(/)1А-/1<б,
\Dft-Df[ = a(t)\Dfa-Df\<6.
Кроме того, ft имеет класс Ср на любом открытом множестве,
где fi и f имеют класс О’. Таким образом, условие (5) также
выполнено. Ц
<5 4. Сглаживание отображений и многообразий 305
Упражнение (а). Разобрать приведенное выше доказательство. Пока-
зать, что, если U открыто в R1" и f (и) <= Н", то ft(U) с Н". Показать, что,
если U открыто в Нт и f(U) cz Нп, то, вообще говоря, неверно, что ft(U) <=
с: Н" Видоизменить построение отображения fi так, чтобы это условие было
выполнено. (Указание: заменить повсюду в доказательстве Ст(е) на Cm(e). П
ПЯт.)
Упр ажнение (Ь). Рассмотреть предыдущую лемму для случая г = 0.
Показать, что заключение леммы выполняется и в этом случае, если опустить
условие | £)/,(%)—Df(x)\ <6, как не имеющее смысла, и принять, что ft
имеет лишь класс С° и, следовательно, является просто гомотопией.
Теорема 4.2. Пусть М и N — многообразия класса Ср и
f: М -* N — отображение класса С' (l^r^p^oo). Пусть
далее 6(х)>0. Существует Ср-отображение h:M->-N, такое,
что
(1)	h представляет собой ^-аппроксимацию f;
(2)	существует Сг-дифференцируемая гомотопия ft между
отображениями f и h, являющаяся б-аппроксимацией отобра-
жения f при любом t.
Доказательство. Пусть {Ui}—локально-конечное покрытие
многообразия М, где для каждого i (th, hi)—координатная си-
стема на М, О, — компакт и f(Ut) содержится в координатной
системе (О/, kt) на многообразии N. Пусть {W\} — открытое по-
крытие многообразия М, такое, что Wi содержится в открытом
множестве V,- и Р, содержится в Ult и пусть б — настолько ма-
лое положительное число, что любая б-аппроксимация отобра-
жения f переводит Ui в Oi.
Положим fQ = f и предположим, что ft-i: М -» N есть С'-ото-
бражение, имеющее класс Ср на (J ... U Wi-i и аппрокси-
мирующее f с погрешностью аппроксимации 6(1 —1/2'-1). Рас-
смотрим отображение gi_i =	переводящее hi(Ui) в
открытое подмножество ki(Oi) пространства R” или Ня. Приме-
няя лемму 4.1, получаем С'-отображение gr. hi(Ui)-*- R” или
Нп класса С°° на hi(Wt), совпадающее с gi-i вне hi(Vt). Если
многообразия М и N обладают краями, то нужно воспользо-
ваться упр. (а) п. 4.1. Пусть gi— достаточно хорошая аппрок-
симация отображения gi-it так что она переводит ht(Ui) в
kt (Oi). Тогда отображение f, корректно определяется формулой
( h-i(x) для х, лежащих вне Vt,
I I (Х) = | .—1	. / \	TI
I kt gfhiix) для х, лежащих в и{.
Ясно, что ft имеет класс Ср на множестве Wi U ... U Wi. (На-
помним, что gi имеет класс Ср на любом открытом множестве,
на котором gi-i имеет класс Ср.) Кроме того, если мы потре-
буем, чтобы \gi(y) — gi-\(y) | и \Dgi(y)— Dgi-i(y) | были до-
статочно малыми, то мы можем считать,что ft является б(х)/2‘-
306 Дополнение. Дж. Манкрс
аппроксимацией отображения fi-i. (Здесь мы, конечно, исполь-
зуем лемму 3.6.)
Положим теперь h(x)— lim ft(x); функция h корректно on-
i->oo
ределена, так как для всех достаточно больших i мы имеем
6(1/) = А+1 (у) = ... на некоторой окрестности точки х. Отобра-
жение h также имеет класс Ср и является 6-аппроксимацией
отображения f.
Чтобы построить дифференцируемую гомотопию между ото-
бражениями f и h, мы поступим следующим образом. Лемма
4.1 дает нам С-дифференцируемую гомотопию между gt—\ и
gi. Из нее мы получаем Сг-дифференцируемую гомотопию
Fi(x,t) между fi-i(x) и Д(х); Fi будет 6/2’-аппроксимацией ото-
бражения Д-i для каждого фиксированного t; Fi постоянно по t
для точек х, лежащих вне Vt. Положим
Fx (х, t) для t 1,
Fi+i(x, t — i) для	4-1.
Отображение F имеет класс Сг на М X R, и для любого ком-
пактного подмножества В cz М существует число п, такое, что
F(x, l) = h(x) для t > п, и х е В. Полагаем
'	f (х)	для
ft (х) =	<	F (х,	tg (л/))	для
.	/г(х)	для
/<0,
о < t < 72,
7г</. 
Упражнение (а). Усилить предыдущую теорему следующим образом.
Пусть А — замкнутое подмножество многообразия М. Предположим, что ото-
бражение f уже имеет класс Ср в некоторой окрестности U множества А.
Тогда мы можем добавить к заключению теоремы следующее утверждение:
(3)	ft(x) = f(x) для хе А.
Указание. В данном выше доказательстве взять покрытие {J7,} вписанным
в покрытие {U, А4\4) многообразия М и выбрать gi = gi-i, если U, cz U.
Упражнение (b). В предположениях предыдущей теоремы пусть В —
замкнутое подмножество открытого множества U в М. Доказать, что суще-
ствует Сг-отображение h: М->-У, имеющее класс О’ в некоторой окрестности
множества В и совпадающее с f вне U, для которого выполнены условия (1)
и (2) предыдущей теоремы.
Упражнение (с). Рассмотреть предыдущую теорему в случае г = 0.
Показать, что заключение теоремы остается в силе, только, конечно, h и ft
будут теперь лишь С°-6-аппроксимациями отображения f.
Следствие 4.3. Пусть М и N — многообразия класса Ср и
f: М N является Сг погружением (1 г р оо). Сущест-
вуют Cp-погружение f\: М—> N и Сг-дифференцируемая гомото-
пия ft между f и fi.
Доказательство. Это следует из теорем 3.10 и 4.2. Напом-
ним читателю, что по принятому нами нашему соглашению
§ 4. Сглаживание отображений и многообразий 307
(см. определение 3.9) требуется, чтобы fa было погружением
для любого I. 
Следствие 4.4. Пусть М и N — многообразия класса Ср и
f:M-*N— некоторое Сг-вложение (l^r^p^oo). Суще-
ствуют Ср-вложение fa: М —» N и дифференцируемая изотопия
между f и fa. 
Следствие 4.5. Пусть М и N— многообразия без края клас-
са Ср и f: М —> N есть Сг-диффеоморфизм (1 г р оо).
Существуют Ср-диффеоморфизм fa: МN и С-дифференцируе-
мая изотопия ft между f и fa, причем ft является диффеоморфиз-
мом для любого t. 
’Упражнение (а). Сформулировать и доказать более сильные ва-
рианты этих трех следствий, получаемые при помощи результатов, данных в
упр. (а) и (Ь) п. 4.2.
* Упражнение (Ь). Пусть Л4 и N— многообразия класса Cr, fB и ft —
С'-отображения М в Ув ft — С1-дифференцируемая гомотопия между f0 и
fi. Пусть, далее, 6(х)> 0. Доказать, что существует С'-дифференцируемая го-
мотопия Ft между fo и fi, такая, что Ft является 6-аппроксимацией отображе-
ния ft для каждого t.
*3адача 4.6. Пусть М и N — многообразия класса С1, f0 и
fi — С1-отображения М в П; и fa — ^-регулярная гомотопия
между ними. Пусть, далее, б(х)>0. Доказать, что существует
С'-дифференцируемая гомотопия ft между f0 и fa, такая, что
Ft является б-аппроксимацией отображения ft для каждого t.
Набросок решения. Рассмотрим сначала такую задачу.
Пусть ft для каждого t есть С'-отображение открытого под-
множества U пространства Нт или R" в пространство Нт или
Rm. Предположим, что ft — (^-регулярная гомотопия между fo
и fa. Пусть А— компактное подмножество множества U и ф—
С°°-функция, как в лемме 4.1, положим
£<(*) = ф (x)ft(x)
И
+ е
А*(х) = J q>(s) gt+s(x)ds,
где е достаточно мало, функция ср положительна на интервале
е
(—в, е) и равна нулю вне него (—8, е), а ^<р=1. Пусть
-е
Ft(x) = ft(x) (1 — ф (х)) + ht (х). Тогда Ft является С’-диффе-
ренцируемой гомотопией между f0 в fa на некоторой окрестности
множества А и совпадает с ft вне некоторой окрестности этого
множества.
308 Дополнение. Дж. Манкрс
Лемма 4.7. Пусть U, V и W — ограниченные открытые под-
множества пространства R"1, такие, что W czV и V с: U. Пусть
далее л — проекция пространства R” на Rm. Предположим, что
f: U -> Rn есть Сг-отображение, такое, что nf: U^-Rm является
вложением. Для заданной функции б(х)> 0 существует С'-вло-
жение h: U -> Rn, такое, что
(1)	h равно f вне V;
(2)	h представляет собой ^-аппроксимацию отображения fi
(3)	h(W) есть С°°-подмногообразие в R";
(4)	если U\ — открытое подмножество в U и f(U\)— С06-под-
многообразие в R", то h(Ui) также будет -подмногообразием
в R".
Доказательство. Ограничение проекции л на f(U) является
гомоморфизмом f(U) на некоторое открытое подмножество О
пространства R"1; пусть g: О -> R" — обратное отображение.
Тогда
g(xl.....xm) = (xl, .... xm, gm+l(x)....gn(x))
и, значит, g имеет класс С', ибо оно равно f (я/)-1.
Далее, если f(Ui)—С°°-подмногообразие в R", то ограниче-
ние отображения g на nf(Ut) имеет класс С°°. (Обратное тоже
верно, как легко следует из теоремы 2.2.) Чтобы показать это,
введем на подмногообразии f(Ui) его индуцированную С°°-
структуру и заметим, что ограничение	есть С°°-отобра-
жение относительно этой структуры, a g представляет собой
композицию обратного к этому ограничению отображения, ко-
торое имеет класс С00, и включения f(Ui) в R", которое тоже
является С°°-отображением.
Рассмотрим отображение g0: О —> R'’-"’, определенное равен-
ством
go(x) = (gm + l(x), .... gn(x)).
Используя лемму 4.1, выберем e-аппроксимацию §о(х) отобра-
жения go, имеющую класс С°° на л/(№) и равную go вне nf(V).
§ 4. Сглаживание отображений и многообразий 309
Кроме того, потребуем, чтобы go было класса С00 на любом от-
крытом подмножестве в О, где таковым является go. Пусть ото-
бражение g:O—>R" определено равенством g (х) = (х, §а (х));
оно представляет собой е-аппроксимацию отображения g.
Определим теперь отображение ft: U -> R" равенством/г (х) =
=gnf(x). Согласно задаче 3.7, если выбрать е должным обра-
зом, то h будет 6-аппроксимацией отображения f = gnf. 
Теорема 4.8. Пусть М — Сг-многообразие без края (1 г)
и f'. М -* R" есть Сг-вложение. Пусть далее 6 (х) > 0. Суще-
ствует Сг-вложение h: М — R", являющееся 8-аппроксимацией
отображения f, такое, что h{M) есть С°°-подмногообразие в R".
Доказательство. Пусть 6 настолько мало, что любая 6-ап-
проксимация вложения f тоже будет вложением. Для каждой
точки х^М отображение df{x) имеет ранг т. Поэтому для
проекции п пространства R" на одну из координатных /п-мер-
ных плоскостей отображение d (nf) (х) также имеет ранг т.
Тогда по теореме об обратной функции af является ^-диффео-
морфизмом некоторой окрестности точки х на открытое под-
множество этой координатной плоскости. Выберем покрытие
многообразия М множествами Ci, такими, что: 1) для некото-
рой координатной системы (Ui, hi), содержащей Ci, множество
hi {Ci) представляет собой единичный m-мерный шар; 2) мно-
жества I nt Ci также покрывают многообразие А! и 3) для про-
екции nt пространства R" на одну из координатных т-мерных
плоскостей Tiif | Ci является вложением. Пусть 6< >» 0 таково,
что любая 61-аппроксимация отображения Ci есть вложение,
и пусть функция 6 (х) настолько мала, что 6 (х) < 6/ для х е Ci,
Тогда, если f': М -* R" является 6-аппроксимацией отображения
f, то n.if' будет 6-аппроксимацией отображения так что
atf' | Ci — вложение. Пусть Wi — открытое покрытие многообра-
зия М, такое, что Wi содержится в открытом множестве Vi и
Vi с: Int Ci.
Положим fQ = f. Рассуждая по индукции, предположим, что
fi-i: М —► Rn есть Сг-отображение, которое служит (1 —
— W-1) б (х)-аппроксимацией отображения f, причем fl-l{Wk)
является С°°-подмногообразием пространства Rn, k < j. По-
строим отображение ff. Применяя лемму 4.7 к отображению
h-ihT1-. Л/(Int Су)-> R",
мы получим отображение fp. М Rn, представляющее собой
б^-аппроксимацию отображения f/_i, равное f/-i вне V/ и та-
кое, что fj(W/) оказывается С°°-подмногообразием пространства
R". Условие (4) леммы 4.1 обеспечивает нам возможность вы-
брать fa так, чтобы fi(Wi,) было С°°-подмногообразием в R",
k < /•
310 Дополнение. Дж. Манкрс
Как и в теореме 4.2, мы полагаем /г(х) — lim fj (х) и легко
/-»«>
убеждаемся, что h удовлетворяет всем требованиям доказывае-
мой теоремы. И
Следствие 4.9. Всякая Сг-дифференцируемая структура 3)
на многообразии М без края содержит некоторую С°°-структуру.
Упражнение (а). Пусть М — С'-миогообразие без края, а W— С"-
многообразие без края. Пусть б(х) >0. Доказать, что, если f: M^-N яв-
ляется Сг-вложением, то существует С'-вложение h: М -> N, служащее 6-ап-
проксимацией отображения f, причем h(M) оказывается С“-подмногообразием
в У, и между отображениями f и h существует Сг-дифференцируемая изотопия.
§ 5. МНОГООБРАЗИЯ С КРАЕМ
Доказательство наших двух главных теорем 4.5 и 4.9 для
случая многообразий с краем требует привлечения дополни-
тельных технических средств.
Прежде всего нам надо доказать теорему о трубчатой ок-
рестности (теорема 5.5), которая утверждает, что всякое Сг-
подмногообразие без края М в евклидовом пространстве имеет
окрестность, которая стягивается на М при помощи ретракции
класса Сг. Если г > 1, то легко найти такую ретракцию класса
Сг-1; грубо говоря, берется плоскость, перпендикулярная к
многообразию М в точке х, и «сжимается» в х. Построение
ретракции класса Сг требует гораздо большей работы. Нужно
сначала изучить многообразия Грассмана (п. 5.1—5.4). Необхо-
дима также одна топологическая лемма (п. 5.7).
Пользуясь этими средствами, мы докажем теорему о ци-
линдрической окрестности края, которая утверждает, что BdAf
имеет окрестность вМ, диффеоморфную BdAf Х[0, 1). Эта тео-
рема в свою очередь используется для построения дифферен-
цируемой структуры на удвоении D(Af) многообразия М
(п. 5.8—5.10).
После этого теоремы для многообразия М с краем сводятся
к соответствующим теоремам для многообразия D(Af), которое
не имеет края (п. 5.11—5.13).
ОПРЕДЕЛЕНИЕ 5.1. Многообразием Грассмана Gp,n назы-
вается множество всех п-мерных подпространств пространства
Rn+₽.
Пусть М(р, q) обозначает множество всех р X ^-матриц; че-
рез M(p,q-,r) обозначается подмножество матриц, имеющих
ранг г. Строки любой матрицы А е М (п, п + р\ п) образуют
множество п линейно независимых векторов в пространстве
Rn+₽. Таким образом, они определяют элемент множества GP,n,
§ 5. Многообразия с краем 311
который мы будем обозначать Х(А). Далее, две матрицы А и В
определяют один и тот же элемент множества Gp, п тогда и
только тогда, когда строки каждой из них являются линейными
комбинациями строк другой, т. е. когда А = СВ для некоторой
невырожденной п X «-матрицы С.
Множество М(п,п Р',^ является открытым подмножест-
вом пространства Rn(n+p) (см. доказательство теоремы 3.10),
так что оно имеет естественную топологию и С°°-дифференци-
руемую структуру. В множестве Gp, п вводится топология отож-
дествления: подмножество V открыто в Gp, п тогда и только
тогда, когда Х-1(К) открыто в М(п, п + р\ п).
Заметим, что A,: М(п, п 4- р; «)-> Gp, п является открытым
отображением. Действительно, пусть U — открытое подмноже-
ство в М(п, п + р; п). Для любой фиксированной матрицы
СеЛ4(п, п;п) отображение С: А —>• С А является гомеоморфиз-
мом пространства М(п,п + р;п) на себя, так что C(U) от-
крыто в М (п, п + р; п). Множество X-1(Z([/)) открыто как
объединением множеств С(U) по всем С е М(п, «; и); следо-
вательно, 1(G) открыто.
Теорема 5.2. Многообразие Грассмана Gp, п является Сх-мно-
гообразием без края размерности рп-, отображение X: М (п, п +
4- р; «)-* Gp, п имеет класс С°°.
Доказательство. (1) Gp,n локально евклидово. Объясним сна-
чала геометрическую идею доказательства. Если ф есть «-мер-
ная плоскость, проходящая через начало координат, то су-
ществует проекция л пространства R"+p на некоторую коорди-
натную n-мерную плоскость, являющаяся линейным изоморфиз-
мом па Ф. Пусть U — множество всех п-мерных плоскостей,
на которых л является линейным изоморфизмом. Каждая «-
мерная плоскость из U однозначно определяет набор из « век-
торов (щ, ..., о„), которые лежат в ней и проектируются при
отображении л в канонический базис координатной п-мерной
плоскости. Обратно, каждый такой набор из n-векторов опре-
деляет некоторую n-мерную плоскость из множества U. Таким
образом, каждый вектор щ имеет р компонент, которые могут
быть выбраны произвольно; так как имеется « таких векто-
ров, множество U гомеоморфно Rnp.
Более точно, пусть 1(Л) элемент общего вида в пространстве
Gp, п. Некоторая n X «-подматрица матрицы А имеет ранг «;
предположим, что она состоит из первых п столбцов. Пусть U
множество матриц вида [PQ], где Р — невырожденная «Х«-
матрица. Ясно, что U является открытым подмножеством в
Rn(”+p) и, следовательно, в М(п, п 4- р; «). Поэтому V = 1(G)—
открытое подмножество в Gp,
312 Дополнение. Дж. Манкре
Пусть ф отображает произвольную матрицу Q е М (п, р) в
матрицу [/Q] е М (п, п 4- р), и пусть ф0 = 1ф. Очевидно, фо
представляет собой непрерывное отображение М(п, р) в Gn,p.
Оно взаимно-однозначно, поскольку 1[/Q(] = X[/Qs] тогда и
только тогда, когда [/Qi]= С[/рг], оно отображает М(п, р) на
V, так как X [PQ] = X [/(Р-1 Q) ] = ф0 (P~'Q).
Пусть <р: U -» М (п, р) отображение, определенное равенством
ф([Р<2]) = P~lQ. Оно постоянно на каждом множестве Л-1 (^),
ибо равенство Л ([РА]) = Л ([P2Q2]) означает, что [PiQi] =
= C[P2Q2], откуда вытекает, что Bf'Q, = (СР2)-1 (CQ2) = P^Qz.
Следовательно, <р индуцирует непрерывное отображение ф0 мно-
жества V в М (п, р); это ф0 является обратным к отобра-
жению ф0, так как Ф0Ф0 (Q) = Ф (UQ]) =/"’Q = Q. Значит,
фо — гомеоморфизм.
(2)	Gp, п имеет С°°-дифференцируемую структуру. Доста-
точно доказать, что любые две координатные окрестности типа
только что построенной окрестности (V, Фо) имеют «пересече-
ние» класса С°°. Пусть ф, ф0, ф1 ф0> О, Р — соответствующие
отображения и открытые множества, определяющие другую ко-
ординатную окрестность указанного типа. Отображение ф дей-
ствует так: оно некоторым образом расставляет столбцы мат-
рицы Q между столбцами единичной матрицы /, поэтому, ко-
нечно, ф имеет класс С°°. Аналогично отображение ф имеет
класс С00 на открытом множестве U в М (п, п 4- Р", п), так как
ф( [jPQ] ) = P~XQ. Следовательно, отображение фофо = фф имеет
класс С°° (на открытом множестве ф(0 П U), где оно опреде-
лено).
(3)	Gp, п хаусдорфово. Пусть Х(А) и X (В)—различные «точ-
ки» пространства Gp,n. Тогда матрица [в] должна быть ранга,
не меньшего n-f- 1. Выберем е >0 так, чтобы любая матрица
размера 2п X (я + р), отличающаяся от нее (поэлементно) не
более чем на в, имела ранг, не меньший п -f- 1. Пусть U обозна-
чает е-окрестность «точки» А, а V обозначает е-окрестность
«точки» В в пространстве М (п, п 4- р\ п). Тогда Х((7) и 1(F)
будут различными окрестностями «точек» А (А) и А (В) соответ-
ственно, ибо Л — открытое отображение,
§ 5. Многообразия с краем 318
(4)	Gp, п имеет счетную базу. Действительно, пространство
Gp,n покрывается (п 4- р) 1/nlpl координатными системами типа
построенной выше. 
•Упражнение (а). Показать, что пространство Gp,n компактно.
•Упражнение (Ь). Показать, что существует С“-диффеоморфизм
Gp, п иа и„, р-
Лемма 5.3. Пусть f: М-* Gp, п есть Сг-отображение. Для лю-
бой заданной точки х&М существуют такая ее окрестность U
и такое Сг-отображение f„: U ->М (п, п + р; п), что kf* = f.
(Это отображение называется поднятием отображения /
над U.)
Доказательство. Пусть (V, фо)— координатная система на
GPt п типа построенной в теореме 5.2, такая, что f (х) лежит в V.
Так как ф0: V -> М (п, р) является С°°-диффеоморфизмом, то
мы просто полагаем
Л W = Ф (фо (f (х)) = [/, Фо/ (х)]. 
•Упражнение (а). Пусть (V, ф0) — координатная система указанного
в теореме 5.2 типа. Показать, что существует диффеоморфизм g пространства
с пространством УХЛ1(л, п; п), такой, что Ag~l представляет собой
естественную проекцию произведения V X М (п, п; п) на V.
Пусть (V, фо) — другая координатная система на Gpn и g — соответст-
вующий диффеоморфизм. Для каждой точки х е V П V обозначим через h„
отображение, переводящее пространство М(п, п; п) в себя, определяемое ра-
венством	j
(х, hx (Р)) — gg~l (х, Р).
Доказать, что h, — это просто умножение на некоторую невырожденную мат-
рицу Ах и что отображение х-*-Ах непрерывно. Все это показывает, что Л:
М (п, п + р; п) -> Gp, п является главным расслоением со слоем и структурной
группой М(п,п;п) (см. [12]).
ОПРЕДЕЛЕНИЕ 5.4. Пусть f: М —► R" и есть Сг-погружение.
Если v — касательный вектор к многообразию М в точке х, то
df(v)— касательный вектор к пространству R" в точке f(x).
Если отождествить 7'(Rn) с R^XR", то df(y) = (f(x),drf(v)) (см.
п. 3.5). Когда вектор v пробегает касательное пространство в
точке х, вектор dof (о) пробегает некоторую т-мерную плоскость,
проходящую через начало координат в Rn. Касательным ото-
бражением t, определяемым погружением, называется отобра-
жение t: At —> Gp, m, сопоставляющее точке х эту m-мерную пло-
скость. (Разумеется, п == m 4- р.)
Пусть (U, h) какая-нибудь координатная система на М.
Тогда локально отображение t задается равенством /(х) =
= i(D(/7H)), где матрица	вычислена в точке A(x), а X
есть проекция пространства М(т, т-\-р, т) на Gp,m. Следова-
тельно, t имеет класс Сг-1.
314 Дополнение. Дж. Манкрс
Аналогичным образом нормальное отображение п, отвечаю-
щее погружению f, определяется как отображение n: М —► Gm, ₽,
сопоставляющее точке х ортогональное дополнение к /п-мерной
плоскости t(x). Так как матрица £>(/й-1) невырождена, ее
можно представить в виде [Р (х) Q (х) ], где Р — невырожденная
tn X m-матрица. Тогда локально отображение п задается ра-
венством п(х) = Х( [Р(х)7]), где /? = — (P_1Q)f. Следовательно,
п также имеет класс С'~х.
Теорема 5.5 (о локальной ретракции). Для всякого ^-вло-
жения f: М —>• R" многообразия без края в евклидово простран-
ство существует Сг-ретракция r\ W-+f(M) некоторой окрестно-
сти W образа f(M) на этот образ. (Напомним, что это значит,
что г(у) = у ДЛЯ у
Доказательство. Рассмотрим нормальное отображение и:
М -» Gm, р и касательное отображение t: М —» Gp, m для вложе-
ния /(р = п — tri). Оба отображения имеют класс Сг~1. Суще-
ствует тонкая С°-окрестность отображения п, такая, что для
любого отображения п, лежащего в этой окрестности, п(х) и
t(x) являются линейно независимыми подпространствами про-
странства R", т. е. их пересечение есть нулевой вектор (см.
упр. (а)). Используя теорему 4.2, выберем отображение n: М -*
—► Gp, m класса Сг, лежащее в этой окрестности. (В случае г = 1
отображение п имеет класс С° и надо воспользоваться упр. (с)
п. 4.2.) Обозначим через t(x) ортогональное дополнение к
п(х); t также является отображением класса СГ.
Пусть Е — подмножество произведения М X R", состоящее
из пар (х, v), таких, что вектор v лежит в пространстве п(х).
(Если бы мы использовали само отображение п вместо п, то Е
было бы тем, что называется нормальным расслоением вложе-
ния f.) Докажем, что Е представляет собой Сг-подмногообразие
в М X R" размерности п.
Для заданной точки х <= М пусть и* и f, суть Сг-поднятия
отображений п и t над некоторой окрестностью этой точки.
Тогда п»(х) = А(х) есть р X «-матрица, a t*(x) = B(x) есть
tn X «-матрица, строки матриц А и В в совокупности образуют
линейно независимое множество. Пусть ((7, h)— координатная
система в точке х, такая, что отображения п* и t* определены
на U, и пусть ft(x) = (u1, ..., um). Определим отображение g:
U X R" -* R"1 X R" равенством
/	Г А (х) 1_1\
g (х, (v1..vn)) =	(х), [у’ ... vn]- L в j J.
§ 5. Многообразия с краем 315
Тогда (t/XRn, g) будет Сг-координатной системой на A4XRn-
Если элемент (х, v) лежит в Е, то вектор v представим в виде
линейной комбинации строк матрицы А (х), так что
••• » 0 •••
для некоторого набора у1, ур. Обратно, если вектор v имеет
такой вид, то элемент (х, о) лежит в Е. Таким образом, (х, о)
лежит в Е тогда и только тогда, когда g(x, v) лежит в A(t/)X
X R". Следовательно, координатное отображение g переводит
пересечение пространства Е с U X R" в открытое подмножество
A(t/)XRP пространства Rm+P, так что Е является ^-подмного-
образием пространства М X R”.
Рассмотрим Сг-отображение М X R” -* R”, которое переводит
(х, и) в /(х)4- V. Пусть F — ограничение этого отображения на
Е. Докажем, что dF имеет ранг п в каждой точке произведения
Л4Х0. Воспользуемся координатной системой g(x, v) =
= («’, ..., ит, ух, ..., ур, 0, ..0) на Е, которая была по-
строена выше. Имеем
Eg~l (и, у) = fh~' {и) + 1У .../]• A (h~l («)),
316 Дополнение. Дж. Манкрс
так что
д (Fg~l)/dy = A(h~l (и)У
и
д (Fg-^/du1 = д ди + ([у1 ... ур] • д (АГГ^/ди*)*.
Последний член обращается в нуль в точках множества
g(M X 0), поскольку в этих точках у = 0. Следовательно,
D (Fg~*) = [D(f/T1) (и) • A (/Г1 (и))‘]
в точках множества g(M'XO). Столбцы матрицы	по-
рождают касательное пространство t(x); строки матрицы А
порождают пространство п(х); в силу выбора п эти простран-
ства линейно независимы.
Но отображение F: Е -♦ R" является на М X 0 гомеоморфиз-
мом и, кроме того, каждая точка из М X 0 имеет окрестность,
которую F гомеоморфно отображает на соответствующее от-
крытое подмножество пространства R" (по теореме об обратной
функции). Отсюда следует, что существует окрестность много-
образия М X 0 в Е, которую F гомеоморфно отображает на от-
крытое подмножество пространства R" (см. лемму 5.7). Суще-
ствует также окрестность многообразия М X 0 в Е, на которой
dF имеет ранг п; пусть V — пересечение этих окрестностей, и
пусть W = F(V). Имеется естественная проекция л прямого про-
изведения М X R" на М. Так как F является С'-диффеоморфиз-
мом V на U7, то FnF~} = г и будет искомой ретракцией W на
f(M). 
Упражнение (а). Построить тонкую С°-окрестность нормального ото-
бражения п, требующуюся в предыдущем доказательстве.
Указание. Используя тот факт, что X — открытое отображение, построить
окрестности подпространств п(хо) и /(х0), состоящие из линейно независимых
подпространств.
Следствие 5.6. Пусть М— многообразие без края и f; M->N
есть Сг-вложение. Для некоторой окрестности W подмногообра-
зия f(M) в N существует Сг-ретракция г:
Доказательство. Пусть g: N—>R4 есть Сг-вложение. Для не-
которой окрестности U подмногообразия gf(M) в R’ существует
Сг-ретракция r0: U-*gf(M). Композиция g-1rog будет искомой
ретракцией, определенной на W = g~lW). 
•Упражнение (а). Пусть М и N — многообразия без края и f:
M-+N есть С'-погружение, г 2. Нормальное расслоение Е погружения f
может быть наиболее просто описано, когда М представляет собой подмного-
образие в R’с индуцированной римановой метрикой. В этом случае Е— это
подпространство в М X R", состоящее из пар (х, о), таких, что о является
§ 5. Многообразия с краем 317
вектором, касательным к Af в точке f(x) и нормальным к подпространству, со-
стоящему из векторов вида df(w), где w — вектор, касательный к М в точке х.
(В общем случае Е описывается как подпространство прямого произведения
M\T(N).) Ясно, что Е представляет собой (/“'-подмногообразие в М X R".
Доказать следующую теорему о трубчатой окрестности'.
Если f: М-+ N с Rp есть (/-вложение, то существуют окрестность U под-
пространства М X 0 нормального расслоения Е и (/“'-диффеоморфизм h этой
окрестности U на некоторую окрестность подмногообразия f(M) в N, такие,
что h | М X 0 = f •
Указание. Рассмотреть отображение F: Е -> Rp, задаваемое формулой
F (х, о) — f (х) -4- о. Пусть г — ретракция некоторой окрестности многообразия
N на N. Взять h — rF.
Лемма 5.7. Пусть А — замкнутое подмножество локально-
компактного пространства X, и пусть отображение f: X —► У яв-
ляется на А гомеоморфизмом, причем каждая точка х е А обла-
дает окрестностью Ux, которую f гомеоморфно отображает на
открытое подмножество пространства У. Тогда f есть гомеомор-
физм некоторой окрестности множества А на некоторое открытое
подмножество в У. (Как всегда, X и У — сепарабельные метри-
ческие пространства.)
Доказательство. Пусть U — объединение окрестностей Ux.
Тогда отображение f является локально взаимно-однозначным
в каждой точке из U. Далее, если В — любое подмножество в U,
такое, что f\B взаимно-однозначно, то f\B — гомеоморфизм.
Действительно, пусть f (х), где точки хп и х принадле-
жат В. Так как множество f(Ux) открыто в У, оно содержит все
элементы последовательности f(xn), начиная с некоторого но-
мера л. Так как f\Ux— гомеоморфизм, последовательность хп
должна сходиться к точке х.
(1)	Докажем, что, если С — компактное подмножество в U
и f взаимно-однозначно на С, то существует окрестность мно-
жества С, на которой замыкание отображения f является вза-
имно-однозначным. Пусть Un обозначает e/n-окрестность мно-
жества С, где е настолько мало, что замыкание О\ компактно и
лежит в U. Допустим, что f не является взаимно-однозначным
ни на каком из множеств Оп. Тогда найдутся точки хп и уп из
On, такие, что хп*£уп и f(xn)~f(yn). Переходя к подпоследо-
вательностям и производя перенумерацию, мы можем считать,
что хп -* х и уп -* у, где х и у — точки из С. Тогда f(x) = f(y) и,
поскольку f взаимно-однозначно на С, х = у. Однако / локально
взаимно-однозначно в точке х, и потому мы не можем иметь
f (хп) = f (уп) для больших л.
(2)	Докажем, что, если С — компактное подмножество в U
и f — взаимно-однозначно на ClM, то существует окрестность V
множества С, такая, что f является взаимно-однозначным на
318 Дополнение. Дж. Манкре
Пусть Un обозначает e/n-окрестность множества С, где е
настолько мало, что Ui компактно и лежит в U; кроме того, мы
можем предполагать (в силу (1)), что f взаимно-однозначно на
Ui. Если f_HQ является взаимно-однозначным ни на одном из
множеств Un U А, то найдутся точки хп из Vn \ А и точки уп из
A\Un, такие, что f(xn) — f(yn). Переходя к подпоследователь-
ностям и производя перенумерацию, мы можем считать, что
хп—*х, где хеС. Тогда f(yn) —*f(x). Так как С U А —гомео-
морфизм, то х. Однако f локально взаимно-однозначно в
точке х, и, следовательно, мы не можем иметь f(xn) = f(yn) для
больших п.
(3)	Теперь непосредственно приступим к доказательству
леммы. Пусть А представлено в виде объединения возрастающей
последовательности X0cz4|CZ ... компактных множеств, где
Ло == 0. Положим Vo = 0, и пусть V„ — окрестность множества
Рп-i U Ап, такая, что Vn — компактное подмножество в U и f
взаимно-однозначно на Vn U А. Согласно (2), мы можем выб-
рать окрестность Vn+i компактного множества Vn U ^«+i, такую,
что Vn+i является компактным подмножеством в U и f взаимно-
однозначно на Vn+i U А.
Пусть V—объединение множеств V„. Тогда V — окрестность
множества А и отображение f взаимно-однозначно на V. 
Лемма 5.8. На всяком Сг-многообразии М существует неот-
рицательная вещественнозначная функция g класса Сг, такая,
что g(x) = 0 и dg(x) имеет ранг 1 в каждой точке х е Bd М.
Доказательство.Пусть {(Ui, hi)} - локально-конечное покры-
тие многообразия М координатными системами и {<рг} —разбие-
ние единицы, подчиненное покрытию {(Л}. Пусть dimAf = m.
Тогда m-я координатная функция Л? (х) равна нулю в точках
хе Ui fl Bd М для каждого i. Далее, если k(x) — (ux, ..., ит) —
другая координатная система в точке х, то производная
dWk~")ldum положительна в точке k(x). Действительно, hik~l
является невырожденным преобразованием некоторого откры-
того множества в Нт, содержащего точку k(x), на некоторое
другое открытое множество в Нт, причем йГА-1 (и', ..., ит~1,0)г&
= 0, так что dfjiTk'^/du1 = 0 в точках пространства R"1-1 для
j < т. Поскольку D(hik~x) — невырожденная матрица, произ-
водная д (/г^А-1)/5ыт должна быть ненулевой в точках простран-
ства R"1-1, а так как h? (х) неотрицательно для всех х, эта про-
изводная должна быть положительной в точках из R'"-1.
Пусть g (х) = У, ф£ (х) • h™ (х). Тогда g(x) = 0 для всех хе
eBdAf. Далее, если k(x) = (u'....ит)—произвольная коор-
§ 5. Многообразия с краем 319
динагная система на М, то
__ V ,т ^(фЛ-1) , v д(фТк~1)
ди'п	дит L, ф‘ дит
Для всякой точки BdAf первый член равен нулю, так как
h? (х) = 0, а второй член строго положителен. Следовательно,
dg(x) имеет ранг 1 в точках х е BdAf. 
Теорема 5.9. Для всякого Сг-многообразия М существует
Сг-диффеоморфизм р некоторой окрестности края Bd М на про-
изведение BdAIXfO, 1), удовлетворяющий условию р(х) = (х, 0)
при х е Bd Af.
Такая окрестность называется цилиндрической окрестностью
края *.
Доказательство. Согласно следствию 5.6, для некоторой
окрестности W края Bd М в Af существует О-ретракция г:
W —»Bd Af. По лемме 5.8 существует неотрицательная Сг-функ-
ция g на Af, такая, что g(x) = 0 и dg(x) имеет ранг 1 для всех
хе BdAf. Определим отображение f: W-* Bd Af Х[0, оо) ра-
венством f(y) = (r(y), g(y)). Если хе BdAf, то f(x) = (x, 0) и
дифференциал df(x) невырожден. Действительно, если k(x) =
— (и\ ..., ип) — координатная система в точке х и h =
= (£|Bd Af)X t, то
ГI *
D(hfk~^ =
d(gk ')	•
dum .
Применяя теорему 1.11, мы получаем, что каждая точка хе
е Bd Af имеет окрестность Ux, которую f гомеоморфно перево-
дит на некоторое открытое подмножество в Bd Af X [0, оо). Так
как f является на Bd М гомеоморфизмом, то из леммы 5.7
следует, что f есть гомеоморфизм некоторой окрестности U гра-
ницы BdAf в W на некоторую окрестность V множества BdAfXO
в BdAf Х[0, оо). Используя упр. (а) п. 2.6, мы можем построить
Сг-функцию ё (х) > 0 на Bd Af, такую, что точка (х, t) из Bd Af X
X[0, оо) лежит в V, если t < 6(х). Пусть s — диффеоморфизм
пространства Bd Af Х[0, оо) на себя, переводящий точку (х, t)
в точку (х, (/ё(х)), и пусть р — sf. Тогда p(U) содержит BdAf X
Х[0, 1) и соответствующее ограничение р будет удовлетворять
требованиям теоремы. И
1 Или воротником. (В оригинале — product neighborhood (окрестность-про-
изведение) .) — Прим. ред.
320 Дополнение 1. Дою. Манкрс
ОПРЕДЕЛЕНИЕ 5.10. Пусть М — (^-многообразие с непу-
стым краем. Напомним, что удвоение D(M) многообразия М —
это объединение множеств Мо = М X 0 и Mi = М X 1 с отожде-
ствлением точек (х, 0) и (х, 1) для всех хе BdAf. Мы можем
ввести дифференцируемую структуру на многообразии D(M)
следующим образом. Пусть р0: £/о —► BdAfoX [0 1) и pi: Ui~+
->BdAfiX(—1, 0] — цилиндрические окрестности края в Мо и
Mi соответственно, U — объединение UQ и Ui в D(M) и Р: U ->
->BdMX(—1, 1) —гомеоморфизм, индуцированный отображе-
ниями ро и pi. Дифференцируемая структура класса С' на D(M)
будет корректно определена, если мы потребуем выполнения
следующих условий;
(1) Р является Сг диффеоморфизмом,
(2) включения Мо и Afi в D(M) являются Сг-вложениями.
Заметим, что так определенная дифференцируемая структу-
ра на D(M) сильно зависит от выбора цилиндрических окрест-
ностей ро и рь Однако дифференцируемые многообразия, соот-
ветствующие различным способам выбора, оказываются, как
мы докажем позднее (см. теорему 6.3), диффеоморфными.
•Упражнение (а). Используя различные выборы цилиндрических ок-
рестностей края Bd Н2, ввести две не тождественные друг другу дифференци-
руемые структуры на удвоении D(H2). Показать, что получающиеся диффе-
ренцируемые многообразия диффеоморфиы, однако соответствующий диффео-
морфизм не может быть выбран как сколь угодно хорошая С-аппроксимация
тождественного отображения иа каждом экземпляре полуплоскости Н2.
•Упражнение (Ь). Показать, что, если М и N суть С'-многообразия,
то произведение М X N обладает дифференцируемой структурой класса Сг,
такой, что каждое из включений М-*-Муу, N-+x%N является Сг-вложе-
ннем.
Теорема 5.11. Всякая дифференцируемая структура S) клас-
са Сг на многообразии М содержит некоторую С°°-структуру.
Доказательство. Мы уже доказали эту теорему для случая,
когда край BdM пуст. Пусть теперь край BdM непуст. Рассмо-
трим многообразие D(M), не имеющее края, и снабдим его диф-
ференцируемой структурой класса Сг, описанной в определении
5.10. Выберем какую-нибудь содержащуюся в ней О-структуру,
и пусть D' обозначает соответствующее дифференцируемое мно-
гообразие.
Рассмотрим отображение Р-1: BdMX(—1, 1)—► D(M), где
Р — отображение из определения 5.10. Заданная О-структура
на BdM содержит некоторую С°°-структуру; обозначим соответ-
ствующее дифференцируемое многообразие через (BdAf)/. Ото-
бражение Р-1 является Сг-диффеоморфизмом С°°-многообразия
(BdM)'X(-1, 1) на некоторое открытое подмножество U в
С°°-многообразии D'.
§ 5. Многообразия с краем 321
Заметим, что существует Сг-диффеоморфизм h многообразия
(Вс1Л1)'Х(—1, 1) на (Л имеющий класс С°° в некоторой окрест-
ности подмногообразия (BdAfJ'XO и совпадающий с Р~1 вне
открытого подмножества (BdAl),X(—‘/г, ’/г). (Здесь мы ис-
пользуем упр. (Ь) п. 4.2.) Поэтому множество A(BdAfXO) яв-
ляется С°°-подмногообразием многообразия D'.
Диффеоморфизм h позволяет построить Сг-диффеоморфизм f
многообразия D' на себя: мы можем просто положить f(x) =
= hP(x) для x^U и f(x) = x для остальных точек. Если i:
M-^AfoCzD] — отображение включения, то fi будет Сг-вложе-
нием многообразия М в многообразие D', а множество fi(M)
будет С°°-подмногообразием в D', откуда и следует требуемый
результат. В
Лемма 5.12. Пусть М и N суть Ср-многообразия без края и
f; M-+N есть Сг-диффеоморфизм. Отождествим для удобства N
с подмножеством NX0 в произведении N X R. Для любой за-
данной положительной функции е на W X R существует положи-
тельная функция 6 на М, такая, что выполнено следующее
условие.
Пусть g — Ср-вложение М в N X R, служащее 6-аппроксима-
цией отображения f. Тогда найдется Ср-диффеоморфизм h про-
изведения N X R на себя, который
(1)	переводит g(M) в N-,
(2)	является е-аппроксимацией тождественного отображения
и равен тождественному отображению вне N X (—2/з, 2/з) -
Доказательство. Пусть 0(/) — монотонная С°°-функция, рав-
ная 1 при t ’/з и нулю при t > 2/3. Пусть k | ₽'(/)] для
всех V, ясно, что k 3. Пусть далее л — проекция произведе-
ния УУ X R на УУ X 0, и пусть б настолько мало, что g(M) лежит
в А^Х(—7з, 7з) и ng— диффеоморфизм М на N'XQ. (Согласно
задаче 3.7, мы можем, беря б достаточно малым, добиться того,
чтобы ng было сколь угодно хорошей аппроксимацией для
я/ = А)
1/2 И Дж. Милнор, Дж, Сташеф
322 Дополнение. Дж. Манкрс
Общая точка образа g(M) имеет вид (у, <р(«/)), где yeN н
Ф — вещественная функция на N, такая, что —'/з < ф(«/)< ’/з-
Поскольку (у, ф(«/)) = g((ng)(у, 0)), то ф есть функция клас-
са Ср.
Определим отображение ft: A/XR—*WXR равенством
ft (У, s) = (у, ф (у, «)),
где
Ф(«/, s) = s — Ф (//)₽( Is |).
Мы имеем |ф(г/)| < ’/з, и, таким образом, р(| s |) = 1, когда
s == <р(у). Следовательно, ft переводит g(M) в N X 0.
Если |s|>2/3, то р(|s|) — 0 и h является тождественным
отображением.
За счет надлежащего выбора б мы можем сделать функцию
ф(;/) сколь угодно близкой к нулевой функции. Действительно,
заметим, что (у, ф(у)) = g(ng)~l(y, 0); используя задачу 3.7,
мы видим, что, если g достаточно близко к f, то ng близко к
rtf = f, (ng~}) близко к f-1 и g(ng_|) близко к ff~l = id. Пусть
б настолько мало, что ср (у) служит е0(у)/2£-аппроксимацией
для нулевой функции, где ео(у) = min е (у, s) по —1 < s < 1.
Чтобы все это имело смысл, надо предварительно вложить мно-
гообразие N в некоторое R₽. Тогда N X R вложится в Rp+1. Так
как |ф(«/) | < е0(«/), го
\\h(y, s) — (y, s)|| = | ф(у, s) —s| <e.0(y),
как и требуется. Пусть v — единичный касательный вектор к
WXR в точке (у, s) и v, у2— его компоненты, касательные к
N X s и у X R соответственно. Имеем
|]dh(у) — у ||<||dh(yj — У11| +1|dh (у2) — у2Ц.
Второй член в правой части этого неравенства меньше ео/2, по-
скольку |дф /ds — 11 — |ф(//)р'(| s |) | < е0/2, а первый член
равен
II ^Ф fai) II = II3 (И) d<p (у,) || < ео/2,
откуда и следует наше утверждение. В
Теорема 5.13. Пусть М и N — многообразия класса Ср и f-.
M-+N есть Сг-диффеоморфизм (1 г р оо). Для любой
заданной функции б(х)>0 существует Ср-диффеоморфизм fr.
M-+JV, являющийся 8-аппроксимацией диффеоморфизма f.
Доказательство. Пусть б настолько мало, что если fi служит
С°-б-аппроксимацией для f и fi (Bd M) cz BdA\ то ft представляет
собой отображение на. Рассмотрим N как подмногообразие
§ 5. Многообразия с краем 323
удвоения D(A/); тогда f будет Сг-вложением М в D(A/). Соглас-
но задаче 3.7, существуют положительные функции 61 и 62 на М
и D(Af) соответственно, такие, что, если g есть 6гаппроксима-
ция для f и h:	D(N) есть 62-аппроксимация тождествен-
ного отображения, то hg является 6-аппроксимацией отображе-
ния f: М —>D(A/).
Пусть g: М—»D(A/) есть С₽-вложение, служащее 61-аппро-
ксимацией для f. Если 61 достаточно мало, то g будет перево-
дить BdAf в цилиндрическую окрестность BdAf Х(—1, 1), кото-
рая используется при введении в D(Af) дифференцируемой
структуры. Теперь мы можем применить предыдущую лемму и
получить Ср-диффеоморфизм h многообразия D(A/) на себя, пе-
реводящий g^Bd А1) на BdAf.
Взяв 6] достаточно малым, мы можем обеспечить, чтобы h
было 62-аппроксимацией тождественного отображения. Тогда
hg = fi отображает М в D(A1) и переводит BdAf в BdAf; из со-
ображений связности следует, что А1 должно переводиться в
подмножество N многообразия D(A/). Поскольку fi имеет класс
Ср, отсюда вытекает доказываемое утверждение. 
*3адача 5.14. Обобщая предыдущую теорему, доказать, что
существует Сг-дифференцируемая изотопия ft между отображе-
ниями f и fi, такая, что ft является диффеоморфизмом А1 на А/
для каждого t.
Указание. Для этого потребуется обобщить лемму 5.12 сле-
дующим образом. Пусть gt есть Сг-дифференцируемая изотопия
между двумя Сг-вложениями А1 в А/ X R, служащая 6-аппро-
ксимацией отображения f при каждом t. Тогда существует
Сг-дифференцируемая изотопия ht, являющаяся диффеоморфиз-
мом N X R на себя для каждого t, удовлетворяющая условиям
(1) и (2) для каждого t и дополнительно удовлетворяющая
условиям:
(3)	если gt(M)dN для некоторого t, то ht представляет со-
бой тождественное отображение;
(4)	если gt имеет класс Ср для некоторого t, то ht тоже
имеет класс Ср.
♦Задача 5.15. Пусть N—многообразие без края и f: М—* N
есть Сг-отображение. Доказать, что любая достаточно хорошая
сильная аппроксимация отображения f дифференцируемо гомо-
топна f.
Точнее, доказать, что для любой заданной функции е(х)> О
найдется функция 6(х)>0, такая, что для всякого ^-отобра-
жения g: M-+N, служащего 6-аппроксимацией отображения f,
существует Сг-дифференцируемая гомотопия ft между fag, яв-
ляющаяся е-аппроксимацией отображения f для каждого t.
7г И*
324 Дополнение. Дж. Манкре
Указание. Пусть N — подмногообразие евклидова простран-
ства Rp и г есть С'-ретракция некоторой окрестности М в R" на
N. Деформировать отображение f в g вдоль прямых линий в Rp,
а затем, применив ретракцию г, перевести эту гомотопию в N.
♦Задача 5.16. Обобщить утверждение задачи 5.15 на случай,
когда N имеет край, при этом дополнительно требуется, чтобы,
если f(x) и g(x) лежат в Bd/V, то ft(x) также лежало в Bd/V
для любого t.
Указание. Вложить Bd N в Rp и продолжить это вложение
до вложения h: U —► Rp+1, где U — некоторая окрестность края
Bd N в D(jV), так что л/г (U) — h (N), где л — проекция Rp+1 на
Rp. Далее, используя задачу 2.11, выбрать какое-нибудь вложе-
ние D (jV) в соответствующее евклидово пространство, совпа-
дающее с h в некоторой окрестности края Bd N. После этого,
применяя технику задачи 5.15, подобрать ретракцию г так, что-
бы она переводила некоторую окрестность точки х в нормаль-
ном пространстве к многообразию D(,V) в точке х в эту точку х.
Вывести отсюда, что ретракция г переводит прямолинейный от-
резок, соединяющий две близкие точки из ft(Bd/V) в ft(BdAZ).
* Упражнение (а). Дать какое-нибудь другое доказательство утвержде-
ния задачи 5.14.
♦Задача 5.17. Пространство X называется локально-стягивае-
мым, если для каждой точки х е X и каждой окрестности U
точки х существует такая окрестность V этой точки, что отобра-
жение включения i: V U гомотопно постоянному отображе-
нию с: V -> х.
Пусть М и N суть (^-многообразия, причем М компактно.
Доказать, что пространство Fr(M, /V) локально-стягиваемо в
С-топологии. Доказать также, что следующие пространства яв-
ляются локально-стягиваемыми в С'-топологии:
(1)	пространство всех Сг-погружений М в У;
(2)	пространство всех Сг-вложений М в У;
(3)	пространство всех Сг-диффеоморфизмов М в М.
ГЛАВА II
ТРИАНГУЛЯЦИИ
ДИФФЕРЕНЦИРУЕМЫХ МНОГООБРАЗИЙ
§ 71. КЛЕТОЧНЫЕ РАЗБИЕНИЯ И КОМБИНАТОРНАЯ ЭКВИВАЛЕНТНОСТЬ
В этом параграфе мы докажем теорему о том, что два ко-
нечных полиэдра в евклидовом пространстве могут быть под-
разделением превращены в симплициальные разбиения таким
образом, что их пересечение окажется подразбиением каждого
из них (теорема 7.10). Но сначала необходимо определить, что
такое евклидово клеточное разбиение, и изучить некоторые свой-
ства клеточных разбиений.
ОПРЕДЕЛЕНИЕ 7.1. Если ц0, vm— линейно независи-
мые точки в пространстве R", то симплексом а = vo ... vm, на-
тянутым на эти точки, называется множество всех точек х вида
x — J^biVi, где b{^Q и ^Ь( = \. Числа bi называются бари-
центрическими координатами точки х. Точка Zoi/(^ + 0 назы-
вается барицентром симплекса о и обозначается а. Гранью сим-
плекса о называется симплекс, натянутый на некоторое подмно-
жество вершин симплекса о. Очевидно, симплекс о гомеомор-
фен шару Вт. Внутренность симплекса а называется открытым
симплексом.
Если А и В — два подмножества пространства R", то их
джойном А* В называется объединение всех замкнутых прямо-
линейных отрезков, соединяющих какую-нибудь точку из Л и
какую-нибудь точку из В при условии, что никакие два таких
отрезка не пересекаются, разве что имеют общую концевую
точку. Ясно, что а = v0 * (vi * (иг * •))•
Симплициальным разбиением 2 К называется всякая совокуп-
ность симплексов в R", удовлетворяющая условиям:
(1)	любая грань симплекса из К принадлежит К\
(2)	пересечение любых двух симплексов из К является
гранью каждого из них;
(3)	каждая точка из |7С| имеет окрестность, пересекающую-
ся лишь с конечным числом симплексов из К. Здесь |7С| обо-
1 Напомним, что § 6 (последний параграф гл. I) при переводе опущен.—
Прим, перев.
2 В оригинале simplicial complex. — Прим, перев.
И Дж. Милнор, Дж. Сташеф
326 Дополнение. Дж. Манкре
значает теоретико-множественное объединение симплексов из
симплициального разбиения К и называется его полиэдром.
(Более общим образом, можно было бы позволить симплек-
сам из К лежать в R°° = |J R", однако данного выше определе-
ния вполне достаточно для наших целей. Фактически мы огра-
ничимся конечномерными симплициальными разбиениями.)
Подразделением (или измельчением) симплициального раз-
биения К называется всякое симплициальное разбиение К', та-
кое, что |Л’/| = |/(| и каждый симплекс из К.' содержится в не-
котором симплексе из К- Подразбиением симплициального раз-
биения К. называется такое подмножество в К, которое само яв-
ляется симплициальным разбиением.
Пусть точка х принадлежит |Л|. Звездой точки х в К назы-
вается объединение внутренностей всех симплексов из К, содер-
жащих эту точку. Это — открытое подмножество полиэдра |/С|.
Оно обозначается через St(x, К). Для произвольного подмно-
жества S полиэдра |Л| мы определяем St(S, К) как объедине-
ние множеств St(x, К) для всех /eS. В случае когда J — под-
разбиение симплициального разбиения К, удобно писать St (7, К)
вместо St(|/|, /().
Пусть а — симплекс ио ... vm- Отображение f: a-*Rp линей-
но, если f (х) = f (£ btvt) = S bif для всех x e о. Пусть те-
перь К и L — симплициальные разбиения. Отображение f:
|/(| —► |L| называется линейным на симплексах, если оно линей-
но переводит каждый симплекс из К в некоторый симплекс из
L. Для краткости мы часто будем в этом случае говорить, что
линейно на симплексах отображение f: К -*L.
Отображение f: K-+L называется кусочно-линейным, если
для некоторого подразделения К' симплициального разбиения К.
отображение f: К' —> L линейно на симплексах. Отображение f:
/С—►£ называется линейным изоморфизмом, если оно является
гомеоморфизмом полиэдра |7С| на полиэдр j L | и линейно пере-
водит каждый симплекс из К в некоторый симплекс из L.
Долгое время стояла знаменитая проблема (часто называе-
мая Hauptvermutung'): следует ли из гомеоморфности полиэд-
ров |К| и |L существование кусочно-линейного гомеоморфиз-
ма полиэдра К| на полиэдр |£|? Были получены следующие
частные ответы: да, если dim/<^2 [11]; да, если | К. | пред-
ставляет собой трехмерное многообразие [1, 8]; да, если К. и L
являются гладкими триангуляциями диффеоморфных многооб-
разий (это мы здесь докажем1 2). Недавно Милнор показал, что
ответ отрицателен, если dim/(^6 [7]. Все еще остается неиз-
1 Основная гипотеза (нем.).— Прим, перев.
2 См. ниже теорему 10.5. — Прим, перев.
§ 7. Клеточные разбиения и комбинаторная эквивалентность 327
вестным, будет ли ответ положительным, если |/<| — многооб-
разие. 1 * * * * * * *
Упражнение (а). Пусть К — симплициальное разбиение. Показать,
что замыкание звезды St(x, К), обозначаемое St(x, К), является полиэдром
некоторого конечного подразбиения К. Мы будем иногда использовать сим-
вол St(x, К) и для обозначения самого этого подразбиения, если это не мо-
жет вызвать недоразумений.
Упражнение (Ь). Показать, что, если f: |К| -► |Д|—кусочно-линей-
ный гомеоморфизм, то существуют подразделения К' и L', такие, что
К' -> L' есть линейный изоморфизм.
ОПРЕДЕЛЕНИЕ 7.2. Пусть с —ограниченное подмножество
пространства R", состоящее из всех точек х, удовлетворяющих
некоторой системе линейных уравнений и линейных неравенств:
i-z (х) = Z апх> >bh i = 1, ..., р;
такое множество с называется (евклидовой) клеткой. Это —
компактное выпуклое подмножество в R". (Выпуклость множе-
ства означает, что оно вместе с любыми двумя точками содер-
жит прямолинейный отрезок, их соединяющий.)
Размерностью клетки с называется минимальная из размер-
ностей плоскостей 0, содержащих с; тот факт, что размерность
клетки с равна т, означает, что с содержит т + 1 линейно не-
зависимых точек и не содержит т-}-2 таких точек. Так как
клетка с должна содержать симплекс, натянутый на эти т 4- 1
точек, она должна иметь внутренние точки относительно плоско-
сти Ф. Обозначим множество этих внутренних точек через Int с,
а остальную часть клетки через Bd с.
Покажем, что существует гомеоморфизм клетки с на т-мер-
ный шар Вт, переводящий Bd с на Sm-1.
Присоединим к системе (уравнений и) неравенств, опреде-
ляющих клетку с, какую-нибудь систему уравнений, определяю-
щих плоскость д9. Некоторые из неравенств могут при этом
1 Вот некоторые другие частичные ответы: да — для полиэдров размер-
ности 3 [*Браун]; да — для односвязных кусочно-линейных многообразий
размерности 5= 5 без 2-кручення в четырехмерных целочисленных когомоло-
гиях [‘Сулливан, 1967, 1970]; да — для кусочно-линейных многообразий раз-
мерности 5 с фундаментальной группой Z и без 2-кручения в четырехмер-
ных целочисленных когомологиях [*Мацумото, 1969]; да — для кусочно-линей-
ных многообразий размерности 5s 5 с нулевой трехмерной группой когомологий
по модулю 2 [*Кёрби, Зибенманн, 1969, 1977]; нет — для кусочно-линейных
многообразий, гомеоморфных тору Тп, п^5 [*Сян, Шейнсон],
[‘Кёрби, Зибенманн, 1977]; нет — для некоторых односвязных кусочно-
линейных многообразий размерности 5= 22 [‘Морита]; существует симпли-
циальное разбиение Кп, п > 5, такое, что полиэдр |К"| гомеоморфен сфере
S", но Кп не гомеоморфен кусочно-линейной границе симплекса <5Дп+1 [‘Кэн-
нон]. — Прим, перев.
П*
328 Дополнение. Дж. Манкрс
стать лишними; пусть L,(x)^6i, i = 1, р,— минимальная
система неравенств, которая вместе с уравнениями для & за-
дает с. Заметим, что для каждого i = 1, ..., р гиперплоскость
Li(x)—bt пересекает SP по плоскости размерности пг—1—в
противном случае эта гиперплоскость содержала бы 9* и соот-
ветствующее неравенство можно было бы отбросить без измене-
ния множества с. Далее, множество Int с совпадает с множе-
ством А тех точек, для которых каждое из этих неравенств яв-
ляется строгим. Действительно, ясно, что А содержится в Int с.
С другой стороны, если точка хо принадлежит пересечению пло-
скости 9 с гиперплоскостью Lj(x) = bi, то в произвольной бли-
зости от Хо найдутся точки из 53, для которых Lj (х) < 6/, так
что точка Хо не принадлежит Int с.
Пусть с — точка из Int с и г — луч в плоскости 9, выходящий
из точки с. Пересечение луча г с клеткой с непусто, компактно
и выпукло, т. е. является замкнутым интервалом. Одной из его
концевых точек служит с, а другой обязательно будет точка
у е Bd с. Каждая точка х, принадлежащая открытому интер-
валу су, заведомо лежит в Int с, ибо Д(с) > Ь, и Li(y) bi, i =
= 1, ..., р, так что Л;(х)> bi. Следовательно, с равно джойну
с * Bd с.
Чтобы закончить доказательство, достаточно показать, что
край Bd с гомеоморфен сфере S'"-1. Не уменьшая общности, мы
можем считать, что 5s есть Rm, а с —начало координат. Отобра-
жение xi—>х/||х|| непрерывно переводит R"1 \ 0 на единичную
сферу; его ограничение на Bd с является, конечно, гомеоморфиз-
мом. 
Лемма 7.3. Пусть с есть m-мерная клетка. Тогда Bd с пред-
ставляет собой объединение конечного множества (пг — ^-мер-
ных клеток, каждая из которых является пересечением некото-
рой (пг — 1) -мерной плоскости с Bd с. Эти клетки однозначно
определяются по клетке с.
Доказательство. Пусть 9— m-мерная плоскость, содержа-
щая клетку с, и пусть с задается уравнениями для 9 в совокуп-
ности с минимальной системой неравенств Ц(х)^ b,, I —
= 1, Р-
Пусть di обозначает множество точек х е с, для которых
Li(x) = bi. Тогда dt — клетка и Bdc представляет собой объеди-
нение таких клеток. Далее, пересечение гиперплоскости
Д(х) = 6,- с плоскостью^1 является (пг—1)-мерной плоскостью,
пересечение которой с Bd с дает как раз di.
Докажем, что di — клетка размерности пг—1. Пусть S обо-
значает подмножество плоскости 9, для которого Lj(x)> bj
при всех J #= I. Ясно, что S выпукло и содержит Int с; в част-
, § 7. Клеточные разбиения и комбинаторная эквивалентность 329
ности, оно содержит некоторую точку х, для которой L((x)>
> bi. Оно также содержит такую точку у, что Li(y)<Z bi. Дей-
ствительно, в противном случае S целиком лежало бы в обла-
сти Li(x)^ bi, так что выбрасывание неравенства L,(x)^ bi из
множества определяющих клетку с неравенств не изменило бы
множества с. В силу своей выпуклости множество S будет со-
держать точку z, такую, что Lt(z)=bi. Таким образом, S(]0i
непусто; поскольку S открыто в 0, то S П открыто в 0i. Так
как S (] 0*t с. di, то di должно быть клеткой размерности пг — 1.
Единственность клеток di доказывается без труда. Граница
Bd с содержится в объединении р плоскостей размерности
m—1. Следовательно, пересечение любой другой (т—1)-мер-
ной плоскости с Bd с лежит в объединении конечного множе-
ства плоскостей размерности меньше m — 1 и потому имеет
размерность меньше пг — 1. Н
ОПРЕДЕЛЕНИЕ 7.4. Пусть с является m-мерной клеткой.
Каждая (т—1)-мерная клетка di, из которых состоит Bdc,
называется ((/и—V)-мерной) гранью клетки с; каждая
(т— 2)-мерная грань клетки di называется (т — 2) -мерной
гранью с и т. д. Для удобства пустое множество также счи-
тается гранью с, равно как и сама клетка с.
Лемма 7.5. Пусть с — клетка, задаваемая некоторой систе-
мой линейных уравнений и неравенств. Если одно из нера-
венств заменить на равенство, то получится система, опреде-
ляющая грань клетки с.
Доказательство. Проведем индукцию по числу m — размер-
ности клетки с. Если m — 0, то лемма тривиальна. Если пг > О,
то пусть 0— /n-мерная плоскость, содержащая клетку с. При-
соединим к системе, определяющей эту клетку, множество урав-
нений для плоскости 0\ ясно, что при этом мы ничего не поте-
ряем в общности. Пусть Li(x)^bi — неравенства, определяю-
щие клетку с, занумерованные так, что те из них, для которых
1 Р, образуют минимальное множество. Заменим теперь
330 Дополнение. Дж. Манкрс
некоторое неравенство L/(x)^bj на равенство. Если j р,
то это определит некоторую (т—1)-мерную грань d, клетки с,
как мы уже доказали выше.
В случае ] > р рассмотрим подмножество клетки с, удов-
летворяющее равенству L, (х) — Ьр Если гиперплоскость £Дх) =
— Ь] содержит она дает тривиальную грань — всю клетку с;
если она не пересекает с, она дает пустую грань. Рассмотрим
теперь промежуточный случай. Пусть е — пересечение клетки
с с указанной гиперплоскостью; это — клетка. Пересечение пло-
скости гР с указанной гиперплоскостью является (т—^-мер-
ной плоскостью, так что в произвольной близости от каждой
точки из е имеются точки у е Ф, для которых L, (у) < Ьр Сле-
довательно, е лежит на границе клетки с.
Так как множество е выпукло, оно должно лежать в неко-
торой (т—1)-мерной грани di. Действительно, допустим, что
это не так, и пусть q — наименьшее целое число, такое, что е
лежит в объединении di U ... U dq. Пусть х — точка из е, не ле-
жащая в d\ U ... U dq-i, и у — точка из е, не лежащая в d9.
Тогда
Lt (х) > bt для i < q и Lq (х) == bq,
Li(y)>bt для i<q и Lq(y)>bq.
Точка z — (х + у) /2 лежит в клетке е, однако £, (г) > bi для
всех i q, так что z не лежит в объединении di U ... U dq в
противоречие с предположением.
Система уравнений и неравенств, определяющая клетку с,
вместе с присоединенным к ней уравнением Li(x)=bi опреде-
ляет (т—1)-мерную клетку di, содержащую е. При этом
клетка е получается из этой системы заменой неравенства
Lj(x)"^bj на равенство. По индуктивному предположению е
является гранью клетки и, следовательно, гранью клетки с. 
ОПРЕДЕЛЕНИЕ 7.6. (Евклидовым) клеточным разбиением
К называется всякая совокупность клеток в R", такая, что:
(1)	каждая грань клетки из К. принадлежит К;
(2)	пересечение двух клеток из К служит гранью каждой
из них;
(3)	каждая точка из |Л| имеет окрестность, пересекающую-
ся лишь с конечным множеством клеток из К. (Здесь |/<| обо-
значает объединение клеток из К.)
Для того чтобы показать, что это определение не является
бессодержательным, заметим, что одиночная клетка с вместе
со всеми своими гранями образует евклидово клеточное раз-
биение. Это следует из предыдущей леммы (см. упр. (а) ниже).
Подразделением евклидова клеточного разбиения К. назы-
вается всякое клеточное разбиение К', такое, что | К.' | = | К. | и
§ 7. Клеточные разбиения и комбинаторная эквивалентность 331
каждая клетка из К'" содержится в некоторой клетке Из К.
Размерностью евклидова клеточного разбиения К называется
наибольшая из размерностей его клеток; р-мерныйостов евкли-
дова клеточного . разбиения К, обозначаемый через Кр, это
совокупность всех клеток из К. размерности не выше р. Легко
проверяется, что Кр является евклидовым подразбиением ев-
клидова клеточного разбиения К.
Упражнение (а). Показать, что, если К состоит из одиночной клетки
вместе со всеми ее гранями, то К — евклидово клеточное разбиение.
Упражнение (Ь). Показать, что симплекс о = о0  ' vm представ-
ляет собой m-мерную клетку н что для симплексов термин «грань» имеет
один и тот же смысл, понимать ли его согласно определению‘7.1 или согласно
определению 7.4. Показать, что симплициальное разбиение — частный случай
евклидова клеточного разбиения.
Лемма 7.7. Пусть евклидовы клеточные разбиения К\ и Х2
таковы, что |/С11 = 1$2'1. Тогда они обладают общим подразде-
лением.
Доказательство. Ясно, что пересечение двух клеток — снова
клетка. Пусть L — совокупность всех клеток вида Ci П с2, где
Ci — клетка из К\, агс2— клетка из /<2. Тогда L — евклидово
клеточное разбиение и |/fi | = |/<2| = |А|. 	.	•
'Упражнение (а). Показать, чтолюбая грань клетки ct П с2 имеет вйД
Ci П с2> где е, — грань с,-, и справедливо обратное утверждение;
Упражнение (Ь). Показать, что L — евклидово клеточное разбиение;
Лемма 7.8. Любое евклидово клеточное разбиение К... обла-
дает евклидовым симплициальным подразделением, .........
Доказательство. Проведем ийдукцию по размерности пг раз-
биения К.. Если пг = 0 или пг1, то уже само К Ъйляется сим-
плициальным разбиением. Рассмотрим общий случай. Пусть
L — симплициальное подразделение (пг—1)-мерного остова
евклидова клеточного разбиения К. Для данной /n-мерной клет-
кй'с из К пусть О1, .... Ор — симплексы из L, лежащие в Bd с.
Вйбёрем какую-нибудь внутреннюю точку с клетки с и при-
соединим' к'' L симплексы Оч •» с, ..., ор»с. (Напомним, что
обозначает»д&бй’н Ф й-в;) Если мы проделаем это для
каждой m-мерной клетки сеК, тов результате"ПбЛучим сим-
плициальное разбиение ../С,. служащее подразделением.. евкли-
дова клеточного разбиения К. V ••	. ___
Часто бывает удобно выбирать в качестве точки с.,центр
(тяжести) клетки с, с тем чтобы, подразделение	опре-
делено канонически,. & уа<е было симплициальным, то
эти’центрь! будут барицентрами симплексов; в этом"случае К'
называется барицентрическим подразделением симплициального
разбиения А.	. ... •
332 Дополнение. Дж. Манкре
Упражнение (а). Проверить, что К' — еймплициальное разбиение и
что оно является подразделением евклидова клеточного рабиения К..
Следствие 7.9. Если симплициальные разбиения К\ и К.2 та-
ковы, что |А1| = |/Сг|, то они имеют общее симплициальное
подразделение.
Теорема 7.10. Пусть К\ и Кя — два конечных симплициаль-
ных разбиения в R". Существуют симплициальные подразделе-
ния К\ и К 2 разбиений К\ и К2 соответственно, такие, что Ki U К
представляет собой симплициальное разбиение.
Доказательство. Прямолинейной триангуляцией простран-
ства R" называется всякое симплициальное разбиение L. такое,
что |£| = R”. Докажем, что некоторое подразделение симпли-
циального разбиения К\ является подразбиением некоторой
прямолинейной триангуляции L\ пространства R".
Пусть oi, Up — симплексы из К\. Выберем какую-ни-
будь прямолинейную триангуляцию ]\ пространства R", содер-
жащую Оь Один из возможных способов построения такой три-
ангуляции Ji состоит в том, что берется произвольная прямо-
линейная триангуляции J пространства R" и подыскивается не-
вырожденное аффинное преобразование hi пространства R", пе-
реводящее один из ее симплексов в симплекс сп; тогда h\(J)
будет требуемым разбиением. (Аффинное преобразование —
это композиция линейного преобразования и переноса.) Анало-
гично, пусть Jt — прямолинейная триангуляция пространства
R", содержащая сп. Обозначим через Li общее подразделение
комплексов Ji, ..., Jp (существующее по следствию 7.9). По-
лиэдр | Ki | является полиэдром некоторого подразбиения симп-
лициального разбиения L\, и это подразбиение будет подразде-
лением симплициального разбиения Ki.
Аналогично, пусть £2 — прямолинейная триангуляция про-
странства R", содержащая в качестве подразбиения некоторое
подразделение симплициального разбиения К2. Пусть £ — об-
щее подразделение прямолинейных триангуляций L\ и £2. Ясно,
что в качестве/С[ и/Сг можно взять подразбиения симплициаль-
ного разбиения L, полиэдрами которых служат |/Ci| и |/С2| со-
ответственно. 
*3адача 7.11. Обобщить эту теорему на случай, когда К\ и
/С2 не являются конечными. Для этого будет необходимо сде-
лать некоторые дополнительные предположения, чтобы избе-
жать случая, когда | К\ | есть множество [0,1]Х0 в R2, а
|Аг| — объединение множеств [О, 1]Х1/П Для n = 1, 2, ... .
ОПРЕДЕЛЕНИЕ 7.12. Доказательство леммы 7.8 обобщает-
ся на следующую ситуацию. Пусть Ki — подразбиение симпли-
§ 8. Погружения и вложения симплициальных разбиений 333
циального разбиения К и Ki — симплициальное подразделение
К\. Мы определим некоторым каноническим образом продол-
жение подразделения К\ до подразделения всего К, при кото-
ром не подразделяются симплексы, лежащие вне St(/G,К). Бу-
дем называть это продолжение стандартным продолжением
подразделения Ki до подразделения всего симплициального
разбиения К.
Любой симплекс из разумеется, принадлежит К', равно
как и любой симплекс из К, лежащий вне St (/и, К). Симплексы
же, внутренности которых лежат в А = St (Ki, К) \ |/(i|, под-
разделяются шаг за шагом следующим образом. Ни одна из
вершин К не лежит в А. Каждый одномерный симплекс а из
К, внутренность которого лежит в А, подразделяется на два
одномерных введением новой вершины — барицентра симплек-
са а. Предположим, что (пг—1)-мерные симплексы уже под-
разделены. Для любого m-мерного симплекса ст его граница
уже подразделена. Пусть ст—его барицентр. Тогда для каж-
дого симплекса s из подразделения границы Bdo включим s* ст
в число симплексов подразделения о. (Соглашение: джойн пу-
стого множества с ст равен ст.) После конечного числа шагов
получим требуемое подразделение симплициального разбие-
ния К. И
Упражнение (а). Проверить, что совокупность симплексов, получен-
ная таким образом, является симплициальным разбиением, полиэдром кото-
рого служит |/С|.
Задача 7.13. Пусть К —симплициальное разбиение й {Д,}—
некоторая локально-конечная совокупность подмножеств поли-
эдра |/С|. Пусть далее Ki, Кг, ... — последовательность сим-
плициальных подразделений К, такая, что Ki+i совпадает с Ki
вне Ai. Это означает, что любой симплекс из Kt, не пересекаю-
щий Ai, является также симплексом из Kt+\. Наконец, пусть
lim Kt обозначает совокупность симплексов о, таких, что о при-
i->oo
надлежит Kt для всех i, больших некоторого целого числа Л/о.
Показать, что эта совокупность будет подразделением К.
Упражнение (а). Пусть К— симплициальное разбиение н б(х)—по-
ложительная непрерывная функция на ]/С|. Доказать, что существует подраз-
деление К' симплициального разбиения К, такое, что диаметр 1 любого симп-
лекса о е К' меньше, чем минимум значений б(х) по всем хе а.
§ 8. ПОГРУЖЕНИЯ И ВЛОЖЕНИЯ СИМПЛИЦИАЛЬНЫХ РАЗБИЕНИЙ
В этом параграфе мы введем понятие Сг-отображения ft
К-*М, где К — симплициальное разбиение, а М — дифферен-
цируемое многообразие. Мы разовьем теорию таких отображе-
1 См. определение 9.2 ниже. — Прим, перев.
334 Дополнение. Дж. Манкре
ний, аналогичную теории для отображений одного многообра-
зия в другое. В частности, мы определим (п. 8.2) дифферен-
циал такого отображения и используем его для определения
(п. 8.3) понятий погружения, вложения и триангуляции (по-
следнее служит аналогом диффеоморфизма). Как и для много-
образий, мы определим (п. 8.5), что такое сильная С'-аппрок-
симация отображения f: К —► М, и докажем фундаментальную
теорему, утверждающую, что всякая достаточно хорошая силь-
ная С'-аппроксимация g отображения, которое является погру-
жением или вложением, сама является погружением или вло-
жением соответственно. (Эта теорема верна также и для триан-
гуляций, если дополнительно предположить, что g переводит
Bd |К| в BdM.)
Начиная с этого места, мы ограничиваемся симплициаль-
ными разбиениями и подразделениями, если явно не оговорено
противное. Целое число г(1 г оо) будет оставаться фикси-
рованным на протяжении всей оставшейся части главы.
ОПРЕДЕЛЕНИЕ 8.1. Пусть К — разбиение. Отображение
f: |К|-»Л1 называется дифференцируемым класса С' относи-
тельно К, если f|o имеет класс Сг для каждого симплекса
о е К. Для кратности мы обычно говорим в этом случае, что
f : К.-+ М имеет класс Сг. Отображение f называется невырож-
денным, если ранг ограничения /|о равен размерности симп-
лекса а для каждого а е К.
Мы хотим обобщить на эту ситуцию понятия погружения и
вложения. Казалось бы, в качестве аналога Сг-вложений мно-
гообразий можно взять невырожденные Сг-гомеоморфизмы раз-
биений. Но так сразу перестает казаться, стоит только взгля-
нуть на приведенный рисунок. Ключевое свойство вложений —
то, что любая достаточно хорошая С'-аппроксимация вложения
также является вложением, — здесь не выполняется, поскольку
в произвольной близости от отображения f находятся отобра-
жения вроде g. Этот пример показывает, что надо поискать бо-
лее подходящее обобщение.
§ 8. Погружения и вложения симплициальных разбиений 335>
ОПРЕДЕЛЕНИЕ 8.2. Пусть f:a->Rn есть Сг-отображение.
Для заданной точки b симплекса о определим отображение.
dfb'- о —> Rn равенством
dfb (х) = Df (Ь) • (х — Ь).
Здесь векторы х и b записываются, как обычно, в виде одно-
столбцовых матриц; матрица Df записана относительно неко-
торой ортонормированной системы координат, выбранной в пло-
скости, натянутой на симплекс о. Отображение dfb не зависит
от этого выбора координат в плоскости симплекса о.
Действительно, пусть R— некоторый луч в симплексе о, на-
чинающийся в точке Ь. Тогда /|/? есть С'-кривая в R", которую
можно считать параметризованной при помощи длины дуги,
вдоль R. Ясно, что dfb(x) — это просто касательный вектор к
этой кривой в точке f{b), умноженный на ||х— Ь\\. Следова-
тельно, вектор dfb(x) не зависит от выбора координат — он за-
висит лишь от метрики в плоскости симплекса о. Далее, из
сказанного выше следует, что dfb\R зависит только от и
не зависит от других значений функции f.
Если теперь f: К —» R" есть (/-отображение, то мы имеем
отображения dfb: о —► R", определенные для каждого симплекса
о е St (Ь,К). Эти отображения совпадают на пересечении лю-
бых двух симплексов из St (ft, К), так как либо один из них
является гранью другого, либо их пересечение представляет
собой объединение лучей, выходящих из точки Ь. Следова-
тельно, отображение
dfb: St (ft, R"
корректно определено и непрерывно. По аналогии со случаем
дифференцируемых многообразий мы называем его дифферен-
циалом отображения f.
ОПРЕДЕЛЕНИЕ 8.3. Пусть М есть Сг-подмногообразие
пространства R” и f: К -+ М имеет класс Сг. Отображение /
называется Сг-погружением, если для каждой точки ft отобра-
жение
dfb: St (ft, K)-+Rn
взаимно-однозначно; (/-погружение, являющееся гомеоморфиз-
мом, называется Сг-вложением, а если оно является гомеомор-
физмом на, то говорят о Сг-триангуляции многообразия М.
Требование взаимной однозначности dfb |о означает, что
матрица (/|сг) имеет в точке b ранг, равный размерности симп-
лекса о. Следовательно, погружение автоматически является
невырожденным отображением. Обратное, вообще говоря, не
верно, как показывает пример, приведенный в п. 8.1. Однако в.
336 Дополнение. Дж. Манкрс
случае, когда f представляет собой гомеоморфизм на, некое
обращение этого утверждения дать можно (см. теорему 8.4).
Упражнение (а). Пусть f: К-+М есть Сг-погружение разбиения К
в многообразие М, a g: M-+N есть С'-погружение многообразия М в много-
образие N. Показать, что композиция gf является С'-погружением разбиения
К в N.
Упражнение (Ь). Показать, что определения С'-погруження, вложе-
ния и триангуляции не зависят от выбора вложения многообразия М в ев-
клидово пространство.
Теорема 8.4. Всякое невырожденное Сг-отображение f: К-*
—> М, являющееся гомеоморфизмом полиэдра |К| на многооб-
разии М, представляет собой Сг-триангуляцию этого многооб-
разия.
Доказательство. Нам нужно доказать, что отображение
•dfb взаимно-однозначно на St (&,/<). Отсутствие взаимной од-
нозначности означает, что некоторые два луча Ri и R2, начи-
нающиеся в точке Ь, отображаются в один луч в пространстве
R", начинающийся в точке /(&). Таким образом, и
суть Сг-кривые на многообразии М, касающиеся друг друга в
точке f(b). Так как отображение f невырожденно, ограничение
dfb на каждый симплекс из St (Ь,К) является взаимно-одно-
значным. Следовательно, /?1 и R2 не принадлежат одному и
тому же симплексу из St(6, К).
Выберем какую-нибудь координатную систему (U,h) на М
в точке f(b). Пусть хп и уп— последовательности точек из R\ и
R2 соответственно, сходящиеся в точке Ь, и х', у'п, Ь' — их об-
разы при отображении hf. Пусть далее s — симплекс из St (b, К),
хю которому проходит луч Ri, и V — открытое множество
St(s, К). Множество hf(V) открыто в Rm; оно содержит точки
х'п, но не содержит точек у'п. Если п достаточно велико, то точки
Хп лежат в V, так что отрезок х'пу'п пересекает множество
7if(7\V) по крайней мере в одной точке zn^b', так как
угол между векторами х'п— Ь' и г/'стремится при п->оо
к нулю, а не к л.	_
Пусть zn обозначает точку в У\К переходящую в точку г'
при отображении hf. Переходя к подпоследовательности и про-
изводя перенумерацию, мы можем считать, что точки zn лежат
в одном и том Же симплексе комплекса К и что единичные
векторы (zn — b) flzn — &|1 сходятся, скажем, к вектору и.
Пусть /?з — луч, вдоль которого направлен вектор и. Лучи R\
и R3 лежат в одном и том же замкнутом симплексе из St(b, К),
а в то же время, как мы сейчас покажем, кривые и
§ 8. Погружения и вложения симплициальных разбиений 337*
й/|/?з касаются друг друга в точке Ь'; это противоречит пред-
положению, что f — невырожденное отображение.
Докажем утверждение о касании. Прежде всего, векторы
(х' — &')/|х'п — Ь' || стремятся к единичному вектору, касатель-
ному к кривой hf(Ri) в точке Ь'. Далее,
i|z„_6i| -i- nzrt-H
Так как угол между векторами х' — Ь' и г' — Ь' стремится к.
нулю, то левая часть этого равенства стремится к вектору,
касательному к кривой hf\Ri в точке Ь'. Правая же часть
стремится к вектору D(hf)(b)-u, который касается кривой
hf |/?3 в точке Ь'. Я
(Приведенный рисунок, к сожалению, вводит в небольшое за-
блуждение, поскольку на нем точка zn лежит на луче /?3, чего.
• мы не можем гарантировать. Доказательство было бы в этом
случае значительно проще.)
Упражнение (а). Показать, что в предположениях теоремы 8.4 раз-
биение К является п-мерным комбинаторным многообразием. Это означает, что.
для каждого й-мерного симплекса s е К линк Lk s = St s \ St s этого симп-
лекса представляет собой комбинаторную сферу размерности п — k—1. т. е.
разбиение Lk s имеет подразделение, изоморфное некоторому подразделению-
границы (п — k)-мерного симплекса а.
Указание. Доказать это сначала для случая, когда s =_t>, где v — вер-
шина разбиения К. Найти линейный изоморфизм h звезды St v с некоторым
разбиением L в пространстве R", такой, что й(п)= 5 и | L |	<т. Найти под-
разделение <т' симплекса о, такое, что включение i: о' -* L линейно. Тогда,
радиальная проекция из точки 5 будет линейным 1 гомеоморфизмом, перево-
дящим Bd о' на Bd|L|.
1 Стандартная ошибка. Радиальное проектирование не является линейным
отображением. Здесь нужно воспользоваться конструкцией псевдоцентральнога
проектирования, см. [*Рурк, Сандерсон]. — Прим, перев.
338 Дополнение. Дж. Манкрс
ОПРЕДЕЛЕНИЕ 8.5. Пусть /:/(—>• R" есть С'-отображение
и 6 — положительная непрерывная функция на К. По аналогии
-с определением 3.5 будем говорить, что отображение g: |/<| —>
—♦ R" служит 8-аппроксимацией отображения f, если
(1)	для некоторого подразделения Д' разбиения К отобра-
жение g: К.’ —► Rn является ^-отображением;
(2)	||f(fe) — g(fe)|| < 8(b) для всех b е | К |;
(3)	lidfs(x)—б/^б(х)||^ 6(fe)||x— fell для всех b е | К | и всех
jc е St (fe, К').
Такие отображения g называются сильными С1 -аппроксима-
циями отображения f.
Заметим, что это определение не зависит от выбора коорди-
натных систем, оно зависит только от метрик ||х — «/|| в евкли-
довом пространстве, содержащем К, и в R". Заметим также,
что, если разбиение К конечно, то функцию б можно, ничего не
меняя, выбрать константой, и мы будем всегда предполагать
в этом случае, что так и делается.
Как и в теореме 3.6, условие (3) выполняется, если матрицы
Якоби отображений fug достаточно близки друг к другу, ибо
II dfb (х) - dgb (х) Н/Н х - Ь || <	РI D (Л о) (L) - D (g | о) (fe) |,
где р — размерность симплекса о, содержащего х.
Пусть f: К —* R" и g: Д’ —> R" суть Сг-отображения, и пусть
V — открытое подмножество полиэдра |К[. Говорят, что g яв-
ляется 8-аппроксимацией отображения f на U, если условия (2)
и (3) выполнены для всех точек 6 е U. При условии, что ото-
бражения fug невырожденны на U, говорят, что g является
угловой а-аппроксимацией для f на U, если угол между векто-
рами dfb(x) и dgb(x) меньше а для всех точек feet/ и всех
точек х #= fe, лежащих в St(fe, Д').
Лемма 8.6. Пусть f: К —> R" — невырожденное Сг-отображе-
ние w а > 0. Для любой точки fe е|/<| существует окрестность
точки fe, на которой отображение dfb служит угловой а-аппрок-
симацией для f.
Доказательство. Достаточно доказать это утверждение для
случая, когда К — одиночный симплекс о. Пусть хе о и и —
произвольный единичный вектор в плоскости симплекса о. Нам
нужно, чтобы угол между векторами Df(x)-u и D(dfb) (х) -и
был меньше а. Но dfb (х) = Df(b) • (х — fe), так что D (dfb) (х) =
— Dj(b). Далее, угол между векторами Df(x)-u и Df(b)-u не-
прерывно зависит от х и и и его значение равно нулю, когда
jc = fe. Так как область изменения вектора и — компактное
§ 8. Погружения и вложения симплициальных разбиений 339
множество, существует окрестность U точки Ь, такая, что этот
угол меньше а, когда х е U, для любого и. 
Лемма 8.7. Пусть f:K-+R.n— невырожденное Сг-отображе-
ние, причем разбиение К. конечно. Для любого заданного а > О
найдется такое 6 > 0, что всякое невырожденное Сг-отображе-
ние g-. К' —* R", являющееся 8-аппроксимацией отображения f
на U, является угловой а-аппроксимацией этого отображения
на U (при любом U).
Доказательство. Пусть е = min || dfb (х) ||/|[х — b ||, где мини-
мум берется по всем &е| К | и всем хе St(6, К), х =/= Ь. Так
как f невырожденно, то е > 0. Положим 6 = ае/л, и пусть
g-	— невырожденное (/-отображение, служащее 6-ап-
проксимацией для f на U. Пусть о е К' и точки Ь, х принад-
лежат симплексу а, причем b^U. Угол 0 между векторами
dfb(x) и dgb(x) тот же самый, что и между векторами v —
— D (f \о) (b)  и и w = D(g\o)(b) • и, где и — (х —• Ь) /\\х — & 11-
Угол между векторами v и w не превосходит || v — w || л/|| v ||,
что меньше 6л/е = а. (Действительно, если угол 0 острый, то
|| v — w ||	|| v || sin 0	|| v || 20/л, если же не острый, то || v — w || >
> IIvII>IIо||0/л.) 
Теорема 8.8. Пусть разбиение К конечно и f:K-+Rn— по-
гружение или вложение класса Сг. Существует S > 0, такое,
что любая 8-аппроксимация отображения f является соответ-
ственно погружением или вложением.
Доказательство. Дадим сначала два предварительных опре-
деления и докажем один частный случай теоремы.
(1)	Пусть tri и аг — два симплекса, таких, что симплекс
о = Gj П о2 служит собственной гранью каждого из них. Угол
от Gi до о2 определяется следующим образом. Пусть о—бари-
центр симплекса о. Рассмотрим угол 0 (у, z) между прямоли-
340 Дополнение. Дж. Манкре
нейными отрезками г/ог и zo, где у принадлежит грани симплек-
са Qi, противоположной a, a z—произвольная точка симплекса
02, отличная от сг. Этот угол ненулевой. Минимум таких углов
0 и называется углом от oi до <И-
Легко видеть, что угол 0 от он до <и отличен от нуля. Дей-
ствительно, если мы продолжим луч, идущий из точки о в
точку z, то он пересечет множество <H\St(cr). Поэтому мы по-
лучим тот же самый минимум, если z будет изменяться лишь
на множестве <т2 \ St (сг); поскольку, таким образом, у и z про-
бегают непересекающиеся компактные множества, угол 0 нену-
левой.
Заметим, что угол 0 от си до аг представляет собой непре-
рывную функцию от вершин симплексов си и сп. Если мы не-
прерывно изменяем эти вершины (не допуская, чтобы симплек-
сы вырождались), то угол 0 также будет изменяться непрерыв-
но (см. упр. (а) ниже).
(2)	Пусть а — собственная (т. е. нетривиальная) грань симп-
лекса <Т1. Определим проекцию щ на о следующим образом.
Прежде всего на самой грани а это —тождественное отображе-
ние. Далее, пусть р е оДо, и пусть si — грань симплекса он,
противоположная о, и сг— барицентр симплекса а. Существуют
однозначно определенные точки у е Si и х е о, такие, что пря-
молинейные отрезки уд и рх параллельны. Проекция си на а
определяется как отображение, переводящее точку р в точку х.
Эта проекция является непрерывным отображением симп-
лекса <и на симплекс а; далее, проекция естественна в том
смысле, что она инвариантна относительно линейных изомор-
физмов симплекса <и на другие симплексы (см. упр. (Ь)).
Для нас будет полезно такое свойство проекции. Пусть симп-
лекс о = си П °2 служит собственной гранью каждого из симп-
лексов <и и аг, и пусть реаДо и <7еог\о. Если проекция
симплекса си на а переводит р в х, то угол между прямолиней-
ными отрезками рх и xq не меньше угла от си до си. Чтобы
убедиться в этом, надо просто взять в симплексе си любую точ-
§ 8. Погружения и вложения симплициальных разбиений 341
ку z, такую, что отрезок oz параллелен х</, и применить опре-
деление угла от ai до 02.
(3)	Теперь докажем один весьма частный случай нашей
теоремы. Пусть L — разбиение, состоящее из двух прямолиней-
ных отрезков 61 и е2 с общей вершиной v, и F: L —► R"— взаим-
но-однозначное линейное отображение. Предположим, что угол
между образами при отображении Fэтих отрезков равен а > 0.
Если G: L' —> R” — невырожденное С'-отображение, являющееся
угловой а/2-аппроксимацией для F, то G взаимно-одно-
значно.
Действительно, пусть 9?— двумерная плоскость, содержащая
Е(Т) (при а л эта плоскость определена однозначно), и пусть
S — прямая линия в плоскости перпендикулярная к бис-
сектрисе угла а (см. рисунок). По условию, никакой вектор
dG&(x) не может быть перпендикулярен прямой 2? и, следова-
тельно, имеет ненулевую проекцию на S. Отсюда вытекает, что,
если мы обозначим через л ортогональную проекцию простран-
ства R" на прямую S, то отображение лй взаимно-однозначно.
Следовательно, и G взаимно-однозначно.
В этом частном случае отражена суть всего доказательства.
Доказательство теоремы. (4) Пусть f — погруже-
ние. Прежде всего выберем 6 настолько малым, чтобы любая
S-аппроксимация отображения f была невырожденным отобра-
жением. Это легко сделать.
Наложим второе условие на 6. Для каждой пары симплек-
сов ai и о2 комплекса К, пересечение о = Oi f| о2 которых яв-
ляется собственной гранью каждого из них, рассмотрим ото-
бражение
dfb: o1U<t2^R'1,
где Ь — произвольная точка симплекса о. Это взаимно-одно-
значное линейное отображение; следовательно, определен не-
нулевой угол от образа симплекса оц до образа симплекса о2.
Этот угол изменяется непрерывно с изменением точки Ь, по-
этому найдется минимальный такой угол a(oi,o2), когда b про-
бегает о. Обозначим через а минимум a(oi,o2) по всем парам
ai, о2 указанного вида. Выберем теперь 6 настолько малым,
чтобы любая 6-аппроксимация g отображения f была угловой
a/6-аппроксимацией для f (лемма 8.7).
342 Дополнение. Дж. Манкре
Докажем, что любая б-аппроксимация g: К' —* R" отображе-
ния / будет погружением.
Пусть	Нам нужно доказать, что отображение
dgb: St (b, K')-+Rn
взаимно-однозначно. Допустим, что dgt>(p) = dgb(q) для неко-
торых точек р и q, принадлежащих St(t>, К'). Тогда отображе-
ние dgb переводит два луча, начинающихся в точке b и прохо-
дящих через точки р и q соответственно, в один и тот же луч
в R". Следовательно, точки р, q на этих лучах, такие, что
dgb(p) = dgb(q), можно считать сколь угодно близкими к
точке Ь.
Далее, существует окрестность U точки Ь, лежащая в
St (б, К'), такая, что dfb(x) является угловой а/6-аппроксима-
цией отображения f(x) для х е U, a dgb(x) — угловой ot/6-ап-
проксимацией отображения g(x) для х е U (лемма 8.6).. Тогда
на множестве U отображение dgb(x) будет угловой «/2-аппрок-
симацией для dfb(x).
Предположим сначала, что точки р и q лежат в одном и
том же симплексе о е К. Выбирая их достаточно близкими к
точке Ь, мы можем тогда добиться того, чтобы прямолинейный
отрезок pq лежал в U. Пусть х — средняя точка отрезка pq,
и пусть 61 = рх, 62 = xq и L = 6i U 62. Так как отображение
dfb линейно на разбиении L, то отрезки dfb(e\) и dfb(e2) обра-
зуют угол, равный л. Далее, dgb является угловой «/2-аппрок-
симацией для dfb на L. Поскольку а л, то применение рас-
смотренного выше частного случая нашей теоремы показывает,
что dgb взаимно-однозначно на L в противоречие с предположе-
нием.
Предположим теперь, что р и q суть внутренние точки раз-
личных симплексов Oi и а2 из К, пересечение Oi П ст2 — о кото-
рых является собственной гранью каждого из них. Пусть х —
образ точки р при проекции симплекса сп на о. Возьмем точки
р и q настолько близкими к точке Ь, чтобы прямолинейный от-
резок ei, соединяющий р и х, и прямолинейный отрезок е2, сое-
диняющий х и q, лежали в U. Ясно, что отображение dfb ли-
нейно на разбиении L = ei (J е2 и dgb служит угловой а/2-ап-
проксимацией для dfb на L.
Мы утверждаем, что угол между прямолинейными отрез-
ками dfb(ei) и dfb(e2) не меньше а; тогда из разобранного част-
ного случая следует, что dgb взаимно-однозначно на L в про-
тиворечие с предположением, что dgb(p) — dgb(q). Докажем
утверждение об угле. Отображение dfb является линейным изо-
морфизмом на Oi, а так как проекция естественна относительно
линейных изоморфизмов, то проекция симплекса dfb(oi) на
симплекс dfb(o) должна переводить dfb(p) в dfb(x). Это озна-
§ 8. Погружения и вложения синплициальных разбиений 343
чает, как замечено выше в (2), что угол между отрезками
dfb(e\) и dfb(e2) не меньше, чем угол от dfb(oi) до dfb(o2), ко-
торый не меньше а.
(5) Пусть теперь f — погружение. Выберем б, как выше.
Для любой заданной точки	существует окрестность V
точки Ь, такая, что всякая б-аппроксимация g: К' -* Rrt отобра-
жения f взаимно-однозначна на V. Это доказывается следую-
щим образом.
Сначала выберем е-окрестность U точки Ь, на которой dfb
служит угловой а/3-аппроксимацией отображения f. Затем под-
берем окрестность V точки Ь, лежащую в U, так, чтобы для
любой пары симплексов Oi, о разбиения К, содержащих точку
b и таких, что о является собственной гранью щ, проекция Oi
на о переводила V П Oi в U.
Поскольку g служит угловой а/6-аппроксимацией для f, оно
является угловой а/2-аппроксимацией для dfb на U. Отсюда
следует, что g взаимно-однозначно на V. Действительно, пред-
положим, что g(p) = g(q), где р, q^V. Если точки р и q ле-
жат в одном и том же симплексе о разбиения К, то рассмотрим
среднюю точку х отрезка pq и положим Ci = рх, е2 = qx. Так
как U есть е-окрестность, то множество U П о выпукло, так
что L = Ci U е2 лежит в U. Далее, отрезки dfb (ei) и dfb(e2) об-
разуют угол, равный л. Поскольку а л, то g взаимно-одно-
значно на L, согласно рассмотренному частному случаю тео-
ремы, что противоречит нашему предположению.
В случае когда точки р и q не лежат в одном и том же
симплексе разбиения К, рассуждения аналогичны. Пусть р е
е Int Oi и q е Int <з2, где симплекс о = щ П а2 является соб-
ственной гранью каждого из симплексов Oi и а2, и пусть х —
образ точки р при проекции Oi на о. Ясно, что х е U. Положим
61 = рх и е2 — qx. Тогда L =. в\ U е2 лежит в U и отрезки
dfb(eP) и dfb(e2) образуют угол не меньше а. Применение част-
ного случая теоремы показывает, что g взаимно-однозначно на
L вопреки предположению.
(6) Наконец, пусть f — вложение. Выберем б, как в (4).
Применяя (5), подберем конечное число компактных множеств
С,, внутренности которых покрывают |К| и на каждом из ко-
торых любая б-аппроксимация g отображения f взаимно-одно-
значна. Согласно упр. (а) п. 3.10, существует такое бо > 0, что,
если g: |К|—Rrt является С°-бо-аппроксимацией отображения
fag взаимно-однозначно на каждом С/, то g — гомеоморфизм.
Следовательно, если g служит одновременно и бо- и б-аппрок-
симацией отображения f, то оно есть вложение. И
Упражнение (а). Пусть отображение f: X X ¥ -+ R непрерывно и А —
компактное подмножество пространства У. Положим t л (х) = min f (х, у).
у^А
344 Дополнение. Дж. Манкрс
Доказать, что отображение (л: X -> R непрерывно. Вывести отсюда, что угол 0
от симплекса <Г1 до симплекса Oj представляет собой непрерывную функцию
от вершин этих симплексов.
Упражнение (Ь). Дать формулу для проекции симплекса щ на а. При
помощи этой формулы показать, что эта проекция непрерывна и естественна
в указанном выше смысле.
Упражнение (с). Обобщить теорему на случай бесконечного разбие-
ния К; в этом случае б будет уже, конечно, положительной непрерывной функ-
цией на |К|.
Упражнение (d). Показать, что для заданной С'-триангуляции f:
К-+М любая ее достаточно хорошая аппроксимация g также будет триан-
гуляцией при условии, что она переводит Bd|K| в Bd М.
§ 9. СЕКУЩЕЕ ОТОБРАЖЕНИЕ, ИНДУЦИРОВАННОЕ ОТОБРАЖЕНИЕМ f
Пусть заданы разбиение К, его конечное подразбиение
и Сг-отображение f: К-* R". Мы хотели бы аппроксимировать
f (^-отображением g некоторого подразделения К' разбиения К
в R", л и ней н ы м на каждом симплексе соответствующего
подразделения Ki разбиения Ki-
В качестве первого шага мы покажем, что, если разбиение
Ki подразделено достаточно аккуратно, то индуцированное ото-
бражение f, секущее отображение g, которое автоматически
является линейным, будет сильной С'-аппроксимацией для f
на (п. 9.1—9.6). Второй шаг будет состоять в доказатель-
стве того, что g можно продолжить на весь полиэдр |А| так,
чтобы оно осталось сильной С’-аппроксимацией для / (п. 9.7—
9.8).
ОПРЕДЕЛЕНИЕ 9.1. Пусть f:K—* R" есть Сг-отображение
и пусть s — произвольный симплекс, содержащийся в некотором
симплексе разбиения К. Линейное отображение Ls:s->-R", со-
впадающее с f на вершинах симплекса s, называется секущим
отображением, индуцированным отображением f.
Аналогично, если К' — подразделение разбиения К, то секу-
щее отображение LK'i К' -> R", индуцированное отображением
f, — это линейное отображение, совпадающее с f на вершинах
К'. Заметим, что, если / переводит какой-нибудь симплекс в
Н" или в R"-1, то и секущее отображение, индуцированное f,
переводит этот симплекс туда же.
ОПРЕДЕЛЕНИЕ 9.2. Радиусом г (о) симплекса о назы-
вается минимальное расстояние от его барицентра б до Bdo.
Диаметром d(o) симплекса о называется длина его наиболь-
шего ребра. Толщиной t(o) симплекса о называется отношение
r(a)/d(o).
$ 9. Секущее отображение, индуцированное отображением f 345
Лемма 9.3. Пусть	есть Сг-отображение и б, to —
положительные числа. Существует в > О, такое, что для лю-
бого, лежащего в о симплекса s, диаметр которого меньше в,
а толщина больше t0, секущее отображение Ls будет 8-аппрок-
симацией ограничения f|s.
Доказательство. Для заданной точки b е о положим
Fb(x)= f(b) + Df(b) • (x — b) и h(x,b) = f(x)—Fb(x). Тогда
ПЛ (x, ft) ||/||x — ft||->0 равномерно при ||x —ft||->0 (см. зада-
чу 1.10 (2)). Далее, имеет место равенство Df(x)—DFb(x)=*
= Df(x) — Df(b). Отсюда следует, что существует такое не за-
висящее от ft положительное число ei, что Fb является 6/2-ап-
проксимацией отображения f на ei-окрестности точки ft. Потре-
буем, чтобы е было меньше, чем еп тогда ||й(х, ft) || < 6/2 для
|| х — ft||<e. Потребуем также, чтобы для ||х— ft|| < е выпол-
нялось неравенство ||й(х, ft) ||/||х— ft||< 6fo.
Докажем, что, если толщина симплекса $ не меньше t0, а
диаметр меньше е, то отображение Ls будет 6/2-аппроксима-
цией ограничения где ft — барицентр симплекса s. Отсюда
будет следовать утверждение леммы, так как Fb | s является
6/2-аппроксимацией для f|s.
(1) Пр едварительный результат. Если L и F —
линейные отображения симплекса s в R" и ||L(x) — F(x) || < р
для всех х, то
|| DL (х)-и- DF (х) • и || < 2p/r (s)
для всех единичных векторов и в плоскости симплекса о.
Действительно, пусть ft — барицентр симплекса $. Поскольку
отображение L линейно, то L(x) = L(b) 4- DL(b) • (х — ft) и
DL(x) = DL(ft). Аналогичные соотношения справедливы для
DF. Поэтому
[DL (х) - DF (х)] • u = [DL (ft) - DF (ft)] • (х - ft)/|| х - ft ||
для некоторой точки хе Bd s. Выражение справа равно
{[L (х) - L (ft)] - [F (х) - F (ft)]}/|| (х - ft) ||,
так что
||DL (х) -u-DF(х) • и|| < 2р/|| х - ft||< 2p/r ($).
(2) Доказательство леммы. Пусть ио, .... va —
вершины симплекса s и x = £aiv/-—его общая точка. Так как
Ls и Fb — линейные отображения, то
Ls (х) = X aA (vt) = £ a(f (uz)
и
Fb W = X “/ft'» (уД
12 Дж. Милнор, Дж. Сташеф
346 Дополнение. Дж. Манкрс
откуда
II Fs (х) — Fb (х) II = II £ ath (х, vt) II < max || h (х, vt) ||.
Но ||/г (х, у) || < 6/2 при ||х — у||< е, следовательно, ||Ls(x) —
— Fs(x)||< 6/2, что есть половина доказываемого утверждения
о 6/2-аппроксимации.
Далее, ||Л(х,1/)||/||х —у|| < 6/0/4 при ||х — у|| < в, так что
II Ls (х) - Fb (х) || < || х - Ь || 6/0/4 < d ($) 6/о/4 < 6г ($)/4,
ибо to r(s)/d(s). На основании предварительного результата
(1) мы заключаем, что Ls является 6/2-аппроксимацией огра-
ничения Fb|s. 
•Упражнение (а). Привести пример, показывающий, что эта лемма
неверна без предположения о том, что толщина симплекса s отграничена от
нуля *.
Лемма 9.4. Для всякого конечного разбиения К существует
to > 0, такое, что К. имеет сколь угодно мелкое подразделение,
минимальная толщина симплексов которого не меньше t0.
Доказательство. Прежде всего заметим, что, если теорема
верна для разбиения К, то она верна для любого разбиения,
изоморфного К. Действительно, пусть	— линейный
изоморфизм. Для каждого симплекса из К. отношение ||/(х) —
— f(#)H/Hx— #11 ограничено сверху и отграничено снизу от
нуля. Выберем числа аир таким образом, что
О < а < ||f (х) - f (#)||/||х-у|| < р,
каковы бы ни были точки х и у, принадлежащие одному и
тому же симплексу разбиения К. Для заданного в > О пусть
К' — подразделение К., симплексы которого имеют диаметр,
меньший в, и толщину, большую to. Тогда симплексы соответ-
ствующего подразделения разбиения К\ имеют диаметр, мень-
ший Ре, и толщину, большую а/о/Р, как читатель легко может
проверить; отсюда вытекает справедливость сделанного утверж-
дения.
Далее, разбиение К изоморфно подразбиению некоторого
«стандартного симплекса» — т. е. симплекса, натянутого на
вершины е0, Bi, ..., ер, где во — начало координат, а в, — век-
торы естественного базиса в пространстве Rp. Следовательно,
нашу лемму достаточно доказать для случая, когда К. — стан-
дартный симплекс.
1 Таким примером может служить хорошо известный «сапог Шварца».—
Прим, перев.
§ 9. Секущее отображение, индуцированное отображением f 347
Пусть J — евклидово клеточное разбиение с |7|= Rp, клетки
которого строятся следующим образом. Для произвольного на-
бора целых чисел io, ii, ..., ip рассмотрим куб
C(i1....ip) = {x	+ 1 для i—l, .... p}
в Rp и пересечем его с областью
/?(/о) = {х|/о<х‘+ ... +хр^/о+ 1}.
Получающееся множество будет клеткой. (На рисунке показан
куб С(0, 0, 0) и его пересечения с областями /?(0), /?(1) и
/?(2),) Евклидово клеточное разбиение I состоит из всех таких
клеток и их граней. Оно имеет два следующих важных для нас
свойства:
(1) каждая клетка евклидова разбиения J получается сдви-
гом в Rp одной из клеток, содержащихся в единичном кубе
С(0, 0, ..., 0).
(2) Для любого положительного целого числа tn симплекс
Sm, натянутый на вершины 0, mei, /пе2, ..., тгр, служит поли-
эдром некоторого подразбиения евклидова клеточного разбие-
ния J.
Теперь превратим клеточное разбиение J в симплициальное
разбиение L, подразделяя его шаг за шагом как описано в
лемме 7.8; на каждом шаге в качестве внутренней точки клет-
ки с, определяющей подразделение, мы используем центр 3
этой клетки. Отсюда вытекает, что условия (1) и (2) выпол-
нены также и для разбиения L, и, значит, его симплексы имеют
минимальную толщину to > 0 и максимальный диаметр d.
Преобразование подобия в пространстве Rp, переводящее
точку х в точку х/т, не изменяет толщины симплексов и уве-
личивает их диаметр в \/т раз. Следовательно, образ симп-
лекса Sm при этом преобразовании будет давать прямолиней-
ную триангуляцию симплекса Si, симплексы которой имеют
толщину не меньше to и диаметр не больше d/m. Поскольку т
произвольно, лемма доказана. В
12*
348 Дополнение. Дж. Манкрс
’Упражнение (а). Пусть К состоит из двумерного симплекса и его
граней, Л1 — барицентрическое подразделение К, Кг — барицентрическое под-
разделение Ki и т. д. Показать, что максимальная толщина симплексов из Кп
стремится к нулю при п оо.
*Нерешенная задача 9.5. Обобщить предыдущую лемму на
случай неконечного разбиения К. Нужно ожидать, что to и е
будут в этом случае непрерывными функциями на |К|, однако
не вполне ясно даже, как сформулировать само утверждение.
Теорема 9.6. Пусть разбиение К конечно и f:K-+Rn есть
Сг-отображение. Для любого заданного S > 0 существует под-
разделение К' разбиения К, такое, что секущее отображение
LK>: К' ->R", индуцированное f, является 8-аппроксимацией
для f.
Более общим образом, верна следующая теорема, немедлен-
но вытекающая из приводимой вслед за ней леммы.
Теорема 9.7. Пусть f: K-+Rn есть Сг-отображение и Kt—
конечное подразбиение разбиения К. Для любого заданного
6 > 0 существует 8-аппроксимация g: К' -♦ R" отображения f,
такая, что:
(1)	на g совпадает с секущим отображением, индуциро-
ванным /;
(2)	вне St(Kb К) g равно f-,
(3)	вне St (Кх, К) К' совпадает с К.
Здесь Кх — подразделение разбиения Кх, индуцированное под-
разделением К', и условие (3) означает, что любой симплекс
из К, лежащий вне St (К), К), входит в К'.
Лемма 9.8. Пусть f: К R" есть Сг-отображение и Кх —
конечное подразбиение комплекса К. Для любого заданного
е > 0 существует 8 > 0, такое, что всякая 8-аппроксимация
g: Kf->-Rnотображения f\Kx может быть продолжена до г-ап-
проксимации h:K'-+Rn отображения f, где К' — стандартное
продолжение подразделения К'х (см. определение 7.12) и h сов-
падает с f вне St (/Ci, К).
Доказательство. Подразделение К' разбиения К уже зада-
но, и отображение h уже определено на |Ki| и на ]/С] \St(/Ci,
К). Остается только продолжить h на каждый симплекс под-
разделения К', внутренность которого лежит в множестве
St(Ki, К) \ |/Ci|, и посмотреть, будет ли полученное продол-
жение хорошей аппроксимацией. Мы произведем это продол-
жение шаг за шагом, начиная с одномерных симплексов, затем
переходя к двумерным, и т. д. По этой причине достаточно
доказать нашу лемму для того частного случая, когда разбие-
ние представляет собой одиночный симплекс.
§ 9. Секущее отображение, индуцированное отображением f 349
Частный случай леммы. Пусть L — комплекс, со-
стоящий из симплекса а и его граней, и пусть L\ = Bd а. Для
любого заданного в > О существует такое б > О, что всякую
б-аппроксимацию g: L\ -> R'! можно продолжить до 8-аппрокси-
мации h: L'—>Rn, где L' — стандартное продолжение подраз-
деления L'i.
Доказательство этого частного случая. Очевидное продолже-
ние отображения g получится, если каждый прямолинейный
отрезок ха линейно отобразить на прямолинейный отрезок
g(x)f(5), где а — барицентр симплекса а. Однако здесь есть
та трудность, что построенное отображение не будет, вообще
говоря, дифференцируемо в точке а. Мы видоизменим это по-
строение, «сводя» g(Bdo) в точку [(a) при помощи гладкой
функции а(0, а не линейной.
Пусть а(0, как обычно, — монотонная С°°-функция, равная
О для ’/з t и 1 для t 2/3. Всякая точка х е о представима
в виде х — ty + (1 — t)cr; где у е Bdo и 0 < t < 1; при этом чис-
ло t и точка у однозначно определены для х =/= а. Если Ц—
любое подразделение границы Bd о и L' — стандартное продол-
жение, то у и t являются С°°-функциями от х на каждом симп-
лексе разбиения L', исключая точку х — а.
Для произвольного Сг-отображения g: L[ -> Rn положим
h (х) = f (х) + а (/ (х)) [g (у (х) — f (у (х))].
Так как а(<(х))=0 для точек х из некоторой окрестности ба-
рицентра 5, то отображение h имеет класс Сг на каждом симп-
лексе разбиения L'. Покажем, что /г автоматически будет хоро-
шей аппроксимацией для f, если g было хорошей аппроксима-
цией для f[Bd а.
Во-первых, заметим, что	Цх) ll^llg(x)—/(х)||, так
что /г будет хорошей С°-аппроксимацией для f, если таковой
было g.
350 Дополнение. Дж. Манкре
Во-вторых, вычислим производную d{h — ft/dx для t '/з.
Она равна
где g и f, как обычно, записываются в виде одностолбцовых
матриц. Поскольку значения a.'(t)-dt/dx и a.(t)-dy/dx ограни-
чены независимо от выбора подразделения L\ и отображения g,
производная d(h — f)/дх будет сколь угодно мала, если только
|g(f/) — №)| и \д8/дУ — ч/ду\ достаточно малы. 
Упражнение (а). Вычислить, насколько малыми должны быть
И-f(t/)| и \dg/dy — df/dy\ для того, чтобы |3(ft —f)/dx| было меньше,
.
Упражнение (Ь). Завершить доказательство леммы, используя дока-
занный выше результат для частного случая.
Упражнение (с). Показать, что справедливо такое дополнение к лем-
ме 9.8. Предположим, что, если f переводит какой-нибудь симплекс О| е К,
в плоскость Ф, то и g тоже переводит этот симплекс в Ф. Доказать, что, если
f переводит какой-либо симплекс <т е К в Ф, то и ft переводит его в Ф.
Упражнение (d). Пусть Ф\, ..., Фл — некоторое конечное множество
плоскостей в Rn. Доказать, что к теореме 9.7 можно сделать следующее добав-
ление: каждый симплекс а е К, который отображением f переводится в одну
из плоскостей фц переводится в эту плоскость и отображением g.
§ 10. ПРИГОНКА ВЛОЖЕННЫХ РАЗБИЕНИЙ
Предположим, что мы имеем Сг-вложения двух разбиений
в дифференцируемое многообразие М, образы которых пере-
крываются. Мы хотим доказать, что, слегка изменив эти вло-
жения, можно «подогнать», «приладить» их образы друг к другу
в том смысле, что после подходящего подразделения они будут
пересекаться по некоторому подразбиению.
Если М — евклидово пространство, это не слишком трудно;
соответствующие построения проводятся в п. 10.2. Основная
идея состоит в том, чтобы (используя результаты § 9) изме-
нить вложения так, чтобы они стали линейными вблизи
зоны перекрытия, ибо, как мы знаем из § 7, два евклидовых
разбиения всегда пересекаются так, как нужно.
Если М не является евклидовым пространством, то надо
привлекать координатные системы на многообразии М, которые
можно рассматривать как евклидово пространство, и проводить
указанное изменение последовательно, шаг за шагом. Процесс
этот, хотя по существу не сложнее, довольно канительный
(пп. 10.3—10.4). Зато после того как технические затруднения
будут преодолены, две главные теоремы этой главы получаются
почти немедленно (п. 10.5—10.6).
§ 10. Пригонка вложенных разбиений 351
ОПРЕДЕЛЕНИЕ 10.1. Пусть fa: Ki -* R", f2: Кг-> Rn —го-
меоморфизмы и fi(|Ki|), f 2 (| Кг |)— замкнутые подмножества
своего объединения. Говорят, что пары (Ki.fi) и (Кг,/г) пере-
секаются по подразбиению, если прообразы множества
А(|К1|)П/г(1Кг|) служат полиэдрами некоторых подразбиений
Ц и Li разбиений Ki и Кг соответственно и f^'fi является ли-
нейным изоморфизмом Li на Л2. Говорят, что они пересекаются
по полному подразбиению, если либо для i == 1, либо для i = 2
разбиение Li содержит каждый симплекс разбиения К/, вер-
шины которого принадлежат Lt. В таком случае существуют
такое разбиение К и такой гомеоморфизм f: К —► R", что сле-
дующая диаграмма коммутативна:
Здесь б и /г — линейные изоморфизмы разбиений Ki и Кг на
соответствующие подразбиения разбиения К, объединение ко-
торых равно К. Пара (К, f) определена однозначно с точностью
до линейного изоморфизма; она называется объединением пар
(Ki, fi) и (Кг, fz). Будем обозначать через L подразбиение
»1(К1)П /г (Кг).
Нас будет интересовать в этой ситуации случай, когда го-
меоморфизмы fi: Ki -* R" и fi- Кг R" являются дополнительно
Сг-вложениями. Отображение f: К -* R" будет в этом случае
невырожденным Сг-гомеоморфизмом, однако оно может не быть
вложением, так как может оказаться нарушенным условие
погружения (см. определение 8.3), т. е. для некоторой точки
b <= | L | отображение dft, может не быть взаимно-однозначным,
хотя само f взаимно-однозначно (см. пример из п. 8.1). Однако
если отображение f/ линейно на St (А/, К/) для / = 1, 2, то
их объединение f обязательно представляет собой вложение,
ибо в этом случае df& = f\Stb для	и f будет взаимно-
однозначным. Этот факт важен для дальнейшего. Другой слу-
чай, когда объединение является вложением, указан в упр. (с).
Упражнение (а). Пусть fa: Ki-+Rn — гомеоморфизм, j = 1, 2. Дока-
зать, что, если fa: К1->йл и fa: Kj-’-R'1 пересекаются по подразбиению, то
fp K{~>Rn и f2:	R" пересекаются по полному подразделению, где
/С] и К2 — барицентрические подразделения разбиений Ki и Ki соответственно.
Упражнение (Ь). Доказать существование и единственность (с точ-
ностью до линейного изоморфизма) объединения (К, f).
352 Дополнение. Дж. Манкрс
Набросок решения. Образовать абстрактное разбиение К, вершинами ко-
торого служат точки (/(у1), где V1 — произвольная вершина разбиения Ki U «
= 1,2). Если v^.. .Vp — симплекс разбиения Л/, то набор {fу (vQ,.. .,fj (v/)}
объявляется симплексом разбиения К. Затем дать геометрическую реализа-
цию этого абстрактного разбиения и определить f. Для доказательства того,
что f — гомеоморфизм, рассмотреть предельное множество отображеия f.
Упражнение (с). Пусть fp. К/ -> R", i = 1, 2, суть Сг-вложения, пере-
секающиеся по полному подразбиению, f: K->R" — их объединение и I/—
включение К/ в К. Если множество |.К| является объединением множеств
Int ii(|/<il) и	то f: K-+Rn представляет собой Сг-вложение.
Лемма 10.2. Пусть f:	есть С-отображение-, Q и А —
подразбиения разбиения Р, объединение которых равно Р;
f\Q и f]А суть Сг-вложения, образы которых замкнуты в R"1,
и пусть А конечно. Для любого заданного б > О существует
8-аппроксимация g; Р' —► R"1 отображения f, такая, что g\Q' и
g\A' пересекаются по полному подразбиению и их объединение
является Сг-вложением.
Кроме того, g совпадает с f, а Р' — с Р вне
St3(r'f (Я), Р) = st (st (st (Г1/ (Я)))),
(все звезды берутся в Р).
Доказательство. Пусть Ро — разбиение, полиэдром которо-
го служит множество St(f~lf(A))', оно состоит из всех симп-
лексов, образы которых пересекают множество /(Я), вместе с
их гранями; поэтому оно содержит Я. Предположим, что б
меньше, чем половина расстояния от множества f(P)\f(Po)
§ 10. Пригонка вложенных разбиений 353
до )(А), так что никакая 6-аппроксимация g отображения f не
может перевести точку из Р\Ро в точку из g{A). Предположим
далее, что 6 настолько мало, что для любой 6-аппроксимации
£:P'-*-Rot отображения f ограничения g\Q' и g|A' являются
Сг-вложениями.
Пусть Pi — подразбиение разбиения Р, полиэдром которого
служит St(P0>P)- По теореме 9.7 существует 6-аппроксима-
ция g: P'-^Rm отображения f, совпадающая на подразбиении
Р[ с секущим отображением, индуцированным f; кроме того, g
совпадает с f, а Р' — с Р вне St (Pi, Р).
Пусть Qi = Pi П Q, так что Р\ == A (J Отображения Q[
и g|A' являются линейными вложениями, так что их образы
представляют собой конечные прямолинейные разбиения в ев-
клидовом пространстве. По теореме 7.10 можно выбрать под-
разделения этих разбиений так, чтобы их объединение было
разбиением. Эти подразделения индуцируют посредством ото-
бражения g-1 подразделение Р'{ разбиения Р(, такое, что g| Qi
и g\A" пересекаются по подразбиению. Возьмем барицентри-
ческое подразделение Р(" разбиения Р?; тогда g |Qf" и glA'"
пересекаются по полному подразбиению (см. упр. (а) п. 10.1).
Продолжим это подразделение разбиения Р( стандартным
образом до подразделения Р"' разбиения Р' (см. определе-
ние 7.12).
Мы утверждаем, что g|Q"' и g\A"' пересекаются по под-
разбиению. Действительно, предположим, что g(oi) пересе-
кает g(az), где oi е Q"' иа2е А'". Тогда симплекс Ст] должен
лежать в |Ро|> согласно нашему первоначальному предполо-
жению относительно б, откуда следует, что Oi лежит в | Qi |.
Однако g\Q\' и g | А'" пересекаются по подразбиению. Значит,
g|Q'" и gl-A"' пересекаются по подразбиению. Аналогичное
рассуждение показывает, что это подразбиение является пол-
ным.
Отсюда вытекает, что объединение g|Q"' и g[A"' есть Сг-
вложение; здесь мы используем замечание, сделанное в конце
п. 10.1. Действительно, если g(bi) = g(bz) для точек t>i e|Q|
и Ьг е | А |, то точка bi должна лежать в |Р0|, согласно вы-
бору 6. Однако g линейно на разбиении Р[", которое содер-
жит St(|P0|, Р'"). Следовательно, объединение отображений
и g|A;,/ представляет собой С'-вложение. В
Следствие 10.3. Пусть М — многообразие без края, являю-
щееся Сг-подмногообразием некоторого евклидова простран-
ства. Утверждение предыдущей леммы сохраняет силу, если
всюду заменить Rm на М и предположить дополнительно, что
f(A) содержится в некоторой координатной системе (U,h)
на М.
364 Дополнение. Дж. Манкрс
Доказательство. Прежде всего возьмем совокупность тех
симплексов из Р, которые пересекаются с f~lf(A), и подразде-
лим их настолько мелко, чтобы диаметр каждого из них был
меньше четверти расстояния от f~lf(A) до f-1(M\U). Продол-
жим это подразделение стандартным образом до подразделе-
ния Р' всего разбиения Р. Ясно, что f переводит St4(f-*(A), Р')
в U. Далее, возьмем подразбиение J разбиения Р', полиэдром
которого является множество St4(f~7(A), Р'), и рассмотрим
(^-отображение hf: J -> R". Применяя предыдущую лемму, по-
лучаем, что существует аппроксимация G: J' -> Rm отображе-
ния hf, такая, что G совпадает с hf, a J' — с J вне
St3(f-7(A), Р'). Поэтому мы можем определить искомое отобра-
жение g, положив g = h~'G на множестве St4(f~lf (А), Р') и
g = f вне множества St3(f-1f(A), Р'); симплексы из Р', лежа-
щие вне J вообще не подразделяются.
Предыдущая лемма гарантирует нам, что G — гомеоморфизм.
Чтобы и g было гомеоморфизмом, достаточно взять его настоль-
ко близким к f, чтобы g(St3(f~}f(A), Р')) и g(P\St4(f~7(А), Р'))
не пересекались. Аналогично, предыдущая лемма гарантирует
нам, что G является Сг-вложением; то, что h~'G тоже будет вло-
жением, следует из упр. (а) 8.3. Наконец, используя упр. (с)
п. 10.1, получаем, что и g будет вложением. 
Упражнение (а). Показать, что в условиях предыдущего следствия
справедливо следующее дополнительное утверждение: g(x) = f(х), если f(x)
лежит вне координатной окрестности (и, й), содержащей /(Д).
Теорема 10.4. Пусть М — многообразие без края, являющее-
ся Сг-подмногообразием пространства R", и пусть f: К-+М и g:
L-+M. суть Сг-вложения, образы которых замкнуты в М. Для
любой заданной функции б (х) > 0 существуют 8-аппроксимации
f': К'-+М и g'\ U-> М отображений fug соответственно, пере-
секающиеся по полному подразбиению, так что их объединение
представляет собой Сг-вложение. (Функция 8 должна быть не-
прерывна на дизъюнктном объединении полиэдров |/С| и |L|.)
Доказательство. Предположим, что g переводит каждый
симплекс из L в некоторую координатную окрестность на М
(см. упр. (а) п. 7.13). Занумеруем симплексы разбиения L:
А[, А2, ...
таким образом, чтобы каждый симплекс предшествовал всем
своим граням. Выберем для каждого номера i окрестность Vi
множества g(A,j в М так, чтобы {?<} было локально-конечной
совокупностью компактных подмножеств в М.
(*) Предположим, что б настолько мало, что для любых
б-аппроксимаций f' и g' отображений fug соответственно мно-
§ 10. Пригонка вложенных разбиений 355
жество g'(Ai) содержится в Vi и не пересекается с множеством
f'f-4M\Vi).
Положим f0 ~ f и go = g.
Индуктивное предположение. Пусть Ki — подразделение раз-
биения К, Li — подразделение разбиения L и fi: Ki~+M, gr.
Lt-+M суть Сг-вложения, являющиеся (1—‘^J^xJ-annpoKcn-
мациями отображений fug соответственно. Далее, если Л обо-
значает подразбиение разбиения Li, полиэдром которого служит
объединение Д111 ... 11Л,-, то мы предполагаем, что отображе-
ния fi: Ki-^M и gi\Ji пересекаются по полному подразбиению
и их объединение представляет собой вложение.
Пусть й: Q-+M есть объединение (Ki, fi) и £/|Л. Это —
Сг-вложение. Рассмотрим Ki и К как подразбиения разбиения Q,
так что Q = Ki U h. Множество A,+1 служит полиэдром некото-
рого подразбиения разбиения Lt, которое мы обозначим также
через Л/+ь пусть Р — разбиение, получаемое отождествлением
каждой точки из В(1Л,+1, с соответствующей точкой из Л. Для
того чтобы Р было разбиением, может понадобиться подразде-
лить At+i; будем считать это сделанным, не изменяя обозначе-
ний. Продолжим й на Р, положив его равным gi на Л,+ь
Теперь применим предыдущее следствие. Отображение й:
Р—>Af является (^-отображением; h\Q и й)Л/+1 суть ^-вложе-
ния, и й(Л/+1) содержится в некоторой координатной системе на
М. Значит, для любого е > 0 найдется такая е-аппроксимация
й': Р'-+М отображения й, что h' | Q' и h'lAf+i будут (^-вложе-
ниями, пересекающимися по полному подразбиению, объедине-
ние которых является вложением. Но это объединение совпадает
с объединением й'|К{ и й'|/< U Л<+1, так что объединение этой
последней пары также является вложением.
Если 8 достаточно мало, то отображение й': К1->М бу-
дет б(x)/2‘+I-аппроксимацией для й, так что ^+1 = й'|/^ будет
(1 — */г/+1) б (х)-аппроксимацией для f, как и требуется.
Далее, если е достаточно мало, то отображение й': 7fU A'i+i~>
-+Л1 можно продолжить до Сг-отображения gi+i-. Li+l-+M, ко-
торое служит б(х)/2/+1-аппроксимацией для gr.	Здесь
мы снова используем лемму 9.8. Таким образом, отображение
gi+V.	является (1 — '/г'*1)б(х)-аппроксимацией для g,
как и требуется. Итак, наше индуктивное предположение выпол-
нено, и, значит, можно считать, что отображения и gt опреде-
лены для всех i.
Теперь хочется положить	и аналогич-
но для g' и L'. Поскольку индуктивное предположение само по
себе не гарантирует существования этих пределов, посмотрим
внимательнее на определения отображений /<+1 и gi+i.
356 Дополнение. Дж. Манкре
Следствие 10.3 говорит нам, что Q' совпадает с Q, a h' — ch
вне St3(ft-1ft(/1,+i), Р). Поэтому ft+i совпадает с ft, a Kt+i — с Ki
для симплексов, лежащих вне St3(/7'gz (А(+1), К(). Но согласно
исходному предположению (*) относительно б, отображение ft
посылает точку х е К в множество gf(Ai+)) тогда и только то-
гда, когда f посылает точку х в V/. Таким образом, мы видим,
что fi+l совпадает с ft, a Kt+i— с Kt вне St3(f_I(V(), К). Эти
множества образуют локально-конечную совокупность подмно-
жеств в К, так что пределы lim ft и limK, существуют (см. за-
дачу 7.13).
Аналогично, g,+i совпадает с gt, a L<+i — с Ц вне St3 '§,Х
X(Ai+1), L;) — St3(A/4.j, L,) c St3(A/+1, А). Следовательно,
интересующие нас пределы существуют и в этом случае. Пре-
дельные отображения автоматически будут б(х)-аппроксимация-
ми для f и g соответственно. То что их объединение является
(/-вложением, проверяется без труда. 
Упражнение (а). Внимательно изучив доказательство теоремы, вы-
вести следующее дополнительное заключение: для любой окрестности V мно-
жества g( |L|) можно выбрать К' и f' так, чтобы К' совпадало с К, а Г —
с f вне
Упражнение (Ь). Используя упр. (а) п. 10.3 и упр. (d) п. 9.8, уси-
лить теорему 10.4 следующим образом. Предположим, что f и g переводят
подразбиения разбиений К и L соответственно в Сг-подмногообразие N много-
образия М, ие имеющее края. Тогда f и g' можно выбрать так, чтобы они
тоже переводили эти подразбиения в N.
Теорема 10.5. Пусть М есть (^-многообразие. Для любых
двух его Сг-триангуляций f: К-+М и g: L-+ М существуют под-
разделения разбиений К и L, линейно изоморфные друг
другу.
Фактически для всякой заданной функции б(х)>0 суще-
ствуют 8-аппроксимации f': К' -+М и g': L'-*M триангуляций f
и g соответственно, являющиеся Сг-триангуляциями многообра-
зия М и такие, что отображение (f')~lg' представляет собой ли-
нейный изоморфизм L' на К'.
Доказательство. В случае, если многообразие М не имеет
Края, выберем б(х)> 0 так, чтобы любые б-аппроксимации ото-
бражений fug были отображениями на; это возможно в силу
леммы 3.11. Наш результат следует тогда из теоремы 10.4.
В случае когда край имеется, рассмотрим М как подмногообра-
зие своего удвоения D(A4); из упр. (Ь) п. 10.4 вытекает, что ото-
бражение f': K/-*D(Af) переводит Bd|K| в BdAl. Если б доста-
точно мало, то /z(Bd|/C|) = BdAl, так что f'(|К|)сМ. Поэтому
для достаточно малых б имеем f'(IK|)« М. Аналогично, если б
достаточно мало, то &'(|L1) = Л1. В
§ 10. Пригонка вложенных разбиений 357
Теорема 10.6. Каждое Сг-многообразие М без края обладает
Сг-триангуляцией. Если многообразие М имеет край, то любая
Сг-триангуляция его края может быть продолжена до Сг-триан-
гуляции всего многообразия М. (Продолжением Сг-триангуля-
ции f: J -> Bd Л4 края многообразия М называется всякая Сг-три-
ангуляция g: L-*M, такая, что отображение g~lf является ли-
нейным изоморфизмом разбиения J на некоторое подразбиение
разбиения L.)
Доказательство. Пусть М — многообразие без края. По-
кроем его m + 1 координатными системами (Ui, hi), i = 0, 1, ...
..., m, выбранными так, что hi(Ui) для каждого i есть объеди-
нение некоторой счетной совокупности (V//) попарно непересе-
кающихся ограниченных множеств в Rm (см. задачу 2.8). Пусть
Ci/ cz Va — замкнутые множества, такие, что совокупность {С,/}
покрывает многообразие М, и пусть Кц для каждой пары индек-
сов / и /— конечное прямолинейное разбиение в Rm, содержа-
щееся в hi(Vtj) и содержащее некоторую окрестность замкну-
оо
того множества /г>(Су). Положим Ki = U Кц- Тогда ЛД1: К, Л4
/-1
будет Сг-вложением, образ которого содержит некоторую окре-
стность множества С^. Пусть gp К'-* Al. суть б, (х)-аппрок-
симации для hpl, i = 0, 1......m, выбранные так, чтобы
(Ку Ео)’ • • •> (^m> Ет) пересекались по полному подразбиению и
их объединение было вложением. Это объединение будет Сг-три-
ангуляцией многообразия М, если б,(х)> 0 выбраны настолько
малыми, что g,(| Ki |) содержит J Сг/ (см. упр. (Ь) п. 3.11).
1
Пусть теперь многообразие М имеет край и f: J—>-Bd Af есть
Сг-триангуляция. Триангулируем пространство |/|Х[0, 1) сле-
дующим образом. Предположим, что J лежит в R". Для каждого
симплекса о е J и каждого целого положительного числа п рас-
смотрим евклидовы клетки оХ [1 — 1/«, 1 — l/(n + 1)] и
оХ(1 — 1/лг), которые содержатся в Rn+1. Совокупность всех та-
ких клеток образует евклидово клеточное разбиение, полиэдром
которого является множество 17| Х[0, 1); это евклидово клеточ-
ное разбиение можно превратить в симплициальное разбиение
при помощи подразделения, не затрагивающего клетки второго
рода оХ(1 — 1/п). Обозначим получившееся симплициальное
разбиение через К.
Пусть Ко—подразбиение разбиения К, полиэдром которого
служит множество |/|Х[0, в/в], и пусть Р; BdA4X[0> l)~*Af —
некоторая цилиндрическая окрестность края многообразия М.
Ограничение на Ко композиции
/Х[0, 1)^ BdMXlO, 1)-Д-А1
358 Дополнение. Дж. Манкрс
представляет собой Сг-вложение g: Ко~>М, образ которого зам-
кнут в М и содержит множество P(BdMX[0, 4/з]) в своей вну-
тренности.
Пусть h: L-+M является Сг-триангуляцией многообразия
IntМ, которое не имеет края. Подразделяя, если надо, разбие-
ние L, мы можем считать, что любой симплекс из L, пересекаю-
щийся с множеством Р (Bd М X (4/б)), не пересекается с множе-
ством P(BdMX[0, 3/4]) (см. упр. (а) п. 7.13). Пусть Lo — под-
разбиение разбиения L, состоящее из симплексов, образы кото-
рых при отображении h пересекают множество M\P(BdMX
Х[0, 4/в)), и их граней. Тогда отображение h: Lo-+M будет
Сг-вложением, образ которого замкнут в М, содержит множество
Af\P(BdMX [0,4/з]) в своей внутренности и содержится в
множестве М \ P(BdMX[0, s/4]).
По теореме 10.4 существуют аппроксимации g': Ко~+М и
h': Lq-*M отображений g и h соответственно, которые пересе-
каются по полному подразбиению и объединение которых яв-
ляется вложением. Согласно упр. (а) п. 10.4, мы можем пред-
положить, что g' совпадает с g, а Ко — с Ко на множестве |/|Х
X [0, ’/а] • Объединение (Ко, gr) и (L'o, h') будет, таким образом,
искомой Сг-триангуляцией многообразия М при условии, что
g'(| Ло |) и Л'(| Lo |) покрывают М.
Но множество g( |/Со|) содержит в своей внутренности мно-
жество P(BdAfX[’/2, 4/в], а А (| Ао|) содержит в своей внутрен-
ности множество М \ P(BdAf Х[0, 3/4]). Применение упр. (Ь)
п. 3.11 показывает, что образу вложений g' и h' будут содер-
жать эти два замкнутых множества, если аппроксимации доста-
точно хороши. Так как g'( |^1) содержит множество P(BdXlX
X [0, */2]) автоматически, то мы видим, что в случае достаточно
хороших аппроксимаций множества g'(|/<o|). и h'(|L0|) действи-
тельно покрывают М. 
СПИСОК ЛИТЕРАТУРЫ*
[1]	Бинг Р. (Bing R. Н.) Locally tame sets are tame, Ann. Math., 1964, 59,
145—158.
[2]	Гуревич В., Волмэн Г. (Hurewicz W., Wallman H.) Теория размерно-
сти.—M.: ИЛ, 1948 (1948).
[3]	Кервер M. (Kervaire М.) A manifold which does not admit any dif-
ferentiable structure, Comment. Math. Helv., 1960, 34, 257—270.
[4]	Манкре Дж. (Munkres J. R.) Obstructions to the smoothing of piece-
wise-differentiable homeomorhisms, Ann. Math., 1960, 72, 521—554.
[5]	Милнор Дж (Milnor J.) On manifolds homeomorphic to the 7-sphere,
Ann. Math., 1956, 64, 399—405. [Имеется перевод: О многообразиях,
гомеоморфных семимерной сфере.—Математика, 1957, 1:3, с. 35—42.]
[6]	— Differential Topology, Princeton Univ., 1958 (mimeographed).
[7]	— Two complexes which are homeomorphic but combinatorially distinct,
Ann. Math., 1961, 74, 575—590.
[8]	Мойз Э. (Moise E. E.) Affine structures in 3-manifolds. V. The triangu-
lation theorem and Hauptvermutung, Ann. Math., 1952, 56, 96—114.
[9]	Моран Д. (Moran D.) Raising the differentiability class of a manifold
in euclidean space (thesis), Univ, of Ill., 1962.
[10]	Морс M. (Morse M.) On elevating manifold differentiability, J. Indian
Math. Soc., 1960, 24, 379—400.
[11]	Папакирьякопулос К. (Papakyriakopoulos C. D.) A new proof of the
invariance of the homology groups of a complex, Bull. Soc. Math.
Gr&e, 1943, 22, 1—154.
[12]	Стинрод H. (Steenrod N.) Топология косых произведений. — M.: ИЛ,
1953 (1951).
[13]	Столлингс Дж. (Stallings J.) The piecewise-linear structure of euclidean
space, Proc. Cambridge Philos. Soc., 1962, 58, 481—488.
[14]	Уайтхед Дж. Г. К. (Whitehead J. H. C.) On C*-complexes, Ann. Math.,
1940, 41, 809-824.
[15]	— Manifolds with transverse fields in euclidean space, Ann. Math.,
1961, 73, 154—212.
[16]	Уитни X. (Whitney H.) Differentiable manifolds, Ann. Math., 1935, 37,
645—680.
[17]	Хокинг Дж., Янг Г. (Hocking J. G., Young G. S.) Topology, Addison-
Wesley, Reading, Mass., 1961.
1 См. подстрочное примечание к стр. 262. — Прим, иерее.
ЛИТЕРАТУРА, ДОБАВЛЕННАЯ ПРИ ПЕРЕВОДЕ'
К основному тексту
Браудер У. (Browder W.) Surgery on simply-connected manifolds, Ergebnisse
Math. 65, Berlin, Springer, 1972.
—	Poincare spaces, their normal fibration and surgery, Invent. Math., 1972,
17, № 3, 191—202.
Бухштабер В. M. Кобордизмы в задачах алгебраической топологии. —
В кн.: Алгебра. Топология. Геометрия (Итоги науки и техники), т. 13,
1975, с. 231—271.
—	Характеристические классы в кобордизмах и топологические приложе-
ния теории однозначных и двузначных формальных групп. — В кн.:
Современные проблемы математики (Итоги науки и техники), т. 10,
1978, с. 5—178.
Бухштабер В. М., Мищенко А. С., Новиков С. П. Формальные группы и их
роль в аппарате алгебраической топологии, УМН, 1971, 26, № 2,
131—154.
Кару би (Karoubi М.) A-theory, Grundlehren math. Wiss. 228, Springer, 1977.
Кёрби P., Зибенманн Л. (Kirby R., Siebenmann L.) Foundational assays on
topological manifolds, smoothings and triangulations, Ann. Math. Stud.
88, Princeton University Press, 1977.
Коннер П., Флойд Э. (Conner P., Floyd E.) Гладкие периодические ото-
бражения.— M.: Мир, 1969 (1964).
Кюйпер Н., Лашеф Р. (Kuiper N., Lashof R.) Microbundles and bundles.
I. Elementary theory, Invent. Math., 1966, № 1, 1—17.
Ликориш У. Б. P. (Lickorish W. B. R.) A representation of orientable com-
binatorial 3-manifolds, Ann. Math., 1962, 76, 531—540.
Постников M. M. Введение в теорию Морса. — М.: Наука, 1971.
Суллнван Д. (Sullivan D.) Inside and outside manifolds, Proc. Int. Congr.
Math. Vancouver 1974, printed in USA, 1975, 1, 533—536.
Уолл 4. (Will С. T. C.) Poincare complexes. I, Ann. Math., 1967, 86,
213—245.
Уэллс P. (Wells R. О.) Дифференциальное исчисление на комплексных мно-
гообразиях.— М.: Мир, 1976 (1973).
Фукс Д. Б. Когомологии бесконечномерных алгебр Ли и характеристиче-
ские классы слоений. — В кн.: Современные проблемы математики
(Итоги науки и техники), т. 10, 1978, с. 179—235.
Хирш М., Мазур Б. (Hirsch М. W., Mazur В.) Smoothing of piecewise linear
manifolds, Ann. Math. Studies, № 80, Princeton Univ. Press, 1974.
1 При ссылках на работы из этого списка ставится звездочка, например
[* Каруби]. — Прим, перев.
Литература, добавленная при переводе 361
К дополнению
Браун Э. М. (Brown Е. М.) The Hauptvermutung for 3-complexes, Trans.
Amer. Math. Soc., 1969, 144, 173—196.
Кёрби P., Зибенманн Л. (Kirby R. C., Siebenmann L C.) On the triangula-
tion of manifolds and the Hauptvermutinung, Bull. Amer. Math. Soc.,
1969, 75, 742—749.
— Foundational essays, Ann. Math. Stud., 1977.
Кэннон Дж. (Cannon J. W.) The recognition problem; what is a topological
manifold? Bull. Amer. Math. Soc., 1978, 84, № 5, 832—866.
Мацумото Ю. (Matsumoto Y.) Hauptvermutung for Л; = Z, J. Fac. Sci.
Univ. Tokyo, 1969, 16, № 2, 165—177.
Морита C. (Morita Sh.). Smoothability of P£-manifolds is not topologically
invariant. Manifolds, Tokyo 1973, Univ, of Tokyo Press, 1975.
Понтрягин Л. С. Гладкие многообразия н их применения в теории гомо-
топий, 2-е изд.,—М.: Наука, 1976.
Рурк К., Сандерсон Б. (Rourke С. Р., Sanderson В. J.) Введение в кусоч-
но-линейную топологию. — М.: Мир, 1974 (1972).
Сулливан Д. (Sullivan D.). On the Hauptvermutung for manifolds, Bull.
Amer. Math. Soc., 1967, 73, 598—600.
— Геометрическая топология. — M.: Мир, 1975 (1970).
Сян У-чун, Шейнсои Дж. (Hsiang Wu-Chung, Shaneson J. L.) Fake tori;
Tipology Manifolds, Chicago, 1970, 18—51.
Уитни X. (Whitney H.) Геометрическая теория интегрирования. — M.: ИЛ,
1960 (1957).
ИМЕННОЙ УКАЗАТЕЛЬ
Адамс Дж. Ф. (J. F. Adams) 44, 49,
113, 205, 211, 212, 237, 238, 262
Адем Дж. (J. Adem) ИЗ, 262
Александров П. С. 205, 262
Андерсон Д. У. (D. W. Anderson)
212 262
Артин Э. (Е. Artin) 238, 262
Атья М. (М. Atiyah) 186, 205, 211,
212, 262
Баум П. (Р. Baum) 210, 263
Бернулли Я. (J. Bernoulli) 234
Бннг Р. (R. Н. Bing) 359
Биркгоф Г. (G. Birkhoff) 35, 265
Бишоп Р. (R. L Bishop) 34, 98, 244,
263
Блантон Дж. Д. (J. D. Blanton) 76,
263
Бой В. (W. Воу) 102, 263
Бордман Дж. (J. М. Boardman) 209,
263
Боревич 3. И. 234, 236, 238, 263
Борель A. (A. Borel) 76, ИЗ, 158, 193,
263
Борсук К. (К. Borsuk) 191
Ботт Р. (R. Bott) 44, 201, 210, 212,
240, 252, 256, 263
Брамфил Г. (G. Brumfiel) 206, 264
Браудер У. (W. Browder) 208, 264,
360
Браун А. Б. (А. В. Brown) 172, 264
Браун Э. (Е. Brown) 212, 262
Браун Э. М. (Е. М. Brown) 327, 360
Бооди.Э. (Е. J. Brody) 202, 264
Бур баки Н. (N. Bourbaki) 257, 264
Бухштабер В. М. 205, 360
Ван дер Варден Б. Л. (В. L. Van der
Waerden) 64, 74, 157, 264
Вей Ж. (J. Vey) 210, 264
Вейль A. (A. Weil) 258
Вейнграм С. (S. Weingram) 65, 265
Вильямсон Р. У. (R. W. Williamson)
206, 264
Волмэн Г. (Н. Wallman) 359
Вуд Дж. (J. Wood) 259, 264
Гальперин С. (S. Halperin) 119, 264
Гамильтон (W. R. Hamilton) 200
Ганнинг Р. (R. С. Gunning) 126, 264
Гильберт Д. (D. Hilbert) 102, 264
Годбийон К. (С. Godbillon) 210, 264
Грейвс Л. (L. Graves) 172, 264
Гуревич В. (W. Hurewicz) 208, 264,
359
Дайер Э. (Е. Dyer) 209, 210, 264
Джеймс И. (I. М. James) 46, 201, 264
Дольд A. (A. Dold) 63, 79, 81, 96,
106—108, ПО, 208, 213, 214, 216,
264
Дугунджн Дж. (J. Dugundji) 59, 66,
264
Зибенманн Л. (L. Siebenmann) 207,
265, 327, 360
Зингер 1 И. (I. Singer) 186, 262
Кан П. (Р. J. Kahn) 186, 264
Капланский И. (I. Kaplansky) 215,
264
Картав А. (Н. Cartan) 223, 264
Карубй М. (М. Karoubi) 205, 211,
264, 360
Квиллен Д. (D. Quillen) 264
Келли Дж. (J. L. Kelley) 25, 35, 59,
60, 264
Кервер М. (М. Kervaire) 44, 206, 237,
оск 970 ЧЦО
Кёрби Р. ’ (R. Kirby) 207, 265, 327,
360
Кистер Дж. (J. М. Kister) 206, 265
Клаузен Т. (Т. Clausen) 236
Кнезер X. (Н. Kneser) 25, 265
Кобаяси С. (S. Kobayashi) 244, 265
» ₽ Сингер. — Прим. ред.
Именной указатель 363
Коннер П. (Р. Conner) 205, 211, 212,
265, 360
Кон-Фоссен С. (S. Cohn-Vossen) 102,
264
Криттенден Р. (R. J. Crittenden) 34,
98, 244, 263
Куммер (Kummer) 237
Кюйпер Н. (N. Kuiper) 206, 360
Кюннет X. (Н. Kiinneth) 223
Кэннон Дж. (J. W. Cannon) 327, 361
Ланделл Э. (А. Т. Lundell) 65, 265
Лашеф Р. (R. К. Lashof) 206, 265,
360
Ленг С. (S. Lang) 31, 74, 98, 215,
265
Ликориш У. Б. Р. (W. В. R. Licko-
rish) 168, 360
Мадсен И. (I. Madsen) 206, 264
Мазур Б. (В. Mazur) 206, 207, 360
Маклейн С. (S. MacLane) 35, 214,
215, 223, 252, 265
Макмахон П. (Р. A. Macmahon) 157,
265
Манкре Дж. (J. R. Munkres) 5, 116,
207, 265, 272, 359
Маховальд М. (М. Mahowald) 237,
265
Мацумото Ю. (Y. Matsumoto) 327,
361
Милграм Р. Дж. (R. J. Milgram) 206,
209, 264, 265
Милнор Дж. (J. W. Milnor) 5, 8, 44,
164, 172, 188, 202, 203, 206, 207, 209,
237, 259, 263, 265, 287, 326, 359
Мищенко А. С. 360
Миядзаки X. (Н. Miyazaki) 66, 265
Мойз Э. (Е. Е. Moise) 359
Моран Д. (D. Moran) 359
Морс М. (М. Morse) 359
Морита С. (Sh. Morita) 327, 361
Мэй Дж. (J. Р. Мау) 188, 209, 266
Нильсен Н. (N. Nielsen) 238, 266
Ннреиберг Л. (L. Nirenberg) 126, 266
Новиков С. П. 164, 189, 190, 202,
207, 209, 212, 266, 360
Номидзу К. (К. Nomizu) 15, 244, 265,
266
Ньюлэндер 9. (A. Newlander) 126,
266
Остманн X. (Н. Ostmann) 71, 266
Папакирьякопулос К- (С. D. Рара-
kyriakopoulos) 359
Петерсон Ф. (F. Р. Peterson) 212,
262, 266
Петре Я. (J. Peetre) 241, 266
Понтрягин Л. С. 7, 8, 47, 64, 167, 266,
287, 361
Постников М. М. 6, 65, 360
Равенель Д. (D. Ravenel) 209, 266
Райт Э. М. (Е. М. Wrignt) 236, 268
Рам Ж., де (О. de Rham) 15, 266
Рамануджан (Ramanujan) 71
Росси X. (Н. Rossi) 126, 264
Ротенберг М. (М. Rothenberg) 265
Рохлин В. А. 168, 189, 266
Рурк К. П. (С. Р. Rourke) 193, 266,
337, 361
Саймонс Дж. (J. Simons) 210, 269
Сандерсон Б. (В, J. Sanderson) 193,
266, 337, 361
Сард A. (A. Sard) 172, 266
Сван Р. (R. Swan) 35, 266
Серр Ж.-П. (J.-P. Serre) 170, 171,
191, 266
Серф Ж. (J. Cerf) 206, 266
Сигал Г. (G. Segal) 209, 266
Симада Н. (N. Shimada) 199, 202,
267
Сингх Варма X. О. (Н. О. Singh
Varma) 269
Смейл С. (S. Smale) 46, 203, 267
Спеньер Э. (Е. Н. Spanier) 40, 73, 86,
89, 95, 96, 107, 108, 113, 171, 191,
213—215, 217, 219, 220, 222, 223,
225, 228, 229, 252, 267
Спивак М. (М. Spivak) 208, 267
Спрингер Дж. (G. Springer) 259, 267
Сташеф Дж. (J. D. Stasheff) 5, 8,
188, 208, 209, 267
Стернберг 1И. (S. Sternberg) 172, 267
Стинрод Н. (N. Steenrod) 13, 15, 17,
23—25, 33, 49, 51, 55, 78, 116, 117,
119, 120, 123, 124, 143, 150, 170,
174, 192, 209, 213, 214, 217, 220, 225,
231, 244, 267, 269, 359
Столлингс Дж. (J. Stallings) 359
Стонг Р. (R. Е. Stong) 48, 164, 184,
205, 210, 267
Сулливан Д. (D. Sullivan) 202, 209,
212, 267, 327, 360, 361
Сян У-чун (Hsiang Wu-Chung) 327,
361
364 Именной указатель
Тамура И. (I. Tamura) 199, 267
Тода X. (Н. Toda) 266
Толедо Д. (D. Toledo) 119, 264
Том Р. (R. Thom) 48, 158, 161, 164,
168, 178, 184, 187, 189, 199, 202, 267
Томас Э. (Е. Thomas) 267
Тэрстон У. (W. Thurston) 210, 268
Хокинг Дж. (J. G. Hocking) 359
Хопф X. (Н. Hopf) 205, 262
Хьюзмоллер Д. (D. Husemoller) 17,
63, 205, 209, 268
Хэфлигер A. (A. Haefliger) 210, 263,
268
У 1 Вэнь-цзунь (Wu Wen-tsun) 36, 65,
66, 112, 187, 188, 268
Уайли С. (S. Wylie) 40, 213, 268
Уайтхед Дж. Г. К. (J. Н. С. White-
head) 49, 58, 59, 64, 55, 116, 171,
191, 197, 201, 217, 264, 267, 268, 359
Уайтхед Дж. У. (G. W. Whitehead)
212, 268
Уитни X. (Н. Whitney) 5, 7, 10, 36,
46, 102, 116, 119, 178, 268, 287, 359,
361
Уолл Ч. (С. Т. С. Wall) 168, 179, 208,
268, 360
Уоллес A. (A. Wallace) 265
Уорнер Ф. (F. Warner) 240, 252, 268
Уэллс Р. (R. О. Wells) 127, 360
Флойд Э. (Е. Floyd) 205, 211, 212,
265, 360
Фогт Р. (R. Vogt) 209, 263
Фукс Д. В. 210, 360
Хайтч И. (J. Heitsch) 256, 263
Харди Г. (G. Н. Hardy) 71, 236, 268
Хёрмандер Л. (L. Hormander) 126,
268
Хилтон П. (Р. J. Hilton) 40, 213, 268
Хирцебрух Ф. (F. Hirzebruch) 33, 36,
179, 181, 184, 188, 189, 212, 234,
255, 262, 268
Хирш М. (М. W. Hirsch) 46, 206, 207,
264, 268, 360
Чепмэн Т. (Т. A. Chapman) 202, 268
Чернявский А. В. 6
Чжень Шен-шень (S. S. Shern) 7, 8,
64, 66, 210, 240, 252, 258, 263, 269
Шафаревич И. Р. 234, 236, 238, 263
Шварц А. С. 189, 266
Швейцер П. (Р. A. Schweitzer) 76,
263
Шевалле К. (С. Chevalley) 34, 269
Шейнсон Дж. (J. L. Shaneson) 327,
361
Ши В. (W. Shih) 212, 269
Штанько М. А. 6
Штаудт К. Г. К., фон (К. G. С. von
Staudt) 236
Штифель Э. (Е. Stiefel) 7, 8, 36, 43,
44, 49, 116, 119, 269
Шуберт X. (Н. Schubert) 66, 269
Шчарба Р. (R. Szczarba) 204, 269
Эйленберг С. (S. Eilenberg) 13, 25,
150, 192, 213, 214, 217, 220, 223, 225,
231, 264, 269
Эпстейн Д. Б. Э. (D. В. A. Epstein)
78, 267
Эресманн Ш. (С. Ehresmann) 7, 25,
64, 269
Янг Г. (G. S. Young) 359
1 = By. — Прим. ред.
предметный указатель
аксиома о накрывающей гомотопии
208
антндиагональ 88
ассоциированное расслоение на мно-
гообразии Штифеля 116
база расслоения 16
базис дифференцируемой структуры
276
базисное пространство 16
барицентр 325
барицентрические координаты 325
барицентрическое подразделение 331
бесконечное многообразие Грассмана
-----Штифеля 61
— проективное пространство 67
бордантность 211
бордизм ориентированный 211
Брауна теорема 172
Бьянки тождество 247
вектор скорости 11, 290
векторное поле 20
— расслоение 16
----- гладкое 17
----- евклидово 23
-----комплексное 124
вещественное проективное простран-
ство 16
включение 291
вложение 277
— класса Сг 335
внешнее когомологическое произведе-
ние 221
-----умножение 79
внутренность многообразия 271
внутренняя точка многообразия с
границей 165
воротник 319
вписанное покрытие 59, 271
вторая фундаментальная форма 34,
Гаусса — Бонне теорема 253
-------обобщенная 258
---2-форма 252
гауссова кривизна 252
гауссово отображение обобщенное 55
геодезические координаты 252
главное расслоение 313
гладкая триангуляция 197
гладкое многообразие 10
--- с границей 165
—	отображение 9
—	— многообразий 12
гладкости структура 15
голоморфное отображение 126
гомотопия дифференцируемая 297
—	регулярная 296
граница многообразия 165, 271
граничная точка многообразия 271
граничный гомоморфизм 214, 218
грань 213, 325, 329
грубая С1-топология 294
группа кобордизмов 50
—	коцепей 218
—	цепей 218
двойственное векторное расслоение
32
— комплексное векторное расслоение
140
двойственность Александера 233
— Пуанкаре 108
двойственный когомологический класс
101
джойн 325
диагональный когомологический
класс 106
диаметр симплекса 344
диффеоморфизм 12, 277
дифференциал отображения 292, 335
дифференциальный оператор 241
дифференцируемая структура 275
366 Предметный указатель
дифференцируемое многообразие 275
— отображение 272
--- относительно разбиения 334
длинная линия 25
Дь£донне теорема 60
евклидова метрика на векторном рас-
слоении 23
евклидово векторное пространство 23
--- расслоение 23
—	клеточное разбиение 330
—	полупространство 270
единичная сфера 27
единичный шар 270
естественность 36, 78, 85, 131
Жирара формула 163
задняя грань 219
звезда 326
измельчение разбиения 152, 326
изоморфизм векторных расслоений 17
—	симплексов линейный 326
—	Тома 79, 84
изотопия 297
инвариантный полином 245
индекс Кронекера 46, 215
—	многообразия 184
индуцированное расслоение 26
интегрирование на многообразии 229
каноническое линейное расслоение
над Рп 19
карта 10
Картана формула 78
касательное многообразие 12
— отображение, определяемое по-
гружением 313
—	пространство И, 290
—	расслоение 18, 291
--- кусочно-линейное 205
касательный вектор 11, 290
квадратичная функция 23
---положительно определенная 23
класс кобордизма 49
— ориентированного кобордизма 166
—	Понтрягина 144
—	Хирцвбруха 189
—	Чокеня 131
—	Штифеля — Уитни 36
—	Эйлера 85
классифицирующее отображение
153—154
—	пространство 136, 206
клетка 327
—	замкнутая 65
—	открытая 65
клеточное разбиение 65, 330
--- конечное 65
ковариантная производная 240
ковариантный тензор второго поряд-
ка 293
когомологическое Х-умноженне 220
когомотопнческая группа многообра-
зия 191
кограница коцепи 214
кограиичный гомоморфизм 218
кокасательное расслоение 240
комбинаторное многообразие 337
компактный носитель 228
комплексифнкация 128, 144
комплексная структура на веще-
ственном расслоении 125
-------- многообразии 126
комплексно-аналитическое отображе-
ние 126
комплексное многообразие 126
—	расслоение 124
компонента вектора 290
конус отображения 95
координатная окрестность 10, 270
—	система 276
координатное пространство 9
косое гомологическое умножение 106
коцепь 214, 218
— с компактным носителем 228
Коши—Римана условия (уравнения)
краевая точка многообразия 271
край многообразия 271
кривая многообразия 271
куб т-мерный 270
кусочно-лннейное касательное рас-
слоение 205
— отображение 193, 326
— расслоение 205, 206
Кюннета теорема 223
лежащее в основе вещественное рас-
слоение 125
лемма о сглаживании 303
линейность на симплексах 193, 326
линейный изоморфизм симплексов
326
линия Александрова 25
линк 337
Липшица —Сильвестра лемма 235
Предметный указатель 367
локальная координатная система 10
— —-----для векторного расслоения
— ориентация многообразия 226
—	параметризация 10
—	тривиальность 17, 124
локально-конечное покрытие 59, 272
— семейство множеств 274
локально-стягиваемое пространство
324
локальный оператор 241
Мазура теорема 206
матрица Якоби 272
микрорасслоение 206
Милнора — Новикова теорема 164
Миядзаки теорема 66
многообразие без края 271
— Грассмана 51, 310
---- бесконечное 57
----комплексное 88, 132
---- стабильное 206
—	дифференцируемое 275
—	топологическое 270
—	Штифеля 51
---- бесконечное 61
—	Шуберта 66
мономы эквивалентные 156
Мориты теорема 59
мультипликативная последователь-
ность 180
----принадлежащая степенному ря-
ду 182
наложение 34
невырожденное отображение (клеточ-
ных разбиений) 334
нормальное отображение, определяе-
мое погружением 3.14
— расслоение 18
----вложения 314
----погружения 31, 316
----подмногообразия 30
---- Спивака 208
носитель 285
— компактный 228
Ньютона формула 162
обобщенная теория гомологий 211
----когомологий 210
обобщенное гауссово отображение 55
объединение пар {Kt, ft) и {Кг, [г)
351
овеществленное расслоение 144
ограничение расслоения 26
ориентация 82
—	многообразия 103, 227
—	расслоения 83
ориентироваииая кобордантность 166
ориентированного объема «-форма
252
ориентированное многообразие 227
—	разбиение 192
ориентированный бордизм 211
—	кобордизм 166, 167
ортогональное дополнение подрас-
слоения 29
ортогональный вектор 130
основная гипотеза (Hauptvermutung)
326
остов 331
паракомпактное пространство 59, 271
параллелизуемое многообразие 18
передняя грань 219
пересекаются по подразбиению 351
----полному подразбиению 351
Петре теорема 241
плоская связность 242, 244
погружение 30, 277
— класса Сг 335
подмногообразие 282
подразбиение 65, 326
подразделение клеточного разбиения
330
— симплициального разбиения 193,
326
подрасслоение 28
полиэдр 326
полный дифференциал 14
— класс Понтрягина 145
----У 112
----Чженя 131
----Штифеля — Уитни 38
— стинродовский квадрат 79
полупространство евклидово 270
последовательность Гизина для век-
торных расслоений 120
послойно гомотопные отображения 59
послойное отображение 27
почти-комплексная структура 126
правило Лейбница 14
предельное множество отображения
287
примарный препятствующий класс
116—117
проективное пространство бесконеч-
ное 57
----вещественное 16, 19
—	— комплексное 133
проективный модуль 35
368 Предметный указатель
проекция векторного расслоения 16
—	касательного расслоения 291
производная 13
—	по направлению 14
простой цикл 192
пространство Пуанкаре 208
—	разбиения 65
—	расслоения 16
—	Тома 169
прямое произведение расслоений 27
прямолинейная триангуляция 332
псевдоцентральное проектирование
337
путь (гладкий) 11
пфаффиан 257
равномерная топология 296
радиус симплекса 344
разбиение единицы 285
---подчиненное покрытию 285
—	целого числа 71
размерность векторного расслоения
17
—	клетки 327
—	клеточного разбиения 331
—	многообразия 271
—	по покрытиям 288
ранг модуля 150
расслоение в смысле Гуревича 208
—	векторное 16
—	конечного типа 64
—	кусочно-линейное 205, 206
рациональное гомологическое много-
образие 192
регулярное значение 172
—	простое число 238
репер 51, 116
риманова метрика 23
--- на многообразии 292
—	связность 250
риманово многообразие 23
род Тодда 189
сапог Шварца 346
свободный цепной комплекс 94
связность 240
—	Леви — Чивиты 250
—	не имеющая кручения 250
—	симметричная 250
— согласованная с метрикой 249
— плоская 242, 244
сглаживание 302
секущее отображение, индуцирован-
ное отображением f 344
сечение векторного расслоения 19
— всюду ненулевое 19
сечения всюду независимые 21
сигнатура многообразия 183
сильная С°-аппроксимация 294
— ^-аппроксимация 293, 338
символ Кристоффеля 250
—	Шуберта 66
симметрическая функция 156
---- элементарная 156
симплекс 325
—	открытый 325
—	сингулярный 213
—	стандартный 213, 346
симплициальное отображение 193
—	разбиение 325
сингулярных гомологий группа 214
—	когомологий группа 214
— цепей группа 213
скалярное произведение 23
складывающее отображение 196
слабая топология 57
слой 17
собственное включение 276
сопряженное комплексное расслоение
139
Спивака расслоение 208
стабильная гомотопическая группа
211
стабильное многообразие Грассмана
206
стандартное продолжение подразде-
ления 333
стандартный симплекс 346
стинродовский квадрат 78
----полный 79
Стоуна теорема 59
структура гладкости 15
структурная группа 244, 313
Сулливана формула 202
сумма Уитни 28
тензор кривизны 244
тензорное произведение векторных
расслоений 32
теорема двойственности 231
----Пуанкаре 108, 114, 230
—	— Уитни 39
—	о локальной ретракции 314
---- неявной функции 280
----произведении для классов Чже-
ня 136
—	— сигнатуре 184
----существовании трубчатой окре-
стности 98
—	~~ трубчатой окрестности 317
----цилиндрической окрестности 166
Предметный указатель 369
—	об изоморфизме 93
----- обратной функции 280
—	периодичности Ботта 211
— Тома об изоморфизме 90
— Уитни о произведении 36
тихоновское пространство 35
толщина симплекса 344
Тома теорема 90, 177
— формула 78—79
тонкая топология 57
— С°-топология 294
— С‘-топология 294
— Сг-топология 296
топологическое многообразие 52
трансверсальность 172, 173
триангуляция 197, 335
— прямолинейная 332
тривиальное расслоение 17
трубчатая окрестность 98
у ( = Ву) формула 82, ПО, 115
Уайтхеда теорема 197
— топология 57, 65
угловая а-аппроксимация 338
удвоение многообразия 272, 320
Уитни теорема 36, 287
универсальное базисное пространство
206
—	комплексное расслоение 136
—	ориентированное расслоение 122
—	расслоение 55
условие локальной тривиальности 17,
124
факторрасслоение 34
фундаментальный гомологический
класс 46, 227
—	когомологический класс 78
функтор 31
—	непрерывный 32
характер Чженя 163
характеристический когомологический
класс 62, 248
характеристическое отображение для
клетки 65
цепь 218
цепное отображение 94
—	правило 273
цилиндрическая окрестность края 319
число Бернулли 234
—	Понтрягина 154
—	Чженя 153
—	Штифеля — Уитни 47
эйлерова характеристика НО
экспоненциальное отображение 98
Эрмита тождество 130
эрмитова метрика на расслоении 130
якобиан 13
^•изоморфизм абелевых групп 170
Сг-вложение 335
Сг-отображенне 272
С'-погружение 335
Сг-подмногообразие 282
Сг-три$нгуляция 335
С°-6-аппроксимация 294
Hauptvermutung 326
К-род 183
fe-сфернческое расслоение 208
К-теория 210
L-род 184
я-репер 51, 116
г-джет 25
6-аппроксимация 293, 338
Х-произведение 221
Х-умножение 220
о-умножение 219
с'»-умножение 229
/-умножение 106
ОГЛАВЛЕНИЕ
Предисловие к русскому изданию..................................... 5
Предисловие........................................................
7
§ 1.	Гладкие многообразия...................................... 9
§ 2.	Векторные расслоения......................................16
Евклидовы векторные расслоения 23
§ 3.	Построение из векторных расслоений новых расслоений .... 26
§ 4.	Классы Штифеля — Уитни....................................35
Следствия из приведенных выше четырех аксиом 37. Алгебры
с делением 44. Погружения 45. Числа Штифеля — Уитни 46
§ В.	Многообразия Грассмана и универсальные расслоения.........50
Бесконечные многообразия Грассмана 56. Универсальное
расслоение уп 57. Паракомпактные пространства 59. Характери-
стические классы вещественных n-мерных расслоений 62
§ 6.	Клеточная структура многообразий Грассмана................64
§ 7.	Кольцо когомологий И* (Gn; Z/2)...........................72
Единственность классов Штифеля — Уитни 75
§ 8.	Существование классов Штифеля — Уитни.....................77
Проверка аксиом 79
§ 9.	Ориентированные расслоения и класс Эйлера.................82
§ 10.	Теорема Тома об изоморфизме..............................82
§ 11.	Некоторые вычисления на гладких многообразиях............97
Нормальное расслоение 97. Касательное расслоение 102. Диаго-
нальный когомологический класс в На (М X Af) 105. Двойствен-
ность Пуанкаре и диагональный класс 108. Класс Эйлера и эйле-
рова характеристика 110. Формула У для классов Шти-
феля — Уитни 110.
§ 12.	Препятствия.............................................116
Последовательность Гизина для векторных расслоений 120.
Ориентированное универсальное расслоение 121. Класс Эйлера
как препятствие 122.
§ 13.	Комплексные векторные расслоения и комплексные многообразия 124
§ 14.	Классы Чженя............................................129
Эрмитовы метрики 130. Построение классов Чженя 130. Комп-
лексные многообразия Грассмана 132. Теорема о произведении
для классов Чженя 136. Двойственные и сопряженные расслое-
ния 139. Касательное расслоение комплексного проективного
пространства 141
§ 15.	Классы Понтрягина.......................................143
Когомологии ориентированного многообразия Грассмана 149
* § 16. Числа Чженя и числа Понтрягина..........................152
Разбиения 152. Числа Чженя 153. Числа Понтрягина 154. Сим-
метрические функции 155. Формула произведения 158. Линейная
независимость чисел Чженя и Понтрягина 161
Оглавление 371
§ 17.	Кольцо ориентированных кобордизмов Q*...................164
Гладкие многообразия с границей 165. Ориентированный кобор-
дизм 166
§ 18.	Пространства Тома н трансверсальность...................169
Пространство Тома евклидова векторного расслоения 169.
Гомотопические группы по модулю Ф 170. Регулярные значения
и трансверсальность 172. Основная теорема 177
§ 19.	Мультипликативные последовательности и теорема о сигнатуре 179
Мультипликативные характеристические классы 186
§ 20.	Комбинаторные классы Понтрягина.........................189
Гладкий случай 190. Комбинаторный случай 192. Некоторые при-
ложения 199
Заключение........................................................205
Негладкие многообразия 205. Гладкие многообразия с дополнитель-
ной структурой 209. Обобщенные теории когомологий 210
Приложение А. Сингулярные гомологии и когомологии.................213
Основные определения 213. Соотношение между гомологиями и кого-
мологиями 215. Гомологин клеточных разбиений 216, ^-умножение 219.
Когомологии произведения пространств 220. Г омологии многообразий 224.
Фундаментальный гомологический класс многообразия 226. Когомоло-
гии с компактными носителями 228. ^-умножение 229
Приложение В. Числа Бернулли......................................234
Приложение С. Связности, кривизна и характеристические классы .... 240
Список литературы ................................................262
Дополнение. Дж. Манкрс. Элементарная дифференциальная топология 270
Глава 1.	Дифференцируемые многообразия........................270
§ 1.	Введение.............................................270
§ 2.	Подмногообразия и вложения...........................282
§ 3.	Отображения и аппроксимации..........................289
§ 4.	Сглаживание отображений н многообразий...............303
§ 5.	Многообразия с краем.................................310
Глава II. Триангуляции дифференцируемых многообразий..........325
§ 7.	Клеточные разбиения и комбинаторная эквивалентность . . 325
§ 8.	Погружения и вложения симплициальных разбиений .... 333
§ 9.	Секущее отображение, индуцированное отображением f . . 344
§ 10.	Пригонка вложенных разбиений.........................350
Список литературы.............................................359
Литература, добавленная при переводе..............................360
Именной указатель.................................................362
Предметный указатель..............................................365
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании кни-
ги, ее оформлении, качестве перевода и
другие просим присылать по адресу:
129820, Москва, И-110, ГСП, 1-й Риж-
ский пер., д. 2, издательство «Мир».
Дж. Милнор,
Дж. Сташеф
ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
Старший научный редактор В. И. Авербух
Младший научный редактор А. Н. Сандерова
Художник И. М. Пучков
Художественный редактор В. И. Шаповалов
Технический редактор Н. И. Борисова
Корректор Н. Н. Баранова
ИБ № 1473
Сдано в набор 15.01.79. Подписано к печати 17.10.79. Формат бОХЭО’/ы. Бумага типограф-
ская № 1. Гарнитура латинскаи. Печать высокая. Объем 11,75 бум. л. Усл. печ.
л. 23,50. Уч.-изд. л. 21,22. Изд. № 1/9795. Тираж 6 500 экз. Заказ № 64. Цена 1 р. 90 к.
Издательство «Мир»
129820, Москва, И-110, ГСП, 1-й Рижский пер., 2.
Ордена Трудового Красного Знамени Ленинградская типография № 2 имени Евгении Со-
коловой «Союзполиграфпрома» при Государственном комитете СССР по делам издательств,
полиграфии и книжной торговли. 198052, Ленинград, Л-52. Измайловский проспект, 29
В ИЗДАТЕЛЬСТВЕ «МИР»
ГОТОВИТСЯ К ВЫПУСКУ
Гомотопическая теория дифференциальных форм: Сб. статей
1977. Пер. с англ., 10 л., 1 р. 20 к.
Сборник содержит работы зарубежных математиков по сим-
плицнальной теории де Рама и ее обобщениям. В целом они
дают хорошее представление о развитии этого нового раздела
алгебраической топологии за последние годы и вместе с тем яв-
ляются удачным введением в предмет. Средн авторов — такие
известные математики, как А. Бусфельд, В. Гугенхейм, Д. Кан,
Д. Леманн, Э. Миллер, Р. Сваи.
Книга представляет интерес для математиков различных спе-
циальностей и будет полезна аспирантам и студентам старших
курсов математических специальностей университетов.
Уважаемый читатель!
Заблаговремеино оформляйте заказы иа интересующие Вас
книги. Заказы принимаются в магазинах, торгующих научно-тех-
нической литературой.
6 ИЗДАТЕЛЬСТВЕ «МИР»
готовится К ВЫПУСКУ
Исследования по метрической теории поверхностей: Сб. ста-
тей 1977. Пер. с англ., 14 л., 1 р. 10 к.
Сборник статей зарубежных математиков содержит новые
результаты в области дифференциальной геометрии, полученные
в последние годы. В статьях первой части рассматривается и
разрешается вопрос об определении римановой метрики по за-
данной ее кривизне. Во второй части сборника приведены статьи,
относящиеся к вопросам изометрических деформаций поверхно-
стей и изометрических погружений метрик. Среди авторов из-
вестные математики — Г. Глюк, Д. Зингер, Р. Коннели, Н. Кюй-
пер.
Книга рассчитана на математиков различных специальностей,
она будет полезным учебным пособием для аспирантов и сту-
дентов старших курсов университетов.
Уважаемый читатель!
Заблаговременно оформляйте заказы на интересующие Вас
книги. Заказы принимаются в магазинах, торгующих научно-тех-
нической литературой.