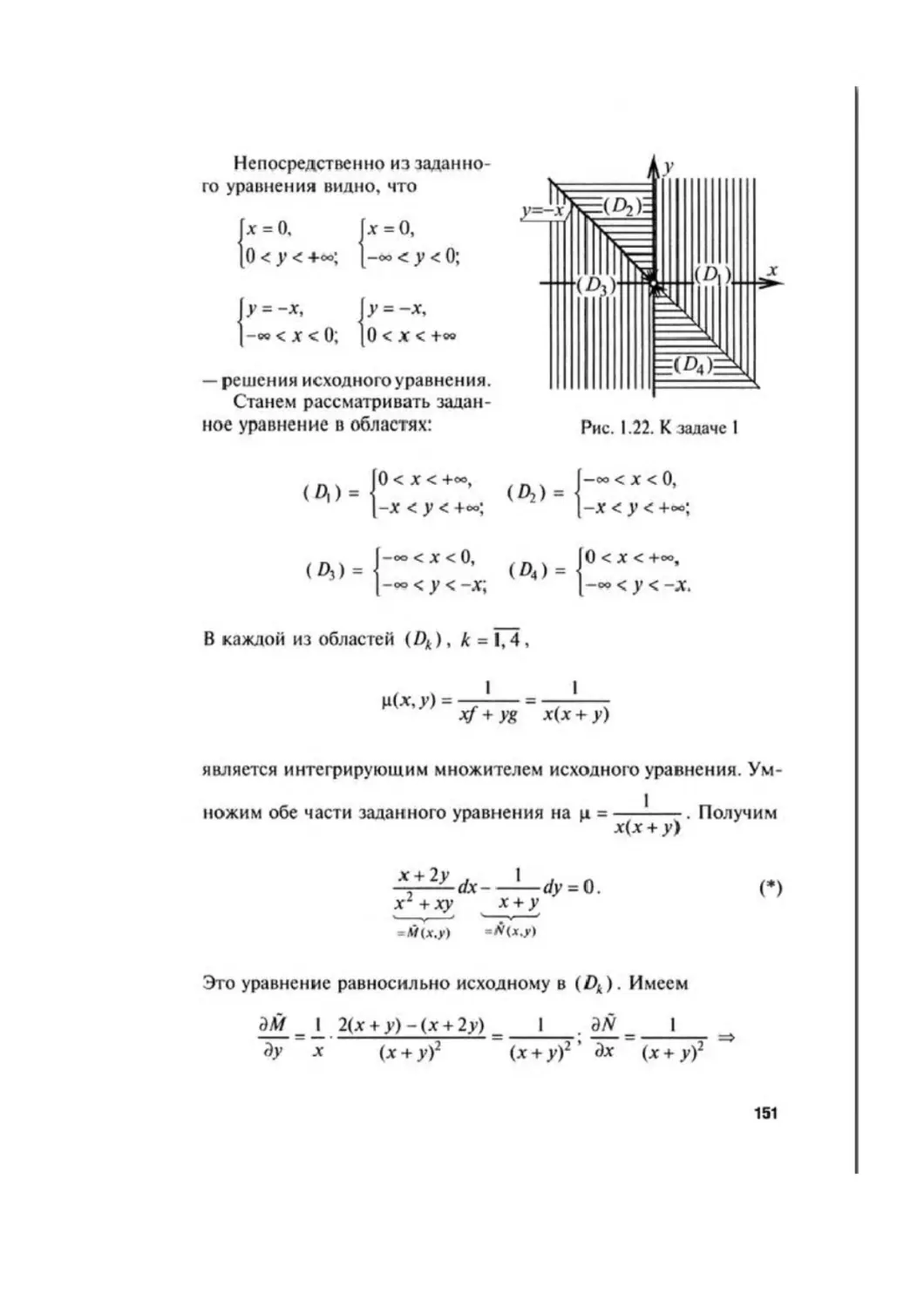
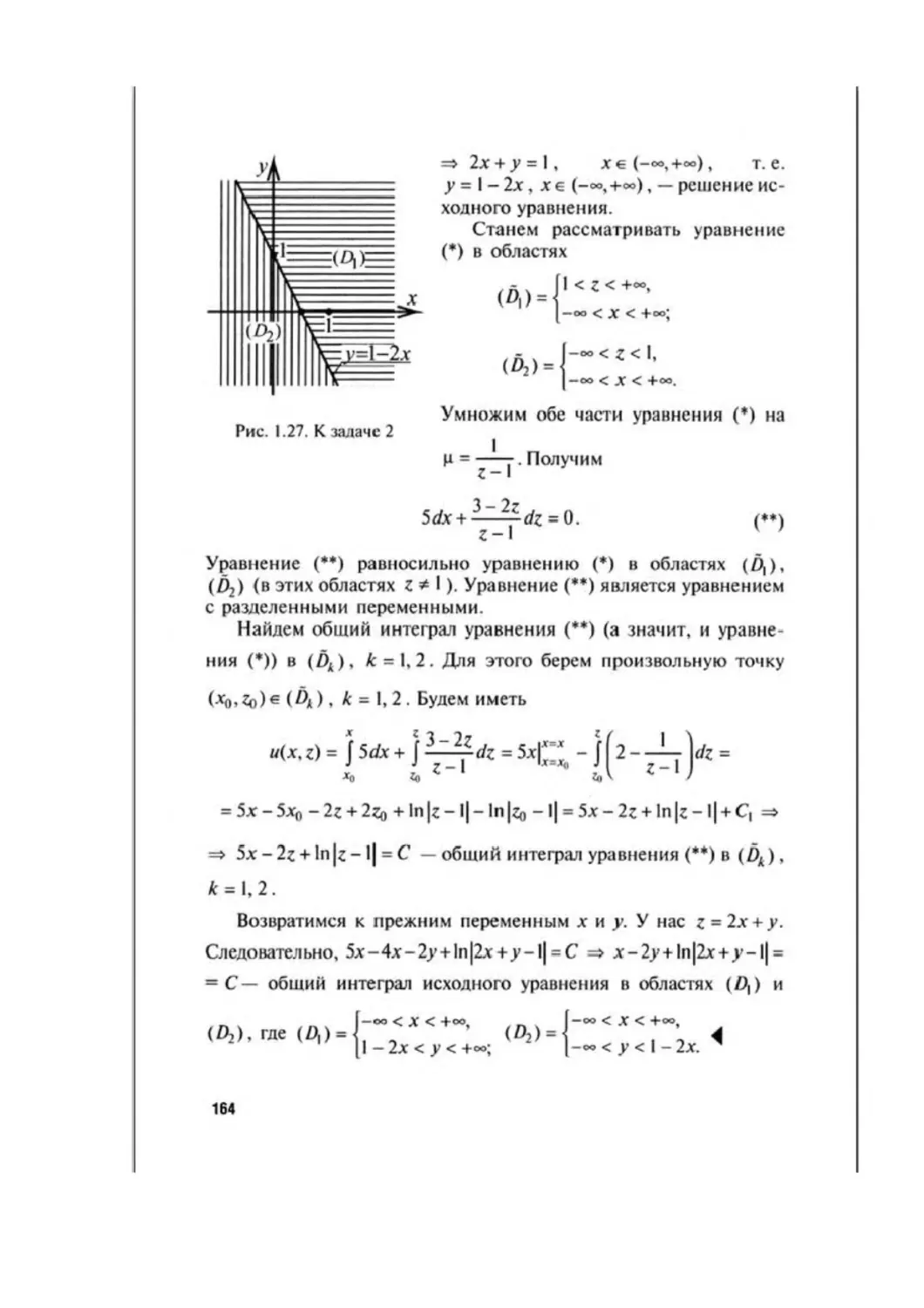
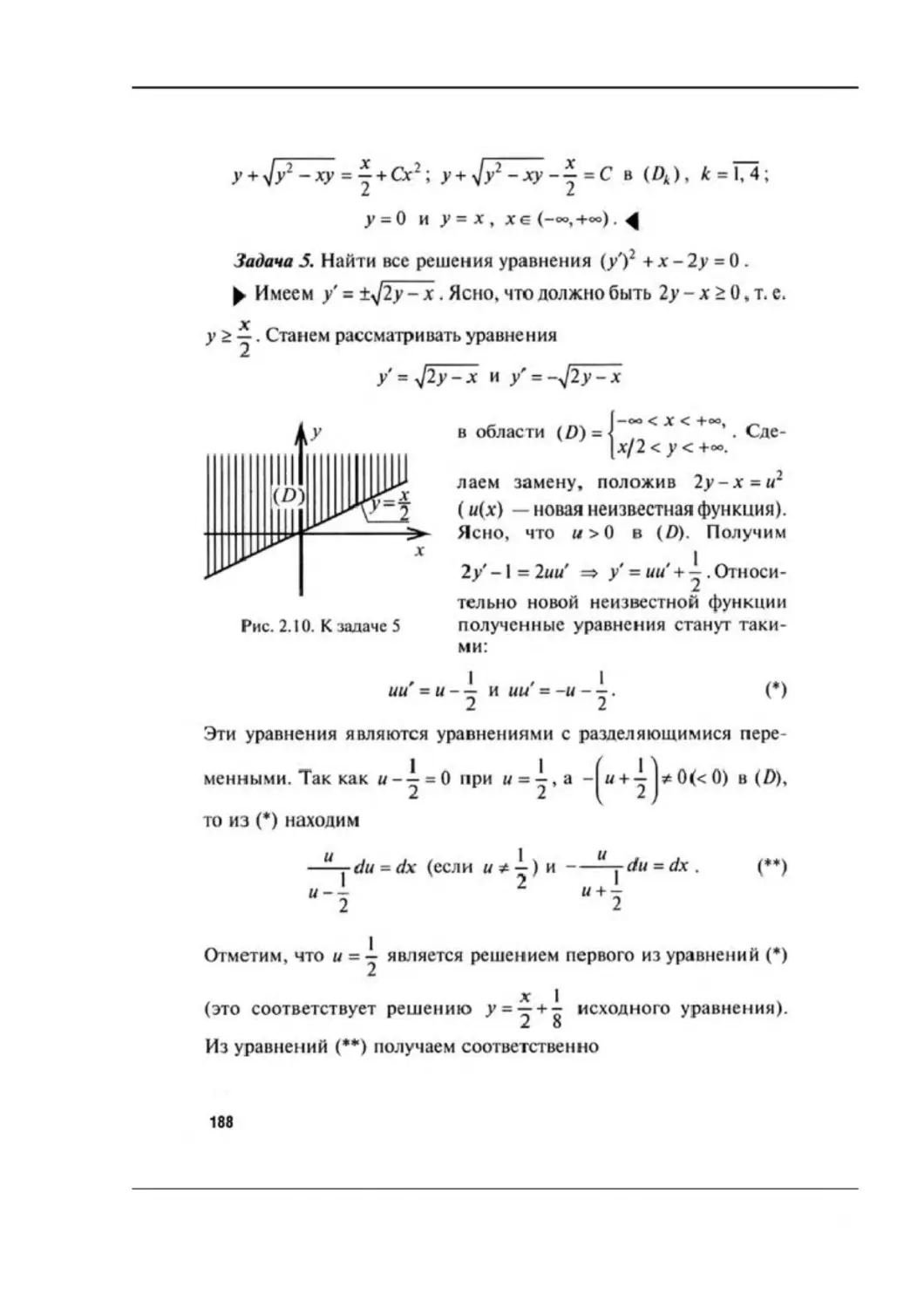
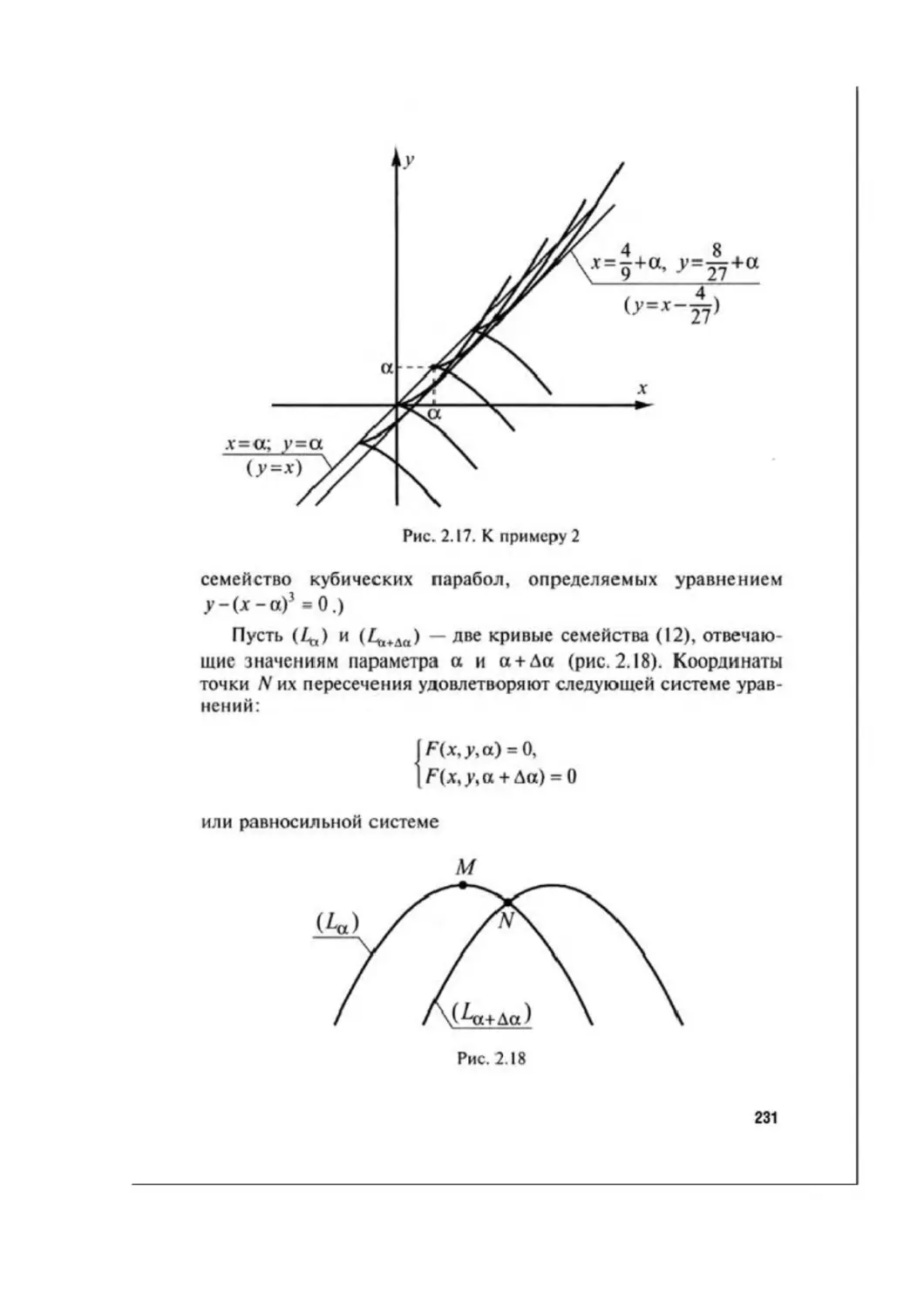
Автор: Аксенов А.П.
Теги: дифференциальные, интегральные и другие функциональные уравнения конечные разности вариационное исчисление функциональный анализ математический анализ высшая математика дифференциальные уравнения
ISBN: 978-5-9916-5873-7
Год: 2016
л
САНКТ-ПЕТЕРБУРГСКИЙ
ПОЛИТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ ПЕТРА ВЕЛИКОГО
А. П. Аксенов
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
Том 1
УЧЕБНИК И ПРАКТИКУМ
ДЛЯ АКАДЕМИЧЕСКОГО БАКАЛАВРИАТА
Рекомендовано Учебно-методическим отделом
высшего образования в качестве учебника для студентов
высших учебных заведений, обучающихся по техническим
направлениям и специальностям
Допущено Министерством образования и науки
Российской Федерации в качестве учебника для студентов
высших учебных заведений, обучающихся по техническим
специальностям
Книга доступна в электронной библиотечной системе
biblio-online.ru
Москва Юрайт 2016
УДК 517.9
ББК 22.161.1я73
А42
Автор:
Аксенов Анатолий Петрович кандидат физико-математических
наук, профессор кафедры высшей математики Института прикладной мате-
матики и механики Санкт-Петербургского государственного политехниче-
ского университета.
Рецензенты:
Кудрявцев Л. Д. — доктор физико-математических наук, профессор,
заведующий кафедрой высшей математики Московского физико-техниче-
ского института, старший научный сотрудник Математического института
имени В. А. Стеклова;
Розанова С. А. — доктор педагогических наук, профессор кафедры выс-
шей математики Московского государственного института радиотехники,
электроники и автоматики;
Карасев В. А. кандидат технических наук, доцент Московского госу-
дарственного института стали и сплавов.
Аксенов, А. П.
А42 Дифференциальные уравнения. В 2 т. Т. 1 : учебник и практикум для
академического бакалавриата / А. П. Аксенов. М.: Издательство Юрайт,
2016. — 241 с. — Серия: Бакалавр. Академический курс.
ISBN 978-5-9916-5873-7
ISBN 978-5-9916-5874-4 (т. 1)
Данная книга представляет собой первый том двухтомного учебника
«Обыкновенные дифференциальные уравнения», который издается в рам-
ках авторского цикла учебников по разделам высшей математики.
Содержание учебника полностью охватывает программу по курсу обык-
новенных дифференциальных уравнений для технических вузов с углуб-
ленным изучением математики. В первый том включены материалы по диф-
ференциальным уравнениям первого порядка.
Разобрано большое количество примеров и задач, разъясняющих основ-
ные идеи, понятия, теоретические <|>акты и их практическое применение. Все
сформулированные теоремы (трудные и простые), как правило, доказываются.
Соответствует актуальным требованиям Федерального госуда|ктвсн-
ного образовательного стандарта высшего образования.
Для студентов высших технических учебных заведений. Может быть
использован для самостоятельной подготовки и повышения квалификации.
УДК 517.9
ББК 22.161.1я73
Все права защищены. Никакая часть данной книги не может быть воспроизведена
Ж в какой бы то ни было форме без пис именного разрешения владельцев авторских, прав,
мв» I Правовую поддержку издательства обеспечивает юридическая компания «,Дельфи ».
ISBN 978-5-9916-5873-7
ISBN 978-5-9916-5874-4 (т.1)
© Аксенов А. П„ 2015
© ООО «Издательство Юрайт», 2016
Оглавление
Предисловие к циклу учебников по высшей математике..........4
Предисловие ................................................8
Введение...................................................12
Глава I. Дифференциальные уравнения первого порядка,
разрешенные относительно производной.......................22
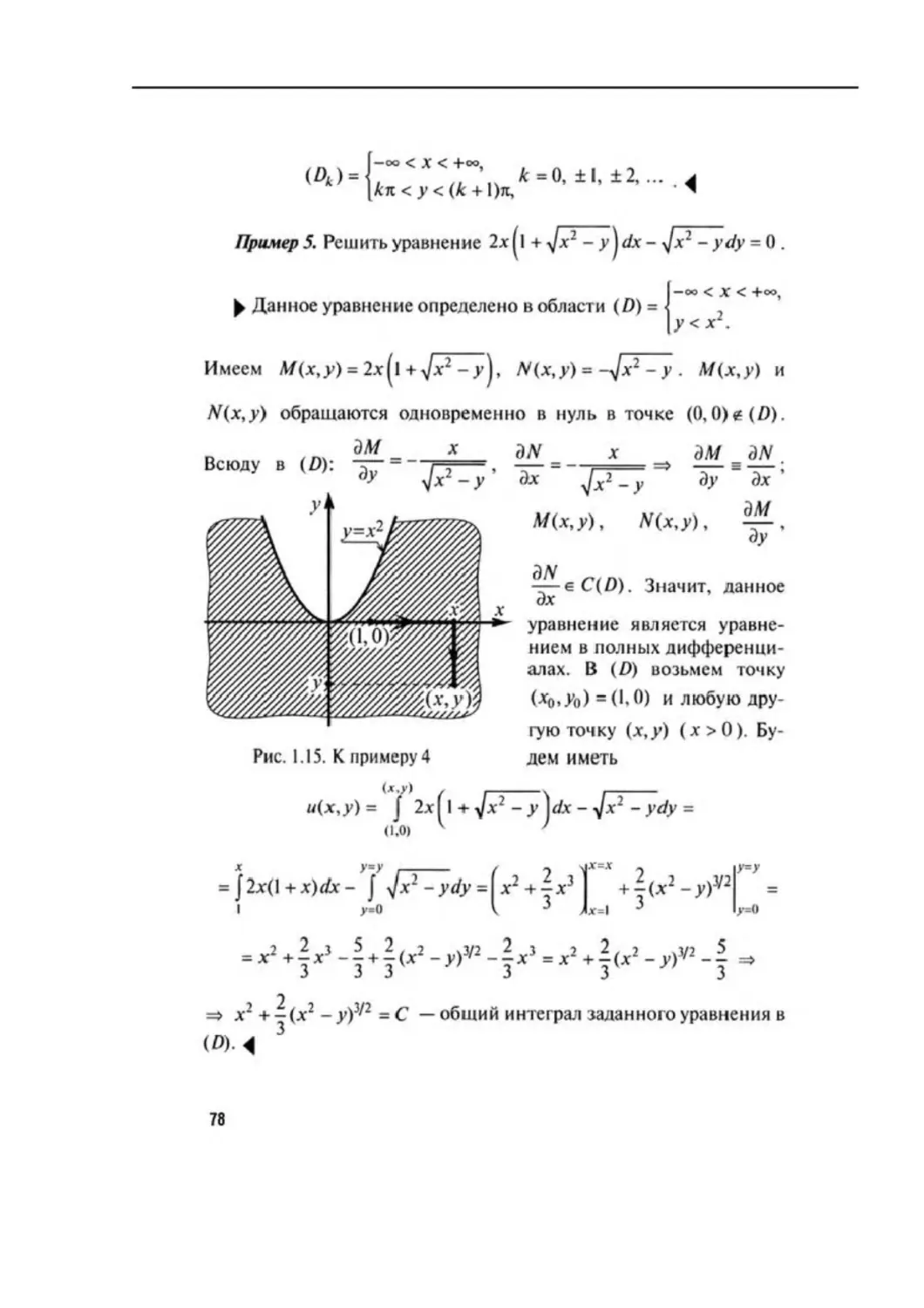
§1 . Основные понятия и определения.....................22
§2 . Существование решения задачи Коши..................34
§3 . Единственность решения задачи Коши.................44
§4 . Общее, частное и особое решения уравнения у' = f(x, у)...................48
§5 . Дифференциальные уравнения первого порядка в
симметричной форме......................................50
§6, Общий интеграл уравнения в симметричной форме.......58
§7 . Уравнение в полных дифференциалах..................66
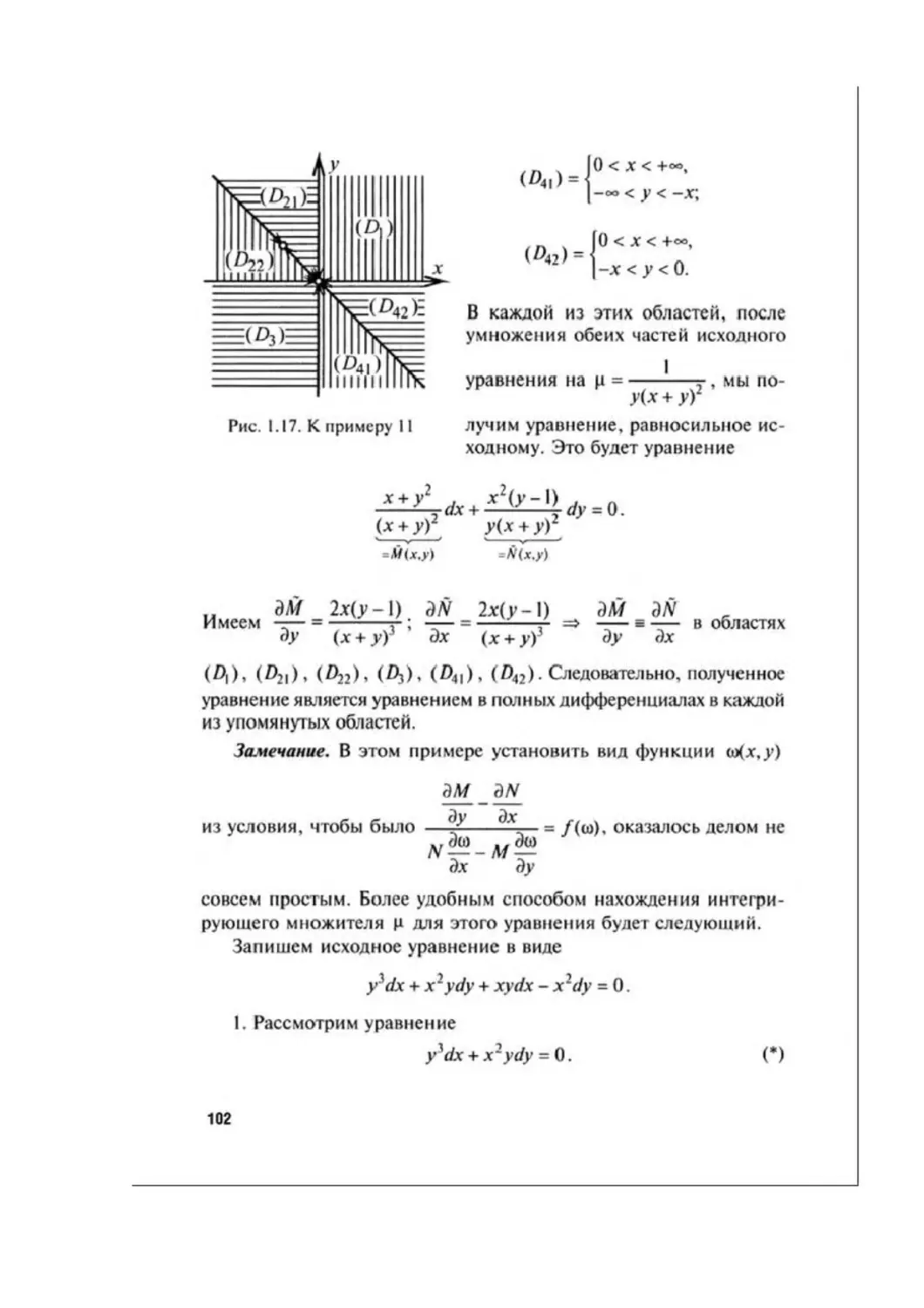
§8, Интегрирующий множитель.............................79
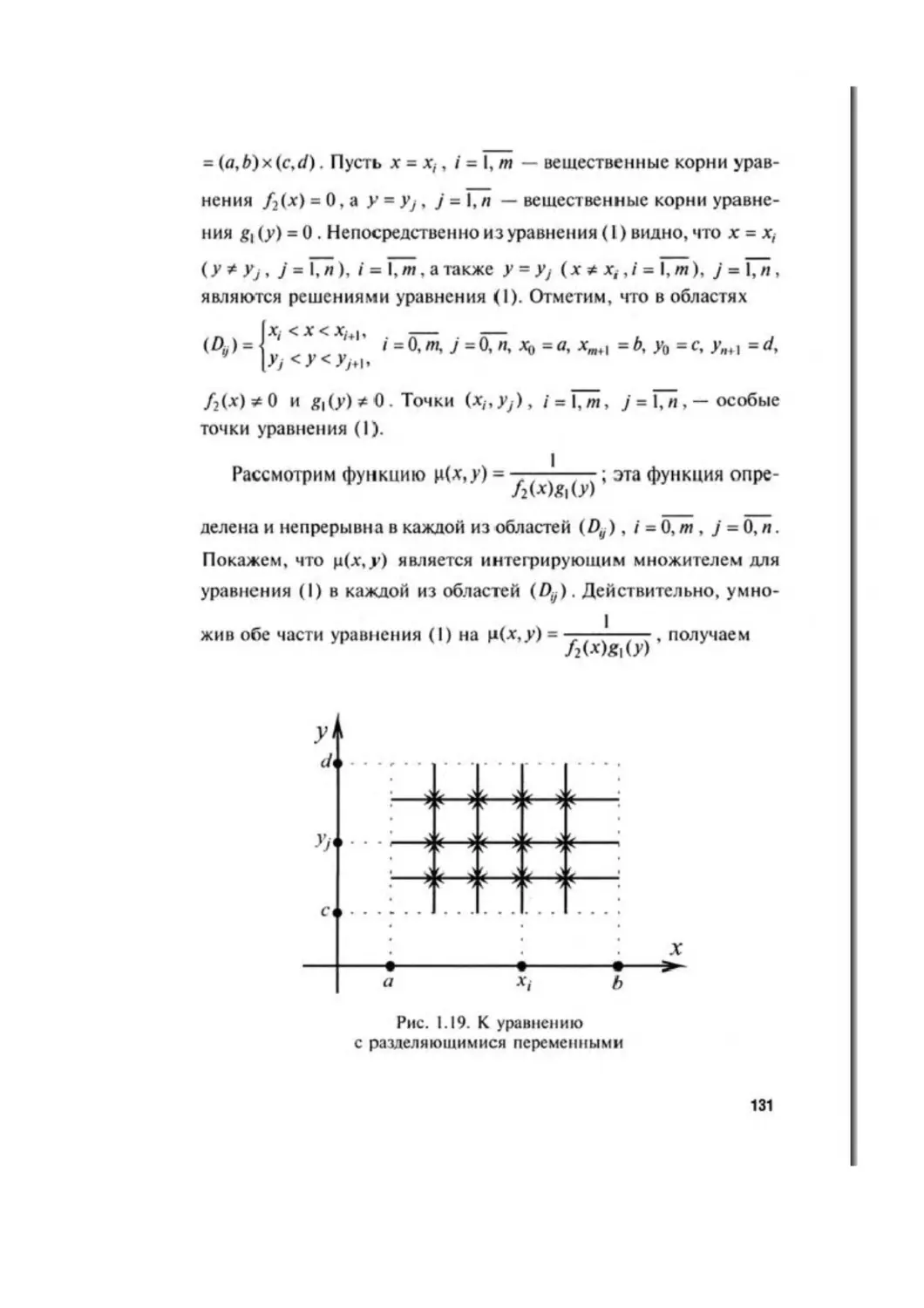
§9 . Уравнения с разделяющимися переменными............130
§10 . Линейные уравнения первого порядка...............134
§11 . Уравнение Бернулли...............................139
§12 . Однородные уравнения........................... 148
§13 . Простейшие уравнения, приводящиеся к однородному.158
Глава 2. Дифференциальные уравнения первого порядка,
не разрешенные относительно производной.......... 173
§1 . Основные понятия и определения....................173
§2 . Метод введения параметра..........................180
§3 . Примеры и задачи к главе 2........................184
§4 . Огибающая и дискриминантная кривая
однопараметрического семейства плоских кривых..........226
§5 . Особое решение обыкновенного дифференциального
уравнения как огибающая семейства интегральных кривых..237
Предисловие к циклу учебников
по высшей математике
Вашему вниманию предлагается цикл книг по разделам выс-
шей математики (математический анализ, обыкновенные диффе-
ренциальные уравнения, теория функций комплексной перемен-
ной), составленных на основе курсов лекций, читаемых автором
в Санкт-Петербургском государственном политехническом уни-
верситете.
Основанием для написания цикла послужило желание дать
достаточное по строгости, глубине и доходчивости изложение
основ высшей математики.
Возникшая еще в древности из практических потребностей
математика выросла к настоящему времени в громадную систему
разветвленных дисциплин. Как и другие науки, она отражает
законы материальной действительности и служит важным инстру-
ментом познания природы. Одной из характерных особенностей
математики является исключительная широта ее применения.
Во-первых, мы постоянно — на производстве, в быту, в обще-
ственной жизни — пользуемся наиболее распространенными поня-
тиями и выводами математики, вовсе не задумываясь об этом. Так,
мы применяем арифметику, считая дни или расходы, а подсчиты-
вая площадь квартиры, используем формулы геометрии. Формулы
эти, конечно, очень простые, но следует знать, что когда-то в древ-
ности они были одним из высших достижений зарождавшейся
тогда математики.
Во-вторых, вся современная техника была бы невозможна без
математики, так как без расчетов не обходится ни одно техниче-
ское усовершенствование. Наконец, почти все науки в той или
иной степени пользуются математикой. Точные науки — механика,
астрономия, физика, а также в большой мере и химия — обычно
выражают свои законы формулами и развивают свои теории,
широко используя математический аппарат. Без математики про-
гресс этих наук был бы просто невозможен.
Приведем несколько примеров особенно блестящих примене-
ний математики в точных науках и технике. Одна из самых дале-
4
ких планет солнечной системы — Нептун была открыта в 1846 г.
на основании математических расчетов. Анализируя “неправиль-
ности” в движении планеты Уран, астрономы Д. Адамс и У. Леве-
рье пришли к выводу, что они вызваны притяжением другой пла-
неты. Леверье на основании законов механики и закона тяготения
вычислил, где эта планета должна находиться, и наблюдатель,
которому он об этом сообщил, увидел ее в телескоп там, где ука-
зал Леверье. Это открытие было триумфом не только механики
и астрономии, но также и математического расчета.
Другой, не менее убедительный пример — открытие электромаг-
нитных волн. Английский физик Дж. Максвелл, обобщая установ-
ленные опытами законы электромагнитных явлений, выразил эти
законы в виде уравнений. Из уравнений он чисто математически
вывел, что могут существовать электромагнитные волны и что они
должны распространяться со скоростью света. Опираясь на это, он
предложил электромагнитную теорию света, которая затем была
всесторонне развита и обоснована.
Но кроме того, вывод Максвелла подтолкнул ученых на пои-
ски электромагнитных волн чисто электрического происхождения,
например испускаемых при колебательном разряде. Такие волны,
действительно, были открыты Г. Р. Герцем. А вскоре А. С. Попов
нашел средства возбуждения, передачи и приема электромагнит-
ных колебаний, вывел их в область широких применений и поло-
жил тем самым начало всей радиотехнике. Таким образом, в откры-
тии радио, ставшего общим достоянием, большую роль сыграли
также результаты чисто математического вывода.
Так от наблюдений наука идет к обобщению, к теории явле-
ний, к формулировке законов и их математическому выраже-
нию. Из этих законов рождаются новые выводы, и, наконец, тео-
рия воплощается в практике, которая в свою очередь дает теории
новые мощные импульсы к развитию.
Замечательно еще и то, что часто даже самые абстрактные
построения математики, возникшие внутри нее самой, уже без
непосредственного влияния со стороны естествознания или тех-
ники находят тем не менее плодотворные применения. Например,
понятие о мнимых числах появилось в алгебре, и долго их реаль-
ный смысл оставался непонятным, на что указывает само их назва-
ние. Однако после того, как им было дано геометрическое толко-
вание, мнимые числа вполне укрепились в математике, и возникла
обширная теория функций комплексной переменной. Эта теория,
так сказать, “мнимых” функций от “мнимых” переменных оказалась
вовсе не мнимым, а очень реальным средством решения вопросов
техники. Так, основная теорема Н. Е. Жуковского о подъемной силе
5
крыла самолета доказывается как раз средствами этой теории. Та же
теория оказывается полезной при решении задач, например о про-
сачивании воды под плотинами — задач, значение которых очевидно
в период строительства крупных электростанций.
В настоящее время благодаря появлению быстродействующих
вычислительных машин произошел большой качественный скачок
в использовании математических методов, которые стали приме-
няться не только в тех областях, где математика использовалась
уже давно, но и в тех областях человеческих знаний, где либо мате-
матика еще совсем недавно применялась мало, либо ее применение
даже не представлялось возможным (медицина, экономика, линг-
вистика, социология и т.п.).
Современный научный работник или инженер должен хорошо
владеть математическими методами исследования, которые могут
применяться в сфере его деятельности. Для того чтобы иметь воз-
можность применять математические методы при изучении того
или иного вопроса, нужно прежде всего уметь правильно использо-
вать математический аппарат, знать границы допустимого исполь-
зования рассматриваемой математической модели.
Свободное владение математическими методами накапливается
и развивается в процессе систематических занятий, в результате
длительной и настойчивой работы. Кто последовательно овладе-
вает математическим аппаратом, приобретает твердое и точное зна-
ние математических фактов, тот легко и просто двигается дальше,
приобретает уверенность в способности и умении справиться
с встречающейся ему задачей, и математика делается послушным
инструментом в его руках.
Большая польза от изучения математики состоит еще и в том,
что оно (изучение) совершенствует общую культуру мышления,
дисциплинирует человека, приучает логически рассуждать, воспи-
тывает точность и обстоятельность аргументации.
Математика учит не загромождать исследование ненужными
подробностями, не влияющими на сущность дела, и наоборот,
не пренебрегать тем, что имеет принципиальное значение для
существа изучаемого процесса.
Овладеть в достаточной .мере математическим .методом, мате-
матической культурой мышления — далеко не простая задача.
Но для того, кто сумеет этого достичь, труд не пропадет зря. Для
него откроются новые перспективы человеческой деятельности,
качественно новые возможности творчества и познания мира.
Помочь в этом и призван предлагаемый цикл учебников.
Автор посчитал полезным сделать изложение вопросов теории
очень подробным и сопроводить его большим числом разобранных
6
примеров и задач. Он исходил из убеждения, что такое построение
курса поможет студентам быстрее овладеть практическими рецеп-
тами решения тех или иных задач, а также понять глубокие общие
идеи, из которых эти рецепты возникают.
Помимо книг, указанных в списках литературы, указанных
в учебниках, для их написания автором использованы материалы
лекций, которые ему посчастливилось слушать в Ленинградском
(ныне Санкт-Петербургском) государственном университете.
С искренней благодарностью автор вспоминает своих учителей —
профессоров В. И. Смирнова, Г. М. Фихтенгольца, А. Ф. Андреева,
Г. М. Голузина, И. П. Натансона, Д. К. Фаддеева, блестящие лекции
которых оставили у него неизгладимое впечатление.
Автор приносит глубокую благодарность доценту кафедры выс-
шей математики СПбГПУ А. В. Ястребову за большую помощь
в работе над циклом книг, а также за целый ряд полезных советов.
Автор выражает свою искреннюю признательность проректору
СПбГПУ В. Н. Козлову за внимание, проявленное им к работе над
учебниками.
7
Предисловие
Данный учебник является вторым в цикле учебников автора
по разделам высшей математики и посвящен теории обыкновен-
ных дифференциальных уравнений. Книга разделена на два тома.
Учебник “Дифференциальные уравнения” составлен на основе
курса лекций, читаемых автором в Санкт-Петербургском государ-
ственном политехническом университете.
Теория дифференциальных уравнений — важнейшая ветвь
математического анализа — имеет дело с такими уравнениями,
где неизвестной является уже не величина, а функция, т.е. закон
зависимости одной величины от другой или от нескольких других
величин.
Большое значение, которое имеют дифференциальные уравне-
ния для математики, и особенно для ее приложений, объясняется
главным образом тем, что к решению таких уравнений может быть
приведено исследование многих физических проблем и техниче-
ских задач. В механике, астрономии, физике, технике с помощью
дифференциальных уравнений были достигнуты огромные успехи
(например, И. Ньютон, исследуя дифференциальные уравнения
движения тел, вывел законы движения планет, установленные
И. Кеплером эмпирически; У. Леверье предсказал существование
планеты Нептун и определил ее положение на небе на основе чис-
ленного анализа тех же уравнений).
Настоящий учебник предназначен для студентов высших тех-
нических учебных заведений. Он может быть использован и для
самостоятельной подготовки и повышения квалификации по дис-
циплинам “Математический анализ”, “Высшая математика”
и “Дифференциальные уравнения”.
Цель книги — помочь студентам в формировании их матема-
тического мышления, выработке практических навыков решения
и исследования дифференциальных уравнений, описывающих эво-
люционные процессы в различных областях естествознания. Для
достижения этой цели автор посчитал необходимым сделать изло-
жение теории очень подробным и сопроводить его большим чис-
лом разобранных примеров и задач. Приведены подробные реше-
8
пня более 250 задач, разъясняющих основные идеи, теоретические
факты и их практическое применение.
Содержание учебника полностью охватывает программу
по курсу обыкновенных дифференциальных уравнений для техни-
ческих вузов с углубленным изучением математики. В первый том
включены материалы по дифференциальным уравнениям первого
порядка.
В учебнике все высказанные теоремы — и трудные, и простые —
как правило, доказываются. Это является следствием убежденно-
сти автора в том, что распространенная тенденция устранять труд-
ности в учебниках и изустных курсах за счет строгости и глубины,
за счет подмены доказательств некоторыми их подобиями — вред-
ная, поскольку фиктивные “доказательства” смазывают трудности
и лишают обучение одной из важнейших его сторон — формирова-
ния у студентов одной из наиболее ценных компетенций — навы-
ков к логически правильному мышлению.
Для успешного овладения материалом обучающиеся должны
хорошо знать школьный курс математики и владеть навыками
логического и алгоритмического мышления, а также математиче-
скими методами решения задач согласно требованиям стандартов
среднего образования.
Согласно последним требованиям ФГОС ВО в результате
изучения курса “Обыкновенные дифференциальные уравнения”
по данному учебнику обучающиеся должны:
знать
• основные понятия, теоретические основы, положения
и методы теории обыкновенных дифференциальных уравнений;
• методы решения прикладных задач, базирующиеся на поста-
новке задач и формулировке начальных и граничных условий для
дифференциальных уравнений, интегрировании дифференциаль-
ных уравнений, исследовании свойств их решений и т.п.;
• современные представления о переводе задач моделирова-
ния реальных процессов и явлений на математический язык тео-
рии дифференциальных уравнений, выборе методов их решения,
в том числе и численных, оценке полученных результатов;
уметь
• использовать полученные знания о математических поня-
тиях, методах и моделях дифференциальных уравнений в практи-
ческой деятельности и при изучении иных естественнонаучных,
общепрофессиональных и специальных дисциплин;
• применять теоретические знания к реальным ситуациям для
математического исследования встречающихся в приложениях
9
эволюционных процессов, а также анализа и интерпретации полу-
ченных результатов;
• выбирать необходимые методы теории дифференциальных
уравнений для решения поставленных задач и реализации алго-
ритмов;
• самостоятельно расширять и углублять полученные матема-
тические знания, изучать новую математическую литературу, обоб-
щать и систематизировать вновь поступающие сведения по теории
дифференциальных уравнений;
• давать самостоятельные оценки эффективности употребляе-
мых алгоритмов решения дифференциальных уравнений;
• самостоятельно формулировать, обосновывать и строго
логически и математически доказывать утверждения теории диф-
ференциалы 1ых уравнений;
владеть
• методами математического моделирования фундаменталь-
ных и прикладных проблем с помощью дифференциальных урав-
нений и выработки наиболее эффективных алгоритмов их реше-
ния;
• навыками решения дифференциальных уравнений, возника-
ющих в ходе математического моделирования реальных процессов
и явлений на практике;
• навыками работы с учебной и научной математической лите-
ратурой для поиска необходимой для решения дифференциальных
уравнений информации;
• современными технологиями анализа и информационной
поддержки решения поставленных задач.
На основе полученных знаний у обучающихся формируются
следующие общекультурные и профессиональные компетенции:
• способность к обобщению, анализу, восприятию информа-
ции, постановке цели и выбору путей ее достижения;
• готовность использовать основные законы и методы теории
дифференциальных уравнений в профессиональной деятельности,
в теоретических и экспериментальных исследованиях;
• способность представить адекватную современному уровню
знаний научную картину мира на основе знания основных поло-
жений, законов и методов теории дифференциальных уравнений;
• умение выявить математическую сущность проблем, воз-
никающих в ходе профессиональной деятельности, привлечь для
решения дифференциальных уравнений, возникающих при моде-
лировании, соответствующий физико-математический аппарат;
• способность разрабатывать математические модели объек-
тов профессиональной деятельности в форме дифференциальных
10
уравнений, применять необходимые для построения моделей зна-
ния принципов действия и математического описания различных
систем (информационных, механических, электронных и т.н.),
а также определять характеристики объектов по разработанным
моделям на базе решения дифференциальных уравнений;
• навыки владения основными приемами математической
обработки и представления экспериментальных данных в виде
дифференциальных уравнений и соответствующих начальных
и граничных условий.
ВВЕДЕНИЕ
Уравнения, с которыми мы встречались до сих пор, служили
преимущественно для отыскания численных значений тех или
иных величин. Однако в приложениях математики часто возника-
ют качественно новые задачи, в которых неизвестной является
сама функция, сам закон зависимости одних переменных от
других. Например, изучая процесс охлаждения тела, мы должны
определить, как будет изменяться с течением времени его темпе-
ратура, при определении движения планеты нам необходимо
определить зависимость ее координат от времени и т. д.
Наиболее важными из уравнений, служащих для разыскания
функций, являются так называемые дифференциальные уравнения.
Под этим названием понимают уравнения, в которые входит не
только сама неизвестная функция, но и ее производные некото-
рых порядков.
Нижеследующие равенства могут служить примерами диффе-
ренциальных уравнений:
dx . . , d2x 2
— + p(j)x = Q(t)\ —г + in х = /I sin cor;
dt dr
du _ d2U d2U _ d2U d2U d2U (Ь
df dx2 ’ dt2 dx2 ’ dx2 dy2
В первых двух из них неизвестная функция обозначена бук-
вой х, а буквой г— независимая переменная; в последних же
трех неизвестная функция обозначена буквой и, и она зависит от
двух аргументов хи г или х и у.
Большое значение, которое имеют дифференциальные урав-
нения для математики и особенно для ее приложений, объясняет-
ся главным образом тем, что к решению таких уравнений может
12
быть приведено исследование многих физических проблем и тех-
нических задач. В механике, астрономии, физике, технике с
помощью дифференциальных уравнений были достигнуты ог-
ромные успехи. Ньютон, исследуя дифференциальные уравнения
движения тел, получил законы движения планет, установленные
Кеплером эмпирически. Леверье в 1846 г. предсказал существова-
ние планеты Нептун и определил ее положение на небе на основе
численного анализа тех же уравнений.
Ниже будет показано, что каждое дифференциальное уравне-
ние определяет, вообще говоря, целый класс функций, ему удов-
летворяющих. Теория дифференциальных уравнений должна дать
возможность получить достаточно полное представление о свой-
ствах всех этих функций. Кроме того, она должна обеспечить
средства для нахождения численных значений функций, если это
потребуется для расчетов.
Если неизвестная функция зависит от одного аргумента, то
дифференциальное уравнение называется обыкновенным диффе-
ренциальным уравнением. В том случае, когда неизвестная функция
зависит от нескольких аргументов и в уравнение входят произ-
водные по нескольким аргументам, дифференциальное уравне-
ние называется уравнением с частными производными. Первые два
из уравнений (I) являются обыкновенными, а последние три —
уравнениями с частными производными.
Теория уравнений с частными производными обладает многи-
ми своеобразными чертами, существенно отличающими ее от
теории обыкновенных дифференциальных уравнений. Основные
идеи, связанные с такими уравнениями, излагаются в курсе мате-
матической физики; мы же в этом пособии будем рассматривать
только обыкновенные дифференциальные уравнения.
Дадим теперь точные определения.
1. Обыкновенным дифференциальным уравнением называется
любое соотношение, связывающее независимую переменную х,
искомую функцию у = у(х) и производные искомой функции
у(х) до некоторого порядка включительно.
Обыкновенное дифференциальное уравнение может быть при-
ведено к виду
F(x,y,y', = 0. (I)
Здесь Е(х,у,у\ ...,у(л)) — известная функция, заданная в неко-
торой области (G) с R”+2.
2. Число п (п е N , п > I), т. е. наивысший из порядков произ-
водных, входящих в (1), называется порядком уравнения.
13
X
Например, уравнение: у' + ху-е 2 =0 является уравнением
первого порядка, а уравнение: у + у* - х = 0 — уравнением второ-
го порядка.
3. Функция у = (р(х) называется решением уравнения (1) в
промежутке (а,Ь) (случаи а = -*>, Ь = +«> не исключаются), если
подстановка функции у = ф(х) в дифференциальное уравнение
(I) превращает последнее в тождество по х на {а,Ь). При этом
предполагается, что функция ф(х) имеет в {а, Ь) непрерывные
производные до порядка п включительно и что точка
(х,ф(х),ф'(х), ф(''*(х)) принадлежит области задания функции
F при любом х из (а, Ь).
Процесс нахождения решений дифференциального уравне-
ния (I) называется интегрированием этого уравнения.
График решения у = ф(х), хе {а,Ь) уравнения (I) на плоско-
сти Оху называется интегральной кривой.
Простейшим примером дифференциального уравнения явля-
ется уравнение: у' = /(х), где /(х) — известная функция, опре-
деленная и непрерывная на некотором интервале (а, Ь) оси Ох, а
у = у(х) — искомая функция независимой переменной х. Реше-
ниями этого уравнения являются первообразные функции для
X
функции /(х) , а именно у(х) = j f(x)dx + С , где х0 и х е (а, Ь),
„ *»
а С— произвольная постоянная.
Придавая постоянной С различные значения, мы получим
бесконечное множество решений уравнения у' = f(x). Отметим,
что иметь бесконечное множество решений — характерное свой-
ство дифференциальных уравнений. В этом смысле приведенный
выше пример типичен. Поэтому, решив дифференциальное урав-
нение, описывающее эволюцию некоторого процесса, нельзя счи-
тать, что мы нашли зависимость между величинами, характеризу-
ющими данный процесс. Чтобы выделить из бесконечного
множества зависимостей ту, которая описывает именно этот про-
цесс, нужно иметь дополнительную информацию, например, знать
начальное состояние процесса. Без этого дополнительного усло-
вия задача недоопределена.
Рассмотрим несколько конкретных задач, приводящих к диф-
ференциальным уравнениям.
Задана 1. В резервуаре имеется р кг водною раствора соли, в
котором содержится q кг соли. В определенный момент включается
14
устройство, непрерывно подающее в резервуар г кг чистой воды в
секунду и одновременно удаляющее из него г кг раствора. При этом
в самом резервуаре жидкость непрерывно перемешивается.
Вопрос: как изменяется со временем количество соли в резер-
вуаре?
Момент начала процесса примем за начало отсчета време-
ни !. Пусть y{t) — искомая функция, выражающая в каждый
момент / количество соли в резервуаре. В силу условия задачи и
соглашения об отсчете времени, имеем: у(0) = q . Это пока един-
ственное значение искомой функции, которое нам известно.
Поначалу кажется, что основная трудность задачи будет со-
стоять в том, что концентрация раствора непрерывно меняется.
Однако, применив надлежащую методику решения, можно из-
влечь пользу из этого “непрерывного” изменения, обратив эту
кажущуюся главную трудность в решающее средство для дости-
жения цели.
Зафиксируем некоторый момент времени t и посмотрим, что
произойдет в резервуаре за промежуток времени от г до г + Д/.
В начале этого промежутка в резервуаре имеется y(f) кг соли,
а в конце — y(t + Д/) кг. Разность y(t) - y(t + Д/) — это количество
соли, которое вытекло с раствором за время Д/. Так как концен-
трация раствора в течение промежутка времени от / до t + ДГ
убывала от —— до + Az^, то
Р Р
— * — гД/ < y(t) - y(t + Д/) < гМ.
Р Р
Разделив все члены этого двойного неравенства на Дг, получаем
У(/ + Д/) r < y(t + bt)-y(t) < y(t) г
Р М р '
Исходя из характера рассматриваемого процесса, можно сделать
вывод, что искомая функция y(t) непрерывна. Но тогда
у(1 + Дг) ——• Переходя в предыдущем неравенстве к преде-
_ у(г+Д/)-у(г) у(г) _
лу при Дг —> 0 , получаем пгп(--—------= —— г. Последнее
означает, что искомая функция y(t) в каждой точке t имеет
производную /(/), причем
£ H-Х'’- (2>
at р
15
(2) — дифференциальное уравнение относительно функции у(г).
Таким образом, наша задача свелась к чисто математической
задаче: найти решение у = y(t) уравнения (2), для которого
у(0) = q . Так как у(г) > 0 , то, разделив обе части уравнения (2) на
y(t), получаем
(In/(/)) = -— => 1пу(г) = --/ + С, ,
dt Р Р
где С, — произвольная постоянная; обозначим ее так: С( =1пС,
С > 0 • Тогда будем иметь
lnj(r) = --/ + 1пС. (3)
Р
Из (3) находим:
у(г) = Се р . (4)
Чтобы из множества функций (4) выделить ту, которая описывает
процесс изменения количества соли в резервуаре, воспользуемся
условием у(0) = q . Это условие дает, что q = С. Таким образом,
окончательно получаем:
y(f) = qe р . 4 (5)
Задача 2. Закон распада радия состоит в том, что скорость
распада пропорциональна наличному количеству радия. Пусть
известно, что в некоторый момент времени / = г0 имелось
граммов ралия. Требуется определить количество радия в любой
момент времени t.
Пусть /?(/) — количество (в граммах) нераспавшегося радия
в момент времени t. Перейдем от момента времени t к моменту
времени t + Д/. В момент t + Д/ количество нераспавшегося ралия
будет равно R(t + Дг). Тогда разность R(t)~ R(t + ДО — это количе-
ство радия, которое распалось за промежуток времени от t до
г + Д/. Отношение ————---------- представляет собой среднюю
скорость распада радия за промежуток времени от г до Г + Д/,
а предел этого отношения при Д/ -> 0, т. е.
S(r)-«(z +а,) Л(г + дг)-Я(О dR(i)
lim--------------= — lim--------------=-------,
д/-»о д/ дг-л д/ dt
есть скорость распада радия в момент /.
16
Так как скорость распада радия пропорциональна его налич-
ному количеству, то получаем
-77 = *Д(,), (6)
где к — постоянная величина. (6) — дифференциальное уравнение
относительно функции /?(/). Таким образом, наша задача свелась
к чисто математической: требуется найти решение R = R(t) урав-
нения (6), для которого Я(/о) = Ry .
Так как /?(/) > 0, то, разделив обе части уравнения (6) на R(t),
получаем -7-(In/?(/)) =-А =>
at
In/?(,) = -*;+In С, (7)
где С — произвольная постоянная (С > 0). Из (7) находим
Я(/)-СГ* (8)
Чтобы из множества функций (8) выделить ту, которая описывает
процесс изменения количества радия, используем условие
/?(г0) = Ry . Положив в (8) t = /0 , получаем Ry = Се~к'а =>
C = V*°. (9)
Подставив теперь в (8) вместо С его значение из (9), будем иметь
Я(П = v - ◄ (Ю)
Задача 3. Тело, имеющее в начальный момент времени /0 =0
температуру Ту , поместили в среду, температура которой поддер-
живается неизменной и равной 7]. Как будет изменяться с тече-
нием времени температура тела?
Обозначим через T(t) температуру тела в момент времени t.
Экспериментально установлено, что скорость изменения темпе-
ра гуры тела пропорциональна разности температур тела и окру-
жающей среды. Это означает, что
77 =-Г (ПО-Г,). (II)
где у > 0 — коэффициент пропорциональности.
Знак минус в правой части (II) соответствует эксперимен-
тальным данным: если T(t)-T} >0, то температура тела убывает
и поэтому скорость изменения температуры < q , если же
dt
17
Т(/)-Г| <0, то температура тела возрастает, а следовательно,
скорость ее изменения положительна.
Итак, процесс охлаждения (или нагревания) тела в среде с
неизменной температурой моделируется уравнением (II). Так как
7j = const, то 7j). Поэтому уравнение (II) мо-
dt dt
жет быть записано в виде
d
^(Т(')-Т,) = -у (Т(1)-Г,) « % -----у
аг / о / ~
(ибо * 0) или в виде
^[|п|Г(О-7-,|] = -у => 1п|Т(/)-7-|| = -уГ + 1пС,
где С >0. Из последнего соотношения находим, что
|Т«) - Г,| = О'”. (12)
I) Пусть То > 7] (тело охлаждается). Тогда T(t)> 7j и, следова-
тельно, имеем из (12): 7(/)-7^ -Се у1 =>
Г(/) = Т, + Се”. (13)
Чтобы из множества функций (13) выделить ту, которая описывает
процесс изменения температуры тела с течением времени, вос-
пользуемся условием 7(0) = 7J). Это условие дает То = 7] + С =>
С = То - 7j. Таким образом, получаем в этом случае (когда TQ > 7j)
Т</> = 7J + - 7J >₽-*. (14)
Из (14) => 7(г)----->7,, монотонно убывая.
2) Пусть 7J, < 7| (тело нагревается). Тогда T(t) < 7] и, следова-
тельно, имеем из (12): 7(/)-7t =-Се 11 =/>
T(t) = 7\-CeT. (15)
Чтобы из множества функций (15) выделить ту, которая описыва-
ет процесс изменения температуры тела с течением времени,
используем условие 7(0) = 7^. Это условие дает 7^ = 7]-С =>
С = 7] - То . Таким образом, получаем в этом случае (когда 7( > 70 )
7(/) = 7;-(7;-Г0)е-’/. (16)
Из (16) => 7(/)----->7, , монотонно возрастая. 4
18
Задача 4. Тело массой т падает вертикально вниз с некоторой
высоты. Сила вязкого трения, действующая на тело, пропорцио-
нальна скорости падения тела, т. е. FTp = -av, где a > 0 — коэф-
фициент трепня.
Вопрос, как изменяется со временем скорость падения тела?
Пусть v(/) — скорость падения тела в момент времени t. На
тело действуют две противоположно направленные силы: сила
тяжести F, = mg и сила вязкого трения Fw = -av. В данном
случае дифференциальное уравнение можно составить, используя
второй закон Н ьютона: та = F = F1 + Fw, т. е.
dv
m— = mg-u\\ (17)
at
так как ускорение а = —. Разделив обе части уравнения (17) на
т, получаем dt
dv
dt
а
=— v + g.
т
Приняв во внимание, что g = const, можем написать
dv т d ( a
dt a. dt\ т
А тогда уравнение (18) принимает вид
где С > 0 — произвольная постоянная. А тогда--v + g
т
a.
СХ Ct —1
Или, так как g-----v > 0 , то----v + g = Се m
m m
a a
Если тело начинает движение с нулевой скоростью, т. е. v(0) = 0 ,
то, положив в (19) t = 0, находим
19
0 = ^.”c^c = g.
a a
Заменив в (19) С на g, мы выделим тем самым из множества
решений дифференциального уравнения (17) то решение, кото-
рое описывает изменение скорости тела с течением времени при
условии, что v(0) = 0 . Таким образом, получаем
ио-а
а
( -И
I -е т
< j
(20)
При свободном падении без трения: — = g => v(/) = gr, т.е.
dt
скорость возрастает линейно (это нам известно). При наличии же
вязкого трения скорость, возрастая, тем нс менее стремится
к постоянной величине: р(г)--> —.
а
Замечание. Даже из приведенного выше небольшого числа
простейших задач становится ясно, что решение каждой из них
состоит из двух этапов. Первый этап решения задачи заканчива-
ется составлением дифференциального уравнения для искомой
функции. Второй этап представляет собой чисто математическую
задачу, а именно: решить полученное дифференциальное уравне-
ние, т. е. найти все его решения или только те, для которых
выполняются определенные дополнительные условия. Следует
отметить, что все многообразие природных процессов и явлений
не сводится к дифференциальным уравнениям нескольких типов.
Мир дифференциальных уравнений богат почти настолько, на-
сколько разнообразен реальный мир.
В этом пособии мы рассмотрим многие типы дифференциаль-
ных уравнений и ознакомимся с методами их решения. Мы увидим,
что дифференциальные уравнения, решаемые в элементарных фун-
кциях, немногочисленны. (Запас элементарных функций оказыва-
ется слишком бедным для того, чтобы дать описание многих физи-
ческих процессов и явлений.) Поэтому весьма часто случается, что
исследование того или иного дифференциального уравнения, встре-
чающегося в физике или механике, побуждает вводить новые клас-
сы функций, подвергать их исследованию и расширять арсенал тех
функций, которые применяются при решении прикладных задач.
В задачу теории дифференциальных уравнений входит также
качественный анализ, т. е. выяснение основных свойств решений
непосредственно по виду уравнения (не решая его).
20
Представим себе, что мы изменяем начальные значения для
искомой функции и производных от нее (изменяем начальное
состояние изучаемого процесса). Тогда будет изменяться и само
решение (будет иначе протекать процесс). Теория должна обеспе-
чить нам возможность судить о том, каким будет это изменение.
В частности, будет ли при малых изменениях начальных данных
мало изменяться и само решение и будет ли оно, следовательно,
устойчивым в этом отношении, или же малые изменения началь-
ных данных могут вызывать большие изменения в самом реше-
нии, и оно будет неустойчивым.
Мы должны также уметь составить качественную и, там, где
можно, количественную картину поведения не только отдельных
решений уравнения, но и всех его решений, взятых вместе.
Наконец, когда потребуется произвести расчет, нужно будет
находить решение уравнения численно. Здесь теория обязана
доставить в руки исследователя методы возможно более эконом-
ного и быстрого вычисления решений.
Глава i
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ПЕРВОГО ПОРЯДКА, РАЗРЕШЕННЫЕ
ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ
§1. Основные понятия и определения
Г. Дифференциальным уравнением первого порядка называ-
ется соотношение вида
F{x,y,y')=0. (I)
Здесь х— независимая переменная; у = у(х) — неизвестная функ-
ция; F(x,y,y'> — известная функция, заданная в некоторой обла-
сти (G) с R1.((I) — дифференциальное уравнение первого порядка
общего вида; оно не разрешено относительно производной.)
В этой главе будем рассматривать уравнения первого порядка,
разрешенные относительно производной, а именно уравнения вида
/ = = (2)
[dx ) ' '
где f{x,y) — известная функция двух переменных, заданная в
некоторой области (О) с R’,
Часто встречается и такая запись дифференциального уравне-
ния первого порядка:
M(x,y)dx + N(x,y}dy = 0. (3)
Здесь М(х>у) и N(x,y) — известные функции переменных х и у,
заданные в некоторой области (D)cR’. (Уравнение (3) имеет
симметричную форму; в нем переменные х и у — равноправные.)
2°. Рассмотрим дифференциальное уравнение первого порядка,
разрешенное относительно производной, т. е. уравнение вида (2):
22
у' = f(x, у).
Пусть функция /(х,у) определена
и непрерывна в некоторой области (D)
плоскости Оху (f(x,y)e C(D)). Будем
говорить в этом случае, что уравнение
у' = f(x,y) задано в области (£)).
Определение. Функция у = ф(х) на-
зывается решением уравнения (2) в про-
межутке {а,Ь), если:
I) ф(х) дифференцируема на (а,Ь),
2) точка (х,ф(х))е (О) для любого хе (а,Ь),
3) ф'(х) = f (х,ф(х)) для любого хе {а,Ь).
Заметим, что функция /(х,ф(х))е С((о,/>)) как суперпозиция
непрерывных функций. У нас ф'(х) = /(х,ф(х)), хе (а, Ь). Сле-
довательно, ф'(х)е С((о, Ь)).
Вывод: любое решение уравнения (2) непрерывно дифферен-
цируемо на промежутке (л, Ь).
График решения у = ф(х), хе (а,Ь), дифференциального
уравнения (2) называется интегральной кривой этого уравнения.
Проекция графика решения на ось ординат называется фазо-
вой кривой (траекторией) дифференциального уравнения.
3°. Отметим, что решение уравнения (2) может быть получено
иногда в неявной форме, т. е. в виде соотношения
ф(х,у) = 0.
(3)
Но при этом предполагается, что соотношение (3) определяет у
как функцию отх: у = ф(х), х е (а, Ь), которая является решением
уравнения (2) на промежутке (а, Ь).
Решение дифференциального уравнения (2) может быть полу-
чено также в параметрической форме:
х = х(/),
У = y(D,
(4)
И в этом случае предполагается, что соотношения (4) определяют
у как функцию от х у = <р(х), х е (а, Ь} , которая является реше-
нием уравнения (2) на промежутке <л, Ь).
23
Пример Л Дано дифференциальное уравнение
Убедиться, что функция у = ф(х), определяемая соотношением
у = arctg (ху) + С , где С— произвольная постоянная, является
решением уравнения (5).
В этом примере f(x,y) =-----!—у => Уравнение (5) опреде-
(х + уУ
лено на всей плоскости Оху, исключая точки прямой у = -х.
У нас у, как функция от х задана неявно соотношением
arctg (х 4-у)-у 4-С = 0 (6)
=f [обозначение]
Видим, что сама функция F и ее частные производные
г, I г' 1 । (Х + У)2
г, =---------=-, К =---------=>- I = —----—=- определены
I 4- (х 4- у)2 |4-(Х4-у)2 I 4-(X 4-у)2
и непрерывны на всей плоскости Оху. Видим, далее, что F'v #0
на всей плоскости Оху, исключая точки прямой: у = -х .
А тогда из теории неявных функций следует, что в окрестности любой
точки (Хо,у0), такой, что у0 # -*о и arctg (*6 + Уо) -Л + с = °,
соотношение (6) определяет единственную непрерывно дифференци-
руемую функцию у = ф(х), х 6 /8 ( /6 = (х0 - 5,хц 4- 5]), причем для
любого хе Г&:
z _ Г<(х,ф(х)) _ 14-(х+ф(х))2 _ I
Гу (А<р(*)) (х + ф(х))2 (х + ф(х))2
I 4- (X 4- ф(Х»2
Видим, что функция у = <р(х), хе /6, определяемая соотношени-
ем (6), является решением уравнения (5). 4
Пример 2. Дано дифференциальное уравнение
Убедиться, что функция у = ф(х), заданная параметрически-
ми уравнениями
24
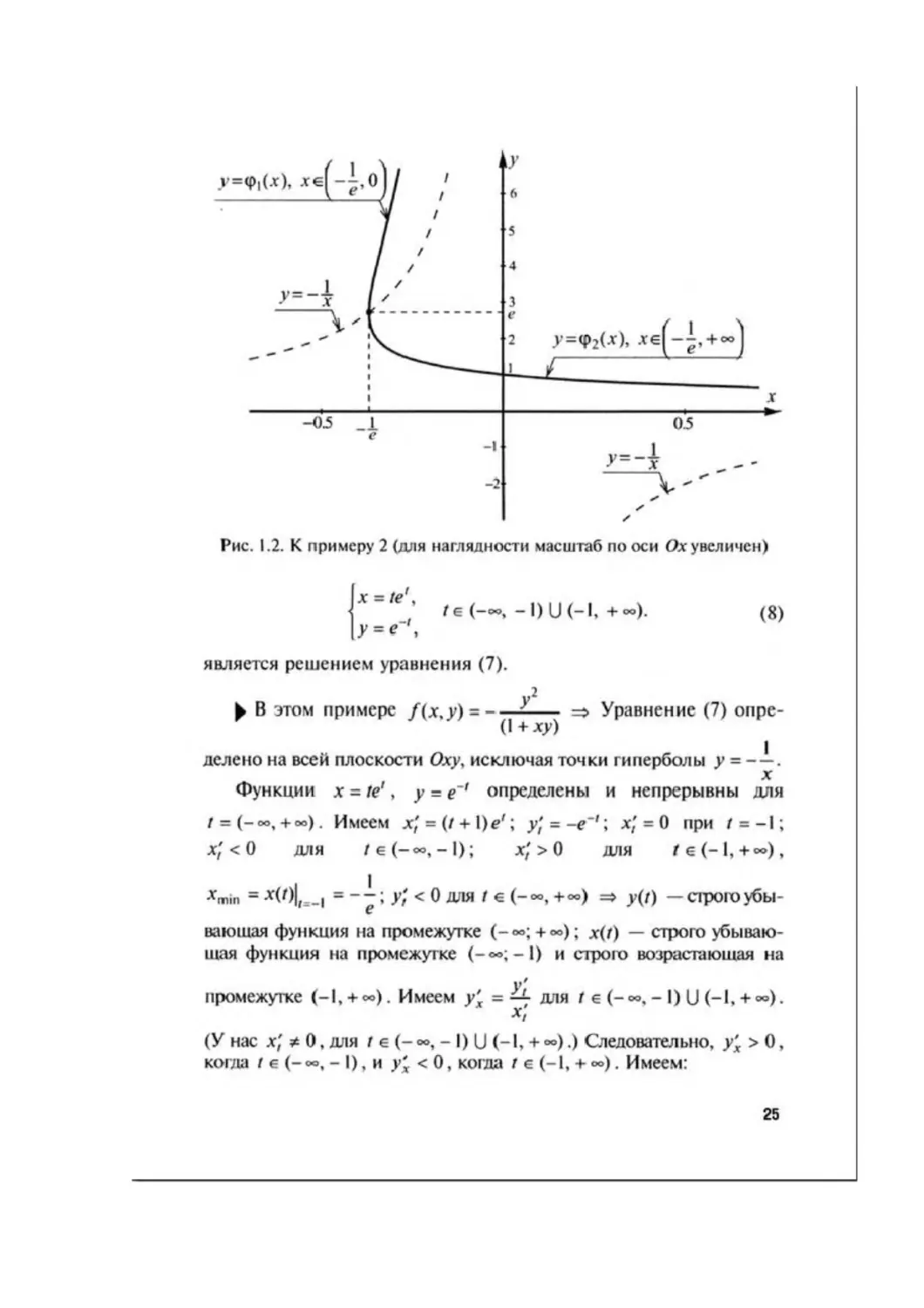
Рис. 1.2. К примеру 2 (для наглядности масштаб по оси Ох увеличен)
х = te',
у = е~',
-l)U(-l, + ~).
(8)
является решением уравнения (7).
V2
Ь В этом примере f(x,y) =---------- => Уравнение (7) опрс-
(1 + ху)
.. г. г 1
делено на всей плоскости Оху, исключая точки гиперболы у = —.
х
Функции х = te', у = определены и непрерывны для
Zsf-oo. + oo). Имеем х, = (/ + 1)е'; у' = -е~'; х’ = 0 при t = -1;
х,'< 0 для /е (-оо,-1); х/> О для Ге(-1,+оо),
xmin = x(0|rs_| = - X < 0 для t € (-оо, +оо) => j(/) _ строго убы-
вающая функция на промежутке (-оо; +<»); х(г) — строго убываю-
щая функция на промежутке (-«»;-|) и строго возрастающая на
промежутке (-1, + оо). Имеем у' = — для t е (-°о, - |) (J (-1, + <~).
(У нас х' * 0, для г е (- оо, - |) (J (-1, + оо).) Следовательно, у' > 0.
когда г е (-оо, - |), и у' < 0, когда t е (-1, + ®о). Имеем:
25
lim x(t) = lim te' = -0; lim x(/)=--;
/-+—» e
lim y(t) = lim e~' = +«>; lim y(r) = e
/ / -> QQ f —| -Q
lim x(t) = —; lim x(t) = lim te' = +«>•
/—♦—i+o e /-»+«• /->+»
lim y(t) = e\ lim y(t) = lim e'1 =0
Вывод: При изменении хот — до 0 функция у(х) возрастает
е
от е до +°°. При изменении х от -- до +°° функция у(х)
е
убывает от е до 0. Функция у = <р(х), определяемая уравнениями
(8), имеет две ветви: у = ф|(х), хе|--,0|, и у = ф,(х),
К е )
хе|--,+~|. Ветвь у = ф>(х) соответствует изменению пара-
Iе /
метра / от до — I; ветвь у = ф2(х) соответствует изменению
параметра / от — I до +°°.
J t I
Имеем у' = ——— => у* = 0 при г = —. Так как у' > 0
(/ + 1)е3 2
3 , л 3
для t < - - и у„ < 0 для --</<-1, то
— точка
перегиба ветви у = ф](х). Так как у^ > 0 для />-1, то ветвь
у = фэ(х), хе +«> , направлена выпуклостью вниз.
Iе )
Итак, параметрические уравнения (8) определяют непрерыв-
но дифференцируемые функции у = ф|(х), хе|--.0|, и
( е J
у = Фз(х), хе|--, +~ |. Покажем, что обе эти функции явля-
\ е /
ются решениями дифференциального уравнения (7).
Действительно, имеем как для /е(-«», -I), так и для
/е (-J, +~):
26
, + у2 _ e 1 t e 21 _
** + (1 + ху) (r + l)e' + l+f
4°. Поле направлений. Говорят,
что в некоторой области задано
поле направлений, если каждой
точке этой области поставлено в
соответствие одно и только одно
направление.
Рассмотрим дифференциальное
уравнение вида (2), т. е. уравнение
у = f(x,y). Пусть (£>)— область, в
которой определена и непрерывна
функция fix,у). Построим в облас-
ти (D) поле направлений следую-
щим образом: в каждой точке
Рис. 1.3
(x0,y0)c(D) проводим отрезок, например, единичной длины,
исходящий из этой точки, так, чтобы он составил с положитель-
ным направлением оси Ох угол а, такой, что tga = f(x0,y0).
Пусть у = ф(х), хе (а, Ь) — решение уравнения (2), график
которого (0 проходит через точку . Так как у = ф(х),
хе (а, Ь),— решение уравнения (2), то ф'(х) =/(х,ф(х)) для
любого хе(й,6), а значит, в частности, ф'(ль) = /(лф<р(-*о)) =
= Но ф'(хь) — тангенс угла наклона касательной к
графику (0 функции у = ф(х) в точке (хь.Л) (см. рис. 1.3). От-
сюда заключаем, что интегральная кривая уравнения (2) в каж-
дой своей точке имеет касательную, совпадающую с направлени-
ем поля в этой точке. Верно и обратное: всякая кривая,
расположенная в области (D) и касающаяся в каждой своей точке
направления, имеющегося в этой точке, является интегральной
кривой уравнения (2).
Замечание. Встречаются случаи, когда в точке (х0,у0) функ-
ция fix,у) представляет неопределенность вида 0/0. В такой
точке нельзя указать никакого разумного направления поля. (Эго —
особая точка поля.)
При изучении поля направлений в области (О) представляют
интерес так называемые изоклины.
27
Изоклиной называется кривая, во всех точках которой направ-
ление поля одинаково. Все интегральные кривые, пересекающие
данную изоклину, в точках пересечения наклонены к оси абсцисс
под одним и тем же углом.
fix, у) = к — уравнение семейства изоклин.
В некоторых случаях по виду правой части уравнения
у'= fix,у) удается найти линию экстремумов и линию точек
перегиба, т. е. линии, во всех точках которых интегральные кривые
этого уравнения имеют соответственно экстремум или перегиб.
Выясним, например, как можно найти уравнение линии экст-
ремумов для решений дифференциального уравнения у' = fix,у)
и как отличить точки минимума от точек максимума.
Пусть у = ф(х) — любое решение уравнения у" = fix,у) на
промежутке {а, Ь). Функция ф(х) непрерывно дифференцируе-
ма, и ее производная в точке экстремума равна нулю:
-/(х,ф(х)) = 0- Следовательно, множество критических
точек решений данного уравнения определяется соотношением
/(х,у) = 0. Пусть х0 — экстремальная точка решения у = ф(х).
Если фж(дсо> >0, то х0 — точка минимума, а если ф,(хп)<0, то
точка х0 — точка максимума. Так как
d2<p d ft < w д/(х’Ф<х)) Э/(х,ф(х>)
vf = f (*> Ф<*)) = —Ч—-+—Ч—- Ф (х) =>
dxl ах Эх ду
. Э/(х0,ф(х0)) Э/(х0,ф(х0)) Э/(х0,ф(х0))
=> Ф (*о) =---г----+-------------ф (х0) =----------- •>
дх ду лг-' дх
то множество точек минимума решений исходного уравнения
у'= fix,у) определяется системой
fix, у) = О,
/х'(х,у)>0,
а множество точек максимума решений — системой
/(х,у) = 0,
/;(x,j)<o. ◄
Изоклины вместе с линиями экстремумов и точек перегиба дают
возможность построить схематически графики интегральных кри-
вых уравнения у' = fix,у).
28
Задача. С помощью изоклин построить приближенную схему
интегральных кривых уравнения
у' = 2х(1-у). (9)
Семейство изоклин для данного уравнения определяется
уравнением 2х(1 - у) = к , где к — действительный параметр. Это
уравнение залает две прямые: х = 0 и у = I (при к = 0) и семей-
ство гипербол у = I (при к * 0)* Заметим, что прямая у = I
является интегральной кривой, так как функция у = I есть реше-
ние исходного дифференциального уравнения. Изоклину х = 0
(т. е. ось ординат) интегральные кривые уравнения (9) пересека-
ют под прямым углом.
(В точках, расположенных на прямой х = 0, имеем у'= 0.
Значит, касательные к интегральным кривым в этих точках па-
раллельны оси абсцисс и, следовательно, перпендикулярны к оси
ординат.)
Так как у' = 0 в точках прямой х = 0, то точки прямой х = 0
являются стационарными критическими точками для инте1раль-
ных кривых уравнения (9). Для исследования на экстремум этих
критических точек находим вторую производную функции
у = у(х). Имеем из (9):
у'(х) = 2(1-у)-2ху'(х)
=> заменив в правой части у его выражением из (9), находим
у'(х) = 2(1 - у) - 2х 2х( I - у) =
= 2(1-у)(1-2х2)=> /|„„ = 2(1-А
Видим, что у'(0) < 0 для у > I и у'(0) > 0 для у < 1. Следователь-
но, точки оси ординат, для которых у > I, являются точками
максимума интегральных кривых, а точки оси ординат, для кото-
рых у<1 являются точками минимума интегральных кривых
уравнения (9). r
Из выражения для у'(х) следует, что у'(х) = 0 при х = ±—.
Так как при переходе через точки х=+— вторая производная
V2 Л
изменяет знак, то точки прямых х = —— и х = — являются
точками перегиба интегральных кривых уравнения (9).
29
Рис. 1.4. К решению задачи о построении
приближенной схемы расположения
интегральных кривых
У нас правая часть уравнения (9): /(х,у) = 0 на линиях х = О
и у = I. Эти линии делят всю плоскость на четыре части:
(Д) =
х > О,
у> 1;
(Д) =
х < О,
у> I;
(Д) = <
х < О,
у< I;
(Д) =
х > О,
у < I.
В каждой из этих четырех областей производная у' имеет опреде-
ленный знак (в каждой области свой знак). Чтобы установить
знак у' в области (Д), / = 1, 2,3,4, достаточно определить знак
функции f(x,y) лишь в одной произвольной точке (х(,у()с (Д).
В нашем примере имеем:
I) /(I, 2) < 0. Значит, у' < 0 в каждой точке области (Д).
2) /(-1,2) > 0. Значит, / >0 в каждой точке области (Д).
3) /(-1,0) < 0. Значит, / <0 в каждой точке области (Д).
4) /(1,0) > 0 . Значит, / > 0 в каждой точке области < Д).
Следовательно, пересекая прямую х=0, интегральные кри-
вые переходят из области возрастания функции у = j(x) в об-
ласть убывания, если у > I (т. е. при переходе из области (Д) в
область (Д)), и из области убывания функции у(х) в область
возрастания, если ><1 (т.е. при переходе из области (Д) в
область (Д)).
30
Рассмотрим еще две изоклины: при к = |, у = I----, и при
I 2х
А=-1, у = 1 + — . Касательные, проведенные к интегральным
2х
кривым в точках их пересечения с указанными изоклинами,
Зя
— соответственно.
образуют с осью абсцисс углы и ------------------
Полученной информации достаточно для построения прибли-
женной схемы интегральных кривых уравнения (9) (см. рис. 1.4).
Можно заметить еще, что уравнение (9) инвариантно относи-
тельно замены х на - х, откуда следует, что картина интегральных
кривых симметрична относительно оси ординат.
5’. Задача Коши. Задача Коши для дифференциального урав-
нения у'-fix, у) состоит в следующем: среди всех решений
этого уравнения найти решение вида у = <р(х), х е (а, Ь), которое
удовлетворяет наперед заданному условию: у = у0 при х = х0, где
числа х0 и у0 такие, что точка (х0,у0)е (D); х0 е (а, Ь).
Геометрически задача Коши означает: среди всех интеграль-
ных кривых дифференциального уравнения у = f(x,y) найти ту,
которая проходит через заданную точку (х0,у0)е (D).
Условие у|х = Jo называется начальным условием, а числа х0
и у0 — начальными данными.
Отметим, что решение задачи Коши может оказаться и не
единственным, так как иногда существует несколько решений
уравнения у'= fix,у), удовлетворяющих заданным начальным
условиям у = уи при х = х0. Эго означает, что через точку (х0, у0)
проходят несколько интегральных кривых несмотря на то, что
уравнение / = fix, у) задает в этой точке только одно направле-
ние поля. Поэтому вопрос о единственности решения задачи
Коши представляет исключительный интерес как для самой тео-
рии дифференциальных уравнений, так и для ее многочисленных
приложений.
Если установлено, что решение задачи Коши единственно,
то, следовательно, других решений, удовлетворяющих тем же
начальным условиям, нет. В вопросах естествознания это приво-
дит к тому, что мы получаем вполне определенный закон явле-
ния, определяемый данным уравнением и заданными начальны-
ми условиями.
6°. Понятие единственности решения задачи Коши. Пусть дано
уравнение
У =Дх, у)
(2)
31
и дано начальное условие
Нг-«.=№-. <2„)
Предполагается, что f(x,y)eC(D), (D)cR2 и что точка
(х0,у0)е (D). Пусть у = ф(х), хе = (хь-б,х0 +5), и у = ф(х),
хе /1 =(л« -5,х0 + 5), — любые два решения задачи (2)— (20).
Тогда: если существует интервал /8 = (х0 - б, х0 + 5} такой, что
ф(х) = ф(х), хе 1&, то говорят, что задача (2)— (20) имеет
единственное решение. Точку (х0,у0)е (D> называют в этом слу-
чае точкой единственности уравнения (2).
(Подчеркнем еще раз, что соотношение ф(х) = ф(х), хе f&,
должно выполняться для любой пары решений задачи (2) — (20>.)
Пусть область (Dt)c(D) и пусть каждая точка (х,у)е (D,)
является точкой единственности уравнения (2). Тогда (£>,) назы-
вают областью единственности уравнения (2).
Пример 1. Пусть имеется уравнение / = 3/^3. Здесь
f(x,y) = Зу^3 — определена и непрерывна на всей плоскости Оху.
Значит, (D) = R2. Легко проверить, что функция: у = (х-С)\
х€ (—о°, + <*>), где С— произвольная постоянная, есть решение
нашего уравнения. Легко видеть, что и функция у = 0,
хе (-«», + оо), — тоже решение нашего уравнения.
Возьмем любую точку (х0,у0) на плоскости Оху, не лежащую
на оси Ох (>’о *0; пусть сначала, для определенности, у0 >0).
Через точку (ль,№) проходят интегральные кривые АВС, АВВС,
4fiiВВС и т.д. Отметим, что любые две из этих интегральных
кривых совпадают на промежутке (хв,+«>). Значит, существует
промежуток (в данном случае это промежуток (хй,+~)), содер-
жащий точку х0, на котором совпадают любые два решения
нашего уравнения, проходящие через точку (х0,р0).
32
Возьмем теперь любую точку (.Хо,Уо), лля которой уо<0.
Через точку (jqj,y0) проходят интегральные кривые АВС , АВВС ,
АВВВС и т. д. Любые две из этих интегральных кривых совпадают
на промежутке (-°°,х^). Значит, существует промежуток (в дан-
ном случае это промежуток <-<»,x^>), содержащий точку х(), на
котором совпадают любые два решения нашего уравнения, про-
ходящие черед точку (х0,у0) -
Вывод; любая точка (х,у) плоскости Оху, не лежащая на оси
Ох, является точкой единственности уравнения у' = Зу^3.
Возьмем любую точку, лежащую на оси Ох, а именно точку
(io,0) (i0 — любое число). Через точку (Д},0) проходят, напри-
мер, две интегральные кривые у = 0 и АВС. Видим, что нельзя
указать промежутка, содержащего точку х0, на котором совпада-
ли бы эти две интегральные кривые.
Вывод: точка (хо,О) не является точкой единственности для
уравнения у' = Зу^3. Так как х0 — любое число, то любая точка
линии у = 0 является точкой неединственности этого уравнения.
В примере I областями единственности уравнения являются
открытая верхняя и открытая нижняя полуплоскости.
33
§2. Существование решения задачи Коши
Пусть дано дифференциальное уравнение
У' = C(D),(D) <= R , (I)
и дано начальное условие
=Лн (x0,y0)e(D), (2)
Будем строить приближенное решение задачи (I)— (2). Пусть
(Z)x) есть проекция области (D) на ось Ох. Возьмем отрезок
/ = [х0 -h,xQ+h] — любой, но такой, чтобы было / с Dx. Обо-
значим Г = [х0, х0 + Л]; Г = [х0 - Л, Ху ]. Разобьем отрезок Г на п
частей ( п > 1) точками х0 < Х| < х2 < ... < х„ = х0 + Л, а отрезок
/‘ — на п частей (п £ I ) точками
Ху - h = х„ < x_(ff_|) < ... < х_| < Ху.
Пусть Х= max {х, -Х/_|}. X — ранг дробления отрезка /.
г =0.-1?-2."..'-(л-1)
Найдем значения функции /(x,j) в точке (х0,у0). Получим
ЧИСЛО /(Xy,Jo).
Интегральная кривая уравнения (I), проходящая через точку
(ху,У’о), имеет касательную в точке (х0,у0) с угловым коэффици-
Рис. 1.7. К построению ломаных Эйлера
34
ентом /(х0,у0). (Считаем, что такая интегральная кривая уравне-
ния (1) существует.) Заменим интегральную кривую на отрезке
касательной к ней в точке (х0,>'0), т. е. прямолинейным
отрезком, заданным уравнением:
Ч'(х) = Уо+/(хЬ,Уо)(х~хь), где хе |Х.ЬХ|).
Имеем 4>(х()) - j’{); V*(x) = /(х0,у0), хе(х_|,Х|]. Рассмотрим точ-
ку (X|,v(X|)), где
V(*l) = .Vo+/(-Wo)(*l -^о)-
Если эта точка принадлежит (D), то в ней определено направле-
ние поля, имеющее угловой коэффициент /(Х|,у(Х|)).
На отрезке [Х|,х2] заменяем интегральную кривую прямоли-
нейным отрезком, имеющим уравнение:
Ц/(Х) = \|/(Х|)+/(Х|,1||(Х|))(Х-Х1),Х€ |хьх2|.
Затем рассматриваем точку (x2,vp(x2)), где
V(x2) = v(xt) + f (х,, v(x,)) (х2 - Х|).
Если точка (х2,у(х2))е (D), то в ней определено направление
ноля, имеющее угловой коэффициент /(х2,у(х2)). На отрезке
[х2,Х}] заменяем интегральную кривую прямолинейным отрез-
ком, имеющим уравнение:
у(х) = \|/(х2)+ /(х2,у(х2))(х-х2),хе |х2,х3].
Продолжая этот процесс аналогичным образом, получим для
V(x) = v(x„_|) + f (x„_|, v(x„_|)) (x - x„_|)
(предполагаем, что на каждом таком шаге прямолинейный отре-
зок, заменяющий интегральную кривую, остается в области (D)).
Рассмотрим теперь точку (х_(,цг(х_|)), где
) = Уо +/(^УоИ*-! --«о)-
Если эта точка принадлежит (D), то на отрезке [х_2,х_(] заменяем
интегральную кривую прямолинейным отрезком, имеющим урав-
нение:
v(x) = v(x_|) + /(x_|,Y(x_|))(x-x_1),X6 |х_2,х_||.
Затем рассматриваем точку (х_2,у(х_2)), где
V(x_2) = V(x_|) + /(x_|,v(x_|))(x_2 -х_|).
35
Если точка (х_2,у(х_2 ))g (D), то на отрезке [х_3,х_2] заменяем
интегральную кривую прямолинейным отрезком, имеющим урав-
нение:
V(x) = v(x_2) + /(x_2,y(x_2))(x-x.2),X6 [x_3,x_2J.
Продолжая этот процесс аналогичным образом, получим для
xgIx^X-^dI
у(х) = ^(х.^.!,) + /(х_(„_,), v(x_(„_n))(x - x_(rt_n).
И здесь предполагается, что на каждом шаге прямолинейный
отрезок, заменяющий интегральную кривую, остается в области
(D). Таким образом, мы получаем ломаную, которая называется
ломаной Эйлера. Ее можно рассматривать как приближенное изоб-
ражение интегральной кривой уравнения (I), проходящей через
точку (х0,у0).
Свойства ломаной Эйлера
Первое свойство. Функция у — у(х), графиком которой явля-
ется ломаная Эйлера, непрерывна на том промежутке, где опреде-
лена. (у(х> — кусочно-линейная функция на промежутке
/ =(х0-й,хь+й].) __
На каждом из промежутков (х_/,хч/_|)), (xz_|,x,), / = |,л,
функция у(х) имеет конечную производную ц/'(х), причем для
любого хе (xJ,x(;_1)): Vz(x) =/(х_</_|),у(х_<(_|))), а для любого
х€(х,.|,х/): v'(x) = /(x,_|,y(x,_|)). В точках х_, и х, , / = I, л - I,
функция у(х) имеет конечные односторонние производные; в
точке х_„ — конечную правостороннюю, а в точке х„ — конеч-
ную левостороннюю производные:
ц/'(х) — ступенчатая функция, определенная на промежутке
/ = [х0 - й, х0 + й]. (Считаем у'(х) = f (х,_|, ц/(х,_|)) для х е [xz_|, х,)
и v'(x) = /(х_(/_|),у(х.</.|))) для хе (х_/,х_</_1)|, / = Гй.)
Так как функция у'(х) ограниченная на промежутке
/ = |х0 - й, х0 + й] и непрерывная там всюду, за исключением
конечного числа точек, то она интегрируема на /. Мы знаем, что,
если значения подынтегральной функции изменить в конечном
числе точек, то от этого интегрируемость не нарушается и вели-
36
чина интеграла не изменяется. Приняв это во внимание, получа-
ем, что для любого хе [х0 -й,х0 +Л] справедливо равенство
У(*) = Уо + J ¥'(*М. (3)
•*b
В самом деле, имеем, например, для хе (х0,х(]:
х
У(^) = Уо + J Лх^УоУЖ = Уо + /(Х(ьУо)(х-хо)'
Для хе |Х|,х2]:
*1 X
У(х) = }’{| + J y'(t)dt + J =
л® Х|
= Уо + f(x0,yQ)(x} -Хр) + J f (х,,у(х,))<// =
~Х1
= v(x,) + /(X| ,V(X|))(X-X|)
и т. д. Предположим, что для хе [Xp,,xJ;
V(x) = у( Хр,) + f (хр,, v(Xp,)} (x - xz_,).
Тогда для xe[Xj,Xp|] будем иметь:
У = = Уо + j + J + ... + j y\t)dt + J y'(0dt =
Ло X| ДГ|_| X,
=*(*1)
= V(*i) + f {x(, y(x, )) (x - x().
Переход от i -1 к / сделан. Следовательно, справедливость равен-
ства (3) установлена.
Определение отрезка Пеано. Рассмотрим прямоугольник с цен-
тром в точке (х0,Уо):
Хо-а^х<Ар+а,
yQ-b<y<yQ+b,
a >Q, b > 0.
37
(Р) — любой, но такой, что (Р)с(Д). Отметим, что (Р) —
ограниченное замкнутое множество и что /(х,у)е С(Р). Значит,
существует число М > 0 такое, что |/(х,у)| < Л/, для любой точки
(х,у)е(Р). Введем в рассмотрение прямые: у = у0 ± М(х - Хо).
Обозначим абсциссы выхода этих прямых из (Р) через x0-h
и х$ + А , а ординаты — через у0 - Н и + Н. Могут реализо-
ваться случаи: а, б и в, изображенные на рис. 1.8.
И Н
Ясно, что h < а , Н < b. Имеем — = М =» А = —. Из рис. 1.8
А М
видим: 1)либо h<a, тогда А = — = — (см. случай а)); 2) либо
Л/ М
h-a, тогда А = — < (см. случаи б) и в)). Следовательно, если
М М
брать А = min
Ь
°' М
, то отрезки прямых (: у = + М(х - х^)
и (А_): у = j’o - М(х -Xq), х е (xq - A, Xq + А] будут лежать в пря-
моугольнике (Р).
Определение. Отрезок / = |х0 - h,xn + А], где А = min
называется отрезком Пеано.
Ь
а, —
М
Второе свойство. Если / = [х0 - А,х0 + А| — отрезок Пеано, то
для любого л (ле N) и для любого разбиения отрезка /точками
X/, соответствующая ломаная Эйлера будет определена на всем
отрезке /.
Исходное звено ломаной имеет угловой коэффициент
/\Хо'Уо)- Так как |/(х,у)| < М всюду в (Р), то, в частности,
|/(х0,/о)| Л/ и, следовательно, это звено на всем отрезке [x0,Xj |
будет оставаться в прямоугольнике (Р). Допустим, что все звенья
ломаной до /-го включительно остаются в прямоугольнике (Р).
Рис. 1.8. К определению отрезка Пеано
38
Тогда для (/ + l)-ro звена ломаной будем иметь: угловой коэффи-
циент (/ + 1)-го звена /(Ху.уСх^)) удовлетворяет неравенству
|/(х,, у(х, )| < М ; для любого хе [х,,х/+1]
X
'♦'(И = То + J ф'(ОЛ => |у(х)- Хо| =
«о
J
я»
£ М | х - Хо | < М h<b.
Значит, (/ + 1)-е звено ломаной остается в (Р). Переход от / к
/ + 1 сделан. Следовательно, приходим к выводу, что ломаная
Эйлера может быть построена на всем отрезке Пеано. «
Третье свойство.Любому, наперед заданному, е>0 отвечает
8>0 такое, что для любой ломаной Эйлера у = ц/(х), хе 1,
задачи (I) — (2) с рангом дробления X < S, имеет место неравен-
ство: |ч^(х)-/(х,У(х)Л<е, хе /.
(В таком случае будем говорить, что функция у = у(х), хе /,
является с -решением задачи (1) — (2).)
Возьмем любое е > 0 . По условию, функция /(х,у) непре-
рывна в прямоугольнике (Р). Следовательно, по теореме Канто-
ра она равномерно непрерывна в (Р). А тогда взятому е>0
отвечает число 8, >0 такое, что для любых двух точек (х,у) и
(Д у) из (Р), для которых |х - х| < б,, |.v - J’| < 5(, будет
|/(ДЯ-/(х,^)|<£. (4)
Возьмем число 5= min
М
и покажем, что это — 5 иско-
мое. В самом деле, построим на отрезке Пеано / = [х0 - h, х0 + Л]
ломаную Эйлера у = у(х) с рангом дробления Х<5. Пусть х —
произвольное, принадлежащее / (пусть, для определенности,
хе/*). Если окажется, что х = х,, то V'(•*,)-/(*/, v(х, )) = 0.
Если xel^.px,) (/ = ],«), то
v'(x) = /(x,_|,v(Vl)).
(5)
Имеем, следовательно, vXx)-/(x,Y(x))s/(X/-i,V(Xm))"
-/(х,ч/(х)). Так как хе [х,_|,х,), то |х - x^J < X < 8 < 8|. Имеем
далее, V(x)-y(xM)= J y'(t)dt =>
39
J y'(t)dt
=> |у(х) - V( Vi )| =
<M \х-хм\< Mk<
Поэтому, принимая во внимание (4), получаем:
|v'(х) - f (х,у(х))| = |/ (х,_,,у(х,_|)) - f (х, v(х))| < £. 4
Определение 1. Последовательность функций .
х е |а, />], называется равномерно ограниченной на промежутке
|а, b], если существует число Л/ >0 такое, что для любого ле N
и для всех хе |о, Л| оказывается: |/„(х)| £ М .
Определение 2. Последовательность функций ,
х е [ff, />], называется равностепенно непрерывной на промежутке
|ff,/>], если любому £>0 отвечает 5>0 такое, что для любых
двух точек х' и х' из |а, Ь|,для которых jx'-x^S, оказывается
|/Л(х')-/„(х')| < е при любом л = 1,2,3, ... .
Пусть bM*)}„eN , хе / = {х0 -h,х0 + Л| — любая последова-
тельность ломаных Эйлера, построенная на отрезке Пеано для
задачи (I) — (2). Покажем, что эта последовательность равномер-
но ограниченная и равностепенно непрерывная на /.
X
► Имеем для любого zigN: ул(х) = у0 + J у' (/) dt, хе/.
ч
У нас у'(х) есть значение.функции/в некоторой точке из (Р).
Но |/(х, у)| < М всюду в (Р). Поэтому |ул (х)| <Л/,хе/,леМ.
А тогда
|v„(x)| =
X
Уо + J Wn(t)dt
*0
j
<|>’0|+Л/|х-х0|<|у0| + Л/Л = Л/,,хе /,ле N.
Отметим, что число Л/, не зависит ни от х, ни от п. Следова-
тельно, последовательность ломаных Эйлера {ч>„ (х)}жГЧ , хе I —
равномерно ограниченная. Покажем, что она и равностепенно
непрерывная на отрезке Пеано /.
Возьмем е>0 — любое. Пусть х' и х' — любые две точки из
отрезка Пеано /. Рассмотрим разность у„(х')-у„(х'). Имеем
х" х' х"
v„(x") - v„(x') = jv;,(Odf- /у;(п<л =>
Xo *0 *'
40
|vn(*")- Vn(x')| =
Jv
x'
< M |x" - x*).
£ e
Положим 8 = —. Если брать xr и x на отрезке / любыми, но
м
такими, для которых |х'-х'|<8, то будем иметь
|у„(х')-V„(x')| < Л/ б => |уя(х'’)-у,,(х')|<Е, ле N . Последнее
означает, что последовательность {'t'„(x)}z|rN, хе 7, равносте-
пенно непрерывная на отрезке Пеано /. 4
Замечание. В книге И.Г. Петровского “Лекции по теории обык-
новенных дифференциальных уравнений” приведено доказатель-
ство теоремы Ар цела — Асколи: из всякой равномерно ограни-
ченной и равностепенно непрерывной на промежутке [о, й|
последовательности функций , хе [я, А], можно выде-
лить подпоследовательность функций {Д (л-)}*, , х е (я, А], рав-
номерно сходящуюся на промежутке [о, А].
Отметим, что если Д (х) е С ([я, А)) и Д (х) =i f(x), хе [я,ft],
то предельная функция /(х)е С(|я, А|). Кроме того, если функ-
ции Д(х), хе|д,А], такие, что |Д (х)|< М, хе |я,А], то и
|/(х)|< М, хе (я,А],
Теорема Пеано (о существовании решения). Пусть дано уравнение:
У' = /(*,У) (I)
и дано начальное условие:
Их-х. =Ah (-Wo)€ (Я). (2)
Тогда, если функция /(xj)eC(A), (P)cR2, то задача (i) —
(2) имеет хотя бы одно решение у = <р(х), которое определено на
отрезке Пеано / = |х^ - А, х0 + й].
(Непрерывности функции /(х,у) в области (7)) достаточно
для существования хотя бы одного решения уравнения (I), удов-
летворяющего условию П =Уо-)
А —AQ
Введем в рассмотрение последовательность {e„}w N , облада-
ющую свойством е„ > 0, для любого п6 N , и ея------>0. Пусть
Л—>*»
для любого не N построена ломаная Эйлера у = у„(х), хе /,
41
такая, что она является е„ -решением задачи (I) — (2). Следова-
тельно, для любого пе N имеет место соотношение
|у;(х)-/(х,ф„(х))|<£Л, хе/ (6)
(см. третье свойство ломаных Эйлера). Обозначим
«х)-/(х,уя(х)) = Дя(х), хе/. (7)
У нас 4G,(x) — кусочно-непрерывная на /, / (х,К|/л(х)) — непре-
рывная на /, как суперпозиция непрерывных функций. Поэтому
функция Д/Г(х) — кусочно-непрерывная на /. Кроме того, из (6)
следует, что: Д„(х)гз0, хе/. Из (7) находим: ц/',(х) =
=/(х,ф„(х)) +Д„(х), хе /, пе N. Функции у'Дх) — интегри-
руемые на любом промежутке |х0,х]с / . Интегрируя обе части
последнего соотношения по х от х0 до х, находим
j ф'(/)Л = ] /(/,уя(0)^+ J Дя(/)</ЛХе Z,rte N, =>
*0*0 *0
=> V«(x) = y0 + J/(z,v„(r))</f + J&n(t)dt,xe !,ne N. (8)
*b *o
У нас последовательность {'Mx)},igN, хе/,— последователь-
ность ломаных Эйлера. Было показано, что она равномерно oipa-
ниченная и равностепенно непрерывная на отрезке Пеано /. Но
тогда по теореме Ариела — Асколи она имеет подпоследователь-
ность {у,, (х)} хе /, обладающую свойством: фи (х) =$ <р(х),
хе/; <р(х)еС(/). Известно, что для любого ие!Ч:
|ф„(х)-у0| < Ь , хе / . Следовательно, |ч% (х)-у0| < Ь, хе / , для
любою к e N. Значит, и |<р(х)- j0| < b, хе /. Отметим, что
4% (*) = Уо + )/('Лл,(0Н'+ |ая<(/)Л,Х€ /, AeN. (9)
Xu *о
Докажем, что функция у = ф(х), хе /, является решением
задачи (1)— (2) на отрезке Пеано. У нас ЧЦ (х) _4 <р(х), хе /.
Покажем, что тогда /(х,ф„х (x))=t /(х.ф(х)), хе /.
42
Возьмем е>0— любое. По условию, функция
/(х, у)_е С(£>) => С(Р) => /(х,у) равномерно непрерыв-
на в (Р) => Взятому е > 0 отвечает 5 > 0 , зависящее только от е ,
такое, что как только |x'-xj<6 и |у'-У|<5, так сейчас же
|/(х',у')-/(х',У)| < £. (Точки (х',/) и (х',у')е (Р).) Так как
у (х) =: <р(х), хе / , то числу 8 > 0 , найденному по е, отвечает
номер К, такой, что как только к > К, так сейчас же
|ф„4 (х) - ф(х)| < 8, для всех хе / .
Рассмотрим разность /(х,фЯ1 (х)) - /(х,ф(х)). Имеем
xp.t ~ ХР = х - х = 0 ’ |-% “ >д| = К* W < 5, для х е /, если
к > К. А тогда |/(х,у„4 (х))-/(х,ф(х))| < е , для всех хе 7, если
к > К. Последнее означает, что /(х,ф„4 (х)) ^/(х,<р(х)), хе / .
Но тогда lim J/(/,ф„4 = jf lim/(/,(0)^ = J/(А <р(/))Л.
X
Покажем теперь, что lim ^Д„4(/)Л = 0. Было отмечено выше,
* ха
что Д„(х) 3 0, хе I. Следовательно, Д„ (х) 4 0, хе /. Это
* &-»<»
означает, что любому сколь угодно малому е > 0 отвечает номер
Л', такой что при к > К будет |д„4 (х)| < е сразу для всех хе J.
JK <'+*
Тогда при к > К :
К. ('Mr
*0
< е{х-х0| £ еЛ. Значит
<
lim |д (0<Л = 0.
Хо
В соотношении (9) перейдем к пределу при к -»<» , Получим
Ф(х) = J/(/,<p(/))rf/ + O, хе / . (10)
43
X
Из (10) видим, что ф(Ло) = Уо и что J /(Лф(О)<^. хе / — есть
Хо
интеграл с переменным верхним пределом от непрерывной фун-
кции. По теореме Барроу, существует производная правой части
(10), равная /(х,ф(х)) для хе /. Но тогда существует производ-
ная и левой части (10): ф'(х), причем
Ф'(х) = /(х,ф(х)), хе/.
Таким образом, получили: функция у = ф(х), хе / ,— решение
задачи (1) — (2) на отрезке Пеано /. 4
§3. Единственность решения задачи Коши
Г. Лемма Гронуола. Пусть
I) функция /(х)е С((«,/>));
2)Дх) удовлетворяет на (а,Ь) неравенству
J
0 < /<х) < Х + ц
.где xsO, и>0 — постоянные числа.
Тогда справедливо неравенство
0 < /(х) < хЛ'Ч хе(а,6>.
► Доказательство проведем для хе [х0,Л> (для хе (д,хп|
оно — аналогичное).
1-й случай: X > 0 .
X
Имеем по условию: 0< /(х) < Х + ц j , хе |х0,/>). Поло-
X х®
жим g(x) = X + pf f(t)dt, хе[ло,/>). Нетрудно понять, что
*0
g(x)e С1 ([х0,/>»; g(xo) = X>0. Имеем g'(x) = g/(x) > 0 ,
xe[xfl,i)=> g(x) — неубывающая на промежутке [х0,/>) =>
g(x)>X>0, хе[х0,/>). Так как я'(х) = р/(х), a /(x)Sg(x),
хе(х0,/>),то g'(x) < м • g(x), хе[х0,/>), =э
777г - ’ хе 1*о.л>.
г» V* )
44
Проинтегрировав последнее неравенство по отрезку
[х(),х| с [х0,Ь), получаем
1п*(л) [х(),b) => =>
g(*o) s(*o)
=> g(x) £ g(x0) = Xep<x"Jto).
=x
Следовательно, и подавно 0< /(x) < Xeg< ,r_Jto), xe[x0,/>>.
2-й случай: A, = 0 .
Имеем по условию в этом случае 0 < /(х) < ц J f(t)dt. хе [х0,/>).
*о
Возьмем последовательность чисел — любую, но такую,
что Х„ >0 для любого ие N и кп------->0. to любого ле N будем
иметь 0 < /(х) < Х„ + р j f(t)dt, х е |х0, Ь). Так как функция /(х)
ч
удовлетворяет последнему неравенству, то получаем предыдущий
случай. Следовательно, будем иметь 0 < /(х) < Х„ем<х‘*0>, хе [х0,д>,
ле N —любое. Переходя в этом неравенстве к пределу при п —»<*> и
приняв во внимание, что к„------»0, получим /(х) = 0, хе [x0,Z>>.
Видим, что и в этом случае лемма доказана.
Определение. Говорят, что функция f(x,y) удовлетворяете
области (D) условию Липшица по у, если существует число L > 0
такое, что для любых двух точек (х,у) и (х,у) из (D) справедливо
соотношение
|/(x,y)-/(x,J)|< £-|у-у|.
Пишут /(х.у)е Lip>,(0).
2\ Теорема единственности. Пусть дано уравнение
У' = Дх,у) (!)
и дано начальное условие
(2)
Пусть функция /(x,y)eC(D) и точка (Хц,у0)е (D). Если
существует окрестность t/(x0,>'0) точки (х0,уй) такая, что
45
f(x,y)e Lipy (U(xQ,y0)), то задача (I) — (2) имеет единственное
решение.
Что задача (1) — (2) имеет решение — это следует из теоре-
мы Пеано. Нужно доказать, что задача (I) — (2) имеет единствен-
ное решение. Рассуждаем от противного, а именно предполагаем,
что задача (I) — (2) имеет не одно, а несколько решений. Возьмем
тогда два любых решения задачи (1) — (2):
У = Ф(х), хе =[хь-Л,х0+Л);
у = ф(х), хе Л =[х0-Л,х0+ й].
п
Так как у = ф(х) , хе /* , и у = ф(х), хе / =, — решения задачи
(1)-(2), то
ф'(х) = /(х,ф(х)),хе /Л;
Ф'(х) = /(х,ф(х)),хе /^.
В левых и правых частях этих тождеств стоят функции, непрерыв-
ные соответственно в промежутках Iи . Интегрируя обе части
первого тождества по промежутку [xo,xj с /^ , а обе части второ-
го — по промежутку |х0,х]с /, получим
п
Ф(х)2Уо + J /(х,ф(х))(Лс,хе /*;
Ф(х) = № + )/(*. Ф(*)) х е I;.
Пусть / = П I = Ясно, что точка Хд е / . Для хе / вычтем из
второго тождества соолиегствующие части первого тождества. Получим
ф(х)-ф(х) = |[/(х,ф(х))-/(х,ф(х))]^,хе 7, =>
*0
По условию, существует окрестность //(х(),у0) точки (Хо,уо)
такая, что /(х,у)е Lipv (£/(х0,у0)). Пусть отрезок / с I (х0 е / )
и такой, что для любого хе / оказывается: точки (х,ф(х)) и
(х,ф(х)) принадлежат £/(х0,у0). Тогда для хе/:
46
|ф(х) - ф(х)| < J L |ф(х) - <р(х)| dx , где L — постоянная Липшица
функции /(х,у) в области щх0,у0). Введем обозначение:
|ф(х)-ф(х)| = /(х), хе Z. Тогда предыдущее неравенство запи-
шется в виде
О < /(х) < L J f(x)dx , х 6 I.
Видим, что функция /(х) удовлетворяет условиям леммы Грону-
ола при X = О и р = L .
Так как X = 0 . то из леммы Гронуола следует, что /(х) = 0 ,
х е / , а это означает, что <₽(х) з ф(х), хе /.
Итак, показано, что существует промежуток /, содержащий точку
х0 , на кагором совпадают любые два решения задачи (I) — (2). После-
днее означает, что задача (I) — (2) имеет единственное решение. 4
Следствие теоремы единственности. Пусть дано уравнение:
y' = f(x,y). Пусть функция f(x,y)e C(D). Пусть (D,)c(D), и
частная производная fy(x,y)e C^D^). Тогда (Dt) является облас-
тью единственности данного уравнения.
Возьмем любую точку (Хо„уо) в области (D,) и покажем,
что эта точка есть точка единственности данного уравнения. Для
этого достаточно показать, что существует окрестность U(xQ,y0)
точки (хо,у’0) такая, что /(х,у)е Lip^ (t/(Xo,y0)). Возьмем неко-
торую окрестность И(д^,у0), такую, что И(х0,у0) с (Д). (Это
сделать можно, ибо (Д) — область.) А затем возьмем окрест-
ность £/(х0,у0) меньшего радиуса. Тогда замкнутый круг, т. е. круг
(7<х0,у0)с И(х0,у0)с(Д). По условию /у'(х,у) е С(Д) =>
f'(x,y)e C(Z7(x0,y0)) => f'(x,y) —ограниченная в (7(х0,у0). Зна-
чит, существует число L > 0 , такое, что |/л'(х,у)| < L в £/(х0,у0) •
Значит, |4(х,у)|^ L в (/(х0,у0).
Пусть (х,У|) и (х,у2) — любые две точки из (/(х0,у0). Имеем
по теореме Лагранжа
f(x, у2) - f(x, у,) = f’(x, у) (у2 - У|), где у е (у,, у2) =>
=> |/(^У2)-/(^У|)| = |/уи»У)| h - л|- ->4
47
Последнее означает, что f(x,y)e Lipy ((/(х0,у0)), а значит, точка
(х0,у0) является точкой единственности для уравнения
у' = fix, у). Так как точка (х0,у0) “ любая из (D,), то (Д)
является областью единственности этого уравнения.
Теперь теорема существования и единственности для уравне-
ния первого порядка может быть сформулирована так.
Пусть имеется уравнение y'=J(x, у).
Если функция Дх, у) непрерывна в области (D) с R2 и имеет
в (D) непрерывную частную производную /}'(х,у), то для любой
точки (х0,у0)е (D) задача (I)—(2) имеет единственное решение.
§4. Общее, частное и особое решения уравнения у' = /(х,у)
Пусть имеется дифференциальное уравнение
(I)
где /(х,у)б C(D); (D)cR2.
I. Пусть (D|)c(D) и (D|) — область единственности для урав-
нения (I). Пусть функция у=<р(х,С) определена, непрерывна и
имеет непрерывную частную производную по х в области (Д)
плоскости (х, С). Пусть дс
Определение. Функция
Рис. 1.9. К определению
общего решения
уравнения (1)
= прс(Д).
у = ф(х,С) называется общим решени-
ем уравнения (1) в области (D(),
если, во-первых, для любой точки
(х0.у0)с(/^) уравнение y0=<p(Afl,C)
имеет одно и только одно решение
С = Со (причем Со е Дс, т. е. Со —
допустимое значение для О, и если,
во-вторых, функция у = ф(х,С0),
х е /6 ( /й = (х0 - 5, х0 + 5)) оказыва-
ется решением уравнения (I) хотя
бы при достаточно малом 5. (Ясно,
что это решение удовлетворяет
условию у| = у0.)
’A-Aq
Геометрически общее решение уравнения (I) представляет
собой однопараметрическое семейство интегральных кривых,
определяемых уравнением у = ф(х,С), которые покрывают всю
область (D|).
48
(Так как через любую точку (х0,у0)е (D,) проходит некото-
рая интегральная кривая из семейства у = ф(х,С), то общее
решение уравнения (I) определяет в любой точке (х0,у0)е (£>|)
линейный элемент (касательную к интегральной кривой в точке
(*0’№))- Следовательно, по общему решению уравнения (I)
можно построить в области (/),) поле направлений.)
II. Определение. Функция у = ф(х), х е / = (а, Ь), называется
частным решением уравнения (I), если:
1) эта функция является решением уравнения (I) в
2) каждая точка интегральной кривой (т. е. каждая точка гра-
фика функции у = ф(х), х е (а, b)) является точкой единственно-
сти для уравнения (I).
Заметим, что если у = ф(х,С) — общее решение уравнения
(I) в (D|), то частные решения этого уравнения в (D,) получа-
ются из общего при конкретных числовых значениях С (каждое
частное решение при своем числовом значении С).
С геометрической точки зрения частное решение есть интег-
ральная кривая, проходящая через заранее заданную точку
(x0,j'0)e (D().
В приведенном ранее примере 2, §1, частными решениями
уравнения у' = Зууз будут части кубических парабол, располо-
женные в открытой верхней полуплоскости, и части кубических
парабол, расположенные в открытой нижней полуплоскости.
III. Определение. Функция у = ф(х), хе(й,/>), называется
особым решением уравнения (I) в области (D), если:
1) эта функция является решением уравнения (I) в (а,Ь)\
2) каждая точка интегральной кривой (т. е. каждая точка гра-
фика функции у = ф(х), хе (а, Ь)) является точкой неедин-
ственности для уравнения (I).
Рис. 1.10. К определению частного решения уравнения (1)
49
Заметим, что особое решение уравнения (I) не может быть
получено из общего решения этого уравнения ни при каком
конкретном (допустимом) числовом значении С.
В примере I, §1, решение у зО, хе (-«>, + «) является осо-
бым решением уравнения у' = Зууз.
§5. Дифференциальные уравнения первого порядка
в симметричной форме
1°. Дифференциальным уравнением первого порядка в симметрич-
ной форме называется уравнение вида:
M(x,y)dx + N(x,y)dy = 0 , (I)
где М(х,у)е C(D) и N(x,y) е C(D), (D)cR2.
Определение.
I. Решением уравнения (1) называется всякая функция вида:
у = ф(х), хе (а,Ь), (2,)
которая удовлетворяет условиям:
I) <р(х)е С’ ((«,6»;
2)точка (х,<р(х))е (О) при любом хе(о,/>);
3) М (х,ф(х))«/х + N (х,ф(х)) <p(x)dx = 0 , хе{а.Ь) и для лю-
бого dx.
11. Решением уравнения (I) называется также всякая функция
вида
х = v(y), ye {c,d), (2„)
которая удовлетворяет условиям:
I) ф(у)е С1 (<c,J>);
2)точка (ф(>’),у)е (D) при любом уе(с,<7);
3) М (у(у),у) y\y)dy+ Н (y(y),y)dysO , ye(c,d) и для лю-
бого dy.
Пусть (х, у) — произвольная точка области (D). Пусть
F(x,y) = (M(x,y)\N(x,y)). Будем считать этот вектор приложен-
ным в точке (х,у). Таким образом в области (D) будет задано
непрерывное векторное поле.
Пусть точка (х0,у0)е (О) и такая, что F(xo,j’o)*O. В этой
точке вектор F имеет вполне определенное направление. Такая
точка называется обыкновенной точкой поля вектора F, а отсюда
и обыкновенной точкой уравнения (1).
Если же F(xo,yo) = 0, го точка (т0,у()) называется особой
точкой поля вектора F, а значит, и особой точкой уравнения (I).
50
Пусть (Я) — совокупность всех особых точек поля вектора F в
области (/)). Покажем, что (Я) — замкнутое множество в (D). Для
этого рассмотрим функцию h(x,y) = М2(х,у) + М2(х,у) . Ясно,
что h(x,y)e C(D) и что А(х,у)эО в (Я). Пусть точка (х0, j’0)e (D)
и является предельной для множества (Я). Но тогда существует
последовательность точек (хк,ук), AgN, такая, что
(хк,ук)е(Н) для любого fccN; (хк,ук) * (хо,Уо) Д™ любого
teN; (хк,ук)-------И^О’Уо)- В силу непрерывности функции
л •«
h(x,y), h(xk,yk)-----*h(x0,y0). У нас h(xk, ук) = 0 при любом
А —
ке N- Следовательно, А(х0,у0) = О => точка (х(),)’())е (Я). Мно-
жество, которое содержит все свои предельные точки, является
замкнутым. Значит, множество (Я) — замкнутое.
Рассмотрим произвольное решение уравнения (I). Пусть это
решение есть решение вида (2j). Тогда, в частности, справедливо
тождество
М (х,ф(х)) dx + /V (х,ф(х)) ф'(х)^х а 0,х € (a,b), dx — любое. (3)
Если ввести в рассмотрение векторы Г(х,ср(х)) = (Л/(х,ф(х));
N (х,ф(х))) и Т(х) = (dx;q'(x)dx), то левую часть тождества (3)
можно рассматривать как скалярное произведение векторов
F(x,ip(x)) и Т(х).
Выясним геометрический смысл вектора Т(х).
Заметим, что решение вида Ц) уравнения (I) можно считать
{X = X,
у = Ф(х) хе(а,Ь)
(х— параметр). Тогда вектор (х' ,у'х) = (1,ф'(х)) является направ-
ляющим вектором касательной к интегральной кривой (2j) в
точке (х,ф(х)), В этом и состоит геометрический смысл вектора
Т(х). Так как соотношение (3) является условием ортогонально-
сти векторов Г(х,ср(х)) и Г(х), то заключаем, что интегральная
кривая (2() располагается в области (D) так, что в каждой своей
точке (х,ф(х)) она ортогональна вектору ^(х,ф(х)).
Пример. Пусть дано уравнение
xdx + ydy = 0. (10)
Здесь Л/(х,у)нх; N(x,y) = y\ М(х,у), Я(х,у)е C(R2). М и N
обращаются одновременно в нуль лишь в точке (0, 0). Значит,
51
Рис. 1.11. К примеру
об ортогональности вектора
Г(х.ф(х)) к интегральным
кривым
н ={(0,0)}; (0)\(Я) =
= R2\{(0,0)}. В любой точке
(х,у)е R2\{(0,0)} вектор
А Л/, /V) = Fix, у). Интегральны-
ми кривыми уравнения (10) яв-
ляются окружности с центром в
начале координат: х2+у2=г2
(рис. 1. 11). Здесь: открытая дуга
-АВС — график решения урав-
нения вида (2(); открытая дуга
-BCD — график решения урав-
нения вида (2ц); открытая дуга
ВС — график решения уравнения и вида (2,), и вида (2Н) (зна-
чит, эти решения взаимно обратны).
Замечание. Пусть функция р(х,у)бС(О) и ц(х,у)*0 в
(£>) \ (//). Наряду с уравнением (I) рассмотрим уравнение
ц(х,у)Л/(х,у) dx + д(х,у)/У(х,у) dy = 0. (Ь
Очевидно, что уравнение (I) равносильно уравнению (I). Следо-
вательно, уравнения (I) и (I) имеют одинаковые решения. Вектор-
ное поле в для уравнения (I) задается вектором
Fi (Л/|(х,у),/V|(x,y)). Ясно, что в любой точке области (D)\(/7)
векторы /| и F коллинеарны (/j || F). => вектор F\ определяет
вектор F с точностью до направления.
2°. Существование решения уравнения (1). Пусть точка (х0, у0) —
обыкновенная точка уравнения (1), т. е. точка (х0,у0)е (D) \(//).
Это означает, что А*Ь,Уо)*б- Следовательно, хотя бы одно из
двух чисел Л/(х0,уп), /У(л0,у0) отлично от нуля. Могут реализо-
ваться следующие случаи.
52
/случай. М(хо,уо) = О\ N(Xq,у0) * 0.
Тогда по теореме о стабильности знака существует окрест-
ность точки (х0,у0): (/(х0,у0) с (D) такая, что /V(x,y)*0 в
^(х0,у0). Умножим обе части уравнения (L) на множитель
/ ч I
М ” У(х,у) (Н(х,у)е С((/) и ц(х,у)*0 в £/(х0,у0)). Полу-
чим уравнение, равносильное уравнению (I), а именно
= 0 или ± = -^1Ы1 (=/(х,»,/€С(4/)). (3)
N(x,y) dx N(x,y)
Уравнение (3) разрешено относительно /.Так как уравнение (3)
удовлетворяет условиям теоремы Пеано, то оно имеет хотя бы
одно решение у = <р(х), хе /; х0 е / и ф(*Ь) = То- Видим, что в
рассматриваемом случае уравнение (I) имеет решение вида (2().
Покажем, что в рассматриваемом случае уравнение (1) не имеет
решения вида (2(|), удовлетворяющего условию х|( ( = х0.
Рассуждаем от противного, а именно допустим, что уравнение
(I) имеет решение вила (2„), удовлетворяющее начальному усло-
вию х|^( = х0. Но тогда для у 6 (у0 -S,+5) и при любом dy
справедливо тождество:
М ^f(y), у) y'(y)dy + N (у(у), у) dy s 0.
Положив здесь у = у0 , получим
л/(-<(! То) /(Уо)+^(*о,Уо) = 0 •
=0 -const const, *0
=0
Видим, что это равенство невозможно. Значит, наше предполо-
жение, что уравнение (1) имеет решение вида (2П) неверно.
И случай. Л/(х0,у0) * 0, ATCW0) = 0.
По теореме о стабильност и знака существует окрестность точки
(*о,То) ’ И(х(),у0) с (D) такая, что М(х,у) * 0 в И(Хо,уо), а пото-
му вместо уравнения (I) будем иметь равносильное уравнение
dx N(x,y) , =
T = -. ^g(x,y);g(x,y eC(V)j. (3
dy M(x,y)
53
Уравнение (3) разрешено относительно х' . По теореме Пеано
заключаем, что через точку (х0,у0) проходит хотя бы одно реше-
ние уравнения (3) (а значит, уравнения (1)). Это решение будет
решением вида (2|(): х = ф(у), уе 7 = (у0 -5,у0 +8); у(у0) = ху.
Отмстим, что решения вида (2^ уравнение (I) в этом случае не
имеет (это устанавливается рассуждениями, аналогичными тем,
которые проведены при рассмотрении случая I).
HI случай. Л/(хь,у0)* 0; Н(Хц,у0) *0.
В этом случае по теореме о стабильности знака существует
окрестность точки (х0,у0): ^(хд.уо) с (£)) такая, что в И^Хо.уь)
одновременно Л/(х,у)*0 и М(х,у)*0. А тогда в ^(хо.уд)
уравнение (I) может быть записано как в виде (3), так и в виде
(3). И, следовательно, по теореме Пеано уравнение (I) имеет как
решение вида (2(): у = ф(х), хе (xfl -8,х0 +8); ф(хь) = у0, так и
решения вида (2„): х = ф(у), у е (у0 -&,у0 +5); ф(Уо) = . Пока-
жем, что при соответствующем подборе интервалов эти решения
взаимно обратны.
Действительно, пусть у = ф(х), х е (х0 - 8, х0 + 8), — решение
уравнения (3) такое, что ф(хь) = у0. Будем считать 8 настолько
малым, что (х,ф(х))е ^(Хо.Уо) для х е (хь - 8; х0 + 8). Тогда
фХх) = -^Х’Ф,(*?*0, хе (л« -8,х0 +8) => функция у = ф(х)
/V(x, ф(х))
строго монотонна на интервале /5 = (хь - 8, х0 + 8) и, следова-
тельно, по теореме о существовании обратной функции, имеет
обратную функцию х = ф(у), ye/s =(у0-8,у0+ 8), причем
ф(Уо)=хо ( /$ — образ 76 при отображении ф). Покажем, что
функция х = у(у), у е /§, является решением уравнения (3). По
теореме о связи между производными взаимнообратных функ-
ций, имеем для любого уе /§:
. I ,, , I ^(у(у),у)
v(у> = -т— => v(у)= —тут——~ ~ ?
ф(х) м (х,ф(х)) Л/(ф(у),у)
(х, ф(х))
Последнее означает, что функция х = ф(у), ye/g, является
решением уравнения (3), таким, что ф(у0) = х0.
Таким образом, доказана следующая теорема.
Теорема. Для любой точки (Хо,уо)б , уравнение (I)
имеет хотя бы одно решение, проходящее через точку (х0,у0).
54
3°. Единственность решения уравнения (1).
Определение. Пусть точка (x$,y0)e(D). Будем говорить, что
уравнение (I) имеет единственное решение с начальными данны-
ми (Ло,у0) в следующих случаях:
1)если оно имеет единственное решение вида (2^ с этими
начальными данными в том смысле, что любые дна решения вида
(2,) совпадают в некоторой окрестности точки Xq;
2)если оно имеет единственное решение вида (2Н) с этими
начальными данными в том смысле, что любые два решения вида
(2Н) совпадают в некоторой окрестности точки у0;
3) если оно имеет единственное решение с этими начальными
данными как вила (2,), так и вида (2Н).
Определение. Пусть функция f(x,y) определена в некоторой
области (D) плоскости х, у. Говорят, что /(х,у) удовлетворяет в
(D) условию Липшица по х, у, если существует постоянная L > О
такая, что для любых двух точек (xt,j|) и (х2,у2) из (D) выполня-
ется неравенство |/(х2, у2) - /(х(, у, )| < L (|х2 - х( | +1у2 - у, |).
Заметим, что если /(х,у)е Lipxy(D>, то одновременно
f(x,y)e Lip(.{D) и f{x,y)e Lipx(D).
Справедливо утверждение:
Если /(х,у)е C’(D) ((D)— область, (D)cR2), то любая
точка (х0,у0) из области (D) имеет окрестность U(x0,yQ) такую,
что /(х.у’)€ Lipx</(D(Xo,yo)).
Возьмем в области (D) любую точку (Xq,j0). Возьмем неко-
торую окрестность И(х0,у0) такую, что И(х0,у0) с: (D) (это сде-
лать можно, ибо (D)— область). Затем возьмем окрестность
^(хо,Уо) такую, чтобы было (7(х0,у0) с И(х0,у0) • По условию
/Дх,у)€ C(D) => Л(Х,у), 4'(х,у)е С((7(х0,у0)) =>
fx(x,y), fy(x,y) — ограниченные в (7(х0,у0). Значит, существует
число £>0 такое, что |/'(х,у)| < L и |/л'(х,у)[ < L всюду в
^(хо,Уо), а следовательно, и в (/(х0,у0).
Пусть (xhy|) и (х2,у2) — любые две точки из (/(х0,у0).
Имеем
Дх2, у2) - /(х,, у,) = |/(х2, у2) - /(х,, у2)] + [/(Х|, у2) - /(Х|, )] =
= У2 )(х2 - х,) + /;(Х|,у)(у2 - у,)
55
(Х€ (Х|,Х2);у€ (У|,У2))-
А тогда
|/(*2»л) - /<х1 »л )| * |/х(*,/2)| h - xi I+|Л'(л ’ jM I» - л I-
s£ S£
< Z.(|x2 -л| + |л -л|)-
Последнее означает, что f(x,y)e Lipx у U(Xq, >0.
Теорема единственности для уравнения (1). Пусть точка
(xQ,y0)e , т.е. (х9,уц) — обыкновенная точка уравне-
ния (I). Пусть существует окрестность U(x0,y0) точки (Хо,уо)
такая, что и(хц,у0)с(О)\(Н) и М(х,у), N(x,y)e
Тогда точка (х0,Уо) — точка единственности для уравнения (1),
р По условию точка (х0,у0) — обыкновенная точка для урав-
нения (I). Значит, хотя бы одно из двух чисел Л/(х0,>0), N(x^,y0)
отлично от нуля. Пусть для определенности W(xo,y0)*0. По
теореме о стабильности знака заключаем, что существует окрест-
ность И(х0,у0) точки (x0,j0) такая, что У(х,у)#0 в И(х0,/0).
(Можно считать, что И(х0,у0)с t/(Xo,j’o).)
Но тогда в И(х<),у0) уравнение (I) может быть записано в виде
^ = ~^4(=/(х.А/и.У)еС(П). (3)
dx А(х,у)
Покажем, что существует окрестность И^х^Уо) точки (х0,у0)
такая, что /(х,у)е Lipv (^(Хц,^)).
Пусть И^— окрестность точки (х0,у0) такая, что
^(хо.уо) с Их^уо). а значит, >₽(х0,>0) с t/(Xo,yo). У нас функ-
ции Л/(х,у), /V(x,y) — непрерывные в области (D). Значит, они
непрерывные в ограниченной замкнутой области ^(ху.Уо), =>
Л/(х,у) и Л/(х,у) — ограниченные в Й'Ч-Хо.Уо) => Существует
число т > 0 такое, что |Л/(х,у)| < т и |/V(x,y)| £ т в И^(х0,у0). У
нас /V(x,y)*O в И(х0,у0). Так как J₽(x0,y0) с И(х0,у0), то
/У(х,у)*0 в Г₽(х0,у0) => существует число К >0 такое, что
|#(л,у)|>АГ в r₽(xb,j0).
По условию, М(хуу), N(x,y)e Lipx>.(4/(хо,уо)). Так как
И/(х0,у0) с (/(х0,у0), то Л/(х,у),/V(x,/)e Lip^f^xo./o)).
Возьмем любые две точки (Х|,У]) и (х2,у2) в Ж(^,у0) и рас-
смотрим разность /(х2,у2) -/(Х|,У|). Имеем
56
|/(X2, J’2 >-/(Х|, >’| )| =
М(х2,у2) Л/(Х|,У|)
Я(х2,у2) /У(Х|,У|)
_ \M(x2,y2)N(Xt,yt)-M(xi,yi)N(x2,y2)\ <
|^(Х|.^)| |W(x2,y2)|
- -рт1л/(х2.>’2)/у(х1.>'|)- М(х},у})/V(x2,y2)| =
л
= ттгI [М(х2. у2) У(Х|,у,) - М(Х|, у,) Л/(Х|, у,)] +
Л
+ [Л/(Х|,У|)/У(хнУ|)- М(хьу{)^(х2,у2)]]<
S А[|Л/(х2,.у2)- Л/(Х|,У| )| + |^(х2,у2)- /V(x,,>’,)|] <
Л
Л
|/(Х2,>2)-/(Х|,>’|)| < 1(|х2 - х,| + |у2
где L = -—— — число, большее нуля. Последнее означает, что
К‘
f(x,y)e Lipr>,(B/(x0,y0)) => /(х,у)е Ыру(И/(х0,у0)). Атогда по
теореме единственности для уравнения, разрешенного относи-
тельно производной, получаем, что точка (хь,Уо) — точка един-
ственности для уравнения (3). Покажем, что из этого следует, что
точка (Хо,.Уо) — точка единственности для уравнения (1). В самом
деле, у нас N(xn,у0) * 0. Могут иметь место следующие два
случая:
I) М(х0,у0) = 0. В этом случае, как мы знаем, уравнение (I)
не имеет решения вида (2Н) с начальными данными (х0,у0),
а решение вида (2,) — единственное. Следовательно, уравнение
(I) имеет единственное решение.
2) ЛЛхо.Уо) * 0. В этом случае уравнение (I) может быть пред-
ставлено как в виде (3), так и в виде (3). Значит, уравнение (I)
имеет как решение вида (2,), так и решение вида (2П). Для
уравнения (3) единственность доказана; совершенно аналогично
устанавливается единственность для уравнения (3). Выше было
57
показано, что при соответствующем подборе интервалов для
решений вида (2() и (2ц) эти решения взаимно обратны. Следова-
тельно, и в этом случае уравнение (I) имеет единственное реше-
ние с начальными данными (х0,у0). 4
Следствие. Если функции М(х,у), N(x,y)e C’(Z)), то любая
точка (х<),у0)е (Z))\(//) является точкой единственности для
уравнения (I).
> Действительно, в этом случае любая точка (хо.Уо) имеет
окрестность l/(x0,y0) a (D) такую, что М(х,у), N(x,y)e Lip, ,.((/).
Но если точка (хо,уо) — обыкновенная, то в ней хотя бы одно из
двух чисел Л/(Хо,уо), М(ха,уо) отлично от нуля, т. е. выполнены
условия теоремы единственности. 4
§6. Общий интеграл уравнения в симметричной форме
Г. Некоторые сведения из теории неявных функций. Пусть фун-
кция F(x,y) определена в области (D) плоскости х, у. Рассмот-
рим уравнение
F(x,y) = 0. (*)
Говорят, что уравнение (*) определяет у как функцию от х, если
существуют интервал / оси Ох и функция у = <р(х), такие, что:
I)точка (х,ф(х))е (£>) при любом хе/;
2) F(x,ip(x)) = 0, хе /.
При этом функция у = ф(х), хе /, называется неявной функ-
цией, определяемой уравнением (*).
Имеют место следующие теоремы:
I. I) Пусть функция F(x,y) определена, непрерывна в прямоу-
х0 - А < х < х0 + А, _ _ _
„ „ ( Л > 0, 5 > 0 — некоторые
у0-В<у<уй + В
числа) и имеет там непрерывные частные производные F*(x,y),
Fy(x,y)-,
2) пусть F(xo,yo) = O;
3) пусть
Тогда существуют числа аи6(0<а<Л; 0 < b < В) такие, что:
а) каждому х из [х0 - а, х0 + а) отвечает одно и только одно у из
[у0 ~Ь,Уо + Ь| такое, что F(x,y) = 0 , т. е. у = ф(х),
х е [ло - a, Xq + а], причем F (х, ф(х)) з 0, х е |х0 - а, х0 + а];
Р) ф(*о) = Уо;
тальнике (/*) =
58
у) ф(х)еС(|х0-д,хь+о]);
б) для любого хе [х<) -л.Хя +а] существует непрерывная про-
изводная ф'(х), причем ф'(х) =-
Э£(х,ф(х))
Эх
3F(x^(x))
Эу
II. I) Пусть функция Г(х,у) определена, непрерывна в пря-
моугольнике (Р) и имеет там непрерывные частные производные
/\(х,у), />(х,у);
2) пусть Г(х0,у0) = 0;
3) пусть ^'(xo.j’o) * 0.
Тогда существуют числа а и Ь (0<а<А,0<Ь<В) такие, что:
а) каждому у из |у0 - Ь,у0 + Ь| отвечает одно и только одно х
из [хо-а.Хо+о] такое, что Г(х,у) = 0, т. е. х = ф(у),
уе |Уо ~^Уо + ^Ь причем F(v(y),y)s0, уе [у0-Ь,_у0 +Ь];
Р) ¥(Уо)=-*Ь;
у) у(у) е С (|у0 - Ь, у0 + 6]);
5) для любого у е [у0 -b,yQ + />| существует непрерывная про-
изводная ф'(у), причем у'(у) = -
ЭГ(у(у),у)
Эу
df(y(y),y)
дх
Замечание. Если уравнение (*) такое, что выполняются одно-
временно условия теорем I и II, то это уравнение (рассматривае-
мое в достаточно малой окрестности U(x0,y0) точки (х0,у0))
определяет неявные функции:
у = ф(х), хе Z& = (х0-б,х0 + 5)
(ф(хо) = Уо; Ф(х)еС(/&); ф'(х)еС(/,))
и
X = v(y), у е /& = (Уо - б, у0 + 5)
(ф(Уо) = •*<>; ф(у)еС(/8); y'(y)eC(/j)),
которые являются взаимно обратными.
59
2\ Определение общего интеграла уравнения в симметричной
форме. Пусть имеется дифференциальное уравнение асимметрич-
ной форме
M(x,y)dx + N(x,y)dy = 0. (I)
Предполагается, что функции М(х,у) и /V(x,y)e C(D), (D)c R2.
Определение. Пусть функция и(х,у)с и пусть С— про-
извольное постоянное число из множества допустимых значений.
(Допустимыми значениями Сявляются значения функции и(х.у)
В <£>).)
I. Соотношение
и(х,у) = С (2)
называется общим интегралом уравнения (1) в области (D), если,
во-первых, для любой точки (х0,у0)е (т. е. для любой
обыкновенной точки уравнения (I)) уравнение:
и(х,у) = и(х0,у0), (3)
рассматриваемое в достаточно малой области £/(х0,.у0), опреде-
ляет хотя бы одну дифференцируемую неявную функцию:
у = ф(х), х е = (х0 - б, х0 + б), (4)
такую, что <р(хо) = у0, м(х,ф(х}) z и(х0,у0), xe/j, и если, во-
вторых, функция у = <р(х), хе /6, хотя бы при достаточно малом
б является решением уравнения (I).
II. Соотношение (2) также называется общим интегралом
уравнения (I) в области (D), если, во-первых, для любой точки
(х0,у0)е уравнение (3), рассматриваемое н достаточно
малой области U(xQ,y0), определяет хотя бы одну дифференци-
руемую неявную функцию:
X = ф(у), у е /5 = (у0 - б, Jo + б), (5)
такую, что у(Уо) = Хо, м(ф(/),у) = и{х^у^), ус /5, и если, во-
вторых, функция х = цг(у), ус /j, является решением уравнения
(1) хотя бы при достаточно малом б.
Из определения общего интеграла уравнения (I) следует, что
для любой точки (х0,у0)б (£))\(Й) общий интеграл (2) опреде-
ляет хотя бы одно решение уравнения (I) с начальными данными
(хо,Уо)’ И частности, если (7))\(Я) — область единственности
для уравнения (I), то общий интеграл (2) содержит в себе все
решения уравнения (I), графики которых лежат в
60
Пусть и(х,у) =С — общий интеграл уравнения (I) в области
(О). Пусть точка (хо,у0) ~ любая из области (D). Рассмотрим
уравнение и(х,у) = и(х0,у0).
Справедливо утверждение.
Любая дифференцируемая неявная функция, определяемая
этим уравнением, график которой лежит в области (£)) (он может
проходить и через особые точки уравнения (I)) является решени-
ем уравнения (I).
Рассмотрим любую дифференцируемую неявную функцию
у = ф(х) , хе (а, Ь), определяемую уравнением w(x,y) = w(x0,y0).
Тогда, в частности, справедливо тождество
u(x,ip(x)) = иСхо,у0), хе (а,Ь). (6)
Покажем, что справедливо тождество
М (х,ф(х))+ А (х,ф(х)) ф'(х) г 0, хе («,/>). (7)
Для этого возьмем произвольную точку х( е (а, Ь) и рассмотрим
точку (х|,ф(х()). Могут иметь место следующие два случая.
1) Точка (Х|,<р(Х|)) — обыкновенная точка уравнения (I). Для
нее, в соответствии с (6), имеем w(x,,(p(X|)) = н(х0,у0). А тогда
уравнение и(х,у) = и(х0,у0) может быть переписано в виде:
и(х,у) = ы(Х|,У|), где У|=ф(х(). И, следовательно, функцию
у = ф(х) можно рассматривать как дифференцируемую неявную
функцию, определяемую уравнением и(х,у) - м(х(,У|) в окрест-
ности точки Х|; причем точка (X|,yt) — обыкновенная точка
уравнения (1). Согласно определению общего интеграла, функ-
ция у = ф(х) на некотором интервале /6 =(xt -5,Х| +5) является
решением уравнения (1>, т. е. на /8 справедливо тождество (7).
В частности, (7) верно при х = Х|. У нас х( — любое из промежут-
ка (о, />). Значит, (7) верно при любом х из (а, />). А это означает,
что у = <р(х), хе (а, Ь) является решением уравнения (1).
2) Точка (x|,q>(xt)) — особая точка уравнения (I). В этом случае
М (х(,ф(Х|)) = N (Х|,ф(Х|)) = 0, а значит, (7) справедливо при
х = Х| ив этом случае. 4
3°. Критерий общего интеграла.
Теорема. Пусть функция и(х,у) е С1 (D), (O)cR2, и такая,
( ди(х,у) f
что — +
\ "X J
(Эи(х,у) Y
*0 в (D) \( Я). Тогда: для того, чтобы
соотношение
61
и(х,у) = С (*)
было общим интегралом уравнения (I) в (D), необходимо и
достаточно, чтобы всюду в (D) было:
<<(х,у) и'(х,у)
Д(х,у) = 7 =0 /**\
М(х,у) N(x,y) * ' ’
Необходимость. Дано: соотношение и(х,у) = С — общий ин-
теграл уравнения (I > в (£>). Требуется доказать, что Д(х,у) а 0 в (D).
Возьмем произвольную точку (х0,у0)е (^) • Могут иметь мес-
то следующие два случая.
I) Точка (х0,у0) — особая точка уравнения (I). Но тогда
M(Wo) = ^(х0,у0) = 0 и> следовательно, Д(х0,у0) = 0.
2) Точка (хо.Уо) — обыкновенная точка уравнения (I). Но
тогда, как мы знаем, общий интеграл уравнения: и(х,у) = С
определяет хотя бы одно решение уравнения (I) с начальными
данными (х0,у0) Пусть это решение есть решение вида, у = ф(х),
хе 1& = (х0 -5,х0 + 5) (эта функция является дифференцируемой
неявной функцией, определяемой уравнением и(х,у) = м(х0,у0),
такой, что <р(хь) = у0; м(х,ф(х)) = и(х0,у0), хе /6). Имеем, сле-
довательно,
и(х,ф(х)) = w(x0,y0), хе /&, (8)
и
Л/(х,ф(х))</х + Л/(х,ф(х)) <p(x)dx = 0, хе /й (9)
(ибо у = ф(х) , хе /б, —решение уравнения (1)). Дифференцируя
тождество (8) по х, получим
и'х (х, ф(х)) + Uy (х, ф(х)) • ф'(х) = О, X € /6. (10)
В частности, при х = х() будем иметь
м;(х0,Ф(х0)) + и;(х0,ф(х0)) ф'(х0) = 0. (10о)
У нас тождество (9) имеет место при любом dx. Поэтому из (9)
следует:
Л/(х,ф(х))+/V(х,ф(х)) ф'(х)а0, хе/5. (II)
Положив в (11) х = Хо, получаем
= (По)
Таким образом, имеем следующую однородную систему двух
линейных уравнений
62
их (*о>ф(*о)) + иу (х0,ф(Хо)) чЛхо) = О,
Л/ (х0, ф(х0)) + N (х0,<р(Хо)) ф (хс) = 0.
(12)
В (12) <(х0,ф(х0)), м;.(х0,ф(х0)), М (хо.фСхо)), Л/(х0,ф(х0)) -
коэффициенты системы. Замечаем, что линейная однородная
система (12) имеет решение, отличное от чисто нулевого,
а именно: (I, ф'(х())) * (0, 0). Но последнее возможно лишь тогда,
когда
Л(Л)’>’о) =
<(х0,ф(х0)) м;.(х0,ф(х0))
М (х0,ф(х0)) (х0,<p(Xq))
= 0.
У нас точка (х(),_у0) — любая из (D), следовательно, Д(х,у) - 0 в
(О). Необходимость доказана.
Достаточность. Дано: Д(х,у) ж 0 в (Z)). Требуется доказать, что
соотношение н(х,у) = С — общий интеграл уравнения (I) в (D).
Покажем, что соотношение и(х,>) = С удовлетворяет опреде-
лению обшего интеграла. Для этого берем произвольную точку
(х0,д’0)е (Р)\(/7) и рассматриваем уравнение: и(х,у) = u(xQ,yn).
Перепишем это уравнение в виде:
и(х,у) -и(х0,у0) =0.
“ обозначение
(13)
Имеем:
I) F(x,y)e С’(Д) (так как u(x,y)e С1 (£)));
2) Г(х0,у0) = 0.
По условию, («'(х,у))2 +(м'.(х,у))‘ * 0 в (Д)\(Я). Так как точка
(х0,>’0)е (Д)\(//), то хотя бы одно из двух чисел м'(х(|,.Уо),
Чу(х0,у0) не равно нулю. Будем считать для определенности, что
w>(*o«>’o) * ° • Но тогда
3) ^'(^.Уо)*0-
Видим, что выполнены условия теоремы об однозначной разре-
шимости уравнения (13) (см. теорию неявных функций). По этой
теореме уравнение (13) определяет единственную дифференциру-
емую неявную функцию у= ф(х), хе /6 = (х^ -5,х0 +5) такую,
что ф(Х0) = Уо и
63
и(х,<р(х)) = и(хс,у0), хе /6 (14)
(точка (х,<р(х))б , хе /8).
По условию, Д(х,.у) = 0 в(Р) =>
<(х,ф(х)) и;(х,ф(х))| * f
И(*,Ч>М) ЛЦх,ч>(х))Г ' <15>
Продифференцируем тождество (14) по х. Будем иметь
«;(х,ф(х)) 1+и'(х,ф(х)) ф'(х) = 0. хе /й;
Из(15) => и' (х,ф(х)) N (х,ф(х)) +
+«'(х,ф(х)) • [-Л/(х,ф(х))] = 0, хе /6.
(16)
Рассматриваем эти два тождества как систему линейных однород-
ных уравнений с коэффициентами: I, ф'(х), У(х,ф(х)),
-М (х,ф(х)). Решениями этой системы для любого хе /5 являют-
ся: «;(х,ф(х)), м'(х,ф(х)).
У нас, по предположению, z/'(x0,y0) # 0 => w'. (х,ф(х)) # 0 ,
х е /6, при достаточно малом 5 -
Было отмечено выше, что точки (х,ф(х))е (D) \ (И) при
хе /8. Значит, точки (х,ф(х)) — обыкновенные для уравнения
(!) при хе /6. Следовательно, система (16) имеет решения, от-
личные от чисто нулевого. Но это возможно лишь тогда, когда
определитель системы равен нулю. т. е. когда
I ф'(х)
/ и л/г / н =0 для хе (,7>
ЛЦх,Ф(-*)) - Л/(х,<р(х))
Из (17) следует, что М (х,ф(х))+ N (х,ф(х))-ф'(х) = 0, хе /б.
Последнее означает, что функция у = ф(х), .хе /5, является
решением уравнения (I). 4
Определение. Пусть функция w(x,y)e C'(D), (D) с RI 2 , такая,
что u(x,y) = C — общий интеграл уравнения (I) в области (D).
Тогда функцию л(х,у) называют интегралом уравнения (I) в (D).
Справедливо утверждение:
Пусть функция м(х,у) — интеграл уравнения (I) в (D). Пусть
(D)\(//) — область единственности для уравнения (I). Тогда на
любом решении уравнения (I): у = ф(х), хе {а.Ь), (рафик кото-
рого лежит в (D)\(//), и(х,ф(х)) = const, хе {а,Ь).
64
Пусть у = ф(х), хе {а,Ь), — произвольное решение урав-
нения (I), график которого лежит в У нас
и(х,у)е C‘(D), <р(х)е С1 => м(х,ф(х))е С1 (<д,/>>). Мы по-
кажем, что и (х, ф(х)) = const, хе <«,/>>, если установим, что
— и(х,ф(х)) а 0 , хе (а,Ь).
dx
Для этого берем произвольную точку х$е(а,Ь) и находим
ф(х0) = _у0. Ясно, что точка (х0,у0)е . Рассмотрим те-
перь уравнение
и(х,у)- и(х0,у0).
По определению общего интеграла, это уравнение определяет
хотя бы одну дифференцируемую неявную функцию у = ф(х),
хе /8, такую, что <р(хо) = у0, и которая при достаточно малом 5
является решением уравнения (I). Ясно, что для хе /6 будет
м(х,ф(х)) = и(х0,у0). (18)
Имеем:
|)у = ф(х), хе(о,д>,— решение уравнения (I), такое, что
Ф(*о) = Jo!
2)у = <р(х), хе /8,— решение уравнения (I), такое, что
ф(*о) = Jo-
Видим, что оба эти решения удовлетворяют одному и тому же
начальному условию у| =Jb, (х0,у0)е (D) \(Н). Так как
XbXq
(D)\(/7) —область единственности уравнения (I), то ф(х)вф(х),
хе /6, по крайней мерс, при достаточно малом 3 • А тогда, в силу
(18), м (х,ф(х)) = и(х0,у0), хе/5=>, -u(x,<p(x)) = O, хе/5, =>
dx
в частности, — м(х,ф(х))
= 0 . У нас точка х0 — любая из (а,Ь)
х=х0
((а,Ь) — промежуток, на котором определено решение у = ф(х)
уравнения (I)). Поэтому получаем
-^-и(х,ф(х))еО,хе (а,Ь).
dx
65
§7. Уравнения в полных дифференциалах
Пусть имеется уравнение:
M(x,y)dx + N(x,y)dy = 0. (1)
M(x,y),N(x,y)e C(D), (D)cR2.
Определение. Уравнение (I) называется уравнением в полных
дифференциалах в области (D), если существует функция
и(х,у)е C'(D) такая, что
du(x,y) = M(x>y)dx+ N(x,y)dy, (х,у)е (D).
Функцию и(х,у) называют в этом случае первообразной по отно-
шению к левой части уравнения (1) в (D).
Рассмотрим уравнение: xdx + ydy = 0. Здесь М(х,у) = х\
N(x,y) = y, M(x,y),N(x,y)eC(R2). Рассмотрим функцию
£
2
и(х,у) =
(х2 +у2); и(х,у)е C'(R2). Имеем du(x,y) = xdx + ydy,
(х,у) € R2. Следовательно, данное уравнение — уравнение в пол-
ных дифференциалах в R2; и(х, у) = -(х2 + у2) — первообразная
для xdx + ydy в R2.
Заметим, что если функция и(х,у) является первообразной
для левой части уравнения (I), то любая первообразная для левой
части уравнения (1) содержится во множестве {и(х,у) + С}, где
С — произвольная постоянная.
В самом деле, пусть функция и(х,у) — первообразная для
левой части уравнения (1) в (О), а й(х,у) — любая другая
первообразная для левой части уравнения (I) в области (/)). Тогда
мы должны иметь du(x,y)= М (x,y)dx + N(x,y)dy и du(x,y) =
= M(x,y)dx + N(x,y)dy. Следовательно, </(и(х,у)-м(х,у)) г 0 в
(D). Но если дифференциал некоторой функции равен тожде-
ственно нулю, то частные производные этой функции по обеим
независимым переменным равны нулю, и, следовательно, сама
функция есть постоянная величина, т. е. й(х,у) -и(х,у) = С в (D)
=> й(х,у) = и(х,у) + С в (£>) 4
Свойства уравнения в полных дифференциалах
Первое свойггво. Пусть (I) — уравнение в полных дифферен-
циалах в области (D). Пусть функция и(х,у) — первообразная его
66
левой части в (/)). Тогда: соотношение и(х,у) = С является общим
интегралом уравнения (I) в области (/)).
► Проверим, что соотношение и(х,у) = С удовлетворяет кри-
терию общего интеграла уравнения (I) в (D).
1. У нас по условию:
du(x,y) = M(x,y)dx + N(x,y)dy, (х,у)е (D) <=>
<=> —dx + — dy • M(x,y)dx+ N(x,y)dy, (x,y)e (£>),
dx dy
при любых dx и dy. Положим (dx,dy) = (1,0>; получим
ux(x,y) = M(x,y). Положим (dx>dy) = (0, l); получим
u'y(x,y) = N(x,y). Так как в (I) M(x,y), N(x,y)e C(D), то заклю-
чаем, что и*х(х,у),и'у(х,у)е C(D) => u(x,y)e C'(D). Имеем далее
(и'(х,у))2 + (и'(х, у))2 = М2(х,у) + N2(x,y) * 0 в (D)\(//) (по
определению множества (Z))\ (//)). Имеем, наконец,
/ . 9
_ Z X UX UV
2. Д(х,у) = у
М N
М(х,у) N(x,y)
М(х,У) М(х,у)
= 0 в (£>).
Видим, что выполнены все условия теоремы (см. критерий обще-
го интеграла). Значит, соотношение и(х,у) = С является обшим
интегралом уравнения (I) в области (О). 4
Второе свойство. — область единственности уравне-
ния (!) (из того, что (I) — уравнение в полных дифференциалах в
(D), следует, что (Р)\(Я) — область единственности этого урав-
нения).
^Возьмем любую точку (х0,у0)е (D)\(//). Покажем, что
любое решение уравнения (1) с начальными данными (х0,у0)
представляет собой в достаточно малой окрестности точки (х0,у0)
неявную функцию, определяемую уравнением:
w(x,y) = и(х0,у0). (2)
В самом деле, пусть функция
у = <р(х), х е /6 = (х0 - 5,х0 + 5), (3)
есть решение уравнения (I) с начальными данными (х0,у0), т. е.
<р(х0) = у0. Тогда, в частности, справедливо тождество:
М (x,(p(x))dx+ Л/(х,ф(х)) ф'(х)б£х = 0, хе /8,
67
а значит, справедливо тождество:
du (х,ф(х)) = 0. хе /5.
Последнее означает, что
zz(х,<р(х)) = C(const), хе /в. (4)
Положим в (4) х = х0. Получим С = «(Хо, j0) . Атогда тождество (4)
означает, что функция (3): у = ф(х), хе /8, есть неявная функция,
определяемая уравнением (2): и(х,у) = m(x0,j0) , рассматриваемым
в достаточно малой окрестности точки (х0,)'()).
Покажем теперь, что уравнение (2), рассматриваемое в доста-
точно малой окрестности точки (х(),у0), определяет единствен-
ную (с точностью до взаимнообратной) неявную функцию. Для
этого перепишем уравнение (2) в виде:
и(х,у)-и(х0,у0) =0.
- обозначение
Имеем: I) Г(х,у)е С'(Z>); 2) F(x^,yo) = 0; 3) F'(xty) = и'у(х,у) =
= h/(x,y) ; F'(x,y) = u'x(x,y) = M(x,y). Следовательно,
[/\4>Wo)]2+[^(*o,>’o)]2 =[A/(x0,y0)]2 + [/V(x0,y0)]2 #0.
Видим, что выполнены все условия теоремы об однозначной
разрешимости уравнения Г(х,у) = 0. Из этого следует, что урав-
нение (2) определяет единственную непрерывно дифференцируе-
мую неявную функцию.
Определение. Область (D) с R2 называется односвязной, если
любой замкнутый самонепересекающийся контур (у). целиком
лежащий в (D). гомотопен точке, причем гомотопия не выводит
контур (у) из области (£)).
Теорема. Пусть функции М(х,у) и N(x,y) определены и
непрерывны в некоторой односвязной области (D)cR‘ и имеют
дМ dN п
там непрерывные частные производные ------- и —. Для того
ф' дх
чтобы уравнение (I) было уравнением в полных дифференциалах,
необходимо и достаточно, чтобы всюду в (D) было:
дМ(х,у) _ dN(x,y)
ду дх ' (5)
68
Необходимость. Дано: (1) — уравнение в полных дифферен-
с ЭМ dN , ч
пиалах. Требуется доказать, что —— = -—, (х,у)е (D).
ду их
По условию, (I)— уравнение в полных дифференциалах. Но
тогда существует функция и(х,у)е Cl(D) такая, что
, ди(Х,у) , ди(х,у) ,
du(x, у) = — dx + — dy =
дх Sy (6)
= M(x,y)dx + N(x,y)dy„ (х,у)е (D).
(7)
Подчеркнем, что (6) должно иметь место при любых значениях dx
и dy. Положив в (6) dx = 0 , a dy # 0 , получаем
/V(x,y) = —.
Эу
Положив в (6) dy = 0 , a dx * 0 , получаем
М(х,у) = ^-.
dx
Дифференцируя обе части (7) по х, а обе части (8> по у, находим:
dN d2u dM d2u d2u d2u
dxdy dydx dxdy
(8)
dx dydx ’ dy
ЭА/
ибо, по условию, -г—
Эу
d2U d2U
и ^-еС(Р). Но тогда, как известно,
dx
dM dN
- . * _ в < D), а значит, —— в ——, (х, у) е ( D). Необходи-
ЭуЭх dxdy dy dx
мость доказана.
Достаточность. Дано: ^. = —, (х,у)е(Д). Требуется до-
ну dx
казать, что (I)— уравнение в полных дифференциалах.
(.Обсудим сначала случай, когда область (D) — прямоуголь-
ник: (D) =
Рассмотрим функцию u(x, у), определяе-
мую равенством:
и(х,у)= J M(x,y)dx+ j H(x0,y)dy,
Лю
(9)
69
Рис. 1.12. К доказательству
теоремы в случае
прямоугольной области
ция /V(xo,.s), как функция от з,
где точка (х0,у0) — произволь-
но выбранная в (D). Покажем,
что функция и(х,у) определена
в (D) и имеет там непрерывные
частные производные и'х(х,у),
м'.(х,у). Для этого возьмем про-
извольную точку (х,у) и закре-
пим ее. Тогда M(t.y), как фун-
кция от / при закрепленном у,
будет определена и непрерывна
на промежутке [х0,х], а функ-
будет определена и непрерывна на
X
промежутке [Уо,у] • Следовательно, функция w(x,y) = | M(t,y)dt +
У
+ j N(X(y,s)ds определена в точке (х.у). У нас точка (х,у)—
Уо
любая из (D). Значит, и(х,у) определена в области (D). Покажем
теперь, что и(х,у) имеет в (Z)) непрерывные частные производные
X
м'(х,у), Му(х.у). Рассмотрим функцию J = j M{tyy)dt. При лю-
•ч,
бом закрепленном у из (c,d) M(t,y) — функция, непрерывная на
X
(д,д). Следовательно, J = J M(t,y)dt — интеграл с переменным
Хо
верхним пределом от непрерывной функции. А тогда по теореме
Барроу существует /' для любого х из (а.Ь), причем /' = М(х,у).
Последнее означает, что всюду в (D) существует и'(х,у), причем
w'(x,y) = М(х,у). Так как Л/(х,у)е C(D) (по условию), то
w'v(x,y)e C(D).
Возьмем теперь любое х из (а,Ь). Тогда для любого у из (c,d)
функция Л/(/,у) определена и непрерывна в прямоугольнике:
[х0,х]х|у-8,у + 5|, где <5>0 — достаточно малое число, и имеет
в этом прямоугольнике непрерывную частную производную
. Видим, что в прямоугольнике [х0,х]х[у-5,у + б] вы-
70
полнены условия теоремы о дифференцировании по параметру
под знаком интеграла J = j M(t,y)dt (у — параметр). По этой
*0
Г' Г' }dM(t,y). X/
теореме J.. существует, причем = —-——at. У нас по уело-
4 3>
ЭЛ/ dtf
вию -----=— в (D), а значит, и в прямоугольнике
ду дх
|х0,х|х(у -&,у + 5|, Следовательно, будем иметь
r _ г dV^y)^ _ ЛГ(г,у)£* = N(x,y)- Н(Хо,у).
dt
*0
у
j /V(X0,$)(fc
Л
Так как
= N(xv,y) для любого у из (c,J), то при-
ходим к выводу, что и\(х,у) существует для любой точки
(x,y)e(D), причем и'у(х,у) = N(x,y), (х,у)е (D) Так как
/V(x,y)e С(Р) (по условию), то u'v(x,y)e C(D). Итак, получили,
что функция и(х,у), определяемая равенством (9), определена в
(D); м(х,у)е С'(/)) и что —= М(х,у)\ — = N(x,y). Значит,
дх ду
M(x,y)dx + N(x,y)dy =
ди(х,у) , ди(х,у) , . . . .
= —dx + —г— <*у = у), (х, у) е (D),
дХ ду
т. е. du(x,y) — дифференциал левой части уравнения (I). Следова-
тельно, (I)— уравнение в полных дифференциалах. Функция
д(х,у), определяемая формулой (9),— первообразная для левой
части уравнения (I).
Замечание. При доказательстве достаточности указан способ
построения функции и(х,у) по ее полному дифференциалу (см.
формулу (9)). Совершенно аналогично для функции w(x,y) мо-
жет быть получена другая формула, а именно:
х у
и(х,У)= J Л/(х,у0)<7х+ J N(x,y)dy. (Ю)
Хо Л
71
При практическом интегрировании дифференциального урав-
нения в полных дифференциалах следует пользоваться как свобо-
дой выбора формулы для и(х,у), так и свободой выбора точки
(х0,у0) в (D). Удачный выбор точки (х0,у0)е (D) и формулы для
и(х,У) нередко упрощает вычисление интегралов.
II. Рассмотрим теперь случай, когда (D)— произвольная од-
носвязная область.
Пусть (х0,уй) и (х,у) — две произвольно выбранные точки в
(D). Пусть кривая .АВ — кусочно-гладкая, соединяющая точки А
и В и лежащая целиком в области (D). Введем в рассмотрение
криволинейный интеграл второго рода:
| М(х, y)dx + N(х,y)dy.
-АВ
Рис. 1.13. К доказательству теоремы
в случае произвольной области
(Н)
Условие в в (D)
ду дх
(при прочих условиях теоре-
мы) является необходимым
и достаточным для того, что-
бы интеграл (II) не зависел
от формы пути интегрирова-
ния .АВ , а зависел лишь от
координат точек А и В. Если
это условие выполнено, и мы
закрепим точку Л(х0,уо),
а точку В(х,у) будем считать
переменной, то интеграл (II)
будет функцией от переменных х и у, т. е. функцией точки В
в области (D):
(х.у)
J M(x,y)dx + W(x,y)dy = и(х,у). (12)
(jWo)
Исследуем свойства этой функции.
Закрепим у и дадим х приращение Дх — любое, но такое, что
Дх * 0 и прямолинейный отрезок, соединяющий точки (х,у) и
(х + Дх,у), лежит в (D). Мы получим
(х+Лх.у) (х.у)
и(х + Дх, у) - и(х, у) = J Mdx + Ndy - J Mdx + Ndy.
(Хв.Л) <Хо->Ъ>
72
Ввиду независимости криволинейного интеграла от формы пути
интегрирования мы можем считать, что путь интегрирования в
первом HHTeipajie состоит из кривой -АВ, соединяющей точки А
и В (той же самой, что и для второго интеграла), и отрезка прямой
ВВ', параллельного оси Ох. Тогда интеграл по -АВ сократится,
и останется:
(х+Лх.у) дг+Дх
и(х + Дх, у) - w(х, у) = J Mdx + Ndy - J М( х, у) dx,
(х.у) X
ибо на прямой ВВ' у не меняется, и dy = 0. Применяя теорему о
среднем, находим:
w(x +Дх,у>-м(х,у) = М(х + 0Дх,у)Дх(О < 0 < 1) =>
и(х + Дх,у)-и(х,у) ... .
—----——-—— = Л/ (х + едх, у)
ди(х,у) = |im и(х + Ьх,у)-и(х,у) =
Эх Лх-»0 Дх
= lim М(х + 0Дх,у) = М(х,у).
Итак, получили
ди(х,у)
Эх
= Л/(х,у). Так как М(х,у)ь C(D) и точка
(х,у) — любая из (D), то заключаем, что и'х(х,у)е C(D). Точно так
_ Эм(х,у) ... .
же мы можем убедиться в том, что --------—=N(x,y) и что
By
«j,(x,y)e С(Р). Следовательно, и(х,у)е C’(D) и
Л/(х, v)dx + N(x,y)dy = 1 dx + ^l^x' -1) dy - du(x.y).
dx dy
Таким образом, оказывается, что при выполнении условия
в (D) левая часть уравнения (1): M{x,y)dx + N(x,y)dy
ay оХ
является полным дифференциалом функции м(х,у), определяе-
мой по формуле (II). 4
73
Замечание. Самое общее выражение функции Ы|(х,у), от ко-
торой полный дифференциал равен M(x,y)dx + N(x,y)dy , дает-
ся формулой
И|(х,>’)*и(х,у) + С, (13)
где С — произвольная постоянная. В самом деле, мы должны иметь
du(x,y) = M(x,y)dx+ N(x,y)dy,
= Л/(х,у)«4х + N(x,y)dy,
откуда d (U| (x, y) - u(x,y)) = 0 в (D). Но если дифференциал неко-
торой функции равен тождественно нулю, то частные производ-
ные этой функции по обеим независимым переменным равны
нулю, и, следовательно, сама функция есть постоянная, т. е.
- и(х,у) С.
Итак, необходимое и достаточное условие для того, чтобы
выражение M(x,y)dx + ?V(x,y)dy было полным дифференциалом
некоторой функции w((x,j) водносвязной области (D), заключа-
ется в том, чтобы в (D) имело место тождество
ЭЛ/(х,у) _ dN(x,y)
ду дх
при выполнении которого функция И|(х,у) определяется по формуле
(*.у)
«|(х,у)= J M(x,y)dx + N(x,y)dy. (14)
(Ч-Уо)
(Предполагается, что функции Л/(х,у), /V(x,y) непрерывны в (D)
дМ dN
и имеют там непрерывные частные производные “““ , .)
Пример 1. Уравнение с разделенными переменными.
Так называются уравнения вида:
f(x)dx + g(y)dy = 0. (15)
(В (15) коэффициент при dx зависит только отх, а коэффициент
при dy зависит только от у.) Предполагается, что /(х)е С((а,/>));
g(y) е С ((c,dY) =* f(x), g(y) е С( D), где (D) = (a, b) х (с, d).
Ь Имеем Л/(х, у) = /(*); jV(x,у) = g(у) =э — = 0; — = 0 в
ду Эх
(D)
дМ _ dN
ду дх
в (Р). Ясно, что (15) является уравнением в
74
полных дифференциалах в (£>). Общим интегралом уравнения (15)
X у
в (D) будет J f(x)dx + J g(y)dy = С, (х0,у0) — любая точка из
<0 >0
(/)).◄
у •>
Пример 2. Решить уравнение — dx + (у + In x}dy - 0.
В этом примере
<D) = l
О < X < +°°,
-оо < у < +оо;
X
N(x,y) = у5 + In х . Л/(х,у) и W(x,y) обращаются в нуль одно-
„ АЧ ЭЛ/ 1 ЭУ I
временно лишь в точке (1,0). Имеем —— = —; -— = -=>
ду х Эх х
ЭЛ/ ЭА ЭЛ/ ЭА о
—— = — в (D). ( ЛЛ /V,-—g C(D)). Значит, данное уравне-
Эу Эх Эу Эх
ние является уравнением в полных дифференциалах в (О).
(D) \ {(1,0)} — область единственности уравнения.
Возьмем х0 = I, у0 = I . По формуле (9) находим
/
4
х ,, у
и(х,у) = j — dx + y3t/y = ylnx|
'*=1
4 .
। У 1
= у1пх + ^---.
4 4
>=1
Это — первообразная для левой
в области (D). А тогда
I У**
w(*,y)+ т = У,пх + т)— тоже первообразная
4 4
части заданного уравнения
u(x,y) + С
(в частности.
для левой части
,4
исходного уравнения в (D) и, следовательно,
общий интеграл данного уравнения в (D).
4
х
Пример 3. Решить уравнение Зх2(I + In y)dx = 2у - -— dy.
► Перепишем заданное уравнение в виде
3x2(l +lny)dr+ --2у dy=0.
У
75
В этом примере (D) =
—о> < X < +°°,
О < У < +оо;
М(х,у) = Зх2(1 + In у);
N(x,y) =---2у \ М(х,у) и /V(x,y) обращаются одновременно в
У
нуль лишь в точке
ЭЛ/ Зх2
Имеем —— =-----
Эу у
Э/V =3?
Эх у
дМ _ 3N ЭМ ZN_________,
~~ = 5“ b(D); Л/(х,у), У(х,у), — , — е C(D). Значит, за-
оу ах ду Эх
данное уравнение является уравнением в полных дифференциалах
в(Я). (Я)\-
— область единственности уравнения.
Возьмем х0 = 0, Уо = I. Точка (х0,у0) = (О, I) е (D). По фор-
муле (10) находим
X
и(х,у) = J 3x2dx
о
+ (х 1пу -ум
1у=1
= х3 + х31п у - у2 + I.
Это — первообразная для левой части заданного уравнения. А тогда
и(х, у) + С , в частности, и(х, у) - I = х3 + х3 In у - у1, — тоже пер-
вообразная для левой части заданного уравнения в (D) и, следова-
тельно, х3 +х3 In у-у2 = С — общий интеграл уравнения.
Пример 4. Решить уравнение
х (x2 + l)cosy , _
----+ 2 ktc + --------—dy-^.
sin у J cos 2y-1
Запишем исходное уравнение в виде
( X -К (x2 + l)cosy , „
----+ 2 k/x + --——-dy = 0.
\siny ) -2 sin" у
Это уравнение определено в областях (Dk) =
-00 < х < +«>,
кп < у < (к + 1)я,
, п . . . Л КН X X - ... . (x2 + l)cosy
к = 0, ± I, ±2, ... ; М(х,у) = --+ 2; N(x,y) = -~----5—-
sin у 2sin*y
76
М(х,у) и /V(x,j) обращаются одновременно в нуль в точках
(~1)*+| 2,(2к + I)- I £ =0, ± I, ± 2, ... (это —особые точки урав-
i 2J
нения). В каждой из областей
(Dk) имеем:
ЭЛ/ _ х cos у
ду sin2 у
dN _ xcos у дМ dW
дх sin2 У ду дх
в (С\), к =0, ±1, ±2,... ;
Л/(х,у), /V(x,y),
ду
-£-eC(Dk), к =0. ±1, ±2__________
Рис, 1.14. К примеру 3
Значит, заданное уравнение является уравнением в полных диффе-
ренциалах в каждой горизонтальной полосе (Dk) ,к = 0, ± 1, + 2,... .
В W
к = 0. ± I, ± 2.
возьмем точку ’) - (2Л +1)-
. По формуле (9) находим
fp_ + 2U- f -^dy =
^siny ’ <2>|2sin^
I I ry
2^Яу=(2Ы)Г
2 sin у
I , (-I)**'
2 sin у 2
xi +1
=>------+ 2x = С — общий интеграл заданного уравнения в каж-
2 sin у
дой из полос
77
—OO < X < 4-00,
kn < у < (к 4- 1)я,
Л =0, ±1, ±2, ...
Пример 5. Решить уравнение 2х (I 4- у]х2 - у 1 dx - у]х2 - ydy = 0 .
Данное уравнение определено в области (D) =
И меем М(х, у) = 2х |I 4- у]х2 - у), Л (х, у) = -yjx2 - у . М(х, у) и
Л(х,у> обращаются одновременно в нуль в точке (0,0>«е (£>).
ЭЛ х дМ _ dN .
дх yjx2 -у ду ~ дх ’
А/(х,у), Л(х,у), ,
ду
ЭЛ г,/п. о
—— еС(£>). Значит, данное
Эх
уравнение является уравне-
нием в полных дифференци-
алах. В (D) возьмем точку
(х0,у0) = 0.0) и любую дру-
гую точку (х,у) (х > 0). Бу-
дем иметь
Рис. 1.15. К примеру 4
2 4х’ -1 ♦ | (х! - - р = X2 + |(х2 - 1
•Z fcj J J J
х2 + -(х2 - у)3/2 = С — общий интеграл заданного уравнения в
(О). 4 1
78
§8. Интегрирующий множитель
Пусть дифференциальное уравнение дано в симметричной
форме:
M(x,y)dx + N(x,y)dy = 0, (1)
М(х,у), N(x,y)e C(D), (D) с R2. Пусть (1) не является уравнени-
ем в полных дифференциалах.
Если существует функция p(x,y) е C(D) и ц(х,_у)#0 в
(£>) \ (//) такая, что после умножения на нес обеих частей урав-
нения (I) получается уравнение
ц(х, у)М(х, y)dx + p(x,y)W (x,y)dy = 0 (2)
в полных дифференциалах в области (£>), то функция ц(х,у)
называется интегрирующим множителем для уравнения (I).
Пусть функция ц(х,у) — интегрирующий множитель уравне-
ния (1) и пусть функция и(х,у)е C'(D) — первообразная левой
части уравнения (2). Так как уравнение (2) равносильно уравне-
нию (I), то справедливы следующие утверждения:
I) соотношение и(х,у)-С — общий интеграл уравнения (1)
в (£>);
2) множество множество точек единственности
для уравнения (I).
Рассмотрим вопрос о нахождении интегрирующего множите-
п a/z \ Kft \ ЭЛ/(х,у)
ля. Пусть Л/(х,у), /V(x,y), —----, ------— непрерывны в
ду дх
односвязной области (/)>. Пусть р(х,у)е С*(Р). При этих услови-
ях было показано:
Для того, чтобы (2) было уравнением в полных дифференциа-
лах, необходимо и достаточно, чтобы всюду в (D) выполнялось
тождество:
ч^Н А// ч^м dN дМ
Л/(х,/)-£•-/V(x, _>’)-£ г ц ----—
ду дх I Эх ду
Эф Л/) = Эф /V)
ду дх
Иначе: Д1я того, чтобы уравнение (I) имело в (Р) интегрирую-
щий множитель ц(х,у), необходимо и достаточно, чтобы функ-
ция р(х, у) была решением уравнения:
а// ч^М .у, (дМ(х,у) dN(x,y)\
/У(х,у)-£-Л/(х,у)тт- = ц- ——----------—— . (3)
Эх Эу I ду Эх I
79
(Можно показать, что если М(х,у), N(x,у)е C'(D), то для
любой точки (х0,.м>)€ существует окрестность t/(x0,y0)
такая, что уравнение (3) имеет решение р(х,у)е С1 (£/(х<>,у0)) и,
следовательно, уравнение (1) имеет в U(x{),yt]) интегрирующий
множитель.)
Отметим, что в общем случае задача по нахождению интегри-
рующего множителя ц(х,у), как решения уравнения в частных
производных (3), не легче, чем задача интегрирования исходного
уравнения (I). Рассмотрим некоторые частные случаи, когда урав-
нение (3) упрощается и интегрирующий множитель для уравне-
ния (I) найти легко.
I. Допустим, что Ц зависит от х и у посредством известной
функции со(х,у), т. е. p = p(to), где <о = (о(х,у) — известная фун-
кция. В этом случае будем иметь
Эр Jp Эш Эр _ zfp fki)
Эх Jco Эх ’ ду dw ду
Поэтому уравнение (3) запишется так:
Эр(,,Эа> ,,Эсо) (дМ dN \
— N-------М— = р--------------I.
d<a[ дх ду) ду дх J
или
d
(4)
дМ dN
ду дх
л/ Э(О ч д(й
W “ М V
Эх ду
Итак, если и зависит только от ю, то уравнением для определения
р является уравнение (4). При этом правая часть (4) должна также
зависеть только от ш. Этот вывод обратим. В самом деле, пусть
дМ dN
ду дх . ,
—т----5“ = V(w)
N--M — ф
Эх Эу I
обозначение
дМ dN
ду дх
(т. е. отношение
N —— М —
Эх ду
есть функция только от со). Тогда (4)
примет вид
80
£(ln|g|) = V(w)^
In|p| = j (0)4/10+ In С , где C > 0 ;
|p| = C^*(u>></“
Соотношение |м| = Ce’v представляет собой бесконечное мно-
жество решений уравнения (4). Для приведения уравнения (I) к
уравнению в полных дифференциалах в качестве интегрирующего
множителя ц достаточно брать лишь какое-нибудь одно из реше-
ний уравнения (4). Так мы и будем поступать всюду и дальнейшем.
Замечание. Из проведенных выше рассуждений вытекает, в
частности, что:
I. Уравнение (I) имеет интегрирующий множитель Ц, зави-
сящий только от х (w = x), если выполнено условие
ЭЛ/ D/V
Дл' = у(х). Тогда |ц| = С^*(Х)Л .
2. Уравнение (I) имеет интегрирующий множитель Ц, зави-
сящий только от у (<о = у), если выполнено условие
ЭЛ/ dN
ду = V(j). Тогда |g| =
— Л?
3. Уравнение (I) имеет интегрирующий множитель ц = р(ху)
ЭЛ/ Э#
(и = х у), если выполнено условие —--— = у(х • у). Тогда
yN - хМ
где <о = х у.
4. Уравнение (I) имеет интегрирующий множитель
ц=ц(х + у) ((о = х + у), если выполнено условие
ЭЛ/ 3N
--— = у(х + у) Тогда |ц| = э где о) = х + у ;
N - Л/
и т. д.
81
II. Пусть ц(х,.у) — интегрирующий множитель уравнения (1)
и пусть и(х,у) — соответствующий ему интеграл этого уравнения.
Тогда все интегрирующие множители уравнения (I) выражаются
формулой Ц(х,у) = ц(х,у) ф(н(х,у)), где <р(г) — произвольная
непрерывно дифференцируемая функция.
Действительно, так как р(х,у) — интегрирующий множитель
уравнения (I), то \tMdx + \iNdy = 0 — уравнение в полных диффе-
дх
ЭфЛ/) Эф/V) /Пч
ренциалах и. следовательно, ———- = —-—- в (О) и
ду дх
ди(х,у) .. Эи(х,у) .. х,
—Эх— = = Умножим обе части уравнения (1)
на функцию ц(х,у). Получим ф(/) цМ dx -кр(Г) gW dy = 0 (здесь
л/
N
дМ Э/V
t = u(x,y)). Рассмотрим разность —--— . Имеем
дМ dN
ду дх
д([1М) .,д<р t d(y.N) Эф
= ф(/)—— + цЛ/-2-ф(/)—=--------»N-^ =
ду ду дх дх
.(д([1М) Э(цЛГ) | , ( ди мди
= Ч>(0 —ч--------— +Ф(/) gAf —-ц# —
I ду дх } ду дх
О в (£>)
= ф'(/) (ц2MN-\rMN} = 0 в(Р) =>
•О b(D)
=> Д(х,у) — интегрирующий множитель уравнения (I).
Принимая во внимание изложенное выше, интегрирующий
множитель уравнения (I) иногда удается найти следующим обра-
зом. Представим уравнение (I) в виде
Л/, (х, у )dx + Nl(x,y)dy + М2(х, y)dx + N2(x,y)dy = 0
и предположим, что удалось найти интегрирующие множители
Hi(x,y) и ц2(х,у) и интегралы «|(х,у) и и2(х,у) соответственно
уравнений
Mi(x,y)dx+ Ni(x,y)dy = 0 и M2(x,y)dx + N2(x,y)dy = 0.
82
Тогда все интегрирующие множители первого из этих уравнений
запишутся в виде (х,у) = Ц|(х,у)ф( (w((x,y)), а второго — в виде
Й2(Х’У) = Мг(х’У)Ф2 (w2<x»y))» где <р| и ф2 — произвольные не-
прерывно дифференцируемые функции.
Если удается подобрать функции ф, и ф2 так, что
Mi(х,>)ф| (Мх,у)) = (и2(х,у)),
то р(х,у) = Ц|(х,у)ф, («| (х,у)) — интегрирующий множитель урав-
нения (I).
Пример 1. Решить уравнение (х2 + у2 + x)dx + ydy = 0.
Здесь Л/(х,у) = х2 +у2 + х ; N(x,y) = y=* М(х,у),
N(x,y)e C(R2). М(х,у) и N(x,y) обращаются одновременно в
нуль в точках: (0,0); (-1,0). Имеем = 2у; 4^- = 0=>
ду дх
дМ dN ~
3—3“ = 2>’-
ду дх
(дМ dN\.
dp _ ( Эу Эх J dp _ 2ydw
н ЭсО , zd<0 ц Эй) . 2 2 х Эй)
и /V —-Л/— и у —-(х~ + / +Х) —
дх ду дх ду
Положим со = х. Тогда — = I; — = 0 и, следовательно,
Эх ду
— = — dx => — = 2dx=t> In hl = 2x + InC => hl=e2xC.
ц у ц
Возьмем, например, ц = е2х (* 0 ). Умножаем обе части исходного
уравнения на р=е2х. Получаем уравнение
(х2 + у2 + х) е2х dx + у е2х dy = 0, равносильное исходному. Име-
=W(x.y) =N(x.r)
ем — = 2уе2х ; = 2уе2х => в в (D) = (R2) => Полу-
Эу Эх Эу Эх
ченное уравнение является уравнением в полных дифференциалах
83
в(£>). R* 2\{(0,0); (-1,0)} — множество точек единственности полу-
ченного и исходного уравнений.
Возьмем в качестве точки (хо,у0) точку (1,0).
X >' X у
и(х,у) = j M(x,ya)dx + jN(x,y)dy = J(x2 + x)e2xdx + jye2xdy =>
ioi о
„2
=> и(х,у) - ~^е2х
х=х
- Jxe
।
x v~
2xdx + [ xe2xdx + — e2x
i 2
)=0
2 * V2
+ У c2x
2
2 j. »2
+ У e^x
2
2
2
[х2 + y2)e2jf =С — общий интеграл исходного уравнения. «
Пример 2. Решить уравнение (х2 + у2 + y)dx - xdy = 0.
Здесь Л/(х, у) = х2 у2 y\N(х, у) =
= -х=> Л/(х,у), jV(x,jp)g C(R2). Л/(х,у)
и N(x,y) обращаются одновременно в нуль
«точках (0,0) и (0, -I). Заметим, что
х = 0.
ПУ
х = О,
х = О,
— решения исходного уравнения. Станем
рассматривать наше уравнение в областях
Рис. 1.16.
К примеру 2
w=
и (О2) =
Имеем
дм _ , ow
— = 2y+l; —
dy dx
dM dN ..
-----— = 2(y+l)
dy dx
ду дх I
dM dN
dp _ dy dx
дх dy
, <4i 2(y + l) ,
dM => — =-r----------г— dm .
ц o(0 . > 2
и -X —-(x*+J)t"
dx dy
84
Положим со = х2 + у1. Тогда — = 2х; -— = 2у и, следовательно,
Эх ду
Jp-------2<у-к1) ---------dm
Р -2х2 - 2у(х2 + у2 +• .у)
2(у+1>
2(у + 1)(х2 + у2)
dw = —у
х2
, did
did =----
ш
с/р _ did
р со
1п|р| = - 1п|со| + In С.
Возьмем, например, р = —, т. е. ц = —--г (р(х,у) определена и
со х + у~
не равна нулю в (D,) U (02)). Умножим обе части исходного урав-
нения на р = —5-у. Получим
х + у
х2 + у2 + у , х
-----------— dx------------
•> ил 2
X" + у X + у
Mix.у) -N(x.y}
dy = 0.
Имеем:
дМ (2у+ 1)(х2 +у2)-2у(х2 + у2 +у) _ х2 - у2
Эу (х2 + у2)2 (х2+у2)2’
3N _ х2 + у2 - 2х2 _ х2 - у2
Эх (х2+у2)2 (х2+у2)2
дМ _ dN
ду дх
(т. е. в (Z)|) U (D2)). Значит, полученное уравнение является урав-
нением в полных дифференциалах в этих полуплоскостях.
I) Возьмем в качестве точки (хь,у0) точку (1,0).
м(х,у) = j М(х,у0 )dx + J N(x,y)dy =
1 о
как в левой, так и в правой открытых полуплоскостях
1
|х=* I . У
. -x -arctg—
х х 0
85
у
=> w(x, у) - х - I - arctg — =>
у
=> х-arctg— = С — общий интеграл уравнения в правой полу-
х
плоскости.
2) Возьмем в качестве точки (Ло,уо) точку (-1,0).
и(х,у) = J M(x,yQ)dx + \N(x,y)dy =
-I о
г ‘f xdy , , у
= -у = + 1-arclS- =»
-I ох + У л
у
=> х-arctg— = С — общий интеграл уравнения влевой полуплос-
X
КОСТИ. 4
Пример 3. Решить уравнение ydy = (xdy + ydx)y/\ + у2 .
^Так как + у2 *0, то исходное уравнение равносильно
уравнению
ydy
= xdy + ydx =>
у dx +
=М(х.у)
= У(х.>)
Здесь М(х,у) = у; N(x.y) = x—; М{х,у), N(xty)e C(R2).
М(х,у) и N(x,y) обращаются одновременно в нуль лишь в точке
(0,0). R2 \{(0,0)} — множество точек единственности исходного
ЭМ . дй , ЭМ dN
уравнения. Имеем -т— = I; — = 1 => -----s— всюду в R-.
ду дх ду дх
Функция и = — оказалась интегрирующим множителем ис-
VI +/
ходно!о уравнения. Возьмем в качестве точки (х0,у0) точку (0,1).
86
X у
и(х,у) = JM(x,y)dx + JN(x0,y)dy -
о I
= xy - + У2 + V2 =>
=> xy - >J\ + у2 = С — обший интеграл уравнения. 4
Пример 4. Решить уравнение
ху2(ху'+ у) = I «- х2у2 dy + (xy3 -\)dx =0.
=N(x,y) = М(х.у)
► Здесь М(х,у) = ху2 -I; N(x,y) = x1y2; M(x,y),N(x,y)e C(R2).
Л/(х,у) и N(x,y) не обращаются одновременно в нуль ни в
одной точке плоскости х, у.
дМ , 2 dtf _ 2 дМ dN 2 дМ dN ^„2.
— = 3ху ; — = 2ху => — -—- = х/ (_ —6C(R-).
ду дх ду дх ' ду дх
(дМ dN},
------------UW ,
rfp _ ( Эу дх j _ xy2da>
ц кг дш .. дол 2 2 / 3
N--M— Х*уг-—(х/-1) —
дх ду дх ду
Положим оз = х. Тогда
дол
дх
^ = 0- - ху2
ду ’ ц х2у2
, du. dx
dx ------------для х х 0
Ц X
=> 1п|ц| = 1п|х|+1пС => |ц|=С|х|.
Возьмем, например, ц = х. Заметим, что исходное уравнение име-
ет решение
х = 0.
-оо < у < -»-оо.
Для х # 0 и для любых у, т. е. в левой и
правой полуплоскостях, ц определена и р * 0 . Поэтому, умножив
обе части заданного уравнения на ц = х, мы получим в каждой из
полуплоскостей уравнение, равносильное исходному:
87
(х2у3 - x) dx + x3y2 dy = 0.
=M(x.» N(x.y)
.. дМ -> 2 2 dN _ 2 2
Имеем-----= Зх у ; — = Зх*у => полученное уравнение являет-
Эу Эх
ся уравнением в полных дифференциалах в обеих полуплоскостях.
I) Возьмем в качестве точки (x0,j0) точку (1,0).
ж у ж у
и(х,у) = J A/(x,y0)dx +J N(x,y)dy = j-xd!x +Jx3y2r/y =
i о io
2 *“* 3 3 y=y 33 2
X X у X у X
— + —— = —--------у —
2 , З л 3 2 2
X=l >=о
х3у3 х2
=> —у—~ общий интеграл уравнения в правой полу-
плоскости.
2) Возьмем в качестве точки (х0,у0) точку (-1,0).
и(х,у)= J M(x,yQ)dx + j N(x,y)dy =
-I о
ж У ,.2 । „3,,3
= J-xdx + jx3y2dy = -~ + l + 3L2L
-I 0 L L 5
у— — = С — общий интеграл уравнения в левой полуплос-
кости .
Заметим, что решение исходного уравнения
х=0,
со-
— оо < У < +оо
держится в общем решении. Оно получается из общего при С = 0. 4
Пример 5. Решить уравнение y2dx - (ху + x3)dy = 0.
^Отметим, что функции М(х,у) = у2', N(х,у) = -ху-х3
определены и непрерывны на всей плоскости х, у и обращаются
одновременно в нуль лишь в точке (0,0). R2 \{(0,0)} — множе-
ство точек единственности заданного уравнения. Из вида уравне-
ния следует, что
88
>’ = 0,
О < х < +~;
У = 0,
-оо < х < 0;
х = 0,
х = 0,
-ОО < у < 0
— решения исходного уравнения. Поэтому искать решения исход-
ного уравнения станем в областях:
(/>,)=
0 < X < + ®о,
0 < у < +«>;
(П2) =
J-oo < X < 0,
|0 < У < +«>;
(£>з) =
-ОО < X < 0.
-оо < у < 0;
(О4) =
0 < X < +оо,
-оо < у < 0.
Имеем:
ЭЛ/ _ эм
— = 2у; — =
ду Эх
-у - Зх2
ЭЛ/
-—-— = 3(у + х*>
Эу Эх
гдМ dN
Эу ’ Эх
(дМ dN\.
—------— k/o) ,
= ( ду Эх ) = 3(у + х2) dw
в дг _ д/ -х(у + х2)—-у2—
Эх ду дх ду
г с. Эй) , Эй) Л
Если положить co = х.тобудем иметь — = I, — = 0 и,следовательно.
Эх ду
</ц 3(у + х2) dx
— = —-------—dx => — = -3—.
Ц - х(у + х2) и х
В качестве ц возьмем, например, ц = — (у нас в каждой из обла-
стей (Dk), к = I, 4: х # 0).
Умножим обе части исходного уравнения на ц = —. Получим
У (У I
уравнение —г dx-1—+1 </у = 0, равносильное исходному в
хД 1,х )
Л(х.у> N(x,y)
89
,п , l П ы ЭЛ?(х,у)_2у Э/V 2у дМ _д/У
(DJ, *=1,4. Имеем —у---------37 = 7 . в
каждой (Dk), к = 1,4. Значит, полученное уравнение является
уравнением в полных дифференциалах в (Dk), к = 1,4.
Найдем общий интеграл заданного уравнения в областях (Dk),
к = I, 4 . Для этого возьмем точку (x0,yft)e (Dk) (* 0 ; у0 * 0).
Будем иметь
х У
и(х,у) = J M(x,y)dx + j N(x0,y)dy =
Хо >0
>’о
У2
2х2
, 2хо
у2
=> — + у = С — общий интеграл заданного уравнения в каждой
у = 0, у = О,
4
из (DJ. Заметим, что решения ’
жатся в семействе —г + у = С при значении С = 0. 4
2х2
Пример 6. Решить уравнение (у - — + — = 0 .
содер-
Здесь М(х,у) = у —; N(xty) = —. Видим, что функция
М(х,у)=у— не определена на линии ‘ ’ а функция
X “°0 < у < +°°,
1 у ~ О,
N(x,y) = — не определена на линии • ’ М(х,у) и
У -оо < х < +°°.
N(x,y) определены и непрерывны в каждой из областей:
90
(Z)|) =
О < x < +«*»,
О < у < +°°;
-« < х < О,
О < у < +°о;
(4) =
< х < О,
< у < О;
О < х < +°°,
-оо < у < 0.
^=0
дх
(DK), к = I, 4 . Имеем ~-
М(х,у) и N(x,y) не обращаются в нуль ни в одной точке областей
ЭЛ/,
ду дх
(ЭМ dNC(D t = | 4);
dy дХ
ал/
t/p _ ( ду
Ki Э<1) 1Z дш
N —-----М —
дх ду
Э<о
дх
МЭсо
х 1ду
<7<о.
Если положить <о = —, то будем
X
Э<о у дю I
иметь — = -А- ; — = -
Эх х2 ду х
т. е.
4* =_____
м _____L
х2
х2
du dot
— =------=>
р со
В качестве интегрирующего
In |р| = - In |w| + In С.
множителя ц возьмем, например,
X —
р =— => М = — (в областях (Dk), к = 1,4, х * О и у * 0 ).
to у
Умножим обе части исходного уравнения на Ц = —. Получим
— х dx
--^dy=Q. М(х,у) и N(x,y) не обращаются одно-
=У<х.»
91
временно в нуль ни в одной точке областей (Dk), к = 1,4. Имеем
ЭЛ/ _ 1 Э/V _ I дМ эй
э7="/; V’аГ вкаждой изобластсй (А)
Найдем общий интеграл заданного уравнения в областях (Dk),
к = 1,4. Для этого возьмем точку (х$,уй)е {Dk) (х0 * 0 и у0 # 0).
Будем иметь
х- *- | \ УХ
и(х,у) = J M(x,y)dx + J N(x0,y)dy = J —х Idx - J -ydy =
•Ч Л *0 \У / To У
y=y
У-Уо
У 2 у 2 у y0
=>-------= С — общий интеграл исходного уравнения в каждой
У 2
из (Dk), к = 1,4.
Пример 7. Решить уравнение (х2 + 3 In y)ydx - xdy = 0 .
► Здесь М(х,у) = (х2 + 31пу)у — определена и непрерывна
I-оо < X < +°°,
п N(x,y) = -x — определена и непрерывна
О < у < +оо;
на R2 => М(х,у) и /V(x,.y) определены и непрерывны в (D);
Л/(х,у) и У(х,у) одновременно обращаются в нуль лишь в точке
(0,1). Из вида заданного уравнения следует, что
х = О,
I < у < +оо
х = 0,
О < у < I
— решения этого уравнения. Поэтому решения наше-
го уравнения станем искать в областях: (D\) =
И (Й2) =
О < X < +оо,
у > 0.
Так как у > 0 в (£>), то заданное уравнение
равносильно уравнению
92
(х2 + 3 In jO dx— dy = {). (*)
',------/ у
=Mt(x.y)
-N^x.y)
Имеем
ЭЛ/, 3. 3N| _ I ЭЛ/, d/V| _ 4.
ду у ’ дх у dy dx y'
ЭЛ', 4
rfp = ay ~ ax rf[a_------------у------- m
I* .^_(xJ+3lny)^
dx dy у dx dy
с r to . 3w n
Если положить co = x, то будем иметь — = 1; — = 0 ;
dx dy
4
- = -l—dx=* — = -4 — => 1п|ц| =-4ln|x| + InC.
И _х ц х 11 11
У
В качестве интегрирующего множителя возьмем, например, фун-
кцию Ц = -т. Заметим, что х * 0 как в (1\), так и в (А). Умно-
х
жим обе части уравнения (*) на р = —т. Получим уравнение
х
( I , Iny А , I , Л
—+ 3— \dx-—^-dy =0,
^Х X ) X у
=М(х.у) •Htx.y)
равносильное исходному в (Z)|)U(^2)- Имеем
dM 3
dy х4 у '
dN 3 dM dN z n 4 t n v „
---= —— => ----=----как в (D,), так и в (/X). Значит, получен-
dx х у dy dx
ное уравнение является уравнением в полных дифференциалах.
Найдем общий интеграл этого уравнения (а следовательно, и ис-
93
ходного уравнения) в областях (Dk), к = I, 2 . Для этого возьмем
точку (х0,у0) е (ДА) (Хо * 0 , у0 > 0 ). Будем иметь
и(х,у) = J M(x,y)dx + J N(x{],y)dy =
Mi
Iny
“Т
•*0
У=У
У=Уо
I In у , 1 . In у ln> ln>() 1 In y l In y,t
1 ' ' 1 1'1 — 1 " ' 1
X X Ло Xq Xq Xq х X3 хо Xq
общий интеграл нашего уравнения в
(D,)U(D2) Ч
Пример 8. Решить уравнение у(у2 + I)dx + х(у2 - х + l)Jy = О .
Здесь М(х,у) = у()Г + 1); N(x,y) = х(у2-х+1) => M,NeC(R:).
Л/(х,у) и Af(x,y) обращаются одновременно в нуль в точках (0,0),
(1,0), Непосредственно из вида данного уравнения заключаем, что
- решения этого уравнения. Поэтому решения исходного уравне-
ния станем искать в областях:
(Р|) =
О < X < +«>,
О < у < +«>;
(02) = ‘
-оо < х < 0,
0 < у < +«>;
-«> < х < 0,
-оо < у < 0;
(Д4) =
0 < х < +°°,
-ОО < у < 0.
Так как у2 + I * 0, то исходное уравнение равносильно уравнению
у dxt Х-—т— юу = 0.
(*)
94
Имеем
дМ, , ЭМ , 2х дМ. Э/V, 2х
Эу Эх у2 +1 Эу Эх у2 +1 ’
ЭЛ/, ЭМ,
d\t _ Эу Эх
ц .» Эш .. Эсо
н У Л/
Эх ду
У2 + I_________
х2 Э(о , Эо)
у2 + I Эх ду
_ _ Э<о Э<о
Если положить w = х у , то будем иметь — = у; —
Эх ду
2х
2х
(/р у2 +1 , d\x 2 ,
р xly Р W
ху - - ху
у + I
В качестве интегрирующего множителя возьмем, например, фун-
I I —
кцию и = —X- => Ц = , , (у нас в каждой области (D,), 4 = 1,4,
со2 х-/
х # 0, у * 0 ).
Умножим
обе части уравнения (*) на ц = 2 2-♦ Получим
уравнение
-М(х.у)
=N(x,y)
равносильное
__ дМ _ I
исходному в (Dk), 4 = 1,4. Имеем ~ »
dN I дМ dN
Ч----—гу =* “г- ~ Т" в каждой из областей (D, ). Следова-
ЭХ х у ду дх *
95
тельно, полученное уравнение является уравнением в полных диф-
ференциалах.
Найдем общий интеграл этого уравнения (а значит, и исход-
ного уравнения) в каждой из областей (Dk), к = 1,4. Для этого
возьмем точку (Хо,у0)е (Z)A) (х0 *0, у0 *0). Будем иметь
* т
и(х,у) = j M(x,y)dx + J N(x^y)dy =
*о Л
— + - + arctgy
у
=------+------------+ — + arctg у +
ху W ЪУ У
I 1 I I
-------------arctg у0 ------+ — + arctg у + G =>
*оУо Jo ху у
=>----+ —+ arctgy = С — общий интеграл исходного уравнения
ху у
в (D*), к =1,4.
Пример 9. Решить уравнение y'dx + (ех -y)dy = 0.
Здесь Л/(х,у) = у2; N(x,y) = ех -у => A/(x,y),W(x,y)e C(R2).
М(х,у) и Н(х,у) не обращаются в нуль одновременно ни в
одной точке из R2. Из самого уравнения легко видеть, что
функция у = 0, хе (-оо,+оо) является решением уравнения. По-
этому станем рассматривать наше уравнение для у # 0, а именно:
для у > 0 и для у < 0 (т. е. в открытых верхней и нижней полу-
плоскостях). Имеем
ЭЛ/
Эу
Э#
Эх е
ЭЛ/ э#
Эу Эх
2у-ех;
96
ЙМ dN
— = » ~ \ du>------------x </«>.
ц », d<0 ,,oW . x . d<0 i Ofc)
(e -y)—-yz^-
dx dy dx dy
г I I I e d(D . d(O I
Если положить co = x + In у , то будет — = I; — = —;
11 dx ду у
= 2У-е' *^-do>.
•* (eK -y)-y2 ~
У
Возьмем в качестве ц, например, функцию ц = е~® ц = е"х • е 1,1
=> ц =----- => Ц =----, если у > 0 и ц =----, если у < 0. Умно-
|у| ех уех уех
жим обе части исходного уравнения на И. Получим (как для открытой
верхней, так и для открытой нижней полуплоскостей) уравнение
уе х dx +
равносильное
исходному.
И меем
dM _х dN .х dM dN
— = е ; —- = е =э — = — всюду в открытых верхней и ниж-
ней полуплоскостях. Значит, полученное уравнение является урав-
нением в полных дифференциалах в отмеченных полуплоскостях.
Найдем общие интегралы нашего уравнения в верхней
и нижней полуплоскостях. Для этого берем точку (х0,у0)е (Dk),
к = I, 2 ((О|) — верхняя, а (Д2) — нижняя полуплоскости; Xq —
любое, а у0 — любое, не равное нулю).
5- уг ~ х у (1 А
w(x,y) = J M(x,y)dx 4- J N(x0,y)dy = J ye'xdx + j-e-*® dy =>
*o л лД^ /
=> u(x,y) = -ye'x|A ' +(ln |y|-e_JCByt
1ж=до г
97
= -уе~х + уе-л° + In |у| - уе 4 - In |у0| + у^ = In |jj - ye х + С, =>
=> ln|y|->’e * = С — общий интеграл уравнения в (О,) U (D2)
Пример 10. Решить уравнение x2y(ydx + xdy) = 2ydx + xdy.
► Здесь M(x,y) = х2у2-2у; /V(x, у) = х3у - х => М(х,у),
N(x,y)e C(R2)- М(х,у) и ЛГ(х,у) обращаются одновременно в
нуль в точке (0,0). Из заданного уравнения непосредственно
видно, что
- решения заданного уравнения. Станем рассматривать исходное
уравнение в областях:
W =
О < х < +«>,
О < у < +«>;
-ОО < X < 0,
О < у < +<»;
О < х < +<»,
-<*<)•< 0.
1. Рассмотрим уравнение
x2y2dx + x*ydy = 0.
Легко видеть, что Ц|(х,у)= . , является интегрирующим мно-
х у
жителем этого уравнения в (Dk). к = 1,4. В самом деле, после
умножения обеих его частей на ц получаем: — + — = 0 — уравне-
X у
ние в полных дифференциалах, ху = С, — общий интеграл уравне-
ния (*) в каждой из областей (£\), к = 1,4 . Тогда все интегриру-
ющие множители уравнения (*) содержатся в формуле
Й1(х,у) = Р|(х,у) ф,(х-у) = ^Ц-<Р|(х у), где <р, — произвольная,
х>у
непрерывно дифференцируемая функция.
98
2. Рассмотрим уравнение
2ydx + xdy = 0. (**)
Легко видеть, что ц2(х,у) = — является интегрирующим множи-
гелем уравнения (♦♦) в (ОА), к = 1,4 , ибо после умножения обеих
частей уравнения (••) на ц2 = —- получаем уравнение в полных
ху
дифференциалах: 2—+ —= 0 => х2у = С2 — общий интеграл
X У __
уравнения (**) в каждой из (Dk), к = I, 4 . Тогда, как мы знаем, все
интегрирующие множители уравнения (**) содержатся в соотно-
шении: Й2(х,у) = ц2(х,у) Ф2(х2у) = ^ ф2(х2у), где Ф2 - произ-
вольная непрерывно дифференцируемая функция.
Попытаемся подобрать функции ф( и ф2 так, чтобы было
Hi (х, у) ф| (ху) = ц2(х, у) • ф2 (х2у),
т. е. чтобы было ——-ф((лу) = —фэ(х2у). Возьмем в качестве функ-
ху2 ху
нии ф|(ху) = I. Тогда фт(х2у) = —5—. Но тогда
ху
Д(х,у) = Ц|(х,у) ф| = ц2(х,у) ф2 =-y-j
будет интегрирующим множителем исходного уравнения в (Dk),
А = 1,4. Проверим это. Умножим обе части исходного уравнения
на
Получим
dy = 0.
=Л'<х.у)
.. ЭЛ/ 2 Э/V 2
Имеем — =——; -г— = -г-
? V2 Зх х’д
ЭЛ/ эй .. ,п , . r-j
— 3 в каждой (D,), к = I, 4.
Эу Эх
99
Найдем общие интегралы исходного уравнения в (Dk), к = 1,4.
Для этого возьмем точку (х«, j0)e (Dk) (х^^О, jo?tO). Будем
иметь
u(xty) = j M(x,y)dx + J N(x0,y)dy =
>b
= ln|x| + -l—In |*b|-“4“ + In И + -4--1П M-
x ly x^y
I
*оЛ
= In |x| + In | vj + -4— + C =>
=> In |x| + In |j | + -у- = С — общий интеграл исходного уравнения
х у
в каждой из областей (Dk), к = 1, 4. «
Пример 11. Решить уравнение у(х + y2)dx + x2(j- \)dy = 0.
Здесь М(х,у) = лу + у3; N(x,y) = х2у- х2 => М. N е C(R2).
М(х,у) и /V(x,y) обращаются одновременно в нуль в точках
(0,0) и (-1,1). Видим непосредственно, что
у = 0, |> = 0,
<
“со < х < 0; [0 < х < +<»;
х = О,
0 < у < +«>;
х = 0,
-СО < у < 0
— решения заданного уравнения. Станем рассматривать исходное
уравнение в областях:
(Д|) =
О < X < +оо,
О < У < 4-оо;
(D2) =
-оо < X < О,
О < У < 4-ое;
(00 =
-ОО < X < О,
-оо < у < 0;
(04) =
О < X < 4-00,
—ОО < у < 0.
100
Имеем
эл/ , 2 dN _ , дм aw , _ 2 п
—— = х + Зу ; —— = 2ху - 2х =>---------— = Зх + Зу - 2ху,
ду дх ду дх
дМ dN
tfg ду дх d (/g _ Зх + Зу2 - 2ху
Ц */ д(0 ./Эю ц -2 2\3(1) . 3ЧЭ(О
В У Л/ в (х*у-х*) —-(ху + уО —
дх ду дх ду
Если положить со=у(х + у)2, то будет: — = 2у(х + у)‘,
дх
^ = (х + у)(х + 3у);
зу
= —2----=----------------------------d„
И (х1у - х1)2у(х + у)- у(х + у)(х + /)(х + Зу)
</g _ Зх 4- Зу2 - 2ху _ d[i _ du
g -у(х + у)2(3х + 3у2 -2ху) g ®
Возьмем в качестве g, например, функцию g = — =----------=-.
® У(х + у)
Умножим обе части исходного уравнения на g =------—у. Заме-
У(х + уу
тим, что умножение на ц сводится к делению обеих частей урав-
нения на произведение у(х + у)2 . У нас в областях (£\), к = !, 4 ,
у # 0. В областях (£>,) и (D?): х + у * 0 . В областях (D2) и (Z)4)
х + у = 0 на прямой у = -х . Отметим, что
У = -х,
-оо < х < - I;
у = -х,
-I < х < 0;
У = -х,
0 < X < +оо
- решения исходного уравнения. Поэтому станем рассматривать
исходное уравнение в областях (D,), (^22)’ (^з)» (^н) •
(О42), где
(^21) =
-ОО < X < 0,
-X < У < +оо;
-оо < X < 0,
0 < у < -х;
(О22) =
101
Рис. 1.17. К примеру 11
О < х < +оо,
—х < у < 0.
(^4?) -
В каждой из этих областей, после
умножения обеих частей исходного
I
уравнения на м =-------т, мы по-
Ях+>’)2
лучим уравнение, равносильное ис-
ходному. Это будет уравнение
х + у2 , х\у-1) , Л
----ах + —— dy = 0.
(х + уГ Я* + У)
-М(х.у') =N(x,y}
Имеем
ЭЛ7 _ 2х(у — I) dN _ 2х(у-\)
dy (x + j)3 ’ Эх (х + у)3
dM dN
---= — в областях
dy dx
(D2|), (Z)22), (At), (A4|), (D42). Следовательно, полученное
уравнение является уравнением в полных дифференциалах в каждой
из упомянутых областей.
Замечание. В этом примере установить вид функции ю(х,у)
dM dN
из условия, чтобы было —- = /(ш), оказалось делом не
,, Эю .. Эю
N —-------------------------М —
dx dy
совсем простым. Более удобным способом нахождения интегри-
рующего множителя р для этого уравнения будет следующий.
Запишем исходное уравнение в виде
y2dx + x2ydy + xydx - x2dy - 0.
I. Рассмотрим уравнение
y2dx + x~ydy = 0. (*)
102
Легко видеть, что р । (х,у) = . является интегрирующим множите-
х у
лем этого уравнения. В самом деле, после умножения обеих его частей
dx dy п . .
на Ц| получаем: —у + -3- = 0 — уравнение в полных дифференциалах
X у
11 г Х+у „ - ..
=>-------= -С => ----- = С — общий интеграл рассматриваемого
х у ху
уравнения в областях (Dk), А: = 1,4,
интегрирующий множитель урав-
нения (*). (ф| — произвольная, непрерывно дифференцируемая фун-
кция.)
2. Рассмотрим уравнение
xydx - x 'dy = 0.
(*•)
Легко видеть, что И2С*>>') = является интегрирующим множи-
х‘у
телем уравнения (♦♦), ибо после умножения обеих частей уравнения
.. * dx dy п
(♦•) на Мг = ~т~ получаем---— = 0 — уравнение в полных диф-
х‘у х у
ференииалах =» — = с — общий интеграл уравнения (**) в облас-
х
тях (Dk), к = 1,4. Значит, р2(х,у) = Мз^У) Ф?
где <р2 — произвольная непрерывно дифференцируемая функция, —
тоже интегрирующий множитель уравнения (*•).
Попытаемся подобрать функции ф, и ф, так’ чтобы было:
Возьмем в качестве функции ф<(О = -г, а в качестве функции
Г
Фг(г) = (I + Z) 2. Тогда ф|[^ + ^-1= Х У 2 , ^2[“]=7--С и»
( ху j (х + уг (х + уГ
следовательно.
103
И|ф|
х-ьу 1 . (у) I
ху ) ^х) у(х + у)2
Вывод: |1(х,у) =-----= — интегрирующий множитель для ис-
у(х + уу
ходного уравнения.
Найдем общие интегралы исходного уравнения в областях:
(Z>i), (Z)21), (£>22)» (ДО» (Ди)» (£>42)• Для этого возьмем точку
(JWo) (х0 * 0; Уо * 0 ; Уо * -х0 )• Будем иметь
х - >’
w(x,y) = J Л/(х,у)</х + j N(xQ,y)dy =
•ч л
х + у2
(х + у)2
У
dx+ J
>0
dy =
У(*о + У)
(Х0+У)2 X0+yj
-(In |у| + Х°^+1) - In |Хо + у|
=> и(х,у) = In |х 4- у| -ь Д - In|х0 + у| -
- -— ------In |у| - 'У(,^'Уо * + In |х0 + у| +
Хо+у х0+у
+ In |у01 + *o(X° +1) - In |х0 + Уо| =
*0 + Уо
104
= In
x + y y-y2 y-y2 + Xo2+Xo
---- T — —----------------т V|
у x + y Xo+y
= In
x + y
, (x + Dy
x + y
= С — общий интеграл исходного уравнения
x + y . (JC + Dy .
------- т 1 *r V ")
У x + y
в областях (D|), (D2]), (D22), (Dj), (Z>4|>, (D42). <
Пример 12. Решить уравнение (x2 - sin2 y)dx + xsin lydy = 0 .
Здесь Л/(х, у) = x2 - sin2 у; V(x, у) =
= xsin2y => A/(x,y),^x,y)eC(R2);
Л/(х,у) и /V(x,y) обращаются одно-
временно в нуль в точках (0,Ал),
к =0, ±1, ± 2, ... , и в точках
^-1,(2А + 1)^, р,(2А + 1)^, А=0.
±1, ±2, ... . Из заданного урав-
нения непосредственно видно, что
г=0’ и • *=0’ ±!’ ±2— “
Ал < у < (к + 1)л,
решения этого уравнения. Станем рас-
1У
2л
п
~х
-л
-2л
Рис. 1.18. К примеру 12
сматривать исходное уравнение в областях: (Dt) =
0 < х < +<»,
—оо < у < +оо
и (О2) =
-ОО < X < 0,
-оо < у < +«>
(это открытые правая и левая полуплоско-
сти). Имеем
дМ . _ d/V . о дМ 3N _ . .
---= -sin 2у; — = sin 2у =>------------= -2 sin 2у;
Эу дх ду дх
105
дМ dN
м у гЭ(,) _ д/ f)tlJ и
дх ду
- 2 sin 2y
_ Э(О . 1 . 2 1д(1)
xsin2y—-(x-sm у) —
dX ду
Если положить а) = х, то будет —
дх
Эй) , Эй) л 2 ,
— = 0; — = — ах. Возьмем
ду И х
в качестве Ц, например, функцию ц = —. Умножим обе части
х
I —
исходного уравнения на р = —г (у нас в областях (Dk), к = I, 2:
х
x * 0 ). Получим уравнение
sin2 у 1 . sin 2у , „
—\dx +------------- dy = 0 , равно-
и*- V
= М(х.у)
, п и ЭЛ/ sin2y
сильное исходному в (ZA), к = I, 2 . Имеем —— =--------;
Эу х2
dN sin2y дМ dN ч , — „ л
—— -----г- => -т— = -г— в (D, ), к - I, 2 . Найдем общие интег-
дх х1 ду дх
ралы полученного (а значит, и исходного) уравнения в областях
(Z>i), (D2). Для этого возьмем точку (х0, у0) (х0 * 0 ). Будем иметь
X . у -
и(х,у) = J M(x,y)dx + J N(x0,y)dy =
л
sin2 у
□
sin2 у
, f sin2 у
dy = х +------
х
sin2 у I _ . _
- хо------i- - —cos 2у + —cos 2у0 =
Хо 2х0 2х0
sin2 у I ( . 2
----------sin" y-t-
X Хо(
r sin 2у
cos2y
2х0
У-Л
,л2 „ cos2y
“ 2
;~2
sin2 у 1 . 2 2 • 2 V г' sin2 у
----— - -—(2sm у + cos у - sin у) + С| = х +--
106
Sin у „ „ r-
=> x +----— = С — общий интеграл исходного уравнения в обла-
х
стях (Д) и (D,).
Пример 13. Решить уравнение х(1п у + 2 In х - l)dy = 2ydx .
Перепишем исходное уравнение в виде
2ydx - х(In у + 2 In л - l)rfy =0.
Ясно, что должно быть х>0 и у>0. Здесь Л/(х,у) = 2у;
N(x,y) = (I - Iny- 2lnx)x => М(х,у), У(х,у)е C{D), где
(О) =
0 < х < +<»,
0 < у < +«>.
Так.как Л/(х,у)#0 в(£>),то Л/(х,у) и N(x.y)
не обращаются в нуль одновременно ни в одной точке области (D).
У нас х #0 для точек (х, у)е (D). Поэтому исходное уравне-
ние равносильно уравнению:
2— dx + (l-1пу-21пх)</у = 0. (*)
х ----------—v------
Имеем
дЛ/, 2 эдг| _ _2
ду х ’ Эх х
ЭЛ/, дЛГ, 4
ду дх X ’
дЛ/| д^ 4
rfp = » ~ Эх ~ dp----------------------------
И “ (l-ln^-Slnx)—-2—
Эх ду дх X ду
Если положить <0 = У, то будет — = 0; — = 1; — = - — dy. Возьмем
дх ду цу
в качестве ц, например, функцию ц = -у. Умножим обе части
уравнения (*) на ц
(у нас для точек (х,у)е (D): у *0). По-
лучим уравнение
107
2 , (l -lny-2lnx 1 . л
— dx + ---------Ц--------k/y = 0,
xy y2 I
*-w-* ______________/
=M(x.y) ^N(x.y)
/пч .. dM 2 dN 2
равносильное исходному в (D). Имеем —— =----=- ; —— =----г
dy ху2 Эх ху2
dM dN e /rx4
— = — в области ( D). Следовательно, полученное уравнение
dy dx
является уравнением в полных дифференциалах.
Найдем общий интеграл этого (а значит, и исходного) уравне-
ния в области (О). Для этого возьмем точку (ль,у0)€ (D) (х0 > 0,
у0 > 0). Будем иметь
и(х,у) = | M(x,y)dx + J N(xOty)dy =
*о №
2 In Xq - I In у 4- I j’
2. 2. 2 In x0 I In у 1 2 . I lny0 I
= — Inx — lnx0 +--------- — + —- +---------lnx0 +--------—-----=
У У У У У У Уо Уо Уо Уо
=> —(1пу + 21пх) = С => 110^_2 = с => у = С1п(х2у) - общий
У У
интеграл исходного уравнения в (D).
Пример 14. Решить уравнение (х2 4j)(2xdfr + cosyd'y) = 2xsinytZx.
Так как х2 + 1 * 0, то исходное уравнение будет равносил ь-
2х
но уравнению 2xdx + cos ydy = —т-sin vdx <=>
X2 4- I
108
_ 2х
2х—-—sin у
х2 + 1
dx + cosy dy = 0.
(*)
•«(XJ)
M(x,y),N(x,y)& C(R2); M, Nобращаются одновременно в нуль в
точках
0, у(2* + 1)1* =0, ±1, ±2,.
/
. Станем рассматривать наше
уравнение в области (^) - (r2) \ • (о» — (2к + 1)
к =0, ±1, ±2, ... -
Имеем
дМ 2х dN
-— =—2~vcosy; —
ду х2 + I дх
дМ dN 2х
—----—- = 5-----COS
ду дх X1 +1
дМ д/У
= » =
ц 0(0 .. 0(0
н /V -— Л/ —
дх ду
2х
cosy
Э(о । _
cosy-- 2х-
дх I
2х
TT-smy
ды
Эу
б/СО.
Если положить (о = х, то будет — = I: — = 0 ; — = —1^—dx .
дх ду И х2 + 1
Возьмем в качестве ц, например, функцию Ц=—J—. Умножим
х +1
обе части уравнения (*) на ц =—у-—. Получим уравнение
х2 +1
cosy
=N(x.y)
dy = 0.
= ЛГ(х./)
равносильное исходному в области
(D). Имеем
дМ
ду
cosy;
дМ _ dN
ду дх
в (D).
Значит, полученное уравнение является уравнением в полных
дифференциалах. Найдем общий интеграл этого (а значит, и ис-
109
холного) уравнения в (D). Для этого берем точку (х0,у0)е (Д).
Будем иметь
* - >' _
U(x,y) = J M(x,y)dx + J M(xQ,y)dy =
, 7. sin у . 2v I I sinyu
= In (I + X~) +------=5- - In (I + Xq )------J-Sin у +------J-Sin у------=
I + X 1 4- Xq I 4- Xq I + Xq
= In (1 +x2) +
, ,, 2v Sm У z-
=> In (I + x ) + —= С — общий интеграл исходного уравнения
I + х
b(D). «
Пример 15. Решить уравнение (2х3у2 — y)dx + (2х2 г3 - x)dy = 0.
► Здесь ЛУ(х,у) = 2х3у2-у, /V(x,y) = 2x2y3-x =э
М(х,у), N(x,y)e C(R’). М(х,у) и /V(x,y) одновременно обра-
щаются в нуль в точках (0,0), (2 *^,2 1/4); (-2 |/4, -2 1/4). Не-
посредственно из заданного уравнения видно, что
у = 0, у = 0, I х = 0, х = 0,
-«><х<0; |0<х<+оо; |0 < у < +«»; -оо<у<0
- решения уравнения. Станем рассматривать исходное уравнение
в областях
(Р|) =
0 < х < +оо,
0 < у < +<«;
(^) =
-оо < X < 0,
0 < У < +оо;
(^з) =
0 < X < 4-00,
<
-оо < у < 0;
(Z>4) =
-ОО < X < О,
-ОО < У < 0.
110
Имеем
дМ . 3 , d/V . з , ЭЛ/ ЭЛТ . 2 2Ч
= 4х у -1; = 4лт - I => = 4ху(х -у );
ду----------------------------дх-ду дх
<*Р =________4ху(х2-у2)_______
ц ,,2 3 ч 3(0 /, 3 2 v 3(0
дх ду
_ д(0 3(0
ли положить со = ху , то будет: — = у; — = х ;
дх ду
dp 4ху(х2 -у2) . 4(х2 - у2) , (7|1 2 ,
— =--------j------------(7 со =--г—=—— do => — = — (7(0.
g ху(2ху -1 -2xjy +1) 2ху(у -х‘) Р <о
Возьмем в качестве ц функцию И = —г =» Ц = у -у. Умножим обе
со х у
части исходного уравнения на и = 2 2 (у нас х * О и у * О в (DA),
к: = I, 4). Получим уравнение 2х
Ь__
=М(х,у)
носильное исходному в (£\), к = I, 4 .
I
2у----- dy = 0, рав-
____2U
N(x.y)
дМ _ I
Имеем -Z------уг;
Зу х2у^
dN I дМ dN —
— = 2 2 => ~~ = в (Dk), к = 1,4. Следовательно, получен-
ное уравнение является уравнением в полных дифференциалах в (Dk).
Найдем общий интеграл этого (а значит, и исходного) уравне-
ния в (Dk). Для этого берем произвольную точку (х0,у0)е (7^),
к = 1,4. Имеем
х - у -
U(x,y)= J M(x,y)dx+ J N(x0,y)dy =
То
X I \ >' 1 \
= J 2х--у- dx + J 2у-----2 Г^ =
41 ху) Д xorJ
in
I
ло>'о
2 I 1
= x + — + y+C, =>
xy
=> x24-y24-—=C — обший интеграл исходного уравнения в
ху
(Dk), *=Г4. <
Пример 16. Решить уравнение (х2у + у)dx + (х3у2 - x)dy = 0.
Здесь М(х,>>) = х2у3 + у ; /V(x,y) = х3у2-х =>
М(х,у), N(x,y)e C(R2). М(х,у) и N(x,y) одновременно обра-
щаются в нуль в точке (0,0). Из заданного уравнения видно
непосредственно, что
у = 0, Jy = O, Jx‘ = O, Jx=O,
-оо < х < 0; [0 < х < 4-оо; оо < у < 0; |0 < у < +«>
— решения уравнения. Станем рассматривать заданное уравнение
в областях:
(А) =
О < X < 4-0»,
О < у < +°о;
(Л) =
-оо < х < О,
О < у < +°о;
< х < О,
< у <0;
(Z>4) =
О < X < +оо,
-оо < у < 0.
ЭЛ/ _ 2 2 । dN 12 2 I dM dN _
Имеем — = 3х2у2+ 1; — = 3xzy -I => -- — = 2;
Эу Эх Эу Эх
дм дм
dii ду Эх , 2 ,
— =----------г— d(O =--------г-----------7—0(0.
ц .. Эсо .z«<0 /22 1\Э(0 /22 «кЭ(0
Н /У Л/ х(х2/-1)-_-у(х2/♦От-
Эх Э_р Эх Эу
112
„ Эш Эш
Если положить w = ху, то будет — = У; — = х ;
дх ду
г/ц _______2dm________ d<n
g xy(x2 у2 - I - x2y2 -1) w
Возьмем в качестве ц, например, функцию ц = — = — , Умножим
w ху
обе части исходного уравнения на Ц = — (у нас х # О и у # О в
ху
(Dk), к = 1,4). Получим уравнение
ху2 +— \dx + 1 х2у~— ]г/>’ = 0, (*)
X J ( У)
равносильное исходному уравнению в областях (Dk), А = 1,4.
В уравнении (*) М(х,у)-ху2 + — ; N(x,y) = х2у~ — => ^-—-2ху\
X У ду
dN эдг
—— = 2ху => ---= — в (Dk), к = I, 4. Следовательно, получен-
дх ду Эх
ное уравнение (*) является уравнением в полных дифференциалах
в областях (Dk), к = Т?4.
Найдем общий интеграл полученного (а значит, и исходного)
уравнения в областях (Dk), к = I, 4 . Для этого берем произволь-
ную точку (х0,у0) в (Dk). Будем иметь
х У
и(х,у) = J M(x,y)dx + J Nix^^ydy =
«о Уо
113
= ^ + ln|x|-^-lnW + ^-lnW-^L
2.2
— общий интеграл уравнения в каждой из
областей (1\), к = I, 4 .
Пример 17. Решить уравнение (х2 -y)dx + x(y+l)dy = O.
► Здесь М(х,у) = х2-у; /V(x,y) = х(у + I) =э M,NeC(R2).
М(х,у), N(x,y) обращаются одновременно в нуль в точке (0,0).
Из самого уравнения непосредственно видно, что
х = 0.
-оо < у < 0
х = 0,
0 < + — решения уравнения. Станем рассматривать заданное
уравнение в областях:
(Я|) =
-°° < х < 0,
—оо < у < +оо;
(А) =
0 < х < +°°,
-оо < у < 4-00
((D)) и (£>2> — открытые левая и правая полуплоскости). Запишем
исходное уравнение в виде
х2dx + xydy + xdy - ydx - 0.
I. Рассмотрим уравнение
x2dx + xydy = 0. (*)
Легко видеть, что функция Ц| =— является интегрирующим
множителем для уравнения (*). В самом деле, после умножения
обеих частей уравнения (♦) на ц( =— получаем: xdx + ydy = 0 —
уравнение в полных дифференциалах => х2 + у1 = С — общий
интеграл уравнения (♦) в (D,) и в (О2) -=$
щ(х,у) = Pt4>i(x2 + у2) — интегрирующий множитель уравнения
114
(*) (ф|(0 — произвольная, непрерывно дифференцируемая
функция).
2. Рассмотрим уравнение
xdy-ydx = 0. (’’)
Легко видеть, что функция Цэ =— является интегрирующим
ху
множителем для уравнения (♦*). Действительно, после умножения
, 1 dy dx „
обеих частей уравнения (•♦) на Ц? =— получаем: —--= 0 =>
ху ух
1п|х|-1п|у| = 1п|С| =>
х
— = С — общий интеграл урав-
У
нения (**) в (Z)|) и в (Р2) => = Р2Ф2 ~ — интегрирую-
ший множитель уравнения (•*) (ф2(г) — произвольная, непре-
рывнодифференцируемая функция). Попытаемся подобрать фун-
кции ф| и ф2 так, чтобы было цДх.зОф^х2+у2) в ц2(х,у)ф21—
э "> 1 ( V
т. е. чтобы было — ф|(х2 + у1) = —<р2 — . Возьмем в качестве фу н-
кции ф|(0 = -р , а в качестве функции Ф2(г) =
. Тогда
ф|(Х2 +/) =
<₽2
== и, следовательно,
+ У
Ц|Ф|(Х2 +/) =Ц2Ф2
в (D,)U(D2)-
Вывод: функция ц =
= — интегрирующий множитель
для исходного уравнения в () U (D2).
115
Умножим обе части исходного уравнения на и = —, 1 (у
x-jx2 + у2
X — У V + |
нас х * 0). Получим уравнение —. ~ dx + . • dy = 0 ,
ху]х2+у2 yjx2+y2
-М(х.у) =N(x.y)
равносильное в (Z\)U(£>2) исходному. Имеем
ЭЛ/ = х(1+у) d/У = х(1 +у) ЭЛ/ _ 3N
ду (х2 + у2 )3/2 ’ Эх (X2 + у2 )у2 ду дх
(Di) U (D2). Следовательно, полученное уравнение является урав-
нением в полных дифференциалах как в (Dt), так и в (О2).
Найдем общий интеграл полученного (а значит, и исходного)
уравнения в (Z)A), Л =1,2. Возьмем произвольную точку
(•*()’Уо)е (At). = I, 2. Имеем
х . >
w(x,y) = J M(x,y)dx+ J N(x0,y)dy =
»o Уо
116
yjx2 + J2 + In
= C — общий интеграл исходного
уравнения в (Dk), к = 1, 2.
Пример !8. Решить уравнение yi(ydx - 2xdy) = x\xdy - 2ydx).
Запишем уравнение в виде
(у3 + 2х3у) dx - (2у2х + х4) dy = 0.
Здесь М(х,у) = 2х3у + у3, A<(x,у) = -2ху2 - х4 => Л/(х,у),
N(x,y)e C(R2); М(х,у) и N(x,y) обращаются одновременно в
нуль в точке (0,0). Непосредственно из уравнения видно, что
у = 0, у = о,
4
0 < х < +«•;
х = 0, х = О,
4
-«о < у < 0; [0 < у < +**
— решения уравнения. Станем рассматривать заданное уравнение
в областях:
W =
0 < X < +оо,
0 < у < +«»;
(О2) =
-ОО < х < 0,
0 < у < +«>;
(Яз) =
-ОО < х < О,
-оо < у < 0;
(Ю =
0 < X < 4-00,
-оо < у < 0.
1. Рассмотрим уравнение
y2(ydx -2xdy) = 0.
117
Легко видеть, что функция Ц| (х, у) = —Ц- является интегрирующим
ху
множителем для уравнения (*). В самом деле, после умножения
dx .dy _
получаем----2 — = 0 —
обеих частей уравнения (*) на Щ = —г
ху*
уравнение в полных дифференциалах =>
Г г к -
— = С — общий интеграл
уравнения (♦) в (ДА), к = I, 4 => Д|(х,у) = Ц| (х,у)ф| —
— ин-
тегрирующий множитель уравнения (*) (<₽|(0 — произвольная, не-
прерывно дифференцируемая функция).
2. Рассмотрим уравнение
х3 (xdy - 2ydx) = 0. (**)
Легко видеть, что функция Мз(х,у) = —— — интегрирующий мно-
житель для уравнения (**). Действительно, после умножения обеих
.. * dy 2dx _
частеи уравнения (*♦) на Рз = -у- получаем —----= 0 — урав-
х2
нение в полных дифференциалах => — = С — общий интеграл
уравнения (♦♦) в (Dk), к = 1,4 => р2(х,у) = ц2(х,у)ф3 —
, У i
— ин-
тегрирующий множитель уравнения (♦*) (ф2(г) — произвольная,
непрерывно дифференцируемая функция).
Попытаемся подобрать функции <p( и ф2 так, чтобы было
У
= ц2 (х, у)Фз _— » т. е. чтобы было
1 - (Н
—гФ| — =
х/ X
47*2 V
118
Возьмем в качестве функции ф](/) = /" , где а — число, пока
неизвестное, а в качестве функции ф2(?) = где Р — число,
пока неизвестное. Тождество (***) примет тогда вид
> J2ot _ I *3 - *2Р>а (2р + а = 3, £ 4
ху3 ха х4у г1' у2 у^2п Р + 2а = 2 3 ’ 3
Значит, ф|(/) = г|/3; ф2(е) — Следовательно,
I
- x4f3yl/3
(у нас х # 0 и у * 0 в (Dk), к = 1,4 ). Умножим обе части исход*
_4 2.
ного уравнения на р = х Зу 3. Получим уравнение
(x-4V3 + 2х*У4'3 )dx - (2x-vy,Л + ^3у'113 )dy=0.
~М(х,у) =N(x.y)
\ Э _____- У — пкг i 4 1 „57
.. оМ 2 , ч о ч , Э/V 2 “т т 8 т т
Имеем —— = —х Зу 3--х3у 3; -— = ±х 3у 3х3у 3 =>
ду 3 3 Эх 3 3
дМ 3N , —
ду ~ дх В (Ла)’
Найдем обший интеграл этого (а значит, и исходного) уравне-
ния в (Dk), к = \, 4. Для этого берем произвольную точку
(х0,у0)е (£>*), к =1,4. Имеем
w(x,y)= J M(x,y)dx+ J N(xa,y)dy =
*0 Уо
= J (x-4'3уV + 2х^у-4,У) dx - } (2ХД1/3у-''3 + xJV7'3) dy =
Xq Уо
-Зх-'/3у2/3
'з^3у^-1хЦ3у^ГУ
< 4 Л-л
119
3 х*3 3
4 уФ у'/3 4 у4/3 х|/3
1 XW UP -> х№ VW
, £ хо______•>>______ л° I 1 3() -s
4 ’ v4/J г,/3 4 ’ г4/3 г|/3
У ло >о ло
3 х*^3 у^3 х3 — 4 у2
-» “<Jt’>> = ; тя’3 тл+С| => "(х->’)=3 5777т+С| =*
= С => х3 - 4у2 = Су • tfxy — общий интеграл исход-
ного уравнения в (Dk), к = I, 4 . 4
Пример 19. Решить уравнение
Здесь Л/(х,у) = у(х + у);
у(х + y)dx + (ху + l)dy = 0.
Э/У
Эх
+1 => Л/(х,у),
™eC<R=).
Эу Эх
N(x,y)eC(R2).
Эу
Л/(х, у) и N(x,y) обращаются одновременно в нуль в точках
(1, - I) и (-1,1). Из заданного уравнения непосредственно видно,
что у = 0 — решение этого уравнения. Станем рассматривать ис-
ходное уравнение
областях (D|) =
в
(02)
Имеем
ЭЛ/ Э/У
Эу Эх
эл/_э/у_
Эу Эх _____________(х + y)d(a___
..ды 1УЭ(1) . ..Эю . ,Э(о
/V —-л/— (ху+ I) — -у(х + у) —
Эх Эу Эх Эу
с г ()<л d[! dy
Если положить <о = у, то будем иметь — = 0 ; — = I; — =----------.
Эх Эу р у
Возьмем в качестве ц, например, функцию |i = — (у нас у *0 в
120
(D*); к = I, 2 ). Умножим обе части исходного уравнения на ц = — .
Получим уравнение
(x + y)dx + x + — L/y = O,
равносильное исходному в областях (Dk), к = 1,2. Здесь
. .0/4 1 ЭЛ/ Э/V дМ dN
М(х,у) = х + у\ /V(x,y) = x + - => — =1, — = 1;
у оу Эх ду дх
Значит, уравнение (•) является уравнением в полных дифференциалах.
Найдем общий интеграл уравнения (*) (а значит, и исходного урав-
нения) в областях (Dk), к = I, 2 . Для этого берем в (Dk), к = I, 2 ,
произвольную точку (х0,у0). Л/(х,у) и /V(x,y) обращаются одно-
временно в нуль в точках (I, -1) и (-1,1). R2 \ {(I, - I); (-1,1)} —
множество точек единственности уравнения (*) (а значит, и исход-
ного уравнения). Имеем
х - у - х у ( I
и(х, у) = J Л?(х,y)dx + J /V (х0,у)dy = J (х + y)dx + П х0 + - р/у =>
*о Л хо лЛ
=* u(x,y) =
т + ху
Лх=х0
'УУо
х1 х2
= + ху - у - ХоУ + ХЬУ + In |у| - хьу0 - In |у01 =
JC2
= у+ ху+ 1п|у| + С| =>
X2
=> у+ ху +• In |у| = С — общий интеграл заданного уравнения в
областях (0|) и (D2). -4
Пример 20. Решить уравнение (х2 + 2х + у)dx + (Зх2у - х)dy = 0 .
Здесь Л/(х, у) = х2 + 2х+ у ; /V(x,y) = Зх2у-х =>
, дМ . d/V , . дМ
Л/(х,у)Л(х,у)еС(К2); -57 = |: эГ = 6ху’1 =* V’
121
C(R2). M(x,y) и N(x,y) обращаются одновременно в нуль
дх
в точках (0,0) и (х. ,у.), где х. = -2,08, у, =— 0,16.
Из заданного уравнения непосредственно видно, что
х = 0,
X = О,
Л — решения этого уравнения.
Станем рассматривать уравнение в областях (Д) =
(D2) =
.. ЭЛ/ ЭУ П/| _ .
Имеем —-----— = 2(1 - Эху);
Эу дх
дМ dN
бф _ ду дх
И
2(1 -3xy)d(a
», Эю .уЭ(о , ..Эсо . 2 л . Эсо
/V —М— Л(Зху-1)— -(х + 2x + j) —
дх ду дх ду
ды , Э<о „ rfu 2dx „
Если положить со = х добудет — = I; — = 0 ; — =-. Возьмем
Эх ду ц х
в качестве м , например, функцию Ц = —у (х # 0 в (Dk), к = I, 2 ).
Умножим обе части заданного уравнения на Ц = —Получим
х2
уравнение
| I + —+ -^- |</х + (3>’|Эу = 0, (♦)
( х х2 ) ( х)
равносильное исходному в областях (/>,) и (£>2). В (*)
М(х,у) = I + - + Д-;
х х2
N(x,y) = Зу - — =>
X
ЭЛ/ = J_ dN 1
Эу х2 ’ Эх ~ х2
ЭЛ/ Э/V „ , —
в (Dk), к = 1, 2. Значит, уравнение (*) является уравне-
нием в полных дифференциалах в (Dk), к = 1,2. Найдем общий
интеграл уравнения (*) (а значит, и исходного уравнения) в обла-
122
стях (Dk), к = I, 2 . Для этого берем произвольную точку (х0,у0) в
(0J. к = 1,2. Имеем
х у
и(х,у) = J M(x,y)dx + J N(x0,y)dy =
ХО >'о
=> и(х,у) = х + 21п|х| - — -х0 - 21п|х0| +
У 3 2 У 3 2 Уо
— + т/ - —-^Уо + —
х0 2 х« 2 х0
=> м(х, у) = х + 2 In |л| - 1 у2 + С| =>
=> х + 21п|х|-- + |у2 - С — общий интеграл исходного урав-
нения в областях (О,) и (Р2). ◄
Пример 21. Решить уравнение xydx - (у3 + х2у + x2)dy = 0.
► Здесь М(х,у) = ху \ N(x,y) =-у3 - х2у - х2 => М(х,у),
м, Ч ^/п2\ dN - - ЭЛ/ dN г 2\
N(x,y)e Сг ; — =х; — = -2ху-2х=> —eC(R),
Эу Эх Эу дх
Щх,у), N(x,y) обращаются одновременно в нуль в точке (0,0).
У = 0,
Из заданного уравнения видно непосредственно, что
у = 0.
п — решения уравнения. Станем рассматривать исход-
123
ное уравнение в областях (0|) = ' -00 < х < +оо, 0 < у <
(О2) = < -оо < X < +оо( -оо < У < 0. дМ dN v Имеем = х(3 + 2у); Эу дх
dM dN
ф ду дх х(3 + 2y)Jli)
U л/d(i) .. dco . з 2 2v<too
H N--M— ~(У +х у + х ) — -ху—
дх ду дх ду
г _ dw n dco , t/ц 3 + 2у ,
Если положить со = у, то будет — = 0; — = I; — =----------ау.
дх ду ц у
е~2у
Возьмем в качестве ц, например, функцию ц = —5- (у нас у * 0 в
(ОА), А =1,2). Умножим обе части заданного уравнения на
е~2у
Р - —5~. Получим уравнение
равносильное исходному в областях (Dk), к = 1,2. В (*)
~ Х£~2у
М(х,у) = -^-; N(x,y) =
2
7
е1у
х‘е
дМ ,
---= -2х
ду
е~2у е 2-
„2 + ,3
dN _
---= ~2х
дх
е
“7з
дМ
dN
ду дх
е ~
~1Л
в (А), Л = I, 2 . Значит, (*) является уравнением в полных диф-
ференциалах. Найдем обший интеграл уравнения (*) в областях
(Dk), к = 1, 2 . (Тем самым мы найдем общий интеграл исходно-
го уравнения в областях (Dk), /с = I, 2 ) Для этого берем произ-
124
вольную точку (х0.у0) в Л = 1,2. Пусть это будет точка
(0,1). Имеем
Х'Хе2у г
о У ।
и(х,у) = j M(x,y)dx + J N(x^y)dy = j
*o Уо L
х2е 2у
2у2
£2
2
х=0
е ’ I
2у2 2 2е2 2у
х2е 2у
х2е~2> е~2
2 + 2
в к
=> -у —+ 1 =С — общий интеграл заданного уравнения в
У
областях (Z)|) и (D2) 4
Пример 22. Решить уравнение (x2 - у2 + y)dx + x(2y - l)rfy = 0 -
Здесь Л/(х,у) = x2-у2 +y ; /V(x, у) = x(2y-1) => M(x.y),
a/z \ r'/r»2\ dM I -» ЭЛ' n i ЭУ /•'7d2\
/V(x,y)e C(RJ; —=l-2y; — = 2y-l => —e C(R ).
Эу Эх Эу Эх
Л/(х,у), /V(x,y) обращаются одновременно в нудь в точках (0,0)
и (0, I). Из
уравнения непосредственно видно, что
х = 0,
-оо < у < 0 “ РСШСНИЯ этого уравнения.
Станем рассматривать исходное уравнение в открытой левой и
заданного
х = 0.
правой полуплоскостях, т. е. в областях (О|)
и
(&) = «
Имеем = 2(1 - 2у);
Эу Эх
ЭЛ/ д^
Эу Эх
р Эо)
.,Эш .. Э<о
2(1 -2у)
</о) =-----------5-------
дх
-----^—dw.
2 2 \ Э(0
-у +х)у
Эу
125
йю Эсо б/ц 2
Если положить со = х, то будет — = I; — = 0; — = —ах. Возьмем
дх ду ц х
в качестве Ц , например, функцию И = —у (у нас х * О в областях
х
— |
(Dk), к = I, 2). Умножим обе части заданного уравнения на ц = -у.
х
Получим уравнение
l-^ + -4]^ + (2---U’=0, (*)
X2 X2 I X X I
х ________I «—
=М(х.у) =/*(х.Я
равносильное исходному уравнению в областях (Dk), к = I, 2. Имеем
=_2у + _1_
ду X2 X2 '
dN _ 2у I
дх х2 X2
дМ _dN
• XS ---
ду дх
в (DJ, * = 1,2.
Значит, (♦) является уравнением в полных дифференциалах.
Найдем обший интеграл уравнения (*) (а значит, и исходного
уравнения) в областях ), к = 1,2. Имеем
х . >'
w(x,y) = J A/(x,y)t/x + J iV(x0,y)^’ =
Ли Л)
dx + J 2
л\
г J2 У г У14. У + У2 У 4.
XX х0 х0 х0 Х„ хь х0
=> х + —— — - С — общий интеграл заданного уравнения в обла-
X X
стях (Z)|) и 4
126
Пример 23. Решить уравнение (2х~уг + y)dx + (х’у - x)dy = 0.
Здесь М(х,у) = 2х2у2 + у ; N(x,y) = х2у - х =э М(х,у),
N(x,y)e C(R2); ^ = 4х2у+1; ^ = Зх2/-1 =>
ду дх ду
dN э
—— € C(R ), Л/(х,у), N(x,y) обращаются одновременно в нуль в
дх
точке (0,0). Из уравнения видно
х = 0.
непосредственно, что
х = 0.
у = о,
У = О,
решении
уравнения. Станем рассматривать исходное уравнение в областях:
(00 =
(00 =
(00 = <
дМ dN
Имеем —----—
ду дх
дМ dN
ф _ ду дх ____________(х2у + 2)</со
Н Осо .z0(O . 3 . Э(О 2 2 \ 0(0
— (ху-х) — -(2х-уг+у) —
дх ду дх ду
_ _ Эсо Осо
Если положить co = ху, то будет — = у; —— = х ;
дх ду
dp (х2у + 2)с/со _ (х2у + 2)dw _ _(/<о
И х’у2 - ху - 2х3у2 - ху -ху(х2у + 2) w *
Возьмем в качестве р , например, функцию ц = — = — (у нас х * О
со ху
и у * 0 в (Dk), к = I, 4 ). Умножаем обе части заданного уравнения
• г.
на ц= —. Получаем уравнение
ху
127
= M(x,y) =N{x.y)
(*)
равносильное исходному в областях (Dk), к = I, 4 . Имеем = 2х;
Эу
dN _ дМ av z Л
= 2х => —— = —— в (/Д), к: = I, 4 . Значит, (*) является уран-
дх ду дХ
нением в полных дифференциалах в (Dk), к = 1,4. Найдем общий
интеграл уравнения (*) (а значит, и исходного уравнения) в обла-
стях (Dk), к = 1,4. Для этого берем произвольную точку (х0,у0)
в(Д*).И меем
w(x,y) = J M{x,y)dx + J N(x0,y)dy =
Xo Л
= x2y + In Ix| - x02y - In |.v0| + x02y -1 n |.r| - x£y0 +
+ In |>’oI = x2y + In |x| - In |y| 4- C| =>
=> x2y + ln|x| - ln|y| = С — общий интеграл исходного уравнения
в каждой из областей (ДА), к = 1,4.
Пример 24. Решить уравнение (2х2уу - l)ydr + (4х2у3 - I)xdy = 0.
► Здесь Л/(х,у) = (2х2у3-1)у; /V(x,y) = (4х2/- 1)х =>
A/(x,y),/V(x,y)eC(R2). ^£ = 8х2у3-1; ^=|2х2/-1 =>
Эу Эх
ЭЛ/ Э/V \ \ е
,--eC(R ). Лт(х,у), 1\(х,у) обращаются одновременно в
ду дх
128
нуль в точке (0.0). Из заданного уравнения видно непосредствен-
но, что
j = 0,
-<х> < х < 0;
х = 0,
0 < у < +оо;
х = 0,
-ОО < у < 0
— решения уравнения. Станем рассматривать исходное уравнение
в областях
(Я2) =
-ОО < X < 0,
0 < у < +оо;
Имеем
дМ
ду дх
0 < X < Ч-оо,
-оо < у < 0.
дМ dN
_ ду дх _____________________-4x~yydaa_______
ц йсо .. Эсо .. з з , йсо /Л 2 4 , Эсо
н N--M — (4х-у -х) — -(2xzy -J1) —
дх ду дх ду
, Эсо Эсо
положить со = ху, то будет — = у; — = х ;
дх ду
d\x -4х2 yydw dp 2d to
И 4х3у4 - ху - 2х3>’4 + ху И со
Возьмем в качестве и, например, функцию Ц = — => М = -—-у (У
со* (ху)
нас х * 0 и у * 0 в областях (Dk), к = I, 4 ). Умножим обе части
заданного уравнения на р = » , . Получим уравнение
ху
2уг - -4- dx + 4ху - -Ц- \dy = 0, (*)
I / -И ХУ )
=М(х.>) =Лг(х.у)
129
равносильное исходному уравнению в областях (Dk), к = 1,4. Имеем
дМ
ду
I dN
Х2у2 ' дх
I _ дМ dN _ ч , —
— => -т- = т- в (DJ. к =1,4.
у ду дх
Значит, (*) является уравнением в полных дифференциалах в (Dk),
к = 1,4 . Найдем общий интеграл уравнения (♦) (а следовательно,
и исходного уравнения) в областях (Dk), А = 1,4. Имеем
и(х,у) = J M(x,y)dx + j N(x0,y)dy =
Ло Л
= 2ху~ + — - 2хоу2 - — + 2хоу2 + — - 2xoJo -
ху Х0у ъу
ху
=> 2ху2 +— = С — общий интеграл исходного уравнения в обла-
ху
стях (Dk), к = I, 4. 4
§9. Уравнения с разделяющимися переменными
Так называются уравнения вида
fi(x)gi(y)dx + f2(x)g2(y)dy =0. (I)
=М(х,у) =N(x.y)
Предполагается, что функции fi(x),f2(x)e C(a,b), (а,Ь) лежит на
оси Ох, а функции gi(y),g2(y)e C(c,d), (c,d) лежит на оси Оу
=> M(x,y) = fi(x)gi(y) -, N(х,у) = f2(x)g2(.y)е C(D). где (£>) =
130
= (a,b)x(c,d). Пусть x = x,, i = I, m — вещественные корни урав-
нения f2(x) = 0, а у = уj;, j = I, fi — вещественные корни уравне-
ния g, (>») = 0 . Непосредственно из уравнения (I) видно, что х = х,
(У * Уу, j = I, fi), / = 1, т, а также у = у, (х * xf, z = I, т), j = I, п,
являются решениями уравнения (I). Отметим, что в областях
<Ч) =
Х.<Х<Х..|, --- ------
7 = 0, ffi, j - 0, л, X. = а, х,
У]<У<У^\,
= ь, у0 =с, уп+| = d,
/Их)* О и g|(y) # 0 . Точки (Х/.д’у), 7 = |,/и, j = I,п,— особые
точки уравнения (I).
Рассмотрим функцию м(х,у) =
—------; эта функция опре-
ЛОФМт)
делена и непрерывна в каждой из областей (DtJ), i = 0, т , j = 0, п.
Покажем, что ц(х,у) является интегрирующим множителем для
уравнения (I) в каждой из областей Действительно, умно-
жив обе части уравнения (I) на p(x,j) = —— -----, получаем
f2(x)g}(y)
Рис. 1.19. К уравнению
с разделяющимися переменными
131
/i(x)
fM
dx +
£?(>’)
Я O')
(2)
dy = 0.
Отметим, что уравнение (2) равносильно уравнению (I) в каж-
дой (Dij) и что (2) — уравнение с разделенными переменными, а
следовательно, (2) — уравнение в полных дифференциалах.
Найдем общий интеграл уравнения (2) (а значит, и уравнения
(1)) в каждой из областей (0^), Дпя этого берем произвольную
точку (х0,у0)е(Д). Будем иметь w(x,j) = [ Д-^г/х +
4 /И*)
и(х,у) = С — общий интеграл в (^).
Пример. Решить уравнение (х2 - l)dy + 2xy2dx = 0 .
Непосредственно из уравнения видим, что
у = 0,
-оо < х < -I;
у = 0, у = 0. х = —I, 1х = -1, х = I,
< < < <
I < X < +«*; 0<у<+оо; |-oo<j<0; 0<у<+«о;
X = I,
-ОО < у < о
решения заданного уравнения. Точки
(-1.0)
и
(1,0) — особые точки уравнения. Станем рассматривать заданное
уравнение в областях:
(Л|) =
(Ю =
1 < X < +оо,
О < у < +<»;
(О2) = <
-I < х < I,
О < у < +»;
(Я3) =
-оо < X < -I,
О < у < +«>;
-оо < X < - I,
—оо < у < 0;
(Я5) =
-I < X < I,
-оо < < 0;
I < X < +оо
-оо < у < О.
W =
Каждая из областей (ДА) ( к = 1,6 ) — область единственности для
заданного уравнения. Рассмотрим функцию ц(х,у) = —т—!; .
У (хz -I)
132
Она определена и непрерывна в каждой (Р*), к = 1,6, и является
интегрирующим множителем для исходного уравнения в (Dk),
к - 1,6. Действительно, умножив обе части заданного уравнения
на p(x,j), получаем: + ^ = О — уравнение в полных диф-
X - I У'
ференциалах. Полученное уравнение равносильно исходному в об-
ластях (РА), к = 1,6 .
Найдем общий интеграл полученного (а значит, и исходного
уравнения) в (Dk), к = 1,6 . Для этого берем произвольную точку
(х(1, у()) е (Р4). Буде м и меть
. . f Ixdx
и[х,у)= ——- +
= Ink'2 -1I--—In kg -1| + —= In |х2 -1|-—+ С| =>
1 1 J7 1 1 Ур 1 1 У
=C| (const >
=> ln|x2-l| — = C — общий интеграл уравнения в (РА),
1 1 У
Рис. 1.20. К примеру
133
§10. Линейные уравнения первого порядка
Так называются уравнения вида
У+ p(x)y = q(x)
(1)
(в (1) у и у' входят в первой степени и не перемножаются).
Считаем, что функции р(х) и q(x) определены и непрерывны в
промежутке (а, Ь). Запишем уравнение (1) в виде, разрешенном
относительно у':
/= - Р(*)У+ <!(*) .
=f(x.y) (обознач.)
Ясно, что f(x,y)eC(D)t где (D) =
а< х <Ь,
—оо < У < 4-00.
Имеем лосе
fy(x,y) =-р(х) => fy(x,y)e C(D). Значит, (D)— область един-
ственности уравнения (Г) (а следовательно, и уравнения (I)).
Вывод: через каждую точку (Хо,у0)е(/)) проходит одна и
только одна интегральная кривая уравнения (I).
Существует несколько методов решения линейного уравнения.
Г. Метод интегрирующего множителя. Покажем, что функция
ц(х) = является интегрирующим множителем для уравне-
ния (I). Для этого перепишем уравнение (1) в виде
[ р(х)у - <?(х)| dx + dy = 0.
(!')
Умножим обе части уравнения (I') на ц(х) = e^plxidx. Получим
(р(Х)у - q(x))dx 4-е-/>( t><y> dy = 0. (2)
,, дМ dN Jp[x)dx . . dM dN
Имеем — = /J(x)eJ I = e P(x) ^(D).
dy dx dy dx
Следовательно, (2) — уравнение в полных дифференциалах.
Так как уравнение (2) равносильно уравнению (I), то, найдя
общий интеграл уравнения (2) в (D), мы найдем тем самым
общий интеграл исходного уравнения (I).
134
Замечание. Формула для общего решения уравнения (1) может
быть получена следующим образом. Умножаем обе части уравне-
ния (I) на ц = Получаем
(/+Р(х)у)е^х)Л = q(x)ejpMdx. (3)
Легко видеть, что уравнение (3) может быть записано в виде
Хр*'*).^*** =, л.е^'’А=/«(х)е»'"',лЛ+С «
^у = е-(«'>л(с + /?(х)е^',лл| <4)
2°. Метод Бернулли. Метод Бернулли нахождения решения ли-
нейного уравнения (I) состоит в следующем: ищем решение у(*)
уравнения (I) в виде произведения двух функций, а именно, в виде
y = u(x)v(x). (5)
Имеем ух = w'v + wv' . Поэтому уравнение (I) запишется так:
w'v + wv' + p{x)uv =q(x) => a'v + u(v' + p(x)v) = q(x). (6)
В качестве функции v(x) берем одно из решений уравнения:
v' + p(x)v = 0 . например,
х(х) = е<р,ж,А. (7)
При таком выборе функции v(x) уравнение (6) примет вид:
axp = g(x), т. е. eJ — = q{*} => </w=g(x)eJ dx =>
dx
и - J^(x)e^/’<,’rf'</x+ C, где С— произвольная постоянная. А тогда
у = u(x)^x) = (с + j<?(x)<-f w”‘ftrfx j.
Видим, что для решения у(х) уравнения (1) снова получена фор-
мула (4).
З.’Метод вариации произвольной постоянной (метод Лагранжа).
Уравнение (I), в котором <у(х)^0, хе(а,Ь), называется линей-
ным неоднородным. Уравнение
У + р(х)у = 0 (8)
135
условимся называть линейным однородным, соответствующим
линейному неоднородному уравнению (I). Рассмотрим сначала
уравнение (8). Оно является уравнением с разделяющимися пере-
менными.
— + p(x)dx = 0 => у = Се /«и
У
где С — произвольная постоянная.
Метод Лагранжа (метод вариации произвольной постоянной)
состоит в том, что решение линейного неоднородного уравнения
(I) ищется в форме, аналогичной форме (9). а именно:
/.CWe’***, (10>
где С(х) уже не постоянная, а искомая функция от х. Из (10)
находим
У = С'(х)е <Иж>Л -р(х)С(х)е >',,,,Л. <П)
Подставив выражения для у и у' из (10) и (I I) в уравнение (I),
получим
C'(x)e~l*x)dx - p(x)C(x)e^p{x)dx + р(х) C(x)e ^p{xjdx = q(x) =>
=У =т
=> С'(х)е lp{')lb = q(x) => С'(х) = ^(х)е^Л’</м =>
=> С(х) = fq(x)elp{xidxdx + C.
Окончательно, согласно равенству (10) для у, получаем
Видим, что и здесь для решения у(х) уравнения (1) получена
формула (4).
Пример]. Решить уравнение y' + ycosx = е ”sinx.
Заданное уравнение — линейное; у и у входят в уравнение
в первой степени и не перемножаются. Здесь р(х) = cosx;
q(x) = e-s,nx => р(х), <?(х)е С(-оо,+оо). Найдем решения этого
уравнения всеми тремя методами.
I. (Метол интегрирующего множителя.) ц(х) = -
_ _ емпл _ интегрирующий множитель для заданного
136
уравнения. Умножаем обе части исходного уравнения на
= esinjr. Так как ц(х) * 0, то получаем равносильное уравне-
ние (y' + ycosx)es'nx = I или -7"(j*s,nx) = I => ves,nx=x + C =>
dx
yesmx ~x -С — общий интеграл заданного уравнения на (R-).
2. (Метод Бернулли.) Станем искать решение заданного урав-
нения в виде
у = u(x)v(x).
И меем у' = uv + uv . Поэтому исходное уравнение запишется так:
w'v + w(v'4-vcosx) = e-s,njr.
В качестве функции v(x) берем одно из решений уравнения
v' + vcosx = 0 => v(x) = e-sinx.
При таком выборе функции v(x) для определения функции
и(х) получаем eun х и'=| ц=х+С.А тогда
у = u(x)v(x) = (х + С)е-япх => уеяпх-х = С.
3. (Метод Лагранжа.) Ищем сначала решения линейного од-
нородного уравнения, соответствующего заданному неоднород-
у'
ному, а именно: уравнения y+ycosx = 0 => — = -cosx =>
у = Се~чпх , где С— произвольная постоянная. Решение исходно-
го уравнения ищем в виде
у = С(х)еяп\ (*)
где С(х) — неизвестная функция, которую нужно найти. Мы
хотим, чтобы (*) была решением заданного уравнения. Но тогда
должно быть
С'(х)е-япх -C(x)e’s,njr cosx + С(х)е"япх cos л = е-япх =>
=> C'(x)s I => C(x) = x + C, где С — произвольная постоянная.
Подставляя это выражение для С(х) в (*), получаем у =
= (х + С)е s,nx => yesinx-x = C — общий интеграл заданного
уравнения. 4
Замечание 2. Некоторые дифференциальные уравнения перво-
го порядка оказываются линейными, если считать у аргументом,
а х(у) неизвестной функцией.
137
Пример 2. Решить уравнение (2х + y)dy = ydx + 4 In ydy.
Отметим сразу, что заданное уравнение определено лишь
в открытой верхней полуплоскости, так как должно быть у > 0 .
Видим, что уравнение не является линейным, если считать
х аргументом, а у(х) неизвестной функцией.
Если же считать у аргументом, а х(у) неизвестной функцией,
то заданное уравнение оказывается линейным. Действительно,
имеем
</х 2 . . In у
-----х - I - 4——
dy У У
(*)
(в (*) х и х'у входят в первой степени). Это уравнение равносильно
исходному, ибо делить на у можно (у нас у > 0 ). В этом уравнении
\ 2 ... . . In у _
Р\у) = —; д(у) = 1-4---. Станем решать полученное уравнен ие
У У
методом интегрирующего множителя. Имеем
l-ltfy ।
ц(у) = = е у = е'21пу = —=. Умножаем обе части (*) на
У
ц = —Получим равносильное уравнение
У
I , 2 I . In у
2 Ху j X — j з ’
У У У У
или
=> х = Су2+2lny-y +I —общее решение исходного уравнения. 4
138
§11.Уравнение Бернулли
Так называется уравнение вида
у'+ р(х)у = q(x)ym, (I)
где т # 0 и т * I, так как при т = О уравнение (1) — линейное,
а при т = I уравнение (I) и линейное, и с разделяющимися
переменными. В (1) р(х) и q(x) — известные функции, опреде-
ленные и непрерывные в некотором промежутке (а,Ь).
Разделим обе части уравнения (1) на ут. Получим
у'"/ + Р(х)у'~т = q(x). (2)
(При переходе от уравнения (I) к уравнению (2) мы делили обе
части (I) на ут. Следовательно, если т > 0, то мы могли поте-
рять решение у = 0 .)
В уравнении (2) делаем замену у1-" = z (z{x) — новая неизве-
стная функция) => z'x = (I - т)у ту'х => У тУх = * (У нас
I — w
т * I). Относительно новой неизвестной функции z(x) уравне-
ние (2) запишется в виде
<Л + p(x)z = q(x) или z'x + (I - m)p(x)z = (I - m)q(x) =>
1 - m
=> z‘x + p(x)z=q(x). (3)
(Здесь положено p(x) = (I -m)p(x); q(x) = (1 -m)q(x).) Видим, что
(3)— линейное уравнение относительно функции z(x). Решая
уравнение (3) и подставляя затем у' т вместо z, получим решение
исходного уравнения.
Пример 1. Решить уравнение / + 2у = у2ех .
Заданное уравнение является уравнением Бернулли. Здесь
р(х) = 2; <Дх) = ех; т = 2(> 0). Непосредственно из уравнения
видно, что у = 0 — решение уравнения. Станем рассматривать
исходное уравнение в открытых верхней и нижней полуплоскос-
тях, т.е, при у >0 и при у < 0, В этих полуплоскостях заданное
уравнение равносильно уравнению, полученному из него делени-
ем обеих его частей на у2, а именно:
139
I / I / , -2 '
Делаем замену: — = Z=> Zx = —~Ух =* УхУ ‘ = ~ZX . Относитель-
У У
но новой неизвестной функции уравнение (*) примет вид
-z'x + 2z = ех => z'x - 2z = -ех. Это — линейное уравнение. Найдем
решение его методом Бернулли. Положим z(x) = u(x)v(x)
Zx = u'xv + uv'x • Будем иметь w'v + u(v'x - 2v) = -ex. В качестве фун-
кции v(x) берем одно из решений уравнения v' -2v = О => v = e2x.
При таком выборе функции v(x> для определения функции и(х)
получаем уравнение: и'хе2х =-ек => и' = -е~х => и(х) = е * + С.
А тогда
z(x) = zz(x)v(x) = е2х(е~х + С) => z(x) = ех + Се2х.
Вспоминаем, что у нас z = — => У- — и, следовательно,
У Z
У = ———^7 у(ех + Се2х) = 1 — общее решение исходного урав-
е + Се
нения в верхней и нижней открытых полуплоскостях. 4
Замечание. Решения уравнения Бернулли можно искать в
виде у(х) = u(x)v(x), не приводя его к линейному уравнению.
Пример 2. Решить уравнение
у' - у tg X = у* COS X.
Заданное уравнение не определено на линиях:
Х = + * = 0,±1,±2....
—«» < у < +°°,
Непосредственно из уравнения видим, что
У = 0,
(2*-1>2<х<(М + 1)р
к =0, ± I, ±2,...
— решения исходного уравнения. Станем рассматривать наше
уравнение в областях:
140
и
-оо < у < 0.
к =0, ±1, ±2,....
Положим в исходном уравнении y-u(x) v(x) => у' =«'v + wv'.
Будем иметь
v + и(у'х - vtgx) = w4v4 cosx.
В качестве функции v(x) берем одно из решений уравнения
v' - v tgx = 0 => v = —!— . При таком выборе функции v(x) для
cosx
определения функции и(х) получаем уравнение
, I 4 COSX , W4 _4 , I
м..------= и ------— => их = —г— => и их =----------------т— о
Л «1 Л / * 9
COS X COS X COS X COS X
=> —r-T = C cos3 x - 3sin xcos2 X =>
U V3
141
=> —г = C cos’ х - 3 sin к cos2 х — общее решение исходного урав-
У
нения в (Dk) и (Ьк), к = 0, ± I, ± 2..
Замечание. Уравнение вида у' + р(х}у + q(x)y2 = г(х) называ-
ется уравнением Риккати. Это уравнение в общем случае не
решается в квадратурах. Однако, если удается найти какое-нибудь
его частное решение у = У|(х), то заменой у = У\ + z (z(x) —
новая неизвестная функция) уравнение Риккати сводится к урав-
нению Бернулли.
Действительно, пусть у = у((х) — какое-нибудь частное ре-
шение уравнения Риккати. Тогда >>|'(х) + р(х)>’,(х) + ^(х)у2(х) s
г(х). Делаем замену у = У\+ Z . Получаем
у'} + р(х)У| + f + p(x)z + <7(Х) (у2 + 2j|Z + г2) = Г(х) =>
=> X + P(x)y'i -г?(х)У|2 + z' +(р(х) + 2y,g(x))z + q(x)z2 = г(х) =>
•Г(х)
=> Z + ~p(x)z = q(x}z2.
А это — уравнение Бернулли относительно неизвестной функции
Z(x). Здесь положено р(х) = р(х)+ 2у|(х)<?(х) — известная функ-
ция; q(x) = -q(x). 4
В задачах 3-7, найдя путем подбора частное решение у = у,(х),
привести заданные уравнения Риккати к уравнениям Бернулли и
решить их.
Задача 3. Дано уравнение x2dy + (ху + х2у2 - 4)dx = 0.
Здесь М(х,у) = ху + х2у2 -4; N(x,y) = х2 => A/,/VeC(R2);
^-х + 2х2у; ^ = 2х => ^,^eC(R2). Л/(х,у) и /V(x,y)
не обращаются одновременно в нуль ни в одной точке. Из задан-
ного уравнения видно непосредственно, что х = 0 — решение
этого уравнения. Станем рассмагривать исходное уравнение для
х*0, т. е. в левой и правой открытых полуплоскостях:
(Д2) =
О < X < +«>,
-оо < у < +оо.
В областях (Dk),
k = I, 2, заданное уравнение равносильно уравнению
142
, I 2 4
У + -У + У =~7- (*)
xx2
Попытаемся искать частное решение у = у((х) уравнения (*)
в виде у(х) = — , где а — постоянное число, пока неизвестное,
х
Подставляя это выражение дпя у(х) в уравнение (*), получаем
=> = 4 =» о = ±2.
2 2
Следовательно, функция у.(х) = — ( а также функция у. = —)
X X
является частным решением уравнения (*).
2
Делаем замену: у = z + — . Получаем
— уравнение Бернулли. Положим z = m(x)v(x) z = w'v + uv'. Бу-
дем иметь uv + и v' + — v = -u2v2 . В качестве функции v(x) берем
одно из решений уравнения у' + —у = О => v = — . При таком выборе
X X5
функции v(x) для определения функции и(х) получаем уравнение
,1 2 1 и I I I С 4х4
и —Г = -и‘ —— =t>---Т = —Г => — =-----г + — => W = --;--.
х5 х10 и‘ Xs и 4х4 4 Сх4 -1
Атогда z = uv = —т----.Следовательно, у = — + —?----вобластях
Сх5 - х х Сх5 - х
(Д) и (D2) (х#0 в (/>,) U (£>2))- <
Задана 4. Решить уравнение (х2у2 + 2)dx + 3x2dy = 0 .
Здесь М(х,у) = х2у2 + 2 ; /V(x,,y) = 3x2 => А/(х,у),
дМ _ 2 dN . дМ 3N х-/о2ч
iV(x,y)eC(R’); V XJ,; а7 = 6хэ 17’17 ( ’
Л/(х,у) и N(x,y) не обращаются в нуль одновременно ни в одной
143
точке плоскости х, у. Из заданного уравнения видно непосред-
ственно, что х = 0 — решение этого уравнения. Станем рассматри-
вать наше уравнение для х * 0, т. е. в левой и правой открытых
полуплоскостях: (D\) =
-оо < х < О,
—оо < у < +оо;
(О2) =
О < X < +оо,
В об-
—оо < у < 4-00.
ластях (Д) и (D2) исходное уравнение равносильно уравнению
(это — уравнение Риккати). Попытаемся найти частное решение
уравнения (*) в виде у = —. Подставляя это выражение для у(х) к
х
уравнение (*), получаем
д д2 I I
х1 3 х2 3 х2
Следовательно, функции у, =— и у. =— являются частными ре-
X X
тениями уравнения (*).
Делаем замену: у = z + — • Получаем
2 I
3 х2
2 1 I 2
--г = --г
3 х 3
(это— уравнение Бернулли). Полагаем г(х) = «(x)v(x) =>
zx = uxv -г uvx. Будем иметь
, f , 2 I ) I 2 2
uxv + “ VX + =-3M'v • в каче-
стве функции v(x) берем одно из решений уравнения
21 --
v' + v = 0 => v(x) = х 3. При таком выборе функции v(x) для
определения функции д(х) получаем уравнение
и'х 3 = ——д2х 3 => - = х3 +С => м = —rJ-.
3 и х,/3+С
144
А тогда z = wv = ——--. Следовательно, у = — + ——------об-
Сх^+х х Сх*3+х
шее решение исходного уравнения в областях (Z)t) и (£>2). (У нас
х*0 в (^)и(Ог).) <
Задача 5. Решить уравнение xdy + {-(2х + I )у + у2 + х2) dx = 0.
> Здесь М(х,у) = -(2х + 1)у+ у2 + х2; N(xty) = x => М(х,у),
Mi \ 1 dN . ЭМ 2х
N(x,y)e C(R); —— = -(2х+ 1)+ 2у; —— = I => —eC(R ).
ду дх ду дх
М(х,у) и /V(x,y) обращаются одновременно в нуль в точках
(0,0) и (0,1). Из уравнения видно непосредственно, что
х = 0, Jx = O, Jx = 0,
I </<+-; |0<у<1; [—</ <0 “ Рсшения Уравнения- Ста-
нем рассматривать наше уравнение для х*0, т. е. в областях
(Д) =
(Дг) =
В областях
(О|) и (D2)
исходное уравнение равносильно уравнению
, 2х+1 I 2
у-------У + -У =-Х (*)
X X
(это — уравнение Риккати). Будем искать частное решение уравне-
ния (*) в виде у -axyb. Подставляя это выражение для у(х) в
уравнение (*), получаем
2х + I . , I . ,j
а-------(ах + />)+— (ах + Ь) = -х =>
=> ах-(2х + 1)(ол: + />) +(ах+ 6)2 = -х2.
Приравниваем коэффициенты при одинаковых степенях х в ле-
вой и правой частях полученного тождества.
х2 | а2 - 2а = -1
х | 2ab-2b = O =>
х° | 62-/> = 0
а = I, b = 0;
а = I, b - I.
145
Следовательно, функции )j = х и =х+1 являются частными
решениями уравнения (*).
Делаем замену: y = z + x. Получаем
, , 2х + I . . I . 2 Л 21 / Z Z'
Z + I-(£ + х) + — (Z + 2ZX + Х) = —X => Z-=-
XX XX
(это— уравнение Бернулли). Полагаем z(x) = u(x)v(x) =>
(у \ V‘
у — и =--------. В качестве фун-
х J х
у
кции v(x) берем одно из решений уравнения v' — = 0 => v(x) = х.
х
При таком выборе функции v(x) для определения функции д(х)
получаем уравнение и'х = -и2х => и = -и1 м(х) = —?—. А тог-
х + С
X X
да г = w(x)v(x) =-—. Следовательно, у = х + —---общее ре-
х+С х + С
шенне исходного уравнения в областях (D|) и
Задача 6. Решить уравнение (х2 + у2 -2xy-5)<Zx + J>’ = 0.
Здесь М(х,у) = х2 + _у2 -2ху-5 ; /V(x,y) = l => М(х,у),
N(x,y)eC(R2); ^ = 2у-2х; <** = 0 => ^.^eC(R2).
ду Эх ду Эх
М(х,у) и N(x,y) не обращаются одновременно в нуль ни в
одной точке плоскости х, у.
Запишем исходное уравнение в виде
у'-2ху + у2 =5-х2. (*)
Попытаемся искать частное решение уравнения (•) в виде
у -ах + b. Подставляя это выражение для у(х) в уравнение (*),
получаем
а - 2х(ох + Ь) + (дх + b)2 s 5-х2.
Приравниваем коэффициенты при одинаковых степенях х в ле-
вой и правой частях полученного тождества.
х
| д2-2д = -1
| 2а6-26=0 =>
| />2+о = 5
6 = 2;
Ь = -2.
146
Следовательно, функции у|(х) = х + 2 и =х-2 являются час-
тными решениями уравнения (*).
Делаем замену: у = z + (x + 2). Получаем
z' + I - 2x(z + х + 2) + (z + х + 2>2 = 5 - х2 => z’ + 4z = -z2
(это — уравнение Бернулли). Полагаем z = w(x)v(x) => z = u'v + uv’.
Будем иметь uv + w(v' + 4v) = —u2v. В качестве функции v(x) берем
одно из решений уравнения v' + 4v = 0 => v(x) = е 4х. При таком
выборе функции v(x) для определения функции м(х) получаем
уравнение
, -4х 2 -8х Г 2 -4х I е 41 С 4
и е = -н е => и - -и е => — =----------+ — => и =-----—.
и 4 4 С-е~*х
а 4
А тогда у = х + 2 + —-----общее решение исходного уравнения
на R2. 4
Задача 7. Решить уравнение
у' + 2еху - у2 = е2х + ех.
(*)
Запишем исходное уравнение в виде разрешенном относи-
тельно у':
t 2 х 2х х
у = у - 2е у + е + е .
=/(*.>>
Имеем f'(x,y) = 2у- 2ех. Видим, что /(х,у) и f'\x,y)e C(R2) =>
множеством точек единственности уравнения является вся плос-
кость х, у. Видим далее, что заданное уравнение — уравнение Рик-
кати. Попытаемся искать частное решение уравнения (*) в виде
у = аех. Подставляя это выражение для у(х) в уравнение (*), по-
лучаем аех + 2ае1х -а2е2х = е2л +ех. Приравниваем коэффициен-
ты при ех и е2х в левой и правой частях полученного тождества:
ех | а = I
е2х | 2а - а2 = I
Следовательно, функция = ех является частным решением урав-
нения (*).
Делаем замену: у = z + ex . Получаем вместо (*) уравнение
147
, 2 1 г' 1
Z = Z => = X + C => z =-----
z X +C
Следовательно, у =ex------— — общее решение исходного урав-
нения на всей плоскости х, у. 4
§12. Однородные уравнения
I°.Определение. Функция и = fix,у), заданная в некоторой
области (D), называется однородной функцией степени р в области
(D), если для каждой точки (х,у)е (D) и для каждого числа t > О
такого, что точка itx,ty}e (D), выполняется тождество
fitx,ty) = tpfix, у).
Примеры.
I) Пусть и = fix, у) = х2 + 5л*у . В этом случае
fitx, ty) = itx)2 + 5(tt) • (ty) = r(x2 + 5xy) = t2fix,y) =>
=> м = f(x,y) — однородная функция степени p = 2.
2) Пусть и = fix, у) = у/2х - 5 у . В этом случае
fitxjy) = 72(a) - 5(ty) = f,2f2x-5y = ly2f(x, у) =>
=> fix,у) — однородная функция степени р = у.
( у А
3) Пусть и = f — .В этом случае
/(«,= f(-
( у I
=> и = f — I — однородная функция степени р = 0.
2’. Формула Эйлера. Пусть функция и = fix, у) определена и
непрерывна в некоторой области (D) и имеет там непрерывные
частные производные f^(x,y), f'.ix,y). Пусть функция и = fix, у)
является однородной функцией степени р в (D). Тогда в каждой
точке (х,у)е (D) имеет место равенство
148
df(x,y) df(X,y) .
\ x + -- --- • у = P f(x,y).
dX dy
Выберем и закрепим любую точку (х0,у0)е (D). В силу основ-
ного тождества (*) будем иметь
f(tx0,tyQ) = tpf(x9,y0) (**)
(/(ttb,%) — сложная функция аргумента /). Продифференцируем
по г обе части (**). Получим
Л'(Ло,/Ио) х0 +/;(Ло,(Ио) № = Р<рЛ f(x0,y0).
В частности, при t = I будем иметь
Л(хо,уо) Хо +//(Ab.>b) >b = РЛхо, Jb).
У нас точка (х0,у0) — любая из области (D). Значит, и для каждой
точки (х,у)е (D) будет xf^x> у) + yf'(x, у) = pf(x,y). <
3’. Определение. Дифференциальное уравнение вида
f(x,y)dx + g(x,y)dy =0 (1)
называется однородным, если функции f(x,y) и g(x,y) являются
однородными одной и той же степени р.
Считаем, что функции /(х,у), g(x,y) определены и непре-
рывны в некоторой области (Z)) и имеют там непрерывные част-
ные производные f'(x,y), fy(x,y), g'x(x,y), gy(x,y).
Пусть (D)e(/J) и (Ь) — множество точек единственности
уравнения (I). Пусть в точках области (Ь) xf(x,y) + yg(x,y) не
обращается в нуль. Покажем, что тогда функция
ц(х,у)= —:------------ является интегрирующим множителем
х/(х,у) +yg(x.y)
для уравнения (I) в (О).
В самом деле, умножим обе части уравнения (1) на ц(х,у).
Получим
—-—dx + —-—dy = 0.
xf + yg xf + yg
ъ V * **- v—
= =N(x.y)
(*)
ЭМ d/V
Рассмотрим разность Имеем
149
ЭЛ/ Э/V _ Э f f ) Э f g )
Эу Эх 3y(x/ + ygJ dx[x/ + ygj"
df . z. \ г ( dg ) dg z \ ( г df dg
dy dy dy J dx dx dx
(V+>£)2
3/ r3g ,3g 3/ ( 3/ df } f( dg 3g)
>^T--y/v--Vv- + ^T- XT" + >'T“ "/ xa+>'^
dy dy dx dx _ ( dx dy J ( Эх dy)
(xf + yg)2 (xf + yg)2
По условию, функции /(x,y), g(x,y) — однородные одной и той
же степени р. Но тогда по формуле Эйлера в каждой точке (х, у) € (Ь)
_ э/ df f 3g 3g n
будет xf-+yf--pf\ yf-= pg. Следовательно, будем
Эх Эу Эх Эу
иметь
g*-jg.<> /•<-<>»/..О >(/>) =, 3*.9*,в(Й).
Эу Эх (xf + yg)2 dy Эх
Значит, (*) является уравнением в полных дифференциалах в (Ь) =>
ц(х,у) = —-------------интегрирующий множитель для урав-
xf(x,y) + yg(x,y)
нения (I).
Замечание. Замена у = их, где и(х) — новая неизвестная фун-
кция, приводит однородное уравнение (I) к уравнению
с разделяющимися переменными.
Задача 1. Решить уравнение (х + 2y)dx - xdy = 0.
► Здесь /(х,у) = х + 2у; g(x,y) = -x => /(x,y),g(x,y) е C(R2).
^• = 2; т^ = -1 => r-.~€C(R2). /(х.у), g(x,y) обращаются
Эу дх ду дх
одновременно в нуль лишь в точке (0,0). /(х,у) и g(x,y) —
однородные одной и той же степени р = I в R2. Имеем
xf (х, у) + yg(x, у) = х(х + 2у) - ху = х2 + ху = х(х + у) = 0
на линиях: х = 0, у = -х .
150
Непосредственно из заданно-
го уравнения видно, что
х = О,
х = 0,
— решения исходного уравнения.
Станем рассматривать задан-
ное уравнение в областях:
Рис. 1.22. К задаче I
(00 =
(00 =
О < X < +«>,
—X < у < +«>;
(00 =
-оо < X < О,
-х < у < +«>;
-ОО < х < О,
< у < -х;
(00 =
О < X < +оо,
-°” < у < -х.
В каждой из областей (00, к = 1,4,
М(х,у) =
I I
V + УХ х(х + у)
является интегрирующим множителем исходного уравнения. Ум-
_ 1
нож им обе части заданного уравнения на ц =---. Получим
х(х + у)
х + 2у , I , л /ж.
——-dx---------dy = 0. (*)
х*+ху Х + у
= М(х,у) =Й(х.у)
Это уравнение равносильно исходному в (00. Имеем
ЭЛ/ __1_ 2(х -г у) - (х -г 2у) = I dN = I
Эу х (х + у)2 (х + у)2 Эх (х + у)2
151
=> ----= — в (Z\), к = I,4. Найдем общий интеграл уравнения
ду Эх
(*) (а значит, и исходного уравнения). Для этого берем произвол ь-
ную точку (Хо.-Уо) в (Pi>, к = 1,4. Будем иметь
«(х.Я = ( М(х,у)dx + ( N(x„,y)dy = J ' * 2 < dx - J
= «(x, /) = (2 In |x| - In |x + - In |x„ + ' =
= 2 In |x| - In |x + j| - 2 In |x„| + In |x„ + >| - In |x0 + + In |x„ + д,| =
= 2 In |x| - In |x + y| 4- C| =>
=> 2 ln|x| - In |x + j'| = С — общий интеграл исходного уравнении в
каждой из областей (Dk), к = 1,4.
Второй способ решения задачи 1.
В заданном уравнении f(x,y) = х + 2у; g(x,y) = -х => /(х,у),
Яад)еС(К!);^ = 2;| = -1 => |^ЛеС(К2).
ду дх ду Эх
Функции /(х,у) , g(x,y) обращаются одновременно в нуль в
точке (0,0). f(x,y) и g(x,y) — однородные функции одной и той
же степени р = I в R2. Непосредственно из заданного уравнения
видно, что
х = 0,
0 < у < +»;
х = 0.
_ — решения исходного урав-
-« < у < и
нения. Станем рассматривать исходное уравнение для х * 0, т. е. в
левой и правой открытых полуплоскостях:
(Д) =
0 < х < +«,
-ОО < у < +оо;
(Д2) =
-оо < X < О,
— ОО < у < +оо.
В заданном уравнении делаем замену: у = и х , где и(х) — новая
неизвестная функция. Будем иметь
152
(х + 2ux)dx - x(udx + xdu) = 0 <=>
(так как х*0 в (D,) и (£>2))
<=>(! + 2u)dx - udx - xdu = 0 <=>
(1 + u)dx-xdu =0. (*•)
Замечаем, что (**) является уравнением с разделяющимися пере-
менными. Непосредственно из уравнения (*•) видно, что
и
и = -1
решения уравнения
— решения исходного уравнения в
(£>i) и в (D2) соответственно.
Станем рассматривать уравнение (**) в областях:
(Д) =
(D2)
(А) = -
(04) = -
В областях (/)*) уравнение
dx du Л z / ч I
-------- = 0 (ц(х,м) = —--
х w+l х(1+и)
(**) равносильно уравнению
— интегрирующий множительурав-
нения (**)) =>
| dx _ “г du
; х /и+1
*1)
In |х||
|Ы=И
'«=«0
=> ln|x| - ln|w + l| = С — общий интеграл уравнения (**) в (ОА),
In |х| - In —
интеграл исходного уравнения в областях
(Д)«
(D2) = <
153
О < x < +°°,
Задача 2. Решить уравнение (у + Jx2 - у2 j dx - xdy = 0.
Здесь f (х,у) = у + у/х2 - у2 ; g(x,y) = -x определены и не-
прерывны
в областях:
(0|)
О < х <
-X < у < Х‘,
(Я2) =
-ОО < X < О,
х < у <-х.
У - 1 г У <*.
ду ' Эх
,^eC((D,)U(D2». /<х,у).
dy dX
g(x,y) обращаются одновременно в нуль лишь в точке (0;0).
/(х, j), g(x,y) — однородные функции одной и той же степени
р = 1 в (0,) U (02)- Следовательно, заданное уравнение является
однородным. Имеем
+ >»(•*»>’) = ху + xyjx2 ~У* ~ху = xdx2 -у2 = О
налиниях х = 0; у = х ; у = -х . Эти линии не входят в (D}) U (02)-
Непосредственно из заданного уравнения видно, что
у = х, у = -х, У = х, у = -х,
< < <
0 < х < +оо; 0 < х < -i-oo; -оо < х < 0; -оо < х < 0
Рис. 1.23. К задаче 2
— решения уравнения. Так как
xf + yg * 0 в (£)j) U (02), то функция
у) = —---= —===== я вл я ется
V + 3'g x-\Jx2—y2
интегрирующим множителем заданно-
го уравнения в (0() U Умножим
обе части исходного уравнения на
И =
==. Получим
154
=W(*.J)
-_£_ = 0.
Jx1 -У1
-Й(х.У)
дМ X dN X дМ dN
dy (%2 - у1 )^2 Эх (x2 - у1 )3/2 dy dx
(Dt) U (D2) => Уравнение (*) является уравнением в полных диф-
ференциалах в (Dt)U(£M- (Отметим, что уравнение (*) в
(Di)U(D2) равносильно исходному уравнению.) Найдем общий
интеграл уравнения (*) (а значит, и исходного уравнения) в
(D|) U (О2). Для этого берем произвольную точку (х0,у0) в (Ок),
к = 1, 2. Будем иметь
х у _
и(х,у) = J M(x,y)dx + J N(x0,y)dy =
хо Уо
или
U(x,y) = J M(x,yQ)dx + j N(x,y)dy =
«о УЬ
-jf-j—фг-
1 г /г2 _ v2 х 1 [3 _ „2
*о ХуX Jq _>'о у X у
Воспользуемся вторым выражением для и(х,у), взяв в качестве
точки (х0,у0) точку (хо,0). где # 0 . Получим
, ч } dx f dy
н(х,у)=
Xb 0 V* - У
- sgn х arcsin —
у=0
= In |xj - In |x0| - sgn x arcsin — = In|x| - sgn x arcsin — + Cj =>
155
=э Inlxl - sgn х arcsin — = С — общий интеграл исходного уравне
X
ния в (D|) U (D,).
у
Задача 3. Решить уравнение у cos In—dx - xdy = 0 .
Ь Должно быть: х*0 и ->0 => Заданное уравнение определе-
х
но в областях: (/}) =
О < х < +<»,
О < у < +«>;
(&) =
-«> < X < О,
„ В этом уравне-
-оо < у < 0.
нии Дх, у) = у cos In — ; g(x,y) = -x f(x,y),g(x,y)e
X
— = cos In —-у sin In —• —• — = cosin —-sin In — ; — = - I =>
ду X X у X X X dX
dy’dx
C((D|) U . f(x,y), g(x,y) не обращаются одно-
временно в нуль ни в одной точке из (Р|) U (Л). Функции f(x,y)
и g(x,y) —однородные одной итой же степени р = 1 в (D|) U
Следовательно, заданное уравнение является однородным в
(D|) U (D2). В (D,)U(D2) выражение
х/ + У£ = xycosln — -ху = ху eosin — — I
обращается в нуль на линиях
у = хе2*", к = 0, ± I, ± 2,
0 < X < +оо.
и на
линиях
у = хе2*", к = 0, ± I, ± 2, ...,
-оо < х < 0.
Подстановкой в заданное
уравнение убеждаемся непосредственно, что эти линии явля-
ются интегральными кривыми. (На рис. 1.24 представлена схе-
ма расположения указанных линий.) В каждой из областей
(^1*) =
0 < х < +»,
хе2"* < у < хе2(*+,)"
(Д«) =
-оо < X < О,
< у < хе2*",
и
156
к = 0, ± I, ± 2, ... , xf + yg *0 и. сле-
I
довательно, функция ц = —:-------=
xf + yg
I
= —------------ является интегриру-
xyl cosin-- I
I х
ющим множителем в (Оц) и в (ДА).
Умножим обе части исходного уравне-
ния на ц. Получим в каждой (Д|А) и в
Рис. 1.24. К задаче 3
(Ь2к), к = 0, ± I, ± 2, ... , уравнение, равносильное исходному:
cos In-
у А
X cos In — - I
, *____d
-Mlx.y)
dx —---------!------г dy = 0.
V
у cos In — - I
. * J
*N(x.y)
Имеем
ЭЛ/
ду
НМ sin |п * Э/У
ду У V
ху cos In — -1
< х J
э/v . .
= — в (Оц) и в (D,k), к = 0, ± 1, ± 2
у
sin In —
__________X .
( ч2
У I
cos In — - 1
X J
... => Уравнение(*)
является уравнением в полных дифференциалах в каждой из обла-
стей (Du) и (Ь2к), 4 = 0, ±1, ±2...Найдем общий интеграл
уравнения (*) (а значит, и исходного уравнения) в областях (Ь1к)
и (D2k). Для этого берем произвольную точку (хь«Уо) в (Рц)»
(Ь2к). Будем иметь
и(х,у)= J M(x,y)dx + J /V(x0,y)^y =
>о
X
dx j- £ ________I______ , t
x :.y y
2
157
ln(y/x)
= I n x| - ctg —----1
-ctg
x=x0
=> U(x,y) = ln|x|-Ctg ln l>',>)-ln|jQ,| +
+ In 07*0) I" №).
2 2 2
In (>’M) r
2 1
= In |х| -ctg
У-Уо
2
=> lnjx|-ctg-------—- = C — общий интеграл заданного уравне-
ния в областях (01Л), (Р2Л), к = 0, ± I, ± 2, .... 4
§13. Простейшие уравнения, приводящиеся к однородному
I. Рассмотрим уравнение вида
dy
dx
(цх + Ь^у + Су
а2х + thy + с2
(I)
Отметим, что если в (1) q = с2 - 0 , то уравнение (I) является од-
нородным, ибо в этом случае у' =
+ t а'+й|7
a, + ^Z
X
= f — , а уравнение / = / -1— однородное. Следовательно,
I х I 1x1
имеет смысл вести обсуждение, когда хотя бы одно из чисел q,c2
отлично от нуля. Это мы и будем предполагать в дальнейшем.
Могут иметь место два случая, а именно: случаи, когда
«I
«2
и когда
"i
а2
= 0.
158
Первый случай. Пусть
а, А)
а2 6,
*0.
' где £ и П — новые переменные, а
У = И + 3-
аир— некоторые постоянные числа, пока неизвестные. Отно-
сительно новых переменных уравнение (1) запишется в виде
Сделаем замену
Я|!; +/>|П + Aja +/>|р +q
+ kn + «2а + + с2
Числа аир выбираем такими, чтобы было
ata + />|P + C| =0,
a2a + &₽ + ci =0-
(2)
(3)
Это всегда можно сделать, так как система (3) имеет и притом
единственное решение, ибо определитель этой системы отличен
от нуля (по условию).
При таком выборе чисел аир будем иметь вместо (2)
*1=
(4) — однородное уравнение. Решив его и возвращаясь к старым
переменным, получим решение исходного уравнения (I).
(4)
Второй случай. Пусть
ai
0|/>j — ОтЬ\
д2
= ^-(=к) => а, =ка,, = кЬэ.
Л
в этом случае запишется в виде
Следовательно, уравнение (1)
41 =
dx
к(агх + thy) + q |
(^x + ^yHcj /
(5)
^П_
П
«I
«2
Ь.
Сделаем замену, положив + = Z (г(х) — новая неизве-
. ~ dz . dy dy I dz „
стная функция). Тогда — = + />, => — =---------Отно-
dx dx dx lh dx th
сительно новой неизвестной функции уравнение (I) будет таким:
159
1 dz
l>2 dx
' kz + c^ + a2
Z+c2 b.
=f\(z) (обозначение)
=> -г sMU) + «2-
(6)
(6) — уравнение с разделяющимися переменными. Решив его и
подставив вместо г его выражение ^х + И^у, найдем решение ис-
ходного уравнения.
Задача I. Решить уравнение (2х -4 у + 6)dx + (х + у- 3)dy = 0 .
► Здесь М(х,у)= 2х-4у + 6 ; W(x,y) = х + у-3 =э М(х,у),
,/V(x,y)eC(R2); ^ = -4; ^ = 1 => V'I7eC<R2)- А/(х’у)’
Эу oX аУ aX
N(x,y) обращаются одновременно в нуль лишь в точке (1,2).
Видим, что у = f
-2х + 4у - 6
х + у-3
и что
Положим
х = £ + а,
У = П + Р-
Будем иметь
(2^ - 4г| + 2а - 4р + 6)^ + (£ + д + а + р - 3)</г| = 0.
Числа аи₽ берем такими, чтобы было
2а-4р + 6 = 0, 1а-2р + 3 = О,
а+Р-3=0 а+0-3=О
ix = £ + l,
А тогда замена приводит к уравнению
1,у = т] + 2
(2£-4r|) (£ +т|)<7г| = 0.
(*)
Здесь /(^,г|) = 2^-4г|; g(£,n) = ^ + H — однородные функции сте-
пени р = I. Следовательно, (*) — однородное уравнение.
160
Имеем /(£,q), g(£,q). -
непрерывны на всей плоскости ^,q;
/(^,q), g(^, q) обращаются одновре-
менно в нуль лишь в точке (0,0). Вы-
ражение
У(^П) + П«(^П) =
= ^-4q) + q(^ + q) =
= 25!-Хп+п2 = й-п)(Д-п)
Рис. 1.25. К задаче I
обращается в нуль на линиях q=^, q = 2^. Во всех остальных
точках плоскости ^,q выражение ^(^,q) + r|g(^,q) # 0 . Непосред-
ственной подстановкой убеждаемся, что
, Л = ^> п=£, ln = 2£, 1п = 2£,
0 <£<+«»; [-«><^<0; |0<^<4-«>; |-оо<^<0
- решения уравнения (*). Станем рассматривать уравнение (*) в
областях:
(Д|) =
0 < ^ < +«>,
-<ю < q <
-ОО < £ < 0,
-оо < q < 2$;
$ < П <
(дз) =
0 < £ < +оо,
2^ < q < +оо;
(Д4) =
В каждой из областей (Д*), к = 1.4 , р(^П) = :-г;—г яв-
^П) + Ч^П)
ляется интегрирующим множителем уравнения (*). Умножим обе
части уравнения (*) на р = ————— • Получим
—4г*--------+---------------dx\ = 0
(^-q)(2^-q) (S-n)(25-q)
=Л(4,п)
161
Отметим, что уравнение (**) равносильно уравнению (*) в (А*),
к = 1,4. Имеем
эм_ У*2»1-2пг = э у<-^п-2Л;
ап й-п)2(2$-п)2 ’ а$ ($-п)г(2$-л)2
в (А*), к = 1,4 => Уравнение (♦♦) является уравнени-
ем в полных дифференциалах в (ДА.), к = 1,4.
Найдем общий интеграл уравнения (*♦) (а значит, и уравне-
ния (*)) в (А*). Для этого берем произвольную точку (^,т|0) в
(ДА), к = 1,4, Будем иметь
и(£,П) = j Л7(£,п)^4- J =
По
If 6 2 hc nff 3 2 \
= J чг----к— + J —---------r =
41^-1 5-nJ .Цп-Зо O-ljoJ
= (31n|2$-n|-2ln|$-n|)p J +(3ln|n-2^,|-2ln|n-^|)|’'" =
S-M ”1“Чо
= 3 In |2£ - nl — 2 In |£ - T||-31n |2£o - nl + 2 ln|£0 - n| +
+31n|n- 2^j|- 2ln|rj-^o|-3ln|n0 - 2^,1 + 2 In|n0 ~£o| =>
=> W(^Ti) = 3ln|2^-n|-2ln|n-q + Cl =>
=> 3 In |2^- T|| - 2ln|^ - r|| = С — общий интеграл уравнения (*) в
(А*), Л=Ё4.
Возвратимся к прежним переменным х и у. У нас £ = х-1;
г| = у-2. Следовательно, 31п|2х-^-21п|х-у +1| =С — общий
инте1рал исходного уравнения в областях:
162
Рис. 1.26. К задаче I
(Я,) =
(Ог) =
2х < у < +<*»;
(£>4> =
-оо < X < I,
2х < у < х + \. ◄
Задача 2. Решить уравнение (2х + у+ I)dx ~(4х + 2у - 3)dy = 0 .
- ►Здесь М(х,у) = 2х +I; /V(x, у) = -4х - 2у 4- 3 => Л/(х,у),
N(x,y)e C(R2); —•»—4 => C(R^ - м(х,у),
dy дх ду дх
N(x,y) не обращаются в нудь ни в одной точке плоскости х, у.
Видим, что у' = f
2х 4- у 4- I
4х + 2у - 3
и что
«I
«2
^2
= 0. Поэтому
2 1
4 2
делаем замену: 2х 4- у = z , где г(х) — новая неизвестная функция.
Относительно новой неизвестной функции заданное уравнение
примет вид
(5z-5)dx + Q-2z)dz = 0 (*)
((*) — уравнение с разделяющимися переменными). Непосредствен-
но видно, что
2=1,
-оо < X < 4-00
решение уравнения
(*)=>
163
Рис. 1.27. К задаче 2
=> 2х + у = I, х €(-«>,+«>), т. е.
у = I - 2х. х е (-оо, 4-оо), — решен ие ис-
ходного уравнения.
Станем рассматривать уравнение
(*) в областях
1 < z < +°°.
-оо < х < +°°;
т
Умножим обе части уравнения (♦) на
Получим
5dx + ——dz = 0.
2-1
Уравнение (••) равносильно уравнению (*) в областях (Д),
(Ь2) (в этих областях 2*1). Уравнение (**) является уравнением
с разделенными переменными.
Найдем общий интеграл уравнения (**) (а значит, и уравне-
ния (*)) в (Ьк), А: = 1,2. Для этого берем произвольную точку
(х0,4)) е ( Ьц), к = I, 2 . Будем иметь
/ \ f с j f 3 — 2Z j е |x=x f I ) j
M(x,z) = I 5dx+ I-------Jz=5xl -J 2------------- \dz =
x L *_| * Л 2-1 I
-*0 4) co \ z
= 5x -5x0 - 2z + 2zo + ln|2-1|- ln|zo -1| = 5x- 2z + ln|z - l| + C| =>
=> 5x - 2? + ln|z - 1| = С — общий интеграл уравнения (*•) в (Dk),
к = 1,2.
Возвратимся к прежним переменным х и у. У нас z = 2х + у.
Следовательно, 5x-4x-2y + ln|2x+y-l| = C => х-2у + 1п|2х + д'-1| =
= С— общий интеграл исходного уравнения в областях (Д) и
(D2), где (Д|) =
-оо < X < +оо,
I - 2х < у < +оо;
(Я2) =
X < +оо,
у < I - 2х.
164
11. Некоторые дифференциальные уравнения можно привести
к однородным заменой у = zk. Число к обычно заранее неизвестно.
Чтобы его найти, нужно в уравнении сделать замену у = zk • Тре-
буя, чтобы полученное после замены уравнение было однород-
ным, находят к, если это возможно. Если же этого сделать нельзя,
то уравнение не приводится к однородному этим способом.
Задача 3. Дано уравнение <х4 + y2)dx - xidy = 0 . Привести
заданное уравнение к однородному.
► Здесь А/(х,у) = х4 + у2; У(х,у) = -х3 => М(х,у),
Л(х,у)е C(R2); ^- = 2у, =-Зх2 C(R2). М(х.у)
ду дХ ду дх
и /V(x,y) обращаются одновременно в нуль лишь в точке (0,0).
Делаем замену: у = zk dy = kzkxdz . Относительно новой не-
известной функции заданное уравнение станет таким:
(х4 -г z^dx-kx^z^ dz=Q. (•)
=/(*.«) =в(х.г)
Уравнение (*) будет однородным, если существует число к такое,
при котором функции f(x,z) и g(x,z) являются однородными
одной и той же степени. Последнее будет лишь тогда, когда
4 = 24 =3 + А:-1 => к = 2.
Вывод: заданное уравнение приводится к однородному заме-
ной у = z2 • При к = 2 уравнение (*) принимает вид
(х4 + z4)dx-2x3ztfz =0.
7(х.г) $(*.«)
7(х,г) и £(х,г) — однородные функции степени р = 4.
Задача 4. Дано уравнение (у3 + xy)dx -2х2dy = 0 . Привести
заданное уравнение к однородному.
► Здесь А/(х,у) = у3+ху; Л^(х,у) = -2х2 => Л/(х,у),
, дМ > dN дМ dN „.„2ч
N(x,y)e C(R ); — = 3у2+х; —- = -4х => -S7’S7eC(R)-
ду дх ду дх
М(х,у) и N(x,y) обращаются одновременно в нуль лишь в точке
(0,0). Делаем замену: у = zk =* dy = kzk''dz . Относительно но-
вой неизвестной функции заданное уравнение станет таким:
165
(zik + xzk)dx-2kx2 *zk 1 dz=O.
af(x,z) =«(x.d
Уравнение (*) будет однородным, если существует число к такое,
при котором функции f(x,z) и g(x,z) являются однородными
одной и той же степени. Это будет лишь тогда, когда
3*=* + 1= 2 + *-1=>* = 1.
Вывод: заданное уравнение приводится к однородному заме-
ной у = zl/2. При к уравнение (*) принимает вид
(ZV2 + xzif2)dx-x2z'if2 dz=O.
=/(х.г)
f(x,z) и g(x,z) — однородные функции степени p =
3
2 ’
Задача 5. Дано уравнение (х2у4 + l)y<Zx + 2xdy = 0 . Привести
заданное уравнение к однородному.
Здесь Л/(х,у) = х2у5+у; N(x,y) = 2x => M(x,y),N(x,y)e C(R2).
ЭЛ/ - 2 4 , dN - дМ(х,у) dN(x,y) r 2 .z. .
—— = 5xzy+l; -r- = 2 => ---------,—------eC(R). M(x,y)
dy dx dy dx
и N(x,y) обращаются одновременно в нуль лишь в точке (0,0).
Делаем замену у = zk => dy = kzk~'dz . Относительно новой неиз-
вестной функции заданное уравнение станет таким:
(х2г4* + \)zk dx + 2kxzk 1 dz=O.
=/(х.г) =$(х.г)
Уравнение (*) будет однородным, если существует число к такое,
при котором функции f(x,z) и g(x,z) являются однородными
одной и той же степени. Это будет лишь тогда, когда
2 + 5* =к = 1 + A--I =>*=-!
2
166
Вывод', заданное уравнение приводится к однородному заме-
ной у = z I 2. При к = -- уравнение (*) принимает вид
(х2?-2 + l)z"l/2 dx-xz'y1' dz =0.
«/(x.d «(*.?)
f{x,z) и — однородные функции степени р = —
Задача 6. Дано уравнение ydx + x(2xy + l)dy = 0. Привести
заданное уравнение к однородному.
► Здесь М(х,у) = у\ N(x,y) = х(2ху+\) => M(x,y),N(x,y)e C(R2).
dM , dN . dM ЭЛТ 2
---= 1; — = 4xy + l => —. —eC(R ), M(x,y) и N(x,y)
dy dx Эу dx
обращаются одновременно в нуль лишь в точке (0,0). Делаем
замену: у = zk =* dy = kzk 'dz Относительно новой неизвестной
функции -заданное уравнение станет таким:
Z^ dx + (2xzk + \)х kzh 'dz=0- (*)
•/<**>
Уравнение (*) будет однородным, если существует число к такое,
при котором функции /(х,г) и g(x,z) являются однородными
одной и той же степени. Это будет лишь тогда, когда
к = 2 +А +Л-I = I + A-1 =>Л = -1.
Вывод', заданное уравнение приводится к однородному заме-
ной у = -. При к = -I уравнение (*) принимает вид
Z
I J (2х , А х , _
- dx - — + 1 \-ydz = 0.
S I z )z2
=f(x.z) -g(x.z)
f(x,z) и g(x,z) — однородные функции степени р = -1.4
Задача 7. Дано уравнение [x-4jy)dx + 2dy = 0 . Привести
заданное уравнение к однородному.
167
► Должно быть у > 0. => Уравнение следует рассматривать
лишь в замкнутой верхней полуплоскости. Имеем
М(х,у) = x-4jy ; N(x,y) = 2 => М(х,у), ЛДх.у) — непрерыв-
~ ЪМ 2 dN „
ны в замкнутой верхней полуплоскости. т~ = и =>
Jy дх
дМ dN
=> ~~, — непрерывны в открытой верхней полуплоскости.
М(х,у) и N(x,y) одновременно не обращаются в нуль ни
в одной точке. Делаем замену: у = Zk => dy = kzk 'dz. Относитель-
но новой неизвестной функции заданное уравнение станет таким:
(х-4zk^2)dx-t-2kzk ' dz =0. (*)
=/(x.t) =«(х.г)
Уравнение (*) будет однородным, если существует число к такое,
при котором функции j\x,z) и g(x,z) являются однородными
одной и той же степени. Это будет лишь тогда, когда
I = - = к - 1 => к = 2.
2
Вывод’, заданное уравнение приводится к однородному заме-
- 2
НОИ у=z .
При к = 2 уравнение (*) принимает вид
(x-4z)dx + 4< dz =0.
/(х,г) и g(x,z) — однородные функции степени р = 1.4
12 А
у2 —- dr-dy - 0. Привести за-
JT I
данное уравнение к однородному.
► Должно быть х#0. => Уравнение следует рассматривать
лишь в открытых левой и правой полуплоскостях. Имеем
2
М(х,у) = у2—N(x,y) = -\ => М(х,у), N(x,y) — непрерыв-
х
дМ _
ны в открытых левой и правой полуплоскостях. ------= 2у;
Эу
168
aw л ал/ aw
— = 0 => — и —- — непрерывны в открытых левой и правой
полуплоскостях.
М(х,у) и W(x,y) одновременно не обращаются в нуль ни в
одной точке. Делаем замену: у - zk => dy = kzk'xdz . Относитель-
но новой неизвестной функции заданное уравнение станет таким:
g(x.g)
=/<x.z)
(*)
Уравнение (*) будет однородным, если существует число к такое,
при котором функции /(х,г) и g(x,z) являются однородными
одной и той же степени. Это будет лишь тогда, когда
2к =-2 = А - I => к =-1.
Вывод: заданное уравнение приводится к однородному заме-
м I
нои у =
Z
При к = -1 уравнение (*) принимает вид
=7(х.г)
+ -у dz = 0 .
Z
/(x,z) и g(x,z) — однородные функции степени /? = -2.«
Задача 9. Дано уравнение (у - у2у]х-х2у2j dx + 2xdy = 0. При-
вести заданное уравнение к однородному.
Здесь Л/(х,у) = у - у2у]х - х2у2 ; W(x,y) = 2х. Должно быть
х-х2у2 >0 <=> х(1-ху2)>0 =>
0 < х < +«>,
Л/(х,у) и W(x,y) обращаются одновременно в нуль лишь в точке
(0,0). Имеем
169
dy
2. ,2
3x2yJ - 2ху. dN _
N(x,y), ™
dy
aw
непрерывны в области
дх
(D) = .
1_. Делаем замену: у = zk => dy = kzk~'dz. От-
носительно новой неизвестной функции заданное уравнение ста-
нет таким:
- z‘k yjx -x2z2k Vx + 2kxz
'^g(xa)
k~'dz =0.
=/(*.€)
Уравнение (*) будет однородным, если существует число к такое,
при котором функции f(x,z) и g(x,z) оказываются однородными
одной и той же степени. Это будет лишь тогда, когда, во-первых.
1=2 + 2А и, во-вторых, к = 2к + - = к =>
Вывод-, заданное уравнение приводится к однородному заме-
ной у = —j=
dZ
При к = -- уравнение (*) принимает вид
dz = O.
в<(х.г)
=/(х.г)
f(x,z) и g(x,z) — однородные функции степени р = -
Задача JO. Дано уравнение
.6 .Л . ..2
) dx -j xydy = 0 .
Привести заданное уравнение к однородному.
Должно быть
170
х6 - у4 > 0 у1 < | х Р « - | х |3/2< у < | х |у2.
M(x,y) = 7x6 -y4 + y2; N(x,y) = -^xy. M(x,y) и N(x,y) обра-
щаются одновременно в нуль лишь в точке (0,0). Имеем
dN 2 ... .. дМ dN
= + 2у; — = --у. Л/(х,у), N(x,y), —, —
,.4 Эх 3 Эу Эх
ЭЛ/
непрерывны в области (£)> = •
Делаем замену:
у = Zk => dy = kzk~ldz • Относительно новой неизвестной функ-
ции заданное уравнение запишется в виде
Ак „2к
:kzk 1 dz = 0.
V / 3
=/(х,г) =«(х.г)
Уравнение (*) будет однородным, если существует число к такое,
при котором функции f(x,z) и r(x,z) оказываются однородными
одной и той же степени. Это будет лишь тогда, когда, во-первых,
Ь = 4к и, во-вторых, 3 = 2к = 2к => Л = —.
Вывод: заданное уравнение приводится к однородному заме-
. 3
ной у = z^2. При = 2 УРавнение (*) принимает вид
(Jxb -zb + z3}dx -xz2 dz=O.
=/(xz)
f(x,z) и #(x,z) — однородные функции степени р =3. 4
Задача 11. Дано уравнение 2ydx + (х2у + 1)хе/у = 0. Привести
заданное уравнение к однородному.
> Здесь Л/(х,у) = 2у; jV(x,y) = (x2y+l)x => M(x,y),N(x,y)e C(R3);
ЭЛ/ « . ЭЛ/ dN 2
— = 2; — = 3xy+l =э —, —€L(R ). Л/(х,у) и У(х,у)
dy dx ду дх
обращаются одновременно в нуль лишь в точке (0,0). Делаем
171
замену у = zk =» dy = kzk 'dz . Относительно новой неизвестной
функции заданное уравнение станет таким:
2?\ dx + (x2zk + \)xkzk 1 dz =0- (*)
Уравнение (*) будет однородным, если существует число к такое,
при котором функции f(x,z) и g(x,z) оказываются однородными
одной и той же степени. Это будет лишь тогда, когда, во-первых,
2 + к = 0 и, во-вторых, к = 2 + 2к - к => к --2.
Вывод: заданное уравнение приводится к однородному заме-
ной у = —т •
Z
При к =-2 уравнение (*) примет вид
2 х (№ \
4 ж--24 ^+i k=o.
z z zL J
. \ J__I
—g(x.z)
f(x,z) и g(x,Z) — однородные функции степени p = -2 .
Глава 2
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ПЕРВОГО ПОРЯДКА, НЕ РАЗРЕШЕННЫЕ
ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ
§1. Основные понятия и определения
Дифференциальное уравнение первого порядка, не разрешен-
ное относительно производной, имеет вид
F(x,y,/) = 0. (I)
Лишь в простейших случаях уравнение (I) удается разрешить
относительно у' и заменить его, следовательно, одним или не-
сколькими уравнениями вида
У = /*(*,А к = \,т. (2)
Так, например, уравнение
у(у')2 +(х-у)/-х = 0 (2)
в результате его решения относительно / распадается для у * О
на два уравнения: у = I и у' = - —, откуда
У
у = х + С; у2 + х2 =С. (*)
Следовательно, все решения уравнения (2) содержатся в форму-
лах (*). Таким образом, семейство интегральных кривых уравне-
ния (2) получается в результате наложения семейств (*) (рис. 2.1).
Мы видим при этом, что через каждую точку (х0, J'o)G r2 \ {<0.0)}
проходят ровно две интегральные кривые уравнения (2).
173
Рис. 2.1
В большинстве же случаев урав-
нение (1) не удается разрешить от-
носительно у'.
Станем рассматривать х,у, у как
координаты точек трехмерного про-
странства. Тогда уравнение (I) будет
определять в этом пространстве не-
которую поверхность (У) (рис. 2.2).
Пусть (D) — проекция поверхности
(5) на плоскость Оху. Ясно, что
только для точек (jc,j’)e(D) суще-
ствуют значения у , которые совместно с х и у удовлетворяют
уравнению (I). Поэтому о решениях уравнения (I) имеет смысл
говорить лишь применительно к области (D).
Возьмем любую точку (х«,у0)е (£>) и рассмотрим уравнение
FCWo»/) = 0-
(3)
Пусть ~ числа, которые являются различными
вещественными корнями уравнения (3). Ради простоты ограни-
чимся рассмотрением случая, когда уравнение (3) имеет конечное
число вещественных корней (рис. 2.3).
Рис. 2.2
174
Пусть (Рк), к = 1,/я, — прямоугольный параллелепипед с цент-
ром в точке (хь.ЯъУ*)- Пусть параллелепипеды (Pk) такие, что
(Р() A (Pt) = 0, /,У = , i * j. Предположим, что в каждом па-
раллелепипеде (РА), к = \,т, функция F(x,y,y') непрерывна и
имеет непрерывные частные производные F^(x,y,y'), Fy(x,y,y'),
F'(x,y,y') и что —
* 0 , к = 1, т. В этом случае точку
-Г* >
(хо.Уо) будем называть обыкновенной точкой уравнения (1). Вся-
кую иную точку области (£)), а также все точки границы области
(D) будем называть особыми точками уравнения (I). Видим, что в
каждом параллелепипеде (Pk)t к = \,т, выполнены условия те-
оремы об однозначной разрешимости уравнения (I) относитель-
но у' (см. теорию неявных функций). Следовательно, существует
окрестность точки М0(х0,у0): йк(х0,у0), к = I, т, в которой урав-
нение (I) определяет у как однозначную непрерывную функцию
от х и у: у = fk (х.у), к = I, т, причем функция /к (х,у) имеет в
175
Видим, таким образом, что если уравнение (1) рассматривать
лишь в параллелепипеде (Рк) (к = 1,/и), то мы будем находиться
в условиях (уже изученного раньше) случая уравнения, разрешен-
ного относительно производной.
Так как в йк(х0,у0) функция fk(x,y) непрерывна и имеет
ЭД(х,у)
непрерывную частную производную —------—, то по теореме о
Эу
существовании и единственности решения уравнения, разрешен-
ного относительно производной, заключаем, что через точку
(х0,у0) проходит одна и только одна интегральная кривая урав-
нения у' = Д(х,у),для которой у'|д/ =у* (к = 1,т).
Общий вывод; если точка (Xo,yo)e (D) является обыкновенной
точкой уравнения (1) и если уравнение (3) имеет т различных
вещественных корней Х.Уг» ••• . то через точку (х0,у0) прохо-
дят ровно т интегральных кривых уравнения (I). Эти кривые
расположены в пределах окрестности u(xQ,yQ) точки (х0,у0), где
т
utxQ.yo) = А М*<ьУо) •
/=1
Так как направления касательных к обсуждаемым кривым в
точке (х<),Уо) различны (поскольку они имеют различные угло-
вые коэффициенты у'\,У2, ••.Ут ), то эти кривые в точке (х0,у0)
не могут касаться друг друга (рис. 2.4). Заметим, что если соотно-
шение (3) определяет бесконечное
Рис. 2.4
множество значений /:
УьУъ -*У*......
то через точку (х0,у0) будет, очевид-
но. проходить бесконечное множество
интегральных кривых с различными
направлениями касательных в этой
точке. (Здесь предполагается, конеч-
но, что точка (х0,у0) — обыкновен-
ная для уравнения (I).)
176
В связи с тем, что соотношение (3) может давать для точки
(•хЬ.Уо) более чем одно значение у', постановка задачи Коши для
уравнения (I) в этом случае нуждается в уточнении. Именно
задача Коши для дифференциального уравнения (I) состоит в
том, чтобы найти решение этого уравнения, которое проходит
через точку (х^,у0) и имеет в этой точке определенное направле-
ние (одно из направлений, задаваемых в этой точке дифференци-
альным уравнением).
Замечание. Если точка Л/О(х0,у0)е (D) является особой точ-
кой для уравнения (I), то одному значению ук, являющемуся
вещественным корнем уравнения (3), может отвечать не одна, а
несколько интегральных кривых уравнения (I), проходящих че-
рез точку Мо(Хц,Уо). Может оказаться также, что значению ук не
будет отвечать никакая интегральная кривая уравнения (I); вмес-
то кривой может получиться точка. Но если одному значению ук
отвечает несколько интегральных кривых уравнения (I), проходя-
щих через точку Л/0(х0,у0), то все эти кривые в точке Л/о имеют
общую касательную (т. е. касаются друг друга в точке Л/0(хо,у0)).
На рис. 2.5 представлена одна из возможных схем расположе-
ния интегральных кривых уравнения (1) в случае, когда точка
Л/0(х0,у0) оказывается особой точкой этого уравнения. Если
геометрическим местом особых точек уравнения (1) оказывается
некоторая линия, то эту линию называют особой линией этого
уравнения.
Из определения особых точек уравнения (I) ясно, что в
области (D) их следует искать среди точек, являющихся проекци-
ями на плоскость Оху тех точек (х,у, >'), в окрестности которых
не выполнены условия теоремы об однозначной разрешимости
уравнения (I) относительно у’ (см. тео-
рию неявных функций).
Точками (х, у, у'), в окрестности ко-
торых не выполнены условия теоремы об
однозначной разрешимое!и уравнения (I)
относительно у’, являются, следователь-
но, либо точки, где одновременно
F(x,y,/) = 0,
F/(x,y,/) =0,
Рис. 2.5
177
либо точки, в окрестности которых нарушено условие существо-
вания и непрерывности функции Л(х, у, у') и ее частных произ-
водных F'(x,y,y'), F'(x,y,y'), F'-(x,y,y')_
Если предполагать, что функция F(x,y,y') и ее частные про-
изводные по всем аргументам всюду существуют и непрерывны,
то особые точки уравнения (I) в области (D) следует искать лишь
среди точек, являющихся проекциями на плоскость Оху тех точек
(х,у,у'), в которых одновременно выполняются соотношения
(4). Допустим, что каждое из уравнений системы (4) определяет
в пространстве х, у, у' поверхность. Пусть это будут поверхности
(5) и (5'). Равенства (4) будут выполняться одновременно вдоль
линии (£) пересечения этих поверхностей (рис. 2.6). Проекция
линии (А) на плоскость Оху будет особой линией уравнения (I).
Заметим, что особая линия уравнения (1) представляет собой
кривую, подозрительную на особое решение этого уравнения.
Особая линия будет особым решением уравнения (1), если, во-
первых, она является интегральной кривой этого уравнения
и если, во-вторых, в каждой ее точке нарушается единственность
решения задачи Коши.
В качестве примера рассмотрим уравнение
у2+(у')2-1 = 0.
Здесь F(x,у,у') = у2 + (у')2 -1, F'x = 0, F’y = 2у, F’y- = 2у'. Видим,
что F(x,y,y') определена, непрерывна и имеет непрерывные част-
ные производные во всем пространстве Охуу'. Станем рассматри-
вать систему
Особая линия.
Рис. 2.6
178
F(A,y,/) = O,
/>'(х,у,/) = О
У1 + (/)2 -1=0,
2/ = 0.
(4)
Линию (£), определяемую системой (4), спроектируем на плос-
кость Оху. Для этого нужно исключить у' из системы (4).
Исключая у' из системы (4), получаем особую линию
У1 =1.
распадающуюся на две прямые: у=1 и у--1. Непосредствен-
ной подстановкой в исходное уравнение функций у = I и у = -I
убеждаемся, что они удовлетворяют этому уравнению. Значит,
у = I и у --I, хе (-<*>, +«»),— интегральные линии.
В нашем примере исходное уравнение удается разрешить отно-
сительно у': y' = ±J\-y2 => в полосе
-со < х < +оо,
находим
-I < у < 1
— - = dx => ± a resin у = х + С => у = ± sin (х + С) —
это общее решение заданного уравнения в области
< х < +*>,
-I < у < 1.
Решения у = I, хе (-<», + <~), и у = -1, хе (-«=, + «»), являются
особыми решениями исходного уравнения, так как в каждой точке
этих решений нарушается единственность решения задачи Коши.
Отметим, что через каждую точку (х0,>'0)е
ходят ровно две интегральные кривые заданного уравнения с
различными направлениями касательных в этой точке.
Рис. 2.7
179
§2. Метод введения параметра
Пусть имеется уравнение
F(x,y,/) = 0. (I)
Пусть (.5)— поверхность, определяемая уравнением (I) в про-
странстве Оху/. Пусть ((7)— некоторая область пространства
Охуу', содержащая внутри себя поверхность (5). Предполагается,
что функция F(x,y,y') определена, непрерывна в области ((7) и
имеет там непрерывные частные производные
^•(х,у,/), F'y(x, у, у'). Пусть, далее, функция у = <р(х) является
решением уравнения (I) в некотором промежутке {а,Ь) и
<у0=ф(х0), /=ф'(х0), причем точка хое(а,Ь), а точка
(Хо’-Уо,/))6 Ш . а следовательно, принадлежит (<7).
Метод введения параметра основывается на следующих двух
леммах.
Лемма 1. Если — *0, то в некоторой окрестности
? Ч*о ГоДО
д(х0) точки х0 существует и непрерывна ф'(х) (м(х0) с {а,Ь)).
У нас (67) — область, и точка (х0,у0,уц)е (G). Следователь-
но, существует параллелепипед (Р), содержащий точку (x0,y0,/j)
и содержащийся в (G), в котором выполнены условия теоремы
об однозначной разрешимости уравнения (I) относительно /
(см. теорию неявных функций). По этой теореме уравнение (I) в
некоторой окрестности И(хо,у0) точки (Хо,у0) определяет /,
как однозначную функцию от х и у.
/ = /(х,у), (2)
причем функция /(х,у) непрерывна и имеет непрерывные част-
ные производные т-иу-в И(х0,.у0). (^(х0,у0) с (D), где (D) —
дх ду
проекция поверхности (5) на плоскость Оху.)
По условию, у = ф(х), х 6 (а,Ь), — решение уравнения (I),
удовлетворяющее условию у|х. л = у0 (т. е. ф(х«) = у0)• Следова-
тельно, существует окрестность м(х0) точки х0, в которой
у = ф(х) является решением уравнения (2) (//(х0) с {а, Ь)). Но
тогда для хе н(х0):
180
Ф'(х) = /(х,ф(х)). (3)
Продифференцируем обе части (3) по х. Получим
ф'(х) = /;(х,ф(х)) + 4'(х, ф(х)) ф'(х). (4)
Здесь /Х(х,<р(х)), //(х,ф(х)), ф'(х) = /(х,ф(х)) — непрерывны в
м(х0) как суперпозиции непрерывных функций. А тогда из (4)
следует, что ф'(х)е С(и(х[})). 4
Лемма 2. Если ф'(х) непрерывна в некоторой окрестности
w(x0) точки х0 (п(х0)с (а,Ь)) и если ф'(хо)*0, то решение
у = ф(х) уравнения (I) представимо в параметрической форме
х = х(/),
y = y(t), (5)
причем функции х(/) и y(t) в некоторой окрестности ^(/0)
точки /0 имеют непрерывные производные и таковы, что
Ух = '•
> Рассмотрим функцию / = ф'(х), xew(x0). По условию,
ф'(х0) * 0. Пусть для определенности ф'(х0) > 0. Так как ф'(х) —
непрерывная, то существует окрестность й(х0) точки х0, в кото-
рой ф'(х) > 0 (й(х0)си(хо)). Но тогда в м(х0) функция г = ф'(х)
строго возрастающая. Следовательно, существует обратная ей
функция х = х(/), определенная в некоторой окрестности И(/о)
точки (/0 =ф'(х0)) и имеющая там непрерывную производную
х,', ибо х' = — = -Д— (ф'(х) * 0).
tx Ф (*)
Подставляя функцию х = х(г> в равенство у = ф(х), получаем
у = Ф(х(/)),т.е. у = y(t).
Ясно, что функция у = y(t) определена и непрерывна в И(/о) как
суперпозиция непрерывных функций и что она имеет в И(/о) не-
прерывную производную у', ибо у, = ф'х(х(/))-х/ (фх(х(/)) —
непрерывна как суперпозиция непрерывных функций, х,' — не-
прерывна по доказанному выше>.
181
Соотношения
X = х(/),
У = У(1),
/€ И(/о),
дают нужное параметрическое представление решения у = ф(х)
уравнения (I). 4
Замечание 1.
1. Если у = ф(х), хе (о. 6), есть решение уравнения (I). по-
_ 3F
дозрительное на особое, то —- = 0 . и, следовательно,
дУ 1(х.ф(Х),ф'(Х))
мы не можем гарантировать существование и непрерывность ф'(х)
(см. лемму I), а значит, не можем применить лемму 2, гарантиру-
ющую возможность нужного параметрического представления
функции у = ф(х) в виде (5).
2. Если уравнение (I) имеет решения вида у = ах + Ь, то
ф'(х) = 0 и, следовательно, лемма 2 не приложима. Значит,
и в этом случае мы не можем гарантировать нужного параметри-
ческого представления этого решения.
Замечание 2. Методом введения параметра / = у очень часто
выгодно искать решения дифференциальных уравнений, не раз-
решенных относительно у', но зато разрешенных относительно х
или у, т. е. уравнений вида
X = g(y,yr) ИЛИ У = /(X, /) . (6)
Этот метод в принципе позволяет найти все решения таких
уравнений, за исключением, быть может, решений вида у = ах + Ь
и решений, подозрительных на особое решение.
Но решения вида у = ах + b, если таковые имеются, могут
быть найдены методом неопределенных коэффициентов, а реше-
ния, подозрительные на особые, — методом, изложенным в пре-
дыдущем параграфе.
В качестве примера для отыскания решений дифференциально-
го уравнения методом введения параметра рассмотрим уравнение
у = хУ + ф(/), (7)
где ф(у') — любая функция, имеющая непрерывную производную
Ф/. ((7) — уравнение Клеро.)
Положим
у' = 1 (т. е. dy = tdx). (8)
182
Тогда
у = хг + ч>(() (9)
и, следовательно, dy = tdx + xdt + y(t)dt. Так как dy = tdx (см. (8)),
то получаем xdt + q>'(t)dt = О или (x + tf(t))dt = 0 . В последнем
соотношении нельзя считать dt = 0 , ибо dt является дифференци-
алом независимой переменной. Поэтому х + ф'(/) = 0 =>
=>х = -ф'(г). (Ю)
В силу соотношений (9) и (10), получаем следующее решение ис-
ходного уравнения (7):
х = -<р'(/),
у = -лр'(О + Ф(О- (11)
Выясним, не имеет ли уравнение (7) решений вида
у = ах + b. (12)
Подстановка в уравнение (7) дает
ах + b = х а + ф(а).
Отсюда видим, что если д = ф(а), где а — любое число (станем
обозначать его через С), то (12) будет решением уравнения (7).
Таким образом, уравнение (7) имеет еще решения вида
у = хС + ф(С). (13)
(Решение (13) определено для всех значений С, при которых
определена функция ф(С); решение (13) представляет собой
функцию от х и С => (13) — общее решение уравнения (7).)
Выясним еще, не имеет ли уравнение (7) решений, подозри-
тельных на особое.
Для нахождения таких решений нужно (как это следует из § I)
рассмотреть систему
Г(х, у, у') = 0, у = ху' + ф(у'),
fy(x.,y,y') = 0 =* 0 = х+ф'(/)
и исключить из нее у'.
Легко видеть, что результат исключения у' из системы (14)
тождествен результату исключения параметра t из системы (II).
Вывод: решение (II) уравнения (7) подозрительно на особое
решение этого уравнения.
183
§3. Примеры и задачи к главе 2
Задача 1. Найти все решения уравнения (у')2 + ху = у1 + ху'.
► Перепишем заданное уравнение в виде (у')2-ху' + (ху-
-?) = 0 =>
Исходное уравнение распадается на два уравнения: у’ + у = х
и у'-у-О. ц = e^dx = ех(* 0) и ц = е = е'х(* 0) — интегриру-
ющие множители для первого и второго из этих уравнений
соответственно. После умножения обеих частей полученных урав-
нений на соответствующие им интегрирующие множители полу-
чаем уравнения
еху' + еху = хех и е ху'-е~ху = 0,
равносильные исходным. Последние могут быть записаны в виде
(еху)х = хех и (е~ху)'х = 0 =>
=> еху = хех - ех + С и е~х у = С =>
=> у = х -1 + Се~х и у = Сех.
Ответ. Все решения заданного уравнения содержатся в фор-
мулах у = х -1 + Се'х; у = Сех .
Задача 2. Найти все решения уравнения ху\ху + у) = 2 у2.
► Перепишем заданное уравнение в виде х2(у')2 + хуу'-
- 2 у2 = 0 => для х * 0 находим
, _ -ху ± Jx2y2 + 8х2у2 _ —ху + Зху -у±3у
У ~ 2х2 " 2х2 " 2х
=> в левой и правой открытых полуплоскостях у' = -2- и у - — ,
X X
,2 , 1
или у + — у = 0 и у —у = 0.Из этих уравнений видно непосред-
ственно, что
у = 0, з=().
„ и • являются решениями каж-
-<*> < х < 0 0 < х < +оо
184
лого из полученных уравнений. Замечаем, что оба уравнения явля-
ются линейными. ц = х2 — интегрирующий множительдля первого
I
из них, а И =--интегрирующий множитель для второго; у нас
х * 0 в областях (D,) =
-ОО < х < О,
—оо < У < +oot
(Pj) =
О < X < +оо,
-ОО < у < 4-00.
После
умножения обеих частей полученных уравнений на соответствую-
щие им интегрирующие множители получаем уравнения
- у у
х‘/ + 2ху = 0 и ----=у=0. Последние могут быть записаны
в виде (х2у)'х = 0 и (L1 = 0 => х2у = С и — = С в (Dk), к = 2.
UJL х
Ответ. Все решения заданного уравнения в. областях (Dk),
к = 1, 2, содержатся в формулах х2у = С и у = Сх. 4
Задача 3. Найти все решения уравнения х(у')2 - 2уу' + х = 0.
у ± \1у2 — х2
Ь Имеем для х#0: у' = -——---------. Ясно, что должно
х
быть у2-х2^О. Легко проверить,
что функции
У = ±Х,
-оо < х < О
У = ±х,
О < х < +°° являются решениями
полученного уравнения. Станем
рассматривать уравнения
и y'^-J^ в
х V х Ух2
Рис. 2.8. К задаче 3
областях:
(£>,) =
(/м =
-ОО < X < О,
-ОО < у < х.
О < X < +оо,
<
X < у < +оо,
(D4) =
О < X < +оо,
-оо < у < -X.
185
Оба этих уравнения являются однородными. Делаем замену:
у = и • х (и(х) — новая неизвестная функция). Тогда у' = хи' + и .
Относительно новой неизвестной функции полученные уравне-
ния станут такими:
хих = V«2 -1 и хих = -Vw2 - I • (*)
Отметим, что в каждой из областей (Dk), к = 1,4 : и2 > I, х * 0.
Следовательно, уравнения (*) равносильны соответственно урав-
нениям
du _ dx
yju2 -1 x
=> In и + л/м2 -11= In |x| + In |C| и In L + Vw2 - 11 = - In |x| + In |C|
=> W + Vw2 -1 = Cx и U + Vm2 - I = — •
X
Возвращаясь к прежним переменным, получаем
У + У2 - х2 = Сх2 и у + Jy2 — х2 - С
в каждой (Z\), к = 1,4.
Ответ. Все решения исходного уравнения содержатся в фор-
мулах: у + yly2 -х2 = Сх2; у + у1у2 -х2 = С в (^), к = 1,4, и
У = х , у = -х , хе (-«о. + оо). <
Задача 4. Найти все решения уравнения х(у')2 -2уу' + у = 0.
, у ± \1 у2 — ху
Ь Имеем для х * 0: у' =---3. Ясно, что должно быть
х
у2 - ху > 0. Легко проверить, что функции
у = 0, у = 0, у = х, у = х,
«
-оо<х<0; 0<х< +»о; -«х><х<0; 0<х< +°°
являются решениями полученного уравнения.
Станем рассматривать уравнения
186
в областях:
(0,) =
О < X < +<»,
х < у < +°°;
(Z>2) =
-ОС < X < О,
О < X < +ОО,
-ОО < у < 0.
Рис. 2.9. К задаче 4
(Р4) =
Оба эти уравнения являются однородными. Делаем замену: у = их
(w(x) — новая неизвестная функция). Тогда у' = и'х + и. Относи-
тельно новой неизвестной функции полученные уравнения ста-
нут такими:
хих = ум2 - и\ хих = -у]и2 - и. (*)
Отметим, что в каждой из областей (Dk), А: = 1,4: х*0
и и2 - и >0. Поэтому уравнения (*) равносильны соответственно
уравнениям
du _ dx du _ dx
yju2 - и x И л/м2 -и х
- In |х| + in |С|;
= - In |.xj + In |C| =>
U-- + yJu2-U=Cx и и--+yju2 -и =— =>
2 2 х
в каждой (), к = 1,4.
Ответ. Все решения исходного уравнения содержатся в фор-
мулах:
187
у + yjy2 - ху = ^+Сх2; у + 7/ - ху -^ = С в (Z\), к = 1,4;
у = 0 и у = х , хе (-«>, +«~). 4
Задача 5. Найти все решения уравнения (/)2 + х - 2у = О .
Имеем у’ = ±у[2у - х . Ясно, что должно быть 2у - х > 0.т. е.
> —. Станем рассматривать уравнения
у' = у]2у-х и у' = -yj2y-x
в области (£)) =
Сде-
лаем замену, положив 2у-х=и2
(и(х) — новая неизвестная функция).
Ясно, что и > 0 в (D). Получим
2у -1 = 2ии
у = ии’ + — . Относи-
2
тельно новой неизвестной функции
полученные уравнения станут таки-
ми:
ии = и — и ии = -и - -
2 2
Эти уравнения являются уравнениями с разделяющимися пере-
« + -J |*0(< 0) в (Z)),
менными. Так как и — = 0 при и = -
2 2
то из (*) находим
и , , . 1 .
----j- du = ах (если и * —) и
“’2
—du - dx .
“+2
Отметим, что и = - является решением первого из уравнений (*)
(это соответствует решению у =
исходного уравнения).
а
Из уравнений (♦♦) получаем соответственно
188
и + - In и —
2
2
= х + С (если и*-) и -и + -1
2 2
Возвращаясь к прежним переменным, находим
4
2
2
, ~ XI
= х + С , если у * — + -,
2 8
и
-у/2у-х + ^\п |
2
Ответ. Все решения исходного уравнения содержатся в фор-
мулах:
2
2
- J2y- х = х + С в (D), где у # у + -;
2
2
2 8’
Задача 6. Найти все решения уравнения (у')3 + (х + 2)еу = 0.
► Имеем у' - -(х + 2)|/3е^3. Это — уравнение с разделяющи-
мися переменными. Так как е^3 * 0, то получаем уравнение
е у!\1у + (х + 2)|/3 dx = 0, равносильное исходному. =>
7 _Z f
=> -Зе^3 + -(х + 2)4/3 = С=э4е 3 = (х + 2)3+С.
4
Ответ. Все решения исходного уравнения содержатся в фор-
муле 4e~y/i = (х + 2)4/3 + С. 4
Задача 7. Найти все решения уравнения (у')2 -2ху' = 8х2.
► Имеем (у*)2 - 2ху -8х2 = 0 => У = х ± Vx2 + 8х2 = х ±Зх.
Видим, что исходное уравнение распадается на два уравнения:
у’ = 4х и у' = -2х => у = 2х2 + С и у = -х2 + С.
Ответ. Все решения исходного уравнения содержатся в фор-
мулах: у = 2х~ +С и у = -х2 + С. 4
189
Задача 8. Найти все решения уравнения (ху' + Зу)2 = 7х.
Из вида уравнения следует непосредственно, что должно
быть х>0. Имеем ху" + 3у = ±474х => для х>0:
, 3 J7
у+-у=±-=.
X >Jx
(*)
Полученные уравнения (*) являются линейными. Они равносиль-
ны исходному в открытой правой полуплоскости, т. е. при х > 0.
^_^Jp(x)dx =ef^ =e31nx _ х3
— интегрирующий множитель для уравнений (*). Отметим, что
ц * 0 для х > 0. После умножения обеих частей уравнений (*) на
|i = № будем иметь
х3у' + Зх2у = ±V7x^2 <=> (х3у)'х =±>/7х5/2 =>
=> х3у = ±-^=х7/2 + С => у = Сх"3 ± ~^= 4х.
Ответ. Все решения исходного уравнения содержатся в фор-
мулах у = Сх~3 + 2
Задача 9. Найти все решения уравнения (у')2 - 2уу' = у2(е* - I).
Имеем
(у')2 - 2уу' + у2 = у2ех <=> (у' - у)2 = у2ех =>
=> у' - у = ±уе^2 => у' = у (I ± е^2 ).
Нетрудно видеть, что функция у = 0, х е (-оо, + «□), является
решением полученных, а также и исходного уравнений. Станем
рассматривать уравнения у =y(l ±е,/2) для у О, т. е. в откры-
тых верхней и нижней полуплоскостях. Эти уравнения в обла-
стях (О|) =
—оо < х < +°°,
-оо < У < О
равносильны
уравнениям
190
— = 1 + е^2 и — = I - ех^ =>
У У
=> In |у| = х + 2ех/2 + In |С| и In |у| = х - 2ел/2 + In |С| =>
=> у = Се**2*"1 и у = Cex~2"f2.
Ответ. Все решения исходного уравнения содержатся в фор-
мулах у = Сех*2е h , у = Сех~2е^' в (D}) U (D2) и у = 0 ,
X € ( — «>, +°°) .
Задача 10. Найти все решения уравнения у'(2у- у') = у2 sin’ х .
Имеем
у'(2у - у') - у2 sin2 х = 0 <=> (у')2 - 2уу‘ + у2(1 - cos2 х) = 0 о
с=> (У ~ У)2 = У2 cos2 х => у' - у = ±у cos х => У = (1 ± cos х)у.
Легко видеть, что функция у = О, хе (-оо, + <~), является реше-
нием полученных, а также и исходного уравнений. Станем рас-
сматривать уравнения
у' = (I + cosx)y и y' = (l-cosx)y (*)
в областях (D|) =
-ОО < X < +°°,
О < у < +оо
И (02) =
-ОО < X < +оо
Уравнения
-оо < у < 0.
(*) в <£>,) U () равносильны соответственно уравнениям
/ /
у У
— = l+cosx и — = l-cosx=>
У У
=> 1п|у| = х + sin х + 1п|С| и ln|jj = x-sinx + ln|C| =>
=>y = Cex*sinx и y = Cex-sinx.
Ответ. Вес решения исходного уравнения содержатся в формулах:
y = Ce**sin*, y = Cex s,,lx в (Dt)U(P2) и у = 0, хе (-~,+оо).
Задача 11. Найти все решения уравнения (у')4 +у2 = у4.
Видим непосредственно, что у = 0, хе (-оо,+оо),— реше-
ние исходного уравнения. Имеем, далее,
(У)4 = у2(у2 - О => (У)2 = ±у>1у2 ~ 1 •
191
Ясно, что если у* 0, то должно быть у2-1^0, т. е. должно
быть: либо уе |1, + «>), либо уе (-«»,!]. Так как левая часть
последнего соотношения неотрицательна, то для уе |1, +«>):
(у')2 - У^У2 ~ । ♦ а для у е (-°о, I]: (у')2 = ~УуУ2 - I • Замечаем, что
функция у = I, хе (-«,+«), является решением первого из полу-
ченных уравнений, а функция у = -1, хе (-<»,+«>), является
решением второго из этих уравнений. Отметим, что обе эти
функции являются решениями исходного уравнения.
Станем рассматривать уравнение
(у')2 = у^У2 - I
в области
Рис. 2.11 . К задаче 11
а уравнение
в области
В области (О,)
следует рассмотреть уравнен ия
у' = ±7у(у2
а в области (D2) — уравнения
Заметим, что если в уравнениях (**) сделать замену у = -у, то
относительно функции у будем иметь уравнения у' = j^J(y2 -1)|/4,
где у е (I, + ~). Видим, что для у получены точно такие же урав-
нения, как и уравнения (*) для функции у. Следовательно, если
будут найдены решения уравнений (*), то тем самым будут найде-
ны и решения уравнений относительно у (а значит, и решения
уравнений (**)). В области (Р,) уравнения (*) равносильны урав-
нениям
р —пт = ±dx = 1 In
Jyty2 - I)*4 2
_arclg£Sl = C±X.
J У
192
Ответ. Все решения исходного уравнения содержатся в фор-
мулах:
у = 0, х е (-оо, + о); у = I, хе (-«>,+«>); у = -1, хе (-«>,+«>). 4
Задача 12. Найти все решения уравнения
х(у - ху’)2 = х( у')2 - 2уу .
Непосредственно из заданного уравнения видно, что у = 0,
хе (-оо, + <»), является его решением. Для х * 0 имеем:
(у-ху')1 = (у')2 -2/- + 2__2_ => (у-хуУ = (/-2.1 -21
X X1 х1 \ X) X1
=> (у- */)2 = u> ,J) -2^. => (х/-у)2(Д--11=2-т =>
X* X* ^Х J X
=> (х/ - у)1 = -2—-, есл и х # ±1.
I -х2
Левая часть последнего соотношения неотрицательна. Следова-
тельно, неотрицательной должна быть и правая часть. А это будет
лишь тогда, когда хе (-1,1).
Станем рассматривать полученное уравнение в областях:
(Д|) =
О < х < I,
О < у < +оо;
(D2) =
-I < х < О,
О < у < +оо;
I < X < О,
оо < у < 0;
(О4) =
0 < х < I,
-оо < У < 0.
В каждой из областей (Dk), к = 1,4, будем иметь
ху' - у = ± — 1 =>у' = 2.±—2—_ => 2_ = 1±— 1 =>
4\- х2 х xVl -х2 У х xVl -х2
193
I 4- Ji *
(Су -1)2 + x2 = I; 2) Cy = x — X => (Су -1)2 + x2 = I.
x
Ответ. Все решения исходного уравнения содержатся в фор-
мулах (Су-1)2 + х2 = I в областях (Dk), к =174, и у = 0.
X G (-°°, «*>) .
Задача 13. Найти все решения уравнения у(ху' - у)2 = у - 2ху'.
Рис. 2.13. К задаче 13
► Из заданного уравнения
видно непосредственно, что фун-
кция у = 0, хе (-«>,+о®), я вл я-
ется его решением. Разрешая ис-
ходное уравнение относительно
у', находим для х * 0 и у * 0:
Из полученных уравнений видим,
что должно быть 1-у2>0 =>
ye |-1,O)U (О, I]. Замечаем, что функции _у = 1, хе (-~,0)U(0, +«>),
и у = -1, хе (-°0, 0) U (0, + оо), являются решениями полученных,
а также исходного уравнений. Станем рассматривать уравнения (*)
в областях
(М) = -
(D,) =
-ОО < X < 0,
О < у < 1,
194
W =
-оо < X < О,
-1 < у < О,
(Д») =
О < х < +«>,
-I < у < О.
Из уравнений (*) находим
хи*в^(^2-|±7|-/)в W,к = М,
Сделаем замену: 1-у2 = и2 (д(х) — новая неизвестная функция;
д#О для уе (-1,0) IJ (0,1)). Относительно функции и(х) полу-
чаем уравнения
-на = -(-д2 ±и) => д' =—(«± I) =>
х х
=> I) 1п|д + 1| = ln|x|+ In |С| => и + I = Сх =э (Сх- I)2 = I - у1;
2) 1п|д - 1| = 1п|х| + 1п|С| => и - I = Сх => (Сх +1)2 = I - у2.
Ответ. Все решения исходного уравнения содержатся в фор-
мулах:
(Сх - I)2 + у2 = I, (Сх + I)2 + у2 = ! в областях (Dk), к = 1,4;
у - 0, хе (-«о, + оо);
>’ = -1, хе (-«,0) U (0, + оо); у = |, хе (-оо,0) U (0, + «). ^
Задача 14. Найти все решения уравнения уу\уу - 2х) = х2 - 2у2.
Сделаем замену, положив у2 =и (д(х) — новая неизвест-
ная функция; и > 0). Тогда =
I , „
-дг. Относительно новой неиз-
2 л
вестной функции исходное уравнение станет таким:
(д')2 - 4хд' + (8д - 4х2) = 0 <=>
<=> (и')2 - 4хи + 4х2 + 8(д - х2) =0 <=> (2х - д')2 + 8(д - х2) = 0 <=>
« (2х - д')2 = 8(х2 - д). (*)
Так как левая часть полученного уравнения неотрицательна, то
неотрицательной должна быть и правая часть этого уравнения,
т. е. должно быть х2 - д > 0 => х2 - у2 > 0 => у2 < х2. Это нера-
венство выполняется в областях:
195
Рис. 2.14. К задаче 14
О < х < +°°,
-х < у < х;
(Д) =
Нетрудно проверить, что функция
и = х2, хе (-<», -+ оо), является реше-
нием уравнения (*) (а значит, функ-
ции У=Х, Xе (-оо, + оо) ; у =-х ,
Х€ (-«о, + оо), являются решениями исходного уравнения). Заме-
тим, что в областях (Z)A), к = 1, 2, х2 - и > 0. Поэтому уравнение
(*) может быть записано в виде
(2x-iZ)2
8{х2 - и)
<=>
1 (2х-ы')
2 У2 /к2 -U
(х2 - и)'
2>1х2 - и
= ±У2 =>
=> Ух2 - и = ±У7х + С => Ух2 - у2 = С ± У2х.
Ответ. Все решения исходного уравнения содержатся в фор-
мулах:
Ух2 - у2 = С±41х в (DJ, Л = 1,2;
у = — х, хе (-°°, + °°); у = х, хе (~°°, + °°). ^
Задача 15. Найти все решения уравнения
(у')2 + 4ху' - у2 - 2х2у = х4 - 4х2.
Имеем
у = -2х ±У4х2 + у2 1х2у 4-х4 -4х2 = -2х± У(у 4-х2)2 =>
=> у 4-2х = ±(у + х2). (*)
Непосредственной проверкой убеждаемся, что функция У = -х2.
хе (-«, + оо), является решением полученных, а также исходного
уравнений. Станем рассматривать уравнения (*) для у * -х2 . Тогда
уравнения (*) будут равносильны уравнениям
/+2х (у4-Х2)' । I . 21 . . । I/-I
-----Г = ±1 => —----= => In у 4-X = ±Х 4-In С =>
у 4-х у 4-х 1 1
196
=>y + x2 = O?tx. (**)
Отметим, что решение у = -л2, х е (-<*>, + оо) , содержится в
соотношении (♦♦) при С = 0.
Ответ. Все решения исходного уравнения содержатся в фор-
муле у = Ceix -х2. 4
Задача 16. Найти все решения уравнения y(y-lxy')2 = 2у'.
► Из заданного уравнения видно, что функция _у=0,
хе (-оо, + ©о), является решением исходного уравнения. Разрешая
исходное уравнение относительно у', находим для х * О и у * 0:
2хуг +1 ± у]4Х}>2 4- 1
4х2у
Из полученных уравнений (*)
заключаем, что должно быть
4ху2 +1 £ 0.
Непосредственной проверкой
убеждаемся, что функции
,Х€ (-оо, 0),
являются решениями уравнений
(*), а также решениями исход-
ного уравнения. Станем рассмат-
ривать уравнения (*) в областях:
Рис. 2.15. К задаче 16
0 < X < +°о,
0 < у < +оо;
(Р2)=
-ОО < X < 0,
w=
0 < X < +оо,
-оо < У < 0.
197
Запишем уравнения (*) в виде
4х2уу' = 2ху2 +1 ± ^4ху2 +1.
(**)
Сделаем замену, положив и = 4ху2 + I (м(х) — новая неизвестная
функция; и(х) > 0 в (Dk), к = 1,4). При такой замене
, * 2 о > и' -4 V2 _ 2 и -1 л
и =4у + 8хуу => уу =——-—; 2ху =----------. Относительно но-
8х 2
вой неизвестной функции уравнения (*•) примут вид
их = 2-Уй(Vw ± l) <=>
du dx
«• d In |Vw ± l| = d In |x| => In |Vn ± l| = In |x| + In |C| =>
=> 4u ± \ =Cx => -Ju = (Cx ? I) =s> ^4xy2 +1 = Cx ? I •
Ответ. Все решения исходного уравнения содержатся в фор-
мулах
^4ху2 + I = Сх + I в (Dk), к = 1,4;
у = ± —, хе (-«о, 0); у = 0 , хе (-~, + °°). 4
27-х
Задача 17. Методом введения параметра решить уравнение
х = (У)3 + У .
► Полагаем y-t (<^>dy-tdx). Тогда х = Г3+/=э
dx = (З/2 + \)dt. У нас dy = tdx. Следовательно, dy = /(З/2 +!)<// =>
х = г3 +/,
— общее решение исходного уравнения в
параметрической форме.
I) Проверим, не имеет ли исходное уравнение решений вида
у = ах + Ь. Подстановка этой функции в заданное уравнение дает
х = а3 + а. Видим, что тождественного равенства не получается.
Значит, исходное уравнение не имеет решений вида у = ах + b.
198
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. Имеем
F(x,y,/) = 0,
F/.(x,j,/) = 0
X-(/)3-j' = 0,
-3(Г)2-1=0=>(/)2=-|
(невозможно).
Следовательно, решений, подозрительных на особое, заданное
уравнение не имеет.
Ответ. Все решения исходного уравнения содержатся в соот-
ношениях
з
4 2
Задача 18. Найти все решения уравнения: х
(методом введения параметра).
Из заданного уравнения находим при у * ±1
х-
(У)2 -1
Полагаем у - t (<=> dy-tdx). Получаем
х = ^~, Ге(-~,-l)U(-U)U(l,+<
г -1
У нас dy = idx. Следовательно,
. 2г(г2 + !) . , (г2 + 1Иг2-1)
dy = —5 rdt dy = 7—7—-
(r2-l)J о2-I)2
<> dy =
(z2 —I)2
=>^’ =---——2 =>У =
2
Таким образом, получили
2
t2 - I
' /е(—. -I) U (-1,1)11(1. +-).
г = _^-|п|?-|| + С,
199
Это — общее решение заданного уравнения в параметрической
форме.
I) Проверим, не имеет ли исходное уравнение решений вида
у = ах + Ь . Подстановка этой функции в заданное уравнение дает
x(tr -1) = 2а. Видим, что тождественного равенства не получает-
ся. Значит, исходное уравнение не имеет решений вида у = ах + b.
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. Для этого вводим в рассмотрение систему
Е(х,у,у') = 0,
г;(х,у,У)=о
х((У)2 - l) - 2/ = 0,
2ху‘ -2 = 0 (невозможно, если х = 0)
, 1
у = —, х * 0;
х
( I А
- х + — =0 (невозможно).
I
Следовательно, решений, подозрительных на особое, заданное
уравнение не имеет.
Ответ. Все решения исходного уравнения содержатся в соот-
ношениях
/е (-оо, -1)U(-I, I) U (I, +-L <
Задача 19. Найти все решения уравнения х = у'у]\ + (у')2 (ме-
тодом введения параметра).
Полагаем у' = t (<=> dy = tdx). Тогда х = /VI + /2 . У нас
dy = tdx. Следовательно,
dy = Vl + /2rf(l + Г2) - - + Z ? => у = -(I + г )3/2 - Vl +t2 + С
2 VI+/2 3
200
Получили, таким образом,
х = /Vi +1\
y = |(i + r2)?/2-ViT7+c, Ze(
I) Проверим, не имеет ли заданное уравнение решений вида
у = ах + b, Подстановка этой функции в заданное уравнение дает
х = ау\ + а2. Видим, что тождественного равенства не получает-
ся. Значит, исходное уравнение нс имеет решений вида у = ах + b .
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое? Для этого рассматриваем систему
1Г(х,у,/) = 0,
\F^.y,y') = 0 ~
х - /Ji + (У)2 =0,
-Jl + (У)2 - , (•* * = 0 =» I + 2(уУ2 = 0 (невозможно).
з/ЖУ)2
Значит, решений, подозрительных на особое, заданное уравнение
не имеет.
Ответ. Все решения заданного уравнения содержатся в соот-
ношениях
/€ (-оо,
Задача 20. Найти все решения уравнения у\х - In у') = I (ме-
тодом введения параметра).
Из заданного уравнения следует, что должно быть у'>0.
Положим у' = t (t > 0). Тогда х = In г + -. У нас dy = tdx. Поэтому
dy = t( - - -L ]dt = dt - — => у = t - In t + C
I / t2 J t
(у нас t > 0). Таким образом, получили
201
, I
X = 1П/ + -,
t
у = t- In t + C,
t G (0, +•<»).
I) Проверим, не имеет ли заданное уравнение решений вида
у = ах + Ь. Подстановка этой функции в заданное уравнение дает
а(х - In а) = I . Видим, что тождественного равенства нет. Значит,
исходное уравнение не имеет решений вида у = ал: + b.
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. С этой целью составим систему
F(x,y,y') = Q,
/у(х,у,У> = 0
у'(х - In /) - I = 0,
х - In у' - I = О
=> У = 1, а значит, х = ! .
х = 1 — не есть решение исходного уравнения. Следовательно,
исходное уравнение не имеет решений, подозрительных на особое.
Ответ. Все решения заданного уравнения содержатся в соот-
ношениях
. I
X = 1п/ + —,
t
у = z - In / + С,
t G (0, + ®о).
Задача 21. Найти все решения уравнения у = (у')2 + 2(у')’
(методом введения параметра).
Положим У = / (<=> dy = tdx ). Тогда
у = /*+2? (*)
=> dy = (2r + 6t2)dt. У нас dy = tdx. Будем иметь, следовательно,
tdx = 2t(\ + 3t)dt. (♦♦)
Замечаем, что если г=0, то из (*): у = 0. Непосредственной
подстановкой в заданное уравнение убеждаемся, что функция
у = 0 , х = (-°0, + «о), является его решением. Для t # 0, из соот-
ношения (**), получаем
dx = 2(1 + 3t)dt =* х = 2/ + 3/2 +С.
Таким образом, получили
х«2/ + 3<’+С, ,е( 0)и(0+„)
у = /2+2?.
202
I) Проверим, не имеет ли заданное уравнение еше решений
вида у = ах + b. Подстановка функции у = ах + b в исходное урав-
нение дает
ах + b = а2 + 2а3 => а = О, Ь = 0.
Получаем, что у s 0, х = (-<», + ««), является решением исходно-
го уравнения (это было отмечено и раньше).
2) Выясним, нс имеет ли заданное уравнение решений, подо-
зрительных на особое. Для этой цели рассматриваем систему
Fix, у, у) = 0,
F'y-(x,y,y') = Q
(/)2 + 2(/)'-у=О,
2/ + 6(/)2 =0
/ = 0,
_ и
>’ = 0
Подстановкой в исходное уравнение убеждаемся, что функ-
ция у = 0 , х = (-оо, + °°), является решением, а функция у = — ,
х = (-«*>, + оо), не является решением заданного уравнения. Реше-
ние у = 0 , х = (-оо, + оо), подозрительно на особое.
Ответ. Все решения исходного уравнения содержатся в соот-
ношениях:
х = 2г + З/2 + С
\ ’ /€ (-«,0)11(0, + «), и у = 0,
у = г + 2г,
X € (—°°, + °°) . ^
Задача 22. Найти все решения уравнения у = In (l + (у')2]
(методом введения параметра).
> Положим у' = t (dy = tdx). Тогда
У=1п(1+/2), /€(-«, + оо) (♦)
=> dy =----7. У нас d\> = tdx . Следовательно, будем иметь
1 + г
/ dx =
2tdt
I +/2
Замечаем, что если t = 0, то из (*): у = 0. Подстановкой в задан-
ное уравнение убеждаемся, что функция у = 0, х = (-оо, + оо),
является его решением. Для t * 0 из соотношения (••) находим
203
dx = 2 dt. => x = 2arctgr + C.
\ + t2
Таким образом, получили
x = 2arctg/ + C,
< , t e (-00,0) U (0, +00).
y = ln(l + r),
1) Проверим, не имеет ли заданное уравнение еще решений
вида у = ах -h b. Подстановка функции у = ах + b в исходное урав-
нение дает
ax + b = in (I + «2).
Приравнивая коэффициенты при одинаковых степенях перемен-
ной х, получаем
а = 0,
• . => а = 0, b = 0.
b = In (1 + а2)
Значит, функция у = 0 , х = (-«•, + «>), является решением задан-
ного уравнения.
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. С этой целью рассматриваем систему
F(x,y,y') = 0,
Fy(xty,y') = 0
In (1 + </)2)-у = 0,
2/ д = 0
I + (У )2
/ = 0,
У = 0
=> у = 0 , х = (-о», + «>),— решение исходного уравнения, подо-
зрительное на особое.
Ответ. Все решения исходного уравнения содержатся в соот-
ношениях:
x = 2arctgr + C, .
, te (-00,0) U (0, + «х»), и у = 0,Х€ (~°°, + оо). 4
у = In (I + г),
Задача 23. Найти все решения уравнения (у' + I)3 = (у - у)2
(методом введения параметра).
Из вида заданного уравнения следует, что должно быть
/ £ -I и что
у'- у = ±(/ + 1)V2 => у = /т(/ + 1)у2.
204
Положим у'= t (с=> dy = tdx), /2-I. Тогда
у = Г?(/ + 1)3/2, />-1. (*)
=> dy = (I + -|(7 + |),/2 jdt. У нас dy = tdx. Поэтому
Гс& = рт|(Г + 1)|/2 dt.
\
Если t = 0, то из (♦) следует, что у = , хе (-оо, + °°). Подста-
новкой в заданное уравнение убеждаемся, что функции у = 1,
хе (-оо, + оо), и у = -I, хе (-оо, + оо), являются его решениями.
Для / * 0 из (••) находим
Таким образом, получили
/е [-1,0)11 (О, + ~).
y = t*(t + 1)3/2,
I) Проверим, не имеет ли заданное уравнение еще решений
вида у = ах + Ь. Подстановка фун кции у = ах + b в исходное урав-
нение дает
(д + 1)3 = (а-ах-Ь)2.
Приравнивая коэффициенты при одинаковых степенях перемен-
ной х, получаем
х2 | а2 = 0,
х | 2о(д“й) = 0, д = 0; Л = ±1.
х° | (b - а)2 = (а + I)3,
Значит, функции у - +1, хе (-<*>, + оо), и у = -I, хе (-оо, + оо),
являются решениями исходного уравнения.
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. С этой целью рассматриваем систему
F(x,y,y') = О,
^'(х,у,У) = 0
(/+1)3-(/-у)2 =0,
3(/+I)2-2(/-j) = 0
205
(/+ I)3 =(/-у)2,
/+1 у'-у
3 2
У = Зу + 2,
(Зу + З)3 =(2у+2)2
=> 27(^ + I)3 = 4(/ +1)2 => у = -I и у--— ,
Непосредственной подстановкой в исходное уравнение убеж-
даемся, что у = -I, хе (-«, + оо), является решением, а у = - — ,
хе (-<», + °°), не является решением заданного уравнения. Реше-
ние у = -I, хе (-«о, + оо), подозрительно на особое. 4
Отпет. Все решения заданного уравнения содержатся в соот-
ношениях
х = In |/| + 3>Jt +1 т - In
te |-l,0) U (0, + оо);
у = /?(/ + 1)у2,
у = -I, хе (-оо, 4- оо);у = |,Х€ (-оо, 4- оо).
Задача 24. Найти все решения уравнения у = (у - 1)е* (мето-
дом введения параметра).
Положим у' = t (<=> dy = tdx). Тогда
j =('-!)*'• С)
=> dy = te’dt. У нас dy = tdx. Поэтому
tdx = te’dt. (**)
Если / = 0, то из (*) следует, что у = -I. Подстановкой в заданное
уравнение убеждаемся, что функция у = -1 , хе (-<», +®о), явля-
ется его решением. Для г * 0 из (*•) находим dx = e’dt =>
х = е‘ 4- С. Таким образом, получили
г — е1 4- С
’ t е (-оо,0) U (О, 4-оо).
[у = (/-!)<
I) Проверим, не имеет ли заданное уравнение еше решений
вида у = ах + b. Подстановка функции у = ах 4- b в заданное урав-
нение дает
206
ax + b = (a- l)e“.
Приравнивая коэффициенты при одинаковых степенях перемен-
ной х, находим
х | о = 0
х° | 6 = (о-1)еа
=> д = 0,6 = -|.
Функция у = -1, хе (-«>, +«>), является решением исходного
уравнения.
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. С этой целью рассматриваем систему
F(x,y,y') = 0.
Гу(х,^,/) = 0
(/- 1)ех -у = О, J/ = 0,
у'еу =0 V = -l
=> функция у = -I, хе (-«о, + оо), является решением исходного
уравнения, подозрительным на особое.
Ответ. Все решения заданного уравнения содержатся в соот-
ношениях
х = в' + С*
re(-~,O)U(O, +оо), и у = -1,
у = (/-!)?',
хе (—°°, + оо).
Задача 25. Найти все решения уравнения (у')4 - (у')2 = У2
(методом введения параметра).
Положим у' = t (dy = tdx). Тогда у2 = /4 - г =>
у2 = r(t2 - I). Ясно, что должно быть |/| > I и / = 0, т. е.
Ге (-оо, - I] (J (I, + оо) и t = 0. Итак, имеем
у = ±ty/t2 -1. (*)
Для / е (-о®, - I) U (1, + °°):
dy = tdx. Поэтому
dy = ±
dt. У нас
tdx = ± V/2
Замечаем, что если t = 0, то из (♦) следует у = 0. Подстановкой в
заданное уравнение убеждаемся, что функция у = 0,
207
x g (-«>, + «>), является его решением. Для г е (-«, -1) U (I, + «)
из (•*) находим
(Jt2 - 1 + V/2 - I - arctg yji2 -1 j + C.
Таким образом, получили
1) Проверим, не имеет ли заданное уравнение еще решения
вила у = ах + Ь. Подстановка функции у = ax + Ь в исходное урав-
н ' дает
в4 - в2 = с2х3 + labx + b2.
Приравниваем коэффициенты при одинаковых степенях пере-
менной х
х2 | а2 = О,
х | 2а b = 0, =>л = 0, Л = 0.
х° I />2 =<?(£?-!)
Значит, функция у=0, хе(-~, +«0, является решением ис-
ходного уравнения.
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. С этой целью рассматриваем систему
F(x,y,/) = 0,
^у(х,у,у') = 0
(Я4+(/)2-/=0,^
4(У)3-2/ = 0
у2 =— (невозможно).
4
Функция _у = 0, хе(-~э,+оо), является решением заданного
уравнения, подозрительным на особое.
208
Ответ. Все решения заданного уравнения содержатся в соот-
ношениях
х = ± (2^t2 - I - arctg - 11 + С,
' ' t € (-°°, - I) U (I, + о»).
у = ±/V/2 -1,
И у = О, X С (-«>, + Од) . 4
Задача 26. Найти все решения уравнения {у')2 -(/)3 = у2
(методом введения параметра).
Положим / = / (о dy = tdx). Тогда у2 = /2 -/3 = /2(1 -г).
Ясно, что должно быть t < I, т. е. t е (-оо, I] =>
y = ±fJTl, (*)
Ге (-оо, 1], => для Ге (— оо, 1):
dy = ±
У нас dy = tdx. Поэтому
tdx = ± I Vl -/ -
Если t = 0 или t = 1, то из (*) следует у = 0. Подстановкой в заданное
уравнение убеждаемся, что функция у = 0 , х е (-оо, + оо), является
решением этого уравнения. Для / е (-оо, 0) U (О, I) находим из (**)
Таким образом, получили
Г е (-оо, O)U(O.I).
209
I) Проверим, не имеет ли заданное уравнение еще решения
вила у = ах + b. Подстановка функции у = ах + Ь в заданное урав-
нение дает
а2 - а* - а2х2 + 2abx + Ь2.
Приравниваем коэффициенты при одинаковых степенях пере-
менной X.
х2 | а2 = О,
х | 2аЬ = 0, => а = 0, Л = 0.
| Ь2=а2-в3
Значит, функция у = 0 , хе (-оо, + «>), является решением исход-
ного уравнения.
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. С этой целью рассмотрим систему
Г(х, у,у') = 0, (у')2 - (у')3 - у2 = 0,
У» /) = 0 2/ - 3( у')2 = 0
у' = 0,
и
у = 0
Подстановкой в исходное уравнение убеждаемся, что функции
2
y = ±—z=, хе(-~, + ~), не являются решениями, а функция
Зл/3
у = 0, хе(-оо, + оо), является решением заданного уравнения
(решение у = 0, х е (-оо, + оо) подозрительно на особое).
Ответ. Все решения заданного уравнения содержатся в соот-
ношениях
re(-oo,0)U(0,l),
и у = 0, х е (-оо, + оо).
Задача 27. Найти все решения уравнения (у')4 = 2уу' + у2 (ме-
тодом введения параметра).
Имеем у2 + 2уу'- (у*)4 = 0 => у = -у' ± у/(у')2 +(у')4 . Поло-
жим y' = t (<=э dy = tdx). Тогда
210
У = -I ± l>J\ + Г , / € (—°°, + 00) .
. У нас dy = tdx. А тогда для t * О
(ft
Таким образом, получили
х = -1пИ± 2^1 + /2 + -ln —- +С,
2 VJ77+1 ге (-«,0) U (0, + оо).
у = -/ ± t>j\ + /2,
При t = 0 получаем из (*): у = 0 , хе (-«>, + «»). Подстановкой в
исходное уравнение функции у=0, хе(-<», + <»), убеждаемся,
что эта функция является решением заданного уравнения.
I) Проверим, не имеет ли заданное уравнение еше решений
вида у = ах + b. Подстановка функции у = ах +• b в исходное урав-
нение дает
а4 = 2а2 х +2 ab + а2х2 + 2abx + Ь2.
Приравниваем коэффициенты при одинаковых степенях пере-
менной х.
х2 | а2 = О,
х | 2а(а + Ь) = 0, => а = 0, Ь = 0.
х° | а4 = Ь(2а + Ь)
Значит, функция j = 0, хе (-«о, +©о), является решением ис-
ходного уравнения.
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. С этой целью рассмотрим систему
211
F(x.y.y') =0,
Fy(x,y,y') = О
/ + 2у/-(/)4 =0,
2у-4(уУ=0
V 2 J
=> исключая у, находим у = 0 и \У = ~рд (невозможно).
Значит, функция у = 0 , хе (-=», + °°), является решением задан-
ного уравнения, подозрительным на особое.
Ответ. Все решения заданного уравнения содержатся в соот-
ношениях
г е (-<*>, 0) U (0, + ©о).
Задача 28. Найти все решения уравнения: (/)2 - 2ху' = х2 -4у
(методом введения параметра).
№ ху' (j’z)2
Имеем у = — + — - — . Положим у = t («=> dy = tdx).
Тогда
X2 X/ t2
y = -r + V-T- ()
4 2 4
У нас dy = tdx. Поэтому
tdx = —dx + -dx + — dt--dt => f— --]dx + ( — - \dt = 0 =>
2 2 2 2 l22J l22J
=> (x - t)(dx + dt) = 0 => x -1 = 0 и d(x + /)=0=>x = r и x + t = C
212
I) Проверим, не имеет ли заданное уравнение решений вида
у = ах + Ь. Подстановка функции у = ах + b в исходное уравнение
дает
а2 - 2ах - х2 - 4(дл + Ь) (невозможно).
Значит, заданное уравнение не имеет решений вида у =ах + Ь.
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. С этой целью рассмотрим систему
F(x,y,y') = 0,
/у(х,У,/) = 0
2 ' / /ч2
* t ху (у)
4 2 4 ’
Исключая из этой системы у , находим у = Значит, функция
хе (-«о, + °°), является решением заданного уравнения,
подозрительным на особое.
Ответ. Все решения заданного уравнения содержатся в соот-
ношениях:
х* | 7 X2
у = —— +Сх —С ,хе (-оо, + <х>), и у = —,хе (-оо, + «О. 4
2 4 2
Задача 29. Найти все решения уравнения 5у + (/)2 = х(х + у')
(методом введения параметра).
Имеем у = + У) “ (У)2 ] • Положим У = / (<=> dy = tdx).
Тогда
у = |[л(л + Г)-/2]. (♦)
У нас dy = tdx. Поэтому будем иметь
tdx = ^[(x + t)dx + x(dx + dt)-2tdt] =>
=> (2/ - x)dt + (4r - 2x)dx = 0 => (2/ - x)(dt + 2dx) = 0 =>
=> It - x = 0 и d(t + 2л) = 0 => x = 2t и 2x +1 = C.
213
I) Проверим, не имеет ли заданное уравнение решений вила
у = ах + Ь. Подстановка функции у = ах + Ь в исходное уравне-
ние дает
5(ах + Ь) + а2 = х(х + а) (невозможно).
Значит, заданное уравнение не имеет решений вида у -ах + Ь.
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое? С этой целью рассмотрим систему
F(x, у, /) = 0, 5у + (у)2 = х(х + /),
^/(*,ЛУ) = О |2/ = х.
х2
Исключая из этой системы у , находим у =-—. Значит, функция
4
х2
, хе(-«, + оо), является решением заданного уравнения,
4
подозрительным на особое.
Ответ. Все решения заданного уравнения содержатся в соот-
ношениях
, С2 х2
У--Х 4-Сх-— ,Х€ (-00, +«), и у =-----,Х€ (-оо, + «) . J
5 4
Задача 30. Найти все решения уравнения х2(у')2 = хуу +-1
(методом введения параметра).
Из заданного уравнения видно, что х * О и / # 0. А тогда
*2(/)2-1
ху'
x2t2 - I
Положим у = t (<=> dy = tdx), t *0. Тогда >’ =--- =>
xt
^y = Xt~li (#)
214
У нас dy = tdx. Поэтому будем иметь
... х dt + tdx ( I А , I j л
tdx - tdx + xdt +-г-3— => x + —=- err + —5- dx = 0 =>
x2t2 ( xr J Xl
x2t2 +1 dx
+ ldt + — = O
t x
(**)
Положим —- = и (u(t) — новая неизвестная функция)
х2
х' л
=> - 2—'т = ut. Относительно новой неизвестной функции уравне-
X
ние (**) станет таким: -l— + - = -t => u'--u = 2t. Полученное
2 t t
уравнение является линейным. Для него интегрирующим множи-
телем будет, например, функция Ц = — • После умножения обеих
частей последнего уравнения на ц будем иметь
и, 2 2
—------и — —
/2 /3 I
и
Т2
/2
Возвращаясь к прежним переменным, получим
—7—г = 1П /2 + С => X2 = -ту---=-.
х2/2 t2 (С + In t2)
Таким образом, получили
I ) Проверим, не имеет ли заданное уравнение решений вида
у = дх + Л. Подстановка функции у-ах+Ь в исходное уравне-
ние дает
х2а2 = ах(ах + b) = I.
215
x I ab = 0,
x° | 1=0 (невозможно).
Значит, исходное уравнение не имеет решений вида у = ах + b.
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. С этой целью рассмотрим систему
F(x, у, У) = 0, х2(у')2 = хуу' + I,
’/;.(х,у,У) = 0 |2х2/«лу.
Исключая из этой системы У, получаем -— = -1 (невозможно).
4
Значит, заданное уравнение не имеет решений, подозрительных на
особое.
Ответ. Все решения заданного уравнения содержатся в соот-
ношении
t с (-°°, 0) U (0, + оо). 4
Задача 31. Найти все решения уравнения (У)’ + у1 = хуу' (ме-
толом введения параметра).
Из заданного уравнения видно непосредственно, что функ-
ция у = 0, хе (—о°, + °о), является его решением. (Заметим, что
у = const#0 не является решением исходного уравнения.) Из
заданного уравнения имеем для у * 0:
Положим У = г (<=> dy -tdx). Будем иметь для t * 0
У нас dy = tdx. Следовательно,
. f 2г , /2 , I , у , dy 2 у3
dy = t — dt—rdy + -dy-4rdt =>-7-—У---г
I у у2 t t2 I dtt t*
216
(это — уравнение Бернулли)
=>4--А=--т- <**>
у3 t у1 2 t*
Положим Д = и (u(t) — новая неизвестная функция). Относи-
У
тельно новой неизвестной функции уравнение (♦♦) будет таким:
, 4 2
ui + ~ и - т
t t4
(это — линейное уравнение). Для него интегрирующим множите-
лем является, например, функция ц = /4 . После умножения обеих
частей последнего уравнения на Ц = /4 получим
<г4 + 4/3м = 2 => (wr4X = 2 => ui4 = 2/ч-С.
1 /4
У нас и = —. Поэтому будем иметь у2 =-----. Таким образом,
у2 2t + C
получили
X = — + —
у t t € (-°°, 0) U (0, + оо).
1) Проверим, не имеет ли заданное уравнение еще решений
вида у = ах 4- Ь. Подстановка функции у = ах + b в исходное урав-
нение дает
а3 + (ах + Ь)2 = ах(ах + Ь).
Приравниваем коэффициенты при одинаковых степенях перемен-
ной х
х2 | а2 -а2,
х | lab = ab, => а = 0, Ь = 0.
х° | о3 + Ь2 = 0
Значит, функция у = 0 , хе (-°°, + «>), является решением задан-
ного уравнения (это было замечено и раньше).
217
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. С этой целью рассмотрим систему
F(xt у, у') = 0, (у')3 + у2 = хуу\
^(х,У,у') = 0 |3(У)2 = ху.
Исключая из этой системы у', находим у = 0 и у = —х3. Непос-
27
редственной подстановкой функций у = 0, хе (-»,+»),
4 з
и у = — х , хе (-«о, + оо), в заданное уравнение убеждаемся, что
у = 0 , Х€ (-
\ А 5
), является решением, а функция у = —х ,
хе (-оо, + о*) , не является решением заданного уравнения. Реше-
ние у = 0, хе (-«, + «>),— подозрительное на особое решение
исходного уравнения.
Ответ. Все решения заданного уравнения содержатся в соот-
ношениях
Г2 у
х = — +—,
* У t t е (-оо, 0) U (0, + оо), и у = 0 , хе (-оо, + оо).
>2(2/ + С) = /\
Задача 32. Найти все решения уравнения 2ху' - у = у' In уу'
(методом введения параметра).
Из заданного уравнения следует, что должно быть уу' >0.
— > г. у In уу' „ ,
Так как у *0, то находим х = -^- +—— . Положим у =/
2у 2
(<=> dy = tdx ), t * 0. Тогда
(должно быть yt > 0). У нас dy = tdx. Поэтому
. I , у dt I dy I dt
dy = t —</y-^-—+ - — +
2t 212 2 у 2 r
| I - — |</y = (1 - - \dt =>
( у) к U
218
=> -—-dyy-—-dt = 0 => (y-t) —+ —]=0=э
У t у t
Заметим, что решение а) представимо в виде у = ±—т=.
de
I) Проверим, не имеет ли заданное уравнение решений вила
у = ах + b. Подстановка функции у = ах + Ь в исходное уравне-
ние дает
2ах - (ах + b) = a In [(ax + />)а]
(такое тождество невозможно). Значит, заданное уравнение реше-
ний вида у = ах + Ь не имеет.
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. С этой целью рассмотрим систему
F(x,y,y') = 0, 12х/-у = y'lnyy',
F'(x, у, у') = 0 2х = In уу' + I.
Исключая из этой системы у', находим у2 =ehl=5 у = ±-=
ve
X с ( —°о, + оо). Подстановкой в исходное уравнение убеждаемся,
ех
что функции у = ±-=, хе С-»», +«>), являются решениями за-
de
данного уравнения. Эти решения — подозрительные на особые
решения.
Ответ. Все решения заданного уравнения содержатся в соот-
з ех
ношениях у - 2cx-clnc; у = ±-т-. хе (-«>; +°°).
de
ху
Задача 33. Найти все решения уравнения у' = е у (методом
введения параметра).
219
Из заданного уравнения следует, что должно быть у*О,
а />0. Прологарифмировав обе части исходного уравнения,
находим
^ = 1пУ=>х = Л1!%.
У У
Положим у' = t (с=> dy = tdx ), t > 0. Тогда
v In г
х = ^~ . '€ (0, +«*>). (*)
У нас dy = tdx. Поэтому
, 7lnr , In г . у . )
dy = г — dy - у -г- dt + Ardt =>
I ' ' ' )
=> (I - InOt/y- —(I -1п/)Л = 0 => (I -Inoftfy-ydt j=0 =>
у
Таким образом, получили у = ех и х = С1п^.
I) Проверим, не имеет ли заданное уравнение решений вида
у = ах + b. Подстановка функции у = ах + Ь в исходное уравне-
ние дает
ах
а = е"** => —-— = In а => ах = (ах + b) In а.
ах+ Ь
Приравниваем коэффициенты при одинаковых степенях г
х° | д1па = 0
Значит, у = ex , хе (-«>, 0) U (0, + <»),— решение исходного урав-
нения (х * 0, так как должно быть у * 0).
220
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. С этой целью рассмотрим систему
Г(х,у,/) = 0,
F'Ax, у,/) = 0
Исключая из этой системы /, находим — = е => У = ех . Значит,
х
решение У = ех , хе (-оо, 0) U (0, + оо). заданного уравнения подо-
зрительно на особое.
Ответ. Все решения заданного уравнения содержатся в фор-
мулах х = С In (у * 0); у = ех , хе (-«>, 0) U (0, + ~) «
Задана 34. Найти все решения уравнения у = ху'-х2(У)3 (ме-
тодом введения параметра).
Положим / = /(<=> dy = tdx). Тогда
j = xr-x2r3. (*)
У нас dy = tdx. Поэтому будем иметь
tdx = tdx + xdt - IxV'dx - 3x1t1dt =>
=> x(l - 3xr)dt = 2xtydx => для x * 0 и / * 0: Д Д x = Дг .
dt It 2/3
Это линейное уравнение. Для него ц = /у2 является интегрирую-
щим множителем. Умножим обе части последнего уравнения на
ц = /3/2. Получаем
л,-/*5+2л=1г-»1 «(л*2); =1/^2 =»
* 2 2 ' 2
=>xz*! = -f-v2+c=>x=a-»2-l.
t2
Таким образом, получили
X/2=CV7-1,
' , , '€ (0, + оо).
у = xt-x t\
221
1) Проверим, не имеет ли заданное уравнение решений вида
у = ах + b. Подстановка функции у = ах + Ь в заданное уравнение
дает
ах + Ь = ах - х‘а\
Приравниваем коэффициенты при одинаковых степенях х
х2 | -а3 = О,
х | а = а, => а = 0, b = 0.
х° | b = О
Функция у = 0, х е (-оо, ч- о»), является решением исходного
уравнения.
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. С этой целью рассмотрим систему
F(x,y,/) = 0,
Гу(х,у,у') =0
у = ху'-х2(у')\
0 = х-3х2(/)2.
2 г—
Исключая из этой системы у', получим у = ±-^=ух , хе (0, + <~).
2 г-
Подстановкой в исходное уравнение убеждаемся, что у = ух
не есть решения заданного уравнения.
Ответ. Все решения заданною уравнения содержатся в соот-
ношениях:
хг = С Ji -1,
t е (0, + <»); у = 0, х е (-°°, + °°).
у = xt - х‘г,
Задана 35. Найти все решения уравнения у = 2ху' + у2(у')'
(методом введения параметра).
Из заданного уравнения видно непосредственно, что функ-
ция у = 0, хе (-*>, + «’}, является его решением, а у = const * 0
решением исходного уравнения не является.
Станем рассматривать заданное уравнение для у * 0 и у’ ? 0.
Имеем для у’ * 0: х =
У У2(/)2
2/ 2
. Положим у’ = t (<=> dy = tdx).
Тогда для / * 0:
222
2.
2t 2
У нас dy = tdx. Следовательно,
dy = / dy - dt - ytI) 2 dy - ty2dt j => ( 1 + yt3 j/y+( + yt* U dt = 0 о
(I з Y dy dt \
I — + yt — + — = 0
I2 b >)
=> 32xJ = -27/, xe <-~.0>
I) Проверим, не имеет ли заданное уравнение еще решения
вида у = ах + b. Подстановка фун кции у = ах + b в исходное урав-
нение лает
ах + Ь = 2ха + (ах + Ь}2а*.
Приравнивая коэффициенты при одинаковых степенях л, полу-
чим а = 0, и b = 0. Следовательно, функция у = 0 , хе (-«>, + «»),
является решением заданного уравнения (это было замечено и
раньше).
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. С этой целью рассмотрим систему
F(x,y,y') = О,
F'(x,y,y') = 0,
2ху' + у2 (у')3 - У = О,
2х + 3>’2(у')2 = 0.
Исключая из этой системы у, получим 27у4 = -З2х3, хе (-«>, 0).
Выше (см. пункт а)) было показано, что функция, определя-
емая этим соотношением, является решением заданного уравне-
ния. Выясним, не будет ли оно особым решением.
223
У нас (см. пункт р)) общее решение заданного уравнения
определяется соотношением
v2 г2
+ [Г(х,ЛС) = 0]
Составим систему уравнений для нахождения дискриминант-
ной кривой:
У С _
F(x,y,C) = 0 Х-2С+Т = 0 х = -^С2
Ге(х,лО = 0 2=2С, (•)
2С2
(*> — параметрические уравнения дискриминантной кривой. Если
в системе (*) исключить параметр “С\ то получим
32х3=-27/. (••)
Следовательно, исследуемое решение исходного уравнения яв-
ляется дискриминантной кривой семейства интегральных кривых
v2 С2
Х-2С+Т = ° [Г(Х'У’С) = °1
В точках кривой (*) имеем: (7\)2 + (/р2 = I + ®
Кроме того F'i = 2 +1 = 3 * 0.
Вывод. Решение, определяемое уравнением (**) является оги-
бающей семейства интегральных кривых исходного уравнения.
Значит оно является особым решением этого уравнения.
Задача 36. Найти все решения уравнения у(у-2х/)5 = (/)2
(методом введения параметра).
Из заданного уравнения видно непосредственно, что функция
у = 0, хе (-«>, + «>) является его решением и что у a const * 0 не
является решением этого уравнения (=> у'^0 для у * 0).
. (v*)2 » (У)^
Имеем (у-2х/)=^—, для у*0 => У~2ху = • ~- =*
У У'
у | |
х = — - —-— . Положим у = г (<_> dy = tdx , t * 0). Тогда
2 У 2 (X)’)1
X=Z.A_L_ (*)
2/ 2(у/)'/з-
224
У нас dy = tdx. Поэтому
dy = t ^-dy--^dt +1 (yt) 4/3 (ydt + tdy)
=> в областях:
(Д) =
0 < t < +oo,
О < у < +oo;
(D2) =
—°° < t < 0,
О < у < +«>;
oo < t < 0,
о» < у < 0;
(Л4) =
О < t <
-00 < у < О
в (DJ,* = I,4, —+ —= 0 => j
t У
Получили, таким образом,
>11
2/ 2 07)1/3 => у2 = 2Сх + Суз.
I) Проверим, не имеет ли заданное уравнение еще решений
вида у = ах + b. Подстановка функции у - ах + b в заданное урав-
нение дает
(ах + Ь)(ах + Ь- 2ах)' = а2 <=> (ах + b)(b- ах)' = а~ => а = О, b = 0.
Функция у = 0, хе (-<*,+«>), является решением заданного
уравнения,
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. С этой целью рассмотрим систему
F(x, у,у') = 0, у(у - 2х/)3 = (У)2,
F;.(x,y,y') = 0 \-6ху(у-2хуг)2 =2у'
/ т чЗ / '\2 >(> - 2х/)3 = (У)2,
у(у-2ху) = (>),
>'( у - 2ху') = -Зхуу' У = - -.
225
Исключая из этой системы у', находим у = 0 и 21 х2 у2 = I.
Непосредственной подстановкой в исходное уравнение убежда-
емся, что функция у = 0, хе (-<», + <~), и функции, определяе-
мые соотношением 27x2j2 = I, являются решениями заданного
уравнения. Они являются подозрительными на особые решения.
Ответ. Все решения заданного уравнения содержатся в соот-
ношениях:
у2 - 1Сх + Су\у = 0,хе (-«, + оо); 21 х2 у2 = 1. 4
§4. Огибающая и дискриминантная кривая
однонара метрического семейства плоских кривых
Г. Некоторые предварительные сведения. Плоские кривые бу-
дем задавать либо параметрическими уравнениями
х = ф(а),
Т = ф(а)
(а — параметр), либо уравнением вида
F(x,j) = 0. (2)
Введем понятия обыкновенной и особой точек кривой.
а) Пусть кривая (L) определяется параметрическими уравне-
ниями (1). Пусть функции х = ф(а), у = у(о) имеют в точке а0
непрерывные производные <р'(а), ф'(«) и пусть <р(а0) = х0,
ф(а0) = у0. (Отметим, что точка М0(х^,у0) е (L).) Точку
Л/(хо,у’о) будем называть обыкновенной точкой кривой (/.), если
(ф'(а0))2 +(/(а0))2 *0 (3)
(т. е. если ф'(а0) и ф'(а0) не обращаются в нуль одновременно).
Если же
(ф'(ао))2+(ф'(ай))2 =0, (4)
то точку Л/о(х0,,Уо) будем называть особой точкой (L).
6) Пусть кривая (L) определяется уравнением (2> и точка
Л/о(*(ьУо)е (М- Пусть функция F(x,y) дифференцируема в не-
которой окрестности точки Мц(х0,у0) и имеет в точке Л/0(Хо.у0)
226
непрерывные частные производные ГД л, у), F'(x,y). Точку
Л/0(х0,у0) будем называть обыкновенной точкой кривой (£), если
в этой точке выполняется соотношение
+(^(ль,^о)) *0 (5)
(т. е.если Г'(х0,у0) и ^•(-Хо.З’о) не обращаются в нуль одновремен-
но). Если же
(^x(Jtb,>b))2 +(^(-*Ь,Л))2 =0.
то точку Л/0(хп,у0) будем называть особой точкой кривой (L).
Убедимся, что если точка Л/о кривой (L) является обыкно-
венной, то в некоторой окрестности этой точки кривая (L) пред-
ставляет собой либо график некоторой дифференцируемой функ-
ции у = /(х), либо график некоторой дифференцируемой
функции x = g(y).
Пусть кривая (£) определяется параметрическими уравне-
ниями (I) и, кроме того, выполнено условие (3). Из условия (3)
следует, что хотя бы одно из двух чисел <р'(ос0), цг'(ао) отлично от
нуля. Пусть для определенности <p'(ao)?tO. Но тогда, в силу
непрерывности функции <р'(а) в точке «о, cp'(a) # 0 в некоторой
окрестности точки а() (см. теорему о стабильности знака). Следо-
вательно, в упомянутой окрестности точки а0 функция х = <р(а)
является дифференцируемой и строго монотонной. При этих
условиях существует дифференцируемая монотонная обратная
функция a=w(x). Подставляя эту функцию в выражение
у = ц/(а), мы убеждаемся, что кривая (L) в некоторой окрестнос-
ти точки Л/(>(Хо,у0) представляет собой график дифференцируе-
мой функции у = /(х) ( = у(со(х))).
Справедливость сформулированного утверждения для случая,
когда кривая (£) определяется уравнением (2), вытекает из того,
что в окрестности обыкновенной точки А/0(х0,у0) выполнены
условия теоремы об однозначной разрешимости уравнения
F(x,y)-0 (либо относительно у, если ГДЛ/о)*0, либо отно-
227
сительно х, если F'(Mn) * 0; см. теорию неявных функций). По-
этому прилегающий к точке Л/о участок кривой (L) представляет
собой график дифференцируемой функции у = /(х) или функ-
ции X = g(y). <4
Замечание /. ► В геометрии точку Мо кривой (Л) называют
обыкновенной, если в некоторой окрестности этой точки кривая
(L) представляет собой график некоторой дифференцируемой
функции, и особой, если в любой окрестности этой точки кривая
(L) не может быть представлена в виде графика дифференцируе-
мой функции. Мы видели, что точка Ма кривой (Л), являющаяся
обыкновенной согласно нашему определению, будет обыкновен-
ной с геометрической точки зрения.
Можно привести примеры, когда точка Л/о кривой (£), явля-
ющаяся особой по нашему определению, будет обыкновенной с
геометрической точки зрения. Таким образом, наше определение
обыкновенной точки является более узким, чем геомегрическое,
но более удобным для приложений.
Введем теперь понятие касания кривых (Ц) и (L,) в их обшей
точке Мо. Будем говорить, что кривые (Ц) и (L,) касаются в их
общей точке Мо, если обе эти кривые имеют в точке Л/о
касательные и эти касательные совпадают.
Пусть кривая (1^) определяется параметрическими уравнени-
ями (1), а кривая (Ц) — уравнением (2), и A/o(-*b->’o) ~ общая
точка этих кривых (при этом координаты х0 и _у0 отвечают
значению а = а0 параметра а). Будем считать, что точка М()
является обыкновенной точкой кривых (£,) и (£,) и эти кривые
касаются в точке Мо. Тогда эти кривые представляют собой в
окрестности точки Л/о графики дифференцируемых функций.
Ради определенности будем считать, что (1^) и (Z^) являются
графиками функций у = /((х) и у = f,(x) соответственно. Так как
по условию кривые и (L,) касаются в точке Л/()(х0,у0), то
угловые коэффициенты касательных в точке Л/() к (рафикам
функций /|(х) и /5(х) равны, т.е.
/|Л(-*ь)= (7)
Используя формулы дифференцирования функций, заданных па-
раметрически, и формулы дифференцирования функций, задан-
ных неявно, получим
У(«о)
/\(*о,Уо)
^(Хо.Уо)
(8)
-
228
Формулы (8) позволяют придать равенству (7) следующий вид:
у'(«о) _ fx'tWo) (9)
<р'(а0) F;(xb,j0)
или
/\(хо^о)ф'(ао)+ ^'(^о,Уо)У'(а0) = 0. (10)
Соотношение (10) мы будем в дальнейшем называть условием
касания в точке Л/() кривых (Z^) и (Aj), заданных соответствен-
но уравнениями (I) и (2). Опуская аргументы функций и исполь-
_ ,, . dx f. . dy
зуя обозначения = а = ’ мы за,,И1Пем условие
касания в следующей форме:
= di)
da у da
Замечание 2. Если в общей точке Л/о кривых (£0 и (1^),
заданных соответственно уравнениями (I) и (2), выполнено ус-
ловие касания (10) и если при этом точка Л/о является обыкно-
венной точкой кривых (Ц) и (1^), то кривые (Ц) и (1^)
касаются в точке Л/() . В самом деле, из соотношений (3) и (5) и из
условия (10) вытекает либо соотношение (9), либо условие
<р'(а0) Ру(хо.Уо) ..
, = , т. е. равенство угловых коэффициентов каса-
у(а0) Рх(хй,у0)
тельных в общей точке Л/о кривых (Ц) и (Li). Это и означает,
что кривые (Ц) и (Li) касаются в точке Мп. Заметим, что
условие касания (10) выполняется также и в случае, когда точка
Л/о является особой точкой по крайней мере одной из кривых
(4|) и (Ln),
Итак, условие касания (10) выполняется как в случае, когда
кривые (£|) и (Ц) касаются в точке Л/о, так и в случае, когда
Л/(| является особой точкой по крайней мере одной из этих
кривых.
2’. Однонараметрическме семейства плоских кривых. Характе-
ристические точки кривых семейства.
Определение. Пусть уравнение
Г(х,у,а) = 0 (12)
для каждого значения а из промежутка (а,Ь) определяет на
плоскости л\ у кривую, причем различным значениям а соответ-
229
Рис. 2.16. К примеру 1
ствуют различные кривые. Тогда это множество кривых называет-
ся однопараметрическим семейством кривых, а параметр а назы-
вается параметром этого семейства.
Рассмотрим примеры однопараметрических семейств плоских
кривых.
Пример 1. Уравнение у-(х-а)2=0 определяет семейство
парабол, получаемых сдвигом по оси Ох параболы у-х1 =0
(рис. 2.16).
Пример 2. Уравнение (у-а)2 -(х-а)3 =0 определяет семей-
ство полукубических парабол, полученных параллельным сдви-
гом вдоль биссектрисы первого координатного угла полукубичес-
кой параболы у2 =х3 (рис. 2.17).
Пусть функция F{x,y,a) является дифференцируемой функ-
цией в области ее задания. В этом случае можно ввести понятие
характеристической точки кривой семейства, определяемой соот-
ношением (12). Точка М(х,у) называется характеристической
точкой кривой семейства (12), отвечающей данному значению а
параметра семейства, если координаты этой точки удовлетворяют
системе уравнений
Г(х,у,а) = О,
F'(x,y,a) = 0.
(13)
Рассмотрим геометрическую интерпретацию характеристической
точки кривой семейства (12). Для простоты ограничимся случаем,
когда любые две кривые семейства пересекаются. (Заметим, что
существуют такие семейства кривых, любые две кривые которых
не пересекаются. Примером такого семейства может служить
230
семейство кубических парабол, определяемых уравнением
у-(х-а)3 =0.)
Пусть и (/^+Да) — две кривые семейства (12), отвечаю-
щие значениям параметра а и а + Ла (рис. 2.18). Координаты
точки N их пересечения удовлетворяют следующей системе урав-
нений:
Г(х,у,а) = 0,
F(x, >’,« +Ла) = 0
или равносильной системе
Рис. 2.18
231
F(x,y,a) = O,
F(x,y,a +Да)- F(x,y,a) Q
Да
Если Да —» 0, то точка N, расположенная на кривой F(x,y,a) = 0 ,
стремится, вообще говоря, к некоторой точке М на этой кривой.
F(x, у,а + Да)- F(x,у,а)
Так как hm —— -------------------------= £.(x,y,a), то коорди-
Ла-Н) * “
Да
наты точки Л/удовлетворяют уравнениям (13), и поэтому точка М
является характеристической точкой кривой семейства.
Итак, характеристическая точка данной кривой — это та точ-
ка, которая служит пределом при Да-> 0 точек пересечения
данной кривой (4J и близкой к ней кривой (Д^да).
3°. Огибающая и дискриминантная кривые однопараметричес-
кого семейства плоских кривых. Пусть однопараметрическое се-
мейство плоских кривых определяется соотношением (12). Будем
считать, что функция Г(х,у,а) является дифференцируемой в
области ее задания.
Определение I. Огибающей однопарамстричсского семейства
кривых (12) называется кривая (Г), которая: 1)в каждой своей
точке касается только одной кривой семейства (12), 2) в разных
точках касается различных кривых этого семейства.
Определение 2. Дискриминантной кривой семейства кривых (12)
называется геометрическое место характеристических точек кри-
вых этого семейства, т. е. кривая, определяемая системой уравне-
ний '
F(x,y,a) =0,
Fa'(x,y,a) = 0.
Оказывается, что при некоторых условиях дискриминантная
кривая семейства кривых (12) является огибающей этого семей-
ства. Выясним эти условия, для чего докажем предварительно
следующую лемму.
Лемма. Пусть точка Л/0(х0, Jo) — характеристическая точка
семейства F(x,y,a) = 0, отвечающая значению параметра а0.
Пусть функции F(x,y,a), F('t(x,y,a) дифференцируемы в неко-
торой окрестности точки (х(),у0,а()) и частные производные этих
функций по х и у, т. е. F'(x,y,a), Г}'(х,у,а), /^(х,у,а),
Fuy(x,y,a), непрерывны в самой точке (Хо,у0,а0). Тогда, если в
точке (х0,у0,аа) якобиан
f;
к
Fay
отличен от нуля, то дискри-
232
минантная кривая, проходящая через точку Mq(Xq,)>0), в некото-
рой окрестности этой точки может быть задана параметрически-
ми уравнениями
х = ф(а), . . . . . .
где ф(а) и ф(а) — дифференцируе-
У = V(a),
мые функции в некоторой окрестности точки а0.
Так как точка Л/0(х0,у0> является характеристической точкой
кривой семейства (12), отвечающей значению параметра а0, то
F(xo,yo.ao) = O.
^a(-v0./o«ao) = 0.
А тогда, принимая еще во внимание условия леммы, видим, что у
нас выполнены все условия теоремы об однозначной разрешимо-
сти системы
F(x,y,a) = О,
v Л относительно х и у (см. теорию неяв-
fa(x,y,a) = О
ных функций). Следовательно, в некоторой окрестности точки
определены две функции
х = Ф(а),у = ц/(а), (14)
являющиеся единственным, непрерывным и дифференцируемым
решением системы
Г(х,у,а) = 0, 1х = ф(а),
Fa'(x,y,a) = 0. Так как кривая y = v(e) со-
стоит из характеристических точек семейства (12), то она является
дискриминантной кривой этого семейства, проходящей черезточ-
ку AfoOWo)- ◄
Отметим, что, в силу единственности решения системы.
F(x,y,a) = О,
F'(x г a)-0 Различные точки дискриминантной кривой, ко-
торая определяется параметрическими уравнениями (14)
(х = ф(а), у = ф(а)), являются характеристическими точками раз-
личных кривых семейства F(x,y,a) = 0 .
Укажем теперь дополнительные условия, при выполнении
которых дискриминантная кривая, проходящая через точку
,Уо), представляет собой огибающую в окрестности этой
точки.
233
Теорема. Пусть кроме условий, сформулированных в лемме,
выполняются еще следующие два условия:
1)в некоторой окрестности точки (х0,у0,а0) производные
Fy> fol Fay и F'a непрерывны;
2) в точке (лсо.Уо>ао) выполняются соотношения
(f/)2+(f;)2*o и f;ui #о.
Тогда дискриминантная кривая, проходящая через характеристи-
ческую точку Л/()(х0,у0), является в некоторой окрестности этой
точки огибающей семейства кривых F(x,y,a) = 0 .
Было показано (см. лемму), что некоторый участок дискри-
минантной кривой, проходящей через точку М0(х^,у0), может
быть представлен параметрическими уравнениями (14) (х = ф(а),
у = у(а)), которые представляют собой решение системы
< Подставим это решение в уравнения системы.
Fa'(x,y,a) = 0.
Получим тождества Л’(ф(а),ф(а),а) = 0 и Гц'(ф(а), y(a),a) = 0.
-х —у =х -у
Продифференцируем полученные тождества по а. Будем иметь
,, dx dy
я +
da da
dx dy
* ____ А /♦ _*
av da
а>\7а т =°‘
Так как Fa' =0, то первое соотношение из (15) примет вид
,, dx dy
•------ь г
* da > da
(15)
(*)
= 0.
Видим, что в каждой точке рассматриваемой дискриминантной
кривой выполняется условие касания (*) этой кривой и соответству-
ющей кривой семейства. Поэтому, в силу замечания 2 из п. Г, для
завершения доказательства теоремы достаточно установить, что каж-
дая характеристическая точка кривой семейства, расположенная в
некоторой окрестности точки Л/0(х0,у0), и каждая точка дискри-
минантной кривой в этой окрестности являются обыкновенными.
234
У нас по условию в точке (хо,у0,а0) выполняется соотноше-
ние (F')' + (F'Y * 0 , которое, в силу непрерывности частных
производных F' и F', будет выполнено и в некоторой окрестно-
сти точки (до,j’o.oto). Следовательно, в этой окрестности все
характеристические точки кривых семейства являются обыкно-
венными.
У нас по условию в точке (х0, Уо,о«): F'a * 0. Но тогда, в силу
непрерывности, F^ 0 и в некоторой окрестности точки
(xft,yrt,a()). А тогда из второго соотношения тождества (15) выте-
« dx dy
кает, что в указанной окрестности производные — и не
da da
обращаются одновременно в нуль. Таким образом, все точки
дискриминантной кривой в некоторой окрестности точки
являются обыкновенными. Из леммы, доказанной
выше, вытекает также, что различные точки дискриминантной
кривой являются характеристическими точками различных кри-
вых семейства. 4
Замечание 1. Рассуждения, приведенные при доказательстве
теоремы, показывают, что в случае, когда выполнены только усло-
вия леммы, в каждой точке дискриминантной кривой выполнено
условие касания этой кривой и кривой семейства. Ранее было
отмечено (см. замечание 2 пункта Г), что условие касания выпол-
няется и тогда, когда обшая точка двух кривых является особой
точкой по крайней мере одной из них. Отсюда вытекает, что
дискриминантная кривая может представлять собой геометриче-
ское место особых точек кривых семейства (если в каждой характе-
ристической точке имеет место равенство (F')2 +(F')2 = 0 ). Отме-
тим, что и сама дискриминантная кривая может иметь особые
. dx dy .
точки (если — и -у- равны нулю одновременно).
da da
Замечание 2. Из доказанной теоремы следует: если все кривые
семейства (12) и дискриминантная кривая этого семейства не
имеют особых точек, то указанная дискриминантная кривая яв-
ляется огибающей семейства кривых (12).
Рассмотрим примеры.
235
Пример 1. Найти дискриминантную кривую семейства
у-(х-а)2 =0.
Имеем F(x,y,a) = у-(х-а)2 ; F^(x,y,a) = 2(х -а). Таким
образом, система (13) имеет вид
F(x,y,a) = О,
Fa'(x,y,a) =0
y-(x-a)2 = 0.
2(х —a)=0
=> х = а; у = 0.
Видим, что характеристические точки имеют координаты
(а,0). Поэтому дискриминантная кривая задается параметриче-
скими уравнениями
х - сх.
j = 0
(дискриминантная кривая — ось Ох).
Имеем, далее, Fx'(x,y,a) =-2(х - a), F'(x,y, а) = I => в точках
дискриминантной кривой (F')2 + (F')2 =0 + 1 = I (*0). Кроме
того, Fa'a = -2 (* 0).
Вывод. Дискриминантная кривая данного семейства кривых,
т. е. ось Ох, является огибающей этого семейства (рис. 2.16). 4
Пример 2. Найти дискриминантную кривую семейства
(у-а)2 -(х-а)3 =0.
Имеем F(x,y,a) = (у-a)’-(х-а)3; F^(x,y,a) = -2(у-а) +
+ 3(х-а)2. Таким образом, система (13) имеет вид
4
F(x,y,a) = 0, (у-a)2 -(х- а)3 =0, х = а, Л-а + 9’
Fn'(x,y,a) = 0 |-2(у-а) + 3(х-а)2 =0 J = a 8
27’
Видим, что дискриминантная кривая представляет собой две
линии, определяемые параметрическими уравнениями:
а + -
х = а,
у = а и
236
(Это — соответственно прямые: у = х и у = х- — •) Имеем, да-
V “ (X
(F')2 + (F'}2 = 0 . Следовательно, эта
у = а у
ветвь дискриминантной кривой представляет собой геометричес-
кое место особых точек кривых заданного семейства. В точках пря-
4
х = <х + —,
9
лее, в точках прямой -
мой
>’ = « + —
27
— t
27
2
(* 0).Крометого,Гаа = --(# 0).
4
Вывод. Ветвь дискриминантной кривой ^ = х~27 является
огибающей заданного семейства кривых (рис. 2.17). 4
§5. Особое решение обыкновенного дифференциального
уравнения как огибающая семейства интегральных кривых
Вспомним, что решение у = <р(х), хе (а,Ь), дифференциаль-
ного уравнения
F(x>y.y') = 0 (I)
называется особым, если в каждой его точке нарушается свойство
единственности, т. е. если через каждую его точку (х0,у0), кроме
этою решения, проходит и другое решение уравнения (I), имею-
щее в точке (х0,у0) ту же касательную, что и решение >’ = ф(х) ,
но не совпадающее с ним в любой, даже сколь угодно малой
проколотой окрестности точки (х0,у0).
График особого решения называют особой интегральной кри-
вой уравнения (I).
Допустим, что общее решение уравнения (1) найдено в виде
Ф(х,у,С) = 0. (2)
Ясно, что (2) определяет однопараметрическое семейство интег-
ральных кривых уравнения (I) (С— параметр).
Справедливо утверждение: если семейство кривых Ф(х,у,С) =
= 0, являющихся интегральными кривыми уравнения (I), имеет
огибающую у = <р(х), то эта огибающая представляет собой осо-
бую интегральную кривую уравнения (1).
Всамом деле, в точках огибающей значения х,у,у‘ совпада-
ют со значениями х,у,у' для интегральной кривой, касающейся
237
огибающей в точке (х,у), и, следовательно, в каждой точке
огибающей значения х,у,/ удовлетворяют уравнению
F(x,y,yf) = 0,т. е. огибающая является интегральной кривой урав-
нения (I).
Далее, в каждой точке огибающей нарушена единственность,
так как через точки огибающей по одному направлению проходят
по крайней мере две интегральные кривые: сама огибающая и
касающаяся ее в рассматриваемой точке интегральная кривая
семейства (2). Следовательно, огибающая является особой интег-
ральной кривой.
Из §4 (пункт У) мы знаем, что если функция Ф(х,у,С)
непрерывно дифференцируема, то огибающая входит в состав
дискриминантной кривой, определяемой системой уравнений
Ф(х, у,С) = 0,
' ЭФ(х,>>,С)
ЭС
В лемме и теореме предыдущего пара!рафа указаны условия,
при выполнении которых некоторая ветвь дискриминантной кри-
вой будет заведомо огибающей.
Пример 1. Решить уравнение у = х + 2у' -(у')2. Выделить осо-
бые решения, если они существуют.
Положим у' = t (<=> dy = tdx). Тогда
у = х + 2/-Г2. (*)
У нас dy = tdx. Поэтому
tdx = dx + 2dt - 2tdt => (t - l)dx + 2(r - l)t/r = 0 =>
=> (f - V)(dx + 2dt) = 0 => / = 1 и x + 2/ = C.
Поэтому решениями исходного уравнения являются функции
у = х + 1, х с (-“о, + <х>) и
х = -2t + С,
у = х+ 2/-Г2.
(**)
1) Проверим, не имеет ли заданное уравнение еще решений
вила у = ах + b. Подстановка функции у = ах + b в заданное урав-
нение дает
2 х | а = I
х° | b = 2а - а2
=> а = I, b = I.
238
Функция у = х + I, хе (-«>, + «>), является решением заданного
уравнения (это решение уже было получено выше).
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. Для этого рассматриваем систему
f(x,y,/) = 0, 1у = х + 2/-(/)2,
Fy(x,y,/) = 0 |2-2/ = О.
Исключая из этой системы у', находим: у = х + I. Значит, функ-
ция у = х + I, хе (-«>, + оо), является решением заданного урав-
нения, подозрительным на особое.
Выясним, будет ли решение у = х + I , хе (-оо, + оо), особым
решением исходного уравнения. Общее решение заданного урав-
нения определяется соотношениями (**). Из первого уравнения
системы (**) находим t = —-—. Подставив это выражение для t
во второе уравнение системы (**), получаем
. (С-х)2 „ (С-х)1 п
у = х + (С - х) - --— => у - С + -----— = 0.
4 4
=Ф(х,у,С)
Составим систему уравнений для нахождения дискриминантной
кривой:
(С-х)2 Л
Ф(х,у,С)=О, У-С+------------=и, (х = С-2,
Ф'с(х,у,С) = 0 t t С -х 0 => J = C-1
Г 2
— параметрические уравнения дискриминантной линии.
С-х
=> у = х+1 — дискриминантная линия. Имеем Ф*. =------—;
Ф'г = I, => В точках прямой
х "" С* 2
x=c-i <ф:)2-<ф;)!=2 <*о>
Вывод. Прямая у = х + 1, хе (-<», + «>), является огибающей
семейства интегральных кривых заданного уравнения. Значит,
239
функция у=х+1, х е (-«о, +«), является особым решением
исходного уравнения. 4
Пример 2. Решить уравнение 8(у')3 - 12(у')I) 2 = 27(у-х). Выде-
лить особые решения, если они существуют.
Заданное уравнение решим относительно у:
>’ = -^(/)3 -^(У)2+х.
Положим у' = t (<=> dy = tdx). Тогда
(*)
У нас dy = tdx. Поэтому
О о о
tdx = -rdt --tdt + dx (t -1)(Л. = -/(/ -!)<?/=>
9 9 9
Поэтому решениями исходного уравнения являются функции
у = х- — .хе (-<», + оо), и
I) Проверим, не имеет ли заданное уравнение еше решения
вида у = ах + b. Подстановка функции у = ах + b в заданное урав-
нение дает
8аЛ -12а2 = 27(ах + b - х) =>
х | 0 = 27(а-1)
х° | 8а3 -12а2 = 27b
Функция у = х- —, хе (-оо, + о«>), является решением заданного
уравнения (это решение уже было получено выше).
2) Выясним, не имеет ли заданное уравнение решений, подо-
зрительных на особое. Для этого рассматриваем систему
240
F(x,y,/) = O,
/у(х,у,/) = О
8</)!-12(/Г =27(у-л),
24(/)2 - 24/ • 0.
Исключая из этой системы у', находим у = х и у = х-. Непос-
27
редственной подстановкой в исходное уравнение убеждаемся, что
функция у = х , хе (-«, + оо) э не является решением этого урав-
. 4
нения, а функция у = х- — , хе (—оо, + оо) , является решением,
причем функция у = х-^, +оо), является решением,
подозрительным на особое. Выясним, будет ли оно особым. Общее
решение заданного уравнения определяется системой уравнений
(**). Исключая из системы (**) параметр t, получаем
(х-С)у2 +С-у = 0 ^Ф(х?<у,С) = (х-С)3/2 + С->’).
Составим систему уравнений для нахождения дискриминантной
кривой:
Ф(х,у,С) = 0,
Фс(х,у,С) = 0
=> ’
(х-С)3/2+С-у = О,
-2<x-C)V2 + l = 0
— параметрические уравнения дискриминантной линии
мой
’ (<t>;)!+(<t>;.)2=2 (#0); фсс=5 <«0).
Вывод. Прямая у = х - — , Х€ (-«>, + , является огибающей
семейства интегральных кривых заданного уравнения. Следова-
4
тельно, решение у = х~ —, хе(-», +«), исходного уравнения
является особым решением этого уравнения. 4
241
Наши книги можно приобрести:
Учебным заведениям и библиотекам:
в отделе по работе с вузами
тел.: (495) 744-00-12, e-mail: vuz@urait.ru
Частным лицам:
список магазинов смотрите на сайте urait.ru
в разделе «Частным лицам»
Магазинам и корпоративным клиентам:
в отделе продаж
тел.: (495) 744-00-12, e-mail: sales@urait.ru
Отзывы об издании присылайте в редакцию
e-mail: red@urait.ru
Новые издания и дополнительные материалы доступны
в электронной библиотечной системе «Юрайт»
biblio-online.ru
Учебное издание
Аксенов Анатолий Петрович
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Том 1
Учебник и практикум для академического бакалавриата
Формат 60x90 ’/»б.
Гарнитура «Petersburg». Печать цифровая.
Усл. печ. л. 15,06. Тираж 1000. Заказ № 5794, 40 экз.
ООО «Издательство Юрайт»
111123, г. Москва, ул. Плеханова, д. 4а.
Тел.: (495) 744-00-12. E-mail: izdat@urait.ru, www.urait.ni