Текст
Н. Н. Поляхов
ппщпшимш
■ Теория воздушных и гребных винтов
■ Теория стационарного обтекания
несущей поверхности
■ Теория нестационарного движения
несущей поверхности
■ Методы решения уравнений
несущей поверхности
Н. Н. Поляхов
АЭРОГИДРОДИНАМИКА
Под редакцией
Е. Н. Поляховой и Н. Н. Поляхова (мл.)
Издание второе
URSS
МОСКВА
ББК 22.253.3 22.3я44 30.13 30.123 30.124
Поляков Николай Николаевич
Аэрогидродинамика / Под ред. Е. Н. Поляховой и Н. Н. Поляхова (мл.).
Сост. Е. Н. Поляховой. Изд. 2-е. — М.: ЛЕНАНД, 2017. — 384 с.
Предлагаемая монография представляет собой первую систематическую подбор¬
ку избранных трудов профессора Санкт-Петербургского университета Николая Нико¬
лаевича Поляхова (1906-1987) — одного из ведущих ученых в области аэрогидроди¬
намики, аналитической механики и истории механики. Первое издание было приуро¬
чено к 110-летию со дня его рождения.
Работы объединены по четырем тематическим разделам: теория воздушных
и гребных винтов; теория стационарного обтекания несущей поверхности; теория не¬
стационарного движения несущей поверхности; методы решения уравнений несущей
поверхности. В основу подборки положена известная монография ученого «Теория
нестационарных движений несущей поверхности». При этом все разделы книги тема¬
тически связаны друг с другом, что позволяет рассматривать ее как монографическое
произведение по теории несущей поверхности, теории винтов и теории крыла конечно¬
го размаха, в котором все вопросы изложены достаточно подробно — от основопола¬
гающих идей до численной реализации методов расчетов.
Книга рассчитана на широкий круг специалистов по аэрогидродинамике, теории
крыла, теории воздушных и гребных винтов. Она будет полезна как сложившимся
ученым, так и молодым специалистам. Поскольку все работы написаны с присущей
Н. Н. Поляхову строгой логикой изложения, данная книга может служить также учеб¬
ным пособием по указанной тематике.
Рецензенты:
ЦНИИ им. акад. А. Н. Крылова (2-е отделение);
проф. С. К. Матвеев (Санкт-Петербургский университет,
кафедра гидромеханики)
Формат 60x90/16. Печ. л. 24. Зак. № АЛ-463.
Отпечатано в ООО «ЛЕНАНД».
117312, Москва, пр-т Шестидесятилетия Октября, 11 А, стр. И.
ISBN 978-5-9710-4174-0 © ЛЕНАНД, 2016
19979 Ю 222943
785971
41
74
НАУЧНАЯ И УЧЕБНАЯ ЛИТЕРАТУРА
URSS
E-mail: URSS@URSS.ru
Каталог изданий в Интернете:
http://URSS.ru
Тел ./факс (многоканальный):
I +7(499)724 25 45
Все права защищены. Никакая часть настоящей книги не может быть воспроизведена или
передана в какой бы то ни было форме и какими бы то ни было средствами, будь то элек¬
тронные или механические, включая фотокопирование и запись на магнитный носитель,
а также размещение в Интернете, если на то нет письменного разрешения владельца.
ОГЛАВЛЕНИЕ
Научное наследие Н. Н. Поляхова (1906-1987 г.). К 90-летию со дня
рождения ученого 5
Раздел I. Теория воздушных и гребных винтов 23
1.1. Теория винта с конечным числом лопастей (1937 г.) —
1.2. Теоретические основы метода расчета кавитирующего вин¬
та (1948 г.) 72
1.3. Обтекание решеток телесных профилей заданной формы
(1952 г.) 90
1.4. Теория решетки пластин по Н. Е. Жуковскому и ее обобще¬
ние на случай произвольного профиля (1956 г.) 96
1.5. Теория несущей винтовой поверхности (1963 г.) 117
Раздел II. Теория стационарного обтекания несущей поверх¬
ности 135
11.1. К теории крыла конечного размаха С. Л. Чаплыгина
(1953 г.) -
11.2. Теория несущей поверхности прямоугольной формы
(1959 г.) 145
И.З. Вихревая теория несущей поверхности (1968 г.) 166
II.4. Приближенная нелинейная теория обтекания тел цилин¬
дрической формы стационарным потоком несжимаемой
жидкости (1971 г.) 180
Раздел III. Теория нестационарного движения несущей по¬
верхности 191
III.1. О распределении давления на поверхности профиля, дви¬
жущегося нестационарно (1952 г.) —
111.2. Теория нестационарных движений несущей поверхности
(1960 г., монография) 197
111.3. Гармонические колебания прямоугольного крыла с цир¬
куляцией, переменной по размаху (1984 г.) 283
111.4. Гармонические колебания крыла с постоянной циркуля¬
цией по размаху (1992 г.) 293
111.5. Обтекание профиля, колеблющегося гармонически с ко¬
нечными амплитудами (1995 г.) 297
Р а з д е л IV. Методы решения уравнений несущей поверхности 306
IV.1. Об интегральном уравнений теории несущих поверхно¬
стей (1973 г.) —
IV.2. О существовании решения интегрального уравнения несу¬
щей поверхности (1975 г.) 316
3
IV.3. О решении интегрального уравнения обтекания несущей
поверхности (1978 г.) 324
IV.4. О построении начального приближения для решения ин¬
тегрального уравнения несущей поверхности (1979 г.) ... 330
IV.5. К вопросу о сходимости метода дискретных вихрей
(1979 г.) 338
IV.6. Заметка о методе дискретных вихрей (1980 г.) 348
IV.7. О методе дискретных вихрей (1980 г.) 350
IV.8. Практический метод расчета нестационарных характери¬
стик крыла с отклоняющейся частью (1986 г.) 356
IV.9. Об интегродифференциальном уравнении для несущей по¬
верхности при нестационарном движении (1987 г.) 365
IV.10. Расчет профиля скорости в круговом канале с прямо¬
угольным поперечным сечением (1989 г.) 370
Список основных научных трудов Н. Н. Поляхова 372
Список статей о Н. Н. Поляхове 377
НАУЧНОЕ НАСЛЕДИЕ Н. Н. ПОЛЯХОВА
(1906 — 1987 г.)
К 90-летию со дня рождения ученого
В 1996 г. исполняется 90 лет со дня рождения Николая Нико¬
лаевича Поляхова—одного из ведущих отечественных ученых
в области аэрогидродинамики, аналитической механики и исто¬
рии механики.
Н. Н. Поляхов родился 17 декабря 1906 г. в Киеве.
Детские и юношеские годы Николая Николаевича прошли в
Киеве. Затем семья переезжает во Владикавказ. В 1922 г. он по¬
ступает на физико-математический факультет Ростовского уни¬
верситета, а через год переводится на математическое отделе¬
ние физико-математического факультета Московского универ¬
ситета, который заканчивает в 1929 г.
Свою научно-исследовательскую деятельность Николай Ни¬
колаевич начинает в 1929 г. в общетеоретическом отделе Цен¬
трального аэрогидро динамического института им. Н. Е. Жуков¬
ского (ЦАГИ) под руководством академика С. А. Чаплыгина,
одновременно занимаясь преподавательской деятельностью в
Текстильном и Энергетическом институтах.
В 1932 г. Н. Н. Поляхов переезжает в Ленинград. С этого вре¬
мени начинается ленинградский период его научно-преподава¬
тельской деятельности: он становится сотрудником кафедры те¬
оретической механики Ленинградского университета, которой
тогда заведовал профессор Н. В. Розе.
В 1933 г. Н. Н. Поляхов утвержден в ученом звании доцента.
С 1934 г. одновременно с работой в университете Николай
Николаевич преподает в Ленинградском политехническом ин¬
ституте на кафедре аэрогидродинамики, читает лекции в Ин¬
ституте гражданского воздушного флота (ГВФ) на факультете
самолетостроения.
В 1937 г. он но представлению ЦАГИ получает ученую сте¬
пень кандидата технических наук без защиты диссертации.
С 1938 г. его работа в Политехническом институте стано¬
вится основной и продолжается вплоть до марта 1942 г., т. е.
до эвакуации института из блокадного Ленинграда на Кавказ.
5
Сам Николай Николаевич по состоянию здоровья был вынужден
остаться в осажденном городе.
В годы блокады с мая 1942 г. он начинает работать учителем
в средней школе, а с 1943 г. заведует кафедрой физики во Вто¬
ром медицинском институте (ныне Санитарно-гигиенический).
В 1947 г. по возвращении в Ленинград из эвакуации Политех¬
нического института Н. Н. Поляхов возобновляет там свою ра¬
боту, совмещая ее с научной деятельностью в ННИИ им. акад.
А. Н. Крылова.
В Политехническом институте Николай Николаевич препо¬
дает на кафедрах аэрогидродинамики и теоретической механи¬
ки, читает общие и специальные курсы по динамике полета са¬
молета, теории решеток, нестационарному движению несущей
поверхности, теории крыла, теории винта и др.
В 1950 г. Н. Н. Поляхов получает ученое звание профессора.
В 1952 г. он возвращается на математико-механический фа¬
культет Ленинградского университета, где сначала в течение 25
лет заведует кафедрой теоретической и прикладной механики,
а затем — кафедрой гидроаэромеханики.
В том же году он блестяще защищает в Москве в Военно-
воздушной академии им. Н. Е. Жуковского докторскую диссер¬
тацию ’’Вихревая теория воздушного гребного винта с конеч¬
ным числом лопастей”.
За заслуги в области научных исследований по аэродинами¬
ке и многолетнюю плодотворную педагогическую деятельность
Н. Н. Поляхов в 1968 г. удостоен почетного звания ’’Заслужен¬
ный деятель науки РСФСР”. Он был награжден двумя орде¬
нами Ленина, орденом Трудового Красного Знамени и шестью
медалями, в том числе медалями ”3а Оборону Ленинграда”,
” За доблестный труд в Великой Отечественной войне”, ”250 лет
Ленинграду” и др.
Обладая широкими знаниями в различных областях науки и
культуры, в совершенстве владея ораторским искусством, Ни¬
колай Николаевич прекрасно читал лекции, много сил и тру¬
да вкладывал в создание университетских и втузовских курсов
лекций по теоретической механике, гидроаэромеханике, исто¬
рии механики, теории несущих поверхностей, динамике полета
и др., многие из которых читаются теперь его учениками в раз¬
ных вузах.
Важным событием в жизни ленинградской школы механики
явился выход в свет в 1984 г. учебного пособия для университе¬
6
тов ’’Теоретическая механика” (в соавторстве с С. А. Зегждой и
М. П. Юшковым) [81]*, подытожившего его 35-летний опыт пре¬
подавания этой фундаментальной науки и отличающегося ори¬
гинальностью изложения. В этой книге глубина современно¬
го изложения предмета удачно сочетается с отражением значи¬
тельности деяний творцов механики прошлых столетий.
Н. Н. Поляхов всегда ведет большую научно-организацион¬
ную и общественную работу. Он подготовил несколько Десят¬
ков докторов и кандидатов наук, с 1954 по 1965 г. был де¬
каном математико-механического факультета ЛГУ, много лет
возглавлял Головной совет по механике Минвуза РСФСР, был
председателем секции истории механики Ленинградского отде¬
ления Советского Национального объединения историков есте¬
ствознания и техники, членом Национального комитета по ме¬
ханике и Президиума Научно-методического совета по теорети¬
ческой механике Минвуза СССР, председателем методической
комиссии Ленинградского университета, заведующим отделе¬
нием механики математико-механического факультета ЛГУ.
Более 30 лет Н. Н. Поляхов руководил общегородской секци¬
ей-семинаром по теоретической механике при Ленинградском
Ломе ученых АН СССР (эта секция ныне носит его имя), се¬
минаром по гидромеханике при Ленинградском кораблестрои¬
тельном институте, в разные годы был председателем и членом
нескольких ученых советов как в ЛГУ, так и в других научных
организациях и вузах.
Много внимания и времени Н.Н. Поляхов уделял журналу
’’Вестник Ленинградского университета”, являясь на протяже¬
нии многих лет ответственным редактором серии ’’Математика,
механика, астрономия”.
Основные исследования Н. Н. Поляховав области аэрогидро¬
механики связаны с развитием теории гребного винта и неста¬
ционарной теории крыла. Уже в начальный период своей на¬
учной деятельности (1929-1945 гг.) Николай Николаевич про¬
являл интерес к нескольким направлениям. В 1929-1930 гг. в
НАГИ им. Н. Е. Жуковского он изучал движение газа со ско¬
ростями, превышающими скорость звука. Первая его статья
на эту тему была включена в монографию В. Л. Александрова
’’Техническая гидромеханика” (см. [1]). В предисловии к этой
книге В. Л. Александров писал: ’’Моя большая загруженность
*См. список работ Н.Н. Поляхова в конце книги.
7
и вследствие этого опасение в запоздании выхода в свет кни¬
ги заставили обратиться к инженеру Н. Н. Поляхову с просьбой
предоставить для помещения в настоящей книге написанную им
ранее статью, дающую обзор современных работ по движению
жидкости со сверхзвуковыми скоростями, т. е. этот вопрос, хо¬
тя и мало еще разработанный, является в настоящее время в
достаточной мере актуальным. За любезное разрешение напе¬
чатать эту статью, а также за просмотр всей книги и сделанные
замечания приношу ему глубокую благодарность”. Книга была
переиздана в 1936 г., а в предисловии к третьему, переработан¬
ному, изданию 1946 г. автор указывает: ”По примеру прежних
изданий глава VIII ” Движение жидкости с большими скоростя¬
ми” вновь переработана Н. Н. Поляховым, за что приношу ему
искреннюю благодарность” (см. [10]).
В 1930 г. Н. Н. Поляхов переходит в группу профессора Вла¬
димира Петровича Ветчинкина. В 1930-1932 гг. он вместе с
В. П. Ветчинкиным занимается подготовкой к переизданию кни¬
ги последнего ’’Динамика самолета”, выступая автором новых
общих глав по аэродинамике, аэродинамическому расчету и те¬
ории гребных винтов, подбирает ряд задач по динамике полета
[2].
Это научное сотрудничество В. П. Ветчинкин отмечает в пре¬
дисловии к переизданию указанной монографии 1933 г.: ’’Главы
II-IV, касающиеся основных сведений по аэродинамике, тео¬
рии винтов и аэродинамическому расчету, были переработа¬
ны мною совместно с Н. Н. Поляховым ... Подготовка рукописи
всего труда к печати была выполнена, главным образом, моим
сотрудником по теоретической группе ИАГИ Н. Н. Поляховым,
которому и выражаю свою искреннюю признательность за по¬
несенные труды” (см. [2]).
С 1932 г. Н.Н. Поляхов совместно с профессором В. П. Вет¬
чинкиным приступает к написанию фундаментального труда по
теории гребных винтов. Началась эта работа с подготовки к
переизданию литографированной монографии В. П. Ветчинкина
’’Теория гребных винтбв”, выпущенной в 1926 г. небольшим ти¬
ражом в качестве учебного курса по теории винтов. В процессе
сотрудничества Н. Н. Поляхов включает в книгу и свои опубли¬
кованные ранее статьи [3, 4, 6].
Монография вышла двумя изданиями: в 1939 г. [5] и в 1940 г.
в окончательном варианте с рядом изменений и дополнений, ка¬
сающихся расчета винта на прочность [7]. Она представляет
8
собой наиболее полное изложение как аэродинамической тео¬
рии винта, так и расчета его на прочность. В этом капитальном
произведении (аэродинамика винта, расчет винта на прочность,
вариационные гребные винты*) собраны все существенные ре¬
зультаты, полученные в то время.
Более полувека эта книга является настольной для гидроме¬
хаников и инженеров-кораблестроителей, занимающихся вопро¬
сами теории движителей.
Н. Н. Поляхов принимал активное участие в научных семина¬
рах ЦАГИ, которые посещал и после переезда в Ленинград.
Уже в начале своей научной деятельности Н. Н. Поляхов со¬
здал серию работ по теории гребных винтов. Они посвящены
осреднениям по полярному углу циркуляции и реальному рас¬
пределению циркуляции.
Если к началу 30-х годов теория крыла конечного размаха с
большими удлинениями нашла уже достаточно полное отраже¬
ние в работах Л.Прандтля, И. Лотца, В. В. Голубева и др., то
теория винта строилась на вихревой теории Н. Е. Жуковского,
предполагавшей равномерное распределение циркуляции по по¬
лярному углу и постоянную циркуляцию вдоль радиуса лопа¬
сти.
Эта теория была обобщена В. П. Ветчинкиным на случай пе¬
ременной циркуляции. Определение циркуляции и сил, действу¬
ющих на лопасть заданной формы, производилось графоанали¬
тически с помощью метода Г. Глауэрта и Г. И. Кузьмина.
Что касается теории конечнолопастного винта, то она опи¬
сывалась лишь формулами общего вида (А. Бетц, Э.Треффц,
Б. Н. Юрьев и др.). Общей теории, аналогичной теории крыла,
не существовало. Вихревая теория несущей линии была осно¬
вана на замене лопасти винта одним присоединенным вихрем.
Однако, как правило, относительная ширина лопасти судовых
гребных винтов достаточно велика, что требовало введения со¬
ответствующих поправок. Н. Н. Поляхов вносит существенный
вклад в создание вихревой теории несущей поверхности. Пред¬
ложенная им замена лопасти системой вихрей позволила полу¬
чить более строгие и полные результаты, учитывающие конеч¬
ные размеры лопасти.
Первоначально в работах Н. Н. Поляхова метод, развитый
*Так назывались винты, проектировавшиеся с одновременным удовле¬
творением требований к прочности лопастей. — Прим. составителей.
9
II. Е. Жуковским для постоянной циркуляции, в аналитическом
виде переносится на случай любой переменной циркуляции.
При этом применительно к лопасти развивается метод, анало¬
гичный методу Глауэрта—Треффца, используемому в теории
крыла для определения циркуляции по заданным геометриче¬
ским и кинематическим характеристикам лопасти.
В общей постановке задачи (при учете центробежных сил в
струе) данный метод приводит к нелинейному интегральному
уравнению, вырождающемуся в простое алгебраическое урав¬
нение при легких нагружениях.
Развивая далее теорию лопасти, Н.Н. Поляхов для опреде¬
ления циркуляции выводит (используя для индуктивной скоро¬
сти интегральную форму Т. Морийя) интегродифференциаль-
ное уравнение, сходное с уравнением теории крыла. Применяя
разработанный им же ранее метод, аналогичный методу Глау-
эрта, он предлагает простой приближенный метод решения это¬
го уравнения [4], который был позднее положен в основу прак¬
тических расчетов гребных винтов.
В 30-е годы Н. Н. Поляхов создал метод практического расче¬
та оптимальных винтов, основанный на строгом доказательстве
теоремы Бетца об оптимальных винтах [5, 6]. Он показал, что
условие Бетца обеспечивает минимальные потери. Отдельно
им исследован случай оптимального винта с учетом профиль¬
ного сопротивления элементов лопасти, позволяющий решить
задачу методом Ритца.
Основные результаты этих работ, дополненные новыми дан¬
ными, были включены в монографии [5] и [7], в 1945 г. эти ре¬
зультаты были опубликованы в США [9].
В 1929-1945 гг. Н. Н. Поляхов, исходя из разработанного им
ранее метода, перешел к созданию нового, более эффективно¬
го метода решения основной задачи как теории крыла, так и
теории винта, строящегося на выделении в выражении для ин¬
дуктивной скорости его главной части, линейной относитель¬
но местной циркуляции. Добавочное слагаемое, зависящее от
закона распределения циркуляции, оказалось малым по сравне¬
нию с основными было легко получено методом последователь¬
ных приближений. Этот метод позволил разрешить до конца
задачу о соосных винтах с учетом их взаимодействия и най¬
ти оптимальную комбинацию последних [13]. Результаты дан¬
ной работы были внедрены в практику расчета соосных винтов.
Развитые методы вихревой теории были обобщены на случай
10
кавитирующих гребных винтов с учетом отрывных течений [14].
В 1947 г. Н.Н. Поляхов защищает докторскую диссертацию
’’Вихревая теория гребного винта с конечным числом лопастей”
[п]. Это фундаментальное исследование явилось фактически
монографией, в которой он последовательно изложил все основ¬
ные задачи в области вихревой теории воздушных винтов и
предложил единый метод решения этих задач, доведя его до
формул, удобных для прикладных расчетов.
Кроме совершенствования математического аппарата разра¬
ботанной им ранее теории в целом, им был освещен ряд смежных
вопросов, а именно: 1) упрощение поверочных и проектировоч¬
ных расчетов винта; 2) теория наивыгоднейших винтов с учетом
лобового сопротивления на элементах лопастей и условий проч¬
ности лопастей; 3) взаимное влияние винта и корпуса самолета;
4) взаимное влияние винта и крыла; 5) теория и расчет соос¬
ных винтов с распространением на них вариационной теории;
6) учет влияния сжимаемости воздуха; 7) постановка задачи об
отыскании наивыгоднейших параметров винта; 8) развитие эф¬
фективных методов решения последней; 9) развитие теории ре¬
шеток, состоящих из профилей конечной толщины.
Оценивая эту работу, профессор В. П. Ветчинкин назвал
Н. Н. Поляхова” ... одним из образованнейших винтовиков Со¬
ветского Союза”.
Исследования в области вихревой теории гребных винтов бы¬
ли позднее продолжены последователями Н. Н. Поляхова, в том
числе В. Ф. Бавиным и Н. Ю. Завадовским, и доведены до паке¬
тов современных компьютерных методик, постоянно используе¬
мых при проектировании винтов гражданских судов и кораблей
ВМФ.
Теория винта получила дальнейшее развитие в серии работ
Н. Н. Поляхова, посвященных методам расчета гидродинамиче¬
ской решетки, составленной из профилей заданной формы, и их
приложениям к задаче об интерференции лопастей винта [11,
18, 20, 23]. Основной отличительной чертой работ этой серии
является возможность конформного отображения решетки про¬
филей на внешность решетки пластин, для которой выражение
скорости имеет простую замкнутую форму. Последнее особен¬
но существенно при большой густоте решетки, когда другие ме¬
тоды расчета непригодны. Применив теорию решетки к задаче
о взаимодействии лопастей гребного винта, Н. Н. Поляхов впер¬
вые построил теорию, описывающую это взаимодействие, особо
И
проявляющееся в случае широколопастных винтов.
Эти результаты положили начало следующему этапу его на¬
учных исследований в области аэродинамики (1947- 1971), свя¬
занному, главным образом, с работами по теории несущей по¬
верхности конечного размаха и нестационарной теории крыла.
Первая группа работ этого периода содержит результаты по
нелинейной теории крыла конечного размаха, причем в качестве
несущей поверхности используются крылья с малым удлинени¬
ем [17, 21, 26].
В работе [30] нашла отражение теория несущей поверхности
винтообразной формы, т. е. теория лопасти как несущей поверх¬
ности. Рассмотренная трехмерная задача позволила вычислить
не только силы и моменты, действующие на несущую поверх¬
ность, но и построить распределение нагрузки по ней. Реше¬
ние задачи основывалось на сочетании теории тонкого профи¬
ля, развитой для плоского потока, с теорией индукции, учи¬
тывающей конечность размаха, и сводилось к решению сингу¬
лярного интегрального уравнения первого рода типа уравнений
Фредгольма в соответствующем классе функций, а для суммар¬
ной циркуляции—к решению интегродифференциалыюго урав¬
нения типа уравнений Прандтля.
Задача о несущей поверхности произвольной в плане фор¬
мы была решена Н. Н. Поляховым в [34] (ранее им анализиро¬
вались только поверхности прямоугольной в плане формы). В
рассматриваемой задаче были известны лишь результаты, от¬
носящиеся к круглому (А. Киннер, Н. Е. Кочин) и эллиптическо¬
му (И.Кринес) крыльям, приводящие к весьма громоздким ре¬
шениям. Предложенный Н. Н. Поляховым новый метод решения
был основан на сведении задачи к сингулярному интегральному
уравнению первого рода с двумя переменными, выражающему
условие непроницаемости, и к интегральному уравнению второ¬
го рода с регулярным ядром. Выделение главной части индук¬
тивной скорости позволило, как и в случае несущей линии, ре¬
шить задачу методом итераций, используя простой метод рас¬
чета, являющийся обобщением известного метода Мультоппа,
но разработанный Н. Н. Поляховым именно для этого случая.
Одновременно метод Мультоппа получил здесь свое строгое
обоснование. Этот и другие методы, примененные в [34], допус¬
кали при использовании методов из [28] обобщение на случай
нестационарных движений.
В работе [36] построена приближенная нелинейная теория об¬
12
текания тел цилиндрической формы стационарным потоком не¬
сжимаемой жидкости. В этой работе впервые с помощью вихре¬
вого метода учтена телесность профиля крыла конечного разма¬
ха. Поскольку результаты расчетов удовлетворительно совпа¬
ли с данными эксперимента, очевидно, что удалось построить
вполне законченную теорию несущей поверхности.
Вторая группа работ этого этапа охватывает исследования
по нестационарной теории крыла [19, 24, 25, 28, 32]. В них рас¬
сматривается нестационарное движение телесного профиля в
плоском потоке, тогда как раньше анализировались только бес¬
конечно тонкие профили. Решалась также задача о распреде¬
лении давления по телесному профилю, с которого сходит вих¬
ревой след в виде некоторой плавной кривой. Это была новая
постановка задачи, так как ранее обычно рассматривалась пла¬
стинка, продолжением которой и служит вихревой след. Затем
в общем виде была изучена задача о силах, действующих на
нестационарно движущийся профиль, причем было установле¬
но, что кроме ранее известных сил на профиль в плоском пото¬
ке действуют силы индукционного характера, подчиняющиеся
уравнениям Праидтля. В частности, в [19] исследуется неста¬
ционарное движение произвольного телесного профиля: здесь
уравнение давления записано без линеаризации, поэтому впер¬
вые при расчете давления принимается во внимание влияние не
только квазистационарных слагаемых, но и вихревого следа.
В [24] анализируется произвольный телесный профиль, с ко¬
торого сходит вихревой след, а анализ нелинейных слагаемых,
связанных со следом, приводит к появлению сил индукционного
характера, причем даже для бесконечно тонкого прямолинейно¬
го профиля сила, направленная вдоль него, оказывается отлич¬
ной от нуля.
В работе [25] решается задача о гармонических колебани¬
ях крыла, конечного размаха в соответствии с вихревой схемой
из метода Бирнбаума, причем удалось получить сравнитель¬
но простое решение, сходное по структуре с уравнением для
стационарного случая. Здесь метод Бирнбаума, развитый для
профиля в плоском потоке, позволил привести уравнение крыла
к уравнению такого же вида, как и в методе Бирнбаума, вслед¬
ствие чего оказалось возможным записать решение для цирку¬
ляции, как постоянной вдоль размаха, так и переменной. Крыло
при этом рассматривалось не как несущая линия, а как несу¬
щая поверхность. Полученные в [25] решения, аналогичные ре¬
13
шениям для стационарного случая, оказались проще и удобнее
в практическом отношении, чем использовавшиеся ранее гро¬
моздкие решения, полученные методами Кюсснера и Чикала.
Упомянутая выше вторая группа работ была включена
Н. Н. Поляховым в монографию ’’Теория нестационарных дви¬
жений несущей поверхности” [28]. Здесь исследование прово¬
дилось в рамках вихревой схемы Кармана—Сирса и была по¬
казана возможность решения основных задач, включая крыло
конечного размаха с не очень малым удлинением, путем реше¬
ния сингулярного интегрального уравнения первого рода, ана¬
логичного уравнению для стационарного случая. Позднее, в
работе [32], это решение было обобщено на случай малых удли¬
нений. Оно применимо и к крылу конечного размаха. В моно¬
графию [28] вошли также и абсолютно новые результаты, как,
например, решение задачи о тонком профиле в постановке Кар¬
мана— Сирса вихревым методом с распространением этого ме¬
тода на случай крыла конечного размаха. В [39] вихревая схема
Бирнбаума обобщена на случай гармонических колебаний кры¬
ла конечного размаха с телесным профилем. Расчеты распреде¬
ления давлений и аэродинамических характеристик оказались в
удовлетворительном соответствии с данными эксперименталь¬
ных исследований.
Более поздние работы Н.Н. Поляхова по аэродинамике по¬
священы в основном созданию целостной теории крыла конеч¬
ного размаха, включающей постановку математической задачи
обтекания и построение вихревой модели; особое внимание уде¬
ляется практическим методам решения. Первые подходы к этой
теории были сделаны в работах [32] и [34], где на основе вихре¬
вых схем Бирнбаума получены решения пространственной за¬
дачи обтекания крыла. Эти решения обеспечивают выполнение
граничных условий данной задачи при минимальных допущени¬
ях, существенно упрощающих расчет, но не нарушающих при
этом физической картины.
Основополагающей среди указанных работ следует считать
статью [37]. В ней дана оригинальная вихревая схема крыла,
конечного размаха, позволяющая записать уравнение непрони¬
цаемости в форме, более простой и удобной для решения кон¬
кретных задач, чем у других исследователей.
Наиболее важным результатом этой работы было преобразо¬
вание исходного интегрального уравнения типа уравнений Ко¬
ши первого рода по формулам обращения в уравнение Фред-
14
гольма второго рода, что позволяет решать данный класс задач
методом итераций, а, главное, гарантирует единственность по¬
лучаемого решения и его соответствие всем граничным услови¬
ям независимо от метода вычисления. По-видимому, это един¬
ственно возможный метод решения задачи обтекания крыла,
полностью соответствующий всем требованиям краевой зада¬
чи для сингулярного уравнения такого вида.
В дальнейшем предложенный Н. Н. Поляховым в [37] Метод
был развит применительно к различным задачам стационарно¬
го и нестационарного обтекания крыла, были сформулированы
условия существования и критерии сходимости итеративного
вычислительного процесса. Все эти вопросы нашли отражение
в публикациях [38, 39, 44, 50, 51, 54-56, 63, 63а] и целом ряде
работ учеников Н. Н. Поляхова разных лет.
Особо следует выделить статьи [44] и [54], которые позволили
подчеркнуть эффективность разработанной методики решения
уравнений теории крыла в практических расчетах, отмечая ее
экономичность при использовании вычислительной техники.
Важное место занимают работы [37, 45, 47, 48, 54], содержа¬
щие анализ метода дискретных вихрей; в них отмечаются недо¬
статочная строгость и корректность решений, получаемых на
его основе.
Н. Н. Поляховым показано, что при преобразовании систе¬
мы алгебраических уравнений задачи обтекания крыла методом
дискретных вихрей к исходному интегральному уравнению не¬
проницаемости в последнее вносится множитель, не зависящий
от порядка системы, но меняющий вид ядра уравнения и, следо¬
вательно, рассматриваемую задачу. Кроме того, Н, Н. Поляхов
установил, что ни при каких условиях решения, полученные с
помощью метода дискретных вихрей, не сходятся к точному ре¬
шению интегрального уравнения, и все доказательства сходи¬
мости содержат ряд чисто математических ошибок. Послед¬
нее представляет особый интерес, поскольку строгости доказа¬
тельств, используемых в методе дискретных вихрей, уделялось
в литературе недостаточно внимания.
Универсальность метода Н. Н. Поляхова подтверждают его
статьи [49, 61], в которых задача обтекания осесимметричных
тел сводится к интегральному уравнению того же типа, что и
уравнение несущей поверхности, в результате чего появляется
возможность использовать при его решении уже хорошо заре¬
комендовавшие себя численные методы.
15
Следует упомянуть работы [5*2. 58-60], в которых вихревые
методы удалось успешно реализовать при решении чисто техни¬
ческой проблемы о движении жидкости в искривленных трубо¬
проводах, причем удачное решение данной задачи использовано
уже применительно к конкретным объектам.
В [55] создан практический метод расчета нестационарных
характеристик крыла с отклоняющейся частью. Работа [62]
представляет собой заявку на изобретение судового руля ново¬
го типа (типа ПН — по начальным буквам фамилий авторов), ко¬
торое позволило бы улучшить управляемость и маневренность
судна путем увеличения боковой силы, действующей на руль,
работающий в струе от гребного винта.
Таким образом, созданные Н. Н. Поляховым методы позволя¬
ют решать широкий спектр задач об обтекании тел различной
конфигурации, т. е. обладают универсальностью и делают эф¬
фективным расчет, что придает им большую практическую зна¬
чимость.
Разными аспектами аэрогидродинамики крыла Н. II. Поляхов
занимался в течение всей творческой жизни. Своей целью при
этом он ставил решение принципиальных вопросов теории ста¬
ционарного и нестационарного движения крыла, а также обосно¬
вание используемых в расчетах численных методов.
Практической разработкой идей Н. Н. Поляхова занимались
его многочисленные ученики. Так, А. И. Пастухов изучал не¬
линейные гидродинамические характеристики тонких крыльев
сложной формы в плане, В. Н. Трещевский—стационарные и
нестационарные характеристики телесных крыльев конечного
размаха, Е. В. Юдин и А. Н. Холодилин занимались приложе¬
нием нестационарной теории крыла к задачам гидродинамики
корабля, В. В. Яковенко выполнял измерения нагрузок на ко¬
леблющемся крыле, О. Ф. Мельникова совместно с Н.Н. Поля¬
ховым проводила исследования решения уравнений теории кры¬
ла численными методами. В соавторстве с 3. Н. Шестерниной
Н. Н. Поляховым были написаны работы, обосновывающие кор¬
ректность и единственность решений задач, в которых исполь¬
зовано интегродифференциальное уравнение в предложенной им
форме. В. И. Николаев рассмотрел характеристики крыла с от¬
клоняющейся частью и разработал судовые рули нового типа.
Многочисленные труды Н.Н. Поляхова в области теории
крыла с определенной долей условности можно сгруппировать
с учетом трех основных направлений: построение теории кры¬
16
ла на основе выделения главной части циркуляции; исследова¬
ние сил и давлений, действующих на крыло в нестационарном
движении; разработка корректных математических методов ре¬
шения уравнений теории крыла. Они завоевали широкую при¬
знательность ясностью постановки задачи, строгостью исполь¬
зуемых методов решения, глубоким физическим анализом и на¬
глядным представлением полученных результатов.
Н. Н. Поляховым создана большая научно-теоретическая
школа в судостроении, к которой принадлежат многие крупные
ученые, развивающие его идеи и методы при исследовании во¬
просов теории корабля, в частности гидродинамического рас¬
чета гребных винтов, крыльевых систем быстроходных судов,
судовых рулей, корпусов и т. д.
Важные научные результаты получены Н. Н. Поляховым и
в области аналитической механики [64-90]: им разработана
единая теория как линейных, так и нелинейных неголономных
систем любого порядка, получены общие уравнения движения
этих систем в произвольном неортогоналыюм неголономном ба¬
зисе, а также формулы, определяющие обобщенные реакции не¬
голономных связей, изучен вопрос об управлении движением с
помощью связей, зависящих от параметров, и установлен новый
обобщенный вариационный принцип типа принципа Гаусса.
Первая публикация Н. Н. Поляхова, посвященная канониче¬
ским уравнениям движения неголономных систем, относится к
1970 г. [68]. Интерес к данной тематике возник у него в 60-е
годы. Сам Николай Николаевич говорил по этому поводу: ” Не¬
сколько особняком стоят мои увлечения историей науки и тео¬
рией движения неголономных систем, которыми я сейчас начал
заниматься’1. Вскоре’’увлечения” переросли в систематические
фундаментальные исследования, его внимание сосредоточилось
на важном вопросе о соотношении между уравнениями движе¬
ния неголономных систем и вариационными принципами меха¬
ники.
Интерес к этим задачам проявился в связи с развитием те¬
ории управляемых систем, в которых часто встречаются нели¬
нейные неголономные связи. В работах [69, 70] Н.Н. Поляхов
развил общую теорию уравнений движения неголономных си¬
стем, не подразделяя их на линейные и нелинейные. Одновре¬
менно им был предложен метод записи уравнений движения при
связях общего вида любого порядка неголоиомности, основан¬
ный на проектировании вектора ускорения изображающей точ¬
17
ки системы на оси должным образом выбранного неголономного
базиса [68-70], описаны способы определения реакций неголо-
номных связей и приведения уравнений движения к канониче¬
ской форме.
В результате этих исследований одновременно с всесторон¬
ним анализом понятия идеальности неголономных связей было
установлено, что в основу аналитической механики может быть
положено линейное преобразование сил по правилу преобразо¬
вания компонент ковариантного вектора. Введение такого пре¬
образования сил позволило сформулировать новый вариацион¬
ный принцип механики, обобщающий принцип Гаусса на него-
лономные системы любого порядка и являющийся в настоящее
время самым общим принципом механики [79]. Этот принцип
непосредственно связан с управляемым движением, неполная
программа которого задана в виде системы дифференциальных
уравнений [80, 82, 83, 88, 89].
Исследования Н.Н. Поляхова по аналитической механике
всегда неразрывно связаны с его преподавательской деятель¬
ностью. Начиная с 1953 г. он читает курс лекций но те¬
оретической механике на отделениях математики и механики
математико-механического факультета Ленинградского универ¬
ситета, включая в них результаты своих научных исследований.
Так, анализируя известный вывод уравнений движения нели¬
нейных неголономных систем, он продемонстрировал его логи¬
ческое несовершенство [69], указав новый, перспективный путь
решения задачи.
В 1975 г. Николай Николаевич предлагает своим учени¬
кам С. А. Зегжде и М. П. Юшкову написать учебное пособие
для механико-математических специальностей университетов
на основе созданного им курса лекций по теоретической меха¬
нике.
Первые две совместные публикации этих авторов [75, 77] бы¬
ли посвящены всестороннему анализу понятия идеальности не¬
голономных связей. Им удалось показать, что ’’...идеальные
связи позволяют написать второй закон Ньютона в том виде,
в каком он пишется для свободной системы. При этом, одна¬
ко, существенно то обстоятельство, что этот закон пишется в
подпространстве, ортогональном подпространству, в котором
ускорение полностью определяется уравнениями связей (про¬
странство реакций)” [77, с. 75]. Эти уравнения динамики ока¬
зались необходимыми условиями минимальности принуждения
18
по Гауссу [75], а в случае неголономных связей первого поряд¬
ка их следствием является однородная линейная дифференци¬
альная форма от контравариантного вектора возможных квази¬
скоростей, коэффициенты которой представляют собой реакции
связей. Результаты текущей работы Н. Н. Поляхова и его соав¬
торов над новым учебником по теоретической механике были
изложены в [76, 78].
Учебное пособие ’’Теоретическая механика” вышло в свет
в 1984 г. [81]. Академик А. Ю. Ишлинский так охарактери¬
зовал этот труд в Предисловии к [87, с. 2]: ’’Тонкий знаток
механики, автор многих серьезных исследований по аэродина¬
мике, Николай Николаевич создал вместе со своими ученика¬
ми С. А. Зегждой и М. П. Юшковым превосходный современный
курс теоретической механики, продолжающий традиции трак¬
татов Аппеля, Суслова, Чаплыгина, Леви-Чивита и Амальди.
В нем, в частности, приводится новая форма уравнений не¬
свободного движения и вводится оригинальный вариационный
принцип для механических систем с нелинейными неголономны-
ми связями любого порядка”.
Это учебное пособие в 1987 г. было удостоено первой премии
Ленинградского университета.
Общий подход к уравнениям Лагранжа первого и второго
рода и установление связи между ними позволили найти но¬
вую, специальную форму уравнений динамики системы твердых
тел, удобную для применения вычислительной техники. Целе¬
сообразным оказалось также введение избыточных координат
и принятие аппарата уравнений Лагранжа с множителями Ла¬
гранжа. Эти результаты были опубликованы в 1989 г. [88], уже
после смерти ученого.
В последние годы жизни Н.Н. Поляхов интересовался про¬
блемами взаимосвязи классической механики с теорией относи¬
тельности и с квантовой механикой. По его мнению, '’специаль¬
ная теория относительности и квантовая механика поставили
перед классической механикой новые задачи, чем ее очень обо¬
гатили, не изменив определений, поучений и аксиом Ньютона”
[87, с. 37].
Будучи разносторонним ученым, Н.Н. Поляхов занимался
исследованиями и в других областях механики: в электромеха¬
нике [72], теории упругости [73, 74]; им опубликованы работы по
методике преподавания теоретической механики [71, 76], исто¬
рии кафедр отделения механики математико-механического фа¬
19
культета Ленинградского университета [65-67, 84]; он является
автором статей, посвященных памяти ученых его учителей и
коллег [15, 16, 27, 31, 33, 35, 42, 57].
Особый интерес Николай Николаевич проявлял к истории ме-
ханики [64-67, 84-86]. Много сил и энергии он отдавал сотруд¬
ничеству с коллективами Института истории естествознания и
техники АН СССР и его филиалов.
Знание иностранных языков (латинского, французского, не¬
мецкого, английского) позволяло ему свободно обращаться к
оригинальным сочинениям И. Ньютона, Ж. Лагранжа, Л. Эйле¬
ра, уточняя и комментируя отдельные места в известных пере¬
водах их трудов. В [86] им была подробно освещена историче¬
ская роль Л. Эйлера в развитии механики. Ло последних дней
Н.Н. Поляхов работал над новым переводом на русский язык
”Математических начал натуральной философии” И. Ньютона,
так и не успев, однако, его завершить.
Глубокое изучение трудов классиков механики позволило
Н.И.Поляхову установить, например, роль результатов
М. В. Остроградского в развитии науки [64], обнаружить, что
вариационный принцип, носящий имя Ф.Журдена, в действи¬
тельности был впервые сформулирован Г. К. Сусловым, осве¬
тить роль А. Пшеборского в обобщении уравнений Маджи на
нелинейные неголономные связи первого порядка и линейные
связи второго порядка [77].
К сожалению, Н. Н. Поляхов не успел приступить к созданию
давно задуманного им учебника по истории механики — этим
творческим планам не суждено было осуществиться.
Многогранность Научной деятельности И. II. Поляхова неод¬
нократно подчеркивалась в статьях, написанных о нем его кол¬
легами и учениками (см., например, [90-92]). Во всей своей
научной, педагогической и общественной деятельности Нико¬
лай Николаевич неизменно выступал как русский гуманист, а
общение с ним всегда оставляло глубокий след.
Все ученики и коллеги Николая Николаевича, имевшие сча¬
стье с ним работать, навсегда сохранят о нем светлую память
не только как о блестящем педагоге и крупном ученом, но и как
о добром, отзывчивом, глубоко интеллигентном человеке, обла¬
давшем высокими нравственными качествами и благородством
души.
Учитывая существенный вклад 11. Н. Поляхова в отечествен¬
ную науку, а также перспективность его научных идей, научная
20
общественность и Редакционно-издательский совет математико¬
механического факультета Санкт-Петербургского университе¬
та приняли решение осуществить поэтапное переиздание из¬
бранных трудов ученого. Необходимость этих публикаций дик¬
туется не только современной научной значимостью его работ,
но и тем, что многие из них стали библиографической редко¬
стью.
Предлагаемая книга включает в себя избранные труды
Н. Н. Поляхова по теории гребного винта и теории крыла, объ¬
единенные тематически в несколько разделов. В основу под¬
борки положена его известная монография ”Теория нестацио¬
нарных движений несущей поверхности’1 [28], изданная в 1960 г.
небольшим тиражом.
Из многочисленных научных работ Н.Н. Поляхова по аэроги¬
дродинамике составителями отобраны двадцать четыре наибо¬
лее значимые. Предлагаемые вниманию читателя работы объ¬
единены в четыре раздела: 1) теория воздушных и гребных пии¬
тов (5 статей); 2) теория стационарного обтекания несущей по¬
верхности (4 статьи); 3) теория нестационарного движения не¬
сущей поверхности (4 статьи и монография); 4) методы решений
уравнения несущей поверхности (10 статей).
Внутри разделов статьи располагаются в хронологической
последовательности.
В конце книги приведен список научных трудов Н.Н. Поля¬
хова* за период с 1932 по 1995 г., в том числе и вышедшие из
печати после его смерти.
Составители надеются, что отобранные для переиздания ста¬
тьи достаточно полно представляют спектр интересов ученого
на протяжении всей его многолетней педагогической и научной
деятельности. Кроме того, будучи собраны воедино, эти ра¬
боты в определенном смысле приобретают новое качество, об¬
условленное высоким научным потенциалом всего творчества
Н. Н. Поляхова и ценностью его научного наследия.
При отборе материалов составители руководствовались не
только их научной значимостью, но и возможностью продемон¬
стрировать корректность и изящество решений задач, выпол¬
ненных ученым в разные периоды его творческой деятельности.
’“Номера в квадратных скобках в заглавиях статей данного издания и
в постатейных указателях литературы соответствуют номерам из =*того
списка.
21
При подготовке материалов к публикации были по возможно¬
сти исправлены опечатки, замеченные в предыдущих изданиях,
а ряд статей снабжен примечаниями или комментариями редак¬
ционного характера с привлечением материалов, сохранивших¬
ся в архиве Н. Н. Поляхова.
Издание рассчитано на широкий круг специалистов по аэ¬
рогидродинамике, теории крыла, теории воздушных и гребных
винтов. Оно будет полезно как сложившимся ученым, так и
молодым специалистам. Действительно, поскольку все разде¬
лы книги тематически связаны друг с другом, она может рас¬
сматриваться как монографическое произведение по теории не¬
сущей поверхности, теории винтов и теории крыла конечного
размаха, в котором все вопросы изложены достаточно подроб¬
но— от основополагающих идей до численной реализации ме¬
тодов расчетов. Поскольку все работы написаны с присущей
Н.Н. По ляхову строгой логикой изложения, данная книга мо¬
жет служить также учебным пособием по указанной тематике.
Как надеются составители, книга поможет сохранить память о
замечательном педагоге и ученом, каким был Н. Н. Поляхов.
Глубокую признательность составители выражают жене уче¬
ного— Наталии Васильевне Нарбут, любезно предоставившей
материалы о жизни и творчестве Николая Николаевича.
Составители приносят свою искреннюю благодарность кол¬
лективу кафедры гидроаэромеханики Санкт-Петербургского
университета, а также коллегами ученикам Н. Н. Поляхова, ока¬
завшим содействие и помощь при подготовке книги к печати.
Раздел I
ТЕОРИЯ ВОЗДУШНЫХ И ГРЕБНЫХ ВИНТОВ
1.1. ТЕОРИЯ ВИНТА
С КОНЕЧНЫМ ЧИСЛОМ ЛОПАСТЕЙ [4]
Проблема винта с конечным числом лопастей давно занима¬
ла внимание гидроаэромехаников. Однако трудности, которые
были связаны с вычислениями индуктивных скоростей винта, не
позволяли довести до конца эту работу, а тем более сделать ее
применимой к расчету гребных винтов.
Впервые вычислить индуктивные скорости, получающиеся у
лопастей винта, в удобной для применения форме, приближенно
удалось японскому ученому Т. Морийя в 1931 г. путем введения
так называемого фактора индукции.* Однако как проектиро¬
вание, так и поверочный расчет гребного винта по формулам
Т. Морийя настолько громоздок, что практически пользоваться
ими весьма сложно. Кроме того, Т. Морийя не дает аналитиче¬
ского способа нахождения фактора индукции и совершенно не
касается вопроса о том, какой тип винта наиболее удобен для
проектирования, а также не касается условий, которым должен
удовлетворять поток позади винта с наибольшим коэффициен¬
том полезного действия.
Автор предлагает способ аналитического нахождения фак¬
тора индукции и устанавливает связь между теорией винта с
конечным числом лопастей и теорией Н. Е. Жуковского.
В Приложении I дается метод аэродинамического расчета
винта с конечным числом лопастей, совершенно не связанный
с графическим вычислением несобственного интеграла, кото¬
рое рекомендуется Т. Морийя и которое чрезвычайно усложня¬
ет весь расчет, делая этот метод практически неприемлемым.
*Мо-рийя Т.// Бюлл. ПАГИ. 1931. Jfc 20 (перевод). Нужно сказать,
что вычислением этих скоростей занимался также Ламб (Proceedings of
Cambridge Philosophical Society. 1923. Vol. 21), но результаты его вычисле¬
ний мало пригодны для применений.
23
Метод, предлагаемый нами, основан на использовании три¬
гонометрических рядов для вычисления интеграла, предложен¬
ного Т. Морийя, и позволяет вести расчет винта по схеме, кото¬
рая требует для своего применения почти столько же времени,
сколько требует расчет по вихревой теории Н. Е. Жуковского.
Метод дал очень хорошее совпадение результатов расчета с ре¬
зультатами эксперимента.
Теоретически метод приложим и к тяжело нагруженным водя¬
ным винтам, но последние при своем расчете требуют не только
учета числа лопастей, но и учета влияния ширины лопасти, ибо
являются широколопастными винтами. Влияние ширины лопа¬
сти на водяных винтах весьма значительно.
В Приложении 2 рассматривается вопрос о винте с наимень¬
шей потерей энергии, который впервые был рассмотрен Бет¬
цем. Мы дали строгое доказательство теоремы Бетца и ука¬
зываем на то, как можно проверить результаты применения по¬
правки Прандтляпри различных видах распределения циркуля¬
ции. Наиболее важным результатом Приложения 2, по нашему
мнению, является установление условия, которому должен удо¬
влетворять поток позади винта с наибольшим к. п. д. Результат,
найденный нами теоретически, подтверждается экспериментом.
Интересно отметить, что винт с наибольшим к. и. д. оказы¬
вается наиболее простым в отношении проектирования и уче¬
та влияния центробежных сил, так как осевая индуктивная ско¬
рость у такого винта постоянна вдоль радиуса.
В отличие от винта типа И ЕЖ в нашем случае циркуляция
по лопасти такова, что она обращается в нуль на конце лопасти
и у втулки, удовлетворяя таким образом физическим условиям
задачи.
Итак, излагается теория винта с конечным числом лопастей,
подтвержденная результатами расчета, дающими хорошее со¬
впадение с экспериментом.
Вихревая теория гребного винта, созданная Н. Е. Жуковским,
основана на замене винта с конечным числом лопастей винтом с
бесконечно большим числом бесконечно топких лопастей. Эта
замена эквивалентна замене винтового вихревого шнура, сходя¬
щего с конца лопасти, боковым вихревым слоем, вихри которо¬
го имеют циркуляцию ^dOds, где Г есть циркуляция винтового
вихря, ds —- элемент длины винтового вихря, выделенного из бо¬
кового вихревого слоя. Метод, предложенный И. Е. Жуковским
для винтов с постоянной циркуляцией (винт типа НЕЖ) в его
24
первой статье по теории гребного винта,* легко обобщается на
винты с переменной циркуляцией. При этом для индуктивных
скоростей, вызываемых вихрями у точки, находящейся в плоско¬
сти винта, получаются следующие значения для окружной ско¬
рости:
при г < 6,
dvt 1 =
при г > 6,
где г— радиус вихревого цилиндрического слоя с элементарной
циркуляцией с/Г, а величина b—расстояние исследуемой точки
от оси винта. Таким образом, точки, лежащие внутри вихревого
слоя, никакой окружной индуктивной скорости от этого слоя не
получают.
Для индуктивной осевой скорости имеем
{О при г < 6,
к ctg в dr , .
— —dr при г > 6,
47гг dr
т. е. вихревой цилиндрический слой, состоящий из геликоидаль¬
ных вихрей, не вызывает у точки, находящейся вне этого слоя в
плоскости винта, никакой осевой индуктивной скорости.
Для индуктивной радиальной скорости получается выраже¬
ние
к ctg f3 dr ^ J cos 0 d6
о
4n2 dr J >/r2 4- d2 - 2rb cos 9
При этом ctg /3 есть котангенс угла, образуемого винтовым вих¬
рем с плоскостью вращения винта. Величина ctg/? есть функция
радиуса г.
Найдем теперь индуктивные скорости, вызываемые в точке
N, лежащей в плоскости винта на расстоянии b от его оси, вих¬
ревым шнуром с элементарной циркуляцией dГ. Для всей лопа¬
сти винта примем известную схему вихревой пелены, состоящей
из элементарных геликоидальных вихрей, образующих винто¬
вую поверхность с радиально-переменным шагом. Воспользу¬
емся формулой Био- Савара, которая дает в векторной форме
следующее выражение для индуктивной скорости:
1 j к
1 dr . г. , 1 dr
dr
dsx dsy dsz
r\x rly ru
*Theorie tourbillonnaire de l’helice propulsive. Pi. I. Paris, 1929.
25
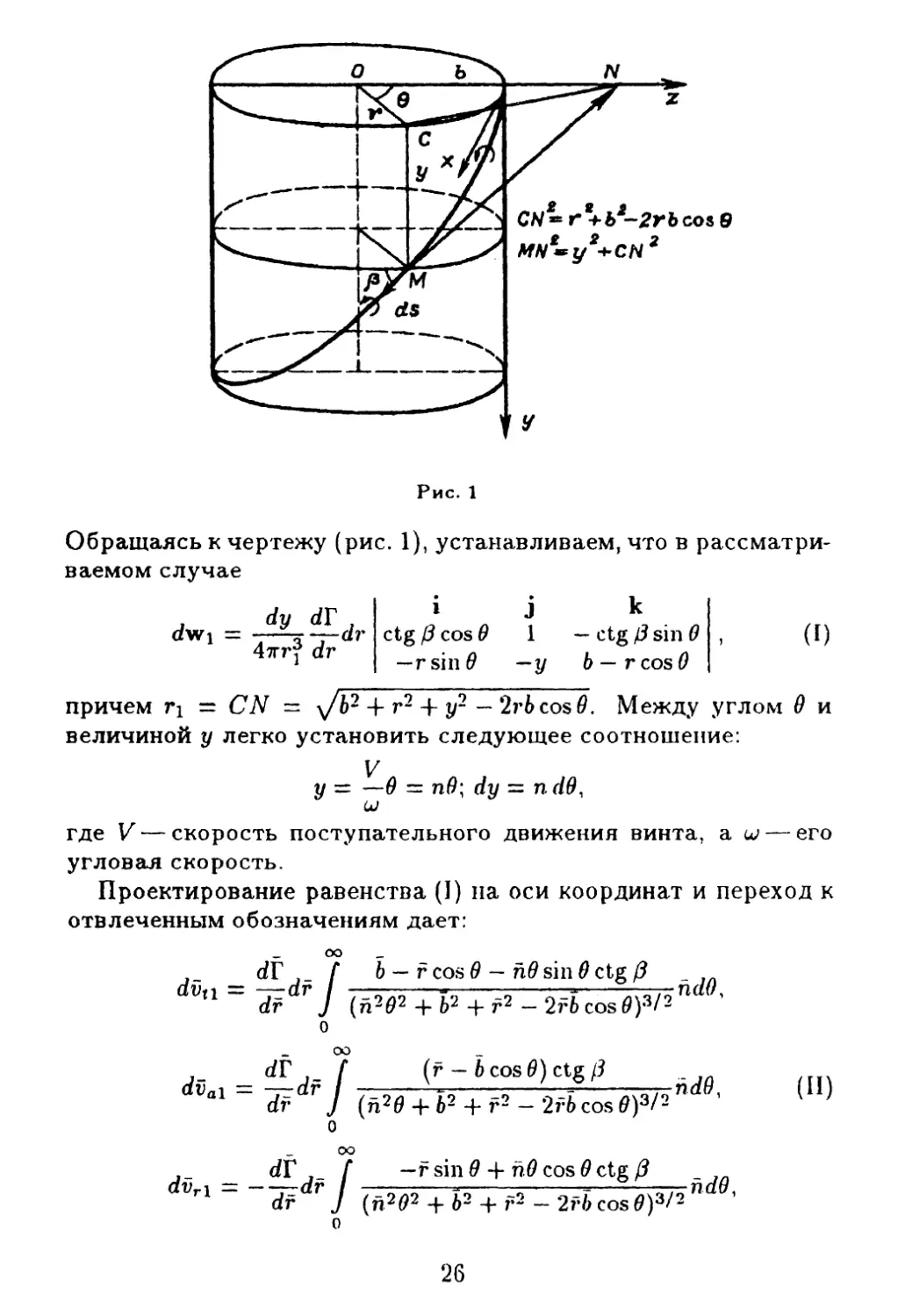
Рис. 1
Обращаясь к чертежу (рис. 1), устанавливаем, что в рассматри¬
ваемом случае
i j k
ctg/?cos0 1 — ctg/?sin0 , (I)
—rsin# — у b—rcosO
причем t*i = CN = yjb2 4- r2 + y2 — 2? 6 cos 0. Между углом 0 и
величиной у легко установить следующее соотношение:
dwi = 1—з “7“
47гг^ аг
т/ = —б = n0; dy = nd9,
и
где К—скорость поступательного движения винта, а — его
угловая скорость.
Проектирование равенства (I) на оси координат и переход к
отвлеченным обозначениям дает:
dv
гг
- dTj- [ 6
dr Г J (n2
6 — г cos 0 — fiQ sin в ctg /3
01 + Ъ'2 + r2 -2гЬсо*в)*/1
ndO,
dva\ = ~df
оо
7
(г — 6 cos в) ctg/3
dr J (n20 + 62 -f r2 — 2r6cos0)3/2
ridO,
(И)
_ dF f —r sin0 + n0cos0ctg/?
rl dr J (n202 -f 62 4* r2 — 2f*6 cos 0)3/2
о
ndO,
26
где
Я’ Я’ Я ыЯ тг ’ 4тгЯ2и/
- Vt - va _ vr
Vi ыЯ’ ыЯ1 иЯ’
Я — радиус винта.
Выражения, стоящие под интегралами (II), обращаются в
бесконечность в точке г = 6 при 0 = 0.
Возьмем функцию
f(p) = 1
где
(п~0~ + г2 + Ь2 — 2r6cos0)3/2
1 1
“ (п202 + 62)3/2 (1 + Р2 - 2Врcos 0)3/2 ’
f _ 6
Р = . Ьм/2' 5 =
(п^ + б2)1^’ (й302 +*2)1/2'
и разложим /(д) = (1 + д2 — 2Spcos0)“3/2 в ряд Тейлора:
f(p) = /(0) + />/40) + §■/"((>) + ^Г'(О) +... (1)
Значения производных, входящих в этот ряд, будут равны
/(0)= 1,
/'(O) = 3Bcos0,
/"(0)= 15В2 cos2 9 — 3,
/"'(0) = 105В3 cos30 — 45В cos в.
Между этими производными легко можно установить следую-
Шее соотношение:
/(*+0(0) = /M(O)B(3 + 2*)coe0-/<t-1)(O)[3fc + i(ifc- 1)], (2)
пользуясь которым получаем
/(IV)(0) = 45(21 В4 cos4 в - 14В2 cos2 0 + 1).
(Эта зависимость устанавливается аналогично формулам для
полиномов Лежандра.)
27
В результате всех указанных преобразований получим для
функции f(p) следующее выражение в виде ряда:
Яр) =
1
63
К-,,
3 /гу
+ 2(б)
1 + ^
5 cos2 9
COS в
3/3 ' "5 (! + И!1!3'2
+
ь2 7
,(i + tF)7/! (l + lr2)
7 cos3 в 3 cos в
УЯ~ L ^3\7/2
+
15
6 U
5/2
+
(I А)
1(1+тН (1+тН
Если в фигурной скобке положить в равным нулю, то коэффи¬
циенты при г/b увеличатся и мы сможем утверждать, что члены
ряда (1) по абсолютной величине соответственно меньше членов
ряда
S(p) = 1 + з£ + 6 (£)2 + ю Q3 +... + rU!
где Ru — остаточный член.
Ряд (IA) сходится равномерно в интервале О ^ 9 <С 7г при
р < 1, при этом
Р =
г
< у,
(й^+б2)1/2 6’
ибо представляет собой не что иное, как разложение функции
[1 + (/>2 — 25/?cos в)]~3/2 в степенной ряд по формуле бинома, при¬
чем в этом разложении сделано приведение относительно р.
Для случая р > 1 мы можем представить функцию f(p) в виде
ряда:
причем
“ D /
Pl (п202+ ^2)1/2' (^2^2 + *=2)1/2-
Оба разложения f(p) и f\{p\) совпадают в точке г = 6 и расхо¬
дятся в этой точке при 0 = 0.
Принимая во внимание разложения (I А) и (3), мы можем на¬
писать индуктивные скорости vt, va и vr на основании формул
(II) при г/6 < 1 в виде
с/Г Г
dvt\ = / [(^ “ г cos 0) — ctg (3 • 7?^ sin 0]/(pi0)nd0,
о
сю
dvai = j(г — bcos в) f(p\0)nd0,
о
оо
с/Г /*
di)rl = ~J=^' I (—?l0cos 0ctg /? + 7~*sin0)/(p10)?~H/0.
(HI)
Аналогичные выражения получаются при т*/6 > 1, только
вместо функции f(piO) под интегралом будет стоять функция
ЛМ).
Найдем скорость Подставляя вместо /i(pi0) ее значение
и выполняя интегрирование самого первого члена:
сю
II
d 77 0
0+г)
3/2
1
h'
•29
в результате получаем в формуле для dvt при r/b < 1
_ , dt dr dt dr 7
Vfl dr b dr b3 J
dr dr f nO sin 0 ctg/3 d nO
_dTdr Г
dr b3 J
3/2
r cos в dnO
M+)T
df dr 7/,
dr b* J \
cos в ■
* Ь;
COS в
1 +
Ml
5/2
+
3i!
+ 2P
5 cos2 в
«♦(г)Г M-tf
+
5 r3
+ 2Ь3
7 cos3 О
3 cos#
Ч*)Г h(f)l
7/2
+
dT dr
~dfT +
(4)
Первый член формулы (4) представляет собой скорость, кото¬
рую мы получили бы, заменив винтовые вихри цилиндрическим
вихревым слоем. Таким образом, второе слагаемое этой форму¬
лы учитывает влияние того факта, что число лопастей конечно.
Это второе слагаемое непосредственно вычислить очень труд¬
но, и поэтому, желая учесть влияние числа лопастей, лучше все¬
го прибегнуть к числовому интегрированию по в, зафиксировав
значения 5,гип. Однако скорость, выражаемая формулой (4),
неполная, так как в этой формуле не учтено влияние вихрей, для
которых г > 6. Эту скорость следует вычислять по формуле
30
dr у
dvt, = — dr <
df
CO
f.2 f J
cos edy-
ctg /?
< [i+(f)T
f sm6d*£ I dTdrJ(b_
I h + (M)213/2 I + df f J \f
пв
ctg 0 sin 6 ) <
)
cos в
5/2
COS в —
dnO
(5)
(см. формулы (3) и (III)).
Заметим, что, принимая схему цилиндрического вихревого
слоя, получаем, что такой слой не вызывает у точки, которая
находится внутри его (6 < г)1 никакой скорости. Полная окруж¬
ная скорость точки, лежащей в плоскости винта, будет равна
fdTd
J df f
dr
j + Д vt,
(6)
r=b
где Avt —поправка на число лопастей.
Переходим к определению скорости dvQ•
Разберем сначала случай b < г. Выполняя в (III) интегриро¬
вание первого члена, получаем
df dr
dval = -гг —
dr г
Ь f cos 0d~
,'~Ч [1 + (?>г
„ dt df [ /, I
3/2
► Ct g/? +
cos 0 ) <
3r
r
cos0
5/2
3 { n0\
+ 5 (t)
5 cos2 0
+
4 PI
.31
Если г < 6, то на оснопании (IA) и (III) имеем:
.j dV dr г f
'li- = cWiT г/
cc#0d&-
Ь
Г " Мт1)
3/2
+
+ ctg/?
dr df
dr Ь
oo
J {I - COS o)
1 +
cos в
5/2
dT <8>
Заметим, что при схеме вихревого слоя элементарная скорость
dvna отсутствует.
Таким образом, для скорости dva можем написать:
У r/f dr J } (IT rdr 3 . _
dv"= J J г?"*"*1'- (!l)
где Дйа—поправка на число лопастей. Первый член формулы
(9) есть не что иное, как индуктивная скорость, которую мы
получили бы, считая, что винт имеет бесконечно большое число
лопастей. Итак, теория винта с бесконечно большим числом
лопастей получается из точной теории как первое приближение,
соответствующее первым членам разложений (4), (5), (7) и (8).
Вычисление поправок Avt и Ava при помощи рядов весь¬
ма громоздко, поэтому для нашего дальнейшего анализа вос¬
пользуемся результатами графического интегрирования, кото¬
рое было применено японским ученым Т. Морийя для нахожде¬
ния индуктивных скоростей. Первоначально напомним прием
вычисления, к которому прибегает упомянутый автор.
Принимая, что ctg/3 % rr и проектируя в точке N скоро¬
сти dvt 1 и dva\, данные формулами (И), на направление, перпен¬
дикулярное относительной скорости W - \Д2 + V~, получаем
dwn 1 = dvt\ sin /? -|- dva\ cos 0 = dvt i
V
-f* dva ]
\Д7+ v- \flr
2 + v
32
или же окончательно
СО _ гу
_ dF j. f (г — 6 cos 9)rb + [r(# sin 0 + cos 9) — 6] K"
duJnl = —a? / — j======(W, (10)
Г о (FV + 62 + r2 - 2rbcose)^\JP + F*
при этом следует помнить, что п = V и, следовательно, nctg/? =
г.
Интеграл (10) был вычислен Т. Морийя* графическим путем
для различных значений V и для разного числа лопастей, при¬
чем для того, чтобы избежать вычислений в точке г . = 6, 0 = 0,
вычислялось отношение, называемое фактором индукции:
dwn
dwnk ~ '
где dwnk есть индуктивная скорость, вызываемая в точке г = 6
прямолинейным вихревым шнуром. Так как в общих случаях
стремление к бесконечности вызвано лишь маленькими отрезка¬
ми вихрей, сбегающих по соседству с точкой г = 6, то порядок
бесконечности будет один и тот же как для прямолинейного, так
и для геликоидального вихря. При этом 1 = 1 в точке г = I.
Как известно из теории крыла,
_ dt dr
dwnk = —
dr f —
и, следовательно,
и>
—(n)
p
где p—радиус нерабочей части лопасти. В работе Т. Морийя
для фактора индукции даны графики, которые он составил пу¬
тем графического вычисления квадратуры (10). Совершенно
очевидно, что семейство кривых V) есть семейство, зави¬
сящее от двух параметров 6 и V = А/7г.
Попробуем, однако, вычислить этот фактор индукции анали¬
тически. Вычисление его произведем не для скорости wn\, а для
скорости vai, что будет несколько проще. Фактором индукции в
этом случае, очевидно, будет величина
dva\
I =
dvk '
*Moriya Т. On the induced velocity and characteristics of propeller // J. Faculty
Eng. Tokyo Imper. Univ. 1932. Vol. 20. N 7. P. 147.
33
где di>k выражается формулой
со
dr. f (f-b)dnO dr df
к ~ df rJ [iаЧ2 + (f - Ь)2]3/2 " df f-b' ( )
0
Формула для фактора индукции будет в нашем случае иметь
вид
со
(г — 6 cos в) ctg Р<1пв
(п7в7 + b7 + г2 - 2гЬ cos 0)3/2 ‘
о
Из этой формулы нетрудно видеть, что фактор I равен единице
в той точке лопасти, для которой г = Ь и в = 0. Действительно,
представим формулу для / в ином виде, исходя из того, что при
очень малых значениях в
v — 6 cos 0 г — 6
(п707 + Ь7 + г2 — 2r£cos0)3/2 [п202 + (6 — г)2]3/2 ’
а именно напишем
/йг
/ = lim <
с—*-0
ctg/3-
[n»e2+(f-6)*]V3
+ /ciT
(f—frcosfl)dnfl
(r-fr)dnfl
CO
или же
I = lim <
t—о
i + '-£VnV + (f-tr-I ^
С ^
(r-fr cos $ )dfi&
n292+b2+r2-2rb cos 0)3/2
i , y/n2e2+(r-fr)2-ng
* fi <*
ctg /3.
В случае, когда г = 6, меняя порядок перехода к пределу, полу¬
чаем (I)f=-h = 1.
Для нахождения приближенного выражения dv'al при b < г
34
воспользуемся формулой (3) и второй формулой (III):
dt dr
d*'al= df Tctg/?
J cosBd—
-J if1
cos2 0 d1J£-
{(b \ f cos 0 i
'*W fe
Ad**
«=>m5/2
о
OO
_ n UO
!G) •/
cosjedм
sjen7/2
L * (i + W
"2/
(i + W
fl2#3\5/2 3
+
_ О OO
Ш ?/
cos3fld^
fiieax9/2
_15 f cos36d!f 15 f cosOd*?
4 (i + *?P)7/2 2/(1 + <^)7/2
/ (i + «JP)
cos 0dAr
+
OO
I/
cos gdS*
(1 + ВД
5/2
- a oo
G) 21/
cos40dS£
nJ93 \ 4/-
* (1 + W
_28 f cos40df f
3 i /1 j. s2#iy9/2 J
{ (1 + W
cos2 Od'-Ф
cos 20df-
+ 4
/
* a + W
8
+
о (l + ^)7/2
+ 15
*-}■
= f fct* Д {1+“‘ 5+“! (?) + 03 (?) +'" }'
(13)
Если в формуле (13) положить cos# = 1, то получим следующий
Ряд:
с df df „Г, 6 /б^2
^ — -гг — ctg /?ч1 + т+ (т) +
аг г I г \ ?• у
!)■*}=
rfr dr ctg /9
dr г 1 — 6/r
так как при cos 0=1
OO _
_ <*Г a f (r-b)dn9 _ dr ctg/? , _ c
Vo1 “ df g ^ J [n202 + (r - 6)2]3/2 df f-Ъ Г “'
0
Перестановка операций разложения в ряд и принятие cos 0=1
35
в рассматриваемом нами случае возможно вследствие равно¬
мерной сходимости ряда, в который была разложена функция
г — 6 cos 0
{п-в2 + г2 + Ь2 - 2 rb cos of!2 '
Таким образом, прибавив и отняв у каждого cosm 0 (где т =
1,2,...) единицу, мы сможем написать:
. dt dr я ( ^ ъ \
*'“' = 5?Tctg'?(rrvf + K“J'
где Rn — остаток, содержащий интегралы типа
cosm в — 1 . пв
I
{(1+т
3*4-1 ^ - »
2 Г
где к,т = 1,2,... Обозначая новые коэффициенты при г/Ь,
(г/6)2,... через В\, Во,... и замечая, что
cos2 в — ~(1 + cos 29),
1 3
cos3 в = - cos 30 + - cos 0, (14)
4 4
1 1 3
cos4 9 — - cos 40 -f - cos 20 4- -,
8 2 8
получаем
- / со sOd^ f cos 0 d ^r-
= 3 / Чл “ / ^ - 1 = «1 - 1.
/ (! + «?) '- / (1 + Ч£)3'-
00 00
11 r cos 2
^2 = — / - n / - 1 = «2 - 1.
Л I . ю
- 15 f cos 20rf^- 3 f cos 20
T/ (i + 4£)v,~*{ (77^
00 -a 00 -o
6 _ 35 f cos3(9105 f cosOd^f
3 = TI (1 + ^r + 1"/ (1 + ^r
f*2
15 f cos Ъв d^j- 105 f cos9d’2f
~»J (1 + W'/=-Ti„ + !*i’/= +
*
Ч-:
0 V • r2 / 0
00
3 f cos 0 d^S-
0 / ^-1 = 03-1.
36
- _ 15 I 21 f cos4flc^ 21^ f
^4 8 | 8 J fi i n3g3\n/- 2 J
cos 26» d'-f
{ (1 + ^)
CO _ oo
7 f cos4Od^f 35 f
6 J (л . n2#iV/2 3 J (i п*е*\9/2
cos 20 d’-*?-
o (i+^r (i+w
cos 2
+
+ 2
/
(i + ^)
— 1 = 04 — 1.
Все интегралы, входящие в выражения для аьа2 и т.д., имеют
вид
г f cos ked^y- _ 2m f cos и du
I 2m4l v / у л nv 2m^i 1
J (l+«2|i) 3 ^ (и2 + г2) a
где
2 = kr/n, и — kO, к, in — 1,2,...
Они могут быть вычислены по следующей формуле:
оо
f cos и du _ c'n A’m(:)
J + “ 1 • 3 • 5 .. .(2?n —
1
1) COS ?// 7Г ’
где /v'm есть бесселева функция мнимого аргумента. В таблицах
даются обычно значения Л’о и A'i, однако 1\т легко вычислить,
воспользовавшись рекуррентной формулой
Кт(~) = Л'т-2(-) - ——;—— ЛГти— 1 (-)-
Итак, все ап могут быть легко вычислены в зависимости от па¬
раметра (кг)/л, и мы при 6 < г сможем найти dv'al по формуле
dr dr _
al = -р — Ctg/?
dr г
i-б/
i ь /ьу ■ AY
- + В,- + Я2 - +йз :
Г Г \Г/ vr/
dV dr I / b
j? f^lcts i ( ?
4
+
+ B3
(14a)
37
или же кратко
iv' -£Л
lVal~ df r-Ь
dr.
(14 6)
Для случая 6 > г получим на основании формулы (8)
1
Ц>+*г)
( 0r cos0 t 3 (r\2
+ Г/1 + ^)5/2 + 2Ш
62
+- n3
6 \bj
15 /f\4
8 \b)
+
5 cos2 9
3/2
1
L(
1 + 4»),/г (i + ^г)
5/2
b2 ) \ b2
7 cos3 0 3 cos 0
LO+er (1 + ^)
21 cos4 9 14 cos2 9
7/2
LO+гГ (*+гГ
+
+
7/3
,n0
)dT'
(>+r)
или же после небольшой перегруппировки и интегрирования
= с‘8^(г)г1+3/
, cos2 9 d~-
■1 + 3 I ^ +
J (1 I П2#2
о P + —
5/2
+
(D
cos 9d¥
f cos° ffdy 9 f
/(^ГГ ° (i + ¥P)
5/2
+
+ Ш’
35 7 cos49d^f 15 f
2 / fl + ^9/2 2 /
35 7 cos4 9 d$r- 15 7 cos29d^-
(Hf)’" 4(. + ¥P)
7/2
38
15
2
cos в d^jr-
Л L 1
7/2
t cos faj
/ (i+fd
15 /f\:
+ tU)
cos bQdlir-
21 ' b-
I
о 0 + r)
11/2
28 /■ cos3 вd*y f cos°0d^
“/ (^W75 « (^r)
00
4
cos 30d^
9/2
cosOdf
(> + rv/!
0
По аналогии с предыдущим можем написать:
+Сз©
dr+Ф ft G) +
1 + ClI +
<R\ 2
ft©
(15)
причем Ci, C2,.. • суть многочлены, стоящие в предыдущей фор¬
муле при тех же степенях г/b, при каких в последней формуле
стоят Ci, С2, ■ • •, но за вычетом единицы. Подставляя вместо
cos20, cos2в и т.д. их выражения из формул (14), получаем
Ci
с -9
2
3 у cos 201
= 5/(Г^)'
cos20rf^
TTi - 1 = С' - >■
ОО
5/
cos ed¥-
00
*-/
cos в d$r
00
-f
12 У
cos39df
i (>+UP)
7/2
(1 + тг)
- 1 = c2 - 1,
s/:
+
39
ft=§
7 f cos 4OdZf 7 f cos 2Od
*1 b+rYr, + ~2j«M?
cos 20 d*£
9/2
oo
■/
cos 29 d^-
{ (> + ^)
7/2
l = Cs-l,
r
C4- 8
21
16
г cos 50 105 f
J 7] + я»»лп/2 + ^
о 11 + -ГГ" o
cos
39 d
пв
+-
105
/■ cos Od^f 35 f cos 39 d^-
/(^W175"'-FfT"
(>+Te)
cos 6 d1^
35 у cos9d*£ f cos9dJ-f
"y/ (i+^r+/(^T.
cos0d*£
- 1 = C4 - 1.
Интегралы, входящие в выражения для Ci, СЧ, известны, и вы¬
числение их не представляет никакого труда.
Формулу (15) можно написать в виде
*ь=§£М1+И)
dt 1\'
сч + с-(д
+ ...
dr г
*dr.
; 16)
Перейдем теперь к выяснению влияния других лопастей вин¬
та, ибо формула (16) дает индуктивную скорость, которую вы¬
зывает лопасть в своих точках.
В случае двухлопастного винта влияние второй лопасти вы¬
разится в том, что во всех предыдущих формулах нужно будет
cos 0 заменить на cos(0 + 7г) = — cos0, в результате чего получим
, d Г dr
di’al = 2— —-7ctS^x
1 / ь
1 + b/f \ r
(17)
40
Точно так же для случая г < Ь
(18)
В случае трехлопастного винта, у которого лопасти образу¬
ют друг с другом углы в 120°, выясним отдельно влияние ка¬
ждой из лопастей (2-й и 3-й) на жидкие частицы, находящие¬
ся на 1-й лопасти, для которых уже была найдена индуктивная
скорость dvai + dvfaj + dv"x, вызываемая у этих частиц самой же
первой лопастью. Порядок обхода лопастей установим в на¬
правлении вращения потока. Влияние 2-й лопасти тогда будет
выражаться формулами того же типа, что и формулы для dv'al
и dv"i, с той лишь разницей, что вместо cos# будет стоять
Для выяснения влияния 3-й лопасти нужно в формулах для dv'a]
и dv"x заменить cos 0 на
В результате влияние обеих лопастей будет выражаться в виде
ряда:
cos
'3
COS -7Г -
1\ 4
(19)
где
а1 = —а 1, а2 — —Яо »
оо __Л оо
105 Г cos3ed^f 45 Г
cos3 Od’lf
а'А — —аА.
41
Лля случая Ь > г точно так же можно написать
+c;(j)
4
+
’♦^c5®-+Cj(;) +
= ^ (20)
dr г - b
при этом
5 7 cos3
c[ = -Cl, C'2 = - bw-c,,
6/ (l+^)7/-
С'г = -c3,
OO _л oo _ _
n, _ 105 f cos3Od^f 35 f cosZed*f ^
4=х/(^гГ‘у. 4'
Общая индуктивная скорость, вызываемая всеми свободными
вихрями винта с тремя лопастями, при г > b будет равна (фор¬
мула (16))
/ j / \ -/ / 1-/ \ ^ 3 1- ^1 0 3 /г» 1 \
(^а1)1>2,з = *>а1 + (rfval)2,3 = -р ——p-rfr = — ~~dr, (21)
а?’ г — о аг г — о
при г < Ь
Wi)i,j,3 = + №",Ь,з = ^ ^ ^Hrfr. (22)
аг г — о аг г — b
В полученной формуле наиболее значительным по величине бу¬
дет первый член, ибо он учитывает скорость, вызываемую вих¬
рями первой лопасти у точек, лежащих на этой же самой лопа¬
сти, т. е. учитывает скорость ’’самоиндукции”.
Переходим к случаю четырехлопастного винта. Будем рас¬
сматривать этот винт как два скрещенных двухлопастных винта
и найдем добавочную индуктивную скорость, происходящую от
2-й и 4-й лопастей (скорость от 1-й и 3-й дается формулами (17)
и (18)). Скорость, получающаяся от 2-й лопасти для случая
г > Ь, будет выражаться в виде ряда, коэффициенты которого
^1,^2)- >dn будут получаться из коэффициентов ai,a2,...,an
путем замены под знаком косинуса величины в на 9 + Ско¬
рость от 4-й лопасти будет получаться путем замены у этих же
42
коэффициентов 9 на 94- §?г. В результате для добавочной индук¬
тивной скорости, происходящей от 2-й и 4-й лопастей, имеем
df df
(<^1)2,4 = 2^Tctg/?
1 + ^2
df 4,4
dr.
dr г — b
Совершенно так же для случая г < 6 можно написать:
(23)
(ВД2,4 = 2^ f ctg/3
[чЧ+*Ф‘+-]®-
_ df 4.4
dr г -Ь
(24)
причем коэффициенты 7 будут получаться из коэффициентов С
путем замены в последних величины 9 на 0 Н- ^ или 0 4- -я* (для
С с нечетными индексами это безразлично).
Для полной индуктивной скорости в случае четырехлопаст¬
ного винта получим при Ь < г
(25)
при этом через 1[ 3 обозначен коэффициент, стоящий при 37^75-
в формуле (17).
Для случая 6 > г
(Л-п \ df 4,з + 4,4 df 4,2,3,4
= Tf -yZb-* = Tf TTb '
гДе /Г,з есть коэффициент при в формуле (8).
Итак, мы видим, что по вышеприведенным формулам можно
найти при заданных значениях г, 6 и тг фактор индукции для вин¬
тов с различным числом лопастей. Вычисление можно провести
с любой степенью точности и составить графики, с которых и
брать значения I.
Для полной скорости va\ получим
7*df Г ) df Г _
6°‘ = J Tf TTldr + J Tf 7=lir'
О v—b
43
где I есть функция от г, 6 и п, меняющаяся при 6 < г как Г,
равная при Ь.= г единице и переходящая в Iй при 6 > г.
Из всего вышеизложенного можно заключить, что основной
формулой для нахождения скорости dva\ при b < г является
формула
где m = 1, 2,...
Влияние второй лопасти получится после замены eos?/?0 на
cos[?ti(0 + 7г)], и, следовательно, в результирующем ряду будут
отсутствовать члены с нечетным значением т. Остальные же
члены удвоятся. Возьмем четырехлопастный винт (два двух¬
лопастных), тогда влияние второй и четвертой лопасти полу¬
чится соответственно при замене cos тО на cos[?n(0 + 7г/2)] и
на cos [т (0 + f71’)]- Нетрудно видеть, что в этом случае в ре¬
зультирующем ряду будут отсутствовать члены, для которых
т = 2(2х +1), где х = 1, 2,..., ибо в этом случае
чему соответствуют значения т = 2, 6, 10,... Эти значения
образуют арифметическую прогрессию с первым членом, рав¬
ным двум, и разностью, равной четырем.
Все члены, для которых т ф 2(2x4- 1), будут в четыре раза
больше, чем в случае однодопастного винта.
Если мы далее образуем восьмилопастный винт, у которого
углы между любыми двумя смежными лопастями равны то
влияние вновь добавленных четырех лопастей можно будет по¬
лучить путем замены под интегралами cos(m0) на cos [in (в + £)],
при этом все выражаются через интегралы вида
cos 2(2х + 1) ^0 4- = — cos[2(2x + 1)0],
cos 2(2х+1) N*)l = -cos[2(2x+ 1)0],
откуда следует, что в ряде, выражающем полную индуктив¬
ную скорость dv'al, будут отсутствовать члены, для которых
ffi = 4(2x4- 1), остальные же будут в восемь раз больше, чем
в случае однолопастного винта. Продолжая указанный процесс
неограниченно и уменьшая Г так, чтобы произведение числа ло¬
пастей на величину Г было неизменно, в пределе получаем
, dt dr
dval ~ ~Г — ctg
аг г
т. е. придем к выражению, следующему из теории Н.Е. Жуков¬
ского. Заметим, что совершенно аналогичным методом можно
доказать, что
dv'b = 0.
Итак, мы видим, что скорости, даваемые теорией Н.Е. Жу¬
ковского, получаются как предельный случай скоростей, рас¬
сматриваемых нами.
Для этих скоростей мы имеем:
dV dr
dvai = — — ctg/?.
dr r
r
Если приближенно положить, что ctg (i = то получим:
г - 1 r/f /-
dva\ — -у —dr,
V dr
или
Для
Г
va=r
vti находим
vt 1 = Г jr.
Из последних двух формул видно, что если на концах рабочей
части лопасти Г — 0, то в этих точках и индуктивные скорости
обращаются в нуль.
ПРИЛОЖЕНИЕ 1
ПОВЕРОЧНЫЙ
АЭРОДИНАМИЧЕСКИЙ РАСЧЕТ ВИНТА
С КОНЕЧНЫМ ЧИСЛОМ ЛОПАСТЕЙ
При поверочном аэродинамическом расчете винта с конеч¬
ным числом лопастей необходимо знание индуктивных скоро¬
стей, вызываемых вихревой системой винта у жидких частиц,
находящихся у лопастей этого винта. Впервые удобную для
практики формулу индуктивной скорости wn\ = >A2i 4- , где
^ti и vai суть тангенциальная и аксиальная составляющие, дал
Т. Морийя.* Его формула имеет вид
1 _
= (26)
Р
где 6 — расстояние точки, в которой вычисляется индукция, от
оси вращения винта; г — радиус элемента винта; I — так назы¬
ваемый фактор индукции, зависящий от г как от аргумента и от
Ь и V (отвлеченная скорость поступательного движения винта)
как от параметров; р—радиус нерабочей части лопасти.
Вычисление фактора I проведено для винтов с двумя, тре¬
мя и четырьмя лопастями путем графического интегрирования
выражения (10). Там же указан способ аналитического нахо¬
ждения величины I для аксиальной скорости dva\.
Замети{Л, что Т. Морийя при вычислении I считает, что ско¬
рость гг„1 нормальна к относительной скорости потока, набега¬
ющего на элемент винта:
W = \Jv2 + г2.
Т. Морийя предлагает получить квадратуру (26) графическим
путем, что, однако, довольно громоздко, ибо подынтегральная
функция обращается в бесконечность при ?‘* = Ь. Кроме того,
отсутствие удобной аналитической формулы для wn\ при раз¬
личных законах распределения циркуляции затрудняет теоре¬
тические исследования в области теории винта. В целях устра¬
нения этого недостатка мы воспользуемся следующим приемом:
так как численные значения фактора I нам известны из графи¬
ков Морийя, то мы можем написать для него интерполяционную
формулу Ньютона:
I = Со 4* C\(v — Г\) + СЧ(г — ri)(7’ ~ ?,2) 4 • • 4 Яп,
где Со, Ci,... —так называемые подъемы функции /, вычисля¬
емые весьма просто; Rn—остаточный член. Полагая г — 77 =
(г — Ь) 4- (г, — 6), после преобразования получаем
I = 1 + Bi(r-6) + S2(f-6)2-f ...
*Mortya Т. On the induced velocity and characteristics of propeller // J. Faculty
Eng. Tokyo Imper. Univ. 1932. Vol. 20. N 7. P. 147.
46
Так как значения / нам известны, то коэффициенты В,- можно
также определять, решая систему п уравнений
п
Ij = 1 + £я,-(г, ~ЬУ' J = 1, 2,...
t=i
Подставляя в формулу (26) вместо / его значение и замечая,
что Г(р) = Г(1) = 0, находим
_ \ fdV df „ }dT, l4J
= TrTTb + bj Tr{f~b)df+
VP p
+ 53/^(f-6)2df+...|. (27)
P )
При вычислении I совершенно достаточно ограничиться пер¬
выми пятью членами.
Лля дальнейших вычислений представим циркуляцию Г в ви¬
де тригонометрического ряда:
Ё = Ап sin пв
и сделаем замену переменного, положив
г = р -f L( 1 — cos 9), b = р + L(1 — cos#'),
где
тогда
dr = L sin 9 d9, r — b ~ L{cos tf7 — cos 9).
Как известно для теории крыла:
. [ dT dr 1 ^ f ,
- П-1 п
cos пв d9
cos 0 — cos 9f
о
__ 7г Ап sin п0'
L ^ П sin 9'
47
Переходим к вычислению следующих интегралов. Интегри¬
руя второй член формулы (27) по частям, находим
1 I
h = ~В2 J jr(r - b)df = В, J Г df =
= B->L
1Г
У Ап J sin n
Osin 9 d9 = BoLA\—.
Далее имеем:
1 _ 1Г
I3 = —B3 J — b)2 = 2B3L2 An j sin n9sin 9 (cos 9‘ —
;-)7T
-cos9)d0 = 2B3L~- ( ^1 costf
1 .. JT
/4 = —B4 J ^-(r — 6)3<ir = 3&i L3 Ип J sin 77^ sin 9 (cosfl'-
-cos9)~d9 = 3B4L3-
Л1 cos2 0' - Л-j cos/?' -f —(Л1 -f Л3)
=-S5 j ~p(r ~ b)4dr — 4B5L4 Л„ J sin nflsin 9 (cos fl'-
p 0
— cos/?)* cW — 2B5L47T
,4j ( cos3 + - cos 0'
-Л2 ^ cos2 0' + i) + “Л3 cos 0' - iЛ4
В результате вместо формулы (27) получаем
Вп "Ь 2 В% L cos 9 -р
7г Ai sin п91 - тг л
»т = т) П —— + L — A\
L ' sm O'
2
48
Для частного случая эллиптического распределения циркуля¬
ции по лопасти все Ап за исключением А\ равны нулю, и мы,
приняв для простоты L = ~, получим
wn 1 = жА\ ^2 -f* — Во 4 Яз cos & 4- ^cos“ в1 4 ^ •
(29)
Вводя сокращенные обозначения, напишем формулу (28) в виде
i sin тгв'
1
где
7Г /
“ I si
sin 0'
+ А1С[ + А2С2 + АгСЬ + А4С'А)< (30)
i). (3'
/2 Г
г* — —
Cl- 2
В2 4- 2S3L cos0' 4- 3R*L2 cos2 0'4 7 4
1
4* 4fisL3 ( cos30' -f - cos0'
5Я3 ^
Я3 + 3B4L cos O' + ABbi2 (jj cos2 O' +
(31)
C’3=^L4(B4 + 4B5Lcos0'y, C\--X-lbBb.
Выведенные формулы тотчас позволяют нам применить к
расчету гребных винтов метод тригонометрических рядов. Дей¬
ствительно, пусть нам даны геометрические характеристики ло¬
пасти и режим работы винта V и пусть требуется найти закон
распределения циркуляции по этой лопасти. Напишем основное
Уравнение связи потока с формой лопасти в виде
Г = CvbWt
или же
Г = BQObW(а 4 |с*о| — До),
где 6 = — хорда сечения лопасти;
W = \/г2 + V2; Boo = (dCy/da)л=Со (близко к тг);
а — геометрический угол атаки элемента; г>о — угол атаки нуле¬
вой подъемной силы; Да = \wn\/W\ — скос потока.
Обозначив для краткости a -f |ао| = 7/, представим циркуля¬
цию в виде тригонометрического ряда и воспользуемся форму¬
лой (30), тогда получим
Задаваясь рядом значений -,0'т и ограничиваясь iv
членами в формуле Г = ^ Ans\nn0\ из формулы (32) легко по¬
лучить т уравнений с т неизвестными, из которых и определим
величины А\, Ло,..., Лш. Зная эти величины, мы легко найдем
индуктивную скорость wn\ в любом сечении винта. Как видно
из формулы (30), эта скорость на концах лопасти отлична от ну¬
ля, хотя Г в этом месте и равна нулю. Заметим, что по теории
Н. Е. Жуковского на конце лопасти при Г(1) = 0 величина гйп\
обращалась бы в ноль.
Указанный нами метод можно применить и к тяжело нагру¬
женным винтам, для чего нужно сделать второе приближение,
выражающееся в том, что в формулу (32) вместо W — у/r~ + V2
нужно подставить
причем и vai взять из первого приближения.
Заметим, что непосредственно из первого приближения сле¬
дует брать только vn, что же касается va\, то его лучше опреде¬
лять, учитывая влияние центробежных сил, которые особенно
большую роль играют для тяжело нагруженных винтов. Для
учета этого влияния воспользуемся уравнением Бернулли так
же, как это делает Н. Е. Жуковский, но в противоположность
Ап sin пв1 = BoobWrj — Boob-j-
7Г / пАп sin n0f
L I sin 9f
откуда
An sinn0'sin0' + Soofry(nsin0' + C^sinfl')
L
= B^bWr) sin O'.
(32)
50
ему мы не будем переходить к винту с бесконечно большим чи¬
слом лопастей. Пусть в бесконечности перед винтом давление
и скорость равны р и W — \Ju2r2 -f V2 и пусть в бесконечно¬
сти позади винта на той же струйке, но прошедшей через винт,
давление будет р2> а скорость W2 = \/(wf2 - vt2)2 + (V + vo2)2,
тогда уравнение Бернулли непосредственно дает
С другой стороны, требуя равновесия между разностью давле¬
ний и центробежными силами, будем иметь
Сравнивая (33) и (34) и замечая, что va\ = ua2/2, получаем
В последних формулах соответствует радиусу струи винта в
бесконечности, гп есть радиус, соответствующий рассматрива¬
емой линии тока в бесконечности. Пренебрегая сжатием струи
и переходя к безразмерным величинам, находим
р W*_ Р2W?
Р+ 2откуда
- V(2Wr2.
(33)
Idp^v^
р dr г
или же
(34)
Лг3 "
Г v ~
(У + vai)vai - vnЫГ2 - + 2 1 -уdr.
f
Если в формуле (35) пренебречь квадратами индуктивных ско¬
ростей, то получим
что соответствует нашим исходным предположениям. Формула
(35) более точная, чем формула (36). Таким образом, мы пер¬
воначально находим vt 1 как бы для легко нагруженного винта и
затем находим vai по формуле более точной, чем (36).
Из сказанного выше следует, что легко нагруженный винт
есть первое приближение; делая ряд последовательных прибли¬
жений, мы сможем произвести поверочный расчет тяжело на¬
груженного винта с Учетом влияния центробежных сил и числа
лопастей. Заметим, что влияние числа лопастей учитывается
вторым слагаемым левой части формулы (32).
Особенностью скорости определяемой по формуле (30),
является то, что она вообще не равна нулю при в = 0 и 0 — 7г,
что соответствует началу и концу рабочей части лопасти, где
циркуляция Г обращается в нуль. Заметим, что согласно тео¬
рии Н. Е. Жуковского, нулевому значению циркуляции Г всегда
соответствует нулевое значение индуктивной скорости wn\. На¬
личие на концах скорости wni ф 0 при Г = 0 создает то явление,
которое носит название концевых потерь и не учитывается тео¬
рией Н. Е. Жуковского.
Обратимся теперь непосредственно к схеме расчета винта.
На основании ряда расчетов, которые были нами произведены,
коэффициенты А\, Ло,. .., Л* убывают настолько быстро, что во
многих случаях достаточно ограничиться тремя коэффициента¬
ми. Приводим коэффициенты А\л Л2,Лз для некоторых из вин¬
тов, поверочный расчет которых производился нами:
Серия винта
V
Ai
M
A3
F2A!Si № 131 ...
0,284
0,251
0,220
0,00358
0,00512
0,006GS
-0,000137
-0,00141
-0,00154
-0,00011
-0,00015
-0,00081
FiAiSj № 1 ...
0,302
0,27
0,0037
0,00533
-0,00087
- 0,0009
-0,00062
-0,0008
F2 Ai Si; h =08 ...
0,275
0,250
0,0031
0,00401
-0,000287
-0,000383
0,00028
0,000208
Построим схему расчета для случая, когда число коэффи¬
циентов Ai равно трем. За относительные радиусы возьмем
г\ = 0,2, го ~ 0,4, г3 = 0,6, ?*4 = 0,8, г5 = 1, этим радиусам
52
будут соответствовать следующие значения 0:
в\ = О, в2- вЯ = 04- ^7Г, 05 = 7Г.
Для случая трех коэффициентов Л, основное уравнение пове¬
рочного расчета винта (см. формулу (32)) будет иметь вид
м
sin2 0 + Boo6-=-(sin0 + С[ sin В)
и
+
+-^2
sin 20 sin 0 -f Вообу (2 sin 20 -f C2 sin 0)
Ju
+
sin 30 sin 0 + Bco^y (3 sin 30 + C3 sin 0)
L/
= BoofcW sin 0.(37)
При расчете винта гораздо удобнее оперировать величиной
Су, а не Воо, и потому в предыдущей формуле лучше сделать
замену:
иОО ч — '-'у »
откуда
Г{у)
и — у
L> со — 1
Ч
где С^} берется для геометрического угла атаки, равного
V
о/д- 7 “ arctg
7 — угол наклона хорды элемента, находящегося на радиусе г,
к плоскости вращения винта, V — безразмерная скорость посту¬
пательного движения винта.. Формула (37) примет вид
Ах
^ - 7Г
sin2 0 + ——b-=r(sin 0 -f Ci)
7/ L
+
(5)
С - 7Г
sin 20 sin 0 Н —6*®-(2 sin 20 -j- Со)
0 L
+
40)
С ' - 7Г
sin 30 sin 0 Ч —6^(3 sin 30 + С3)
0 L
+Д3
где Cj = C'j sin 0, »= 1,2,3.
53
При указанном выше выборе относительных радиусов г бу¬
дем иметь
и, следовательно, 1т/L = 7,85. Величины, стоящие множителями
при {Су9^)/т}у одинаковы на одних и тех же относительных ради¬
усах для всех винтов с одним и тем же числом лопастей, влияние
последних заключено в коэффициентах С*, которые вычислены
нами для двухлопастных винтов в соответствии с графиками
Т. Морийя. Изменение этих коэффициентов в зависимости от V
даны на рис. 2, причем второй индекс при С,- показывает тот
относительный радиус г, для которого берется С*, так, напри¬
мер, С12 соответствует коэффициенту Ci, взятому для в2 = тг/З,
и т.д.
Из рис. 2 видно, что с увеличением V коэффициенты С, убы¬
вают, что вполне естественно, так как увеличение V влечет за
собой увеличение шага винтовых вихрей и при значительных V
эти вихри вблизи лопасти ведут себя почти как прямолинейные
вихри. При V = оо все С, = 0, так как в этом случае вихри
прямолинейны и уравнение (32) должно совпасть с уравнением
теории крыла, для которого С, = 0. Нужно заметить, что, одна¬
ко, уже при V — 0,5 влияние коэффициентов Сг мало.
Взяв = 7г/3, 0з = 7г/2, 04 = 27г/3, получим следующую си¬
стему уравнений:
+ Ао
Н-Аз
0 +
7Г
Ьз-ь2(0 + с32)
L 7/2
1+'^^ + ^] +
1 1П \ /.
= С<‘>62Й^, (38)
7Г -
1 + Т-^Ml+Cis)
+ а2
0 +
°^6з(0 + С23)
L 1?з
+
+-<4з
— 1 +
к С.
(я)
Уз
L г) з
Ы~3 + С’зз)
= С^’&зИЛз, (39)
54
Рис. 2
На
+
А~Л^2
7Г С\
($)
-Z + 7 —М-^3 + Са4)
4 L 7/4
+
+>1з
0 +
1г С
Ы
У 4
L Щ
64(0 4* С34)
= с<;>64ю,^. (40)
основании всего изложенного схема поверочного расчета
55
винта при данном V будет следующая:
1) на выбранных радиусах винта Г{ вычисляются значения
угла 7i наклона хорды элемента к плоскости вращения;
2) на этих же радиусах вычисляются значения угла притека-
ния струй ft по формуле
t?
ft = arctg т;
Vi
3) вычисляются значения геометрического угла атаки =
7, — ft, по которым находятся значения С^ и Су9^/?};
4) определяются значения Ап из системы уравнений (40), по
которым и находятся значения циркуляции Г;
5) определяются значения tUni, va\ = wni cos/? и vt\ = tZvii sin/?;
6) и наконец находятся значения
^ = Р'= Г [(F— Vti) - H(V + e,i)], (41)
L = Г = Г [(V7 + ) + //(г - |.„ )] Г, (42)
по которым определяются а и /? для заданного значения V' = ^ А.
Указанная схема годится, разумеется, при любом выборе от¬
носительных радиусов; изменение ?%• будет отражаться только
на С,*. При нашем выборе относительных радиусов г* = 0,2; 0,4
и т.д. производить вычислений для г\ = 0,2 и ?’5 = 1 не надо,
так как на этих радиусах по условию Г = 0. Приведенная выше
схема расчета при заранее вычисленных С, чрезвычайно про¬
ста, и расчет по ней требует столько же времени, сколько и по
теории Н. Е. Жуковского, а иногда и меньше. Нужно сказать,
что поверочный расчет винта путем задания для каждого эле¬
мента ряда значений а весьма неудобен и при расчете по теории
Н. Е. Жуковского, Действительно, на одном и том же радиусе
г, задают обычно десять значений угла а, для всех этих значе¬
ний вычисляются индуктивные скорости, с косы потока и т.д.,
и, наконец, величину Л; пусть этих величии будет п, тогда для
одного и того же радиуса придется произвести 10п вычисли¬
тельных операций. Если число радиусов взято равным пяти, то
всего вычислительных операций для построения характеристи¬
ки винта нужно будет произвести 50/j. По нашему методу расчет
ведется при заданном V и вычисляются циркуляция, индуктив¬
ные скорости и т.д. на каждом радиусе винта. Если число ре¬
жимов равно пяти, что совершенно достаточно для построения
56
характеристики винта, а число радиусов также равно пяти, то
вычислительных операций придется произвести 25т?.
Если относительные радиусы выбрать гак, как это сделано
нами выше, то выпадут еще вычисления для радиусов гj = 0,2,
r5 = 1, и всего будет 15п операций. Однако при вычислении ко¬
эффициентов Ai циркуляции нужно будет решать систему урав¬
нений (32), но даже в случае четырех неизвестных это решение
отнимает немного времени; выше мы указывали, что во многих
случаях достаточно вычислить только три коэффициента.*
ПРИЛОЖЕНИЕ 2
О НАИВЫГОДНЕЙШЕМ ВИНТЕ
С КОНЕЧНЫМ ЧИСЛОМ ЛОПАСТЕЙ
Известно, что при проектировании гребного винта по вихре¬
вой теории необходимо задаться законом распределения цирку¬
ляции по лопасти этого проектируемого винта.
Однако какой закон распределения принимать в том или ином
случае является нерешенным вопросом. Очень часто применя¬
ется эллиптический закон, которому в тригонометрическом ря¬
ду циркуляции
оо
Г = sin пО
соответствуют
А\ ф 0, Ао = Аз = ... = Ап ~ 0,
при этом радиус любого элемента винта выражается через в
при помощи формулы
г = p-f L(i — cos0),
где р—радиус нерабочей части лопасти; L = — половина
рабочей части лопасти.
Особого интереса заслуживает так называемая ’’наивыгод-
нейшая” циркуляция по Прандтлю, которая при заданной тяге
Дает наименьшую потерю энергии. Впервые вопрос о винте с
наименьшей потерей энергии был поставлен Бетцем в 1918 г.
о оригинале статьи приведены результаты расчета по относитель¬
ной теории” для трех американских винтов, совпадающие с данными экс-
ПеРимента лучше, чем результаты расчета по Н. Е. Жуковскому.
57
применительно к легко нагруженным винтам. Прандтль допол¬
нил работу Бетца и указал, как найти закон распределения цир¬
куляции по лопасти наивыгоднейшего винта и как следует по¬
ступать в случае тяжело нагруженных винтов. Бетц принимает,
что полезная мощность винта выражается формулой
где к — число лопастей.
Потерянная же энергия, соответствующая индуктивной ско¬
рости, равна
Из приведенных формул видно, что Бетц пренебрегает индук¬
тивными скоростями va\ и vti там, где они входят в сумме с
основными скоростями движения элементов винта. Это пре¬
небрежение как раз эквивалентно случаю легко нагруженного
винта. В действительности следует писать:
В своей статье, помещенной в ’’Handbuch der Physik” (1927, Bd 7),
Бетц указывает, что для тяжело нагруженных винтов нужно
пользоваться зависимостями вида (44) и (45), и формулирует
условие, при котором винт с заданной тягой будет иметь наи¬
меньшую потерю энергии. Свою формулировку Бетц базирует
на соображениях, которые никак нельзя назвать строгим доказа¬
тельством условия оптимальности винта. Здесь мы дадим новое
(43)
при этом
W = у/ш2г2 + У2, w„ilW.
(44)
(45)
где
Wt = >/(wr-!/tl)2 + (V + »ei)2) Wnliw,.
58
Рис. 3
и строгое доказательство этого предложения, исходя из совер¬
шенно иных соображений.
Итак, требуется найти условие, которому соответствует ми¬
нимальное значение интеграла (45) при том, что интеграл (44)
имеет постоянное значение. Будем считать, что свободные вих¬
ри уходят в бесконечность, представляя собой винтовые линии
постоянного шага и диаметра. Каждая из этих линий на ради¬
усе г образует с плоскостью, параллельной плоскости вращения
винта, угол
иг - vn
Л = "с‘*г+7^
В действительности винтовые линии представляют собой линии
переменного шага, составляющие в бесконечности с плоскостью
вращения угол
иг - Vi2
/?2 = arctg — ,
V + va2
радиус этих линий также меняется вследствие сжатия струи за
винтом. Предположения, сформулированные выше, эквивалент¬
ны тому, что мы пренебрегаем переменностью шага и радиуса
винтовых вихрей.
Вихревая пелена, образованная в бесконечности винтовыми
вихрями, может быть рассматриваема как поверхность разры¬
ва потенциала Ф того течения, которое имеет место вне этой
Поверхности. Циркуляция, соответствующая элементу винта,
59
находящемуся на каком-нибудь радиусе г, будет раина разно-
сти потенциалов, имеющих место в точках, лежащих на атом
радиусе с разных сторон поверхности разрыва, т.е. будет рав¬
на (рис. 3)
Что касается скорости wni, то считая, что она направлена пер¬
пендикулярно скорости Wi и равна половине скорости далеко
за винтом, можем написать:
(представляет собой производную по нормали). Обозначая да¬
лее для краткости
ц>г- Vt\ - Vtu
можно записать формулы (44) и (45) в виде
где df\ есть элемент винтовой поверхности, описанной в единицу
времени отрезком dr и, следовательно, равный
Пусть имеем два распределения циркуляции Г вдоль лопастей
винта, которые соответственно дают потенциалы Ф' и Ф". Со¬
ставим течение с потенциалом Ф" — Ф' и будем считать, что при
переходе от первого течения ко второму индуктивные скорости
настолько малы, что изменением их можно пренебречь, когда
они входят в сумме с основными скоростями wr и У (напомним,
что применительно к легко нагруженным винтам Бетц пренебре¬
гает самими скоростями, а не их изменением). В этих предпо¬
ложениях потерянная энергия винта, соответствующая течению
Ф" — Ф', будет равна:
Г = Фв - ФА - Ф.
ЫФ
о
60
Нетрудно показать, что Е'" > 0 при всяких Ф" и Ф'. Действи¬
тельно, обозначая для краткости Ф" —ф' = у< и применяя первую
формулу Грииа, получаем
, dip
(Ш
+
(*
dx )
dr + JJj ipV2\l)dT,
где г есть объем жидкости с основанием /ь отброшенной в еди¬
ницу времени вдоль нормали, V2 — оператор Лапласа. Так как
жидкость несжимаема, то
и, следовательно,
//v’Z7f//l ~ JJJ^gra<t>0
Выражение (48) можно написать в виде
к п г к
1 /.
Но согласно третьей формуле Г рииа
II (ф,^ + ф,,^)^ = ///(ф,у2ф,( - ф"у2ф/)с,г-
где
и, следовательно,
У2Ф' = V-Ф" = О
61
откуда
£"'=£,+к-р£//-и^..
1 /i
Рассмотрим течение с потенциалом Ф", полученное следующим
образом. Пусть вихревая пелена опускается вниз как твердое
тело с некоторой скоростью 2w\. Тогда скорость по направле¬
нию нормали к d/i, образуемая набегающим потоком жидкости,
будет равна
ЛФ"
—-— = 2wi cos /?i (49)
ап
и, следовательно,
R
JJ Ф— 2wi jj Ф' cos /?idfi = 2wi j Ф'И^ cos fiidr.
h h о
Так как W\ cos/?i = Vu, to
k „ R
I = pt^JJф'^7dfl = 2pWl J*'Vt'dr = 2pTE'x'
1 h 0
где E[ есть полезная мощность винта, соответствующая тече¬
нию с потенциалом Ф'. С другой стороны, мы имеем
£? = fE// =™tjj ♦'%*== 'г
1 /. 1 /1
где #2 — полезная мощность, соответствующая течению с по¬
тенциалом Ф". По условию полезные мощности винтов должны
быть неизменны, т. е. Е\ = Е2, и потому
Я'" = - Е2 > 0, (50)
откуда
Щ < Е'2.
Таким образом, поток, создаваемый винтом с наименьшей по¬
терей энергии, будет таков, как будто вихревая пеленав беско¬
нечности за винтом затвердела и двиг ается в осевом направле¬
нии со скоростью 2w\.
Еще раз отметим, что необходимым предположением в приве¬
денном нами доказательстве является то, что мы пренебрегаем
62
вариациями индуктивных скоростей там, где они входят в сум¬
ме со скоростями иг и V. Этого предположения не надо делать,
если ограничиться случаем легко нагруженного винта, который
первоначально и рассматривался Бетцем.
Обобщение результатов, имеющих место для легко нагружен¬
ного винта, на винты тяжело нагруженные возможно только при
введении вышеупомянутого условия о вариациях индуктивных
скоростей. Идея и метод приведенного нами строгого доказа¬
тельства условия оптимума тяжело нагруженного винта заим¬
ствована из теории крыла.
Для индуктивных скоростей в плоскости винта, соответству¬
ющих найденному условию, получим
с • о (К + Ьа)(шг — Vt)
Vti = Wi cos ft smft = Wi—— -T— (51)
(V + va)2 + {u>- vty
Vai =Wx COS2 ft = Wi ^2 , 7~~ \2- (52)
(v + t>ai)2 + (wr-vn)2
Из этих двух формул путем исключения легко найти:
ыг(У + и>1)
vt 1 = Ц>1 -2 v , у,}-; Го 1 (53)
и1г- -f (V 4- wi)-
*> о
и~т~
vai = Wi , , (54)
ы-г- + (V + w\ )-
Что касается к. п. д. рассматриваемого винта, то он для ка¬
ждого элемента будет один и тот же, ибо
V иг — vt _ V
^ЭЛ V + va иг V + w\
Переходим теперь к вопросу о распределении циркуляции по
лопасти винта с наименьшей потерей энергии. Если при про¬
ектировании винта заданы его мощность Т, диаметр Д угло¬
вая скорость и и скорость его поступательного движения V, то
кривую распределения циркуляции следует строить, используя
формулу (32) предыдущей статьи, согласно которой, задавшись
значениями во,..., 0'т, сможем написать следующую систему
Уравнений:
’jT^i^<L + Alc<m +
L \ sin в'т
+ АзСзт I = W cos 0т (55)
63
с m| 1 неизвестными, где (?т? -f 1)-м неизвестным является w.
Присоединяли полученным уравнениям формулу для мощности
,Л-. 7Г
m *
Т An {V + wn cos- /J) sill n0'{}> +L-L cos O') sin 0'<I0',
получаем возможность определить w и все Ап.
Выражение для мощности можно также представить в виде
T = LV ^(р+ L)A\ - L^-
7Г
2 +
+wL
Г
YlAn J
n=i i
cos2 ^9 sin пО'(р + L — L cos O') sin O'dO*. (56)
Интеграл, входящий в эту формулу, следует вычислять графи¬
чески или по формуле Симпсона для различных значений V и
п, так как
COS" /? =
[}) -f L( 1 - cos 0)]2
г2-hK2 [р + L(1 -cos0)]2 + V2
Заметим, что при практических вычислениях удобнее всего при¬
нять р = 0,2, тогда L = 0,4. Обозначим значения этого инте¬
грала соответственно со значением 77 через 1\, /2,...,/П1 тогда
будем иметь:
Т — V L
где
А'Лр+L)-
— -f L( Л*| /j -f Л/о “h • • •),/Г i (5 О
4. Ло
л', = |ь л; = — и т.д.
и>1 “
В соответствии с этими обозначениями формулу (35) лучше на¬
писать в виде
* /Еп=1 пл; sin
cos /?та = у
L \ sin О'м
-f А\ C'lrn + ЛоС-jm “h ЛзС3m ) -
(58)
Лля того чтобы точно знать значение циркуляции в пяти точ¬
ках rm = 0,2; 0,4; 0,6; 0,8; 1, достаточно вычислить всего лишь
три коэффициента А\, Л2, Л3, задавшись, например, значением
г\ = 0,4, чему соответствует в\ — 7г/3, затем = 0,6 (#', = тг/2) и
г3 = 0,8 (0£ = 2тг/3).
64
Напомним, что на границах Г = 0, т. е. Г(0,2) = Г(1) = 0, если
радиус нерабочей части р = 0,2. Итак, с достаточной для прак¬
тики степенью точности можно коэффициенты А'т определить
из системы
А\(Си + 1) + .4'2(С21 + 2) + A'3C3l = - cos/?!,
7Г
А'^Су, + 1.) + А‘2С22 + А'3(С3-> - 3) = - cos02, (59)
7Г
Л[(С13 + 1) + ^2(^23 ~ 2) + Л3С33 = — cos/?3-
7Г
Значения С** берутся из графиков.*
Приведенный здесь метод позволяет проверить приближен¬
ные формулы, данные Прандтлем и Гольдштейном для построе¬
ния кривой циркуляции по лопасти винта с наименьшей потерей
энергии.
Заметим, что, найдя из формулы (57) w, мы сможем всегда
улучшить полученные нами результаты, заменив V па V 4- й>ь
что имеет смысл сделать для тяжело нагруженного винта.
Помимо винта с наименьшей потерей энергии специального
интереса заслуживает винт с- наибольшим осевым к. п. д. Как
известно, к. п. д. винта выражается формулой
V Р
V =
где
/
1
Г(г - vt\)dv\ (60)
Т = J Г( К + I’ai )rdr.
(61)
Р
Очевидно, что i) будет иметь наибольшее значение прй задан¬
ном Р, когда Т будет иметь наименьшее значен ие. Таким об ра¬
зом, задача о винте с 7/тах сводится к нахождению минимума
интеграла. (61) при условии, что интеграл (60) сохраняет посто¬
янное значение. Л ля решения этой задачи нам придется ввести
Некоторые предположения, а именно: будем считать, что при
См. оригинал данной статьи [4].
переходе с дуги экстремали (индекс') на дугу допустимой ли¬
нии (индекс") f} Гfv'tldr меняется настолько незначительно, что
jp
можно положить
1 1
J Г'v'ndf = J f^dr, (62)
р р
а также
W[ = W[‘ и Wnl cos fix = Val (63)
(последнее предположение мы делали и при рассмотрении винта
с наименьшей потерей энергии). Заменим, как и в предыдущем
случае, Г = Ф и Wn\ = d$/dn, тогда на основании сделанных
предположений получим
1
т = j Ф (v + ^ COS /?1^ rdf. (64)
Р
Что касается условия неизменяемости тяги при варьировании
Ф, то запишем его в виде
1 1
Р = J Ф'(г - v'ti)df = j Ф"(г - v't\)dv
р р
В силу условия (62) последняя формула дает:
1 1
J Ф,rdr = j Ф"rdr.
(65)
(66)
р р
Рассмотрим, как и в предыдущем случае, течение с потенциалом
Ф" — Ф', тогда мощность этого течения будет равна
1
rrfr,
откуда после раскрытия скобок и учета условия (66) получим
На основании соображений, высказанных выше, можно утвер¬
ждать, что Т"' > 0 при любых Ф;/ и Ф'. Кроме того, применение
формулы Грина дает
1 1
/d*" _ [ (1Ф*
ф' —cos/?irdr= / Ф"—-cos/?irdr,
ап J dn
р Р
и мы в результате имеем
1 1
/dФf f dФ"
Ф'-^-со s/?ircfr + I Ф" -j-- cos 0i г dr -
р
1
/^Ф'
ф,/-^— c°s 0i г dr.
Р
Предположим далее, что течение с потенциалом Ф' обладает
свойством
<*ф/ Л -
-Г—COS Pi = t>ei = const,
dn
тогда будем иметь
i i
/dФt f
Ф"-^— cos 0\ г dr = 2va\ I Фn r dr = I\,
я я
1 1
I Ф' -j— cos 0\ г dr = va\ I Ф 'г dr — U.
Р Р
На основании условия (46) очевидно, что 1\ = 2/э, и, следова¬
тельно,
1 1
/dФff f dФ,
Ф" —-— cos 0i г dr — / Ф' —- cos /?i rdr.
dn J dn
P P
Добавляя и отнимая в правой части этого равенства величины
которые равны между собой согласно условию (66), получаем
1 1
Т'" = J Ф" (v + ^ cos/i,^ rdf - У Ф' (\7 + ~ cos 8^ rdf > О,
Р Р
или же V" = Т" - Г > 0, откуда V < Г".
Итак, из всех винтов, обладающих одинаковой тягой, наи¬
более выгодным в отношении к. п. д. оказывается тот, который
отбрасывает позади себя жидкость с постоянной вдоль радиуса
скоростью Vai .
Совершенно очевидно, что если принять, что wn\ _L W\, то
скорость уц в этом случае будет равна
- * а ^ + Ьа\
= va\ tg/?l = Vai- —,
Г - Vti
откуда
Val(V + Vai) = Vti(r - vn).
Гораздо более строго будет определение vt\ из условия (35),
которое учитывает влияние центробежных сил:
1
/2
l-j-dr.
f
Из этого условия видно, что wn 1 не перпендикулярно \V[. Гели
считать, что wn\ _L W, то тогда получим совсем прос тое равен¬
ство
Vf \ = Va\tgP = Val~. (68)
Графики Морийя вычислены именно при этом последнем пред¬
положении. Для того чтобы улучшить результаты Морийя,
можно поступить так: найдя первоначально vai по графикам
Морийя, найти затем Ьц по формуле (68) и, подставив найденное
значение йп в формулу (35), вычислить va\ в новом приближе¬
нии по формуле
(69)
f’al (V + u"l ) = v{i Г - (>t\ + 2V- J v, —,
p
или же, если va\ — const, то по формуле
v"\iy + Vai) = Vn>' - v‘,l< (70)
68
где що есть окружная скорость на конце винта (?• = 1) (значки '
и " показывают порядок приближения).
Укажем теперь, как найти распределение циркуляции по ло¬
пасти винта с наибольшим к. п. д., чему соответствует по дока¬
занному выше vai = const.
Пусть нам даны мощность винта Т) его диаметр D, его угло¬
вая скорость oj и скорость его поступательного движения V, то¬
гда для случая va\ = const мы можем написать:
T = (V + vt
>al)j
Гг dr;
полагая, что
получаем
= Е'4-
sin п9,
I
T = L(v + va 1) Е*/ sin пв(р + L — L cos в) sin
OdO,
A\(p + L) — A? —
откуда после интегрирования имеем
T=L(V + val)
Эту формулу лучше переписать в следующем виде
Т = L(V + t>ai )i>ai
где
A[(L + p)-l-AU
ж
2'
(71)
А\ = 4i, л; = ^1.
t>ai ~
Лля определения всех А вместо системы уравнений (59) бу¬
дем иметь следующую систему:
А\(Сп + 1)4- Ло(С21 + 2) + Л3С31 + ... — ■—
^i(C12 + 1) + ДС22 + ^:з(Сз2 - 3) + .,. =
L I
7Г COS fli
L 1
(72)
^1 (Сиз + 1) + Л'2(С2з “ 2) + АзГзз + ...— —
L 1
7Г COS /?3 ’
69
так как
Val
U>n\ =
COS p
и cos /? в первом приближении принимается равным
г
cos/? =
у/f2 + V2
Найдя из системы (52) значения
А\ = Л'2 = -^-, = — и т.д.,
Va\ Va\ Val
мы йз формулы (51) легко определим va\ и, найдя затем vti> смо¬
жем cos/? заменить во втором приближении на
а Г - t;ti
cos Р — —, , ■ ■■■
yj(f + Vn)2 + {V -f tial)2
Это приближение следует делать только для тяжело нагружен¬
ных винтов. Зная новые значения cos/?, из системы (72) найдем
новые значения А[} А2> и т.д. Поскольку значения циркуляции
на каждом радиусе г нам будут известны на основании преды¬
дущих рассуждений, тягу наивыгоднейшего винта найдем путем
численного интегрирования выражения
1
Р = J Г(f-vt)dr.
Р
Ло сих пор мы нигде не принимали во внимание влияние про¬
фильного сопротивления, и, следовательно, циркуляция, най¬
денная нами, будет лишь приближенно удовлетворять задаче
проектирования винта.
Для учета профильного сопротивления следует идти методом
последовательных приближений.
Как известно, мощность винта Т с учетом профильного со¬
противления выражается формулой
1 1
Т = J Г(К + va\)rdr + J цТ(г — vxi)rdT\ (73)
Р Р
где ц = сх/су определяется характером дужки, которая ставит¬
ся на заданном радиусе г винта и которую выбирают согласно
условию
Г = CybWu (74)
70
а также в соответствии с условием прочности, беря то или иное
значение для Ь. Таким образом, дужку можно выбрать (а, следо¬
вательно, знать /х) только располагая значением Г(7Т), которое,
в свою очередь, зависит от /1.
Ввиду того, что значение второго интеграла формулы (53)
мало по сравнению с первым интегралом этой же формулы, мы
в первом приближении указанным интегралом пренебрежем и,
следовательно, получим возможность определить приближенно
Г в виде ряда:
Г = ^2 An sin
п
а также найти va и vt.
Зная Г, мы, пользуясь формулой (74), можем выбрать дуж¬
ки, которые необходимы для осуществления этой циркуляции,
и тем самым определить значения fi. Зная же Г', у! и v't (штрихи
показывают номер приближения), мы легко вычислим интеграл
1
Р
Лалее во втором приближении будем решать ту же задачу,
что и раньше, по формуле (71) брать не значение Т, которое
равно мощности мотора, а значение Т' = Т - 7£.
1.2. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
МЕТОДА РАСЧЕТА
КАВИТИРУЮЩЕГО ВИНТА [14]*
В работе рассматриваются общие теоремы для кавитирую¬
щего гребного винта при условии, что кавитационные зоны за¬
мыкаются на конечном расстоянии от его лопастей. Показыва¬
ется, что при этом допущении выражения для сил, действующих
на элементы гребного винта, и вызванных скоростей сохраняют
ту же форму, какую они имеют в случае некавитирующего вин¬
та. Влияние кавитации на силы и скорости сказывается, таким
образом, лишь посредством коэффициентов Су и Сг, значения
которых при развитой кавитации существенно отличаются от
их значений при обычном обтекании.
Проблема расчета кавитирующих гребных винтов связана с
решением двух самостоятельных задач:
1) об общих зависимостях, которым подчиняется кавитирую¬
щий гребной винт;
2) о теоретическом подсчете коэффициентов подъемной силы
и силы лобового сопротивления элементов, из которых соста¬
влена лопасть винта.
Для решения первой задачи необязательно знать решение
второй, ибо коэффициенты Ст и Су, фигурирующие в расчете
лопасти винта, могут быть определены опытным путем для раз¬
личных элементов при различных скоростных режимах и раз¬
ных углах атаки. В этом смысле соотношение между первой
и второй задачей совершенно такое же, как и в случае некави¬
тирующего винта, который рассчитывается по данным коэффи¬
циентам Сх и Су} в то время как теоретический расчет Ст (а
также Су на больших углах атаки) еще не доведен до конца. В
настоящей работе рассматривается только первая задача.
Известно, что кавитация на профиле крыла, обтекаемого по¬
током капельной жидкости, наступает тогда, когда местные да¬
вления на крыле становятся настолько малыми, что в жидко¬
сти преобладающее значение получают силы нормального на¬
тяжения. Капельные жидкости не выдерживают растяжения и
разрываются. Если бы жидкость не испарилась, насыщая про¬
странство внутри воздушных пузырьков, всегда имеющихся в
*В работе излагаются результаты теоретического исследования кави¬
тирующих гребных винтов, проведенного в ЦНИИ им. акад. А. Н. Кры¬
лова в 1945 г.
72
ней, то кавитация или разрыв в жидкости наступал бы теорети¬
чески при давлении р = 0. В действительности пары жидкости
способствуют ее разрыву, особенно при высоких температурах,
и этот разрыв наступает при давлении р < pj, где р<* — давление
паров, способных насыщать пространство при заданной темпе¬
ратуре. Давление р<* мало при низких температурах и сильно
повышается при повышении температуры. При температуре ки¬
пения оно делается равным внешнему давлению, которое скла¬
дывается из атмосферного давления и давления столба жидко¬
сти, находящегося над данной площадкой. Область кавитации
ограничена пленкой поверхностного натяжения, которая ведет
себя как упругая пленка и потому способна выдерживать давле¬
ния большие, чем р<*. Считая жидкость идеальной, а движение
установившимся, мы можем на основании уравнения Бернулли
написать
К — — — ^ t — 9
а “ vk - v/ьк1' * ~ рУ2 ’
где Vk — скорость, соответствующая давлению, при котором на¬
ступает кавитация. Полученное отношение есть критерий, по¬
зволяющий судить о наступлении кавитации.
Во всех точках, для которых Ка < 1 (£ > 0), кавитация от¬
сутствует, и наоборот, кавитация появляется в тех точках, для
которых Ка = 1. Больше единицы число Ка быть не может.
Если жидкость течет впереди крыла со скоростью то ка¬
витация на профиле наступит гораздо раньше, чем число А’а0о>
равное
К - 1 f - -уРсо ~Pd
t'aco “ л=——> Чоо — * тгп >
УПЧоо pV£
Достигнет единицы, ибо на профиле всегда будут точки, в ко¬
торых V > Voo и, следовательно, Ка > Каоо• Опыт показывает,
что на профиле, обтекаемом капельной жидкостью, может обра¬
зоваться кавитационная зона, замыкающаяся как на самом про¬
филе (первая стадия кавитации), так и за профилем при более
значительных скоростях Voo (вторая стадия).
Теорема о силах, действующих
на кавитирующий профиль
в плоском потоке
Существует мнение, что для кавитирующего профиля теоре¬
ма Н. Е. Жуковского о подъемной силе даже в обобщенном виде
73
неприменима. Предполагают, что кавитирующий профиль не¬
льзя заменять системой присоединенных вихрей, поскольку на
профиле происходит какой-то сложный процесс, сопровождае¬
мый разрывом плотности жидкости. То, что профиль нельзя
заменить системой присоединенных вихрей — несомненно спра¬
ведливо, но доказательство теоремы о силах, действующих на
профиль, можно получить, основываясь на двух теоремах: на
теореме импульсов и теореме энергии. Часто в тех случаях,
когда дифференциальные уравнения рассматриваемого явления
не могут быть составлены или проинтегрированы, теорема им¬
пульсов и теорема энергии дают возможность узнать характер
движения в его общих чертах, не вдаваясь в детали явления.
При доказательстве теорем о силах, действующих на кавити¬
рующее крыло или кавитирующий гребной винт, будем считать,
что жидкость идеальна и несжимаема, а движение стационарно.
Кавитационную зону будем считать сначала имеющей конеч¬
ные размеры. Случай зоны, простирающейся в бесконечность,
разберем особо; он вряд ли может существовать в действитель¬
ности. Всюду в кавитационной области будем считать давление
р равным pd.
Случай ограниченной зоны
Для доказательства теоремы поместим профиль D решетку,
ось которой возьмем, для простоты, перпендикулярной напра¬
влению вектора скорости Uqq невозмущенного поступательного
движущегося потока (рис. 1).*
Пусть расстояние между профилями по оси у равно h. Возь¬
мем контрольную поверхность, образованную двумя плоскостя¬
ми, параллельными оси у, и двумя идентичными линиями то¬
ка, расстояние между которыми, очевидно, равно h. Применяя
уравнение расхода, получим (см. рис. 1)
[/„ = 1/2= У, (1)
где U<i—проекция полной скорости Ц на ось х.
*В случае ограниченной зоны кавитации можно не прибегать к те¬
ории решетки, а воспользоваться тем же приемом, каким пользуется
Н. Е. Жуковский для случая изолированного профиля, поскольку в бес¬
конечности в обоих случаях имеют место одинаковые условия. Мы поль¬
зуемся теорией решетки потому, что ее удобно применять и для случая
кавитационной зоны, тянущейся в бесконечность.
74
Рис. 1
Совершенно ясно, что наличие ограниченной кавитационной
зоны никак не может отразиться ни на теореме импульсов, ни
на теореме энергии. Действительно теорема импульсов для оси
у дает:
-У + ph(v2 + Voo)U = 0*, (2)
так как поверхности, взятые в виде линий токов, совершенно
идентичны и, следовательно, интегралы от импульса и коли¬
чества движения, взятые по этим поверхностям, в сумме дают
нуль.
Нетрудно, однако, видеть, что величина циркуляции, вычи¬
сленной для контура abed, равна
^abed — ^ + J Vsds + v2h + J V3ds.
be da
Так как эти интегралы в силу идентичности условий на Ьс и
ad равны по величине и прямо противоположны по знаку, то
Г abed =Ч-Л(^оо + Vo).
"‘Знак плюс стоит в скобках потому, что скорости vcс и v2 направлены
в противоположные стороны (см. рис. 1).
75
С другой стороны, циркуляция по замкнутому контуру abllcfg
Llcda (см. рис. 1), который не пересекается никакими вихрями,
равна нулю, и потому
Г fgLkf + Г abcd = О,
или же
Г fgLkf — + ^2),
но циркуляция Г fgLkf есть вычисленная с обратным знаком цир¬
куляция Г, взятая по контуру кавитационной зоны и по той ча¬
сти контура профиля, которая соприкасается с капельной жид¬
костью. Итак,
г = Л(г)то + t>2),
откуда на основании формулы (2)
У = рЩ». (3)
Переходим к вычислению силы сопротивления X. Восполь¬
зовавшись уравнением импульсов, получим
x = (p-p2)h.
Далее из уравнения Бернулли находим
x = ph?Ldk' (4)
Так как контуры с циркуляцией Г ведут себя по отношению
к бесконечно удаленным точкам как сосредоточенные вихри с
той же циркуляцией,* то в силу симметрии на ab и cd имеем
|р2| = |voo| = М и, следовательно, X = 0. Если расстояние ме¬
жду лопатками увеличивается, стремясь к бесконечности, то v
будет стремиться к нулю, тогда как циркуляция вокруг профи¬
ля Г = 2hv всегда будет оставаться конечной величиной. Если
направление скорости в бесконечности V00 совпадает с напра¬
влением оси аг, т. е. \4о = f^oo, то для изолированного профиля
получим
У = />1^00, Л' = 0.
Это обстоятельство позволяет нам пользоваться при вычи¬
слении Г зависимостью, известной из теоремы крыла:
Г = (4а)
*В теории решеток доказывается, что vcю = — г/2 = Г/(2h). Эта же зави¬
симость получается и для решетки, составленной из дискретных вихрей.
76
где b — длина хорды профиля, а Су берется из опыта при задан¬
ном числе кавитации А'аСо
Случай зоны, тянущейся в бесконечность
Рассмотрим теперь случай, когда кавитационная зона тянет¬
ся в бесконечность, имея там вид полосы шириной е вдоль оси
у (рис. 2). Уравнение количества движения в проекциях на ось
у в этом случае следует записать так:
причем согласно уравнению расхода Uoody = {/г^Уг-
Рис. 2
Из рис. 2 видно, что циркуляция по замкнутому контуру
abclkfgLda равна нулю, а потому
Г^аЫ = -FlkfgL = Гьд/Ы-
Но ввиду идентичности скоростных условий на da и Ьс
Г Ldabcl = Г Ld + Га£ + Г с/ = Г Lgfkl = Г'.
С другой стороны,
jvxdy=rab, / vody — J vody2 + J Vods = Г Ld -j- F*,
a b Ld Ld Ld
77
J v2dy = J v2dy2 + j v2dc = Тс; = Г",
cl cl cl
где de = dy — dy2 есть величина сжатия струйки, имеющей ши¬
рину dy вследствие сжатия потока на величину е.
Таким образом, получим
У = pUoo (Гаъ + Гс/ + Ги) -f pUooFc = pUooF, (5а)
где
Г = Га, + Гс, + TLd + Г, =Г/ + ГС;
Ге = J V2de + J v2de = v^e
Ld cl
(^2 — среднее значение v2).
Формула (5а) дает теорему Н. Е. Жуковского для случая ка¬
витационной зоны, простирающейся до бесконечности. Величи¬
на Г*, появляющаяся вследствие сжатия потока на величину ел
формально может рассматриваться как циркуляция, взятая по
отрезку IL = £, замыкающему контур Lgjkl.
Переходим теперь к определению силы сопротивления X, для
чего составим уравнение импульсов:
- Qoo = -X + J Poody - j p2dy = -X + Ip, (6)
ab cd
где Qoo и Q2 — количества движения втекающей и вытекающей
жидкости. Уравнение расхода для элементарной струйки будет
иметь вид
U2dy2 = Uoody = U^idi/2 + de),
и потому
Qoo - Р J U^dy = pUoo ( J U2dyo + j U2dyn j ,
ab \cl Ld /
Q2 = p I / Uldy, + f UHy2 I =pUool / u*dy+ f Uidy) =
\cl Ld / \cl Ld /
= pUoo I j u2dy2 + J U2dy2 j + pUoo I J Vide + j Unde) =
\cl Ld / 'cl Ld '
— Qi 4- Qc.
78
Отсюда имеем
Ql ~~ Q\ ~ Qt — pUoo
| J Unde + J Un
\cl Ld
где U% —значение заключающееся между значением {/2max =
Uk и значением U2 на линии тока Ьс (или ad).
Что касается импульса давлений, то на основании уравнения
Бернулли его можно записать в виде
Ip = J(Рос - Pl)dy = | j(U* - Ul)dy + J(U2 - Ul)dy +
+ J(U2-Ul)dy
IL
(7)
С другой стороны,
P
2
U2 dy +
\cl Ld
а потому
T _ Q2- Qoc
lP ~ о
J U%dy- J U^dy \ = 2
+ £ / Uldy = ZUooUSe + \u\t. (7a)
IL
Подставив в формулу (6) вместо Qn — Q00 и Ip их значения (7) и
(7а), получим
X = £d/t (ик -UO0jf-)> £eUk(Uk - {/«),
ui V Ukih)-
При увеличении шага решетки, т. е. при h —► 00, vn —*• i>oo О,
выбирая ось х по направлению 14о, получаем
X^^eVtlV-Vnr,), т,= Ц-,
Y = рГКто.
(8)
(9)
79
Таким образом, в рассматриваемом нами случае, как всегда,
мы можем пользоваться формулами
г = ^CybVoo
Что касается силы сопротивления Х) то это есть сила со¬
противления давления, к которой в реальной жидкости будет
добавляться еще сопротивление трения, действующее на часть
контура профиля, соприкасающуюся с капельной жидкостью.
Заметим, что разобранная задача имеет много общего с зада¬
чей о сопротивлении тела, обтекаемого с образованием «мерт¬
вой» зоны (Кирхгоф, Жуковский, Леви-Чивита). Однако в этой
задаче на границе мертвой зоны скорость, в случае неограни¬
ченного потока, равна Voo, а не V* и, следовательно, т] = 1,
что дает для X нулевое значение при всяком конечном е. Та¬
ким образом, мертвая зона, соответствующая сопротивлению,
не равному нулю, не может быть зоной постоянной ширины; на¬
оборот, с бесконечным удалением от тела ее поперечное сечение
должно бесконечно возрастать.
В случае кавитационной зоны величина е будет оставаться
конечной, если Vqq ф V*. Это следует иметь в виду при описании
второй стадии кавитации с помощью схемы Кирхгофа.
Рассмотрим сначала случай слабонагруженного пекавитиру-
ющего винта. Здесь, как известно, с лопастей будут сбегать
вихри, образующие вихревую пелену, которая, если считать ин¬
дуктивные скорости малыми по сравнению с V и иг, имеет вид
вихри этой пелены будут иметь элементарную циркуляцию
Не следует думать, что отбрасывание индуктивных скоро¬
стей, указанное выше и приводящее к тому, что вихревая пеле¬
на совпадает с твердой винтовой поверхностью шагового угла
13, приводит непременно к случаю так называемой оптимальной
Случай гребного винта
с конечным числом лопастей
винтовой поверхности с шаговым углом 0 = arctg Отдельные
80
циркуляции в смысле Ветца. Этой циркуляции соответствует
такое распределение скоростей по лопасти, какое получилось
бы, если бы затвердевшая вихревая пелена двигалась в осевом
направлении с постоянной скоростью. В общем случае циркуля¬
ция вихрей, лежащих на нашей винтовой поверхности, отлична
от оптимальной, а распределение скоростей отлично от полу¬
чающегося при движении твердой винтовой поверхности.
Если мы начнем увеличивать относительную скорость W =
y/V2 +ы2г2, то настанет такой момент, когда вихри, сбегаю¬
щие с лопасти, начнут кавитировать. Это произойдет от того,
что внутри вихревых шнуров давление будет сильно понижено.
Таким образом, мы получим то, что Прандтль называет ’'по¬
лым вихрем”, указывая, что физически вихревое течение имеет
смысл только тогда, когда оно ограничено изнутри ядром конеч¬
ных размеров. Это ядро может быть твердым телом, оно может
состоять из вращающейся жидкости, в которой нет потенциала,
оно может, наконец, состоять и из другой (более легкой) жидко¬
сти, не принимающей во вращении никакого участия, например
из воздуха (полый вихрь). ”Во всех таких случаях мы имеем
дело с течением, в котором уже заранее имеется циркуляция,
вызванная какой-нибудь посторонней причиной”.*
При дальнейшем увеличении скорости начнут кавитировать
не только завихренные, но и другие линии тока, причем основ¬
ной циркуляционный характер движения жидкости сохранит¬
ся, т. е. в жидкости будут существовать винтовые поверхности
(след прошедших лопастей), вдоль которых будет идти кавита¬
ционная зона, причем эти поверхности будут являться поверх¬
ностями разрыва радиальной скорости (рис. 3 и 4). В случае
некавитирующей жидкости эти поверхности можно считать бес¬
конечно тонкими; при кавитации они будут представлять собой
зоны малой, но конечной толщины. Известно, что поверхность
разрыва скорости ведет себя как система вихревых шнуров с
осями, перпендикулярными плоскости, в которой лежит вектор
радиальной скорости Vr. Всюду вне указанных зон движение
будет потенциально, причем при переходе с одной стороны по¬
верхности на другую потенциал будет давать скачок, равный
ф+ - ф- = Г,
гДе Г — циркуляция, взятая по части контура профиля и границе
*Прандтлъ JI. Физика упругих и жидких тел. М., 1935.
81
Рис. 3
Рис. 4
кавитационной зоны (рис. 5). Если кавитационная зона замы¬
кается на конечном расстоянии от элементов лопасти, а опыт
показывает именно такое замыкание, то в бесконечности за вин¬
том мы будем иметь бесконечно тонкие поверхности разрыва
скорости. В дальнейшем будем считать, что кавитация замы¬
кается на конечном расстоянии от лопастей винта. Лля полу¬
чения выражения для сил, действующих на лопасти винта, сле¬
дует воспользоваться, гак же как это мы делали в случае изо¬
лированного профиля, теоремой импульсов и теоремой живых
сил. При применении этих теорем сделаем некоторые предпо¬
ложения относительно массы жидкости, отбрасываемой винтом
в единицу времени. Так как в случае легкого нагружения мы
считаем, что вихревые и кавитационные зоны имеют вид пра¬
вильных винтовых поверхностей, то нам, следовательно, нужно
рассматривать жидкость, заключенную в объеме т между дву¬
мя смежными винтовыми поверхностями, которые простирают¬
ся до бесконечности, цилиндром бесконечно большого радиуса
и двумя плоскостями (П* и Пз), перпендикулярными к оси винта
и отстоящими друг от друга на расстояние, численно равное V.
В этом случае теорема импульсов для числа лопастей к дает
вектор упора винта*
Преобразуя этот тройной интеграл в двойной по формуле Гри-
*Встчинкин В. П., Поляхов Н. Н. Теория и расчет воздушного гребного
винта. М., 1940. 520 с.
т
82
Рис. 5
на, можно записать
где поверхность S\ ограничивает объем г жидкости; п° — еди¬
ничный вектор нормали к элементу dS\. Так как при г ^ R
(R—радиус винта) Ф+ — Ф“ = 0 и течение в плоскостях П1 и ГЬ
одинаково, то интегралы, взятые в этих плоскостях, взаимно
уничтожаются, и останутся интегралы, взятые лишь по винто¬
вым поверхностям площадью S и радиусом R. Таким образом,
поскольку dS = Wdrdt, а интегрирование по времени I соверша¬
ется от нуля до единицы.
Или в дифференциальной форме
что дает подъемную силу элемента.
Совершенно очевидно, что на отбрасывание вышеуказанной
массы жидкости должна затрачиваться определенная энергия,
т*е. винт должен иметь потери, или, иначе говоря, лопасть
Должна обладать некоторым сопротивлением. Эти потери рав¬
ны кинетической энергии отброшенной жидкости:
я
S
о
jdR = pYWvfdr,
к
(10)
Г
83
Преобразуя этот интеграл по формуле Грина и замечая, что
жидкость несжимаема, получаем
5 О
ИЛИ
dE- hpT^-Wdr. (11)
2 an
Обозначая через dR, силу сопротивления всех к элементов
лопасти, будем иметь:
1 1 dФ
(.2)
Эта сила, как следует из формулы (11), направлена по линии
действия вектора относительной скорости W и представляет
собой индуктивное сопротивление элемента лопасти. Проекти¬
руя силы dR и dR, на направление скорости V и скорости wr,
получаем элементарную силу тяги dP, элементарную силу со¬
противления вращению dQ и элементарную мощность dT в виде
dP = крГ(и>г — wni sin /?)dr,
dQ = fc/?r(V + wny cos /?)dr, (13)
dT = kpT(V -f wnx cos f3)wrdr,
где
1 ЛФ
^ni ““ 2 dn
Мы получили обычные формулы теории гребного винта, опе¬
рируя только теоремой импульсов и теоремой живых сил, зная
состояния лишь на пограничной поверхности и не зная явлений,
происходящих внутри этой поверхности. Заметим при этом, что
циркуляция Г = Ф+ — Ф~ есть не что иное, как циркуляция во¬
круг профиля вместе с границей кавитационной зоны, так же
как в случае одного профиля. Это следует из рис. б, из которо¬
го видно, что
Fabcda — “Г LkJgL = Г.
Но в силу идентичности условий на линиях тока ad и Ьс
Tad -f Г be = О, Г ah — Фб — фа — 0, Г cd — Ф+ — Ф“
и, следовательно,
Г = Г abed а = ^ cd = Ф+ ~ Ф” .
84
Рис. б
Скорость шП2 = ^ — нормальная составляющая скорости,
получающейся на поверхности разрыва скорости vr, т. е. на по¬
верхности двойного слоя, или, что то же, на вихревой поверхно¬
сти. Таким образом, эту скорость мы имеем право вычислять по
обычной формуле Био — Савара, известной из гидродинамики.
Все вышеприведенное позволяет высказать следующее поло¬
жение: если вихревые системы кавитирующего и некавитирую-
Щего винтов в бесконечности эквивалентны (т. е. имеют одина¬
ковые Г), то винты динамически также эквивалентны.
Отметим, что на лопастях винтов мы будем иметь в этом слу¬
чае совершенно различные геометрические углы атаки элемен¬
тов лопасти.
Лля случая легкого нагружения можно, как известно, поль¬
зоваться линеаризированным уравнением Бернулли
(V + VaJlV ~ (wr - vn)vtx « Vvai ~ Urvtl =
= Wwni cos(W, wni) = 0,
гДе wni —полная индуктивная скорость. Из этой формулы вид¬
85
но, что wni 1_ W, следовательно,
v*i = Wnj sin/?, иа, = wni cos/?
и формулы (13) примут вид
dP = крТ(шг — Vt^dr, dT = Я:/>Г( V + v0l)wrdr. (14)
Рассматривая эти формулы, можно заключить, что если речь
идет о силах, действующих на винт, то лопасти последнего мо¬
гут быть заменены прямолинейными ’’несущими” вихрями, на
которых имеет место скорость tvni = wn2/2. Только в этом смы¬
сле и можно говорить о скоростях в ’’плоскости” винта.
Таким образом, для реального винта, независимо от того,
является он широколопастным или узколопастным, всегда мож¬
но подыскать такую систему ’’несущих” прямолинейных вихрей,
которая создаст ту же самую систему свободных вихрей, что и
винт, и даст те же самые значения тяги и мощности.
Из формул (10) и (11) непосредственно следует
Эту формулу, описывающую влияние индукции через посред¬
ство индуктивного сопротивления, можно было получить иначе,
сделав предположение, что масса жидкости, отбрасываемая в
единицу времени винтом, протекает между винтовыми поверх¬
ностями с шаговым углом
т. е., иначе говоря, ее можно было бы получить, учитывая вли¬
яние индукции через посредство изменения шага винтовых вих¬
рей, или, что то же, изменения скорости течения жидкости
вследствие наличия индуктивных скоростей. Лействительно,
мы можем написать
п
о
где
R
86
где dS\ = W\drdt, и интегрирование по времени t произвести от
нуля до единицы. Последний интеграл есть количество движе¬
ния жидкости с массой чщ = причем т\ ограничено двумя
смежными винтовыми поверхностями с шаговым углом /?*, ци¬
линдром бесконечно большого радиуса, плоскостью ГЦ, перпен¬
дикулярной оси винта, и поверхностью, точки которой отстоят
от П1 на расстояние W\, если считать вдоль винтовых линий, а
вдоль оси— на расстояние V + vai.
В случае винтов, для которых мало и скорости в беско¬
нечности va2 и vt2 значительны, мы не можем считать, как это
мы делали выше, что шаговый угол вихрей равен /? = arctg^.
Считая, что этот угол в бесконечности равен /?г5 мы должны
записать теорему импульсов в виде
/=1
где F\ — контрольная поверхность, совпадающая с плоскостью
Рассматривая расход через площадку rzdvdrn, где da — по¬
лярный угол, можно написать:
dm = p(V + Va7)r2dcrdr2 = p(V + vai)ridadr\,
здесь vai— скорость, которая была бы в том случае, если бы
радиус вихревой поверхности R\ был равен радиусу винта.
Сделав указанную замену переменного и обычное преобразо¬
вание тройного интеграла в двойной, имеем
где dsi есть элемент кривой, по которой вихревые поверхности,
после преобразования переменных, будут пересекать контроль¬
ные плоскости; ni — единичный вектор нормали к площадкам
Разлагая силу dR на направление скорости W и направле¬
ние, перпендикулярное радиусу винта и скорости W, получим
формулы типа (12) и (10):
Пь
R = кр I TniWidsi, dR = IcpTniWidsi,
о
Wds.
dRi = kpTvfnidr, dR = kpTWdr.
87
С другой стороны, написав для суммарного индуктивного со¬
противления dRt знакомое нам выражение через кинетическую
энергию, получим
Ло сих пор мы не учитывали того обстоятельства, что давле¬
ние р2 в бесконечности за винтом на данном радиусе г2 не равно
Роо—давлению в бесконечности перед винтом. Если эту раз¬
ность давлений учитывать, то теорему импульсов в проекции
на ось винта нужно написать так:
причем интегрирование в плоскости П2 следует распространить
на вихревую область и ее ближайшую среду. Величина роо по¬
стоянна, величина же р2 есть функция от гз и полярного угла <т,.
а потому интеграл давления точно вычислить довольно трудно.
Имея в виду, что влияние его невелико, можно приближенно вы¬
числить этот интеграл для случая осредненного по окружности
потока. В этом случае, как известно,
причем вычисления следует вести способом последовательных
приближений, взяв за первое приближение данные расчета без
учета поправки на разность р^ — ро. Тогда мы сможем найти
величины го/гх и vi2 по формулам:
Итак, если считать, что кавитационные зоны не тянутся в бес¬
конечность, то теорема импульсов и теорема энергии позволяют
установить для расчета винта формулы того же вида, какой мы
имеем в случае некавитирующего винта. Значения величин CV
и Су, входящих неявно в эти формулы, при одних и тех же углах
атаки у лопастей сравниваемых винтов будут различны, так же
как и индукционные скорости.
dTLi = крТ
откуда
Р =
88
Таким образом, кавитирующий винт с заданными профилями
ведет себя, при тех же А, как винт некавитирующий, но имею¬
щий совершенно другие профили; последние дают те же самые
значения Сх, Су, что и кавитирующие профили.
Результаты проведенного исследования позволяют сделать
расчет кавитирующего винта методом вихревой теории. В ра¬
боте показано, что если предположить замыкание кавитацион¬
ных зон на конечном расстоянии от лопасти, то между вызван¬
ными скоростями и нагрузкой элементов лопасти винта сохра¬
няются обычные соотношения вихревой теории. При этом уси¬
лия, действующие на элемент, должны определяться с учетом
кавитационных характеристик профиля. Таким образом, влия¬
ние кавитации на величины вызванных скоростей проявляется
только через изменение коэффициента подъемной силы Су.
В результате оказывается, что при расчете кавитирующего
винта могут быть довольно просто применены существующие
методы вихревой теории, если только известны изменения коэф¬
фициентов подъемной силы и сопротивления профилей, соста¬
вляющих лопасть. Следовательно, для расчета кавитирующих
винтов необходимо знать указанные характеристики профилей.
Следует, однако, помнить, что формула 2Г = CybW справед¬
лива до тех пор, пока справедлива гипотеза плоских сечений,
т.е. теория несущей линии. Последнюю же можно применять
лишь в случаях, когда лопасти винта сравнительно узкие. Это
относится в одинаковой мере как к кавитирующим, так и к не¬
кавитирующим винтам.
1.3. ОБТЕКАНИЕ РЕШЕТОК
ТЕЛЕСНЫХ ПРОФИЛЕЙ
ЗАДАННОЙ ФОРМЫ [18]
В настоящей работе дается способ расчета решетки профи¬
лей заданной формы и выноса, одинаково применимый для лю¬
бых густот q. В основе этого способа лежит конформное ото¬
бражение решетки некоторых овалов с выносом п/2 на дан¬
ную решетку. Для осуществления этого отображения необ¬
ходимо предварительно знать отображение указанной решетки
овалов на решетку пластин с выносом тг/2, которая по способу
Н. Е. Жуковского [1] отображается на решетку пластин с произ¬
вольным выносом. Все эти вспомогательные отображения легко
выполняются и табулируются. Вследствие этого расчет решет¬
ки телесных профилей оказывается простым и мало отличается
по форме от расчета изолированного профиля.
Известно, что в результате наложения поступательного пото¬
ка, текущего параллельно действительной оси £о со скоростью,
численно равной единице, на решетку диполей, расположенных
на этой оси так, что их моменты обращены навстречу потоку,
получается течение около решетки овалов с выносом п/2. По¬
тенциал этого течения имеет вид
ч > t . о nR 7Г(о
F«0) = Со + - sin- — ctg —,
7Г с с
где R — расстояние от диполя до критических точек.
Приняв функцию F(Cо) за отображенную функцию С, возмож¬
но на плоскости С получить решетки частного вида профилей с
выносом п/2. В случае профилей произвольной формы отобра¬
жающую функцию следует взять в виде
оо
c=F(co)+i:^+^)i/r^.
п = О
где |/| и д суть модуль и аргумент ctg(7r£o/0* При обходе вокруг
диполя по какому-нибудь овалу величина д будет изменяться от
нуля до 2п.
Остановившись в плоскости Со на решетке овалов, для кото¬
рых |/| есть постоянная величина (называем эту решетку «вспо-
90
могательной» решеткой), получим
со
£ = Ф0(р, в) + ^(а„ cos пд — 6n sin пг)) 4- ао,
71 = 1
оо
г, = Фо(Р, в) + £(*п cos пд + ап sin пд) -f
п = 1
где р и в — полярные координаты точек овала, а постоянная |/|л
включена в ап и Ьп. В частности, для решетки пластин с вы¬
носом 7г/2 коэффициенты ап и Ьп представляют собой коэффи¬
циенты Фурье для функции Фо- Таким образом, для различных
значений густоты q этой решетки можно составить таблицы или
графики функции i?), приняв длину пластинки за единицу.
Н. Е. Жуковский [1] показал, что внешность решетки пластин с
шагом t и выносом тг/2 отображается на внешность пластин с
произвольным выносом /3 и тем же шагом при помощи формулы
-: = т= =*■(-Ъ± *
+ ^<7'Csin/?, (1)
где С отнесено к половине длины пластинки и при переходе с
верхней стороны пластинки на нижнюю знак перед корнем ме¬
няется на обратный. При гравном нулю, и £, заключенном в
пределах ( — 1, 4-1), мнимая часть z\ равна, нулю. Это означает,
что «первая» пластинка, на которой помещено начало коорди¬
нат системы £, 77, перейдет в «первую» пластинку плоскости z\.
Для этой пластинки формула (1) примет вид
cos[3 ( тг(7 / 0 7rq\ 0 7Гq\
^—In I COS у С ± у COS- у(, - COS- у 1 +
4-у sin /? = £1 cos в 4- у sin /3. (2)
Так как £ известно в зависимости от q и то легко составить
таблицы и графики для функции £i(g, г?) и на основании форму-
лы (2) установить соотношение между точками пластинки z\ и
точками овала, плоскости Со-
91
Концам первой пластины плоскости z\ соответствует некото¬
рое значение равное е, которое будет определяться из условия
Условие (3) будет выполняться в точках (-К, +0) и (—е, —0).
Густота новой решетки будет равна
По этой формуле легко построить графики для функции q{q\, /?)..
В случае решетки телесных профилей с шагом t и выносом 0
можно написать z ~ z\ + Az, где z\ относится к решетке пла¬
стин, a Az — искомая функция, которую в плоскости Со можно
представить в виде ряда по степеням |/|е*1’, что в результате
даст:
где х* определяется формулой (2), в которой С и —известные
функции от q и д. Для этих функций, как указывалось, легко
составить таблицы.
Система уравнений (5) имеет тот же вид, который получается
в задаче отображения изолированного профиля на круг. Если
профиль тонкий и малоизогнутый, то в первом приближении для
х* можно взять x\(q\, i9). Это позволит найти y*[x(q\, i?)] и, сле¬
довательно, найти ап, Ьп, а затем поправку Ax*(gi, 1?)квеличине
sin2 Ц- - sin2 ft
sin
- 40 = 0,
откуда
• щ • а • *q
sm—e = sin/?sin —.
z z
(3)
oo
x* =Xi(q\ 0) + £>» cosm? — bn sin m?) + ao,
n = l
oo
(5)
»• = £<» n cos m3 + an sin nfl) + 6q,
n = 1
Таким образом, во втором приближении получим:
х\ = x^qi, ti) + Ax’(qu i?).
92
Эту зависимость при практическом расчете лучше всего пред¬
ставить графически, выбрав ао так, чтобы начало координат
было в середине профиля. Густота решетки во втором прибли¬
жении окажется равной
Для получения в первом приближении решетки профилей с за¬
данной густотой q можно взять решетку пластин с густотой q\}
равной q — Aq\.
Таким образом, мы получим, что на решетку пластин с выно¬
сом тг/2 и густотой q будет отображаться решетка профилей с
густотой q и решетка пластин с густотой причем выносы этих
решеток будут одинаковы и равны /?. В случае сильно искри¬
вленных профилей нужно сначала взять решетку так называе¬
мых «теоретических» профилей, близких к заданным, и отобра¬
зить их на решетку пластин того же шага и выноса. Это всегда
можно сделать, ибо решетки теоретических профилей строятся
обычно путем отображения их на решетку кругов, которую лег¬
ко отобразить на решетку пластин. Таким образом возможно
установить зависимость координат теоретического профиля от
переменного после чего основные формулы задачи будут
иметь вид
где индексом ”т” отмечены координаты теоретического профи¬
ля.
Решение этой системы ничем не отличается от ее решения в
случае тонкого профиля, для которого за первое приближение
берется пластинка. Если конформное отображение заданной ре¬
шетки на решетку пластин с выносом тг/2, лежащую в плоскости
С, известно, то построение потока около заданной решетки не
представляет труда, так как поток около пластин известен.
Согласно Н. Е. Жуковскому [1], скорость на пластинках в
плоскости С будет равна
q2 = qi + Aqi.
ОО
х = хт(^) + ^(an cos пд — Ьп sin п(?) + ао,
п — 1
00
(6)
У = Ут(^) + sin пд + bn cos пд) + Ь0,
П = 1
Цро sin Ц-j + £ cos
93
На профилях решетки в плоскости z тогда получим
и«)| = на-^- = на
Ж
d£/dti
dx
Id
2
Производные, входящие в это выражение, могут быть найде¬
ны, поскольку х и £ известны как функции д. Так как, кроме
того, в результате конформного отображения на пластинах нам
будет известно местоположение точки, соответствующей задне¬
му острому концу профиля, то определение циркуляции Г, со¬
гласно постулату С. А. Чаплыгина, не представляет труда.
Производные от ctg(?r£o/0 в бесконечности перед и за решет¬
кой овалов равны нулю, поэтому
Таким образом, при переходе от плоскости £о к плоскости с
величина вектора скорости на бесконечном удалении от оси ре¬
шетки остается неизменной, направление же этого вектора ме¬
няется, а именно, он поворачивается на угол 0 + 7г/2. Это тот
самый угол, который составляет ось решетки профилей с осью
решетки овалов в результате отображения.
Из формулы (7) следует
где и —проекции скорости невозмущенного потока плос¬
кости z на оси х, у. Нетрудно убедиться, что система (б) экви¬
валента следующему интегральному уравнению:
о
В случае, когда теоретический профиль близок к заданному,
влияние интеграла мало и его не нужно вычислять с большой
С = ±*0О
- giOM-ir/2)
и, следовательно,
IXОС — v'oo COS 0 — sill 0,
Vco = -(«'со C0S 0 + v'oo S]n P)'
94
точностью. Вследствие этого при малых густотах, когда вспо¬
могательные овалы близки к окружностям, можно вычислять д
на этих окружностях.
Во время окончания этой работы вышла из печати работа
С. В. Валландера [2], посвященная той же задаче, но решаемой
иным способом.
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Жуковский Н. Е. Вихревая теория гребного винта. Статья 3//Избр.
соч. Т. 2. М., 1948.
2. Валландер С. В. Расчет обтекания решетки профилей//Докл. АН
СССР. 1952. Т. 82. Jfs 3. С. 345.
1.4. ТЕОРИЯ РЕШЕТКИ ПЛАСТИН
ПО Н. Е. ЖУКОВСКОМУ И ЕЕ ОБОБЩЕНИЕ
НА СЛУЧАЙ ПРОИЗВОЛЬНОГО ПРОФИЛЯ [23]*
В настоящей работе решается задача об обтекании решетки
профилей произвольной формы, причем в основу решения кла¬
дется работа Н. Е. Жуковского [1] об обтекании решетки пла¬
стин. Приводится подробное решение задачи с доведением ее
до расчетной схемы, а также дается обобщение тех приемов,
которые были получены в [2].
Пусть дана решетка пластин с шагом причем пластины рас-
положенывдоль действительной оси£ и имеют длину 2а (рис. 1).
Допустим, что на эту решетку набегает плоский потенциаль¬
ный поток, текущий в бесконечности перед и за решеткой вдоль
оси г} с постоянной скоростью Vqq. Поместим начало коорди¬
нат в середине пластинки и выясним некоторые общие свой¬
ства вектора комплексной сопряженной скорости У*(С). Функ¬
ция V^(C) должна быть нечетной относительно £, периодической
функцией с периодом t, обращающейся в постоянную величи¬
ну Vqo при т) = ±оо. На самих пластинках мнимая часть этой
функции должна быть равна нулю. При f = ±а эта функция
должна обращаться в бесконечность, оставаясь ограниченной
во всех остальных точках полосы, заключенной между прямы¬
ми £ = ±t/2. При /, стремящемся к бесконечности, К*(С) должно
стремиться к значению сопряженной скорости для изолирован¬
ной пластинки. Эта скорость, как известно, равна
V*(C) = «-*'» = -tv соС/х/С5^,
где С = £ + tty —комплексная координата. Нетрудно проверить,
что указанным условиям удовлетворяет функция
Решение Н. Е. Жуковского
4"
а
Рис. 1
(1)
•Печатается с сокращениями.
96
Рис. 2
Действительно, обозначая (рис. 2)
|5| =
с • я-С
S = Sin :
t
■
sin
t
= УС
7Г a
smT’
tgv?
COS'1
*1
t ’
ITT}
получаем
5-5a = |5i|e*>*; S +Sa = |S2|e^,
\S\
u — IV = —tv
#1Ш
+ г sin (^p —
cos ^ip —
<Pl + <p 2
2
+
¥>1 +^2
(2)
При ?7 = +0 и 0 ^ |£| ^ a на верхней стороне пластинки р =
У>2 = 0, <р\ = 0 и потому
у*(0 = «(*. +0) = -
too sin ^
/• 2 я-a • 2 *£
Vsm т ~s,n т
При замене f на — £ скорость будет менять знак. С нижней сто¬
роны 0 < |£| < а, <р — <р2 = 0, Ч>\ — —я имеем
sin^
u(£, -0) = «оо
^/sin2 ™ — sin2 Ц
При |£| > а, т) = 0 составляющая и равна нулю и линии тока
°ртогонально пересекают ось При ц = ±оо <р = <р\ = <ръ =
±1г/2 и потому
У* = —п.’со, т. е. и = 0, v — Vqq.
97
Переходя с одной пластинки на другую, т. е. заменяя £ на
£ + обнаруживаемого знаки у sin ^ и у радикала меняются
одновременной функция V*(Q) возвращается к своему значению.
Если на решетку набегает поток, текущей в бесконечности со
скоростью Voo так, что Uoo = Voo sin 0, Voo = Voo cos 0У то ком¬
плексная сопряженная скорость будет равна
Н. Е. Жуковскому принадлежит плодотворная идея принять
функцию F(С) за отображающую функцию. Так как мнимая
часть этой функции на контуре пластинок постоянна, то при
конформном отображении на плоскости z\ = F(С) снова полу¬
чится решетка пластин. Исследуем эту решетку.
Приняв в формуле (4) постоянную интегрирования равной
где А = {ira)/ty £ = (/а. Заменяя в выражении (5) С на С + I, т. е.
переходя в плоскости £ с одной пластинки на другую, получаем,
с учетом изменения знака радикала, что z\ прирастет на величи¬
ну Дz\ = или Ах\ = tsin/3, Ау\ = t cos/?, откуда видно,
что в плоскости мы получим решетку пластин с выносом — 0
(рис. 3), причем ось £ при преобразовании поворачивается от¬
носительно пластинки на угол тг/2 — 0 против часовой стрелки.
Для точек самой пластинки имеем
V*
sin Zf
(3)
— = sin 0 — cos 0
оо
Интегрирование выражения (3) дает
(4)
^lncos^
j-, будем иметь
- 1 , (6)
98
Рис. 3
где верхний и нижний знаки соответствуют верхним и нижним
точкам. Эта величина достигает максимума при f, равном не¬
которому £, определяемому из условия равенства нулю произ¬
водной от х\ по
Приравнивая нулю указанную производную в точке £ = е,
получаем
sinAe
/-V ■■-"i'-Trf = tgft
± Vsin А — sin Af
откуда
|sin Ае| = sin sin А. (8)
Это условие будет выполняться в точках (+£, -fO) и (— еч —0),
как это видно из формулы (8). Ллина пластинки 21\ в плоскости
Z\ окажется тогда равной
21\ = xi(+£, +0) - х’ 1 ( 6, -0) = 2?sin/? +
2tcosf3. cos Хе + \/cos2 Ac — cos2 A
+ In г ,
7Г COS A
откуда густота новой решетки определится формулой
2/i 2 Л _ . Л cos Хё + \Zcos“ Хё - cos- А
01 = — = — [ Xs sin р + cos р In
t 7Г \ cos А
(9)
Начало координатной системы ху совпадает с серединой пла¬
стинки.
99
Действительно, вычисления дают:
+0) + ^i(—£, —0) = 0,
откуда
zi(+e, +0) = —ari(—е, -0) =
Решетка пластин с нулевым выносом
В случае решетки с нулевым выносом скорость и — iv долж¬
на быть периодической функцией с периодом it, обращающейся
в tioo — ivоо при £ = ±оо. На самих пластинках мнимая часть
этой функции должна быть равна нулю. При £ = ±а эта функ¬
ция должна обращаться в бесконечность. При неограниченном
возрастании it скорость и — iv должна стремиться к значению
скорости для изолированной пластинки.
Нетрудно видеть, что указанным условиям удовлетворяет
функция
Выбирая постоянную С так, чтобы при £ = а второе слагаемое
обращалось в ноль, находим
U — IV — Иоо — IV оо
и — iv = Uoo — IVoo
y/stflf -sh2¥
Положив tioo = Voo cos/?, t/oo = Voo sin/?, получим
и — IV =
и — IV
оо
Отсюда, интегрируя, имеем
arccos
c.h Л С
chA ’
(Ю)
100
Рис. 4
где А и С имеют тот же смысл, что и раньше. Заменяя в этой
формуле £ на £ + И, т.е. переходя в плоскости Q с одной пла¬
стинки на другую, получаем
^ v. .ч t sin ft ch(A<T + <тг)
z\((, + it) — cos /?•((,+ *0 Ч arccos — =
7Г cli A
_ _ .. t sin ft ( ch \iQ
— cos ft • (C + it) 4 arccos ( —-
7Г V ch A
. t sin ft cliA( -Q
— cos ft 4 arccos — + tie и.
7Г ch A
Таким образом,
~i« + *0 - -i(C) = ite~i/},
и, следовательно, в плоскости z\ мы имеем решетку пластин с
выносом — ft (рис. 4).
При г} = 0 формула (10) дает
t sin/? ch А£
xi = £ cos p 4- ■ arccos —.
7Г ch A
(ii)
Эта величина достигает своего максимального значения при £,
Равном некоторому £, которое будет определяться из уравнения
sh Аё = cos ftsh X = cos /?sh — <7, (12)
101
аналогичного уравнению (8). В соответствии с этим для густо¬
ты решетки в плоскости z\ будем иметь
2 Л . chAA /10
qi = — Аб: cos р -f sin р arccos --- . (13)
7Г \ cli Л /
Отметим, что все вышенаписанные формулы можно получить
из формул предыдущего раздела путем замены t на it и Р на
pi/2 - Р. На основании формулы (13) легко построить графики,
показывающие изменение q\ в зависимости от Р и q = (2а)// =
(2А )/*.
Построение потока
В случае решетки с нулевым выносом комплексная скорость
будет определяться формулой, получающейся из формулы (1)
путем замены t на it:
ch ^
и - П> = «00 - П'оо (14)
' /
V^f-sh2?
Применяя при отыскании скорости циркуляционного потока те
же рассуждения, что и при выводе формулы (1), получаем
ch^-
Vr*(C) = щ - ivr =А «==, (15)
где А — некоторая постоянная. Для отыскания этой постоян¬
ной вычислим циркуляцию вокруг пластинки, считая ее поло¬
жительной при обходе контура против часовой стрелки:
Г = <f V*(C)dC = -2.4 / - —=
/ . sh* +а
= -2Л-агс5т —
= -2 At,
откуда А = —Г/(21) и, следовательно,
гТ ch^-
Мг — IVг - — -
2<
102
(16)
0з этой формулы, в частности, вытекает, что в бесконечно¬
сти справа и слева от оси решетки поток течет со скоростью
±Г/(2*)- Полная скорость течения около решетки без выноса
будет выражаться формулой
и - iv = Uoo — г— 1 ■■ JL: —У . (17)
2^-sh2^
t
Так как решетка пластин с выносом /? и густотой q\ получа¬
ется из решетки с нулевым выносом путем конформного отобра¬
жения при помощи формулы (5), то скорости на плоскости z\
будут определяться по формуле
и _ iv — Voosh^ - ^ch-^
их - ivi = = - ========= . (18)
<*С cos/?y sh2™ — sh2^* — sin/Jsh^-
B точках С = знаменатель этого выражения обращается в
ноль, что соответствует передней и задней кромкам пластины в
плоскости Z\ .
Для того чтобы скорость в точке -f£ была конечна, необхо¬
димо, согласно постулату С. А. Чаплыгина, приравнять нулю
выражение
. о ж а о же . же Г же _
sh'T ~sk~T - '”shT ■ TtchT = °'
откуда для циркуляции получаем
2< / / 2 Л-а ,тге 7ге\
r = Sf(i“”\/sh T-sh-y-''~>bTj'
Подставляя вместо shy1 его значение и производя вычисления,
находим
Г - —2t th— V°° CQS P ~~U°° sin ^ -
2 ^1 - th2^ sin2 /?
= . (.9)
2 ^/l-th2f sin2/?
Покажем, что величина a — /? есть угол атаки пластинки в
Плоскости г,. Для этой цели выясним, как преобразуется в
103
результате конформного отображения скорость в бесконечном
удалении от оси решетки. Имеем
«loo - ivloo = (и - iy)c=00(rfC/^i)c=co = (« - iv)(=Qoet0,
uioo + ivioo = (и + iv)(=Ooe~t0, (19a)
откуда следует, что вектор скорости поворачивается вме¬
сте с осью решетки на угол — /3 и не изменяет относительно ее
своей ориентировки. Так как в результате отображения ось со¬
ставляет с направлением пластинки угол 7г/2 — /3 (см. рис. 4), то
угол атаки а\ в плоскости z\ будет равен а — 0. Таким образом,
о th^
Г = -7Г -2/1^00 sin«1 — ■ т- -2 -== = Гиэх(дь /?), (20)
^l-th2^sin2iS
где Гиз есть циркуляция вокруг изолированной пластинки, рав¬
ная —7Г • 2l\Voo sinai. Поправка на влияние решетки, как видно
из формулы (20), зависит от gi и 0, причем густота qi связана с
густотой q формулой (13).
Решетка овалов и ее отображение
на решетку профилей
Известно, что внешность окружности радиусом Я, лежащей
в плоскости Со, отображается на внешность телесного профиля,
лежащего в плоскости г, при помощи формулы
==^+tajLi^- <21>
П — 1
Таким образом, разность z — Со разлагается в плоскости кру¬
га в ряд по степеням 1 /Со- С гидродинамической точки зрения
функция 1/Со есть потенциал диполя, для которого окружности
являются линиями равного значения модуля |Со|- В случае ото¬
бражения решетки профилей на решетку некоторых овалов (ха¬
рактеристика которых дана ниже) того же шага и выноса фор¬
мула (21) должна быть обобщена. Ее непосредственное обоб¬
щение получается использованием выражения для потенциала
решетки диполей, которое имеет вид
Жо) = ^с«А
где г = teif}.
104
Таким образом, разность z — Со разлагается в плоскости ова¬
лов в ряд
ап -f- ibn
-г(Со) - Со = У/
/г
п = 1
где
/i(Co) = |/i|ew=th
т
Разложение периодической на решетке аналитической функции
F(Co) в ряд по степеням cth^2- можно обосновать совершенно
так же, как обосновывается разложение F(Со) в ряд по степеням
1/Со в случае изолированного профиля. Для этой цели следует
воспользоваться формулой
/
cth^^-dCo = 2ir,
г
из которой непосредственно вытекает формула для аналитиче¬
ской функции, принимающей на контуре значение F((o)> а в бес¬
конечности перед и за решеткой имеющей постоянные значения,
равные по величине и противоположные по знаку (обобщенная
формула Коши):
ПСо) =
и
Так как
г и <о z z Со 2а
/1 = til = MlTTgoCch <>0 = ?0 = ,
г 1а т
то действительная и мнимая части функции будут равны
sh '2nqo£o sin2nq0rj0
(f — = —, = = —. (11)
ch 27T^oCo ~ cos 2irqofjo ch 27T7o£o — cos 27rgo^o
Поэтому
(23)
sh 2nqo£0
Возьмем овал, на котором |Д| постоянна, так что
+ ’Ф2 = Л2 = const.
Подставляя вместо qз и V’ их значения и определяя А из условия
6 = £отах = 1/2 при щ = 0, получаем
. сЬ2тгдо£о ch 2д</оСо
cos2irq0T)o = —— = —: (24)
ch 27rg0^omax ch
105
и, следовательно,
\ С1Г27Гд0£о - 1
Из формулы (25) непосредственно вытекает, что
(25)
(26)
и, следовательно,
th 27rg0£o = cos д th 7rq0.
(27)
Так как на основании (24) и (26)
cos 27гдот?о =
1
cos ^ \/l + ch27T(/o tg2 д
то
tg 27гдо^о = sin д sh 7Г7о-
(28)
Формулы (27) и (28) позволяют непосредственно выразить £о, Щ
как функции д и параметра 70.
Если внешность рассматриваемой решетки овалов отобража¬
ется на внешность решетки пластин без выноса, лежащей в плос¬
кости С, то в этом случае
при этом постоянные |/i|n включены в коэффициенты ап и in,
а знак волны (тильда) показывает, что все линейные величины
отнесены к размеру 2£отах- Так как ?)о(^, (1о) есть функция из-
вестиая, то коэффициенты ап и Ьп легко определяются как коэф¬
фициенты тригонометрического ряда. Отсюда непосредственно
вытекает возможность найти £ как функцию г) и 70, затем найти
7 как функцию 70 и, наконец, вычислить значения функций
оо
i = €о(0, 9о) + ^(an cos пд + bn sinrn?) 4- а0,
П = 1
ОО
О = V0(i9, д0) + 5^(Ьп cos пО — а„ sin ni?) + bo,
Mo ch 7rg0^i
max
106
sh irq0i — cos f3 sh тгдо^тах = cos в sh ^.
После этого составление функции ij, устанавливающей coot-
тствие точек решетки пластин с выносом 0 и решетки овалов,
; представляет труда. Лействительно, на основании формулы
1) имеем
xi = £ cos 0 + sin 0F{d, д0), (29)
>ичем значения густоты q\ зависят от 0 и qo*
Решетка телесных профилей
В случае решетки телесных профилей с шагом t и выносом 0
эжно написать:
z = Z\ + Az,
[е z\ относится к решетке пластин, a Az — искомая функция,
•торую в плоскости Со можно представить в виде ряда по сте¬
пям cth^. В результате получим
х = хi(t?, 0, до) + ]Г(а„ cos ml + />„ sin ml) + a0,
4 = 1
00
у = ]T(fcn cos ml — cin sin ???^) -f bo,
и = l
e i\ известно и определяется формулой (29). При расчете
офиля удобнее иметь дело с координатами х и у, отнесенными
)азмерам хорды профиля Ь. Так как густота решетки д равна
, то ясно, что
£ ~qo - У - flo
х = 7 = х —, У=т = У—-
од од
стема уравнений (30) имеет тот же вид, что и в задаче отобра¬
ния изолированного профиля на круг. Эту систему следует
хктически решать методом последовательных приближений,
с в случае изолированного профиля. Если профиль тонкий и
яоизогнутый, то за первое приближение можно взять х % х\.
к как xi —известная функция г), 0 и до, то в первом прибли-
*ии станет известна функция </[x(i?)], разлагая которую в ряд
рье, легко найти коэффициенты ап и Ьп и затем определить
В оригинале статьи приведены графики величин £(<j), q0), q(qo)*
* 9о)> Я\((3, go).
107
поправку Ах к величине х\. Таким образом, во втором прибли¬
жении будем иметь
z2 = xi(^) 4- Azi(tf).
Построив график этой функции и определив по нему хтах и
£min, можно найти густоту решетки во втором приближении по
формуле
42 = 9i + Д?ь
где q\ как функция от qy /3 известна (13). Для получения во вто¬
ром приближении решетки профилей с густотой q2, равной q,
следует взять решетку пластин с густотой q — Aq\ и снова най¬
ти Аж как функцию д. Для получения следующего приближения
надо разложить в тригонометрический ряд функцию у[хо{^)\ и
найти поправку Ах2) и т- Д- Таким образом, в процессе последо¬
вательных приближений придется находить поправки Aq и соот¬
ветственно с ними исправлять густоту получающихся решеток
так, чтобы окончательно получить решетку с заданной густо¬
той q. В случае сильно искривленных профилей нужно снача¬
ла взять решетку так называемых «теоретических» профилей,
близких к заданным, и отобразить их на решетку пластин то¬
го же шага и выноса. После этого основные формулы задачи
будут иметь вид
00
х = хт + ^^(an cos пд + Ьп sin ml) + ао,
п:1 о»)
У = Ут 4- У^(Ьп СОs ml - а„ sin ml) 4- b0,
n = 1
где индексом ”т” отмечены координаты теоретического профи¬
ля. Решение этой системы ничем не отличается от ее реше¬
ния в слу'чаё тонкого малоизогнутого профиля, для которого за
первое приближение берется пластинка. Для получения реше¬
ток, составленных из так называемых «теоретических» профи¬
лей, можно Использовать отображающие функции, найденные
для изолированных профилей. Впервые это было осуществле¬
но Э.Л. Блохом [3] применительно к отображению внешности
решетки овалов, близких к кругам, на внешность решетки про-
^ дальнейшем прием Э. JI. Блоха был усовершенствован
Е. И. Умновым [4].
108
Если за исходную решетку принять решетку пластин, то к
построению решетки, составленной из теоретических профилей,
м0жно подойти, исходя из следующих рассуждений.
Известно, что внешность изолированной окружности ради¬
усом R отображается на внешность пластинки длиной 4R при
помощи формулы
С — Со + Д2/Со,
причем сама пластинка оказывается расположенной на действи¬
тельной оси. Если желательно получить пластинку, наклонен¬
ную к оси £ под углом /?, то достаточно воспользоваться пре¬
образованием
z\ = С cos /3 — sin 0 \Ja2 —С2 =
= + i sin 0 (С - \/C2 ~ a2) = Co + Я2/Со,
причем
Со = <o'-i0 = e-^(C + v/C73^)/2.
Функция, отображающая внешность окружности на внешность
профиля, имеет вид
г = 21( C) + F(l/Co).
откуда следует, что функция, отображающая внешность пла¬
стинки, лежащей в плоскости С, на внешность профиля, может
быть взята в виде
= г, (С) + F[isin 0 (С - n/C2 - «2)1 = + F(z[). (32)
Для изолированных профилей вид функции может счи¬
таться известным. Заметим, что функция
z[ = isin 0 (С - \/С2 - а2)
гидродинамически представляют собой потенциал возмущенно¬
го движения, вносимого пластинкой в поступательный поток, на¬
бегающий на нее под углом атаки 0. В случае отображения
вНешности решетки пластин с шагом t и нулевым выносом на
рещетку некоторых телесных профилей с шагом t и выносом 0*,
Не равным 0, можно, обобщая формулу (31), написать:
z = :i(Q + F(z[)<
где
/ • Ai
= sm0 I -arccos^^ + H I,
109
Функция z[ есть периодическая функция £ с периодом /, сле¬
довательно, функция F(z[) есть также периодическая функция с
тем же периодом. Контуру профиля соответствует контур пла¬
стинки, для которой у\ = 0, 7/ = 0, и потому точки профиля
определяются комплексной координатой:
Если взять одно и то же значение х\ для изолированной пла¬
стинки и для пластинки в решетке, то ему будут соответство¬
вать разные значения £ и, следовательно, разные значения z\,
выражаемые равенством
Так как функция F(z[) отличает профиль от пластинки, то
разным z[y при заданном яь будут соответствовать разные про¬
фили. Таким образом, взяв функцию для случая изоли¬
рованного профиля и подставив вместо z\ (£) его значение (33),
мы получим решетку с некоторыми телесными профилями, не
совпадающими по форме с изолированным профилем. Подби¬
рая должным образом изолированный профиль, можно постро¬
ить профиль в решетке, близкий заданному.
Так же, как и в случае изолированного профиля, система (31)
эквивалентна интегральному уравнению
ках, для которых, при изменении <р через равные промежутки,
точки на контуре профиля распределяются весьма неравномер¬
но, что затрудняет использование аппарата тригонометриче¬
ских рядов. Самый простой способ вычисления этого интеграла
состоит в замене подынтегральной функции кусочно-постоянной
z = Х\ *4“ F sin0 [ — arccos
V ж ch-p
t chf
+ if • (33)
Разделение действительной и мнимой частей дает:
* = *»(£) +^(О. У = fyiO-
:[ = xi - /£ sin /3.
функцией, построенной по значениям Ат/ = у — ут, взятым в се¬
рединах частичных промежутков *?*..+! — т?*, на которые разбит
интервал интегрирования. В этом случае формула (34) дает:
где
0>пк —
tf 1с+1
(35)
причем tfn+i/2 берется в серединах частичных промежутков.
Для к = п главное значение соответствующего интеграла рав¬
но нулю. Коэффициенты ап* могут быть подсчитаны раз и на¬
всегда для стандартного разбиения интервала интегрирования
(О, 27г) при разных длинах частичных промежутков. Как показа¬
ли практические расчеты, формула (35) удобна для применения.
При решении уравнения (34) можно также использовать прие¬
мы, рассмотренные в работе [5].
Так как обтекание решетки пластин известно, то в случае, ко¬
гда установлено конформное соответствие между точками плос¬
кости решетки пластин и точками плоскости решетки профи¬
лей, определение скоростей на контуре профиля не представля-
ет труда. Согласно формуле (17) скорость на пластинках в плос¬
кости £ равна
как в результате конформного отображения известна зависи¬
мость я(£) и, кроме того, дано уравнение контура профиля
Распределение скоростей
на поверхности профиля в решетке
На профилях решетки при этом будем иметь
1
Производные dx/d£ и dy/dx могут считаться известными, так
111
у =: f(x). To обстоятельство, что отображающая функция для
решетки профилей имеет вид
г - 2i +5Zc'nCth"~7^ - -1 + 51 (7^je in<>'
аналогичный виду отображающей функции для изолированного
профиля, позволяет использовать в задачах, связанных с решет¬
кой, методы, развитые для изолированного профиля. Так, на¬
пример, используя метод ”малых вариаций” кривой давления,
известной для данного профиля, можно построить профиль с
заданной кривой давления. Действительно, для двух близких
профилей, находящихся в решетке и отображающихся на одну
и ту же решетку овалов, можем написать так же, как и для изо¬
лированного профиля:
z = z + Д Z,
V(S) = VobKo)^, v*(z) = v;*B(Co)^,
где V^*B(Co) — комплексная сопряженная скорость в плоскости
овалов.
Таким образом, dz/dz — V*(z)/V*(z), откуда имеем dAz/dz =
V*/V* — 1, Az — z — z, и, следовательно,
В
А
Разделяя действительную и мнимую части, получаем
В В
Ах = J{Rdx — Idy), Ат/ = J(Idx + Rdy),
А А
где R и / представляют собой действительную и мнимую части
выражения
К* t V'-V* AV*
R + г I — 1 — г — —=—.
V* Vm V*
Если скорости V* и V* близки друг к другу по направлению
и образуют между собой малый угол <5q, то
V*
v* iv*!
(cos 6а + i sin 6а)
112
V”
R + il — — 1 =
V*
(cos 6a + i sin 6a) — 1,
и, следовательно,
Y1
V*
откуда, ввиду малости угла 6а, получим
Яю!П-1,
\vi IV'-l
Так как \V*\ и \V*\ нами задаются, то величина R в Первом
приближении может считаться известной. Она будет функцией
I?, и потому мнимая часть определится формулой
2*
4$) = J
Для того чтобы вновь полученный профиль замыкался, необхо¬
димо, чтобы Дг, найденное для задней кромки, при следовании
от передней кромки к задней по стороне профиля было равно
Д2, найденному при следовании по нижней его стороне, т. е. не¬
обходимо, чтобы выполнялось условие
Rx + Их = j ^ - l) dz = О
и, следовательно, чтобы Я1 и 1\ были равны нулю. В плоскости
решетки овалов будет иметь место разложение
V'-V* 4„.un*Co ,
“ о о,
R -f il = = ]P(an + ibn)cthn—р +
и потому
/
V* - V*
dz = 0,
1/"
если ao = a\ = 61 = 0. При этом условии действительная часть
R представится в виде
сю
R = ^(an cos 711? + bn sin ni?).
n = 2
Если при заданном распределении \V\ и \V\ величины ao, а\, b\
Не получаются равными нулю, то необходимо из задаваемого
значения R вычесть величину ao -f ci\ cos t? + &i sin 1? и этим задать
113
новое распределение скоростей, которое может лучше отвечать
требуемым условиям. Так же, как и в случае изолированного
профиля, R\ представляет собой изменение подъемной силы, а
1г —изменение сопротивления при переходе от одного профиля
к другому. Эти величины в нашем случае, как указывалось вы¬
ше, равны нулю. Таким образом, отражение решетки профилей
на решетку овалов, на которых модуль cth^ сохраняет посто¬
янное значение, является непосредственным обобщением прие¬
ма, при помощи которого внешность изолированного профиля
отображается на внешность круга. При этом вид всех расчет¬
ных формул остается тем же, что и в случае изолированного
профиля [5, 6].
Преобразование
основного интегрального уравненил
Если за теоретический профиль взять пластинку, для кото¬
рой уг = 0, то уравнение (34) примет вид
2тг
1 f i) — <р
X- = х-г + — / У ct6 —2— ^ +
О
Преобразуем это уравнение, выразив переменную <р через пе¬
ременную Функцию у(<р) всегда можно представить в виде
суммы:
У = Ун + .Ум,
где
со со
Ун = - а" sin П<^’ У'* = 5Z cos пЧ> + &0-
п = 1 п = 1
Кроме того, ctg = 5|,-'-У-+$|П 0 и, следовательно,
А и Z COS кр — cost/
Так как в плоскости (Jo мы рассматриваем овалы, па которых
модуль / = th^ имеет постоянное значение, то в плоскости
/ = Л + *7г будем иметь дело с окружностью радиусом |/| = С.
Преобразование S = / + С2/f отобразит внешность этой окруж¬
ности на внешность прямолинейного отрезка длиной 4С\ при¬
чем точкам, лежащим на этом отрезке, будет соответствовать
$' := 2С cos <р = / cos у?.
На основании изложенного
С другой стороны, внешность решетки пластин густотой 2а//,
имеющая нулевой вынос, отображается при помощи функции
на внешность прямолинейного отрезка длиной 21. Таким обра¬
зом,
7Г
/2 — s2 y4ds'
/2“ “72 7Т7’
где
«'-s th^f-th^- t th^-th^ ch2=f
7Г 1 d£' _ я- ch^
sh^chIf ~ ~l chZ^
следовательно,
115
Основное интегральное уравнение задачи примет вид
•с = *i(£) + /(£).
Следует отметить, что эта форма основного уравнения задачи,
хотя и более наглядна, чем форма (36), однако для практиче¬
ских расчетов менее удобна. Все приведенные рассуждения без
всяких изменений применимы и к уравнению (34).
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Жуковский Н. Е. Вихревая теория гребного винта. Статья 3//Избр.
соч. Т. 2. М., 1948.
2. Поляхов Н. Н. Обтекание решеток телесных профилей заданной фор¬
мы//Докл. АН СССР. 1952. Т. 84. № 2. С. 233-236. [18*]
3. Блох Э. Л. Исследование плоской решетки, составленной из теорети¬
ческих профилей конечной толщины//Труды ЦАГИ. 1947. Вып. 611.
4. Умное Е. И. Потенциальное обтекание несжимаемой жидкостью ре¬
шеток из теоретических профилей//Труды Моск. авиац. ин-та. 1952.
№ 205.
5. Симонов Л. А. Расчет обтекания крыловых профилей и построение
профиля по распределению скоростей//Прикл. мат. и мех. 1947. Т. 11.
Вып. 1.
6. Betz A. Anderung der Profilform zur Erzielung einer vorgegebenen Anderung
der Druckverteilung // Luftfahrtforschung. 1934. Jfe 11.
1.5. ТЕОРИЯ
НЕСУЩЕЙ ВИНТОВОЙ ПОВЕРХНОСТИ [30]
Общие соображения.
Поле индуктивных скоростей
Теория несущей поверхности (крыла или лопасти) отлича¬
ется от теории несущей линии тем, что учитывает изменение
индуктивных скоростей, вызываемых свободными вихрями на
всем протяжении от передней до задней кромок сечения, а также
учитывает эффект конечности размаха присоединенных вихрей.
Теория несущей линии считает эти скорости постоянными, что
приводит к повороту всего потока на некоторый угол, называе¬
мый углом скоса.
Теория крыла прямоугольной формы в плане строится до¬
вольно просто, как теория вихревой несущей поверхности [1].
В настоящей работе делается попытка распространить ме¬
тод, использованный в указанной работе, на случай винтовой
лопасти. Лопасть при этом рассматривается как часть пра¬
вильной винтовой поверхности.
Рассмотрим сначала одну лопасть (рис. 1) радиусом R (АЕ =
AF = Я, АВ = г, AD — а — г cos Д0, N'D = h).
А'
Рис. 1
Пусть присоединенные вихри, совпадающие с радиусами вин¬
товой поверхности, имеют постоянную, вдоль радиусов плот-
117
ность 7, которая изменяется вдоль винтовой линии так, что у
есть функция дуги s. Присоединенный вихрь, проходящий че¬
рез некоторую точку iV, лежащую на винтовой линии радиусом
г, вызывает в точке N\ лежащей на этой же линии, индуктивную
скорость
j(s) ds
(sin— smv?i),
где h есть длина перпендикуляра, опущенного из точки N* на
рассматриваемый радиус.
Из рис. 1 непосредственно видно,
sin<pi = cos Д0[1 + (АО)2 tg2 <р}~1!2, г' = г'/Л,
sin <^>2 = (г; cos АО — 1) [1 + г 2 — 2r' cos АО + г 2(Д0)2 tg2
где АО — угол между радиусами; ip — шаговый угол. Индуктив¬
ная скорость, вызываемая радиальным вихрем в точке N*, будет
равна
7(s)ds A0(sin <£>о — sin <р\)
4 яг г АО
\Js\n2 АО + (AOtg<p)2
Кроме того, г АО ~ Ascos<p, где As =~NNf— дуга винтовой ли¬
нии CN'. Если дуговая координата, отсчитываемая на винтовой
поверхности, для точки N' есть s', а для точки N есть s, то пол¬
ная скорость в точке N* будет
, , 7 1 (sin — sin <р\ )A9ds
2 ' Г—I1)
ns s cos<pysm2A0+(A0tgp)~
Вектор этой скорости будет направлен перпендикулярно плос¬
кости AN'E. Проекция ее на плоскость AFE, на направление
DB, равна
= rAStgvм = A»tg Viw' _
^ y4iir АО -f (АО tg^)2
Лля проекций вектора dw' на направление радиуса и перпенди¬
кулярное ему получим
. , tg ф АО sin АО dw* . , tg <р АО cos АО dirf
dwr = -v-- dw[ =
yjsin2 Дв + (Д0 tg <p)2 sin2 AO + (AO tg <p)2
118
Точно так же проекция на направление Nf В найдется по форму¬
ле
. , sm АО dw'
dwn =
yjsin2 Ав + (A0 tg v?)2
Наконец, проекция на нормаль к винтовой поверхности в точке
N' будет
. . , ... cos<p(sin Ав + AOtg2 у? cos A0)dwf
dw = dwa cos cp -f dwt sin <p = ... = ,
ysm2A« + (A«tg»»P
откуда на основании (1) имеем
, . 7(s)ds (sin<p2 ~ sin (pi )Л0 , . A Л 0 A
dw" = + *,)><”"** + Л**' *“•**> =
= g> Щ *-M)ds
2тг s' — s
При этом следует заметить, что
s' — 5
Ав = -— cos<p.
г
Если радиусы, соответствующие передней и задней кромкам,
образуют угол Д0а> то можно написать
а л 2а
Д0а = — cos <р
г*'
и потому
Для г = Д имеем
°ткуда
Д0 = -Д0а.
2а
(Д0а)я = ~JfCOS у?Д)
s' - s aR
Ав = r-cos^fi.
а К
Обозначая s'/a — ^ Л’/а — а/?/Я = 1/^ получаем
На основании изложенного находим
2 у/\ 4- (AOtgip)2 у/1 + г - — 2г' cos АО + (г' Al!Hg<р)'2
(sin Д0 + Дб tg2 <р cos Д0) Дб
sin2 Дб *f (Дб tg<p)2
(3)
х
Отсюда видно, что когда Дб —► 0, то J\ —* 1. Вообще говоря,
О $ J\ ^ 1, так как представляет собой отношение скорости, вы¬
зываемой прямолинейным вихрем конечного размахав заданной
точке, к скорости, вызываемой в этой точке вихрем бесконечно¬
го размаха.
Лля того чтобы учесть влияние других лопастей и получить
J2, «/з и т. д., достаточно под знаком sin и cos заменить АО на Дб+
^г(>* — 1), где х есть номер лопасти, причем основная лопасть
имеет х = 1. Окончательно для скорости получим
где J = Ji + J2 + <7з + .. .
Заметим, что при (Д£)/А —► 0 величины Jo, </3 и т.д. стре¬
мятся к нулю, а потому J = J] стремится к единице. Условие
непроницаемости элемента лопасти на радиусе г будет иметь
вид
где —проекция скорости W* набегающего потока на нормаль
к элементу лопасти. Скорость потока может быть представлена
формулой
где т° и а0 — единичные векторы касательного и осевого на¬
правлений, vt и va — индуктивные скорости, создаваемые си¬
стемой свободных вихрей лопасти, тс —угловая скорость вра¬
щения винта, V — скорость поступательного движения судна,
W — скорость набегающего потока без учета вызванных рабо--
той винта скоростей, w — индуктивная скорость. Скорости гн ^
— а
y{s)J(г', у, As, A)ds
(5)
W' = (ыг' - 1»,)т° + (V + t,e)a° = W + w,
120
шг'
Рис. 2
va в различных точках профиля разные и меняются в зависимо¬
сти от sf.
Из рис. 2 видно, что
= (wr* — vt)sin(<p' - tff) - (V + va)cos(<^>/ — tf'),
где ^ — шаговый угол профиля, i?' — угол наклона касательной
к оси х. С другой стороны,
и)г* — W cos /?, К = sin /?,
и потому
= И7 sin(a — г?') — [i;t sin(^>' — д') -b va cos(<p' — *?')] =
= W sin(<* - i?') + Win(s'). (5a)
Переходим к определению скорости Win(s'). Так как мы рас¬
сматриваем винт с постоянной циркуляцией, то на радиусе R с
конца каждого присоединенного вихря с циркуляцией у(s)ds бу¬
дет сходить свободный винтообразный вихрь, обладающий той
*е Циркуляцией. В первом приближении можно предположить,
Что этот вихрь имеет тот же шаговый угол <£>я, что и рассматри¬
ваемая лопасть, которая является частью правильной винтовой
Поверхности.
Пусть точка 7V', лежащая на лопасти, имеет координаты г'
и а положение радиального присоединенного вихря харак¬
теризуется углом в, тогда индуктивные скорости, вызываемые
121
свободными вихрями в точке ЛГ', будут
dvt =
dva —
7 (s)ds
4тгЯ
j(s)ds
4ttR
£
x = l
к
£
*=1
[ Ft«(?, вх)с10х Г Ftx(r', Oi )dOj
J #1, tgfiR) J ^(r1, Oi, tg0R)
0 0
OO 00
f Fax(f', 9i )d$ f FM(f,tel)d$l
J V*(r', 0i, tg/Зд) У Ф(г', 0Ь tg/?fi
(6)
где
(7)
= (01 sin x -j- COS 01 x - r')ig0R,
Fax(f', 0l) = (1 ~ f'cOS0ix)tg/?rt,
Ф(г', 01, tg/Зл) = (01 tg2 (iR + 1 + f 2 - 2f/cos0ix)3/2,
- + ^ « tgy-R, 0lx = 01 + ~{x- 1),
luH — vt к
к— число лопастей.
Сумма первых интегралов, стоящих в каждой из скобок, даст
величины, которые мы обозначим соответственно через ки*{ и
kv. Эти величины являются функциями параметров г* и <р и не
зависят от в' — в. Вторые слагаемые в скобках дадут величины,
которые будут зависеть от f', <pR и АО = О* — 0, поэтому можем
записать
dvt - + e't(r', <pR% As)],
dva -
4nR
k~f(s)ds ф
4ttR
1>:,[1 +£a(r\ IpR, As)] Ctg ipR,
где АО определяется формулой (2).
Для получения полной тангенциальной скорости необходимо
к скорости dv't добавить скорость, вызываемую осевым вихрем.
В случае fc-лопастного винта получим
Хаким образом,
dvf; =
lcy(s)ds ^ 1 (s' — s) cos (fft sin <p
4тгг' Л / i] , / 's‘-s • ^
Y COS- <p -+■ ( COS (fn sin <p)
(7a)
Полные скорости будут:
A:7(s)ds
dvt —
(1 -f + £:'/ -f r'r^s') —
47Г r'
_ + £,) = dvti(l + £,),
47Г r
ib'vf
dva = 4я.?1/ «al ct6 P ( 1 +£a) = <W(1 + £a
(8)
где v** = l-t-f't)*!- Из полученных формул видно, что dvt\ и dvai
представляют собой значения скоростей dvt и dva при s = s', ко¬
гда St — с а = 0. Проекция элементарной индуктивной скорости
на нормаль и к профилю (см. рис. 2) найдется по формуле
dtunc = dvt sin(<y?' - i)') + dva cos(<£>' - tf'),
где <p' -—шаговый угол элемента; ?/' - угол, образуемый норма¬
лью к профилю с перпендикуляром к его хорде. Подставляя
вместо dvt и dva их значения, получаем
dwnc = [v** ( 1 + £t ) sin(¥?' - I1)') sill (fi +
47Г7*' sin tp
+ ^ai(l +£a)cos(^' - tf')cosy?] =
.hSs)dLw';,(l + e) = 7(s)fi (V, <p,
4ят' simp \ A )
(9)
где
w* t = v** sin(<£>' — flf) sin p + v*i cos(p* - i?') cos <p «
« Vt* sin2 p 4-1;*! cos2V-
® теории H. E. Жуковского, которая имеет дело со скоростями,
°сРедненными по полярному углу, лежащему в плоскости ”вих-
Ревого донышка”, величины v**, v*a^ и равны единице.
123
Переходя к безразмерным координатам и интегрируя (9), на¬
ходим
+1
kw*}a [ ... As\
Wnc = wn 1 + -— / t(s)£-( Г , ip, — rfs, (10)
4irr' sin <p J \ A )
-1
или на основании теоремы о среднем
Wnc = Wnl(l +£*)>
где
wn\ = ~———wnl\ е =e[r,<pt—-— ,
4 тгг'sin \ * J
причем величина 5* зависит от s'.
Основное интегральное
уравнение задачи
На основании изложенного уравнение непроницаемости (5)
элемента можно записать в виде
+1
h / ЧЧг =w [sin<“_ "'|" А“* *’■ Чг).
-1
где
(П)
-Ы
Wnc
= W /7(s)/l (г~'’ Чг)ds
с W
-i
есть скос потока, вызываемый в точках профиля системой сво¬
бодных вихрей лопасти, причем следует отметить, что знак вол¬
нистой черточки над s здесь опущен. В дальнейшем мы так же
будем его опускать, помня, однако, что длина s измеряется в
долях длины а. Функция J ^г', как указывалось выше,
обращается в единицу при s = s', При этом можно заметить,
что при s —► s' функция J = 1 — J стремится к нулю как (s' — s)2,
так что функция
стремится к нулю при s —► s' и, следовательно, непрерывна в
промежутке (—1, +1). Имея это в виду, перепишем уравнение
124
(И)
где
в виде
-hi
1 f = ^fsin(a __ ,?') _ дас + Догп],
Z7T J S — S
-1
(11а)
-1 -1
можно рассматривать как дополнительный скос потока, зави¬
сящий от s' и А. Этот скос получается вследствие индукции
присоединенных вихрей, имеющих конечный размах. Полагая
h - f\ - F (г', <р, —д—^ - (12)
запишем уравнение (11а) в виде
— J ~71~ = w sin (а - у?') + j 7 (s)F ^г', <р, —у—) (12a)
-i -i
Обращая интеграл, стоящий в левой части, для случая, когда
7(—1) = оо, 7(0) = 0, получаем
7Г V 1 + <*
1 4- sf W sin(a — duels'
1 -
<т — s'
+
+
МШ
T+V F nr)ds>
(13)
a - s'
-1 L-i
Первое слагаемое этой формулы представляет собой вихревую
плотность 7оо при А = со, второе учитывает влияние конечности
размаха. Вводя обозначение
А(^,*) = -у — ,
-1
Получаем для определения 7(а) интегральное уравнение Фред-
гольма второго рода
+ 1
7(о') + у|уу J s)ds = 7oo(<r).
-1
(14)
125
Рассмотрим более подробно отдельные слагаемые, входящие в
это уравнение.
Примем прежде всего sin(a — д*) & а — i)'(s*). Замечая, что
Ядро К(<т, s) уравнения (14) будет непрерывно. Решение этого
уравнения способом итераций или путем замены его системой
линейных алгебраических уравнений весьма громоздко.
Ввиду того, что нас интересует не столько 7, сколько цирку¬
ляция Г, которая выражается формулой
умножим обе части уравнения (14) на adcr и запишем интеграл
по <т:
-1
получаем
где
-1
-1
-1 L-1
Подставляя вместо К (сг, s) его значение, имеем
-1 -1 -1
но так как
то
т* -ГА
Г = Гоо + 2a J J j(s)yJ —д—J ds'ds.
-1 -1
126
или на основании (12)
+ 1 +з
Г=Г„ + 2аУ|т(.)У^
-1 -1
fcaw*(l + е)
47гг' sin р
Отсюда
+ 1 +1
тгЬи)* Г
Г
?*' sin р
-1-1
где
/з Г , V, ——
ds'ds.
7гЬю*Г f [ j 1 4- s' ( . \ ,
= Г<^ - ——- + a / / 7 s)W 7 /2 - — ds ds,
?*'sinp / J V 1 - fi \ r'smp/
7 k2a
0 —
4irR
Обозначая
-hi
a j lis)e(r'’ <P, ~X“) = Г£(г/’ ~T~) = Ге+’
-1
+ 1
о J 7(s)h(r’, <p, ~д"~) ds =' Г/о^г', p, “p2') ~
-1
и замечая, что
+1 +i
Г00 -a j joo(s)ds = 2а7г1У ^а - j у d'(sf)dsf —
-1 -1
= 2тга1У(аг -f ао),
получаем из (16)
Г = Гоо — 2cnrW(Aai + 6а£ — 8а\),
где
6Г и>1
Да/ =
^ _ 6Г <Л _ /Л
^ “ / * 7 Т т г — * _
г snip 2(lTtW 2(ПТГ sin р vv j
-1
+ i
2аг' sin р W ’
+ 1
ЬГм» [ jl + s' ..
sili<pW J У 1 — s' 1
x Г/* Г
d»aA =
27raW 2тга1У
Эти величины представляют собой соответственно: 1) скос по¬
тока по теории несущей линии; 2) скос потока вследствие не¬
равномерности скоростей, вызываемых на профиле свободными
вихрями; 3) скос потока вследствие конечной радиальной про¬
тяженности присоединенных вихрей. Из формулы (17) имеем
Для больших Л, т. е. для случая несущей линии, Jt и J\ равны
нулю. Первая из этих поправок учитывает так называемую кри¬
визну потока, происходящую от того, что скорость, вызываемая
свободными вихрями на профиле, непостоянна. Она увеличи¬
вается от передней кромки к задней, вследствие чего влияние
кривизны потока будет способствовать уменьшению циркуля¬
ции. Поправка J\ связана с индукцией, вызываемой присоеди¬
ненными вихрями. Рассмотрим сначала основную лопасть. Ей
соответствует согласно (116) скос потока
который будет всегда положителен, так как представляет со¬
бой разность скосов, индуцируемых системой присоединенных
вихрей бесконечного и конечного размахов. Величине Aani бу¬
дет соответствовать по (17а) величина 6а\\ и приращение цир¬
куляции на величину Jx\T. Влияние остальных лопастей про¬
является в том, что они вызывают в точках основной лопасти
дополнительный скос, которому соответствуют в формуле (4)
факторы Ji, «/3,... Наличие у основной лопасти соседних лопа¬
стей приводит к тому, что она находится между двумя свобод¬
ными границами. Эти границы имеют в первом приближении
вид винтовых поверхностей с параметром т. е. являются
поверхностями, идентичными с основной поверхностью, из ко¬
торой выделена лопасть; они получаются из основной путем ее
поворота на углы 1). Ранее было показано, что влияние
свободных границ на элемент лопасти приводит к уменьшению
циркуляции. Если принять гипотезу цилиндрических сечений
и положить Ji равным единице, то циркуляция около элемента
выразится формулой (см. [2])
+1 _ +1
2жа\¥^21'
-1 -1
Г = tt2iraW(a + а'0 — Да; — 6ас),
(19)
128
где -/ • I
г sin <р , жо
x = — th— $ 1,
7Г6 Г Sill (р
причем а{) > Qq3. Если не вводить предположения, что J\ равно
единице, что соответствует случаю малого удлинения лопасти,
то в первом приближении, если учитывать влияние конечно¬
сти размаха присоединенных вихрей основной лопасти, следует
принять формулу
Г = 2ir>caW{ct 4- ог'0 — А— 6а£ + £c*ai)>
откуда получим
г = . ■ ,*Г~ . (20)
1 + ^?—(1 + Л)-Л1
г sin <р
Для определения Г можно пользоваться и формулой (18), кото¬
рая более точна, чем (20). Однако формула (20) гораздо более
наглядна, так как из нее отчетливо видно влияние свободных
границ, малости удлинения и кривизны.
Для определения е* и /£ в первом приближении можно заме¬
нить в формуле (16а) величину у величиной Aoy/(l — s)/( 1 + s).
Тогда, полагая s = — cos 0, получаем
Т 7Г
в* = i J е( 1 + cos 6)d0, = /2(1 + cos 0)d0
о 0
и, следовательно,
T T
Je = J(l- cose')e'd6' = тге**, Jx = J{ 1 - cosO^fUO' = тг/2**,
0 0
где значок ** соответствует второму приближению. По этим
формулам могут быть подсчитаны раз и навсегда J€ и J\ для
разных значений г' и Как показывают вычисления, для гру¬
бой оценки влияния малости удлинения можно взять
1/А).
Следует заметить также, что для определениям можно в первом
приближении рассматривать винт Н. Е. Жуковского. Для этого
пинта при f' < 1
2т
(1 — rf cos 6)d0
= ± f
2irJ
г, v/g2 + г?
129
где
r\ — 1 4- г 2 — 2г' cos 0;
1 Дя
г/ = — (s' - s) sill <р = i5' tgy? — COSV?R-
Лля в этом случае можно принять выражение (см. (7а))
„ 1 (s'-s) cos<p R simp
£t €t Д ’ j ~—з r
у cos2 v? + (cos sin <p)4
Случай переменной циркуляции
Допустим, что плотность распределения присоединенных
вихрей 7 изменяется по закону 7 = у{s)f(v), тогда
+ а
Г = /(г) J 7(S)ds = f{r)Г.
— а
Индуктивная скорость dw'n, вызываемая одним присоединенным
вихрем в точке N', выразится формулой
* = т j = д„ (2,,
О 1 + (=^
4ягh J Г, . ,,_,/^сЛйч213/2 4nh
о
где по-прежнему
h = r'y4in2 Д0 + (Д0)2 tg2 v?, г'АО = (5' — s)cos<^>,
и, следовательно, как обобщение формулы (1) получим
, 7(s) 1 F{r\ A0)A0ds y(s) F\ds
dwn — — -■—■■ — - ■ — ■■■■.=- rr .
4n s' — s / . 2 л л , / a a * 47Г s' — s
cos
<^^/sin2 Д0 -h (Д0 tgV)
Если функция /(г) задана, то вычисление Ji не представляет
труда. Однако очень часто бывает необходимо определить вид
функции f(r). В этом случае задача становится очень сложной
и для ее приближенного решения необходимо сначала задать в
первом приближении /(г), которую затем надо определить бо¬
лее точно в следующем приближении.
130
Имея это в виду, напишем формулу (21) в виде
r')ds f f(r) d—
47гЛ У Дг') Г ,£_£ГЛсЛвч 213/2 4я-л
, , _ т(*)/(г')^ / /(Г) ^Л~Г ГДУ 7(*)/(г;) „
- 7-Т / Т7Т77Т I7177T = —7ТТ—/f2
[l + (^-C'..cosA0)2]‘
(22)
и будем считать, что функция /(г) может быть представлена в
обычной для теории несущей линии форме
оо
/[г(ф)\ = А\ sin гр + А2 sin 2ф + .. . = Лп sin пф,
П — 1
причем г = 1~-~У, Предполагая далее, что искомое распре¬
деление циркуляции близко к эллиптическому, вычислим инте¬
грал, входящий в формулу (22), для
f(r) _ sinV’ _ у/1 - (г/L)2
/(?■') sinф' у/1 - (z'/L1)2’
где 2 — г — L, L = 1/2.
Таким образом, вместо формулы (1а) будем иметь
iTM/tgwr;. у, д«/л)
п 2тг s'-s
где
1 sin Ав + Д0 cos А9 tg2 у? /, As\
1 _ 2 sin2 Д<? + (Aetg ip)2 2 V ’ ^ Т/ ’
причем Fo(rf, <р, As/Л) известна. Соответствующие выражения
для J21 ^3) • •• можно получить аналогичным способом. Основ¬
ное интегральное уравнение задачи будет того же вида, а имен¬
но (см. (12а))
* -/ *
2^ J 7^g' ’_S^S = lV siii(o - д') - w,ic(r', s') 4- J 7(i''> s)f2ds, (23)
-l -i
где по-прежнему
f _ i i-j
h 2ж s' -s'
131
Выясним теперь вид зависимости wnc(r\ s').
Один винтообразный свободный вихрь, сходящий в точке с
координатами г, 0, будет иметь циркуляцию —7(s)^pdrds, и по¬
тому вместо формул (6) получим
dv, = Ms)Js 1
47Г R г
Р
+ Ф<2 (j, tgV?r, х)]^’
P
+ Фа2 tg(fir, dr,
где Фп, Ф<2, Фаь Фа2 выражаются так же, как в формулах (6), с
той лишь разницей, что вместо tgtpR будет стоять tg (prt а вме¬
сто г' — отношение г'/г. Согласно теории ’’несущей линии” мы
имели бы
4irR г' у г dr
Р
1
^ kj(s)ds ctgipf { df(r)
iv"' “ J IF
P
поэтому весьма удобно записать dvt и dva в виде
dvt — dt;ti
dva = dvai
l + £, (j, 9, V,. x)] ■
,l + £“ (?’ ‘fr’t)]-
где St и ea представляют собой отношение интегралов, завися¬
щих от распределения циркуляции и содержащих Фп, Ф*2, Фл1>
Ф«2-
В первом приближении можно взять для £t и еа их значения
в случае постоянной циркуляции или какой-либо другой, близ-
кой по предположению к искомой, например эллиптической или
132
«наивыгоднейшей» в смысле Бетца. Отметим, что основные ве¬
личины dvti и dva\ должны быть взяты для случая переменной
циркуляции, подлежащей определению. Проецируя dvt и dva на
цормаль к профилю в точке N', находим, как и ранее,
dwn = dwni + €tdvt\sin(^; — i?') + eadva\ cos(<p' — d'):
Так как согласно теории несущей линии
dvti « dwni sin <р, dva\ « dit;ni cos <p,
to = dwni(l -be), где e « £t sin2 y> + £a cos2 Интегрируя (23),
получаем
= ^nl(l + £*)■
Заметим, что скорость wn\ выражается формулой
_ кГ 1
Wnl 47rr'xsin<^’
причем х—поправка типа поправки Гольдштейна. Исходя из
изложенного, представим основное интегральное уравнение за¬
дачи (23) в виде
1 f 7(г , s)ds _ |ysin^a _ _ Wnl(i +£*) +
27Г J s' — s
-i
+ J 7(r', s)h <P, <Pr, —д—^ ds, (24)
-1
который совпадает с видом уравнения (Г2а), полученного для
постоянной циркуляции.
Произведя все те операции, которые были сделаны примени¬
тельно к уравнению (12а), получим
г — .
г1 sin <р х v 7
Эта формула по внешнему виду совпадает с формулой (18). Од¬
нако после предпринятого вывода видно, что содержание ее не¬
вольно иное.
Для определния постоянной циркуляции формулу (18) нужно
было применить лишь один раз в каком-нибудь выбранном се¬
янии. Для выполнения условия непроницаемости в остальных
сечениях нужно из формулы (18) найти зная которое, опре¬
делить в каждом сечении необходимое значение а и затем иай ги
шаговый угол элемента по формуле
<р' = а -1- arctg( V"/г).
Этот угол может не совпасть с шаговым углом правильной вин¬
тообразной вихревой поверхности, которую мы брали в самом
начале наших рассуждений. Получаемое расхождение не мо¬
жет повлечь за собой ощутительной ошибки в определении Г,
так как мы пользовались предположением о правильной винто¬
вой поверхности, на которую как бы сносили присоединенные
свободные вихри лишь для приближенного учета влияния вели¬
чин J и е.
В формуле (25) величина Гоо задана с самого начала в ка¬
ждом сечении, для которого выполняется условие непроницае¬
мости (24). Строго говоря, величины Je и J\ зависят от закона
распределения Г вдоль радиуса. Однако так как они играют
роль поправок в формуле (25), то самым простым приемом бу¬
дет, если взять их для случая постоянной циркуляции (или эл¬
липтической) и для
7 = Ао ctg(0/2),
а затем, найдя Г, исправить Je и J\. То же самое можно сказать
о <р' и х-
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1, Поляхов Н, H.t Пастухов А. И. Теория несущей поверхности прямо¬
угольной формы//Вестн. Ленингр. ун-та. 1959. № 13. С. 93-110. [26*]
2. Поляхов Н. Н. Влияние кривизны потока на работу элемента гребного
винта//Вестн. Ленингр. ун-та. 1962. № 1. С. 134-141. [29]
Раздел II
ТЕОРИЯ
СТАЦИОНАРНОГО ОБТЕКАНИЯ
НЕСУЩЕЙ ПОВЕРХНОСТИ
П.1. К ТЕОРИИ КРЫЛА
КОНЕЧНОГО РАЗМАХА С. А, ЧАПЛЫГИНА [21]
Известно, что в 1913 г. С. А. Чаплыгин сделал доклад в Мо¬
сковском математическом обществе ”О вихревой теории крыла
конечного размаха”. Этот доклад был стенографически записан
В. П. Ветчинкиным, и его материалы были частично опублико¬
ваны в книге В. В. Голубева [1], а также в статье [2].
Следует отметить, что формулы С. А. Чаплыгина для подъ¬
емной силы и индуктивного сопротивления крыла были опубли¬
кованы без вывода.
В настоящей работе дается вывод формул С. А. Чаплыгина,
которые, оказываясь нелинейными, могут быть применены к
расчету крыльев малых удлинений при введении некоторых до¬
бавочных соображений.
Будем, следуя С. А. Чаплыгину, предполагать, что с концов
Крыла сбегают вихри, расстояние между которыми п бесконеч¬
ности равно /пр, меньше размаха крыла /.
Воспользуемся для определения подъемной силы и индук¬
тивного сопротивления крыла теоремой импульсов и теоремой
энергии. Для этого в бесконечности перед и за крылом прове¬
дем контрольные плоскости, перпендикулярные к направлению
скорости невозмущенного потока. Допустим также, что вихри
Перпендикулярны к этим плоскостям. Координатные оси рас¬
положим так, как показано на рис. 1. Течение всюду будет по-
ТеНциальным (при этом точки ±/пр/2 будут особыми точками),
И скорость отбрасывания жидкости вниз w будет равна <9Ф/ду,
гДе ф — потенциал обтекания.
135
У
г-Фв-Фн
Рис. 1
Часть подъемной силы крыла, вызванная указанным отбра¬
сыванием, на основании теоремы импульсов будет равна
Yi=-pjJJwdr, (1)
Т
где интегрирование распространяется на объем жидкости, ле¬
жащей вне разреза длиной /пр и заключенной между двумя плос¬
костями, расстояние между которыми численно равно То¬
гда будем иметь
У\ = -pVco J[ (2)
s
где Voo — скорость набегающего невозмущенного потока. В на¬
писанном двойном интеграле интегрирование распространено
на всю площадь контрольной плоскости 5.
Применяя к выражению (2) формулу Остроградского и инте¬
грируя по всей площади, лежащей вне разреза /пр, получим
*i = -pVoо j *da,
3
где $ — контур, охватывающий разрез длиной /пр, причем свер¬
ху от разреза ds = +dz, снизу от него ds = — dz. Ввиду того,
что вблизи точечных вихрей с координатами z = ±/пр/2 скоро¬
сти становятся неограниченно большими, при интегрировании
эти точки нужно обойти по кружкам сколь угодно малого ради¬
уса и в окончательной формуле положить эти радиусы равными
нулю.
136
В результате интегрирования будем иметь
Yi = -pVoo (- f*.dz+ f Фнdz 1 =
V L t J
+Ц/2 +li/2
= pVo0 j (*.-*H)dz = pV00 J Tdz,
-/l/2 -/l/2
причем /1 = /пр — 2C, где С — радиус кружка, по которому обхо¬
дятся точки Т/Пр/2 (см. рис. 1).
Интегралы по самим кружкам, вследствие противоположного
вращения вихрей, друг друга уничтожат. Переходя к пределу,
окончательно находим
-И пр/2
Y\ = pVoo j Tdz. (3)
— fnp/2
В частности, в случае постоянной циркуляции
Yx =рУооГ1ар. (4)
Если позади крыла тянутся вихревые шнуры радиусом г0, то
считал, что они все время направлены по скорости Voo и, следо¬
вательно, не участвуют в движении вниз со скоростью wy надо
из полученного выше выражения для Y\, учитывающего количе¬
ство движения всей жидкости, вычесть силу, соответствующую
количеству движения жидкости, текущей внутри вихревых шну¬
ров. Эта сила будет равна
У2 = 2pVcx>'nrlwc, (5)
гДе wc — индуктивная скорость центра вихря, равная .
— 7Г1 п р
Таким образом, окончательно получаем
Y = Y1-Y7 = pVooTlnp(l-r20/l2np). (б)
® формуле С. А. Чаплыгина вместо го//„р стоит половина этой
Величины, что можно получить, предположив скорость опуска-
НИя вихрей равной ги/2. Следует отметить, что эта величина
°Чень мала и практически ею можно пренебрегать по сравне¬
нию с единицей.
137
Для определения индуктивного сопротивления воспользуем¬
ся теоремой живых сил. Мощность, затрачиваемая на преодо¬
ление сопротивления, будет равна
где т\ — объем, по которому производилось интегрирование при
нахождении подъемной силы Хц, за исключением объема, за¬
нятого вихревыми шнурами.
Преобразовывая написанный интеграл по формуле Остро¬
градского и производя вычисления, аналогичные вышеизложен¬
ным для подъемной силы, получаем
причем w*—среднее значение индуктивной скорости w на от¬
резке 1\. Эту скорость легко определить по формуле
Таким образом, учитывая влияние двух вихрей, будем иметь
Хи^1Л. (И)
27Г г о
Если вихри опускаются вниз со скоростью wc, то живая сила,
соответствующая этому движению, будет равна
i /2
(8)
-(,/2
где /х = /пр - 2г0.
При постоянной циркуляции будем иметь
(9)
+ii/2
/
-!i/2
откуда
(12)
138
Принятое выше допущение о том, что сбегающие с концов
крыла вихри являются цилиндрами с радиусом г0, дает возмож¬
ность вычислить составляющую индуктивного сопротивления,
возникающую в результате пониженного давления внутри вих¬
ря. Нетрудно видеть, что эта составляющая для одного вихря
может быть представлена в виде
Го 1Г Го
^3. = j J(Poo - p)rd$dr = 2ir j(Poo-p)rdrt (13)
0 0 0
где Poo — давление в невозмущенном потоке, а р — давление в не¬
которой точке внутри вихревого ядра, вычисляемое по формуле
рГ2(2г^ — г2)
Р ~ Р°°
Подставив последнее выражение в формулу (13), получим
lXai = JfeH^lrdr =
0
го
3pjr^
4тг
откуда
3 рГ2
<м>
Таким образом, окончательно для индуктивного сопротивле¬
ния можно написать формулу
Xi = Л’к + X2i + X3i = ZL^ + jj>- + Infjg'J (15)
Последнее выражение полностью соответствует полученному
С. А. Чаплыгиным, однако, если предполагать, что, как и цри
вычислении подъемной силы, вихревые шнуры не обладают ско¬
ростью скоса, то можно записать
/2 Л
(16)
Легко видеть, что выражение (16) практич!ески не отличается
от формулы (15), ибо, как указывалось выше, величина г$//%р
пренебрежимо мала по сравнению с 1п(/2р/го).
139
V
Рис. 2
В своем исследовании С. А. Чаплыгин считал, что вихревые
шнуры за крылом не параллельны скорости Voo, & направлены
параллельно скорости Vi, представляющей собой геометриче¬
скую сумму Voo + w/2, причем индуктивная скорость w напра¬
влена перпендикулярно плоскости, в которой лежат оси скошен¬
ных вихрей. Предположение, что вихри направлены по скоро¬
сти Vx, можно оправдать тем соображением, что накрыло более
всего влияют близлежащие к нему участки вихрей, на которых
скорость близка к скорости Vi. В бесконечности за крылом
вихри должны быть направлены по скорости V2 = V^ + V.
Применяя при этих новых условиях теорему импульсов, по¬
лучим для полной силы, действующей на крыло, следующее вы¬
ражение:
Эта сила, согласно теореме Н. Е. Жуковского, направлена пер¬
пендикулярно скорости Vi. Подъемная сила и индуктивное со¬
противление крыла будут получаться как проекции силы R на
направление скорости Voo и на направление, к ней перпенди¬
кулярное (рис. 2). При этом под Да следует подразумевать
средний по размаху скос потока. Проецируя, получим
Если величину среднего по размаху крыла угла скоса при-
R — prVilnp-
(17)
)=/>г К*ЛР 1-(^) • (18)
140
ближенно положить равной*
Да = * = %!1 « -J—Ilnfnp
У V'oo 2/ПрК» 7Г Г0 2/npVoo
то
У = *>ГУ„1„Р (1 - j£) -
SrlnpVn I 2 l'if
Это и есть окончательная формула С. А. Чаплыгина для подъ¬
емной силы с учетом нелинейного слагаемого.
В случае крыла со значительным удлинением при небольших
углах атаки второе слагаемое может быть отброшено по сравне¬
нию с первым ввиду малости величины Гз//пр. В случае малых
удлинений такое отбрасывание производить нельзя. Кроме то¬
го, если в первом случае Г определялась как линейная функция
а, то во втором случае она должна определяться по нелинейной
формуле.
Интересно отметить, что если величину Г определить по фор¬
муле
г =Гл + г vY~ i\+ г+1п^И - (20)
4тгУ0О/Пр \2 /йр 7*5 J
где Гл —циркуляция, найденная по линейной теории, то форму¬
ла для подъемной силы приобретает вид
/2
У = РГМпр + 8^- { - + ^ + 1п^ ) (21)
и дает хорошие совпадения с экспериментом для всех удлине¬
ний, как больших, так и малых.
Заметим, что формула (20) может быть также записана сле¬
дующим образом:
г= Гл + -^-= Гл(1 + Дал), (22)
Р*оо *пр
где Дал — скос потока, найденный по линейной теории.
Формулу (22) можно получить, предположив, что вследствие
Перетекания жидкости с нижней поверхности крыла на верхнюю
нихри отклонены от вектора Voo на угол Да вверх. Физиче¬
ски это возможно только для участков вихрей, непосредственно
’“Более точно было бы принять, что -ln^* a ~ (см. (28)).
141
примыкающих к крылу, однако влияние этих участков и явля¬
ется наиболее существенным.
Заменяя крыло П-образным вихревым цилиндром, С. А. Чап¬
лыгин приближенно определял длину несущей его части как 2/3
абсолютного размаха крыла. Лалее, имея в виду крыло конеч¬
ного, но большого размаха, С. А. Чаплыгин дал лишь весьма
приближенную оценку радиуса свободных вихрей (порядка тол¬
щины крыла).
Более точный способ определения указанных величин был
предложен В. В. Голубевым [1]. Напомним вкратце эти сообра¬
жения.
Как известно, современная линейная теория воспроизводит
силовые характеристики крыльев большого удлинения с прак¬
тически достаточной точностью. Применяя метод тригономе¬
трических разложений, подъемную силу прямоугольного крыла
можно найти по формуле
У = p^CiaVllb, (23)
где С\ — первый коэффициент тригонометрического разложе¬
ния циркуляции Гл:
00
Гл =тгУ0О6а]Г С„ sin пв. (24)
1
Подставляяв это выражение в = тг/2, для среднего сечения кры¬
ла получаем
со
гп0 = irVoobaJ^Cni-l)^. (25)
1
Подставляя выражение (25) в (21), можно найти величину /пр в
первом приближении, если приравнять линейную часть форму¬
лы С. А. Чаплыгина для подъемной силы к правой части линей¬
ной формулы (23):
^пр тг Ci
1 4 £Г £„(-1) а
(26)
Соотношение между приведенной длиной крыла и радиусом
вихревого шнура можно определить из следующих соображе¬
ний.
142
Принимая, как и в линейной теории, что свободные вихри на¬
правлены по скорости невозмущенного потока (уравнение (11)),
Л',, =
27Г г0
Подставляя сюда значение Г из (20), приближенно можно напи¬
сать
Хи = ^1п^.
2тг го
(27)
Если в этом выражении заменить Гл на Гло по формуле (25),
а затем приравнять правые части выражения (27) и линейной
формулы для индуктивного сопротивления:
то получим
Xi= p\v™h2a2lt,nC"'
|п*пр _ ^г“> П^п
’•о " 4 Z?Cn(-1)^
(28)
Приняв в первом приближении указанный способ определе¬
ния го//Пр и /пр и обозначив
Я г2 /2
х - - + + 1п-^
2 /2 г2 ’
z пр г0
приведем формулы С. А. Чаплыгина к следующему виду:
Су = yCia7)
(29)
(30)
где
7 = 1 +
,к\2С\
£с„(-1)^
L 1
\а
ж2СЬ2
причем Су в формуле (30) определяется по выражению (29).
143
Легко видеть, что конструктивно формула для коэффициента
подъемной силы очень близка к соответствующим выражени¬
ям, полученным В. В. Голубевым [3] и Г.Ф.Бураго [4]. Кроме
того, из последней формулы видно, что поправка 6, в отличие
от обычного случая, является функцией не только удлинения,
но и угла атаки крыла.
Расчеты показывают, что формула (29) дает результаты, ко¬
торые весьма удовлетворительно согласуются с эксперимен¬
тальными кривыми, полученными для крыльев различных удли¬
нений с симметричным профилем. При этом величина циркуля¬
ции вокруг крыла корректировалась коэффициентом кото¬
рый определялся по результатам испытания крыла большого
удлинения, пересчитанным на бесконечный размах.
Из изложенного следует, что теория крыла конечного раз¬
маха, предложенная С. А. Чаплыгиным еще в 1913 г., является,
по существу, нелинейной теорией, дающей хорошие результаты
не только для крыльев больших удлинений, но и для крыльев с
удлинениями меньше А = 1,5. Таким образом, С. А. Чаплыгину
несомненно принадлежит приоритет в создании теории крыла
конечного размаха в наиболее общей форме.
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Голубев В. В. Теория крыла аэроплана конечного размаха. М., 1931.
2. Работы С. А. Чаплыгина по теории индуктивного сопротивления//
Прикл. мат. и мех. 1941. Т. 5. Вып. 2.
3. Голубев В. В, К теории крыла малого удлинения//Изв. АН СССР.
Отд. техн. наук. 1947. № 3.
4. Бураго Г. Ф. Приближенная теория крыльев малых удлинений //Тру¬
ды Научно-технической конференции ВВА им. Н. Е. Жуковского. Т. 3.
М., 1944.
II.2. ТЕОРИЯ НЕСУЩЕЙ ПОВЕРХНОСТИ
ПРЯМОУГОЛЬНОЙ ФОРМЫ [26]*
Экспериментальные исследования прямоугольных, пластинок
показывают, что с уменьшением их относительного удлинения
до А < 2 возрастание подъемной силы и момента с увеличением
угла атаки становится нелинейным. При этом на нелинейность
моментной кривой, помимо параболического характера измене¬
ния подъемной силы, существенное влияние оказывает И пере¬
мещение центра давления.
Известно, что современные теории для пластинок конечного
размаха можно разделить на две группы:
1) теории несущей линии, применяемые в случае пластинок
с большими удлинениями и основанные на предположении, что
индуктивные скорости, создаваемые свободными вихрями, оди¬
наковы для всех точек пластинки, что и позволяет заменять ее
одним присоединенным вихрем;
2) теории несущей поверхности, охватывающие работы двух
направлений: использующие методы теории потенциала (Кин-
нер, Кринес, Кочин) и основанные на замене поверхности си¬
стемой вихрей конечного размаха, распределенных по средней
линии профиля с некоторой плотностью 7.
Настоящая работа относится к последнему направлению, и
потому кратко рассмотрим лишь работы, использующие тео¬
рию вихрей.
Если при малых углах атаки принять, что свободные вихри,
сходящие с концов, направлены по скорости невозмущенного по¬
тока Voo, то для подъемной силы элемента получится обычная
формула Н. Е. Жуковского, линейная относительно циркуляции
Г:
dY = pWoodL,
где dL — элемент размаха.
Если принять, что свободные вихри направлены в бесконеч¬
ности по линиям тока относительного движения, то для подъем¬
ной силы получаются формулы, нелинейные относительно Г [1].
Что касается циркуляции Г в этом случае, то она по теории не¬
сущей линии будет линейной функцией а, а по теории несущей
Поверхности — нелинейной.
*Соавт. А. И. Пастухов. Печатается с сокращениями.
145
Наконец, если принять, при малых углах атаки, что свобод¬
ные вихри совпадают с плоскостью пластинки, то для подъем¬
ной силы получится нелинейная формула относительно Г. Что
же касается зависимости Г от угла атаки, то она будет линей¬
ной. (Это будет видно из дальнейшего.)
С точки зрения изложенного, теория несущей поверхности,
развитая в упрощенной форме Бол леем [2], являлась нелиней¬
ной теорией, так как автор предполагал, что свободные вихри
пластинки, сходящие со всех точек ее боковых кромок, отклоне¬
ны от направления скорости К» на угол, равный половине угла
атаки. Недостатком этой работы является то, что для плотно¬
сти распределения присоединенных вихрей по пластинке Бол-
лей применяет одночленное выражение у — 7осЧ$(0/2), взятое им
для случая бесконечного размаха. Это допущение исключило
возможность подсчета перераспределения нагрузки по пластин¬
ке и связанного с этим изменения аэродинамического момента.
Теоретическая зависимость для подъемной силы, полученная
Боллеем, дает удовлетворительное совпадение с экспериментом
лишь в области весьма малых удлинений (А < 0,2).
Вихревая схема Боллея учитывает влияние вихревых слоев,
получающихся в плоскостях, перпендикулярных плоскости пла¬
стинки, вследствие пересечения этих плоскостей со свободны¬
ми вихрями. В случае пластинки конечного размаха протяжен¬
ность этих вихревых слоев вверх от нее будет конечна. В про¬
стейшем случае, если считать, что плотность вихрей в указан¬
ных вихревых слоях постоянна и эти слои тянутся в бесконеч¬
ность, можно для приближенного учета их влияния привлечь
схему отрывного течения Кирхгофа, использованную Бетцем
для случая нулевого удлинения. Однако в отличие от метода
Бетца теория Боллея учитывает как течение от вышеуказанных
вихревых слоев, так и течение, вызываемое присоединенными
вихрями. Таким образом, схема Боллея учитывает как цирку¬
ляционное течение вокруг пластинки, так и течение, близкое к
отрывному течению Кирхгофа.
Для определения не только силовых, но и моментных харак¬
теристик пластинки нами была предпринята попытка обобще¬
ния теории тонкого профиля на вихревую поверхность конечно¬
го размаха.
Основным уравнением теории тонкого профиля при бесконеч¬
ном размахе является интегральное уравнение
146
составленное в предположении, что присоединенные вихри* с
плотностью 7(1) распределены по средней линии профили, при¬
чем величина dy/dx (ось х направлена вдоль хорды длиной 2а,
ось у — нормально к хорде) учитывает влияние кривизны про¬
филя.
Для случая конечного размаха ядро этого уравнения при¬
нимает вид где Ко есть функция, учитывающая конеч¬
ность размаха присоединенных вихрей. Кроме того, в правой
части этого уравнения, составленного для неизогнутой пластин¬
ки (dy/dx = 0), появляемся скос потока, вызванный свободными
вихрями (Аас) и меняющийся вдоль этой пластинки. В отличие
от скоса; получаемого по теории несущей линии (Дал), в данном
случае скос можно представить в виде
Дас = Дал(1 + Л’1), (2)
где К1 —функция, учитывающая отличие Аас от Дол в зависи¬
мости от удлинения и угла атаки.
Скос Дос, рассматриваемый как функция х, играет в урав¬
нении (1) ту же роль, что и производная dy/dx, учитывающая
влияние кривизны профиля. Заметим, что этот скос в отличие
от dy/dx является неизвестной функцией, зависящей от распре¬
деления 7 вдоль пластины.
Решение полученного таким образом интегрального уравне¬
ния, в отличие от уравнения Воллея, разыскивалось в общей
форме
Ограничиваясь в этой сумме конечным числом членов, можно
Приближенно заменить решение интегрального уравнения зада¬
чи решением системы линейных алгебраических уравнений, по¬
ручающихся для коэффициентов Лп.
Целью настоящей работы, основанной, как и [2], на использо¬
вании теории несущей поверхности, является отказ от замены
основного интегрального уравнения задачи системой алгебраи¬
ческих уравнений и определение коэффициентов Ап как коэффи¬
циентов ряда Фурье. Это упрощение достигается путем введе¬
ния некоторых добавочных гипотез и приводит к существенному
уменьшению объема вычислительной работы при определении
силовых и моментных характеристик.
Заметим, что использование в этом исследовании некоторых
допущений позволяет, в отличие от работы [2], распространить
метод на случай переменной по размаху циркуляции.
Интегральное уравнение задачи
и его решение для случая
постоянной циркуляции
Пусть на пластинку прямоугольной формы в плане под углом
атаки а набегает поступательный поток несжимаемой жидкости,
текущей в бесконечности со скоростью К».
Поместим начало координат в среднем сечении пластинки и
направим оси так, как показано на рис. 1. Будем первоначаль¬
но предполагать, что циркуляция по размаху постоянна и, сле¬
довательно, поверхность пластинки покрыта присоединенными
вихрями, параллельными размаху, циркуляция каждого из ко¬
торых постоянна вдоль размаха.
Рис. 1
В соответствии с принятой схемой с концов пластинки бу¬
дут сбегать свободные вихри, являющиеся продолжением при¬
соединенных. Будем приближенно считать, что оси этих вихрей
направлены по скорости невозмущенного потока К».
Возьмем какое-нибудь сечение пластинки, находящееся на
расстоянии Z* от плоскости ху, и рассмотрим условия ее непро-
148
ницаемости. При этом будем считать, что указанное сечение
представляет собой отрезок прямой длиной 2а.
В некоторой точке с координатами я7, 0, zf прямолинейный
присоединенный вихрь, проходящий через точку с координатой
х, будет вызывать, согласно формуле Вио — Савара, скорость
+L
7(x)dx Г [уo*ri]
Jv”= -sr У —■iz- (4)
— £,
где 7о — единичный вектор присоединенного вихря; 7(2) — ин¬
тенсивность присоедйненного вихря в точке с координатой я;
П — расстояние от элемента присоединенного вихря с длиной
dz до рассматриваемой точки (см. рис. 1).
В проекциях.на оси будем иметь
dv„ = -
7 (x)dx
47Г
+L
L /
-L
(я' — x)dz
х)2 + _ 2)2]3/2
27Г я' — я
(5)
причем
Л'(Ь, х' - х, г') = ^
+
У(х'- х)2 + (L + г')2
L-z'
+
VV - х)2 + (L - г')2
Вся система присоединенных вихрей, распределенных по пла-
стинке, дает скорость
4а
1 ii
1 Г Ar(L, я' - я, z')y(x)dx
(6)
где функция A”(L, я7 — я, г7) учитывает то обстоятельство, что
присоединенные вихри имеют конечный размах, равный разма¬
ху 2L.
Для каждого заданного сечения я7 и z' можно написать
7К(1. = K.(L х, У) 7ТЩ* т
J х' — х J х — х
149
или, вводя обозначения х' = х'/а, zf — z'/а и А = L/a, вместо (7)
получаем
+1
/
-1
А'(А, х' — ху z')y(x)dx
х' — х
= Л-(А, ?7Ш, т
J xf — х
-1
где А*(А, х'у г')— некоторое значение функции А'(А, х' — х, z') в
промежутке от —1 до -1-1 (от —а до -fa). Точное определение К*
возможно лишь в результате вычисления интегралов, входящих
в левую и правую части (8),
Одним из простейших законов распределения вихревой плот¬
ности 7 является закон
7(0) = 2КооЛ0 ctg^,
(9)
где в = arecos(—х). Для этого простейшего закона можно пере¬
писать (8) в виде
/
Л'(А, 9' — в, г') ctg | sin 9d9
cos в — cos в'
= Л'*(А, 9\
(10)
где cos 0 = —х; cos<?' = — х'\
А'(А, в' - в, :') = -
у/ (cos 9 — cos 9')2 + (А + :')2
А - г'
+
y/(cos<? — cos#')2 + (А — г')2
Выделяя особенность, находим
7Г
/
Л **> Ц.О(.+ со!У = [А'*(А, 9', z') - 1]тг. (11)
cos 9 — cos 9 v
Можно показать, что при Р —> 0* функция - соТё-ёо*в'— стремит¬
ся к нулю, и, следовательно, подынтегральная функция в (10) не
имеет особенности, что облегчает численное интегрирование.
Такое интегрирование было произведено, и коэффициенты
А"*(А, в*у z') были вычислены для диапазона удлинений А -
0,2 -г 1,4.
150
Рис. 2
Перейдем к вычислению скоростей, вызываемых в некоторой
точке N* свободными вихрями, которые будем предполагать на¬
правленными по скорости Voo-
Из рис. 2 следует, что пара свободных вихрей будет в рас¬
сматриваемой точке вызывать в направлении оси у скорость
L-z
47Г
+
(L — -г')2 + (х* — x)2sin~ а
(х' — я) COS O'
1 +
+
+
L +
(L + г')2 4- (x* — x)2 sin a
1 +
(x/ — x) cos a
)
(12)
Если бы точка N' лежала на линии присоединенного вихря,
т. е. х' = х, то мы получили бы
7(x)cte
атл = cos а
47Г
1
L-z1
+
1
(13)
L + V
Эта скорость и входит всегда в теорию несущей линии, когда
величина размаха 2L велика по сравнению с х' — х. Для даль¬
нейших рассуждений скорость d.vc удобно представить в виде
dvc - с/г;л[1 + Ki(x' - х, L, z', or)], (14)
151
где К\(х' — a;, L, г1, а) выражается формулой
Kiix'-x, L, z',a) =
L2 - z 2
L-z'
2L (L — z')2 + (*' — x)2 sin2 a
(x' — x) cos a
1 +
y/(x'- Xy + (L - z')\
L + z'
(L + z02 + (x' — x)2 sin a
1 +
(x' — x) cos a
y/(x' — x)2 + (L 4- z')2
- 1.
Для всей вихревой скорости vc будем иметь
Vc = (г^7 + ГТ7) /7(х)[ 1 + Of)]rfar.
(15).
Полученный интеграл можно записать в виде
j 7(х)[1 + Ki(x' - х, L, z', a)\dx =
— a
+a
= [1 + K[{x\ L, z\ a)] J 7(x)dx = [1 + K^x', /, z\ о)]Г, (16)
где K*(x\ L, 2', a) есть некоторое значение K\(xf - х, L, о).
Это значение приближенно можно взять для случая вихревой
плотности, изменяющейся по закону (9).
Таким образом, получим
/0
Ki(6' — в, A, z', a)ctg - sin $d$ =
о
ТГ
= А'Г(0', A, S', о) J ctg ^sinOd0 = Л7(0', A, z\ a)x, (17)
о
152
где
(Л — z')2 + (cos в1 — cos в)2 sin2 а
х 1 +
>/(А — z')2 + (cos(9 — cos#')2
A + z'
(cos 0 — cos 0') cos а
+
(A -f z')2 + (cos 0' — cos в)2 sin2 а
x 1 +
^/(A + z')2 + (cos0 — cos0')2
(cos0 — cos 0')cosa
По формуле (16) было произведено численное интегрирование
в том же диапазоне относительных удлинений А, что и при вы¬
числении коэффициентов /С^(А, 0', zf),
В соответствии с выражениями (15)-(17) скорость, вызван¬
ная свободными вихрями по нормали к пластинке, представится
в виде
Граничные условия обтекания пластинки конечного размаха
можно выразить в виде равенства в рассматриваемой точке нор¬
мальных к пластинке компонентов скорости набегающего пото¬
ка и скоростей, индуцируемых несущими и свободными вихря¬
ми. На основании (18) запишем условие непроницаемости пла¬
стинки:
Условие непроницаемости (19) и представляет собой инте¬
гральное уравнение задачи.
Так как К* и приближенно нам известны, то величина
7(я) может быть найдена известными способами из полученного
Уравнения как функция аиил.
Известно, что если величину у(х) взять в виде ряда
г;с = i^l + ZifO?', А, а)].
(18)
^ = v^sma-V„(l + K;). (19)
Аж J X — X
— а
153
то уравнение (19) можно записать так:
со 1
А0 - A, cos пв' = —
sin о - тг-(1 + Ль
Г ОС
(21)
откуда
1 . } dff v„ } (1 + Л'Г)^'
° 7TSmaj !<• nVaoj Л'*
cos nO'dO1 2vn f (1 + /ij) cos nO'dO*
(22)
—2 . /* cos nO'dO* 2vn f
l„ = Tsm aJ—^ + —j
4*
’TV'oo
0 0
Л'*
Величина ил при постоянной по размаху циркуляции выража¬
ется в виде
v' = icosa(ih + Th)' (23)
коёффициенты Ao,Ai,..., Ап выражаются, следовательно, че¬
рез циркуляцию Г, которая пока еще не определена.
Лля ее определения имеем
Г = J ч(х)<1х = 2Ус»ак(А0 + ^). (24)
— а
Подставляя в эту формулу вместо Ао и А\ их значения, дава¬
емые выражениями (22), и полагая zf = 0, получаем уравнение
для определения Г:
Г 1 — COS в1 ,
Г = 2aVoo sin а / — rffl'-
J Л О
7Г
-2av* cos a J
(1 + Л’о)(1 - cos#') ,
л*
(25)
р с/
где v* = представляет собой скорость скоса по линейной
теории в точке zf = 0, для которой берутся коэффициенты К о 11
Л7о- Отсюда
(26)
Г= Гс
1 + /2(Л, а)/А’
154
где
7Г
О
7Г
7Г
О
После того как определены величины Ло, Ап, позволя¬
ющие вычислить функцию 7(0), а также найдена величина г>л, по
выражению (18) можно определить величину sin а как функцию
от z. Таким образом, при постоянной по размаху циркуляции
условие непроницаемости будет выполняться во всех сечениях
прямоугольной перекрученной пластинки.
При достаточно больших относительных удлинениях значе¬
ния функций /г(А) и /г(А. а) будут близки к единице, и мы по¬
лучим формулу, даваемую теорией несущей линии для случая
постоянной по размаху циркуляции:
Таким образом, функция /i(A) учитывает влияние на величи¬
ну циркуляции относительного удлинения, функция fo(А, о) —
влияние относительного удлинения и угла атаки. В силу по¬
следнего, как видно из формулы (26), циркуляция Г при избран¬
ном направлении свободных вихрей (по направлению скорости
Voo) оказывается нелинейной функцией угла атаки а.
Если бы мы направили свободные вихри по пластинке, как
это принято в работе Вигардта [3], коэффициент /\'^0 и функция
/2 оказались бы не зависящими от угла атаки а, а следователь¬
но, циркуляция, как указано в начале статьи, была бы линейной
функцией угла атаки.
Вообще же по поводу угла ’’заклинения” свободных вихрей
следует заметить следующее. Поскольку теории поверхностей
Конечного размаха базируются на схематических вихревых си¬
стемах, воспроизводящих лишь главные черты исследуемого
явления, постольку при назначении направления свободных вих¬
рей достаточно воспользоваться некоторым эффективным углом
заклинения’. Очевидно, что величина его будет зависеть как
°т выбранной вихревой схемы, так и от тех упрощений, кото-
Pbie вводятся при ее математическом анализе. В нашем случае
155
угол ”заклинения” свободных вихрей относительно плоскости
пластинки принят равным углу атаки а. Проведенные расчеты
показывают, что для широкого диапазона относительных удли¬
нений это значение угла ’’заклинения” дает вполне достаточное
приближение к экспериментальным данным.
Возвращаясь к решению основного интегрального уравнения
задачи, заметим, что поскольку для определения циркуляции Г
нами получена формула (25), определение коэффициентов Ап не
требует решения системы уравнений и сводится к вычислению
их значений по формулам (22), что не представляет трудности.
Рассмотрим случай прямоугольной пластинки с переменной
по размаху циркуляцией. Будем искать 7(х, z) в классе функ¬
ций, которые можно представить в виде 7(х, z) = 7(2)7(2). То¬
гда индуктивная скорость, вызываемая одним присоединенным
вихрем в точке пластинки с координатами х', 0, будет выра¬
жаться формулой
где 7J* есть некоторое среднее значение 71 (г) в промежутке от
—L до +Х, a K(xf — х, z\ L) имеет прежнее значение.
Значение 7J можно приближенно определить для заданного
типа распределения циркуляции по размаху, например для слу¬
чая эллиптической циркуляции.
Для более грубой оценки 7J можно взять равным интеграль¬
ному среднему значению 71 (z) по размаху. В частности, для
случая эллиптического распределения циркуляции 7* = 7i(0)f-
Вся система присоединенных вихрей, распределенных по пла-
Пластинка с переменной циркуляцией
7(х) К(х' - х, z', L)y!
2ж х* — х
156
стинке, дает скорость
1 [ К(х'- х, z', L)~f(x)yl
Vn = - — I J.'-L^dz =
x’ — X
+a
'n~~h!'
— a
.-£*•<,W.
— a
где A'*(x' — x, z', L) — некоторое среднее значение К в интервале
от —а до +а, удовлетворяющее соотношению (28).
Используя этот же закон распределения интенсивности для
свободных вихрей, можно вызываемую ими в направлении оси
у индуктивную скорость записать в виде
-a-L
— z, х' — х, a)]dxdz =
+L ( -4-а
cos a f 1 ^7i(z)
47Г
-L
+A'i(z' — z, x' — x, a)]dx|cfz =
+■£
cos a [ 1 r , . Ч,9Г .
= —4Г J + Л‘(г "
(29)
-L
где А*(г' — z, x', a) — некоторое среднее значение A'i(z' — z, x' —
Qr) в интервале от —a до +a, удовлетворяющее соотношению
j + K^Z> ~ Z'X' ~ X’ Q№X =
— a
+Д
= [1 + K\{s' - z, x\ a)] J 7(x)~^dx.
157
Выражение (29) можно записать следующим образом:
-L
или коротко
vc = (i.+xrw=(i + *rn^U + «).
(30)
где в определяется из равенства г = —L cos в, а Г есть значение
циркуляции в сечении zf.
Из полученных формул следует, что вычисление коэффициен¬
тов К* и К”, а следовательно, и функций /i(A, z*) и /о(A, z*л о)
в случае переменной циркуляции представляет значительные
трудностй. Если, однако, предположить, что эффект малости
удлинения, выражаемый этими функциями, мало зависит от ти¬
па распределения циркуляции, то формулу (30) можно записать
в виде
где коэффициент К* = /v'J* (ж', zf} L, а) берется для случаяпосто-
янной по размаху циркуляции. В этом случае вместо уравнения
(25) получим
причем /i(A, z') и /г(А, г', а) в соответствии со сделанными вы¬
ше предположениями берутся в различных точках размаха для
случая постоянной по размаху циркуляции. Полученное при
указанных допущениях уравнение (32) является обобщением из¬
вестного интегродифференциального уравнения Прандтля. При
достаточно больших А значения функций /i(A, z') и /о(A, z', о)
становятся равными единице, и мы получаем обычное уравне¬
ние теории Прандтля.
(31)
— L
г= Гоо/^А, z') +
/о(А, а)а Г дГ dz
2 j сЪ z‘-z
I
(32)
Расчетные формулы
и сравнение результатов расчета
с экспериментальными данными
Примем в соответствии с формулой (30), что линейная часть
скорости скоса по направлению нормали к пластинке, вызывае¬
мая свободными вихрями, определяется выражением
Г cos а ., /Л„.
= 77-7—х(1+ 6). (33)
4Lsin в
Для циркуляции в среднем сечении zf = 0 на основании уравне¬
ния (32) получим
Го = Гоо 1 * (34>
* 2Л( + "о)/2(А, <*)
или, полагая приближенно 1 60 & 1 и вводя обозначение
г(^ = ттшту (м|
найдем
Го = Гсо/'СА, а).
Если теперь для упрощения расчетов принять, что значения
функций /i(A, zf) и /о(A, z*, а) постоянны вдоль размаха и равны
их значениям в среднем сечении /1 (А) и /о(А, а) соответственно,
то для циркуляции в произвольном сечении можно получить
Г = Г~Т7ТЖЗ' (361
1 ^ 2Л sin 9
ИЛИ
г - г 8'пЧ1 + £Ых><*)} П7)
sin 8 + ^/2(А, а)
Для подъемной силы, действующей в целом, можно написать
+L
Y = pV'оо J Гйг. (38)
-L
Заменяя в этой формуле циркуляцию Г по выражению (37) и
Учитывая, что dz = L sin 8d0, находим
У = рУооГоЬ j Sln4l+r)f' (39)
J sm0 + 5х/з(А, а)
159
Переходя к безразмерной форме и заменяя Го по (36), получаем
Су = 27г/*(А, ar)esina, (40)
где значения функции /*(А, а) определяются по формуле (35), а
коэффициент
1 / sin2 9 [1 + ^/2(А, а)] -
2 J sin0-f ^/2(А, а)
играет роль коэффициента полноты эпюры распределения по
размаху циркуляции или подъемной силы. Произведенные рас¬
четы показывают, что коэффициент е практически не зависит от
угла атаки и возрастает с увеличением удлинения А, оставаясь
в диапазоне удлинений А = 0,2 -г 1,4 больше соответствующего
коэффициента для эллиптического закона распределения цир¬
куляции (тг/4).
Лля случая переменной циркуляции будем иметь
7(ж, г) = 7(1)71 (г).
Лля функции 7(х) можно написать разложение
Q ^
7(х) = /ioctg - + ^A„sinn0, (41)
П
и поэтому
7(ж, г) = А0 ctg - + An sin пв,
П
где каждое Ап равно уг(г)Ап.
Уравнение (18), выражающее собой условие непроницаемо¬
сти, сохранит свой вид, однако под знаком интеграла вместо
функции 7(я) будет стоять функция 7(2, z). Точно так же сохра¬
нят свой вид формулы (22) и (24).
Функция 7i(z) для середины пластины (z = 0) может быть
принята равной единице. Действительно,
+а +а
Г(г) = J у(х, z)dx = 71(2) j 7(x)dx.
-а —а
+<•
Обозначая интеграл / 7(x)dx через Го, будем иметь Г(г) =
-а
-yi(^г)Го- Если теперь потребовать, чтобы Г0 равнялось цирку-
ляции T(z) при z = 0, то в этом случае следует положить 71 (~)
при z = 0 равной единице.
160
Из сравнения формул (24) и (35), взятых для среднего сечения
на основании изложенного, получим
Ао + ^Ai = /*(А, a)sina. (42)
В соответствии с (42) формула (40) для коэффициента подъем¬
ной силы перепишется в виде
И-
Су = 2тге [Ао + ^Аг]. (43)
Выражение для нормальной силы, согласно обобщенной тео¬
реме Н. Е. Жуковского, можно написать в виде
+L +а
N
-L -а
+Ь +а
-Р J J y(x)yi(z)Vdxdz, (44)
причем V есть проекция полной скорости в данной точке на на¬
правление его хорды, т. е.
V = Voo cos a -h v'c sin а, (45)
где — скорость скоса, вызываемая системой свободных вих¬
рей в данной точке по направлению, перпендикулярному скоро¬
сти потока К»•
Подставив это значение V в выражение (44), получим
+L +я
N ~ pVoo cos a J J y(x)yi(z)dxdz+
-L-a
+L +а
+psin а J J y(x)yi(z)v'c(x, z)dxdz,
или
-L-a
+ L + a
N = pVooCOsa J J y(x)y\(z)dxdz -f
-L-a
+L
+/W* sin a j j y(x)y\(z)dxdz, (46)
-L -a
161
где v* — среднее (в смысле обобщенной теоремы о среднем) зна¬
чение скорости скоса потока, вызванной свободными вихрями.
Выражение (46) можно переписать в виде
* \ +L +а
N = (cos а + sin а J // 7(x)yi(z)dxdz, (47)
°° -i-а
ИЛИ
N = ^1 + tg У cos а. (48)
Величина ^ tga невелика по сравнению с единицей, и поэтому
не будет большой погрешностью принять для упрощения рас¬
четов, что скорость V* равна среднему по хорде значению ско¬
рости скоса в среднем сечении z = 0, т. е.
^ = ^(1 + /<Госр),
* со У оо
где
= Гр 7ГГ(Л, а) ;
Уоо 4LVCO 2А
или в соответствии с формулой (42)
vn тг Ло 4- \А\
sin а, (49)
Вводя обозначение
X = (l + у~ tg a) cos а
(50)
(51)
и используя для вычисления коэффициента подъемной силы
формулу (42), можно получить выражение для коэффициента
нормальной силы
Сп = Чтгех ^Л0 4- -А\
Как видно из изложенного, выражение для момента аэроди¬
намических сил, действующих на пластинку, можно записать
следующим образом:
+£ -fa
Mz — р J j 7(2)71(z)xVdxdz, (52)
— L —a
162
где, как и ранее, через V обозначена проекция полной скорости
в данной точке на направление хорды, определяемая выражени¬
ем (44). В соответствии с этим после несложных преобразова¬
ний формулы (52) получим
где V**—некоторое среднее значение скорости скоса потока,
вызванной свободными вихрями, которая, вообще говоря, отли¬
чается от среднего значения скорости в формуле (46).
После замены вихревой плотности 7(2:) рядом (41) внутрен¬
ний интеграл выражения (53) приводится к виду
Учитывая, что выражение для v**/Voo входит в формулу (53) с
малым множителем sin о, не будет большой погрешностью при¬
нять
В этом случае аэродинамический момент можно выразить фор-
-L
В соответствии с выражениями (55) и (56) для коэффициента
Момента можно написать
Относительное положение центра давления при выбранном
Начале отсчета определяется формулой
cos a т—- sin а
Voo
(54)
— а
-L
где на основании предыдущего
+L
z)dz = 2 Le: (56)
(57)
(58)
163
Положение центра давления относительно передней кромки
будет равно
Л Л _ _ ^4 о ~^4*> / 2
Q = 0,50- 0.25—--=д, (59)
тогда для коэффициента момента относительно передней кром¬
ки получим
Ст = CnCd = 2weX (о,50 - 0,25^^) , (60)
или
с„ = С,х (о,50 - 0.257^7^|) ■ №)
Полученные выражения для коэффициентов подъемной силы
и момента содержат только первые три коэффициента ряда для
вихревой плотности. Очевидно, что остальные коэффициенты
определяют изменение распределения плотности, не оказываю¬
щее влияния на подъемную силу и аэродинамический момент.
При практическом использовании формул (43) и (60) в них
вводился эмпирический коэффициент
(dCyJda)x=OQ Goo
Ъг ~ 27’
учитывающий меньшую по сравнению с теорией величину цир¬
куляции.
Для сравнения с продувками крыльев с профилями NACA-
0021 и NACA-0015 принималось среднее для них значение =
0,90, при сравнении с результатами эксперимента для плос¬
ких пластинок эмпирический коэффициент не вводился. Здесь
уместно заметить, что сравнение теоретических результатов с
экспериментальными данными для телесных профилей и пла¬
стинок конечной толщины не противоречит теории тонкого про¬
филя, так как последняя предполагает плавное обтекание сред¬
ней линии профиля, по которой распределяются присоединен¬
ные вихри.
Экспериментальная проверка полученных формул (рис. 3)
показывает практически достаточное согласие расчетных ре¬
зультатов с результатами испытаний пластинок и крыльев в
широком диапазоне удлинений Л = 0,4 Ч-1,5 (i — NACA-0015, 2^
NACA-0021 — эксперимент ЛГУ; 3—расчет).* Это позволяет
*В оригинале статьи приведены также графики Су для Л = 0,2 и Ст
для Л =г 0,4 4- 1,5.
164
Рис. 3
предполагать, что результаты настоящего исследования найдут
применение для расчета аэродинамических характеристик кры¬
льев малых удлинений.
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Поляхов Н. Н., Пастухов А. И. К теории крыла конечного размаха
С. А. Чаплыгина//Тр. ЛПИ. 1953. № 5. С. 168-175. [21*]
2. Bollty W. A non-linear theory and its application to rectangular wing of small
aspect ratio//ZAMM. 1939. № 1.
3. Wieghardt. Uber Auftriebsverteilung des einfachen Rechteckfliigels iiber die
Tiefe // ZAMM. 1939. Bd 19. H. 5.
II.3. ВИХРЕВАЯ ТЕОРИЯ
НЕСУЩЕЙ ПОВЕРХНОСТИ [34]*
В предлагаемой работе дано обобщение методов, развитых в
работе [1] для случая прямоугольной пластинки при некоторых
частных видах распределения циркуляции, на случай пластин¬
ки произвольной формы в плане. Получено интегральное урав¬
нение второго рода для вихревой плотности, удовлетворяющей
требуемым граничным условиям.
Вихревая схема и индуктивные скорости
Пусть в стационарном, поступательно движущемся потоке
идеальной несжимаемой жидкости находится слабо изогнутая
«несущая» поверхность. Известно, что вследствие ее малой
изогнутости можно в первом приближении удовлетворять усло¬
вия непроницаемости не в точках поверхности, а в их проекциях
на плоскость, нормаль к которой составляет с нормалями к по¬
верхности малые углы. Таким образом, нас будет интересовать
в дальнейшем лишь плоская поверхность. Первоначально мы
возьмем ее в виде системы полосок прямоугольной формы, ле¬
жащих в плоскости xz (рисунок). Пусть таких полосок будет
п, а ширина их будет одинакова и равна Д*. Предположим да¬
лее, что каждая полоска покрыта системой П-образных вихрей с
плотностью 7„, где и = 1, 2,..., п, причем плоскость, в которой
лежат эти вихри, совпадает с плоскостью полоски.
-Мл—
. -v гг—- -! \
—
V: 1
Tid*i n\
„ *"* » _г~—
* —К—
— ! -и ,
х' 1
i *1 f
j
'г
*Соавт. А. И. Пастухов. Печатается с сокращениями.
166
Один П-образный вихрь с номером V будет вызывать в точке
JV7, лежащей в середине полоски с номером т, скорость
Л 2 dx i л П
Д Д*и,т — л , _ (fv + l /*') _ (/y + l /д)>
где
47Г х' — Ху
Л =
47Г
(1)
Z' — Z„
^/(z' - z„)2 + (Z' - z„)2
Л =
1 +
Z - z„
V^z' - z„)2 + (г' - z„)2
z' — zv
Так как zv+\ — zv + Az, то при достаточно малом Az можно
написать
dfy
+1 fu ^ о
azv
что позволит представить (1) при v ф т в виде
yudx \ х* — xv 1
(2)
+
4тт ^ Я? (z'-z„)2
(z* Z|/)31 2(z'-z„)\
Щ J ^ j
1 +
(3)
где
Ru = V(x' -x^ + iz' -z„)2.
В полоске с номером т = и скорость на основании (1) пред¬
ставится формулой
А Ч
—A iui =
l\dxx
2е
lirix'-Xx) yj(X' - хг)2 + Е1
+
7idxi2
47Г £
1 +
X — Х\
ч/(х/_х,)2+£2
(4)
так как zm+i = zf + £, zm = z' — е. В формуле (4) для краткости
обозначено ут = 7i и xm = ^1 •
Суммирование действия всех П-образных вихрей даст пол¬
ную скорость в точке N'. Увеличивая неограниченно число по-
л°сок, получаем возможность исследовать «несущую» поверх-
1G7
ность, ограниченную некоторой кривой. Прежде чем перехо¬
дить к такому суммированию, отметим следующие тождества:
1 +
X ~ Х\
yj(x' - Х\)2 + е2
L + z' L-z'
+L
/dz f dz f ipdz f ipdz
(7^)2 + J (FTip + J -Щ+ J -Щ< (5)
— L z'+e — L z'-fc
где
X — X\
r?. b
x — X\
[(*' - n)2 + (L + Z')2]1/2 ’ [(x' - Xi)2 + (L - Z')2]1/2’
1
+
(z' - z)2 (x' — Xl)2e
— xi)dz
-L
- xx)dz
1 2s f (xf — x
c'-Xi 7(1:' - art)2 + e2 ~ J Я?
-(7+7)^
\-L *'+£ /
G-£ +t\
*/
:4« /
(x' — xi)dz
(5a)
2 {[(*'■
L + z'
L-г'
Kl " ' an)2 + (L + z>y-YI- ' l(x' - xi)2 + (L - z')2]1/2
Принимая во внимание (5) и (5a) и вводя безразмерные вели¬
чины z = z/L, z = zf/L, x = х/аь x' = x'/ai, Ai — L/a\ (cm-
рисунок), сможем записать формулу (4) в виде
2 7l K\dxx 71(1 Kcl)dxx yxdxx
~A ^ = r.jrzr, + -2,A7(1 - {■»)• + 47ч *
z'-f +1\ _ /*'“* +1
(l + /i)dz TiAidi,
(2' - z)2
168
, X - *l
Л [(*'-*i)2 + Af(z'-x)3]3/3’
/,= /1[(i'-x1) + 2A?(2'-2)2],
1-2'
/Cl =
+
\/(x' - II)2 + A?(l + x')2
1 + 2'
J?' — Xj
>/(x' - Xi)2 + Aj(l - 2;)2_
Выясним теперь суммарное действие на точку ЛГ' всех 11-
образных вихрей, присоединенные части которых проходят че¬
рез точки, отстоящие от линии передних кромок на одно и то же
относительное расстояние 1 + £, или, что то же, на расстояние
£ от середины полосок. Если передняя кромка рассматривае¬
мой полоски отстоит от оси z на расстояние хп, то координату
х ”присоединенного” участка вихря можно записать в виде (см.
рисунок)
X = х„(г) + а(г) +£а(2),
откуда
х-х„-а _1jU$+1
а
где хп — абсцисса передней кромки; а — полудлина полоски. Яс¬
но, что
х' - х = хП1 - хп + (1 -а)(1 + £) + (£' - О.
х' — х\ = dx = ad£, dx\ = d£, d = a/aj,
причем xnl — хп и 1 — a представляют собой функции от z} кото¬
рые обозначим соответственно через p(z) и q(z). Эти функции
полностью характеризуют форму пластинки. Для пластинки, у
которой а постоянна, х' — х = p(z) -f £' — £. Для прямоугольной
пластинки р = 0 и х' — х = f.
На основании (3) и (6) можно записать при неограниченном
Увеличении числа полосок
^ = lL ^с1 + Al
^ 2яг £ 2ttAi 1 - z2 4ir
. + + (7)
47гА! \ J J I {z‘ — z)2
,-1 r'+*
169
где
7 = 7a/ai = 7a, /1 = (/);
1Г = Х! ) J\ — \J /T — fl 1
/l {f)x = r1 j
^ [(i'-a:)2 + A2(r'-2)2]3/2-
Здесь черточки над x и z для краткости опущены, но следует по¬
мнить, что х измеряется в долях a, a z — в долях L. Знак минус
включен в 7. Интегралы, входящие в формулу (7), криволиней¬
ные и вычисляются вдоль кривых £ = const, при этом
есть функция z. Каждая из таких кривых представляет собой
геометрическое место точек, отстоящих на одно и то же отно¬
сительное расстояние от линии передней кромки. В формуле
(7) можно устремить е к нулю и понимать входящие в нее инте¬
гралы в смысле их главного значения. Это относится только ко
второму интегралу, так как первый интеграл не имеет особенно¬
стей относительно z' — z и, следовательно, его главное значение
совпадает с обычным. Второй интеграл в смысле главного зна¬
чения будет существовать, если предположить, что функция
в промежутке z' — rj ^ z ^ z* + 77, где г) сколь угодно мало, есть
аналитическая функция. Выделяя в формуле (7) слагаемое с
особенностью (£' — £)~1 и выполняя интегрирование по £, полу-
чаем
х' - х - p(z) + [1 - a(z)](l + О + (С - О
Ф = 7(1 + /) = <$! +
<ЭФ
д:
“Ку-Р7
-1
2тг А, 1 -
7i# , [
(*< /• Т г» \ 1
(8)
х, - А'сх -
170
Xi — регулярная функция, так как 1 — Кi при £ —^ £' стремится к
нулю как (£' — £)2. Знак V.P. перед интегралом показывает, что
интеграл следует понимать в смысле его главного значения.
Формула (8) позволяет вычислить скорость гс, если задан за¬
кон распределения плотности 7 и форма пластинки.
Интегральное уравнение
обтекания несущей поверхности
Если потребовать, чтобы величина w(Nf) удовлетворяла ус¬
ловию непроницаемости
w(N') = Voo*in{*-0i) = f'(t'i *')■
где Vqq — скорость невозмущенного потока; а — местный угол
атаки и д' = arctg(dy/dx)x=zx‘ считаются заданными, то исполь¬
зование формулы (8) даст*
i =w. --■) - »■ (®)
где w есть сумма всех членов правой части (8), за исключени¬
ем первого. Интеграл, входящий в (9), может быть обращен,
если предварительно указан класс функций, к которому должно
принадлежать искомое 71. Этот класс устанавливается в зави¬
симости от того, каким условиям должно удовлетворять 71 на
концах отрезка [—1, 4*1]. Такими условиями могут быть [2, § 88]:
1) 71 обращается в ноль на обоих концах как (1 — £
2) 7i обращается в бесконечность на обоих концах как (1 —
£'2Г1/2;
3) 7i обращается в бесконечность на одном конце и в ноль на
другом как У(1 - £')/(1 + £'].
Отсюда видно, что замена интегрального уравнения (9) си¬
стемой алгебраических уравнений не может привести к какому-
то определенному решению. Решение будет совершенно неопре¬
деленным, пока не указан класс функций, в котором оно отыс¬
кивается, и не гарантировано выполнение требуемых концевых
Условий.
*3десь символ V.P. перед интегралом опущен.
171
Производя обращение интеграла (9) при условии (3) и заме¬
няя обозначение £ на /, получаем
+1
71
где
2 /1 - / У ЯТё 14о Sin(a -1?')
-1 т
(10)
или в раскрытом виде
/ Т-*
71 =7оо - ~2 "ГТгууТ//71^’ ^П)
-1
где
У /1 + £' l-i-xi+Ф +/(£*-0i)(l-za)cfc
*=/vi^f /-* d(‘- *='vp'/ _
-1 " ’ -1
(Z' - z?
Интегральное уравнение (11) принадлежит к типу уравнений
второго рода, и поэтому его можно пытаться решать методом
итераций. Однако прежде чем обсуждать этот вопрос, несколь¬
ко преобразуем это уравнение.
Другая форма представления скорости w
Рассмотрим интегралы
z —
-S
dy{z, О dz
, h
+i-
-1
ду(г, £) dz
(12)
dz z* — z' J dz z* — z'
-1 2;+£
где 7 обладает свойством
7(±l,O = 0. (13)
Так как интегралы не имеют особенностей, то можно написать
Ji = —р—
Z — Z
_ ! у*2 -
— 1 J (z'-z)2
ydz у(z' - е, О
J2 = -
Г — Z
+ 1
-1.
+ 1
z —e
{ idz
J (z'-z?i
-1
+1
(14)
[ ldz - Т(г' + £, Q _ f id:
z,+e J (z'-z)2 e J (z'-z)2^
z'+e
г'+е
172
откуда
J=J'+J>~2f-{j + j)w^' <16>
\-l :'+f/
где т(£> z; ± e) = 71 =F (dy/dz)z‘€ 4- ..., а через 71 обозначено
7(z', f). Кроме того,
; = TT?+rb+ (/ + /) (T^F' (17>
и потому
+1
Шп 4ТГЛ!
-1
+ 1
7i 1 1 \, D f (7 - 7i)<fc
27rAi
-1
С другой стороны, если взять частный вид распределения
плотности
= J_VP =
л 4ttAi J dz z'-z
-l
+ 1
1 L_VP / (7 - 7i)<^
^ 1 - z'2 4Я-А, J (z‘ - z)2
(18)
7 =7r
У1-?
vi
то для получим
Ti 71
= = 7o\/l--2, (19)
i-vp
J (г' -
-1
Из формул (18) и (20) следует
4A1vT^?2 l-*'2
+i
(7* ~ 7i)d~
47rAi Т * J (z' — z)2
(20)
+1
/ _ 71 _J_A/P f (7 -7*V> ,on
“;л_4А1ч/Г^ 4jrA, J (z'-z)2 ‘ (21)
-1
Для эллиптического распределения 7 интеграл в этой фор¬
муле обращается в ноль. Для распределений, близких к элли¬
птическому, интеграл будет мал по сравнению с первым сла-
гаемым. Для того чтобы величина w\ сохраняла конечное, не
173
равное нулю значение при z' — ±1, необходимо, чтобы обра¬
щалось в этих точках в ноль порядка — £ 2^ —► 0.
Таким образом, будем иметь
w> = Л \ L_vp +[(7-V)dz =
я 2тгА 1 \ -z'2 4жХг J (z'-z)2
-1
+ 1
_ 71 1_у р [ (7-7*)<**
4А1Л/Г^75 4жХ, ’ J (z'-z)2 ‘
-1
Обращаясь теперь к формуле (7), запишем ее в виде
7i 1
(22)
/ 7i ^1 ,
w = Ь
2ж
_ J_v Р
4тгА! ‘ J (z'-z
-1
41 +1
+vJw-^-zkveT-
-1 -1
2irAj 1 — z'2
(1 + hd) -f
7(/ ~ A’ci) ~ 7i (/i ~ A'ci )dz
(z'-z)2
откуда на основании (22) после небольших преобразований по¬
лучим
.../ 7i Л’г , 7i(l + ^ci) , А
W — —— Н .. , -|
+ 1
2тге-^ ' 4A1N/T^72 ’ 4тг/(7 f
-1
. vр угО-Ы-ъ</,-к«)ь +
4ttAi J (z' - z)-
-1
-1 -1
+ f)dz
, Ат = 7-7*'
-1
Так как
vT^ А. 7vT^75-7l4/I^
7 =71-77=77, Д7 = —
vT-^2
174
то выражение для w после выделения особенности (£' — £) 1 и
интегрирования по ( можно представить в виде
+1 +1
”=^/^Т + 5л^Ы/Т1(, + “' + ф1+ф2Ж' (23)
-1
где
2(l-/ii)AiVT-772
*■=—.
Ф •п /'{КМ!*' - *)*/- Ф] - - vi]}d
=w
(Z'-Z?
(24)
j +/ (£ЯХ - ft) (А?(У - zff - / - l]dz
. (25)
-1
R= Vl~z2, Ri = V 1 - r'2, v = f-KcX.
Интегральное уравнение (11) заменится теперь уравнением
71 = 7”'2Л7Tih^yiTi J ут'l)d(' {Щ
-1
где
+ 1 I
-f УС\ -f- Ф1 + Ф2 ,г/
-1 Т
причем Фх и Ф2 даются формулами (24) и (25). Если бы рас¬
пределение ух вдоль линии ^ — С было эллиптическим, то ве¬
личина Ф2 была бы равна нулю. В случае, когда это распре¬
деление близко к эллиптическому, величина Ф2 будет мала по
сравнению с единицей и ее в первом приближении можно отбро¬
сить. Тогда уравнение (26) превратится в интегральное урав¬
нение Фредгольма второго рода, решение которого можно най¬
ти одним из известных приближенных способов. Найдя таким
образом 7i(£, z), мы получим возможность найти Фо и сделать
следующее приближение. Первое приближение в какой-то мере
Позволит судить, насколько искомое 7 отклоняется от эллипти¬
ческого.
175
Для того чтобы сделать полученные результаты более на¬
глядными и качественно сравнимыми с результатами теории
несущей линии, отметим, что
+1 j / -1-1
J \/у“|7|ГГ] =*’ ГЛ*) = J
-1 ' -1
и, кроме того,
+1 Г+1
У у—(■-Г—*
-1 L-1
#=-!( 1 + хЦ-ФП.
«1
где и Ф* — значения х\ иФь взятые для некоторых значений
£ * и £*. Точно так же
+1/ +1 ,
1 / I Г /1+£' 1
*j I j V 1-*'?-/
-1 V-1 1
+1
■+1
/
(f^i -71Я)02<**
(г' - г)2
> <Ц =
1 /* (ГЯ, - ГiR)<p?,dz
Gl J
-1
где ^2 = ^i(*; -~z)2f — / — а есть значение <£о для некоторых
£ * и вообще говоря, отличных от предыдущих. При такой
форме представления интеграла, входящего в уравнения (26),
мы получим
71 = 7оо ~
\ /Г=7
r=^Vi + /x
1 + УС-
2ЬуД
+1 (г._ д) <p*dz
(z> - z)2
(27)
откуда
»Г!
г, = Гво -
2Ai\/l — z2
. 1 V (£*-*)«*
(28)
176
Если бы мы имели прямоугольную пластинку большого удли¬
нения Аь то величины и Ф* были бы малы по сравнению с
единицей, а было бы близко к —1, что непосредственно сле¬
дует из стремления / и / к нулю при неограниченном возраста¬
нии Ai и z ф г*. Вследствие этого уравнение (28) превратится в
уравнение
Г =г , 1 1,0 7<г -п*
+ _LVp [LrzD^ (29)
2тгА! J (z'-z)2 ’ ( '
2AiV1--172 2тгА!
-1
которое представляет собой интегральное уравнение теории не¬
сущей линии. Это уравнение переходит в обычное интегродиф-
ференциальное, если принять во внимание (18) и (21). Если в
(29) интеграл приближенно заменить конечной суммой, то по¬
лучится система уравнений
п
ЬщГm ■— Гqm + ^ (30)
i/ = l
предложенная Мультоппом. В этой системе знак штриха при
сумме указывает, что при суммировании следует пропустить
слагаемое, соответствующее и — т. Необходимо отметить, что
уравнению (29) соответствует представление индуктивной ско¬
рости wn в виде
+1
dr dz
w„
dz zf — z
4Ln/1 -V* 4ttL
Здесь первое слагаемое есть не nio иное, как главная часть
скорости, определяемая местной циркуляцией Гь а интеграл
Учитывает ту добавку, которая получается вследствие откло¬
нения циркуляции в точках z -ф- z* от эллиптической, принима¬
ющей при z = z* значение Г\. По сути дела этот прием вы¬
деления главной части скорости, определяемой через местную
и лежит в основе вывода интегрального уравнения (26). С
Физической стороны такое выражение скорости представляется
°пРавданным, так как средняя по сечению скорость прежде все-
Го Должна зависеть от нагрузки в этом сечении, которая пропор¬
циональна циркуляции. Формулу (28) рационально представить
177
в виде
Г =
Ш—’
где
6 = б! + 67 = х\ +
-1
Так как, вообще говоря, 1 + Ь ф 0 при 2 = ±1, то Г и 7 обраща¬
ются в этих точках в ноль. Если бы мы знали , то расчет
7i и Г*1 был бы аналогичным расчету по теории несущей линии.
Чтобы решать задачу методом итераций, можно взять значе¬
ния х\ и Ф1 при £' == 0,5 и £ = —0,5, что соответствует предпо¬
ложению Вейзингера, которое строго выполняется только для
случая неизогнутой пластинки бесконечного размаха. Высшие
приближения будут находиться по формуле (26).
В заключение отметим, что основное интегральное уравне¬
ние задачи было получено путем рассмотрения системы прямо¬
угольных полосок, каждая из которых покрывалась системой 11-
образных вихрей, и последующего предельного перехода. Этот
переход приводил к тому, что условие непроницаемости могло
быть выполнено во всех точках несущей поверхности. Напо¬
мним, что точки Nf, в которых выполнялось это условие пер¬
воначально, до перехода к пределу, выбирались на серединной
линии полоски. Совокупность таких точек, лежащих на перед¬
них кромках полосок, в пределе переходила в некоторую кри¬
вую, форма которой зависит от характера предельного перехо¬
да. Если контур, ограничивающий несущую поверхность, дани
представляет собой плавную кривую, то разбиение поверхности
на элементарные прямоугольные полоски удобнее производить
следующим образом: 1) разбить поверхность прямыми с = const
на трапецеидальные полоски шириной Д^г; 2) для каждой по¬
лоски построить серединную линию; 3) на каждой серединной
линии построить прямоугольную полоску шириной Д-.
Таким образом, контур несущей поверхности будет аппрокси¬
мироваться ступенчатой ломаной, построенной по методу среД'
них ординат. Предельный переход от системы прямоугольных
полосок к площади, ограниченной плавной кривой, позволил,
как мы видели, найти плотность 7 в классе функций, отвечаю'
щих вполне определенным граничным условиям.
178
Наконец, нужно отметить, что все приведенные выше рассу¬
ждения относились к малым углам атаки, что позволяло счи¬
тать плоскость П-образных вихрей совпадающей с плоскостью
xz. В случае больших углов атаки такого рода предположение
делать нельзя. Для прямоугольных пластинок в предположе¬
нии постоянной циркуляции, дающей два концевых сосредото¬
ченных вихря, вполне достаточно, как показывают расчеты [1],
считать, что эти вихри направлены по скорости невозмущенно¬
го потока Voo. В случае переменной циркуляции, когда свобод¬
ные вихри сходят со всех точек поверхности, представляется,
что эти вихри должны лежать вследствие обтекания на самой
поверхности. Однако эти рассуждения с физической стороны не
вполне справедливы, и вот почему. Система свободных вихрей,
образующаяся около несущей поверхности, физически зарожда¬
ется в пограничном слое, образовавшемся около нее. Скорости
vy внутри слоя, за исключением точек, лежащих на поверхно¬
сти, не равны нулю, и потому свободные вихри, вообще говоря,
не будут прилегать к поверхности, а будут направлены к ней
под некоторыми углами. Так как пограничный слой имеет в на¬
правлении нормали к поверхности малое протяжение, то можно
источники, порождающие свободные вихри, снести на поверх¬
ность, введя тем самым присоединенные вихри и направив сво¬
бодные вихри под некоторыми углами к ней. Точно указать зна¬
чения этих углов заранее нельзя, но, имея в виду интегральный
эффект действия вихрей, можно в первом приближении выбрать
Для них некоторое среднее значение, дающее хорошее совпаде¬
ние данных расчетов и эксперимента. К таким значениям сле¬
дует отнести угол, равный а/2, что было принято еще Боллеем
в его работе 1939 г. Вообще же по поводу угла «заклинения»
следует заметить, что поскольку теории несущей поверхности
базируются на схематизации явления в рамках идеальной жид¬
кости, постольку при назначении направлений свободных вих¬
рей достаточно воспользоваться некоторым эффективным углом
«заклинения». Очевидно, что величина его будет зависеть как
от выбранной вихревой схемы, так и от тех упрощений, которые
вводятся при ее математическом анализе.
УКАЗА ТЕЛЬ ЛИТЕРА ТУРЫ
Поляхов Н. Н., Пастухов А. И. Теория несущей поверхности прямо¬
угольной формы//Вестн. Ленингр. ун-та, 1959. № 13. С. 93-110. [26*]
2* Мусхелишвили Н. И. Сингулярные интегральные уравнения. М., 1946.
II.4. ПРИБЛИЖЕННАЯ НЕЛИНЕЙНАЯ
ТЕОРИЯ ОБТЕКАНИЯ ТЕЛ
ЦИЛИНДРИЧЕСКОЙ ФОРМЫ
СТАЦИОНАРНЫМ ПОТОКОМ
НЕСЖИМАЕМОЙ ЖИДКОСТИ [36]*
Постановка задачи и основные уравнения
Подавляющее большинство работ по теории несущей поверх¬
ности посвящено исследованию тонких тел. При практическом
использовании результатов этих работ обычно вводятся эмпи¬
рические поправки, позволяющие учесть влияние формы профи¬
ля тела на суммарные гидродинамические характеристики. Ме¬
жду тем для ряда задач представляет интерес систематическое
исследование расчетным путем влияния формы профиля цилин¬
дрической поверхности конечного размаха как на подъемную
силу и продольный момент, так и на распределение давления
по поверхности.
В настоящей работе рассматривается плавное обтекание ци¬
линдрических тел малого удлинения (А ~ 1,0) прямоугольной
формы в плане с профилем конечной толщины. На основе схе¬
матизированной вихревой модели предлагается приближенный
способ расчета распределения давления по хорде, а также подъ¬
емной силы и продольного момента. В работе в силу особенно¬
стей гидродинамики цилиндрических тел указанных удлинений
[1] рассматривается течение в меридиональном (среднем по раз¬
маху) сечении тела.
Заменим тело в каждом поперечном сечении вихревым пря¬
моугольником, с углов которого сбегают прямолинейные сво¬
бодные вихри. Примем, что свободные вихри располагаются в
плоскости торцов под некоторым углом /? к хорде. Такая вихре¬
вая схема эквивалентна, очевидно, замене тела двумя система¬
ми П-образных вихрей: присоединенные вихри одной системы
размещаются по контуру тела параллельно размаху, присоеди¬
ненные вихри второй—располагаются по торцам перпендику-
лярно хорде и имеют размах, равный текущей толщине профи¬
ля. На рис. 1 и далее в формулах указанные системы вихрей
отмечены соответственно индексами I и II.
*Соавт. В. Н. Трещевский. Печатается с сокращениями.
180
Рис. 1
В работе принята следующая система координат (см. рис. 1).
Начало координат помещено на задней кромке профиля. Дуго¬
вая координата контура в меридиональном сечении отсчитыва¬
ется от нижней к верхней поверхности; ее текущее значение (по¬
ложение элементарного вихря) обозначено s, фиксированное —
s', /. Абсциссу носика обозначим хн. Профиль задается табли¬
цей координат (я, у) и углом нормали относительно хорды u;(s).
Длина контура обозначена 2L, размах тела—/. Далее исполь¬
зуются безразмерные линейные величины, полученные делени¬
ем размерных величин на L.
Граничные условия на поверхности тела (условия непротека-
ния) удовлетворяются на контуре в меридиональном сечении и
по линии хорды на торцах. Условия непротекания записывают¬
ся в виде
С,с>') + Усвов >') + Сис>') + ^обп(5') + Vojs') = О,
кU., (*')+С., (*') + ^о6м (*') = 0 (1)
и образуют систему интегральных уравнений относительно вих¬
ревой плотности 71 и у11. В этих формулах VrnpMcn, ^свобп—
составляющие индуктивных скоростей от присоединенных и
свободных вихрей в меридиональной плоскости, нормальные к
контуру; VnPncn > К:воб,ч—составляющие индуктивных скоро¬
стей от присоединенных и свободных вихрей на линии хорд,
Нормальные к торцам тела.
Используя формулу Био — Савара и производя необходимые
геометрические построения, можно получить следующие выра¬
жения для входящих в систему (1) величин:
I/1 (s') = — / J ^ ■ cos S(s, s')rfs, (2)
пристЛ > 2тг J r(s, s') ^(Ь/2)2 4- r2 V
181
'/с1Воб„(«/)= ^/4(e)
(b/2)cos8i(s')ds
(i/2)2 + [(а: - х') sin 0 - (у - у') cos 0]2
(х - х') cos 0 + (у - у') sin/? ^
[ ч/(&/2)2 + г2
(Л - J_ (V2)cos“sin“'
прис»( j_ 4тг/7 С }(6/2)2 + (а: — а?'):
(3)
у + у'
+
у-У
VW2)2 + (х - х')2 + (у + у')2 л/(6/2)2 + г2
(i/2)cosii(s)ds
rfs, (4)
^6>') = ^/7И(«)
(fc/2)2 4- [(х — х') sin /3 — (у — yf) cos /?]2
(х — х') cos/? 4- (г/ — у1)sin/3
+ 1
у/(6/2)2 + г2
(х — х') cos 0 Л-У sin 0
у/у2 + (х - г')2
smu ;
(5)
+ 1
(х — х') cos 0 — у sin /?
X I .i-- . , + 1
s/b2 + (x - x')2 + у
1
ycos0
(x - x')sm0 - у cos0
b2 + [(a; — x') sin 0 — у cos 0}2 *
da, (6)
^присП1 (* ) - 4^ /7 (s)
У
X — X
*-*' yV + (x - i')2
У
b2 + (x - X')2 ^62 + (X - X')2 + y2
(I,) = h / r"w {
Silica
(7)
у COS 0
(x — x') cos/? 4- 2/sin 0 t ^ (x — x')sin/3 — у cos/?
4- 1 — T7 7 —:—r rrr X
у/у2 + (x - x')2 J i2 + [(x x') sin 0 у cos 0\2
(x — x1) cos 0 — j/ sin 0
y/b2 + (x - x1)2 + y2
182
+ 1
■ sin ш ds;
(8)
Рис. 2
Von(s') = cos(o-w'),
-ТП(^„„»,и) = TU(5iMpxiI) = yll(xf) при x, = x(s,). (9)
В приведенных формулах costf = sin(y> — a/), <p = arccos
COS 61 = 8in(w' - /?), r = ^/(x - x')2 +"(y ~У)2.
Составляющие скорости и вихревая плотность отнесены к
скорости набегающего потока Vo. Схема скоростей в мериди¬
ональной плоскости поясняется рис. 2.
Решение уравнении
и определение давлений на поверхности тела
и суммарных гидродинамических характеристик
Преобразуем уравнения системы (1). Первое уравнение с
учетом формул (2)-(5) для индуктивных скоростей может быть
приведено к виду
1- £ylFi(x, у, х\ y')ds + j yllF2(x, у, х', y')ds +
+ cos(a - и) = 0, (10)
причем i*2 — регулярная функция, a F\ содержит особенность
типа jzjj. Выделим эту особенность:
+ ^ yuF2ds + cos(a — w1) — 0. (11)
183
Можно показать, что ^Fi — 7377) —*■ 0 при s -+ s'.
Преобразуем аналогично второе уравнение системы (1), за¬
писав его в виде
£ yllFsds — £ y^F^ds = О,
где F4 — регулярная функция, F3 терпит разрыв при х = х*. Вы¬
делим особенность 7—7:
f х ^ xfdS f (^3 ~ ж~ж^) dS ~ / y^F+ds = 0, (12)
f р3 —- ] —+ 0 при х —► х'.
\ х — х1)
Таким образом, исходная система уравнений принимает вид
hfy>7h3s+hfy'f'ds+
+ ^ / 7ПЛ^ + cos(a - u/) = 0, (13)
f yl1 x -x,(is + f У11 - <j> j'Uds = 0, (14)
где /,■ — регулярные функции.
Будем искать распределение вихревых плотностей 71 и 711 в
классе следующих функций:
п п
71 = sin n^, 711 = 53 вп sin п<р, (15)
1 1
обеспечив на задней кромке тела выполнение условия 7Г(0) = 0.
При использовании представлений (15) несобственные интегра-
лы в (13), (14) могут быть обращены с помощью формулы (см.,
например, [2])
sin 9d0 d(p
cos p cos <p — cos ф
о 0
В координатах s = 2 sin2 |, s' = 2 sin2 f, / = 2 sin2 ^ эта формула
принимает вид
Умножим обе части уравнения (13) на и проин-
у з(2 —л;) ^
тегрируем полученное выражение по s' в пределах от 0 до 2;
умножим уравнение (14) на 2 V^1" Ы j^rp и проинтегрируем
\/Х (Ги — X ) г
/х^Хп-Х1) 1
по х' в пределах от 0 до хн. В результате с учетом формулы (16)
получим следующую систему уравнений:
i/п I 1 ( f I/ \ / /w у/Ч? ~~ 0 ^
г (0 + T,j j У (.)«.(.. • № / РГ7
О о
2 2
4*
1 У У / /\j
^2 / I rl{s)x2(s, s)ds
о о
\/ s'(2 — s')
'l( 2 - /) rf
VV(2 - s') / - s' ~
+
2 [ , /ч У/(2^7) ds'
= I cos (a — Ы )—^====7 7,
» J Js'(2 - s') I - S'
О V V /
дг н 2 .
IIzi 4 , 1 [[ 11/ \ / t\j V ^(xh *"/r) dx*
(17)
JF 2 ——————
^ f f 1/ \ / /\j \//r(^H ~ /x) dx*
-wjjy (*)--(*. * = °-
oo v
Входящие в эти формулы величины х* — регулярные функции:
xj(s, s') =
1
+
(Ь/2) cos 5
г^(Ь/2)2 + г2 “ в - в'
(Ь/2) cosbi
+
(Ь/2)2 + [(х — x')sin 0 — (у — у1) cos/?]2
(х - x')cos/? + (у - у') sin /? 1
^(W + r2
/\ (Ь/2) sin ш'
x2(s, S ) = 0,5—— ; ГГ^Г X
(Ь/2)2 + (х - х')2
У + У'
У(Ь/2)2 + (х - х')2 + (у - г/)2
185
+
у-У
+
^(Ь/2У- + (Х-Х‘У~+(У-У')2
(6/2) cos 61
(6/2)2 + [(* - х')2 sin /3 — (у — у1) cos /?р
(х — х1) cos /3 + (у — у') sin /?
v/(6/2)2 + г2
+1
smw
x3(s, s') =
X — X
(x - x')y/y2 + (x - *')2
У
b2 + (x- x')2 ^62 + (x - x')2 + У2
sm w +
{(*-
1
x') sin /? — у cos/?
(x — x') cos/3 + y'Sin/?
4/y2 + (x - x')2
+ 1
(x — x') sin /3 — у cos /3
62 + [(x — x') sin /3 — у cos /3]2
(x — x') cos /3 4- у sin /3
ч/б2 + (x - x')2 + У2
■ + 1
sinu; ,
>£4(5, S ) —
1
(x — x7) sin j3 — у cos /3
(x — x') sin /3 — у cos /3
b2 + [(x — x') sin /3 — у cos /Зр
(x — x')cos/3 + ysin/3
v/(*-x')2+F
(x — x') cos /3 4- у sin /3
ч/б2 -f (x - x'pTy^
+ 1
+ 1
Система (17) интегральных уравнений типа Фредгольма II рб-
да с регулярным ядром при выполнении расчетов решалась пу¬
тем сведения ее к системе алгебраических уравнений [3]. При
этом интегрирование по s, х осуществлялось методом трапеций,
а. по sf и х' — методом средних ординат. Длина контура разби¬
валась на 22 интервала, хорда—на 11 интервалов, так что ка¬
ждой расчетной точке х* соответствовала пара точек на конту'
Ре: 5*«ерхи и 5»нижн' Расчетные точки размещались в серединах
указанных интервалов. Таким образом, система интегральных
уравнений заменялась системой 33 линейных уравнений, реше¬
нием которой определялись значения 7J и 7*1 в расчетных точ¬
ках, С целью облегчения вычислительных трудностей, обусло-
186
вленных изменением взаимного расположения свободных вих¬
рей и расчетных точек в плоскости торца при изменении угла
Р заклинения свободных вихрей, влияние граничного условия
по линии хорд на течение в меридиональной плоскости оцени¬
валось в предположении /? = 0 (п. 3).
Распределение полной касательной скорости V(l) и безраз¬
мерного давления р(1) по контуру тела в его меридиональном
сечении может быть вычислено по формулам
Коэффициенты подъемной силы и момента могут быть опреде¬
лены на основе теоремы Жуковского ”в малом” по формулам
где т = 2L/x„, к = Сп/Су, е — коэффициент полноты эпюры
распределения гидродинамической нагрузки по размаху, «(«)--
плечо расчетной точки относительно начала координат.
ровались в пределах: удлинение А = 0,5 -т- 5,0; толщина профиля
продольного сечения 6 = 6 30 %- Коэффициенты гидродинами¬
ческих характеристик рассматривались в диапазоне углов ата-
х
(х — я') cos/? -4- (2/ — у1) sin/?
\/W 2)2 + r2
+ 1 +
V if 1 if if if
l>/(fc/2)2 + (*-*,)3-+(v-V')2= v/(6/2)2 + r2j
P(l) = 1 - V-(l).
У + у' , У-У1
Результаты расчетов и их сопоставление
с экспериментальными данными
Параметры тел цилиндрической формы при расчетах варьи-
ки а = 0-30°.
187
Был произведен контрольный расчет обтекания цилиндра
бесконечного размаха с эллиптическим профилем относитель¬
ной толщиной 6 = 10% при а = 18°, сопоставление результатов
которого с эпюрой давлений, полученной методом конформных
отображений, свидетельствует о достаточной точности предла¬
гаемого приближенного метода в этом предельном случае.
При исследовании тел цилиндрической формы конечного раз¬
маха наиболее сложным и трудно разрешимым вопросом оказа¬
лось назначение угла заклинения свободных вихрей. Расчеты
показали, что при удлинениях А < 1,0 ориентация свободных
вихрей оказывает существенное влияние на суммарные и рас¬
пределенные характеристики. При удлинениях А > 1,5 4-2,0 вы¬
бор угла заклинения и конфигурации свободных вихрей с ука¬
занных позиций большого значения не имеет.
Сложность вихревой зоны вблизи поверхности тел малого
удлинения заставляет прибегать к весьма приближенным прие¬
мам построения ее расчетной модели. Элементарные вихревые
нити считают прямолинейными, а их угол заклинения принима¬
ют постоянным по хорде. Поскольку уже на небольшом удале¬
нии в направлении нормали от поверхности крыла свободные
вихри должны быть направлены по скорости невозмущенного
потока (0 = а), а на поверхности тела прилегать к ней при
условии плавного обтекания (0 = 0), можно полагать, что значе¬
ние угла 0, обусловливающее удовлетворительное соответствие
расчетных и экспериментальных значений гидродинамических
характеристик, должно лежать в указанных пределах.
В соответствии со сказанным в процессе расчетов было вы¬
брано значение угла заклинения, обеспечивающее в диапазоне
удлинений А = 0,6 4- 1,5 и углов атаки а = 0 4- 30° соответствие
расчетных и экспериментальных данных с точностью до 10%
по суммарным характеристикам. Это значение оказалось зави¬
сящим от удлинения и угла атаки и имеет вид 0 = у/Ха2, что
согласуется с приведенной выше оценкой этой величины. Сопо¬
ставление теоретических и экспериментальных данных для это¬
го случая расчета приведено на рис. 3 для Су{а) и ?пг(а)*.
С целью исключения условности в выборе угла заклинения
свободных вихрей были произведены расчеты, в которых угол
0 рассматривался как переменный по хорде и определялся из
*В оригинале статьи приведены также графики распределения давле¬
ний по нижней и верхней сторонам цилиндрической поверхности, а также
по хорде (в плоскости торца).
188
Рис. 3
условия схода вихря в направлении проекции местной скорости
на плоскость торца крыла. Необходимые при этом значения
индуктивных скоростей на торцах определялись, согласно Вол-
лею [4], как половины индуктивных скоростей в меридиональном
сечении цилиндрического тела удвоенного размаха. Вычисле¬
ния при этом производились путем последовательных прибли¬
жений, практическая сходимость которых оказалась достаточно
хорошей. Результаты расчета во втором-третьем приближении
не зависят от выбора угла 0 в первом приближении, однако от¬
личаются от экспериментальных данных, причем различие тем
больше, чем меньше удлинение тела. Например, при А = 1,0
указанное несоответствие Су и mz опытным данным при боль¬
ших углах атаки составляет 15-20%. Такое расхождение, по-
видимому, является закономерным, поскольку принятая вихре¬
вая схема не может в полной мере воспроизвести сложной кар¬
тины обтекания тела малого удлинения в широком диапазоне
углов атаки. Отметим, что углы заклинения, полученные в этих
расчетах, изменялись по длине контура в пределах 0 — 0,5а.
Оценивая возможности изложенного метода в целом, можно
считать, что принятая схема правильно отражает влияние фор¬
мы профиля, а также других параметров тел цилиндрической
формы конечного размаха на их гидродинамические характе¬
ристики и распределение давлений по хорде в среднем сечении
и может использоваться для сравнительных расчетов. Уместно
Добавить, что схема расчета легко обобщается на ряд важных
в практическом отношении и достаточно сложных для экспери¬
ментального исследования случаев движения, например вблизи
границы раздела сред и по круговой траектории с постоянной
Циркуляцией.
189
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Полях о в Н. И., Пастухов А. И. Теория несущей поверхности прямо¬
угольной формы//Вестн. Ленингр. ун-та, 1959. № 13. С. 93-110. [26*]
2. Трихомч Ф. Интегральные уравнения. М., 1960.
3. Мчхлин С. Г., Смолицкич X. Л. Приближенные методы решения диф~
ференциальных и интегральных уравнений. JI., 1965.
4. Bollcy W. A non-linear wing theory and its application to rectangular wings of
small aspect ratio //ZAMM. 1939. Bd 19. H. 1.
Послесловие составителей. Теорией обтекания про¬
филя конечной толщины Н. Н. Поляхов начал заниматься еще в
50-е годы. В частности, совместно с Е. Б. Юдиным им было вы¬
полнено теоретическое исследование распределения давления
по профилю лопасти гребного винта. Публикуемая в насто¬
ящем издании работа Н. Н. Поляхова и В. Н. Трещевского [36]
об обтекании крыла конечного размаха с телесным профилем
была развита ими в [39] на случай нестационарного движения.
Излагаемая в [39] теория гармонических колебаний крыла бази¬
руется на вихревой схеме Бирнбаума, причем присоединенные
вихри, как*и в стационарном случае, располагаются на контуре
профиля, а свободные поперечные вихри перемещаются по нему
к задней кромке, образуя за ней вихревой след. Одновременно в
докторской диссертации В. Н. Трещевского (1975 г.), выполнен¬
ной под руководством Н. Н. Поляхова, были рассмотрены во¬
просы аэродинамики крыла экраноплана—скоростного транс¬
портного средства, движущегося над границей раздела сред, и
на основе указанных выше исследований выполнены практиче¬
ские расчеты стационарных и нестационарных характеристик
низколетящих крыльев с новыми типами профилей, позволяю¬
щими максимально использовать положительный эффект влия¬
ния экрана.
Раздел III
ТЕОРИЯ
НЕСТАЦИОНАРНОГО ДВИЖЕНИЯ
НЕСУЩЕЙ ПОВЕРХНОСТИ
III.1. О РАСПРЕДЕЛЕНИИ ДАВЛЕНИЯ
НА ПОВЕРХНОСТИ ПРОФИЛЯ,
ДВИЖУЩЕГОСЯ НЕСТАЦИОНАРНО [19]
Пусть некоторая плоская фигура (тело) движется в идеаль¬
ной, несжимаемой жидкости. Допустим, что скорость поступа¬
тельного движения этой фигуры равна Vc, а угловая скорость
ее равна ш. Свяжем неизменно с нашей фигурой систему ко¬
ординат ХУ, начало которой поместим в центре вращения С,
и отнесем ее движение к неподвижной системе координат XoYq.
Движущееся тело будет вызывать в жидкости некоторое поле
скоростей V, которое будет иметь потенциал Ф. На контуре
при этом должно выполняться следующее условие для функции
тока:
Ф = ucy-vcx- |(х2 + у2) + Фг + Ф., (1)
где Фр, Фя—граничные значения функций тока, соответствую¬
щих потокам, которые вызываются циркуляцией вокруг конту¬
ра и вихревым следом, всегда образующимся при переменной
во времени циркуляции; ис, vc — проекции скорости Vc на оси
У-
Допуская, что конформное отображение внешности плоской
фигуры на внешность круга известно, можем записать выраже¬
ние для потенциала Ф на контуре круга в виде
Ф(0, /) = + vc(0$2 + и(*)Фз + тг-0 + ФД0, О,
Z7T
есть значение полярного угла для точек окружности, а
Фг, Фз суть функции 9, которые, на основании формулы
191
Шварца, будут равны:
2тг 2тг
— If в — f . — —1 f в — f {
*1 = й J yets —<<*>. = 2? J * '‘8 — if.
0 0
2jt
Фз = 2^- J(x2 + У2) Ctg 9—^dip.
0
Величина Фа(0, f) есть потенциал, вызываемый в точках ок¬
ружности вихревым следом. Из сказанного следует, что потен¬
циал абсолютного, возмущенного движения жидкости в какой-
либо точке плоскости ЛоУо будет выражаться формулой
ф(<> *0, Уо) = Ue®l(z, у) + исФ2(*. у) +
+ шФ3(я, у) + ГФг(г, у) + Ф,(<, *, у), (2)
т. е. будет являться функцией ис, гс, ы, ж, у, которые суть функ¬
ции времени, причем координаты х, р однозначно выражаются
через абсолютные координаты хо, Уо и время f.
Интеграл Лагранжа для точек плоскости XqYo будет иметь
вид
дФ и2 + г2 р р„о
<9* + 2 % р ’
здесь гг и v — проекции скорости возмущенного движения жид¬
кости на оси х, уу а роо—значение давления в бесконечности,
где возмущения отсутствуют. На основании формулы (2) имеем
дФ _ дФ dx дФ dy дФ duc дФ dvc дФ du dr дФ5
dt дх dt ^ ду dt ^ дис dt ^ dvc dt ди dt ^ 1 dt dt
но дФ/дх — Uy дФ/ду = и, dx/dt = —(ис — шу), dy/dt = —(t>c + их),
а потому
Р = Poo +Р (uc ~ u*y)u + (vc +wx)v -
и2 -f г;21
2
duc dvc _ du> ^ dF дФЛ
-О (Ф.-Jf + + Фз-^ + «т-^ + ж)
(3)
Для определения циркуляции необходимо использовать усло¬
вие конечности скорости V на заднем остром конце профиля
192
Нормальная составляющая этой скорости всегда конечна и рав¬
на:
Vn = (ис - иу) cos(nx) + (vc + wx) cos(ny).
Тангенциальная составляющая на заднем остром конце про¬
филя может обращаться в бесконечность. Лля того чтобы она
была конечна, достаточно найти циркуляцию Г из условия
<1Ф \ ^ ,г
Rd9 )в=Й1 Vе RdO + Vc RM RdO + Rd6) f=ti 2irR ^ ’
где 0\ соответствует заднему концу. Из этого равенства следу¬
ет, что циркуляция Г складывается из той циркуляции Гк, ко¬
торая была бы в отсутствие вихревого следа, и той циркуляции
Г', которую следует наложить на профиль при наличии потока,
вызванного следом. Определение Гк, а также скоростей, соот¬
ветствующих движению при отсутствии следа, не представляет
труда. Более сложным является нахождение Г' и скоростей,
вызываемых на профиле вихревым следом.
Так как в дальнейшем мы будем рассматривать нетолстые
и несильно изогнутые телесные профили, обтекаемые при не¬
больших углах атаки, то за линию вихревого следа в первом
приближении можно принять линию тока, получающуюся при
обтекании профиля с углом атаки, дающим нулевую подъем¬
ную силу. При конформном отображении внешности профиля
на внешность круга указанная линия перейдет в прямую, начи¬
нающуюся в задней критической точке круга. Если направле¬
ние этой прямой принять за направление оси абсцисс, то вихре¬
вой след в плоскости круга будет расположен на действитель¬
ной полуоси.
Пусть преобразование
°тображает внешность круга на внешность профиля; тогда для
т°чек вихревого следа (г/ = 0) имеем
(4)
ГДе R — радиус круга.
193
В случае нетолстых и малоизогнутых профилей для точек
следа приближенно можно положить
я2 ^ 6П
+ у, = 2^ «г- (;))
^ П — 1 ^
Известно, что при обтекании окружности потоком, создавае¬
мым точечным вихрем с циркуляцией 7(£, лежащим на дей¬
ствительной оси на расстоянии —£ от центра этой окружности,
на ее контуре возникают скорости, определяемые выражением
7(С> 0#
2тгЯ
Л )
V f2 + #2 + 2fi£cos0,/’
где 9— полярный угол, образуемый радиусом R с осью Для
того чтобы скорость в точке 9 = 7г была равна нулю, достаточ¬
но наложить на взятое течение еще течение с соответственным
образом подобранной циркуляцией. Выполняя эту операцию и
учитывая формулу (5), получаем для скорости на окружности
выражение
W, 0+ - ]ъ(*„ <)
7Г J V У xs Х$ + COS 9
I N
dxa, (6)
где
* =iL- 7l(* o = 7« n—= —
* 2R' 71 ( *’ ’ \/x, rff dx5 dxs 2R
Дополнительная циркуляция, соответствующая этому рас¬
пределению скоростей, будет равна
r' = 2Rj ~ i)
i
Так как конформное отображение круга на профиль известно,
то определение добавочной скорости Vf на профиле не предста¬
вляет труда, если предварительно найдено Vo-
Скорости возмущенного потока всегда можно представить в
виде
и — ик + и , v -=■ vK + v*,
194
где первые слагаемые соответствуют движению с квазипостоян-
цой циркуляцией, а вторые — влиянию следа и добавочной цир¬
куляции Г'. Подставив эти выражения в формулу (3), получим
Р = Рк + р[{ис -иу- ик)и' 4- (vc + шх - vK)i/] -
,/2
и2 + v 2 (дФ$ Л dr\
-р——-р{-аГ + Фгл)'
где рк есть давление при движении с квазипостоянной циркуля¬
цией.
Так как нормальная к профилю добавочная скорость V„ равна
нулю, то
p = p.+pW.V + «г=_,
где WK —мгновенная относительная скорость при давлении рк.
Определение величин, отмеченных индексом к, известно. Ве¬
личину же дФs/di лучше всего определять по формуле
дФ,
dt
причем ФЛ(0, /) = 0. В случае гармонически колеблющегося
профиля имеем
Г = Г0 + Re(>4e-"/VAil')1 (7)
Т) = -£1 = -Аке(Ле-“"е,А^), (8)
где с — длина полу хорды профиля; v — частота колебания; Л —
число Струхаля, равное vc/Vc\ А — амплитуда колебания цир¬
куляции, равная Г] + /Го. Способ определения А известен [1],
вследствие чего становится возможным определение Vo(0, t).
Формула (6) на основании равенств (7) и (8) примет вид
со ,
гАе~ш j е'Аг’ (
х3 4- COS 0 I
(9)
Вычисления Г' хорошо известны [1] и затабулированы. Вы¬
числение интеграла, содержащего в, можно произвести прибли¬
женно, учитывая, что |z,| ^ 1. После этого вычисление dVo/dt
195
и ЭФs/dt не представляет труда, в частности
где через /(0, А) обозначен интеграл, входящий в формулу (9).
Л о сих пор предполагалось, что связь между £ и х3 дает¬
ся приближенной формулой (5), из которой следует, что |£|
yjx\ — (2Я)2. Если, для достижения большей точности, жела¬
тельно приближенно учесть влияние малого слагаемого S =:
входящего в формулу (4), то величину £ следует опре¬
делять из уравнения £ = \/{х8 — 6)2 — (2R)62, которое можно ре¬
шить методом итераций, выразив предварительно 6 приближен¬
но конечным числом членов. В этом случае формулы (6), (7) и
(9) сохранят свой вид, но в них следует заменить х8 на х3 - <5.
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Некрасоё А. И. Теория крыла в нестационарном потоке. М., 1947.
III.2. ТЕОРИЯ НЕСТАЦИОНАРНЫХ ДВИЖЕНИЙ
НЕСУЩЕЙ ПОВЕРХНОСТИ [28]*
Введение
Кирхгоф [1], а также Томсон и Тэт [2], по-видимому, впервые
доставили и частично решили задачу о неустановившемся дви¬
жении твердого тела в идеальной несжимаемой жидкости. Ими
была установлена структура потенциала скоростей возмущен¬
ного движения жидкости, вызываемого телом, й получены выра¬
жения для сил и моментов, действующих со стороны жидкости
на это тело. Указанные авторы рассматривали случаи только
однозначного потенциала, так что циркуляционный поток около
движущегося тела отсутствовал.
Кирхгоф показал, что потенциал возмущенного движения
жидкости, вызванного движущимся в ней телом, может быть
представлен в виде
Ф = 1>1$1 + + ^зФз + Ф4 + и^Фб + ^зФб»
где vi, г>2, vs — проекции скорости V поступательного движе¬
ния тела; wi,W2j<*>3— проекции угловой скорости и? этого те¬
ла на оси координат, движущиеся вместе с телом; функции
Фх, Ф2, -.Фб суть функции координат точки, в которой вычи¬
сляется потенциал.
Силы и моменты оказываются при этом линейными функция¬
ми i>x, v2> г>з, ыь иг, w3, а также произведений (i, к = 1, 2, 3).
Естественно, что множители, стоящие при щ и VjUJk в вы¬
ражениях для сил, имеют размерность массы и потому назы¬
ваются присоединенными массами. Точно так же множители,
стоящие в выражениях для моментов при величинах, имеющих
размерность углового ускорения, называются присоединенны¬
ми моментами инерции. Как присоединенные массы, так и при¬
соединенные моменты инерции зависят только от геометриче¬
ской формы тела. Вычисление их довольно громоздко, но для
некоторого вида тел, например для эллипсоида, доводится до
элементарных формул.
В 1922 г. Прандтль [3] сформулировал для плоскости за-
Дачу о неустановившемся движении профиля при переменной
Циркуляции, указав, что в этом случае позади профиля должен
°бразовываться вихревой след, форма которого так же, как и
^Монография, 1960 г.
197
плотность распределения 7 его вихрей, неизвестны. Точное ре¬
шение этой задачи Прандтль охарактеризовал как безнадежно
трудное. Первое приближенное решение задачи было найде¬
но в 1924 г. Бирнбаумом [4], который рассмотрел бесконечно
тонкую слабо изогнутую пластинку, движущуюся с постоянной
скоростью U вдоль оси х и совершающую гармонические коле¬
бания в направлении оси у и вращательные гармонические ко¬
лебания около начала координат. Считая, что амплитуды коле¬
бания весьма малы, Бирнбаум предположил, что вихревой след
является прямолинейным и совпадающим с осью х и что вихри
этого следа в абсолютной системе отсчета неподвижны. При¬
соединенные вихри, которые имеют плотность т](х, t), Бирнбаум
считает распределенными по хорде пластинки, совпадающей с
осью х, и представляет силы, действующие на профиль, форму¬
лами, имеющими такой же вид, как и в стационарном случае:
+а +а
Y = pU J rfdx, X = р J rjv'dx — aY, (I)
где v* — скорость, складывающаяся из скорости, индуцируемой
вихрями следа, и скорости, происходящей от колебания; второе
слагаемое второй формулы есть обычная подсасывающая сила.
Для того чтобы формулы для А" и У имели указанный вид,
Бирнбауму пришлось предположить, что непосредственно око¬
ло бесконечно тонкого профиля кроме присоединенных вихрей
существуют еще свободные вихри с некоторой плотностью е.
Эту плотность следует определить так, чтобы удовлетворялись
основные уравнения гидромеханики. Так как в относительном
движении полная нормальная к профилю скорость равна нулю,
то для относительной скорости, касательной к профилю, сверху
и снизу от него получим
sv; + idv* _ 1 дРв
dt 2 ds pds
дУ» j дУн2 = 1 дри
dt 2 ds pds
откуда
198
Обозначая VB — V» = 7, (VB + VH)/2 = К*, будем иметь
07 д(7^*) _ 1 дАр
dt ^ ds р ds
В стационарном случае, когда вихревая плотность 7 не зависит
от времени, получим
Ар = pyV*y
и, следовательно, на элемент профиля длиной ds действует эле¬
ментарная сила
dR — p^V'ds. (II)
В нестационарном случае положим, 7 = т] + е, тогда
'д(|/ + б) 5(еУ*) d(r)V*) _ 1 дАр
dt ds ds pds
Потребовав, чтобы силовые воздействия на профиль были
связаны только с присоединенными вихрями, ПОДЧИНИМ плот¬
ность е условию
тогда получим (II), откуда вытекают формулы
dX = pv*rjds, dY = pu*r)ds.
Для слабо изогнутого профиля, имеющего малый угол атаки,
можно принять ds % dx, V0 « U = const, г* = i/ — v, где v —
постоянная скорость, и потому получим
•fa +а
Л' = р J rjv'dx — — Р J w'dx — а У,
-а -а
+а
У = pU j t)dx — pU Гг;,
— а
где а = v/м — мгновенный угол атаки.
Уравнение (III) примет при этом вид
Таким образом, для любого момента времени t изменение
плотности присоединенного вихря равно (с обратным знаком)
изменению плотности свободного. Так как в относительном
движении присоединенный вихрь неподвижен, а свободные дви¬
жутся с относительной скоростью (7, то свободный вихрь будет
последовательно проходить мимо присоединенных, начиная от
передней кромки. Если к моменту t свободный вихрь имеет ко¬
ординату ж, то это значит, что от некоторого присоединенного
вихря т; с координатой х' он удалился на расстояние х — ж', за¬
тратив на это перемещение время
Отсюда следует, что d/dt = djdV, dt' = dx*/U и
£(Xl = W (*',<_ ^77^) dx'-
-a
После того как свободный вихрь прошел заднюю кромку, его
интенсивность на расстоянии £ от начала координат для момен¬
та t будет равна
•-*-¥■)*■ (IV)
— а
Заметим, что в абсолютном движении вихри следа неподвиж¬
ны, а пластинка движется вдоль оси х со скоростью U.
Условие непроницаемости контура будет иметь вид
1 Jцмь = ^/ _£,■\_(V)
2тг J х\ — х \ dx 1 /
-а
где а — мгновенный угол атаки; dy\/dx\—тангенс угла накло¬
на касательной линии профиля к оси х\\ — индуктивная ско¬
рость, вызываемая свободными вихрями.
Бирнбаум получил решение уравнения (V) для случая гар¬
монических колебаний, но оно весьма громоздко.
В дальнейшем усовершенствованию решения Бирнбаума был
посвящен ряд работ Кюсснера, которые позволили значительно
продвинуть вперед задачу о нестационарном движении крыла-
200
Весьма интересной оказалась вышедшая в 1925 г. работа
Вагнера [5], который рассматривал случай прямолинейного не-
установившегося движения пластинки, высказав некоторые со¬
ображения относительно случая ее вращения. Он изучает об¬
текание прямолинейной пластинки поступательным потоком и
потоком, вызываемым вихревым следом. Применяя способ кон¬
формного отображения и выполняя постулат С. А. Чаплыгина,
он получает
где 7 — плотность вихрей следа. Вагнер решает это интеграль¬
ное уравнение относительно у для случаев: а) когда движение
возникает внезапно из состояния покоя и скорость, достигая по¬
стоянного значения за малый промежуток времени, остается да¬
лее постоянной; б) когда равноускоренное движение началось
из состояния покоя.
Общие выражения для сил и моментов Вагнер устанавлива¬
ет на основе теоремы импульсов и теоремы моментов. В случае
неизогнутой пластинки, для которой им было изучено обтека¬
ние, вызываемое вихревым следом, Вагнер получает следую¬
щие выражения для нормальной силы и момента относительно
середины:
гДе t^oo = Vqo sin а есть относительная скорость, перпендикуляр¬
ная пластинке и равная (с обратным знаком) скорости переме¬
щения пластинки vc в направлении оси у. Из формулы (VII)
видно, что
гДе индексом к отмечены величины, относящиеся к движению в
°тсутствии следа, т. е. к квазистационарному движению.
В 1926 г. С. А, Чаплыгин [6] устанавливает общие формулы
сил и моментов, которые действуют на плоскую фигуру,
(VI)
а
а
(VII)
I
а
Y = Yk + Y„ М = Мк + М„
201
движущуюся в идеальной несжимаемой жидкости произволь¬
ным образом. С. А. Чаплыгин вводит систему координат х, уп
неизменно связанную с плоской фигурой, и предполагает, что
она движется поступательно с некоторой скоростью Vc и враща¬
ется вокруг начала координат с угловой скоростью о>. Восполь¬
зовавшись интегралом Лагранжа— Коши для абсолютного дви¬
жения жидкости и преобразовав его так, чтобы в него явно вхо¬
дил квадрат полной относительной скорости, С. А. Чаплыгин
получает для главного вектора сил давления следующее выра¬
жение:
Y + iX.-,J г-т +
L L L
+ ip(iu + w2)S(x - iy) + ipS[(iic - ivc) - iu;(uc - iuc)], (VIII)
где z = x + iy; z* = x — iy\ S — площадь фигуры, ограничива¬
емой контуром профиля; х и у --координаты ее центра тяже¬
сти; ис и vc — проекции скорости начала координат на оси х, у\
F\ —комплексный потенциал, который можно представить в ви¬
де F\ = F — Fn, причем F — потенциал возмущенного движения
жидкости, a Fn = (t/c — ivc)z.
Для момента С. А. Чаплыгин получает выражение
+pS(xvc - уйс) + pSw(xuc + yvc) - 2ры/0. (IX)
Несколько позднее аналогичные формулы были получены Ка-
рафоли [7] (1928 г.) и Глауэртом [8] (1929 г.). Существует мне¬
ние, что формулы С. А. Чаплыгина установлены для случая по¬
стоянной циркуляции. Мнение это совершенно ошибочное, так
как формулы получены в общем виде только путем использова¬
ния интеграла Лагранжа — Коши и тождественных преобразо¬
ваний, позволяющих выразить давление р через производные от
потенциала Fi(z). Вышеупомянутое мнение сложилось на осно¬
вании того, что, переходя к рассмотрению примеров, в част¬
ности эллипса и профилей авиационного типа, С. А. Чаплыгин
считал циркуляцию около этих профилей постоянной во време¬
ни и показал, что и в этом случае в выражения для сил Л и
У входят слагаемые типа pTvr и рТис (силы Н. Е. Жуковского)
202
^ слагаемые, содержащие линейным образом tic, а также
произведения итс и uvc (силы Кирхгофа).
В 1929 г. Глауэрт помимо работы, в которой он устанавлива¬
ет формулы, аналогичные формулам С. А. Чаплыгина, опубли¬
ковал работу, которую он сам характеризует как применение
результатов Вагнера к случаю гармонического колебания пря¬
молинейной пластинки. Глауэрт исходит из условия, что вихри
следа имеют плотность 7(0?, t), причем
Считая, что вихревой след есть продолжение пластинки и про¬
стирается до бесконечности, он получает обобщенные резуль¬
таты Вагнера в виде
и дает способ определения циркуляции Г и плотности 7 для
случая гармонических колебаний пластинки.
Глауэрт устанавливает также значение для подсасывающей
силы, действующей на пластинку, но при этом не точно учиты¬
вает влияние следа.
Работы С. А. Чаплыгина, Вагнера и Глауэрта представляли
собой существенное достижение в области нестационарной тео¬
рии крыла. Если С. А. Чаплыгин установил общие формулы для
силы и момента, но ограничился при рассмотрении примеров
лишь случаем постоянной циркуляции, ,т,о Вагнер и Глауэрт для
^изогнутой пластинки установили вид силы и момента, проис¬
ходящих от переменности циркуляции во времени и вычислили
Нх для случаев равноускоренного прямолинейного движения и
^лых колебаний около состояния прямолинейного движения.
х
а
со
а
со
V X" — а~
а
со
а
203
Теория нестационарного движения пластинки с переменной
циркуляцией в постановке Вагнера и Глауэрта с некоторы¬
ми небольшими дополнениями (введение так называемых обоб¬
щенных сил, выражение некоторых интегралов, встречавших¬
ся у Глауэрта, через функции Бесселя, анализ подсасываю¬
щей силы и некоторые другие вопросы) была дана Бюргерсом
и Карманом в 1935 г. [9]. В 1935 г. также появилась рабо¬
та М. В. Келдыша и М. А. Лаврентьева [10], посвященная теории
колеблющейся пластинки с переменной циркуляцией. Авторы
шли путем иным, чем Глауэрг, и получили для добавочной си¬
лы У, нормальной к пластинке, то же самое выражение, что и
Глауэрт, а для подсасывающей силы — несколько иное выраже¬
ние, учитывающее более точно влияние вихревого следа. Авто¬
ры также выразили некоторые характерные интегралы задачи
через функции Бесселя и дали анализ тянущей силы пластинки.
В 1935 г. появилась также работа Л И. Седова [11], в кото¬
рой автор устанавливает выражения для силы и момента, дей¬
ствующих на нестационарно движущийся профиль, и выражает
их через интегралы, содержащие производные от комплексно¬
го потенциала возмущенного движения F. Воспользовавшись
интегралом Лагранжа — Коши, Л. И. Седов получает для глав¬
ного вектора силы в подвижных осях следующее выражение:
X + гУ = ipTVc - ipzm Г -f
d_
+ Tt
пт
JlSf) , I dF .
„—+/,SVc + ,pJz-SId=
dz
+
(XII)
где Vc = uc + ivc\ z = x + iy — комплексная координата центра тя¬
жести профиля; zm —комплексная координата точки схода вих¬
ревого следа, т. е. задней кромки профиля, а звездочка указы¬
вает на сопряженную величину.
Формулу для силы, так же как и формулу для момента, мож¬
но получить из формул С. А. Чаплыгина, если в них подставить
вместо F\ его значение F\ = F — Fn = F — V*z и произвести неко¬
торые тождественные преобразования. Так, для силы получим
204
X + iY = i(Y - iX) = i(Y + iA')* =
+ ipVcT — pu J
dF- . 8F
z ——dz tp ~:: z
dz
8t
L
ч-i (?)-
— pS(Vc + ivVc) — ipS(u> — iw )z.
Точки В и А лежат сверху и снизу от вихревого следа непосред¬
ственно за задней кромкой профиля, и, следовательно,
. 3F*
V-
— ipZm Г •
Так как = ucdy — vcdx — v(xdx + ydy), то
/* /Ш \
р z ( -щ- + iwdty ) = pS[Vc + iuz + iv(Vc + iwz)].
L
Это выражение равно по величине и противоположно по знаку
сумме двух последних слагаемых в формуле для X + ?У.
На основании изложенного можно написать
X + iY =
+
L
. [ fddF .
,pJ iU*+"
+ ipVc Г — гт +
dF\
,u7h)d‘ +
+ pS(Vc + iu>Vc) + ipS{u> + iu>7)z.
Вводя обозначение da/dt = a + iuja, где a — вектор, записан¬
ный, как комплексное число, получим формулу (XII). Точно так
Же можно получить и формулу для М. JI. И. Седовым были так¬
же даны формулы для присоединенных масс и вычислены коэф¬
фициенты присоединенных масс для крыла Н. Е. Жуковского. В
случае постоянной циркуляции JI. И. Седов показал, что
X + iY = X0 + tYo + ipTWk, М = Mo + Re[-i*5(i>rW*)],
гДе Xo+iYo и Mo соответствуют движению без циркуляции;
205
Wk = Vc + iukо, причем k0 есть комплексная координата кон¬
формного центра тяжести.
В 1936 г. [12] и более подробно в 1939 г. [13] JI. И. Седов рас¬
смотрел случай неустановившегося движения бесконечно тон¬
кого, мало изогнутого крыла, которое в первом приближении
может быть заменено прямолинейным отрезком, являющимся
линией разрыва скоростей и давлений. Вихревой след с плот¬
ностью вихрей 7 = будет представлять собой как бы про¬
должение этого отрезка. Используя аппарат интеграла Коши,
Л. И. Седов получает формулы для силы У и момента М, а так¬
же интегральное уравнение Вагнера—Глауэрта (VI), (XI) для
определения 7.
Первые слагаемые в выражениях для У и М представляют
собой силу и момент, которые получились бь: при квазистаци-
онарном рассмотрении, когда отсутствует вихревой след, по¬
следние же слагаемые, учитывающие влияние вихревого следа,
имеют такой же вид, как и в случае неизогнутой пластинки:
00 00
У = П - PU'ca J ^Х_а2 . М = Мк + 1-Риу- J
7 dx
\/х~ — or
где ufc = uc + da/dt, так как предполагается, что длина пластинки
может измениться, а это, естественно, изменяет относительную
скорость сбегания следа на величину dajdt. Величины У* и Мл
выражаются интегралами, которые содержат под своим знаком
нормальную составляющую Vn скорости на профиле. Эта ско¬
рость определяется формой крыла и условиями его движения и
может считаться заданной величиной.
В 1938 г. Карман и Сирс [14] опубликовали работу по вихре¬
вой теории бесконечно тонкого мало изогнутого профиля, заме¬
няемого прямолинейным вихревым отрезком, с которого cyiojx^т
прямолинейный вихревой след с плотностью вихрей 7 = —•
Авторы, используя теорему импульсов и теорему моментов,
приходят к формулам для силы У и момента М, которые имеют
вид
оо со
7 dx
У = П - pUca J М = Мк + l~pUca2 J
Следует заметить, что определение У* и Мл не представля¬
ет трудностей, и для нахождения их нет надобности переходить
206
X теории тонкого профиля. Главной задачей теории нестацио¬
нарного движения с переменной циркуляцией является как раз
определение тех дополнительных сил и моментов, которые свя¬
заны с потоком, создаваемым вихревым следом. Что касается
последних, то для них теория тонкого профиля ничего не дает
кроме слагаемых Вагнера. Этот результат можно было предви¬
деть заранее, так как след, являющийся продолжением хорды
профиля, вызывает на контуре в первом приближении нормаль¬
ные скорости, такие же, как и на хорде, и, следовательно, в
выражение для этих скоростей не будет входить кривизна про¬
филя.
В своей работе Карман и Сирс решают задачу Глауэрта о
гармонически колеблющейся пластинке и путем использования
так называемой функции Теодорсена придают решению Г лау¬
эрта более компактный вид, удобный для вычислений.
В 1947 г. появилась монография А. И. Некрасова [15] ”Тео-
рия крыла в нестационарном потоке”, в которой автор подробно
излагает работы Кармана—Сирса, Бирнбаума и Л. И. Седова
для случая крыла бесконечного размаха, а также работы и Чи¬
кала для случая крыла конечного размаха. В монографии рас¬
сматриваются, кроме того, случаи апериодического движения
и влияние сжимаемости (метод Поссио). Эта очень хорошая и
полезная для справок монография, ввиду своей энциклопедич¬
ное™, несколько трудна для чтения.
Книга Л. И. Седова [16] ”Плоские задачи гидродинамики и
аэродинамики”, вышедшая в 1950 г., содержит результаты, опу¬
бликованные автором в 1935 и 1939 гг. с добавлением результа¬
тов, полученных М. В. Келдышем и М. А. Лаврентьевым (1935 г.)
и М. Л. Хаскиндом (1944 г.) для силы тяги, развивающейся на
неизогнутой пластинке. Теория крыла конечного размаха в кни¬
ге не рассматривается.
Несколько особняком стоят интересные исследования
В. Голубева [17], посвященные теории машущего крыла с ко¬
нечной амплитудой, в которых вместо вихревого следа автор
Нводит вихревую дорожку типа дорожки Кармана.
Предлагаемая небольшая книга является попыткой изложить
Те°рию нестационарного движения крыла бесконечного и конеч¬
но размаха по возможности в общей и простой форме. В осно¬
ву Кладется (при бесконечном размахе) представление потенци¬
ей Ф абсолютного возмущенного движения жидкости в форме,
207
аналогичной форме Кирхгофа:
Ф = исФ] + усФ2 + и>Ф3 + ГФ4 4- Фл,
где Ф, —потенциал обтекания плоского контура потоком, созда¬
ваемым вихревым следом, и интеграл Лагранжа—Коши, запи¬
санный в виде
г/ ч / ч , u2 + v2 5Ф
Р = Роо+ p[{Uc - иу)и + (vc + U>x)v] - Р
где и и v — проекции скорости возмущенного движения на оси
подвижной системы.
Использование этих формул позволяет сразу получить силы,
действующие на контур, как сумму сил Н. Е. Жуковского, сил
Кирхгофа и сил, связанных с наличием вихревого следа. Среди
последних, кроме сил, связанных с производной дФs/dt, иссле¬
дуются еще силы, связанные с интегралом, который содержит
под своим знаком величину (и — it>)2. Исследование этого ин¬
теграла при наличии следа почему-то не производилось, между
тем он играет существенную роль и приводится, как было ранее
показано [18], к силам индукционного характера, которые под¬
чиняются формулам Прандтля, полученным для стационарного
потока. Это освобождает, в случае бесконечно тонких профи¬
лей, от необходимости вводить дополнительно подсасывающую
силу.
При рассмотрении сил, связанных с дФ3/д1, не делается сра¬
зу переход к бесконечно тонкому профилю, как это дано у всех
авторов, а рассматривается телесный профиль, след которого
расположен по ”нулевой” линии тока стационарного движения,
и при конформном отображении сечения на внешность круга пе¬
реходит в действительную полуось. Такого рода обобщение по¬
зволяет подойти к вопросу о распределении давления по неста¬
ционарно движущемуся профилю. При построении вихревой те¬
ории бесконечно тонкого профиля автор исходил из обычного
интегрального уравнения Бирнбаума—Глауэрта для стацио¬
нарного случая, но при этом в правую часть уравнения вводил
скорость, индуцируемую вихревым следом. Этот же прием был
использован и при построении теории крыла конечного размаха,
которая получилась значительно проще, чем теории Кюсснер&
[19] и Чикала [20].
Так как эта монография не преследует обзорных и энциклО'
педических целей, то некоторые вопросы в ней не затронуть1
208
совсем, например апериодическое движение и применение по¬
тенциала ускорений. Нестационарные движения крыла в сжи¬
ваемой жидкости также не вошли в книгу.
Г лава 1. ТЕОРИЯ
НЕСТАЦИОНАРНЫХ ДВИЖЕНИЙ ПРОФИЛЯ
В ПЛОСКОМ ПОТОКЕ
1. Постановка задачи
Пусть некоторая плоская фигура (тело) движется в идеаль¬
ной несжимаемой жидкости, находящейся в плоскости хоу0. До¬
пустим, что скорость поступательного движения этой фигуры
равна Vc, а угловая скорость вращения ее относительно полюса
С равна и. Предположим, кроме того, что жидкость до момента,
когда тело начало двигаться, находилась в покое. Свяжем неиз¬
менно с нашей фигурой систему координат ху> начало которой
совместим с полюсом С) и отнесем ее движение к неподвижной
системе координат хоуо (рис. 1).
Рис. 1
Движущаяся фигура будет вызывать в жидкости некоторое
Поле скоростей V, причем это поле будет иметь потенциал Ф.
Йа бесконечном удалении от тела скорость V и потенциал Ф
Возмущенного движения жидкости следует положить равными
209
нулю. На контуре самого тела должно при этом выполняться
условие
— = — = (ис - иу) cos(nx) + (vc + их) cos(пу),
где ds есть элемент дуги контура; dn — элемент внешней норма¬
ли; Ф — функция тока; х, у — координаты точек контура, ис, vc •—
проекции Vc на оси х) у. Так как cos(nx) = dy/ds) cos (пу) =
—dx/ds, то интегрирование дает
ф = ~ - — (т2 + у2) + const, (1)
причем черточка указывает, что берется контурное значение Ф.
Потенциал Ф и функция тока Ф представляют собой гармони¬
ческие сопряженные функции, поэтому, зная на контуре функ¬
цию Ф, мы имеем возможность определить контурное значение
потенциала Ф. Если допустить, что известно конформное ото¬
бражение внешности плоской фигуры на внешность круга, т.е.
считать, что нам известны х yl у как функции полярного угла у?
и радиуса г, мы можем написать, воспользовавшись формулой,
непосредственно вытекающей из формулы Шварца [13]:
2п
Ф(0, Я) = 2^ J *(¥>. Я) ctg (2)
О
где R есть радиус окружности и интеграл берется в смысле его
главного значения.*
*ПР имечание составителей. При выводе формулы (2) следУ'
+ - Л —'
ет иметь, в виду, что Ф(0, R) = (Лп cos + bnsinntf), где sin пи -
f т7-<:А^ = & f corfn^ctgi(e-vMv; cosn* = / sinnY>ctgi(0"
0 0 о
2тг
Окончательно: Ф(в, R) = ~ f Л) ctg ^(0 —
* о
210
Имея в виду формулу (1), получаем
Ф = иеФ1(0, R) + VW R) + и;Ф3(в, R) + Ф9(в, Я), (3)
а функция Ф, есть действительная часть произвольной аналити¬
ческой функции Fs(z), мнимая часть которой принимает на кон¬
туре постоянное значение. В случае наличия вокруг контура
циркуляционного течения с постоянной во времени циркуляци-
Зная потенциал Ф на контуре круга, можно найти его зна¬
чения и в любой точке вне круга, а следовательно, и в любой
точке вне плоского контура, отображение внешности которого
на внешность круга нам известно. Из формулы (3) непосред¬
ственно можно заключить, что потенциал Ф будет иметь вид
обтекающему контур так, что на нем Ф, = const. Таким образом,
потенциал Ф есть функция координат х, у, скоростей иСу vCy ш и
Циркуляции Г, которые изменяются во времени.
Следует особо отметить, что потенциал Ф есть потенциал аб¬
солютного возмущенного движения жидкости в некоторой точ¬
ке Af, которая неподвижна относительно системы отсчета хоуо,
Сраженный через х, у, tzc, vc, о; и Г, меняющиеся с течением
вРемени.
где
о
2тг
(За)
О
о
ей Г функция Ф, будет равна т^в, так как в этом случае
Ф = исФ,(а;, у) + г>сФ2(х, у) + ыФ3(х, у) +
+ ГФ4(х, у) + Ф,(х, у, <),
(4)
ГФ4 соответствует циркуляционному течению; Ф, — течению,
211
Рассмотрим пример. Пусть эллипс с полуосями а и b дви-
жется в идеальной несжимаемой жидкости. Известно, что внещ,
ность окружности радиусом R отображается на внешность эл¬
липса при помощи формул
х = (R + с2/R) cos <р = a cos у>,
у = {R — c2/R) sin (р = b sin у?,
где с—радиус вспомогательного круга, так что
^ = Д, 2с2 = (а — b)R = —•
Согласно формулам (За) будем иметь
ф! = — bcos9, Ф2 = —asinfl,
2*
_ 1 //О О »9 • 9 \ ^ , (1^ 6^
Ф3 — — — / (a cos 92 + 6 sin <р) ctg —-—dp = sin 29.
4л* J 2 4
* о
Таким образом, при постоянной циркуляции
/ а2-Ь2 \ Г
ф = — I uc6 cos в + vca sin 9 -j- и sin 29 } + — 9.
V 4 / 2тг
В частности, для пластинки
( • Л «2 • „Л г„
Ф = — I rcasin0 +w —sm20J + 2^0'
Касательная составляющая абсолютной скорости на самом
эллипсе будет определяться по формуле
с/Ф 1 <1Ф
V =
где ds— элемент длины дуги эллипса, равный
ds = \f dx2 + dy2 = \/a2 sin2 9 + b2 cos2 OdO,
и, следовательно,
ue £ sin 9 — ve cos 9 — ua1:V cos 29 +
V =
■^^1^9+^cos^e
212
В частности, в случае пластинки b = 0, и потому
vc cos в+^ыа cos 20-^
sin0
Для того чтобы эта скорость не обращалась в бесконечность
на заднем конце пластинки, т. е. при в = тг, следует определить
циркуляцию Г из условия
Если пластинка вращается не вокруг своей середины, а отно¬
сительно произвольного центра (рис. 3), то можно считать, что
Движение состоит из поступательного движения со скоростью
К, равной ljRq, и вращения около середины с угловой скоро¬
стью ы < 0. Отсюда вытекает, что
(4а)
Обозначим (рис. 2) vc = — Vasina, тогда получим
Г = 2naVe sin a 4* и>тга?.
( u>a Г \ I
V = [ Vc sin a cos 9 -f — cos 29 + -— ) -г—т.
\ 2 27ra J sin 9
2жа J sin 9'
Г \ 1
)
Если потребовать, чтобы скорость на левом конце была конеч-
На> то получим
Рис. 3
В случае, когда передний конец обращен в сторону вогнуто¬
сти, в найденной формуле следует заменить а на —а. Предыду¬
щую формулу удобно написать в виде
Г = tt\Vc (sinо — ±Л ,
V 4 До /
где / = 2а.
При малых углах Г = TtlVc(ot - ао), где ао = Так выража¬
ется циркуляция около профиля, движущегося поступательно со
скоростью Vc и имеющего угол атаки нулевой подъемной силы,
равной ао.
2. Случай движения с переменной циркуляцией
Если на движущийся профиль наложена циркуляция, изменя¬
ющаяся со временем, то позади этого профиля должен образо¬
вываться так называемый вихревой след, представляющий со¬
бой систему вихрей, оси которых перпендикулярны плоскости
движения. Действительно, представим себе, что перед движу-
щимся профилем находится некоторый контур С (рис. 4). Цир¬
куляция по этому контуру будет равна нулю, так как в жидко¬
сти, по предположению, отсутствуют вихри. Представим себе
далее, что при своем движении профиль входит в соприкоснове¬
ние с контуром С, который деформируется и принимает форму
habcdefh, изображенную на рис. 5, а.
214
Рис. 4
Так как циркуляция Го по контуру С равна нулю, то
Г/1а6 = Г bcdefh'
Если предположить, что непосредственно за задней кромкой
точки h и 6 совпадают, то циркуляция ГнаЪ будет являться цир¬
куляцией вокруг профиля, которую мы обозначим через Г. Та¬
ким образом, получим, что Г -f Г1 = 0, где Г1 = Tbcdejh•
При дальнейшем движении профиля контур hab перейдет в
некоторый контур hh'ab'b и предыдущее равенство перейдет в
следующее (рис. 5, 6)\ Г + 6Г + Г3 + Г1 = 0, где 6Г есть при¬
ращение циркуляции Г, а Г, = Циркуляция Гх, взятая
но контуру bcdefh, при этом не изменится, так как для этого
контура должна выполняться теорема Томсона, а потому будем
иметь: Г, = ~6Г. Из этого равенства видно, что если цирку¬
ляция вокруг взятого профиля изменяется в процессе движения,
т° в области ЛЛ'б'б должны появиться вихри.
Если мы представим себе, что границы hh* и bb* могут быть
неограниченно сближены друг с другом, то в пределе получим
вМесто области hh'b'b линию разрыва скоростей, эквивалентную
системе непрерывно распределенных по ней точечных вихрей
vPHc. 6). Найдем плотность этих вихрей. Предположим, что
215
Рис. 6
циркуляция Г получила бесконечно малое приращение dr за
промежуток времени dt, в течение которого задняя кромка про¬
филя прошла расстояние ds, тогда плотностью вихревого слоя
будет называться величина
-
7 “ ds ~ V ~dt'
Из изложенного следует, что если в идеальной жидкости дви¬
жется некоторый профиль, циркуляция которого непрерывно из¬
меняется со временем, то позади этого профиля должен образо¬
вываться вихревой след с плотностью у.
В дальнейшем, имея в виду некоторое упрощение задачи, бу¬
дем предполагать, что в неподвижной системе отсчета вихри
следа остаются неподвижными, а их плотность у— неизменной.
3. О силах,
действующих на плоский контур
при нестационарном движении
Чтобы определить силы, действующие на плоскую фигуру
при нестационарном движении, необходимо сначала установить
выражения для гидродинамического давления р, имеющего ме-
сто в точках этой фигуры.
Воспользовавшись интегралом Лагранжа, для случая отсут¬
ствия массовых сил получим
дФ0(t, д0, у0) у^_ р_
dt 2 р Л
где V — скорость абсолютного возмущенного движения жидко¬
сти. Считая, что жидкость в бесконечном удалении от тела не
возмущена, получим, что функция f(t) приводится к постоянной
Роо/р* Таким образом, будем иметь
V2 <9Ф0(<, *о, Уо)
Р-Роо- Ртг ~ Р
2 r dt
216
Потенциал Фо абсолютного возмущенного движения жидко¬
сти есть функция времени t и координат жо, уо. Если этот по¬
тенциал выразить через координаты в подвижной системе ху> то
ф как функция от t, ху у, иС) vc, и и Г представится выражением
(4). При таких условиях частную производную дФо/dt следует
вычислять по формуле
дФо (1Ф дФ . дФ . дФ .
dt dt dx Х ду ^ дис Uc
дФ дФ дФ • дФ$
+ ЖГс'Ус + Ж;ш + дТг+~дГ-
Но
i = -(uc - шу), у = ~(ve + их),
дФ дФ
!h~u' ~ду ~V'
и на основании (4) для точек, лежащих на контуре, получим
= йсФ1 + veФ2 + шФз + ГФ4 -
01
дФ,
- и{ис - шу) - v(vc + шх) +
где
дФ дФ ж дФ ж дФ ж
!Ые~ 15 дье ~ 2’ дш~ з; ЭГ ~ 4'
После указанных преобразований интеграл Лагранжа при¬
мет вид
Р = Р« + />[(ис - + (Vc + шх)у] - р
u2 + v2
2
дФ
- р-~ - р(йеФг + ьсФ2 + шФ3 + ГФ4). (5)
at
Переходим теперь к определению сил, действующих на пло-
217
Рис. 7
скую фигуру. Из рис. 7 следует, что
X = - j pdy — ~Р j[(uc - + (vc + u>x)v]dy +
+1/
L
Y = J pdx — P Ji(uc “ wy)u 4 (t>c 4 ujx)v\dx —
L L
где
9'Ф 9Ф.
2 •> I j
' +»-+2ЖМ*’
4 Ф4Г + Ф\йс + Фоvc 4- Фз^
(6)
(6а)
Э* dt
и интегралы берутся по контуру плоской фигуры.
Замечая, что
ЭФ ЭФ
с/Ф = dx 4 dy = — i>dx 4 urfy,
Эх Эг/
и принимая во внимание, что на контуре выполняется условие
ЛФС = (ис — wy)dy — (г>с 4u>x)dx = —vdx 4 udy — f/Ф,
получаем
(г/с — ujy)dy = (vc 4 ux)dx — vdx 4 udy
и, следовательно,
(uc — uy)udy = (vc 4 ux)udx 4 u2dy — uvdx,
(vc + u)x)vdx = (uc — uy)vdy 4 ггcfx — uvdy.
(бб)
218
£сли подставить эти выражения в формулы (G), то будем иметь
есть циркуляция по контуру плоской фигуры. Первые слага¬
емые написанных формул представляют собой проекции силы
prVc (силы Н. Е. Жуковского) на оси подвижной системы ху.
Направление этой силы получается путем поворота направле¬
ния скорости поступательного движения плоской фигуры Vc на
прямой угол в сторону циркуляции.
Вторые слагаемые полученных формул представляют собой
силы, связанные только с вращением фигуры. Следует отме¬
тить, что эти силы существуют даже тогда, когда циркуляция
Г равна нулю. Действительно, известно, что конформное ото¬
бражение внешности круга радиусом R на внешность плоской
фигуры дается формулой
при этом круг считается лежащим в плоскости С- Для контура
плоской фигуры будем иметь
L
L
L
где 6Ф = udx -b vdy и, следовательно, интеграл
L
L
п-О
00
х = '2R cos в -h cos пв 4- Ьп sin пв) + ао
п = 1
со
(8а)
П = 1
Принимая во внимание, что
г
Ф = ксФг + г>сФ2 + и/Ф3 + — в + Ф,,
(9)
219
получаем
Х^г = —ри>Г I xdbi — —риао Г,
L
(Ю)
Ywг = -риГ / ус1Ф4 = — ры60Г,
откуда полная сила Rwг выразится по формуле
ДыГ = = рГи>с0.
Выражения типа
J xd^i, J yd$i (i = 1, 2, 3),
L
вообще говоря, не равны нулю, что приводит к наличию силы
Я** даже в случае, если Г равно нулю.
Интересно также отметить, что сила г обращается в ноль
при наличии циркуляции, если фигура вращается вокруг цен¬
тра, для которого ао и 6о равны нулю.
Все изложенное хорошо иллюстрируется на примере эллип¬
са. Предположим, что Ф3 равно нулю, в этом случае
фг = — &cos0, Ф2 — — asintf, Фз = — ^(a2 — 62)sin 2в,
В частности, для пластинки Хш = р7гыа2ус, Yw = 0. Силы
Н. Е. Жуковского в этом случае, при постоянной во времени
циркуляции, будут
х = a cos в, у = 6 sin 0, а0 = 60 = 0.
Отсюда следует, что Rwг равно нулю и
L
L
= — pYvc = ру^2та — р7ги>а2ус,
Yj - />Гцс = —рисус2,ка + ртгисгис.
220
Переходим теперь к оценке других слагаемых. Рассмотрим
последние слагаемые наших формул. Производную д'Ф/dt мож¬
но, очевидно, представить в виде
dt dt + 4 + dt ’
где
Фт = «СФ1 + Vc$2 + ^Ф4.
Выясним сначала силы, связанные с дФm/dt. Для них будем
иметь выражения
(П)
Хт = Р J ~~§jrdy = -(mu«с + mi2tic + тп\зы1),
Ym = -р J = ~(m2i«c + m2ovc + m23wO.
L
где / — некоторый произвольный линейный размер;
mu = -р J Ф\dy\ mi2 = -р J mi3 = -р J Ф3dy\
L L L
тп 21 = р J Ф \dx] Ш22 = pj Фз^«; тзз — Р J &ddx.
L L L
Очевидно, что величины mt* имеют размерность массы и
потому могут быть названы ”присоединенными” массами. Не¬
трудно видеть, что силы Хт и У'т обращаются в нуль при равно¬
мерном движении тела и совершенно не зависят от циркуляции
Г. В частности, для эллипса
а2 - 62
фг = —6 cos 9, Ф2 = —а sin в, Ф3 = sin 29,
4
с/х = —а sin 0cf0, dy = Ь cos 0</0,
следовательно,
2ir
тц — —p j Фгdy = />62 J cos2 = p7r62,
0
2rr
m22 = P J Ф2<1х — pa2 J sin2 9d9 = ртга2,
L 0
mi 0 = mi3 = 771-21 = m23 = 0.
221
Можно убедиться, что ранее найденные силы Хш. и Yw могут
быть выражены через присоединенные массы плоской фигуры,
если Г и Ф, равны нулю. Действительно, для этих сил имеем
выражения
Хш = —pu> J xdi, Yw = -ры J ydФ.
L L
В случае, когда Г и Ф, равны нулю,
Ф = исФ1 4" Vc&2 4“ ^Фзт
где Фх, Ф2, Фз — однозначные функции. На основании этого по¬
сле интегрирования по частям получим
Хш = ры / Фdx = ры lucj $\dx + vc J Ф2С/ж 4- w j i^dx J =
I» \ L L L /
= ы(тг\ис 4- m22^c 4* тззы/), (12)
Yu, — pu> J Фdy = pw I tic J i\dy 4- vc J indy 4- ы J Ф3dy j =
L \ L L L /
= -ы(?лц uc 4* mi2Vc 4- mi3U>/). (13)
4. Исследование сил,
связанных с вихревым следом
Исследуем прежде всего интегралы
Xi = ^ j[(и2 - u2)dy+ 2uvdx],
L
Yi = IJ[{v2 - tr)cfx - 2uvdy],
г
объединяемые в комплексе
R- = A'i - г У; = *-£j(u- ivfdz (14)
L
222
Рис. 8
и входящие в формулы (7). Покажем, что силы, выражаемые
этими интегралами, носят характер индуктивных сил. Будем
предполагать, что вихревой след, сходящий с острого конца
профиля, представляет собой линию разрыва тангенциальных
скоростей. Вводя натуральную систему координат, оси ко¬
торой направлены по касательной и нормали к линии следа
(рис. 8), получаем
и — iv — {vt — ivn)e~1^.
Рассмотрим интеграл
I = J (и — iv)2dz,
L
взятый по замкнутому контуру / (см. рис. 8). Этот контур будем
мыслить состоящим из контура ABC самого профиля, из участ¬
ка CD, идущего по следу с верхней его стороны, участка DE, где
следа нет, окружности EGF, радиус которой можно взять сколь
Угодно большим, участка FH, совпадающего с £D, и, наконец,
Участка НА, идущего по следу с нижней его стороны. Так как
ннутри контура ABCDEGFHA нет никаких особенностей, то
1(1) = I(ABC) + I(CD) + ЦОЕ) +
+I(EGF) + 1(FH) + I(HA) = 0.
Но интегралы, взятые вдоль DE и FH, друг друга уничтожат,
как вдоль DE скорость, а следовательно, и подынтеграль¬
ная функция не терпят разрыва. Интеграл по окружности EGF
223
будет стремиться к нулю при неограниченном возрастании ее
радиуса в предположении, что скорость возмущения имеет на
большом удалении порядок 1/Д. Это предположение эквива¬
лентно гипотезе присоединенного вихря. Таким образом, при
Д —► оо получаем
I(ABC) = f (и — iv)2dz ~ — f (и — iv)2dz — f {и — iv)2dz =
ЛВС CD НА
= j [(и - iv)2 - (и - iv)l]dz,
CD
где (tt—iv)\ и (и—iv)^ суть значения функции (ц—iv)2 при подходе
к следу с верхней и нижней сторон.
Как было показано ранее,
и — iv = (v* — ivn)e~l{*, (14а)
и потому, замечая, что при переходе через вихревой слой нор¬
мальные составляющие скорости не терпят разрыва, получаем
I (и - iv)2dz = - f [(v2B - v2J - 2ivn(vtB - vtH)]e-2,,,<fe.
ABC CD
Разность vtB — viH есть не что иное, как напряженность у вих¬
ревого слоя, поэтому
I(ABC) = j (u - iv)2dz = -2 J тК - iv*n)e~2'ndz,
ЛВС CD
где vj1 = (vtB + i>tH)/2, = vn — скорости на самом следе. Пере¬
ходя к проекциям и и v, находим
1{АВС) = -2 J 7(и* -iv‘)ds,
CD
так как
и* - iv* = («; - м£)е-" И (f2 = ds е".
На основании изложенного выражение для силы
Д* = Xi - iYi
примет вид
Д* — J (и — iv)2dz = —ip J у(и* — iv*)ds,
ЛВС CD
224
т
Рис. 9
CD
CD
что эквивалентно векторной формуле
r, = р J (-у х v;)*,
(16)
CD
точка D может мыслиться лежащей сколь угодно далеко.
Скорость V* вызывается в фиксированной точке следа вихря¬
ми этого следа и, кроме того, системой присоединенных вихрей
профиля. Будем считать, что вихри эти распределены по конту¬
ру профиля с линейной плотностью 7П. Обозначая скорость, вы¬
званную вихрями следа, через V*, а вихрями профиля — через
V*, запишем V* = VJ -f V*.
Как видно из рис. 9, скорость, вызываемая в точке N следа,
будет выражаться формулой
где 7' есть плотность вихрей следа в точке N\ а г— расстояние
где п — расстояние от точки профиля, в которой помещается
вихрь 7П, до точки N, а интегрирование совершается по кон-
ТУРУ профиля. Сила, действующая на профиль, на основании
ЛГ'ЛГ. Скорость же V* представится в виде
ЛВС
Формулы (16) будет равна
CD CD
CD ABC
225
Первый интеграл равен нулю, так как каждому значению подын¬
тегрального выражения, взятого для точки N и учитывающего
влияние вихря, который помещен в точке N', соответствует рав¬
ное по величине и противоположное по знаку значение, взятое
для точки N* и учитывающее влияние вихря, который помещен
в точке N.
Таким образом, сила R, будет выражаться формулой
CD ABC
Так как 7 = 7k, 7П = 7пк, где к есть орт оси z, то можно
написать
Ri = pj(yiXln)dSi, (17)
L
где
= (Па)
2тг J г\
CD
есть индуктивная скорость, вызываемая вихрями следа на кон¬
туре профиля. Формула(17) совпадаете обычной формулой, да¬
ваемой теорией крыла конечного размаха для сил индуктивно¬
го сопротивления. Лля вычисления силы R, необходимо знать
плотность вихрей следа 7, а также плотность 7П присоединен¬
ных вихрей профиля, которые распределены по его контуру.
Заметим, что формулу (17) можно еще установить и другим
путем. Начнем, для простоты, со случая бесконечно тонкой ду¬
ги. На основании формул (14) и (14а) будем иметь
Щ = у J(и - iv)2dz = — J(vt - 2rn)2e“2lt?cb,
L L
причем контур интегрирования будет составляться из верхней
и нижней сторон обтекаемой дуги, которая является поверхно¬
стью разрыва тангенциальной составляющей скорости. В соот¬
ветствии с этим можем написать
Щ = Y /KW‘B ” vt*)~ 21упЫ - ytH)]e~2,,>d.z.
Lb
Введя обозначения
^tB — 7п ) Vt — ^h)i Vn — vnB — vnH,
226
получим
Щ = ip J 7nK - iv^)e~'^dsi = ip J yn(u* - ivm)dsl.
Lb Lb
Скорости и* и v* представляют собой скорости возмущения,
взятые на обтекаемой дуге. Это будут скорости, индуцируемые
в точках этой дуги свободными вихрями следа и присоединен¬
ными вихрями 7п профиля. Из полученной формулы вытекает
R-i = Р j (У * х ‘1n)dsi,
Lb
причем V* = V, + V* есть индуктивная скорость, вызываемая
на профиле свободными и присоединенными вихрями.
Легко убедиться, что
/
(v; х 7n)dSl = о,
п
Lb
следовательно,
Ri=p j(ViX-r„)dslt (176)
LB
где Vt- выражается формулой (17а).
Для распространения формулы (176) на случай замкнутого
контура следует рассматривать этот контур как предельный
случай дуги, начало и конец которой стремятся к совпадению.
Такого рода подход приведет формулу (176) к виду (17).
Переходим теперь к рассмотрению величин, зависящих от
ГФ4 + дФз/dt. Из формул (7) и (ба) имеем
а'; + iv; = -ip J (гф4 + ^ dz.
(18)
L
Так как циркуляционный поток и поток, создаваемый вихревым
следом, обтекают профиль, то функции тока Фг и Ф„ на конту¬
ре профиля имеют постоянное значение. Отсюда следует, что
формула (18) может быть записана в виде
а; + гт; = -ipj(tF4 + ^j dz, (19)
L
гДе F4 и Fs — комплексные потенциалы.
227
Рис. 10
Отобразим конформно внешность профиля на внешность кру-
га и предположим, что вихревой след профиля таков, что при
отображении переходит в действительную полуось —£ (рис. 10).
Общее представление о форме такого следа профиля можно себе
составить на основе того, что нулевая линия тока, которая полу-
чается при стационарном обтекании профиля поступательным
потоком при угле атаки, дающем нулевую циркуляцию, перехо¬
дит при отображении в контур круга и действительную полуось.
Ясно, что след указанного вида вряд ли может существовать в
действительности. Однако при движениях, мало уклоняющих¬
ся от прямолинейных и происходящих при малых углах атаки,
приближенно можно принять, что вихревой след расположен на
описанной нулевой линии тока.
Из гидродинамики известно, что два вихря с циркуляци¬
ей 6Г,, вращающиеся в противоположные стороны, имеют ли¬
нии тока в виде окружностей радиусом Я2, причем (рис. 11)
|C'||Cil = Я2, где |С'| и | — расстояния этих вихрей от центра
окружности. Комплексный потенциал указанной системы вих¬
рей будет
где С = Ле1*—комплексная координата точки, лежащей на
окружности.
Помещение в центр окружности вихря с тем же направлени¬
ем, что и наружный вихрь, не изменит формы линии тока, ко¬
торая останется окружностью, но сделает циркуляцию вокруг
этой окружности равной нулю. Очевидно, что такая комбина¬
ция вихрей дает комплексный потенциал
2*г С-Ci
Так как при безотрывном обтекании твердой окружности он»
является линией тока, то можно утверждать, что комплексны!1
228
Рис. 11
потенциал 6FS является потенциалом бесциркуляционного обте¬
кания окружности потоком, создаваемым изолированным вих¬
рем. Если вихри расположены непрерывно вдоль кривой Е так,
что 6Г8 = То^сг', то потенциал обтекания окружности потоком,
создаваемым таким вихревым следом, будет
Конформное соответствие ( = CU) предполагается извест¬
ным, поэтому, зная Е,(С), мы всегда можем найти функцию
Fa(z) = F[£(z)]. Заметим, кроме того, что
где 7 и dsf—вихревая плотность и элемент длины вихревого
следа в плоскости профиля, есть не что иное, как циркуляция
всех вихрей следа, которая в случае, если профиль начал дви¬
гаться из состояния покоя (Го = 0), должна быть равна с обрат¬
ным знаком циркуляции вокруг профиля, т. е.
5
На основании сделанных замечаний формулу (19) можно за¬
писать в виде
(20)
£
5
229
где к указывает, что интегрирование в плоскости совершается
по контуру круга. Но
С -C_dz
CldC
г(С)1п
с - С
с-си
Л'
к
(22)
ибо написанная подстановка дает — 2m'.?o, где zq относится к
задней кромке.
Так как
Я2 . ^ Сп
КС) - С + -^- + ]Г]7Г + Со’
4 п = 1 4
то, замечая, что
/j^L-п / 1 <*с = о . i
У С-С' ’ У С" С-С' С'"’
*/^L = чЛс [ 1 dc = О
Ус-С( 11 У С’1 С-С!
(23)
находим
7i - —27гг ^С5 + — + ^2 + 2хг(с0 - io)-
Интегрирование по С выполнено, поэтому вместо теперь мож¬
но всюду писать С-
Полагая со = го, С = ге>в> Cl = ^ге%в< получаем
v/ . д ? (2R2 „ ^
X, + 'Y, =~lpQi I 7о I—«** + £
_ \ 71 = 1
<70
Спе~'пв
da =
-41
7 f(s)ds,
& О
где через f(s) обозначено выражение, стоящее в предшествуй
щем интеграле в круглых скобках.
230
Так как в неподвижной системе отсчета местоположение вих¬
ря и его напряженность у ds неизменны, то при интегрировании
вдоль следа плотность у будем считать функцией только коор¬
динат. Если же след рассматривать в подвижной системе коор¬
динат, связанной с профилем, то у будет функцией координат и
времени.
В абсолютной системе координат вихри следа неподвижны и
имеют плотность, не зависящую от времени. Напротив, если мы
будем из неподвижной системы наблюдать за движущимся про¬
филем, то расстояние s, отсчитываемое вдоль следа от задней
кромки профиля до вихря, будет изменяться с течением време¬
ни, и потому
Lf\.<t\ 1 - ^L— - _'Lv
dt ds dt ds c’
а значит, в случае бесконечно длинного следа, когда si = оо,
получим
оо
X', + iY: = -ip J iVc^ds. (24)
«О
Особенно просто вести вычисления для случая пластинки, с
которой сходит вихревой след, являющийся ее продолжением.
В этом случае все сп равны нулю, cos# = -1 и
следовательно, полагая s = —х = х\, получаем
откуда
г2 — х\г + R2 = О,
= \ (*1 ± .
где а = 2Я, причем точкам, лежащим вне круга, соответствует
верхний знак перед радикалом. Тогда
1 2
г Х\ + уХ]
Формула (24) в этом случае даст при ис = const
А-; = 0, =
231
В более общем случае при следе, совпадающем с отрицатель¬
ной осью £, получим
оо
V' I -V/ • & [ 2Я2 ^ |\пап + *^п
*. + ‘П = -.Ода у 1. — + D-1) -jr-
d L n_l J
откуда
Д п=1
у/ _ ^ Г [2Д2 V"V 1\п ап
» L п—1 j
Коэффициенты аЛ и 6П определяются обычным способом при
конформном отображении внешности профиля на внешность
круга.
Для тонкого мало изогнутого профиля можно приближенно
принять £i « £l + i и, следовательно,
Ь = J(*i + \jx\-a7)-
Тогда получим
о°
Y' - л— f гГ| 1чп б.»_
а
= ^ f>i )n+lnfr" / ^ J(xi)
n —1 а
у;=^/т( +
= (у,')пл + ду;,
(25)
(25а)
где (У/)пл соответствует случаю неизогнутой пластины, для ко-
торой все а„ и 5П равны нулю.
232
5. Определение циркуляции
Скорость на профиле в проекции на касательное направление
будет выражаться формулой
/ (1Ф± </Фг </Фз Г d^A 1
Vs ~ U ~ dO lh ~ Vе do +Vc d9 + w de + 2x + ~df) ds/dO'
Для того чтобы в особой точке преобразования, для которой
ds/dO равно нулю, скорость vs не обращалась в бесконечность,
необходимо найти Г из условия
* ( d$ 1
r = -2’T'^*'+v‘
d ф2 йФ3 dф
~do' + u~do’ + ~do
(26)
где вь соответствует заднему острому концу профиля.
Выше мы выбрали направление осей (и?| так, что вь оказался
равным 7г.
Если бы вихревого следа не было, то циркуляция определи¬
лась бы из условия
{ dФl dФ2 dФз\
г‘ = -2Ч“'^ + ^ + “лг),=,.' ,26а|
Таким образом, циркуляция Г при наличии вихревого следа
складывается из циркуляции Г* и дополнительной циркуляции
Г', которую надо наложить на профиль, чтобы удовлетворить
постулату С. А. Чаплыгина при обтекании профиля потоком, со¬
здаваемым вихревым следом. Как видно из формулы (26), эта
Циркуляция равна
Г' = -2it№s/d6)(,=eb.
Найдем сначала скорость ——г, получающуюся на окружно-
RdO
°ти при обтекании ее потоком, который создается одним изоли¬
рованным вихрем с циркуляцией <5ГЛ. На основании формулы
(20) имеем
dF’=tE±l(1+ <•' <
2 xi С V
dC 2xi с V ' с -с
Где ( = Rei«t £ = r'eie\ = BLeie'.
Таким образом,
d( 2тг i < ^
6Г, 1
с-а
2xi С
1 -
CJ-C(C' + Ci) + C,Cn
г' - R?/г'
г' + R2/г' — 2/£cos(0 — O')
233
Рис. 12
В особой точке угол в равен я, и потому скорость там будет
равна
\ 6Г' 1 Л
Г —
г' + —■ + 2Я cos 0'
Для того чтобы скорость в этой точке была равна нулю, доста¬
точно на окружность наложить циркуляцию (рис. 12)
гг = -<г- 0 - ?+т£?тй^) ■
Тогда общая скорость на окружности будет
1
1
,г' + В?/г' -2Нсо*в\ г'+ №/r' + 2ftcos(fl-ei)J ’
где 0[ — в' — тг.
В случае вихревого следа с плотностью вихрей 70 получим
г' - Я2/г'
- 1 )d<T,
ОО
J ( г' -f Я2/г' — 2Я cos 9
S0
-m-ss/»(''■-т) [? + л«7^
(27)
2Я cos 0,
1
da.
(28)
г' + Я2 /г' + 2Я cos(0 - 0',) J
причем интеграл берется вдоль линии вихревого следа в плоС'
кости С- При интегрировании, следовательно, г и 0't должны
234
быть известны как функции а. Можно, конечно, воспользовать¬
ся и равенствами
г 2 — £2 -f г)~у г* cos в] — , da = с/£;>/1 + (drj/di')2.
Особенно простой вид написанные формулы примут в случае,
когда drf/d? мало по сравнению с единицей. Действительно,
тогда da « d£> cos^ w 1. Замечая, что приближенно для вихрей
в следе в плоскости г можно принять (опуская штрихи у г')
xi « (г + Я2/г) cosflj « г + Я2/г
и, следовательно,
r = (xi + \Ai - а2)/2, (28a)
г - Я2/г = yxf-a2, (286)
находим
(29)
причем интеграл берется вдоль действительной оси xi в плос¬
кости профиля. Точно так же
„(я, „) = -L / 7 (JEH-jME*L) Jtl.
2nRJ \ * X] — я xi + acosPy
6. Окончательное выражение для сил
Из формулы (29) имеем
со со
j ydx 1 = J 7(1-1, ~ r/’
a a
а потому величина силы У/ для пластинки примет вид
или
oo
Y, = puca / - рГ ue.
J y/xf — a-
Замечая, что первое слагаемое в общей формуле для силы
У5, т. е. слагаемое, дающее силу Н. Е. Жуковского, выражается
формулой
Yj = рГис = рГ кис + рГ'ис, (30)
где Г* — квазистационарная циркуляция, получаем
Yj + У/ = РГкис + риса 1 Tfa
J \/xl a
a
Таким образом, силы, связанные со следом, окончательно вы¬
разятся для пластинки слагаемыми
сю
/ydx 1
V
у «Г j ” Я *"
a
Для случая тонкого мало изогнутого профиля, для которого
приближенно выполняются равенства (286) и (29), будем иметь
X, = Х[ - рГЧ, (30а)
оо
f y(xi, t)dx
J \/x i — a2
У, = puca j + ay;, (306)
a
где X' и ДУ/ даются формулами (25) и (25а).
Из предшествующего ясно, что общие выражения для сил,
действующих на профиль при нестационарном движении, будут
иметь вид
А = Xjk + Хш + Хт + Xj + XSy (ЗОв)
У = Yjk+Y„+Ym+Yj+Y„
причем Xjk и Yjk определяются, согласно теореме Н. Е. Жуков-
ского, для квазистационарного значения циркуляции.
Для остальных составляющих выше были найдены соотвсТ'
ствующие выражения. Относительно Xw и Yw следует заметить,
236
4»io в них содержится влияние следа. Действительно, так как
дф = d$k + d$9 4- ЛФГ/, то
Хш = -ри> j х((1Ф}с 4- (1Ф3 4 (1ФГ>) = Л'*,* 4 Хшя 4 Л*Г',
L
П, = —pu J у((1Фк + (1Ф3 4 (1Фг*) = 4- У^г'-
L
В комплексной форме
+ in, = -puJ zd^Fk *Fr')dz -puj "j*. (30r)
L L
Пользуясь разложениями, полученными выше для Х3 и Ул,
будем иметь выражение
2 Я2 ^ сп
х,ш + iY,u = -pu> [ + 53 4e'in' ^ (30д)
Г ' Г4
м — 1
В частности, в случае пластинки, для которой Сп — 0 и
г= 4 \fx\ — а2^/2, получим
оо
x4w = ры j 7 - а2^ dxi, YJU) = 0. (ЗОе)
а
Заметим, что все силы, зависящие от следа, требуют знания
плотности вихрей следа 7(24, t).
7. Распределение давления
на поверхности профиля
Так как конформное отображение внешности круга на внеш¬
ность профиля известно, то определить скорость V'(u', г/), ко-
т°рая получается на профиле при обтекании его потоком, со-
3Даваемым вихревым следом на профиле, можно по формуле
гДе и0 дается формулой (28). Скорости возмущенного потока
°к°До профиля всегда можно представить в виде и = щ 4 и*,
v ^ vk + v\ где первые слагаемые соответствуют движению с
237
” квазипостоянной” циркуляцией, а вторые — влиянию следа и
добавочной циркуляции.
Подставляя эти выражения в формулу (5), получаем
Р = Рк + р[{ис -и>у- ик)и' + (vc + их - vk)v'] -
и2 + v2 (дФа dr .
-Р о Р
(дФ* л. dr*
(_¥‘ + 'лф4)’
где рк — давление, соответствующее движению с ”квазипосто-
янной” циркуляцией.
Так как нормальные составляющие V„ равны нулю, то
r = n + mv-p^-f(^. + ^ + §*t), (31)
где Wk —мгновенная относительная скорость, которой соответ¬
ствует давление рк\
Wk = V(uc -wy- IZJt)2 + {vc +WI - Vk)2.
Определение величин, отмеченных индексом Аг, известно. Вели¬
чину дФ3/дЬ лучше всего находить по формуле
«ф •(»•<)= у
dt J dt
причем Ф,(0, t) равно нулю.
Таким образом, если известна величина 7(5), то всегда мож¬
но найти Vq(9, t) и затем построить распределение давления по
профилю.
8. Вычисление моментов
Вычисление моментов относительно начала координат, дей¬
ствующих на профиль, следует производить по формуле
= J(xdY - ydX),
М
L
где dX = —pdy\ dY = pdx, p дается формулой (5), так что
dX = —Poody - p[{uc - шу)и + (vc + ux)v]dy +
+
2 \
238
dY = +poodx + p[{uc — wy)u + (ve + u>x)v]dx -
- I (u! + »2 - 2^) ix,
причем через д'Ф/dt обозначено выражение
дФ ,/dt + ГФ4 + йсФ1 + иеФ2 +и>Фз.
Использовав, как и при вычислении сил, формулы (6а), получим
dX = -poody - p{vc + шх)<5Ф +
+ ^[(u2 ~ u2)dy + 2uvdx)dy + Р-^^У^
dY — +poadx + p(uc — ыу)6Ф +
4- ^[(^2 — u2)dx - 2uvdy]dx — p^-^-dx.
Отмечая, что выражения
dP = 2 uvdx + (v2 — u2)dy, dQ = (i>2 — u2)dx — 2 uvdy
представляют собой соответственно действительную и мнимую
части комплексной величины
dP — idQ — i{u — iv)2(dx + idy) = i(dF/dz)2dz,
для элементарного момента dM находим
dM = xdY — ydX = pao(xdx + ydy) + p(ucx -f vcy)6Ф +
P д'Ф
+ 2 (xdQ ~ ydp) ~ p~df(xdx + ydy)-
Ho xdQ — ydP есть не что иное, как действительная часть выра¬
жения
iz{dP - idQ) = -z{dF/dzfdz,
и Потому
dM = poo(xdx + ydy) + p(ucx -I- vcy)6Ф —
- rRe
p д'Ф.
~ 2~дГ y^y)>
239
откуда после интегрирования по контуру профиля получим
М = р j(исх + ьсу)6Ф - ^Re J zdz ~
L L
f д'Ф
-p I -^-(xdx + ydy). (32)
L
Так как 8Ф можно представить в виде 6Ф = 8Фк + 6ФЛ 4- 6Фг', где
<5Ф* соответствует квазистационарному течению, а <5Ф5 и <5Фр> —
течению от наличия вихревого следа, то первое слагаемое фор¬
мулы (32) представится в виде
р j (исх + усу)«5Ф = Р J (“сх + г>су)6(Фк + Фг<) +
L L
+р j\исх + усу)6Ф, = Мк + Mr- + М*.
L
Величина
Мк = pj(ucx + ьсу)6Фк (33)
L
есть момент, найденный в предположении, что движение проис¬
ходит в отсутствие следа, т. е. как бы при постоянной во вре¬
мени циркуляции, найденной для зафиксированных, мгновенных
значений ис, гс, так как
8Фк = ис6Ф1 4- ьс6Ф2 4- их$Фз 4- Гк6Ф4-
Мы умеем определять Ф\, Фо, Фз и Ф4 на контуре круга как функ¬
ции в, поэтому определение Мк не представляет труда, если мы
знаем х(в) и у(в) согласно формулам (8а).
Так как 6Фр/ = ^50, то
2тг
Мг< = рJ[исх(в) 4- vcy(0)]60 = р(иса0 4 Мо)Г'’ (34^
о
Это выражение есть момент силы рУсГ\ проходящей через точ-
ку с координатами ао и Ьо, относительно начала координат.
Момент М* у выраженный формулой
М* = р j(исх 4 усу)8Ф3,
240
^ожет быть несколько преобразован. Действительно, так как
функция Ф, на контуре профиля постоянна, то можно написать
М* = р J(исх + vcy)^-dz = р Re j zdzj ,
где V* = «с - ivc-
Переходя в плоскость £, будем иметь
М* — р Re
,•/
dFs( С)
dC '
(СК
Ж) _ J_ / Л, _1 L_W
ic 2jti У \С С - С С-Cl/ ’
где на основании формулы (20)
dR
~dC
Е
причем, как и раньше, есть длина дуги вихревого следа, про¬
веденная из начала этого следа в точку, где помещается вихрь
с циркуляцией 70daf (см. рис. 11); — комплексная координата
точки Nf. Так как
R2
ТО
-.-Чй/.\Khzh-гУ>
da У
Произведя интегрирование по переменному С с учетом фор-
мУл (23), получим
М; = -Re
Или, так как
с
241
то, опуская значок штриха, будем иметь
м; = -Re |Pv; J70 fcl + е2’Г) + f] ^
с/я > .
(35)
Если вихревой след профиля таков, что он при конформном
отображении внешности профиля на внешность круга переходит
в отрицательную действительную полуось £i, то г = <т = и
Г 2 Я2 °°
где 6 = |С|-
В частности, для пластинки сп = О, V* = ис и
со
м:
dt 1 (36)
f* f ш AC
= Puc J 70-j^-dtb
(37)
В этом случае, переходя в плоскость с, имеем z — С + Я2/С, и
потому для точек следа х\ = + R~ /£i и, следовательно,
А/* = рис J 7 (ii - - a-^j dx
(38)
Переходим ко второму интегралу формулы (32), а именно к
интегралу
Рассмотрим сначала бесконечно тонкий профиль, т. е. дугу. В
этом случае можем написать
м, = -|^е J[(vt - ivn)l - (v< - ivn)2„]ze~2,9dz,
i.
причем интеграл берется по верхнему разрезу. Замечая, как
и раньше, что vtB - ь1и = уп, v* = (vtB + «т)/2, < = vnB =
получаем
А/,- = —pRe J y„(v* - 1ь*п)е~г9 zdsi =
i-
= -pRe J 7„(u* - n>’ )(x + iy)dsi,
242
откуда
Mi = -Р / 7n(u*x + v*y)dsi<
или векторно
Mi = pJ [rx(V? х7пРь
ГДе V* = V, + Vn есть индуктивная скорость, вызываемая на
профиле системой свободных и присоединенных вихрей. Можно
убедиться, что
т. е. момент М» есть главный момент элементарных индуктив¬
ных сил dUi = p(V, х 7п)^51-
Лля телесного замкнутого профиля можно получить формулы
того же вида, устремляя к совпадению начало и конец дуги.
Переходим, наконец, к третьему интегралу формулы (32).
Этот интеграл имеет вид
и окончательно получаем
М izzp
L
±){xdx + ydy). (40)
L
Из (40) видно, что будет существовать момент Мт, не завися¬
щий от влияния следа:
гДе щ — Uc) ll2 - уС) г/3 = ш.
Так как величины Фк как функции полярного угла в вычи¬
тать умеем, то вычисление момента Мт не представляет труда,
243
если мы знаем х(0) и у(в) в результате конформного отображе¬
ния. В частности, для эллипса
9 I 9
а~ — 6"
£ = acos0, y = 6sin0, xda: -f 2/dy = sin 2Qd0,
-62 .
кроме того,
фх = — 6cos0, ф2 = — a sin Ф3 = — -—sin 29
4
и, следовательно,
Afm = !£(«>-6>)Ъ.
Наконец, из формулы (40) вытекает выражение для момента,
связанного с наличием следа:
м:
д
~рт
д
~рт
д
г
dt
У70
J(Fr + F,)d
х2 + у2
1 у с -С' ад
-—г / lilt -
2тгг У С - <,{
к
где z — х — гу w
с{ лц
а-с d(zz)
dC
da\
= -/-«№>
к
1
- I dc, - 2irizoz0.
.С-С С-С{
к
Так как
г>2 00
г(С) = С+-^- + Х]7^’ = ^ + "Г + S
4 п = 0 ^ ”—nS
ID2 00 -
XL . V > Сп
71 = О
ТО
^ я2 ^ ^ с„, Я2 X я4
<< + T< + S^c + Tt+« +
оо оо
+&Y -^ + Y^c + r2Y ^ + yys^L
4—j спС с п СпС
М = 1 4 4 71 = 1 4 71 = 1 4 4 Ц и 4 4
(41)
+ CqCo-
244
f(poMe того, ££ = Rr и, следовательно,
p4 i °° i 00
« = 2Я! + с + 75-^ E г„с'"+,) + 52 «"-‘Ч
n = l
СЮ СО -
Cn Сп 1
п = 1
+*JE^ + E^^EES+^°
n = l S п = 1 S м I/ 4
Бели это выражение умножить на - jrjf) <*С и полученный
многочлен проинтегрировать вдоль окружности К, то, исполь¬
зуя формулы
о / п .у»
J С - С ' J С - Ci Cl ’
А' К
М _#_ = _??[* [ 1 <*с
J сп с - с' с,п ’ J сп с - с;
к к
при п > 0, опуская знак штриха и принимая с0 = г0, находим
?4 '
^(О = -2”' (с? + ^т) + 2*1
-ЁчкГкг'я’)^-
со р2 00
ЕлС Сух ч ^
£П + 1 ' /“п — 1
_ п — 1 S п-2 S
-ЕЕ|
^(1 ( ^ -и — Ц
V /1
ГЕ + ^1
(42)
причем двойная сумма вычисляется только при и > [л.
В результате для М' имеем
м = -р-Ц.
2dtJ
то Ч +
2 '
гДе через Д обозначено выражение, стоящее в формуле (42) в
Квадратных скобках. Так как для точек, лежащих на следе, £ =
Ге<<>, Ci = (Я2/г)е-'Л то
245
Если форма вихревого следа позади профиля такова, что
при конформном отображении внешности профиля на внешность
круга этот след переходит в действительную отрицательную
полуось: — £ = £i, для которой 9 = 7г, то
Е
В частности, для пластинки будем иметь
к=“'I/■"’тИ1 = ~4'vsЛ (*• ■ -а2) =
R а
= -£/т (*. - (’ - ^Г=г) =
ОО р
Н / Ц11 - 7^ (У^17 - *0
Л
ОО ОО
{''-'I*17')11'
ра2
Из изложенного следует, что полный момент, происходящий
от влияния следа для случая пластинки, будет следующий:
2 °°
м, = м; + м: =
ОО
[ jucdx\
) v^f^‘
Если мы имеем дело не с пластинкой, а с профилем, то в случае,
когда профиль не очень толст и не очень сильно изогнут, для
точек следа можно приближенно принять
1 ^ 2*J - \Jx\ — а2
г а2
и тогда для полного момента получится выражение
ОО
*- = т
ОО
/ 7«с<&1 _
J
•246
^ oo
о° r
-pJ2Cn I
n = l {
00
p [ д Д
+ 2 J (43)
a
Итак, момент относительно начала координат будет равен
М = Mk + Мт + М{ + Мр/ + М3 , (44)
причем суммируемые моменты выражаются соответственно
формулами (33), (41), (39), (34), (43).
Первые два момента находятся известным способом. Следу¬
ющие три требуют знания плотности вихрей следа у. Опреде¬
ление этой величины в общем случае представляет собой весь¬
ма сложную задачу. Однако для некоторых частных случаев
эта задача доводится до конца, например, когда тонкое мало
изогнутое крыло движется при малом угле атаки с постоянной
скоростью Vc и совершает гармонические колебания бесконечно
малой амплитуды в направлении, перпендикулярном направле¬
нию, которое дает нулевую подъемную силу при стационарном
движении (см. рис. 12).
9. Гармонические колебания профиля
Рассмотрим сначала неизогнутую пластинку (рис. 13). Пусть
эта пластинка движется вдоль своей длины с постоянной скоро¬
стью ис и, кроме того, имеет скорость vc в направлении, перпен¬
дикулярном ис. Пусть скорость ve выражается формулой
vc = vo -f v\ cos vt -f t>2 sin vt, (45)
гДе и го — заданные постоянные величины, a v — частота
колебания.
О
* (!) " 1 ■ ■
х +а 1 -а 1&с
Рис. 13
Если бы явление развивалось квазистационарно, то цирку¬
ляция вокруг пластинки выражалось бы формулой (4а) при cj,
Равном нулю, т. е.
Г* = —27Г avc = Го* + Ги- cos vt + Г ok sin vt, (46)
247
где Го* = — 2iravo, Ti* — — 2wavi, Гпк = —2жагь.
При рассмотрении движения пластинки как нестационарного
процесса мы должны определять Г из условия (см. § 5)
г = Г* + Г', (47)
где Г' выражается формулой
оо
Г'
(48)
причем, согласно определению,
7(хь 0 = -
дГ
1_д£
дх\ ис dt
Будем искать Г в виде, напоминающем формулу (46), а имен¬
но
Г = Го 4- Гх cos vt + Г2 sin vt, (49)
где Го, Гх и Г2 — неизвестные величины. В некоторый момент
t*, предшествующий моменту t, циркуляция Г будет тогда вы¬
ражаться формулой Г = Го + Гх соsvt' + r2sin vt', или, так как
пластинка движется с постоянной скоростью ис (см. рис. 13),
t* = t — (xi — а)/ис, откуда
^ ис dt'
Г1 sin v ( t —
xi — a
- Г2 cos
V
Uc
(
sin vt ( Г1 cos v
X\ — a
— cos vt ( Г1 sin v ——- + Го cos
Г 2 sin
xi — a
Uc )
Uc Uc
Подставляя это значение 7 в формулу (48), получаем
Г' = crsin vt [riC(<r) — Г2*?(сг)] - cos vt [Гi5(<r) 4- Г2С(сг)],
где обозначено: <т = va/ue (число Струхаля),
00
5(cr) = J ~ l) sin<r(ii - 1)<Ии
1
ОО
С(<?) = J ~ *) cos<T(*i ~ •
(50)
(51)
248
Да основании изложенного условие (47) примет вид
Го + Г\ cos vt + Г2 sin vt = Г ojl* 4- Г u cos vt + Гок sin vt +
+ <r{sinut [riC(<r) - Г25(<г)] - cos vt [riSV) + Г2(<г)С(сг)]}.
Приравнивая коэффициенты при sinW и cos vt, получаем
Го = Го*,
Гi = Tlfc - <т[Гi5(<r) + Г2С(<т)], (52)
Г2 = Г2* + 1г[Г1С(<7)-Г25И]
и, следовательно,
Г - Ги ~ ~ Г- г п - л-<г \
1 ' l + torS + aHSi + C2) u(
г r2t + tr(rlfcC+r2fc5) ^ n . , ( }
2 1 + 2crS + <г2(53 + С2) 2к( 2*‘
Таким образом, коэффициенты Г1 и Г2 полностью определя¬
ются через посредство Ги и Г2ь которые известны, и безраз¬
мерный параметр сг (число Струхаля), функцией которого явля¬
ются величины 5 и С. Очевидно, что, зная Г\ и Г2, можно по
формуле (49) найти значение циркуляции Г для любого момента
времени.
Из формул (52) видно, что они представляют собой соответ¬
ственно действительную и мнимую части выражения
откуда
где
Гх - *Г2 = ги. - *Ги - «г(Гг - iT2)(C - iS),
r = ттЬ- (54)
Г* = Г, - iTj, п. = Г и - *т«,
ЕГ = С -iS = e'°j (\/|4т - >) di I •
1
Циркуляция Г(/), выражаемая формулой (49), может быть то¬
гда представлена в виде
Г = ro + RefrV"*), (55)
Точно так же
Г* = Г0* + Л е(Г*кеш).
249
В соответствии с этим для общности и краткости записи мож¬
но ввести комплексные циркуляции
Г = Го + Г*.. = rofc +
тогда комплексная плотность вихрей следа будет
(5б>
а вместо (48) получим
00
г' = —1<тГ*eivieio J e~ias* ~ *) dii =
1
= -iaT'e^e** E{,
где E\ = e~iaE\
Аналогично находим Г = Г* + Г , откуда на основании (55)
Г* = Г£ — г<тГ*е“'Е* и, следовательно, как и раньше,
Г’ = . (57)
\ + ioe'°E\ ' '
Ясно, что действительная и мнимая части этого выражения да¬
ются формулами (53). Действительно, умножая числитель и
знаменатель выражения (57) на 1 — icr(C 4- /S), получаем
Г--г Г г;ц - >>(с + is)]
г "г‘”,Гг - IT2rfT?W+c4’ (
откуда и следуют формулы (53).
Итак, для того чтобы вычислить Г\ и Го, а. следовательно, и
полную циркуляцию Г, необходимо знать численные значения
функций S(ct) и С{<т), выражаемых интегралами (51). Эти значе¬
ния могут быть получены путем использования таблиц функций
Бесселя.
Начнем с исследования интеграла
сю
* = т-‘Ь"
1
Его можно записать также в виде
Цолагая х\ = ch77, получаем
ОО
Я* = f e->ch4(ch77 +l)dr,-^
О
Таким образом, вычисление Е{ свелось к вычислению извест¬
ных интегралов вида J e""l<7ch,7ch(nr/)d7; при п = 0 и n = 1.
о
В частности, как известно, интеграл
о
называется первой функцией Ганкеля, а комплексно сопряжен¬
ный интеграл
причем Jn{&), являющаяся действительной частью, называется
бесселевой функцией первого рода, a Nn((r) — функцией Нейма¬
на (бесселевой функцией второго рода). Лля обеих этих функ¬
ций при разных п существуют таблицы точных значений.
На основании изложенного имеем
ОО
со
ОО
(59)
или
°тсюда
Ел = eiaЕ\ -C-iS=~ [ЛИ + No(<г)~
-i(Nt И - ./оИ)]<’,<* - -г-.
мг
С = —^[(Л + Nq)cos(t + (N1 — У0) sin сг],
(60)
Эти формулы позволяют найти величины С и S, так как для
функций Jn и АГЛ существуют таблицы, и, следовательно, опре~
деление Ti и Г2 по формулам (53) не представляет труда. На
основании (59) можно записать выражение (57) для Г* в виде
Г (б1)
отсюда вытекает (см. формулу (56))
tv r*keivte-iaei
j(t, Xi) = —ттт TJ7-. (62)
«с f <х(Я<2) - )
Поэтому сила У,, выражаемая, как мы знаем, формулой
оо
„ [tixut)dxl
Y, = риса / - ,
J - 02
представится в виде
Aut
где
v D J 2Гке*"‘ f e~taXld£i
= />«cRe{n.e'v‘F(<T)} = pucRe{f*F(<r)}, (63)
OO
2 f e~laTldx^ -*
вд=м/жт' r‘ = r:'e'"
Для того чтобы явно выделить влияние Г*, функцию F(<r)
можно заменить функцией вида Fi(cr) - 1 = F(<r). Тогда будем
иметь
У, = —рисКеГ*к + pocRe {f\.Fi(<7)}.
Если обозначить F\(a) = га(<т) + m(o), то, имея в виду, что
Г ^ = (Г1 jt — гТг*)*11'1 = Г\к cos vt -f Ггл sin 1^/ Ч-
-И*(Г \к sin vt — Г о к cos vt),
получим
Г д. ) = (Ги- cos vt -f Г 2Jb sin vt)m — (Ги sin у/ — Г2* cos W)n ^
+ *[(rusm vt - Г2fc cos vt)m + (Tu- cos vt+ Г2^ sin vt)n]
252
jj следовательно,
Ys = -рис(Г\к cos vt + Г-2*.. sin vt) +
+ /жс[(Гu-m + Г2*n) cos i/l + (Г2А-Н1 - Гn.n)sin vt). (64)
Значения функций тп(<т) и п(сг), являющихся действительной
и мнимой частями функции .Fi(cr), которая называется функцией
Теодор сена, приведены в таблице. С помощью этой таблицы на
основании формулы (64) легко подсчитать значение У,.
а
т(<г)
п(сг)
а
т(<г)
п(<г)
оо
0,5000
0,0000
0,56
0,5857
0,1428
10,0
0,5006
0,0124
0,54
0,5895
0,1453
5,0
0,5024
0,0246
0,52
0,5936
0,1480
4,0
0,5037
0,0305
0,50
0,5979
0,1507
3,0
0,5063
0,0400
0,48
0,6026
0,1535
2,5
0,5087
0,0473
0,46
0,6076
0,1563
2,0
0,5130
0,0577
0,44
0,6130
0,1592
1,5
0,5210
0,0736
0,42
0,6187
0,1621
1,2
0,5300
0,0877
0,40
0,6250
0,1650
1,1
0,5342
0,0936
0,38
0,6317
0,1679
1,0
0,5394
0,1003
0,36
0,6390
0,1709
0,98
0,5406
0,1017
0,34
0,6469
0,1738
0,94
0,5431
0,1047
0,32
0,6556
0,1766
0,90
0,5459
0,1078
0,30
0,6650
0,1793
0,86
0,5490
0,1112
0,28
0,6752
0,1819
0,82
0,5523
0,1147
0,26
0,6865
0,1842
0,80
0,5541
0,1165
0,24
0,6989
0,1862
0,78
0,5560
0,1184
0,22
0,7125
0,1877
0,76
0,5581
0,1203
0,20
0,7276
0,1886
0,74
0,5602
0,1223
0,18
0,7442
0,1887
0,72
0,5624
0,1243
0,16
0,7628
0,1875
0,70
0,5648
0,1264
0,14
0,7834
0,1849
0,68
0,5673
0,1286
0,12
0,8063
0,1801
0,66
0,5699
0,1308
0,10
0,8319
0,1723
0,64
0,5727
0,1330
0,08
0,8604
0,1604
0,62
0,5756
0,1354
0,06
0,8902
0,1426
0,60
0,5788
0,1378
0,04
0,9267
0,1160
0,58
0,5822
0,1402
0,02
0,9637
0,0752
Отметим, что сумма Уц- + У,, если учесть, что Ул
РГ'0ис + рдс(Ги cos vt + ^jtsiniT)- будет иметь вид
Yk + У, = рус[Го + (Гu-»n + ГзА:Ч) cos vt +
+ (Г2лт - Гu-n) sin W].
= рГц/с =
(65)
253
10. Применение вихревого метода
В случае бесконечно тонкого профиля (т.е. дуги) формула
для дополнительной циркуляции Г', найденная нами при помо¬
щи конформного отображения, может быть найдена непосред¬
ственно, если использовать вихревой метод. Помимо определе¬
ния Г' этот метод позволяет найти также плотность слоя при¬
соединенных вихрей, входящих в выражения для R, и Mt .
Действительно, представим себе, что нам дан мало изогну¬
тый, бесконечно тонкий профиль (дуга), позади которого тя¬
нется вихревой след, мало отклоняющийся от прямой, которая
является продолжением хорды профиля (рис. 14). Покроем мы¬
сленно нашу дугу непрерывно распределенными по ней вихрями
с плотностью 7„, а линию следа—вихрями с плотностью 7. Так
как рассматриваемая дуга и ее вихревой след очень мало укло¬
няются от оси абсцисс, то при вычислении индуктивных скоро¬
стей можно считать, что вихревой слой расположен на оси х\ и
скорости в точках дуги в первом приближении равны скоростям
в точках, являющихся проекциями точек дуги на ось х\.
Условие непроницаемости профиля в этом случае можно за¬
писать в виде
+а +оо
J_ f 7n(*i, t)dx 1 _v+2_f 7(»i. t)dxi (f)6j
2ir J x\ - x\ en 2ж J x\ - x\
— a +<2
где Vcn = V^sin(a — i?') = Vcf{x\, f). Делая известную замену
переменного х\ = — acos0, dx 1 = asin9d9, полагая
254
и принимая во внимание, что
п
/
cos пв<10 sin пО*
= 7Г-
cos0 —cos#7 sinfl'
вместо (66) получаем
= /(<?', *)+Да,(0',f)-
Отсюда имеем
О L а
х. = -1/ГЛГ()+ * ?2<£ь^1
я-У 2я-Кс У *г - *',(£')
cos пв'ёв'
+<J
Г = J yn(xi,t)dxi = 2iraVe(A0 + Ai/2).
— a
Таким образом,
Г = 2a VC,
J -cos0')<M' +
о
1 f , }(i-cose')de>
^cJl(xnt)dXlJ
2%VC
®i - х[(в')
(68)
(69)
(70)
Если бы вихревой след отсутствовал, то отсутствовало бы
второе слагаемое в квадратной скобке формулы (70). Поэтому
можно утверждать, что величина
ТГ
2a Vc J /(«',*)( 1 - cosO’W = Г*
255
есть квазистационарная циркуляция, а величина
ОО 7Г
г.» а [ / м f(i-coSe')de'
Г - - / 7(хь<)^1 / 7777т- (71)
X у J XI- х[(в') ’
а О
— добавочная циркуляция, которую нужно наложить на про¬
филь, чтобы выполнить постулат С. А. Чаплыгина при наличии
вихревого следа.
Вычислим интеграл
f (1 — cos 9f)d9f
~aJ Xi-х'^в')
Имеем
_ Г (1-cosflQrfg' j (1_- zo&#)dV
J x 1 4- a cos 0* J x
4- cos O'
о 0
dO1
— 7Г.
Xl + COS
0
Сделаем замену переменного, положив г = tg(0'/2), тогда
Л/ 1 — ~2 |Л/ 2dz
cos в = -, <Л? =
dz
/l= f de' _ 2 /
У *1 +COS0' У (1+г2)^1 + ^
ОО
f dz
~ 2у (*1 + 1) + 22(Х) - 1)’
или
dz 2 7 d (ч/itrF") __
Zi +
00
2
1 f dz - 2 /
1 = ’ 1/ i + ftrb2 1
+ (\/ё?~)
= *Y\/*i - L
256
Следовательно,
7Г
— 7Г = 7Г
О
Отсюда вытекает, что Г', выражаемое формулой (71), примет
Эта формула совпадает с ранее полученной формулой для не¬
изогнутой пластинки (29).
Мы видим, что в рамках вихревой теории тонкого профиля
эта формула остается справедливой и для случая слабо ис¬
кривленного профиля. Разумеется, численное значение Г' для
искривленного профиля будет другое, чем для неискривленной
пластинки, так как различны будут, в рассматриваемом случае,
величины Гjb, через которые выражается 7.
Отметим, наконец, что величина
представляет собой не что иное, как индуктивную скорость, вы¬
званную на профиле вихрями следа. Эта скорость создает скос
потока Да, = Vns/Vc, которому и соответствует добавочная цир¬
куляция Г'. В тех случаях, когда мы умеем определять величи¬
ну Г(*), например в случае колебаний профиля, всегда можно
найти 7, равное — — ^7, и затем, определив коэффициенты Лп,
найти величину 7П.
Посмотрим теперь, как можно представить уп при помощи од¬
ной интегральной формулы. Имея в виду, что согласно формуле
вид
ОО
(716)
ОО
(72)
а
(68)
о
получаем
откуда, принимал во внимание (69), находим
,Л/ .ч . O' sin в' } /(в, I) + АаЛв, t) ,Л
7п(0',О = 21'с Uoctg- Г1-1-2-* • (?3)
\ 2 ж J cos 9 — cos в' J '
)
7Г
А0 = i j[f(e, <) + Да5(0, *)]<Ю
и, следовательно,
ж
М*. о = / [/(*, о+д.,(«, 01 (=•* £ - cos;i!l<i,) <*> =
о
“ V * / 0 - JSfTSSr) '»+ *«•<»• 'И* ■
о
2Vc t o' ft в f(0,t) + Aa,(O,t) . aja
— ctg — / tg sm OdO.
7Г 2 J 2 cos 0 — cos 0'
о
Замечая, что ху = —acos0, х'г = —a cos 0', получаем
„ = ^ Hi / я»,. 0 + A..fe.,0^ (74)
ж Ц a + X\ J \J a - Xi Xi - x\
' -a
Отсюда видно, что 7П = ynk + Уп, где через 7пл- обозначена ква-
зистационарная вихревая плотность, а
Y^l[tIK7jHEb^ld,u ,75)
K\a + x\J \l a-xi х\-х\
1 —а
t;n* дается формулой (72), которую во избежание путаницы в
обозначениях при дальнейших интегрированиях запишем
оо
1 [ yd£
vn, = ~ / т , -a ^ xi ^ +a, a ^ ^ оо.
2тг J S-xi
a
Тогда формула (75) представится в виде
Применяя метод неопределенных множителей, находим
+а
j | /- . dx
-JM
*1 (£ - *i)(*i - *i)
— а
+а
_ 1 [ Га + Xi dx\
f - *i J У a-x i ^ - ii +
— a
+<*
f [a + x i
£ — x\ J \ a — xi xi — x['
— a
Сделав известную нам замену переменных xi = — acosfl, х'х =
-acosfl', будем иметь (см. (68) и (71а))
+а тг
sin 0У0
=
_ [ [а + Х\ dxi _ Г О
° J У a-x i ii-i', J g2
COS в — COS 0'
— a
+a
j_ f la + x 1 _ /* (1 — cos0)d0 _ ^
J a — X1 f-ii У £ + a cos 0
-a 0 '
На основании этого интеграл / примет вид
f _ я- /£ + д
£ ~ Х\У £ — а’
и поэтому
I 00 /
' = I а ~ gi / /1+£
7п v)j а + х\ J У £ - а £ - х[
а
Так как интегрирование по xi выполнено, то, вводя вместо £
°бозначение xi, получаем
уп = 1 kIK 7 j'EH Л!Ё1_, ^ « +в. ,76)
тг У а + Xj J у х\ — а х\ — х\
а
Заметим, что при помощи вихревого метода можно весьма
пРосто получить выражение для силы У'а, действующей на бес¬
конечно тонкий слабо изогнутый профиль. В самом деле, как
259
мы видели ранее (см. § 4),
У* = ~Р1Й J^Г + = ~p§i^r + +
L
’Ш /*< “'*'■'
+"\.
L
где и' = д(Фг + ^s)/dx\. Взяв за начало отсчета дуг точку
х[ = у[ = 0, получим для рассматриваемого типа профилей
где 7' = < -
На основании (76) имеем
+а оо /
— а
НО
7 ГЕЕ. _Ii±L = _ +
J у а + хi *i - i'j У у а + ij
-а —а
— а
+а
+ *i J \1—у—^-Г = *\1—А\1Ч-а1-^
— а
и потому
оо
У* = РЪ1 J (\/х1 “°2 - *i)
а
Если бы мы имели вместо вихревого следа один изолированный
вихрь с циркуляцией 6Г, — 76x1, находящийся на расстоянии я
от начала координат, то элементарная сила ($У/ равнялась бы
где /(*i) = \Д? - а2 - zi.
260
Так как рассматриваемый вихрь остается неподвижным и
циркуляция его неизменна во времени, то при профилях, дви¬
жущихся вдоль оси — яь получим
сл//_ ст- df{*i)dxi _ ГГ1 ( ХХ Д _
dxi dt - рис6Г’{,/х1-а1~ )~
= -рисЬТ, fJXl +--a- - Л + pUca-y~==,
\у XI -а ) - а2
где ие = —dxi/dt.
В случае непрерывно распределенного вихревого следа бу¬
дем иметь
= -^сГ' + риса
[ ydxi
J
где Г' есть добавочная циркуляция, определяемая формулой
(716). Сила
V [ ydxi
ттта
U
уже знакома нам (см. § 9).
Точно так же можно было бы получить и силу, зависящую от
ускорений и присоединенных масс.
11. Вычисление силы X
Выше мы видели, что сила X может быть представлена в виде
(см. формулу (ЗОв))
X = Xjk + Xw + Xm + Xi + x5,
гДе отдельные слагаемые определялись при помощи формул
Xj k ” pvc Г к,
Хш — —ри J х<1(Фк + Ф, + ФгО = Хшк + Xw3 + Хц,г',
L
Хт = “(тц11с + m\2Vc + 7П1зй;/),
причем X' следует находить, применяя формулу (25), а
применяя формулу (ЗОг).
Лля случая тонкого симметричного профиля можно принять
имея в виду формулу (ЗОе), что
-fa оо
X = Хк + р J TnMz'i - рш J у - \Jx\ -а2^ dxi - pT'vc, (77)
— a a
где через X* обозначено выражение, соответствующее квази-
стационарному рассмотрению. Определение X* известно, и мы
на нем не останавливаемся. Индуктивная скорость, входящая в
формулу (77), будет выражаться так:
оо
_ 1 f ydxi
V> ~ 2тг J х\- х\
а
В случае гармонических колебаний величины 7, 7П и Г' могут
быть найдены способами, изложенными выше, что позволяет
найти силу X.
Действительно, в этом случае имеем
оо
Хш, - рш j у ^Xi - yjx\ - a2) dx 1 =
а
= ршаа[{Т\Сш — ^Su^sin^ — (TiS^ + ГэСц,) cos W],
где
Сш = ]cos^X! - 1) (ii - х/^м)
1
СО
Sw = j sin a{x\ — 1) ^Xi — \jx\— l) di\.
Или же
ICO
-pwaffiTV"4 j - l) dx
Для скорости v, в точке с абсциссой х\ получим
ОО
г,, = -L ( = ^-[(TxCi-Г 2Si) sin vt-{Г xSi + T.Ci) cos
27Г J xi - 2тга
a
262
И.
где
mj
/■ cos cr(i! - l)dii [ sin<T(xi - l)d±i
Ci= : ; bi = I Г (Xj < 1).
J *1 - x\ J xi - x[
l l
Если положить 7n = 7ni cos vt + yn2 sin vt, то для X{ получим
{+<2
cos vt sin vt J[j„i(riCi - r2Si)-
+a
-7n2(rt5j + r2C,)]dii+sin2 vt J 7„2(Г1&-
— а
+a 1
-ra5i)rf*i - cos214 J 7ai(ri5,- + ГаСОА?; I
Из этой формулы видно, что среднее за период значение Х{ бу¬
дет выражаться так:
" +а 4а
Xi- = {к J 7п2(ГгС< “ Г25-)^1 " / 7«i(riSi + Г2С,•)*?',
а —а
Если, в частности, имея в виду приближенный характер ре¬
шения задачи, для заданного момента времени t принять, что
скорость Vi одинакова во всех точках хорды профиля и равна ее
значению в некоторой точке с абсциссой х\, то Xicp примет вид
Аг.«-^(г? + г22)5,((т, art).
Составляющая Xjk = — рГкУс при поступательных колебаниях
(см. формулы (45) и (46)) будет иметь следующее среднее за
ПеРиод значение:
Ц?*)ср = P*a(v\ + 1>2) = piravl, = + Г^) = ^Г2,.
Наконец сила X,, равная в первом приближении — pT'vc, на
°сновании формул (45), (46) и (50) даст
*.«„ = -^ИПГ» - Г2Г,*)С + (Г2Г2* + Г,Ги)5].
263
Напомним, что, согласно формулам (53), Fi = Ги*( 1 -<теО, Г2 ==
Г*2/ь(1 + (TS2), и потому при малых а можно написать
Хср«^[1-<т(5 + 5,-.)].
47г а
Г лав а 2. ТЕОРИЯ
НЕСТАЦИОНАРНОГО ДВИЖЕНИЯ ПЛАСТИНКИ
КОНЕЧНОГО РАЗМАХА
12. Пластинка
с постоянной циркуляцией по размаху
Теорию нестационарного движения пластинки конечного раз¬
маха будем строить путем обобщения теории нестационарного
движения пластинки бесконечного размаха и теории стационар¬
ного движения пластинки конечного размаха. Очевидно, что
обе упомянутые теории должны получаться из теории, которую
мы хотим построить, как частные случаи.
Предположим, что пластинка в плане имеет форму прямо¬
угольника и обладает постоянной по размаху циркуляцией. Се¬
чения пластинки плоскостями, перпендикулярными ее размаху,
могут иметь различную кривизну, которую будем считать ма¬
лой в смысле теории тонкого профиля. Допустим, кроме того,
что пластинка движется с постоянной скоростью и вдоль хор¬
ды среднего сечения и имеет в перпендикулярном направлении
скорость V.
Будем рассматривать взятую пластинку как вихревую несу¬
щую поверхность так же, как мы это делали в случае бесконеч¬
ного размаха. Для этой цели представим себе, что она замене¬
на системой вихревых линий, которые параллельны размаху и
проведены через точки хорды среднего сечения. При осях, пока¬
занных на рис. 15, вихревая несущая поверхность будет лежать
В ПЛОСКОСТИ X\Z.
Так же, как и при стационарном движении, мы должны допу¬
стить, что с боковых сторон пластинки сходят свободные вих¬
ри, направленные по линиям тока относительного движения
При малых углах атаки можно в первом приближении считать,
что свободные вихри лежат в плоскости x\z и являются ка*
бы продолжением системы присоединенных вихрей 7П. Физи¬
чески боковые вихри являются не вихревыми линиями, а вих¬
ревыми шнурами, имеющими конечный радиус е. Однако А31*1
264
Рис. 15
определения на пластинке индуктивных скоростей, вызываемых
такими шнурами, в первом приближении достаточно рассматри¬
вать лишь вихревые линии, совпадающие с осью вихревых шну¬
ров. Расстояние 2Ь\ между этими осями должно, следователь¬
но, быть несколько больше размаха пластинки 2L.
Если бы пластинка имела бесконечный размах, то интеграль¬
ное уравнение, выражающее непроницаемость бесконечно тон¬
кого профиля, как мы уже знаем, имело бы вид
+а оо
'y(xi,t)dxi
1 [ 7п(*ъ t)dx 1 _ , 1 [
T*j O + s У г, - г',
где
Ven « Vc (а - dy\/dy\).
В случае прямоугольной пластинки конечного размаха, соста¬
вленной из бесконечно тонких профилей, присоединенные вих-
Ри, как уже было указано, имеют размах 2X,, и потому условие
непроницаемости следует записать в виде
■fa оо
[ Кп7п(х\, t)dx\ ( dy[\ 1 f I<y(xi,t)dxi
W + v‘”
"“a a
<78)
Kn есть коэффициент, зависящий от х\ —х\, z[, L\ и учитыва¬
вший, что присоединяемые вихри имеют конечный размах; К —
*°эффициент, учитывающий, что свободные поперечные вих¬
265
ри следа имеют также конечный размах; Цп нормальная ско¬
рость, вызываемая свободными продольными вихрями.
Для того чтобы установить вид коэффициента Л'п, рассмо¬
трим присоединенный вихрь с циркуляцией yndx\, проходящий
через точку N параллельно размаху, и найдем индуктивную
скорость, вызываемую в точке N с координатами х'г, 0, z'. Эта
скорость на основании закона Био — Савара будет равна
4тг J г°
-Ly
где г = (х[ — xi)i + (z* — z)k. В проекции на ось у получим
dv п = -
47г(х
+L1
7nd*i f
i-*i) J '
(4^I
H^)!]
3/2 *
(79)
Полагая -r-r^ = tg<p, находим
причем
так что
Tn^i 1
47Г
V?2
*1 - *1 J
ч>\
cos tpdip = — —-(sinv?2 — sin
47г(х1 — X])
ladxi 1
27r(xj — xi) 2
+
Li+z'
VVi -Х.Г- + (L\ +
Lx - z'
+
v/(x' -Xl)a + (Li-r')2
7 A'n(x, - xj, 2', Li)
27Г
и, следовательно,
Xi - X]
+<*
dx 1
1 f inKndx\
Vn 27Г J x\ - Xi
(80)
(81)
266
Заметим, что при Ь\ —* оо Кп —► 1. При zf = 0, т. е. в середине
пластинки,
Из полученных формул видно, что при больших удлинениях ве¬
личина Кп может быть принята равной единице, что всегда ис¬
пользуется в так называемой теории ”несущей линии”.
Величина К имеет тот же вид, что и Л'п, с той лишь разницей,
что Яь входящее в Л", изменяется в промежутке +а ^ х\ ^ +оо.
При таком условии А', которое при z' = 0 запишем в виде
будет стремиться к нулю при возрастании х\. При больших
удлинениях влияние величины х\, заключенной в пределах — 1 ^
х\ ^ +1, будет мало, и для А'о можно в этом случае приближенно
принять
следовательно, скорость может быть представлена в виде
где7х = A'o(*i, ^i)7- Отсюда видно, что при большом, но конеч¬
ном удлинении влияние вихревого следа эквивалентно влиянию
вихревого следа с плотностью 71, получающегося у крыла бес¬
конечного удлинения.
Выясним теперь величину и направление скорости V*, созда¬
ваемой свободными продольными вихрями. Будем считать, что
Углы атаки малы и, следовательно, можно предположить, что
Указанные вихри совпадают с плоскостью пластинки и скорость
перпендикулярна ей. Особенностью рассматриваемой зада¬
чи является то, что циркуляция Г свободного бокового продоль¬
ного вихря должна изменяться вдоль него, т. е. этот вихрь дол¬
жен быть вихрем с переменной циркуляцией. Это обстоятель¬
но следует из того, что вводимые нами присоединенные вихри
где
оо
а
267
Рис. 16
7fn(xi) 0 должны в каждый заданный момент времени образовы¬
вать со свободными вихрями замкнутую систему (рис. 16), для
чего должно выполняться условие
7п(*ь 0 = -dr{xi)/dxi.
В каком-либо сечении xi = const при — а <С х\ ^ -fa циркуляция
r(^i) бокового вихря будет
гI
Г(*1, <) = - j ya(xi,t)dxi = j 7п(ц, t)dx\.
Ti -а
В сечении х\ — -fa циркуляция вихря становится равной цирку¬
ляции вокруг крыла, поскольку
+ а
Г(а, t) =r J 7п(^ь t)dx\.
Так как циркуляция Г изменяется во времени, то позади задней
кромки циркуляция продольного свободного вихря будет изме¬
няться вдоль его длины.
268
Если пластинка движется с постоянной скоростью ис, то Г
для момента т. е. для сечения хх = может быть записана в
виде
Отсюда видно, что производная dY/dt' не равна нулю и, сле¬
довательно, в точке xi = £ от свободного вихря отделяется по¬
перечный свободный вихрь с циркуляцией Вихри этого
вида и образуют пелену свободных поперечных вихрей, с кото¬
рой мы встречались в случае пластинки бесконечного размаха,
движущейся нестационарно.
Участок свободного бокового вихря с циркуляцией Г(<, xi),
тянущийся от задней кромки до бесконечности, будет вызывать
в точке N' с координатами х', 0, z' скорость
, 1 1 ГУ'ХгКЬг-г'^хх
Vi 4*J [(*',- *, г- + а, -*')2]3/2
со
4я- L\ - z' J
П<,*1
3/2'
*i=« |l +
(83)
(84)
(йЗ)1
Второй концевой вихрь даст скорость
„ _ 11 1 Г(г'хМ(т?&)
Vi " 4*1,+2/ J Г /*._*' \213/2
Прлная скорость будет равна
Vi = + i>". (85)
Ь частности, для середины, т. е. при zf — 0, имеем
«o = -Vr / 7 "3fV (86)
2w£i У Г /Х]_Х'\21 '
*■=■ [■ + (V1) j
В случае гармонического колебания пластинки, как и в слу¬
чае бесконечного размаха, можно положить
Г = Г*е,‘,('"£^!') + Го,
269
откуда
T*eiuietu'
vi0 = - -
2тгЬ\
со iuZl-f±, (xiZx[\
e ,e d(-Tr±) Го
J ’ (4?)T
. \2T3/2 2vLx '
или
ViO = -■
2irL\
*i=“ p +
oo e-ia{i
/
- M^)]
,42]3/2 2icL\ ’
где x, = xj/a, x, = x'j/a, A, = Ii/a, a = va/ue.
Полагая -1 = tgy, будем иметь
V{ о = --
2icL\
2
J е~гаХ' cos (pd(p —
. • -*i
arctg -5—1
Гр
27rZ/ j
В точке x[ = 1, т. e. на заднем конце пластинки, получим
ж/2
ЩО =
2ttL
tJ
-iaXi tgv> cos — ;r—7- = -^-(Го + ГТое*"1),
27rLi
2ttLi
*/2
где Fo = / e*"t<7Al fcg(p cos
о
Участки свободных вихрей, тянущиеся от —а до -И и обла¬
дающие циркуляцией Г(х1} J), дадут в точке N* сечения zf = О
скорость
2irL]. J Г /11_х'\2l3/2
- [i + fV1)
На основании теоремы о среднем получим
Abu = -
27rLi
a — i
■ +
>/(a - X| )2 4- if >/(a 4- x'J2 4- Lf
где Гт есть некоторое среднее значение Г(хь t). При боль¬
ших удлинениях величина Дг>г0 будет иметь значение, близкое
Г m 2
к —
2ira Л? ‘
270
Для пластинки конечного размаха, находящейся в стационар¬
ном потоке (|/ = 0), наиболее хорошо развита так называемая
теория несущей линии, которая предполагает, что удлинение
настолько велико, что можно пренебрегать изменением ско¬
рости Vi в зависимости от х\ и в промежутке —а ^ х[ ^ +а
считать vt всюду постоянной, а в сечении z* = 0 — равной
Точно так же теория несущей линии пренебрегает и влиянием
добавочной скорости Дг^, которая вызывается участками сво¬
бодных вихрей с циркуляцией r(xi). Мы видели, что эта ско¬
рость должна быть порядка
Для пластинки конечного размаха с большим удлинением в
нестационарном потоке мы сохраним допущения, указанные вы¬
ше для стационарного случая, так как нет никаких оснований
для отказа от них. При этих условиях уравнение непроницае¬
мости пластинки можно записать в виде
1 / 7п(*ь t)dx! [ dy'A 1 f Ку(хи t)dxi
T,j =v4'*~1а) + Г,)—^ »"<87>
—a a
Из этого уравнения следует, что jn можно представить так:
7п = ik + i + 7«,
где 7; соответствует влиянию поперечных, а 7,—продольных
свободных вихрей.
В соответствии с этим можно утверждать, что полная цир¬
куляция Г может быть представлена в виде Г = Г* + Г' + Г,-.
Величину Г* мы находить умеем. Найдем теперь Г' и Г*. Пер¬
вая из этих величин определяется по формуле (71), но теперь
вместо 7(яь t) будет стоять Л'о(*ь ^1)т(-сь 0- Таким образом,
Г' = a j К0[хх, Aib(xi, t) ""i ~ dxi' ^88^
1
® случае гармонических колебаний в направлении, перпендику¬
лярном плоскости пластинки, для полной комплексной циркуля-
получим
00
Г' = —гсгГ*е“'*е|<т J К0(хь Ai)e-V*‘ ~ *) <89)
1
271
Наконец, величина Г* найдется по формуле типа формулы
(70), в которую следует добавочно ввести слагаемое
Определение действительной части Г*, которое может инте¬
ресовать нас при решении конкретных задач, не представляет
труда, если заранее подсчитаны величины С\, S\, А\ и В\, за¬
висящие от удлинения Ai и параметра а. Таким образом, цирку¬
ляция Г, постоянная по размаху пластинки, определяется про¬
сто. Заметим, однако, что если бы мы начали строить такую
пластинку с постоянной циркуляцией согласно формулам (90),
то она получилась бы перекрученной, причем элементы ее при
z* ф 0 имели бы больший угол атаки а, чем центральный эле¬
мент (zf — 0).
Действительно, уравнение непроницаемости (87) должно вы¬
полняться во всех сечениях пластинки. Мы удовлетворили это¬
му уравнению в сечении z* = 0, что позволило найти величину
о
где Да,- = Fq(ct, Ai). Таким образом, будем иметь
2тгVCL
Собирая вместе все найденные циркуляции, получаем
Г = Г0 4- Г*еш =
откуда
1 + 1/А! ’ 1 + itre” Е\ 4- Fq(<t, А, )/Хх ’
(90)
где
1
1
оо
оо
272
р. Однако то обстоятельство, что мы знаем Г, позволяет найти
равное — — §7, а также величины уп, Vi(t, Ab z') и, наконец,
величины
00
К{Аь г', *1)7(11, *)d*i
МЛ„г',0 = ^/
XI - х\
1
+1
(91)
<92>
-1
Так как v, и v, зависят от z', то для того чтобы удовлетворить
уравнению непроницаемости при z' ф 0, необходимо определить
угол а из формулы (87), т. е. взять его в виде
a(f,)=^ ++Ж) •
(93)
откуда и следует, что пластинка будет перекручена. Если мы
хотим, чтобы она была не перекручена, необходимо предполо¬
жить, что 7п есть функция не только от хь но и z', т. е. мы
приходим к пластинке с переменной циркуляцией.
13. Пластинка
с переменной циркуляцией по размаху
Будем считать пластинку по-прежнему прямоугольной и по¬
пробуем удовлетворить основному условия непроницаемости,
взяв плотность вихрей уп в виде уп = /(-)7m(^i), где f(z) есть
безразмерная функция, на которую мы наложим обычное усло¬
вие для случая конечного размаха, а именно условие, что f(z)
обращается в ноль на концах, т. е. при z = Совершенно
очевидно, что циркуляция около какого-либо сечения пластин-
ки будет выражаться формулой
+Л
Если пластинка имеет большое удлинение, то можно исхо-
^ть из предположения, что скорость, вызываемая в точке (х'2, 0)
Сечения z' вихрем, который проходит через точку N, будет та-
же, какую вызывает в этой точке вихрь, имеющий постоян¬
ную по размаху циркуляцию rm/(z'). При этом предположении
273
получим
*1
— а
Переходим теперь к определению скорости, вызываемой сво¬
бодными продольными вихрями. Продольный вихрь, который
начинается в точке (ari, 0) сечения ^ (см. рис. 16) и является как
бы продолжением присоединенного вихря, обладающего цирку¬
ляцией 7n(xi, z)dxi, имеет циркуляцию
oz
Циркуляцию свободного продольного вихря, тянущегося вдоль
прямой у — 0, z = const, будет изменяться вдоль его длины и
равняться при -а $ х\ $ а
d.T(xu *,t) = J ^dzdxа = dz^p- J 7t)dx 1 =
— a —a
Непосредственно за задней кромкой циркуляция продольного
вихря будет
с/Г(а, z> t) = Гт(а, t)~^ds.
На промежутке от +a до +оо циркуляция вихря также будет
изменяться вдоль его длины. Если скорость ис постоянна, то в
этом случае, как и ранее, будем иметь
</Г(£1, z, t) = rfT
При большом удлинении Л мы пренебрежем влиянием пр0'
дольных вихрей, имеющих протяженность от —а до +а, а так#е
пренебрежем в этом же промежутке изменениями индуктивн0#
скорости, вызываемой свободными продольными вихрями, и
числим индуктивную скорость в точке N'(a, 0, zf). Для эт°
274
скорости будем иметь
ОО
[ <Л>ь г, t)(z - z‘)dXl
Vt 4ж J [(а - zi)2 + (z - г')2]3/2
а
1 Л/(г) dz 7Г"»(«г,
47Г dz z - г' J Г / N 213/2 ’
• [l+N
В случае гармонических колебаний полагаем, как и ранее,
Гт = Г0т +
что дает
^ —1<7(X, — 1
4^0
1
1 dr0 dz еш dr* h(a, z - z')
, ,v<r* f Vi r
* " 4эг dr 2 - г' | J Г . A2-|3/2 +Гот
• + (**)
47Г cf* 2 — 2; 47Г c/z 2 — 2'
Полная скорость будет тогда выражается формулой
1 <*Г0 ^ еш dr* /i((7, z - z') ,
dz.
(94)
_ __1_ f dr о dz _ Г
V% 47Г J dz Z — 2; 47Г J
dz
— L -L
Свободные поперечные вихри в рассматриваемом случае бу-
Дут также иметь переменную вдоль своего размаха напряжен¬
ность 7 = — Скорость, вызываемая ими в точке Nf с коор¬
динатами 0^ * * будет выражаться формулой
, 1 7тт(«.,1)1+/ ,,
”*=4i/^rWr , <95)
Ь 1 + ^
^Дс 7m — —L Hjzl
/т uc at •
275
Эту формулу удобно переписать в виде
Г .. 1 7к„,.',о
4ir J ii-x'i ] У Г / , \213/:г
dx 1, (96)
где /(2, z') = f(z)/f(z'). Обозначая выражение, стоящее в фи¬
гурных скобках, через 2/l'(xi — х\, г'), получаем
_ 1 ‘7l(xi, х\ t)A'(xi - x'i, z')
V’-2iJ
a
Основное интегральное уравнение задачи будет иметь вид
1 / 7n(*i, г', t)dxi лг ( dy\\
г*} = ЧJ*j+ ■ "
—а
Поступая, как и ранее (см. формулу (70)), находим
Г = Г* + a j 7(хь z', t)K(xx - Xj, z') ^ | “ ^ dxi - 2rtTn>,.
1
В случае гармонических колебаний, полагая Г = Г0 + rVw,
Г* = Го* + Г\etv\ будем иметь
Г0 + r*eivt = rok + Г*кеш-
— icr Г
W'j^yil±T_^Wll +
1
a +t dT0 dx eiyta+fLdr Ixdz
+ 2 J ИГ ГП7 + “2“ J d7 г - V ’
откуда следует
Го — Го* +
— L
а [ с1Г о dz
I
2 J dz z-z>'
-L
(97)
276
г. _ г. , а / hdz
Г ~ 2 J ~dz 7^7' ~
-L
00
- «rrV* J e~i9*' - l) *<**1- (98)
1
Рассмотрим интеграл
ОО
h = Г*(г') j - l) = Г*^(<т, A, z');
1
подставляя Л\ получаем
Если бы циркуляция была распределена по пластинке согласно
закону полуэллипса, то мы имели бы
f(z) _ у/1 - (z/L)-
/(*') yi-Cz'/L)2’
или же, полагая, что z = — Lcosy?,
/(г) _ sin у?
/(z') sin<£>'
В более общем случае распределения циркуляции
оо
/(2) = sin п<р
П — 1
и, следовательно,
J + ЕГ=3Лп sil1^
/(г) _ sin ip А\siny _ sin у 1 -f r
f(z') sin ip' t ^ £?=3 An sin mp‘ sin^'l + r'’
A\ sin
277
Для пластинки, у которой плоскость ху является плоскостью
симметрии, А2 — Л\ — ~ А2к = 0, и потому суммирование в
написанных суммах начинается с п — 3, причем А$ часто мало
по сравнению с А\. Вследствие этого для первого приближения
можно принять
входящий в формулу (98). В этом интеграле функция /] имеет,
как мы видели выше, следующий вид:
Ввиду того, что свободные продольные вихри сходят особенно
интенсивно вблизи концов пластинки и, как показывает экспе¬
римент, сворачиваются в сосредоточенные концевые вихри, в
написанном интеграле для первого приближения можно заме¬
нить :наА = Ь/а. При такой замене интеграл v^ примет вид
f(z') sinv?' y/l-(z'/L)2'
f(z) _ sin<? s/\ - (z/L)2
Таким образом, получим
где z = z/ay A — L/a.
Рассмотрим теперь интеграл
+L>
oo
О
рели бы циркуляция была распределена по какому-нибудь дру¬
гому закону Г*(г), то мы имели бы
/,(А, гг, г') Vd(r - r;j d-
- v" + 4. J —iT '-'z-f
-L
Учитывая, что интеграл понимается в смысле его главного
значения, и потребовав, чтобы выполнялись условия
г*(*0 = г
г *(L) = r;(i) = г*(-х) = r;(-L) = о,
после интегрирования по частям получим
„* - „* + А / г(г)-г,(г)
•1 ~ " + 4тг J (г - г1)2
-L
Если предположить, что циркуляция r3(z) подчинена элли¬
птическому закону
r; = r;mV/i -(z/l)2,
ТО
4тг ^/1 _ {z'/Lf
и, следовательно, так как Г^(г') = Г*^'),
а _ r*(z')/i(l + <r) ,VL^7^ Г (Г* - r;)dz
vn = ======, о =
“ 4L\/1 4- (z' / L)2 ’ я- J (z-z1)2
Для эллиптической циркуляции величина S равна нулю, а для
Циркуляций, близких к эллиптической, будет мала по сравне¬
нию с единицей.
На основании изложенного интегродифференциальное урав¬
нение (98) примет вид
°ТкУда
I-* _ г» <т, *') iere,aГ*
г - г*- 2Vi-(Wi)!< ’“ 11
Г*
р* =
тг/х(1 + *) i*e"El
2\у/1 ~{z'/L)2 v/1 - {z'/\)2
279
Определение Г* из этого уравнения следует вести методом по¬
следовательных приближений, выбирая в первом приближении
бит для случая эллиптической циркуляции, для которой они
равны нулю.
В заключение заметим, что изложенное обобщение вихревой
теории тонкого профиля на случай пластинок конечного раз¬
маха с большим удлинением может быть распространено и на
случай малых удлинений. Это можно сделать так же, как и
для стационарного случая [23]. Прежде всего следует отме¬
тить, что основное интегральное уравнение (78) остается без
изменений. Однако, если для больших удлинений можно было
положить Кп(хj, х'и,Х) равным единице, то для малых удлине¬
ний этого сделать нельзя. В подобном случае множитель Кп
может быть в первом приближении заменен некоторым коэффи¬
циентом значения которого сосчитаны раз и навсегда
для простейшего закона распределения вихревой плотности уп.
Величина Av,o при малых удлинениях также должна быть учте¬
на. Для нее можно получить выражение
А^О = л, <7),
где /\ * — коэффициент, численные значения которого для перво¬
го приближения находятся сравнительно просто. При указан¬
ных преобразованиях интегральное уравнение (78) приобретает
знакомую нам структуру, и потому для Г* можно получить вы¬
ражение, имеющее тот же характер, что и формула (90). Однако
это выражение будет содержать множители, которые учитыва¬
ют влияние малости удлинения вследствие того, что К * не при¬
нималось равным единице, а К* не принималось равным нулю
Отметим, что основной целью при решении задачи о неста¬
ционарном движении несущей поверхности, как при большом,
так и при малом удлинениях, являлось решение основного ин¬
тегрального уравнения (78), т. е. получение функции 7П, удовле¬
творяющей постулату С. А. Чаплыгина на задней кромке пла¬
стинки и обращающейся в бесконечность на передней. Суще¬
ствуют, однако, и другие методы приближенного решения той
же задачи, например метод Лоуренса—Гербера [24], а так*6
метод С. М. Белоцерковского [25].
280
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
\. Kirckhoff G. Uber die Bewegung eines Rotationskorpers in einer Flussigkeit.
Teil LXXI. Berlin, 1869; Vorlesungen iiber mathematische Physik. Mechanik.
Vorlesung. 19. 1876.
2. Thomson W.t Tail W. Natural philosophy, Cambridge, 1912.
3. Prandtl L. Uber die Entstehung von Wirbeln in einer idealen Fliissikeit. Vortrage
zur Hydro- und Aerodynamik. Berlin, 1924.
4. Bimbaum W. Das ebene Problem des schlagenden Flugeln // ZAMM. 1924. N 4.
5. Wagner H. Uber die Entstehung des dynamischen Auftriebs von lYagflugeln//
ZAMM. 1925. N 5.
6. Чаплыгин С. А, О влиянии плоскопараллельного потока воздуха на дви¬
жущееся в нем цилиндрическое крыло//Труды ЦАГИ. 1926. Вып. 19;
Собр. соч. Т. 2. М., 1948.
7. Carafoli Е. Aerodynamique des ailes d’avion. Paris, 1928.
8. Glauert H. The force and moment on an oscillating airofoil//Rep. and Mem.
1929. P. 1215-1242.
9. Karman Т., Burgers J. M. Aerodynamic theory. Vol. 2. Berlin, 1935.
10. Келдыш М. В., Лаврентьев М. А. К теории колеблющегося кры¬
ла//Технич. заметки ЦАГИ. 1935. 45.
И. Седов Л. Я. К теории неустановившихся движений внутри жидко¬
сти //Труды ЦАГИ. 1935. Вып. 229.
12. Седов Л. И. Теория нестационарного глиссирования и движения кры¬
ла со сбегающими вихрями//Труды ЦАГИ. 1936. Вып. 252.
13. Седов Л. Я. Теория плоских движений идеальной жидкости. М., 1939.
14. Кагтап Т., Sears W. R. Airofoil theory for non-uniform motion // J. Aeronaut.
Sci. 1938. N 5.
15. Нехрасов А. Я. Теория крыла в нестационарном потоке. М., 1947.
16. Седов Л. Я. Плоские задачи гидродинамики и аэродинамики. М.,
1950.
17. Голубев В. В. Лекции по теории крыла. М., 1949.
18. Поляхов Н. Н. Об индуктивных силах при нестационарном движении
крылового профиля//Вестн. Ленингр. ун-та. 1956. X? 7. С. 87-93. [24]
19. Поляхов Н. Н. О распределении давления на поверхности профиля,
движущегося нестационарно//Докл. АН СССР. 1952. Т. 87. № 6.
С. 901-904. [19*]
20. Поляхов Я. Я. Теория крыла конечного размаха, колеблющегося гар¬
монически // Вестн. Ленингр. ун-та. 1957. № 19. С. 87-97. [25]
21. Kussner Н. G. Allgemeine Tragflachentheorie: Luftfahrt-Forschung. Berlin,
1940.
22. Cicala P. Sul moto stazionario di un’ala di allungamento finito. Atti d. Reale
Accad. Naz. d. Lincei Ser. VI. 1937. Vol. XXVI.
23. Поляхов H. Я., Пастухов А. Я. Теория несущей поверхности прямо¬
угольной формы//Вестн. Ленингр. ун-та. 1959. № 13. С. 93-110.
[26*]
**. Лоуренс, Гербер. Аэродинамические силы, действующие на колеблю¬
щееся крыло малого удлинения //Сборник переводов иностранной ли¬
тературы. Механика. Вып. 2. М., 1954.
Велоцерховский С. М. Пространственное неустановившееся движение
несущей поверхности//Прикл. мат. и мех. 1955. Вып. 4.
281
Здесь указываются лишь работы, упомянутые в тексте. Во-
лее подробную библиографию по нестационарному движению
можно найти в книге А. И. Некрасова [15] и в сжатой обзор¬
ной статье Тимана ”La theorie des profils minces en ecoulement non
stationnaire en fluide incompressible ou compressible”. Publ. Scient.
et Techn. Ministere Air, N 296. 1955. Интересна также книга:
Robinson, Laurmann. Wing theory. Cambridge, 1956.
III.3. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
ПРЯМОУГОЛЬНОГО КРЫЛА С ЦИРКУЛЯЦИЕЙ,
ПЕРЕМЕННОЙ ПО РАЗМАХУ [50]*
Предлагаемое ниже решение задачи о малых гармонических
колебаниях слабоизогнутого прямоугольного в плане крыла в
поступательном потоке идеальной несжимаемой жидкости осно¬
вано на результатах работы [1]. При решение принята вихревая
схема Бирнбаума, вихревой след предполагается расположен¬
ным в плоскости xz, скорость набегающего потока Vqq парал¬
лельна оси х (рисунок).
Воспользуемся безразмерными величинами х = х/а, z = z/L,
у = V/a и введем следующие обозначения: уп — плотность
присоединенных вихрей; (х, z)— координаты присоединенного
вихря; (х', zf) — координаты точки расчета; (£, z) — координаты
точек вихревого следа; —djn/dz — плотность вихревого шну¬
ра, сбегающего в точке (х, z)\ —8yn/dt— индуцированная плот¬
ность; V00(at—dy/dx)etTi —вертикальная составляющая скорости
набегающего потока на крыле.
Теперь скорость, вызванную присоединенными вихрями,
Можно записать в виде
Уп = 4*JdXJ [(*' - * j* + А*У - г)2р/2 dz•
-1 -1
Скорость, вызванная вихревыми шнурами плотности —дуn/dz,
*Соавт. 3. Н. Шестернина.
283
будет равна
1 оо 1
\ г г _ г z' _ ?\
Vi = —JdxJ dij [(-/_^)2Эг+л2(,,_5)2]з/2^-
-1 X -1
Индуцированная скорость равна
1 оо 1
V. = ±Jd,]«j di.
-1 X -1
Пользуясь условием непроницаемости крыла
Уп = Voo (а - ^ еш + Vi + Vit,
запишем уравнение для ип:
1 };-} 7п(*'-*) ;-_Уоо ( dy\ iut ,
4тг j J [{х' - if + A2(z' - z)2]3/2 A \ dx)e
-1 -1
-1 X - 1
1 °o 1 Л
+ hM*J (I)
-1 x — 1
Зададим вихревую плотность */п в виде
7п = 7(ж)7(г)е"", (2)
где t' — время образования индуцированного вихря, связанное с
временем расчета f зависимостью tf = t — (£ — x)/Vоо, тогда
Как и в работе [1], будем считать у (г) заданным в виде ряда
7(z) = 70 + 72 22 + ... + 72п^2", (4)
Причем на границах крыла у(z) должно удовлетворять условию
7(±1) = 0, или 7о + 72 + • • • + 72п = 0. (5)
Используем полученные в [1] выражения для интегралов:
[(*'-О2
-1
[ ai(2' z) __ j (с j)
J [(*/ _ ^)2 + A2(z'-2)2]3/2 ^ ’ )}
1
/
7(z)(x' - x)
[(*' - x)2 + А2(г1 - г)2]з/2
-l
z' - 1
= _2_(
x' — X \ [(x' —
+
x)2 + A2(z' — l)2]1/2
f, + 1 \{ x ~2 ,
2 [ (70 + 72 = +
[(x' — x)2 + А2(г' + l)2]1/2
+ ... + 72n5'2n) +J22(x, x', *'),
где Ji(£, x', z') и J22(i, z') непрерывны относительно разно¬
стей x‘ — £ и x' — x соответственно, содержат в качестве параме¬
тров 7о, 72,..., 72„ и имеют вид
J\ = — г (e[Gl + . . . + (—l)*G2Jt + l + • • • + ( —l)n_1G2n-l] +
х' — X \
+f[G7 + ... + (-1 )k-'cH.-1G2k + ... + (-lr-^-^an]-
E2k-l[G2k+l + • • • + ( — 1)кСп-1&2п- J — . . . — ■Е12»-зС?Зп-1 +
\g2 + ... + + .. ■ + (-1 )n-lC%-1AkiG2n+
+Fn
+^i(Gat+ • • • +(-l)fc^G2n) +... + л?е2„
+'.•• + Fk-i[Al(G2k +
4- ... 4- (—l)n kCn kG2n) 4- A^Gon] 4-... 4- Fn_i>l”G2n| ,
285
Зп
— ~—г •Ге[ЛГ 1 -(-... + (—1)* 1 Л'2*_г + .. • + (—1)" lA'2n-i]-
X X I
-Л-А'г + ... + (-1)*A'2t + ... + (-1)"А2п] - ... -
-^t-ifAWU-l)1 + • • • + (-1)п'*-1С”Г*-1А-2„_1]
1
-^2п-зА2п_1 — Fo
+Al(-l)fc-1C*"1) + ... + А2п(Л? + (-l)1*?* Л?'1 + - • • +
+(-l)xC^rl + • • • + (-1)"-*С"-‘Л*)А2п] - Fn-ij4JJA'2„|.
Здесь Ck— число сочетаний, Ak — коэффициенты разложения
на простейшие дроби
= (-l)2fc”2(x7 - х)2*"2 (2ky2kClkZi~ +
+ ,..+ 2 пггпС?;:;^”-1-»),
Gik = («'m + ••. + 2«n„Cgi"1'-,-‘u-,>)
Кп = <-l)*V - *)!* («» + ... + ЪпСЦг'2"-и),
(vP7
+ 1
- х)2 + А2(~' - 1)2 ^(х' - Х)2 + A2(Z' + 1)2
А,
е = (х' — х)
1
у/(? - X)2 + А2(*/ - 1)2
1
v/(i'-i)3 + A2(5'+l)2
F - 2 In v^7~~ + + + ^
у/(£' - х)2 + А2(г' - I)2 + А(г' - 1) ’
286
Е 2*-3 —
1
2к - 3
р' - х)2 + A2(z' - l)2]24^ - р' - х)2 + A2(z' + I)2]24?2
* (х' - х)2*-3
+A(z' - I)]*"1] - У(х' - х)2 + А2(г' - I)2 - А(г' - I)]4*1} -
+А(*' + I)]4'1 - У{х> - х)2 + А2(У + I)2 - А (г1 +. I)]4'1}.
Подставив в (1) полученные значения 1\ и I22 и сократив на etvt,
получим интегральное уравнение относительно v(x):
1
J_ f 7(*)
47Г J (х' - х)
-1
г' - 1
+
vP' - х)2 + Ар' - I)2
z' + 1
v/(x'-x)2 + A2(2'+ l)2
х (70 + 72^ 2 + ... + 72n- 2n)rfi =
Koo
A
(a _ §) - i; / ^/22(i’
-1
1 00
+ ib J^">di J ' f/)e_,v^~d£ +
-1 f
1 00
+ —-==— /
4 7Г К oo J J
-1 J?
1 00
-1
l
x/(x' - x)2 + A2(z' - l)2
+
+
z' + l
i/(x' — x)2 + A2(f' + l)2
287
х(70 + 7зг “ + ... + 72„2 "п)е"
(6)
Все слагаемые правой части уравнения (б) кроме последне¬
го— непрерывные функции аргумента (х'-х), что следует из не¬
прерывности функций й(х), 1\(х, х', г') и /22(2, х', г'). Покажем,
Воспользуемся тем, что
$ 1, a v(x) в силу не-
e-iv((-x)/V
прерывности достигает на интервале [—1, 1] своего наибольшего
значения М, и оценим подынтегральное выражение последнего
слагаемого уравнения (6):
7(*)
z' - 1
\/{х' — х)2 -)- A2(z' — I)2
+
z'+l
\/{х' — х)2 + А2(z' 4- I)2
'2„)|
D
— iv ^ , _*п
е (70 + 7гг +
?_-\
- х)3 + ХЦГ - I)2
+
+
z'+l
у/W - х)* +\Ц5'+ I)3
где D = М(7о + 7з^2 + • •. + 72п^2’1), откуда следует
ОО 1
7(х)
/!
z' -1
+
У(х'-02 + Л2(5'-1)2
z+1
+
у/{х' _Оа + А2(5' + 1)2
еих
X (7о + 722<2 + • • • + 72п'
J2 п>
<т
4/(2' — х)2 + A2(z' — I)2 — A(z* — 1) |
\/(*'-*)2 + А2(г'-1)2 + А(г'-1)
+ 1п
х/(х' - х)2 + А2(г' + I)2 + А(=' + 1)
Последняя функция имеет при х' — х особенность вида 1п|х' — я]'
Таким образом, сходимость последнего слагаемого при х —* х
288
полностью определится сходимостью интеграла I:
1
Г)
J
-? /
-1
, х)2 + A2(z' - 1)2 - \{? - 1) |
v/(i' - х)2 + A2(z' - 1)2 + А (z' - 1)
+ 1п
у/(х' - х)2 + А Цг> + 1)2 - А (г' + 1)
v/(x' - х)2 + A2(z' + I)2 + A(z' + 1)
dx.
Разобьем интервал [—1, 1] на два: [—1, ж'] и [ж', 1] и запишем
соответственно два несобственных интеграла / и /:
X
=-?/
-1
у/(х; - х)2 + A2(z' - 1)* - A(z' - 1)
^/(х' - х)2 -f A2(z' - I)2 + A(z - 1)
+ 1п
s/(i' - х)2 + А2(г + I)2 - A(f' + 1)
^(х' - х)2 + A2(z' + I)2 + A(z' + 1)
d(x' — ж),
У(*' — *02 + А2(г' — I)2 — A(z' — 1)
у/(х' - х)2 + A2(z' - I)2 + A(z' - 1)
y/jx1 - if + A2(z' + lp - A(z' + 1)
+ ln-
d(x' - x),
y/(x> - x)2 + A2(z' + l)2 + A(z' + 1)
которые вычисляются одинаково интегрированием по частям:
(х'+ 1)1п
\J(x' + I)2 + A2(z' - I)2 - A(z' - 1)
+
у/{х> + 1)2 + A2(z' - 1)2 + A(z' - 1)
+ 2(г' - 1) 1п|г' - 1| - 2(г' - l)ln|vV + I)2 + А2(г' - I)2 -
- (*/■+ 1)| + (*' + j) ln \/(y + 1 )2+,A*(z' + l)2_-A(z' + l)
\/(х'+1)г + А2(5' + 1)2 + A(z' + 1)
+ 2(z' + l) In |z'+l|-2(z' + l)x
х In \у/{х' + l)2 + A2(z' + I)2 - (*' + 1)|]. (7)
Аналогично вычисляется второй интеграл. Сложив получен-
289
ные результаты, найдем выражение для ./ = /+/:
D
J =
(х' + 1) In
yV-f 1)2 + A2(f'-1)-'-A(z'-l)
V(*' + 1)2 + A2(5'-1)2 + A(z' - 1)
-2(z' - 1) In |\/(*' + l)2 + A2(z'-l)2 - (*' + 1)| -
_ 1} b y/(*' - l)2 + A2(2' - l)2 - A(z1 - 1)
v/(i' - l)2 + A2(5' - l)2 + A(z' - 1)
+2(z' - 1) In\y/(i>+ - 1)| +
y/(x> + l)2 + А2(z' + l)2 - A(? -I- 1)
+ (x7 + 1) in . ш - . - . ■ ■
\/(i' + l)2 + A2(z' + l)2 + A (z‘ + 1)
-2(г* + 1) In |\/(x' + l)2 + A2(z' + l)2 — (*' + 1)| -
_ 1} ln +
v/(x'-l)2 + A2(z'+l)2 + A( zf + 1)
+ 2(z' + 1) ln |у/(х> - l)2 + A2(z' + l)2 - (*' - 1)|], (8)-
которое остается ограниченным при всех значениях х* и zf. Сле¬
довательно, ограниченным будет и последнее слагаемое уравне¬
ния (6), но в этом случае вся правая часть уравнения (6) будет
интегрируемой по х' функцией, а само уравнение (6) становится
а
уравнением вида / jr^dx = Ф(х'), где Ф(х;) — интегрируемая
— а
функция. Как показано в работе [2, § 88], к уравнениям такого
вида можно применить формулу обращения
2 [a^l f ф(х,)
vi,) = i:y7TiJ V7r7—,dx'
— а
что позволит преобразовать уравнение (6) в уравнение типа
Фредгольма II рода относительно &(х):
7(0(7о + 72z'2 + ... + 72n z'~n) =
1 /1 - I } /1 + *' Ф(х') ,
= 7" _ » V ТТ7 У V ТТ"? ¥^1 '
(9)
290
1 1
Ф(х') = — J y(x)Jo2dx +
J7(x)dxJ
-1 X
1 OO
+ ¥z! J +VzJ j FT
-1
1 OO
— 1 X
z'~ 1
— 1 X
Zf + 1
V(*' - 02 + л2(^ - !)2 v/(^'-02-bA2(^ + l)2
xe ^ (70 + • • • + 72n^,2n)^-
(10)
Уравнение (9) может быть решено методом итерации. Схо¬
димость процесса итераций для уравнений такого вида показа¬
на в работе [3]. Критерий сходимости существенно упрощается
для конкретных п. Полученные в процессе итераций решения
содержат параметры vо, vo,..., V2п> которые можно определить
с помощью граничных условий (5) так же, как это сделано для
стационарного случая в работе [1]. Воспользуемся тем, что гра¬
ничные условия (5) должны выполняться при любых приближе¬
ниях, начиная с первого, поскольку в качестве нулевого прибли¬
жения предполагается взять i/nо = ^оо(Л тогда для любых
значений I кроме значения / = —1, требующего дополнитель¬
ного анализа, при z = ± 1 первое приближение (/, 1) должно
быть равно нулю. Вычислим ип\ для п значений / при г = 1
или z = — 1, при этом слева согласно (5) получим ноль, а спра¬
ва для каждой точки (/^, 1) — некоторую линейную комбинацию
чисел ио, V2, • •., V2n\ п точек дадут п линейных уравнений отно¬
сительно и о, 1^2, • • • 1 vm, еше одно уравнение даст само условие
(5). Полученная система п + 1 уравнений позволит определить
все параметры vq, ..., ^2п- После того как все вычислены,
плотность уп(/, z) легко вычисляется для любого z при любом
приближении.
Итак, задачу о гармонических колебаниях прямоугольного
кРыла удалось свести к решению уравнения Фредгольма II рода
при выполнении всех граничных условий. При v = 0 нестацио-
Нарная задача переходит в стационарную, а уравнение (8) — в
аНалогичное уравнение для стационарной задачи (см. уравне-
ние(18)в[1]).
291
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Полжхов Н. Шестерична 3. Н. Стационарное обтекание прямоуголь¬
ного крыла с циркуляцией, переменной по размаху //Вестн. Ленингр
ун-та. 1980. N* 13. С. 85-92. [46]
2. Мусхелчшвчли Н. И. Сингулярные интегральные уравнения. М.; Л.
1946. 448 с.
3. Полжхов Н. Н., Шестерична 3. Н. О существовании решения инте¬
грального уравнения несущей поверхности//Вестн. Ленингр. ун-та.
1975. № 19. С. 102-107. [38*]
III4. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ КРЫЛА
С ПОСТОЯННОЙ ЦИРКУЛЯЦИЕЙ
ПО РАЗМАХУ [63]*
в несжимаемой идеальной жидкости рассматривается неста¬
ционарное движение прямоугольной гибкой пластинки с по1
стоянной циркуляцией по размаху. Предполагается, что кры¬
ло имеет достаточно большое относительное удлинение Ао =
1/а (4 ^ Ао ^ 8) и применима гипотеза плоских сечений [1].
Вводятся две системы координат: XYZ — абсолютная, непо¬
движная система, syz — относительная, неизменно связанная с
крылом натуральная система. Ввиду постоянства циркуляции
все величины рассматриваются в среднем сечении крыла при
z = 0.
Крыло движется с постоянной скоростью до по горизонтали
и совершает конечные гармонические колебания со скоростью
vm cosi/t в вертикальном направлении. Задняя кромка движется
по заданной траектории, которая определяется уравнением
w vm а •
Уо = sin а —, Ао = uot,
щ а а
где (vm/uo)(a/cr) — конечная величина, <т = va/uo — число Стру-
халя, V — частота колебаний.
Для обеспечения безотрывного обтекания крыла на параме¬
тры движения накладываются следующие ограничения:
о ^ 4, vm/uo ^ 0,3.
Во время движения сечение крыла меняет свою форму таким
образом, что задняя кромка всегда направлена по касательной
к траектории. Отметим, что экспериментальные исследования
Движения рыб [2, 3] и наблюдения за полетом птиц подтвержда¬
ет, что наблюдаемые в природе изменения формы сечения кры-
ЛД при движении происходят именно таким образом.
*Соавт. JI. Ю. Уразаева. Предлагаемая статья отражает переход к но-
Е°Му классу задач, связанных с обтеканием крыльев переменной геоме¬
трии. Наряду с работай Н.Н. Поляхова ’’Обтекание профиля, колеблю¬
щегося гармонически с конечными амплитудами”, публикуемой ниже, она
А*ет возможность исследовать задачи значительно более высокого класса
Сл°Жности, нежели широко известные задачи о плоских и слабоизогнутых
п°верхностях. — Прим. составителей.
293
Согласно предложенной модели сечение крыла изменяется по
следующему закону:
Хпл = Х0 + (а - s) cos до, Упл = У0 + (а - s) sin g0,
где s — натуральный параметр дуги, qo — угол наклона каса¬
тельной к сечению крыла, причем
Величина нормальной составляющей скорости точек сечения
будет равна
Vn„n = VeT sin ((ft - go) + qoa( 1 + cos0),
Будем рассматривать пластинку как вихревую несущую по¬
верхность. Движение крыла сопровождается сходом свободных
поперечных и продольных вихрей следа. В отличие от случая
колебаний с бесконечно малыми амплитудами вихри следа не
сносятся на прямую, параллельную оси ОХ} учитывается кри¬
волинейная форма следа. Принимается, что продольные вихри
покидают пластинку при z = ±/ и тянутся от передней кром¬
ки на некотором расстоянии от крыла, как и поперечные вихри,
сходящие с задней кромки. Затем вихревой след за крылом сво¬
рачивается, образуя шахматную дорожку Кармана [5]. Исходя
из экспериментальных данных [4], примем расстояние, на кото¬
ром след за крылом будет непрерывным, равным 7га/<т.
Дополнительная скорость, возникающая за счет влияния до¬
рожки, равна [5] ь! = 0Д06> где Г0 = J у3dXl —интенсив¬
ность вихря дорожки, / = Л/0,2806 — расстояние между вихрями
дорожки, которое находится из условия устойчивости дорожки,
Л = 2avm/(uo<r) — высота дорожки, у$ = F интенсивность
поперечных вихрей следа.
Крыло непроницаемо, имеет место уравнение
Vt ~ <Pm Sgn(cOSI/t)
«О =
где
2va/a
ir a/a
Kipn(s, t) = Vcn(s, t) + Vsn(s, t) - v:„(s, t)
294
где Vnpn — нормальная составляющая индуктивной скорости,
рызываемой присоединенными поперечными вихрями, V9n, —
нормальные составляющие индуктивных скоростей, вызывае¬
мых соответственно поперечными и продольными вихрями сле¬
да.
Так как квадрат величины максимального прогиба рассма¬
триваемого сечения пренебрежимо мал, то нормальная соста¬
вляющая индуктивной скорости, вызываемой присоединенными
вихрями профиля, имеет такой же вид, как и для прямолинейной
пластинки.
Используя гипотезу плоских сечений и обращая известным
образом уравнение непроницаемости [1], отбросив бесконечно
малые величины, получим следующее интегродифференциаль-
ное уравнение относительно величины циркуляции:
здесь Гк — квазистационарная циркуляция, Г' — дополнитель¬
ная циркуляция, возникающая за счет конечности размаха кры¬
ла и нестационарности движения.
При определении Гк, Г' учтены конечность амплитуды ко¬
лебаний крыла, изменение формы сечения крыла при движе¬
нии, конечность размаха крыла. В соответствии с наблюдаемой
физической картиной вихревой след предполагается конечным,
сворачивающимся в шахматную дорожку Кармана на некото¬
ром расстоянии от крыла. Разрешая эти уравнения, определим
величины сил, связанных с влиянием вихревого следа, Ха, Ys:
Г = 2 a J(Ven + Vsn - K„)(l - cos в' - (4/Ag)cos2 tf)d#,
О
Г=ГК + Г', Гк = 2а VCn(l — cos#' — (4/Aq) cos 20/)d0/,
о
Г = Г' 4- Г'
* 4 ПООЛ. ВИХ D • 4 П
прод. вихр
поп.вихр >
Х,=-рГ'(Усп-и'8тп),
irfa
У, = рГ'(к' cos <ft + Уст) - арио 7,/(cos <р) 1 dX[,
о
X[=X0-X[, X[ = X[/a,
295
D = ро cos(<pt - q) + у cos 2(у>, - flr) + />о л/Р,
Р = 1 + Y + ро COS ((fit - ?),
р0 = {Хх2 + ?12у/\ Y{ = Y0-Y',
COS (£> = — COS <r(JVo — Xj),
Wo
, ♦ *1
cos = — cos vt, q = arctg
Up Aj
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Поляхов H. Н. Теория нестационарных движений несущей поверхно¬
сти. Л., 1960. 84 с. [28*]
2. Козлов Л. Ф. Теоретическая биогидродинамика. Киев, 1983.
3. Кокша&схий Н. Б. Очерк биологической аэро- и гидродинамики. М.,
1974.
4. Головкин В. А. //Уч. зап. ЦАГИ. 1972. Т. 11. С. 1-11.
5. Голубее В. В. Лекции по теории крыла. М.; Л., 1949.
III.5. ОБТЕКАНИЕ ПРОФИЛЯ,
КОЛЕБЛЮЩЕГОСЯ ГАРМОНИЧЕСКИ
С КОНЕЧНЫМИ АМПЛИТУДАМИ [63ц]*
Предлагаемая работа подготовлена к печати на основе ма¬
териалов, найденных в архиве покойного профессора Н.Н. По¬
ляхова. Задуманная им, но по какой-то причине не доведенная
до реализации решения, эта его работа даже в незавершенном
виде представляет большой теоретический интерес как содер¬
жащая совершенно новый подход к решению нелинейной задачи
о нестационарном движении слабо искривленного профиля при
отсутствии срыва потока. Датировка положенных в основу ста¬
тьи материалов относит их ориентировочно к 1984-85 г. Учи¬
тывая преемственность тематики и хронологическое распреде¬
ление материалов научного наследия Н.Н. Поляхова [1], эту не¬
завершенную статью можно с достаточной степенью достовер¬
ности считать продолжением его монографии ”Теория нестаци¬
онарных движений несущей поверхности” [2].
Рассматриваемый частный случай гармонических колебаний
пластинки с конечными амплитудами решается путем учета
влияния нелинейности следа с помощью введения коэффици¬
ента cos/? для вихревой плотности следа, где /? — угол между
радиус-вектором, проведенным из точки вихревого следа в точ¬
ку профиля, и осью Ох. Ось Ох направлена от середины О
хорды профиля в сторону, противоположную скорости посту¬
пательного движения профиля, ось Оу перпендикулярна к ней.
Введенный коэффициент позволяет свести нелинейную задачу к
интегральному уравнению, вид которого очень близок уравне¬
нию, соответствующему прямолинейному следу, что позволяет
Использовать ранее проверенные алгоритмы решения.
Кроме того, построенные уравнения дают возможность вычи¬
слять составляющую вихревой интенсивности, вызванную сле¬
дом, на профиле (причем отдельно определять влияние линей¬
ной части следа) и учитывать составляющую, вызванную не¬
линейностью следа. Этот прием весьма удобен в практических
Расчетах, так как позволяет строить более оптимальные вычи¬
слительные алгоритмы.
Предлагаемый метод не имеет аналогов и, по-видимому, ни-
КеМ не использовался. Он позволяет четко оценивать качество
*Соавт. О. Ф. Мельникова, 3. Н. Шестернина.
297
получаемых результатов, обеспечивает единственность реше¬
ния и достаточно быструю сходимость итеративного процес¬
са, поскольку ядро, входящее в основное интегральное уравне¬
ние, аналогично хорошо исследованному ядру соответствующе¬
го уравнения при линейном следе [3]. В этом большое преиму¬
щество предлагаемого метода перед методом дискретных вих¬
рей.
Полученные уравнения Н.Н. Поляхов, вероятно, предпола¬
гал решать методом итераций. Хотя в работе нет детальных
указаний, как реализовать этот метод, тем не менее просма¬
тривается рекомендация принимать в качестве нулевого на¬
чального приближения к искомому решению величину Гк —
квазистационарную циркуляцию, значение которой должно
уточняться за счет вычисления итеративной поправки. Этот
прием использовался в других работах Н. Н. Поляхова и обыч¬
но обеспечивал достаточно быструю сходимость [4, 5].
Известно, что задача о плоском неустановившемся движении
профиля в идеальной несжимаемой жидкости более или менее
удовлетворительно решается для случая колебаний со столь
малой амплитудой, что вихри следа, тянущиеся за профилем,
могут быть снесены на кривую, которая при конформном ото¬
бражении внешности профиля на внешность круга переходит в
действительную полуось. В случае пластинки такой след явля¬
ется продолжением пластинки.
Если не делать предположения о малости амплитуды коле¬
баний, то вихревой след (без учета собственного движения его
вихрей вследствие взаимной индукции) должен быть близок к
синусоиде, которая является траекторией задней кромки про¬
филя, поскольку при нестационарном движении профиля с его
задней кромки сходят вихри, которые, по предложению, в непо¬
движной системе отсчета остаются неподвижными. Так как в
относительном движении жидкость обтекает контур, то для то¬
го чтобы сошедший вихрь имел абсолютную скорость, равную
нулю, следует предположить, что он сходит с переносной скоро¬
стью, равной скорости относительного движения, направленной
по линии тока. Если мы имеем профили, у которых задняя кром¬
ка есть точка заострения, т. е. профили типа Н. Е. Жуковского,
то вихрь, сходящий с задней кромки, будет сходить по касатель¬
ной к этой кромке, или, что то же самое, по направлению линии
тока.
В дальнейшем при построении приближенного следа буДе1И
298
предполагать, что элемент следа, примыкающий к задней кром-
совпадает с элементом ’’квазистационарной” линии тока, ко¬
торый всегда можно построить, зная мгновенное значение ско¬
рости движения профиля vq. В случае пластинки, совершающей
колебания конечной амплитуды, элемент следа, примыкающий
к задней кромке, будет являться продолжением пластинки. Обо¬
значим длину этого участка через е.
Если пластинка вдоль своей длины движется равномерно со
скоростью ис> а в перпендикулярном направлении совершает ко¬
лебания с частотой I/ и амплитудой А по закону у = Asinvt =
As\n(ux/uc) со скоростью vc = Ai/cos vi, то след будет иметь
синусоидальную форму.
Условие непроницаемости пластинки с длиной хорды профи¬
ля 2/ будет иметь вид
где 7 — плотность присоединенных вихрей, vcn(x', t) — проекция
скорости в точке N* на нормаль к пластинке, —проекция на
нормаль в точке Nf индуктивной скорости г', вызванной вихря¬
ми следа. Эта скорость будет выражаться интегралом
где 7,— плотность вихрей следа, г = >/(х' — х5)2 + у;. Кроме
того,
здесь d5— угол между касательной к элементу ds и осью Ох, а
Координата х3 соответствует точкам следа.
Таким образом,
1 f y(x,zt)dx
27Г J х* — х
/
= Vcn(x', t) - v'n(z', t)
(1)
CO
(2)
j (-0
у, = A sm(i/x,/uc), y’s = (u/uc)Acos(ux,/uc),
cos(3 = (x' - x,)/r,
ds = dx,\/\ + (dys/dxt)2 = dx,\J 1 + tg2 d, = dxsyj 1 + j/'2, (2')
OO
i. f 7* cos0\/1 + fa
(3)
r
299
причем
dr(t) dt _ 1 dr{t)
dt ds vc dt
1 dnt)
1 dr(t)
vc\/l + (vc/«c)2 9t
(3')
Введем момент времени V) предшествующий ” настоящему” мо¬
менту t и равный
Рассматривая конечные амплитуды колебания, будем все же
ограничиваться такими значениями vcmax> при которых угол
атаки
меньше своего критического значения акр, т. е. имеет место
безотрывное обтекание. Так как уравнение (1) линейно, то най¬
денное из него 7 будет иметь вид 7 = ук + 7', где ук соответству¬
ет квазистационарному случаю, когда след отсутствует, 7' —
добавочная вихревая плотность, соответствующая наличию по¬
тока, создаваемого следом. Величина 7к(я', t) может считаться
известной.
На основании изложенного для определения 7' получим сле¬
дующее интегральное уравнение:
где скорость v'n выражается формулой (2). Очевидно, что в по-
токе со скоростями v'n должно иметь место обтекание рассма¬
триваемого контура, и, следовательно, мы должны потребовать
выполнение постулата С. А. Чаплыгина, т. е. условия конечно¬
сти касательных скоростей на заднем конце. Обращая интеграл
из (4) в классе функций, удовлетворяющих указанному постула-
ту, получим
(3"
ttmax ^ ^в^шах — ^сшах/^с
шах
(5)
Подставляя вместо v'n его выражение из (2), находим
300
-I
X' — X
oo
hj
7,(s) cos (ids
2tt J y(x* - X,)2 + yj
»(-!)
dx',
причем согласно (3')
1
дг(?)
(6)
(в')
as uc^i + (vc/ucy ev ’
где согласно (3") t' = f — (я, — /)/uc — момент времени, предше¬
ствующий ’’настоящему” моменту t, а ^
Очевидно, что если Г можно представить в виде произведе¬
ния двух функций fi(t) и /г(х,), т. е.
Г(0 = r[t - (х, - /)/««] = МШ*.), (7)
то из (6') следует
1 аг cost?, аг
7а — ~
«е>/1 + tg21?,Л' «с а*,'
ч&у
1 q Уз dys t
tgtis = — = Т~ = 2/ (**)» cosi/, =
х 5 йх 9
-1/2
(7')
(7")
Переставив в (6) порядок интегрирования по х и по sy получим
У(х) =
; (3dx
+/
__ 1 jl + х у* ^ jf у/ — х' cos /3d.
1Г2У I — х J ^5 J V f + я' (х' — х)^/(х' - х,)2 -f у?
з(-/) L-J
Подставляя сюда вместо cos/? его выражение из (2'), имеем
оо
ds.
= / 7'U)*
5(~/)
■f/
Г // — х' dx'
J у l + х' (х1 - х)(х' - х,)[1 + (у,/(х, - х'))2]
ds.
301
Полная добавочная циркуляция Г', удовлетворяющая посту,
лату С. А. Чаплыгина, представится теперь в виде
+ J оо
Г' = j y'(x)dx = J 7,(s)
-l *(-0
] —
dx'
*»)[i + {y*Kx*-x')Y]
L*(-o
Лелая общую замену переменных
х =
+/ .
f jl + x dx
ds.
= — I cos в, I ±x = 1(1 =f cos 0) = 2/sin = tg2 -
2 t — x I
и вычисляя интеграл
+/ тг
/ // -h х dx ^ f в sin Ode _
— xx' — x J ^2 cos 0 — cos
0
находим циркуляцию
Г +' /
f [EZ
J V / + *' (r' -
.-i
dx'
)[1 + (Vs/(x' ~ £s))2]
(8)
r' = i /т.(.)
Если величина (j/s/(i; — i,))2 мала по сравнению с едини¬
цей, то внутренний интеграл в (8) вычисляется точно. Дей¬
ствительно, сделав замену переменного г' = —/ cos в, получаем
dx1 = IsinOdO, l—x1 = /(l+cosfl') — 2/cos2 у, /+х' = /(1—cos#') =
2/sin2 у, после чего вычисляем внутренний интеграл отдельно:
У ГГ-ГГ dx' Г в' IsinO'de'
Jsl + x'x' — х, J ® 2 I cos 9' + x,
-l о
j (1+cos e')de' _ _ j(l + cos0')d9' _
J COS0' + X,/l J cos 6' -t- X,
[ X, + COS0'-X, + 1 , f
-- 7Г7-- de - ~ж +
J COS в' + Xs J
dd'
cos 9' + x,
= (x, - l)Ji - JT,
302
где обозначение J\ очевидно, ах, = . Положим z — tg тогда
cos#' = (1 *“ ~2)/(1 + z2), (19' = 2с/с/(1 4- г2). Теперь вычисляем Ji:
dz
(1 + *2)[*. + (1 -*»)/(!+ *3)]
, / * _ 2 f !*£
J (x, + 1) + z2(x, - 1) X, + 1J 1 + (x, - l)/(xs + l)z2
0 0
d [n/(*. -1)/(*. +1)*] _ ж
2 f
о 1 + [\/(*« “ !)/.(*• + 1)*]
Возвращаемся к интегралу J:
J — {х, — l)7l - 7Г = ж [\/(х, + l)/(x, - 1) - l],
следовательно,
оо
r°~l Jъ^ [v/(** + !)/(*« - !)- 1
dx.
(9)
При величине (у,/(х' — х,))2, соизмеримой с единицей, удобно
записать выражение для Г в следующем виде с учетом (7"):
ОО
Г' = Г0 + ДГ'о = Г'0 +
1
.1 + (Vs/(x' - X,))7 costf,
-1
dr,.(10)
Интеграл из (10) можно вычислять приближенно, имея в ви-
ДУ, что подынтегральная функция, стоящая в фигурных скобках,
асимптотически стремится к нулю с возрастанием х,. Величина
ДГ(, есть та добавочная циркуляция, которую следует наложить
на пластинку для того, чтобы учесть влияние непрямо линейно¬
сти следа.
Займемся определением7, в (10). Если скорость vC) перпенди¬
кулярная пластинке, изменяется по закону vc = v\ cos vt-\-v2 sin vty
To квазистационарная циркуляция будет выражаться формулой
Гк = —2tt/(i;i cos vt 4- vo sin vt).
303
В соответствии с этими истинную циркуляцию Г будем искать
в виде
Г = Г\ cos vt + Г2 sin vt = Re(r*eII/t),
где Ti и Г2— неизвестные постоянные, для которых Гх — /Го -
Гф.
В момент времени t\ предшествующий моменту t, величина
Г будет выражаться формулой
Г = Гх cost/t* + Г2sin= RefFV1'* ).
Так как пластинка движется вдоль своей длины с постоянной
скоростью иСу то в силу (3") V = t — (х5 — 1)/ис и, следовательно,
в соответствии с (7;) получим
1_дГ_
us dt'
V
Uc
"|-х . Л х*-1\ т- Л х*~1Х
1 1 Sin V I t 1 — 12 cos V [t
V uc ) \ UC ) m
= ^-Re = Re
— €iut
tlc
= Re —Г*е 7,
uc
y3 =
(H)
Подставляя (11) в (10) и пользуясь выражением (7/у) для cos??,,
определяем циркуляцию Г':
г = ri+{ir‘"’ / ’’ [/ £prir«'*'
v 1 L-/
где
P ( „ , _ v/l + {dy,/dx,¥
Fx{x.,y.)- l + {ys/ix,_Xs)r !•
Что касается Tq, to это слагаемое соответствует прямоли¬
нейному следу и согласно (9) имеет вид
Г'п = —Re
(13)
Окончательно с помощью (12) и (13) для циркуляции Г' получим
Г' = <rRe [iTV"'^ + -Ы].
304
Здесь cr — ~— число Струхаля,
ОО
т-'Ь'
1
оо
J2 = j e-i<i'-^F2(x,)dx„
1
с/=г 1 / /1 ” y>(x,))di,
Ыг‘> = *J VTTF '
-1
УКА ЗА ТЕ ЛЬ ЛИТЕРА ТУРЫ
1. Зегэюда С. А., Мельникова О. Ф., Поляхов И. И. (мл.) и др. На¬
учное наследие профессора Николая Николаевича Поляхова (1906-
1987 г.)//Вестн. С.-Петербург, ун-та. Сер. 1. 1992. Вып. 4. С. 3-19.
[92]
2. Поляхов Н. Н. Теория нестационарных движений несущей поверхно¬
сти. Л., 1960. 84 с. [28*]
3. Поляхов Н. Н., Шестернина 3. Н. О существовании решения инте¬
грального уравнения несущей поверхности//Вестн. Ленингр. ун-та.
1975. № 19. С. 102-107. [38*]
4. Поляхов Н. Н., Мельникова О. Ф. О решении интегрального уравнения
обтекания несущей поверхности//Вестн. Ленингр. ун-та. 1978. Jfe 1.
С. 123-128. [43*]
5. Поляхов Н. НМельникова О. Ф. О построении начального при¬
ближения для решения интегрального уравнения несущей поверхно¬
сти//Вестн. Ленингр. ун-та. 1979. № 1. С. 104-110. [44*]
Раздел IV
МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ
НЕСУЩЕЙ ПОВЕРХНОСТИ
IV.1. ОБ ИНТЕГРАЛЬНОМ УРАВНЕНИИ ТЕОРИИ
НЕСУЩИХ ПОВЕРХНОСТЕЙ [37]
В настоящей работе, являющейся продолжением и обобще¬
нием работы [1], устанавливается новая форма интегрального
уравнения несущей поверхности и рассматривается способ его
приближенного решения.
1. Составление основного уравнения
Пусть дана несущая поверхность, представляющая собой со¬
вокупность прямоугольных полосок, лежащих в плоскости у — О
и покрытых непрерывно распределенной системой П-образных
вихрей с плотностью 7. Длина каждой полоски вдоль оси х рав¬
на 2а, ширина равна dz} размах вдоль оси z есть 2L.
Индуктивная скорость, вызываемая одним П-образным вих¬
рем, который расположен так, как показано на рисунке, в точке
306
]\Г;(х;, 0, z*), лежащей в середине полоски с номером fc, равна [1]
7(х, z)dxd
4тг
7(х, z)dxdz
47r(z' — z)2
(х' — х)а
Z Г х' — х 1
~ 1 Л3 + (г' - г)2
(i + ^). я! = (*' - «)г + <»' - *)г
Сделаем замену переменных, положив х = ха + а(г) + £а(г), х' =
x'n + a' + Z'a', тогда
Х~а, ■- = р(*) + g(z)(l + £) + - С
*'п -* , а
Р = - . 7=1--,
а' а7
где хп есть координата передней кромки в сечении z, а штри¬
хами отмечены величины, взятые в сечении г7. Очевидно, что
р характеризует относительный сдвиг, a q — относительное су¬
жение полосок. Вихри всех полосок, за исключением полоски с
номером к, внутри которой лежит точка Лг/, дадут скорость
(z'-c +1
/+
-1 гЧ£
где все z отнесены к величине L и
7tf,*)(l + /)dz
/ =
(1)
[(Р + 7(1 + О + С - О2 + A'2(z' - г)2]1/2 ’
7 = 7 а/а7, А7 = L/a'.
Вихри полоски с номером А: вызовут скорость
lkd£> Хе
(2)
—dw2 =
2т(£'-0 \/(С-02 + А'2£2
+
+
1 +
Ук<Ц
2тгА'е 'и у/(? - ^)2 + А'2е2
= 2^I) + 2^7(1 + /)’
307
(3)
Воспользуемся приближенным равенством
V-C 1
е +J+J (z-z'y-
которое будет тем более точным, чем меньше е. Тогда получим
j... _ IkKtdt , 7ii<% „ , ,
~dW2 - wF=l)+ T\'Vi -7*(1 + fn
, ^ ('Г, f\ 7*(1+ /')<**
4тгА' у]| +J J {z'-zY ’
t* =Tit(0-
>/1 - z'2
В результате, выделяя особенность и интегрируя, будем иметь
” = Ь??/^Л'К'<4»
где
~1 -1
2A4lrKi|v^_
z'-s +1'
(г-е +1\
/*/
-1 z'+e /
(*' - ^)2
z'+£ '
z' —£ 1
hi
*7к \ J J J (*' - г)2
■1 z'+e.
есть регулярная функция, так как I — К€ обращается в ноль как
(С-О2 при£->£'•
Интегралы, стоящие в первых скобках, могут быть найдены
численно при заданных £, z*. Интегралы, стоящие во вторых
скобках, могут быть найдены лишь после того, как будут най¬
дены в первом приближении значения у во всех сечениях.
308
На основании (4) уравнение непроницаемости в точке Nf при¬
мет вид интегрального уравнения
-•'> - 4<5)
-1 -1
где F — заданная функция. Уравнение такого вида получалось
и раньше, но теперь его ядро К более простое, что важно для по¬
лучения приближенного решения (см. [1]). Интегральное урав¬
нение (5) допускает бесчисленное множество решений. Из этого
множества необходимо выделить решение, которое соответству¬
ет плавному течению около задней кромки, что приводит к тре¬
бованию обращения в ноль плотности 7 * на этой кромке. Обра¬
щение в ноль должно иметь строго определенный порядок, так
как главное значение интеграла, входящего в левую часть урав¬
нения (5), существует только в определенных классах функций,
в которых интеграл допускает обращение. Формулы обращения
имеют вид (см. [2, § 88])
, ,п _ /Т^т 2 У / 1-К' ф<Ц‘
а) 7*( ) yi+lnJ \Л_£, с_г
-1 1
б) ук(1) = ч/l - Г- - [ у -— ;
в) 7t(0
+ 1
?-1
-1
где через Ф обозначена правая часть (5).
Обращая сингулярный интеграл уравнения (5) при условии
выполнения постулата С. А. Чаплыгина (7(4-1) = 0) по формуле
а), получаем
+ 1
(6)
-1
/ +1
w(,) =- SwbW ш / ■ '• *'«•
где Yoo соответствует бесконечному удлинению и
, У / 1+с т,?, ~~'ис
309
Это уравнение можно пытаться решать методом итераций, при¬
няв, что в выражении для К в первом приближении 7 = 7*.
Тогда (6) превратится в уравнение Фредгольма второго рода с
регулярным ядром- Для получения решения методом итераций
удобно представить его в виде
7к(0 = 7к (О + Ат fc = 7* (0 у J _ I у J + £
где Дт*(±1) = 0.
После подстановки уравнение (6) примет вид
А/ (I\ — 7oofc ~ Ayook (
где
+1
Лт”‘ = VTT7 /(7‘ -
-1 1
При решении уравнения (7) методом итераций в нулевом при¬
ближении следует взять 7* равным 7* (Д700* = 0). Это позволит
найти в первом приближении 7* во всех сечениях z*k, т. е. найти
7(£, z), затем найти разности 7(£, z) — 7*(5, z) и Д7* и перейти
к вычислению второго приближения. Расчет становится совер¬
шенно элементарным, если при вычислении J\ и Д7 воспользо¬
ваться гипотезой Вайзингера и положить £' — £ равным единице,
а £' равным —0,5. Из формулы (7) видно, что при г9 —► ±1 ве¬
личина 7(/, zf) обращается в нуль как (1 — г 2)0,5, а производная
—в бесконечность как (1 —.г 2)-0,5. Можно убедиться, что эти
краевые условия являются прямым следствием вихревого мето¬
да. Действительно, вихревая пелена, соответствующая кривой
£ = const, пересекаясь в бесконечности с перпендикулярной ей
плоскостью Треффца, дает прямолинейный отрезок (—1, 1), по¬
крытый вихревым слоем с плотностью дуjdz. Индуктивная ско¬
рость в точках этого отрезка равна
2тг J дг z1 — z
-1
310
Так как циркуляция около рассматриваемого отрезка вслед¬
ствие симметрии равна нулю, то интеграл следует обращать
по формуле в), которая в данном случае будет иметь вид
ду 2 1 у* л/1 — z2w(z')dzt
dz ж x/l - z2 J z'-z
-1
что соответствует сформулированным выше краевым условиям.
Из изложенного видно, что краевые условия для у как на перед¬
ней кромке, так и на задней, и на боковых являются следстви¬
ем введения вихревой системы, для которой характерно появле¬
ние сингулярных интегралов, допускающих строго определен¬
ные условия на краях области интегрирования.
2. Замена интегрального уравнения
системой алгебраических уравнений
Эта операция должна быть осуществлена, разумеется, с со¬
блюдением краевых условий, указанных выше. Наличие сингу¬
лярного интеграла в уравнении (5) требует искать решение в
виде
7*=*oJy^| + i№. (8)
где rjk(±l) должно обращаться в ноль как \/1 — £2 при f —*• ±1.
Подставляя (8) в (5), получаем, удаляя индекс к:
(9)
где Кг = А({, z9)/[2\${\ - *#2)0,5]-
Лля вычисления последних интегралов в левой и правой ча¬
стях уравнения (9) разобьем промежуток интегрирования на
N частичных промежутков (—l,£i), (£i, £2)1 • • •, (t/v-ь !)• В ка¬
ждом частичном промежутке будем считать известной функцию
z;), приняв в первом приближении у & у*. В первом и
Последнем промежутках аппроксимируем т) по параболическому
закону:
_ / 1-KI - / i-е
311
а в остальных —по линейному:
*-€т-1
“Пт — ^]т — 1 (IJm ^)т — 1 )
£т-1
где г) — значения rf в точках деления. При указанной аппрокси¬
мации второй интеграл левой части уравнения (9) примет вид
1 V 1с 1 ЛГ“1 1C
л m-lc m=l
"1 чтя — 1
причем Cfm) представляемые интегралами, весьма просто вы¬
числяются аналитически для любых включая интервал, со¬
держащий особенность. Точно так же интеграл правой части
приводится к виду
/+1 N-1 N„x
! m = lc ^ m=l
~1 U-i
Интегралы, входящие в С^, можно вычислить по формулам ме¬
ханических квадратур, так как они не имеют особенностей. В
результате уравнение (9) приведется к следующей системе ал¬
гебраических уравнений:
N— 1
А.СЖ', *')+ £ ^СЖ, г') = Ftf, z'). (10)
/* = 1
Неизвестными здесь являются Ло, ^лт-i- Число их
равно числу промежутков и потому, если взять внутри каждого
точку с координатой получится система, позволяющая най¬
ти все неизвестные. Плотность у определяется по формуле (8).
Найденное приближенное решение будет удовлетворять требу¬
емым краевым условиям вихревого метода.
3. О методе дискретных вихрей
Существует два понимания этого метода. Одно принадлежит
Фолкнеру и состоит в том, что несущая поверхность разбивает¬
ся на ряд полос, параллельных направлению движения. Каждая
полоса покрывается конечным числом П-образных вихрей с цир¬
куляциями Гтп, где т — номер полосы, п — номер точки в этой
312
полосе. В каждом сечении величины Гтп связываются с коэф¬
фициентами разложения плотности ут в ряд
£ = - cos в, Ах = Ахо + Axizm + AX2Z„ + ..X = 0, 1,...
Связь между Гтп и AXfi устанавливается путем приравнива¬
ния в каждом сечении суммарных циркуляций, происходящих
от дискретного и непрерывного распределений. То же самое
делается с индуктивными скоростями в заданных точках. Этим
путем можно выразить через Ах^ все Гтп, а следовательно, и
полную индуктивную скорость. Интегральное уравнение зада¬
чи Фолкнер явно не пишет, а для определения AXfl использует
систему уравнений, выражающую условие непроницаемости в
различных точках взятых сечений. В рассматриваемом методе
удовлетворены краевые условия, отвечающие вихревому мето¬
ду-
Другой подход к методу дискретных вихрей состоит в том,
что разложение (11) не вводится, а циркуляции П-образных вих¬
рей (обычных прямоугольных или перекошенных) оставляются
в условиях непроницаемости, так что получается система алге¬
браических уравнений не относительно Ахкак у Фолкнера, а
относительно Г:. Эта система имеет вид
где i есть номер вихря, j — номер точки, причем нумерация идет
подряд. Кроме того, отрезки несущих вихрей расположены на
0,25Л, а условие непроницаемости выполняется в точках 0,75Л,
где Л — длина частичных промежутков, на которые разбиты се¬
чения z = const.
На примере плоского стационарного потока, который будет
описываться уравнением (5) при нулевом значении интеграла
правой части (Л = оо), можно убедиться, что система (12) не
Дает правильного решения задачи. Действительно, эта система,
Получаемая из интегрального уравнения, будет иметь вид
где
т
(12)
»=i
313
Во-первых, замена ядра по формуле (13) в промежутке, где оно
становится неограниченным (£* —координаты дискретных вих¬
рей), совершенно недопустима, а во-вторых, если и принять для
исходной системы структуру (12). то о соответствии между (12)
и (13) теория интегральных уравнений говорит следующее (см.
[3, с. 12]): «даже если определитель системы (12) не равен ну¬
лю и она имеет единственное решение, то система (13) будет
иметь бесконечно много решений, поскольку однозначно опреде¬
лены только средние значения функции у на интервалах ( — 1, £г),
(£ь Ы и т.д.».
Известно, что для того чтобы выбрать из бесконечного мно¬
жества решений какое-то одно, отвечающее физическим услови¬
ям, необходимо выдвинуть краевые условия, соответствующие
вихревому методу. Их выполнение должно быть гарантирова¬
но, но этого не дает система (12), в которой никак не отражены
условия на краях. Следует помнить, что аппроксимирующая
функция должна удовлетворять тем же краевым условиям, что
и аппроксимируемая. Считается, что обращение в ноль вихре¬
вой плотности на задней кромке в пределе будет автоматически
выполняться, если последние контрольные точки в каждом сече¬
нии взять между задней кромкой и последним дискретным вих¬
рем. Доказательства этого утверждения нет. При этом следует
помнить, что важно не просто обращение в ноль, а обращение в
ноль строго определенного порядка. Выбор последней точки не
соответствует структуре особенного интеграла и потому не мо¬
жет дать требуемого порядка обращения в ноль. Действитель¬
но, этот интеграл существует только в смысле главного зна¬
чения, которое получается для точки, лежащей между двумя
участками вихревого слоя, чему в дискретной схеме соответ¬
ствует точка, лежащая между двумя вихрями. Этому условию
не удовлетворяет «последняя» точка. Таким образом, систе¬
ма (12) не может заменить исходное интегральное уравнение с
соответствующими ему краевыми условиями. Поэтому утвер¬
ждение, что метод дискретных вихрей в теории несущей поверх¬
ности «приводит во всех случаях к замене двух- или трехмер¬
ных интегродифференциальных уравнений системами алгебра¬
ических» (см. [4, с. 222]), неверно. Такая замена для уравнений
первого рода без гарантированного выполнения строго опреде¬
ленных краевых условий незаконна. Решение зависит от харак¬
тера расположения вихрей и расчетных точек, который назна¬
чается совершенно произвольно.
314
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Поляхов Я. Я., Пастухов А. И. Вихревая теория несущей поверхно¬
сти//Вестн. Ленингр. ун-та. 1968. № 19. С. 121-131. [34*]
2. Мусхелишвили Я. И. Сингулярные интегральные уравнения. М.; Л.,
1946. 448 с.
3. Трчкоми Ф. Интегральные уравнения. М., 1960. 200 с.
4. Белоцерковсхий С. М., Схрипач Б. Я., Табачнихов В. Я. Крыло в неста¬
ционарном потоке газа. М., 1971. 767 с.
IV.2. О СУЩЕСТВОВАНИИ РЕШЕНИЯ
ИНТЕГРАЛЬНОГО УРАВНЕНИЯ
НЕСУЩЕЙ ПОВЕРХНОСТИ [38]*
В работе [1] для тонкого слабоизогнутого крыла, проекция
поверхности которого на плоскость xz такова, что может быть
покрыта системой П-образных вихрей, получено интегральное
сингулярное уравнение, определяющее плотность 7(f, z) систе¬
мы этих вихрей. При выводе уравнения был использован изло¬
женный в работе [2, § 88] метод обращения сингулярных интегра¬
лов при условии, что искомая функция в особой точке принад¬
лежит строго определенному классу функций, в данном случае
она должна обращаться в ноль порядка у/1 — £ в задней кром¬
ке и в бесконечность вида 1 /\Л~+Т в передней кромке. Здесь
£ = £(я) зависит от формы крыла и подобрано так, что £ = — 1
соответствует передней кромке крыла, а £ = +1 — задней.
Рассматриваемое в работе [1] и ниже уравнение непригодно
для крыльев, поверхность которых не может быть аппроксими¬
рована ступенчатой фигурой. Обозначения и система коорди¬
нат здесь приняты те же, что ив [1].
В настоящей работе сделан анализ ядра интегрального урав¬
нения несущей поверхности, полученного в [1]:
1
7‘ = Т” - 2.AV1 -*'W"
7* = 7оо -
2ttAV1 - г'2
1
7(С г')^, (1)
-1
где 7оо соответствует бесконечному удлинению;
(1 + л-
2А(1 - А'е)\Л - г'2 1
7Г
/
L-1
*Соавт. 3. Н. Шестернина.
316
+
1
/
z'+e
Kc =
z —
I
(7-7*)(!+/)
(z' - z)2
dz -f
-l
(7-7*)(l+/)
(*' - -i2 '
A'e
<*C,
/ =
[(e-02 + A'2£2]l/2’
p(z)+g(z)(l + 0 + (C~0
(N*) + «0)0 + 0 + С - <£]2 + А'2(г' - z)2}1/2 ’
/' = /U^r. 7* =7
/ \ хп / 4 | ®
^ )= a' ’ »(*-)=‘-7-
Рассмотрим ядро V;(£i /, 2/) интегрального уравнения (1), по¬
лагая крыло прямоугольным, что, не нарушая общности, упро¬
стит его, поскольку в этом случае и! = а, я' = хп, р = 0, q = О,
А' = А, 7 = 7,
с-*
КС - О2 + А2(г' - г)2]’/2 ’ f' [(С - O' + A2e2]i/2 ’
C~f
7 = У к
1 — 22
П^Т2
После этого ядро ^*(С /> 21) может быть записано как
1
Ж=
1
7Г
-1
Z* — £
1-с с-/
*(С - О
f у/г^и-п^, Г
J W - .->* J‘+ J W -,)» J-
i'+C
уЬ-7
7Г7 *
(2' - z)2
g£z -f-
L-i
317
►/
z'+t
dz
df'.
(2)
Анализ ядра удобно начать с его третьего и четвертого слага¬
емых, содержащихся в фигурных скобках.
Рассмотрим третье слагаемое, переписав его несколько ина¬
че:
1.
п
z —
/
уг^(/-л
L-i
(с-о
I
/
>/Г^(/-Л
(*' - ■г)2
dz
f VI -z7Rj t [VI-
J (2>-z)*dZ+ J (*'-
.-1 гЧе
dz
где
Я =
[(*' - О2 + A2*2]1/2 [(*' - О2 + A2(r' - z)2]l/2 *
При z' — z —► £ величина R стремится к нулю, оставаясь положи¬
тельной, так как |z' — z\ > £, и, как показывает непосредственный
подсчет, не превышает ^ для всей области крыла. Поскольку
рассматриваемый интеграл имеет переменную особую точку z',
его удобнее рассматривать отдельно для г', лежащих внутри
интервала [-1, 1], и для г* = ±1.
Вначале оценим данный интеграл для значений zf внутри
[— 1, 1], пользуясь положительностью подынтегральной функции
как в первом, так и во втором слагаемых. Для оценки поведения
интеграла заменим подынтегральные выражения более
простыми функциями хе(г^-гУ» превышающими данные на всей
области крыла, но сохраняющими те же особые точки. После
этого сходимость всего третьего слагаемого определится схо-
димостью в смысле главных значений интеграла
1
' z'-с
[
7Г АбГ
J (
.-1
е
-и
7гХе {
Z —С 1
Г dz Г dz
J (г' - ;)2 + J (ТЗ
1 + г' + 1
'+г
1
-г-
(3)
318
что не превышает по модулю если принять (£' — £) эквива¬
лентным е2 при £ 0 и 0.
При z' = — 1 несобственный интеграл (3) можно записать как
*lzl f dz =*'-*( 1 » М
J (—1 - г)2 7гАс \ 2 £/
-1+«
откуда видно, что при тех же допущениях относительно е и (£' —
£) он меньше Аналогично оценивается интеграл и при z' =
1. Итак, третье слагаемое для всех г' на интервале [—1, 1] не
превышает
Для анализа четвертого слагаемого
у/\ — z,<l
(*' - *)2
+
I
/
? (y-rty/if^d + f)^
(*' - zY
(4)
наложим дополнительное условие на 7(£, z): будем считать, что
у((, z) имеет вид A(£)B(z)y/l — z^, где .Д(£) и B(z) имеют ограни¬
ченные на (-1, 1) производные и не обращаются в ноль. Теперь
несобственный интеграл (4) примет следующий вид:
1
Z —
/
L-i
[Л(С)Я(г') - A{QB(z)}V1-^(1 + /)
(.z'-zf
dz -f-
, I IMCiBiz1) - Л(()В(,)\УГ- 7‘(1 + !) л
+ J <*' - --)3
г'+е
(5)
Разложим 4(f')B(z') — Л(£)Б(г) в ряд Тейлора по степеням
(С - О и (*' - г):
Л(С)5(г')-Л(05(с) =
+
2!
-(С-£Г +
319
+4^^(^0з + ет£!(.,_г)з+
+лчет(?,.?)(г,:г)1+...
В силу ограниченности всех производных от Л(£) и B(z) мож¬
но записать
ит*') - л(ов(х) | ^ a{ob\z')^A+
+ м
1!
|с - с, ic - с2 , i^-*!2, \?-w-z\ ]
1!
2!
2!
2!
1C - С3 , IC-CV-*!
+ !^1Г~+П ”3! - +
где М — верхняя граница всех производных от Л(£) и B(z).
Заменим выписанным рядом стоящую под интегралом (5) раз¬
ность Л(£')#(г') — A(£)B(z), кроме того, заменим сумму 1 + / ее
верхней границей, равной двум. Получившиеся в результате
замены интегралы можно переписать, разбив их па три груп¬
пы: первая группа—интегралы, содержащие Л^')#'^')^' — z)
в числителе, вторая группа—интегралы, содержащие |£' — £|, и
третья группа — интегралы, не содержащие |£' — £|, но в числи¬
теле которых имеется |z' — z|n, где п > 1.
Итак, получим
г —
I
-1
'[Л(С)В(*') - Л(0Д(г)}/Г=^(1 4- /)
(*' - -~)2
dz +
+
[Л(С)В(-') - Л(0В(--)]\А^(1 + Л
г'+е
(z'-zY-
dz £
2Л(С)В'(С)
+ 2 М
I / &
. — 1 г'+£
'Г к'-(\,‘Г , ,
} <7^)5* + J (7Г1)=2!‘,- + ' +
.-1 -1
320
+ 2 М
+ 7 (737)?dz+ J (z'_^2irf‘ + ---
г'+ff z'+f
г zy-f 1 1
/с/г / z' — z , f dz f z — z' .
J 2! + J —* + ••■+ J 2! + у -3TJj+ -
. — 1 —1 z'+e z'4*£
Для первой группы интегралов можно получить аналитиче¬
ское выражение
ч/ГГ?-
-1 z'-K
dz =
Уо~»?
+ z' arctg у
Уо+i)
здесь у = у У° ^ соответствует z' — с и имеет вид
h-2J\-(z'-£)3-(z'-e)3
Уо — ?7 = у у—(z'^Fp ’ а 2/о + ^? соответствует z'+£ и име¬
ет вид т/о -f г) = -■Чс|2~~ *Z’ Вычисляя несобственные
интегралы в смысле главных значений при с —* 0, получаем
+1
/&+/&■=
'+£
VTZ’T? (z' - 1 - ч/Г-Т2)(г' + 1 + ч/Г-z75)
г In
\(z> _ 1 + v/1 - z'2)(z' + 1 - ч/1 - г'2)
4- г'я\
321
Для последнего выражения при всех значениях z1 верхней гра¬
ницей будет служить 7г.
Группа слагаемых, содержащая (£'— £), после интегрирования
образует ряд
2М
1-Z'
+
1 + Z1
(1 - Z')2!
е (l + z')2!
+ о(К'-*13)1,
который обращается в ноль порядка с при (£# — £) —*■ 0 для всех
z1 на интервале [—1, 1] в силу эквивалентности |£' — и е2.
Последняя третья группа слагаемых после интегрирования
по z дает сумму двух рядов
2 М
Z* — Z
z -€
(z> - zf
г' — с
(*' - z)n
zJ-e
2!
3!2
-i
^ ' (п + 1)!п
-1
+ 2 М
2!
+
2п-
г'+е
л*'-
3!2
■)"
(п + 1)!п
+
'+£
Лля обоих рядов, стоящих в скобках, мажорирующим рядом
является ряд 1 + 52~=i(l/3)n, сумма которого равна 3/2, и, сле¬
довательно, верхняя граница обоих рядов не превышает 6М, а
все четвертое слагаемое ядра уравнения будет ограничено по
модулю величиной
1
—шах
7Г
(шт)<2’м+Ш)-
Второе слагаемое ядра 3 имеет особенность в
точке £' =• £ и не превышает 2А/7Г при разностях |£; — £| больших
единицы и меньших или равных двум. Для исследования этого
выражения при малых (£' — £) разложим в ряд Тейлора по сте¬
пеням (£' — £) функцию и убедимся в ее эквивалентности
функции —гт~,—h—тттз 1 что позволяет получить оценку всего
322
второго слагаемого при |£' — £| < 1:
т.е. при любом значении разности (£' — £) все второе слагае¬
мое не превышает 2А/7Г. Здесь при оценке, как и прежде, была
использована эквивалентность (£' — £) и е2.
Первое слагаемое ядра 1 + /;, как это видно из самой функции
/', не может превысить двух.
Теперь, просуммировав ограничения всех слагаемых ядра,
можно получить оценку всего ядра
№(£. I, г')| 5$ 7Г
„ 2А 2л- .
2 + 1- — + -шах
ТТ А
^(шт) (2т"+6")
Ограниченность ядра ведет к ограниченности интеграла
1
f т(£> I* на всей области крыла, а требуемые по-
-1
рядки нуля при ( = 1 и бесконечности при f = — 1 обеспечи¬
ваются множителем, стоящим перед интегралом. Для сходимо¬
сти процесса итераций согласно работе [3] необходимо, чтобы
1
2^1 / ^ ~)\d£ ^ т < т- е- выполнение условия
-1
1
А
2А 27г 1 ( 1 \
2+v + т + жтах (щщ)(2'"+ш)
^ 771 < 1.
Поскольку в систему ограничений для т/»(£, /, г') входят па¬
раметры 7(f, z), то для каждого приближения ограниченность
ядра следует проверять отдельно и заново проверять величину
т.
Итак, рассматриваемое интегральное уравнение при выпол¬
нении указанных условий допускает решение методом итера¬
ций, причем каждое приближение является функцией требуемо¬
го класса.
УКАЗА ТЕЛЬ ЛИТЕРА ТУРЫ
1. Поляхов Н. Н. Об интегральном уравнении теории несущих поверхно¬
стей//Вестн. Ленингр. ун-та. 1973. № 7. С. 115-121. [37*]
2. Мусхелишвили Н. И. Сингулярные интегральные уравнения. М.; Л.,
1946. 448 с.
3. Соболев С. П. Уравнения математической физики. М., 1954. 444 с.
323
IV.3. О РЕШЕНИИ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ
ОБТЕКАНИЯ НЕСУЩЕЙ ПОВЕРХНОСТИ [43]*
1. Теоретические предпосылки задачи
Рассматривается задача обтекания крыла конечного размаха
невязким несжимаемым потоком. Крыло в плане представляется
гладкой поверхностью малой кривизны, что позволяет рассма¬
тривать лишь плоскую поверхность, лежащую в плоскости xz.
Поверхность крыла разбивается на систему N прямоуголь¬
ных полосок шириной dz. Предполагается, что каждая полос¬
ка покрыта системой П-образных вихрей с плотностью 7* (к =
1, 2,..., N). Плоскость, в которой лежат эти вихри, совпадает
с плоскостью полоски.
Вихревая плотность 7* (i = 1, 2,..., N) определяется из усло¬
вия непротекания, которое, как показано в [1], имеет вид следу¬
ющего интегрального уравнения:
= П(' -ШтЬ?J^ <4
-1 -1
где F(Z', zf) = Vasina — заданная функция, a — угол атаки.
Уравнение (1) — сингулярное интегральное уравнение относи¬
тельно вихревой плотности 7*(£)- Ядро Л'(£» £', z') согласно [1]
представляет собой регулярную функцию параметров £, г' в
[—1, +1] и искомой функции 7*(£)-
Рассмотренные ниже численные методы решения уравнения
(1) реализованы при допущении, что ядро К в первом прибли¬
жении не зависит от 7.
Искомое решение должно удовлетворять краевым условиям:
обращению в нуль вихревой плотности 7* на задней кромке и
на торцах крыла, а также стремлению 7* к бесконечности на
передней кромке крыла.
В работе рассмотрены три приближенных метода решения
уравнения (1).
2. Замена интегрального уравнения
системой алгебраических уравнений
Интегральное уравнение (1) заменяется системой алгебраи¬
ческих уравнений с соблюдением сформулированных выше кра-
*Соавт. О. Ф. Мельникова. Печатается с сокращениями.
324
евых условий. В силу этого решение уравнения (1) ищется в
виде
(2)
где *lk(0\t=±i Должно обращаться в ноль как y/l — £2.
Искомую функцию т)к(0 аппроксимируем по параболическо¬
му закону вблизи концов £ = ±1 и кусочно-линейной функцией
внутри интервала ( — 1, -f 1). Кроме того, введем допущение, что
ядро Л'(£, ?') может быть заменено кусочно-линейной функ¬
цией аргументов £, {' € [—1, +1].
В результате подстановки (2) в (1) с учетом принятой аппрок¬
симации интегральное уравнение (1) приведется к следующей
системе алгебраических уравнений:
JV-1
АоСо(С, z'k) + J2 VnCmit'n, z'k) = F(&, 4)
(3)
m = 1
относительно неизвестных Aq, г)x, 7/2,. fy/v-i- Коэффициенты
Cm(m = 0, 1, ... N — 1) вычисляются по формулам
c, = i
1 + iv^
где
Ci =
2л-
— 1 — у/п — 0,5 In
Cm = C'm + С" ,
1—v/n - 0,5
CL =
1
27Г
(n — m + 0,5) In
(11 — m — 1,5) In
n — m — 0,5
+ (n — 2,5) In
n — m — 1,5
n—2,5
71—1,5
7i — m + 0, 5
С' — —
LN~1 ~ 277
1 + \/jV - 71 4- 0,5 In
— (n — N — 0,5) In
77 — m — 0,5
, m = 2,3, 2;
1 - ^N- ti + 0,5
1 + v/W - n + 0,5
71 — TV + 0,5
n-JV + 1,5
325
С[' = —-- (bK{i) + 22К{1) + 8/\(йЛ ,
60AV1 - г 2 ' '
^К(т-\) + 4Л-(т) + Л-(т+1)^ ^
(5Я(Л_2) + 22А'<*_1) + 8А'(ЛГ>) .
;(т + 1)
Здесь А = — значение ядра К(£, zf) в фиксиро¬
ванной точке £т = £/—€т; я— номер координаты = Л(п — 0,5).
Вихревая плотность 7*(£) определяется по формуле (2) в резуль¬
тате решения системы (3). Следует отметить, что найденное
решение удовлетворяет требуемым краевым условиям.
Изложенный метод имеет ряд недостатков, которые снижают
эффективность его применения для данной задачи:
1) Анализ точности полученного решения оказывается весьма
затруднительным.
2) При решении систем уравнений с разными порядками тре¬
буется заново для каждой системы проводить вычисления коэф¬
фициентов, что ввиду сложности их выражений является трудо¬
емкой процедурой, в то время как значения ряда коэффициентов
и их вес в результатах решения оказываются несущественными.
3) С увеличением числа дроблений происходит накопление
числовой погрешности при решении системы алгебраических
уравнений. В результате погрешность может превзойти то
уточнение решения, которое может быть получено вследствие
увеличения порядка системы.
При численной реализации метода итераций в качестве ну¬
левого приближения к искомой функции 7*(£) берется решение
уравнения
3. Итеративный метод решения
интегрального уравнения несущей поверхности
-1
получаемого в результате замены ядра:
к* (г1) = же, z')\
326
При этом значение циркуляции Г(г') вычисляется по формуле
Гоо
Г(С') =
1 + тЬ
т к-
где Гоо —значение циркуляции для крыла бесконечного разма¬
ха.
Решение уравнения (4) согласно [2] запишется в виде
7fc(«
о • Л ^ /1-^
= 2 Sin а 1 ) ч /
V ,K* + 2\'y/T=7*JVl+i
Итеративный процесс решения уравнения (1) строится следую¬
щим образом. Рассматривается уравнение
rj = W. *•> - * 2'ж(5)
-1 -1
которое при заданных значениях т[0*(£) представляет собой
уравнение плоского потока. После введения тригонометриче¬
ских координат £ = — cos0, = — cos#' решение уравнения (5)
ищется в виде
в °°
7*(0) = Л0 ctg - + ^ sin п0, (6)
М — 1
где коэффициенты Aq, Ап вычисляются по формулам
Aq = 2F(#', zf) -
2ttAV1 -г"2
о \0
1 III (0)
70\ z')smOdOU#y (7)
Ап = у- - --у - / ( / у[°\в)К(9у О*, г')$\х\в(1в I cos nOdO.
7tA'v1 — z 2 J \J I
0 \o /
Очередное приближение к искомой функции 7*^(0) вычисля¬
ется по (6) с учетом коэффициентов (7), где вместо значений 7^0)
Подставляются 7**~1^— значения искомой функции из предыду-
Щей итерации.
327
Как показывают расчеты, итеративный процесс носит двух¬
сторонний характер, т. е. два соседних приближения распола¬
гаются с разных сторон от искомого решения. Для ускорения
сходимости итеративного процесса в качестве исходного оче¬
редного приближения удобно брать среднеарифметическое ме¬
жду двумя соседними приближениями.
Численные расчеты показали, что в результате трех-четырех
итераций получаются значения 7*(£) с удовлетворительной сте¬
пенью совпадения.
Решение интегрального уравнения (1) методом итераций не
требует введения специальной процедуры анализа точности, по¬
скольку он осуществляется на каждой итерации и является кри¬
терием окончания итеративного процесса.
Трудоемкость вычислительных работ метода итераций суще¬
ственно ниже, чем в методе системы алгебраических уравнений.
4. Решение уравнения несущей поверхности
на основе его регуляризации
Согласно [2] сингулярное уравнение (1) преобразуется к экви¬
валентному интегральному уравнению
»(,)=?»<«*«■ '•*'*• т
-1
где7сх> —вихревая плотность, которая соответствует крылу бес¬
конечного удлинения.
При найденных значениях у (т. е. при условии, что ядро есть
функция только координат и не зависит от 7) уравнение (8) пред¬
ставляет собой уравнение Фредгольма II рода, решение которо¬
го может быть найдено любым известным методом.
В данной работе было получено решение уравнения (8) ме¬
тодом последовательных приближений по методике, данной в
[1]. Расчеты первого приближения показали, что значения 7*(£)
имеют несущественные отклонения от значений 7*, найденных
описанными в п. 2 и 3 способами.
Численная реализация этого метода требует увеличения объ¬
ема вычислительной работы (по сравнению с методом итераций,
изложенным в п. 3), вызванного необходимостью предваритель¬
ного анализа и выбора метода вычисления двойного интеграла,
содержащего особенность в подынтегральной функции.
328
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Поляхов Н. Н. Об интегральном уравнении теории несущих поверхно¬
стей //Вестн. Ленингр. ун-та. 1973. № 7. С. 115-121. [37*]
2. Му схелишв ил и Н. И. Сингулярные интегральные уравнения. М., 1962.
582 с.
IV.4. О ПОСТРОЕНИИ
НАЧАЛЬНОГО ПРИБЛИЖЕНИЯ
ДЛЯ РЕШЕНИЯ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ
НЕСУЩЕЙ ПОВЕРХНОСТИ [44]*
Уравнение обтекания несущих поверхностей произвольных
форм в плане представляет собой сингулярное интегральное
уравнение вида [1]
-1
относительно вихревой плотности 7* (О для каждого сечения
z§ = zk ^ 1* 2, N; N — число сечений). Здесь z') —
заданная функция;
+1
= J (-2)
-1
зависимость Л'(£, г'), которую в дальнейшем будем называть
ядром интегрального уравнения (1), дается формулой
2Л'(1-А,)/П^
М«,«,*)-! + /
+1>
1 I ( + j \ (f -nVT^dz
* \ J J (*' - -)2
-1 г+е
г'-с +1
hi
*7к \ J J I (:' - г)2
■1 г'+с
при следующих введенных обозначениях:
p(z)+q(z){l + £)+£'-€
(3)
/ =
Г = А. = А'Е
J ПТ» \ 9 , Л '9-9 ’ С
yiHiw’ \/(е-о2 + л'2е2
*Соавт. О. Ф. Мельникова. Печатается с сокращениями.
330
/т-S'
1' = то
Ф) = 1»'М<И-1*1)4.*.. ф> =
(функции p(z) и q(z) определяют форму крыла, характеризуя
величину стреловидности и сужения соответственно);
А'(*') = Ло
1 - |г'|(1 -aLy
Л0 = L/ao — корневое удлинение; dj, = аь/ац — относительное
сужение. Геометрические параметры (2ао — корневая хорда,
2ai — концевая хорда, L — полуразмах крыла и \п — угол перед¬
ней стреловидности) считаются заданными.
Для нахождения решения уравнения (1) может быть исполь¬
зован предложенный в [2, 3] метод итераций. Данная работа по¬
священа вопросу построения начального приближения, от каче¬
ства которого зависит эффективность итеративного процесса.
При этом построение начального приближения искомой функ¬
ции должно обеспечивать выполнение требуемых краевых усло¬
вий.
Как показано в [2], интеграл (2) существует (по крайней мере,
в смысле главного значения) для всех значений £', zf £ ( — 1, 1).
Следовательно, можно записать
= = (4)
f 7k(t№ К
-1
+ 1
где Г*,* = а' / 7jb(£)df — циркуляция, определенная для сечения
-1
zf = z'k, половина хорды которого есть а'. Ясно, что z')
представляет собой в силу существования интеграла (2) конеч¬
ную величину для каждого значения £', z* £ (—1, 1).
Обозначим через £*(£', z*) то значение £, при котором
Эта запись правомочна, поскольку, как показано в [2], ядро
/\(£, £', zf) вблизи точки £ = £' имеет порядок ^j^asign(£' — £)
и, следовательно, может принимать значения из промежутка
—оо < К < +оо при изменении £ в пределах (— 1, +1).
331
С учетом (4) уравнение (1) для слабоизогнутой пластины за¬
пишется так:
1 7т*КК _ v • ,,,,
2т J ~ ( - ) —
~1
<5)
где Voo — скорость набегающего потока; № — угол наклона каса¬
тельной к оси £; а — угол атаки.
Обращая интеграл, входящий в уравнение (5), в классе функ¬
ций, стремящихся к бесконечности при £ —► — 1 и к нулю при
£ —> +1, получим [4]
Т*(0 = 7оо(0-
+1
/1 А-f К(?+ (Г ~’\ Г
(6)
IWa' ДЦ У А + Г
2*\'y/T=lFVi + iJ V1^' *'-*
-1 т
где
7оо(0 = 2^00 sin ^
— вихревая плотность, соответствующая крылу бесконечного
размаха; / — текущая координата на оси £.
Обозначая интеграл, входящий в (6), через
t'-i
-1
можно записать
*й=^м-гйетга,||'Л (9)
Умножая обе части равенства (9) на a'dl и интегрируя, будем
иметь
г‘(г')-г“--2тТ7Г1т
-1
где
Гсоц = 2Tra'Voo Sin а (11)
332
— циркуляция, соответствующая крылу бесконечного размаха
для сечения z' = zfk.
Обозначая интеграл, входящий в (10), через
+i I
*»(*') = J (12)
-1
и применяя к нему обобщенную теорему о среднем, имеем
К0(*') = »Я(Г,г')-
Тогда из (10) получаем следующее выражение для циркуляции:
г‘<г'>у • Sr.jp - <13>
+ 2AVl - г'2
С другой стороны, если принять во внимание, что в случае
отсутствия сужения ядро /\'(£, z') содержит £ и £' только в
комбинации £' — то, воспользовавшись гипотезой Вайзингера
[5] (т. е. положив в (1) £ = 1), получим возможность записать
формулу для циркуляции в виде
<М>
2AV1 - -'2
Сравнивая (13) и (14), получаем
Д(/‘,/) = */*(£'-£, г')|{,_<=1 • (15)
Итак, для вычисления циркуляции Гjt(z') исходное интеграль¬
ное уравнение (1) может быть преобразовано к форме (13). При
этом в рамках допустимости применения гипотезы Вайзингера
в качестве представления /?(/*, z') могут быть взяты значения
ядра К при £' — £ = 1 (в случае крыла без сужения). Заме¬
тим, что последнее ограничение, требующее отсутствия суже¬
ния, относится только к знаменателю формулы (14). Действи¬
тельно, как видно из (11), выражение для Г со* содержит хорду
крыла a'(z'), благодаря чему осуществляется учет стреловидно¬
сти и сужения при вычислении циркуляции. Влияние сужения
приближенно может быть учтено и в знаменателе формулы (14),
если положить, согласно гипотезе Вайзингера, что центр давле¬
ния находится в точке £ = —0,5, чему соответствует = +0,5.
333
Таким образом, допущение об отсутствии сужения относится
лишь к способу приближенного вычисления значений ядра /v,
и полученную формулу (14) можно рассматривать как некото¬
рое приближение для вычисления циркуляции, значения кото¬
рой могут быть в дальнейшем уточнены.
Воспользуемся полученным результатом (9) для построения
начального приближения вихревой плотности т*(£) при реали¬
зации итеративного процесса решения уравнения (1).
Из (9), учитывая (7), (11), (13) и (15), получаем
7*(0 — Too* ~
— Too*
и окончательно
1
./
1 -
2AV1 - *'2
2А
Vl - z'2 + 1гК({1 z')|f,
где
xi(/, *') = !-
7*(0 = 7oofc*i(/, -')>
Д(/, -')
(16)
(17)
2AV1 - г'2 + кК(£> - г')
Формулы (16), (17) позволяют при найденных значениях
#(/, г;) достаточно легко вычислить значения вихревой плотно¬
сти 7*(/). Покажем, что (16) обеспечивает выполнение краевых
условий задачи. Поскольку (см. (7)) т*(—1) = оо и 7*(+1) = 0,
то остается показать, что 7*|z/_-f;1 = 0. Как видно из (17), это
условие будет выполнено, если удастся установить, что
да *')иТ1 = я(Г*')ит1.
Для доказательства рассмотрим уравнение
7*(/) = 7оо*(/)-
(18)
которое получается в результате обращения (см. [4]) исходно¬
го интегрального уравнения (1). Если решение уравнения (19)
334
искать в виде
7к(0 = 7 kit) + ATfc(0 = 7к(0
+ АЪ(0, (20)
где 7к(0 — начальное приближение, Ду*(£)— итерационная по¬
правка, то (19) примет вид
Too*
7к(0 =
1 +
Щ, *')
2AV1 - г'2
(21)
где
/(', О = ;
(22)
Из (21) непосредственно следует, что 7fc(0l*'=^i = 0 при всех
/ / —1, так как, вообще говоря, при z' — 1 интеграл 1(1, z') ф 0.
Зависимость (21), представленная в виде
7к(1) = 7оо*(0*з(Л -'), (23)
где
Ы1, =
1
1 +
(24)
2AV1 - *'2
является иной формой записи исходного уравнения (1) и, следо¬
вательно, в рамках использования гипотезы Вайзингера будет
тождественна формуле (16), т. е. при £ = 1 будет иметь место
равенство xj(/, z') = хг(/, z'). В результате получаем
1 -
R(l, *')
2А
■y/F=7* + irK(t'-t, z')\
k'-e=i
2А'^/ГГ72 + щ z')\
(25)
откуда при z' = ^1 вытекает соотношение (18), необходимое для
обеспечения в (16) краевого условия 7fc(/)lZ'=^i =
335
Таким образом, показано, что (16), (17) могут быть использо¬
ваны для вычисления вихревой плотности, при этом вследствие
(18) требуемые условия выполняются.
Для построения неизвестной зависимости Я(/, zf) можно вос¬
пользоваться в силу равенства (25) методом последователь¬
ных приближений, т. е. формулой (20). Тогда, положив в (22)
Ат*(0 — 0) получим
/(/, ^ = г
В результате из (25) будет следовать, что в первом приближе¬
нии можно взять
= (26)
Итак, использование гипотезы Вайзингера позволяет сравни¬
тельно просто выбрать первое приближение для решения исход¬
ного интегрального уравнения (1), записанное в форме (16). При
этом гарантируется выполнение требуемых краевых условий.
Численные значения 7* (О могут быть найдены по формуле
(21) методом последовательных приближений, где в качестве
начального приближения 7л-(О берется значение вихревой плот¬
ности, которое получается из (21) с учетом (7) и (26), т. е.
- (С\ _ 2 К* sin а /7-Т
7*(0 Y1+*'
2А'ч/Г^7*
Значения вихревой плотности, вычисленные по (27), могут
быть уточнены по (20) с итерационной поправкой Д7л(£), кото¬
рая учитывается в /(/, г').
Однако численная реализация итеративной формулы (21) тре¬
бует значительного объема вычислительной работы, вызванной
необходимостью предварительного анализа и выбора метода
вычисления двойного интеграла (22), содержащего особенности
в подынтегральной функции.
Поэтому для дальнейшего уточнения решения (27) был ис¬
пользован итеративный процесс, предложенный в [6]. Приме¬
нение этого метода для вычисления вихревой плотности в слу¬
чае крыла прямоугольной формы показало, что использование
в качестве начального приближения формулы (27) обеспечивает
быструю практическую сходимость итеративного процесса.
336
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Поляхов Н. И. Об интегральном уравнении теории несущих поверхно¬
стей//Вестн. Ленингр. ун-та. 1973, № 7. С. 115-121. [37*]
2. Мельникова О. Ф. О приближенных методах решения интегрального
уравнения несущей поверхности с учетом стреловидности // Специаль¬
ные вопросы аэрогазодинамики летательных аппаратов: Межвуз сб.
Л., 1976. С. 74-82.
3. Поляхов Я. Н., Шестпернина 3. Н. О существовании решения инте¬
грального уравнения несущей поверхности//Вестн. Ленингр. ун-та.
1975. № 19. С. 102-107. [38*]
4. Мусхелишвили Н. Н. Сингулярные интегральные уравнения. М., 1962.
582 с.
5. Weissinger J. Uber die Auftriebsverteilung von Pfeilfliigeln// Zentralplatt fur
wissenschaftliches Berichtswissen der Luftfahrtforschung des Generalluftzeug-
meisters: Forschungsbericht. Berlin; Adlershof, 1942. N 1553. S. 544-561.
6. Поляхов Я. Я., Мельникова О. Ф. О решении интегрального уравнения
несущей поверхности//Вестн. Ленингр. ун-та. 1978. 1. С. 123-128.
[43*]
IV.5. К ВОПРОСУ О СХОДИМОСТИ
МЕТОДА ДИСКРЕТНЫХ ВИХРЕЙ [45]*
В последние годы появились работы, в которых широко ис¬
пользуется для расчетов аэродинамических характеристик ча¬
стей самолета в дозвуковом потоке метод дискретных вихрей с
жестко обусловленным расположением точек размещения этих
вихрей и точек удовлетворения условию непроницаемости. Наи¬
более полно этот подход изложен в работах [1-3].
В настоящей работе излагается историческое развитие мето¬
да дискретных вихрей и дается анализ попыток доказать равно¬
мерную сходимость решений, полученных этим методом, к име¬
ющимся теоретическим решениям.
Впервые общеизвестная схема решения задачи о крыле в ста¬
ционарном потоке, состоящая в замене крыла системой дискрет¬
ных вихрей и удовлетворении условию непроницаемости в ко¬
нечном числе точек поверхности крыла, была предложена в ра¬
боте [4] для решения задачи о прямоугольном крыле. Крыло
было разбито по хорде на п частей, и к каждой части как к са¬
мостоятельному крылу была применена теория несущей линии:
в каждой части вихревая несущая линия с циркуляцией Г,-(у)
расположена на 1/4 местного интервала, а точка выполнения
граничных условий — на 3/4 интервала. Циркуляция на концах
крыла Г ,(±6/2) предполагалась равной нулю (6—размах кры¬
ла, у = 0 соответствует середине крыла). Вызванная вихревой
системой скорость в точке А(х*, у*) равна
Г,(у) предполагалась или эллиптически распределенной, тогда
число расчетных точек равно числу вихрей, или записанной в
*Соавт. 3. Н. Шестернина.
—1 О
X
где
6
У — 2 cos<P>
. Ь
У = 2 cos v7 -
338
виде ряда
Г*(у) = Г* sin <р( 1 + aj1)siny> +
-f a^sin3<£> + Ь a^sin(2r — 1)у>),
тогда число расчетных точек равно т — пт и неизвестными
г* (!) (2) (г) о
являются Г», а] , а- а} \ В этих случаях удается изба¬
виться от сингулярности при ip —* <р*, но она остается при
х —* х*. При решении сделано допущение, по признанию авто¬
ра ничем не обоснованное, что сингулярность интегралов при
х х* не влияет на решение.
Таким образом, в работе [4] указано на качественное искаже¬
ние картины при данной схеме из-за невозможности полностью
учесть сингулярность уравнения и выполнить условия Жуков¬
ского— Чаплыгина. Поэтому там же предложен второй при¬
ближенный метод, основанный на непрерывном распределении
по крылу вихрей плотности 7, причем 7 ищут в виде ряда спе¬
циального вида, указанного Бирнбаумом:
ж, ч) = J~^ + awi-c- + a3<:Vi-<;2 +
+ >ЦСа\Л-<С2 +
где £=£(1 + С)» У = f 77> который позволил избавиться от син¬
гулярности в интегродифференциальном уравнении крыла.
Лальнейшее развитие метод дискретных вихрей получил в
работе [5], где он был применен для стреловидного крыла. По¬
добно предыдущему крыло заменено системой вихрей с цирку¬
ляцией Г,•(?/), которую ищут в виде ряда ^7 = + М +
С,- г,2 + ...)•
Более интересной вихревой моделью стреловидного крыла
является модель, предложенная в работе [6], где крыло разделе¬
но по размаху на к частей и каждая часть заменена системой из
п П-образных вихрей, расположенных равномерно с интервалом
(1 /n)t(y), где t(y) — местная хорда. Вихри интенсивностью Гцс
расположены на расстоянии 1/4 от передней кромки своего ин¬
тервала, а точки расчета — на расстоянии 3/4. Интенсивность
339
Г,* определяется в виде ряда
4^— = n/1"1?2 {ct8 f(«o + bov + c0,г + ...) +
+ sin ip(ai + biT) + ciT/2 +
Таким образом, к середине 40-х годов была хорошо разра¬
ботана методика расчета крыла с помощью дискретно распре¬
деленных вихрей и непосредственного удовлетворения усло¬
виям непроницаемости, но не было дано обоснование суще¬
ствования решения, удовлетворяющего условиям Чаплыгина —
Жуковского, и не доказана сходимость процесса при возраста¬
нии числа вихрей п.
В появившихся позже работах [1-3, 7, 8] этот метод был ши¬
роко использован без анализа и устранения тех слабых мест
данной теории, на которые указывал еще автор [4].
Первая попытка доказать сходимость решения, полученного
методом дискретных вихрей, к теоретическому была сделана
для профиля, рассматриваемого в работе [9]. В ней для тонко¬
го профиля в стационарном потоке методом дискретных вихрей
было получено решение, выражающее вихревую интенсивность
через число вихрей N и номер вихря п:
7п тг(2ЛГ-2п+ 1)!(2п — 2)!
Va “ 22N~2[(N — п)!(п — I)!]2*
Далее без ссылки на источник автором использована форму¬
ла N1 (2тг)i/2j\riV+1/2e“;v, которая существенно отличается от
приведенной в работе [10]:
N! = r(N+l) = (N+l)fr+l/2e~i)f-1(2x)»e^^T, О<0< 1, (1)
но даже в том случае, если использовать формулу автора, то
вместо выражения
.JV-1 Ч 1/2 Г / /3\"-Vl/21
l+(2iV)-1 f 1 С»» (4) )
»Л-Сп-(|)
Сп-Ш
AM
Тп_ _ 2 /1 - Сп - ’щ \ г/‘ Г
Va е V Сп - 577 У I
1
2*0-<»-&)
2N—2N(„ —3/4
3/2
1 +
2JV(1-C„-4W)
340
где п = N£n + 3/4, £n = хп/с, с — длина хорды. Последнее выра¬
жение при N —► оо не сходится к 2^/(1 — С)/С* соответствующему
точному значению Уп/Va, так как
3/2
2ЛГ-2ЛГ<„-3/4
L1 2(JV - п)
3/2 г J -j 2(N—n)
и при сколь угодно большом N принимает в зависимости от
п любые, даже бесконечно большие значения (при n = N) и,
следовательно, ни в коем случае не стремится к е.
Если использовать для N1 формулу (1), то получим
но, что это выражение близко к е~1 при больших значениях п, но
не является таковым при начальных п. даже при больших зна¬
чениях N. Таким образом, увеличение числа интервалов при¬
ближает к теоретическому решению лишь первый множитель
чек, близких к передней кромке (при малых п), и дают близкую
к теоретической картину обтекания задней кромки (при боль¬
ших п). Указанная закономерность хорошо прослеживается и в
таблице сравнения теоретических значений у с вычисленными
по методу дискретных вихрей уп, приведенной в работе [9], хотя
асимптотическая формула для N1 и взята неверно.
Итак, анализ работы [9] показывает, 4fa полученное мето¬
дом дискретных вихрей значение уп не может быть приведено к
теоретическому значению у = 2у/(1 — £)/£ Для любых ( из ин¬
тервала [0, 1] путем увеличения числа дискретных вихрей.
Иное доказательство сходимости этого метода предложено в
I з 1
Где к = — 2(2Л/-2Л/С„-1/2) + ЛГ(„ +1/2 “ N(„'+3/4'
, то очевид-
341
работе [11], где рассмотрено уравнение
ъ
(2)
X - Хо
а
и для него сделаны следующие утверждения:
Первое. Решение уравнения (2) методом дискретных вих¬
рей единственно и обладает требуемыми свойствами, посколь¬
ку ими обладает решение, полученное методом регуляризации,
изложенным в [12].
Второе. Решение, полученное методом дискретных вихрей
при возрастании числа вихрей, стремится к точному решению,
данному в [12]:
Рассмотрим каждое из этих утверждений отдельно.
Первое. Решение (3) получено для уравнения (2) при опре¬
деленных дополнительных требованиях, предъявляемых к по¬
ведению функции вблизи концов, что отражено в самой форме
решения, и выполнение именно этих требований позволило по¬
добрать решение в форме (3). Таким образом, решение (3) не
есть общее решение уравнения (2), а лишь одно из частных ре¬
шений. Уравнение (2) есть уравнение типа Фредгольма I рода и,
следовательно, имеет бесконечное множество решений. Любое
численное его решение дает одно из частных решений, но при
методе дискретных вихрей в решение невозможно ввести какие-
либо дополнительные требования, поэтому нет никаких основа¬
ний утверждать, что полученное решение совпадает с (3). Един¬
ственным оно также быть не может, так как это противоречит
свойствам решений уравнений Фредгольма I рода.
Второе. При доказательстве сходимости решения, получен¬
ного методом дискретных вихрей, к решению (3) авторы [11] ис¬
пользовали метод, близкий к предложенному в работе [9], ана¬
лиз недостатков которого дан выше. Подобно [9] в работе [11]
используется особенность расположения точек приложения вих¬
ря и точек расчета, расстояние между которыми равно половине
интервала А = afr/n, что позволяет записать j{xi) в виде
6 — X X — Хо
(3)
а
(4)
342
к-1 / * ч п — к
Р?(п)=
771 — 1 4 ' 171 = 1 '
после чего Пт=\ О ~ 5йг) и Пт=* (* + 55?) преобразуются по
формуле
0?+1)Ы + 2). ..(0 + П)
«I ~ L'(l3 + 1) 1 ’ (5)
для /? = 1/2 и /3 = —1/2, при этом дана ссылка на монографию
[13]. Но в монографии [13, с. 9] приведена формула
= п^+±с.«>-'+<*»'-'-■), <«>
и в дальнейшем там пользуются или (6), полагая п достаточно
большим, или ее предельной формой
lim 4- 2)...(/? Ч- гг) 1
П-+СО п\пР Г(/3 Н- 1)
Однако применять формулу (6) к обоим произведениям
и ПГЛ одновременно нельзя, так как при больших п величи¬
на к может принимать любые значения от 1 до п, и поэтому
или к или п — к не будут стремиться к бесконечности, т. е. не¬
льзя отбрасывать как малую величину Y^=i с»п^~р + 0(п^"р~1)
в формуле (6) и, следовательно, утверждать существование рав¬
номерной сходимости Р^(п) к yJjfEji что делает недопустимой
замену yjна \Jвозможную лишь для (п — к) —► со
и к —> оо. Но тогда нет и стремления 7(х, ) из формулы (4) при
ть —► оо к решению 7(х), данному формулой (3).
Итак, ни о эквивалентности решений (3) и (4), ни о равномер¬
ной сходимости решения (4) к решению (3) говорить нельзя.
Все сказанное выше касалось сравнения двух методов реше¬
ния, но следует особо сказать о математической обоснованно¬
сти метода дискретных вихрей.
В работах [3, 11], рассматривая простейшую форму сингу-
ъ
лярного интеграла f ~^dx из уравнения профиля для доказа¬
тельства сходимости метода, аппроксимируют этот интеграл
квадратурной формулой прямоугольников, которая применима
343
лишь для функций, ограниченных на всем интервале, включая
концы. Но функция разрывна в каждой точке интерва¬
ла и остается таковой в том случае, если предположить, как
это и сделано, что 7(х) удовлетворяет условию Гельдера Н(а):
|т(*г) - 7(*i)l < а|*2 - *i|a, 0 < а < 1.
Последнее позволило получить оценку
j Jl±dt - у лШ
J Т. — ГГл *
X Xq ^0
< **н° {£ [»+ 5(17^] +(«VSI+I)}
Ah 4|7(*о)||Ь-о|
- *о|1-а |*о —а||Ь—*о|
h.
Но даже при использовании условия Гельдера полученная оцен¬
ка справедлива для фиксированного х0, а в рассматриваемом
случае xq может принимать любые значения на [а 4- Л/2; Ь — Л/2]
и, следовательно, отношение не стремится равномер¬
но к нулю при Л —► 0, так как для точек, близких к передней и
задней кромкам, h/\b — (6 — Л/2)| = 2 при любых Л, т. е. разница
между интегралом и его приближением не может стать малой
для всех значений х одновременно. Поскольку на решении и
анализе этого интеграла основаны все остальные результаты,
то приведенные далее в работе [3] выкладки не доказывают рав¬
номерной сходимости рассматриваемого метода.
Указанные в работе [3] величины € и 6, на которые требуется
уменьшить интервал [а, Ь], чтобы уже в интервале [а 4- е, Ь — й]
обеспечить равномерную сходимость решения, не меняют сути
дела, поскольку невозможно дать теоретически обоснованных
значений этих величин, так как они зависят от Л. Необходи¬
мость вводить упомянутые € и 6, к тому же, лишает смысла
главную задачу — нахождение данным методом решения, удо¬
влетворяющего определенным условиям именно на концах ин¬
тервала [а, 6].
Итак, в рассмотренных работах [3, 9, 11] равномерная схо¬
димость нарушается на концах интервала, что, по-видимому, и
характерно для данного метода, поскольку именно на концах ин¬
тервала требуется выполнение определенных условий для 7, ко¬
торые никоим образом не учитываются видом решаемого урав¬
344
нения непроницаемости и, следовательно, не могут отразиться
в решении.
Исключение из рассмотрения участков, близких к концам ин¬
тервала, позволяет утверждать равномерную сходимость чи¬
сленного решения к теоретическому внутри интервала, но от¬
сутствие точного метода для определения величины этих участ¬
ков и их зависимость от h не дают возможности установить,
в каких пределах можно вести расчет с требуемой точностью.
Тем более остается открытым вопрос о выполнении граничных
условий на концах интервала.
В дополнение к сказанному хотелось бы напомнить о работе
[14], где строго доказана невозможность получить единствен¬
ное решение задачи обтекания тела методом источников и сто¬
ков, который с математической точки зрения аналогичен методу
дискретных вихрей.
Несколько слов о работах [15] и [16]. В работе [15] в слу¬
чае дискретной системы вихрей у; написано выражение для вы¬
званной ими скорости и показано, что при возрастании числа
присоединенных вихрей оно сходится к интегралу, входящему в
уравнение непроницаемости; существования и единственности
решения этого уравнения автор не касался.
Работа [16] является обзором существующих методов реше¬
ния задачи о несущей поверхности, в ней для доказательства
сходимости метода дискретных вихрей изложено содержание
работы [9], разбор которой дан выше. Кроме того, автор предла¬
гает пользоваться для численного решения уравнения (2) обоб¬
щенной формулой Коши, но не приводит необходимой для этой
формулы системы ортогональных с весом р — полиномов
РП) а указывает лишь Pi = х + 1/2, которого явно недостаточно
для построения решения. А поскольку решение не построено,
то не приходится говорить о его сходимости.
Из изложенного видно, что попытка доказать сходимость ре¬
шения системы алгебраических уравнений, написанных для дис¬
кретной системы вихрей, не содержащих в себе краевых усло¬
вий, к решению интегрального уравнения задачи с учетом та¬
ких условий не может быть признана удовлетворительной. Не¬
допустимо выполнение этих условий только в пределе лишь за
счет выбора особого положения расчетных точек. Удовлетво¬
рение краевых условий должно быть гарантировано для всяко¬
го конструируемого приближения решения при любом выборе
345
расчетных точек. Между тем известно, какому решению будут
принадлежать средние по частичным промежуткам значения 7JJ,
найденные из системы упомянутых выше алгебраических урав¬
нений, и каким краевым условиям это приближенное решение
удовлетворяет. Эти значения очень сильно могут изменяться
в зависимости от выбора расчетных точек. Выше было пока¬
зано, что и в пределе краевое условие на переднем конце не
выполняется, так как рассматриваемая последовательность не
стремится к требуемому выражению. Невозможно поэтому со¬
гласиться с утверждением, высказанным в статье [17], что метод
дискретных вихрей строго обоснован. К сожалению, он никак
не обоснован с точки зрения теории приближенного решения
краевых задач математической физики и теории интегральных
уравнений Фредгольма первого рода. Заметим, наконец, что с
теоретической стороны непонятно, почему нужно интегральное
уравнение краевой задачи заменять системой алгебраических
уравнений, получаемой вопреки методам математической фи¬
зики без учета граничных условий, когда для такой замены су¬
ществуют рациональные методы [18] и [19], позволяющие учесть
эти условия.
В заключение отметим, что, как показали расчеты [20-22],
практически наиболее удобным при решении интегрального
уравнения теории несущей поверхности является метод итера¬
ций, если за нулевое приближение взять решение, которое по¬
лучается при применении к регуляризированной части ядра до¬
пущения Вайзингера.
Изложенный выше материал публикуется в порядке дискус¬
сии.
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Белоцерковскич С. М. Тонкая несущая поверхность в дозвуковом по¬
токе газа. М., 1965. 442 с.
2. Белоцерковскчй С. М., Скрипач Б. К., Табачников В. Г. Крыло в неста¬
ционарном потоке газа. М., 1971. 767 с.
3. Белоцерковскич С. М., Скрипач Б. К. Аэродинамические производ¬
ные летального аппарата и крыла при дозвуковых скоростях. М., 1975.
424 с.
4. Wieghardt К. Uber die Auftriebsverteilung des einfaches Rechteckflugels iiber
die Tiefe//Z. Ang. Math. Mech. 1939. Bd 19. S. 257-270.
5. Schlichting H., Ткотпаз H. H, В. M. Note on the calculation of lift distribution
of swept wings // Royal Aircraft Establishment Rep. 1947. N Aero 2236. P. 371 -
377.
346
6. Falkener V. M. The calculation on aerodynamic loading on surfaces of any
shap//Rep. Memor Aero Res. 1943. N 1910.
7. Белоцерковский С. М. Пространственное неустановившееся движение
несущей поверхности // Прикл. мат. и мех. 1955. Т. 19. Вып. 4. С. 410-
420.
8. Белоцерковский С. М., Гиневский А. С., Полонский Я. Е. Аэродинами¬
ческие силы, действующие на решетку профилей при нестационарном
обтекании//Промышленная аэродинамика. 1961. Вып. 20. С. 137-167.
9. Dc Joung J. Convergence proof of discrete-panel wings theories // J. Aircraft.
1971. Vol. 8. N 10. P. 837-839.
10. Учттеккер Э. Т., Батсон JJotc. H, Курс современного анализа. Т. 2.
М., 1963. 516 с.
11. Лчфанов И, K,f Полонский Я. Е, Обоснование численного метода
дискретных вихрей решения сингулярных интегральных уравнений //
Прикл. мат. и мех. 1975. Т. 39. Вып. 4. С. 742-746.
12. Мусхелишвили П. И. Сингулярные интегральные уравнения. М.; Л
1946. 448 с.
13. ХарЬи Г. Расходящиеся ряды. М., 1951. 504 с.
14. Валландер С. В., Липких Ю. В. Замечания об уравнениях, связанных
с методом источников и стоков // Вестн. Ленингр. ун-та. 1968. Jf* 19.
С. 24-29.
15. Воробьев Я. Ф. О дискретной вихревой схеме крыла конечного разма¬
ха //Изв. Сиб. АН СССР. 1972. № 13. Вып. 3. С. 59-68.
16. Мишкевич В: Г, О методах непрерывного и дискретного вихревых
слоев в теории несущей поверхности//Материалы по обмену опытом.
Научно-техн. общ. им. акад. А. Н. Крылова. Вып. 217. Гидродинамика
высоких скоростей. 1974. С. 34-58.
17. Белоцерковский С. М., Ништ М. И. Отрывные течения и нелинейные
характеристики тонких несущих поверхностей j j Итоги науки и техни¬
ки. Т. 2. М., 1978.
18. Лаврентьев М. А. О построении потока, обтекающего дугу заданной
формы //Труды ЦАГИ. 1932. № 118.
19. Поляхов Я. Я. Об интегральном уравнении теории несущих поверхно¬
стей //Вестн. Ленингр. ун-та. 1973. № 7. С. 115-121. [37*]
20. Мельникова О. Ф., Поляхов Я. Я. О применении гипотезы Вайзингера
при расчете обтекания стреловидной пластины//Ленинградский ин¬
ститут авиационного приборостроения. Межвуз. сб. Вып. 108. Л.,
1976. С. 68-74. [41]
21. Мельникова О. ФПоляхов Я. Я. О решении интегрального уравнения
несущей поверхности//Вестн. Ленингр. ун-та. 1978. № 1, С. 123-128.
[43*]
22. Поляхов Н. Н., Шестернина 3. Н. О существовании решения инте¬
грального уравнения несущей поверхности//Вестн. Ленингр. ун-та.
1975. № 19. С. 102-107. [38*]
347
IV.6. ЗАМЕТКА О МЕТОДЕ
ДИСКРЕТНЫХ ВИХРЕЙ [47]
Интегральное уравнение обтекания слабо изогнутой дуги
имеет вид
Если отрезок (—/, /) разбить на п равных частей длиной h и ап¬
проксимировать неизвестную функцию 7 в каждом промежутке
с номером i/ = 1,2,. ,.,п по формулам
где 7 — значения 7(х) в точках деления, то уравнение (1) приве¬
дется к системе п — 1 алгебраических уравнений:
п — 1
где Г|, = /iTv, /г, и = 1, 2,..., п. Выражения для а^ получены в
[1]. Они зависят только от разностей /х — v. Если бы мы стали
рассматривать Г„ как напряженность изолированных вихрей,
помещенных в точках х„, то, вычислив индуктивные скорости в
серединах отрезков хИ — xM_i, получили бы систему вида (3), но
с коэффициентами
Коэффициенты а^и и аЦ1/ различны, и разность между ними тем
больше, чем меньше разность \/л — 1/\} т. е. чем ближе промежуток
с номером v к точке х' . Наиболее всего будут расходиться avv
и аии, причем расхождение это не зависит от п. Если начать
неограниченно увеличивать число делений, то система (3) вер¬
нется к уравнению (1), а система с коэффициентами а^и к нему
не придет. Она может привести лишь к уравнению того же типа,
но с ядром вида х(х/ — х)"1, где множитель х более всего будет
отклоняться от единицы в особом интервале. Таким образом,
(1)
(3)
1 1
а>“' 2тг 0,5 + ц — v
348
схема дискретных вихреи приводит к решению другой задачи,
чем поставленная первоначально. Выделяя в новом уравнении
сингулярный интеграл и обращая его, получим связь между ре¬
шениями обоих уравнений
-/ L/ т
dt,
где xi = 1 — х, и концевые условия при х = ±1 будут удовле¬
творены. Таким образом, способ дискретных вихрей не может
быть улучшен за счет увеличения числа делений.
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Мельникова О. Ф., Поляхов Н. Я. О решении интегрального уравнения
несущей поверхности//Вестн. Ленингр. ун-та. 1978. № 1. С. 123-128.
[431
IV.7. О МЕТОДЕ ДИСКРЕТНЫХ ВИХРЕЙ [48]
Метод дискретных вихрей, предложенный Вигхардом и
Шлихтингом, нашел довольно широкое применение в числен¬
ных методах расчета несущих поверхностей вследствие того,
что он приводит к сравнительно правдоподобным результатам
при достаточно простом алгоритме решения. Однако попыт¬
ки теоретически обосновать его и показать, что в предельном
случае бесконечного числа вихрей он приводит к точному реше¬
нию интегрального уравнения плоской задачи теории несущей
поверхности с выполнением требуемых краевых условий, не мо¬
гут быть признаны удовлетворительными.
В данной статье производится сравнение интегрального
уравнения несущей поверхности с интегральным уравнением,
полученным по способу дискретных вихрей. Решения этих
уравнений оказываются различными. Показывается, что этот
метод является принципиально приближенным и в предельном
случае приводит к решению интегрального уравнения, не со¬
впадающего с основным уравнением
Для того чтобы в этом убедиться, построим решение уравне¬
ния (1). Предварительно выполним аппроксимацию неизвестной
функции 7(х), учитывая, что она должна обращаться в нуль на
разделен равномерно точками —/ = хо, xi,..., xn_i, х„ = +/ на л
частичных отрезков и точкам деления соответствуют значения
7ь 72) • • •) 7n-i функции 7(х). Значения этой функции в проме¬
жутке от Х{/_1 до х„(|/ =1,2,.. .п) будем обозначать через 7„(х)
и примем
(1)
задней кромке при х = +/ как (/ —х)*1/2 и в бесконечность на пе¬
редней кромке при х = —/ как (/ + х)”1/2. Пусть отрезок [—/, +/]
7„(x) = 7„_i
Ъ -7г-1
хи — x„_i
(х Xy_i), i/ = 2, 3, ,..., п- 1, (2)
350
Тогда уравнение (1) можно записать в следующей форме:
1 Jb.IHE.[EI^-+
2nj ПЧ l-Xl \ l + xx' -х
-t
n — 1 *> . .. +J
. 1 f 7u(x)dx 1 f yn(x)dx _ ,
i/~2
*v-l *n+l
Вычисление первого интеграла затруднено тем, что функция 71
становится неограниченной вблизи точки х = —Лля устра¬
нения этого неудобства представим тождественно первый инте¬
грал в виде
1 / // + *i // - a?
1 27г J V / — zi V / 4* х х1 — х
-I
i/=2_
Первое слагаемое в правой части (3') вычисляется и оказывает¬
ся равным остальные могут быть вычислены по обыч¬
ным квадратурным формулам, причем в особом интервале, в
котором х обращается в я', величину можно аппроксими¬
ровать, в частности по линейному закону.
Пользуясь приближенным представлением (2), можем также
вычислить и остальные интегралы уравнения (3). В результате
формула (3) примет вид
п
У! lva\iv = /i = 1, 2,..., п, (4)
i/=l
или
= (5)
U-1
где /i = l>2,...,n;A = 21/п — величина частичного промежутка;
Г„ = 7vh\ коэффициенты а^ = а^(х^) получены в [1] и зависят
исключительно от разности и — что соответствует взаимным
расстояниям между точками хи и х*^.
351
Обратимся теперь к методу дискретных вихрей [2]. Если рас¬
сматривать Г*, как напряженность вихря, помещенного в точке
Ху, то полная индуктивная скорость в точке х^, находящейся
в середине отрезка [хд_1, х^], будет определяться следующим
выражением:
п
и>„ = £ (6)
i/=i
где ^ i
~ 2^0,5 + /*-^’ -
Тогда согласно теории дискретных вихрей [2] уравнение непро¬
ницаемости будет иметь вид
1 п —
-53г"а^ = /(**•) = л*!.). ^ = 1,2,...,п,
V — 1
или же
п
= л*'„)- (7)
*/=1
Сравнивая систему (7) с системой (4), полученной из (1), от¬
метим, что эти системы аналогичны по форме, но отличаются
выражениями для коэффициентов аЦи и а^и приуу. Расхождения
в значениях аЦи и а^и будут наиболее значительны при разно¬
сти v — fi = 0, т. е. в элементах, стоящих по главной диагонали
определителя системы (в коэффициентах ац, «зз,...). При
больших же значениях разности г/ — /4 различие между соответ¬
ствующими коэффициентами сглаживается. Это объясняется
тем, что расстояние между точкамии х^ достаточно велики
и элемент вихревого слоя с номером v обоснованно может быть
заменен напряженностью суммарного вихря с Гу. В случае, ко¬
гда рассматривается элемент, близкий к точке х'м, указанного
рода замена элемента вихревого слоя сосредоточенным вихрем
будет давать существенные ошибки, причем это свойство будет
оставаться и при увеличении числа дробления.
Например, непосредственными подсчетами удалось устано¬
вить, что значения коэффициентов аМь, и могут отличаться
друг от друга почти на 14%.
Таким образом, система алгебраических уравнений (4) и си¬
стема (7) отличаются матрицами коэффициентов, что может по¬
влечь за собой значительное расхождение в векторах решений
[3].
352
Перейдем теперь к вопросу об идентичности интегральных
уравнений, получаемых из систем (4) и (7). Очевидно, что
обратный переход от системы (4) к интегральному уравнению
(1) будет получаться с той степенью приближения, которая бы¬
ла допущена в результате применения указанной аппроксима¬
ции (2). Точность этой аппроксимации может быть увеличена
за счет увеличения числа делений, а также использования вме¬
сто взятой в (2) формулы трапеций любой другой формулы ме¬
ханических квадратур.
Построим интегральное уравнение на основе системы (7):
здесь зависимость х(х, х') есть функция искажения ядра в ре¬
зультате того, что коэффициенты отличаются от коэффи¬
циентов а^, а функция 7(2:) соответствует вихревой плотности,
определяемой системой (7). Очевидно, что множитель х(х, х')
более всего будет отклоняться от единицы в особом интервале,
в котором лежит точка х'м.
Таким образом, теория ’’дискретных вихрей” приводит рас¬
сматриваемую задачу к интегральному уравнению (8), отлич¬
ному от интегрального уравнения (1) и тем самым решает фак¬
тически другую задачу, т. е. метод ’’дискретных вихрей” пред¬
ставляет собой метод приближенный, который не может быть
улучшен за счет увеличения числа самих вихрей. При этом
нет основания утверждать, что указанный метод автоматиче¬
ски удовлетворяет краевым условиям в результате выбора рас¬
четных точек. Эти краевые условия могут быть гарантированы
лишь путем обращения сингулярного интеграла в требуемом
классе функций.
Решения этих двух задач —уравнения (1) и уравнения (8) —
могут оказаться близкими. Действительно, представляя (8) в
виде
где xi(x*, xf) = 1 — х(х, х'), и обращая затем интеграл слева в
классе функций, удовлетворяющих требуемым краевым уело-
(8)
-И
1 J j(x)dx
2к J х‘ — х
J
353
виям, получим уравнение
т(*) = 7(*) + ]~+~ j 7(ОФ(*. (9)
где функция
Ф(х, О =
/У
будет непрерывной. Уравнение (9) есть уравнение Фредгольма
второго рода, решение которого 7(х) в случае, когда коэффици¬
ент искажения ядра х(х, г') близок к единице, может не слишком
сильно отличаться от значений искомой функции 7(х).
Непосредственные расчеты 7(2) путем решения системы (7)
также показывают, что указанные выше различия в коэффици¬
ентах систем (7) и (4) не очень сильно сказываются на значе¬
ниях у(х) для точек, удаленных от концов промежутка [—/, +/].
Поэтому система (7) может использоваться для приближенных
расчетов. Однако при этом следует иметь в виду, что результат
решения получается приближенный й нет возможности оценить
заранее допускаемую ошибку.
Итак, метод дискретных вихрей в ряде случаев может давать
достаточно хорошие результаты, однако гораздо более стро¬
гим, надежным и устойчивым для исследования крыла конеч¬
ного размаха, как показывают расчеты [1], является метод ите¬
раций при решении интегрального уравнения теории несущих
поверхностей. Решение интегрального уравнения методом ите¬
раций не требует введения специальной процедуры анализа точ¬
ности, так как этот анализ осуществляется на каждой итерации
и является критерием окончания итеративного процесса. Сле¬
дует также отметить, что решение задачи путем сведения ее
к системе алгебраических уравнений может привести к классу
некорректно поставленных задач [4], тогда как итерационное ре¬
шение интегрального уравнения второго рода, к которому сво¬
дится основное уравнение теории несущих поверхностей, таким
дефектом не обладает.
354
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Поляхов Н. Я., Мельникова О. Ф. О решении интегрального уравнения
обтекания несущей поверхности//Вестн. Ленингр. ун-та. 1978. № 1.
С. 123-128. [43ф]
2. Белоцерковскии С. М. Расчет обтекания крыльев произвольной формы
в плане в широком диапазоне углов атаки //Мех. жидкости й газа.
1968. № 4. С. 32-45.
3. Фаддеев Д. К., Фаддеева В. Я. К вопросу о решении линейных алгебра¬
ических систем //Журн. вычислит, математики и мат, физики. 1974.
Т. 1. Na 3. С. 539-559.
4. Тихонов А. Я., Арсенин В. Я. Методы решения некорректных задач.
М., 1974. 201 с.
IV.8. ПРАКТИЧЕСКИЙ МЕТОД РАСЧЕТА
НЕСТАЦИОНАРНЫХ ХАРАКТЕРИСТИК КРЫЛА
С ОТКЛОНЯЮЩЕЙСЯ ЧАСТЬЮ [55]*
Рассматривается обтекание идеальной жидкостью тонкого
прямоугольного крыла с удлинением А = 0,5 — 3,0, имеющего
отклоняющуюся часть по всему размаху. Такое крыло являет¬
ся естественной схематизацией судового руля за рудерпостом.
Известен ряд работ, в которых излагаются методы опреде¬
ления сил, действующих на крылья такого вида, но одни из
них позволяют определить только стационарные характеристи¬
ки [3, 4], другие — нестационарные, но требуют больших затрат
машинного времени [1,2]. В работе предлагается сравнительно
простой и экономный метод решения этой задачи.
Течение жидкости будем считать безвихревым везде кроме
непосредственной близости к крылу и его следу. Тогда реше¬
ние задачи сведется к определению потенциала возмущенных
скоростей жидкости из уравнения Лапласа при следующих на¬
чальных и граничных условиях:
1) в начальный момент времени все характеристики течения
известны;
2) на несущей поверхности (крыле) выполняется условие не¬
проницаемости;
3) на задней кромке выполняется постулат Жуковского —
Чаплыгина;
4) на бесконечности возмущенные скорости равны нулю;
5) при переходе через поверхность следа за несущей поверх¬
ностью функция давления не претерпевает разрыва.
Закон движения крыла будем считать произвольной аперио¬
дической функцией времени. Функции, описывающие движение
частей крыла, будем полагать непрерывными.
Решение задачи получим вихревым методом. Вихревую мо¬
дель построим как обобщение на нестационарный случай мо¬
дели Боллея, приняв, что циркуляция постоянна по размаху
(рис. 1).
Примем следующие термины: А В — несущий (присоединен¬
ный) собственный вихрь; AD и ВС — свободные собственные
вихри; EF — отошедший поперечный вихрь; ЕК и FM — ото¬
шедшие свободные вихри. Свободные вихри будем считать пря-
*Соавт. В.М.Журава, В. И. Николаев.
356
Рис. 1
молинейными, наклоненными на углы заклинивания к передней
и задней частям крыла ар/, где р = 1, если вихрь расположен на
передней части крыла, р = 2 — если на задней; / = 1 — если угол
определяется относительно передней части крыла, / = 2 — если
относительно задней. Пусть оц—угол атаки передней части,
аг — задней, тогда 6 = а? — а\ есть угол излома крыла.
Пусть в момент времени т интенсивность несущего вихря GK
у(х} т) изменится на Тогда в соответствии с известной те¬
оремой от GK отделится вихрь противоположной циркуляции
и образуется вихревая рамка GiGnK^Ki- С це¬
лью некоторого упрощения заменим вихревую рамку двумя П-
образными вихрями, у которых поперечные стороны есть G\K\
и G2Л2• Свободные вихри изображены штриховыми линиями*
Строго говоря, такая замена не вполне равноценна, поскольку
свободные вихри не совпадают, но можно показать, что соот¬
ветствующая ошибка мала. Отошедший вихрь стелется по не¬
сущей поверхности и превращается в след, который будем счи¬
тать прямолинейным.
Введем прямоугольные системы координат, взяв их начало
на оси излома поверхности посередине размаха 2L: поточную
OX\Y\Zi и местную OXYZ. В поточной системе ось ОХ\ со¬
впадает с вектором скорости набегающего потока г>оо, ось OZ\
совпадет с осью излома крыла. В местной системе,ось OZ со¬
впадает с OZ\y ось ОХ лежит в плоскости поверхности, ось OY
перпендикулярна большей части крыла.
357
Обозначим координаты середины отошедших вихрей через
£ — вдоль ОХ, £ — вдоль OY, х и у — координаты середины соб¬
ственных вихрей в местной системе. Очевидно, что х = х(х, <5),
У = у(я, 5), 6 = 6(<) функции £(х, О» С(®* 0» *(*> Of 2/(ж> 0 непре¬
рывные.
Условие непроницаемости выполним в среднем интегральном
смысле по размаху на контрольных линиях с координатами х'
(см. рис. 1). В [7] показано, что в этом случае точность вы¬
числения углов заклинивания не имеет особого значения и их
можно получить по эмпирическим формулам, например:
СЩ = 0,7(*i + 0,76\/б, 6*22 = 0,7 Of 2 (1)
или
с*ц = 0,7ai + 0 J6\/bi е*22 = 0,7с*2 ” 0,76>/а?. (2)
Здесь а — координата передней кромки, а < 0, 6 — координата
задней кромки, |а| + 6 = 1. Формулы (1) — для случая, когда
неподвижна передняя кромка крыла, (2) — когда задняя кромка
неподвижна.
Пусть функция 7(х, I) задает распределение плотности цир¬
куляции по хорде в момент времени t. Уравнение задачи полу¬
чим как выражение для условия непроницаемости:
ь
J у(х, t)I<cp(x\ х, t)dt =
-а
-а О
+ 2v\[voofa(x, t) + x'fu(x, <)]• (3)
Здесь Кср(х', х, t) определяет среднюю по размаху вызванную
скорость на контрольной линии х1 от собственного П-образного
вихря единичной интенсивности, К0(х\ х, t)—то же от отошед¬
шего вихря. Функции /<*(*, 0 й /w(^i О определяют угловые ско¬
рости и углы атаки частей поверхности.
Граничными условиями являются следующие:
— на передней кромке 7(2, t) имеет бесконечность порядка
(х - а)-1/2;
— на задней кромке — нуль порядка (Ь - х)1/2;
358
— в окрестности точки излома (х = 0) функция у(х, t) имеет
особенность, порядок которой следует определить.
Указанные особенности следуют из сущности вихревого ме¬
тода, зависимость же циркуляции от времени никаких новых
особенностей не порождает.
Определим порядок особенности в точке излома.
Известно, что распределение скорости потенциального тече¬
ния вблизи угла излома подчиняется степенному закону: U(х) =
с|х|т. Специальное исследование показало, что т можно вычи¬
слять по интерполяционной формуле:
При отсутствии излома (6 = 0), при обтекании прямого угла (6 =
7г/2) и передней кромки крыла (6 = -тг) формула дает известные
значения т: 0, —1/3 и —1/2.
Следуя предложению работ [8] и [9], примем для y(x,t) пред¬
ставление, показанное на рис. 2. Разобьем хорду на п панелей
с хордами Дх = 1/п. Пусть 7, есть плотность циркуляции в
точках деления, N— точка излома крыла. Она совмещена со
стыком панелей. Учитывая граничные условия, причем: для
первой панели
для панелей с номерами < i ^ п — 1 (внутренние
панели, не прилегающие к кромкам и точке излома)
Х{ — X
у(х) = Ji + (7i - 7«-i)-дж
(5)
слева от точки излома
(6)
справа от точки излома
х - хдг+1
Ах
(7)
для последней панели
7(х) = 7„_iх/пл/Ь - х.
(8)
В точке N принята фиктивная плотность jn Для того, чтобы
при 6 = 0 в ее окрестности получить такое же распределение
циркуляции, как для остальных внутренних панелей.
Решение (3) получим численно с помощью метода колокации,
сведя (3) к линейной системе. Этот путь далеко не единствен¬
ный (см. [8, 9]), однако он представляется наиболее простым и
наглядным. Непрерывный процесс изменения кинематических и
динамических характеристик представим как дискретный. То¬
гда углы атаки будут изменяться скачком, как это принято в [1,
2]. Скачок происходит непосредственно после каждого расчет¬
ного момента времени г. В момент скачка угла атаки скачком
изменяется циркуляция.
После подстановки формул (4) — (8) в уравнение (3) и приве¬
дения его к дискретному виду получаем
Левая часть (9) есть вектор-строка неизвестных плотностей 7* в
точках деления хорды i = 1, 2,..., л - 1. Подстановка в (9) п — 1
значения координат контрольных линий х1 (удобнее это обозна¬
чение заменить на xj, где и — признак контрольной линии, j —
ее номер) дает п — 1 уравнение, линейное по ц. Коэффициенты
-гг'Жср^- С, г) - (г? - гг1) х
х Ko(xj - С. »з) + 2xVooA [fa(x, t) + xffw{x, <)] . (9)
360
системы Tji есть сумма интегралов 7},- = lj\ + />21 где Ij\ и 2
имеют вид
Правая часть (3) для r-го расчетного момента определяется
по известным решениям в) для всех предшествующих мо¬
ментов s < г. Ее вычисление подробно изложено в [б].
Распределение п контрольных линий может быть различным,
однако наиболее целесообразно распределить их следующим
образом: n-ю линию совместить с задней кромкой (это гаранти¬
рует выполнение постулата Жуковского — Чаплыгина не в пре¬
деле, а при любом конкретном п, что обеспечивается распре¬
делением (8)), остальные линии следует совместить с точками
деления хорды.
Определим функции /\0 и КСр.
В [6] показано, что средняяпо размаху скорость на контроль¬
ной линии от П-образного вихря с координатами середины £
и С определяется формулой
с*з — угол заклинивания.
Лля Кср имеем ту же формулу, но вместо £ и С следует под¬
ставить координаты середин собственных вихрей х и у.
Функции х и у получены из геометрических соображений:
при х1- < 0 (передняя часть крыла)
х
х - gj-i
Д*
А'ср-£> С <*3, t)dx.
где
(Ю)
В (11) и (12) х есть координата середины собственного вихря в
местной системе (ось ОХ имеет излом), х и у — координаты той
же точки в местной системе, связанной с передней или задней
частями крыла.
Функции £ = £(я, t) и £ = С(я, t) имеют сложный вид в связи с
тем, что взаимное расположение Xj-й контрольной линии и ото¬
шедшего вихря зависит от того, от какого собственного вихря
отделился отошедший, на какой части поверхности он находит¬
ся в рассматриваемый момент времени или уже превратился в
след. Приведем эти формулы в дискретном виде. Пусть рц —
путь, проходимый отошедшим вихрем вдоль ломаной оси ОХ за
г — s интервалов времени:
Здесь Ь — а — хорда, к — кратность (число панелей, проходимых
вихрем за один временной интервал).
Момент схода гсх вихря с поверхности в след:
где s — момент отделения вихря от собственного; —коорди¬
ната собственного вихря.
В итоге имеем для £ и £:
при х*< < О
(13)
г О, X) < О
{xrj + Рк) sin 6(0, xj + pt>0
(14)
п — 1
(15)
362
- (Xj +Pfc)sin6(0, *} + Р*<0
Q = ч °’ xj + P* > 0
(16)
Если в (11)-(16) положить 6 = 0 и c*i = «2, то как частный
случай получим соответствующие формулы в [6].
Решение линейной системы (9) получим, задавая г = 1, 2,...
При г = 1 вихревого следа еще нет и сумма в правой части
равна нулю. При г > 1 сумма определяется решениями в пред¬
шествующие моменты времени s < 1.
Гидродинамические коэффициенты можно вычислить непо¬
средственно, зная наборы у,■ для каждого г или, что удобнее,
проинтегрировав по хордам панелей и получив наборы цирку¬
ляций Г[\ Коэффициенты вычисляются по формулам:
для передней части
Решения системы (9) подчиняются принципу суперпозиции.
Удерживая в правой части различные комбинации слагаемых,
можно вычислить все комбинации нестационарных гидродина¬
мических сил кроме непосредственно связанных с присоединен¬
ными массами и присоединенными моментами инерции.
Для проверки метода были выполнены специальные расчеты.
Эксперимент выполнялся с моделями рулей за рудерпостами.
Профиль — NACA-0021. Результаты обобщены в виде формул,
приведенных в [3]. Удлинения комплексов были равны 1,41 и 1,0
относительные хорды рудерпоста — 0,22 и 0,44 соответственно.
1. Белоцерковский С. М., Нигит М. И. Отрывное и безотрывное обтекание
тонких крыльев идеальной жидкостью. М., 1978. 352 с.
2. Белоцерковский С. М., Скрипач Б. К., Табачников В. Г. Крыло в неста¬
ционарном потоке газа. М., 1971. 768 с.
Су 1 = 2 cos2 O'! (г) ^2 ri. Cmi = 2cosori(r) ^ Г,-х}\
для задней части
УКАЗА ТЕЛЬ ЛИТЕРА ТУРЫ
363
3. Воиткунский Я. И., Першчц Р. Я., Титов И. А. Справочник по теории
корабля. Изд. 2-е. Л., 1973. 512 с.
4. Ермоленко С. Л. Расчет аэродинамических характеристик крыльев
малого удлинения с закрылком или отклоняющимся носком по всему
размаху//Аэродинамика крыльев летательных аппаратов. М., 1969.
С. 29-54.
5. Завиша Я. В., Декип Я. Г. Нагрузка рулевой машины на заднем ходу
судна//Судостроение. Респ. межвед. сб. № 28. Киев; Одесса, 1979.
С. 75-77.
6. Николаев В. И. Метод расчета нестационарных характеристик прямо¬
угольного* крыла малого удлинения //Труды Николаевского корабле-
строит. ин-та. Вып. 152, 1979. С. 85-96,
7. Николаев В. И. К вопросу о расчете гидродинамических характери¬
стик крыльев малого удлинения (А = 0,5 — 2,5)//Судостроение. Рес-
публ. межвед. сб. X® 29. Киев; Одесса, 1980. С. 43-45.
8. Полжхов Я. Н.% Мельникова О. Ф. О решении интегрального уравнения
обтекания несущей поверхности // Вестн. Ленингр. ун-та, 1978. Jf* 1.
С. 123-128. [43*]
9. Полжхов И. И. Об интегральном уравнении теории несущей поверхно¬
сти//Вестн. Ленингр. ун-та, 1973. Вып. 2. 7. С. 115-121. [37*]
IV.9. ОБ ИНТЕГРОДИФФЕРЕНЦИАЛЬНОМ
УРАВНЕНИИ ДЛЯ НЕСУЩЕЙ ПОВЕРХНОСТИ
ПРИ НЕСТАЦИОНАРНОМ ДВИЖЕНИИ [56]
В предлагаемой работе рассматривается несущая поверх¬
ность, представляющая собой совокупность прямоугольных по¬
лосок с размахом Az, лежащих в плоскости у = 0, Каждая из
таких полосок покрыта непрерывно распределенной системой
вихрей П-образной формы, имеющих плотность 7(2, z). Длина
каждой полоски 2а, а размах всей поверхности вдоль оси z ра¬
вен 2L. В случае стационарного прямолинейного движения в
направлении оси х с концов каждого присоединенного вихря с
размахом Az сходят два бесконечно длинных парных свободных
вихря плотностью 7, параллельных оси х, причем пространство
между ними, т. е. полоса шириной Az, свободно от поперечных
вихрей. В случае нестационарного движения плотность 7 будет
зависеть не только от х и z, но и от времени t. Свободные боко¬
вые вихри будут иметь переменную по своей длине плотность
7(2, z, *). Вследствие этого в полосе между парными вихрями
будут существовать свободные поперечные вихри с плотностью
/? = —ду/дх, где х относится к точкам продольного свободного
вихря. Если расстояние присоединенного вихря от начала коор¬
динат равно 2, то поперечный свободный вихрь с координатой
х должен был образоваться в момент времени
когда присоединенный вихрь проходил через точку, удаленную
в момент t от начала координат на расстояние xf — 2. При¬
чем само начало движется со скоростью и. Если и = const, то
промежуток времени t — т будет равен (2 — х)/и. Таким обра¬
зом, при нестационарном движении вихря с размахом Az позади
него будет простираться вихревой «листок» с таким же разма¬
хом, покрытый свободными поперечными с плотностью /?(х, z)
и ограниченный П-образными вихрями. Эта система вихрей бу¬
дет вызывать в точке Nf(xf, О, z') скорости, подчиненные закону
Био — Савара.. Лля случая стационарного движения, а следова¬
тельно, и квазистационарного, вычисления приведены в работе
[1]. Лля нестационарного движения, сопровождаемого вихре¬
вым следом, вычисления дают следующее выражение для ин-
е
(и
365
дуктивной скорости dv вдоль оси у:
УК, z')Kcdj 7'К, z')Ied(j
2*-К' - О 4А'УТ^Т2
, —i_v*t 1_L_
4ttAV1 - г'2
УК, *')#
(г' - г)2 +
(y~’y')Idz Xy'dt
- г)2 4зг
-1
j Ipdz. (2)
Здесь
. _ 7 VI - 22
х — координата присоединенного вихря, принадлежащего по¬
лоске, заключенной между прямыми z = Chz = C + Аг, а -
длина полоски, хп — координата ее передней кромки. То же са¬
мое относится к полоске «штрихованной», в середине которой
лежит точка N'. Значения z отнесены к полуразмаху L. Ве¬
личина у' есть нестационарная плотность вихря в точке (£, z')
«штрихованного» сечения. Функция Ке равна
где 2е — ширина «штрихованной» полоски, А' = L/a. Далее,
/ = h 4- /2, где
А'е
\Л?-02 + А,2е
h 1 + Vlp + Ж 1 + 0 + С -Я2 + УЧ=' - -)2 ’
p(z) + q(z){ 1 +Q + К' - О
(3)
Р ='(*П-*")/«'. Я = 1 - a(z)/a'(z'),
(4)
€=«'
366
причем х и соответственно £ есть координата точки, лежащей
на продольном боковом вихре, с плотностью, изменяющейся в
зависимости от (,
= 7(0 - 7'(0, Л. = 1 + V((, _У+ х,,е, = (5)
h, = т* = (6)
ОО
— х
У [(Х>.-х)* + (Z> - z)2]3/2dl- (7>
f=ar
Если движение принять квазистационарным, то интеграл 1р бу¬
дет равен нулю и выражение (2) дает возможность сразу найти
скорость v. Следует отметить, что это выражение позволяет пе¬
рейти к пределу при е —► 0 и рассматривать интегралы в смысле
главного значения. Вычисление их будет показано ниже.
Используя выражение (2), можно составить уравнение непро¬
ницаемости в точке N*. Действительно, это уравнение, вообще
говоря, имеет вид
v = Voon. (8)
Подставляя вместо v его значение и выделяя интеграл с особен¬
ностью, можно привести это уравнение к виду, который являет¬
ся обобщением стационарного случая на нестационарный. Для
стационарного случая уравнение было получено в работе [1].
Внешний вид его остается тем же, но значения входящих в него
выражений будут другими. Уравнение приводится к виду
1 1
°°п 4А'\/Г^_г'2 У
-1 -1
(9)
где
I-IC С/ '\-т J.T 2А'(1-Я,)>Л-75
£ > г> ~ ) — he + he
1Г(С-0
1 1
_1VP fVi^(i-h)dz i
» 7 (2'-2)2 n' 7
-1 -1
a'27T=T2
j Ifidz. (10)
-1
367
В стационарном случае последнее слагаемое в (10) пропадает, а
выражение для /2 превращается в ноль, так что 1 = 1\. Уравне¬
ние (9) есть интегродифференциальное вследствие наличия ин¬
теграла 1р. Если приближенно взять 0 « -дук/дх, где ук —
квазистационарная плотность, то (9) приведется к интеграль¬
ному уравнению того же типа, который имеет место в стацио¬
нарном случае, но с добавочным «скосом» потока, зависящим
от 1р. Это уравнение можно решать путем приведения его к
системе алгебраических линейных уравнений [1, 2] с гаранти¬
рованным выполнением краевых условий при £ = ±1 или же
привести его к интегральному уравнению Фредгольма второ¬
го рода с регулярным ядром [3] путем обращения сингулярного
интеграла левой части в соответствующем классе функций, от¬
вечающих краевым условиям. Как показывают сравнительные
расчеты [4], уравнение (9) удобнее всего решать методом ите¬
раций, рассматривая его правую часть как некоторый плоский
перекошенный поток, вызванный влиянием всех свободных вих¬
рей. При этом скорость скоса учитывается интегралом, стоя¬
щим в правой части уравнения. Расчеты на ЭВМ показывают
хорошую практическую сходимость итераций.
При численном решении рассматриваемой задачи приходит¬
ся встречаться с вычислением интеграла вида
-1 -1
где F(z) и F*(z) — аналитические функции и F{zf) = F*(<r'). Пу¬
тем непосредственных вычислений можно убедиться, что
<**>
\-1 *'+е/ -1
Лля получения этой формулы достаточно при е ф 0, т. е. до
перехода к пределу е —► 0, воспользоваться интегрированием
по частям с учетом условий Ф(±1) = 0, Ф(~') = 0. Если ввести
замену z = — cos <р и представить Ф в виде
N
Ф(— cos <р) = ^ Вп sin тир, 0 ^ <р $ 7г,
п = 1
368
то формулу (11) можно привести к виду
J_yp f _Щ<Р,) + Т,п=Л”‘-1)Вп*тп‘рг
4ж * / (z — z')2 4siny?'
-l
Ф(^) = W) - ^ V) = 0.
Если коэффициенты Bn выразить по формулам Бесселя:
2 } 2 М~1
Вп = - / Ф sin n$d6 « — sin п0ц,
* о
где М — число делений промежутка (0, тг), то интеграл (11) пре¬
образуется к форме
М-1
и?1) = ^2 фцал?1)’
»=i
которая удобна при решении уравнения (9) методом итераций
[5, б].
УКАЗА ТЕЛЬ ЛИТЕРА ТУРЫ
1. Поляхов Н. Н. Об интегральном уравнении теории несущих поверхно¬
стей//Вестн. Ленингр. ун-та. 1973. № 7. С. 115-121. [37*]
2. Каландия А. И. Математические методы двумерной упругости. М.,
1973.
3. Смирнов В. И. Курс высшей математики. Т. 4. М., 1951.
4. Мельникова О. Ф., Поляхов Н. Н. О построении начального при¬
ближения для решения интегрального уравнения несущей поверхно-
сти//Вестн. Ленингр. ун-та. 1979. Jfs 1. С. 104-110. [44*]
5. Поляхов Н. И., Шесшернина 3. Н. О существовании решения инте¬
грального уравнения несущей поверхности//Вестн. Ленингр. ун-та.
1975. № 19. С. 102-107. [38]
6. Поляхов П. Н., Шесшернина 3. Н. Гармонические колебания прямо¬
угольного крыла с циркуляцией, переменной по размаху//Вестн. Ле¬
нингр. ун-та. 1984. № 19. С. 44-50. [50*]
369
IV.10. РАСЧЕТ ПРОФИЛЯ СКОРОСТИ
В КРУГОВОМ КАНАЛЕ С ПРЯМОУГОЛЬНЫМ
ПОПЕРЕЧНЫМ СЕЧЕНИЕМ [60]*
В настоящей работе на основании результатов, полученных
в [1, 2], предложен метод расчета профиля скорости в круговом
канале с прямоугольным поперечным сечением. Для случая ги¬
дродинамически стабилизированного режима изотермического
течения вязкой несжимаемой жидкости определена корректиру¬
ющая функция, которая в сумме с распределением скорости для
двухмерного (плоского) течения в круговом канале [1] дает про¬
филь продольной составляющей в поперечном сечении кругово¬
го канала.
Введем систему ортогональных координат, оси у и z которой
лежат в плоскости произвольного поперечного сечения канала
на линиях симметрии, а ось х совпадает с осевой линией кана¬
ла и направлена вниз по течению. Пусть ось z перпендикулярна
плоским боковым стенкам канала, а ось у направлена вдоль ра¬
диуса осевой линии канала.
Если размеры поперечного сечения приняты равными 2h и ‘2а,
то координаты поперечного сечения канала будут задаваться
системой неравенств |у| ^ h и \z\ ^ а.
Будем искать продольную составляющую скорости в виде
суммы и = V(y) -f W(y, z), где V(y) — распределение скорости
двухмерного течения из [1]:
в = дхр/(2рх2)\ дхр— продольный градиент давления, ^ — ди¬
намическая вязкость, х = Я'1—радиус осевой линии канала;
Я = 1+ху, #i = Я(-Л), Но = Я(+Л); W(y, z) — решение краевой
задачи
Уравнение для W получено из уравнений Навье — Стокса и
уравнения неразрывности.
*Соавт. В. А. Разумов, В. Л. Мовсесян.
+ In# , (1)
V(±/i) = О,
(2)
(02, + *н~1ду - х~Н~2 + d]z)W = о,
W(|y| ^h,z = ±о) = -V(y),
W(y = ±h, |г| ^ a) = 0.
(3)
(4)
(5)
370
Выполняя разделение переменных W(y, z) = F(y)G(z), из (3)
(5) имеем
H2F" + xHF' + (А2Я2 - x2)F = 0, (6)
G" - A2G = 0, (7)
где А — константа разделения в задаче Штурма—Лиувилля,
Собственные функции этой задачи имеют вид
Wn(y, z) = Dndi(\nZ)Zi{\nr), (8)
где решение уравнения (7)
Zi(Anr) = ^{ХппШХпГ) - Ji(Ann)tfi(A„r) (9)
является цилиндрической функцией первого порядка, г = (1 +
>гу)/х, J1 и Ni—функции Бесселя и Неймана первого поряд¬
ка, Г\ — (1 - x/i)/x и r*2 = (1 + xh)/x—радиусы внутренней и
внешней цилиндрических поверхностей кругового канала. Соб¬
ственные значения Ап определяются из уравнения следующего
вида:
N](Xnri)Ji(Xnr2) - Ni{Xnr2)J\(Xnri) = 0. (10)
Вычисляя Dn с учетом (2), (4) и (5), находим корректирую¬
щую функцию
\\г/ ^ [Zo(Anr)-Z0(Anr1)]ch(Anz)Z1(Anr)
~ A3[r22Z02(Anr2)-r?Z2(Anrn)]c.h(Ana)’ U'
где Zo — цилиндрическая функция нулевого порядка, q = —4x6/.
Окончательно из (11) с учетом (1) получим формулу для рас¬
чета профиля скорости в поставленной задаче.
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Разумов В. А., Мовсесян В. Л., Агафонова О. Г., Поляхов Н. Н. Гидроди¬
намика ламинарных течений вязкой несжимаемой жидкости в плоских
и щелевых криволинейных каналах постоянной геометрии//Пробле¬
мы экономии топливно-энергетических ресурсов на промпредприлти-
ях и ТЭС: Межвуз. сб. науч. тр. Л., 1988. С. 18-23. [58]
2. Разумов В. А., Мовсесян В. Л., Паулич Т. М., Поляхов //. Н. Расчет
профиля скорости для ламинарного течения вязкой несжимаемой жид¬
кости в каналах с прямоугольным поперечным сечением//Проблемы
экономии топливно-энергетических ресурсов на промпредприятиях и
ТЭС: Межвуз. сб. науч. тр. Л., 1988. С. 42-47. [59]
371
СПИСОК ОСНОВНЫХ НАУЧНЫХ ТРУЛОВ
Н.Н. ПОЛЯХОВА*
Аэрогидродинамика
1. Движение жидкости с большими скоростями//Александров В. JI.
Техническая гидромеханика. М., 1932. 216 с. С. 183-200.
2. Аэродинамический расчет самолета, расчет гребного винта и ряд
заметок по динамике полета// Ветчинкин В. П. Динамика самолета.
Ч. 1, 2. Изд. 2-е, перераб. и доп. М.; Л., 1933. 409 с. С. 42-87.
3. К теории гребного винта: 1. Обобщение теории винта типа НЕЖ на
винты с переменной циркуляцией. 2. О винте с произвольным рас¬
пределением циркуляции по лопасти. 3. Распределение циркуляции
по лопасти произвольной формы в плане. 4. Сжатие струи за вин¬
том // Труды ЦАГИ им. Н. Е. Жуковского. 1935. Вып. 184. С. 1 -32.
4. * Теория винта с конечным числом лопастей: 1. Теория винта с конеч¬
ным числом лопастей. 2. Поверочный аэродинамический расчет вин¬
та. 3. О наивыгоднейшем винте с конечным числом лопастей //Труды
ЦАГИ им. Н.Е.Жуковского. 1937. Вып. 324. С. 1 -48.
5. Теория и расчет воздушного гребного винта с конечным числом лопа¬
стей. Ч. 1. Аэродинамика//Труды ИАГИ им. Н. Е. Жуковского. 1939.
Вып. 366. С. 1 - 224. (Совм. с В. П. Ветчинкиным).
6. О наивыгоднейшем винте//Труды ЦАГИ им. Н. Е. Жуковского. 1939.
Вып. 455. С. 1-33.
7. Теория и расчет воздушного гребного винта (Аэродинамика и проч¬
ность). М., 1940. 520 с. (Совм. с В. П. Ветчинкиным).
8. О влиянии винта на крыло//Труды Ленингр. политехи, ин-та. 1942.
№ 1. С. 162-173.
9. The minimum energy loss propeller//Techn. Memoranda Nath. Adv. Comm.
Aeronaut (NACA). 1945. N 1067. P. 25-29.
10. Движение жидкости с большими скоростями//Александров В. Л.
Техническая гидромеханика. М.; Л., 1946. 431 с. С. 348-410.
11. Вихревая теория воздушного гребного винта с конечным числом лопа¬
стей: Докт. дис. М., Военно-воздушн. академия им. Н. Е. Жуковского,
1947. 280 с.
12. К вопросу о расчете крыла конечного размаха//Труды Ленингр.
ин-та авиац. приборостроения. 1947. Т. 1. С. 17-30.
13. О соосных винтах, вращающихся в разные стороны //Труды Ленингр.
ин-та авиац. приборостроения. 1947. Т. 1. С. 38-49.
*Список составлен по хронологическому принципу. Звездочкой отме¬
чены работы, вошедшие в настоящее издание.
372
14. * Теоретические основы метода расчета кавитирующего винта//Тру¬
ды ЦНИИ им. А. Н. Крылова. 1948. Вып. 34. С. 1 -18.
15. Владимир Петрович Ветчинкин. 1888- 1950//Судостроение. 1951. №2
(194). С. 34.
16. Работы В. II. Ветчинкина по теории и расчету винтов// Изв. АН
СССР (ОТН). 1952. № 5. С. 771-775.
17. Некоторые вопросы теории крыльев конечного размаха (несущая по¬
верхность) // Бюлл. ВВМИУ им. Ф. Э. Дзержинского. 1952. N* 3. С. 7-
31. (Совм. с А. И. Пастуховым).
18. * Обтекание решеток телесных профилей заданной формы // Докл. АН
СССР. 1952. Т. 84. № 2. С. 233-236.
19. * О распределении давления на поверхности профиля; движущегося
нестационарно// Докл. АН СССР. 1952. Т. 87. № 6. С. 901-904.
20. Вихревая теория гребного винта с точки зрения теории jtetueтки//
Труды Ленингр. политехи, ин-та. 1953. № 5. С. 45-48.
21. * К теории крыла конечного размаха С. А. Чаплыгина//Труды Ле¬
нингр. политехи, ин-та. 1953. № 5. С. 168-175. (Совм. с А. И. Па¬
стуховым).
22. Работы В. П. Ветчинкина по теории и расчету гребных винтов и ветря¬
ных двигателей //Труды по истории техники. 1954. Вып. 4. С. 52-58.
23. * Теория решетки пластин по Н. Е. Жуковскому и ее обобщение на слу¬
чай произвольного профиля//Вестн. Ленингр. ун-та. 1956. Jfs 1.
С. 125-144.
24. Об индуктивных силах при нестационарном движений крылового про¬
филя// Вестн. Ленингр. ун-та. 1956. № 7. С. 87-93.
25. Теория крыла конечного размаха, колеблющегося гармонически //
Вестн. Ленингр. ун-та. 1957. № 19. С. 87-97.
26. * Теория несущей поверхности прямоугольной формы//Вестн. Ле¬
нингр. ун-та. 1959. № 13. С. 93-110. (Совм. с А. И. Пастуховым).
27. Работы В. П. Ветчинкина по гребным винтам и прочности самолета//
Ветчинкин В. П. Избранные труды. Т. 2. Гребные винты. Прочность
самолета. М., 1959. С. 3-8. (Совм. с Н. В. Зволинским).
28. * Теория нестационарных движений несущей поверхности. Л., 1960.
84 с. (Монография).
29. Влияние кривизны потока на работу элемента гребного винта//
Вестн. Ленингр. ун-та. 1962. № 1. С. 134-141.
30. * Теория несущей винтовой поверхности//Вестн. Ленингр. ун-та.
1963. № 13. С. 92-105.
31. Леонид Николаевич Сретенский (К шестидесятилетию со дня рожде¬
ния)// Успехи матем. наук. 1963. Т. 18. Вып. 1. С. 192-205. (Совм. с
Я. И. Секкерж-Зенковичем, В. И. Смирновым, С. П. Финиковым).
32. Теория нестационарных движений крыла малого удлинения//Труды
Ленингр. кораблестроит. ин-та. 1964. Вып. 45. С. 45-55. (Совм. с
А. Н. Холодилиным).
33. Константин Иванович Страхович//Инж.-физич. журн. 1965. Т. 8.
№ 3. С. 409-410. (Совм. с С. В. Валландером, И. П. Гинзбургом,
П. П. Юшковым).
34. * Вихревая теория несущей поверхности//Вестн. Ленингр. ун-та.
1968. № 19. С. 121-131. (Совм. с А. И. Пастуховым).
373
35. Константин Иванович Страхович // Инж.-физич. журн. 1969. Т. 16.
№ 2. С. 373-374. (Совм. с А. В. Лыковым, И. П. Гинзбургом, В. А. Зыси-
ным, В. Ф. Рисом, П.П. Юшковым).
36. * Приближенная нелинейная теория обтекания тел цилиндрической
формы стационарным потоком несжимаемой жидкости//Вестн. Ле¬
нингр. ун-та. 1971. Jfc 7. С. 98-106. (Совм. с В. Н.Трещевским).
37. * Об интегральном уравнении теории несущих поверхностей//Вестн.
Ленингр. ун-та. 1973. № 7. С. 115-121.
38. * О существовании решения интегрального уравнения несущей поверх¬
ности//Вестн. Ленингр. ун-та. 1975. № 19. С. 102-107. (Совм. с
3. Н. Шестерниной).
39. Theorie der instationaren Bewegung ernes Flugels kleiner Spannweite mit einem
Profil endlicher Dicke//Experim. und Mathem. Metoden der Grundlagen-
forsch. in der SchifTstechnik: Schiffstechn. Symp. Rostock Universitat. Rostock,
1975. S. 231-236. (Совм. с В. H. Трещевским).
40. К вопросу о гашении ветрового волнения в среде с естественной тур¬
булентностью//Вестн. Ленингр. ун-та. 1976. ДО* 19. С. 115-122. (Совм.
с К.К.Ляпиным, В. А. Разумовым).
41. О применении гипотезы Вайзингера при расчете обтекания стре¬
ловидной пластины//Специальные вопросы аарогазодин&мики лета¬
тельных аппаратов. Вып. 108. Л., ЛИАП, 1976. С. 68-74. (Совм. с
О. Ф. Мельниковой).
42. Сергей Васильевич Валландер//Вестн. Ленингр. ун-та. 1976. № 13.
С. 5-9. (Совм. с Р. Г. Баранцевым, 3. И. Боревичем, А. А. Грибом).
43. * О решении интегрального уравнения обтекания несущей поверхно¬
сти // Вестн. Ленингр. ун-та. 1978. .№ 1. С. 123-128. (Совм. с
О. Ф. Мельниковой).
44. * О построении начального приближения для решения интегрального
уравнения несущей поверхности//Вестн. Ленингр. ун-та. 1979. № 1.
С. 104-110. (Совм. с О. Ф. Мельниковой).
45. * К вопросу о сходимости метода дискретных вихрей // Вестн. Ле¬
нингр. ун-та. 1979. № 7. С. 75-81. (Совм. с 3. Н. Шестерниной).
46. Стационарное обтекание прямоугольного крыла с циркуляцией, пере¬
менной по размаху//Вестн. Ленингр. ун-та. 1980. № 13. С. 85-92.
(Совм. с 3. Н. Шестерниной).
47. * Заметка о методе дискретных вихрей//Вестн. Ленингр, ун-та. 1980.
№ 19. С. 109-110.
48. * О методе дискретных вихрей //Специальные вопросы аэрогазодина¬
мики летательных аппаратов. Вып. 145. Л., ЛИАП, 1980. С. 3-8.
49. Об улучшении точности численного решения интегрального урав¬
нения осесимметричного обтекания тел вращения // Вестн. Ленингр.
ун-та. 1982. № 13. С. 67-72. (Совм. с О. Ф. Мельниковой).
50. * Гармонические колебания прямоугольного крыла с циркуляцией, пе¬
ременной по размаху//Вестн. Ленингр. ун-та. 1984, № 19. С. 44-50.
(Совм. с 3. Н. Шестерниной).
51. Теория нестационарного движения крыла. Справочник по теории ко¬
рабля: В 3 т. / Под ред. Я. И. Войткунского. Т. 1. Гидромехани¬
ка. Сопротивление движению судов. Судовые движители. Л., 1985.
С. 165 — 177. (Совм. с В. Н. Трещевским).
374
52. Ламинарное течение жидкости между эквидистантными стенками по¬
стоянной кривизны. Лепонир. в ВИНИТИ 12 июля 1985 г. № 5003-85.
М., 1985. 12 с. (Совм. с В. А. Разумовым, В. Л. Мовсесяном).
53. Гидравлическое сопротивление при ламинарном течении вязкой Жид¬
кости между эквидистантными стенками постоянной кривизны. Лепо¬
нир. в ВИНИТИ 7 августа 1985 г. № 5870-85. М., 1985. 12 с. (Совм. с
B. А. Разумовым и В. Л. Мовсесяном).
54. Оценка точности определения индуктивной скорости в теории несу¬
щей поверхности//Вопросы моделирования процессов газовой дина¬
мики и аэродинамики. Ташкент, ТПИ, 1985. С. 55-58. (Совм. с
О. Ф. Мельниковой).
55. * Практический метод расчета нестационарных характеристик крыла
с отклоняющейся частью. Лепонир. в ЦНИИ ’’Румб” 1 октября 1986 г.
Л., 1986. 10 с. (Совм. с В.М.Журавой, В. В. Николаевым).
56. * Об интегродифференци&льном уравнении для несущей поверхности
при нестационарном движении//Вестн. Ленингр. ун-та. Сер. 1. 1987.
Вып. 3. № 15. С. 75-78.
57. Аэродинамика крыла в работах С. А. Чаплыгина // История механи¬
ки в России/Под ред. А. Н. Боголюбова, И.З.Штокало. Киев, 1987.
C. 355-358.
58. Гидродинамика ламинарных течений вязкой несжимаемой жидко¬
сти в плоских и щелевых криволинейных каналах постоянной гео¬
метрии//Проблемы экономии топливно-энергетических ресурсов на
предприятиях и ТЭС. Л., ЛТИЦБП, 1988. С. 18-23. (Совм. с
B. А. Разумовым, В. Л. Мовсесяном, О. Г. Агафоновой).
59. Расчет профиля скорости для ламинарного течения вязкой несжи¬
маемой жидкости в каналах с прямоугольным поперечным сечени¬
ем //Проблемы экономии топливно-энергетических ресурсов на пред¬
приятиях и ТЭС. Л., ЛТИЦБП, 1988. С. 42 - 47. (Совм. с В. А. Разумо¬
вым, В. Л. Мовсесяном, Т.М.Паулич).
60. * Расчет профиля скорости в круговом канале с прямоугольным попе¬
речным сечением //Проблемы экономии топливно-энергетических ре¬
сурсов на предприятиях и ТЭС. Л., ЛТИЦБП, 1989. С. 26-27. (Совм.
с В. А. Разумовым, В. Л. Мовсесяном).
61. Приближенный метод расчета параметров обтекания тел вращения
под углом атаки //Вопросы аэродинамики и управления летательных
аппаратов. Л., ЛИАП, 1989. С. 3-14. (Совм. с О. Ф. Мельниковой).
62. Руль судовой типа ПН. Заявка на изобретение от 12 апреля 1991 г.
(Совм. с В. И. Николаевым).
63. * Гармонические колебания крыла с постоянной циркуляцией по раз¬
маху// Вестн. С.-Петербург, ун-та. Сер. 1. 1992. Вып. 3. № 15. С. 102-
104. (Совм. с Л. Ю. Уразаевой).
63а. * Обтекание профиля, колеблющегося гармонически с конечными ам¬
плитудами//Вестн. С.-Петербург, ун-та. Сер. 1. 1995. Вып. 1. (№ 1).
C. 89-94. (Совм. с О. Ф. Мельниковой, 3. Н. Шестерни ной).
375
Теоретическая механика.
История механики
64. Примечания к работам М. В. Остроградского по механике// Избран¬
ные труды М. В. Остроградского / Под ред. акад. В. И. Смирнова. М.,
1958. С. 512-540.
65. Развитие кафедры механики в Петербургском-Ленинградском универ¬
ситете//Очерки по истории Ленинградского университета. Вып. 1.
Л., 1962. С. 20-28.
66. Основные этапы развития механики на кафедрах Ленинградского уни¬
верситета за 1917-67 гг. //Вестн. Ленингр. ун-та. 1967. № 13. С. 5-20.
(Совм. с И. П. Гинзбургом, А. А. Грибом, Л. М. Качановым).
67. Математика, механика, астрономия в Петербургском-Ленинградском
университете//Вестн. Ленингр. ун-та. 1969. № 1. С. 5-28. (Совм. с
К. Ф. Огородниковым, В. И. Смирновым).
68. Канонические уравнения для неголономных систем // Вестн. Ленингр.
ун-та. 1970. № 1. С. 120-122.
69. Уравнения движения механических систем при нелинейных неголо¬
номных связях в общем случае // Вестн. Ленингр. ун-та. 1972. № 1.
С. 125-132.
70. О дифференциальных принципах механики, получаемых из уравнений
движения неголономных систем//Вестн. Ленингр. ун-та. 1974. № 13.
С. 106-114.
71. Опыт преподавания раздела теоретической механики ’’Движение под
действием случайных сил” в Ленинградском университете// Теорети¬
ческая механика: Сб. научно-методических статей. Вып. 4. М., 1974.
С. 25-31. (Совм. с П. Е.Товстиком).
72. Приложение неголономной механики к теории электромеханических
систем // Вестн. Ленингр. ун-та. 1977. № 13. С. 137-146. (Совм. с
А. Ю. Львовичем).
73. Растяжение плоскости с решеткой разрезов без выноса//Вестн. Ле¬
нингр. ун-та. 1981. № 7. С. 85-90. (Совм. с Н. Н. Поляховым (мл.)).
74. Растяжение плоскости с вырезом заданной формы//Вестн. Ленингр.
ун-та. 1981. № 13. С. 55-59. (Совм. с Н. Н. Поляховым (мл.)).
75. Уравнения динамики как необходимые условия минимальности при¬
нуждения по Гауссу//Колебания и устойчивость механических си¬
стем: Прикладная механика. Вып. 5. Л., 1981. С. 9-16. (Совм. с
С. А. Зегждой, М. П. Юшковым).
76. Рациональное построение раздела аналитической механики в общем
курсе механики//V Всесоюзн. съезд по теор. и прикл. механике:
Аннотации докл. Алма-Ата, 1981. С. 163. (Совм. с С. А. Зегждой,
М. П. Юшковым).
77. Принцип Суслова — Журдена как следствие уравнений динамики//
Теоретическая механика: Сб. научно-методических статей. Вып. 12.
М., 1982. С. 72-79. (Совм. с С. А. Зегждой, М. П. Юшковым).
78. Определение реакций голономных связей как прямая задача меха¬
ники// Вестн. Ленингр. ун-та. 1982. № 1. С. 65-70. (Совм. с
С. А. Зегждой, М. П. Юшковым).
376
79. Обобщение принципа Гаусса на случай неголономных систем высших
порядков//Докл. АН СССР. 1983. Т. 269. № 6. С. 1328-1330. (Совм. с
С. А. Зегждой, М. П. Юшковым).
80. Линейные преобразования сил и обобщенный принцип Гаусса//
Вестн. Ленингр. ун-та. 1984. № 1. С. 73-80. (Совм. с С. А. Зегждой,
М. П. Юшковым).
81. Теоретическая механика: Учеб. пособие для студентов механико¬
математических специальностей университетов. Л., 1984. 536с. (Совм.
с С. А. Зегждой, М. П. Юшковым).
82. Управление движением при помощи связей, зависящих от параме¬
тров// Вестн. Ленингр. ун-та. 1985. № 8. С. 56-60. (Совм. с
С. А. Зегждой, М. П. Юшковым).
83. Управление движением и дифференциальные принципы механики//
VI Всесоюзн. съезд по теор. и прикл. механике: Аннотации докл.
Ташкент, 1986. С. 519. (Совм. с М. П. Юшковым).
84. Развитие механики в Петербургском университете//История меха¬
ники в России/Под ред. А. Н. Боголюбова, И.З.Штокало. Киев, 1987.
С. 177-178.
85. Научное наследие Д. К. Бобылева // История механики в России / Под
ред. А. Н. Боголюбова, И.З.Штокало. Киев, 1987. С. 274-275.
86. Исследования Л. Эйлера по аналитической механике первого петер¬
бургского периода//Развитие идей Леонарда Эйлера и современная
наука / Под ред. Н. Н. Боголюбова, Г. К. Михайлова, А. П. Юшкевича.
М., 1988. С. 229-232.
87. Что привнесли теория относительности и квантовая механика в клас¬
сическую механику? Препринт № 330. Ин-т проблем механики АН
СССР. М., 1988. 38 с.
88. Специальная форма уравнений динамики системы твердых тел//
Докл. АН СССР. 1989. Т. 309. №4. С. 805-807. (Совм. с С. А. Зегждой,
М. П. Юшковым).
89. Использование дифференциальных принципов механики в задачах
управления с неполной программой движения//Вестн. Ленингр.
ун-та. Сер. 1. 1990. Вып. 2. № 8. С. 64-66. (Совм. с С. А. Зегждой,
М. П. Юшковым).
СПИСОК СТАТЕЙ О Н. Н. ПОЛЯХОВЕ
90. Николай Николаевич Поляхов (К 80-летию со дня рождения) // Вестн.
Ленингр. ун-та. Сер. 1. 1986. Вып. 4. С. 3-6.
91. Николай Николаевич Поляхов (Памяти ученого)//Вопросы истории
естествознания и техники. М., 1987. Вып. 4. С. 166-167.
92. Научное наследие профессора Николая Николаевича Поллхова (1906-
1987 гг.) /Авт.: Зегжда С. А., Мельникова О. Ф., Поляхов Н. Н. (мл.),
Поляхова Е. Н., Товстик П. Е., Трещевский В. Н., Шестернина 3. Н.,
Юшков М. П. // Вестн. С.-Петербург, ун-та. 1992. Сер. 1. Вып. 4. № 22.
С. 3-19.
377
URSS.ru URSS.ni URSS.m URSS.ru
Представляем Вам следующие книги:
URSS
Серия «Физико-математическое наследие: квантовая механика»
уБлохинцев Д. И. Основы квантовой механики.
у Блохинцев Д. И. Принципиальные вопросы квантовой механики.
уФлюгге 3. Задачи по квантовой механике.
у Фок В. А. Квантовая физика и строение материи.
у Мотт НСнеддон И. Волновая механика и ее применения.
у Блохинцев Д. И. Квантовая механика: Лекции по избранным вопросам.
у Родимое Б. Н. Автоколебательная квантовая механика.
у Бройль Л. де. Введение в волновую механику.
Серия «Физико-математическое наследие: история физики»
у Франкфурт У. И. Обшая теория относительности: Исторические очерки.
уХволъсон О. Д. Популярные лекции об основных гипотезах физики.
у Франкфурт У. И. Закон сохранения и превращения энергии.
уБуфеев В. А. Кто и как создал теорию относительности: История создания и развития
понимания теории относительности.
у Болотовский Б. М. Оливер Хевисайд (1850—1925).
уГуриков В. А. Становление прикладной оптики: XV—XIX вв.
у Соколовская (Новокшанова) 3. К. Василий Яковлевич Струве.
у Столетов А. Г. Ньютон, Гельмгольц, Ковалевская.
уРозенбергер Ф. История физики в четырех книгах.
уФренкель В. Я., Явелов Б. Е. ЭЙНШТЕЙН: Изобретения и эксперимент.
уГуриков В. А. Возникновение и развитие оптико-электронного приборостроения.
у Житомирский С. В. Архимед.
у Космодемьянский А. А. Константин Эдуардович Циолковский (1857—1935).
у Космодемьянский А. А. Очерки по истории механики.
у Веселовский И. Н. Очерки по истории теоретической механики.
уРожанская М. М. Механика на средневековом Востоке.
у Щербаков С. В. Исторический очерк развития учения о движении небесных тел.
Серия «Физико-математическое наследие: философия физики»
уМиткевич В. Ф. Основные физические воззрения: Сборник докладов и статей.
у Бунге М. Философия физики.
у Бунге М. Причинность: Место принципа причинности в современной науке.
у Кассирер Э. Теория относительности Эйнштейна.
у Пуанкаре Л. Эволюция современной физики.
уГрюнбаум А. Философские проблемы пространства и времепи.
у Чудинов Э. М. Философские проблемы современной физики.
у Лазарев П. П. Физические основания принципа относительности.
у Кузнецов Б. Г. Принцип дополнительности.
у Кузнецов Б. Г. Принципы классической физики.
у Бом Д. Причинность и случайность в современной физике.
у Кузнецов Б. Г. Развитие научной картины мира в физике XVII—XVIII вв.
у Кузнецов Б. Г, Разум и бытие.
URSS.ru ilRSS.ru URSS.ru liRSS.ru
Представляем Вам следующие книги:
s Кононович Э. В., Мороз В. И. Общий курс астрономии.
s Спиридонов О. Я. Фундаментальные физические постоянные: От начал физики
до космологии.
URSS
s Тарасов Л. В., Тарасова А. Я. Беседы о преломлении света.
sСпиридонов 0. 77. Биографии физических констант.
sЛоренц Х.А. КУРС ФИЗИКИ.
уфрова А. Почему происходит то, что происходит: Окружающий мир глазами ученого.
s Тарасов Л. В. Четырнадцать лекций о лазерах.
s Гааз А. Волны материи и квантовая механика.
✓ Эльясберг П. Е. Измерительная информация: Сколько ее нужно? Как ее обрабатывать?
у Розенблат Г. М. Механика в задачах и решениях.
sКвасников И. А. Молекулярная физика.
✓Джашитов В. Э., Панкратов В. М., Голиков А. В. Мультимедийный курс теоретической
механики: Теория и компьютерный эксперимент.
s Уле О. Почему и потому: Учебпик физики в вопросах и ответах.
✓ Тиндаль Дж. Физика в простых уроках.
^Конобеев Ю. В. и др. (ред.) Физики продолжают шутить.
sИсаев 77. С. Обыкновенные, странные, очарованные, прекрасные... Об истории
РАЗВИТИЯ ТЕОРЕТИЧЕСКИХ ИДЕЙ В ФИЗИКЕ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ.
sГартман 3. Занимательная физика, или Физика во время прогулки,
у Тисандье Т. Научные развлечения.
s Вердеревская Н. 77., Егорова С. П. Сборник задач и вопросов по физике.
✓ Баиыачев Ю.А., Богданов Д. Л. Фундаментальные эксперименты физики: Курс лекций.
✓Сачков И. Н. Электромагнетизм: Эффекты, история, парадигма.
у Киселев А. 77. Элементарная физика для средних учебных заведений. Со многими
упражнениями и задачами: Акустика, оптика, магнетизм, электричество, гальванизм,
механический отдел, приложения.
s Пятницкий Л. Н. Безопасность дорожного движения глазами физика.
✓ Тарасов Л. В. Введение в кваптовую оптику.
sЛебедев В. И. Исторические опыты по физике.
sПерельман М. Е. Наблюдения и озарения, или Как физики выявляют законы природы:
ОТ АРИСТОТЕЛЯ ДО НИКОЛЫ ТЕСЛЫ.
✓Хволъсон О. Д. Популярные лекции об электричестве и магнетизме.
sВеников В. А., Веников Г. В. Теория подобия и моделирования: Применительно
к задачам электроэнергетики.
s Николаев О. С. Физика и астрономия: Курс практических работ для средней школы.
sМакеева Г. Я., Цедрик М. С. Физические парадоксы и занимательные вопросы.
✓ Торчигин В. Я., Торчигин А. В. Шаровая молния: От невероятного к очевидному.
✓ Точидловский И. Я. Что можно в школе сделать и показать по физике.
s Миткевич В. Ф. (.Академик АН СССР) Физические основы электротехники.
URSS.ru URSS.ru URSS.ru URSS.ru
' '<
ruURSS.ru URSS.ru URSS.ru
со
ШЩ0
T-
и
-.4 -
шт
тт
Представляем Вам следующие книги:
sКабисов К. С., Камалов Т. Ф., Лурье В. А. Колебания и волновые процессы.
s Кирхгоф Г. Механика. Лекции по математической физике.
sДобролюбов А. И. Скольжение, качение, волна.
мрсс
sЗельдович Я. Б. Теория ударных волн и введение в газодинамику. ипот
^Мейз Дж. Теория и задачи механики сплошных сред.
sСелезнев В. Е., Прялов С. Н. Численное моделирование течений в магистральных
системах.
s Самарский А. А., Вабищевич П. Н. Численные методы решения задач
конвекции—диффузии.
sСокольников И. С. Тензорный анализ: Теория и применения в геометрии и в МСС.
/Гликлих Ю. Е. Глобальный и стохастический анализ в задачах математической физики.
s Ильюшин А. А., Ломакин В. А., Шмаков А. П. Задачи и упражнения по механике
сплошной среды.
s Грац Ю. В. Лекции по гидродинамике.
s Шам и н Р. В. Математические вопросы волн-убийц.
sЛещенко А. П. Фундаментальная строительная механика упругих систем: Теория,
практика, примеры. Научно-практическое пособие для инженеров, проектировщиков
и научных работников.
/Шулейкин В. В. Очерки по физике моря.
s Пятницкий Л. Н. Природа турбулентности и обратная задача.
sЕрохин В. Г., Маханько М. Г. Сборник задач по основам гидравлики и теплотехники.
s Свалов А. М. Проблемы добычи нефти и газа. Капиллярные эффекты в подземной
гидродинамике: Новые результаты.
s Власов А. А. Статистические функции распределения.
s Шулейкин В. В. Физика моря.
sЛионе Ж.-Л. Некоторые методы решения нелинейных краевых задач.
sАбурджаниа Г. Д. Самоорганизация нелинейных вихревых структур и вихревой
турбулентности в диспергирующих средах.
s Билля А. Теория вихрей.
^Планк М. Введение в теоретическую физику: Механика деформируемых тел. Пер.
с нем.
■/Звягин В. Г., Турбин М. В. Математические вопросы гидродинамики вязкоупругих сред.
sПопов И. В., Фрязинов И. В. Метод адаптивной искусственной вязкости численного
решения уравнений газовой динамики.
s Бобылев Д. К. Очерк теории водяпых течений, выработанной Буссинеком.
^Галавкин В. В. Синергетическая физика, или Мир наоборот.
s Щербаков Ю. В. Теория полета дирижаблей: Краткий курс.
sIOh А. А. Моделирование турбулентных течений.
s Климонтович Ю.Л. Турбулентное движение и структура хаоса.
уЖелиговский В. А. Математическая теория устойчивости магнитогидродинамических
режимов к длинномасштабным возмущениям.
s Селезнев В. Е., Алешин В. ВКлишин Г. С. Методы и технологии численного
моделирования газопроводных систем.
s Селезнев В. Е., Прялов С. Н. Методы построения моделей течений в магистральных
трубопроводах и каналах.
sЖуковский Н. Е. О гидравлическом ударе в водопроводных трубах.
ru URSS.ru URSS.ru URSS.ru
nj'ssun nj-ssun nJSSMIl njssun nj'SSUn
iijsstm njssMn nj'ssun nj-ssun nj-ssHn
URSS.ru URSS.ru URSSm URSS.ru
Представляем Вам следующие книги:
s Кривошапко С. Н., Иванов В. Н. Энциклопедия аналитических поверхностей.
^Секованов В. С. Что такое фрактальная геометрия?
^Жукарев А. С. и др. Задачи повышенной сложности в курсе общей физики.
■/Федер Е. ФРАКТАЛЫ. URSS
s Иванов Б. Н. Законы физики.
s Петров К П. О достижениях аэродинамики летательных аппаратов,
у' Бойз Ч. Мыльные пузыри.
s Петров Ю. И. Парадоксы фундаментальных представлений физики.
sОлемской А. И. Синергетика сложных систем: Феноменология и статистическая теория.
s3umoh А. Д. Что такое адгезия.
sЭглит М. Э. Лекции по основам механики сплошных сред.
s Губанков В. Н. Солитоны.
sБыков Л. В., Молчанов А. М., Щербаков М. А., Янышев Д. С. Вычислительная механика
сплошных сред в задачах авиационной и космической техники.
sМалинецкий Г. Г. (ред.) Нелинейность в современном естествознании.
sHeimapK Ю. И, Ланда П. С. Стохастические и хаотические колебания.
s Киселев А. П. Элементарная физика для средних учебных заведений. Со многими
упражнениями и задачами: Введение, основные сведения из механики, тяжесть,
жидкости, газы, теплота.
s Вебстер А. Г. Механика материальных точек, твердых, упругих и жидких тел. В 2 т.
sКраснов Н. Ф. Аэродинамика: Основы теории. Аэродинамика профиля и крыла.
s Краснов Н. Ф. Аэродинамика: Методы аэродинамического расчета.
sАндрианов И. ВБаранцев Р. Г., Маневич Л. И. Асимптотическая математика
и синергетика: Путь к целостной простоте.
^ Гухман А. А. Введение в теорию подобия.
^Лагалли М. Векторное исчисление в применении к математической физике.
sПетров Ю. И. Заблуждения и ошибки фундаментальных концепций физики.
s Иванов Б. Н. Мир физической гидродинамики: От проблем турбулентности
до физики космоса.
s Эйхенвальд А. А. Теоретическая физика: Механика твердого тела.
^Кляцкин В. И. Очерки по динамике стохастических систем.
sБардзокас Д. И., Зобнин А. И., Сеник И. А., Фильштинский М.Л. Задачи по теории
термопьезоэлектричества с подробными решениями.
sБеляков И. С., Носко А. П. Неидеальный тепловой контакт тел при трении.
s Циолковский К Э. Труды по воздухоплаванию.
s Коровайцев А. В., Коровайцева Е.А., Столярчук В. А. Структурный подход в расчетах
прочности и устойчивости простейших элементов конструкций летательных аппаратов.
s Циолковский К Э. Труды по ракетпой технике.
✓ Подосенов С. А., Потапов А. А., Фоукзон Дж., Менъкова Е. Р. Неголономные,
фрактальные и связанные структуры в релятивистских сплошных средах,
электродинамике, квантовой механике и космологии. В 3-х кн.
✓Лермит Р. Проблемы технологии бетона.
s Работное Ю. Н. Введение в механику разрушения.
✓ Тывес Л. И. Динамика виброударных моделей механизмов и рабочих процессов: Точные
методы нелинейной механики. Метод припасовывания.
✓Старченко И. Б. Динамический хаос в гидроакустике.
и
и
вя:
■ ■
S--''
09
URSS.ru URSS.ru URSS.ru URSS.ru
ill
Ев
ru
URSS.ru
URSS.ru
URSS.ru
Ш
Ж
09
URSS
Представляем Вам следующие книги:
s Перельман М. Е. А почему это так? Физика в гостях у других наук.
sПерельман М. Е. А почему это так? Физика вокруг нас.
s Пригожий И., Стенгерс И. Время. Хаос. Квант. К решению
парадокса времени.
s Гарднер М. Загадки Сфинкса и другие математические головоломки.
sСвердлик А. Г. Как эмоции влияют на абстрактное мышление и почему математика
невероятно точна: Как устроена кора головного мозга, почему её возможности
ограничены и как эмоции, дополняя работу коры, позволяют человеку совершать
научные открытия.
s Перельман Я. И. Обманы зрения: Коллекция оптических иллюзий.
s Раков Д. Л., Печейкина Ю.А. Парадоксальный мир невозможных фигур
и оптических иллюзий.
sПригожий Стенгерс И. Порядок из хаоса. Новый диалог человека с природой.
у Владимиров Ю. С. Пространство-время: явные и скрытые размерности.
sСпиридонов О. П. СВЕ'Е ФИЗИКА. ИНФОРМАЦИЯ. ЖИЗНЬ: О природе
уникального явления, его роли в изучении Вселенной, в появлении жизни и об
изобретательном гении человечества.
sKau, Е.А. Фуллерены, углеродные нанотрубки и нанокластеры: Родословная форм
и идей.
s Федин С. Н. Математики тоже шутят.
s Попова А. П. Занимательная астропомия.
✓ Тимердинг Г. Е. Золотое сечение.
^Ген. Меладзе. Легкомысленные записки ученого с большой дороги: Научный блеф-клуб.
sXeau М. П. Неистовая Вселенная: от Большого взрыва до ускоренного расширения,
от кварков до суперструн.
s Вигнер Э. Инвариаптность и законы сохранения. Этюды о симметрии.
sЛанге В. П. Физические опыты и наблюдения в домашней обстановке.
Закгейм А. Ю. Системность — симметрия — эволюция в физике, химии, биологии.
sЛанге В. Н. Физические парадоксы, софизмы и занимательные задачи: Электричество
и магнетизм. Колебания и волны. Оптика. Теория относительности. Атомная и ядерная
физика.
s Архангельская И. Д., Чернин А. Д., Розенталь И.Л. Космология и физический вакуум.
Тел./фанс:
+7 (499) 724-25-45
(многоканальный)
E-mail:
URSS@URSS.ru
http://URSS.ru
Наши книги можно приобрести в магазинах:
«НАУКУ - ВСЕМ!» (м. Профсоюзная, Нахимовский пр-т, 56. Тел. (499) 724-2545)
«Библио-Глобус» (м. Лубянка, ул. Мясницкая, 6. Тел. (495) 625-2457)
«Московский дом книги» (м. Арбатская, ул. Новый Арбат, 8. Тел. (495) 203-8242)
«Молодая гвардия» (м. Полянка, ул. Б. Полянка, 28. Тел. (495) 238-5001,
(495) 780-3370)
«Дом научно-технической книги» (Ленинский пр-т, 40. Тел. (495) 137-6019)
«Дом книги на Ладожской» (м. Бауманская, ул. Ладожская, 8, стр.1.
Тел. (495) 267-0302)
«Санкт-Петербургский Дом книги» (Невский пр., 28. Тел. (812) 448-2355)
«Книжный бум» (г. Киев, книжный рынок «Петровка», ряд 62, место 8
(павильон «Академкнига»). Тел. +38 (067) 273-5010)
Сеть магазинов «Дом книги» (г. Екатеринбург, ул. Антона Валека, 12.
Тел. (343) 253-5010)
URSS.ru
URSS.ru
URSS.ru
URSS.ru
URSS.ru URSS.ru URSS.ru URSS.ru URSS.ru
05
05
10
Ш
05
05
С.
5?
05
05
ю
05
URSS
Уважаемые читатели! Уважаемые авторы!
Наше издательство специализируется на выпуске научной и учеб¬
ной литературы, в том числе монографий, журналов, трудов ученых
Российской академии наук, научно-исследовательских институтов
и учебных заведений. Мы предлагаем авторам свои услуги на выгод¬
ных экономических условиях. При этом мы берем на себя всю ра¬
боту по подготовке издания — от набора, редактирования и верстки
до тиражирования и распространения.
Среди вышедших и готовящихся к изданию книг мы предлагаем Вам следующие:
sАганов А. В., Сафиуллин Р. К., Скворцов А. Таюрский Д. А. Физика вокруг нас:
КАЧЕСТВЕННЫЕ ЗАДАЧИ ПО ФИЗИКЕ. Около 1500 задач с подробными
решениями.
s Грин Б. Скрытая реальность: Параллельные миры и глубинные законы Космоса.
sПфаундлер Л. ФИЗИКА ОБЫДЕННОЙ ЖИЗНИ.
s Рэндалл Л. Закручепные пассажи: Проникая в тайны скрытых
размерностей пространства.
s Грин Б. Ткань космоса: Пространство, время и текстура реальности.
✓ Вайнберг С. Мечты об окончательной теории: Физика в поисках самых
фундаментальных законов природы.
sKpyuianoe А. А., Мамчур Е.А. (ред.) Будущее фундаментальной науки:
Концептуальные, философские и социальные аспекты проблемы.
sСерый А. А., Серая Е. И. Изобретая инструменты науки будущего: Ускоряющая науку
ТРИЗ: Физика ускорителей, лазеров, плазмы.
s Перельман Я. И. Занимательная астрономия.
s Перельман Я. И. Физическая хрестоматия: Пособие по физике и книга для чтения:
Введение. Начальные сведения из механики. Жидкости. Газы. Теплота.
s Франкфурт У. И. Очерки по истории специальной теории относительности.
✓ Пенроуз Р. Новый ум короля. О компьютерах, мышлении и законах физики.
s Федин С. Н., Чирок Л. М. (ред.) Ученые — авторы издательства URSS шутят.
✓ Горобец Б. С., Золотов Ю.А., Федин С. Н. Ученые шутят.
^Грин Б. Элегантная Вселенная. Суперструны, скрытые размерности и поиски
окончательной теории.
s Ушаков И. А. История науки сквозь призму озарений. В 8 кп.
Кн. 1. Пути познания Вселенной.
Кн. 2. Сначала было числоЕ
Кн. 3. Колдовство геометрии.
Кн. 4. От арифметики до алгебры: Таинственная страна Аль-Джебр.
Кн. 5. Вероятность и статистика: Этот случайный, случайный, случайный мирЕ
Кн. 6. От счетных машин до ЭВМ: Как люди научили машины «думать».
Кн. 7. Покорение океана и неба: Икары и Ихтиандры.
Кн. 8. Покорение космоса: Небо без границ.
По всем вопросам Вы можете обратиться к нам:
тел. +7 (499) 724—25—45 (многоканальный)
или электронной почтой URSS@URSS.ru
Полный каталог изданий представлен
в интернет-магазине: http://URSS.ru
Научная и учебная
литература
URSS.ru
lURSS.ru
lURSS.ru
URSS.ru
nJ'SSHR nj'SSUn nj'ssun IM'SSUR iM'SStm
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
В РЕШЕНИЯХ ЗАДАЧ
ИЗ СБОРНИКА
Вышли пособия • Динамика материальной точки
с решениями задач # динамика материальной системы
к следующим " г
разделам: • Аналитическая механика
• Кинематика
• Системы с качением. Неголономные связи
• Устойчивость равновесия. Малые колебания.
Устойчивость движения
IPS'SsT'
каршчикаюз
мишки ёщ
теоретическом
механики
Компьютерное математическое моделирование, анимация и динамическая
одно- двух- и трехмерная визуализация
Издательская группа I
URSS
Книга 4 Теория и компьютерный эксперимент: 29 лекций с раздаточным материалом.
24 компьютерные модели физических систем с широким диапазоном настроек.
Книга Практикум и компьютерный эксперимент: 120 практических
JL и учебно-исследовательских задач. 35 компьютерных моделей
Николай Николаевич
ПОЛЯХОВ
Один из ведущих отечественных специалистов в области аэро¬
гидромеханики (авиация, кораблестроение), аналитической меха¬
ники и истории науки. Автор многих работ, посвященных теории
и расчету авиационных и судовых гребных винтов, а также теории
стационарных и нестационарных движений несущей поверхности
крыла самолета.
Наше издательство предлагает следующие книги
МАТЕМАТИЧЕСКАЯ ТЕОРИЯ
УСТОЙЧИВОСТИ
МАГНИТОГИДРО¬
ДИНАМИЧЕСКИХ
РЕЖИМОВ
К ДЛИННОМАСШТАБНЫМ
ВОЗМУЩЕНИЯМ
СПЛОШНЫХ СРЕД
В ЗАДАЧАХ в
НАУКА г/*
ссср
А. Н. Крм.нш МОИ
ВОСПОМИНАНИЯ
ТЕОРИЯ
С АМООРГ АВИЗОВАННОЙ
КРИТИЧНОСТИ ' Щ
Издательская группа
117335, Москва, Телефон/факс
Нахимовский (многоканальный)
проспект, 56 +7 (499) 724 25 45
Отзывы о настоящем издании, а также обнаруженные
опечатки присылайте по адресу URSS@UR3S.ru.
Ваши замечания и предложения будут учтены
и отражены на web-странице этой книги на сайте
http://URSS.ru
19979 Ю 222943
Каталог изданий
в Интернете:
http://URSS.ru
E-mail: URSS@URSS.ru
Методы
АЭРОДИНАМИЧЕСКОГО
РАСЧЕТА
тшшейн
Жизнь
РОССИЯ
XX! ВЕК
Как работает
природа
БЕСЕДЫ О