Текст
JVLG.tfyревич
СИГНАЛОВ
М. С. ГУРЕВИЧ
СПЕКТРЫ
РАДИОСИГНАЛОВ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО ЛИТЕРАТУРЫ
ПО ВОПРОСАМ СВЯЗИ И РАДИО
МОСКВА 1963
УДК 535.33 : 621.396.001 + 004
।
АННОТАЦИЯ
В книге рассматриваются спектры различных радиосигна-
лов и некоторые способы борьбы со взаимными помехами в
каналах радиосвязи при наиболее распространённых видах
модуляции. Описываются также методы измерения ширины-
полосы частот, занимаемой каналами радиосвязи, на передаю-
щих центрах и контрольных станциях.
Книга может быть использована широким кругом радиол
инженеров и научных работников, а также аспирантами и
студентами старших курсов радиотехнических специальностей
высших учебных заведений для углублённого изучения вопроса
и в качестве пособия при проведении расчётов и измерений-
v . '
ПРЕДИСЛОВИЕ
'Ж
W. ' • s
' Радиосвязь играет весьма важную роль в общей сети элек-
4роснязи СССР. Дальнейшее развитие радиосвязи во многом оп-
арпрлится тем, насколько успешно будут разрешены следую-
|ййа проблемы:
< ’ О увеличение пропускной способности й повышение помехо-
^дЩищённости систем радиосвязи;
2) более экономное использование полосы частот, отводимой
радиоканалу, которое позволило бы разместить в ограниченном
йас^отном диапазоне наибольшее число каналов с наименьшими
4^йМными помехами.
Чтобы успешно решить эти проблемы, нужно изучить спект-
/радиосигналов и, в частности, рассмотреть возможность
’Ййеньшения ширины полосы частот радиоканала, которая яв-
’Йя^тся важнейшим показателем, характеризующим систему, ра-
^освязи и эффективность использования спектра радиочастот.
>1‘. Несмотря на то, что к изучению спектров радиосигналов дав-
^э-проявляется усиленный интерес, многие вопросы из этой об-
лети исследованы ещё совершенно нёдостаточно. Настоящая
рйптга написана на основании исследований, проводимых авто-
.в течение ряда лет.*
Автор благодарит рецензентов Г. А. Левина, X. А. Лившица
^^!(ветственного редактора В. М. Розова за ценные замечания,
Которые были учтены при работе над. рукописью, а также всех
Шй;,в той или иной мере содействовавших написанию книги.
'С, Автор понимает, что сложность и новизна вопросов, рассмат-
риваемых в книге, может «явиться причиной ошибок и упущений
Йрудет благодарен за все замечания, которые помогут в даль-
.Мёйшем улучшить книгу. Замечания по книге -следует найрав-
ййть в Связьиздат (Москва-центр, Чистопрудный бульвар, 2).
АВТОР
ВВЕДЕНИЕ
§ В.1. СПЕКТР РАДИОЧАСТОТ Й
ЕГО ИСПОЛЬЗОВАНИЕ
Если проследить за развитием ра-
диотехники, то можно видеть
громадные достижения в использо-
вании электромагнитных колебаний
в весьма широком диапазоне частот
от -20-103 гц до 10й гц. Передача
сигналов при помощи радиоволн
применяется в радиосвязи, радиове-
щании, телевидении, радиолокаций,
радионавигации,' телемеханике, те- ;
леизмерениях. Электрические и ма-
основную гнитные поля высокой частоты ис-
пользуют в промышленности и ме-
дицине; • Одно лишь это пёрёчислё- ;
нйе показывает, что использование
радиочастот тесно соприкасается со
Рассмотрены причины недо-
статка радиочастот и меро-
приятия, улучшающие исполь-
зование спектра.
Показано, что ширина поло-
сы играет важную роль среди
других параметров, опреде-
ляющих пропускную способ-
.. ность канала радиосвязи.
Определены понятия ширины
полосы, занимаемой излуче-
нием, необходимой ширины по-
лосы и внеполосного излуче-
ния.
Обоснована целесообразность
«энергетического» определения
ширины полосы, занимаемой
излучением, как полосы ча-
стот, содержащей <
часть излучаемой мощности.'
Перечислены основные . воп-
росы, которые автор стремится
-поставить и разрешить в книге.,
всей народнохозяйственной и культурной жизнью страны. .
Теневой стороной быстрого прогресса радиосвязи, радиове-
щания и смежных областей является.всё возрастающая загрузка
частотного спектра. Множество жизненно важных служб-пё--
регружает каналы, создавая всё увеличивающийся уровень
взаимных помех, а быстрый рост потребителей усугубит нехват-
курадиочастот в ближайшие годы. Поэтому радиоспектр дол-ч
жен рассматриваться как ограниченное достояние, которое нуж-
но благоразумно использовать и заботливо охранять. < '
Есть много причин, из-за которых используемый сейчас столь
широкий спектр частот не удовлетворяет, потребности радио--
служб.
Первая и наиболее важная из них, пожалуй, состоит в том,
что частоты выше 30 Мгц распространяются иначе, чем более’
низкие частоты. Частоты ниже 30 Мгц используют преимуще-'
ственно для связи на расстояния в несколько тысяч километров,;
а также когда необходимо экономично обслужить радиовещание
ём широко разбросанную аудиторию. Частоты выше-,30 Мгц при-;,
меняют для связи на расстояния, не превышающиеста километ-
ров и при не слишком больших мощностях передатчиков. Следов
вательно, для передачи сообщенйй-на большие расстояния без
ретрансляций можно использовать полосу лишь в 30 Мгц из об-
спектра шириной в один миллион мегагерц. Этим объяс-
' СЙ сильная перегрузка? спектра частот, лежащих ниже
^^гц. " '.•
причина заключается в том, что многие из новых
а именно вещание на ультракоротких волнах с частот-
;%№йибдуляцией. телевидение и радиолокация требуют каналов,
^у^угвенно более широких, чём каналы старых служб. Так
ЧМ радиостанция занимает полосу, которая в 20 раз шире
Mgibcbi радиовещательной станции с амплитудной модуляцией
аЮЙ'):". Телевизионный канал в 600 раз шире канала вещания по
^особу AM. Радиолокационная станция занимает полосу в не- -
’.^^Дько тысяч раз более широкую, чем полоса, необходимая для
Ш^бтелегоаФной связи.
!^В-третьих, верхнюю часть спектра (частоты свыше
^Щ1гц) использовать, трудно. Достижимые в этой области
’^ё'вбт мощность передатчика и чувствительность приёмника
Распространение некоторых частот осложнено неоднор.од-
«^^"составом атмосферы. Так, при частотах свыше 30 000 Мгц
^ШЙЙЫЙ' дождь может вывести из строя линию связи,
Втёртой, причиной загруженности спектра являются труд-
Йй/перемещения некоторых служб из уже «обжитых» ими
^йаэонов частот в новые, ещё мало освоенные.
ЖЙКйййе технические препятствия стоят на пути наиболее пол- .
^мЙВ^дспользования спектра?
^?!эд»^Метим сначала тот факт, что системы связи успешно дей-
уют лигрь тогда, когда отношение сигнала к. помехе значи-
ло превышает единицу. За последнее время, правда, появи-
корреляционные методы, позволяющие работать при отно-
си сигнала к помехе, меньшем единицы, однако при этом
ительно увеличивается время занятости кайала. Поэтому
аЖОйтически уровень сигнала должен превышать уровень по-
’величину от 10 до 50 дб.'' ' - . ' -
^^Радиостанции создают значительные помехи на расстояниях,
]нргд превышающих зону обслуживания. Даже при наиболее
|она.льном территориальном. размещений радиостанций и не-
фшйх условиях распространения радиоволн каждый пере-
йк создаёт значительные помехи приёму другого передать,
^^работающего на той же частоте, в радиусе, превышающем
^рй: раза радиус зоны его обслуживания. Практически нцког-
* нельзя разместить территориально передатчики, руковбдст-
''^Ь'/лишьгеометрическими соображениями. Уровни сигналов
йй^ёх,фактически меняются в зависимости от атмосферных ус-
в/частности, бтсостояния ионосферы (для частот ниже
|рно 50 Мгц) и состояния тропосферы (ддя частот выше
Эти изменения могут быть весьма значительными, при-
:рнймогут носить: спорадический или периодический харак-
и их почти невозможно предопределить в:деталях.: Кроме
того, суточные и сезонные изменения условий распространения,
в частности для частот ниже 25 Мгц, требуют присвоения ра*
диостанциям многих классов нескольких частот, которые исполь-
зуют попеременно в зависимости от времени дня или года и
покрываемого расстояния.
Улучшить использование спектра можно передачей сигналов
лишь в тех направлениях, где находятся приёмники, и приёмом,
сигналов лишь с того направления, на котором находится при-
нимаемая станция, т. е. применением направленных антенн. Н а-
правленные антенны широко используют в -магистраль-
ной радиосвязи и значительно меньше в подвижных службах.
Они могут и должны более широко применяться во всех обла-
стях радиосвязи и вещания.
'Таким образом, мы коснулись технической проблемы разме-
щения многих станций, использующих одну и ту же частоту, с
минимальными взаимными помехами. В одинаковой степени
важно, чтобы каждая станция использовала наименьшую часть
спектра. Если мы хотим обеспечить максимальную занятость
спектра, то ширина полосы, занимаемая передачей, должна быть
возможно более узкой и тесно заполненной частотными состав-
ляющими сигналов, а защитные полосы и частотные допуски—
. , уменьшены до минимальных значений.
'Рассмотрим сначала вопрос о ширине полосы, занимаемой
передатчиками различных видов, и о том, как заполнен канал
частотными составляющими.
При 'всех полезных методах модуляции энергия концент-
рируется в определённых участках полосы частот, занимаемой'
Передачей; при этом плотность распределения частотных состав-
ляющих в канале зависит от метода модуляции. В некоторых
службах соответствующим выбором или видоизменением метода
модуляции можно увеличить плотность частотных составляю-
щих и улучшить использование спектра.
В течение последнего времени много изучали методы моду-
ляции, чтобы определить, насколько эффективно они - исполь-
зуют занятый канал и насколько эффективно1 противостоят воз-
действию помех, попавших в этот канал.
Методы модуляции совершенствовались путём подавления
Частотных составляющих, которые повторяют информацию, со-
держащуюся в другой части составляющих. Например, приме-
няют системы модуляции, в которых несущая и одна боков с я
полоса полностью подавлены. Очень часто радиостанции, осо-
бенно связные, излучают спектр частот в несколько раз более
широкий, чем это нужно, из-за неисправного состояния аппара-
z туры или неправильно установленного режима.
Далее, остановимся на вопросе о частотных допусках. Мож-
.6 ''' ’
яаЩй преувеличения сказать, что любой технический метод ог-
^Оййения ширины полосы, занимаемой передачей, не улучшит
да^Йьзования частотного спектра до тех пор, как не уменыпат-
^^ущественно допуски на нестабильность частоты передат-
^ж>чень ещё велики и допуски на нестабильность частоты для
^огёмников; приёмники многих служб к тому же имеют недо-
^доцйяую избирательность. Частотные нестабильности передат-
-^йпв^.я приёмников заставляют применять разносы между
^йалами, значительно превышающие занимаемую ширину по-
.которая, как правило, во много раз больше, чем необхо-
ширина полосы. '
^’Необходимость повышения эффективности использования
^а^-дтного спектра требует проведения ряда научно-техниче-
мероприятий:
’ Систематически изыскивать способы наиболее рациональ-
ней.Размещения максимального количества станций с наймень-
взаимными помехами во всех диапазонах частот.
. '^ ‘Ограничить ширину полосы, занимаемой передачей, до
’ -^даёний, близких к необходимой ширине полосы. Частотные
' $э^ски на отклонение несущей должны составлять малую часть
^ф^Йны" канала.
Устранить недостатки аппаратуры, из-за которых прихо-
Жйф&я увеличивать ширину защитных полос, а именно: повысить
'^Н^йльность несущей частоты передатчика и гетеродинов приём-
избирательность приёмников', установить надлежащую
модуляции. . •
^Внедрить наиболее эффективные методы модуляции, обе-
ШМйвайщие наилучшее использование занимаемого канала
<^^бенно широкополосных служб, таких как УКВ ЧМ вещание
Йтелевидение).
Ограничить уровень помех, создаваемых станцией за пре-
Делами её зоны обслуживания, снижая мощность передатчиков,
Ж^Ййляя, гармонические излучения, синхронизируя несущие
. где это имеет практический смысл) и используя направлен-
, здЙОнтенны.
; ’^^Усовершенствовать методы контроля и наблюдения за за-
’Йадбстью 'спектра, в частности, контроля за шириной полосы,
.’йЭД^маемой излучением.
на большое практическое значение изучения спект-
^^фйдйбсигнал'о®, эта тема разработана ещё совершенно недо-
Причина этого заключается в теоретических и прак-
•ЙЯ^кйх трудностях, которые встречаются при изучении . р.а.с-
^матриваемого вопроса. Достаточно сказать, что не так уж дав-
W ®i 1930 г., такой авторитетный учёный и радиоинженер, .как,
7
Флеминг, поднял на страницах журнала «Nature» полемику *)>
утверждая, что реальной является только «модулированная не-
сущая», а боковые полосы — это вычислительный приём, мате-
матическая фикция, которой ничего не соответствует в действи-
тельности.
Как правильно указывает С. М. Рытов, 'выводы отсюда
касались отнюдь не высоких материй, а самых насущных и
практических вопросов. Так как, по мнению Флеминга, имеется
одна единственная несущая частота, то нет никаких оснований
к установлению частотных разносов между радиостанциями, и
густота заселения «эфира» ограничивается только избиратель-
ностью приёмников. Хотя Флеминг, разумеется, не смог последо-
вательно защитить свою неверную точку зрения, однако отрица-
ние им реальности боковых частот несомненно задержало разра-
ботку вопроса о ширине полосы, занимаемой каналами радио-
связи. Ошибочные выступления по этому вопросу встречаются
в литературе и после дискуссии с Флемингом.
В области развития спектральных представлений советские
учёные имеют значительные достижения. Ещё в 1917 г. Н. Н. Ан-
дреев провёл капитальное научное исследование и создал моно-
графию (Л 1], трактующую на современном уровне вопросы при-
менения спектральных представлений к анализу электрических
колебаний.
Большую роль в этой области сыграли работы Л. И. Ман-
дельштам и его учеников Г. С. Горелика и С. М. Рытова,
а в последние годы книга А. А. Харкевича [Л23]. Решение
задач, непосредственно связанных с использованием радиоча-
стот, содержится в работах М. В. Шулейкина [Л22], В. А. Ко-
тельникова [Л4], В. И. Сифорова [Л7].
§ В.2. ШИРИНА ПОЛОСЫ ЧАСТОТ КАК ФИЗИЧЕСКАЯ
ХАРАКТЕРИСТИКА СИГНАЛА
Чтобы установить количество сведений, которое может быть
передано посредством сигнала, и выяснить соотношения между
характеристиками сигнала и свойствами канала связи, необхо-
димо ввести некоторые величины, которые позволили бы охарак-
теризовать сигнал с физической точки зрения [Л28].
Если сигнал представляется некоторой функцией времени, то,
определив так или иначе эту функцию, мы определяем и сиг-
нал. Однако такое полное описание сигнала не всегда нужно.
В ряде случаев достаточно ограничиться более общим описанием
сигнала, определив лишь небольшое количество обобщённых
>) Подробные данные по этой полемике содержатся в работах С. М. Ры-
това [Л8] и [ЛЮ].
8
измерений. Обычно в теории связи для описания общих свойств
сигнала принимают три измерителя: его продолжительность, пре-
вышение сигнала над помехой и ширина полосы частот сигна-
ла. Последняя величина даёт представление о многих важных
свойствах сигнала и является весьма удобной. Произведение
/этих трёх величин обычно называют объёмом сигнала. Если
^принять, что помехи представляют собой шумы с равномерно
распределённым спектром в полосе пропускания фильтра и под-
. чиняются нормальному закону распределения, то для идеальной
системы пропускная способность канала, как известно, будет
,,равна
р Л Д/
C = Flog2—двоичных единиц в секунду, (В.1>
где С — пропускная способность канала,
F — ширина полосы канала,
Р — мощность сигнала,
N — мощность помех.
< Из приведённой формулы видно, что увеличить пропускную-
способность канала можно, либо увеличивая ширину полосы,
.либо увеличивая мощность сигнала по сравнению с мощностью-
Йомех. И, в свою очередь, если мы удовлетворены существующей
.пропускной способностью канала, то можем уменьшить ширину
полосы за счёт увеличения отношения сигнала к помехе, т. е. за
счёт увеличения мощности передатчика. Следует, однако, отме-
тить, что экономия ширины полосы обходится очень дорогой
ценой, так как логарйфм меняется очень медленно в зависимо-
сти от изменения мощности Р. Например, при отношении сиг-
‘нала к помехе, равном 30 <56, для того, чтобы компенсировать
уменьшение ширины полосы на 10%, необходимо увеличить мощ-
ность передатчика в два раза.
, Из ф-лы (В.1) можно видеть, какую важную роль играет
ширина полосы среди других параметров, определяющих про-
пускную способность канала связи: изменение ширины полосы
'„в идеальной системе связи сказывается на пропускной способ-
ности канала значительно сильнее, чем изменение мощности пе-
редатчика. Этот вывод весьма важен: он говорит о необходимо-
сти бережного отношения к использованию ширины полосы, так
как известно, что увеличение мощностей достигается путём зна-
чительных капиталовложений.
§ В.З. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ, ОТНОСЯЩИЕСЯ
К СПЕКТРАМ РАДИОСИГНАЛОВ
Чтобы рассмотреть вопросы, связанные с размещением ка-
налов связи в диапазонах радиочастот, необходимо точно опре-
делить ширину полосы частот, занимаемой каждым из каналов.
9>
Радиотелеграфные сигналы имеют конечную продолжитель-
ность, вследствие чего их спектры простираются по частоте до
бесконечности. Поэтому передача таких сигналов теоретически
занимает бесконечно широкую полосу частот. Однако это тео-
ретическое положение не приводит нас к какому-либо практиче-
скому выводу, так как наибольшая часть энергии сигнала, ис-
пользуемого в радиосвязи, концентрируется в относительно уз-
кой полосе частот и части спектра, удалённые от централь-
ной частоты, не являются существенными для поддержания
связи.
Чтобы практически определить «место», занимаемое переда-
чей, мы вынуждены выбрать, причём в достаточной мере произ- .
вольно, ту часть излучаемой мощности, которая предназначает-
ся для осуществления связи. Если эта часть мощности выбрана,
то можно, исходя из распределения энергии в спектре частот,
определить часть спектра, которая содержит эту мощность, и та-
ким образом определить ширину занимаемой полосы, т. е. ши-
рину канала, который это излучение занимает.
Практически ширину занимаемой полосы можно определить'
двояким путём:
1) по значению частоты со*, при которой значение модуля
спектра |F(®)| составляет некоторую долю от максимального
его значения, т. е.
|f(M __ 1
d ’
где d> 1;
2) по значению частоты и ограничивающей область спект-
ра, в которой заключена основная часть всей его мощности.
Иногда первое определение ширины полосы называют «гео-
метрическим», а второе — «энергетическим». Приняв любое из
этих определений, можно получить значение ширины полосы, в
той или иной степени учитывающее наиболее важную часть
спектра, формирующую данный сигнал. Для каждой из форм
сигналов можно установить соответствие между относительным
содержанием мощности в данной полосе и уровнями спектраль-
ных компонентов на краю этой полосы.
В Регламенте радиосвязи [Л43] и в рекомендациях Между-
народного консультативного комитета по радио (МККР) [Л40]
содержится следующее «энергетическое». определение занимае-
мой ширины полосы: шириной занимаемой полосы называется
ширина такой полосы частот, за нижним и верхним пределами
которой средние излучаемые мощности равняются каждая 0,5%
всей средней мощности данного излучения.
В некоторых случаях, например, при использовании много- '
канальных систем с частотным уплотнением значение 0,5% мо-
жет привести к известным затруднениям при практическом при-
10
щенении определений ширины занимаемой и необходимой поло-
сы частот; в таких случаях может оказаться полезным другое
процентное содержание.
Следует отметить, что численное значение коэффициента —
0,5% —в определении Регламента радиосвязи и МККР выбрано
произвольно и не имеет теоретических обоснований. Можно лишь
установить, что процентное содержание мощности в полосе
должно быть менее 100%, поскольку при передаче сигнала ко-
нечной продолжительности его мощность распределена в беско-
нечной полосе частот. С практической точки зрения коэффициент
0,5% во многих случаях удобен, так как полоса, содержащая
99% излучаемой мощности, примерно соответствует полосе, не-
обходимой для качественного воспроизведения сигналов с прием-
лемым для практики скруглением.
Несмотря на произвольный выбор коэффициента 0,5%, вы-
шеприведённое определение ширины полосы удобно для широ-
кого пользования и его следует предпочитать, как принятое по
международному соглашению. Введение какого-либо нового оп-
ределения для широкого пользования затруднило бы возмож-
ность взаимного сравнения результатов измерений и излишне
усложнило бы измерительное дело.
Поэтому мы принимаем и в дальнейшем будем использовать
Определение ширины занимаемой полосы, принятое Регламен-
„ том радиосвязи и МККР.
Уменьшить ширину полосы, занимаемой излучением сигна-
, лов заданной продолжительности, можно только за счёт изме-
нения их формы. Известно, что скруглённые сигналы занимают
меньшую ширину полосы, чем прямоугольные. Опыт показы-
вает, что сигналы, скруглённые до некоторой степени, при приё-
ме легче воспроизводить с требуемым качеством. Однако чрез-
мерное скругление может ухудшить качество принимаемых сооб-
мцений, например относительное число ошибок может превысить
норму. Таким образом, мы подошли к понятию необходимой ши-
рины полосы- Регламент радиосвязи [Л43] и МККР [Л40] реко-
мендуют необходимой шириной полосы считать минимальное
значение ширины полосы, занимаемой излучением, достаточное
при данном классе излучения, чтобы обеспечить передачу сооб-
. Щения с такой скоростью и такого качества, которые требуются
для системы, используемой при определённых условиях.
В приложении I дана таблица значений необходимой ширины
полосы для различных классов излучений, составленная на ос-
новании данных, содержащихся в [Л43}.
Излучение является совершенным, если ширина занимаемой
полосы равна необходимой ширине полосы. Это означает, что
при передаче используются сигналы, скруглённые до такой сте-
/ пени; чтобы обеспечить связь требуемого качества. Использо-
вание более широкой полосы излишне, но зато использование
11
более узкой полосы может привести к недопустимому ухудше-
нию качества.
Ширина занимаемой полосы и необходимая ширина полосы
представляют собой два важных фактора, которые следует учи-
тывать, распределяя частоты для передатчиков и определяя ши-
рину полосы 'пропускания приёмников, предназначенных для
приёма этих передач.
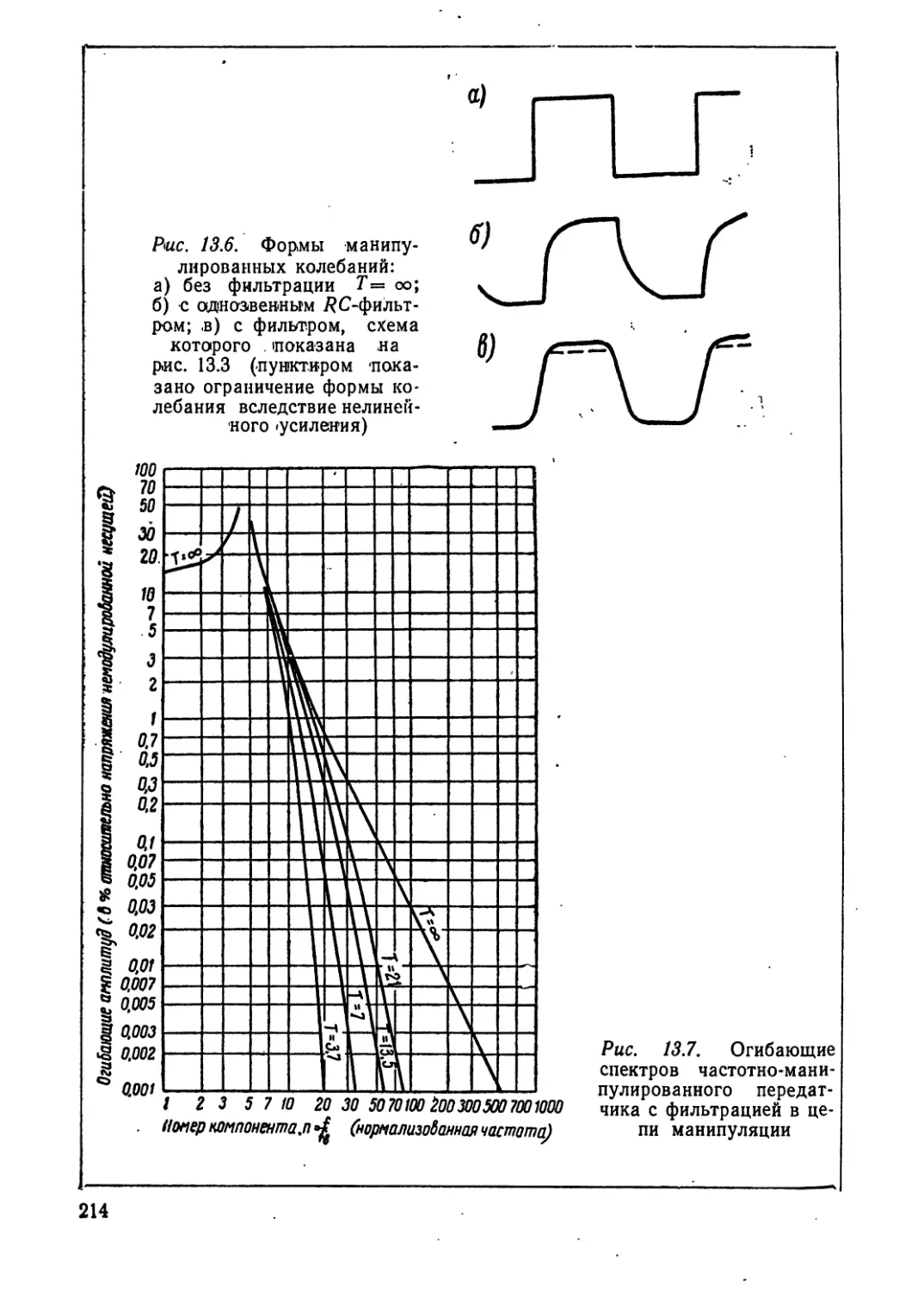
^лучение за лрйя,ла«а необго
симой полосы
ИВВВИВ Излучена е за предела на
занимаемой полосы
Рис. В.1. Кривые, поясняющие определение ширины зани-
маемой полосы, необходимой ширины полосы и внеполос-
ного излучения. Спектр предполагается симметричным:
Д/я — необходимая ширина полосы; — ширина зани-
маемой полосы
12
. Однако спектры радиосигналов не ограничиваются полосой,
занимаемой излучением, а, как следует из принятого выше опре
.- деления, 1% мощности, излучается вне этой полосы. Хотя эта
часть излучения не воздействует на приёмник, настроенный на
!i частоту излучения, но она может создавать помехи в соседних
каналах. Отсюда возникает понятие внеполосного излучения.
Обычно [Л 40] внеполосным излучением считается мощность,
•излучаемая за пределами необходимой ширины полосы.
С Такое излучение, как, например, подавленная несущая, ко-
,вторая полезна для нормального действия приёмного устройства,
''Относится к необходимой ширине полосы, а не к внеполосному
'излучению.
Понятие внеполосного излучения удобно для определения от-
яосительного несовершенства излучения (рис. В.1).
. . V-
В.4. ВОПРОСЫ, РАССМАТРИВАЕМЫЕ В КНИГЕ
1. Какое представление сигналов в математической форме
наиболее приемлемо для решения практических задач, связан-
ных с исследованием спектров?
2. Какую форуму следует придать сигналу для того, чтобы
-при его передаче использовалась наименьшая полоса частот?
3. Какую полосу частот занимает передача сигналов различ-
ных форм?
. 4. Каково соотношение между шириной полосы, занимаемой
.• ^передачей, и временем установления сигналов?
5. Как форма сигнала влияет на излучения за пределами по-
' „лосы частот, занимаемой передачей?
6. Какую полосу частот занимают импульсные излучения при
*'наиболее употребительных видах манипуляции?
/ у- 7. Как спектр сигнала и пропускная способность канала свя-
зи зависят от времени замедления в канале?
8. Как связаны спектры, регулярных и случайных последо-
>; вательностей сигналов?
" 9. Как определять ширину полосы, занимаемой передачей
'.« .последовательности случайных сигналов, соответствующей реаль-
. ;'ному сообщению?
’ 10. Как различные характеристики спектров радиосигналов
и, радиоприёмников влияют на взаимные помехи между кана-
: "'Лами?
11. Как практически формировать сигналы в радиопередат-
• никах?
1 12. Каковы предпочтительные методы измерения ширины по-
~ лосы, занимаемой радиотелеграфными излучениями?
13
ГЛАВА ПЕРВАЯ
ПРЕДСТАВЛЕНИЕ СИГНАЛОВ В МАТЕМАТИЧЕСКОЙ
ФОРМЕ И ПОНЯТИЕ СПЕКТРА
В главе
требования,
удовлетворять
сигналов, и показано, что для
решения большинства • практи-
ческих задач целесообразно
представить сигналы g(t) в ви-
де СУММЫ
g(t) = Vanyn(t). (А)
Рассмотрены преимущества и
недостатки представления сиг-
налов посредством экспонен-
циальных функций и показано,
как такое представление при-
водит к понятию спектра.
Показано, что разложение
вида (А) возможно лишь в
случае, если система функций
y(t) является полной; если к
тому же эта система является
ещё и ортогональной, то вы-
числение коэффициентов ап уп-
рощается.
Рассмотрено представление
сигналов в виде ряда смещён-
ных функций и указано, что
применение этого метода осо-
бенно полезно при рассмотре-
нии спектров непериодических
сигналов.
§1.1. ОБЩИЕ СООБРАЖЕНИЯ О
ПРЕДСТАВЛЕНИИ СИГНАЛОВ
сформулированы
которым должно
представление
Гробы представить сигнал в мате*
матической форме, скажем в
виде абстрактного символа G, необ-
ходимо прежде всего точно опреде-
лить те его свойства, которые жела-
тельно отразить при представлении.
Рассмотрим, например, сигнал речи.
Можно интересоваться его формой,
разборчивостью или смысловым со-
держанием. Конечно, эти три аспек-
та сигнала находятся в каком-то со-
отношении между собой, но это не
означает, что хорошее представле-
ление одного из этих аспектов, ска-
жем его формы, соответствует хоро-
шему представлению другого аспек-
та, например содержания.
Поэтому на представление сигна-
лов необходимо наложить некото-
рые ограничения. Первое из них со-
стоит в том, что мы будем пытаться
охарактеризовать тот аспект G,
его «формой» и задаётся в виде
который обычно называется
функции времени. Далее потребуем, чтобы наше представление
облегчало расчёты, анализ схем и рассмотрение процессов, про-
исходящих при формировании и прохождении сигналов.
Если G задано в виде функции времени g(t), то к такому
представлению предъявляется ещё одно требование: оно долж-
но позволить разложить задачу, для рассмотрения которой мы
ввели данное представление, на составные части, которые ре-
шить легче, чем первоначальную задачу. Затем мы должны,
иметь возможность сложить эти отдельные части вместе, чтобы
14
Получить решение общей задачи. Такая процедура может быть
названа логической суперпозицией.
. Чтобы решить большинство практических задач посредством
введения сложных сигналов, действующих в сложных системах,
необходимо производить не только логическую суперпозицию,,
но и сам процесс или явление разложить на составные части,
•г. е. произвести физическую суперпозицию. А для этого-
'сигналы в описываемых процессах должны быть, по крайней
мере приближённо, линейными. Поэтому даже при рассмотрении
. ' таких принципиально нелинейных систем, как модуляторы, обыч-
но стараются свести нелинейную задачу к линейной с меняю-
щимися по времени параметрами.
В линейной задаче логическая процедура, описанная ранее,
сводится к представлению g(t) как взвешенной суммы последо-
вательности выбранных определённым образом форм колебаний
Уп (t), т. е. в виде
V. = (1.1)
Функции y(t) выбирают такими, чтобы решать интересующие
нас задачи было бы наиболее легко.
§ 1.2. ИСПОЛЬЗОВАНИЕ ЭКСПОНЕНЦИАЛЬНЫХ ФУНКЦИЙ
Под экспоненциальными функциями понимаются функции
вида Aept, где A, p=pi + ip2—любые комплексные числа, a t—
действительное время. Использование этого класса функций для
выражения сигнала в виде суммы более простых функций явля-
ется наиболее изученным и полезным. На основании известной
формулы Эйлера
Аер/ = AePli (cos р2/ + i sin p2t)
эспоненциальные функции просто выражаются через синусои-
дальные и косинусоидальные функции. Этот класс функций об-
ладает тем свойством, что он инвариантен относительно опера-
ций. дифференцирования и интегрирования.
Решение линейных дифференциальных уравнений с постоян-
ными коэффициентами сводится к алгебраическим операциям
над функциями этого класса, благодаря чему можно использо-
вать операционное исчисление.
Исходя из представления сигнала в виде суммы экспоненци-
альных и, в частности, гармонических функций и появилось по-
нятие спектра. Синусоидальные колебания дополняют наши ин-
.15
туитивные представления о внешних воздействиях на реальные
физические системы и позволяют концентрировать внимание на
существенных особенностях системы, которые не были бы оче-
видными при других представлениях.
Вместе с тем, хотя представление сигнала посредством экспо-
ненциальных функций значительно упрощает решение задач,
такое представление приводит к некоторым методологическим
трудностям. Мы, например, говорим относительно реакции си-
стемы в ограниченной области спектра, тогда как это в прин-
ципе невозможно. Кроме того, в любом достаточно сложном
случае мы приходим лишь окольным путём к тому, чтобы пред-
ставить себе, что происходит в какой-либо области времени, со-
ответствующей действительному сигналу.
Остановимся более подробно на представлении сигналов в
виде суммы экспонентов. Основное свойство экспоненциальных
функций
х(/) = Лер/ (1.2)
состоит в том, что они являются собственными функциями стаци-
онарных линейных преобразований. Поясним это. Предположим,
что мы имеем дело с преобразованием Т (например, с операци-
ей фильтрования), которое преобразует x^(t) в y{(t) и x2(t) в
Уг(1). Символически это можно записать в виде
У1 = ТХ1 ) . (1.3)
Уъ = Тх2 )
Преобразование называется линейным, если соблюдается
принцип суперпозиции, т. е. если соблюдается соотношение
7 (ал + а2х2 + ... + аахп) — а{Г4- а2Тх2 + • • • + апТхп. (1.4)
Мы будем называть преобразование «стационарным», если
его действие является независимым от начала отсчёта време-
ни, т. е. если из того, что
Тх (0 = y(t), (1.5)
следует, что
Tx(t + z)=.y(t + x)
для всех преобразуемых функций x(t). х
Можно показать, что по отношению к экспоненциальным вы-
ражениям вида (1.2) стационарное линейное преобразование
Т сводится к умножению преобразуемой функций x(t) на ком-
плексное число z(p), зависящее лишь от экспонента р, т. е.
7[х(/)]=г(р)х(0. (1.5)
16
?' функция x(t), для которой Tx(t) =const • x(t), называется
собственной функцией преобразования, а константа — соответ-
ствующим собственным значением. В равенстве (1.6) z(p) —
собственное значение, соответствующее собственной функции
x(t) = ept.
Линейные стационарные преобразования имеют в качестве
собственных функций экспоненциальные функции ept, и это
важно по следующей причине. Если найдено раз и навсегда пра-
вило для вычисления собственных значений, то для любой функ-
ции
*(0 = 2Л*е^
преобразованная функция находится в виде
Tx(0 = ^(p*)ep*',
так как для линейного преобразования Т выполняется свойст-
во суперпозиции (1.4) и ePftZ являются собственными функци-
ями преобразования 7 [т. е. 7,ер*/= z(pA)ep*z ].
Если же приходится применять несколько линейных преоб-
разований последовательно, то преобразованную функцию нахо-
дят в виде
ТгТ2.. .Tnx(t) = 2МР*).. .zMAke^ , (1.7)
- где Zi(pft) . . . (z„pk)— собственные значения, соответствующие
собственной функции ePft< для линейных преобразований
Т\... Тп; причём Zi(p4) — преобразование Ть zn (рА) — преоб-
разование Тп.
Произведение линейных преобразований сигнала можно
свести к простому умножению также и в случае, когда функцией
x(t) задаются в виде интеграла экспоненциальных выражений
вместо суммы их, т. е. в виде
x(t)=^f(p)eptdp.
С
Тогда
T1T2...T„x(0=p1(p)z2(p)...z/I(p)f(p)ep<dp. (1.8)
С
Преобразование в последней форме хорошо известно: при
соответствующем выборе пути интегрирования С=(—ioo , +ioo )
выражение (1.8) становится преобразованием Фурье, f(p) —
2-730 17
спектрам сигнала и zlt z2, . . ., zn — характеристиками пе-
редачи фильтров Т], 72,..., Тп, причём р — и».
Для систем с сосредоточенными параметрами, состоящих из
ограниченного числа элементов, операция Т описывается обык-
новенными интегро-дифференциальными уравнениями с посто-
янными^ коэффициентами, причём z(p) принимает вид рациональ-
ной дроби
2(р) = -^-,
Q(p)
(1-9)
где Р и Q — полиномы с конечным числом членов.
Поскольку число ступеней свободы (независимых видов на-
копления энергии) в электрическом фильтре мало, то число
полюсов и нулей в z(p) также мало. Расположение этих полю-
сов и нулей может дать теоретически несложную картину воз-
действия фильтра на сигнал.
Переходной процесс в такой системе можно вычислить по
формуле
п
(1.10)
Вышеприведённые линейные преобразования могут оказать-
ся полезными только в том случае, если сигналы u(t) могут
быть представлены в виде суммы экспоненциальных выражений
(1.7) или интегралов (1.8). Многие физические сигналы при-
надлежат к тем классам функций, которые могут быть пред-
ставлены в виде ряда (см. гл. 6, 7) или интеграла Фурье (см.
гл. 2, 3 и 5), т. е. спектра любого вида. Однако принципиаль-
ная возможность представления сигнала в виде спектра ещё не
означает практической целесообразности такого представления,
так как вычислительные операции могут оказаться слишком
сложными. Существуют и такие сигналы, для которых обычное
представление спектра в виде ряда или интеграла Фурье совер-
шенно несостоятельно не только с точки зрения удобства, но и
с принципиальной стороны. Все случайные функции времени от-
носятся к такого рода сигналам. Таким примером является
речь. Можно представить посредством экспонентов любой ко-
нечный участок речи u(t), но если говорящий во время речи
включает в неё новый материал, который совершенно отличает-
ся от соответствующего f(p), то интервал анализа неопределённо
расширяется и амплитудный спектр f(p) перестаёт существо-
вать.
Для случайных функций обычно вводится более удобное по-
нятие энергетического спектра, который связан со статистйче-
18
Ш'
«ж .
«Ш&ими параметрами сигнала, а именно с его функцией автокор-
й^еляции (теорема Хинчина).
Звание энергетического спектра является для многих задач
От°ль же полезным, как и знание самого сигнала. Однако сигнал
Жз энергетического спектра не может быть восстановлен. Поэто-
йШУ необходимо найти некоторые другие способы представления
^сигнала.
1.3. ОРТОГОНАЛЬНОСТЬ И ПОЛНОТА
•З^' . При представлении сигнала в виде (1.1) необходимо преж-
де-, всего уметь определять коэффициенты ап. Определить эти
коэффициенты значительно проще, если семейство функций yn(t)
^представляет собой ортогональную систему.
Если рассматривается сигнал g(t) на интервале (ti, t2) и
^функции уп (t) удовлетворяют условиям:
t1
J Ут (0 Уп (О dt = 0 при т ф п, (1.11)
(1.12)
^.система функций yn(J) называется ортогональной и нормиро-
^'авной [поскольку интеграл (1.12) равен единице] или орто-
*Шррмированной.
./.^.Коэффициенты а„ в разложении (1.1) определяют из фор-
'../ЗЙуДы*
а*= о-13)
-ч^':'{Далее при представлении сигналов в виде ряда (1.1) необ-
ходимо, чтобы разность
g(t) — ^akyk(f)
л-1
/была мала в определённом смысле. Обычно «малость» этой
/ Разности определяется, как «малость» интеграла
Я (0 —
Л-1
dt.
(1Л1)
19
Если предел интеграла (1.14) при п->оо равен нулю, то мы
будем говорить, что ряд справа в равенстве (1.1) «сходится в
среднем» к функции g(t).
После того, как мы условились, в каком смысле должны схо-
диться ряды вида (1.1), возникают два вопроса: существуют ли
функции, к которым сходятся эти ряды в указанном смысле и бу-
дут ли эти функции единственными. Ответы на эти вопросы мож-
но получить, используя понятие полноты ортогональной системы
функций.
Ортогональная система функций вида yn(t) называется пол-
ной, если к ней нельзя присоединить ни одной функции, орто-
гональной одновременно всем уп (t) и не равной тождественно
нулю, т. е. из равенства
t,
§g(t)yn(t)dt = О
h
при любом п должно следовать, что g(t) = O.
Если функции уп (t) составляют полную систему, то легко
показать, что ряды %anyn(t) сходятся в среднем только к
одному пределу; действительно, пусть
и
g2(/) = Sa„t/„(0-
По ф-ле (1.13) для коэффициентов ак ряда получим
^2
— gMyk(t)dt = ak — ак = °
К
при любом k.
Из последнего равенства на основании свойства полноты
системы yk(t) следует, что
Ях (0 — ^2 (0 25 °,
или
Таким образом, мы ответили на второй из поставленных выше
вопросов и показали, что двух различных функций, к которым
могли бы сходиться в среднем ряды (1.1), не может быть.
Ответ на первый вопрос, с точки зрения математика, являет-
ся более сложным; для инженера же это менее трудно, так как
инженеру чаще приходится искать представления в виде ряда
для известного сигнала, чем решать обратную задачу и забо-
20
Чтиться о том, чтобы известный ряд сходился к некоторому сиг-
налу.
Ответ на первый вопрос даёт фундаментальная теорема о раз-
ложении функции в обобщённый ряд Фурье, которая утверж-
дает, что если числовый ряд сходится, то существует
для любого функционального ряда вида (1.1) с коэффициента-
ми а„ функция g(t) с интегрируемым квадратом на отрезке /j,
/2) к которой сходится ряд (1.1) в среднем *)•
Ответ на вопрос о том, какими свойствами должна обладать
функция, представленная рядом (1.1), даёт вторая часть тео-
ремы Рисса-Фишера, которая утверждает, что всякая функция
с интегрируемым квадратом на отрезке Л, t2 разлагается в ряд
вида (1.1), который сходится к ней в среднем.
Частный случай полной ортонормированной системы на ин-
тервале (0; 2 л) — система вида
—, —i=sin/, ‘ — cos/, i sin 2/, cos 2/...
2it у it /it /к Yit
По этой системе обычно раскладывают функции с интегрируе-
мым квадратом на интервале (0; 2 л) и периодически продол-
женные на всю числовую ось в обычный ряд Фурье, который
сводится к ним в среднем.
Другим примером полной ортогональной системы функций в
интервале —оо, 4-оо являются функции вида
зт2хг(/—
2kF (t £— )
\ 2F /
по которым функции с ограниченным спектром, определяемые
от —оо до4-оо, разлагаются в ряд Котельникова
+оо sm2itr 11-
-оо 2tcF | t —
(1.15)
При представлении функций g(t) в виде ряда (1.15) .возни-
кают трудности, заключающиеся в том, что обычные сигналы
имеют конечную продолжительность. Поэтому они могут быть
представлены рядом (1.15) лишь приближённо. Приближение
заключается в том, что приходится продолжать сигнал за пре-
’) Мы привели здесь в несколько видоизменённой форме одно из ут-
верждений теоремы Рисе а -Фишера.
21
делы интервала его существования любым произвольным об-
разом. Наиболее естественным, с точки зрения инженера, счи-
тать, что вне заданного интервала g(t) равно нулю. Но при
этом сигнал имел бы неограниченный спектр, который приш-
лось обрезать и представить сигнал в виде ряда (1.15) лишь
приближённо. Таким образом, перед нами возникает альтерна-
тива: либо ограничиваться' рассмотрением сигналов, единствен-
ным образом продолжаемых за пределы интервала существо-
вания (например, аналитические сигналы, которые определяют-
ся своими значениями и значениями всех своих производных в
какой-либо точке интервала существования), либо удовлетво-
риться приближением, получаемым при обрезании спектра.
В некоторых случаях мы получаем сигнал, решив дифферен-
циальное уравнение, как, например, при определении формы
сигнала конечной продолжительности, занимающего наимень-
шую полосу частот. При этом решение дифференциального урав-
нения обычно представляется-в виде ряда по собственным функ-
циям дифференциального уравнения.
•
§ 1.4. МЕТОД СМЕЩЁННЫХ ФУНКЦИЙ
Для представления сигналов можно использовать метод
смещённых функций, который состоит в следующем. По некото-
рым соображениям выбирают элементарный сигнал y(t) и из
него образуют смещённые функции уп (t) по формуле
yn(f) = y(f—
где 0 — интервал смещения, »
п — номер смещённой функции.
При .некоторых ограничениях, налагаемых на сигнал, его
можно представить в виде ряда
g(t)=^anyn(i)- О-16)
п
Такое представление возможно для функций, определённых
при —оо< t < 4- оо, если система смещённых функций являет-
4 со
ся полной и J i/2(/) dt имеет конечное значение. Сигнал
g(i) должен обладать конечной энергией, т. е.
+ оо
f g*(t)dt < + оо..
-00
22
^Ж^Многие сигналы, используемые в системах связи, представ*
.Й'яют собой естественный ряд смещённых функций, например, те-
'/^Ьрафные сигналы, состоящие из импульсов произвольной фор-
.•мы, но одинаковой длительности.
~*.;'Рднако не всякий сигнал конечной продолжительности мо-
.^ет быть представлен в виде ряда (1.16), так как если сигнал
-ЖО длится от момента времени /1 до tt, то в промежутке
..^/2-тЛ) укладывается лишь конечное число смещённых функций
' фиксированной продолжительности. Как известно из теории ря-
,:дрв; любая конечная система функций не может быть полной и,
ёйедовательно, правая часть (1.16) не сможет, вообще говоря,
’^ходиться к левой в среднем.
. '-. Для представления сигналов конечной продолжительности
Зюжно пользоваться функциями вида
t 12хт~
^л(О = ^(^-и0)е *, (1.17)
12wn —
. e
-г^де множитель e зависит от частоты--.
V Л .0
т^дТогда разложение сигнала примет вид
= (1Л8)
f?'П
^Разложение (1.18) позволяет представить сигнал конечной
^продолжительности g(t) в виде разложения по функциям
смещённым как по времени, так и по частоте.
>‘Й^у1римером применения метода смещённых функций являет*
ся ‘ряд Котельникова (1.15). Из предыдущих рассуждений яс-
' Долито так разложить можно только функции, известные на
^.ерконёчном интервале —оо</< + оо, а применить этот ряд
‘Для/ представления сигналов конечной продолжительности
* ;Мр>кно лишь с некоторой степенью приближения.
• .и'Преимущество метода смещённых функций особенно прояв-
;\,;Д^гся при рассмотрении спектров непериодических сигналов,
. Например, случайных последовательностей сигналов. Спектры
..^цх сигналов как амплитудные, так и энергетические можно
'/^.представить в виде произведения двух спектральных функций,
« одна из которых зависит лишь от формы элементарного сигна-
.Да^ а другая от характера передаваемой информации.
ГЛАВА ВТОРАЯ
СИГНАЛЫ КОНЕЧНОЙ ПРОДОЛЖИТЕЛЬНОСТИ,
СОДЕРЖАЩИЕ МАКСИМАЛЬНУЮ ДОЛЮ ЭНЕРГИИ
В ЗАДАННОЙ ПОЛОСЕ ЧАСТОТ
В начале главы рассмот-
рены соотношения между сиг-
налами и спектрами и показа-
но, что используемые в радио-
связи сигналы наиболее целесо-
образно рассматривать как
сигналы конечной продолжи-
тельности. Далее теоретически
рассмотрен вопрос о том, ка-
кую форму должен иметь им-
пульс конечной продолжитель-
ности для того, чтобы в задан-
ной полосе частот содержалась
максимальная доля полной
энергии спектра.
Определена ширина по-
лосы, содержащей 93% полной
энергии импульса оптимальной
формы. Выведена асимптоти-
ческая формула для определе-
ния импульсов оптимальной
формы при большом содержа-
нии энергии в полосе частот
и показано, что в этом случае
импульс имеет форму кривой
типа распределения Гаус-
са, ограниченной интервалом
т т
времени —
§2.1. НЕКОТОРЫЕ СООТНОШЕНИЯ
МЕЖДУ СИГНАЛАМИ И СПЕКТРАМИ
Ш ироко известен тот факт, что
функцию времени и её спектр
нельзя одновременно ограничить до
произвольно малых значений. Это
можно показать, изменяя шкалу в
интегральном преобразовании Фурье
[Л 17, стр. 19].
00
f (2.1)
—со
Если U(t) представляет собой
некоторый импульс, то U (М) при
Х>1 представляет собой более уз-
кий импульс той же формы; и спект-
1 11 ш \ ,
ральное распределение — / I—I в л
л \ к /
раз шире, чем первоначальный
спектр Такое соотношение
между функцией времени и -соответ-
ствующим ей частотным спектром определяется тем, что пере-
менные t и о) входят в виде произведения в показатели подын-
тегральных выражений прямого >и обратного преобразований
Фурье.
Другое соотношение между формой импульса и его спектром
состоит в следующем: невозможно одновременно ограничить
ширину полосы и продолжительность импульса до конечных ин-
тервалов с тем, чтобы они исчезали всюду за пределами интер-
валов. Это соотношение можно установить следующим образом.
24
Если
|t/(O|<Me-*1'1, (2.2)
то
А(Р)= J U(t)zptdt (2.3)
^00
будет представлять собой аналитическую функцию в области
a<Rep<a. Этот результат содержится в [Л5, стр. 3] и осно-
вывается на теореме о том, что равномерно сходящиеся интег-
ралы от аналитических функций сами являются аналитическими
функциями [Л20, стр. 118]. Из аналитичности fi(p) следует, что
все нули этой функции на мнимой оси должны быть изолирован-
ными точками [Л20, стр. 106].
Если функция U(t) равна нулю вне конечного интеграла t,
то она при соответствующем выборе параметра а удовлетворяет
^условию (2.2), и поэтому на основании теоремы о том, что все
. нули fi(p) являются изолированными точками, f(oj) может ис-
чезать лишь в изолированных точках, но не в конечном интерва-
. ле частот.
Л. И. Мандельштам поставил задачу о нахождении произве-
дения продолжительности импульса на ширину его спектра. Эта
задача при достаточно общих предположениях была решена в
1934 г. А. Г. Майером и Е. А. Леонтович в [Л6], где показано су-
ществование зависимости между этими двумя величинами, подоб-
ной соотношению неопределённости в физике, и произведена
' оценка нижней границы их произведения.
Методика работы в [Л6] была основана на рукописи П. С. Но-
викова, которая не была опубликована и по-видимому утеряна.
Позднее Г. М. Жислин в [Л41] строго обосновал методику, ис-
пользованную в [Л6].
В 1946 г. Габор в [ЛИ] повторно рассмотрел эту задачу, наз-
вав среднеквадратичные значения функции времени и её спект-
ра, сосредоточенные вокруг некоторого среднего значения, «эф-
фективной продолжительностью», а сосредоточенные вокруг не-
которой средней частоты — «эффективной шириной спектра».
Следует отметить, что «эффективная продолжительность» и «эф-
фективная ширина спектра» из-за своей приблизительности ма-
ло полезны при описании свойств действительных сигналов, ис-
пользуемых для радиосвязи. Кроме того, эти величины неудобно
вычислять, не говоря уже о том, что определение «эффективной
ширины спектра» для импульсов некоторых форм приводит к
расходящимся интегралам.
Используемые в радиосвязи сигналы наиболее целесообразно
рассматривать как сигналы конечной продолжительности, т. е.
25
как сигналы, начинающиеся и заканчивающиеся в определённые
моменты времени и равные нулю всюду вне интервала, заклю-
чающегося между этими моментами времени. Такое рассмотре-
ние хорошо отображает действительный характер сигналов и
вместе с тем позволяет математически корректно исследовать
их, например, применять метод «смещённых» функций, опреде-
лять оптимальную форму импульса и т. д.
Обычно рассматриваемые и синтезируемые формы импульсов
(например, прямоугольный, трапецеидальный, косинусоидаль-
ный и др.) относятся к сигналам конечной продолжительности.
Получающийся в реальном фильтре сигнал, у которого задний
край асимптотически приближается к нулю, также можно с лю-
бой степенью точности представить в качестве сигнала конечной
продолжительности. ,
Учитывая приведённые соображения, мы будем рассматри-
вать в качестве сигналов импульсы конечной продолжительно-
сти. Ниже рассматривается вопрос о том, какую форму должен
иметь импульс конечной продолжительности для того, чтобы в
заданной полосе частот содержалась максимальная доля пол-
ной энергии спектра. Для импульса такой формы находят рас-
пределение энергии в полосе частот и определяют ширину поло-
сы частот, содержащей 99% полной энергии спектра, т. е. шири-
ну полосы, соответствующую общепринятым международным
определениям (см. § В.З).
§ 2.2. СОСТАВЛЕНИЕ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ
Пусть заданы длительность импульса т и полоса частот
—(оо<®< + шо. Мы хотим определить форму импульса U(t), при
которой частичная энергия спектра в указанной полосе
(2.4)
составляет максимальную долю полной энергии импульса
= [f(Mf*(i<“)= f U4t)dt.
J J
(2.5)
Аналогичная задача приближённо решалась в (Л 18]. Бла-
годаря новой методике решения задачи, автору данной книги
26
тел -
-’Д'
удалось получить её точное решение и использовать табулиро
ванные функции.
ч Здесь f(ico) — амплитудный спектр импульса
2
/(i<o)= f U(t)e~iatdt,
(2.6)
. 2
2 2
/(ia>)/* (i<o) = f f U(t)U (s)ei<a(t~s) dtds.
2 2
Ь V Подставляя в (2.4) интеграл (2.7), меняя порядок
фования и интегрируя по ю, находим
* ‘К '
MS ‘
•22
IF(a>o)=— f f <7(Ot/(s)?in<°o(f~—
те J J t — S
(2.7)
интегри-
(2.8)
АД Таким образом, сформулированное условие сводится к вариа-
ционной задаче: определить при заданных <оо и т функцию U(t),
£^ри которой
, 2 + 2
Ц7 (©о)=— f f и ф и (s) dtds (2.9)
ЧЗ/ * те J J t — s
4/" 2 2"
,г.Д1меет максимум, если
•v.,% Нормировка Wn0M =4, очевидно, не снижает общности за-
ч,:Дачи.
в [ЛЗ, стр. 118] доказано, что вариационная задача (2.9) в
силу симметричности и положительной определённости ядра
, Ч K(/,s) = — sina>o(/-s) (2.10)
‘ к t-s
J, • 27
при любых конечных ио и г имеет решение. При этом
£/мя(0 = Ф1(0, (2-И)
где есть первая фундаментальная функция (с наименьшим
положительным числом щ) интегрального уравнения Фред-
гольма
т
+
U(t) = ? f — sintt>o(<~— U(s)ds. (2.12)
J It t — s
т
“ T
Достигающийся при этом максимум в полосе — но<и< + но
равен
max W (а>0) = — = *i,
или
§ 2.3. ОПРЕДЕЛЕНИЕ ГРАНИЦ ДЛЯ ЧАСТИЧНОЙ ЭНЕРГИИ СИГНАЛА
Прежде чем приступить к решению интегрального ур-ния (2.9),
определим границы для частичной энергии, т. е. для величины «ь
При перечисленных выше свойствах ядра (2.10) фундамен-
тальные функции ур-ния (2.12) образуют полную ортонормиро-,
ванную систему { фп (t)} на интервале (-----1” ’ ’ ^Ри
этом по [ЛЗ, стр. 128] ядро можно представить в виде ряда
Фп(0Фд(8)
(2-И)
п=1
Полагая в последней формуле t—s и интегрируя почленно,
находим
(2.15)
Аналогично, заменяя квадрат ядра двойной суммой и учиты-
вая ортонормированность фундаментальных функций, получим
23
"1" 2 "1" 2 оо оо
si= J J = =
_ 2 т л=1 л=1
2 2
W = S2=ff ^[4kSi(4k)-2sin2(2^Cl(4k)<4n(^
(2.13)
Рис. 2.1. Пределы, в которых заключается мак-
симальная частичная энергия сигнала конечной
продолжительности, и приближённые значения W
\Для рассматриваемого ядра интегралы (2.15) и (2.16) берут-
ся элементарно:
Sl = — , <2.174
к
$2 = (4Л Si 4Л — 2 sin2 2k + Ci 4k — С - In 4k), (2.18)
29
где Si и Ci обозначают интегральные синус и косинус, а
С=0,577216... — постоянная Эйлера.
Величины (2.17) и (2.18) оказываются выраженными через
единственный параметр
Л=-^ = —Д/с, (2.19)
2 2
где Д/ — полная ширима полосы в герцах: Д/ = —5— 2 ш0.
2 л
В качестве верхнего предела для величины (2.10) прини-
маем согласно (2.16)
1?(А)=»3,(А). (2.20)
Чтобы найти нижний предел, учитываем, что из-за положи-
тельности фундаментальных, чисел [ЛЗ, стр. 122]
(ОО \ 2 00
2». >2’"=^-“?-
п-2 / л-2
Решая последнее неравенство относительно Xi, находим
W (А) = + ]/ . (2.21)
Обе границы для частичной энергии сигнала представлены на
рис. 2.1.
§ 2.4. ПРИБЛИЖЁННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ
ПОСРЕДСТВОМ РАЗЛОЖЕНИЯ ЯДРА
Чтобы решить ур-ние (2.12), воспользуемся частным случа-
ем формулы на стр. 398 в [Л 15]
50 J 1 (®оО 1 (“оО
_1_ sino0(/-s) _ yi / . _1_ \ Л+Т-----”+ т —. ,2 22)
к t — s и\ 2 ) /7
п=0
Разложение (2.22) позволяет построить последовательность
вырожденных ядер, аппроксимирующих ядро (2.10). При вырож-
денном ядре [ЛЗ, стр. 106], решение интегрального уравнения
сводится к квадратурам и решению системы лйнейных алгебраи-
ческих уравнений.
30
ч *
$ Сделаем предварительно подстановку
/ = VqX
^обозначим
< 1/(0 = t/i (®оО- (2.23)
У В согласии с определением (2.19) ур-ние (2.12) примет вид
t/i(x) = t4 U^y) sin(x у) dy. (2.24)
J X — У
, —k
%,
Удерживая в ф-ле (2.22) N членов ряда, ищем приближённое
^решение ур-ний (2.24) в виде суммы
l/.W-g
m=0
г . W
m+ т
(2.25)
^" ’Заменяя в (2.24) ядро указанным приближением, a U[(x)
^цо ф-ле (2.25) и приравнивая коэффициенты при функциях Бес-
>^еёля равных индексов в правой и левой частях, получаем систе-
му .однородных линейных уравнений
< ‘ 1*2 ....(2-26)
. л-0 '
Ж? Коэффициенты симметричной матрицы ||РП> т || равны
4-Л
Pmt п = Рп, tn ~ ~~ ( J j (х) J । (x)dx,
2 J_k п+Т т+т
(2.27)
•?4i- -
'л^'А А
’^‘.Значения интегралов (2.27) приведены в [Л15, стр. 167—168]
гЛ<в [Л14, стр. 237].
^m;n
1 с-
— Si
тс
/п-1
(2£)-V 1 (*)-vJ2m+ ‘ W ’ <2-28>
jhJ V 2 v
л-о
Гл
Рд, т = 0
(2.29)
п+т нечётно,
ж..
1
31
i 1 2 1 \2
Г/ , (4)7 , m-
J 1 (k)J ] (k)
-J j (k)J , (A)|
m+ Л---7Г I
2 2 J
m-H 1
(2.30)
если n+m. чётно.
Из ф-лы (2.29) заключаем, что система (2.26) распадается
на две независимые системы уравнений: для ат с чётными и
с нечётными т. Если учесть, что в ф-ле (2.25) чётность функций
соответствует чётности индексов, то полученный результат ста-
новится физически очевидным.
Решение Ui(x) задачи, поставленной в § 2.2, должно быть
чётно относительно середины отрезка — k х < k. Можно до-
казать непосредственно, что оптимальная функция имеет впол-
не определённую чётность. Действительно, в противном случае
сигнал можно представить в виде суммы чётного и нечётного им-
пульсов, энергии которых складываются линейно. Поэтому, вы-
бирая из двух импульсов тот, у которого отношение (2.13) боль-
ше, найдём, что сумма импульсов не является оптимальной. Не-
чётное решение имеет нуль амплитудного спектра в центре за-
данной полосы, что противоречит, если не математической, то,
во всяком случае, физической постановке задачи. Поэтому мы
полагаем ат = 0 при нечётном т.
Дальше рассчитываем по обычной схеме. При известных ко-
эффициентах (2.28) и (2.30) требуем обращения в нуль опре-
относительно р,. Определив его наименьший положительный ко-
рень, находим коэффициенты а2да и из ф-л (2.26) и (2.13 — опти-
мальную форму импульса и достижимую при этой форме долю
частичной энергии.
При 77=0 ао¥=О, при m>Q система (2.26) вырождается в
одно уравнение, из которого находим
Ро,о = — Si (2k) - J2. (k).
7Г 4-
(2-31)
Нулевое приближение к искомой форме импульса определя-
ется с точностью до произвольного множителя а0.
. (2.32)
32
жЙ'Как отмечалось выше, случай N=\ ие уточняет ф-л (2.31)
«2-32)- „
^1:;При ^=2, когда оптимальное решение ищем в виде
К' (Л(х) = -^
Ж;-- : У X
Ц^йучаем уравнение второй
''Эить **
Л W4
. 2
степени,
T J
из которого можно опреде-
рРо.о — 1
P^0,2
Р^2.0
pA.2
2
5
= 0,
(2.33)
/^Раскрыв определитель (2.33), без труда находим меньший из
:де>ух корней (РО2 = ^2,о)
p. =
0,0
2 4 .
*ТР«’
<
2 (Л),0 P2,2 ^0,2)
(2.34)
^а/При ц=р.1 оптимальная форма сигнала имеет вид
" 1 М + -~^— Л м],
Г 1 — 5^2,2 Т J
2 2
— произвольная постоянная.
им
(2.35)
*’4
Л'
’?W
•M
ж
aQ
И i?* Sf'4
W =
Рис, 2.2. Форма импульса конечной продолжительности,
< занимающего наименьшую полосу частот, при ^=3,6; 5 и 20:
Кривые при 6=3,6 и 6=5 (штриховая линия) рассчитаны
по формуле £7(6,K)—Yndn (k) Рл(Х), кривые при 6=5
’ (сплошная линия) и 6=20 по приближённой формуле
'Ж,: У [k, Х)^е 2
^*30
33
Коэффициенты, входящие в ф-лы (2.34) и (2.35), получаем из
общих ф-л (2.28) — (2.30):
POiO = — Si (2А) — J2. (А),
К —
2
Ро,2 = -^ГЛ (А)Л (A)-j±(A)j ±(А)] —LjL(k)JL(k), (2.36)
L 2 2 2 2 J d 2 2
P22 = 2_r_LSi(2A)-j21 (6)-±.Рб (fe)‘ •
5 it 4- 2 4-
Ha рис. 2.2 дан график правой части (2.13) по данным вто-
рого приближения.
§ 2.5. РЕШЕНИЕ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ ПОСРЕДСТВОМ
ПРИВЕДЕНИЯ ЕГО К КРАЕВОЙ ЗАДАЧЕ ДИФФЕРЕНЦИАЛЬНОГО
УРАВНЕНИЯ
Преобразуем интегральное ур-ние (2.12), введя новые пе-
U(X) = р/ f и(v) dv,
J x(k — v)
(2.37)
где
В приложении II показано, что каждое решение интеграль-
ного ур-ния (2.37) является ограниченным решением однород-
ного линейного дифференциального уравнения типа Лиувилля
U (X) s -±- [(X2 -1) + (АХ)2 U (X) = CU (X). (2.38)
uA 1 uA J
Интегральное ур-ние (2.37) удобно приводить к краевой за-
даче дифференциального ур-ния (2.38) потому, что в числовых
расчётах для определения сигнала оптимальной формы Uoam(t)
и максимума энергии в полосе частот max W(соо) мы сможем
использовать табулированные коэффициенты dn, содержащиеся
в [Л9].
Покажем, что каждое ограниченное решение u(k, X) диф-
ференциального ур-ния (2.38), соответствующее наименьшему
собсФвенному значению Со константы разделения С, является ре-
34
^Дением интегрального ур-ния (2.37). Функция ы(М) может
быть представлена при IX|< 1 в виде ряда
«(Л,К) = 2Х(Л)РЛ(Х). (2.39)
п
В ф-ле (2.39) параметр k может принимать любое положи-
тельное значение, коэффициенты dn (k) табулированы в (2.9)
для k •< 5, а функции Рп (Л) являются полиномами Лежандра
> соответствующих степеней л=0, 1, 2, 3.... Штрих над S озна-
чает, что суммируют только по чётным п, начиная с нуля.
/. В приложении III показано, каким образом определяются
коэффициенты dn(k).
‘ Функции u(k, X), являющиеся ограниченными решениями
Дифференциального ур-ния (2.32), можно, с другой стороны, раз-
Држить для любых значений Л в сходящийся ряд по -сферическим
/функциям Бесселя для
п
«(*,Х) = р(4)--!---V'(-I)2 (2.40)
' 2'«.(ч
В ф-ле (2.40) и в дальнейшем штрих над S имеет то же зна-
чение, что ив ф-ле (2.39), a p(k), коэффициент пропорциональ-
ности, не зависящий от Л. Функции /„ независимой переменной
Д представляют собой сферические Бесселевы функции, опреде-
ляемые равенствами
(2.42)
,-й удовлетворяющие соотношениям:
in («),♦«--sin (z — -у-);
/ (г) ~ zn =_______________—_____
nt". in\ (2n^l)l 1*3-5... (2n^ 1)
.. .Коэффициенты dn(k) имеют те же значения, «
Ф-ле (2.39). Это можно проверить, если для коэффициентов
из равенства (2.40) вывести рекуррентное соотношение,
Подобно тому, как выведено -соотношение (2.15) для коэффици-
ента равенства (2.39) в 'Приложении III. Оба соотношения име-
совершенно одинаковый вид.
(2.43)
ЧТО и в
35
Величину р(/г) можно получить, полагая %=0 в (2.40) и учи-
тывая соотношение (2.43)
РА= °)- (2-44)
“0 («)
Выведем теперь формулу для определения шах 1У((оо) = А-
Заменим в ур-нии (2.39) аргумент к на р, умножим обе части
полученного равенства на е1кХ|1 и проинтегрируем его по р в пре-
делах от —1 до 4-1
+ 1 +1
pje'^dp- J ^dn(k)Pn(p)eik*dp =
-1 -1 n
’+1
= J]k(^)Jel^Pn(p)dp. (2.45)
n —I
Известно (Л36, стр. 583], что
+1
Je'^P„(p)dp = 2f/e(«). (2.46)
— 1
Учитывая (2.40) и (2.46), можно переписать равенство (2.45)
в следующем виде:
р 2^dn(k)
Ju (/с, p)ewdp =——u(A,X). • (2.47)
--1
Учтём, <что u(k, р) представляет собой чётную функцию р
и подставим значение р(А) из (2.44) в ур-ние (2.47), тогда по-
следнее можно записать в следующем виде:
+1
f cos (АХр) и (k, р) dp й= 2 и (k, X). (2.48)
ы - J и (k, 0)
—1
Далее из чётности u(k, р) следует, что sin(AXp) >u(k, р) бу-
дет нечётной функцией р и, следовательно,
+ 1.
J sin (АХр) u(Ap) dp = 0. (2.49)
-1
.36
г
Г
gU Сложим почленно равенства (2.48) и (2.49)
+1
f u (А, р) [cos (AXp) + sin (AXp)] dy. = и (k, X). (2.50)
ч-<; ’ J и («, О) . .
Заменив в (2.50) аргументы л на ц и ц на v, получим
t +1
$ a f и (k, v) [COS (Apv) 4- sin (kpv)] dv = ^---- И (k, p). (2.51)
'/</ W \K f \j)
J.' Умножим обе части (2.51) на
^проинтегрируем
’1—1
[cos (AXp) + sin (AXp)]
по p в пределах от —1 до +1:
+i
[cos (AXp) 4- sin (AXp)] J и (A, v) [cos (Apv) 4- sin (Apv)] dv.dp =
— 1
-Ч-1
= -2^(^ f U (A, p) [cos (AXp) 4- Sin (AXp) dp]. (2.52)
u (n j 0) J
—1
л/, Преобразуем левую и правую части (2.52).
Левая часть. Изменим порядок интегрирования :
§4';.+1 +1. ] .
Йfcos s*n (^4*)] J ы (&, v) [c°s (^v) + sin (Apv) dv dp =
+i г +1
j |u (k, v)J [cos (AXp) 4- sin (AXp)] [cos (Apv) 4- sin (Ap)] dp dv;
J [cos (AXp) + sin (AXp)] [cos (Apv) 4- sin (Apv)] dp
i/''si; 2 sin A (k v)
• A(X —v) ‘
|Йй;Поэтому левую часть равенства (2.52) можно написать в
+i"' +1
Ьл u(А, V)d*«-“[«(v) jfoy~v) dv. (2.54)
g// / J j я (a — v) kJ n(X—-\)
37
Правая часть. Учтя равенство (2.51), напишем
+1
f U(ft, И) [cos (k\|*)+sin (AXfOJ& X)- (2-55)
»> 0) J L“(«>0) j
Приравнивая правые части (2.54) и (2.55), получим .
— f и (v) sin*(X~~v) dv = Г Г и (k, к),
k J *(Х —v) L u(k, 0) J '
откуда
и (к) = и (v) sink£~±<b. (2.56)
W 2Ц(Л) J x(X —v) V '
— 1
Таким образом, мы показали, что решение и (Л) дифферен-
циального ур-ния (2.38), соответствующее наименьшему соб-
ственному значению Со константы разделения С, является ре-
шением интегрального ур-ния (2.37).
z _ та? (6,0)
2Ad§(*)
или в соответствии с нормировкой
u(k, 0)=Ро(0) = 1, (2.57)
принятой в [Л9],
и максимальная энергия >в полосе частот, определяемая в соот-
ветствии с ур-ниями (2.13) и (2.58), будет равна
max W (k) = Ц- = —-. (2.59)
р. тс
Аналогично можно доказать, что каждое ограниченное реше-
ние дифференциального ур-ния (2.38) (при любом собствен-
ном значении Ст константы разделения С) является решени-
ем интегрального ур-ния (2.37).
В приложении II доказано, что каждая собственная функ-
sin£(X — v)
ция ядра-------*----- является ограниченным решением диффе-
it (X v)
ренциального ур-ния (2.38), соответствующим' некоторому зна-
чению Сж константы разделения С.
38
Таким образом, совокупность решений интегрального урав-
нения (2.37) совпадает с совокупностью ограниченных решений
дифференциального ур-ния (2.38).
у Расчёты по ф-ле (2.59) показывают, что при 6=3,6 доля
энергии в заданной полосе достигает 99% (точнее 99,15%). Та-
ким образом, ширина полосы частот, занимаемой «идеальным»
•импульсом, составляет
Д/^-2--3,6 = — (гц).
(2.60)
На рис. 2.2 приведён график uovn (%) для случая 6=3,6,
. рассчитанный по ф-ле (2.39).
На рис. 2.3 построены графики функции u(k, Л) при 6=
=04-5 и дана соответствующая таблица.
у Выясним, каково соотношение, о котором упоминалось ра-
внее, между «эффективной продолжительностью» импульса и
^эффективной шириной спектра» для полученного нами «иде-
:ального» импульса.
'; По определению
Г 1—
= |2 л (и—и)* J — «эффективная продолжительность» импуль*
са,
: _______j_
Д/ = [2л (/ — /)2]2 — «эффективная ширина спектра»,
Определим «эффективную продолжительность» «идеального»
Импульса. В соответствии с ф-лой (2.39)
+00 +1
у'. J uu*dk=§ u2dk = - (2.62)
AS it P
На основании ф-лы (П.Ш.4) получим:
+°о +1
uu*Kdk = С и2ХА =
-00 -1
= [ УрлР„ (*) РЧ [-377 Рп-г (к) + Pn+l (к)] d’K = 0. (2.63)
Л/ ЛшА шЛ [бП ^Г* 1 ч * J
— 1 л п
б)
X и (k, X) при
Л=1 *-2 л=з Л=5 Л-5
0 1 1 1 1 1
0,1 0,9985 0,9945 0,9893 0,9842 0,9786
0,2 0,994 0,978 0,958 0,937 0,919
0,25 0,990 0,965 0,934 0,905 0,876 1
0,3 0,986 0,950 0,907 0,865 0,826
0,4 0,975 0,912 0,839 0,770 0,707
0,5 0,961 0.865J 0,957 0,659 0,574
0,6 0,944 0,810 0,664 0,540 0,439
0,7 0,924 0,748 0,565 0,420 0,312
0,75 9,913 0,714 0,514 0,362 0,255
0,8 0,901 0,679 0,463 0,307 0,203
0,9 0,876 0,607 0,363 0,205 0,115
0,95 0,862 0,569 0,314 0,160 0,080
1 0,8481 0,5315 0,2675 0,1193 0,0502
Рис. 2.3, а) Форма сигнала и (k, X), содержащего мак-
симальную долю энергией заданной полосе частот при
б) Значения функции u(ktX) —^dn(k)Pn (К)
40
Учитывая, что
(2.64) получим
(2.64)
^Йбсле интегрирования
п п— 1 2
= у d„d„_2
L4 I л 2n4-l 2n —3 2n—1
n
n2 2
\ а2\ п‘ 2 I <п<н)а 2 1 _|_
"Г ”[(2л4 I)2 2л — 1 (2п-& I)2 2п>з]
. л j * +1 л 4-2 2 ]
"Г " "+22п4-1 2п4-5 2п\ЬЗ| ’
учитывая, что первое слагаемое в фигурных
(2.65)
|^гЙли, .
r^(|>65) фактически равно третьему, получим
В >’............. ч-Г “2 г »•
скобках
iO!
ad%=y | ~ " 1-^—-
I(2л4-1)2 [2л—1
п
+ 4dndrt+2 — <^П(п.±2)
л (2л 4-1) (2л 43) (2л 45)
(п^1)а
2л фЗ
(2.66)
^Обозначив
-00
, получим, в соответствии с (2.62)
J uu*di
' -оо
£Jl(2n4-l)2
Ш -------------
(п^1)2
2п «4е 3
(п<М)(п^2) |
n+2(2n^l)(2n4-3)(2n^5) (
Л';'
Шг-’
У'-?-/
п
(2.67)
Д/-1Л2*/’.
Далее нам следует определить «эффективную ширину спек-
ра» «идеального» импульса. Однако этого сделать нельзя, так
как «'идеальный» импульс имеет на краях разрывы, а спектр
функции, имеющей разрывы, как это будет показано в гл. 5,
убывает при возрастании частоты пропорционально —, т. е. мы
(О
должны определить «эффективную ширину спектра» импульса,
выражаемого в виде
причём
Нт <р (®) =/= о,
со—*-°О
ибо ф(ш) является периодической функцией.
Поэтому
J = J <p2(co)do>.
— СО -00
(2.68)
Поскольку подынтегральная функция в (2.68) всюду поло-
жительна и не стремится к нулю при о)->со, то интеграл (2.68)
расходящийся, и определить «эффективную ширину спектра»
невозможно. Это лишний раз подтверждает неудобство понятия
«эффективная ширина спектра».
§ 2.6. ИССЛЕДОВАНИЕ СИГНАЛОВ и (А, К) ПРИ БОЛЬШИХ
ЗНАЧЕНИЯХ ПАРАМЕТРА k
Заменим переменные в ур-нии (2.38)
X/Т = х\ тогда U(К) = U= V(*)> (2.69)
и ур-ние (2.38) принимает вид
— О^г-1+*ау (х) = Т V <*>♦ (2J0)
dx [\ k /dx } k
При А->-оо(2.70) обратится в уравнение вида
_ + (х) = B0V (х), (2.71)
dx2
где
(2.72)
А->оо k
42
причём через Со обозначено наименьшее собственное значение
-Константы разделения С.
Решением ур-ния (2.71) является функция
< Vo(x)=Toe 2 (2.73)
:при
0е Во = 1, (2.74)
• в чём можно убедиться, если подставить (2.73) в (2.71) и про-
верить.
, Из (2.72) и (2.74) получаем, что
*♦00 k
С. (Л)— k при k-+<x>.
. Если выбрать нормировку (2.57), то
_ ал
М и(k, vo(k, k) = e 2 . (2.75)
Числовой расчёт показывает, что сигнал иопт (t), ограничен-
ней интервалом времени—достаточно хорошо
Представляется асимптотической ф-лой (2.75) при k > 5, что
Соответствует полосе частот, содержащей не менее 99,94% лол-
фЗй энергии спектра.
У Таким образом, мы пришли к заключению, что «идеальный»
.Импульс выражается на участке —1<С X -С +1 в соответствии
Н'ф-лой (2.75) кривой типа распределения Гаусса при условии,
С^о в заданной полосе частот содержится не менее чем 99,94%
'Полной энергии спектра.
ГЛАВА ТРЕТЬЯ
ПОЛОСА ЧАСТОТ, ЗАНИМАЕМАЯ ПРИ
ПЕРЕДАЧЕ ИМПУЛЬСОВ
В главе рассмотрено рас-
пределение энергии импульсов
различных форм в полосе ча?
стот и определены численные
значения ширины полосы
частот, занимаемой при их пе-
редаче. Даны формулы и по-
строены графики функции рас-
пределения энергии в полосе
частот прямоугольных, трапе-
цеидальных, треугольных, ко-
синусоидальных, косинус-квад-
ратных и косинус-кубичных им-
пульсов.
Подробно исследованы низ-
кочастотные и высокочастотные
косинусоидальные импульсы.
В частности, рассмотрен во-
прос о влиянии начальной фа-
зы импульсов на ширину поло-
сы, занимаемой при,их переда-
че. Даны графики зависимо-
сти ширины полосы, занима-
емой при передаче косинусои-
дальных импульсов с различ-
ными начальными фазами, от
числа периодов косинусоиды,
из которых состоит импульс.
Результаты расчётов ис-
пользованы . для оценки им-
пульсов различных форм в
отношении занимаемой ими
полосы частот. Показано,
что импульс, состоящий из по-
лупериода косинусоиды, зани-
мает весьма узкую полосу ча-
стот и близок к «идеальному».
§ 3.1. РАСПРЕДЕЛЕНИЕ ЭНЕРГИИ
ИМПУЛЬСА В ПОЛОСЕ ЧАСТОТ
П усть задан U(t) — импульс
• продолжительностью т. Спектр
f(i<o) импульса U(t) вычисляется
при помощи интеграла Фурье:
т/2
/(!•)» J 6/(/)е"ы dt, (3.1)
-т/2
где U(t) = Q при |/| >-у
Спектральная плотность энергии
импульса будет равна:
т/2 т/2
f/* = j j l/(/i)£/(G)X
-т/2 —т/2
Xe-i«>(G-/.)d4d/at (з.2)
Частичная энергия в полосе ча-
стот —<в, +® выражается формулой
4-ц> 4-оо
н=4- f =~ \ff
—<о —.00
*d®.
(3.3)
Для удобства введём функцию распределения энергии в поло-
се частот следующего вида:
44
£ В отношении функции т| нужно сделать следующие замеча-
$ния:
fc;;: 1. Она является монотонно возрастающей функцией, т. е.
^Непрерывно возрастает или, в крайнем случае, остаётся по-
йётоянной при увеличении со.
jh . 2. Функция т) между двумя любыми значениями со пропор-
циональна содержащейся в этой области частот энергии функ-
!;ции U(t).
3. Максимальное значение функции т] равно единице.
Рассмотрим распределение энергии импульсов различных
%форм в полосе частот и определим ширину полосы частот, за-
снимаемой передачей этих импульсов.
7§ 3.2. ПРЯМОУГОЛЬНЫЙ ИМПУЛЬС
Функция времени описывается выражением:
«К
Л т . т
Л при—
Щ/) =
(3.5)
О при И >-|
Спектральная плотность энергии импульса равна:
(3.6)
?-.где со — ширина полосы, т — продолжительность импульса.
Относительная частичная энергия в полосе частот выражает-
формулой
7] = — Si (сот)
я
(ОТ
2 sin2-—
2
(ОТ
(3-7)
;Или, введя единственный параметр
- (ОТ
к =-----------------------------,
2
(3.8)
ж?
|жЦ1редставляющий собой половину произведения продолжительно-
сти импульса на ширину полосы, .
46
получим
2
где J1(A)=(4V
— \ J
п У /
71 = — Si(2A)-Ja. (k), (3.9)
К _L_
2
sin k — Бесселева функция с индексом, рав-
ным половине.
Рис. 3.1. Распределение энергии «идеаль-
ного» (W) и прямоугольного (tj) импульса
в полосе частот
Как видно из рис. 3.1,
в центральной части
спектра (при малых зна-
чениях k) единичного сиг-
нала конечной продолжи-
тельности нельзя скон-
центрировать энергию,
большую, чем энергия
прямоугольного импуль-
са. Однако при увеличе-
нии k энергия прямо-
угольного импульса нара-
стает значительно мед-
леннее, чем энергия иде-
ального импульса.
Ширина полосы, зани-
маемой передачей (прямо-
угольного импульса (вы-
раженная в единицах k),
равна:
А/як 32,2.
§ 3.3. ТРАПЕЦЕИДАЛЬНЫЙ И ТРЕУГОЛЬНЫЙ ИМПУЛЬСЫ
Функция времени трапецеидального импульса описывается
выражением:
46
Спектральная плотность энергии равна:
//* = (---(3.11)
\ О-*1И2 4 4 ) ' '
а относительная частичная энергия в полосе частот выражается
формулой
_______1______(___cos 2k .
«(1-5)41 + 2$) I +
sin2fc 2cos.2fe. , 4Si2^ +
А» k
cos 2£k sin 2gfe . 2 cos 2$fe
?k» + ik
{-4S12U
_/| , аз Г 2cos(l +5)fe . sin(l +$)fe . cos(l +$)fe
' 7 I (i + e)8*8 (i + e)8*2 "r (i + $)fe "r
4- Si (i + $) л] — (i — n» [—2col(1~^fe _ _
v J ' L (i-e)8*8 (i-e)2*8
—<312>
$ =—, k =— и т, ^показаны на рис. 3.2.
т 2
л. Рис. 3.2. Распределение энергии прямоугольного, трапецеидального и тре-
2 угольного импульсов в полосе частот
47
Полагая |=0, получаем формулу для определения относи-
тельной частичной энергии треугольного импульса:
1 Г cos 2k — 4 cos k -ф- 3 , sin 2k — 2 sin A .
= T [----------5--------+-------k‘------+
+ ?.<=?? а.~ “s *>. 4.2 (2 Si — Si t)l. (3.13)
k J
Рассмотрим прямоугольный импуЛьс, фронты которого бу-
дем наклонять, уменьшая ть При этом (прямоугольник будет по-
следовательно превращаться в трапецию, а затем, как крайний
случай, в треугольник. Как при этом будет изменяться распреде-
ление энергии в полосе частот? Ответ на этот вопрос зависит от
того, о какой ширине полосы идёт речь. Как видно из графиков
рис. 3.2, при k менее приблизительно двух увеличение наклона
фронтов импульсов уменьшает процент энергии, сосредоточен-
ной в заданной полосе частот. При значениях k, больших приб-
лизительно 3,5, наклон фронтов импульса увеличивает процент
энергии, сосредоточенной в заданной полосе частот. И, нако-
нец, существует область значений 2,04-3.5, в которой содер-
жание энергии мало зависит от наклона фронтов импульса.
Ширина полосы частот, занимаемой передачей трапецеидаль-
ного и треугольного импульсов, будет равна:
g 0,0 0,5 " 0,8
Af (в единицах k) ' 4,1 6,2 10,2
Таким образом, ширина полосы частот, занимаемой переда-
чей (т. е. полоса частот, содержащая 99% энергии импульса),
уменьшается при увеличении наклона фронтов импульсов.
§ 3.4. ИМПУЛЬС, ИМЕЮЩИЙ ФОРМУ ОТРЕЗКА КОСИНУСОИДЫ.
КОСИНУСОИДАЛЬНЫЙ ИМПУЛЬС
Импульсом, имеющим форму отрезка косинусоиды, будем на-
зывать функцию {/(/), совпадающую с функцией coscoq/ в некото-
ром интервале 4, h и равную нулю всюду вне этого интервала.
Модуль частотного спектра определяют из выражения
5 (ш) = V [Al(®)J8 + [JV(w)]8, (3.14)
где для всех значений ш, за исключением о> = и>0:
М. = —J— (sin Ata — sin Д4) 4—~ (sin - sin Bx4), (3.15)
2Л1 2»!
48
g-;
N (<o) = — (cos — cos A4) —
I;; ----(cos ВЛ — cos Bj/i),
< A = <i> + oi0; Bi = w — «>o-
*, При a> = w0
M (ш0) = (ir:(1 —1— (sin 2<n0Z2 — sin 2(00^),
2 4<i>0
N (®0) =---------— (cos 2o>0/2 — cos 2<i>ofi).
4t0o
(3.16)
(3.17)
(3.18)
(3.19)
Энергию в полосе угловых частот
Йлить по формуле
от 0 до ® можно
опреде-
J[S(<o)]4© =
fe1 ~ [si AitQ — Si (-|- BitQ)
sin8 Л^р
2
sin8-^
_____2_
Bi Л1
COS <оо (/2 + /1) (
2w0 ( L X
“Ь Ci Ci Ad — sin <W()/o [Si (~|“ (Bi^o) — Si A^o])»
* -1 j
|£де t0 = tt — ti и верхний знак соответствует (u<w0, а
йнак ш > we.
|| Если в импульсе содержится целое число полупериодов часто-
мы соо и он начинается с минимума косинусоиды,.?, е. при ?i= — ,
№
(3.20)
нижний
( sin8-<^
№/о = 100 = — --------—
I (1 —g)p
_____2
(1<Н)Р
[2 2
+ Si(l+«)p-Si[±(l-a)p] +
a) 0 — Ci (1 + a) p
(3.21)
»
— , P=2ny=©o6, Y — число периодов частоты ®o> co-
me
, н — "WV f —WU*U.» Y ’ 1X1^147 **TUVIVIMI wu, V.V
Держащееся в импульсе. Различные знаки перед 'некоторыми
Дренами ур-ния (3.21) соответствуют тем же значениям, что и
|||ур-нии (3.20).
IF'
49
Если импульс начинается с максимума косинусоиды (^ = 0),
то перед членом в ур-нии (3.21) вместо плюса будет
стоять минус.
Обозначим нижний и верхний края полосы частот, занимае-
мой передачей, соответственно через ей и сог- Тогда ширину по-
лосы, занимаемой передачей импульса, имеющего форму отрез-
ка косинусоиды, можно найти по формуле
А/ = 4" Ь - = V- (“2 - <3-22>
Крайние частоты coj и сог полосы частот рассчитывают из
ур-ния (3.21), в котором левую часть полагают равной соответ-
ственно 0,005 и 0,995, поскольку мощности внеполосной переда-
чи, расположенные по обе стороны от полосы, занимаемой пере-
дачей, принимают равными друг другу.
На рис. 3.3 показан пример двух импульсов одинаковой про-
должительности (у = 2), но отличающихся начальными фазами.
Спектры этих импульсов рассчитаны по ф-лам (3.14) — (3.19).
Как видно из рисунка, изменение начальной фазы «перекаши-
вает» спектр: если импульс начинается с нулевого значения ко-
синусоиды, то боковые лепестки, расположенные справа от цент-
ральной части спектра, превышают лепестки, расположенные
слева от центра; если же импульс начинается с максимума ко-
синусоиды, то, наоборот, левые лепестки превышают правые.
На рис. 3.4—3.6 изображены графики функции К°/о=/(а)
для импульсов различной продолжительности, в которых содер-
жится целое число периодов частоты coo- На рис. 3.4 и 3.5 пока-
заны также кривые спектральной плотности соответствующих
импульсов. Из графиков видно, что при увеличении длительно-
сти импульсов кривая К%=/(а) по своей форме приближается
к ступенчатой.
На рис. 3.7 и 3.8 изображены графики для определения соот-
ветственно нижнего и верхнего краёв полосы, занимаемой пере-
дачей импульсов различной продолжительности. Графики рас-
считаны по ф-ле (3.21) и относятся к импульсам, начинающимся
с нулевого значения косинусоиды
\ 2ш0 /
На рис. 3.9 дан график ширины полосы, занимаемой пере-
дачей, которая соответствует разности значений аг—ai из двух
предыдущих графиков. Здесь же для сравнения показан гра-
фик ширины полосы передачи для импульсов, начинающихся с
максимального значения косинусоиды (^ = 0). Сравнение обоих
графиков рис. 3.9 показывает, что при коротких импульсах (ма-
лые значения у) величина начальной фазы значительно влияет
на ширину полосы передачи. При увеличении длительности им-
50
Рис. 3.3. Сравнение импульсов, имеющих
форму отрезка косинусоиды одинаковой
продолжительности, с различными началь-
ными фазами
Рис. 3.4. Спектр имлульса, имеющего фор-
му «отрезка косинусоиды, и содержащаяся в
нём энергии. Энергия----------, спектраль-
ная плотность-----------------
пульсов начальная фаза меньше влияет на ширину полосы, я,
как видно на рисунке, обе кривые сближаются между собой.
При у=1/2 получаем частный случай, при котором импульс
имеет форму полуволны косинусоиды. Последний импульс бу-
Рис. 3.5. Спектр импульса, имеющего форму отрез-
ка косинусоиды, и содержащаяся в нём энергия.
Энергия----------, спектральная плотность ......
дем называть косинусоидальным. Для него функция времени
описывается выражением
t/(/) = (л п A cos — t т при < t < .. (3.23)
0 при |/| > ~
и формула для определения относительной частичной энергии в
полосе частот имеет вид
1
'*11 = —
К
+ Si 2 + 4) - Si 4) +
—k
тс
In
Fнижняя
т0
(3.25)
W-
035-
0S-
085-
08-
075-
07-
065‘
06-
055-
' 05-
! 045-
! 04-
035-
' 03-
025-
02-
015 \
Of-
005-
0-
В1!!ИП1!%ЗЕЯЙЯ
__ишззезйз
1ИЕ30Е2
45
5
О
625
М-гО-ЖОО"
0^^0^85
азгшо/в
90
JS*2jrr^t0
0 20 30 60 SO 60 10 80 90 00 00
Рис. 3.8. Верхний край полосы, за-
нимаемой излучением импульсов, име-
ющих форму отрезков косинусоиды
различной продолжительности
Рис. 3.7. Нижний край полосы, за-
нимаемой излучением импульсов,
имеющих форму отрезков косинусои-
ды различной продолжительности
——k
2
®И0ЕЗЕЗЕЗ
НШЕИИЯМШЕ
ИЕИЕЗЕЕИ^Е
Ширина полосы, занимаемой передачей косинусоидального
импульса, равна (в единицах k):
Д/«4,0.
54
55
§ 3.5. ИМПУЛЬСЫ С КОСИНУС-КВАДРАТНЫМ СКРУГЛЕНИЕМ
В этом параграфе определяют распределение энергии в по-
лосе частот и ширину полосы, занимаемой при передаче сим-
метричными импульсами, центральная часть которых представ-
ляет собой прямоугольник, а края скруглены по закону, опреде-
лённому выражением cos2/. Форма этих импульсов показана на
рис. 3.10. Мы будем называть их импульсами с косинус-квадрат-
ным скруглением. Импульсы с косинус-квадратным скругле-
нием, у которых центральная прямоугольная часть отсутствует
(рис. 3.11) будем называть косинус-квадратными импульсами.
Эти импульсы исследуют, чтобы ответить на вопрос о том,
в каких случаях целесообразно скруглять края импульсов по
закону cos2/ и когда лучше использовать трапецеидальные им-
пульсы. Функция времени импульса с косинус-квадратным
скруглением описывается выражением
A cos2 —-— (t -|- —при-----— < t < ——
’-Ч\ 2/ г 2 2
£/(/) = { А
(3.26)
ПРИ + + t
A cos2 —-— (t — —
т-сД 2 У
Рис. 3.10. Распределение энергии импульса с косинус-квадратным скруглени-
56
Спектральная плотность энергии импульса равна:
(3.27)
где $ = — и k = — .
т 2
Формула для определения относительной частичной энергии
в лолосе частот имеет вид
= И & + в^ + с <*>] > <3-28)
к М- о?)
где
k
А (*) = f i------‘ М, (3.29)
k
«И-Нг------------(3.30)
J p — (i—e)2 (—) k
о L \ 15 / J
k
~ f r--------1 / <3-31)
о L \ TC / J
Формулы для вычисления нетабличных интегралов A(k),
и C(k) даны в приложении IV. Проверка показывает, что при
Л->оо сумма A(k) + B(k) + C(k) приводит к значению, удовле-
творяющему известной теореме Рэлея.
При , где п=1, 2, 3... и т. д., каждый из интегралов
п
A(k), B(k) и C(k) имеет бесконечный разрыв в точке k=—— .
(1—6)
Однако это неважно, так как сумма всех трёх интегралов ® точ-
ке разрыва остаётся конечной, что впрочем ясно и из физиче-
ских соображений. Главные значения несобственных интегралов
определяют без затруднения.
При £= (2x11 разрывы в интегралах A(k), B(k) и C(k)
п
отсутствуют, причём упрощаются приведённые в приложении IV
58
формулы для определения этих интегралов. Это во многих слу-
чаях облегчает вычисления, особенно для наиболее важных
практически значении g, близких к единице, когда точки g =-.
п
которые можно рассчитывать по упрощённым формулам, распо-
лагаются достаточно тесно.
На рис. 3.10 построены графики A(k), B(k) и C(k) при
значениях 5=0,3; 0,5 и 0,8. Значения этих функций иормирова-
4
ны относительно --------, вследствие чего на графиках вве-
я(34-5е)
дены новые обозначения A' (k), В' (k) и С' (k). При 5=0,3 ин-
тегралы имеют разрывы; при 5=0,5 и 0,8 разрывов нет.
При 5=0 B(k) = C(k)=0 и получается импульс, который в
начале настоящего параграфа назвали косинус-квадратным.
Формула (3.28) для косинус-квадратного импульса принимает
вид
>12 = ^(--^=^-sina^ + 4Si2A + Si2(K + A)-
Зя I k (я2 — Л2)
— Si2(« — £)+ — Г1п —
к — £
— Ci 2 (я + А) + Ci 2 (* — £)]}• (3.32)
На основании ф-л (3.28) — (3.31) вычисляют ширину поло-
сы, занимаемой при передаче импульсов (т. е. ширина полосы
частот, содержащей 99% полной энергии импульса):
5 0,0 0,3 0,5 0,8
Д/ (в единицах k) 4,4 6,5 6,9 . 12,0
Таблицы [JI27], которые использовались при вычислениях, со-
держат значения Si (х) и Ci (х) для 0 100. Чтобы вычис-
лить значения Si (х) и Ci (х) при х> 100, которые встречаются
при определении значений г], близких к 0,99 (т. е. при определе-
нии ширины полосы, занимаемой передачей), используют фор-
мулы:
Si (х)«1,57 079 633 - 0----A) Sin х — A) cos х>
Ci w ~ (т - i)sln Л - Gr -1)cos *•
получающиеся из асимптотических рядов.
На основании ф-лы (3.12) рассчитывают ширину полосы,
занимаемой при передаче трапецеидальных импульсов.
Как видно из табл. 3.1, при передаче импульсов с косинус-
квадратным скруглением занимается (при рассмотренных зна-
' ) 59
чениях I) несколько большая полоса, чем при передаче трапе-
цеидальных импульсов.
ТАБЛИЦА 3.1 -
Ширина полосы импульсов с крсинус-квадратным скруглением
и трапецеидальных импульсов
Форма импульса Ширина полосы (в единицах В)1) при £
0,0 0,3 0,5 0,8 1,0
Импульс с косинус-квад- ратным скруглением 2,8 4,2 4,4 7,7 20,6s)
Трапецеидальный импульс 2,6s) 2,5 3,9 6,5 20,6s)
О В—скорость манипуляции, выраженная в бодах. Для перехода от единиц k к едини-
цам В, применяемым в электросвязи, полученные выше значения ширины полосы для коси-
нус-квадратного импульса поделены на — .
2
*) Треугольный импульс.
*) Прямоугольный импульс. *
Из ф-л (3.11) и (3.27) видно, что при больших значениях k
огибающая частотного спектра трапецеидальных импульсов
убывает пропорционально —, а для импульсов с косинус-квад-
k2
ратным скруглением — пропорционально-^-. Поэтому импуль-
й3
сы с косинус-квадратным скруглением имеют преимущество пе-
ред трапецеидальными импульсами, так как у них внеполосные
излучения при больших расстройках более быстро убывают.
§ 3.6. КОСИНУС-КУБИЧНЫЙ ИМПУЛЬС
В § 3.4 и 3.5 рассмотрены косинусоидальные и косинус-квад-
ратные импульсы, т. е. импульсы, формируемые по закону пер-
вой и второй степеней косинуса. Иногда можно получить некото-
рые преимущества, формируя импульсы по закону более высо-
ких степеней косинуса, в частности третьей. Ниже рассчиты-
вается ширина полосы частот, занимаемой при передаче таких
импульсов, которые назовём косинус-кубичными.
Импульс продолжительностью — —, -|—, формируемый
по закону третьей степени косинуса, описывается функцией
60
U(t) =
A cos8 — t
T
0
Спектральную плотность
выражения
при —— <7 < -Ь —
2 2
(3.33)
при И > у
энергии импульса определяют из
//* =
(3.34)
а относительную частичную энергию в полосе частот из выра
жения
—J4_U»-20^)fe- а k 9 2Л) _
-чН(т-‘-)(т*-)
— Si (к — 24)] + Si (Зтг + 24) — Si (3* — 24) +
Рис, 3.11, Распределение энергии косинусоидального, коси-
нус-кв адратного и косивус-кубичного импульсов .в полосе
частот 61
Ширина полосы, занимаемой при передаче косинус-кубично-
го импульса (в единицах k), равна:
Д/«5,2.
На рис. 3.11 показано распределение в полосе частот энергии
косинусоидального (при т = -i-J, косинус-квадратного и коси-
нус-кубичного импульсов, рассчитанное соответственно по
ф-лам (3.25), (3.32) и (3.35).
Из кривых рис. 3.11 видно, что любое заданное значение q
достигается быстрее при меньших степенях косинуса. Поэтому
импульс, формируемый по закону высоких степеней косинуса,
занимает более широкую полосу частот, чем импульс, форми-
руемый по закону низких степеней косинуса. Косинусоидальный
импульс (при y = как видно из результатов расчётов, отно-
сится к сигналам, занимающим наиболее узкую полосу частот,
и весьма близок к «идеальному».
ГЛАВА ЧЕТВЁРТАЯ
ШИРИНА ПОЛОСЫ, ЗАНИМАЕМОЙ ПЕРЕДАЧЕЙ,
И ВРЕМЯ УСТАНОВЛЕНИЯ СИГНАЛОВ
Рассмотрены соотношения
между шириной полосы, зани-
маемой передачей, и временем
установления сигналов.
Указано, что во многих слу-
чаях желательно использовать
сигналы, имеющие, не только
наменьшую полосу частот, но
и наименьшее время установ-
ления. Поэтому введён общий
критерий, который позволяет
оценить сигналы одновремен-
но как со стороны занимаемой
полосы частот, так и со сторо-
ны времени установления. Этот
критерий определён в виде
§ 4.1. ОБЩИЕ СООБРАЖЕНИЯ
В гл. 2 определена форма сигна-
ла, занимающего наименьшую'
полосу частот, и в гл. 3 «найдены
численные значения ширины поло-
сы, занимаемой передачей сигналов
различных форм. Однако сигналы,
занимающие наименьшую полосу
частот, не всегда оптимальны для
практического применения. Ширину
полосы уменьшают скруглением сиг-
налов, которое иногда может за-
труднить их интерпретацию в месте
приёма. В частности, в телеграфии
желательно использовать сигналы,
не только занимающие наименьшую
полосу частот, но и имеющие паи-
меньшее время установления. Иног-
да важно время установления сиг-
налов, в других же случаях более
важным фактором является эконо-
мия ширины полосы. Поэтому же-
лательно рассматривать сигналы по-
где (д — ширина полосы и
время установления сигнала.
Определяется численное зна-
чение введённого критерия для
импульсов различных форм.
Показано, что если критерием
качества считать наименьшее
значение ку, то оптимальными
будут иные формы импульсов,
чем те, которые занимают наи-
меньшую полосу частот.
каждому из этих показателей в от-
дельности, а также выработать общий критерий, позволяющий.
оценивать сигналы одновременно с обеих точек зрения.
§ 4.2. ОПРЕДЕЛЕНИЕ ВРЕМЕНИ УСТАНОВЛЕНИЯ СИГНАЛА
Поскольку мы намереваемся установить соотношение между
шириной полосы, занимаемой передачей, и временем установле-
ния сигналов, то вначале необходимо сформулировать определе-
63
ние каждой из этих величин, которое удовлетворяло бы логиче-
ским соображениям и которое можно использовать практически.
Повторим данное в § В.З определение МКК.Р для ширины по-
лосы: шириной занимаемой полосы называется ширина такой
полосы частот, за нижним и верхним пределами которой средние
излучаемые мощности равняются каждая 0,5 % всей средней
мощности данного излучения. МККР [Л40] определяет время
установления сигнала, как время, в течение которого телеграф-
ный ток проходит от одной десятой до девяти десятых (или на-
оборот) значения, достигаемого в установившемся состоянии.
Для несимметричных сигналов могут быть два различных зна-
чения, соответствующих времени установления в начале и в кон-
це сигнала.
Однако это определение относится лишь к телеграфным сиг-
налам и поэтому является частным. Оно также не учитывает
других параметров переходного процесса, как, например, коле-
бательность, выбросы и т. д., которые характеризуют форму сиг-
нала. Коэффициенты 0,1 и 0,9 выбраны произвольно, как и коэф-
фициенты для ширины полосы. Вместе с тем, с практической точ-
ки зрения такое определение удобно, из-за чего и получило ши-
рокое распространение. Всё сказанное в § В.З относительно пре-
имуществ международного определения ширины относится и к
времени установления сигнала. В дальнейшем будем использо-
вать определения ширины полосы и времени установления сиг-
нала, принятые МККР.
§ 4.3. ОБЩИЙ КРИТЕРИЙ ОЦЕНКИ СИГНАЛА
Введём общий критерий оценки сигнала, учитывающий одно-
временно и занимаемую полосу частот и время установления сиг-
нала. Уравнения, выражающие зависимость спектральной плот-
ности энергии от занимаемой полосы частот и продолжительно-
сти сигналов (см- гл. 3), симметричны относительно каждого из
этих показателей в отдельности. Поэтому для характеристики
сигнала обычно вводится общий показатель
*=р (4.1)
где со — ширина занимаемой полосы,
т — продолжительность сигнала.
Чем меньше k, тем лучше используется полоса частот и про-
должительность сигнала. Но, как мы уже указывали выше, во
многих случаях желательно использовать сигналы, имеющие
наименьшее время установления.
64
Представим продолжительность сигнала в виде
Т ~ ХОСН “1“ (4*2)
где т0Сц — продолжительность установившегося сигнала,
Ту — время установления сигнала.
Для упрощения считаем, что время нарастания сигнала рав-
но времени убывания.
Подставляя (4.2) в (4.1) и введя обозначения:
получим
*=Л« + 2*у. (4.4)
Критерий характеризует использование полосы частот и
время установления сигнала.
§ 4.4. ЧИСЛЕННЫЕ ЗНАЧЕНИЯ ky
Прямоугольный, трапецеидальный и тре-
угольный импульсы. Формулы для определения ширины
полосы, занимаемой передачей этих импульсов, приведены в
гл. 3. На рис. 4.1 дан график зависимости ширины полосы, выра-
5—730
Рис. 4.1. Полоса частот, занимаемая передачей
трапецеидальных импульсов
65
женной в единицах k, от 5 = tj/т; п — продолжительность
вершины импульса, т — продолжительность основания импульса.
Случай £=0 соответствует треугольному импульсу; если
£=1,0, то импульс принимает прямоугольную форму. Как видно
из рис. 4.1, при изменении £ от 0,0 до 0,3 ширина полосы, зани-
маемой передачей, практически не изменяется, а при изменении
£ от 0,6 до 1 — изменяется наиболее сильно.
Время установления сигнала будет равно:
.-^- = 0,4(1-5),
k, = 0,4(1 — l)k.
На рис. 4.2 изображён график зависимости =/(£.).
Косинусоидальный импульс! при у= —1
Функция времени описывается выражением:
U (0 — cos — t при —— < t < —;
2 2
£/(0 = 0 при |0
£
Ко с и н у с-к в а д р а т н ы й
описывается выражением:
£/(0 = cos2 — t
т
импульс. Функция
времени
•с ъ
при---------< t < —;
г 2 2
£/(0 = 0
при |0
Л!
66
Ширина полосы, занимаемой передачей, 6=4,4 (см. § 3.5).
Время установления импульса
JL = = о,294,
т т
где t\ и tz определяют из уравнений:
cos2 0,1 >
cos2 — /г = 0,9
т
И
6= ^-6 =0,30.
л т
Косинус-кубичный импульс. Функция времени опи-
сывается выражением:
U(t) = cos9 — t
пРи-т<О<т;
U(t)~ о
при И > у •
Ширина занимаемой полосы 6=3,6 (см. § 3.6).
Время установления импульса
-^- = ^—^ = 0,263,
т т
где /1 и tz определяют из уравнений:
cos’—Л» 0,1,
т
cos9—/, = 0,9
И
ь =-*-Л=1,4.
Л т
Б*
67
«Идеальный» импульс. Так условно назвали в гл. 2
импульс конечной продолжительности, содержащий максималь-
ную долю энергии в заданной полосе частот.
Ширина полосы, занимаемой передачей «идеального» импуль-
са, &=3,6 (см. § 2.5).
Время установления определяется по ф-ле (2 39):
= 0,365
т
И
=-^-Л = 1,31.
Л т
Сравнение полученных данных позволяет оценить различ-
ные формы сигналов посредством общего критерия ky. Наилуч-
шим с точки зрения критерия ky является прямоугольный им-
пульс, хотя он и занимает наиболее широкую полосу частот, а
«идеальный» импульс, занимающий наименьшую полосу частот,
является одним из худших.
ГЛАВА ПЯТАЯ
ФОРМИРОВАНИЕ СИГНАЛОВ С ЦЕЛЬЮ
УМЕНЬШЕНИЯ ВНЕПОЛОСНЫХ ИЗЛУЧЕНИЙ
Показано, что форму сигна-
лов нужно выбрать, учитывая
не только занимаемую полосу
и время установления, но и
скорость убывания внеполос*
ных излучений при возрастании
частоты.
Выведены формулы, выра-
жающие спектральную плот-
ность через скачки функции
и её производных, из которых
видно, что величина спектраль-
ных компонентов зависит от
вида скачков (т. е. от того,
имеются ли скачки функции
или её производных), а также
от количества скачков и их
расположения. Скорость убы-
вания частотного спектра при
возрастании частоты зависит
лишь от вида скачков, но не
зависит от количества скач-
ков данного вида.
Для сигнала конечной про-
должительности U(t) показа-
но, что если U(t),
не имеют скач.
ков, a U (t) всюду конечна,
то спектральная плотность убы-
вает при возрастании частоты
С
<о не медленнее, чем •
Исследованы новые (сфор-
мированные по закону /1-й сте-
пени косинуса и др.) формы
импульсов, спектры которых
убывают при возрастании ча-
* С
стоты не медленнее, чем "п+1,
где п > 4.
В конце главы приведена
таблица основных показателей,
характеризующих импульсы
различных форм.
§ 5.1. ПРЕДВАРИТЕЛЬНЫЕ
ЗАМЕЧАНИЯ
g гл. 2 рассмотрен вопрос о том,
какую форму должен иметь им-
пульс конечной продолжительности
для того, чтобы в заданной полосе
частот содержалась максимальная
доля полной энергии спектра.
Однако, как было показано в
гл. 4, сигналы, занимающие наи-
меньшую полосу частот, не всегда
являются наилучшими для практи-
ческого применения: во многих слу-
чаях желательно использовать сиг-
налы, не только занимающие наи-
меньшую полосу частот, но и имею-
щие наименьшее время установ-
ления.
Формы сигналов можно оценить
также, исходя из желательности ос-
лабления внеполосных излучений.
Как указывалось в § В.З, в соответ-
ствии с международным определе-
нием, шириной полосы, занимаемой
излучением, называется полоса ча-
стот, содержащая 99% излучаемой
мощности, а под внеполосными из-
лучениями понимается мощность,
излучаемая за пределами занимае-
мой полосы. Поэтому мощность вне-
полосного излучения всегда посто-
янна и составляет 1% всей мощно-
сти, излучаемой передатчиком.
В первом приближении (не
учитывая энергии, воспринимае-
69
мой приёмником из полосы, занимаемой соседним каналом) мож-
но считать, что взаимные помехи создают лишь внеполосные из-
лучения соседних каналов. Но поскольку процентное содержа-
ние мощности во внеполосном излучении постоянно, то умень-
шить взаимные помехи посредством воздействия на спектр сиг-
нала можно, лишь распределяя соответствующим образом вне-
полосное излучение в полосах частот, занимаемых соседними
каналами. Практически желательно, чтобы спектр внеполосного
излучения убывал с наибольшей скоростью. Ниже мы рассмот-
рим, насколько это практически осуществимо. Мы покажем,
что асимптотическое поведение спектра при высоких частотах
существенно определяется свойствами непрерывности сигнала и
что можно выбрать форму сигнала, обеспечивающую желатель-
ную скорость убывания частотного спектра внеполосных излу-
чений при возрастании частоты.
Как будет показано в гл. 9, задача уменьшения взаимных по-
мех сводится к задаче нахождения элементарного сигнала, ко-
торый при передаче той же самой системой создавал бы помехи
минимальной энергии. Поэтому мы будем рассматривать внепо-
лосные излучения, создаваемые элементарными сигналами.
Прежде чем анализировать возможность уменьшения внепо-
лосных излучений посредством воздействия на форму элементар-
ного сигнала, рассмотрим эту проблему с точки зрения следст-
вий, вытекающих из теории Шеннона о пропускной способности
канала.
§ 5.2. РАССМОТРЕНИЕ ВОЗМОЖНОСТИ УМЕНЬШЕНИЯ ЭНЕРГИИ
ВНЕПОЛОСНЫХ ИЗЛУЧЕНИЙ С ТОЧКИ ЗРЕНИЯ ТЕОРИИ
ШЕННОНА О ПРОПУСКНОЙ СПОСОБНОСТИ КАНАЛА
Формула (В-1), полученная Шенноном для определения про-
пускной способности канала, основывается на разложении сиг-
нала в ряд Котельникова-
sin
(5.1)
-00
2*F
Элементарная функция
“('-v-)
70
?'этого ряда не равна нулю ни в каком конечном интервале вре-
. мени.
5 Сигнал U(t), известный на бесконечном интервале времени,
можно разложить в ряд Котельникова (5.1), причём его спектр
будет заключаться в конечной полосе частот. Реальные сигна-
лы конечной продолжительности можно лишь приближённо ап-
проксимировать посредством ряда Котельникова (5.1).
Рис. 5.1. Воаможяость аппроксимации сигнала
конечной продолжительности
Пусть продолжительность сигнала .U(t) равна (^—ti) (см.
рис. 5.1); для аппроксимации этого сигнала его можно продол-
жить за пределы интервала существования (t2—^) (см. пунк-
тарную линию на рис. 5.1) и тем самым сделать его бесконечным,
а затем этот бесконечный сигнал разложить в ряд Котельнико-
ва (5.1).
Конечно, мы можем продолжить сигнал U(i) вне интервала
(^2—Л) различным образом; каждому продолжению будет со-
ответствовать свой ряд Котельникова. Но если мы хотим, чтобы
аппроксимация была возможно более точной, то мы должны
: продолжить его так, чтобы спектр внеполосных излучений убы-
вал наиболее быстро, а для этого, как будет показано далее, не-
' обходимо, чтобы сигнал был продолжен наиболее гладко, т. е.
чтобы наибольшее число производных сигнала не имело скач-
ков.
Продолженный таким способом сигнал имеет сплошной
спектр в определённой конечной полосе частот, за пределами ко-
торой он равен нулю и поэтому не создаёт помехи для соседних
каналов. Однако в действительности такой способ продолже-
' ния предполагает, что сигнал известен в течение бесконечно
большого промежутка времени и поэтому бесполезно передавать
его по какому бы то ни было каналу электросвязи.
Теория Шеннона, таким образом, относится лишь к предель-
ному случаю неограниченно долго передаваемых сигналов. Но
71
при определённых условиях, которые часто удовлетворяются на
практике, амплитуды сигнала приближённо подчиняются стати-
стическому распределению Гаусса. Эти условия заключаются в
том, что случайная функция, представляющая собой сигнал,
должна быть стационарной, характеристическая функция её за-
кона распределения (т. е. преобразование Фурье от закона рас-
пределения) должна быть ограниченной вначале (при нуле) и
значения функции в различные моменты квантования или пере-
ключения должны быть независимыми [Л25, гл. 13, стр. 513]. Та-
кой достаточно гладко продолженный сигнал можно во многих
случаях хорошо аппроксимировать рядом Котельникова (5.1).
Этот сигнал может иметь очень малые внеполосные излучения.
Пример сигнала, который имеет малые внеполосные излуче-
ния — человеческая речь. Такого рода сигнал изучался многи-
ми авторами [Л40, том III], которые считают, что для достаточ-
но продолжительного периода времени и достаточно большого
числа различных голосов статистическое распределение речи
является приблизительно распределением Гаусса, приближаясь
в этом отношении к «белому» шуму, который точно удовлетво-
ряет поставленным выше математическим условиям. Таким об-
разом, внеполосные излучения речи можно уменьшить до очень
малых значений, но их нельзя свести к нулю, так как речь всё
же неточно подчиняется распределению Гаусса и, кроме того, она
продолжается конечный промежуток времени.
Внеполосное излучение речи можно уменьшить при помощи
фильтра, не ухудшая значительно разборчивость. Это уменьше-
ние будет тем более значительным, чем больше звеньев с опре-
делёнными характеристиками имеет фильтр.
В отличие от речи, телеграфные сигналы, которые обычно
имеют только два различных уровня, нельзя аппроксимировать
распределением Гаусса; они поэтому являются значительным
источником взаимных помех.
Чтобы получить телеграфные сигналы, приближающиеся к
распределению Гаусса при амплитудной манипуляции, следо-
вало бы использовать такую систему кодирования, при которой
различные знаки соответствовали различным уровням сигнала.
Однако это привело бы к техническим трудностям. Теоретиче-
ский сигнал Шеннона соответствует амплитудам, разность кото-
рых для двух соседних моментов времени, по крайней мере,
равна уровню шума. На основании известной теоремы из теории
вероятностей закон распределения суммы большого числа ма-
лых и независимых случайных величин имеет в качестве предела
закон Гаусса. Таким образом, если сигналы представляют собой
сумму большого числа малых и независимых сигналов с раз-
личным уровнем, наблюдающихся в случайные моменты време-
ни, то эти сигналы подчиняются закону распределения Гаусса-
72
§ 5.3. ИНТЕГРАЛЬНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ, ВЫРАЖЕННОЕ
ЧЕРЕЗ СКАЧКИ ФУНКЦИИ И ЕЁ ПРОИЗВОДНЫХ
Ниже преобразование Фурье выражается через скачки функ-
ции времени и её производных. Аналогичные результаты были
получены В. А. Котельниковым и опубликованы в [Л 16}.
Пусть .U(t) будет функцией конечной продолжительности —
представленной в различных частях области своего су-
ществования прямой линией или параболой р-й степени: у=С0+
. ,+Cptp. Для упрощения будем предполагать, что
функция U.(t) является чётной.
Пусть далее .(/(О или любая из её производных имеют скач-
ки , /в1/« , /',в точках си, аг,..., определяемые
как
/«. = (7(а1 + О)-(7(а1-О),
+ 0) - U' (ах - 0) и т. д.
Преобразование Фурье функции ,U(t) имеет вид
Г г
т т
/(ш)= J U (7) cos со/ dt = 2 J U (t) cos ®tdt. (5.1а)
_ т о
2
Интегрируя (5.1а) по частям, получим
— [U (t) sin а)/] —- f U' (/) sin со/ dt. (5.2)
(0 J
Предположим, что .U(t) имеет скачок в точке аь Первый член
(5.2), если взять его в пределах от 0 до (ai—0) и от (ои + 0) до
т/2, имеет вид
U (— ) sin —-----------U (ах + 0) sin ajto + (7 (<4 — 0) X
\ 2 / 2
. , . 2 Г г г / X X •
X sin а,® — 0 = — I/ — | sin ------------------------------
J <0 L k 2 ) 2
/«, sin а»
За пределами интервала интегрирования от нуля до т/2
функция ,(7(0 равна нулю. Поэтому — (/(-^представляет со-
бой скачок в точке ; если имеются также другие скачки при
аа, а8,...,а(,..., аж, то ясно, что, разделив интервал интегрирования
73
на части от 0 от ои до аг и т. д., получим первый член (5.2)
в виде
— Li sin a,(i>,
«1
где суммированы все скачки функции U(t), включая точку-^-.
Если мы таким же образом проинтегрируем второй член (5.2)
по частям, то получим
2 Г t/'(/) cos
<0 I со
2
2 С
----- I *
Ci)2 J
О
(5.3)
Точно также значение первого члена выражения (5-3) будет
равно:
— — Lt cos azco,
«1
где Га1 представляет собой скачок U'(t) при f=ai и суммирова-
ние распространяется на все скачки. Подобным путём, если про-
интегрируем второй член (5.3) по частям, получим
2 Г СТ (0 sin «>* ~
Ci)2 I Ci)
+ -4-f^"(0sin<o/dt
Ci)8 J
Значение первого члена этого выражения будет равно'
ak
-I'ii Sin a,«.
Ci)8
al
Продолжая подобным же образом, получим в качестве окон-
чательного результата, что
ak ak ;
f (ю) =-— V./ai sin afl)-У /«• cos axw 4-
«1 “1
*k и ' 4
+ ^^^sinV°+ cosa^u) — .... (5.4)
«1 «1
74
Этот ряд конечен, так как если р представляет собой высшую
степень любой параболической дуги, то (р+1)-ая производная
U<p+l\t) будет всюду равна нулю, так что нет скачков /?+1 или
любых высших порядков. Однако ф-лу (5.4) можно использовать
и в случае бесконечного ряда, если этот ряд сходится.
Из ф-лы (5.4) видно, что величина спектральных компонен-
тов зависит от количества скачков и от их вида (т. е. имеются
ли скачки в функции или в её определённых производных), а
также от расположения скачков. Так, например, скачки самой
функции и её чётных производных при значениях t, близких к
нулю, дают малые значения спектральных компонентов, убываю-
щих обратно пропорционально нечётным степеням частоты. Но
, ч скачки такого же вида и той же величины при значениях t, близ-
ТС
ких к —, существенно увеличивают эти спектральные компо-
ненты.
Скорость убывания частотного спектра с возрастанием ча-
стоты зависит лишь от вида скачков, но не зависит от количест-
ва скачков данного вида.
$ 5.4. СООТНОШЕНИЕ МЕЖДУ ФОРМОЙ ИМПУЛЬСА И СКОРОСТЬЮ
УБЫВАНИЯ ВНЕПОЛОСНЫХ ИЗЛУЧЕНИЙ
Скорость убывания спектра с возрастанием частоты со
можно оценить посредством ограничивающей кривой, ниже ко-
торой расположены все максимумы спектральной плотности,
выражаемой посредством интегрального преобразования Фурье.
Докажем, что такая ограничивающая кривая при достаточно
больших значениях © убывает пропорционально , где (/г—1) —
порядок первой из имеющих скачки производных функции
U(t), описывающей сигнал конечной продолжительности.
Исходя из физических соображений, будем предполагать,
что преобразование Фурье для функции U(i) существует.
Интервал — ~ , на котором функция U(t) отлична
от нуля, можно подразделить на конечное число областей,
в 'каждой из которых функция будет иметь один знак и будет
либо монотонно возрастать или убывать, либо оставаться неиз-
менной.
Рассмотрим значение преобразования Фурье (5.1а) в любой
из этих областей при достаточно больших значениях <в. На ко-
ротком интервале длиной — подынтегральное выражение бу-
75
дет положительно и будет вносить в интеграл некоторое слагае-
мое, которое обозначим Sj. На следующем участке длиной —
подынтегральное выражение будет отрицательно и будет вно-
сить слагаемое — 32 и т. д. до где St соответствует послед-
нему полному полупериоду в рассматриваемой области. Теперь
мы получили сумму членов
Si — 32 + S3 — • • •
которые попеременно положительны и отрицательны, а по ве-
личине либо монотонно возрастают, либо монотонно убывают.
Известно, что в любом случае такая сумма не может превы-
шать либо Si, либо 3; в зависимости от того, какая из этих ве-
личин является большей. Ясно также, что ни один из этих чле-
нов не может превышать М — t, где М— наибольшее значение
со
U(t) в рассматриваемом интервале.
К этому значению, возможно, следует добавить два слагае-
мых, получаемых при интегрировании по неполным интервалам
в начале и конце области. Каждое из этих слагаемых не может
превышать М— т, так что значение f U (/)’cos <&tdt в рассматри-
о>
о , ЗМлт _
ваемои области не может превышать -----------. Суммируя по
<о ,
остальным областям, получаем, что интеграл в целом на интер-
't . , т С
вале интегрирования----+~» не может превышать — , где
С —некоторое постоянное число. Тот же, результат, очевидно, по-
лучается для интеграла, содержащего sin®/.
На основании рассмотренного можно доказать, что если U(t)
не имеет скачков и если U'(t) всюду конечна (второе условие
включает в себя и первое), тогда преобразование Фурье не пре-
С
вышает—-.
Следует отметить, что предположение об отсутствии скачков
по величине функции U(t) имеет в виду также и то, что на кон-
цах интервала----—, +— функция принимает нулевые значе-
2 2
ния, т. е.и(•—^-\ = U = 0.
2 / \ 2 /
Интегрируя (5.1а) по частям, получим
Л- Т
,, ч Г и (Osin®/ 12 1 f
/ (ш) = ——----------------------1 U'(t) sin <at dt.
L ** J— — ш J
2 _ т
T
76
Если U(t) не имеет скачков, то первый член исчезает. Инте-
т
2
грал J U'(t) sin со/ dt представляет собой преобразование
Г
2
•Фурье для функции U'(t), и оно, как мы видели, будет меньше,
С
чем — , где С — некоторое постоянное число.
Подобным же образом можно доказать, что если U(t) и
V'(t) не имеют скачков и если U"(t) всюд^ конечна, то преобра-
зование Фурье/(<о) должно быть меньше — .
Продолжая это рассуждение, придём к заключению, . что
если U(t), U'(t),..., Uin~iy(t) не имеют скачков, a U^tt) всюду
е ' 1 С
конечна, то спектр убывает не медленнее, чем ——7.
§ 5.5. ФОРМА СИГНАЛА КОНЕЧНОЙ ПРОДОЛЖИТЕЛЬНОСТИ,
СПЕКТР КОТОРОГО УБЫВАЕТ НЕ МЕДЛЕННЕЕ, ЧЕМ С/шп+1
Определим, какую форму, должен иметь сигнал для того,
чтобы соответствующий ему спектр убывал не медленнее, чем
Всегда можно выбрать такую функцию U(t), которая вместе
со своими производными не имела бы скачков внутри области
своего существования----—,+ —. Например, этому условию
2 2
удовлетворяют гармонические функции, многочлен и т. д. Но,
кроме этого, ещё необходимо, чтобы U(t) со всеми своими произ-
водными до заданного порядка были равны нулю в точках±
Для выполнения этих условий можно выбрать функцию вида:
U (t) = A cos" — (/) при —— < t < + —
х 2 2
</(0 = 0
при И > Д-
(5-5)
При таком выборе функции в точках ±-^- не будет скач-
ков в (я—1)-й производной; ноп-я производная будет содержать
член вида sinft—-t, который в точках+ “ не будет равен нулю,
t 2
77
хотя все остальные члены n-й производной и обратятся в нуль.
Поэтому функция, удовлетворяющая условиям (5.5), обеспечит
, с
убывание частотного спектра не медленнее, чем —.
Введём обозначение k=^-. Спектральная плотность для
функции (5.5) при различных значениях п будет:
при п= 1 (косинусоидальные импульсы)
fi (°>) = -у- ---COS ki
(5.6)
при п=2 (косинус-квадратные импульсы)
. , ч Ат х2 . ,
/2 (о>) =-----------------------------sin я;
/2V ' 2 А(п2 —А2)
при п—3 (косинус-кубичные импульсы):!
2
(5.7)
COS k',
(5.8)
/з(ш)-=^
&
при других значениях п>2:
е i \ с t \ л2'1-1 (2л)!
Лл (<*>) = к («)-------у5-2----------
г2*-1 (J ($*«’—а2)
J-2
, f/, Л»п(2л4.1)!
/2л+1 (®) = fl (<“)----------
S-1
(5.9)
Кроме того, чтобы найти f„ (со) можно воспользоваться рекур-
рентной формулой
- . , - , , п (п — 1) Л*
f „ (ш) = fn_o (ш)-1i--
На рис. 5.2 показаны огибающие спектров косинусоидально-
го, косинус-квадратного и косинус-кубичного импульсов, рас-
считанные в децибелах при А-^-= 1.
(5.Ю)
78
Иногда желательно иметь сигнал с плоской вершиной, т. е.
сигнал, состоящий из прямоугольной части при (—у-, + -у-) и
\ -6 Л /
краёв при (---— , ——) и ( — , —). В этом случае, если мы
\ 2 2 / \ 2 2 /
Рис. 5.2. Огибающие спектров косинусоидально-
го, косинус-квадратного и коси-нус-кубичного им-
пульсов (в децибелах при Дт/2==1)
хотим, чтобы спектр убывал не медленнее, чем —должны
удовлетворяться следующие условия:
79
Поскольку все производные горизонтальной прямой, описы-
вающей центральную часть импульса, повсюду равны нулю, то
необходимо, чтобы функция U(t) и на участках I----—, — -у-]и
\ 2 2 /
t'l _2_\
2*2/
удовлетворяла бы условиям (3.11).
Чтобы найти форму краёв сигнала с плоской вершиной и же-
лательной скоростью убывания внеполосных излучений, рассмот-
рим сигнал вида:
U (0 = A cos" —— (t 4- —
т — \ 2 /
U (t) = А
U (/) = A cos» ——
т — \ 2 /
(5.12)
Из последнего выражения видно, что при (='---— значение
U" (0 =# 0, и таким образом скругление по закону п-й степени ко-
синуса при п>2 не увеличивает скорости убывания спектра по
сравнению с косинус-квадратным скруглением. Поэтому будем
искать такое дополнение <р(7) к U(t), которое устраняет скачок
U"(t) в точке---у и не создаёт скачка в точке —. Получен-
ная нами функция для формирования сигнала будет иметь вид
Un (t) = A [cos» + + <р (/)
(5.14)
Будем искать <f(t) в виде
(<г \ П / т, \ 2
t 4- —) И 4-v) п₽и п>3>
(5.15)
80
где В = const, определяемая далее так, чтобы устранялся ска-
чок U" (t) в точке t = —у-.
Как видно из (5.15), при t =-----— и при t — —— <?(/) = 0.
2 2
Найдём:
(0 = пвIt + vV’1 Р+vf + 2В(' + v) (' + VУ <5-16>
и
?"(0 = n(tt_i)B(/+-L-y-2(/ + i-y +
\ / \ " /
+ 4"В + у) (' + у )“-‘ + 2В (« + -у)” <517>
Из (5.16) и (5.17) видно, что
Чтобы устранить скачок в Ui (—"2”)’ полагаем
. с';'(-т) = и"(-т)+’"(-т) = 0- <5-19>
Поскольку, как следует из (5.13),
у (— _±А — ~Anni
\ 2/ (т-Тх)’ ’
то (5.19) принимает вид
t,“(-T)'-^+2B(V-)”=()- (5-20)
Из (5.20) определяем:
& _ п2п~1 Лд*
(х_Т1)«+2
6—730
81
При этом (5.14) принимает вид
Аналогичным путём получаем
i'li (*) = А [cosn—— (t — v) +
L ’ — 4 \ 2 /
Для этого сигнала спектральная плотность при п = 3 будет
/(ш) = — -4[г cos (A — <p) + riCos(U — (5.23)
2
где
г = V р2 + q2 cos <р = ;
П = Pi.+ fl’i ; cos<p!=^-;
e = 2L; d=_^_;
т i-e
p = 3d«f_______2-_______+ ?^-6<«2Л;
\ (4А2 —9<f)(4# —d2) 8## /
9d«
it2# ’
_ 9d3(20d2 —Зя2#)
P1 ~ 8##
_ _ 3d* / ,28# ^9# 9 \
91 2# \4(4# — 9d2)(4# — d4)+ ## 7'
При k = 0 ф-ла (5.23) принимает вид
/(0)=-ilL.4L2(-1-~6) 4-J-----------^L(i_e)l (5.24)
' v ' 2 L 3k 2 320 \ 'J V '
82
Первые два члена в квадратных скобках (5.24) соответствуют
импульсу, края которого скруглены по косинус-кубичному за-
кону, а средняя часть прямоугольная. Третий член появляется
вследствие «дополнения» импульса.
Скорость убывания частотного спектра, выражаемого ур-нием
(5.23), зависит от р и pi, так как q и qi убывают при возраста-
нии k пропорционально Как видно из выражений для р и
«5
Pi, эти величины убывают пропорционально ; таким обра-
Л4
зом, функция U(t), определяемая ур-ниями (5.21) и (5.22), обес-
печивает скорость убывания частотного спектра не медленнее,
с
чем —.
с
Подобным же образом, чтобы получить большие, чем —,
скорости убывания, можно функцию <р(/) в выражении (5.14)
искать в виде
. ’M'+T)”[B('+t)s+4+f)’+
4-... 4- В„_3 (t 4- -у-) ]» (5.25)
где В, Bi, В^..., В(л_3) — постоянные, определяемые из условий,
что
Un (!) = A [cos'1 (t 4- 4- ? (/)]
не имеет, вместе со своими производными до (п—1) включи-;
тельно, скачков на интервалах [-, — -y-J и [-5-, .
Откуда получаем при---— t — и л = 4
2 2
Ut(t) = A cos1
32хЧ^0,5)«р4*у)’ J
8
(1-6)*
1-6
; ~ (5.26)
и при л=5
Vn(t)
1.0
-0.50 -045 -MJ) -035 -0.30 -025 -020 T
Рис. 5.3. Формы сигналов с прямоугольной частью, спект-
С
ры которых убывают не медленнее, чем--------------
84
Ub (i) = A cos5
10
80к*(/ + 0,5р(^-|-У
2 (1-S)’
60 —
(5.27)
рассчи-
i-e (i-ер J
На рис. 5.3 показаны графики Uz(t), .U^t) 'и U^t),
тайные по ф-лам (5.21), (5.26) и (5.27).
Результаты определения ширины полосы, времени установле-
ния, критерия ky и скорости убывания спектра, полученные в
гл. 2—5, сведены для удобства обозрения в табл. 5.1. Ширина
полосы в этой таблице выражена в единицах = у и в едини-
цах В, где В — скорость манипуляции в бодах. Для перехода от
единиц k к единицам В численные значения ширины полосы пс
делены на —.
2
Сравнение этих основных показателей позволяет оценить ра
смотренные формы импульсов с различных точек зрения.
ТАБЛИЦА.
Сравнение импульсов различных форм
№ пп. Форма импульса Ширина полосы Время устано- вления Критерий качества импульса Ско- рость убыва- ния спектра
в единицах
k В ту ь = ТУ ь У т 1
*n+1
1 • Идеальный* 3,6 2,3 0,365 1,31 1
2 Прямоугоаьный 32- 20,6 0,000 0,00 1 k
— Т —
85
Продолжение
№ пп. Форма импульса Ширина полосы Время устано- вления Критер 1й качества импульса Ско- рость убыва- ния спект- ра
в единицах
k в 1 *я+|
3 Трапецеидальный, (,’0,8 I—Т-4 (•0,5 -1ST Л 10,2 6,5 0,080 0,82 1 А8
4 6,2 3,9 0,200 1,24 1 fe2
5 Треугольный (•0,0 4,1 2,6 0,400 1,64 1 ft2
6 КоьимусоиВальный (без преноушьной части/ 4,0 2,5 0,324 1,25 1 k‘
86
Продолжение
№ пп. Форма импульса Ширина полосы Время устано- вления Критерий качества импульса Ско- рость убыва- ния спект- ра
в единицах
k В ту г 1 kn+i
7 С косинус-квадратным скруглением $•06 Л 12,0 7,7 0,059 0,707 1 &
8 S-4S L- г -J 6,9 4,4 0,147 1,015 1 k3
9 Косинус -квадратный $•0.0 -Л 4,4 2,8 0,294 1,30 1 k3
10 Косинус-кубичный ( без прямоугольной части) 5,2 3,3 0,263 1,40 1
87
ГЛАВА ШЕСТАЯ
ПОЛОСА ЧАСТОТ, ЗАНИМАЕМАЯ ПЕРЕДАЧЕЙ
РАДИОТЕЛЕГРАФНЫХ СИГНАЛОВ
ПРИ АМПЛИТУДНОЙ
И ЧАСТОТНОЙ МАНИПУЛЯЦИЯХ
Изложен метод расчёта
ширины полосы, занимаемой
передачей .радиотелеграфных
сигналов при амплитудной и
частотной манипуляции. Рас-
смотрение основано на спект-
рах периодических сигналов
(«телеграфных точек»).
Показано, что, применяя
даже простейший формирую-
щий контур, можно при ампли-
тудной манипуляции снизить в
несколько раз ширину полосы
передачи. Определена шири-
на полосы частотно-манипули-
рованиой передачи при прямо-
угольных -и скруглённых сигна-
лах. Результаты расчётов срав-
нены с результатами, по-
лучаемыми при использовании
эмпирической формулы МККР.
Установлено численное со-
отношение между шириной по-
лос, занимаемых передачей
прямоугольных сигналов при
амплитудной и частотной ма-
нипуляциях, и показано, что
если индекс частотной манипу-
ляции /п<16, то передача с ча-
стотной манипуляцией зани-
мает меньшую полосу, чем с
амплитудной, и, наоборот, при
т>16 амплитудно-манипулиро-
ванная передача лучше исполь-
зует полосу частот.
§ 6.1. ШИРИНА ПОЛОСЫ, ЗАНИМАЕ-
МОЙ ПЕРЕДАЧЕЙ ПРИ
АМПЛИТУДНОЙ МАНИПУЛЯЦИИ
U усть периодическая функция
с периодом 1 р=----, соответствую-
щая низкочастотному сигналу, пред-
ставлена рядом
fl (0 = а0 + di cos (pt — <?х) +
-|- a2cos(2p/ —ф2) + ...
... + a„cos(npt — <?„) + ...=
00
= аа + J] ап cos (npt — <p„). (6.1)
Л=1
Найдём среднеквадратичное зна-
чение функции за период Тр, т. е.
ТР
(6.2)
1 р
88
Коэффициенты ряда (6.1) удовлетворяют уравнениями:
1 ?
a0== y j
b
tp
a„cos®„ •= — ( Д (f) cos npt dt
tp J
T?
<Vin <p„ = -2- (' Д (/) sin npt dt
* P d
0
Можно записать, что
т,
(6.3)
т
)Л(0Х
о
р
00
X Оо + 2 ta« C0S ®n C0S ПР{ + an sin ?л sin nP^ dt'
n = l
Из (6.4) получаем
т,
(6.4)
т
р 00
= a0-J- I Л(/)Л +Va„cos<р„ X
‘Р j тр J
О ' О л-1
ГР оо ТР
X — ( ЛW cos npt dt + У ал sin <р„ — f fi (/) sin npt dt.
'p ’ Л» 'nJ
О 0
(6-5)
Или в соответствии с (6.3) низкочастотный сигнал можно
представить в виде
т у
+ (6'6>
Р О Л“1
Далее, пусть дан амплитудно-манипулированный сигнал.
Ширина полосы, занимаемой передачей высокочастотных сигна-
лов, может быть получена при рассмотрении случая, соответ-
ствующего низкочастотному сигналу.
Высокочастотный амплитудно-манипулированный сигнал
можно представить в виде
/ (0 = /1 (0 sin (at + ф) = [а0 + di cos (p/ — ?i)+...+
4-ал cos (пр/ —<?„)+...] sin (©Н-ф), (6-7)
89
где угловая частота со соответствует несущей, а ряд в квадрат-
ных скобках — низкочастотному сигналу.
Выражение (6.7) можно переписать в форме
0°
f (t) = а0 sin (a>t + ф) + у J] а„ cos [(ш — пр) / + ф — <?„] 4-
Л = 1
+ у a«cos К" + пр) 14- Ф + <р„].
п-1
В соответствии с ур-нием (6.2) высокочастотный
можно представить в виде
т
(6-8)
сигнал
оо
Лв1
00
УА
(6.9)
что распределение
2те
где Т=-----период высокой частоты.
(О
Сравнивая ур-ния (6.6) и (6.9), видим,
энергии в высокочастотном сигнале такое же, как и в низкоча-
стотном, за исключением множителя у, который содержится
в ур-нии (6.9). В дальнейшем, в соответствии с этим, будут рас-
смотрены только спектры низкочастотных сигналов.
Прямоугольные сигналы. Форма сигналов показана
на рис.
6.1.
fit)
*1— Т —............
Рис. 6.1. Прямоугольные сигналы
При манипуляции прямоугольными сигналами
ДО-
1 при 0 < t < у-
0 при у < / < Г
о
8
О
2
2
Г
1
t
(6.10)
90 -
Разложение выражения (6.10), соответствующего низкоча-
стотному сигналу, в ряд Фурье даёт
1 , 2
2 я
/(О = 7_ + -Z-[sin^ + 4-sin3^ +
о
+ 4-sin5p/+... + ——-sin(2n — l)p/+...l. (6.11)
о zn — 1 J
Мощность, которая соответствует компонентам, находящим-
ся в 'полосе передачи, будет с учётом ф-лы (6.11) равна:
Р = — +— • 471 + — + — 0,99. (6.12)
4 2 я» I 3» 5» „2 I 2 v
Из ф-лы (6.12) находим, что «1=21.
Если через В обозначить скорость манипуляции, выражен-
ную в бодах, то ширина полосы, занимаемой передачей, будет
равна-
А/в=21В.
Скругл’ённые сигналы. Рассмотрим сигнал, изобра-
жённый на рис. 6.2 и представленный функцией
/(0 =
О в пределах
t
от t = — со
от t = 0 .
от t — т
до / = о
до / = т
до t = 4-00
. (6.13)
Сигналы такой формы могут быть получены посредством про-
стейшего формирующего контура (рис. 6.3), состоящего из сопро-
тивления R и ёмкости С.
Постоянная времени контура, определяющая собой степень
скругления сигнала, равна:
в = RC.
(6-14)
91
B практических условиях 0 выбирается достаточно малой
по сравнению с продолжительностью сигнала так, чтобы отноше-
0 х 11
ние — было порядка—-н—.
Пусть периодическое напряжение прямоугольной формы,
представленное рядом (6.11), прилагается в зажимам /, 2 кон-
тура (рис. 6.3) и с зажимов /' 2' этого контура снимается скруг-
лённое напряжение. Форма периодических сигналов на выходе
контура приближается к изображённой на рис. 6.2, однако для
. наглядности это изобра-
жение утрировано: в дей-
ствительности же сигнал
в большинстве случаев
получается значительно
менее скруглённым.
Определим среднее
значение мощности за пе-
риод частоты манипуля-
ции Г. Если —
т
но мало, то (
R
Vt
U2
, г
Рис. 6.3. . Формирующий контур
для получения скруглённого сигнала
достаточ-
т
о
J — е
о
(6.15)
Проинтегрировав, получим
(6.16)
Обратимся к соотношению между выходным и входным на-
пряжениями контура (рис. 6.3), которое в установившемся со-
стоянии описывается уравнением
(“У’ТтЧ^- <6Л7>
у «! / 14-
Если (о=пр, где
p = = 4 (6.18)
92
является основной угловой частотой манипуляции, то
=. (6.19)
Если ко входу формирующего контура приложить прямо-
угольный сигнал (6.10), то на выходе контура будем иметь на-
пряжение
и, (0 = ~ + •— [ / - - -—~ s*n Pt +
2V ’ 2 « |yi + P-p2 0s и
4- — . _ -1. ----sin3pt-\—- ——- ——sin5pt + .. . 1. (6.20)
3 /1Ч-38-Р202 5 Kl + 52-p20« J
Фазовые соотношения между отдельными компонентами на-
пряжения в данном случае не представляют интереса. Средне-
квадратичное значение этого напряжения определяет мощность
P = ±f[/(/)]2^ = _L + _L._LV----------1---,_L. (6.21)
Т J u v 4 2 л2 Д 14- л2р2 02 л2 V
О n=l
0 1
Если принять —= —, то из ф-лы (6.16) получим
Р = . (6.22)
Мощность в полосе передачи, вычисленная по ф-ле (6.21),
равна 99%’ общей мощности, определённой по ф-ле (6.16), т. е.
N
— + — V------------5---= —-0,99 = 0,470. (6.23)
4 Ц-л’р’02 40
Л=1
Из равенства (6.23) находим, что для определения полосы
частот, содержащей 99% мощности, необходимо принимать в
расчёт 1, 3 и 5-ю гармоники, т. е. ширина полосы будет равна
A f = 5В. (6.24)
Произведя аналогичные вычисления для других значений — ,
т
получим следующие значения ширины полосы частот, занимае-
мой передачей:
при От = — А / = ЗВ;
4,6
при От = i. Д/ = 7В.
93
Расчёты показыв.ают, что, применяя даже простейший фор-
мирующий контур, можно снизить в несколько раз ширину по-
лосы передачи. Для практических целей обычно применяют фор-
мирующие Контуры более сложного вида. Ширину полосы пере-
дачи, получаемой при их использовании, можно определить по-
добным же методом в каждом отдельном случае.
§ 6.2. ШИРИНА ПОЛОСЫ, ЗАНИМАЕМОЙ ПЕРЕДАЧЕЙ
ПРИ ЧАСТОТНОЙ МАНИПУЛЯЦИИ
Прямоугольные сигналы. Как известно [Л2], при
манипуляции без разрыва фазы прямоугольными тачками сиг-
нал можно представить следующим рядом:
с /j\ 2 ( tn * f tz * \ . .
f (t) = — 1 — sm — m । cos <o 14-
k I m2 \ 2 /
+—cos(тт) icos(o>-/,)<—cos(<b+p)/i —
- sin(i"™) tcos —2p)f+cos —
-~2232cos(tm) tcoscos+эд+
+.......................................), (6.25)
где p — частота манипуляции,
2D
m =-------индекс частотной модуляции,
В
D — отклонение частоты (половина разности между рабо-
чими частотами).
При целых значениях т ф-лу (6.25) можно записать в более
компактном виде:
+ оо
7 (О = 2 ~пг^тг sin 0 + m) -J- cos [(“ + nP) t +(«+"»)
Л=—ОС
(6-26).
В соответствии с ф-лой (6.26) амплитуда n-го компонента
спектра равна:
А -А = —
Ап~ -« «
sin (п 4 т)
ла —та
(6.27)
94
Определим среднее значение мощности за период частоты
манипуляции. Если т — целое число или половина целого чис-
ла, то
cos2 2 к Dt dt +
т
У cos2 (— 2 к D) t dt =
т
2
т
2
cos2 к D dt = —.
2
(6.28)
С другой стороны,
(/<')!"*-4- S
О л=—оо
2л
я л2 — т2
— sin2—+ 2m2 V
m2 2 LA
> л=1 L
sin (n -4- m) -y-
n2 —m2
(6.29)
Из ф-л (6.28) и (6.29) получаем, что мощность в полосе пе-
редачи равна:
4
Я2
Л1
— sin2 — +2/л2У!
т2 2
л "]2
sin (п ф- т) —
п2 — тг
= 0,99. (6.30)
Из выражения (6.30) можно найти пгй компонент спектра,
при котором это равенство удовлетворяется, т. е. определить но-
мер последнего компонента, который входит в полосу, содержа
щую 99% мощности сигнала.
Для определения ширины полосы, занимаемой передачей
последовательности равных и прямоугольных частотно-манипу-
лированных сигналов, МККР рекомендует следующую формулу
[Л40]:
д (2,бР-ф 1,4В с точностью до 2°/0 для 2<m<8 j zgзх\
l2,2D-f-3,lB с точностью до 2% для 8</п<20]
Э5
Формулу (6.31) удобнее представить несколько иначе, чем
это сделано в рекомендации МККР, а именно: выразить шири-
ну полосы через индекс частотной модуляции в единицах скоро-
сти манипуляции В; тогда получим
. , ((1,3/и + 1,4) В с точностью до 2% для QO.
1(1,1 tn -f- 3,1) В с точностью до 2°/о для 8 20)
Скруглённые сигналы. Рассмотрим случай частотной
манипуляции одной частотой, соответствующий наибольшему
скруглению, которое можно получить, формируя сигналы. Такой
передаче соответствует с точностью до постоянного коэффи-
циента амплитуды функция
f (t) — sin (ш t 4- <ро + т sin. р/), (6.33)
где t представляет собой время, а со, фо, Р и т — константы, ко-
торые могут принимать любые действительные и положитель-
ные значения.
Известно, что функцию (6.33) можно разложить в сходящий-
ся ряд синусоидальных функций времени, т. е. представить в
виде дискретного бесконечного спектра,
+ 00
/(0 = J] J„(m)sin[(u)4-np)/ + <р0], (6.34)
П=—оо
где п — целое число и /„ (т) означает функцию Бесселя первого
рода, порядка п и аргумента т.
Итак, средняя мощность, соответствующая каждой частоте,
равна квадрату амплитуды Jп(т) с точностью до постоянного
коэффициента, независимого от п; общая мощность, соответ-
ствующая ряду (6.34), выражается, с точностью до того же са-
мого постоянного коэффициента амплитуды, формулой
00
j2(m) + 2^ Щт), (6.35)
Л=1
поскольку
/_„('П) = (-1)Я/Л(щ).
Ряд (6.35) сходится при любом значении т, и его сумма, не-
зависимая от т, имеет [Л 15, стр. 40] весьма простой вид:
00
^(/n) + 2j J2(/n) = l. (6.36)
n=l
96
Обычно считается, что дискретные частоты, мощность на ко-
торых составляет не менее 0,25%i общей мощности излучения,
включаются в полосу, занимаемую передачей. Поэтому ширину
полосы, занимаемой передачей, определяют наименьшие целые
значения п, положительные или равные нулю, которые удовлет-
воряют следующим двум условиям:
J 0,005,
р-П+1
•^+9 (т) С 25 • 10 4 или | Jn+q (m)| < 0,05,
(6.37)
(6.38)
где q — любое целое положительное число.
Выражение (6.38) содержит в себе бесконечное число усло-
вий, поскольку q, является произвольным положительным чис-
лом. Поэтому заменим его двумя условиями, которые уже не
будут заключать в себе этой неопределённости.
Из [Л 13] следует, что любая функция 7Л (т), для которой
т — произвольная постоянная и п — переменно, достигает своей
максимальной амплитуды (после того как она совершает не-
сколько колебаний1 *), амплитуда и псевдопериод которых увели-
чивается) при п=п1; эта максимальная амплитуда является по-
ложительной, причём nt<m. Для «1 справедливо приближённое
равенство
1
п.1 ~ т — 0,8086 т 3 . (6.39)
Далее эта функция, оставаясь положительной, уменьшается
с увеличением п и быстро стремится к нулю.
Максимальная амплитуда уменьшается с ростом т по зави-
симости
J (tn) as 0,6749 —. (6.40)
т3
Таким образом, для n+lS»^, если Jn+i <0,05, то тем бо-
лее Jn-tqfm) <0,05. Следовательно, (6.38) можно заменить двумя
неравенствами:
n-(-l>n1;Jn+1(m)<0,05. (6.41)
Кроме того, если ЛДт) <0,05, то мы видим, что оба условия
(6.41) утрачивают своё значение, поскольку ] Jn (т) | <0,05 для
любых целых п.
1) Число этих колебаний возрастает с увеличением т.
7—730
97
Из ур-ния (6.40) следует, что случай, когда оба условия ут-
рачивают своё значение, имеет место при т >2460. Естествен-
но, что условие (6.37) при этом всё ещё сохраняет свою силу.
Обратимся сначала к неравенствам (6.41). Таблицы [Л14]
для 0<>п~С29 непосредственно дают решения при целых зна-
чениях т. .
Чтобы решить неравенство (6.37), прежде всего выразим
каждый член его левой части в виде ряда Неймана [Л 15, стр. 43]:
?1(2р+<?)! Кр+М2
(6-42)
Таким образом, мы представили левую часть (6.37) в виде
ряда с положительными членами, являющимися абсолютно схо-
дящимися рядами. Далее можно сгруппировать вместе члены,
содержащие т в одинаковой степени. В результате такой груп-
пировки получим
ОО
Р-п+1
/ т2 \«+1
\~4/
К«+1)12
т2
~4~ )
<?1(2п+<?+1)! 1(«+<?+1)!]2
00 (2л + 2?+1)!
/и*
2п + 3 т2 . (2п + 4)(2п + 5)
(п4-2)2 4 + 2 [(п 4-2) («4-3)1*
(6.43)
Последнее выражение представляет собой убывающую функ-
цию своего индекса п+1 и стремится к нулю при возрастании п.
Знакопеременный ряд (6.43) удобно применять лишь от зна-
чений ш=0 до т=4. При больших значениях т применять его
затруднительно, поскольку ряд медленно сходится.
Чтобы решить неравенство (6.37), поступим следующим об-
разом в зависимости от значений т:
1) для 0<тп<4 используем знакопеременные ряды (6.43);
2) для 5<^т<29 применим таблицы [Л14].
В заключение остаётся лишь одновременно учесть неравенст-
ва (6.37) и (6.41). Для малых значений т условие (6.41) более
ограничивающее, чем (6.37). Для больших значений т условие
(6.37) определяет собой п.
Таким образом, мы определили ширину полосы, занимаемой
передачей частотно-манипулированных сигналов при прямо-
угольной и скруглённой формах сигналов. На рис. 6.4 произве-
дено сравнение результатов обоих расчётов; график 1 соответ-
ствует синусоидальным сигналам, а график 2 относится к пря-
моугольным сигналам.
98
§ 6.3. СРАВНЕНИЕ ПОЛОС, ЗАНИМАЕМЫХ ПРИ ОБОИХ ВИДАХ
МАНИПУЛЯЦИИ
Воспользовавшись произведёнными расчётами, можно уста-
новить численное -соотношение между шириной полос, зани-
маемых передачей при амплитудной и частотной манипуляции.
Проще всего такое сравнение провести для сигналов прямо-
угольной формы. .Как видно из расчётов § 6.1, ширина полосы,
занимаемой передачей при амплитудной манипуляции, равна
Д/а = 21 В. Из графика 2 на рис. 6.4 видно, что такая ширина по-
лосы при частотной -манипу-
ляции соответствует индексу
модуляции т =16.
При этом критическом
значении индекса модуля-
ции значения ширины поло-
сы, занимаемой в каждом
случае, равны между собой.
При т <16 передача с час-
' тотной манипуляцией зани-
мает меньшую полосу, чем с
амплитудной, и, наоборот,
при /п>16 передача с ам-
плитудной манипуляцией
: лучше использует полосу ча-
стот.
На радио-связях получи-
ло значительное распростра-
нение отклонение частоты
D = 500 гц. При т=16
В= 2-500 = б2 5 бод
16
ъ?(S едаяицахб)
Рис. 6.4. Ширина полосы, занимаемой
излучением, при частотной манипуля-
ции синусоидальными (1) «и прямоуголь-
ными (2) периодическими -сигналами
Таким образом, при £>=500 гц частотная манипуляция с точ-
ки зрения занимаемой полосы частот выгоднее, чем амплитуд-
ная при скоростях, превышающих 62,5 бод.
Также можно сравнить и другие формы импульсов. При
скруглении импульсов критическое значение индекса модуляций
т уменьшится и частотная манипуляция будет иметь преимуще-
ство перед амплитудной в отношении занимаемой полосы частот
при меньших индексах модуляции, т. е. при больших скоростях
работы, чем это было при использовании прямоугольных им-
пульсов. * “j
ГЛАВА СЕДЬМАЯ
СПЕКТРЫ РАДИОТЕЛЕГРАФНЫХ СИГНАЛОВ
РАЗЛИЧНЫХ ФОРМ ПРИ ЧАСТОТНОЙ
МАНИПУЛЯЦИИ
Рассчитаны спектры и
определена ширина занимае-
мой полосы частот частотно-
модулированных сигналов для
двух форм модулирующих им-
пульсов: с установлением ло
линейному закону (трапецеи-
дальные) и по синусоидально-
му закону. При выводе расчёт-
ных «формул применен тот же
метод, что <и в [Л13] и [Л21].
Рассмотрены внеполос-
ные излучения частотночмоду-
лированных сигналов при раз-
личных формах модулирующих
импульсов и . показано, что
компоненты спектра частотно-
манипулированных сигналов
наиболее типичной формы при
высоких частотах прямо про-
порциональны компонентам
спектра манипулирующей функ-
ции и обратно пропорциональ-
ны номеру компонента.
Показано, что хотя обе
формы рассмотренных импуль-
сов практически равноценны в
отношении занимаемой ими по-
лосы частот, однако следует
предпочитать импульсы с уста-
новлением по синусоидальному
закону, так как они имеют
ббльшую скорость убывания
внеполосных излучений.
§7.1. ТРАПЕЦЕИДАЛЬНЫЕ
ИМПУЛЬСЫ
на рис. 7.1 при
В [Л35] приводятся результаты
чисто экспериментального ис-
следования спектров частотно-мани-
пулированных сигналов при трапе-
цеидальном и синусоидальном
скруглениях манипулирующих им-
пульсов.
Рассмотрим частотно-манипули-
рованный трапецеидальный импульс:
/(0 = sin[©/ = ?(0], (7.1)
d<s
для которого определяется
ломаной трапецеидальной линией,
показанной
Ф(0)=0.
Обозначим частоту повторения
импульсов, соответствующую перио-
ду 2т, через Q, индекс частотной мо-
дуляции т= — и g= . Обо-
ft т
значения т, Ti и ф,' показаны на
рис. 7.1.
Поскольку о и Q в общем слу-
чае не находятся в рациональном
соотношении, то f (0 нельзя пред-
ставить в виде ряда Фурье. Но мы можем представить эту функ-
цию в виде
/ (0 — sin © t cos <р (t) + cos © t sin <p (t),
где ф (0 и — являются периодическими и их период состав-
dt
(7.2)
100
ляет 2т. Тогда соэф(/) и sin<p(/) можно разложить в ряд Фурье
с периодом 2т.
Рис. 7.1. Частотная манипуляция трапецеидаль-
ными (импульсами
Функция
—*— чётная. Поэтому <p(t) — нечётная функция/;
cos <р(/)—чётная функция / и sin<p(7) — нечётная функция /.
Разложения cos<p(/) и sin<p(/) в ряд Фурье имеют вид:
cos<p(/) =-у +yja„cosnw— = 4- JJancosnQ/, (7.3)
л=! л=!
sin «р (/) = ba sin п it — = bn sin п 2 /, (7.4)
П=1 П=1
где ап и Ъп — коэффициенты Фурье, которые вследствие сим-
метричности ф относительно /=0 выражаются в виде:
ап = — f cos n S/cos<p(/)d/ >=— f (cos [<р (/) — п 2/] 4-
т J т J
О О
4- cos [<?(/) 4- п 2 /]}<//, (7.5)
bn = — f sin п Q / sin <р (/) dt = — С cos [<р (/) — л Q /] —
т J т J
о о
— cos (<р(/) 4- п О /])<//. (7.6)
101
Подставляя (7.3) и ,(7.4) в (7.2), получим
оо
2/0) = aosin®/4-2(ал[sin(о>4-п£2)/ + sin(«> — пй)/] 4-
П=1
4- bn [sin (ш 4- п И) t — sin (ш — п й) /]} =
ОО
= aosina>f 4- 2 [(а„4- £„)sifi(<o 4- яй)/4- (а„ — bn) sin (« — nQ)/].
П=1
(7.7)
Обозначив
_^. = Св; (7.8)
можем записать (7.7) в более компактном виде
+°О
/0)= 2 СЛзЩ« + яС)Л (7.9)
п=—оо
где
С„ = —[cos [<?(/) —пй/] Л. (7.10)
T J
о
Разложение функции <р (/) в интервале (0, т) будет различным
в трёх различных подынтервалах:
Функция изменяется в соответствии с формой модули-
рующего сигнала, показанного на рис. 7.1, т. е.
тй при *1 2 1
dy d/ ~ (т—2/) •с — Тх при 2 т — тх "" 2 • (7.U)
— /пй при 2 т — тх 2 < т
Подобным же выражением будет описываться изменение
—в течение второй половины периода от т до 2т.
dt
Периодический компонент фазового угла <р определится из
выражения
102
<?(/) =
tn Q t при 0 < t < -y-
772 О г А л. / 21 пл»» 3 л. y'
4(,-„) t4f"P"
mS3(t — t) при 2*~T1 <t<т
(7.12)
Аналогичное выражение получается и для второй половины
периода. Таким образом, в соответствии с выражением (7.10)
X
TC„=jcos[<p/ — nQ t\dt = Ix + Z2 + Z8, (7.13)
о
где
л
2
Л = J cos [(m — n)Qt]dt, (7.14)
о
2
Л = J cos {«[41 (t -t) -1|] - 4n (т-t,)/}) dt, (7.15)
*1
2
x
Is= J cos {Q [mx— (m+ «)/]}<//. (7.16)
2x—Tt
2
Вычислить Zi и Z3 нетрудно. Обозначив
aa = (n-mk)^- , (7.17)
An = I^±h.i (7.18)
получим
A- “ 77^.)" (m cos ["(1 - !> T ]s,n “ -
— nsin n(l—5) -yl cosan|. (7.19)
Рассмотрим далее интеграл Z2, выраженный ф-лой (7.15).
Чтобы исключить член первой степени t под знаком косинуса,
заменим переменную
Откуда
т г 2т 2 2т ‘
(7.20)
(7.21)
103
Полагаем
₽ = Гп- ?а(1-£) 1— . (7.22)
Гл L 2 m 2 J 2
Использовав ур-ния (7.21) и (7.22) и обозначив -у = Вя, по-
лучим из (7.15):
____(n+m) V£
В"=Г-^Г f cos( ^u>+?a)dU. (7.23)
r Z tn J ________ \ z /
(»-m)
Введя интегралы Френеля
S(x) = J sin-J t2df,
о
C(x) = J cos-^- tsdf,
о
(7.24)
получим, что
2tn (C0S {C ~2m-
Общая амплитуда n-го компонента будет
|СЯ| = |Л„ + В„|. (7.26)
Поскольку
= L„ = Pn-n* I 727)
Л^-=(-1)^п; В_„-(-1)лВя J’
то, следовательно,
|C_J = ICJ- Р-28)
§ 7.2. ИМПУЛЬСЫ С СИНУСОИДАЛЬНЫМ СКРУГЛЕНИЕМ
Достаточно полно теоретически рассмотрен спектр сигналов,
модулированных по частоте несимметричными импульсами с
синусоидальным скруглением в [Л21].
Из сравнения рис. 7.1 и рис. 7.2 видно, что рассматриваемые
импульсы отличаются от трапецеидальных лишь на интервале
("2”’ j’ Поэтому мы воспользуемся результатами вычисле-
на
ний интегралов Ц и 13, а также значений Ап, и заново рассчи-
таем интеграл который для рассматриваемого случая будем
обозначать /'2, и D„ = —.
Рис. 7.2. Частотная манипуляция -импульсами с
синусоидальным скруглением
Частота и фаза в интервале
кону:
изменяются по за-
dt
2т—тх
~~2
(7.29)
4-mQ
It
(7.30)
Откуда
(’-H
I'2= J cos [ср(/) — nQ/] dt =
2
к —n£lt\dt.
(7.31)
105
Введём обозначения:
(7.32)
t 1
ф=(/П$—Zl)-y
Тогда
2
2 — f cos {л (1 — О у — т (1 — 6) cos у — ф} dy. (7.33)
ТС J
те
“Т"
Подынтегральное выражение можно разложить, пренебрегая
нечётным ком1П01нентом. так как пределы интегрирования сим-
метричны. В результате 'получим
/2=,21<1^)сгаф
* тс
2
J cos [к (1 — £) у] cos [т (1 — 5) cos у] dy
о
2т(1—е)
тс
2
sin ф cos [п (1 — 5) у] sin [т (1 — 5) cos у] dy . (7.34)
'о
Интегралы в ф-ле (7.34) можно выразить через известные
[Л 15, стр. 338, 339] функции Ангера и Вебера. Но посколь-
ку эти функции недостаточно табулированы, это оказалось бы
мало полезным в нашем случае, когда требуется определить
численные значения интегралов. Для числовых расчётов более
удобно воспользоваться частным случаем функций Ломмеля
v(z), а именно s_1(V (г) и s0 у(а)([Л15, стр. 377] и приложе-
ние V). Графики этих функций построены нами и показаны на
рис. n.V.l. и П.У.2. Тогда
D. = — -----------— [v cos ф sin v s (z) +
" 2 те n L \ 2 / -1’’4
4- sin ф cos f — v s0>v (z)l, (7.35)
\ 2 / * |
где
/ \ _ 2__________z’______.______Z®________
SO.V W— —м»)(за_vS)(52 *—
(7.36)
106
s , (z) =----ч-----------------------------------h. • (7.37)
-M'' ^(2’ —v«) ч2(22 — ч2)(42 — м«) '
v=n(l— 5)
И
z= m(l — 5).
Легко убедиться, что
D_n = (—!)” Dn. (7.38)
Поэтому, учитывая, что в соответствии с ф-лой (7.27)
Л_„ = (—1)ПЛ„,
получим, что
|Яя| = |£-„ | = |Л„ + о„| = |Л_„ +р_п |. (7.39)
Если v = n(l—5) — целые числа, то s_lv(z) или sOv(z) ста-
новятся гнеопределёнными. Чтобы определить в этих случаях
значения интегралов в ф-ле (7.34), воспользуемся выражениями
[Л15, стр. 30]:
тс
2 -у (»-1)Т
Jn (z) = — (— 1) I cos ny sin (z cos y) dy (7.40)
те J
0
(n — нечётное);
It
-Lrty
Jn (z) = — (— 1) I cosny cos (z cos y) dy (7.41)
те J
0
(n—чётное)
Формула (7.34) после подстановки в неё значений интегра-
лов из (7.40) и (7.41) принимает вид:
при v нечётном
г _2г(1-£)
— v cos ф sin
ч -8Шф/п(1_е)(2)^-(-1)2 ° °];
(7.42)
107
при v чётном
— sin ф cos (v у) sO v
(7.43)
§ 7.3. РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ ШИРИНЫ ПОЛОСЫ
Амплитуды компонентов спектра трапецеидальных импуль-
сов и импульсов с синусоидальным скруглением вычислялись
по ф-лам (7.19), (7.25) и (7.35) для индексов модуляции
2D
т= — =1-~-24 (0,5). Такие значения т были выбраны, чтобы
В
охватить все практически применяемые в радиотелеграфной свя-
зи скорости манипуляции В и отклонения частоты D. Параметр
$ = — был принят равным 0,9; 0,8 и 0,7, что соответствует
т
времени установления сигнала, значительно меньшему, чем ис-
правляющая способность стартстопного телеграфного аппарата
(равная 35-4-40%).
На основании полученных результатов была вычислена ши-
рина полосы, занимаемой излучением, которая определялась из
суммы квадратов амплитуд компонентов, содержащей 99%i из-
лучаемой мощности. Таким образом, ширина полосы, занимае-
мой излучением, выражается в значениях п— — , которые и
В
приведены в виде функций индекса модуляции т в приложе-
нии VI.
Из табл. n.VI.l видно следующее:
а) Трапецеидальные импульсы и импульсы с синусоидаль-
ным скруглением при одинаковых значениях § почти для всех
значений т занимают одинаковую полосу частот, и лишь для
небольшого числа т импульсы с синусоидальным скруглением
занимают несколько более широкую полосу частот, чем трапе-
цеидальные.
б) При /п<2 скругление импульсов не уменьшает полосу
частот, занимаемую излучением. Небольшое скругление
(£=0,7), незначительное по сравнению с исправляющей способ-
ностью стратстопного телеграфного аппарата, обеспечивает
выигрыш по ширине занимаемой полосы более 30%. при /п=3 и
порядка 10% при /п=24.
в) Использование значений £<0,7, а при малых т и £<0,8
уже не уменьшает ширину занимаемой полосы, так как при этом
достигаются пределы, соответствующие синусоидальному сигна-
лу (см. гл. 6).
108
§ 7.4. ВНЕПОЛОСНЫЕ ИЗЛУЧЕНИЯ ПРИ РАЗЛИЧНЫХ ФОРМАХ
СИГНАЛОВ
Частотно-манипулированный сигнал можно представить в
виде (7.9), и если на функцию — не налагать дополнитель-
dt
ных условий относительно её чётности, то (7.10) будет иметь вид
2т
С„ = — [cos [ср (t) - п Q d t. (7.44)
2т J
о
Представим (7.44) в виде
2к
Сп = — f[cos<p(/)cosnQ/4-sin<p(/)sinnQ/] dt. (7.45)
2т J
о
и разобьём (7.45) на сумму двух интегралов:
2т
Сп... = — [cos ф (t) cos п □ t dt, (7.46)
п \1) 2т )
о
2т
Cn(2) = — f sin<Р (t) sinп Q t dt. (7.47)
2т
О
Рассмотрим (7.46) в случае, когда манипулирующая функция
представляет собой прямоугольный импульс, т. е.
на интервале 0 и на интервале -у <т.
При этом (7.46) принимает вид
С — —
Gn(l) ~ х
2
I cosmQtcosnQtdt +
"-о
+ J cos tn Q (т—t) cos n£ltdt .
T
Если m — чётное число, то, поскольку Q=—
(7-48)
cos mQ(x —1) = cos mQt;
109
поэтому (7.48) можно представить в виде
СЛ(1)~
= у- Jcos(m+ п)Й/Й + Jcos(m — n)Qtdt .
О о
(7.49)
Если п=#±/п, то из (7.49) получаем, что Ся(1) = 0,
Если п = ± т, то Ся(1) — 1/2.
Если т — нечётное число, то cos т £2 (т — /) = — cos т £2 /; по-
этому (7.48) можно представить в виде:
при п =# ± т
С — —
sin (m 4- п)
£
п) Q
sin(/n — n)-y
(m — n)Q
0
___2m
~ u (m2 — n2)
±—-—
w (m2 — n2)
при n — нечётном
при n — чётном;
Таким образом, мы рассмотрели равенство (7.46) при усло-
вии, что манипуляцию производим прямоугольными импульса-
ми. При этом же условии (7.47) примет вид
tn Q t sin п Q t dt +
+ Jsin/nQ(T —/)sinnQtdt .
T
(7.50)
Если m—чётное число, то sinmQ(t — /) =—sin m £2/; поэ-
тому (7.50) можно представить в виде.
110
sin/га £2/sin га £2/4/
с_______J_
Ь«(2)~ т
— I sin m £2 / sin га £2 / d/
О при любом чётном n, в том числе и при п— + т
+ 2m
~ я (т2 — п2)
+ 2п
л (ffl2 — П2)
при нечётном п.
Если т—нечётное число,то при п#= +/га значение sin/ra£2(t—/)==
= sintnQt, поэтому (7.50) можно представить в виде
С — —
»(2)— ,
2 т
J sin /га £2 t sin га £2 t dt 4- Jsin /га £2 t sin га £21 dt
0 _r_
2
~ f sin m £2 t sin ra £21 dt =
T J
0
0 при n ± m
1/2 при n = ± tn.
Выберем в качестве манипулирующего сигнала наибо-
лее типичную функцию, которая позволила бы в то же время
легко аппроксимировать компоненты излучаемого спектра при
высоких частотах. Такой является функция с горизонтальными
центральными частями, продолжительности которых составляют
более половины от общей продолжительности сигнала, а пере-
ходный процесс между этими областями является непрерывным
и монотонным. Если наложить это ограничение на — , то <р(/)
dt
будет иметь форму, близкую к треугольной со скруглёнными
вершинами.
Пусть /га — четное число. Если манипулирующая функция
удовлетворяет вышеуказанным ограничениям, то sin<p(/) будет
иметь форму, подобную полученной для прямоугольной модулях
ции, с изменениями в области sin<p(Z) ~ —<р(/) (с точностью
до знака).
Известно, что на величину высокочастотных компонентов
спектра сильно влияет область быстрого изменения функции, т. е.
та область, где sintpf/)’» —<р(/). Поэтому при определении
111
высокочастотных компонентов спектра можно заменить sin (0
2т
на —ф(/) или просто на <р(0, поскольку sinn£ltdt=Q.
о
Таким образом, получим
2т
cn(2) = 7-f'PWsinnQ/dt (7.51)
<я»т> s
Проинтегрировав (7.51) по частям, получим
С — 1
п <2> 2т
-----— cosnTC • ср (2 т) Н 5— ср (0) 4-
и Q ti Q
2т
Н—— cosnQ/Л
лй J dt
о
(7.52)
Учитывая, что при выбранной нами аппроксимации манипу-
лирующей функции ф(0) =<р(2т) =0. получим (7.52) в виде
С ,п\ -- ------ ------
(п^т) <п^т)
2т
Р*- cos 11 Q t dt =
J di
о
2т
f-^-cosnQ/d/.
1____1_
п& 2 т
б
(7.53)
Компоненты спектра манипулирующей функции
рая выбирается чётной, будут иметь вид
d-f
dt
, кото-
2т
Mn= —— Г-^-cosnQM/.
я 2t J dt
0
(7.54)
Сравнивая (7.53) и (7.54), видим, что
с„ =Ц-м„.
(7.55)
Если т— нечётное число и n #= + tn, то [qm. ур-ние (7.46)]
2т
Сп = Сп (1) = JC0S Т W C0S П Q t dt-
о
(7.56)
112
Здесь cos (t) изменяется в области, где аргумент f?(t) бли-
зок к ‘ Представим (7.56) в виде
2т
О
— <p(Z) cosnQ tdt.
(7-57)
Поскольку —?(/) близко к нулю, то sin —
L 2 J 2
— ф(^) ~~~—ф(0 и выражение (7.57) принимает вид
J
2т
СП = Сп(П = + (6 cosn Й tdt. (7.58)
.Проинтегрировав (7.58) по частям, получим
2т
(7-59)
Компоненты спектра манипулирующей функции , которая
для данного случая выбирается нечётной, будут иметь вид
2т
Мп = — sin й t dt.
2т J dt
о
(7.60)
Сравнивая (7.59) и (7.60), снова получаем выражение типа
(7.55)
С„ =± — Мп.
(п^>т) п Q
(7.61)
Если т не целое число, а манипулирующая функция удовле-
творяет те же ограничения, что и при целых т, то функция
sirKp (t) будет иметь форму, подобную -полученной для прямо-
угольных сигналов с изменениями в области, где ф(/) близко к
mu
-р-. В этой области:
mu
2
sin <f> (/) = sin /+ <p (t)
, mu . Г mu
+ cos—sin <p(0——
. т к
Sin COS ср (t)
mu
~2~
2 L’ ' '
mu "I mu
--- cos-----
2 J 2
(7.62)
113
8-730
и
COS Ср (t) ~ COS + Гер (f)
tTl It / ,\
= cos--------COS (p (t)
2
mn
T
• /7Z * • / >\
— sin-------Sin <p(0
2
m u Г /^\
—-[fW
(7.63)
Подставив в (7.46) и (7.47) значения coscp (7) и sinq>(7) соот-
ветственно из (7.63) и (7.62), после преобразований получаем:
2т
(л^>т) ~ sin — !_ №. sin П Q, t dt, (7.64) 2 nQ 2т J dt 0 2т
Сл(2)~ (л>т) cos~~~ —- — cosn Q t. (7.65) 2 лй 2т J dt 0
Для нецелых значений т синусоидальный и косинусоидаль-
ный компоненты спектра манипулирующей функции — будут
dt
соответственно иметь вид:
2т
м (1} = — sin л й t dt,
Л(1) 2 т J dt
о
2т
о
(7.66)
(7.67)
Сравнивая (7.64) с (7.66) и (7.65) с (7.67), получаем, что
1
п Q
C„0)«sin
/И ТС
(7.68)
^Л(1)
и
fflit 1 ,.
~ cos--------------М„
2 nil
(7.69)
^л(2)
(л>т)
Таким образом, мы доказали, что в общем случае (при лю-
бом значении т) компоненты спектра сигналов, модулирован-
ных по частоте импульсами наиболее типичной формы, при вы-
соких частотах прямо пропорциональны компонентам спектра
114
модулирующей функции и обратно пропорциональны номеру
компонента.
В § 7.3 было показано, что трапецеидальные импульсы и им-
пульсы с синусоидальным скруглением практически равноцен-
ны по занимаемой их передачей полосе.частот. Однако из рас-
смотренного в настоящем параграфе видно, что скорость убы-
вания внеполосных излучений частотно-манипулированных сиг-
; налов определяется формой -манипулирующей функции, а, как
показано в гл. 5, импульсы с синусоидальным скруглением име-
ют большую скорость убывания внеполосных излучений, чем
трапецеидальные. Поскольку при выборе формы импульсов
следует учитывать не только ширину занимаемой полосы, но и
скорость убывания внеполосных излучений, то импульсы с сину-
соидальным скруглением имеют преимущества по сравнению
с трапецеидальными.
ГЛАВА ВОСЬМАЯ
СООТНОШЕНИЕ МЕЖДУ ШИРИНОЙ ПОЛОСЫ,
ЗАНИМАЕМОЙ ПЕРЕДАЧЕЙ, И ВРЕМЕНЕМ
ЗАМЕДЛЕНИЯ СИГНАЛОВ
В гл. 5 была рассмотрена
возможность уменьшения энер-
гии внеполосных излучений
с точки зрения теории Шеннона
о пропускной способности кана-
ла. В этой главе рассмотрено
понятие замедления сигнала и
те ограничения, которые оно
налагает на пропускную спо-
собность канала.
Поскольку бесконечно замед-
ленные сигналы нереальны, то
возникает вопрос, нельзя ли
получить сигналы с конечным
временем замедления, котррые
давали бы нам преимущества
в использовании полосы частот.
Выведена формула для опре-
деления пропускной способно-
сти канала связи при конечном
времени замедления, из которой
видно, что при малом времени
замедления пропускная спо-.
собность канала уменьшается
по сравнению с пропускной
способностью канала, в кото-
ром время замедления беско-
нечно велико.
Определена форма сигнала с
ограниченным спектром, содер-
жащего максимальную долю
энергии в заданной полосе ча-
стот, и показано, что решение
этой задачи приводит к тому
же интегральному уравнению и
той. же форме импульса, что
и для сигнала конечной продол-
жительности.
§ 8.1. ПРОПУСКНАЯ СПОСОБНОСТЬ
КАНАЛА И ВРЕМЯ
ЗАМЕДЛЕНИЯ
pj ропускная способность канала,
ограниченного шириной полосы
F, в случае, если сигнал и помеха
представляют собой белый шум, как
мы уже упоминали во введении, вы-
ражается по Шеннону [Л28] форму-
лой
„ ci
С = F log2 —!— , двоичных единиц
N
в секунду, (8.1)
где Р — мощность сигнала,
Л' — мощность помех.
Если сигнал g(t) не содержит
частот, превышающих полосу ча-
стот F, и известен на интервале вре;
мени —оо-5-4-оо, то его можно пред-
ставить в виде ряда Котельникова
+ оо
Л = —ОО
(8-2)
116
Из (8.2) видно, что если мы будем воспроизводить через про-
межутки времени т= — бесконечно короткие импульсы, пред-
2F
ставляющие собой значение функции g(t) в эти моменты време-
ни, то эти импульсы будут передаваться без искажений ампли-
туды.
Рассмотрим (рис. 8.1) единичный сигнал вида
g(0 = gosin22”X(Z~/? • М
2п г Iq)
Рис. 8.1. Элементарный сигнал при передаче
через идеальный фильтр
Он достигает максимума в момент времени t=tQ, причём про-
межуток времени от 0 до to представляет собой время замедления
импульса. Через промежутки времени т импульс принимает ну-
левые значения. Поэтому, если мы хотим, чтобы максимальные
значения импульсов не искажались за счёт соседних импульсов,
то следует передавать нужные нам импульсы через промежутки
времени —L. Скорость передачи импульсов будет равна
В= —= 2F бод.
Откуда F= ; или, учитывая, что мы обычно по высокой ча-
стоте определяем полосу Д/=2В, получаем, что Af=B, т. е., каза-
лось бы, что мы имеем очень хорошую систему передачи, которая
превосходит даже при двухполосной работе все существующие
системы, поскольку для обычной двухполосной AM Д/= (34-5) В,
а для идеального импульса Д/=2,3 В. Такая система не созда-
вала бы за пределами полосы каких-либо внеполосных излу-
чений.
117
Из-за помех в канале связи каждый импульс может обес-
печивать т= yZfiA выборов ступеней амплитуд. Поэтому с по-
мощью п таких импульсов можно обеспечить пт выборов в се-
кунду, и скорость передачи •
С = log2mn = log2 тв
или, поскольку
то
(8.4)
Если мы имеем выбор из двух положений (обычная телегра-
фия), то
С = В.
(8.5)
Рассмотрим, каким образом можно было бы получить сигнал
g(t), определяемый ур-«ием (8.2) и представляющий собой по-
следовательность смещённых по времени на промежуток —
элементарных сигналов вида (8.3).
Допустим, что для этой цели мы используем полосовой
фильтр с характеристиками передачи:
|z(a>) | = z0 = const
?.(«») = <°/о
z (<о) = z0 е1"/‘
(8-6)
где to — время замедления фильтра.
Однако идеальный фильтр, описываемый характеристиками
передачи (8.6), может воспроизвести функцию вида (8.3), толь-
ко при бесконечно большом времени замедления t0, так как
зависимость между z(co) и t0 позволяет получить ступенчатое
ограничение полосы частот при Ft0= оо. Поэтому, если F конеч-
но, то to должно быть бесконечно и, наоборот, конечное время
замедления to предусматривает, строго говоря, бесконечную по-
лосу частот. Поскольку ф-ла (8J) выведена, исходя из представ-
ления сигнала в виде ряда Котельникова (8.2), который может
быть получен при помощи идеального фильтра (8.6) только при
бесконечно большом времени замедления, то эта формула верна
только при t0— оо.
118
Вопрос, каким образом определить пропускную способность
канала для систем с конечным временем замедления, будет рас-
сматриваться далее.
§ 8.2. ХАРАКТЕРИСТИКИ СИСТЕМЫ СВЯЗИ, ОБЕСПЕЧИВАЮЩЕЙ
ПЕРЕДАЧУ СИГНАЛОВ С КОНЕЧНЫМ ВРЕМЕНЕМ ЗАМЕДЛЕНИЯ
Чтобы получить элементарный сигнал gp (t) с конечным
. временем замедления, к сигналу (8.3) добавим сигнал вида
при t < О
&(0=
sin 2я Г (/^о)
2xf (/-Но)
при £>0
(8-7)
Тогда получим сигнал,
показанный на рис. 8.2.
Сигнал gp(t)=g(t) +
+ёг(1) равен нулю при
/<0 и имеет тот же са-
мый максимум, равный go,
/что и сигнал g(t)‘, время
..замедления его конечно и
равно to.
Рассмотрим, какую ха-
рактеристику передачи
должен иметь фильтр,
чтобы при бесконечно ко-
ротком импульсе на его
входе получился бы на
его выходе сигнал gp (t).
Обозначим характеристи-
ку передачи этого фильт-
ра Zi((o) и фазовую ха-
рактеристику ф1 (со) так,
что
«!<<») = (w)| (8.8)
।
Рис. 8.2. Элементарный сигнал gp(t) с
конечным временем замедления /0
Тогда спектр Q(co) выходного сигнала gp(t) будет
e(a)) = l.z1(«>) = |zi(a>)|e-w<“). (8.9)
119
С другой стороны,
2(®) = р>(0е“1ш'Л. (8.10)
о
Подставляя в ф-лу (8.10) значения gp (t) — g (t) -F gz (/) из
ур-ний (8.3) и (8.7), получим, сравнивая по отдельности действи-
тельные и мнимые части в равенстве (8.10):
| Zi (to) | cos [ср (ш)] = Re J gp (/) e_w dt;
о
I Zi (ш) I sin [cp (co)] = Im J gp (/) e-w dt;
0
00 2
Im \gp(f)fi~Mdt ;
6
ср (co) = arc cos
Re JgP(Oe"w di
0___________
I Z1 (to) I
Откуда получаем:
При to > 2kF
I Zi (ш) | cos [tp («.)] = 0
и ср (co) == -^-при всех частотах.
I Zi (со) | sin [<р (со)] =
= — [Ci (<о + 2к F) to — Ci (со — 2nF) ^0]cos to to —
К
---— [— Si (to + 2к F) to + Si (to — 2к F) /0] sin to t0- (8.11)
При to < 2k F
I Zi (<o) | cos [cp (to)] = cos to t0;
| Zi (co) | sin [cp (to)] = sin to /о + — [Ci (o>+2k F) t0 — Ci (2k F—a>) t0!X
Xcos co t0----— [к + Si (co + 2k F) to — Si (co — 2k F) /o] sin co to- (8.12)
К
120
Далее примем
|21(ш)| = 1-
На рис. 8.3 показана функция | zx (<о) | для некоторых значений
2nFt0, причём | Zi (ш) | выражено в децибелах в зависимости от
Рис. 8.3. Спектр передачи zj (со) при передаче через систему с .конеч-
ным временем замедления t0
При 2п Ft0 = оо функция | zx (и) | имеет вид прямоугольника.
При 2к Ft о = О
I zi (ш) I — 1 / 1 + f — In “ -2эт—\ при<о<2к/:' (8.13)
I/ \ те 2те F — о> /
И
|Zi(w)|= — In
к
to 2те F
2nF — «о
при ф > 2к F.
(8.14)
Из рис. 8.3 видно, что при уменьшении времени замедления
to спектр передачи / Z\ (со) | убывает всё медленее с увеличе-
нием о и вследствие этого ширина полосы передачи неограничен-
но увеличивается. Если границу полосы частот установить на
некотором определённом уровне, например 40 дб, то ширина
полосы изменяется приблизительно обратно пропорционально
121
времени замедления to. Таким образом, действительная ширина
полосы сигнала с конечным временем замедления t0 всегда
будет шире, чем F.
В табл. 8.1 приведено отношение действительных значений
ширины полосы Го к F на уровне — 40 дб.
Приведённые в табл. 8.1 данные соответствуют значениям
ширины полосы, получающимся при 2nFto, если 2nFto крат-
но —. Если же применять произвольные значения 2nFt0, то
ширина полосы может принимать только большие значения,
так как импульсы будут начинаться не с нуля.
TAB ЛИ ЦА 8.1
ТАБЛИЦА 8.2
2кГ/в F на уровне -40 дб Ft, ft
0 63,8 0 0,0157
ТС 2,61 1,305 0,383
2тс 1,86 1,86 0,537
Зтс 1,58 2,37 0,632
4тс 1,44 2,88 0,694
5тс 1,36 3,40 0,736
бтс 1,30 3,90 0,769
7тс 1,26 4,41 0,793
§ 8.3. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА С УЧЁТОМ
ВРЕМЕНИ ЗАМЕДЛЕНИЯ
Если действительная ширина полосы Fo при конечном вре-
мени замеделения to будет больше, чем F, то это соответствую-
щим образом отразится и на пропускной способности канала.
Если ввести коэффициент
h(F,t0) = -^-,
Го
где F — первоначальная ширина полосы, соответствующая эле-
ментарному бесконечно замедленному сигналу, из которого
составляется ряд Котельникова (8.2), a Fo— действительная
ширина полосы элементарного сигнала с конечным временем
замедления, то пропускная способность канала будет равна
122
C^FhiF, /0)log2^ (8.15)
двоичных единиц в секунду, причём всегда коэффициент Л<1.
Функция h(t) вычисляется в соответствии с табл. 8.1, и её
трафик показан на рис. 8.4. Из табл. 8.2, в которой приведены
значения этой функции, видно, что при небольшом времени за-
медления пропускная способность канала значительно умень-
Рис. 8.4. Коэффициент уменьшения пропускной
способности канала при конечном времени за-
медления
шается по сравнению с пропускной способностью канала с бес-
конечным временем замедления, определяемой из ур-ния (8.1).
•Однако Л быстро возрастает и достигает 1/2 для значений Ft^.
близких к 2. И только при значительно больших значениях Ft,h
'близких к 10, величина h достигает значений, приближающих-
ся к 1. .
В телеграфии замедления, не ведущие к значительному .
уменьшению пропускной способности канала, имеют такой же
порядок, что и замедления, получаемые в некоторых существую-
щих многократных системах.
В канале передачи речи с шириной Полосы 3,5 кгц время за-
медления составляет
. 10-1000 '
tn — -------~3 мсек.
3500
Следовательно, уже при времени замедления в несколько
миллисекунд практически достигается предельная величина
пропускной способности канала, определяёмая по формуле
123
Шеннона (8.1). Системы связи со значительно меньшим време-
нем замедления, чем указанные выше, при тех же значениях ши-
рины полосы будут иметь значительно меньшую пропускную
способность канала.
Пропускная способность канала с весьма небольшим време-
нем замедления может быть в принципе повышена искусствен-
ным увеличением времени замедления.
§ 8.4. ФОРМА СИГНАЛА С ОГРАНИЧЕННЫМ СПЕКТРОМ,
ЗАНИМАЮЩЕГО НАИМЕНЬШУЮ ПОЛОСУ ЧАСТОТ
Пусть на вход фильтра подаётся сигнал G(t) конечной про-
должительности —+“ , причём характеристика фильтра тако-
ва, что все частоты спектра выходного сигнала g(t) за предела-
ми полосы угловых частот —<оо, +соо не воспроизводятся.
Определим, какую форму должен иметь входной сигнал
G(t), чтобы в полосе —«ю, +а>о содержалась наибольшая доля
его полной энергии.
Выходной сигнал g(t) можно получить из спектра Q(co) это-
го сигнала при помощи обратного преобразования Фурье
g(f)= J 2(ш)е1<о/с(<о =
—ш»
+ ^-
Г 2? J 6№~мс1т-еы(1ш =
— а» о т0
2
+ —
2 4-<»)о
J G (х) т J еМ*~d а) =
то —О'о
2
2
1 Г sin <00 (/— т)
тс J (/ — т)
G(x)dT.
(8.16>
Выражение (8.16) связывает входной сигнал G(t) фильтра с
выходным сигналом g(t) для случая, когда спектр сигнала огра-
ничен.
124
Решим вариационную задачу по ^определению максимальной -
энергии «у—, или просто W, поскольку по принятой нормировке
поли
wnoM = l-
co
J «W
W =
(8-17)
2
2
(0
где, учитывая (8.16)
2
2
2
2
‘ sina)0 (/ — х)
л (t — х)
2
X 8-1п^Цу) G (х) G (у) dxdy= С
*(< — у) J
то
2 2
Т (8.18)
j* G(x)G(y)dxdy [</а /3];
/о
2
С _СО8Ш0^-20 d 0
J (t-x)(t-y)
-оо
С cos (о0 (2/ — х — у)
J У-*)(‘-у)
+ оо
cos <о0 (2/— х — у) Г coso>0(2/ — х —у) dt =
/—X J t—y
= 2xsin<fl0(y x)°j (8 20)
„ (х — у)
Подставляя значение J2 из (8.19) и Js из (8.20) в (8.18) и за-
тем учитывая (8.16), получим
+ оо 2 2
J ga(t)dt= у у G(x)G(y)dxdy
—00 ' Т. т.
Sina>0(X —у)
л(х —у)
2 2
+ Т .
= J G(t)g(t)dt. (8.21)
—It
2 125
+ оо
Перепишем (8.17), подставив в него значение j g (/) dt иэ
—оо
(8.21)
+ + 2i
. +оо 2
J g*(‘)dt J G(i)g(t)dt
—*оо _ Т0
W =--------------=-------------------. (8.22)
2 2
J G*(Od/ j G2(/)d/
2 2
Чтобы решить вариационную задачу по определению, макси-
мума энергии в полосе частот — <оо + ш0 после ограничения спек-
тра сигнала, возьмём первую вариацию (8.22) и приравняем её
нулю:
J (bg-G-t-lG-g)dt J Ga(0<«— j 2G *G dt
8W = —--------------------------------------____-
+ ~2
2
J G*(t)dt
2
J G(t)g(t)di
=0;
откуда
+ 11 +21
2 2
J (IgG + tG g)dt J G(t)g(t)dt
2G-ZG dt
+ ^-
2
J G«(0^
(8.23)
Найдём значение %g(t) из выражения (8.16)
+ —
2
^(o« f sin;/-T) 8G(t)dt.
J It (/ — t)
4
(8.24)
2
126
, ' (Ядро остаётся неизменным, так как нас интересует прира
щение не аргумента, а входного сигнала.)
Покажем, что
J G-tgdt= f g-lGdt. (8.25)
__то _ то
2 2
Г Выпишем левую часть (8.25) и подставим в неё значение
"Mg (О из (8-24)
+ T-i + 21 + 2i
‘ 2 2’2
j Gtgdt= f G(t) f sinM'~T) 8G(t)fiHd/==
T r * * V - T)
• T0 _ To T0 '
2 2 2
" + ^ + ’-1
2 2
< = f f s—“*(<~T)G(/)-5G(T)-dt-rft
2 2
i Выпишем правую часть (8.25) и подставим в неё значение g
:< из равенства (8.16):
:v; + 21 + 2i + Ii
2 2 2
; f gbGdt— f f G(t)aG(i)-dtdt =
*' ~ _ it (t T J
__ 21 _ 11 — IL ‘ ' 7
2 2 2 у
Л: ' . +21 + 21
2 2
= f f sinmo(/-t)Q(/) gG(
!• J, J, Kit — t)
_ 2»__Il ' '
2 2
t. e. левая часть выражения (8.25) равна его правой части, и
д. равенство (8.25) доказано.
Возвратимся к равенству (8.23).
На основании (8.25) сумма членов в числителе левой части
(8.23) равна
J (8£-G+8G.g)# = 2-f g-*G dt,
127
и равенство (8.23) можно переписать в виде
2
J giGdt
__ ^0_
2
+ —
2
J GlGdt
'Со
То
—?----------------г,
+^-
2
J G*(t)dt
— I®.
2
(8.26)
2
откуда
2
J [£-1ГО-]80Л = 0.
_^о_
2
(8.27)
Уравнение (8.27) представляет собой интеграл от произведе-
ния двух функций, одна из которых — 8G — является произ-
вольной. Это выражение равно нулю; поэтому выражение в
квадратных скобках тоже должно равняться (в пределах ин-
тегрирования) нулю.
Следовательно,
g(f) — WG(t)
(8.28)
в пределах интегрирования
— </<+—.
2 2
Докажем также обратное соотношение.
Если входной сигнал G(t) и выходной сигнал g(t) связа-
ны посредством равенства (8.28), то W будет равен доле энер-
гии, которая определяется ограничением спектра и переходом
G(t) + g(t).
На основании (8.28)
g(t) — WG(t) = Q,
поэтому
+ —
2
J te(/)-HW)W) л=о
__ I®.
2
128
или
2 2
f g d) RO dt - W J G (t) • 8G (0 = 0
2
, Откуда, учитывая (8.21) и (8.26),
2
получаем
2
j g(t)bG(t)dt
W = —---------------
2
j G(t)g(t)dt
-1®.
2
2
j G(t)iG(t)dt
2
J с2(/)Л
_ 21
2
j £а('И
2
J <з’(0^
2
т. e. мы получили то же самое W, что и при фильтрации путём
ограничения спектра, и обратное соотношение доказано.
< Получим теперь интегральное уравнение для определения
формы сигнала, заданная доля энергии которого сосредоточена
. в наименьшей полосе частот. Из (8.28) видно, что входной сир
нал G(t) и выходной сигнал g(t) пропорциональны на интер-
вале — —</<+—.
; 2 2
Подставим в (8.16) значение G(t) из ур-ния (8.28). Такая
подстановка возможна, так как (8.16) позволяет получить беско-
. нечный выходной сигнал g(t) интегрированием конечного сиг-
• нала G(t). Этот конечный сигнал можно заменить на интервале
интегрирования — -у-</<-(- ~ бесконечным сигналом(/).
Очевидно, что в ур-ние (8.16) нельзя было бы подставить вмес-
то g(t) его значение WG(t) из ур-ния (8.28), так как при этом
мы заменили бесконечный сигнал конечным. Итак,
9—730
129
2
f sina,e(t~T)G(z)dT = WG(t)
J к(/ —t)
T
ИЛИ
2
’ sin <o0 (t— t)
it (t — t)
g (T) d t.
(8.29)
Уравнение (8.29) получено для выходного сигнала g(t), а
входной сигнал G(t) получается из (8.28) на интервале его су-
ществования— -у-<^<+ -у-.
Таким образом, мы получили то же самое интегральное
уравнение, что и при решении задачи об определении макси-
мальной доли энергии в заданной полосе частот для сигнала ко-
нечной продолжительности [см. ур-ние (2.12)].
Этот результат очень интересен, так как он показывает, что
форма бесконечного сигнала, занимающего наименьшую полосу
частот, совпадает с формой сигнала (на интервале его сущест-
вования), содержащего максимальную долю энергии в заданной
полосе частот.
Рассмотрим случай другой фильтрации сигнала, а именно:
1. На вход фильтра Fi подаётся сигнал G(i) конечной про-
должительности—+ -у-; на выходе этого фильтра получа-
ется сигнал g(t), ограниченный полосой угловых частот
—4*<Оо.
2. Ограничитель срезает часть сигнала g(t) за пределами
интервала —— < t <4- — .
г 2 2
3. Сигнал gz(t) вторично отфильтрован (после ограничи-
теля) посредством фильтра Гг с такими же характеристиками,
как и фильтр Fi.
Выберем G(t) таким образом, чтобы содержание энергии в
сигнале после его фильтрации по частоте и ограничения по вре-
мени было бы наибольшим.
Введём W' — коэффициент содержания энергии, получаемой
в результате первой фильтрации и ограничения по времени:
130
+ —
2
J S4t)dt
_ T°
W' = —----------. (8.30)
+ —
2
j Ga (0 dt
2
Используя равенство (8.16), представим интеграл в числи-
теле правой части (8.30) в следующем виде:
+ +2®. 4-—
2 2 2
[g2(t)dt= J g(i)dt G{x)dx =
__т® то ТО
2 2 2
2
= (8.31)
— I®.
2
где
+ T-i
2
^(/)= f-n“;('~e)g(6)de =
Г sin<o0(/—0)
J «(/-в)
Sina>8(0 —%)
it (0 — t)
(8.32)
2 L 2
Из (8.30) и (8.31) следует, что
2
J g^)G(t)dt
т__________
4-^
2
J о»(ОЛ
(8.33)
9»
131
Таким образом, видно, что (8.33) имеет таков же вид, как я
(8.22) при замене IF на IF' и g(t) на g^it). Поэтому все даль- -•
нейшие рассуждения по поводу равенства (8.28) остаются в
силе и для этого случая, т. е.
g^t) = W'G(t) (8.34)
в пределах —< t < + .
Подставив значение G(t) из равенства (8.34) в равенство
(8.32), получим
2
3 sin top (/ — 0)
I 7С(/-^0)
re
2
^70-(е~т) gt(x)dx. (8.35)
Л (v — Т|
Случаю двойной фильтрации по частоте соответствует зна-
чение (0 из ур-ния (8.35) и значение G(t) из ур-ния (8.34).
При этом коэффициент содержания энергии в сигнале после
фильтраций и ограничения по времени будет равен W', что сле-
дует из соотношения, получаемого на основании (8.31) и (8.34):
J Я2 W dt = J g2 (t) G (t) dt=W' j G2 (/) dt. (8.36)
Покажем, что интегральн'ые ур-ния (8.29) и (8.35) имеют
одинаковые собственные функции, а соответствующие этим
функциям собственные значения связаны равенством
IF' = IF2;
иначе говоря, покажем, что если <р(/) является решением интег-
рального ур-ния (8.29), т. е. если
sin <oq (/ — т)
*(*—т)
ср (т) d х,
(8.37)
то ср (t) является также решением интегрального ур-ния (8.35) при
IF' = IF2 или
132
ч--
2
Г sin o>t (t — 0) sin<o0(0— t) , q
J «(/ — 6) я(0 — т) °
- 2
<t (t) d t.
(8.38)
Преобразуем правую часть (8.38), меняя порядок интегриро-
вания и используя равенство (8.37):
1
1Р
sin «>о (t — 6) sin ар (О — t)
я(/ — 0) ж(0 — т)
<р (т) d т =
dB
sin «>0(0 — т)
я (0 — т)
sin «>о(* —0)^g_
K(t — 0)
2
= — f IF<p(0) sin<”o(<~e)d0=
U7« J ' «(/ —0)
2
Итак, мы показали, что правая часть (8.38) равна его левой
части, и равенство (8.38) доказано. Таким образом, поставлен-
ная здесь задача двойной фильтрации с ограничением по вре-
мени сводится к тому же интегральному уравнению, что и за-
' дача по определению оптимальной формы сигнала, которую мы
рассматривали в начале настоящего параграфа.
В § 2.2. выяснено, какую форму должен иметь импульс ко-
нечной продолжительности, чтобы в заданной полосе частот со-
держалась максимальная доля полной энергии спектра. Здесь
показано, что форма импульса, который подвергается двойной
фильтрации по частоте и ограничивается по времени, опреде-
ляется таким же интегральным уравнением.
ГЛАВА ДЕВЯТАЯ
СООТНОШЕНИЯ МЕЖДУ СПЕКТРАМИ
РЕГУЛЯРНЫХ И СЛУЧАЙНЫХ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ СИГНАЛОВ
В этой главе спектры пред-
ставлены в виде произведения
двух спектральных функций:
спектра элементарного сигна-
ла, который можно назвать
фактором формы, и спектра
1=п . .
4 = 1
который далее будет назы-
ваться фактором повторения.
Вычислен фактор повторения
для двух важных частных слу-
чаев: 1) последовательности
одинаковых сигналов, следую-
щих через равные про-
межутки времени; 2) последо-
вательности одинаковых сигна-
лов, следующих через случай-
ные промежутки времени.
Показано, что /?(<о) явля-
ется спектром бесконечно ко-
ротких импульсов. Если мо-
менты времени появления
этих импульсов распределены
хаотично, то /?(<о) является
спектром белого шума.
Рассмотрены энергетиче-
ские соотношения между спек-
трами регулярных и случай-
ных последовательностей сиг-‘
налов, а также спектрами эле-
ментарных сигналов. Показано,
что если ширина полосы до-
статочно велика, то средняя
мощность спектра R (со) дей-
ствительных сообщений не за-
висит от R(со). Подсчитана
ширина полосы, для которой,
в случае обычной телеграфии
предыдущий вывод практиче-
ски справедлив.
134
§ 9.1. ПРЕДВАРИТЕЛЬНЫЕ
ЗАМЕЧАНИЯ
Обычно при определении ширины
полосы, занимаемой передачей
импульсных радиосигналов, основы-
ваются на спектрах периодической
последовательности импульсов рав-
ной продолжительности, следующих
через одинаковые промежутки вре-
мени («телеграфных точек»). Этот
метод использован нами в гл. 6.
Такой подход оправдывается тем,
что «телеграфные точки» передают
по тракту для проверки действия
аппаратуры. Такие простые формы
сигналов также позволяют доста-
точно легко определить воздействие
на схему, имитирующую приёмник,
подверженный помехам. Но во
всех случаях эксплуатации линий
радиосвязи 'передаются не «теле-
графные точки», а действительные
сообщения, представляющие собой
случайные последовательности, сиг-
налов. Кроме того, поскольку метод
исследования «телеграфных точек»
позволяет легко рассчитывать и из-
мерять, то целесообразно опреде-
лить соотношения между спектрами
«телеграфных точек» и действитель-
ных сообщений.
Если будет найдено соотношение
между спектрами случайных после-
довательностей сигналов и спектрами регулярных последователь-
ностей сигналов, поступающих от того же самого передатчика,
то теоретические проблемы исследования взаимных помех мо-
гут быть упрощены.
§ 9.2. ПРЕДСТАВЛЕНИЕ СООБЩЕНИЯ ПОСРЕДСТВОМ ЭЛЕМЕНТАРНЫХ
СИГНАЛОВ, СМЕЩЁННЫХ ВО ВРЕМЕНИ
Допустим, что передатчик удовлетворяет «принципу наложе-
ния», заключающемуся в следующем: если E(t) — элементар-
ный сигнал, подаваемый на вход передатчика, создающий на
выходе передатчика сигнал g(t), начинающийся в момент /=0,
то «принцип наложения» удовлетворяется, когда входной сиг-
нал E(t—ti)+E(t—12) + ... +E(t—tn) создаёт на выходе сигнал
g (t—1\) +g (t—t2) + .. .4- g(t—in) независимо от последователь-
ности t2,...; ln. Преобразование E в g обладает аддитивными
. свойствами и линейно в пределах максимальной амплитуды, по-
даваемой на нормально действующий передатчик.
Для телеграфного передатчика эта максимальная амплиту-
да соответствует E(t); элементарные сигналы следуют один за
' . другими так, что результирующая максимальная амплитуда не
превышает амплитуд элементарных сигналов.
Для радиотелефонного передатчика максимальная ампли-
туда может во много раз превышать амплитуду элементарного
сигнала. В этом случае можно аппроксимировать любую задан-
ную форму сигнала наложением со сдвигом по времени конеч-
ной последовательности сигналов E{t{),..., E(tn), если элемен-
тарный сигнал E(t) правильно выбран и достаточно мал. Такая
форма количественного разложения передаваемого сигнала
практически реализуется в системах кодово-импульсной моду-
ляции.
Для того чтобы представить сообщение, передаваемое в по-
следовательные моменты времени t2,..., t п, будем считать,
что известен элементарный сигнал gt (t) =Atg{t—tj) и что задана
последовательность этих моментов времени.
Если спектр элементарного сигнала gt (t) обозначить
+ 00
2о(«>)= J е~М g^Odt, (9.1)
— 00
\ то спектр, соответствующий сообщению, передаваемому в после-
довательные Моменты времени t2,..., tn, будет
135
Q(ш)=< J ^Alg(t-Qdt^^Al J e-lm< g(t-t^dt.
—оо iel /el —oo
(9.2)
Поскольку каждый из сигналов g(t—t{) при t<t{ равен ну-
лю, то
2(<o) = 2A+f g(f-t])dt. (9.3)
/-1 tt
Заменим в (9.3) переменную t = Q + tt, тогда dt = dQ и
2 (ш) = 2 4 [ е-'“(в+/') g (в) d в.
i-l о
Следовательно"
2 (ш) = 2*4 J° е-’шее-1о>^(0)а в = 2Л,el“\f е-,вв g^dB =
Z-1 О 1=1 о
= 20(о))24е-’^. (9.4)
i=i
Как видно из выражения (9.4.), спектр последовательности
сигналов можно рассматривать как произведение двух спектров:
первый — спектр элёментарного сигнала Qo(®)> который назо-
зём фактором формы, и второй, заключённый под знаком сум-
мы:
/?(«)= 24 е-1^, (9.5)
i—l
который назовём фактором повторения.
§ 9.3. СПЕКТР /? (®)
Поскольку вычислить фактор формы, как показано в гл. 3,
нетрудно, то обратимся к фактору повторения (9.5) и вычислим
его для двух важных частных случаев.
1-й случай. Конечная последовательность одинаковых
сигналов, следующих через равные промежутки времени.
Такие последовательности могут встречаться среди других
136
случайных сигналов, и поэтому, как будет видно из дальнейше-
„ го, этот случай важен для экспериментального определения ши-
рины полосы, занимаемой передачей случайных сигналов.
Рассмотрим спектр конечной последовательности п элемен-
. тарных сигналов продолжительностью т, идентичных по форме
' и посылаемых через равные интервалы времени Т (при т<7;
рис. 9.1).
пт
Рис. 9.1. Последовательность .повторяемых сигналов
к; Каждый из элементарных сигналов определяется выраже-
•&’ нием
Г! <[/-(k-1)7]
. при 0 <7— (k—1) 7<л и £=1; 2; 3; . .п.
Последовательность п сигналов определяется в таком случае
выражением
G(0 = 2 (9.6)
»' Л-1
5 а спектр выражается уравнением
• ' Q(o>)=+J° G(t)e~Mdt= jg(/)e-M j} j e-i(*-,)<or. (9.7)
/• —co -О л-1 A—1
; Как и в общем случае (9.4), спектр последовательности рав-
ноотстоящих сигналов (9.7) состоит .из произведения фактора
формы и фактора повторения, причём последний в данном слу-
. чае имеет вид
/(W=jew =-----------А-е . (9.8)
I 4-1 sinT
у График функции /?(а>) при п>1 представляет собой беско-
; нечную последовательность лепестков, расположенных на оси со.
Лепестки, центры которых соответствуют угловым частотам
Z 137
m2 7т
(где /п=0; ±1; ±2, и т. д.), будем называть главны-
ми. Главные лепестки идентичны один другому, их максималь-
ные ординаты равны п и их ширина, измеренная на оси со, рав-
на — . Положения угловых частот <аг соответствующих цент-
рам главных лепестков, фиксированы и не зависят от числа
сигналов (п).
Между двумя соседними главными лепестками находятся
второстепенные лепестки, число которых тем больше, чем больше
Тт 2п
п. Их ширина на оси со разд а---, а максимальные ординаты
зависят от местоположения по отношению к главным лепест-
кам.
На рис. 9.2 показаны отрезки кривой, представляющей мо-
дуль фактора повторения |/?(<«>) | для значений п, равных 3,
5 и 10. Эти кривые простираются до бесконечности в обе сторо-
ны оси абсцисс. Как видно из этого рисунка, при возрастании п
относительная величина второстепенных лепестков уменьшается
и при п-> оо имеем
<оГ
sinn —
lim£(a>) = lim-------
П-+ОО n-+<X) sin--------
2
(9.9)
Выражение (9.9), как и известная S-функция, обладает
фильтрующим действием, и таким образом, предельный переход
при п -► со в выражении (9.9) соответствует переходу от
сплошного спектра конечной последовательности сигналов к ди-
скретному спектру периодически повторяющихся сигналов.
2-й случай. Конечная последовательность одинаковых сиг-
налов, следующих через случайные промежутки времени.
Если последовательность tb t2, ... tn случайна, то для каждо-
го значения со фактор повторения /?(со) представляет собой сум-
му п векторов случайной амплитуды, фазы которых распреде-
лены хаотично. Вероятность амплитуд суммарного вектора рас-
считывают как известную задачу о случайных перемещениях
[Л 15, стр. 460]. В интересующем нас случае, когда амплитуды
всех составляющих равны единице, вероятность того, что ре-
зультирующая амплитуда превышает г, определяется выраже-
нием
00
(rx) J" (х) dx.
(9.10)
138
При п>3 интеграл (9.10) не выражается в известных функ-
циях, за исключением случая г—1, и (9.10) надо определять чис-
ленным интегрированием при помощи различных разложений.
Подобные вычисления произведены в работе [Л 12] для значе-
ний п, заключающихся между 2 и 12. Действительные сообще-
ние. 9.2. Графики функции R (<о) при п—3; 5 и 10
ния обычно содержат значительно больше 12 элементарных сиг-
, налов, однако расчёты показывают, что при п>10 закон распре-
деления амплитуд 7? (со) выражается с хорошим приближением
законом Рэлея, действительным для бесконечного числа состав-
- ляющих.
139
Плотность распределения вероятностей для закона Рэлея
имеет вид Р (*) =-у е-2* . (9.11> о*
Если рассматривать нормализованный фактор повторения
/?0(ш) = -М(ш), (9.12>
У «
то можно принять за переменную
У = ~^- (9.13>
У п
Поскольку, с другой стороны, теория случайного перемеще-
ния [Л 12] показывает, что о= то плотность распределе-
ния вероятностей нормализованной амплитуды у принимает вид
р(г/)=2уе *.
(9.14>
Вероятность того, что р=0, равна нулю. Наиболее вероятно
значение у=р=. Максимальная величина у, соответствующая
случаю, когда все составляющие находятся в фазе и склады-
ваются арифметически, равна У~п. Вероятность этого случая
ничтожна.
Среднеквадратичное значение у равно единице, а его сред-
нее значение (математическое ожидание) равно KjL. Учиты-
вая это. получаем как частный случай из нашего |рассмотрения
известную теорему, сформулированную и доказанную Н. Н. Анд-
реевым [Л 1]: спектр ряда импульсов совпадает со спектром од-
ного импульса, если импульсы следуют друг за другом беспоря-
дочно. Действительно, поскольку фактор повторения может рас-
сматриваться «в среднем» как величина постоянная, то, как
видно из ур-ния (9.4), спектр достаточно длинной последова-
тельности беспорядочно повторяемых сигналов определяется
фактором формы йо(ш).
§ 9.4. СИГНАЛ, СООТВЕТСТВУЮЩИЙ ФАКТОРУ ПОВТОРЕНИЯ
Выясним, какому сигналу соответствует спектр Я(<о). Для
этого получим обратное преобразование Фурье от спектра
140
, /?((o) с точностью до постоянного коэффициента —
' 2л
+оо + оо п
у 7?(ш)е*ш<4ш= у 2Ae”i<“/,eWd(B =
г —оо — оо*в1
п + оо
(9.15)
1-1 - СО
Каждый из интегралов, входящих в сумму (9.15), является
расходящимся, но его можно преобразовать
4-оо 0 4 00
—оо —оо О
В первом из полученных интегралов заменим <»=—ш, тогда
4-Q0 0 4-00
у J е-1“('-/04<в4. J е1ш(^)^ =
— оо 4 оо О
4- оо
о
Представим последний интеграл (при S>0) в виде
J [е«»('-'/) + e-H'-'i)] d Ш=
О
V +Р° r -8«+Ы(-М
= lira [е ' "
e-S<o41<е(/—tt)
23
=lim i--------1.
s-olsa+ ('-</)’J
- (9.16)
В полученном выражении при t =/= t\ предел равен нулю, а
ири t=ti предела не существует.
Чтобы проинтегрировать (9.16), заменим переменные /=•-// +
4- S 0; тогда при t = 4<х>
0=4-оо; dt=SdQ я
Пт С —---------d/ = lim f —d0==
S-+o J s«44*-O’ s-o J S84-Sa0’
r - 00 — 00
+ 00
=lim f -^-=2arctg0
$->0 J
— 00
=Иш
s-o|_ -s^iK-f,)
= 2« .
(9.17)
141
Соотношения (9.16) и (9.17) определяют 6-функцию для
£=Л(2л — коэффициент, опущенный в Выражении (9.15)).
Следовательно, можно написать
+ 00 п п
f (9.18)
-ooi=l Z=1
Таким образом, спектр 7? (со) является спектром бесконечно ко-
ротких импульсов, передаваемых в моменты времени t\, tz..., tn.
Если эти моменты времени распределены хаотично, то А1 (со) —
равномерный спектр шума, распространяющийся на все значе-
ния о. В этом и заключается физический смысл спектра (<о).
В обычных телеграфных системах моменты времени
Л, tz, ...,tn распределены не случайно. Во-первых, потому что
элементарные сигналы g(t) не перекрываются, что может быть
выражено в виде условия
= , (9.19)
где В обозначает телеграфную скорость, выраженную в бодах.
Во-вторых, в случаях кодов Морзе, Бодо, телетайпов и аналогич-
ных им аппаратов все интервалы tt — tK являются кратными
1/В. Можно считать, что сигналы этих аппаратов соответству-
ют наложению на моменты времени t{ условия
ti— t% ti — /3 t% = • • • = tn tn—i " Т. (9.20)
Если число моментов времени tt конечно и равно п, то усло-
вие (9.20) соблюдается для обычной передачи.
§9.5. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
ДЛЯ РАЗЛИЧНЫХ СПЕКТРОВ
Если g(t) представляет собой переменный • электрический
ток и если не учитывать безразмерный коэффициент e-i at, то
видно, что интеграл (9.1), определяющий й0((о). имеет размер-
ность количества электричества. Энергия спектра й(со) увеличи-
вается с возрастанием продолжительности g(t) и с возраста-
нием п, так как к сумме Ао(со) добавляются новые положитель-
ные слагаемые. Различные спектры, соответствующие различ-
ным значениям п, можно сравнивать лишь в том случае, если
нормализовать спектры так, чтобы их энергия стала одинако-
вой.
142
Энергия, содержащаяся в спектре й(о), согласно теореме
Парсеваля пропорциональна
^ = +^[g(t-h)+g(t-Q+ . . .+g{t-Q\2dt. (9.21)
о
Амплитуды спектра нужно нормализовать посредством коэф-
фициента — . Если все элементарные сигналы полностью пере-
крываются друг другом, то W2 достигает своего максимального
значения
4- оо 4-00
W2MaKC = J n2g(f)dt = n2 J g(t)dt. (9.22)
о о
Если, как в случае телеграфии, сигналы не перекрываются,
' то все интегралы, соответствующие удвоенным произведениям
разлагаемого квадрата, обращаются в нуль и W2 достигает
своего минимального значения
4-оо 4- оо
W2MaH = J ng (/) dt = п j g (t) dt. (9.23)
о о
/ В общем случае телефонии и аналогичных случаях W мо-
жет оказаться пропорциональным любому значению, заключаю-
щемуся между п2 и п. Точное значение W нужно определять пе-
ред каждым сравнением спектров. Для обычной радиотелефо-
нии, для которой среднее значение суммы ^g(t—Q равно ну-
лю, практически спектры легко привести к определённым уров-
ням. Это достигается посредством сравнения уровней несущих,
которые представляют собой постоянные члены, добавляемые
к спектрам й (со), которые для упрощения записи здесь нами
опускаются.
Для большего множества сообщений при условии, что рас-
пределение моментов времени tL случайно, среднюю мощность
спектра переключения /?(©) в малой ширине полосы Д/= Аи> -
можно определить как произведение второго момента закона
вероятности (9.14) на . Поскольку, как мы уже установи-
ли ранее, среднеквадратичное значение у равно единице, то
средняя мощность спектра переключения J?(<o) в рассматривае-
мой малой полосе численно равна В общем случае (9.4)
, средняя мощность спектра й(©) равна й^ (<о).
143
Таким образом, элементарные мощности спектра случайного
сигнала и спектра единичного элементарного сигнала g(t) рав-
ны между собой при одинаковой ширине полосы А/, центриро-
ванной на одной и той же угловой частоте со.
Рассмотрим далее последовательность из п сигналов, перио-
дически повторяющихся в течение времени пТ. Период явле-
ния равен Т, а его частота равна -±- ; если ширина полосы А/ до-
статочно велика, то количество спектральных линий на данной
ширине полосы будет равно &f_T. Каждая из этих линий спектра
имеет амплитуду, равную ]/п . Поэтому общая энергия спект-
ра переключения /?(<о) в такой ширине полосы А/ составляет
— Aj Т, а средняя мощность численно равна -£• .
Следовательно, в случае периодического сигнала мощность, в
полосе Af численно равна как для случайного, так и для
единичного сигналов, рассмотренных ранее. Разумеется, эти со-
отношения справедливы для тех случаев, когда ширина полосы
достаточно велика по сравнению с разностью частот, которые
соответствуют двум соседним спектральным линиям, так что
мощность пропорциональна ширине полосы.
Полученные соотношения справедливы, во-первых, толь-
ко для спектров, которые нормализованы посредством числово-
го коэффициента W, определяемого ур-нием (9.20). Если теле-
графные сигналы не перекрываются, спектры нормализуют пу-
тём введения коэффициента Уп. На практике эта нормализа-
ция осуществляется автоматически, если использовать одно и то
же измерительное устройство, постоянная времени которого учи-
тывает одно и то же число элементарных сигналов, и если ско-
рость передачи остаётся постоянной. В случае более сложных
сигналов (например, для телефонии) мощности спектров можно
сравнивать только тогда, если одновременно с измерениями
спектральных компонентов измерять при помощи интегрирую-
щего устройства энергию сигнала, определяемую ур-нием (9.21),
и корректировать соответствующим образом полученные резуль-
таты.
Во-вторых, предыдущие выводы справедливы при усло-
вии выполнения закона распределения вероятностей (9.14).
Определим в более общем виде мощность случайного сигна-
ла, подчиняющегося закону Рэлея, интегрируя квадрат
модуля в полосе а>2—е>ь Энергия в полосе сог—©i будет равна
J /?(<») J?*(a>)d<o,
<0,
(9.24)
144
где Я* (со) обозначает величину, сопряжённую с /?(<о).
Тогда’
п п
R (ш) 7?* (w)= -Lе~Ыг е+’ш// =
' 1=1 *=1
= 1 +-^^cos<o(^ — ti). (9.25)
П W
Количество функций созш(/г—tj) равно числу сочетаний из п
по 2, т. е.
„2 п(« —1)
" 2
Поскольку здесь, согласно условию, t^htj и
> 00
J СОЗ<в/4ш = 0 При t
о
то средняя мощность спектра 7? (<в) в соответствии с ур-нием (9.25)
будет равна
<|> О) р
lira — С1?(ш) Я*’(о>) d<o=lim — f 1 +
СО—>ОО Ш J О)->ОО J
О О L
=lim 1 -j- J-. —
со->00 ш п
1т^=/ О
С другой стороны, как мы уже упоминали,
(9.26)
j2^2+1e-^z/= L. (9.27)
<. °
Сравнивая (9.26) и (9.27), видим, что
00 (О
С 2y2+I е~у‘dy — lim — ( 7? (co) 7?* (u>)d <u. (9.28)
J co—>oo w J
U 0
Таким образом, мы доказали, что применённый ранее метод
определения мощности даёт правильные результаты. Равенство
(9.28) является предельным соотношением, и поэтому практиче-
ски оно справедливо для достаточно большой ширины полосы.
Отсюда следует, что если ширина полосы достаточно велика, то
10—730 . 145
средняя мощность фактора повторения, подчиняющегося зако-
ну (9.14), не зависит от R(a).
Количественно оценим ширину полосы, для которой в случае
обычной телеграфии можно практически считать, что предыду-
щий вывод справедлив; Для рассматриваемого случая телегра-
фии ' '
tK — — I) при&>/ ит=—. (9.29)
В
Из (9;29) видно, что
1 < 1
tK-ti ’
и, следовательно, можно записать, что
•sin<ofa-/f)j ---I----. (9.30)
L it . т (к О
Известно1), что
V— = С + In и + —-------V------------------------— , (9.31)
Li k 2n J
Л=1 I A=2
где C = 0,577216 . . . —постоянная Эйлера; f
i ' ,
Ak = J x (1 — x) (2 — x) (3 — x). . . (k — 1 — x) dx;
. o
Л2 = —, A3 = — , At = ~, Л5 = — ;
2 12 ’ 3 12 80 8 20
поэтому
n—1
Jj-L<ln(n-1)+1.' (9.32)
*=i * '
Далее оценим интеграл (9.24) в соответствии с (9.25)
«0t COf
J (со) 7?* (о>) d со = J
. 2 TI sin ш (t — tA /л nnv
= ш2 — о>1 4- — V / . (9.33)
п AJ ti—tj
1.+-
п
COSш (fi — fj) do> =
>) См. [JI19, стр. 16].
.146
На основании (9.30) и (9.33) .
шг — □>, + — У sln*>(f< —М < +
t £J
+ -ЧУ—L^ + yi_!_1 = +AV-JL.. '
n Zj t (‘ — /) Zj t (/ — О n T Zj i — /
[>>/ i>j i<j
(9-34)
Поскольку
Si^S-b .'9-36>
i—j &=1
то в соответствии с (9.32)
L—Ц<п[1п(п —1)+1]. <9.36)
(»-/)
• i>i
На основании (9.33), (9.34), и (9.36) можно записать, что
; 7? , 4
I /? (ш) (ш) d ш. < ш2—шх4-[1п(п— 1)+JJ. (9.37)
J т
Ш1 • • *
Из' (9.37) видно, что вывод, который мы делали йз (9.28)
.относительно независимости средней мощности фактора повто-
рения от /?((о) является справедливым при условии
<о2 — «>1» — [In (п—1) + 1 ].. (9,38)
Неравенство (9.38) можно переписать в лиде
Д / » — [In (и — 1) +1J. (9.39)
7С ....
При п=10 находим, что — >2-
„ в
’ При п=100 находим, что
Отсюда видно, что предыдущие выводы справедливы только
при достаточно коротких сообщениях, если учесть, что ширина
^полосы обычно бывает задана. Следует также учесть, что при
выводе (9.39)'было использовано неравенство (9.30), которое не
^учитывает знака левой части '.(9.30,).. Поэтому правая часть
10» 147
(9.30) может оказаться меньшей, чем по произведённому расчё-
ту, и в практических случаях можно довольствоваться меньши-
ми значениями ширины полос, чем это получается из (9.39).
Кроме того, в практических условиях измерений прибор учи-
тывает не действительное число п, соответствующее передавае-
мому сообщению, а гораздо меньшее, определяемое постоянной
времени измерительного прибора. Поэтому при измерениях
можно ограничиться ещё меньшей шириной полосы, определяе-
мой конструкцией прибора.
§ 9.6. ВЫВОДЫ
1. Передачу действительных сообщений можно представить
в виде, который приводит к удобному выражению спектра.
Спектр можно рассматривать как произведение двух спектраль-
ных функций, одна из которых зависит только от применяемой
системы передачи, а другая от передаваемого сообщения. Эта
последняя зависимость соответствует сигналам переключения
элементарного сигнала, характеризующего систему, и имеет вид
спектра белого шума, если сообщение является совершенно слу-
чайным и длится достаточно долго.
2. Энергия спектров, соответствующих отдельному элемен-
тарному сигналу и периодически повторяющимся элементарным
сигналам, идентично распределяется по одним и тем же полосам
Частот, при условии, что ширина полос не слишком мала..
3. Спектр, соответствующий случайному сообщению, имеет
то же самое распределение энергии по полосам частот, что и
предыдущие спектры.
4. Если сигналы не являются совершенно случайными, в ча-
стности, если моменты их переключения или квантования опре-
деляются, как в обычных телеграфных системах, то предыдущие
соотношения справедливы только в том случае, если ширина
полосы не слишком мала, и если используемое для измерения
энергии устройство имеет не слишком большую постоянную вре-
мени.
5. Прежде чем сравнивать спектры, их следует привести к
одной и той же шкале (нормализовать). В случае телеграфии
нормализуют путём введения числового коэффициента. В более
сложных случаях, как, например, телефонии, следует измерять
энергию сигнала в каждом отдельном случае.
ГЛАВА ДЕСЯТАЯ
ПОЛОСА ЧАСТОТ, ЗАНИМАЕМАЯ ПЕРЕДАЧЕЙ
СЛУЧАЙНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ СИГНАЛОВ
Рассмотрены трудности, воз- §
никающие при определении ши-
рины полосы, занимаемой .пере-
дачей случайной последователь-
ности радиотелеграфных сигна-
лов и намечены пути их преодо-
ления:
1. Установление соотноше-
ний между спектрами периоди-
ческих и случайных последова-
тельностей сигналов.
2. Определение «средней»
ширины полосы посредством
функции корреляции.
Далее на основе энергетиче-
ского спектра радиотелеграф-
ных сигналов двух видов рас-
считана «средняя» ширина по-
лосы. Расчёты показывают, что
ширина полосы, определяемая
таким способом, сильно зависит
от закона распределения сиг-
налов.
10.1. ТРУДНОСТИ, ВОЗНИКАЮЩИЕ
ПРИ ОПРЕДЕЛЕНИИ ШИРИНЫ
ПОЛОСЫ, ЗАНИМАЕМОЙ пе-
редачей СЛУЧАЙНОЙ ПОС-
ЛЕДОВАТЕЛЬНОСТИ СИГНА-
ЛОВ
гт о определению МККР [Л40] ши-
риной полосы, занимаемой пе-
редачей, называется (полоса частот,
содержащая 99% передаваемой
мощности. Однако при применении
этого определения к случайным по-
следовательностям сигналов возни-
кают затруднения, которые рассмот-
рим специально. !
Прежде всего отметим, что по-
стоянные времени контуров приём-
ников, на которые воздействуют им-
пульсные радиосигналы, достаточно
малы для того, чтобы сигналы могли
считаться раздельными. Иными словами, интервалы времени
между сигналами достаточно продолжительны для того, чтобы
воздействие одного сигнала было бы практически равно нулю к
моменту приёма следующего сигнала.
При этих условиях пределы занимаемой ширины полосы, со-
, держащей 99% общей мощности сигнала, нужно определять на
основе непрерывного спектра, выражаемого в виде интеграла
Фурье. Теоретически полосу, определяемую таким образом, мож-
но во многих случаях рассчитать (см. гл. 2 и 3). Однако неиз-
вестна аппаратура, при помощи которой можно было бы экспе-
риментально определить непрерывный спектр>изолированного
сигнала; вследствие этого невозможно точно определить на ос-
нове экспериментальных данных и ширину полосы, занимаемой
передачей.
149
Поскольку непосредственно экспериментально исследовать
непрерывный спектр сигнала невозможно, то можно рассчитать
(см. гл. 6 и 7) и экспериментально определить дискретный
спектр периодической последовательности сигналов.
Известно, что линии ряда Фурье пропорциональны ампли-
тудам непрерывного спектра сигнала при соответствующих ча-
стотах, нд интервалы выбора, которые зависят от частоты повто-
рения, не всегда являются наилучшими с точки зрения восста-
новления огибающей непрерывного спектра. Кроме того, преде-
лы. занимаемой полосы частот редко точно совпадают с линия-
ми дискретного спектра и могут определяться с точностью до од-
ной линии с каждой стороны, т. е. всегда возможна неточность
порядка четырёх частот повторения. Любая интерполяция меж-
ду двумя линиями затруднена, так как энергия распределяется
различно В непрерывном и линейчатом спектрах.
Тем не менее ширину полосы, занимаемой передачей на прак-
тике, относительно удобно приблизительно определять, суммируя
мощность, содержащуюся в каждой линии ряда Фурье, до до-
стижения 99% .полной мощности.
Однако и этот приближённый метод трудно применить к
сигналам, продолжительность и моменты появления которых слу-
чайны. Дело в том, что при передаче таких сигналов общая излу-
чаемая мощность изменяется в процессе передачи. Например,
для прямоугольных сигналов кода Морзе среднеквадратичное
значение тока в антенне меняется от 0,707/иакс (для точек) до
0,866/маке (для тире), т. е. более чем на 20%. Отсюда следует,
что и ширина полосы, занимаемой передачей, которая содержит
99% общей мощности излучения, постоянно изменяется в про-
цессе передачи, и поэтому определение ширины полосы, реко-
мендуемое МККР, в данном случае неприменимо.
Поэтому нужно изыскать новые методы и определения, ко-
торые в принципе дали бы результаты, не слишком отличающие-
ся от теоретических значений, и которые можно применять на
практике. Можно наметить два пути в этом направлении:
1. Установить соотношения между спектрами периодичес-
ких и случайных последовательностей сигналов с тем, чтобы оп-
ределить, насколько простой способ исследования периодических
последовательностей сигналов позволяет приблизиться к спект-
рам действительных сообщений. В гл. 9 мы установили такие
соотношения для двух частных случаев, имеющих практическое
значение. ,
2. Определить энергетические спектры случайных последова-
тельностей сигналов посредством функции корреляции.
Поскольку ни ряд, ни интеграл Фурье не применимы к нере-
гулярным сигналам, заданным при — оо </< + оо , то невоз-
150 ‘ •
можно найти спектральную плотность для функции, соответству-
ющей неопределённо долго передаваемой последовательности
случайных сигналов: само понятие спектральной плотности в
его обычном смысле по отношению к случайным сигналам теряет
своё содержание. В этом случае обычно вводят понятие спект-
ральной плотности среднего (по времени) квадрата случайной
функции или, как упрощённо называют эту характеристику,
энергетического спектра функции G(t). Энергетический спектр
может быть получен через функцию корреляции, поскольку
связь между этими двумя характеристиками устанавливается
на основе известной теоремы Хинчина. В [Л44] подробно рас-
смотрены энергетические спектры различных импульсных слу-
чайных процессов. Воспользовавшись энергетическим спектром,
можно определить «среднюю» ширину полосы, занимаемой пере-
дачей.
Энергетический спектр имеет более ограниченное значейие,
чем спектральная плотность непериодического сигнала; «сред-
няя» ширина полосы, определяемая на основе энергетического
спектра, во многих случаях будет меньше, чем истинная шири-
на,' соответствующая элементарным сигналам, наиболее опас-
ным с точки зрения межканальных помех. Кроме того, по энер-
. гетическому спектру нельзя восстановить исходную функцию,
как это можно сделать по спектральной плотности непериодиче-
ских сигналов. Однако часто определить «среднею» ширину по-
лосы наиболее просто, так как функции корреляции во многих
•случаях можно определить аналитически или экспериментально.
§ 10.2. ОПРЕДЕЛЕНИЕ ШИРИНЫ ПОЛОСЫ ПОСРЕДСТВОМ
ФУНКЦИИ КОРРЕЛЯЦИИ
; . Рассмотрим случай ручной телеграфной передачи кодом
. Морзе, когда прямоугольные точки, тире и промежутки между
ними не равны друг другу. При этих условиях случайное появ-
ление точек и тире не обязательно равной продолжительности
достаточно хорошо соответствует действительным условиям. Та-
ким образом, мы будем иметь телеграфную передачу, при ко-
торой сигнал равен либо +1, либо —1, причём передача про-
изводится с некоторой средней скоростью, которую мы выразим
в бодах и обозначим через В. Функция, соответствующая пере-
даче, будет принимать значение либо +1, либо —1 в бесконеч-
ном ряде событий, происходящих случайно со средней частотой
появления В событий <в единицу времени.
В [Л.26] определяется функция корреляции такой передачи
ф(ы)=е-2В“ (10.1)
151
и показывается, что энергетический спектр функции имеет вид
те 4оа 4“
Функция 0 (<в), определяющая относительную мощность, со-
держащуюся в полосе частот от нуля до о, выражается форму-
лой
(О
' Рис. 10.1. Графики 0(<о) и
На рис. 10.1 показаны графики функций 0(<в) и её произ-
водной по о, т. е. (©). При помощи функции 0 (о) можно»
определить ширину полосы, занимаемой передачей сигналов.
Для этого приравняем правую часть ур-ния (10.2) величине
0,99:
— arc tg—=0,99.
it s 2В
Так как <в определяет собой ширину полосы угловых ча-
стот, Отсчитываемых от нуля, то о> = 2л ДД где Д/— ширина
полосы передачи; из таблиц тригонометрических функций нахо-
дим, что (
Д/^18В. . (10.4)
Как показано в гл. 6, при передаче периодических последо-
вательностей -прямоугольных сигналов со скоростью В ширина
полосы, занимаемой передачей, равна
Д/ = 21В. • (10.5)
152
Из сравнения ф-л (10.4) и (10.5) видно, что сделанное до-
пущение относительно случайного появления точек и тире ие-
обязательно равной продолжительности приводит к несколько’
меньшей ширине полосы, чем та, которая получается для пе-
риодических последовательностей сигналов.
Рассмотренный метод можно распространить и на другие-
виды телеграфной работы. В частности, есть ещё и другой тип;
случайного телеграфного сигнала, который интересно проана-
лизировать. Ось времени делят на интервалы т равной про-
должительности. В произвольно выбранном 'интервале значение
сигнала не зависит от значений в других интервалах и равно-
вероятно будет либо +1, либо —1.
Энергетический спектр телеграфного сигнала такого типа
равен [Л.26] '
(со \ 2
sin— \
—. (10.6)
. 26 J
Функция ©(о) выражается формулой
(10.7>
Введём обозначение k — — = —,
2В 2
тогда ф-ла (10.7) примет вид
---|-sin2£ -|- Si 2k
(Ю.8),
. Из сравнения ф-лы (10.8) с ф-лой (3.7) видно, что для рас-
сматриваемой последовательности случайных сигналов распре-
деление энергии импульса по полосе частот, а следовательно, и:
ширина занимаемой полосы частот будут такими же, как и при:
передаче прямоугольного импульса.'
Полученный результат показывает, что если для случайного
сигнала первого вида мы имели, как видно из ф-лы (10.4), не-
которое уменьшение ширины полосы частот, по сравнению с пе-
редачей периодической последовательности сигналов, то для
сигнала второго вида такого уменьшения не наблюдается. Та-
ким образом, определение «средней» полосы частот показывает,
что её значение зависит от закона распределения сигналов.
ЛАВА ОДИННАДЦАТАЯ
УМЕНЬШЕНИЕ ВЗАИМНЫХ ПОМЕХ МЕЖДУ
КАНАЛАМИ РАДИОСВЯЗИ ПРИ ПЕРЕДАЧЕ
СЛУЧАЙНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ СИГНАЛОВ
"Рассмотрена возможная ме-
тодика изучения проблемы
взаимных помех и показано,
что анализ свойств действи-
тельных сообщений облегчает^
ся. если они представлены в
виде последовательности функ-
ций, смещённых по времени.
. Показано, что энергетиче-
ский спектр сигнала, представ-
ленного в виде ряда смещён-
ных функций, представляет со-
•бой произведение двух спект-
ральных функций: первая из
них является энергетическим
•спектром элементарного сигна-
ла, а вторая представляет со-
бой энергетический спектр пе-
реключения импульсов.
На основе рассмотрения
энергетического спектра кор->ч
релированной и некоррелиро-
ванной последовательности сиг-
налов, смещённых по времени,
•определена возможность умень-
шения помех при передаче слу-
чайной последовательности сиг-
налов; в частности, показано,
что в этих условиях уменьшить
взаимные помехи — значит
найти элементарный сигнал, ко-
торый при передаче той же, си-
стемой создавал бы помехи ми-
нимальной энергии.
§ 11.1. ВОЗМОЖНАЯ МЕТОДИКА
ИЗУЧЕНИЯ ПРОБЛЕМЫ
ВЗАИМНЫХ ПОМЕХ
Т^исло каналов, которое можно
разместить в данной полосе
частот, зависит от необходимого
разноса по частоте между соседни-
ми каналами. Этот разнос, в свою
очередь, определяется взаимными
помехами между каналами. Такие
явления, как колебания напряжен-
ности поля,, приводят к необходи-
мости дополнительно увеличивать
разнос.
Взаимные помехи зависят от. ши-
рины полос, занимаемой излучени-
ем, и, следовательно, от распределе-'
ния энергии в полосе частот, зани-
маемой полезной передачей. Но что-
бы определить взаимные помехи, не-
достаточно знать распределение
энергии в полосе частот, занимае-
мой передачей, необходимо ещё
знать закон убывания энергии вне-
полосных излученйй.
ТакилМ образом, чтобы умень-.
шить взаимные помехи между кана-
лами радиосвязи, необходимо уменьшить ширину полосы, зани-
маемой излучением, и увеличить скорость убывания внеполос-
ных излучений, т. е. необходимо использовать данные, которые
зависят от всего спектра сообщения.
Однако, если даже мы и .располагаем этими данными, то
этого недостаточно для решения проблемы взаимных помех, по-
154
'скольку помехи сильно зависят от вида мешающего излучения
и от вида полезного излучения, которое должен воспринять при-
ёмник, подвергающийся помехам, а также от характеристик это/
. го приёмника. Подобная постановка задачи чрезвычайно услож-
няет её решение, так как обычно невозможно полностью учесть
все действующие "факторы. Поэтому необходимо использовать
более простые, но достаточно общие схемы, учитывающие
реальные условия.
Обычно помехи создаются излучениями при передаче дейст-
вительных сообщений. Поэтому методы представления излуче-
ний, используемые при изучении этих проблем, должны позво-
лять рассматривать передаваемые сигналы в виде случайных
величин.
Свойства действительных сигналов легче анализировать, если
сигналы представлены в виде последовательности функций. Что-
бы выявить случайный характер сигналов и рассмотреть про-
блему взаимных помех, особенно полезно использовать пред-
ставление действительных сигналов в виде последовательности
функций, смещённых по времени.
Для многих классов излучений можно, таким образом, уста-
новить простое соотношение между излучённым радиосигналом
и сигналом, поданным на вход модулятора.
Если сигнал, предназначенный для передачи, представлен
(как, например, при телеграфии) в виде ряда дискретных напря-
жений, то нетрудно представить его в виде последовательности
функций, смещённых по времени. При этом излучение полностью
определяется, если определён элементарный сигнал, представ-
’ ляемыи обычно в виде импульса, модулирующего несущую, и
один из параметров элементарного сигнала (амплитуда, часто-
та, продолжительность и т. д.) имеет коэффициент, пропорцио-
нальный дискретным и случайным напряжениям первичного
; сигнала.
В другом случае (наиболее простым примером которого яв-
ляется телефония)', сигнал определяется непрерывной функцией
времени, и здесь можно использовать тот же метод путём изме-
1 нения одного из пардметров, связанных’ с элементарным сигна-
лом, как функции непрерывного параметра, определяющего
. 'сигнал.
В гл. 9 нами использованы амплитудные спектры (преобра-
зования Фурье) последовательностей смещённых по времени эле-
Iментарных сигналов, чтобы представить действительные сооб-
;; щения и установить соотношения между регулярными и слу-.
’ /чайными последовательностями сигналов» В настоящей главе
показывается, что, используя энергетические спектры последо-
i вательностей смещённых по времени сигналов при рассмотре-
V; нии проблем уменьшения взаимных помех, можно сделать ряд
- полезных выводов для различных практических случаев,
V'' 1S5
§ 11.2. ЭНЕРГЕТИЧЕСКИЙ СПЕКТР СИГНАЛА, ПРЕДСТАВЛЕННОГО
В ВИДЕ РЯДА СМЕЩЁННЫХ ФУНКЦИЙ
Пусть сигнал 'Представлен в виде .ряда смещённых функций
п
Z— п
Найдём энергетический спектр функции G(t);
+ ПТ 2
2.(<e) = lim — — ( G(t)e~ia>i dt =
пт-хяпт 2к J V
—пТ
= lim — Q(w).Q*(<d), (11.2)
, «Г—>оо пТ
где Q(co) — преобразование Фурье функции G(t), 2*(<в)' — со-
пряжённое выражение Q(со), а Т — интервалы времени между
импульсами.
В гл. 9 было показано, что
2 (ш) = Qo (<о) £ Л, е~1 ш/‘, . (11.3>
1—п
где Qo(®) — спектр элементарного сигнала.
Поэтому
п
Qe (ш) = lim 4 Qo (ш) 2S (ш) V А Ак е~1 “ >• (11.4}
лТ->оо nl ЬЛ
i, к=—п
Поскольку Т ограничено, то (11.4) можно переписать в виде
п
Q,(w) = lim 420(ш)2’(а)) '
п ->оо nl
i, к=—п
п
= lim 1q;W20W lim-L V ДЛке-1ш(/‘-/'£) =
д->оо I п-><п п Ut
i, к=—п
п
= 12.W^) lim -I- V ^4е-и,'^)= '
Т ' л-> оо п АшЛ
it к=—п
п
= £2эО(«0 Пт - У Д4е-1Ш(^)> (1'1.5)
д->00 ьЛ
156
. где.£2эо(ш) = -у- So (®) SJ 6°) Энергетический Спектр единич- .
ного импульса.
Таким образом, из (11.5) видно, что энергетический спектр
сигнала, представленного в виде ряда смещённых функций, пред-
, ставляет собой произведение двух спектральных функций:
первая из них Й,о(®) — является энергетическим спектром эле-
ментарного сигнала, а вторая функция имеет вид
Нт
Л-*0О
Учитывая ф-лы (9.4) и (9.11), последнее выражение можно
переписать в виде
lim Я0(ш) Яо(“) = #эо(ш), (116)
00
, где Ro (со) — нормализованный спектр переключения импульсов
(фактор повторения),
» /?,о(со) — энергетический нормализованный спектр переклю-
чения импульсов.
§ 11.3. СПЕКТР НЕКОРРЕЛИРОВАННЫХ СИГНАЛОВ
В обычных телеграфных системах моменты времени t2 .... tn
распределены не случайно по следующим причинам.
Во-первых, элементарные сигналы не перекрываются, что
можно выразить в виде условия
(11.7)
где В — телеграфная скорость, выраженная в бодах,
ат — продолжительность элементарного сигнала. '
Во-вторых, в случаях кодов Морзе, Бодо, телетайпов и ана-
логичных им аппаратов все интервалы —tK) являются крат-
ными — . Можно считать, что в этих аппаратах на моменты
времени появления сигналов налагаются условия
tl = t2 — t1—t3 — ti=...=tn — tn_l = T. (11.8)
Как показано в § 9.4. спектру /?0 (ш) переключения импульсов
соответствует сигнал
п
(11.9)
/=—п
157
Чтобы найти функции автокорреляции ф(и) сигнала (11.9),
введём вспомогательные функции Gn(t) и фп(и):
G(0 =
G(t)
О
при
ft > пТ
при всех L < Q
(НЛО)
+ оО
фл(«) = -^г[олЮбл(* + «)^ =
Л/ J
+ оо Л — 00 Я
=j * • 2 л з (t - о)'2 а 8 « - 'i+°) dt=
— i=—n
п + оо
= ^Г 2 AlAi J.8V“O8(f-/v+'.u)dL
iA=—n — оо
L(ll.ll)
Используя известное соотношение для 8-функций
+оо
J f(W-/i)d/ = /(0), (П.12)
"00
получим, ЧТО
п
фл(«)=4 5 А^Ц^-ti+u). (11.13)
П1 ЛШ
iA—п
Заменим в (11.13) О = (Т, тогда
< п
фл(ы)=^ 2 мимт <1114)
Из (11.14) ВИДНО, ЧТО фл(и) отлично от нуля только в точ-
ках, где и кратно Т. '
Найдём функцию автокорреляции ф (и) сигнала (11.9), являю-
щейся пределом, к которому стремится функция <|»„(ы) при л->оо
п
<|> (и) = lira А- V —i)T-+-w].=
л~>оо nl *
t,i=—п
( п п \ •
lim 4. Г Л?8(«)+ V] ДДМ^-ОГ+и] =
«-►оо nl. Ы лл!
i,i=—п
п п
iA---п
При
п ,
= 8 (u) lim
Лг->00
Л--п
п
4- VAI+ lim 4 V А48[(‘-1)Г+и]. (11.15>
Пл ЛшЛ П->00 п*
-►оо - .---
Z,i«—п
’458
На основании известной теоремы Хинчина энергетический1
спектр сигнала (11.9) будет равей*:
00
7?э0 (ш) = 4 j ф. (и) cos <iiudu —
о • х
П
lira ,-L V
Л->00 nl Ы
it\—n
n oo
X cos rnudu = lim — V] д^ f 8 (•«) cos <ou du +
П-+ 00 ПТ Ы 1 J
|Л=—n 0
n
+ lim — V AlAi ( 8[(i — i)T + «]cos<o« du. (11.16)
«-►oo “ J t
0
Op
Или, поскольку J 3(u)cos(i)udw=l'zH, учитывая (11Д2), окон*
• - Q
чательно получаем
n П'
R^) = lim А Vh? + lim — V ^Acosw(i— i) 7.(11.17)
Z - tlT {ал ad
i=—n i—n
" Первый член в правой части (11.17) представляет собой сред-
нюю мощность некоррелированных сигналов. Второй член той
же части обращается в тождественный нуль только в тех слу-.
чаях, когда, обращается в нуль второй член в правой частц
(11.15). Первый член в правой частй (11.15) не зависит от мо--
ментов переключения, а второй член там же не равен нулю толь-
/ко в точках, кратных ±7’. Если функция автокорреляции ф(«)>
/выражаемая ф-лой (11.15), периодически (через период Т) рб,
в ращается в нуль, то в правой части ф-лы (11.15) остаётся толь-
tKo первый член. В. этом случае второй член в правой части
\( 11.17), который получается из второго члена в правой части
' (Г1.Д5), также обращается в нуль и спектр сигнала (11.9) будет
. содержать только компоненты, не зависящие от частоты.
* Из (11.5) видно, что энергетический спектр ряда смещённых
^функций можно представить в виде произведения двух спект-
ральных функций. Первая из них 2э0 (со) — энергетический
-спектр элементарного сигнала, а вторая, как видно из ф-лы
•(11.17), равна 7?э0 (со). Эта вторая спектральная функция, пред-
ке, 159
t) - .
'Ставляющая собой преобразование Фурье функции корреляции
Некоторого сигнала (11.9), равна постоянной величине, если
функция автокорреляции (11.15) периодически принимает ну-'
левые значения, причём период равняется времени, разделяю-
щему два последующих момента переключения. В этом случае
спектр последовательности сигналов идентичен спектру элемен-
тарного сигнала, что упрощает определение взаимных помех:
квадратичный интегратор на выходе приёмника, подверженного
помехам, даёт непосредственно энергию, воспринимаемую при-
ёмником.
При настройке приёмника с достаточно узкой полосой на
значительно удалённую от центра спектра частоту, где спектр
элементарного сигнала обычно изменяется в зависимости от
частоты достаточно медленно, приёмный фильтр отделяет часть
спектра, имеющую приблизительно постоянный уровень во всей
полосе фильтра.
Если последовательность сигналов не только не коррелиро-
вана, но, кроме того, элементарные сигналы принимают в мо-
менты переключения независимые значения, то, как можно до-
казать [Л25, стр. 513}, сигнал, действующий на выходе приёмни-
ка, подверженного помехам, представляет собой «белый» гаус-
сов шум. Единственный результат воздействия тогда заключает-
ся в увеличении уровня шумов на выходе приёмника, подвергаю-
щегося помехам. При равной энергии в заданной полосе частот
эта помеха вызывает наибольшие потери пропускной способно-
сти рассматриваемого канала.
X.
/
§ 11.4. СПЕКТР^ КОРРЕЛИРОВАННЫХ СИГНАЛОВ
Если сигналы коррелируются между собой в моменты пе-
реключения, то, как видно.из ф-лы (11.17). к средней энергии
сигнала, не зависящей от частоты, добавляется член, завися-
щий от частоты. „
Интересно расвмотреть. воздействие этого члена на приёмник,
если приёмник, как и для случая некоррелированных сигналов,
имеет достаточно узкую полосу пропускания и настроен на ча-
стоту, значительно удалённую от центральной части спектра.
Энергия, попадающая в фильтр, будет периодически меняться
при удалении частоты настройки от средней частоты сигнала; она
также будет периодически меняться при изменении ширины по-
лосы приёмника.
Поэтому в случае коррелированных сигналов величина по-
мехи, испытываемой приёмником, сложно зависит не только от
статистических свойств сигнала, но и от характеристик приём-
ника и, в частности, от ширины его полосы.
.160
§ 11.5. ВЫВОДЫ
1. Воздействие помехи на приёмник зависит не только от
энергии, принимаемой от мешающей станции, но и от статисти-
ческого характера передаваемых сообщений, а также и от типа
приёмника.
2. Если приёмник настроен на частоту, достаточно удалён-
ную от центра мешающего спектра, и его полосу пропускания
можно считать прямоугольной, то при некоррелированных по-
следовательностях сигналов воздействие мешающей станции
легко определяется. Если, кроме того, мешающий сигнал имеет
независимые амплитуды, то помеха уподобляется тепловому шу-
му. Она увеличивает собственный шум канала и вызывает наи-
большую потерю пропускной способности канала.
3. Если последовательность сигналов не коррелирована, то
её спектр можно непосредственно сопоставить со спектром эле-
ментарных сигналов, передаваемых той же самой передающей
системой.
4. В случае коррелированной последовательности сигналов
спектр колеблется относительно спектра элементарного сигна-
ла. Эти колебания сложно зависят от характеристик приёмни-
ка, в особенности, если его полоса пропускания широка.
В этом случае, чтобы измерить мешающее воздействие пере-
дач, лучше всего заменить такой сигнал лйбо «белыми» шумами,
модулирующими передатчик (для радиотелефонного передатчи-
ка), либо периодической последовательностью сигналов (для ра-
диотелеграфного передатчика).
5. Уменьшение энергии помехи сводится к нахождению эле-
ментарного сигнала, который при передаче той же самой систе-
мой создавал бы помехи минимальной энергии.
11—730
ГЛАВА ДВЕНАДЦАТАЯ
ВЗАИМНЫЕ ПОМЕХИ МЕЖДУ СИСТЕМАМИ
РАДИОСВЯЗИ, ИСПОЛЬЗУЮЩИМИ
АМПЛИТУДНУЮ, ЧАСТОТНУЮ ИЛИ ФАЗОВУЮ
МОДУЛЯЦИЮ
Рассмотрено влияние типа
излучения, в частности формы
его спектра, и характеристик
избирательности приёмника на
уровень взаимных помех в си-
стемах радиосвязи- с амплитуд-
ной, частотной и фазовой моду-
ляциями.
Определён уровень взаимных
помех при различных значе-
ниях крутизны р у убывания
спектра сигнала и крутизна
кривой избирательности
приёмника.
Показано, что взаимные по-
мехи в системах радиосвязи
минимальны, если асимптотиче-
ские крутизны Ру и Pr равны
между собой.
Выведены соотношения меж-
ду мощностью мешающего из-
лучения и его максимальной
амплитудой, из которых видно,
что при достаточно больших
расстройках мощность мешаю-
щего сигнала пропорциональна
квадрату его максимальной
амплитуды и что это соотно-
шение не зависит от величины
расстройки.
§ 12.1. ИСХОДНЫЕ ПРЕДПОЛОЖЕНИЯ
Ц роводимое ниже рассмотрение
основывается на той концепции,
что источником взаимных помех яв-
ляется энергия, излучаемая передат-
чикам и воспринимаемая приёмни-
ком как на частотах, заключённых
в желательных полосах передатчи-
ка и приёмника, так и на частотах,
находящихся далеко за пределами
этих полос.
Пусть имеем приёмник, настро-
енный на частоту fo, и передатчик,
излучающий несущую частоту
/г=/о+А/о, причём сигнал модули-
руется по амплитуде, по частоте или
по фазе. Изобразим совокупность
этих устройств на схеме рис. 12.1
и рассмотрим свойства каждого из
этих элементов в отдельности и си-
стемы связи в целом.
На выходе совершенного моду-
лятора получается сигнал, общий
вид которого
ит (0=At (0 cos [2к fT t + <P (/)],
(I2.l>
где M(t) — функция модуляции по амплитуде,
Ф (/) — функция модуляции по частоте или фазе;
по своему характеру обе эти функции изменяются медленно
по сравнению с cos2njTt, и поэтому ширина полосы частот, за-
162
ключающей в себе основную часть энергии спектра, очень мала
по сравнению с fT .
Допустим, что спектр энергии внеполосных излучений этого
сигнала убывает в среднем со скоростью рт дб на октаву изме-
нения частоты.
Рис. 12.1. Эквивалентная схема системы радиосвязи
Далее предположим, что излучаемый сигнал имеет вид
п
= 2 ® cos [2я fr (0 + ф (12.2)
i
Хотя высокочастотные ступени передатчика, работающие
обычно в режиме класса «С», создают гармоники несущей, ко-
торые не устраняются полностью выходными контурами пере-
датчика, но основной компонент излучаемого сигнала
«1 (0 = Мг (/) cos [2тс fT t + <pi (/)] (12.3)
очень мало отличается от (12.1). Это различие определяется из-
бирательностью и нелинейностью низкочастотных и высокоча-
стотных ступеней передатчика и постоянными времени цепей мо-
дуляции. Так как мы рассматриваем отклонения A/о, малые по
сравнению с fo, то можно пренебречь гармониками несущей и не
делать различия между излучаемым сигналом (12.1) и основным
его компонентом (12.3).
Если функции Afj(/) и M(t), а также <pi(/) и <р(/) не будут
абсолютно идентичными, то спектры их сигналов будут несколь-
ко отличаться один от другого. Допустим, что это отличие бу-
дет особенно проявляться в области их внеполосных излучений,
причём среднее убывание спектра сигнала (12.3), равное р и дб
на октаву, будет превышать рт. Это значит, что передатчик мож-
но характеризовать кривой избирательности, средняя асимпто-
тическая крутизна которой равна:
Рт^Ри-Рт,^-’ Х12.4)
QKfJl
Как показано на рис. 12.1, эта избирательность вводится по-
средством фильтра FT.
11* 163
Далее предположим, Что кривая избирательности приёмника
за пределами его полосы пропускания стремится принять по-
стоянную крутизну pR дб на октаву, причём ширина полосы про-
пускания приблизительно равна ширине полосы, занимаемой из-
лучением сигнала (12.3).
Будем также допускать, что ступени высокой и промежуточ-
ной частоты приёмника достаточно линейны, чтобы их можно
было характеризовать линейным фильтром F R , объединяющим
в себе их избирательности.
Наконец, предположим, что демодулятор является линейным,
или, точнее говоря, не будем принимать его в расчёт.
§ 12.2. ИЗМЕНЕНИЕ ЭНЕРГИИ ВЗАИМНЫХ ПОМЕХ
ПРИ РАЗЛИЧНЫХ РАССТРОЙКАХ
Построим в одинаковом масштабе на шкале частот кривую
избирательности приёмника и огибающую спектра энергии по-
мехи (рис. 12.2). Обозначим через W н основную часть энергии
Рис. 12.2; Относительное положение кривой избиратель-
ности . приёмника и спектра .мешающего сигнала
компонентов этого спектра, расположенных в непосредственной
близости от частоты /о- Через WR обозначим энергию компонен-
тов спектра помехи, попадающих в полосу пропускания приём-
ника.
Рассмотрим, как изменяется энергия, воспринимаемая приём-
ником, при увеличении отклонения Д/о-
Учитывая, что спектр энергии помехи на выходе фильтра FR
- получается путём умножения каждого компонента спектра ме-
шающего сигнала на соответствующее затухание, определяемое
из кривой избирательности приёмника, можно непосредственно
• из рис. 12.2 вывести следующие соотношения:
1) Если ру<рл>то при увеличении Д/о сверх некоторого зна-
чения преобладает'действие компонентов спектра, расположен-
ных вблизи частоты настройки приёмника /о- Энергия, восприни-
.164
маемая приёмником, становится тогда приблизительно равной
WR, а кривая, выражающая её изменение в зависимости от
Д/о, стремится принять крутизну, равную ру дб на октаву.
2) Если PV>PR то при увеличении Д/о сверх некоторого зна-
чения преобладает действие компонентов, расположенных вбли-
зи несущей частоты fr излучаемого сигнала. Воспринимаемая
приёмником энергия приближается к и кривая её измене-
ния принимает крутизну, равную pR дб на октаву. Излучаемый
сигнал воздействует на приёмник так, как будто спектр сигнала
ограничен. Величина pR при этом значительно влияет на уро-
вень взаимных помех.
3) Если Ри=рЛ,то трудно выделить преобладающее влияние
WH или WR и поэтому нужно рассматривать спектр сообщения
в целом. Рассматривая этот случай как граничный для двух
других, можно сделать вывод, что кривая изменения энергии,
воспринимаемой приёмником, стремится принять крутизну
Ри ~Pr дб на октаву.
Таким образом, крутизна кривой pw, выражающей изменение
энергии, воспринимаемой приёмником, в зависимости от откло-
нения Д/о, удовлетворяет соотношению
Pw ~
ра при ру<рд]
PR при Рц > PRi
(12.5)
Соотношение (12.5) очень важно, так как оно показывает, ка-
ким путём можно уменьшить взаимные помехи и, следовательно,
работать при меньших разносах между соседними каналами.
; Для этого нужно сделать так, чтобы внеполосные излучения пе-
редатчика убывали бы со скоростью не меньшей, чем крутизна
' кривой избирательности приёмника, не ухудшая, разумеется, при
этом избирательности приёмников. Существующие в настоящее
время системы связи весьма несовершенны в этом смысле и не
удовлетворяют этим требованиям. В настоящее время асимпто-
‘ тическая крутизна кривых избирательности многих профессио-
: нальных приёмников превышает 60 дб на октаву, тогда как сред-
няя скорость убывания внеполосных излучений некоторых радио-
передатчиков остаётся порядка 12 дб на октаву. Следовательно,
. при конструировании передатчиков нужно увеличивать скорость
убывания внеполосных излучений.
Рассмотренные выше соотношения получены, исходя из пред-
« положения, что приёмник чувствителен к энергии мешающего
* излучения. Однако могут существовать и такие системы связи,
в которых приёмное устройство чувствительно не к энергии сиг-
: нала, а к его форме. Например, приёмный телеграфный аппа-
165
рат чувствителен к форме напряжения, подведённого к его вход-
ным зажимам, и срабатывает тогда, когда это напряжение до-
стигает определённой величины. В этих случаях целесообразно
соотнести максимальную амплитуду реакции приёмника на ра-
диотелеграфную передачу и соответствующую принимаемую
энергию. Это позволяет судить о том, нисколько принятый энер-
гетический критерий является универсальным и сопоставимым с
амплитудным критерием.
В последующих разделах мы рассмотрим соотношение меж-
ду максимальной амплитудой А и энергией W сигнала, переда-
ваемой через фильтр F
§ 12.3. СООТНОШЕНИЕ МЕЖДУ МАКСИМАЛЬНОЙ АМПЛИТУДОЙ А
И ЭНЕРГИЕЙ СИГНАЛА W, ПЕРЕДАВАЕМОЙ ЧЕРЕЗ ФИЛЬТР
F*, ЭКВИВАЛЕНТНЫЙ ПРИЁМНИКУ
Чтобы определить это соотношение, воспользуемся следую-
щим методом:
1) Предположим, что передатчик передаёт в интервале вре-
мени от до /2 сигнал вида
u(t) = M\t)cos [2к fTt -h <p (/)], (12.6)
а до момента времени Л и после момента /г передатчик не излу-
чает.
2) Найдём спектральную функцию Q (/), соответствующую пе-
редаваемому сигналу u(t).
3) В предыдущем параграфе мы приблизительно установили
границы полосы частот, содержащей те компоненты Q (f), дейст-
вием которых на приёмник нельзя пренебрегать. Эта полоса ча-
стот зависит от соотношения между скоростью рт убывания
спектра внеполосных излучений помехи и крутизной pR скатов
кривой избирательности приёмника.
Зная границы этой полосы частот и аналитическую форму
Q(f), попытаемся определить функцию Qi(f), которая приблизи-
тельно совпадает со спектром сигнала, искомого в этой полосе,
и равна нулю вне этой полосы. При этих условиях обратное пре-
образование Фурье от функции (f) даёт на выходе приёмного
фильтра FR сигнал
UK (0 = 2 JQx (/) е’2’ft df, (12.7)
о
причём интегрируют только по положительной полуоси частот и
166
поэтому требуется знание функции Qi(f) только в этой области
частот.
Энергия W этого сигнала выражается через интеграл
(12.8)
где Qf (/) — выражение, сопряжённое Qi(f).
Интегралы (12.7) и (12.8) позволяют выразить А и W как
функции 21(f); из них мы выведем соотношение между этими
величинами.
§ 12.4. СООТНОШЕНИЕ МЕЖДУ Л И IF ПРИ Pu<Pr
Спектр излучаемого сигнала U(t) выражается через преоб-
разование Фурье в виде
t,
Й (f) = j(/(/) е— 12vlt dt. (12.9)
Исходя из (12.6), можно представить й (f) в виде суммы
К
t,
, Г M(t) _ 1Т (Пе- 1 2х (/г +f) t dt.
J 2
h
(12.10)
Предполагается, что модулирующие функции M(t) и <p(f) из-
меняются медленно по сравнению с cos 2л fTt и рассматривае-
мые отклонения Д/г=/г—f всегда меньше несущей частоты; по-
скольку мы рассматриваем только область положительных ча-
стот, то вторым интегралом ф-лы (12.10) можно пренебречь по
сравнению с первым.
Полагая
, (12.11)
2
можно (12.9) записать в виде
Q(/) = JC(/)e’2’^'d/
ti
(12.12)
167
и, повторно интегрируя по частоте этот интеграл, как было в
гл. 5 по отношению к функции U(t), получаем ряд
Q^= X (—1 +1 е‘2x4*
q-o (i2nhfT) 941
-t.
, (12.13)
где С(?) (0—q-я производная от C(t).
Рассмотрим, что произойдёт при увеличении Д/г.
В § 12.1 мы допускали, что огибающая излучаемого спектра
в области внеполосных излучений убывала в среднем на по-
стоянную величину ру дб на октаву при увеличении частоты. Это
значит, что если Д/г велико, то в выражении Q(f) можно выне-
1
сти в виде множителя член --- , где
А/?
(12.14)
Из этого следует:
а) что члены ряда, соответствующие значениям q, меньшим
п—1, равны нулю, т. е- можно записать
=о при t=ii, t=t2 и 0<4 < п — 1; (12.15)
б) что ряд (12.13) сходится, начиная с этого члена, к выра-
жению.
Й (/) -> —(тР?— [C^-’Va) е12’4 fr —
v/ (i2itA fT)n '
-C(n-1)(/1)e12,t4^4 (12.16)
причём п — целое число и Ру, определяемое в соответствии с
(12.14), кратно 6.
Рассмотрим далее рис. 12.3, где на оси частот показаны
Д/о и Д/Г,уже определённые, и Д/в, которая равна ширине по-
лосы пропускания приёмника.
Выражение (12.8) принимает вид
Wr = 2 J О(Д/г)2*(Д/г)й(Д/7.). (12.17)
Д/о 2
168
Положим
О-1» = С(я“1)(4) = т1е'8'”‘; (12.18)
/2 — h = х и 8 т2 — 8 nti == 8/п,
где б/П] и 6/«2 — значения фазы С(я ° (t) в моменты времени 6
и tz соответственно. Поэтому можно переписать (12.16) в виде
(-1)"
(i2rc Д/Г)п
Й(Д/Г) =
[/п2 е’(2х Чт *'»«> _ т1 е‘ <2lt Vr м »'»*>].
(12.19)
Рис. 12.3. Относительное положение центральной частоты при-
ёмника, /о полосы приёмника Д/в и несущей частоты fT ме~
тающего сигнала"
Откуда
а(л«Е,(4М = [(-Й77?»]х
1 — 2/П1/”2 cos(2«Д/Гт + 8т)
/ИрЬ т2
(12.20)
Поскольку мы предполагаем, что Д/о>Д/в, то Д/г практиче-
ски не изменяется в полосе пропускания приёмника и равно
Afo- Поэтому, заменив в первом множителе правой части (12.20)
Д/Т на Afo и подставив (12.20) в (12.17), получаем
д/в
= Г
. (2^/0)2n .
2^со5(2кД/гг+8т)Ъ(Д/г). (12.21)
тр*
л,
Д/е- —
Вычислив интеграл в (12.21) и обозначив
k = —у- = 1С Д/ВТ,
16S
подобно тому, как это было сделано в § 2.3, получаем
- w = Г2(«? + /»2)Д^'|
* L (2геД/о)8" -|Л
Г< 2т1т2 sin£ /о А £ . * ч 1
X 1-------Т • Т" cos (2те А/0х + М •
4- k
Из этого выражения можно получить величину средней энер-
гии:
(12.22)
r 2(m^m22)AfB
Rcp
(12.23)
и энергию верхнего и нижнего пределов
sinfc
1 ± 2 У 2
т1 +т1
(12.24)
разделяющей верхний
Теперь определим порядок величины,
и нижний пределы.
Если ширина полосы приёмника равна ширине полосы, зани-
маемой излучением, то, как мы видели в § 3.2, для импульсов
прямоугольной формы 6=32, для трапецеидальных импульсов с
приемлемым для практики скруглением 6=12. В области зна-
чений, близких к 6=12, функция
6=10,9, равный 0,091. Поскольку
2/П1 т2 < j
имеет максимум при
то оба предела WRMaKC и WRMUH различаются между собой не бо-
лее чем на 1 дб, т. е. на величину, которой можно пренебречь.
В практических условиях различие между WRMaKC и WRMUK
ещё меньше, так как, поскольку необходимо иметь допуск на не-
стабильность частоты передатчика, приём ведётся в более широ-
кой полосе, чем полоса, занимаемая излучением.
Если же ширина црлосы приёмника Д/в уменьшается, то в
(12.17) можно считать Й(Д/Г) постоянным и равным Q(Afo).
Вынося 2 (Д/о) 2* (Д/о) из-под знака интеграла в (12.17), полу-
чаем
’^ = 2Д/вЙ(Д/0)2*(Д/0). (12.25)
При этом приёмник действует как анализатор спектра излу-
чаемого сигнала.
170
Рассчитаем максимальную амплитуду сигнала А.
Сигнал, спектр которого является частью спектра передачи,
попадающей в полосу пропускания приёмника, определяется при
помощи интеграла (12.7), который здесь можно переписать в
виде
UK(t)=2 f 2(Д/г)е12’'Д/г'</(д/г). (12.26)
Заменяя Q(A/r) его значением из (12.19) и предполагая, как
и ранее, что Д/О^>Д/В и, следовательно, А/T~&.f0, приходим после
вычисления полученного интеграла к следующему выражению:
_ л Г sinit Д/д(/2 —О I (2« Д/, +«m,) _
(12«Д/0)л [_ хД/в(/,-/)
_ sin к Д/в(\-0 l(2«4/,/x | 2</,/ (12.27)
2 «ад-0 J
из которого видно, что сигнал UR(t) получается в виде алге-
браической суммы двух колебаний одной и той же частоты fo>
сдвинутых по фазе между собой и различно модулируемых по
амплитуде. Эта модуляция .осуществляется значительно более
низкими частотами, чем частота несущей /о- и амплитуда А яв-
ляется максимумом модуля UR (t).
Из (12.27) получаем квадрат модуля:
17/ /л 12 ( 2 , 2 Sin’к Д/в (/2-О
i-Wf +mi t.AfB
-2т,т. = cos(2.ДМ + М1
к д/в (^2 О я дДв (^1—О J
(12.28)
и находим его максимальное значение.
На рис. 12.4 показаны полученные экспериментальным путём
значения UR(t) при передаче модулирующих сигналов прямо-
угольной формы (верхняя осциллограмма) и при различных рас-
стройках. Эти значения хорошо совпадают с результатами вы-
числений по ф-ле (12.28).
Из осциллограмм видно, что даже при не очень широкой по-
лосе фильтра (km 16) и не очень больших расстройках функ-
ция I UR (t) | имеет вид двух разделённых импульсов, максиму-
171
Увеличено в 10 раз.
Фильтр построен
на частоту пере-
дачи
Расстройка 250 гц
Расстройка 500 atf
Расстройка 750 г$
Рис. 12.4. Воспроизведение сигналов при расстрой-
ке фильтра. Ширина полосы фильтра—245 гц; ско-
рость манипуляции—50 бод; форма сигналов—
прямоугольная
Модулирующий
сигнал
Расстройка 1000 гц
172
МЫ которых соответствуют моментам времени t\ и В общем
случае максимальные значения этих импульсов могут быть не
равны между собой.
Искомое максимальное значение UR (t) в первом приближении
равно J UR (ti) |, если т\>т2 или | U R{t^ |, если /П2>/Пь
Предположим, что /П1>/П2,| UR (tj) | • Тогда из ф-лы
(12.28) при t=ti, учитывая, что t2—Л=т, получим
4(А/в)8 raisin2k
(2и Д/0)2л L k*
+m2i — 2ш! m2 • 1 • cos (2k Д/о т-j- 8/n)j=
4 (Д fB)* r/m2 \2sin2£ , , o ли sin ft /o . r , « \ 1
=------— — I-----------1—2—*-— cos (2it ДЛ r 4- 8/n) .
(2кД/0)2« LUi / A* mt k 4 /о -r / j
(12.29)
Поскольку m1>'/na, to
л - ! m2 \2 sin2 к
Пренебрегая I —I —— по сравнению с остальными чле-
нами в квадратных скобках правой части (12.29), получим при-
ближённое равенство:
Л2_ JXMbH,Ff _2cos(2« Д/от 4- 8/и)1. (12.30)
(2гсД/в)2Л L mi k J '
Из ур-ния (12.30) получаем квадрат среднего значения:
,2 _4(Д/в)2/га1
ср (2кД/0)2л
и двух крайних его пределов
»2макс___ д2 /< . л т2 sin k'
Ямин — лср I 1 х 7
\ rnx k .
(12.31)
(12.32)
173
Пределы в (12.32) расположены очень близко один от дру-
1 /и2 1
того, так как мы полагаем, что к> 1 и — >1.
Из ур-ний (12.23) и (12.31) получаем равенство
9 2/п?(Д/д)2
A2CP=-1--B Wcp, (12.33)
ml "Ь т2
которое связывает Аер и Wep.
Как мы уже видели, А и W очень мало отклоняются от сред-
него значения. Таким образом, доказано, что при Ри<Рк мак-
симальная амплитуда реакции приёмника на радиотелеграфную
передачу практически пропорциональна корню квадратному из
соответствующей принимаемой энергии при коэффициенте про-
порциональности, не зависимом от А/о.
§ 12.5. СООТНОШЕНИЕ МЕЖДУ А И W- ПРИ Ри>Рн
В § 12.2. мы показали, что если р£/>р/?,то при достаточно
больших расстройках Д/о наибольшая часть энергии, восприни-
маемой приёмником, поступает за счёт основной части излучае-
мого спектра-
Рис. 12.5. Относительное положение полосы приёмника AfB и
«основной» части AfB спектра мешающего сигнала
Обозначив через Д/д ширину основной части спектра Q(f),
практически равную ширине полосы, занимаемой излучением
(рис. 12.5), и через Z(f) коэффициент передачи фильтра FR, эк-
вивалентного приёмнику, можно определить Qi(f) как функцию,
равную
Рх(/) = Z (/)□(/) (12.34)
в интервале частот
(12-35)
и равную нулю за пределами этого интервала.
174
Далее, предполагая, что несущая частота /г постоянна, а ча-
стота настройки fo приёмника переменна, введём переменную-
величину:
bfT = fT-f.
Заметим, что 2(f) зависит только от Д/у, так как излучаемый
спектр центрируется на частоте fT, а коэффициент передачи
Z(f), центрированный на частоте f0, зависит от отклонения
Д/о—Д/т
Уравнение (12.34) можно теперь записать в виде
21 (Д /г) = Z (Д /0 - A fT) 2 (Д fr). (12.36)
Переход от ур-ния (12.34) к ур-нию (12.36) соответствует пе-
реносу начала отсчёта частот из нуля в точку fT. Новая перемен-
ная частота обозначена нами Д/г. Поэтому интервал (12.35)
теперь будет
д f' д <
__^<д/г<-^. (13.37)
Можно считать, что в пределах полосы &f'B усиление на всех
частотах одинаково и определяется только значением коэффи-
циента передачи фильтра при данной расстройке, т. е. значением:
Zo(Afo). При этом предположении спектр Qi(f) выходного сиг-
нала фильтра выражается через спектр Q(f) входного сигна-
ла в следующем виде:
Р1(Д/Г) = 2О(Д/О)Й(Д/Г). (12.38)
Затем получим сигнал UR(t) на выходе фильтра. Для этого
произведём обратное преобразование Фурье от Qi(f), т. е. на ос-
новании (127) и (12.38) получим
UR(t)= ( 21(Д/Г)е12ж44(/(Д/Г) =
2
= 2о(Д/о) J 2(Д/г)е12яЛ/т^(Д/г)=
= 2о(Д/о)С/г(О. (12-39)
175
Далее, на основании (12.8) и (12.38) получим значение энер-
хии W на выходе фильтра:
W- [ 21(Д/Х(Д-/7.)^(Д/Г) =
2
~ |Z0 (Д fг)|* J 2 (Д Д.) Q* (Д /г) d (Д fT) = |Z0 (Д fT)\* WT.
-LLs.
2
(12.40)
Из (12.39) видно, что сигнал на входе и выходе фильтра
ямеет одинаковую форму. Из этого выражения можно получить
.соотношение для определения А:
. ’1^(0| = Ио(Д/о)||{/г(01
или, обозначив через Ат максимальную амплитуду излучаемого
.сигнала, можем записать
Л = |г0(Д/0)|Лг. (12.41)
-Сравнивая (12.40) и (12.41), получаем выражение
А2 = А2г
W
(12.42)
которое показывает, что максимальная амплитуда реакции
приёмника на радиотелеграфную передачу пропорциональна
корню квадратному из соответствующей принимаемой энергии
так же, как и максимальная амплитуда передаваемого сигнала
пропорциональна корню квадратному из излучаемой энергии,
причём коэффициент пропорциональности не зависит от Д/о-
Суммируй выше сказанное, можно сказать, что если:
176
а) приёмник с шириной полосы Afs настроен на частоту
Д/о> а кривая его избирательности имеет асимптотическую кру-
тизну ркдб)окт-,
б) передатчик, спектр которого имеет ширину, близкую к
Д/в, настроен на частоту fo+Д/о, а внеполосные излучения убы-
вают со скоростью ри дб/окт.;
в) Ру>рди отклонение Д/о столь велико, что им можно пре-
небречь по сравнению с Д/в; то при этих условиях сигнал и его
спектр не деформируются, а затухание сигнала определяют по
кривой избирательности приёмника.
Исходя из изложенного, можно сделать следующие выводы.
1. При достаточно больших расстройках кривая изменения
мощности, воспринимаемой приёмником, стремится принять
либо крутизну Ру убывания спектра сигнала, либо крутизну pR
кривой избирательности приёмника.
Если Ру <pR, то энергия, воспринимаемая приёмником, ста-
новится приблизительно равной WR (см. рис. 12.2), а кривая,
выражающая её изменение в зависимости от расстройки, стре-
мится принять крутизну Ру d6joKT\ центральная часть сигнала
не воспроизводится, а началу и концу его соответствуют им-
пульсы, величина и вид которых зависят от законов нарастания
и убывания сигнала.
Если Ру >рЛ, то энергия, воспринимаемая приёмником, рав-
на WH, сигнал и его спектр не деформируются, а затухание сиг-
нала определяется по кривой избирательности приёмника.
Если Ру=Рв, то трудно выделить, преобладает влияние WH
или WR, и поэтому нужно рассматривать спектр сообщения в це-
лом.
2. Равенство (12-5) заключает в себе три утверждения:
а) если Pu=PR, то PW=PV=PR,
б) если РуС.Рд, то Р1Г=Ру<Ря;
в) если Pu>PR, то’Р^Ри>Рк-
Эти утверждения означают, что крутизна кривой изменения
мощности помех, поступающих в приёмник, в зависимости от
расстройки не может превышать наименьшей из величин ри или
pR. Поэтому, если, например, крутизну риудалось довести до
значений рв,то нет смысла ещё дальше её увеличивать, так как
в этом случае pw, которая до этого определялась рц, при даль-
нейшем увеличении ри будет определяться pR.
Такое же положение будет и в другом случае: если мы по-
пытаемся увеличить pR до значений, больших, чем ру.
12—730 177
Следовательно, взаимные помехи будут убывать наиболее
быстро при увеличении разноса тогда, когда асимптотические
крутизны ри и pR представляющие собой передатчик и приём-
ник, одинаковы.
3. Если расстройка между несущей частотой мешающего из-
лучения и частотой настройки приёмника, подверженного поме-
хам, достаточно велика, то мощность мешающего сигнала при
изменении расстройки остаётся пропорциональной квадрату его
максимальной амплитуды. Поэтому в этих условиях безразлич-
но, определяем ли мы отношение сигнал/помеха по мощности
или по максимальной амплитуде.
§ 12.6. ОПРЕДЕЛЕНИЕ РАЗНОСА МЕЖДУ КАНАЛАМИ
Рассмотренный в предыдущих параграфах метод можно ис-
пользовать для определения разноса по частоте между соседни-
ми каналами, необходимого для того, чтобы взаимные помехи
не превышали заданных значений. Ниже приводятся построен-
ные в соответствии с этим методом кривые, показывающие за-
висимость затухания мешающего сигнала от разноса между
средней частотой, на которую настроен приёмник, и средней ча-
стотой спектра мешающего сигнала. Это затухание представ-
ляет собой отношение средней мощности, воспринимаемой в дей-
ствительности от источника мешающего сигнала при расстройке,,
к средней мощности, которая воспринималась этим же .приёмни-
ком, если он был бы настроен на мешающий сигнал.
Приводимые кривые относятся к различным классам излу-
чения и к различным приёмникам. К полученным из кривых зна-
чениям разноса следует добавить разнос из-за нестабильности
Центральная
частота
Рис, 12.6. Огибающая частотного спектра, принятого для теоретического
рассмотрения радиотелефонной передачи; Т — отношение разноса частот
(измеренного от центральной частоты) к необходимой ширине полосы
178
12*
179
частоты передатчиков. Таблица. допустимых отклонений часто-
ты передатчиков содержится в [Л43, стр. 336]. На рис. 12.6 по-
казана огибающая частотного спектра радиотелефонной пере-
дачи. На рис. 12.7 и 12.8 показаны использованные для расчётов
характеристики приёмников-
Мы рассмотрим случай, когда высокочастотная часть ис-
пользуемого приёмника имеет достаточно большой линейный ди-
намический диапазон, и не будем учитывать некоторые нелиней-
ные явления, которые особенно значительно проявляются при
сильных взаимных помехах.
Рассмотрим предлагаемые кривые для различных классов из-
лучений.
а) Тел егр аф и ая связь с амплитудной манипу-
ляцией (А1)1). В основу расчёта был положен дискретный
спектр, создаваемый последовательностями однородных теле-
графных сигналов, а именно, точек равной продолжительности.
Предполагалось, что первоначальная прямоугольная форма сиг-
налов изменялась при прохождении через простейший фильтр,
состоящий из ёмкости и сопротивления. Постоянная времени
фильтра, определяющая собой скорость нарастания и убывания
сигналов, составляет одну двадцатую часть от продолжительно-
сти элементарного сигнала. Из рис. 12.9—12.10 определяется ми-
нимальный разнос, который нужно поддерживать между часто-
тами двух телеграфных излучений с амплитудной манипуляцией
как функцию желаемого затухания мешающего сигнала.
б) Телеграфия посредством амплитудной
манипуляции модулирующей звуковой часто-
ты (А2). Расчётные кривые рис. 12.11 построены, исходя из
предположения, что модуляция осуществляется одной частотой
*) Обозначение излучений см. в приложении VII.
180
1000 гц и манипулируется лишь напряжение модулирующей ча-
стоты.
в) Телефония (АЗ). Если две системы двухполосной те-
леграфии работают на смежных каналах и поля обоих сигналов
равны между собой, то помеха будет помещаться на наклонной
части характеристики затухания фильтра приёмника. При этом
помеха будет вызываться биениями между несущей полезного
сигнала и неравными боковыми полосами мешающей станции.
Кроме того, поскольку боковая полоса мешающей станции, рас-
положенная ближе всего к каналу полезного сигнал а, может пре-
вышать по амплитуде несущую помехи, то возможна дополни-
тельная. помеха от биений между собой компонентов боковой
полосы. Первый тип помехи вносит разборчивый переходный
разговор, хотя со значительными искажениями, а второй тип —
только неразборчивый переходный разговор; допуск её мо-
жет быть увеличен на 10 дб по сравнению с помехой первого
типа. Отсюда следует, что можно принимать во внимание лишь
помехи, получающиеся вследствие биений между несущей и бо-
ковыми полосами мешающей станции. Переходный разговор
между другими компонентами обычно удаляется при помощи
фильтров звуковой частоты.
Если две несущие отличаются по частоте на величину, пре-
восходящую более чем в два раза наивысшую частоту модуля-
ции, то уровень разборчивого переходного разговора, по сравне-
нию с желательным сигналом, равен с достаточно хорошим при-
ближением отношению двух амплитуд несущих. Это означает,
что при равных полях относительная величина несущей помехи
определяется затуханием фильтра приёмника.
Кроме того, в рассматриваемом случае при работе с двумя
боковыми полосами величина низкочастотного компонента по-
мехи ещё более уменьшается потому, что биения происходят
между ослабленной несущей помехи и её боковыми полосами,
которые также ослабляются в фильтре приёмника. Это’справед-у
ливо как для линейных, так и для квадратичных детекторов.
Для построения кривых был принят частотный спектр, изо-
бражённый на рис. 12.6, и введён коэффициент W, равный от-
ношению ширины полосы приёмника, который подвергается ме-
шающему действию, к необходимой ширине полосы телефонной
передачи. На рис. 12.12 построены для различных приёмников
отношения минимального разноса между соседними каналами
к необходимой ширине полосы мешающего излучения, выра-
женные в децибелах. Эти два графика были использованы для
построения кривых на рис. 12.13—12.15, при помощи которых оп-
ределяют необходимый разнос между центральными частотами
желательного и мешающего сигналов при различных значениях
затухания мешающего сигнала.
181
Рис. 12.9. Изменение мощности, принимаемой от мешающего передатчика, в
Частотные характеристики приёмника даны пунктиром: е — разнос между
шающее излучение — телеграфия А1. Характеристики приёмника: а) ширина
— 10 дб!ок,т\ б) ширина полосы при неравномерности в 6 дб — 3 кгц, измене-
1,5 кгц, изменение затухания — 15 дб!окт\ г) ширина полосы при неравномер-
182
зависимости от разноса между каналами.
соседними частотами; Ьм— затухание мешающего сигнала, дб; ъВ = —. Ме-
полосы при неравномерности в 6 дб — 1 кгц, изменение затухания —
ние затухания — 20 дб)окт\ в) ширина полосы при неравномерности в 6 дб —
ности в 6 дб — 1 кгц, изменение затухания — 30 дб/окт
183
затухание мешающего сигнала, дб; . Мешающее излучение — телегра-
фия А1. Характеристики приёмника: а) ширина полосы <при неравномерно-
сти в 6 дб — 3 кгц, изменение затухания — 30 дб[окт; б) ширина полосы
при неравномерности в 6 дб — 3 кгц, изменение затухания — 90 дб/окт
184
напряжения модулирующей частоты 1000 гц. Частотная характеристика
приёмника дана пунктиром: е — разнос между соседними частотами;
тВ = —; b — затухание мешающего сигнала, дб. Мешающее излуче-
ние — телеграфия А2.
Характеристики приёмника: а) ширина полосы при (неравномерности в
6 дб — 2 кгц, изменение затухания — 15 дб[окт; б) ширина полосы при
неравномерности в 6 дб — 3 кгц, изменение затухания — 20 дб!окт
185
<ъ|о
r -7'
Рис. 12.12. Изменение мощности, принимаемой от мешающего передатчика,
в зависимости от разноса между каналами: е — разнос между соседними
частотами; b — затухание мешающего сигнала, дб.
Ширина полосы приёмника
W—
Необходимая ширина полосы помехи (в).
v Мешающее излучение — телефония АЗ.
\ Изменение затухания соответствует кривой:
а)— -------120 дб/окт; б) ---------30 дб!окт;
---------30 дб/окт; --------15 дб)окг
_____________________________________________20 дб!окт\
Рис. 12,13. Изменение мощности, принимаемой от мешающего передатчика, в
ника дана пунктиром: е — разнос между соседними частотами; В — необходи-
Ьм — затухание мешающего сигнала, об. Характеристики приёмника: а) ши-
120 дб/окт; б) ширина полосы при неравномерности в 2 дб — 3 кгц, измене-
6 кгц, изменение затухания — 20 дб!окт\ г) ширина полосы при неравномерно-
188
-зависимости от разноса между каналами. Частотная характеристика приём-
ная ширина полосы мешающего сигнала. Мешающее излучение—телефония АЗ
•рина полосы при неравномерности в 2 дб — 10 кгц, изменение затухания—
ние затухания — 120 дб!окт\ в) ширина полосы при неравномерности в 2 дб —
сти в 2 дб — 6 кгц, изменение затухания — 40 дб/окг
189
Рис. 12.14. Изменение мощности, принимаемой от мешающего передатчика, в
ника дана пунктиром: е — разнос между соседними частотами; В — необхо-
ния АЗ; Ьм — затухание мешающего сигнала, дб. Характеристики приёмника:
ния — 30 дб!окт; б) ширина полосы при неравномерности в 6 дб — 2 кгц,
6 дб — 3 кгц, изменение затухания —20 дб)окт; г) ширина полосы при не-
190
зависимости от разноса между каналами. Частотная характеристика приём-
димая ширина полосы 'мешающего сигнала. Мешающее ’излучение — телефо-
а) ширина полосы при неравномерности в 6 дб — '1,5 кгц, изменение затуха-
изменение затухания — 15 дб/окт; в) ширина полосы при неравномерности в
равномерности в 6 дб — 1 кгц, изменение затухания — 30 дб/окт
191
Рис. 12.15. Изменение мощности, принимаемой от мешающего передатчика,
в зависимости от разноса между каналами. Частотная характеристика при-
ёмника дана пунктиром: е — разнос между соседними частотами; В — необ-
ходимая ширина полосы мешающего сигнала. Мешающее излучение — теле-
фония, Ьм*— затухание мешающего сигнала, дб. Характеристики приёмника:
а) ширина полосы при неравномерности в 6 дб — 2 кгц, изменение затухания—
30 дб!окт; б) ширина полосы при неравномерности в 6 дб — 3 кгц, изменение
затухания----------------30 дб/окт----------90 дб!окт
192
Рис. 12.17. Изменение мощности, принимаемой от мешающего передатчика, в
ника дана пунктиром: е — разнос между соседними частотами: Ьм — зату-
Характеристики приемника: а) ширина полосы отри неравиомерности в 6 дб —
ности в 6 дб — 2 кгц, изменение затухания — 20 дб!окт\ в) ширина полосы при
полосы при неравномерности в 2 дб — 6,5 кгц, изменение затухания —
194
зависимости от разноса между каналами. Частотная характеристика приём-
хание мешающего сигнала, Мешающее излучение—телеграфия А1.
2 кгц, измерение затухания — 115 дб/окт; б) ширина полосы при неравномер-
неравномерности в 2 дб — 6 кгц, изменение затухания — 40 дб/окт\ г) ширина
60 дб/окт
13*
195
496
зависимости от разноса между каналами. Частотная характеристика приемни-
ка дана пунктиром: е — разнос между соседними частотами; Ьм—затуха-
ние мешающего сигнала, дб; Мешающее излучение — телеграфия А'1.
Характеристики приёмника: а) ширина полосы при неравномерности в 6 дб —
10 кгц, изменение затухания — 20 дб)окт; б) ширина полосы при неравномер-
ности в 6 дб — 10 кгц, изменение затухания — 20 дб/окт
0
Ю
20
30
*0
30
60
70
60
90
100
110
120
е.кгц
ЮО
мешающего сигнала, дб; хВ = —. Мешающее излучение — телеграфия А2.
1 кгц, изменение затухания — 10 дб!окт; б) (ширина полосы при -неравномер-
неравномерности в 6 дб — 1 кгц, (изменение затухания — 30 дб!окт; г) ширина
60 дб/окт
198
зависимости от разноса между каналами. Частотная характеристика приём-
частоты 1000 гц: е — разнос между соседними частотами; Ьм—затухание
Характеристики приемника: а) ширина .паласы при <нерав1номерности в 6 дб—
пости в 6 дб — Я,5 кгц, изменение затухания 15 дб/окт; в) ширина полосы при
полосы при неравномерности в 2 дб — 6,5 кгц, изменение затухания —
199
Рис. 12.20. Изменение мощности, принимаемой от мешающего передатчика, в
ника дана пунктиром. Амплитудная модуляция напряжений модулирующей
мешающего сигнала, дб;ъВ = . Мешающее излучение — телеграфия А2.
10 кгц, изменение затухания —20 дб/окт\ б) ширина полосы при неравномер-
при неравномерности в 6 дб — 6 кгц, изменение затухания — 20 дб)окт\
ния — 20 дб/окт
200
Зависимости от разноса между каналами. Частотная характеристика приём-
Яастоты 1000 гц: е — разнос между соседними частотами; Ьм—затухание
Характеристики приёмника: а) ширина полосы при неравномерности в 6 дб—
йости в 2 дб—10 кгц, изменение затухания — 40 дб!окт\ в) ширина полосы
7 Ширина полосы при неравномерности в 2 дб — 6 кгц, изменение затуха-
201
зависимости от разноса между каналами. Частотная характеристика приёмни-
ка дана пунктиром: е — разнос между соседними частотами; Ьм—затуха-
ние мешающего сигнала, дб, Девиация частоты ±425 гц. Мешающее излуче-
ние—телеграфия с частотной манипуляцией.
Характеристики приемника: а) ширина полосы при неравномерности в 6 дб—
1 кгц, изменение затухания — 30 дб!окт; б) ширина полосы при неравномер-
ности в 6 дб — 3 кгц, изменение затухания — 30 дб/окт
202
г) Фототелеграфия (А4). Для фототелеграфа рассмат-
ривается лишь случай, когда несущая частота модулирована по
амплитуде поднесущей, частота которой меняется в зависимо-
сти от модуляции в пределах от 1500 до 2300 гц. Предполагает-
ся, что форма сигналрв прямоугольная, общее число белых и
чёрных элементов, переданных в секунду, равно 1000. На
рис. 12.16 показаны кривые, позволяющие определить мини-
мальный разнос между несущими частотами двух фототеле-
графных излучений в зависимости от затухания мешающего сиг-
нала.
д) Помехи между излучениями различных
классов. Для различных случаев были рассчитаны кривые,
при помощи которых можно определить необходимые разносы
между частотами двух телеграфных излучений различных клас-
сов, а также между частотами телеграфного и телефонного из-
лучений, которые подвергаются мешающему действию телеграф-
ного излучения. Эти кривые показаны на рис. 12.11—12.21.
ГЛАВА ТРИНАДЦАТАЯ
ФОРМИРОВАНИЕ СИГНАЛОВ В ПЕРЕДАТЧИКАХ
В главе рассмотрены практи-
ческие соображения относитель-
но выбора формы импульсов
для радиосвязей и показано
что выбор формы импульса в
каждом отдельном случае оп-
ределяется конкретными тре-
бованиями, предъявляемыми к
системе связи, и условиями, в
которых она работает.
Показаны скелетные схемы
использования фильтров в це-
лях минипуляции передатчиков.
Дана схема, обеспечивающая
желательные характеристики
фильтра.
Приведены спектральные ха-
рактеристики, получающиеся
после фильтрации при ампли-
тудной и частотной манипуля-
циях, из которых видно, что
фильтрация значительно улуч-
шает использование спектра
радиочастот.
Описано нелинейное устрой-
ство для формирования сигна-
лов.
§ 13.1. ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ
ПО ВЫБОРУ ФОРМЫ ИМПУЛЬ*
СОВ
В ы8ор оптимальной формы сиг-
нала— большая и многосторон-
няя задача. Здесь мы рассмотрим
лишь .некоторые соображения, выте-
кающие в основном из требований
лучшего использования спектра ра-
диочастот.
Мы полагаем, что оптимальной
формой импульса является та, кото-
рая для данных условий распрост-
ранения и* типа излучения обеспе-
чит требуемое качество передачи со-
общений при наилучшем использо-
вании мощности передатчика и
спектра радиочастот.
Выбор оптимальной формы сиг-
нала затруднён тем, что эффектив-
ность использования спектра радио-
частот и выгоду, получаемую при лучшем использовании мощно-
сти передатчика, трудно выразить в одинаковых единицах, хотя,
как можно видеть из ф-лы (В.1), имеются некоторые возможно-
сти в этом направлении. В самом деле, если бы модель, для
которой действительна ф-ла (В.1) была реальностью, то мы име-
ли систему, в которой ширина полосы и отношение сигнала к по-
мехе взаимозаменяемы; тогда экономия в ширине полосы,
равная 10%, была бы равносильна увеличению мощности пере-
датчика в два раза.
Однако реальные системы радиосвязи далеки от таких
идеальных и не позволяют увеличивать пропускную способность
канала за счёт увеличения ширины полосы передачи или увели-
чения отношения сигнала к помехе в той мере, как возможно в
идеальной системе. В реальных системах радиосвязи, помимо
204
ширины полосы и отношения сигнала к помехе, на пропускную
способность канала влияет ещё ряд других факторов, например,
“ замирания, нестабильность частоты передатчиков и приёмников
и пр. При выборе системы радиосвязи следует учитывать про-
стоту и реализуемость устройства, а также стоимость оборудо-
вания и монтажа. Такого рода факторы не учитываются ф-лой
(В.1). Поэтому «а практике приходится рассматривать не-
которые действующие факторы, хотя и трудносопоставимые, но
позволяющие приблизиться к оптимальной форме сигнала.
При амплитудной манипуляции прямоугольными периодиче-
скими сигналами огибающая частотного спектра убывает при
возрастании частоты со скоростью только 6 дб на октаву, вслед-
ствие чего энергия спектра распределяется по значительной по-
лосе частот.
Проиллюстрируем это на численном примере.. Предположим,
что передают со скоростью 200 бод. Амплитуды компонентов
спектра будут следующие:
Частота, гц Компоненты спектра
Амплитуда
(отсчитывается lot несущей) Абсолютное значение дб
0 1 —6,0
100 2тс 1 —9,9
300 тс 1 —19,5
500 Зк 1 —23,9
5тс
700 1 —26,8
7тс
900 1 —29,0
1100 9те 1 —30,8
и т. д Птс
- Таким образом, огибающая спектра при отклонении от несу-
щей на 1000 гц уменьшается на 30 дб по отношению к уровню
v неманипулированной несущей, что весьма благоприятно. Одна-
Ко при дальнейшем отклонении частоты ещё на 1000 гц., т. е.
всего на 2000 гц от несущей, огибающая уменьшается ещё лишь
на 6 дб, что составляет в общем 36 дб; при отклонении частоты
205
ещё на одну октаву, т. е. до 4000 гц, огибающая будет ниже
уровня несущей всего только на 42 дб. Очевидно, что при такой
скорости убывания спектра с возрастанием частоты будут весь-
ма значительные помехи в соседних каналах.
Из этого примера следует, что необходимо формировать сиг-
налы для уменьшения мешающих воздействий в соседних кана-
лах. В обычном передатчике амплитудная манипуляция произво-
дится в задающих ступенях, и ограничение в последующих сту-
пенях, действующих в режиме класса С, делает неэффективным;
формирование сигнала .непосредственно после манипулируемой
ступени. Поэтому в. обычном передатчике, чтобы сформировать
сигналы, необходимо перевести последующие ступени в режим
класса В, что хотя и несколько понижает коэффициент полез-
ного действия передатчика, но зато повышает общую излучае-
мую мощность. Если высоту импульса анодного тока считать
постоянной, то при изменении угла отсечки от 75 до 90° колеба-
тельная мощность увеличивается на 9%, а коэффициент полез-
ного действия уменьшается на 5°/о. Угол отсечки, близкий к 90°,
позволяет работать с меньшими величинами возбуждения. Ре*
жим класса В полезен также тем, что уменьшает гармоники.
Частотная манипуляция позволяет легче сформировать сиг*
налы, так как при этой манипуляции нелинейность усилителя пе-
редатчика не создаёт на его выходе боковых частот, отсутствую*
щих во входном напряжении.
В гл. 6 определены значения ширины полосы, занимаемой пе*
редачей частотно-манипулированных прямоугольных и синусои-
дальных сигналов, т. е. рассмотрены два предельных случая наи-
большего и наименьшего скруглений. Сравнение полученных дан-
ных показывает, что при частотной манипуляции формирование
сигналов не уменьшает ширину полосы столь значительно, как
при амплитудной. Однако нельзя пренебрегать при частотной ма*
нипуляции формированием сигналов, так как оно значительно
уменьшает внеполосные излучения.
Рассмотрим соображения, определяющие выбор формы сиг*
налов при амплитудной и при частотной манипуляции. При ам*
плитудной манипуляции, как показано в гл. 6, ширина полосы
частот, занимаемой передачей, определяется полосой частот мо-
дулирующего сигнала. Поэтому прежде всего следует учесть воз*
можность использования «идеального» импульса, занимающего
наименьшую полосу частот. Но, вместе с тем, следует помнить,
что у этого импульса есть особенности:
1) скруглённая вершина;
2) малая скорость убывания внеполосных излучений при воз-
растании частоты.
Рассмотрим значение этих особенностей «идеального» им*
пульса с практической стороны, учитывая что в обычных уело*
виях приёма, когда применяются ограничители, лишь нижняя
206
часть импульсов определяет величину выходного напряжения
приёмника. При импульсах со скруглённой или заострённой вер-
шиной длительность сигналов на выходе приёмника будет ме«
няться, что может вызвать преобладания и сбои. Если учесть,
что МККР для амплитудной манипуляции рекомендует время
установления — =0,2, то «идеальный» импульс, у которого
*с
=0,365, мало подходит для работы в условиях замираний.
Более подходящим для этих условий будет трапецеидальный
импульс или импульс с косинус-квадратным скруглением при
значении £ не менее 0,5. Исключение составляет случай, когда
условия приёма стабильные (замираний нет); при этом можно ис-
пользовать импульс со скруглённой вершиной, близкий к «иде-
альному». Следует также иметь в виду, что скругление сигналов
уменьшает энергию, сосредоточенную в импульсе. Покажем это
на примере. Для импульсов, сформированных по закону n-й сте-
пени косинуса, энергия в импульсе, отнесённая к длительности
импульса, будет равна при различных значениях п:
Форма импульса
косинусоидальный
косинус-квадратный
косинус-кубичный
Энергия
в импульсе1)
1
2
3
8
5
16
Приведённые цифры показывают, что если при формирова-
нии импульса желательно сохранить в нем прежнюю энергию, то
необходимо увеличить мощность передатчика. Естественно, что
увеличить установочную мощность маломощных передатчиков в
большинстве случаев легче, чем мощных.
Всегда желательно увеличить скорость убывания внеполос-
ных излучений, но не во всех случаях бывает ясно, к каким прак-
тическим значениям следует стремиться. Если бы приёмники
имели характеристики избирательности, близкие к прямоуголь-
ным, а мощность мешающего передатчика соседнего канала
была такой же, как и мощность желательного передатчика, то
отношение сигнала к помехе в ближайшем соседнем канале не
превышало бы приблизительно 23 дб, даже при условии, что в
*) Энергия, сосредоточенная в прямоугольном импульсе, принята за еди-
ницу.
207
этом канале сосредоточена вся энергия внеполосового излуче^
ния, т. е. условия приёма были бы сравнительно благоприятные.
Однако на практике характеристика избирательности при-
ёмников не прямоугольная, а мощность мешающего передатчика
может во много раз превышать мощность желательного пере-
датчика. Задача ещё усложняется необходимостью иметь за-
щитные допуски по частоте из-за нестабильности частот пере-
датчика и приёмника.
Следует также учесть, что скорость убывания спектра с ча-
стотой ещё не достаточно характеризует сигнал; важно также,
чтобы те частоты, при которых спектр начинает быстро убывать,
были бы не слишком высокими, т. е. чтобы уже в ближайшем со-
седнем канале внеполосные излучения были сильно ослаблены.
Рассмотрение импульсов, формируемых по закону n-й степени
косинуса, показывает, что при п=1 убывание, пропорциональ-
ное 1/£2, начинается при £>л/2 и при каждом увеличении п на
единицу начало быстрого убывания спектра отодвигается по
оси k на л/2. Учитывая, что для линий, подверженных действию
замираний, ширина канала составляет не менее 2,5лД уже в
ближайшем соседнем канале убывание спектра, пропорцио-
нальное l/kn+l, можно получить при п, не превышающем 3,
т. е. при косинус-кубичных импульсах.
Для сигналов, форма которых определяется выражениями
/5.21) и (5.22), спектр начинает убывать пропорционально 1/£4
при Л>5/(1—£).
Из приведённого выше следует, что импульс, близкий по фор-
ме к «идеальному», можно рекомендовать в тех условиях, ког-
да мощность передатчика невелика, а используемые приёмники
имеют хорошую характеристику избирательности.
Импульсы со скруглённой вершиной и с большой скоростью
убывания внеполосных излучений, например косинус-кубичные,
можно использовать в следующих условиях;
1) стабильные условия распространения;
2) малая излучаемая мощность;
3) наличие приёмников с невысокой избирательностью.
Если первое из перечисленных условий не удовлетворяется,
т. е. поле сигнала неустойчиво, то, чтобы увеличить скорость
убывания внеполосных излучений, можно корректировать края
сигнала, как это описано в § 5.4.
При частотной манипуляции, как видно из гл. 7, целесооб-
разно использовать трапецеидальные импульсы и импульсы с
синусоидальным скруглением, занимающие достаточно узкую
полосу частот и имеющие высокую скорость убывания внеполо-
сных излучений.
208
Таким образом, выбор формы импульсов в каждом отдель-
ном случае определяется конкретными требованиями, предъяв-
ляемыми к системе связи, и условиями, в которых она работает.
§ 13.2. ЛИНЕЙНЫЕ ФИЛЬТРЫ В ЦЕПЯХ МАНИПУЛЯЦИИ
На рис. 13.1 изображена скелетная схема использования
фильтра в цепях манипуляции передатчика.
Рис. 13.1. Скелетная схема использования фильтра в це-
пях манипуляции передатчиков
Линейный электрический фильтр, подобно любой линейной
системе, можно определить либо его частотной характеристи-
кой, либо переходным процессом, получающимся при подаче на
его вход единичного толчка или единичного импульса. В элек-
тросвязи наиболее развит расчёт фильтров по частотной харак-
теристике. Телевидение же и импульсная техника требуют оп-
ределять временные характеристики, и в настоящее время уже
успешно развивается метод проектирования фильтров, имеющих
заданные временные характеристики.
В настоящей книге мы не рассчитываем фильтры, а лишь оп-
ределяем основные показатели для желательного фильтра в це-
пи манипуляции и рассматриваем пример фильтра, обеспечива-
ющего эти показатели. В практических условиях для желатель-
ного фильтра в цепи манипуляции должны быть определены
три основных показателя:
а) переходный процесс в фильтре, который определяется хо-
дом частотной характеристики фильтра в области низких ча-
стот приблизительно до точки с затуханием 20 дб:
б) отношение ширины полосы фильтра к частоте манипуля-
ции, которое мы будем называть относительной полосой фильт-
ра, т. е.
т =А
1в
где Afc— ширина полосы фильтра на уровне 6 дб;
fB — частота манипуляции (гц)-,
14—730 209
в) внеполосное затухание, т. е. ход частотной характери-
стики за пределами точки с затуханием 20 дб.
Сравнение переходных процессов в фильтрах с различными
частотными характеристиками, которое здесь нами не приводит-
ся, показывает, что независимо от формы частотной характери-
стики скорость возрастания функций манипуляции на выходе
фильтра (при подаче на его вход единичного толчка или единич-
ного импульса) определяется шириной полосы фильтра, Д/с;
напряжения меняются от отжатия к нажатию приблизительно
„„ .0,4
в 0,7 раза в период времени, равный независимо от
других показателей фильтра. Характер -и скорость дальнейшего
(после точки, при которой амплитуда равна 0,7) хода переход-
ного процесса определяются показателем а).
Поскольку имеется много различных систем связи, то мы сна-
чала рассмотрим общие соображения, влияющие на выбор по-
казателей а), б), в), и затем определим характеристики фильтра,
приемлемые для различных случаев.
Показатель а) определяет величину взаимных помех, ко-
торые создаются в области, значительно удалённой от полосы
частот, необходимой для передачи желательной информации.
Этот показатель важен для амплитудно-манипулированных
передатчиков, так как он определяет пиковое значение напря-
жения сигнала и выброс свидетельствует о неполном использо-
вании средней мощности передатчика. При частотной манипу-
ляции соблюдение минимального выброса не так важно, как
при амплитудной, так как при частотной манипуляции выброс в
мгновенной частоте не создаёт пику в амплитуде напряжения вы-
сокой частоты или в какой-либо степени характеризует использу-
емую среднюю мощность передатчика. Однако если передатчик
предназначают для многократной работы посредством исполь-
зования нескольких частот, то важно, чтобы фильтр имел мини-
мальное время установления и наименьший выброс, что обеспе-
чит большую точность при определении каждого значения ча-
стоты.
С точки зрения передачи информации, при работе двумя ча-
стотами точная форма манипулирующего напряжения (форма
переходного процесса) несущественна, если приёмное устрой-
ство позволяет соответствующим образом использовать приня-
тый сигнал. В практических условиях обычное устройство для
приёма частотно-манипулированных колебаний достаточно раз-
деляет частоты, и в нём сигнал поэлементно интегрируется, что
позволяет использовать переходный процесс с наименьшим вы-
бросом и наименьшим временем установления. Преимущество
такого переходного процесса в том, что манипулирующее напря-
жение имеет одинаковую форму для даиного фильтра при ме-
210
£ няющихся скоростях манипуляции; в результате не будет ка-
ких-либо впадин в амплитуде, которые могут совпасть с точкой
:? выбора сигнала в приёмнике, если такой выбор производится.
Следовательно, можно считать, что в большинстве случаев
“ желателен фильтр, обеспечивающий переходный процесс с наи-
меньшим временем установления и с наименьшим выбросом;
это и будет предполагаться при рассмотрении других показате-
лей.
П о к а з а т е л ь б), т. е. Т, наилучшим образом определяется
после рассмотрения влияния Т на форму манипулирующего ко-
лебания. Выбор показателя б) зависит от выбора а). Исследова-
ние кривых различных переходных процессов в фильтрах, ко-
торое здесь нами не приводится, показывает, что различным
• значениям Т соответствует следующая плоская часть кодовой
посылки:
7'= 1,6 0% (косинусоидальный импульс)
Т=3,2 50%
Т=16 90%
Т= 00 100% (прямоугольный импульс)
Если применяемая система связи очень хорошо синхронизи-
рована и высокостабильна по частоте, то желательно выбрать
малое значение Т, порядка 2 или 3. При использовании старт-
стопной телеграфной аппаратуры и значительном уходе несу-
щей частоты желательно использовать Т от 4 до 16, в зависимо-
сти от стабильности.
Действительная форма колебания на выходе приёмника по-
лучается после прохождения через фильтр нижних частот в
приёмнике, который должен иметь, по крайней мере, такую же
ширину, как и фильтр передатчика. Если в цепи манипуляции
передатчика и на выходе детектора в приёмнике используются
; одинаковые фильтры, то относительная полоса каждого из них
. должна быть увеличена приблизительно в 1,4 раза.
Л. Показатель в) выбирают, учитывая следующее: экономи-
ческие соображения (количество и тип используемых звеньев
фильтра), разнос между соседними каналами по частоте и ха-
рактериетики избирательности приёмников, используемых в со-
седних каналах.
Действительная характеристика фильтра, удовлетворяющего
основным предъявленным выше требованиям, должна быть
плавной кривой, лежащей внутри заштрихованной области
, рис. 13.2. Для амплитудно-манипулированного передатчика на
' частоте, превышающей в четыре раза ширину полосы фильтра
Afc затухание должно быть не менее 40 дб. Для частотно-мани-
' пулированного передатчика затухание на этой частоте должно
.быть 40 дб при /п<5 и 30 дб при ш>5. При таких частотных
2Н
характеристиках обеспечивается переходный процесс с выбро-
сом менее 4%' от общего изменения напряжения.
Рас, 13.2. Критерий проектирования фильтра ма-
нипуляции для амплитудно- и частотно-манипули-
рованных передатчиков
На рис. 13.3 показана электрическая схема фильтра, обес-
печивающая желательные характеристики. Этот фильтр рас-
считан на частоту манипуляции 60 гц и частота среза его выбра-
на равной 200 гц. Частотная характеристика его по форме про-
межуточна между косинус-квадратной и гауссовой кривыми.
Действительные значения ёмкостей, индуктивностей и доброт-
Рис. 13.3. Схема электрического фильтра в цепи ма
нипуляции
ностей Q = d)L/R, а также входные и нагрузочные сопротивле-
ния должны поддерживаться с точностью от 5 до 10%, если же-
лательно получить соответствующий переходный процесс. Ес-
ли Q индуктивностей необходимо значительно уменьшить, то
вместо шунта лучше включить последовательное сопротивление,
212
увеличивающее внеполосные затухания фильтра. Чтобы по-
лучить наилучший переходный процесс, важно включить во
входную цепь фильтра последовательное сопротивление 560 ом,
показанное на схеме рис. 13.3.
На рис. 13.4 показаны формы манипулирующих напряжений,
Л/с
получаемых на выходе фильтра при различных значениях Т = —’
/в
где Д/с— полоса пропускания фильтра на уровне 6 дб, fB —
частота манипуляции.
На рис. 13.5 показа-
ны огибающие спектров
на выходе амплитудно-
манипулированного пере-
ра, создаваемого передатчиками при
амплитудной манипуляции1. Частота
манипуляции — 60 гц.
------Прямоугольное колебание без
фильтрации.
------Колебание при одн оз венном RC-
фильтре Т=3,3.
------Колебание при четырёхзвенном
LC-фильтре и нелинейном усилителе.
------Колебание при четырёхзве-нном
LC-фильтре Т=3,3
Рис. 13.4, Формы манипули-
рованных колебаний на вы-
ходе фильтра
1 датчика для четырёх видов колебаний, показанных на рис. 13.6:
1) без фильтрации; 2) с фильтром, состоящим из одного зве-
на RC; 3) с фильтром, схема которого показана на рис. 13.3
при Т=3,3 и 4) при тех же условиях, как и в предыдущем случае,
,, но при ограничении -в передатчике. Как -видно из кривых, одно-
213
a)
Рис. 13.6. Формы манипу-
лированных колебаний:
а) без фильтрации Т= оо;
б) с одноэвенным /?С-фильт-
ром; .в) с фильтром, схема
которого . доказана на
рис. 13.3 (пунктиром 'пока-
зано ограничение формы ко-
лебания вследствие нелиней-
ного «усиления)
Рис. 13.7. Огибающие
спектров частотно-мани-
пулированного передат-
чика с фильтрацией в це-
пи манипуляции
214
•ячеечный 7?С-фильтр значительно менее эффективен три ограни*
чении внеполосных излучений, чем рационально спроектирован-
ный LC-фильтр. Также очевидно, что даже небольшое ограни-
чение или нелинейность ступеней, включённых после фильтра
манипуляции, вновь заметно увеличивает количество энергии,
проникающей в соседний канал.
Из полученных расчётным путём кривых рис. 13.7 видно, что
фильтрация при частотной манипуляции значительно умень-
шает величину внеполосных излучений.
Следует подчеркнуть, что желательные частотные характе-
ристики фильтра (см. рис. 13.2) можно получить при 'помощи
многих других конфигураций фильтра. Иногда на практике
можно ограничиться фильтрами более простой конструкции, чем
на рис. 13.3.
§ 13.3. НЕЛИНЕЙНОЕ УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ СИГНАЛОВ
Ниже приводится описание устройства для формирования
сигналов в цепях манипуляции, рассчитать которое легче, чем
линейный электрический фильтр.
Рис. 13.8. Схема устройства для скругления сигналов в цепи манипуляции
Принцип работы устройства следующий: прямоугольный
; , сигнал сначала преобразуют в трапецеидальный, вводя посто-
янную времени в моменты установления сигнала. Это дости-
'гается при помощи перезаряда конденсатора. Углы трапеции
: затем скругляют, для чего используют нелинейность характе-
ристик ламп манипуляции и усилителя высокой частоты.
Схема устройства показана на рис. 13.8. Напряжение низ-
кой частоты, поступающее от отдельного гетеродина Н, пода-
1/. 215
ётся через манипулятор на первичную обмотку трансформа-
тора Тр. Напряжение - низкой частоты, снимаемое с каждой из
двух вторичных обмоток, выпрямляется. Полученное таким об-
разом постоянное напряжение служит для подачи смещения на
сетки двух триодов Л\ и Л 2, так что. когда один из них открыт,
то второй заперт. При замыкании манипулятора М между точ-
ками А и В получается напряжение (Л, а между точками С и
Д — напряжение U2. Лампа Л2 запирается, причём её сетка
доводится до отрицательного потенциала (—.U2). Лампа Л\ на-
оборот, открывается, поскольку напряжение U\ противоположно
напряжению смещения и равно ему по величине. Эта лампа
проводит ток и заряжает по экспоненциальному закону конден-
сатор С через сопротивление R\. Напряжение UE — Up на за-
жимах конденсатора С достигло бы величины — U6, если не
было ограничителя Д6- В действительности же этот ограничи-
тель начинает действовать, как только напряжение UE — UFдо-
стигает величины — t/6. Следовательно, на сетке манипулирую-
щей лампы Л3 получаем напряжение, которое в виде функции
времени представлено кривой abc на рис. 13.9.
Рис. 13.9. Напряжение на сетке лампы Л3 как
функция времени
При размыкании манипулятора М напряжения U\ и U2 ста-
новятся равными нулю. Лампа Л1 запирается напряжением
смещения U3. Лампа Л2 открывается, причём потенциал её
сетки становится таким же, как и потенциал катода. Ток, про-
ходящий через эту лампу, заряжает конденсатор С по экспо-
ненциальному закону. Если бы не было ограничителя Д$, то
напряжение на зажимах конденсатора С достигло бы величи-
ны + U5. В действительности же этот ограничитель начинает
действовать, как только UE — UF становится положительном, и
поэтому на сетке манипулирующей лампы Л3 получается на-
пряжение, которое в виде функции времени представлено кри-
вой cde на рис. 13.9.
216
Таким образом, получаем трапецеидальные сигналы, крутиз-
ну участков db и cd которых можно регулировать, изменяя по-
стоянную времени устройства, например придавая различные
значения ёмкости конденсатора С. Для скругления углов в точ-
ках а, Ь, с и d, что позволит увеличить скорость убывания вне-
полосных излучений, используют крутизну характеристики анод-
ного тока /а в зависимости от сеточного напряжения Ue лампы
Л3 (рис. 13.10).
Рис. 13.10. Изменение 1а как функции Uc
Манипулирующее устройство воздействует на лампу (см.
рис. 13.8), которая находится в высокочастотной цепи. Напря-
жение U7 с сопротивления R3 подаётся на сетку лампы Л4 по-
следовательно с напряжением смещения Ug, причём напряжение
на сетке этой лампы в каждый момент времени равно —(U7+
+.U3). Выходное напряжение высокой частоты будет максималь-
ным при минимуме 07, и таким образом сигнал опрокидывает-
ся. В усилителе высокой частоты углы b и с будут соответство-
вать максимальной амплитуде сигнала, а углы а и d—нулю.
ГЛАВА ЧЕТЫРНАДЦАТАЯ
ИЗМЕРЕНИЕ ШИРИНЫ ПОЛОСЫ ЧАСТОТ,
ИЗЛУЧАЕМОЙ РАДИОТЕЛЕГРАФНЫМИ
ПЕРЕДАТЧИКАМИ
В главе рассмотрены мето-
ды измерения ширины -поло-
сы частот, занимаемой -радио-
телеграфными излучениями, а
также скелетные схемы
соответствующих приборов.
Рассчитаны численные зна-
чения уровней <на краю по-
лосы частот, содержащей
99% излучаемой мощности,
при амплитудной и частотной
манипуляциях.
Рассмотрены методы, ко-
торые могут быь использованы
.для дистанционных измерений
ширины полосы излучения, • и
желательные характеристики
измерительных устройств.
Даны практические со-
веты по экспериментальному
определению ширины поло-
сы, занимаемой передачей слу-
чайной (последовательности
сигналов.
§ 14.1. МЕТОДЫ ИЗМЕРЕНИЯ
ШИРИНЫ ПОЛОСЫ ИЗЛУЧЕНИЯ
В настоящее время, чтобы изме-
рить ширину полосы излучения
на частотах ниже 30 Мгц, исполь-
зуют три описанных ниже основных
метода [Л40].
Первый метод состоит в
полном анализе спектра передачи
при помощи узкополосного фильтра
с фиксированной частотной харак-
теристикой, причём частоту каждого
спектрального компонента устанав-
ливают равной центральной частоте
фильтра, преобразуя частоту вруч-
ную или автоматически. На рис. 14.1
показана в качестве .примера ис-
пользования первого метода изме-
рения скелетная схема, спектраль-
ного анализатора. Спектральный анализатор представляет со-
бой прибор с повторяющейся развёрткой по звуковой частоте, в
котором развёртывают частотные компоненты и измеряют их
уровни по гетеродинному принципу. Частотные компоненты по-
являются в виде вертикальных отклонений («выбросов») на
экране электронно-лучевой трубки и располагаются на горизон-
тальной оси в последовательности их частот. Высота отклоне-
ния является мерой величины компонента, которого оно пред-
ставляет. При применении трубки с длительным послесвечением
на экране получается спектр частот в виде непрерывной линии.
Выход генератора развёртки подключают к усилителю горизон-
тального отклонения (ось X), а также к реактивному элементу,
посредством которого изменяют частоту местного генератора.
218
Реактивный элемент имеет несколько обмоток, одна из которых
включена в мостовую схему, имеющую в одном из плеч лампу ге-
нератора развёртки. К этой обмотке подводят пилообразное
напряжение, позволяющее изменять частотный диапазон. Ам-
плитуду пилообразного напряжения устанавливают вручную.
Вторая обмотка реактивного элемента питается постоянным
Рис. 14.1. Первый метод измерения ширины полосы излучения.
Скелетная схема спектрального анализатора
током, величина которого определяет рабочую точку кривой на-
магничивания материала сердечника, обеспечивая таким обра-
зом линейность изменения частоты местного генератора.
К балансному модулятору подводятся выход местного ге-
нератора изменяющейся частоты и исследуемый сигнал, вслед-
ствие чего на выходе балансного модулятора появляется сиг-
нал разностной частоты (нижняя боковая полоса) 100 кгц.
Чтобы разделить частотные компоненты спектра после ба-
лансного модулятора, включён фильтр с переменной шириной
полосы. После усиления до требуемого уровня сигнал с часто-
той 100 кгц выпрямляют и подводят в виде импульса постоян-
ного тока к усилителю отклоняющего напряжения вертикальных
пластин (ось У).
Для количественного анализа в приборе предусмотрен
внутренний калибратор. Он состоит из генератора синусои-
дального напряжения с частотой 1000 гц и схемы, преобразую-
щей синусоидальное напряжение в последовательность прямо-
угольных импульсов известной амплитуды. Отношение сигнала
к паузе выбрано таким образом, что амплитуда нечётных гар-
моник значительно превышает амплитуду чётных гармоник,
так что нечётные гармоники можно легко сосчитать для опре-
деления положения спектральных компонентов сигнала на шка-
ле частот.
219
Первый метод'измерения, хотя и позволяет экспериментально
определить ширину полосы излучения, однако имеет следующие
существенные недостатки: а) Аппаратура достаточно сложна -и
требует тщательного обращения, б) Местный генератор пере-
менной частоты должен быть высокостабилен, чтобы избежать
смещения шкалы частот, в) Уровни во всех звеньях измеритель-
ного тракта необходимо тщательно поддерживать, г) Все ви-
ды помех сильно снижают точность результатов измерений;
д) Трудно выбрать благоприятное значение промежутка време-
ни для проведения анализа спектра. Устанавливать время ана-
лиза больше 20—30 сек нежелательно, так как за это время мо-
гут измениться условия измерений, а при небольшом промежутке
времени и при достаточно узком анализирующем фильтре ско-
рость развёртки влияет на результаты отсчёта, что отражается
на точности измерений, е) Метод не позволяет непосредственно
отсчитывать ширину полосы излучения, определяемой в соот-
ветствии с требованиями Регламента радиосвязи; чтобы опре-
делить эту величину, необходимо знать форму сигнала и рас-
считать уровень на краю полосы частот, содержащей 99% 'из-
лучаемой мощности, соответствующей данной форме сигнала,
а затем на рассчитаном уровне измерить ширину полосы. По-
скольку в практических условиях трудно установить точное соот-
ношение между формой сигнала и уровнем на краю полосы
излучения, то это усложняет получение результатов измере-
ний и снижает их точность. На рис. 14.2 и 14.3 показаны об-
разцы спектрограмм, полученных по первому методу.
Второй метод измерения ширины полосы.излучения со-
стоит в непосредственном измерении той части энергии, кото-
рая содержится в частотных компонентах, удалённых от цент-
ральной частоты спектра, с целью определения относительной
мощности внеполосного излучения.
Частотные компоненты выпрямленного сигнала выделяются
фильтром высоких частот, частота среза которого может изме-
няться. На рис. 14.4 показана скелетная схема измерения шири-
ны полосы, занимаемой амплитудно-манипулированными сигна-
лами, по второму методу. Передатчик модулируется точками.
Вход измерителя ширины полосы присоединяется к эквивален-
ту антенны. Входной сигнал проходит через регулятор напряже-
ния и преобразуется линейным детектором. Если переключатель
поставлен в положение Красная черта, то индикатор показывает
общую мощность тока, проходящего через детектор. Показание
индикатора устанавливается соответствующим Красной черте
регулятором входного напряжения, а также подбором величины
связи между передатчиком и измерителем, после чего входной
уровень поддерживается постоянным. Далее переключатель пе-
реводит в положение %’. При этом часть выходной мощности де-
220
to
to
Рис. 14.2, Амплитудная манипуляция (Al).
Прямоугольные точки. Скорость работы:
а) 141 бод, б) 282 бод
Рис. 14.3. Частотная манипуляция (F1).
Прямоугольные точки, а) Разнос частот
500 гц, скорость работы 47 бод; б) разнос
частот 1000 гц, скорость работы 141 бод
тектора, которая соответствует частотам, более высоким, чем ча-
стота среза фильтра, проходит через фильтр и усилитель и воз-
действует на измерительный прибор. Таким образом, в дополне-
ние к измерению всей излучаемой мощности измеряется также
мощность, соответствующая частотам за пределами определён-
ной полосы. Измерительный прибор, имеющий линейную шкалу»
Рис. 14.4. Второй метод измерения ширины полосы излучения. Скелетная
схема измерителя ширины полосы для AM сигналов
градуирован в значениях мощности, соответствующей частотам
внутри заданной полосы. В качестве измерительного прибора ис-
пользуют индикатор средних значений, что позволяет непосред-
ственно измерять мощность.
На рис. 14.5 дана скелетная схема измерения ширины полосы,
занимаемой частотно-манипулированными сигналами по этому
же методу. Сигналы проходят через регулятор уровня, детекти-
руются и усиливаются разделительным усилителем. Далее, если
переключатель находится в положении Красная черта, то изме-
ряется общая мощность сигнала. В остальном схема действует
так же, как и схема амплитудно-манипулированных сигналов
(см. рис. 14.4). Недостаток прибора описанного типа — необхо-
димость смены фильтров в зависимости от используемых скоро-
стей работы.
В [Л29] описан другой прибор для измерения ширины поло-
сы по второму методу. Скелетная схема его показана на
рис. 14.6. Сигнал поступает одновременно на преобразователи
Mi и М2 и детекторы Да и Дь. После калибровки прибора, ко-
торая описывается ниже, генератор Gi настраивают на частоту
105 кгц, а генератор G2 — на частоту 95 кгц. После линейного
преобразования частоты сигнал поступает на одинаковые поло-
совые фильтры Fi и F2 с полосой пропускания 5-5-15 кгц.
В результате фильтрации на усилитель У1 поступает только
нижняя боковая полоса сигнала, а на усилитель У2 — только
верхняя боковая полоса. Каналы Mt — Ft—У1 и М2—F2—У2 об-
222
Рис. 14.5. Второй метод измерения ширины .полосы излучения. Скелетная
схема измерителя ширины полосы для ЧМ сигналов
* Рис. 14.6. Второй метод измерения ширины полосы излучения. Вариант
скелетной схемы прибора
222k
ладают усилением около 23 дб в полосе пропускания фильтров
Выпрямленные напряжения, получаемые от квадратичных де-
текторов Дх и Дг, действуют в противоположных направлениях
по отношению к выходным напряжениям детекторов Да и Дь.
Эти напряжения используют для управления реактивными лам-
пами Rx и /?2, которые изменяют частоту генераторов Gx и G2.
Если напряжение от детектора Дх (Дг) больше, чем напряжение
от детекторов Дд, (ДД то частота генератора Gx (G2) изменяет-
ся таким образом, что разность между частотой генератора и
промежуточной частотой приёмника (100 кгц) уменьшается. В
результате спектральные компоненты, удалённые от центра по-
лосы, затухают, и напряжение, управляющее частотой генерато-
ра, уменьшается.
Перестройка генераторов Gx и G2 прекращается, когда мощ-
ность, потребляемая обоими детекторами, становится одинако-
вой, т. е. когда полная мощность сигнала равна той части мощ-
ности каждой из боковых полос, которая лежит вне действи-
тельной ширины полосы и усилена на 23 дб. Таким образом,
мощность сигнала в Дан Дь (100% в каждом случае) сравни-
вается с частями мощности, достигающими детекторов Дх и До
(0,5% в каждом случае).
Сумма изменений частоты, производимых генераторами Gx и
G2, получаемая на преобразователе 2И3, соответствует действи-
тельной ширине полосы. Её можно отсчитывать непосредствен-
но по шкале S резонансного контура О, который при помощи
ручки настраивается на максимальное показание вольтметра V j.
Шкала S измерителя ширины полосы, соответствующая измене-
нию ёмкости переменного конденсатора, калибрована от 0 до
5250 гц. Такие пределы достаточны для измерения ширины по-
лосы, занимаемой излучением при обычных скоростях телегра-
фирования.
Измеряют следующим образом. После присоединения при-
бора к приёмнику и включения питающих напряжений приём-
ник настраивают на слух на частоту измеряемого сигнала. За-
тем в приёмнике устанавливают такой уровень сигнала, посту-
пающего в прибор, чтобы стрелка вольтметра Vf отклонилась
к крайнему правому делению шкалы. При этом переключатели
Ра и Рь установлены в положение 2. Как видно из скелетной
схемы рис. 14.6, если переключатели Ра и Рь находятся в по-
ложении 2, то сигнал не поступает на детекторы Дх и Д2; к де-
текторам же Да и Дь он подводится, вследствие чего реактив-
ные лампы изменяют частоту генераторов G{ и G2, так, что раз-
ность между частотами этих генераторов и промежуточной ча-
стотой приёмника увеличивается. В результате калибровки гене-
раторы Gi и G2 оказываются настроенными соответственно на
частоты 105 и 95 кгц. При точной настройке приёмника на ис-
224
следуемый сигнал показания вольтметра Vs одинаковы при
обоих положениях переключателя Ps.
После настройки приёмника и калибровки измерителя мож-
но приступить к измерениям. Переключатели Ра и Рь ставят
теперь в положение 1, резонансный контур О настраивают на
максимальное показание вольтметра Vj, и действительную ши-
рину полосы отсчитывают непосредственно по шкале S. '
Третий метод измерения ширины полосы излучения со-
стоит в делении всей занятой полосы на узкие полосы примерно
по 100 гц, причём для каждой из узких полос предусматривает-
ся узкополосный фильтр; выход каждого из фильтров подклю-
чается либо постоянно к отдельному измерительному прибору, ли-
бо автоматически поочерёдно к общему измерительному при-
бору.
Годной
1-й
фильтр
1-и
- выпрями
тель
. ....-in <.« u ТГ-
цсили- - - фильтр - йыпряпи
тель ---------- тель
2-й
27-й
27-й
фильтр тель
Делитель
гтз
{накопляю-
щий/Мен-
I сатор
| 2>-fl ‘
шкопляю-
Щийнонден-
I сатор
Генератор^—\модулятор
3000герц . i .
Полосойой
Источник,
постоянного
напряжения
фильтр
[выпрямитель]
Рис. 14.7. Третий метод ширины полосы излучения. Скелетная схема
прибора
Принцип действия прибора поясняется рис. 14.7. Исследуе-
мое напряжение через усилитель подают на параллельно вклю-
чённые узкополосные фильтры (в данной схеме число'их равно
27), которые охватывают полосу частот от 40 гц до 16 000 гц. Вы-
ходные напряжения фильтров через выпрямители подводят к
накопляющим конденсаторам и поочерёдно передают переклю-
чателем на модулятор, где выходные напряжения модулируют
напряжение генератора частоты 3000 гц и, таким образом, пре-
образовываются в переменные напряжения. Благодаря этому
на экране осциллоскопа спектр частот получается в виде линий
различной высоты, что удобно для наблюдения. Полосовой
фильтр, настроенный на частоту 3000 гц, задерживает мешаю-
15—730 225
щие гармоники. Выпрямитель служит для того, чтобы луч на
экране трубки отклонялся только вверх, а не вниз.
Механически связанные переключатели Pi и Р2 приводятся
в движение мотором. Переключатель Р2 снимает с делителя
скачкообразно изменяющееся 'постоянное напряжение, так что
подключению к трубке определённого фильтра соответствует оп-
ределённое напряжение на пластинах горизонтального отклоне-
ния (ось X). Поэтому напряжения тональной частоты, соответ-
ствующие отдельным фильтрам, изображаются рядом вертикаль-
ных линий различной длины, расположенным на оси развёртки.
Каждая линия повторяется приблизительно 20 раз в секунду,
поэтому глаз воспринимает картину, как неподвижное изображе-
ние спектра частот. Этот метод пригоден главным образом для
исследования непериодических сигналов, например, телефонных
передач.
В соответствии с рекомендацией МККР [Л40], при измерени-
ях ширины полосы необходима следующая точность.
Периодические сигналы класса А1 (телегра-
фия с амплитудной м а н ипу л я цией). При первом
методе измерения используют лабораторную аппаратуру и аппа-
ратуру с автоматической развёрткой. Лабораторную аппаратуру
можно применять при стабильной амплитуде и частоте испыту-
емых сигналов. Амплитуды измеряют калиброванным аттенюа-
тором с отсчётом относительно постоянного уровня; частоты из-
меряют частотомером. При достаточной стабилизации ампли-
туды и частоты точность измерений зависит только от точности
аттенюатора и частотомера. При измерениях амплитуды можно
достигнуть погрешности не более ±1%, однако практически
можно допустить погрешность ±5%.
При применении аппаратуры с автоматической развёрткой,
если скорость развёртки частоты достаточно мала, то можно
полностью использовать высокую избирательность фильтра. Бла-
годаря этому амплитуды компонентов, близких к несущей ча-
стоте, могут быть измерены с точностью ±2 дб, а амплитуды
удалённых компонентов — с меньшей точностью, особенно при
узком фильтре и небольшой скорости передачи.
Точность измерения отклонений частоты зависит от линейно-
сти развёртки и от ширины исследуемой полосы. Однако в слу-
чае периодических сигналов расстояние по частоте между ком-
понентами известно, если известна величина скорости передачи.
Точность аппаратуры, применяемой при втором методе из-
мерения, зависит от точности измерения отношения мощностей
и от крутизны скатов кривой затухания фильтра высоких частот.
Погрешность измерения отношения мощностей составляет при-
мерно ±0,1%. Ошибки, вносимые фильтрами, зависят от типа
используемых фильтров.
226
В аппаратуре, применяемой при третьем методе измерения,
можно обеспечить погрешность порядка ±1%, если частоты ком-
понентов приблизительно соответствуют средним частотам филь-
тров.
Периодические сигналы класса F1 (телегра-
фия с частотной манипуляцией). При измерениях
спектров сигналов типа F1 могут быть достигнуты те же точно-
сти, что и при измерениях спектров сигналов типа А1. По реко-
мендации МККР аппаратура, применяемая при анализе спект-
ров передатчиков, работающих в диапазоне средних и коротких
волн, действующая по первому методу, должна иметь следую-
щие характеристики.
Ширина полосы фильтра устанавливается в зависимости
главным образом от характеристик исследуемого сигнала. Она
должна быть мала по сравнению с шириной измеряемого спект-
ра; желательно, чтобы ширина полосы фильтра в статическом
режиме не превышала 25 гц. Частотная характеристика затуха-
ния фильтра должна иметь крутые скаты до затуханий порядка
60 дб-
Развёртка должна быть достаточно медленной, чтобы кривая
реакции фильтра по возможности приближалась к статической
характеристике. Допустимая величина скорости развёртки зави-
сит главным образом от ширины полосы анализирующего фильт-
ра. (Для фильтра с шириной полосы 10 гц допустимая скорость
развёртки обычно меньше 100 гц в секунду.)
Область измеряемых частот должна охватывать достаточно
удалённые компоненты спектра, которые желательно измерить.
Представляется, что достаточна максимальная развёртка до
30 кгц. Для анализа узкополосных передач развёртка должна
быть уменьшена до 1 кгц.
Аппаратура должна позволять измерять компоненты, ампли-
! туды которых различаются по крайней мере на 60 дб. Можно
раздельно измерять большие и малые компоненты калиброван-
/ ным аттенюатором или калиброванной шкалой осциллоскопа.
Стабильность частоты генераторов, входящих в схему при-
бора, должна быть такова, чтобы общий уход частоты за время
измерений был мал по сравнению с эффективной разрешающей
способностью фильтра.
: § 14.2. ОПРЕДЕЛЕНИЕ УРОВНЕЙ ДЛЯ ИЗМЕРЕНИЯ ШИРИНЫ
ПОЛОСЫ ЧАСТОТ, ЗАНИМАЕМОЙ РАДИОТЕЛЕГРАФНЫМИ
ИЗЛУЧЕНИЯМИ
Чтобы определить действительные значения ширины полосы
, излучения в тех случаях, когда измеряют по первому методу,
15* 227
необходимо знать численные значения уровней на краю полосы
частот, содержащей 99%; излучаемой мощности. Ниже рассчи-
таны значения этих уровней для случаев амплитудной и частот-
ной манипуляции.
Для амплитудной манипуляции прямоугольными сигналами
мы уже получили из ф-лы (6.12) значение компонента на краю
полосы п=21. Поэтому уровень на краю полосы, занимаемой из-
лучением, будет
Рис. 14.8. Уровень на краю полосы ча-
стот, содержащей 99% излучаемой мощ-
ности, при передаче прямоугольных пе-
риодических частотно-модулированных
сигналов
полосы частот, содержащей
99%
tf,56=101og10 —=
\ тс2 }
“101оЧ^)=~36’4Ж-
\ ** XI /
(14.1)
Если форма сигналов не
прямоугольна, то уровни
для определения ширины
полосы, занимаемой излуче-
нием, можно определить
подобным же методом.
В табл. 14.1 приведены рас-
считанные и полученные
экспериментально значения
уровней для сигналов раз*
личных форм.
Для прямоугольных сиг-
налов при частотной мани-
пуляции пгй компонент
спектра можно определить
из выражения (6.30). На
рис. 14.8 показан рассчитан-
ный таким путём график из-
менения уровня N на краю
излучаемой мощности при
передаче прямоугольных частотно-манипулированных сиг-
налов, в зависимости от индекса манипуляции. На рисунке
N, дб=10 1g nf , где «1 — крайний компонент полосы частот,
содержащей 99% 'изучаемой мощности; D — девиация; В—ско-
рость манипуляции в бодах; т=~£--------индекс модуляции.
Уровень рассчитан по отношению к немодулированной несущей,
П1 — определён из соотношения
— — sin2
ж та .
Л«1
те “р1
sin(n^m) —
X
л2 — т2
0,99
2
228
ТАБЛИЦА 14.1
Уровень на краю полосы частот, содержащей 99% излучаемой мощности
(амплитудная манипуляция)
№ пп. Форма сигнала Уровень ниже неманипули- рованной несущей, который соответствует ширине Г полосы, занимаемой излучением {дб} 1римечание
1 прямоугольный J L —36,4 Расчёт- ные зна- чения
2 3 Трапецеидальный j>T,4 —30,8 —25,0
4 5 С носинуС'кбадратным скруглением LLd т- Lt -J —29,7 -21,3
229
Продолжение
Уровень ниже неманипули-
рованной несущей, который
соответствует ширине
полосы, занимаемой
излучением (дб)
от —34 до —30
от —30 до —25
Примечание
Экспери-
менталь-
ные зна-
чения
График рис. 14.8, так же, как и данные табл. 14.1 можно ис-
пользовать для отсчёта уровней при измерениях.
§ 14.3. ДИСТАНЦИОННЫЕ ИЗМЕРЕНИЯ ШИРИНЫ ПОЛОСЫ ЧАСТОТ,
ИЗЛУЧАЕМОЙ РАДИОПЕРЕДАТЧИКАМИ
Результаты измерений ширины полосы излучения, произве-
дённых в непосредственной близости от передатчика, часто силь-
но отличаются от результатов измерений, произведённых в зна-
чительном отдалении от него. Причиной этого являются труд-
ности, возникающие при дистанционных измерениях, вследствие
чего точность таких измерений значительно снижается.
Между тем следует отметить, что дистанционные измерения
на контрольных станциях во многих случаях весьма желатель-
ны, поскольку они позволяют централизованно контролировать
большую группу передатчиков. Поэтому ниже рассматриваются
особенности условий дистанционных измерений, методы, кото-
рые могут быть использованы для этой цели, и желательные ха-
рактеристики измерительных устройств.
Дистанционные измерения ширины полосы контрольными
станциями во многом отличаются от измерений вблизи передат-
чика:
1) Излучение может часто наблюдаться при наличии помех
"от других станций и шумов и искажаться глубокими и частыми
замираниями, в том числе и селективными.
230
2) Контрольные станции должны наблюдать на всех часто-
тах, которые относятся к сфере их действия, за. большим коли-
чеством различных передатчиков многих служб с разнообразны-
ми видами излучения. Это требует большей гибкости и мобиль-
ности оборудования, чем при наблюдении лишь одного пере-
датчика.
3) Наблюдатель не может управлять временем начала рабо-
ты, её продолжительностью или видом излучения; он ограничен
тем, что измеряет такой сигнал, какой он принимает, и в то вре-
мя, 'пока идёт передача. Поэтому измерять нужно быстро; в
случаях сомнений или неуверенности оператор часто бывает ли-
шён возможности повторить измерения.
Вопреки этим трудностям, связанным с выполнением измере-
ний в точке, удалённой от передатчика, очень часто контроль-
- ные станции удовлетворительно анализируют излучаемый спектр
и измеряют ширину полосы излучения. Объясняется это в зна-
чительной степени тем, что окончательная цель измерений, про-
изводимых контрольными станциями, обычно отличается от це-
’ пи измерений вблизи передатчика. Измерения, производимые
контрольными станциями, предназначены в первую очередь для
надзора и контроля; цель их — определить, совпадает ли излу-
' чаемый спектр с установленными нормами, и если не совпадает,
то какова амплитуда и протяжённость спектра, существующего
. вне назначенной полосы. Анализ спектра, производимый вблизи
; передатчика, обычно преследует более широкие цели.
Рассмотрим основные причины, ограничивающие точность из-
мерений на контрольных станциях.
Получаемая точность ограничивается стабильностью частоты
; передатчика и точностью измерения частоты в анализаторе ча-
стотного спектра.
При анализе спектра важно точно определить относитель-
ный уровень отдельных компонентов спектра по отношению к
уровню компонента, имеющего максимальный уровень. Поэто-
му точность измерения этих уровней сильно влияет на точность
измерений ширины полосы. *
Помехи обусловливают предел, ниже которого измерения не-
возможны или дают неуверенные результаты. Таким образом,
этот предел лимитирует количество передатчиков, которые конт-
L рольная станция может наблюдать удовлетворительным обра-
зом. Характер и величина ошибки измерений, которая вызы-
4, вается помехами, зависит от используемого метода измерений и
соотношения между уровнями сигнала и помехи. Это соогноще-
; ние может изменяться ото дня ко дню, от сезона к сезону и за-
висит от глубины замираний, существующих во время наблю-
- дения сигнала.
231
Селективные замирания также могут влиять на предел точ-
ности, с которой можно измерять амплитуду наблюдаемого
спектра. Поскольку можно предполагать, что в течение длитель-
ного периода времени величина замираний на всех частотах из-
лучаемого спектра будет одна и та же, то. основная часть оши-
бок, происшедших вследствие селективного замирания, может
быть усреднена, если измерять в течение достаточно продолжи-
тельного периода времени. Трудности возрастают при увеличе-
нии ширины спектра. Однако широкие спектры излучаются боль-
шей частью в области частот свыше 50 Мгц, где селективные за-
мирания не являются определяющим фактором. Но при часто-
тах свыше 50 Мгц может быть разница в распространении ча-
стот, находящихся внутри широкой измеряемой полосы.
Если рассматривать в качестве ограничивающего фактора
точность самого анализатора, то, чтобы определить ошибку,
свойственную этому прибору, нужно наблюдать сигналы с изве-
стным спектром. Практически применим анализатор, который
различает в пределах .10%'' измеряемой амплитуды сигналы, от-
дельные компоненты спектра которых расположены с интерва-
лами, не меньшими, чем принятая разрешающая способность
фильтра.
Спектр излучения, с которым приходится иметь дело на конт-
рольных станциях, может изменяться по ширине от нескольких
герц до 6 Мгц в зависимости от используемого излучения и несу-
щей частоты. Если наблюдения ограничиваются каналами радио-
спектра при частотах ниже приблизительно 50 Мгц, то можно
считать, что большинство встречающихся сигналов будет иметь
ширину полосы, меньшую, чем примерно 25 кгц. Если контроль-
ным' станциям приходится измерять ширину полосы на более вы-
соких частотах, то ширина излучаемой полосы частот может до-
стигать 6 Мгц и более.
Описанные выше три метода измерения ширины полосы при-
менимы также и для измерений на контрольных станциях (т. е.
в точках, удалённых от передатчика). Ни один из этих методов
не может быть признан наилучшим при всех обстоятельствах
при использовании на контрольных станциях.
Первый метод имеет то преимущество, что он позволяет
легко и быстро измерять в широком диапазоне частот. На осно-
ве этого метода можно легко создать прибор, сочетающий в себе
переменную область измеряемых частот, ручную и автоматиче-
скую развёртки и переменную разрешающую способность анали-
затора. Можно также получить удовлетворительный амплитуд-
ный диапазон и свести к минимуму действие помех. Использова-
ние электронно-лучевой трубки обеспечивает быструю и чёткую
индикацию. Однако большие скорости развёртки, необходимые
для индикации случайных и неповторяющихся компонентов
232
спектра, получаются ценой уменьшения разрешающей способ-
ности. Тем не менее может быть получен практический ком-
промисс этих параметров и создан практически пригодный
прибор.
Второй метод имеет то преимущество, что он позволяет
непосредственно измерять ширину полосы, содержащей 99% из-
лучаемой мощности. Измерительный прибор получается сравни-
тельно простым и дешёвым. Однако этот метод уступает другим
методам по чувствительности к помехам и по возможности из-
мерять спектры разной ширины и при разных видах работы.
Точно так же точность, получаемая при измерениях в условиях
замираний, значительно уменьшается. Поэтому второй метод ог-
раниченно применяется на контрольных станциях.
Третий метод анализа спектра требует подключения ис-
следуемого сигнала к большому количеству фильтров, что, с од-
ной стороны, усложняет и удорожает устройство, а с другой
стороны, ограничивает выбор допусков, необходимых для дости-
жения соответствующей точности. Изменять область измеряе-
мых частот и разрешающую способность можно весьма ограни-
ченно и лишь путём значительного усложнения и без того слож-
ного устройства. Однако поскольку анализируют одновременно
многими фильтрами, то выполняют это быстрее, а результаты
анализа не искажаются переходными процессами. Благодаря
этому облегчается индикация неповторяющихся компонентов
спектра.
Из предыдущего обсуждения можно заключить, что измери-
тельное устройство, пригодное для использования на контроль-
ных станциях, должно обладать по крайней мере следующими
характеристиками.
1. Лёгкость и быстрот^ действия. Поскольку долж-
ны контролироваться передатчики, действующие в течение раз-
ного времени и в разных диапазонах частот, причём сигналы на-
блюдаются при различном уровне помех, то потеря времени
при переходе от наблюдения одного сигнала к наблюдению дру-
гого и время самого измерения должны быть наименьшими. На-
до отметить, что это требование не всегда легко соблюсти. С од-
ной стороны, желательно, чтобы индикация спектра производи-
лась одновременно с приёмом сигнала. С другой стороны, что-
бы успеть выбрать наиболее благоприятное время для испыта-
ний ,в зависимости от условий распространения и помех от дру-
гих станций и чтобы иметь достаточно времени для получения
спектра из временной функции и для точного измерения шири-
ны полосы, запись сигнала и измерение ширины полосы должны
быть разделены во времени. При этом сигнал может записывать
оператор на контрольной станции, а измерять ширину полосы
можно в централизованном порядке в лаборатории.
23»
2. Широкий диапазон , частот. Очевидно, что чем
шире диапазон частот, охватываемый прибором, тем меньше по-
требуется измерительных устройств. Ширина диапазона частот
определяется приёмником, который должен быть достаточно
высокого качества. Опыт показывает, что такие приёмники мо-
гут перекрывать достаточно широкую область частот, вплоть до
50 Мгц.
3. Минимальная область измеряемых частот.
Эта область связана с шириной полосы частот, разворачиваемой
перед анализатором. Как указывалось выше, ширина полос,
встречающаяся при контроле большого числа излучений и
служб, сильно различается между собой. Для сохранения макси-
мальной разрешающей способности в каждом из измерений же-
лательно, чтобы область измеряемых частот была бы не больше,
чем это необходимо для расположения на частотной шкале же-
лаемой части спектра. Этими соображениями определяется мини-
мальное значение области измеряемых частот (1 кгц).
В диапазоне частот меньше приблизительно 30 Мгц наблю-
дают спектры, ширина которых не превышает 25 кгц. Если ис-
следуют также компоненты внеполосного излучения, то жела-
тельно, чтобы величина развёртки превышала величину ширины
полосы в 3—4 раза; тогда максимальная величина развёртки
будет составлять 100 кгц.
При измерениях на частотах свыше 30 Мгц могут встречать-
ся сигналы, занимающие значительно более широкие полосы
частот. Спектр таких излучений может потребовать максималь-
ных величин развёртки, превышающих 6 Мгц. Для наблюдения
в деталях отдельных частей спектра таких широких излучений
желательно, чтобы минимальная величина развёртки была по-
рядка 10 кгц. о .
4. Переменная скорость развёртки. Чтобы мак-
симально использовать анализатор, скорость развёртки должна
быть переменной. Максимальная скорость развёртки ограничи-
вается необходимой величиной наибольшей развёртки и разре-
шающей способностью анализатора. Может потребоваться из-
менять скорость ют одной развёртки в 60 сек до 10 развёрток в
1 сек.
Если в качестве индикатора используют электронно-лучевую
трубку, то послесвечение её экрана будет играть значительную
роль в определении наименьшей скорости развёртки.
Оптимальную скорость развёртки определяют компромис-
сом между характеристиками спектра излучения и анализато-
ра. Малые скорости развёртки позволяют более детально иссле-
довать данный спектр, но увеличивают вероятность того, что пе-
реходные процессы и неповторяющиеся явления не будут об-
234
наружены. Большие скорости развёртки уменьшают точность
наблюдения амплитуды и разрешающую способность прибора.
Предпочтительны анализаторы, которые сочетают переменную
скорость развёртки (при максимальных и минимальных преде-
лах, определённых выше) с удовлетворительной разрешающей
способностью и точностью.
5. Остановка автоматической развёртки. Что-
бы можно было исследовать отдельные части спектра при по-
мощи ручного управления, необходимо предусмотреть оста-
новку автоматической развёртки.
6. Переменная разрешающая с п ос о б н ос ть. Под
разрешающей способностью понимают способность анализатора
отделять или различать два соседних сигнала или компонента
спектра; так как требования, предъявляемые к анализатору, ме-
няются в процессе работы контрольных станций, то разрешаю-
щая способность прибора должна быть регулируемой. Благо-
даря этому можно выбрать оптимальную скорость развёртки и
достаточно точно воспроизвести амплитуду. Разрешающая спо-
собность около 50 гц на уровне —60 дб может считаться жела-
тельной для анализаторов, используемых при частотах ниже
30 Мгц.
7. Соответствующий амплитудный диапазон.
Диапазон амплитуд должен быть таким, чтобы в приёмное уст-
ройство и анализатор не вводилась бы нелинейность, которая
может повлечь за собой появление ложных спектральных ком-
понентов или искажения относительных амплитуд истинных
компонентов. Практически достижим без особых трудностей ди-
намический диапазон около 60 дб.
8. Относительная нечувствительность к по-
мехам. Как указывалось выше, помехи очень затрудняют из-
мерение спектра излучения в точках, удалённых от передатчика.
Помехи можно разделить на две большие группы: а) помехи от
других передатчиков, работающих в тех же или близких кана-
лах; б) атмосферные и индустриальные помехи. Для удовлетво-
рительного результата измерений нужно исключить или компен-
сировать оба вида помех.
Меры для уменьшения и исключения помех от других пере-
датчиков обычно рассматривают как внешние по отношению к
самому анализатору. К таким мерам относится, например, ис-
пользование направленных приёмных антенн. Однако, если
спектры желательного и мешающего сигналов располагаются
близко по шкале частот, то анализатор должен разделить их
между собой.
Анализатор должен быть спроектирован таким образом,
чтобы помехи, попадающие на его вход, не производили бы лож-
ной индикации интенсивности спектральных компонентов. Такая
235
ложная индикация может возникнуть, например, вследствие пе-
рекрёстной модуляции внутри анализатора между желательным
и мешающим сигналами.
9. Соответствующий индикаторный прибор.
При дистанционных измерениях нужна быстрая индикация. Наи-
более предпочтительным индикаторным прибором является
электронно-лучевая трубка с послесвечением. Спектр можно
сфотографировать на экране трубки.
В заключение следует подчеркнуть, что поскольку спектры
измеряют на контрольных станциях в условиях замираний и при
наличии помех от других станций и шумов, то особенно важно
измерять быстро и оперативно. Если уровень сигналов достато-
чен для перекрытия уровня помех, то, используя существующие
методы измерения и измерительные приборы, можно получить
точность измерений, сравнимую с той, которая получается вбли-
зи передатчика.
§ 14.4. ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ ПО ЭКСПЕРИМЕНТАЛЬНОМУ
ОПРЕДЕЛЕНИЮ ШИРИНЫ ПОЛОСЫ, ЗАНИМАЕМОЙ
ПЕРЕДАЧЕЙ СЛУЧАЙНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ СИГНАЛОВ
При исследовании спектральным анализатором спектра, по-
лучаемого при передаче случайной последовательности сигналов,
показания индикаторного прибора обычно колеблются во вре-
мени. Поэтому возникает вопрос, какие из показаний должны
учитываться при определении ширины полосы, занимаемой пере-
дачей.
Известно, что если передают сигналы одинаковой формы, но
различной продолжительности, т. е. сигналы, которые подчи-
няются тем же самым законам нарастания и убывания, имеют
одинаковые максимальные амплитуды и отличаются ликпь своей
продолжительностью, то более короткому сигналу будет соответ-
ствовать более широкая полоса. Поэтому, если мы интересуемся
шириной полосы, занимаемой передачей элементарного сигнала
используемого кода, то надо учитывать наибольшие показания
индикаторного прибора. Однако следует всё же выяснить, при
каких условиях эти показания достигнут тех же значений, что и
для периодических последовательностей сигналов. Исследова-
ния, которые здесь не приводятся, показывают, что если есть
последовательность одинаковых сигналов, то чтобы достичь с
большой точностью стационарного состояния, которое соответ-
ствовало бы передаче периодических сигналов, необходимо вре-
мя:
236
где F — ширина полосы фильтра спектрального анализатора,
выраженная в герцах.
Если, например, ширина полосы фильтра спектрального ана-
лизатора F=10 гц и скорость передачи В=20 бод, то, чтобы
установить показания индикаторного прибора, нужно иметь по-
следовательность сигналов:
п — Т В— — — 2'2Q_ 4 сигнала
F F 10
Следовательно, если в передаваемом тексте встречаются до-
статочно длинные последовательности элементарных сигналов
(в рассматриваемом примере не менее четырёх), то при переда-
че этих сигналов будет максимальное показание индикаторного
прибора, соответствующее спектру элемента сигнала исполь-
зуемого кода.
Если передаваемый текст не содержит достаточно длинных
последовательностей одинаковых сигналов, то получаемая ши-
рина полосы будет меньше, чем определённая ранее. Другие
комбинации сигналов будут недостаточными для нахождения
предельных значений,, соответствующих спектру периодических
сигналов.
Очевидно, что при использовании, например, кода Морзе
большинство обычных текстов (кроме цифровых) содержит не-
большое количество последовательностей необходимой длитель-
ности для достижения предельной кривой. Поэтому время наб-
людения должно быть достаточно длительным, а полоса фильт-
ра анализатора возможно более широкой.
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ I
ШИРИНА ПОЛОСЫ, НЕОБХОДИМАЯ ДЛЯ РАЗЛИЧНЫХ
КЛАССОВ ИЗЛУЧЕНИЙ
При составлении таблицы применены следующие обозначения:
Вп — необходимая ширина полосы, гц;
В — телеграфная скорость, бод;
N — максимально возможное число белых и чёрных элементов, передавае-
мых в секунду, при факсимиле и телевидении;
М — максимальная частота модуляции, гц;
С — поднесущая частота гц;
D —'половина разности между максимальной и минимальной величинами
мгновенной частоты. Мгновенная частота — это скорость изменения
фазы;
t — продолжительность импульса, сек;
К —общий числовой коэффициент, меняющийся при излучении; он зависит
от допустимого искажения сигнала.
Таблица П.1.1
Описание и класс излучения Необходимая ширина полосы, гц Примеры и пояснения
Телеграфия незатухаю- щими колебания (А1) I. Амплитудная модуляция Вп = ВК, К=5 для ли- ний, подверженных зами- ранию, К = 3 для линии без замирания Код Морзе, 25 слов в минуту, В = 20, К = 5, Вп— 100 гц. Для четырёх- канальной временной мно- гократной системы с се- мизначным кодом при 42,5 бода на канал В=170, К= =5; ширина полосы, 850 гц
Тональная телеграфия (А2) ВЛ=ВК^-2М, К=5для линий, подверженных за- миранию, К=3 для лийий без замирания Код Морзе, 25 слов в минуту, В=20, М= 1000, К=5, Вл=2100 гц
Телефония (АЗ) Вп=М — для передачи на одной боковой полосе, Вп=2М—для передачи на двух боковых полосах Для однополосной теле- фонии при пониженной несущей М = 3000, Вп = =3000 гц. Для телефонии на двух боковых полосах М=3000 гц, Вп=6000 гц. Для телефонии на двух независимых боковых по- лосах М = 3000, вп = =6000 гц
238
Продолжение
Описание и класс излучения Необходимая ширина полосы, гц Примеры и пояснения
Радиовещание (АЗ) Вп = 2М, М= 40004- -4-10 000 в зависимости от желаемого качества Речь и музыка, М = =4000, В„=8000 гц
Факсимиле, несущая частота модулирована зву- ковой частотой и манипу- лирована (А4) Bn=KN+%M, К=1,5 N равно окружности ба- рабана, умноженной на число линий, приходящих- ся на единицу длины и на скорость вращения бара- бана, в оборотах в секун- ду. Диаметр барабана — 70 мм, число линий на миллиметр — 5, скорость вращения барабана — 1 оборот в секунду, N = = 1100, М = 1900, Вп = = 5450 гц
Телевидение (передача изображения и звукового сопровождения) (А5 и F3) Изменяется в зависимо- сти от принятой системы телевидения Число строк—625, число строк в секунду— 15 625, Вп видеосигнала— 5 Мгц. Общая ширина полосы сигналов изображения — 6,25 Мгц. Ширина полосы излучения ЧМ звукового сопровождения, включая защитную полосу частот, —0,75 Мгц, общая шири- на полосы—7 Мгц
II. Частотная модуляция
Частотная (F1) телеграфия Вп =2,60-4-0,5£>В 2D для 1,5 < — < 5,5; Вп = 2,1D4" 1,9В 2D для 5,5 <— < 20 В Четырёхканальная вре- менная многократная си- стема с семизначным ко- дом, 42,5 бода на канал; В = 170, D =200, 2D -^-=2,35, поэтому Вл= =2,6Р-Н),55В=613 гц
Частотная (F3) телефония Вп = 2М 4- 2DK. Нор- мально К = 1, но иногда необходимы более высо- кие значения К Для средних условий частотной телефонии D = = 15 000, М = 3000, Вл=36 000 гц
239
Продолжение
Описание и класс излучения Необходимая ширина полосы, гц Примеры и пояснения
Радиовещание (F3) B„ = 2M^-2Dtf D=75000, /И=15000, при /<=1 £„=180000 гц
Факсимиле (F4) Bn=KN^2M+2, /<=1,5 (См. факсимиле, ампли- тудная модуляция). Диа- метр барабана — 70 мм, количество линий на мил- лиметр—скорость вра- щения—'! оборот в секун- ду, W = 1100, М = 1900, D=10000, Вп=25 450 гц
Двойное частотное те- леграфирование (ДЧТ)(Р6) / [ Если каналы не синхрони- зированы, то Вл=2,6£-ф- 4-2,75В, причём В озна- чает скорость канала, имеющего наибольшую скорость. Если каналы синхронизованы, то шири- на полосы такая же, как для F1, причём В озна- чает скорость любого из обоих каналов Система ДЧТ с разно- сом между частотами в 400 гц, каналы не син- хронизованы, при манипу- ляции в 170 бод в каж- дом канале, D=600, В = =170, Вл=2027 гц
III. Импульсная модуляция
Немодулированные им- пульсы (РО) о п „ Вп =2 д зависит от отношения длительности импульса ко времени на- растания импульса; 1<К< ю При t = 3-10—с, К=6, £„=4-10е гц
Модулированные им- пульсы (Р2 или РЗ) Вп зависит от типов применяемой модуляции, многие из которых ещё разрабатываются
ПРИЛОЖЕНИЕ II
ПРИВЕДЕНИЕ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ К КРАЕВОЙ
ЗАДАЧЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
Покажем, что интегральное ур-ние (2.37)
+1
С sin k (X — v)
^(Х) = н' ----./ (П.П.1)
J 7С (X--V)
— 1
приводится к краевой задаче дифференциального уравнения типа Лиувилля.
Рассмотрим следующее однородное линейное дифференциальное уравнение
dr dU(X)l
Dxt/(X)= — (X’-D—^U(AX)’l/(X) = Cl/(X), (П.П.2)
dk [ ok J
где C — постоянный действительный параметр, называемый обычно констан-
той разделения.
Уравнение (П.П.2) — самосопряжённое уравнение типа Лиувилля. Оно
обладает решениями а (%), отличными от нуля, дважды дифференцируемыми и
ограниченными в интервале —1 < X < -М, только для некоторых дискрет-
ных значений С/ константы разделения С. Соответствующие решения
Ul (М будем называть далее ограниченными решениями дифференциально-
го ур-ния (П.П.2).
Известно [Л36, § 6.3)] что дискретные значения С/ можно пронумеровать
в возрастающем порядке, начиная от наименьшего значения Со и что огра-
ниченные решения ил(%), соответствующие константе разделения номера п,
в наиболее часто встречающихся случаях обладают п нулями в интервале
-4 <%< + !. '
Если un(k) является частным решением дифференциального ур-ния
(П.П.2), то общий интеграл этого дифференциального уравнения, будет
х п
,.С
а Ф о I------------ ,
J (на-1)[Мр)]2
о
(П.П.З)
где а и b — произвольные постоянные.
Из ф-лы (П.П.З) следует, что все ограниченные решения дифференци-
ального ур-ния (П.П.2), соответствующие одному и тому же значению» Сп
константы разделения С, пропорциональны друг другу и что неограниченные
решения этого уравнения имеют две логарифмические особенности в точках
±1.
С другой стороны, два различных ограниченных решения ур-ния (П.П.2),
соответствующие двум различным значениям Ст и Сп константы разделе-
ния С, ортогональны, так как
(Рт— ^п) J ит (X) Цп (X) dk — j |wOT(X) £(1—X2) ] —
—I —1
-“n(x)4k-xa)^rlldx=o’ (ППЛ)
ал L «А j;
что легко проверить двойным интегрированием по частям.
16—730 241
Наконец, можно доказать [Л.36, § 6.3], что последовательность всех огра-
ниченных решений ур-ния (П.П.2) ц/(X), которые предполагаются нормированными
/ +1 ч
< f [w/(X)]adX=l к образует полную ортонормированную систему. Это значит
I —1 J
что любую функцию U (X), дважды дифференцируемую и ограниченную на зам-
кнутом интервале —1 < Х< ф1, можно представить на этом интервале в виде
абсолютно и равномерно сходящегося ряда
^о)= 2а*и(Х)’ (ПЛЕ5>
/=0
где
+1
az = j l/(X)«z(X)dX.
—1
Покажем, что каждое решение интегрального ур-ния (П.П.1) является
решением дифференциального ур-ния (П.П.2). Для этого сначала докажем
вспомогательное соотношение
-1 -1
где
d Г dU М 1
D.t7(v)= — 0а-1) —U(W)
av [ av j
и U(у) — произвольная дважды дифференцируемая и ограниченная на ин-
тервале —4<v<4-l функция.
Действительно,
+1 +1
С sin£(X — v) ГГ sin £ (X —
— 1 —1
Существует равенство
sin £(X — v) sin k (X — v)
* к (X — v) v z (X — v)
В самом деле,
sinA(X —\) d Г d sin£(X—v)1 sin£(X —v)
Я(Х_,)-----L(X “° dX «(X —v) "J*( "(X-v)
2£Xv x a 2Xv sin £ (X—v) t r2£cos£(X— v)
- - c” 4 (l * .(>->) * .(>_,)
2sin#(X—-v) k2 sin A; (X — v)
7C (X —r v)3 ic (X — v)
(П.П.8)
(П.П.9>
242
Последнее выражение симметрично относительно X и v и, следовательно,
равенство (П.П.8) справедливо. Поэтому равенство (ПЛ 1.7) можно записать
в виде
л f sin£(X—* м) „ t 4 f sin£(X — v)1 rf, x J
D* J J h’^X-v)
—1 — 1
+ 1
P Г sin£(X— v) 1
= J |D, uw • (П.11.10)
— 1
Пусть G(v) и Fi(v) произвольные дважды дифференцируемые и ограничен-
ные на интервале —11<^<-ф1 функции. Тогда можно написать равенство
+1 +1
С d Г dFMl Г d Г dGMl
\ ~Г Ь’-П—Г2 I ^)“Т (va-l) —Г2"\<Ь>, (П.П.11)
J dv I dv J J dv [ dv J
. -1 -1
. - которое проверяется интегрированием по частям его левой и правой частей.
Выпишем и преобразуем левую часть равенства (П.П.6), используя ра-
венство (П.П.10) и (П.П.11)
П+1 ~ sin£(X_v)T„, ч л
D,----3---4t/(v <Ь =
я(Х —v) J
—1
+ 1
nd Г d sin^(X — v)l sin£(X — v) ) r
y v -------------m \ s —n—r u <v)-
dv [ dv те(Х*—v) J 7c(X—-v) J
—1
J dv L dv тс (X v) J J тс (X — v)
> —1 . — 1
f* sinA(X^v) d[ . /f ... .. sinfe(X-v) tt<
= I —7—;—ЗГ 0 — I)-j—'рЧ| (H—7—— t/O)<fr =
J ic(X—*v) dk [ du J J it (a — v)
—1 —1
+1
p sin&(X—(df dU (v) 1 )
- У -"(jL,) (57[<'Л j+WOMp'--
- Г
J к (A—>v)
т. e. в результате преобразований мы получили из левой части (ПЛ 1.6) его пра-
• вую часть и тем самым доказали это равенство.
Теперь докажем, что каждое решение интегрального ур-ния (ПЛ 1.1) яв-
Ш ляется решением дифференциального ур-ния (П.П.2). Пусть (%) — соб-
ственная функция интегрального ур-ния (П.П.1), соответствующая собствен-
ному значению рп, т. е.
’ 16е 243
(П.П.12)
—1
Функция фот (%) является дважды дифференцируемой и ограниченной иа
интервале —1 < X < +1, поскольку ©тим условиям удовлетворяет ядро ин-
тегрального ур-ния (П.ПЛ). Поэтому она удовлетворяет соотношению
(П.П.6), т. е.
(X) = (4 J “
— 1
+ 1
, C sin k (X — v)
= ^J K(X_V) (п.п.13)
Из (П.П.13) непосредственно следует, что Dx (%) является собствен-
ной функцией интегрального ур-ния (П.П.1). Следовательно, Dx Ф™ (X) и фот(Х)
пропорциональны, т. е.
Фт (X) = (X),
где Ст — коэффициент пропорциональности, зависящий от tn.
Последнее выражение показывает, что (%) является решением диф-
ференциального ур-ния (П.П.2).
Таким образом, Mbf доказали, что каждая собственная функция ядра
sin£(X — v) J
----------- является ограниченным решением дифференциального ур-ния
тс (X v)
(П.П.2), соответствующим некоторому значению Ст константы разделе-
ния С. z
ПРИЛОЖЕНИЕ III
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ dn
Полиномы Лежандра Рп (Ь) определяются равенствами
1 dn(\* — 1)л
(П.ш.1)
и удовлетворяют соотношениям ортогональности
+1 J Pm(X)P„(X)dX = • —1 0 при т п 2 (П.Ш.2) л при m - л 1 2л-ф 1
Для полиномов Лежандра справедливы рекуррентные формулы:
х
(2л<ф1) f РпМ-------Рп-М + Рп+гЮ, (П.Ш.З)
—1
(2л ♦ 1) ХРЯ (X) = n P„_t (X) (n 1) Pn+l (X). (П .111.4)
Полиномы являются решениями дифференциальных уравнений
-^[(X’-l)^^]-n(n4U)/>„(X) = 0. (П.Ш.5)
аК [_ ад J
Подставим в ур-ние (2.38) значение u(kf К) из равенства (2.39), тогда
получим
2 dn [<** - о w 2 dn {k} Рп (Х)" с 2' dn (k} Рп (Х)-
п п п
(П.Ш.6)
Заменим в (П.Ш.6) Г(Ха — 1)^У" I на п(п^1)Рп(к) в соответствии
аК |_ ак J
с (П.Ш.5) и внесём Xs под знак^ ; тогда (П.Ш.6) примет вид
2' dn (k) п (п «ф 1) Р„ (X) 4- 2’ dn (k) W>n (X) = С 2' dn (*) Рп (М- (П.П1.7)
п п п
245
Из соотношения (П.Ш.4) видно, что
<пш»
Умножив обе части равенства (ПЛПи8) на %, получим
(Х) “ 5тЬхр«->(Х) ♦ (Х) р«+1(Х)* (niIL9)
Применив далее ф-лу (П.Ш.8) к и [ХРп+1(Х), получим
хр«->(Х) = 7 р»-2(Х) ♦ 5ГП р"(Х) (П IIL10)
л 1 п 2
хр^ (X)=dhPn(X) Ъ-^Гз Р-*(Х)- <пшп>
Подставим (П.Ш.10) и (П.П1.11) в (П.Ш.9), тогда
w“2тЬр-Ч ♦
»(п—1) р
(2я4-1)(2л—1) я~2
"<Нп ш^2±1р ш =
2п^ЗР” ^2п4-3 Р"+2
(»♦!)* ~
‘ [4Па—1 (2п4* 1)(2п3)
(п4И)(л*2)
Ч2«4-1)(2п4-3) п+2{
п«
РпЮ +
(П.Ш.12)
Заменив в (П.Ш.7) ХЯРП(Х) его выражением из (П.Ш.12) и разбив во вто-
ром члене полученного выражения суцму на отдельные слагаемые, получим
Jk (4) а („ +1) Р, W+Л- Щ'd. (4)(2„"^,)(2’>_,)
п п
♦2
п
ОЧИ)8 ]
42/14-1Х2л 4-3)]
РП(Х)4
* Я dn(k) (2n41)(2«V3j Ря+2(Х) " С S'dn (k) Рп (Х)- (П1П13)
п п
246
Приравняем коэффициенты при РЛ(Х) в (П.III. 13); при этом учитываем,
что в 2 будет входить и РЛ(Х), если вместо п взять (п^2), а в
П '
2 ? п+2 W будет входить Рп (X), если вместо п взять (п — 2). В результате
Л
получим
(*) П (П «И) * И dn+2 (k) *
7 [(2n—l)(2n^3)j (2л — 3)(2n — 1) J \
откуда
Г (n —l)n 2n*4-2n-l (n^l)(n*2) ] =
L(2n — 3)(2n— p n~2 ♦ (2n — l)(2n 4-3) " * (2n 3)(2n 4- 5) n+2 J
= [C — n(n>l)]d„. (П. Ill, 15)
Этой рекурсивной формулой определяются коэффициенты dn(k) при за-
данном С»Со(^) с точностью що произвольного множителя, который удоб-
но выбрать таким образом, чтобы
и(£,0) = Ро(О)=? 1. (П.Ш.16)
При составлении таблиц [Л9] учитывались условия (П.Ш.16), поэтому их
можно использовать, определяя коэффициенты dn.
Чтобы определить коэффициент dn по ф-ле <(П.III. 15), задаёмся d0 из
условий
и (А, X) = и (к, 0) - 2' dn (k) Рп (X) = 2' dn (А) Рп (0) - 1. (П.ш. 17)
п Л
Считая dn известным, подставляем в (П.ШЛ5) n=0; в результате по
лучаем
[1 2
°’dn-2^~rd9-^ —~d9
О 10
= Cd0,
откуда
(П.III.18)
Далее, через do выражают Л, de, de,..;
Подставляя их в (П.П1.17) определяют d0, а вместе с ним и остальные
коэффициенты. Методика определения константы разделения С описана в
с:^[Л9, стр. 15—17].
Ниже приводится таблица коэффициентов dn при различных значени-
ях k.
247
КОЭФФИЦИЕНТЫ dn РАСЧЕТА ФОРМЫ СИГНАЛА и (А, X), СОДЕРЖАЩЕГО
k max W (А) •/• (А) + d. (А) -<*.(*) + d^k)
0 0 1 0 0 0
0,1 6,36 0,00333 0,99945 0,001110 0,00000019
0,2 12,68 0,01331 0,99778 0,004429 0,00000304
0,4 25,02 0,05296 0,99122 0,017532 0,00004802
0,5 30,97 0,08242 0,98637 0,027180 0,00011623
0,6 36,72 0,11810 0,98053 ' 0,38768 0,00023849
0,8 47,53 0,20739 0,96608 0,067281 0,0007339
1,0 57,26 0,31900 0,94837 0,10195 0,0017316
1,2 65,78 0,45073 0,92796 0,14147 0,0034449
1,4 73,07 0,60010 0,90547 0,18446 0,0060801
1,5 76,26 0,68058 0,89363 0,20680 0,0078006
1,6 79,15 0,76447 0,88152 0,22949 0,0098150
1,8 84,10 0,94120 0,85672 0,27526 0,014783
2,0 88,05 1,12773 0,83162 0,32059 0,021062
2,2 ’ 91,14 1,32174 0,80669 0,36450 0,028673
2,4 93,50 1,52117 0,78230 0,40625 0,037582
2,5 94,46 1,62238 0,77040 0,42614 0,042500
2,6 95,28 1,72433 0,75874 0,44531 0,047710
2,8 96,61 1,92986 0,73620 0,48135 0,058940
3,0 97,58 2,13673 0,71480 0,51422 0,071137
3,2 98,28 2,34419 0,69460 0,54392 0,084149
3,4 98,79 2,55172 0,67559 0,57052 0,097824
3,5 98,99 2,65540 0,66653 0,58271 0,10486
3,6 99,15 2,75899 0,65775 0,59419 0,11201
3,8 99,41 2,96581 0,64103 0,61513 0,12657
4,0 99,59 3,17207 0,62537 0,63356 0,14138
4,2 99,72 337775 0,61068 0,64969 0,15631’
4,4 99,80 3,58286 0,69690 0,66376 0,17127
4,5 99,83 3,68521 0,59033 0,67009 0,17873
4,6 99,86 3,78743 0,58396 0,67598 0,18616
4,8 99,90 3,99150 0,57179 0,68654 0,20092
5,0 s 99,94 4,19514 0,56032 0,69561 0,21548
248
Таблица П.П1.1
МАКСИМАЛЬНУЮ ДОЛЮ ЭНЕРГИИ В ЗАДАННОЙ ПОЛОСЕ ЧАСТОТ
+ (k) - di.(*) + dit (£) - rfu (A)
0 О 0 0 0.
0,00000000 0,000000000 .0,000000000 0,000000000 0,000000000
0,00000000 0,000000000 0,000000000 0,000000000 0,000000000
0,00000006 0,000000000 0,000000000 0,000000000 0,000000000
0,00000021 0,000000000 0,000000000 0,000000000 0,000000000
0,00000062 ,0,000000001 0,000000000 0,000000000 0,000000000
0,00000338 0,000000009 0,000000000 0,000000000 p,000000000
0,000012439 0/100000049 0,000000000 0,000000000 0,000000000
0,000035561 0,000000203 0,000000001 , 0,000000000 0,000000000
.0,000085205 0,000000663 0,000000003 0,000000000 /0,000000000
0,00012530 0,000001118 0,000000006 0,000000000 0,000000000
0,00017908 0,000001816 01,000000012 0,000000000 0,000000000
0,00034007 0,000004354 0,000000036 0,000000000 0,000000000
0,00059551 0,000009388 0,000000094 0,000000000 p,000000000
0,00097590 . 0,0000185'58 0,000000225 0,000000002 0,000000000
0,0015133 0,000034127 ‘•0,000000492 0,000000005 .0,000000000
0,0018509 0,000045205 0,000000706 0,000000008 0,000000000
0,0022397 ' 0,000059042 0,000000996 0,000000012 0,000000000
0,0031852 0,000096952 0,000001890 0,000000026 0,000000000
10,0043773 0,00015220 0,000003398 0,000000053 0,000000000
0,0058391 0,00022976 j0,000005815 0,000000103 .0,000000001
0,0075896 0,00033517 0,000009538 0,000000189 0,000000003
0,0085776 0,00040017 0,000012042 0,000000253 0,000000004
0,0096427 0,00047440 0,000015071 0,000000334 0,000000005
0,0120080 0,00065377 0,000023036 0,000000567 0,000000010
.0,014689 0,00087978 0,000034182 <0,000000930 0,00000019
0,017687 0,0011590 0,000049391 . 0,000001476 0,00000033
0,020997 0,0014981 0,000069681 0,000002276 0,00000055
0,022768 0,0016920 0,000082085 0,000002798 0,00000071
.0,024614 0,0019032 0,000096202 0,000003420 0,00000090
0,028526 0,0023806 0,00013023 0,000005019 0,00000143
0,032721 0,0029359 0,00017318 0,000007208 0,00000223
249
ПРИЛОЖЕНИЕ IV
1) A(k) =
ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ A(k), B(k) и C(k)
k
1 sin* 2 * 4 A sin2 A A
(AV? ** d =Sl2k~ A “ 4(A2—d2)
3 lk-±-d cos2d f 3 Г M ,1 cos2(A«^d)
♦ed^lA-d* 8 { d [C12(A-d)-Ci2(A4d)j4 4
4- 4 2 Si (A 4 d) 4 2Si (A — d) } 4 — ~^Si 2 (A 4 d)4
^Si(A-d)]^^in^^)_-Sin;(fe-d)-Ci(A^d)^2Ci(A-d)):
йфа k — a J
k
2) В (k) = p-
1 2sin^sin?A tt 2'sin£sing£
ZW ——dk— I
о
_(l_6)Si(l-6)A^(14.e)Si(l«H)^-M-Ci [(1-6)A4-«14
4a t
4- Ci [(1 — e) A — «] — cos [(14- 6) d] [Ci (1 4 5)(A 4 d) — Ci (1 4 6)(A — d)] —
- sin [(1 4 6) d][Si (14- 6)(* 4 4 Si (1 4 6)(A — d)]j 4
1-6 ( cos[(1-6)A4k] cos[(1 — 6)А —к]
Ae5A4/’4 (i-ejA-K -4Si[(l-6)*4«]4
4 Si [(1 — 6) A — k]| 4 (cos [(14 5М1Г C°h Ltwfe
J 4 ( [ (1 «Нкя-фа)
соз(1фЁ)(& — d)
* * Si (* * Ф rf) Si (I Wk - d) -
.in гл J.Я1Г sin(i>e)(^^d) sin(n>e)(*-d)
45)d][ (i4ex*4<0 * (145)(*-d) +
4Ci(i 4g)(A4-d) — Ci(146)(A—d)
k
3) C(A)= f-:----
4
___sin2^.,- r
2]2 kt dk-t
sin2 £k'
Ik .
о L \ » / J
k 3 I k 4- d I cos 28d ( 3
4тг71п—[Ci2e(A-d)-ci2e(A4>d)H
4$ (ft* — d*) 8l~d | h — d I 05 (a
cos 2£ (k Ф d) cos 2$ (k — d) )
4---;17 4-----A . ' 4 26 [Si 2? (A 4 d) 4 Si 26 (A - d)J 4
йф a «—« J
< S * * В-4F [ - v >si 2 <s *si * <“ - “и -
05 ( d K^>d
- sin^7d) ~25 lCi 26 (ft ♦d) ~Ci 26 (k" ‘Ч) •
те
В интегралах A (k)t В (k) и С (k)d = j—- .
250
ПРИЛОЖЕНИЕ V
ФУНКЦИИ ЛОММЕЛЯ
Рассмотрим дифференциальное уравнение вида:
' V, у-h**', (n.V.l)
где
d
у — искомая функция,
z — аргумент искомой функции,
k и ц — постоянные.
Частным решением ур-ния (II.V.1) является функция вида
Г 2р*+з 1
у “k Lwi)’->a “ [(н-м)’-*а][(^з)’->»] ♦•••]“
(II.V.2
Обозначения (. . .) ж+ j во второй строке равенства (П.У.2) означают
произведение (т+1) множителей, первый из которых равен выражению в
скобках, а каждый из последующих множителей на единицу больше предыду-
щего.
В третьей строке равенства (П.У.2) введена гамма-функция посредством
умножения числителя и знаменателя на
г(т'-4”+т)г(т'*т’*т)' <n-v-2)
Для краткости запишем выражение в правой части (П.У.2) в виде
У = (г)-
25»
Таким образом, вводится функция Ломмеля (z). Эта функция
становится, очевидно, неопределённой, если какое-нибудь из чисел ji±v ока-
зывается нечётным отрицательным числом.
Для функций Ломмеля v(z) справедливы следующие рекуррентные
формулы:
^+2,,(«) = ^+I- «И 4 1)а - *21 ,(г). (TT.V.3)
Далее, легко ^проверить, что
[ z’s^, (г)] = (р 4 * — 1) г- S(1_h (г). (ILV.4)
Действительно, подставим в правую и левую части выражения (II.V.4)
значение
2^+1 2^+3
® = (1,4,1)»-?» ~ [(|Л 4-1)» ->а][(р 4-3)»-?»] '♦’•••’(nV,5)
получающееся из первой строки ф-лы (П.У.2). Подстановка значения
s (z) в левую часть выражения (П.У.4) даёт
d / г, ( г1*'4'*_________________z't+3______ |\ _
dz V Чр41)2-*2 “ • • fj-
d ( г^4”4’1 ^+’+3
= d71 Wl)a-1 “ [(р41)2-*2][(р43)2-?2] * ' ’ ’ J =
_ (р4?4 1)г|х+'' (р 4 * 4 3) z|t+v+2
(р41)2-*2 “ [(р41)а-?2][(р43)2-?2] • •“
2|Х+* 2|х+^+2
р —*4 1 (р4*4 1)(н—*4 1)(р—*43) ‘
Подставив значение в правую часть выражения (П.У.4), по-
лучим
(|» 4 * — 1) г’ 8ц_ J, v_j(z) =
( г9" z9+2 1
= (и тФ- v - 1) ZV \------ -----------------------------? =
1р» - (? - I)2 [р3 - (V - 1)3][(р 4 2)а - (?-!)’] • 7
_ (р4у_ 1)гр+» (р4?—1)г»ч-,4~2__________________________
Ра-(?-1)а — [р»—(? - 1)»][(р 4 2)а—(? — I)2] “
_ (р4?~ 1) г(‘,+'1 __________(^,-1)гмн2_____________________
— (р 4 * — 1)(р 4 •* — О (н 4 * — 1)(и—? 41)(р 4^4 1)(и — *43)
2Р-+* 2|a+v+2
р —*41 (р— *4 1)(м 4 * 41)(|< — *43)^
т. е. .равенство (II.V.4) доказано.
252
Из равенства (FI.V.4) следует, что
vz’-1 (n.V.6)
Разделим обе части равенства »(П.У.6) на zv ; тогда получим
Ч*(г) "7 W v “ 0 Vl. v-i (П.У.7)
и аналогично получается
^,vW —“S|X„vW= (Р —V—1) S|X-I, v+i(2)- (П.У.8)
Вычитая из равенства (П.У.7) равенство (П.У.'8), получаем
2v
— з^(г)= (П.У.9)
Нас интересует частный случай функций $и^(г) (см. гл. 7), при р=0;—1,
т. е* so,v (2) и s—i,v(2)» которые в соответствии с ф-лой [(П.У.5), имеют вид
z ______________2?_______ ___________г?____________
S0,v (2) = р —V2 (p_v2)(3a_v2) (Р— V2)(32 —V2)(52 —v2) * * * ’
(n.V.10)
1 z2 z4
S-l., (z) = — ^2 ^•^2’ —\»)"~va(28 —^)(4a —№) ^ ’ ’ (n-V>11)
В таблицах П.У.1 и П.У.2 даны значения, а па рис. П.У.1 и П.У.2
(см. вклейку) построены графики функций sOtV (z) и s_j v (z), рассчитанные по
ф-лам (П.У.10) и (П.У.П).
В соответствии с выражением (П.У.9) sO v (z) и s_Iv (z) связаны между
собой соотношением
у so,v (г) “О’ — 1)8-1, ,-1 (г) 4-04-1) 8-1, ,+1 (z),
которое облегчает проверку результатов вычислений по ф-лам (П.У.10) и
(П.У.Ш).
253
ФУНКЦИИ
2 0,1 0,2 0,3 0,4 0.5
0,05 —99,93735 —24,98422 —11,10401 —6,24593 —3,99733
0,1 —99,74953 —24,93691 —11,08271 —26,23273 —3,98934
0,15 —99,43688 —24,85815 —11,04726 —6,21343 —3,97603
0,20 —99,00000 —24,74810 —10,99773 —6,18506 —3,95744
0,25 —98,43980 —24,60697 —10,93420 —6,14867 —3,93360
0,30 —97,75702 —24,43502 —10,85680 —6,10435 —3,90455
0,35 —96,95326 —24,23256 —10,76567 —6,05216 —3,87034
0,40 —96,02992 —23,99998 —10,660.98 —5,99220 —3,83106
0,45 —94,98872 —23,73772 —10,54294 —5,92460 —3,78676
0,50 —93,83162 —23,44627 —10,41177 —5,84948 —3,73753
0,55 —92,56078 —23,12617 —10,26770 —5,76697 —3,68348
0,60 —91,17855 —22,77802 -^10,11101 —5,67724 —3,62469
0,65 —89,68756 —22,40249 — 9,94200 —5,58047ж —3,56128
0,70 —88,09055 —22,00026 — 9,66097 —5,47681 —3,49337
0,75 —86,39051 —21,57208 — 9,56828 —5,36648 —3,42109
0,80 —84,59061 —21,11877 — 9,36428 —5,24967 —3,34458
0,85 —82,69418 —20,64114 — 9,14935 —5,12662 —3,36398
0,90 —80,70477 —20,14012 — 8,92390 —4,99755 —3,17944
0,95 —78,62603 —19,61662 — 8,68833 —4,86271 —3,09112
1,0 —76,46187 -^19,07160 — 8,44310 —4,72233 —2,99919
1,05 —74,21623 —18,50609 — 8,18867 -4,57669 —2,90382
1,10 —71,89330 -17,92113 — 7,92549 —4,42606 —2,80519
1,15 —69,49733 —17,31780 — 7,65406 —4,27071 —2,70349
1,20 —67,03277 —16,69720 — 7,37489 —4,11095 —2,59890
1,25 -64,50411 —16,06050 — 7,08847 —3,94706 —2,59890
254
Таблица FIN./
ЛОММЕЛЯ s_j, v (в)
0.6 0,7 0,8 0,9 1,0 1,1 1,2
—2,77587 —2,03937 —1,56134 —1,23360 —0,99917 —0,82571 —0,69376
—2,77015 —2,03501 —1,55785 —1 ,-28070 —0,99667 —0,82249 —0,69173
—2,76063 —2,02776 -1,55205 —1,22588 —0,99251 —0,81980 —0,68835
—2,74733 —2,01762 —1,54395 —1,21913 —0,98670 —0,81463 —0,68362
—2,73028 —2,00463 —1,53355 —1,21048 —0,97925 —0,80801 —0,67756
—2,70949 —1,98879 —1,52089 -1,19994 —0,97018 —0,79995 —0,67018
—2,68503 —1,97016 —1,50599 — 1,18754 —0,95950 —0,79046 —0,66149
—2,65692 —1,94875 —1,48887 —1,17330 —0,94723 —0.77957 -0,25151
—2,62524 —1,92461 —1,46956 —1,15724 —0,93341 —0,76728 —0,64027
> —2,59003 —1,89779 —1,44812 —1,13940 —0,91805 —0,75364 -0,62778
—2,55136 —1,86834 —1,42458 —1,11981 —0,90119 —0,73866 —0,61407
—2,50931 —1,83631 —1,39897 —1,09851 —0,88285 —0,72238 —0,59917
—2,46397 —1,80177 —1,37136 —1,07555 —0,86309 —0,70483 —0,58312
—2,41541 —1,76480 —1,34180 - — 1,05096 —0,84193 —0,68604 —0,56593
-2,36372 —1,72544 —1,31035 —1,02480 —0,81942 —0,66607 —0,54765
—2,30901 — 1,68379 —1,27706 —0,99713 —0,79561 —0,64492 —0,52832
—2,25138 —1,63992 —1,24199 —0,96798 —0,77053 —0,62267 —0,50797
—2,19094 —1,59390 — 1,20523 —0,93743 —0,74425 —0,59935 —0,48665
—2,12781 -1,54585 —1,16685 -0,90552 —0,71681 —0,57501 —0,46410
—2,06210 —1,49584 —1,12690 —0,87233 —0,68827 —0,54969 —0,44127
• —1,99394 —1,44397 —1,08547 —0,83790 —0,65867 —0,52346 —0,41731
—1,92346 —1,39034 —1,04265 —0,80232 —0,62810 —0,49635 —0,39255
—1,85079 — 1,33505 —0,99851 —0,76567 —0,59660 ' —0,46842 —0,36706
t -*—1,77606 —1,27821 —0,95314 —0,72799 -0,56424 —0,43974 —0,34088
—1,69942 —1,21993 —0,90692 —0,68937 —0,53106 —0,41037 —0,31405
255
Продолжение
1,3 1,4 1.6 1.6 ’ 1»7
0,05 —0,59108 —0,50957 —0,44381 —0,38995 -0,34524
0,1 —0,58916 —0,50770 —0,44190 —0,38793 —0,34291
0,15 —0,58597 —0,50458 —0,43874 —0,38454 —0,33902
0,20 —0,58150 —0,50022 -0,43431 —0,37981 —0,33359
0,25 —0,57578 —0,49464 —0,42864 —0,37375 -0,32663
0,30 —0,56881 —0,48783 —0,42173 —0,36638 —0,31816
0,35 —0,56061 —0,47983 —0,41361 —0,35770 —0,30819
0,40 —0,55119 —0,47064 —0,40428 —0,34774 —0,29675
0,45 —0.54058 ' -0,46028 —0,39376 —0,33652 —0,28386
0,50 —0,52879 —0,44878 —0,38209 —0,32406 -0,26956
0,55 —0,51585 —0,43616 —0,36929 —0,31040 —0,25388
0,60 —0,50180 —0,42245 —0,35538 -0,29556 —0,23684
0,65 —0,48665 —0,40767 —0,34040 —0,27958 —0,21851
0,70 —0,47044 —0,39187 —0,32436 —0,26249 —0,19890
0,75 —0,45320 —0,37506 —0,30733 —0,24432 —0,17807
0,80 —0,43488 —0,35730 —0,28932 —0,22513 —0,15607
0,85 —0,41580 —0,33860 —0,27039 —0,20495 —0,13294
0,90 —0,39571 -0,31903 —0,25056 —0,18383 -0,10874
0,95 —0,37474 —0,29861 —0,22988 -0,16181 —0,08354
1,0 —0,35295 —0,27740 —0,20840 —0,13895 —0,05736
1,05 —0,33038 —0,25542 —0,18617 —0,11529 —0,03030
1,10 —0,30707 -0,23275 —0,19323 —0,09089 —0,00240
1,15 —0,28308 —0,20942 —0,13964 —0,06581 —0,02628
1,20 —0,25845 —0,18547 —0,11543 —0,04009 —0,05566
1,25 —0,23324 —0,16096 —0,09068 —0,01380 —0,08568
256
Продолжение
1.8 1.9 2,0 2.1 2,2 2,3 2,4
—0,30726 -0,27523 —0,22814 -0,20722 —0,18941 —0,17386
—0,30458 —0,26991 —0,23229 —0,20907 —0,19050 —0,17460
—0,29952 —0,26106 5 —0,23918 -0,21213 —0,19233 —0,17582
—0,29245 —0,24869 —0,24881 -0,21641 —0,19488 —0,17754
—0,28338 —0,23284 —0,26114 -0,22190 -0,19815 —0,17974
—0,27235 —0,21355 -0.27615 —0,22857 —0,20212 —0,18241
-0,25937 —0,19086 —0.29380 —0.23641 —0,20679 -0,18555
—0,24447 —0,16482 —0,31404 -0,24540 —0,21214 -0.19915
—0,22770 —0,13552 - 0,35682 —0,25552 —0,21816 —0,19319
—0,20908 -0,10300 —0,36207 —0,26674 —0.22493 —0,19767
—0,18868 —0,06735 —0,38974 —0,27902 -0,23213 —0,20253
—0,16652 —0,02866 —0,41976 —0,39233 —0.24004 —0,20789
—0,14267 +0,01299 —0,45202 —0,00665 -0.24854 —0,21359
-0,11718 4-0,05746 , —0,48648 —0,32192 ' —0,25761 —0,21967
—0,09011 +0,10470 —0,52303 —0,33312 —0,26772 -0,22610
—0,06151 +0,15456 -0,56153 —0,35519 —0,27734 -0,23238
—0,03148 +0.20690 —0,60200 -0,37308 —0,23794 —0.23997
—0,00003 +0,26164 —0.64424 -0.39175 —0,29900 —0,24735
+0,03265 +0,31861 —0,63814 -0,41116 —0,21048 -0,25502
+0,06660 +0,37768 —0,73360 -0,43123 —0,32233 -0.26293
+0,10169 +0,43872 —0,78050 —0,45193 —0,33456 —0,27103
+0,13783 +0,50157 —0,82874 —0,47319 -0,34710 —0.27942
+0,17497 +0,56610 —0.87816 —0,49495 —0,35993 —0,28793
+0,21299 +0,63208 —0,92363 -0,51716 —0,37298 —0,29661
+0,25181 +0.69943 —0,98004 —0,53975 —0,38627 —0,30540
17—730 257
Продолжение
V 2,5 2,6 2,7 2,8 2,9
0,1)5 —0,16018 —0,14806 —0,13727 —0,12763 —0,11898
0,1 —0,16071 —0,14847 —0,13759 —0,12788 —0,11918
0,15 —0,16160 —0,14913 —0,13811 —0,12830 —0,11951
0,20 —0,16283 —0,15006 — 0,13883 —0,12887 —0,11908
0,25 —0,16442 —0,15126 —0,13976 —0,12961 —0,12058
0,30 —0,16634 —0,15271 —0,14083 -0,13051 —0,12131
0,35 —0,16860 —0.15441 —0,14221 —0,13156 -0.12216
0,40 —0,17119 —0,15636 -0,14372 —0,13276 —0,1.2312
0,45 —0,17410 —0,15855 -0,14542 —0,13411 —0,12423
0,50 —0,17733 —0,16097 -0,14730 -0,13560 —0,12543
0,55 —0,18085 —0,16362 —0,14935 -0,13723 —0,12674
0,60 —0,18467 —0.16648 —0,15157 -0,13899 —0,12816
0,65 —0,18876 —0,16355 —0,15394 —0,14087 —0,12368
0,70 —0,19312 —0,17282 -0,15647 —0,14287 —0,13128
0,75 —0,19774 —0,17628 —0,15914 —0,14397 —0,13298
0,80 —0,20259 -0.17991 -0,16194 —0,14718 —0,13475
0,85 —0,20766 —0,18370 -0,16486 —0,14948 —0,13658
0,90 —0,21234 —0,18764 —0.16789 —0,15186 —0,13849
0,95 —0,21841 —0,19172 -0,17102 —0,15432 —0,14045
1,0 —0,224о6 —0,19592 —0,17424 —0,15684 —0,14245
1,05 —0,22986 —0,20023 —0,17754 -0,15941 —0,14449
1,10 —0,23579 —0,20464 —0,18090 —0,16203 —0,11656
1,15 —0,21184 —0,20212 —0,18431 -0,16468 —0,14865
1,20 —0,24799 —0,21366 —0,18777 —0,16736 —0,15075
1,25 -0,25421 -0,21825 — 0,13125 —0,17005 —0,15285
258
Продолжение
3,0 3,1 3,2 3,3 3,4 3,5 3.6
-0,11117 —0,10411 —0,09770 —0,09186 —0,08653 —0,08166 -0,07718
-0,11133 —0,10425 —0,09781 —0,09196 -0,08662 —0,08173 —0,07725
—0,11161 —0,10448 —0,09801 —0,09213 —0,08676 —0,08185 —0,07735
—0,11199 —0,10480 —0,09828 —0,09236 —0,08696 —0,08203 —0,07750
—0,11249 —0,10521 —0,09862 -0,09265 —0,08721 —0,08224 -0,07769
—0,11308 —0,10571 —0,09904 -0,09301 —0,08751 —0,08250 —0,0779
—0,11378 -0,10629 —0,09953 -0,09342 —0,08787 —0,08281 —0,0781
-0,11458 —0,10695 —0,10009 —0,09389 —0,08827 —0,08315 —0,07847
-0,11548 —0,10770 —0,10071 —0,09442 -0.08872 —0,08353 —0,07879
-0,11647 —0,10852 —0,10140 —0,09500 —0,08921 —0,08394 —0,07914
—0,11754 —0,10941 —0,10214 —0,09562 -0,08973 —0,08439 —0,07951
—0,11870 —0,11037 —0,10294 —0,09629 —0,09030 —0,08486 —0,07990
—0,11994 —0,11139 -0,10379 -0.09700 - 0,£089 —0,08535 —0,08030
-0,12125 -0,11246 —0,10468 -0,09774 —0,09151 —0,08586 —0,08071
—0,12263 —0,11359 —0,10562 —0,09852 —0,09215 -0,08638 —0,08113
-0,12406 —0,11477 —0,10659 -0,09932 —0,09280 —0,08691 —0,08154
-0,12555 -0,11599 —0,10758 -0,10013 —0,09347 —0,08745 —0,08195
—0,12709 -0.11724 —0,10860 -0,10097 —0,03414 —0,08798 —0,08234
—0,12867 —0,11852 —0,10364 -0,10181 —0,09481 —0,108849 —0,08271
—0,13027 —0,11981 —0,11069 -0,10265 —0,09547' -f0,08900 —0,08306
-0,13191 -0,12113 —0,11175 —0,10349 —0,09613 —0,08348 —0,08337
—0,13355 —0,12444 —0,11280 —0,10431 —0,09676 —0,08994 —0,08365
—0,13521 —0,12376 —0,11334 -0,10513 -0,09736 —0,09036 —0,09387
-0,13681 -0,12507 —0,11486 -0,10591 —0,09795 —0,09073 —0,08404
—0,13852 —0,12636 —0,11587 -0,10667 ! —0,09848 -04)9106 —0,08415
17*
•259
Продолжение
0,1 0,2 0,3 0,4 0,5
1,30 —61,91600 — 15,40835 —6,79536 —3,77934 —2,38185
1,35 —59,27316 —14,74345 —6,49607 —3,60811 —2,26980
1,40 —56,58044 —14,06550 —6,19119 —3,43369 —2,15567
1,45 —53,84269 —13,37627 —5,88122 —3,25639 —2,03967
1,50 —51,06495 —12,67698 -5,56676 —3,07655 —1,92203
1,55 —48,25220 —11,96892 —5,24840 —2,89647 —1,80294
1,60 —45,40952 —11,25337 —4,92668 —2,71051 —1,68263
1,65 —42,54204 —10,52162 —4,60220 —2,52500 —1,56134
1,70 —39,65489 — 9,80495 —4,27556 —2,33862 —1,43927
1,75. —36,75323 — 9,07468 —3,94732 —2,15065 — 1,31664
1..80 —32,84224 — 8,34210 —3,61808 —1,96250 —1,19369
1,85 —30,92709 — 7,60853 -3,28843 —1,77414 —1,07062
Is,90 —28,01290 — 6,87525 -2,95895 -1,58591 —0,94767
1,95 —25,10481 — 6,14356 —2,63023 —1,39814 —0,82506
2,0 —22,20790 5,41473 —2,30826 —1,21119 —0,70300
; 2,05 —19,32722 — 4,69008 -4,97739 —1,02536. —0,58141
2,10 —16,46778 — 3,97081 —1,65439 —0,84099 —0,46140
2,15 —13,63446 — 3,25819 — 1,33443 —0,65837 —0,34229
2,20 —10,83213 — 2,55345 —1,01806 —0,47787 —0,22458
2,25 — 8,06556 — 1,85776 —0,70583 —0,29976 —0,10848
2,30 — 5,33941 — 1,17234 —0,39825 —0,12437 0,00581
2,35 -г- 2,65823 — 0,49829 —0,09585 —0,04801 0,11809
2,40. — 0,02651 i 0,16323 0,20086 —0,21711 0,22819
960
Продолжение
0,6 0,7 0,8 0,9 1,0 1,1 1.2
— 1,62102 —1,16031 —0,85994 —0,64989 —0,49716 —0,38034 —0,28668
—1,54100 —1,09947 —0,81050 —0,60961 —0,46258 —0,34973 —0,25877
—1,45949 —1,03752 -0,76110 -0,56861 -0,42750 —0,31860 —0,23040
—1,37669 —0,97458 —0,71090 —0,52700 —0,39169 —0,28701 - 0,20161
—1,29270 —0,91077 —0,66004 —0 48481 —0,35552 —0,25502 —0,17248
— 1,20771 —0,84621 —0,60858 —0,44216 —0,31896 —0,22270 —0,14307
—1,12188 —0,78102 —0,55663 —0,39912 —0,28207 —0,19011 —0,11342
—1,03535 —0,71533 —0,50431 —0,35577 —0,24494 -0,15731 —0,08359
—0,94828 —0,64923 —0,45167 —0,31220 —0,20763 —0,12439 -0,05366
—0,86085 —0,58288 —0,39886 -0,26848 —0,17021 —0,09137 —0,02368
—0,77319 —0,51639 —0,34594 —0,22471 —0,13276 —0,58335 +0,00630
—0,68551 —0,44986 —0,29303 —0,18095 —0,09535 —0,02538 —0,03621
—0,59789 —0,38346 —0,24022 —0,13729 —0,05805 +0,00747 0,06598
—0,51055 —0,31726 —0,19762 —0,09385 —0,02093 +0,04014 0,09558
—0,42363 —0,25143 —0,13532 —0,05065 0,01594 0,07256 0,12491
—0,33731 —0,18605 —0,08340 —9,00781 0,05247 0,10468 0,15394
—0,25170 —0,12124 —0,03198 0,03460 0,08863 0,13642 0,18263
—0,16698 —0,05715 0,01887 0,07652 0,12432 0,16773 0,21088
—0,08329 +0,00613 0,06903 0,11783 0,15948 0,19855 0,23867
—0,00078 0,06850 0,11844 0,15848 0,19406 0,22883 0,26592
0,08041 0,12983 0,16699 0,19842 0,22797 0,25848 0,29260
0,16013 0,19000 0,21460 .0,23753 0,26917 0,28749 0,31863
0,23826 0,24894 0,26118 0,27577 0,29359 0,31577 0,34399
Продолжение
1,3 1,4 1,5 1,6 1,7
1,30 —0,20749 —0,13575 —0,6542 0,01300 0,11626
1,35 —0,18127 —0,11049 -0,03972 0,04027 0,14735
1,40 —0,15462 —0,08462 -0,01363 0,06792 0,17886
1,45 —0,12759 —0,05841 0,01280 0,09592 0,21073
1,50 —0,10026 —0,03191 0,03949 0,12418 0,24289
1,55 -0,07266 —0,00518 0,06640 0,15265 0,27524
1,60. —0,04487 0,01174 0,09347 0,18126 0,30774
1.65 —0,01693 0,04877 0,12065 0,20996 0,34028
1,70 +0,01109 0,07586 • 0,14787 0,23866 0,37282
t,75 +0,03914 0,10297 0,17506 0,26733 0,40528
1,80 0,06716 0,13002 0,20219 0,27589 0,43754
1,85 0,09510 0,15676 0,22918 0,32427 0,46958
Г.,90 0,12289 0,18375 0,25597 0,35250 0,50130
11,95 0,15049 0,21034 0,28251 0,38025 0,53264
2,0 0,17782 0,23660 0,30875 0,40772 0,56352
2,05 0,20485 0,26256 0,33462 0,43477 0,59387
2,.10 0Г23152 0,28813 0,36007 0,46135 0,62361
2,15 0,25775 0,31326 0,38504 0,48738 0,65268
2,20 0,28352 0,33792 0,40950 0,51280 0,68103
2,25 0,30877 0,36202 0,43337 0,53757 0,70856
2,30 0,33343 0,38553 0,45661 0,56162 0,73521
2,35 0,35747 0,40842 0,47916 0,58491 0,76095
2,40 0,38085 0,43060 0,50098 0,60739 0,78569
262
Продолжение
1,8 1,9 2.0 2,1 2,2 2,3 2,4
0,29134 0,76795 —1,03224 —0,56266 —0,39971 —0,31420
0,33149 0,83747 —1,08511 —0,58583 —0,41329 —0,32325
0,037214 0,90781 — 1,13847 —0,60919 —0,42694 —0,33226
0,41323 0,97883 —1,19220 —0,63267 —0,44066 —0,34128
0,45465 1,05033 —1,24616 —0,65621 —0,45438 —0,35027
0,49628 1,12215 --1,30020 —0,67975 —0,46806 —0,35924
0,53804 1,19409 —1,35418 —0,70321 —0,48168 -0,36812
0,57983 1,23597 — 1,40792 —0,72652 —0,49517 —0,37690
0,62155 1,33765 —1,46134 —0,74962 —0,50851 —0,38554
0,66310 1,40890 -1,51421 —0,77246 —0,52165 —0,39404
0,70438 1,47958 — 1,56635 —0,79495 —0,53455 — 0,40234
0,74528 1,54951 — 1,61789 —0,81703 —0,54717 —0,41042
0,78573 1,61849 —1,66838 —0,83864 -0,55946 —0,41826
0,82481 1,68637 —1,71779 —0,85970 -0,57139 —0,42583
0,86481 1,75296 —1,76598 —0,88016 —0,58294 —и,43310
0,90326 1,81810 —1,81282 —0,89996 —0,59403 —0,44004
0,94086 1,88163 — 1,85815 -0,91902 -0,60466 —0,44663
0,97752 1,94339 —1,90186 —0,93730 —0,61478 —0,45283
1,01316 2,00321 -1,94381 —0,95474 —0,62434 -0,45864
1,04767 2,06092 —1,98388 —0,97127 -0,63332 —0,46403
1,08098 2,11640 —2,02195 -0,98685 —0,64168 —0,46897
1,11300 2,16951 —2,05789 —1,00140 —0,64940 —0,47342
1 1,14367 2,22006 —2,09163 —1,01490 —0,65645 —0,47740
263
Продолжение
2 2,5 2,6 2,7 2,8 2,9
1,30 —0,26050 —0,22287 —0,19474 —0,17274 —0,15493
1,35 —0,26681 -0,22751 —0,19823 —0,17541 —0,15701
1,40 -0,27315 —0,23214 —0,20171 —0,17807 —0,15905
1,45 —0,27974 —0,23676 —0,20516 —0,18069 —0,16105
1,50 —0,28576 —0,24133 —0,20857 —0,18326 —0,16300
1,55 —0,29201 —0,24586 —0,21193 —0,18822 —0,16490
1,60 —0,29818 —0,25031 —0,21521 —0,18822 —0,16672
1,65 —0,30426 —0,25467 —0,21841 —0,19095 —0,16846
1,70 —0,31023 —0,25894 -0,22151 —0,19285 —0,17012
1,75 —0,31606 —0,26307 -0,22450 —0,19503 —0,17167
1,80 —0,32172 —0,26707 —0,22737 —0,19708 —0,17311
1,85 —0,32721 -0,27092 —0,23009 —0,19900 —0,17444
1,90 —0,33250 —0,27459 —0,23266 —0,20079 —0,17563
1,95 —0,33757 —0,27807 —0,23507 —0,20243 —0,17669
2,0 —0,34240 —0,28136 —0,23730 —0,20390 —0,17759
- 2,05 —0,34696 —0,28452 —0,23935 —0,20521 —0,17835
2,10 —0,35125 —0,28725 —0,24118 —0,20633 —0,17894
2,15 —0,35523 —0,28983 —0,24281 —0,20727 —0,17935
2,20 —0,35891 —0,29215 —0,24420 —0,20801 —0,17958
2,25 —0,36224 —0,29419 —0,24536 —0,20853 —0,17963
2,30 —0,36523 —0,29594 —0,24628 —0,20884 —0,17948
2,35 —0,36785 —0,29739 —0,24693 —0,20893 —0,17913
2,40 —0,37007 —0,29852 —0,24733 —0,20878 —0,17857
264
Продолжение
3,0 3,1 3,2 3,3 3,4 3,5 3,6
—0,14015 —0,12763 —0,11684 —0,10739 —0,09897 —0,09134 —0,08420
-0,14175 —0,12887 -0,11777 —0,10806 -0,09942 —0,09155 —0,08416
—0,14332 —0,13006 —0,11866 —0,10868 —0,09980 —0,09170 —0,08405
—0,14485 —0,13121 —0,11949 —0,10925 —0,10011 —0,09177 —0,08384*
—0,14632 -0,13230 —0,12027 —0,10974 —0,10035 —0,09175 —0,08354
—0,14774 —0,13333 —0,12097 —0,11017 —0,10052 —0,09165 —0,08313
—0,14908 -0,13428 —0,12160 —0,11051 —0,10059 —0,09145 —0,08260
—0,15034 —0,13516 -0,12215 -0,11078 —0,10058 —0,09114 —0,08196
v\ —0,15151 —0,13594 —0,12216 —0,11094 —0,10046 —0,09073 —0,08119
-0,15259 —0,13663 —0,12296 —0,11100 -0,10023 —0,09020 —0,98029
—0,15355 —0,13721 —0,12322 —0,11095 —0,09990 —0,08954 —0,07925
—0,15441 —0,13768 —0,12336 —0,11080 —0,09944 —0,08876 —0,07806
—0,15514 —0,13804 —0,12339 —0,11052 -0,09886 —0,08784 —0,07672
—0,15574 -0,13826 —0,12329 —0,11011 —0,09815 —0,08678 —0,07522
-0,15621 —0,13836 —0,12305 —0,10958 —0,09730 —0,08558 —0,07356
—0,15652 —0,13831 —0,12268 —0,10890 —0,09630 —0,08422 -0,07173
—0,15668 —0,13811 —0,12217 —0,10808 —0,09517 —0,08271 —0,06972
-0,15668 —0,13776 —0,12151 —0,10711 —0,09387 —0,08103 —0,06754
—0,15651 —0,13726 —0,12069 —0,10600 —0,09243 —0,07920 -0,06517
—0,15618 —0,13658 —0,11972 —0,10472 —0,09082 —0,07718 —0,06262
—0,15565 —0,13574 —0,11858 —0,10327 —0,08994 —0,07500 —0,05987
—0,15494 —0,13472 —0,11728 —0,10167 -0,08710 —0,07264 —0,05693
—0,15404 —0,13352 —0,11579 —0,09989 —0,08499 —0,07010 —0,05379
265
Продолжение
0,2 0,4 0,6 с,8 1,0 1,2 1,4
2,5 1,44436 0,54428 0,38916 0,35096 0,35584 0,39246 0,47275
2,6 2,66309 0,85499 0,53213 0,43569 0,41430 0,43764 и,51164
2,7 3,81066 1,14723 0,66621 0,51482 0,46853 0,47919 0,54695
2,в 4,88097 1,41919 0,79054 0,58780 0,51817 0,51680 0,57839
2,9 5,86729 1,66919 0,90436 0,65417 0,56289 0,55020 0,60572
3,0 6.76398 1,89581 1,00699 0,71352 0,60239 0,57916 0,62873
•3,1 7,56619 2,09780 1,09784 0,76552 0,63640 0,60346 0,64724
•3,2 8,26983 2,27410 1,17643 0,80983 0,66477 0,62300 0,66112
3,3 8,87176 2,42391 1,24240 0,84630 0,68733 0,63761 0,67028
•3,4 9,36959 2,54664 1,29549 0,87473 0,70397 0,64725 0,67465-
3,5 9,76190 2,64194 1,33551 0,89505 0,71463 0,65187 0,67424
*3,6 10,04811 2,70967 1,36246 0,90724 0,71935 0,65151 0,66906
•3,7 10,22850 2,74992 1,37637 . 0,91137 0,71815 0,64621 0,65918
3,8 10,30425 2,76303 1,37741 0,90754 0,71114 0,63606 0,64472
3,9 10,27737 2,74954 1,36536 0,89592 0,69846 0,62123 0,65282
4,0 10,15070 2,71019 1,34209 0,87680 0,68032 0,60186 0,60268
4,1 9,92781 2,64594 1,30659 0,85045 0,65694 0,57818 0,57550
4,2 9,61311. 2,55795 1,25989 0,81725 0,62863 0,55043 0,54453
4,3 9,21165 2,44757 1,20268 0,77761 0,59567 0,51891 0,51009
4,4 8,72911 2,31628 1,13565 0,73199 0,55844 0,48394 0,47246
4,5 8,17184 2,16574 1,05975 0,68092 0,51732 0,44581 0,43195
4,6 7,54662 1,99774 0,977548 0,62493 0,47274 0,40493 0,38904
4,7 6,86078 1,81422 0,88409 0,56463 0,42511 0,36165 0,34398
4,8 6,12197 1,61716 0,78648 0,50061 0,37492 0,31637 0,29722
266
Продолжение
1.6 1.8 2,0 2,2 2.4 2,6 2,8 3.0
0,64967 1,20059 —1,03853 —0,48378 —0,29981 —0,20776 —0,15165
0,68811 1,25119 —1,05738 -0,48799 -0,29972 -0,20573 —0,14843
0,72235 1,29493 —1,07112 -0,48987 —0,29818 -0.20265 —0,14437
0,75209 1,33138 —1,07948 —0,48933 —0,29514 —0,19848 —0,13944
0,77708 1,36012 — 1,08223 —0,48628 —0,29055 -0,19320 —0,13364
0,79707 1,38035 —1,07921 —0,48067 —0,28440 —0,18682 —0,12696
0,81188 1,39329 —1,07029 —0,47244 —0,27665 —0,16930 -0,11940
0,82140 1,39729 —1,05541 —0,42159 —0,26732 —0,17068 —0,11098
0 82553 1,39274 —1,03455 -0,44812 —0,25642 —0,16097 -0,10174
0,82421 1,37958 —1.С0776 —0,43208 —0,24399 —0,15021 —0,09168
0,81743 1,35778 —0,97511 —0,41351 —0,23007 -0,13842 —0,08087
0,80536 1,32776 —0,93677 —0,39252 -0,21472 —0,12568 —0,06935
0,78796 1,23940 —0,89293 —0,36917 —0,19802 —0,11202 —0,05717
0,76544 1,24309 -0,84386 -0,34362 -0,18005 —0,09756 —0,04441
0,73797 1,18915 —0,78986 —0,31602 —0,16093 —0,08233 —0,03113
0,70579 1,12799 —0,73124 —0,28652 -0,14076 —0,06645 —0,01741
0,66916 1,06009 —0,66841 —0,25534 -0,11967 —0,05002 —0,00335
0,62841 0,98595 —0,60183 —0,22266 —0,09778 —0,03313 +0,01099
0,58387 0,90618 -0,53191 —0,18871 -0,07527 -0,01589 +0,01549
0,53593 0,82138 —0,45924 —0,15371 —0,05227 0,00159 0,04008
0,48496 0,73225 —0,38425 —0,11794 —0,02893 0,01915 0,05462
0,43142 0,63947 —0,30753 —0,08162 —0,00542 0,03671 0,06904
0,37575 0,54379 —0,22965 —0,14502 —0,01809 0,05413 0,08322
0,31839 0,44598 -0,15118 —0,00841 0,04142 0,07130 0,09706
267
Продолжение-
3,2 3,4 3,6 3,8 4,0 4,2 4,4
' 2,5 —0,11229 —0,08023 —0,04693 0,01289 —0,15217 —0,09899
2,6 —0,10806 —0,07477 —0,03925 0,02698 —0,16368 -0,10413
2,7 —0,10310 —0,06858 -0,03076 0,04229 —0,17590 —0,10953
' 2,8 —0,09737 -0,06166 —0,02148 0,05881 —0,18877 —0,11518
2,9 —0,09090 —0,05403 —0,01140 0,07646 —0,20225 —0,12103
3,0 —0,08365 —0,04568 —0,00057 0,09524 —0,21629 —0,12706
3,1 —0,07567 —0,03663 0,01101 0,11506 -0,23081 —0,13324
3,2 —0,06698 —0,02693 —0,02328 0,13583 —0,24575 —0,13953
3,3 -0,05758 —0,01660 0,03619 0,15748’ —0,26101 —0,14589
3,4 —0,04753 —0,00567 0,04969 0,17989 —0,27651 -0,15227
3,5 —0,03687 —0,00577 0,06370 0,20295 —0,29214 —0,15862
3,6 —0,02564 -0,00770 0,07817 0,22652 —0,30778 -0,16491
3,7 —0,01390 .0,03004 0,09298 0,25045 —0,32334 —0,17105
3,8 —0,00172 0,04273 0,10809 0,27459 —0,33865 —0,17702
3,9 0,01081 0,05569 0,12337 0,29879 —0,35367 —0,18274
4,0 0,02367 0,06884 0,13874 0,32288 —0,36819 -0,18815
4,1 0,03671 0,08208 0,15409 0,34671 —0,38211 —0,19321
4,2 0,04990 0,09535 0,16939 0,37002 —0,30529 —0,19784
4,3 0,06313 0,10854 0,18427 0,39270 —0,40761 —0,20200
4,4 0,07632 0,12156 0,19888 0,41454 -0,41892 —0,20562
4,5 0,08936 0,13431 0,21304 0,43535 —0,42911 —0,20865
4,6 0,10217 0,14670 0,22659 0,45499 —0,43803 —0,21104
4,7 0,11465 0,15863 0,23948 0,47324 —0,44556 -0,21273
4,8 0,12671 0,17002 0,25154 0,4899 • —0,45162 —0,21369
268
Продолжения
4,6 4,8 5,0 5,2 5,4 5,6 5,8
—0,07773 -0,06506 —0,05617 —0,04935 —0,04377 —0,03884 —0,03344
—0,08077 —0,06706 —0,05755 —0,05030 —0,04439 -0,03913 —0,03316
—0,08393 -0,06912 -0,05895 —0,05125 —0,04498 —0,03936 —0,43274
—0,08720 —0,07122 —0,06035 —0,05218 —0,04552 -0,03950 —0,03214
-0,09056 —0,07335 —0,06175 —0,05307 —0,04601 —0,03955 —0,03136
-0,09398 —0,07550 —0,06314 —0,05393 —0,04643 —0,03947 —0,03035
t 1 -0,09745 —0,07764 -0,06449 —0,05472 —0,04676 —0,03931 —0,02910
t —0,10093 —0,07976 -0,06578 -0,05545 —0,04700 —0,03898 —0,02759
t * —0,10441 —0,08183 —0,06701 —0,05608 —0,04712 —0,03849 —0,02578
I: -0,10785 —0,08382 —0,06816 —0,05661 —0,04711 —0,03782 —0,02365
i —0,11121 —0,11448 —0,08575 —0,08755 —0,06919 —0,07011 —0,05702 —0,05729 —0,04696 —0,04665 —0,03696 —0,03589 —0,02117 —0,01832
I —0,11761 —0,08921 —0,07088 -0,05741 —0,04615 —0,03459 —0,01508
-0,12057 —0,09070 —0,07149 —0,05736 —0,04547 —0,03304 -0,01142
—0,12332 —0,09201 —0,07191 -0,05712 —0,04458 —0,03123 —0,00732
—0,12583 —0,09310 —0,07213 —0,05667 —0,04346 —0,02915 -0,00277
—0,12806 —0,09395 —0,07213 —0,05600 —0,04211 —0,02678 +0,00226
—0,12997 —0,09454 —0,07189 —0,05510 —0,04051 —0,02410 +0,00778
-0,13154 —0,09484 —0,07139 —0,05395 —0,03864 —0,02111 +0,01380
—0,13273 —0,09483 —0,07061 —0,05254 —0,03651 —0,01781 +0,02032
-0,13349 —0,09449 —0,06955 —0,05086 —0,03410 -0,01417 +0,02736
—0,13382 —0,09380 —0,06818 —0,04889 —0,03140 —0,01021 0,03491
-0,13366. —0,09274 —0,06650 —0,04664 —0,02841 —0,00591 0,04297
—0,13302 —0,09129 —0,06450 —0,04409 —0,02512 —0,00128 0,05152
269
Продолжение
V Z 0,3 0,6 0,9 1,2 1,5
4,95 2,24156 0,63051 0,33805 0,24562 0,22359
5,1 1,66654 0,46636 0,24639 0,17276 0,14447
5,25 1,07139 0,29740 0,15281 0,09916 0,06547
5,4 —0,46273 0,12738 0,05932 0,02633 —0,01188
5,55 —0,12668 —0,04047 —0,03237 —0,04453 —0,08631
5,7 —0,70530 —0,20267 —0,12043 -0,11201 —0,15645
5,85 —1,25596 —0,35646 —0,20344 —0,17504 —0,22126
6,00 -1,76851 —0,49910 —0,27991 —0,23261 —0,27971
6,15 —2,23579 —0,62860 —0,34888 —0,28401 —0,33113
6,30 —2,65165 —0,74333 —0,40953 —0,32867 —0,37503
6,45 —3,013570 —0,84270 -0,46155 —0,36641 —0,41129
6,60 —3,32148 —0,92669 —0,50503 —0,39738 -0,44017
6,75 —3,57992 —0,99668 —0,54074 -0,42223 —0,46239
6,90 —3,79771 —1,05516 -0,57015 —0,44210 —0,47931
7,05 —3,99018 —1,10648 —0,59558 —0,45890 —0,49296
7,20 —4,17985 -1,15595 —0,62055 —0,47536 —0,50329
270
Продолжение-
1.8 2.0 2.1 2.4 2.7 3,0
0,29689 —0,19173 0,04595 0,08640 0,11699
0,14750 0,05213 0,09880 0,11399 0,13557
0,00021 0,28914 0,14834 0,13986 0,15254
—0,14219 0,51502 0,19669 0,16353 0,16757
—0,27752 0,7264'« 0,24012 0,18467 0,18043
—0,40239 0,91966 0,27893 0,20292 0,19091
—0,51795 1,09215 0,31259 0,21805 0,19885
—0,61954 1,24139 0,34052 0,22983 0,20413»
—0,70708 1,36598 0,36281 0,23818 0,20674.
—0,77980 1,46502 0,37904 0,24312 0,20674.
—0,73771 0,53887 0,38950 0,24477 0,20427.
—0,88144 1,58893 0,39498 0,23344 0,19959
—0,91259 0,61813 0,39498 0,23958 0,19311
—0,93377 0,63115 0,39190 О, 23388 0,18539-
—0,94898 1,63483 0,38691 0,22731 0,17718
—0,96384 1,63870 0,38225 । 0,22113 i 0,1695а
271
Продолжение
3,3 3.6 3,9 4,0 4,2
4,95 0,16203 0,26794 0,99778ч —0,45769
5,1 0,17675 0,28196 1,02376 —0,45983
5,25 .0,18965 0,29331 1,04051 —0,45781
5,4 0,20045 0,30172 1,04729 —0,45146
5,55 0,20899 0,30703 1,04381 —0,44064
5,7 0,21509 0,30905 1,02964 —0,42535
5,85 0,21864 0,30772 1,00493 —0,40564
6,00 0,21726 0,30302 ' 0,96961 —0,38171
6,15 0,21798 0,2 9 506 0,92438 —0,35386
6,30 0,21388 0,28401 0,87005 —0,32255
6,45 0,21750 0,27022 0,80773 —0,28835
6,60 0,19913 0,25405 0,73915 —0,25208
6,75 0,18920 0,23621 0,66635 —0,21473
6,90 0,17830 0,21747 0,59227 —0,17763
7,05 0,16717 0,19890 0,52039 —0,14235
7,20 0,15689 0,18187 0,45533 —0,11096
272
Продолжение
iee* 4,5 4,8 5,1 5,4 5,7 6,3
—0,16431 —0,08837 —0,04983 —0,01964 0,02772 —0,09826
—0,16161 —0,08452 —0,04512 —0,01351 0,03763 —0,10539
—0,15735 —0,07972 —0,03971 —0,00674 0,04882 —0,11270
—0,15151 —0,07398 —0,03360 0,00061 0,06065 —0,12007
—0,14407 —0,06730 —0,02684 0,00851 0,07305 —0,12743
—0,13508 —0,05974 —0,01948 0,01688 0,08588 —0,13466
—0,12455 —0,05136 —0,01156 0,02565 0,09900 —0,14164
ч —0,11264 —0,04224 —0,00321 0,03468 0,11224 —0,14823
—0,09946 —0,03249 0,00550 0,04388 0,12539 —0,15426
—0,08524 —0,02227 0,01442 0,05308 0,13821 —0,15960
—0,07021 —0,01173 0,02339 0,06213 0,15043 —0,16403
—0,05471 —0,00113 0,03220 0,07079 0,16173 —0,16733
—0,03914 —0‘, 00929 0,04067 0,07884 0,17176 —0,1692
- —0,02399 0,01918 0,04848 0,08597 0,18003 —0,16954
—0,00991 0,02815 0,05331 0,09185 0,18608 —0,16779
"ч \>- —0,00233 0,03567 0,06071 0,09603 0,18919 —0,16356
•" ’’г H;v &
'18-730 273
к-Ъ.
Продолжение
v Z 6,6 6,9 7,2 7,5
4,95 —0,05854 —0,04296 —0,03361 —0,02622
5,1 —0,06135 —0,04432 —0,03416 —0,02606
5,25 —0,06415 —0,04551 —0,03459 —0,02571
5,4 —0,06689 —0,04677 —0,03488 —0,02516
5,55 —0,06951 —0,04780 —0,03499 —0,02437
5,7 —0,07196 —0,04865 —0,03490 —0,02333
5,85 -0,07419 —0,04928 —0,03458 —0,02200
6,00 —0,07614 —0,04966 —0,03400 —0,02034
6,15 —0,07772 —0,04972 —0,03312 —0,01833
6,30 —0,07888 —0,04944 —0,03190 —0,01593
6,45 —0,07951 —0,04876 —0,03031 —0,01310
6,60 —0,07953 —0,04761 —0,02828 —0,00981
6,75 —0,07882 —0,04592 —0,02580 —0,00600
6,90 —0,07725 —0,04361 —0,02276 —0.00161
7,05 —0,07466 —0,04049 —0,01911 4-0,00346
7,20 —0,07085 —0,03670 —0,01472 т 0,00930
274
Продолжение
7,8 8,1 8,4 8,7 9,0
—0,01554 —0,04464 —0,02587 —0,02142 —0,01870
—0,01376 —0,04963 —0,02728 —0,02226 —0,01928
—0,01158 —0,05530 —0,02884 ' —0,02317 —0,01989
—0,00896 —0,06171 —0,03055 —0,02414 —0,02054
—0,00585 —0,06892 —0,03242 —0,02519 —0,02122
—0,00222 —0,07697 —0,03446 —0,02630 —0,02193
—0,00199 —0,08591 —0,03666 • —0,02749 —0,02267
-0,00681 —0,09580 —0,03904 —0,02874 —0,02343
. +0,01230 —0,10667 —0,04160 —0,03006 —0,02422
0,01849 —0,11858 —0,04434 —0,03144 —0,02503
0,02545 —0,13159 —0,04727 —0,03289 —0,02586
0,03325 —0,14576 —0,05040 —0,03442 —0,02670
0,04194 —0,16122 —0,05375 —0,03601 —0,02757
0,05164 —0,17805 —0,05732 —0,03769 —0,02846
0,06250 —0,19649 —0,06118 —0,03947 -0,02939
0.07468 —0,21681 —0,06535 —0,04 >37 —0,03037
•
18* , 275
ФУНКЦИИ
v 2 0 0,1 0,2 0,3 0,4
0,05 0,04999 0,05049 0,05207 0,05493 0,05951
0,10 0,09989 0,10090 0,10405 0,10977 0,11892
0,15 0,14963 0,15114 0,15586 0,16442 0,17812
0.20 0,19911 0,20111 0,20740 0,21879 0,23702
0,25 0,24827 0,25078 0,25861 0,27281 0,29552
0,30 0,29701 0,30001 0,30937 0,32635 0,35352
0,35 0,34526 0,34875 ' 0,35962 0,37936 0,41092
0,40 0,39293 0,39689 0,40928 0,43172 0,46763
0,45 0,43996 0,44439 0,45824 0,48336 0,52354
0,50 0,48625 0,49115 0,50644 0,53419 0,57857
•0,55 0,53174 0,53709 0,55381 0,58413 0,63263
, 0,60 0,57634 0,58214 0,60025 0,63308 0,68562
>0,65 0,62000 0,62623 0,64569 0,68099 0,73745
0,70 0,66263 0,66928 0,69007 0,72775 0,78804
0,75 0,70417 0,71123 0,73330 0,77331 0,83732
0,80 0,74455 0,75201 0,77531 0,81757 0,88518
0,85 0,78371 0,79155 0,81606 0,86049 0,93157
0,90 0,92158 0,82979 0,85545 0,90198 0,97640
0,95 0,85811 0,86668 0,89344 0,94198 1,01961
1.0 0,89324 0,90215 0,92997 . 0,98042 1,06112
1,05 0,92692 0,93615 0,96498 1,01726 1,10087
1,10 0,95909 > 0,96863 0,99841 1,05241 1,13880
1.15 0,98971 0,99954 1,03023 1,08585 1,17484
1,20 1,01874 1,02883 1,06037 1,11752 1,20896
1,25 1,04613 1,05647 1,08879 1,14738 1,24110
276
Таблица ПУ.2
V ЛОММЕЛЯ sQ v U)
0,5 0,6 0,7 0,8 0,9 1,0 1,1
0,06665 0,07810 0,09801 0,13885 0,26308 —0,23802
\ Л* i*4 , 0,13318 0,15607 0,19585 0,27745 0,52568 —0,47558
6'-; 0,19949 0,23377 0,29334 0,41555 0,78730 —0,71223
* 0,26545 0,31106 0,39032 0,55291 1,04750 —0,94750
•'!' 0,33096 0,38781 0,48661 0,68926 1,30577 —1,18095
0,39590 0,46388 0,58204 0,82430 1,56166 —1,41213
» < 0,46017 0,53916 0,67644 0,95805 1,81470 ‘ —1,64060
0,52364 0,61350 0,76966 1,08998 2,06440 —1,86590
h.v 0,58623 0,68679 0,86153- 1,21997 2,31035 —2,08763
fei 0,64781 0,75887 0,95188 1,34778 2,55208 —2,30534
0,70829 0,82966 1,04057 1,47318 2,78915 —2,51863
*;5Й'. 0,76756 0,89900 1,12743 1,59595 3,02113 —2,72708
£.Г' 0,82553 0,96681 1,21232 1,71588 3,24763 —2,93033
0,88209 1,03294 1,29508 1,83274 3,46821 —3,12793
Ъ : 0,93716 1,09731 1,37559 1,94635 3,68249 -3,31957
0,99064 1;15978 1,45370 2,05651 3,89009 —3,50485
гдС *t * 1,04244 1,22028 1,52928 2,16301 4,09063 —3,68344
1,09249 1,27867 1,60220 2,26570 4,28379 —3,85500
1,14070 1,33490 1,67234 2,36437 4,46920 —4,01922
vX;!’. 1,18698 1,38885 1,73958 2,45887 4,64655 —4,17578
•*. 1,23128 1,44044 1,80382 2,54905 4,81553 —4,32441
Л:. 1,27352 1,48958 1,86496 2,63474 4,97586 —4,46483
' 1,31363 1,53621 1,92288 2,71580 5,12726 —4,59677
'jJ- 1,35157 1,58023 1,97750 2,79212 5,26948 —4,72003
.,7' ' Г 1,38725 1,62161 2,02874 2,86357 5,40230 —4,83437
5 277
>-r-
t£>;, '
Продолжение
V 2 1,2 1,3 1,4 1.5 1.6
0,05 —0,11360 —0,07244 —0,05207 —0,03999 —0,03204
0,10 —0,22697 —0,14473 —0,10402 —0,07988 —0,06400
0,15 —0,33990 —0,21672 —0,15575 —0,11960 —0,09582
0,20 —0,45215 —0,28828 —0,20715 —0,15905 —0,12742
0,25 -0,56350 —0,35923 —0,25811 —0,19815 —0,15871
0,30 —0,67373 —0,42945 —0,30852 —0,23681 —0,18963
0,35 —0,78263 —0,49879 —0,35827 —0,27495 —0,22012
0,40 —0,88998 —0,56711 —0,40727 —0,31247 —0,25008
0,45 —0,99557 —0,63426 —0,45538 —0,34930 —0,27947
0,50 —1,09918 —0,70012 —0,50253 —0,38535 —0,30821
0,55 —1,20062 —0,76454 —0,54862 —0,42054 —0,33622
0,60 —1,29962 —0,82740 —0,59354 —0,45480 —0,36346
0,65 —1,39618 —0,88856 —0,63718 —0,48805 —0,38985
0,70 —1,48991 —0,94790 —0,67949 —0,52021 —0,41532
0,75 —1,58071 —1,00531 —0,72033 —0,55122 —0,43982
0,80 —1,66839 —1,06066 —0,75965 —0,58100 —0,46329
0,85 —1,75278 —1,11384 —0,79736 —0,60949 —0,48568
0,90 —1,83371 —1,16476 —0,83336 —0,63662 —0,50693
0,95 —1,91103 —1,21329 —0,86759 —0,66234 —0,52699
1,0 —1,98460 — 1,25935 —0,90000 —0,68658 —0,54583
1,05 —2,05426 —1,30284 —0,93047 —0,70929 —0,56338
1,10 —2,11991 —1,34367 —0,95897 —0,73043 -0,57960
1,15 —2,18139 —1,38178 —0,98544 —0,74994 —0,59446
1,20 • —2,23860 — 1,41707 —0,00982 —0,76777 —0,60793
1,25 —2,29144 —1,44949 —0,03205 —0,78390 —0,61996
278
Продолжение
1,7 \\ 1,8 1,9 2,0 2,1 2,2 2,3- X
—0,02644 —0,02231 —0,01915 —0,01663 —0,01466 —0,01301 —0,01165
—0,05282 —0,04457 —0,03824 —0,03327 —0,02926 —0,02598 —0,02325
—0,07907 —0,06670 —0,05723 —0,04978 —0,04377 —0,03885 —0,03475
—0,10513 —0,08867 —0,07606 —0,06614 —0,05814 —0,05158 —0,04612
—0,13093 —0,11040 —0,09468 —0,08229 —0,07232 —0,06413 —0,05730
- —0,15640 —0,13185 —0,11303 —0,09821 \ —0,08626 —0,07644 —0,06824
\ —0,18150 —0,15295 —0,13107 —0,11383 —0,09992 —0,08848 —0,07891
—0,20614 —0,17365 —0,14874 -0,12910 —0,11324 —0,10020 —0,08925
—0,23028 —0,19386 —0,16599 -0,14398 —0,12620 -0,11154 —0,09923
—0,25385 —0,21363 —0,18279 —0,15844 —0,13874 —0,12248 —0,10880
—0,27680 —0,23282 —0,19907 —0,17240 —0,15082 —0,13297 —0,11792
и —0,29906 —0,25139 —0,21479 —0,18585 —0,16239 —0,14297 —0,12653
’ —0,32059 —0,26930 —0,22990 —0,19873 —0,17343 -0,15243 -0,13463
' —0,34132 —0,28651 —0,24437 —0,21099 —0,18388 —0,16133 —0,14215
' —0,36121 —0,30296 —0,25815 —0,22262 —0,19371 —0,16963 —0,14907
/ —0,38021 —0,31861 —0,27119 —0,23356 —0,20289 —0,17728 —0,15534
—0,39827 —0,33342 —0,28347 —0,24377 —0,21139 —0,18426 —0,16094
—0,41533 —0,34735 —0,29494 -0,25324 —0,21915 —0,19054 —0,16583
Л— 0,43138 —0,36036 -0,30556 —0,26192 —0,22616 —0,19608 —0,17000
—0,44634 —0,37241 —0,31531 —0,26977 —0,23240 —0,20085 —0,17339
—0,46019 —0,38347 —0,32418 —0,27678 —0,23782 —0,20484 —0,17599
> —0,47289 —0,39350 —0,33206 —0,28291 —0,24241 —0,20800 —0,17778
; —0,48443 —0,40247 -0,33899 -0,28814 -0,24613 —0,21033 -0,17873
—0,49473 1 —0,41037 —0,34495 -0,29245 —0,24899 —0,21181 —0,17883
—0,50381 —0,41717 —0,34989 —0,29582 —0,25092 —0,21240 —0,17805 1
279
Продолжение
V Z 2,4 2,5 2,6 2,7 2,8
0,05 —0,01050 —0,00952 -0,00867 -0,00794 —0,00729
0,10 —0,02094 —0,01898 —0,01728 —0,01581 —0,01449
0,15 —0,03129 —0,02834 —0,02578 —0,02353 —0,02151
0,20 —0,04150 —0,03754 —0,03410 -0,03106 —0,02823
0,25 —0,05151 —0,04654 —0,04220 —0,03830 —0,03459
0,30 —0,06128 -0,05528 —0,05000 —0,04520 -0,04048
0,35 —0,07077 —0,06372 —0,05746 -0,05169 -0,04581
0,40 —0,07992 —0,07180 —0,06453 —0,05770 —0,05049
0,45 —0,08869 —0,07947 —0,07114 —0,06317 —0,05444
0,50 -0,09704 —0,08670 —0,07725 -0,06803 —0,05757
0,55 - —0,10493 —0,09342 —0,08280 -0,07223 -0,05981
0,60 —0,11230 -0,09961. —0,08776 —0,07571 —0,06106
0,65 -0,11913 —0,10521 —0,09205 —0,07841 —0,06126
0,70 -0,12538 -0,11019 -0,09565 —0,08027 —0,06033
0,75 -0,13100 —0,11450 —0,09851 —0,08125 —0,05820
0,80 —0,13596 -0,11811 —0,10058 -0,08128 —0,05480
0,85 —0,14022 —0,12098 —0,10183 —0,08033 —0,05007
0,90 —0,14376 —0,12308 -0,10221 —0,07835 —0,04395
0,95 —0,14654 —0,12436 —0,10170 —0,07530 -0,03639
1,0 —0,14853 -0,12482 —0,10026 -0,07113 —0,02734
1,05 —0,14972 —0,12441 —0,09786 -0,06583 —0,01674
1,10 —0,15007 —0,12311 —0,09446 —0,05935 —0,00456
1,15 -0,14956 —0,12091 —0,09005 —0,05166 4-0,00924
1,20 —0,14816 —0,11777 —0,08462 —0,04275 0,02469
1,25 —0,14588 —0,11369 —0,07813 —0,03257 0,04183
280
Продолжение
2,9 3,0 3,1 3,2 3,3 3,4 3,5 3,6
—0,00672 —0,00583 —0,00542 —0,00506 —0,00474 —0,00445 —0,00418
—0,01327 -0,01180 —0,01091 -0,01016 -0,00951 —0,00892 —0,00838
—0,01947 —0,01806 —0,01653 —0,01535 —0,01433 —0,01343 -0,01261
—0,02517 —0,02475 —0,02234 —0,02065 -0,01923 -0,01800 —0,01689
—0,03018 —0,03200 —0,02341 -0,02611 -0,02425 —0,02265 —0,02123
—0,03434 —0,03995 -0,03481 —0,03177 —0,02940 -0,02740 -0,02565
—0,03750 —0,04875 —0,04159 -0,03766 —0,03472 —0,03227 —0,03016
—0,03948 —0,05852 —0,04882 —0,04383 -0,04022 —0,03729 —0,03478
—0,04014 —0,06939 —0,05655 -0,05031 -0,04593 —0,04245 —0,03952
—0,03931 —0,08149 —0,06484 —0,05713 -0,05189 —0,04780 —0,04439
-0,03686 —0,09494 —0,07375 —0,06432 —0,05810 -0,05333 —0,04941
—0,03263 —0,10986 -0,08333 —0,07193 —0,06460 -0,05908 —0,05459
-0,02649 —0,12636 —0,09364 —0,07998 —0,07140 -0,06504 —0,05995
-0,01830 —0,14455 -0,10471 —0,08850 —0,07852 -0,07125 —0,06548
-0,00794 -0,16454 —0,11661 —0,09752 -0,08599 —0,07770 —0,07121
+0,00470 —0,18641 -0,12936 —0,10706 —0,09381 —0,08442 —0,07714
0,01975 —0,21026 -0,14301 -0,11715 -0,10201 —0,09142 —0,08327
0,03731 —0,23617 -0,15761 -0,12781 -0,11060 —0,09870 —0,08963
0,05748 —0,26423 -0,17317 —0,13906 -0,11960 —0,10627 —0,09621
0,08033 —0,29447 -0,18975 -0,15091 —0,12901 -0,11415 —0,10302
0,10595 —0,32701 —0,20734 —0,16340 —0,13884 —0,12334 —0,11006
0,13444 -0,36187 —0,22599 -0,17651 -0,14912 —0,13084 -0,11735
0,16584 -0,39910 -0,24570 —0,19028 —0,15981 —0,13965 —0,12486
0,20019 —0,43869 -0,26650 —0,20469 -0,17097 —0,14880 —0,13262
0,23757 —0,48076 —0,28842 —0,21977 —0,18256 —0,15825 —0,14063
281
Продолжение
Z 0 o.i 0,2 0,3 0,4
1,30 1,07183 1,08241 1,11546 1,17537 1,27120
1,35 1,09583 1,10663 1,14034 1,20146 1,29922
1,40 1,11808 1,12907 1,16339 1,22562 1,32516
1,45 1,13856 1,14972 1,18460 1,24782 1,34892
1,50 1,15724 1,16856 1,20392 1,26802 1,37052
1,55 1,17411 1,18556 1,22134 v 1,28620 1,38994
1,60 1,18913 1,20070 1,23685 1,30235 1,40711
1,65 1,20230 1,21397 ' 1,25041 1,31645 1,42207
1,70 1,21362 1,22535 1,26203 1,32848 1,43476
1,75 1,22307 1,23486 1,27169 1,33845 1,44520
1,80 1,23064 1,24247 1,27940 1,34634 1,45338
1,85 1,23635 1,24818 1,28514 1,35216 1,45929
1,90 1,24018 1,25200 1,28895 1,35590 1,46296
1,95 1,24215 1,25396 1,29081 1,35760 1,46437
2,00 1,24227 1,25402 1,29073 1,35723 1,46356
2,05 1,24056 1,25225 1,28873 1,35485 1,46053
2,10 1,23704 1,24863 1,28484 1,35044 1,45531
2,15 1,23172 1,24319 1,27906 1,34405 1,44792
2,20 1,22462 1,23596 1,27143 1,33569 1,43840
2,25 1,21577 1,22698 1,26199 1,32541 1,42677
2,30 1,20522 1,21627 1,25075 1,31323 1,41309
2,35 1,19299 1,20385 1,23776 1,29921 1,39739
2,40 1,17911 1,18977 1,22307 1,28336 1,37971
282
Продолжение
0,5 0,6 0,7 0,8 0,9 1,0 1,1
1,42063 1,66025 2,07652 2,93002 5,52550 -4,93959
1,45169 1,69614 2,12077 2,99140 5,63886 —5,03550
1,48035 1,72918 2,16143 3,04760 5,74225 -5,12197
1,50658 1,75936 • 2,19842 3,09854 5,83547 -5,19882
1,53037 1,78663 2,23172 3,14415 5,91843 —5,26596
1,55167 1,81095 2,26126 3,18438 5,99099 -5,32326
1,57045 1,83230 2,28702 3,21915 6,05305 —5,37068
1,58672 1,85065 2,30899 3,24846 6,10458 -5,40812
1,60044 1,86599 2,32714 •3,27228 6,14549 —5,43555
1,61160 1,87832 2,34143 3,29057 6,17577 -5,45295
1,62022 1,88762 2,35189 3,30335 6,19541 -5,46032
1,62629 1,89391 2,35851 3,31061 6,20443 —5,45770
1,62980 1,89716 2,36131 3,31237 6,20287 —5,44510
1,63078 1,89744 2,36029 3,30866 6,19076 —5,42261
1,62925 1,89471 2,35550 3,29952 6,16821 —5,39030
1,62521 1,88906 2,34695 3,28498 6,13531 —5,34825
/ 1,61870 1,88046 2,33470 3,26514 6,09217 —5,29663
1,60975 1,86897 2,31878 3,24004 6,03895 —5,23554
1,59839 1,85464 2,29926 3,20977 5,97578 —5,16517
1,58467 1,83752 2,27618 3,17443 5,90286 -5,08567
1,56862 1,81765 2,24964 3,13410 5,82039- —4,99725
/ 1,55029 1,79510 2,21970 3,08889 5,72256 —4,90014
1,52975 1,76993 2,18642 3,03895 5,62766 —4,79455
283
Продолжение
2 1.2 1.3 1.4 1,5 1.6
1,30 —2,33981 —1,47896 -1,05210 —0,79827 —0,63053
1,35 —2,38360 -1,50543 —1,06991 —0,81087 —0,63961
1 ;40 —2,42277 —1,52886 —1,08546 —0,82166 -0,64718
1,45 —2,45723 -1,54919 —1,09870 —0,83061 —0,65322
1,50 —2,48692 —1,56639 —1,10962 —0,83771 —0,65770
1,55 —2,51180 -1,58043 —1,11819 —0,84293 —0,66061
1,60 —2,53182 -1,59128 —1,12440 —0,84628 —0,66196
1,65 —2,54697 —1,59894 —1,12823 —0,84773 —0,66173
1,70 —2,55722 —1,60337 —1,12966 -0,84728 —0,65991
1,75 • —2,56256 -1,60459 —1,12873 —0,84493 —0,65652
1,80 —2,56300 —1,60259 —1,12540 —0,84069 —0,65154
1,85 —2,55854 -1,59740 —1,11970 —0,83456 -0,64500
1,90 —2,54921 —1,58900 -1,11164 —0,82256 —0,63689
1,95 —2,53506 —1,57745 —1,10124 —0,81670 -0,62725
2,0 -2,51610 — 1,56276 —1,08851 —0,80500 —0,61607
2,05 —2,49241 —1,54497 — 1,07349 —0,79148 —0,60339
2,10 —2,46403 —1,52413 —1,05621 —0,77618 -0,58922
2,15 -2,43104 -1,50027 —1,03673 —0,75912 —0,57361
2,20 -2,39353 —1,47346 -1,01507 -0,74033 -0,55656
2,25 —2,35160 -1,44376 —0,99127 —0,71988 —0,53814
2,30 -2,30530 -1,41124 —0,96539 —0,69780 —0,51836
2,35 —2,25479 —1,37597 —0,93750 -0,67410 —0,49727
2,40 -2,20017 —1,33802 -0,90764 —0,64887 -0,47491
284
Продолжение
1,7 1,8 1,9 2,0 2,1 2,2 2,3
-0,51160 —0,42283 —0,35380 —0,29821 —0,25195 —0,21211 -0,17638
-0,51811 —0,42734 -0,35667 -0,29964 -0,25206 —0,21090 —0,17381
—0,52331 -0,43069 —0,35847 в—0,30009 —0,25121 —0,20879 —0,17033
-0,52719 —0,43285 —0,35919 -0,29951 —0,24942 —0,20574 —0,16593
-0,52972 -0,43382 —0,35882 -0,29794 -0,24666 —0,20176 —0,16060
-0,53091 —0,43358 —0,35737 —0,29534 —0,24294 —0,19685 —0,15433
-0,53072 -0,43216 —0,35482 -0,29172 —0,23825 —0,19099 -0,14714
-0,52919 -0,42951 -0,35115 —0,28708 —0,23258 -0,18420 -0,13901
—0,52627 —0,42564 —0,34640 —0,28142 —0,22595 -0,17646 —0,12997
-0,52201 —0,42057 —0,34054 —0,27474 —0,21836 —0,16780 -0,11999
—0,51637 —0,41429 -0,33359 —0,26704 —0,20980 -0,15822 —0,10911
-0,50939 —0,40682 —0,32556 -0,25835 —0,20029 —0,14771 -0,09733
—0,50106 -0,39816 —0,31645 —0,24866 —0,18986 -0,13631 —0,08465
—0,49140 —0,38833 —0,30627 —0,23798 —0,17850 —0,12402 -0,07111
—0,48043 —0,37733 —0,29505 —0,22634 —0,16623 —0,11085 —0,05671
—0,46817 —0,36519 —0,28280 —0,21376 —0,15306 -0,09684 —0,04147
—0,45464 —0,35195 —0,26955 —0,20024 —0,13904 —0,08199 —0,02543
—0,43986 —0,33760 —0,25532 -0,18583 —ft,12416 —0,06634 —0,00860
—0,42387 -0,32218 -0,24011 —0,17054 —0,10847 —0,04991 0,00099
—0,40669 —0,30571 —0,22398 —0,15438 —0,09198 —0,03272 0,02731
—0,38836 -0,28825 —0,20695 -0,13742 —0,07473 —0,01481 0,04633
—0,36891 —0,26982 —0,18904 —0,11965 —0,05673 =0,00380 0,06601
—0,34838 —0,25043 —0,17030 —0,10113 —0,03805 —0,02306 0,08632
285
Продолжение
** 9 2,4 2,5 2,6 2,7 2,8
1,30 —0,14269 —0,10864 —0,07057 -0,02114 0,06066
1,35 —0,13857 —0,10260 -0,06193 +0,00842 0,08121
1,40 -0,13352 —0,09559 -*0,05220 +0,00560 0,10349
1,45 -0,12753 —0,08758 —0,04137 0,02091 0,12750
1,50 -0,12059 —0,07857 —0,02944 0,03753 0,15325
1,55 -0,11270 -0,06856 —0,01640 0,05544 0,18073
1,60 -0,10386 —0,05754 —0,00227 0,07466 0,20993
1,65 -0,09408 —0,04554 —0,01297 0,09516 0,24083
1,70 -0,08335 -0,03255 —0,02928 0,11693 0,27343
1,75 —0,07169 -0,01858 0,04667 0,13996 0,30767
1,80 -0,05911 —0,00365 0,06512 0,16423 0,34354
1,85 -0,04562 0,01224 0,08460 0,18970 0,38100
1,90 —0,03122 0,02907 0,10510 0,21636 0,42002
1,95 -0,01595 0,04681 0,12659 0,24417 0,46054
2,0 +0,00018 0,06544 0,14906 0,27310 0,50249
2,05 0,01715 0,08493 0,17244 0,30309 0,54583
2,10 0,03492 0,10526 0,19673 0,33411 0,59050
2,15 0,05348 0,12640 0,22188 0,36613 0,63642
2,20 0,07280 0,14832 0,24786 0,39907 0,86356
2,25' 0,09284 0,17096 0,27463 0,43291 0,73177
2,30 0,11356 0,19431 0,30213 0,46756 0,78104
2,35 0,13495 0,21831 0,33032 0,50298 0,83125
2,40 0,15694 0,24295 0,35915 0,53912 0,88231
286
Продолжение
А 2,9 3,0 3,1 3,2 3,3 3,4 3,5 3,6
0,27798 —0,52529 -0,31142 —0,23552 -0,19461 —0,16804 —0,14888
0,32147 0,36804 -0,57226 —0,62174 —0,33553 —0,36078 —0,25191 -0,26899 —0,20710 —0,22004 —0,17814 —0,18855 -0,15735 —0,16607
0,41771 —0,67368 —0,38711 —0,28671 —0,23340 -0,19929 -0,17501
°- 0,47048 —0,72809 -0,41453 -0,30508 —0,24722 —0,21031 —0,18417
0,52631 —0,78489 —0,44304 —0,32409 —0,26143 —0,22165 —0,19355
0,58519 —0,84411 -0,47260 —0,34373 —0,27608 —0,23326 —0,20313
V 0,64710 —0,90572 —0,50320 -0,36399 -0,29111 —0,24516 —0,21292
\ 0,71198 -0,96958 —0,53482 —0,38481 -0,30653 —0,25732 —0,22289
ч" 0,77978 -1,03574 —0,56743 —0,40623 —0,32233 —0,26974 —0,23304
0,85041 —1,10408 —0,60102 —0,42817 —0,33847 —0,28239 —0.24334
£ 0,92385 -1,17454 —0,63548 —0,45067 -0,35495 —0,29525 —0,25379
& 0,99998 -1,24697 —0,67082 —0,47362 —0,37172 —0,30833 —0,26438
«г 1,07872 —1,32139 —0,70699 —0,49707 —0,38881 -0,32157 —0,27509
1... * 4 1,15995 -1,39763 —0,74392 -0,52090 —0,40613 -0,33500 -0,28589
1,24352 —1,47561 —0,78156 -0,54516 —0,42370 —0,34854 -0,29677
1,32940 —1,55512 —0,81987 —0,56979 —0,44145 —0,36222 —0,30773
Г 1,41742 —1,63617 —0,85879 —0,59469 —0,45940 —0,37598 —0,31871
1,50744 —1,71859 —0,89826 -0,61989 —0,47748 —0,38982 —0,32971
1,59926 -1,80213 —0,93818 -0,64528 —0,49568 —0,40368 —0,34071
b‘ 1,69280 — 1,88682 —0,97849 —0,67088 -0,51393 —0,41756 —0,35168
1,78790 -1,97240 — 1,01912 —0,69659 —0,53224 -0,43144 -0,36259
к'. 4 «Л 1- Й-.< 1,88435 —2,05877 —1,05999 —0,72240 —0,55054 =0,44525 —0,37344 287
Продолжение
V 2 0 0,2 0,4 0,6 0,8
2,5 1,14662 1,18870 1,33864 1,71198 2,92532
2,6 1,10807 1,14802 1,29034 1,64442 2,79435
2,7 1,06390 1,10147 1,23527 1,56792 2,6J?29
2,8 1,01452 1,04950 1,17397 1,48321 2,48552
2,9 0,96043 0,99261 1,1070 1,39108 2,31054
3,0 0,90212 0,93132 1,03513 1,29240 2,12389
3,1 0,84013 0,86622 0,95884 1,18803 1,92726
3,2 0,77503 0,79786 . 0,87887 1,07889 1,72235
3,3 . 0,70737 0,72687 0,79593 0,96596 1,51095
3,4 0,63776 0,65385 0,71074 0,85018 1,29484
3,5 0,56678 0,57943 0,62399 0,73256 . 1,07584
3,6 0,49503 0,50422 0,53645 0,61405 0,85579
3,7 0,42310 0,42888 0,44882 0,49563 0,63648
. 3,8 0,35159 0,35397 0,36182 0,37829 0,41971
3,9 0,28106 0,28014 0,27614 0,26295 0,20721
4,0 0,21208 0,20795 0,19246 0,15054 0,00066
4,1 0,14518 0,13796 0,11145 0,04191 —0,19832
4,2 0,08086 0,07070 0,03370 —0,06210 —0,38822
4,3 0,01960 0,00668 -0,04020 —0,16070 —0,56759
4,4 —0,03813 —0,05363 —0,10970 —0,25319 -0,73514 •
4,5 —0,09195 —0,10981 —0,17432 —0,33889 —0,88965
4,6 —U, 14148 —0,16148 —0,23361 —0,41723 —1,03005
4,7 —0,18640 —0,20829 —0,28719 —0,48767 —1,15540
4,8 —0,22643 -0,24995 —0,33471 —0,54977 —1,26490
288
Продолжение
-r 1,0 1,2 1,4 1,6 1,8 ' 2,0
—2,07911 —0,84231 —0,42657 —0,20901 —0,06195
- —1,94319 —0,76997 -0,37374 —0,16430 —0,02016
—1,79365 —0,69121 —0,31687 —0,11667 —0,02390
—1,63179 —0,60673 —0,25641 —0,06651 0,06989
—1,45903 —0,51724 —0,19287 —0,01421 0,11743
. —1,27686 -0,42351 —0,12679 0,03978 0,16614
—1,08685 —0,32632 —0,05870 0,09502 "• 0,21562
—0,89061 —0,22649 0,01082 0,15107 0,26547
-0,68982 —0,12486 0,08120 0,20745 0,31526
—0,48614 —0,02228 0,15185 0,26369 0,36457
-0,28127 —0,08042 0,22217 0,31934 0,41302
—0,07694 0,18237 0,29160 0,37390 0,46016
0,12521 0,28273 0,35956 0,42695 0,50562
0,32354 0,38071 0,42549 0,47803 0,54901
b ' 0,51643 0,47547 0,48884 0,52673 0,58994 ’
0,70235 0,56628 0,54911 0,57264 0,62809
0,87984 0,65241 0,60580 0,61536 0,66310
1,04751 0,73318 0,65847 0,65456 0,69468
Л/ 1,20411 0,80797 0,70669 0,68992 0,72257
1,34841 0,87619 0,75008 0,72113 0,74653
1,47938 0,93734 0,78832 0,74795 0,76633
1,59609 0,99099 0,82109 0,77018 0,78181
1,69773 1,03674 0,84818 0,78762 0,79286
t / 1,78363 1,07427 0,86938 / 0,80015 0,79934
19—730
289
Продолжен^.
z V 2,2 2,4 2,6 2,8 3,0
2,5 0,06343 0,20264 0,41853 0,98664
2,6 0,10598 0,25030 0,47984 1,09325
2,7 0,15042 . 0,29957 0,54260 1,20132
2,8 0,19636 0,35006 0,60631 1,30998
2,9 0,24347 0,40137 0,67049 1,41832
3,0 0,29134 0,45308 0,73457 1,52544
3,1 0,33961 0,50478 0,79803 1,63038
3,2 0,38784 0,55601 0,86033 1,73220
3,3 0,43566 0,60635 0,92090 1,82996
3,4 0,48266 0,65536 0,97921 1,92275
3,5 0,52840 0,70258 1,03470 2,00962
3,6 0,57254 0,74764 1,08689 2,08976 i
3,7 0,61466 0,79010 1,13525 2,16229
3;8 0,65442 0,82960 1,17933 2,22644
3,9 0,69144 0,86572 ' 1,21866 2,28147
4,0 0J2540 0,89817 1,25285 2,32672
4,1 0,75599 0,92659 1,28153 2,36163
4,2 0,78294 0,95072 1,30435 2,38564
- 4,3 0,80599. 0,97034 1,32104 2,39833
4,4 0,82495 0,98518 1,33136 2,39939
4,5 0,83959 0,99510 1,33513 2,38858
4,6 0,84981 0,99996 1,33223 2,36572
4,7 0,85546 0,99965 1,32257 2,33078
4,8. 0,85650 0,99417 1,30614 2,28381
290
¥' л, w*' |L ’ Продолжение
3,2 3,4 3,6 3,8 4,0
*•^1 ' 1
й- —1,14215 —0,58699 —0,39480 —0,29408 * —0,22994
—1,22435 —0,62299 —0,41556 —0,30718 —0,23823
?! —1,30581 -0,65819 —0,43551 —0,31944 —0,24565
к Г —1,38587 —0,69224 —0,45440 —0,33069 —0,25204
—1,46375 —0,72483 —0,47205 —0,34077 —0,25726
ч«’ ; &• • —1,53878 —0,75558 —0,48823 -0,34952 ‘ —0,26120
4 —1,61012, —0,78417 —0,50270 —0,35679 -0,26374
> —1,67704 —0,81624 —0,51526 —0,36242 —0*26474
v,y к,. —1,73882 , —0,83345 —0,52571 —0,36626 —0,26411
—1,79480 —0,85349 —0,53383i —0,36817 -0,26173
—1,84419 —0,87006 —0,53946 —0,36804 —0,25750
£• —1,88640 —0,88286 —0,54244 -0,36574 -0,25137
—1,92080 —0,89162 —0,54259 —0,36117 —0,24324
1* t —1,94690 —0,89611 -0,53979 —0,35426 —0,23306
i*. V £• —1,96407 —0,89613 -0,53391 —0,34493 -0,22081
to £’ —1,97196 —0,89151. —0,52488 —0,33313 —0,20644
lh’ 1’ —1,97017 —0,88208 —0,51261 -0,31884 -0,18996
?’ \. —1,95846 —0,86775 —0,49706 —0,30204 -0,17139
1 —1,93652 —0,84845 —0,47824, —0,28274 —0,15074
—1,90424 —0,82416 —0,45614 —0,26098 —0,12806
% t —1,86157 —0,79488 —0,43079 —0,23680 —0,10343
1 —1,80859 —0,76067 , —0,40229 —0,21029 —0,07694
k; jt- -1,74533 -0,7216? —0,37068 . —0,18153 z —0,04867
к —1,67204 " -0,67793 -0,33614 —0,15066 —0,01876
4
Л*-1 Й ti 19* t 291
f: l,f <
Продолжение
* 2 4,2 4,4 4,6 4,8 5,0
2,5 —0,18331 —0,14465 —0,10501 —0,03775
2,6 —0,18800 —0,14593 —0,10186 —0,02433
2,7 —0,19170 —0,14606 —0,09718 —0,00820
2,8 —0,19430 —0,14492 —0,09085 —0,01080
2,9 —0,19569 —0,14241 —0,08276 0,03284
3,0 —0,19575 —0,13841 —0,07277 0,05809
3,1 —0,19439 —0,13284 —0,06081 0,08668
3,2 —0,19149 ,—0,12559 - —0,04677 0,11871
3,3 —0,18696 —0,11658 —0,03058 0,15434
3,4 -0,18073 —0,10577 —0,01217 0,19353
3,5 —0,17270 —0,09305 0,00850 0,23639
3,6 —0,16284 —0,07842 0,03147 0,28293
3,7 —0,15111 —0,06185 0,05674 0,33310
3,8 -0,13744 —0,04329 0,08431 0,38680
3,9 —0,12183 —0,02277 0,11414 0,44403
4,0 —0,10427 —0,00030 0,14620 0,50458
4,1 —0,08480 —0,02409 0,18038 0,56827
4,2 —0,06342 —0,05033 0,21662 0,63489
4,3 —0,04019 —0,07835 0,25478 0,70429
4,4 —0,01518 —0,10807 0,20473 0,77606
4,5 —0,01152 —0,13936 0,33629 0,84990
4,6 0,03982 0,17210 ' 0,37928 0,92547
4,7 0,06959 0,20614 0,42351 1,00242
4,8 0,10071 0,24132 0,46874 1,38027
292:
Продолжение
5,2 5,4 5,6 5,8 6,0
—0,20532 —0,14609 —0,12091 —0,10506 —0,09342
—0,22754 —0,15854 • —0,12984 —0,11208 —0,09920
—0,25184 —0,17189 —0,13929 —0,11943 —0,10519
—0,27832 —0,18618 «0,14928 —0,12712 —0,11139
—0,30706 —0,20143 —0,15980 —0,13514 —0,11780
—0,33811 —0,21766 —0,17087 —0,14348 —0 Л2439
—0,37154 —0,23490 —0,18248 —0,15213 —0,13117
—0,40736 —0,25309 —0,19459 —0,16108 —0,13810
—0,44558 —0,27226 —0,20722 -0,17030 —0,14516
—0,48617 —0,29236 —0,22031 —0,17977 ‘ —0,15231
—0,52911 —0,31337 —0,23385 —0,18944 —0,15954
—0,57432 —0,33523 —0,24779 —0,19927 —0,16680
—0,62171 —0,35789 —0,26206 —0,20925 —0,17403
—0,67113 —0,38126 —0,27663 —0,21929 -0,18121
—0,72243 —0,40527 -0,29143 . —0,22937 —0,18828
—0,77549 —0,42983 —0,30636 —0,23939 —0,19517
—0,83001 —0,45479 —0,32139 —0,24929 —0,20183
—0,88582 —0,48002 —0,33636 —0,25903 —0,20820
» —0,94263 —0,50539 -0,35122 —0,26849 —0,21422
—1,00012 —0,53077 —0 ,(36586 —0,27760 —0,21978
—1,05801 —0,55599 —0,38015 —0,28632 —0,22485
—1,11593 —0,58088 —0,39403 —0,29449 —0,22935
—1,17352 —0,60527 —0,40731 —0,30208' —0,23319
—1,23040 —0,62&93 —0,41989 —0,30893 —0,23629
293
Продолжение
X. V z ,0 0,3 0,6 0,9 . 1,0 1,2
4,95 —0,27678 —0,33747 —0,62653 —2,98999 1,88187
5,13 —0,31502 —0,37893 —0,68286 —3,16208 1,94243
5,25 —0,34083 —0,40648 —0,71827 —3,25689 1,96488
5,4 —0,35411 —0,42002 —0,73271 —3,27459 1,97959
5,55 —0,35504 Д0,41975 —0,72652 —3,21686 1,89759
5,7 T-0,34398 —0,40612 —0,70046 —3,08673 I4,81063
5;85 —0,32157 —0,37983 —0,6^561 —2,88852 1,69102
6,0 —0,28856 —0,34179 —0,59336 —2,62768 £1,54166
6,15 —0,24599 —0,29306 —0,51538 —2,31062 1,36586
6,3 —0,19490 —0,23486 —0,42352 1,16725
6,45 —0,13640 —0,16850 —0,31974 —1,53634 0,94957
6,6 —0,07169 —0,09524 —0,20604 —1,09395 0,71657
6,7$ —0,00186 —0,01636 —0,08425 —0,62418 0,47176
6,9 0,07215 4-0,06712 —0,04401 —0,13300 0,21811
7,05 0,14965 0,15436 0,17756 0,37530 --0,04229
7,2 < . 0,23027 i 0,24510 0,31591 0,89889 • —0,30859
294,
. (
Продолжение
1,5 1,8 2,1 2,4 2,7 3,0
0,97447 0,80955 0,81721 0,97619 1,57370
0,98709 0,80759 0,80402 0,94666 1,49952
0.98373 r0,79435 0,78074 0,90600 1,40790
0,96460 0,77015 0,74778 ' . 0,85481 1,30009,
0,93031 0,73550 0,70572 0,79387 1,17764.
0,88171; 0,6911.0 0,65530 , 0,72416 . 1,04238
0,81989. 0,63781 0,59740 0,64678 0,89636
0,74615 . 0,57666 0,53303 0.563Q1 . 0,74181
0,60201 0,50877 0,46328 0,47418 0,58107
0,56903 0,43535 , ^38933 0,33168 0,41654
0,46887 0,35758 v 0,31228 0,28686 0,25Q54
0,36315 0,27668 0,23326 0,19100 0,08522
0,25337 0,19371 0,15328. 0,09530 0,07748
0,14080' 0,10959 0,07317; 0,00063 0,23614
0,02630 0,02491 0,00658 —0,09239 —0,38991 . - :
—0,08978 —0,06013 —0,08581 —0,18375 —0,53881
i j
. 295
Продолжение
3,3 3,6 3,9 4,2 4,5
4,95 —0,91927 —0,27910 —0,03279 0,14956 0,39663
5,1 —0,81442 —0,21639 0,01885 0,20049 0,45790
5,25 —0,69779 . —0,14872 0,07318 0,25286 0,51949
5,4 —0,57082 —0,07699 0,12948 0,30600 0,58052
5,55 —0,43521 —0,00212 0,18701 0,35911 0,64008
5,7 —0,29286 ф0,07483 0,24496 0,41147 0,69726
45»85 —0,14579 Н, 15280 0,30248 0,46226 0,75114
<6,0 —0,00390 ФО,23066 0,35874 0,51073 0,80079
6,15 —0,15403 4-0,30729 0,41292 0,55611 0,84|537
6,3 0,30250 40,38161 0,46425 0,59775 0,88418
6,45 0,44732 : .4-0,45263 0,51203 0,63499 0,91655
•6,6 0,58670 4-0,51948 0,55565 0,66742 0,94208
6,75 0,71916 4-0,58147 0,59470 0,69470 0,96048
«,9 0,74370 4-0,63818 0,62893 0,71673 0,97180
7,05 0,95992. 4-0,68955 > 0,65843 0,73369 0,97645
7.2 1,06826 . 0,73594 0,6836Q 0,74611 0,97530
1 1 i i i i i i i i 1 !
29Ц
Продолжение
4,8 5,0 5,1 5,4 5,7 6,0
1,19769 —2,59431 —0,66272 —0,36996 —0,23940
1,31457 —2,77014 —0,69382 —0,38030 —0,24042
1,42907 —2,93667 —0,72150 —0,38808 -0,23915
1,53945 —3,09047 —0,74518 —0,39297 —0,23531
1,64376 —3,22884 —0,76412 -0,39466 -0,22871
1,74029 —3,34870 —0,77770 —0,39279 -0,21918
1,82722 —3,44705 -0,78540 —0,38717 —0,20658
1,90275 —3,52128 —0,78667 —0,37755 —0,19081
1,96551 —3,56944 —0,78110 —0,36377 —0,17185
- 2,01407 —3,58954 —0,76848 —0,34581 —0,14973
2,04754 —3,58039 —0,74865 —0,32368 —0,12456
2,06525 —3,54146 —0,72169 -0,29754 —0,09656
2,06702 —3,47345 —0,68784 —0,26766 -0,06602
2,05341 —3,37781 —0,64774 —0,23450 —0,03342
2,02552 —3,25755 —0,60229 —0,19874 -0,00064
1,98571 —3,11732 —0,55281 —0,16126 0,03533
20—730
297
Продолжение
\ ** Z \ 6.3 6,6 6,9 7,0 • 7,2
4,95 —0,15126 —0,05409 0,35572 —0,38068
5,1 . —0,14493 —0,03640 0,43926 -0,42507
5,25 —0,13615 —0,01546 0,53275 -0,47324
5,4 —0,12474 0,00890 0,63631 —0,52499
5,55 —0,11054 0,03678 0,75003 —0,58023
5,7 —0,09346 0,06822 0,87371 —0,63873
5,85 —0,07345 0,10316 1,00681 —0,70016
6,0 —0,05048 0,14153 1,14868 —0,76404
6,15 —0,02461 0,18317 1,29851 —0,82989
6,3 0,00403 0,22777 1,45484 —0,89705
6,45 0,03526 0,27498 1,61637 —0,96462
6,6 0,06877 0,32432 1,78089 —1,03159
6,75 0,10416 0,37508 1,94625 —1,09691
6,9 0,14093 0,42648 2,10920 —1,15907
7,05 0,17834 0,47748 2,26614 1,21640
7,2 0,21547 0,52679 - 2,41239. —1,26687
298
Продолжение
7.5 7,8 8,1 8,4 8,7
—0,21111 —0,15864 -0,12884 —0,10692 —0,08425
—0,22899 —0,16941 —0,13598 —0,11140 —0,08527
—0,24789 —0,18054 —0,14316 —0,11564 —0,08552
—0,26775 —0,19196 —0,15028 —0,11953 —0,08483
—0,28845 —0,20357 —0,15726 —0,12295 —0,08304
—0,30987 —0,21526 —0,16398 —0,12579 —0,07997
—0,33181 —0,22690 —0,17032 —0,12792 —0,07541
—0,35412 —0,23833 —0,17614 —0,12917 —0,06914
—0,37645 —0,24935 —0,18128 —0,12939 —0,06094
—0,39862 —0,25979 -0,18556 —0,12840 —тО,05055
—0,42019 —0,26940 —0,18880 —0,12601 -40,03771
—0,44081 —0,27789 —0,19077 —0,12200 —0,02214
—0,45998 —0,28498 —0,19122 —О', 11612 —0,00352
—0,47715 —0,29032 —0,18987 —0.108Ц —0,01854
—0,49167 —0,29344 —0,18641 —0,09766 —0,04442
—0,50281 I —0,29393 —0,18042 —0,08436 —0,07466
299
ПРИЛОЖЕНИЕ V
Таблица П.У1.1
ШИРИНА ПОЛОСЫ, ЗАНИМАЕМОЙ ИЗЛУЧЕНИЕМ ТРАПЕЦЕИДАЛЬНЫХ
ИМПУЛЬСОВ И ИМПУЛЬСОВ С СИНУСОИДАЛЬНЫМ СКРУГЛЕНИЕМ
ПРИ ЧАСТОТНОЙ МАНИПУЛЯЦИИ
т Ширина полосы в единицах n—^f/B
прямо- угольные импульсы 1 трапецеидальные импульсы при И» Равном 1 t импульсы с синусоидальным скруглением при £, равном
0,7 0,8 0,9 0,7 0,8 0,9
1.0 2 2 2 2 2 2 2
1,5 3 3 3 3 3 3 3
2,0 3 3 3 — 3 3 3
2,5 5 4 4 5 4 4 5
3,0 6 4 4 6. 4 4 6
3,5 6 5 5 6 5 5 6
4,0 7 5 5 7 5 5 7
4,5 8 6 6 7 6 6 7
5,0 8 6 6 8 6 6 8
5,5 9 7 7 8 7 7 8
6,0 9 7 7 9 7 7 9
6,5 10 8 8 9 8 8 9
7,0 10 9 9 10 8 10 10
7,5 И 9 9 10 9 10 10
8,0 И 10 10 11 — 11 И
8,5 13 10 10 11 10 11 И
9,0 14 11 И 12 11 12 12
9,5 14 11 11 12 11 12 13
10,0 15 12 12 13 12 13 13
10,5 15 12 12 13 12 13 14
11,0 16 13 13 14 12 14 14
11,5 16 13 13 14 13 14 15
12,0 17 14 14 15 14 15 15
12,5 17 14 14 16 14 15 16
13,0 18 15 16 16 15 16 16
13,5 18 15 16 17 15 16 17
14,0 19 16 17 17 16 17 17
14,5 19 16 17 18 16 17 18
15,0 20 17 18 18 — 18 18
15,5 21 17 ‘ 18 19 17 18 19
16,0 21 18 19 19 18 19 19
16,5 22 18 19 20 18 19 20
17,0 22 19 20 20 19 20 20
17,5 со -сч — 19 21 21 19 20 21
300
Продолжение
Ширина полосы в единицах п=Ц/В
т прямо- угольные импульсы трапецеидальные импульсы ' при £, равном импульсы с синусоидальным скруглением при £, равном
0,7 0,8 0,9 0,7 0,8 0,9
18,0 23 20 21 21 -- 21 21
18,5 24 20 22 22 20 21 22
19,0 24 21 22 22 21 22 22
19,5 25 21 23 23 21 23 23
20,0 25 22 23 23 22 23 23
20,5 26 22 24 24 22 24 24
21,0 26 23 •24 24 23 24 24
21,5 27 23 25 25 24 25 25
22,0 27 24 25 25 24 25 25
22,5 28 24 26 26 — 26 26
23,0 28 .25 26 26 — 26 26
23,5 29 25 27 27 27 27
24,0 29 26 27 27 — 27 27
ПРИЛОЖЕНИЕ VII
КЛАССИФИКАЦИЯ ИЗЛУЧЕНИИ
В соответствии с Регламентом радиосвязи [Л43] излучения классифици-
руют и обозначают, учитывая следующие характеристики:
1. Тип модуляции основной несущей частоты.
2. Тип передачи.
3. Дополнительные характеристики.
1. Типы модуляции основной несущей частоты: Обозначение
а) амплитудная А
б) частотная (или фазовая) F
в) импульсная Р
2. Типы передачи:
а) отсутствие какой-либо модуляции, предназначенной
для передачи сообщения О
б) телеграфирование без использования модулирующей
звуковой частоты 1
в) телеграфирование посредством амплитудной манипуля-
ции одной или нескольких модулирующих звуковых частот
или посредством амплитудной манипуляции модулированного
излучения (особый случай: модулированное излучение без ма-
нипуляции) 2
г) телефония (включая радиовещание) 3
д) факсимиле (при помощи модулирующей. основной не-
сущей частоты непосредственно или при помощи модулиро-
ванной по частоте поднесущей) 4
е) телевидение (только изображение) 5
ж) двойное частотное телеграфирование (ДЧТ) 6
з) тональная телеграфия (многократная) 7
и) случаи, не предусмотренные выше 9
3. Дополнительные характеристики:
а) две боковые полосы никакого
б) одна боковая полоса:
ослабленная несущая частота, А
полная несущая частота Н
подавленная несущая частота J
в) две независимые боковые полосы В
г) остаточная боковая полоса С
д) импульсная передача:
модуляция по амплитуде D
модуляция по ширине (или длительности) Е
модуляция по фазе (или положению) F
кодово-импульсная модуляция G ,
Классификация типичных излучении дана в табл. П.УПЛ.
Таблица ПУП Л
КЛАССИФИКАЦИЯ ТИПИЧНЫХ ИЗЛУЧЕНИЙ
Тип передачи Дополнительные характеристики Обозначение
I. Амплитудная модуляция несущей частоты Телеграфирование без применения мо- дулирующей звуковой частоты (ам- плитудная манипуляция) Телеграфирование посредством ампли- тудной манипуляции модулирующей звуковой частоты или модулирующих звуковых частот, или посредством амплитудной манипуляции модули- рованного излучения (частный случай: постоянное модулированное по амп- литуде излучение) Телефония Факсимиле (с модуляцией основной несущей частоты непосредственно или при помощи модулированной по частоте поднесущей) Телевидение Многократная триальная телеграфия Случаи, не предусмотренные выше, например, комбинированная пере- дача телефонии и телеграфии II. Частотная (или фазовая) модуля- ция несущей частоты Телеграфирование (частотная мани- пуляция) без применения модуляции звуковой частоты, одна из двух ча- стот излучается в любое время Телеграфирование посредством ампли- тудной манипуляции модулирующей звуковой частоты или посредством При отсутствии модуля- ции Две боковые полосы Одна боковая полоса; не- сущая частога ослаб- лена Одна боковая полоса; не- сущая частота подав- лена Две независимые боко- вые полосы Одна боковая полоса; не- сущая частота ослаб- лена Остаточная боковая по- лоса Одна боковая полоса; не- сущая частота ослаб- лена Две независимые боковые полосы АО А1 А2 АЗ АЗА A3J АЗВ А4 А4А А5С А7А А9В F1 F2
303
Продолжение
Тип передачи Дополнительные характеристики Обозначение
амплитудной манипуляции излуче- ния, модулированного по частоте (частотный случай, излучение, моду- лированное по частоте без манипу- ляции) Телефония Факсимиле при помощи непосредствен- ной модуляции несущей частоты Телевидение Двойное частотное телеграфирование (ДЧТ) Случаи, не предусмотренные выше, в которых основная несущая моду- лируется по частоте III. Импульсная модуляция несущей частоты Несущая импульсов без применения модуляции, предназначенной для передачи сообщения (например, радиолокация) Телеграфирование посредством ампли- тудной манипуляции несущей им- пульсов без применения [модуляции звуковой частоты Телеграфирование посредством ампли- тудной манипуляции одной или нескольких модулируемых звуковых частот или посредством амплитуд- ной манипуляции модулированной несущей импульсов (частный случай: модулированная несущая импульсов без манипуляции) Звуковая частота или звуковые частоты, мо- дулирующие амплитуду импульсов Звуковая частота или звуковые частоты, мо- дулирующие ширину импульсов Звуковая частота или звуковые частоты, мо- дулирующие фазу (или положение) импульсов F3 F4 F5 F6 F9 Р0 P1D P2D Р2Е P2F
Телефония Модуляция амплитуды импульсов P3D
304.
Продолжение
Тип передачи Дополнительные характеристики Обозначение
Случаи, не предусмотренные импульсной модуляцией несущей частоты выше, с основной Модуляция ширины (или длительности) импуль- сов Модуляция фазы (или по- ложения) импульсов Кодово-импульсная моду- ляция (после амплитуд- но-импульсной модуля- ции и отбора импульс- ных посылок) РЗЕ P3F P3G Р9
ЛИТЕРАТУРА
1. Андреев Н. Н. Электрические колебания и их спектры. М., 1917.
2. Balth. van der Pol. Frequency modulation. Proc, of the IRE, t. 8
№ 7, 1930, стр. 1195.
3. Курант iP., Гильберт Д. Методы математической физики. ГИТТЛ,
1933, 1.
4. Котельников В. А. О пропускной способности «эфира» и прово-
локи в электросвязи. Материалы к I Всесоюзному съезду по вопросам тех-
нической реконструкции связи и развития слаботочной промышленности. М.,
Связьиздат, 1934.
5. R. Е. А. С. Paley and N. Wiener — Fourier transforms in the comple
domain, American Mathematical Society, New York, 1934.
6. Майер А. Г. и ЛеонтовичЕ. А. Об одном неравенстве, связан-
ном с интегралом Фурье. Доклады Академии наук СССР, т. IV, № 7, 1934,
стр. 354.
7. С и фор о в В. И. Об уплотнении эфира и проволоки при фазовой те-
леграфной передаче. В кн. Ленинградский электротехнический институт свя-
зи, научно-технический сборник. Выл. 15. Связьиздат, 1936, стр. 24.
8. Рыто в С. М. Модулированные колебания и волны. Труды ФИАН,
т. II, вып.’ 1, 1938.
9. Stratton I. A., Morse Р. М., Chu L. J., Hutner R. A. Elliptic
cylinder and spheroidal wave functions, The Technology Press, M. I. T., 1941
10. P ы т о в С. M. О некоторых «-парадоксах», связанных со спектраль-
ными разложениями. Успехи физических наук XXIX, вып. Л—2, 1946.
11, Gabor D. Theory of communication, ЛЕЕ, (III), v. 93, № 26, 1946
стр. 429.
12. Slack M. The probability distributions of sinusoidal oscillations com-
bined in random phase. Journal IEE, ч. Ill, t. 93, № 22, 1946, стр. 76.
13. Corrin'gton M. S. Variation of bandwidth with modulation index.
Proc, of the IRE,1 t. 35, № 10, 1947, стр. 1013.
14. Янке Б., Эм де Ф. Таблицы функций с формулами и кривыми.
ГИТТЛ, 1948.
15. В атсон Г. Н. Теория бесселевых функций, ч. 1. ИЛ, 1949.
/6. Котельников В. А. и Николаев А. М. Основы радиотех-
ники, ч. 1. М., Связьиздат, 1950.
17. Бу-ни-мо в и ч В. И. Флуктуационные процессы в радиоприёмных
устройствах, Изд. «Советское радио», 1951.
18. J. Н. Н. Chalk. The optimume pulse-shape for pulse communi-
cation. Proc. IEE, t. 87, 1950, стр. 88.
19. Рыжик И. M. и Г р а д ш т е й н И. С. Таблицы интегралов, сумм,
рядов и проведений. Изд. 3-е. М.-Л., Гостехиздат, 1951.
20. Титчмарш Е. Теория функций. ГТТЛМ, Л., 1951.
21. CawthraW. A. and Thomson W. Е. Bandwidth of sinusoidal
carrier wave, frequency-modulated by a rectangular with half-sine-wave
build-up. Proc. IEE, ч. Ill, № 51, t. 98, 1951, c. 69.
22. M. В. Шулейкин. Сборник статей под ред. акад. Б. А. Введенского.
Изд. «Советское радио», ’ 1952.
23. Харкевич А. А. Спектры и анализ. Гостехникотеоретиздат, 1952.
24. Таблицы интегралов Френеля, под ред. В. А. Диткина. Изд. Ин-та
точной механики и вычислительной техники АН СССР, М., 1953.
25. В 1 a n c-Lapierre Aet Fortet R.—Theorie des fonctions aleatoires, Masson
et Cie. Paris, 1953.
306
26. Р а й с С. Теория флуктуационных шумов. В сборнике под редакцией
Н. А. Железнова. ИЛ, 1953, стр. 88.
27. Таблицы интегрального синуса и косинуса, под ред. В. А. Диткина.
Изд. Ин-та точной механики и вычислительной техники АН СССР, М., 1954.
28. X а р к е в и ч А. А. Очерки общей теории связи. М., Гостехиздат, 1955.
29. Н е 1 b i п g Н. Pomiary widma radioteleraficznego, Prace Instytuty
Lacznosci Zeszyt 1 (2), Rok II Warszawa, 1955, c. 23.
30. Гу-ревич M. С. Сигналы конечной продолжительности, содержащие
максимальную долю энергии в заданной полосе частот. «Радиотехника и элек-
троника», т. 1, 3, 1956, стр. 313.
31. Гуревич М. С. Полоса частот, занимаемая при передаче импуль-
сов. «/Радиотехника и электроника», т. II, 1, 1957, стр. 38.
32. Харкевич А. А. О возможностях сжатия спектра сигнала. «Элек-
тросвязь», № 4, апрель «1957, стр. 3.
33. X а р к е в и ч А. А. О вычислении спектров случайных процессов. Ра-
диотехника», т. 12, № 5, май, 4957, стр. 5.
34. Гуревич М. С. Новый метод измерения ширины полосы частот,
излучаемой радиотелеграфными передатчиками. «Вестник связи», 12, 1957,
стр. 27.
35. А 11 n a 11 I. W. and Jones E. D. J. An investigation of the spectra
of binary frequency-modulated signals with various build-up wave-forms.
Proc. IEE. pt. B, No. 14, vol. 104, March 1957, c. 111.
36. Морс Ф. M. и Ф e ш 6 a x Г. Методы теоретической физики, т. I.
ИЛ, 1958.
37. Гуревич М. С. Измерение ширины полосы частот, излучаемой ра-
диотелеграфными передатчиками. «Измерительная техника», № 1, 1958.
стр. 62.
38. Гуревич М. С. Спектр радиочастот и его 'использование. «Вестник
связи», № 4, 1958. стр. 11.
39. Г у р е в и ч М. С. Полоса частот, занимаемая передачей случайной по-
следовательности сигналов. «Радиотехника», т. 13, № 11, 1958, стр. 18.
40. С. С. I. R. Documents of the IX th Plenary Assembly (Los Angeles,
1959), ITU, Geneva, vol. 1, 11, 111, 1959.
40. Ж и с л и н Г. M. К задаче об оценке произведения продолжительно-
сти сигнала на ширину его полосы. Известия высших учебных заведений. Ра-
диофизика, т. 3, № 5, 1960, стр. 860.
42. Гуревич М. С. Косинус-кубичные импульсы. «Радиотехника»,
т. 15, № 5, 1960, стр. 60.
43. Регламент радиосвязи 1959 г. Связьиэдат, 1961.
44. Л евин Б. Р. Теория случайных процессов и её применение в радио-
технике. М., Изд. «Советское радио», 1957.
307
ОГЛАВЛЕНИЕ
Стр.
Предисловие..................................................... 3
Введение .......................................................... 4
§ В.1. Спектр радиочастот и его использование...................... 4
§ В.2. Ширина полосы частот как физическая характеристика сигнала 8
§ В.З. Основные понятия и определения, относящиеся к спектрам ра-
диосигналов ....................................................... 9
§ В.4. Вопросы, рассматриваемые в книге 13
ГЛАВА 1. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ В МАТЕМАТИЧЕСКОЙ ФОРМЕ
И ПОНЯТИЕ СПЕКТРА
§ 1.1. Общие соображения о представлении сигналов..................14
§ 1.2. Использование экспоненциальных функций .... 15
§ 1.3. Ортогональность и полнота...................................19
§ 1.4. Метод смещённых функций.....................................22
ГЛАВА 2. СИГНАЛЫ КОНЕЧНОЙ ПРОДОЛЖИТЕЛЬНОСТИ, СОДЕРЖАЩИЕ
МАКСИМАЛЬНУЮ ДОЛЮ ЭНЕРГИИ В ЗАДАННОЙ ПОЛОСЕ ЧАСТОТ
§ 2.1. Некоторые соотношения между сигналами и спектрами ... 24
§ 2.2. Составление интегрального уравнения.........................26
§ 2.3. Определение границ для частичной энергии сигнала . 28
§ 2.4. Приближённое решение интегрального уравнения посредством
разложения ядра....................................................30
§ 2.5. Решение интегрального уравнения посредством приведения его
к краевой задаче дифференциального уравнения .... 34
§ 2.6. Исследование сигналов u(k, к) при больших значениях пара-
метра k........................................................... 42
ГЛАВА 3. ПОЛОСА ЧАСТОТ, ЗАНИМАЕМАЯ ПРИ ПЕРЕДАЧЕ ИМПУЛЬСОВ
§ 3.1. Распределение энергии импульса в полосе частот..............44
§ 3.2. Прямоугольный импульс.................................. . 45
§ 3.3. Трапецеидальный и треугольный импульсы......................46
§ 3.4. Импульс, имеющий форму отрезка косинусоиды. Косинусои-
дальный импульс................................................... 48
§ 3.5. Импульсы с косинус-квадратным скруглением..................56
§ 0.6. Косинус-кубичный импульс....................................60
308
Стр.
ГЛАВА 4. ШИРИНА ПОЛОСЫ, ЗАНИМАЕМОЙ ПЕРЕДАЧЕЙ, И ВРЕМЯ
УСТАНОВЛЕНИЯ СИГНАЛОВ
§4.1. Общие соображения....................................... 63
§ 4.2. Определение времени установления сигнала..................63
§ 4.3. Общий критерий оценки сигнала.............................64
§ 4.4. Численные значения ky...................................
ГЛАВА 5. ФОРМИРОВАНИЕ СИГНАЛОВ С ЦЕЛЬЮ УМЕНЬШЕНИЯ
ВНЕПОЛОСНЫХ ИЗЛУЧЕНИЙ
§ 5.1. Предварительные замечания ................................69
§ 5.2. Рассмотрение возможности уменьшения энергии внеполосных из-
лучений с точки зрения теории Шеннона о пропускной способно-
сти канала........................................................70
§ 5.3. Интегральное преобразование Фурье, выраженное через скачки
функции и её производных......................................; 73
§ 5.4. Соотношение между формой импульса и* скоростью убывания вне-
полосных излучений................................................75
§ 5.5. Форма сигнала конечной продолжительности, спектр которого
убывает не медленнее, чем С/(ол+1.................................77
ГЛАВА 6. ПОЛОСА ЧАСТОТ, ЗАНИМАЕМАЯ ПЕРЕДАЧЕЙ РАДИОТЕЛЕГРАФНЫХ
СИГНАЛОВ ПРИ АМПЛИТУДНОЙ И ЧАСТОТНОЙ МАНИПУЛЯЦИЯХ
§6.1. Ширина полосы, занимаемой передачей при амплитудной ма-
нипуляции ........................................................88
§ 6.2. Ширина полосы, занимаемой передачей при частотной манипу-
ляции ........................................................... 94
§ 6.3. Сравнение полос, занимаемых при обоих видах манипуляции . 99
ГЛАВА 7. СПЕКТРЫ РАДИОТЕЛЕГРАФНЫХ СИГНАЛОВ РАЗЛИЧНЫХ
ФОРМ ПРИ ЧАСТОТНОЙ МАНИПУЛЯЦИИ
§7.1. Трапецеидальные импульсы ................................100
§ 7.2. Импульсы с синусоидальным скруглением . ..............104
§ 7.3. Результаты вычислений ширины полосы......................108
§ 7.4. Внеполосные излучения при различных формах сигналов ... 109
ГЛАВА 8. СООТНОШЕНИЕ МЕЖДУ ШИРИНОЙ ПОЛОСЫ, ЗАНИМАЕМОЙ
ПЕРЕДАЧЕЙ, И ВРЕМЕНЕМ ЗАМЕДЛЕНИЯ СИГНАЛОВ
§8.1. Пропускная способность канала и время замедления . . . 116
§ 8.2. Характеристики системы связи, обеспечивающей передачу сигна-
лов с конечным временем замедления . . ................119
§ 8.3. Пропускная способность канала с учётом времени замедления . 122
§ 8.4. Форма сигнала с ограниченным спектром, занимающего наи-
меньшую полосу частот.......................................... 124
309
Стр.
ГЛАВА 9. СООТНОШЕНИЯ МЕЖДУ СПЕКТРАМИ РЕГУЛЯРНЫХ И СЛУЧАЙНЫХ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ СИГНАЛОВ
§ 9.1. Предварительные замечания................................134
§ 9.2. Представление сообщения посредством элементарных сигналов,
смещённых во времени................................135
§ 9.3. Спектр R (со)........................................136
§ 9.4. Сигнал, соответствующий фактору повторения .... 140
§ 9.5. Энергетические соотношения для различных спектров . 142
§ 9.6. Выводы...................................................148
ГЛАВА 10. ПОЛОСА ЧАСТОТ, ЗАНИМАЕМАЯ ПЕРЕДАЧЕЙ СЛУЧАЙНОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ СИГНАЛОВ
§ 10.1. Трудности, возникающие при определении ширины полосы, за-
нимаемой передачей случайной 'последовательности сигналов . 149
§ 10.2. Определение ширины полосы посредством функции корреляции 151
ГЛАВА И. УМЕНЬШЕНИЕ ВЗАИМНЫХ ПОМЕХ МЕЖДУ КАНАЛАМИ РАДИОСВЯЗИ
ПРИ ПЕРЕДАЧЕ СЛУЧАЙНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ СИГНАЛОВ
§ 11.1. Возможная методика изучения проблемы взаимных помех . 154
§ 11.2. Энергетический спектр сигнала, представленного в виде ряда
смещённых функций..............................................156
§ 11.3. Спектр некоррелированных сигналов .... . . 157
§ 11.4. Спектр коррелированных сигналов................. . . 160
§ 11.5. Выводы..................................................161
ГЛАВА 12. ВЗАИМНЫЕ ПОМЕХИ МЕЖДУ СИСТЕМАМИ РАДИОСВЯЗИ,
ИСПОЛЬЗУЮЩИМИ АМПЛИТУДНУЮ, ЧАСТОТНУЮ ИЛИ ФАЗОВУЮ
МОДУЛЯЦИЮ
§ 12.1. Исходные предположения..................................162
§ 12.2. Изменение энергии взаимных помех при различных расстройках 164
§ 12.3. Соотношение между максимальной амплитудой А и энергией
сигнала W, передаваемой через фильр F, эквивалентный при-
ёмнику .........................................................166
§ 12.4. Соотношение между А и W при Ру<Р%.......................167
§ 12.5. Соотношение между А и W при ри>Р% ...... .174
§ 12.6. Определение разноса между каналами......................178
ГЛАВА 13. ФОРМИРОВАНИЕ СИГНАЛОВ В ПЕРЕДАТЧИКАХ
§ 13.1. Практические соображения по выбору формы импульсов . 204
§ 13.2. Линейные фильтры в цепях манипуляции....................209
§ 13.3. Нелинейное устройство для формирования сигналов . , • 215
310
Стр.
ГЛАВА 14. ИЗМЕРЕНИЕ ШИРИНЫ ПОЛОСЫ ЧАСТОТ, ИЗЛУЧАЕМОЙ
РАДИОТЕЛЕГРАФНЫМИ ПЕРЕДАТЧИКАМИ
§ 14.1. Методы измерения ширины полосы излучения.............218
§ 14.2. Определение уровней для измерения ширины полосы частот,
занимаемой радиотелеграфными излучениями.....................227
§ 14.3. Дистанционные измерения ширины полосы частот, излучаемой
радиопередатчиками.................................... .... 230
§ 14.4. Практические соображения по экспериментальному определе-
нию ширины полосы, занимаемой передачей случайной последо-
вательности сигналов.........................................236
ПРИЛОЖЕНИЯ
Приложение I. Ширина полосы, необходимая для различных клас-
сов излучений . <. •....................................238
Приложение II. Приведение интегрального уравнения к краевой
задаче дифференциального уравнения.................... 241
Приложение III. Определение коэффициентов dn...............245
Приложение IV. Формулы для вычисления интегралов A(k)t B(k)
и C(k)................................................ 250
Приложение V. Функции Ломмеля (г)...........................'251
Приложение VI. Ширина полосы, занимаемой излучением трапе-
' цеидальных импульсов и импульсов с синусоидальным скруглени-
ем при частотной манипуляции.................................300
Приложение VII. Классификация излучений ...... 302
Литература...................................................306
Моисей Сергеевич Гуревич
СПЕКТРЫ РАДИОСИГНАЛОВ
Отв. редактор В, М, Розов Техн, редактор С. Ф. Романова
Редактор Г. И. Вейцман # Корректор А. 3. Боровая
Сдано в набор 22/ХП 1963 г. Подписано в печ. 25/IV 1963 г.
Форм. бум. 60x90/16 20,25 печ. л. (включая 2 вклейки) 17,57 уч.-изд. л.
Т-03823 Тираж 7500 экз. Зак. изд. 10062 Цена 1 руб. 08 коп.
Связьиздат, Москва-центр, Чистопрудный бульвар, 2.
Типография Связьиздата, Москва-центр, ул. Кирова, 40. Зак. тип. 730
1 12 я 1 1 3,0 1 1 i j j 1
г
1
2 2--2,4
2--4,<з 1--1, 2-7,2 8 I
2-3,0 /I2'
2 = ^ ',ц •
/ z=t '.0 ...
1-1,2 1 2-5,4 fr'- V? skf 6.6
2’54 h 6 \ ^}=7 2 Z =54 /г 7.2 2-72 1'6,6 [2 = 6,0 2=4,8 2 = 4,2
'— Z=3.6 2=3,0 2 = 7,2 2-5,4
2*2/ 4 *^2-< о,6, : г 7 *А А \Z*2A 2*0,6 . J 1=1,6 2-7,2 2-3,0 2*6,0 2*3,6 Z^t2 z< y°V3’b6 24 2=7,2 7 -54 2 = 5.0 *<?79 9
•. , rL >±L
2*0,6 t = '0,4
r 2=5,4
2 >6,0 *4,2/ 2*4,8
2Г х 7,2-2 ' '„гГг< ,11) 11 и
1 * 1 1
г=Jo г* f-8 1 (
1 -
у Z‘2,
'2-7,2]
| 1 i
Z‘ 7,<9 *2 L ^,21
Рис. П.У.1. Функции Ломмеля—sItV (г)
Зак 730
3,0
2,5
2,0
1,5
to
0
-1.0
4,5
'2,0
5 2=// 2=2,4
I2’ 2-42 0,6
2=4,2 Z -4,8 2=7.2
ПГ 3,0 2=3.6 z-- -6,6
z=4,e 2 = 5,4 2 = 2 112=7,2 12 = 1 16
2=6,0 Г J к 1=5.4
> 24 2 =6,0 ♦
Z =4.2 V- 2=7.2 J m =4,8 /1/ 2=6. 0
'z=3,t 2 = 7.2 \\У 2=6.6 X fz=66L 2=1,8 7/ / II
2 =6.6 / 1=4.2
'2=1,2 ; =3,6
^1=6. —Q \ 2=3,0 z = 2 s< 7Я
1 2=<j 16 -—i Ьцб' J 2=0.6 I 5 7 J ^2-60 9 Z-S.4
\z =4,2 И 2 = 7,2 / Z=\2 Z=3‘ ° /
2^7,2 i =3fi /L 2=3,4
4 Z=£ ‘^'-L 1-Д 2 2=6,0^ 1 > /
\\\ 2-6, 6 2=3,0 2 1 Ip = 1.8 / I / 1=6,6 1
2=4,8 2 = I / 3,o-L j L_ 2=4,8 1 = 7.2
2 =
1|Z4 4 I 2=3,1 ? r4 1 7 - /. 0 _
Lz=i,t 2 2 = 5.4
Z=6 ,0 | 2 :=i,e
7 2=0,6 2 = 5
/ - , ,, , 2 '=7.2 Ld
4 '' ' .1-S.k . 2=^1 2=6,0
Рис. FI.V.2. Функции Ломмеля sOv(z)
Зак 730